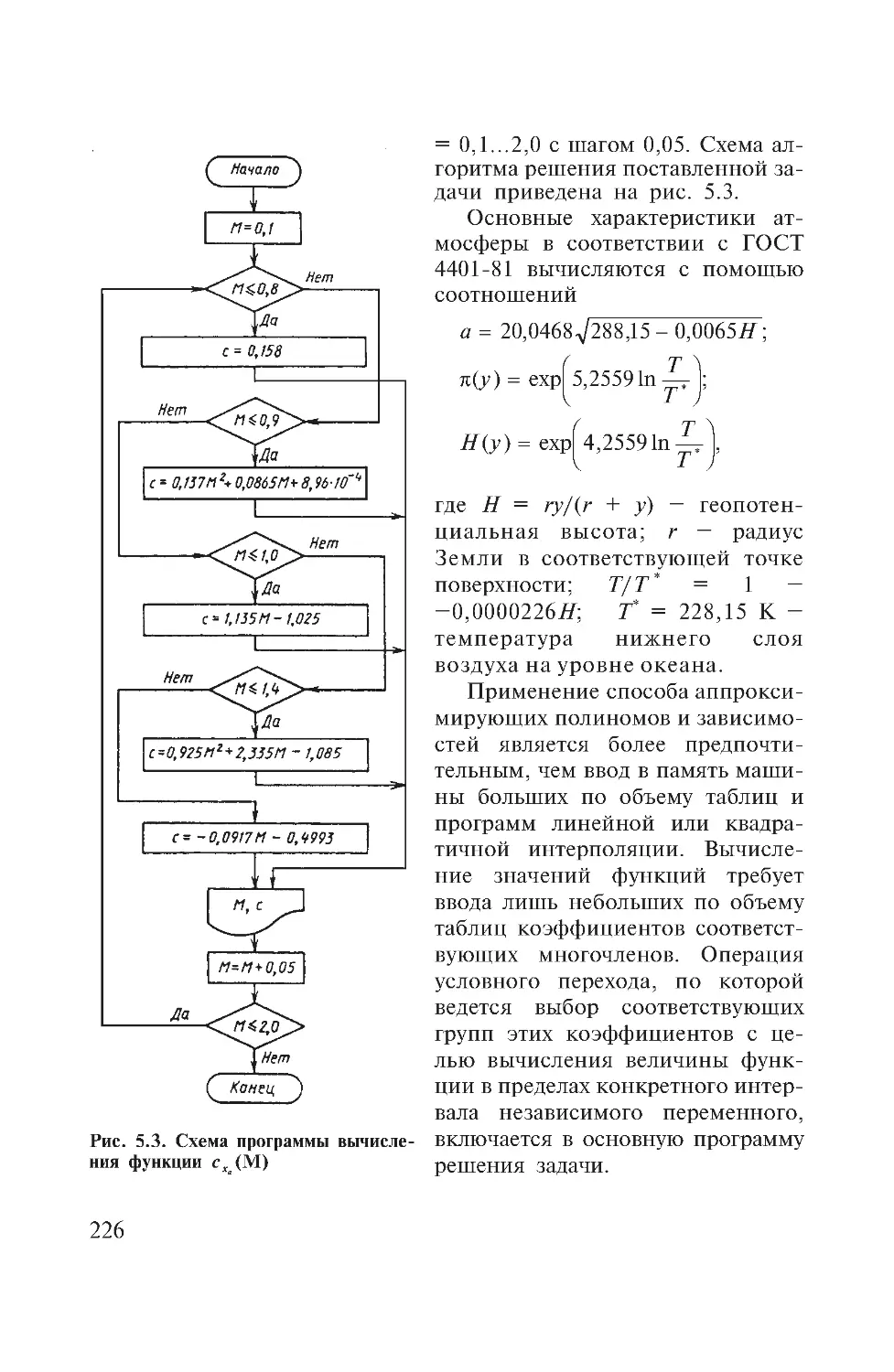
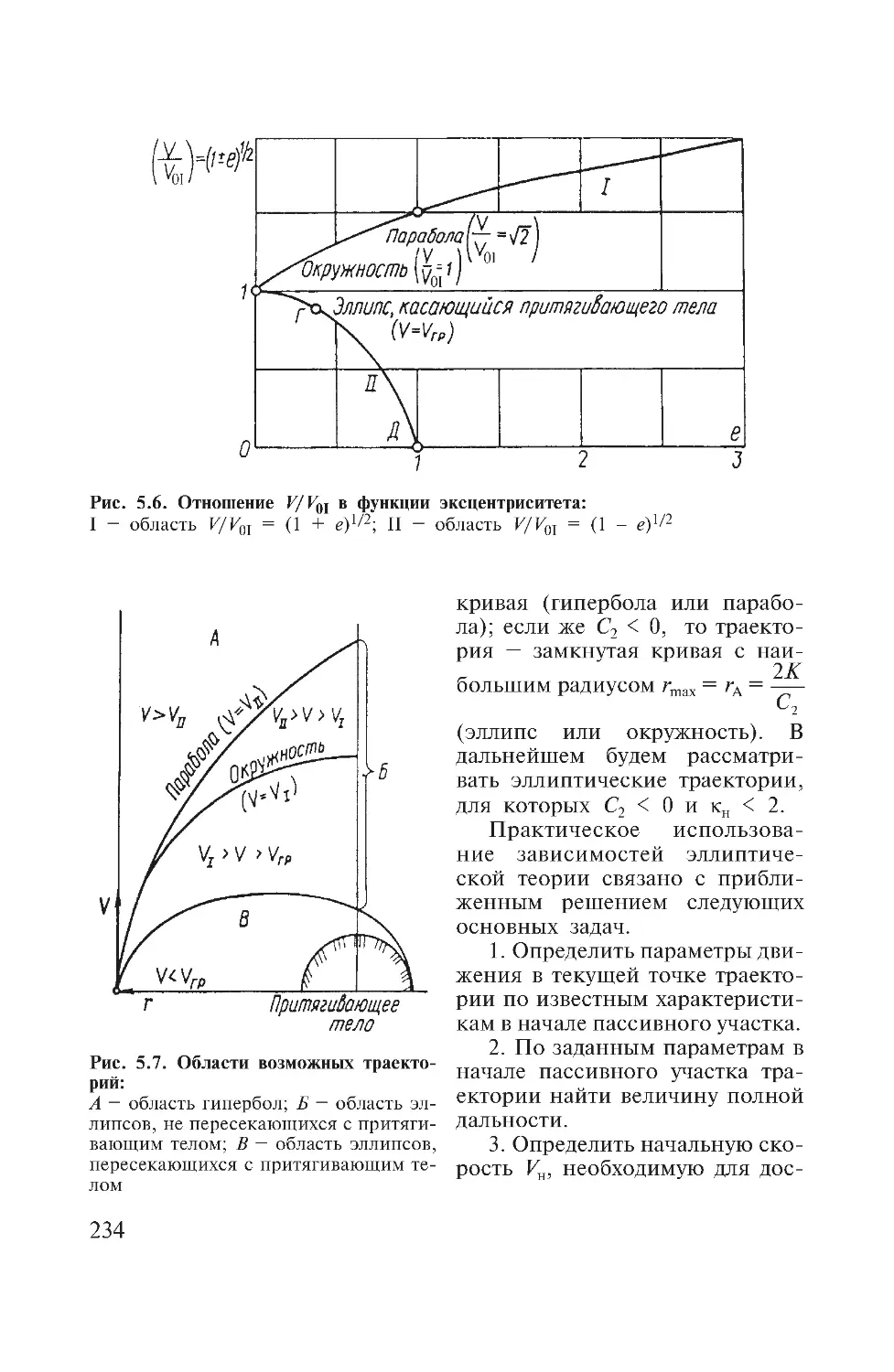
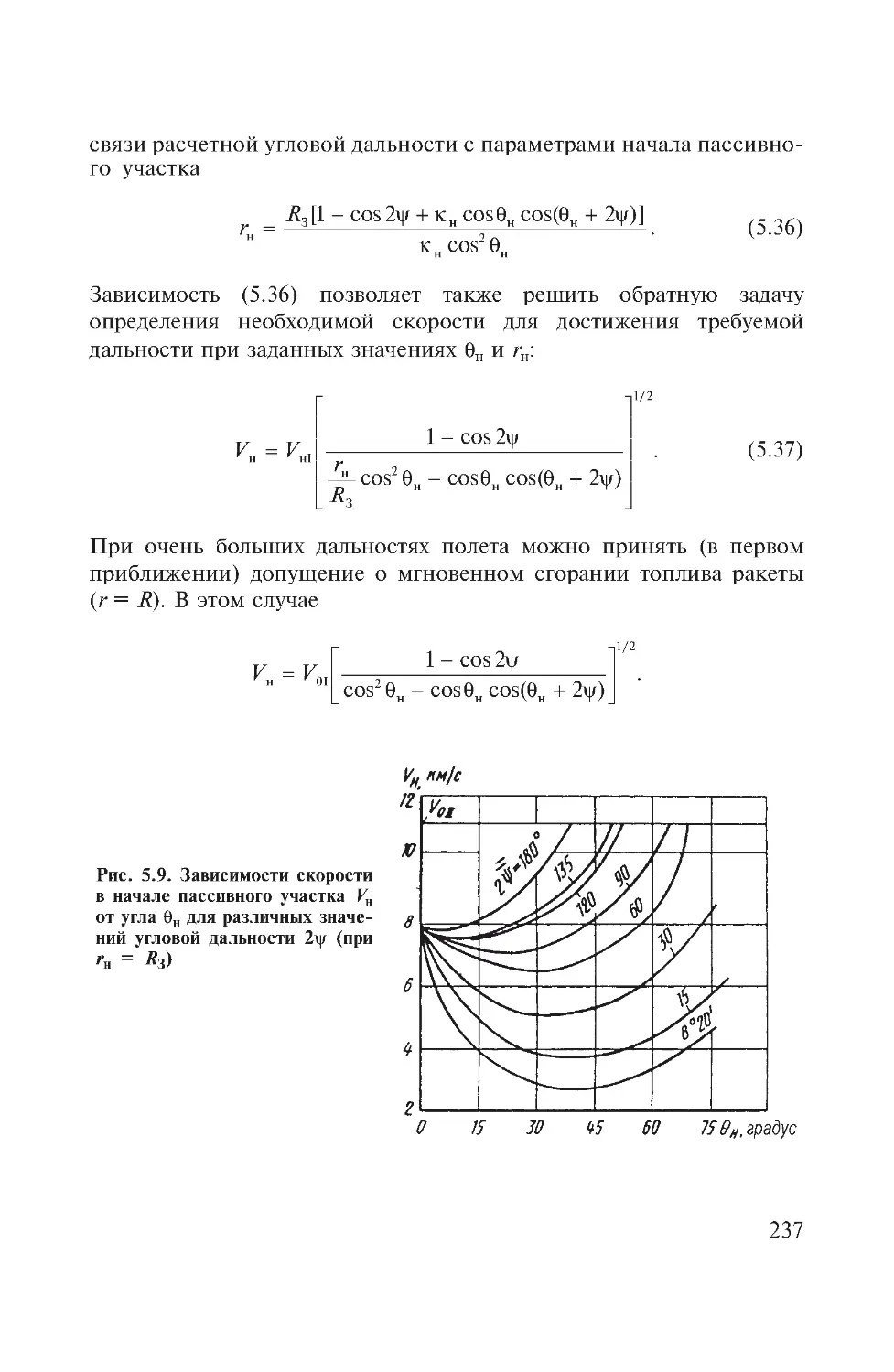
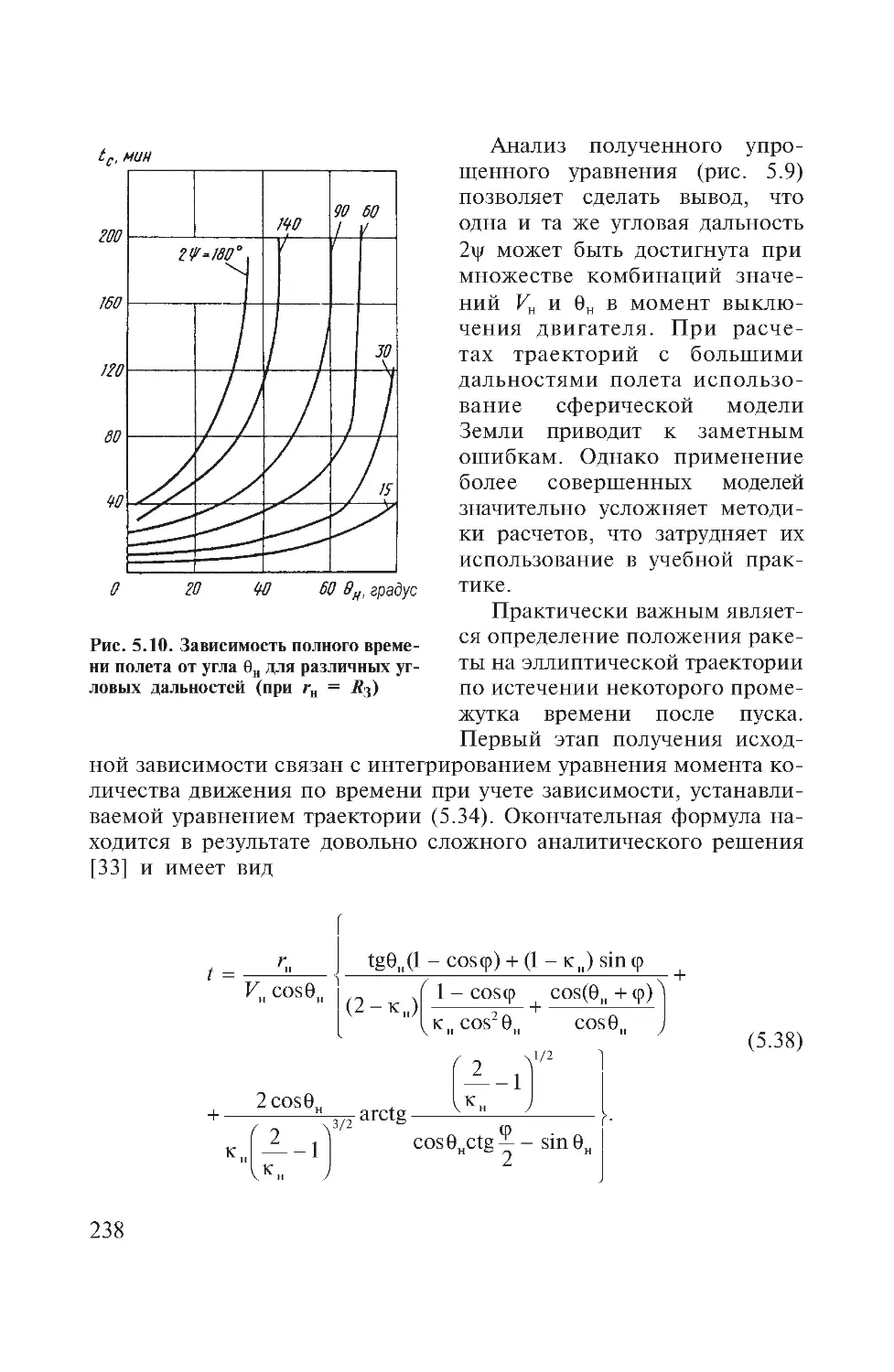
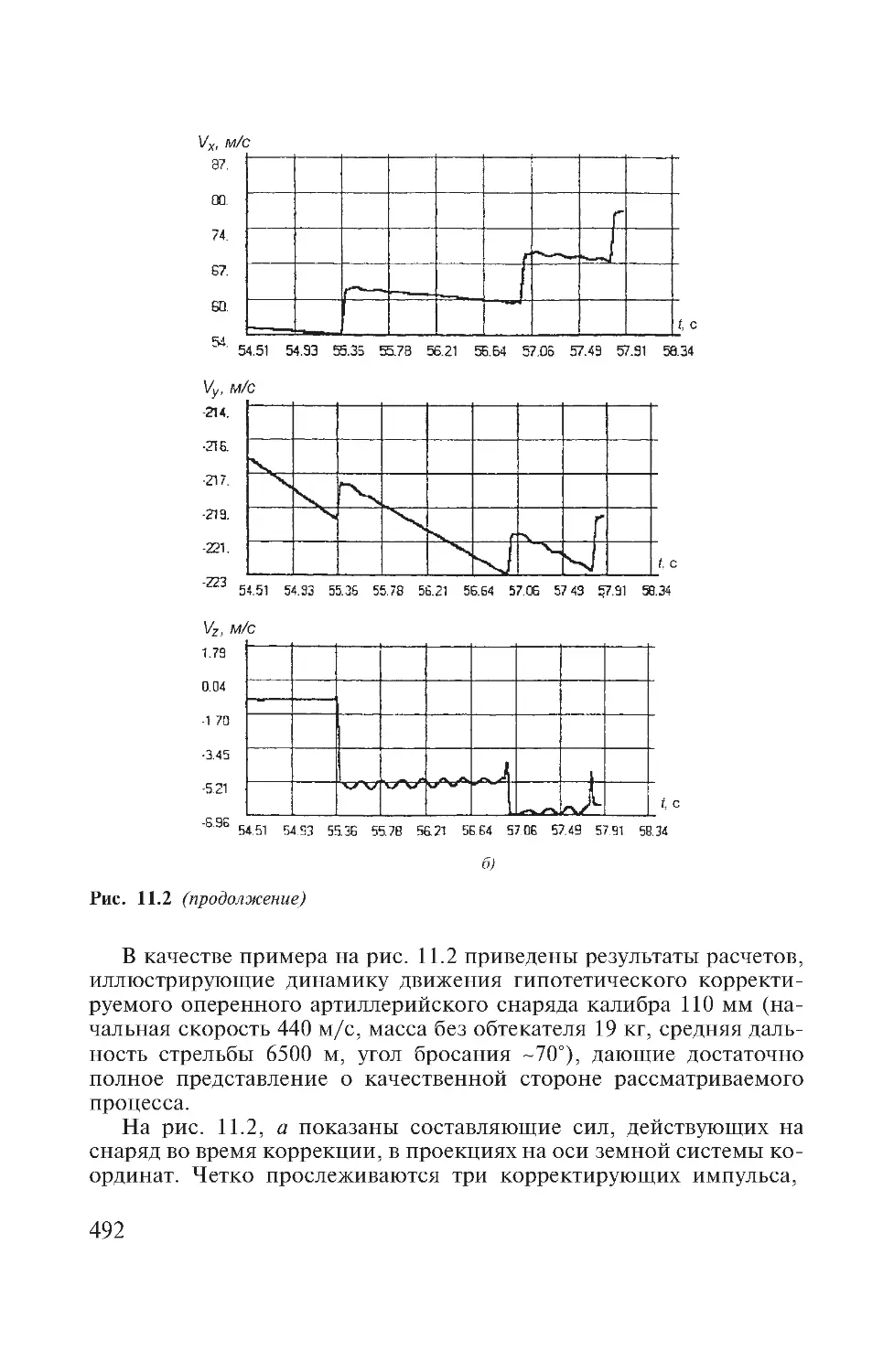
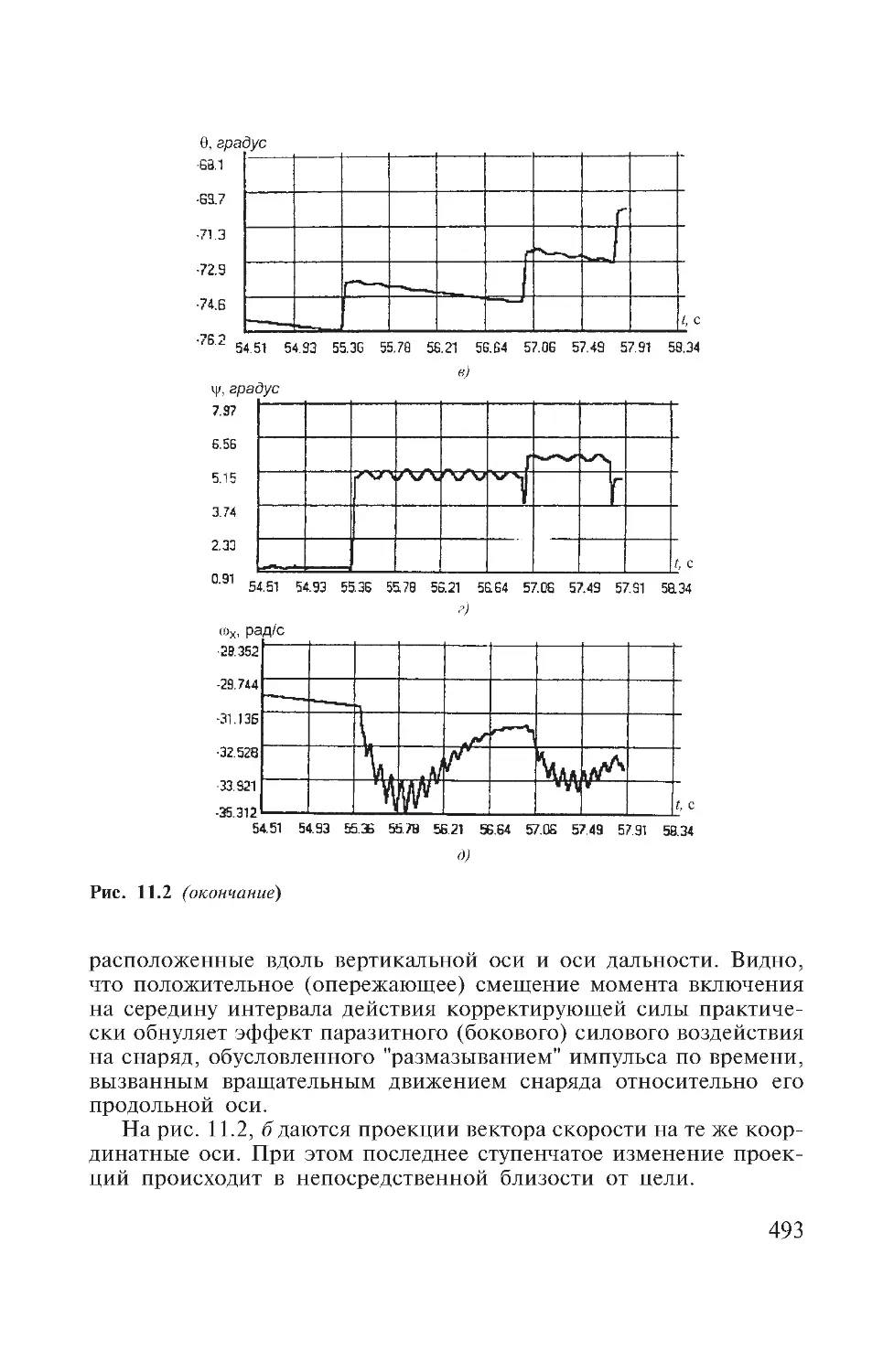
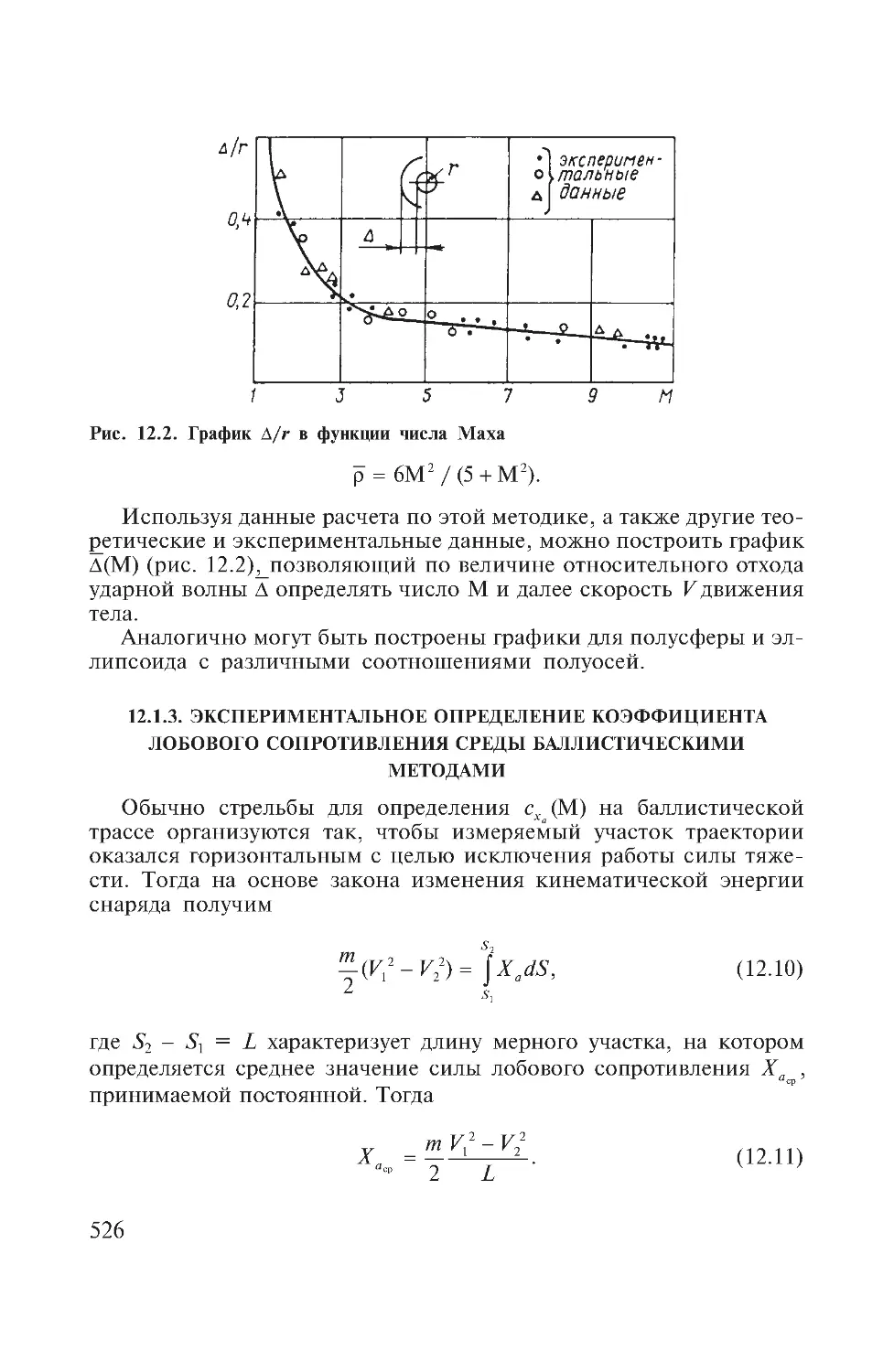
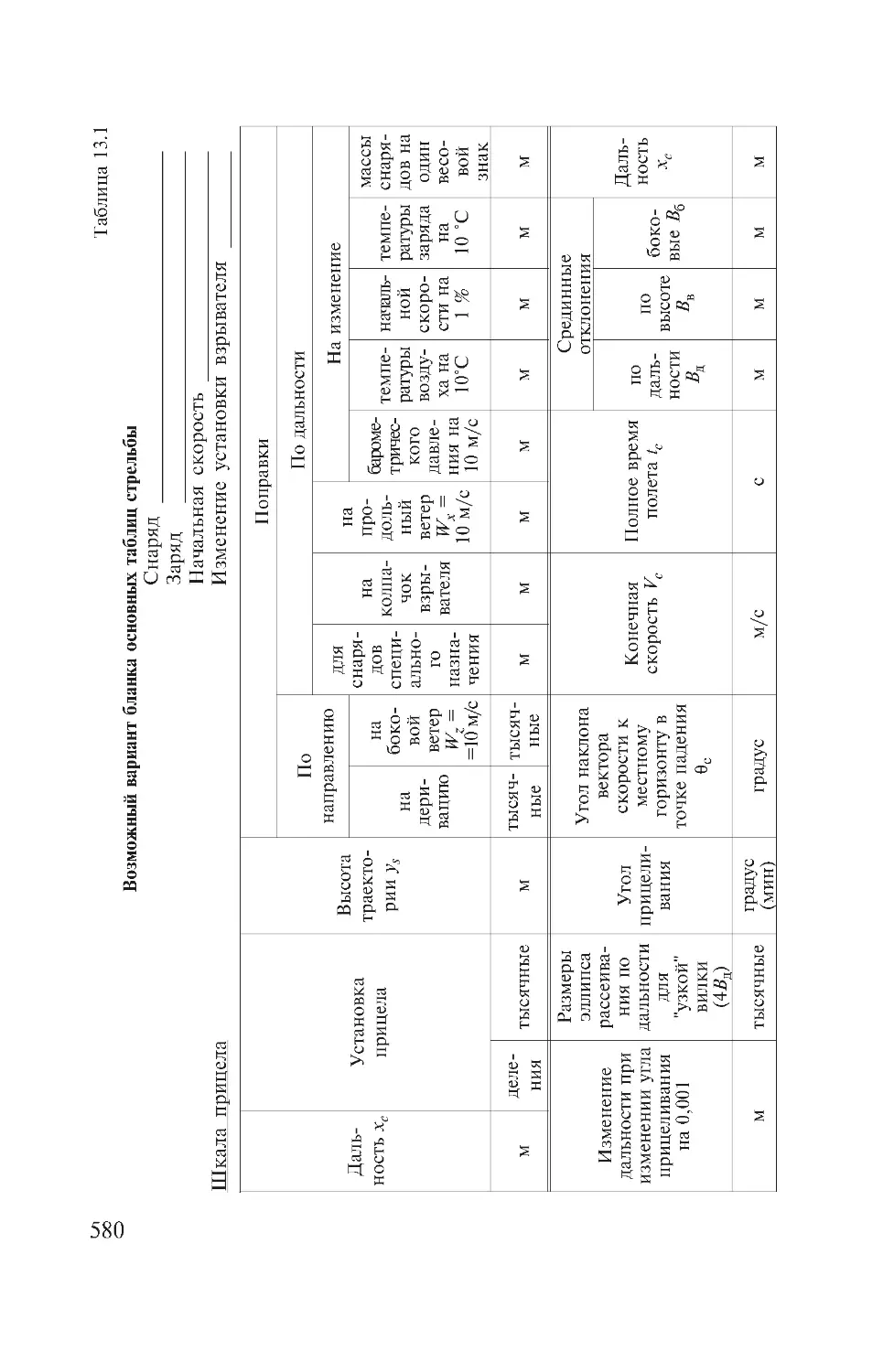
Author: Дмитриевский А.А. Лысенко Л.Н.
Tags: пищевое производство баллистика
ISBN: 5-217-03252-9
Year: 2005
Text
ДЛЯ ВУЗОВ
À.À . Äìèòðèåâñêèé,
Ë.Í. Ëûñåíêî
ÌÎÑÊÂÀ
«ÌÀØÈÍÎÑÒÐÎÅÍÈÅ»
2005
ÂÍÅØÍßß
ÁÀËËÈÑÒÈÊÀ
Äîïóùåíî Ìèíèñòåðñòâîì îáðàçîâàíèÿ
ÐÔ â êà÷åñòâå ó÷åáíèêà äëÿ ñòóäåíòîâ
âûñøèõ ó÷åáíûõ çàâåäåíèé, îáó÷àþùèõñÿ
ïî ñïåöèàëüíîñòè «Áàëëèñòèêà» íàïðàâ-
ëåíèÿ ïîäãîòîâêè «Ãèäðîàýðîäèíàìèêà è
äèíàìèêà ïîëåòà»
4-å èçäàíèå,
ïåðåðàáîòàííîå è äîïîëíåííîå
ÓÄÊ [623.54; 623.451](075.8)
ÁÁÊ 39.62-01ß-73
Ä53
Ðåöåíçåíòû: êàôåäðà "Èíôîðìàöèîííî-óïðàâëÿþùèå êîì-
ïëåêñû" ÌÀÈ; ä-ð òåõí. íàóê, ïðîôåññîð Í.Ì. ÌÎÍ×ÅÍÊÎ
Äìèòðèåâñêèé À.À., Ëûñåíêî Ë.Í .
Ä53
Âíåøíÿÿ áàëëèñòèêà: Ó÷åáíèê äëÿ ñòóäåíòîâ âóçîâ.
–
4-å
èçä., ïåðåðàá. è äîï. – Ì .: Ìàøèíîñòðîåíèå, 2005. 608 ñ.; èë.
ISBN 5-217-03252-9
Èçëîæåíû òåîðåòè÷åñêèå îñíîâû âíåøíåé áàëëèñòèêè ñíàðÿäîâ è ðà-
êåò, ìåòîäèêè ðàñ÷åòà ïàðàìåòðîâ èõ äâèæåíèÿ, îïðåäåëåíèÿ õàðàêòåðè-
ñòèê òî÷íîñòè ñòðåëüáû, à òàêæå ìåòîäû áàëëèñòè÷åñêîãî îáåñïå÷åíèÿ èñ-
ïûòàíèé.
Çíà÷èòåëüíîå âíèìàíèå óäåëåíî áàëëèñòè÷åñêîìó ïðîåêòèðîâàíèþ
ðàññìàòðèâàåìûõ òèïîâ áîåïðèïàñîâ, âûáîðó è ðàñ÷åòó îïòèìàëüíûõ òðà-
åêòîðèé, âûïîëíåíèþ óñëîâèé óñòîé÷èâîñòè äâèæåíèÿ.
Ïî ñðàâíåíèþ ñ ïðåäûäóùèì èçäàíèåì (3-å èçä. 1991 ã.) ó÷åáíèê ñó-
ùåñòâåííî ïåðåðàáîòàí è äîïîëíåí íîâûìè ìàòåðèàëàìè.
Äëÿ ñòóäåíòîâ âóçîâ è ñïåöèàëèñòîâ â îáëàñòè ðàêåòíî-àðòèëëåðèéñêîé
òåõíèêè.
ÁÁÊ 39.62-01ß-73
Ó×ÅÁÍÎÅ ÈÇÄÀÍÈÅ
ÄÌÈÒÐÈÅÂÑÊÈÉ Àíäðåé Àëåêñàíäðîâè÷,
ËÛÑÅÍÊÎ Ëåâ Íèêîëàåâè÷
ÂÍÅØÍßß ÁÀËËÈÑÒÈÊÀ
Ðåäàêòîð Í.À . Ëåîíòüåâà
Õóäîæåñòâåííûé ðåäàêòîð Ò.Í . Ãàëèöûíà
Òåõíè÷åñêèå ðåäàêòîðû Ò.È . Àíäðååâà, Ñ.À. Æèðêèíà
Êîððåêòîð Â.Î. Êàáàíîâà
Ëèöåíçèÿ ÈÄ 1 05672 îò 28.08 .01
Ñäàíî â íàáîð 29.04 .04 . Ïîäïèñàíî â ïå÷àòü 04.02.05.
Ôîðìàò 60x88 1/16.
Ãàðíèòóðà Íüþòîí Ñ Áóìàãà îôñåòíàÿ.
Ïå÷àòü îôñåòíàÿ.
Óñë. ïå÷. ë . 37,24.
Ó÷. - èçä. ë. 33,05. Òèðàæ 1000 ýêç.
Çàêàç
.
ÎÀÎ “Èçäàòåëüñòâî “Ìàøèíîñòðîåíèå”,
107076, Ìîñêâà, Ñòðîìûíñêèé ïåð., 4
Îòïå÷àòàíî â ÃÓÏ ÏÏÏ “Òèïîãðàôèÿ “Íàóêà” ÐÀÍ”,
128009, Ìîñêâà, Øóáèíñêèé ïåð., 6
ISBN 5-217-03252-9 © À.À . Äìèòðèåâñêèé, Ë.Í . Ëûñåíêî, 2005
© Èçäàòåëüñòâî "Ìàøèíîñòðîåíèå", 2005
Ó÷åíûì-àðòèëëåðèñòàì Ðîññèè, îñíîâàòåëÿì
âñåìèðíî èçâåñòíîé îòå÷åñòâåííîé øêîëû
âíåøíåé áàëëèñòèêè, ïðîñëàâèâøåé ñåáÿ âî âðå-
ìÿ Âåëèêîé Îòå÷åñòâåííîé âîéíû è ïðîäåìîí-
ñòðèðîâàâøåé íåèññÿêàåìûé ïîòåíöèàë íà âñåõ
ýòàïàõ îñíàùåíèÿ Ñîâåòñêîé Àðìèè âûñîêîýô-
ôåêòèâíûìè ñðåäñòâàìè ðàêåòíî-àðòèëëåðèé-
ñêîãî âîîðóæåíèÿ, íàøèì âåëèêèì ïðåäøåñò-
âåííèêàì è äîðîãèì ó÷èòåëÿì ïîñâÿùàåòñÿ
ÈÇ ÏÐÅÄÈÑËÎÂÈß Ê ÏÅÐÂÎÌÓ ÈÇÄÀÍÈÞ*
Íà ïðîòÿæåíèè ìíîãèõ ëåò âíåøíÿÿ áàëëèñòèêà áûëà íàóêîé,
èçó÷àþùåé äâèæåíèå ìèí è ñíàðÿäîâ ñòâîëüíûõ àðòèëëåðèéñêèõ
ñèñòåì. Ñ ðàçâèòèåì ðàêåòíîé òåõíèêè è ñîâåðøåíñòâîâàíèåì òåî-
ðèè ïîëåòà ðàêåò è ñíàðÿäîâ êðóã âîïðîñîâ âíåøíåé áàëëèñòèêè ñó-
ùåñòâåííî ðàñøèðèëñÿ. Çíà÷èòåëüíîå ðàçâèòèå ïîëó÷èëè ïðîåêò-
íûå áàëëèñòè÷åñêèå ðàñ÷åòû. Ïðèìåíåíèå âûñîêîïðîèçâîäèòåëü-
íîé âû÷èñëèòåëüíîé òåõíèêè íåèçìåðèìî ïîâûñèëî âîçìîæíîñòè
áàëëèñòè÷åñêèõ èññëåäîâàíèé.
Âíåøíÿÿ áàëëèñòèêà, â îñíîâå êîòîðîé ëåæàò çàêîíû òåîðåòè÷å-
ñêîé ìåõàíèêè, òåñíî ñâÿçàíà ñ àýðîäèíàìèêîé, ãðàâèìåòðèåé è ìå-
òåîðîëîãèåé, òåîðèåé âåðîÿòíîñòåé è ìàòåìàòè÷åñêîé ñòàòèñòèêîé.
Áàëëèñòè÷åñêèé ðàñ÷åò äàåò âñå íåîáõîäèìûå äàííûå î òðàåêòî-
ðèÿõ è ïàðàìåòðàõ äâèæåíèÿ, èñõîäÿ èç êîòîðûõ ìîæíî ñóäèòü î
òàêòèêî-òåõíè÷åñêèõ õàðàêòåðèñòèêàõ ðàêåòíîãî èëè àðòèëëåðèé-
ñêîãî êîìïëåêñà â öåëîì.
Ðàçóìååòñÿ, ñîäåðæàíèå ó÷åáíèêà äàëåêî íå èñ÷åðïûâàåò âñåãî
ìíîãîîáðàçèÿ ïðîáëåì, ñòîÿùèõ ïåðåä âíåøíåé áàëëèñòèêîé. Ñî-
âðåìåííîå ñîñòîÿíèå íàóêè î äâèæåíèè ðàêåò è àðòèëëåðèéñêèõ
ñíàðÿäîâ ðàçëè÷íûõ òèïîâ òàêîâî, ÷òî ìíîãèå èç ðàññìàòðèâàåìûõ â
êíèãå âîïðîñîâ ìîãóò ñëóæèòü ïðåäìåòîì ñàìîñòîÿòåëüíûõ òåîðåòè-
÷åñêèõ è ýêñïåðèìåíòàëüíûõ èññëåäîâàíèé.
3
*
Ì.: Ìàøèíîñòðîåíèå, 1972.
ÏÐÅÄÈÑËÎÂÈÅ Ê ×ÅÒÂÅÐÒÎÌÓ ÈÇÄÀÍÈÞ
Âíåøíÿÿ áàëëèñòèêà îòíîñèòñÿ ê ÷èñëó ñòàðåéøèõ ïðèêëàäíûõ
íàóê âîåííî-òåõíè÷åñêîé íàïðàâëåííîñòè. Èñòîðèÿ åå ðàçâèòèÿ íå-
ðàçðûâíî ñâÿçàíà ñ ñîçäàíèåì è áîåâûì ïðèìåíåíèåì îãíåñòðåëü-
íîãî îðóæèÿ, äàòèðóåìûìè ñåðåäèíîé XIV âåêà.
 íà÷àëüíûå ãîäû ïîÿâëåíèÿ îãíåñòðåëüíîãî îðóæèÿ âîïðîñû,
êàñàþùèåñÿ áàëëèñòèêè, à òàêæå ïðàâèë ïðîâåäåíèÿ ñòðåëüá, ðåøà-
ëèñü ãëàâíûì îáðàçîì èñõîäÿ èç ïðàêòèêè è íàêîïëåííîãî îïûòà.
Äëÿ îðãàíèçàöèè "ïóøå÷íîãî äåëà" â XV è XVI âåêàõ â Ðîññèè
áûëè ó÷ðåæäåíû "Ïóøå÷íûé äâîð" è "Ïóøå÷íûé ïðèêàç".
Ïåðâûì àâòîðîì îïóáëèêîâàííîãî òðóäà ïî áàëëèñòèêå, îáîá-
ùèâøèì îïûò êàê ðóññêèõ, òàê è èíîñòðàííûõ àðòèëëåðèñòîâ XVI
âåêà, ïðèíÿòî ñ÷èòàòü "ïóøêàðñêèõ äåë ìàñòåðà" Îíèñèìà Ìèõàé-
ëîâà, íàïèñàâøåãî â 1620 ã. "Óñòàâ ðàòíûõ, ïóøå÷íûõ è äðóãèõ äåë,
êàñàþùèõñÿ äî âîåííîé íàóêè", ÿâèâøèéñÿ öåííûì âêëàäîì â
ïðàêòèêó âåäåíèÿ ñòðåëüá.
Ïåðâîå ðåøåíèå çàäà÷è î äâèæåíèè ñíàðÿäà ñ ó÷åòîì ñèëû ñî-
ïðîòèâëåíèÿ âîçäóøíîé ñðåäû áûëî ïîëó÷åíî â 1753 ã. ÷ëåíîì Ïå-
òåðáóðãñêîé àêàäåìèè íàóê Ëåîíàðäîì Ýéëåðîì. Îïóáëèêîâàííàÿ â
1755 ã., ýòà ðàáîòà ñòàëà, ïî ñóùåñòâó, ïåðâûì òåîðåòè÷åñêè îáîñíî-
âàííûì èññëåäîâàíèåì ïî ðàñ÷åòó òðàåêòîðèé ñâîáîäíî áðîøåííî-
ãî òåëà â âîçäóõå, âûïîëíåííûì â Ðîññèè.
 1836 ã. ïðîôåññîðîì Àðòèëëåðèéñêîé àêàäåìèè Â.À. Àíêó-
äîâè÷åì (1792–1856) áûë èçäàí ó÷åáíèê "Òåîðèÿ áàëëèñòèêè, ñî-
äåðæàùàÿ ïðèëîæåíèå ìàòåìàòè÷åñêîãî àíàëèçà ê îïðåäåëåíèþ
ðàçëè÷íûõ îáñòîÿòåëüñòâ, ñîïðîâîæäàþùèõ äâèæåíèå òÿæåëûõ
òåë, áðîøåííûõ êàêîé-íèáóäü ñèëîé", ñûãðàâøèé ñóùåñòâåííóþ
ðîëü â ìåòîäè÷åñêîì îáåñïå÷åíèè ïðåïîäàâàíèÿ ñîîòâåòñòâóþ-
ùåé äèñöèïëèíû.
Îãðîìíîå âëèÿíèå íà ðàçâèòèå áàëëèñòèêè è ïîäãîòîâêó ñïåöèà-
ëèñòîâ íå òîëüêî â Ðîññèè, íî è ïðàêòè÷åñêè âî âñåõ ñòðàíàõ Åâðî-
ïû îêàçàëè ó÷åáíèêè, âûïóùåííûå â ñâåò â 1870 ã. íà ðóññêîì è â
1872 ã. íà ôðàíöóçñêîì ÿçûêàõ âûäàþùèìñÿ ó÷åíûì-àðòèëëåðè-
ñòîì, îñíîâàòåëåì ðóññêîé íàó÷íîé øêîëû áàëëèñòèêè, ãåíåðàëîì
îò àðòèëëåðèè, ÷ëåíîì-êîððåñïîíäåíòîì Ïåòåðáóðãñêîé àêàäåìèè
íàóê Í. . Ìàèåâñêèì (1823–1892).
Àðòèëëåðèéñêèé êîìèòåò Ãëàâíîãî àðòèëëåðèéñêîãî óïðàâëåíèÿ
(ÃÀÓ), ïðîðåöåíçèðîâàâ íàïèñàííûé ïðîôåññîðîì Í. . Ìàèåâ-
ñêèì ó÷åáíèê, òàê îïðåäåëèë â 1873 ã. åãî çíà÷åíèå: "... ðàññìàòðè-
âàåìîå ñî÷èíåíèå ïî ïîëíîòå è îáñòîÿòåëüíîñòè èññëåäîâàíèÿ âî-
4
ïðîñîâ ... ïðåâîñõîäèò âñå èìåþùèåñÿ ïî ýòîìó ïðåäìåòó èçûñêàíèÿ
è, ìîæíî ñêàçàòü, ïðåäñòàâëÿåò â íàñòîÿùåå âðåìÿ ïîñëåäíåå ñëîâî
íàóêè áàëëèñòè÷åñêîé".
Í. . Ìàèåâñêèé ñ 1852 ã. è ïðàêòè÷åñêè äî êîíöà ñâîåé æèçíè
çàíèìàëñÿ ïåäàãîãè÷åñêîé äåÿòåëüíîñòüþ â Ìèõàéëîâñêîé àðòèëëå-
ðèéñêîé àêàäåìèè. Îí ïîäãîòîâèë çíà÷èòåëüíûé îòðÿä ó÷åíèêîâ,
ñòàâøèõ âïîñëåäñòâèè êðóïíûìè ó÷åíûìè-àðòèëëåðèñòàìè.
Ñ èìåíåì îäíîãî èç íèõ, ãåíåðàë-ëåéòåíàíòà Í.À. Çàáóäñêîãî
(1853–1917), ñâÿçàíî ïîÿâëåíèå ñëåäóþùåãî èçäàíèÿ ó÷åáíèêà ïî
êóðñó "Âíåøíÿÿ áàëëèñòèêà", ñîñòîÿâøååñÿ â 1895 ã.
Ýòîò êóðñ ïî÷òè 30 ëåò îñòàâàëñÿ îñíîâíûì ðóêîâîäñòâîì ïî áàë-
ëèñòèêå. Ïîñëå ó÷åáíèêîâ Í. . Ìàèåâñêîãî ýòî áûëà íàèáîëåå ïîë-
íàÿ ðàáîòà, îòðàçèâøàÿ âñå íîâûå äîñòèæåíèÿ áàëëèñòè÷åñêîé íàó-
êè, êîòîðûìè îòìå÷åíà ïîñëåäíÿÿ ÷åòâåðòü XIX âåêà.
 íà÷àëå XX âåêà â ÷èñëå âàæíåéøèõ çàäà÷, ïîñòàâëåííûõ ïåðåä
âíåøíåé áàëëèñòèêîé, îêàçàëàñü çàäà÷à ïîâûøåíèÿ òî÷íîñòè
ñòðåëüáû íà áîëüøèå äàëüíîñòè, îñîáåííî ïðè ñòðåëüáå ïî íåâèäè-
ìûì öåëÿì. Ýòî ïîòðåáîâàëî ñîâåðøåíñòâîâàíèÿ ìåòîäèê ïðîâåäå-
íèÿ îïûòíûõ ñòðåëüá è ñîñòàâëåíèÿ òàáëèö ñòðåëüáû. Íàèáîëåå ñó-
ùåñòâåííûé âêëàä â ðåøåíèå òàêîãî ðîäà çàäà÷ íà òîò ïåðèîä âíåñ
êðóïíûé ðóññêèé àðòèëëåðèñò Â.Ì. Òðîôèìîâ, âîçãëàâëÿâøèé äåÿ-
òåëüíîñòü Ãëàâíîãî àðòèëëåðèéñêîãî ïîëèãîíà ñ 1910 ïî 1918 ã.
Áîëüøîå çíà÷åíèå èìåëè òàêæå òåîðåòè÷åñêèå èññëåäîâàíèÿ ïðî-
ôåññîðà Àðòèëëåðèéñêîé àêàäåìèè Ñ.Ã. Ïåòðîâè÷à, îïóáëèêîâàí-
íûå â 1904 ã.
Íåîáõîäèìîñòü óòî÷íåíèÿ âëèÿíèÿ ñîïðîòèâëåíèÿ âíåøíåé ñðå-
äû íà äâèæåíèå ñíàðÿäîâ äàëüíîáîéíîé àðòèëëåðèè è çåíèòíûõ
ñèñòåì ïîòðåáîâàëà ðàçðàáîòêè óíèâåðñàëüíîãî ïîäõîäà ê ðàñ÷åòó
òðàåêòîðèé íà îñíîâå ÷èñëåííîãî èíòåãðèðîâàíèÿ äèôôåðåíöèàëü-
íûõ óðàâíåíèé äâèæåíèÿ.
Ïðèîðèòåòíûå ðàáîòû â ýòîì íàïðàâëåíèè âíåøíåé áàëëèñòèêè
ïðèíàäëåæàò àêàäåìèêó À.Í. Êðûëîâó. Ýòè èññëåäîâàíèÿ áûëè ïðî-
äîëæåíû Â.Â. Ìå÷íèêîâûì, Í.À. Óïîðíèêîâûì, Ã.Â. Îïîêîâûì,
Á.Í. Îêóíåâûì, Ñ.À. Êàçàêîâûì è äð.
 ñîâåòñêèé ïåðèîä ðàçâèòèå âíåøíåé áàëëèñòèêè ñâÿçûâàþò
ïðåæäå âñåãî ñ äåÿòåëüíîñòüþ ñîçäàííîé â 1918 ã. Êîìèññèè îñîáûõ
àðòèëëåðèéñêèõ îïûòîâ (ÊÎÑÀÐÒÎÏ) âî ãëàâå ñ Â.Ì. Òðîôèìî-
âûì.  ñîñòàâ Êîìèññèè âõîäèëè òàêèå âûäàþùèåñÿ ó÷åíûå, êàê
Í.Å. Æóêîâñêèé, Ñ.À. ×àïëûãèí, À.Í. Êðûëîâ. Çíà÷èòåëüíûé âêëàä
â åå äåÿòåëüíîñòü âíåñëè êðóïíûå ó÷åíûå-àðòèëëåðèñòû Í.Ô . Äðîç-
äîâ, Ã.Ï. Êèñíåìñêèé è äð.
ÊÎÑÀÐÒÎÏ â óñëîâèÿõ ïîñëåâîåííîé ðàçðóõè è îñòðîé íåõâàòêè
êâàëèôèöèðîâàííûõ êàäðîâ óñïåøíî ñïðàâèëàñü ñ ïîñòàâëåííûìè
çàäà÷àìè. Ðàáîòû, âûïîëíåííûå ýòîé êîìèññèåé â 1920-å ãîäû, à çà-
5
òåì åå ïðååìíèêàìè – Àðòèëëåðèéñêèì íàó÷íî-èññëåäîâàòåëüñêèì
èíñòèòóòîì (ÀÍÈÈ ÐÊÊÀ) è Àðòèëëåðèéñêîé àêàäåìèåé, ñòàëè íà-
ó÷íûì ôóíäàìåíòîì äëÿ ïåðåâîîðóæåíèÿ àðòèëëåðèè Êðàñíîé Àð-
ìèè â 1930-å ãîäû.
Ñôîðìèðîâàëàñü ñîâåòñêàÿ íàó÷íàÿ øêîëà àðòèëëåðèéñêèõ ó÷å-
íûõ è êîíñòðóêòîðîâ, ñîçäàâøèõ ëó÷øóþ â ìèðå àðòèëëåðèþ, çàñëó-
æåííî ïîëó÷èâøóþ íåîôèöèàëüíûé òèòóë "áîãà âîéíû".
Ïîä ðóêîâîäñòâîì Í.È . Òèõîìèðîâà, Â.À. Àðòåìüåâà, Á.Ñ. Ïåò-
ðîïàâëîâñêîãî, Ã.Ý . Ëàíãåìàêà áûëè ñêîíñòðóèðîâàíû ïåðâûå ñî-
âåòñêèå áîåâûå ðåàêòèâíûå ñíàðÿäû íà òâåðäîì òîïëèâå, êîòîðûå ñ
íåêîòîðîé äîðàáîòêîé ýôôåêòèâíî ïðèìåíÿëèñü íà ïîëå áðàíè
Âåëèêîé Îòå÷åñòâåííîé âîéíû, íàâîäÿ ïàíèêó â ðÿäàõ ïðîòèâíèêà.
Áîëüøèõ äîñòèæåíèé äîáèëèñü ïðîåêòíî-êîíñòðóêòîðñêèå êîë-
ëåêòèâû, âîçãëàâëÿâøèåñÿ âûäàþùèìèñÿ ó÷åíûìè-àðòèëëåðèñòàìè
Â.Ã. Ãðàáèíûì, Á.È . Øàâûðèíûì, È.È. Èâàíîâûì, Ô.Ô . Ïåòðîâûì
è äðóãèìè ñîâåòñêèìè êîíñòðóêòîðàìè.
Ñâîèìè óñïåõàìè ñîâåòñêàÿ øêîëà âíåøíåé áàëëèñòèêè îáÿçàíà
è íàó÷íûì òðóäàì Â.Ï. Âåò÷èíêèíà, Ä.À . Âåíòöåëÿ, Á.Í. Îêóíåâà,
ß.Ì. Øàïèðî, Ô.È. Ôðàíêëÿ, Â.Ñ. Ïóãà÷åâà è ìíîãèõ äðóãèõ.
Âî âòîðîé ïîëîâèíå XX âåêà ðàçëè÷íûìè àâòîðàìè è àâòîðñêèìè
êîëëåêòèâàìè, ïðåäñòàâëÿþùèìè âåäóùèå áàëëèñòè÷åñêèå íàó÷íûå
øêîëû ÑÑÑÐ, áûëî íàïèñàíî è îïóáëèêîâàíî çíà÷èòåëüíîå êîëè÷åñò-
âî ìîíîãðàôèé, ó÷åáíèêîâ è ó÷åáíûõ ïîñîáèé, êîòîðûå â òîé èëè èíîé
ñòåïåíè îòðàæàëè ñîäåðæàíèå ýòîé èíòåðåñíåéøåé äèñöèïëèíû è íà
êîòîðûõ âîñïèòûâàëîñü íåñêîëüêî ïîêîëåíèé ñîâåòñêèõ è ðîññèéñêèõ
ñïåöèàëèñòîâ.
 îäíîì ðÿäó ñ èìåíàìè Ä.À. Âåíòöåëÿ, Á.Í. Îêóíåâà, ß.Ì. Øà-
ïèðî, Ë.Á. Êîìàðîâà, Ñ.È. Åðìîëàåâà, À.Ä . ×åðíîçóáîâà,
Í.Ì. Ìîí÷åíêî, Â.Ä . Êèðè÷åíêî, Æ.Ï. Ïàðøèíà, áåçóñëîâíî, ñòî-
èò èìÿ óøåäøåãî èç æèçíè àâòîðà ýòîãî ó÷åáíèêà – Àíäðåÿ Àëåê-
ñàíäðîâè÷à Äìèòðèåâñêîãî (1913–1992). À.À. Äìèòðèåâñêèé âíåñ
îãðîìíûé âêëàä â ðàçâèòèå áàëëèñòèêè ìèíîìåòíûõ ñèñòåì, îñòà-
âàÿñü äî êîíöà ñâîèõ äíåé êðóïíåéøèì àâòîðèòåòîì â ýòîé îáëàñòè.
 ãîäû âîéíû îí áûë ãëàâíûì êîíñòðóêòîðîì ìèíîìåòíîãî çàâîäà,
â 1948 ã. ïåðåøåë íà ïðåïîäàâàòåëüñêóþ ðàáîòó â ÌÂÒÓ
èì. Í.Ý. Áàóìàíà. Áîëåå òðèäöàòè ëåò âîçãëàâëÿÿ êàôåäðó áàëëèñòè-
êè ÌÂÒÓ (ñ 1956 ïî 1987 ã.), À.À. Äìèòðèåâñêèé ñîçäàë îäíó èç
êðóïíåéøèõ íàó÷íûõ øêîë, ïðåäñòàâèòåëè êîòîðîé õîðîøî èçâåñò-
íû ñâîèìè òðóäàìè íå òîëüêî â ÑÑÑÐ, íî è çà ðóáåæîì.
Âûäåðæàâøèé ïðè åãî æèçíè òðè èçäàíèÿ, ó÷åáíèê "Âíåøíÿÿ
áàëëèñòèêà" ïîëó÷èë âûñîêóþ îöåíêó ñïåöèàëèñòîâ, áûë óäîñòîåí
ðÿäà íàãðàä è ïðåìèé, ïåðåèçäàí íà èíîñòðàííûõ ÿçûêàõ.
Íàñòîÿùåå, ÷åòâåðòîå, èçäàíèå çàäóìûâàëîñü ó÷åíèêàìè
À.À . Äìèòðèåâñêîãî êàê äàíü ïàìÿòè êðóïíîìó ó÷åíîìó è ïðåêðàñíî-
6
ìó ïåäàãîãó. Â ñèëó óêàçàííîãî îáñòîÿòåëüñòâà â ïðåäëàãàåìîì âíèìà-
íèþ ÷èòàòåëÿ èçäàíèè ïî âîçìîæíîñòè ñîõðàíåíû áåç èçìåíåíèé ìà-
òåðèàëû è ðàçäåëû, ëè÷íî íàïèñàííûå À.À. Äìèòðèåâñêèì äëÿ òðåòüå-
ãî èçäàíèÿ (ãë. 1 ...3). Íå ïðåòåðïåëè òàêæå ñóùåñòâåííûõ èçìåíåíèé
íàïèñàííûå ïîä íàó÷íûì ðóêîâîäñòâîì À.À. Äìèòðèåâñêîãî åãî àñïè-
ðàíòîì Ñ.Ñ . Áîãîäèñòîâûì ãë. 7 è çíà÷èòåëüíàÿ ÷àñòü ãë. 11 . Èìåííî
ïî ýòèì ñîîáðàæåíèÿì ñîõðàíåíî è èìÿ À.À. Äìèòðèåâñêîãî êàê ñîàâ-
òîðà ó÷åáíèêà, âûïóñêàåìîãî â ñâåò áîëåå ÷åì ÷åðåç äåñÿòü ëåò ïîñëå
åãî ñìåðòè.
Áûëî áû íåïðàâèëüíûì, îäíàêî, ñ÷èòàòü íàñòîÿùåå èçäàíèå èñ-
êëþ÷èòåëüíî ìåìîðèàëüíûì. Äàííàÿ êíèãà ÿâëÿåòñÿ ó÷åáíèêîì,
óäîâëåòâîðÿþùèì, êàê ïðåäñòàâëÿåòñÿ, âñåì òðåáîâàíèÿì, êîòîðûì
äîëæíà óäîâëåòâîðÿòü ñîâðåìåííàÿ ó÷åáíàÿ ëèòåðàòóðà. Åå ñîäåðæà-
íèå ïîëíîñòüþ ñîîòâåòñòâóåò ïðîãðàììå êóðñà "Âíåøíÿÿ áàëëèñòè-
êà", ÿâëÿþùåãîñÿ îñíîâîïîëàãàþùåé äèñöèïëèíîé ñïåöèàëüíîñòåé
"Áàëëèñòèêà" è "Äèíàìèêà ïîëåòà è óïðàâëåíèå äâèæåíèåì ëåòà-
òåëüíûõ àïïàðàòîâ".
Ðåøåíèåì ó÷åáíî-ìåòîäè÷åñêîãî îáúåäèíåíèÿ (ÓÌÎ) âóçîâ ïî
óíèâåðñèòåòñêîìó ïîëèòåõíè÷åñêîìó îáðàçîâàíèþ äàííîå èçäàíèå
ðåêîìåíäîâàíî òàêæå â êà÷åñòâå îñíîâíîãî ó÷åáíèêà ïî êóðñó
"Âíåøíÿÿ áàëëèñòèêà" äëÿ îáó÷àþùèõñÿ ïî ñïåöèàëüíîñòÿì
"Ñòðåëêîâî-ïóøå÷íîå, àðòèëëåðèéñêîå è ðàêåòíîå îðóæèå" è "Ñðåä-
ñòâà ïîðàæåíèÿ è áîåïðèïàñû".
Åñòåñòâåííî, ÷òî çà ãîäû, ïðîøåäøèå ïîñëå âûõîäà â ñâåò òðåòüå-
ãî èçäàíèÿ ó÷åáíèêà (1991), âíåøíÿÿ áàëëèñòèêà ïîïîëíèëàñü íî-
âûìè ðåçóëüòàòàìè, áåç çíàíèÿ êîòîðûõ ïîäãîòîâêà ñïåöèàëèñòîâ
ñîîòâåòñòâóþùåãî ïðîôèëÿ íå ìîæåò áûòü ïðèçíàíà ïîëíîöåííîé.
Îáúåêòèâíîñòè ðàäè íåîáõîäèìî, ïðàâäà, îòìåòèòü, ÷òî ïðîøåä-
øèå ãîäû, õàðàêòåðèçóåìûå êðóïíûìè ñîöèàëüíûìè ïîòðÿñåíèÿìè,
âûñîêèì óðîâíåì ýêîíîìè÷åñêîé íåñòàáèëüíîñòè â ñòðàíå, íåîïðåäå-
ëåííîñòüþ â ñìåíå ïðèîðèòåòîâ â îáëàñòè âîåííîãî ñòðîèòåëüñòâà, íå
ñïîñîáñòâîâàëè áóðíîìó ðàçâèòèþ áàëëèñòè÷åñêèõ íàó÷íûõ øêîë è
ñåðüåçíîìó ïðîãðåññó â îáëàñòè äàííîé íàóêè.
Âìåñòå ñ òåì íèêàêèå îáñòîÿòåëüñòâà è ñóáúåêòèâíûå ôàêòîðû íå
ìîãëè ïîìåøàòü ïîñòóïàòåëüíîìó äâèæåíèþ â ðàçâèòèè íàóêè è òåõ-
íèêè âîîáùå è, â ÷àñòíîñòè, â òåõ èõ ðàçäåëàõ, êîòîðûå ñîïðèêàñàëèñü
è îêàçûâàëè íåïîñðåäñòâåííîå âîçäåéñòâèå íà ðàçâèòèå âíåøíåé áàë-
ëèñòèêè. Ïðåæäå âñåãî ýòî êàñàåòñÿ äàëüíåéøåãî ïðîãðåññà â îáëàñòè
ñîçäàíèÿ âûñîêîýôôåêòèâíîé âû÷èñëèòåëüíîé òåõíèêè è ìåòîäîâ âû-
÷èñëèòåëüíîé ìàòåìàòèêè, çàñòàâèâøèõ ïåðåñìîòðåòü íåêîòîðûå ñëî-
æèâøèåñÿ ïðåäñòàâëåíèÿ, ïî-èíîìó îöåíèòü ïðèîðèòåòû è âîçìîæ-
íûå ïóòè ðåøåíèÿ çàäà÷ ïîäãîòîâêè èñõîäíûõ äàííûõ äëÿ ïðîâåäåíèÿ
ñòðåëüá.
7
 ïîñëåäíèå ãîäû ñòàë äîñòóïåí äëÿ øèðîêîãî ÷èòàòåëÿ ðÿä ðå-
çóëüòàòîâ, ãëàâíûì îáðàçîì ìåòîäè÷åñêîãî õàðàêòåðà, â îáëàñòè
òåîðèè óñòîé÷èâîñòè äâèæåíèÿ, ïðåäñòàâëÿþùèõ èíòåðåñ ñ òî÷êè
çðåíèÿ èçëîæåíèÿ ìàòåðèàëà.
Åùå áîëåå ïîâûñèëàñü òåõíè÷åñêàÿ îñíàùåííîñòü è ìåòîäè÷å-
ñêàÿ îáåñïå÷åííîñòü áàëëèñòè÷åñêîãî ýêñïåðèìåíòà.
Äàëüíåéøåå ðàçâèòèå ïîëó÷èëè îòäåëüíûå ðàçäåëû áàëëèñòèêè
êîððåêòèðóåìûõ è óïðàâëÿåìûõ àðòèëëåðèéñêèõ ñíàðÿäîâ.
Ïî âîçìîæíîñòè âñå ýòî ó÷òåíî â íîâîì èçäàíèè ó÷åáíèêà.
Ïîìèìî ñâåäåíèé, ñîñòàâëÿþùèõ ñîäåðæàíèå îñíîâíûõ ðàçäåëîâ
êóðñà, â íàñòîÿùåå èçäàíèå, êàê è â ïðåäûäóùèå, âêëþ÷åíû íåêîòîðûå
ìàòåðèàëû äëÿ ôàêóëüòàòèâíîãî èçó÷åíèÿ, âûäåëåííûå â òåêñòå ìåëêèì
øðèôòîì.
Ïðèâåäåííûé ñïèñîê ëèòåðàòóðû, íåñêîëüêî ðàñøèðåííûé ïî
ñðàâíåíèþ ñ ïðåäûäóùèìè èçäàíèÿìè çà ñ÷åò âêëþ÷åíèÿ â íåãî ðàíåå
íåäîñòóïíûõ äëÿ øèðîêîãî ÷èòàòåëÿ ðàáîò, ñîäåðæèò ïåðå÷åíü èñ-
ïîëüçîâàííûõ ïðè íàïèñàíèè ó÷åáíèêà èñòî÷íèêîâ. Ðàáîòû, ðåêî-
ìåíäîâàííûå äëÿ áîëåå ãëóáîêîãî èçó÷åíèÿ äèñöèïëèíû, îòìå÷åíû
çâåçäî÷êàìè.
Ïðè ïîäãîòîâêå ðóêîïèñè ÷åòâåðòîãî èçäàíèÿ êíèãè ê ïå÷àòè áûëè
ó÷òåíû çàìå÷àíèÿ ðåöåíçèðóþùåé êàôåäðû è ðåöåíçåíòà, äåéñòâè-
òåëüíîãî ÷ëåíà Ðîññèéñêîé àêàäåìèè ðàêåòíûõ è àðòèëëåðèéñêèõ
íàóê, çàñëóæåííîãî äåÿòåëÿ íàóêè è òåõíèêè ÐÑÔÑÐ, äîêòîðà òåõíè-
÷åñêèõ íàóê, ïðîôåññîðà Í.Ì. Ìîí÷åíêî, âêëàä êîòîðîãî â ñîâåðøåí-
ñòâîâàíèå ìàòåðèàëîâ ó÷åáíèêà äàëåêî âûõîäèò çà ðàìêè ôîðìàëüíûõ
ôóíêöèé îôèöèàëüíîãî ðåöåíçåíòà. Åãî äîáðîæåëàòåëüíàÿ êðèòèêà è
ñîâåòû ÿâèëèñü îïðåäåëÿþùèìè ïðè îòáîðå è ïåðåîñìûñëèâàíèè èñ-
òèííîé öåííîñòè ïðèâëåêàåìûõ ê ðàññìîòðåíèþ ìàòåðèàëîâ.
Ñ÷èòàþ ñâîèì äîëãîì ïîáëàãîäàðèòü ãëàâíîãî ðåäàêòîðà ëèòåðàòó-
ðû ïî àâèàöèè, ðàêåòíîé òåõíèêå è êîñìîíàâòèêå èçäàòåëüñòâà "Ìà-
øèíîñòðîåíèå" Ë.À. Ãèëüáåðãà, âûñòóïèâøåãî èíèöèàòîðîì ïåðåèçäà-
íèÿ ó÷åáíèêà. Áåç åãî ïîääåðæêè îíî âðÿä ëè îêàçàëîñü áû âîçìîæ-
íûì.
Íàêîíåö, õîòåë áû âûðàçèòü ïðèçíàòåëüíîñòü êîëëåãàì, ïðèíÿâ-
øèì ó÷àñòèå â îáñóæäåíèè ðóêîïèñè è ñïîñîáñòâîâàâøèì óëó÷øå-
íèþ åå ñîäåðæàíèÿ, à òàêæå îêàçàâøèì ñîäåéñòâèå â ôèíàíñîâîé
ïîääåðæêå èçäàíèÿ.
Äåéñòâèòåëüíûé ÷ëåí Ðîññèéñêîé àêàäåìèè
ðàêåòíûõ è àðòèëëåðèéñêèõ íàóê,
çàñëóæåííûé äåÿòåëü íàóêè ÐÔ,
ëàóðåàò ïðåìèè Ïðåçèäåíòà ÐÔ,
äîêòîð òåõíè÷åñêèõ íàóê, ïðîôåññîð Ë. Ëûñåíêî
ÎÑÍÎÂÍÛÅ ÎÁÎÇÍÀ×ÅÍÈß
Âåêòîðû âûäåëÿþòñÿ ïðÿìûì ïîëóæèðíûì øðèôòîì; ìàòðèöû
ëèáî îáîçíà÷àþòñÿ áîëüøèìè ïîëóæèðíûìè áóêâàìè (À, Â, Ñ),
ëèáî ïðåäñòàâëÿþòñÿ â âèäå ÷àñòíûõ ïðîèçâîäíûõ îò âåêòîðîâ
∂
∂
f
x
⎛
⎝⎜⎞
⎠⎟.
Ñêàëÿðíûå èëè âåêòîðíûå ôóíêöèè ñêàëÿðíûõ èëè âåêòîð-
íûõ ïåðåìåííûõ îáîçíà÷àþòñÿ ñëåäóþùèì îáðàçîì: x(t); x(t);
f(x); f(x, t).
Îñíîâíûå îáîçíà÷åíèÿ ñîîòâåòñòâóþò ÃÎÑÒó 20058–80 "Äèíà-
ìèêà ëåòàòåëüíûõ àïïàðàòîâ â àòìîñôåðå" è ÃÎÑÒó 4401–81 "Àòìî-
ñôåðà ñòàíäàðòíàÿ. Ïàðàìåòðû".
À – àçèìóò
à – ñêîðîñòü çâóêà
àà – óñêîðåíèå öåíòðà ìàññ ËÀ â àáñîëþòíîì äâèæåíèè
àå – óñêîðåíèå öåíòðà ìàññ êîðïóñà ËÀ â ïåðåíîñíîì äâèæåíèè
ar – óñêîðåíèå öåíòðà ìàññ ñèñòåìû "êîðïóñ – òîïëèâî
–
ãàçû"
îòíîñèòåëüíî êîðïóñà ðàêåòû
ñ – áàëëèñòè÷åñêèé êîýôôèöèåíò, èíòåãðàë ïëîùàäåé
CR – àýðîäèíàìè÷åñêèé êîýôôèöèåíò ñóììàðíîé àýðîäèíàìè-
÷åñêîé ñèëû
cx, cy, cz – êîýôôèöèåíòû àýðîäèíàìè÷åñêèõ ñèë
F – ðàâíîäåéñòâóþùàÿ âíåøíÿÿ ñèëà
Fêîð – êîðèîëèñîâà ñèëà
Fp – ðàâíîäåéñòâóþùàÿ ðåàêòèâíàÿ ñèëà
F(V), G(V),K
V
a
⎛
⎝⎜⎞
⎠⎟ – ôóíêöèè ñèëû ñîïðîòèâëåíèÿ âîçäóõà
g – óñêîðåíèå ñâîáîäíîãî ïàäåíèÿ
gò – óñêîðåíèå îò ñèëû òÿãîòåíèÿ
à – ìîìåíò ïîâåðõíîñòíîãî òðåíèÿ
Í – ãåîïîòåíöèàëüíàÿ âûñîòà
H(y) – ôóíêöèÿ èçìåíåíèÿ ïëîòíîñòè âîçäóõà â çàâèñèìîñòè îò
âûñîòû
III
xyz
iii
,, – ìîìåíòû èíåðöèè ËÀ îòíîñèòåëüíî îñåé ïðèíÿòîé
ê ðàññìîòðåíèþ ñèñòåìû êîîðäèíàò
III
xy
xz
yz
ii
ii
ii
,, – öåíòðîáåæíûå ìîìåíòû èíåðöèè
K – âåêòîð êèíåòè÷åñêîãî ìîìåíòà òåëà
L – ëèíåéíàÿ äàëüíîñòü ïî ïîâåðõíîñòè Çåìëè
Ì – ÷èñëî Ìàõà
Ìä – äåìïôèðóþùèé ìîìåíò
9
Ìñò – ñòàáèëèçèðóþùèé ìîìåíò
MF – ñóììàðíûé ìîìåíò âíåøíèõ ñèë îòíîñèòåëüíî öåíòðà
ìàññ ËÀ
m – ìàññà äâèæóùåãîñÿ òåëà (ðàêåòû, ñíàðÿäà)
mx, my, mz – êîýôôèöèåíòû àýðîäèíàìè÷åñêèõ ìîìåíòîâ
Ï – ïîòåíöèàë ñèëû òÿæåñòè
Ïò – ïîòåíöèàë ñèëû çåìíîãî òÿãîòåíèÿ
Ïö – ïîòåíöèàë öåíòðîáåæíîé ñèëû èíåðöèè
Жòÿãà
ð – äàâëåíèå âîçäóõà
Q – âåêòîð êîëè÷åñòâà äâèæåíèÿ òåëà
Qi – îáîáùåííàÿ ñèëà
q – ñêîðîñòíîé íàïîð
S – õàðàêòåðíàÿ ïëîùàäü
T = tc = tï – ïîëíîå âðåìÿ ïîëåòà
ÒÏ – êèíåòè÷åñêàÿ ýíåðãèÿ òåëà ïåðåìåííîé ìàññû
Va – ñêîðîñòü öåíòðà ìàññ ËÀ â àáñîëþòíîì äâèæåíèè
Ve – ñêîðîñòü öåíòðà ìàññ ËÀ â ïåðåíîñíîì äâèæåíèè
Vr – ñêîðîñòü öåíòðà ìàññ ñèñòåìû "êîðïóñ – òîïëèâî
–
ãàçû" îò-
íîñèòåëüíî êîðïóñà ðàêåòû
Vxc
= u – ïðîåêöèÿ ñêîðîñòè öåíòðà ìàññ ËÀ íà îñü OXc ñòàðòîâîé
ñèñòåìû êîîðäèíàò
Vyc
= w – ïðîåêöèÿ ñêîðîñòè öåíòðà ìàññ ËÀ íà îñü OYc
Xa – ñèëà ëîáîâîãî ñîïðîòèâëåíèÿ
Xp, Yp, Zp – óïðàâëÿþùèå ñèëû, äåéñòâóþùèå â íàïðàâëåíèè ñâÿ-
çàííûõ îñåé ËÀ
xc – ãîðèçîíòàëüíàÿ äàëüíîñòü
Ya – àýðîäèíàìè÷åñêàÿ ïîäúåìíàÿ ñèëà
ó – ãåîìåòðè÷åñêàÿ âûñîòà
ys – âûñîòà òðàåêòîðèè
Za – àýðîäèíàìè÷åñêàÿ áîêîâàÿ ñèëà
α – óãîë àòàêè
β – óãîë ñêîëüæåíèÿ
γ – óãîë êðåíà
ε – óãîë ìåñòà
θ – óãîë íàêëîíà òðàåêòîðèè
θ – óãîë òàíãàæà
λ* – äîëãîòà
λ – äîëãîòà ëèíèè óçëîâ
π(y) – ôóíêöèÿ èçìåíåíèÿ äàâëåíèÿ ñ âûñîòîé
ρ – ïëîòíîñòü âîçäóõà
τ – âèðòóàëüíàÿ òåìïåðàòóðà
φã – ãåîãðàôè÷åñêàÿ øèðîòà
10
φãö – ãåîöåíòðè÷åñêàÿ øèðîòà
Ψ – óãîë ïóòè
ψ – óãîë ðûñêàíèÿ
Ω – óãëîâàÿ ñêîðîñòü âðàùåíèÿ Çåìëè
ω – âåêòîð óãëîâîé ñêîðîñòè êîðïóñà ñíàðÿäà (ðàêåòû) îòíîñè-
òåëüíîé áàçîâîé ñèñòåìû êîîðäèíàò
Íèæíèå èíäåêñû
ê – êîíå÷íàÿ âåëè÷èíà
ö–öåëü
Âåðõíèå èíäåêñû
ο – åäèíè÷íûé âåêòîð (opò), îïòèìàëüíîå çíà÷åíèå
ò – çíàê òðàíñïîíèðîâàíèÿ âåêòîðà èëè ìàòðèöû
* – íîìèíàëüíîå çíà÷åíèå, ëîêàëüíàÿ ïðîèçâîäíàÿ
Ïðî÷èå îáîçíà÷åíèÿ, ïðèíÿòûå â ó÷åáíèêå, ïîÿñíåíû â òåêñòå.
ÂÂÅÄÅÍÈÅ
Òåðìèí "áàëëèñòèêà", èçíà÷àëüíî îïðåäåëÿþùèé íàóêó î äâèæå-
íèè ñâîáîäíî áðîøåííîãî òåëà, èìååò ãðå÷åñêîå ïðîèñõîæäåíèå â
ñèëó ñîçâó÷íîñòè ñî ñëîâîì "ba'llo", îçíà÷àþùèì â ïåðåâîäå "áðî-
ñàþ". Îò íåãî æå ïîøëî è íàçâàíèå äðåâíèõ ìåòàòåëüíûõ óñòàíîâîê
"áàëëèñò", ïðåäíàçíà÷åííûõ äëÿ ìåòàíèÿ êàìíåé, òÿæåëûõ ñòðåë,
áî÷åê ñ ãîðÿùåé ñìîëîé è ò.ä ., èñïîëüçóåìûõ âïëîòü äî êîíöà
V âåêà ïðè îñàäå êðåïîñòåé è ïîðàæåíèè èõ çàùèòíèêîâ.
Ñ âîçíèêíîâåíèåì àðòèëëåðèè, ñòðåëêîâîãî îðóæèÿ, à òàêæå íå-
óïðàâëÿåìûõ ðàêåò ïîä "áàëëèñòèêîé" ñòàëè ïîíèìàòü íàóêó î äâè-
æåíèè àðòèëëåðèéñêèõ ñíàðÿäîâ, ìèí, ïóëü è íåóïðàâëÿåìûõ ðàêåò.
Ïîÿâëåíèå óïðàâëÿåìûõ áàëëèñòè÷åñêèõ ðàêåò, ïîëåò êîòîðûõ, çà
èñêëþ÷åíèåì îòíîñèòåëüíî íåáîëüøîãî àêòèâíîãî ó÷àñòêà, ñîâåð-
øàåòñÿ ïî òðàåêòîðèè ñâîáîäíî áðîøåííîãî òåëà, ïðèâåëî ê èñ-
ïîëüçîâàíèþ òåðìèíà "áàëëèñòèêà" è ïðè èçó÷åíèè çàêîíîìåðíî-
ñòåé äâèæåíèÿ óïðàâëÿåìûõ ðàêåò äàëüíåãî äåéñòâèÿ, à òàêæå êîð-
ðåêòèðóåìûõ áîåïðèïàñîâ ðàçëè÷íîãî òèïà.
Ðàñïðîñòðàíåíèå îäíîãî òåðìèíà (à òî÷íåå, ïîíÿòèÿ) íà ñòîëü
øèðîêèé êðóã çàäà÷ äâèæåíèÿ "ñâîáîäíî áðîøåííûõ" îáúåêòîâ, åñ-
òåñòâåííî, ïîòðåáîâàëî äàëüíåéøåé äåòàëèçàöèè â íàçâàíèè îñíîâ-
íûõ íàïðàâëåíèé (ðàçäåëîâ) áàëëèñòèêè.
Íà ñîâðåìåííîì ýòàïå ðàçâèòèÿ îáñóæäàåìîé íàóêè ïðåäñòàâëÿ-
åòñÿ âîçìîæíûì äîñòàòî÷íî ñòðîãî ðàçäåëèòü èõ, ïî êðàéíåé ìåðå ñ
òî÷êè çðåíèÿ íàçâàíèé è õàðàêòåðà ðåøàåìûõ çàäà÷.
Ñ ó÷åòîì ñëîæèâøåéñÿ òåðìèíîëîãèè ïðèíÿòî ðàçëè÷àòü:
âíóòðåííþþ áàëëèñòèêó, èçó÷àþùóþ äâèæåíèå ñíàðÿäîâ, ìèí,
ïóëü è ò.ä . â êàíàëå ñòâîëà îðóæèÿ ïîä äåéñòâèåì ïîðîõîâûõ ãàçîâ, à
òàêæå äðóãèå ïðîöåññû, ïðîèñõîäÿùèå ïðè âûñòðåëå â êàíàëå ñòâî-
ëà èëè êàìåðå ñãîðàíèÿ ðàêåòû;
ïðîìåæóòî÷íóþ áàëëèñòèêó, ÿâëÿþùóþñÿ ïîäðàçäåëîì âíóòðåí-
íåé áàëëèñòèêè, èçó÷àþùóþ ïðîöåññû ïåðèîäà ïîñëåäåéñòâèÿ, îïðå-
äåëÿþùåãî äåéñòâóþùóþ íà îòêàòíûå ÷àñòè îðóäèÿ ñèëó, ïóòü è
ñêîðîñòü äâèæåíèÿ ýòèõ ÷àñòåé, óñêîðåíèå è ïóòü ñíàðÿäà ïðè âûëå-
òå èç êàíàëà ñòâîëà èëè ðàêåòû ïðè ñõîäå ñ íàïðàâëÿþùåé, âðåìÿ
äåéñòâèÿ íà ñíàðÿä èñòåêàþùèõ èç êàíàëà ñòâîëà ãàçîâ, íà÷àëüíûå
12
óñëîâèÿ äâèæåíèÿ ñíàðÿäà èëè ðàêåòû, äåéñòâèå íàäóëüíûõ ãàçîîò-
âîäíûõ óñòðîéñòâ è äð.;
âíåøíþþ áàëëèñòèêó, èçó÷àþùóþ äâèæåíèå íåóïðàâëÿåìûõ ëåòà-
òåëüíûõ àïïàðàòîâ (ñíàðÿäîâ, ìèí, ïóëü, íåóïðàâëÿåìûõ ðàêåò,
àâèàáîìá è ò.ä.) ïîñëå ïðåêðàùåíèÿ èõ ñèëîâîãî âçàèìîäåéñòâèÿ ñî
ñòâîëîì îðóæèÿ èëè íàïðàâëÿþùåé ïóñêîâîé óñòàíîâêè, à òàêæå
ôàêòîðû è óñëîâèÿ, âëèÿþùèå íà ýòî äâèæåíèå;
ýêñïåðèìåíòàëüíóþ áàëëèñòèêó (âíóòðåííþþ è âíåøíþþ), çàíè-
ìàþùóþñÿ èññëåäîâàíèåì ðåàëüíûõ ïðîöåññîâ, ïðîèñõîäÿùèõ ïðè
ãîðåíèè ïîðîõà, äâèæåíèè ñíàðÿäîâ, ðàêåò (èëè êîíñòðóêòèâíî ïî-
äîáíûõ èì ìîäåëåé) è ò.ä .;
áàëëèñòèêó óïðàâëÿåìûõ è êîððåêòèðóåìûõ ðàêåò è ñíàðÿäîâ, èçó-
÷àþùóþ äâèæåíèå áàëëèñòè÷åñêèõ ëåòàòåëüíûõ àïïàðàòîâ ïî òðàåê-
òîðèÿì, ðåàëèçàöèÿ ãðàíè÷íûõ óñëîâèé êîòîðûõ îïðåäåëÿåòñÿ ïðè-
íÿòûì çàêîíîì íàâåäåíèÿ èëè êîððåêöèè è óñëîâèÿìè ïîñëåäóþ-
ùåãî ñâîáîäíîãî äâèæåíèÿ â áåçâîçäóøíîì ïðîñòðàíñòâå è/èëè â
àòìîñôåðå.
Íåñìîòðÿ íà î÷åâèäíûå ðàçëè÷èÿ â ñîäåðæàòåëüíîé ñòîðîíå ïå-
ðå÷èñëåííûõ ðàçäåëîâ áàëëèñòèêè, áîëüøèíñòâî èç íèõ (çà èñêëþ-
÷åíèåì, ìîæåò áûòü, âíóòðåííåé è ïðîìåæóòî÷íîé áàëëèñòèêè)
îáúåäèíÿåò òî, ÷òî îáúåêòîì èññëåäîâàíèÿ ÿâëÿåòñÿ ñâîáîäíîå äâè-
æåíèå òåëà, ò.å . äâèæåíèå, íå îãðàíè÷åííîå íèêàêèìè ìåõàíè÷åñêè-
ìè ñâÿçÿìè.
Ñëåäîâàòåëüíî, áàëëèñòèêà èìååò äåëî ñ íàèáîëåå îáùèì âèäîì
ìåõàíè÷åñêîãî äâèæåíèÿ – äâèæåíèåì òâåðäîãî òåëà, îáëàäàþùåãî
øåñòüþ ñòåïåíÿìè ñâîáîäû.  ðÿäå ñëó÷àåâ íà ýòî äâèæåíèå íàêëà-
äûâàþòñÿ ñîïóòñòâóþùèå ýôôåêòû, îáóñëîâëåííûå âíåøíèìè óñ-
ëîâèÿìè ïîëåòà, êîððåêòèðóþùèìè âîçäåéñòâèÿìè, èçìåíåíèåì
ìàññû ðåàêòèâíîãî ñíàðÿäà (ðàêåòû), ïåðåìåùåíèåì åãî öåíòðà
ìàññ âäîëü êîðïóñà è ò.ä .
Ðàññìàòðèâàÿ äâèæåíèå ëåòàòåëüíîãî àïïàðàòà (ËÀ) ïîä äåéñòâè-
åì ïðèëîæåííûõ ê íåìó ñèë (àýðîäèíàìè÷åñêîé, ãðàâèòàöèîííîé è
ðåàêòèâíîé), âíåøíÿÿ áàëëèñòèêà ñòàâèò öåëüþ ïîëó÷åíèå èñõîä-
íûõ äàííûõ äëÿ ïðîåêòèðîâàíèÿ àðòèëëåðèéñêèõ è ðàêåòíûõ êîì-
ïëåêñîâ, áîåïðèïàñîâ ê íèì; ìåòîäè÷åñêîãî îáåñïå÷åíèÿ èñïûòà-
íèé íîâûõ ñèñòåì; ñîñòàâëåíèÿ òàáëèö ñòðåëüáû, ïî êîòîðûì ðåøà-
þòñÿ çàäà÷è ïðèöåëèâàíèÿ, îáîáùåíèÿ ðåçóëüòàòîâ ñòðåëüáû è
áàëëèñòè÷åñêèõ ðàñ÷åòîâ äëÿ ñïåöèàëèçèðîâàííûõ ÝÂÌ ïîäãîòîâ-
êè äàííûõ; ïðîâåäåíèÿ òðàåêòîðíûõ èçìåðåíèé, îöåíêè òî÷íîñòè
ñòðåëüáû è ò.ä .
Ñîçäàíèå íîâîé ñèñòåìû âñåãäà íà÷èíàåòñÿ ñ áàëëèñòè÷åñêîãî ïðîåê-
òèðîâàíèÿ è ðåøåíèÿ çàäà÷ âíåøíåé è âíóòðåííåé áàëëèñòèêè. Âíåøíÿÿ
áàëëèñòèêà îïðåäåëÿåò ôîðìó òðàåêòîðèè, íàèáîëüøèå è íàèìåíüøèå
13
óãëû áðîñàíèÿ, òðåáîâàíèÿ ê çíà÷åíèþ ïåðåãðóçêè. Âûÿâëåíèå óñëîâèé
óñòîé÷èâîñòè äâèæåíèÿ ñíàðÿäîâ ðàçëè÷íîé êîíñòðóêöèè îòíîñèòñÿ ê
îäíîé èç ãëàâíûõ çàäà÷ âíåøíåé áàëëèñòèêè. Òåîðèÿ ïîïðàâîê, îñíî-
âàííàÿ íà ó÷åòå îòêëîíåíèé äåéñòâèòåëüíûõ óñëîâèé ñòðåëüáû îò íîìè-
íàëüíûõ, ïîçâîëÿåò ïðîèçâåñòè óòî÷íåíèå óñòàíîâîê, îïðåäåëÿþùèõ íà-
÷àëüíûå óñëîâèÿ ñòðåëüáû ïî íåïîäâèæíûì è ïîäâèæíûì öåëÿì. Ðàñ÷åò
ðàññåèâàíèÿ ñíàðÿäîâ è îæèäàåìîé òî÷íîñòè ñòðåëüáû äàåò âîçìîæíîñòü
îöåíèòü ïðåäïîëàãàåìûé ðàñõîä ñíàðÿäîâ ïðè ðåøåíèè òîé èëè èíîé
òàêòè÷åñêîé çàäà÷è.
Âàæíîé ïðîáëåìîé âíåøíåé áàëëèñòèêè ÿâëÿåòñÿ ó÷åò âëèÿíèÿ
äâèæåíèÿ íîñèòåëÿ âîîðóæåíèÿ (êîðàáëÿ, ñàìîëåòà è äð.) íà îïðåäåëå-
íèå íà÷àëüíûõ óñëîâèé ñòðåëüáû. Ïðè ñòðåëüáå ïî ïîäâèæíûì öåëÿì
ìåòîäàìè âíåøíåé áàëëèñòèêè ðàññ÷èòûâàþòñÿ óãëû óïðåæäåíèÿ è èõ
èçìåíåíèå â ïðîöåññå äâèæåíèÿ öåëè.
Áàëëèñòè÷åñêèå ðàñ÷åòû ïðîâîäÿòñÿ â íåñêîëüêî ïðèáëèæåíèé.
Íà ñòàäèè áàëëèñòè÷åñêîãî ïðîåêòèðîâàíèÿ îáû÷íî èñïîëüçóþòñÿ
óïðîùåííûå ìîäåëè äâèæåíèÿ, ó÷èòûâàþùèå ëèøü îñíîâíûå ôàê-
òîðû.  ïðîöåññå êîíñòðóèðîâàíèÿ ñèñòåì (êîìïëåêñà) ýòè ðàñ÷åòû
ïîâòîðÿþòñÿ ñ ââåäåíèåì â íèõ íîâûõ óòî÷íÿþùèõ äàííûõ.
Íåñìîòðÿ íà îïðåäåëåííûå îñîáåííîñòè áàëëèñòè÷åñêèõ çàäà÷
äëÿ ðàçëè÷íûõ êëàññîâ ðàêåò è ñíàðÿäîâ, ïîñòàíîâêà ýòèõ çàäà÷ è
ïîñëåäóþùèå èõ ðåøåíèÿ âî ìíîãîì îñòàþòñÿ îáùèìè. Äâèæåíèå
ðàêåò è ñíàðÿäîâ ïîä÷èíÿåòñÿ îäíèì è òåì æå çàêîíàì ìåõàíèêè è
îïèñûâàåòñÿ îäíîòèïíûìè äèôôåðåíöèàëüíûìè óðàâíåíèÿìè.
×àùå âñåãî ðàçëè÷àþòñÿ ëèøü ïðàâûå ÷àñòè óðàâíåíèé, ñîäåðæàùèå
êîíêðåòíûé êîìïëåêñ äåéñòâóþùèõ ñèë è ìîìåíòîâ.
Âíåøíÿÿ áàëëèñòèêà ðàêåò ïðåäïîëàãàåò íåîáõîäèìîñòü âûäåëå-
íèÿ äëÿ èçó÷åíèÿ àêòèâíîãî ó÷àñòêà òðàåêòîðèè, íà êîòîðîì äâèæå-
íèå ËÀ îñóùåñòâëÿåòñÿ çà ñ÷åò èñòå÷åíèÿ èç ñîïëîâîãî áëîêà ãàçî-
âîé ñòðóè, îáðàçóþùåéñÿ îò ñãîðàíèÿ òîïëèâà, íàõîäÿùåãîñÿ âíóò-
ðè åãî êîðïóñà. Ïîñëå ïðåêðàùåíèÿ äåéñòâèÿ ðåàêòèâíîé ñèëû
(ïàññèâíûé ó÷àñòîê òðàåêòîðèè) ðàñ÷åò äâèæåíèÿ ðåàêòèâíîãî ñíà-
ðÿäà (ðàêåòû) ïðàêòè÷åñêè ïîëíîñòüþ ñîâïàäàåò ñ ðàñ÷åòîì òðàåê-
òîðèé îáû÷íûõ àðòèëëåðèéñêèõ ñíàðÿäîâ ïîñòîÿííîé ìàññû.
Ðàññìàòðèâàåìûå â ó÷åáíèêå àðòèëëåðèéñêèå è ðåàêòèâíûå ñíà-
ðÿäû*
, ÿâëÿþùèåñÿ îñíîâíûì îáúåêòîì èçó÷åíèÿ âíåøíåé áàëëè-
ñòèêè, îáëàäàþò îïðåäåëåííûìè îñîáåííîñòÿìè, íå ïîçâîëÿþùèìè
â ïîëíîé ìåðå ðàñïðîñòðàíÿòü ðåçóëüòàòû, ïîëó÷åííûå ïðè èõ èñ-
14
*
 ñëó÷àå, åñëè ïîñòàíîâêà çàäà÷è íå òðåáóåò äåòàëèçàöèè òèïà ñíàðÿäà
(ðàêåòû), äàëåå â òåêñòå èñïîëüçóåòñÿ îáîáùàþùåå ïîíÿòèå – ëåòàòåëüíûå
àïïàðàòû.
ñëåäîâàíèè, íà óïðàâëÿåìûå áàëëèñòè÷åñêèå ðàêåòû. Òåì íå ìåíåå
äàëüíåéøåå ðàçâèòèå ýòèõ ðåçóëüòàòîâ ñîçäàåò îñíîâó äëÿ òåîðåòè-
÷åñêèõ èññëåäîâàíèé áàëëèñòèêè óïðàâëÿåìûõ ËÀ. Ýòî òåì áîëåå
ñïðàâåäëèâî äëÿ êîððåêòèðóåìûõ àðòèëëåðèéñêèõ ñíàðÿäîâ, îòíî-
ñÿùèõñÿ ê ïðîìåæóòî÷íîìó êëàññó áîåïðèïàñîâ.
 íàñòîÿùåì ó÷åáíèêå â òîé èëè èíîé ñòåïåíè ïîëíîòû èçëîæå-
íèÿ ðàññìàòðèâàþòñÿ âñå îñíîâíûå âîïðîñû âíåøíåé áàëëèñòèêè
ËÀ.
Çàäà÷è âíåøíåé áàëëèñòèêè ïðèíÿòî ïîäðàçäåëÿòü íà ïÿòü ãðóïï
(ïÿòü îñíîâíûõ çàäà÷). Ñôîðìóëèðóåì èõ.
Ïåðâàÿ çàäà÷à ñîñòîèò â ðàñ÷åòå òðàåêòîðèé äâèæåíèÿ ËÀ ïî çàðà-
íåå èçâåñòíûì äàííûì. Äëÿ åå ðåøåíèÿ íåîáõîäèìî ïðåæäå âñåãî ïðà-
âèëüíî îïðåäåëèòü ñèëû, äåéñòâóþùèå íà ËÀ â ïîëåòå, è èõ âåëè÷èíó
â êàæäûé ìîìåíò âðåìåíè. Äàëåå ñëåäóåò ñîñòàâèòü äèôôåðåíöèàëü-
íûå óðàâíåíèÿ äâèæåíèÿ ËÀ ñ ó÷åòîì âñåõ äåéñòâóþùèõ ñèë.  ðå-
çóëüòàòå èõ ðåøåíèÿ ïðè çàäàííûõ íà÷àëüíûõ óñëîâèÿõ íàõîäÿòñÿ îñ-
íîâíûå ïàðàìåòðû äâèæåíèÿ è êîîðäèíàòû öåíòðà ìàññ â ôóíêöèè
âðåìåíè, ïî êîòîðûì ìîæåò áûòü ïîñòðîåíà òðàåêòîðèÿ. Ïåðâóþ çàäà-
÷ó èíîãäà íàçûâàþò îñíîâíîé èëè ïðÿìîé çàäà÷åé âíåøíåé áàëëèñòèêè.
×èñëî ñèë, äåéñòâóþùèõ íà ËÀ â ïðîöåññå äâèæåíèÿ, õàðàêòåð èõ èç-
ìåíåíèÿ â ïîëåòå, à òàêæå ÷èñëî óðàâíåíèé, îïèñûâàþùèõ äâèæåíèå
è èõ âèä, çàâèñÿò îò íàçíà÷åíèÿ ËÀ, åãî êîíñòðóêöèè, ñïîñîáà ñòàáè-
ëèçàöèè â ïîëåòå è ïðåäïîëàãàåìîé òðàåêòîðèè äâèæåíèÿ, à òàêæå îò
ýòàïà æèçíåííîãî öèêëà èçäåëèÿ, äëÿ êîòîðîãî ïðîâîäÿòñÿ ñîîòâåòñò-
âóþùèå áàëëèñòè÷åñêèå èññëåäîâàíèÿ.
Âòîðàÿ, èëè òàê íàçûâàåìàÿ îáðàòíàÿ, çàäà÷à, âàæíûì ýëåìåíòîì
êîòîðîé ÿâëÿåòñÿ îòûñêàíèå îïòèìàëüíûõ ðåæèìîâ è òðàåêòîðèé
äâèæåíèÿ, ñîñòîèò â îïðåäåëåíèè ïðîåêòíûõ áàëëèñòè÷åñêèõ ïàðà-
ìåòðîâ äâèæåíèÿ ïî çàäàííûì òàêòèêî-òåõíè÷åñêèì õàðàêòåðèñòè-
êàì è òðåáîâàíèÿì áîåâîãî ïðèìåíåíèÿ, ïðåäúÿâëÿåìûì ê ðàêåò-
íîé èëè àðòèëëåðèéñêîé ñèñòåìå.
Ðàñ÷åò ñòàáèëèçàöèè è óñòîé÷èâîñòè äâèæåíèÿ ËÀ ðàçëè÷íîãî
íàçíà÷åíèÿ îòíîñèòñÿ ê òðåòüåé çàäà÷å âíåøíåé áàëëèñòèêè. Åñëè
ðàêåòà èëè ñíàðÿä íåóñòîé÷èâû â ïîëåòå, òî íåëüçÿ îæèäàòü, ÷òî îíè
"ïðàâèëüíî" ïîëåòÿò â çàäàííîì íàïðàâëåíèè.
Ïðîåêòíûå ðàñ÷åòû âåäóòñÿ, êàê ïðàâèëî, äëÿ èäåàëüíî âûïîëíåííî-
ãî ñíàðÿäà ïðè ñðåäíèõ ìåòåîðîëîãè÷åñêèõ óñëîâèÿõ, ïðèíÿòûõ çà íîìè-
íàëüíûå. Îäíàêî â äåéñòâèòåëüíîñòè ïîÿâëÿåòñÿ ðÿä ôàêòîðîâ, âûçû-
âàþùèõ îòêëîíåíèå ñíàðÿäà îò ðàñ÷åòíîé òðàåêòîðèè. Ðàññåèâàíèå òðà-
åêòîðèé îòäåëüíûõ âûñòðåëîâ èëè ïóñêîâ ðàêåò ìîæåò áûòü îáóñëîâëåíî
êàê êîíñòðóêòèâíûìè è òåõíîëîãè÷åñêèìè ïðè÷èíàìè (íàïðèìåð, âû-
15
çûâàåìûì èìè ó ðàêåò ýêñöåíòðèñèòåòîì ñèëû òÿãè), òàê è îòêëîíåíèÿ-
ìè óñëîâèé ïîëåòà îò ðàñ÷åòíûõ, íàïðèìåð èçìåíåíèåì ìåòåîôàêòîðîâ,
íåðàâíîìåðíûì ðàçãàðîì êðèòè÷åñêîãî ñå÷åíèÿ ñîïëà, "óíîñîì" ìàññû
òåïëîçàùèòû ïîêðûòèÿ ñ ãîëîâíîé ÷àñòè áàëëèñòè÷åñêîé ðàêåòû è äð.
Èçó÷åíèå ôàêòîðîâ, âëèÿþùèõ íà ðàññåèâàíèå òðàåêòîðèé ËÀ, îïðåäå-
ëåíèå ñòåïåíè èõ âîçäåéñòâèÿ è ðàññìîòðåíèå ñïîñîáîâ óìåíüøåíèÿ
ðàññåèâàíèÿ è ïîâûøåíèÿ òî÷íîñòè ñòðåëüáû ÿâëÿåòñÿ ÷åòâåðòîé çàäà÷åé
âíåøíåé áàëëèñòèêè.
Ïÿòàÿ çàäà÷à ôîðìóëèðóåòñÿ êàê ðàçðàáîòêà ìåòîäè÷åñêîãî îáåñ-
ïå÷åíèÿ ñîñòàâëåíèÿ òàáëèö ñòðåëüáû è îïåðàòèâíûõ àëãîðèòìîâ
ïîäãîòîâêè èñõîäíûõ äàííûõ äëÿ ïðîâåäåíèÿ àðòèëëåðèéñêîé
ñòðåëüáû èëè ïóñêîâ ðàêåò.
Ïðè ðåøåíèè çàäà÷ âíåøíåé áàëëèñòèêè ðàêåò è ñíàðÿäîâ áîëü-
øåå ÷èñëî äåéñòâóþùèõ ôàêòîðîâ ñ ìåíüøèì êîëè÷åñòâîì äîïóùå-
íèé ìîæåò áûòü ó÷òåíî ÷èñëåííûì èíòåãðèðîâàíèåì äèôôåðåíöè-
àëüíûõ óðàâíåíèé äâèæåíèÿ ËÀ ñ èñïîëüçîâàíèåì ÝÖÂÌ. Òîëüêî
íåáîëüøîé êëàññ ñðàâíèòåëüíî ïðîñòûõ çàäà÷ ìîæåò ðåøàòüñÿ òàá-
ëè÷íûìè èëè àíàëèòè÷åñêèìè ìåòîäàìè.
Îòðàáîòêà ëþáîãî òèïà áîåïðèïàñà ïîñëå ñîçäàíèÿ îïûòíîãî îá-
ðàçöà òðåáóåò ïðîâåäåíèÿ áîëüøîãî îáúåìà ýêñïåðèìåíòàëüíûõ èñ-
ñëåäîâàíèé, â òîì ÷èñëå ëåòíûõ èñïûòàíèé.
Âûïîëíåíèå îïåðàöèé, íàïðàâëåííûõ íà íåïîñðåäñòâåííîå ðå-
øåíèå çàäà÷ ñòðåëüáû (ïîëèãîííîé èëè áîåâîé), ïðåäïîëàãàåò íåîá-
õîäèìîñòü îñóùåñòâëåíèÿ òàê íàçûâàåìîé ïîëíîé ïîäãîòîâêè: òî-
ïîãåîäåçè÷åñêîé, êîòîðàÿ çàêëþ÷àåòñÿ â òîïîãðàôè÷åñêîé ïðèâÿçêå
ïîëîæåíèÿ öåëè è îãíåâîé ïîçèöèè, ìåòåîðîëîãè÷åñêîé è ñîáñò-
âåííî áàëëèñòè÷åñêîé, ó÷èòûâàþùåé ðåçóëüòàòû òîïîïðèâÿçêè è
âëèÿíèå âîçìóùàþùèõ ôàêòîðîâ, íàïðèìåð èçìåíåíèÿ òåìïåðàòó-
ðû çàðÿäà è ñîîòâåòñòâåííî íà÷àëüíîé ñêîðîñòè ñíàðÿäà.
Òàêèì îáðàçîì, ïåðå÷åíü âîïðîñîâ, ñîñòàâëÿþùèõ ñîäåðæàíèå âíåø-
íåé áàëëèñòèêè, ïîçâîëÿåò âûäåëèòü â íåé òðè ãëàâíûõ íàïðàâëåíèÿ –
ïðîåêòíóþ áàëëèñòèêó, ýêñïåðèìåíòàëüíóþ âíåøíþþ áàëëèñòèêó, áàëëè-
ñòè÷åñêîå îáåñïå÷åíèå ñòðåëüá (èëè "èñïîëíèòåëüíóþ áàëëèñòèêó").
Ïðîåêòíàÿ áàëëèñòèêà ñîñòàâëÿåò òåîðåòè÷åñêóþ îñíîâó íà÷àëüíî-
ãî ýòàïà ïðîåêòèðîâàíèÿ ëåòàòåëüíûõ àïïàðàòîâ ðàçëè÷íîãî íàçíà÷å-
íèÿ, ïîýòîìó â ýòîé ÷àñòè îíà òåñíî ñòûêóåòñÿ ñ êóðñàìè ïðîåêòèðî-
âàíèÿ è êîíñòðóèðîâàíèÿ, à èíîãäà è âêëþ÷àåòñÿ â íèõ â êà÷åñòâå ñî-
ñòàâíîé ÷àñòè.
Áàëëèñòè÷åñêîå îáåñïå÷åíèå ñòðåëüá ñëóæèò áàçîâûì ðàçäåëîì òåî-
ðèè ñòðåëüáû è ÿâëÿåòñÿ, ïî ñóùåñòâó, îäíèì èç âàæíåéøèõ ýëåìåíòîâ
ýòîé ñìåæíîé âîåííîé íàóêè.
16
ÐÀÇÄÅË I
ÓÑËÎÂÈß ÏÎËÅÒÀ
ÐÀÊÅÒ È ÑÍÀÐßÄÎÂ,
ÌÀÒÅÌÀÒÈ×ÅÑÊÈÅ ÌÎÄÅËÈ
ÈÕ ÄÂÈÆÅÍÈß
Ãëàâà 1
ÑÈËÛ È ÌÎÌÅÍÒÛ,
ÄÅÉÑÒÂÓÞÙÈÅ ÍÀ ËÀ Â ÏÎËÅÒÅ
Äåéñòâóþùèå íà ðàêåòó ñèëû è ìîìåíòû ìîæíî óñëîâíî ðàçäåëèòü íà âíåøíèå è
âíóòðåííèå.Êâíåøíèì îòíîñÿò ñèëû è ìîìåíòû, âûçûâàåìûå âîçäåéñòâèåì âíåø-
íåé ñðåäû. Ýòî àýðîäèíàìè÷åñêèå ñèëû è ìîìåíòû è ñèëû, îïðåäåëÿåìûå âëèÿíèåì
Çåìëè. Ïîä âëèÿíèåì Çåìëè â äàëüíåéøåì áóäåì ïîíèìàòü ñîâìåñòíîå äåéñòâèå íà
ËÀ (ïðè ðàññìîòðåíèè åãî îòíîñèòåëüíîãî äâèæåíèÿ) ñèëû òÿãîòåíèÿ, öåíòðîáåæ-
íîé ñèëû èíåðöèè è êîðèîëèñîâûõ ñèë, îïðåäåëÿåìûõ âðàùåíèåì Çåìëè. Ê âíóòðåí-
íèì ìîæíî îòíåñòè ñèëû è ìîìåíòû, îïðåäåëÿåìûå îòäåëåíèåì ìàññû îò ðàêåòû
(ò.å . ðåàêòèâíûå ñèëû è èõ ìîìåíòû) è âûçûâàåìûå ïåðåìåùåíèåì ðàáî÷åãî âåùå-
ñòâà (òîïëèâà è ãàçîâ) âíóòðè êîðïóñà (êîðèîëèñîâû ñèëû, âîçíèêàþùèå ïðè êîëåáà-
íèÿõ ðàêåòû, à òàêæå âàðèàöèîííûå ñèëû, ïðîÿâëÿþùèåñÿ ïðè íåñòàöèîíàðíîì
äâèæåíèè ìàññ âíóòðè êîðïóñà, è èõ ìîìåíòû). Ïîñëåäíèå îáû÷íî îòíîñÿò ê âòîðî-
ñòåïåííûì (äîïîëíèòåëüíûì) ôàêòîðàì.
Óïðàâëÿþùèå ñèëû è ìîìåíòû â çàâèñèìîñòè îò ïðèíöèïà ðàáîòû è êîíñòðóê-
öèè óïðàâëÿþùèõ îðãàíîâ ìîæíî ñ÷èòàòü êàê âíåøíèìè, òàê è âíóòðåííèìè. Íå-
óïðàâëÿåìûå ðàêåòû è ñíàðÿäû íå èñïûòûâàþò âîçäåéñòâèÿ óïðàâëÿþùèõ ñèë, ñâî-
áîäíûé ïîëåò ïðåäïîëàãàåò òàêæå îòñóòñòâèå òÿãè.
Ïðè ðàñ÷åòå ïàðàìåòðîâ äâèæåíèÿ ËÀ ïðèõîäèòñÿ ïåðåõîäèòü îò âåêòîð-
íîãî ïðåäñòàâëåíèÿ äåéñòâóþùèõ íà ðàêåòó èëè ñíàðÿä ñèë ê ñêàëÿðíîé ôîðìå
èõ çàïèñè â ïðîåêöèÿõ íà îñè âûáðàííîé ñèñòåìû êîîðäèíàò. Ïðè ýòîì â ñî-
ñòàâëåíèè óðàâíåíèé äâèæåíèÿ ËÀ ó÷àñòâóþò ñèëû, çàäàííûå â ñèñòåìå êîîð-
äèíàò, ñâÿçàííîé ñ Çåìëåé (ñèëà òÿãîòåíèÿ è âåñ), â ñèñòåìå êîîðäèíàò, ñâÿ-
çàííîé ñ âåêòîðîì ñêîðîñòè ËÀ è îòñëåæèâàþùåé åãî äâèæåíèå ïî òðàåêòî-
ðèè (àýðîäèíàìè÷åñêèå ñèëû), è, íàêîíåö, â ñèñòåìå êîîðäèíàò, íåïîñðåäñòâåííî
ñâÿçàííîé ñ êîðïóñîì ËÀ (òÿãà).
17
1.1 . ÑÈÑÒÅÌÛ ÊÎÎÐÄÈÍÀÒ È ÓÃËÛ, ÎÏÐÅÄÅËßÞÙÈÅ
ÏÎËÎÆÅÍÈÅ ËÀ Â ÏÐÎÑÒÐÀÍÑÒÂÅ
1.1.1. ÎÁÙÀß ÕÀÐÀÊÒÅÐÈÑÒÈÊÀ ÑÈÑÒÅÌ ÊÎÎÐÄÈÍÀÒ
Ïðîñòðàíñòâåííîå ïîëîæåíèå ËÀ êàê òâåðäîãî òåëà îïðåäåëÿ-
åòñÿ òðåìÿ ëèíåéíûìè êîîðäèíàòàìè è òðåìÿ óãëàìè. Êàê ïðà-
âèëî, ñèñòåìû äèôôåðåíöèàëüíûõ óðàâíåíèé äâèæåíèÿ çàïèñû-
âàþòñÿ îòíîñèòåëüíî ïðàâîé ñèñòåìû êîîðäèíàò. Ïðè ïðîâåäå-
íèè ðàñ÷åòîâ ÷àùå âñåãî èñïîëüçóþòñÿ ïðÿìîóãîëüíûå,
öèëèíäðè÷åñêèå è ñôåðè÷åñêèå ñèñòåìû êîîðäèíàò.  ýêñïåðè-
ìåíòàëüíîé áàëëèñòèêå ñèñòåìû êîîðäèíàò äëÿ îïðåäåëåíèÿ ïðî-
ñòðàíñòâåííîãî ïîëîæåíèÿ ËÀ âûáèðàþòñÿ â çàâèñèìîñòè îò ìå-
òîäà ïðèáîðíîé ðåàëèçàöèè èçìåðåíèé.
Äëÿ ðåøåíèÿ çàäà÷ òåîðèè ïîëåòà ËÀ, äâèæóùèõñÿ â ïîëå çåìíî-
ãî òÿãîòåíèÿ, èñïîëüçóþòñÿ äâå áîëüøèå ãðóïïû ñèñòåì êîîðäèíàò,
ðàçëè÷àþùèåñÿ ðàñïîëîæåíèåì íà÷àëà ñèñòåìû îòñ÷åòà. Ê ïåðâîé
ãðóïïå îòíîñÿòñÿ ñèñòåìû êîîðäèíàò, ñâÿçàííûå ñ Çåìëåé èëè äðó-
ãèìè òî÷êàìè ïðîñòðàíñòâà, êî âòîðîé – ñâÿçàííûå ñ ËÀ.
Îáû÷íî ïðèìåíÿåòñÿ íåñêîëüêî ðàçíîâèäíîñòåé çåìíûõ ñèñ-
òåì êîîðäèíàò. Çà èõ íà÷àëî ìîæåò ïðèíèìàòüñÿ öåíòð ìàññ
Çåìëè, òî÷êà ñòàðòà èëè äðóãàÿ íåïîäâèæíàÿ îòíîñèòåëüíî Çåì-
ëè òî÷êà.
Äëÿ èññëåäîâàíèÿ àáñîëþòíîãî äâèæåíèÿ ÷àñòî ïðèìåíÿåòñÿ
èíåðöèàëüíàÿ ñèñòåìà êîîðäèíàò ÎèÕèYèZè.  îáùåì ñëó÷àå ïîä èíåð-
öèàëüíîé ñèñòåìîé êîîðäèíàò ïîíèìàþò ñèñòåìó, îñè êîòîðîé íå
èçìåíÿþò ñâîåãî íàïðàâëåíèÿ â ïðîñòðàíñòâå. Èíåðöèàëüíàÿ ñèñòå-
ìà êîîðäèíàò ó÷àñòâóåò òîëüêî â ïîñòóïàòåëüíîì äâèæåíèè Çåìëè
âîêðóã Ñîëíöà, è ïîëîæåíèå åå îñåé íå çàâèñèò îò ñóòî÷íîãî âðàùå-
íèÿ Çåìëè (â îòëè÷èå îò ñèñòåì êîîðäèíàò, ñâÿçàííûõ ñ Çåìëåé è
âðàùàþùèõñÿ âìåñòå ñ íåé, èñïîëüçóåìûõ ïðè èçó÷åíèè îòíîñè-
òåëüíîãî äâèæåíèÿ ðàêåò).
Çåìíàÿ ñèñòåìà êîîðäèíàò O0X0Y0Z0 èìååò íà÷àëî â òî÷êå O0 è
îñè, çàôèêñèðîâàííûå ïî îòíîøåíèþ ê Çåìëå. Ïðÿìîóãîëüíàÿ
ñèñòåìà êîîðäèíàò, êîòîðàÿ ñâÿçàíà ñ Çåìëåé è íà÷àëî êîòîðîé
ñîâìåùåíî ñ öåíòðîì ìàññ Çåìëè, à îäíà èç îñåé íàïðàâëåíà íà
ñåâåð ïî îñè âðàùåíèÿ Çåìëè, íàçûâàåòñÿ ãåîöåíòðè÷åñêîé ñèñòå-
ìîé êîîðäèíàò.
Åñëè öåíòð ìàññ Çåìëè âûáðàí çà íà÷àëî ñôåðè÷åñêîé ñèñòåìû
êîîðäèíàò, òî åå íàçûâàþò ãåîöåíòðè÷åñêîé ñôåðè÷åñêîé ñèñòåìîé
êîîðäèíàò.
Ñèñòåìû êîîðäèíàò ñ íà÷àëîì íà ïîâåðõíîñòè Çåìëè íàçûâàþò-
ñÿ òîïîöåíòðè÷åñêèìè.
18
Íîðìàëüíîé çåìíîé ñèñòåìîé
êîîðäèíàò O0XgYgZg íàçûâàþò ñèñ-
òåìó, íà÷àëî êîòîðîé O0 ôèêñèðî-
âàíî ïî îòíîøåíèþ ê Çåìëå, îñü
O0Yg íàïðàâëåíà ââåðõ ïî ìåñòíîé
âåðòèêàëè, à íàïðàâëåíèÿ îñåé
O0Xg è O0Zg âûáèðàþòñÿ â ñîîòâåò-
ñòâèè ñ ðåøàåìîé çàäà÷åé. Ñòàð-
òîâàÿ ñèñòåìà êîîðäèíàò O0XcYcZc
ÿâëÿåòñÿ ðàçíîâèäíîñòüþ òîïî-
öåíòðè÷åñêîé ïðÿìîóãîëüíîé ñèñ-
òåìû êîîðäèíàò äëÿ íàçåìíîé àð-
òèëëåðèéñêîé èëè ðàêåòíîé ñèñ-
òåìû (ðèñ. 1.1). Íà÷àëî ñòàðòîâîé
ñèñòåìû êîîðäèíàò îïðåäåëÿåòñÿ
ïîëîæåíèåì ïóñêîâîé óñòàíîâêè
è ñîâïàäàåò ñ öåíòðîì ìàññ ðàêå-
òû, ïîäãîòîâëåííîé ê ïóñêó. Ïðè
ýòîì êîîðäèíàòíàÿ îñü O0Yc íàïðàâëåíà âåðòèêàëüíî ââåðõ, à îñè
O0Xc è O0Zc ëåæàò â ïëîñêîñòè ñòàðòîâîãî ãîðèçîíòà, ïðè÷åì îñü
O0Xc óêàçûâàåò íàïðàâëåíèå ñòðåëüáû. Âåðòèêàëüíàÿ ïëîñêîñòü
O0YcXc, ïðîõîäÿùàÿ ÷åðåç âåêòîð íà÷àëüíîé ñêîðîñòè, íàçûâàåòñÿ
ïëîñêîñòüþ ïóñêà èëè ñòðåëüáû, à èíîãäà – ïëîñêîñòüþ áðîñàíèÿ.
Ïîëîæåíèå ïëîñêîñòè ïóñêà îòíîñèòåëüíî Çåìëè îïðåäåëÿåòñÿ àçè-
ìóòîì ïóñêà èëè àçèìóòîì ñòðåëüáû À ñ .
Äëÿ îïðåäåëåíèÿ ïðîñòðàíñòâåííîãî ïîëîæåíèÿ ðàêåòû èëè âîç-
äóøíîé öåëè îòíîñèòåëüíî ïîâåðõíîñòè Çåìëè ÷àñòî èñïîëüçóþò
òîïîöåíòðè÷åñêóþ ñôåðè÷åñêóþ ñèñòåìó êîîðäèíàò (ðèñ. 1.2). Ïîëî-
æåíèå öåíòðà ìàññ ðàêåòû Ð çàäàåòñÿ ìîäóëåì ðàäèóñ-âåêòîðà r,íà-
çûâàåìûì èíîãäà íàêëîííîé äàëüíîñòüþ, è äâóìÿ ïîëÿðíûìè óãëà-
ìè: àçèìóòîì À, îòñ÷èòûâàåìûì ïî ÷àñîâîé ñòðåëêå â ìåñòíîé ãîðè-
çîíòàëüíîé ïëîñêîñòè îò íàïðàâëåíèÿ íà ñåâåð, è óãëîì ìåñòà q,îò-
ñ÷èòûâàåìûì â âåðòèêàëüíîé ïëîñêîñòè. Ïðè ñîñòàâëåíèè óðàâíå-
íèé äâèæåíèÿ â ñôåðè÷åñêîé ñèñòåìå êîîðäèíàò â ðÿäå ñëó÷àåâ ñ
öåëüþ ñîõðàíåíèÿ åäèíñòâà íàïðàâëåíèé îòñ÷åòà óãëîâ â ãîðèçîí-
òàëüíîé ïëîñêîñòè âìåñòî àçèìóòà À óäîáíåå ââîäèòü óãîë À*, îòñ÷è-
òûâàåìûé îò íàïðàâëåíèÿ íà ñåâåð ïðîòèâ ÷àñîâîé ñòðåëêè. Íà ðè-
ñóíêå êîîðäèíàòíûìè ïîâåðõíîñòÿìè ñôåðè÷åñêîé ñèñòåìû êîîðäè-
íàò ÿâëÿþòñÿ: ñôåðà ðàäèóñîì r ; âåðòèêàëüíàÿ ïëîñêîñòü, ïðîõîäÿ-
ùàÿ ÷åðåç ðàäèóñ r ; êîíóñ ñ âåðøèíîé â òî÷êå O0 è óãëîì ïðè âåð-
øèíå, ðàâíûì 180° – 2q. Êîîðäèíàòíûå ëèíèè: (r) – ïðÿìàÿ ðàäè-
óñ-âåêòîðà; (q) – îêðóæíîñòü áîëüøîãî êðóãà ñôåðû, ïðîõîäÿùàÿ
÷åðåç çàäàííóþ òî÷êó Ð ;(À*) – îêðóæíîñòü, îáðàçîâàííàÿ ïðè ñå÷å-
19
Ðèñ. 1.1 . Ñòàðòîâàÿ ñèñòåìà êîîðäèíàò
íèè ñôåðû ïëîñêîñòüþ, ïàðàëëåëüíîé ïëîñêîñòè O0XgZg è ïðîõîäÿ-
ùåé ÷åðåç çàäàííóþ òî÷êó. Êîîðäèíàòíûå îñè [r], [q]è[A*] êðèâî-
ëèíåéíîé ñèñòåìû êîîðäèíàò ÿâëÿþòñÿ êàñàòåëüíûìè ê êîîðäèíàò-
íûì ëèíèÿì.
Áîëüøàÿ ãðóïïà ïîäâèæíûõ êîîðäèíàò îáúåäèíåíà îáùèì ïðè-
çíàêîì – ðàñïîëîæåíèåì íà÷àëà êîîðäèíàò â õàðàêòåðíîé òî÷êå
äâèæóùåãîñÿ ËÀ, îáû÷íî â öåíòðå ìàññ. Íàïðàâëåíèÿ îñåé ïîäâèæ-
íîé îðèåíòèðîâàííîé ñèñòåìû êîîðäèíàò OXèYèZè íåèçìåííû â ïðî-
ñòðàíñòâå (îòíîñèòåëüíî çâåçä). Îñè ïîäâèæíîé çåìíîé ñèñòåìû êî-
îðäèíàò OX0Y0Z0 íàïðàâëåíû òàê æå, êàê è ñîîòâåòñòâóþùèå èì îñè
çåìíîé (íåïîäâèæíîé îòíîñèòåëüíî Çåìëè) ñèñòåìû êîîðäèíàò
O0X0Y0Z0. Â íîðìàëüíîé ñèñòåìå êîîðäèíàò OXgYgZg, ñâÿçàííîé ñ ËÀ,
îñü Yg íàïðàâëåíà ââåðõ ïî ìåñòíîé âåðòèêàëè è â îòëè÷èå îò îñè
O0Yg íîðìàëüíîé çåìíîé ñèñòåìû êîîðäèíàò èçìåíÿåò ñâîå íàïðàâ-
ëåíèå â ïðîñòðàíñòâå â ïðîöåññå äâèæåíèÿ ËÀ îòíîñèòåëüíî Çåìëè.
Îñè OXg è OZg íîðìàëüíîé ñèñòåìû êîîðäèíàò ïàðàëëåëüíû ïëîñ-
êîñòè ìåñòíîãî ãîðèçîíòà è íàïðàâëåíû òàê, ÷òîáû óäîáíî áûëî ðå-
øàòü ïîñòàâëåííóþ çàäà÷ó.
Îñè ñâÿçàííîé ñèñòåìû êîîðäèíàò OXYZ: ïðîäîëüíàÿ îñü OX íàõî-
äèòñÿ â ïëîñêîñòè ñèììåòðèè ËÀ èëè â ïëîñêîñòè, ïàðàëëåëüíîé åé,
åñëè íà÷àëî êîîðäèíàò Î ïîìåùåíî âíå ïëîñêîñòè ñèììåòðèè (äëÿ
îñåñèììåòðè÷íûõ àïïàðàòîâ îñü OX íàïðàâëåíà ïî îñè ñèììåò-
ðèè ê íîñîâîé ÷àñòè ËÀ); íîðìàëüíàÿ îñü OY ðàñïîëàãàåòñÿ â
ïëîñêîñòè ñèììåòðèè èëè ïàðàëëåëüíî åé è íàïðàâëåíà ê âåðõ-
íåé ÷àñòè ËÀ; ïîïåðå÷íàÿ îñü OZ íàïðàâëåíà âïðàâî, ïåðïåíäèêó-
ëÿðíî ïëîñêîñòè ñèììåòðèè.  ñêîðîñòíîé (àýðîäèíàìè÷åñêîé) ñèñ-
òåìå êîîðäèíàò OXaYaZa ñêîðîñòíàÿ îñü OXa ñîâïàäàåò ñ âåêòîðîì
20
Ðèñ. 1 .2 . Òîïîöåíòðè÷åñêàÿ ñôåðè÷å-
ñêàÿ ñèñòåìà êîîðäèíàò
âîçäóøíîé ñêîðîñòè ëåòàòåëüíîãî àïïàðàòà (âåêòîðîì ñêîðîñòè ËÀ
îòíîñèòåëüíî àòìîñôåðû V), îñü ïîäúåìíîé ñèëû OYa ðàñïîëàãàåòñÿ
â ïëîñêîñòè ñèììåòðèè ËÀ èëè â ïëîñêîñòè, åé ïàðàëëåëüíîé. Áî-
êîâàÿ îñü OZa äîïîëíÿåò äâå íàçâàííûå îñè äî ïðàâîé ñèñòåìû
êîîðäèíàò.
Íà÷àëî òðàåêòîðíîé ñèñòåìû êîîðäèíàò OXêYêZê îáû÷íî ïîìåùå-
íî â öåíòðå ìàññ ëåòàòåëüíîãî àïïàðàòà, îñü OXê íàïðàâëåíà ïî âåê-
òîðó çåìíîé ñêîðîñòè ËÀ (ñêîðîñòè ËÀ îòíîñèòåëüíî Çåìëè Vê), îñü
OYê – ââåðõ îò ïîâåðõíîñòè Çåìëè â âåðòèêàëüíîé ïëîñêîñòè, ïðî-
õîäÿùåé ÷åðåç îñü OXê, îñü OZê – ãîðèçîíòàëüíî. Ïðè áåçâåòðèè íà-
ïðàâëåíèÿ ñêîðîñòíîé îñè OXa è îñè OXê òðàåêòîðíîé ñèñòåìû êî-
îðäèíàò ñîâïàäàþò, òàê êàê ïðè ýòîì ñîâïàäàþò âåêòîðû âîçäóøíîé
è çåìíîé ñêîðîñòåé.
1.1.2. ÎÏÐÅÄÅËÅÍÈÅ ÂÇÀÈÌÍÎÉ ÎÐÈÅÍÒÀÖÈÈ
ÑÈÑÒÅÌ ÊÎÎÐÄÈÍÀÒ
Ñâÿçü ìåæäó ñêîðîñòíîé è ñâÿçàííîé ñèñòåìàìè êîîðäèíàò îñó-
ùåñòâëÿåòñÿ ñ ïîìîùüþ óãëà àòàêè α, óãëà ñêîëüæåíèÿ β, ïðîñòðàí-
ñòâåííîãî óãëà àòàêè αï è àýðîäèíàìè÷åñêîãî óãëà êðåíà φï. Óãîë
àòàêè – óãîë ìåæäó ïðîåêöèåé âåêòîðà âîçäóøíîé ñêîðîñòè íà
ïëîñêîñòü ñèììåòðèè ËÀ OXY è ïðîäîëüíîé îñüþ OX. Óãîë ñêîëüæå-
íèÿ – óãîë ìåæäó âåêòîðîì âîçäóøíîé ñêîðîñòè è ïëîñêîñòüþ ñèì-
ìåòðèè ËÀ (ðèñ. 1 .3). Ïðîñòðàíñòâåííûé óãîë àòàêè – óãîë ìåæäó
ïðîäîëüíîé îñüþ ËÀ è âåêòîðîì ñêîðîñòè. Ñ ïðîñòðàíñòâåííûì óã-
ëîì àòàêè íåïîñðåäñòâåííî ñâÿçàíà ñèñòåìà êîîðäèíàò OXïYïZï,ó
êîòîðîé ïëîñêîñòü OXïYï ñîâïàäàåò ñ ïëîñêîñòüþ ïðîñòðàíñòâåííî-
ãî óãëà àòàêè (ðèñ. 1 .4). Îñü OXï ñèñòåìû ñîâïàäàåò ñ ïðîäîëüíîé
îñüþ ËÀ, îñü OYï ëåæèò â ïëîñêîñòè ïðîñòðàíñòâåííîãî óãëà àòàêè,
îñü OZï äîïîëíÿåò ñèñòåìó äî ïðàâîé. Óãîë ìåæäó íîðìàëüíîé îñüþ
OY è îñüþ OYï íàçûâàþò àýðî-
äèíàìè÷åñêèì óãëîì êðåíà.
Ñâÿçü ìåæäó íîðìàëüíîé
OXgYgZg è ñâÿçàííîé OXYZ
ñèñòåìàìè êîîðäèíàò îñó-
ùåñòâëÿåòñÿ ñ ïîìîùüþ óã-
ëîâ ðûñêàíèÿ, òàíãàæà è
êðåíà (ðèñ. 1.5).
Óãîë ðûñêàíèÿ ψ – óãîë
ìåæäó îñüþ OXg è ïðîåêöèåé
ïðîäîëüíîé îñè OX íà ãîðè-
çîíòàëüíóþ
ïëîñêîñòü
OXgZg. Ó íåêîòîðûõ ËÀ óãîë
21
Ðèñ. 1.3 . Ñõåìà âçàèìíîãî ðàñïîëîæåíèÿ ñêî-
ðîñòíîé è ñâÿçàííîé ñèñòåì êîîðäèíàò
ðûñêàíèÿ ìîæåò îïðåäåëÿòüñÿ â çàâèñèìîñòè îò ïðèáîðíîé ðåàëèçà-
öèè èçìåðåíèé â ïëîñêîñòè, ïåðïåíäèêóëÿðíîé ïëîñêîñòè áðîñà-
íèÿ XgO0Yg è ïðîõîäÿùåé ÷åðåç ïðîäîëüíóþ îñü ËÀ OX. Åñëè óãîë
ðûñêàíèÿ, îïðåäåëÿåìûé â óêàçàííîé íàêëîííîé ïëîñêîñòè, îáî-
çíà÷èì ÷åðåç ψí, òî, ñîãëàñíî ðèñ. 1.6, sinψí = sinψ cosθ.
Óãîë òàíãàæà θ – óãîë ìåæ-
äó ïðîäîëüíîé îñüþ OX èãî-
ðèçîíòàëüíîé
ïëîñêîñòüþ.
Ñëåäóåò ðàçëè÷àòü óãîë òàíãà-
æà ïî îòíîøåíèþ ê ñòàðòîâîé
ãîðèçîíòàëüíîé
ïëîñêîñòè,
ò.å . ïî îòíîøåíèþ ê íîðìàëü-
íîé çåìíîé ñèñòåìå êîîðäè-
íàò, è ìåñòíûé óãîë òàíãàæà,
èçìåðÿåìûé îò ïëîñêîñòè
ìåñòíîãî ãîðèçîíòà. Ýòî ðàç-
ëè÷èå öåëåñîîáðàçíî ó÷èòû-
âàòü ïðè îïðåäåëåíèè õàðàê-
òåðèñòèê äâèæåíèÿ ËÀ, ïðåä-
íàçíà÷åííûõ äëÿ ïîëåòà íà
áîëüøèå
äàëüíîñòè (ñì.
ðèñ. 1.5).
22
Ðèñ. 1 .4. Ñõåìà âçàèìíîãî ðàñïîëîæåíèÿ ñèñòåìû êîîðäèíàò, ñâÿçàííîé ñ ïðîñòðàí-
ñòâåííûì óãëîì àòàêè, è ñâÿçàííîé è íîðìàëüíîé çåìíîé ñèñòåì êîîðäèíàò ïðè áåç-
âåòðèè
Ðèñ. 1.5 . Ñõåìà âçàèìíîãî ðàñïîëîæåíèÿ
ñâÿçàííîé è íîðìàëüíîé ñèñòåì êîîðäèíàò
ïðè ïåðâîì ïîâîðîòå îòíîñèòåëüíî îñè OYg
Î÷åâèäíî, ïðè θ = 0 ïîëó÷èì
ψí=ψ.
Óãîë êðåíà γ – óãîë ìåæäó ïî-
ïåðå÷íîé îñüþ OZ è îñüþ OZg,
ñìåùåííîé â ïîëîæåíèå, ñîîò-
âåòñòâóþùåå íóëåâîìó óãëó ðûñ-
êàíèÿ.
Ñâÿçü ìåæäó íîðìàëüíîé ñèñ-
òåìîé êîîðäèíàò OXgYgZg è ñêîðîñò-
íîé OXaYaZa îñóùåñòâëÿåòñÿ ñ ïî-
ìîùüþ òàê íàçûâàåìûõ ñêîðîñò-
íûõ óãëîâ ðûñêàíèÿ, òàíãàæà è
êðåíà. Ñêîðîñòíîé óãîë ðûñêàíèÿ
ψa – ýòî óãîë ìåæäó îñüþ OXg è
ïðîåêöèåé ñêîðîñòíîé îñè íà ãî-
ðèçîíòàëüíóþ ïëîñêîñòü OXg Zg . Ñêîðîñòíîé óãîë òàíãàæà θa – ýòî óãîë
ìåæäó ñêîðîñòíîé îñüþ OXa è ãîðèçîíòàëüíîé ïëîñêîñòüþ OXg Zg . Ñêî-
ðîñòíîé óãîë êðåíà γa – ýòî óãîë ìåæäó áîêîâîé îñüþ OZa è îñüþ OZg, ñìå-
ùåííîé â ïîëîæåíèå, ñîîòâåòñòâóþùåå íóëåâîìó ñêîðîñòíîìó óãëó ðûñ-
êàíèÿ.
Ïîëîæåíèå òðàåêòîðíîé ñèñòåìû êîîðäèíàò îòíîñèòåëüíî íîð-
ìàëüíîé îïðåäåëÿåòñÿ äâóìÿ óãëàìè θ è Ψ: θ – óãîë íàêëîíà (âîçâû-
øåíèÿ) òðàåêòîðèè (óãîë ìåæäó çåìíîé ñêîðîñòüþ ËÀ è ãîðèçîí-
òàëüíîé ïëîñêîñòüþ); Ψ – óãîë ïóòè (óãîë ìåæäó îñüþ OXg è ïðîåê-
öèåé çåìíîé ñêîðîñòè ËÀ íà ïëîñêîñòü OXgZg – ïóòåâîé ñêîðîñòüþ
Vï).
Ïðè áåçâåòðèè âåêòîðû çåìíîé è âîçäóøíîé ñêîðîñòåé ñîâïàäóò.
Ñëåäîâàòåëüíî, óãîë íàêëîíà òðàåêòîðèè θ áóäåò ðàâåí ñêîðîñòíîìó
óãëó òàíãàæà θa, à óãîë ïóòè Ψ – ñêîðîñòíîìó óãëó ðûñêàíèÿ ψa.
Ïðîåêöèè âåêòîðà çåìíîé ñêîðîñòè Vê íà îñè íîðìàëüíîé çåì-
íîé ñèñòåìû êîîðäèíàò íàéäåì èç ðèñ. 1 .7:
VV
VV
VV
x
y
z
g
g
g
=
=
=
ê
ê
ê
cos cos ;
sin ;
cos sin .
θ
θ
θ
Ψ
Ψ
(1.1)
Ïðè ðàññìîòðåíèè "ïëîñêèõ çàäà÷", êîãäà Ψ = 0, ãîðèçîíòàëüíàÿ
è âåðòèêàëüíàÿ ïðîåêöèè ñêîðîñòè ñîîòâåòñòâåííî èìåþò âèä
VuV
VwV
x
y
g
g
==
==
ê
ê
cos ;
sin .
θ
θ
(1.2)
23
Ðèñ. 1.6 . Óãëû ðûñêàíèÿ, èçìåðÿåìûå â
ãîðèçîíòàëüíîé è íàêëîííîé ïëîñêîñòÿõ
Óãëîì âåòðà ΨW íàçûâàåòñÿ óãîë ìåæäó îñüþ OXg è ïðîåêöèåé
âåêòîðà ñêîðîñòè âåòðà W íà ãîðèçîíòàëüíóþ ïëîñêîñòü. Íàêëîíîì
âåòðà θW íàçûâàåòñÿ óãîë ìåæäó âåêòîðîì ñêîðîñòè âåòðà è ãîðèçîí-
òàëüíîé ïëîñêîñòüþ.
Óãëîâàÿ îðèåíòàöèÿ îäíèõ êîîðäèíàòíûõ îñåé îòíîñèòåëüíî
äðóãèõ, ïðèíèìàåìûõ çà îïîðíûå èëè áàçîâûå, ìîæåò áûòü îñóùåñò-
âëåíà ñ ïîìîùüþ ýéëåðîâûõ óãëîâ ïîâîðîòà.
 ïðîöåññå ïîäãîòîâêè ê ïóñêó è âî âðåìÿ ïîëåòà ËÀ óãëû Ýéëå-
ðà ìîãóò áûòü èçìåðåíû ïîñðåäñòâîì òðåõîñíîé ãèðîñòàáèëèçèðî-
âàííîé ïëàòôîðìû. Îñü âðàùåíèÿ íàðóæíîé ðàìêè ïëàòôîðìû âñå-
ãäà íàïðàâëÿåòñÿ ïî ïðîäîëüíîé îñè îáúåêòà. Îñü âðàùåíèÿ ïëàò-
ôîðìû âîêðóã âíóòðåííåé ðàìêè äîëæíà ñîâïàäàòü ñ îñüþ,
îòíîñèòåëüíî êîòîðîé îñóùåñòâëÿåòñÿ ïåðâûé ïîâîðîò íà îäèí èç
óãëîâ Ýéëåðà. Ïåðâîé îñüþ ïîâîðîòà âûáèðàåòñÿ îñü, îòíîñèòåëüíî
êîòîðîé ñèñòåìà êîîðäèíàò â ïðîöåññå ïîëåòà ìîæåò ïîâîðà÷èâàòü-
ñÿ íà áîëüøèé óãîë. Äëÿ ËÀ ñàìîëåòíîé ñõåìû (íîðìàëüíàÿ ñèñòåìà
êîîðäèíàò OXgYgZg) ïåðâîé îñüþ ïîâîðîòà ÿâëÿåòñÿ îñü OYg ïîâîðî-
òà íà óãîë ðûñêàíèÿ ψ. Ñõåìó ïîñëåäîâàòåëüíîãî ïîâîðîòà íà óãëû
Ýéëåðà ìîæíî ïðîñëåäèòü íà ðèñ. 1 .5 . Äëÿ ËÀ ñ âåðòèêàëüíûì ñòàð-
òîì è ïðîãðàììíûì èçìåíåíèåì óãëà òàíãàæà ïåðâîé îñüþ ïîâîðî-
òà ÿâëÿåòñÿ îñü OZg ïîâîðîòà íà óãîë òàíãàæà (ðèñ. 1 .8).
24
Ðèñ. 1 .7. Ñõåìà âçàèìíîãî ðàñïîëîæåíèÿ ñêîðîñòíîé, òðàåêòîðíîé è íîðìàëüíîé
ñèñòåì êîîðäèíàò ïðè áåçâåòðèè
Íàïîìíèì, ÷òî óãëû Ýéëåðà
íå çàâèñÿò äðóã îò äðóãà, ò.å. ïðè
èçìåíåíèè îäíîãî óãëà äâà äðó-
ãèõ íå èçìåíÿþòñÿ.
1.1 .3. ÊÎÎÐÄÈÍÀÒÍÛÅ
ÏÐÅÎÁÐÀÇÎÂÀÍÈß
Ñ ÏÎÌÎÙÜÞ ÌÀÒÐÈÖ
ÍÀÏÐÀÂËßÞÙÈÕ ÊÎÑÈÍÓÑÎÂ
Ïðåîáðàçîâàíèÿ, ñâÿçàííûå ñ
ïåðåõîäîì îò îäíîé ñèñòåìû êî-
îðäèíàò ê äðóãîé, îñóùåñòâëÿ-
þòñÿ ñ ïîìîùüþ ìàòðèö íàïðàâ-
ëÿþùèõ êîñèíóñîâ, êîòîðûå
èíîãäà íàçûâàþò òàáëèöàìè ïå-
ðåõîäíûõ êîñèíóñîâ. Ìàòðèöó
óäîáíî îáîçíà÷àòü äâóìÿ èíäåêñàìè, íàïðèìåð A1
(2)
, ãäå íèæíèé èí-
äåêñ ñîîòâåòñòâóåò îñíîâíîé íåïîäâèæíîé ñèñòåìå êîîðäèíàò, à
âåðõíèé – ñèñòåìå, îïðåäåëÿåìîé ïîñëåäîâàòåëüíûì ïîâîðîòîì íà
ýéëåðîâû óãëû îòíîñèòåëüíî íåïîäâèæíîé ñèñòåìû. Ýëåìåíòû ìàò-
ðèöû, ÿâëÿþùèåñÿ ôóíêöèÿìè ýéëåðîâûõ óãëîâ ïîâîðîòà, òàêæå
óäîáíî îáîçíà÷àòü äâîéíûì èíäåêñîì, íàïðèìåð aij, ãäå i – íîìåð
ñòðîêè, j – íîìåð ñòîëáöà:
A
xyz
1
(2)
=
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
2
0
2
0
2
0
11
12
13
21
22
23
31
32
33
aaa
aaa
aaa
⎥
⎥
⎥
⎥
x
y
z
1
0
1
0
1
0
.
(1.3)
Êàæäûé ýëåìåíò ìàòðèöû ðàâåí ïðîåêöèè åäèíè÷íîãî âåêòîðà,
íàïðàâëåííîãî ïî îäíîé êîîðäèíàòíîé îñè íåïîäâèæíîé ñèñòåìû,
íà ñîîòâåòñòâóþùóþ îñü äðóãîé (ïîäâèæíîé) ñèñòåìû, ò.å ., äðóãèìè
ñëîâàìè, êàæäûé ýëåìåíò ìàòðèöû åñòü ñêàëÿðíîå ïðîèçâåäåíèå
åäèíè÷íûõ âåêòîðîâ, îïðåäåëÿåìûõ ñîîòâåòñòâóþùèìè ñòðîêîé è
ñòîëáöîì, íàïðèìåð a11 = xx
1
0
2
0
.
Åñëè íåîáõîäèìî îñóùåñòâèòü
ïåðåõîä îò âòîðîé ñèñòåìû êîîðäèíàò ê ïåðâîé, òî ñëåäóåò
âîñïîëüçîâàòüñÿ
òðàíñïîíèðîâàííîé
ìàòðèöåé. Ñëîæíûé
ïîñëåäîâàòåëüíûé ïåðåõîä îò ïåðâîé ñèñòåìû êîîðäèíàò êî âòîðîé è
îò âòîðîé ê òðåòüåé âûïîëíÿåòñÿ ïî ïðàâèëó ïåðåìíîæåíèÿ ìàòðèö:
25
Ðèñ. 1.8 . Ñõåìà âçàèìíîãî ðàñïîëîæåíèÿ
ñâÿçàííîé è íîðìàëüíîé çåìíîé ñèñòåì
êîîðäèíàò ïðè ïåðâîì ïîâîðîòå îòíîñè-
òåëüíî îñè OZg
AAA
1
3
2
3
1
2
()
() ().
=⋅
(1.4)
Ïðè îñóùåñòâëåíèè ýòîé îïåðàöèè ñëåäóåò ïîìíèòü, ÷òî
ïðîèçâåäåíèå ìàòðèö â îáùåì ñëó÷àå íåêîììóòàòèâíî, ò.å .
ïåðåìåñòèòåëüíûé çàêîí íå ñîáëþäàåòñÿ:
CABBA
=⋅≠⋅
.
Òåîðåìó óìíîæåíèÿ ìàòðèö ìîæíî ðàñïðîñòðàíèòü íà ñëó÷àé
ïðîèçâîëüíîãî ÷èñëà ñèñòåì êîîðäèíàò (n):
AAA AA
11
2
1
2
3
1
2
n
n
n
n
n
=⋅⋅
⋅
⋅
−−
−
...
.
() ()
(1.5)
Ïðîèçâåäåíèå ìàòðèö àññîöèàòèâíî:
ABC ABC
⋅⋅=⋅⋅
()().
×òîáû ïîëó÷èòü ìàòðèöó ïåðåõîäà îò èñõîäíîé ñèñòåìû êîîðäè-
íàò ê êîíå÷íîé, íåîáõîäèìî ñîñòàâèòü ýëåìåíòàðíûå ìàòðèöû ïî-
ñëåäîâàòåëüíîãî ïîâîðîòà íà îäèí óãîë è ïåðåìíîæèòü èõ. Ñîñòà-
âèì òàê íàçûâàåìóþ ìàòðèöó òðåõ ïîâîðîòîâ ïåðâîãî ðîäà, âçÿâ â
êà÷åñòâå ïðèìåðà ìàòðèöó (òàáëèöó íàïðàâëÿþùèõ êîñèíóñîâ) ïå-
ðåõîäà îò íîðìàëüíîé ñèñòåìû êîîðäèíàò OXgYgZg ê ñâÿçàííîé
OXYZ. Ïîâîðîòû áóäåì îñóùåñòâëÿòü ïðîòèâ ÷àñîâîé ñòðåëêè, ò.å. â
ïîëîæèòåëüíîì íàïðàâëåíèè, â ñëåäóþùåé ïîñëåäîâàòåëüíîñòè:
θ →ψ→γ. Îáîçíà÷èâ AA
1
2
=
θ , ïîëó÷èì äëÿ ïåðâîãî ïîâîðîòà íà
óãîë θ
Aθ
θθ
θθ
=−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
cos
sin
sin
cos
;
0
0
001
(1.6)
äëÿ âòîðîãî ïîâîðîòà íà óãîë ψ
AA
2
3
0
01
0
0
()
cos
sin
sin
cos
;
==
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
ψ
ψψ
ψψ
(1.7)
äëÿ òðåòüåãî ïîâîðîòà íà óãîë γ
AA
3
4
10
0
0
0
()
cos
sin
sin
cos
.
==
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
γ
γγ
γγ
(1.8)
26
Ïîìíÿ, ÷òî ïåðåìåñòèòåëüíûé çàêîí íå âûïîëíÿåòñÿ, ïîëó÷èì
óðàâíåíèå ìàòðè÷íîãî ïåðåõîäà îò OXgYgZg ê OXYZ. Ñîõðàíèâ äëÿ
îáùíîñòè íóëåâûå çíà÷åíèÿ ýëåìåíòîâ ìàòðèö, íàõîäèì
AA
γψ
γγ
γγ
ψψ
⋅=
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
−
10
0
0
0
0
01
cos
sin
sin
cos
cos
sin
0
0
0
sin
cos
cos
sin
sin sin
cos
sin co
ψψ
ψψ
γψγ γ
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
=
−
s
cos sin
sin
cos cos
.
ψ
γψγγψ
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
Ïðîèçâåäåíèå ìàòðèö èìååò âèä
AAAA AA
1
4
0
0
001
()
cos
sin
sin
cos
⋅⋅⋅=⋅⋅
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
γψθ γψ
θθ
θθ⎥
⎥
⎥
.
(1.9)
 ðåçóëüòàòå ïåðåìíîæåíèÿ ïîëó÷èì ìàòðèöó ïåðåõîäà îò
íîðìàëüíîé ñèñòåìû êîîðäèíàò ê ñâÿçàííîé:
AA
1
4()
cos cos
cos sin
sin
sin sin cos
cos sin
==
=
−
−
ψθ
ψθ
ψ
γψθγθγψθγθγψ
γψθ γ
sin sin sin
cos cos
sin cos
cos sin cos
sin sin
+
+θ
γ
ψ
θ
γ
θ
γ
ψ
cos sin sin
sin cos
cos cos
.
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
(1.10)
Ôîðìóëà ïåðåõîäà èìååò âèä
X
Y
Z
X
Y
Z
g
g
g
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=⋅
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
A
.
(1.11)
Ñîõðàíÿÿ äâîéíóþ èíäåêñàöèþ ýëåìåíòîâ ìàòðèöû ïåðåõîäíûõ
êîñèíóñîâ aij â ñîîòíîøåíèè (1.3), ïîëó÷èì ñëåäóþùóþ ñâÿçü ìåæäó
åäèíè÷íûìè âåêòîðàìè (ïî îñÿì êîîðäèíàò):
xxyz
yxyz
z
0
11
0
12
0
13
0
0
21
0
22
0
23
0
0
=++
=++
aaa
aaa
ggg
ggg
;
;
=++
aaa
ggg
31
0
32
0
33
0
xyz
.
(1.12)
27
Ïåðåõîäÿ îò ñâÿçàííîé ñèñòåìû ê
íîðìàëüíîé, èìååì
xxyz
yxyz
z
g
g
g
aaa
aaa
a
0
11
0
21
0
31
0
0
12
0
22
0
32
0
0
1
=++
=++
=
;
;
3
0
23
0
33
0
xyz
++
aa
.
(1.13)
Ñâÿçü ìåæäó ãåîöåíòðè÷åñêèìè ïðÿìî-
óãîëüíûìè è ãåîöåíòðè÷åñêèìè ñôå-
ðè÷åñêèìè êîîðäèíàòàìè (ðèñ. 1 .9) âû-
ðàæàåòñÿ ïðîñòûìè ñîîòíîøåíèÿìè
xr
yr
zr
0
0
0
=
=
=
cos
sin ;
sin ;
cos
cos ,
φλ
φ
φλ
ãö
ãö
ãö
(1.14)
ãäå φãö, λ – ãåîöåíòðè÷åñêèå øèðîòà è äîëãîòà ïîëîæåíèÿ ðàêåòû
ñîîòâåòñòâåííî.
Ïåðåõîä îò îñåé êðèâîëèíåéíîé ñôåðè÷åñêîé ñèñòåìû êîîðäè-
íàò ê îñÿì çåìíîé ñèñòåìû êîîðäèíàò O0XgYgZg îñóùåñòâëÿåòñÿ ñ ïî-
ìîùüþ òàáë. 1 .1 .
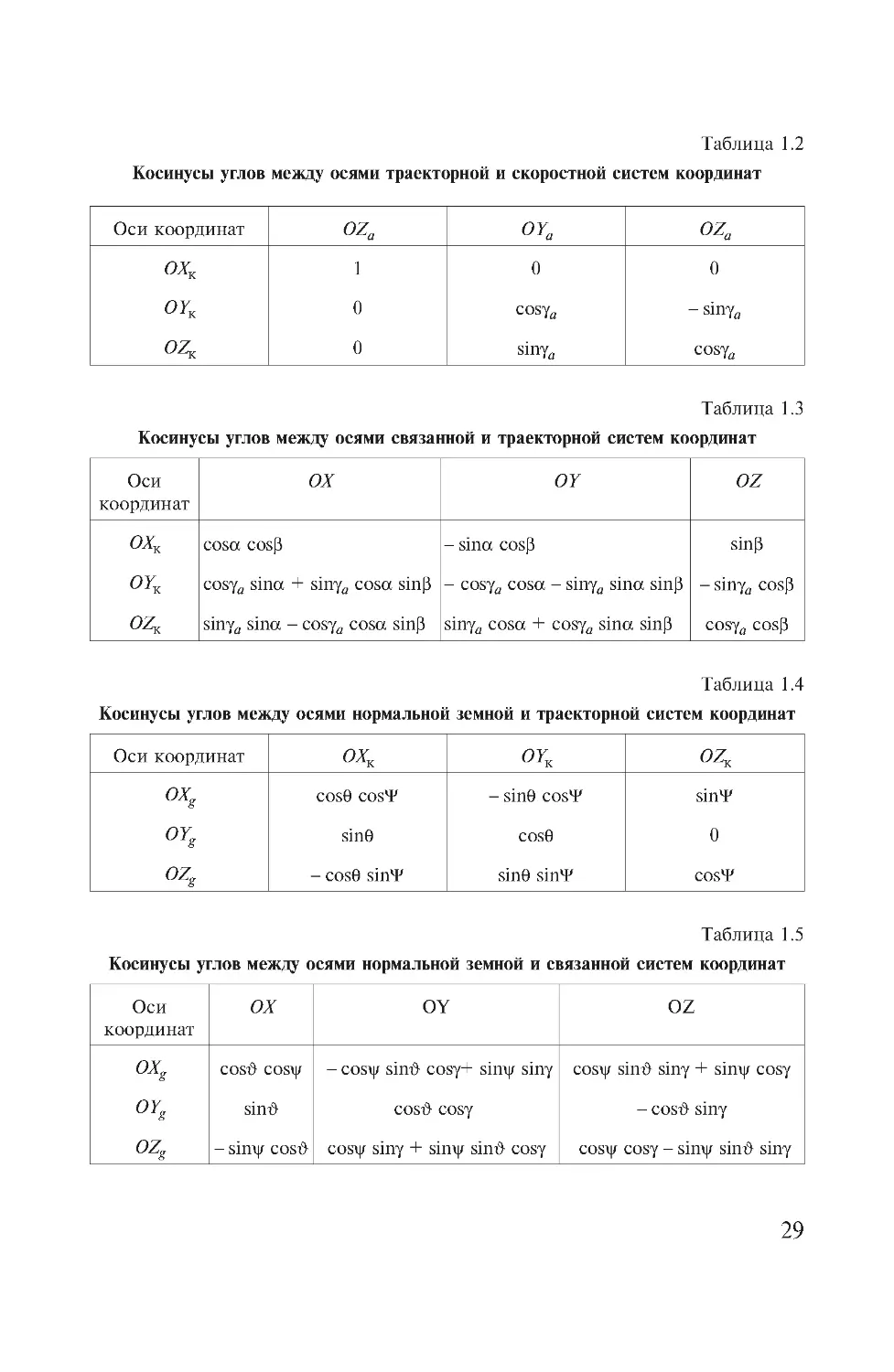
Ìàòðèöû ïåðåõîäíûõ êîñèíóñîâ äàíû â òàáë. 1 .2 ...1.6.
Äëÿ âðàùàþùèõñÿ ËÀ (íàïðèìåð, òóðáîðåàêòèâíûõ ñíàðÿäîâ)
ïîëîæåíèå ñâÿçàííîé ñèñòåìû êîîðäèíàò îòíîñèòåëüíî îïîðíîé,
íàïðèìåð ïîäâèæíîé îðèåíòèðîâàííîé, îïðåäåëÿåòñÿ òðåìÿ óãëàìè
Ýéëåðà: óãëîì ñîáñòâåííîãî âðàùåíèÿ îòíîñèòåëüíî ïðîäîëüíîé
îñè φ, óãëîì íóòàöèè δ è óãëîì ïðåöåññèè ν. Ïðè ñîâìåùåíèè âåê-
òîðà êèíåòè÷åñêîãî ìîìåíòà K ñ âåêòîðîì çåìíîé ñêîðîñòè öåíòðà
ìàññ Vê ïîëó÷èì ñõåìó äâèæåíèÿ Ýéëåðà – Ïóàíñî (ðèñ. 1 .10). Íà
ñõåìå âìåñòî óãëîâ φ è ν ïîêàçàíû âåêòîðû óãëîâûõ ñêîðîñòåé •φ è •ν .
Òàáëèöà 1.1
Êîñèíóñû óãëîâ ìåæäó îñÿìè êðèâîëèíåéíîé
è íîðìàëüíîé çåìíîé ñèñòåì êîîðäèíàò
Îñè êîîðäèíàò
O0Xg
O0Yg
O0Zg
[r]
cosq cosA
sinq
cosq sinA
[q]
−sinq cosA
cosq
−sinq sinA
[A]
−sinA
0
cosA
28
Ðèñ. 1 .9. Ñõåìà âçàèìíîãî ðàñïî-
ëîæåíèÿ ãåîöåíòðè÷åñêèõ ïðÿìî-
óãîëüíîé è ñôåðè÷åñêîé ñèñòåì
êîîðäèíàò
Òàáëèöà 1.2
Êîñèíóñû óãëîâ ìåæäó îñÿìè òðàåêòîðíîé è ñêîðîñòíîé ñèñòåì êîîðäèíàò
Îñè êîîðäèíàò
OZa
OYa
OZa
OXê
100
OYê
0
cosγa
−
sinγa
OZê
0
sinγa
cosγa
Òàáëèöà 1.3
Êîñèíóñû óãëîâ ìåæäó îñÿìè ñâÿçàííîé è òðàåêòîðíîé ñèñòåì êîîðäèíàò
Îñè
êîîðäèíàò
OX
OY
OZ
OXê
cosα cosβ−
sinα cosβ
sinβ
OYê
cosγa sinα + sinγa cosα sinβ−cosγa cosα−sinγa sinα sinβ − sinγa cosβ
OZê
sinγa sinα−cosγa cosα sinβ sinγa cosα + cosγa sinα sinβ
cosγa cosβ
Òàáëèöà 1.4
Êîñèíóñû óãëîâ ìåæäó îñÿìè íîðìàëüíîé çåìíîé è òðàåêòîðíîé ñèñòåì êîîðäèíàò
Îñè êîîðäèíàò
OXê
OYê
OZê
OXg
cosθ cosΨ−
sinθ cosΨ
sinΨ
OYg
sinθ
cosθ
0
OZg
−
cosθ sinΨ
sinθ sinΨ
cosΨ
Òàáëèöà 1.5
Êîñèíóñû óãëîâ ìåæäó îñÿìè íîðìàëüíîé çåìíîé è ñâÿçàííîé ñèñòåì êîîðäèíàò
Îñè
êîîðäèíàò
OX
OY
OZ
OXg
cosθ cosψ−
cosψ sinθ cosγ+ sinψ sinγ cosψ sinθ sinγ + sinψ cosγ
OYg
sinθ
cosθ cosγ−
cosθ sinγ
OZg
− sinψ cosθ cosψ sinγ + sinψ sinθ cosγ
cosψ cosγ−sinψ sinθ sinγ
29
Òàáëèöà 1.6
Êîñèíóñû óãëîâ ìåæäó îñÿìè ñêîðîñòíîé è ñâÿçàííîé ñèñòåì êîîðäèíàò
Îñè êîîðäèíàò
OX
OY
OZ
OXa
cosα cosβ−
sinα cosβ
sinβ
OYa
sinα
cosα
0
OZa
−
cosα sinβ
sinα sinβ
cosβ
 ñëó÷àå ñâîáîäíîãî íåîðãàíèçîâàííîãî äâèæåíèÿ, êîãäà òðèãî-
íîìåòðè÷åñêèå ôóíêöèè íàçâàííûõ âûøå óãëîâ ìîãóò ìåíÿòü çíàêè,
îðèåíòàöèþ ëåòàòåëüíîãî àïïàðàòà â ïðîñòðàíñòâå óäîáíî îïðåäå-
ëÿòü ñîñòàâëÿþùèìè êâàòåðíèîíîâ. Êâàòåðíèîíû Ðîäðèãà – Ãàìèëü-
òîíà ξ0, ξ1, ξ2, ξ3 äîëæíû óäîâëåòâîðÿòü ñîîòíîøåíèþ
ξξξξ
0
2
1
2
2
2
3
2
1
+++ =
.
Ïðîèçâîäíûå ïî âðåìåíè ïàðàìåòðîâ ξ1, ξ2 è ξ3
ñâÿçàíû ñ óãëîâûìè ñêîðîñòÿìè óðàâíåíèåì
•
•
•
,
•
(
ξ
ξ
ξ
ω
ω
ω
ξω
ξ
1
2
3
1
2
1
2
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=−
A
x
y
z
a
tt
)(),
oξ
(1.15)
ãäåω=ωx+ωy+ωz;ξ=ξ1+ξ2+ξ3,
Aξ
03
2
301
210
ξ−
ξξ
ξξ−
ξ
−ξ
ξξ
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
,
(1.16)
"B"
îçíà÷àåò îïåðàöèþ êâàòåð-
íèîííîãî óìíîæåíèÿ. Âåêòîð
óãëîâîé ñêîðîñòè âðàùåíèÿ ñâÿ-
çàííîé ñèñòåìû êîîðäèíàò îòíî-
ñèòåëüíî èíåðöèàëüíîé ñèñòåìû
îáîçíà÷àåòñÿ Ω, à îòíîñèòåëüíî
âûáðàííîé ñèñòåìû êîîðäèíàò,
ñâÿçàííîé ñ Çåìëåé, îáîçíà-
÷àåòñÿ ω. Ïðîåêöèè óãëîâîé
ñêîðîñòè ω íà îñè ñâÿçàííîé
ñèñòåìû êîîðäèíàò OXY íàçû-
âàþòñÿ ñîîòâåòñòâåííî ñêîðî-
30
Ðèñ. 1.10. Ñõåìà óãëîâîãî äâèæåíèÿ ËÀ:
•
φ – âåêòîð ñîáñòâåííîé óãëîâîé ñêîðî-
ñòè ËÀ îòíîñèòåëüíî ïðîäîëüíîé îñè;
•
ν – âåêòîð óãëîâîé ñêîðîñòè ïðåöåñ-
ñèè; δ – óãîë íóòàöèè; K – âåêòîð ìî-
ìåíòà êîëè÷åñòâà äâèæåíèÿ; Vê – âåê -
òîð çåìíîé ñêîðîñòè ËÀ
ñòüþ êðåíà ωx , ñêîðîñòüþ ðûñêàíèÿ ωy , ñêîðîñòüþ òàíãàæà ωz .
Ïîäîáíûì îáðàçîì îáîçíà÷àþòñÿ ñîñòàâëÿþùèå óãëîâîé ñêîðîñòè
ËÀ è â äðóãèõ ñèñòåìàõ êîîðäèíàò.
1.2 . ÂËÈßÍÈÅ ÏÎËß ÒßÃÎÒÅÍÈß ÇÅÌËÈ
È ÅÅ ÂÐÀÙÅÍÈß ÍÀ ÏÎËÅÒ ÐÀÊÅÒ È ÑÍÀÐßÄÎÂ
1.2 .1. ÏÎÒÅÍÖÈÀË ÑÈËÛ ÇÅÌÍÎÃÎ ÒßÃÎÒÅÍÈß,
ÔÎÐÌÀ È ÐÀÇÌÅÐÛ ÇÅÌËÈ
Ïîòåíöèàëüíîé ôóíêöèåé èëè ïîòåíöèàëîì íàçûâàþò ôóíêöèþ
Ï(x, y, z), ïîëíûé äèôôåðåíöèàë êîòîðîé ðàâåí ýëåìåíòàðíîé ðà-
áîòå ñèëû, äåéñòâóþùåé íà òî÷êó:
dd
x
dx
y
dy
z
dz
ÏFr
=
ÏÏÏ
=++
∂
∂
∂
∂
∂
∂
.
(1.17)
Ïðîåêöèè íà îñè êîîðäèíàò ðàâíîäåéñòâóþùåé ïðèëîæåííûõ ê
òî÷êå ñèë ñîîòâåòñòâåííî èìåþò âèä
Fx
Fy
Fz
xyz
===
∂∂∂∂∂∂
ÏÏÏ
/;
/;
/.
(1.18)
Ïîòåíöèàë äëÿ òî÷å÷íîé åäèíè÷íîé ìàññû, íàõîäÿùåéñÿ âíå
Çåìëè íà ðàññòîÿíèè l îò ýëåìåíòàðíîé ìàññû Çåìëè dM,ïîçàêîíó
òÿãîòåíèÿ Íüþòîíà îïðåäåëÿåòñÿ âûðàæåíèåì
df
d
M
l
Ïò
=
/, (1.19)
ãäå f – ãðàâèòàöèîííàÿ ïî-
ñòîÿííàÿ; l – ðàññòîÿíèå ìåæäó
òî÷êîé ñ åäèíè÷íîé ìàññîé
(òî÷êà Ð) è òî÷êîé ñ ýëåìåíòàðíîé
ìàññîé dM (ðèñ. 1.11). Ïîòåíöèàë
ñèëû òÿãîòåíèÿ Çåìëè äëÿ òî÷å÷-
íîé åäèíè÷íîé ìàññû ïîëó÷àþò
èíòåãðèðîâàíèåì ïî âñåé ìàññå
Çåìëè M:
31
Ðèñ. 1 .11 . Êîîðäèíàòû òî÷å÷íîé åäèíè÷-
íîé ìàññû, íàõîäÿùåéñÿ âíå Çåìëè
Ïò
=
∫fdMl
M
/.
(1.20)
Ïîëîæåíèÿ òî÷êè Ð âíå Çåìëè è òî÷êè ýëåìåíòàðíîé ìàññû Çåìëè
dM îïðåäåëÿþòñÿ ñôåðè÷åñêèìè êîîðäèíàòàìè: r, φãö, λ äëÿ òî÷êè Ð ;
ρ, ′′
φλ
ãö
,
äëÿ òî÷êè ýëåìåíòàðíîé ìàññû dM. Ïîòåíöèàë,
ïðåäñòàâëåííûé ÷åðåç ñôåðè÷åñêèå êîîðäèíàòû, èìååò âèä
Ïr
f
dM
lr
M
(, ,)
(,,,,,)
.
φλ
φλρφλ
ãö
ãö
ãö
=
′′
∫
(1.21)
Íàïèñàííûé èíòåãðàë ìîæåò áûòü âû÷èñëåí òîëüêî ïðèáëèæåííî,
òàê êàê íåèçâåñòíû òî÷íî ôîðìà Çåìëè è ïëîòíîñòü âåùåñòâà Çåìëè
μÇ, êîòîðàÿ ñóùåñòâåííî èçìåíÿåòñÿ ïî âñåìó åå îáúåìó. Îáîçíà÷àÿ
óãîë ìåæäó ρ è r ÷åðåç ψ, ïîëó÷èì
lrr
=+
−
22
2
ρρψ
cos .
(1.22)
 ïðîöåññå ïîëåòà ðàêåòû îòíîñèòåëüíî Çåìëè áóäóò èçìåíÿòüñÿ
âåëè÷èíû r è ψ, à ñëåäîâàòåëüíî, è âåëè÷èíà l. Î÷åâèäíî, ÷òî
ïîòåíöèàë, èçìåíÿâøèéñÿ â ïðîöåññå äâèæåíèÿ ðàêåòû â íåêîòîðûõ
ïðåäåëàõ, ìîæåò áûòü âû÷èñëåí ïðèáëèæåííî ïðè ââåäåíèè
ðàçëè÷íîãî ðîäà äîïóùåíèé. Íàèáîëåå ñóùåñòâåííûå äîïóùåíèÿ
êàñàþòñÿ ôîðìû Çåìëè, åå ðàçìåðîâ è ðàñïðåäåëåíèÿ ìàññ.
Çà áîëåå áëèçêóþ ê ðåàëüíîé ôîðìå Çåìëè ïðèíèìàþò ôèãóðó,
íàçûâàåìóþ ãåîèäîì. Ãåîèä – ýòî ôèãóðà, îãðàíè÷åííàÿ óðîâåííîé
ïîâåðõíîñòüþ ïîòåíöèàëà ñèëû òÿæåñòè, âî âñåõ òî÷êàõ êîòîðîé
çíà÷åíèå ïîòåíöèàëà îäèíàêîâî è êîòîðàÿ ñîâïàäàåò ñ ïîâåðõíî-
ñòüþ îêåàíîâ, íàõîäÿùèõñÿ â íåâîçìóùåííîì ñîñòîÿíèè, ò.å . ïðè
îòñóòñòâèè ïðèëèâîâ, îòëèâîâ, àòìîñôåðíûõ è êàêèõ-ëèáî äðóãèõ
âîçìóùåíèé. Òî÷íîå ìàòåìàòè÷åñêîå îïèñàíèå ãåîèäà íåâîçìîæíî.
Ïðè ïðîâåäåíèè ðàçëè÷íîãî ðîäà âû÷èñëèòåëüíûõ ðàáîò (ãåîäåçè-
÷åñêèõ, àñòðîíîìè÷åñêèõ è áàëëèñòè÷åñêèõ) â êà÷åñòâå ïîñëåäîâà-
òåëüíûõ ïðèáëèæåíèé ê ãåîèäó ïðèíèìàþò: ñôåðè÷åñêóþ ìîäåëü
Çåìëè – ñôåðó, ñôåðîèäàëüíóþ ìîäåëü – ñôåðîèä (ýëëèïñîèä âðà-
ùåíèÿ), òðåõîñíûé ýëëèïñîèä.
 Ðîññèè â òå÷åíèå äëèòåëüíîãî âðåìåíè ïðè ïðîâåäåíèè àñòðî-
íîìî-ãåîäåçè÷åñêèõ ðàáîò áûë ïðèíÿò ñôåðîèä Áåññåëÿ.  1924 ã. ïî
ìåæäóíàðîäíîìó ñîãëàøåíèþ ëó÷øèì ñôåðîèäîì áûë ïðèçíàí
ñôåðîèä Õåéôîðäà. Âî ìíîãèõ ñëó÷àÿõ îêàçûâàåòñÿ óäîáíûì èñ-
ïîëüçîâàòü òàê íàçûâàåìûé íîðìàëüíûé ñôåðîèä, ïðåäëîæåííûé
À. Êëåðî.
32
Ðàçìåðû, îïðåäåëÿþùèå ñôåðîèä (åãî îñè), âû÷èñëÿëèñü íà îñ-
íîâàíèè ãðàäóñíûõ èçìåðåíèé äëèí äóã ìåðèäèàíîâ. Òàê êàê ôèãóðà
Çåìëè îòëè÷íà îò ñôåðîèäà, òî â ðàçíûõ ìåñòàõ íà îäíîé è òîé æå
øèðîòå äóãè ìåðèäèàíîâ èìåþò ðàçíóþ êðèâèçíó. Ïîýòîìó îïðåäå-
ëåííûå â ãðàäóñàõ ðàçìåðû ýëëèïñîèäà çàâèñÿò îò ìåñòà èçìåðåíèÿ.
Ýòèì îáúÿñíÿþòñÿ èìåþùèåñÿ ðàçëè÷èÿ â ÷èñëåííûõ çíà÷åíèÿõ ïà-
ðàìåòðîâ çåìíîãî ñôåðîèäà, ïîëó÷åííûõ îòäåëüíûìè àâòîðàìè.
Ñîâåòñêèå ãåîäåçèñòû ïîä ðóêîâîäñòâîì Ôåîäîñèÿ Íèêîëàåâè÷à
Êðàñîâñêîãî (1878–1948) ñ ïîìîùüþ ãðàäóñíûõ èçìåðåíèé ÑÑÑÐ,
Çàïàäíîé Åâðîïû è ÑØÀ îïðåäåëèëè ðàçìåðû äâóõîñíîãî ýëëèï-
ñîèäà (ñôåðîèäà), êîòîðûé èñïîëüçîâàëñÿ â ãåîäåçè÷åñêèõ ðàáîòàõ â
ÑÑÑÐ è áûë íàçâàí çåìíûì ýëëèïñîèäîì Êðàñîâñêîãî. Íà îñíîâà-
íèè òåõ æå ðàáîò áûëè ïîëó÷åíû ðàçìåðû òðåõîñíîãî ýëëèïñîèäà.
Äëÿ äâóõîñíîãî ýëëèïñîèäà Êðàñîâñêîãî áîëüøàÿ ïîëóîñü (ñðåä-
íèé ðàäèóñ ýêâàòîðà) ïðèíèìàåòñÿ ðàâíîé à = 6 378245 ì, ìàëàÿ ïî-
ëóîñü b = 6 356863 ì. Ðàçíîñòü ìåæäó îñÿìè ñôåðîèäà ñîñòàâëÿåò
≈ 42800 ìì. Ñæàòèå ñôåðîèäà a =(a – b)/a = 1/298,3 = 0,003352.
Êâàäðàò ïåðâîãî ýêñöåíòðèñèòåòà laba
1
2222
=−
()
/= 0,006693. Êâàä-
ðàò âòîðîãî ýêñöåíòðèñèòåòà labb
2
2222
=−
()
/= 0,006739.
Äëÿ ñôåðè÷åñêîé ìîäåëè Çåìëè îñíîâíîé ãåîïîñòîÿííîé âåëè÷è-
íîé ÿâëÿåòñÿ ðàäèóñ çåìíîé ñôåðû. Îí ìîæåò áûòü îïðåäåëåí ïî-ðàç-
íîìó. Åñëè âçÿòü ñðåäíåå àðèôìåòè÷åñêîå òðåõ ïîëóîñåé ýëëèïñîèäà
Êðàñîâñêîãî, òî ïîëó÷èì 6 371118 ì. Ðàäèóñ ñôåðû, ïîâåðõíîñòü êîòî-
ðîé ðàâíà ïîâåðõíîñòè çåìíîãî ýëëèïñîèäà, áóäåò ðàâåí 6 371110 ì.
Âñå ìåòîäû äàþò áëèçêèå ê ïîñëåäíåìó ðåçóëüòàòû.
Îáùåå âûðàæåíèå äëÿ ïîòåíöèàëà ñèëû çåìíîãî òÿãîòåíèÿ,
ïðàêòè÷åñêè ïðèãîäíîå äëÿ ðàçëè÷íûõ ìîäåëåé ãåîèäà, ïîëó÷àþò,
ðàçëîæèâ âûðàæåíèå äëÿ Ïò â ðÿä ñôåðè÷åñêèõ ôóíêöèé. Ïðåäâàðè-
òåëüíî ðàññìîòðèì áîëåå ïðîñòîé âûâîä, õîðîøî ïîÿñíÿþùèé ôè-
çè÷åñêèé ñìûñë ïåðâûõ ÷ëåíîâ ðàçëîæåíèÿ. Èç ôîðìóëû (1.22) ïî-
ëó÷èì
11
1
1
2
l
r
rr
rr
=
+
⎛
⎝⎜⎞
⎠⎟−
=
⎛
⎝⎜⎞
⎠⎟
ρρ
ψ
ρ
ψ
cos
,.
F
(1.23)
Ðàçëîæåíèå íàïèñàííîé ôóíêöèè â áèíîìèàëüíûé ðÿä ìîæåò
áûòü ïðåäñòàâëåíî â âèäå ñóììû ÷ëåíîâ, âêëþ÷àþùèõ â ñåáÿ ïîëè-
íîìû Ëåæàíäðà Pn(cosψ):
ρρ
ψ
rrr
P
n
n
n
⎛
⎝⎜⎞
⎠⎟= ⎛
⎝⎜⎞
⎠⎟
=
∞
∑
1
0
(cos ).
(1.24)
33
Îáùåå âûðàæåíèå äëÿ ïîëèíîìà ñòåïåíè n èìååò âèä
P
n
d
d
n
n
nn
n
(cos )
!
[(cos ) ]
[(cos ) ]
.
ψ
ψ
ψ
=
−
1
2
1
2
(1.25)
Äëÿ îòäåëüíûõ çíà÷åíèé n áóäåì èìåòü
P0
1
(cos) ;
ψ=
P1(cos ) cos ;
ψψ
=
P2
2
3
2
1
2
(cos )
cos
;
ψψ
=−
P3
3
5
2
3
2
(cos )
cos
cos ;
ψψψ
=−
P4
42
35
8
15
4
3
8
(cos )
cos
cos
;
ψψψ
=−+
...........................................
Èñïîëüçóÿ (1.24), èç (1.20) ïîëó÷èì
Ïò
=
⎛
⎝⎜⎞
⎠⎟
=
∞
∑∫f
rr
Pd
M
n
n
n
M
ρ
ψ
(cos )
.
0
Îãðàíè÷èìñÿ òðåìÿ ÷ëåíàìè ðàçëîæåíèÿ è ïðåäñòàâèì ïîòåíöèàë
ñóììîé òðåõ èíòåãðàëîâ:
Ïò
=+
+
−
⎛
⎝⎜
⎞
⎠⎟
⎡
⎣⎢
∫
∫
∫f
r
dM
r
dM
r
dM
M
M
M
11
3
2
1
2
2
22
ρψ
ρψ
cos
cos
⎤
⎦⎥ . (1.26)
Çíà÷åíèå ïåðâîãî èíòåãðàëà î÷åâèäíî: dM M
M
=
∫ . Îñòàëüíûå èí-
òåãðàëû ìîãóò áûòü âçÿòû â êîíå÷íîì âèäå, åñëè íàëîæèòü íåêîòî-
ðûå îãðàíè÷åíèÿ íà ðàñïðåäåëåíèå ìàññû è ôîðìó Çåìëè. Ïðè ðàâ-
íîìåðíîì ðàñïðåäåëåíèè ìàññû ïî îáúåìó Çåìëè, âûðàæàÿ cosψ ÷å-
ðåç êîîðäèíàòû ÷àñòèöû ìàññû dM è âíåøíåãî òåëà åäèíè÷íîé
ìàññû â ñèñòåìå êîîðäèíàò, öåíòð êîòîðîé ïîìåùåí â öåíòðå ìàññ
Çåìëè, íàéäåì ρψ
cos
.
dM
M
=
∫
0
34
Âëèÿíèå íåñôåðè÷íîñòè Çåìëè íà ðàñïðåäåëåíèå ìàññû ìîæíî
õàðàêòåðèçîâàòü ìîìåíòàìè èíåðöèè Çåìëè, îïðåäåëåííûìè îòíî-
ñèòåëüíî îñåé ãåîöåíòðè÷åñêîé ñèñòåìû êîîðäèíàò. Åñëè îáîçíà-
÷èòü ÷åðåç  ìîìåíò èíåðöèè îòíîñèòåëüíî ãëàâíîé îñè O0Y0, ñîâ-
ïàäàþùåé ñ îñüþ âðàùåíèÿ Çåìëè, à ÷åðåç À è Ñ – ìîìåíòû èíåð-
öèè îòíîñèòåëüíî ãëàâíûõ îñåé O0X0, O0Z0, ëåæàùèõ â
ýêâàòîðèàëüíîé ïëîñêîñòè, è ñâÿçàòü ïðÿìîóãîëüíûå è ñôåðè÷åñêèå
ãåîöåíòðè÷åñêèå êîîðäèíàòû òî÷êè Ð è ÷àñòèöû dM îáû÷íûì îáðà-
çîì, íàïðèìåð òàê:
Xr
Yr
Zr
0
0
0
pã
ö
pã
ö
pã
ö
=
=
=−
cos
cos ;
sin ;
cos
sin ,
φλ
φ
φλ
(1.27)
òî ïîëó÷èì
ρψ
φ
22
2
3
2
1
2
1
4
23
1
3
4
cos
(
)( sin
)
(
−
⎛
⎝⎜
⎞
⎠⎟ =+
−
−
+
+
∫
dM
ACB
M
ãö
CA
−
)cos cos
2
2
φλ
.
ãö
(1.28)
Îáîçíà÷àÿ ñóììó íåó÷òåííûõ ÷ëåíîâ ðàçëîæåíèÿ ÷åðåç Ïòí, ïîëó÷èì
ôîðìóëó äëÿ òàê íàçûâàåìîãî "íîðìàëüíîãî ïîòåíöèàëà Çåìëè"
Ïòã
ö
ãö
=+
+
−
−
+
+−
fM
r
f
r
ACB
f
r
CA
4
23
1
3
4
3
2
3
2
()
(
s
i
n
)
()
c
o
s
φ
φ cos
.
2λ+Ï òí
(1.29)
 ôîðìóëå (1.29) ïåðâîå ñëàãàåìîå ïðåäñòàâëÿåò ñîáîé ïîòåíöèàë
ñèëû òÿãîòåíèÿ Çåìëè ñ ðàâíîìåðíûì èëè ñôåðè÷åñêèì ðàñïðåäå-
ëåíèåì ìàññû – òàê íàçûâàåìûé ïîòåíöèàë íüþòîíîâñêîãî ïðèòÿ-
æåíèÿ. Âòîðîå ñëàãàåìîå çàâèñèò îò øèðîòû φãö è ó÷èòûâàåò âëèÿ-
íèå ïîëþñíîãî ñæàòèÿ Çåìëè, òðåòüå – ó÷èòûâàåò çàâèñèìîñòü ðàñ-
ïðåäåëåíèÿ ìàññû Çåìëè îò äîëãîòû, ò.å . îòðàæàåò âëèÿíèå
áîêîâîãî ñæàòèÿ. Ïîñëåäóþùèå ñëàãàåìûå (îáîçíà÷åííûå Ïòí) ó÷è-
òûâàþò íåñèììåòðè÷íîñòü ðàñïðåäåëåíèÿ ìàññû â ñåâåðíîé è þæ-
íîé ÷àñòÿõ Çåìëè, à òàêæå äðóãèå íåðàâíîìåðíîñòè â ãðàâèòàöèîí-
íîì ïîëå Çåìëè.
Åñëè ïðåäïîëîæèòü, ÷òî Çåìëÿ – ïðàâèëüíûé ýëëèïñîèä âðàùå-
íèÿ ñ ðàâíîìåðíûì ðàñïðåäåëåíèåì ìàññû âîêðóã îñè âðàùåíèÿ,
35
ò.å . À = Ñ, òî ñ äîáàâëåíèåì åùå îäíîãî ïîëèíîìà ïðåäñòàâèì ïî-
òåíöèàë â òàêîì âèäå:
Ïòã
ö
ãö
=+⋅
−
+
+⋅
−
ππ
φ
π
φ
02
3
2
4
5
4
1
2
31
1
8
35
30
rr
r
(sin
)
( sin
sin
) ....
2
3
φãö ++
(1.30)
Êîýôôèöèåíòû π0, π2, π4, íàçûâàåìûå ãåîïîñòîÿííûìè, ïî äàííûì
ðàáîòû È.Ä. Æàíãîëîâè÷à [47], ïðèíèìàþòñÿ ðàâíûìè
ππ
π
0
14
2
2
25
2
4
36
3 9859 10
177 10
23 10
=⋅
=
−
⋅
=⋅
,;
,
;
,
ì/ñ
ì/c
35
ì/ñ
72
.
 áîëüøèíñòâå ñëó÷àåâ îêàçûâàåòñÿ äîñòàòî÷íîé óïðîùåííàÿ
ôîðìóëà
Ïòã
ö
=+⋅
−
ππ
φ
02
3
2
1
2
31
rr
(sin
).
(1.31)
Ïðè áîëåå ïîëíîì ðàññìîòðåíèè ïîòåíöèàëà ñèëû òÿãîòåíèÿ Çåìëè
ïðåäïî÷èòàþò çàâèñèìîñòü äëÿ åãî îïðåäåëåíèÿ ïðåäñòàâëÿòü ðÿäîì
ñôåðè÷åñêèõ (øàðîâûõ) ôóíêöèé, êîòîðûå âûðàæàþòñÿ ÷åðåç
ïðèñîåäèíåííûå ôóíêöèè Ëåæàíäðà. Äëÿ òðèãîíîìåòðè÷åñêîé
ôóíêöèè ζ ïðèñîåäèíåííàÿ ôóíêöèÿ Ëåæàíäðà èìååò âèä
P
d
d
P
nm
m
m
m
n
()()
(),
ζζ
ζ
ζ
=−
12
(1.32)
ãäå èíäåêñ n îïðåäåëÿåò ñòåïåíü ïîëèíîìà, èíäåêñ m – ïîðÿäîê
ïðîèçâîäíîé.
Ãðàâèòàöèîííûé ïîòåíöèàë ñèëû òÿãîòåíèÿ Çåìëè, âûðàæåííûé
÷åðåç ñôåðè÷åñêèå ôóíêöèè, èìååò âèä
Ïò
ý
=+
×
⎧⎨
⎩
×
⎛
⎝⎜⎞
⎠⎟
+
=
∞
=
∑
∑
fM
r
R
r
Cm
C
n
m
N
n
nm
nm
1
1
0
12
(c
o
s
s
i
λ
n)(
s
i
n),
mP
nm
λφ
ãö
⎫
⎬
⎭
(1.33)
36
ãäå C1nm è C2nm – áåçðàçìåðíûå ÷èñëîâûå êîýôôèöèåíòû; Rý –
ýêâàòîðèàëüíûé ðàäèóñ Çåìëè.
Åñëè ïðèíÿòü ðàñïðåäåëåíèå ìàññû ïî îáúåìó Çåìëè ñèììåòðè÷-
íûì îòíîñèòåëüíî åå îñè âðàùåíèÿ, òî âûðàæåíèå (1.33) ìîæåò
áûòü ïðèâåäåíî ê áîëåå óäîáíîìó âèäó:
Ïò
ý
ãö
ý
=+
⎛
⎝⎜⎞
⎠⎟
+
⎧
⎨
⎩⎪
+
⎛
⎝⎜⎞
⎠⎟
fM
r
C
R
r
P
Ñ
R
r
120
2
20
30
(sin )
φ
3
30
40
4
40
PC
R
r
P
(sin )
(sin)....
φφ
ãö
ý
ãö
+
⎛
⎝⎜⎞
⎠⎟
+
⎫
⎬
⎭
(1.34)
Áåçðàçìåðíûå ïàðàìåòðû Cn0 îïðåäåëÿþòñÿ óðîâåííîé ïîâåðõíîñòüþ
è óãëîâîé ñêîðîñòüþ Çåìëè. Âåëè÷èíû Pn0(sinφãö) íàçûâàþòñÿ
çîíàëüíûìè ñôåðè÷åñêèìè ôóíêöèÿìè.
Äëÿ îðèåíòèðîâêè ïðèâåäåì äàííûå, õàðàêòåðèçóþùèå ïîëå
ïðèòÿæåíèÿ Çåìëè, ïîëó÷åííûå ñ ïîìîùüþ ãåîäåçè÷åñêèõ ñïóòíè-
êîâ [124]:
Kf
M
a
C
==
=
±
=−
⋅
398603 2
1 2982 02
1082 645
2
20
,;
:
(
,
,
)
;
,
êì /c
3
10
2546 10
164910
6378 165
6
30
6
40
6
−−
−
=⋅
=⋅
=
;,;
,;
,
C
CR
ý
êì.
Åñëè Çåìëþ ðàññìàòðèâàòü êàê ñôåðó ñî ñðåäíèì ðàäèóñîì RÇ,â
êîòîðîé ìàññà ðàñïðåäåëåíà ðàâíîìåðíî ïî îáúåìó, òî èç (1.29)
èìååì Ïò = fM/r = K/r. Ñëåäîâàòåëüíî, â ýòîì ñëó÷àå ïîòåíöèàëüíîå
(ãðàâèòàöèîííîå) ïîëå Çåìëè áóäåò öåíòðàëüíûì, à óñêîðåíèå îò
ñèëû ïðèòÿæåíèÿ, äåéñòâóþùåå â íåì íà òåëî åäèíè÷íîé ìàññû,
ìîæåò áûòü çàïèñàíî êàê gò = − dÏò/dr = K/r 2. Çíàê "ìèíóñ" çäåñü ïî-
ñòàâëåí ïîòîìó, ÷òî âåêòîð r, ïî íàïðàâëåíèþ êîòîðîãî áåðåòñÿ
ïðîèçâîäíàÿ dÏò/dr, è âåêòîð gò íàïðàâëåíû â ïðîòèâîïîëîæíûå
ñòîðîíû.
Ñðàâíèâàÿ çíà÷åíèÿ gò äëÿ ðàäèóñîâ r è RÇ, ïîëó÷èì çàâèñèìîñòü
g
g
R
r
ò
ò
ý
0
2
=
⎛
⎝⎜⎞
⎠⎟ , êîòîðàÿ õàðàêòåðèçóåò èçìåíåíèå óñêîðåíèÿ ñèëû ïðè-
òÿæåíèÿ â öåíòðàëüíîì ãðàâèòàöèîííîì ïîëå ïî ìåðå óäàëåíèÿ îò
åãî öåíòðà.
37
1.2.2. ÑÈËÀ ÒßÆÅÑÒÈ È ÅÅ ÏÎÒÅÍÖÈÀË
Ñèëó òÿæåñòè ìîæíî ïðåäñòàâèòü êàê
FFF
=+
òö
,
(1.35)
ãäå Fò – âåêòîð ñèëû çåìíîãî ïðèòÿæåíèÿ; Fö – âåêòîð öåíòðîáåæíîé
ñèëû èíåðöèè.
 ñôåðè÷åñêèõ ãåîöåíòðè÷åñêèõ êîîðäèíàòàõ öåíòðîáåæíàÿ ñèëà
èíåðöèè, äåéñòâóþùàÿ íà òåëî ìàññîé m â íàïðàâëåíèè, ïåðïåíäè-
êóëÿðíîì îñè âðàùåíèÿ Çåìëè, èìååò âèä
Fm
r
öã
ö
=Ω
2
cos ,
φ
(1.36)
ãäå Ω – óãëîâàÿ ñêîðîñòü Çåìëè.
Íàïðàâëåíèå ñèëû òÿæåñòè ñîâïàäàåò ñ íàïðàâëåíèåì îòâåñà, ò.å .
ñ âåðòèêàëüþ â ðàññìàòðèâàåìîé òî÷êå çåìíîé ïîâåðõíîñòè. Óãîë
ìåæäó íîðìàëüþ n ê ïîâåðõíîñòè è ýêâàòîðèàëüíîé ïëîñêîñòüþ
Çåìëè íàçûâàåòñÿ ãåîãðàôè÷åñêîé øèðîòîé φã, êîòîðàÿ îòëè÷àåòñÿ îò
ãåîöåíòðè÷åñêîé øèðîòû φãö (ðèñ. 1 .12). Ãåîãðàôè÷åñêàÿ äîëãîòà îò-
ñ÷èòûâàåòñÿ îò íà÷àëüíîãî ìåðèäèàíà, çà êîòîðûé ïðèíÿò ìåðèäèàí
Ãðèíâè÷à. Ñâÿçü ìåæäó ãåîöåíòðè÷åñêîé è ãåîãðàôè÷åñêîé øèðîòà-
ìè óñòàíàâëèâàåòñÿ ïî ïðèáëèæåííîé ôîðìóëå
tg
tg
ãö
ã
φφ
=−
()
,
11
2
l
(1.37)
ãäå l1 – ïåðâûé ýêñöåíòðèñèòåò.
Ðàçíîñòü ìåæäó óãëàìè φã −φãö ìîæåò áûòü íàéäåíà òàêæå èç çà-
âèñèìîñòè
φφαφ
ãã
ö
ã
−=
sin
.
2
(1.38)
Íàèáîëüøåå çíà÷åíèå ðàçíîñòè φã −φãö ðàâíî 11,5′ ïðè φã = 45°.
Ïîòåíöèàë ñèëû òÿæåñòè òàêæå ìîæíî ïðåäñòàâèòü êàê ñóììó
ïîòåíöèàëîâ ñèëû çåìíîãî ïðèòÿæåíèÿ è öåíòðîáåæíîé ñèëû èíåð-
öèè, îïðåäåëÿåìîé ñóòî÷íûì âðàùåíèåì Çåìëè:
ÏÏÏ
òö
=+.
(1.39)
Ó÷èòûâàÿ, ÷òî dÏö = Födrö, ãäå rö = rcosφãö, ïîëó÷èì ïîòåíöèàë
öåíòðîáåæíîé ñèëû èíåðöèè, îòíåñåííîé ê åäèíèöå ìàññû, â âèäå
Ïöã
ö
=
1
2
222
Ωrcos
.
φ
(1.40)
38
Åñëè èñïîëüçîâàòü äëÿ Ïò ôîðìóëó (1.31), òî
Ï
ãö
ãö
=+
−
+
ππ
φφ
02
3
22
2
2
2
31
1
2
rr
r
(sin
)
cos .
Ω
(1.41)
Ïîëó÷èì òåïåðü ôîðìóëó äëÿ îïðåäåëåíèÿ óñêîðåíèÿ ñâîáîäíîãî
ïàäåíèÿ. Ïî ñâîéñòâó ïîòåíöèàëà, íàéäåííîãî äëÿ åäèíè÷íîé ìàñ-
ñû, èìååì
gS
S=∂ ∂
Ï/,
(1.42)
ãäå gS – ïðîåêöèÿ óñêîðåíèÿ ñâîáîäíîãî ïàäåíèÿ íà íàïðàâëåíèå S;
∂Ï/∂S – ïðîèçâîäíàÿ îò ïîòåíöèàëà ñèëû òÿæåñòè, âçÿòàÿ ïî
íàïðàâëåíèþ S.  íåêîòîðûõ ñëó÷àÿõ âåêòîð óñêîðåíèÿ ñâîáîäíîãî
ïàäåíèÿ g óäîáíî çàäàâàòü â êîñîóãîëüíûõ ñèñòåìàõ êîîðäèíàò.
39
Ðèñ. 1.12. Ñõåìà îïðåäåëåíèÿ ïîëîæåíèÿ ìåñòíîé âåðòèêàëè ïðè ãåîãðàôè÷åñêîé
øèðîòå φã è ðàçëîæåíèå âåêòîðà óñêîðåíèÿ ñâîáîäíîãî ïàäåíèÿ ïî îñÿì êîñîóãîëü-
íîé ñèñòåìû êîîðäèíàò
Íàïðèìåð, â êîîðäèíàòíîé ñèñòåìå, îáðàçîâàííîé ðàäèóñ-âåêòîðîì
r è óãëîì φãö, èìååì
grS
=+
gg
r
*
,
oo
φφãö
(1.43)
ãäågr
*
è gφ – ïðîåêöèè g íà íàïðàâëåíèÿ êîîðäèíàò Sr è S φ ãö
; r°èS ãö
φ
o
–
ñîîòâåòñòâóþùèå îðòû.
Äëÿ êîîðäèíàòíîé ñèñòåìû (ðàäèóñ-âåêòîð r – âåêòîð óãëîâîé
ñêîðîñòè Çåìëè Ω) àíàëîãè÷íî ïðåäûäóùåìó ìîæíî íàïèñàòü
gr
=+
gg
r
*
.
oo
ΩΩ
(1.44)
Ïðîåêöèè óñêîðåíèÿ ñâîáîäíîãî ïàäåíèÿ g r
*
è gφ áóäåì íàõîäèòü ïî
ôîðìóëàì g
Sr
r
r
*
==
∂
∂
∂
∂
ÏÏ
èg
Ï
Sr
φ
φ
∂
∂
∂
∂φ
=
ãö
Ï
ãö
1
.
Äèôôåðåíöèðóÿ (1.41)
ïîî÷åðåäíî, ïîëó÷èì
g
rr
r
g
r
r
*
(sin
)cos;
s
=−
−
−
+
=
ππ
φφ
π
φ
0
2
2
3
22
2
2
4
2
3
2
31
3
ãö
ãö
Ω
in cos
sin
cos .
φφ
φφ
ãö
ãö
ãö
ãö
−Ω
2
r
(1.45)
Ïîëàãàÿ â ôîðìóëàõ (1.45) Ω = 0, ìîæíî ïîëó÷èòü âûðàæåíèå äëÿ
îïðåäåëåíèÿ ñîñòàâëÿþùèõ âåêòîðà gò ïî óêàçàííûì íàïðàâëåíèÿì.
Íàéäåì òåïåðü ñîñòàâëÿþùèå gr è gΩ, ó÷èòûâàÿ, ÷òî
gg
gg
r
r
r
Ω
Ω
=
′==
−
φ
φ
φ
φ
π
φφ
/cos ,
sin
sin
.
ãö
ãö
ãö
ãö
tg
32
4
22
2
(1.46)
Òàê êàê gr
*
è′g
r
èìåþò ïðîòèâîïîëîæíûå íàïðàâëåíèÿ, òî
ggg
rr
r
g
r
rrr
=−
′=−
−
−
+
=
*
(sin
);
si
ππ
φ
π
0
2
2
4
22
2
4
3
2
51
3
ãö
Ω
Ω
ns
i
n
.
φφ
ãö
ãö
−Ω
2
r
(1.47)
 áîëüøèíñòâå ïðèáëèæåííûõ ðàñ÷åòîâ íå äåëàþò ðàçíèöû ìåæ-
äó íàïðàâëåíèåì ðàäèóñ-âåêòîðà ê óñëîâíîìó öåíòðó Çåìëè è íà-
ïðàâëåíèåì îòâåñà â òî÷êå ñòàðòà.
40
Âûáåðåì â êà÷åñòâå íàïðàâëåíèÿ S íîðìàëü ê ïîâåðõíîñòè ñôå-
ðîèäà, íà êîòîðóþ âåêòîð óñêîðåíèÿ g ïðîåöèðóåòñÿ ïîëíîé âåëè-
÷èíîé. Îáîçíà÷àÿ íàïðàâëåíèå íîðìàëè ê ñôåðîèäó ÷åðåç n, áóäåì
èìåòü
gg
n
n
==
∂
∂
Ï
.
(1.48)
Ââèäó òîãî ÷òî ðàçíîñòü óãëîâ φãö è φã ìàëà, ïðîèçâîäíóþ ïî íà-
ïðàâëåíèþ n çàìåíÿþò ïðîèçâîäíîé ïî íàïðàâëåíèþ r:
∂
∂
∂
∂
ÏÏ
rn
=
()
.
^
nr
(1.49)
Ó÷èòûâàÿ ïðîòèâîïîëîæíîñòü íàïðàâëåíèé îòñ÷åòà äëÿ n è r è
ìàëîñòü óãëà ìåæäó n è r, ìîæíî çàïèñàòü
−≤
≤−
1
0 999995
cos(
)
^
,,
nr
ãäå ÷èñëî 0,999995 ñîîòâåòñòâóåò íàèáîëüøåé ðàçíîñòè óãëîâ φã −
−φãö = 11,5′. Ó÷èòûâàÿ ìàëîå îòëè÷èå cos( )
^
nr îò åäèíèöû, ïîëó÷èì
g = ∂Ï/∂n = −∂Ï/∂r. Äàëåå, çàìåíèâ â ïåðâîé ôîðìóëå (1.45) ôóíêöèè
πi èõ çíà÷åíèÿìè π0 = fM è π2 = f(A − B), ïðèäåì ê âûðàæåíèþ
g
fM
r
f
r
AB
r
=+
−
−
−
24
22
2
3
2
31
()
(
s
i
n)c
o
s
.
φφ
ãö
ãö
Ω
(1.50)
Äëÿ ñôåðè÷åñêîé ìîäåëè Çåìëè áåç ó÷åòà åå âðàùåíèÿ èç (1.50)
ïîëó÷èì g = fM/r
2
= gò.
 ôîðìóëó (1.50) ÷àñòî ââîäÿò âåëè÷èíû
μ=
−
==
AB
R
q
R
fMR
R
fM
ý
2
ý
ý
2
ý
è
ΩΩ
22
3
/
.
Âåëè÷èíà μ èìååò ðàçìåðíîñòü ìàññû, à q – áåçðàçìåðíûé ïàðà-
ìåòð Çåìëè, ðàâíûé îòíîøåíèþ óñêîðåíèÿ öåíòðîáåæíîé ñèëû ê
óñêîðåíèþ ñâîáîäíîãî ïàäåíèÿ â ïëîñêîñòè ýêâàòîðà. Ðàñ÷åòû ïî-
êàçûâàþò, ÷òî μ = 0,0011M; q = 0,003468. Ââîäÿ â (1.50) âåëè÷èíû μ
è q, ïîëó÷èì
g
fM
rM
R
r
q
r
R
=+
−
−
⎡
⎣⎢
⎤
⎦⎥
2
2
2
2
3
2
1
3
2
13
μ
φφ
'
(s
i
n)c
o
s
ý
ãö
ý
3
ãö
.
(1.51)
41
 ïðàêòèêå ïðåäâàðèòåëüíûõ ðàñ÷åòîâ äëÿ îïðåäåëåíèÿ óñêîðåíèÿ
ñâîáîäíîãî ïàäåíèÿ g0 íà ïîâåðõíîñòè Çåìëè íàõîäèò ïðèìåíåíèå
ôîðìóëà
gg
00
2
1
=+
ýã
ö
(s
i
n)
,
βφ
(1.52)
ãäå g0ý – óñêîðåíèå ñâîáîäíîãî ïàäåíèÿ íà ýêâàòîðå ïðè φãö =0.
Âåëè÷èíà β íàçûâàåòñÿ êîýôôèöèåíòîì Êëåðî. ×èñëåííî g0ý =
= 9,78034 ì/ñ2 è β = 0,005280 01 [124].  òåõ ñëó÷àÿõ, êîãäà ìîæíî
ïðèíÿòü g = const, îáû÷íî áåðóò g = 9,81 ì/ñ2. Äëÿ ñôåðè÷åñêîé ìî-
äåëè Çåìëè g ≈ g0(RÇ/r)2. Ïðè òî÷íûõ ðàñ÷åòàõ èñïîëüçóþò
g = 9,80665.
1.2.3. ÂËÈßÍÈÅ ÂÐÀÙÅÍÈß ÇÅÌËÈ ÍÀ ÏÎËÅÒ ÐÀÊÅÒ È ÑÍÀÐßÄÎÂ
Çåìëÿ ñîâåðøàåò â ïðîñòðàíñòâå ñëîæíîå äâèæåíèå – ãîäîâîå
îáðàùåíèå âîêðóã Ñîëíöà è ñóòî÷íîå âðàùåíèå îòíîñèòåëüíî ñâîåé
îñè; çåìíàÿ îñü â ñâîþ î÷åðåäü ñîâåðøàåò íóòàöèîííîå è ïðåöåññè-
îííîå äâèæåíèå. Îäíàêî ïðè èññëåäîâàíèè äâèæåíèÿ ðàêåò è ñíà-
ðÿäîâ ââèäó êðàòêîâðåìåííîñòè èõ ïîëåòà ñ÷èòàþò, ÷òî äâèæåíèå
Çåìëè ïî îðáèòå âîêðóã Ñîëíöà ìîæíî ïðèíÿòü çà ïðÿìîëèíåéíîå
ðàâíîìåðíîå ïîñòóïàòåëüíîå äâèæåíèå: íóòàöèîííûå êîëåáàíèÿ
Çåìëè è åå ïðåöåññèþ íå ó÷èòûâàþò, òàê êàê ýòè äâèæåíèÿ õàðàêòå-
ðèçóþòñÿ î÷åíü ìàëûìè óãëîâûìè ñêîðîñòÿìè (ïåðèîä ïðåöåññèîí-
íîãî äâèæåíèÿ – 26000 ëåò, ïåðèîä íóòàöèîííûõ êîëåáàíèé –
18,6 ãîäà ïðè àìïëèòóäå, íå ïðåâûøàþùåé 9,2′′). Ó÷èòûâàþò òîëüêî
ñóòî÷íîå âðàùåíèå Çåìëè, êîòîðîå ÿâëÿåòñÿ ïðàêòè÷åñêè ðàâíîìåð-
íûì; îäèí îáîðîò ñîâåðøàåòñÿ çà 23 ÷ 56 ìèí 4 ñ ñ óãëîâîé ñêîðî-
ñòüþ
Ω=
⋅+ ⋅+
=⋅
−
2
236056604
729210 1
5
π
()
,/
ñ
.
Âëèÿíèå ñóòî÷íîãî âðàùåíèÿ Çåìëè íà ïîëåò ðàêåò è ñíàðÿäîâ
ëåãêî ïðîñëåäèòü, åñëè ðàññìîòðåòü èõ äâèæåíèå â èíåðöèàëüíîé
ãåîöåíòðè÷åñêîé ñèñòåìå êîîðäèíàò.  ìîìåíò âûñòðåëà (ïóñêà) íà-
÷àëüíóþ ñêîðîñòü ðàêåòû â îòíîñèòåëüíîì äâèæåíèè îáîçíà÷èì V0,
à â àáñîëþòíîì äâèæåíèè îáîçíà÷èì Va0 = V0 + Vïåð0, ãäå Vïåð0 –ïå
-
ðåíîñíàÿ ñêîðîñòü ðàêåòû, îïðåäåëÿåìàÿ âðàùàòåëüíûì äâèæåíèåì
Çåìëè ñ óãëîâîé ñêîðîñòüþ Ω è çàâèñÿùàÿ îò ãåîãðàôè÷åñêîé øèðî-
òû ìåñòà ðàñïîëîæåíèÿ ñòàðòîâîé ïîçèöèè (çäåñü è äàëåå ýëåìåíòû
òðàåêòîðèè öåíòðà ìàññ â àáñîëþòíîì äâèæåíèè áóäåì îòìå÷àòü èí-
äåêñîì à).
42
Î÷åâèäíî, Vïåð0 = Ωr0cosφãö0, ãäå r0 – ðàññòîÿíèå ñòàðòîâîé ïîçè-
öèè îò óñëîâíîãî öåíòðà Çåìëè; φãö0 – ãåîöåíòðè÷åñêàÿ øèðîòà ðàñ-
ïîëîæåíèÿ ñòàðòîâîé ïîçèöèè.
Íà ïîëþñàõ Vïåð0 = 0; íà ýêâàòîðå Vïåð0 ≈ 1674 êì/÷ (465 ì/ñ).
Çåìëÿ âðàùàåòñÿ îòíîñèòåëüíî ïîëÿðíîé îñè ñ çàïàäà íà âîñòîê,
ïîýòîìó ïðè çàïóñêå â âîñòî÷íîì íàïðàâëåíèè Va0 > V0, θa0 < θ0,à
ïðè çàïóñêå â çàïàäíîì íàïðàâëåíèè (ïðîòèâ âðàùåíèÿ Çåìëè) Va0 <
< V0, θa0 > θ0 (ðèñ. 1.13).
Ïðè ñâîáîäíîì ïîëåòå òðàåêòîðèÿ àáñîëþòíîãî äâèæåíèÿ ðàêå-
òû êëàññà "ïîâåðõíîñòü – ïîâåðõíîñòü" â ïåðâîì ïðèáëèæåíèè, ò.å .
äëÿ ñôåðè÷åñêîé ìîäåëè Çåìëè ñ ðàâíîêîíöåíòðè÷åñêèì ðàñïðåäå-
ëåíèåì ìàññ, ÿâëÿåòñÿ ïëîñêîé êðèâîé è åå ïëîñêîñòü çàíèìàåò íå-
èçìåííîå ïîëîæåíèå â ïðîñòðàíñòâå. Â òî æå âðåìÿ â ðåçóëüòàòå
âðàùåíèÿ Çåìëè ïîëîæåíèå öåëè â èíåðöèàëüíîì ïðîñòðàíñòâå èç-
ìåíÿåòñÿ. Çà ïîëíîå âðåìÿ ïîëåòà ðàêåòû öåëü èçìåíèò ñâîå ïîëî-
æåíèå íà âåëè÷èíó
∆Ω
LR
t
öÇ
ïã
ö
=
cos ,
φ
(1.53)
ãäå ∆Lö – ïåðåìåùåíèå öåëè ïî äîëãîòå; tï – ïîëíîå âðåìÿ ïîëåòà;
φãö – ãåîöåíòðè÷åñêàÿ øèðîòà öåëè, êîòîðàÿ îñòàåòñÿ íåèçìåííîé â
ïðîöåññå âðàùåíèÿ Çåìëè.
Ìåñòî ñòàðòà è ìåñòî ïàäåíèÿ ðàêåòû (ñíàðÿäà) êëàññà "ïîâåðõ-
íîñòü – ïîâåðõíîñòü" íàõîäÿòñÿ íà Çåìëå; íàáëþäåíèå çà ïîëåòîì
ðàêåòû îñóùåñòâëÿåòñÿ ñ ïóíêòîâ, ðàñïîëîæåííûõ íà çåìíîé ïî-
43
Ðèñ. 1 .13. Çàâèñèìîñòü íà÷àëüíîé àáñîëþòíîé ñêîðîñòè äâèæåíèÿ ðàêåòû îò íà-
ïðàâëåíèÿ åå çàïóñêà
âåðõíîñòè. Ïîýòîìó ÷àñòî ðàñ÷åò òðàåêòîðèé äâèæåíèÿ ðàêåò è ñíà-
ðÿäîâ ïðîâîäÿò â ñèñòåìå êîîðäèíàò, ñâÿçàííîé ñ Çåìëåé, ò.å . â îò -
íîñèòåëüíîì äâèæåíèè. Óñòàíîâèì ñâÿçü íà÷àëüíûõ óñëîâèé áðîñà-
íèÿ â àáñîëþòíîì è â îòíîñèòåëüíîì äâèæåíèÿõ, èñïîëüçóÿ
ãåîöåíòðè÷åñêóþ èíåðöèàëüíóþ ñèñòåìó êîîðäèíàò O0XèYèZè è ãåî-
öåíòðè÷åñêóþ çåìíóþ ñèñòåìó êîîðäèíàò O0X0Y0Z0; îñè O0Yè è O0Y0
ñîâìåñòèì ñ âåêòîðîì Ω.
Äâèæåíèå ðàêåòû â ïåðâîé ñèñòåìå êîîðäèíàò áóäåò àáñîëþò-
íûì, âî âòîðîé – îòíîñèòåëüíûì . Äëÿ îïðåäåëåíèÿ ïîëîæåíèÿ ðà-
êåòû â èíåðöèàëüíîé ñèñòåìå êîîðäèíàò èñïîëüçóåì îáû÷íûå ñôå-
ðè÷åñêèå êîîðäèíàòû ra, φãöa, λa, à â ñâÿçàííîé ñ Çåìëåé – r, φãö, λ.
Ñâÿçü ìåæäó äîëãîòîé â àáñîëþòíîì è îòíîñèòåëüíîì äâèæåíèÿõ
çàäàåòñÿ ñîîòíîøåíèåì
λλ
a
t
=+
Ω.
(1.54)
Íà÷àëüíûìè óñëîâèÿìè äëÿ îïðåäåëåíèÿ òðàåêòîðèè îòíîñèòåëüíîãî
äâèæåíèÿ öåíòðà ìàññ ðàêåòû â ìîìåíò âðåìåíè t = t0 áóäóò âåëè÷èíû
r0, φãö0, λ0, íà÷àëüíàÿ ñêîðîñòü V0 è óãîë áðîñàíèÿ θ0 (ðèñ. 1.14). Çà
óãîë áðîñàíèÿ ïðèíèìàþò óãîë ìåæäó âåêòîðîì íà÷àëüíîé ñêîðîñòè
è åãî ïðîåêöèåé íà ïëîñêîñòü, êàñàòåëüíóþ ê ñôåðå â òî÷êå áðîñàíèÿ
Ð0. Äëÿ ñôåðè÷åñêîé ìîäåëè Çåìëè ïëîñêîñòüþ áðîñàíèÿ íàçûâàþò
ïëîñêîñòü, ïðîõîäÿùóþ ÷åðåç âåêòîð íà÷àëüíîé ñêîðîñòè è öåíòð
Çåìëè. Ëèíèÿ O0K ïåðåñå÷åíèÿ ïëîñêîñòè áðîñàíèÿ Á ñ ïëîñêîñòüþ
ýêâàòîðà íàçûâàåòñÿ ëèíèåé óçëîâ. Äîëãîòà ëèíèè óçëîâ îïðåäåëÿåòñÿ
â ïëîñêîñòè ýêâàòîðà óãëîì λ 0
*
ìåæäó îñüþ è ëèíèåé óçëîâ.
Íàêëîíåíèå ïëîñêîñòè áðîñàíèÿ ê ïëîñêîñòè ýêâàòîðà îïðåäåëÿåòñÿ
óãëîì χ. Çíà÷åíèÿ íàçâàííûõ óãëîâ â íà÷àëüíûé ìîìåíò âðåìåíè
îáîçíà÷èì ÷åðåç λ 0
*
è χ0. Èç ñåêòîðà P0O0P0ý è ïðÿìîóãîëüíîãî
ñôåðè÷åñêîãî òðåóãîëüíèêà P0KP0ý áóäåì èìåòü
cos
cos
sin ;
arcsin(
),
χφλ
λ
χ
φ
0
∗
00
0
0
0
==
−
ãö
0
ãö
Ac
t
g
t
g
(1.55)
ãäå óãîë À0 – àçèìóò ñòðåëüáû ïðè îòíîñèòåëüíîì äâèæåíèè,
îòñ÷èòûâàåìûé îò ìåðèäèàíà Ì, ïðîõîäÿùåãî ÷åðåç òî÷êó Ð0.
Íàéäåì íà÷àëüíûå óñëîâèÿ ïðè àáñîëþòíîì äâèæåíèè. Ïóñòü â
íà÷àëüíûé ìîìåíò âðåìåíè èíåðöèàëüíûå ãåîöåíòðè÷åñêèå êîîð-
äèíàòû ñîâïàäàþò ñ îñÿìè êîîðäèíàò, ñâÿçàííûìè ñ Çåìëåé, è òîãäà
òî÷êà Ð0 îêàæåòñÿ ñîâìåùåííîé ñ ïëîñêîñòüþ O0XèY è. Íà÷àëüíàÿ
ñêîðîñòü â àáñîëþòíîì äâèæåíèè
VVV
a00
0
=+
ïåð
,
(1.56)
44
ãäå ïåðåíîñíàÿ ñêîðîñòü òî÷êè
Ð0, ðàâíàÿ Vïåð0 = Ωr0cosφãö0,
êîëëèíåàðíà
êàñàòåëüíîé
ê
ïàðàëëåëè Ï â òî÷êå Ð0.
Ïîìåñòèì â òî÷êó Ð0 íà÷àëî
òîïîöåíòðè÷åñêîé çåìíîé ñèñ-
òåìû êîîðäèíàò, îñü OYò0 íà-
ïðàâèì ïî ðàäèóñó r0, îñü OXò0 –
íà ñåâåð, îñü OZò0 – ïî êàñàòåëü-
íîé ê ïàðàëëåëè â òî÷êå ïóñêà.
 òîïîöåíòðè÷åñêîé ñèñòåìå
êîîðäèíàò (ðèñ. 1.15) óêàæåì
àçèìóò ñòðåëüáû À0 è óãîë áðî-
ñàíèÿ θ0 â îòíîñèòåëüíîì äâè-
45
Ðèñ. 1 .14 . Ñõåìà îïðåäåëåíèÿ íà÷àëüíûõ óñëîâèé ñòðåëüáû â àáñîëþòíîì è îòíîñè-
òåëüíîì äâèæåíèÿõ
Ðèñ. 1 .15. Âçàèìîñâÿçü âåêòîðîâ íà-
÷àëüíûõ ñêîðîñòåé, àçèìóòîâ è óãëîâ
áðîñàíèÿ â àáñîëþòíîì è îòíîñèòåëü-
íîì äâèæåíèÿõ
æåíèè è ïîñòðîèì âåêòîðíóþ ñóììó ñêîðîñòåé (íà ðèñ. 1 .14 è 1.15
ìåðèäèàí è ïàðàëëåëü, ïðîõîäÿùèå ÷åðåç òî÷êó Ð0, îòìå÷åíû áóêâà-
ìè Ì0 èÏ0). Èç ðèñ. 1 .15 íàõîäèì
VV
VV
V
aa
aa
000 0
00
000
0
sin
sin ;
cos cos
cos
cos
;
c
θθ
θθ
α
=
=
AA
0
os sin
cos
cos
sin
.
θφ
θ
000 000 0
AA
ãö
+=
ΩrV
aaa
(1.57)
Èç ïåðâîãî ðàâåíñòâà íàõîäèì óãîë áðîñàíèÿ â àáñîëþòíîì äâè-
æåíèè
θθ
a
a
V
V
0
0
0
0
=
⎛
⎝⎜
⎞
⎠⎟
arcsin
sin
,
(1.58)
èç âòîðîãî – àçèìóò ñòðåëüáû
A arccos
A
a
aa
V
V
0
0
0
00
0
=
⎛
⎝⎜
⎞
⎠⎟
cos cos
cos
.
θ
θ
(1.59)
Èç òðåòüåãî ðàâåíñòâà, ïðîâîäÿ ïðåîáðàçîâàíèÿ, ïîëó÷èì ôîð-
ìóëó äëÿ ðàñ÷åòà ìîäóëÿ íà÷àëüíîé ñêîðîñòè
VVV
r
r
a00
2
00
00
0
2
0
2
0
2
=+
+
ΩΩ
cos
cos sin
cos
.
φθ
φ
ãö
ãö
A
(1.60)
Âîçâðàùàÿñü ê ðèñ. 1.14, èç ñôåðè÷åñêîãî ïðÿìîóãîëüíîãî òðå-
óãîëüíèêà KaP0P0ý íàõîäèì íàêëîíåíèå ïëîñêîñòè áðîñàíèÿ â àáñî-
ëþòíîì äâèæåíèè (Áà) ê ïëîñêîñòè ýêâàòîðà:
cos
cos
sin
χφ
a00
0
=
ãö
A
(1.61)
è äîëãîòó ëèíèè óçëîâ
λλ
χφ
aa
00
00
*
arcsin(
).
=−
ctg tg ãö
(1.62)
Ó÷èòûâàÿ â ñîîòâåòñòâèè ñ ôîðìóëîé (1.53) ïîïðàâêó íà âðàùå-
íèå Çåìëè ∆Lö, ïîëó÷èì ïîëîæåíèå ìåñòà öåëè â ìîìåíò ïóñêà ðà-
êåòû – òî÷êó Ö íà ïàðàëëåëè Ïö (ðèñ. 1.16). Äîëãîòà äåéñòâèòåëüíî-
ãî ïîëîæåíèÿ öåëè â èíåðöèàëüíîé ñèñòåìå êîîðäèíàò â ìîìåíò ïà-
äåíèÿ ãîëîâíîé ÷àñòè ðàêåòû ðàññ÷èòûâàåòñÿ ïî ôîðìóëå (1.54) è
ðàâíà λöà = λö + Ωtï.
Öåíòðàëüíûé óãîë 2ψ â ïëîñêîñòè òðàåêòîðèè àáñîëþòíîãî äâè-
æåíèÿ, ñîîòâåòñòâóþùèé ïîëíîé äàëüíîñòè ïîëåòà (óãëîâàÿ äàëü-
46
íîñòü), ìîæåò áûòü îïðåäåëåí â ïðîöåññå ðàñ÷åòà òðàåêòîðèè. Íà
ðèñ. 1.16 òðàåêòîðèþ ðàêåòû â àáñîëþòíîì äâèæåíèè èçîáðàæàåò
ïëîñêàÿ êðèâàÿ P0Ö′, â îòíîñèòåëüíîì äâèæåíèè – êðèâàÿ äâîÿêîé
êðèâèçíû P0Ö. Òàêèì îáðàçîì, ïðè ðàññìîòðåíèè òðàåêòîðèè â îò-
íîñèòåëüíîì äâèæåíèè äàëüíîñòü äî öåëè ïî çåìíîé ïîâåðõíîñòè
ðàâíà Ð0Ö.
Îïðåäåëèì óñêîðåíèå ðàêåòû â îòíîñèòåëüíîì äâèæåíèè.
Ïåðåíîñíîå óñêîðåíèå íàõîäèòñÿ (ðèñ. 1.17) ïî ôîðìóëå
ar
ïåð
ãö
=Ω
2
cos .
φ
(1.63)
Âåêòîð ïåðåíîñíîãî (öåíòðîñòðåìèòåëüíîãî) óñêîðåíèÿ íàïðàâëåí
îò öåíòðà ìàññ ðàêåòû ê îñè âðàùåíèÿ Çåìëè ïî êðàò÷àéøåìó ðàññòîÿ-
íèþ. Èìåÿ â âèäó, ÷òî â äàëüíåéøåì áóäåò ñîñòàâëåíî óðàâíåíèå îòíî-
ñèòåëüíîãî äâèæåíèÿ ðàêåòû â ãåîöåíòðè÷åñêèõ çåìíûõ êîîðäèíàòàõ,
íàïèøåì ïðîåêöèè ïåðåíîñíîãî óñêîðåíèÿ íà ýòè îñè êîîðäèíàò:
ax
aaz
xy
z
ïåð
ïåð
ïåð
00
2
00
0
2
0
=−
=
=−
ΩΩ
;; . (1.64)
Êîðèîëèñîâî óñêîðåíèå îïðåäåëÿåòñÿ ïî ôîðìóëå
aêîð
= 2VV
ΩΩ
sin(
).
^
(1.65)
47
Ðèñ. 1 .16 . Òðàåêòîðèÿ äâèæå-
íèÿ ðàêåòû îòíîñèòåëüíî âðà-
ùàþùåéñÿ Çåìëè (Λ0 – äîëãîòà
òî÷êè ïóñêà P0; λö – äîëãîòà
ïîëîæåíèÿ öåëè â ìîìåíò ïóñêà
â ñâÿçàííîé ñ Çåìëåé ãåîöåí-
òðè÷åñêîé ñèñòåìå êîîðäèíàò):
1 – â îòíîñèòåëüíîì äâèæå-
íèè; 2 – â àáñîëþòíîì äâèæå-
íèè
Âåêòîð êîðèîëèñîâà óñêîðåíèÿ ïåðïåíäèêóëÿðåí ïëîñêîñòè, îï-
ðåäåëÿåìîé âåêòîðàìè Ω è V. Íàïðàâëåíèå aêîð â ñîîòâåòñòâèè ñ ïðà-
âèëîì âåêòîðíîé àëãåáðû áåðåòñÿ òàêèì, ÷òîáû âåêòîðû aêîð, Ω è V
ñîñòàâèëè ïðàâóþ òðîéêó îðòîâ. Ïðè ýòîì íåîáõîäèìî, ÷òîáû íà-
áëþäàòåëü, ñìîòðÿùèé ñ êîíöà âåêòîðà àêîð, âèäåë ïîâîðîò Ω ê V,
ïðîèñõîäÿùèé ïî ìàëîé ÷àñòè îêðóæíîñòè ïðîòèâ ÷àñîâîé ñòðåëêè.
Òàê êàê V â ïðîöåññå äâèæåíèÿ ðàêåòû áóäåò èçìåíÿòü íàïðàâëåíèå,
òî è âåêòîð aêîð ìîæåò áûòü íàïðàâëåí ðàçëè÷íûì îáðàçîì. Åñëè
ïðèíÿòü, ÷òî íàïðàâëåíèÿ èçâåñòíûõ ñîñòàâëÿþùèõ V ñîîòâåòñòâó-
þò ïîëîæèòåëüíîìó íàïðàâëåíèþ êîîðäèíàòíûõ îñåé, òî ìîæíî óñ-
òàíîâèòü âåëè÷èíó è íàïðàâëåíèå ñîñòàâëÿþùèõ aêîð â òîé æå ãåî-
öåíòðè÷åñêîé çåìíîé ñèñòåìå êîîðäèíàò. Èñïîëüçóÿ (1.65) è ïðàâè-
ëî îïðåäåëåíèÿ íàïðàâëåíèÿ aêîð, ïîëó÷èì
aa
êîð
êîð
xz
zx
00
00
22
==
−
ΩΩ
VV
;.(1.66)
Òàê êàê Ω è Vy 0 êîëëèíåàðíû, òî aêîð y 0 =0.
Ïðè îïðåäåëåíèè íàïðàâëåíèÿ aêîð â ïðîñòðàíñòâå ìîæíî òàêæå
âîñïîëüçîâàòüñÿ ïðàâèëîì Æóêîâñêîãî, â ñîîòâåòñòâèè ñ êîòîðûì
íàïðàâëåíèå aêîð ìîæíî íàéòè, ïîâåðíóâ íà óãîë π/2 â ñòîðîíó ïåðå-
íîñíîãî âðàùåíèÿ ïðîåêöèþ âåêòîðà V íà ýêâàòîðèàëüíóþ ïëîñ-
êîñòü Vý. Íàïðèìåð, ïðè ñòðåëüáå âäîëü ìåðèäèàíà èç ñåâåðíîãî ïî-
ëóøàðèÿ â þæíîå âåêòîð aêîð áóäåò íàïðàâëåí íà âîñòîê êîëëèíåàð-
íî êàñàòåëüíîé ê ïàðàëëåëè äî òåõ ïîð, ïîêà ïðîåêöèÿ âåêòîðà V íà
ýêâàòîðèàëüíóþ ïëîñêîñòü áóäåò íàïðàâëåíà îò öåíòðà Çåìëè; êàê
48
Ðèñ. 1 .17. Ðàçëîæåíèå âåêòîðà îòíîñèòåëüíîé ñêîðîñòè, ïåðåíîñíîãî è êîðèîëèñîâà
óñêîðåíèé ïî îñÿì ïðÿìîóãîëüíîé ãåîöåíòðè÷åñêîé ñèñòåìû êîîðäèíàò
òîëüêî ïðîåêöèÿ V ïîëó÷èò íà-
ïðàâëåíèå ê öåíòðó Çåìëè, âåê-
òîð aêîð ïîâåðíåòñÿ íà çàïàä
(ðèñ. 1 .18). Î÷åâèäíî, ÷òî òðàåê-
òîðèÿ ðàêåòû â îòíîñèòåëüíîì
äâèæåíèè èç-çà äåéñòâèÿ ïåðå-
íîñíîé è êîðèîëèñîâîé ñèë
èíåðöèè (à òàêæå ââèäó åùå íå-
êîòîðûõ ôàêòîðîâ) áóäåò ÿâ-
ëÿòüñÿ êðèâîé äâîÿêîé êðèâèç-
íû, ò.å . ðàêåòà ïðè äâèæåíèè
áóäåò ñìåùàòüñÿ âáîê îòíîñè-
òåëüíî ïëîñêîñòè ñòðåëüáû.
Ïåðåíîñíîå (öåíòðîáåæíîå)
óñêîðåíèå ñêëàäûâàåòñÿ ñ óñêî-
ðåíèåì ñèëû çåìíîãî òÿãîòå-
íèÿ â îáùåå óñêîðåíèå ñâîáîä-
íîãî ïàäåíèÿ (ñì. ïîäðàçä. 1 .2 .2).
Êîðèîëèñîâî óñêîðåíèå îñòà-
åòñÿ åäèíñòâåííûì ôàêòîðîì, ó÷èòûâàþùèì âëèÿíèå âðàùåíèÿ
Çåìëè íà îòíîñèòåëüíîå äâèæåíèå ðàêåòû. Äëÿ ñôåðîèäàëüíîé ìî-
äåëè Çåìëè íàèáîëüøåå çíà÷åíèå êîðèîëèñîâà óñêîðåíèÿ ñîñòàâëÿ-
åò ïðèìåðíî 1,5 % óñêîðåíèÿ ñâîáîäíîãî ïàäåíèÿ íà êàæäóþ òûñÿ÷ó
ìåòðîâ ýêâàòîðèàëüíîé ïðîåêöèè Vý îòíîñèòåëüíîé ñêîðîñòè ËÀ.
Ïðîâåäåííûå ðàñ÷åòû ïîêàçûâàþò, ÷òî âëèÿíèå âðàùåíèÿ Çåìëè íà
ïîëåò ñíàðÿäîâ öåëåñîîáðàçíî ó÷èòûâàòü íà÷èíàÿ ñ äàëüíîñòè
ñòðåëüáû ïðèìåðíî 10000 ì.
1.3 . ÇÅÌÍÀß ÀÒÌÎÑÔÅÐÀ È ÅÅ ÑÂÎÉÑÒÂÀ
1.3.1. ÑÒÐÓÊÒÓÐÀ ÀÒÌÎÑÔÅÐÛ
Îñíîâíûå ôèçè÷åñêèå ïàðàìåòðû àòìîñôåðû – ïëîòíîñòü âîçäó-
õà, òåìïåðàòóðà, áàðîìåòðè÷åñêîå äàâëåíèå, âëàæíîñòü, ñêîðîñòü
çâóêà è âåòåð – ñóùåñòâåííûì îáðàçîì âëèÿþò íà õàðàêòåðèñòèêè
äâèæåíèÿ ðàêåò è ñíàðÿäîâ. Äëÿ èçó÷åíèÿ àòìîñôåðû ñîçäàíà øè-
ðîêàÿ ñåòü ìåòåîñòàíöèé, ðàññåÿííûõ ïî âñåìó çåìíîìó øàðó. Èñ-
ñëåäîâàíèÿ ïðîâîäÿòñÿ ñ ïîìîùüþ ìåòåîðîëîãè÷åñêîé àïïàðàòóðû,
óñòàíàâëèâàåìîé íà øàðàõ-çîíäàõ, ðàäèîçîíäàõ, ñïåöèàëüíî îáîðó-
äîâàííûõ ñàìîëåòàõ, ìåòåîðîëîãè÷åñêèõ ðàêåòàõ è ñïóòíèêàõ Çåì-
ëè; ðåçóëüòàòû èçìåðåíèé ïîäâåðãàþòñÿ ñòàòèñòè÷åñêîé îáðàáîòêå
è îáîáùàþòñÿ.
Àòìîñôåðó Çåìëè ïî õèìè÷åñêîìó ñîñòàâó ïðèíÿòî íàçûâàòü
àçîòíî-êèñëîðîäíîé, îíà ñîäåðæèò ≈76 % àçîòà, ≈21 % êèñëîðîäà,
49
Ðèñ. 1.18 . Íàïðàâëåíèå êîðèîëèñîâûõ
óñêîðåíèé è ñèë ïðè äâèæåíèè ËÀ âäîëü
ìåðèäèàíà
≈3 % âîäÿíîãî ïàðà, âîäîðîäà, óãëåêèñëîãî ãàçà è ðÿäà äðóãèõ ãàçîâ.
Èçâåñòíî íåñêîëüêî ïðèíöèïîâ ïîñòðîåíèÿ ñõåì êëàññèôèêàöèè
àòìîñôåðû ïî ñëîÿì. Ïî ñîñòàâó âîçäóõà àòìîñôåðó ïîäðàçäåëÿþò
íà ãîìîñôåðó è ãåòåðîñôåðó. Â ãîìîñôåðå, ïðîñòèðàþùåéñÿ äî âû-
ñîò ≈95000 ì, ñîñòàâ âîçäóõà ñ âûñîòîé ïî÷òè íå èçìåíÿåòñÿ.
Ïîñêîëüêó òåìïåðàòóðà âîçäóõà ÿâëÿåòñÿ îñíîâíûì ïàðàìåòðîì,
îïðåäåëÿþùèì õàðàêòåðèñòèêè ñîñòîÿíèÿ àòìîñôåðû, íàèáîëüøèé
èíòåðåñ äëÿ áàëëèñòèêè ïðåäñòàâëÿåò ñõåìà ïîñòðîåíèÿ àòìîñôåðû
ïî õàðàêòåðó ðàñïðåäåëåíèÿ òåìïåðàòóðû ñ âûñîòîé. Â ýòîé ñõåìå
àòìîñôåðó Çåìëè ïîäðàçäåëÿþò íà ïÿòü îñíîâíûõ ñëîåâ, íàçâàííûõ
ñôåðàìè.
Íèæíèé ñëîé – òðîïîñôåðà, ïðîñòèðàþùàÿñÿ â ñðåäíèõ øèðîòàõ
äî âûñîò ≈11000 ì, à â ýêâàòîðèàëüíûõ îáëàñòÿõ – äî âûñîò
≈16000 ì. Âûñîòà òðîïîñôåðû çàâèñèò îò âðåìåíè ãîäà: óâåëè÷èâà-
åòñÿ ëåòîì è óìåíüøàåòñÿ çèìîé. Â òðîïîñôåðå ñîäåðæèòñÿ ≈75 %
âñåé ìàññû àòìîñôåðû è îñíîâíàÿ ÷àñòü âîäÿíîãî ïàðà.  òðîïîñôå-
ðå ôîðìèðóþòñÿ âñå ÿâëåíèÿ ïîãîäû. Îòëè÷èòåëüíàÿ ÷åðòà òðîïî-
ñôåðû – ïîíèæåíèå òåìïåðàòóðû âîçäóõà ñ óâåëè÷åíèåì âûñîòû.
Îäíàêî çèìîé è ëåòîì ïîñëå ÿñíûõ õîëîäíûõ íî÷åé ìîãóò íàáëþ-
äàòüñÿ òåìïåðàòóðíûå èíâåðñèè, ïðè êîòîðûõ òåìïåðàòóðà ñ óâåëè-
÷åíèåì âûñîòû ñíà÷àëà âîçðàñòàåò, à çàòåì íà÷èíàåò óáûâàòü.  òðî-
ïîñôåðå èìåþò ìåñòî çíà÷èòåëüíûå ãîðèçîíòàëüíûå è âåðòèêàëü-
íûå òå÷åíèÿ âîçäóøíûõ ìàññ – âåòðû. Âàæíûì îáñòîÿòåëüñòâîì,
îïðåäåëÿþùèì óñëîâèÿ áîåâîãî ïðèìåíåíèÿ àðòèëëåðèè è íåäàëü-
íîáîéíûõ ðàêåò, ÿâëÿåòñÿ íàëè÷èå â òðîïîñôåðå ïîñòîðîííèõ (íå
ãàçîîáðàçíûõ) âêëþ÷åíèé: îñàäêîâ âñåõ òèïîâ, ïûëåâèäíûõ îáðàçî-
âàíèé è ò.ä .
Ñëåäóþùèé ñëîé – ñòðàòîñôåðà, ïðîñòèðàþùàÿñÿ â ñðåäíèõ
øèðîòàõ îò ≈11000 äî ≈50000 ì. Ñòðàòîñôåðà äî âûñîò ≈30000 ì
õàðàêòåðèçóåòñÿ ïîñòîÿíñòâîì òåìïåðàòóðû; íà áîëüøåé âûñîòå
ïî ìåðå ïðèáëèæåíèÿ ê âåðõíåé ãðàíèöå ñòðàòîñôåðû òåìïåðàòó-
ðà âîçðàñòàåò, ïðè÷åì èìåþò ìåñòî çíà÷èòåëüíûå ñóòî÷íûå è
ìåæñóòî÷íûå êîëåáàíèÿ. Èçìåíåíèå òåìïåðàòóðíîãî ãðàäèåíòà
ìåæäó òðîïîñôåðîé è ñòðàòîñôåðîé ïðîèñõîäèò â îòíîñèòåëüíî
óçêîì ñëîå, íàçûâàåìîì òðîïîïàóçîé. Òîëùèíà ñëîÿ òðîïîïàóçû
êîëåáëåòñÿ îò íåñêîëüêèõ ñîòåí ìåòðîâ äî ≈2000 ì. Â ýòîì ñëîå
íàáëþäàþòñÿ ìîùíûå ïåðåìåùåíèÿ âîçäóøíûõ ìàññ (òàê íàçû-
âàåìûå ñòðóéíûå òå÷åíèÿ) ñ çàïàäà íà âîñòîê ñî ñêîðîñòÿìè, äî-
õîäÿùèìè äî ≈110 ì/ñ (400 êì/÷).
Îáëàñòü ñòðóéíûõ òå÷åíèé â àòìîñôåðå õàðàêòåðèçóåòñÿ áîëüøè-
ìè ñêîðîñòíûìè ãðàäèåíòàìè â âåðòèêàëüíîì è ãîðèçîíòàëüíîì íà-
ïðàâëåíèÿõ.
50
Íàä ñòðàòîñôåðîé ðàñïîëîæåíà ìåçîñôåðà, êîòîðàÿ ïðîñòèðàåòñÿ
îò âûñîòû ≈50000 äî ≈90000 ì. Îíà õàðàêòåðèçóåòñÿ ïîíèæåíèåì
òåìïåðàòóðû äî âåðõíåé ãðàíèöû ñëîÿ è ïîâûøåííîé òóðáóëåíòíî-
ñòüþ.
Òåðìîñôåðà – ýòî ñëîé àòìîñôåðû îò ≈90000 äî ≈500000 ì, õàðàê-
òåðèçóþùèéñÿ íåïðåðûâíûì ïîâûøåíèåì êèíåòè÷åñêîé òåìïåðàòó-
ðû.  âåðõíåé ÷àñòè òåðìîñôåðû íà âûñîòàõ 400000...500000 ì êèíå-
òè÷åñêàÿ òåìïåðàòóðà âîçäóõà äîñòèãàåò ≈1500 Ê.
Ñëîé, ðàñïîëîæåííûé îò âûñîò 500000 ì äî âíåøíåé ãðàíèöû
àòìîñôåð, ò.å . ïðèìåðíî äî 2 000000...3 000000 ì, íàçûâàåòñÿ ýêçî-
ñôåðîé.  ýêçîñôåðå âîçäóõ î÷åíü ðàçðåæåí. Ïåðåõîäíûå ñëîè ìåæ-
äó íàçâàííûìè ñôåðàìè íîñÿò ñîîòâåòñòâåííî íàçâàíèÿ ñòðàòîïàó-
çû, ìåçîïàóçû è òåðìîïàóçû.
1.3.2. ÑÒÀÍÄÀÐÒÍÛÅ ÀÒÌÎÑÔÅÐÛ
Èññëåäîâàíèÿ ïîêàçàëè, ÷òî ôèçè÷åñêèå ïàðàìåòðû àòìîñôåðû
çíà÷èòåëüíî èçìåíÿþòñÿ â çàâèñèìîñòè îò êëèìàòè÷åñêèõ óñëîâèé,
âðåìåíè ãîäà è âûñîòû. Íàïðèìåð, â ñëîå àòìîñôåðû ñ âûñîòîé äî
5000 ì ñîäåðæèòñÿ îêîëî 50 % âñåé ìàññû âîçäóõà, à ñ âûñîòîé äî
20000 ì – ïðèìåðíî 95 %. Áàëëèñòè÷åñêèå ðàñ÷åòû ïðîâîäÿòñÿ äëÿ
íîðìàëüíûõ ìåòåîóñëîâèé, ñîîòâåòñòâóþùèõ ñðåäíèì ñòàòèñòè÷å-
ñêèì îïûòíûì äàííûì èëè ñòàíäàðòíûì àòìîñôåðàì. Îòêëîíåíèå
ìåòåîóñëîâèé îò èõ íîðìàëüíûõ çíà÷åíèé ó÷èòûâàåòñÿ îòäåëüíî â
òåîðèè ïîïðàâîê.
Äî 1920 ã. â íàøåé ñòðàíå ïîëüçîâàëèñü óñëîâíîé àòìîñôåðîé,
ïîëó÷åííîé ïóòåì îáðàáîòêè ïðèçåìíûõ ìåòåîðîëîãè÷åñêèõ óñëî-
âèé â ðàéîíå Ìîñêâû. Â 1920 ã. áûëà ïðèíÿòà ìåæäóíàðîäíàÿ ñòàí-
äàðòíàÿ àòìîñôåðà (ÌÑÀ). Äëÿ àðòèëëåðèéñêîé ïðàêòèêè â 1927 ã.
ââåëè íîðìàëüíóþ àðòèëëåðèéñêóþ àòìîñôåðó (ÍÀÀ). Â 1949 ã.
áûëè îïóáëèêîâàíû ïîäðîáíûå òàáëèöû ñòàíäàðòíîé àòìîñôåðû
(ÃÎÑÒ 4401-48). Ñ ðàçâèòèåì àâèàöèè è ðàêåòíîé òåõíèêè âîçíèêëà
íåîáõîäèìîñòü è ïîÿâèëèñü òåõíè÷åñêèå âîçìîæíîñòè èññëåäîâà-
íèÿ âåðõíèõ ñëîåâ àòìîñôåðû. Ê êîíöó 1950-õ ãã . áûë íàêîïëåí
áîëüøîé ýêñïåðèìåíòàëüíûé ìàòåðèàë, êîòîðûé ïîçâîëèë êîîðäè-
íàöèîííîìó êîìèòåòó ÀÍ ÑÑÑÐ âûñòóïèòü ñ ïðîåêòîì íîâîé ñòàí-
äàðòíîé àòìîñôåðû. Ñíà÷àëà áûëà ïðèíÿòà âðåìåííàÿ ñòàíäàðòíàÿ
àòìîñôåðà, à ïîçæå
–
ñòàíäàðòíàÿ àòìîñôåðà ÑÀ-81 (ÃÎÑÒ
4401-81). Ïîñëåäíÿÿ ïîëó÷èëà ðàñïðîñòðàíåíèå ïðè ðåøåíèè øè-
ðîêîãî êðóãà çàäà÷ äèíàìèêè ïîëåòà. Òåì íå ìåíåå äî íàñòîÿùåãî
âðåìåíè, ñîãëàñíî ÃÎÑÒ 24288-80, ðàñ÷åòû òàáëèö ñòðåëüáû è ïîä-
ãîòîâêè èñõîäíûõ äàííûõ íà ïóñê ðàêåò Ñóõîïóòíûõ âîéñê îñóùåñò-
51
âëÿþòñÿ èñêëþ÷èòåëüíî ïî ÍÀÀ ñ ââåäåíèåì â íåå íåçíà÷èòåëüíûõ
êîððåêöèé äëÿ âûñîò ñâûøå 27000 ì.
 îòëè÷èå îò ÍÀÀ â ÑÀ-81 âûñîòà íàä ïîâåðõíîñòüþ çàäàåòñÿ ÷å-
ðåç òàê íàçûâàåìóþ ãåîïîòåíöèàëüíóþ âûñîòó.
 ìåòåîðîëîãèè ãåîïîòåíöèàëüíóþ âûñîòó âûðàæàþò ÷åðåç "ãåî-
ïîòåíöèàëüíûå" ìåòðû. Äëÿ óäîáñòâà èçó÷åíèÿ ðàñïðåäåëåíèÿ äàâ-
ëåíèÿ â àòìîñôåðå â ðàñ÷åòíûå ôîðìóëû ââîäÿò ãåîïîòåíöèàë, õà-
ðàêòåðèçóþùèé ïîòåíöèàëüíóþ ýíåðãèþ ÷àñòèöû, ðàñïîëîæåííîé
â äàííîé òî÷êå Φ(x, y, z). Ïîâåðõíîñòü, ñîîòâåòñòâóþùàÿ óðàâíåíèþ
Φ(x, y, z) = const, íàçûâàåòñÿ èçîïîòåíöèàëüíîé èëè ãåîïîòåíöèàëü-
íîé. Äëÿ ïåðåíîñà åäèíèöû ìàññû ñ ïîâåðõíîñòè, èìåþùåé ïîòåí-
öèàë Φ1, íà áëèçêóþ ïîâåðõíîñòü, èìåþùóþ ïîòåíöèàë Φ2, íåîáõî-
äèìî ïðîäåëàòü åäèíè÷íóþ ðàáîòó dΦ = g(h)dh, èìåÿ â âèäó, ÷òî Φ2 =
=Φ2 + dΦ. Èíòåãðèðóÿ, ïîëó÷èì Φ = ghdh
h
().
0
∫ Ðàçäåëèâ Φ íà ñòàí-
äàðòíîå (ò.å . ñîîòâåòñòâóþùåå íóëåâîé âûñîòå) óñêîðåíèå ñâîáîäíî-
ãî ïàäåíèÿ gc, ïîëó÷èì ãåîïîòåíöèàëüíóþ âûñîòó, èìåþùóþ ðàç-
ìåðíîñòü äëèíû:
H
gg
ghdh
h
==
∫
Φ
cc
1
0
().
(1.67)
×òîáû óñòàíîâèòü çàâèñèìîñòü ìåæäó ãåîïîòåíöèàëüíîé è ãåî-
ìåòðè÷åñêîé âûñîòàìè, íåîáõîäèìî íàéòè çàâèñèìîñòü g(h). Â
ÑÀ-81 çíà÷åíèå g(h) âû÷èñëÿëîñü áåç ó÷åòà öåíòðîáåæíîãî óñêîðå-
íèÿ ïî ôîðìóëå äëÿ ñôåðè÷åñêîé ìîäåëè Çåìëè g = g
R
Rh
c
Ç.ñ
Ç.ñ
+
⎛
⎝⎜
⎞
⎠⎟
2
, ãäå
gñ = 9,81 ì/ñ2, òîãäà êàê â ÍÀÀ íîðìàëüíîå óñêîðåíèå ñâîáîäíîãî
ïàäåíèÿ g0 = 9,80665 ì/ñ2.
Ïîñëå èíòåãðèðîâàíèÿ (1.67) ïîëó÷åíû çàâèñèìîñòè
H
Rh
Rh
h
RH
RH
=
+
=
−
Ç.ñ
Ç.ñ
Ç.ñ
Ç.ñ
è. (1.68)
Ïðè âû÷èñëåíèè ïàðàìåòðîâ, ïîìåùåííûõ â òàáëèöàõ ÑÀ, ïðèíÿòà
âåëè÷èíà RÇ.ñ = 6 356766 ì.
Ôîðìóëû, îïðåäåëÿþùèå èçìåíåíèå äàâëåíèÿ ñ èçìåíåíèåì âû-
ñîòû, îñíîâàíû íà ãèïîòåçå î âåðòèêàëüíîì ñòàòèñòè÷åñêîì ðàâíî-
52
âåñèè àòìîñôåðû. Ïî ýòîé ãèïîòåçå âåñ ãîðèçîíòàëüíîãî ñëîÿ âîçäó-
õà ýëåìåíòàðíîé òîëùèíû dh è åäèíè÷íîé ïëîùàäè óðàâíîâåøèâà-
åòñÿ ýëåìåíòàðíîé ðàçíîñòüþ dp äàâëåíèé, äåéñòâóþùèõ íà âåðõíåå
è íèæíåå îñíîâàíèÿ ñëîÿ:
dp gdh
=−ρ
.
(1.69)
Óðàâíåíèå ñîñòîÿíèÿ äëÿ èäåàëüíîãî ãàçà:
p
RT
M
=
ρ
,
(1.70)
ãäå R – óíèâåðñàëüíàÿ ãàçîâàÿ ïîñòîÿííàÿ; Ì – ìîëÿðíàÿ ìàññà
âîçäóõà. Äëÿ âûñîò äî 94 êì çíà÷åíèå ìîëÿðíîé ìàññû îñòàåòñÿ
ïîñòîÿííûì è R/M = R
*
,ãäåR
*
–
óäåëüíàÿ ãàçîâàÿ ïîñòîÿííàÿ. Òîãäà
pR
T
=ρ
*
.
(1.71)
 çàâèñèìîñòè îò õàðàêòåðà èçìåíåíèÿ òåìïåðàòóðû àòìîñôåðà
ÑÀ-81 ïî âûñîòå ðàçáèòà íà ðÿä ñëîåâ; òåìïåðàòóðà â êàæäîì ñëîå
àïïðîêñèìèðóåòñÿ ëèíåéíîé ôóíêöèåé ãåîïîòåíöèàëüíîé âûñîòû
TT HH
=+
−
**
()
,
β
(1.72)
ãäå β = dT/dH – ãðàäèåíò òåìïåðàòóðû ïî ãåîïîòåíöèàëüíîé âûñîòå;
T* è H* – òåìïåðàòóðà è ãåîïîòåíöèàëüíàÿ âûñîòà íèæíåé ãðàíèöû
ñîîòâåòñòâóþùåãî ñëîÿ. Èñïîëüçóÿ óðàâíåíèÿ (1.69)...(1.71) è
èíòåãðèðóÿ (1.69), ìîæíî ïîëó÷èòü äëÿ èçîòåðìè÷åñêèõ ñëîåâ (β =0)
ln
(
),
*
*
p
p
g
RT
HH
⎛
⎝⎜⎞
⎠⎟ =−
−
c
(1.73)
èëè
pp
g
RT
HH
=−−
⎡
⎣⎢
⎤
⎦⎥
**
exp
(
).
c
(1.74)
Äëÿ ñëîåâ ñ ëèíåéíî èçìåíÿþùåéñÿ òåìïåðàòóðîé (β≠0)
ln
ln
()
,
*
**
*
p
p
TH
H
T
g
R
⎛
⎝⎜⎞
⎠⎟=
−−
⎛
⎝⎜
⎞
⎠⎟
−
β
β
c
53
èëè
pp
T
HH
g
R
=+−
⎡
⎣⎢
⎤
⎦⎥
−
*
*
*
()
.
1
β
β
c
(1.75)
Ïëîòíîñòü îïðåäåëÿåòñÿ èç óðàâíåíèÿ ñîñòîÿíèÿ
ρ= pRT
/( ).
*
(1.76)
Óäåëüíûé âåñ
γρ
=
g.
(1.77)
Ñêîðîñòü çâóêà
a
kRT
M
T
==
0
20 046796
,,
(1.78)
ãäå k
0
= cp/cv = 1,4 – ïîêàçàòåëü àäèàáàòû.
Ïî ïðèâåäåííûì ôîðìóëàì âû÷èñëåíû òàáëèöû, ñîäåðæàùèå
îñíîâíûå õàðàêòåðèñòèêè àòìîñôåðû: òåìïåðàòóðó (T, Kèt, °Ñ),
äàâëåíèå ð (Ïà è ìì ðò.ñò .), ïëîòíîñòü âîçäóõà, óñêîðåíèå ñâîáîäíî-
ãî ïàäåíèÿ, ñêîðîñòü çâóêà. Ïðèâåäåíû òàêæå îòíîñèòåëüíûå âåëè-
÷èíû p/pc, ρ/ρc è äð. Èíäåêñîì "ñ" îòìå÷åíû çíà÷åíèÿ ïàðàìåòðîâ
äëÿ ñðåäíåãî óðîâíÿ ìîðÿ (íóëåâîé âûñîòû). Çíà÷åíèÿ òåìïåðàòóð-
íûõ ãðàäèåíòîâ äëÿ ñòàíäàðòèçîâàííîé ÷àñòè àòìîñôåðû ÑÀ-81
ïðèâåäåíû â òàáë. 1 .7.
Çàâèñèìîñòü òåìïåðàòóðû îò ãåîìåòðè÷åñêîé âûñîòû ïðèâåäåíà
íà ðèñ. 1 .19.
Äëÿ ó÷åòà âëàæíîñòè âîçäóõà âìåñòî èñòèííîé Ò ââîäèòñÿ óñëîâ-
íàÿ òåìïåðàòóðà τ. Ïîëó÷èì óïðîùåííûå çàâèñèìîñòè äëÿ ðàñ÷åòà
óäåëüíîãî âåñà è äàâëåíèÿ âîçäóõà. Äëÿ óäåëüíîãî âåñà Ï = ρg ñóõîãî
âîçäóõà èç (1.1) ïîëó÷àåì
Ï=pRT
/.
(1.79)
Âìåñòî áàðîìåòðè÷åñêîãî äàâëåíèÿ ð, èçìåðÿåìîãî â Ïà, ââåäåì
äàâëåíèå, èçìåðÿåìîå â ìì ðò.ñò . è îáîçíà÷àåìîå h. Òàê êàê p =
=
10 333
760
h = 13,6h, òî ñîîòâåòñòâåííî
54
Òàáëèöà 1.7
Çíà÷åíèÿ òåìïåðàòóðíûõ êîýôôèöèåíòîâ
H*,êì
T*,Ê
β, Ê/êì
−2
301,15
−6,5
0
288,15
−6,5
11
216,65
0,0
20
216,65
1,0
32
288,65
2,8
47
270,65
0,0
51
270,65
–
Ï=136,.
*
h
RT
(1.80)
Äàâëåíèå âëàæíîãî âîçäóõà h ìîæåò áûòü îïðåäåëåíî êàê ñóììà
ïàðöèàëüíûõ äàâëåíèé ñóõîãî âîçäóõà hñ.â è âîäÿíîãî ïàðà å:
hhe
=+
ñ.â
.
(1.81)
Óäåëüíûé âåñ âëàæíîãî âîç-
äóõà â åäèíèöå îáúåìà (ì3) íàõî-
äèòñÿ ïî àíàëîãè÷íîé çàâèñèìî-
ñòè
ÏÏÏ
ñ.â
=+
å.
(1.82)
Ñ÷èòàÿ ñ äîñòàòî÷íîé äëÿ
ïðàêòèêè òî÷íîñòüþ, ÷òî ïðè
îäèíàêîâûõ
äàâëåíèè
è
òåìïåðàòóðå ïëîòíîñòü âîäÿíîãî
ïàðà ðàâíà
ïðèìåðíî 5/8
ïëîòíîñòè
ñóõîãî
âîçäóõà,
ïîëó÷èì
Ïå
e
RT
=⋅
5
8
13 6,
(1.83)
55
Ðèñ. 1.19. Çàâèñèìîñòü òåìïåðàòóðû îò
ãåîìåòðè÷åñêîé âûñîòû äëÿ ñòàíäàðò-
íîé àòìîñôåðû ÑÀ-81
è îêîí÷àòåëüíî
Ï=−
⎛
⎝⎜⎞
⎠⎟
136
1
3
8
,.
h
RT
e
h
(1.84)
Äëÿ ó÷åòà âëàæíîñòè âîçäóõà â áàëëèñòè÷åñêèå ðàñ÷åòû ââîäÿò
"âèðòóàëüíóþ" òåìïåðàòóðó
τ=
−
Ò
å
h
()
1
3
8
(1.85)
è â ïîñëåäóþùåì âìåñòî ðåàëüíîãî âëàæíîãî âîçäóõà, õàðàê-
òåðèçóþùåãîñÿ ïàðàìåòðàìè h,Ï
,Ò è å, ðàññìàòðèâàþò óñëîâíûé
ñóõîé âîçäóõ ñ õàðàêòåðèñòèêàìè h,Ïèτ. Ýòîò óñëîâíûé âîçäóõ
îêàçûâàåò ïî÷òè òàêîå æå ñîïðîòèâëåíèå äâèæóùåìóñÿ â íåì
ñíàðÿäó, êàê è ðåàëüíûé âîçäóõ. Ñòðîãî ãîâîðÿ, ïîäîáíàÿ çàìåíà ñ
òåîðåòè÷åñêîé òî÷êè çðåíèÿ íå âïîëíå êîððåêòíà, ïîñêîëüêó íå
îòðàæàåò àäåêâàòíî èñòèííîãî èçìåíåíèÿ ñêîðîñòè çâóêà. Ñëåäóåò
ó÷èòûâàòü, îäíàêî, ÷òî âëèÿíèå âèðòóàëüíîé äîáàâêè íà ñêîðîñòü
çâóêà ñòàíîâèòñÿ çàìåòíûì òîëüêî ïðè âûñîêîé âëàæíîñòè è
òåìïåðàòóðå âîçäóõà íå íèæå 35...40° Ñ. Ñ ó÷åòîì τ ôîðìóëû äëÿ
óäåëüíîãî âåñà è ïëîòíîñòè èìåþò âèä
Ï=136,/()
;
*
hRτ
(1.86)
ρτ
= 136,/( )
.
*
hgR
(1.87)
Çíà÷åíèÿ äàâëåíèÿ è ïëîòíîñòè ðàññ÷èòûâàþòñÿ ïî ôîðìóëå h =
=he
ON
R
dy
y
−
∫1
0
è ñëåäóþùåìó èç ôîðìóëû (1.79) âûðàæåíèþ
Ï=
∫−
136
1
0
,.
h
R
e
ON
R
dy
y
τ
τ
(1.88)
Åñëè îòíåñòè ýòîò óäåëüíûé âåñ ê íîðìàëüíîìó óäåëüíîìó âåñó
âîçäóõà ó ïîâåðõíîñòè Çåìëè, òî ìîæíî ïîëó÷èòü áåçðàçìåðíóþ
ôóíêöèþ èçìåíåíèÿ óäåëüíîãî âåñà ñ âûñîòîé. Ïóñòü ó ïîâåðõíîñòè
Çåìëè
ÏON
ON
ON
h
R
= 136,,
τ
(1.89)
56
òîãäà
Ï
ÏON
ON
R
dy
e
y
=
∫−
τ
τ
τ
1
0
.
(1.90)
Ñîîòâåòñòâåííî ìîæíî íàïèñàòü è äëÿ äàâëåíèÿ
h
h
e
ON
R
dy
y
=
∫−
1
0
τ
.
(1.91)
Äëÿ ëèíåéíîé çàâèñèìîñòè τ = f(y) ïîëó÷èì
h
h
y
Hyy
ON
ON
RG
ON
ON
==
⎛
⎝⎜⎞
⎠⎟
==
π
τ
τ
π
τ
τ
()
,
()().
1
1
Ï
Ï
(1.92)
Äëÿ ñëîæíûõ òåìïåðàòóðíûõ çàâèñèìîñòåé τ = f(y) èíòåãðàë â
ïðàâîé ÷àñòè ôîðìóëû (1.88) áåðåòñÿ îäíèì èç ÷èñëåííûõ ìåòîäîâ.
Ïðè ðåøåíèè ðÿäà ïðàêòè÷åñêèõ çàäà÷, íàïðèìåð ïðè áàëëèñòè-
÷åñêîì ïðîåêòèðîâàíèè, äëÿ âû÷èñëåíèÿ áåçðàçìåðíîé ôóíêöèè
èçìåíåíèÿ ïëîòíîñòè ñ âûñîòîé óäîáíî ïîëüçîâàòüñÿ ýìïèðè÷åñêè-
ìè ôîðìóëàìè.
Èçâåñòíû ôîðìóëû:
Â.Ï. Âåò÷èíêèíà
Hy
y
y
()
;
=
−
+
20000
20000
(1.93)
ëèíåéíàÿ
Hy
ky
()
;
=−
1
(1.94)
ãèïåðáîëè÷åñêàÿ
Hy
ky
()
;
=
+
1
1
(1.95)
ïîêàçàòåëüíàÿ
Hye
ky
().
=
−
(1.96)
57
Âî âñåõ ôîðìóëàõ y èìååò ðàçìåðíîñòü "ìåòðû"; â ïîñëåäíèõ òðåõ
ôîðìóëàõ êîýôôèöèåíò k = 0,0001.
1.4 . ÀÝÐÎÄÈÍÀÌÈ×ÅÑÊÈÅ ÑÈËÛ È ÈÕ ÌÎÌÅÍÒÛ
1.4.1. ÂÅÊÒÎÐ ÀÝÐÎÄÈÍÀÌÈ×ÅÑÊÎÃÎ ÑÎÏÐÎÒÈÂËÅÍÈß
È ÎÁÓÑËÎÂËÅÍÍÛÉ ÈÌ ÌÎÌÅÍÒ
Ïðè ïîëåòå ðàêåòû èëè ñíàðÿäà â àòìîñôåðå íà íèõ äåéñòâóåò ñî-
ïðîòèâëåíèå âîçäóõà, íàçûâàåìîå àýðîäèíàìè÷åñêèì.
Àýðîäèíàìè÷åñêàÿ ñèëà RA ñêëàäûâàåòñÿ èç ñèë äàâëåíèÿ âîçäó-
õà, íàïðàâëåííûõ ïî íîðìàëÿì ê ïîâåðõíîñòè ËÀ, è ñèë òðåíèÿ âîç-
äóõà, êàñàòåëüíûõ ê íåé. Ðàâíîäåéñòâóþùàÿ ñèëà RA ïðèëîæåíà ê
ËÀ â òî÷êå, êîòîðóþ íàçûâàþò öåíòðîì äàâëåíèÿ (ðèñ. 1.20). Îáû÷-
íî öåíòð äàâëåíèÿ íå ñîâïàäàåò ñ öåíòðîì ìàññ ËÀ è ñèëà RA îòíî-
ñèòåëüíî íåãî ñîçäàåò ìîìåíò M. Ñèëó RA, ïðèëîæåííóþ â öåíòðå
ìàññ ðàêåòû, íàçûâàþò ïîëíîé àýðîäèíàìè÷åñêîé ñèëîé, à ìîìåíò
M – ïîëíûì àýðîäèíàìè÷åñêèì ìîìåíòîì.  îñíîâíîì äåéñòâèå
àýðîäèíàìè÷åñêîé ñèëû ïðèâîäèò ê óìåíüøåíèþ ñêîðîñòè ïîëåòà
ðàêåòû. Äåéñòâèå ìîìåíòà M âûçûâàåò âðàùàòåëüíîå äâèæåíèå ðà-
êåòû âîêðóã öåíòðà ìàññ. Íàóêà, èçó÷àþùàÿ ÿâëåíèÿ, ñîïðîâîæäàþ-
ùèå âçàèìîäåéñòâèå ËÀ ñ íàáåãàþùèì ïîòîêîì âîçäóõà, íàçûâàåòñÿ
àýðîäèíàìèêîé [9].
Ìû ïðèâåäåì òîëüêî ñâåäåíèÿ, íåïîñðåäñòâåííî ñâÿçàííûå ñ
ïðàêòè÷åñêèì ïðèìåíåíèåì âî âíåøíåé áàëëèñòèêå ôîðìóë äëÿ
ðàñ÷åòà àýðîäèíàìè÷åñêèõ ñèë è ìîìåíòîâ.
Äëÿ îïðåäåëåíèÿ RA èñïîëüçóþò ôîðìóëó
Rq
S
C
AR
=
(,
,
)
,
M,Reαβ
(1.97)
ãäåq=ρV
2
2
/ – ñêîðîñòíîé
íàïîð íàáåãàþùåãî íåâîçìó-
ùåííîãî ïîòîêà; S – õàðàêòåðíàÿ
ïëîùàäü
ðàêåòû; CR
–
áåçðàçìåðíûé
àýðîäèíàìè÷å-
ñêèé êîýôôèöèåíò, çàâèñÿùèé â
îñíîâíîì îò ôîðìû ðàêåòû,
÷èñëà Ìàõà Ì = V/a, ÷èñëà
Ðåéíîëüäñà Re = Vdρ/μ, óãëîâ
àòàêè α è ñêîëüæåíèÿ β.
Åñëè ïðè âû÷èñëåíèè RA îêà-
æåòñÿ íåîáõîäèìûì ó÷èòûâàòü
58
Ðèñ. 1.20. Ñõåìà ïðèâåäåíèÿ ïîëíîé
àýðîäèíàìè÷åñêîé ñèëû ê öåíòðó ìàññ
(ÖÌ) ðàêåòû äëÿ ñëó÷àÿ ïëîñêîãî äâè-
æåíèÿ
èçìåíåíèå óãëîâ α è β âî âðåìåíè èëè óãëîâûå ñêîðîñòè ðàêåòû ωi
îòíîñèòåëüíî i-õ îñåé, ò.å . íåñòàöèîíàðíîñòü îáòåêàíèÿ êîðïóñà ðà-
êåòû âîçäóõîì, òî ñëåäóåò ïîä çíàê ôóíêöèè CR â ôîðìóëå (1.97)
âíåñòè âåëè÷èíû •
,
•
,
αβωi è âðåìÿ t. Ïîëíûé àýðîäèíàìè÷åñêèé ìî-
ìåíò îïðåäåëÿåòñÿ ôîðìóëîé
Mq
S
l
m
=
,
(1.98)
ãäå l – õàðàêòåðíàÿ äëèíà ðàêåòû (íàïðèìåð, äëèíà ðàêåòû îò åå äíà
äî âåðøèíû êîíóñà); m – áåçðàçìåðíûé àýðîäèíàìè÷åñêèé
êîýôôèöèåíò, çàâèñÿùèé îò ôîðìû ðàêåòû, åå ïîëîæåíèÿ íà
òðàåêòîðèè, ñêîðîñòè âðàùàòåëüíîãî äâèæåíèÿ, âðåìåíè è äð.
1.4.2. ÑÎÑÒÀÂËßÞÙÈÅ ÏÎËÍÎÉ ÀÝÐÎÄÈÍÀÌÈ×ÅÑÊÎÉ ÑÈËÛ
È ÏÎËÍÎÃÎ ÀÝÐÎÄÈÍÀÌÈ×ÅÑÊÎÃÎ ÌÎÌÅÍÒÀ
Äëÿ îïðåäåëåíèÿ îòäåëüíûõ ñîñòàâëÿþùèõ RA è Ì ïðèìåíÿþò
çàâèñèìîñòè, àíàëîãè÷íûå (1.97) è (1.98). Ïðîåêöèè ñèëû RA îáî-
çíà÷àþòñÿ ñëåäóþùèì îáðàçîì. Íà îñè ñâÿçàííîé ñèñòåìû êîîðäè-
íàò OXYZ : X – àýðîäèíàìè÷åñêàÿ ïðîäîëüíàÿ ñèëà (áåðåòñÿ ñ îáðàò-
íûì çíàêîì), Y – àýðîäèíàìè÷åñêàÿ íîðìàëüíàÿ ñèëà; Z – àýðîäè-
íàìè÷åñêàÿ ïîïåðå÷íàÿ ñèëà. Íà îñè ñêîðîñòíîé ñèñòåìû
êîîðäèíàò OX Y Z
aaa
: Xa – ñèëà ëîáîâîãî ñîïðîòèâëåíèÿ (áåðåòñÿ ñ
îáðàòíûì çíàêîì), Y a – àýðîäèíàìè÷åñêàÿ ïîäúåìíàÿ ñèëà, Za –
àýðîäèíàìè÷åñêàÿ áîêîâàÿ ñèëà. Íà îñè ñèñòåìû êîîðäèíàò
OXïYïZï, ñâÿçàííîé ñ ïðîñòðàíñòâåííûì óãëîì àòàêè, – ñîîòâåòñò -
âåííî Xï, Yï, Zï.
Ïðîåêöèè ïîëíîãî ìîìåíòà àýðîäèíàìè÷åñêèõ ñèë íà îñè ñêîðî-
ñòíîé è ñâÿçàííîé ñèñòåì êîîðäèíàò èìåþò ñëåäóþùèå îáîçíà÷å-
íèÿ. Íà îñè ñâÿçàííîé ñèñòåìû êîîðäèíàò: Mx – àýðîäèíàìè÷åñêèé
ìîìåíò êðåíà; My – àýðîäèíàìè÷åñêèé ìîìåíò ðûñêàíèÿ; Mz –
àýðîäèíàìè÷åñêèé ìîìåíò òàíãàæà. Íà îñè ñêîðîñòíîé ñèñòåìû êî-
îðäèíàò ñîîòâåòñòâåííî MMM
xyz
aaa
,, ñ òåìè æå íàçâàíèÿìè.
Ïîñêîëüêó ó ïðîåêöèé Ì íàçâàíèÿ ñîâïàäàþò, òî îáÿçàòåëüíî
íàäî îãîâàðèâàòü, ê êàêîé ñèñòåìå êîîðäèíàò îíè îòíîñÿòñÿ.
 àýðîäèíàìè÷åñêèõ ðàñ÷åòàõ óäîáíåå èìåòü äåëî íå ñ ñîñòàâ-
ëÿþùèìè ñèë è ìîìåíòîâ,àñèõêîýôôèöèåíòàìè. Â ñîîòâåòñòâèè
ñ ôîðìóëàìè (1.97) è (1.98) äëÿ ñâÿçàííîé ñèñòåìû êîîðäèíàò ìîæ-
íî çàïèñàòü
XqScMqSlm
YqScMqSlm
ZqScMqSlm
xx
x
yy
y
zz
z
==
==
==
;;
;;
;,
(1.99)
59
ãäå cx, cy, cz, mx, my, mz – ñîîòâåòñòâóþùèå áåçðàçìåðíûå
êîýôôèöèåíòû ñèë è ìîìåíòîâ.
Ñîñòàâëÿþùèå RA è Ì â ñêîðîñòíîé ñèñòåìå êîîðäèíàò îïðåäå-
ëÿþòñÿ ïî ôîðìóëàì, àíàëîãè÷íûì ôîðìóëàì (1.99), íî èìåþùèì
èíäåêñ "à" â îáîçíà÷åíèÿõ ñèë, ìîìåíòîâ è èõ êîýôôèöèåíòîâ. Â
íàçâàíèÿ êîýôôèöèåíòîâ âêëþ÷àþò íàèìåíîâàíèÿ òåõ ñèë è ìî-
ìåíòîâ, êîòîðûå îíè îïðåäåëÿþò. Íàïðèìåð, c
xa
–
êîýôôèöèåíò
ëîáîâîãî ñîïðîòèâëåíèÿ; cx – êîýôôèöèåíò ïðîäîëüíîé ñèëû; mz a
–
êîýôôèöèåíò ìîìåíòà òàíãàæà â ñêîðîñòíîé ñèñòåìå êîîðäèíàò;
mz – êîýôôèöèåíò ìîìåíòà òàíãàæà â ñâÿçàííîé ñèñòåìå êîîðäè-
íàò.
Ïðè ïðîâåäåíèè òåîðåòè÷åñêèõ ðàñ÷åòîâ è ýêñïåðèìåíòîâ â àýðî-
äèíàìè÷åñêèõ òðóáàõ àýðîäèíàìè÷åñêèå êîýôôèöèåíòû îïðåäåëÿ-
þòñÿ â êàêîé-ëèáî îäíîé ñèñòåìå êîîðäèíàò. Ïåðåõîä ê äðóãèì ñèñ-
òåìàì êîîðäèíàò îñóùåñòâëÿåòñÿ ñ ïîìîùüþ ìàòðèö íàïðàâëÿþùèõ
êîñèíóñîâ.
Çíà÷åíèÿ àýðîäèíàìè÷åñêèõ ñèë îòëè÷àþòñÿ îò àýðîäèíàìè÷å-
ñêèõ êîýôôèöèåíòîâ ýòèõ ñèë íà qS, à çíà÷åíèÿ ìîìåíòîâ îò êîýô-
ôèöèåíòîâ ìîìåíòîâ – íà qSl, ïîýòîìó ôîðìóëû, ïî êîòîðûì âåäåò-
ñÿ ïåðåñ÷åò êîýôôèöèåíòîâ ñèë è ìîìåíòîâ èç îäíîé ñèñòåìû êî-
îðäèíàò â äðóãóþ, áóäóò òàêèìè æå, êàê è äëÿ ïåðå÷åòà ñàìèõ ñèë è
ìîìåíòîâ.
 ñëó÷àå íåóñòàíîâèâøåãîñÿ äâèæåíèÿ àýðîäèíàìè÷åñêèå êîýô-
ôèöèåíòû ñèë è ìîìåíòîâ çàâèñÿò íå òîëüêî îò íàçâàííûõ âûøå îñ-
íîâíûõ ïàðàìåòðîâ (1.97), íî è îò õàðàêòåðèñòèê íåñòàöèîíàðíîñòè
îáòåêàíèÿ. Íàïðèìåð, äëÿ êîýôôèöèåíòîâ ïîäúåìíîé è áîêîâîé
ñèë íàïèøåì òàêèå ôóíêöèîíàëüíûå çàâèñèìîñòè:
cf
t
cf
yx
y
z
z
=
=
(,,
•
,
•
,
,
,
, , ...);
(,,
αβ
αβωωω
αβ
M, Re,
M,
000
Re,
•
,
•
,
,
,
, , ...),
αβωωω
xyz
t
000
(1.100)
ãäå ωωω
xyz
000
,, – ïðèâåäåííûå óãëîâûå ñêîðîñòè ËÀ îòíîñèòåëüíî
íåïîäâèæíûõ çåìíûõ îñåé; •
,
•
αβ– ïðèâåäåííûå óãëîâûå ñêîðîñòè
ËÀ; Ì – ÷èñëî Ìàõà.
Ïðèâåäåííûå óãëîâûå ñêîðîñòè, ÿâëÿþùèåñÿ áåçðàçìåðíûìè âå-
ëè÷èíàìè, ðàâíû
••
,
••
;
;;
αα ββ
ωωωωωω
==
===
l
V
l
V
l
V
l
V
l
V
xxyyzz
000000
èò.ï
.
(1.101)
60
Àýðîäèíàìè÷åñêèå ìîìåíòû ìîæíî ïðåäñòàâèòü êàê Mz = Y∆l; My =
=Z∆l, ãäå ∆l – ðàññòîÿíèå ìåæäó öåíòðîì ìàññ è öåíòðîì äàâëåíèÿ.
Ïðèíèìàÿ äëÿ Y è Z çàâèñèìîñòè, àíàëîãè÷íûå (1.99) è (1.100),
ïîëó÷èì ñîîòíîøåíèÿ äëÿ îïðåäåëåíèÿ ìîìåíòîâ, âûðàæåííûå ÷å-
ðåç êîýôôèöèåíòû ñîîòâåòñòâóþùèõ àýðîäèíàìè÷åñêèõ ñèë:
Mq
S
l
l
l
c
zy
=
∆
(, , ,Re,
•
,
•
, ...);
αβ
αβ
M
(1.102)
Mq
S
l
l
l
c
yz
=
∆
(, , ,Re,
•
,
•
, ...).
αβ
αβ
M
(1.103)
Íàéòè äëÿ êîýôôèöèåíòîâ àýðîäèíàìè÷åñêèõ ìîìåíòîâ çàâèñè-
ìîñòè, êîòîðûå îòðàæàëè áû âñå îïðåäåëÿþùèå ôàêòîðû, î÷åíü
ñëîæíî, ïîýòîìó îáû÷íî ó÷èòûâàþò òå ôàêòîðû, êîòîðûå îêàçûâà-
þò íà ìîìåíòû ñóùåñòâåííîå âëèÿíèå.
Ïðîâåäåííûå àýðîäèíàìè÷åñêèå èññëåäîâàíèÿ ïîêàçàëè, ÷òî äëÿ
îïðåäåëåíèÿ êîýôôèöèåíòà àýðîäèíàìè÷åñêîãî ìîìåíòà òàíãàæà â
ñâÿçàííîé ñèñòåìå êîîðäèíàò ìîæíî îãðàíè÷èòüñÿ çàâèñèìîñòüþ
mf
zz
=
(,,
•
).
αωα
(1.104)
Ôîðìóëà (1.104) ñïðàâåäëèâà ïðè íåáîëüøèõ èçìåíåíèÿõ ÷èñëà Ì.
Íàäî èìåòü â âèäó, ÷òî ïðè çíà÷èòåëüíîì èçìåíåíèè Ì ôîðìà
êðèâîé mz(α) ñóùåñòâåííî èçìåíÿåòñÿ, è ýòî íóæíî ó÷èòûâàòü.
Ïðåîáðàçóåì âûðàæåíèå (1.104). Ïðèðàâíèâàÿ ïîëíûé äèôôå-
ðåíöèàë ñóììå ÷àñòíûõ äèôôåðåíöèàëîâ è âûïîëíÿÿ çàìåíó dm ≈
≈∆mz=mz−mz0
, ïîëó÷èì
mm
mmm
zz
zz
z
z
z
=+
++
0
∂
∂α
α
∂
∂ω
ω
∂
∂α
α
•
•
,
(1.105)
ãäå mz0
–
àýðîäèíàìè÷åñêèé êîýôôèöèåíò mz ïðè íóëåâûõ çíà÷åíèÿõ
α,ωzè
•
.
α
Äëÿ îáîçíà÷åíèÿ ÷àñòíûõ ïðîèçâîäíûõ êîýôôèöèåíòîâ ñèë è
ìîìåíòîâ ââåäåì Aλ, ãäå A – ñèìâîë ðàññìàòðèâàåìîãî êîýôôèöè-
åíòà ñèëû èëè ìîìåíòà; λ – ñèìâîë âåëè÷èíû, ïî êîòîðîé áåðåòñÿ
ïðîèçâîäíàÿ, íàïðèìåð cc
yy
aa
α
∂∂
α
=
/ – ÷àñòíàÿ ïðîèçâîäíàÿ êîýô-
ôèöèåíòà àýðîäèíàìè÷åñêîé ïîäúåìíîé ñèëû ïî óãëó àòàêè.
×àñòíûå ïðîèçâîäíûå ïî óãëàì òèïà mm
zz
α
∂∂
α
=
/ íàçûâàþòñÿ
ñòàòè÷åñêèìè ïðîèçâîäíûìè. Ïðîèçâîäíûå ïî óãëîâûì ñêîðîñòÿì
61
òèïà mm
zz
z
z
ω
∂∂
ω
=
/;
mm
zz
•
/•
α
∂∂
α
=
íàçûâàþòñÿ âðàùàòåëüíûìè ïðî-
èçâîäíûìè.
Óïðîñòèâ çàïèñü (1.105), ïîëó÷èì
mmmm m
zzz z
zz
z
=++
+
0
α
ω
α
αωα
•
•
.
(1.106)
Äëÿ êîýôôèöèåíòà ìîìåíòà ðûñêàíèÿ ïðèìåíÿþò ôîðìóëó, àíà-
ëîãè÷íóþ íàïèñàííîé äëÿ êîýôôèöèåíòà ìîìåíòà òàíãàæà:
mmmmm
yy
yxyyy
x
y
=+
++
β
ω
ω
β
βω ωβ
•
•
,
(1.107)
ãäå mm
yy
β∂∂
β
=
/ – ñòàòè÷åñêàÿ ïðîèçâîäíàÿ;
mm
yy
x
x
ω
∂∂
ω
=
/;
mm mm
yy
y
yy
y
ω
β
∂∂
ω
∂∂
β
==
/;/
•
•
–
âðàùàòåëüíàÿ ïðîèçâîäíàÿ.
Ïðè íóëåâûõ çíà÷åíèÿõ βω ω β
,,,
•
xy àýðîäèíàìè÷åñêèé êîýôôè-
öèåíò my 0
= 0, ïîýòîìó îí íå âêëþ÷åí â ôîðìóëó (1.107).
 íàïèñàííûõ âûøå ôîðìóëàõ ñëàãàåìûå, ñîäåðæàùèå óãëîâûå
ñêîðîñòè •
,
•
αβè ω i , õàðàêòåðèçóþò ñîïðîòèâëåíèå âîçäóõà êîëåáàíè-
ÿì è âðàùåíèþ ëåòàòåëüíîãî àïïàðàòà. Ýòî ñîïðîòèâëåíèå âûçûâà-
åò çàòóõàíèå (äåìïôèðîâàíèå) âðàùàòåëüíûõ ïåðåìåùåíèé. Ïîýòî-
ìó âðàùàòåëüíûå ïðîèçâîäíûå ìîãóò áûòü íàçâàíû òàêæå ïðîèçâîä-
íûìè äåìïôèðîâàíèÿ.
Àýðîäèíàìè÷åñêèé ìîìåíò êðåíà Mx = gSlmx. Ïðè çàôèêñèðî-
âàííîì ÷èñëå Ì áåçðàçìåðíûé êîýôôèöèåíò mx îïðåäåëÿåòñÿ ôóíê-
öèîíàëüíîé çàâèñèìîñòüþ
mf
xx
y
z
=
(,,,,)
.
αβωωω
(1.108)
Ðàñêðûòèå ýòîé ôóíêöèîíàëüíîé çàâèñèìîñòè ïðè ó÷åòå âçàèì-
íîãî âëèÿíèÿ îïðåäåëÿþùèõ ïàðàìåòðîâ ïðèâîäèò ê ñëîæíîìó îá-
ùåìó âûðàæåíèþ äëÿ êîýôôèöèåíòà àýðîäèíàìè÷åñêîãî ìîìåíòà
êðåíà:
mmm
m
m
m
m
xxx
x
xx
xy
x
y
y
x
y
=++
++
++
0
2
2
β
ω
ω
β∂
∂α∂β
αβ
ω
ω
∂
∂α∂ω
αω+
∂
∂β∂ω
βω
2
mx
z
z.
(1.109)
62
Çäåñü mx 0
–
ñîñòàâëÿþùàÿ êîýôôèöèåíòà àýðîäèíàìè÷åñêîãî
ìîìåíòà êðåíà, îïðåäåëÿåìàÿ àýðîäèíàìè÷åñêîé àñèììåòðèåé ËÀ;
mx
β β – ñîñòàâëÿþùàÿ êîýôôèöèåíòà, îïðåäåëÿåìàÿ ñêîëüæåíèåì;
∂
∂α∂β
αβ
2
mx
–
ñîñòàâëÿþùàÿ êîýôôèöèåíòà ìîìåíòà êðåíà,
îïðåäåëÿåìàÿ âçàèìíûì âëèÿíèåì êðûëüåâ è îïåðåíèÿ; mxx
x
ω
ω–
êîýôôèöèåíòû äåìïôèðóþùåãî ìîìåíòà êðåíà, ñîçäàâàåìîãî
êðûëüÿìè è îïåðåíèåì; mxy
y
ω
ω,
∂
∂α∂ω
αω
2
mx
y
y,
∂
∂β∂ω
βω
2
mx
z
z – ñîñòàâëÿþùèå
ñïèðàëüíîãî ìîìåíòà êðåíà, âîçíèêàþùåãî ïðè âðàùåíèè ËÀ âîêðóã
îñåé OY è OZ.  ôîðìóëó (1.109) íå âêëþ÷åíû ñëàãàåìûå âûñøèõ
ïîðÿäêîâ îòíîñèòåëüíî óãëîâ α è β.
Êàê âèäíî èç ôîðìóëû (1.109), êîýôôèöèåíò àýðîäèíàìè÷åñêîãî
ìîìåíòà êðåíà â çíà÷èòåëüíîé ñòåïåíè îïðåäåëÿåòñÿ òàê íàçûâàå-
ìûìè ïåðåêðåñòíûìè àýðîäèíàìè÷åñêèìè ïðîèçâîäíûìè. Âçàèì-
íîå âîçäåéñòâèå ïðîäîëüíîãî è áîêîâîãî äâèæåíèé ïðîÿâëÿåòñÿ
îñîáåííî ñèëüíî ïðè êðåíå è âðàùåíèè îòíîñèòåëüíî ïðîäîëüíîé
îñè ËÀ ñ ðàçâèòûìè íåñóùèìè ïîâåðõíîñòÿìè. Õàðàêòåðíûå àýðî-
äèíàìè÷åñêèå òî÷êè: ôîêóñ ïî óãëó àòàêè – òî÷êà íà îñè OX ñâÿçàí-
íîé ñèñòåìû êîîðäèíàò, îòíîñèòåëüíî êîòîðîé àýðîäèíàìè÷åñêèé
ìîìåíò òàíãàæà îñòàåòñÿ ïîñòîÿííûì ïðè ìàëûõ èçìåíåíèÿõ óãëà
àòàêè, ò.å. ∂mz/∂α = 0. Íàïðàâëåíèå îñè OX âûáèðàåòñÿ òàê, ÷òîáû
ïðè íóëåâîì çíà÷åíèè óãëà àòàêè ïîäúåìíàÿ ñèëà ËÀ áûëà áëèçêà ê
íóëþ. Ïîëîæåíèå ôîêóñà ïî óãëó ñêîëüæåíèÿ îïðåäåëÿåòñÿ ðàâåí-
ñòâàìè ∂my/∂β =0è∂mx/∂β = 0, ïî îòêëîíåíèþ îðãàíîâ óïðàâëåíèÿ
òàíãàæîì – ðàâåíñòâîì ∂mz/∂δâ = 0, ïî óãëó ðûñêàíèÿ – ðàâåíñòâàìè
∂my/∂δí =0è∂mx/∂δí =0
.
 íåêîòîðûõ ñëó÷àÿõ âåêòîð ïîëíîãî ìîìåíòà àýðîäèíàìè÷åñêèõ
ñèë óäîáíî ïðåäñòàâëÿòü â âèäå ñóììû
MMM
=+
ñò
ä,
(1.110)
ãäå Mñò – ñòàáèëèçèðóþùèé èëè îïðîêèäûâàþùèé ìîìåíò; Mä –
äåìïôèðóþùèé ìîìåíò.
Íàçâàíèå ìîìåíòà Mñò îïðåäåëÿåòñÿ õàðàêòåðîì åãî äåéñòâèÿ
íà óãîë àòàêè α èëè ñêîëüæåíèÿ β. Åñëè ìîìåíò óâåëè÷èâàåò ýòè
óãëû, îí íàçûâàåòñÿ îïðîêèäûâàþùèì, åñëè óìåíüøàåò – ñòàáè-
ëèçèðóþùèì. Ìîìåíò äåìïôèðîâàíèÿ Mä äåéñòâóåò ïðîòèâ íà-
ïðàâëåíèÿ âðàùåíèÿ ïðè êîëåáàíèÿõ îòíîñèòåëüíî öåíòðà ìàññ.
Îí ñòðåìèòñÿ çàòîðìîçèòü (ïîãàñèòü) êîëåáàíèÿ ðàêåòû è åå âðà-
63
ùåíèå. Îòäåëüíî âçÿòûé ìîìåíò äåìïôèðîâàíèÿ ìîæåò áûòü
ïðåäñòàâëåí âûðàæåíèåì
Mq
S
l
m
l
V
qSl m
ii
i
i
ii
ä==
|| ||,
ωω
ω
ω
i
(1.111)
ãäå ||
mi
i
ω
–
ñîîòâåòñòâóþùàÿ âðàùàòåëüíàÿ ïðîèçâîäíàÿ.
 íåêîòîðûõ ñëó÷àÿõ ìîìåíòû äåìïôèðîâàíèÿ ïðåäñòàâëÿþò çà-
âèñÿùèìè îò ïåðâîé ñòåïåíè ñêîðîñòè ïîëåòà:
Mq
S
l
mS
V
lm
ii
i
i
i
i
ää
==
||
||.
ω
ωρω
2
(1.112)
Çäåñü mäi íàçûâàþò êîýôôèöèåíòîì äåìïôèðîâàíèÿ; îí ðàâåí mäi =
=
1
2
mi
i
ω
.
Ïðè ðåøåíèè çàäà÷ ïðîñòðàíñòâåííîãî äâèæåíèÿ
êîýôôèöèåíò äåìïôèðîâàíèÿ äîëæåí áûòü îïðåäåëåí ïî âñåì òðåì
ñâÿçàííûì îñÿì (mäx, mäy, mäz). Êîýôôèöèåíòû è ìîìåíòû
äåìïôèðîâàíèÿ ËÀ ìîãóò áûòü ïðåäñòàâëåíû êàê ñóììû
ñîîòâåòñòâóþùèõ êîýôôèöèåíòîâ îñíîâíûõ êîíñòðóêòèâíûõ óçëîâ
ËÀ. Íàïðèìåð, ÷òîáû íàéòè äåìïôèðóþùèé ìîìåíò ðàêåòû
ñàìîëåòíîé ñõåìû îòíîñèòåëüíî îñè OZ, íóæíî îïðåäåëèòü îáùèé
äåìïôèðóþùèé ìîìåíò êàê ñóììó äåìïôèðóþùèõ ìîìåíòîâ
îïåðåíèÿ, êðûëüåâ è êîðïóñà. Ó ðàêåò è ñíàðÿäîâ, íå èìåþùèõ ðåçêî
âûñòóïàþùèõ ïîâåðõíîñòåé, ò.å. áåñêðûëûõ è íåîïåðåííûõ,
êîýôôèöèåíò äåìïôèðîâàíèÿ êîðïóñà áóäåò îäèíàêîâ ïî
ýêâàòîðèàëüíûì îñÿì, à ðàçíèöà â äåìïôèðóþùèõ ìîìåíòàõ áóäåò
îïðåäåëÿòüñÿ ðàçíèöåé çíà÷åíèé ωz è ωy.
 ïðîöåññå íåâîçìóùåííîãî ñáàëàíñèðîâàííîãî ïîëåòà ðàêåòû
(îïåðåííîãî ñíàðÿäà) ïðîèñõîäÿò ïëàâíûå èçìåíåíèÿ óãëîâ àòàêè è
ñêîëüæåíèÿ. Ïðè ýòîì, êàê ïîêàçàëè ìíîãèå èññëåäîâàíèÿ, óãëîâûå
ñêîðîñòè ìàëî âëèÿþò íà ïîëíûé âåêòîð àýðîäèíàìè÷åñêèõ ñèë è
åãî ñîñòàâëÿþùèå. Ïîýòîìó àýðîäèíàìè÷åñêèå êîýôôèöèåíòû äëÿ
ïîäúåìíîé è áîêîâîé ñèë ÷àñòî îïðåäåëÿþò áåç ó÷åòà óãëîâûõ ñêî-
ðîñòåé, êîòîðûå áûëè âêëþ÷åíû íàìè â áîëåå ïîëíûå ôóíêöèî-
íàëüíûå çàâèñèìîñòè (1.100), íî îáÿçàòåëüíî ó÷èòûâàþò èõ ïðè îï-
ðåäåëåíèè àýðîäèíàìè÷åñêèõ êîýôôèöèåíòîâ ìîìåíòîâ. Ïðèíÿòî
òàêæå äëÿ óïðîùåíèÿ ñ÷èòàòü, ÷òî ïðè ìàëûõ α è β ïîäúåìíàÿ è áî-
êîâàÿ ñèëû íå çàâèñÿò äðóã îò äðóãà. Ñ ó÷åòîì îòìå÷åííûõ óïðîùå-
íèé ïîëó÷àþò
ccc
yyy
=+
0
α
α;
(1.113)
64
cc
zz
=
ββ.
(1.114)
Äëÿ ËÀ ñàìîëåòíîé ñõåìû cc
yy
=
0
ïðè α = 0; äëÿ îñåñèììåòðè÷íûõ
ËÀ cy0
0
=
.
Ïðè ðàñ÷åòå õàðàêòåðèñòèê äâèæåíèÿ îñåñèììåòðè÷íûõ ËÀ â
ïåðâîì ïðèáëèæåíèè ìîæíî ïðèíÿòü (â ñêîðîñòíûõ îñÿõ)
Y
V
ScZ
V
Sc
ay
az
aa
==
ρ
α
ρ
β
αβ
22
22
;;
(1.115)
M
V
Slm
V
Slm
zz
yy
aa
aa
==
ρ
α
ρ
β
αβ
22
22
;.
Μ
(1.116)
Êîýôôèöèåíò ëîáîâîãî ñîïðîòèâëåíèÿ â îáùåì âèäå ìîæíî
ïðåäñòàâèòü êàê cx a
= f(M, Re, α, β). Çàâèñèìîñòü cx a
îò Re íà÷èíàåò
çàìåòíî ïðîÿâëÿòüñÿ ïðè çíà÷èòåëüíîì èçìåíåíèè âûñîòû ïîëåòà, â
ñâÿçè ñ ÷åì íåîáõîäèì ïåðåñ÷åò cx a
íà ðàçëè÷íûå âûñîòû. Âëèÿíèå α
è β ó÷èòûâàþò ÷åðåç êîýôôèöèåíò èíäóêòèâíîãî ñîïðîòèâëåíèÿ
ccc
xi
xi
xi
aa
a
=+
() ().
αβ
(1.117)
Ïîëíûé êîýôôèöèåíò ëîáîâîãî ñîïðîòèâëåíèÿ
ccc
xxx
i
aaa
=+
0
,
(1.118)
ãäå cxa0
–
êîýôôèöèåíò ëîáîâîãî ñîïðîòèâëåíèÿ ïðè ñîâïàäåíèè
ïðîäîëüíîé îñè è âåêòîðà ñêîðîñòè öåíòðà ìàññ ËÀ, ò.å . ïðè óñëîâèè
α=β=0.
Äëÿ ËÀ, èìåþùèõ îòíîñèòåëüíî ïëîñêèå òðàåêòîðèè, íàïðèìåð
äëÿ ðàêåò êëàññà "çåìëÿ – çåìëÿ", êîãäà ìîæíî ñ÷èòàòü β = 0, ÷àùå
âñåãî îãðàíè÷èâàþòñÿ áîëåå ïðîñòîé çàâèñèìîñòüþ
ccc
xxx
i
aaa
=+
0
().
α
(1.119)
Ïðè ïîëåòå ñ îòíîñèòåëüíî íåáîëüøèìè óãëàìè àòàêè
Xq
S
c
ax
a
=
(M).
(1.120)
65
1.4.3. ÏÐÈÂÅÄÅÍÈÅ ÀÝÐÎÄÈÍÀÌÈ×ÅÑÊÈÕ ÑÈË È ÌÎÌÅÍÒÎÂ
Ê ÝÒÀËÎÍÍÛÌ ÔÓÍÊÖÈßÌ ÑÎÏÐÎÒÈÂËÅÍÈß
Äëÿ ËÀ, áëèçêèõ ïî àýðîäèíàìè÷åñêîé ôîðìå, ãðàôèêè çàâèñè-
ìîñòåé cx a
(M) òàêæå îêàçûâàþòñÿ ïîõîæèìè, ÷òî ïîçâîëÿåò â ðÿäå
ñëó÷àåâ ïîëüçîâàòüñÿ íà íà÷àëüíîì ýòàïå ïðîåêòèðîâàíèÿ àýðîäè-
íàìè÷åñêèìè êîýôôèöèåíòàìè, îïðåäåëåííûìè äëÿ ñóùåñòâóþ-
ùèõ, õîðîøî ñåáÿ çàðåêîìåíäîâàâøèõ îáúåêòîâ. Òàê êàê òîæäåñò-
âåííîå ïîäîáèå ìîæíî èìåòü íå âñåãäà, òî â ðàñ÷åò ââîäÿò êîýôôè-
öèåíò ïðîïîðöèîíàëüíîñòè i, íàçûâàåìûé êîýôôèöèåíòîì ôîðìû:
i
cVa
cVa
x
x
a
a
=
(/)
(/)
,
ýò
(1.121)
ãäåcVa
xa
(/)– íåèçâåñòíûé àýðîäèíàìè÷åñêèé êîýôôèöèåíò äëÿ
âíîâü ïðîåêòèðóåìîãî îáúåêòà; cVa
xaýò
(/)– àýðîäèíàìè÷åñêèé
êîýôôèöèåíò
èçâåñòíîãî,
àýðîäèíàìè÷åñêè
ïîõîæåãî
íà
ïðîåêòèðóåìûé è õîðîøî ñåáÿ çàðåêîìåíäîâàâøåãî îáúåêòà
(ýòàëîííîãî).
Åñëè èçâåñòíî çíà÷åíèå cVa
xaýò
(/)äëÿ êàêîé-ëèáî ðàêåòû (èëè
ñíàðÿäà), òî äëÿ ðàêåòû, áëèçêîé ïî àýðîäèíàìè÷åñêîé ôîðìå,
ìîæíî ïðèíÿòü
X
V
SicVa
ax
a
=
ρ2
2
ýò
(/).
(1.122)
Åñëè ôîðìû ðàêåò (ñíàðÿäîâ) è óñëîâèÿ ïîëåòà íåòîæäåñòâåííî
ïîäîáíû, òî, î÷åâèäíî, i ≠ 1 è çàâèñèò îò îòíîøåíèÿ V/a. Óñòàíî-
âèòü òî÷íî ýòó çàâèñèìîñòü ìîæíî îïûòíûì ïóòåì èëè ïîëó÷èâ òåî-
ðåòè÷åñêè çíà÷åíèå cVa
xaýò
(/)äëÿ âíîâü ïðîåêòèðóåìîãî îáúåêòà,
íî ïðè ýòîì òåðÿåòñÿ ïðåèìóùåñòâî ââåäåíèÿ êîýôôèöèåíòà ôîðìû
i. Ïîýòîìó ïðèíÿòî îïðåäåëÿòü çíà÷åíèå i ïðèáëèæåííî, ïîëàãàÿ
åãî ïîñòîÿííûì äëÿ äàííîé òðàåêòîðèè.
×èñëåííîå çíà÷åíèå i çàâèñèò îò ôîðìû âíîâü ïðîåêòèðóåìîãî
îáúåêòà è çíà÷åíèé cVa
xaýò
(/)äëÿ èçâåñòíûõ òèïîâ îáúåêòîâ (ðàêåò,
ñíàðÿäîâ), ñ êîòîðûìè íîâûé îáúåêò ñðàâíèâàåòñÿ. Ïîýòîìó âñåãäà
íåîáõîäèìî óêàçûâàòü, ïî êàêîìó ýòàëîííîìó çàêîíó ñîïðîòèâëå-
íèÿ âîçäóõà îïðåäåëÿåòñÿ êîýôôèöèåíò i. Óäîáíî èñïîëüçîâàòü i â
êà÷åñòâå êîýôôèöèåíòà ñîãëàñîâàíèÿ ðàñ÷åòà ïî îïðåäåëåíèþ äàëü-
íîñòè ñòðåëüáû ñ îïûòîì.  ýòîì ñëó÷àå i áóäåò ó÷èòûâàòü íå òîëüêî
ôîðìó ñíàðÿäà, íî è âñå ôàêòîðû, íå îòðàæåííûå â äàííîì ðàñ÷åòå,
íàïðèìåð îòëè÷èå ÷èñëîâûõ çíà÷åíèé êîýôôèöèåíòîâ ôîðìû, ïî-
ëó÷åííûõ ïðè ñòðåëüáå, îò ýòàëîííîãî çíà÷åíèÿ êîýôôèöèåíòà, à
66
òàêæå ðàçëè÷íûå õàðàêòåðèñòèêè êîëåáàíèé îòíîñèòåëüíî öåíòðà
ìàññ ïðè ðàçëè÷íûõ íà÷àëüíûõ óñëîâèÿõ ñòðåëüáû.
 óðàâíåíèå (1.122) âõîäèò ïëîòíîñòü ρ (êã/ì3). Åñëè ïåðåéòè ê
óäåëüíîìó âåñó Ï (Í/ì3), ïîëó÷èì
X
d
VicVa
ax
a
=
π
2
2
8
Ï
g
ýò
(/).
(1.123)
Óìíîæèì è ðàçäåëèì ïðàâóþ ÷àñòü óðàâíåíèÿ (1.123) íà ïðîèç-
âåäåíèå QÏON ⋅103. Â ðåçóëüòàòå áóäåì èìåòü
X
Q
g
id
Q
VcVa
a
ON
ON
xa
=⋅
⋅
2
3
3
2
10
810
Ï
Ï
Ï
ýò
π
(/). (1.124)
 ïîëó÷åííîé çàâèñèìîñòè ìíîæèòåëü
id
Q
c
2
3
10
⋅=íàçûâàåòñÿ
áàëëèñòè÷åñêèì êîýôôèöèåíòîì, à ÷ëåí
FV
VcVa
VcVa
ON
x
x
aa
()
(/) ,
(/)
=
⋅
=⋅
−
π
810
474 10
3
24
2
Ï
ýò
ýò
(1.125)
ÿâëÿåòñÿ ôóíêöèåé ñîïðîòèâëåíèÿ âîçäóõà. Çäåñü íåîáõîäèìî
îòìåòèòü, ÷òî â àðòèëëåðèè áîëåå ðàïðîñòðàíåíî âûðàæåíèå
áàëëèñòè÷åñêîãî êîýôôèöèåíòà ci
dm
=⋅
−
21
103
,
ïîñêîëüêó ïðè
ïåðåõîäå ê ñèñòåìå ÑÈ Q äîëæíî âûðàæàòüñÿ â íüþòîíàõ, ÷òî ÷àñòî
ïðèâîäèò ê ïóòàíèöå, îáóñëîâëåííîé äèàïàçîíîì çàäàíèÿ c â
Òàáëèöàõ âíåøíåé áàëëèñòèêè (ÒÂÁ), èìåþùåãî âåëè÷èíó, ìíîãî
áî'ëüøóþ äåñÿòè.
Ïîñëå ïðåîáðàçîâàíèé ïîëó÷èì óäîáíóþ ôîðìóëó
Xm
c
H
y
F
V
a
=
()(),
(1.126)
â êîòîðîé ïðîèçâåäåíèå cH(y)F(V ) èìååò ôèçè÷åñêèé ñìûñë
óñêîðåíèÿ ñíàðÿäà îò ñèëû ñîïðîòèâëåíèÿ âîçäóõà è îáîçíà÷àåòñÿ
÷åðåç J.
Ïðèìåíÿÿ ôîðìóëó (1.126) äëÿ ðàêåò íà ó÷àñòêå ðàáîòû äâèãàòåëÿ
(àêòèâíîì ó÷àñòêå ïîëåòà), ñëåäóåò èìåòü â âèäó, ÷òî m è c ïåðåìåí-
íû è ðàâíû ñîîòâåòñòâåííî
67
m
QQd
t
g
t
=
−
∫ ñåê
0
;
(1.127)
c
id
QQd
t
t
=
⋅
−
∫
23
0
10
ñåê
,
(1.128)
ãäå Qñåê – ñåêóíäíûé ðàñõîä òîïëèâà. Ïîñëå ïðåîáðàçîâàíèé
âûðàæåíèÿ (1.126) ïîëó÷èì äëÿ ËÀ ñ ïåðåìåííîé ìàññîé
X
id
g
HyFV
a
=⋅
2
3
10 ()().
(1.129)
Èíîãäà âìåñòî ôóíêöèè F(V ) èñïîëüçóåòñÿ ôóíêöèÿ
GVFVV
VcVa
xa
()()/,
(/)
==
⋅
−
474 104
ýò
(1.130)
èëè ôóíêöèÿ
KVaFVV
cVa
xa
(/) ()/ ,
(/).
==
⋅
−
24
474 10 ýò
(1.131)
Äëÿ ðàêåò (ñíàðÿäîâ), ðàçëè÷íûõ ïî ôîðìå, ðàçëè÷íû è ôóíêöèè
F(V )èG(V ). Ïðè ïðîâåäåíèè áàëëèñòè÷åñêèõ ðàñ÷åòîâ ÷èñëîâîå
çíà÷åíèå êîýôôèöèåíòà ôîðìû i äîëæíî âûáèðàòüñÿ ïðèìåíèòåëü-
íî ê èñïîëüçóåìîé ôóíêöèè F(V ) èëè G(V ). Äëÿ ñíàðÿäîâ ñòâîëü-
íûõ àðòèëëåðèéñêèõ ñèñòåì èçâåñòíû ýìïèðè÷åñêè óñòàíîâëåííûå
òèïîâûå ôóíêöèè F(V ), èíîãäà íàçûâàåìûå íå ñîâñåì ïðàâèëüíî
çàêîíàìè ñîïðîòèâëåíèÿ âîçäóõà.
Èçâåñòíû, â ÷àñòíîñòè, "çàêîíû" Íüþòîíà, Ìàèåâñêîãî è Çàáóä-
ñêîãî, Ãàðíüå è Äþïþè, Ñèà÷÷è, ðàçðàáîòàííûå ñîâåòñêèìè ó÷åíû-
ìè "çàêîíû 1930 ã. è 1943 ã." Ýìïèðè÷åñêèå çàâèñèìîñòè äëÿ òèïî-
âûõ ôóíêöèé F(V )èG(V ) çàäàþòñÿ â âèäå ñïåöèàëüíûõ òàáëèö.
Ïðè èñïîëüçîâàíèè â ðàñ÷åòàõ óæå èìåþùèõñÿ òàáëèö äëÿ F(V )
è G(V ) è ïðè ñîñòàâëåíèè òàáëèö äëÿ íîâûõ òèïîâûõ ôóíêöèé ñëå-
äóåò ó÷èòûâàòü, ÷òî ñêîðîñòü çâóêà a çàâèñèò îò òåìïåðàòóðû âîçäóõà
è, ñëåäîâàòåëüíî, èçìåíÿåòñÿ ñ âûñîòîé. Êàê èçâåñòíî, a = kgRτ,
ãäå k – ïîêàçàòåëü àäèàáàòû.
Åñëè äëÿ îòíîñèòåëüíî êîðîòêèõ òðàåêòîðèé (Xc £ 50 êì) ïðè-
íÿòü g = const, à k – íå çàâèñÿùèì îò òåìïåðàòóðû, òî îêàæåòñÿ, ÷òî
ñêîðîñòü çâóêà ïðîïîðöèîíàëüíà τ. Äëÿ òîãî ÷òîáû èìåòü òàáëèöû
ôóíêöèè F(V ) èëè G(V ) ñ îäíèì âõîäîì, íåîáõîäèìî èõ ðàññ÷èòû-
68
âàòü äëÿ îäíîé ôèêñèðîâàííîé ñêîðîñòè çâóêà, ñîõðàíÿÿ ïðè ýòîì
ðàâåíñòâî
cVacVa
xx
O
N
aa
(/) (/ ),
=
τ
èëè
VaV a
ON
//
,
=
τ
(1.132)
ãäå aON – ñêîðîñòü çâóêà ïðè íîðìàëüíûõ óñëîâèÿõ, ïðèíèìàåìàÿ
ïîñòîÿííîé ïðè âû÷èñëåíèè òàáëèö; Vτ – óñëîâíàÿ òàáëè÷íàÿ
ñêîðîñòü.
Î÷åâèäíî, ÷òî
VV
a
a
V
ON
ON
τ
τ
τ
==.
(1.133)
Ñëåäîâàòåëüíî, èñïîëüçóÿ ôîðìóëó (1.125), ïîëó÷èì
FV
V
c
V
a
ON
x
ON
a
(),
.
=⋅
⎛
⎝⎜⎞
⎠⎟
−
474 1042
τ
τ
τ
τ
ýò
(1.134)
Îáîçíà÷àÿ
FV
Vc
V
a
x
ON
a
(),
,
ττ
τ
=⋅
⎛
⎝⎜⎞
⎠⎟
−
474 1042
ýò
(1.135)
èìååì
FV
FV
ON
()
().
=
τ
τ
τ
(1.136)
Ñîîòâåòñòâåííî
GV
GV
ON
()/(),
=ττ
τ
(1.137)
è, ñðàâíèâàÿ (1.135) è (1.137), ïîëó÷èì
GV
FV
V
() ().
τ
τ
τ
=
(1.138)
Ïðè ó÷åòå âëàæíîñòè âîçäóõà ïîñðåäñòâîì ââåäåíèÿ âèðòóàëüíîé
òåìïåðàòóðû åãî óäåëüíûé âåñ îïðåäåëÿåòñÿ ôîðìóëîé (1.79).
69
Ïðè ýòîì ôóíêöèÿ èçìåíåíèÿ ïëîòíîñòè ñ âûñîòîé ðàâíà
Hy
h
h
ON
ON
ON
()
,
==
Ï
Ï
τ
τ
ò.å. çàâèñèò îò îòíîøåíèÿ äàâëåíèé è âèðòóàëüíûõ òåìïåðàòóð. Åñëè
òåïåðü âåðíóòüñÿ ê ôîðìóëå (1.126) è ïîäñòàâèòü â íåå âûðàæåíèÿ äëÿ
F(V )èH(y), òî ïîëó÷èì
Xm
c
h
h
FV
a
ON
=
(),
τ
(1.139)
èëè
Xm
c
y
F
V
a
=π
τ
()( ).
(1.140)
Åñëè â (1.126) ñ ïîìîùüþ (1.137) ââåñòè ôóíêöèþ G(Vτ), òî áóäåì
èìåòü
Xm
c
Hy
V
G
V
a
=
ττ
()(),
(1.141)
ãäå Hy Hy
ON
τ
τ
τ
()().
=
Äëÿ ýòîé ôóíêöèè òàêæå ñîñòàâëåíû òàáëèöû
ñ âõîäíîé âåëè÷èíîé y.
Ïðè ðàñ÷åòå õàðàêòåðèñòèê äâèæåíèÿ âðàùàþùèõñÿ àðòèëëåðèé-
ñêèõ ñíàðÿäîâ îáû÷íî ñ÷èòàþò, ÷òî ñíàðÿäû óñòîé÷èâû íà òðàåêòî-
ðèè è äâèæóòñÿ ñ ìàëûìè óãëîâûìè îòêëîíåíèÿìè ïðîäîëüíîé îñè
ñíàðÿäà îò âåêòîðà ñêîðîñòè (óãîë íóòàöèè δ íà ðèñ. 1.10); ïëîñêîñòü
óãëà δ âðàùàåòñÿ. Ëîáîâîå ñîïðîòèâëåíèå (òàíãåíöèàëüíóþ ñîñòàâ-
ëÿþùóþ Rò ïîëíîãî âåêòîðà àýðîäèíàìè÷åñêèõ ñèë) ñ÷èòàþò íåçà-
âèñèìûì îò δ è îïðåäåëÿþò ïðè δ = 0, à íîðìàëüíóþ ñîñòàâëÿþùóþ
RN è îïðîêèäûâàþùèé ìîìåíò Ì ïðèíèìàþò ïðîïîðöèîíàëüíûìè
óãëó δ (ðèñ. 1.21). Êðîìå òîãî, óäîáíî ïðè ðàñ÷åòàõ â ôîðìóëû äëÿ
íàçâàííûõ àýðîäèíàìè÷åñêèõ õàðàêòåðèñòèê ââåñòè êàëèáð ñíàðÿäà
d, ôóíêöèþ H(y) è ñîîòâåòñòâóþùèå àýðîäèíàìè÷åñêèå êîýôôèöè-
åíòû Ki(V/a). Ñ ó÷åòîì ýòîãî ïîëó÷èì
XRR
id
g
HyVK
V
a
YZR
dl
g
H
aA
aaN
===⋅
⎛
⎝⎜⎞
⎠⎟
== =⋅
ò
2
32
3
10
10
()
;
()
;
()
yVK
V
a
MMM
dh
g
HyVK
V
a
N
yz
M
2
2
32
10
⎛
⎝⎜⎞
⎠⎟
=== ⋅
⎛
⎝⎜⎞
⎠⎟
δ
δ.
(1.142)
70
Àýðîäèíàìè÷åñêèå êîýôôèöèåíòû K
V
a
⎛
⎝⎜⎞
⎠⎟,K
V
a
N
⎛
⎝⎜⎞
⎠⎟èK
V
a
M
⎛
⎝⎜⎞
⎠⎟ ìî-
ãóò áûòü îïðåäåëåíû ïî äàííûì îïûòíûõ ñòðåëüá. Âåëè÷èíà h ≈∆l
ñîîòâåòñòâóåò óñëîâíîìó ðàññòîÿíèþ ìåæäó öåíòðîì äàâëåíèÿ è
öåíòðîì ìàññ ñíàðÿäà è îïðåäåëÿåòñÿ îáû÷íî ïî ýìïèðè÷åñêèì
ôîðìóëàì.  êà÷åñòâå ïðèìåðà ìîæíî ïðèâåñòè èçâåñòíóþ ôîðìóëó
Ãîáàðà
hhhd
=+
−
1 057
016
,,
,
ã
ãäå h1 è hã (ñì. ðèñ. 1.21) – ðàçìåðû, õàðàêòåðèçóþùèå ïîëîæåíèå
öåíòðà ìàññ ñíàðÿäà è äëèíó åãî ãîëîâíîé (îæèâàëüíîé èëè
êîíè÷åñêîé) ÷àñòè ñîîòâåòñòâåííî.
Òîëüêî áûñòðîâðàùàþùèìñÿ ñíàðÿäàì ïðèñóùè àýðîäèíàìè÷å-
ñêèå õàðàêòåðèñòèêè – ñèëà Ìàãíóñà RÌà, ìîìåíò ñèëû Ìàãíóñà
MÌà è ìîìåíò ïîâåðõíîñòíîãî òðåíèÿ Ã. Ñèëà Ìàãíóñà ÿâëÿåòñÿ ñî-
ñòàâëÿþùåé ãëàâíîãî âåêòîðà àýðîäèíàìè÷åñêèõ ñèë. Îíà ïðîïîð-
öèîíàëüíà ïðîèçâåäåíèþ ωxδ. Ìåõàíèçì âîçíèêíîâåíèÿ ýòîé ñèëû
âèäåí èç ðèñ. 1.22. Ïðè âñòðå÷å ÷àñòèö íàáåãàþùåãî íà ñíàðÿä ñî
ñêîðîñòüþ V ïîòîêà âîçäóõà ñ ÷àñòèöàìè âîçäóõà, óâëå÷åííûìè âî
âðàùåíèå ïîâåðõíîñòüþ ñíàðÿäà, ñîçäàåòñÿ ðàçíîñòü ïðèñòåííîãî
äàâëåíèÿ. Â ðåçóëüòàòå ïåðåðàñïðåäåëåíèÿ äàâëåíèÿ ïî ïîâåðõíîñòè
ñíàðÿäà ïîÿâëÿåòñÿ äîïîëíèòåëüíàÿ ñèëà, ïåðïåíäèêóëÿðíàÿ ïëîñ-
71
Ðèñ. 1.21. Ñõåìà ïðèâåäåíèÿ ãëàâíîãî âåêòîðà ïîëíîé àýðîäèíàìè÷åñêîé ñèëû ê
öåíòðó ìàññ (ÖÌ) âðàùàþùåãîñÿ ñíàðÿäà
êîñòè óãëà íóòàöèè δ è íàïðàâëåííàÿ â ñòîðîíó, îáðàòíóþ îáëàñòè
ñìåøåíèÿ âñòðå÷íûõ ïîòîêîâ. Äëÿ îïðåäåëåíèÿ ñèëû è ìîìåíòà
Ìàãíóñà ìîãóò áûòü èñïîëüçîâàíû ôîðìóëû
R
dl
g
HyVK
V
a
M
dl
g
HyVK
x
Ma
Ma
Ma
=⋅
⎛
⎝⎜⎞
⎠⎟
=⋅
2
3
3
3
10
10
()
;
()
ωδ
Ix
V
a
⎛
⎝⎜⎞
⎠⎟ωδ,
(1.143)
ãäå KMa, K
V
a
I
⎛
⎝⎜⎞
⎠⎟ – îïûòíûå àýðîäèíàìè÷åñêèå êîýôôèöèåíòû.
Òàê êàê â îáùåì ñëó÷àå âåêòîð ñèëû Ìàãíóñà íå ïðîõîäèò ÷åðåç
öåíòð ìàññ, ïîÿâëÿåòñÿ ìîìåíò ýòîé ñèëû. Âëèÿíèå RMa è åå ìîìåí-
òà íà ïîëåò ñíàðÿäîâ èçó÷åíî ñðàâíèòåëüíî ìàëî.
Ñèëû ïîâåðõíîñòíîãî òðåíèÿ óìåíüøàþò óãëîâóþ ñêîðîñòü ñîá-
ñòâåííîãî âðàùåíèÿ ñíàðÿäà îòíîñèòåëüíî ïðîäîëüíîé îñè. Ìî-
ìåíò äåìïôèðîâàíèÿ ñòðåìèòñÿ ïîãàñèòü êîëåáàíèå ïðîäîëüíîé
îñè ñíàðÿäà, ò.å . óìåíüøèòü ñîñòàâëÿþùóþ óãëîâîé ñêîðîñòè, ïåð-
ïåíäèêóëÿðíóþ ê åãî ïðîäîëüíîé îñè. Ìîìåíò ïîâåðõíîñòíîãî òðå-
íèÿ è äåìïôèðóþùèé ìîìåíò ìîãóò áûòü îïðåäåëåíû ïî ôîðìóëàì
Ã
Ã
ä
=⋅
⎛
⎝⎜⎞
⎠⎟
=⋅
⎛
⎝
dl
g
HyVK
V
a
M
dl
g
HyVK
V
a
x
D
2
3
3
3
10
10
()
;
()
ω
⎜⎞
⎠⎟Ω,
(1.144)
72
Ðèñ. 1 .22. Ñõåìà îáðàçîâàíèÿ ñèëû Ìàãíóñà
ãäå K
V
a
K
V
a
D
Ã
⎛
⎝⎜⎞
⎠⎟⎛
⎝⎜⎞
⎠⎟
,
–
àýðîäèíàìè÷åñêèå êîýôôèöèåíòû; Ω –
ñîñòàâëÿþùàÿ óãëîâîé ñêîðîñòè ñíàðÿäà, ïåðïåíäèêóëÿðíàÿ
ïðîäîëüíîé îñè. Êàê ïîêàçûâàþò ðàñ÷åòû è îïûò, ìîìåíò Ã
ñóùåñòâåííî óìåíüøàåò óãëîâóþ ñêîðîñòü âðàùåíèÿ ñíàðÿäà â
ïðîöåññå ïîëåòà.
 âûðàæåíèÿ (1.142)...(1.144) äëÿ àýðîäèíàìè÷åñêèõ ñèë è ìî-
ìåíòîâ, äåéñòâóþùèõ íà àðòèëëåðèéñêèé ñíàðÿä, âõîäÿò òèïîâûå
ôóíêöèè ñîïðîòèâëåíèÿ K
V
a
⎛
⎝⎜⎞
⎠⎟,K
V
a
N
⎛
⎝⎜⎞
⎠⎟,K
V
a
Ma
⎛
⎝⎜⎞
⎠⎟,K
V
a
M
⎛
⎝⎜⎞
⎠⎟,K
V
a
I
⎛
⎝⎜⎞
⎠⎟,
K
V
a
Ã
⎛
⎝⎜⎞
⎠⎟, K
V
a
D
⎛
⎝⎜⎞
⎠⎟ , ïî êîòîðûì íàêîïëåí áîëüøîé ýêñïåðèìåíòàëü-
íûé ìàòåðèàë íà îñíîâå îáðàáîòêè ðåçóëüòàòîâ îïûòíûõ ñòðåëüá
(ñì., íàïðèìåð, [21, 118]). Ýêñïåðèìåíòàëüíûå çíà÷åíèÿ ýòèõ ôóíê-
öèé ïîëó÷åíû ïðè óñëîâèè ìàëûõ óãëîâ íóòàöèè è ëèíåéíîé çàâè-
ñèìîñòè ñèë RN, RMa è ìîìåíòîâ M, MMa îò óãëà δ.  òåõ ñëó÷àÿõ, êî-
ãäà óãîë íóòàöèè íå ìîæåò áûòü ïðèíÿò ìàëûì, ìîæíî çàäàòü çàâè-
ñèìîñòü àýðîäèíàìè÷åñêèõ êîýôôèöèåíòîâ â âèäå K
V
a
i
;s
i
n
.
δδ
⎛
⎝⎜⎞
⎠⎟
Ïðè ýêñïåðèìåíòàëüíîì îïðåäåëåíèè àýðîäèíàìè÷åñêèõ êîýôôè-
öèåíòîâ â àýðîäèíàìè÷åñêèõ òðóáàõ îáû÷íî â êà÷åñòâå õàðàêòåðíî-
ãî ðàçìåðà è ïëîùàäè èñïîëüçóþò äëèíó ñíàðÿäà l è ïëîùàäü ìèäå-
ëåâîãî
ñå÷åíèÿ S = πd 2/4. Â
ýòîì
ñëó÷àå, îáîçíà÷èâ
πÏON d
g
HyVl
8
2
22
() =47410
2
2
22
,(
)
⋅
−
d
g
HyVl = φ1(V, y); V/a = M, âûðà-
æåíèÿ äëÿ ñèë è ìîìåíòîâ ìîæíî çàïèñàòü â âèäå
RV
y
l
c
RV
y
lc
R
NN
òò
Ma
(M
M,
=
=
=
−
−
φδ
φδ
δ
1
2
1
2
(,)
,);
(,)sin();
φω
δ
δ
φδ
δ
1
1
1
1
(,)() sin (,);
(,) sin (,
Vy lV
c
MV
y
lm
x
M
−
−
=
MaM
M);
(,) sin ( ,);
(,)
( ,);
MV
ym
VyV m
x
x
Ma
Ma
Ã
M
ÃM
=
=
−
φωδ δ
φωδ
1
1
1
DV
y
Vm
D
=
−
φδ
1
1
(,)
(,)
.
ΩM
(1.145)
Òîãäà ïåðåõîä ê òèïîâûì ôóíêöèÿì ñîïðîòèâëåíèÿ ñîîòâåòñò-
âóþùèõ ñèë è ìîìåíòîâ ïðè ìàëûõ óãëàõ íóòàöèè (sinδ≈δ; ci(M, δ) ≈
73
≈ c i(M); mi(M, δ) ≈ mi(M)) ñ ó÷åòîì îáîçíà÷åíèÿ
d
lON
8103
⋅
πÏ
≈
≈ 2,11⋅103dl −1
= φ2(d, l) ìîæåò áûòü îñóùåñòâëåí ïî ôîðìóëàì
cd
l
l
d
i
K
c
dldlK
c
NN
ò
Ma
MM
MM
() (,) ();
() (,) ();
=
=
−
−
φ
φ
2
1
2
22
(),
();
() (,) ();
()
MM
MM
M
Ma
Ma
=⋅
=
=
−
211 103
2
1
K
md
l
d
h
K
m
MM
φ
φ2
2
2
22
(,)();
() (,) ();
() (,)
dlK
md
l
K
m
dldlK
I
D
M
MM
M
ÃÃ
=
=
−
φ
φ
D()
.
M
(1.146)
1.5 . ÒßÃÀ ÐÀÊÅÒÍÎÃÎ ÄÂÈÃÀÒÅËß
Òÿãîé ðàêåòíîãî äâèãàòåëÿ íàçûâàåòñÿ ðàâíîäåéñòâóþùàÿ ðåàê-
òèâíîé ñèëû è ñèë äàâëåíèÿ îêðóæàþùåé ñðåäû, äåéñòâóþùèõ íà
åãî âíåøíèå ïîâåðõíîñòè, çà èñêëþ÷åíèåì ñèë âíåøíåãî àýðîäèíà-
ìè÷åñêîãî ñîïðîòèâëåíèÿ. Ðàâíîäåéñòâóþùàÿ ãàçî- è ãèäðîäèíà-
ìè÷åñêèõ ñèë, äåéñòâóþùèõ íà âíóòðåííèå ïîâåðõíîñòè ðàêåòíîãî
äâèãàòåëÿ ïðè èñòå÷åíèè èç íåãî âåùåñòâà, íàçûâàåòñÿ ðåàêòèâíîé
ñèëîé.
Îïðåäåëèòü òÿãó â ïîëåòå ìîæíî òîëüêî êîñâåííûì ðàñ÷åò-
íî-ýêñïåðèìåíòàëüíûì ïóòåì. Ïîýòîìó òÿãà îïðåäåëÿåòñÿ â ñòàòè-
÷åñêèõ óñëîâèÿõ íà ñïåöèàëüíûõ ñòåíäàõ. Ñîâìåñòíîå äåéñòâèå ñèë,
âêëþ÷àÿ êîðèîëèñîâû, çàâèñÿùèå îò êîëåáàíèé ðàêåòû, äâèæåíèÿ
ãàçîâ è ïåðåìåùåíèÿ öåíòðà ìàññ ïðè âûãîðàíèè òîïëèâà, ìîæåò
áûòü ýêñïåðèìåíòàëüíî îïðåäåëåíî â àýðîäèíàìè÷åñêîé òðóáå, ãäå
ðàêåòó ñ ðàáîòàþùèì äâèãàòåëåì ñëåäóåò çàêðåïèòü øàðíèðíî òàê,
÷òîáû ïðîäîëüíàÿ îñü ðàêåòû ìîãëà ñîâåðøàòü êîëåáàíèÿ. Øàðíèð-
íîå êðåïëåíèå âíîñèò çíà÷èòåëüíûå èñêàæåíèÿ â îáòåêàþùèé ðàêå-
òó âíåøíèé ïîòîê, ÷òî ñíèæàåò òî÷íîñòü ðåçóëüòàòîâ. Ðàñïîëàãàÿ
ïðîäîëüíóþ îñü ðàêåòû ïî ïîòîêó òàê, ÷òîáû èç àýðîäèíàìè÷åñêèõ
ñèë äåéñòâîâàëî òîëüêî ëîáîâîå ñîïðîòèâëåíèå, ìîæíî èçìåðèòü íà
îïîðàõ ðàêåòû ñóììàðíóþ äåéñòâóþùóþ ñèëó, íàçûâàåìóþ ýôôåê-
òèâíîé òÿãîé äâèãàòåëÿ:
PPX
q
dt
ýô
âàð
=−−
δ
,
(1.147)
ãäå Ð – ñòåíäîâàÿ òÿãà.
74
Åñëè ïðèíÿòü ñêîðîñòü âíåøíåãî ïîòîêà ðàâíîé íóëþ, òî íà îïî-
ðàõ ðàêåòû áóäåò îïðåäåëåíà ñòåíäîâàÿ òÿãà äâèãàòåëÿ.
Îòäåëüíî èçìåðèòü ðåàêòèâíóþ ñèëó íå ïðåäñòàâëÿåòñÿ âîçìîæ-
íûì, è åå îïðåäåëÿþò âìåñòå ñ ñèëàìè ñòàòè÷åñêîãî äàâëåíèÿ, äåé-
ñòâóþùèìè â íàïðàâëåíèè ïðîäîëüíîé îñè ðàêåòû.
Óêðåïëåííàÿ íà ñòåíäå ðàêåòà óäåðæèâàåòñÿ îò ïåðåìåùåíèÿ îñåâîé
ñèëîé ′P , êîòîðàÿ ðàâíà òÿãå, íî íàïðàâëåíà ïðîòèâîïîëîæíî åé: ′
P=
= −P. Íà íàðóæíóþ ïîâåðõíîñòü ðàêåòû äåéñòâóþò ñèëû, îïðåäåëÿåìûå
àòìîñôåðíûì äàâëåíèåì ð, ñîîòâåòñòâóþùèì âûñîòå, íà êîòîðîé ðàñïî-
ëîæåíà ðàêåòà. Ïî âåëè÷èíå îíè ðàâíû ïðîèçâåäåíèþ äàâëåíèÿ íà ïëî-
ùàäü è íàïðàâëåíû ïåðïåíäèêóëÿðíî òîé ïëîùàäêå, íà êîòîðóþ äåéñò-
âóþò. Âñå ñèëû, äåéñòâóþùèå íà áîêîâóþ ïîâåðõíîñòü ðàêåòû, óðàâíî-
âåøèâàþò äðóã äðóãà. Íî ïðè ðàáîòàþùåì äâèãàòåëå àòìîñôåðíîå
äàâëåíèå íå äåéñòâóåò íà âûõîäíîå ñå÷åíèå ñîïëà, ÷åðåç êîòîðîå ïàðàë-
ëåëüíî îñè ðàêåòû OX èñòåêàþò ãàçû ñî ñêîðîñòüþ Wîòí, è ïîÿâëÿåòñÿ
ïðèëîæåííàÿ ê êîðïóñó íåóðàâíîâåøåííàÿ ñèëà pSa , íàïðàâëåííàÿ â ñòî-
ðîíó èñòå÷åíèÿ ãàçîâ (Sa – ïëîùàäü âûõîäíîãî ñå÷åíèÿ ñîïëà).  âûõîä-
íîì ñå÷åíèè ñîïëà äåéñòâóåò ïðîòèâîïîëîæíî íàïðàâëåííàÿ ñèëà paSa,
ãäå pa – äàâëåíèå èñòåêàþùèõ èç ñîïëà ãàçîâ â ýòîì ñå÷åíèè (ñèëà ñîïðî-
òèâëåíèÿ èñòå÷åíèþ ãàçîâ).
Òàêèì îáðàçîì, ïðèìåíèòåëüíî ê ñòåíäîâûì èñïûòàíèÿì ïîëó-
÷èì ôîðìóëó äëÿ ðàñ÷åòà òÿãè
P
dm
dt
WS
pp
aa
=+
−
îòí
()
.
(1.148)
Ñäåëàâ â óðàâíåíèè (1.148) çàìåíó
dm
dt
Q
g
=
ñåê
, íàéäåì âûðàæåíèå äëÿ
òÿãè â äðóãîé ôîðìå:
P
Q
g
WS
pp
aa
=+
−
ñåê
îòí
()
.
(1.149)
 ñëó÷àå, êîãäà ìîæíî ïðèíÿòü p ≈ 0, èìååì
P
Q
g
WS
p
aa
=+
ñåê
îòí
.
(1.150)
Åñëè ðàêåòà ðàñïîëîæåíà ó ïîâåðõíîñòè Çåìëè íà íóëåâîì óðîâ-
íå, òî äëÿ íîðìàëüíûõ ìåòåîóñëîâèé (y =0;p = pON) åå òÿãà ðàâíà
P
Q
g
WS
pp
aaO
N
=+
−
ñåê
îòí
()
.
(1.151)
75
Åñëè óñëîâèÿ îòëè÷íû îò íîðìàëüíûõ, òî ïðè y = 0 èìååì P = P0.
Ñðàâíèâàÿ ôîðìóëû (1.149) è (1.151), ïîëó÷èì
PPSp pp
ON
aON
ON
=+
−
(/)
.
1
(1.152)
Òàê êàê π(y)=p/pON, îêîí÷àòåëüíî áóäåì èìåòü
PP Sp
y
ON
aON
=+
−
[(
)
]
.
1π
(1.153)
Âûíîñÿ â ïðàâîé ÷àñòè ôîðìóëû (1.149) çà ñêîáêè Qñåê/g, ïîëó-
÷èì óïðîùåííóþ ôîðìóëó äëÿ òÿãè
P
Q
g
WmW
ee
==
ñåê
ñåê
,
(1.154)
ãäå
WW
Sg
Q
pp
e
a
a
=+
−
îòí
ñåê
()
(1.155)
–
âåëè÷èíà, íàçâàííàÿ ôðàíöóçñêèì ó÷åíûì Ï. Ëàíæåâåíîì
ýôôåêòèâíîé ñêîðîñòüþ èñòå÷åíèÿ ãàçîâ.
Ðàñ÷åòû ïîêàçûâàþò, ÷òî â ôîðìóëå (1.155) âòîðîå ñëàãàåìîå ïî
ñðàâíåíèþ ñ ïåðâûì ìàëî è ñîñòàâëÿåò îáû÷íî íå áîëåå 10...15 %,
ïîýòîìó ýôôåêòèâíàÿ ñêîðîñòü èñòå÷åíèÿ îïðåäåëÿåòñÿ â îñíîâíîì
ñêîðîñòüþ ãàçà â âûõîäíîì ñå÷åíèè ñîïëà Wîòí.
Åñëè îòíåñåì òÿãó ê ñåêóíäíîìó ðàñõîäó òîïëèâà, òî ïîëó÷èì
ôîðìóëó, îïðåäåëÿþùóþ óäåëüíûé èìïóëüñ òÿãè:
PJ
P
Q
y==
y
ñåê
.
(1.156)
Èç (1.149) èìååì
P
W
g
S
Q
pp
y
a
a
=+
−
îòí
ñåê
()
.
(1.157)
Îòñþäà âèäíî, ÷òî ñ óìåíüøåíèåì äàâëåíèÿ îêðóæàþùåãî ðàêå-
òó âîçäóõà óäåëüíûé èìïóëüñ òÿãè óâåëè÷èâàåòñÿ. Óäåëüíûé èì-
ïóëüñ òÿãè ïåðåìåíåí ïî âûñîòå è â êîñìîñå áîëüøå, ÷åì íà Çåìëå,
íà 10...15 %.
Âûðàæåíèå äëÿ óäåëüíîãî èìïóëüñà Jy ìîæåò áûòü òàêæå ïîëó÷å-
íî èç îáùåãî âûðàæåíèÿ, îïðåäåëÿþùåãî èìïóëüñ òÿãè, åñëè âçÿòü
76
We = const è îòíåñòè ïîëíûé èìïóëüñ òÿãè ê âåñó òîïëèâà Qò, ñãî-
ðåâøåãî çà âðåìÿ ðàáîòû äâèãàòåëÿ tê:
J
Q
Pdt
W
Qg
Qdt
e
tt
y
òò
ñåê
êê
==
∫∫
1
00
.
(1.158)
Ïðè Qñåê = const ïîëó÷èì Qdt
t
ñåê
ê
0
∫ =Qñåêtê = Qò, è òîãäà
JWg
e
y=
/.
(1.159)
Èç ñîïîñòàâëåíèÿ (1.155) è (1.157) òàêæå ñëåäóåò, ÷òî
PJ
W
g
y
e
==
y
.
(1.160)
1.6 . ÄÎÏÎËÍÈÒÅËÜÍÛÅ È ÓÏÐÀÂËßÞÙÈÅ ÑÈËÛ
È ÌÎÌÅÍÒÛ
1.6.1 . ÄÎÏÎËÍÈÒÅËÜÍÛÅ ÑÈËÛ È ÌÎÌÅÍÒÛ
Äîïîëíèòåëüíûå ñèëû è ìîìåíòû ìîæíî ðàçäåëèòü íà äâå áîëü-
øèå ãðóïïû: âíåøíèå (àýðîäèíàìè÷åñêèå) è âíóòðåííèå. È òå è
äðóãèå âîçíèêàþò ïðè ïðîñòðàíñòâåííîì êðèâîëèíåéíîì ïîëåòå è
ðàçëè÷íîãî ðîäà êîëåáàíèÿõ ËÀ.
Ê âíåøíèì äîïîëíèòåëüíûì ñèëàì è ìîìåíòàì îáû÷íî îòíîñÿò
ðàçëè÷íîãî ðîäà äåìïôèðóþùèå àýðîäèíàìè÷åñêèå ñèëû è ìîìåí-
òû; àýðîäèíàìè÷åñêèå ñèëû è ìîìåíòû, âûçâàííûå ñêîñîì ïîòîêà è
åãî çàïàçäûâàíèåì; ïåðåêðåñòíûå àýðîäèíàìè÷åñêèå ñèëû è ìîìåí-
òû, à ê âíóòðåííèì äîïîëíèòåëüíûì ôàêòîðàì – âíóòðåííèé ìî-
ìåíò äåìïôèðîâàíèÿ, îïðåäåëÿåìûé êîðèîëèñîâûì óñêîðåíèåì, è
äðóãèå ñèëû è ìîìåíòû, âûçâàííûå ïåðåìåùåíèåì òîïëèâà è ðàáî-
÷èõ ãàçîâ âíóòðè êîðïóñà ðàêåòû. Áîëüøèíñòâî äîïîëíèòåëüíûõ ñèë
è ìîìåíòîâ îïðåäåëÿåòñÿ óãëîâûìè ñêîðîñòÿìè ËÀ îòíîñèòåëüíî
åãî öåíòðà ìàññ.
Äåìïôèðóþùèå è ïåðåêðåñòíûå àýðîäèíàìè÷åñêèå ñèëû è ìî-
ìåíòû ðàññìîòðåíû âûøå. Ïåðå÷èñëèì çäåñü âíóòðåííèå äîïîëíè-
òåëüíûå ñèëû è èõ ìîìåíòû îòíîñèòåëüíî öåíòðà ìàññ: Ðãàç, Ìãàç –
ñèëà è ìîìåíò, îïðåäåëÿåìûå äâèæåíèåì ãàçîâ âíóòðè êîðïóñà ðà-
êåòû; Ðãàç.êîð, Ìãàç.êîð – ñèëà Êîðèîëèñà è ìîìåíò ýòîé ñèëû, îïðåäå-
ëÿåìûå äâèæåíèåì ãàçîâ âíóòðè êîëåáëþùåãîñÿ êîðïóñà ðàêåòû.
77
Ðàêåòû ñ äâèãàòåëåì íà æèäêîì òîïëèâå èñïûòûâàþò âëèÿíèå
äîïîëíèòåëüíûõ ñèë è ìîìåíòîâ, îïðåäåëÿåìûõ äâèæåíèåì êîìïî-
íåíòîâ òîïëèâà âíóòðè êîðïóñà ðàêåòû. Ïðè äâèæåíèè â ïëîòíûõ
ñëîÿõ àòìîñôåðû âëèÿíèå âíóòðåííèõ äîïîëíèòåëüíûõ ñèë è ìî-
ìåíòîâ íåçíà÷èòåëüíî ïî ñðàâíåíèþ ñ äåéñòâèåì îñíîâíûõ è äî-
ïîëíèòåëüíûõ âíåøíèõ àýðîäèíàìè÷åñêèõ ñèë è ìîìåíòîâ, è èõ â
ðàñ÷åòàõ íå ó÷èòûâàþò. Ïðè ïðîåêòíûõ ðàñ÷åòàõ õàðàêòåðèñòèê äâè-
æåíèÿ öåíòðà ìàññ ËÀ äîïîëíèòåëüíûå ñèëû è ìîìåíòû îáû÷íî íå
ó÷èòûâàþòñÿ.
1.6.2 . ÓÏÐÀÂËßÞÙÈÅ ÑÈËÛ È ÌÎÌÅÍÒÛ
Óïðàâëåíèå ðàêåòàìè è ñíàðÿäàìè â ïîëåòå îñóùåñòâëÿåòñÿ ñèñ-
òåìîé óïðàâëåíèÿ, íåîòúåìëåìîé ÷àñòüþ êîòîðîé ÿâëÿþòñÿ èñïîë-
íèòåëüíûå îðãàíû, èëè îðãàíû óïðàâëåíèÿ. Èñïîëíèòåëüíûå îðãà-
íû, èëè ðóëè, êàê èõ ÷àñòî íàçûâàþò, ñîçäàþò óïðàâëÿþùèå ñèëû è
ìîìåíòû. Ïî ïðèíöèïó ñîçäàíèÿ óïðàâëÿþùèõ ñèë è ìîìåíòîâ îð-
ãàíû óïðàâëåíèÿ ïðèíÿòî ðàçäåëÿòü íà òðè òèïà: àýðîäèíàìè÷åñêèå,
ãàçîäèíàìè÷åñêèå è ñìåøàííûå. Àýðîäèíàìè÷åñêèå (âîçäóøíûå),
èëè, êàê èõ èíîãäà íàçûâàþò, ñàìîëåòíûå, îðãàíû óïðàâëåíèÿ ðàáî-
òàþò òîëüêî â ïëîòíûõ ñëîÿõ àòìîñôåðû ïðè âçàèìîäåéñòâèè ñ ïî-
òîêîì âîçäóõà, îáòåêàþùèì ËÀ. Ãàçîäèíàìè÷åñêèå îðãàíû óïðàâëå-
íèÿ ìîãóò ðàáîòàòü è â íèæíèõ, è â âåðõíèõ ñëîÿõ àòìîñôåðû (êîñ-
ìè÷åñêîì ïðîñòðàíñòâå), òàê êàê îíè ôóíêöèîíèðóþò çà ñ÷åò
ýíåðãèè, âûäåëÿþùåéñÿ ïðè ñãîðàíèè òîïëèâà.
Ìíîãèå èç óïðàâëÿåìûõ îáúåêòîâ, íàïðèìåð ðàêåòû, ñàìîëåòû,
ñíàðÿäû, óïðàâëÿåìûå òîðïåäû è àâèàáîìáû, èìåþò òîëüêî àýðîäè-
íàìè÷åñêèå îðãàíû óïðàâëåíèÿ. Íåêîòîðûå ðàêåòû èìåþò êîìáè-
íèðîâàííûå îðãàíû óïðàâëåíèÿ, ñîñòîÿùèå èç ðàçëè÷íîãî ðîäà
àýðîäèíàìè÷åñêèõ è ãàçîäèíàìè÷åñêèõ óñòðîéñòâ. Àýðîäèíàìè÷å-
ñêèå îðãàíû óïðàâëåíèÿ îáû÷íî äåëÿòñÿ íà ðóëåâûå ïîâåðõíîñòè
(ðóëè), ïîâîðîòíûå êðûëüÿ è ïðåðûâàòåëè âîçäóøíîãî ïîòîêà (èí-
òåðöåïòîðû).
Ïðèíöèï äåéñòâèÿ ðóëåé è ïîâîðîòíûõ êðûëüåâ ñîñòîèò â òîì,
÷òî îíè, îòêëîíÿÿñü îò ñâîåãî íåéòðàëüíîãî ïîëîæåíèÿ è ïîâîðà÷è-
âàÿñü îòíîñèòåëüíî ñâÿçàííûõ îñåé ËÀ, èçìåíÿþò â ïðîöåññå ïîëå-
òà ñâîè óãëû àòàêè, ÷òî âûçûâàåò èçìåíåíèå óãëà àòàêè (èëè ñêîëü-
æåíèÿ) ËÀ â öåëîì.
Äëÿ ó÷åòà â óðàâíåíèÿõ äâèæåíèÿ óïðàâëÿþùèõ ñèë è ìîìåí-
òîâ íåîáõîäèìî âûäåëÿòü ñîñòàâëÿþùèå àýðîäèíàìè÷åñêèõ êîýô-
ôèöèåíòîâ, îïðåäåëÿåìûå ïîâîðîòîì óïðàâëÿþùèõ îðãàíîâ. Íà-
ïðèìåð, äëÿ ðóëåé òàíãàæà (âûñîòû) è ðûñêàíèÿ (íàïðàâëåíèÿ)
ïðîäîëüíàÿ, íîðìàëüíàÿ è ïîïåðå÷íàÿ óïðàâëÿþùèå ñèëû ñîîò-
âåòñòâåííî ðàâíû
78
XS
q
ccc
Y Sqc
Z Sqc
xxc
yz
pp
â
í
pp âpp
pp
â
p
í
p
â
=+
+
==
()
;
;
δδ
δ
δδ
δ
p
í
í
δ
δ,
(1.161)
ãäå Sp – õàðàêòåðíàÿ ïëîùàäü ðóëåé; q – ñêîðîñòíîé íàïîð; ñx p
í
δ
,c
xp
â
δ
,
cyp
â
δ
, czp
í
δ
–
ñîîòâåòñòâóþùèå ÷àñòíûå ïðîèçâîäíûå; δí è δâ – óãëû
îòêëîíåíèÿ ñîîòâåòñòâóþùèõ îðãàíîâ óïðàâëåíèÿ (ðóëåé).
Ìîìåíòíûå õàðàêòåðèñòèêè îïðåäåëÿþòñÿ ñ ó÷åòîì óãëîâûõ ñêî-
ðîñòåé ïîâîðîòà óïðàâëÿþùèõ îðãàíîâ:
mmm
mmm
yyy
zzz
pp
í
p
í
pp
âp
â
íí
ââ
=+
=+
δδ
δδ
δδ
δδ
•
•
•
;
•
.
(1.162)
Ìîìåíòû óïðàâëÿþùèõ ñèë
MS
q
l
mMS
q
l
m
yy
zz
pp
pp
==
;. (1.163)
 çàâèñèìîñòè îò íàçíà÷åíèÿ ðàêåòû èëè ñíàðÿäà è èõ àýðîäèíà-
ìè÷åñêîé êîìïîíîâêè âîçäóøíûå ðóëè ìîãóò ðàçìåùàòüñÿ â ðàç-
ëè÷íûõ ìåñòàõ êîðïóñà (ðèñ. 1.23). Äëÿ íàãëÿäíîñòè íà ðèñóíêå ðóëè
çàøòðèõîâàíû.
Ýôôåêòèâíîñòü îðãàíà óïðàâëåíèÿ îïðåäåëÿåòñÿ ïðèðàùåíèåì
ñîîòâåòñòâóþùåãî ìîìåíòà (èëè åãî êîýôôèöèåíòà) ïðè ïîëíîì îò-
êëîíåíèè îðãàíà óïðàâëåíèÿ îò åãî íåéòðàëüíîãî ïîëîæåíèÿ. Òàê,
ýôôåêòèâíîñòü îðãàíà óïðàâëåíèÿ òàíãàæîì îöåíèâàåòñÿ ∆mzâ –
ïðèðàùåíèåì êîýôôèöèåíòà ìîìåíòà òàíãàæà ïðè èçìåíåíèè óãëà
δâ íà ïîëíóþ âåëè÷èíó; ýôôåêòèâíîñòü îðãàíà óïðàâëåíèÿ êðå-
79
Ðèñ. 1.23. Ñõåìû ðàñïîëîæåíèÿ ðóëåé íà êîðïóñå ðàêåòû:
à – íîðìàëüíàÿ; á – "áåñõâîñòêà"; â – "óòêà"
íîì – ïðèðàùåíèåì ∆mxý, îïðåäåëÿåìûì ïîëíûì óãëîì îòêëîíåíèÿ
δý; ýôôåêòèâíîñòü îðãàíà óïðàâëåíèÿ ðûñêàíèåì – ïðèðàùåíèåì
∆myí, îïðåäåëÿåìûì ïîëíûì óãëîì îòêëîíåíèÿ δí. Ñîîòâåòñòâóþ-
ùèå êîýôôèöèåíòû ýôôåêòèâíîñòè îðãàíîâ óïðàâëåíèÿ îïðåäåëÿ-
þòñÿ ÷àñòíûìè ïðîèçâîäíûìè
m
m
m
m
m
m
z
z
x
x
y
y
δδδ
∂
∂δ
∂
∂δ
∂
∂δ
âýí
âýí
===
;;,
îòíîñÿùèìèñÿ ê ñòàòè÷åñêèì ïðîèçâîäíûì.
Ãëàâà 2
ÒÅÎÐÅÒÈ×ÅÑÊÈÅ ÎÑÍÎÂÛ ÑÎÑÒÀÂËÅÍÈß
ÌÀÒÅÌÀÒÈ×ÅÑÊÈÕ ÌÎÄÅËÅÉ ÄÂÈÆÅÍÈß ËÀ
Ïîä ìîäåëüþ ïîíèìàþò óïðîùåííîå ìàòåìàòè÷åñêîå îïèñàíèå ðàññìàòðèâàå-
ìîé äèíàìè÷åñêîé ñèñòåìû èëè ïðîöåññà, â ÷àñòíîñòè ïðîöåññà äâèæåíèÿ ËÀ, ïî-
çâîëÿþùåå ïðîèçâîäèòü ðàçëè÷íûå òåîðåòè÷åñêèå èññëåäîâàíèÿ â çàâèñèìîñòè îò
ïîñòàâëåííîé çàäà÷è è ïðèíèìàåìûõ äîïóùåíèé. Ñîñòàâëåíèå ìîäåëåé, õàðàêòåðè-
çóþùèõ ñîñòîÿíèå ËÀ, îñíîâûâàåòñÿ íà èçâåñòíûõ ìåòîäàõ êëàññè÷åñêîé òåîðåòè-
÷åñêîé ìåõàíèêè è ðàêåòîäèíàìèêè. Õàðàêòåð ïðåäñòàâëåíèÿ ìîäåëåé ðàçëè÷àåòñÿ
â çàâèñèìîñòè îò óðîâíÿ ðàñïîëàãàåìîé èíôîðìàöèè î âíåøíèõ óñëîâèÿõ ïîëåòà è
íåîáõîäèìîé ñòåïåíè äîñòîâåðíîñòè îòðàæåíèÿ ìîäåëüþ ðåàëüíîãî ôèçè÷åñêîãî
ïðîöåññà.
2.1. ÊËÀÑÑÈÔÈÊÀÖÈß È ÔÎÐÌÛ ÏÐÅÄÑÒÀÂËÅÍÈß
ÌÀÒÅÌÀÒÈ×ÅÑÊÈÕ ÌÎÄÅËÅÉ
2.1.1 . ËÀ ÊÀÊ ÄÈÍÀÌÈ×ÅÑÊÀß ÑÈÑÒÅÌÀ
Ïîëó÷åíèå ìàòåìàòè÷åñêèõ ìîäåëåé, îïèñûâàþùèõ ñîñòîÿíèå
ËÀ, èìååò ñâîåé öåëüþ, êàê ïðàâèëî, îïðåäåëåíèå èñêîìûõ ïàðà-
ìåòðîâ äâèæåíèÿ: êîìïîíåíòîâ ñêîðîñòè äâèæåíèÿ öåíòðà ìàññ, óã-
ëîâîé ñêîðîñòè ËÀ îòíîñèòåëüíî åãî öåíòðà ìàññ, óãëîâ, õàðàêòåðè-
çóþùèõ îðèåíòàöèþ àïïàðàòà, è, íàêîíåö, êîîðäèíàò öåíòðà ìàññ,
ïî êîòîðûì ìîæåò áûòü ïîñòðîåíà òðàåêòîðèÿ. Ïîä òðàåêòîðèåé ËÀ
ïðèíÿòî ïîíèìàòü íåïðåðûâíóþ ëèíèþ, êîòîðóþ îïèñûâàåò öåíòð
80
ìàññ ËÀ îòíîñèòåëüíî âûáðàííîé áàçîâîé ñèñòåìû îòñ÷åòà (ñèñòå-
ìû êîîðäèíàò).  êà÷åñòâå íåçàâèñèìîé ïåðåìåííîé (ãëàâíîãî àðãó-
ìåíòà) â ìàòåìàòè÷åñêèõ ìîäåëÿõ äâèæåíèÿ ËÀ âûñòóïàåò òåêóùåå
âðåìÿ.
Îñíîâó ìàòåìàòè÷åñêèõ ìîäåëåé, õàðàêòåðèçóþùèõ ñîñòîÿíèå
ËÀ, ñîñòàâëÿþò äèôôåðåíöèàëüíûå óðàâíåíèÿ äâèæåíèÿ. Äëÿ
òîãî ÷òîáû ïîëó÷èòü èõ ðåøåíèå â êîíå÷íîé ôîðìå, äîëæíû
áûòü îäíîçíà÷íî çàäàíû íà÷àëüíûå óñëîâèÿ è îïðåäåëåíû ñèëû,
ñòîÿùèå â ïðàâûõ ÷àñòÿõ äèôôåðåíöèàëüíûõ óðàâíåíèé. Ïðè
ýòîì íåñóùåñòâåííî, â êàêîé ôîðìå çàäàþòñÿ âîçäåéñòâèÿ (äå-
òåðìèíèðîâàííûé èëè ñòîõàñòè÷åñêèé ïîäõîä); âàæíî, ÷òîáû
ïðèíÿòàÿ ìîäåëü ñèë õàðàêòåðèçîâàëàñü ïîëíîé èíôîðìàöèåé îá
èõ çíà÷åíèÿõ íà ðàññìàòðèâàåìîì èíòåðâàëå âðåìåíè. Èìåííî
ýòà ïîëíàÿ ñîâîêóïíîñòü ñèë, îïðåäåëÿþùàÿ âèä âõîäíûõ âîç-
äåéñòâèé, áóäåò õàðàêòåðèçîâàòü ñîñòîÿíèå ËÀ â äàííûé è ïîñëå-
äóþùèå ìîìåíòû âðåìåíè ÷åðåç åãî ôàçîâûå êîîðäèíàòû.
Îáû÷íî ñèñòåìû, òåêóùåå ñîñòîÿíèå êîòîðûõ îäíîçíà÷íî îïðå-
äåëåíî, åñëè èçâåñòíû èõ íà÷àëüíîå ñîñòîÿíèå è âõîäíûå âîçäåéñò-
âèÿ íà ðàññìàòðèâàåìîì èíòåðâàëå âðåìåíè, ò.å .
xx
() [,,(),(,)],
tt
ttt
t
=φ
η
000
(2.1)
íàçûâàþò äèíàìè÷åñêèìè ñèñòåìàìè.
 ôóíêöèîíàëüíîé çàâèñèìîñòè (2.1) ìíîæåñòâî çíà÷åíèé âåê-
òîðà ñîñòîÿíèÿ x(t) õàðàêòåðèçóåò îáëàñòü âîçìîæíûõ ñîñòîÿíèé
ñèñòåìû, à ñëåäîâàòåëüíî, è åå òðàåêòîðèé â ïðîñòðàíñòâå. Êîìïî-
íåíòû âåêòîðà x(t) íàçûâàþòñÿ ïåðåìåííûìè ñîñòîÿíèÿ. Ôóíêöèÿ φ
ïðåäñòàâëÿåò ñîáîé ïåðåõîäíóþ ôóíêöèþ ñîñòîÿíèÿ ñèñòåìû, η(t)îï-
ðåäåëÿåò õàðàêòåð âõîäíûõ âîçäåéñòâèé. Îãðàíè÷åíèÿ, íàêëàäûâàå-
ìûå â êàæäîì êîíêðåòíîì ñëó÷àå íà η(t0, t), äèêòóþòñÿ óñëîâèÿìè
ðåøàåìîé çàäà÷è, õàðàêòåðèñòèêàìè âíåøíåé ñðåäû è äðóãèìè ôàê-
òîðàìè.
Ïåðåõîäíàÿ ôóíêöèÿ ñîñòîÿíèÿ ñèñòåìû, ìîäåëü êîòîðîé ïðåä-
ñòàâëÿåòñÿ â ôîðìå äèôôåðåíöèàëüíûõ óðàâíåíèé äâèæåíèÿ, åñòü
íå ÷òî èíîå, êàê ðåøåíèå ýòèõ óðàâíåíèé äëÿ âñåõ t ∈ T, ãäå ìíîæå-
ñòâî ìîìåíòîâ âðåìåíè Ò ÿâëÿåòñÿ ìíîæåñòâîì âåùåñòâåííûõ ÷è-
ñåë. Äèíàìè÷åñêàÿ ñèñòåìà, óäîâëåòâîðÿþùàÿ ïåðåõîäíîé ôóíêöèè
ñîñòîÿíèÿ òàêîãî òèïà, íàçûâàåòñÿ îáûêíîâåííîé äèíàìè÷åñêîé ñèñ-
òåìîé.
Ïðåäñòàâëåíèå ËÀ â êà÷åñòâå äèíàìè÷åñêîé ñèñòåìû ïîçâîëÿåò
ðàññìàòðèâàòü íåóïðàâëÿåìûé ïîëåò ðàêåò è ñíàðÿäîâ êàê ÷àñòíûé
ñëó÷àé óïðàâëÿåìîãî ïîëåòà ñ ïðèâëå÷åíèåì ýôôåêòèâíûõ ìåòîäîâ,
áàçèðóþùèõñÿ íà ïîíÿòèè ïðîñòðàíñòâà ñîñòîÿíèé, ðàçðàáîòàííûõ
ãëàâíûì îáðàçîì äëÿ óïðàâëÿåìûõ äèíàìè÷åñêèõ ñèñòåì. Àíàëèç
81
äèíàìèêè íåóïðàâëÿåìûõ ðàêåò è ñíàðÿäîâ êàê îáûêíîâåííûõ äè-
íàìè÷åñêèõ ñèñòåì îáåñïå÷èâàåò îïðåäåëåííóþ ïðååìñòâåííîñòü
ïî îòíîøåíèþ ê ñîîòâåòñòâóþùèì ìåòîäàì, è îñîáåííî â òîì ñëó-
÷àå, êîãäà çàäà÷à ïî ñâîåé ïîñòàíîâêå òðåáóåò "ñøèâàíèÿ" ðåçóëüòà-
òîâ èññëåäîâàíèÿ íåóïðàâëÿåìîãî è óïðàâëÿåìîãî äâèæåíèÿ, â ÷àñò-
íîñòè ïðèìåíèòåëüíî ê ðàçäåëÿþùèìñÿ è êîððåêòèðóåìûì áîåïðè-
ïàñàì.
 ïðîöåññå ïîëåòà îáû÷íî èìååò ìåñòî ñóùåñòâåííîå èçìåíåíèå
äèíàìè÷åñêèõ, ìàññîâûõ è äðóãèõ õàðàêòåðèñòèê ËÀ. Âàðèàöèè ýòèõ
õàðàêòåðèñòèê îáóñëîâëèâàþòñÿ ñóùåñòâåííûìè ñåêóíäíûìè ìàñ-
ñîâûìè ðàñõîäàìè òîïëèâà, ïåðåìåùåíèåì ËÀ ñ ïåðåìåííîé ñêîðî-
ñòüþ â àòìîñôåðå, ïëîòíîñòü êîòîðîé ìåíÿåòñÿ ñ âûñîòîé, íåñòà-
áèëüíîñòüþ ãåîôèçè÷åñêèõ ïîëåé Çåìëè è ò.ä. Âñå ýòî äàåò îñíîâà-
íèå ðàññìàòðèâàòü ËÀ êàê íåñòàöèîíàðíóþ äèíàìè÷åñêóþ ñèñòåìó.
Áîëåå òîãî, äëÿ ïîäàâëÿþùåãî áîëüøèíñòâà ñëó÷àåâ ïðèõîäèòñÿ
èìåòü äåëî ñ íåëèíåéíûìè íåñòàöèîíàðíûìè äèíàìè÷åñêèìè ñèñòå-
ìàìè. Íåëèíåéíîñòü óðàâíåíèé äâèæåíèÿ îïðåäåëÿåòñÿ ðÿäîì âõî-
äÿùèõ â íèõ íåëèíåéíûõ çàâèñèìîñòåé. Íàïðèìåð, çàâèñèìîñòè
àýðîäèíàìè÷åñêèõ ñèë è ìîìåíòîâ îò ïàðàìåòðîâ äâèæåíèÿ, âðå-
ìåííûå çàâèñèìîñòè ìàññîâûõ è èíåðöèîííûõ õàðàêòåðèñòèê,
ñêà÷êîîáðàçíî èçìåíÿþùèåñÿ â ðåçóëüòàòå ðàçäåëåíèÿ ñòóïåíåé,
îòäåëåíèÿ ýëåìåíòîâ êîíñòðóêöèè ðàêåòû è äð.
Îòñþäà ìû äåëàåì âûâîä, ÷òî ìàòåìàòè÷åñêèå ìîäåëè ËÀ êàê íå-
ëèíåéíûå íåñòàöèîíàðíûå îáûêíîâåííûå äèíàìè÷åñêèå ñèñòåìû
äîëæíû èìåòü äîñòàòî÷íî âûñîêèé ïîðÿäîê. Ââèäó òîãî ÷òî ïîðÿäîê
ñèñòåìû äèôôåðåíöèàëüíûõ óðàâíåíèé, îïèñûâàþùèõ äâèæåíèå
ìàòåðèàëüíîé ñèñòåìû ñ êîíå÷íûì ÷èñëîì ñòåïåíåé ñâîáîäû, ðàâåí
óäâîåííîìó êîëè÷åñòâó ñòåïåíåé ñâîáîäû äàæå â ïðîñòåéøåì ñëó-
÷àå ðàññìîòðåíèÿ ËÀ êàê òâåðäîãî òåëà, ñèñòåìà äèôôåðåíöèàëüíûõ
óðàâíåíèé åãî äâèæåíèÿ áóäåò èìåòü 12-é ïîðÿäîê. Ïîýòîìó ðåøå-
íèå ëþáîé çàäà÷è èññëåäîâàíèÿ äèíàìèêè ËÀ íåîáõîäèìî íà÷èíàòü
ñ îáîñíîâàíèÿ ðàöèîíàëüíîé ìàòåìàòè÷åñêîé ìîäåëè ïîëåòà. Òîëü-
êî ïîñëå ýòîãî îñóùåñòâëÿåòñÿ åå ñîñòàâëåíèå èëè óïðîùåíèå äî
òðåáóåìîãî óðîâíÿ ñõåìàòèçàöèè èçâåñòíîé áîëåå ïîëíîé ñèñòåìû
äèôôåðåíöèàëüíûõ óðàâíåíèé.
2.1 .2. ÂÎÇÌÎÆÍÛÅ ÂÈÄÛ ÌÀÒÅÌÀÒÈ×ÅÑÊÈÕ ÌÎÄÅËÅÉ
Ïî ñâîåìó ïîñòðîåíèþ ìîäåëè äåëÿòñÿ íà ìîäåëè ñ îïðåäåëåí-
íîé, íåîïðåäåëåííîé è ñìåøàííîé ñòðóêòóðàìè.
Ê ìîäåëÿì ñ îïðåäåëåííîé ñòðóêòóðîé (èëè îïðåäåëåííûì ìîäå-
ëÿì) îòíîñÿòñÿ ìîäåëè, îòâå÷àþùèå ïîëíîìó (äåòåðìèíèðîâàííîìó
èëè ñòîõàñòè÷åñêîìó) óðîâíþ èíôîðìàòèâíîñòè î ñîñòîÿíèè èñ-
ñëåäóåìîãî ËÀ. Ïðèìåíåíèå äàííûõ ìîäåëåé ïðåäïîëàãàåò íàëè÷èå
82
ñâåäåíèé î õàðàêòåðå äâèæåíèÿ, îñóùåñòâëÿåìîãî â ðàìêàõ ðåàëè-
çóåìîé ñõåìû ïðè îòñóòñòâèè èëè ïðè íàëè÷èè âîçìóùåíèé, âåëè-
÷èíà êîòîðûõ çàðàíåå èçâåñòíà.  ñëó÷àå, êîãäà âîçìóùåíèÿ íîñÿò
ñëó÷àéíûé õàðàêòåð, èñïîëüçóþò ïîíÿòèå ñòîõàñòè÷åñêîé îïðåäåëåí-
íîé ìîäåëè, äëÿ êîòîðîé ïàðàìåòðû ðàñïðåäåëåíèÿ âåðîÿòíîñòè ñëó-
÷àéíûõ âîçìóùåíèé äîëæíû áûòü çàäàíû. Ïðè ïðåäïîëîæåíèè î
òîì, ÷òî ñëó÷àéíûå âîçìóùåíèÿ íå äåéñòâóþò, îïðåäåëåííàÿ ìîäåëü
íàçûâàåòñÿ äåòåðìèíèðîâàííîé. Åñëè îòñóòñòâóåò äîñòîâåðíàÿ èí-
ôîðìàöèÿ î âîçìîæíîì ñîñòîÿíèè ñèñòåìû, ðàçðàáîòêà æåñòêîé,
ò.å . îäíîçíà÷íî çàäàííîé ðàñ÷åòíîé, ñõåìû îêàçûâàåòñÿ íåâîçìîæ-
íîé. Äàííàÿ ñèòóàöèÿ ñîîòâåòñòâóåò íåîïðåäåëåííîìó óðîâíþ èí-
ôîðìàòèâíîñòè, êîòîðîìó îòâå÷àþò äåòåðìèíèðîâàííûå èëè ñòîõàñ-
òè÷åñêèå íåîïðåäåëåííûå ìîäåëè. Íàêîíåö, ñìåøàííûå ìîäåëè çà-
íèìàþò ïðîìåæóòî÷íîå ïîëîæåíèå ìåæäó îïðåäåëåííûìè è
íåîïðåäåëåííûìè ìîäåëÿìè. Äëÿ íèõ õàðàêòåðíî òî, ÷òî õîòÿ äâè-
æåíèå ËÀ ïîä äåéñòâèåì âîçìóùåíèé è ñóùåñòâåííî îòëè÷àåòñÿ îò
ðàñ÷åòíîãî, íî îñòàåòñÿ â ïðåäåëàõ îáëàñòè äåéñòâèÿ ïðèíÿòîé ðàñ-
÷åòíîé ñõåìû, îïðåäåëÿåìîé ââåäåííîé ìîäåëüþ è çàäàííûìè äî-
ïóñòèìûìè ìíîæåñòâàìè, ê êîòîðûì ïðèíàäëåæàò óêàçàííûå âîç-
ìóùåíèÿ. Ïðè ýòîì ëþáàÿ èíàÿ èíôîðìàöèÿ î õàðàêòåðå è âîçìîæ-
íûõ çíà÷åíèÿõ äåéñòâóþùèõ âîçìóùåíèé îáû÷íî îòñóòñòâóåò.
Íåîïðåäåëåííûå è ñìåøàííûå ìîäåëè èñïîëüçóþòñÿ â ðàìêàõ òåî-
ðåòèêî-èãðîâîãî (ìèíèìàêñíîãî) ïîäõîäà ê ðåøåíèþ èññëåäóåìûõ
çàäà÷ [35].
Îïðåäåëåííûå è ñìåøàííûå ìîäåëè çàäàþòñÿ, êàê ïðàâèëî, â
âèäå äèôôåðåíöèàëüíûõ óðàâíåíèé äâèæåíèÿ (äåòåðìèíèðîâàííûõ
èëè ñòîõàñòè÷åñêèõ) èëè â âèäå êîíå÷íûõ àíàëèòè÷åñêèõ çàâèñèìî-
ñòåé. Íåîïðåäåëåííûì ìîäåëÿì â áîëüøåé ñòåïåíè îòâå÷àåò ñõåìà
ïðåäñòàâëåíèÿ êîìïîíåíòîâ âåêòîðà ñîñòîÿíèÿ ñèñòåìû â âèäå êà-
êèõ-ëèáî ôîðìàëüíûõ ðàçëîæåíèé. Ïîìèìî ôîðìàëüíûõ ïðèìåíÿ-
þò òàêæå ôàêòîðíûå ìîäåëè [17].  ñâîþ î÷åðåäü ìîäåëè, ïðåäñòàâ-
ëåííûå â âèäå äèôôåðåíöèàëüíûõ óðàâíåíèé, ïîäðàçäåëÿþòñÿ íà
ëèíåéíûå è íåëèíåéíûå. Íàêîíåö, â çàâèñèìîñòè îò õàðàêòåðà èçìå-
íåíèÿ (íåïðåðûâíîãî èëè äèñêðåòíîãî) àðãóìåíòà, â ôóíêöèè êîòî-
ðîãî ïðîèñõîäèò ðàçâèòèå ïðîöåññà (îáû÷íî âðåìåíè), ìîäåëè ïîä-
ðàçäåëÿþò íà íåïðåðûâíûå è äèñêðåòíûå.
Ïðèìåðîì ôóíêöèîíàëüíîãî ïðåäñòàâëåíèÿ îïðåäåëåííîé ìîäå-
ëè îáûêíîâåííîé äèíàìè÷åñêîé ñèñòåìû êàê íåñòàöèîíàðíîãî íå-
ëèíåéíîãî óïðàâëÿåìîãî îáúåêòà, ïîäâåðæåííîãî äåéñòâèþ âîçìó-
ùåíèé ηi(t), ìîæåò ñëóæèòü ìîäåëü âèäà
d
dt
tttt
tt
tt
xx
u
yx
u
() [, (), (), ()];
() [, (), ()],
=
=
φη
τ
ψ
(2.2)
83
ãäå u(t) – âåêòîð óïðàâëåíèÿ èëè (áîëåå øèðîêîå ïîíÿòèå) âåêòîð
âõîäíûõ ïåðåìåííûõ; y(t) – âåêòîð âûõîäíûõ ïåðåìåííûõ ñèñòåì.
Ìàòåìàòè÷åñêàÿ ìîäåëü ëèíåéíîé íåñòàöèîíàðíîé ñèñòåìû ñ
íåïðåðûâíûì âðåìåíåì áóäåò èìåòü âèä
d
dt
tt
tt
tt
t
t
t
xA
xB
uF
xx
yC
() ()() ()() ()();
();
()
=++
=
=
η
00
()() ()(),
tt tt
xD
u
+
(2.3)
ãäå A, B, F, C è D – ìàòðèöû ñîîòâåòñòâóþùèõ ðàçìåðíîñòåé,
ÿâëÿþùèåñÿ ôóíêöèÿìè âðåìåíè.
Äëÿ ÷àñòíîãî ñëó÷àÿ ñòàöèîíàðíîé ñèñòåìû (îáúåêòà ñ ïîñòîÿí-
íûìè ïàðàìåòðàìè) óêàçàííûå ìàòðèöû èìåþò ïîñòîÿííûå, íå çà-
âèñÿùèå îò âðåìåíè ýëåìåíòû.
Äâèæåíèå ëèíåéíîãî îáúåêòà ñ äèñêðåòíûì âðåìåíåì îïèñûâà-
åòñÿ ðàçíîñòíûì óðàâíåíèåì òèïà
∆xA
xB
uF
xx
() ()() ()() ()();
().
tt
tt
tt
t
=++
=
η
00
(2.4)
Âñå îáîçíà÷åíèÿ, íàèìåíîâàíèÿ è ñìûñë âåêòîðîâ, à òàêæå ìàòðèö
ñîõðàíÿþòñÿ òàêèìè æå, êàê è äëÿ äèíàìè÷åñêèõ ñèñòåì ñ
íåïðåðûâíûì âðåìåíåì. Ïîñêîëüêó ïîä t â îáúåêòàõ ñ äèñêðåòíûì
âðåìåíåì ïîíèìàåòñÿ íîìåð òàêòà, ïðèíèìàþùåãî öåëî÷èñëåííûå
çíà÷åíèÿ, t =0,1,2,...,n, òî ïðîèçâîäíàÿ çäåñü çàìåíÿåòñÿ ïåðâîé
ðàçíîñòüþ
∆xx
x
=+
−
()(
)
.
tt
1
(2.5)
Ïðè ýòîì ñ öåëüþ èñêëþ÷åíèÿ íåäîðàçóìåíèé, êàñàþùèõñÿ
òðàêòîâêè ðàçìåðíîñòè âåëè÷èíû t, â ðàçíîñòíîì óðàâíåíèè
ïîñëåäíþþ ÷àñòî çàìåíÿþò íà k.
Ïåðåõîä îò íåëèíåéíûõ ìîäåëåé ê ëèíåéíûì îñóùåñòâëÿåòñÿ ïó-
òåì ëèíåàðèçàöèè èñõîäíîé íåëèíåéíîé ìîäåëè. Äëÿ ïðîâåäåíèÿ
ëèíåàðèçàöèè âûäâèãàþòñÿ òðåáîâàíèÿ âûïîëíåíèÿ ðÿäà óñëîâèé.
Îñíîâíûì ÿâëÿåòñÿ òðåáîâàíèå, êàñàþùååñÿ ìàëîñòè îòêëîíåíèé
ïàðàìåòðîâ âîçìóùåííîãî äâèæåíèÿ îò èõ íîìèíàëüíûõ çíà÷åíèé.
Îáû÷íî ïðèíèìàåòñÿ, ÷òî åñëè îòêëîíåíèÿ âõîäíûõ ïàðàìåòðîâ
ñèñòåì è âûçûâàåìûå èìè îòêëîíåíèÿ δx(t) íå ïðåâîñõîäÿò 3...5 %
íîìèíàëà, òî òàêîå òðåáîâàíèå âûïîëíÿåòñÿ. Ýòî äàåò îñíîâàíèå
ïðåäñòàâëÿòü âîçìóùåííîå äâèæåíèå â âèäå ëèíåéíîé êîìáèíàöèè
84
uuu
xxx x
() () (),
;
()()()()
*
*
ttt
t
t
t
ttt t
=+≤
≤
=+
=
δ
δ
01
0
ïðè
xx
*
() (),
tt
00
+δ
(2.6)
ãäå ïàðàìåòðû, îáîçíà÷åííûå çâåçäî÷êîé, îòâå÷àþò íîìèíàëüíîìó
íåâîçìóùåííîìó äâèæåíèþ. Ïîäñòàíîâêà ñèñòåìû óðàâíåíèé (2.6) â
èñõîäíóþ ñèñòåìó (2.2) ïðè η(t)=0èååïîñëåäóþùåå ðàçëîæåíèå â
ðÿä Òåéëîðà ïðèâîäèò ê âûðàæåíèþ
•
() •()
•
() [(),();] [(),(
**
*
*
*
xxxxu
xu
x
ttt tt
ttt
=+=
+
δφ
Φ
);
]•() [(), ;]() (),
.
**
tt
t tt tttt
δδ
δ
xx
u
u
u
++
≤
≤
ΦΦ
01
(2.7)
Çäåñü δΦ(t) – îñòàòî÷íûé ÷ëåí ðàçëîæåíèÿ, ó÷èòûâàþùåãî òîëüêî
ëèíåéíûå ÷ëåíû; Φx è Φu – ÿêîáèàíû (êâàäðàòíûå ìàòðèöû ÷àñòíûõ
ïðîèçâîäíûõ – âåñîâûõ êîýôôèöèåíòîâ) ôóíêöèè φ îòíîñèòåëüíî x
è u ñîîòâåòñòâåííî. Èñõîäíûå ïðåäïîñûëêè äàþò îñíîâàíèå ñ÷èòàòü
δΦ(t) íåñîèçìåðèìî ìàëûì ïî îòíîøåíèþ ê óäåðæèâàåìûì ÷ëåíàì
ëèíåéíîãî ðàçëîæåíèÿ. Òîãäà ëèíåàðèçîâàííîå äèôôåðåíöèàëüíîå
óðàâíåíèå ñîñòîÿíèÿ ïðèîáðåòàåò âèä
d
dt
tt
tt
t
t
t
t
[()] ()()()(),
.
δδδ
xA
xB
u
=+≤
≤
01
(2.8)
 çàäà÷àõ, ñâÿçàííûõ ñ èññëåäîâàíèåì äèíàìèêè ñèñòåì ïðè îò-
ñëåæèâàíèè íîìèíàëüíîé òðàåêòîðèè, õàðàêòåð ñîáñòâåííî íîìè-
íàëüíîãî äâèæåíèÿ ÷àñòî íå ïðåäñòàâëÿåò èíòåðåñà. Ïîýòîìó â (2.6)
ìîæíî ïîëîæèòü x*(t) = 0, è òîãäà x(t)=δx(t), ÷òî ïðèâîäèò ê êàíî-
íè÷åñêîé ôîðìå ìàòåìàòè÷åñêîé ìîäåëè ñîñòîÿíèÿ ëèíåéíîé íå-
ñòàöèîíàðíîé ñèñòåìû òèïà (2.3):
d
dt
tt
tt
tt
xA
xB
uxx
() ()() ()(), ()
.
=+
=
00
(2.9)
Äëÿ òîãî ÷òîáû çàïèñàòü ñîîòâåòñòâóþùèå óðàâíåíèÿ äëÿ íå-
óïðàâëÿåìîé äèíàìè÷åñêîé ñèñòåìû (íåóïðàâëÿåìîãî ËÀ), äîñòà-
òî÷íî ïîëîæèòü â ðàññìîòðåííûõ çàâèñèìîñòÿõ u(t) = 0. Òîãäà
ôóíêöèîíàëüíîå ñîîòíîøåíèå (2.2) ïðèìåò âèä
d
dt
tttt
tttt
xF
x
yx
() [; (), ()];
() [; (); ()],
=
=
η
ψ
(2.10)
85
à óðàâíåíèå (2.9) – âèä
d
dt
tt
tt
xA
xxx
() ()(), ()
.
==
00
(2.11)
Èç ñòðóêòóðû óðàâíåíèÿ (2.11) ñëåäóåò, ÷òî äëÿ íåóïðàâëÿåìîãî
äâèæåíèÿ ôàêòîðîì,
"ïîðîæäàþùèì" ïðîöåññ îòêëîíåíèé îò
íîìèíàëà, ÿâëÿåòñÿ çàäàííàÿ â âèäå íà÷àëüíûõ óñëîâèé
ñîâîêóïíîñòü îòêëîíåíèé ïàðàìåòðîâ x0 (íà÷àëüíûõ çíà÷åíèé
îòêëîíåíèé ïåðåìåííûõ ñîñòîÿíèÿ ËÀ).
×òîáû ïîëó÷èòü ìîäåëü, îòâå÷àþùóþ ñòîõàñòè÷åñêîé ñèñòåìå,
íà ïåðâûé âçãëÿä ìîæåò ïîêàçàòüñÿ äîñòàòî÷íûì ïðîñòî äîáàâèòü ê
ïðàâîé ÷àñòè äåòåðìèíèðîâàííîãî óðàâíåíèÿ ñîñòîÿíèÿ ñèñòåìû
ñîîòâåòñòâóþùóþ ñëó÷àéíóþ ñîñòàâëÿþùóþ. Îäíàêî ýòî íå òàê.
Äåéñòâèòåëüíî, ðàññìîòðèì äëÿ îáùíîñòè äåòåðìèíèðîâàííóþ ìî-
äåëü ñîñòîÿíèÿ ñèñòåìû
d
dt
tttt
xx
() [; (), ()],
=φ
η
(2.12)
â êîòîðîé η(t) ïðåäñòàâëÿåò ñîáîé âåêòîð äåòåðìèíèðîâàííûõ
âõîäíûõ âîçäåéñòâèé, à òàêæå "ñòîõàñòè÷åñêóþ" ìîäåëü.
d
dt
tttt t
xx
x
() [;(),()] (,),
*
=+
φη
η
(2.13)
ãäå η
*
(x, t) – ñëó÷àéíûé ïðîöåññ ñ çàäàííûìè ñâîéñòâàìè. Ê ÷èñëó
òàêèõ
ñâîéñòâ äîëæíû áûòü
îòíåñåíû:
íåïðåðûâíîñòü,
íåçàâèñèìîñòü η*(t)èη(τ) ïðè t ≠τè íàëè÷èå êîíå÷íîé
(îãðàíè÷åííîé) äèñïåðñèè, îïðåäåëÿþùåé ðàçáðîñ (îòêëîíåíèÿ).
Óñëîâèå êîíå÷íîé äèñïåðñèè âûòåêàåò èç ðåàëüíûõ ñâîéñòâ
äåéñòâóþùèõ íà ËÀ âîçìóùåíèé; íåïðåðûâíîñòü åñòü ñëåäñòâèå
âûáîðà êëàññà ìîäåëè â âèäå ñèñòåìû äèôôåðåíöèàëüíûõ
óðàâíåíèé. Òðåáîâàíèå íåçàâèñèìîñòè η
*
(t)èη
*
(τ) äèêòóåòñÿ òåì, ÷òî
â ïðîòèâíîì ñëó÷àå ðàñïðåäåëåíèå dx/dt áóäåò çàâèñåòü íå òîëüêî îò
òåêóùåãî ñîñòîÿíèÿ (÷òî íåîáõîäèìî äëÿ äàííîé ìîäåëè), íî è îò åãî
ïðåäûñòîðèè.
Ïðè îãîâîðåííûõ óñëîâèÿõ èíòåãðàë îò η*(τ) ñóùåñòâóåò, à åãî
ìàòåìàòè÷åñêîå îæèäàíèå ðàâíî íóëþ, ò.å . M ητ τ
*
().
d=
∫ 0 Ñóùåñòâó-
åò è ñðåäíèé êâàäðàò ïðîèçâîäíîé, êîòîðûé â ñèëó îãðàíè÷åííîñòè
äèñïåðñèè è íåçàâèñèìîñòè η*(t)èη*(τ) áóäåò òàêæå ðàâåí íóëþ íà
86
îñíîâàíèè íåðàâåíñòâà Øâàðöà: M[η*2(t)] = 0. Ïðè ýòîì ìîäåëü ñèñ-
òåìû â ôîðìå (2.13) íå áóäåò óäîâëåòâîðÿòü ñòîõàñòè÷åñêîé ìîäåëè
ñîñòîÿíèÿ ñ æåëàåìûìè ñòàòèñòè÷åñêèì ñâîéñòâàìè. ×òîáû ïîëó-
÷èòü êîððåêòíóþ ñòîõàñòè÷åñêóþ ìîäåëü ñîñòîÿíèÿ ñèñòåìû ñ íå-
ïðåðûâíûì âðåìåíåì, ñëåäóåò èñïîëüçîâàòü ñòîõàñòè÷åñêèå äèôôå-
ðåíöèàëüíûå óðàâíåíèÿ.  ýòîì ñëó÷àå îñëàáëÿåòñÿ òðåáîâàíèå ê êî-
íå÷íîñòè äèñïåðñèè äåéñòâóþùåãî âîçìóùåíèÿ. Åñòåñòâåííî, ýòî
ïðèâîäèò ê ñíèæåíèþ óðîâíÿ àäåêâàòíîñòè ïîëó÷àåìîé ìîäåëè ïî
îòíîøåíèþ ê ðåàëüíîìó ïðîöåññó, íî ïîçâîëÿåò óïðîñòèòü ïðîöåññ
èññëåäîâàíèÿ. Ïîñêîëüêó η*(t) â ñòîõàñòè÷åñêèõ ìîäåëÿõ íå èìååò
êîíå÷íîé äèñïåðñèè: Dη*(t) →∞, òî íå áóäåò åå èìåòü è ïðîèçâîäíàÿ
dx/dt. Ñëåäîâàòåëüíî, îæèäàòü ñóùåñòâîâàíèÿ ïðîöåññà dx/dt ìû íå
ìîæåì.  ñâÿçè ñ ýòèì ñòîõàñòè÷åñêèå äèôôåðåíöèàëüíûå óðàâíå-
íèÿ çàïèñûâàþòñÿ â ôîðìå
dt
d
tt
d
xx
x
=+
φσ
η
(,) (,)
.
*
(2.14)
Ñòîõàñòè÷åñêîå äèôôåðåíöèàëüíîå óðàâíåíèå áóäåò íàçûâàòüñÿ
ëèíåéíûì, åñëè ôóíêöèÿ φ ëèíåéíàÿ ïî x è σ íå çàâèñèò îò x.
2.2. ÏÐÈÍÖÈÏÛ ÑÎÑÒÀÂËÅÍÈß ÓÐÀÂÍÅÍÈÉ
ÄÂÈÆÅÍÈß ËÀ
1.2 .1. ÓÐÀÂÍÅÍÈß È.Â. ÌÅÙÅÐÑÊÎÃÎ
 îáùåì ñëó÷àå áóäåì ñ÷èòàòü, ÷òî ïðè äâèæåíèè ïðîèñõîäèò îä-
íîâðåìåííîå ïðèñîåäèíåíèå ÷àñòèö ê òåëó è èõ îòäåëåíèå îò íåãî.
Õàðàêòåðíûì ïðèìåðîì òàêîé ìîäåëè ìîæåò ñëóæèòü ìîäåëü ËÀ ñ
âîçäóøíî-ðàêåòíûì äâèãàòåëåì, ÷åðåç çàáîðíûé äèôôóçîð êîòîðî-
ãî ïîñòóïàåò âñòðå÷íûé ïîòîê âîçäóõà, íåîáõîäèìûé äëÿ ðàáîòû
äâèãàòåëÿ. Îäíîâðåìåííî ñ çàáîðîì âîçäóõà èç ñîïëà äâèãàòåëÿ íà-
çàä âûòåêàþò ñ áîëüøîé ñêîðîñòüþ ïðîäóêòû ñãîðàíèÿ òîïëèâà,
ñîçäàâàÿ òÿãó.
 ïðîöåññå ïðèñîåäèíåíèÿ è îòäåëåíèÿ ÷àñòèö ìàññà òåëà íåïðå-
ðûâíî èçìåíÿåòñÿ. Äîïóñòèì, ÷òî ñêîðîñòè ïðèñîåäèíåíèÿ è îòäå-
ëåíèÿ ÷àñòèö íå çàâèñÿò îò ñêîðîñòè äâèæåíèÿ òåëà. Ïóñòü â ðàñ-
ñìàòðèâàåìûé ìîìåíò âðåìåíè t òåëî èìååò ìàññó m + dm2 è äâèæåò-
ñÿ ñ àáñîëþòíîé ñêîðîñòüþ Va. Çà ïðîìåæóòîê âðåìåíè dt ìàññà òåëà
èçìåíèòñÿ çà ñ÷åò ïðèñîåäèíåíèÿ ýëåìåíòàðíîé ìàññû dm1 è îòäå-
ëåíèÿ ìàññû dm2. Ñîãëàñíî ãèïîòåçå, ïðèíÿòîé È.Â. Ìåùåðñêèì,
ïðèñîåäèíåíèå è îòäåëåíèå ÷àñòèö ïðîèñõîäèò çà áåñêîíå÷íî ìà-
ëûé ïðîìåæóòîê âðåìåíè, ïîäîáíî óäàðó. Ïîñëå ïðèñîåäèíåíèÿ
÷àñòèöà äâèæåòñÿ ñî ñêîðîñòüþ îñíîâíîé ìàññû òåëà, à îòäåëèâøàÿ-
87
ñÿ ÷àñòèöà, ïîëó÷èâ ñêîðîñòü, ñðàçó òåðÿåò âçàèìîäåéñòâèå ñ îñíîâ-
íîé ìàññîé òåëà. Ýòî òàê íàçûâàåìàÿ ãèïîòåçà êîíòàêòíîãî âçàèìî-
äåéñòâèÿ.
Íà ðàññìàòðèâàåìóþ ñèñòåìó òðåõ ìàññ äåéñòâóþò âíåøíèå
ñèëû, ðàâíîäåéñòâóþùàÿ êîòîðûõ ðàâíà ΣFi. Â ðåçóëüòàòå âçàèìî-
äåéñòâèÿ ìåæäó ñîáîé ìàññ m, dm1 è dm2 è ïîä äåéñòâèåì ñèëû ΣFi
ñêîðîñòü ñîåäèíåííîé ìàññû m + dm1 áóäåò îïðåäåëÿòüñÿ êàê ñóììà
Va + dVa. Àáñîëþòíóþ ñêîðîñòü äâèæåíèÿ ìàññû dm1 ïåðåä ïðèñîå-
äèíåíèåì îáîçíà÷èì ÷åðåç Ua, à àáñîëþòíóþ ñêîðîñòü ìàññû dm2
ïîñëå îòäåëåíèÿ – ÷åðåç Wa.
Íàéäåì èçìåíåíèå êîëè÷åñòâà äâèæåíèÿ ñèñòåìû ìàññ m1, dm1 è
dm2 çà ïðîìåæóòîê âðåìåíè dt è ïðèðàâíÿåì åãî ê èìïóëüñó âíåø-
íèõ ñèë:
mdmd
md
dm
dt
aaa
aa
aa
a
()[
()
]().
VVV VV
UW
V
F
+−+ +
−
−+
−=
1
2
Σ
(2.15)
Ïðåíåáðåãàÿ ñëàãàåìûì âòîðîãî ïîðÿäêà ìàëîñòè dm1dVa, äåëÿ
îáå ÷àñòè óðàâíåíèÿ íà dt è ïðîâîäÿ ïðåîáðàçîâàíèÿ, ïîëó÷èì óðàâ-
íåíèå äâèæåíèÿ òåëà ïåðåìåííîé ìàññû â ôîðìå
m
d
dt
dm
dt
dm
dt
a
aa
aa
V
VU
WVF
+−
+−
=
=
12
0
()() ,
Σ
(2.16)
èëè
m
d
dt
dm
dt
dm
dt
a
aa
aa
V
FU
VW
V
=+
−−
−
Σ
12
()( )
.
(2.17)
Åñëè îáîçíà÷èòü, êàê ýòî áûëî ñäåëàíî È. . Ìåùåðñêèì, ÷åðåç
•
,
x•
,
y •z ïðîåêöèè ñêîðîñòè îñíîâíîé ìàññû m íà îñè ïðÿìîóãîëüíîé
ñèñòåìû êîîðäèíàò, ÷åðåç X, Y, Z – ïðîåêöèè ðàâíîäåéñòâóþùåé
âñåõ ñèë íà òå æå îñè êîîðäèíàò, ÷åðåç α1, β1, γ1 – ïðîåêöèè ñêîðîñòè
ïðèñîåäèíÿþùåéñÿ ÷àñòèöû è ÷åðåç α2, β2, γ2 – ïðîåêöèè ñêîðîñòè
îòäåëÿþùåéñÿ ÷àñòèöû, òî, ïðîåöèðóÿ óðàâíåíèå (2.16) íà îñè êî-
îðäèíàò, ïîëó÷èì
mx
dm
dt
x
dm
dt
xX
my
dm
dt
y
d
+−
−−
−
=
+−
−
1
1
2
2
1
1
0
(• )(
•
);
(•)
αα
βm
dt
yY
mz
dm
dt
z
dm
dt
zZ
2
2
1
1
2
2
0
0
(• );
(• )(
•
).
−−
=
+−
−−
−
=
β
γγ
(2.18)
88
Ýòè óðàâíåíèÿ áûëè îïóáëèêîâàíû È. . Ìåùåðñêèì â 1904 ã. è
íàçâàíû åãî èìåíåì ïî ïðåäëîæåíèþ ïðîôåññîðà À.À. Êîñìîäåìü-
ÿíñêîãî [58]. Âõîäÿùèå â óðàâíåíèÿ (2.18) ñëàãàåìûå
dm
dt
x
1
1
(• ),
−α
dm
dt
x
2
2
(•)
−α È. . Ìåùåðñêèé íàçâàë ïðîåêöèÿìè íà êîîðäèíàòíûå
îñè "ïðèáàâî÷íîé ñèëû".
Òàêèì îáðàçîì, È. . Ìåùåðñêèé ïîêàçàë, ÷òî óðàâíåíèÿ äâèæå-
íèÿ òåëà ïåðåìåííîé ìàññû ìîæíî çàïèñàòü òàê æå, êàê è óðàâíåíèÿ
äâèæåíèÿ òåëà ïîñòîÿííîé ìàññû, âêëþ÷èâ â ÷èñëî äåéñòâóþùèõ
ñèë ïðèáàâî÷íóþ ñèëó.
Åñëè â (2.17) îáîçíà÷èòü îòíîñèòåëüíûå ñêîðîñòè ïðèñîåäèíå-
íèÿ ÷àñòèö ÷åðåç Uîòí = U a − Va è îòäåëåíèÿ ÷àñòèö – ÷åðåç Wîòí =
= Wa − Va, òî ýòî óðàâíåíèå ïðèìåò âèä
m
d
dt
dm
dt
dm
dt
a
VFUW
=+
−
Σ
12
îòí
îòí
.
(2.19)
Ïåðåìåííàÿ ìàññà äâèæóùåãîñÿ òåëà ðàâíà m = m0 +
dm
dt
dt
t
1
0
−
∫
−
∫dm
dt
dt
t
2
0
.
Åñëè ïðèñîåäèíåíèÿ ÷àñòèö íåò, ò.å .
dm
dt
dt
t
1
0
0
=
∫
,òîèç
(2.19) ïîëó÷èì óðàâíåíèå äâèæåíèÿ ËÀ ñ ðåàêòèâíûì äâèãàòåëåì
îáû÷íîãî òèïà
m
d
dt
dm
dt
a
V
FW
=−
Σ
îòí
,
(2.20)
ãäå
dm
dt
m
dm
dt
==
|•|
2
–
ñåêóíäíûé ìàññîâûé ðàñõîä ðàáî÷åãî âåùåñòâà.
Çàìåòèì, ÷òî ïðè îòäåëåíèè ÷àñòèö îò ìàññû m ñàìà ïðîèçâîäíàÿ
dm/dt èìååò çíàê ìèíóñ.
Äëÿ îïðåäåëåíèÿ äâèæåíèÿ ðàêåòû âåðòèêàëüíî ââåðõ Ìåùåð-
ñêèì áûëî ïðåäëîæåíî óðàâíåíèå
mx
mgp
dm
dt
WR
x
=−
+−
−
ãî
ò
í
(•),
(2.21)
ãäå g – óñêîðåíèå ñâîáîäíîãî ïàäåíèÿ; Rx
(•)
–
ñîïðîòèâëåíèå
âîçäóõà. Ïîëó÷èâ óðàâíåíèå (2.21), Ìåùåðñêèé íå ðàñêðûë
ñîäåðæàíèÿ ñëàãàåìîãî pã, íàçâàâ åãî äàâëåíèåì ãàçîâ.
89
2.2.2. ÎÑÍÎÂÍÛÅ ÒÅÎÐÅÌÛ ÄÈÍÀÌÈÊÈ ÒÅË ÏÅÐÅÌÅÍÍÎÉ
È ÏÎÑÒÎßÍÍÎÉ ÌÀÑÑ, ÏÐÈÍÖÈÏ ÇÀÒÂÅÐÄÅÂÀÍÈß
Ê ÷èñëó îñíîâíûõ òåîðåì, èñïîëüçóåìûõ ïðè ñîñòàâëåíèè óðàâíå-
íèé äâèæåíèÿ ñíàðÿäîâ, îòíîñÿòñÿ òåîðåìû îá èçìåíåíèè êîëè÷å-
ñòâà äâèæåíèÿ, èçìåíåíèè êèíåòè÷åñêîãî ìîìåíòà, èçìåíåíèè êè-
íåòè÷åñêîé ýíåðãèè.
Ðàñïðîñòðàíåíèå íà äèíàìèêó ðàêåò, ïðèíàäëåæàùèõ êëàññó òåë
ïåðåìåííîãî ñîñòàâà (ìàññû), óêàçàííûõ âûøå êëàññè÷åñêèõ òåîðåì
ïðîâîäèòñÿ íà îñíîâå òàê íàçûâàåìîãî ïðèíöèïà çàòâåðäåâàíèÿ,
ôîðìóëèðóåìîãî ñëåäóþùèì îáðàçîì [26, 37, 70]: óðàâíåíèÿ äâèæå-
íèÿ òåëà ïåðåìåííîãî ñîñòàâà ìîæíî ïðåäñòàâëÿòü â ôîðìå óðàâíå-
íèé äâèæåíèÿ òåëà ïîñòîÿííîãî ñîñòàâà, èìåþùåãî ìãíîâåííî çà-
ôèêñèðîâàííóþ (çàòâåðäåâøóþ) ìàññó.  ÷èñëî ñèë, äåéñòâóþùèõ
íà òåëî â ðàññìàòðèâàåìûé ìîìåíò, âêëþ÷àþòñÿ âíåøíèå, ðåàêòèâ-
íûå ñèëû Êîðèîëèñà è âàðèàöèîííûå ñèëû.
Èìåÿ â âèäó, ÷òî äëÿ òåëà ïåðåìåííîé ìàññû âåêòîðû êîëè÷åñòâà
äâèæåíèÿ è êèíåòè÷åñêîãî ìîìåíòà îòíîñèòåëüíî îñåé îïîðíîé
ñèñòåìû êîîðäèíàò îïðåäåëÿþòñÿ êàê
QV
KV
=
=×
=
=
∑
∑
m
m
n
n
νν
ν
νν
ν
ν
ρ
1
1
;
()
,
ìàòåìàòè÷åñêàÿ çàïèñü òåîðåì îá èçìåíåíèè êîëè÷åñòâà äâèæåíèÿ è
êèíåòè÷åñêîãî ìîìåíòà òåëà ïåðåìåííîãî ñîñòàâà áóäåò èìåòü âèä
d
dt
t
d
dt
r
r
r
QFFq Q
F
KMM K
=++
−
+−
⎛
⎝⎜⎞
⎠⎟+
=++
−+
−
*
()
;
()
δ
∂
δ
ê
ê
Kr
t∂
⎛
⎝⎜⎞
⎠⎟.
(2.22)
 ïðèâåäåííûõ ñîîòíîøåíèÿõ F è Ì – ñîîòâåòñòâåííî ãëàâíûé
âåêòîð è ãëàâíûé ìîìåíò âñåõ âíåøíèõ ñèë, äåéñòâóþùèõ íà òåëî â
ìîìåíò âðåìåíè t; Fê = −
=
∑m
n
νν
ν
aê
1
–
âåêòîð êîðèîëèñîâûõ ñèë
èíåðöèè: Mê – ãëàâíûé ìîìåíò ýòèõ æå êîðèîëèñîâûõ ñèë,
ñâÿçàííûõ ñ äâèæåíèåì ÷àñòèö (ãàçà èëè æèäêîñòè) âíóòðè òåëà; F* =
= Sa(pa − p0) – ãëàâíûé âåêòîð ñèë, îáóñëîâëåííûõ âîçäåéñòâèåì
àòìîñôåðíîãî äàâëåíèÿ è äàâëåíèÿ ãàçà íà ñðåçå ñîïëà;
90
δ
∂
δ
∂
QqQ
r
r
r
tt
+=
*
–
èçìåíåíèå êîëè÷åñòâà äâèæåíèÿ îòíîñèòåëüíî
ñâÿçàííîé ñèñòåìû êîîðäèíàò, ïðåäñòàâëÿþùåå ñîáîé ëîêàëüíóþ
(îòíîñèòåëüíóþ) ïðîèçâîäíóþ
δ
νν
ν
dt
mr
n
V,
=
∑1
ãäå Vνr – âåêòîð ñêîðîñòè
÷àñòèöû ñ ìàññîé mν îòíîñèòåëüíî êîðïóñà òåëà, qr – ãëàâíûé âåêòîð
ðåàêòèâíûõ ñèë,
δQr
dt
–
ãëàâíûé âåêòîð âàðèàöèîííûõ ñèë,
îáóñëîâëåííûé íåñòàöèîíàðíîñòüþ ïðîöåññîâ äâèæåíèÿ ÷àñòèö
(ìàññ) âíóòðè êîðïóñà òåëà; Kr è
δKr
dt
–
ñîîòâåòñòâåííî ãëàâíûé
ìîìåíò ðåàêòèâíûõ ñèë è ãëàâíûé ìîìåíò âàðèàöèîííûõ ñèë; ρν –
ðàäèóñ-âåêòîð ÷àñòèöû ñ ìàññîé mν îòíîñèòåëüíî íà÷àëà îïîðíîé
ñèñòåìû êîîðäèíàò.
Ðàññìîòðèì îòäåëüíî ñóììó F* − qr −
δQr
dt
â ïåðâîì óðàâíåíèè
(2.22).  ýòîé ñóììå qr îïðåäåëÿåòñÿ êàê ãåîìåòðè÷åñêàÿ ñóììà ýëå-
ìåíòàðíûõ ðàñõîäîâ:
qV
V
d
S
rn
r
S
=
∫∫ρ
.
Ñïðîåöèðîâàâ äàííîå âåêòîðíîå âûðàæåíèå íà ïðîäîëüíóþ îñü ËÀ,
ñîâïàäàþùóþ ñ ïðîäîëüíîé îñüþ ðàêåòíîãî äâèãàòåëÿ, ïîëó÷èì
qV
V
d
SW
S
rn
xa
a
a
S
==
−
∫∫ ρρ
2
,
ãäå ρa – ïëîòíîñòü èñòåêàþùèõ ãàçîâ; Wa – ñêîðîñòü èñòå÷åíèÿ ãàçîâ
÷åðåç ïëîùàäü Sa âûõîäíîãî ñå÷åíèÿ ñîïëà.
Èìåÿ â âèäó, ÷òî gρaWaSa = Qñåê, ïîëó÷èì
−=
q
Q
g
W
ra
ñåê
,
è, ñëåäîâàòåëüíî,
Fq
Q
Wp
p
Q
*
().
−−
=
+−−
r
r
aa
a
r
dt
Q
g
S
dt
δδ
ñåê
91
Ó÷èòûâàÿ, ÷òî äëÿ ðàññìàòðèâàåìîãî êëàññà ðàêåò âåëè÷èíîé
δQr
dt
ìîæíî ïðåíåáðå÷ü, ïîëó÷èì
d
dt
Q FPF
=++
ê
.
(2.23)
Àíàëîãè÷íûì îáðàçîì ìîæíî ïåðåéòè ê ñëåäóþùåé çàïèñè òåîðåìû
î ãëàâíîì ìîìåíòå êîëè÷åñòâ äâèæåíèÿ ðàêåòíîãî ËÀ:
d
dt
K
MMM
=++
äâ
ê
,
(2.24)
ãäå Ì – ãëàâíûé ìîìåíò âñåõ âíåøíèõ ñèë, çà èñêëþ÷åíèåì
àòìîñôåðíîãî äàâëåíèÿ è äàâëåíèÿ ãàçîâ â âûõîäíîì ñå÷åíèè ñîïëà
äâèãàòåëÿ, îòíîñèòåëüíî öåíòðà ìàññ ËÀ; Mäâ – ãëàâíûé ìîìåíò òÿãè
äâèãàòåëåé, âêëþ÷àþùèé ïîìèìî ìîìåíòîâ ÷èñòî ðåàêòèâíîãî
ïðîèñõîæäåíèÿ äîïîëíèòåëüíûå ìîìåíòû, âûçâàííûå àòìîñôåðíûì
äàâëåíèåì, äàâëåíèåì ãàçà â âûõîäíîì ñå÷åíèè ñîïëà è (ïðè
íåîáõîäèìîñòè ó÷åòà) íåñòàöèîíàðíîñòüþ äâèæåíèÿ ãàçà è æèäêîãî
íàïîëíèòåëÿ âíóòðè êîðïóñà ðàêåòû.
Óðàâíåíèÿ (2.23) è (2.24) îòðàæàþò ôîðìóëèðîâêó ïðèíöèïà çà-
òâåðäåâàíèÿ äëÿ ðåàêòèâíûõ àïïàðàòîâ êàê òåë ïåðåìåííîãî ñîñòà-
âà.
Êèíåòè÷åñêàÿ ýíåðãèÿ ðàêåòû êàê òåëà ïåðåìåííîãî ñîñòàâà îï-
ðåäåëÿåòñÿ ñóììîé êèíåòè÷åñêèõ ýíåðãèé òî÷åê ïåðåìåííîãî ñîñòà-
âàTï=
mVa
n
νν
ν
2
12
.
=
∑ Èñïîëüçóÿ ðàâåíñòâî Vaν = Va + Vrν, ïîñëå ñîîòâåò-
ñòâóþùèõ ïðåîáðàçîâàíèé ìîæíî ïîëó÷èòü
TT
mV
mVV
a
ar
ï
=+
−
2
2
,
(2.25)
ãäå m – ìàññà ìãíîâåííî çàòâåðäåâøåé ðàêåòû â ìîìåíò âðåìåíè t ;
T=
mVa
n
νν
ν
2
12
=
∑ – êèíåòè÷åñêàÿ ýíåðãèÿ ñèñòåìû ìàòåðèàëüíûõ òî÷åê,
ïðèíàäëåæàùèõ ðàêåòå, â åå äâèæåíèè îòíîñèòåëüíî öåíòðà ìàññ.
Ïîñêîëüêó öåíòð ìàññ ïåðåìåùàåòñÿ îòíîñèòåëüíî êîðïóñà, âî
ìíîãèõ ñëó÷àÿõ îêàçûâàåòñÿ óäîáíûì îïðåäåëÿòü êèíåòè÷åñêóþ
ýíåðãèþ ðàêåòû ÷åðåç ñêîðîñòè â ïåðåíîñíîì è îòíîñèòåëüíîì äâè-
æåíèÿõ. Òàê êàê Va = Ve + Vr,òî
92
TT
mV
mV
er
ï
=+
−
22
2
.
(2.26)
Òàêèì îáðàçîì, êèíåòè÷åñêàÿ ýíåðãèÿ ðàêåòû â åå àáñîëþòíîì
äâèæåíèè êðîìå Ò ñîäåðæèò ðàçíîñòü êèíåòè÷åñêèõ ýíåðãèé öåíòðà
ìàññ, îáëàäàþùåãî ìàññîé ìãíîâåííî çàòâåðäåâøåé ðàêåòû, â åãî
ïåðåíîñíîì è îòíîñèòåëüíîì äâèæåíèÿõ.
Äèôôåðåíöèàë êèíåòè÷åñêîé ýíåðãèè òåëà ïåðåìåííîãî ñîñòàâà
ìîæåò áûòü ïîëó÷åí íåïîñðåäñòâåííûì äèôôåðåíöèðîâàíèåì ðà-
âåíñòâà
dTd
mV
dmV
mV dV
a
n
a
aa
n
ï=
⎛
⎝⎜
⎞
⎠⎟ =+
==
=
∑∑
νν
ν
νν
ννν
ν
ν
2
1
2
1
22
.
1
n
∑
(2.27)
Ðàçäåëèâ ïðàâóþ è ëåâóþ ÷àñòè ðàâåíñòâà íà dt, ïîëó÷èì âòîðîå
ñëàãàåìîå åãî ïðàâîé ÷àñòè â âèäå
mV
dV
dt
a
n
d
νν
ν
ν
=
∑1
.
Óðàâíåíèå äâèæåíèÿ òî÷êè ïåðåìåííîé ìàññû ïðåäñòàâèì êàê
m
d
dt
a
ν
ν
ννν
V
FRF
=++
p,
(2.28)
ãäå Fν – ðàâíîäåéñòâóþùàÿ âíåøíèõ àêòèâíûõ ñèë, ïðèëîæåííûõ ê
òî÷êå ν; R ν – ðàâíîäåéñòâóþùàÿ âñåõ âíóòðåííèõ àêòèâíûõ ñèë,
ïðèëîæåííûõ ê òî÷êå ν; Fpν – ðåàêòèâíàÿ ñèëà, ïðèëîæåííàÿ ê
òî÷êå ν.
Ïðåíåáðåãàÿ äåéñòâèåì âíóòðåííèõ ñèë è ïðîâîäÿ çàìåíó â
(2.27), ïîëó÷èì
dT
dt
FV
FV
dm
dt
V
aa
a
n
n
n
ï
p
=++
=
=
=
∑
∑
∑νν νν νν
ν
ν
ν
2
1
1
1
2
.
(2.29)
Îáîçíà÷àÿ Vaν =
dS
dt
ν
, ãäå dSν – ýëåìåíòàðíûé ïóòü ÷àñòèöû ìàññîé
mν, è âîçâðàùàÿñü ê äèôôåðåíöèàëàì, áóäåì èìåòü
dTAA
dmV
F
a
n
ïp
=++
=
∑
δδ
νν
ν
2
1
2
,
(2.30)
93
ãäå δAF è δAp – ñîîòâåòñòâåííî ýëåìåíòàðíûå ðàáîòû âíåøíèõ è
ðåàêòèâíûõ ñèë, ïðèëîæåííûõ ê ðàêåòå.
Ïîñëåäíåå ñëàãàåìîå ïðàâîé ÷àñòè – êèíåòè÷åñêàÿ ýíåðãèÿ, îï-
ðåäåëÿåìàÿ èíòåíñèâíîñòüþ èçìåíåíèÿ òî÷åê ìàññû mν, ïðèíàäëå-
æàùèõ òåëó, è èõ àáñîëþòíûìè ñêîðîñòÿìè.
Êèíåòè÷åñêóþ ýíåðãèþ ðàêåòû ðàññìàòðèâàþò òàêæå è â òîì ñëó-
÷àå, êîãäà ñîñòàâëÿþò óðàâíåíèÿ äâèæåíèÿ ðàêåòû â îáîáùåííûõ
êîîðäèíàòàõ. Åñëè ïîëîæåíèå òåëà ïåðåìåííîé ìàññû îïðåäåëÿåòñÿ
íåçàâèñèìûìè îáîáùåííûìè êîîðäèíàòàìè q1, q2,...
,qs è
rr
νν
=
(,,...,
,),
qq qt
s
12
òî óðàâíåíèÿ äâèæåíèÿ ìîãóò áûòü çàïèñàíû â ôîðìå óðàâíåíèé
Ëàãðàíæà âòîðîãî ðîäà [58]
d
dt
T
q
T
q
QP
d
dt
T
q
T
∂
∂
∂
∂
∂
∂
∂
ï
ïï
•
;
•
11
11
2
⎛
⎝⎜⎞
⎠⎟ −=
+
⎛
⎝⎜⎞
⎠⎟−
ï
∂
∂
∂
q
QP
d
dt
T
2
22
=+;
................................
•
ï
q
T
q
QP
ss
ss
⎛
⎝⎜⎞
⎠⎟ −=
+
∂
∂
ï
,
(2.31)
ãäåQσ=ΣF
r
q
ν
ν
σ
∂
∂
–
îáîáùåííàÿ ñèëà, îïðåäåëÿåìàÿ âíåøíèìè
ôàêòîðàìè; Pσ =
dm
dt
W
V
q
a
n
ν
ν
ν
σ
ν
∂
∂•
=
∑1
–
îáîáùåííàÿ ñèëà, îïðåäåëÿåìàÿ
ïðèòîêîì ìåõàíè÷åñêîé ýíåðãèè ê çàòâåðäåâøåìó òåëó ïåðåìåííîé
ìàññû ïðè îòáðàñûâàíèè ÷àñòèö; σ =1,2,...,s.
Ïîñëåäíåå ëåãêî ïîêàçàòü, åñëè çàìåíèòü Wν = λ(t)Vaν. Òîãäà
ôóíêöèÿ, õàðàêòåðèçóþùàÿ ïðèòîê ìåõàíè÷åñêîé ýíåðãèè, èìååò
âèä Ï=
=
∑λ
νν
ν
()t
dm
dt
Va
n
2
1
2
èPσ=
∂
∂σ
Ï
q
.
Êèíåòè÷åñêàÿ ýíåðãèÿ ñíàðÿäà â åãî âðàùàòåëüíîì äâèæåíèè îò-
íîñèòåëüíî öåíòðà ìàññ ìîæåò áûòü âûðàæåíà ÷åðåç ìîìåíòû èíåð-
öèè ñíàðÿäà è ïðîåêöèè ìãíîâåííîé óãëîâîé ñêîðîñòè ñíàðÿäà íà
ñîîòâåòñòâóþùèå îñè:
TA
p
B
q
C
r
=+
+
1
2
222
[]
,
(2.32)
94
ãäå A = Iz; B = Iy; C = Ix – ìîìåíòû èíåðöèè ñíàðÿäà îòíîñèòåëüíî åãî
ãëàâíûõ îñåé èíåðöèè z, y, x; p, q, r – ïðîåêöèè ìãíîâåííîé óãëîâîé
ñêîðîñòè ñíàðÿäà íà íàçâàííûå îñè.
Òàê êàê ìîìåíòû èíåðöèè ñíàðÿäà îòíîñèòåëüíî ýêâàòîðèàëü-
íûõ îñåé îäèíàêîâû (A = B), òî ïîñëåäíåå ðàâåíñòâî ìîæåò áûòü
ïðåäñòàâëåíî â ñëåäóþùåì âèäå:
TA
p
qC
r
=+
+
1
2
222
[()].
(2.33)
Ïðè ñîñòàâëåíèè äèôôåðåíöèàëüíûõ óðàâíåíèé âðàùàòåëüíîãî
äâèæåíèÿ ñíàðÿäà ÷àñòî èñïîëüçóþò óðàâíåíèå Ëàãðàíæà â
îáîáùåííûõ êîîðäèíàòàõ (óðàâíåíèå Ëàãðàíæà 2-ãî ðîäà), êîòîðîå â
ýòîì ñëó÷àå èìååò âèä
d
dt
T
q
T
q
Q
ii
i
∂
∂
∂
∂
•
.
⎛
⎝⎜⎞
⎠⎟ −=
(2.34)
Ñóùåñòâåííî óïðîùàåòñÿ òàêæå è çàâèñèìîñòü (2.30) äëÿ âû÷èñëåíèÿ
èçìåíåíèÿ êèíåòè÷åñêîé ýíåðãèè ñíàðÿäà.
2.2.3. ÂÅÊÒÎÐÍÛÅ ÓÐÀÂÍÅÍÈß ÏÎÑÒÓÏÀÒÅËÜÍÎÃÎ ÄÂÈÆÅÍÈß ËÀ
ÊÀÊ ÒÅËÀ ÏÅÐÅÌÅÍÍÎÉ ÌÀÑÑÛ
Îáîçíà÷èì ñêîðîñòü è óñêîðåíèå öåíòðà ìàññ ñèñòåìû (êîðïóñ
ðàêåòû – òîïëèâî
–
ãàçû) â àáñîëþòíîì äâèæåíèè ÷åðåç Va è aa.
Äâèæåíèå êîðïóñà è æåñòêî ñâÿçàííûõ ñ íèì ÷àñòåé (ò.å . è òîé òî÷-
êè òåëà, ñ êîòîðîé â äàííûé ìîìåíò âðåìåíè ñîâïàäàåò öåíòð ìàññ)
îòíîñèòåëüíî íåïîäâèæíîé ñèñòåìû êîîðäèíàò áóäåò ïåðåíîñíûì.
Ñêîðîñòü è óñêîðåíèå öåíòðà ìàññ êîðïóñà â ïåðåíîñíîì äâèæåíèè
îáîçíà÷èì ÷åðåç Ve è ae = dVe/dt. Ñêîðîñòü è óñêîðåíèå öåíòðà ìàññ
ñèñòåìû "êîðïóñ – òîïëèâî
–
ãàçû" îòíîñèòåëüíî êîðïóñà ðàêåòû
îáîçíà÷èì ÷åðåç Vr è ar. Èç ìåõàíèêè òåë ïåðåìåííîãî ñîñòàâà ñëå-
äóåò, ÷òî ïðîèçâåäåíèå ìàññû òåëà íà ïåðåíîñíîå óñêîðåíèå åãî
öåíòðà ìàññ ðàâíî ðàâíîäåéñòâóþùåé âñåõ âíåøíèõ è ðåàêòèâíûõ
ñèë, äåéñòâóþùèõ íà òåëî, ò.å.
me
a=+
ΣΣ
FF
p.
(2.35)
Ñêîðîñòü è óñêîðåíèå öåíòðà ìàññ ðàêåòû â àáñîëþòíîì äâèæå-
íèè ñîîòâåòñòâåííî èìåþò âèä
VVV
V
aer
aer
r
=+
=++ ×
;(
)
.
aaa2 ω
(2.36)
Èç ïîñëåäíåãî ðàâåíñòâà îïðåäåëèì ae è ïîäñòàâèì åãî â (2.35).
Òîãäà óðàâíåíèå äâèæåíèÿ öåíòðà ìàññ ñèñòåìû "êîðïóñ – òîïëè-
95
âî – ãàçû", íàïèñàííîå â âåêòîðíîé ôîðìå, ïîëó÷èì â ñëåäóþùåì
âèäå:
mm
d
dt
mm
a
a
rr
aa
==
+
+
+×
V
FF
V
ΣΣ
p
2( ).
ω
(2.37)
Ïðè âûâîäå óðàâíåíèé (2.17) è (2.18) ïðåäïîëàãàëîñü, ÷òî âçàè-
ìîäåéñòâèå îñíîâíîãî òåëà ñ ïðèñîåäèíÿþùèìèñÿ èëè îòäåëÿþùè-
ìèñÿ ÷àñòèöàìè ïðîèñõîäèò ìãíîâåííî.  äåéñòâèòåëüíîñòè ïðî-
öåññ âçàèìîäåéñòâèÿ ËÀ ñ ïîäâèæíûìè ïðèñîåäèíÿþùèìèñÿ èëè
îòäåëÿþùèìèñÿ ãàçîâûìè ïîòîêàìè ñëîæíåå. Ó ðàêåò ñ äâèãàòåëÿ-
ìè íà æèäêîì è òâåðäîì òîïëèâå îòäåëÿþùèåñÿ ÷àñòèöû ïîëó÷àþò
îòíîñèòåëüíóþ ñêîðîñòü åùå â êàìåðå ñãîðàíèÿ äâèãàòåëÿ äî ìî-
ìåíòà âûõîäà ÷àñòèöû çà ïëîñêîñòü íàðóæíîãî ñå÷åíèÿ ñîïëà, ò.å .
äî ïîòåðè ñâÿçè ñ îñíîâíîé ìàññîé ðàêåòû. Êðîìå òîãî, ó ðàêåò íà
æèäêîì òîïëèâå ãîðþ÷åå è îêèñëèòåëü ïåðåìåùàþòñÿ â ïðîöåññå
ðàáîòû äâèãàòåëÿ âíóòðè êîðïóñà ðàêåòû. Ïðè âçàèìîäåéñòâèè äâè-
æóùèõñÿ ïîòîêîâ ñ êîðïóñîì, êîëåáëþùèìñÿ â ïîïåðå÷íîì íàïðàâ-
ëåíèè, âîçíèêàåò êîðèîëèñîâà ñèëà Fêîð. Çàïèøåì óðàâíåíèå äâèæå-
íèÿ öåíòðà ìàññ ðàêåòû ñ ó÷åòîì ýòîé ñèëû:
m
d
dt
mm
a
rr
V
FFF
V
=++++×
ΣΣ
pê
î
ða2().
ω
(2.38)
Äîáàâèì â ïîñëåäíåå óðàâíåíèå ñëàãàåìîå, ó÷èòûâàþùåå íåñòà-
öèîíàðíîñòü äâèæåíèÿ ìàññ âíóòðè ðàêåòû. Ïóñòü êîëè÷åñòâî äâè-
æåíèÿ òîïëèâà è ãàçîâ, ïåðåìåùàþùèõñÿ âíóòðè êîðïóñà, â ìîìåíò
âðåìåíè t ðàâíî qâàð, à â ìîìåíò âðåìåíè t + dt ðàâíî qâàð + δqâàð. Î÷å-
âèäíî, çà ïðîìåæóòîê âðåìåíè dt èçìåíåíèå êîëè÷åñòâà äâèæåíèÿ
ïîäâèæíûõ ìàññ ñîñòàâèò δqâàð, è óðàâíåíèå äâèæåíèÿ ðàêåòû çàïè-
øåòñÿ â áîëåå ïîëíîé ôîðìå:
m
d
dt
mm
dt
a
rr
V
FFF
V
q
=++
++ ×+
ΣΣΣ
pê
î
ð
âàð
a2()
.
ω
δ
(2.39)
Ñîñòàâëÿþùóþ (δqâàð)/dt ïðèíÿòî íàçûâàòü âàðèàöèîííîé ñèëîé.
Óðàâíåíèå (2.39) ñîîòâåòñòâóåò ðàññìîòðåííîìó âûøå ïðèíöèïó
çàòâåðäåâàíèÿ.
Âàðèàöèîííûå ñèëû è ìîìåíòû îòðàæàþò íåñòàöèîíàðíîñòü
äâèæåíèÿ ìàññ âíóòðè êîðïóñà ðàêåòû. Îäíàêî â áîëüøèíñòâå ñëó-
÷àåâ ïðîöåññ ïåðåìåùåíèÿ ðàáî÷åãî òåëà âíóòðè ðàêåòû ìîæíî ïðè-
íèìàòü çà êâàçèñòàöèîíàðíûé è âàðèàöèîííûå ñèëû íå ó÷èòûâàòü
ââèäó ìàëîñòè.
Ñèëû Êîðèîëèñà, îáóñëîâëåííûå äâèæåíèåì ìàññ âíóòðè êîðïó-
ñà ðàêåòû è åå êîëåáàíèÿìè, íà äâèæåíèå öåíòðà ìàññ ïî÷òè íå îêà-
çûâàþò âëèÿíèÿ. Ñèëû Êîðèîëèñà, ïîÿâëÿþùèåñÿ ïðè ðàññìîòðå-
96
íèè îòíîñèòåëüíîãî äâèæåíèÿ ðàêåòû â ñâÿçàííîé ñ Çåìëåé ñèñòåìå
êîîðäèíàò, îêàçûâàþò çàìåòíîå âëèÿíèå íà åå ïîëåò òîëüêî ïðè
äâèæåíèè ñî ñêîðîñòÿìè, ïðåâûøàþùèìè 600...700 ì/ñ.
 èíåðöèàëüíîé ñèñòåìå êîîðäèíàò óðàâíåíèå äâèæåíèÿ öåíòðà
ìàññ ëåòàòåëüíîãî àïïàðàòà çàïèñûâàåòñÿ â âèäå
m
d
dt
a
V
FF
=+
ΣΣ
p,
(2.40)
ãäå ΣF è ΣFp – âåêòîðû ñóììû âíåøíèõ è ðåàêòèâíûõ ñèë. Óðàâíåíèå
äâèæåíèÿ öåíòðà ìàññ ëåòàòåëüíîãî àïïàðàòà îòíîñèòåëüíî
ïîäâèæíîé, ñâÿçàííîé ñ Çåìëåé ñèñòåìû êîîðäèíàò áóäåò èìåòü âèä
mm
m
aa
a
=
++−
+−
ΣΣ
FF
pï
å
ðê
î
ð
()
()
,
ãäå maïåð è maêîð – ïåðåíîñíàÿ è êîðèîëèñîâà ñèëû èíåðöèè,
îïðåäåëÿåìûå âðàùåíèåì Çåìëè.
Äëÿ ïðÿìîóãîëüíîé ñèñòåìû êîîðäèíàò ñ íà÷àëîì â óñëîâíîì
öåíòðå Çåìëè ïðè íàïðàâëåíèè âåêòîðà óãëîâîé ñêîðîñòè Çåìëè Ω
ïî îñè OY0 ïîëó÷èì
aïåð
=×
+××
d
dt
Ω
ΩΩ
rr
()
.
(2.41)
Åñëè ïðèíÿòü Ω = const, òî ïåðåíîñíîå óñêîðåíèå ðàâíî
aïåð
=××
ΩΩ
()
,
r
(2.42)
à êîðèîëèñîâî óñêîðåíèå, îïðåäåëÿåìîå âðàùåíèåì Çåìëè, ðàâíî
aêîð
=×
2(
),
ΩV
(2.43)
ãäå V – îòíîñèòåëüíàÿ ñêîðîñòü ËÀ.
Î÷åíü ÷àñòî óðàâíåíèÿ äâèæåíèÿ öåíòðà ìàññ çàïèñûâàþòñÿ îò-
íîñèòåëüíî ïîäâèæíîé ñèñòåìû êîîðäèíàò OX Y Z
iii
*
, ñâÿçàííîé ñ ðà-
êåòîé. Âîñïîëüçóåìñÿ ïðàâèëîì ïåðåõîäà îò íåïîäâèæíîé ñèñòåìû
êîîðäèíàò ê ïîäâèæíîé:
m
d
dt
m
d
dt
m
a
ai
ai
V
V
VFF
=+
×
=
+
[],
ωΣ
Σ
p
(2.44)
97
*
 äàëüíåéøåì èíäåêñ i çàìåíÿåòñÿ íà èíäåêñ ñîîòâåòñòâóþùåé âûáðàí-
íîé ñèñòåìû êîîðäèíàò.
ãäå
d
dt
ai
V
–
ïðîèçâîäíàÿ âåêòîðà ñêîðîñòè öåíòðà ìàññ ðàêåòû â
ïîäâèæíîé ñèñòåìå êîîðäèíàò.
Äëÿ çåìíûõ ñèñòåì êîîðäèíàò
m
d
dt
mm
V
FF
=+−
−
ΣΣ
pï
å
ðê
î
ð
aa
.
(2.45)
Åñëè ω – óãëîâàÿ ñêîðîñòü îñåé ïîäâèæíîé ñèñòåìû êîîðäèíàò
îòíîñèòåëüíî îñåé, ñâÿçàííûõ ñ Çåìëåé, òî
d
dt
d
dt
VV
V
=+
×
*
,
ω
(2.46)
ãäå
d
dt
*
–
V
ëîêàëüíàÿ ïðîèçâîäíàÿ.
Òîãäà âåêòîðíîå óðàâíåíèå äâèæåíèÿ öåíòðà ìàññ ËÀ ñ ó÷åòîì
âëèÿíèÿ âðàùåíèÿ Çåìëè áóäåò èìåòü âèä
m
d
dt
mm
*
.
V
VFF
+×
⎛
⎝⎜
⎞
⎠⎟=+ −
−
ωΣ
Σ
pï
å
ðê
î
ð
aa
(2.47)
Äëÿ ëþáîé ïðÿìîóãîëüíîé ñèñòåìû êîîðäèíàò OXiYiZi, íà÷àëî
êîòîðîé ñîâïàäàåò ñ öåíòðîì ìàññ ËÀ, íà îñíîâàíèè (2.44) ìîæíî
íàïèñàòü òðè ñêàëÿðíûõ óðàâíåíèÿ äâèæåíèÿ öåíòðà ìàññ ðàêåòû
•
;
VVV
F
m
F
m
xi
yi zi
zi yi
xi
xi
+−=
+
ωω
Σ
Σp
•
;
VVV
F
m
F
m
yi
zi xi
xi zi
yi
yi
+−=
+
ωω
ΣΣ
p
(2.48)
•
,
VVV
F
m
F
m
zi
xi yi
yi xi
zi
zi
+−=
+
ωω
ΣΣ
p
ãäå Vxi, Vyi, Vzi – ïðîåêöèè âåêòîðà ñêîðîñòè öåíòðà ìàññ ðàêåòû íà
îñè ñâÿçàííîé ñ íèì ñèñòåìû êîîðäèíàò; ωxi, ωyi, ωzi – ïðîåêöèè
âåêòîðà óãëîâîé ñêîðîñòè ñâÿçàííîé ñèñòåìû êîîðäèíàò íà
âûáðàííûå i-å îñè ïîäâèæíîé ñèñòåìû êîîðäèíàò, íàïðàâëåíèå
êîòîðûõ íåèçìåííî â ïðîñòðàíñòâå è ñîâïàäàåò ñ íàïðàâëåíèåì îñåé
íåïîäâèæíîé ñèñòåìû êîîðäèíàò; ΣFxi, ΣFyi, ΣFzi, ΣFpxi, ΣFpyi, ΣFpzi –
98
ïðîåêöèè âíåøíèõ è ðåàêòèâíûõ ñèë, äåéñòâóþùèõ íà ËÀ, íà îñè
ñèñòåìû êîîðäèíàò OXiYiZi.
2.2.4 . ÓÐÀÂÍÅÍÈß ÂÐÀÙÀÒÅËÜÍÎÃÎ ÄÂÈÆÅÍÈß ËÀ
×òîáû ñîñòàâèòü óðàâíåíèÿ âðàùàòåëüíîãî äâèæåíèÿ ðàêåòû îò-
íîñèòåëüíî îñåé, ïðîõîäÿùèõ ÷åðåç öåíòð ìàññ è âðàùàþùèõñÿ ïî
îòíîøåíèþ ê ðàêåòå ñ óãëîâîé ñêîðîñòüþ ω*
, ïðè âðàùåíèè ñàìîé
ðàêåòû ñ óãëîâîé ñêîðîñòüþ ω, íàäî âîñïîëüçîâàòüñÿ èçâåñòíûì
óðàâíåíèåì
d
dt
d
dt
KK
K
=+
+×
*
*
[(
)],
ωω
(2.49)
ãäå dK/dt – ïðîèçâîäíàÿ îò êèíåòè÷åñêîãî ìîìåíòà, âû÷èñëåííàÿ
îòíîñèòåëüíî íåïîäâèæíîé ñèñòåìû êîîðäèíàò;
d
dt dt
*
–
KK
=
δ
ïðîèçâîäíàÿ îò êèíåòè÷åñêîãî ìîìåíòà, âû÷èñëåííàÿ îòíîñèòåëüíî
i-é ñèñòåìû êîîðäèíàò OXiYiZi (ëîêàëüíàÿ ïðîèçâîäíàÿ).
Åñëè ñèñòåìà êîîðäèíàò OXiYiZi íå ïåðåìåùàåòñÿ îòíîñèòåëüíî
ðàêåòû, òî ω* =0è
d
dt
d
dt
R
KK
KM
=+
×
=
*
,
ω
(2.50)
ãäå ÌR – ðåçóëüòèðóþùèé ìîìåíò ñèñòåìû ñèë.
Ïðîåêöèè âåêòîðíîãî ðàâåíñòâà (2.50) íà îñè êîîðäèíàò, ñâÿçàí-
íûå ñ ËÀ, ìîãóò áûòü ïðåäñòàâëåíû ÷åðåç ïðîåêöèè íà ýòè îñè âåê-
òîðà ìîìåíòà êîëè÷åñòâà äâèæåíèÿ K:
K
K
K
x
y
z
I
x
y
z
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
A
ω
ω
ω
,
(2.51)
ãäå ÀI – òåíçîð èíåðöèè ËÀ, âûðàæåííûé ìàòðèöåé èíåðöèè:
AI
xx
yx
z
yx
y
yz
zx
zy
z
III
III
III
=
−−
−−
−−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
.
(2.52)
99
Ïðîåêöèè êèíåòè÷åñêîãî ìîìåíòà K íà îñè êîîðäèíàò XiYiZi èìå-
þò âèä
KIII
KIII
xx
xx
y
yx
z
z
yy
yy
z
z
ii
ii
i
ii
i
i
ii
ii
i
i
=−−
=−−
ωωω
ωω
;
yxx
zz
zz
x
xz
y
y
iii
ii
ii
i
ii
i
i
KIII
ω
ωωω
;
,
=−−
(2.53)
ãäå III
xyz
iii
,,–
ìîìåíòû èíåðöèè ðàêåòû îòíîñèòåëüíî îñåé Xi, Yi, Zi;
Ixy
ii
,I
xz
ii
, Iyz
ii
–
öåíòðîáåæíûå ìîìåíòû èíåðöèè, îïðåäåëÿåìûå
îòíîñèòåëüíî êîîðäèíàòíûõ ïëîñêîñòåé.
Ïðè îïðåäåëåíèè îñåâûõ è öåíòðîáåæíûõ ìîìåíòîâ èíåðöèè
ìîæåò áûòü ó÷òåíî ïåðåìåùåíèå öåíòðà ìàññ (íà÷àëà êîîðäèíàò) è
âðàùåíèå îñåé êîîðäèíàò îòíîñèòåëüíî êîðïóñà [55]:
Im
y
z
Iz
x
Im
xi
i
y
i
i
n
n
z
ii
i
=+
=
+
=
=
=
∑
∑ννν
νν
ν
ν
ν
()
;()
;
22
22
1
1
()
;
;
xyII m
yz
II
iix
yy
x
i
i
n
n
xz
ii
ii
ii
νν
ν
ν
ν
ν
ν
22
1
1
+=
=
=
=
=
∑
∑
zx
ii
yz
zy
ii
n
n
ii
ii
ii
mxz I
I
myz
==
=
=
=
∑
∑ ννν
ννν
ν
ν
;.
1
1
(2.54)
Î÷åâèäíî, îñåâûå è öåíòðîáåæíûå ìîìåíòû èíåðöèè â ïðîöåññå
ðàáîòû äâèãàòåëÿ è äâèæåíèÿ ðàêåòû áóäóò ïåðåìåííûìè âåëè÷èíà-
ìè, çàâèñÿùèìè îò âðåìåíè.
Óðàâíåíèÿ âðàùàòåëüíîãî äâèæåíèÿ îòíîñèòåëüíî öåíòðà ìàññ
çàïèøåì, èñïîëüçóÿ ôîðìóëû (2.50) è (2.53):
II
II
I
xx
zyyzx
yy
xz
xz
ii
i
iii
i
ii
ii
ii
•
()(
•
)
(
ωω
ω
ω
ω
ω
+−
−
−
−
−
•
)()
;
ωω
ω
ωω
zx
yy
z
zyxx
ii
ii
i
iiii
IM
M
++−
=
+
22
p
II
II
I
yy
x
zxz
x
yx yz
xz
ii
i iii
i
ii
ii
ii
•
()(
•
)
(
ωω
ω
ω
ω
ω
+−
−
++
+
••
)(
•
);
ωω
ωω
ω
xzy
z
zx
yyy
iii
i
ii
iii
IM
M
22
−−
−
=+
p
(2.55)
II
II
I
zz
y xxy
xx
yz
yz
ii
i
iii
ii
ii
ii
•
()(
•
)
(•
ωω
ω
ω
ω
ω
ω
+−
−
−
−
−
yx
zx
y
yxzz
ii
ii
i
iiii
IM
M
++−
=
+
ωω
ωω
)()
.
22
p
Ïðàâûå ÷àñòè óðàâíåíèé ñîäåðæàò ïðîåêöèè ñóììû ìîìåíòîâ
îòíîñèòåëüíî öåíòðà ìàññ âñåõ ñèë, äåéñòâóþùèõ íà ðàêåòó, íà ñî-
îòâåòñòâóþùèå îñè êîîðäèíàò. Ìîìåíòû êîðèîëèñîâûõ ñèë è äî-
100
ïîëíèòåëüíûé ìîìåíò, îïðåäåëÿåìûé ïåðåìåùåíèåì öåíòðà ìàññ
ðàêåòû îòíîñèòåëüíî êîðïóñà, ïðè ðåøåíèè ìíîãèõ áàëëèñòè÷åñêèõ
çàäà÷ ââèäó ìàëîñòè íå ó÷èòûâàþòñÿ.
Åñëè ïîäâèæíûå îñè êîîðäèíàò ñîâìåñòèòü ñ ãëàâíûìè öåíò-
ðàëüíûìè îñÿìè èíåðöèè OXYZ, òî ìàòðèöà (2.52) ïðåâðàòèòñÿ â
äèàãîíàëüíóþ:
AI
x
y
z
I
I
I
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
00
00
00
,
(2.56)
à åå ýëåìåíòû Ix, Iy, Iz áóäóò ãëàâíûìè öåíòðàëüíûìè ìîìåíòàìè
èíåðöèè. Ïðîåêöèè óðàâíåíèÿ (2.50) íà îñè ñâÿçàííîé ñèñòåìû
êîîðäèíàò ïðè ýòîì çàïèøóòñÿ â âèäå
AA
A
I
x
y
z
I
x
y
z
x
y
M
M
•
•
•
ω
ω
ω
ω
ω
ω
ω
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
+
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
Σ
Σ
ΣMz
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
,
(2.57)
ãäå
Aω
ωω
ωω
ωω
=−
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
0
0
0
zy
zx
yx
;
(2.58)
ΣMx, ΣMy, ΣMz – ñóììû ïðîåêöèé ìîìåíòîâ âñåõ âíåøíèõ è
ðåàêòèâíûõ ñèë íà îñè ñâÿçàííîé ñèñòåìû êîîðäèíàò; •
,
•
,
•
–
ωωω
xyz
ñîñòàâëÿþùèå âåêòîðà óãëîâîãî óñêîðåíèÿ.
Îïðåäåëÿÿ èç (2.55) óãëîâûå óñêîðåíèÿ, çàïèøåì äèíàìè÷åñêèå
óðàâíåíèÿ âðàùàòåëüíîãî äâèæåíèÿ ËÀ îòíîñèòåëüíî öåíòðà ìàññ â
ïðîåêöèÿõ íà îñè ñâÿçàííîé ñèñòåìû êîîðäèíàò:
•
•
•
ω
ω
ω
ω
x
y
z
I
-
x
y
z
I
M
M
M
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
−
−
AA
A
11
Σ
Σ
Σ
AI
x
y
z
ω
ω
ω
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
,
(2.59)
ãäåAI
−1
–
ìàòðèöà, îáðàòíàÿ ê AI. Ïåðåõîäÿ ê ñêàëÿðíûì óðàâíåíèÿì,
ïîëó÷èì óðàâíåíèÿ âðàùàòåëüíîãî äâèæåíèÿ â âèäå äèíàìè÷åñêèõ
óðàâíåíèé Ýéëåðà
101
•
;
•
;
ωω
ω
ωω
ω
x
xx
x
zy
x
yz
y
yy
y
xz
y
xy
MM
I
II
I
MM
I
II
I
=
+
−
−
=
+
−
−
p
p
•
.
ωω
ω
z
zz
z
yx
z
yx
MM
I
II
I
=
+
−
−
p
(2.60)
2.2.5. ÏÐÎÅÊÖÈÈ ÂÅÊÒÎÐÍÛÕ ÓÐÀÂÍÅÍÈÉ ÍÀ ÍÎÐÌÀËÜ
È ÊÀÑÀÒÅËÜÍÓÞ Ê ÒÐÀÅÊÒÎÐÈÈ
Óñêîðåíèå ðàêåòû ïðè ïëîñêîì êðèâîëèíåéíîì äâèæåíèè ìîæ-
íî ïðåäñòàâèòü êàê ñóììó òàíãåíöèàëüíîãî àτ è íîðìàëüíîãî àn óñ-
êîðåíèé. Ýòè óñêîðåíèÿ íàïðàâëåíû ïî íàòóðàëüíûì (åñòåñòâåí-
íûì) îñÿì ñèñòåìû êîîðäèíàò Oτn. Òàíãåíöèàëüíîå óñêîðåíèå
•
V íà-
ïðàâëåíî ïî êàñàòåëüíîé ê òðàåêòîðèè. Íîðìàëüíîå óñêîðåíèå V2/ρ
íàïðàâëåíî ïî íîðìàëè ê òðàåêòîðèè â ñòîðîíó ìãíîâåííîãî öåíòðà
êðèâèçíû. Êðèâèçíà òðàåêòîðèè 1/ρ ìîæåò áûòü ïðåäñòàâëåíà êàê
1/ρ =|dθ/dS|, ãäå dθ – ýëåìåíòàðíîå èçìåíåíèå óãëà íàêëîíà êàñà-
òåëüíîé ê òðàåêòîðèè; dS – ýëåìåíòàðíûé îòðåçîê êðèâîé.
Ïðîâîäÿ çàìåíó è ïðåîáðàçîâàíèÿ, ïîëó÷èì ôîðìóëó äëÿ ìîäóëÿ
íîðìàëüíîãî óñêîðåíèÿ
an
V
V
d
dt
dt
dS
V
d
dt
==
=
2
2
ρ
θθ
.
(2.61)
Çíàê ïðîèçâîäíîé dθ/dt çàâèñèò îò ôîðìû òðàåêòîðèè: åñëè θ
óáûâàåò ñ âîçðàñòàíèåì äóãè, òî dθ/dt < 0, åñëè íàîáîðîò, òî dθ/dt >0.
Ïîñêîëüêó äëÿ òðàåêòîðèé ðàêåò è ñíàðÿäîâ êëàññà "ïîâåðõíîñòü –
ïîâåðõíîñòü" âñåãäà
•
,
θ<0 òî â ïîñëåäóþùåì ôîðìóëó äëÿ
íîðìàëüíîãî óñêîðåíèÿ áóäåì çàïèñûâàòü â âèäå
anV
d
dt
V
d
dt
==
−
θθ
.
(2.62)
Èíà÷å, çíàê ìèíóñ åñòü ñëåäñòâèå òîãî, ÷òî ïðè ðàññìîòðåíèè
äâèæåíèÿ â ïðàâîé ñèñòåìå êîîðäèíàò OXcYc ïîëîæèòåëüíîìó
íàïðàâëåíèþ îñè n ñîîòâåòñòâóåò îòðèöàòåëüíîå íàïðàâëåíèå ëèíèè
îòñ÷åòà óãëîâ θ.
Ñõåìà äåéñòâóþùèõ íà ðàññìàòðèâàåìóþ â êà÷åñòâå ïðèìåðà
êðûëàòóþ ðàêåòó îñíîâíûõ ñèë, ïðèâåäåííûõ ê öåíòðó ìàññ, ïðåä-
102
ñòàâëåíà íà ðèñ. 2 .1. Ïðîåêöèè ñèë íà êàñàòåëüíóþ è íîðìàëü âíå-
ñåì â òàáë. 2.1 . Îáîçíà÷åíèÿ ñèë è óãëîâ âçÿòû èç ðèñ. 2.1 . Çíàê ïå-
ðåä ïðîåêöèåé ïîêàçûâàåò íàïðàâëåíèå ñîñòàâëÿþùåé äàííîé
ñèëû. Åñëè íàïðàâëåíèå ñîñòàâëÿþùåé ñîâïàäàåò ñ íàïðàâëåíèåì
îñè êîîðäèíàò, òî ñòîèò ïëþñ, åñëè íå ñîâïàäàåò – ìèíóñ. Óïðàâ-
ëÿþùèå ñèëû ïðèâåäåíû ê öåíòðó ìàññ, ïàðû ñèë íà ðèñóíêå íå ïî-
êàçàíû.
 òàáë. 2.1 èñïîëüçóþòñÿ îáîçíà÷åíèÿ: Õð è Yð – ñóììû ñèë, ñîç-
äàâàåìûõ îäíîòèïíûìè ðóëÿìè; Ð – ñóììàðíàÿ òÿãà âñåõ äâèãàòå-
ëåé; mg = Q – âåñ èëè ñèëà òÿæåñòè.
Òàáëèöà 2.1
Ñîñòàâëÿþùèå îñíîâíûõ ñèë, äåéñòâóþùèõ
íàËÀïîîñÿìτèn
Ñèëà
Êàñàòåëüíàÿ ñîñòàâëÿþ-
ùàÿ (ïðîåêöèÿ íà îñü τ)
Íîðìàëüíàÿ ñîñòàâëÿþ-
ùàÿ (ïðîåêöèÿ íà îñü n)
Òÿãà
P cos (α−ξ)
−P sin (α−ξ)
Ëîáîâîå ñîïðîòèâëåíèå
Xa
0
Ïîäúåìíàÿ ñèëà
0
Ya
Âåñ
− mg sinθ
mg cosθ
Ïîòåðÿ òÿãè íà ðóëÿõ
−Xp cos(θ−θ)
Xp sin(θ−θ)
Óïðàâëÿþùàÿ ñèëà
−Yp cos(θ−θ)
−Yp sin(θ−θ)
103
Ðèñ. 2 .1 . Ñõåìà äåéñòâèÿ ñèë íà äâèæóùèéñÿ ËÀ ïðè ðàáîòå ñòàðòîâîãî äâèãàòåëÿ:
τ° – íà ïðàâëåíèå êàñàòåëüíîé ê òðàåêòîðèè; n° – í à ïðàâëåíèå íîðìàëè ê òðàåê-
òîðèè
Íàïèøåì óðàâíåíèÿ äâèæåíèÿ â ïðîåêöèÿõ íà êàñàòåëüíóþ è
íîðìàëü:
mV
P
Xmg
X
Y
mV
a
•
cos(
)
sin
cos(
) sin( );
•
=−
−
−−
−
−−
−
αξ
θ
θθ
θθ
pp
θα
ξθθ
θθ
θ
=−
−
−
+
+
−
−
−
PY
m
g
XY
a
sin( )
cos
sin( )
cos(
).
pp
(2.63)
 óðàâíåíèè âðàùàòåëüíîãî äâèæåíèÿ áóäåì ó÷èòûâàòü ñëåäóþ-
ùèå ìîìåíòû:
ìîìåíò àýðîäèíàìè÷åñêèõ ñèë Mz, êîòîðûé ïðèáëèæåííî ðàâåí
ïðîèçâåäåíèþ Ya lö.ä, ãäå lö.ä
–
ðàññòîÿíèå ìåæäó öåíòðîì ìàññ (ÖÌ)
è öåíòðîì äàâëåíèÿ (ÖÄ);
ìîìåíò óïðàâëÿþùèõ ñèë Mpz, êîòîðûé ïðèáëèæåííî ðàâåí Yp lp,
ãäå lp – ðàññòîÿíèå îò öåíòðà äàâëåíèÿ óïðàâëÿþùèõ îðãàíîâ äî
öåíòðà ìàññ êðûëàòîé ðàêåòû.
Óðàâíåíèå âðàùàòåëüíîãî äâèæåíèÿ â ýòîì ñëó÷àå áóäåò èìåòü
âèä
IMM
zz
z
•
•
,
θ=
+p
(2.64)
ãäå Iz – ýêâàòîðèàëüíûé ìîìåíò èíåðöèè ðàêåòû îòíîñèòåëüíî îñè
OZ, êîòîðàÿ â ðàññìàòðèâàåìîì ñëó÷àå ñîâïàäàåò ñ îñüþ OZc.
Äëÿ èññëåäîâàíèÿ óïðàâëÿåìîãî ïîëåòà, óñòîé÷èâîñòè äâèæåíèÿ
è ñòàáèëèçàöèè ËÀ ê ïðèâåäåííûì óðàâíåíèÿì íåîáõîäèìî äîáà-
âèòü óðàâíåíèÿ óïðàâëåíèÿ, îïèñûâàþùèå ðàáîòó ñèñòåìû óïðàâëå-
íèÿ. Ïðè ýòîì óïðàâëåíèè ïîëåòîì ïî ðàçëè÷íûì ïàðàìåòðàì ðàêå-
òà äîëæíà èìåòü îðãàíû óïðàâëåíèÿ, ñ ïîìîùüþ êîòîðûõ ìîæåò èç-
ìåíÿòüñÿ ñîîòâåòñòâóþùèé ïàðàìåòð äâèæåíèÿ ðàêåòû. Íàïðèìåð,
ïðè óïðàâëåíèè ïî óãëîâûì ïàðàìåòðàì θ, ψ è γ ðàêåòà èìååò ñîîò-
âåòñòâóþùèå óïðàâëÿþùèå îðãàíû – ðóëè òàíãàæà (âûñîòû), ðûñêà-
íèÿ (íàïðàâëåíèÿ) è êðåíà. Ïðè óïðàâëåíèè ïî ìîäóëþ ñêîðîñòè
ðàêåòà äîëæíà èìåòü èñïîëíèòåëüíûå îðãàíû, îáåñïå÷èâàþùèå
âîçìîæíîñòü âëèÿòü íà V ïóòåì èçìåíåíèÿ òÿãè èëè ëîáîâîãî ñî-
ïðîòèâëåíèÿ (íàïðèìåð, ñîïëî ñ öåíòðàëüíûì òåëîì èëè ðàçëè÷íî-
ãî ðîäà àýðîäèíàìè÷åñêèå òîðìîçíûå ùèòêè è çàêðûëêè).  îáùåì
ñëó÷àå ïîëîæåíèå èñïîëíèòåëüíîãî óïðàâëÿþùåãî îðãàíà â ïðîöåñ-
ñå ïîëåòà ðàêåòû çàâèñèò îò ìíîãèõ ïàðàìåòðîâ. Ê íèì îòíîñÿòñÿ
èçìåíåíèÿ íàçâàííûõ âûøå óãëîâ, óãëîâûõ ñêîðîñòåé, êîîðäèíàò
öåíòðà ìàññ è ò.ä . Äëÿ îáåñïå÷åíèÿ çàïðîãðàììèðîâàííîãî èçìåíå-
íèÿ îïðåäåëÿþùåãî ïàðàìåòðà èñïîëíèòåëüíûé îðãàí äîëæåí óñòà-
íàâëèâàòüñÿ â ïîëîæåíèå, ñîîòâåòñòâóþùåå ðàçíîñòè ìåæäó èçìå-
ðåííûì è ïðîãðàììíûì çíà÷åíèÿìè ïàðàìåòðîâ. Íàïðèìåð, ïðè
óïðàâëåíèè â âåðòèêàëüíîé ïëîñêîñòè íåîáõîäèìî çíàòü çàâèñè-
ìîñòü ìåæäó óãëîì ïîâîðîòà óïðàâëÿþùåãî îðãàíà δâ è óãëîì ïîâî-
104
ðîòà ïðîäîëüíîé îñè ËÀ. Â íàøåì ïðèìåðå íåîáõîäèìî èìåòü çàâè-
ñèìîñòü δ = f(∆θ), ãäå ∆θ – èçìåíåíèå óãëà òàíãàæà.
Äîïîëíèòåëüíûå ñëîæíîñòè, íå îòðàæåííûå â íàïèñàííûõ óðàâ-
íåíèÿõ, çàêëþ÷àþòñÿ â òîì, ÷òî ñèëû è ìîìåíòû âçàèìîñâÿçàíû ñ
õàðàêòåðèñòèêàìè äâèæåíèÿ ñëîæíûìè çàâèñèìîñòÿìè, ïðèâåäåí-
íûìè â ãë. 1.
2.2.6 . ËÈÍÅÀÐÈÇÀÖÈß ÓÐÀÂÍÅÍÈÉ ÄÂÈÆÅÍÈß ÐÀÊÅÒ È ÑÍÀÐßÄÎÂ
Ìàòåìàòè÷åñêèé ñìûñë ëèíåàðèçàöèè ñîñòîèò â òîì, ÷òî èñêî-
ìîå îòêëîíåíèå ýëåìåíòîâ îò ðàñ÷åòíûõ çíà÷åíèé, îïðåäåëÿþùèõ
íîìèíàëüíîå (îïîðíîå) äâèæåíèå, íàõîäèòñÿ ïîñðåäñòâîì ðàçëîæå-
íèÿ ñîîòâåòñòâóþùèõ ôóíêöèé â ðÿä Òåéëîðà ïî ñòåïåíÿì îòêëîíå-
íèÿ ýëåìåíòà. Íàïîìíèì ôîðìóëó ðàçëîæåíèÿ â ðÿä Òåéëîðà äëÿ
ôóíêöèè ìíîãèõ àðãóìåíòîâ, ê êîòîðîé îòíîñÿòñÿ ýëåìåíòû òðàåê-
òîðèé ðàêåò. Ïðè íàïèñàíèè ðåçóëüòàòîâ ðàçëîæåíèÿ âîñïîëüçóåìñÿ
óñëîâíûìè îáîçíà÷åíèÿìè ïîëíûõ äèôôåðåíöèàëîâ ôóíêöèè ìíî-
ãèõ ïåðåìåííûõ
dA
d
d
df
m
n
n
n
=+
+
+
⎛
⎝⎜
⎞
⎠⎟
∂
∂ξ
ξ∂
∂ξ
ξ
∂
∂ξ
ξξ
ξξ
12
1
2
KK
(,,,)
.
(2.65)
Ôîðìóëà ðàçëîæåíèÿ èìååò âèä
ff
f
nn
n
(,,,) (
;
;;
)
(,
**
*
*
ξξξ
ξδξξδξξδξ
ξ
12
1
12
2
1
KK
=+
+
+=
=
ξξ∂
∂ξ
δξ
∂
∂ξ
δξ
∂
∂ξ
δξ
2
1
1
2
2
1
1
**
**
*
,,)
!
KK
n
n
n
++
+
+
⎛
⎝⎜
⎞
⎠⎟×
×f
n
n
n
(,,,)
!
**
*
**
*
ξξξ
∂
∂ξ
δξ
∂
∂ξ
δξ
∂
∂ξ
δξ
12
1
1
2
2
1
2
KK
++
+
+
⎛
⎝⎜
⎞
⎠⎟×
×+
+
+
+
2
12
1
1
2
2
1
3
f
n
(,,,)
!
**
*
**
ξξξ
∂
∂ξ
δξ
∂
∂ξ
δξ
∂
∂ξ
KK
n
n
n
fR
*
**
*
(,,,) ,
δξ
ξξξ
⎛
⎝⎜
⎞
⎠⎟×
×+
3
12
K
(2.66)
ãäå ξi*
–
ðàñ÷åòíûå (íîìèíàëüíûå) çíà÷åíèÿ îïðåäåëÿþùèõ
ïàðàìåòðîâ.
Îòêëîíåíèå ôóíêöèè f(ξ1, ξ2, ..., ξn), âûçâàííîå îòêëîíåíèÿìè
ïàðàìåòðîâ îò ðàñ÷åòíûõ çíà÷åíèé δξ1, δξ2, ..., δξn, áóäåò ðàâíî
δξξξ ξδξξδξξδξ
ξ
1
ff
f
nn
n
(,,,) (
,
,,
)
(
**
*
*
12
1
2
2
1
KK
=+
+
+−
−
,,, )
.
**
ξξ
2K
n
(2.67)
105
Ïåðâûé ÷ëåí ðàçëîæåíèÿ (2.66) è âòîðîé ÷ëåí ðàçëîæåíèÿ (2.67)
ðàâíû è èìåþò ðàçíûå çíàêè, ïîýòîìó îáùàÿ ôîðìóëà äëÿ îòêëîíå-
íèÿ ôóíêöèè f(ξ1, ξ2, ..., ξn) ìîæåò áûòü ïîëó÷åíà â ñëåäóþùåì âèäå:
δξξ ξ
∂
∂ξ
δξ∂
∂ξ
δξ
∂
∂ξ
δξ
f
n
n
n
(,,,)
!***
12
1
1
2
2
1
1
KK
=+
+
+
⎛
⎝⎜
⎞
⎠⎟
+
++
+
+
f
n
n
(,,,)
!
**
*
**
*
ξξξ
∂
∂ξ
δξ
∂
∂ξ
δξ
∂
∂ξ
δξ
12
1
1
2
2
1
2
K
K
nn
f
⎛
⎝⎜
⎞
⎠⎟
+
++
+
+
2
12
1
1
2
2
1
3
(,,,)
!
**
*
**
ξξξ
∂
∂ξ
δξ
∂
∂ξ
δξ
∂
K
K
∂ξ
δξ
ξξξ
n
nn
fR
*
**
*
(,,,) .
⎛
⎝⎜
⎞
⎠⎟
+
3
12
K
(2.68)
×èñëî ÷ëåíîâ ðàçëîæåíèÿ, ñîõðàíÿåìîå â ðàñ÷åòàõ, çàâèñèò îò
òðåáóåìîé òî÷íîñòè îïðåäåëåíèÿ îòêëîíåíèÿ. Ïåðåõîä ê ëèíåéíîé
ôîðìå ìîäåëè ïðåäïîëàãàåò ñîõðàíåíèå òîëüêî ëèíåéíûõ ÷ëåíîâ
ðàçëîæåíèÿ.  ýòîì ñëó÷àå ôîðìóëà (2.68) ïðèìåò âèä
δξξ ξ
∂
∂ξ
δξ
∂
∂ξ
δξ
∂
f
ff
n
(,,,)
**
12
1
1
2
2
KK
=
⎛
⎝⎜⎞
⎠⎟ +⎛
⎝⎜⎞
⎠⎟ ++f
n
n
∂ξ
δξ
⎛
⎝⎜⎞
⎠⎟
*
.
(2.69)
Íàéäåì âûðàæåíèå äëÿ îòêëîíåíèÿ ïðîèçâîäíîé âèäà δ
ξd
dt
. Òàê
êàê δ
ξξξ
d
dt
d
dt
d
dt
=−
⎛
⎝⎜⎞
⎠⎟
*
,àξ=ξ*+δξ,òîïîëó÷èì
δ
ξ
ξδξ ξ
δξ
d
dt
d
dt
d
dt
d
dt
⎛
⎝⎜⎞
⎠⎟ =+
−
⎛
⎝⎜⎞
⎠⎟=
()
.
*
*
(2.70)
Òàêèì îáðàçîì, åñëè ìû èìååì ñèñòåìó íåëèíåéíûõ äèôôåðåí-
öèàëüíûõ óðàâíåíèé äâèæåíèÿ, ñîñòàâëåííóþ èç n óðàâíåíèé âèäà
d
dt
f
d
dt
f
n
n
ξξξξ
ξ
ξξξ
1
112
2
212
=
=
(,,,)
,
(,,,)
,
K
K
(2.71)
òî íà îñíîâàíèè (2.69) è (2.70) îíà ëåãêî ïðèâîäèòñÿ ê ñèñòåìå
ëèíåéíûõ óðàâíåíèé â îòêëîíåíèÿõ
106
d
dt
fff
δξ
∂
∂ξ
δξ∂
∂ξ
δξ∂
∂ξ
1
1
1
1
1
2
2
1
3
=
⎛
⎝⎜⎞
⎠⎟ +⎛
⎝⎜⎞
⎠⎟ +⎛
⎝⎜
**
⎞
⎠⎟+
=
⎛
⎝⎜⎞
⎠⎟ +⎛
⎝⎜⎞
⎠⎟
*
**
,
δξ
δξ
∂
∂ξ
δξ
∂
∂ξ
δξ
3
2
2
1
1
2
2
2
K
d
dt
ff
+
⎛
⎝⎜⎞
⎠⎟+
∂
∂ξ
δξ
f2
3
3
*
,
..............................
K
...............
(2.72)
Åñëè îïîðíîå äâèæåíèå èçâåñòíî, ò.å . ýëåìåíòû ξ1*(t), ξ2*(t), ξ3*(t)
è äðóãèå çàäàíû, òî áóäóò èçâåñòíû â ôóíêöèè âðåìåíè è ÷àñòíûå
ïðîèçâîäíûå âèäà
∂
∂ξ
fi
i
⎛
⎝⎜⎞
⎠⎟
*
, ñòîÿùèå â ñèñòåìå (2.72) ïðè îòêëîíåíèÿõ
δξi ýëåìåíòîâ.
Èñïîëüçóÿ èçëîæåííûé ìåòîä, ïðîâåäåì ëèíåàðèçàöèþ ñèñòåìû
äèôôåðåíöèàëüíûõ óðàâíåíèé, îïèñûâàþùèõ ïðîñòîé ñëó÷àé ïðî-
äîëüíîãî äâèæåíèÿ íåóïðàâëÿåìîãî îïåðåííîãî ðåàêòèâíîãî ñíàðÿ-
äà. Âîçüìåì èçâåñòíóþ íàì ñèñòåìó äèôôåðåíöèàëüíûõ óðàâíåíèé
(2.63). Ñ÷èòàÿ, ÷òî òÿãà íàïðàâëåíà ïî îñè ðàêåòû (ò.å . ïîëîæèâ óãîë
ξ = 0), è ïðèíèìàÿ Xp = Yp = 0, ïîñëå ïðåîáðàçîâàíèé èç (2.63) è
(2.64) ïîëó÷èì
m
dV
dt
PX
Q
mV
d
dt
PY
QI
d
dt
a
az
=−
−
=+
−
cos
sin ;
sin
cos ;
αθ
θ
αθ
θ2
2=M.
(2.73)
Ïðè ëèíåàðèçàöèè áóäåì ñ÷èòàòü, ÷òî ìàññà è ìîìåíò èíåðöèè
äëÿ îïîðíîãî è âîçìóùåííîãî äâèæåíèé èçìåíÿþòñÿ ïî âðåìåíè
îäèíàêîâî:mt mt It It
zz
()()()().
*
*
==
è
Êðîìå òîãî, áóäåì ïðåíåáðåãàòü âëèÿíèåì èçìåíåíèÿ âûñîòû íà
àýðîäèíàìè÷åñêèå õàðàêòåðèñòèêè è òÿãó. Äëÿ ìàëûõ çíà÷åíèé δy ýòî
âëèÿíèå íåñóùåñòâåííî, ïîñêîëüêó ôóíêöèè H(y), ρ(y), π(y)èa(y), êî-
òîðûìè îíî ó÷èòûâàåòñÿ ïðè ðàñ÷åòàõ, èçìåíÿþòñÿ ìåäëåííî.
Òàêèì îáðàçîì, ìîæíî çàïèñàòü
m
dV
dt
dV
dt
PX
Q
mV
d
dt
V
d
a
−
⎛
⎝⎜
⎞
⎠⎟ =−
−
−
*
*
(cos)
(si
n);
δα
δδθ
θ
θ
δα
δδθ
θθ
*
*
(si
n)
(cos)
;
dt
PY
Q
I
d
dt
d
dt
a
z
⎛
⎝⎜
⎞
⎠⎟ =+
−
−
⎛2
2
2
2
⎝⎜
⎞
⎠⎟ =δMz.
107
Ïðè ïðèíÿòûõ óïðîùåíèÿõ îòêëîíåíèÿ àýðîäèíàìè÷åñêèõ ñèë è
ìîìåíòîâ áóäóò çàâèñåòü òîëüêî îò äâóõ âåëè÷èí – îòêëîíåíèÿ ñêî -
ðîñòè ïîëåòà δV è îòêëîíåíèÿ óãëà àòàêè δα. Åñëè îáîçíà÷èòü
Xf
VXf
V
Yf
VYf
V
aa
aa
*
*
(;);
(;);
(;);
(;);
**
**
==
==
11
22
αα
αα
Mf
VMf
V
zz
*
(; );
(;),
**
==
33
αα
òî, ðàçëàãàÿ ïðèâåäåííûå çàâèñèìîñòè â ðÿä ïî ôîðìóëå (2.66),
ïîëó÷èì ñ ó÷åòîì òîëüêî ëèíåéíûõ ÷ëåíîâ
δ
∂
∂
δ
∂
∂α
δα
δ
XXX
X
V
V
X
YYY
aaa
aaa
=−=
⎛
⎝⎜⎞
⎠⎟ +⎛
⎝⎜⎞
⎠⎟
=−=
*
**
*
;
∂
∂
δ
∂
∂α
δα
δ
∂
∂
Y
V
V
Y
MMM
M
V
aa
zzz
z
⎛
⎝⎜⎞
⎠⎟ +⎛
⎝⎜⎞
⎠⎟
=−=
⎛
⎝⎜⎞
**
*
;
⎠⎟ +⎛
⎝⎜⎞
⎠⎟
**
.
δ
∂
∂α
δα
V
Mz
(2.74)
Çíà÷îê * ïîêàçûâàåò, ÷òî äàííàÿ âåëè÷èíà îòíîñèòñÿ ê îïîðíîìó
äâèæåíèþ, îïèñûâàåìîìó íåëèíåéíîé ìîäåëüþ. Ââåäåì ñîêðàùåí-
íóþ çàïèñü ÷àñòíûõ ïðîèçâîäíûõ
∂
∂ξ
ξ
A
A
i
i
⎛
⎝⎜⎞
⎠⎟=
*
è ïåðåïèøåì ôîðìóëó (2.74) â ñëåäóþùåì âèäå:
δδδ
α
δ
δ
α
δδδ
α
ααα
XXVX YY
VY mmVm
aa
V
aa
a
V
az
z
V
z
=+
=
+
=+
;;.
Ïîäîáíûì æå îáðàçîì íàéäåì îòêëîíåíèÿ äëÿ ÷ëåíîâ, ñîäåðæà-
ùèõ òÿãó Ð:
δ
α
αδαδ
α
αδα
(si
n)c
o
s ;(co
s)
s
in.
**
PP PP
==
−
Ñ÷èòàÿ âåñ ðàêåòû Q ïîñòîÿííûì, ïîëó÷èì δ(Q sinθ)=Q cosθ* δθ;
δ(Q cosθ)=− Q sinθ* δθ. Èìåÿ â âèäó, ÷òî
dV
dt
dV
dt
d
dt
V
V
d
dt
V
d
dt
V
d
dt
V
d
dt
dV
d
−=
−=++
*
*
*
*
*
;
δ
θθ
δθδ
θ
dt
V
d
dt
δθ
δθ
≈
*
108
(áåç ó÷åòà ÷ëåíîâ âòîðîãî ïîðÿäêà ìàëîñòè);
d
dt
d
dt
d
dt
2
2
2
2
2
2
θθ
δθδθδθδα
−=
=
−
*
,
è
à òàêæå ïðèíèìàÿ â ñèëó ìàëîñòè óãëà α*, ÷òî sinα* ≈α*, cosα* ≈ 1,
ïîëó÷èì ñëåäóþùóþ ñèñòåìó ëèíåàðèçîâàííûõ óðàâíåíèé:
m
dV
dt
XVPXQ
Q
mV
d
dt
a
V
a
δ
δα
θ
δ
αθ
δ
θ
δθ
α
=−
−
+
−
−
(
cos )
cos
;
**
*
*
−
⎛
⎝⎜
⎞
⎠⎟ =+
+
−
+
d
dt
YdVPYQ
Q
I
d
a
V
a
z
δα
θδα
αδθ
δ
α
(s
i
n
)
s
i
n
;
**
2
θ
δδ
α
α
dt
mVm
z
V
z
2=+
.
(2.75)
Ýòà ñèñòåìà ñîñòîèò èç ëèíåéíûõ îäíîðîäíûõ äèôôåðåíöèàëü-
íûõ óðàâíåíèé ñ êîýôôèöèåíòàìè, ÿâëÿþùèìèñÿ èçâåñòíûìè
ôóíêöèÿìè âðåìåíè.
Ïðè èñïîëüçîâàíèè ìåòîäà ëèíåàðèçàöèè óðàâíåíèé äâèæåíèÿ,
â îñíîâå êîòîðîãî ëåæèò óñëîâèå äîñòàòî÷íîé ìàëîñòè âîçìóùåíèé,
íåîáõîäèìî çíàòü, êàêîâà òî÷íîñòü ïîëó÷àåìûõ ðàñ÷åòîì ðåçóëüòà-
òîâ èëè, èíà÷å, êàêèìè ïðåäåëàìè äîëæíû áûòü îãðàíè÷åíû èññëå-
äóåìûå âîçìóùåíèÿ, ÷òîáû ïîãðåøíîñòè ðàñ÷åòà ïî óðàâíåíèÿì â
îòêëîíåíèÿõ íå ïðåâîñõîäèëè äîïóñòèìûõ. Èñ÷åðïûâàþùèé îòâåò
íà ýòîò âîïðîñ ìîæåò áûòü ïîëó÷åí ïóòåì ñðàâíåíèÿ ðåçóëüòàòîâ
ïðèáëèæåííîãî è òî÷íîãî ðåøåíèé, îäíàêî èç-çà òðóäîåìêîñòè ïî-
ñëåäíåãî òàêîé ìåòîä îöåíêè òî÷íîñòè íå èìååò øèðîêîãî ïðèìåíå-
íèÿ. Ïîýòîìó ÷àñòî èñïîëüçóþò ìåíåå ñòðîãèå, íî áîëåå ïðîñòûå
êîñâåííûå èëè ïðèáëèæåííûå ìåòîäû îöåíêè ïîãðåøíîñòåé. Îä-
íèì èç íèõ ÿâëÿåòñÿ îöåíêà ñóììû R ÷ëåíîâ ðàçëîæåíèÿ, îòáðàñû-
âàåìûõ ïðè ëèíåàðèçàöèè èñõîäíûõ óðàâíåíèé, ñ ïîìîùüþ êîòî-
ðîé ìîæíî îðèåíòèðîâî÷íî óñòàíîâèòü äîïóñòèìóþ îáëàñòü âîçìó-
ùåíèé åùå äî âûïîëíåíèÿ ðàñ÷åòîâ. Ïðîâåäÿ ïîäîáíîãî ðîäà
àíàëèç äëÿ âñåõ ÷ëåíîâ èñõîäíûõ óðàâíåíèé, ìîæíî óñòàíîâèòü
îáîáùåííûå ïðåäåëüíûå çíà÷åíèÿ âîçìóùåíèé, âíóòðè êîòîðûõ
òî÷íîñòü ðàñ÷åòà ïî ëèíåàðèçîâàííûì óðàâíåíèÿì áóäåò óäîâëåòâî-
ðèòåëüíîé.
Ãëàâà 3
ÑÎÑÒÀÂËÅÍÈÅ ÄÈÔÔÅÐÅÍÖÈÀËÜÍÛÕ
ÓÐÀÂÍÅÍÈÉ ÄÂÈÆÅÍÈß ÐÀÊÅÒ È ÑÍÀÐßÄÎÂ
Êîíêðåòíûé âèä ìàòåìàòè÷åñêîãî îïèñàíèÿ ïðîöåññà äâèæåíèÿ ËÀ çàâèñèò îò
äîïóùåíèé, ïîëîæåííûõ â îñíîâó ñîñòàâëåíèÿ ìàòåìàòè÷åñêîé ìîäåëè, âûáðàííîé
ñèñòåìû êîîðäèíàò è ñèñòåìû äåéñòâóþùèõ ñèë.
Ïðè äâèæåíèè òåë â âîçäóõå ñâÿçü ìåæäó îñíîâíûìè âèäàìè äâèæåíèé (ïîñòó-
ïàòåëüíûì è âðàùàòåëüíûì, ïðîäîëüíûì è ïîïåðå÷íûì) ïðîÿâëÿåòñÿ ÷åðåç ðåàêòèâ-
íûå è àýðîäèíàìè÷åñêèå ñèëû è ìîìåíòû.  çàâèñèìîñòè îò ïîñòàíîâêè çàäà÷è ïðè
ñîñòàâëåíèè óðàâíåíèé ïðîñòðàíñòâåííîãî äâèæåíèÿ ËÀ ó÷èòûâàþòñÿ èíåðöèîí-
íûå, àýðîäèíàìè÷åñêèå è ðåàêòèâíûå ïåðåêðåñòíûå ñâÿçè, à ïðè ñîñòàâëåíèè óðàâ-
íåíèé ïðîñòðàíñòâåííîãî äâèæåíèÿ â ðàñøèðåííîé ïîñòàíîâêå äîëæíû ó÷èòûâàòü-
ñÿ òàêæå ïåðåêðåñòíûå ñâÿçè ñèñòåìû óïðàâëåíèÿ ïî êàíàëàì òàíãàæà, ðûñêàíèÿ,
êðåíà è ñâÿçè, îáóñëîâëåííûå ïîÿâëåíèåì óïðàâëÿþùèõ ñèë.
Äëÿ áàëëèñòè÷åñêèõ ðàêåò, êàê ïîêàçûâàþò òåîðåòè÷åñêèå è ýêñïåðèìåíòàëü-
íûå èññëåäîâàíèÿ, ðàçäåëåíèå äâèæåíèé íà ïîñòóïàòåëüíîå äâèæåíèå öåíòðà ìàññ è
âðàùàòåëüíîå îòíîñèòåëüíî öåíòðà ìàññ è ðàçäåëåíèå ïîñòóïàòåëüíîãî äâèæåíèÿ
íà ïðîäîëüíîå è áîêîâîå ïîçâîëÿþò ïîëó÷èòü ïðàêòè÷åñêè ïðèåìëåìóþ òî÷íîñòü
ðàñ÷åòîâ, ðåçóëüòàòû êîòîðûõ õîðîøî ñîãëàñóþòñÿ ñ ðåçóëüòàòàìè îïûòíûõ
ñòðåëüá. Åñòåñòâåííî, ÷òî ðàçäåëüíîå ðàññìîòðåíèå äâèæåíèé âîçìîæíî òîëüêî
ïðè ñóùåñòâåííûõ óïðîùåíèÿõ.
3.1 . ÓÐÀÂÍÅÍÈß ÏÐÎÑÒÐÀÍÑÒÂÅÍÍÎÃÎ ÄÂÈÆÅÍÈß
ÐÀÊÅÒ ÍÀ ÀÊÒÈÂÍÎÌ Ó×ÀÑÒÊÅ ÒÐÀÅÊÒÎÐÈÈ
3.1.1. ÈÑÕÎÄÍÀß ÑÈÑÒÅÌÀ ÓÐÀÂÍÅÍÈÉ ÏÐÎÑÒÐÀÍÑÒÂÅÍÍÎÃÎ
ÄÂÈÆÅÍÈß ÐÀÊÅÒÛ
Äâèæåíèå ðàêåòû áóäåì ðàññìàòðèâàòü â íîðìàëüíîé çåìíîé
ñèñòåìå êîîðäèíàò O0XgYgZg. Ïðè ýòîì äëÿ óïðîùåíèÿ çàäà÷è âëèÿ-
íèå âðàùåíèÿ Çåìëè ó÷òåì ââåäåíèåì ïîñòîÿííîãî ïî âåëè÷èíå è
íàïðàâëåíèþ óñêîðåíèÿ ñâîáîäíîãî ïàäåíèÿ, ïðåíåáðåãàÿ êîðèîëè-
ñîâûì óñêîðåíèåì; êðèâèçíó Çåìëè òàêæå ó÷èòûâàòü íå áóäåì. Ïðè
ýòèõ äîïóùåíèÿõ ñèñòåìà óðàâíåíèé ìîæåò áûòü íàïèñàíà íà îñíî-
âàíèè óðàâíåíèé (2.48) è (2.60). Â îòñóòñòâèå âåòðà âîçäóøíàÿ ñêî-
ðîñòü ðàâíà çåìíîé: V = Vê.
Ïðîùå âñåãî çàïèñàòü ñèñòåìó óðàâíåíèé äëÿ îïðåäåëåíèÿ ñêî-
ðîñòè V ïîñòóïàòåëüíîãî äâèæåíèÿ öåíòðà ìàññ ðàêåòû îòíîñèòåëü-
íî Çåìëè â ïðîåêöèÿõ íà îñè òðàåêòîðíîé ñèñòåìû êîîðäèíàò, òàê
110
êàê â ýòîé ñèñòåìå VV
xê
=
,
Vyê
=
==
Vzê
0. Òîãäà óðàâíåíèÿ (2.48)
óïðîñòÿòñÿ è áóäóò èìåòü âèä
•
/;
/;
/.
VFm
VF
m
VF
m
x
zy
yz
=
=
=−
Σ
Σ
Σ
ω
ω
êê
êê
(3.1)
Ñ öåëüþ îïðåäåëåíèÿ ïðîåê-
öèé óãëîâîé ñêîðîñòè äâèæåíèÿ
òðàåêòîðíîé ñèñòåìû êîîðäèíàò
OXêYêZê îòíîñèòåëüíî íåïîäâèæ-
íîé ñèñòåìû O0XgYgZg íà îñè òðà-
åêòîðíîé ñèñòåìû êîîðäèíàò âîñ-
ïîëüçóåìñÿ ðèñ. 3.1, èç êîòîðîãî
ñëåäóåò
ωθ
ωθ
ω
θ
xyz
êêê
===
•
sin ;
•
cos ;
•
.
ΨΨ
(3.2)
Ïîäñòàâëÿÿ ω y ê
è ωzê
â (3.1), ïîëó÷èì ñèñòåìó
•
;•
;
•
cos
.
V
F
m
V
F
m
V
F
m
xy
z
==
=−
Σ∆
Ψ
Σ
êê
ê
θ
θ
(3.3)
Ïðè íàïèñàíèè ïðàâûõ ÷àñòåé óðàâíåíèé (3.3) áóäåì ó÷èòûâàòü
ñîñòàâëÿþùèå òÿãè, ñèëû òÿæåñòè, àýðîäèíàìè÷åñêèõ è óïðàâëÿþ-
ùèõ ñèë.
Àýðîäèíàìè÷åñêóþ ñèëó RA çàäàäèì ñîñòàâëÿþùèìè Xa, Ya, Za â
ñêîðîñòíîé ñèñòåìå êîîðäèíàò. Òîãäà, âîñïîëüçîâàâøèñü òàáëèöåé
íàïðàâëÿþùèõ êîñèíóñîâ (ñì. òàáë. 1 .2) è ôîðìóëàìè ïåðåõîäà, ïî-
ëó÷èì ïðîåêöèè àýðîäèíàìè÷åñêîé ñèëû íà îñè òðàåêòîðíîé
ñèñòåìû êîîðäèíàò:
RXX
RYY Z
RZY
Ax
a
Ay
a
a
a
a
Az
a
ê
ê
ê
ê
ê
ê
=−
=−
==
−
==
;
cos
sin ;
sin
γγ
γγ
aaa
Z
+
cos .
(3.4)
111
Ðèñ. 3 .1 . Ñõåìà âçàèìíîãî ðàñïîëîæå-
íèÿ òðàåêòîðíîé è íîðìàëüíîé ñèñòåì
êîîðäèíàò
Ïóñòü òÿãà çàäàíà ïðîåêöèÿìè íà ñâÿçàííûå îñè êîîðäèíàò Px,
Py, Pz. Ïîäîáíîå ïðåäñòàâëåíèå òÿãè óäîáíî ïðè ðàñ÷åòàõ õàðàêòåðè-
ñòèê äâèæåíèÿ ðàêåò äëÿ ïîñëåäóþùåãî ó÷åòà ãàçîäèíàìè÷åñêèõ
óïðàâëÿþùèõ ñèë, êîòîðûå ïðîÿâëÿþòñÿ ïðè îòêëîíåíèè âåêòîðà
òÿãè îò ïðîäîëüíîé îñè ðàêåòû. Óïðàâëÿþùèå ñèëû, ñîçäàâàåìûå
îòäåëüíûìè ãàçîäèíàìè÷åñêèìè îðãàíàìè óïðàâëåíèÿ, ìîãóò áûòü
âêëþ÷åíû â ñîñòàâëÿþùèå òÿãè ïî ñâÿçàííûì îñÿì. Êðîìå òîãî, ýòî
äàåò âîçìîæíîñòü ó÷åñòü âëèÿíèå ýêñöåíòðèñèòåòà òÿãè íà õàðàêòå-
ðèñòèêè äâèæåíèÿ ðàêåòû.
Çàïèøåì óïðàâëÿþùèå àýðîäèíàìè÷åñêèå ñèëû, ñîçäàâàåìûå
îäíîòèïíûìè àýðîäèíàìè÷åñêèìè îðãàíàìè óïðàâëåíèÿ, â ïðîåê-
öèÿõ íà îñè ñâÿçàííîé ñèñòåìû êîîðäèíàò ΣXp, ΣYp, ΣZp.
Ïîëüçóÿñü òàáëèöåé íàïðàâëÿþùèõ êîñèíóñîâ (ñì. òàáë. 1.3) è
ôîðìóëàìè ïåðåõîäà, ïîëó÷èì óðàâíåíèÿ äëÿ âû÷èñëåíèÿ ïðîåêöèé
òÿãè è óïðàâëÿþùèõ ñèë íà òðàåêòîðíûå îñè:
PX PX
PY
PZ
xx
yz
êê
pp
p
−=
−
−
−+
+−
ΣΣ
ΣΣ
()
c
o
s
c
o
s
()
s
i
n
c
o
s
(
αβ
αβ
p)sin ;
β
PY PX
PY
yx
a
a
y
êê
pp
−=
−
+
+
++
ΣΣ
Σ
(
)(sin cos
sin cos sin )
(
αγ γαβ
p
p
)(cos cos sin sin sin ) (
)sin cos ;
γα γαβ
γβ
aa
za
PZ
−−
+
Σ
(3.5)
PZ PX
PY
zxaa
y
+=
−
−
+
++
ΣΣ
Σ
pp
p
ê
()
(
s
i
n
s
i
n
c
o
s
c
o
s
s
i
n
)
(
γα γαβ
)(sin cos
cos sin sin)(
)cos cos .
γα γαβ
γβ
aa
za
PZ
++
+
Σ
p
Òàê êàê ìû íå ó÷èòûâàåì ïåðåìåí÷èâîñòü ñèëû òÿæåñòè è êðè-
âèçíó ïîâåðõíîñòè Çåìëè, òî ïðîåêöèè ñèëû òÿæåñòè íà òðàåêòîð-
íûå îñè êîîðäèíàò î÷åâèäíû:
QQQQQ
xyz
êêê
=−
=−
=
sin ;
cos ;
.
θθ
0
(3.6)
Ïîäñòàâëÿÿ ïîëó÷åííûå çíà÷åíèÿ ñîñòàâëÿþùèõ âñåõ ó÷èòûâàå-
ìûõ íàìè ñèë èç (3.5), (3.6) è óãëîâûõ ñêîðîñòåé (3.2) â îñíîâíûå
óðàâíåíèÿ (3.1), ïðèõîäèì ê ñèñòåìå óðàâíåíèé, îïèñûâàþùåé äâè-
æåíèå öåíòðà ìàññ ðàêåòû â òðàåêòîðíîé ñèñòåìå êîîðäèíàò:
•
()
;
V
m
PXXQ
xx
=−
−
+
1
êê
ê
pê
Σ
(3.7)
V
m
PYYQ
yy
•
()
;
θ=
+
++
1
êê
ê
pê
Σ
(3.8)
V
m
PZZ
z
•
cos
(
).
ΨΣ
θ=−
+
+
1
êê
pê
(3.9)
112
Óðàâíåíèÿ âðàùàòåëüíîãî äâèæåíèÿ ðàêåò îáû÷íî çàïèñûâàþò â
ïðîåêöèÿõ íà ñâÿçàííûå îñè. Ëþáàÿ äðóãàÿ íå ñâÿçàííàÿ ñ ðàêåòîé
ñèñòåìà êîîðäèíàò ïåðåìåùàåòñÿ îòíîñèòåëüíî ðàêåòû, à ýòî ïðè-
âîäèò ê íåîáõîäèìîñòè ó÷èòûâàòü ïðè èññëåäîâàíèè åå äâèæåíèÿ
ïåðåìåííîñòü ìîìåíòîâ èíåðöèè äàæå ïðè m = const, ÷òî âíîñèò èç-
ëèøíèå óñëîæíåíèÿ. Çàïèøåì óðàâíåíèÿ âðàùàòåëüíîãî äâèæåíèÿ
â ïðîåêöèÿõ íà ñâÿçàííûå îñè êîîðäèíàò, ïðåäïîëàãàÿ, ÷òî îíè ñîâ-
ïàäàþò ñ ãëàâíûìè öåíòðàëüíûìè îñÿìè èíåðöèè:
II
IMM
xx
zyyz
x
x
•
()
;
ωω
ω
+−
=
+
ΣΣ
p
(3.10)
II
IMM
yy
x
zxz
y
y
•
()
;
ωω
ω
+−
=
+
ΣΣ
p
(3.11)
II
IMM
zz
yzxy
z
z
•
()
,
ωω
ω
+−
=
+
ΣΣ
p
(3.12)
ãäå ΣMx, ΣMy, ΣMz – ñóììû ïðîåêöèé ìîìåíòîâ âíåøíèõ ñèë è òÿãè
íà ñâÿçàííûå îñè êîîðäèíàò (áåç ó÷åòà óïðàâëÿþùèõ ñèë); ΣM x
p,
ΣM yp
, ΣMzp
–
ñóììû ïðîåêöèé ìîìåíòîâ óïðàâëÿþùèõ ñèë íà
ñâÿçàííûå îñè êîîðäèíàò.
Äëÿ îñåñèììåòðè÷íûõ ðàêåò äèíàìè÷åñêèå óðàâíåíèÿ âðàùà-
òåëüíîãî äâèæåíèÿ ìîæíî ïðèíÿòü â óïðîùåííîì âèäå:
IM
M
II
IMM
II
xx
x
yy
x
zxz
y
zz
x
y
•
;
•
()
;
•
(
ω
ωω
ω
ω
=+
+−
=
+
+
ΣΣ
ΣΣ
p
p
yxx
y
z
IM
M
z
−=
+
).
ωωΣ
Σp
(3.13)
Ïðè ðàáîòàþùåì äâèãàòåëå âñëåäñòâèå èçìåíåíèÿ ìàññû ðàêåòû
èç-çà ðàñõîäà òîïëèâà ìîìåíòû èíåðöèè áóäóò ïåðåìåííûìè âåëè-
÷èíàìè. Çíà÷åíèÿ Ix, Iy, Iz äëÿ ðàêåòû îïðåäåëÿþòñÿ òàê æå, êàê è
äëÿ âñÿêîãî ñëîæíîãî òåëà, ò.å . âû÷èñëÿþòñÿ íà îñíîâàíèè ïîäðîá-
íûõ ÷åðòåæåé ðàêåòû è ïðè èçâåñòíîì çàêîíå èçìåíåíèÿ åå ìàññû â
ïîëåòå. Ðàáîòà ïî ðàñ÷åòíîìó îïðåäåëåíèþ ìîìåíòîâ èíåðöèè è èõ
èçìåíåíèþ êðîïîòëèâà è òðóäîåìêà, ïîýòîìó èõ ïðèíèìàþò ïîñòî-
ÿííûìè ïðè ïðèáëèæåííûõ áàëëèñòè÷åñêèõ ðàñ÷åòàõ. Ïðè áîëåå
òî÷íûõ ðàñ÷åòàõ, ñâÿçàííûõ ñ èññëåäîâàíèåì óñòîé÷èâîñòè è óïðàâ-
ëÿåìîñòè, ïåðåìåí÷èâîñòü ìîìåíòîâ èíåðöèè íåîáõîäèìî ó÷èòû-
âàòü. Ýêñïåðèìåíòàëüíûå ìåòîäû îïðåäåëåíèÿ ìîìåíòîâ èíåðöèè
ñëîæíûõ òåë, äàþùèå áîëåå òî÷íûå ðåçóëüòàòû â ñðàâíåíèè ñ ðàñ-
÷åòíûìè, äîñòàòî÷íî ïîäðîáíî ðàçðàáîòàíû â ìåõàíèêå, è ìû èõ
êàñàòüñÿ íå áóäåì.
Äëÿ óñòàíîâëåíèÿ ñâÿçåé ìåæäó ïðîèçâîäíûìè
•
,
θ•
,
ψ •γ è óãëîâûìè
ñêîðîñòÿìè ωx, ωy è ωz âîñïîëüçóåìñÿ ôîðìóëàìè ïåðåõîäà (ðèñ. 1 .5)
113
ωψθγωψθγ
θγ
ω ψθγ
xy
z
=+
=
+
+=
−
+
•
sin
•
;
•
cos cos
•
sin ;
•
cos sin
•
cos .
θγ
(3.14)
Ðåøàÿ ýòè óðàâíåíèÿ ñîâìåñòíî, ïîëó÷èì
•
sin
cos ;
θωγωγ
=+
yz
(3.15)
•
cos
(cos s
i
n)
;
ψ
θ
ωγ
ωγ
=−
1
yz
(3.16)
•
(cos s
i
n)
.
γωθ
ωγωγ
=−
−
xyz
tg
(3.17)
Ïðè îïðåäåëåíèè àýðîäèíàìè÷åñêèõ ñèë â ïðîöåññå ðåøåíèÿ
ïðîñòðàíñòâåííîé çàäà÷è äâèæåíèÿ ðàêåòû íàäî çíàòü çíà÷åíèÿ óã-
ëîâα,βèγa.
Îïðåäåëÿÿ ìàòðèöó íàïðàâëÿþùèõ êîñèíóñîâ ïîñëåäîâàòåëüíî-
ãî ïåðåõîäà îò ñâÿçàííîé ñèñòåìû êîîðäèíàò ê ñêîðîñòíîé, îò ñêî-
ðîñòíîé – ê òðàåêòîðíîé, îò òðàåêòîðíîé – ê çåìíîé è ïðèðàâíèâàÿ
åå äèàãîíàëüíûå ýëåìåíòû ê äèàãîíàëüíûì ýëåìåíòàì ìàòðèöû íà-
ïðàâëÿþùèõ êîñèíóñîâ íåïîñðåäñòâåííîãî ïåðåõîäà îò ñâÿçàííîé
ñèñòåìû êîîðäèíàò ê çåìíîé, ïîëó÷èì ñëåäóþùèå ñîîòíîøåíèÿ
ìåæäó óãëàìè:
sin
sin cos cos
cos (sin cos
cos sin sin );
θθ
α
βθαγ αβγ
=++
aa
(3.18)
sin cos
sin cos cos
cos (sin cos
sin sin cos
ψγ
βγ
βθ
γθ
=+
+
+
ΨΨ
a
a
βψ
θ
γ
)cos
•
sin sin ;
−
(3.19)
cos sin
sin cos cos
sin sin .
θγ γβθβθ
=−
a
(3.20)
Åñëè òåïåðü èñïîëüçîâàòü âûðàæåíèÿ äëÿ ïðîåêöèé âåêòîðà ñêîðîñòè
öåíòðà ìàññ ðàêåòû íà îñè ñèñòåìû êîîðäèíàò O0XgYgZg (ñì. ðèñ. 1.7),
òî ïîëó÷èì
dxdtV
g/c
o
s
c
o
s
;
=θ
Ψ
(3.21)
dydtV
g/s
i
n
;
=θ
(3.22)
dzdtV
g/c
o
s
s
i
n
.
=−
θΨ
(3.23)
Ñîîòâåòñòâåííî ðàññòîÿíèå îò íà÷àëà êîîðäèíàò äî öåíòðà ìàññ
ðàêåòû (íàêëîííàÿ äàëüíîñòü) ðàâíî
114
rxyz
ggg
=+
+
222
.
(3.24)
Óðàâíåíèÿ (3.7)...(3.12) è (3.15)...(3.24) âìåñòå ñ óðàâíåíèåì
mm md
t
t
=−
∫00
| •|,
(3.25)
îïðåäåëÿþùèì èçìåíåíèå ìàññû, áóäóò ñîñòàâëÿòü ñèñòåìó èç 17
óðàâíåíèé, îïèñûâàþùóþ ïðîñòðàíñòâåííîå äâèæåíèå ðàêåòû. Ýòà
ñèñòåìà óðàâíåíèé ìîæåò ïðèìåíÿòüñÿ äëÿ ðàçëè÷íûõ öåëåé. Ïðîùå
åå èñïîëüçîâàòü äëÿ ðåøåíèÿ ïðÿìîé çàäà÷è âíåøíåé áàëëèñòèêè. Â
ýòîì ñëó÷àå, åñëè áóäóò èçâåñòíû âñå ãåîìåòðè÷åñêèå, âåñîâûå,
èíåðöèîííûå,
àýðîäèíàìè÷åñêèå
õàðàêòåðèñòèêè ðàêåòû,
õàðàêòåðèñòèêè, îïðåäåëÿþùèå ðàáîòó åå äâèãàòåëÿ, çàêîíû
èçìåíåíèÿ óïðàâëÿþùèõ ñèë ΣXt
pê
(),ΣYt
pê
(),ΣZt
pê
()è ìîìåíòîâ ΣM x
p,
ΣM yp
, ΣM zp è íà÷àëüíûå óñëîâèÿ ïîëåòà, óðàâíåíèÿ ñèñòåìû ìîãóò
áûòü òåì èëè èíûì ñïîñîáîì ïðîèíòåãðèðîâàíû.
 ðåçóëüòàòå ðåøåíèÿ áóäóò íàéäåíû âñå ïàðàìåòðû äâèæåíèÿ
ðàêåòû:
Vtt txtyt
z
tr
ttt
gg
g
(); (); (); (); ();
(); (); (); (); (
θ
θψγ
Ψ
tt
ttttt
m
t
axyz
); ();
(); (); (); (); (); ().
α
βγωωω
Ðåøåíèå ïîëíîé ñèñòåìû óðàâíåíèé, îïèñûâàþùåé ïðîñòðàíñò-
âåííûé ïîëåò óïðàâëÿåìîé ðàêåòû, ÿâëÿåòñÿ ñëîæíûì è òðóäîåì-
êèì; ÷àùå âñåãî ïðè ðåøåíèè ïðàêòè÷åñêèõ çàäà÷ ðàññìîòðåííóþ
èñõîäíóþ ñèñòåìó óïðîùàþò.
3.1.2 . ÓÏÐÎÙÅÍÍÛÅ ÑÈÑÒÅÌÛ ÓÐÀÂÍÅÍÈÉ,
ÎÏÈÑÛÂÀÞÙÈÅ ÏÐÎÑÒÐÀÍÑÒÂÅÍÍÎÅ ÄÂÈÆÅÍÈÅ ÐÀÊÅÒ
 ÏËÎÒÍÛÕ ÑËÎßÕ ÀÒÌÎÑÔÅÐÛ ÎÒÍÎÑÈÒÅËÜÍÎ ÍÎÐÌÀËÜÍÎÉ
ÇÅÌÍÎÉ ÑÈÑÒÅÌÛ ÊÎÎÐÄÈÍÀÒ
Ïðè èäåàëüíîé ðàáîòå ñèñòåìû óïðàâëåíèÿ è ñîîòâåòñòâåííî â
îòñóòñòâèå ïåðåõîäíûõ ïðîöåññîâ, ïðåíåáðåãàÿ óãëîâûìè ñêîðîñòÿ-
ìè ωx, ωy, ωz è ïðîèçâîäíûìè ïî âðåìåíè •
,
•
,
•
,
αβγ
•
,
•
,
•
,
δδδ
âíý
èç ïðåäû-
äóùèõ ðàâåíñòâ ìîæíî ïîëó÷èòü ôóíêöèîíàëüíûå çàâèñèìîñòè
Mx(V, y, γ, δý)=0;My(V, y, β, δí)=0;Mz(V, y, α, δâ) = 0. Ýòè çàâèñèìî-
ñòè, íàçûâàåìûå áàëàíñèðîâî÷íûìè, îòðàæàþò ðàâåíñòâî ìîìåíòîâ
óïðàâëÿþùèõ ñèë ìîìåíòàì âñåõ îñòàëüíûõ ñèë, äåéñòâóþùèõ íà
ðàêåòó. Óãëû àòàêè, ñêîëüæåíèÿ, êðåíà, îïðåäåëÿåìûå áàëàíñèðî-
115
âî÷íûìè çàâèñèìîñòÿìè, íàçûâàþòñÿ áàëàíñèðîâî÷íûìè óãëàìè αá,
βá è γá, äâèæåíèå ðàêåòû ïî òðàåêòîðèè ñ òàêèìè óãëàìè – äâèæåíè-
åì â áàëàíñèðîâî÷íîì ðåæèìå. Ïðè áàëàíñèðîâî÷íîì ðåæèìå ïîëåòà
ïðåäïîëàãàåòñÿ ìãíîâåííàÿ ðåàêöèÿ ËÀ íà îòêëîíåíèÿ îðãàíîâ
óïðàâëåíèÿ (δí , δâ) ïî íàïðàâëåíèþ è âûñîòå ñîîòâåòñòâåííî, ïðè-
÷åì óãëû àòàêè, ñêîëüæåíèÿ è êðåíà ïðèíèìàþò ñâîè áàëàíñèðî-
âî÷íûå çíà÷åíèÿ. Çàâèñèìîñòè ìåæäó áàëàíñèðîâî÷íûìè óãëàìè
ËÀ è îðãàíîâ óïðàâëåíèÿ ìîæíî óñòàíîâèòü äâóìÿ ïóòÿìè.
Åñëè èçâåñòíû íåçàâèñèìûå àýðîäèíàìè÷åñêèå õàðàêòåðèñòèêè
ËÀ è åãî îðãàíîâ óïðàâëåíèÿ, òî äëÿ äâèæåíèÿ â ïðîäîëüíîì íà-
ïðàâëåíèè èìååì
qSlm qSlm
z
z
+=
pppp 0.
(3.26)
Îñòàâëÿÿ òîëüêî ñòàòè÷åñêèå ÷ëåíû ïðè ðàçäåëüíîì ó÷åòå
àýðîäèíàìè÷åñêèõ ìîìåíòîâ, çàïèøåì
δ
α
α
δ
â.á
á
ppp p
â
=−
+
qSlm m
qSlm
zz
z
()
.
0
(3.27)
Ïîäîáíûì îáðàçîì ìîæåò áûòü ïîëó÷åíà çàâèñèìîñòü δí.á = f(βá).
Åñëè ñóììàðíûé ìîìåíò, äåéñòâóþùèé íà ËÀ, îïðåäåëÿåòñÿ ïðè
ñîâìåñòíîì èçìåíåíèè óãëà àòàêè è óãëà îòêëîíåíèÿ óïðàâëÿþùèõ
îðãàíîâ, òî ïðè ó÷åòå ñòàòè÷åñêèõ ÷ëåíîâ ïîëó÷èì
δα
δ
α
â.á
p
á
â
=−
+
1
0
m
mm
z
zz
()
.
(3.28)
Êîýôôèöèåíò àýðîäèíàìè÷åñêîé ïîäúåìíîé ñèëû ìîæåò áûòü
ïðåäñòàâëåí â âèäå
ccc c
yyy y
áâ
â
=++
0
α
δ
αδ
.
(3.29)
Íà íà÷àëüíûõ ýòàïàõ ïðîåêòèðîâàíèÿ áîëåå óäîáíî âîñïîëüçîâàòüñÿ
ôîðìóëîé
ccc
yy
y
á
â.á
á
á
â
=+
⎛
⎝⎜⎞
⎠⎟
⎡
⎣
⎢
⎤
⎦
⎥
α
δδ
α
α.
(3.30)
Óãëû αá, βá è γá ìåäëåííî èçìåíÿþòñÿ ïî òðàåêòîðèè; èõ òåêóùèå
çíà÷åíèÿ çàâèñÿò îò ïîëîæåíèÿ ðóëåé, ñêîðîñòè äâèæåíèÿ ðàêåòû è
116
âûñîòû åå ïîëåòà. Êàê ïðàâèëî, çíà÷åíèÿ óêàçàííûõ óãëîâ, à òàêæå
óãëà γa íåâåëèêè, ÷òî ïîçâîëÿåò îïóñòèòü â óðàâíåíèÿõ ÷ëåíû,
ñîäåðæàùèå ïðîèçâåäåíèÿ ýòèõ óãëîâ. Ïðè ýòîì ñèñòåìà óðàâíåíèé
áóäåò èìåòü âèä
•
[(
)cos cos (
) sin cos
()
V
m
PX
PY
PZ
xy
z
=−
−
+
+
++
1
páá
páá
p
αβ
αβ
sin
sin ];
βθ
áê
−−
XQ
•
[(
)sin cos (
) cos cos
(
θα
γ
γ
α
=−
+
+
+
++
1
mV
PX
PY
PZ
xa
y
z
pá
páá
p )sin cos
cos ];
γβ
θ
a
YQ
áê
+−
•
cos
[( )cos cos sin
()
s
i
n
c
Ψ=−
−
−
+
++
1
mV
PX
PY
xa
ya
θ
γαβ
γ
pá
á
p
os
(
) cos cos
];
αγ
β
ápá
ê
++
+
PZ
Z
za
MMMMMM
xyz
xyz
+≈+≈+≈
ppp
000
;;;
(3.31)
sin
sin cos cos
cos sin cos ;
θθ
αβθ
αγ
=+
áá
áa
sin cos
sin cos cos
cos (sin cos
sin sin
ψγ
βγ
ββ
γ
áá
á
á
=++
+
ΨΨ
a
a
θβ ψθγ
cos)cossinsin;
áá
−
cos sin
sin cos cos
sin sin ;
θγ γβθβθ
áá
á
á
=−
•
coscos ;•
sin;•
cos sin ;
xV
yV zV
gg
g
==
=
−
θθ
θ
ΨΨ
rxyz
m
mm
d
t
ggg
t
=+
+=
−
∫
222
0
0
;|
•
|.
Ïîëó÷åííàÿ ñèñòåìà ñîñòîèò èç 14 óðàâíåíèé, ñîäåðæàùèõ 14 íå-
èçâåñòíûõ. Åñëè ïðåäïîëîæèòü, ÷òî â ïðîöåññå ïîëåòà óãëû αá, βá, γá,
à òàêæå γa íå ïðåâîñõîäÿò âåëè÷èí, ïðè êîòîðûõ ìîæíî ïðèíÿòü
sinαá ≈αá; sinγá ≈γá; cosαá ≈ 1; cosγá ≈ 1; sinβá ≈βá; sinγa ≈γa; cosβá ≈ 1;
cosγa ≈ 1, òî â ñèñòåìå (3.31) âèä óðàâíåíèé ñóùåñòâåííî óïðîñòèòñÿ
è îíà çàïèøåòñÿ â ôîðìå
•
[()
()s
i
n
]
;
V
m
PXPY PZ XQ
xy
z
=−
−
++
+−
−
1
pp
áp
á
ê
αβθ
117
•
[(
)(
)(
)
cos ];
θα
γ
θ
=
−
++−+ +
−
1
mV
PX PYPZYQ
xy
z
a
pá
á
p
ê
•
cos
[
()()()]
;
Ψ=−
−
−
++
++
+
1
mV
PX PY PZZ
xy
a
z
θ
βγ
pá
p
p
ê
MMMMMM
xyz
xyz
+=+=+=
ppp
000
;;;
sin
sin
cos ;
θθ
αθ
=+
á
(3.32)
sin
sin
cos ( cos
sin )
cos sin ;
ψβ
θ
γ
θ
γ
ψ
θ
=+
+−
ΨΨ
áá
a
γθγθ
βθ
áá
cos
cos
sin ;
=−
a
•
coscos ;•
sin;•
cos sin ;
xV
yV zV
gg
g
==
=
−
θθ
θ
ΨΨ
rxyz
m
mm
d
t
ggg
t
=+
+=
−
∫
222
0
0
;|
•
|.
Åñëè ðàññìàòðèâàåòñÿ äâèæåíèå ïðîâîðà÷èâàþùåéñÿ ðàêåòû, òî
ωx ≠ 0, à ïðàâîìåðíîñòü äîïóùåíèÿ ωy ≈ωz ≈ 0 íåîáõîäèìî ïðîâåðÿòü
äîïîëíèòåëüíûìè èññëåäîâàíèÿìè.
Ñóùåñòâåííî óïðîñòèòü ñèñòåìó óðàâíåíèé, îïèñûâàþùóþ ïðî-
ñòðàíñòâåííîå äâèæåíèå, ìîæíî äëÿ îñåñèììåòðè÷íûõ ðàêåò è ñíà-
ðÿäîâ, ó êîòîðûõ òÿãà íå ñîçäàåò ìîìåíòà îòíîñèòåëüíî öåíòðà ìàññ
è íàïðàâëåíà ïî ïðîäîëüíîé îñè ðàêåòû, ò.å . êîãäà Ð = Px; Py = Pz =
=0
.
Óïðàâëÿþùèå ñèëû ΣXp, ΣYp, ΣZp ó÷òåì â íåÿâíîì âèäå, âêëþ÷èâ
èõ ñîîòâåòñòâåííî â ÷ëåíû, ó÷èòûâàþùèå ëîáîâîå ñîïðîòèâëåíèå,
ïîäúåìíóþ è áîêîâóþ ñèëû. Òîãäà áóäåì èìåòü
•
(coscos
s
in);
•
[(si
nco
sco
ss
V
m
PX
Q
mV
P
a
a
=−
−
=+
1
1
αβ
θ
θα
γ
α
insin)
cos
sin
cos ];
•
cos
[(si
n
βγ
γγθ
θ
a
aaaa
YZQ
mV
P
+
+−−
=
Ψ
1
αγ αβγ
γγ
sin
cos sin cos )
sin
cos ].
aa
aaaa
YZ
−+
++
(3.33)
118
Èç (3.10)...(3.12) ïîëó÷èì
IM
MI
I
IM
MI
I
xx
x
z yyz
yy
y
x
z
x
y
•
();
•
()
ωω
ω
ωω
=+−
−
=+−
−
ΣΣ
ΣΣ
p
p
zx
zz
z
y xxy
IM
MI
I
z
ω
ωω
ω
;
•
().
=+−
−
ΣΣ
p
(3.34)
Åñëè óãëîâûå ñêîðîñòè ωy, ωz ðàêåòû (ñíàðÿäà) âî âðàùàòåëüíîì
äâèæåíèè ìàëû è ωx = 0, òî óðàâíåíèÿ (3.34) ìîæíî çàìåíèòü áàëàí-
ñèðîâî÷íûìè çàâèñèìîñòÿìè. Èç ïîñëåäíèõ íàéäåì áàëàíñèðîâî÷-
íûå óãëû αá, βá, êîòîðûå ââåäåì â (3.33). Äîïîëíèòåëüíî, êàê è
ðàíüøå, áóäåì ïðèíèìàòü sinαá ≈αá, sinβá ≈βá, sinγa ≈γa, à êîñèíóñû
ýòèõ óãëîâ ïðèðàâíÿåì ê åäèíèöå. Äëÿ âû÷èñëåíèÿ ïîäúåìíîé è áî-
êîâîé ñèë ïðèìåì ëèíåéíûå çàâèñèìîñòè
YYZZ
aa
a
a
==
−
αβ
αβ
áá
;,
(3.35)
ãäå
Yq
S
cZq
S
c
ay
az
aa
αα
ββ
==
;|
|
.
(3.36)
Ââîäÿ ïðèíÿòûå óïðîùåíèÿ, èç (3.33) ïîëó÷èì
•
sin ;
V
PX
m
g
a
≈
−
−θ
(3.37)
•
()() c
o
s
;
θ
αβ
γ
θ
αβ
≈
++
+
−
PY
PZ
mV
g
V
aa
a
áá
(3.38)
•
()( )
cos
.
Ψ≈
+−
+
PY
PZ
mV
aa
a
αβ
αγ
β
θ
áá
(3.39)
Èç óðàâíåíèé (3.18), (3.19) è (3.20) ñëåäóåò ñîîòâåòñòâåííî
sin
sin
cos (
);
(cos s
i
θθθ
α
β
γ
ψβ
θ
γ
≈+
+
≈+
áá
á
sin
sin + cos
a
a
ΨΨ
n);
.
θ
γβθ
a
≈
átg
(3.40)
Óðàâíåíèÿ (3.21)...(3.25) îñòàíóòñÿ áåç èçìåíåíèÿ.
Òàêèì îáðàçîì, â ðåçóëüòàòå ïðîâåäåííûõ óïðîùåíèé ïîëó÷èì
ñèñòåìó èç 11 óðàâíåíèé, íåèçâåñòíûõ æå â íåé îñòàíåòñÿ 13:
Vtt txtyt
z
tr
ttt
gg
g
(); (); (); (); ();
(); (); (); ();
θ
θψα
Ψ
á (); (); (); ().
ttt
m
t
a
βγ
á
119
Ñèñòåìà ìîæåò áûòü ðåøåíà, åñëè ê íàïèñàííûì óðàâíåíèÿì äî-
áàâèòü êèíåìàòè÷åñêèå óðàâíåíèÿ, çàäàþùèå ìåòîä óïðàâëåíèÿ.
Íàïðèìåð, ïðèíÿòü äëÿ äâóõ èç ýòèõ íåèçâåñòíûõ âåëè÷èí îïðåäå-
ëåííûé çàêîí èõ èçìåíåíèÿ ïî âðåìåíè (ïðîãðàììó), â ÷àñòíîñòè
çàäàòü θ(t)èψ(t).
 óðàâíåíèÿõ (3.38) è (3.39) ÷ëåíû, ñîäåðæàùèå ïðîèçâåäåíèÿ
ìàëûõ óãëîâ βáγà è αáγa, çíà÷èòåëüíî ìåíüøå îñòàëüíûõ ñëàãàåìûõ, è
ïðè ïðîâåäåíèè ïðèáëèæåííûõ ðàñ÷åòîâ èõ ìîæíî îïóñòèòü. Òîãäà
âìåñòî óðàâíåíèé (3.38) è (3.39) áóäåì èìåòü
•
()c
o
s
;
θ
αθ
α
≈
+
−
PY
mV
g
V
a
á
(3.41)
•
()
cos
.
Ψ≈
+
PZ
mV
a
ββ
θ
á
(3.42)
Ïîëó÷åííûå ðàíåå ñèñòåìû äèôôåðåíöèàëüíûõ óðàâíåíèé ìîãóò
áûòü ïåðåïèñàíû ïðèìåíèòåëüíî ê äâèæåíèþ íåóïðàâëÿåìîé ðàêå-
òû, åñëè îïóñòèòü â íèõ ÷ëåíû, ñîäåðæàùèå óïðàâëÿþùèå ñèëû è
ìîìåíòû. Íàïðèìåð, äëÿ ìàëûõ α, β, γ è γa, à òàêæå íåçíà÷èòåëüíûõ
óãëîâûõ ñêîðîñòåé ωx, ωy è ωz, ïîçâîëÿþùèõ ïðåíåáðå÷ü ÷ëåíàìè
âòîðîãî ïîðÿäêà ìàëîñòè, èìååì
•
( cos cos
sin cos
sin
sin );
•
V
m
PPP
X
Q
m
xyz
=−
+
−
−
=
1
1
αβ
αβ
β
θ
θ
ê
V
PPP
YQ
xa
y
a
z
a
( sin cos
cos cos
sin cos
cos );
−+
−+
+−
αγ
γα γβ
θ
ê
•
cos
( cos sin
sin cos
cos cos
Ψ=−
+
+
+
1
mV
PPPZ
xa
ya
za
θ
γβ γα γβê);
•
;•
;•
.
IM
IM
IM
xx
xyy
yzz
z
ωωω
===
(3.43)
Îñòàëüíûå 11 óðàâíåíèé ñèñòåìû ïðèìóò âèä
•
sin
cos ;
θωγωγ
=+
yz
•
cos
(cos s
i
n)
;
ψ
θ
ωγ
ωγ
=−
1
yz
•
(cos s
i
n)
;
γωθ
ωγωγ
=−
−
xyz
tg
120
sin
sin cos cos
cos sin cos ;
θθ
α
βθ
α
γ
=+
a
sin cos
sin cos cos
cos (sin cos
sin sin cos
ψγ
βγ
βθ
γθ
=+
+
+
ΨΨ
a
a
βψ
θ
γ
)cossi
ns
in;
−
cos sin
sin cos cos
sin sin ;
θγ γβθβθ
=−
a
(3.44)
•
cos cos ;
•
sin ;
•
cos sin ;
xV
yV
zV
rxyz
g
g
g
gg
=
=−
=
=+
+
θ
θ
θ
Ψ
Ψ
22
g
t
mm md
t
2
0
0
;
| •|.
=−
∫
3.1.3 . ÑÈÑÒÅÌÛ ÓÐÀÂÍÅÍÈÉ ÄÂÈÆÅÍÈß ÖÅÍÒÐÀ ÌÀÑÑ ÐÀÊÅÒÛ
Ñ Ó×ÅÒÎÌ ÂÐÀÙÅÍÈß ÇÅÌËÈ
Ðàññìîòðèì äëÿ íåïîäâèæíîé àòìîñôåðû äâèæåíèå ðàêåòû êàê
ìàòåðèàëüíîé òî÷êè, ïîìíÿ, ÷òî â ýòîì ñëó÷àå âåêòîðû V, RA è P íà-
ïðàâëåíû ïî îäíîé ëèíèè. Ñèñòåìó óðàâíåíèé ñîñòàâèì â ãåî-
öåíòðè÷åñêîé ñèñòåìå êîîðäèíàò O0X0Y0Z0, óäîáíîé äëÿ ó÷åòà âëèÿ-
íèÿ ôîðìû Çåìëè è åå âðàùåíèÿ. Ïîëîæåíèå ðàêåòû áóäåì îïðåäå-
ëÿòü êîîðäèíàòàìè x, y, z*, ãåîöåíòðè÷åñêîé øèðîòîé φãö è äîëãîòîé
λ (ñì. ðèñ. 1 .9). Äèôôåðåíöèàëüíîå óðàâíåíèå äâèæåíèÿ öåíòðà
ìàññ â èíåðöèàëüíîé ñèñòåìå êîîðäèíàò èìååò âèä m(a + aïåð +
+ aêîð)=ΣF. Â îòíîñèòåëüíîì äâèæåíèè ma = ΣF − maïåð − maêîð. ×òî-
áû ñîñòàâèòü ñêàëÿðíûå óðàâíåíèÿ, îïðåäåëèì ïðîåêöèè âõîäÿùèõ
â ýòè çàâèñèìîñòè âåëè÷èí íà êîîðäèíàòíûå îñè.
Ïðîåêöèÿ òÿãè íà êîîðäèíàòíûå îñè áóäåò ðàâíà ïðîèçâåäåíèþ
òÿãè íà êîñèíóñ óãëà ìåæäó íàïðàâëåíèåì âåêòîðà ñèëû è ñîîòâåòñò-
âóþùåé îñüþ. Êîñèíóñû óãëîâ áóäóò ðàâíû ñîîòâåòñòâåííî Vx/V;
Vy/V; Vz/V, ãäå Vx, Vy è Vz – ïðîåêöèè îòíîñèòåëüíîé ñêîðîñòè äâè-
æåíèÿ öåíòðà ìàññ ðàêåòû íà îñè êîîðäèíàò:
V VVV
xyz
=−
+
222
.
Ïðîåêöèè òÿãè îïðåäåëÿþòñÿ ïî ôîðìóëàì
121
*Çäåñü è íèæå èíäåêñ 0 ó îñåé êîîðäèíàò îïóùåí.
PP
VVPP
VVPP
VV
xxyyzz
===
/;
/;
/.
Ïðîåêöèè ñèëû ñîïðîòèâëåíèÿ âîçäóõà íà êîîðäèíàòíûå îñè áó-
äóò ðàâíû ñèëå RA, óìíîæåííîé íà êîñèíóñû óãëîâ, ò.å .
R
V
ScV R
V
ScV R
V
ScV
AR
x
AR
y
AR
z
xyz
===
ρρρ
222
;;.
(3.45)
Ñîñòàâëÿþùèå ñèëû ïðèòÿæåíèÿ Çåìëè îïðåäåëèì ñ ïîìîùüþ
ôîðìóëû äëÿ óñêîðåíèÿ ñèëû ïðèòÿæåíèÿ, ïîëó÷åííîé äëÿ ñôåðè-
÷åñêîé ìîäåëè Çåìëè: gg
R
r
òò
Ç
=
0
2
2 . Ñîîòâåòñòâóþùèå ñîñòàâëÿþùèå:
Fm
g
R
r
x
r
Fm
g
R
r
y
r
Fm
g
R
r
z
r
xy
z
òò
0
Ç
2
òò
0
Ç
2
2
òò
0
Ç
2
==
=
;;
,
2
(3.46)
ãäå x/r, y/r, z/r – êîñèíóñû óãëîâ ìåæäó íàïðàâëåíèåì ñèëû Fò è
áàçèñíûìè îñÿìè êîîðäèíàò.
Èñïîëüçóÿ ýòè ôîðìóëû, ïîëó÷èì ñèñòåìó äèôôåðåíöèàëüíûõ
óðàâíåíèé, îïèñûâàþùèõ äâèæåíèå öåíòðà ìàññ ðàêåòû îòíîñè-
òåëüíî âðàùàþùåéñÿ Çåìëè:
•
;
•
VP
V
Vm
V
ScV
m
g
R
r
xV
VP
V
V
x
x
Rx
x
z
y
y
=−
−
+
−
=
1
2
1
2
1
3
2
ρ
ò0
Ç
2
ΩΩ
m
V
ScV
m
g
R
r
y
VP
V
Vm
V
ScV
m
g
R
Ry
z
z
Rz
−−
=−
−
ρ
ρ
2
1
1
2
1
3
ò0
Ç
2
ò0
Ç
;
•
2
r
zV
zx
3
2
2
+−
ΩΩ.
(3.47)
Óñòàíîâèì ñâÿçü ìåæäó ïîëîæåíèåì ðàêåòû â âûáðàííîé ïðÿìî-
óãîëüíîé ñèñòåìå êîîðäèíàò è åå ãåîöåíòðè÷åñêèìè øèðîòîé è äîë-
ãîòîé. Èç ðèñ. 1.9 ïîëó÷èì
xr
yr
zr
==
=
cos
sin ;
sin ;
cos
cos .
φλ
φ
φλ
ãö
ãö
ãö
(3.48)
Äèôôåðåíöèðóÿ (3.48) äâàæäû ïî âðåìåíè, ïðåîáðàçîâûâàÿ ïî-
ëó÷åííûå äèôôåðåíöèàëüíûå óðàâíåíèÿ â ñîîòâåòñòâèè ñ çàâèñè-
ìîñòÿìè (3.47) è ïîìíÿ, ÷òî
•
•
•
;• ••;
•
•••
;
•
;
•
,
Vx
VyVzVx
Vy
Vz
xyz xyz
=== ===
è
122
ïðèõîäèì ê ñèñòåìå äèôôåðåíöèàëüíûõ óðàâíåíèé, êîòîðàÿ
îïèñûâàåò òðàåêòîðèþ îòíîñèòåëüíîãî äâèæåíèÿ ðàêåòû â ñâÿçàííîé
ãåîöåíòðè÷åñêîé ñôåðè÷åñêîé ñèñòåìå êîîðäèíàò. Ó÷èòûâàÿ
ãðîìîçäêîñòü ñèñòåìû, çàïèøåì åå â âèäå ôóíêöèîíàëüíûõ
çàâèñèìîñòåé
rf
r
r
t
frr
=
=
1
2
(, ,,
•
,
•
,
•
,);
(, ,,
•
,
•
,
φλ φλ
φφ
λ
φ
ãö
ãö
ãö
ãö
ãö
•
,);
(, ,,
•
,
•
,
•
,).
λ
λφ
λ
φ
λ
t
frr
t
ãö
ãö
ãö
=
3
(3.49)
Ñëîæíîñòü ðåøåíèÿ óðàâíåíèé î÷åâèäíà, íî òðóäíîñòè ïðåîäî-
ëåâàþòñÿ ñ ïîìîùüþ ýëåêòðîííûõ âû÷èñëèòåëüíûõ ìàøèí.
Ïåðåéäåì òåïåðü ê ðàññìîòðåíèþ âîçìîæíîñòè ñîñòàâëåíèÿ äè-
íàìè÷åñêèõ óðàâíåíèé äâèæåíèÿ öåíòðà ìàññ ËÀ îòíîñèòåëüíî òðà-
åêòîðíîé ñèñòåìû êîîðäèíàò ïðè òåõ æå èñõîäíûõ ïðåäïîñûëêàõ,
êàñàþùèõñÿ ó÷åòà âðàùåíèÿ Çåìëè.
Áóäåì èìåòü â âèäó, ÷òî òðàåêòîðíàÿ ñèñòåìà êîîðäèíàò ïðè ñî-
âìåùåíèè îñè OYê ñ ìåñòíîé âåðòèêàëüþ, ïðîõîäÿùåé ÷åðåç öåíòð
ìàññ äâèæóùåãîñÿ ËÀ, âðàùàåòñÿ â ïðîñòðàíñòâå îòíîñèòåëüíî êî-
îðäèíàò, ñâÿçàííûõ ñ Çåìëåé.  êà÷åñòâå ïîñëåäíèõ âîçüìåì íîð-
ìàëüíóþ çåìíóþ ñèñòåìó êîîðäèíàò OgXgYgZg. Â ñîîòâåòñòâèè ñ
(2.46) èìååì
d
dt
d
dt
VV
V
êê
ê
=+
×
*
,
ω
ãäå â ðàññìàòðèâàåìîì ñëó÷àå ω –
âåêòîð óãëîâîé ñêîðîñòè âðàùåíèÿ òðàåêòîðíûõ êîîðäèíàò îòíîñè-
òåëüíî çåìíûõ;
d
dt
*
–
Vê ëîêàëüíàÿ ïðîèçâîäíàÿ âåêòîðà Vê â òðàåê-
òîðíîé ñèñòåìå êîîðäèíàò.
Ïîäñòàâëÿÿ ïîñëåäíåå ðàâåíñòâî â (2.45), ïîëó÷èì
m
d
dt
mm
x
*
.
V
VFF
ê
êð
ï
å
ð
ê
î
ð
+×
⎛
⎝⎜
⎞
⎠⎟=+ −
−
ωΣ
Σ
aa
(3.50)
Âåêòîð óãëîâîé ñêîðîñòè òðàåêòîðíîé ñèñòåìû êîîðäèíàò îòíî-
ñèòåëüíî çåìíîé îïðåäåëÿåòñÿ ñóììîé âåêòîðîâ óãëîâûõ ñêîðîñòåé:
ωθ
λ
φ
=+
++
•••
•
,
Ψ
ãö
(3.51)
ãäå
•
λè•
–
φãö
âåêòîðû óãëîâûõ ñêîðîñòåé èçìåíåíèÿ äîëãîòû è
øèðîòû, îïðåäåëÿþùèõ ïîëîæåíèå öåíòðà ìàññ äâèæóùåãîñÿ ËÀ â
123
ñôåðè÷åñêèõ
ãåîöåíòðè÷åñêèõ
êîîðäèíàòàõ;
•
Ψè
•
–
θ
âåêòîðû
ïðîèçâîäíûõ ïî âðåìåíè óãëà ïóòè è
óãëà íàêëîíà òðàåêòîðèè.
Ñâÿçü óãëîâîé êîîðäèíàòû φãö ñ
îñüþ OYg äëÿ ñëó÷àÿ, êîãäà ïëîñ-
êîñòü OXgYg íîðìàëüíûõ êîîðäèíàò
ïðîõîäèò ÷åðåç îñü âðàùåíèÿ Çåìëè,
ïîêàçàíà íà ðèñ. 3.2. Ñõåìà âçàèìíî-
ãî ðàñïîëîæåíèÿ òðàåêòîðíûõ è íîð-
ìàëüíûõ çåìíûõ êîîðäèíàò ïðèâåäå-
íà íà ðèñ. 1 .7, 1.12.
Ïðîåêöèè óãëîâûõ ñêîðîñòåé íà
îñè òðàåêòîðíîé ñèñòåìû êîîðäèíàò
îïðåäåëèì, ïîëüçóÿñü ìåòîäèêîé,
èçëîæåííîé â ðàáîòå [71]. Âåêòîð óã-
ëîâîé ñêîðîñòè îïðåäåëèòñÿ ÷åðåç
åãî ñîñòàâëÿþùèå, íàïðàâëåííûå ïî
íîðìàëüíûì îñÿì, ñëåäóþùèì îáðà-
çîì (ñì. ðèñ. 3 .2):
••
(cos s
i
n)
.
λλφ
φ
=+
xy
gg
oo
ãö
ãö (3.52)
Èìåÿ â âèäó, ÷òî âåêòîð •φ
ãö ïåðïåíäèêóëÿðåí ïëîñêîñòè óãëà φãö,
ïîëó÷èì
•
.
φφ
gg
=−z
o
ãö
(3.53)
Ïîëüçóÿñü ìàòðèöåé ïåðåõîäà îò íîðìàëüíîé çåìíîé ñèñòåìû
êîîðäèíàò ê òðàåêòîðíîé (ñì. òàáë. 1.4), ïîëó÷èì âûðàæåíèÿ äëÿ
âåêòîðîâ •φ
ãöè
•
λ ÷åðåç èõ ñîñòàâëÿþùèå, íàïðàâëåííûå ïî îñÿì
òðàåêòîðíîé ñèñòåìû êîîðäèíàò [71]:
••
[ (cos cos cos sin
sin )
(cos c
λλφ
θφθ
φ
=+
+
+−
x
y
êã
ö
ã
ö
êã
ö
o
o
Ψ
os sin
sin
cos )
(cos sin )];
••
[
ΨΨ
θφθ φ
φφ
++
=−
ãö
ê
ãö
ãö
ãö
ê
z
x
o
oo
o
(sin cos) (sin sin)
cos ].
−+
+
ΨΨΨ
θθ
yz
êê
(3.54)
Âåêòîðû
•
Ψè
•
θ âûðàçèì ÷åðåç èõ ïðîåêöèè íà îñè òðàåêòîðíîé
ñèñòåìû êîîðäèíàò:
124
Ðèñ. 3.2. Ñõåìà âçàèìíîãî ðàñïîëî-
æåíèÿ îñåé OXg, OYg è âåêòîðîâ Ω è
•
λ
••
(s
i
n
c
o
s)
;
••
.
ΨΨ
=+
=
xy
z
êê
ê
oo
o
θθ
θθ
(3.55)
Ïîëüçóÿñü ôîðìóëîé (3.51) è ïîñëåäóþùèìè, ïîëó÷èì ïðîåêöèè
âåêòîðà ω íà îñè òðàåêòîðíîé ñèñòåìû êîîðäèíàò:
ωλφ
θφθφ
θ
xê
ãö
ãö
ãö
=+
+
+
•
(cos cos cos sin
sin) •sin cos
•
s
ΨΨ
Ψ
in;
•
( cos cos sin
sin
cos )
•
sin si
θ
ωλφ
θφθ
φ
yê
ãö
ãö
ãö
=−
+
−
−
Ψ
Ψn
•
cos ;
•
(cossin)•cos
•
.
θθ
ωλφ
φ
θ
+
=−
+
Ψ
ΨΨ
zê
ãö
ãö
(3.56)
Ìíîæèòåëü ëåâîé ÷àñòè âåêòîðíîãî ðàâåíñòâà (2.45), îïðåäåëÿþùèé
îòíîñèòåëüíîå óñêîðåíèå, ìîæåò áûòü ïðåäñòàâëåí â âèäå âåêòîðíîãî
ïðîèçâåäåíèÿ ïî ñîîòâåòñòâóþùèì îñÿì òðàåêòîðíîé ñèñòåìû
êîîðäèíàò:
aê
ê
ê
ê
êêê
êêê
êêê
êê
=+
×
=+
d
dt
d
dt
VVV
xyz
xy
**
V
V
V
xyz
ω
ωωω
ooo
zê
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
.
(3.57)
Äëÿ îñåé òðàåêòîðíîé ñèñòåìû êîîðäèíàò
d
dt
Vx
xy
z
*
•
;;
;
V
VV
V
ê
êêê
êê
ê
êê
ê
V
==
=
=
o
0
ïðîåêöèè îòíîñèòåëüíîãî óñêîðåíèÿ ñîîòâåòñòâåííî ðàâíû:
aV
aVaV
xy
z
zy
êê
êêê ê
êê
ê
êê
==
=
−
•
;;.
ωω
Ïîäñòàâëÿÿ â ïîñëåäíèå ðàâåíñòâà ôîðìóëû äëÿ ñîñòàâëÿþùèõ
óãëîâûõ ñêîðîñòåé èç (3.56), ïîëó÷èì
aV
aV
aV
x
y
z
êê
ê
ê
ãö
ãö
ê
ê
ê
ê
=
=−
+
=−
•
;
(•
cos
sin
•
cos
•
);
λφ
φ
θ
ΨΨ
êã
ö
ãö
ãö
[ •(cos
cos sin
sin
cos)•sin sin
•
c
−+
+−+
λφ
θ
φθ
φ
θ
Ψ
ΨΨ
os ].
θ
(3.58)
125
Âûðàçèì òåïåðü óãëîâûå ñêîðîñòè •
,
•
φλ
ãö
÷åðåç ïðîåêöèè
îòíîñèòåëüíîé ñêîðîñòè Vê íà îñè íîðìàëüíîé çåìíîé ñèñòåìû
êîîðäèíàò:
•
cos cos ;
•
cos sin
cos
.
φθ
λθ
φ
ãö
êê
ãö
==
−
V
r
V
r
Ψ
Ψ
(3.59)
Ïîäñòàâëÿÿ ïîñëåäíåå ðàâåíñòâî â (3.58), ïîëó÷èì óñêîðåíèå â
ëåâîé ÷àñòè óðàâíåíèÿ (2.45) â ïðîåêöèÿõ íà îñè òðàåêòîðíîé ñèñòå-
ìû êîîðäèíàò:
dV
dt
V
dV
dt
V
V
r
dV
dt
V
õy
z
ê
ê
ê
ê
ê
2
ê
ê
êê
ê
==
−
=−
•
;
•
cos ;
•
cos
θθ
Ψθφθ
.
+
V
r
ê
2
ãö
tg sin cos
Ψ2
(3.60)
Íàéäåì ïðîåêöèè ñëàãàåìûõ ïðàâîé ÷àñòè óðàâíåíèÿ (2.45) íà òå
æå îñè. Ïðîåêöèè òÿãè è óïðàâëÿþùèõ ñèë îïðåäåëÿþòñÿ ñèñòåìîé
ðàâåíñòâ (3.5). Ñîñòàâëÿþùèå àýðîäèíàìè÷åñêèõ ñèë çàäàþòñÿ ñèñ-
òåìîé ðàâåíñòâ (3.4).
Ó÷èòûâàÿ ñôåðîèäàëüíóþ ôîðìó Çåìëè, ïëîòíîñòü âîçäóõà, âõî-
äÿùóþ â âûðàæåíèÿ äëÿ ñîñòàâëÿþùèõ ñèë RA, ñëåäóåò îïðåäåëÿòü
ïî ìåñòíîé âûñîòå Í:
Hra
e
e
=−
−
−
1
1
2
2
cos
,
φãö
(3.61)
ãäå à è å – áîëüøàÿ ïîëóîñü è ýêñöåíòðèñèòåò çåìíîãî ñôåðîèäà
ñîîòâåòñòâåííî.
Ïðîåêöèè ïåðåíîñíîãî è êîðèîëèñîâà óñêîðåíèé íà îñè çåìíîé
ãåîöåíòðè÷åñêîé ñèñòåìû êîîðäèíàò, ó êîòîðîé îñü O0Y0 ñîâïàäàåò
ñ îñüþ âðàùåíèÿ Çåìëè, îïðåäåëÿþòñÿ ôîðìóëàìè (1.64) è (1.66).
Íàõîæäåíèå ïðîåêöèé íàçâàííûõ óñêîðåíèé íà îñè òðàåêòîðíîé
ñèñòåìû êîîðäèíàò çíà÷èòåëüíî ñëîæíåå.
Óñêîðåíèå ñèëû çåìíîãî òÿãîòåíèÿ è ïåðåíîñíîå óñêîðåíèå â
ôîðìóëàõ (1.44) è (1.47) îáúåäèíåíû â îáùåå óñêîðåíèå ñâîáîäíîãî
ïàäåíèÿ, êîòîðîå ïðåäñòàâëåíî â êîñîóãîëüíîé ñèñòåìå êîîðäèíàò,
îáðàçîâàííîé ðàäèóñ-âåêòîðîì r è âåêòîðîì Ω. Îáîçíà÷èâ â ôîðìó-
ëàõ (1.47) ñëàãàåìûå, îïðåäåëÿåìûå óñêîðåíèåì ñèëû çåìíîãî òÿãî-
òåíèÿ, ñîîòâåòñòâåííî ÷åðåç gòr è gòΩ, íàïèøåì
ggrggr
rr
=+
=−
òò
ã
ö
ΩΩ
ΩΩ
22
;s
i
n
.
φ
(3.62)
126
Äëÿ ïåðåõîäà ê òðàåêòîðíîé ñèñòåìå êîîðäèíàò âîñïîëüçóåìñÿ
íàïðàâëÿþùèìè êîñèíóñàìè äëÿ îïðåäåëåíèÿ ïðîåêöèé âåêòîðîâ
•
Ψ
è λ íà òå æå îñè (ñì. ôîðìóëû (3.54) è (3.56)). Ó÷èòûâàÿ çíàêîì "ìè-
íóñ" ïðîòèâîïîëîæíîñòü íàïðàâëåíèé âåêòîðîâ gr, gΩ è r, Ω, ïîëó-
÷èì
ggg
gg
xr
yr
ê
ê
ãö
ãö
=−
−
+
=−
sin
(cos cos cos sin
sin );
c
θφθ
φ
θ
Ω
Ψ
os
( cos cos cos sin
sin );
cos
si
θφθ
φ
θ
φ
−−
+
=−
g
gg
z
Ω
Ω
Ψ
ãö
ãö
ãö
ê
nΨ.
(3.63)
Ïðîåêöèè êîðèîëèñîâîé ñèëû íà îñè òðàåêòîðíîé ñèñòåìû îï-
ðåäåëèì èç ñîîòíîøåíèÿ âèäà
mm
m
V
xyz
aêîð
ê
êêê
ê
êê
00
=×
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
22
()
.
Ω
ΩΩΩ
V
xyz
ê
ooo
(3.64)
Òàê êàê íàïðàâëåíèÿ âåêòîðîâ Ω è
•
λ ñîâïàäàþò (ñì. ðèñ. 3.2), òî ñ
öåëüþ îïðåäåëåíèÿ ïðîåêöèé âåêòîðà Ω âîñïîëüçóåìñÿ ðàíåå
ïîëó÷åííîé ôîðìóëîé (3.54):
ΩΩ
Ψ
=+
+
+−
[ (cos cos cos sin
sin )
(cos cos
x
y
êã
ö
ã
ö
êã
ö
o
o
φθ
φ
θ
φΨ
Ψ
sin
sin
cos )
(cos sin )].
θφθ φ
++
ãö
ê
ãö
z
o
(3.65)
Èìååì VV
yz
êê
êê
==
0, è, ñëåäîâàòåëüíî, ïðîåêöèè êîðèîëèñîâîé
ñèëû íà îñè òðàåêòîðíîé ñèñòåìû êîîðäèíàò ðàâíû
ma
ma
V
V
ma
x
yz
z
êîð
êîð
ê
ê
ãö
êîð
ê
êê
ê
=
==
=−
0
22
2
;
cos
sin ;
ΩΩΨ
φ
VV
y
ê
ê
ãö
ãö
ê
ΩΩΨ
=+
2 (cos cos sin
sin
cos ).
φθ
φ
θ
(3.66)
×òîáû óïðîñòèòü âèä ôîðìóë, îáúåäèíèì ñîñòàâëÿþùèå îñíîâ-
íûõ äåéñòâóþùèõ ñèë ïî òðàåêòîðíûì îñÿì, èñïîëüçóÿ (3.4) è
(3.63):
FPXRm
g
xx
A
xx
êêêêê
ð
=+++
Σ
;
FPYRm
g
yy
A
yy
êêêêê
ð
=+++
Σ
;
127
FPZRm
g
zz
A
zz
êêêêê
ð
=+
++
Σ
.
Ïðèìåíèâ ôîðìóëó (2.46) è ôîðìóëû äëÿ îòäåëüíûõ ñëàãàåìûõ,
íàïèøåì óðàâíåíèÿ äâèæåíèÿ öåíòðà ìàññ ËÀ â ïðîåêöèÿõ íà îñè
òðàåêòîðíîé ñèñòåìû êîîðäèíàò, âûäåëèâ ÷ëåíû, îïðåäåëÿåìûå
âðàùåíèåì Çåìëè è åå êðèâèçíîé:
•
sin
(cos cos cos sin
sin );
•
V
F
m
gg
F
x
r
y
=+
−
+
=
ê
ãö
ãö
θφθ
φ
θ
θ
Ω
Ψ
ê
ãö
ãö
m
g
V
g
V
V
r
r
−−
−
+
++
cos
( cos cos sin
sin
cos )
cos
θφθ
φθθ
Ω
Ψ
−
=−
+
+
+
2ΩΨ
Ψ
Ω
cos
sin ;
•
cos
cos
sin
cos
φ
θ
φψ
θ
ãö
ãö
ê
t
F
mV
g
V
V
r
z
gt
g
ãö
ãö
ãö
φθφθ
φ
sin cos
(cos cos
sin ).
ΨΩΨ
+−
2
(3.67)
Ê íàïèñàííûì òðåì óðàâíåíèÿì ñëåäóåò äîáàâèòü óðàâíåíèÿ (3.59)
è î÷åâèäíûå óðàâíåíèÿ rxyz
ggg
=+
+
222
;m=mm
t
0−|
•
|.
3.2 . ÓÏÐÎÙÅÍÍÛÅ ÑÈÑÒÅÌÛ ÓÐÀÂÍÅÍÈÉ
ÏÐÎÄÎËÜÍÎÃÎ È ÁÎÊÎÂÎÃÎ ÄÂÈÆÅÍÈÉ ËÀ
ÍÀ ÀÊÒÈÂÍÎÌ Ó×ÀÑÒÊÅ ÒÐÀÅÊÒÎÐÈÈ
3.2.1 . ÐÀÇÄÅËÅÍÈÅ ÄÂÈÆÅÍÈß ÍÀ ÏÐÎÄÎËÜÍÎÅ È ÁÎÊÎÂÎÅ
Ïðè ðàçäåëåíèè ñëîæíîãî äâèæåíèÿ ðàêåò íà ïðîäîëüíîå è áî-
êîâîå ïðèíèìàþò, ÷òî â ïåðâîì ïðèáëèæåíèè ïðîäîëüíîå äâèæåíèå
íå çàâèñèò îò áîêîâîãî. Â ñîîòâåòñòâèè ñ ýòèì â óðàâíåíèÿõ äëÿ îï-
ðåäåëåíèÿ õàðàêòåðèñòèê ïðîäîëüíîãî äâèæåíèÿ ó÷èòûâàþò òîëüêî
òå ñèëû è ìîìåíòû, êîòîðûå äåéñòâóþò â ïëîñêîñòè ñòðåëüáû. Ïðè
îïðåäåëåíèè æå õàðàêòåðèñòèê áîêîâîãî äâèæåíèÿ ðàêåòû ñ÷èòàòü
åãî íåçàâèñèìûì îò ïðîäîëüíîãî íåëüçÿ, ïîýòîìó â óðàâíåíèÿ
âêëþ÷àþòñÿ âñå ñèëû è ìîìåíòû, êîòîðûå â òîé èëè èíîé ñòåïåíè
ìîãóò âûçûâàòü îòêëîíåíèå ðàêåòû îò ïëîñêîñòè ñòðåëüáû. Íà îñíî-
âàíèè ââåäåííûõ ðàíåå ïðåäïîëîæåíèé, êàñàþùèõñÿ âîçìîæíîñòè
ïðåíåáðåæåíèÿ ÷ëåíàìè âòîðîãî ïîðÿäêà ìàëîñòè, ïîëó÷èì, èñ-
128
ïîëüçóÿ èñõîäíóþ ìîäåëü, ñèñòåìó óðàâíåíèé, îïèñûâàþùóþ ïðî-
äîëüíîå (ïëîñêîå) äâèæåíèå óïðàâëÿåìîé ðàêåòû:
•
[(
)cos (
) sin
sin ];
•
[(
V
m
PX
PY
XQ
mV
P
xy
x
=−
−
+−
−
=
1
1
pp
ê
ααθ
θ−+
+
+
−
=+
=
XP
YY
Q
IM
M
y
zz
z
z
z
pp
ê
ð
)sin (
)cos
sin ];
•
;•
;
αα
θ
ωθ
ω
sin
sin cos
cos sin
sin( );
cos ;
sin ;
θθ
αθ
αθ
α
θθ
=+=
+
==
xV yV
gg
rxy
m
mm
d
t
gg
t
=+
=
−
∫
22
0
0
;|
•
|.
(3.68)
Òðèãîíîìåòðè÷åñêîå ñîîòíîøåíèå â ñèñòåìå (3.68), ñâÿçûâàþ-
ùåå óãëû θ, θ è α, â ðÿäå ñëó÷àåâ óäîáíåå çàìåíèòü ðàâåíñòâîì
θθα
=+.
(3.69)
Åñëè â ïåðâûõ äâóõ óðàâíåíèÿõ óïðàâëÿþùèå ñèëû íåèçâåñòíû,
òî ê ñèñòåìå ñëåäóåò äîáàâèòü óðàâíåíèÿ óïðàâëåíèÿ. Ïîëó÷åííàÿ
ñèñòåìà óðàâíåíèé áóäåò çàìêíóòîé è ìîæåò áûòü ðåøåíà.
Íàïèøåì òåïåðü ñèñòåìó óðàâíåíèé äëÿ îïðåäåëåíèÿ õàðàêòåðè-
ñòèê áîêîâîãî äâèæåíèÿ ðàêåòû, ïðåäïîëàãàÿ, ÷òî ïîëåò áåç êðåíà
(γ=0):
•
cos
[(
)cos sin (
)sin
(
Ψ=−
−
−
++
+
++
1
mV
PX
PY
PZ
xa
ya
z
θ
γβ
γ
pp
p )cos
];
•
;•
cos
;
sin
sin cos cos
β
ω
θ
ω
ψβ
+
=+
=
=
Z
IM
M
yy
y
y
y
ê
p
Ψ
Ψ
1
γβ
θ
γ
θ
β
γβ
θ
aa
ag
z
++
==
−
cos (sin cos
sin sin cos );
sin
;•
Ψ
tg tg
Vcossin .
θΨ
(3.70)
Óðàâíåíèÿ (3.70), îïèñûâàþùèå òîëüêî áîêîâîå äâèæåíèå, íå
ìîãóò ðåøàòüñÿ ñàìîñòîÿòåëüíî, áåç ó÷åòà îñíîâíûõ âåëè÷èí, îïðå-
äåëÿåìûõ ïðîäîëüíûì äâèæåíèåì. Íàïðèìåð, ïåðâîå óðàâíåíèå ÿâ-
ëÿåòñÿ îñíîâíûì ïðè îïðåäåëåíèè ïàðàìåòðîâ áîêîâîãî äâèæåíèÿ,
íî îíî ðåøàåòñÿ, åñëè òîëüêî èçâåñòíû m(t), V(t)èθ(t). Àýðîäèíà-
ìè÷åñêèå ñèëû è ìîìåíòû, äåéñòâóþùèå â áîêîâîì íàïðàâëåíèè,
129
òàêæå íå ìîãóò áûòü îïðåäåëåíû, åñëè íåèçâåñòíû ñêîðîñòü è âûñî-
òà ïîëåòà.
Ñèñòåìà (3.70) ïîëó÷èëàñü ñëîæíîé; êðîìå òîãî, ïðè áîëüøèõ θ
íåîáõîäèìî ïðîâåðÿòü ïðåäåëû ïðèìåíèìîñòè ôîðìóëû, îïðåäå-
ëÿþùåé γa. Ñóùåñòâåííî óïðîñòèòü ñèñòåìó ìîæíî, åñëè âîñïîëüçî-
âàòüñÿ èñêóññòâåííûì ïðèåìîì è ïðèíÿòü θ = θ = 0 â óðàâíåíèÿõ,
îïðåäåëÿþùèõ óãëîâûå ïàðàìåòðû äâèæåíèÿ ðàêåòû. Òàêîå äîïó-
ùåíèå ðàâíîñèëüíî ïðåäïîëîæåíèþ, ÷òî ðàêåòà ëåòèò â ãîðèçîí-
òàëüíîì ïîëîæåíèè, åå ïðîäîëüíàÿ îñü ñîñòàâëÿåò ñ âåêòîðîì ñêî-
ðîñòè öåíòðà ìàññ óãîë β, à óãîë γa =0
.
×òîáû ïîëó÷èòü ðåçóëüòàòû, áëèçêèå ê äåéñòâèòåëüíûì, â óðàâ-
íåíèÿõ óñëîâíîé ãîðèçîíòàëüíîé òðàåêòîðèè äâèæåíèÿ öåíòðà ìàññ
ðàêåòû ñêîðîñòü ðàêåòû äîëæíà áûòü ïðèíÿòà ðàâíîé V cosθ. Ýòà âå-
ëè÷èíà íàõîäèòñÿ ïðè ðåøåíèè ñèñòåìû óðàâíåíèé, îïèñûâàþùèõ
ïðîäîëüíîå äâèæåíèå öåíòðà ìàññ ðàêåòû (ñíàðÿäà). Ïðè ïðèíÿòûõ
äîïóùåíèÿõ èç (3.70) ñëåäóåò
Ψ=−
−
−
++
+
=+
1
mV
PX
PZ
Z
IM
M
xz
yy
y
cos
[( )si
n(
)cos ];
•
θ
ββ
ω
pp
ê
py
y
g
zV
;•
;
sin
sin cos
cos sin
sin(
);
•
cos
ψω
ψβββ
=
=+=
+
=−
ΨΨΨ
θsin .
Ψ
(3.71)
Ïðåäïîñëåäíåå ðàâåíñòâî ìîæíî çàìåíèòü ñóììîé óãëîâ
ψΨβ
=+
.
(3.72)
Åñëè â ïåðâîì óðàâíåíèè íåèçâåñòíû óïðàâëÿþùèå ñèëû, òî ê
ñèñòåìå (3.71) ñëåäóåò äîáàâèòü óðàâíåíèÿ óïðàâëåíèÿ.
Óïðàâëåíèå ïîëåòîì ðàêåò, êàê ïðàâèëî, îñóùåñòâëÿåòñÿ ïî òðåì
ðàçäåëüíûì êàíàëàì: ïî òàíãàæó, ðûñêàíèþ è êðåíó. Íåñìîòðÿ íà
òî ÷òî êàæäûé êàíàë óïðàâëåíèÿ ðåøàåò ñàìîñòîÿòåëüíûå çàäà÷è,
èõ ðàáîòà îêàçûâàåòñÿ âçàèìîçàâèñèìîé, ÷òî ïðîÿâëÿåòñÿ ÷åðåç äè-
íàìè÷åñêèå õàðàêòåðèñòèêè ðàêåòû, äèíàìè÷åñêèå è êèíåìàòè÷å-
ñêèå õàðàêòåðèñòèêè äâèæåíèÿ è ïåðåêðåñòíûå ñâÿçè. Ïîýòîìó ïðè
ðåøåíèè çàäà÷ ïî îïðåäåëåíèþ õàðàêòåðèñòèê äâèæåíèÿ óïðàâëÿå-
ìûõ ðàêåò ðàçäåëåíèå äâèæåíèÿ âîçìîæíî òîëüêî ïîñëå òîãî, êàê
óñòàíîâëåíà åãî ïðàâîìåðíîñòü íà îñíîâàíèè ïðåäâàðèòåëüíîãî
àíàëèçà êîíêðåòíûõ õàðàêòåðèñòèê ðàêåòû, åå ñèñòåìû óïðàâëåíèÿ
è óñëîâèé äâèæåíèÿ.
130
3.2.2. ÓÐÀÂÍÅÍÈß ÏÐÎÄÎËÜÍÎÃÎ
ÄÂÈÆÅÍÈß ÓÏÐÀÂËßÅÌÎÉ
ÐÀÊÅÒÛ Â ÖÅÍÒÐÀËÜÍÎÌ
ÃÐÀÂÈÒÀÖÈÎÍÍÎÌ ÏÎËÅ
Ñîñòàâèì ñèñòåìó óðàâíå-
íèé, îïèñûâàþùóþ äâèæåíèå
öåíòðà ìàññ óïðàâëÿåìîé áàë-
ëèñòè÷åñêîé ðàêåòû íà àêòèâ-
íîì ó÷àñòêå ïëîñêîé òðàåêòî-
ðèè ïðèìåíèòåëüíî ê ñôåðè÷å-
ñêîé ìîäåëè Çåìëè. Âëèÿíèå
âðàùåíèÿ Çåìëè ó÷òåì ÷àñòè÷-
íî, òîëüêî ÷åðåç óñêîðåíèå
ñâîáîäíîãî ïàäåíèÿ, ïîëàãàÿ â
ïåðâîì ïðèáëèæåíèè, ÷òî îíî
íàïðàâëåíî â öåíòð Çåìëè è
èçìåíÿåòñÿ â ñîîòâåòñòâèè ñ
çàâèñèìîñòüþ g = g0(RÇ/r)2,
àíàëîãè÷íîé çàâèñèìîñòè äëÿ
gò, ïîëó÷åííîé ðàíåå äëÿ öåí-
òðàëüíîãî
ãðàâèòàöèîííîãî
ïîëÿ. Óïðàâëÿþùèå ñèëû Õð è
Yð îòäåëüíî ó÷èòûâàòü íå áó-
äåì, à âêëþ÷èì èõ â ÷ëåíû,
ó÷èòûâàþùèå ëîáîâîå ñîïðî-
òèâëåíèå è ïîäúåìíóþ ñèëó.
Âåêòîð òÿãè íàïðàâèì ïî ïðî-
äîëüíîé îñè ðàêåòû. Ñèñòåìó
óðàâíåíèé ñîñòàâèì â ïðîåê-
öèÿõ íà îñè ïðÿìîóãîëüíîé
ñòàðòîâîé ñèñòåìû êîîðäèíàò OXY (OXcY c) (ñì. ðèñ. 3 .3). Ïðîåê-
öèþ âåêòîðà ñêîðîñòè íà îñü OX îáîçíà÷èì ÷åðåç u, à ïðîåêöèþ
íà îñü OY – ÷åðåç w. Ïðîåêöèè ñèëû òÿæåñòè íà òå æå îñè îáî-
çíà÷èì ñîîòâåòñòâåííî ÷åðåç gx è gy : gx = g sinγ; gy = g cosγ.Çà-
ïèñàâ óðàâíåíèÿ äâèæåíèÿ â ïðîåêöèÿõ íà âûáðàííûå îñè êîîð-
äèíàò è äîáàâèâ îáû÷íûå êèíåìàòè÷åñêèå è òðèãîíîìåòðè÷åñêèå
ñîîòíîøåíèÿ, î÷åâèäíûå èç ðèñ. 3 .3, ïîëó÷èì ñèñòåìó óðàâíå-
íèé
du
dt
PX
Y
m
g
dw
dt
P
aa
=
+−
−
−
=
+
cos(
) cos
sin
sin ;
sin( )
θα
θ
θ
γ
θα−+
−
XY
m
g
aa
sin
cos
cos ;
θθ
γ
131
Ðèñ. 3.3 . Ñõåìà ñèë, äåéñòâóþùèõ íà
áàëëèñòè÷åñêóþ ðàêåòó äàëüíåãî äåéñò-
âèÿ ïðè ðàññìîòðåíèè åå îòíîñèòåëüíîãî
äâèæåíèÿ â öåíòðàëüíîì ãðàâèòàöèîííîì
ïîëå
dx
dt
u
dy
dt
w
w
u
x
Ry
Vuw
r Ryx
=== =
+
=+ =++
;;;
;
;()
tg
tg
Ç
Ç
θγ
22
22
0
2
;
(/).
ggR r
=
Ç
(3.73)
Åñëè ê íàïèñàííûì óðàâíåíèÿì äîáàâèòü óðàâíåíèå, çàäàþ-
ùåå ïðîãðàììíûé óãîë òàíãàæà (α + θ)=θ = θ ïð, çàâèñèìîñòü
äëÿ îïðåäåëåíèÿ ïîäúåìíîé ñèëû è óðàâíåíèå, îïèñûâàþùåå èç-
ìåíåíèå ìàññû ðàêåòû m(t), òî ñèñòåìà ìîæåò áûòü ïðîèíòåãðè-
ðîâàíà ÷èñëåííî.
3.2.3 . ÓÐÀÂÍÅÍÈß ÏÐÎÄÎËÜÍÎÃÎ ÄÂÈÆÅÍÈß ÐÀÊÅÒÛ
 ÏËÎÑÊÎÏÀÐÀËËÅËÜÍÎÌ ÃÐÀÂÈÒÀÖÈÎÍÍÎÌ ÏÎËÅ
Ïðè ðàñ÷åòå òðàåêòîðèé äëÿ ñðàâíèòåëüíî íåáîëüøèõ äàëüíîñòåé
âî ìíîãèõ ñëó÷àÿõ ìîæíî íå ó÷èòûâàòü êðèâèçíó Çåìëè, à åå âðàùå-
íèå ó÷èòûâàòü ïðèáëèæåííî ÷åðåç óñêîðåíèå ñâîáîäíîãî ïàäåíèÿ,
ïðåäïîëàãàÿ åãî ïîñòîÿííûì ïî âåëè÷èíå è íàïðàâëåíèþ, ò.å. ñ÷è-
òàÿ ãðàâèòàöèîííîå ïîëå Çåìëè ïëîñêîïàðàëëåëüíûì.  ýòîì ñëó÷àå
â ñèñòåìå (3.73) ñëåäóåò ïîëîæèòü γ = 0, òîãäà äëÿ àêòèâíîãî ó÷àñòêà
òðàåêòîðèè ïîëó÷èì ñèñòåìó óðàâíåíèé
du
dt
PX
Y
m
dw
dt
PX
Y
m
g
aa
aa
=
−−
=
−+
−
()
c
o
ss
i
n
;
()
s
i
ns
i
n
;
θθ
θθ
du
dt
w
dx
dt
uV
uw
w
u
==
=
+
=
;;
;
.
22
θ arctg
(3.74)
 êà÷åñòâå óïðàâëÿþùåé ìîæåò áûòü âûáðàíà ôóíêöèÿ, ñâÿçàí-
íàÿ ñ ïîäúåìíîé ñèëîé Ya è ââîäÿùàÿ ñîîòâåòñòâóþùèå îãðàíè÷å-
íèÿ íà óãîë àòàêè α.
Ïðè îòñóòñòâèè óïðàâëåíèÿ èëè âûêëþ÷åíèè åãî ïî êàêèì-ëèáî
ïðè÷èíàì ïîëåò ðàêåòû ñòàíîâèòñÿ íåóïðàâëÿåìûì.  ýòîì ñëó÷àå
ñèñòåìó óðàâíåíèé, îïèñûâàþùóþ äâèæåíèå öåíòðà ìàññ, ìîæíî
ïîëó÷èòü èç ñèñòåìû (2.63), îïóñòèâ ÷ëåíû, ó÷èòûâàþùèå âëèÿíèå
óïðàâëåíèÿ. Ó áîëüøèíñòâà íåóïðàâëÿåìûõ ðàêåò âåêòîð òÿãè ñîâ-
ïàäàåò ñ îñüþ ðàêåòû, ò.å . ξ = 0. Åñëè ó÷åñòü, ÷òî ïðè ìàëûõ óãëàõ
àòàêè cosα≈1, sinα≈0, Ya ≈ 0, è äîáàâèòü îáû÷íûå êèíåìàòè÷åñêèå
132
ñîîòíîøåíèÿ, òî ïîëó÷èì ñèñ-
òåìó óðàâíåíèé, îïèñûâàþùóþ
äâèæåíèå öåíòðà ìàññ íåóïðàâ-
ëÿåìîé ðàêåòû:
dV
dt
PX
m
g
d
dt
g
V
dy
dt
V
dx
dt
V
a
=
−
−
=−
=
=
sin ;
cos
;
sin ;
cos
θ
θθ
θ
θ.
(3.75)
Ïðè ïðèíÿòûõ äîïóùåíèÿõ âåêòîðû òÿãè è ëîáîâîãî ñîïðî-
òèâëåíèÿ, äåéñòâóþùèå íà ìàòåðèàëüíóþ òî÷êó ìàññîé m, ñîâïà-
äàþùóþ ñ öåíòðîì ìàññ íåóïðàâëÿåìîé ðàêåòû, è âåêòîð ñêîðî-
ñòè åå öåíòðà ìàññ ëåæàò íà îäíîé ïðÿìîé (ðèñ. 3 .4). Èñõîäÿ èç
ðèñ. 3.4, íàïèøåì
du
dt
PX
m
a
=
−
cos .θ
Óìíîæèâ è ðàçäåëèâ ïðàâóþ ÷àñòü óðàâíåíèÿ íà m0V, ïîëó÷èì
du
dt
=
1
μ
(D − E )u. Îáû÷íî îáîçíà÷àþò tg θ = ð, è òîãäà
dp
dt
d
dt
=
1
2
cos
.
θ
θ
Èñïîëüçóÿ âòîðîå óðàâíåíèå ñèñòåìû (3.75), ïîëó÷èì dp/dt = −g/u,à
èç òðåòüåãî óðàâíåíèÿ ñèñòåìû (3.75) ïîëó÷èì
dy
dt
Vu
p
==
sin
cos
cos
.
θ
θ
θ
×åòâåðòîå óðàâíåíèå ñèñòåìû (3.75) îñòàíåòñÿ áåç èçìåíåíèÿ. Â
ðåçóëüòàòå áóäåì èìåòü ñèñòåìó óðàâíåíèé â ôîðìå, óäîáíîé äëÿ
ïðîâåäåíèÿ ïðàêòè÷åñêèõ ðàñ÷åòîâ àêòèâíûõ ó÷àñòêîâ òðàåêòîðèé
íåóïðàâëÿåìûõ ðàêåò:
du
dt
DEu
dp
dt
g
u
dy
dt
up
dx
dt
u
=−
=
−
=
=
1
μ
()
; ; ;.(3.76)
Èñõîäÿ èç ðèñ. 3.4 èëè ïîëàãàÿ â ñèñòåìå (3.74) Ya = 0, ìîæíî òàêæå
ïîëó÷èòü
133
Ðèñ. 3.4 . Ñõåìà ñèë, äåéñòâóþùèõ íà
ìàòåðèàëüíóþ òî÷êó, ñîâïàäàþùóþ ñ
öåíòðîì ìàññ íåóïðàâëÿåìîé ðàêåòû
du
dt
PX
m
dw
dt
PX
m
g
a
a
=
−
=
−
−
()
c
o
s
,
()
s
i
n
.
θ
θ
Ïîñëå ïðåîáðàçîâàíèé ïðèäåì ê ñèñòåìå
du
dt
DEu
dw
dt
PX
m
g
dy
dt
w
dx
dt
uV
u
a
=−
=
−
−
==
=
1
μ
θ
()
;
()
s
i
n
;
;; 22
+w.
(3.77)
3.2.4. ËÈÍÅÉÍÛÅ ÓÐÀÂÍÅÍÈß ÁÎÊÎÂÎÃÎ È ÏÐÎÄÎËÜÍÎÃÎ
ÑÒÀÁÈËÈÇÈÐÓÅÌÛÕ ÄÂÈÆÅÍÈÉ Â ÍÎÐÌÀËÜÍÎÉ ÔÎÐÌÅ
Íåëèíåéíûå óðàâíåíèÿ ïðîäîëüíîãî óïðàâëÿåìîãî äâèæåíèÿ â
íîðìàëüíîé çåìíîé ñèñòåìå êîîðäèíàò èìåþò âèä (ðèñ. 3 .5)
myP
Y
X
Y
mg
mx
P
ga
a
j
j
m
g
••
sin
cos
sin
cos
;
••
c
=+− +
−
=
=
∑
θθθ θ
p
1
os
sin
cos
sin ;
•
•
.
θθθ θ
θ
−−
+
=+
=
∑
YXY
IMM
aa
j
j
m
zzz
p
p
1
(3.78)
134
Ðèñ. 3 .5. Ñõåìà äåéñòâèÿ ñèë è óãëû, îïðåäåëÿþùèå ïîëîæåíèå ËÀ â ïðîäîëüíîì
ïëîñêîì äâèæåíèè
Ïîìèìî ââåäåííûõ îáîçíà÷åíèé, ñîîòâåòñòâóþùèõ ÃÎÑÒó
20058–80, èñïîëüçóåì ñëåäóþùèå îáîçíà÷åíèÿ óïðàâëÿþùèõ ñèë:
YY
j
m
=
=
∑ δδ.
1
Ðàññìîòðèì ñòàáèëèçèðîâàííûé ãîðèçîíòàëüíûé ïîëåò ñ ìàëû-
ìè çíà÷åíèÿìè óãëîâ θ, θ è α, ïîëîæèâ
sin
; sin
; sin
;
cos
cos
cos
.
θθθθαα
θθα
=≈≈
≈≈=
1
Ñóììó ìîìåíòîâ â ïðàâîé ÷àñòè óðàâíåíèÿ âðàùàòåëüíîãî äâè-
æåíèÿ ïðåäñòàâèì â çàâèñèìîñòè îò α, δ è óãëîâûõ ñêîðîñòåé
•
θè•
.
α
Ñòàâÿ â äàëüíåéøåì öåëüþ ðåøåíèÿ òîëüêî çàäà÷è ñòàáèëèçàöèè
âûñîòû ïðè ïîñòîÿííîé ñêîðîñòè ïîëåòà, îïóñòèì âòîðîå óðàâíåíèå
(3.78), îñóùåñòâèâ ïðåîáðàçîâàíèå ïåðâîãî è òðåòüåãî óðàâíåíèé
ýòîé ñèñòåìû.  ðåçóëüòàòå ïîëó÷èì
d
dt
dy
dt
y
d
dt
m
I
m
I
m
I
m
z
z
z
z
z
z
z
z
θ
θ
θ
αθα
α
ω
αδ
==
=+ ++
•
;
•
;
•
•
•
•
δ
θαδθ
αδ
I
dy
dt
P
m
Y
m
Y
m
X
m
g
z
a
;
•
.
=+ +−−
(3.79)
Ïðè ïðîâåäåíèè ïîñëåäóþùèõ ïðåîáðàçîâàíèé èñïîëüçóåì
ñîîòíîøåíèÿ ïàðàìåòðîâ äâèæåíèÿ
αθθαθθ θ
=−
=−
≈
;• ••
;•
.
yV
Ñ èõ ó÷åòîì ïîñëåäíåå óðàâíåíèå ñèñòåìû (3.78) ïðåîáðàçóåì ê âèäó
dy
dt
P
m
P
m
Y
m
Y
m
X
m
g
PY
m
PX
mV
y
Y
a
a
•
•
=+++−−
=
=
+
+
−
+
αθαδθ
α
αδ
αδ
m
g
δ−
.
(3.80)
Äàëåå ïðåäñòàâèì
d
dt
PY
mV
PX
mV
y
Y
mV
g
V
z
a
α
θθω
α
δ
αδ
=−=
−
+
−
−
−+
••
•
.
2
(3.81)
135
Ìàëûì ñëàãàåìûì (P − Xà)/(mV
2
) ìîæíî ïðåíåáðå÷ü. Ïîýòîìó
îêîí÷àòåëüíî
d
dt
PY
mV
g
V
Y
mV
z
α
ωα
+δ
αδ
=−
+
−
.
(3.82)
Âòîðîå óðàâíåíèå ñèñòåìû (3.79) ïðåîáðàçóåì ñëåäóþùèì îáðàçîì:
d
dt
d
dt
mm
I
m
I
mPY
ImV
zzz
z
z
z
z
z
z
z
•
()
••
θω
ω
ω
αα
α
α
==
+
+−
+
⎡
⎣
⎢
⎤
⎦
⎥+
+−
⎛
⎝⎜
⎞
⎠⎟+
α
δ
αα
δ
α
m
I
mY
ImV
m
IV
g
z
z
z
z
z
z
••
.
(3.83)
Çàïèøåì ñèñòåìó
dydty
dy
dt
PY
m
PX
mV
y
Y
m
g
d
dt
mm
a
zz
z
/•;
•
•
;
=
=
+
+
−
+−
=
+
αδ
ω
α
δ
ω
z
z
z
z
z
z
z
z
z
z
I
m
I
mPY
ImV
m
I
m
•
()
αα
α
α
δ
ωα
⎛
⎝⎜
⎞
⎠⎟ +−
+
⎡
⎣
⎢
⎤
⎦
⎥+
+−
•
;.
αδ
α
αδ
δ
α
ωαδ
Y
ImV
m
IV
g
d
dt
PY
mV
g
V
Y
mV
z
z
z
z
⎛
⎝⎜
⎞
⎠⎟ +=
−
+
+−
(3.84)
Ââåäåì ñëåäóþùèå îáîçíà÷åíèÿ:
yxyx x
x
xxu
z
=== =
=
===
123
4
5
6
;• ;;
•
;
;•
;.
θθ
ω
ααδ
Òîãäà, îñóùåñòâèâ çàìåíó, ïîëó÷èì ñèñòåìó óðàâíåíèé â íîðìàëüíîé
ôîðìå, ñîîòâåòñòâóþùåé âåêòîðíîìó óðàâíåíèþ òèïà ïåðâîãî
óðàâíåíèÿ ñèñòåìû (2.71):
dxdtx
dxdtmPY
VPXxYumgdx
a
12
2
11
2
/;
/[
()()
;
=
=+
+−+
+
−−
αδ
α
34
4
1
4
1
/;
/[]
[
(
)
(
••
dtx
dxdtImmxm
mV mP
zzz
z
z
z
=
=+
+
−
−−
α
ω
αα
{
}
++
+−
+
==−
−−
Yx
mm
Vm
Y
u
Vm
g
dxdtxx
zzz
α
δαα
)]
[() ]
;
/
••
5
11
5
6
4()
( )()
.
mV
PYxmVYuVg
−−
−
−−
+
1
5
11
αδ
(3.85)
136
Ïåðåõîäÿ ê ðàññìîòðåíèþ áîêîâîãî
äâèæåíèÿ â ïðåäïîëîæåíèè ìàëîñòè óãëîâ
ψ, β è Ψ (ðèñ. 3.6), çàïèøåì sinψ≈ψ; sinβ≈
≈β; sinΨ≈Ψ. Êîñèíóñû ýòèõ óãëîâ ïðèìåì
ðàâíûìè åäèíèöå, òîãäà
•
sin
,
zV
V
=−
=−
ΨΨ (3.86)
îòêóäà
Ψ=−
•
/.
zV
(3.87)
Óðàâíåíèÿ ñòàáèëèçèðóåìîãî áîêîâîãî
äâèæåíèÿ ïðåäñòàâèì â âèäå
dz
dt
P
m
Z
m
X
m
Z
m
a
•
;
=−
+
+
+
ψβ
δ
βδ
Ψ
(3.88)
I
d
dt
mm mm
yy
y
y
y
y
2
2
ψ
ψβδ
β
ω
βδ
=+
++
•
•
.
•
(3.89)
Ó÷èòûâàÿ ñîîòíîøåíèå óãëîâ ψ = β + Ψ,
íàéäåì
dz
dt
PZ
m
XZ
mV
z
Z
m
a
•
•
;
=−
−
−
−
+
ψδ
βδ
(3.90)
d
dt
mm
I
m
I
mPZ
ImV
yy
y
y
y
y
y
y
•
•
()
•
ψ
ψ
ω
ββ
ββ
=
+
⎛
⎝⎜
⎞
⎠⎟ ++
−+
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
+
++
−+
⎡
⎣
⎢
⎤
⎦
⎥++
ψ
ββ
βδβ
m
IV
mXZ
ImV
z
m
I
mZ
y
y
ya
y
y
y
y
()
•
•
2
δ
δ
ImV
y
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
.
(3.91)
Ïîäñòàâèì â ïîëó÷åííîå âûðàæåíèå (3.91) çíà÷åíèå •z èç (3.86):
137
Ðèñ. 3.6 . Ñõåìà äåéñòâèÿ ñèë
è óãëû, îïðåäåëÿþùèå ïîëî-
æåíèå ËÀ â áîêîâîì ïëîñêîì
äâèæåíèè
d
dt
d
dt
mm
I
m
I
mPZ
yyy
y
y
y
y
y
•
•
(
••
ψω
ψ
ω
ββ
ββ
==
+
⎛
⎝
⎜⎜
⎞
⎠
⎟⎟ ++
−+)
()
(
•
ImV
m
IV
mXZ
ImV
y
y
y
ya
y
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
+
++
−+
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
−
ψ
ββ
β
2
V
m
I
mZ
ImV
mm
I
y
y
y
y
yy
y
y
Ψ)
•
•
++
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
+
⎛
⎝
⎜⎜
⎞
⎠
⎟⎟
ββ
δ
ω
β
δ=
=
•
()
••
ψβ
ββ
β
δβ
δ
++
−+
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
++
m
I
mPZ
ImV
m
I
mZ
ImV
y
y
y
y
y
y
y
y
⎛
⎝
⎜⎜
⎞
⎠
⎟⎟δ,
(3.92)
à â âûðàæåíèè (3.90) çàìåíèì ψ ñóììîé óãëîâ β + Ψ:
dz
dt
PZ
m
PZ
m
XZ
mV
z
Z
m
PZ
m
PX
m
a
a
•
•
=−
−
−
−
−
−
+=
=
−+
+
−
βββ
δ
β
βδ
β
Ψ
V
z
Z
m
•
.
+
δ
δ
(3.93)
Ó÷èòûâàÿ äàëåå, ÷òî
•
•
•
,
βψ
=−
Ψ
(3.94)
ïîëó÷èì
d
dt
V
dz
dt
V
PZ
m
PX
mV
z
Z
m
yy
a
βωωβ
δ
βδ
=+
=+
−+
+
−
+
⎛
⎝⎜
⎞
⎠⎟=
=
11
•
•
ωβ
δ
βδ
z
a
PZ
mV
PX
mV
z
Z
mV
+
−+
+
−
+
2
•
.
(3.95)
Ïðåíåáðåãàÿ ñëàãàåìûì •z (P − Xa)/(mV
2
), çàïèøåì îêîí÷àòåëüíî
d
dt
PZ
mV
Z
mV
y
βωβ
δ
ββ
=+
−+
+
.
(3.96)
Òàêèì îáðàçîì, ñèñòåìà óðàâíåíèé áóäåò èìåòü âèä
dz
dt
z
dz
dt
PX
mV
z
PZ
m
Z
m
d
dt
mm
a
yyy
y
==
−
−
−
+
=
+
•
;
•
•
;
•
βδ
ω
β
βδ
ω
I
m
I
mPZ
ImV
m
I
y
y
y
y
y
y
y
y
⎛
⎝
⎜⎜
⎞
⎠
⎟⎟ ++
−+
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
+
+
ωβ
ββ
β
δ
•
()
+
+
⎛
⎝⎜
⎞
⎠⎟ =+
−+
+
mZ
ImV
d
dt
PZ
mV
Z
mV
y
y
y
βδ
βδ
δ
βωβ
δ
;.
(3.97)
138
Îáîçíà÷èâ z = x1; • ;
zx
=
2ψ=x3;•
;
ψ=x4 β=x5;
•
;
β=x6 δ = u, çàïè-
øåì
dxdtx
dx
dt
PX
mV
x
PZ
m
x
Z
m
u
dxdtx
dx
a
12
2
25
34
/;
;
/;
=
=
−
−
−
+
=
βδ
4
4
dt
mm
I
x
m
I
mPZ
ImV
yy
y
y
y
y
y
y
=
+
⎛
⎝
⎜⎜
⎞
⎠
⎟⎟ ++
−+
⎡
⎣
⎢
⎤
ω
ββ
ββ
•
()
⎦
⎥++
⎛
⎝⎜
⎞
⎠⎟
==+
−+
+
x
m
I
mZ
ImV
u
dx
dt
xx
PZ
mV
Z
y
y
y
y
5
5
6
4
δβ
δ
β
β
;
δ
mV
u.
(3.98)
3.2.5. ÑÈÑÒÅÌÛ ÓÐÀÂÍÅÍÈÉ ÏÐÈ ÎÒÍÎÑÈÒÅËÜÍÛÕ
ÁÅÇÐÀÇÌÅÐÍÛÕ ÀÐÃÓÌÅÍÒÀÕ
Ñòðåìëåíèå óïðîñòèòü ðåøåíèå çàäà÷ âíåøíåé áàëëèñòèêè è
ñäåëàòü âîçìîæíûì ïðèìåíåíèå ðàçëè÷íîãî ðîäà ðàñ÷åòíûõ òàáëèö,
ñîêðàùàþùèõ âðåìÿ ðåøåíèÿ, ïðèâåëî ê ðàçðàáîòêå ñèñòåì óðàâíå-
íèé, ó êîòîðûõ â êà÷åñòâå íåçàâèñèìûõ ïåðåìåííûõ ïðèíèìàþòñÿ
îòíîñèòåëüíûå áåçðàçìåðíûå âåëè÷èíû.
Ïðèâåäåì ñèñòåìó óðàâíåíèé, êîòîðàÿ îïèñûâàåò äâèæåíèå öåí-
òðà ìàññ íåóïðàâëÿåìûõ ðàêåò è â êîòîðîé èñïîëüçóåòñÿ íåçàâèñè-
ìàÿ ïåðåìåííàÿ
λ=
∫Qdt
Q
t
ñåê
0
0
.
(3.99)
Âîçüìåì ïåðâîå óðàâíåíèå ñèñòåìû (3.75) è çàìåíèì â íåì Ð è Õà
èõ âûðàæåíèÿìè. Ó÷èòûâàÿ òàêæå (3.99), ïîëó÷èì
dt
Q
Q
d
=
0
ñåê
λ.
(3.100)
Ïîñëå ïîäñòàíîâêè áóäåì èìåòü
Q
Q
dV
d
QW
Q
cHyFV g
e
ñåê
ñåê
0
λ
θ
=−
−
()() sin.
(3.101)
139
Òåêóùåå çíà÷åíèå Q = Q0 − Qdt
t
ñåê
.
0
∫ Îòíîñèòåëüíàÿ ìàññà
Q
Q
Qdt
Q
m
m
t
0
0
00
11
=−
=−=
=
∫ ñåê
λμ
.
(3.102)
Áàëëèñòè÷åñêèé êîýôôèöèåíò ðàêåòû ìîæíî âûðàçèòü ÷åðåç îò-
íîñèòåëüíóþ ìàññó:
c
id
Q
id
Q
cc
=⋅=
⋅
−
=
−
=
2
3
23
0
00
10
10
11
()
,
λλ
μ
(3.103)
ãäå
c
id
Q
0
2
0
3
10
=⋅
.
Ðàçäåëèâ â (3.101) ïðàâóþ è ëåâóþ ÷àñòè íà Qñåê/Q0 è ïîäñòàâèâ â
ïîñëåäíèå òðè óðàâíåíèÿ ñèñòåìû (3.75) âûðàæåíèå äëÿ ∆t ïî ôîð-
ìóëå (3.100), ïîëó÷èì
dV
d
Wc
H
y
F
V
g
Q
Q
d
d
Q
e
λλλ
θ
θ
λ
=
−
−
−
+
⎡
⎣⎢
⎤
⎦⎥
=−
11
00
()() sin
;
ñåê
0
00
Q
g
V
dx
d
Q
Q
V
dy
d
Q
Q
V
ñåê
ñåê
ñåê
cos
;
cos ;
sin .
θ
λ
θ
λ
θ
==
(3.104)
Ñèñòåìà ïðèìåíÿåòñÿ ïðè áàëëèñòè÷åñêîì ïðîåêòèðîâàíèè.
Ïðîèíòåãðèðîâàâ åå, ìîæíî óáåäèòüñÿ, ÷òî ïåðâîå ñëàãàåìîå ïðàâîé
÷àñòè ïåðâîãî óðàâíåíèÿ áóäåò ñîîòâåòñòâîâàòü ôîðìóëå
Ê.Ý. Öèîëêîâñêîãî äëÿ îïðåäåëåíèÿ ñêîðîñòè äâèæåíèÿ ðàêåòû áåç
ó÷åòà ñèëû ñîïðîòèâëåíèÿ âîçäóõà è ñèëû òÿæåñòè. Âòîðîé ÷ëåí
áóäåò ó÷èòûâàòü âëèÿíèå ñîïðîòèâëåíèÿ âîçäóõà, òðåòèé – âëèÿíèå
ñèëû òÿæåñòè.
Äëÿ óïðàâëÿåìûõ ðàêåò ñèñòåìó óðàâíåíèé äâèæåíèÿ áåðóò â íå-
ñêîëüêî èíîì âèäå. Ïðè ïîñòîÿííîì ñåêóíäíîì ðàñõîäå | •|
m = const
èç (3.24) ïîëó÷èì mm mt
=−
0 | •|.Ïðè ýòîì îòíîñèòåëüíàÿ ìàññà ðàêå-
140
òûμ==−
m
m
m
m
t
0
1
|•|
÷àñòî âûáèðàåòñÿ â êà÷åñòâå íåçàâèñèìîé ïåðå-
ìåííîé.
Îáîçíà÷èì τô = mm
0 /| •|, è òîãäà t = τô(1 −μ). Âåëè÷èíà τô èìååò
ðàçìåðíîñòü âðåìåíè (ñ) è íàçûâàåòñÿ ôèêòèâíûì âðåìåíåì. Îïðå-
äåëÿÿ èç ïîñëåäíåãî ðàâåíñòâà dt = −τôdμ è ïðîâîäÿ çàìåíó â ñèñòåìå
òèïà (3.75), ïîëó÷èì
dV
d
PX
m
g
dy
d
V
dx
d
V
a
μμ
ττθ
μ
τθ
μ
τ
=−
−
+
=−
=−
0
ôô
ôô
sin ;
sin ;
cos θ.
(3.105)
Î÷åâèäíî, ÷òî â ðàññìàòðèâàåìîì ñëó÷àå âòîðîå óðàâíåíèå ñèñ-
òåìû (3.75) äîëæíî áûòü îïóùåíî è çàìåíåíî ïðîãðàììíûì óãëîì
òàíãàæà, ïðåäñòàâëÿåìûì â ôîðìå θ = θ ïð(μ).
3.2.6 . ÓÐÀÂÍÅÍÈß ÄÂÈÆÅÍÈß Â ÏÅÐÅÃÐÓÇÊÀÕ
Ïðè âûïîëíåíèè çàäàííîé ïðîãðàììû ïîëåòà èëè ïðè íàâåäå-
íèè ðàêåòû (ò.å . âî âðåìÿ ìàíåâðà) èçìåíÿþòñÿ âåëè÷èíà è íàïðàâ-
ëåíèå ñêîðîñòè äâèæåíèÿ öåíòðà ìàññ ðàêåòû. Â ñîîòâåòñòâèè ñ
ýòèì ïîä ìàíåâðåííîñòüþ ðàêåò ïîíèìàþò áûñòðîòó èçìåíåíèÿ ñêî-
ðîñòè ïîëåòà ïî âåëè÷èíå è íàïðàâëåíèþ. Îöåíèâàþò ìàíåâðåí-
íîñòü âñåõ òèïîâ ËÀ, ðàêåò è ñíàðÿäîâ ñ ïîìîùüþ ïåðåãðóçîê. Ïå-
ðåãðóçêà, òàê æå êàê è ñêîðîñòü, âåëè÷èíà âåêòîðíàÿ. Ïîä ïåðåãðóç-
êîé ïîíèìàþò îòíîøåíèå ðåçóëüòèðóþùèõ ñèë, äåéñòâóþùèõ íà ËÀ
(çà èñêëþ÷åíèåì ãðàâèòàöèîííûõ è èíåðöèîííûõ), ê ïðîèçâåäåíèþ
ìàññû ËÀ íà óñêîðåíèå ñâîáîäíîãî ïàäåíèÿ:
n
RRP
==
+
mg
mg
A
.
(3.106)
Ìîäóëü âåêòîðà ïåðåãðóçêè n ÿâëÿåòñÿ âåëè÷èíîé áåçðàçìåðíîé,
÷òî äåëàåò åå óäîáíîé äëÿ ñðàâíèòåëüíûõ îöåíîê. Ïåðåãðóçêè îïðå-
äåëÿþòñÿ ýíåðãåòè÷åñêèìè ðåñóðñàìè ðàêåòû, âîçìîæíîñòÿìè åå
àýðîäèíàìè÷åñêîé ñõåìû, ýôôåêòèâíîñòüþ îðãàíîâ óïðàâëåíèÿ è
ñèñòåìû óïðàâëåíèÿ â öåëîì. Ñóììàðíûé âåêòîð ïåðåãðóçêè ìîæåò
îïðåäåëÿòüñÿ åãî ñîñòàâëÿþùèìè ïî îñÿì ïðèíÿòîé ñèñòåìû êîîð-
äèíàò. Â ñâÿçíîé ñèñòåìå êîîðäèíàò
141
n
R
mg
n
R
mg
n
R
mg
x
x
y
y
z
z
===
;;
(3.107)
–
ñîîòâåòñòâåííî ïðîäîëüíàÿ, íîðìàëüíàÿ è ïîïåðå÷íàÿ ïåðåãðóçêè.
 ñêîðîñòíîé ñèñòåìå êîîðäèíàò
n
R
mg
n
R
mg
n
R
mg
x
x
y
y
z
z
a
a
a
a
a
a
===
;;
(3.108)
–
ñîîòâåòñòâåííî òàíãåíöèàëüíàÿ, íîðìàëüíàÿ ñêîðîñòíàÿ è áîêîâàÿ
ïåðåãðóçêè.
Òàíãåíöèàëüíàÿ ïåðåãðóçêà õàðàêòåðèçóåò èçìåíåíèå ñêîðîñòè
ïî âåëè÷èíå, à ïåðåãðóçêè, âçÿòûå ïî íîðìàëè ê âåêòîðó ñêîðî-
ñòè, – èçìåíåíèå íàïðàâëåíèÿ âåêòîðà ñêîðîñòè ËÀ, ò.å . ìàíåâð ïî-
ñëåäíåãî. Ïðè àíàëèçå óñëîâèé, îáåñïå÷èâàþùèõ ìàíåâðåííîñòü
ËÀ, ðàññìàòðèâàþòñÿ îáû÷íî òîëüêî ïåðåãðóçêè nz a
è nya
.
Íàéäåì ñâÿçü ìåæäó âèäîì ñî-
âåðøàåìîãî ðàêåòîé ìàíåâðà è
ïåðåãðóçêàìè, íåîáõîäèìûìè äëÿ
åãî îñóùåñòâëåíèÿ. Ïðè ïðîåêòè-
ðîâàíèè ñèñòåì óïðàâëåíèÿ èñ-
õîäíûì ÿâëÿåòñÿ ïðîâåäåíèå ïîä-
ðîáíîãî àíàëèçà ñ öåëüþ óñòàíî-
âèòü ïîòðåáíûå âèäû òðàåêòîðèé
(ò.å . ìàíåâðîâ), êîòîðûå ïîçâîëÿ-
þò ïðîåêòèðóåìîé ðàêåòå âûïîë-
íèòü ïîñòàâëåííûå òàêòèêî-òåõ-
íè÷åñêèå òðåáîâàíèÿ.
Íà ðèñ. 3.7 ïîêàçàíà òðàåê-
òîðèÿ ñáëèæåíèÿ ðàêåòû ñ ìà-
íåâðèðóþùåé â âåðòèêàëüíîé
ïëîñêîñòè öåëüþ, ïîñòðîåííàÿ
äëÿ ïðèíÿòîãî ìåòîäà íàâåäåíèÿ
ïî çàäàííûì òðàåêòîðèè öåëè è
ñêîðîñòè ðàêåòû. Ïîäîáíàÿ òðà-
åêòîðèÿ, ïîñòðîåííàÿ áåç ðàñ-
êðûòèÿ ñèñòåìû ñèë, îáóñëîâèâ-
øèõ åå ôîðìó, ïîçâîëÿåò óñòà-
íîâèòü õàðàêòåðèñòèêó, êîòîðàÿ
äàåò âîçìîæíîñòü ïåðåéòè ê îï-
ðåäåëåíèþ äåéñòâóþùèõ íà ðà-
êåòó ñèë. Òàêîé êèíåìàòè÷åñêîé
142
Ðèñ. 3 .7 . Èçìåíåíèå ðàäèóñà êðèâèçíû
òðàåêòîðèè ïðè ñáëèæåíèè ïî êðèâîé
ïîãîíè óïðàâëÿåìîé ðàêåòû ñ öåëüþ
õàðàêòåðèñòèêîé ìàíåâðà ðàêåòû ÿâëÿåòñÿ ðàäèóñ êðèâèçíû òðà-
åêòîðèè r.
Èç ðèñ. 3 .7 âèäíî, ÷òî ïðåäñòàâëåííàÿ íà íåì òðàåêòîðèÿ ñáëè-
æåíèÿ ðàêåòû ñ öåëüþ õàðàêòåðèçóåòñÿ ïîñòåïåííûì óâåëè÷åíèåì
êðèâèçíû èëè, ÷òî àíàëîãè÷íî, óìåíüøåíèåì ðàäèóñà êðèâèçíû îò
âåëè÷èíû r0 â íà÷àëüíîé òî÷êå òðàåêòîðèè äî âåëè÷èíû râ â òî÷êå
âñòðå÷è ðàêåòû ñ öåëüþ. Ïðèìåíèòåëüíî ê òðàåêòîðíîé ñèñòåìå êî-
îðäèíàò ìîæíî íàïèñàòü ñëåäóþùèå âûðàæåíèÿ äëÿ ðàäèóñîâ êðè-
âèçíû:
r
dS
d
V
d
dt
yê
ê
==
⎛
⎝⎜⎞
⎠⎟
−
θ
θ
1
;
(3.109)
r
dS
d
V
d
dt
zê
ê
=−
=
−
⎛
⎝⎜⎞
⎠⎟
−
Ψ
Ψ
1
.
(3.110)
Ïðè ýòîì áûëî ïðèíÿòî, ÷òî r > 0 â ñëó÷àå, êîãäà èçîáðàæàþùèé
åãî îòðåçîê, íàïðàâëåííûé îò òî÷êè òðàåêòîðèè ê öåíòðó êðèâèçíû,
ñîâïàäàåò ñ ïîëîæèòåëüíûì íàïðàâëåíèåì ñîîòâåòñòâóþùåé îñè
êîîðäèíàò.
Âõîäÿùèå â âûðàæåíèÿ (3.109) è (3.110) óãëîâûå ñêîðîñòè dθ/dt è
d Ψ/dt ìîæíî âûðàçèòü ÷åðåç ñîîòâåòñòâóþùèå ïåðåãðóçêè íà îñíî-
âàíèè ñèñòåìû äèôôåðåíöè-
àëüíûõ óðàâíåíèé, îïèñû-
âàþùèõ äâèæåíèå öåíòðà
ìàññ ðàêåòû.
Ïóñòü ïëîñêîñòü óãëà àòà-
êè α âåðòèêàëüíà, à ïëîñ-
êîñòü óãëà ñêîëüæåíèÿ β åé
ïåðïåíäèêóëÿðíà, òîãäà ñ
ó÷åòîì ðèñ. 3 .8 ìîæíî íàïè-
ñàòü ñèñòåìó óðàâíåíèé ïðî-
äîëüíîãî è áîêîâîãî äâèæå-
íèé öåíòðà ìàññ óïðàâëÿå-
ìîé ðàêåòû â òðàåêòîðíîé
ñèñòåìå êîîðäèíàò. Ïðè
ýòîì óïðàâëÿþùèå ñèëû
îáúåäèíèì ñ àýðîäèíàìè÷å-
ñêèìè ñèëàìè Xa, Y ê, Zê;ëå-
âûå è ïðàâûå ÷àñòè óðàâíå-
íèé ïîäåëèì íà âåñ ðàêåòû
Q = mg.  ðåçóëüòàòå ïîëó÷èì
143
Ðèñ. 3.8. Âçàèìíîå ðàñïîëîæåíèå ñèñòåì êî-
îðäèíàò, ïðèìåíÿåìûõ ïðè âûâîäå óðàâíåíèé
äâèæåíèÿ â ïåðåãðóçêàõ
1
g
dV
dt
PX
mg
a
=
−
−
cos cos
sin ;
αβ
θ
(3.111)
V
g
d
dt
PY
mg
V
g
d
dt
PZ
mg
θα
θ
θ
αβ
=
+
−−
−=
−+
sin
cos
cos
cos sin
ê
ê
Ψ
.
(3.112)
Èç íàïèñàííûõ óðàâíåíèé, ñîãëàñíî îïðåäåëåíèþ, âûäåëèì è
óïðîñòèì âûðàæåíèÿ äëÿ ïåðåãðóçîê, ñäåëàâ âñëåäñòâèå ìàëîñòè óã-
ëîâ çàìåíó
sin
; sin
; cos cos
.
ααββαβ
≈≈≈
≈
1
Òîãäà ïðîåêöèè âåêòîðà ïåðåãðóçêè â òðàåêòîðíîé ñèñòåìå
êîîðäèíàò áóäóò èìåòü âèä
n
PX
mg
PX
mg
x
aa
ê
=
−
≈
−
cos cos
;
αβ
n
PY
mg
PY
mg
yê
êê
=
+
≈
+
sin
;
αα
n
PZ
mg
PZ
mg
zê
êê
=
−+
≈
−+
cos sin
.
αβ
β
(3.13)
Ââîäÿ ïðîåêöèè âåêòîðà ïåðåãðóçêè â ôîðìóëû (3.111), (3.112),
çàïèøåì
n
g
dV
dt
n
V
g
d
dt
n
V
g
d
dt
xy
z
êê
ê
=+
=+
=−
1
sin ;
cos ;
cos
.
θ
θ
θ
θ
Ψ
(3.114)
Îòñþäà
d
dt
g
V
n
d
dt
g
V
n
yz
θ
θ
θ
=−
=
−
(c
o
s
)
;
cos
.
êê
Ψ
(3.115)
Ïîäñòàâèâ ñîîòâåòñòâåííî âûðàæåíèÿ (3.115) â óðàâíåíèÿ äëÿ
ðàäèóñîâ êðèâèçíû (3.109) è (3.110), ïîëó÷èì
144
n
r
V
g
y
y
ê
ê
=+
12
cos ;θ
(3.116)
n
r
V
g
z
z
ê
ê
=
12
cos
.
θ
(3.117)
Ïàðàìåòðû òðàåêòîðèè V, θ è Ψ îïðåäåëÿþò çíà÷åíèå è íàïðàâ-
ëåíèå âåêòîðà ñêîðîñòè, à èõ ïðîèçâîäíûå, âûðàæåííûå ÷åðåç ïåðå-
ãðóçêè, õàðàêòåðèçóþò ñïîñîáíîñòü ËÀ èçìåíÿòü âåëè÷èíó è íà-
ïðàâëåíèå ñêîðîñòè äâèæåíèÿ öåíòðà ìàññ.
Çàâèñèìîñòè (3.116) è (3.117) ïîêàçûâàþò, ÷òî ðàêåòà ìîæåò
âûïîëíèòü ìàíåâð, õàðàêòåðèçóþùèéñÿ ðàäèóñîì êðèâèçíû r,
òîëüêî â òîì ñëó÷àå, åñëè áóäóò ñîçäàíû íåîáõîäèìûå ïåðåãðóç-
êè nyê
è nzê
, ïðè÷åì ìàíåâð ñ ìåíüøèì ðàäèóñîì êðèâèçíû, ò.å.
áîëåå ðåçêèé, ìîæåò áûòü îñóùåñòâëåí ïðè ïðî÷èõ ðàâíûõ óñ-
ëîâèÿõ çà ñ÷åò óâåëè÷åíèÿ íîðìàëüíûõ ïåðåãðóçîê. Ïðè èññëå-
äîâàíèè ïåðåãðóçîê îïðåäåëÿþò òàê íàçûâàåìûå òðåáóåìûå ïåðå-
ãðóçêè, íåîáõîäèìûå äëÿ ïîëó÷åíèÿ òðàåêòîðèé çàäàííîãî âèäà.
Ñ ýòîé öåëüþ ïî ôîðìóëàì (3.109) è (3.110) îïðåäåëÿþò òðàåê-
òîðèþ, èìåþùóþ íàèìåíüøèé ðàäèóñ êðèâèçíû. Åñëè äëÿ ýòîé
òðàåêòîðèè íàéòè ôóíêöèè V(t), θ(t)èΨ(t), òî òðåáóåìûå ïåðå-
ãðóçêè ìîæíî âû÷èñëèòü ïî ôîðìóëàì (3.114).
Ïåðåãðóçêè, êîòîðûå ìîæåò èìåòü ñáàëàíñèðîâàííûé ËÀ ïðè
ìàêñèìàëüíîì îòêëîíåíèè îðãàíîâ óïðàâëåíèÿ, íàçûâàþò ðàñïîëà-
ãàåìûìè. Ðàñïîëàãàåìûå ïåðåãðóçêè – ýòî íàèáîëüøèå ïåðåãðóçêè,
êîòîðûå ðåàëüíî ìîãóò áûòü ïîëó÷åíû ðàêåòîé. Íàäî èìåòü â âèäó,
÷òî óñòàíîâëåíèå ðàñïîëàãàåìûõ ïåðåãðóçîê äîëæíî ïðîâîäèòüñÿ ñ
ó÷åòîì òùàòåëüíîãî àíàëèçà èõ âëèÿíèÿ íà ðàáîòó áîðòîâîé óïðàâ-
ëÿþùåé àïïàðàòóðû, ïðî÷íîñòè êîðïóñà è àãðåãàòîâ ðàêåòû. Íàè-
áîëüøèå çíà÷åíèÿ íîðìàëüíûõ ðàñïîëàãàåìûõ ïåðåãðóçîê äîñòèãà-
þòñÿ ñáàëàíñèðîâàííûìè ËÀ ïðè ìàêñèìàëüíûõ çíà÷åíèÿõ óãëîâ
àòàêè è ñêîëüæåíèÿ [ñì. (3.113)].
Ðàêåòà ìîæåò äâèãàòüñÿ ïî ïðîãðàììíîé òðàåêòîðèè èëè ïî òðà-
åêòîðèè íàâåäåíèÿ òîëüêî â òîì ñëó÷àå, åñëè íåîáõîäèìûå äëÿ åå
ïîëó÷åíèÿ òðåáóåìûå ïåðåãðóçêè áóäóò ìåíüøå èëè (â ïðåäåëüíîì
ñëó÷àå) ðàâíû ðàñïîëàãàåìûì ïåðåãðóçêàì, êîòîðûå ìîãóò áûòü ñîç-
äàíû ðàêåòîé:
() ();() ().
nnnn
yyzz
êê
êê
òð
òð
≤≤
(3.118)
Èíäåêñ "ò" ñîîòâåòñòâóåò òðåáóåìûì ïåðåãðóçêàì, èíäåêñ "ð" –
ðàñïîëàãàåìûì.
145
Íî óñëîâèÿ (3.118) íåëüçÿ ñ÷èòàòü äîñòàòî÷íûìè. Äâèæåíèå ðà-
êåò â ðåàëüíûõ óñëîâèÿõ âñåãäà ñîïðîâîæäàåòñÿ ðàçíîãî ðîäà êðàò-
êîâðåìåííûìè èëè äëèòåëüíûìè âîçìóùåíèÿìè, êîòîðûå îòêëîíÿ-
þò ðàêåòó îò ðàñ÷åòíîé òðàåêòîðèè. Äëÿ îáåñïå÷åíèÿ óñòîé÷èâîñòè
äâèæåíèÿ ðàêåòû åå ñèñòåìà óïðàâëåíèÿ äîëæíà îáëàäàòü âîçìîæ-
íîñòüþ ïàðèðîâàòü ýòè âîçìóùåíèÿ.
Ñëåäîâàòåëüíî, ïðè óñòàíîâëåíèè ñâÿçè ìåæäó òðåáóåìûìè è
ðàñïîëàãàåìûìè ïåðåãðóçêàìè íóæíî îáÿçàòåëüíî ïðåäóñìàòðèâàòü
çàïàñ ïåðåãðóçîê ()
nyê ç
è()
,
nzê ç
êîòîðûé íåîáõîäèì äëÿ îñóùåñòâëå-
íèÿ çàäàííîãî ïîëåòà ðàêåòû ïðè äåéñòâèè íà íåå ñëó÷àéíûõ âîçìó-
ùåíèé. Ñ ó÷åòîì ýòîãî óñëîâèÿ (3.118) ïðèìóò âèä
() () ();() () ().
nnnnnn
yyyzzz
êêê
êêê
òçð
òçp
+≤
+≤
(3.119)
3.3. ÌÎÄÅËÈ ÄÂÈÆÅÍÈß ÓÏÐÀÂËßÅÌÛÕ
È ÍÅÓÏÐÀÂËßÅÌÛÕ ÐÀÊÅÒ
ÍÀ ÏÀÑÑÈÂÍÎÌ Ó×ÀÑÒÊÅ ÒÐÀÅÊÒÎÐÈÈ
3.3.1 . ÓÐÀÂÍÅÍÈß ÑÂÎÁÎÄÍÎÃÎ ÄÂÈÆÅÍÈß ËÀ ÏÎÑÒÎßÍÍÎÉ
ÌÀÑÑÛ Â ÏËÎÒÍÛÕ ÑËÎßÕ ÀÒÌÎÑÔÅÐÛ
Ïðè ñâîáîäíîì ïîëåòå â ïëîòíûõ ñëîÿõ àòìîñôåðû íà ËÀ ïî-
ñòîÿííîé ìàññû äåéñòâóþò äâå ãðóïïû ñèë – àýðîäèíàìè÷åñêèå
ñèëû è ñèëû, îïðåäåëÿåìûå âëèÿíèåì Çåìëè. Ñèñòåìà óðàâíå-
íèé, îïèñûâàþùàÿ ïðîñòðàíñòâåííûé ïîëåò íåóïðàâëÿåìîãî ËÀ,
ìîæåò áûòü ïîëó÷åíà èç îáùåé ñèñòåìû óðàâíåíèé (3.7)...(3.12),
(3.15)...(3.24), åñëè â íèõ îïóñòèòü óïðàâëÿþùèå ñèëû è ìîìåí-
òû è ïîëîæèòü m = const è P = 0. Ó õîðîøî ñòàáèëèçèðîâàííûõ
ËÀ èçìåíåíèå óãëîâ α è β, âûçâàííîå êîëåáàíèÿìè ËÀ îòíîñè-
òåëüíî öåíòðà ìàññ, ïðèâîäèò ê íåçíà÷èòåëüíûì îòêëîíåíèÿì
öåíòðà ìàññ îò ðàñ÷åòíîé òðàåêòîðèè, ïîëó÷åííîé áåç ó÷åòà êî-
ëåáàíèé.
Çàìåòíîå âëèÿíèå íà ôîðìó òðàåêòîðèè öåíòðà ìàññ ËÀ ïðè ñâî-
áîäíîì ïîëåòå ìîãóò îêàçûâàòü âîçìóùàþùèå ôàêòîðû, íå ó÷òåí-
íûå â óðàâíåíèÿõ (3.7)...(3.12) è (3.15)...(3.24).
Ñèñòåìó óðàâíåíèé, îïèñûâàþùóþ óïðàâëÿåìûé ïîëåò öåíòðà
ìàññ áàëëèñòè÷åñêîé ðàêåòû (èëè åå ãîëîâíîé ÷àñòè) íà ïàññèâ-
íîì ó÷àñòêå òðàåêòîðèè ñ ó÷åòîì âëèÿíèÿ ñèëû ñîïðîòèâëåíèÿ
âîçäóõà, ëåãêî ïîëó÷èòü èç ñèñòåìû (3.73), åñëè ïðèíÿòü Ð =0è
m = const:
146
du
dt
XY
m
g
dw
dt
XY
m
g
aa
aa
=−
+
−
=−
−
−
cos
sin
sin ;
sin
cos
c
θθ
γ
θθ
os;
;;
;
;;
(
γ
θγ
dy
dt
w
dx
dt
uV
uw
w
u
x
Ry
rRy
==
=
+
=
+
=+
22
tg
tg=
Ç
Ç
);
;(
)
.
22
0
2
+
=
⎛
⎝⎜⎞
⎠⎟ +==
x
gg
R
r
t
Ç
ïð
αθθθ
(3.120)
Ðàñ÷åò ïàðàìåòðîâ äâèæåíèÿ ðàêåòû íà ïàññèâíîì ó÷àñòêå
òðàåêòîðèè, â êîòîðîì ïðèíÿòî ðàçëè÷àòü âîñõîäÿùóþ è íèñõîäÿùóþ
âåòâè, ïðîâîäèòñÿ ëèáî äî òî÷êè ïåðåñå÷åíèÿ òðàåêòîðèè ñ
ïîâåðõíîñòüþ Çåìëè, ëèáî äî òî÷êè, íàõîäÿùåéñÿ íà çàäàííîé
âûñîòå hâ íàä ïîâåðõíîñòüþ Çåìëè. Ïðè ðåøåíèè ïëîñêîé çàäà÷è â
ñòàðòîâîé ñèñòåìå êîîðäèíàò äëÿ ñôåðè÷åñêîé ìîäåëè Çåìëè
êîîðäèíàòû òî÷êè ïåðåñå÷åíèÿ òðàåêòîðèè ñ ïîâåðõíîñòüþ Çåìëè xc
è yc äîëæíû ïðèíàäëåæàòü îêðóæíîñòè, îòâå÷àþùåé óðàâíåíèþ x
2
+
++=
().
yRR
ÇÇ
22
Ïîëó÷àåìûå â ïðîöåññå ðåøåíèÿ ñèñòåìû (3.120)
êîîðäèíàòû õ è y ïîäñòàâëÿþòñÿ â íàïèñàííîå óðàâíåíèå
îêðóæíîñòè. Äëÿ îêîí÷àíèÿ ñ÷åòà íà âûñîòå hâ êîîðäèíàòû xc è yc
äîëæíû îòâå÷àòü óðàâíåíèþ îêðóæíîñòè
xyR Rh
222
++=+
()( )
.
ÇÇ
â
Îïðåäåëåíèå òî÷êè ïåðåñå÷åíèÿ òðàåêòîðèè ñ ïîâåðõíîñòüþ îáú-
åìíîé ìîäåëè Çåìëè â âèäå ýëëèïñîèäà òðåáóåò ñàìîñòîÿòåëüíîãî
ðàññìîòðåíèÿ ñ ó÷åòîì øèðîòû è äîëãîòû ìåñòà ïóñêà è ìåñòà ïðè-
çåìëåíèÿ. ×òîáû íàïèñàòü óïðîùåííóþ ìîäåëü íåâîçìóùåííîãî
äâèæåíèÿ íåóïðàâëÿåìîãî ËÀ, äîñòàòî÷íî âîñïîëüçîâàòüñÿ óðàâíå-
íèÿìè (3.7) è (3.8), à òàêæå óðàâíåíèåì (3.12).  ðåçóëüòàòå ïîëó÷èì
â ðàçâåðíóòîé ôîðìå ñèñòåìó óðàâíåíèé, îïèñûâàþùóþ ïðîäîëü-
íîå äâèæåíèå íåóïðàâëÿåìîãî ËÀ ñ ó÷åòîì êîëåáàíèé åãî ïðîäîëü-
íîé îñè îòíîñèòåëüíî öåíòðà ìàññ:
dV
dt
c
S
m
Vg
d
dt
c
S
m
V
g
V
x
y
a
a
=−
−
=−
ρ
θ
θρ
α
θ
α
2
2
2
sin ;
cos
;
147
d
dt
I
m
Sl
VmS
l
V
d
dt
d
dt
d
z
z
zz
z
z
ω
ρ
αρ
θ
θ
ω
α
ω
=−
+
⎛
⎝⎜
⎞
⎠⎟
=
1
2
22
;
;
x
dt
V
dy
dt
V
yg
==
=
−
cos ;
sin ;
.
θθ
α
θ
θ
(3.121)
Äëÿ îïåðåííûõ íåâðàùàþùèõñÿ ñíàðÿäîâ è ìèí â óðàâíåíèÿõ
(3.10)...(3.12) ìîæíî îïóñòèòü ÷ëåíû, ñîäåðæàùèå ïðîèçâåäåíèå óã-
ëîâûõ ñêîðîñòåé.
Åñëè ìîìåíòû àýðîäèíàìè÷åñêèõ è âîçìóùàþùèõ ñèë èçâåñòíû,
òî êàæäîå èç ýòèõ óðàâíåíèé ìîæåò ðåøàòüñÿ ñàìîñòîÿòåëüíî.
3.3.2. ÓÏÐÎÙÅÍÍÛÅ ÓÐÀÂÍÅÍÈß ÏÐÎÄÎËÜÍÎÃÎ ÄÂÈÆÅÍÈß
ÖÅÍÒÐÀ ÌÀÑÑ ËÀ Â ÀÒÌÎÑÔÅÐÅ
Ïðè ðåøåíèè ðÿäà çàäà÷ ìîæíî ïîëàãàòü, ÷òî íåóïðàâëÿåìûé
ËÀ ñîâåðøàåò òîëüêî ïðîäîëüíîå äâèæåíèå â îäíîðîäíîì ïëîñ-
êîïàðàëëåëüíîì ïîëå ïðèòÿæåíèÿ, â íåïîäâèæíîé àòìîñôåðå è ñ
ïðåíåáðåæèìî ìàëûìè óãëàìè àòàêè.  ýòîì ñëó÷àå òðàåêòîðèÿ
ñíàðÿäà – ïëîñêàÿ êðèâàÿ. Ñèñòåìà óðàâíåíèé, îïèñûâàþùàÿ
òàêîå äâèæåíèå öåíòðà ìàññ ËÀ, ïðè äîïóùåíèè, ÷òî cosα≈ 1,
sinα =0èYa = 0, ìîæåò áûòü ïðåäñòàâëåíà â ñëåäóþùåì âèäå:
dV
dt
X
m
g
d
dt
g
V
dy
dt
V
dx
dt
V
a
=−
−
=−
==
sin ;
cos
;
sin ;
cos
θ
θθ
θθ
.
(3.122)
Ïåðâûå äâà óðàâíåíèÿ (3.122) íàïèñàíû â ñêîðîñòíîé (ñîâïà-
äàþùåé â äàííîì ñëó÷àå ñ òðàåêòîðíîé) ñèñòåìå êîîðäèíàò, ò.å . â
ïðîåêöèÿõ íà êàñàòåëüíóþ è íîðìàëü ê òðàåêòîðèè. Âî ìíîãèõ ñëó-
÷àÿõ îêàçûâàþòñÿ óäîáíûìè äëÿ ðåøåíèÿ ñèñòåìû óðàâíåíèé, âû-
ðàæåííûå â ïðÿìîóãîëüíîé ñòàðòîâîé ñèñòåìå êîîðäèíàò. Â ñîîò-
âåòñòâèè ñ ðèñ. 3 .9 èìååì
du
dt
= −Xa cosθ. Óìíîæàÿ ÷èñëèòåëü è çíàìå-
íàòåëü ïðàâîé ÷àñòè íà V, ïîëó÷èì du/dt = Xau/(mV). Çíà÷åíèå
ïîëíîé ñêîðîñòè ïî èçâåñòíîé âåëè÷èíå u ìîæåò áûòü íàéäåíî êàê
V=up
12
+ , ãäå p =tgθ. Ïîýòîìó â êà÷åñòâå âòîðîãî óðàâíåíèÿ ðàñ-
ñìàòðèâàåìîé ñèñòåìû âîçüìåì äèôôåðåíöèàëüíîå óðàâíåíèå
dp
dt
d
dt
g
u
==
−
().
tgθ
(3.123)
148
Îáîçíà÷àÿ äëÿ ïðîñòîòû íàïèñà-
íèÿ E = Xa/(mV) è äîáàâëÿÿ
êèíåìàòè÷åñêèå ñîîòíîøåíèÿ,
ïîëó÷èì
èçâåñòíóþ
ñèñòåìó
óðàâíåíèé
du
dt
Eu
dp
dt
g
u
dy
dt
up
dx
dt
u
=−
=−
==
;
;
;.
(3.124)
Åñëè âîñïîëüçîâàòüñÿ äëÿ Xa
ðàâåíñòâîì (1.126) è ââåñòè
ôóíêöèþ G(V),
òî
ïåðâîå
óðàâíåíèå ñèñòåìû áóäåò èìåòü
âèä
du
dt
cHyGVu Eu
=−
=−
()()
, (3.125)
ãäå E = cH(y)G(V).
Äëÿ ó÷åòà èçìåíåíèÿ ñêîðîñòè çâóêà ñ âûñîòîé ñëåäóåò âîñïîëü-
çîâàòüñÿ (1.141), è òîãäà du/dt = −cHτ(y)G(Vτ)u. Ñîîòâåòñòâåííî
Ec
HyGV
=
ττ
()( ).
(3.126)
Âòîðîå óðàâíåíèå ñèñòåìû (3.124) ìîæåò áûòü çàìåíåíî
äèôôåðåíöèàëüíûì óðàâíåíèåì äëÿ îïðåäåëåíèÿ âåðòèêàëüíîé
ñîñòàâëÿþùåé ñêîðîñòè dw/dt = −Xa sinθ/m − g . Ââîäÿ ñîñòàâëÿþùóþ
ñêîðîñòè w = V sinθ, áóäåì èìåòü ñèñòåìó óðàâíåíèé
du
dt
Eu
dw
dt
Ewg
dy
dt
w
dx
dt
u
=−
=−
−
=
=
;;
;
.
(3.127)
Ñèñòåìû óðàâíåíèé ïðè íåçàâèñèìîé ïåðåìåííîé t öåëåñîîáðàç-
íî èñïîëüçîâàòü äëÿ ðàñ÷åòà õàðàêòåðèñòèê äâèæåíèÿ çåíèòíûõ ñíà-
ðÿäîâ ïîñòîÿííîé ìàññû. Äëÿ ðàñ÷åòà õàðàêòåðèñòèê äâèæåíèÿ ðà-
êåò êëàññà "çåìëÿ – çåìëÿ" çà íåçàâèñèìóþ ïåðåìåííóþ áåðóò t (âðå-
149
Ðèñ. 3.9. Óïðîùåííàÿ ñõåìà ñèë, äåéñò-
âóþùèõ íà ñíàðÿä ïîñòîÿííîé ìàññû,
äâèæóùèéñÿ â âîçäóõå ïðè g = const
ìÿ) èëè êîîðäèíàòó õ. Ñèñòåìó óðàâíåíèé ïðè àðãóìåíòå õ ïîëó÷èì,
ïðîâåäÿ î÷åâèäíûå ïðåîáðàçîâàíèÿ ïåðâîãî è âòîðîãî óðàâíåíèé
ñèñòåìû (3.124):
du
dt
du
dt
dt
dx
Eu
u
E
dp
dx
dp
dt
dt
dx
g
uu
==
−
⎛
⎝⎜⎞
⎠⎟ =−
==
−
();
1
1
=−
g
u
2.
(3.128)
Ñëåäîâàòåëüíî, ñèñòåìà óðàâíåíèé ïðè íåçàâèñèìîé ïåðåìåííîé õ
áóäåò èìåòü âèä
du
dx
E
dp
dx
g
u
dy
dx
p
dt
dxu
=−
=−
=
=
;;
;
.
2
1
(3.129)
Ñ öåëüþ ïîëó÷åíèÿ íåêîòîðûõ ïðèáëèæåííûõ àíàëèòè÷åñêèõ ðå-
øåíèé îñíîâíîé çàäà÷è âíåøíåé áàëëèñòèêè ËÀ ïîñòîÿííîé ìàññû
èñïîëüçóåòñÿ ñèñòåìà óðàâíåíèé ïðè íåçàâèñèìîé ïåðåìåííîé θ.
Ïðåäñòàâèì
du
d
du
dt
dt
d
Eu
V
g
EV
g
θθ
θ
==
−
−
⎛
⎝⎜
⎞
⎠⎟=
cos
.
2
Âûðàçèâ Å èç ñîîòíîøåíèÿ (3.125), áóäåì èìåòü
du
d
c
g
HyVFV
θ
=
() ().
(3.130)
Ââåäÿ ïðîìåæóòî÷íûå ïðîèçâîäíûå, ïîëó÷èì ñîîòâåòñòâåííî
dx
d
dx
dt
dt
d
V
V
g
V
g
dy
d
dy
dx
dx
d
θθ
θ
θ
θ
==−
⎛
⎝⎜
⎞
⎠⎟ =−
=
cos
cos
;
2
θ
θ
=−
⎛
⎝⎜⎞
⎠⎟
tg
V
g
2
.
Ñëåäîâàòåëüíî, ñèñòåìà óðàâíåíèé ïðè àðãóìåíòå θ áóäåò èìåòü âèä
du
d
c
g
HyVFV
dy
d
V
g
dx
d
V
g
dt
d
V
g
θθ
θ
θθ
==
−
=−
=−
() ();
;
;
co
2
2
tg
s
.
θ
(3.131)
150
Ïðè ó÷åòå èçìåíåíèÿ ñêîðîñòè çâóêà â çàâèñèìîñòè îò âûñîòû
ïåðâîå óðàâíåíèå ñèñòåìû (3.131) ñëåäóåò çàìåíèòü ñëåäóþùèì:
du
d
c
g
HyVFV
θ
τ
=
() ().
(3.132)
 ñèñòåìàõ (3.122), (3.124), (3.127) è (3.129) ñîâîêóïíûìè (ò.å .
ïîäëåæàùèìè ñîâìåñòíîìó ðåøåíèþ) ÿâëÿþòñÿ ïåðâûå òðè óðàâíå-
íèÿ. Â ñèñòåìå (3.131) ñîâîêóïíûìè ÿâëÿþòñÿ òîëüêî äâà ïåðâûõ
óðàâíåíèÿ. Ïðè äîïîëíèòåëüíûõ óïðîùåíèÿõ, íàïðèìåð ïðè H(y) ≈
≈ H(yñð), â ïåðâîì óðàâíåíèè ìîæíî ðàçäåëèòü ïåðåìåííûå. Ýòî
ñâîéñòâî ñèñòåìû (3.131) ïîçâîëÿåò èñïîëüçîâàòü åå äëÿ ïðèáëè-
æåííûõ àíàëèòè÷åñêèõ ðåøåíèé.
Ðåøåíèåì óðàâíåíèÿ (3.130) ÿâëÿåòñÿ ôóíêöèîíàëüíàÿ çàâèñè-
ìîñòü V = f(θ), êîòîðàÿ îïðåäåëÿåò ãîäîãðàô ñêîðîñòè öåíòðà ìàññ
ËÀ. Ïîýòîìó ïðèíÿòî (3.130) íàçûâàòü óðàâíåíèåì ãîäîãðàôà ñêîðî-
ñòè.
 íàñòîÿùåé ãëàâå ïðè ñîñòàâëåíèè âñåõ ïðåäûäóùèõ óðàâíåíèé
ïðåäïîëàãàëîñü g = const. Îäíàêî òàêîå äîïóùåíèå ñïðàâåäëèâî ïðè
ðàñ÷åòå òðàåêòîðèé äâèæåíèÿ ðàêåò, ïðåäíàçíà÷åííûõ äëÿ ñòðåëüáû
íà îòíîñèòåëüíî ìàëûå äàëüíîñòè. Ñèñòåìó óðàâíåíèé, îïèñûâàþ-
ùóþ ñâîáîäíûé ïîëåò öåíòðà ìàññ ËÀ ïîñòîÿííîé ìàññû, ïðåäíà-
çíà÷åííîãî äëÿ ñòðåëüáû íà áîëüøèå äàëüíîñòè, ìîæíî ïîëó÷èòü èç
(3.120), åñëè ïðèíÿòü, ÷òî ïðîãðàììà èçìåíåíèÿ óãëà òàíãàæà îòñóò-
ñòâóåò è Ð =0:
du
dt
XY
m
g
dw
dt
XY
m
g
aa
aa
=−
+
−
=−
−
−
cos
sin
sin ;
sin
cos
c
θθ
γ
θθ
os;
;;;
;;
γ
θ
γ
dx
dt
u
w
u
gg
R
r
dy
dt
w
x
Ry
===
⎛
⎝⎜⎞
⎠⎟
=
+
tg
tg=
Ç
Ç
0
2
IM
Vuw
rRy
zz
•
•
;
;;
(
)
.
θ
αθθ
=
=−
=
+
=
+
Σ
22
2
Ç
(3.133)
Åñëè ïîëîæèòü α =0,Ya =0,òî
du
dt
X
m
g
dw
dt
X
m
g
aa
=−
−
=−
−
cos
sin ;
sin
sin .
θ
γ
θ
γ (3.134)
151
Îñòàëüíûå óðàâíåíèÿ (3.133) îñòàíóòñÿ áåç èçìåíåíèÿ. Äëÿ
îòíîñèòåëüíî íåáîëüøèõ äàëüíîñòåé ìîæíî ïîëîæèòü γ =0èg = g0 =
= const, òîãäà èç (3.133) ïîëó÷èì
du
dt
XY
m
dw
dt
XY
m
g
dx
dt
u
aa
aa
=−
+
=−
−
−
=
cos
sin
;
sin
cos
;
θθ
θθ
;;;
.
dy
dt
w
w
u
Vuw
==
=+
θ arctg
22
(3.135)
3.3.3. ÓÐÀÂÍÅÍÈß, ÎÏÈÑÛÂÀÞÙÈÅ ÑÂÎÁÎÄÍÎÅ ÄÂÈÆÅÍÈÅ
ÖÅÍÒÐÀ ÌÀÑÑ ËÀ ÁÅÇ Ó×ÅÒÀ ÑÎÏÐÎÒÈÂËÅÍÈß
ÂÍÅØÍÅÉ ÑÐÅÄÛ
Äëÿ ïðèáëèæåííîãî ðàñ÷åòà íåáîëüøèõ òðàåêòîðèé ñâîáîäíîãî
ïîëåòà, ïðîõîäÿùèõ â áåçâîçäóøíîì ïðîñòðàíñòâå èëè â ñðåäå, îêà-
çûâàþùåé ïðåíåáðåæèìî ìàëîå ñîïðîòèâëåíèå, â òîì ñëó÷àå, êîãäà
ìîæíî íå ó÷èòûâàòü ïåðåìåííîñòü g, êîðèîëèñîâî óñêîðåíèå è êðè-
âèçíó Çåìëè, èñïîëüçóþòñÿ óðàâíåíèÿ, ó÷èòûâàþùèå òîëüêî ñèëó
òÿæåñòè. Ïðè ìàëûõ ñêîðîñòÿõ äâèæåíèÿ òåë â âîçäóõå (ïðèìåðíî äî
50 ì/ñ) ìîæíî ñ÷èòàòü, ÷òî ñèëà ñîïðîòèâëåíèÿ âîçäóõà îòñóòñòâóåò
è òåëî ëåòèò êàê áû â áåçâîçäóøíîì ïðîñòðàíñòâå.  ýòîì ñëó÷àå
åäèíñòâåííîé äåéñòâóþùåé íà òåëî ñèëîé áóäåò ñèëà òÿæåñòè. Äèô-
ôåðåíöèàëüíûå óðàâíåíèÿ äâèæåíèÿ, ñîñòàâëåííûå â ïðîåêöèÿõ íà
îñè ïðÿìîóãîëüíîé ñòàðòîâîé ñèñòåìû êîîðäèíàò, ïðè ýòîì èìåþò
âèä
dx dt
dy dt
g
22 22
0
/;/ .
==
−
(3.136)
Óðàâíåíèÿ (3.136) ÿâëÿþòñÿ èñõîäíûìè óðàâíåíèÿìè â òàê
íàçûâàåìîé ïàðàáîëè÷åñêîé òåîðèè äâèæåíèÿ ñíàðÿäîâ ïîñòîÿííîé
ìàññû. Îáùèå óðàâíåíèÿ (3.47) ïîçâîëÿþò ïîëó÷èòü ñèñòåìó
äèôôåðåíöèàëüíûõ óðàâíåíèé, îïèñûâàþùèõ ïîëåò áàëëèñòè÷åñêîé
ðàêåòû èëè åå ãîëîâíîé ÷àñòè áåç ó÷åòà âðàùåíèÿ Çåìëè íà
ïàññèâíîì, íåóïðàâëÿåìîì ó÷àñòêå ïîëåòà çà ïðåäåëàìè ïëîòíûõ
ñëîåâ àòìîñôåðû. Åñëè â ñèñòåìå óðàâíåíèé (3.47) Vz,
•
θzèΩ
ïðèðàâíÿòü ê íóëþ è îïóñòèòü ÷ëåíû, ó÷èòûâàþùèå òÿãó è
àýðîäèíàìè÷åñêîå ñîïðîòèâëåíèå, òî ïîëó÷èì ðàññìàòðèâàåìûé
ñëó÷àé, îòâå÷àþùèé ïëîñêîé òðàåêòîðèè äâèæåíèÿ îòíîñèòåëüíî
èíåðöèàëüíîé ñèñòåìû êîîðäèíàò OèXèYè:
152
•
;
•
.
Vg
R
r
x
Vg
R
r
y
x
y
è
è
ò
Ç
è
ò
Ç
è
=−
=−
0
2
3
0
2
3
Èç ðèñ. 3.10 ñëåäóåò
xr yr
èè
==
sin ;
cos ,
γγ
(3.137)
è òîãäà
•
sin ;
•
cos .
Vg
R
r
Vg
R
r
x
y
è
è
ò
Ç
ò
Ç
=−
⎛
⎝⎜⎞
⎠⎟
=−
⎛
⎝⎜⎞
⎠⎟
0
2
0
2
γ
γ
(3.138)
Ïîìíÿ, ÷òî
••
•
xV
x
è
è
=
è•• •
,
yV
y
è
è
=
è
äâàæäû
äèôôåðåíöèðóÿ
(3.137), ïåðåéäåì ê ïîëÿðíûì êîîðäèíàòàì r è γ:
••
sin
••
cos
•
sin
••
cos
s
rrrrg
R
r
γγγγγγγ
+−+=
⎛
⎝⎜⎞
⎠⎟
2
2
0
2
ò
Ç
in ;γ (3.139)
•
•
cos
••
sin
•
cos
•
•
sin
c
rrrrg
R
r
γγγγγγγ
−−
−
=
⎛
⎝⎜⎞
⎠⎟
2
2
0
2
ò
Ç
os .γ (3.140)
Óìíîæàÿ ÷ëåíû óðàâíåíèÿ (3.139) íà sinγ, à ÷ëåíû óðàâíåíèÿ
(3.140) – íà cosγ è ñêëàäûâàÿ, ïîëó÷èì
••
•
.
rr
g
R
r
−=
−
⎛
⎝⎜⎞
⎠⎟
γ2
0
2
ò
Ç
(3.141)
Åñëè, äàëåå, óìíîæèòü ÷ëåíû óðàâíåíèÿ (3.139) íà cosγ, à ÷ëåíû
óðàâíåíèÿ (3.140) – íà sinγ è âû÷åñòü èç âòîðîãî óðàâíåíèÿ ïåðâîå, òî
ïîëó÷èì 20
••
.
rr
γγ
+= Óìíîæàÿ ïîñëåäíåå óðàâíåíèå íà r è
ïðåîáðàçîâûâàÿ, çàïèøåì ñèñòåìó óðàâíåíèé
153
Ðèñ. 3 .10. Ñõåìà äåéñòâèÿ ñèëû òÿãîòå-
íèÿ â öåíòðàëüíîì ãðàâèòàöèîííîì ïîëå
••
•
;(•).
rrg
R
r
d
dt
r
−=
−
⎛
⎝⎜⎞
⎠⎟
=
γγ
2
0
2
2
0
ò
Ç
(3.142)
Ýòî èçâåñòíûå äèôôåðåíöèàëüíûå óðàâíåíèÿ äâèæåíèÿ ñíàðÿäà
ïîñòîÿííîé ìàññû â öåíòðàëüíîì ãðàâèòàöèîííîì ïîëå Çåìëè áåç
ó÷åòà ñîïðîòèâëåíèÿ âîçäóõà è âðàùåíèÿ Çåìëè, çàïèñàííûå â
ïîëÿðíûõ êîîðäèíàòàõ r è γ. Ñèñòåìà óðàâíåíèé (3.142) ÿâëÿåòñÿ
îñíîâîé ýëëèïòè÷åñêîé òåîðèè, ïîçâîëÿþùåé ïðèáëèæåííî
îïðåäåëÿòü õàðàêòåðèñòèêè äâèæåíèÿ áàëëèñòè÷åñêèõ ðàêåò íà
âíåàòìîñôåðíîì ó÷àñòêå ïîëåòà.
Óäîáíî çàïèñàòü ýòó ñèñòåìó â ôîðìå óðàâíåíèé Ëàãðàíæà âòî-
ðîãî ðîäà (2.27), âçÿâ â êà÷åñòâå îáîáùåííûõ êîîðäèíàòû r è γ èó÷-
òÿ, ÷òî íà ñíàðÿä äåéñòâóåò îäíà âíåøíÿÿ ñèëà òÿãîòåíèÿ Çåìëè.
 ñîîòâåòñòâèè ñ ðèñ. 3.10
Vrr
=+
•
•
22
2
γ
(3.143)
è êèíåòè÷åñêàÿ ýíåðãèÿ ñíàðÿäà
T
m
rr
=+
2
22
2
(• •).
γ
(3.144)
Äèôôåðåíöèàëüíîå óðàâíåíèå äëÿ êîîðäèíàòû r íàïèøåì, ïîëó-
÷èâ ïðåäâàðèòåëüíî çíà÷åíèÿ ñëàãàåìûõ èç ñèñòåìû óðàâíåíèé
(2.31):
∂
∂
γ
∂
∂
∂
∂
T
r
mr
T
r
mr
d
dt
T
r
mr
Fg
m
r
==
⎛
⎝⎜⎞
⎠⎟=
=−
−
•
;•
•
;
•
•
•
;
2
òò
mg
R
r
ò
Ç
0
2
⎛
⎝⎜⎞
⎠⎟.
 ðåçóëüòàòå ïîëó÷èì ïåðâîå óðàâíåíèå ñèñòåìû óðàâíåíèé
(3.142)
••
•
.
rr
g
R
r
−=
−
⎛
⎝⎜⎞
⎠⎟
γ2
0
2
ò
Ç
Äèôôåðåíöèàëüíîå óðàâíåíèå äëÿ êîîðäèíàòû γ ïîëó÷èì, ïîäñòàâèâ
â (2.27) çíà÷åíèÿ
∂
∂γ
∂
∂γ
γ
γ
TT
mr
F
==
=
00
2
;•
•
.
èò
Ýòî áóäåò âòîðûì óðàâíåíèåì ñèñòåìû (3.142).
154
3.4. ÑÂÎÁÎÄÍÛÉ ÏÎËÅÒ ÀÐÒÈËËÅÐÈÉÑÊÈÕ ÑÍÀÐßÄÎÂ
3.4.1 .ÓÐÀÂÍÅÍÈß ÄÂÈÆÅÍÈß ÑÍÀÐßÄÀ  ÂÅÊÒÎÐÍÎÉ ÔÎÐÌÅ
Ïðè âûâîäå óðàâíåíèé äâèæåíèÿ îñåñèììåòðè÷íûõ ËÀ, â òîì
÷èñëå àðòèëëåðèéñêèõ ñíàðÿäîâ, ñòàáèëèçèðóåìûõ âðàùåíèåì èëè ñ
ïîìîùüþ îïåðåíèÿ, ñëåäóåò ó÷èòûâàòü, ÷òî ïîâîðîò ñíàðÿäà íà ïðî-
èçâîëüíûé óãîë êðåíà íå èçìåíÿåò îðèåíòàöèþ âåêòîðîâ àýðîäèíà-
ìè÷åñêèõ ñèë è ìîìåíòîâ, äåéñòâóþùèõ íà ñíàðÿä â ïîëåòå. Íà-
ïðàâëåíèÿ âåêòîðîâ àýðîäèíàìè÷åñêèõ ñèë è ìîìåíòîâ çàâèñÿò îò
âçàèìíîãî ðàñïîëîæåíèÿ ïðîäîëüíîé îñè è âåêòîðà ñêîðîñòè öåí-
òðà ìàññ ñíàðÿäà, ïîýòîìó íàèáîëåå ïðîñòî àýðîäèíàìè÷åñêèå ñèëû
è ìîìåíòû îïèñûâàþòñÿ â ñèñòåìå êîîðäèíàò, ñâÿçàííîé ñ ïðî-
ñòðàíñòâåííûì óãëîì àòàêè.
Äëÿ íàõîæäåíèÿ îðèåíòàöèè âåêòîðîâ àýðîäèíàìè÷åñêèõ ñèë è
ìîìåíòîâ ââåäåì åäèíè÷íûå âåêòîðû: x
o
–
îðò îñè OX ñâÿçàííîé
ñèñòåìû êîîðäèíàò è x ê
o
–
îðò îñè OXê òðàåêòîðíîé ñèñòåìû êîîð-
äèíàò, êîòîðûå îïðåäåëÿþò ñîîòâåòñòâåííî îðèåíòàöèþ ïðîäîëü-
íîé îñè ñíàðÿäà è âåêòîðà ñêîðîñòè. Óãîë íóòàöèè δ ìåæäó íèìè ëå-
æèò â ïëîñêîñòè, íàçûâàåìîé â áàëëèñòèêå ïëîñêîñòüþ ñîïðîòèâëå-
íèÿ.
Âåêòîð RA ïîëíîé àýðîäèíàìè÷åñêîé ñèëû, äåéñòâóþùåé íà àð-
òèëëåðèéñêèé ñíàðÿä, ïðåäñòàâëÿþò îáû÷íî â âèäå ñóììû òðåõ êîì-
ïîíåíò:
RRRR
AN
=++
òÌ
à
,
ãäå Rò (Xa)
–
ñèëà ëîáîâîãî ñîïðîòèâëåíèÿ (òàíãåíöèàëüíàÿ
ñîñòàâëÿþùàÿ ïîëíîãî âåêòîðà àýðîäèíàìè÷åñêèõ ñèë); RN –
íîðìàëüíàÿ ñîñòàâëÿþùàÿ ïîëíîãî âåêòîðà àýðîäèíàìè÷åñêèõ ñèë;
RÌà – ñèëà Ìàãíóñà.
Èñïîëüçóÿ âûðàæåíèÿ äëÿ ýòèõ ñèë (ñì. ãë. 1), ìîæíî ïðåäñòà-
âèòü èõ â âèäå
XR
x
x
R
a
ON
N
d
g
HyVc
V
a
mf
==
−
⎛
⎝⎜⎞
⎠⎟ =−
=
òò
ê
ê
Ï
Ï
π
δ
π
8
2
2
1
()
;
;
oo
ON
N
d
g
HyVc
V
a
mVf
8
2
2
2
()
;
()
(
δ
⎛
⎝⎜⎞
⎠⎟ ××=
××
xxx
xxx
êêê
oo
o
oo
ê
Ìà
Ìà
ê
Ï
o
oo
o
);
()
;
Rx
x
x
=
⎛
⎝⎜⎞
⎠⎟ ×=
×
π
δ
ON dl
g
HyVrc
V
a
mVf
8
2
3
xê
o
.
155
Ñèëà Ìàãíóñà RÌà íàïðàâëåíà ïî âåêòîðó xx
oo
× ê ïðè ïðàâîì
âðàùåíèè ñíàðÿäà. Ìîäóëè âåêòîðîâ äåéñòâóþùèõ ñèë ïðèâåäåíû â
(1.145). Êîýôôèöèåíòû f1, f2, f3 áóäóò îïðåäåëÿòüñÿ âûðàæåíèÿìè
f
d
mg
HyVc
V
a
f
d
mg
HyVc
ON
ON
N
1
2
2
2
2
8
8
=
⎛
⎝⎜⎞
⎠⎟
=
π
δ
π
Ï
Ï
ò
()
;;
()V
a
f
dl
mg
Hyrc
V
a
ON
;;
() ;.
δ
π
δ
⎛
⎝⎜⎞
⎠⎟
=
⎛
⎝⎜⎞
⎠⎟
3
2
8
Ï
Ìà
Âåêòîð ÌÀ ïîëíîãî àýðîäèíàìè÷åñêîãî ìîìåíòà, äåéñòâóþùåãî íà
àðòèëëåðèéñêèé ñíàðÿä, ïðåäñòàâèì â âèäå ñóììû ÷åòûðåõ
êîìïîíåíò:
MMDÃM
A=+
+
+
ñò
Ìà
.
Çäåñü Ìñò – âåêòîð îïðîêèäûâàþùåãî (èëè ñòàáèëèçèðóþùåãî)
ìîìåíòà; D – âåêòîð ýêâàòîðèàëüíîãî äåìïôèðóþùåãî ìîìåíòà; Ã –
âåêòîð ìîìåíòà ïîâåðõíîñòíîãî òðåíèÿ (÷àñòî íàçûâàåìîãî â
áàëëèñòèêå âåêòîðîì àêñèàëüíîãî òóøàùåãî ìîìåíòà); ÌÌà – âåêòîð
ìîìåíòà Ìàãíóñà:
Mx
x
x
x
D
ñò
ê
ê
Ï
=
⎛
⎝⎜⎞
⎠⎟ ×=
×
=
π
δ
ON
M
dl
g
HyVm
V
a
Af
8
2
2
4
()
;
.
oo
oo
−∇
⎛
⎝⎜⎞
⎠⎟=
=
π
δ
π
Ï
Ï
Ma
ON
D
ON
dl
g
Hy Vm
V
a
Af
dl
g
8
8
22
7
22
()
;
;
ΩΩ
M
HyVrm
V
a
Crf
x
()
;
()
()
;
Ma
ê
ê
δ
⎛
⎝⎜⎞
⎠⎟ ××=
=×
×
xxx
xxx
Ã
oo
o
ooo
5
=
⎛
⎝⎜⎞
⎠⎟ =−
π
δ
Ï
Ã
ON dl
g
HyVm
V
a
rC
r
f
8
22
6
();
,
xx
oo
ãäå À = Iy = Iz – ýêâàòîðèàëüíûé ìîìåíò èíåðöèè ñíàðÿäà; Ñ = Ix –
îñåâîé (àêñèàëüíûé) ìîìåíò èíåðöèè ñíàðÿäà; r = r x
o
–
ñîñòàâëÿþùàÿ âåêòîðà óãëîâîé ñêîðîñòè ñíàðÿäà ïî ïðîäîëüíîé îñè;
156
Ω – ñîñòàâëÿþùàÿ âåêòîðà óãëîâîé ñêîðîñòè ñíàðÿäà,
ïåðïåíäèêóëÿðíàÿ ê ïðîäîëüíîé îñè.
Âçàèìíàÿ îðèåíòàöèÿ âåêòîðîâ äåéñòâóþùèõ ñèë è ìîìåíòîâ ïî-
êàçàíà íà ðèñ. 3 .11. Âûðàæåíèÿ äëÿ ìîäóëåé âåêòîðîâ ìîìåíòîâ ñî-
îòâåòñòâóþò (1.145).
Êîýôôèöèåíòû f4, f5, f6, f7 áóäóò îïðåäåëÿòüñÿ âûðàæåíèÿìè
f
dl
Ag
HyVm
V
a
f
dl
Cg
Hy
ON
M
ON
4
2
2
5
22
8
8
=
⎛
⎝⎜⎞
⎠⎟
=
π
δ
π
Ï
Ï
()
;;
()Vm
V
a
f
dl
Cg
HyVm
V
a
f
ON
Ma
Ã
Ï
;;
() ;;
δ
π
δ
⎛
⎝⎜⎞
⎠⎟
=
⎛
⎝⎜⎞
⎠⎟
=
6
22
7
8
π
δ
ÏON
D
dl
Ag
HyVm
V
a
8
22
()
;.
⎛
⎝⎜⎞
⎠⎟
Èñïîëüçóÿ òîæäåñòâî, ñïðàâåäëèâîå äëÿ 3 ïðîèçâîëüíûõ âåêòîðîâ:
abc acbab
c
××=⋅
−⋅
( )()(),
(3.145)
157
Ðèñ. 3.11. Îïðåäåëåíèå âçàèìíîé îðèåíòàöèè âåêòîðîâ äåéñòâóþùèõ íà ñíàðÿä ñèë
è ìîìåíòîâ
ìîæíî ïðåîáðàçîâàòü âûðàæåíèÿ äëÿ âåêòîðîâ RN è MMa:
Rx
x
xx
x
x
x
Mx
N
mVf
mVf
Crf
=×
×
=−
⋅
=
22
5
êê
ê
ê
Ma
oo
o
oo
o
o
() [()
]
;
oo
o
o
o
o
o
××=
⋅
()[
()]
.
xx
xxx
-
x
êê
ê
Crf 5
Ñ ó÷åòîì ïðèâåäåííûõ âûðàæåíèé äëÿ ñèë è ìîìåíòîâ, äåéñòâóþùèõ
íà àðòèëëåðèéñêèé ñíàðÿä, íà îñíîâàíèè òåîðåì îá èçìåíåíèè
âåêòîðîâ êîëè÷åñòâà äâèæåíèÿ è êèíåòè÷åñêîãî ìîìåíòà (Q è K)
ìîæåì çàïèñàòü óðàâíåíèÿ äâèæåíèÿ â âåêòîðíîé ôîðìå [98]:
d
dt
mf
Vf
Vf
Q
Qxx
x
x
xx
x
g
+×= −
+
−
⋅
+×+
ω
{[
(
)
]}
12
3
êê
ê
ê
oo
o
o
oo
o
;
[()
]
d
dt
Af
Crf
Crf
Af
K
Kx
xx
x
x
xx
+×=
×+
⋅
−
−
−
ω
45
6
êê
ê
oo
o
o
oo
o
7Ω.
(3.146)
Çäåñü ω – óãëîâàÿ ñêîðîñòü ïîäâèæíîé ñèñòåìû êîîðäèíàò.
Ïðåîáðàçóåì ïåðâîå óðàâíåíèå ñèñòåìû (3.146), èñïîëüçóÿ
ñîîòíîøåíèå Q = mVx ê
o
. Áóäåì èìåòü
dV
dt
V
d
dt
Vf
Vf
x
x
xx
xxx
x
ê
ê
êê
êê
o
o
oo
oo
o
o
++
×
=
−
+
+−
⋅
ω
1
2[( )]
+×
+
Vf3xx g
oo
ê
.
(3.147)
Óìíîæèâ ýòî óðàâíåíèå ñêàëÿðíî íà x ê
o
, ïîëó÷èì
dVdtf
/.
=−
+⋅
1 gxê
o
(3.148)
Ïîäñòàâèì (3.148) â (3.147), òîãäà
d
dt
V
f
x
xg
x
g
x
xxx
x
ê
êê
ê
êê
o
oo
o
oo
o
o
+×=
−
⋅
+
+−
⋅
−
ω
1
2
[()
]
[( )]
+×
f 3xx
oo
ê
.
(3.149)
×òîáû îïðåäåëèòü ïîëîæåíèå öåíòðà ìàññ ñíàðÿäà â ñòàðòîâîé
ñèñòåìå êîîðäèíàò, áóäåì èñïîëüçîâàòü ðàäèóñ-âåêòîð öåíòðà ìàññ
ñíàðÿäà rc, äëÿ êîòîðîãî ñïðàâåäëèâà êèíåìàòè÷åñêàÿ çàâèñèìîñòü
d
dt
V
r
x
c
ê
=
o
,
(3.150)
158
ãäå
d
dt
rc
–
ïðîèçâîäíàÿ â íåïîäâèæíîé (ñòàðòîâîé) ñèñòåìå
êîîðäèíàò.
Òàêèì îáðàçîì, äâèæåíèå öåíòðà ìàññ ñíàðÿäà îïèñûâàåòñÿ
óðàâíåíèÿìè (3.148)...(3.150).
Âåêòîð ìîìåíòà êîëè÷åñòâà äâèæåíèÿ ñíàðÿäà èìååò âèä
Kx
=+
CrA
o
Ω.
Ëèíåéíàÿ ñêîðîñòü êîíöà âåêòîðà x
o
ðàâíà
d
dt
x
x
o
o
−×
⎛
⎝⎜
⎞
⎠⎟ω , ïîýòîìó
ñîñòàâëÿþùàÿ óãëîâîé ñêîðîñòè ñíàðÿäà Ω, ïåðïåíäèêóëÿðíàÿ åãî
îñè, ñ ó÷åòîì (3.144) ìîæåò áûòü ïðåäñòàâëåíà ñëåäóþùèì
îáðàçîì:
Ω=×
−
×
⎛
⎝⎜
⎞
⎠⎟ =×−
⋅+
x
x
x
xxxx
o
o
o
ooo
o
d
dt
ωω
ω
•
().
Ââîäÿ îáîçíà÷åíèå 2à = Cr/A, âòîðîå óðàâíåíèå ñèñòåìû (3.146)
ìîæåì ïðèâåñòè ê âèäó
22
2
2
•
••
••
()(•)
•
aa
a
x
xxxxx
xx
x
o
o
o
o
oo
oo
o
+ +×−
⋅−
⋅+
+×
ωω
ω
ω
−
−⋅
×= ×+
⋅
−
−
−
()
()
[
()]
xx
x
xx
x
x
x
oo
o
oo
o
o
o
ωω
fa
f
af
45
6
2
2
êê
ê
x xxxx
o
ooo
o
−×
−⋅
+
f7[
•
()]
.
ωω
(3.151)
Óìíîæàÿ ýòî óðàâíåíèå ñêàëÿðíî íà x
o
, ïîëó÷èì
•
.
af
a
=−
6
(3.152)
Ñ ó÷åòîì ýòîãî óðàâíåíèå (3.151) ïðåîáðàçóåòñÿ ê ñëåäóþùåìó:
xxxx
xxx
x
x
oo
o
o
o
o
o
o
o
×+−+×+
⋅−
⋅+
+
•••
(•
)()(•)
•
22
7
af
ωω
ω
ω+
×=
×+
⋅
−
−
−×
+
22
45
7
afa
f
f
ω
ω
xx
xx
x
x
x
xx
oo
o
o
o
o
o
oo
êê
ê
[()
]
(•).
(3.153)
Óðàâíåíèÿ (3.152) è (3.153) îïðåäåëÿþò âðàùàòåëüíîå äâèæåíèå
ñíàðÿäà. Ïîëíàÿ ñèñòåìà óðàâíåíèé äâèæåíèÿ â âåêòîðíîé ôîðìå
áóäåò èìåòü âèä
159
•
;
•
[()
][(
Vf
Vf
=⋅
−
+×=
−
⋅
+−
−
gx
xxg
x
g
xx
x
ê
êê
ê
ê
o
oo
o
oo
o
1
1
2
ω⋅
+
×
=
×+−+×
xx
xx
rx
xxxx
x
c
êê
ê
ê
oo
o
o
o
oo
o
o
o
)]
;
•
;
•
(•
f
a
3
22
V
ω+⋅
−
⋅
+
++×=×+
f
afa
f
7
45
22
xx
xx
xx
xx
oo
o
o
oo
o
)()(•)
•
[(
ωω
ωω
ê
o
o
oo
oo
⋅−
−×
+
=−
xxx
xx
êê
ê
)]( )
;
•
.
f
af
a
7
6
ω
(3.154)
3.4.2 . ÓÐÀÂÍÅÍÈß ÄÂÈÆÅÍÈß ÀÐÒÈËËÅÐÈÉÑÊÎÃÎ ÑÍÀÐßÄÀ
 ÔÎÐÌÅ Â.Ñ. ÏÓÃÀ×ÅÂÀ
Äëÿ òîãî ÷òîáû ïîëó÷èòü óðàâíåíèÿ ïðîñòðàíñòâåííîãî äâè-
æåíèÿ àðòèëëåðèéñêîãî ñíàðÿäà â ôîðìå Â.Ñ. Ïóãà÷åâà, áóäåì
èñïîëüçîâàòü ñòàðòîâóþ ñèñòåìó êîîðäèíàò OXcYcZc äëÿ îïðåäåëå-
íèÿ ïîëîæåíèÿ öåíòðà ìàññ ñíàðÿäà è òðàåêòîðíóþ ñèñòåìó êî-
îðäèíàò OXêYêZê äëÿ îïðåäåëåíèÿ îðèåíòàöèè ïðîäîëüíîé îñè
ñíàðÿäà îòíîñèòåëüíî âåêòîðà ñêîðîñòè (ñì. ðèñ. 3.12). Ïîëîæå-
íèå âåêòîðà ñêîðîñòè öåíòðà ìàññ ñíàðÿäà V (èëè x ê
o
) â ñòàðòî-
âîé ñèñòåìå êîîðäèíàò áóäåì íàõîäèòü ñ ïîìîùüþ óãëà θ íàêëî-
160
Ðèñ. 3.12. Ñõåìà âçàèìíîé îðèåíòàöèè ïðîäîëüíîé îñè ñíàðÿäà è âåêòîðà ñêîðîñòè
íà âåêòîðà ñêîðîñòè ê ãîðèçîíòó è óãëà Ψí ïîâîðîòà âåêòîðà
ñêîðîñòè, îïðåäåëÿåìîãî â íàêëîííîé ïëîñêîñòè. Ïîëîæèòåëüíîå
íàïðàâëåíèå ïîñëåäíåãî ïîêàçàíî íà ðèñ. 3 .12. Òîãäà âåêòîðû è
ïðîèçâåäåíèÿ âåêòîðîâ, âõîäÿùèå âî âòîðîå è ÷åòâåðòîå óðàâíå-
íèÿ ñèñòåìû (3.154), áóäóò èìåòü ñëåäóþùèå ïðîåêöèè íà îñè
òðàåêòîðíîé ñèñòåìû êîîðäèíàò:
xx
êí
oo
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=−
⎡
⎣
⎢
1
0
0
0
1
2
3
;;•
•
z
z
z
ω
θ
Ψ
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
−
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
;
sin
cos ;
g
g
g
θ
θ
0
ωθ
×=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
×=
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
×
xx
xx
ê
í
ê
oo
oo
00
3
2
•
•
;;
Ψ
z
z
x
o
=
−
−
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
=
z2
•••
•
•••
•
•••
•
zz
z
zz zz
zz zz
32
3
31 31
12 12
⎥
⎥
⎥
×=
−+
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
;
(••
)
•
•
;
ω
θ
θ
x
o
zz
z
z
23
1
Ψ
Ψ
í
1
í
xx
x
oo
o
×=
+
−
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
×=
−
•
•
••
•
••
••
;
ω
θ
θ
zz
z
z
23
1
1
0
Ψ
Ψí
ê
z
z
zz zz
zz zz
zz
3
2
23 23
31 31
12
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
×=
−
−
−
;
•
••
••
•
xx
oo
•
.
zz
12
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
Ñêàëÿðíûå ïðîèçâåäåíèÿ âåêòîðîâ, âõîäÿùèå âî âòîðîå è ÷åòâåðòîå
óðàâíåíèÿ (3.154), èìåþò âèä
gx
xx
x
x
⋅=
−
⋅=
⋅
=−
⋅=
êê
í
oo
o
o
o
gz
z
z
z
sin ;
;
••
;
•
••
θω
θ
ωθ
13
2
3
Ψ
−
z2
•
•
.
Ψí
Ïðîåöèðóÿ âòîðîå è ÷åòâåðòîå óðàâíåíèÿ (3.154) íà îñè OYê è
OZê, ïîëó÷èì
161
•
cos
;
•
;
•••
•
θθ
=−
+
+
=−
+
−
−
gV
fz fz
fz fz
zz zz
1
22 33
32 23
313
Ψí
122
1
7
2
3
22
3
2
22
+−++
−
−−
−
az
zz
fzz
zz
zz
•
(••)(
•
•
)(•• •
θθ
θ
Ψí
•
) •••
(•••
ψθ
íí
−+
=
=−
+
−
−
−
Ψ
Ψ
2
2
1
43
521 731 31
az
fz afzz fzz zz
í
í
);
•••
••
(••
)(•
•
zz zz
az
zz
fzz
z
12 12
3
31
733
2
22
−+
−+
+
−
−
Ψθ
ΨΨ
Ψ
íí
í
)(•••
•
) •••
−−
+
+=
=+
−
zzz
a
z
fz afzz f
33
2
1
42
531 7
2
2
θθ
(•••).
zz zz
12 12
−+
θ
(3.155)
Ïðîåöèðóÿ òðåòüå óðàâíåíèå ñèñòåìû (3.154) íà îñè ñòàðòîâîé
ñèñòåìû êîîðäèíàò, ïîëó÷èì
•
cos
sin ;•
sin;•
sin .
xV
yV zV
ñí
ñ
c
í
=−
=
=
22
θθ
ΨΨ
(3.156)
Îáúåäèíÿÿ (3.155) è (3.156) è ó÷èòûâàÿ, ÷òî äëÿ ïðîåêöèé âåêòîðà x
o
íà îñè OXêYêZê ñïðàâåäëèâî ñîîòíîøåíèå zzz
1
2
2
2
3
2
1
++=
, çàïèøåì
ïîëíóþ
ñèñòåìó
óðàâíåíèé
ïðîñòðàíñòâåííîãî äâèæåíèÿ
àðòèëëåðèéñêîãî ñíàðÿäà â ôîðìå Â.Ñ . Ïóãà÷åâà [98]:
1
2
3
1
1
22 33
3
)•
sin
;
)•
cos
;
)•
Vgf
gV
fz fz
fz
=−
−
=−
+
+
=−
−
θ
θθ
Ψí2
2
3
+ fz;
42
2
31 31
2
21
723
2
) •••••
(••)(
•
•
zzzzaz
zzfzz
z
−+
−+
+
−
−
θθ
Ψí)(
•
••
•
) •••
(
−−
−
+=
=−
+
−
zzz
a
z
fz afzz f
23
2
1
43
521 7
2
2
θθ
ΨΨ
íí
zz zz
zz zz
az
zz
31 31
12 12
3
31
52
2
••
•
);
) •••••
(••
+−
−+
−+
Ψ
Ψ
í
í
+−
−−
−
+
+=
=
fzz
zz
zz
a
z
f
733
23
3
2
1
2
)(•
•
)(•••
•
) •••
θ
θθ
ΨΨ
Ψ
íí
42
531 712 12
2
z
afzzfzz zz
+−−
+
(•••);
θ
(3.157)
6
71
8
9
6
12
2
3
2
22
)•
;
);
)•
cos
sin ;
)•
af
a
zz
z
xV
y
=−
=−−
=−
cí
c
θΨ
=
=
V
zV
sin ;
)•
sin .
θ
10 cí
Ψ
162
×òîáû èññëåäîâàòü ñèñòåìó (3.157) àíàëèòè÷åñêèìè èëè ÷èñëåí-
íûìè ìåòîäàìè, åå ïðèâîäÿò ê íîðìàëüíîé ôîðìå Êîøè. Îáîçíà-
÷èì
uzuz
2233
==
•
;
•
.
Ïðèíèìàÿ, ÷òî êîýôôèöèåíòû cN è cÌà çàâèñÿò òîëüêî îò V/a è δ,
ìîæíî ïîëó÷èòü âûðàæåíèÿ äëÿ
••
θè
••
:
Ψí
••
(si
n
c
o
s)(
•
sin )
(•
θθ
θθ
=−
+
++
+
++
−−
gVg
f
fgV
fz
f
2
12
1
22
3
2
gV
fzfzfz
fzfzfz
−
++
=
−
+−+
1
332233
322332
sin )
••
;
••
••
•
θ
ψí
•
,
fz
23
ãäå
••
•••
;
•
ff
V
V
f
y
y
f
z
z
f
z
z
ff
2
22 22
3
3
=+ ++
=
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
ñ
c
2
2
3
3
V
V
f
y
y
f
z
z
f
z
z
•
•••
.
+++
∂
∂
∂
∂
∂
∂
333
ñ
c
2
2
3
3
Äèôôåðåíöèðóÿ ñåäüìîå óðàâíåíèå ñèñòåìû (3.157), ïîëó÷èì
•
••
.
z
zz zz
zz
1
22 33
2
2
3
2
1
=−
+
−−
Îòêóäà íàéäåì
••
•••
•••
(••
z
zzzzzz
zz
zz zz
1
22332
2
3
2
2
2
3
2
223
1
=−
+++
−−
−
+
3
2
2
2
3
232
1
)
()
.
/
−−
zz
Ñ èñïîëüçîâàíèåì ïðèâåäåííûõ âûðàæåíèé äëÿ •z 1 è ••
z1 ÷åòâåðòîå è
ïÿòîå óðàâíåíèÿ ñèñòåìû (3.157) ïðåîáðàçóþòñÿ ê âèäó
zzu
zu
zz
V yzzuu
232
2
2
3
2
2
3
2
1
2323
1
1
•
()
•
(,,,,,,,
+−
−−
=Φ θc
a
zu zzu
zz
V yzzu
);
()
••
(,,,,,,
1
1
3
2
2 233
2
2
3
2
2
232
−+
−−
=Φ θc
ua
3,)
,
(3.158)
163
ãäå
Φ1 33
7
2 422
7
33
227 2
2
1
=+
+−−
+−+
−
−
(• )(
•
)(
fffz ffff
zf
uff zz
3
2
3
2
2
12
3
1
2
222
1
)
( sin
cos )
cos
u
augVg
f
zz
agV
z
+
++
+
−
−
−−
θθ
θ2
3
2
2
1
22 33
2
2
3
2
72
21
−+
+−
−−
−
−
+
+
−
z
ug
V
fzf
zzz
fzg
[(c
o
s
)
][
θ
Vz
f
z
zg
Vf
z
f
z
z
z
f
−−
−+
−
+
−
−
1
33
2
2
3
21
22 3323
cos
(
)]
sin (
)
•
θθ
322
2
3
2
223 322 322 332
2
zzzfzuzuzfzuzuz
af
(
)
()
()
(
+
+−−++
+
223352
2
2
3
2
73
22 33
2
2
3
2
3
1
1
zf
zf
z zzf
z
zu zu
zz
z
+− −−−
+
−−
−
−
)
uu
zz
z
zu zu
zz
2
2
3
2
2
2
3
2
3
22 33
2
2
2
3
232
1
1
+
−−
−
+
−−
()
()
;
/
Φ2
2
1
1
742
1
2
=+
++
−
−
−−
−
gVg
f
gV
fffgV
( sin
cos )
cos
(•
sin
θθθ
θ
f
ffzfgV
fffzff
zz
2
272
3
1
33
7
327 2
2
3
1
−
−−
+
+−
+−
−
−
)(
•
sin
)(
θ
2
23
3
3
3
23 32
2
2
3
2
73
22
1
)
[()
]
[
uf
u
au
u
fz fz
zz
fz gV
+−
−−+
−
−
−
+
−
−−
−+
−
−+
+
1
33
2
2
3
2
2
13
21
2
cos
(
)]
(si
n
c
o
s)
θ
θθ
zf
zz
gVg
f
z gVsin(
)
•
()( )
θfzfzz
fzzz fzu zuz
22 333
2
332
2
3
2
223 323
++
++
−−+++
−
+
+−
−
−
fzu zuz afz fz
fzzzfz
322 333
32 23
53
2
2
3
2
72
2
1
()(
)
zu zu
zz
z
uu
zz
z
zu zu
22 33
2
2
3
2
2
2
2
3
2
2
2
3
2
2
22 33
11
+
−−
−
+
−−
−
+
(
)
()
.
/
2
2
2
3
232
1−−
zz
Ðàçðåøàÿ óðàâíåíèÿ (3.158) îòíîñèòåëüíî •u2 è •
,
u3 ìîæíî ïðèâåñòè
ñèñòåìó (3.157) ê íîðìàëüíîìó âèäó [98]:
1
2
3
1
1
22 33
3
)•
sin
;
)•
cos
;
)•
Vgf
gV
fz fz
fz
=−
−
=−
+
+
=−
−
θ
θθ
Ψí2
2
3
22
222
1
32
22
2
3
2
4
51
+
=
=−
+
−
−
fz
zu
uz
z
z
z
z
;
)•
;
)•[()
]
(
ΦΦΦ
);
/
−12
6
71
8
33
313
1
32
22
2
3
212
)•
;
)•[()
]
()
;
/
zu
uz
z
z
z
z
=
=−
+
−
−
−
ΦΦΦ
)•
;
af
a
=−
6
164
(3.159)
9
10
11
22
)•
cos
sin ;
)•
sin ;
)•
sin .
xV
yV
zV
ñí
c
ñí
=−
=
=
θ
θ
Ψ
Ψ
Ñèñòåìà (3.159), ïîëó÷åííàÿ Â.Ñ. Ïóãà÷åâûì, ÿâëÿåòñÿ íàèáîëåå
îáùåé ñèñòåìîé óðàâíåíèé, îïèñûâàþùèõ ïðîñòðàíñòâåííîå äâè-
æåíèå àðòèëëåðèéñêîãî ñíàðÿäà ïðè ïåðå÷èñëåííûõ âûøå ñèëàõ è
ìîìåíòàõ. Ñèñòåìà ïîëó÷åíà áåç êàêèõ-ëèáî îãðàíè÷åíèé íà ôàçî-
âûå êîîðäèíàòû, îïðåäåëÿþùèå äâèæåíèå àðòèëëåðèéñêîãî ñíàðÿ-
äà, ïîýòîìó ïðè èçâåñòíûõ çàâèñèìîñòÿõ àýðîäèíàìè÷åñêèõ êîýô-
ôèöèåíòîâ îò V/à è δ îíà ìîæåò áûòü èñïîëüçîâàíà ïðè ïðîèçâîëü-
íûõ çíà÷åíèÿõ óãëîâ íóòàöèè.
 ñèñòåìå (3.159) óðàâíåíèÿ 3,9è11ìîãóò èíòåãðèðîâàòüñÿ íå-
çàâèñèìî îò îñòàëüíûõ. Ïîñëå òîãî êàê â ðåçóëüòàòå èíòåãðèðîâàíèÿ
ñèñòåìû (3.159) áóäóò íàéäåíû âåëè÷èíû z2 è z3, ìîæíî îïðåäåëèòü
óãëû, çàäàþùèå îðèåíòàöèþ ïðîäîëüíîé îñè îòíîñèòåëüíî âåêòîðà
ñêîðîñòè.
Åñëè ïîëîæåíèå ïðîäîëüíîé îñè ñíàðÿäà çàäàåòñÿ ñ ïîìîùüþ óã-
ëîâ Ýéëåðà – óãëîâ íóòàöèè δ è ïðåöåññèè ν (ñì. ðèñ. 3.12), òî îðò x
o
îñè OX ñâÿçàííîé ñèñòåìû êîîðäèíàò áóäåò èìåòü ñëåäóþùèå ïðî-
åêöèè íà îñè OXêYêZê:
x
o
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
z
z
z
1
2
3
cos
sin cos
sin sin
δ
δν
δν
.
(3.160)
Åñëè ïîëîæåíèå ïðîäîëüíîé îñè ñíàðÿäà çàäàåòñÿ óãëàìè δ1 è δ2
(ñì. ðèñ. 3.12), òî
x
o
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
z
z
z
1
2
3
21
21
1
cos cos
sin cos
sin
δδ
δδ
δ
⎤
⎦
⎥
⎥
⎥
.
(3.161)
Çíàÿ z2 è z3, èç (3.160) ìîæåì íàéòè óãëû íóòàöèè è ïðåöåññèè:
δν
=−
−
=
arccos
;
,
12
2
3
2
3
2
zz
z
z
arctg
(3.162)
à èç ñîîòíîøåíèé (3.161) íàéäåì
δδ
13
2
2
2
2
3
2
1
==
−−
arcsin ;
.
z
z
zz
arctg
(3.163)
165
Òàêèì îáðàçîì, ñîîòíîøåíèÿ (3.162) èëè (3.163) ïîçâîëÿþò îïè-
ñàòü ãåîìåòðè÷åñêóþ êàðòèíó óãëîâîãî äâèæåíèÿ ïðîäîëüíîé îñè
ñíàðÿäà îòíîñèòåëüíî âåêòîðà ñêîðîñòè ïî çíà÷åíèÿì z2 è z3, ïîëó-
÷åííûì â ðåçóëüòàòå èíòåãðèðîâàíèÿ ñèñòåìû (3.159).
3.4.3 . ÓÐÀÂÍÅÍÈß ÏÐÎÑÒÐÀÍÑÒÂÅÍÍÎÃÎ ÄÂÈÆÅÍÈß
ÀÐÒÈËËÅÐÈÉÑÊÎÃÎ ÑÍÀÐßÄÀ ÏÐÈ ÌÀËÛÕ ÓÃËÀÕ ÍÓÒÀÖÈÈ
 ðàáîòå [98] íà îñíîâå òùàòåëüíîãî àíàëèçà ÷ëåíîâ, âõîäÿùèõ â
óðàâíåíèÿ (3.157), è èõ ïîðÿäêîâ ïîêàçàíî, ÷òî ïðè ìàëûõ óãëàõ íó-
òàöèè δ ñèñòåìà (3.157) ìîæåò áûòü çàìåíåíà ïðèáëèæåííîé, ïîëó-
÷åííîé èç (3.157) îòáðàñûâàíèåì ÷ëåíîâ áîëåå âûñîêîãî ïîðÿäêà
ìàëîñòè, ÷åì óäåðæèâàåìûå:
•
sin
;
•
cos
;
•
Vgf
gV
fz fz
fz fz
=−
−
=−
+
+
=−
+
−
θ
θθ
1
1
22 33
32 23
Ψí
;
•••• •
()
−
+−+++=
=−
+
za
zf
zf
za
fzf
z
fz af
3
22332
22 33
43
5
22
2zf
za
Vg
za
zf
zf
za
fz
27
3
1
2
32233
23
2
22
++
+ +++
−
•
cos ;
•••• •
(
θ
−=
=+
−
+
fz
fz afz fz
32
42
53 72
2
)
(• );
θ
•
;
;
•
cos
sin ;
•
sin ;
•
af
a
zz
z
xV
yV
=−
=−−
=−
=
6
12
2
3
2
22
1
cí
c
θ
θ
Ψ
zV
cí
=
sin .
Ψ
Ïðè ìàëûõ óãëàõ íóòàöèè δ, à ñëåäîâàòåëüíî, è ïðè ìàëûõ óãëàõ
δ1 è δ2 ìîæåì â óðàâíåíèÿõ äâèæåíèÿ (3.164) ïåðåéòè îò íàïðàâëÿþ-
ùèõ êîñèíóñîâ z2 è z3 íåïîñðåäñòâåííî ê óãëàì.
Òàê êàê ïðè ìàëûõ δ1 è δ2
sin
; cos
( ,),
δδδ
iiii
≈≈
=
11
2
â ñîîòâåòñòâèè ñ (3.161) ïîëó÷èì
zz
zz
22
1
22
31
1
3
1
=≈
≈
=≈≈
sin cos
;••
;
sin
;••
.
δδδ δ
δδδ
166
(3.164)
Ïðè ìàëûõ δ èìååì z 1
2
1
2
=≈
−
cos
,
δ
δ
îòêóäà
z1
222
1
=≈
−
cos
.
δδ
Ñ ó÷åòîì ýòîãî ñåäüìîå óðàâíåíèå ñèñòåìû (3.164) ìîæíî ïðèâåñòè ê
âèäó
δδδ
2
1
2
2
2
=+
.
 ðåçóëüòàòå ñèñòåìà (3.164) ïðåîáðàçóåòñÿ ñëåäóþùèì îáðàçîì:
•
sin
;
•
cos
;
•
Vgf
gV
ff
ff
=−
−
=−
+
+
=−
+
−
θ
θθ
δ
δ
δδ
1
1
22 31
32 21
Ψí
;
••
()
•
()
•
()
()
δδδ δ
1++ −+
−
++
+−
ff af
a
ff
aff
27
1
3
234
1
52
22
2
δθ
δδδ
2
1
227
2
3
134
2
22
=−
++++−+
−
agV
ff af
a
ff
cos ;
••
()( )
•
()
δδ
θ
25
2
1
7
2
−−
=
−
aff
f
() •;
•
;
;
•
cos
sin ;
•
sin ;
•
af
a
xV
yV
z
=−
=+
=−
=
6
2
1
2
22
δδδ
θ
θ
2
2
cí
c
c
Ψ
=Vsin .
Ψí
Òàê êàê êîýôôèöèåíòû f1, ..., f7 ÿâíî çàâèñÿò îò ñêîðîñòè öåíòðà
ìàññ, ââåäåì îáîçíà÷åíèÿ:
fVcf V
cfa
c
fVmfV
mfV
m
f
N
M
1
2
23
4
2
5
6
7
2
===
===
=
òÌ
à
Ìà
Ã
;;;
;;;
VmD ,
ãäå
ñ
d
mg
Hyc
V
a
ñ
d
mg
Hyc
V
a
ON
N
ON
N
òò
Ï
Ï
=
⎛
⎝⎜⎞
⎠⎟
=
⎛
π
δ
π
8
8
2
2
() ,;
()⎝⎜⎞
⎠⎟
=
⎛
⎝⎜⎞
⎠⎟
;
();
ñ
dl
mg
A
C
Hyc
V
a
ON
Ìà
Ma
Ï
π
8
2
167
(3.165)
m
dl
Ag
Hym
V
a
m
dl
Cg
Hym
M
ON
M
ON
=
⎛
⎝⎜⎞
⎠⎟
=
π
π
Ï
Ï
Ma
Ma
8
8
2
22
();
()V
a
m
dl
Cg
Hym
V
a
m
dl
ON
D
ON
⎛
⎝⎜⎞
⎠⎟
=
⎛
⎝⎜⎞
⎠⎟
=
;
();
ÃÃ
Ï
Ï
π
π
8
8
22
22
Ag
Hym
V
a
D
().
⎛
⎝⎜⎞
⎠⎟
Òîãäà, ïîäñòàâëÿÿ â ïðàâóþ ÷àñòü ïÿòîãî óðàâíåíèÿ ñèñòåìû
(3.165) çíà÷åíèå
•
θ èç âòîðîãî óðàâíåíèÿ ñèñòåìû è ïðåíåáðåãàÿ ÷ëå-
íàìè ïîðÿäêà f7 f2δ2 è f7 f3δ1 â ïÿòîì óðàâíåíèè, îêîí÷àòåëüíî ïîëó-
÷èì ñèñòåìó â ñëåäóþùåì âèäå:
•
sin
;
•
cos
;
•
VgV
c
gV
Vc
ac
ac
N
=−
−
=−
+
+
=−
−
θ
θθ
δ
δ
2
1
21
2
2
ò
Ma
í
Ψ
Ma
Ma
Ma
δδ
δδδ
21
112
2
21
4
+
++ −+
−
−+
Vc
Vcm
ac
ac
N
ND
;
••
()
•
()
•
(
Vm
aVm
c
aVg
MN
2
12
1
22
)() c
o
s
;
δδθ
+−
=
−
−
Ma
•
•
()
•
()
•
()
δδδ
δ
221
22
2
21
42
++++−
−+
−
Vcm
ac
ac Vm
aV
ND
M
Ma
Ma
()c
o
s
;
•
;
•
cos
sin ;
•
mcm
g
aV
m
a
xV
y
ND
Ma
Ã
cí
c
−=
=−
=−
=
δθ
θ
1
22
Ψ
V
zV
sin ;
•
sin ;
.
θ
δδδ
2
2
cí
2
=
=+
Ψ
1
2
Ñèñòåìà (3.166) ìîæåò áûòü èñïîëüçîâàíà äëÿ àíàëèòè÷åñêîãî
(ïðè ñîîòâåòñòâóþùèõ äîïóùåíèÿõ) èëè ÷èñëåííîãî èññëåäîâàíèÿ
ïðîñòðàíñòâåííîãî äâèæåíèÿ àðòèëëåðèéñêîãî ñíàðÿäà ïðè ìàëûõ
óãëàõ íóòàöèè.
168
(3.166)
Êîíòðîëüíûå âîïðîñû
1.  ÷åì ñîñòîèò ðàçëè÷èå ìåæäó ñâÿçàííûìè è èíåðöèàëüíûìè ñèñòå-
ìàìè êîîðäèíàò? Êàêèå óãëû îïðåäåëÿþò âçàèìíóþ îðèåíòàöèþ îñåé ñêî-
ðîñòíîé è ñâÿçàííîé ñèñòåì êîîðäèíàò?  êàêîì ñëó÷àå îñè òðàåêòîðíîé è
ñêîðîñòíîé ñèñòåì ñîâïàäàþò? Íàðèñóéòå ñõåìó ñèñòåì êîîðäèíàò è óãëîâ,
îïðåäåëÿþùèõ ïîëîæåíèå ËÀ îòíîñèòåëüíî ìåñòíîãî ãîðèçîíòà. ×åì îáó-
ñëîâëåíà íåîáõîäèìîñòü ïðèìåíåíèÿ êâàòåðíèîíîâ?
2. ×åì îòëè÷àåòñÿ òÿãà îò ðåàêòèâíîé ñèëû? Êàê èçìåíÿåòñÿ çíà÷åíèå
óäåëüíîãî èìïóëüñà òÿãè ñ èçìåíåíèåì âûñîòû? Êàêàÿ ðàçíèöà ìåæäó òåëîì
ïåðåìåííîé ìàññû è òåëîì ïåðåìåííîãî ñîñòàâà? Íàçîâèòå ñîñòàâëÿþùèå
àáñîëþòíîé ñêîðîñòè è óñêîðåíèÿ öåíòðà ìàññ ñèñòåìû "êîðïóñ – òîïëè-
âî – ãàçû". Êàê íàïðàâëåí âåêòîð óñêîðåíèÿ ñâîáîäíîãî ïàäåíèÿ ïðèìåíè-
òåëüíî ê ýëëèïñîèäàëüíîé ìîäåëè Çåìëè íà ýêâàòîðå è íà ïîëþñå? Êàê èç-
ìåíÿåòñÿ óñêîðåíèå ñèëû òÿãîòåíèÿ Çåìëè â öåíòðàëüíîì ãðàâèòàöèîííîì
ïîëå ïî ìåðå óäàëåíèÿ îò åãî öåíòðà? Íàïèøèòå âåêòîðíóþ ñóììó ñîñòàâ-
ëÿþùèõ ñèëû òÿæåñòè.
 ÷åì çàêëþ÷àåòñÿ âëèÿíèå âðàùåíèÿ Çåìëè íà ïîëåò ðàêåò è ñíàðÿäîâ?
Ïåðå÷èñëèòå íàçâàíèÿ ñëîåâ àòìîñôåðû ïðè èõ êëàññèôèêàöèè ïî õàðàêòå-
ðó ðàñïðåäåëåíèÿ òåìïåðàòóðû ñ âûñîòîé. Êàêèå "ñòàíäàðòíûå àòìîñôåðû"
âàì èçâåñòíû? Äàéòå îïðåäåëåíèå "âèðòóàëüíîé" òåìïåðàòóðû è ïîÿñíèòå
ñìûñë åå ââåäåíèÿ. ×òî ïîíèìàåòñÿ ïîä "ïîëíîé àýðîäèíàìè÷åñêîé ñèëîé"?
 ÷åì çàêëþ÷àåòñÿ ñìûñë ïðèâåäåíèÿ àýðîäèíàìè÷åñêèõ ñèë è ìîìåíòîâ ê
ýòàëîííûì ôóíêöèÿì ñîïðîòèâëåíèÿ?
3. Ñôîðìóëèðóéòå îñíîâíûå òåîðåìû äèíàìèêè òåë ïåðåìåííîé è ïî-
ñòîÿííîé ìàññ. Äàéòå îïðåäåëåíèå ïðèíöèïà çàòâåðäåâàíèÿ.
Íàçîâèòå îñíîâíûå ìàòåìàòè÷åñêèå ìîäåëè äâèæåíèÿ ËÀ. Êàêèå ñèëû è
ìîìåíòû íåîáõîäèìî ó÷èòûâàòü ïðè ñîñòàâëåíèè äèôôåðåíöèàëüíûõ óðàâ-
íåíèé ïðîñòðàíñòâåííîãî äâèæåíèÿ ðàêåò è ñíàðÿäîâ? Êàê âëèÿåò âðàùå-
íèå Çåìëè íà ïîëåò ãîëîâíîé ÷àñòè ðàêåòû äàëüíåãî äåéñòâèÿ ïðè ïóñêå ðà-
êåòû âäîëü ýêâàòîðà íà çàïàä è íà âîñòîê? Ñîñòàâüòå óðàâíåíèÿ äâèæåíèÿ
öåíòðà ìàññ ËÀ íà àêòèâíîì (ïàññèâíîì) ó÷àñòêå ïîëåòà â âåðòèêàëüíîé
ïëîñêîñòè, èñïîëüçóÿ òðàåêòîðíóþ è ñòàðòîâóþ ñèñòåìû êîîðäèíàò.
ÐÀÇÄÅË II
ÈÑÑËÅÄÎÂÀÍÈÅ ÌÀÒÅÌÀÒÈ×ÅÑÊÈÕ
ÌÎÄÅËÅÉ ÄÂÈÆÅÍÈß ËÅÒÀÒÅËÜÍÛÕ
ÀÏÏÀÐÀÒÎÂ È ÌÅÒÎÄÛ ÐÅØÅÍÈß ÇÀÄÀ×
ÂÍÅØÍÅÉ ÁÀËËÈÑÒÈÊÈ
Ãëàâà 4
ÓÑÒÎÉ×ÈÂÎÑÒÜ ÄÂÈÆÅÍÈß ÐÀÊÅÒ È ÑÍÀÐßÄÎÂ
Çàäà÷à îáåñïå÷åíèÿ óñòîé÷èâîñòè äâèæåíèÿ ñíàðÿäîâ ïðèîáðåëà îñîáóþ àê-
òóàëüíîñòü â íà÷àëå âòîðîé ïîëîâèíû XIX âåêà â ñâÿçè ñ íàñòóïëåíèåì íîâîãî
ýòàïà â ðàçâèòèè âíåøíåé áàëëèñòèêè, ñâÿçàííîãî ñ ïîÿâëåíèåì íàðåçíîé àð-
òèëëåðèè, âåäóùåé îãîíü ïðîäîëãîâàòûìè âðàùàþùèìèñÿ ñíàðÿäàìè.
Ïåðâûå ðåçóëüòàòû â òåîðèè óñòîé÷èâîñòè äâèæåíèÿ âðàùàþùèõñÿ ñíàðÿ-
äîâ áûëè ïîëó÷åíû Í.Â. Ìàèåâñêèì.
Äàëüíåéøåå ðàçâèòèå òåîðèÿ äâèæåíèÿ àðòèëëåðèéñêîãî ñíàðÿäà îòíîñè-
òåëüíî åãî öåíòðà ìàññ ïîëó÷èëà â òðóäàõ àêàäåìèêà À.Í. Êðûëîâà, ïðîôåñ-
ñîðîâ Ä.À. Âåíòöåëÿ, Á.Í . Îêóíåâà, ß.Ì . Øàïèðî è äð.
 1940 ã. ä. ò. í., ïðîôåññîðîì (ïîçäíåå àêàäåìèêîì) Â.Ñ . Ïóãà÷åâûì áûëà
îïóáëèêîâàíà ðàáîòà [98], îêàçàâøàÿ ñóùåñòâåííîå (åñëè íå îïðåäåëÿþùåå)
âëèÿíèå íà ïîñëåäóþùåå ðàçâèòèå ìåòîäîâ èññëåäîâàíèÿ óñòîé÷èâîñòè âðà-
ùàþùèõñÿ ñíàðÿäîâ.
Ïîÿâëåíèå è øèðîêîå ïðèìåíåíèå (âî âðåìÿ âòîðîé ìèðîâîé âîéíû) ðåàê-
òèâíûõ ñíàðÿäîâ ïîâëåêëî çà ñîáîé íåîáõîäèìîñòü ðàçðàáîòêè òåîðåòè÷åñêîãî
îáîñíîâàíèÿ ïðàêòè÷åñêèõ ñïîñîáîâ îáåñïå÷åíèÿ èõ óñòîé÷èâîñòè. Íà÷àëüíûé
ýòàï ýòèõ èññëåäîâàíèé îñóùåñòâëÿëñÿ ïîä ðóêîâîäñòâîì àêàäåìèêà Ñ.À . Õðè-
ñòèàíîâè÷à.
Îäíàêî íàèáîëåå îáùèå ïðèíöèïû âûáîðà ðåøåíèé, îòâå÷àþùèõ óñòîé÷è-
âûì ñîñòîÿíèÿì ËÀ êàê äèíàìè÷åñêîé ñèñòåìû, áûëè ñôîðìóëèðîâàíû âûäàþ-
ùèìñÿ ðóññêèì ìàòåìàòèêîì è ìåõàíèêîì Àëåêñàíäðîì Ìèõàéëîâè÷åì Ëÿïó-
íîâûì (1857–1918).
 òåîðèè äèíàìè÷åñêèõ ñèñòåì ïðè àíàëèçå âîçìîæíûõ äâèæåíèé èñïîëüçó-
þòñÿ è äðóãèå îïðåäåëåíèÿ è ìåòîäû èññëåäîâàíèÿ óñòîé÷èâîñòè, îòëè÷íûå îò
ïðåäëîæåííûõ À.Ì . Ëÿïóíîâûì. Íàïðèìåð, èçâåñòíû ïîäõîäû ê îöåíêå óñòîé-
÷èâîñòè ïî Ëàãðàíæó, Ëàïëàñó, Ïóàññîíó, Áèðêãîôó. Îäíàêî ïîíÿòèå óñòîé-
÷èâîñòè, ââåäåííîå À.Ì . Ëÿïóíîâûì, íàèëó÷øèì îáðàçîì îòâå÷àåò õàðàêòåðó
îáñóæäàåìûõ çàäà÷. Èìåííî ýòèì îáúÿñíÿåòñÿ ñîâðåìåííîå ãëóáîêîå ïðîíèêíî-
170
âåíèå èäåé è ìåòîäîâ À.Ì. Ëÿïóíîâà â ðàçäåë âíåøíåé áàëëèñòèêè, èçó÷àþùèé
óñòîé÷èâîñòü äâèæåíèÿ ðàêåò è ñíàðÿäîâ.
Ñëåäóåò, ïðàâäà, îòìåòèòü, ÷òî â îïðåäåëåíèè À.Ì . Ëÿïóíîâà óñòîé÷è-
âîñòü ðàññìàòðèâàåòñÿ íà áåñêîíå÷íîì ïðîìåæóòêå âðåìåíè. Âî ìíîãèõ æå
ïðèêëàäíûõ çàäà÷àõ áàëëèñòèêè òðåáóåòñÿ îáåñïå÷èòü óñòîé÷èâîñòü ëèøü íà
êîíå÷íîì èíòåðâàëå âðåìåíè.  ýòèõ ñëó÷àÿõ ââîäÿò â ðàññìîòðåíèå ïîíÿòèå
"òåõíè÷åñêîé óñòîé÷èâîñòè".
4.1 . ÎÁÙÈÅ ÏÎÍßÒÈß ÎÁ ÓÑÒÎÉ×ÈÂÎÑÒÈ ÄÂÈÆÅÍÈß
È ÑÒÀÁÈËÈÇÀÖÈÈ ÐÀÊÅÒ È ÑÍÀÐßÄÎÂ
4.1 .1. ÓÑÒÎÉ×ÈÂÎÑÒÜ ÒÐÀÅÊÒÎÐÈÉ ÐÀÊÅÒ È ÑÍÀÐßÄÎÂ
Ïðè èñïîëüçîâàíèè ìàòåìàòè÷åñêèõ ìîäåëåé, îïèñûâàþùèõ
ïîëåò ðàêåò è ñíàðÿäîâ, âîçíèêàåò âîïðîñ î âîçìîæíîñòè ðàñ-
ïðîñòðàíåíèÿ ìàòåìàòè÷åñêèõ ðåçóëüòàòîâ, ïîëó÷åííûõ äëÿ íåêî-
òîðîé ñõåìàòèçèðîâàííîé ìîäåëè, íà ðåàëüíûé ôèçè÷åñêèé ïðî-
öåññ. Ïðåäïîëîæèì, ÷òî ðåçóëüòàò âåñüìà ÷óâñòâèòåëåí ê ìàëåé-
øåìó èçìåíåíèþ ñòðóêòóðû ìîäåëè.  òàêîì ñëó÷àå ñêîëü
óãîäíî ìàëîå èçìåíåíèå ýòîé ñòðóêòóðû (íàïðèìåð, ïðàâûõ ÷àñ-
òåé äèôôåðåíöèàëüíûõ óðàâíåíèé äâèæåíèÿ) ïðèâîäèò ê ìîäåëè
ñ ñîâåðøåííî äðóãèìè ñâîéñòâàìè. Òàêèå ðåçóëüòàòû îïàñíî ðàñ-
ïðîñòðàíÿòü íà èññëåäóåìûé ïðîöåññ. Òàêèì îáðàçîì, âîçíèêàåò
âîïðîñ îá îïðåäåëåíèè òåõ ñâîéñòâ ìàòåìàòè÷åñêîé ìîäåëè ËÀ,
êîòîðûå ìàëî ÷óâñòâèòåëüíû ê íåáîëüøîìó èçìåíåíèþ ñòðóêòó-
ðû ìîäåëè è, ñëåäîâàòåëüíî, ìîãóò âîñïðèíèìàòüñÿ êàê ñâîéñòâà
ðåàëüíîãî ïðîöåññà.
Âûáîð òàêèõ ñâîéñòâ ìàòåìàòè÷åñêèõ ìîäåëåé ËÀ êàê äèíàìè÷å-
ñêèõ ñèñòåì ñâÿçàí ñ ïîíÿòèåì ãðóáîñòè, èëè ñòðóêòóðíîé óñòîé÷è-
âîñòè, ââåäåííûì À.À. Àíäðîíîâûì è Ë.Ñ. Ïîíòðÿãèíûì. Åùå ðàç
ïîä÷åðêíåì, ÷òî ýòî ïîíÿòèå õàðàêòåðèçóåò ìîäåëü äèíàìè÷åñêîé
ñèñòåìû, êîòîðàÿ ÿâëÿåòñÿ ñòðóêòóðíî óñòîé÷èâîé, åñëè ïðè ëþáîì
äîñòàòî÷íî ìàëîì èçìåíåíèè ìîäåëè ïîëó÷àåòñÿ ñèñòåìà, ýêâèâà-
ëåíòíàÿ èñõîäíîé, ò.å. åñëè îñòàþòñÿ íåèçìåííûìè êà÷åñòâåííûå
õàðàêòåðèñòèêè âîçìîæíûõ äâèæåíèé ñèñòåìû.
 îòëè÷èå îò ëèíåéíûõ ñèñòåì íåëèíåéíàÿ äèíàìè÷åñêàÿ ñèñòå-
ìà, îïèñûâàþùàÿ äâèæåíèå ËÀ, ìîæåò áûòü óñòîé÷èâîé ïðè îäíèõ
ðåæèìàõ ïîëåòà è íåóñòîé÷èâîé ïðè äðóãèõ. Äðóãèìè ñëîâàìè, îäíè
äâèæåíèÿ èëè ñîñòîÿíèÿ ðàâíîâåñèÿ ìîãóò áûòü óñòîé÷èâûìè, à
äðóãèå äâèæåíèÿ èëè ñîñòîÿíèÿ ðàâíîâåñèÿ òîé æå ñàìîé ñèñòå-
ìû – íåò . Ïîýòîìó íåëüçÿ ãîâîðèòü îá óñòîé÷èâîñòè èëè íåóñòîé÷è-
âîñòè ËÀ êàê íåëèíåéíîé ñèñòåìû âîîáùå, à ìîæíî ãîâîðèòü òîëü-
171
êî îá óñòîé÷èâîñòè èëè íåóñòîé÷èâîñòè ðàçëè÷íûõ ðåæèìîâ äâèæå-
íèÿ.  ñâÿçè ñ ýòèì ïîíÿòèå óñòîé÷èâîñòè îòíîñÿò íå ê ñèñòåìå, à ê
íåêîòîðîìó äâèæåíèþ ñèñòåìû, íàçûâàÿ åãî ïî òåðìèíîëîãèè
À.Ì. Ëÿïóíîâà íåâîçìóùåííûì.
 áàëëèñòèêå íåâîçìóùåííûì äâèæåíèåì íàçûâàþò äâèæåíèå, êî-
òîðîå ñîâåðøàëè áû ðàêåòà èëè ñíàðÿä â ñòàíäàðòíîé àòìîñôåðå
èëè â áåçâîçäóøíîì ïðîñòðàíñòâå ïðè äåéñòâèè íà íèõ çàðàíåå ïðå-
äóñìîòðåííûõ, ïîä÷èíÿþùèõñÿ îïðåäåëåííûì çàêîíîìåðíîñòÿì
ñèë. Ñîîòâåòñòâóþùàÿ íåâîçìóùåííîìó äâèæåíèþ òðàåêòîðèÿ íà-
çûâàåòñÿ íåâîçìóùåííîé èëè íîìèíàëüíîé.
Îäíàêî â ðåàëüíûõ óñëîâèÿõ äâèæåíèå ðàêåò è ñíàðÿäîâ ïðîèñ-
õîäèò ïðè äåéñòâèè äîïîëíèòåëüíûõ, ñëó÷àéíûõ ôàêòîðîâ, êîòîðûå
îáû÷íî ïðè ðàñ÷åòå íîìèíàëüíûõ òðàåêòîðèé íå ïðèíèìàþòñÿ âî
âíèìàíèå (ðàçáðîñ íà÷àëüíûõ óñëîâèé, îòêëîíåíèå òåìïåðàòóðû
âîçäóõà îò íîðìàëüíûõ óñëîâèé, âåòåð è åãî ïîðûâû, ïóëüñàöèÿ òÿãè
äâèãàòåëÿ, íåïðîãðàììíûå óïðàâëÿþùèå ñèëû è ò.ï.) . Äåéñòâèÿ
ýòèõ âîçìóùàþùèõ ôàêòîðîâ ïðèâîäÿò ê òîìó, ÷òî ðàêåòà è ñíàðÿä
áóäóò äâèãàòüñÿ íå ïî íîìèíàëüíîé òðàåêòîðèè, à îòêëîíÿÿñü îò íåå
áîëåå èëè ìåíåå çíà÷èòåëüíî â çàâèñèìîñòè îò âåëè÷èíû è íàïðàâ-
ëåíèÿ äåéñòâèÿ âîçìóùåíèÿ. Äâèæåíèå, îòðàæàþùåå äåéñòâèå âîç-
ìóùàþùèõ ôàêòîðîâ, íàçûâàþò âîçìóùåííûì äâèæåíèåì, à ñîîòâåò-
ñòâóþùóþ åìó òðàåêòîðèþ – âîçìóùåííîé òðàåêòîðèåé.
 ñîîòâåòñòâèè ñ èíòóèòèâíûìè ïðåäñòàâëåíèÿìè îá óñòîé÷èâî-
ñòè äâèæåíèå ËÀ ìîæåò áûòü íàçâàíî óñòîé÷èâûì, åñëè îíî îáëàäà-
åò ñâîéñòâîì âîçâðàùàòüñÿ ïîñëå ïðåêðàùåíèÿ äåéñòâèÿ âîçìóùàþ-
ùèõ ôàêòîðîâ ê íåâîçìóùåííîìó äâèæåíèþ. Îïðåäåëåíèå àñèìï-
òîòè÷åñêîé óñòîé÷èâîñòè äâèæåíèÿ ïî Ëÿïóíîâó ôîðìàëèçóåò òàêîå
ïðåäñòàâëåíèå. Åñëè ðå÷ü èäåò, íàïðèìåð, î äâèæåíèè öåíòðà ìàññ
íåóïðàâëÿåìîé ðàêåòû èëè ñíàðÿäà, òî îáåñïå÷èòü òàêîãî ðîäà óñ-
òîé÷èâîñòü, î÷åâèäíî, íå óäàåòñÿ. Êàêèìè áû íè áûëè âîçìóùåíèÿ,
óâîäÿùèå öåíòð ìàññ ðàêåòû îò íîìèíàëüíîé òðàåêòîðèè, îíè íå
ïîëó÷àþò ïðÿìîãî ïðîòèâîäåéñòâèÿ.
Ìîæíî ñ÷èòàòü, ÷òî äâèæåíèå ðàêåòû óñòîé÷èâî, åñëè ìàëûå
âîçìóùåíèÿ ïðèâîäÿò ê ìàëûì îòêëîíåíèÿì îò íîìèíàëüíîé òðà-
åêòîðèè. Åñëè îòêëîíåíèÿ îñòàþòñÿ ìàëûìè ïðè t →∞, òî òàêîå
ïðåäñòàâëåíèå îá óñòîé÷èâîñòè ìîæåò áûòü ôîðìàëèçîâàíî ñ ïîìî-
ùüþ îïðåäåëåíèÿ óñòîé÷èâîñòè ïî Ëÿïóíîâó.
Íà ïðàêòèêå ñ÷èòàþò, ÷òî äâèæåíèå ËÀ áóäåò óñòîé÷èâûì, êîãäà
îòêëîíåíèå ðåàëüíîé òðàåêòîðèè îò íîìèíàëüíîé íå ïðåâûøàåò äî-
ïóñòèìîãî ïðåäåëà çà âðåìÿ ïîëåòà. Òàêîé ïîäõîä ñâÿçàí ñ èñïîëü-
çîâàíèåì ïîíÿòèÿ òåõíè÷åñêîé óñòîé÷èâîñòè. Äåéñòâèòåëüíî, òàê
êàê âðåìÿ ïîëåòà ðàêåòû èëè ñíàðÿäà îãðàíè÷åíî, òî íåò íåîáõîäè-
ìîñòè òðåáîâàòü îáåñïå÷åíèÿ óñòîé÷èâîñòè åãî äâèæåíèÿ ïî Ëÿïó-
172
íîâó, ò.å. îãðàíè÷åííûõ îòêëîíåíèé íà áåñêîíå÷íîì èíòåðâàëå âðå-
ìåíè. Äîñòàòî÷íî, ÷òîáû çà âðåìÿ ïîëåòà îòêëîíåíèÿ áûëè ìåíüøå
ïðåäåëüíî äîïóñòèìûõ, ò.å. òðåáîâàíèå óñòîé÷èâîñòè ïî Ëÿïóíîâó â
ïðàêòè÷åñêèõ çàäà÷àõ ìîæåò îêàçàòüñÿ ÷ðåçìåðíî æåñòêèì.  òî æå
âðåìÿ äâèæåíèå, íåóñòîé÷èâîå ïî Ëÿïóíîâó, íà îãðàíè÷åííîì èí-
òåðâàëå âðåìåíè ìîæåò óäîâëåòâîðÿòü êðèòåðèþ òåõíè÷åñêîé óñòîé-
÷èâîñòè.
Ïðè èññëåäîâàíèè óñòîé÷èâîñòè äâèæåíèÿ ðàêåò è ñíàðÿäîâ
îáû÷íî ðàññìàòðèâàþò îòäåëüíî óñòîé÷èâîñòü äâèæåíèÿ öåíòðà
ìàññ è óñòîé÷èâîñòü âðàùàòåëüíîãî äâèæåíèÿ îòíîñèòåëüíî öåíòðà
ìàññ. Îáåñïå÷åíèå ïîñëåäíåé ÿâëÿåòñÿ íåîáõîäèìûì óñëîâèåì óñ-
òîé÷èâîñòè äâèæåíèÿ öåíòðà ìàññ è íåðàçðûâíî ñâÿçàíî ñ ïîíÿòèåì
óãëîâîé ñòàáèëèçàöèè ðàêåò è ñíàðÿäîâ.
4.1.2. ÑÏÎÑÎÁÛ ÑÒÀÁÈËÈÇÀÖÈÈ ÍÅÓÏÐÀÂËßÅÌÛÕ ÐÀÊÅÒ
È ÑÍÀÐßÄÎÂ
 ïðîöåññå ïîëåòà âåêòîð ñêîðîñòè ëåòàòåëüíîãî àïïàðàòà V(t)
ïîâîðà÷èâàåòñÿ, îòñëåæèâàÿ äâèæåíèå ïî òðàåêòîðèè.  ðåçóëüòàòå
óñòîé÷èâûå ðàêåòà è ñíàðÿä äîëæíû íåïðåðûâíî èçìåíÿòü ñâîå óã-
ëîâîå ïîëîæåíèå îòíîñèòåëüíî öåíòðà ìàññ, êàê ïîêàçàíî íà
ðèñ. 4.1 . Åñëè ïðîäîëüíàÿ îñü êîðïóñà ñíàðÿäà èëè íåîïåðåííîé ðà-
êåòû îòêëîíèòñÿ îò íàïðàâëåíèÿ äâèæåíèÿ õîòÿ áû íà íåçíà÷èòåëü-
íûé óãîë, òî âîçíèêíåò ðàâíîäåéñòâóþùàÿ àýðîäèíàìè÷åñêàÿ ñèëà
RA, äåéñòâóþùàÿ íà ðàêåòó èëè ñíàðÿä è ïðèëîæåííàÿ â öåíòðå äàâ-
ëåíèÿ (ÖÄ), êîòîðûé íàõîäèòñÿ ìåæäó ãîëîâíîé ÷àñòüþ ËÀ è åãî
öåíòðîì ìàññ (ðèñ. 4.2, à). Ýòî ïðèâåäåò ê ïîÿâëåíèþ îòíîñèòåëüíî
öåíòðà ìàññ îïðîêèäûâàþùåãî ìîìåíòà Ì, êîòîðûé ïðè äâèæåíèè
íåñòàáèëèçèðîâàííîé ðàêåòû ïî òðàåêòîðèè âûçîâåò åå áåñïîðÿäî÷-
íîå äâèæåíèå îòíîñèòåëüíî öåíòðà ìàññ è êàê ñëåäñòâèå çíà÷èòåëü-
173
Ðèñ. 4 .1. Ñõåìà ïîñëåäîâàòåëüíûõ ïîëîæåíèé îïåðåííîãî ñíàðÿäà íà òðàåêòîðèè
ïðè ïðàâèëüíîì ïîëåòå
íîå èñêàæåíèå òðàåêòîðèè. Òàêèì îáðàçîì, ïîëîæåíèå êîðïóñà ñíà-
ðÿäà, ïðè êîòîðîì åãî îñü ñîâïàäàåò ñ íàïðàâëåíèåì äâèæåíèÿ,
ìîæíî îõàðàêòåðèçîâàòü êàê ïîëîæåíèå íåóñòîé÷èâîãî ðàâíîâåñèÿ,
ïîñêîëüêó ìàëåéøåå îòêëîíåíèå îñè ñíàðÿäà îò íàïðàâëåíèÿ âåêòî-
ðà V âûçîâåò óâåëè÷åíèå ýòîãî îòêëîíåíèÿ. ×òîáû ïðåäîòâðàòèòü
ýòî ÿâëåíèå è îáåñïå÷èòü ïðàâèëüíîå ïîëîæåíèå ïðè ïîëåòå (ãîëîâ-
íîé ÷àñòüþ âïåðåä), ðàêåòó è ñíàðÿä íåîáõîäèìî ñòàáèëèçèðîâàòü.
Ïðèìåíèòåëüíî ê íåóïðàâëÿåìûì ðàêåòàì è ñíàðÿäàì ñóùåñòâó-
þò äâà îñíîâíûõ "ïàññèâíûõ" ìåòîäà ñòàáèëèçàöèè – ñòàáèëèçàöèÿ
âðàùåíèåì è ñòàáèëèçàöèÿ îïåðåíèåì.
Ñòàáèëèçàöèÿ ðàêåò è ñíàðÿäîâ îïåðåíèåì çàêëþ÷àåòñÿ â òîì, ÷òî
íà õâîñòîâîé ÷àñòè ïðîäîëãîâàòîãî êîðïóñà óêðåïëÿþòñÿ ðàçíîîá-
ðàçíûå ïî ñâîèì êîíñòðóêòèâíûì ôîðìàì è ðàçìåðàì ñòàáèëèçàòî-
ðû. Ïðè ñîîòâåòñòâóþùåì âûáîðå ðàçìåðîâ ñòàáèëèçàòîðîâ â ñëó÷àå
α≠0 ðàâíîäåéñòâóþùàÿ àýðîäèíàìè÷åñêàÿ ñèëà RA áóäåò äåéñòâî-
âàòü òàê, êàê ïîêàçàíî íà ðèñ. 4.2, á (äëÿ äâèæåíèÿ â âåðòèêàëüíîé
ïëîñêîñòè).
Î÷åâèäíî, ÷òî îáóñëîâëåííûé ñèëîé RÀ ìîìåíò Ì áóäåò ñòðå-
ìèòüñÿ óìåíüøèòü óãîë α è ïðèâåñòè êîðïóñ â òàêîå ïîëîæåíèå, ïðè
êîòîðîì îñü OX ñîâïàäåò ñ âåêòîðîì ñêîðîñòè V, à ñàì ìîìåíò Ì
ñòàíåò ðàâíûì íóëþ, ò.å . áóäåò îêàçûâàòü ñòàáèëèçèðóþùåå (èëè
âîññòàíàâëèâàþùåå) âîçäåéñòâèå. Ïîëîæåíèå êîðïóñà, êîòîðîå õà-
ðàêòåðèçóåòñÿ çíà÷åíèåì α = 0 è îòíîñèòåëüíî êîòîðîãî ìîìåíò Ì
ñòàáèëèçèðóåò êîðïóñ, áóäåò ÿâëÿòüñÿ ïîëîæåíèåì óñòîé÷èâîãî ðàâ-
íîâåñèÿ.
Åñëè óêàçàííîå ÿâëåíèå ðàññìàòðèâàòü òîëüêî â ñòàòèêå, òî äëÿ
ìîìåíòà Mz ìîæíî (ïðè ìàëûõ α) ïðèíÿòü çàâèñèìîñòü Mq
S
l
m
zz
=
α
α
(ñì. ãë . 1). Èñõîäÿ èç ýòîãî âûðàæåíèÿ íàõîäèì ïðèçíàê, îïðåäå-
ëÿþùèé õàðàêòåð äåéñòâèÿ Mz íà ðàêåòó èëè ñíàðÿä.
174
Ðèñ. 4 .2. Ñõåìà äåéñòâèÿ àýðîäèíàìè÷åñêîãî ìîìåíòà:
à – íà íåîïåðåííûé ñíàðÿä (ðàêåòó); á – íà îïåðåííûé ñíàðÿä
Äëÿ îïðîêèäûâàþùåãî ìîìåíòà, çíàê êîòîðîãî ñîâïàäàåò ñî çíà-
êîì óãëà α, èìååì mz
α
> 0; äëÿ ñòàáèëèçèðóþùåãî ìîìåíòà mz
α
<0.
Ïðîèçâîäíàÿ mz
α
ñâÿçàíà ñ êîýôôèöèåíòîì ïîäúåìíîé ñèëû ñîîò-
íîøåíèåì
mc
ll
l
zy
a
αα
≈
−
ö.ì
ö.ä
,
(4.1)
ãäå l – ïîëíàÿ äëèíà ðàêåòû; lö.ì è lö.ä
–
ñîîòâåòñòâåííî ðàññòîÿíèÿ îò
âåðøèíû ðàêåòû äî öåíòðà ìàññ è öåíòðà äàâëåíèÿ (ñì. ðèñ. 4.2, á).
Òàê êàê cya
α
> 0 òî, î÷åâèäíî, çíàê ïðîèçâîäíîé ñîâïàäàåò ñî çíà-
êîì ðàçíîñòè (lö.ì
–
lö.ä). Èñõîäÿ èç ýòîãî óñëîâèÿ ñòàòè÷åñêîé óñ-
òîé÷èâîñòè èëè íåóñòîé÷èâîñòè ðàêåòû (ñíàðÿäà) ìîæíî ñôîðìóëè-
ðîâàòü ñëåäóþùèì îáðàçîì:
lö.ì
–
lö.ä < 0 – ðàêåòà èëè ñíàðÿä ñòàòè÷åñêè óñòîé÷èâû;
lö.ì
–
lö.ä > 0 – ðàêåòà èëè ñíàðÿä íåóñòîé÷èâû;
lö.ì
–
lö.ä = 0 – ðàêåòà èëè ñíàðÿä íàõîäÿòñÿ â ñîñòîÿíèè áåçðàç-
ëè÷íîãî ðàâíîâåñèÿ.
Ïðè äâèæåíèè ñíàðÿäà ïî òðàåêòîðèè ñêîðîñòü åãî ïîëåòà è îðè-
åíòàöèÿ îòíîñèòåëüíî âåêòîðà ñêîðîñòè íåïðåðûâíî èçìåíÿþòñÿ,
÷òî ïðèâîäèò ê èçìåíåíèþ ïîëîæåíèÿ ÖÄ îòíîñèòåëüíî êîðïóñà.
Êðîìå òîãî, íà àêòèâíîì ó÷àñòêå òðàåêòîðèè âñëåäñòâèå ðàñõîäà òîï-
ëèâà ïðè ðàáîòå äâèãàòåëÿ öåíòð ìàññ ðàêåòû òàêæå ñìåùàåòñÿ îò-
íîñèòåëüíî ñâîåãî íà÷àëüíîãî ïîëîæåíèÿ. Ýòè ïðè÷èíû ìîãóò âû-
çâàòü ñóùåñòâåííîå èçìåíåíèå çíà÷åíèÿ lö.ì
–
lö.ä è, ñëåäîâàòåëüíî,
ïðîèçâîäíîé mz
α
, îïðåäåëÿþùåé ñòåïåíü óñòîé÷èâîñòè ðàêåòû. Îò-
ñþäà ñëåäóåò, ÷òî äëÿ îáåñïå÷åíèÿ óãëîâîé ñòàáèëèçàöèè ðàêåòû â
ïîëåòå íåîáõîäèìî, ÷òîáû ïî âñåé òðàåêòîðèè âûïîëíÿëîñü óñëîâèå
mz
α
< 0 è íåðàâåíñòâî ||| |
.
mm
zz
αα
≥ äîï
Èíûìè ñëîâàìè, ñòàáèëèçèðîâàííàÿ îïåðåíèåì ðàêåòà (èëè ñíà-
ðÿä) äîëæíà îáëàäàòü çàïàñîì "ñòàòè÷åñêîé" óñòîé÷èâîñòè. Çàïàñ
ñòàòè÷åñêîé óñòîé÷èâîñòè îáû÷íî õàðàêòåðèçóþò âûðàæåííîé â
ïðîöåíòàõ âåëè÷èíîé mz
cy
, êîòîðàÿ íàõîäèòñÿ èç ñîîòíîøåíèÿ
m
m
c
ll
l
cñ
z
c
z
y
y
a
==
−
=−
||( )%(
)%,
α
α
ö.ì
ö.ä
ö.ì
ö.ä
100
100
(4.2)
ãäå ñö.ä
–
êîýôôèöèåíò öåíòðà äàâëåíèÿ; ñö.ì
–
êîýôôèöèåíò öåíòðà
ìàññ.
Ïðèíÿòî ñ÷èòàòü, ÷òî íåóïðàâëÿåìûå îïåðåííûå ðàêåòû è ñíàðÿ-
äû ÿâëÿþòñÿ õîðîøî ñòàáèëèçèðîâàííûìè, åñëè îíè îáëàäàþò çàïà-
ñîì ñòàòè÷åñêîé óñòîé÷èâîñòè mz
cy
=10 15
K
%.
175
Èññëåäóåì õàðàêòåð äâèæåíèÿ (ïîëàãàÿ, ÷òî îíî ñîâåðøàåòñÿ
òîëüêî â ïëîñêîñòè ñòðåëüáû) íåóïðàâëÿåìîãî ñòàòè÷åñêè óñòîé÷è-
âîãî ñíàðÿäà îòíîñèòåëüíî åãî öåíòðà ìàññ. Äëÿ ïðîñòîòû ðàññìîò-
ðèì ó÷àñòîê òðàåêòîðèè, ïðè äâèæåíèè ïî êîòîðîìó ìîæíî ñ÷èòàòü
mz
α
= const, θ = const.  ýòîì ñëó÷àå áåç ó÷åòà äåìïôèðîâàíèÿ óðàâ-
íåíèå äâèæåíèÿ îòíîñèòåëüíî öåíòðà ìàññ çàïèøåòñÿ â âèäå
d
dt
2
2
2
0
α
ωα
+=
c
,
(4.3)
ãäå ω
α
α
c
2
==
M
I
Sql
I
m
z
zz
z
||–êîýôôèöèåíò, êîòîðûé ìîæåò áûòü
ðàññ÷èòàí çàðàíåå ïî èçâåñòíîé òðàåêòîðèè öåíòðà ìàññ îïåðåííîãî
ñíàðÿäà.
Ïîëàãàÿα=α0è••
αα
=
0 â ïðåäåëàõ íåáîëüøîãî ó÷àñòêà òðàåêòî-
ðèè äëÿ íà÷àëüíûõ óñëîâèé ïðè t0 = 0, ïîëó÷èì ðåøåíèå óðàâíåíèÿ
(4.3) â âèäå
ααω
α
ω
ω
=+
0
0
cos( )
•
sin( ).
c
c
c
tt
(4.4)
Ïóòåì íåñëîæíûõ ïðåîáðàçîâàíèé ýòî ðåøåíèå ìîæåò áûòü
ïðèâåäåíî ê áîëåå óäîáíîìó âèäó
ααωε
=+
m
t
sin(
),
c
(4.5)
ãäå ñäâèã ïî ôàçå îïðåäåëÿåòñÿ óðàâíåíèåì
ε
ωα
α
= arctg c0
0
•
.
(4.6)
Ðåøåíèå ïîêàçûâàåò, ÷òî ïðè ïðèíÿòûõ äîïóùåíèÿõ äâèæåíèå
ñòàòè÷åñêè óñòîé÷èâîãî îïåðåííîãî ñíàðÿäà îòíîñèòåëüíî öåíòðà
ìàññ ïðåäñòàâëÿåò ñîáîé ïëîñêèå ãàðìîíè÷åñêèå êîëåáàíèÿ, õàðàê-
òåðèçóþùèåñÿ àìïëèòóäîé
α
α
ω
α
m
=
⎛
⎝⎜⎞
⎠⎟+
•
0
2
0
2
ñ
(4.7)
è ïåðèîäîì Ò =2π/ωñ.
176
Ãðàôèêè èçìåíåíèÿ óãëà α ïî
âðåìåíè ïðèìåíèòåëüíî ê ïîëó-
÷åííîìó ðåøåíèþ ïðåäñòàâëåíû
íà ðèñ. 4.3.
 ðàññìîòðåííîì âûøå ñëó-
÷àå ïðè àíàëèçå êîëåáàòåëüíîãî
äâèæåíèÿ îïåðåííûõ ñòàòè÷åñêè
óñòîé÷èâûõ ðàêåò è ñíàðÿäîâ ìû
íå ó÷èòûâàëè äåìïôèðóþùèé
ìîìåíò Mäz. Ïðèðîäà ýòîãî ìî-
ìåíòà áûëà ðàññìîòðåíà â ãë. 1,
è çäåñü îòìåòèì òîëüêî, ÷òî äåé-
ñòâèå Mäz ïðèâîäèò ê çàòóõàíèþ
êîëåáàòåëüíîãî äâèæåíèÿ, îáó-
ñëîâëåííîãî íà÷àëüíûìè âîçìó-
ùåíèÿìè è ìîìåíòîì Mz. Õàðàê-
òåð èçìåíåíèÿ óãëà α ïðè ó÷åòå
äåìïôèðîâàíèÿ ïîêàçàí íà ðèñ. 4.3 (êðèâàÿ 2).
Òàêèì îáðàçîì, â ïëîòíûõ ñëîÿõ àòìîñôåðû îïåðåííûå ðàêåòû è
ñíàðÿäû äâèæóòñÿ ïî òðàåêòîðèè òàê, ÷òî èõ ïðîäîëüíàÿ îñü ïëàâíî
"ñëåäèò" çà âåêòîðîì V, ïîêà êàêèå-ëèáî âîçìóùåíèÿ âíîâü íå âîç-
áóäÿò êîëåáàíèé.
Ñòàáèëèçàöèÿ ñíàðÿäîâ âðàùåíèåì. Ïðè äâèæåíèè ïî òðàåêòîðèè
ñíàðÿäà, áûñòðî âðàùàþùåãîñÿ îòíîñèòåëüíî ñâîåé ïðîäîëüíîé
îñè, àýðîäèíàìè÷åñêèå ñèëû, ñîçäàâàÿ ìîìåíò, ñòðåìÿòñÿ îïðîêè-
íóòü ñíàðÿä, íî îí, êàê âîë÷îê, íå îïðîêèäûâàåòñÿ, à äâèæåòñÿ óñ-
òîé÷èâî. Ïðîäîëüíàÿ îñü ñíàðÿäà, "ñëåäÿ" çà êàñàòåëüíîé ê òðàåêòî-
ðèè, êîëåáëåòñÿ â ïðîöåññå äâèæåíèÿ îòíîñèòåëüíî äèíàìè÷åñêîé
îñè ðàâíîâåñèÿ. Àðòèëëåðèéñêèé ñíàðÿä ïîëó÷àåò âðàùåíèå â êàíà-
ëå ñòâîëà âñëåäñòâèå äâèæåíèÿ âûñòóïîâ âåäóùåãî ïîÿñêà ñíàðÿäà
ïî âèíòîîáðàçíûì íàðåçàì ñòâîëà. Ðàêåòû, ñòàáèëèçèðóþùèåñÿ
âðàùåíèåì, íàçûâàþòñÿ òóðáîðåàêòèâíûìè ñíàðÿäàìè (ÒÐÑ); îíè
âðàùàþòñÿ çà ñ÷åò èñòå÷åíèÿ ãàçîâ èç êîñî ðàñïîëîæåííûõ ñîïåë.
Óãëîâàÿ ñêîðîñòü àðòèëëåðèéñêîãî ñíàðÿäà èëè ÒÐÑ äîëæíà ðàñ-
ñ÷èòûâàòüñÿ òàê, ÷òîáû ïðè äâèæåíèè ïî òðàåêòîðèè åãî ïðîäîëü-
íàÿ îñü íåïðåðûâíî "ñëåäèëà" çà íàïðàâëåíèåì äâèæåíèÿ öåíòðà
ìàññ ñíàðÿäà, îòêëîíÿÿñü îò ïîñëåäíåãî â ïðåäåëàõ äîïóñòèìûõ óã-
ëîâ.
Êàê ïîêàçàëè ìíîãèå èññëåäîâàíèÿ, äâèæåíèå ñíàðÿäîâ è ðà-
êåò îòíîñèòåëüíî èõ öåíòðîâ ìàññ ìîæíî ðàññìàòðèâàòü îòäåëü-
íî îò ïîñòóïàòåëüíîãî äâèæåíèÿ ïî òðàåêòîðèè, ñ÷èòàÿ, ÷òî âñå
õàðàêòåðèñòèêè ïîñëåäíåãî ÿâëÿþòñÿ èçâåñòíûìè ôóíêöèÿìè
âðåìåíè V(t), θ(t), yg(t) è ò.ä. Ïðè ýòîì äëÿ èíæåíåðíûõ ðàñ÷åòîâ
177
Ðèñ. 4 .3 . Èçìåíåíèå ñî âðåìåíåì óãëà α:
1 – áåç ó÷åòà äåìïôèðîâàíèÿ; 2 – ñ ó÷å-
òîì äåìïôèðîâàíèÿ
óñòîé÷èâîñòè âðàùàþùåãîñÿ ñíàðÿäà äîñòàòî÷íî â ïåðâîì ïðè-
áëèæåíèè ó÷åñòü òîëüêî îïðîêèäûâàþùèé ìîìåíò Mz, êîòîðûé
ÿâëÿåòñÿ îñíîâíûì ôàêòîðîì, îïðåäåëÿþùèì õàðàêòåð âðàùà-
òåëüíîãî äâèæåíèÿ [37].
Ïåðâûå òåîðåòè÷åñêèå ðåçóëüòàòû ïî îöåíêå óñëîâèé óñòîé÷èâî-
ñòè óãëîâîãî äâèæåíèÿ áûñòðîâðàùàþùèõñÿ ñíàðÿäîâ áûëè ïîëó÷å-
íû Í. . Ìàèåâñêèì [82], êîòîðûé ïðèâåë ýòó çàäà÷ó ê èçâåñòíîìó â
òåîðåòè÷åñêîé ìåõàíèêå ñëó÷àþ Ëàãðàíæà–Ïóàññîíà äâèæåíèÿ
ñèììåòðè÷íîãî òÿæåëîãî òåëà ñ îäíîé çàêðåïëåííîé òî÷êîé, â ïðåä-
ïîëîæåíèè, ÷òî äëÿ ìàëûõ îòêëîíåíèé îñè ñíàðÿäà îò êàñàòåëüíîé
ê òðàåêòîðèè ñèëû ñîïðîòèâëåíèÿ âîçäóõà èãðàþò êàê áû ðîëü âåñà.
Ìàèåâñêèé, èñïîëüçóÿ ïðèáëèæåííûé àíàëèç, ïîëó÷èë óñëîâèå óñ-
òîé÷èâîñòè âðàùàòåëüíîãî äâèæåíèÿ ñíàðÿäà äëÿ íàñòèëüíûõ òðà-
åêòîðèé, êîòîðîå Í.Ã. ×åòàåâ íàçâàë íåîáõîäèìûì óñëîâèåì óñòîé-
÷èâîñòè è ñòðîãèé âûâîä êîòîðîãî áûë äàí À.Í. Êðûëîâûì [64].
Í.Ã. ×åòàåâ, ðàññìàòðèâàÿ äâèæåíèÿ ñíàðÿäà íà íà÷àëüíîì ó÷àñòêå
òðàåêòîðèè ïðè äåéñòâèè îïðîêèäûâàþùåãî ìîìåíòà, ñ ïîìîùüþ
ïðÿìîãî ìåòîäà Ëÿïóíîâà ïîêàçàë, ÷òî ïðè âûïîëíåíèè óñëîâèÿ
Ìàèåâñêîãî óãëîâîå äâèæåíèå ñíàðÿäà ñ íóëåâûì óãëîì íóòàöèè óñ-
òîé÷èâî ïî Ëÿïóíîâó [127]. Â.Ñ. Ïóãà÷åâ, èñïîëüçóÿ ïåðâûé ìåòîä
Ëÿïóíîâà, óñòàíîâèë, ÷òî ïðè ïîëíîé ñèñòåìå ñèë, äåéñòâóþùèõ íà
àðòèëëåðèéñêèé ñíàðÿä, äâèæåíèå, ñîîòâåòñòâóþùåå èäåàëüíî ïðà-
âèëüíîìó ïîëåòó, íåóñòîé÷èâî ïî Ëÿïóíîâó [98].
Ýòè êëàññè÷åñêèå â áàëëèñòèêå ðåçóëüòàòû ïðèâîäÿòñÿ íèæå (ñì.
ïîäðàçä. 4 .3).  êà÷åñòâå èñõîäíûõ óðàâíåíèé äâèæåíèÿ ñíàðÿäà
ïðèíÿòû óðàâíåíèÿ äâèæåíèÿ, çàïèñàííûå â ôîðìå Â.Ñ. Ïóãà÷åâà.
Äîñòàòî÷íûå óñëîâèÿ óñòîé÷èâîñòè äâèæåíèÿ àðòèëëåðèéñêîãî
ñíàðÿäà (ïî òåðìèíîëîãèè Í.Ã. ×åòàåâà), à òàêæå âëèÿíèå íà óñòîé-
÷èâîñòü ðàçëè÷íûõ ñèë, äåéñòâóþùèõ íà ñíàðÿä, ðàññìàòðèâàþòñÿ
ñàìîñòîÿòåëüíî â ãë. 8 .
4.2 . ÓÑÒÎÉ×ÈÂÎÑÒÜ ÄÂÈÆÅÍÈß ÏÎ ËßÏÓÍÎÂÓ
4.2.1. ÎÏÐÅÄÅËÅÍÈÅ ÓÑÒÎÉ×ÈÂÎÑÒÈ ÏÎ ËßÏÓÍÎÂÓ
Ïóñòü äâèæåíèå ËÀ îïèñûâàåòñÿ ñèñòåìîé îáûêíîâåííûõ äèô-
ôåðåíöèàëüíûõ óðàâíåíèé âèäà
•
(,,,);
....................
•
(,,
yYty y
yYt
y
n
nn
111
1
=
=
K
K,)
,
yn
(4.8)
178
ãäå y1,..., yn – ïåðåìåííûå, õàðàêòåðèçóþùèå ñîñòîÿíèå ñèñòåìû, â
íàøåì ñëó÷àå – õàðàêòåðèñòèêè äâèæåíèÿ ËÀ.
Íåêîòîðîå âïîëíå îïðåäåëåííîå äâèæåíèå, ïîäëåæàùåå èññëå-
äîâàíèþ íà óñòîé÷èâîñòü, íàçûâàåòñÿ íåâîçìóùåííûì äâèæåíèåì.
Ïóñòü åìó ñîîòâåòñòâóåò ÷àñòíîå ðåøåíèå óðàâíåíèÿ (4.8) y1 =
= ξ1(t); ...; yn = ξn(t), óäîâëåòâîðÿþùåå íà÷àëüíûì óñëîâèÿì (t = t0)
yyt
yyt
nnn
11
01
0
00
==
==
ξ
ξ
();
...............
().
(4.9)
Äðóãèå âîçìîæíûå ïðè òåõ æå ñèëàõ äâèæåíèÿ ñèñòåìû (4.8) yi = yi(t)
(i =1
,
... , n), ñ êîòîðûìè áóäåò ñðàâíèâàòüñÿ íåâîçìóùåííîå
äâèæåíèå, íàçûâàþò âîçìóùåííûìè. Èì îòâå÷àþò äâèæåíèÿ ñ
èçìåíåííûìè íà÷àëüíûìè óñëîâèÿìè:
yt yt
t
t
nn
n
11
01
0
0
=+
=+
=
ξε ξε
();; ()
.
K
ïðè
(4.10)
Âåëè÷èíû ε1,...,εn áóäåì íàçûâàòü âîçìóùåíèÿìè. Ðàçíîñòè
ïåðåìåííûõ, îòâå÷àþùèõ âîçìóùåííîìó è íåâîçìóùåííîìó
äâèæåíèþ, ðàâíû
xyt ti
n
iii
=−
=
()(),,,.
ξ
1K
(4.11)
Ïåðåìåííûå xi íàçûâàþò îòêëîíåíèÿìè èëè âàðèàöèÿìè âåëè÷èíû yi.
Åñëè âñå îòêëîíåíèÿ ðàâíû íóëþ (xi =0,i =1,..., n), òî âîçìóùåííîå
äâèæåíèå yi(t) áóäåò ñîâïàäàòü ñ íåâîçìóùåííûì ξi(t). Íà÷àëüíûå
çíà÷åíèÿ îòêëîíåíèé xi0 ïðåäñòàâëÿþò ñîáîé âîçìóùåíèÿ ñèñòåìû
xx
intt
iii
===
=
00
1
ε(,
,
)
.
K
ïðè
(4.12)
Äâèæåíèå, îïèñûâàåìîå ðåøåíèåì ξi(t), íàçûâàåòñÿ óñòîé÷èâûì ïî
Ëÿïóíîâó, åñëè ïðè âñÿêîì ïðîèçâîëüíî çàäàâàåìîì ÷èñëå À >0,êàê
áû ìàëî îíî íè áûëî, ìîæåò áûòü âûáðàíî òàêîå ïîëîæèòåëüíîå
÷èñëî Λ, ÷òî ïðè âñÿêèõ âîçìóùåíèÿõ xi0, óäîâëåòâîðÿþùèõ óñëîâèþ
xxx
x
ni
i
n
10
2
20
2
0
2
0
2
1
+++= ≤
=
∑
K
Λ,
(4.13)
è ïðè ëþáîì t ≥ t0 áóäåò âûïîëíÿòüñÿ íåðàâåíñòâî
xxxxA
ni
i
n
1
2
2
222
1
+++ =
<
=
∑
K
.
(4.14)
 ïðîòèâíîì ñëó÷àå äâèæåíèå íåóñòîé÷èâî.
179
Ñõåìà îïðåäåëåíèÿ óñòîé÷èâîñòè ïî Ëÿïóíîâó ïîêàçàíà íà
ðèñ. 4.4 . Âîçìóùåííîå ðåøåíèå yi(t), íà÷èíàþùååñÿ ïðè t = t0 âîê-
ðåñòíîñòè íåâîçìóùåííîãî ðåøåíèÿ, îïðåäåëÿåìîãî âåëè÷èíîé δ,
ïðè t →∞íå ïîêèäàåò îêðåñòíîñòü íåâîçìóùåííîãî ðåøåíèÿ ξi(t),
îïðåäåëÿåìîãî âåëè÷èíîé À. Ïðàêòè÷åñêè óñòîé÷èâîñòü äàííîãî
íåâîçìóùåííîãî äâèæåíèÿ îçíà÷àåò, ÷òî ïðè äîñòàòî÷íî ìàëûõ íà-
÷àëüíûõ âîçìóùåíèÿõ âîçìóùåííîå äâèæåíèå áóäåò ñêîëü óãîäíî
ìàëî îòëè÷àòüñÿ îò íåâîçìóùåííîãî.
Åñëè ïðè âûïîëíåíèè óñëîâèé (4.13) è (4.14) âûïîëíÿåòñÿ òàêæå
óñëîâèå
lim
(),
t
i
i
n
xt
→∞
=
=
∑2
1
0
(4.15)
òî íåâîçìóùåííîå äâèæåíèå ξi(t) íàçûâàåòñÿ àñèìïòîòè÷åñêè
óñòîé÷èâûì.
 ñîîòâåòñòâèè ñ îïðåäåëåíèåì äâèæåíèÿ, óñòîé÷èâîãî ïî Ëÿïó-
íîâó, äëÿ îöåíêè óñòîé÷èâîñòè íåîáõîäèìî âûÿñíèòü ïîâåäåíèå îò-
êëîíåíèé xi(t) ïðè t →∞. Ïîýòîìó ðåøåíèå âîïðîñà îá óñòîé÷èâîñòè
ïî Ëÿïóíîâó ïðèâîäèò ê èññëåäîâàíèþ äèôôåðåíöèàëüíûõ óðàâíå-
íèé (ìîäåëåé) âîçìóùåííîãî äâèæåíèÿ.
Èç (4.11) èìååì yi(t)=xi(t)+ξi(t); i =1,..., n. Ïîäñòàâèâ ýòè çíà-
÷åíèÿ â èñõîäíóþ ñèñòåìó (4.8), ïîëó÷èì
•
•
(,,,)
,
,,.
xY
t
x xin
iii
nn
+=
+
+=
ξξξ
11
1
KK
(4.16)
180
Ðèñ. 4 .4 . Îïðåäåëåíèå óñòîé÷èâîñòè äâèæåíèÿ ïî Ëÿïóíîâó
Ðàñêëàäûâàÿ ïðàâûå ÷àñòè ýòèõ óðàâíåíèé â ðÿäû Òåéëîðà ïî
ñòåïåíÿì xi, íàéäåì
•
•
(,,,)
xY
t
Y
x
x
Y
x
iii
n
ii
n
+=
+
⎛
⎝⎜⎞
⎠⎟ ++⎛
⎝⎜⎞
ξξξ∂
∂
∂
∂
1
10
1
KK
⎠⎟+
0
xX
ni
*
,
(4.17)
ãäåXi
*
–
ñîâîêóïíîñòü ÷ëåíîâ, çàâèñÿùèõ îò îòêëîíåíèé â ñòåïåíè
âûøå ïåðâîé; íèæíèé èíäåêñ 0 ïðè ÷àñòíûõ ïðîèçâîäíûõ îçíà÷àåò,
÷òî îíè âû÷èñëÿþòñÿ ïðè xi = 0, ò.å . ïðè íåâîçìóùåííûõ çíà÷åíèÿõ
àðãóìåíòîâ.
Òàê êàê â íåâîçìóùåííîì äâèæåíèè ôóíêöèè ξi(t) äîëæíû óäîâ-
ëåòâîðÿòü óðàâíåíèÿì (4.8), ò.å .
•
(,,,)
,
,,,
ξξξ
ii
n
Yt
i
n
==
1
1
KK
(4.18)
îêîí÷àòåëüíî ïîëó÷èì
•
(,,,),
xXtx x
ii
n
=
1K
(4.19)
ãäå Xi (t, x1,..., xn)= ∂
∂
∂
∂
Y
x
x
Y
x
xX
in
n
ni
10
1
0
⎛
⎝⎜⎞
⎠⎟ ++⎛
⎝⎜⎞
⎠⎟+
K
*
.
Óðàâíåíèÿ (4.19) íàçûâàþòñÿ äèôôåðåíöèàëüíûìè óðàâíåíèÿìè
âîçìóùåííîãî äâèæåíèÿ. Åñëè â ýòèõ óðàâíåíèÿõ îòáðîñèòü ÷ëåíû
Xi
*
, òî ïîëó÷àòñÿ óðàâíåíèÿ
•
;
............
x
Y
x
x
Y
x
x
n
n
1
1
10
1
1
0
=
⎛
⎝⎜⎞
⎠⎟ ++⎛
⎝⎜⎞
⎠⎟
∂
∂
∂
∂
K
................
•
x
Y
x
x
Y
x
n
nn
n
=
⎛
⎝⎜⎞
⎠⎟ ++⎛
⎝⎜⎞
⎠⎟
∂
∂
∂
∂
10
1K
0
xn,
(4.20)
íàçûâàåìûå óðàâíåíèÿìè ïåðâîãî ïðèáëèæåíèÿ.
Òàêèì îáðàçîì, àíàëèç óñòîé÷èâîñòè íåâîçìóùåííîãî äâèæåíèÿ
ξi(t), ñîîòâåòñòâóþùåãî ÷àñòíîìó ðåøåíèþ ñèñòåìû (4.8), ñâîäèòñÿ
ê àíàëèçó óñòîé÷èâîñòè íóëåâîãî ðåøåíèÿ (ïîëîæåíèÿ ðàâíîâåñèÿ)
óðàâíåíèé âîçìóùåííîãî äâèæåíèÿ (4.19), òàê êàê ïðè õ1 = õ2 = ...=
=xn = 0 âñå ôóíêöèè xi îáðàùàþòñÿ â íóëü:
Xt
i(,)
.
00
≡
(4.21)
181
Åñëè óðàâíåíèÿ âîçìóùåííîãî äâèæåíèÿ àâòîíîìíû, ò.å. ôóíêöèè Xi
ÿâíî îò âðåìåíè íå çàâèñÿò, òî áóäåì èìåòü
•
(,,)
.
xXx x
ii
n
=
1K
(4.22)
4.2 .2. ÏÅÐÂÛÉ ÌÅÒÎÄ ËßÏÓÍÎÂÀ.
ÓÑÒÎÉ×ÈÂÎÑÒÜ ÏÎ ÏÅÐÂÎÌÓ ÏÐÈÁËÈÆÅÍÈÞ
Ïåðâûì Ëÿïóíîâ íàçâàë òàêîé ìåòîä èññëåäîâàíèÿ, ïðè êîòîðîì
óäàåòñÿ ïîñòðîèòü ðåøåíèå çàäàííîé ñèñòåìû äèôôåðåíöèàëüíûõ
óðàâíåíèé âîçìóùåííîãî äâèæåíèÿ, ïîêàçûâàþùåå, óñòîé÷èâî íó-
ëåâîå ðåøåíèå èëè íåò.
Ïðè îïðåäåëåíèè óñòîé÷èâîñòè ïðåäïîëàãàåòñÿ, ÷òî âîçìóùàþ-
ùèõ ñèë íåò â òîì ñìûñëå, ÷òî âîçìóùåííûå äâèæåíèÿ ïðîèñõîäÿò
ïîä äåéñòâèåì òåõ æå âíåøíèõ ñèë, êîòîðûå ó÷èòûâàëèñü ïðè îïðå-
äåëåíèè íåâîçìóùåííîãî äâèæåíèÿ.
Çàäà÷à îá óñòîé÷èâîñòè ïðè âîçìóùàþùèõ ñèëàõ íå èìååò ñìûñ-
ëà, åñëè ýòè ñèëû íè÷åì íå îãðàíè÷åíû. Åñëè æå âîçìóùåíèÿ, äåé-
ñòâóþùèå íà ËÀ, ìåíÿþòñÿ îò ñëó÷àÿ ê ñëó÷àþ òàê ìàëî, ÷òî èõ èç-
ìåíåíèå íå âëèÿåò íà ëèíåéíûå ÷ëåíû â ôóíêöèÿõ Xi, òî âîçíèêàåò
ïðàêòè÷åñêè âàæíàÿ çàäà÷à îá óñòîé÷èâîñòè ïî ïåðâîìó ïðèáëèæå-
íèþ (ò.å. ïî óðàâíåíèÿì ïåðâîãî ïðèáëèæåíèÿ) íåçàâèñèìî îò ÷ëå-
íîâ âûøå ïåðâîãî ïîðÿäêà ()
.
*
X i Òî åñòü ñòàâèòñÿ âîïðîñ îá îïðåäå-
ëåíèè óñëîâèé, ïðè âûïîëíåíèè êîòîðûõ óðàâíåíèÿ ïåðâîãî ïðè-
áëèæåíèÿ äàþò ïðàâèëüíóþ îöåíêó óñòîé÷èâîñòè äâèæåíèÿ.
Îáîçíà÷èâ â óðàâíåíèÿõ ïåðâîãî ïðèáëèæåíèÿ (4.20)
∂
∂
∂
∂
Y
x
a
Y
x
ai
n
i
i
i
n
in
10
1
0
1
⎛
⎝⎜⎞
⎠⎟=
⎛
⎝⎜⎞
⎠⎟ ==
;;
,
,,,
KK
ìîæíî çàïèñàòü èõ â âèäå
•
;
...................
•
xa
xa
x
xa
xa
nn
nn
11
1
11
11
=+
+
=+
+
K
K
nnn
x.
(4.23)
Ðàññìîòðèì ñëó÷àé àâòîíîìíîé ñèñòåìû, êîãäà âñå êîýôôèöè-
åíòû óðàâíåíèé (4.23) – ïîñòîÿííûå ÷èñëà . ×àñòíîå ðåøåíèå ýòèõ
óðàâíåíèé ìîæåò áûòü íàéäåíî â ôîðìå
xA
exA
e
t
nn
t
11
==
λλ
;;
,
K
(4.24)
182
ãäå À1,..., An, λ – ïîñòîÿííûå ÷èñëà . Äèôôåðåíöèðóÿ (4.24), íàéäåì
ïðîèçâîäíûå
•
;;•
.
xAe xA
e
t
nn
t
11
==
λλ
λλ
K
(4.25)
Ïîäñòàâèâ (4.24) è (4.25) â óðàâíåíèÿ (4.23) è ñîêðàòèâ èõ íà îáùèé
ìíîæèòåëü e
λt
, ïîëó÷èì
()
;
()
aA
a
Aa
A
aAaA
aA
nn
nn
11
1
122
1
211
22
2
2
0
−++
+=
+−+
+=
λ
λ
K
K
0
11 22
;
...............................
(
aA aA
a
nn
n
++
+
K
nn
A
−=
λ).
0
(4.26)
Ýòà ñèñòåìà ëèíåéíûõ îäíîðîäíûõ àëãåáðàè÷åñêèõ óðàâíåíèé
îòíîñèòåëüíî ïîñòîÿííûõ À1,..., An äîëæíà èìåòü ðåøåíèå, îòëè÷-
íîå îò íóëÿ (èíà÷å âñå xi ≡ 0). Ïîýòîìó îïðåäåëèòåëü ýòîé ñèñòåìû
äîëæåí áûòü ðàâåí íóëþ:
aaa
aa
a
aaa
n
n
nn
n
n
11
12
1
21
22
2
12
0
−
−
−
=
λ
λ
λ
K
K
KK
K
K
K
.
(4.27)
Ïîëó÷åííîå óðàâíåíèå îòíîñèòåëüíî λ íàçûâàåòñÿ õàðàêòåðèñòè-
÷åñêèì. Õàðàêòåðèñòè÷åñêîå óðàâíåíèå ñîäåðæèò íåèçâåñòíîå ÷èñ-
ëî λ â ñòåïåíè n. Ñëåäîâàòåëüíî, îíî èìååò n êîðíåé: λ1, λ2,..., λn.
Åñëè ñðåäè êîðíåé õàðàêòåðèñòè÷åñêîãî óðàâíåíèÿ íåò ðàâíûõ ìåæ-
äó ñîáîé, òî âñåãäà ñóùåñòâóåò íåîñîáîå ëèíåéíîå ïðåîáðàçîâàíèå
za
xza
x
ii
n
i
n
nii
i
n
11
11
==
==
∑∑
;;
,
K
(4.28)
ãäå aji – ïîñòîÿííûå ÷èñëà, êîòîðîå ïðèâîäèò óðàâíåíèÿ ïåðâîãî
ïðèáëèæåíèÿ (4.23) ê âèäó
•
;
..........
•
.
zz
zz
nn
n
11
1
=
=
λ
λ
(4.29)
183
Ïåðåìåííûå z1,..., zn íàçûâàþòñÿ êàíîíè÷åñêèìè ïåðåìåííûìè. Òàê
êàê êîýôôèöèåíòû aji – ïîñòîÿííûå ÷èñëà, òî èç óñòîé÷èâîñòè
äâèæåíèÿ îòíîñèòåëüíî ïåðåìåííûõ xi ñëåäóåò óñòîé÷èâîñòü
äâèæåíèÿ îòíîñèòåëüíî ïåðåìåííûõ zi, è íàîáîðîò. Ïðè ñäåëàííûõ
âûøå ïðåäïîëîæåíèÿõ î êîðíÿõ λ óðàâíåíèÿ (4.29) èíòåãðèðóþòñÿ
íåçàâèñèìî äðóã îò äðóãà è èõ ðåøåíèå èìååò âèä
zz
ezz
e
t
nn
tn
11
0
0
1
==
λλ
;;
,
K
(4.30)
ãäå zi0 – çíà÷åíèå ïåðåìåííûõ ïðè t = 0.  îáùåì ñëó÷àå λk = νk + iμk.
Åñëè νk ≠ 0èμk ≠ 0, òî êîðåíü êîìïëåêñíûé; åñëè νk =0èμk ≠ 0–
÷èñòî ìíèìûé; åñëè μk = 0 – âåùåñòâåííûé; åñëè μk = νk =0–
íóëåâîé. Òîãäà
||| |||
.
()
ee
e
e
kk
kk
k
ti
t
t
i
t
λν
μν
μ
==
+
Òàê êàê ||
|
c
o
ss
i
n|,
et
i
t
it
kk
k
μ
μμ
=+=
1òî
||.
ee
kk
tt
λν
=
(4.31)
Èç ðàâåíñòâà (4.24) ñëåäóåò, ÷òî ïðè t →∞
||,
;
||,
;
||,
e
e
e
k
k
k
t
k
t
k
t
λ
λ
λ
ν
ν
ν
→<
==
→∞
00
10
åñëè
åñëè
åñëè k>0.
(4.32)
Òàêèì îáðàçîì,
äëÿ ëèíåéíîé
àâòîíîìíîé
ñèñòåìû,
õàðàêòåðèñòè÷åñêîå óðàâíåíèå êîòîðîé íå èìååò êðàòíûõ êîðíåé,
âîïðîñ îá óñòîé÷èâîñòè ðåøàåòñÿ â çàâèñèìîñòè îò çíàêà
âåùåñòâåííîé ÷àñòè âñåõ êîðíåé õàðàêòåðèñòè÷åñêîãî óðàâíåíèÿ.
À.Ì. Ëÿïóíîâ ñôîðìóëèðîâàë óñëîâèÿ, ïðè êîòîðûõ çàêëþ÷åíèå
îá óñòîé÷èâîñòè äâèæåíèÿ ìîæíî ñîñòàâèòü ïî óðàâíåíèÿì ïåðâîãî
ïðèáëèæåíèÿ, äîêàçàâ òåîðåìû îá óñòîé÷èâîñòè è íåóñòîé÷èâîñòè
ïî ïåðâîìó ïðèáëèæåíèþ:
åñëè âåùåñòâåííûå ÷àñòè âñåõ êîðíåé õàðàêòåðèñòè÷åñêîãî óðàâ-
íåíèÿ ïåðâîãî ïðèáëèæåíèÿ îòðèöàòåëüíû, òî íåâîçìóùåííîå äâè-
æåíèå àñèìïòîòè÷åñêè óñòîé÷èâî íåçàâèñèìî îò ÷ëåíîâ âûøå ïåð-
âîãî ïîðÿäêà ìàëîñòè;
åñëè ñðåäè êîðíåé õàðàêòåðèñòè÷åñêîãî óðàâíåíèÿ íàéäåòñÿ õîòÿ
áû îäèí ñ ïîëîæèòåëüíîé âåùåñòâåííîé ÷àñòüþ, òî íåâîçìóùåííîå
184
äâèæåíèå íåóñòîé÷èâî íåçàâèñèìî îò ÷ëåíîâ âûøå ïåðâîãî ïîðÿäêà
ìàëîñòè.
Ýòè äâå òåîðåìû îá óñòîé÷èâîñòè ïî ïåðâîìó ïðèáëèæåíèþ ðå-
øàþò çàäà÷ó â äâóõ ñëó÷àÿõ – êîãäà âåùåñòâåííûå ÷àñòè âñåõ êîðíåé
õàðàêòåðèñòè÷åñêîãî óðàâíåíèÿ îòðèöàòåëüíû è êîãäà âåùåñòâåí-
íàÿ ÷àñòü õîòÿ áû îäíîãî êîðíÿ ïîëîæèòåëüíà.  äðóãèõ ñëó÷àÿõ
(îíè íàçûâàþòñÿ îñîáûìè èëè êðèòè÷åñêèìè), íàïðèìåð êîãäà âå-
ùåñòâåííûå ÷àñòè íåêîòîðûõ êîðíåé ðàâíû íóëþ, äëÿ îöåíêè óñ-
òîé÷èâîñòè äâèæåíèÿ îäíèõ óðàâíåíèé ïåðâîãî ïðèáëèæåíèÿ íå-
äîñòàòî÷íî. Âîçíèêàåò íåîáõîäèìîñòü â ó÷åòå âëèÿíèÿ íåëèíåéíûõ
÷ëåíîâ.
4.2.3. ÂÒÎÐÎÉ ÌÅÒÎÄ ËßÏÓÍÎÂÀ
Âòîðîé ìåòîä Ëÿïóíîâà ÿâëÿåòñÿ îäíèì èç íàèáîëåå ýôôåêòèâ-
íûõ ìåòîäîâ èññëåäîâàíèÿ óñòîé÷èâîñòè. Îí îñíîâàí íà ïðèìåíå-
íèè ôóíêöèé Ëÿïóíîâà, îïðåäåëÿåìûõ äëÿ èññëåäóåìîé ñèñòåìû
óðàâíåíèé âîçìóùåííîãî äâèæåíèÿ, è íå ïðåäïîëàãàåò íåîáõîäè-
ìîñòè íàõîæäåíèÿ îáùåãî ðåøåíèÿ ýòèõ óðàâíåíèé. Äàííîå îáñòîÿ-
òåëüñòâî äàëî Í.Ã. ×åòàåâó îñíîâàíèå íàçâàòü åãî ïðÿìûì ìåòîäîì.
Åãî òàêæå íàçûâàþò ìåòîäîì ôóíêöèé Ëÿïóíîâà, ïî ñâîéñòâàì êî-
òîðûõ ñóäÿò îá óñòîé÷èâîñòè èëè íåóñòîé÷èâîñòè âîçìóùåííîãî
äâèæåíèÿ.
Ñâîéñòâà ôóíêöèé Ëÿïóíîâà. Ôóíêöèÿ V(t, x1,..., xn)=V(t, x), ãäå
x – âåêòîð-ñòðîêà ñ ñîñòàâëÿþùèìè x1, ..., xn, áóäåò íàçûâàòüñÿ
ôóíêöèåé Ëÿïóíîâà, åñëè îíà óäîâëåòâîðÿåò äâóì îáùèì òðåáîâà-
íèÿì:
îíà äîëæíà ÿâëÿòüñÿ âåùåñòâåííîé, îäíîçíà÷íîé è íåïðåðûâíîé
ôóíêöèåé â îáëàñòè
tt xA
i
i
n
≥≤
=
∑
0
2
1
,,
(4.33)
ãäå À – íå ðàâíàÿ íóëþ âåëè÷èíà, è èìåòü â ýòîé îáëàñòè
íåïðåðûâíûå ÷àñòíûå ïðîèçâîäíûå ïåðâîãî ïîðÿäêà ïî âñåì
ïåðåìåííûì;
ïðè âñÿêîì t ≥ t0 çíà÷åíèå ôóíêöèè â íà÷àëå êîîðäèíàò äîëæíî
îáðàùàòüñÿ â íóëü:
Vt
(,, ,)
.
000
K
=
(4.34)
Ïðè ýòîì îáëàñòü ïåðåìåííûõ t è õi íàçûâàþò îáëàñòüþ At,à
ìíîæåñòâî òî÷åê (x1,..., xn), óäîâëåòâîðÿþùèõ óñëîâèþ
185
xA
i
i
n
2
1
≤
=
∑,
íàçûâàþò îáëàñòüþ À èëè ìíîæåñòâîì, îãðàíè÷åííûì ñôåðîé À,
óðàâíåíèå êîòîðîé èìååò âèä
xA
i
i
n
2
1
=
=
∑.
Åñëè â îáëàñòè At ôóíêöèÿ V êðîìå íóëåâîãî ìîæåò ïðèíèìàòü
çíà÷åíèÿ òîëüêî îäíîãî çíàêà, òî îíà íàçûâàåòñÿ çíàêîïîñòîÿííîé
(ïîëîæèòåëüíîé èëè îòðèöàòåëüíîé). Åñëè æå çíàêîïîñòîÿííàÿ
ôóíêöèÿ îáðàùàåòñÿ â íóëü òîëüêî â òîì ñëó÷àå, êîãäà âñå õ1, õ2, ...,
xn ðàâíû íóëþ (ò.å . â åäèíñòâåííîé òî÷êå ôàçîâîãî ïðîñòðàíñòâà
âîçìóùåííîé ñèñòåìû – â íà÷àëå êîîðäèíàò), òî ôóíêöèÿ V íàçûâà-
åòñÿ çíàêîîïðåäåëåííîé (ñîîòâåòñòâåííî îïðåäåëåííî-ïîëîæèòåëü-
íîé èëè îïðåäåëåííî-îòðèöàòåëüíîé).
Ôóíêöèè, ïðèíèìàþùèå è ïîëîæèòåëüíûå è îòðèöàòåëüíûå
çíà÷åíèÿ, íàçûâàþòñÿ çíàêîïåðåìåííûìè ôóíêöèÿìè.
Ââåäåííûå òàêèì îáðàçîì ôóíêöèè V íàçûâàþòñÿ ôóíêöèÿìè
Ëÿïóíîâà.
Èç óêàçàííûõ îïðåäåëåíèé ñëåäóåò, ÷òî çíàêîîïðåäåëåííàÿ
ôóíêöèÿ èìååò ïðè õ1 = ... = xn = 0 ýêñòðåìóì: â ñëó÷àå îïðåäåëåí-
íî-ïîëîæèòåëüíîé ôóíêöèè – ìèíèìóì, â ñëó÷àå îïðåäåëåííî-îò -
ðèöàòåëüíîé – ìàêñèìóì.
Ïóñòü ôóíêöèÿ V = V(x) íåïðåðûâíà âìåñòå ñî ñâîèìè ïðîèçâîä-
íûìè è ÿâëÿåòñÿ çíàêîîïðåäåëåííîé. Òîãäà ïðè õ1 = õ2 = ... = xn =0
îíà áóäåò èìåòü èçîëèðîâàííûé ýêñòðåìóì, à çíà÷èò, âñå ÷àñòíûå
ïðîèçâîäíûå ïåðâîãî ïîðÿäêà, âû÷èñëåííûå â ýòîé òî÷êå, áóäóò
ðàâíû íóëþ (íåîáõîäèìîå óñëîâèå ñóùåñòâîâàíèÿ ýêñòðåìóìà):
∂
∂
V
x
in
i
⎛
⎝⎜⎞
⎠⎟ ==
01
,,
,
.
K
(4.35)
Ðàçëîæèì ôóíêöèþ V â ðÿä Ìàêëîðåíà ïî ñòåïåíÿì x1,..., xn:
VV
V
x
x
V
xx
xx
i
i
ji
ji
i
=+
⎛
⎝⎜⎞
⎠⎟+
⎛
⎝⎜⎞
⎠⎟+
=
()
.
0
1
2
0
2
0
1
∂
∂
∂
∂∂
K
n
j
n
i
n
∑
∑
∑
=
=
1
1
(4.36)
Ñ ó÷åòîì âûðàæåíèé (4.34) è (4.35) ïîëó÷èì
Vc
x
x
jiji
i
n
j
n
=+
=
=
∑
∑1
21
1
K.
(4.37)
186
Ïîñòîÿííûå êîýôôèöèåíòû cji = cij îïðåäåëÿþòñÿ ðàâåíñòâàìè
c
V
xx
ij
n
ji
ji
=
⎛
⎝⎜⎞
⎠⎟
=
∂
∂∂
2
0
12
,,
,, ,.
K
(4.38)
Èç (4.37) âèäíî, ÷òî ðàçëîæåíèå çíàêîîïðåäåëåííîé ôóíêöèè V â ðÿä
ïî ñòåïåíÿì x1,..., xn íå ñîäåðæèò ÷ëåíîâ ïåðâîé ñòåïåíè. Åñëè
êâàäðàòè÷íàÿ ôîðìà
1
21
1
cxx
jiji
i
n
j
n
=
=
∑
∑
(4.39)
ïðèíèìàåò ïîëîæèòåëüíûå çíà÷åíèÿ è â íóëü îáðàùàåòñÿ òîëüêî ïðè
õ1 = õ2 = ... = xn = 0, òî íåçàâèñèìî îò ÷ëåíîâ âûñøåãî ïîðÿäêà ïðè
äîñòàòî÷íî ìàëûõ ïî ìîäóëþ xi ôóíêöèÿ V òàêæå áóäåò ïðèíèìàòü
ïîëîæèòåëüíûå çíà÷åíèÿ è â íóëü áóäåò îáðàùàòüñÿ òîëüêî ïðè
x1 = ... = xn = 0. Òàêèì îáðàçîì, åñëè êâàäðàòè÷íàÿ ôîðìà (4.39)
îïðåäåëåííî-ïîëîæèòåëüíà, òî ôóíêöèÿ V áóäåò îïðåäåëåí-
íî-ïîëîæèòåëüíîé.
Êðèòåðèé Ñèëüâåñòðà. Ðàññìîòðèì ìàòðèöó êîýôôèöèåíòîâ êâàä-
ðàòè÷íîé ôîðìû (4.39)
Ñ=
ññ
ñ
ññ
ñ
cc
c
n
n
nn
11
12
1
21
22
2
12
K
K
K
....................
nn
(4.40)
è ñîñòàâèì èç íåå n ãëàâíûõ äèàãîíàëüíûõ ìèíîðîâ
∆∆
∆
11
12
11
12
21
22
11
1
==
=
c
cc
cc
cc
c
n
n
;
;;
..............
K
K
nn
n
c
1K
.
(4.41)
 ëèíåéíîé àëãåáðå äîêàçûâàåòñÿ êðèòåðèé Ñèëüâåñòðà [27]: äëÿ òîãî
÷òîáû êâàäðàòè÷íàÿ ôîðìà áûëà îïðåäåëåííî-ïîëîæèòåëüíîé,
íåîáõîäèìî è äîñòàòî÷íî, ÷òîáû âñå ãëàâíûå äèàãîíàëüíûå ìèíîðû
∆1, ∆2,..., ∆n ìàòðèöû åå êîýôôèöèåíòîâ áûëè ïîëîæèòåëüíû, ò.å .
∆∆
∆
12
00
0
>>
>
;;
;.
K
n
(4.42)
187
Òàêèì îáðàçîì, êðèòåðèé Ñèëüâåñòðà (4.42) äëÿ êâàäðàòè÷íîé ÷àñòè
(4.39) ôóíêöèè V ÿâëÿåòñÿ äîñòàòî÷íûì óñëîâèåì îïðåäåëåííî-
ïîëîæèòåëüíîñòè ñàìîé ôóíêöèè V (4.37).
Åñëè ôóíêöèÿ V îïðåäåëåííî-îòðèöàòåëüíà, òî (−V ) áóäåò îïðå-
äåëåííî-ïîëîæèòåëüíîé. Ïîýòîìó óñëîâèåì îïðåäåëåííî-îòðèöà-
òåëüíîé ôóíêöèè V ñëóæèò êðèòåðèé Ñèëüâåñòðà äëÿ ìàòðèöû (−Ñ):
∆∆∆
123
000
<><
,,,
,
K
(4.43)
ò.å. çíàêè îïðåäåëèòåëåé ∆i äîëæíû ÷åðåäîâàòüñÿ.
Îñíîâíûå òåîðåìû ïðÿìîãî ìåòîäà Ëÿïóíîâà. Îäíîâðåìåííî ñ
ôóíêöèåé V ðàññìîòðèì åå ïîëíóþ ïðîèçâîäíóþ ïî âðåìåíè t, âçÿ-
òóþ â ïðåäïîëîæåíèè, ÷òî ïåðåìåííûå xi (i =1,..., n) óäîâëåòâîðÿþò
äèôôåðåíöèàëüíûì óðàâíåíèÿì âîçìóùåííîãî äâèæåíèÿ (4.22).
Èìååì
•
••
•
.
V
dV
dt
V
x
x
V
x
x
V
x
x
n
n
=
=++
+
∂
∂
∂
∂
∂
∂
1
1
2
2K
(4.44)
Ïîäñòàâëÿÿ â (4.44) âìåñòî •x i ïðàâûå ÷àñòè óðàâíåíèé âîçìóùåí-
íîãî äâèæåíèÿ (4.22), ïîëó÷èì
•
.
V
V
x
X
V
x
X
V
x
X
n
n
=++
+
∂
∂
∂
∂
∂
∂
1
1
2
2K
(4.45)
Çíàíèå ïðîèçâîäíîé
•
V ïîçâîëÿåò íàãëÿäíî ïðîñëåäèòü çà äâèæåíèåì
èçîáðàæàþùåé òî÷êè â ôàçîâîì ïðîñòðàíñòâå âîçìóùåííîé ñèñòåìû
(4.22).
Äëÿ ëþáîé îïðåäåëåííî-ïîëîæèòåëüíîé ôóíêöèè V óðàâíåíèå
Vxxc
n
(,,)
1K
=
èçîáðàæàåò îäíîïàðàìåòðè÷åñêîå ñåìåéñòâî çàìêíóòûõ ïîâåðõíî-
ñòåé â ôàçîâîì ïðîñòðàíñòâå âîçìóùåííîé ñèñòåìû. Ïðè ýòîì
âáëèçè íà÷àëà êîîðäèíàò çíà÷åíèþ ñ1, ìåíüøåìó ñ, ñîîòâåòñòâóåò
ïîâåðõíîñòü, öåëèêîì ëåæàùàÿ âíóòðè îáëàñòè, îãðàíè÷åííîé
ïîâåðõíîñòüþ, ñîîòâåòñòâóþùåé áîëüøåìó çíà÷åíèþ ïàðàìåòðà. Ïðè
ñ → 0 ïîâåðõíîñòü ñòÿãèâàåòñÿ â òî÷êó – íà÷àëî êîîðäèíàò.
Èç ãåîìåòðè÷åñêèõ ñîîáðàæåíèé ÿñíî, ÷òî åñëè ïðè äâèæåíèè
ñèñòåìû èçîáðàæàþùàÿ òî÷êà â ôàçîâîì ïðîñòðàíñòâå â îêðåñòíî-
ñòè íà÷àëà êîîðäèíàò ìîæåò äâèãàòüñÿ òîëüêî âîâíóòðü ëþáîé ïî-
âåðõíîñòè V(x1,..., xn)=c èëè ïî íåé è íå ìîæåò âûõîäèòü èç îãðàíè-
188
÷åííîé ýòîé ïîâåðõíîñòüþ îáëàñòè íàðóæó, òî ñèñòåìà óñòîé÷èâà
(ðèñ. 4.5, à). Åñëè æå èçîáðàæàþùàÿ òî÷êà ìîæåò äâèãàòüñÿ òîëüêî
âîâíóòðü ëþáîé ïîâåðõíîñòè V(x1, x2,..., xn)=c (ñì. ðèñ. 4.5, á), òî
ñèñòåìà àñèìïòîòè÷åñêè óñòîé÷èâà.
Åñëè èçîáðàæàþùàÿ òî÷êà äâèæåòñÿ âîâíóòðü ïîâåðõíîñòè
V(x1,..., xn)=c, òî îïðåäåëåííî-ïîëîæèòåëüíàÿ ôóíêöèÿ V(x1,..., xn)
óáûâàåò ïðè äâèæåíèè ñèñòåìû è, ñëåäîâàòåëüíî, åå ïîëíàÿ ïðîèç-
âîäíàÿ ïî âðåìåíè îòðèöàòåëüíà. Åñëè èçîáðàæàþùàÿ òî÷êà äâè-
æåòñÿ ïî ïîâåðõíîñòè V(x1,..., xn)=c, òî ïîëíàÿ ïðîèçâîäíàÿ ôóíê-
öèè V ïî âðåìåíè ðàâíà íóëþ.
Òàêèì îáðàçîì, ïîëíàÿ ïðîèçâîäíàÿ ôóíêöèè V(x1,..., xn) ïîñòî-
ÿííî-îòðèöàòåëüíà, åñëè èçîáðàæàþùàÿ òî÷êà ìîæåò äâèãàòüñÿ
òîëüêî âîâíóòðü ëþáîé ïîâåðõíîñòè V = c èëè ïî íåé, è îïðåäåëåí-
íî-îòðèöàòåëüíà, åñëè èçîáðàæàþùàÿ òî÷êà ìîæåò äâèãàòüñÿ òîëüêî
âíóòðü ïîâåðõíîñòè V = c .
Ïðèâåäåííûìè ãåîìåòðè÷åñêèìè ñîîáðàæåíèÿìè èëëþñòðèðó-
þòñÿ îñíîâíûå òåîðåìû Ëÿïóíîâà îá óñòîé÷èâîñòè è íåóñòîé÷èâî-
ñòè äâèæåíèÿ.
Òåîðåìà Ëÿïóíîâà îá óñòîé÷èâîñòè. Åñëè äëÿ äèôôåðåíöèàëüíûõ
óðàâíåíèé âîçìóùåííîãî äâèæåíèÿ ìîæíî íàéòè çíàêîîïðåäåëåí-
íóþ ôóíêöèþ V, ïðîèçâîäíàÿ
•
V êîòîðîé â ñèëó ýòèõ óðàâíåíèé
áûëà áû çíàêîïîñòîÿííîé ôóíêöèåé ïðîòèâîïîëîæíîãî ñ V çíàêà
èëè òîæäåñòâåííî ðàâíà íóëþ, òî íåâîçìóùåííîå äâèæåíèå óñòîé-
÷èâî.
Òåîðåìà Ëÿïóíîâà îá àñèìïòîòè÷åñêîé óñòîé÷èâîñòè. Åñëè äëÿ
äèôôåðåíöèàëüíûõ óðàâíåíèé âîçìóùåííîãî äâèæåíèÿ ìîæíî
íàéòè çíàêîîïðåäåëåííóþ ôóíêöèþ V, ïðîèçâîäíàÿ
•
V êîòîðîé â
189
Ðèñ. 4 .5. Òðàåêòîðèÿ äâèæåíèÿ èçîáðàæàþùåé òî÷êè â ôàçîâîì ïðîñòðàíñòâå:
à – óñòîé÷èâîé ñèñòåìû; á – àñèìïòîòè÷åñêè óñòîé÷èâîé ñèñòåìû
ñèëó ýòèõ óðàâíåíèé áûëà áû çíàêîîïðåäåëåííîé ôóíêöèåé ïðîòè-
âîïîëîæíîãî ñ V çíàêà, òî íåâîçìóùåííîå äâèæåíèå àñèìïòîòè÷å-
ñêè óñòîé÷èâî.
À.Ì. Ëÿïóíîâûì áûëè äîêàçàíû äâå òåîðåìû î íåóñòîé÷èâîñòè
äâèæåíèÿ. Í.Ã. ×åòàåâ îáîáùèë ýòè òåîðåìû è äîêàçàë òåîðåìó, èç
êîòîðîé êàê ÷àñòíûé ñëó÷àé âûòåêàþò òåîðåìû Ëÿïóíîâà.
Òåîðåìà ×åòàåâà î íåóñòîé÷èâîñòè äâèæåíèÿ. Åñëè äèôôåðåíöè-
àëüíûå óðàâíåíèÿ âîçìóùåííîãî äâèæåíèÿ ïîçâîëÿþò íàéòè ôóíê-
öèþ V, äëÿ êîòîðîé â ñêîëü óãîäíî ìàëîé îêðåñòíîñòè íóëÿ ñóùåñò-
âóåò îáëàñòü V > 0, è åñëè ïðîèçâîäíàÿ
•
V ôóíêöèè V, âû÷èñëåííàÿ â
ñèëó ýòèõ óðàâíåíèé, ïîëîæèòåëüíà âî âñåõ òî÷êàõ îáëàñòè V >0,òî
íåâîçìóùåííîå äâèæåíèå íåóñòîé÷èâî.
Çàìåòèì, ÷òî ïðÿìîé ìåòîä äàåò äîñòàòî÷íûå óñëîâèÿ óñòîé÷èâî-
ñòè, ò.å . íåâûïîëíåíèå ýòèõ óñëîâèé åùå íå îçíà÷àåò, ÷òî äâèæåíèå
ñèñòåìû íåóñòîé÷èâî.
Ïîñòðîåíèå ôóíêöèè Ëÿïóíîâà. Ïðàêòè÷åñêîå ïðèìåíåíèå ýòîãî
ìåòîäà ÷àñòî îñëîæíÿåòñÿ òðóäíîñòüþ íàõîæäåíèÿ ôóíêöèè Ëÿïó-
íîâà V(x1, ..., xn). Îáùèõ ðåêîìåíäàöèé ïîñòðîåíèÿ ôóíêöèè Ëÿïó-
íîâà äëÿ ïðîèçâîëüíûõ ñèñòåì íå ñóùåñòâóåò.
Âìåñòå ñ òåì äëÿ ìíîãèõ êëàññîâ çàäà÷ ðàçðàáîòàíû ðåãóëÿðíûå
ñïîñîáû ïîñòðîåíèÿ ôóíêöèé Ëÿïóíîâà. Îáçîð îñíîâíûõ ñïîñîáîâ
ïðèâåäåí â ðàáîòå [107]. Ðàññìîòðèì çäåñü ñïîñîá ïîñòðîåíèÿ ôóíê-
öèé Ëÿïóíîâà, èñïîëüçîâàâøèéñÿ ïðè ðåøåíèè áàëëèñòè÷åñêèõ çà-
äà÷, ïðåäëîæåííûé Í.Ã. ×åòàåâûì.
Äëÿ ñëó÷àåâ, êîãäà èçâåñòíû ïåðâûå èíòåãðàëû óðàâíåíèé âîçìó-
ùåííîãî äâèæåíèÿ, Í.Ã. ×åòàåâ ïðåäëîæèë ñïîñîá ïîñòðîåíèÿ
ôóíêöèè Ëÿïóíîâà â ôîðìå ñâÿçêè ïåðâûõ èíòåãðàëîâ.
Ïðåäïîëîæèì, ÷òî óðàâíåíèÿ âîçìóùåííîãî äâèæåíèÿ (4.22) äî-
ïóñêàþò ïåðâûé èíòåãðàë:
Fxx
h
n
(,,)
,
1K
==
const
(4.46)
äëÿ êîòîðîãî ðàçíîñòü F(x)–F(0) ÿâëÿåòñÿ îïðåäåëåííî-ïî-
ëîæèòåëüíîé ôóíêöèåé ïåðåìåííûõ x1,...,xn. Òîãäà â êà÷åñòâå
ôóíêöèè Ëÿïóíîâà ìîæíî âçÿòü ôóíêöèþ
VFxxF
n
=−
(,,) ()
.
1
0
K
(4.47)
Äåéñòâèòåëüíî, ïðîèçâîäíàÿ ôóíêöèè V ïî âðåìåíè â ñèëó
óðàâíåíèé âîçìóùåííîãî äâèæåíèÿ ñîãëàñíî (4.46) òîæäåñòâåííî
ðàâíà íóëþ, è, ñëåäîâàòåëüíî, ýòà ôóíêöèÿ áóäåò óäîâëåòâîðÿòü âñåì
óñëîâèÿì òåîðåìû Ëÿïóíîâà îá óñòîé÷èâîñòè äâèæåíèÿ.
190
 íåêîòîðûõ ñëó÷àÿõ óðàâíåíèÿ äâèæåíèÿ äîïóñêàþò íåñêîëüêî
ïåðâûõ èíòåãðàëîâ:
FxxhFxxh
nk
n
k
11
1
1
(,,) ;; (,,)
,
KK
K
==
(4.48)
ïðè÷åì íè îäèí èç íèõ íå ÿâëÿåòñÿ îïðåäåëåííî-ïîëîæèòåëüíîé
ôóíêöèåé.  îáùåì ñëó÷àå
VF
F
F
F
FF
kkk
k
=−+
+−+
+−+
+
λλ
μμ
111
11
2
1
2
00
0
[(
)
][(
)
]
[(
)
]
K
K
[(
)
]
,
FF
kk
22
0
−
(4.49)
ãäå λ1, ..., λk, μ1, ..., μk – íåîïðåäåëåííûå ïîñòîÿííûå. Åñëè ýòè
ïîñòîÿííûå óäàñòñÿ ïîäîáðàòü òàêèì îáðàçîì, ÷òî ôóíêöèÿ V áóäåò
îïðåäåëåííî-ïîëîæèòåëüíîé, òî îíà áóäåò óäîâëåòâîðÿòü âñåì
óñëîâèÿì òåîðåìû Ëÿïóíîâà îá óñòîé÷èâîñòè äâèæåíèÿ. Çàìåòèì,
÷òî îäèí èç 2k êîýôôèöèåíòîâ λi, μi ìîæíî âûáðàòü ïðîèçâîëüíî.
×àñòî ôóíêöèþ óäàåòñÿ ïîñòðîèòü ñ ïîìîùüþ ëèíåéíîé ñâÿçêè
èíòåãðàëîâ, ïîëàãàÿ μi =0.
4.3. ÓÑÒÎÉ×ÈÂÎÑÒÜ ÄÂÈÆÅÍÈß
ÁÛÑÒÐÎÂÐÀÙÀÞÙÅÃÎÑß ÑÍÀÐßÄÀ
4.3.1. ÏÅÐÂÛÅ ÈÍÒÅÃÐÀËÛ ÓÐÀÂÍÅÍÈÉ ÄÂÈÆÅÍÈß ÑÍÀÐßÄÀ
ÎÒÍÎÑÈÒÅËÜÍÎ ÖÅÍÒÐÀ ÌÀÑÑ
ÍÀ ÍÀ×ÀËÜÍÎÌ Ó×ÀÑÒÊÅ ÒÐÀÅÊÒÎÐÈÈ
Ðàññìîòðèì äâèæåíèå àðòèëëåðèéñêîãî ñíàðÿäà íà íà÷àëüíîì
ó÷àñòêå òðàåêòîðèè, ïðåíåáðåãàÿ åå êðèâèçíîé, ïðè äåéñòâèè òîëü-
êî îïðîêèäûâàþùåãî ìîìåíòà.
Óðàâíåíèÿ, îïèñûâàþùèå äâèæåíèå ñíàðÿäà îòíîñèòåëüíî öåí-
òðà ìàññ ïðè ýòèõ äîïóùåíèÿõ, ìîãóò áûòü ïîëó÷åíû èç îáùèõ óðàâ-
íåíèé äâèæåíèÿ ñíàðÿäà â ôîðìå Â.Ñ. Ïóãà÷åâà (3.157), åñëè â íèõ
ïîëîæèòü
fffff
2356
7
00
===== ==
;••
•
.
θθ
(4.50)
 ýòîì ñëó÷àå óðàâíåíèÿ 4...7 ñèñòåìû (3.157), îïèñûâàþùèå
äâèæåíèå ñíàðÿäà âîêðóã öåíòðà ìàññ, ìîãóò èíòåãðèðîâàòüñÿ è
191
èññëåäîâàòüñÿ íåçàâèñèìî îò óðàâíåíèé, îïèñûâàþùèõ äâèæåíèå
öåíòðà ìàññ. Òàêèì îáðàçîì, èç ñèñòåìû (3.157) áóäåì èìåòü [38]
zzzzaz
fz
zz zz
az fz
31 31
2
43
12 12
342
2
2
•
••
••
;
•
••
••
−+=
−
−+ =;
;
•
.
zzz
a
1
2
2
2
3
2
1
0
++=
=
(4.51)
Ñëîæèì ïåðâîå è âòîðîå óðàâíåíèÿ ñèñòåìû (4.51), ïðåäâàðèòåëüíî
óìíîæèâ èõ ñîîòâåòñòâåííî íà z2 è z3. Ïîëó÷èì
z
z
zz
z
za
z
zz
z
132 123
22 33
20
•••
•
(••
),
−+
+=
îòêóäà ñëåäóåò
zzzza
zz zz
z
32 23
22 33
1
20
•••
•
••
.
−+
+
=
(4.52)
Ïðîäèôôåðåíöèðîâàâ ïî âðåìåíè îáå ÷àñòè òðåòüåãî óðàâíåíèÿ
ñèñòåìû (4.51), ìîæåì ïîêàçàòü, ÷òî
zz zz
z
z
22 33
1
1
••
•
.
+
=−
(4.53)
Ñ ó÷åòîì (4.53) óðàâíåíèå (4.52) èìååò âèä
−+
+=
zzzzaz
32 23
1
20
•
••
••
.
(4.54)
Çàìåòèì, ÷òî óðàâíåíèå (4.54) ìîæåò áûòü çàïèñàíî â ôîðìå
d
dt
zzzzaz
(••).
−+
+=
32 23
1
20
(4.55)
Ñëåäîâàòåëüíî, âûðàæåíèå
−+
+==
zzzzaz
h
32 23
1
1
2
••
const
(4.56)
ïðåäñòàâëÿåò ñîáîé ïåðâûé èíòåãðàë ñèñòåìû (4.51).
Óìíîæàÿ òåïåðü ïåðâîå óðàâíåíèå ñèñòåìû (4.51) íà •
,
z3 à âòî-
ðîå–íà
•
z 2 è ñêëàäûâàÿ, ïîëó÷èì óðàâíåíèå
−+
++=+
•
•
(••
)(
••• •
•
•
)(••
zzz zz zzz zz
fzz z
22 33
133 22
4 33 2z2),
(4.57)
192
êîòîðîå ñ ó÷åòîì (4.53) ïðèìåò âèä
••••
•
••
•
••
.
zzzzzzfz
112233410
+++ =
(4.58)
Çàìåòèì, ÷òî ëåâàÿ ÷àñòü óðàâíåíèÿ (4.58) ïðåäñòàâëÿåò ñîáîé
ïðîèçâîäíóþ ïî âðåìåíè:
d
dt
zzz f
z
1
2
0
1
2
2
2
3
2
41
(•••).
+++
⎡
⎣⎢
⎤
⎦⎥=
(4.59)
Òàêèì îáðàçîì, âûðàæåíèå
1
21
2
2
2
3
2
41
2
(•••)
zzz f
z
h
+++==
const
åñòü âòîðîé ïåðâûé èíòåãðàë ñèñòåìû (4.51).
Òðåòüå óðàâíåíèå ïðåäñòàâëÿåò ñîáîé òðèâèàëüíûé ïåðâûé èíòå-
ãðàë, íàçûâàåìûé â äèíàìèêå òâåðäîãî òåëà èíòåãðàëîì êîñèíóñîâ
èëè ãåîìåòðè÷åñêèì ïåðâûì èíòåãðàëîì, òàê êàê îí âûðàæàåò ðà-
âåíñòâî åäèíèöå ñóììû êâàäðàòîâ íàïðàâëÿþùèõ êîñèíóñîâ (z1, z2,
z3), îïðåäåëÿþùèõ îðèåíòàöèþ ïðîäîëüíîé îñè ñíàðÿäà â òðàåêòîð-
íîé ñèñòåìå êîîðäèíàò.
 ðåçóëüòàòå îò ñèñòåìû (4.51) ìîæíî ïåðåéòè ê ñèñòåìå ÷åòûðåõ
ïåðâûõ èíòåãðàëîâ
−+
+=
−+
++=
zzzzazh
zzz f
zh
z
32 23
11
1
2
2
2
3
2
412
2
1
2
••
;
(•••);
1
2
2
2
3
2
03
1
++= ==
zz aah
;.
(4.60)
4.3 .2. ÍÅÎÁÕÎÄÈÌÎÅ ÓÑËÎÂÈÅ ÓÑÒÎÉ×ÈÂÎÑÒÈ ÓÃËÎÂÎÃÎ
ÄÂÈÆÅÍÈß ÀÐÒÈËËÅÐÈÉÑÊÎÃÎ ÑÍÀÐßÄÀ
 êà÷åñòâå íåâîçìóùåííîãî óãëîâîãî äâèæåíèÿ àðòèëëåðèéñêîãî
ñíàðÿäà, óñòîé÷èâîñòü êîòîðîãî õîòèì óñòàíîâèòü, ïðèìåì òàêîå
äâèæåíèå, ïðè êîòîðîì âåêòîð ñêîðîñòè öåíòðà ìàññ è åãî ïðîäîëü-
íàÿ îñü ñîâïàäàþò, ò.å .
δδ δδ
12120
() () •()
•
().
tttt
====
(4.61)
Îò óðàâíåíèé âðàùàòåëüíîãî äâèæåíèÿ â ïåðåìåííûõ zi (i =1,2,3)
ïåðåéäåì íåïîñðåäñòâåííî ê óðàâíåíèÿì â óãëàõ δ1 è δ2, îïðåäå-
193
ëÿþùèì îðèåíòàöèþ ïðîäîëüíîé îñè ñíàðÿäà â òðàåêòîðíîé ñèñòåìå
êîîðäèíàò [38]. Äëÿ ýòîãî óìíîæèì ïåðâîå óðàâíåíèå ñèñòåìû (4.51)
íà ()
,
13
2
−
z à âòîðîå – íà z2z3 è, ñêëàäûâàÿ èõ, ïîëó÷èì
z
zzzz
zz zzzz
a
32
2
3
2
113
2
3 1232
11
21
()
••
()
•
••
•
[(
−−
−
−
+
+
+−
zz zzz
fzz z
3
2
2 233
432
2
3
2
1
)••
]()
.
+=+
−
(4.62)
 ñîîòâåòñòâèè ñ (3.161) èìååì
zzz
12
1
22
2
31
===
cos cos ;
sin cos ;
sin .
δδ
δδ
δ
Äâàæäû äèôôåðåíöèðóÿ ýòè âûðàæåíèÿ ïî âðåìåíè, íàéäåì •z i è ••
zi
(i = 1, 2, 3). Ïîäñòàâèâ ñîîòâåòñòâóþùèå âûðàæåíèÿ äëÿ zi,
•
zi è••
ziâ
(4.62), ïîñëå íåñëîæíûõ ïðåîáðàçîâàíèé ïîëó÷èì
••
cos cos
•
sin cos cos
•
cos c
δδδδδ δδ
δδ
1
2
122
2
1
3
12
2
3
1
2
−+
+a
os
sin cos cos .
δ
δδδ
241
2
1
2
2
=−f
Ðàçäåëèâ îáå ÷àñòè ïîñëåäíåãî óðàâíåíèÿ íà (−cos
2
δ1 cosδ2), ìîæåì
ïðèâåñòè åãî ê âèäó
•••
sin cos
•
cos
sin cos .
δδδδ δδ δδ
12
2
11 21412
2
+−
=
af
(4.63)
Àíàëîãè÷íî ïîäñòàâëÿÿ zi,
•
,
zi
•
•
z i âî âòîðîå óðàâíåíèå ñèñòåìû (4.51),
ïîëó÷èì
•
•
cos
••
sin
sin .
δδδ
δδδ δ
212
11142
22
−+
=
af
(4.64)
Äëÿ íåâîçìóùåííîãî äâèæåíèÿ (4.61) óðàâíåíèÿìè âîçìóùåííîãî
äâèæåíèÿ ÿâëÿþòñÿ óðàâíåíèÿ (4.63) è (4.64), äëÿ êîòîðûõ
ñóùåñòâóþò, êàê áûëî ïîêàçàíî âûøå, ïåðâûå èíòåãðàëû h1 è h2.
Íàéäåì èõ âûðàæåíèÿ â ïåðåìåííûõ δ1 è δ2, ïîäñòàâëÿÿ â ïåðâûå äâà
óðàâíåíèÿ ñèñòåìû (4.60) çàâèñèìîñòè zi è •z i îò óãëîâ δ1 è δ2:
•
sin
•
sin cos cos
cos cos
;
(•
δδδδδδ
δδ
δ
122112
121
1
2
1
2
−+
=
ah
2
2
22
14122
++
=
•
cos )
cos cos
.
δδ δδ
fh
(4.65)
Äëÿ ðåøåíèÿ çàäà÷è îïðåäåëåíèÿ óñòîé÷èâîñòè íåâîçìóùåííîãî
äâèæåíèÿ (4.61) Í.à . ×åòàåâ èñïîëüçîâàë ïðÿìîé ìåòîä Ëÿïóíîâà è
194
ïîñòðîèë ôóíêöèþ Ëÿïóíîâà â âèäå ñâÿçêè ïåðâûõ èíòåãðàëîâ (4.65)
óðàâíåíèé âîçìóùåííîãî äâèæåíèÿ (4.63) è (4.64) (ñì. [127]).
Óìíîæèì ïåðâûé èíòåãðàë h1 íà (−2f4), à h2 –íà2à è ñëîæèì:
Wa
a
f
f
=⋅
+
+
−
−
1
2
22
2
1
2
2
2
1412
41
(••
cos )
cos cos
•
sin
δδδ
δδ
δδ
24
211 2
412 24
2
22
22
+−
−⋅
=
−
f
af
a
hf
•
sin cos cos
cos cos
δ δδδ
δδ
h1.
(4.66)
Ðàçëîæèì â ðÿä Òåéëîðà òðèãîíîìåòðè÷åñêèå ôóíêöèè, âõîäÿùèå â
(4.66):
sin
!
;cos
!
(,)
.
δδδ
δ
δ
ii
i
i
i
i
=−+
=
−
+=
32
3
1
2
12
KK
Óäåðæèâàÿ ÷ëåíû ðÿäà, èìåþùèå ïîðÿäîê δi è δ i
2
, ïîëó÷èì
cos
;
sin cos cos (
2
1
1
2
2
1
2
11 21
1
2
1
δ
δ
δ
δδδδ
=−+
⎛
⎝⎜
⎞
⎠⎟=−+
=
KK
+−+
⎛
⎝⎜
⎞
⎠⎟ −+
⎛
⎝⎜
⎞
⎠⎟ =+
=
KKK
K
);
cos cos
1
1
2
1
1
2
1
2
2
2
1
12
δδ
δ
δδ1
1
2
1
1
2
1
22
1
2
2
2
1
2
2
2
−+
⎛
⎝⎜
⎞
⎠⎟ −+
⎛
⎝⎜
⎞
⎠⎟=
−−+
δδ
δδ
KK
K
.
(4.67)
Ïîäñòàâëÿÿ â âûðàæåíèå äëÿ ôóíêöèè W çíà÷åíèÿ ïðîèçâåäåíèé
(4.67), íàéäåì åå ïåðâîå ïðèáëèæåíèå:
Wa
faf a
f
afa
f
+=
−
++
++
+
42
2
41
2
412
42
2
2
2
421
41
••
••
δδ
δδ
δδ
δδ
2
2
+=+
KK
W
.
(4.68)
Çäåñü W2 ïðåäñòàâëÿåò ñîáîé êâàäðàòè÷íóþ ôîðìó îòíîñèòåëüíî
ïåðåìåííûõ δ1, δ2,
•
,
δ1
•
,
δ2 ñîñòîÿùóþ èç äâóõ îäíîòèïíûõ
êâàäðàòè÷íûõ ôîðì. Äîñòàòî÷íî ðàññìîòðåòü îäíó èç íèõ:
wafa
f
21
2
412
42
2
2
=−
+
••
.
δδ
δδ
(4.69)
Ñîãëàñíî êðèòåðèþ Ñèëüâåñòðà (4.42), ôîðìà w2 áóäåò
îïðåäåëåííî-ïîëîæèòåëüíîé òîãäà, êîãäà ïîëîæèòåëüíûìè áóäóò
195
ãëàâíûå äèàãîíàëüíûå ìèíîðû åå îïðåäåëèòåëÿ.  íàøåì ñëó÷àå
äîëæíû âûïîëíÿòüñÿ óñëîâèÿ
a
af
fa
f
aff
>
−
−
=−
>
00
4
44
2
44
2
;.
(4.70)
Åñëè íåðàâåíñòâà (4.70) óäîâëåòâîðåíû, òî äëÿ íåâîçìóùåííî-
ãî âðàùàòåëüíîãî äâèæåíèÿ ñíàðÿäà (δ =δ =δ δ
2
11
2
0
••
)
==ôóíêöèÿ
W +4af4 = W2 + ... áóäåò îïðåäåëåííî-ïîëîæèòåëüíîé ïî êðàéíåé
ìåðå â äîñòàòî÷íî ìàëîé îáëàñòè ÷èñëåííûõ çíà÷åíèé ïåðåìåííûõ
δ1, δ2,
•
,
δ1
•
.
δ2 Òàê êàê ôóíêöèÿ W ñòðîèëàñü â âèäå ëèíåéíîé ñâÿçêè
ïåðâûõ èíòåãðàëîâ, òî ïîëíàÿ ïðîèçâîäíàÿ ïî âðåìåíè ôóíêöèè
(W +4af4) ñîãëàñíî òî÷íûì óðàâíåíèÿì âîçìóùåííîãî äâèæåíèÿ
(4.63), (4.64) áóäåò ðàâíà íóëþ. Òàêèì îáðàçîì, ïðè âûïîëíåíèè íå-
ðàâåíñòâ (4.70) èìåþò ìåñòî óñëîâèÿ òåîðåìû ïðÿìîãî ìåòîäà Ëÿïó-
íîâà îá óñòîé÷èâîñòè äâèæåíèÿ è, ñëåäîâàòåëüíî, ðàññìàòðèâàåìîå
íåâîçìóùåííîå äâèæåíèå (4.61) ÿâëÿåòñÿ óñòîé÷èâûì.
Ïåðâîå èç íåðàâåíñòâ (4.70), î÷åâèäíî, âûïîëíÿåòñÿ, òàê êàê
à=à0=
C
A
r
2
0
0 > . Âòîðîå íåðàâåíñòâî, ïîëó÷åííîå âïåðâûå
Í. . Ìàèåâñêèì, ñ ó÷åòîì òîãî, ÷òî f4 > 0, ìîæåò áûòü çàïèñàíî â
âèäå
af
2
4
0
−>
.
(4.71)
Òàê êàê âûðàæåíèå (4.68) ÿâëÿåòñÿ èíòåãðàëîì òî÷íûõ óðàâíåíèé
âîçìóùåííûõ äâèæåíèé ñíàðÿäà, òî ïîñòðîåííàÿ ôóíêöèÿ ðàçðåøàåò
âîïðîñ îá óñòîé÷èâîñòè â òîé êîíå÷íîé îáëàñòè ôàçîâîãî
ïðîñòðàíñòâà ïåðåìåííûõ δ1, δ2,
•
,
δ1
•
,
δ2 ãäå óðàâíåíèÿ W = const
îáðàçóþò ñèñòåìó çàìêíóòûõ, ñòÿãèâàþùèõ â íà÷àëî êîîðäèíàò
îãðàíè÷åííûõ ïîâåðõíîñòåé.
Ïðåäñòàâëÿåò ñóùåñòâåííûé èíòåðåñ ïðîâåðêà ñïðàâåäëèâîñòè
êðèòåðèÿ óñòîé÷èâîñòè Í.Â. Ìàèåâñêîãî â ôîðìå (4.71) äëÿ îáùåãî
ñëó÷àÿ îïèñàíèÿ âîçìóùåííîãî äâèæåíèÿ îñè âðàùàþùåãîñÿ ñíà-
ðÿäà â âèäå äèôôåðåíöèàëüíûõ óðàâíåíèé óãëîâîãî äâèæåíèÿ â
íîðìàëüíîé ôîðìå, ýêâèâàëåíòíûõ óðàâíåíèþ
d
dt
tA
t tBC
xx
ωω
()()()
,
+=
+
(4.72)
ãäå Amq
S
lI
xx
x
=
−
||–
ω
21
ïîëÿðíûé àýðîäèíàìè÷åñêèé òóøàùèé
ìîìåíò; Bmq
S
I
xx
=
−
||–
0
1
àýðîäèíàìè÷åñêèé ìîìåíò îò êîñî
ïîñòàâëåííîãî îïåðåíèÿ; CMI
x
=
−
γ
1
–
ðåàêòèâíûé êðóòÿùèé ìîìåíò.
196
Èñõîäíûå óðàâíåíèÿ äâèæåíèÿ îñè ñíàðÿäà ìîãóò áûòü çàïèñàíû
[14] ñëåäóþùèì îáðàçîì:
••• •
;
••• •
δδ δδδ
δδδ
γ
121
12
11
21
22
22
0
++−−
=+
−+
a bceQQ
ab
g
P
2212 2
0
−+= +
ceQQ
g
P
δδ
γ,
(4.73)
ãäå êîýôôèöèåíòû èìåþò âèä
ab
c
e
=+ =++
=+
−
+−−
=−
αξ λμχ
βαξχλμλμ
ξ
11
111
1
44
2
4
;;
()(
•
•
);
αλμχξξ
11
42
()•
,
+−−
(4.74)
à âîçìóùàþùèå ÷ëåíû – âèä
Q
g
V
d
dt
g
V
Q
g
V
g
g
11
00
21
0
0
0
2
2
=+
⎛
⎝⎜⎞
⎠⎟
=−
χθ
θ
α
θ
cos
cos ;
cos
;
Q
Q
P
P
P
11
1
1
2111
442
442
γ
γ
εχ
εα
ηε
γ
ηχ
ηα
εη
=−
+
−
+
=+
++
(
•
);
(
•
)γP,
(4.75)
âåëè÷èíû êîòîðûõ îïðåäåëÿþòñÿ ÷åðåç êîýôôèöèåíòû, ïðèâåäåííûå
â òàáë. 4.1, çàèìñòâîâàííîé èç [14].
Àíàëîãè÷íî ïðåäûäóùåìó áóäåì ðàññìàòðèâàòü âîçìóùåííîå
äâèæåíèå âðàùàþùåãîñÿ ñíàðÿäà òîëüêî ïîä äåéñòâèåì îïðîêèäû-
âàþùåãî ìîìåíòà.
Ïåðåõîä îò îäíîðîäíûõ äèôôåðåíöèàëüíûõ óðàâíåíèé (4.73) ê
íîðìàëüíûì óðàâíåíèÿì â ôîðìå Êîøè ïðèâîäèò ê ïîëó÷åíèþ ïðè
ââåäåíèè îáîçíà÷åíèé
õ1=δ1,x21
=
•
,
δx3=δ2èx42
=
•
δ
ñëåäóþùåé ñèñòåìû:
•
;
•
;
•
;
•
,
xx
xc
xa
x
xx
xa
xc
x
12
214
34
42
3
2
2
=
=−
=
=+
(4.76)
197
198
Òàáëèöà 4.1
Òàáëèöà êîýôôèöèåíòîâ
1
Ñèëîâûå
êîýôôèöèåíòû
Âûðàæåíèÿ êîýôôèöèåíòîâ
Êîýôôèöèåíòû ñèë
è ìîìåíòîâ
1
λ=
P
mV
2
ñèëû òÿãè
2
μ
ρ
α
=
c
V
S
mV
ya
2
2
2
íîðìàëüíîé
àýðîäèíàìè÷åñêîé ñèëû
3
ξ
ρ
ω
αω
=
||
c
V
Sl
mV
z
x
a
x
2
2
àýðîäèíàìè÷åñêîé ñèëû
Ìàãíóñà
4
ε=λsin(δ3+φP)
ñèë, âîçíèêàþùèõ ïðè
íàëè÷èè àñèììåòðèè
ðåàêòèâíîé ñèëû
5
η=λcos(δ3+φP)
6
Ìîìåíòíûå
êîýôôèöèåíòû
αω
1
2
=
I
I
x
y
x
ãèðîñêîïè÷åñêîãî ìîìåíòà
7
β
ρ
α
1
2
2
=
m
V
Sl
I
z
y
îïðîêèäûâàþùåãî èëè
ñòàáèëèçèðóþùåãî
àýðîäèíàìè÷åñêîãî
ìîìåíòà
8
χ
ρ
ω
1
2
2
2
2
=
−
||
m
V
SLI
I
y
y
y
ì
ýêâàòîðèàëüíîãî òóøàùåãî
ìîìåíòà (ïåðâûé ÷ëåí) è
ìîìåíòà îò ðåàêòèâíîé
ñèëû Êîðèîëèñà
9
ξ
ρ
ω
ξξ
α
αω
1
1
2
1
1
2
=
′=
m
V
Sl
I
y
y
x
x
,
àýðîäèíàìè÷åñêîãî
ìîìåíòà Ìàãíóñà
10
λ1=
−
Pxx
I
a
y
()
ö.ì
ìîìåíòîâ, âîçíèêàþùèõ
ïðè íàëè÷èè àñèììåòðèè
ðåàêòèâíîé ñèëû
11
ε1=λ1sin(δ3+φP)
12
η1=λ1cos(δ3+φP)
13
A
m
V
Sl
I
x
x
x
1
2
2
=
||
ωρ
ïîëÿðíîãî òóøàùåãî
ìîìåíòà
Ïðèìå÷àíèå: φP åñòü óãîë, õàðàêòåðèçóþùèé àñèììåòðèþ (ýêñöåíòðèñèòåò) ðåàêòèâíîé
ñèëû.
ãäå, ñîãëàñíî çàâèñèìîñòÿì (4.74) è äàííûì òàáëèöû 4.1,
a
I
I
bc
mqSl
I
e
x
y
x
z
y
==
>===
>=
αω
β
α
11
2
00
00
,,
,.
(4.77)
Óìíîæèâ, ñëåäóÿ [14], âòîðîå óðàâíåíèå ñèñòåìû (4.76) íà õ2,à
÷åòâåðòîå – íà õ4 è ïî÷ëåííî ñëîæèâ, íàéäåì
xx xx cxx cxx
22 44
12
34
••
.
+=+
(4.78)
Èñêëþ÷àÿ èç ïðàâîé ÷àñòè âåëè÷èíû õ2 è õ4, èñïîëüçóÿ ïåðâîå è
òðåòüå óðàâíåíèÿ ñèñòåìû, ïîëó÷èì
xxxxcxxxx
22 44
11 33
••
(••
),
+=+
(4.79)
èëè
xxc
xxh
2
2
4
2
1
2
3
2
1
+−+==
().
const
(4.80)
Âûðàæåíèå (4.80) åñòü èíòåãðàë ñèñòåìû (4.76). ×òîáû íàéòè âòîðîé
èíòåãðàë, óìíîæèì âòîðîå óðàâíåíèå ñèñòåìû íà −õ3, à ÷åòâåðòîå –
íà õ1. Ïîñëå ïî÷ëåííîãî ñëîæåíèÿ ðåçóëüòàòîâ óìíîæåíèÿ èìååì
−+=
+
xx xx
axx xx
32 14
34 12
2
••
()
,
÷òî ýêâèâàëåíòíî
d
dx
xx xx
a
d
dt
xx
()
(
)
,
−+=
+
23 14
3
2
1
2
îòêóäà
xxxxaxx
h
14 23
1
2
3
2
2
−−+
=
=
().
const
(4.81)
Òàêèì îáðàçîì ïîëó÷èì âûðàæåíèå âòîðîãî èíòåãðàëà ñèñòåìû
(4.76).
Ïðèíèìàÿ â âûðàæåíèÿõ èíòåãðàëîâ ñèñòåìû (4.76) çíà÷åíèÿ
õ1=õ2=õ3=õ4=0,íàéäåìh1=h2=0
.
199
Ñëåäîâàòåëüíî, F1(0, 0, 0, 0) = F2(0, 0, 0, 0) = 0 è ðàçíîñòè
FxFFxxxcxx
FxF F
111 2
2
4
2
1
2
3
2
22
0
0
()()()
();
() ()
−=
=
+
−
+
−=
21
4
2
31
2
3
2
()
()
xx
xx
xa
xx
=−−+
(4.82)
ïðåäñòàâëÿþò êâàäðàòè÷íûå ôîðìû ïåðåìåííûõ.
Äàëåå ñëåäóåò îñóùåñòâèòü èõ ïðîâåðêó íà çíàêîîïðåäåëåííîñòü.
Äëÿ ýòîãî â ñîîòâåòñòâèè ñ êðèòåðèåì Ñèëüâåñòðà íåîáõîäèìî ðàñ-
ñìîòðåòü ìàòðèöû êîýôôèöèåíòîâ êâàäðàòè÷íîé ôîðìû è âû÷èñ-
ëèòü çíà÷åíèÿ ãëàâíûõ ìèíîðîâ äëÿ ýòèõ ìàòðèö.
Ìàòðèöà êîýôôèöèåíòîâ ïåðâîé (âåðõíèé èíäåêñ "1") êâàäðà-
òè÷íîé ôîðìû èìååò ýëåìåíòû
ccc
cc ccccc
11
1
33
1
22
1
44
1
12
1
13
1
14
1
21
1
23
1
1
==
−
==
=====
;;
c
ccc ccc
24
1
31
1
32
1
34
1
41
1
42
1
43
1
0
=
=== ====
,
à çíà÷åíèÿ ãëàâíûõ ìèíîðîâ ìàòðèöû ïðèîáðåòàþò âèä
∆∆∆∆
3
1
1
1
2
12
4
12
0000
=
−
<=
−
<=>
=>
cccc
;;;.
Ïîëó÷àåì, ÷òî íè îäíî èç óñëîâèé êðèòåðèÿ Ñèëüâåñòðà íå
âûïîëíÿåòñÿ, è, ñëåäîâàòåëüíî, ðàññìàòðèâàåìàÿ êâàäðàòè÷íàÿ
ôîðìà íå ÿâëÿåòñÿ çíàêîîïðåäåëåííîé.
Âòîðàÿ êâàäðàòè÷íàÿ (âåðõíèé èíäåêñ "2") ôîðìà (4.82) èìååò
ìàòðèöó ñ ýëåìåíòàìè
cca
cc
cc
cc
11
2
33
2
14
2
41
2
23
2
32
2
12
2
13
05
05
==
−
==
==
−
=
;,
;,
;
2
21
2
22
2
31
2
34
2
42
2
43
2
44
2
0
===
======
cc
ccccc .
Ñîîòâåòñòâóþùèå çíà÷åíèÿ ãëàâíûõ ìèíîðîâ òàêîâû:
∆∆∆∆
1
2
2
2
3
2
4
2
0
4
1
16
=−
=
=
=
a
a
;;;.
Òàêèì îáðàçîì, êâàäðàòè÷íûå ôîðìû (4.82) íå ÿâëÿþòñÿ
çíàêîîïðåäåëåííûìè, è, ñëåäóÿ Í.à . ×åòàåâó, ôóíêöèþ Ëÿïóíîâà
áóäåì èñêàòü â ôîðìå ñâÿçêè èíòåãðàëîâ (4.49), îãðàíè÷èâàÿñü
ëèíåéíûìè ÷ëåíàìè è ïîëàãàÿ λ1 =1,λ2 = −λ:
VxFxFx
() () ().
=−
12
λ
(4.83)
200
Ïîäñòàâëÿÿ çíà÷åíèÿ ôóíêöèé F1(x)èF2(x) èç (4.82) â (4.83),
ïîëó÷àåì êâàäðàòè÷íóþ ôîðìó
Vx ac
xx
xxx
xac
xx
(
)
()
(),
=−−
++ +−+
λλλ
λ
1
2
142
2
23
3
2
4
2
(4.84)
èìåþùóþ ìàòðèöó êîýôôèöèåíòîâ ñ ýëåìåíòàìè
ñña
c
cc
cc
cc
11
33
14
41
23
32
22
44
05
05
1
==−
==
−
==
==
λλ
λ
;,
;,
;;
cccccccc
12
13
21
24
31
34
42
43
0
========
.
Ãëàâíûå ìèíîðû ýòîé ìàòðèöû ïðèíèìàþò çíà÷åíèÿ
∆∆
∆∆
∆∆
∆
12
31
2
41
3
22
44
4
==−
=
−
−
⎛
⎝⎜
⎞
⎠⎟ =+
−
−
λλ
λλ
λ
λ
ac
ac
ac
;;
⎛
⎝⎜
⎞
⎠⎟.
Àíàëèç ïîëó÷åííûõ çíà÷åíèé ãëàâíûõ ìèíîðîâ äàåò îñíîâàíèå
ñ÷èòàòü, ÷òî óñëîâèÿ êðèòåðèÿ Ñèëüâåñòðà ∆1 >0,∆2 >0,∆3 >0,∆4 >0
âûïîëíÿþòñÿ â ñëó÷àå, åñëè âåëè÷èíà λ > 0 è èìååò ìåñòî íåðàâåíñòâî
λ
λ
ac
−−
>
2
4
0,
(4.85)
òàê êàê èç íåãî ñëåäóåò è ñïðàâåäëèâîñòü óñëîâèÿ
λac
− >0.
(4.86)
Ïðåäñòàâèì íåðàâåíñòâî (4.85) â ýêâèâàëåíòíîì âèäå:
λλ
2
440
−+<
ac.
Çíàê êâàäðàòíîãî òðåõ÷ëåíà áóäåò ïðèíèìàòü îòðèöàòåëüíîå
çíà÷åíèå òîëüêî â òîì ñëó÷àå [14], êîãäà âåëè÷èíà λ ëåæèò ìåæäó
äåéñòâèòåëüíûìè ïîëîæèòåëüíûìè êîðíÿìè êâàäðàòíîãî óðàâíåíèÿ
λλ
2
440
−+
=
ac.
(4.87)
Àíàëèç ðåøåíèÿ
λ12
2
22
,
=±
−
aa
c
(4.88)
ñâèäåòåëüñòâóåò, ÷òî îáà êîðíÿ áóäóò ïîëîæèòåëüíûìè, åñëè
ac
2
0
−>
.
(4.89)
201
Òàêèì îáðàçîì, åñëè âåëè÷èíà λ, âõîäÿùàÿ â âûðàæåíèå (4.83),
óäîâëåòâîðÿåò óñëîâèþ
22
22
()()
,
aac
aac
−−
<
<+−
λ
(4.90)
òî ôóíêöèÿ Ëÿïóíîâà áóäåò îïðåäåëåííî-ïîëîæèòåëüíîé, à åå
ïðîèçâîäíàÿ â ñèëó âèäà óðàâíåíèé âîçìóùåííîãî äâèæåíèÿ áóäåò
ðàâíà íóëþ.
 ðåçóëüòàòå èìååì, ÷òî äëÿ ñèñòåìû (4.76) âûïîëíåíû óñëîâèÿ
òåîðåìû Ëÿïóíîâà îá óñòîé÷èâîñòè. Íåðàâåíñòâî (4.89), îáåñïå÷èâ-
øåå òðåáóåìîå ñâîéñòâî ôóíêöèè Ëÿïóíîâà, è ÿâëÿåòñÿ êðèòåðèåì
óñòîé÷èâîñòè óãëîâîãî äâèæåíèÿ ñíàðÿäà Í. . Ìàèåâñêîãî â ðàìêàõ
ðåøåíèÿ çàäà÷è â ðàññìîòðåííîé ïîñòàíîâêå.
Ïðèíèìàÿ âî âíèìàíèå ñîîòíîøåíèÿ (4.77), ïåðåïèøåì åãî â
âèäå
αβ
1
2
1
0
−>
è ïîñëå ïîäñòàíîâêè âûðàæåíèé äëÿ α1 è β1 èìååì
I
I
qSl
I
m
x
y
x
y
z
2
2
2
4
0
ω
α
−>
.
(4.91)
Âåðíåìñÿ òåïåðü ê àíàëèçó óñëîâèÿ óñòîé÷èâîñòè Í. . Ìàèåâñêîãî,
ïîëó÷åííîãî íà îñíîâå îáùèõ óðàâíåíèé äâèæåíèÿ áûñòðîâðà-
ùàþùåãîñÿ àðòèëëåðèéñêîãî ñíàðÿäà â ôîðìå Â.Ñ . Ïóãà÷åâà.
 ñîîòâåòñòâèè ñ (4.71) îíî çàïèñûâàåòñÿ â âèäå a2 − f4 >0.Íà-
ïîìíèì, ÷òî â ýòîì âûðàæåíèè a
C
A
r
=
2
,ãäåA=Iz=Iy;C=Ix–ìî
-
ìåíòû èíåðöèè ñíàðÿäà îòíîñèòåëüíî åãî ãëàâíûõ îñåé; |r |=rx° =
=|ωx| – îñåâàÿ ñîñòàâëÿþùàÿ åãî óãëîâîé ñêîðîñòè, à
f
dl
Ig
HyVm
V
a
Vm
ON
y
MM
4
2
22
8
=⋅
⎡
⎣⎢
⎤
⎦⎥=
π
δ
Ï
()
;
,
ïðè÷åì êîýôôèöèåíò
m
V
a
dld hK
V
a
MM
;(
,
);
.
δφ
δ
⎡
⎣⎢
⎤
⎦⎥=
⎡
⎣⎢
⎤
⎦⎥
−
2
1
202
Ïîñëå ïîäñòàíîâêè ïîëó÷àåì
f qSl
I
dl
h
d
K
V
a
y
M
42
=⋅
⎡
⎣⎢
⎤
⎦⎥
φδ
(,)
;.
(4.92)
 âûðàæåíèè (4.92), íàéäåííîì äëÿ ãèðîñêîïè÷åñêè óñòîé÷èâîãî
àðòèëëåðèéñêîãî ñíàðÿäà, ìíîæèòåëü φδ
2(,)
;
dl
h
d
K
V
a
M
⎡
⎣⎢
⎤
⎦⎥ ïî ñâîåìó
ñìûñëó ýêâèâàëåíòåí çíà÷åíèþ ñòàòè÷åñêîé ïðîèçâîäíîé mz
α
äëÿ
ñòàòè÷åñêè óñòîé÷èâîãî âðàùàþùåãîñÿ ñíàðÿäà. Ïîä÷åðêíåì, ÷òî
âûðàæåíèå (4.92), âîîáùå ãîâîðÿ, íåóäîáíî äëÿ ïðàêòè÷åñêîãî
èñïîëüçîâàíèÿ.
Õîòÿ ýòî âûðàæåíèå è ñîäåðæèò íåêóþ ïîñòîÿííóþ φ2(d, l )=
=⋅
211 103
,
d
l
è òèïîâóþ ôóíêöèþ ñîïðîòèâëåíèÿ ìîìåíòà K
V
a
M
;,
δ
⎡
⎣⎢
⎤
⎦⎥
îáîëüùàòüñÿ âèäèìîé ïðîñòîòîé åãî îïðåäåëåíèÿ íå ñòîèò. Äåëî â
òîì, ÷òî, âî-ïåðâûõ, ýêñïåðèìåíòàëüíûå èññëåäîâàíèÿ, ïî êîòîðûì
íàêàïëèâàëñÿ ñòàòèñòè÷åñêèé ìàòåðèàë äëÿ çàäàíèÿ óêàçàííîé
ôóíêöèè, ïðîèçâîäèëèñü íà óðîâíå 40-õ ãîäîâ ïðîøëîãî âåêà (ò.å .
ÿâíî íå äëÿ ñîâðåìåííûõ òèïîâ ñíàðÿäîâ), âî-âòîðûõ, ñîîòâåòñò-
âóþùèå ýêñïåðèìåíòàëüíûå çíà÷åíèÿ ýòîé ôóíêöèè ïîëó÷åíû ïðè
óñëîâèè ìàëûõ óãëîâ íóòàöèè è ëèíåéíîé çàâèñèìîñòè M(δ), ò.å. íà
ñàìîì äåëå ïðèõîäèòñÿ çàìåíÿòü K
V
a
M
;δ
⎡
⎣⎢
⎤
⎦⎥íàK
V
a
M
⎡
⎣⎢
⎤
⎦⎥.Íîèýòîíå
ñàìîå ãëàâíîå, ïîñêîëüêó â âûðàæåíèå (4.92) âõîäèò âåëè÷èíà h ≈∆l,
ñîîòâåòñòâóþùàÿ óñëîâíîìó ðàññòîÿíèþ ìåæäó öåíòðîì äàâëåíèÿ è
öåíòðîì ìàññ ñíàðÿäà, îïðåäåëÿåìàÿ èñêëþ÷èòåëüíî ïî ýìïèðè÷å-
ñêèì ôîðìóëàì (òèïà ôîðìóëû Ãîáàðà, ñì. ï. 1.4.3), êîòîðûå äëÿ
âíîâü ïðîåêòèðóåìûõ áîåïðèïàñîâ, åñòåñòâåííî, îòñóòñòâóþò.
Òåì íå ìåíåå ïîëó÷åíèå âûðàæåíèÿ f4 â ôîðìå (4.92) ïðåäñòàâëÿ-
åò îïðåäåëåííûé ìåòîäè÷åñêèé èíòåðåñ, òàê êàê îíî äàåò îñíîâàíèå
ñ÷èòàòü óñëîâèå óñòîé÷èâîñòè Í. . Ìàèåâñêîãî óíèâåðñàëüíûì è
èíâàðèàíòíûì ïî îòíîøåíèþ ê ôîðìàì ïðåäñòàâëåíèÿ ìîäåëåé
äâèæåíèÿ ñíàðÿäà.
×òî æå êàñàåòñÿ ïðàêòè÷åñêèõ àñïåêòîâ åãî èñïîëüçîâàíèÿ, òî
áîëåå ïðåäïî÷òèòåëüíîé, èìåÿ â âèäó ðàâåíñòâà (4.77), ÿâëÿåòñÿ
ôîðìà îáùåèçâåñòíîãî êðèòåðèàëüíîãî êîýôôèöèåíòà ãèðîñêîïè-
÷åñêîé óñòîé÷èâîñòè
σ
β
α
2
1
1
2
10
=−
>.
203
4.3.3. ÒÐÀÊÒÎÂÊÀ ÏÎÍßÒÈß ÍÅÓÑÒÎÉ×ÈÂÎÑÒÈ ÄÂÈÆÅÍÈß
ÀÐÒÈËËÅÐÈÉÑÊÎÃÎ ÑÍÀÐßÄÀ ÏÎ ËßÏÓÍÎÂÓ
Ðåøàÿ îáùóþ çàäà÷ó îá óñòîé÷èâîñòè äâèæåíèÿ àðòèëëåðèéñêîãî ñíàðÿ-
äà, Â.Ñ . Ïóãà÷åâ äîêàçàë [98] åãî íåóñòîé÷èâîñòü (ïî Ëÿïóíîâó) ïðè "ïðà-
âèëüíîì" ïîëåòå ñíàðÿäà íà áåñêîíå÷íîì èíòåðâàëå âðåìåíè, ò.å . ïðè t →∞.
Ýòîò ðåçóëüòàò ïðåäñòàâëÿåò ñóùåñòâåííûé èíòåðåñ íå òîëüêî ñ òåîðåòè-
÷åñêîé òî÷êè çðåíèÿ, íî è ñ òî÷êè çðåíèÿ ïðèëîæåíèé, ïðåæäå âñåãî ñ ïîçè-
öèé åãî ïðàêòè÷åñêîé òðàêòîâêè.
Ðàññìîòðèì ñèñòåìó óðàâíåíèé ïðîñòðàíñòâåííîãî äâèæåíèÿ ñíàðÿäà â
ôîðìå Â.Ñ . Ïóãà÷åâà (3.157). Ïðè áîëüøèõ çíà÷åíèÿõ íåçàâèñèìîé ïåðå-
ìåííîé (t →∞) çíà÷åíèå çàâèñèìîé ïåðåìåííîé yc →−∞
. Äëÿ òîãî ÷òîáû èç-
áàâèòüñÿ îò áåñêîíå÷íîãî (ïî àáñîëþòíîé âåëè÷èíå) çíà÷åíèÿ yc ïðè t = ∞,
öåëåñîîáðàçíî [98] îñóùåñòâèòü ñëåäóþùóþ çàìåíó:
we
yc
=
.
(4.93)
Òîãäà ïðè yc →−
∞èìååì w → 0. Ñ ó÷åòîì (4.93) ñîâìåñòíî ðåøàåìûå
óðàâíåíèÿ ñèñòåìû (3.157) ïðèìóò âèä
Vgf
gV
fz fz
ww
V
z
.
.
.
.
=−
−
=−
+
+
=
=
−
sin
;
cos
;
sin ;
θ
θθ
θ
1
1
22
33
2
u
zu
uz
z
z
z
z
u
2
33
22
2
1
32
22
2
3
2
1
2
3
1
;
;
[()
]
()
;
.
.
.
=
=−
+
−
−
−
ΦΦΦ
=−
+
−
−
=−
−
[()
]
()
;
.
ΦΦΦ
131
32
2
2
2
3
2
1
2
6
1
zzzzz
af
a
.
(4.94)
Ïîëîæåíèÿ ðàâíîâåñèÿ ñèñòåìû (4.94), èëè îñîáûå çíà÷åíèÿ ïåðåìåííûõ V,
θ, w, z2, z3, u2, u3, à, îïðåäåëÿþòñÿ èç óñëîâèÿ ðàâåíñòâà íóëþ ïðàâûõ ÷àñòåé
óðàâíåíèé (4.94):
qf
qV
fz fz
wV
uu
sin
;
cos
;
sin
;
;
θ
θ
θ
+=
−−=
=
==
−
1
1
22 33
23
0
0
0
0
Φ221
32
2
131
32
2
0
0
0
−+
=
−+
=
=
zzz
zzz
a
()
;
()
;
.
ΦΦ
ΦΦΦ
(4.95)
204
Ôóíêöèè Φ1 è Φ2 çàâèñÿò îò âûðàæåíèÿ 1 2
2
3
2
−−
zz
, ïîëîæèòåëüíûå çíà-
÷åíèÿ êîòîðîãî ñîîòâåòñòâóþò ïîëåòó ñíàðÿäà ãîëîâíîé ÷àñòüþ âïåðåä, à îò-
ðèöàòåëüíûå – ïîëåòó ñíàðÿäà, ïåðåâåðíóâøåãîñÿ ãîëîâíîé ÷àñòüþ íàçàä
(c
o
s
.
12
2
3
2
1
−− ==
zz z δ Ïðè cosδ >0δ∈[0;
π
2
]; ïðè cosδ <0δ∈ [
π
2
; π]).
Ðàññìîòðèì ñëó÷àé ïîëîæèòåëüíûõ çíà÷åíèé z1, ò.å . ïîëåò ñíàðÿäà ãî-
ëîâíîé ÷àñòüþ âïåðåä. Ðåøåíèÿìè ñèñòåìû (4.95), î÷åâèäíî, ÿâëÿþòñÿ çíà-
÷åíèÿ ïåðåìåííûõ
wzzuua
VV
======
==
=
−
2323
0
2
;
;/
,
**
θθπ
(4.96)
ãäå V*
–
ïðåäåë ñêîðîñòè öåíòðà ìàññ ñíàðÿäà ïðè t →∞, êîòîðûé ìîæåò áûòü
íàéäåí èç óñëîâèÿ ðàâåíñòâà âåñà è ñèëû ñîïðîòèâëåíèÿ âîçäóõà (ðèñ. 4 .6),
ò.å. èç ïåðâîãî óðàâíåíèÿ ñèñòåìû (4.95) ïðè θ = π/2.
Çàìåòèì, ÷òî ðåøåíèå ñèñòåìû (4.96) îïèñûâàåò èäåàëüíî ïðàâèëüíûé
ïîëåò ñíàðÿäà, òàê êàê èç óñëîâèÿ z2 = z3 = 0 ñëåäóåò, ÷òî z1 = cosδ =1è,ñëå-
äîâàòåëüíî, óãîë íóòàöèè δ = 0. Ïîýòîìó ðåøåíèå (4.96) ìîæåò áûòü ïðèíÿ-
òî çà íåâîçìóùåííîå äâèæåíèå, ïîäëåæàùåå èññëåäîâàíèþ íà óñòîé÷èâîñòü
ïî Ëÿïóíîâó.
×òîáû ïîëó÷èòü óðàâíåíèÿ âîçìóùåííîãî äâèæåíèÿ, âûïîëíèì çàìåíó
ïåðåìåííûõ [38]
VV
=+
=+=
−
+
**
;/
vθθθπθ
2
è ðàçëîæèì ïðàâûå ÷àñòè óðàâíåíèé (4.94) ïî ñòåïåíÿì v, θ, w, z2, z3, u2, u3, a.
Íîâûå ïåðåìåííûå v è θ õàðàêòåðèçóþò îòêëîíåíèÿ ñêîðîñòè è óãëà íàêëîíà
âåêòîðà ñêîðîñòè îò íåâîçìóùåííûõ çíà÷åíèé.
Ó÷èòûâàÿ, ÷òî âåëè÷èíû f3,
•
f3è
•
f2 (âûðàæåíèÿ äëÿ f2 è f3 ñì. â ïîä-
ðàçä. 3 .4.1) îáðàùàþòñÿ â íóëü
ïðè âûïîëíåíèè ðàâåíñòâ (4.96),
ìîæåì ïðèâåñòè ñèñòåìó (4.94) ê
âèäó
vv
.
.
=−
−
−
−
+
=−
+
+
−
f fwf
zf
zX
qV
fzX
11
12
132
143
1
1
202
2
*
*
;
;
θθ
wV
wX
zu
zu
.
.
.
=−
+
=
=
3
2
2
3
3
*
;
;
;
(4.97)
205
Ðèñ. 4.6. Ê îïðåäåëåíèþ óñòîé÷èâîñòè äâè-
æåíèÿ àðòèëëåðèéñêîãî ñíàðÿäà ïî Ëÿïóíîâó
ug
V
g
Vf ff
f
gVfzf
.
2
11
70
40
20 70
1
202
20
=−
−
+
−
+
+−
+
−−
−
()
(
)(
v
fuX
uff
fzff
uX
af
702
4
34
02
0
7
0
32
07
0
35
);
()
();
*
*
+
=−
−+
+
=−
.
60
6
aX
+
*
.
Ñèñòåìà (4.97) – ýòî ñèñòåìà óðàâíåíèé âîçìóùåííîãî äâèæåíèÿ, â êîòîðîé
Xi
*
(i =1,...,6) ïðåäñòàâëÿþò ñîáîé ñîâîêóïíîñòü ÷ëåíîâ ðàçëîæåíèÿ âûøå
ïåðâîãî ïîðÿäêà îòíîñèòåëüíî ïåðåìåííûõ v, θ, w, z2, z3, u2, u3, a. Êðîìå òîãî,
êîýôôèöèåíòû f11, f12, f13, f14 îáîçíà÷àþò ñîîòâåòñòâåííî çíà÷åíèÿ
ïðîèçâîäíûõ
∂
∂
f
V
1,
∂
∂
f
w
1,
∂
∂
f
z
1
2
,
∂
∂
f
z
1
3
, à fi0 (i =2,..., 7) – çíà÷åíèÿ ôóíêöèé fi ïðè
w=z2=z3=0èV=V
*
.
Îòáðàñûâàÿ â ïðàâûõ ÷àñòÿõ óðàâíåíèé (4.97) íåëèíåéíûå ÷ëåíû X i
*
, ïî-
ëó÷èì óðàâíåíèÿ ïåðâîãî ïðèáëèæåíèÿ. Õàðàêòåðèñòè÷åñêîå óðàâíåíèå
(4.27) â äàííîì ñëó÷àå áóäåò èìåòü âèä
[]
[]
−−
−
−
−
⎡
⎣⎢
⎤
⎦⎥
−−
−
ff
f
g
V
f
V
11
12
13
20
0
00
00
0
000
000 0
λ
λ
λ
λ
00
000 0
0
70
40
20 70
20
−−
⎛
⎝⎜⎞
⎠⎟
⎡
⎣⎢
⎤
⎦⎥
−+
⎡
⎣⎢
⎤
⎦⎥
g
V
g
V
ff
f
f
g
V
f
000
−
−
−−
−
−
f
ff
fff
14
20
70
40
20 70
000
00 00
00 00
01 00
010
00
0
λ
λ
[]
[
][
]
[]
.
00
000
0
20
70
60
−−
−
−−
=
ff
f
λ
λ
(4.98)
Ðàñêðûâàÿ îïðåäåëèòåëü, óðàâíåíèå ìîæíî ïðèâåñòè ê âèäó
206
()
()
()
[()
]
fVf
ffff
f
11
60
2
20
70
40
20 70
3
++ +++−
+×
×+
λλλ
λ
λ
λg
V
ff fffg
V
f
g
V
f
++
⎛
⎝⎜
⎞
⎠⎟ −−−
⎛
⎝⎜
⎞
⎠⎟−
⎡
⎣
20
70
2
40
20 70
70
40
λλ
⎢
⎤
⎦⎥=0.
(4.99)
Îíî èìååò ïÿòü êîðíåé
λλλ
11
12
360
==
−
=
−
fVf
;;;
(4.100)
λ
λ
42
0
7
0
2
0
7
0
2
40
52
0
7
0
1
2
4
1
2
=−
+
+
−
+
=−
+
−
()
();
()
(
fffff
fff
20
70
2
40
4
−+
ff
).
(4.101)
Ïåðâûå ÷åòûðå êîðíÿ îòðèöàòåëüíû, à ïÿòûé – ïîëîæèòåëåí (λ5 > 0), òàê êàê
()()(),
ff f ff fffff
20
70
2
40
20
70
2
40
20 70
20
70
44
−+=++− >+
ïîñêîëüêó äëÿ àðòèëëåðèéñêîãî ñíàðÿäà îáû÷íî f40 > f20 f70. Äëÿ îïðåäåëåíèÿ
îñòàëüíûõ êîðíåé óðàâíåíèé (4.99) íåîáõîäèìî íàéòè êîðíè ïîëèíîìà
F
g
V
ff fffg
V
f
()
λλ
λ
λ
2
=+
+
⎛
⎝⎜
⎞
⎠⎟ −−−
⎛
⎝⎜
⎞
⎠⎟−
3
20
70
40
20 70
70
g
V
f40 .
Ó÷èòûâàÿ, ÷òî f40 > 0, ìîæåì óñòàíîâèòü çíàêè çíà÷åíèé ïîëèíîìà F(λ) ïðè
λ→±∞. Ïóñòü Ì – äîñòàòî÷íî áîëüøîå ïîëîæèòåëüíîå ÷èñëî. Òîãäà
FMFMF
g
V
f
() ;() ;()
.
−<
>
=
−
<
00
00
40
Âîçìîæíîå èçìåíåíèå F(λ) ïîêàçàíî íà ðèñ. 4.7. Òàêèì îáðàçîì, îäèí èç
êîðíåé ïîëèíîìà F(λ) ïîëîæèòåëåí (λ6 > 0). Îñòàëüíûå äâà ëèáî
îòðèöàòåëüíûå (λ8 < λ7 < 0), ëèáî êîìïëåêñíî-ñîïðÿæåííûå ñ îòðèöàòåëüíîé
äåéñòâèòåëüíîé ÷àñòüþ.
 ðåçóëüòàòå ïîëó÷àåì, ÷òî õàðàêòåðèñòè÷åñêîå óðàâíåíèå èìååò
øåñòü êîðíåé ñ îòðèöàòåëüíûìè è äâà ñ ïîëîæèòåëüíûìè äåéñòâèòåëü-
íûìè ÷àñòÿìè.
Òàêèì îáðàçîì, â ñèëó òåîðåìû Ëÿïóíîâà î íåóñòîé÷èâîñòè ïî ïåðâîìó
ïðèáëèæåíèþ (ñì. ïîäðàçä. 4 .2.2) íåâîçìóùåííîå äâèæåíèå, îïèñûâàþùåå
èäåàëüíî ïðàâèëüíûé ïîëåò áûñòðîâðàùàþùåãîñÿ àðòèëëåðèéñêîãî ñíàðÿ-
äà (4.96), ÿâëÿåòñÿ íåóñòîé÷èâûì.
Âûâîä î íåóñòîé÷èâîñòè äâèæåíèÿ âðàùàþùåãîñÿ ñíàðÿäà íà áåñêîíå÷-
íîì èíòåðâàëå âðåìåíè, ïîëó÷åííûé Â.Ñ . Ïóãà÷åâûì, îáúÿñíèì ñ ôèçè÷å-
ñêîé òî÷êè çðåíèÿ. Òàê êàê ñêîðîñòü âðàùåíèÿ ñíàðÿäà âîêðóã ïðîäîëüíîé
207
îñè óìåíüøàåòñÿ ïðè t →∞, òî ñ íåêîòîðîãî ìîìåíòà âðåìåíè îïðîêèäû-
âàþùåìó ìîìåíòó áóäåò ïðîòèâîñòîÿòü íåäîñòàòî÷íûé ãèðîñêîïè÷åñêèé
ìîìåíò è óãîë íóòàöèè íà÷íåò óâåëè÷èâàòüñÿ.
Ñ òî÷êè çðåíèÿ ïðàêòèêè íåîáõîäèìî, ÷òîáû îòêëîíåíèå îñè ñíàðÿäà îò
êàñàòåëüíîé ê òðàåêòîðèè áûëî êàê ìîæíî ìåíüøå â òå÷åíèå âñåãî âðåìåíè
ïîëåòà îò íà÷àëüíîãî ìîìåíòà t0 äî êîíå÷íîãî ìîìåíòà âðåìåíè Ò. Òàêèì
îáðàçîì, ìû ïðèõîäèì ê çàäà÷å îá óñòîé÷èâîñòè äâèæåíèÿ íà êîíå÷íîì èí-
òåðâàëå âðåìåíè.
 îïðåäåëåíèè óñòîé÷èâîñòè ïî Ëÿïóíîâó ïðåäïîëàãàåòñÿ íåîãðàíè÷åí-
íûé ïîëóèíòåðâàë èçìåíåíèÿ âðåìåíè t ∈ [t0;+∞[, à òàêæå çàâèñèìîñòü ÷èñ-
ëà Λ, îïðåäåëÿþùåãî îáëàñòü âîçìîæíûõ íà÷àëüíûõ âîçìóùåíèé (4.13), îò
÷èñëà À (ôîðìóëà (4.14)). Ïðàêòè÷åñêè òðåáóåòñÿ îáåñïå÷èòü âûïîëíåíèå
óñëîâèé, çàäàâàåìûõ íåðàâåíñòâàìè (4.13) è (4.14) ïðè t ∈ [t0; T].
Í.à . ×åòàåâ äàë ïîñòàíîâêó çàäà÷è î (Λ, A, t0, T)-óñòîé÷èâîñòè, êîòîðàÿ
ïîëó÷àåòñÿ èç çàäà÷è Ëÿïóíîâà ïðè ôèêñèðîâàííûõ çàäàííûõ çíà÷åíèÿõ âå-
ëè÷èí Λ, A, t0, T.  ðàìêàõ ðàçðàáîòàííîãî èì ïîäõîäà çàäà÷à îá óñòîé÷èâî-
ñòè äâèæåíèÿ çà îãðàíè÷åííûé ïðîìåæóòîê âðåìåíè ïðè äåéñòâèè ñîîòâåò-
ñòâóþùèì îáðàçîì îãðàíè÷åííûõ âîçìóùàþùèõ ñèë ìîæåò áûòü ñâåäåíà ê
çàäà÷å óñòîé÷èâîñòè ïî Ëÿïóíîâó.
Ïðèìåðîì ðåøåíèÿ òàêîé çàäà÷è, ãäå ïî çàäàííîìó îãðàíè÷åíèþ À íà
òåêóùèå çíà÷åíèÿ ôàçîâûõ êîîðäèíàò âûáèðàþòñÿ äîïóñòèìûå íà÷àëüíûå
âîçìóùåíèÿ (Λ), ÿâëÿåòñÿ ðåøåíèå Í.Ã. ×åòàåâûì çàäà÷è î äîñòàòî÷íûõ óñ-
ëîâèÿõ óñòîé÷èâîñòè ñíàðÿäà, ïîñòàíîâêà êîòîðîé äàíà â ãë. 7.
Ðàçëè÷íûå îáîáùåíèÿ îïðåäåëåíèé òåõíè÷åñêîé óñòîé÷èâîñòè è íåóñ-
òîé÷èâîñòè äâèæåíèÿ ðàññìàòðèâàþòñÿ â ðàáîòàõ [2, 107] è äð.
208
Ðèñ. 4 .7 . Âîçìîæíûå ãðàôèêè F(λ):
à – ïîëèíîì èìååò òðè äåéñòâèòåëüíûõ êîðíÿ; á – ïîëèíîì èìååò îäèí äåéñòâè-
òåëüíûé è äâà êîìïëåêñíûõ êîðíÿ
Ãëàâà 5
×ÈÑËÅÍÍÎÅ ÈÍÒÅÃÐÈÐÎÂÀÍÈÅ ÓÐÀÂÍÅÍÈÉ
ÄÂÈÆÅÍÈß ËÀ È ÏÐÈÁËÈÆÅÍÍÛÅ ÌÅÒÎÄÛ
ÐÅØÅÍÈß ÇÀÄÀ× ÂÍÅØÍÅÉ ÁÀËËÈÑÒÈÊÈ
Ñëîæíîñòü óïðàâëÿåìîãî è íåóïðàâëÿåìîãî ïîëåòà ðàêåò è ñíàðÿäîâ, òðåáîâà-
íèå áûñòðîòû è âûñîêîé òî÷íîñòè ðàñ÷åòîâ õàðàêòåðèñòèê äâèæåíèÿ, à òàêæå
áîëüøîé îáúåì âû÷èñëåíèé ñîçäàþò íåîáõîäèìîñòü øèðîêîãî èñïîëüçîâàíèÿ ïðè ðå-
øåíèè çàäà÷ áàëëèñòèêè ñîâðåìåííîé öèôðîâîé âû÷èñëèòåëüíîé òåõíèêè.
Îñîáåííîñòü èíòåãðèðîâàíèÿ óðàâíåíèé âíåøíåé áàëëèñòèêè, àäåêâàòíî îòðà-
æàþùèõ óñëîâèÿ ðåàëüíîãî ïîëåòà (ñîñòàâëåííûõ áåç ââåäåíèÿ ñóùåñòâåííûõ äîïó-
ùåíèé), çàêëþ÷àåòñÿ â ñëîæíîñòè ñàìèõ óðàâíåíèé, à òàêæå â òîì, ÷òî ôóíêöèè,
îïðåäåëÿþùèå ñèëó ñîïðîòèâëåíèÿ âíåøíåé ñðåäû, ñèëó òÿãè è íåêîòîðûå äðóãèå âå-
ëè÷èíû, íå èìåþò ïðîñòîãî àíàëèòè÷åñêîãî âûðàæåíèÿ.  ñâÿçè ñ ýòèì óðàâíåíèÿ
ïîëåòà ðåøàþòñÿ îáû÷íî ìåòîäàìè ÷èñëåííîãî èíòåãðèðîâàíèÿ.
×àùå äðóãèõ â áàëëèñòè÷åñêèõ ðàñ÷åòàõ èñïîëüçóþò ìåòîäû Ýéëåðà, Ðóí-
ãå–Êóòòà, Àäàìñà–Øòåðìåðà.
 Ðîññèè ÷èñëåííîå èíòåãðèðîâàíèå óðàâíåíèé âíåøíåé áàëëèñòèêè âïåðâûå îñó-
ùåñòâèë À.Í . Êðûëîâ. Èì æå ïðåäëîæåíû âû÷èñëèòåëüíûå ñõåìû, àäàïòèðîâàííûå
ê ðåøåíèþ îáñóæäàåìûõ çàäà÷.
 ñîâðåìåííîé ïðàêòèêå áàëëèñòè÷åñêèõ ðàñ÷åòîâ èñïîëüçóåòñÿ ìåòîä êîíå÷-
íûõ ðàçíîñòåé, ïðåäñòàâëÿþùèé ñîáîé ìîäèôèêàöèþ óæå óïîìèíàâøåãîñÿ ìåòîäà
Àäàìñà–Øòåðìåðà, ïîëó÷èâøóþ íàçâàíèå ìåòîäà Àäàìñà–Êðûëîâà.
×èñëåííûå ìåòîäû ïîçâîëÿþò ïðîèíòåãðèðîâàòü ëþáóþ èç ïðèâåäåííûõ âûøå
ñèñòåì äèôôåðåíöèàëüíûõ óðàâíåíèé ñ íåîáõîäèìîé òî÷íîñòüþ. Âìåñòå ñ òåì ýòè
ìåòîäû òðóäîåìêè, è èõ öåëåñîîáðàçíåå âñåãî èñïîëüçîâàòü äëÿ âûïîëíåíèÿ òî÷íûõ
áàëëèñòè÷åñêèõ ðàñ÷åòîâ. Íà íà÷àëüíûõ ýòàïàõ ïðîåêòèðîâàíèÿ òðåáîâàíèÿ ê
òî÷íîñòè áàëëèñòè÷åñêèõ ðàñ÷åòîâ íèæå. Äëÿ ïîäîáíûõ ðàñ÷åòîâ ìîãóò ïðèìå-
íÿòüñÿ ðàçëè÷íûå àíàëèòè÷åñêèå è òàáëè÷íûå ìåòîäû ðåøåíèÿ çàäà÷ âíåøíåé áàë-
ëèñòèêè.
 çàâèñèìîñòè îò õàðàêòåðà ïðèíèìàåìûõ äîïóùåíèé àíàëèòè÷åñêèå ìåòîäû
ðåøåíèÿ çàäà÷ âíåøíåé áàëëèñòèêè ìîæíî ðàçäåëèòü íà ÷åòûðå îñíîâíûå ãðóïïû.
Ê ïåðâîé ãðóïïå ñëåäóåò îòíåñòè ìåòîäû ðåøåíèÿ ñèñòåì óðàâíåíèé, â êîòîðûõ
÷ëåíû, ó÷èòûâàþùèå ñîïðîòèâëåíèå ñðåäû, îïóùåíû.
Êî âòîðîé ãðóïïå îòíåñåì ìåòîäû, â êîòîðûõ ñèëà ñîïðîòèâëåíèÿ âîçäóõà ó÷è-
òûâàåòñÿ â óðàâíåíèÿõ â âèäå êàêîé-ëèáî àíàëèòè÷åñêîé ôóíêöèè, îòðàæàþùåé
çàâèñèìîñòü ìåæäó ñèëîé ñîïðîòèâëåíèÿ âîçäóõà è ñêîðîñòüþ äâèæåíèÿ öåíòðà
ìàññ ËÀ.  ïîäîáíûõ ðåøåíèÿõ, êàê ïðàâèëî, ó÷èòûâàþòñÿ òîëüêî îäíà-äâå àýðîäè-
íàìè÷åñêèå õàðàêòåðèñòèêè, íàïðèìåð òîëüêî ëîáîâîå ñîïðîòèâëåíèå è ïîäúåìíàÿ
ñèëà, ñâÿçü ìåæäó êîòîðûìè äàåòñÿ â âèäå ñïåöèàëüíîé ôóíêöèè – ïîëÿðû ËÀ, îïè-
ñûâàåìîé àíàëèòè÷åñêèì âûðàæåíèåì.
209
 òðåòüþ ãðóïïó âõîäÿò ìåòîäû, îñíîâàííûå íà èñêóññòâåííûõ ïðåîáðàçîâàíè-
ÿõ îñíîâíûõ äèôôåðåíöèàëüíûõ óðàâíåíèé äâèæåíèÿ, ïðèâîäÿùèõ ê ðàçäåëåíèþ ïå-
ðåìåííûõ. Îäíàêî ðàçäåëåíèå ïåðåìåííûõ íå âñåãäà ïîçâîëÿåò ïîëó÷èòü ðåøåíèå â
êîíå÷íîì âèäå, äàþùåì ÷èñëåííûé ðåçóëüòàò. Âî ìíîãèõ ñëó÷àÿõ îêàçûâàåòñÿ íåîá-
õîäèìûì ïðåäñòàâëÿòü èíòåãðàëû â âèäå òàáëèö èëè ãðàôèêîâ. Ïîäîáíûå ïðåîáðà-
çîâàíèÿ íå îáëàäàþò íåîáõîäèìîé ñòðîãîñòüþ ðåøåíèÿ è òðåáóþò ââåäåíèÿ ñîãëà-
ñóþùèõ êîýôôèöèåíòîâ è èñïîëüçîâàíèÿ âñïîìîãàòåëüíûõ òàáëèö.
Ê ÷åòâåðòîé ãðóïïå îòíîñÿòñÿ ìåòîäû ðåøåíèÿ, â êîòîðûõ çàðàíåå çàäàåòñÿ
âèä ôóíêöèè, îïðåäåëÿþùèé èçìåíåíèå òîé èëè èíîé õàðàêòåðèñòèêè äâèæåíèÿ.
Íàïðèìåð, ìîæåò áûòü ôèêñèðîâàí âèä çàâèñèìîñòè ñêîðîñòè äâèæåíèÿ öåíòðà
ìàññ ËÀ îò âðåìåíè V(t). Ýòè ìåòîäû òðåáóþò äîïîëíèòåëüíîãî çàäàíèÿ çàêîíà ñî-
ïðîòèâëåíèÿ ñðåäû èëè ïðîâåäåíèÿ ïîñëåäîâàòåëüíûõ ïðèáëèæåíèé ïðè âû÷èñëåíèè
îïðåäåëåííûõ èíòåãðàëîâ, ñîäåðæàùèõ ôóíêöèè îò ñèëû ñîïðîòèâëåíèÿ âîçäóõà.
Êàæäûé èç ìåòîäîâ ïðèìåíèì äëÿ êîíêðåòíûõ óñëîâèé ïîëåòà ñíàðÿäà, îòâå÷àþ-
ùèõ äîïóùåíèÿì, ïðèíÿòûì ïðè ñîñòàâëåíèè äèôôåðåíöèàëüíûõ óðàâíåíèé äâèæå-
íèÿ.
5.1 . ÏÎØÀÃÎÂÛÅ ÌÅÒÎÄÛ ÈÍÒÅÃÐÈÐÎÂÀÍÈß
È ÏÐÀÊÒÈÊÀ ÈÕ ÏÐÈÌÅÍÅÍÈß
5.1.1. ×ÈÑËÅÍÍÎÅ ÈÍÒÅÃÐÈÐÎÂÀÍÈÅ ÐÀÇÍÎÑÒÍÛÌ ÌÅÒÎÄÎÌ
Ìåòîäû ÷èñëåííîãî èíòåãðèðîâàíèÿ ïîçâîëÿþò âû÷èñëèòü çíà-
÷åíèå èíòåãðàëà îò ôóíêöèè, çàäàííîé òàáëè÷íî. Äëÿ ýòîé öåëè èñ-
ïîëüçóåòñÿ òàê íàçûâàåìàÿ èíòåðïîëèðóþùàÿ ôóíêöèÿ, êîòîðàÿ ïîä
çíàêîì èíòåãðàëà çàìåíÿåò äåéñòâèòåëüíóþ ôóíêöèþ, àíàëèòè÷å-
ñêèé âèä êîòîðîé íåèçâåñòåí. Ïðè óñëîâèè, ÷òî òàêàÿ çàìåíà ïðîèñ-
õîäèò íà ìàëîì ó÷àñòêå êðèâîé, òî÷íîñòü èíòåãðèðîâàíèÿ ìîæåò
áûòü äîñòàòî÷íî âûñîêîé.
Ïðåäïîëîæèì, ÷òî èìååòñÿ ôóíêöèÿ y = f(x). Òîãäà ïðèðàùåíèå
îïðåäåëåííîãî èíòåãðàëà â ïðåäåëàõ îò xn äî xn+1 åñòü
∆Jy
d
x
n
x
x
n
n
=
+
∫.
1
(5.1)
Ñàìîé ïðîñòîé ÿâëÿåòñÿ ëèíåéíàÿ èíòåðïîëèðóþùàÿ ôóíêöèÿ
()
( )()
()
,
yyyyxxxx
nn
n
nn
n
−−
=
−−
+
−
+
−
1
1
1
1
(5.2)
ãäå xn+1 − xn = hx – øàã èçìåíåíèÿ àðãóìåíòà; yn+1 − yn = ∆yn – ðàçíîñòü
ìåæäó n-ì è n + 1-ì çíà÷åíèÿìè ôóíêöèè.
210
Èç ôîðìóëû (5.2) èñêîìóþ âåëè÷èíó ôóíêöèè, ñîîòâåòñòâóþ-
ùóþ àðãóìåíòó õ, çàäàäèì â âèäå
yy hxxy
nx
nn
=+
−
−1
().
∆
(5.3)
Ïðè ëèíåéíîì èíòåðïîëèðîâàíèè ïëîùàäü ïîä êðèâîé, èçîáðà-
æàþùåé ôóíêöèþ f(x), áóäåò ðàçáèòà íà ðÿä òðàïåöèé. Èíòåãðèðî-
âàíèå ïî ìåòîäó òðàïåöèé äàåò ñóùåñòâåííóþ îøèáêó è, êàê ïðàâè-
ëî, íàõîäèò îãðàíè÷åííîå ïðèìåíåíèå ïðè áàëëèñòè÷åñêèõ ðàñ÷å-
òàõ.
Ïðîñòåéøèì ìåòîäîì ÷èñëåííîãî èíòåãðèðîâàíèÿ ÿâëÿåòñÿ ìå-
òîä Ë. Ýéëåðà. Ïóñòü òðåáóåòñÿ íàéòè ðåøåíèå äèôôåðåíöèàëüíîãî
óðàâíåíèÿ ïåðâîãî ïîðÿäêà ′ =
yf
x
y
x
(, )ïðè íà÷àëüíûõ óñëîâèÿõ
x=x0,y=y0.
Ïðè èíòåãðèðîâàíèè øàã èçìåíåíèÿ àðãóìåíòà hx âûáèðàåòñÿ
òàê, ÷òîáû â ïðåäåëàõ ýòîãî øàãà ôóíêöèÿ f(x, y) ñîõðàíÿëà ïîñòîÿí-
íîå çíà÷åíèå. Çàìåíÿÿ ïðîèçâîäíóþ îòíîøåíèåì ìàëûõ êîíå÷íûõ
ïðèðàùåíèé, ìîæíî çàïèñàòü
′=≈
y
dy
dx
y
x
x
∆
∆
.
Äëÿ ïåðâîãî ó÷àñòêà èíòåãðèðîâàíèÿ ∆x0 = x1 − x0 = hx, ∆y0 =
=y1−y0,èòîãäà
fxy
yy
hx
(,)
.
00
10
=
−
 ðåçóëüòàòå ïðåîáðàçîâàíèÿ áóäåì èìåòü
yyh
fxy
x
10
0
0
=+ (,)
.
Ïîâòîðÿÿ îïåðàöèþ äëÿ ïîñëåäóþùèõ ó÷àñòêîâ èíòåãðèðîâàíèÿ,
ïîëó÷àþò ïîñëåäîâàòåëüíûå çíà÷åíèÿ ôóíêöèé
yyh
fxy
yyh
fxy
x
x
21
1
1
32
2
2
=+
=+
(, );
(,)
.
 îáùåì âèäå ôîðìóëà ÷èñëåííîãî èíòåãðèðîâàíèÿ äèôôåðåí-
öèàëüíîãî óðàâíåíèÿ ïåðâîãî ïîðÿäêà ïî ìåòîäó Ë. Ýéëåðà çàïè-
øåòñÿ ñëåäóþùèì îáðàçîì:
yyh
f
x
y
nn
x
n
n
+=+
1
(,)
.
(5.4)
Ïðè ðåøåíèè çàäà÷ âíåøíåé áàëëèñòèêè ìåòîä Ë. Ýéëåðà ìîæåò
ïðèâåñòè ê çíà÷èòåëüíûì îøèáêàì. Òî÷íîñòü ìåòîäà ïîâûøàåòñÿ ñ
211
óìåíüøåíèåì øàãà èíòåãðèðîâàíèÿ, îäíàêî ïðè ýòîì óâåëè÷èâàåò-
ñÿ îáùèé îáúåì âû÷èñëåíèé è ïðîèñõîäèò íàêîïëåíèå îøèáîê â
ïðîöåññå èíòåãðèðîâàíèÿ. Ïîýòîìó â íàèáîëåå ðàñïðîñòðàíåííûõ
ìåòîäàõ ÷èñëåííîãî èíòåãðèðîâàíèÿ óðàâíåíèé âíåøíåé áàëëèñòè-
êè èñïîëüçóþòñÿ ñïåöèàëüíûå èíòåðïîëèðóþùèå ôóíêöèè, ïîçâî-
ëÿþùèå óâåëè÷èâàòü øàã èíòåãðèðîâàíèÿ ïî ñðàâíåíèþ ñ èíòåãðè-
ðîâàíèåì ïî ìåòîäó òðàïåöèé è ìåòîäó Ë. Ýéëåðà ïðè ñîõðàíåíèè
íåîáõîäèìîé òî÷íîñòè.
Èíòåðïîëèðóþùàÿ ôóíêöèÿ ñîñòàâëÿåòñÿ â âèäå öåëîãî ìíîãî-
÷ëåíà, ñòåïåíü êîòîðîãî íà åäèíèöó ìåíüøå ÷èñëà çàäàííûõ çíà÷å-
íèé ôóíêöèè íà ðàññìàòðèâàåìîì ó÷àñòêå èíòåðïîëèðîâàíèÿ. Êðè-
âàÿ, ñîîòâåòñòâóþùàÿ ìíîãî÷ëåíó, äîëæíà ïðîõîäèòü ÷åðåç âñå èñ-
ïîëüçóåìûå òî÷êè, íîñÿùèå íàçâàíèå óçëîâ èíòåðïîëÿöèè.
Âûïîëíåíèå ýòèõ óñëîâèé îáóñëîâëèâàåò åäèíñòâåííîñòü èíòåðïî-
ëèðóþùåé ôóíêöèè. Èíòåðïîëÿöèîííûå ôîðìóëû îáåñïå÷èâàþò
âîçìîæíîñòü ïðèáëèæåííîãî âû÷èñëåíèÿ çíà÷åíèé ôóíêöèè äëÿ
çíà÷åíèé àðãóìåíòà, îòëè÷íûõ îò óçëîâ èíòåðïîëèðîâàíèÿ. Ïðè
ýòîì ðàçëè÷àþò èíòåðïîëèðîâàíèå, êîãäà àðãóìåíò õ ëåæèò âíóòðè
çàäàííîãî èíòåðâàëà xn − xn+1, è ýêñòðàïîëèðîâàíèå, êîãäà çíà÷åíèå
àðãóìåíòà íàõîäèòñÿ çà ïðåäåëàìè ýòîãî èíòåðâàëà.
Íàèáîëåå óíèâåðñàëüíîé ÿâëÿåòñÿ èíòåðïîëèðóþùàÿ ôóíêöèÿ Ëà-
ãðàíæà. Ïðè åå èñïîëüçîâàíèè íà âûáîð óçëîâ èíòåðïîëÿöèè íå íà-
êëàäûâàåòñÿ êàêèõ-ëèáî ñïåöèàëüíûõ îãðàíè÷åíèé. Èíòåðïîëÿöè-
îííàÿ ôîðìóëà Ëàãðàíæà èìååò âèä
yfx
xxxx xx
xxxx xx
y
m
m
=≈
−−
−
−−
−
() ()
()
()
()
()
()
12
0102 0
0
K
K
+
+
−−
−
−−
−
+
+
()
()
()
()
()
()
(
xxxx xx
xxxx xx
y
m
m
02
1012 1
1
K
K
K
K
xxxx xx
xxxx xx
y
m
mmm
m
m
−−
−
−−
−
−
−
01
1
01
1
)( )(
)
()
()
()
.
K
K
(5.5)
Èçâåñòíû è äðóãèå èíòåðïîëÿöèîííûå ôîðìóëû: ïåðâàÿ è âòîðàÿ
ôîðìóëû Íüþòîíà, ôîðìóëû Ãàóññà, Áåññåëÿ, Ñòèðëèíãà. Èíòåðïî-
ëÿöèîííûå ôîðìóëû Íüþòîíà, ñîñòàâëÿåìûå ñ èñïîëüçîâàíèåì
òàáëèö êîíå÷íûõ ðàçíîñòåé, ïîëó÷àþòñÿ ïðè óñëîâèè ïîñòîÿíñòâà
øàãà àðãóìåíòà: hx = const.
Åñëè íåêîòîðàÿ ôóíêöèÿ y − f(x) çàäàíà òàáëè÷íî ñ èçìåíåíèåì
àðãóìåíòà ÷åðåç ïîñòîÿííûé øàã hx, òî êîíå÷íîé ðàçíîñòüþ ôóíê-
öèè ïåðâîãî ïîðÿäêà, èëè ïåðâîé ðàçíîñòüþ, íàçûâàåòñÿ âåëè÷èíà
∆y = ∆f(x)=f(x + hx) − f(x). Âòîðàÿ ðàçíîñòü ôóíêöèè ∆2y = ∆2f(x)=
=∆[∆f(x)] è ò.ä . ×òîáû ñîñòàâèòü òàáëèöó êîíå÷íûõ ðàçíîñòåé, ñëå-
212
Òàáëèöà 5.1
Ãîðèçîíòàëüíàÿ òàáëèöà êîíå÷íûõ ðàçíîñòåé ôóíêöèè âèäà y = f(x)
xy∆y
∆2y
∆3y
xn−3
yn−3
∆yn−3
∆2yn−3
∆3yn−3
xn−2
yn−2
∆yn−2
∆2yn−2
∆3yn−2
xn−1
yn−1
∆yn−1
∆2
1
yn−
*
∆3
1
yn−
*
x
yn
*
∆yn
*
∆2yn
∆3yn
xn+1
yn+1
∆yn+1
∆2yn+1
xn+2
yn+2
∆yn+2
xn+3
yn+3
äóåò èç êàæäîãî çíà÷åíèÿ ôóíêöèè âû÷åñòü åìó ïðåäøåñòâóþùåå è
ïîëó÷åííûé ðåçóëüòàò çàïèñàòü â ñòîëáöå ñïðàâà â îäíîé ñòðîêå ñ
âû÷èòàåìûì, ïðèäàâ åìó íîìåð ïîñëåäíåãî (òàáë. 5.1). Ñîñòàâëåííóþ
ïîäîáíûì îáðàçîì òàáëèöó íàçûâàþò ãîðèçîíòàëüíîé òàáëèöåé
êîíå÷íûõ ðàçíîñòåé ôóíêöèè.
Ââîäÿ íîâóþ ïåðåìåííóþ
ξ=
−
xx
hx
0,
ãäå õ0 – íà÷àëüíîå çíà÷åíèå àðãóìåíòà, íàïèøåì ôîðìóëó äëÿ ïåðâîãî
èíòåðïîëèðóþùåãî ïîëèíîìà Íüþòîíà ñòåïåíè íå âûøå n:
Pxy y
y
y
n
()
()
!
()
()
!
(
=+
+
−
+
+
−−
++
00
2
0
3
0
1
2
12
3
ξξξ
ξξξ
ξ
∆∆
∆K
ξξ
−−
+
11
0
)()
!
.
K
n
n
yn∆
(5.6)
Âòîðàÿ èíòåðïîëÿöèîííàÿ ôîðìóëà Íüþòîíà ïðèìåíÿåòñÿ äëÿ
èíòåðïîëèðîâàíèÿ â êîíöå èçâåñòíûõ çíà÷åíèé ôóíêöèè (ò.å . äëÿ
ýêñòðàïîëèðîâàíèÿ):
Pxy y
y
y
nnn
n
n
()
()
!
()
()
!
=+
+
+
+
+
++
−−
−
ξ
ξξ
ξξξ
∆∆
∆
1
2
2
3
1
2
12
3
30
11
++
++
−
K
K
ξξ
ξ
()( )
!
,
n
n
yn∆
(5.7)
ãäå yn – ïîñëåäíåå èçâåñòíîå çíà÷åíèå ôóíêöèè.
213
Ïðè íàëè÷èè òàáëèöû êîíå÷íûõ ðàçíîñòåé ôóíêöèè èíòåðïîëè-
ðóþùàÿ ôóíêöèÿ ñîñòàâëÿåòñÿ â ñëåäóþùåì ïîðÿäêå.
1. Âûïèñûâàåòñÿ ñòðîêà ïîñëåäîâàòåëüíûõ ýëåìåíòîâ, ò.å . ÷èñåë
èç òàáëèöû ðàçíîñòåé, íåïîñðåäñòâåííî çàâèñÿùèõ îò ïðåäûäóùèõ
÷èñåë (ñòðîêîé íàçûâàþò òàêóþ ñîâîêóïíîñòü ïîñëåäîâàòåëüíûõ
ýëåìåíòîâ, â êîòîðóþ èç êàæäîãî ñòîëáöà áåðåòñÿ òîëüêî ïî îäíîìó
ýëåìåíòó).
2. Ïåðåä êàæäûì ýëåìåíòîì ñòðîêè, êðîìå ïåðâîãî, ñòàâèòñÿ êî-
ýôôèöèåíò â âèäå äðîáè. Åå çíàìåíàòåëü åñòü ôàêòîðèàë, ïîðÿäîê
êîòîðîãî ðàâåí ïîðÿäêó ýëåìåíòà, à â ÷èñëèòåëå ñîäåðæèòñÿ ñòîëüêî
ñîìíîæèòåëåé âèäà ξ –,
i êàêîâ ïîðÿäîê ðàçíîñòè.
3. Ïåðâûé ìíîæèòåëü ÷èñëèòåëÿ äîëæåí èìåòü âèä ξ – i0, ãäå i0 –
èíäåêñ ïðåäûäóùåãî ýëåìåíòà êîíå÷íîé ðàçíîñòè (íàïðèìåð, åñëè
ïðåäûäóùèé ýëåìåíò èìååò íîìåð – 3, òî èíäåêñ i0 = –3).
Âñå ïîñëåäóþùèå ñîìíîæèòåëè óáûâàþò íà åäèíèöó.
Èñïîëüçóÿ ýòî ïðàâèëî, ïîëó÷èì â êà÷åñòâå ïðèìåðà èíòåðïîëÿ-
öèîííóþ ôîðìóëó äëÿ ëîìàíîé ñòðîêè, îòâå÷àþùåé çíà÷åíèþ àðãó-
ìåíòà xn:
yyy
y
y
nn
n
n
=+
+
−
+
+−
−−
ξξ
ξξξ
ξ
1
1
2
11
3
2
1
3
1
!
()
!
()()
!
.
∆∆
∆
(5.8)
Ôîðìóëà (5.8) îòâå÷àåò ëîìàíîé ñòðîêå ïîñëåäîâàòåëüíûõ ýëå-
ìåíòîâ, è êîíå÷íûå ðàçíîñòè, èñïîëüçîâàííûå äëÿ åå íàïèñàíèÿ,
îòìå÷åíû â òàáë. 5 .1 çâåçäî÷êîé.  ñëó÷àå íåçàâèñèìîé ïåðåìåííîé
ξ èç (5.1) ïîëó÷èì ïðèðàùåíèå îïðåäåëåííîãî èíòåãðàëà äëÿ îäíîãî
øàãà èíòåãðèðîâàíèÿ â âèäå
∆Jhy
d
nx
=
∫ξ,
0
1
(5.9)
òàêêàêdξ=dx/hx.
Äëÿ íàõîæäåíèÿ ∆Jn ìîæíî âîñïîëüçîâàòüñÿ îäíîé èç èíòåðïî-
ëÿöèîííûõ ôîðìóë, ñîñòàâëåííûõ íà îñíîâàíèè ñòðîê ïîñëåäîâà-
òåëüíûõ ýëåìåíòîâ. Òàê, íàïðèìåð, ïîäñòàâèâ çíà÷åíèå y èç ôîðìó-
ëû (5.8) â (5.9), ìîæíî ïîëó÷èòü ñëåäóþùåå âûðàæåíèå äëÿ âû÷èñ-
ëåíèÿ ïðèðàùåíèÿ îïðåäåëåííîãî èíòåãðàëà:
∆∆
∆
∆
Jhyyy
h
nx
n
n
n
n
=+−
−
⎛
⎝⎜
⎞
⎠⎟
−−
1
2
1
12
1
24
2
1
3
1.
(5.10)
214
Àíàëîãè÷íî äëÿ ãîðèçîíòàëüíîé ñòðîêè ïîñëåäîâàòåëüíûõ ýëå-
ìåíòîâ
∆∆
∆
∆
Jhyyy
y
nx
n
n
n
n
=+− +
⎛
⎝⎜
⎞
⎠⎟
−
1
2
1
12
1
24
2
1
3
.
(5.11)
Ïðè èñïîëüçîâàíèè íàêëîííîé ýêñòðàïîëÿöèîííîé ñòðîêè ôîð-
ìóëà ïðèîáðåòàåò âèä
∆∆
∆
∆
Jhy y
y
y
nx
n
n
n
n
=++
+
⎛
⎝⎜
⎞
⎠⎟
−−
−
1
2
5
12
3
8
1
2
2
3
3.
(5.12)
Ïîñëåäíÿÿ ôîðìóëà ïîçâîëÿåò èíòåðïîëèðîâàòü âïåðåä (ýêñòðà-
ïîëèðîâàòü), îñíîâûâàÿñü íà õàðàêòåðå ïðåäûäóùåãî èçìåíåíèÿ
ôóíêöèè.
Ïðèáàâëÿÿ ðàçíîñòü ôóíêöèè ∆yn, îïðåäåëåííóþ ïî ñîîòâåòñò-
âóþùåé ôîðìóëå, ê èçâåñòíîìó çíà÷åíèþ yn, ïîëó÷àåì ïîñëåäóþ-
ùåå èñêîìîå çíà÷åíèå ôóíêöèè
yyy
nnn
+=+
1
∆.
(5.13)
Ôîðìóëû, ñîäåðæàùèå ðàçíîñòè òðåòüåãî ïîðÿäêà, ìîãóò áûòü
ïðèìåíåíû äëÿ íàðàùèâàíèÿ ñòðîê, åñëè èçâåñòíî íå ìåíåå ÷åòûðåõ
íà÷àëüíûõ çíà÷åíèé ïðîèçâîäíîé. Ïåðâîå çíà÷åíèå îïðåäåëÿåòñÿ
íà÷àëüíûìè óñëîâèÿìè x = x0 è y = y0 ïî èíòåãðèðóåìîìó äèôôå-
ðåíöèàëüíîìó óðàâíåíèþ. Íåäîñòàþùèå íà÷àëüíûå çíà÷åíèÿ ïðî-
èçâîäíûõ îáû÷íî íàõîäÿò ñïîñîáîì ïîñëåäîâàòåëüíûõ ïðèáëèæå-
íèé, ñóòü êîòîðîãî èçëîæåíà íèæå.
Ïóñòü çàäàíî äèôôåðåíöèàëüíîå óðàâíåíèå ïåðâîãî ïîðÿäêà
′=
y x f(x, y), êîòîðîå äàëåå áóäåì çàïèñûâàòü â âèäå y ′ = f(x, y). Íà-
÷àëüíûå çíà÷åíèÿ x0 è y0 èçâåñòíû, ñëåäîâàòåëüíî, èçâåñòíî çíà÷å-
íèå ′
y 0. Îïðåäåëåíèå íåäîñòàþùèõ ýëåìåíòîâ òàáëèöû ðàçíîñòåé íà-
÷èíàåòñÿ ñ ïåðâîãî ïðèáëèæåíèÿ
∆∆
yh
yyy y
00
100
=
′
=+
;.
Ïî èçâåñòíîìó çíà÷åíèþ y1 íàõîäèì ′ =
yf
x
y
11
1
(, )è âû÷èñëÿåì
∆′=
′−
′
yyy
010
.
Ïðè âûïîëíåíèè âòîðîãî ïðèáëèæåíèÿ ïî èçâåñòíûì èç ïåðâîãî
ïðèáëèæåíèÿ ′
y0, ′
y1 è ∆ ′y 0 îïðåäåëÿåì
∆∆∆
yhy yyy y
x
000
1
0
0
1
2
=
′+
′
⎛
⎝⎜
⎞
⎠⎟ =+
,
215
è
∆∆∆
yhy yyy y
x
110
2
1
1
1
2
=
′+
′
⎛
⎝⎜
⎞
⎠⎟ =+
,.
Ïîäñòàâëÿÿ â èñõîäíîå óðàâíåíèå èçâåñòíûå x1, y1 è x2, y2, íàõî-
äèì ′
y1è ′
y2,àòàêæå∆ ′ =
′−
′
yyy
010
;∆′=
′−
′
yyy
121
; ∆∆∆
2
′=
′−
′
yyy
010
. Òðåòüå
ïðèáëèæåíèå ÿâëÿåòñÿ êîíòðîëüíûì. Ïî çíà÷åíèÿì
∆∆
∆
∆∆
yhyyy
yhy y
x
x
000
2
0
111
1
2
1
12
1
2
1
=
′+
′−
′
⎛
⎝⎜
⎞
⎠⎟
=
′+
′−
,
12
2
0
∆′
⎛
⎝⎜
⎞
⎠⎟y
îïðåäåëÿåì y1 è y2 è âû÷èñëÿåì ′
y1, ′
y2,∆ ′y0,∆ ′y1,∆
2
′
y0.
 êà÷åñòâå ïðèìåðà ïðèâåäåì ðåçóëüòàòû ðàñ÷åòà õàðàêòåðèñòèê
äâèæåíèÿ íåóïðàâëÿåìîé ðàêåòû ìåòîäîì êîíå÷íûõ ðàçíîñòåé.
Òðåáóåòñÿ îïðåäåëèòü õàðàêòåðèñòèêè äâèæåíèÿ ËÀ, èìåþùåãî
ñëåäóþùèå êîíñòðóêòèâíûå ïàðàìåòðû:
d=0,5ì;m0=1174êã;|•|
m =86,59êã/ñ;ñ1=Ð0/m0=148ì/ñ2;ñ2=
= SaPON/m0 = 16,15 ì/ñ2; tk = 2,8 ñ ïðè íà÷àëüíûõ óñëîâèÿõ V0 =
=50ì/ñ;θ0=40,6°;õ0=y0=0
.
Êîýôôèöèåíò ëîáîâîãî ñîïðîòèâëåíèÿ cx a
()
M íà ó÷àñòêå äåéñò-
âèÿ àêòèâíûõ ñèë ïðèâåäåí â òàáë. 5 .2.
Ñèëà ëîáîâîãî ñîïðîòèâëåíèÿ íà ïàññèâíîì ó÷àñòêå çàäàíà
òèïîâîé ôóíêöèåé G(Vτ), çíà÷åíèÿ êîòîðîé ïðèâåäåíû â
òàáë. 5 .3.
Òàáëèöà 5.2
Êîýôôèöèåíòû ñèëû ëîáîâîãî ñîïðîòèâëåíèÿ â ôóíêöèè ÷èñåë Ìàõà
M
0,01
0,55
0,60
0,70
0,80
0,90
1,00
1,02
cxa
0,30
0,30
0,33
0,42
0,54
0,68
0,82
0,85
M
1,06
1,08
1,10
1,20
1,30
1,40
1,50
1,60
cxa
0,87
0,86
0,86
0,83
0,80
0,77
0,74
0,71
M
1,70
1,80
1,90
2,30
2,90
cxa
0,68
0,65
0,62
0,50
0,31
216
Òàáëèöà 5.3
Çíà÷åíèÿ òèïîâîé ôóíêöèè ñîïðîòèâëåíèÿ
Vτ, ì/ñ
200
220
240
260
280
G(Vτ)
0,1466
0,1611
0,1753
0,1900
0,2098
Vτ, ì/ñ
300
320
340
360
380
G(Vτ)
0,2430
0,3474
0,5099
0,6111
0,6718
Vτ, ì/ñ
400
420
440
460
480
G(Vτ)
0,7141
0,7480
0,7770
0,8028
0,8257
Vτ, ì/ñ
500
520
540
560
580
600
G(Vτ)
0,8472
0,8671
0,8856
0,9033
0,9203
0,9363
×òîáû âûïîëíèòü ðàñ÷åòû, íåîáõîäèìû òàêæå çíà÷åíèÿ ôóíê-
öèé π(y), H(y), a(y) äëÿ àêòèâíîãî ó÷àñòêà è Hτ(y), ττ
ON /–äëÿ
ïàññèâíîãî ó÷àñòêà òðàåêòîðèè. Îíè çàäàþòñÿ â âèäå ñïåöèàëü-
íûõ òàáëèö. Äëÿ óäîáñòâà âûïîëíåíèÿ ðàñ÷åòîâ â òàáë. 5.4, 5.5
ïðèâîäÿòñÿ ôðàãìåíòû òàáëèö, ñîäåðæàùèå íåîáõîäèìûé ÷èñëî-
âîé ìàòåðèàë.
Òàáëèöà 5.4
Èçìåíåíèå ïî âûñîòå ôóíêöèé π(y), H(y)èa(y)
y,ì
0
100
200
300
400
π(y)
1,000
0,9882
0,9765
0,9649
0,9535
H(y)
1,000
0,9904
0,9849
0,9715
0,9622
a(y), ì/ñ
340,7
339,9
339,5
339,1
338,8
y,ì
500
600
700
800
900
1000
π(y)
0,9421
0,9309
0,9198
0,9087
0,8978
0,8879
H(y)
0,9529
0,9437
0,9345
0,9254
0,9164
0,9075
a(y), ì/ñ
338,4
338,0
337,6
337,2
336,8
336,4
217
Òàáëèöà 5.5
Èçìåíåíèå ïî âûñîòå ôóíêöèé Hτ(y)è ττ
ON/
y,ì
0
200
400
600
800
1000
Hτ(y)
1,000
0,97
0,9583
0,9371
0,9171
0,8976
ττ
ON/
1,000
1,002
1,004
1,007
1,009
1,011
y,ì
1200
1400
1600
1800
2000
2200
Hτ(y)
0,8775
0,8587
0,8400
0,8210
0,8032
0,7839
ττ
ON/
1,014
1,016
1,018
1,021
1,023
1,026
y,ì
2400
2600
2800
3000
Hτ(y)
0,7677
0,7500
0,7334
0,7164
ττ
ON/
1,028
1,031
1,033
1,733
Äëÿ àêòèâíîãî ó÷àñòêà òðàåêòîðèè èíòåãðèðóåìàÿ ñèñòåìà óðàâ-
íåíèé èìååò âèä
•
()
;
•
;•
;•
,
uD
E
u
p
g
u
yp
uxu
=−
=
−=
=
1
μ
(5.14)
ãäåμ=m/m0;D=P/(m0V);E=Xa/(m0V);p=tgθ;u=Vcosθ.
Íà÷àëüíûå óñëîâèÿ äëÿ ïðèâåäåííîé ñèñòåìû âû÷èñëÿþò ñ ïî-
ìîùüþ ñîîòíîøåíèé u0 = V0 cosθ0; p0 =tgθ0.
Ðàñ÷åò ïàññèâíîãî ó÷àñòêà óäîáíî âûïîëíÿòü, èíòåãðèðóÿ ñèñòå-
ìó äèôôåðåíöèàëüíûõ óðàâíåíèé, çàïèñàííóþ ïî àðãóìåíòó õ:
′=−
=−
′=
′=
uc
H
y
G
Vp
'
y
u
yp
t
u
xx
x
x
x
ττ
()( );
;
;
,
2
1
(5.15)
ãäå Vu
p
ON
τ
ττ
=+
/.
12
Îòìåòèì íåêîòîðûå îñîáåííîñòè ðåøåíèÿ ñèñòåìû (5.15).
Íà÷àëüíûå óñëîâèÿ èíòåãðèðîâàíèÿ ñîîòâåòñòâóþò êîíå÷íûì
çíà÷åíèÿì ýëåìåíòîâ òðàåêòîðèè, ïîëó÷åííûì ïðè ðàñ÷åòå àêòèâ-
íîãî ó÷àñòêà.  òîì ñëó÷àå, åñëè çàäàííîå âðåìÿ tk íå ïîïàäàåò íà óç-
ëîâîå çíà÷åíèå àðãóìåíòà, ýëåìåíòû òðàåêòîðèè íàõîäÿò ñ ïîìî-
ùüþ ôîðìóë èíòåðïîëÿöèè.
218
Äëÿ îïðåäåëåíèÿ "ðàçãîííûõ" òî÷åê èñïîëüçóþò ñáëèæåíèÿ, êî-
òîðûå âûïîëíÿþò ïî òîé æå ñõåìå, ÷òî è äëÿ àêòèâíîãî ó÷àñòêà. Õà-
ðàêòåð èçìåíåíèÿ îñíîâíûõ ýëåìåíòîâ òðàåêòîðèè â ïðîöåññå äâè-
æåíèÿ ËÀ èëëþñòðèðóþò ïîêàçàííûå íà ðèñ. 5 .1 ãðàôèêè çàâèñèìî-
ñòåéy=f1(x),V =f2(x),p =f3(x), ′ =
ux f4(x), êîòîðûå ïîñòðîåíû ïî
ðåçóëüòàòàì ðàñ÷åòîâ äëÿ ðàññìîòðåííîãî ïðèìåðà.
5.1.2. ÒÎ×ÍÎÑÒÜ ÐÀÑ×ÅÒÎÂ È ÂÛÁÎÐ ØÀÃÀ ÈÍÒÅÃÐÈÐÎÂÀÍÈß
Ïîãðåøíîñòü ðåçóëüòàòîâ ðàñ÷åòîâ õàðàêòåðèñòèê äâèæåíèÿ ËÀ
îïðåäåëÿåòñÿ ñëåäóþùèìè òèïîâûìè ãðóïïàìè îøèáîê.
1. Ïîãðåøíîñòè ïîñòàíîâêè çàäà÷è, îïðåäåëÿåìûå ñòåïåíüþ
ïðèáëèæåíèÿ ìàòåìàòè÷åñêîé ìîäåëè ê äåéñòâèòåëüíîìó ïðîöåññó
äâèæåíèÿ. Ýòà ãðóïïà îøèáîê, íàçûâàåìàÿ ïîãðåøíîñòÿìè çàäà÷è,
îáóñëîâëèâàåòñÿ óñòàíîâëåííûìè äîïóùåíèÿìè è âûáîðîì ñèñòå-
ìû óðàâíåíèé.
2. Ïîãðåøíîñòè ìåòîäà ðåøåíèÿ, íàïðèìåð ââåäåíèå àïïðîêñè-
ìèðóþùèõ ôóíêöèé äëÿ ñèëû ñîïðîòèâëåíèÿ âîçäóõà, çàìåíà ÷èñ-
ëåííîãî ðåøåíèÿ ïðèáëèæåííûì àíàëèòè÷åñêèì è ò.ä .
3. Ïîãðåøíîñòè ââåäåíèÿ â ðåøåíèå ðÿäîâ èëè äðóãèõ ìàòåìàòè-
÷åñêèõ ïîñëåäîâàòåëüíîñòåé è èñïîëüçîâàíèÿ òîëüêî èõ íà÷àëüíûõ
219
Ðèñ. 5.1 . Õàðàêòåð èçìåíåíèÿ îñíîâíûõ ïàðàìåòðîâ äâèæåíèÿ è ýëåìåíòîâ òðàåêòî-
ðèè â ïðîöåññå äâèæåíèÿ ËÀ
÷ëåíîâ. Òàêèå ïîãðåøíîñòè íàçûâàþòñÿ îñòàòî÷íûìè è îáóñëîâëè-
âàþòñÿ âåëè÷èíîé ñóììû îïóùåííûõ ÷ëåíîâ ðÿäà.
4. Îøèáêè çàäàíèÿ èñõîäíûõ äàííûõ, íàïðèìåð îïðåäåëåíèÿ
àýðîäèíàìè÷åñêèõ õàðàêòåðèñòèê. Òàêèå ïîãðåøíîñòè íàçûâàþò-
ñÿ íà÷àëüíûìè.
5. Òåõíè÷åñêèå ïîãðåøíîñòè âû÷èñëåíèé, ê êîòîðûì îáû÷íî îò-
íîñÿò ïîãðåøíîñòè îêðóãëåíèÿ è áîëüøóþ ãðóïïó ïîãðåøíîñòåé
äåéñòâèé íàä ïðèáëèæåííûìè ÷èñëàìè.
Ðàçëè÷íûå îáëàñòè áàëëèñòè÷åñêèõ èññëåäîâàíèé è ðàçëè÷íûå
ìåòîäû ðåøåíèÿ áàëëèñòè÷åñêèõ çàäà÷ èìåþò ñâîè ñïåöèôè÷åñêèå
îøèáêè. Ïðè ïðèìåíåíèè ìåòîäà êîíå÷íûõ ðàçíîñòåé ïîãðåøíîñòü
âû÷èñëåíèé îïðåäåëÿåòñÿ â îñíîâíîì îøèáêàìè àïïðîêñèìàöèè,
îøèáêàìè ìàòåìàòè÷åñêèõ äåéñòâèé è îøèáêàìè îêðóãëåíèÿ. Ïî-
ãðåøíîñòè ìàòåìàòè÷åñêèõ äåéñòâèé çàâèñÿò îò îáùåé ñõåìû ðåøå-
íèÿ è ïðàêòè÷åñêè íåóñòðàíèìû. Îøèáêè ìàòåìàòè÷åñêèõ äåéñòâèé
è îøèáêè îêðóãëåíèÿ îáû÷íî ìàëî ñêàçûâàþòñÿ íà òî÷íîñòè îêîí-
÷àòåëüíûõ ðåçóëüòàòîâ ïðè ðàñ÷åòå òðàåêòîðèé.
Îøèáêè àïïðîêñèìàöèè âûçûâàþòñÿ çàìåíîé äåéñòâèòåëüíîé
ôóíêöèè èëè åå ïðîèçâîäíîé èíòåðïîëèðóþùåé ôóíêöèåé. Âåëè-
÷èíà îøèáêè àïïðîêñèìàöèè îïðåäåëÿåòñÿ ïîðÿäêîì óäåðæèâàå-
ìîé ðàçíîñòè â èíòåðïîëèðóþùåé ôóíêöèè è øàãîì àðãóìåíòà.
 ïðîöåññå íàðàùèâàíèÿ ñòðîê îøèáêè àïïðîêñèìàöèè, ìàòåìàòè-
÷åñêèõ äåéñòâèé è îêðóãëåíèÿ íàêàïëèâàþòñÿ. Âûáîð øàãà èíòåãðè-
ðîâàíèÿ ÿâëÿåòñÿ âàæíûì ýòàïîì âñåãî ðàñ÷åòà, òàê êàê åãî çíà÷å-
íèåì îïðåäåëÿåòñÿ íå òîëüêî òî÷íîñòü, íî è òðóäîåìêîñòü ðàñ÷åòîâ.
Ïðè ìàëîì øàãå èíòåãðèðîâàíèÿ ìîæíî îòêàçàòüñÿ îò èñïîëüçî-
âàíèÿ ðàçíîñòåé ïðîèçâîäíûõ âûñîêèõ ïîðÿäêîâ (âòîðîãî è âûøå),
îäíàêî ïðè ýòîì âîçðàñòàåò ÷èñëî ðàñ÷åòíûõ òî÷åê è â ïðîöåññå ðàñ-
÷åòîâ óâåëè÷èâàåòñÿ íàêîïëåíèå îøèáîê. Ïðè áîëüøîì øàãå ñîêðà-
ùàåòñÿ îáúåì âû÷èñëåíèé, íî óìåíüøàåòñÿ òî÷íîñòü.
Âûáîð ðàçìåðà øàãà èíòåãðèðîâàíèÿ çàâèñèò îò ìíîãèõ âåëè÷èí
è îïðåäåëÿåòñÿ àáñîëþòíîé è îòíîñèòåëüíîé îøèáêàìè êîíå÷íîãî
ðåçóëüòàòà. Íåîáõîäèìîñòü óìåíüøåíèÿ øàãà â ïðîöåññå ðàñ÷åòîâ
îáû÷íî ñâÿçàíà ñ ðåçêèì èçìåíåíèåì îäíîé èç âåëè÷èí, íàïðèìåð
èçìåíåíèåì âåëè÷èíû ñõ(Ì) â îáëàñòè ñêîðîñòåé äâèæåíèÿ ËÀ,
áëèçêèõ ê ñêîðîñòè çâóêà. Ïîñëå ïðîõîæäåíèÿ îáëàñòè çâóêîâûõ
ñêîðîñòåé ïðè äàëüíåéøåì ïëàâíîì èçìåíåíèè ñõ(Ì) øàã èíòåãðè-
ðîâàíèÿ öåëåñîîáðàçíî âíîâü óâåëè÷èâàòü. Êàê ïðàâèëî, ñòàíäàðò-
íûå ïðîãðàììû èíòåãðèðîâàíèÿ íà ÝÂÌ èìåþò ïðîöåäóðû àâòîìà-
òè÷åñêîãî âûáîðà øàãà ïî çàäàííîìó çíà÷åíèþ îøèáêè.
Ïðè èíòåãðèðîâàíèè ñèñòåì (5.14) è (5.15), îïèñûâàþùèõ äâè-
æåíèå öåíòðà ìàññ íåóïðàâëÿåìîé ðàêåòû ïðè îòíîñèòåëüíî íå-
áîëüøèõ äàëüíîñòÿõ, øàã ïî âðåìåíè ìîæíî âçÿòü ðàâíûì ht =
= 0,1...0,5 ñ. Äëÿ çåíèòíûõ ðàêåò è ñíàðÿäîâ â çîíå âñòðå÷è ñ ìàíåâ-
220
ðèðóþùåé öåëüþ èíîãäà îêàçûâàåòñÿ íåîáõîäèìûì ïðèíÿòü ht =
= 0,01...0,001 ñ.
Ïðè èíòåãðèðîâàíèè ñèñòåìû óðàâíåíèé, îïèñûâàþùåé äâèæå-
íèå öåíòðà ìàññ ñíàðÿäà è êîðîòêîïåðèîäè÷åñêèå êîëåáàòåëüíûå
äâèæåíèÿ îòíîñèòåëüíî öåíòðà ìàññ, øàã èíòåãðèðîâàíèÿ äëÿ ìà-
ëûõ ñíàðÿäîâ ñîñòàâëÿåò ht = 0,001...0,0005 ñ.
Òî÷íîñòü ðàñ÷åòîâ çàâèñèò îò êîëè÷åñòâà âåðíûõ çíà÷àùèõ
öèôð, êîòîðîå îïðåäåëÿåòñÿ èç íåðàâåíñòâà
∆≤10k
,
(5.16)
ãäå k = m − n +1;∆ – àáñîëþòíàÿ ïîãðåøíîñòü ÷èñëà; m – ñòàðøèé
äåñÿòè÷íûé ðàçðÿä ÷èñëà; n – ÷èñëî âåðíûõ çíà÷àùèõ öèôð.
Ïðèìåð. Ïóñòü ïðèáëèæåííîå ÷èñëî L = 12480 êì äîëæíî áûòü âû÷èñëå-
íî ñ îòíîñèòåëüíûìè òî÷íîñòÿìè δL = 1 %; 0,1 %; 0,01 % è 0,001 %.
Îïðåäåëèì, ñêîëüêî â êàæäîì ñëó÷àå ñëåäóåò áðàòü âåðíûõ çíàêîâ ïðè
ðàñ÷åòàõ. Àáñîëþòíàÿ ïîãðåøíîñòü â êàæäîì ñëó÷àå îïðåäåëèòñÿ ïî ôîðìó-
ëå ∆L = LδL/100 è áóäåò ðàâíà
∆∆
∆∆
LL
LL
12
34
125 10
125 10
12
51
0
01
2
51
0
32
1
=<
=<
=<
=<
;,;
,;,
0
.
Ðàñ÷åòíîå ÷èñëî â ïîçèöèîííîé çàïèñè èìååò âèä
12480110 210 410 810 010
43210
=⋅
+⋅+⋅+⋅+⋅
.
Ñëåäîâàòåëüíî, ñòàðøèé äåñÿòè÷íûé ðàçðÿä m = 4. ×èñëî âåðíûõ çíà-
êîâ, ñîãëàñíî ôîðìóëå n = m − k + 1, äëÿ êàæäîãî ðàñ÷åòíîãî ñëó÷àÿ ðàâíî
n1 =2;n2 =3;n3 =4èn5 = 5. Ñ ó÷åòîì îäíîãî çàïàñíîãî çíàêà ïðîìåæóòî÷-
íûå ðàñ÷åòû íóæíî âåñòè ñîîòâåòñòâåííî ñ òðåìÿ, ÷åòûðüìÿ, ïÿòüþ è øå-
ñòüþ âåðíûìè çíàêàìè. Ïðàâèëüíàÿ çàïèñü ÷èñëà L â êàæäîì ñëó÷àå áóäåò
èìåòü âèä
LL
LL
=⋅
=⋅
=⋅
=
125 10
1248 10
1 2480 10
1 2480
44
4
,;
,
,;
,
êì
êì;
êì
0 104
⋅
êì.
5.1.3. ÐÅØÅÍÈÅ ÎÑÍÎÂÍÎÉ (ÏÅÐÂÎÉ) ÇÀÄÀ×È ÂÍÅØÍÅÉ
ÁÀËËÈÑÒÈÊÈ ÍÀ ÝÂÌ
Ðàñ÷åòû íà ÝÂÌ ïî îòëàæåííûì ïðîãðàììàì äàþò âîçìîæíîñòü
ïîëó÷èòü áîëüøîé ïî îáúåìó ìàòåðèàë, êîòîðûé èñïîëüçóåòñÿ ïðè
ïðîâåäåíèè èññëåäîâàíèé è ïðîåêòèðîâàíèè ËÀ.
Ïî ñâîåé ñòðóêòóðå ñóùåñòâóþùèå ìåòîäû ÷èñëåííîãî èíòåãðè-
ðîâàíèÿ óðàâíåíèé äâèæåíèÿ ËÀ ìîãóò áûòü ïîäðàçäåëåíû íà îäíî-
221
øàãîâûå, ìíîãîøàãîâûå è ìåòîäû ïðîãíîçà è êîððåêöèè (ïðåäèê-
òîð-êîððåêòîð-ìåòîäû). Òèïè÷íûìè äëÿ îäíîøàãîâûõ ÿâëÿþòñÿ
ìåòîäû Ðóíãå–Êóòòà ðàçëè÷íûõ ïîðÿäêîâ. Ìåòîä Ýéëåðà îòíîñèòñÿ
ê ìåòîäàì ïåðâîãî ïîðÿäêà, ñòàíäàðòíûé ìåòîä Ðóíãå–Êóòòà – ê
ìåòîäàì ÷åòâåðòîãî ïîðÿäêà. Ìåòîäû Ðóíãå–Êóòòà îáëàäàþò ñëå-
äóþùèìè äîñòîèíñòâàìè è íåäîñòàòêàìè [40]:
èìåþò îäíîòèïíóþ âû÷èñëèòåëüíóþ ñõåìó;
íå òðåáóþò ðàñ÷åòà "ðàçãîííûõ" òî÷åê;
ïîçâîëÿþò ëåãêî èçìåíÿòü øàã èíòåãðèðîâàíèÿ â ïðîöåññå
ñ÷åòà;
õîðîøî ïðèñïîñîáëåíû äëÿ èíòåãðèðîâàíèÿ äèôôåðåíöèàëüíûõ
óðàâíåíèé ñ ðàçðûâíûìè ïðàâûìè ÷àñòÿìè;
òðåáóþò ìíîãîêðàòíîãî âû÷èñëåíèÿ ïðàâîé ÷àñòè íà îäíîì
øàãå;
íå îáåñïå÷èâàþò íàäåæíîãî êîíòðîëÿ ïðàâèëüíîñòè âû÷èñëå-
íèé.
 áèáëèîòåêå ìàòåìàòè÷åñêîãî îáåñïå÷åíèÿ ÏÝÂÌ ïðåäñòàâëå-
íû ñòàíäàðòíûå ïîäïðîãðàììû èíòåãðèðîâàíèÿ äèôôåðåíöèàëü-
íûõ óðàâíåíèé, îñíîâàííûå íà ìåòîäå Ðóíãå–Êóòòà, â òîì ÷èñëå
âêëþ÷àþùèå ìîäèôèêàöèþ Ãèëëà äëÿ êîìïåíñàöèè íàêàïëèâàå-
ìûõ îøèáîê îêðóãëåíèÿ.
Ìíîãîøàãîâûì ÿâëÿåòñÿ ðàññìîòðåííûé âûøå ìåòîä Àäàì-
ñà–Êðûëîâà.
Ìåòîäû ïðîãíîçà è êîððåêöèè, ê êîòîðûì îòíîñÿò ìîäèôèöèðî-
âàííûå ìåòîäû Ýéëåðà, Ìèëíà, Õåììèíãà è äð., èìåþò ñëåäóþùèå
îñîáåííîñòè:
îáåñïå÷èâàþò íàäåæíûé êîíòðîëü ïðàâèëüíîñòè âû÷èñëåíèé íà
êàæäîì øàãå;
ðåæå, ÷åì îäíîøàãîâûå ìåòîäû, îáðàùàþòñÿ ê ñ÷åòó ïðàâûõ ÷àñ-
òåé íà îäíîì øàãå (ìåòîä Õåììèíãà – äâà ðàçà âìåñòî ÷åòûðåõ ðàç â
ñòàíäàðòíîì ìåòîäå Ðóíãå–Êóòòà);
â ïðîöåññå ñ÷åòà íà ÝÂÌ íåñêîëüêî áîëüøå, ÷åì â ñëó÷àå ñòàí-
äàðòíîãî ìåòîäà Ðóíãå–Êóòòà, çàãðóæàþò ïàìÿòü ìàøèíû;
òðåáóþò âû÷èñëåíèÿ "ðàçãîííûõ" òî÷åê ïðè èçìåíåíèè øàãà èí-
òåãðèðîâàíèÿ.
Âûáîð øàãà èíòåãðèðîâàíèÿ äëÿ ðàñ÷åòà ýëåìåíòîâ äâèæåíèÿ
ìîæåò áûòü îñóùåñòâëåí ïóòåì ÷èñëåííîãî ýêñïåðèìåíòà, à òàêæå
íà îñíîâàíèè ñëåäóþùèõ ðåêîìåíäàöèé:
ïðè èíòåãðèðîâàíèè óðàâíåíèé ïëîñêîãî äâèæåíèÿ ËÀ ñ ó÷åòîì
äåéñòâèÿ àêòèâíûõ ñèë øàã èíòåãðèðîâàíèÿ ïî âðåìåíè âûáèðàþò
ðàâíûì ht = 0,1...0,5 c ïðè V0 <50ì/ñ è ht = 0,5...1,0 ñ ïðè V0 >
> 50 ì/ñ;
222
ïðè èíòåãðèðîâàíèè óðàâíåíèé ïëîñêîãî äâèæåíèÿ ËÀ ìàëîé
äàëüíîñòè íà ïàññèâíîì ó÷àñòêå øàã èíòåãðèðîâàíèÿ ïî êîîðäèíàòå
õ âûáèðàþò â ïðåäåëàõ hx =50
...500 ì;
ïðè èíòåãðèðîâàíèè óðàâíåíèé ïðîñòðàíñòâåííîãî äâèæåíèÿ ñ
ó÷åòîì êîëåáàíèé ËÀ øàã èíòåãðèðîâàíèÿ ïî âðåìåíè ïðèõîäèòñÿ
âûáèðàòü äîñòàòî÷íî ìàëûì.  çàâèñèìîñòè îò õàðàêòåðà ïðîöåññà
îí ìîæåò èçìåíÿòüñÿ îò 0,01...0,05 ñ äî 0,001...0,005 ñ.
Íåîáõîäèìîñòü èñïîëüçîâàíèÿ ìàëîãî øàãà äëÿ èíòåãðèðîâàíèÿ
ðÿäà ñèñòåì äèôôåðåíöèàëüíûõ óðàâíåíèé îñîáåííî îñòðî ñòàâèò
âîïðîñ î ïðàâèëüíîñòè âûáîðà ìåòîäà ÷èñëåííîãî èíòåãðèðîâàíèÿ
ñ öåëüþ îáåñïå÷åíèÿ íàèìåíüøèõ çàòðàò ìàøèííîãî âðåìåíè ïðè
çàäàííîé òî÷íîñòè âû÷èñëåíèé.
5.1.4. ÑÎÑÒÀÂËÅÍÈÅ ÏÐÎÃÐÀÌÌÛ ÈÍÒÅÃÐÈÐÎÂÀÍÈß ÓÐÀÂÍÅÍÈß
ÄÂÈÆÅÍÈß ËÀ ÍÀ ÝÂÌ
Ïðîöåññó ñîñòàâëåíèÿ ïðîãðàììû äëÿ ñ÷åòà íà ÝÂÌ ïðåäøåñò-
âóåò ýòàï ïîäãîòîâêè çàäà÷è, íà êîòîðîì ðåøàþò âîïðîñû, ñâÿçàí-
íûå ñ îñîáåííîñòÿìè ÷èñëåííîé ðåàëèçàöèè ìåòîäà è âîçìîæíîñòÿ-
ìè ðàáîòû â ïðîãðàììèðóåìîì ðåæèìå. Îòìåòèì íåêîòîðûå ïîäãî-
òîâèòåëüíûå äåéñòâèÿ.
1. Èíòåãðèðóåìàÿ ñèñòåìà äîëæíà áûòü ðàçðåøåíà îòíîñèòåëüíî
ïðîèçâîäíûõ, ò.å. íàïèñàíà â íîðìàëüíîé ôîðìå Êîøè.
2. Íåîáõîäèìî âûáðàòü ñïîñîá çàäàíèÿ è âîñïðîèçâåäåíèÿ íà
ÝÂÌ çíà÷åíèé àýðîäèíàìè÷åñêèõ ôóíêöèé è ïàðàìåòðîâ àòìîñôå-
ðû: òàáëè÷íûé, ñ èñïîëüçîâàíèåì ñïëàéí-èíòåðïîëÿöèè, ñïîñîá
àïïðîêñèìèðóþùèõ ïîëèíîìîâ è äð. Ïðè ýòîì ñëåäóåò èìåòü â
âèäó, ÷òî èç-çà èñïîëüçîâàíèÿ èíòåðïîëèðóþùèõ ôóíêöèé ïðèõî-
äèòñÿ ïðîâîäèòü äîïîëíèòåëüíûå ðàñ÷åòû ïî ïðîâåðêå ïðàâèëüíî-
ñòè ïîëó÷åííûõ çàâèñèìîñòåé.
3. Íåîáõîäèìî âûáðàòü ìåòîä ÷èñëåííîãî èíòåãðèðîâàíèÿ, îáåñ-
ïå÷èâàþùèé ïîëó÷åíèå ðåçóëüòàòîâ ñ÷åòà ñ çàäàííîé òî÷íîñòüþ è
âûñîêèì áûñòðîäåéñòâèåì.
Ìåòîä êîíå÷íûõ ðàçíîñòåé, ïðèìåíÿåìûé äëÿ ðó÷íîãî ñ÷åòà,
ïëîõî àäàïòèðóåòñÿ ê îñóùåñòâëåíèþ âû÷èñëèòåëüíîãî ïðîöåññà íà
ÝÂÌ. Îí èñïîëüçóåò äâå ðàçëè÷íûå ñõåìû ðàñ÷åòà (îäíó – äëÿ íàðà-
ùèâàíèÿ ñòðîêè), ïîýòîìó íåäîñòàòî÷íî ïðèñïîñîáëåí äëÿ èçìåíå-
íèÿ øàãà â ïðîöåññå âû÷èñëåíèé. Ìåòîä Ýéëåðà è åãî ìîäèôèêàöèè
ïðè ðåàëèçàöèè íà ÝÂÌ òðåáóþò íåáîëüøèõ çàòðàò ìàøèííîãî âðå-
ìåíè, íî, êàê ïðàâèëî, îáëàäàþò íåâûñîêîé òî÷íîñòüþ. Ïðåäïî÷òå-
íèå ïðè ðàñ÷åòå ýëåìåíòîâ äâèæåíèÿ ËÀ îòäàåòñÿ ìåòîäó Ðóí-
ãå–Êóòòà, åãî ìîäèôèêàöèÿì è ìåòîäàì ïðîãíîçà è êîððåêöèè. Îíè
îáåñïå÷èâàþò âûñîêóþ òî÷íîñòü ïîëó÷åííûõ ðåçóëüòàòîâ, îôîðìëå-
223
íû â âèäå ñòàíäàðòíûõ ïîäïðîãðàìì è âõîäÿò â ñîñòàâ ìàòåìàòè÷å-
ñêîãî îáåñïå÷åíèÿ áîëüøèíñòâà ÝÂÌ.
4. Èñïîëüçîâàíèå ÝÂÌ äëÿ èíòåãðèðîâàíèÿ ñèñòåìû ïîçâîëÿåò
àâòîìàòèçèðîâàòü ïðîöåññ âû÷èñëåíèÿ ýëåìåíòîâ òðàåêòîðèè â õà-
ðàêòåðíûõ òî÷êàõ (k, s, c). Ïðè ñîñòàâëåíèè ïðîãðàììû äëÿ ýòîé
öåëè ìîãóò áûòü âûáðàíû îáðàòíàÿ èíòåðïîëÿöèÿ, óìåíüøåíèå
øàãà èíòåãðèðîâàíèÿ ïðè ïðîâåäåíèè âû÷èñëåíèé â îêðåñòíîñòè
õàðàêòåðíûõ òî÷åê ñ ïîñëåäóþùåé îáðàòíîé èíòåðïîëÿöèåé, óìåíü-
øåíèå øàãà è èçìåíåíèå åãî çíàêà ïðè ïðîâåäåíèè âû÷èñëåíèé â
ðàéîíå õàðàêòåðíûõ òî÷åê. Âûáîð ïðîöåäóðû äîëæåí îáåñïå÷èòü
ïîëó÷åíèå ðåçóëüòàòîâ ñ çàäàííîé òî÷íîñòüþ.
5. Äëÿ çàâåðøåíèÿ ïðîöåññà ñ÷åòà ïðåäóñìàòðèâàåòñÿ óñëîâèå
âûõîäà èç ïðîãðàììû èíòåãðèðîâàíèÿ, ñîñòàâëåííîå ñ ó÷åòîì îñî-
áåííîñòåé äâèæåíèÿ ËÀ.
 êà÷åñòâå ïðèìåðà ïðèâåäåì ñèñòåìó äèôôåðåíöèàëüíûõ óðàâ-
íåíèé äâèæåíèÿ äëÿ àêòèâíîãî ó÷àñòêà
du
dt
cc
ym
um
Vcc V
Hyu
mm
dp
xa
=+−
−
{[(
)
]
}/
()(
)(
)/
;
12
0
3
0
1π
M
//
;
/;
/.
dt gu
dxdtudydtup
=−
==
(5.17)
Çäåñü ñ1 = Ð0/m0; c2 = Sa pON/m0; c3 = SρON/(2m0).
Ïðèâåäåì òàêæå ïðèìåð ïðåäñòàâëåíèÿ ôóíêöèè cx a
()
M ñ ïîìî-
ùüþ àïïðîêñèìèðóþùèõ ïîëèíîìîâ (òàáë. 5.6).
Äëÿ àïïðîêñèìàöèè ôóíêöèè ñòðîÿò åå ãðàôèê è ïî âèäó ãðàôè-
êà âûáèðàþò íà íåì õàðàêòåðíûå ó÷àñòêè (ðèñ. 5 .2).  íàøåì ñëó÷àå
òàêèõ ó÷àñòêîâ îêàçàëîñü ïÿòü: ó÷àñòêè I, III, V ìîãóò áûòü îïèñàíû
ëèíåéíîé çàâèñèìîñòüþ cx a
= aM2 + b, à ó÷àñòêè II, IV – êâàäðàòè÷-
íîé çàâèñèìîñòüþ âèäà cx a
= aM2 + bÌ+ñ. Êîýôôèöèåíòû ýìïèðè-
÷åñêèõ ôîðìóë ìîæíî âû÷èñëèòü ñ ïîìîùüþ îäíîãî èç ìåòîäîâ ìà-
Òàáëèöà 5.6
Òàáëèöà êîýôôèöèåíòîâ c xa
()
M
Ì
0,1
0,8
0,1
1,2
1,3
1,4
cxa
0,158
0,158
0,325
0,385
0,381
0,371
M
1,6
1,8
2,0
cxa
0,351
0,332
0,316
224
òåìàòè÷åñêîé òåîðèè îáðàáîòêè
ðåçóëüòàòîâ ýêñïåðèìåíòà: ìåòîäîì
âûáðàííûõ òî÷åê, ìåòîäîì ñðåä-
íèõ êâàäðàòîâ, ìåòîäîì íàèìåíü-
øèõ êâàäðàòîâ. Âîñïîëüçóåìñÿ ìå-
òîäîì âûáðàííûõ òî÷åê è ïîñòðî-
èì àïïðîêñèìèðóþùóþ ôîðìóëó
äëÿ ó÷àñòêà IV, êîòîðûé çàäàåòñÿ
íà èíòåðâàëå Ì = 1,0...1,4. Äëÿ
ýòîãî â óðàâíåíèå ïàðàáîëû ïîä-
ñòàâëÿþò ïîñëåäîâàòåëüíî êîîð-
äèíàòû òðåõ òî÷åê (ïî ÷èñëó íåèç-
âåñòíûõ êîýôôèöèåíòîâ, âõîäÿ-
ùèõ â ôîðìóëó). Âîçüìåì äâå ãðà-
íè÷íûåòî÷êèäëÿÌ=1,0è1,4è
îäíó âíóòðåííþþ äëÿ Ì = 1,2.
Ïîëó÷àåì ñëåäóþùóþ ñèñòåìó àë-
ãåáðàè÷åñêèõ óðàâíåíèé:
abc
abc
ab
c
++=
++=
++
=
0325 144 12
0 385
196 14
0371
,;
,
,
,;
,,
,
.
Èç ðåøåíèÿ ñèñòåìû íàõîäÿò íåèçâåñòíûå êîýôôèöèåíòû.
Îêîí÷àòåëüíûé âèä àïïðîêñèìèðóþùåãî ïîëèíîìà äëÿ IV ó÷àñòêà
ñëåäóþùèé:
cxa
=+
−
0 925
2335 1085
2
,,
,
.
MM
Ïîäîáíûì ñïîñîáîì íàõîäÿò óðàâíåíèÿ äëÿ îñòàëüíûõ ó÷àñòêîâ.
Îáùèé âèä çàâèñèìîñòè cx a
():
M
cxa
=
++
−
−
0158
0 137
0 865 0 000898
135 1025
09
2
,,
,,,
,
,,
,
,
MM
M
25
2335 1085
0 0917 0 4993
01
0
2
MM
M
M
+−
−+
⎧
⎨
⎪
⎪⎪
⎩
⎪
⎪
⎪
≤≤
,,
,
,,
,
,,
;
8
0,8 M 0,9;
0,9<M 1,0;
1,0<M 1,4;
1,4<M 2,0.
≤≤
≤
≤
≤
×òîáû ïðîâåðèòü ïðàâèëüíîñòü ïîëó÷åííûõ ñîîòíîøåíèé, ñî-
ñòàâèì ïðîãðàììó âû÷èñëåíèÿ çíà÷åíèé ôóíêöèè cx a
()
MäëÿÌ=
225
Ðèñ. 5 .2. Ïðèìåð çàâèñèìîñòè c xa
(Ì)
= 0,1...2,0 ñ øàãîì 0,05. Ñõåìà àë-
ãîðèòìà ðåøåíèÿ ïîñòàâëåííîé çà-
äà÷è ïðèâåäåíà íà ðèñ. 5 .3.
Îñíîâíûå õàðàêòåðèñòèêè àò-
ìîñôåðû â ñîîòâåòñòâèè ñ ÃÎÑÒ
4401-81 âû÷èñëÿþòñÿ ñ ïîìîùüþ
ñîîòíîøåíèé
aH
y
T
T
=−
=
⎛
⎝⎜
⎞
⎠⎟
20 0468 288 15 0 0065
5 2559
,,
,
;
()exp, ln ;
*
π
Hy
T
T
()exp, ln ,
*
=
⎛
⎝⎜
⎞
⎠⎟
4 2559
ãäå H = ry/(r + y) – ãåîïîòåí-
öèàëüíàÿ âûñîòà; r – ðàäèóñ
Çåìëè â ñîîòâåòñòâóþùåé òî÷êå
ïîâåðõíîñòè; T/T * =1–
– 0,0000226H; T * = 228,15 Ê –
òåìïåðàòóðà
íèæíåãî
ñëîÿ
âîçäóõà íà óðîâíå îêåàíà.
Ïðèìåíåíèå ñïîñîáà àïïðîêñè-
ìèðóþùèõ ïîëèíîìîâ è çàâèñèìî-
ñòåé ÿâëÿåòñÿ áîëåå ïðåäïî÷òè-
òåëüíûì, ÷åì ââîä â ïàìÿòü ìàøè-
íû áîëüøèõ ïî îáúåìó òàáëèö è
ïðîãðàìì ëèíåéíîé èëè êâàäðà-
òè÷íîé èíòåðïîëÿöèè. Âû÷èñëå-
íèå çíà÷åíèé ôóíêöèé òðåáóåò
ââîäà ëèøü íåáîëüøèõ ïî îáúåìó
òàáëèö êîýôôèöèåíòîâ ñîîòâåòñò-
âóþùèõ ìíîãî÷ëåíîâ. Îïåðàöèÿ
óñëîâíîãî ïåðåõîäà, ïî êîòîðîé
âåäåòñÿ âûáîð ñîîòâåòñòâóþùèõ
ãðóïï ýòèõ êîýôôèöèåíòîâ ñ öå-
ëüþ âû÷èñëåíèÿ âåëè÷èíû ôóíê-
öèè â ïðåäåëàõ êîíêðåòíîãî èíòåð-
âàëà íåçàâèñèìîãî ïåðåìåííîãî,
âêëþ÷àåòñÿ â îñíîâíóþ ïðîãðàììó
ðåøåíèÿ çàäà÷è.
226
Ðèñ. 5.3 . Ñõåìà ïðîãðàììû âû÷èñëå-
íèÿ ôóíêöèè c xa
(Ì)
5.2 . ÏÐÈÁËÈÆÅÍÍÛÅ ÀÍÀËÈÒÈ×ÅÑÊÈÅ
È ÒÀÁËÈ×ÍÛÅ ÌÅÒÎÄÛ
5.2.1. ÏÀÐÀÁÎËÈ×ÅÑÊÀß ÒÅÎÐÈß
Ïðè äâèæåíèè ñíàðÿäà ïîñòîÿííîé ìàññû â óñëîâíîì ïëîñêîïà-
ðàëëåëüíîì ïîëå òÿãîòåíèÿ ïðè g = g0 = const â îòñóòñòâèå ñèëû ñî-
ïðîòèâëåíèÿ âîçäóõà òðàåêòîðèÿ ñíàðÿäà îïèñûâàåòñÿ ñèñòåìîé
äèôôåðåíöèàëüíûõ óðàâíåíèé ••() ;
xt=0
••
(),
ytg
=−
ðåøåíèå êîòîðîé
îïðåäåëÿåòñÿ íà÷àëüíûìè óñëîâèÿìè ïîëåòà õ0 = y0 =0,V0 è θ0.
Ïîñëåäîâàòåëüíî äâàæäû èíòåãðèðóÿ óêàçàííûå óðàâíåíèÿ, ïî-
ëó÷èì
•
;;
•
;,
.
xCxCC
tyC g
tyCCt g
t
==
+=
−
=
+
−
13
12
4
2
2
05
Èç âûðàæåíèÿ •
cos
xV
C
==
θ 1 ñëåäóåò, ÷òî ðàññìàòðèâàåìîå äâè-
æåíèå ñíàðÿäà õàðàêòåðèçóåòñÿ ïîñòîÿíñòâîì çíà÷åíèÿ âäîëü òðàåê-
òîðèè ãîðèçîíòàëüíîé ïðîåêöèè âåêòîðà ñêîðîñòè. Èç íà÷àëüíûõ
óñëîâèé íàõîäèì Ñ3 = Ñ4 =0;Ñ1 =
•
x0 =V0cosθ0;C2=
•
y0 = V0 sinθ0.
Ïîäñòàâëÿÿ çíà÷åíèÿ êîíñòàíò â âûðàæåíèÿ äëÿ õ è y, ïîëó÷èì
óðàâíåíèå òðàåêòîðèè â ïàðàìåòðè÷åñêîì âèäå: x = V0t cosθ0; y =
= V0t sinθ0 − 0,5gt 2, èëè, èñêëþ÷èâ ïàðàìåòð t ïîäñòàíîâêîé t =
= x/(V0 cosθ0) â óðàâíåíèå äëÿ y, îïðåäåëèì
yx
g
x
V
=−
−−
tgθθ
0
2
0
22
0
1
2
cos
.
(5.18)
Ñîïîñòàâëåíèå óðàâíåíèÿ (5.18) ñ îáùèì âèäîì óðàâíåíèÿ êðèâîé
âòîðîãî ïîðÿäêà Ax2 +2Bxy + Cy2 +2Dx +2Ey + F = 0 ïîêàçûâàåò, ÷òî
ó óðàâíåíèÿ (5.18) äèñêðèìèíàíò B
2
−
AC = 0 è, ñëåäîâàòåëüíî,
êðèâàÿ, îïèñûâàåìàÿ óðàâíåíèåì (5.18), ÿâëÿåòñÿ ïàðàáîëîé. Èñõîäÿ
èç ýòîãî ðàññìàòðèâàåìûé ìåòîä ðåøåíèÿ ÷àñòî íàçûâàþò
ïàðàáîëè÷åñêîé òåîðèåé äâèæåíèÿ ñíàðÿäà.
Íàéäåì ñîîòíîøåíèÿ, ïîçâîëÿþùèå ðàññ÷èòàòü õàðàêòåðèñòèêè
äâèæåíèÿ ñíàðÿäà â ïðîèçâîëüíîé òî÷êå ïàðàáîëè÷åñêîé òðàåêòîðèè.
Äèôôåðåíöèðóÿ (5.18) ïî õ, ïîëó÷àåì çàâèñèìîñòü äëÿ îïðåäåëåíèÿ
óãëà íàêëîíà âåêòîðà ñêîðîñòè ê ãîðèçîíòó
tg
tg
θθθ
=
′=−
−−
yg
x
V
x
00
22
0
cos
.
(5.19)
Ñêîðîñòü ñíàðÿäà â ïðîèçâîëüíîé òî÷êå òðàåêòîðèè íà âûñîòå y
îïðåäåëèì èç óðàâíåíèÿ "æèâûõ ñèë" (mV 2)/2 − ()
mV0
2
/2 = −mgy,
îòêóäà ñëåäóåò
227
VVg
y
=−
0
2
2.
(5.20)
Èç ïîñëåäíåé ôîðìóëû âèäíî, ÷òî ñêîðîñòè ñíàðÿäà â äâóõ òî÷êàõ,
ëåæàùèõ íà îäèíàêîâîé âûñîòå íà âîñõîäÿùåé è íà èñõîäÿùåé
âåòâÿõ òðàåêòîðèè, îäèíàêîâû.
Âðåìÿ äâèæåíèÿ ñíàðÿäà îïðåäåëÿåòñÿ çàâèñèìîñòüþ
txV
=
/( cos ).
00
θ
(5.21)
Íàéäåì çíà÷åíèÿ õàðàêòåðèñòèê äâèæåíèÿ ñíàðÿäà â òî÷êå ïàäåíèÿ
ñ, èñïîëüçóÿ óñëîâèå yc = 0. Ïðè ýòîì èç óðàâíåíèé (5.18)...(5.21)
ñîîòâåòñòâåííî ïîëó÷àåì: ïîëíóþ äàëüíîñòü ïîëåòà
xV
g
c
=
0
2
0
2
sin /;
θ
(5.22)
òàíãåíñ óãëà ïàäåíèÿ tgθc = −tgθ0; ñêîðîñòü ïàäåíèÿ Vc = V0; ïîëíîå
ïîëåòíîå âðåìÿ
tVg
c
=200
sin/.
θ
(5.23)
Ïîëó÷åííûå çàâèñèìîñòè ïîêàçûâàþò, ÷òî äëÿ ïàðàáîëè÷åñêîé
òðàåêòîðèè â òî÷êå ïàäåíèÿ |θc|=θ0; Vc = V0.
Õàðàêòåðèñòèêè äâèæåíèÿ äëÿ âåðøèíû òðàåêòîðèè íàõîäÿòñÿ
èç óñëîâèÿ tgθs = 0 (èëè θs = 0). Ïðè ýòîì èç (5.19) ñëåäóåò
xV
g
s
=
0
2
0
22
sin /( ),
θ
(5.24)
ò.å.xs=xc/2.
Àíàëîãè÷íî èç (5.21) ïîëó÷àåì ts = V0 sinθ0/g, ò.å . tt
sc
=
1
2
. Òàê êàê
â âåðøèíå òðàåêòîðèè ñîñòàâëÿþùèå ñêîðîñòè •
cos
xV
s
=
00
θè
•
sin
,
yV
g
t
ss
=−
=
00
0
θ
òî ïîëíàÿ ñêîðîñòü Vxy
ss
s
=+
=
••
22
V0cosθ0.Âû-
ñîòó òðàåêòîðèè ys íàéäåì, ïîäñòàâèâ âûðàæåíèå äëÿ xs â îñíîâíîå
óðàâíåíèå (5.18):
yV
g
s
=
0
22
0
2
sin /( ).
θ
(5.25)
Ïîëåçíî ïðèâåñòè âûðàæåíèå äëÿ ys ê âèäó
y
x
s
c
=
40
tgθ .
(5.26)
228
Àíàëèç çàâèñèìîñòåé, îïðåäåëÿþùèõ ýëåìåíòû òðàåêòîðèè â
âåðøèíå è â òî÷êå ïàäåíèÿ, ïîêàçûâàåò, ÷òî ïàðàáîëè÷åñêàÿ òðàåê-
òîðèÿ ÿâëÿåòñÿ ñèììåòðè÷íîé êðèâîé.
Ïðè ïðèáëèæåííûõ ðàñ÷åòàõ òðàåêòîðèé ñ ó÷åòîì ñîïðîòèâëå-
íèÿ àòìîñôåðû ÷àñòî ôóíêöèþ èçìåíåíèÿ ïëîòíîñòè âîçäóõà ñ âû-
ñîòîé áåðóò ñî ñðåäíèì çíà÷åíèåì H(y)=H(yñð).  êà÷åñòâå ïåðâîãî
ïðèáëèæåíèÿ ñðåäíþþ âûñîòó òðàåêòîðèè ìîæíî îïðåäåëÿòü, ïîëü-
çóÿñü âûâîäàìè ïàðàáîëè÷åñêîé òåîðèè:
y
x
ydx
x
x
gx
V
dx
cc
x
x
c
c
ñð
tg
==
−
⎛
⎝⎜
⎞
⎠⎟
∫
∫11
2
0
2
0
22
0
0
0
θ
θ
cos
.
Ïîñëå èíòåãðèðîâàíèÿ è ïðåîáðàçîâàíèé ïîëó÷èì
yy
s
cp
=
2
3
.
(5.27)
Çàâèñèìîñòè ïàðàáîëè÷åñêîé òåîðèè ÿâëÿþòñÿ ïðåäåëüíûìè ïî
îòíîøåíèþ ê çàâèñèìîñòÿì, îïðåäåëÿþùèì äâèæåíèå ñíàðÿäà â àò-
ìîñôåðå, ïðè ñòðåìëåíèè ê íóëþ ñîïðîòèâëåíèÿ âîçäóõà.
Ïàðàáîëè÷åñêàÿ òåîðèÿ ìîæåò ïðèìåíÿòüñÿ äëÿ ðàñ÷åòîâ õàðàê-
òåðèñòèê äâèæåíèÿ ñíàðÿäîâ ïîñòîÿííîé ìàññû çà ïðåäåëàìè ïëîò-
íûõ ñëîåâ àòìîñôåðû (íà âûñîòàõ áîëåå 20 êì). Îäíàêî ïðè ðàñ÷åòå
îòíîñèòåëüíî áîëüøèõ ó÷àñòêîâ òðàåêòîðèé ñëåäóåò ïîìíèòü, ÷òî
çàâèñèìîñòè ïàðàáîëè÷åñêîé òåîðèè ïîëó÷åíû áåç ó÷åòà èñêðèâëå-
íèÿ çåìíîé ïîâåðõíîñòè è ïåðåìåííîñòè g è ðàñ÷åò ïî íèì ìîæåò
ïðèâåñòè ê çàìåòíûì îøèáêàì.
5.2.2. ÝËËÈÏÒÈ×ÅÑÊÀß ÒÅÎÐÈß
Âíåøíÿÿ áàëëèñòèêà ðàññìàòðèâàåò äâèæåíèå òåëà ïîñòîÿííîé
ìàññû íà ó÷àñòêàõ áîëüøîé ïðîòÿæåííîñòè â öåíòðàëüíîì ãðàâèòà-
öèîííîì ïîëå Çåìëè îòíîñèòåëüíî èíåðöèàëüíîé ñèñòåìû êîîðäè-
íàò. Ïðè ýòîì òðàåêòîðèè ïðåäñòàâëÿþò ñîáîé ýëëèïòè÷åñêèå òðàåê-
òîðèè Êåïëåðà, êîòîðûå ìàòåìàòè÷åñêè îïèñûâàþòñÿ ñèñòåìîé
óðàâíåíèé (3.142), ïîääàþùåéñÿ äîñòàòî÷íî ïðîñòîìó àíàëèòè÷å-
ñêîìó ðåøåíèþ. Â ýòîé ñèñòåìå âòîðîå óðàâíåíèå âûðàæàåò çàêîí
ñîõðàíåíèÿ ìîìåíòà êîëè÷åñòâà äâèæåíèÿ â öåíòðàëüíîì ãðàâèòà-
öèîííîì ïîëå. Èíòåãðèðóÿ åãî, íàõîäèì ñâÿçü ìåæäó ïàðàìåòðàìè
íà÷àëà ïàññèâíîãî ó÷àñòêà è òåêóùèìè ïàðàìåòðàìè òðàåêòîðèè
Crr
V
r
V
1
2
==
=
•
cos
cos .
γθθ
íí
í
(5.28)
229
Çäåñürí=rk,àVíèθí–íà-
÷àëüíûå ïàðàìåòðû äâèæå-
íèÿ òåëà â àáñîëþòíîé
ñèñòåìå êîîðäèíàò; θí è θ –
óãëû íàêëîíà âåêòîðîâ Ví è
V ê ìåñòíûì ãîðèçîíòàì
(íîðìàëÿì ê ðàäèóñàì rí è r
ñîîòâåòñòâåííî).
Çàâèñèìîñòü (5.28), âû-
ðàæàþùàÿ îäèí èç çàêîíîâ Êåïëåðà, íîñèò íàçâàíèå èíòåãðàëà ïëî-
ùàäåé. Ôèçè÷åñêèé ñìûñë ââåäåííîãî ïîíÿòèÿ çàêëþ÷àåòñÿ â òîì,
÷òî ïëîùàäè, "îòìåòàåìûå" ðàäèóñ-âåêòîðîì çà îäèíàêîâûå ïðîìå-
æóòêè âðåìåíè, ðàâíû (ðèñ. 5.4).
Èíòåãðèðóÿ ïåðâîå óðàâíåíèå (3.142) ñ ó÷åòîì âòîðîãî óðàâíåíèÿ
ýòîé ñèñòåìû, ïîëó÷èì
•
•
,
rr
K
r
C
22
2
2
2
+=+
γ
(5.29)
îòêóäà
CV
K
r
V
K
r
2
22
22
=− =−
í
í
,
(5.30)
ãäå K = fM – ãðàâèòàöèîííûé ïàðàìåòð Çåìëè (ñì. ï. 1.2.1).
Âûðàæåíèå (5.30) íàçûâàþò èíòåãðàëîì ýíåðãèè èëè èíòåãðàëîì
"æèâûõ ñèë".
Äëÿ äâóõ òî÷åê òðàåêòîðèè V
K
r
V
K
r
1
2
1
2
2
2
22
−=
−
, è ïîñëå óìíîæå-
íèÿ âñåõ ÷ëåíîâ óðàâíåíèÿ íà m/2 áóäåì èìåòü
mV
mV
Km
r
Km
r
2
2
1
2
21
22
=+
−
,
ò.å. êèíåòè÷åñêàÿ ýíåðãèÿ òåëà âî âòîðîé òî÷êå ðàâíà êèíåòè÷åñêîé
ýíåðãèè â ïåðâîé òî÷êå ïëþñ èçìåíåíèå ïîòåíöèàëüíîé ýíåðãèè
ïîëîæåíèÿ.
Óðàâíåíèå òðàåêòîðèè òåëà â öåíòðàëüíîì ãðàâèòàöèîííîì ïîëå
ìîæåò áûòü ïîëó÷åíî èç óðàâíåíèé äâèæåíèÿ (3.142). Ïîäñòàâëÿÿ â
(5.29) •γ èç (5.28) è èìåÿ â âèäó, ÷òî
•
,
r
dr
d
d
dt
C
r
dr
d
==
γ
γ
γ
1
2
230
Ðèñ. 5 .4. Ê ïîíÿòèþ èíòåãðàëà ïëîùàäåé
ïîëó÷èì
d
Cr
CCr Kr
γ=
−+
1
2
21
22
2
/
//
.
Îêîí÷àòåëüíîå ðåøåíèå ýòîãî óðàâíåíèÿ èìååò âèä
r
p
e
s
=
−−
1c
o
s
()
.
φφ
(5.31)
Ïîëó÷åííàÿ çàâèñèìîñòü ÿâëÿåòñÿ óðàâíåíèåì êîíè÷åñêîãî ñå÷åíèÿ â
ïîëÿðíûõ êîîðäèíàòàõ.
 óðàâíåíèè (5.31) φ è φs – ïîëÿðíûå óãëû, îòñ÷èòûâàåìûå îò ðà-
äèóñ-âåêòîðà rí, îïðåäåëÿþùèå ñîîòâåòñòâåííî ïîëîæåíèÿ òåêóùåé
òî÷êè òðàåêòîðèè è åå âåðøèíû; pC K
=
1
2
/–ôîêàëüíûé ïàðàìåòð
êîíè÷åñêîãî ñå÷åíèÿ;
eC
C
K
=+
12
1
2
2 – ýêñöåíòðèñèòåò.
(5.32)
Äëÿ ïàðàìåòðà ð ÷àñòî èñïîëüçóþò è äðóãîå, ïðîèçâîäíîå, âûðà-
æåíèå pr
=κ
θ
íí
í
cos ,
2
ãäåκí
íí
2
=
rV
K
–
áåçðàçìåðíîå îòíîøåíèå óäâî-
åííîé êèíåòè÷åñêîé ýíåðãèè ê ïîòåíöèàëüíîé ýíåðãèè â òî÷êå òðà-
åêòîðèè, ñîîòâåòñòâóþùåé íà÷àëó ïàññèâíîãî ó÷àñòêà.
Ïîñëå ïîäñòàíîâêè çíà÷åíèé Ñ1 è Ñ2 â âûðàæåíèå (5.32) ïîëó÷à-
åì ôîðìóëó äëÿ îïðåäåëåíèÿ òåêóùåé ñêîðîñòè â ôóíêöèè îñíîâ-
íûõ ïàðàìåòðîâ òðàåêòîðèè V
K
r
e
2
2
2
11
1
=±
−
−
⎛
⎝
⎜⎜
⎞
⎠
⎟⎟
cos
.
θ
Äëÿ òî÷åê òðàåêòîðèè, êîòîðûå ðàñïîëîæåíû íà ôîêàëüíîé îñè
êîíè÷åñêîãî ñå÷åíèÿ è â êîòîðûõ θ = 0 (cosθ = 1), ïîëó÷åííîå óðàâ-
íåíèå èìååò âèä
V
K
r
e
2
1
=±
()
.
(5.33)
Çàâèñèìîñòè (5.31) è (5.33) ïîçâîëÿþò èññëåäîâàòü âëèÿíèå íà-
÷àëüíûõ óñëîâèé íà âèä òðàåêòîðèé è ñêîðîñòè äâèæåíèÿ ËÀ.
Ðàññìîòðèì âîçìîæíûå ñëó÷àè.
1. Ñëó÷àé å = 0. Ïðè ýòîì èç (5.31) ñëåäóåò, ÷òî òåëî áóäåò
äâèãàòüñÿ ïî îêðóæíîñòè, óðàâíåíèå êîòîðîé â ïîëÿðíûõ êîîð-
231
äèíàòàõ èìååò âèä r = p = rí. Ñêîðîñòü VK
r
I=
/ íîñèò íàçâà-
íèå êðóãîâîé è ÿâëÿåòñÿ ñêîðîñòüþ, êîòîðóþ íåîáõîäèìî ñîîá-
ùèòü òåëó, ÷òîáû îíî ñòàëî ñïóòíèêîì Çåìëè.  ÷àñòíîì, óñëîâ-
íîì, ñëó÷àå V0I = 7,906 êì/ñ ïðè r = RÇ = 6371 êì. Ýòà ñêîðîñòü
íàçûâàåòñÿ ïåðâîé êîñìè÷åñêîé ñêîðîñòüþ. Ââåäåííûé âûøå ïà-
ðàìåòð κí ìîæåò áûòü âûðàæåí ÷åðåç âåëè÷èíó êðóãîâîé ñêîðî-
ñòè, ñîîòâåòñòâóþùåé ðàäèóñó rí:
κí
í
2
í
í
íI
==
⎛
⎝⎜⎞
⎠⎟
V
Kr
V
V
/
.
2
Îòñþäà âèäíî, ÷òî äâèæåíèþ òåëà ïî îêðóæíîñòè ñîîòâåòñòâóåò
çíà÷åíèå κí =1.
2. Ñëó÷àé 0 < e < 1. Ñîãëàñíî (5.31) áóäóò èìåòü ìåñòî ýëëèïòè÷å-
ñêèå òðàåêòîðèè. Îäíàêî âîçìîæíû äâà ðàçëè÷íûõ âàðèàíòà, òàê
êàê â ôîðìóëå (5.33) ïåðåä çíà÷åíèåì ýêñöåíòðèñèòåòà ñòîÿò äâà
çíàêà:
à) åñëè ïðèíÿòü, ÷òî V
K
r
eV
2
1
=+
=
(),
Ï
2
òî áóäåì èìåòü ýëëèïñ, ó
êîòîðîãî ïðèòÿãèâàþùèé öåíòð ñîâïàäàåò ñ ôîêóñîì, áëèæàéøèì ê
òî÷êå ñî ñêîðîñòüþ VÏ. Äëÿ ðàññìàòðèâàåìîãî âàðèàíòà ýòà òî÷êà
òðàåêòîðèè – ïåðèãåé. Òåëî, äâèæóùååñÿ â ïåðèãåå ñ òàêîé ñêîðî-
ñòüþ, áóäåò ñïóòíèêîì, òàê êàê ýëëèïñ íå ïåðåñåêàåòñÿ ñ ïðèòÿãè-
âàþùèì òåëîì;
á) åñëè V
K
r
eV
2
1
=−
=
(),
A
2
òî áóäåì èìåòü ýëëèïñ, ó êîòîðîãî
ïðèòÿãèâàþùèé öåíòð ñîâïàäàåò ñ äàëüíèì ôîêóñîì. Ñêîðîñòü VA
õàðàêòåðèçóåò òî÷êó, íàçûâàåìóþ àïîãååì òðàåêòîðèè.  ýòîì ñëó-
÷àå òðàåêòîðèÿ ìîæåò ïåðåñåêàòüñÿ ñ ïðèòÿãèâàþùèì òåëîì, íî ìî-
æåò è íå ïåðåñåêàòüñÿ. Ãðàíè÷íîå çíà÷åíèå VÀãð ëåãêî îïðåäåëÿåòñÿ,
ïîñêîëüêó ñêîðîñòü VÀãð äîëæíà áûòü ðàâíà ñêîðîñòè â àïîãåå òàêî-
ãî ýëëèïñà, êîòîðûé â ïåðèãåå êîñíåòñÿ ïîâåðõíîñòè Çåìëè. Èñ-
ïîëüçóÿ óñëîâèå VÏ RÇ = VÀãð rÀãð = Ñ1, ïîäñòàâèì â íåãî VÏ è VÀ è
ïîñëå ïðåîáðàçîâàíèé ïîëó÷èì
VV
R
rR
Àãð
I
Ç
Àãð
Ç
=
+
2
.
Åñëè VA > VÀãð – ýëëèïñ íå ïåðåñåêàåòñÿ ñ ïðèòÿãèâàþùèì òåëîì;
VA = VÀãð – ýëëèïñ êîñíåòñÿ ïðèòÿãèâàþùåãî òåëà; VA < VÀãð – ýëëèïñ
ïåðåñåêàåòñÿ ñ òåëîì (ýòîò âàðèàíò ñîîòâåòñòâóåò òðàåêòîðèÿì
232
áàëëèñòè÷åñêèõ ðàêåò äàëüíåãî äåéñòâèÿ (ÁÐÄÄ)). Äëÿ ýëëèïñîâ
ïàðàìåòð κí <2.
3. Ñëó÷àé å = 1. Òðàåêòîðèÿ ÿâëÿåòñÿ ïàðàáîëîé. Åñëè ïðèäàòü
ðàêåòå ïàðàáîëè÷åñêóþ ñêîðîñòü, îíà ïðåîäîëååò ñèëó çåìíîãî òÿãî-
òåíèÿ. Èç óðàâíåíèÿ ñêîðîñòè (5.33) ñëåäóåò
V
K
r
V
II
I
==
2
2;
ïðèr=RÇ=6371êìV0II=V02
I
= 11,80 êì/ñ, ýòî – âòîðàÿ
êîñìè÷åñêàÿ ñêîðîñòü.
Ïàðàáîëè÷åñêîé òðàåêòîðèè ñîîòâåòñòâóåò ïàðàìåòð κí =2
.
4. Ñëó÷àé e > 1. Ñîãëàñíî (5.31) òðàåêòîðèÿ áóäåò ãèïåðáîëîé,
ïðè ýòîì κí >2.
Äëÿ ïîÿñíåíèÿ ðàññìîòðåííûõ âàðèàíòîâ ïðèâåäåíû ðèñ. 5 .5 ...5.7.
Íà ðèñ. 5 .5 ïîêàçàíû âèäû òðàåêòîðèé òåëà â çàâèñèìîñòè îò âåëè-
÷èíû ïàðàìåòðà κí . Ãðàôèêè ôóíêöèè V/V0I =(1± å)1/2 èç (5.33), èçî-
áðàæåííûå íà ðèñ. 5 .6, ïîçâîëÿþò óñòàíîâèòü âèä òðàåêòîðèè òåëà â
çàâèñèìîñòè îò ñîîòíîøåíèÿ ýêñöåíòðèñèòåòà å è ñêîðîñòè V â òî÷-
êå òðàåêòîðèè íà ôîêàëüíîé îñè
êîíè÷åñêîãî ñå÷åíèÿ. Èçìåíå-
íèå õàðàêòåðà òðàåêòîðèè òåëà,
óäàëåííîãî îò ïðèòÿãèâàþùåãî
öåíòðà íà ðàññòîÿíèå r, â çàâè-
ñèìîñòè îò ñêîðîñòè ýòîãî òåëà
(ïðèV⊥r) ïîêàçàíî íàðèñ. 5.7.
Ââåäåíèå ïîíÿòèÿ "ïàðàáî-
ëè÷åñêîé ñêîðîñòè" ïîçâîëÿåò
äàòü åùå îäíî òîëêîâàíèå ñëà-
ãàåìîìó (mK)/r â âûðàæåíèè
äëÿ èíòåãðàëà ýíåðãèè. ßñíî,
÷òî
mK
r
K
r
mm
V
==
2
22
2
II
–
êèíå-
òè÷åñêàÿ ýíåðãèÿ òåëà â òî÷êå ñ
ðàäèóñîì r, íåîáõîäèìàÿ äëÿ
ïðåîäîëåíèÿ ïîëÿ òÿãîòåíèÿ
Çåìëè.
Äëÿ êîíñòàíòû Ñ2 àíàëîãè÷íî
ìîæíî ïîëó÷èòü âûðàæåíèå Ñ2 =
=VV
íí
I
I
22
–,
èç êîòîðîãî ñëåäóåò,
÷òî åñëè Ñ2 >0,òîr →∞è òðàåê-
òîðèÿ òåëà åñòü ðàçîìêíóòàÿ
233
Ðèñ. 5.5 . Ñåìåéñòâî õàðàêòåðíûõ òðàåê-
òîðèé ïîëåòà íà áîëüøèõ âûñîòàõ:
1 – ãèïåðáîëà; 2 – ïàðàáîëà; 3 – ýëëèïñ
êðèâàÿ (ãèïåðáîëà èëè ïàðàáî-
ëà); åñëè æå C2 < 0, òî òðàåêòî-
ðèÿ – çàìêíóòàÿ êðèâàÿ ñ íàè-
áîëüøèì ðàäèóñîì rmax = rA =
2
2
K
C
(ýëëèïñ èëè îêðóæíîñòü). Â
äàëüíåéøåì áóäåì ðàññìàòðè-
âàòü ýëëèïòè÷åñêèå òðàåêòîðèè,
äëÿ êîòîðûõ C2 <0èκí <2.
Ïðàêòè÷åñêîå èñïîëüçîâà-
íèå çàâèñèìîñòåé ýëëèïòè÷å-
ñêîé òåîðèè ñâÿçàíî ñ ïðèáëè-
æåííûì ðåøåíèåì ñëåäóþùèõ
îñíîâíûõ çàäà÷.
1. Îïðåäåëèòü ïàðàìåòðû äâè-
æåíèÿ â òåêóùåé òî÷êå òðàåêòî-
ðèè ïî èçâåñòíûì õàðàêòåðèñòè-
êàì â íà÷àëå ïàññèâíîãî ó÷àñòêà.
2. Ïî çàäàííûì ïàðàìåòðàì â
íà÷àëå ïàññèâíîãî ó÷àñòêà òðà-
åêòîðèè íàéòè âåëè÷èíó ïîëíîé
äàëüíîñòè.
3. Îïðåäåëèòü íà÷àëüíóþ ñêî-
ðîñòü Ví, íåîáõîäèìóþ äëÿ äîñ-
234
Ðèñ. 5 .6 . Îòíîøåíèå V/V0I â ôóíêöèè ýêñöåíòðèñèòåòà:
I – îáëàñòü V/V0I =(1+e)1/2; II – îáëàñòü V/V0I =(1− e)1/2
Ðèñ. 5 .7. Îáëàñòè âîçìîæíûõ òðàåêòî-
ðèé:
À – îáëàñòü ãèïåðáîë; Á – îáëàñòü ýë-
ëèïñîâ, íå ïåðåñåêàþùèõñÿ ñ ïðèòÿãè-
âàþùèì òåëîì; Â – îáëàñòü ýëëèïñîâ,
ïåðåñåêàþùèõñÿ ñ ïðèòÿãèâàþùèì òå-
ëîì
òèæåíèÿ òðåáóåìîé äàëüíîñòè
ïîëåòà ïðè èçâåñòíûõ çíà÷åíèÿõ
rí è θí â íà÷àëå ïàññèâíîãî ó÷à-
ñòêà òðàåêòîðèè.
4. Ïî çàäàííîé äàëüíîñòè ïî-
ëåòà è rí ðàññ÷èòàòü îïòèìàëü-
íûé óãîë θí.îïò, ïðè êîòîðîì
äàëüíîñòü áóäåò äîñòèãàòüñÿ ïðè
ìèíèìàëüíîé íà÷àëüíîé ñêîðî-
ñòè Ví min.
5. Ïðè èçâåñòíûõ çíà÷åíèÿõ
rí è Ví íàéòè çíà÷åíèå óãëà íàè-
áîëüøåé äàëüíîñòè θí max.
Äëÿ ðåàëüíûõ ÁÐÄÄ äëèíà
ïîñëåäíåãî ó÷àñòêà òðàåêòîðèè –
ó÷àñòêà âõîäà â ïëîòíûå ñëîè àò-
ìîñôåðû ñîñòàâëÿåò ìåíåå 5 %
îáùåé äàëüíîñòè ïîëåòà. Ïîýòî-
ìó äîïóùåíèå î òîì, ÷òî ðàêåòà
äâèæåòñÿ çäåñü òàê æå, êàê è ïî
ýëëèïòè÷åñêîé òðàåêòîðèè, äàåò
õîðîøåå ïåðâîå ïðèáëèæåíèå
äëÿ îïðåäåëåíèÿ äàëüíîñòè è
îöåíîê ïðîìàõà. Ó÷èòûâàÿ ýòî,
ïðè äàëüíåéøèõ âûâîäàõ áóäåì
ðàññìàòðèâàòü ñõåìó äâèæåíèÿ,
ïðåäñòàâëåííóþ íà ðèñ. 5 .8, ãäå Í′Ö – ýëëèïòè÷åñêèé ó÷àñòîê òðà-
åêòîðèè.
 äèôôåðåíöèàëüíûõ óðàâíåíèÿõ äâèæåíèÿ ïåðåéäåì îò íåçàâè-
ñèìîé ïåðåìåííîé t ê íåçàâèñèìîé ïåðåìåííîé φ. Ïðåîáðàçîâàíèå
èìååò âèä
d
dt
d
d
d
dt
rV
r
d
d
==
•
;
cos
.
φ
φ
θ
φ
íí
í
2
Ñäåëàâ åùå îäíó çàìåíó ρ =1/r, çàïèøåì ïåðâîå óðàâíåíèå ñèñ-
òåìû (3.142) äëÿ ðàññìàòðèâàåìîãî ñëó÷àÿ òàê:
d
dr
2
22
1
ρ
φ
ρ
κθ
+=
íí
í
cos
.
Ïîñòîÿííûå èíòåãðèðîâàíèÿ íàõîäÿòñÿ èç íà÷àëüíûõ óñëîâèé
235
Ðèñ. 5 .8. Óïðîùåííàÿ ñõåìà òðàåêòîðèè
ïîëåòà áàëëèñòè÷åñêîé ðàêåòû äàëüíåãî
äåéñòâèÿ
ρ
ρ
φ
θ
í
í
í
í
í
d
tg
==
−
11
r
d
r
;.
Ðåøåíèå ïîëó÷åííîãî óðàâíåíèÿ ÿâëÿåòñÿ î÷åâèäíûì:
rí
íí
í
í
ρ
φ
κθ
θφ
θ
=
−
+
+
1
2
cos
cos
cos(
)
cos
.
Ïðîâåäÿ îáðàòíóþ çàìåíó ρ íà 1/r, ïîëó÷èì óðàâíåíèå ýëëèïòè-
÷åñêîé òðàåêòîðèè
r
r
=
−+
+
κθ
φκθθφ
íí
í
ííí
cos
cos
cos cos(
)
.
2
1
(5.34)
Õîòÿ òàêàÿ ôîðìà çàïèñè ñëîæíåå îáùåïðèíÿòîé (5.31), îíà îáëàäàåò
òåì ïðåèìóùåñòâîì, ÷òî íåïîñðåäñòâåííî è êîñâåííî âêëþ÷àåò â
ñåáÿ ïàðàìåòðû Ví, θí è rí, õàðàêòåðèçóþùèå ïîëîæåíèå è âåëè÷èíó
ýíåðãèè ðàêåòû â ãðàíè÷íîé òî÷êå, ñîîòâåòñòâóþùåé íà÷àëó
ïàññèâíîãî ó÷àñòêà ïîëåòà. Çàâèñèìîñòü (5.34) ñîâìåñòíî ñ
ïðèâåäåííûìè â ïðåäûäóùåì ïîäðàçäåëå ñîîòíîøåíèÿìè ïîçâîëÿåò
äîñòàòî÷íî ïðîñòî îïðåäåëÿòü ýëåìåíòû òðàåêòîðèè ïî èçâåñòíûì
íà÷àëüíûì äàííûì. Ïîñëåäóþùèå çàäà÷è òàêæå ñâîäÿòñÿ ê ðåøåíèþ
ïîëó÷åííûõ ðàíåå ñîîòíîøåíèé.
Ïðè îïðåäåëåíèè ïàðàìåòðîâ äâèæåíèÿ, ñîîòâåòñòâóþùèõ òî÷-
êàì ïàäåíèÿ ãîëîâíîé ÷àñòè ðàêåòû, ñëåäóåò èìåòü â âèäó, ÷òî ïîëî-
æåíèå öåëè îòíîñèòåëüíî íà÷àëà ïàññèâíîãî ó÷àñòêà òðàåêòîðèè ðà-
êåòû îäíîçíà÷íî îïðåäåëÿåòñÿ óãëîâîé äàëüíîñòüþ äî öåëè 2ψ.
Ñâÿçü ìåæäó óãëîâîé è ëèíåéíîé äàëüíîñòüþ L (äëÿ ñôåðè÷åñêîé
ìîäåëè Çåìëè) âûðàæàåòñÿ ñîîòíîøåíèåì
LR
=2Çψ,
(5.35)
ãäå 2ψ – óãîë îòíîñèòåëüíîãî ïîëîæåíèÿ öåëè â ðàäèàíàõ. Ïðèâåäåì
ðÿä ÷èñëîâûõ çíà÷åíèé óãëîâ ψ è ñîîòâåòñòâóþùèõ èì âåëè÷èí
ëèíåéíîé äàëüíîñòè ïîëåòà L ïðè RÇ = 6371 êì:
ψ,ãðàäóñ... 5
8
15
30
607590
L,êì ..... 556 890 1668 3336 6672 8340 10008
Óñëîâèåì ïîïàäàíèÿ â öåëü ÿâëÿåòñÿ ñîáëþäåíèå ðàâåíñòâà r =
=RÇ ïðè φ =2ψ. Ïîäñòàâèâ ýòî óñëîâèå â (5.34), ïîëó÷èì óðàâíåíèå
236
ñâÿçè ðàñ÷åòíîé óãëîâîé äàëüíîñòè ñ ïàðàìåòðàìè íà÷àëà ïàññèâíî-
ãî ó÷àñòêà
r
R
í
Çí
í
í
íí
=
−+
+
[ cos
cos cos(
)]
cos
.
12
2
2
ψκθθψ
κθ
(5.36)
Çàâèñèìîñòü (5.36) ïîçâîëÿåò òàêæå ðåøèòü îáðàòíóþ çàäà÷ó
îïðåäåëåíèÿ íåîáõîäèìîé ñêîðîñòè äëÿ äîñòèæåíèÿ òðåáóåìîé
äàëüíîñòè ïðè çàäàííûõ çíà÷åíèÿõ θí è rí:
VV
r
R
íí
I
í
Ç
íí
í
=
−
−+
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
12
2
2
cos
cos
cos cos(
)
ψ
θθθψ
⎥
12
/
.
(5.37)
Ïðè î÷åíü áîëüøèõ äàëüíîñòÿõ ïîëåòà ìîæíî ïðèíÿòü (â ïåðâîì
ïðèáëèæåíèè) äîïóùåíèå î ìãíîâåííîì ñãîðàíèè òîïëèâà ðàêåòû
(r = R).  ýòîì ñëó÷àå
VV
íI
íí
í
=
−
−+
⎡
⎣⎢
⎤
⎦⎥
0
2
12
12
2
cos
cos
cos cos(
).
/
ψ
θθθψ
237
Ðèñ. 5.9. Çàâèñèìîñòè ñêîðîñòè
â íà÷àëå ïàññèâíîãî ó÷àñòêà Ví
îò óãëà θí äëÿ ðàçëè÷íûõ çíà÷å-
íèé óãëîâîé äàëüíîñòè 2ψ (ïðè
rí=RÇ)
Àíàëèç ïîëó÷åííîãî óïðî-
ùåííîãî óðàâíåíèÿ (ðèñ. 5 .9)
ïîçâîëÿåò ñäåëàòü âûâîä, ÷òî
îäíà è òà æå óãëîâàÿ äàëüíîñòü
2ψ ìîæåò áûòü äîñòèãíóòà ïðè
ìíîæåñòâå êîìáèíàöèé çíà÷å-
íèé Ví è θí â ìîìåíò âûêëþ-
÷åíèÿ äâèãàòåëÿ. Ïðè ðàñ÷å-
òàõ òðàåêòîðèé ñ áîëüøèìè
äàëüíîñòÿìè ïîëåòà èñïîëüçî-
âàíèå ñôåðè÷åñêîé ìîäåëè
Çåìëè ïðèâîäèò ê çàìåòíûì
îøèáêàì. Îäíàêî ïðèìåíåíèå
áîëåå ñîâåðøåííûõ ìîäåëåé
çíà÷èòåëüíî óñëîæíÿåò ìåòîäè-
êè ðàñ÷åòîâ, ÷òî çàòðóäíÿåò èõ
èñïîëüçîâàíèå â ó÷åáíîé ïðàê-
òèêå.
Ïðàêòè÷åñêè âàæíûì ÿâëÿåò-
ñÿ îïðåäåëåíèå ïîëîæåíèÿ ðàêå-
òû íà ýëëèïòè÷åñêîé òðàåêòîðèè
ïî èñòå÷åíèè íåêîòîðîãî ïðîìå-
æóòêà âðåìåíè ïîñëå ïóñêà.
Ïåðâûé ýòàï ïîëó÷åíèÿ èñõîä-
íîé çàâèñèìîñòè ñâÿçàí ñ èíòåãðèðîâàíèåì óðàâíåíèÿ ìîìåíòà êî-
ëè÷åñòâà äâèæåíèÿ ïî âðåìåíè ïðè ó÷åòå çàâèñèìîñòè, óñòàíàâëè-
âàåìîé óðàâíåíèåì òðàåêòîðèè (5.34). Îêîí÷àòåëüíàÿ ôîðìóëà íà-
õîäèòñÿ â ðåçóëüòàòå äîâîëüíî ñëîæíîãî àíàëèòè÷åñêîãî ðåøåíèÿ
[33] è èìååò âèä
t
r
V
=
−+
−
−
−
í
íí
íí
í
í
tg
cos
(c
o
s)( )
s
i
n
()cos
co
θ
θφκ
φ
κ
φ
κ
11
2
1
s
cos(
)
cos
cos
2
2
2
1
θ
θφ
θ
θ
κ
κ
í
í
í
í
í
í
+
+
⎛
⎝⎜
⎞
⎠⎟
+
⎧
⎨
⎪⎪
⎩
⎪
⎪
+
−
⎛
⎝⎜⎞
⎠⎟
−
⎛
⎝⎜⎞
⎠⎟
−
⎫
⎬
⎪
⎪
⎭
⎪
⎪
32
12
2
1
2
/
/
cos
sin
.
arctg
ctg
í
íí
κ
θ
φ
θ
(5.38)
238
Ðèñ. 5 .10 . Çàâèñèìîñòü ïîëíîãî âðåìå-
íè ïîëåòà îò óãëà θí äëÿ ðàçëè÷íûõ óã-
ëîâûõ äàëüíîñòåé (ïðè rí = RÇ)
Ïîëíîå âðåìÿ ïîëåòà tc âû÷èñëÿåòñÿ ïðè ïîäñòàíîâêå çíà÷åíèÿ
φ =2ψ â óðàâíåíèå (5.38):
t
r
V
r
R
ñ
=
−+
−
−
+
⎧
⎨
í
íí
íí
í
í
Ç
tg
cos
(c
o
s)( )
s
i
n
()
θ
θψ
κ
ψ
κ
121 2
2
⎪⎪
⎩
⎪
⎪
+
−
⎛
⎝⎜⎞
⎠⎟
−
⎛
⎝⎜⎞
⎠⎟
2
2
1
2
1
32
12
cos
cos
/
/
θ
κ
κ
κ
í
í
í
í
arctg
θψθ
íí
ctg −
⎫
⎬
⎪
⎪
⎭
⎪
⎪
sin
.
(5.39)
Ãðàôè÷åñêîå èçîáðàæåíèå çàâèñèìîñòè âðåìåíè ïîëåòà ïî áàëëèñ-
òè÷åñêîé òðàåêòîðèè (ïðè rí = RÇ) îò óãëà θí äëÿ ðàçëè÷íûõ óãëîâûõ
äàëüíîñòåé ïðåäñòàâëåíî íà ðèñ. 5.10.
5.2.3 . ÔÎÐÌÓËÀ Ê.Ý . ÖÈÎËÊÎÂÑÊÎÃÎ ÄËß ÐÀÑ×ÅÒÀ
ÌÀÊÑÈÌÀËÜÍÎÉ ÑÊÎÐÎÑÒÈ ÏÎËÅÒÀ ÐÀÊÅÒÛ
Óðàâíåíèÿ äâèæåíèÿ ËÀ ïåðåìåííîé ìàññû íàèáîëåå ïðîñòî èí-
òåãðèðóþòñÿ â ñëó÷àå, êîãäà â äîïîëíåíèå ê ïðåäïîëîæåíèþ îá îò-
ñóòñòâèè ñîïðîòèâëåíèÿ âîçäóõà íå ó÷èòûâàåòñÿ è äåéñòâèå ñèëû òÿ-
æåñòè.
 ýòîì ñëó÷àå óðàâíåíèå äâèæåíèÿ ðàêåòû äëÿ ïðÿìîëèíåéíîãî
ïîëåòà áóäåò èìåòü âèä
mV
P
•
.
=
(5.40)
Ïîäñòàâëÿÿ â (5.40) çíà÷åíèÿ Ð è m, îïðåäåëÿåìûå ïî ôîðìóëàì
(1.154) è (3.25), ïîëó÷èì
dVW
Qdt
QQd
t
e
tk
=
−
∫
ñåê
ñåê
0
0
.
Èíòåãðèðóÿ ýòî óðàâíåíèå, íàéäåì ñêîðîñòü ðàêåòû â ìîìåíò
âðåìåíè t:
VW
Q
QQd
t
e
tk
=
−
⎛
⎝
⎜
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
⎟
∫
ln
,
0
0
0
cåê
(5.41)
239
èëè
VW
m
m
V
e
==
ln
,
0
Ö
(5.42)
ãäå m0 è m – íà÷àëüíàÿ è òåêóùàÿ ìàññû ðàêåòû. Ôîðìóëà (5.42)
ìîæåò áûòü çàïèñàíà â äðóãîì âèäå:
m
m
e
VWe
0
=
−
/
.
(5.43)
Ó÷èòûâàÿ, ÷òî Qdt Q
tk
ñåê
ò
=
∫
,
0
ïîëó÷èì ôîðìóëó, îïðåäåëÿþùóþ
íàèáîëüøóþ ñêîðîñòü, êîòîðóþ ìîæåò èìåòü ðàêåòà áåç ó÷åòà äåéñò-
âèÿ íà íåå ñèëû òÿæåñòè è ñèëû ñîïðîòèâëåíèÿ âîçäóõà:
VW
Q
QQ
e
max
ln
.
=
−
0
0ò
(5.44)
Åñëè ïðåäñòàâèòü íà÷àëüíûé âåñ ðàêåòû êàê Q0 = Qï + Qò, ãäå Qï –
ïàññèâíûé âåñ ðàêåòû, òî
VW
Q
Q
e
max
ln
;
=+
⎛
⎝⎜⎞
⎠⎟
1ò
ï
(5.45)
VW
Q
Q
e
max
ln
.
=−
−
⎛
⎝⎜⎞
⎠⎟
1
0
ò
(5.46)
Äëÿ ïðàêòè÷åñêèõ ðàñ÷åòîâ ìîæíî âîñïîëüçîâàòüñÿ òàáóëèðîâàí-
íîé ôóíêöèåé k(λ)=−ln(1 −λ), ãäå λ=∫QdtQ
t
ñåê
/.
0
0
Òîãäà V =
= We k(λ).
Ôîðìóëà (5.42) âïåðâûå áûëà âûâåäåíà Ê.Ý. Öèîëêîâñêèì è íà-
çâàíà åãî èìåíåì.
5.2.4. ÏÐÈÁËÈÆÅÍÍÛÅ ÌÅÒÎÄÛ ÐÀÑ×ÅÒÀ ÒÐÀÅÊÒÎÐÈÉ ÑÍÀÐßÄÎÂ
ÏÎÑÒÎßÍÍÎÉ ÌÀÑÑÛ
Àíàëèòè÷åñêèå ìåòîäû ðàñ÷åòà òðàåêòîðèé ñíàðÿäîâ ïîñòîÿííîé
ìàññû â âîçäóõå îáû÷íî îñíîâûâàþòñÿ íà ñèñòåìå óðàâíåíèé
(3.131), çàïèñàííîé ïðè íåçàâèñèìîì θ. Íàèáîëüøèå òðóäíîñòè âû-
çûâàåò îïðåäåëåíèå ñêîðîñòè äâèæåíèÿ öåíòðà ìàññ ñíàðÿäà. Ñêî-
ðîñòü íàõîäÿò ïóòåì èíòåãðèðîâàíèÿ óðàâíåíèÿ ãîäîãðàôà (3.130).
Ïðåäñòàâèì åãî â âèäå
240
dV
d
EV
g
(cos)
,
θ
θ
=
2
(5.47)
ãäå E
X
mV
a
=
0
.
Åñëè äëÿ îïðåäåëåíèÿ Õà âîñïîëüçîâàòüñÿ (1.126), òî
ïîëó÷èì
E
VS
m
cxa
=
ρ
20
(Ì).
(5.48)
Åñëè âîñïîëüçîâàòüñÿ (1.131), òî áóäåì èìåòü
E
c
V
HyFV
=
()().
(5.49)
 ïåðâîì ñëó÷àå èç (5.47) ñëåäóåò
dV
d
y
V
mg
Sc
ON
ON
xa
(cos) ()
(
θ
θ
ρ
ρ
ρ
=
3
0
2
M).
(5.50)
Îäíîâðåìåííàÿ çàìåíà ôóíêöèé ρ/ρON(y)ècx a
(M) àíàëèòè÷åñêèìè
çàâèñèìîñòÿìè íå ïðèâîäèò ê ðàçäåëåíèþ ïåðåìåííûõ â óðàâíåíèè
(5.50) è íå äàåò ðåøåíèÿ â êîíå÷íîì âèäå.
Åñëè äàæå ïðèíÿòü cc
xx
aa
(,
M)
const
≈=
÷òî ïðèâîäèò ê êâàäðà-
òè÷íîé çàâèñèìîñòè ñèëû ëîáîâîãî ñîïðîòèâëåíèÿ âîçäóõà
X
SV
c
ax
a
=
ρ2
2
,
(5.51)
òî ïåðåìåííûå â óðàâíåíèè (5.50) âñå ðàâíî íå ìîãóò áûòü ðàçäåëåíû,
ïîñêîëüêó â (5.51) îñòàåòñÿ ôóíêöèÿ ρ(y).
Åñëè èñïîëüçîâàòü (5.49), òî ïîëó÷èì ïåðâîå óðàâíåíèå ñèñòåìû
(3.132) â âèäå
dV
d
c
VFV
g
(cos) ()
,
θ
θ
=
1
(5.52)
ãäå c1 = cH(y).
Èññëåäîâàíèÿ ïîêàçûâàþò, ÷òî äëÿ ïðèáëèæåííîãî èíòåãðèðî-
âàíèÿ óðàâíåíèÿ (5.52) ïðè îáåñïå÷åíèè ïðèåìëåìîé òî÷íîñòè ðàñ-
÷åòà ñëåäóåò áðàòü H(y) ≈ H(yñð), à ôóíêöèþ ñîïðîòèâëåíèÿ âîçäó-
õà – îïèñûâàòü îäíîé èç àíàëèòè÷åñêèõ çàâèñèìîñòåé
FV abV
n
()=+
(5.53)
241
èëè
FV BVn
(),
=
(5.54)
ãäå a, b, B, n – ïîñòîÿííûå ýêñïåðèìåíòàëüíûå êîýôôèöèåíòû.
Ïîñëåäíÿÿ çàâèñèìîñòü áûëà ïðåäëîæåíà Í. . Ìàèåâñêèì è
Í.À. Çàáóäñêèì. Çíà÷åíèÿ ïîêàçàòåëÿ ñòåïåíè n äëÿ ðàçëè÷íûõ äèà-
ïàçîíîâ ñêîðîñòè V èìåþò ñëåäóþùèå çíà÷åíèÿ:
V, ì/ñ ... 0 ...240 240 ...295 295...375 375...419 419...550 550...800 800 ...1000
n
.. ..2
3
5
3
2
1,70
1,55
Êîýôôèöèåíòû Bi äëÿ êàæäîãî ó÷àñòêà ïîäáèðàþòñÿ òàê, ÷òîáû
ôóíêöèÿ F(V ) áûëà íåïðåðûâíîé.
Ïîäñòàâèì (5.53) â (5.52) è ðàñêðîåì ïðîèçâîäíóþ â ëåâîé ÷àñòè
óðàâíåíèÿ
dV
d
cV
g
ab
V
dV
d
V
g
cag
cb
g
n
(cos) ()
:
cos
(s
i
n
)
θ
θ
θθ
θ
=+
=+
+
1
1
1
cos
.
θ
Vn+1
Ââåäåì ïîäñòàíîâêó V*V
n
= 1, èç êîòîðîé äèôôåðåíöèðîâàíèåì
ïîëó÷èì
dV
dV
nV
n
=−
−−
*
.
1
(5.55)
Ïîñëå çàìåíû è ïðåîáðàçîâàíèé áóäåì èìåòü ëèíåéíîå äèôôå-
ðåíöèàëüíîå óðàâíåíèå ïåðâîãî ïîðÿäêà
dV
d
nNV
ncM
*
*
()
(),
θ
θθ
+=
1
(5.56)
ãäå
N
ag
g
M
c
g
()
sin
cos
;()
cos
.
θ
θ
θ
θ
θ
=
+
=−
1
 ñîîòâåòñòâèè ñ îáùèì ïðàâèëîì ðåøåíèÿ äèôôåðåíöèàëüíûõ
óðàâíåíèé íàçâàííîãî òèïà íàéäåì ðåøåíèå óðàâíåíèÿ (5.56) â âèäå
242
Vn
c
e
e
Mdk
nNd
nNd
*
()
()
()
=
∫∫
+
⎛
⎝
⎜
⎜⎜
⎞
⎠
−
∫
1
00
0
θθ
θθ
θ
θ
θ
θ
θ
θ
θθ
⎟
⎟⎟
.
(5.57)
Èç (5.57) è (5.55) äëÿ íà÷àëüíûõ óñëîâèé θ = θ0 è V = V0 ïîëó÷èì
kV
n
=1
0
/;
îïðåäåëèâ V* èç (5.55), íàéäåì òàêæå çíà÷åíèå èñêîìîé
ñêîðîñòè
V
nV
=
1
*
.
(5.58)
Ðàññìîòðèì àíàëèòè÷åñêîå ðåøåíèå, âîñïîëüçîâàâøèñü äëÿ îï-
ðåäåëåíèÿ ôóíêöèè F(V) ôîðìóëîé (5.54). Òîãäà èç (5.52) áóäåì
èìåòü
dV
d
cBV
g
n
(cos)
.
θ
θ
=
+
1
1
(5.59)
Ðàçäåëèì ïåðåìåííûå, óìíîæèâ ÷èñëèòåëü è çíàìåíàòåëü ïðàâîé
÷àñòè ïðåäûäóùåãî ðàâåíñòâà íà cos
n+1
θ:
dV
V
cB
g
d
nn
(cos)
(cos)
cos
.
θ
θ
θ
θ
++
=
1
1
1
Ïîñëå èíòåãðèðîâàíèÿ áóäåì èìåòü
11
1
00
1
1
0
nV
V
cB
g
d
nn
n
(cos) (cos)
cos
.
θθ
θ
θ
θ
θ
−
⎡
⎣⎢
⎤
⎦⎥=
+
∫
(5.60)
Èíòåãðàë ïðàâîé ÷àñòè ìîæåò áûòü âçÿò â ýëåìåíòàðíûõ ôóíêöèÿõ.
Èçâåñòíû ðåøåíèÿ äî n = 5, ïðèâåäåííûå, íàïðèìåð, â [34, 57]. Äëÿ
îïðåäåëåíèÿ êîîðäèíàò è âðåìåíè äâèæåíèÿ âîñïîëüçóåìñÿ òðåìÿ
ïîñëåäíèìè óðàâíåíèÿìè ñèñòåìû (3.131). Èç óðàâíåíèÿ dy/dθ =
=-V
2
tgθ/g ïîëó÷èì
yy
V
g
tgd
=+
∫0
2
0
θθ
θ
θ
.
(5.61)
Èç óðàâíåíèÿ dx/dθ = −V 2/g íàéäåì
243
xx
V
g
d
=+
∫0
2
0
θ
θ
θ
.
(5.62)
Èç óðàâíåíèÿ dt/dθ = −Vg cosθ ïîëó÷èì
tt
V
g
d
=+
∫0
0
θ
θ
θ
θ
cos
.
(5.63)
Ñëîæíîñòü ôîðìóë äëÿ îïðåäåëåíèÿ ñêîðîñòè (5.57) è (5.58) èëè
(5.60) íå ïîçâîëÿåò âçÿòü èíòåãðàëû ïðàâûõ ÷àñòåé (5.61)...(5.63) â
êîíå÷íîì âèäå.
Ðàññìîòðèì ðåøåíèå îñíîâíîé çàäà÷è âíåøíåé áàëëèñòèêè ïðè
àïïðîêñèìàöèè ôóíêöèè F(V ) îäíî÷ëåííîé êâàäðàòè÷íîé çàâèñè-
ìîñòüþ F(V )=BV 2. Ýòî ðåøåíèå ïîëó÷èëî íàçâàíèå ìåòîäà Ýéëåðà
[45].
 ïåðâîì óðàâíåíèè ñèñòåìû (3.131) îáîçíà÷èì b = BcH(yñð). Òî-
ãäà óðàâíåíèå ãîäîãðàôà áóäåò èìåòü âèä
du
d
b
g
u
θθ
=
3
3
cos
. Ïðîèíòåãðè-
ðîâàâ, ïîëó÷èì
1
2
1
2
0
22
3
0
uu
b
g
d
−=
∫θ
θ
θ
θ
cos
,
(5.64)
ãäå u0 = V0 cos(θ). ×òîáû óïðîñòèòü äàëüíåéøåå ðåøåíèå, îáû÷íî
ââîäÿò âñïîìîãàòåëüíóþ ôóíêöèþ ε(θ)= dθθ
θ
/cos ,
3
0
∫
è òîãäà
112
2
0
2
0
uu
b
g
=−
−
[() ( )].
εθ εθ
(5.65)
Åñëè ïîñòîÿííûå âåëè÷èíû, çàâèñÿùèå îò íà÷àëüíûõ óñëîâèé,
ñãðóïïèðîâàòü âìåñòå è îáîçíà÷èòü ε(V0, θ0)=εθ
(),
0
0
2
2
+
g
bu
òî ïîëó-
÷èì
u
g
bV
2
00
0
2
1
=
−
εθε
θ
(,) ()
.
(5.66)
Äëÿ ôóíêöèè ε(θ), âõîäÿùåé â (5.66), ìîæåò áûòü çàïèñàíà
àíàëèòè÷åñêàÿ çàâèñèìîñòü
244
εθ
θ
θ
θ
θ
πθ
θ
() cos
sin
cos
ln
.
== ++
⎛
⎝⎜⎞
⎠⎟
⎡
⎣⎢
⎤
⎦⎥
∫d
32
0
1
24
2
tg
Îïðåäåëèâ u, ñêîðîñòü ñíàðÿäà íàéäåì ïî ôîðìóëå V = u/cosθ.
Ïîäñòàâëÿÿ (5.66) â îñòàëüíûå óðàâíåíèÿ ñèñòåìû (3.131), ïîëó-
÷èì ñîîòâåòñòâåííî ïîñëå èíòåãðèðîâàíèÿ
y
b
d
V
x
b
d
V
=
−
=
∫1
2
1
2
00
2
00
0
tgθθ
εθε
θθ
θ
εθ
θ
θ
[( , ) ()]cos
;
[(,)()
]c
o
s
;
[( , ) ()]cos
.
−
=
−
∫
∫
εθ
θ
θ
εθε
θθ
θ
θ
θ
θ
2
00
2
0
0
1
2
t
bg
d
V
(5.67)
Èíòåãðàëû, ñîäåðæàùèåñÿ â ïðàâûõ ÷àñòÿõ óðàâíåíèé (5.67), â
êîíå÷íîì âèäå íå áåðóòñÿ, íî
ÿâëÿþòñÿ ôóíêöèÿìè îäíèõ è
òåõ æå âåëè÷èí, ÷òî ìîæåò ñëó-
æèòü îñíîâàíèåì äëÿ îïðåäåëå-
íèÿ èõ ñ ïîìîùüþ ñïåöèàëüíûõ
òàáëèö [22].
Ìåòîä ïñåâäîñêîðîñòè îòíî-
ñèòñÿ ê òðåòüåé ãðóïïå àíàëèòè-
÷åñêèõ ìåòîäîâ, òàê êàê â åãî îñ-
íîâå ëåæèò äîïîëíèòåëüíîå ïðå-
îáðàçîâàíèå óðàâíåíèÿ ãîäî-
ãðàôà ñêîðîñòè (3.130). Â óðàâ-
íåíèå ãîäîãðàôà äëÿ ðàçäåëåíèÿ
ïåðåìåííûõ ââîäèòñÿ ôóíêöèÿ
F(U ), ãäå U – âåëè÷èíà, èìåþ-
ùàÿ ðàçìåðíîñòü ñêîðîñòè è íà-
çûâàåìàÿ ïñåâäîñêîðîñòüþ. Çíà-
÷åíèå
U îïðåäåëÿåòñÿ
ïî
ðèñ. 5.11:
U
V
=
cos
cos
.
θ
θ0
(5.68)
Âåêòîð ïñåâäîñêîðîñòè ïà-
ðàëëåëåí íà÷àëüíîé ñêîðîñòè è
èìååò òó æå ãîðèçîíòàëüíóþ
245
Ðèñ. 5.11. Ïîñòðîåíèå âåêòîðà ïñåâäî-
ñêîðîñòè
ïðîåêöèþ u, ÷òî è äåéñòâèòåëüíàÿ ñêîðîñòü V. Òàê êàê ïðîñòàÿ çàìå-
íà F(V )íàF(U ) äàåò çíà÷èòåëüíûå îøèáêè, òî â óðàâíåíèå ãîäîãðà-
ôà ââîäÿòñÿ äîïîëíèòåëüíûå ïîïðàâî÷íûå êîýôôèöèåíòû.
Ïîäñòàíîâêà èìååò îáùèé âèä
HyFV kFU
()() (),
=
(5.69)
ãäå k – ïîïðàâî÷íûé ìíîæèòåëü, êîìïåíñèðóþùèé îøèáêó.
Äëÿ íàñòèëüíûõ òðàåêòîðèé, õàðàêòåðèçóþùèõñÿ ìàëûìè óãëàìè
áðîñàíèÿ è áîëüøèìè íà÷àëüíûìè ñêîðîñòÿìè, óãîë θ ìàëî èçìå-
íÿåòñÿ ïî òðàåêòîðèè, à H(y) ≈ 1.  ýòîì ñëó÷àå äîñòàòî÷íî ïðèíÿòü
k=1/cos.
θ
(5.70)
Äëÿ çåíèòíûõ òðàåêòîðèé òàêæå õàðàêòåðíû áîëüøèå íà÷àëüíûå
ñêîðîñòè è ñëàáîå èçìåíåíèå cosθ ïî òðàåêòîðèè, íî H(y) ≠ 1, è ïî-
ýòîìó íåîáõîäèìà ïîäñòàíîâêà äðóãîãî âèäà:
HyFV Hy FU
()() ( )()cos
cos
,
≈
ñð
θ
θ
0
(5.71)
ò.å.
kHy
=
()cos
cos
.
ñð
θ
θ
0
(5.72)
Äëÿ ñðåäíèõ óãëîâ áðîñàíèÿ è ñêîðîñòåé, õàðàêòåðíûõ äëÿ
òðàåêòîðèé ñíàðÿäîâ ïîëåâûõ àðòèëëåðèéñêèõ ñèñòåì, ïîäñòàíîâêà
íåñêîëüêî ñëîæíåå ïðåäûäóùèõ:
HyFV FU
()() ()cos
cos
,
≈β
θ
θ
2
0
(5.73)
ò.å.
k=β
θ
θ
cos
cos
,
2
0
(5.74)
ãäå β – äîïîëíèòåëüíûé ÷èñëåííûé ïîïðàâî÷íûé ìíîæèòåëü.
Ïîñëåäíÿÿ çàìåíà íîñèò íàçâàíèå ïîäñòàíîâêè Ñèà÷÷è.
246
Ïðè èçâåñòíîé ïñåâäîñêîðîñòè äåéñòâèòåëüíàÿ ñêîðîñòü îïðåäå-
ëÿåòñÿ èç ðàâåíñòâà (5.68):
V
U
=
cos
cos
,
θ
θ
0
(5.75)
à åå ãîðèçîíòàëüíàÿ ïðîåêöèÿ ðàâíà
uU
=
cos .
θ0
(5.76)
Ââåäåì ïîäñòàíîâêó (5.73) â óðàâíåíèå ãîäîãðàôà ñêîðîñòè, çà-
ìåíèì ñ′ = ñβ è ðàçäåëèì ïåðåìåííûå:
dg
c
dU
UFU
θ
θθ
cos
cos
()
.
22
0
=
′
(5.77)
Ïîñëå èíòåãðèðîâàíèÿ áóäåì èìåòü
tg tg
θθ
θ
−=
′
∫
0
2
00
g
c
dU
UFU
U
U
cos
().
(5.78)
Èíòåãðàë â ïðàâîé ÷àñòè ìîæåò áûòü âçÿò òîëüêî ÷èñëåííî.
Ïðàêòè÷åñêè ðàñ÷åò òðàåêòîðèè ìåòîäîì ïñåâäîñêîðîñòè âåäåòñÿ ñ
èñïîëüçîâàíèåì ñïåöèàëüíûõ òàáëèö, ïðè÷åì ñ öåëüþ ïîâûøåíèÿ
òî÷íîñòè ïðèìåíÿþòñÿ ñïåöèàëüíûå ïîïðàâî÷íûå òàáëèöû íà âå-
ëè÷èíó c′. Äëÿ óäîáñòâà ñîñòàâëåíèÿ òàáëèö è ðàáîòû ïî íèì ââåäå-
íû ôóíêöèè
IUk
gdU
UFU
IVk
gdU
UFU
U
V
U
U
()
() ()
(),
=−
=−
∫
∫10
1
22
0
è
í
í
ãäåV0=U0.
Ïðåîáðàçóÿ (5.78), ïîëó÷èì
tg
tg
() () cos
[() ()].
θθ
θ
=−
′
−
0
2
0
0
1
2c
IU IV
(5.79)
Ïðîèíòåãðèðóåì îñòàëüíûå óðàâíåíèÿ (3.131). Óðàâíåíèå
dt
d
u
g
θθ
=−
1
2
cos
ïðåîáðàçóåì ñ ó÷åòîì (5.77). Ïîñëå èíòåãðèðîâàíèÿ áóäåì èìåòü
247
t
c
dU
FU
V
U
=
′
∫
1
00
cos
().
θ
Ââîäÿ ôóíêöèþ
TUk
dU
FU
U
U
()
(),
=−
∫2
í
ïîëó÷èì
t
c
TU TV
=
′
−
1
0
0
cos
[() ( )].
θ
(5.80)
Âîçüìåì óðàâíåíèå
dx
d
u
g
θθ
=−
2
2
0
cos
.
Ðàçäåëèâ â íåì ïåðåìåííûå è ó÷èòûâàÿ (5.77), ïîëó÷èì
dx
UdU
cFU
=−
′()
.
(5.81)
Ïðîèíòåãðèðîâàâ, áóäåì èìåòü
x
c
UdU
FU
V
U
=−
′
∫1
0
().
Ââîäÿ ôóíêöèþ
DUk
UdU
FU
U
U
()
()
,
=−
∫3
í
ïîëó÷èì
x
c
DU DV
=
′
−
1
0
[() ()].
(5.82)
Äëÿ îïðåäåëåíèÿ îðäèíàòû òðàåêòîðèè áóäåì èñõîäèòü èç îáû÷íîãî
ðàâåíñòâà dy =tgθdx. Ïîäñòàâëÿÿ â ýòî ðàâåíñòâî (5.79) è (5.81) è
èíòåãðèðóÿ, ïîëó÷èì
248
yx
x
c
AU AV
DU DV
IV
=−
′
−
−
−
⎡
⎣⎢
⎤
⎦⎥
tgθ
θ
0
2
0
0
0
0
2cos
() ()
() ()
(), (5.83)
ãäå
AUk
IU UdU
FU
U
U
()
()
()
.
=−
∫4
í
×òîáû îïðåäåëèòü tgθ, t, x è y ïî ôîðìóëàì (5.79), (5.80), (5.82) è
(5.83), íåîáõîäèìî âîñïîëüçîâàòüñÿ òàáëèöàìè ñïåöèàëüíûõ ôóíê-
öèé I(U ), T(U ), D(U )èA(U ), íàçûâàåìûõ îñíîâíûìè ôóíêöèÿìè.
Âõîäíîé âåëè÷èíîé â òàêèõ òàáëèöàõ ïðèíèìàåòñÿ ïñåâäîñêîðîñòü
U. ×èñëåííûå çíà÷åíèÿ ôóíêöèé îïðåäåëÿþòñÿ ïðèíÿòîé äëÿ ñèëû
ñîïðîòèâëåíèÿ âîçäóõà çàâèñèìîñòüþ F(U ) è ïîñòîÿííûìè ÷èñëàìè
Uí è Ki, êîòîðûå âûáèðàþòñÿ ñ òàêèì ðàñ÷åòîì, ÷òîáû òàáëè÷íûå
çíà÷åíèÿ ôóíêöèé áûëè óäîáíû ïðè ïðîâåäåíèè âû÷èñëåíèé. Äëÿ
êðàòêîñòè îñíîâíûå ôóíêöèè ÷àñòî îáîçíà÷àþò òîëüêî ïåðâûìè
áóêâàìè; èíäåêñ ó áóêâû îáîçíà÷àåò ïîëîæåíèå ðàññìàòðèâàåìîé
òî÷êè íà òðàåêòîðèè [130]. Ìåòîä ïñåâäîñêîðîñòè ïîçâîëÿåò âû÷èñ-
ëÿòü õàðàêòåðèñòèêè äâèæåíèÿ â ëþáîé òî÷êå òðàåêòîðèè, â òîì
÷èñëå â âåðøèíå è â òî÷êå ïàäåíèÿ.
Äëÿ òî÷êè ïàäåíèÿ îðäèíàòà òðàåêòîðèè ðàâíà íóëþ. Ïîäñòàâëÿÿ
â (5.83) yñ = 0 è ïðåîáðàçîâûâàÿ, ïîëó÷èì
sin
.
2
1
0
0
0
0
θ=
′
−
−
−
⎡
⎣⎢
⎤
⎦⎥
c
AA
DD
I
c
c
(5.84)
Âûäåëèòü â ÿâíîì âèäå èç ýòîãî óðàâíåíèÿ ïñåâäîñêîðîñòü â òî÷-
êå ïàäåíèÿ Uc íå ïðåäñòàâëÿåòñÿ âîçìîæíûì. Ðåøèòü åãî îòíîñè-
òåëüíî Uñ ìîæíî ïîäáîðîì, çàäàâàÿñü ïðèìåðíûìè âåëè÷èíàìè Uc.
Îïðåäåëèâ Uc, íàéäåì è îñòàëüíûå ýëåìåíòû òðàåêòîðèè â òî÷êå ïà-
äåíèÿ:
x
c
DDt
c
TT
c
ccc
c
c
=
′
−=
′
−
=−
′
11
1
2
0
0
0
0
()
;
cos
()
;
cos
θ
θθ
tg
tg
2
0
0
θ
()
.
II
c
−
(5.85)
 âåðøèíå òðàåêòîðèè θs =0ètgθs = 0; òîãäà èç (5.79) ïîñëå ïðå-
îáðàçîâàíèÿ ïîëó÷èì
249
Ic
I
s
=
′
+
sin
.
200
θ
(5.86)
Ïîëüçóÿñü òàáëèöàìè îñíîâíûõ ôóíêöèé, ïî Is íàéäåì Ds, Ts, As;
ïî íà÷àëüíûì óñëîâèÿì ïðè U0 = V0 íàéäåì D0, T0 è À0, ïîñëå ÷åãî,
ïðèìåíÿÿ ôîðìóëû (5.80), (5.82) è (5.83), ïîëó÷èì
t
c
TTx
c
DD
yx
x
c
ss
s
s
ss
s
=
′
−=
′
−
=−
′
11
2
0
00
0
cos
()
;()
;
co
θ
θ
tg
s
.
2
0
0
0
0
θ
AA
DD
I
s
s
−
−
−
⎛
⎝⎜
⎞
⎠⎟
(5.87)
Ýëåìåíòû òî÷êè ïàäåíèÿ ìîæíî íàéòè, èçáåæàâ ðåøåíèÿ óðàâ-
íåíèÿ (5.84), ìåòîäîì ïîäáîðà. Èç ðàâåíñòâà (5.82) äëÿ òî÷êè ïàäå-
íèÿ D(Uc)=c′xc − D(V0) ñëåäóåò, ÷òî Uc = f(c′xc; V0). Ñ ó÷åòîì ýòîãî
âûðàæåíèå â êâàäðàòíûõ ñêîáêàõ èç óðàâíåíèÿ (5.84) ìîæíî ðàñ-
ñìàòðèâàòü êàê íåêîòîðóþ ôóíêöèþ f0 ýòèõ æå àðãóìåíòîâ:
AU AV
DU DV
IV fcxV
c
c
c
() ()
()()()(;)
−
−
−=
′
0
0
000
è çàïèñàòü (5.84) â ôîðìå
′
=
′
cf
c
x
V
c
sin
(;).
200 0
θ
(5.88)
Äëÿ f0(c′xc; V0) ñîñòàâëåíû òàáëèöû.
Ïî íà÷àëüíûì äàííûì ìîæíî íàéòè âåëè÷èíó ñ′sinθ0;ïîíåéè
ïî âåëè÷èíå V0, ïîëüçóÿñü òàáëèöàìè, íàõîäÿò ïðîèçâåäåíèå c′xc è
äàëåå xc.
Ïîäîáíûì îáðàçîì ìîæíî ïîëó÷èòü è íåêîòîðûå äðóãèå ôóíê-
öèè îò ñ′õñ è V0 [130]:
f
V
x
ff
V
t
fV
c
c
c
1
00
2
2
0
3
0
4
0
2
==
=
=
sin
;
||;
sin
;
cos
θθ
θ
θ
θ
tg
tg
0
5
6
0
V
fx
x
fy
x
cc
s
c
s
c
cos
;;.
θθ
==
tg
(5.89)
Ôóíêöèè f0,...,f6 íàçûâàþòñÿ âñïîìîãàòåëüíûìè ôóíêöèÿìè. Ýòè
ôóíêöèè, êðîìå f5 è f6, ïðèãîäíû äëÿ âû÷èñëåíèÿ õàðàêòåðèñòèê
äâèæåíèÿ â ëþáîé òî÷êå òðàåêòîðèè.  ýòîì ñëó÷àå ïðîèçâåäåíèå ñ′õ
íå èìååò èíäåêñà. Íàïðèìåð, äëÿ òåêóùåãî çíà÷åíèÿ õ êîîðäèíàòà y
îïðåäåëÿåòñÿ ïî ñëåäóþùåé ôîðìóëå:
250
yx
fcxV
fcxV
c
=−
′
′
⎡
⎣⎢
⎤
⎦⎥
tgθ0
00
00
1
(;)
(;)
.
(5.90)
Èñêóññòâåííîå ïðåîáðàçîâàíèå óðàâíåíèÿ ãîäîãðàôà ñêîðîñòè ñ
çàìåíîé ôóíêöèè F(V )íàF(U ) äàåò õîðîøèå ïî òî÷íîñòè ðåçóëüòà-
òû ïðè ðàñ÷åòå òðàåêòîðèé, ó êîòîðûõ cosθ ìàëî èçìåíÿåòñÿ âäîëü
òðàåêòîðèè, è ìîæíî ïðèíÿòü H(y) ≈ 1. Äëÿ êîðîòêèõ íàñòèëüíûõ
òðàåêòîðèé (ïðè áîëüøèõ íà÷àëüíûõ ñêîðîñòÿõ è ìàëûõ óãëàõ áðî-
ñàíèÿ), êîãäà ìîæíî ïðèíÿòü cosθ≈cosθ0 ≈ 1, î÷åâèäíî, ÷òî β =1,
c′=cèU=V.Òîãäà
x
c
DV DV
yx
t
g
x
c
AV AV
DV DV
I
=−
=−
−
−
−
1
2
0
0
0
0
[() ()];
() ()
() ()
θ
();
[() ( )].
V
t
c
TV TV
0
0
1
⎡
⎣⎢
⎤
⎦⎥
=−
(5.91)
Ïðè ðåøåíèè îáðàòíûõ çàäà÷ óãîë áðîñàíèÿ îïðåäåëÿåòñÿ èç óñ-
ëîâèÿ yc = 0 ïî ôîðìóëå
sin
() ()
() ()
().
2
1
0
0
0
0
θ=
−
−
−
⎡
⎣⎢
⎤
⎦⎥
c
AV AV
DV DV
IV
Ñ óâåëè÷åíèåì óãëà áðîñàíèÿ è óìåíüøåíèåì íà÷àëüíîé ñêîðî-
ñòè îøèáêà îïðåäåëåíèÿ ýëåìåíòîâ òðàåêòîðèè â òî÷êå ïàäåíèÿ óâå-
ëè÷èâàåòñÿ. Êîìïåíñàöèÿ îøèáîê îñóùåñòâëÿåòñÿ ââåäåíèåì ïî-
ïðàâî÷íîãî êîýôôèöèåíòà β. Ñòðîãî ãîâîðÿ, äëÿ êàæäîãî ýëåìåíòà
òðàåêòîðèè ñëåäóåò ââîäèòü ñâîé ïîïðàâî÷íûé êîýôôèöèåíò βx, βy,
βθ, βz. Ïðè âûïîëíåíèè ïðàêòè÷åñêèõ ðàñ÷åòîâ ïîëüçóþòñÿ îäíèì
êîìïåíñèðóþùèì ìíîæèòåëåì βx, ïðèâîäÿùèì â ñîîòâåòñòâèå ïîë-
íûå äàëüíîñòè, ðàññ÷èòàííûå ìåòîäîì ïñåâäîñêîðîñòè, è îäíèì èç
áîëåå òî÷íûõ ìåòîäîâ. Ýòîò êîýôôèöèåíò β íàçâàí ãëàâíûì êîýô-
ôèöèåíòîì.
Òàáëèöà çíà÷åíèé êîýôôèöèåíòà β [22, 130] äëÿ ñòðåëêîâîãî
îðóæèÿ è àðòèëëåðèè ìàëûõ êàëèáðîâ (ïðè ñ > 1) ñîñòàâëåíà ïî
âõîäíûì ÷èñëàì θ0 =6...30 ° è Xc = 1000...7000 ì. Êîýôôèöèåíò β â
òàáëèöå èçìåíÿåòñÿ â óçêèõ ïðåäåëàõ îò 0,97 äî 1,06.
Äëÿ ñðåäíèõ è áîëüøèõ êàëèáðîâ (ïðè ñ < 1) ß.Ì. Øàïèðî ñîñòà-
âèë òàáëèöû ñ âõîäàìè ñ = 0,2...1,0; V0 = 300...1000 ì/ñ è θ0 =5...60°.
Òàáëèöû ñîñòàâëåíû ïóòåì îáðàáîòêè ðåçóëüòàòîâ ðàñ÷åòîâ òðàåêòî-
251
ðèé, ïðîâåäåííûõ ìåòîäîì ÷èñëåííîãî èíòåãðèðîâàíèÿ [22, 130].
 çàâèñèìîñòè îò ñêîðîñòè è óãëà áðîñàíèÿ ãëàâíûé êîýôôèöèåíò
ñîãëàñîâàíèÿ β ñóùåñòâåííî èçìåíÿåòñÿ (îò 0,609 äî 1,329 äëÿ θ0 =
= 60° è îò 0,984 äî 1,039 äëÿ θ0 = 5°) . Ïðè ñîãëàñîâàíèè ïîëíûõ äàëü-
íîñòåé îøèáêà â îïðåäåëåíèè îñòàëüíûõ ýëåìåíòîâ äîõîäèò äî 5 %
(ïðè θ0 =30
...40°).
5.2 .5. ÏÎÄÎÁÈÅ ÒÐÀÅÊÒÎÐÈÉ
È ÒÀÁËÈ×ÍÛÅ ÌÅÒÎÄÛ ÐÅØÅÍÈß
 ïðàêòèêå áàëëèñòè÷åñêèõ ðàñ÷åòîâ ïðèìåíÿþòñÿ òàáëè÷íûå ìåòîäû ðå-
øåíèÿ, ñ ïîìîùüþ êîòîðûõ ìîæíî íàéòè ïàðàìåòðû äâèæåíèÿ â õàðàêòåð-
íûõ òî÷êàõ òðàåêòîðèé, íàïðèìåð â âåðøèíå èëè òî÷êå ïàäåíèÿ. Îñîáåííî
øèðîêî èñïîëüçóþòñÿ áàëëèñòè÷åñêèå òàáëèöû äëÿ ðàñ÷åòà ýëåìåíòîâ òðàåê-
òîðèé ñíàðÿäîâ ñòâîëüíîé àðòèëëåðèè, íàçûâàåìûå Òàáëèöàìè âíåøíåé
áàëëèñòèêè. Ýòè æå òàáëèöû ìîãóò áûòü èñïîëüçîâàíû è äëÿ ðàñ÷åòà ïàñ-
ñèâíûõ ó÷àñòêîâ òðàåêòîðèé ðàêåò. Èññëåäîâàíèå ñèñòåì óðàâíåíèé (3.129)
è (3.131) ïîêàçûâàåò, ÷òî ýëåìåíòû òðàåêòîðèè îïðåäåëÿþòñÿ òðåìÿ ïàðà-
ìåòðàìè: íà÷àëüíîé ñêîðîñòüþ V0, áàëëèñòè÷åñêèì êîýôôèöèåíòîì ñ,óã-
ëîì áðîñàíèÿ θ0. Ðàññ÷èòàâ áîëüøîå êîëè÷åñòâî òðàåêòîðèé, ìîæíî ñîñòà-
âèòü òàáëèöû ýëåìåíòîâ òðàåêòîðèé, âçÿâ â êà÷åñòâå âõîäîâ çíà÷åíèÿ V0, c è
θ0.  òàáëèöàõ îáû÷íî äàþòñÿ çíà÷åíèÿ ïîëíîé äàëüíîñòè õñ, âûñîòû òðàåê-
òîðèè ys, ïîëíîãî âðåìåíè ïîëåòà tc, ñêîðîñòè â òî÷êå ïàäåíèÿ Vc è óãëà íà-
êëîíà êàñàòåëüíîé ê òðàåêòîðèè â òî÷êå ïàäåíèÿ θc.
Äëÿ ðàñ÷åòà òðàåêòîðèé çåíèòíîé ñòðåëüáû ê òðåì âõîäíûì ïàðàìåòðàì
äîáàâëÿåòñÿ ÷åòâåðòûé – âðåìÿ äâèæåíèÿ.
Ñ ïîìîùüþ òàáëèö çåíèòíîé ñòðåëüáû ìîæíî äëÿ òðàåêòîðèè, îïðåäå-
ëÿåìîé V0, ñ è θ0, íàéòè çíà÷åíèÿ xt, yt è Vt, îòâå÷àþùèå âðåìåíè ïîëåòà ñíà-
ðÿäà t1, t2, t3 è ò.ä.
Áàëëèñòè÷åñêèå òàáëèöû èñïîëüçóþòñÿ äëÿ ðàñ÷åòà òðàåêòîðèé ñíàðÿäîâ
ïðè íîðìàëüíûõ ìåòåîðîëîãè÷åñêèõ óñëîâèÿõ. Ïðåäåëû ïðèìåíèìîñòè òàá-
ëèö ìîãóò áûòü ðàñøèðåíû, åñëè âîñïîëüçîâàòüñÿ òåîðèåé ïîäîáèÿ òðàåêòî-
ðèé. Ôðàíöóçñêèé ó÷åíûé Ï. Ëàíæåâåí óñòàíîâèë çàâèñèìîñòü ìåæäó õà-
ðàêòåðèñòèêàìè äâóõ òðàåêòîðèé ñíàðÿäîâ ïîñòîÿííîé ìàññû, äëÿ êîòîðûõ
çíà÷åíèÿ òåìïåðàòóðû è äàâëåíèÿ îêðóæàþùåãî âîçäóõà, ñîîòâåòñòâóþùèå
íà÷àëó òðàåêòîðèé, ðàçëè÷íû. Ïðåäïîëîæèâ, ÷òî òåìïåðàòóðà âîçäóõà îòëè-
÷àåòñÿ íà ïîñòîÿííóþ âåëè÷èíó îò òåìïåðàòóðû, îïðåäåëÿåìîé ëèíåéíîé
çàâèñèìîñòüþ, è ÷òî èçìåíåíèå äàâëåíèÿ âîçäóõà ïîä÷èíÿåòñÿ ãèïîòåçå î
âåðòèêàëüíîì ðàâíîâåñèè àòìîñôåðû, ìîæíî ïîêàçàòü, ÷òî òðàåêòîðèè áó-
äóò ïîäîáíû, åñëè ó íèõ îäèíàêîâû òðè îïðåäåëÿþùèõ ïàðàìåòðà
cc
h
h
VV
ON
ON
*
,
==
0
00
0
τ
τ
τ
è θ0, ãäå h0 è τ0 – äàâëåíèå è òåìïåðàòóðà â íà÷àëü-
íîé òî÷êå òðàåêòîðèè. Ó äâóõ ïîäîáíûõ òðàåêòîðèé êîîðäèíàòû x è y áóäóò
252
ñîîòíîñèòüñÿ, êàê òåìïåðàòóðû â íà÷àëüíîé òî÷êå òðàåêòîðèè τ01 è τ02, ñêî-
ðîñòè è âðåìÿ ïîëåòà áóäóò ñîîòíîñèòüñÿ, êàê êîðíè êâàäðàòíûå èç îòíîøå-
íèÿ òåìïåðàòóð â íà÷àëüíîé òî÷êå; óãëû íàêëîíà êàñàòåëüíîé áóäóò ðàâíû,
ò.å.
x
x
y
y
t
t
V
V
i
i
i
i
i
i
i
i
1
2
01
02
1
2
01
02
1
2
01
02
1
2
===
=
τ
τ
τ
τ
τ
τ
τ
;;;
01
02
1
2
1
τ
θ
θ
;.
i
i
=
(5.92)
Ôîðìóëû Ëàíæåâåíà ïðèìåíÿþòñÿ, íàïðèìåð, ïðè ðàñ÷åòå òðàåêòîðèé
ñíàðÿäîâ ñòâîëüíûõ ñèñòåì äëÿ óñëîâèé, ñîîòâåòñòâóþùèõ óñëîâèÿì
ñòðåëüáû â ãîðàõ, äëÿ ðàñ÷åòà ïàññèâíûõ ó÷àñòêîâ òðàåêòîðèé ðàêåò è ò.ï.
Íà÷àëî ïàññèâíîãî ó÷àñòêà òðàåêòîðèè ðàêåòû êëàññà "ïîâåðõíîñòü – ïî-
âåðõíîñòü" èíîãäà íàõîäèòñÿ íà çíà÷èòåëüíîé âûñîòå, ïîýòîìó íåïîñðåäñò-
âåííîå èñïîëüçîâàíèå áàëëèñòè÷åñêèõ òàáëèö ìîæåò ïðèâåñòè ê ñóùåñòâåí-
íûì îøèáêàì. Îáîçíà÷èì ãîðèçîíòàëüíóþ äàëüíîñòü ïàññèâíîãî ó÷àñòêà
òðàåêòîðèè, ðàññ÷èòûâàåìîãî ïî áàëëèñòè÷åñêèì òàáëèöàì, ÷åðåç õ2, ýëå-
ìåíòû íà÷àëà ýòîãî ó÷àñòêà ñíàáäèì èíäåêñîì k, à êîíöà – èíäåêñîì k ′
(ðèñ. 5.12). Èç óñëîâèÿ ïîäîáèÿ òðàåêòîðèé ìîæíî ïîëó÷èòü ñëåäóþùèå
ôîðìóëû:
xc
V
yc
V
k
ON
xk
k
s
k
ON
yk
k
k
2
2
=
=
=
′
τ
τ
θ
τ
τ
θ
θ
τ
τ
Φ
Φ
Φ
(,,);
(,,);
*
*
θτ
τ
θ
τ
τ
θ
τ
τ
(,,);
(,,);
(
*
*
*
cV
Vc
V
tc
kk
k
k
ON
Vk
k
k
k
ON
t
′
′
=
=
Φ
Φ ,,)
;
;,
*
V
cc
h
h
VV
kk
k
ON
kk
ON
k
τ
τ
θ
τ
τ
==
ï
(5.93)
ãäå cc
h
h
VV
k
ON
kk
ON
k
*
;.
==
ï
τ
τ
τ
 ýòèõ ôîðìóëàõ ñèìâîëàìè Vk, θk, hk è τk îáîçíà÷åíû ñîîòâåòñòâåííî
ñêîðîñòü, óãîë áðîñàíèÿ, áàðîìåòðè÷åñêîå äàâëåíèå è âèðòóàëüíàÿ òåìïåðà-
òóðà â òî÷êå íà÷àëà ïàññèâíîãî ó÷àñòêà òðàåêòîðèè, ò.å . â êîíöå àêòèâíîãî
ó÷àñòêà.
253
Áàëëèñòè÷åñêèé êîýôôèöèåíò äëÿ ïàññèâíîãî ó÷àñòêà ðàâåí ñï =
=
−
⋅
id
QQ
2
0
3
10
ò
. Çíà÷åíèÿ ôóíêöèé Φx, Φy, Φθ, ΦV è Φt áåðóòñÿ èç îáû÷íûõ áàë-
ëèñòè÷åñêèõ òàáëèö ïî âõîäíûì äàííûì ñ*, Vτk è θk. Òàê, íàïðèìåð, Φx(c*,
Vτk, θk) ÿâëÿåòñÿ ôóíêöèåé äàëüíîñòè, îïðåäåëåííîé ïî áàëëèñòè÷åñêèì
òàáëèöàì äëÿ ÷èñëåííûõ çíà÷åíèé âåëè÷èí, óêàçàííûõ â ñêîáêàõ. Óñëîâèÿ
ïîäîáèÿ òðàåêòîðèé ñïðàâåäëèâû â ïðåäåëàõ ëèíåéíîãî èçìåíåíèÿ òåìïå-
ðàòóðû ñ âûñîòîé.
Ãëàâà 6
ÐÅØÅÍÈÅ ÎÏÒÈÌÈÇÀÖÈÎÍÍÛÕ ÇÀÄÀ×
ÁÀËËÈÑÒÈÊÈ
 îáùåì ñëó÷àå çàäà÷à îïòèìàëüíîãî óïðàâëåíèÿ äâèæåíèåì ËÀ ïîäðàçäåëÿ-
åòñÿ íà äâå, îò÷àñòè íåçàâèñèìûå ïîäçàäà÷è.
Ïåðâàÿ, ôîðìóëèðóåìàÿ êàê îïòèìàëüíîå ïðîãðàììèðîâàíèå îïîðíîãî äâè-
æåíèÿ, ñâîäèòñÿ ê îïðåäåëåíèþ íîìèíàëüíîé òðàåêòîðèè ËÀ, óäîâëåòâîðÿþ-
ùåé íåêîòîðûì íàïåðåä çàäàííûì òðåáîâàíèÿì ïðè íàëîæåííûõ îãðàíè÷åíèÿõ.
Âòîðàÿ ïîäçàäà÷à ñâîäèòñÿ ê ñîáñòâåííî ñèíòåçó îïòèìàëüíîãî óïðàâëå-
íèÿ. Åå ñóùíîñòü çàêëþ÷àåòñÿ â íàõîæäåíèè â ðåçóëüòàòå ìàòåìàòè÷åñêîãî
èññëåäîâàíèÿ íàèëó÷øåãî çàêîíà óïðàâëåíèÿ, ñâÿçûâàþùåãî äîïóñòèìûå â
ñìûñëå òåõíè÷åñêîé ðåàëèçóåìîñòè óïðàâëÿþùèå âîçäåéñòâèÿ ñ òåìè êîîðäè-
íàòàìè âîçìóùåííîãî äâèæåíèÿ ËÀ, êîòîðûå ëèáî äîñòóïíû ïðÿìûì èçìåðå-
íèÿì, ëèáî ÿâëÿþòñÿ ôóíêöèÿìè èçìåðÿåìûõ ïàðàìåòðîâ, ïîëó÷àåìûìè â ëþ-
áîé òåêóùèé ìîìåíò âðåìåíè.
254
Ðèñ. 5 .12 . Ñõåìà äåëåíèÿ òðàåêòîðèè íà îòäåëüíûå ðàñ÷åòíûå ó÷àñòêè
Öåíòðàëüíîå ìåñòî â áàëëèñòèêå çàíèìàåò çàäà÷à îïòèìàëüíîãî ïðîãðàì-
ìèðîâàíèÿ îïîðíîãî äâèæåíèÿ êàê ïîäçàäà÷à êîëè÷åñòâåííîãî è êà÷åñòâåííîãî
àíàëèçà îïòèìàëüíûõ ðåæèìîâ äâèæåíèÿ, ñóùåñòâîâàíèÿ è åäèíñòâåííîñòè
ðåøåíèé, à òàêæå òåõíèêè (â øèðîêîì ïîíèìàíèè ýòîãî òåðìèíà) èõ îñóùåñò-
âëåíèÿ. Çàìåòíàÿ ðîëü ïðè ýòîì îòâîäèòñÿ èññëåäîâàíèþ êðàåâûõ çàäà÷ áàëëè-
ñòèêè, âûòåêàþùèõ èç îáùåé ïîñòàíîâêè çàäà÷è ñòðåëüáû ñíàðÿäàìè è ðàêå-
òàìè ïî çàäàííîé öåëè.
Äîñòàòî÷íî îáùèìè ìåòîäàìè îïòèìèçàöèè ïðè ýòîì ÿâëÿþòñÿ ìåòîäû
êëàññè÷åñêîãî âàðèàöèîííîãî èñ÷èñëåíèÿ.
Àïïàðàò êëàññè÷åñêîãî âàðèàöèîííîãî èñ÷èñëåíèÿ îñíîâûâàåòñÿ íà ïðåä-
ñòàâëåíèè ýêñòðåìàëè â âèäå òî÷êè ïðîñòðàíñòâà ôóíêöèé. Âàðèàöèîííûå
ñâîéñòâà ýòîé òî÷êè õàðàêòåðèçóþòñÿ óðàâíåíèÿìè Ýéëåðà. Äëÿ òîãî ÷òîáû
íàéòè â êàêîì-ëèáî ñìûñëå îïòèìàëüíóþ òðàåêòîðèþ, ïðèõîäèòñÿ ðåøàòü
êðàåâóþ çàäà÷ó, ïîäáèðàÿ íà÷àëüíûå çíà÷åíèÿ ìíîæèòåëåé Ëàãðàíæà.  áîëü-
øèíñòâå ñëó÷àåâ ýòî îêàçûâàåòñÿ âåñüìà ñëîæíûì ïðîöåññîì, íå ñîîòâåòñò-
âóþùèì ïî òðóäîåìêîñòè òðåáóåìîé òî÷íîñòè è íàäåæíîñòè ïîëó÷åííîãî ðå-
øåíèÿ. Áîëåå ïðîñòî ñîîòâåòñòâóþùèå îöåíî÷íûå ðåçóëüòàòû ìîãóò áûòü
íàéäåíû ñ ïîìîùüþ ìåòîäà äèíàìè÷åñêîãî ïðîãðàììèðîâàíèÿ. Ïîñëåäíèé ìå-
òîä, îñíîâîïîëàãàþùèé âêëàä â ðàçâèòèå êîòîðîãî âíåñ Ð. Áåëëìàí, òàê æå
êàê è "ïðèíöèï ìàêñèìóìà", ðàçðàáîòàííûé ïðåäñòàâèòåëÿìè îòå÷åñòâåííîé
øêîëû ñîâåòñêèõ ìàòåìàòèêîâ ïîä ðóêîâîäñòâîì Ë.Ñ. Ïîíòðÿãèíà, ïðèíÿòî
ïðè âñåé óñëîâíîñòè ïîäîáíîé êëàññèôèêàöèè îòíîñèòü ê íåêëàññè÷åñêèì ìå-
òîäàì âàðèàöèîííîãî èñ÷èñëåíèÿ. Çàäà÷è îïòèìàëüíîãî óïðàâëåíèÿ, ðåøàåìûå
ñ èñïîëüçîâàíèåì ïðèíöèïà ìàêñèìóìà, ñîñòàâëÿþò îñíîâó ïðîáëåìû ñèíòåçà,
ò.å . îòíîñÿòñÿ ê ðàçðÿäó âòîðîé ãðóïïû ïðîáëåì îïòèìàëüíîãî óïðàâëåíèÿ
äâèæåíèåì ËÀ.
Îòäåëüíûé êëàññ îïòèìàëüíûõ çàäà÷ âíåøíåé áàëëèñòèêè ñîñòàâëÿþò
ïðîñòåéøèå ýêñòðåìàëüíûå çàäà÷è ïðîãðàììèðîâàíèÿ îïîðíîãî äâèæåíèÿ íà
îñíîâå îòûñêàíèÿ ãëàäêîé ôóíêöèè îäíîãî ïåðåìåííîãî áåç îãðàíè÷åíèé.
6.1 . ÊÐÀÅÂÛÅ ÇÀÄÀ×È ÁÀËËÈÑÒÈÊÈ
6.1.1. ÎÁÙÀß ÕÀÐÀÊÒÅÐÈÑÒÈÊÀ ÊÐÀÅÂÛÕ ÇÀÄÀ× ÁÀËËÈÑÒÈÊÈ
È ÌÅÒÎÄÎÂ ÈÕ ÐÅØÅÍÈß
Óïðàâëåíèå îãíåì àðòèëëåðèè è ïóñêàìè ðàêåò, îñóùåñòâëÿåìîå
ñ öåëüþ ïîâûøåíèÿ ýôôåêòèâíîñòè áîåâîãî ïðèìåíåíèÿ êîìïëåê-
ñîâ àðòèëëåðèéñêîãî è ðàêåòíîãî âîîðóæåíèÿ, ïðåäïîëàãàåò îïðåäå-
ëåíèå òàê íàçûâàåìûõ óñòàíîâîê äëÿ ñòðåëüáû.
Ïîä óñòàíîâêàìè äëÿ ïðîâåäåíèÿ ñòðåëüá èëè ïóñêîâ áàëëèñòè-
÷åñêèõ ðàêåò ïðèíÿòî ïîíèìàòü ñîâîêóïíîñòü äàííûõ èç ÷èñëà
èìåþùèõñÿ íà øêàëàõ ïðèöåëîâ è äðóãèõ óñòðîéñòâ, ïðåäíàçíà÷åí-
íûõ äëÿ íàâåäåíèÿ ñòâîëüíîé ñèñòåìû èëè íàñòðîéêè êîíòóðà
255
óïðàâëåíèÿ áàëëèñòè÷åñêîé ðàêåòû òàêèì îáðàçîì, ÷òîáû îáåñ-
ïå÷èòü ïðîõîæäåíèå ñðåäíåé òðàåêòîðèè êàê ìîæíî áëèæå ê êîíå÷-
íîé òî÷êå äâèæåíèÿ (â ÷àñòíîñòè, ê öåëè) â êîíêðåòíûõ óñëîâèÿõ
ïîëåòà.
Îïðåäåëåíèå óñòàíîâîê, òàêèì îáðàçîì, âñåãäà â òîé èëè èíîé
ñòåïåíè ñâÿçàíî ñ ðàñ÷åòîì òàê íàçûâàåìîé ïîïàäàþùåé òðàåêòî-
ðèè.
 îòëè÷èå îò ñëó÷àÿ êëàññè÷åñêèõ ïîïàäàþùèõ òðàåêòîðèé, îò-
íîñÿùåãîñÿ ê êëàññó çàäà÷ Êîøè, â ðàìêàõ êîòîðûõ ÷àñòíîå ðåøåíèå
èùåòñÿ äëÿ èçâåñòíûõ íà÷àëüíûõ ïàðàìåòðîâ äâèæåíèÿ, èçâåñòíûõ
èñõîäíûõ äàííûõ è ïðè èçâåñòíîì âðåìåíè îêîí÷àíèÿ ðàñ÷åòà, îï-
ðåäåëåíèå èñõîäíûõ äàííûõ íà ïóñêè óïðàâëÿåìûõ áàëëèñòè÷åñêèõ
ðàêåò (ðåàêòèâíûõ ñíàðÿäîâ) îòíîñèòñÿ ê êëàññó îáðàòíûõ çàäà÷.
Ïîñëåäíèå îòëè÷àþòñÿ îò çàäà÷ Êîøè (ïðÿìûõ çàäà÷) òåì, ÷òî
ðàñ÷åò äâèæåíèÿ ðàêåòû îñóùåñòâëÿåòñÿ èñõîäÿ èç òðåáîâàíèÿ îï-
ðåäåëåíèÿ âñåõ èëè ÷àñòè óïðàâëÿþùèõ ïàðàìåòðîâ (àçèìóòà ïðèöå-
ëèâàíèÿ, âðåìåíè îáíóëåíèÿ òÿãè äâèãàòåëüíîé óñòàíîâêè, ïðî-
ãðàìì óïðàâëåíèÿ èëè íåêîòîðûõ èõ ïàðàìåòðîâ) ïî îãîâîðåííûì
êðàåâûì óñëîâèÿì.  êà÷åñòâå êðàåâûõ óñëîâèé ìîãóò áûòü çàäàíû
êîîðäèíàòû òî÷åê ñòàðòà è öåëè. Äîïîëíèòåëüíî â êà÷åñòâå ãðàíè÷-
íûõ óñëîâèé ìîãóò çàäàâàòüñÿ êîîðäèíàòû òî÷åê ïðèöåëèâàíèÿ äëÿ
ñáðàñûâàåìûõ íà Çåìëþ îòäåëÿþùèõñÿ óñêîðèòåëåé, ñòóïåíåé ðàêå-
òû, ãîëîâíîãî îáòåêàòåëÿ.
Òðàåêòîðèþ, óäîâëåòâîðÿþùóþ çàäàííûì ãðàíè÷íûì óñëîâèÿì ñ
ó÷åòîì êîíñòðóêòèâíûõ îãðàíè÷åíèé, íàêëàäûâàåìûõ ðàçðàáîò÷èêà-
ìè êîìïëåêñà âîîðóæåíèÿ íà âûáîð ôîðìû òðàåêòîðèè, è íàçûâàþò
ïîïàäàþùåé òðàåêòîðèåé. Èìåííî íà ïîëåò â îêðåñòíîñòè ýòîé òðàåê-
òîðèè "íàñòðàèâàþò" ñèñòåìó óïðàâëåíèÿ óñòàíîâî÷íûå äàííûå íà
ïóñê. Ïî ñâîåìó ìàòåìàòè÷åñêîìó ñîäåðæàíèþ çàäà÷à ðàñ÷åòà ïîïà-
äàþùåé òðàåêòîðèè ÿâëÿåòñÿ êðàåâîé çàäà÷åé (â îáùåì ñëó÷àå – ìíî-
ãîòî÷å÷íîé) ñ ïîäâèæíûì (èç-çà âðàùåíèÿ Çåìëè èëè âîçìîæíîãî ìà-
íåâðà öåëè) ïðàâûì êîíöîì. Îñîáåííîñòè èñïîëüçîâàíèÿ â ïðîöåññå
ðåøåíèÿ ýòîé çàäà÷è ïðîãðàììíûõ ôóíêöèé è îðèåíòàöèÿ íà áàëëè-
ñòè÷åñêîå îáåñïå÷åíèå (ÁÎ) ïîäãîòîâêè äàííûõ íà ïóñêè ðàêåò ïðèâ-
íîñÿò â õàðàêòåð çàäà÷è íåêîòîðóþ ñïåöèôèêó.
Ñ òî÷êè çðåíèÿ ñóùåñòâóþùåé êëàññèôèêàöèè îáðàòíûå çàäà÷è
ÁÎ îòíîñÿòñÿ ê êðàåâûì çàäà÷àì èëè çàäà÷àì ïîèñêà ýêñòðåìóìà
ôóíêöèè ìíîãèõ ïåðåìåííûõ.
Âîîáùå ãîâîðÿ, îáñóæäàåìûå çàäà÷è â ðàññìàòðèâàåìîé ïîñòà-
íîâêå íå ïîëíîñòüþ ñîîòâåòñòâóþò ñòðîãîìó ìàòåìàòè÷åñêîìó îïðå-
äåëåíèþ êðàåâîé çàäà÷è.
Äåéñòâèòåëüíî, åñëè â òåîðèè äèôôåðåíöèàëüíûõ óðàâíåíèé ïîä
êðàåâîé çàäà÷åé äëÿ óðàâíåíèÿ, íàïðèìåð, 2-ãî ïîðÿäêà âèäà fx
(••
,
•
,
x
x, C, t) = 0 ïîíèìàþò çàäà÷ó ðåøåíèÿ ýòîãî óðàâíåíèÿ ïðè çàäàííûõ
256
çíà÷åíèÿõ çàâèñèìîé ïåðåìåííîé õ = õ0 ïðè t = t0 (íà ëåâîì êîíöå)
è x = xê ïðè t = tê (íà ïðàâîì êîíöå) è çàäàííîì çíà÷åíèè êîíñòàíòû
Ñ, òî ïðè ÁÎ ïîä êðàåâîé çàäà÷åé äëÿ ýòîãî æå óðàâíåíèÿ óæå ïîíè-
ìàåòñÿ çàäà÷à îòûñêàíèÿ êîíñòàíòû Ñ ïðè çàäàííûõ ãðàíè÷íûõ óñ-
ëîâèÿõ.
 ñâÿçè ñ ýòèì êðàåâûå çàäà÷è ÁÎ, îáû÷íî ïîíèìàåìûå â îáîá-
ùåííîì ñìûñëå (ñì. èçëîæåííîå âûøå), ïîëó÷èëè íàçâàíèå "îáîá-
ùåííûõ êðàåâûõ çàäà÷" [83].
Ïîäîáíûå äâóõòî÷å÷íûå êðàåâûå çàäà÷è â ïîäàâëÿþùåì áîëü-
øèíñòâå ñëó÷àåâ ïðèâîäÿò ê íåîáõîäèìîñòè ðåøåíèÿ ñèñòåì òðàíñ-
öåíäåíòíûõ óðàâíåíèé.
Ê ÷èñëó îáû÷íî ïðèìåíÿåìûõ ïðè ýòîì ÷èñëåííûõ ìåòîäîâ îò-
íîñÿòñÿ: ìåòîä Íüþòîíà è åãî ìîäèôèêàöèè, ãðàäèåíòíûå ìåòîäû ñ
ëèíåéíûì è êâàäðàòè÷íûì ïðîãíîçîì øàãà, ìåòîä Ñòåôôåíñîíà è
äð.
 êà÷åñòâå êðèòåðèàëüíîé ôóíêöèè (ýêñòðåìóì êîòîðîé äîëæåí
áûòü ïîëó÷åí â ðåçóëüòàòå ïîèñêà ðåøåíèÿ), êàê ïðàâèëî, âûñòóïàåò
âåëè÷èíà ìèíèìèçèðóåìîãî ñóììàðíîãî ðàñõîäà òîïëèâà.
Àíàëèç èñõîäíûõ äàííûõ äàåò îñíîâàíèå óñòàíîâèòü [116], ÷òî
ñðåäè íèõ ïðèñóòñòâóþò äâå ãðóïïû äàííûõ:
îïðåäåëÿåìûå â ïðîöåññå ðåøåíèÿ çàäà÷è îòûñêàíèÿ ïîïàäàþ-
ùåé òðàåêòîðèè (àçèìóò ïðèöåëèâàíèÿ À0, íàñòðîå÷íûå ïàðàìåòðû
ïðîãðàìì óïðàâëåíèÿ óãëàìè òàíãàæà θïð è ðûñêàíèÿ ψïð, âåëè÷èíà
òÿãè äâèãàòåëÿ Ð è äð.);
îïðåäåëÿåìûå ïðè èçâåñòíûõ ïàðàìåòðàõ ïîïàäàþùåé òðàåêòî-
ðèè (ðàñõîä êîìïîíåíòîâ òîïëèâà ïî ñòóïåíÿì, çíà÷åíèÿ ÷àñòíûõ
ïðîèçâîäíûõ êîíå÷íîãî ïðîìàõà ïî ïàðàìåòðàì äâèæåíèÿ â êîíöå
àêòèâíîãî ó÷àñòêà, àïðèîðíûå õàðàêòåðèñòèêè òî÷íîñòè ïîëåòà è
äð.) .
Åñëè îáîçíà÷èòü âñå èñõîäíûå äàííûå, îïðåäåëÿåìûå íà ñòàäèè
ðàçðàáîòêè ïðåäïîëåòíîãî ÁÎ, ÷åðåç N, òî äàííûå, êîòîðûå îïðåäå-
ëÿþòñÿ òîëüêî â ïðîöåññå ðàñ÷åòà ïîïàäàþùåé òðàåêòîðèè è áåç êî-
òîðûõ îíà íå ìîæåò áûòü íàéäåíà (íàçûâàåìûå óñòàíîâî÷íûìè äàí-
íûìè), áóäóò õàðàêòåðèçîâàòüñÿ âåêòîðîì n, ïðè÷åì n ⊂ N.
Åñëè ðàçìåðíîñòü k âåêòîð-ñòîëáöà n óñòàíîâî÷íûõ äàííûõ ñîîò-
âåòñòâóåò ðàçìåðíîñòè l âåêòîð-ñòîëáöà ãðàíè÷íûõ óñëîâèé q, ò.å .
k = l, òî èìååì êðàåâóþ çàäà÷ó. Åñëè æå k > l, òî ïðèõîäèì ê ïîñòà-
íîâêå çàäà÷è ïîèñêà óñëîâíîãî ýêñòðåìóìà ôóíêöèé ìíîãèõ ïåðå-
ìåííûõ.  ñëó÷àå åñëè k < l, ðåøåíèå çàäà÷è îòñóòñòâóåò è äëÿ òîãî,
÷òîáû ñäåëàòü åå êîððåêòíîé, íåîáõîäèìî óìåíüøèòü ÷èñëî ãðàíè÷-
íûõ óñëîâèé äî âûïîëíåíèÿ óñëîâèÿ k ≥ l [83].
Ïîìèìî óæå óêàçàííûõ â âåêòîð óñòàíîâî÷íûõ äàííûõ áóäóò âõî-
äèòü ñ÷åòíîå êîëè÷åñòâî çíà÷åíèé àðãóìåíòîâ ïðèöåëèâàíèÿ À0i,
257
íàñòðîå÷íûå ïàðàìåòðû óïðàâëÿþùåé ôóíêöèè Φ*
, ïî êîòîðîé ôîð-
ìèðóåòñÿ ãëàâíàÿ êîìàíäà íà îáíóëåíèå òÿãè ÄÓ, è ðÿä äðóãèõ âåëè-
÷èí, çàâèñÿùèõ îò ðåàëèçóåìîãî ïðèíöèïà è çàêîíà óïðàâëåíèÿ. Èõ
êîëè÷åñòâî äëÿ ðàçëè÷íûõ òèïîâ áàëëèñòè÷åñêèõ ðàêåò (ÁÐ) áóäåò
ðàçëè÷íûì.
Ñëåäóþùèì âàæíûì àñïåêòîì ðåøàåìîé çàäà÷è ÿâëÿåòñÿ îïðå-
äåëåíèå âëèÿíèÿ óñòàíîâî÷íûõ äàííûõ íà êîíå÷íûé ïðîìàõ. Âëèÿ-
íèå òîãî èëè èíîãî ïàðàìåòðà èç ìíîæåñòâà ïàðàìåòðîâ n íà êà-
êóþ-ëèáî ôóíêöèþ ýòèõ ïàðàìåòðîâ â ïåðâîì ïðèáëèæåíèè ìîæíî
îöåíèòü íà îñíîâå ìåòîäîâ òåîðèè ÷óâñòâèòåëüíîñòè.
Ïîñêîëüêó âåêòîð ãðàíè÷íûõ óñëîâèé â êîíöå àêòèâíîãî ó÷àñòêà
âûâåäåíèÿ îäíîçíà÷íî îïðåäåëÿåòñÿ (â äåòåðìèíèðîâàííîé ïîñòà-
íîâêå) àëãåáðàè÷åñêè çàäàííûìè ôóíêöèÿìè âåêòîðà óñòàíîâî÷íûõ
äàííûõ, ò.å . q = q(n), òî îöåíèâàòü âëèÿíèå óñòàíîâî÷íûõ äàííûõ íà
ãðàíè÷íûå óñëîâèÿ íàèáîëåå óäîáíî ñ ïîìîùüþ êâàäðàòíîé ìàòðè-
öû âëèÿíèÿ âèäà Qn =
∂
∂
q
n
i
j
⎧
⎨
⎩
⎫
⎬
⎭
ïðè ij
,
= 1,..., k äëÿ ñëó÷àÿ êðàåâîé çà-
äà÷è è ïðÿìîóãîëüíîé ìàòðèöû Qn =
∂
∂
q
n
i
j
⎧
⎨
⎩
⎫
⎬
⎭
ïðèi=1,..., kèj=1,..., l
äëÿ ðåøåíèÿ çàäà÷è ïîèñêà óñëîâíîãî ýêñòðåìóìà çàäàííîé ôóíê-
öèè.
Ìåòîäû ïîñòðîåíèÿ ñîîòâåòñòâóþùèõ ìàòðèö âëèÿíèÿ ðàññìîò-
ðåíû â [83]. Òàì æå ïðèâåäåíî ïîäðîáíîå îïèñàíèå ïðèìåíÿåìûõ
íà ïðàêòèêå àëãîðèòìîâ îïðåäåëåíèÿ óñòàíîâî÷íûõ äàííûõ è ïðåä-
ñòàâëåíà äîñòàòî÷íî ïîëíàÿ õàðàêòåðèñòèêà ìàòåìàòè÷åñêèõ è òåõ-
íîëîãè÷åñêèõ ìåòîäîâ ðåøåíèÿ êðàåâûõ çàäà÷ è çàäà÷ ïîèñêà óñëîâ-
íîãî ýêñòðåìóìà ïðèìåíèòåëüíî ê ÁÎ ïóñêà ðàêåò.
Çäåñü æå ìû îãðàíè÷èìñÿ êðàòêèì èçëîæåíèåì ñõåìû íàèáîëåå
èñïîëüçóåìîãî ïîäõîäà ê îïðåäåëåíèþ óñòàíîâî÷íûõ äàííûõ ìåòî-
äîì Íüþòîíà ïðèìåíèòåëüíî ê ðåøåíèþ êðàåâîé çàäà÷è (k = l ).
Ïîñêîëüêó çàäà÷à îïðåäåëåíèÿ ïîïàäàþùåé òðàåêòîðèè äëÿ äàí-
íîé ïîñòàíîâêè îòíîñèòñÿ ê ÷èñëó îáðàòíûõ çàäà÷ áàëëèñòèêè, ò.å .
ê çàäà÷å îïðåäåëåíèÿ îáðàòíîé ôóíêöèè n(q) êàêîãî-òî îäíîãî âà-
ðèàíòà çàäàíèÿ âåêòîðà q, îáîçíà÷àåìîãî qçàä, òî îíà ñâîäèòñÿ, ïî
ñóùåñòâó, ê ðåøåíèþ çàäà÷è íàõîæäåíèÿ êîðíåé ñèñòåìû òðàíñöåí-
äåíòíûõ óðàâíåíèé âèäà
φ()().
nq
nq
=−
çàä
Ïîëîæèì, ÷òî â íåêîòîðîé âûïóêëîé îáëàñòè Φ, ñîäåðæàùåé
ðàñøèðåíèå n(*) ñèñòåìû òðàíñöåíäåíòíûõ óðàâíåíèé, ôóíêöèè φi(n),
i =1,..., k, íåïðåðûâíû, èìåþò íåïðåðûâíûå ÷àñòíûå ïðîèçâîäíûå
258
ïåðâîãî ïîðÿäêà è â òî÷êå n = n(*) ìàòðèöà Qn =
⎧
⎨
⎩
⎫
⎬
⎭
=
⎧
⎨
⎩
⎫
⎬
⎭
∂φ
∂
∂
∂
i
j
i
j
n
q
n
;
i , j =1,..., k, íå âûðîæäåíà.
Òîãäà â îêðåñòíîñòè n îíà áóäåò èìåòü îáðàòíóþ ìàòðèöó Qn
−1
.
 ýòîì ñëó÷àå ðåøåíèå n(*) áóäåò è ðåøåíèåì âåêòîðíîãî óðàâíå-
íèÿn=nQn
n
(*)
().
−
−1
φ Åñëè n(0) åñòü íåêîòîðîå íà÷àëüíîå ïðèáëèæå-
íèå äëÿ ðåøåíèÿ n(*)
, òî äëÿ îòûñêàíèÿ ïîñëåäíåãî ñ íåêîòîðîé íà-
ïåðåä çàäàííîé òî÷íîñòüþ ε ìîæíî ïîñòðîèòü èòåðàöèîííûé ïðî-
öåññ òèïà
nn
Q
nn
n
() ()
() ()
()()
.
mm
m
m
+−
=−
11
φ
Èòåðàöèîííûé ìåòîä ïîèñêà ðåøåíèÿ, â êîòîðîì èñïîëüçóåòñÿ
ñõåìà ïîñëåäîâàòåëüíûõ ïðèáëèæåíèé óêàçàííîãî òèïà, íàçûâàåòñÿ
ìåòîäîì Íüþòîíà.
Ïîñðåäñòâîì îñóùåñòâëåíèÿ îáðàòíûõ ïðåîáðàçîâàíèé çàïèñàí-
íîå âûøå âåêòîðíîå óðàâíåíèå ìîæåò áûòü ïðèâåäåíî ê ñèñòåìå ëè-
íåéíûõ àëãåáðàè÷åñêèõ óðàâíåíèé, ðàçðåøàåìûõ îòíîñèòåëüíî ýëå-
ìåíòîâ âåêòîðà n(m+1):
∂
∂
∂
∂
q
n
n
q
n
nq
i
j
m
j
m
j
k
i
j
m
j
m
⎛
⎝⎜⎞
⎠⎟
=
⎛
⎝⎜⎞
⎠⎟
+
+
=
∑
()
()
()
()
1
1
ii
m
j
k
qn
ik
m
çàä
−
==
=
∑
(),
,,;
,
,
,.
()
1
10
1
2
KK
Ïðîöåññ îïðåäåëåíèÿ êîðíåé n(*) ñèñòåìû òðàíñöåíäåíòíûõ
óðàâíåíèé, ê êîòîðîìó, òàêèì îáðàçîì, ñâîäèòñÿ ðàñ÷åò óñòàíîâî÷-
íûõ äàííûõ, çàêàí÷èâàåòñÿ, êîãäà ðàçíîñòü q(n) − qçàä ≤ε.
6.1.2 . ÎÑÎÁÅÍÍÎÑÒÈ ÏÎÑÒÀÍÎÂÊÈ È ÐÅØÅÍÈß ÊÐÀÅÂÛÕ ÇÀÄÀ×
ÐÀÑ×ÅÒÀ ÓÑÒÀÍÎÂÎ×ÍÛÕ ÄÀÍÍÛÕ ÁÀËËÈÑÒÈ×ÅÑÊÈÕ ÐÀÊÅÒ
Ðàñ÷åò ïîïàäàþùåé òðàåêòîðèè, ðàññìàòðèâàåìîé â êà÷åñòâå áà-
çîâîé, ïðîâîäèòñÿ ñ öåëüþ îïðåäåëåíèÿ àçèìóòà ïðèöåëèâàíèÿ è
âðåìåíè ïîäà÷è êîìàíäû íà âûêëþ÷åíèå äâèãàòåëÿ è îòäåëåíèå
(åñëè ïðåäóñìîòðåíî) ãîëîâíîé ÷àñòè (Ã×), îáåñïå÷èâàþùåé ïðî-
õîæäåíèå ñ çàäàííîé òî÷íîñòüþ íîìèíàëüíîé òðàåêòîðèè ÷åðåç
òî÷êó ñòàðòà è òî÷êó öåëè.
Ïðè ðàñ÷åòå ïîïàäàþùåé òðàåêòîðèè ÁÐ äîëæíû áûòü çàäàíû
ñëåäóþùèå îñíîâíûå èñõîäíûå äàííûå:
õàðàêòåðèñòèêè àòìîñôåðû, ãðàâèòàöèîííîãî ïîëÿ, ñèëû ïðèòÿ-
æåíèÿ è ôèãóðû Çåìëè;
259
àýðîäèíàìè÷åñêèå, ãåîìåòðè÷åñêèå, öåíòðîâî÷íûå è âåñîâûå õà-
ðàêòåðèñòèêè ðàêåòû â öåëîì è äâèãàòåëåé, âêëþ÷àÿ ïåðåõîäíûå
ó÷àñòêè íàáîðà è ñïàäà òÿãè, äëÿ âñåõ ñòóïåíåé;
õàðàêòåðèñòèêè ñèñòåìû óïðàâëåíèÿ, â òîì ÷èñëå îñîáåííîñòè
ðåàëèçóåìîãî ìåòîäà íàâåäåíèÿ, çàäåðæêè âêëþ÷åíèÿ ïðèáîðîâ è
äðóãèå îñîáåííîñòè ðàáîòû ñèñòåìû óïðàâëåíèÿ (ÑÓ);
âðåìåííàÿ ñõåìà ðàáîòû äâèãàòåëÿ è äðóãèõ ñèñòåì ÁÐ (öèêëî-
ãðàììà ïîëåòà);
ïðîãðàììà èçìåíåíèÿ âî âðåìåíè óãëîâ òàíãàæà, ðûñêàíüÿ è êà-
æóùåéñÿ ñêîðîñòè (åñëè êîíñòðóêöèÿ ÁÐ ïðåäóñìàòðèâàåò âîçìîæ-
íîñòü ðåãóëèðîâàíèÿ êàæóùåéñÿ ñêîðîñòè, ÷òî õàðàêòåðíî íå äëÿ
âñåõ òèïîâ ðàêåò);
ãåîäåçè÷åñêèå êîîðäèíàòû òî÷åê ñòàðòà è öåëè.
Ïåðå÷èñëåííûå èñõîäíûå äàííûå óñëîâèìñÿ íàçûâàòü äàëåå ïà-
ðàìåòðàìè ìàòåìàòè÷åñêîé ìîäåëè äâèæåíèÿ ÁÐ.
Ñèñòåìà äèôôåðåíöèàëüíûõ óðàâíåíèé, îïèñûâàþùàÿ äâèæå-
íèå öåíòðà ìàññ ðàêåòû íà àêòèâíîì è ïàññèâíîì ó÷àñòêàõ òðàåêòî-
ðèè, ñîñòàâëÿåòñÿ ñ ó÷åòîì òðåáîâàíèé ïî äîïóñòèìîé âåëè÷èíå
îøèáîê â îïðåäåëåíèè äàííûõ íà ïóñê. Ýòî íàêëàäûâàåò îãðàíè÷å-
íèÿ íà âûáîð ÷àñòíûõ ìàòåìàòè÷åñêèõ ìîäåëåé, âõîäÿùèõ â ìàòåìà-
òè÷åñêóþ ìîäåëü äâèæåíèÿ (ÌÌÄ), ñîñòàâëÿþùóþ îñíîâó äëÿ ðå-
øåíèÿ ðàññìàòðèâàåìîé êðàåâîé áàëëèñòè÷åñêîé çàäà÷è (ÊÁÇ).
Ñ÷èòàåòñÿ, ÷òî ïîãðåøíîñòü ðàñ÷åòà òî÷êè ïàäåíèÿ, âû÷èñëÿåìîé â
ðåçóëüòàòå ñîâìåñòíîãî ðåøåíèÿ óêàçàííîé ñèñòåìû äèôôåðåíöè-
àëüíûõ óðàâíåíèé, íå äîëæíà ïðåâûøàòü ìàëîé âåëè÷èíû (äëÿ áàë-
ëèñòè÷åñêèõ ðàêåò äàëüíåãî äåéñòâèÿ – ïîðÿäêà 30 ìåòðîâ). Âëèÿ-
íèå âðàùàòåëüíîãî äâèæåíèÿ ðàêåòû íà åå ïîñòóïàòåëüíîå äâèæå-
íèå ïðè ðåøåíèè ðàññìàòðèâàåìîãî êëàññà çàäà÷ ÁÎ ïóñêîâ íå
ó÷èòûâàåòñÿ, à ñ÷èòàåòñÿ, ÷òî ÑÓ ñïîñîáíà ïðàêòè÷åñêè ìãíîâåííî
îòðàáàòûâàòü çàäàííûå ïðîãðàììû âðàùàòåëüíîãî äâèæåíèÿ íà
ïðîòÿæåíèè âñåãî ïîëåòà.
Ïðè ðàçðàáîòêå òàêîé ÌÌÄ íåîáõîäèìî ó÷èòûâàòü äâà ÷ðåçâû-
÷àéíî âàæíûõ îáñòîÿòåëüñòâà. Ïåðâîå ñîñòîèò â òîì, ÷òî ïðè ìîäå-
ëèðîâàíèè ïîëåòà íà àêòèâíîì ó÷àñòêå òðàåêòîðèè òðåáîâàíèÿ ê
òî÷íîñòè çàäàíèÿ ïîâåðõíîñòíûõ ñèë (òÿãè ÄÓ è àýðîäèíàìè÷åñêèõ)
ìîãóò áûòü íå î÷åíü âûñîêè. Êàê ïðàâèëî, âïîëíå äîñòàòî÷íî èñ-
ïîëüçîâàòü ìîäåëü ñòàíäàðòíîé àòìîñôåðû. Ïðè÷èíà, ñ îäíîé ñòî-
ðîíû, ñîñòîèò â òîì, ÷òî èíåðöèàëüíàÿ íàâèãàöèîííàÿ ñèñòåìà, êî-
òîðàÿ âõîäèò â ñîñòàâ ÑÓ âñåõ ñîâðåìåííûõ ÁÐ, ìîæåò èçìåðÿòü ñòå-
ïåíü îáóñëîâëåííûõ ýòèì ôàêòîðîì îòêëîíåíèé ôàêòè÷åñêîé
òðàåêòîðèè îò ðàñ÷åòíîé. Ñ äðóãîé ñòîðîíû, êîíñòðóêòèâíî î÷åíü
ñëîæíî îáåñïå÷èòü îòêëîíåíèÿ óäåëüíîé òÿãè è ñåêóíäíîãî ðàñõîäà
òîïëèâà ÄÓ îòíîñèòåëüíî èõ ðàñ÷åòíûõ çíà÷åíèé, à òàêæå îòêëîíå-
íèÿ êîýôôèöèåíòîâ àýðîäèíàìè÷åñêèõ ñèë, êîòîðûå ïðèâîäèëè áû
260
ê ìåíüøèì âîçìóùåíèÿì òðàåêòîðèè, ÷åì ðàññìàòðèâàåìîå âëèÿ-
íèå ìîäåëåé àòìîñôåðû. Íî íåëüçÿ äîïóñêàòü ñëèøêîì ãðóáûõ óï-
ðîùåíèé ïðè ìîäåëèðîâàíèè ïîâåðõíîñòíûõ ñèë (ìîäåëèðîâàòü ïî-
ëåò ñîâñåì áåç ó÷åòà àòìîñôåðû èëè ñ èçîòåðìè÷åñêîé àòìîñôåðîé),
â ýòîì ñëó÷àå ìîãóò èìåòü ìåñòî ñëèøêîì áîëüøèå çàòðàòû òîïëèâà
íà ñîîòâåòñòâóþùóþ êîððåêöèþ òðàåêòîðèè.
Âàæíî ïîíèìàòü, ÷òî âëèÿíèå ðàññìîòðåííûõ ïîãðåøíîñòåé
ÌÌÄ êàñàåòñÿ â ïåðâóþ î÷åðåäü íå òî÷íîñòíûõ õàðàêòåðèñòèê ÁÐ, à
ýíåðãåòè÷åñêèõ (ïðè ïóñêàõ íà ïðåäåëüíûå äàëüíîñòè íåêîððåêò-
íûé ó÷åò óêàçàííûõ ôàêòîðîâ ìîæåò ïðèâåñòè ê íåøòàòíîìó çàâåð-
øåíèþ ïîëåòà èç-çà íåäîñòàòêà òîïëèâà). Íàðÿäó ñ ýòèì íåîáõîäè-
ìî îñîçíàâàòü, ÷òî ñîñòàâ ÌÌÄ, èñïîëüçóåìûõ ïðè ðåøåíèè ÊÁÇ,
äîëæåí áûòü óâÿçàí ñî ñòðóêòóðîé âîçìóùàþùèõ ôàêòîðîâ, ó÷òåí-
íûõ ïðè ïðîåêòèðîâàíèè ÁÐ â ñîñòàâå òàê íàçûâàåìûõ ãàðàíòèéíûõ
çàïàñîâ òîïëèâà. Òàêèì îáðàçîì, ñóùåñòâóåò ôóíêöèîíàëüíàÿ ñâÿçü
ìåæäó èñõîäíûìè äàííûìè, èñïîëüçóåìûìè ïðè ðåøåíèè ðàçëè÷-
íûõ çàäà÷ ÁÎ ïóñêîâ ÁÐ íà ðàçëè÷íûõ ýòàïàõ ñîçäàíèÿ, ýêñïåðè-
ìåíòàëüíîé îòðàáîòêè è ïëàíèðîâàíèÿ áîåâîãî ïðèìåíåíèÿ ðàêåò-
íûõ êîìïëåêñîâ.
Âòîðîå âàæíîå îáñòîÿòåëüñòâî, êîòîðîå íåîáõîäèìî ó÷èòûâàòü
ïðè ðàçðàáîòêå ÌÌÄ äëÿ ðåøåíèÿ ÊÁÇ, ñîñòîèò â òîì, ÷òî èíåðöè-
àëüíûå íàâèãàöèîííûå ñèñòåìû ïðèíöèïèàëüíî íå ìîãóò èçìåðÿòü
âîçìóùåíèÿ, ñâÿçàííûå ñ ïðèðîäîé ãðàâèòàöèè. Ïîýòîìó ìàòåìàòè-
÷åñêèå ìîäåëè ãðàâèòàöèîííîãî ïîëÿ Çåìëè, èñïîëüçóåìûå ïðè ðàñ-
÷åòå ïîïàäàþùèõ òðàåêòîðèé, äîëæíû áûòü êàê ìîæíî áîëåå òî÷-
íûìè. Ëþáîå îòêëîíåíèå òðàåêòîðèè, âûçâàííîå íåàäåêâàòíîñòüþ
ìàòåìàòè÷åñêîãî ìîäåëèðîâàíèÿ ãðàâèòàöèîííîãî óñêîðåíèÿ, íå
áóäåò çàôèêñèðîâàíî íàâèãàöèîííûìè ïðèáîðàìè è ïðèâåäåò ê îò-
êëîíåíèþ òî÷êè ïàäåíèÿ îò òî÷êè ïðèöåëèâàíèÿ. Ââèäó òîãî ÷òî
ãðàâèòàöèîííîå óñêîðåíèå â ïðîöåññå âû÷èñëåíèÿ êîîðäèíàò öåí-
òðà ìàññ ËÀ äâàæäû èíòåãðèðóåòñÿ, ïîãðåøíîñòü åãî ìîäåëèðîâà-
íèÿ áóäåò íîñèòü íàðàñòàþùèé ñî âðåìåíåì õàðàêòåð. Â ñâÿçè ñ òåì,
÷òî íà ïàññèâíîì ó÷àñòêå óïðàâëåíèå ïîëåòîì îòñóòñòâóåò, âñå ñêà-
çàííîå ïî ïîâîäó ìîäåëèðîâàíèÿ ãðàâèòàöèîííîãî óñêîðåíèÿ íà àê-
òèâíîì ó÷àñòêå ñëåäóåò îòíåñòè êî âñåì ÷àñòíûì ìàòåìàòè÷åñêèì
ìîäåëÿì ïàññèâíîãî ó÷àñòêà. Íà ýòîì ó÷àñòêå ïîëåòà îòêëîíåíèÿ
ïîâåðõíîñòíûõ ñèë îò èõ ðàñ÷åòíûõ çíà÷åíèé óæå íå êîìïåíñèðó-
þòñÿ ðàáîòîé ÑÓ. Â ðåçóëüòàòå íåîáõîäèìî ïîëüçîâàòüñÿ ìîäåëÿìè
àòìîñôåðû, ó÷èòûâàþùèìè ñåçîííûå èçìåíåíèÿ êëèìàòà, à òàêæå
ëîêàëüíûå îñîáåííîñòè àòìîñôåðû, îáóñëîâëåííûå ãåîãðàôè÷å-
ñêèì ïîëîæåíèåì îáúåêòà ïîðàæåíèÿ è ñîîòâåòñòâóþùèõ åìó òî÷åê
ïðèöåëèâàíèÿ. Êðîìå òîãî, òðåáóåòñÿ êàê ìîæíî áîëåå òî÷íî ìîäå-
ëèðîâàòü çíà÷åíèÿ àýðîäèíàìè÷åñêèõ ñèë è ïðîöåññ èçìåíåíèÿ
261
ôîðìû è ìàññû Ã× âî âðåìÿ âîçäåéñòâèÿ íà íåãî àýðîäèíàìè÷åñêî-
ãî íàãðåâà.
Ïîñëåäíåå îáñòîÿòåëüñòâî óñóãóáëÿåòñÿ ïðèðîäîé àëãîðèòìà
ðåøåíèÿ ÊÁÇ. Ðàñ÷åò ïîïàäàþùåé òðàåêòîðèè ÁÐ îñíîâàí íà
ìíîãîêðàòíîì ÷èñëåííîì èíòåãðèðîâàíèè óïîìÿíóòîé âûøå
ñèñòåìû óðàâíåíèé äâèæåíèÿ ðàêåòû íà àêòèâíîì è ïàññèâíîì
ó÷àñòêàõ òðàåêòîðèè. Îáåñïå÷åíèå ïîïàäàíèÿ ìîäåëèðóåìîé
òî÷êè ïàäåíèÿ â òðåáóåìóþ îêðåñòíîñòü òî÷êè ïðèöåëèâàíèÿ
îñóùåñòâëÿåòñÿ öåëåíàïðàâëåííûì ïîäáîðîì íîìèíàëüíîãî âðå-
ìåíè âûêëþ÷åíèÿ äâèãàòåëÿ (tê) è àçèìóòà ïðèöåëèâàíèÿ (À0)ñ
ïîñëåäîâàòåëüíûì óòî÷íåíèåì ýòèõ ïàðàìåòðîâ îò îäíîé èòåðà-
öèè ðåøåíèÿ ÊÁÇ ê äðóãîé. Ïðàâèëüíî îðãàíèçîâàâ èòåðàöèîí-
íûé ïðîöåññ (ïðè ìîäåëèðîâàíèè ïóñêîâ â ïðåäåëàõ äîïóñòèìî-
ãî äèàïàçîíà äàëüíîñòåé), âñåãäà ìîæíî îáåñïå÷èòü åãî ñõîäè-
ìîñòü. Ýòî îçíà÷àåò, ÷òî åñëè, íàïðèìåð, â ÌÌÄ èñïîëüçóþòñÿ
àýðîäèíàìè÷åñêèå õàðàêòåðèñòèêè Ã×, îøèáî÷íî âçÿòûå äëÿ Ã×
äðóãîé ðàêåòû, òî â õîäå ðåøåíèÿ ÊÁÇ áóäóò ïîäîáðàíû òàêèå
çíà÷åíèÿ ïàðàìåòðîâ tê èÀ0, ÷òî êîîðäèíàòû ìîäåëèðóåìîé
òî÷êè ïàäåíèÿ íå áóäóò îòëè÷àòüñÿ îò çàäàííûõ êîîðäèíàò òî÷-
êè ïðèöåëèâàíèÿ áîëåå, ÷åì ýòî òðåáóåòñÿ ïî óñëîâèþ ïðåêðà-
ùåíèÿ èòåðàöèîííîãî ïðîöåññà. ÊÁÇ â ýòîé ãèïîòåòè÷åñêîé ñè-
òóàöèè áóäåò óñïåøíî ðåøåíà. Ïî ðåçóëüòàòàì åå ðåøåíèÿ ìîæ-
íî áóäåò ïîäãîòîâèòü âñå íåîáõîäèìûå óñòàíîâî÷íûå äàííûå íà
ïóñê. À â ðåàëüíîì ïóñêå, åñëè ïðåäïîëîæèòü, ÷òî ýòîò ïóñê
áóäåò ïðîèñõîäèòü â ãåîôèçè÷åñêèõ óñëîâèÿõ, òî÷íî ñîîòâåòñò-
âóþùèõ íîìèíàëüíîé òðàåêòîðèè, Ã× îòêëîíèòñÿ îò òî÷êè ïðè-
öåëèâàíèÿ èìåííî íà òàêîå ðàññòîÿíèå, êîòîðîå ñîîòâåòñòâóåò
îøèáêå, äîïóùåííîé ïðè ìîäåëèðîâàíèè ñèë, äåéñòâóþùèõ íà
ïàññèâíîì ó÷àñòêå ïîëåòà.
Ïîýòîìó ðàñ÷åò ïîïàäàþùèõ òðàåêòîðèé, îñóùåñòâëÿåìûé íå-
ïîñðåäñòâåííî â èíòåðåñàõ ïîäãîòîâêè óñòàíîâî÷íûõ äàííûõ íà
ïóñêè ðàêåò, âûçûâàåò íåîáõîäèìîñòü â ïðèíÿòèè ñïåöèàëüíûõ
ìåð ïî êîíòðîëþ àäåêâàòíîñòè ÌÌÄ, èñïîëüçóåìûõ äëÿ ðåøå-
íèÿ ÊÁÇ.
Ïîñêîëüêó îòûñêàíèå ðåøåíèÿ òðåáóåò ïîñëåäîâàòåëüíîãî èí-
òåãðèðîâàíèÿ äâóõ ñèñòåì íåëèíåéíûõ äèôôåðåíöèàëüíûõ óðàâíå-
íèé (íà àêòèâíîì è ïàññèâíîì ó÷àñòêàõ ïîëåòà), òî ÿñíî, ÷òî ðåøå-
íèå ïîñòàâëåííîé çàäà÷è ìîæåò áûòü òîëüêî ÷èñëåííûì è äîëæíî
âêëþ÷àòü èòåðàöèîííûé ïðîöåññ ïîñëåäîâàòåëüíîãî óòî÷íåíèÿ èñ-
êîìûõ ïàðàìåòðîâ tê èÀ0.  ñâîþ î÷åðåäü ýòî îçíà÷àåò, ÷òî óñïåõ ðå-
øåíèÿ â çíà÷èòåëüíîé ìåðå çàâèñèò îò òîãî, íàñêîëüêî óäà÷íî âû-
áðàíî ïåðâîå ïðèáëèæåíèå ýòèõ ïàðàìåòðîâ è íàñêîëüêî ýôôåêòèâ-
íà ïðîöåäóðà èõ ïîñëåäîâàòåëüíîãî óòî÷íåíèÿ.
262
6.1.3. ÄÂÓÕÒÎ×Å×ÍÛÅ ÊÐÀÅÂÛÅ ÇÀÄÀ×È ÂÍÅØÍÅÉ ÁÀËËÈÑÒÈÊÈ
Ïðè ïîëåòå íåóïðàâëÿåìîãî ËÀ ïî áàëëèñòè÷åñêîé òðàåêòîðèè
åãî çàäà÷à â ïîäàâëÿþùåì áîëüøèíñòâå ñëó÷àåâ ìîæåò ñ÷èòàòüñÿ
âûïîëíåííîé, åñëè óêàçàííàÿ òðàåêòîðèÿ, íà÷àëî êîòîðîé ñîîòâåò-
ñòâóåò òî÷êå ïðåêðàùåíèÿ ìåõàíè÷åñêîé ñâÿçè ñíàðÿäà èëè ðàêåòû
ñî ñòâîëîì èëè íàïðàâëÿþùåé ïóñêîâîé óñòàíîâêè, äîñòèãíåò íà-
ìå÷åííîãî ê ïîðàæåíèþ îáúåêòà. Õîòÿ ðå÷ü çäåñü èäåò î äâèæåíèè
íåóïðàâëÿåìîãî ËÀ, ðåàëèçàöèÿ áàëëèñòè÷åñêîé äâóõòî÷å÷íîé êðè-
âîé òåì íå ìåíåå òðåáóåò ôîðìèðîâàíèÿ ñîîòâåòñòâóþùåãî óïðàâ-
ëÿþùåãî âîçäåéñòâèÿ.
 êà÷åñòâå òàêîãî óïðàâëÿþùåãî âîçäåéñòâèÿ ïðèìåíèòåëüíî ê
îáû÷íûì àðòèëëåðèéñêèì ñíàðÿäàì è íåóïðàâëÿåìûì ðàêåòàì ñëå-
äóåò ðàññìàòðèâàòü ïàðàìåòðè÷åñêîå óïðàâëåíèå (ò.å. óïðàâëåíèå
ïàðàìåòðàìè äâèæåíèÿ). Äåéñòâèòåëüíî, äëÿ ïîëó÷åíèÿ òðåáóåìîé
òðàåêòîðèè ñíàðÿäó íåîáõîäèìî ñîîáùèòü òðåáóåìîå çíà÷åíèå âåê-
òîðà ñêîðîñòè â òî÷êå, ñîîòâåòñòâóþùåé íà÷àëó áàëëèñòè÷åñêîãî
äâèæåíèÿ, ïðèíèìàåìîé çà íà÷àëüíóþ. Âåêòîð ñêîðîñòè ìîæåò
áûòü îïðåäåëåí, åñëè çàäàíû åãî ïðîåêöèè íà îñè âûáðàííîé îðòî-
ãîíàëüíîé ñèñòåìû êîîðäèíàò, ëèáî åñëè îãîâîðåíà âåëè÷èíà ìîäó-
ëÿ V è çàäàí óãîë íàêëîíà âåêòîðà V ê ìåñòíîìó ãîðèçîíòó θ (äëÿ
ñëó÷àÿ ïëîñêîãî äâèæåíèÿ). Êðàåâûå çàäà÷è ñ ïàðàìåòðè÷åñêèì
óïðàâëåíèåì îòíîñÿòñÿ ê ÷èñëó ïðîñòåéøèõ êðàåâûõ äâóõòî÷å÷íûõ
çàäà÷ äèíàìèêè ïîëåòà.
Ó àýðîäèíàìè÷åñêè óïðàâëÿåìûõ ËÀ ê óêàçàííûì ïàðàìåòðàì
óïðàâëåíèÿ äîáàâëÿþòñÿ òàêæå óãëû (óïðàâëÿþùèå ôóíêöèè) îò-
êëîíåíèÿ àýðîäèíàìè÷åñêèõ ðóëåé. Íàëè÷èå ïîñëåäíèõ ïîçâîëÿåò
ËÀ îñóùåñòâëÿòü ìàíåâð â ïðîöåññå ïîëåòà, ðåàëèçóÿ äâèæåíèå ïî
òðàåêòîðèè, îòëè÷àþùåéñÿ îò áàëëèñòè÷åñêîé. Åñëè íà áîðòó ê òîìó
æå èìååòñÿ äâèãàòåëüíàÿ óñòàíîâêà (íàïðèìåð, â ñëó÷àå óïðàâëÿå-
ìîãî àêòèâíî-ðåàêòèâíîãî ñíàðÿäà (ÓÀÐÑ), òî ïðè îáåñïå÷åíèè
âîçìîæíîñòè åå ðåãóëèðîâàíèÿ (ôîðñèðîâàíèÿ è/èëè äðîññåëèðîâà-
íèÿ òÿãè äâèãàòåëÿ) â ñîâîêóïíîñòè ñ èñïîëüçîâàíèåì óïðàâëÿþùèõ
ïàðàìåòðè÷åñêèõ âîçäåéñòâèé è âîçäåéñòâèé, ôîðìèðóåìûõ àýðîäè-
íàìè÷åñêèìè îðãàíàìè óïðàâëåíèÿ, ìîæåò áûòü ðåàëèçîâàíà ïðàê-
òè÷åñêè ëþáàÿ, òåîðåòè÷åñêè íàèáîëåå ñëîæíàÿ ïðîãðàììà îïîðíî-
ãî äâèæåíèÿ. Ñ öåëüþ èëëþñòðàöèè ïðîñòåéøåãî ïîäõîäà, ñâÿçàí-
íîãî ñ ðåøåíèåì äâóõòî÷å÷íîé êðàåâîé çàäà÷è âíåøíåé
áàëëèñòèêè, ðàññìîòðèì äâèæåíèå ñíàðÿäà ïîñòîÿííîé ìàññû â
ðàìêàõ äîïóùåíèé, îòâå÷àþùèõ ïàðàáîëè÷åñêîé òåîðèè (ñì.
ï. 5 .2 .1). Âîñïîëüçîâàâøèñü ñòàíäàðòíûìè óðàâíåíèÿìè äâèæåíèÿ
ìàòåðèàëüíîé òî÷êè ïîñòîÿííîé ìàññû â ïëîñêî-ïàðàëëåëüíîì
ïîëå òÿãîòåíèÿ, ïîëó÷èì ñåìåéñòâî èíòåãðàëüíûõ êðèâûõ, îòâå÷àþ-
ùèõ ñîîòíîøåíèÿì âèäà
263
xCtCyCtC g
t
=+
=+−
12 34
2
05
;,
,
(6.1)
ãäå Ci (i =1,..., 4) – ïîñòîÿííûå èíòåãðèðîâàíèÿ. Èç ñåìåéñòâà (6.1)
ìîæåò áûòü âûáðàíà êðèâàÿ, óäîâëåòâîðÿþùàÿ ãðàíè÷íûì óñëîâèÿì,
çàäàííûì â âèäå
txyt
tT
x
x
yy
kk
k
===
=
===
000
00
:,;
:,, (6.2)
ãäå Ò ïðèíèìàåòñÿ çà ïàðàìåòð.
Èç (6.1) è (6.2) íàõîäèì
xx
Tt
k
=
−1
;
(6.3)
yy gTTtgt
k
=+
−
−
(,) ,
.
05
05
21
2
(6.4)
Ïðè èññëåäîâàíèè êà÷åñòâà äâèæåíèÿ (6.3), (6.4) ïî äâóõòî÷å÷-
íîé êðèâîé áóäåì èñõîäèòü èç òîãî î÷åâèäíîãî ñâîéñòâà, ÷òî ÷åðåç
äâå òî÷êè ìîæíî ïðîâåñòè áåñ÷èñëåííîå ìíîæåñòâî ïàðàáîëè÷å-
ñêèõ òðàåêòîðèé, êàæäàÿ èç êîòîðûõ áóäåò îáëàäàòü ïðèñóùèìè
òîëüêî åé îïðåäåëåííûìè ñâîéñòâàìè. Â ýòîì íåòðóäíî óáåäèòüñÿ,
èìåÿ â âèäó âûðàæåíèå (5.22) äëÿ ïîëíîé äàëüíîñòè ïîëåòà, ñîãëàñ-
íî êîòîðîìó îäíà è òà æå äàëüíîñòü õñ ìîæåò äîñòèãàòüñÿ ïðè ìíî-
æåñòâå ñî÷åòàíèé V0 è θ0, îïðåäåëÿåìûõ èç óñëîâèÿV 0
2
0
2
sin
.
θ=const
Óêàçàííûå ñâîéñòâà ìîãóò áûòü çàðàíåå îãîâîðåíû ïðè ôîðìóëè-
ðîâêå êà÷åñòâà äâèæåíèÿ. Íàïðèìåð, ìîæíî ïîòðåáîâàòü äîñòèæå-
íèÿ çàäàííîé äàëüíîñòè õñ ïðè îáåñïå÷åíèè ìàêñèìàëüíîé èëè ìè-
íèìàëüíîé âûñîòû ïîëåòà (ïîëîæåíèÿ âåðøèíû òðàåêòîðèè), ìè-
íèìàëüíîé íà÷àëüíîé ñêîðîñòè è ò.ä . Âûáîð êðèòåðèÿ äîëæåí
îïðåäåëÿòüñÿ êîíêðåòíûì ñîäåðæàíèåì è öåëåâûì íàçíà÷åíèåì ðå-
øàåìîé ïðèêëàäíîé çàäà÷è.  çàâèñèìîñòè îò åãî êîíêðåòíîãî âû-
ðàæåíèÿ áóäóò èìåòü ìåñòî è ðàçëè÷íûå êîíå÷íûå ðåçóëüòàòû ðåøå-
íèÿ.
Äëÿ ïðèäàíèÿ îïðåäåëåííîñòè ïîñëåäóþùåìó àíàëèçó âûäåëèì
èç ðàññìàòðèâàåìîãî ñåìåéñòâà òðàåêòîðèé òàêóþ, êîòîðàÿ îáåñïå-
÷èâàëàñü áû ïðè ìèíèìàëüíûõ çàòðàòàõ ýíåðãèè, ò.å . ïðè ìèíèìàëü-
íîé íà÷àëüíîé ñêîðîñòè. Ïîñêîëüêó êîíöû äâóõòî÷å÷íîé êðèâîé
ôèêñèðîâàíû, åäèíñòâåííîé âåëè÷èíîé, ïðèíèìàåìîé â êà÷åñòâå
ïàðàìåòðà óïðàâëåíèÿ, ìîæåò ñëóæèòü âðåìÿ äâèæåíèÿ Ò. Èñïîëü-
çóÿ åãî ïðîèçâîë â ðàìêàõ äàííîé ïîñòàíîâêè çàäà÷è, áóäåì ñ÷èòàòü
V0 ôóíêöèåé ýòîãî ïàðàìåòðà.
Òîãäà, ó÷èòûâàÿ, ÷òî V0 â ôóíêöèè Ò ìîæåò áûòü ïðåäñòàâëåíà
êàê
264
VTxy g
T
kk
0
12
2
2
1
2
05
=+
+
−
(( ,)
),
/
(6.5)
ïîëó÷èì äëÿ ïðîäîëæèòåëüíîñòè ïîëåòà
Tg
x
y
kk
=+
−
212212
()
/
(6.6)
çíà÷åíèå
Vg
y
x
y
kkk
0
22
1
2
min
/
(( ))
.
=+
+
(6.7)
Äëÿ íàéäåííîé ñêîðîñòè çàêîí äâèæåíèÿ ñíàðÿäà ïî äâóõòî÷å÷íîé
òðàåêòîðèè, óäîâëåòâîðÿþùèé ãðàíè÷íûì óñëîâèÿì (6.2), áóäåò
èìåòü âèä [24]
xtg
xxy
kkk
=+
−
05 22 212
,(
);
/
(6.8)
y
yxy g
xy
tg
t
kkk
kk
=
++
+
−
(( ))
()
,.
/
/
22
1
2
22
1
2
2
2
05
(6.9)
Äàííîå äâèæåíèå ÿâëÿåòñÿ åäèíñòâåííûì.
Åñòåñòâåííî, âîçíèêàåò âîïðîñ: äëÿ âñåõ ëè ïðîèçâîëüíûõ ñòðóê-
òóð ìàòåìàòè÷åñêèõ (äèôôåðåíöèàëüíûõ) ìîäåëåé ñîñòîÿíèÿ ËÀ
ìîæåò áûòü ïîëó÷åíî ðåøåíèå êðàåâîé çàäà÷è (ò.å . ñóùåñòâóåò è ÿâ-
ëÿåòñÿ ëè åäèíñòâåííîé äâóõòî÷å÷íàÿ êðèâàÿ, óäîâëåòâîðÿþùàÿ çà-
äàííûì ñâîéñòâàì)?
Îòâåò íà ýòîò âîïðîñ äàåò ñëåäóþùàÿ òåîðåìà, èçâåñòíàÿ êàê òåî-
ðåìà Áåðíøòåéíà: åñëè ôóíêöèè F, F
F
y
y=
∂
∂
èF
F
y
y′
=
′
∂
∂
äèôôåðåíöè-
àëüíîãî óðàâíåíèÿ
′=
′
yFx
yy
(,, )
(6.10)
íåïðåðûâíû â êàæäîé êîíå÷íîé òî÷êå (x, y) äëÿ ëþáîãî êîíå÷íîãî y ′
è åñëè ñóùåñòâóþò òàêàÿ êîíñòàíòà Ñ > 0 è òàêèå îãðàíè÷åííûå â
êàæäîé êîíå÷íîé ÷àñòè ïëîñêîñòè xy ôóíêöèè
kkx
y kxy
11
2
00
=≥
≥
(,) ; (,)
,
(6.11)
÷òî
Fxyy CFxyy ky k
y(,,) ;|(,,)| () ,
′>
′≤
′
+
1
2
2
(6.12)
265
òî ÷åðåç ëþáûå äâå òî÷êè ïëîñêîñòè A(a, a1), B(b, b1), èìåþùèå
ðàçëè÷íûå àáñöèññû (a ≈ b), ïðîõîäèò îäíà è òîëüêî îäíà
èíòåãðàëüíàÿ êðèâàÿ y = φ(x) óðàâíåíèÿ (6.10).
6.1.4. ÏÎÑÒÀÍÎÂÊÀ ÇÀÄÀ×È ÎÏÐÅÄÅËÅÍÈß ÌÍÎÃÎÒÎ×Å×ÍÎÉ
ÊÐÈÂÎÉ Â ÊÐÀÅÂÛÕ ÇÀÄÀ×ÀÕ ÓÏÐÀÂËßÅÌÎÃÎ ÏÎËÅÒÀ
Áîëåå ñëîæíûì ÿâëÿåòñÿ âîïðîñ î ñóùåñòâîâàíèè è åäèíñòâåííîñòè ðå-
øåíèé äëÿ íåáàëëèñòè÷åñêîé (ìíîãîòî÷å÷íîé) êðèâîé ïðèìåíèòåëüíî ê îá-
ùåìó ñëó÷àþ íåëèíåéíîé ìîäåëè ñîñòîÿíèÿ óïðàâëÿåìîãî ËÀ.
Õàðàêòåðíûì ïðèìåðîì òàêîé êðèâîé ÿâëÿåòñÿ òðàåêòîðèÿ óïðàâëÿåìî-
ãî ñíàðÿäà, ñòàðòóþùåãî ñ ïîäâèæíîãî íîñèòåëÿ (íà÷àëüíàÿ òî÷êà), âûõîäÿ-
ùåãî â ôèêñèðîâàííîé ïðîìåæóòî÷íîé òî÷êå íà òðàåêòîðèþ ãîðèçîíòàëü-
íîãî ïîëåòà, ñîâåðøàþùåãî ïîëåò ïî íåé äî äðóãîé ôèêñèðîâàííîé òî÷êè è
ïèêèðóþùåãî ïðè äîñòèæåíèè ïîñëåäíåé íà öåëü (÷åòâåðòàÿ (êîíå÷íàÿ)
ôèêñèðîâàííàÿ òî÷êà òðàåêòîðèè).
Ïóñòü èìååòñÿ ìîäåëü, îïèñûâàþùàÿ ñîñòîÿíèå èññëåäóåìîãî ïðîöåññà
÷åðåç îáîáùåííûå êîîðäèíàòû
qf
t
q
q
qq
nn
()
()
(;,,,,
)
=
′′
′
−
K
1
(6.13)
ñ êðàåâûìè óñëîâèÿìè
xa
k
m
r
r
r
kk
()
(),,
,
,
;,
,
,,
==
=
−
01
2
0
11
KK
(6.14)
ãäåa≤a1<a2<...<am<b;1≤m≤n; rn
k
k
m
=
=
∑.
1
Áóäåì ñ÷èòàòü
bba
r
rr
rr
k
kk
00
120
0
+++
+++
==
=
=
KK
K
()
.
Ââåäåì â ðàññìîòðåíèå ôóíêöèè
Pt
Pt
btj
n
nj
i
ij
n
01
11
2
(),,()(),
,,,,
==
−
=
−+
=
∏
KK
(6.15)
ãäå ∏ – çíàê ïðîèçâåäåíèÿ.
Ïîëîæèì
φ=
=
−
−
−
−
−
(;,,)[;(),, ()
()
ty y ftPty
cbtP
nn
j
i
in
i
ij
11
1
1
KK
(),
,(
)(
)
]
.
()
ty
cbtPty
i
j
n
i
in
i
ni
i
i
n
1
1
1
1
1
K
K
=
−
−
−
−
=
∑
∑−
(6.16)
Òîãäà ñïðàâåäëèâà äîêàçàííàÿ â [15] ñëåäóþùàÿ òåîðåìà: ïóñòü ôóíêöèÿ f(t,
y,..., yn) îïðåäåëåíà â îáëàñòè, äëÿ êîòîðîé a ≤ t ≤ b; −∞ < yi < ∞ (i =1,2,..., n),
266
è òàêîâà, ÷òî ôóíêöèÿ (6.16) íåïðåðûâíà ïî t è óäîâëåòâîðÿåò óñëîâèþ
Ëèïøèöà ïî ïåðåìåííûì y1, y2,..., yn ñ êîýôôèöèåíòàìè L1(t),..., Ln(t),
èìåþùåìó âèä
|(;,,) (;,,)| ()| |,
φφ
η
ηη
tyy
t
Lty
at
nn
i
i
i
i
n
11
1
KK
−≤
−
≤≤
=
∑
bLt
i
,(
),
≥0
(6.17)
ãäå ïåðåìåííûå ηi îïðåäåëåíû â òîé æå îáëàñòè, ÷òî è yi. Êðàåâàÿ çàäà÷à
(6.13), (6.14) áóäåò èìåòü åäèíñòâåííîå, îïðåäåëåííîå íà [a, b] ðåøåíèå, åñëè
âûïîëíÿåòñÿ íåðàâåíñòâî
sup
!
()
!(
),
atb
i
i
n
n
iL
t
≤≤
=
−<
∑
1
11
1
ãäå sup îáîçíà÷àåò âåðõíþþ ãðàíü ôóíêöèè (äîñòèæåíèå êîòîðîé
ñîîòâåòñòâóåò åå ìàêñèìóìó). Ñëåäñòâèåì äàííîé òåîðåìû ÿâëÿåòñÿ ðÿä
èçâåñòíûõ òåîðåì ñóùåñòâîâàíèÿ è åäèíñòâåííîñòè ðåøåíèÿ êðàåâîé çàäà÷è,
îòâå÷àþùåé óñëîâèÿì (6.13), (6.14). Òàê, â ñëó÷àå m = 1 îíà âûðîæäàåòñÿ â
çàäà÷ó Êîøè.  çàêëþ÷åíèå îáñóæäåíèÿ ïðèâåäåííîé òåîðåìû îòìåòèì, ÷òî
â ðÿäå ñëó÷àåâ óäîáíî ïðîâåðÿòü óñëîâèå Ëèïøèöà íå äëÿ ôóíêöèè φ(t, y1,...
... ,yn), à íåïîñðåäñòâåííî äëÿ ïðàâîé ÷àñòè óðàâíåíèÿ (6.13).
Íåòðóäíî çàìåòèòü, ÷òî óêàçàííàÿ òåîðåìà ñòðîãî ðàñïðîñòðàíÿåòñÿ
òîëüêî íà ñëó÷àé ñòàöèîíàðíûõ ñèñòåì. Ìîäåëè æå ËÀ, òåì áîëåå óïðàâëÿå-
ìûõ, èìåþò íåñòàöèîíàðíûé õàðàêòåð (ñì. ãë . 2).  ñâÿçè ñ ýòèì ïîëó÷åíèå
ãàðàíòèðîâàííîãî ðåøåíèÿ êðàåâîé çàäà÷è â ðàìêàõ åå ïîñòàíîâêè, óäîâëå-
òâîðÿþùåé ðàññìîòðåííîé òåîðåìå, òðåáóåò â ïîäàâëÿþùåì áîëüøèíñòâå
ñëó÷àåâ "çàìîðàæèâàíèÿ" êîýôôèöèåíòîâ ëèáî çàìåíû èõ íåêîòîðûìè îñ-
ðåäíåííûìè çíà÷åíèÿìè. Ââèäó íåïðåðûâíîñòè ïðàâûõ ÷àñòåé óðàâíåíèé
ïî âñåì ïåðåìåííûì, à òàêæå íåïðåðûâíîñòè ñàìèõ óïðàâëÿþùèõ ôóíêöèé
ïðåäñòàâëÿåòñÿ âîçìîæíûì ðàñïðîñòðàíèòü âûâîäû òåîðåìû è íà ñëó÷àé
äîñòàòî÷íî ìàëîé îêðåñòíîñòè ïåðåìåííûõ çíà÷åíèé êîýôôèöèåíòîâ ìîäå-
ëåé îáúåêòà è ïðèíÿòûõ ïàðàìåòðîâ óïðàâëÿþùèõ ôóíêöèé.
6.2 . ÎÁÐÀÒÍÛÅ ÇÀÄÀ×È ÄÈÍÀÌÈÊÈ ÏÎËÅÒÀ
6.2 .1. ÊÎÍÖÅÏÖÈß ÎÁÐÀÒÍÛÕ ÇÀÄÀ× ÄÈÍÀÌÈÊÈ ÏÎËÅÒÀ
 îòëè÷èå îò îñíîâíîé (ïðÿìîé) çàäà÷è, ñòàâÿùåé öåëüþ îïðåäå-
ëåíèå òðàåêòîðèè ïîä äåéñòâèåì çàäàííîé ñèñòåìû ñèë, îáðàòíàÿ
çàäà÷à ôîðìóëèðóåòñÿ êàê îïðåäåëåíèå ñèë ïî çàäàííûì ñâîéñòâàì
267
äâèæåíèÿ. Â òàêîé ïîñòàíîâêå êîíöåïöèÿ îáðàòíûõ çàäà÷ ìåõàíèêè
áûëà ñôîðìóëèðîâàíà åùå È. Íüþòîíîì, Æ. Ëàãðàíæåì, À. Ïóàíêà-
ðåèäð.
Ðàçâèòèå ðàêåòîäèíàìèêè ïîòðåáîâàëî ðåøåíèÿ îáðàòíûõ çàäà÷
äèíàìèêè òî÷êè (òåëà) ïåðåìåííîé ìàññû, ïðèîðèòåò â îáëàñòè ïî-
ñòàíîâêè êîòîðûõ ïðèíàäëåæèò È. . Ìåùåðñêîìó. Ñóùåñòâåííûé
âêëàä â ðàçâèòèå äàííîãî êëàññà çàäà÷ âíåñëè À.À. Êîñìîäåìüÿí-
ñêèé è Ä.Å . Îõîöèìñêèé. Â òðàêòîâêå À.À. Êîñìîäåìüÿíñêîãî îá-
ðàòíûå çàäà÷è äèíàìèêè òî÷êè ïåðåìåííîé ìàññû ôîðìóëèðîâà-
ëèñü êàê çàäà÷è, â êîòîðûõ ïî çàäàííûì âíåøíèì ñèëàì è çàäàííî-
ìó çàêîíó äâèæåíèÿ íåîáõîäèìî îïðåäåëèòü çàêîí èçìåíåíèÿ
ìàññû, îáåñïå÷èâàþùèé çàäàííîå äâèæåíèå.  îïðåäåëåííîì
ñìûñëå ê òðàêòîâêå îáðàòíûõ çàäà÷ äèíàìèêè À.À. Êîñìîäåìüÿí-
ñêîãî ïðèìûêàåò è ïîäõîä À.À. Äìèòðèåâñêîãî ê îïðåäåëåíèþ íà-
÷àëüíûõ óñëîâèé äâèæåíèÿ òåë ïîñòîÿííîé ìàññû ïî áàëëèñòè÷å-
ñêîé òðàåêòîðèè íà îñíîâå ðåøåíèÿ îáðàòíûõ çàäà÷ âíåøíåé áàëëè-
ñòèêè [37].
Âåñüìà ïëîäîòâîðíûì îêàçàëîñü ýòî íàïðàâëåíèå è ïðè èññëå-
äîâàíèè ìíîãèõ êëàññè÷åñêèõ çàäà÷ òåîðèè àâòîìàòè÷åñêîãî
óïðàâëåíèÿ ïîëåòîì, â ðåøåíèå êîòîðûõ ñóùåñòâåííûé âêëàä
âíåñ Ï.Ä. Êðóòüêî. Äåòàëüíûé àíàëèç ýâîëþöèè êîíöåïöèé îáðàò-
íûõ çàäà÷ è èõ ïðèìåíåíèÿ â àíàëèòè÷åñêîé ìåõàíèêå, äèíàìèêå
óïðàâëÿåìîãî äâèæåíèÿ è â òåîðèè àâòîìàòè÷åñêîãî óïðàâëåíèÿ îò
åå ñòàíîâëåíèÿ êàê íàó÷íîé äèñöèïëèíû äî ñîâðåìåííîãî ñîñòîÿ-
íèÿ äàí â [63]. Çäåñü ìû îãðàíè÷èìñÿ ëèøü îáñóæäåíèåì íåêîòîðûõ
÷àñòíûõ çàäà÷, èìåþùèõ íåïîñðåäñòâåííîå îòíîøåíèå ê äèíàìèêå
ïîëåòà ðàêåò è ñíàðÿäîâ.
6.2.2. ÐÅØÅÍÈÅ ÊÐÀÅÂÛÕ ÇÀÄÀ× ÄÈÍÀÌÈÊÈ ÓÏÐÀÂËßÅÌÎÃÎ ÏÎËÅÒÀ
ÍÀ ÎÑÍÎÂÅ ÊÎÍÖÅÏÖÈÈ ÎÁÐÀÒÍÛÕ ÇÀÄÀ×
Îñíîâûâàÿñü íà ðåçóëüòàòàõ, ïîëó÷åííûõ Â.Ò. Òàðàíåíêî, è ñëå-
äóÿ [63], ðàññìîòðèì êðàåâóþ çàäà÷ó: ïðèìåíèòåëüíî ê ìîäåëè ñî-
ñòîÿíèÿ ËÀ âèäà
m
dV
dt
mgn
mV
d
dt
mgn
x
y
=−
=−
(s
i
n
)
;
(cos cos)
;
θ
θ
γθ
268
mV
d
dt
mgn
dx
dt
V
dy
dt
V
dz
d
y
cos
sin ;
cos cos ;
sin ;
θγ
θ
θ
Ψ
Ψ
=−
=
=
t
Vm
m
m
t
=−
=
−
cos sin ;
| •|,
θΨ0
(6.18)
ãäå ñîñòàâëÿþùèå âåêòîðà ïåðåãðóçêè n
mg
PX
xa
=−
1
[cos ];
α
ny=
=+
1
mg
PY
a
[si
n
],
α
òðåáóåòñÿ íàéòè óïðàâëÿþùèå ôóíêöèè Ð(t), α(t)è
γ(t), ïðè êîòîðûõ ËÀ çà âðåìÿ tk = Ò ïåðåìåñòèòñÿ èç çàäàííîãî
íà÷àëüíîãî (t = 0) ôàçîâîãî ñîñòîÿíèÿ
xx
yy
zz
xx
yy
z
() ;() ;() ;•()
•
; •()
•
; •()
000000
00000
======
•
z 0 (6.19)
â òðåáóåìîå êîíå÷íîå (tk = T ) ñîñòîÿíèå
xt
xytyztz
xt
xyty
kT kTkT
kT kT
();();();
•
()•;
•
()•;
•
===
==
ztz
kT
()•
.
=
(6.20)
 äàííîé ïîñòàíîâêå ñôîðìóëèðîâàííàÿ çàäà÷à ìîæåò áûòü ðåøåíà
íà îñíîâå ìåòîäîâ îáðàòíûõ çàäà÷ äèíàìèêè.
Ââåäåì â ðàññìîòðåíèå íåêîòîðîå îïîðíîå (îáîçíà÷àåìîå âåðõ-
íèì èíäåêñîì "*") äâèæåíèå, óäîâëåòâîðÿþùåå ãðàíè÷íûì óñëîâè-
ÿì è òàêîå, ÷òî ôóíêöèè x*(t), y
*
(t)èz*(t) ÿâëÿþòñÿ äâàæäû äèô-
ôåðåíöèðóåìûìè ïî âðåìåíè. Ñ÷èòàÿ îïîðíîå äâèæåíèå çàäàííûì,
íàéäåì äëÿ íåãî óïðàâëÿþùèå ôóíêöèè P(t), α(t)èγ(t) ïóòåì ïîä-
ñòàíîâêè x*(t), y
*
(t)èz*(t) â èñõîäíóþ ñèñòåìó (6.18) âìåñòî x(t), y(t)
è z(t) è ïîñëåäóþùåãî èñêëþ÷åíèÿ ïðîìåæóòî÷íûõ ïåðåìåííûõ.
 ðåçóëüòàòå ìîãóò áûòü ïîëó÷åíû âûðàæåíèÿ äëÿ âñåõ ïðàâûõ ÷àñ-
òåé äèôôåðåíöèàëüíûõ óðàâíåíèé, à ñëåäîâàòåëüíî, è äëÿ ñòîÿùèõ
â ëåâûõ ÷àñòÿõ ïðîèçâîäíûõ. Èìåÿ ýòî â âèäó, íàéäåì
sin
•
/;s
in
•
/( cos );
•••
.
θθ
==
−
=
+
+
yV
zV
Vxyz
Ψ
222
(6.21)
Äèôôåðåíöèðóÿ äàëåå ïî âðåìåíè âûðàæåíèå äëÿ êâàäðàòà ñêîðîñòè,
ìîæíî ïîëó÷èòü
269
d
dt
Vx
x
y
y
z
z
() (•••••••••).
2
2
=+
+
(6.22)
Èç ïåðâûõ äâóõ ñîîòíîøåíèé (6.21) èìååì
θθ
() arcsin(• / ), ( ) arcsin( •/( cos )).
ty
V
tz
V
==
−
Ψ
(6.23)
Òàêèì îáðàçîì, âûðàæåíèÿ (6.22) è (6.23) îïðåäåëÿþò òðè
ïåðåìåííûõ ñîñòîÿíèÿ ËÀ ÷åðåç èçâåñòíûå ôóíêöèè. Ýòî äàåò
îñíîâàíèå ñ÷èòàòü
•
(),
Vt θ(t)èΨ(t) çàäàííûìè.
Äëÿ îïðåäåëåíèÿ ñîñòàâëÿþùèõ âåêòîðà ïåðåãðóçêè è óãëà êðåíà
γ ïðåäâàðèòåëüíî íåîáõîäèìî óñòàíîâèòü çíà÷åíèÿ ïðîèçâîäíûõ
•
()
θt
è
•
():
Ψt
•
()
•
•
•
•
cos
; •()
(••••••)cos
•
.
θ
θ
t
Vy Vy
V
t
xz zx
x
=
−
=
−
2
2
2
Ψ
Ψ
(6.24)
Ñ÷èòàÿ
•
(),
Vt
•
()
θtè
•
()
Ψ t èçâåñòíûìè, èç ïåðâûõ òðåõ óðàâíåíèé (6.18)
ïîëó÷àåì
n
V
g
n
V
g
g
xy
=+=
+
⎛
⎝⎜
⎞
⎠⎟=
+
sin
•
;
cos
•
cos ;
•
cos
•
θ
γ
θθγ
θ
θ
1
tg
Ψ
V
cos
.
θ
(6.25)
Ïîñëåäíåå ñîîòíîøåíèå (6.25) íåïîñðåäñòâåííî îïðåäåëÿåò îäíó èç
èñêîìûõ óïðàâëÿþùèõ ôóíêöèé. Äâå äðóãèå ôóíêöèè P(t)èα(t)
ìîãóò áûòü íàéäåíû èç ñëåäóþùèõ ñîîòíîøåíèé:
Pt
mgn X
mgn Y
t
mgn Y
mgn X
xa
ya
ya
x
()(
)(
);
()
=+
+−
=
−
+
22
α
arctg
a
.
(6.26)
Ïðèâåäåííûå ñîîòíîøåíèÿ äëÿ óïðàâëÿþùèõ ôóíêöèé â ïðèí-
öèïå îáåñïå÷èâàþò ðåøåíèå ïîñòàâëåííîé êðàåâîé çàäà÷è. Ïðè
ýòîì ñóùåñòâåííî, ÷òî èõ âûðàæåíèÿ ïîëó÷åíû [63] â çàìêíóòîé
ôîðìå â ðåçóëüòàòå âûïîëíåíèÿ êîíå÷íîãî ÷èñëà îïåðàöèé áåç èí-
òåãðèðîâàíèÿ óðàâíåíèé äâèæåíèÿ ËÀ.
270
6.2.3. ÏÐÈÁËÈÆÅÍÍÎÅ ÎÏÐÅÄÅËÅÍÈÅ ÏÀÐÀÌÅÒÐÈ×ÅÑÊÎÃÎ
ÓÏÐÀÂËÅÍÈß ÄÀËÜÍÎÑÒÜÞ ÑÒÐÅËÜÁÛ ÏÐÈ ÐÅØÅÍÈÈ ÎÁÐÀÒÍÛÕ
ÇÀÄÀ× ÂÍÅØÍÅÉ ÁÀËËÈÑÒÈÊÈ ÄËß ÑÒÂÎËÜÍÛÕ ÑÈÑÒÅÌ
Êëàññè÷åñêàÿ òðàêòîâêà îáðàòíîé çàäà÷è âíåøíåé áàëëèñòèêè
çàêëþ÷àåòñÿ â îïðåäåëåíèè õàðàêòåðèñòèê äâèæåíèÿ, ñîîòâåòñòâóþ-
ùèõ íà÷àëó òðàåêòîðèè, ïî èõ çàäàííûì çíà÷åíèÿì â êîíöå òðàåêòî-
ðèè.  ÷àñòíîñòè, äëÿ òðàåêòîðèé ñíàðÿäîâ ïîëåâûõ àðòèëëåðèéñêèõ
ñèñòåì â êà÷åñòâå îñíîâíûõ õàðàêòåðèñòèê îáû÷íî çàäàåòñÿ ïîëíàÿ
äàëüíîñòü õñ è ïîëåçíûé (èëè ïîëíûé) âåñ ñíàðÿäà. Ìîäóëü ñêîðî-
ñòè Vc è óãîë ïàäåíèÿ θc, êàê ïðàâèëî, çàäàþòñÿ íà îñíîâàíèè óñëî-
âèÿ íåîáõîäèìîãî äåéñòâèÿ ñíàðÿäà ïî öåëè [34]. Äëÿ ñíàðÿäîâ ïî-
ñòîÿííîé ìàññû èçâåñòíî íåñêîëüêî ïðèáëèæåííûõ ðåøåíèé îá-
ðàòíîé çàäà÷è. Âñå ðåøåíèÿ ïðåäïîëàãàþò èñïîëüçîâàíèå ìåòîäà
ïîñëåäîâàòåëüíûõ ïðèáëèæåíèé. Ðàññìîòðèì ðåøåíèå, îñíîâàííîå
íà ìåòîäå ïñåâäîñêîðîñòè (ñì. ãë. 5).  óêàçàííîì ìåòîäå ãðàíè÷íûå
õàðàêòåðèñòèêè òðàåêòîðèè ñâÿçàíû ÷åòûðüìÿ îñíîâíûìè óðàâíå-
íèÿìè. Îñòàâëÿÿ â ñòîðîíå îïðåäåëåíèå âðåìåíè ïîëåòà, çàïèøåì
îñòàâøèåñÿ óðàâíåíèÿ â ñëåäóþùåì âèäå:
x
c
DU DV
c
AU AV
DU DV
cc
c
c
=
′
−
=
′
−
−
1
2
1
0
0
0
[( ) ()];
sin
() ()
()(
θ
0
0
2
0
1
0
2
)
();
(c
o
s)[() ()
−
⎡
⎣⎢
⎤
⎦⎥
−
′
−
−
IV
cI
U
I
V
cc
tg=tg0
θθ
θ
].
Íàïîìíèì, ÷òî ñ′ = ñβ; Uc = Vc cosθc cos
−1
θ0, ãäå β – êîýôôèöèåíò
ñîãëàñîâàíèÿ, îïðåäåëÿåìûé ïî èçâåñòíûì òàáëèöàì [22] ïî âõîäàì
xc, θc äëÿ ñëó÷àÿ ñ >1èïîñ, V0 è θ0 äëÿ ñëó÷àÿ ñ ≤ 1.
Ïðîùå âñåãî ðåøåíèå ìîæåò áûòü ïîëó÷åíî, åñëè çàäàíû c, V0, xc
è òðåáóåòñÿ îïðåäåëèòü θ0.  ýòîì ñëó÷àå â ïåðâîì ïðèáëèæåíèè íå-
îáõîäèìî ïðèíÿòü ñ′≈ñ è îïðåäåëèòü D(Uc)=cxc + D(V0). Âõîäÿ â
òàáëèöû ïî D(Uc), ìîæíî îïðåäåëèòü Uc è äàëåå ñ ïîìîùüþ âòîðîé
ïðèâåäåííîé âûøå ôîðìóëû íàéòè θ0. Âî âòîðîì ïðèáëèæåíèè ïî c,
V0 è θ0 íàõîäèòñÿ êîýôôèöèåíò β, è ðåøåíèå ïîâòîðÿåòñÿ.
Åñëè êðîìå ñ è äàëüíîñòè õñ çàäàí óãîë θ0 è òðåáóåòñÿ îïðåäåëèòü
V0, òî òàêæå èìåþòñÿ âñå íåîáõîäèìûå âåëè÷èíû äëÿ ðåøåíèÿ çàäà-
÷è.  ýòîì ñëó÷àå V0 íàõîäèòñÿ ìåòîäîì ïîäáîðà ñ ïîìîùüþ ïåðâîé
è âòîðîé èç ïðèâåäåííûõ ôîðìóë.
Ðåøåíèå ïî îïðåäåëåíèþ θ0 óñëîæíÿåòñÿ, åñëè êðîìå ñ è V0 çàäà-
íû êîíå÷íûå ýëåìåíòû òðàåêòîðèè xc, Vc è θc â âèäå íåðàâåíñòâ òèïà
õñ > xc min; Vc > Vc min; θc > θc min.  ýòîì ñëó÷àå òðåáóåòñÿ îñóùåñòâèòü
271
ðÿä ïîñëåäîâàòåëüíî ïîâòîðÿþùèõñÿ ðàñ÷åòîâ ïî ïåðâîé è âòî-
ðîé ôîðìóëàì è îïðåäåëèòü Uc (ïîäáîðîì). Ïðè ýòîì íåðàâåíñòâà
xc > xc min; θc > θc min äîëæíû ïðîâåðÿòüñÿ ïàðàëëåëüíûìè ðàñ÷åòàìè
ïî ïåðâîé è òðåòüåé ôîðìóëàì. Àíàëîãè÷íûå çàäà÷è ïî îïðåäåëå-
íèþ îäíîé âåëè÷èíû èç ÷åòûðåõ ñ, V0, θ0, xc ïðè òðåõ çàäàííûõ, à
òàêæå çíà÷åíèé Vc è θc ëåãêî ðåøàþòñÿ ïðè èñïîëüçîâàíèè âñïîìî-
ãàòåëüíûõ ôóíêöèé (5.88), (5.89). Ïðèáëèæåíèÿ, ñâÿçàííûå ñ óòî÷-
íåíèåì ñ′, äîëæíû ïîâòîðÿòüñÿ è â ýòîì ñëó÷àå.
Äðóãèì ìåòîäîì ðåøåíèÿ îáðàòíûõ çàäà÷ âíåøíåé áàëëèñòèêè
äëÿ àðòèëëåðèéñêèõ ñèñòåì ÿâëÿåòñÿ ìåòîä, îñíîâûâàþùèéñÿ íà
èñïîëüçîâàíèè áàëëèñòè÷åñêèõ òàáëèö, ñîäåðæàùèõ ïàðàìåòðû
òî÷êè ïàäåíèÿ xc, θc è Vc. Âõîäàìè â òàáëèöû ñëóæàò c, V0, θ0. Îïðå-
äåëåíèå V0 èëè θ0 ïî òðåì èçâåñòíûì çíà÷åíèÿì xc, c è θ0 èëè ñîîò-
âåòñòâåííî V0 (òðåì èçâåñòíûì èç ÷åòûðåõ) âåäåòñÿ ìåòîäîì îáðàò-
íîãî ëèíåéíîãî èíòåðïîëèðîâàíèÿ.
Ñóùåñòâåííî áîëåå ñëîæíûì îêàçûâàåòñÿ ðåøåíèå îáðàòíûõ çà-
äà÷ âíåøíåé áàëëèñòèêè äëÿ àêòèâíî-ðåàêòèâíûõ ñíàðÿäîâ (ÀÐÑ).
Îïðåäåëåíèå íà÷àëüíîãî óãëà òðàåêòîðèè íàèáîëüøåé äàëüíîñòè θ0
è ìåñòà âêëþ÷åíèÿ ðåàêòèâíîãî äâèãàòåëÿ (òî÷êà Í) íà òðàåêòîðèè
íåóïðàâëÿåìîãî ñíàðÿäà, ïðîõîäÿùåé â ïëîòíûõ ñëîÿõ àòìîñôåðû,
ïðåäñòàâëÿåò ñîáîé ìíîãîïàðàìåòðè÷åñêóþ ñëîæíóþ çàäà÷ó. Ïîë-
íàÿ äàëüíîñòü çàâèñèò îò V0, θ0, c0, Ví , θí , yí, àýðîäèíàìè÷åñêîãî êî-
ýôôèöèåíòà ëîáîâîãî ñîïðîòèâëåíèÿ (èëè áàëëèñòè÷åñêîãî êîýô-
ôèöèåíòà ñíê), òÿãè Ð è âðåìåíè ðàáîòû äâèãàòåëÿ íà ó÷àñòêå òðàåê-
òîðèè Í–Ê . Äàëüíîñòü, ñîîòâåòñòâóþùàÿ ó÷àñòêó òðàåêòîðèè îò
òî÷êè Ê äî âñòðå÷è ñ öåëüþ, îïðåäåëÿåòñÿ çíà÷åíèÿìè Vê, θê, yê è ñê.
Òàêèì îáðàçîì, ñóììàðíàÿ äàëüíîñòü áóäåò çàâèñåòü îò îäèííàäöàòè
äèñêðåòíûõ âåëè÷èí è äâóõ ôóíêöèé cx a
(M) è P(y). Î÷åâèäíî, ÷òî
âûáîð ïàðàìåòðîâ, îïðåäåëÿþùèõ â ýòèõ óñëîâèÿõ íàèáîëüøóþ
äàëüíîñòü ñòðåëüáû, ïðåäñòàâëÿåò ñîáîé âåñüìà òðóäîåìêóþ çàäà÷ó,
åäèíñòâåííûé ïóòü ðåøåíèÿ êîòîðîé – ðàñ÷åò ñåìåéñòâà òðàåêòî-
ðèé.
Ïðè îòíîñèòåëüíî íåáîëüøèõ äàëüíîñòÿõ ñòðåëüáû, õàðàêòåðíûõ
äëÿ ñòâîëüíûõ àðòèëëåðèéñêèõ ñèñòåì, ñóììàðíàÿ äàëüíîñòü îïðå-
äåëÿåòñÿ âòîðûì ïàññèâíûì ó÷àñòêîì òðàåêòîðèè. Ýòî ïîçâîëÿåò
óïðîñòèòü ñðàâíèòåëüíûå ðàñ÷åòû ïî îïðåäåëåíèþ íà÷àëüíîãî (îðó-
äèéíîãî) óãëà íàèáîëüøåé äàëüíîñòè.
Ïðè ïðîâåäåíèè ðàñ÷åòîâ ïðèíèìàþò ñëåäóþùåå äîïóùåíèå:
VVV
êíö
=+
P,
(6.27)
ãäå VP ö – ñêîðîñòü, îïðåäåëåííàÿ ïî ôîðìóëå Ê.Ý . Öèîëêîâñêîãî;
Ví – ñêîðîñòü ñíàðÿäà â ìîìåíò âêëþ÷åíèÿ äâèãàòåëÿ.
272
Ìîìåíò âêëþ÷åíèÿ äâèãàòåëÿ íà òðàåêòîðèè âûáåðåì ïî óãëó
íàèáîëüøåé äàëüíîñòè äëÿ âòîðîãî ïàññèâíîãî ó÷àñòêà òðàåêòîðèè.
Äëÿ ñðåäíèõ è áîëüøèõ êàëèáðîâ è äëÿ ñêîðîñòåé Vê, íå ïðåâûøàþ-
ùèõ 600 ì/ñ, áåç áîëüøîé ïîãðåøíîñòè ìîæíî ïðèíÿòü θí = 45°.
Îáîçíà÷èì îòíîñèòåëüíûé âåñ ðàêåòíîãî çàðÿäà ÷åðåç
μQ
Q
Q
=
ð
0
,
(6.28)
ãäå Qp – âåñ ðàêåòíîãî çàðÿäà; Q0 – íà÷àëüíûé âåñ ñíàðÿäà.
Òîãäà ïî ôîðìóëå Ê.Ý . Öèîëêîâñêîãî ñêîðîñòü
Vw
Pe
Q
ö=
−
⎛
⎝⎜⎞
⎠⎟
ln
.
1
1μ
(6.29)
Ñ÷èòàÿ, ÷òî êîýôôèöèåíò ôîðìû ñíàðÿäà íå èçìåíèòñÿ ïðè ñãî-
ðàíèè ðàêåòíîãî çàðÿäà, ìîæíî äëÿ âòîðîãî ïàññèâíîãî ó÷àñòêà ïî-
ëîæèòü
cñ
Q
ê
=
−
0
1
1μ
.
(6.30)
Ïðè ïðèíÿòûõ äîïóùåíèÿõ íà÷àëüíûé óãîë òðàåêòîðèè íàèáîëü-
øåé äàëüíîñòè ìîæíî íàéòè ñðàâíåíèåì ðåçóëüòàòîâ ðàñ÷åòîâ, ïðî-
âîäèìûõ ïî ñëåäóþùåé ìåòîäèêå. Ïðè çàäàííûõ çíà÷åíèÿõ V0, c0, α
äëÿ ðàçëè÷íûõ θ0 ðàññ÷èòûâàþò ïåðâûé ïàññèâíûé ó÷àñòîê òðàåêòî-
ðèè äî äîñòèæåíèÿ òî÷êè ñ óãëîì θí = 45° . Ïðè ðàñ÷åòå âòîðîãî ïàñ-
ñèâíîãî ó÷àñòêà ñ íà÷àëüíûìè óñëîâèÿìè Vê = Ví + VPö; θê = θí =
= 45°; ñê îïðåäåëÿåòñÿ ïîëåòíàÿ äàëüíîñòü õñ. Çàòåì ðàñ÷åòû ïîâòî-
ðÿþòñÿ ïðè âàðüèðîâàíèè âåëè÷èí V0, c0, μQ. Ïîëüçóÿñü îïèñàííîé
ìåòîäèêîé, À.À. Äìèòðèåâñêèé ñîñòàâèë òàáëèöû îñíîâíûõ õàðàê-
òåðèñòèê òðàåêòîðèè, êîòîðûå ñîîòâåòñòâóþò òî÷êå âêëþ÷åíèÿ äâè-
ãàòåëÿ è ïðè êîòîðûõ ñëåäóåò îæèäàòü ïîëó÷åíèÿ äàëüíîñòè ñòðåëü-
áû, áëèçêîé ê íàèáîëüøåé [34]. Â òàáëèöàõ äàíû:
îðóäèéíûé óãîë âîçâûøåíèÿ θ0;
êîîðäèíàòû òî÷êè âêëþ÷åíèÿ äâèãàòåëÿ xí è yí;
çàäåðæêà âðåìåíè âêëþ÷åíèÿ äâèãàòåëÿ èëè âðåìÿ äâèæåíèÿ
ñíàðÿäà íà ïåðâîì ïàññèâíîì ó÷àñòêå òðàåêòîðèè tí;
ñêîðîñòü ñíàðÿäà â ìîìåíò âêëþ÷åíèÿ äâèãàòåëÿ Ví.
Äëÿ êàæäîé èç ýòèõ âåëè÷èí ñîñòàâëåíû ñàìîñòîÿòåëüíûå òàáëè-
öû. Âõîäîì â òàáëèöû ÿâëÿþòñÿ ñëåäóþùèå èõ çíà÷åíèÿ: V0 â ïðåäå-
ëàõ 50...600 ì/ñ; ñ0 â ïðåäåëàõ 0,0...1,5; μQ â ïðåäåëàõ 0,05...0,30.
273
Îïîðíûå òî÷êè äëÿ ñîñòàâëåíèÿ òàáëèö ðàññ÷èòàíû ìåòîäîì
÷èñëåííîãî èíòåãðèðîâàíèÿ. Äàííûå òàáëèö ìîãóò áûòü èñïîëüçî-
âàíû êàê èñõîäíûå äëÿ ñðàâíåíèÿ ðàçëè÷íûõ âàðèàíòîâ òðàåêòîðèé.
Ðàáîòà ïî òàáëèöàì ñâîäèòñÿ ê ëèíåéíîìó èíòåðïîëèðîâàíèþ ïî
òðåì âõîäàì.
Ñëåäóåò èìåòü â âèäó, ÷òî êðèâàÿ xc max = f(θ0) â ïðåäåëàõ óãëîâ,
áëèçêèõ ê ïðèâåäåííûì â òàáëèöàõ, èìååò ïîëîãèé ìàêñèìóì. Ïî-
ýòîìó äîïóñòèìî íåêîòîðîå îòêëîíåíèå îò çíà÷åíèé, äàííûõ â òàá-
ëèöàõ, òàê êàê îíî íå ïðèâîäèò ê çàìåòíîìó óìåíüøåíèþ äàëüíîñòè
ñòðåëüáû. Ïðè ìàëûõ ñ0 è V0 çíà÷åíèÿ xí , yí è âðåìÿ tí îêàçûâàþòñÿ
íåáîëüøèìè (õí è yí – ïîðÿäêà íåñêîëüêèõ äåñÿòêîâ ìåòðîâ è äàæå
ìåíüøå). Ýòè öèôðû ïðèâåäåíû â òàáëèöàõ äëÿ îáùíîñòè ðåøåíèÿ
âî âñåì äèàïàçîíå âõîäíûõ ïàðàìåòðîâ.
6.3 . ÏÐÎÑÒÅÉØÈÅ ÝÊÑÒÐÅÌÀËÜÍÛÅ ÇÀÄÀ×È
ÏÐÎÃÐÀÌÌÈÐÎÂÀÍÈß ÎÏÎÐÍÎÃÎ ÄÂÈÆÅÍÈß
6.3 .1. ÎÏÐÅÄÅËÅÍÈÅ ÎÏÒÈÌÀËÜÍÎÃÎ ÓÃËÀ ÁÐÎÑÀÍÈß
ÄËß ÁÀËËÈÑÒÈ×ÅÑÊÈÕ ÒÐÀÅÊÒÎÐÈÉ
Ïðèìåðîì îïòèìàëüíûõ òðàåêòîðèé ðàññìàòðèâàåìîãî òèïà ÿâ-
ëÿþòñÿ áàëëèñòè÷åñêèå òðàåêòîðèè íàèáîëüøåé äàëüíîñòè èëè íàè-
ìåíüøåé ñêîðîñòè. Çàäà÷à îïðåäåëåíèÿ òàêèõ îïîðíûõ òðàåêòîðèé
ðåøàåòñÿ â àíàëèòè÷åñêîì âèäå òîëüêî ïðèìåíèòåëüíî ê ýëåìåíòàð-
íûì ìîäåëÿì ËÀ ïîñòîÿííîé ìàññû, îïèñûâàþùèì èõ äâèæåíèå
áåç ó÷åòà ñîïðîòèâëåíèÿ âíåøíåé ñðåäû â óñëîâíîì îäíîðîäíîì
ïëîñêîïàðàëëåëüíîì èëè öåíòðàëüíîì ãðàâèòàöèîííîì ïîëå.
Íàèáîëåå ïðîñòî çàäà÷à ðåøàåòñÿ â ïåðâîì ñëó÷àå äëÿ ïàðàáîëè-
÷åñêîé òðàåêòîðèè. Ñîãëàñíî ôîðìóëå (5.22) íàèáîëüøàÿ äàëüíîñòü
xc = xc max áóäåò äîñòèãàòüñÿ ïðè sin 2θ0 = 1. Íàéäåííûé èç ýòèõ óñëî-
âèé óãîë íàçûâàåòñÿ óãëîì íàèáîëüøåé äàëüíîñòè θ0 max(θ0, xmax). Î÷å-
âèäíî, ÷òî äëÿ ðàññìàòðèâàåìîãî ñëó÷àÿ îí ðàâåí 45°.
 ðàìêàõ ýëëèïòè÷åñêîé òåîðèè ïðè g ≠ const äëÿ öåíòðàëüíîãî
óãëà φs è íà÷àëüíîãî ðàäèóñ-âåêòîðà rí èìååì
tg
íí
2
òÇ
2
íí
2
í
0
φ
θ
θ
s
rV
gR rV
=
−
1
2
20
2
sin
cos
.
(6.31)
Âçÿâ ïðîèçâîäíóþ
d
d
s
θ
φ
í
tg
()è ïðèðàâíÿâ åå ê íóëþ, íàéäåì
ìàêñèìóì ôóíêöèè. Ïîñëå íåñëîæíûõ ïðåîáðàçîâàíèé ïîëó÷èì
274
sin
.
θímax
òÇí
2
òÇí
2
0
=
−
−
gRV
gRV
0
2
(6.32)
Ñ óâåëè÷åíèåì ñêîðîñòè óãîë
íàèáîëüøåé äàëüíîñòè, îïðåäå-
ëÿåìûé ïî (6.32), áóäåò óìåíü-
øàòüñÿ (ïî îòíîøåíèþ ê óãëó 45°,
îòâå÷àþùåìó ìàëûì íà÷àëüíûì
ñêîðîñòÿì), äîñòèãàÿ íóëÿ ïðè
ïåðâîé êîñìè÷åñêîé ñêîðîñòè
(ðèñ. 6.1).
Ïðåäñòàâëÿåò èíòåðåñ ðåøå-
íèå ïî îòûñêàíèþ ìèíèìàëüíîé
íà÷àëüíîé ñêîðîñòè ËÀ, íåîáõî-
äèìîé äëÿ ïðåîäîëåíèÿ çàäàííîé
äàëüíîñòè ïîëåòà ïðè èçâåñòíîì
rí. Çàäà÷à â äàííîé ïîñòàíîâêå
ñâîäèòñÿ ê íàõîæäåíèþ óãëà θí opt,
ïðè êîòîðîì äîñòèãàåòñÿ κí min.
Ïðîäèôôåðåíöèðîâàâ óðàâíå-
íèå (5.37) ïî θí è ïðèðàâíÿâ ïîëó÷åííîå âûðàæåíèå ê íóëþ, ïîñëå
ïðåîáðàçîâàíèé èìååì
275
Ðèñ. 6.1 . Çàâèñèìîñòü óãëà íàèáîëüøåé
äàëüíîñòè θí max îò ñêîðîñòè Ví
Ðèñ. 6 .2. Çàâèñèìîñòü îïòèìàëüíîãî
íà÷àëüíîãî óãëà θí opt îò óãëîâîé äàëü-
íîñòè ψ ïðè ðàçëè÷íûõ çíà÷åíèÿõ ðà-
äèóñà rí:
1–rí=1,05RÇ;2–1,02RÇ;3–RÇ
Ðèñ. 6 .3. Ïðèìåðíàÿ çàâèñèìîñòü óãëà
íàèáîëüøåé äàëüíîñòè θ0max îò íà÷àëü-
íîé ñêîðîñòè è êàëèáðà ñíàðÿäà
θ
ψ
ψ
íopt
íÇ
arctg
sin2
=
−
⎛
⎝⎜
⎞
⎠⎟
1
22
rR
/c
o
s
.
Òðàåêòîðèþ, ñîîòâåòñòâóþùóþ
óãëó θí opt, íàçûâàþò òðàåêòîðè-
åé ìèíèìàëüíîé ñêîðîñòè. Çàâè-
ñèìîñòü îïòèìàëüíîãî óãëà θ0
îò óãëîâîé äàëüíîñòè äëÿ íå-
ñêîëüêèõ çíà÷åíèé rí ïðèâåäå-
íà íà ðèñ. 6.2.
Ïðè ó÷åòå ñîïðîòèâëåíèÿ
ñðåäû íàõîæäåíèå ñîîòâåòñò-
âóþùåãî ðåøåíèÿ òðåáóåò
ïðèìåíåíèÿ ÷èñëåííûõ ìåòî-
äîâ ïîèñêà ýêñòðåìóìà ôóíê-
öèè. Íàèáîëåå ïðîñòîé ïóòü –
ïîñëåäîâàòåëüíîå ïðîâåäåíèå
áîëüøîãî ÷èñëà ðàñ÷åòîâ òðà-
åêòîðèé äëÿ ðàçëè÷íûõ çíà÷å-
íèé θ0 è ïîñòðîåíèå ãðàôèêîâ
õñ = f(θ0). Íåîáõîäèìî èìåòü â
âèäó, îäíàêî, ÷òî äàæå äëÿ àð-
òèëëåðèéñêîé ñèñòåìû ïðè
äâèæåíèè ñíàðÿäà â âîçäóõå
óãîë íàèáîëüøåé äàëüíîñòè
áóäåò çàâèñåòü íå òîëüêî îò íà-
÷àëüíîé ñêîðîñòè, íî è îò êà-
ëèáðà, ìàññû è ôîðìû ñíàðÿäà, îáúåäèíÿåìûõ ôîðìóëîé áàëëè-
ñòè÷åñêîãî êîýôôèöèåíòà. Èç ðèñ. 6.3 ñëåäóåò, ÷òî â çàâèñèìîñòè
îò êàëèáðà óãîë íàèáîëüøåé äàëüíîñòè ìîæåò èçìåíÿòüñÿ â øèðî-
êèõ ïðåäåëàõ – îò 30 äî 55° . Åùå áËëüøèå òðóäíîñòè âñòðå÷àþòñÿ
ïðè îïðåäåëåíèè îïòèìàëüíîãî ñî÷åòàíèÿ ïàðàìåòðîâ, îáåñïå÷è-
âàþùèõ ìàêñèìàëüíóþ äàëüíîñòü ñòðåëüáû ïðè ñëîæíûõ òðàåêòî-
ðèÿõ óïðàâëÿåìûõ è íåóïðàâëÿåìûõ ÀÐÑ è ðàêåò. Ïðèìåð èçìåíå-
íèÿ îñíîâíûõ õàðàêòåðèñòèê ñëîæíîé îïîðíîé òðàåêòîðèè ïðåä-
ñòàâëåí íà ðèñ. 6.4. Î÷åâèäíî, ÷òî âûáîð ïàðàìåòðîâ,
îïðåäåëÿþùèõ â ýòèõ óñëîâèÿõ íàèáîëüøóþ äàëüíîñòü ñòðåëüáû,
ðåæèì ðàñõîäà òîïëèâà è ôîðìó òðàåêòîðèè, ïðåäñòàâëÿåò ñîáîé
âåñüìà òðóäîåìêóþ çàäà÷ó.
276
Ðèñ. 6.4. Ïðèìåð èçìåíåíèÿ ïî âðåìåíè îñ-
íîâíûõ õàðàêòåðèñòèê îïîðíîé òðàåêòîðèè:
1 – óãîë òàíãàæà; 2 – óãîë íàêëîíà òðàåê-
òîðèè; 3 – ñêîðîñòíîé íàïîð; 4 – ñêî-
ðîñòü; 5 – óñêîðåíèå, îáóñëîâëåííîå ðàáî-
òîé äâèãàòåëÿ; 6 – äàëüíîñòü; 7 – âûñîòà
(6.33)
277
6.3.2. ÌÀÊÑÈÌÀËÜÍÀß ÄÀËÜÍÎÑÒÜ ÃÎÐÈÇÎÍÒÀËÜÍÎÃÎ
ÏËÀÍÈÐÓÞÙÅÃÎ ÏÎËÅÒÀ ÎÏÅÐÅÍÍÎÃÎ ÓÏÐÀÂËßÅÌÎÃÎ ÑÍÀÐßÄÀ
Ðåøåíèå çàäà÷è óâåëè÷åíèÿ äàëüíîñòè ñòðåëüáû óïðàâëÿåìûìè
ñíàðÿäàìè ñîïðÿæåíî ñ íàõîæäåíèåì óñëîâèé, îáåñïå÷èâàþùèõ
ìàêñèìàëüíóþ ïðîòÿæåííîñòü ãîðèçîíòàëüíîãî èëè íàêëîííîãî
ïëàíèðîâàíèÿ íà ïàññèâíîì ó÷àñòêå òðàåêòîðèè. Ìû îãðàíè÷èìñÿ
àíàëèçîì íàèáîëåå ïðîñòîãî ñëó÷àÿ îïðåäåëåíèÿ äàëüíîñòè ãîðèçîí-
òàëüíîãî ïëàíèðóþùåãî ïîëåòà ñíàðÿäà â ñïîêîéíîé (ïðè áåçâåò-
ðèè) àòìîñôåðå, îñíîâûâàÿñü ãëàâíûì îáðàçîì íà ðåçóëüòàòàõ è âû-
âîäàõ ðàáîòû [118]. Èìåÿ â âèäó ðèñ. 6.5, èñõîäíûå óðàâíåíèÿ äâèæå-
íèÿ öåíòðà ìàññ ñíàðÿäà ïðåäñòàâèì â ôîðìå
m
dV
dt
X
mV
d
dt
Ym
g
dx
dt
V
dy
dt
yt
a
a
=−
=−
==
==
;
;
(cos );
[()
θ
θ1
0c
o
n
s
t
]
.
(6.34)
Óñëîâèå äâèæåíèÿ ñíàðÿäà íà ïîñòîÿííîé âûñîòå (y = const) â
ðàññìàòðèâàåìîì ñëó÷àå ìîæåò áûòü âûïîëíåíî òîëüêî ïðè dθ/dt =0,
÷òîäàåòθ=θ0=constâòå÷å-
íèå âñåãî âðåìåíè ãîðèçîí-
òàëüíîãî ïëàíèðîâàíèÿ (ÃÏ).
Òîãäà èç âòîðîãî óðàâíåíèÿ
ñèñòåìû (ïðè
•
θ=0) èìååì
Ya = mg, è, ñëåäîâàòåëüíî,
c
V
Sm
g
ya
α
α
ρ2
2
=
.
 ñèëó èçìå-
íåíèÿ (óìåíüøåíèÿ) ñêîðîñòè
ïîëåòà íà ïàññèâíîì ó÷àñòêå
òðàåêòîðèè äëÿ âûïîëíåíèÿ
óêàçàííîãî ðàâåíñòâà òðåáóåò-
ñÿ îáåñïå÷èòü óïðàâëåíèå óã-
ëîâûì äâèæåíèåì ñíàðÿäà
α(t) ≈θ(t) çà ñ÷åò ðåãóëèðîâà-
íèÿ ïîëîæåíèÿ âîçäóøíîãî
ðóëÿ δ(t). Ðàññìàòðèâàÿ òîëüêî
Ðèñ. 6 .5 . Îïðåäåëåíèå óñëîâèé ãîðèçîíòàëü-
íîãî ïëàíèðîâàíèÿ ñíàðÿäà íà ïàññèâíîì
ó÷àñòêå òðàåêòîðèè
óñòàíîâèâøèéñÿ ðåæèì ïîëåòà, èç ñîîòíîøåíèÿ
I
d
dt
MM
zz
z
•
θ
=+
=
óïð
0
(6.35)
íàéäåì
cxx cxx
yy
αδ
αδ
áòä
òä
.
ð
p
()()
,
−=
−
−
îòêóäà
αδ
δ
α
á
òä
.
ð
òä
p
=−
−
−
c
c
xx
xx
y
y
,
(6.36)
ãäå õò, õä è õä.ð
–
êîîðäèíàòû öåíòðà ìàññ, öåíòðà äàâëåíèÿ è öåíòðà
äàâëåíèÿ ðóëÿ, îòñ÷èòûâàåìûå îò íîñêà ñíàðÿäà. Ïîäñòàâèâ (6.36) â
âûðàæåíèå c
V
Sm
g
ya
α
α
ρ2
2
=
, íåòðóäíî ïîëó÷èòü ñâÿçü ìåæäó V è óãëîì
ïîâîðîòà ðóëåé òàíãàæà
V
mgc
Scc
xx
xx
y
yy
a
2
2
δ
ρ
α
δα
=−
−
−
ð
òä
òä
.
ð
.
(6.37)
 âûðàæåíèè (6.37) îòíîøåíèå cc
yy
a
αα
/,
ÿâëÿþùååñÿ ôóíêöèåé
àýðîäèíàìè÷åñêîãî êà÷åñòâà K è óãëà àòàêè:
c
cK
y
ya
α
α
α
=+
1
12
á,
(6.38)
âîçðàñòàåò ñî âðåìåíåì â ñèëó óâåëè÷åíèÿ αá. Îäíàêî K
−
<<
1
1
αá
2
,
ïîýòîìó â ïåðâîì ïðèáëèæåíèè çíà÷åíèå ccxx
yy
a
αα
/[( )]
òä
−
ìîæíî
ïðèíÿòü ïîñòîÿííûì. Ïðè îòíîñèòåëüíî ìàëûõ èçìåíåíèÿõ
ñêîðîñòè çíà÷åíèÿ cy p
δ
è õä.ð òàêæå ìîæíî ïðèíÿòü êîíñòàíòàìè,
ïîýòîìó
Vc
2
1
δ= =const.
(6.39)
Èìåÿ â âèäó òðåòüå óðàâíåíèå (6.34), çàïèøåì
xt Vdt
t
()
,
=
∫0
(6.40)
278
à èç ïåðâîãî óðàâíåíèÿ ïîëó÷èì
dt
m
SVc
dV
xa
=−
2
2
ρ
.
(6.41)
Çàìåíèâ cc
xx
aa
()
M
ñð
≈
ñðåäíèì ïîñòîÿííûì çíà÷åíèåì êîýôôè-
öèåíòà íà ðàññìàòðèâàåìîì èíòåðâàëå ãîðèçîíòàëüíîãî ïîëåòà,
íàéäåì îêîí÷àòåëüíî
x
m
Sc
V
V
xa
ã.ï
ñð
=
2
0
ρ
ln.
(6.42)
Î÷åâèäíî, ÷òî îòêëîíåíèå óãëà δ íå ÿâëÿåòñÿ áåñïðåäåëüíûì. Íà
óïðàâëÿþùóþ ôóíêöèþ δ(t) ñëåäóåò íàëîæèòü îãðàíè÷åíèå òèïà
δ(t) ≤δïð. Ïîýòîìó
()
ln
ln
,
x
m
Sc
V
ñ
m
Sc
ñV
xx
aa
ã.ï ïð
ïð
ïð
ñð
ñð
==
22
0
1
20
ρ
δ
ρ
ρδ
(6.43)
ãäå c
Sc
mg
c
c
xx
xx
y
y
y
a
2
2
=
−
−
ð
òä
.
ð
òä
δα
α
.
Ïðîäèôôåðåíöèðîâàâ (6.43) ïî ρ è ïðèðàâíÿâ ïðîèçâîäíóþ ê
íóëþ, ïîëó÷èì ðàâåíñòâî
12
0
20
−=
ln(
),
cV σρ
ïð opt
(6.44)
èç êîòîðîãî íåòðóäíî íàéòè âåëè÷èíó ρopt è îòâå÷àþùóþ åìó
ìàêñèìàëüíóþ äàëüíîñòü ãîðèçîíòàëüíîãî ïîëåòà [118]
()
l
n
.
x
m
Sc
cV
xa
ã.ï max
opt
opt ïð
ñð
=
2
20
ρ
ρδ
(6.45)
6.4 . ÂÀÐÈÀÖÈÎÍÍÛÅ ÇÀÄÀ×È ÐÀÊÅÒÎÄÈÍÀÌÈÊÈ
È ÁÀËËÈÑÒÈÊÈ
6.4.1. ÏÎÑÒÀÍÎÂÊÀ È ÊËÀÑÑÈÔÈÊÀÖÈß ÇÀÄÀ× ÂÀÐÈÀÖÈÎÍÍÎÃÎ
ÈÑ×ÈÑËÅÍÈß È ÎÏÒÈÌÀËÜÍÎÃÎ ÓÏÐÀÂËÅÍÈß
Ïîñòàíîâêà ëþáîé çàäà÷è, îòíîñÿùåéñÿ ê êëàññè÷åñêîìó âàðèà-
öèîííîìó èñ÷èñëåíèþ èëè ê ñîâðåìåííîé òåîðèè îïòèìàëüíîãî
279
óïðàâëåíèÿ, ïðåäïîëàãàåò íåîáõîäèìîñòü çàäàíèÿ òðåõ ýëåìåíòîâ:
ôóíêöèîíàëà (êðèòåðèÿ êà÷åñòâà), îãðàíè÷åíèé íà ôàçîâûå êîîð-
äèíàòû è óïðàâëåíèå, à òàêæå ãðàíè÷íûõ óñëîâèé.
Êðèòåðèè êà÷åñòâà â ðàññìàòðèâàåìûõ çàäà÷àõ ìîãóò èìåòü òðè
âîçìîæíûå ôîðìóëèðîâêè:
èíòåãðàëüíóþ
Jtt f
tttt
d
t
t
t
1
0
[(),()] [;(),
•
(), ()] ;
xu
xxu
=
∫
ê
(6.46)
òåðìèíàëüíóþ
Jtf
tttt
20
0
[()] [;(); , ()];
xx
x
êê
ê
=
(6.47)
ñìåøàííóþ (èíòåãðîòåðìèíàëüíóþ)
Jtt JttJt
312
[(),()] [(),()] [()].
xu
xu
x
=+
ê
(6.48)
Îãðàíè÷åíèÿ, êàê ïðàâèëî, óêëàäûâàþòñÿ â äâà âîçìîæíûõ âàðè-
àíòà èõ çàäàíèÿ:
ôóíêöèîíàëüíûå ñîîòíîøåíèÿ â âèäå ðàâåíñòâ è íåðàâåíñòâ
G
tttt
G
tttt
1
2
0
0
[; (),
•
(), ()] ;
[; (),
•
(), ()] ,
xxu
xxu
=
<
(6.49)
ïðè÷åì ôóíêöèîíàëüíûå ñîîòíîøåíèÿ òèïà (6.49), íî íå çàâèñÿùèå
îò ïðîèçâîäíîé âåêòîðà ôàçîâûõ êîîðäèíàò è âåêòîðà óïðàâëåíèÿ,
íàçûâàþòñÿ ôàçîâûìè îãðàíè÷åíèÿìè;
íåôóíêöèîíàëüíûå ñîîòíîøåíèÿ òèïà
uu
u
u
(),
().
min
max
tU
t
∈≤
≤
(6.50)
Ãðàíè÷íûå óñëîâèÿ çàäàþòñÿ âûäåëåíèåì â ïðîñòðàíñòâå ñîñòîÿ-
íèé íåêîòîðîãî ìíîæåñòâà, êîòîðîìó äîëæíû ïðèíàäëåæàòü êîíöû
òðàåêòîðèé x(t0)èx(tê). Ïðè ýòîì ïðèíÿòî ðàçëè÷àòü:
çàêðåïëåííûå ãðàíè÷íûå óñëîâèÿ, êîãäà ñîîòâåòñòâóþùèå çíà÷å-
íèÿ çàêðåïëåíû íà îáîèõ êîíöàõ îòðåçêà [t0, tê], à ñàì îòðåçîê ïðåä-
ïîëàãàåòñÿ ôèêñèðîâàííûì;
ñâîáîäíûé ïðàâûé èëè ëåâûé êîíåö, êîãäà ñîîòâåòñòâóþùèé êîíåö
îòðåçêà [t0, tê] ñ÷èòàåòñÿ ôèêñèðîâàííûì, íî óñëîâèÿ íà ôàçîâóþ
òðàåêòîðèþ íå íàêëàäûâàþòñÿ:
ïåðèîäè÷åñêèå, êîãäà îòðåçîê [t0, tê] ôèêñèðîâàí è ôàçîâûå êîîð-
äèíàòû ïðèíèìàþò ðàâíûå çíà÷åíèÿ íà êîíöàõ: x(t0)=x(tê).
280
 íàèáîëåå îáùåé ïîñòàíîâêå, îõâàòûâàþùåé áîëüøèíñòâî çà-
äà÷ âàðèàöèîííîãî èñ÷èñëåíèÿ è îïòèìàëüíîãî óïðàâëåíèÿ, èõ ìà-
òåìàòè÷åñêàÿ ôîðìóëèðîâêà ñâîäèòñÿ [52] ê ñëåäóþùåìó:
òðåáóåòñÿ íàéòè íèæíþþ (âåðõíþþ) ãðàíü ôóíêöèè
Jtt
[(), ()] inf(sup)
xu→
(6.51)
ïî âñåì x(t)èu(t), óäîâëåòâîðÿþùèì îãðàíè÷åíèþ
G
tttt
G
tttt
1
2
0
0
[; (),
•
(), ()] ;
[; (),
•
(), ()] ;
xxu
xxu
=
≤
(6.52)
u()
tU
∈
(6.53)
è ãðàíè÷íûì óñëîâèÿì
(,(); ,())
.
ttt t
00
xx
êê
Ã
∈
(6.54)
Ïðè ýòîì, åñëè ôóíêöèîíàë (6.51) ÿâëÿåòñÿ èíòåãðàëüíûì, çàäà-
÷à (6.51)...(6.54) íàçûâàåòñÿ çàäà÷åé Ëàãðàíæà, åñëè ôóíêöèîíàë
òåðìèíàëüíûé, òî – çàäà÷åé Ìàéåðà è, íàêîíåö, åñëè ôóíêöèîíàë
ñìåøàííûé, òî – çàäà÷åé Áîëüöà. Îòëè÷èòåëüíîé îñîáåííîñòüþ çà-
äà÷ êëàññè÷åñêîãî âàðèàöèîííîãî èñ÷èñëåíèÿ ÿâëÿåòñÿ òî, ÷òî â
íèõ âñå ôóíêöèè ïðåäïîëàãàþòñÿ ãëàäêèìè.
 çàäà÷àõ îïòèìàëüíîãî óïðàâëåíèÿ ïîäîáíîå ïðåäïîëîæåíèå â
îòíîøåíèè ôóíêöèè u(t) â áîëüøèíñòâå ñëó÷àåâ ÿâëÿåòñÿ íåïðàâî-
ìåðíûì. Íàëè÷èå â íèõ íåôóíêöèîíàëüíûõ îãðàíè÷åíèé èãðàåò
âåñüìà ñóùåñòâåííóþ ðîëü. Ñàìî ïî ñåáå ìíîæåñòâî U, çàäàþùåå
îãðàíè÷åíèå (6.53), ìîæåò áûòü, íàïðèìåð, äèñêðåòíûì ìíîæåñò-
âîì. Ïî èçëîæåííûì ïðè÷èíàì â îòëè÷èå îò çàäà÷ âàðèàöèîííîãî
èñ÷èñëåíèÿ ñòàíäàðòíûì äîïóùåíèåì â çàäà÷àõ îïòèìàëüíîãî
óïðàâëåíèÿ ÿâëÿåòñÿ äîïóùåíèå î íåïðåðûâíîñòè ïî ñîâîêóïíîñòè
ïåðåìåííûõ è ãëàäêîñòè ïî ïåðåìåííûì t è x.
Îñíîâíûìè ìåòîäàìè ðåøåíèÿ çàäà÷ îïòèìàëüíîãî óïðàâëåíèÿ,
ïîëó÷èâøèìè øèðîêîå ðàñïðîñòðàíåíèå, ñëóæàò ïðèíöèï ìàêñèìó-
ìà Ïîíòðÿãèíà è ìåòîä äèíàìè÷åñêîãî ïðîãðàììèðîâàíèÿ Áåëëìàíà.
Ñóùíîñòü ïðèíöèïà ìàêñèìóìà çàêëþ÷àåòñÿ â òîì, ÷òî îí ïðåä-
ñòàâëÿåò âîçìîæíîñòü ïðè ðåøåíèè âàðèàöèîííûõ çàäà÷ ñ îãðàíè-
÷åíèÿìè òèïà íåðàâåíñòâ âûäåëèòü èç âñåõ òðàåêòîðèé, íà÷èíàþ-
ùèõñÿ â òî÷êå x0(t0) è ïðèõîäÿùèõ â òî÷êó x(tê), èçîëèðîâàííûå òðà-
åêòîðèè, óäîâëåòâîðÿþùèå ñôîðìóëèðîâàííûì â íåì íåîáõîäèìûì
óñëîâèÿì îïòèìàëüíîñòè. Ïðè ðåøåíèè ñ ïîìîùüþ ïðèíöèïà ìàê-
ñèìóìà âàðèàöèîííûõ çàäà÷ ñ ïîäâèæíûìè êîíöàìè â ðÿäå ñëó÷àåâ
281
ïðèõîäèòñÿ ñòàëêèâàòüñÿ ñ íåîáõîäèìîñòüþ èññëåäîâàíèÿ òàê íàçû-
âàåìûõ îñîáûõ ðåøåíèé (íåðåãóëÿðíûé ñëó÷àé), ñîîòâåòñòâóþùèõ
óñëîâèþ îáðàùåíèÿ â íóëü âåêòîðà ãðàäèåíòà grad f(x) â íåêîòîðûõ
òî÷êàõ ãèïåðïîâåðõíîñòè ïðîñòðàíñòâà Õ, îïèñûâàåìîé óðàâíåíèåì
fxx xn
(,,,) .
12
0
K
=
(6.55)
Îñíîâîé äèíàìè÷åñêîãî ïðîãðàììèðîâàíèÿ, ïðåäñòàâëÿþùåãî ñîáîé
â òåîðèè îïòèìàëüíîãî óïðàâëåíèÿ àíàëîã òåîðèè Ãàìèëüòîíà –
ßêîáè, ñëóæèò óðàâíåíèå Áåëëìàíà. Îïðåäåëÿþùèì ïîëîæåíèåì
ïðè âûâîäå óðàâíåíèÿ Áåëëìàíà ÿâëÿåòñÿ òî, ÷òî, êàêîâû áû íè áûëè
ïåðâîíà÷àëüíîå ñîñòîÿíèå ñèñòåìû è îòâå÷àþùåå åìó ðåøåíèå â
íà÷àëüíûé ìîìåíò, ïîñëåäóþùèå ðåøåíèÿ äîëæíû óäîâëåòâîðÿòü
óñëîâèþ îïòèìàëüíîñòè îòíîñèòåëüíî ñîñòîÿíèÿ, ïîëó÷èâøåãîñÿ â
ðåçóëüòàòå ïåðâîãî ðåøåíèÿ. Äàííîå ïîëîæåíèå ïîëó÷èëî íàçâàíèå
ïðèíöèïà îïòèìàëüíîñòè Áåëëìàíà [35]. Ïðèíöèï îïòèìàëüíîñòè
ôàêòè÷åñêè óòâåðæäàåò, ÷òî îòðåçîê íåêîòîðîé îïòèìàëüíîé
òðàåêòîðèè åñòü òàêæå îïòèìàëüíàÿ òðàåêòîðèÿ. Äàííîå óòâåðæäåíèå,
áóäó÷è ýêâèâàëåíòîì òîãî, ÷òî ëþáàÿ ÷àñòü ìèíèìàëè ñàìà ÿâëÿåòñÿ
ìèíèìàëüþ íåêîòîðîé çàäà÷è, êàê äîêàçàíî â òåîðèè Ãàìèëüòîíà –
ßêîáè, äàåò îñíîâàíèå ñ÷èòàòü, ÷òî îñíîâíûå ïîëîæåíèÿ ìåòîäà
äèíàìè÷åñêîãî ïðîãðàììèðîâàíèÿ ñïðàâåäëèâû äëÿ ìíîãèõ çàäà÷ îá
ýêñòðåìóìå êîíå÷íî-èíòåãðàëüíîãî ôóíêöèîíàëà çàäà÷è Áîëüöà.
Îáñóæäàåìûå ñîâðåìåííûå ìåòîäû ðåøåíèÿ çàäà÷ îïòèìàëüíîãî
óïðàâëåíèÿ ÿâëÿþòñÿ àíàëèòè÷åñêèìè êàê â ñìûñëå ïðèíöèïèàëü-
íîãî ïîëó÷åíèÿ çàìêíóòîãî ðåøåíèÿ, òàê è â ñìûñëå ïîëó÷åíèÿ
ôóíêöèîíàëüíûõ çàâèñèìîñòåé, íà îñíîâå êîòîðûõ ÷èñëåííûìè
ìåòîäàìè âîçìîæíî îòûñêàíèå ðåøåíèÿ.
 ñèëó ñóùåñòâåííîé íåëèíåéíîñòè èñõîäíîé ìîäåëè ñîñòîÿíèÿ
ËÀ áåç åå çíà÷èòåëüíûõ óïðîùåíèé ïîëó÷åíèå àíàëèòè÷åñêîãî ðå-
øåíèÿ (â òðàäèöèîííîì ñìûñëå) â ïîäàâëÿþùåì áîëüøèíñòâå ñëó-
÷àåâ îêàçûâàåòñÿ íåâîçìîæíûì. Äàííîå îáñòîÿòåëüñòâî ïðèâîäèò ê
íåîáõîäèìîñòè øèðîêîãî èñïîëüçîâàíèÿ ÷èñëåííûõ ìåòîäîâ îïòè-
ìèçàöèè. Ïîñëåäíèå ïîäðàçäåëÿþòñÿ íà ïðÿìûå è íåïðÿìûå. Ïåðâûå
ïðåäïîëàãàþò ïîñòðîåíèå èòåðàöèîííûõ ïðîöåäóð ïîñëåäîâàòåëü-
íîãî èçìåíåíèÿ (óâåëè÷åíèÿ, óìåíüøåíèÿ) ôóíêöèîíàëà J[x(t),
u(t)], âòîðûå áàçèðóþòñÿ íà èñïîëüçîâàíèè íåîáõîäèìûõ óñëîâèé
ýêñòðåìóìà âûáðàííîãî ôóíêöèîíàëà.  ïîñëåäíåì ñëó÷àå èñõîäíàÿ
çàäà÷à òðàíñôîðìèðóåòñÿ â êðàåâóþ äëÿ ñèñòåìû 2n + k óðàâíåíèé
(ãäå n – ïîðÿäîê ñèñòåìû, k – ÷èñëî äîïîëíèòåëüíûõ óðàâíåíèé,
ñîîòâåòñòâóþùèõ ââîäèìûì îãðàíè÷åíèÿì íà ôàçîâûå êîîðäèíà-
282
òû). Ê ãðóïïå íåïðÿìûõ ìåòîäîâ ðåøåíèÿ îòíîñÿòñÿ è ðàññìîòðåí-
íûå âûøå àíàëèòè÷åñêèå ìåòîäû, èñïîëüçîâàíèå êîòîðûõ, åñòåñò-
âåííûì îáðàçîì, òàêæå ïðèâîäèò ê íåîáõîäèìîñòè ðåøåíèÿ êðàå-
âîé çàäà÷è.
6.4 .2. ÎÏÒÈÌÀËÜÍÎÅ ÏÐÎÃÐÀÌÌÈÐÎÂÀÍÈÅ ÎÏÎÐÍÎÃÎ ÄÂÈÆÅÍÈß
ÍÀ ÎÑÍÎÂÅ ÌÅÒÎÄΠÊËÀÑÑÈ×ÅÑÊÎÃÎ ÂÀÐÈÀÖÈÎÍÍÎÃÎ
ÈÑ×ÈÑËÅÍÈß
Íà÷íåì àíàëèç ñ ðàññìîòðåíèÿ çàäà÷è îïðåäåëåíèÿ çàêîíà ðàñ-
õîäà òîïëèâà ËÀ (èçìåíåíèÿ ìàññû ðàêåòû) ïî âðåìåíè, ïðè ðåàëè-
çàöèè êîòîðîãî ïðîéäåííûé àïïàðàòîì ïóòü ïî íàêëîííîé ïðÿìîé
áóäåò íàèáîëüøèì. Ïîñêîëüêó ôóíêöèÿ óïðàâëåíèÿ, â êà÷åñòâå êî-
òîðîé â ðàìêàõ äàííîé çàäà÷è âûñòóïàåò ïðîãðàììà èçìåíåíèÿ ðàñ-
õîäà òîïëèâà ïî âðåìåíè (ïðè îáùåé ôèêñèðîâàííîé ìàññå mò), íå-
ïîñðåäñòâåííî íå ñâÿçàíà ñ ïðîéäåííûì ËÀ ïóòåì, äëÿ ôîðìóëè-
ðîâêè îïòèìèçèðóåìîãî ôóíêöèîíàëà (èíòåãðàëüíîãî ïîêàçàòåëÿ
êà÷åñòâà) ïðåäâàðèòåëüíî âûïîëíèì ñëåäóþùèå âñïîìîãàòåëüíûå
ïðåîáðàçîâàíèÿ. Âîñïîëüçîâàâøèñü ïåðâûì óðàâíåíèåì ñèñòåìû
(3.75), ïîëîæèì â íåì θ = θ0 = const, òÿãó ïðåäñòàâèì â âèäå ñëåäóþ-
ùåãî óïðîùåííîãî ñîîòíîøåíèÿ: Ð = −
dm
dt
W e, à ñîïðîòèâëåíèå âîç-
äóõà çàäàäèì ôóíêöèîíàëüíîé çàâèñèìîñòüþ Ra(V, ρ). Òîãäà
m
dV
dt
dm
dt
WRV m
g
ea
=−
−
−
(,)
sin .
ρθ
0
(6.56)
Ïóñòü ìàññà ðàêåòû èçìåíÿåòñÿ ïî çàâèñèìîñòè m = m0u, ãäå u –
ôóíêöèÿ, õàðàêòåðèçóþùàÿ èçìåíåíèå ìàññû ðàêåòû (ðàñõîä
òîïëèâà) â ïðîöåññå ðàáîòû äâèãàòåëÿ. Çàìåíèâ â óðàâíåíèè (6.56)
çíà÷åíèå m íà m0u è ðàçäåëèâ âñå ÷ëåíû íà ïîñòîÿííóþ âåëè÷èíó m0,
ïîëó÷èì
u
dV
dt
du
dt
W
RV
m
ug
e
a
=−
−
−
(,)
sin .
ρ
θ
0
0
Âûïîëíèì çàìåíó ïåðåìåííûõ, ââåäÿ çíà÷åíèå ýëåìåíòàðíîãî ïóòè
ðàêåòû ds ïî ïðÿìîé, íàêëîí êîòîðîé ê ãîðèçîíòàëüíîé ïëîñêîñòè
îïðåäåëÿåòñÿ óãëîì θ. Ïîäñòàâëÿÿ
dV
dt
V
dV
ds
du
dt
uV
dV
ds
V
==
′
è
283
â (6.56), çàïèøåì
uV
dV
ds
VuW
dV
ds
RV
m
ug
Ve
a
=−
′
−−
(,)
sin .
ρ
θ
0
0
(6.57)
Ïðåîáðàçóÿ è èíòåãðèðóÿ, ïîëó÷èì âûðàæåíèå äëÿ ôóíêöèîíàëà
Jtt su
V
uu
WV
d
V
ug
mRV
Ve
a
[(), ()] [( )]
()
sin
(,
xu ==
+′
+
−
θ00
1
ρ)
.
V
V0
∫
(6.58)
Öåëü ïîñëåäóþùåãî ðåøåíèÿ – íàéòè òàêóþ ôóíêöèþ u(V), ïðè
êîòîðîé çíà÷åíèÿ èíòåãðàëà, âûðàæàþùåãî çàêîí èçìåíåíèÿ ìàññû
ðàêåòû â ïðîöåññå åå äâèæåíèÿ, è ïóòè ðàêåòû s áóäóò ìàêñèìàëüíû-
ìè. Èññëåäîâàíèå â ðàññìàòðèâàåìîì ïðèìåðå ïðîâîäèòñÿ äëÿ ãðà-
íè÷íûõ óñëîâèé: ïðè t = 0 ñêîðîñòü ðàêåòû V = V0 è u = 1, ò.å . ìàññà
m=m0;ïðèt=têñîîòâåòñòâåííîV=Vêèm=mê.
Ñôîðìóëèðîâàííàÿ çàäà÷à âàðèàöèîííîãî èñ÷èñëåíèÿ ðåøàåòñÿ
ñ ïîìîùüþ äèôôåðåíöèàëüíûõ óðàâíåíèé Ýéëåðà, îïðåäåëÿþùèõ
íåîáõîäèìîå óñëîâèå ýêñòðåìóìà ôóíêöèîíàëà. Åñëè ôóíêöèÿ
y(x)=F [x, y(x), ′y x ] â ïðåäåëàõ îò x1 äî x2 îäíîçíà÷íà, òðèæäû äèô-
ôåðåíöèðóåìà, íåïðåðûâíà ñàìà è íåïðåðûâíû åå ÷àñòíûå ïðîèç-
âîäíûå, òî âàðèàöèÿ ôóíêöèîíàëà îáðàùàåòñÿ â íóëü, åñëè èñêîìàÿ
ôóíêöèÿ îòâå÷àåò óðàâíåíèþ Ýéëåðà
dF
dy
d
dx
F
yx
−
′
⎛
⎝⎜⎞
⎠⎟=
∂
∂
0,
(6.59)
ãäå äëÿ íàøåãî ñëó÷àÿ F – ïîäûíòåãðàëüíîå âûðàæåíèå ôóíê-
öèîíàëà (6.58). Ýòî óñëîâèå ÿâëÿåòñÿ íåîáõîäèìûì. Èíòåãðàëüíûå
êðèâûå óðàâíåíèÿ Ýéëåðà y = y(x, c1, c2) íàçûâàþòñÿ ýêñòðåìàëÿìè.
Òîëüêî íà ýêñòðåìàëÿõ ìîæåò äîñòèãàòüñÿ ýêñòðåìóì ôóíêöèîíàëà.
×òîáû îïðåäåëèòü ôóíêöèþ, ïðè êîòîðîé ìîæåò áûòü ïîëó÷åí
ýêñòðåìóì, ñëåäóåò ïðîèíòåãðèðîâàòü óðàâíåíèå Ýéëåðà. Ïðîèçâîëüíûå
ïîñòîÿííûå íàõîäÿòñÿ èç ãðàíè÷íûõ óñëîâèé y(x1)=y1 è y(x2)=y2.
Òðóäíîñòè ïðàêòè÷åñêîãî ðåøåíèÿ çàêëþ÷àþòñÿ â òîì, ÷òî äèô-
ôåðåíöèàëüíîå óðàâíåíèå Ýéëåðà ÿâëÿåòñÿ óðàâíåíèåì âòîðîãî ïî-
ðÿäêà è åãî ðåøåíèå íå âñåãäà ìîæåò áûòü ïîëó÷åíî â êîíå÷íîì
âèäå. Åñëè ðåøåíèå è èìååò êîíå÷íûé âèä, òî åãî íåîáõîäèìî äî-
ïîëíèòåëüíî ïðîâåðèòü íà äîñòàòî÷íûå óñëîâèÿ.  êàæäîé êîíêðåò-
íîé çàäà÷å äîëæåí áûòü îãîâîðåí èëè êàê-òî äîïîëíèòåëüíî îïðå-
äåëåí êëàññ ôóíêöèé, â ïðåäåëàõ êîòîðîãî èùåòñÿ ýêñòðåìàëü.
284
Îòûñêàíèå ýêñòðåìóìà óñëîæíÿåòñÿ äëÿ ôóíêöèîíàëîâ, ñîäåð-
æàùèõ íåñêîëüêî ôóíêöèé íåçàâèñèìîãî ïåðåìåííîãî. Â ýòîì ñëó-
÷àå ñîñòàâëÿåòñÿ è ðåøàåòñÿ ñèñòåìà äèôôåðåíöèàëüíûõ óðàâíå-
íèé, â êîòîðîé ÷èñëî óðàâíåíèé ñîîòâåòñòâóåò ÷èñëó ôóíêöèé. Èñ-
ïîëüçóÿ ñêàçàííîå, íàéäåì ýêñòðåìóì ôóíêöèîíàëà (6.58). Â íàøåì
ñëó÷àå ïîäûíòåãðàëüíàÿ ôóíêöèÿ èìååò âèä
F
uu
WV
ug
mRV
Ve
a
=
+′
+
⎡
⎣⎢
⎤
⎦⎥
−
()
sin
(,)
.
θρ
00
1
(6.60)
Äëÿ ïîäñòàíîâêè â óðàâíåíèå Ýéëåðà íàéäåì
∂
∂
∂
∂
∂
∂
F
u
F
u
d
dV
F
u
VV
,,
′′
⎛
⎝⎜⎞
⎠⎟
è
èìåÿ â âèäó, ÷òî ïåðåìåííûìè âåëè÷èíàìè ÿâëÿþòñÿ V, Ra(V, ρ)è
ôóíêöèÿ u, çàâèñÿùàÿ îò V. Òîãäà
∂
∂θρ
θ
θ
F
u
V
ug
mRV
uu
WV
g
ug
a
Ve
=
+
−
+′
−
sin
(,)
()
s
i
n
[s
i
n
00
1
0
0+
′
=
+
−
−
mRV
F
u
WV
ug
mRV
d
dV
F
a
V
e
a
0
12
0
1
(, )]
;
sin
(,)
;
ρ
∂
∂θρ
∂
0
∂θρ
∂ρ
∂
0
′
⎛
⎝⎜⎞
⎠⎟=
+
−
−
−
u
W
ug
mRV
WVm
RV
V
e
a
e
a
sin
(,)
(
(,)
0
1
0
1
V
ug
ug
mRV
V
a
−
′
+
−
sin )
[s
i
n
(,)
]
.
θ
θρ
0
0
12
Ïîäñòàâëÿÿ ïðàâûå ÷àñòè íàïèñàííûõ óðàâíåíèé â (6.59) è óìíî-
æàÿ ïîñëå ïîäñòàíîâêè âñå íà [ug sinθ0 + mRV
a
0
12
−
(, )],
ρ ïîëó÷èì
uu
V
mWg
VWRV V
W
RV
V
e
ea
e
a
==
−
+
⎡
⎣⎢
⎤
⎦
()
sin
()
(
,
) (,)
1
00
θ
ρ
∂ρ
∂
⎥. (6.61)
Ðàñêðîåì çíà÷åíèå ïîñëåäíåãî ñëàãàåìîãî â ïðàâîé ÷àñòè
ôîðìóëû (6.61):
VW
RV
V
VWS
V
c
V
a
V
e
ae
xa
∂ρ
∂
∂
∂
ρ
(,)
.
=
⎛
⎝⎜⎞
⎠⎟
⎡
⎣⎢
⎤
⎦⎥
2
2
Èìåÿ â âèäó, ÷òî ρ åñòü ôóíêöèÿ òîëüêî âûñîòû, è ïðîâîäÿ
äèôôåðåíöèðîâàíèå, ïîëó÷èì
285
VW
RV
V
V
WSy c
V
a
V
c
V
a
e
a
ex
x
a
a
∂ρ
∂
ρ
∂
(,)
()
=
⎛
⎝⎜⎞
⎠⎟+
⎛
⎝⎜⎞
⎠⎟
2
2
2
∂V
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
.
Ïîäñòàâëÿÿ ïîñëåäíåå ðàâåíñòâî â (6.61), ïðèäåì ê óðàâíåíèþ
ýêñòðåìàëè, îïðåäåëÿþùåé ôóíêöèþ u(V ) , ïðè êîòîðîé èìååò ìå-
ñòî ìàêñèìóì ïóòè:
()
uV
yVS
mWg
c
V
a
VWV
W
c
V
a
e
xe
e
x
a
a
() ()
sin
=
⎛
⎝⎜⎞
⎠⎟ ++
⎛
⎝
ρ
θ
∂
2
00
2
⎜⎞
⎠⎟
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
∂V
.
(6.62)
Äàííàÿ çàâèñèìîñòü íå ìîæåò áûòü íåïîñðåäñòâåííî èñïîëüçîâàíà
äëÿ ðåøåíèÿ íàøåé çàäà÷è, òàê êàê ìû ïîëó÷èëè ôóíêöèþ â
çàâèñèìîñòè îò ñêîðîñòè äâèæåíèÿ ðàêåòû V, à áîëüøèíñòâî ñèñòåì
óðàâíåíèé îïèñûâàåò äâèæåíèå ðàêåòû ïðè íåçàâèñèìîé
ïåðåìåííîé t.
Ïðåäñòàâèì
du
dt
du
dV
dV
dt
u
dV
dt
V
==
′
.
Ïðîâåäÿ ñîîòâåòñòâóþùóþ
çàìåíó â (6.56), ïîëó÷èì
()[
s
i
n(
,
)
]
,
uu
W
dV
dt
ug
mRV
Ve
a
+′
=−
+
−
θρ
00
1
îòêóäà
t
uu
Wd
V
ug
mRV
Ve
a
V
V
=
+′
+
−
∫()
sin
(,)
.
θρ
00
1
0
(6.63)
Äëÿ òîãî ÷òîáû âçÿòü èíòåãðàë, íåîáõîäèìî ïîäñòàâèòü â íåãî
ïðàâóþ ÷àñòü (6.61) è ïðîèçâîäíóþ ′uV , êîòîðóþ ïðåäâàðèòåëüíî ïî-
ëó÷èì òàêæå èç (6.61):
′==
×
×++
u
d
dV
u
mWg
RVV
RV
V
VW
R
V
e
a
a
e
()
sin
(,)
(,)
1
00
2
θ
ρ
∂ρ
∂
∂aV
äV
(,)
.
ρ
2
⎡
⎣⎢
⎤
⎦⎥
(6.64)
286
Ïðèíèìàÿ, êàê è ðàíüøå, g = const, ïîëó÷èì èç (6.63) ðàáî÷óþ
ôîðìóëó äëÿ t:
t
VV
g
W
g
VWc
V
a
VV
e
ex
a
=
−
+×
×
+
⎛
⎝⎜⎞
⎠⎟ ++
0
00
2
2
1
2
4
sin
sin
()(
θθ
W
c
V
a
V
VV Wc
V
a
e
x
ex
V
V
a
a
)
()
∂
∂
⎛
⎝⎜⎞
⎠⎟
+
⎧
⎨
⎪⎪
⎩
⎪
⎪
+
⎛
⎝⎜⎞
⎠⎟+
∫
2
0
K→
→
+
⎛
⎝⎜⎞
⎠⎟
⎡
⎣⎢
⎤
⎦⎥
⎛
⎝⎜
⎞
⎠⎟ ⎫⎬
⎭
+
K
W
V
c
V
a
Vd
V
WVc
ex
ex
a
2
22
2
2
∂∂
∂a
V
a
V
⎛
⎝⎜⎞
⎠⎟
⎡
⎣⎢
⎤
⎦⎥
∂
.
Ïðè çàäàíèè êîíêðåòíîé ôóíêöèè Ra(V, ρ), îïðåäåëÿþùåé ñèëó
ñîïðîòèâëåíèÿ âîçäóõà, èíòåãðàë â (6.65) ìîæåò áûòü âçÿò ÷èñëåííî,
ïîñëå ÷åãî îïðåäåëÿåòñÿ çàâèñèìîñòü t(V ) . Çàâèñèìîñòü u(V ) íàõî-
äèòñÿ èç ôîðìóëû (6.61) ïîñëå ïîäñòàíîâêè â íåå ïðîèçâîäíîé
∂Ra(V, ρ)/∂V îò êîíêðåòíîé ôóíêöèè Ra(V, ρ). Èìåÿ çíà÷åíèÿ u(V )
è t(V ) , ìîæíî óñòàíîâèòü èñêîìóþ çàâèñèìîñòü u(t), êîòîðàÿ îïðå-
äåëÿåò èçìåíåíèå ìàññû ðàêåòû âî âðåìåíè è ïðè êîòîðîé ïóòü ðà-
êåòû s áóäåò íàèáîëüøèì.
Åñëè ïîëîæèòü ρ = const è ââåñòè äëÿ Ra(V, ρ) àíàëèòè÷åñêóþ
ôóíêöèþ, ïðè êîòîðîé ìîæåò áûòü âçÿò èíòåãðàë â âûðàæåíèè
(6.63), òî çàâèñèìîñòü t(V ) ïîëó÷èò êîíå÷íûé âèä. Íàïðèìåð, â [58]
ïðè îïðåäåëåíèè ñèëû ñîïðîòèâëåíèÿ âîçäóõà ïðèíÿòû ïîñòîÿííû-
ìè ïëîòíîñòü âîçäóõà ρ è êîýôôèöèåíò ëîáîâîãî ñîïðîòèâëåíèÿ cx a
.
Òîãäà
RV SVc BV
RV
V
BV
RV
V
B
ax
aa
a
()
;
();
().
==
=
=
1
2
22
22
2
2
ρ
∂
∂
∂
∂
Ïðîâåäÿ çàìåíó ôóíêöèé ïîä èíòåãðàëîì â (6.63), áóäåì èìåòü
t
g
VVW
VWd
V
VVW
e
e
e
V
V
=−
+
+
+
⎡
⎣
⎢
⎤
⎦
⎥
∫
12
2
0
0
0
sin
()
()
.
θ
(6.66)
287
(6.65)
Èíòåãðèðîâàíèå äàåò èçâåñòíóþ ôîðìóëó, ñâÿçûâàþùóþ âðåìÿ
ñî ñêîðîñòüþ äâèæåíèÿ ðàêåòû:
t
g
VVW
VVW
VVW
e
e
e
=−
+
+
+
⎡
⎣⎢
⎤
⎦⎥
12
2
0
0
00
sin
ln
()
()
.
θ
(6.67)
×àñòî ïðåäïîëàãàþò, ÷òî ãðàíè÷íûå òî÷êè íàõîäÿòñÿ íà îïðåäå-
ëåííûõ ëèíèÿõ èëè ïîâåðõíîñòÿõ.  ýòèõ ñëó÷àÿõ íàõîæäåíèå ïðî-
èçâîëüíûõ ïîñòîÿííûõ ïðè ðåøåíèè óðàâíåíèé Ýéëåðà òðåáóåò äî-
ïîëíèòåëüíûõ óñëîâèé, êîòîðûå íàçûâàþòñÿ óñëîâèÿìè òðàíñâåð-
ñàëüíîñòè.
Ýêñòðåìóì ôóíêöèîíàëà ìîæåò äîñòèãàòüñÿ íà ýêñòðåìàëÿõ ñ óã-
ëîâûìè òî÷êàìè. Ìåæäó óãëîâûìè òî÷êàìè îòäåëüíûå ãëàäêèå îò-
ðåçêè äîëæíû áûòü èíòåãðàëüíûìè êðèâûìè óðàâíåíèÿìè Ýéëåðà.
Êîîðäèíàòû óãëîâûõ òî÷åê äîëæíû óäîâëåòâîðÿòü äîïîëíèòåëüíûì
óñëîâèÿì Âåéåðøòðàññà – Ýðäìàíà.
Ïðè óïðîùåíèè ìîäåëè ËÀ âîçìîæíîñòè àíàëèòè÷åñêèõ ðåøå-
íèé, åñòåñòâåííî, ðàñøèðÿþòñÿ. Ðàññìîòðèì â êà÷åñòâå ïðèìåðà çà-
äà÷ó ïî îïðåäåëåíèþ îïòèìàëüíîãî óãëà íàêëîíà âåêòîðà òÿãè ê ãî-
ðèçîíòó θ. Îíà ôîðìóëèðóåòñÿ ñëåäóþùèì îáðàçîì: íàéòè ôóíê-
öèþ èçìåíåíèÿ óãëà θ(t), ïðè êîòîðîé âðåìÿ ïîëåòà ðàêåòû áóäåò
íàèìåíüøèì. Ïðèâåäåì ðåøåíèå ýòîé âàðèàöèîííîé çàäà÷è â ôîð-
ìå Ìàéåðà [123] äëÿ îáùåãî ñëó÷àÿ, êîãäà çàäàíû îáå êîîðäèíàòû
íà÷àëà è êîíöà ó÷àñòêà x0, y0 è xê, yê, ò.å . äëÿ çàäà÷è ñ çàêðåïëåííû-
ìè êîíöàìè.
Äëÿ ðåøåíèÿ èñïîëüçóåì óïðîùåííóþ (α = 0) ìîäåëü ïðîäîëüíî-
ãî äâèæåíèÿ öåíòðà ìàññ ðàêåòû â âèäå ñèñòåìû äèôôåðåíöèàëüíûõ
óðàâíåíèé
•
cos ;
•
sin
;•
;•
,
V
P
m
V
P
m
gxVyV
xy
x
y
==
−
=
=
θθ
(6.68)
ïîëó÷åííîé â ïðåäïîëîæåíèè, ÷òî Ra(V, ρ) = 0. Êðîìå òîãî, áóäåì
ñ÷èòàòü, ÷òî Ð = const è g = g0 = const. Óðàâíåíèÿ îãðàíè÷åíèé,
ñîîòâåòñòâóþùèå ýòîé ñèñòåìå, ïðåäñòàâèì â âèäå
GVV
GVV
g
GxV G
xy
x
12
34
00
0
=−
=
=−
+=
=−=
=
••
cos
;
••
sin
;
•
;
òò
θθ
•
,
yVy
−=
0
(6.69)
ãäå
•
Vò
= P/m.
 ñîîòâåòñòâèè ñ ôîðìóëèðîâêîé óñëîâèÿ íàïèøåì îñíîâíîé
ôóíêöèîíàë îáùåé çàäà÷è
288
JttTu
d
t
t
[(), ()] [()] .
xu ==
∫
θ
0
ê
(6.70)
Ïîëüçóÿñü èçâåñòíûìè ïðàâèëàìè ðåøåíèÿ, ïðåäñòàâèì âûðàæå-
íèå äëÿ ïîäûíòåãðàëüíîé ôóíêöèè âñïîìîãàòåëüíîãî ôóíêöèîíàëà
Fdt
t
*
:
0
ê
∫
FG
G
G
G
*
.
=+
+++
111223344
λλλλ
(6.71)
Íåèçâåñòíûìè áóäóò ôóíêöèè x, y, Vx, Vy, θ, λi. ×òîáû íàéòè
ýêñòðåìóì âñïîìîãàòåëüíîãî ôóíêöèîíàëà, ñîñòàâèì óðàâíåíèÿ
Ýéëåðà,
ïðåäâàðèòåëüíî
ïîëó÷èâ
÷àñòíûå
ïðîèçâîäíûå,
íåîáõîäèìûå äëÿ ñîñòàâëåíèÿ óðàâíåíèé:
∂
∂
∂
∂
∂
∂
λ∂
∂
λ
∂
∂
λ∂
F
x
F
y
F
V
F
V
F
V
xy
x
***
*
*
;;;;
•
;
===
−
=
−
=
00 34
1
F
V
F
V
F
y
*
**
•
;
•
(s
i
n
c
o
s)
;•
.
∂
λ
∂
∂θ
λθλθ
∂
∂θ
=
=−
=
2
12
0
ò
(6.72)
 ñîîòâåòñòâèè ñ (6.59) óðàâíåíèÿ Ýéëåðà áóäóò èìåòü âèä:
•
λ30
=
äëÿ íåèçâåñòíîé x(t); •λ 4 0
=
äëÿ íåèçâåñòíîé y(t); ñîîòâåòñòâåííî
•
,
λλ
13
=−
•
λλ
24
=−
äëÿ íåèçâåñòíûõ Vx(t), Vy(t)èλ1 sinθ−λ2 cosθ =0
äëÿ íåèçâåñòíîé θ(t). Ðåøåíèå ýòèõ óðàâíåíèé ïðèâîäèò ê çàâèñè-
ìîñòÿì
λλλ
λ
θ
113 2243 34 4
24
13
=
+
=
+
=−
=−
=
+
+
cc
tcc
t
c
c
cc
t
cc
t
;;
;
;
tg
.
(6.73)
Îáîçíà÷èâ ccc
11
4
*
/,
=
ñcc
22
4
*
/,
=
ccc
33
4
*
/,
=
ïîëó÷èì
tg θ=
+
+
ct
cc
t
2
13
*
**
.
(6.74)
Ðàññìîòðèì äâà ÷àñòíûõ ñëó÷àÿ èçìåíåíèÿ ãðàíè÷íûõ óñëîâèé. Åñëè
ïðè ñôîðìóëèðîâàííîé âûøå îáùåé çàäà÷å ïðàâûé êîíåö
289
ýêñòðåìàëè íå îãðàíè÷åí â íàïðàâëåíèè âåëè÷èíû õ, òî ÷àñòíàÿ
çàäà÷à ôîðìóëèðóåòñÿ òàê: íàéòè ôóíêöèþ èçìåíåíèÿ óãëà íàêëîíà
âåêòîðà òÿãè ê ãîðèçîíòó ïðè çàäàííîé âåëè÷èíå êîíå÷íîé îðäèíàòû
yê.  ðàññìàòðèâàåìîì ñëó÷àå íà÷àëî ýêñòðåìàëè ñîîòâåòñòâóåò
çàäàííûì çíà÷åíèÿì x0 è y0, êîíåö ýêñòðåìàëè îãðàíè÷åí îðäèíàòîé
yê, ïðè ýòîì, î÷åâèäíî, V y ê
= 0, îãðàíè÷åíèå •
–
x Vx = 0 îòñóòñòâóåò, è
òîãäà âåëè÷èíà λ3 = −c3 = 0. Èñêîìàÿ ôóíêöèÿ θ(t), ïîëó÷åííàÿ èç
(6.73), áóäåì èìåòü âèä
tgθ= +
cc
t
24
**
**
(),
(6.75)
ãäå
cc
c
cc
c
22
1
44
1
**
**
,.
==
Âî âòîðîì ÷àñòíîì ñëó÷àå îáå êîîðäèíàòû òî÷êè k íå çàôèêñèðî-
âàíû; òîãäà îãðàíè÷åíèÿ •
;
xV
x
−=
0 •yVy
−=
0 â (6.69) îêàçûâàþòñÿ
ëèøíèìè è âåëè÷èíû λ3 = λ4 = −c3 = −c4 = 0. Èñêîìàÿ ôóíêöèÿ θ(t),
ïîëó÷åííàÿ èç (6.73), áóäåò èìåòü âèä
tg
tg
const
θ
λ
λ
θ
=== =
•
•
.
2
1
2
1
0
c
c
(6.76)
Ïðèâåäåì åùå îäèí ïðèìåð ðåøåíèÿ çàäà÷è, óñëîâèå êîòîðîé
ôîðìóëèðóåòñÿ ñëåäóþùèì îáðàçîì: íàéòè ôóíêöèþ èçìåíåíèÿ
óãëà θ(t), ïðè êîòîðîé ñêîðîñòü ïîëåòà â êîíöå àêòèâíîãî ó÷àñòêà
òðàåêòîðèè áóäåò íàèáîëüøåé. Î÷åâèäíî, îñíîâíûì êðèòåðèåì îï-
òèìèçàöèè áóäåò ñêîðîñòü â êîíöå àêòèâíîãî ó÷àñòêà òðàåêòîðèè Vê.
 öåëÿõ óïðîùåíèÿ çàäà÷è îáû÷íî âûáèðàþò â êà÷åñòâå îñíîâíîãî
ôóíêöèîíàëà êâàäðàò êîíå÷íîé ñêîðîñòè VVV
õy
ê
êê
222
=+ èëè
Jtt
VV VVd
tFd
t
xx
yy
tt
[(), ()] ( ••
).
*
xu =−
+
=
∫∫
2
00
êê
(6.77)
Ó÷èòûâàÿ îãðàíè÷åíèÿ (6.69), íàïèøåì ïîäûíòåãðàëüíóþ ôóíêöèþ
âñïîìîãàòåëüíîãî ôóíêöèîíàëà:
FV
V
V
Vt
V
P
m
tV
P
m
xx
yy
x
y
*
(••
)(
)
(
•
cos )
()(•
=−
+
+
−
+
+−
2
1
2
λθ
λ
sin
).
θ+g
(6.78)
290
Ïðîèçâîäíûå, íåîáõîäèìûå äëÿ ñîñòàâëåíèÿ óðàâíåíèé Ýéëåðà,
èìåþò âèä
∂
∂
∂
∂
∂
∂
λ
F
V
V
F
V
V
d
dt
F
V
V
x
x
y
y
x
x
**
*
•
;
•
;
•
•
=−
=−
⎛
⎝⎜⎞
⎠⎟ =−
+
22
2
1
12
22
;
•
;•
;
•
**
*
∂
∂
λ∂
∂
λ
∂
∂
F
V
V
F
V
V
d
dt
F
V
x
x
y
y
y
=−
+
=−
+
⎛
⎝⎜⎞
⎠⎟=
=−
+
=
−
)
=
20
21
2
•
;(
s
i
n
c
o
s
;
•
.
**
V
FP
m
F
y
λ∂
∂θ
λθλθ
∂
∂θ
(6.79)
Óðàâíåíèÿ Ýéëåðà ïðèìóò âèä
•
;
•
;s
i
nc
o
s.
λλ λθ
λθ
121 2
00
0
==
+=
(6.80)
Ðåøàÿ ýòè óðàâíåíèÿ, ïîëó÷èì
λλθ
λ
λ
θ
112 2
2
1
2
1
0
===
=
=
=
cc
c
c
;;
.
tg
tg
const
(6.81)
Ñðàâíèâàÿ ñ (6.76), çàêëþ÷àåì, ÷òî ïîëó÷èëè òîò æå ðåçóëüòàò, ÷òî è
ïðè îïòèìèçàöèè âðåìåíè ïîëåòà è ñâîáîäíîì ïðàâîì êîíöå
291
Ðèñ. 6 .6 . Îïòèìàëüíàÿ òðàåêòîðèÿ ËÀ ïðè ïîñòîÿííîì íàïðàâëåíèè âåêòîðà òÿãè
ýêñòðåìàëüíîé òðàåêòîðèè. Ôîðìà òðàåêòîðèè áóäåò èìåòü âèä,
ïðåäñòàâëåííûé íà ðèñ. 6.6 .
6.4.3. ÎÏÐÅÄÅËÅÍÈÅ ÎÏÒÈÌÀËÜÍÎÃÎ ÓÏÐÀÂËÅÍÈß ÄÂÈÆÅÍÈÅÌ ËÀ
ÍÀ ÎÑÍÎÂÅ ÏÐÈÍÖÈÏÀ ÌÀÊÑÈÌÓÌÀ
Ïðåäâàðèòåëüíî îáñóäèì ñëåäóþùóþ ïðîñòóþ çàäà÷ó. Òðåáóåòñÿ
óñòàíîâèòü äîïóñòèìîå óïðàâëåíèå u(t), t0 ≤ t ≤ tê (îïðåäåëÿþùåå ñå-
êóíäíûé ìàññîâûé ðàñõîä òîïëèâà ðàêåòû, ñîâåðøàþùåé ãîðèçîí-
òàëüíûé ïîëåò u(t)=−dm/dt), òàêîå, ÷òî ïðè íåôèêñèðîâàííîì tê –
– t0 ôóíêöèîíàë J[x(t), u(t)]= −
∫Vdt
x
t
t
0
ê
äîñòèãàë áû ýêñòðåìàëüíîãî
çíà÷åíèÿ.
Ââåäåì ñëåäóþùèå äîïóùåíèÿ: óñêîðåíèå ñâîáîäíîãî ïàäåíèÿ
ïîñòîÿííî; θ = θ = θ0 = 0; ñèëà òÿæåñòè óðàâíîâåøèâàåòñÿ ïîäúåì-
íîé ñèëîé, ñîçäàâàåìîé ïîâîðîòíûì êðûëîì; ïîëåò îñóùåñòâëÿåòñÿ
íà ïîñòîÿííîé âûñîòå (ρ = const).
Ñèëó àýðîäèíàìè÷åñêîãî ñîïðîòèâëåíèÿ ïðåäñòàâèì â âèäå
RVcAc
V
ScS
V
c
V
S
ax
y
x
xx
y
x
aa
a
a
()(
)
=+
=
+
+
0
2
2
0
2
2
24
2
2
1
2
4
ρ
ρ
ρ
21
2
2
2
2
A
SV
BVC
c
V
x
x
y
x
a
ρ
=+,
(6.82)
ãäå À – êîýôôèöèåíò, îáû÷íî íàçûâàåìûé [10] êîýôôèöèåíòîì
"îòâàëà" ïîëÿðû, îïðåäåëÿåìûé ïðè ñâåðõçâóêîâûõ ñêîðîñòÿõ ïîëåòà
êàê
A≈−
−
()
,
41
21
M
àòÿãó–ââèäå
P
dm
dt
Wu
W
ee
=−
=
.
Òîãäà óðàâíåíèÿ ñîñòîÿíèÿ áóäóò èìåòü ñëåäóþùèé âèä:
m
dV
dt
uW
X
dm
dt
u
x
ea
=−
=
−
;,
(6.83)
ãäå ìíîæåñòâî U çíà÷åíèé óïðàâëåíèÿ u(t) çàäàåòñÿ íåðàâåíñòâàìè
292
0≤≤
uu
max
,
(6.84)
ïðè÷åì umax – ôèêñèðîâàííàÿ ïîñòîÿííàÿ âåëè÷èíà.
Àëãîðèòì îòûñêàíèÿ îïòèìàëüíîãî óïðàâëåíèÿ ïðè èñïîëüçîâà-
íèè ïðèíöèïà ìàêñèìóìà [84] ñëåäóþùèé: êðîìå îñíîâíîé ìîäåëè
ñîñòîÿíèÿ, ðàñøèðåííîé çà ñ÷åò ïðåîáðàçîâàíèÿ èíòåãðàëüíîãî
ôóíêöèîíàëà
d
dt
tttt
xf
xu
pp
() [; (), ()],
=
(6.85)
â ðàññìîòðåíèå ââîäèòñÿ äîïîëíèòåëüíàÿ ñèñòåìà äèôôåðåí-
öèàëüíûõ óðàâíåíèé
d
dt
f
x
i
i
i
i
i
n
ψ
∂
∂
ψ
=−
=
∑ (,)
xu
p
p
0
(6.86)
îòíîñèòåëüíî âñïîìîãàòåëüíûõ (ñîïðÿæåííûõ) ïåðåìåííûõ. Ñîñòàâ-
ëÿåòñÿ ôóíêöèÿ H (ψ, xp, u)= ψ ii
i
n
f (,)
,
xu
p
=
∑0
íàçûâàåìàÿ ôóíêöèåé
Ïîíòðÿãèíà. Åå âåðõíèé ïðåäåë ðàâåí ãàìèëüòîíèàíó (ôóíêöèè
Ãàìèëüòîíà)
Í() (
ψψ
,,
s
u
p ,,)
,
p
u
p
xu
xu
=
∈U
H
ïðè÷åì âåêòîð-ôóíêöèþ ψ =[ψ1, ψ2,..., ψn]
ò
âñåãäà íîðìèðóþò,
ïîëàãàÿ, íàïðèìåð, ψ0 = −=
10
0
(• ).
ψ
Ïðåäïîëàãàåòñÿ, ÷òî ôóíêöèÿ Í
ÿâëÿåòñÿ âûïóêëîé ôóíêöèåé ïî u(t), è, ñëåäîâàòåëüíî, îïòèìàëüíîå
óïðàâëåíèå ñóùåñòâóåò è ïðîèçâîäíûå
∂ψ
∂
Í((), (),())
()
ttt
t
xu
u
uu
p
=
=0
(6.87)
ìîãóò áûòü âûðàæåíû àíàëèòè÷åñêè.  ðåçóëüòàòå ðåøåíèå èñõîäíîé
îïòèìàëüíîé çàäà÷è ñâîäèòñÿ ê ðåøåíèþ êðàåâîé çàäà÷è äëÿ
ãàìèëüòîíîâîé ñèñòåìû
d
dt
t
d
dt
t
x
x
p
ò
p
ò
()
;()
.
=
⎡
⎣⎢
⎤
⎦⎥
=−
⎡
⎣
⎢
⎤
⎦
⎥
∂
∂ψ
ψ
∂
∂
(6.88)
293
 ðàññìàòðèâàåìîé èñõîäíîé ñèñòåìå (6.83) óïðàâëåíèå u(t) âõîäèò
ëèíåéíî â óðàâíåíèÿ ñîñòîÿíèÿ, ïîýòîìó íà îñíîâàíèè (6.83) è
âûðàæåíèÿ äëÿ ôóíêöèîíàëà J[x(t), u(t)] = −
∫Vdx
x
t
tê
0
çàïèøåì
Í(, ,)
(
),
ψψ
ψψψ
xu
p
=−
−
+
−
−−
01
1
1
1
2
VX
VW
mu
xa
x
e
(6.89)
à ñîïðÿæåííóþ ñèñòåìó – êàê
•
;
•
/;
•
/
ψ
ψψψ
∂∂
ψψ
∂∂
0
101
222
0
=
=+
=
−
+
⎛
⎝⎜
⎞
XV
m
uW
X
m
Xm
m
ax
eaa
⎠⎟.
(6.90)
Èìåÿ â âèäó îãðàíè÷åíèå (6.84), ïîëó÷èì, ÷òî, åñëè u(t)
ýêñòðåìàëüíî, îíî áóäåò ïðèíèìàòü çíà÷åíèÿ u(t)=umax è u(t)=0,
èñõîäÿ èç çíàêà ôóíêöèè ïåðåêëþ÷åíèÿ σk(t), îïðåäåëÿåìîé óñëîâèåì
(6.87). Ïî ñâîåìó ôèçè÷åñêîìó ñìûñëó σk( t) – ôóíêöèÿ ïåðå-
êëþ÷åíèÿ äëÿ k-é óïðàâëÿþùåé ïåðåìåííîé – ïðåäñòàâëÿåò ñîáîé
ñêàëÿðíóþ ôóíêöèþ, îïðåäåëÿþùóþ óñëîâèå ïåðåêëþ÷åíèÿ uk(t)ñî
çíà÷åíèÿ uk min íà çíà÷åíèå uk max èëè íàîáîðîò. Ïîñêîëüêó σk(t)
íåïðåðûâíà, îíà ïðîõîäèò ÷åðåç íóëü âñÿêèé ðàç, êîãäà åå çíàê
èçìåíÿåòñÿ íà îáðàòíûé. Èìåÿ â âèäó (6.89) è óñëîâèå ∂ H/(∂u)=0,
çàïèøåì
σψ
ψ
() ()
()
tt
W
m
t
e
=−
12
(6.91)
è ñîîòâåòñòâåííî
utu
t
ut
t
(),
();
(),
().
max
=>
=<
åñëè
åñëè
σ
σ
0
00
(6.92)
Ðàññìîòðèì òåïåðü âîçìîæíîñòü ïîÿâëåíèÿ îñîáîãî óïðàâëåíèÿ, ÷òî
ñîîòâåòñòâóåò îáðàùåíèþ σ(t) â íóëü íà ïðîìåæóòêå íåíóëåâîé
ïðîäîëæèòåëüíîñòè. Äëÿ ýòîãî âû÷èñëèì ïðîèçâîäíóþ [dσ(t)]/dt ïðè
σ(t) = 0. Ïðè ýòîì áóäåì èñõîäèòü èç òîãî, ÷òî äëÿ ýêñòðåìàëüíîãî u(t)
294
H (ψ(t), x(t)) = 0. Òîãäà, ïîäñòàâèâ âûðàæåíèå ψ2 èç (6.91) â (6.89),
íàéäåì
−−
+=
−
ψψ
σ
01
1
0
Vt X tVtV
tut
xa
x
x
()
[; ()]
()() .
(6.93)
Êàê ñëåäóåò èç ïîëó÷åííîãî ñîîòíîøåíèÿ, ïðè Xa [t; Vx(t)]>0ψ0 ≠ 0,
åñëè σ(t) = 0, ïðè÷åì åñëè Vx(t)>0,m(t)>0,ψ0 < 0, òî ñîãëàñíî (6.93)
ψ1(t) > 0. Èìåÿ â âèäó
dt
dt
tVtm
t
t
x
σ
ψ
σ
()
() [ (), ()],
()=
=
0
1Λ
(6.94)
ãäå
Λ[(),()]
Vt mt
WV
Vm
B
WV
WV
Vm
g
C
x
ex
x
ex
ex
x
=
++
+
−
⎛
⎝⎜
⎞
3
3
22
42
2
⎠⎟,
ïðèäåì ê âûâîäó, ÷òî çíàê ïðîèçâîäíîé ñîâïàäàåò ñî çíàêîì
âûðàæåíèÿ Λ[Vx(t), m(t)].
Ãåîìåòðè÷åñêèì ìåñòîì îñîáûõ òî÷åê ÿâëÿåòñÿ êðèâàÿ, óäîâëå-
òâîðÿþùàÿ ðàâåíñòâó
Λ[(),()] ,
Vt mt
x
=0
(6.95)
ïîñêîëüêó òîëüêî íà ýòîé êðèâîé â òå÷åíèå íåíóëåâîãî ïðîìåæóòêà
âðåìåíè ìîæåò èìåòü ìåñòî σ(t)=0.
Óðàâíåíèåì êðèâîé ÿâëÿåòñÿ ñîîòíîøåíèå âèäà
mV
B
Cg
WV
WV
x
ex
ex
=
+
+
2
2
3
.
(6.96)
Óêàçàííàÿ êðèâàÿ äåëèò êâàäðàíò Vx >0,m > 0 íà äâå îáëàñòè, òàêèå,
÷òî
dt
dt
Vt mt
dt
dt
V
t
x
t
x
σ
σ
σ
σ
()
,((
),()) ;
()
,(
()
()
=
=
=∈
<
0
0
0
0
Λ
(), ())
;
()
,((
),())
()
tmt
dt
dt
Vt mt
t
x
∈
>∈
=
îáëàñòè I
îá
σ
σ
0
0
ëàñòè II.
(6.97)
295
Áóäó÷è íåïðåðûâíîé, ôóíêöèÿ σ(t) ïðîõîäèò ïðè ïåðåìåíå çíàêà
÷åðåç íóëü, â ýòîò ìîìåíò ïðîèñõîäèò ïåðåêëþ÷åíèå [73]. Ïðè ýòîì â
êàæäîé îáëàñòè ìîæåò áûòü íå áîëåå îäíîãî ïåðåêëþ÷åíèÿ: umax → 0â
îáëàñòè I; −umax → 0 â îáëàñòè II. Âåðîÿòíîñòü ïîÿâëåíèÿ îñîáîãî
óïðàâëåíèÿ òåì âûøå, ÷åì áîëüøå â ðàññìàòðèâàåìîé çàäà÷å òÿãà
äâèãàòåëÿ ïî ñðàâíåíèþ ñ âåëè÷èíîé Xa.
Ïîëó÷åíèå çàìêíóòîãî ðåøåíèÿ òèïà ðàññìîòðåííîãî âûøå, êî-
íå÷íî, ïðåäñòàâëÿåòñÿ âîçìîæíûì òîëüêî â îòäåëüíûõ, äîñòàòî÷íî
ïðîñòûõ ÷àñòíûõ ñëó÷àÿõ.  ïîäàâëÿþùåì áîëüøèíñòâå ïðàêòè÷å-
ñêè âàæíûõ è îáëàäàþùèõ îáùíîñòüþ çàäà÷ ïðèõîäèòñÿ îãðàíè÷è-
âàòüñÿ ïîñòðîåíèåì âû÷èñëèòåëüíîãî àëãîðèòìà, îáåñïå÷èâàþùåãî
îòûñêàíèå ýêñòðåìóìà èñõîäíîãî ôóíêöèîíàëà â ðåçóëüòàòå ÷èñëåí-
íîãî ñ÷åòà íà ÝÂÌ.
Ïðîèëëþñòðèðóåì ýòî íà ñëåäóþùåì ïðèìåðå. Ðàññìîòðèì çàäà-
÷ó óïðàâëåíèÿ äâèæåíèåì áàëëèñòè÷åñêîãî ËÀ â àòìîñôåðå ïðè ïî-
ëåòå íà ìèíèìàëüíóþ è ìàêñèìàëüíóþ äàëüíîñòè ïðè îãðàíè÷åíèè,
íàêëàäûâàåìîì íà âåëè÷èíó àýðîäèíàìè÷åñêîãî êà÷åñòâà àïïàðàòà:
cc
Kc
yy
y
aa
min
max
max
(),
<<
êîòîðàÿ ïîçâîëÿåò îöåíèòü åãî ìàíåâðåííûå
âîçìîæíîñòè.
Ïðèìåì ñëåäóþùèå äîïóùåíèÿ: äâèæåíèå îñóùåñòâëÿåòñÿ â âåð-
òèêàëüíîé ïëîñêîñòè â öåíòðàëüíîì ãðàâèòàöèîííîì ïîëå g=
=
+
⎛
⎝⎜⎞
⎠⎟
g
R
Ry
0
2
Ç
Ç
; ñïðàâåäëèâ ýêñïîíåíöèàëüíûé çàêîí èçìåíåíèÿ
ïëîòíîñòè ïî âûñîòå (ρ = ρ0 e−βy); êîýôôèöèåíò ñèëû ëîáîâîãî ñî-
ïðîòèâëåíèÿ îïðåäåëÿåòñÿ çàâèñèìîñòüþ cc
c
xx
y
aa
a
=+
≈
−
0
12
025
,M
≈=
cx a 0 const.
Òðåáóåòñÿ îïðåäåëèòü çàêîí èçìåíåíèÿ óïðàâëÿþùåãî ïàðàìåòðà
α(t) ïðè îãðàíè÷åíèè
cV
S
mg
n
cV
S
mg
y
y
y
aa
αα
αρ
αρ
min
max
||
,
22
22
≤≤
(6.98)
äîñòàâëÿþùèé ìèíèìóì (ìàêñèìóì) ôóíêöèîíàëó
Jtt
R
Ry
Vd
t
t
t
[(), ()]
cos .
xu=
+
∫Ç
Ç
ê
θ
0
(6.99)
Ââåäåì ñëåäóþùèå îáîçíà÷åíèÿ ïåðåìåííûõ ñîñòîÿíèÿ: V = x1, θ =
= x2, y = x3, x = x4. Ïîñòîÿííûå âåëè÷èíû îáúåäèíèì â êîýôôèöèåíòû
kcS
m
kS
m
xa
10
0
1
20
1
05
05
==
−−
,;
,
.
ρρ
296
Òîãäà óðàâíåíèÿ ñîñòîÿíèÿ ËÀ ïðèìóò âèä
•
exp()sin;
•
exp( )
xk
x xgx
xk
x
ux
x
Rx
11
1
2
32
22
1
3
1
=−
−
=+
+
β
β
Ç
31
2
312
4
3
12
−
⎛
⎝⎜
⎞
⎠⎟
=
=
+
g
x
x
xxx
x
R
Rx
xx
cos ;
•
sin ;
•
cos ,
Ç
Ç
(6.100)
ãäå óïðàâëåíèå uc c
yy
aa
==
α
α
;RÇ=R =6371êì.
 ïðèíÿòûõ îáîçíà÷åíèÿõ ôóíêöèîíàë (6.99) ïåðåïèøåì êàê
Jtt
R
Rx
xx
t
tê
[(), ()]
cos .
xu=
+
∫ 312
0
Ãðàíè÷íûå óñëîâèÿ çàäàäèì â âèäå
tx
txx
txx
txx
t
01
01
0
2
02
0
3
03
0
4
0
00
==
=
=
=
:() ;() ;() ;();
tê ñâîáîäíî: x3(tê)=R; x1(tê), õ2(tê), õ4(tê) – var .
 îáùåì ñëó÷àå îïòèìàëüíàÿ òðàåêòîðèÿ ìîæåò ñîäåðæàòü êàê
ó÷àñòêè, íà êîòîðûõ âûïîëíÿåòñÿ óñëîâèå ðåãóëÿðíîñòè
∂∂
nc
yy
a
/,
≠ 0 òàê è ó÷àñòêè ñ îñîáûì óïðàâëåíèåì (/
)
.
∂∂
nc
yy
a
=0
Äëÿ ðåãóëÿðíîãî ñëó÷àÿ ôóíêöèÿ H çàïèñûâàåòñÿ â âèäå
H=
+
⎡
⎣⎢
⎤
⎦⎥ −+
+
+
ψψ
β
ψ
0
3
121
1
1
2
32
R
Rx
xxk
x xgx
cos
[exp()sin]
221
3
3
1
1
23
1
kxu x
R
Rx
xg
x
x
exp( )
cos
[s
βψ
+
+
−
⎛
⎝⎜
⎞
⎠⎟
⎡
⎣
⎢
⎤
⎦
⎥+
−
in ],
x2
(6.101)
à îòâå÷àþùàÿ åé ñîïðÿæåííàÿ ñèñòåìà – â âèäå
297
•
;
•
cos
exp( )
exp(
ψ
ψψ
ψβ
ψβ
0
10
3
21
1
1
3
22
0
=
=−
+
+−
−
R
Rx
xk
xx
ku
x
Rx
xg
x
xk
g
x
3
3
1
2
2
322
0
1
1
1
2
)c
o
s
sin
+
+
−
⎛
⎝⎜
⎞
⎠⎟
⎡
⎣
⎢
⎤
⎦
⎥−
−+
−
ψ
u
c
nc
x
x
R
Rx
xg
y
yy
a
a
∂∂
∂∂
β
ψψ
ψ
H/
/
exp( );
•
sin
cos
3
20
1
3
21
=
+
+
x
x
Rx
gx
x
x
x
2
2
1
3
1
1
23
12
+
+
+
−
⎡
⎣⎢
⎤
⎦⎥
−
−
ψψ
sin
cos ;
(6.102)
•
()
cos
sin
exp( )
ψψ
ψ
ββ
30
1
3
2
21
3
21
2
13
2
=
+
−
+
+
x
R
Rx
x
g
Rx
xxk x
⎡
⎣⎢
⎤
⎦⎥+
+
+
−
+
+
ψβ
2
1
3
2
2
2
13
12
2
x
Rx
x
gx
xRx
xku
()
cos
cos
()
exp()
/
exp( ),
β
β
∂∂
∂∂
β
x
kg xu
c
nc
x
y
yy
a
a
3
20
1
13
⎡
⎣⎢
⎤
⎦⎥−
−
−
H/
ãäå
∂∂
∂∂
ψ
H/c
nc
gx
y
yy
a
a
/
.
=
−
101
1
Èìåÿ â âèäó ãðàíè÷íûå óñëîâèÿ äëÿ èñõîäíîé ñèñòåìû, çàïèøåì
ψψ
12
0
êê
==
.
(6.103)
Ñîîòíîøåíèÿ (6.103) ÿâëÿþòñÿ óæå ãðàíè÷íûìè óñëîâèÿìè äëÿ
ñèñòåìû (6.102).
Èç óñëîâèé ψ0ê = −1è•ψ 0 0
=
ñëåäóåò, ÷òî ψ0 = −1 íà âñåé òðàåêòî-
ðèè. Ïîñêîëüêó êîíå÷íîå âðåìÿ íå çàôèêñèðîâàíî, òî H = 0. Çàäàâ
ψ10 è ψ20 è ïðèðàâíÿâ ê íóëþ (6.101), âîçìîæíî íàéòè ψ30. Â ðåçóëü-
òàòå ïîñòàâëåííàÿ âàðèàöèîííàÿ çàäà÷à ñâåëàñü ê êðàåâîé çàäà÷å
äëÿ ñèñòåìû îáûêíîâåííûõ äèôôåðåíöèàëüíûõ óðàâíåíèé (6.100) è
(6.102), ðåøàåìîé ìåòîäîì ïîñëåäîâàòåëüíûõ èòåðàöèé. Ìàêñè-
ìàëüíàÿ äàëüíîñòü ïîëåòà ïðè ýòîì ñîîòâåòñòâóåò óñëîâèþ
298
H→min,
cya
ìèíèìàëüíàÿ – óñëîâèþ H → max .
cya
Çíàê ôóíêöèè îïòè-
ìàëüíîãî óïðàâëåíèÿ u(t) îïðåäåëÿåòñÿ çíàêîì ïåðåìåííîé ψ2(t),
ò.å .
utc
t
ya
0
2
()
().
=
α
αψ
extr sign
(6.104)
Åñëè α(t) ïðèíèìàåò íóëåâîå çíà÷åíèå, òî c y a
= 0 è ïðîèçâîäíàÿ
∂∂
nc
yy
a
/ òàêæå ïðèíèìàåò íóëåâîå çíà÷åíèå, ÷òî ïðè |ny|=|ny|extr
ïðèâîäèò ê íåðåãóëÿðíîìó ñëó÷àþ. Ïðè cx a 0
= const íåðåãóëÿðíûé
ó÷àñòîê ñâîäèòñÿ ê êîíå÷íîìó ÷èñëó èçîëèðîâàííûõ òî÷åê ñ îñîáûì
óïðàâëåíèåì, ïîñêîëüêó áàëëèñòè÷åñêàÿ òðàåêòîðèÿ â ýòîì ñëó÷àå
íå ìîæåò áûòü èçîïåðåãðóçî÷íîé. Íåêîòîðûå âîïðîñû îïðåäåëåíèÿ
íåîáõîäèìûõ óñëîâèé ýêñòðåìóìà â íåðåãóëÿðíîì ñëó÷àå è ïîèñêà
îòâå÷àþùèõ åìó îïòèìàëüíûõ óïðàâëåíèé äëÿ îáñóæäàåìîãî òèïà
çàäà÷ ðàññìîòðåíû â [51].
6.4.4 . ÐÀÑ×ÅÒ ÒÐÀÅÊÒÎÐÈÈ ÍÀÊËÎÍÍÎÉ ÌÀÊÑÈÌÀËÜÍÎÉ
ÄÀËÜÍÎÑÒÈ ÏÎËÅÒÀ ÏËÀÍÈÐÓÞÙÅÃÎ ËÀ ÌÅÒÎÄÎÌ
ÄÈÍÀÌÈ×ÅÑÊÎÃÎ ÏÐÎÃÐÀÌÌÈÐÎÂÀÍÈß
Îñíîâó ñîáñòâåííî ìåòîäà äèíàìè÷åñêîãî ïðîãðàììèðîâàíèÿ
ñîñòàâëÿåò äîïóùåíèå î ñóùåñòâîâàíèè ôóíêöèè V[x(t), t], èìåþ-
ùåé ñìûñë ýêñòðåìóìà îïòèìèçèðóåìîãî ôóíêöèîíàëà J[x(t), u(t)]:
Vtt
Jtt
tU
[(),] min [(), ()].
()
xx
u
u
=
∈
(6.105)
Ïóñòü â êà÷åñòâå òàêîãî ôóíêöèîíàëà çàäàí ñìåøàííûé ôóíêöèîíàë
òèïà (6.48)
Jtt f
tt td
ttt
êê
t
tê
3[(),()] [;(),()] [;()].
xu
xu
x
=+
∫
φ
Òîãäà
−=
=+
∈
∂
∂
∂
∂
Vtt
t
ft tt
Vtt
tU
((),)
min [(),(),]
((),)
()
x
xu
x
u
x
Ft tt
i
i
i
n
[(), ()
,],
xu
=
∑
⎧
⎨
⎩
⎫
⎬
⎭
1
(6.106)
èëè â îáùåì âèäå
m
in
,
,,(
),
()
u
x
tU
H
VV
t
Vut
∈
⎡
⎣⎢
⎤
⎦⎥
⎧
⎨
⎩
⎫
⎬
⎭
=
∂
∂
∂
∂
0
(6.107)
299
÷òî ôîðìàëüíî ÿâëÿåòñÿ çàïèñüþ óðàâíåíèÿ Ãàìèëüòîíà – ßêîáè.
Ñèìâîë Í îçíà÷àåò ôóíêöèþ Ãàìèëüòîíà, ïðè÷åì äëÿ êðèòåðèÿ,
çàäàííîãî â ôîðìå (6.46), è ïðè ñâÿçÿõ, íàêëàäûâàåìûõ ïðàâûìè
÷àñòÿìè óðàâíåíèé ñîñòîÿíèÿ
d
dt
tFt tt
xx
u
() ((), (),),
=
ãàìèëü-
òîíèàí èìååò âèä
H
V
fV
t
=+
+
∂
∂
∂
∂
x
F
,
ãäå
∂
∂
V
x
F ïðåäñòàâëÿåò ñîáîé ñêàëÿðíîå ïðîèçâåäåíèå, ðàâíîå
âòîðîìó ñëàãàåìîìó â (6.106).
Áîëüøèå âîçìîæíîñòè ìåòîä äèíàìè÷åñêîãî ïðîãðàììèðîâàíèÿ
ïðåäîñòàâëÿåò ïðè ðåøåíèè ïðàêòè÷åñêèõ çàäà÷ ïî îïðåäåëåíèþ
îïòèìàëüíîãî óïðàâëåíèÿ ïðèìåíèòåëüíî ê äèñêðåòíûì ñèñòåìàì
(ñèñòåìàì ñ äèñêðåòíûì âðåìåíåì). Ìåòîä ÿâëÿåòñÿ, ïî ñóùåñòâó,
ìíîãîøàãîâîé (ìíîãîýòàïíîé) âû÷èñëèòåëüíîé ïðîöåäóðîé, è åãî
ïðèìåíåíèå äëÿ îïòèìèçàöèè îòíîñèòåëüíî ñëîæíûõ ñèñòåì ñòàëî
âîçìîæíûì òîëüêî íà îñíîâå øèðîêîãî èñïîëüçîâàíèÿ ñîâðåìåí-
íîé âû÷èñëèòåëüíîé òåõíèêè.
Íà ðàññìàòðèâàåìîì èíòåðâàëå âðåìåíè äâèæåíèå óïðàâëÿåìîé
ñèñòåìû äîëæíî îïèñûâàòüñÿ ñèñòåìîé äèôôåðåíöèàëüíûõ óðàâíå-
íèé, ïðèâåäåííûõ ê êîíå÷íî-ðàçíîñòíîìó âèäó, ò.å ., êàê îáû÷íî,
ïðè ÷èñëåííîì èíòåãðèðîâàíèè ïðîèçâîäíàÿ çàìåíÿåòñÿ îòíîøå-
íèåì ïåðâîé ðàçíîñòè ôóíêöèè ê êîíå÷íîìó ìàëîìó èíòåðâàëó èç-
ìåíåíèÿ àðãóìåíòà. Àëãîðèòì ñâîäèòñÿ ê ïîýòàïíîìó ïëàíèðîâà-
íèþ ìíîãîøàãîâîãî ïðîöåññà, ïðè êîòîðîì íà êàæäîì ýòàïå ñ ó÷å-
òîì ðàçâèòèÿ âñåãî ïðîöåññà îïòèìèçèðóåòñÿ òîëüêî îäèí øàã, ò.å .
ïðè ïðèíÿòèè ðåøåíèÿ ó÷èòûâàåòñÿ áóäóùåå. Îäíàêî ëþáîé óïðàâ-
ëÿåìûé ïðîöåññ áóäåò èìåòü ïîñëåäíèé, n-é, øàã, ïðèíÿòèå ðåøå-
íèÿ íà êîòîðîì íå çàâèñèò îò áóäóùåãî. Ïîýòîìó íà ýòîì øàãå âû-
áèðàåòñÿ óïðàâëåíèå, ïîçâîëÿþùåå ïîëó÷èòü íàèâûñøèé ýôôåêò.
Ñïëàíèðîâàâ ýòîò øàã, ê íåìó ïðèñîåäèíÿþò ïðåäïîñëåäíèé, (n –
1)-é, øàã, ê êîòîðîìó â ñâîþ î÷åðåäü ïðèñîåäèíÿþò (n – 2)-é øàã, è
ò.ä .  êîíå÷íîì èòîãå "ðàçâîðà÷èâàÿ" ïðîöåññ îò êîíöà ê íà÷àëó,
ïðèõîäèì â íà÷àëüíîå ñîñòîÿíèå ñèñòåìû x(t0)=x0.
×òîáû ñïëàíèðîâàòü n-é øàã, íåîáõîäèìî çíàòü ñîñòîÿíèå ñèñòå-
ìû íà (n – 1)-ì øàãå . Åñëè îíî íåèçâåñòíî, òî, èñõîäÿ èç õàðàêòåðà
ïðîöåññà, ñëåäóåò ïðèíÿòü òó èëè èíóþ ãèïîòåçó î âîçìîæíûõ ñî-
ñòîÿíèÿõ ñèñòåìû íà ýòîì øàãå. Äëÿ êàæäîãî ïðåäïîëîæåíèÿ çàòåì
âûáèðàåòñÿ îïòèìàëüíîå óïðàâëåíèå íà ïîñëåäíåì øàãå. Òàêîå
óïðàâëåíèå íàçûâàåòñÿ óñëîâíî îïòèìàëüíûì.
300
Áóäåì ñ÷èòàòü, ÷òî ïëàíèðóåòñÿ íåêîòîðûé n-øàãîâûé ïðîöåññ.
Ïðåäïîëîæèì, ÷òî íà (n – 1)-ì øàãå ñäåëàíî íåñêîëüêî ïðåäïîëî-
æåíèé î âîçìîæíûõ ñîñòîÿíèÿõ ñèñòåìû xn–1, 1, xn–1, 2, ..., xn–1, m
.Íà
ïîñëåäíåì øàãå äëÿ êàæäîãî èç ýòèõ ñîñòîÿíèé ìîæåò áûòü íàé-
äåíî m óñëîâíî îïòèìàëüíûõ óïðàâëåíèé uu
nn
,
*
,
()
,
11
1
−
ux
nn
,
*
,
()
,
21
2
−
K
K,( )
.
,
*
,
ux
nmnm
−1
Òàêèì îáðàçîì, n-é øàã ìîæíî ñ÷èòàòü ñïëàíèðîâàí-
íûì. Àíàëîãè÷íî ñëåäóåò ïîñòóïèòü è íà (n – 1)-ì øàãå, òîëüêî óñ-
ëîâíî îïòèìàëüíîå óïðàâëåíèå íåîáõîäèìî óæå âûáèðàòü, ó÷èòûâàÿ
âûáðàííûå óñëîâíî îïòèìàëüíûå óïðàâëåíèÿ íà ýòîì øàãå, è ò.ä .
Äëÿ ïåðâîãî øàãà (â îòëè÷èå îò âñåõ îñòàëüíûõ) ïðåäïîëîæåíèé î
âîçìîæíîì ñîñòîÿíèè ñèñòåìû íå äåëàåòñÿ, òàê êàê ñîñòîÿíèå x(t0)
èçâåñòíî. Îïòèìàëüíîå óïðàâëåíèå äëÿ íåãî âûáèðàåòñÿ ñ ó÷åòîì
âñåõ óñëîâíî îïòèìàëüíûõ óïðàâëåíèé äëÿ âòîðîãî øàãà. Äâèãàÿñü
îò x0 ê x(tê) â åñòåñòâåííîì, ò.å . îáðàòíîì ïî îòíîøåíèþ ê ïåðâîíà-
÷àëüíîìó, íàïðàâëåíèè, ìîæíî ïîëó÷èòü èñêîìîå îïòèìàëüíîå
óïðàâëåíèå äëÿ ïðîöåññà â öåëîì.
Ïðèìåíèòåëüíî ê ðåøåíèþ çàäà÷è îïðåäåëåíèÿ îïòèìàëüíîé ïî
ïðîòÿæåííîñòè òðàåêòîðèè ïëàíèðîâàíèÿ ñåìåéñòâî âîçìîæíûõ
òðàåêòîðèé, îòâå÷àþùèõ óñëîâíî îïòèìàëüíûì óïðàâëåíèÿì, ïðåä-
ñòàâëÿåòñÿ ãðàôè÷åñêè â ïîëå VH, ãäå H = y – òåêóùàÿ âûñîòà, V –
ñêîðîñòü ïîëåòà. Äâèæåíèå îò x0 íà êàæäîì øàãå ïðåäïîëàãàåò âîç-
ìîæíûì ïåðåìåùåíèå íà îäíó êëåòêó âïðàâî (óâåëè÷åíèå V) èëè
ââåðõ (óâåëè÷åíèå Í). Âåëè÷èíà "øàãà êëåòêè" îïðåäåëÿåò òî÷íîñòü
ôîðìèðîâàíèÿ ïðîãðàììû ïîëåòà. Ñëåäóåò ïîä÷åðêíóòü, îäíàêî,
÷òî ðàññìîòðåííàÿ êàíîíè÷åñêàÿ ñõåìà âû÷èñëèòåëüíîãî àëãîðèòìà
ìåòîäà òðåáóåò î÷åíü áîëüøèõ çàòðàò âðåìåíè. Ñóùåñòâåííîãî ñî-
êðàùåíèÿ îáúåìà âû÷èñëåíèé ìîæíî äîáèòüñÿ, åñëè âîñïîëüçîâàòü-
ñÿ ïîäõîäîì, äåòàëüíî ðàññìîòðåííûì â [132]. Äàëüíåéøåå èçëîæå-
íèå ðåøåíèÿ îáñóæäàåìîé çàäà÷è îñíîâûâàåòñÿ íà ðåçóëüòàòàõ óêà-
çàííîé ðàáîòû.
Ïóñòü èñêîìîå "ïîëå" âûðàæàåòñÿ â âèäå ìàòðèöû À:
A=
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
aa
a
aa
a
aa
a
n
n
mm
m
n
11
12
1
21
22
2
12
K
K
KK
KK
K
,
òî äëÿ òîãî ÷òîáû èç ïîëîæåíèÿ àm1 ïîñëåäîâàòåëüíî ïåðåéòè â
ïîëîæåíèå a1n, ñäâèãàÿñü íà êàæäîì øàãå íà îäíó êëåòêó âïðàâî èëè
íà îäíó êëåòêó ââåðõ è ïðèòîì òàê, ÷òîáû ñóììà âñåõ âñòðåòèâøèõñÿ
íà ïóòè ýëåìåíòîâ áûëà ìèíèìàëüíîé, íåîáõîäèìî ñîñòàâèòü
301
âñïîìîãàòåëüíóþ ìàòðèöó Â, êàæäûé ýëåìåíò êîòîðîé âû÷èñëÿåòñÿ
ïî ñëåäóþùåìó ðåêóððåíòíîìó ñîîòíîøåíèþ:
ba bb
ij
ij
ij
ij
=+
+−
min[ ; ].
,,
11
(6.108)
Òàê êàê ìàòðèöà  äîëæíà èìåòü ÷èñëî ñòðîê è ñòîëáöîâ, ðàâíîå
÷èñëó ñòðîê è ñòîëáöîâ ìàòðèöû À,òî
bab b
jjj j
111
1
00
=+
=
+
,
;;
(6.109)
babb ba
in
in
inin
n
n
=+
=
=
−+
11 11
0
,,
;;. (6.110)
Ðåêóððåíòíîå ïðàâèëî (6.108) ïðåäïîëàãàåò, ÷òî ïðè ðàñ÷åòå ìàòðèöû
 ñëåäóåò äâèãàòüñÿ îò êîíå÷íîãî ïîëîæåíèÿ ê íà÷àëüíîìó.
Ïðèìåì, ÷òî â ìàòðèöå
B=
bbb
bbb
bbb
n
n
mm
m
11 12
1
21
22
2
12
K
K
K
...................
n
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
ýëåìåíòû bij â ñâîþ î÷åðåäü îïðåäåëÿþòñÿ ïî ðåêóððåíòíîé ñõåìå
b
ab
bb
ij
ij
ij
ij
ij
=
+
+
−−
+
min
,
(max)
,,
,
11
1
(6.111)
ãäå àij õàðàêòåðèçóåò ðàññòîÿíèå, êîòîðîå ïðîéäåò ËÀ íà ïîñòîÿííîé
âûñîòå ïðè èçìåíåíèè ÷èñëà Ì íà ∆Ì; bij – äàëüíîñòü ïîëåòà ïðè
ïëàíèðîâàíèè ËÀ ñ ïîñòîÿííûì ÷èñëîì Ì ïðè èçìåíåíèè âûñîòû
íà ∆H. Ïðåäïîëàãàÿ òåïåðü, ÷òî äâèæåíèå ËÀ óäîâëåòâîðÿåò ìîäåëè
âèäà
m
dV
dt
Xm
g
mV
d
dt
Ym
g
dH
dt
V
dx
dt
V
a
a
=−
−
=−
=
=
sin ;
;
sin ;
(co
θ
θ
θ
s)
,
θ≈1
302
ïðîàíàëèçèðóåì õîä ðåøåíèÿ ïîñòàâëåííîé çàäà÷è îïðåäåëåíèÿ
îïòèìàëüíîé ïðîãðàììû ïîëåòà, îáåñïå÷èâàþùåé ìàêñèìàëüíóþ
íàêëîííóþ äàëüíîñòü ïëàíèðîâàíèÿ ïðè óïðàâëåíèè çà ñ÷åò
èçìåíåíèÿ óãëà àòàêè cy a
α
α. Äëÿ òîãî ÷òîáû ñôîðìèðîâàòü
ìàêñèìèçèðóåìûé ôóíêöèîíàë,
ïðåäâàðèòåëüíî
íåîáõîäèìî
âûïîëíèòü [132] ñëåäóþùèå ïðåîáðàçîâàíèÿ.
Èìåÿ â âèäó, ÷òî dt = dH(V sinθ)–1
, â ðåçóëüòàòå çàìåíû àðãóìåíòà
â ïåðâîì óðàâíåíèè ñèñòåìû è ïîñëåäóþùèõ ïðåîáðàçîâàíèé ïîëó-
÷èì
dV
dH
gn
dH
dt
g
V
x
=
⎛
⎝⎜⎞
⎠⎟−
−1
.
(6.112)
Ðàçäåëèâ ïåðåìåííûå è âçÿâ èíòåãðàë, çàïèøåì
x
V
gn
dV
n
dH
xx
VH
VH
=+
⎛
⎝⎜
⎞
⎠⎟
∫
1
00
êê
.
Èòàê,
Jtt
V
gn
dV
n
dH
xx
VH
VH
[(), ()]
,
xu =+
⎛
⎝⎜
⎞
⎠⎟
∫
1
00
êê
(6.113)
è òðåáóåòñÿ íàéòè êðèâóþ φ(V, H ) = 0, äîñòàâëÿþùóþ ìàêñèìóì
ôóíêöèîíàëó (6.113). Âñå äîïóñòèìûå êðèâûå φ(V, H ) çàìåíÿþòñÿ â
îáëàñòè VH ëîìàíûìè, íà êàæäîì îòðåçêå êîòîðûõ ëèáî V, ëèáî Í
ïîñòîÿííà. Îïòèìàëüíàÿ òðàåêòîðèÿ íàõîäèòñÿ â êëàññå êðèâûõ,
àïïðîêñèìèðóþùèõ óêàçàííûå ëîìàíûå. Äëÿ åå íàõîæäåíèÿ
íåîáõîäèìî îïðåäåëèòü âñå aij è bij. Ñ ýòîé öåëüþ âñÿ îáëàñòü ÌÍ
ðàçáèâàåòñÿ íà ïðÿìîóãîëüíèêè ñî ñòîðîíàìè, ïàðàëëåëüíûìè îñÿì
ÌèÍ. Çäåñü Ì = V/a. Ïðèðàùåíèÿ ∆X âû÷èñëÿþòñÿ íà êàæäîé
ñòîðîíå êàæäîãî ïðÿìîóãîëüíèêà. Íà èõ ãîðèçîíòàëüíûõ ñòîðîíàõ
Í=const,∆H=0èìååì
aX
a
gn
ij
x
==
∆
∆
2
MM
,
(6.114)
ãäå à – ñêîðîñòü çâóêà.
303
Âûðàæåíèå äëÿ îïðåäåëåíèÿ îñåâîé ïåðåãðóçêè èìååò âèä
()
n
X
mg
cA
c
V
mg
S
x
a
xy
aa
≈
−
=−
+
0
2
2
2
ρ
.
(6.115)
Ó÷èòûâàÿ óñëîâèå Ya = mg, íàéäåì
c
mg
VS
mg
aS
ya
==
22
22
2
ρρ
M
è ïîñëå ïîäñòàíîâêè
ncA
mg
aS
aS
mg
xx
a
=−
+
⎛
⎝⎜
⎞
⎠⎟
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
0
22
2
22
2
2
ρ
ρ
M
M
.
(6.116)
Òîãäà
a
mg
gSc
A
mg
aS
ij
xa
=−
+
⎛
⎝⎜
⎞
⎠⎟
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
2
2
0
22
2
∆M
M
M
ρ
ρ
.
(6.117)
Íà âåðòèêàëüíûõ ñòîðîíàõ ïðÿìîóãîëüíèêîâ ∆M = 0, ïîýòîìó
bX
H
n
ij
x
==
∆
∆
.
(6.118)
Äàííîå âûðàæåíèå íå ÿâëÿåòñÿ ÿâíîé ôóíêöèåé θ, õîòÿ è î÷åâèäíî,
÷òî bij = f(θ), ïîñêîëüêó
dV
dt
gnx
=−=
(s
i
n
).
θ0
(6.119)
Óêàçàííîå îáñòîÿòåëüñòâî ëåãêî îáõîäèòñÿ [132] ïðè äîáàâëåíèè
óðàâíåíèÿ
mV
d
dt
Ym
g
a
θ
θ
=−
=
cos
,
0
(6.120)
îòðàæàþùåãî òîò ôàêò, ÷òî àïïàðàò ïëàíèðóåò íà ñîîòâåòñòâóþùåì
ó÷àñòêå ëîìàíîé íå òîëüêî ñ ïîñòîÿííîé ñêîðîñòüþ, íî è ñ
ïîñòîÿííûì, õîòÿ è ìàëûì, óãëîì íàêëîíà âåêòîðà ñêîðîñòè ê
304
ìåñòíîìó ãîðèçîíòó. Èç (6.119) è (6.120) èìååì nx = sinθ; ny = cosθ;
nn
n
xy
Σ=+
=
+=
22
2
2
1
sin
cos
,
θθíî, ñ äðóãîé ñòîðîíû,
ncc
VS
mg
xy
aa
Σ=+
22
2
2
ρ
.
Ïîýòîìó
1
2
22
2
=+
cc
VS
mg
xy
aa
ρ
,
îòêóäà
V
mg
Scc
xy
aa
2
22
2
=
+
ρ
.
(6.121)
Ïîäñòàâèâ â (6.121)
ccA
cc
cc
A
xx
yy
xx
aa
aa
aa
=+
=
−
0
22
0
è,
íàõîäèì îêîí÷àòåëüíî
V
mgS
cA
cc
xx
x
aa
a
4
222
22
1
0
4
=
+−
−
/
[()
]
.
ρ
(6.122)
Èç (6.122) âûòåêàåò çàâèñèìîñòü
n
kk
k
x
=−
−
11
2
2
24
,
(6.123)
ãäå
k
VS
Amg
k
c
A
VS
mg
xa
1
2
2
0
22
2
1
2
=
=+
⎛
⎝⎜⎞
⎠⎟
ρ
ρ
;
.
305
Îïðåäåëåíèå îïòèìàëüíîé ïðîãðàììû ïîëåòà ñâîäèòñÿ òåïåðü ê
âûáîðó íà êàæäîì øàãå ìíîãîýòàïíîãî ïðîöåññà óïðàâëåíèé, îòâå-
÷àþùèõ íàèìåíüøåìó èç äâóõ çíà÷åíèé nx, âû÷èñëÿåìûõ ïîýòàïíî
ïî (6.123).  ðàáîòå [132] ïðèâåäåíû ðåçóëüòàòû ðàñ÷åòîâ, èëëþñò-
ðèðóþùèå ðàáîòîñïîñîáíîñòü èçëîæåííîãî àëãîðèòìà.
Ãëàâà 7
ÈÑÑËÅÄÎÂÀÍÈÅ ÓÃËÎÂÎÃÎ ÄÂÈÆÅÍÈß
ÐÀÊÅÒ È ÑÍÀÐßÄÎÂ*
Èññëåäîâàíèå óãëîâîãî äâèæåíèÿ ïðîâîäèòñÿ â ïðåäïîëîæåíèè, ÷òî ïàðà-
ìåòðû äâèæåíèÿ öåíòðà ìàññ ñíàðÿäà èçâåñòíû è öåíòð ìàññ ñíàðÿäà äâèæåò-
ñÿ ïî ïëîñêîé òðàåêòîðèè, à åãî îñü ñîâïàäàåò ñ êàñàòåëüíîé ê òðàåêòîðèè â
òå÷åíèå âñåãî âðåìåíè ïîëåòà.
Âàæíåéøåé çàäà÷åé àíàëèçà óãëîâîãî äâèæåíèÿ ÿâëÿåòñÿ îïðåäåëåíèå óñëî-
âèé óñòîé÷èâîãî ïîëåòà ðàêåò è ñíàðÿäîâ. Îò òîãî, íàñêîëüêî óñïåøíî ðåøåíà
çàäà÷à îáåñïå÷åíèÿ óñòîé÷èâîãî è ïðàâèëüíîãî ïîëåòà ñíàðÿäà, òðåáóåìîãî ðå-
æèìà åãî óãëîâîãî äâèæåíèÿ ïî òðàåêòîðèè, çàâèñÿò êàê õàðàêòåðèñòèêè
òî÷íîñòè ñòðåëüáû, òàê è îáùàÿ ýôôåêòèâíîñòü àðòèëëåðèéñêèõ è ðàêåòíûõ
ñèñòåì.
7.1 . ÄÂÈÆÅÍÈÅ ÎÒÍÎÑÈÒÅËÜÍÎ ÖÅÍÒÐÀ ÌÀÑÑ
ÑÍÀÐßÄÎÂ, ÑÒÀÁÈËÈÇÈÐÎÂÀÍÍÛÕ ÂÐÀÙÅÍÈÅÌ
7.1.1. ÓÃËÎÂÎÅ ÄÂÈÆÅÍÈÅ ÂÐÀÙÀÞÙÅÃÎÑß ÑÍÀÐßÄÀ
ÏÎÄ ÄÅÉÑÒÂÈÅÌ ÒÎËÜÊÎ ÎÏÐÎÊÈÄÛÂÀÞÙÅÃÎ ÌÎÌÅÍÒÀ
Óðàâíåíèÿ äâèæåíèÿ ñíàðÿäà îòíîñèòåëüíî öåíòðà ìàññ ìîãóò áûòü ïî-
ëó÷åíû èç îáùèõ óðàâíåíèé ïðîñòðàíñòâåííîãî äâèæåíèÿ.  ï. 4.3.1 ïîêàçà-
íî, êàê ìîæíî ïîëó÷èòü óðàâíåíèÿ âðàùàòåëüíîãî äâèæåíèÿ èç îáùåé ñèñ-
òåìû â ôîðìå Â.Ñ . Ïóãà÷åâà äëÿ óãëîâ δ1 è δ2 (ñì. ðèñ. 3.12). Îò óðàâíåíèé
(4.51) âðàùàòåëüíîãî äâèæåíèÿ ñ ïåðåìåííûìè z1, z2, z3 ìîæíî ïåðåéòè ê
óðàâíåíèÿì äëÿ óãëîâ íóòàöèè δ è ïðåöåññèè ν â ñîîòâåòñòâèè ñ (3.160):
zz
z
12
3
==
=
cos ;
sin cos ;
sin sin .
δδ
νδ
ν
306
*
Ìàòåðèàëû ãëàâû, íàïèñàííîé ê.ò .í ., ñíñ Ñ.Ñ . Áîãîäèñòîâûì, îðèåíòè-
ðîâàííûå â îñíîâíîì íà ôàêóëüòàòèâíîå èçó÷åíèå, äàþòñÿ â ðåäàêöèè
òðåòüåãî èçäàíèÿ ó÷åáíèêà [38].
Äèôôåðåíöèðóÿ äâàæäû ïî âðåìåíè, íàõîäèì
•
•
sin;• •
cos cos
•
sin sin ;
•
•
cos si
zz
z
12
3
=−
=
−
=
δδ δδνννδ
δδn
•
sin cos ;•• ••
sin
•
cos ;
••
••
cos co
ννδν δδδδ
δδ
+=
−
−
=
z
z
1
2
2
s
•
sin cos
•
•
cos sin
•
sin cos
••
sin s
νδδνδ
νδν
νδν
νδ
−−
−
−−
2
2
2
in;
••
••
cos sin
•
sin sin
•
•
cos cos
•
ν
δδνδ δνδ
νδν
ν
z3
2
2
=−+
−
−
2
sin sin
••
sin cos .
δννδν
+
Óìíîæèâ ïåðâîå óðàâíåíèå ñèñòåìû (4.51) íà (−z3), à âòîðîå – íà z2 è
ñêëàäûâàÿ, ïîëó÷èì
−+
++−
−−
=
zzzzzzzz
azz zz
fz
13
2
2
2
122 33
32 23
43
2
2
()( )
(••
)(+z2
2
).
(7.1)
Ïîäñòàâëÿÿ âûðàæåíèÿ äëÿ zi, zi
•
,zi
••
(i = 1, 2, 3) â óðàâíåíèÿ (4.55) è (7.1),
ïîñëå ïðåîáðàçîâàíèÿ îò ñèñòåìû (4.51) ïåðåéäåì ê ñèñòåìå â óãëàõ δ è ν:
d
dt
a
af
(• sin
cos) ;
•
•
•
sin cos
•
sin
si
νδ
δ
δνδδ νδ
2
4
20
2
+=
−+
=
n;
.
δ
a
C
A
r
C
A
r
===
22
0
const
(7.2)
Óðàâíåíèÿ (4.63), (4.64) è (7.2) îïèñûâàþò óãëîâîå äâèæåíèå ñíàðÿäà íà
îòíîñèòåëüíî êîðîòêîì ó÷àñòêå òðàåêòîðèè, êîãäà ìîæíî ïðåíåáðå÷ü åãî
êðèâèçíîé.
Èç ïîëíîé ñèñòåìû óðàâíåíèé â ôîðìå Â.Ñ . Ïóãà÷åâà ìîæíî ïîëó÷èòü
óðàâíåíèÿ óãëîâîãî äâèæåíèÿ ñíàðÿäà äëÿ êðèâîëèíåéíîãî ó÷àñòêà òðàåêòî-
ðèé. Ñ÷èòàÿ, ÷òî òðàåêòîðèÿ ñíàðÿäà – ïëîñêàÿ êðèâàÿ (
•
,
•
•
),
ΨΨ
íí
==
00
è
ïîëàãàÿ â ñèñòåìå (3.157)
fffff
2356
7
0
=====
,
÷åòâåðòîå è ñåäüìîå óðàâíåíèÿ ýòîé ñèñòåìû çàïèøåì â âèäå
12
2
2
31 31
2
213
23
1
) •••••
(• •)
••
•
zzzzaz
zzzzz
az
−+
−+
−
+
θθθ•
;
) ••••••
••
••
•
θ
θθθ
=−
−+
−
−+
fz
zz zz
az
zzz
43
12 12
3
33
3
2
22
2=−
=
++=
fz
a
zzz
42
1
2
2
2
3
2
30
41
;
)•;
).
(7.3)
307
Óìíîæàÿ ïåðâîå óðàâíåíèå (7.3) íà ()
,
13
2
−
z à âòîðîå – íà z2z3 è ñêëàäûâàÿ
èõ, ïîëó÷èì
z
zzzz
zz zzzz
a
33
2
2
2
113
2
3 1232
11
21
()
••
()
•••
•
[(
−−
−
−
+
+
+−
zz zzz
zzz zzz
zz
3
2
2 233
3
2
32 23
2
3
13
21
)••
]•[( )••
]
(
+−
−+−
−
θ
12
1
1
3
22
13
2
432
2
3
2
−+
−
=
+
−
za
z
zf
z
z
z
)•
()
•
()
.
θθ
(7.4)
Çàäàâàÿ îðèåíòàöèþ ïðîäîëüíîé îñè ñíàðÿäà â òðàåêòîðíîé ñèñòåìå
êîîðäèíàò óãëàìè δ1 è δ2 è äèôôåðåíöèðóÿ âûðàæåíèÿ (3.161) ïî âðåìåíè,
íàéäåì zi, zi
•
,zi
••
(i = 1, 2, 3) äëÿ ýòîãî ñëó÷àÿ è ïîäñòàâèì â óðàâíåíèå (7.4).
Ïîñëå ïðåîáðàçîâàíèé áóäåì èìåòü
−−
+
••
cos cos
•
sin cos cos
•
cos c
δδδδδδδ δδ
1
2
122
2
1
3
122
3
1
2a
os
••
sin cos cos
•
sin cos cos
δ
θ
δδδδθδδδ
2
21
3
12
2
1
3
12
2
−
−−
+
+2
3
12 41
2
1
2
2
af
•
cos cos
sin cos cos .
θδδ
δδδ
=−
(7.5)
Àíàëîãè÷íî, ïîäñòàâëÿÿ âûðàæåíèÿ äëÿ zi è ïðîèçâîäíûõ âî âòîðîå
óðàâíåíèå ñèñòåìû (7.3), íàéäåì
(•• ••)cos (
•
•
)•
sin cos
•
cos
δθδδθ
δδδ
δδ
2
2
12
11
11
2
2
+−
+
+
+a
= f421
sin cos .
δδ
(7.6)
Ðàçäåëèâ îáå ÷àñòè óðàâíåíèÿ (7.5) íà (−cos2δ1 cosδ2), à óðàâíåíèÿ (7.6) – íà
cosδ1 è îáúåäèíÿÿ èõ, ïîëó÷èì ñèñòåìó, îïèñûâàþùóþ óãëîâîå äâèæåíèå
ñíàðÿäà íà êðèâîëèíåéíîì ó÷àñòêå òðàåêòîðèè ïðè äåéñòâèè òîëüêî
îïðîêèäûâàþùåãî ìîìåíòà:
••
(• •)sin cos
(• •)cos
sin co
δδθδδ δθδ
δ
12
2
112
141
2
++
−
+
=
af
s;
(•• ••)cos (
•
•
)•
sin
•
sin
δ
δθδδθ
δδδ
δ
2
21
2
1
1
1
4
22
+−
++
=
af2
0
22
;
.
a
C
A
r
C
A
r
===
const
(7.7)
Óðàâíåíèÿ (7.2) è (7.7) ïîëó÷åíû áåç êàêèõ-ëèáî îãðàíè÷åíèé íà çíà÷åíèÿ
óãëîâ δ, δ1 è δ2.
Ïðè ìàëûõ óãëàõ íóòàöèè δ è ñîîòâåòñòâåííî ìàëûõ δ1 è δ2 ñèñòåìû
óðàâíåíèé (7.2) è (7.7) ìîæíî óïðîñòèòü. Èç ïåðâîãî óðàâíåíèÿ (7.2)
ñëåäóåò
•
sin
cos
.
νδ
δ
2
2
+=
=
ad
const
(7.8)
Êîíñòàíòà d çàâèñèò îò íà÷àëüíûõ óñëîâèé. Ðàññìàòðèâàÿ äâèæåíèå ïðè
íà÷àëüíûõ óñëîâèÿõ δ = δ0 =0;••
δδ
=
0ïðèt=0,ïîëó÷èì
308
da
=2.
Òîãäà (7.8) ìîæíî ïðèâåñòè ê âèäó
•
(c
o
s) (c
o
s
)
.
νδ
δ
12
1
2
−=
−
a
(7.9)
Ïðè ìàëûõ δ èìååì cosδ≈1, sinδ≈δ è ïåðâûå äâà óðàâíåíèÿ ñèñòåìû (7.2)
çàïèøóòñÿ ñëåäóþùèì îáðàçîì:
•
;••
.
νδδδ
=+
−
=
aaf
2
4
0
(7.10)
Ïðè ìàëûõ óãëàõ δ1 è δ2, ïîëàãàÿ sinδi ≈δi, cosδi ≈ 1(i = 1, 2), ïåðâûå äâà
óðàâíåíèÿ ñèñòåìû (7.7) ìîæíî óïðîñòèòü, ïðåíåáðåãàÿ ÷ëåíàìè áîëåå
âûñîêîãî ïîðÿäêà ìàëîñòè ((
••
)
δθδ
2
2
1
+
è(
••
)• ):
δθδ
δ
21
1
+
•••
•
;
•••
•
•
.
δδδ θ
δδδθ
12
4
1
21
4
2
22
2
−−
=
+−=
−
afa
af
(7.11)
Îáîçíà÷èâ â (7.10)
σ=−
14
2
fa
/,
(7.12)
âòîðîå óðàâíåíèå ýòîé ñèñòåìû ïðèâåäåì ê âèäó
•
•
.
δσ
δ
+=
a
2
0
(7.13)
Êîýôôèöèåíòû f4 è σ ÿâëÿþòñÿ ïåðåìåííûìè âî âðåìåíè. Äëÿ íåáîëüøèõ
èíòåðâàëîâ âðåìåíè V ≈ const, òîãäà ìîæíî ïðèíÿòü, ÷òî f4 ≈ const, a ≈ const, è,
ñëåäîâàòåëüíî, σ≈ const.
Õàðàêòåðèñòè÷åñêîå óðàâíåíèå, ñîîòâåòñòâóþùåå (7.13), èìååò ñëåäóþ-
ùèé âèä: λ2 + a2σ = 0. Ïðè σ > 0 ïîëó÷èì èçâåñòíîå ðåøåíèå
δ
σσ
=+
−
Ce
Ñe
iat
iat
12
.
Îïðåäåëèâ ïðîèçâîëüíûå ïîñòîÿííûå, ïîëó÷èì ôîðìóëó äëÿ óãëà íóòà-
öèè
δ
δ
σ
σ
=
•
sin
.
0
a
at
(7.14)
Òàêèì îáðàçîì, ïðè σ > 0 óãîë íóòàöèè âûðàæàåòñÿ ÷åðåç òðèãîíîìåòðè-
÷åñêèé ñèíóñ è äâèæåíèå ïðîäîëüíîé îñè ñíàðÿäà íîñèò õàðàêòåð ãàðìîíè-
÷åñêèõ êîëåáàíèé ñ ïåðèîäîì Ta
= 2πσ
/( ) è îãðàíè÷åííîé àìïëèòóäîé
δδσ
max
•
/( ).
=
0
a
Ïðåöåññèîííîå äâèæåíèå â ñîîòâåòñòâèè ñ (7.10) ïðåäñòàâ-
309
ëÿåò ñîáîé âðàùåíèå ïëîñêîñòè ñî-
ïðîòèâëåíèÿ âîêðóã êàñàòåëüíîé
òðàåêòîðèè ïî÷òè ñ ïîñòîÿííîé óã-
ëîâîé ñêîðîñòüþ •
.
ν==
a
C
A
r
2
0 Èçìå-
íåíèå óãëà íóòàöèè îïðåäåëÿåòñÿ óðàâ-
í å íèåì (7.14) è ïðîèñõîäèò â ïëîñ-
êîñòè ñîïðîòèâëåíèÿ. Íà ó÷àñòêàõ
òðàåêòîðèè, áëèçêèõ ê ïðÿìîëèíåé-
íûì, ñëîæíîå ïðîñòðàíñòâåííîå
äâèæåíèå ïðîäîëüíîé îñè âðàùàþ-
ùåãîñÿ ñíàðÿäà ñîâåðøàåòñÿ îòíî-
ñèòåëüíî âåêòîðà V è äëÿ íà÷àëüíûõ
óñëîâèé ν =0,δ0 =0,
•
δ00
≠ ìîæåò
áûòü íàãëÿäíî ïðîèëëþñòðèðîâàíî
ãðàôèêîì, ïîñòðîåííûì â ïîëÿðíûõ
êîîðäèíàòàõ δ = f(ν) (ðèñ. 7.1). Óãîë δ
èçîáðàæàåòñÿ ðàäèóñ-âåêòîðîì, ïî-
ëîæåíèå êîòîðîãî îïðåäåëÿåòñÿ óã-
ëîì ν. Åñëè ðàññìàòðèâàòü äâèæåíèå
îñè ñíàðÿäà â çàâèñèìîñòè îò âðåìå-
íè, òî ãðàôèêè ôóíêöèé δ(t)èν(t)
áóäóò èìåòü âèä, ïðåäñòàâëåííûé íà
ðèñ. 7.2, à. Ïðè îáðàáîòêå îïûòíûõ äàííûõ óäîáíåå ðàññìàòðèâàòü ëèøü àá-
ñîëþòíóþ âåëè÷èíó óãëà íóòàöèè δ, ïîýòîìó ãðàôèê δ(t) ÷àñòî ñòðîÿò òîëüêî
â ïîëîæèòåëüíîé ïîëóïëîñêîñòè: â ýòîì ñëó÷àå ãðàôèê ν(t) ïîëó÷èò ñòóïåí-
÷àòûé âèä, òàê êàê ïðè ïåðåõîäå δ ÷åðåç íóëü óãîë ν ïðåòåðïåâàåò ðàçðûâ,
ðàâíûé ±π. Ïîñòðîåííûå ïîäîáíûì îáðàçîì ãðàôèêè δ(t)èν(t) ïðè ðàçðûâå,
âçÿòîì ðàâíûì −π, ïðåäñòàâëåíû íà ðèñ. 7.2, á. Ïðè èçìåíåíèè íà÷àëüíûõ
óñëîâèé ãðàôèêè δ = f(ν), δ(t)èν(t) áóäóò èìåòü âèä, îòëè÷íûé îò ïîêàçàí-
íîãî íà ðèñ. 7.1 è 7.2.
Èíòåãðèðîâàíèå óðàâíåíèÿ (7.12) ïðè σ > 0 ïðèâåëî ê ôîðìóëå (7.13),
îïðåäåëÿþùåé ãàðìîíè÷åñêèå êîëåáàíèÿ ïðîäîëüíîé îñè ñíàðÿäà ñ îãðàíè-
÷åííîé àìïëèòóäîé. Èíòåãðèðîâàíèå (7.12) ïðè σ < 0 ïðèâåäåò ê çàâèñèìî-
ñòè
δ
σσ
=−
+
−
Ce
e
at
at
()
.
||
||
Îïðåäåëèâ ïîñòîÿííóþ èíòåãðèðîâàíèÿ, ïîëó÷èì
δ
δ
σ
σ
=
•
||
(||).
0
a
at
sh
Òàêèì îáðàçîì, ïðè σ < 0 óãîë íóòàöèè îïðåäåëÿåòñÿ ôóíêöèåé, íåîãðà-
íè÷åííî âîçðàñòàþùåé ñ ðîñòîì âðåìåíè, ÷òî ÿâëÿåòñÿ ïðèçíàêîì íåóñòîé-
310
Ðèñ. 7 .1 . Çàâèñèìîñòü δ = f(ν) äëÿ ïðÿìî-
ëèíåéíîãî ó÷àñòêà òðàåêòîðèè áûñòðî-
âðàùàþùåãîñÿ ñíàðÿäà ïðè δ0 =0è
•
δ0≠0
÷èâîñòè äâèæåíèÿ ñíàðÿäà. Ñëåäî-
âàòåëüíî, óñëîâèå ïðàâèëüíîãî äâè-
æåíèÿ
âðàùàþùèõñÿ
ñíàðÿäîâ
ìîæåò áûòü âûðàæåíî íåðàâåíñòâîì
σ=−
>
10
4
2
fa
/,(7.15)
â êîòîðîì êîýôôèöèåíò σ íàçû-
âàåòñÿ êðèòåðèåì ãèðîñêîïè÷åñêîé
óñòîé÷èâîñòè ñíàðÿäà íà íà÷àëüíîì
ïðÿìîëèíåéíîì ó÷àñòêå òðàåêòîðèè.
Óñëîâèå óñòîé÷èâîñòè, èñõîäÿ èç σ >
> 0, ìîæíî çàïèñàòü åùå è êàê
fa
4
2
1
/.
<
(7.16)
 ãë. 4 áûëî ïîêàçàíî, ÷òî óñëîâèå
(7.15)
ÿâëÿåòñÿ
íåîáõîäèìûì
óñëîâèåì óñòîé÷èâîñòè óãëîâîãî
äâèæåíèÿ ñíàðÿäà íà íà÷àëüíîì
ó÷àñòêå òðàåêòîðèè.
Âåëè÷èíû, îò êîòîðûõ çàâèñèò f4,
îïðåäåëÿþòñÿ âî ìíîãîì ðàçìåðàìè
ñíàðÿäà, åãî íàçíà÷åíèåì è õàðàêòå-
ðèñòèêàìè äâèæåíèÿ öåíòðà ìàññ:
f4=
⎛
⎝⎜⎞
⎠⎟
⎡
⎣⎢
⎤
⎦⎥
fdVAlHy m V
a
M
22
,,,
,()
,
,ïî-
ýòîìó âàðüèðîâàòü âåëè÷èíó f4, ÷òîáû îáåñïå÷èòü âûïîëíåíèå íåðàâåíñòâà
(7.16), ïðàêòè÷åñêè íåâîçìîæíî. Çíà÷èòåëüíî ïðîùå ïðè çàäàííîì f4 îáåñ-
ïå÷èòü âûïîëíåíèå óñëîâèÿ ãèðîñêîïè÷åñêîé óñòîé÷èâîñòè ñíàðÿäà ñîîò-
âåòñòâóþùèì âûáîðîì ïàðàìåòðà à èëè íà îñíîâàíèè ôîðìóëû (7.9) óãëî-
âîé ñêîðîñòè r0.
Ðàññìîòðèì äâèæåíèå ñíàðÿäà ïðè ïðîèçâîëüíûõ íà÷àëüíûõ óñëîâèÿõ,
ïîëàãàÿ â ñèñòåìå (7.11) íà íà÷àëüíîì ó÷àñòêå òðàåêòîðèè
•
,.
θθ
==
00
Ââåäÿ
êîìïëåêñíóþ ïåðåìåííóþ z = δ2 + iδ1, óìíîæèâ ïåðâîå óðàâíåíèå (7.11) íà i
è ñëîæèâ ñî âòîðûì, çàïèøåì
•••
•
(••)( )
.
δδδδδδ
21 124
21
20
++−−+=
iaif i
Ó÷èòûâàÿ, ÷òî ii
i
••
(••),
δδδδ
21 21
− = + ïîëó÷èì
•••
.
zi
a
zf
z
−−
=
20
4
(7.17)
Ââîäÿ êîýôôèöèåíò ãèðîñêîïè÷åñêîé óñòîé÷èâîñòè σ, óðàâíåíèå ïðèâåäåì ê
âèäó
311
Ðèñ. 7 .2. Çàâèñèìîñòè δ(t)èν(t):
à – â ïëîñêîñòè ñîïðîòèâëåíèÿ; á –â
ïîëîæèòåëüíîé ïëîñêîñòè
•••
().
zi
a
zaz
−−
−
=
210
2
σ
(7.18)
Õàðàêòåðèñòè÷åñêîå óðàâíåíèå λ2 − 2iaλ−a2(1 −σ) = 0 áóäåò èìåòü ñëåäóþùèå
êîðíè:
λσ
σ
σ
12
22
11
,
()
()
.
=±
−+
−
=±−= ±
ia
a
a
iaa
ia
Çàïèøåì îáùèé èíòåãðàë óðàâíåíèÿ (7.18)
zC
e
Ce
ia
t
ia
t
=+
+−
1
1
2
1
()
()
,
σσ
(7.19)
ãäå Ñ1, Ñ2 – ïîñòîÿííûå èíòåãðèðîâàíèÿ, ÿâëÿþùèåñÿ êîìïëåêñíûìè
÷èñëàìè, îïðåäåëÿåìûìè èç íà÷àëüíûõ óñëîâèé
CeC e
ii
11 22
12
==
ρρ
εε
;.
Ñ ó÷åòîì ýòîãî èìååì
ze
e
ia
t
ia
t
=+
++
−+
ρρ
σε
σε
1
1
2
1
12
[()
[()]
.
(7.20)
Îáîçíà÷àÿ
ωσ
ωσ
12
11
=+
=−
aa
()
,()
(7.21)
è èñïîëüçóÿ ôîðìóëó eix = cosx + i sinx, çàïèøåì (7.20) â âèäå
zt
t
it
=+
++
+
++
+
ρωερ ωε
ρωερ
111
222
111
2
cos(
) cos(
)
[ sin(
) sin(
)].
ωε
22
t+
(7.22)
Ó÷èòûâàÿ, ÷òî z = δ2 + iδ1, íàéäåì âûðàæåíèÿ äëÿ óãëîâ δ1 è δ2:
δρωερωε
δρωερ
11112 22
21 112
=+
++
=+
+
sin(
) sin(
);
cos(
)
tt
t
cos(
).
ωε
22
t+
(7.23)
Ïîëàãàÿ, ÷òî â íà÷àëüíûé ìîìåíò âðåìåíè t =0
δδδδδδδδ
11
022
011
022
0
====
;;
••
;••
,
ïîäñòàâèì ýòè çíà÷åíèÿ â âûðàæåíèÿ (7.23) äëÿ δ1 è δ2 è èõ ïðîèçâîäíûå:
312
δρωερωε
δρ ωε
1
01 112 22
20
1
1
1
=+
++
=+
+
sin(
) sin(
);
cos(
)
tt
t
ρωε
δρ
ω ωερ
ωωε
222
1
01
1 112
222
cos(
);
•
cos(
)
cos(
)
t
tt
+
=+
++
;
•
sin(
)
sin(
).
−=
++
+
δρ
ω ωερ
ωωε
2
01
1 112
222
tt
(7.24)
Ðåøàÿ ñèñòåìó (7.24) îòíîñèòåëüíî ρ1, ρ2, ε1, ε2, ïîëó÷èì
ρ
σ
δω
δδω
δ
ρ
σ
δω
12
0
2
1
0
2
10
220
2
22
0
1
1
2
1
2
=+
+
−
=+
a
a
(•
)(
•
);
(•
δδω
δ
ε
δω
δ
δω
δ
10
2
10
120
2
1
10
210
20
220
)(
•
);
•
•
;
+−
=−
+
−
arctg
ε
δω
δ
δω
δ
2
10
110
20
120
=−
+
−
arctg
•
•
.
(7.25)
Íà ðèñ. 7 .3 ïðåäñòàâëåí ãðàôèê äâèæåíèÿ ïðîäîëüíîé îñè ñíàðÿäà â êî-
îðäèíàòàõ δ1 è δ2. Òî÷êà Ì ïðåäñòàâëÿåò ñîáîé ïðîåêöèþ òî÷êè ïåðåñå÷åíèÿ
ïðîäîëüíîé îñè ñíàðÿäà ñî ñôåðîé åäèíè÷íîãî ðàäèóñà, ïðîâåäåííîãî èç
öåíòðà ìàññ ñíàðÿäà íà êîîðäèíàòíóþ ïëîñêîñòü δ1Oδ2. Âåêòîð ñêîðîñòè
öåíòðà ìàññ ñíàðÿäà äëÿ ðàññìàòðèâàåìîãî ðåøåíèÿ îäíîðîäíîãî óðàâíå-
íèÿ (7.18) ïðîåöèðóåòñÿ â òî÷êó, ñîîòâåòñòâóþùóþ íà÷àëó ïðÿìîóãîëüíîé
ñèñòåìû δ1 è δ2. Äâèæåíèå òî÷êè Ì íà êîîðäèíàòíîé ïëîñêîñòè ìîæåò áûòü
ïðåäñòàâëåíî êàê ãåîìåòðè÷åñêàÿ ñóììà äâóõ äâèæåíèé: âðàùåíèÿ òî÷êè Ì
ïî êðóãó ñ ðàäèóñîì ρ1 îòíîñèòåëüíî ìãíîâåííîãî öåíòðà âðàùåíèÿ è ïåðå-
íîñíîãî êðóãîâîãî äâèæåíèÿ ìãíîâåííîãî öåíòðà âðàùåíèÿ ïî îêðóæíîñòè
ñ ðàäèóñîì ρ2. Óãëîâûå ñêîðîñòè ω1 è ω2 îïðåäåëÿþòñÿ âûðàæåíèÿìè (7.21).
Î÷åâèäíî, ÷òî ω1 > ω2.
Ïðîåêöèè ðàäèóñ-âåêòîðîâ íà êîîðäèíàòíûå îñè δ1 è δ2 ñîîòâåòñòâåííî
ðàâíûδ1=δ12+δ11;δ2=δ22+δ21,ãäå
δρωεδρωε
δρω
11
1
1
1
12
2
2
2
21
1
1
=+
=+
=+
sin(
);
sin(
);
cos(
tt
t εδρωε
12
22 22
);
cos(
).
=+
t
(7.26)
Òðàåêòîðèÿ òî÷êè Ì â ñóììàðíîì äâèæåíèè íà êîîðäèíàòíîé ïëîñêîñòè
δ1Oδ2 áóäåò ýïèöèêëîèäîé, ïîñòðîåííîé íà îêðóæíîñòè ðàäèóñà ρ2 −ρ1.Âå-
ëè÷èíû ðàäèóñ-âåêòîðîâ ρ1 è ρ2, èõ ñîîòíîøåíèå è ïîñòîÿííûå ε1 è ε2,îò
êîòîðûõ çàâèñÿò íà÷àëüíûå ïîëîæåíèÿ ðàäèóñ-âåêòîðîâ, îïðåäåëÿþòñÿ íà-
÷àëüíûìè óñëîâèÿìè. Äëÿ îáùåãî ñëó÷àÿ íà÷àëüíûõ óñëîâèé óãëû íóòàöèè
è ïðåöåññèè ìîãóò áûòü íàéäåíû ïîñëå òîãî, êàê δ1 è δ2 áóäóò îïðåäåëåíû ïî
ôîðìóëàì
δδδ νδδ
2
1
2
2
2
12
=+
=
;/
.
tg
313
 çàâèñèìîñòè îò íà÷àëüíûõ
óñëîâèé âîçìîæíû ðàçëè÷íûå
âèäû äâèæåíèé îñè ñíàðÿäà
îòíîñèòåëüíî âåêòîðà ñêîðîñ-
òè. Õàðàêòåð âîçìîæíîãî èçìå-
íåíèÿ óãëà íóòàöèè δ êàê ôóíê-
öèè óãëà ïðåöåññèè ν äëÿ ðàçëè÷íûõ íà÷àëüíûõ çíà÷åíèé •ν0 ïðè çàäàííîì
δ= δ0 ïîêàçàí íà ðèñ. 7.4.
×òîáû îïðåäåëèòü õàðàêòåð äâèæåíèÿ ïðîäîëüíîé îñè ñíàðÿäà íà êðèâî-
ëèíåéíîì ó÷àñòêå òðàåêòîðèè, íåîáõîäèìî íàéòè îáùèé èíòåãðàë ñèñòåìû
(7.11), êîòîðàÿ ïîñëå ââåäåíèÿ êîìïëåêñíîé ïåðåìåííîé z = δ2 + iδ1 ìîæåò
áûòü ïðåäñòàâëåíà â âèäå óðàâíåíèÿ
•••
••
•
.
zi
a
zf
zi
a
−−
=−
22
4
θθ
(7.27)
Ïðèíèìàÿ, êàê è ðàíåå, äîïóùåíèå î ïîñòîÿíñòâå êîýôôèöèåíòîâ à è f4,
íàéäåì ÷àñòíûé èíòåãðàë íåîäíîðîäíîãî óðàâíåíèÿ (7.27). Ðåøåíèå îáû÷íî
èùóò â âèäå ðÿäà
zz
a
z
a
z
p=+ +
+
00
1
202
11
K.
(7.28)
Èññëåäîâàíèÿ ïîêàçûâàþò, ÷òî à – áîëüøîé ïàðàìåòð è ÷ëåíû ðÿäà áû-
ñòðî óáûâàþò. Ôóíêöèè îò âðåìåíè z0, z01, z02 ïîäëåæàò îïðåäåëåíèþ. Âîçü-
ìåì ïðîèçâîäíûå zp
•
èzp
••
è âìåñòå ñ z ïîäñòàâèì èõ â (7.27):
314
Ðèñ. 7.3 . Ãðàôèê çàâèñèìîñòè δ2 = f(δ1) äëÿ
ïðÿìîëèíåéíîãî ó÷àñòêà òðàåêòîðèè áûñòðî-
âðàùàþùåãîñÿ ñíàðÿäà ïðè δ0 ≠ 0,
•
δ≠0
Ðèñ. 7.4 . Âîçìîæíûå âèäû ãðàôèêà
δ(ν) äëÿ ðàçëè÷íûõ íà÷àëüíûõ óñ-
ëîâèé
•
••
(/) ••
(/)
zi
a
za
fa
z
a
zi
za
fa
z
00
2
4
2
00
10
14
2
01
2
1
2
−−
+−−
+
+−−
+
=
−
1
2
1
2
202
02
4
2
02
a
zi
a
zfa
z
i
a
•••
(/)
••
•
.
K
θθ
 ïîëó÷åííîì óðàâíåíèè ñëàãàåìûå 1
2
01
z
••
,
1
2
02
z
••
è2
1
02
i
a
z
•
îáû÷íî ÿâëÿþòñÿ
÷ëåíàìè âòîðîãî ïîðÿäêà ìàëîñòè, êîòîðûìè ìîæíî ïðåíåáðå÷ü.
Ïðèðàâíÿåì êîýôôèöèåíòû ïðè à ñ îäèíàêîâîé ñòåïåíüþ â ïðàâîé è ëå-
âîé ÷àñòÿõ ïîñëåäíåãî óðàâíåíèÿ.
Êîýôôèöèåíòû ïðè à2 :
f
a
z
4
20
0
=
; êîýôôèöèåíòû ïðè à: −−
=
•
22
02
4
201
izf
a
zi
•
;θ
êîýôôèöèåíòû ïðè à0:
•••
•
•
.
zi
z
f
a
z
00
1
4
202
2
−−
=
−
θ
Èç òðåõ ïîñëåäíèõ óðàâíåíèé íàõîäèì
zz
ia
f
z
a
f
i
a
f
z
00
1
2
4
02
2
4
2
4
01
0
2
2
==
−
=−
;
•
;
•
•
•
.
θθ
(7.29)
Âîçüìåì ïðîèçâîäíóþ ïî t îò âòîðîãî óðàâíåíèÿ ñèñòåìû (7.29) è ïîä-
ñòàâèì z
.
01 â òðåòüå óðàâíåíèå. Ïîñëå ïðåîáðàçîâàíèÿ áóäåì èìåòü
z
a
f
a
f
f
f
02
2
4
4
4
2
4
4
4
=−
−
⎛
⎝⎜⎞
⎠⎟
•
••
•
•
.
θθ
θ
θ
Ïîäñòàâëÿÿ z0, z01 è z02 â (7.28), ïîëó÷èì
zi
a
ff
a
f
f
f
p=−
+−
−
⎛
⎝⎜⎞
⎠⎟
24
44
2
4
2
4
4
•
•••
•
•
•
.
θ
θθ
θ
(7.30)
Ó÷èòûâàÿ îáùèé âèä êîìïëåêñíîé ïåðåìåííîé, íàïèøåì
zi
ppp
=+
δδ
21
.
(7.31)
Ñðàâíèâàÿ (7.30) è (7.31), ïîëó÷èì
δθ
1
4
2
p=−
a
f
•
;
(7.32)
315
δ
θθ
θ
2
4
2
4
2
4
4
4
p=−
−
⎛
⎝⎜⎞
⎠⎟
•••
•
•
•
.
f
a
f
f
f
(7.33)
Èç ðàñ÷åòîâ ñëåäóåò, ÷òî óãîë δ1p
çíà÷èòåëüíî áîëüøå óãëà δ2p è ÿâëÿåòñÿ
ãëàâíîé ñîñòàâíîé ÷àñòüþ óãëà δp.Ðå-
øåíèå çàäà÷è î äâèæåíèè âðàùàþùåãî-
ñÿ ñíàðÿäà íà êðèâîëèíåéíîì ó÷àñòêå
òðàåêòîðèè ïîêàçûâàåò, ÷òî â ýòîì ñëó-
÷àå ýïèöèêëîèäà ñòðîèòñÿ îòíîñèòåëü-
íî äèíàìè÷åñêîé îñè ðàâíîâåñèÿ (îòíî-
ñèòåëüíî òî÷êè D íà ðèñ. 7.5). Òî÷êà D
ïðåäñòàâëÿåò ñîáîé ïðîåêöèþ íà ïëîñ-
êîñòü èçîáðàæåíèÿ òî÷êè ïåðåñå÷åíèÿ
äèíàìè÷åñêîé îñè ðàâíîâåñèÿ ñî ñôå-
ðîé åäèíè÷íîãî ðàäèóñà. Äëÿ êàæäîãî
ìîìåíòà âðåìåíè ïîëîæåíèå òî÷êè D íà
êîîðäèíàòíîé ïëîñêîñòè îïðåäåëÿåòñÿ
çíà÷åíèÿìè óãëîâ δ1p è δ2p, âû÷èñëÿå-
ìûìè ïî ôîðìóëàì (7.32) è (7.33). Óãëû δ1p è δ2p îòñ÷èòûâàþòñÿ îò íà÷àëà
êîîðäèíàò Î, ïðåäñòàâëÿþùåãî ñîáîé ïðîåêöèþ íà ïëîñêîñòü èçîáðàæåíèÿ
òî÷êè ïåðåñå÷åíèÿ êàñàòåëüíîé ê òðàåêòîðèè ñî ñôåðîé åäèíè÷íîãî ðàäèó-
ñà. Ïðè ïîñòåïåííîì îòêëîíåíèè äèíàìè÷åñêîé îñè ðàâíîâåñèÿ îò âåêòîðà
ñêîðîñòè (òî÷êè D îò òî÷êè Î) êðèâàÿ, îïèñûâàåìàÿ ðàäèóñîì ρ2, ïîëó÷àåò
âèä ñïèðàëè (â îòëè÷èå îò îêðóæíîñòè íà ðèñ. 7.3).
Òàêèì îáðàçîì, ïîëó÷åíû âûðàæåíèÿ äëÿ óãëîâ, õàðàêòåðèçóþùèõ ïîëî-
æåíèå îñè äèíàìè÷åñêîãî ðàâíîâåñèÿ. Òàê êàê δ1p >> δ2p, òî â ïåðâîì ïðè-
áëèæåíèè ìîæíî ñ÷èòàòü, ÷òî
δδ
θ
pp
≈=
1
4
2
a
f
|•|.
(7.34)
Ïîäñòàâëÿÿ âòîðîå óðàâíåíèå ñèñòåìû (3.122) â (7.34) è ïðåîáðàçóÿ ïî-
ñëåäíåå, ïîëó÷èì
δ
θ
p=
⎛
⎝⎜⎞
⎠⎟
k
HyVm
V
a
M
cos
()
.
3
(7.35)
Óãîë δð îïðåäåëÿåò ïîëîæåíèå äèíàìè÷åñêîé îñè ðàâíîâåñèÿ, îòíîñè-
òåëüíî êîòîðîé ïðîèñõîäèò ïåðèîäè÷åñêîå êîëåáàòåëüíîå äâèæåíèå ïðî-
äîëüíîé îñè âðàùàþùåãîñÿ ñíàðÿäà. Åñëè òðàåêòîðèÿ äâèæåíèÿ ñíàðÿäà
316
Ðèñ. 7.5 . Çàâèñèìîñòü δ2 = f(δ1) äëÿ
êðèâîëèíåéíîãî ó÷àñòêà òðàåêòîðèè
öåíòðà ìàññ áûñòðîâðàùàþùåãîñÿ
ñíàðÿäà ïðè óâåëè÷èâàþùåìñÿ çíà÷å-
íèè óãëà δð
ïðèáëèæàåòñÿ ê ïðÿìîé è |
•
|,
θ≈ 0 òî δp = 0 ñîãëàñíî (7.34) è êîëåáàíèÿ ïðî-
äîëüíîé îñè ñíàðÿäà áóäóò ñîâåðøàòüñÿ îòíîñèòåëüíî âåêòîðà ñêîðîñòè
äâèæåíèÿ öåíòðà ìàññ.
Óñëîâèå óñòîé÷èâîñòè âðàùàþùåãîñÿ ñíàðÿäà (7.16) ïîëó÷åíî äëÿ äâè-
æåíèÿ íà ïðÿìîëèíåéíîì ó÷àñòêå òðàåêòîðèè. Ñ óâåëè÷åíèåì êðèâèçíû
òðàåêòîðèè äèíàìè÷åñêàÿ îñü ðàâíîâåñèÿ áóäåò âñå áîëüøå îòêëîíÿòüñÿ îò
âåêòîðà ñêîðîñòè íà óãîë δp. Óãîë δp îïðåäåëÿåòñÿ ôîðìóëîé (7.35).
Àíàëèç âåëè÷èí, âõîäÿùèõ â ôîðìóëó (7.35), ïîêàçûâàåò, ÷òî óãîë δð
âäîëü êðèâîëèíåéíîãî ó÷àñòêà òðàåêòîðèè èçìåíÿåòñÿ òàêèì îáðàçîì, ÷òî â
ðàéîíå âåðøèíû òðàåêòîðèè, ãäå çíà÷åíèå cosθ áëèçêî ê íàèáîëüøåìó, à
H(y)V 3 – ê íàèìåíüøåìó, îí äîñòèãàåò íàèáîëüøåãî çíà÷åíèÿ. Ïðè íåïðà-
âèëüíîì âûáîðå ñêîðîñòè âðàùåíèÿ ñíàðÿäà óãîë δp â âåðøèíå òðàåêòîðèè
ìîæåò ñòàòü íàñòîëüêî áîëüøèì, ÷òî ýòî ïðèâåäåò ê ïîòåðå ñíàðÿäîì óñòîé-
÷èâîñòè. Ñëåäîâàòåëüíî, óãîë δp íåîáõîäèìî ðàññìàòðèâàòü êàê ñàìîñòîÿ-
òåëüíûé êðèòåðèé, îöåíèâàþùèé óñòîé÷èâîñòü âðàùàþùèõñÿ ñíàðÿäîâ íà
êðèâîëèíåéíîì ó÷àñòêå òðàåêòîðèè. Ñîïîñòàâëÿÿ çàâèñèìîñòè (7.35) è
(7.15) äëÿ êðèòåðèåâ óñòîé÷èâîñòè σ è δð, ïîëó÷àåì ïðîòèâîðå÷èâîñòü ïî-
ñëåäíèõ.
Äåéñòâèòåëüíî, ñ öåëüþ ïîâûøåíèÿ óñòîé÷èâîñòè âðàùàþùèõñÿ ñíàðÿ-
äîâ íà íà÷àëüíîì ïðÿìîëèíåéíîì îòðåçêå òðàåêòîðèè åãî óãëîâóþ ñêîðîñòü
r=
•
φ íåîáõîäèìî óâåëè÷èâàòü. Ýòî âûçîâåò ñîîòâåòñòâóþùåå óâåëè÷åíèå •ν è
óãëà δð è, ñëåäîâàòåëüíî, ïðèâåäåò ê óìåíüøåíèþ óñòîé÷èâîñòè ñíàðÿäà â
âåðøèíå òðàåêòîðèè.
Ñîâìåñòèòü îáà óñëîâèÿ óñòîé÷èâîñòè äëÿ ñíàðÿäîâ, äëèíà êîòîðûõ 5-6
êàëèáðîâ, óäàåòñÿ ïðè óãëàõ áðîñàíèÿ äî 60...65°.
 ýòîì ñëó÷àå äëÿ îáåñïå÷åíèÿ óñòîé÷èâîñòè ñíàðÿäà âäîëü âñåé òðàåê-
òîðèè äîñòàòî÷íî âûáðàòü åãî óãëîâóþ ñêîðîñòü â íà÷àëå ïàññèâíîãî ó÷àñòêà
òàê, ÷òîáû êðèòåðèé óñòîé÷èâîñòè σ áûë ðàâåí σ í
= 060 066
,,
.
K
Îòìåòèì åùå îäíó îñîáåííîñòü òðàåêòîðèé ñíàðÿäîâ, ñòàáèëèçèðóåìûõ
âðàùåíèåì. Ñóùåñòâîâàíèå óãëà δp ïðèâîäèò ê òîìó, ÷òî ïðîäîëüíàÿ îñü
ñíàðÿäà áËëüøóþ ÷àñòü âðåìåíè ïîëåòà íàõîäèòñÿ ïî îäíó èç ñòîðîí âåêòîðà
V è ñíàðÿä îòêëîíÿåòñÿ âáîê îò íà÷àëüíîé ïëîñêîñòè ñòðåëüáû. Ñèñòåìàòè-
÷åñêîå áîêîâîå îòêëîíåíèå áûñòðîâðàùàþùèõñÿ ñíàðÿäîâ íàçûâàåòñÿ äåðè-
âàöèåé. Ïðè ïðàâîì âðàùåíèè ñíàðÿäà äèíàìè÷åñêàÿ îñü ðàâíîâåñèÿ îòêëî-
íÿåòñÿ âïðàâî îò âåêòîðà (åñëè ñìîòðåòü ïî íàïðàâëåíèþ äâèæåíèÿ) è ýòî
ïðèâîäèò ê ïðàâîé äåðèâàöèè. Ïðè ëåâîì âðàùåíèè ñíàðÿä áóäåò óõîäèòü
âëåâî îò ïëîñêîñòè ñòðåëüáû, ò.å . äåðèâàöèÿ áóäåò ëåâîé. Äåðèâàöèÿ ñíàðÿ-
äà ìîæåò áûòü îïðåäåëåíà îïûòíûì ïóòåì èëè ðàñ÷åòîì. Èç òåîðåòè÷åñêèõ
ôîðìóë (ïðèìåíèòåëüíî ê ñíàðÿäàì ïîñòîÿííîé ìàññû) èçâåñòíû ôîðìóëû
À.Í. Êðûëîâà, Â.È . Îñòàïîâè÷à è Ï.Ï . Áåðåñíåâà, ôîðìóëà Ä.À . Âåíòöåëÿ
è ìåòîä ðàñ÷åòà, ïðåäëîæåííûé Â.Í. Ïåðøèíûì. Îäíîé èç íàèáîëåå èñ-
ïîëüçóåìûõ ÿâëÿåòñÿ ôîðìóëà À.Í. Êðûëîâà:
317
zf
g
Q
C
hRd
Vd
t
t
=−
∫
2
00
0
π
η
φφ
()
,
(7.36)
ãäå R – ïîëóêàëèáð ñíàðÿäà; φ – óãîë ìåæäó êàñàòåëüíîé ê òðàåêòîðèè è
âåðòèêàëüþ; Ñ – îñåâîé ìîìåíò èíåðöèè ñíàðÿäà.
Ôîðìóëà ñîäåðæèò âåëè÷èíû, îïðåäåëÿåìûå èç îïûòà: íåèçâåñòíóþ òî÷-
íî âåëè÷èíó h, ïðîïîðöèîíàëüíóþ ðàññòîÿíèþ ìåæäó öåíòðîì ìàññ è öåí-
òðîì äàâëåíèÿ ñíàðÿäà, è êîýôôèöèåíò ñîãëàñîâàíèÿ ñ îïûòîì f. Äëÿ îäíî-
òèïíûõ ñíàðÿäîâ è òðàåêòîðèé ôîðìóëà äàåò óäîâëåòâîðèòåëüíûå ðåçóëüòà-
òû. Áîëåå îáùåé ÿâëÿåòñÿ ôîðìóëà Â.Í . Ïåðøèíà, ó÷èòûâàþùàÿ ÿâëåíèå
çàòóõàíèÿ óãëîâîé ñêîðîñòè ñíàðÿäà âî âðåìÿ ïîëåòà.
Ðàññìîòðèì ðàñ÷åòíîå îïðåäåëåíèå äåðèâàöèè. Óðàâíåíèå äâèæåíèÿ
öåíòðà ìàññ ñíàðÿäà ïî îñè OZg ñèñòåìû êîîðäèíàò OXgYgZg áóäåò èìåòü âèä
Q
g
zRX
gza
•
•
cos
=−
(VZ
ag
∧
),
(7.37)
ãäå Rz
–
áîêîâàÿ ñèëà, îáóñëîâëåííàÿ óãëîì δp.
Ìîæíî ñäåëàòü çàìåíó cos(
)/,
VZ
ag
g
zV
∧
•
=
è òîãäà
z
g
Q
R
g
Q
X
z
V
gza
g
••
=−
•
.
(7.38)
Âûïîëíÿÿ çàìåíó g
Q
Xc
H
y
F
V
a
=
()( )è ïîìíÿ, ÷òî G(V)=F(V )/V, ïîëó-
÷èì
••
()()•
.
z
g
Q
Rc
Hy
G
Vz
gz
g
=−
(7.39)
Ó÷èòûâàÿ îòíîñèòåëüíî íåáîëüøóþ êðèâèçíó òðàåêòîðèè, îïðåäåëÿå-
ìóþ äåðèâàöèåé, ìîæíî âîñïîëüçîâàòüñÿ çàâèñèìîñòüþ, ñïðàâåäëèâîé äëÿ
ïëîñêîé òðàåêòîðèè: cH y G V u u
() () •/.
=
Òîãäà èç (7.39) ìîæíî íàïèñàòü
••
••
,
z
uz
u
g
Q
R
g
g
z
−=
(7.40)
èëè
u
d
dt
z
u
g
Q
R
g
z
⎛
⎝⎜⎞
⎠⎟=
.
(7.41)
Èíòåãðèðóÿ (7.40), ïîëó÷èì
318
z
g
Q
udt
R
u
dt
g
t
z
t
=
∫∫
00
.
(7.42)
Ðàñêðîåì ñîäåðæàíèå Rz. Îáû÷íî ïðåäïîëàãàåòñÿ, ÷òî ñèëà, îòêëîíÿþ-
ùàÿ âðàùàþùèéñÿ ñíàðÿä îò ïëîñêîñòè áðîñàíèÿ, ïðîïîðöèîíàëüíà óãëó
δp; òîãäà â ñîîòâåòñòâèè ñ îáùåé òåîðèåé àýðîäèíàìè÷åñêîãî ïîäîáèÿ
R
dl
g
HyVc
zN
=⋅
1033
().
δp
(7.43)
Ââîäÿ â (7.43) çíà÷åíèå δp è ïîëüçóÿñü (7.34), ðàñêðîåì çíà÷åíèÿ âåëè÷èí
à è f4; çíà÷åíèå |
•
|θ îïðåäåëèì êàê îáû÷íî. Êðîìå òîãî, áóäåì ïîìíèòü, ÷òî
cosθ = u/V. Òîãäà, íå ó÷èòûâàÿ çàòóõàíèå âðàùåíèÿ ïîä äåéñòâèåì ìîìåíòà
ïîâåðõíîñòíîãî òðåíèÿ, ïîëó÷èì äëÿ ðàñ÷åòà äåðèâàöèè ñëåäóþùåå âûðàæå-
íèå:
z
gl
h
Vud
t
c
m
dt
V
N
M
t
t
=
∫
∫
πμ
η
2
0
2
0
0
.
(7.44)
Èìåÿ îïûòíûå àýðîäèíàìè÷åñêèå õàðàêòåðèñòèêè c V
a
N
⎛
⎝⎜⎞
⎠⎟, m
V
a
M
⎛
⎝⎜⎞
⎠⎟ èïî-
ëó÷åííûå ðàñ÷åòîì äëÿ ïëîñêîé òðàåêòîðèè çíà÷åíèÿ V = V(t)èu = u(t),
ìîæíî âû÷èñëèòü èíòåãðàë ïðàâîé ÷àñòè (7.44) è ðàññ÷èòàòü äåðèâàöèþ [34].
7.1.2. ÄÎÑÒÀÒÎ×ÍÛÅ ÓÑËÎÂÈß ÓÑÒÎÉ×ÈÂÎÑÒÈ ÓÃËÎÂÎÃÎ
ÄÂÈÆÅÍÈß ÑÍÀÐßÄÀ
 ãë. 4 áûëî ïîêàçàíî, ÷òî óñëîâèå óñòîé÷èâîñòè Ìàèåâñêîãî
(4.71) èëè (7.15) ÿâëÿåòñÿ íåîáõîäèìûì â òîì ñìûñëå, ÷òî â îãðàíè-
÷åííîé îáëàñòè ôàçîâîãî ïðîñòðàíñòâà ïåðåìåííûõ δ1, δ2,
•
,
δ1
•
δ2 âîê-
ðåñòíîñòè íà÷àëà êîîðäèíàò âûïîëíåíèå ýòîãî óñëîâèÿ îáåñïå÷èâà-
åò óñòîé÷èâîñòü äâèæåíèÿ ïî Ëÿïóíîâó. Òàê êàê ýòà îáëàñòü îãðàíè-
÷åíà, òî ðå÷ü èäåò îá óñòîé÷èâîñòè â ìàëîì.
Ñ ïðàêòè÷åñêîé òî÷êè çðåíèÿ âàæíî, ÷òîáû óãîë íóòàöèè δ âî âñå
âðåìÿ ïîëåòà íå ïðåâîñõîäèë íåêîòîðîãî ïðåäåëüíî äîïóñòèìîãî
çíà÷åíèÿ:
δδ
()
[; ],
tt
T
<∈
äîï
ïðè
0
(7.45)
ãäå Ò – ïîëíîå âðåìÿ ïîëåòà ñíàðÿäà.
Íåîáõîäèìî óñòàíîâèòü, ïðè êàêèõ íà÷àëüíûõ óãëîâûõ âîçìóùå-
íèÿõ â ìîìåíò âûëåòà ñíàðÿäà èç êàíàëà ñòâîëà áóäåò âûïîëíÿòüñÿ
óñëîâèå (7.45).
319
Ýòà çàäà÷à áûëà ïîñòàâëåíà è ðåøåíà Í.Ã. ×åòàåâûì [126] äëÿ
ðÿäà ïðàêòè÷åñêè àêòóàëüíûõ ñëó÷àåâ. Óñëîâèÿ, ïîçâîëÿþùèå ïî
çàäàííîìó îãðàíè÷åíèþ δäîï óñòàíîâèòü äèàïàçîí èçìåíåíèÿ íà-
÷àëüíûõ óãëîâûõ âîçìóùåíèé, ïðè êîòîðûõ ýòî îãðàíè÷åíèå íå íà-
ðóøàåòñÿ, Í.Ã. ×åòàåâ íàçâàë äîñòàòî÷íûìè óñëîâèÿìè óñòîé÷èâîñòè
âðàùàòåëüíîãî äâèæåíèÿ ñíàðÿäà.
Ðàññìîòðèì äâèæåíèå àðòèëëåðèéñêîãî ñíàðÿäà íà íà÷àëüíîì
ó÷àñòêå òðàåêòîðèè, ñ÷èòàÿ ñêîðîñòü äâèæåíèÿ åãî öåíòðà ìàññ è óã-
ëîâóþ ñêîðîñòü âîêðóã ïðîäîëüíîé îñè ïîñòîÿííûìè âåëè÷èíàìè.
 ï. 4 .3 .1 áûëî ïîêàçàíî, ÷òî äâèæåíèå ñíàðÿäà îòíîñèòåëüíî öåí-
òðà ìàññ ìîæíî îïèñàòü ñèñòåìîé ÷åòûðåõ ïåðâûõ èíòåãðàëîâ (4.60),
òðè èç êîòîðûõ çàïèñûâàþòñÿ â âèäå
zzzzazh
zzz f
zh
zz
23 32
11
1
2
2
2
3
2
41
2
1
2
2
22
••
;
•••
;
−+=
+++ =
+2
2
3
2
1
+=
z
.
(7.46)
Èç ïåðâîãî âûðàæåíèÿ (7.46) ñëåäóåò
(••
)( ).
zz zz
haz
23 32
2
11
2
2
−=
−
Âîçâåäÿ â êâàäðàò, èìååì
zz
zzzzzzhaz
2
2
3
2
2323 3
2
2
2
11
2
22
••
•
•
()
.
−+
=
−
(7.47)
Äèôôåðåíöèðóÿ ïî âðåìåíè òðåòèé ïåðâûé èíòåãðàë (7.46), íàéäåì
zzzzzz
1122330
•••
.
++=
Ïîñëå ïåðåíîñà âòîðîãî è òðåòüåãî ñëàãàåìûõ â ïðàâóþ ÷àñòü ýòîãî
ðàâåíñòâà è âîçâåäåíèÿ åãî â êâàäðàò ïîëó÷èì
22323 1
2
1
2
2
2
2
2
3
2
3
2
zzzz zz zz zz
••
•
•
•
.
=−−
Ïîäñòàâèâ ýòî âûðàæåíèå â (7.47), ïîñëå ïðåîáðàçîâàíèé áóäåì
èìåòü
•••
.
zzz
z
zz
ha
z
zz
2
2
3
2
1
2
1
2
2
2
3
2
1
2
2
3
2
2
+=
+
+
−
+
Òàêêàêzz z
2
2
3
2
1
2
1
+=
−
,òî
320
•••
()
.
zzz
z
z
ha
z
z
2
2
3
2
1
2
1
2
1
2
11
2
1
2
1
2
1
+=
−
+
−
−
(7.48)
Ïîäñòàâëÿÿ (7.48) âî âòîðîå âûðàæåíèå (7.46) è ïðåîáðàçóÿ, ïîëó÷èì
•
()
(
)
()
.
zhf
zzha
z
1
2
24
11
2
11
2
221
2
=−
−
−
−
(7.49)
Ïðàâàÿ ÷àñòü (7.49) ïðåäñòàâëÿåò ñîáîé ïîëèíîì òðåòüåé ñòåïåíè
îòíîñèòåëüíî z1 = cosδ. Îáîçíà÷èì
fzhfzzhaz
()(
)( )(
).
12
4
11
2
11
2
221
2
=−
−
−
−
(7.50)
Ïîëèíîì f(z1) îòðèöàòåëåí ïðè z1 →−∞, z1 = ±1 è ïîëîæèòåëåí ïðè
z1 → +∞ è z1 = z10 = cosδ0 (òàê êàê •z 1 ïî ôèçè÷åñêîìó ñìûñëó äîëæíà
áûòü äåéñòâèòåëüíîé âåëè÷èíîé). Îòñþäà ñëåäóåò, ÷òî òðè êîðíÿ
ýòîãî ïîëèíîìà z11, z12, z13 äåéñòâèòåëüíû è ëåæàò ñîîòâåòñòâåííî â
èíòåðâàëàõ
zz
z
zz
11
10
12
10
13
11
1
∈−
∈
+
∈+∞
];[;];[;];[.
Ïîýòîìó f(z1) ìîæíî ïðåäñòàâèòü â âèäå
fz fzzzzzz
(
)()
()
()
.
14
11
111
211
3
2
=−−−
Òàê êàê z1 = cosδ è ïðèíèìàåò çíà÷åíèÿ âñåãäà â èíòåðâàëå îò −1äî
+1, òî äëÿ íàøåé çàäà÷è îïðåäåëÿþùèì áóäåò èíòåðâàë [z11; z12],
âíóòðè êîòîðîãî òîëüêî è ìîæåò èçìåíÿòüñÿ ïåðåìåííàÿ z1 (z1 ∈ [z11;
z12]).
Äðóãèìè ñëîâàìè, óãîë δ áóäåò êîëåáàòüñÿ ìåæäó çíà÷åíèÿìè
δmax = arccosz11 è δmin = arccosz12, ò.å.
arccos
arccos .
min
max
z
z
12
11
=<
<=
=
δδδ
Ñëåäîâàòåëüíî, óãëû íóòàöèè
áóäóò îñòàâàòüñÿ ìàëûìè â
òå÷åíèå ïîëåòà ñíàðÿäà, åñëè
êîðíè f(z1), z11 è z12 ïîëèíîìà
áóäóò áëèçêè ê åäèíèöå, òàê êàê â
ýòîì ñëó÷àå z1 = cosδ îêàæåòñÿ
áëèçêèì ê åäèíèöå è, ñëåäîâà-
òåëüíî, δ áóäåò ïðèíèìàòü ìàëûå
çíà÷åíèÿ (ðèñ. 7.6). Íàéäåì
321
Ðèñ. 7 .6. Ãðàôèê ïîëèíîìà f(z1)
óñëîâèÿ, ïðè êîòîðûõ óãîë íóòàöèè îñòàåòñÿ ìàëîé âåëè÷èíîé, ò.å .
óñëîâèÿ, ïðè êîòîðûõ êîðíè ïîëèíîìà z11 è z12 áóäóò áîëüøå (1 −∆),
ãäå ∆ – ïðîèçâîëüíî ìàëàÿ âåëè÷èíà (ñì. ðèñ. 7.6):
cos
.
δ=>−
z11∆
(7.51)
Íåðàâåíñòâî (7.51) áóäåò âûïîëíåíî, åñëè
10
1
−−
<
∆z
.
(7.52)
Íåðàâåíñòâî (7.52) âûïîëíÿåòñÿ, åñëè âñå êîðíè ïîëèíîìà F(x)=
=−f(1 −∆ −x) îòðèöàòåëüíû. Ââåäåííûé òàêèì îáðàçîì ïîëèíîì F(x)
èìååò âèä
Fxh
aax
hf
fx
()[()][
()
][(
=−− +
−
−
−
+
+−
−
1
2
24
4
21
2
221
211
∆∆
∆)() ]
.
22
21
+−−
∆xx
Ðàñêðûâàÿ ñêîáêè, ïîñëå ïðåîáðàçîâàíèé ïîëó÷èì
Fxfxaxaxa
()
,
=+
+
+
24
3
1
2
23
(7.53)
ãäå
aha f
aa
ha
f
12
4
4
21
4
2
24 61
42
12
2
=+−
−
=−
−
−
−
−
−
()
;
[()
]()
∆
∆∆
∆
21
221
21
221
24
31
2
24
()
[()
]
;
[()
]
[(
−−
−
=−−−−
−
∆∆
∆∆
hf
aha
hf)][()].
112
−−
∆
Óñëîâèå îòðèöàòåëüíîñòè êîðíåé ïîëèíîìà F(x), ñîãëàñíî òåîðåìå
Ãóðâèöà, èìååò âèä
aa
af
aa
11
24
33
0200
>−>>
;;
.
(7.54)
Ïîäñòàâëÿÿ â (7.54) çíà÷åíèÿ a1, a2, a3, ïîëó÷èì
2466 0
2464 22
22
2
2
44
24
12
haff
hafa
ha hf
+−+ >
+−
−
−
−
∆;
()
[
(
)
(
44
1
2
2
2
4
2
41
22
2246
44
22
)](
)
{(
)[()(
−−
+
++
−
+
−
−
fha
haf fa
ha 22
16246
32
0
2
24
42
2
4
2
4
23
1
hf
fhaf
f
ha
−+
++
−
+>
−
)]}
();
()
∆
∆∆
2
12
4
2
2
4
2
4
3
422
22
24620
+−
−
−
+
++−+>
[( )(
)]
()
aha
hf
haf f
∆
∆∆.
(7.55)
322
Åñëè íåðàâåíñòâà (7.55) âûïîëíÿþòñÿ äëÿ ëþáîãî t ∈ [0; T], òî
îáåñïå÷èâàåòñÿ ìàëîñòü óãëîâ íóòàöèè â òå÷åíèå âñåãî âðåìåíè
ïîëåòà ñíàðÿäà, òàê êàê áóäåò âûïîëíÿòüñÿ óñëîâèå
11
11
12
−<
<<<
∆zz
cos
,
δ
(7.56)
îòêóäà ñëåäóåò, ÷òî
01
<<
−
=
δδ
arccos (
).
∆
äîï
(7.57)
Íåðàâåíñòâà (7.55) ïðåäñòàâëÿþò ñîáîé (ïî òåðìèíîëîãèè
Í.à . ×åòàåâà) äîñòàòî÷íûå óñëîâèÿ äëÿ óñòîé÷èâîñòè óãëà íóòàöèè.
Ïîêàæåì, êàê ìîæíî èñïîëüçîâàòü ýòè óñëîâèÿ â ïðàêòè÷åñêèõ
çàäà÷àõ. Âõîäÿùèå â (7.55) ïåðâûå èíòåãðàëû h1 è h2 çàâèñÿò îò íà-
÷àëüíûõ óñëîâèé. Äëÿ èäåàëüíîãî îðóäèÿ, ó äóëüíîãî ñðåçà êîòîðîãî
ñíàðÿä èìååò δδ
000
==
•
, âñå íåðàâåíñòâà (7.55) óäîâëåòâîðÿþòñÿ îä-
íîâðåìåííî è íåçàâèñèìî îò ∆, åñëè âûïîëíÿåòñÿ óñëîâèå Ìàèåâ-
ñêîãî a2 − f4 > 0. Äåéñòâèòåëüíî, äëÿ íà÷àëüíîãî ìîìåíòà âðåìåíè
ìîæåì íàïèñàòü
22
2
21
0
2
20
2
30
2
410
1
2030 3020
hzzz f
z
hzzzz a
=+++
=−+
•••
;
••
z 10.
Ñ ó÷åòîì âûðàæåíèé äëÿ •z i ïîëó÷èì
22
2
20
2
0
22
040
10
2
00
hf
ha
=+
+
=+
•
•
sin
cos ;
•
sin
cos .
δνδ
δ
νδ
δ
(7.58)
Åñëè δδ
000
==
•
, òî 2h2 =2f4 è h1 =2a. Ïîäñòàâëÿÿ ýòè çíà÷åíèÿ
ïåðâûõ èíòåãðàëîâ â (7.55), ìîæíî ïðèâåñòè ýòè íåðàâåíñòâà ê âèäó
46
0
32
64
32
2
44
2
4
2
4
2
4
2
4
23
();
() ()
aff
af
faf f
−+>
−+
−+>
∆
∆∆
∆
0
42
0
2
4
2
4
3
;
()
.
af
f
−+>
∆∆
(7.59)
Òàê êàê ïî ñîäåðæàíèþ çàäà÷è f4 è ∆ – ÷èñëà ïîëîæèòåëüíûå, âñå
íåðàâåíñòâà áóäóò óäîâëåòâîðÿòüñÿ íåçàâèñèìî îò ∆, åñëè à
2
−
f4 >0.Â
ýòîì ñìûñëå óñëîâèå Ìàèåâñêîãî ÿâëÿåòñÿ óñëîâèåì óñòîé÷èâîñòè
ñíàðÿäà íà ïðÿìîëèíåéíîì ó÷àñòêå òðàåêòîðèè â áåñêîíå÷íî ìàëîì.
323
Äëÿ ðåàëüíîãî îðóäèÿ, êîãäà íà÷àëüíûå çíà÷åíèÿ δ0 è
•
δ0 â ìîìåíò
âûëåòà îòëè÷íû îò íóëÿ, íåðàâåíñòâà (7.55) îïðåäåëÿþò ðàññìàòðè-
âàåìîå îòêëîíåíèå ∆ (ñì. ðèñ. 7 .6) êàê íàèìåíüøåå çíà÷åíèå, óäîâ-
ëåòâîðÿþùåå íåðàâåíñòâàì (7.55).  ïðàêòè÷åñêè àêòóàëüíîì ñëó÷àå
δ0 =0
,
•
δ00
> ïåðâûå èíòåãðàëû ñîãëàñíî (7.58) ðàâíû
hah f
12
0
2
4
22
2
==
+
,
•
δ
è íåðàâåíñòâà (7.55) ìîæíî çàïèñàòü â âèäå
•
();
[• ()
]
•
{[•
δ
δδ
δ
0
22
44
0
22
40
2
0
2
46
0
24
2
+−+ >
−+
−
+
aff
af
∆
+−−
−+− +
4
81
643
2
2
4
2
40
2
40
22
4
2
4
2
()
]
•
}[
•
()
]
af
ffa
ff
δδ
∆∆
∆
3
0
2
0
22
4
2
4
3
0
242
0
>
−+
+−+>
;
•
[• ()
]
.
δδ
∆∆
∆
af
f
(7.60)
Àíàëèç ýòèõ íåðàâåíñòâ ïîêàçûâàåò, ÷òî ïåðâîå èç íèõ óäîâëåò-
âîðÿåòñÿ íåçàâèñèìî îò ∆, åñëè
saf
=−>
2
4
0.
Åñëè æå ïðè ýòîì âåëè÷èíà s óäîâëåòâîðÿåò åùå óñëîâèþ
(•)
•
,
sf
+−≥
δδ
0
22
40
2
20
(7.61)
òî
∆<
+
20
2
0
2
•
/( •).
δδ
s
(7.62)
Ñ ó÷åòîì (7.56) ïîñëåäíåå îòíîøåíèå öåëåñîîáðàçíî âûáèðàòü
ìåíüøå ïðåäåëüíîãî äîïóñêà äëÿ çíà÷åíèÿ óãëà íóòàöèè. Ïðè çàäàí-
íûõ äîïóñêå δäîï è íà÷àëüíîé ñêîðîñòè íóòàöèè
•
δ0 íåðàâåíñòâî (7.62)
îïðåäåëèò âåëè÷èíó íóæíîãî çàïàñà óñòîé÷èâîñòè s, çàâèñÿùåãî îò
óãëîâîé ñêîðîñòè âðàùåíèÿ âîêðóã ïðîäîëüíîé îñè a
Cr
A
=
⎛
⎝⎜⎞
⎠⎟
2
. Èíà-
îáîðîò, ïðè íàéäåííûõ çàïàñàõ óñòîé÷èâîñòè s è çàäàííûõ ïðåäåëü-
íûõ îòêëîíåíèÿõ ∆ ñîîòíîøåíèå (7.62) îïðåäåëÿåò äîïóñòèìóþ âå-
ëè÷èíó íà÷àëüíûõ âîçìóùåíèé
•
.
δ0
324
7.1.3 . ÂËÈßÍÈÅ ÑÒÐÓÊÒÓÐÛ ÄÅÉÑÒÂÓÞÙÈÕ ÑÈË ÍÀ ÓÑÒÎÉ×ÈÂÎÑÒÜ
ÄÂÈÆÅÍÈß ÑÍÀÐßÄÎÂ, ÑÒÀÁÈËÈÇÈÐÓÅÌÛÕ ÂÐÀÙÅÍÈÅÌ
Èññëåäîâàíèå óãëîâîãî äâèæåíèÿ ñíàðÿäà ïðè äåéñòâèè òîëüêî
îïðîêèäûâàþùåãî ìîìåíòà ïîçâîëÿåò îïðåäåëèòü îñíîâíûå êà÷åñò-
âåííûå õàðàêòåðèñòèêè äâèæåíèÿ è â ïåðâîì ïðèáëèæåíèè ïîëó-
÷èòü êîëè÷åñòâåííûå îöåíêè èçìåíåíèÿ óãëîâûõ êîîðäèíàò ñíàðÿ-
äà. Íåîáõîäèìî ðàññìîòðåòü, êàê âëèÿþò íà óñòîé÷èâîñòü äâèæåíèÿ
äðóãèå ñèëû è ìîìåíòû, ïðåæäå âñåãî ýêâàòîðèàëüíûé äåìïôèðóþ-
ùèé ìîìåíò, ìîìåíò Ìàãíóñà è ïîâåðõíîñòíîãî òðåíèÿ.
Äëÿ îïèñàíèÿ óãëîâîãî äâèæåíèÿ â ýòîì ñëó÷àå ìîæíî èñïîëüçî-
âàòü óðàâíåíèÿ 3...5 ñèñòåìû (3.166):
••
()
•
()
•
(
)
δδδ
δ
112
2
2
1
21
4
2
++ −+
−
+
++
Vcm
ac
ac
ma
V
ND
M
Ma
Ma
v
()c
o
s
;
••
()
•
()
•
mc
a
Vg
Vcm
ac
N
ND
Ma
Ma
−=
−
++ ++
−
δθ
δδ
2
1
22
2
21δ
δδ
θ
1
2
2
21
4
2
−+
+−−
=
=−
(
)()c
o
s
;
•
ac
Vm
aVm c
mg
aV
m
a
MN
D
Ma
Ma
ã
.
(7.63)
Ïåðâûå äâà óðàâíåíèÿ ýòîé ñèñòåìû, ââåäÿ âåêòîð δ =[δ1; δ2]
ò
, ìîæíî
ïðèâåñòè ê âèäó
••• •
,
δδδδδ
++++=
BGCP ∆
(7.64)
ãäå îáîçíà÷åíî
BGC
P
=
⎡
⎣⎢
⎤
⎦⎥=
−
⎡
⎣⎢
⎤
⎦⎥ =⎡
⎣⎢
⎤
⎦⎥
=
−
⎡
⎣⎢
b
b
g
g
c
c
p
p
0
0
0
0
0
0
0
0
;;;
⎤
⎦⎥ =⎡
⎣⎢
⎤
⎦⎥
=+=+=
−
;;
()
;()
;(
∆
∆
∆
1
2
2
21
4
bVcmgacc
ac
ND
Ma
Ma+
=−
=
−
=
−
Vm
pa
V
mc
a
Vg
m
g
M
ND
2
1
1
2
22
);
(
);
cos ;
cos .
Ma
∆∆
θθ
Óðàâíåíèå (7.64) èñïîëüçóþò ïðè àíàëèçå óñòîé÷èâîñòè óãëîâîãî
äâèæåíèÿ ïî âèäó ìàòðèö äåéñòâóþùèõ îáîáùåííûõ ñèë, âõîäÿùèõ â
óðàâíåíèÿ äâèæåíèÿ.
Àíàëèçó ðàçëè÷íûõ âîçìóùàþùèõ ñèë, âëèÿþùèõ íà óñòîé÷è-
âîñòü äâèæåíèÿ, ñ òî÷êè çðåíèÿ èõ ôèçè÷åñêîé ïðèðîäû è ñòðóêòó-
ðû äåéñòâóþùèõ ñèë ïîëîæèëè íà÷àëî ðàáîòû Òîìñîíà è Òåéòà
[144], ñôîðìóëèðîâàâøèõ ðÿä îáùèõ òåîðåì, ñòðîãîå äîêàçàòåëüñòâî
325
êîòîðûõ äëÿ ïðàêòè÷åñêè âàæíûõ ñëó÷àåâ áûëî äàíî Í.Ã. ×åòàåâûì.
Ýòè ðåçóëüòàòû ïîçâîëÿþò óãëóáèòü ôèçè÷åñêîå ïðåäñòàâëåíèå î
âëèÿíèè ðàçëè÷íûõ ñèë íà óñòîé÷èâîñòü äâèæåíèÿ, ïîëó÷èòü êà÷å-
ñòâåííûå îöåíêè îòäåëüíûõ ôàêòîðîâ, âëèÿþùèõ íà óñòîé÷èâîñòü.
 îñíîâó êëàññèôèêàöèè äåéñòâóþùèõ íà ñèñòåìó îáîáùåííûõ
ñèë ïîëîæåíû óðàâíåíèÿ Ëàãðàíæà 2-ãî ðîäà
d
dt
T
q
T
q
Qqq i
n
ii
i
∂
∂
∂
∂
•
(,
•
), ,,,
⎛
⎝⎜⎞
⎠⎟ −=
=
1K
(7.65)
ãäå Ò – êèíåòè÷åñêàÿ ýíåðãèÿ ñèñòåìû.
Ðàññìîòðèì ñëó÷àé ëèíåéíîé çàâèñèìîñòè ñèëû Q =[Q1, ..., Qn]
ò
îò âåêòîðîâ îáîáùåííûõ êîîðäèíàò q =[q1, ..., qn]
ò
è ñêîðîñòåé •q
QC
qB
q
=−
−
11
•
,
(7.66)
ãäå Ñ1 è Â1 – èçâåñòíûå ìàòðèöû ðàçìåðà n×n. Ìàòðèöû Ñ1 è Â1
ìîæíî ïðåäñòàâèòü â âèäå ñèììåòðè÷åñêèõ Ñ0 è Â0 è
êîñîñèììåòðè÷åñêèõ Ð0 è G0 ÷àñòåé:
CCPBBG
100100
=+
=+
;.
Òîãäà âåêòîð îáîáùåííîé ñèëû Q ìîæíî ïðåäñòàâèòü â âèäå ñóììû
QKRDÃ
=+++
,
(7.67)
ãäåK= −C0q;R= −P0q;D= −Bq
0
•
;Ã= −Gq
0
•
. Ñèëà K ñ ñèììåòðè÷íîé
ìàòðèöåé C0 =||cij || íàçûâàåòñÿ ïîòåíöèàëüíîé èëè êîíñåðâàòèâíîé,à
êâàäðàòè÷íàÿ ôîðìà ÏC
q
q
=⋅
1
20
áóäåò îïðåäåëÿòü ïîòåíöèàëüíóþ
ýíåðãèþ ñèñòåìû. Ýëåìåíòû ñèëû R = −P0q, ëèíåéíî çàâèñÿùèå îò
êîîðäèíàò q ñ êîñîñèììåòðè÷åñêîé ìàòðèöåé êîýôôèöèåíòîâ Ð,
íàçûâàþòñÿ íåêîíñåðâàòèâíûìè ïîçèöèîííûìè ñèëàìè. Ñèëû D = −Bq
0
•
íàçûâàþòñÿ äèññèïàòèâíûìè ñèëàìè, à êâàäðàòè÷íàÿ ôîðìà
FB
q
q
=⋅
1
20
••
,
åñëè îíà íåîòðèöàòåëüíà, íàçûâàåòñÿ ôóíêöèåé
ðàññåèâàíèÿ èëè äèññèïàòèâíîé ôóíêöèåé Ðýëåÿ. Åñëè êâàäðàòè÷íàÿ
ôîðìà F îïðåäåëåííî-ïîëîæèòåëüíà, òî äèññèïàöèÿ íàçûâàåòñÿ
ïîëíîé, â ïðîòèâíîì ñëó÷àå – íåïîëíîé. Ñèëû à = −G0q, ëèíåéíî
çàâèñÿùèå îò ñêîðîñòåé •q è èìåþùèå êîñîñèììåòðè÷åñêóþ ìàòðèöó
êîýôôèöèåíòîâ G0, íàçûâàþòñÿ ãèðîñêîïè÷åñêèìè ñèëàìè.
326
Óðàâíåíèÿ äâèæåíèÿ (7.66) ïðèâîäÿòñÿ ê âèäó
AqBqCqQ
•••
,
()
++=
11
2
(7.68)
ãäå À – îïðåäåëåííî-ïîëîæèòåëüíàÿ ìàòðèöà; Q(2)
–
âåêòîð
îáîáùåííûõ ñèë, ñîäåðæàùèé êîîðäèíàòû qi è •q i â ñòåïåíè âûøå
ïåðâîé.
Èñïîëüçóÿ ïðåäñòàâëåíèå Q â âèäå (7.67), ïîëó÷èì
AqBqGqPqQ
•
•••
.
()
++ +=
000
2
(7.69)
Óðàâíåíèå äâèæåíèÿ (7.69) ñ ïîìîùüþ ïðåîáðàçîâàíèÿ q = Sz, ãäå
S – îðòîãîíàëüíàÿ ìàòðèöà ïðåîáðàçîâàíèÿ, ìîæíî çàïèñàòü â âèäå
•
•••
,
zB
zG
zC
zP
zZ
++++=
(7.70)
ãäå  – ñèììåòðè÷åñêàÿ ìàòðèöà; G è P – êîñîñèììåòðè÷åñêèå
ìàòðèöû, à Ñ – äèàãîíàëüíàÿ ìàòðèöà (Â = S
ò
B0S;G=S
ò
G0S;P=
=S
ò
P0S;C=S
ò
C0S;Z=S
ò
Q(2)S).
 ðåçóëüòàòå ïîòåíöèàëüíûå, äèññèïàòèâíûå, ãèðîñêîïè÷åñêèå è
íåêîíñåðâàòèâíûå ïîçèöèîííûå ñèëû ïðåîáðàçóþòñÿ â ñèëû òîé æå
ñòðóêòóðû. Óïîòðåáëåíèå çäåñü òåðìèíàëà "ñèëà" íîñèò óñëîâíûé
õàðàêòåð (ñì. [85]) â òîì ñìûñëå, ÷òî ÷ëåíû óðàâíåíèÿ (7.65), òðàê-
òóåìûå êàê ñèëû (îáîáùåííûå ñèëû), íå ïðåäñòàâëÿþò ñîáîé ðåàëü-
íûå ñèëû, à ïîëó÷èëèñü â ðåçóëüòàòå íåêîòîðûõ ìàòåìàòè÷åñêèõ
ïðåîáðàçîâàíèé.
Ðàññìîòðèì âëèÿíèå ãèðîñêîïè÷åñêèõ, äèññèïàòèâíûõ è íåêîí-
ñåðâàòèâíûõ ïîçèöèîííûõ ñèë (ñì. óðàâíåíèå (7.64)) íà óñòîé÷è-
âîñòü äâèæåíèÿ ñíàðÿäà îòíîñèòåëüíî öåíòðà ìàññ. Åñëè íà ñíàðÿä
äåéñòâóþò òîëüêî ïîòåíöèàëüíûå ñèëû (îïðåäåëÿåìûå â îñíîâíîì
îïðîêèäûâàþùèì ìîìåíòîì), ò.å . ñíàðÿä íå çàêðó÷åí âîêðóã ïðî-
äîëüíîé îñè, óðàâíåíèå (7.64) èìååò âèä
••
.
δδ
+=
C∆
(7.71)
Ïåðåõîäÿ ê ñêàëÿðíûì óðàâíåíèÿì
•
•
;••
()
,
δδ δδ
1
11 122
2212
+= +=
=
=
cc
c
c
c
∆∆
(7.72)
ìîæíî íàïèñàòü õàðàêòåðèñòè÷åñêèå ÷èñëà λi ýòîé ñèñòåìû:
λλ
12
134
2
,,
;.
=±−
=±−
cc
327
Òàê êàê ñ < 0, òî äâà èç ÷åòûðåõ êîðíåé äåéñòâèòåëüíû è ïîëîæè-
òåëüíû, ñëåäîâàòåëüíî, äâèæåíèå âèäà
δδ δδ
12120
() () •()
•
()
tttt
====
(7.73)
îêàçûâàåòñÿ íåóñòîé÷èâûì ïî òåîðåìå Ëÿïóíîâà î íåóñòîé÷èâîñòè
äâèæåíèÿ ïî ïåðâîìó ïðèáëèæåíèþ. Ïî òåðìèíîëîãèè Ïóàíêàðå
÷èñëà ci â óðàâíåíèÿõ ñèñòåìû âèäà (7.72) íàçûâàþòñÿ
êîýôôèöèåíòàìè óñòîé÷èâîñòè ñèñòåìû, à ÷èñëî îòðèöàòåëüíûõ ÷èñåë
ci – ñòåïåíüþ íåóñòîé÷èâîñòè. Ñóùåñòâåííûì îêàçûâàåòñÿ íå ÷èñëî
ýòèõ ÷èñåë, à åãî ÷åòíîñòü. Òàê, â ñëó÷àå ñèñòåìû (7.72) ñòåïåíü
íåóñòîé÷èâîñòè ÷åòíà è ðàâíà äâóì. Âîçíèêàåò âîïðîñ, íåëüçÿ ëè
ñòàáèëèçèðîâàòü
íåóñòîé÷èâîå äâèæåíèå,
ïðèñîåäèíèâ
ê
ïîòåíöèàëüíûì ñèëàì ãèðîñêîïè÷åñêèå.
Îäíî èç íåîáõîäèìûõ óñëîâèé ãèðîñêîïè÷åñêîé ñòàáèëèçàöèè
ôîðìóëèðóåò ïåðâàÿ òåîðåìà Òîìñîíà–Òåéòà–×åòàåâà [85]: åñëè íå-
óñòîé÷èâîñòü èçîëèðîâàííîãî ïîëîæåíèÿ ðàâíîâåñèÿ ñèñòåìû ïðè
îäíèõ ïîòåíöèàëüíûõ ñèëàõ èìååò íå÷åòíóþ ñòåïåíü, òî ãèðîñêîïè-
÷åñêàÿ ñòàáèëèçàöèÿ ðàâíîâåñèÿ íåâîçìîæíà ïðè ëþáûõ ÷ëåíàõ, ñî-
äåðæàùèõ êîîðäèíàòû è ñêîðîñòè â ñòåïåíè âûøå ïåðâîé.
 ðàññìàòðèâàåìîì ñëó÷àå ñòåïåíü íåóñòîé÷èâîñòè ÷åòíàÿ è ãè-
ðîñêîïè÷åñêàÿ ñòàáèëèçàöèÿ ðàâíîâåñèÿ âîçìîæíà. Ñ÷èòàÿ, ÷òî
ñíàðÿä çàêðó÷åí âîêðóã ïðîäîëüíîé îñè, çàïèøåì (7.64) â ñëåäóþ-
ùåì âèäå:
•
••
,
δδδ
++=
GC∆
(7.74)
èëè â ñêàëÿðíîì âèäå
•
••
;
•••
.
δδδ δδδ
121
11
212
22
−+=++=
gc
gc
∆∆
(7.75)
Õàðàêòåðèñòè÷åñêîå óðàâíåíèå ýòîé ñèñòåìû
λλ
42
12
2
120
+++ +=
()
gcc c
c
íå èìååò êîðíåé ñ ïîëîæèòåëüíîé âåùåñòâåííîé ÷àñòüþ, åñëè äëÿ λ2
îíî èìååò îòðèöàòåëüíûå êîðíè, ò.å. åñëè
gcc
gcc
cc
cc
2
12
2
12
2
12
12
04
0
0
++>
++−>
>
;(
)
;
.
(7.76)
Ó íàñ c1 = c2 = c < 0, è íåðàâåíñòâà (7.76) âûïîëíÿþòñÿ, åñëè
gc
2
40
+>
.
(7.77)
328
Ñ÷èòàÿ, ÷òî ãèðîñêîïè÷åñêèå ñèëû ôîðìèðóþòñÿ çà ñ÷åò âðàùåíèÿ
âîêðóã ïðîäîëüíîé îñè, à ïîòåíöèàëüíûå îáóñëîâëåíû òîëüêî
îïðîêèäûâàþùèì ìîìåíòîì, áóäåì èìåòü g =2a; ñV
mf
M
=−
=−
2
4;è
òîãäà íåðàâåíñòâî (7.77) ñâåäåòñÿ ê ïîëó÷åííîìó ðàíåå óñëîâèþ
Ìàèåâñêîãî
af
2
4
0
−>
.
Íàëîæèì òåïåðü íà ñèñòåìó (7.74) äèññèïàòèâíûå ñèëû ñ ïîëíîé
äèññèïàöèåé, çàäàâàåìûå ìàòðèöåé Â. Åå ýëåìåíòû îïðåäåëÿþòñÿ
ñîâìåñòíûì äåéñòâèåì ýêâàòîðèàëüíîãî äåìïôèðóþùåãî ìîìåíòà è
ïîäúåìíîé ñèëû (îòîáðàæåííûõ ñîîòâåòñòâåííî â êîýôôèöèåíòàõ
mD è cN):
••• •
.
δδδδ
+++=
BGC ∆
(7.78)
Îòâåò íà âîïðîñ îá óñòîé÷èâîñòè ïîëîæåíèÿ ðàâíîâåñèÿ (7.73)
ñèñòåìû (7.78) äàåò ÷åòâåðòàÿ òåîðåìà Òîìñîíà–Òåéòà–×åòàåâà [85],
èç êîòîðîé ñëåäóåò, ÷òî èçîëèðîâàííîå ðàâíîâåñèå, íåóñòîé÷èâîå
ïîä äåéñòâèåì ïîòåíöèàëüíûõ ñèë, îñòàåòñÿ íåóñòîé÷èâûì ïðè
äîáàâëåíèè ãèðîñêîïè÷åñêèõ ñèë è ñèë äèññèïàòèâíûõ, åñëè
ïîñëåäíèå îáëàäàþò ïîëíîé äèññèïàöèåé. Èìååì
•
•••
;••• •
.
δδδδ δδδδ
11211
22122
+−+= +++=
bgc
bgc
∆∆
(7.79)
Ñòðîãîå äîêàçàòåëüñòâî òîãî, ÷òî äèññèïàòèâíûå ñèëû ðàçðóøàþò
ãèðîñêîïè÷åñêóþ ñòàáèëèçàöèþ àðòèëëåðèéñêîãî ñíàðÿäà, äàíî
×åòàåâûì [127], ïîñòðîèâøèì äëÿ ñèñòåìû âèäà (7.79) ôóíêöèþ
Ëÿïóíîâà. Îïðåäåëèì õàðàêòåð óãëîâîãî äâèæåíèÿ ñíàðÿäà ïðè
äåéñòâèè ýêâàòîðèàëüíîãî äåìïôèðóþùåãî ìîìåíòà, ïðåíåáðåãàÿ
âëèÿíèåì íîðìàëüíîé ñèëû, ñèëû Ìàãíóñà è èçìåíåíèåì ñêîðîñòè
öåíòðà ìàññ íà óãëîâîå äâèæåíèå ñíàðÿäà. Â ñèñòåìå (7.79)
bVmfgacVm f
DM
=== =
−=
−
7
2
4
2
;;
.
Ââîäÿ êîìïëåêñíûé óãîë δ = δ2 + iδ1 è ïðåäñòàâëÿÿ f4 = a
2
(1 −σ),
ñèñòåìó (7.79) çàïèøåì â ôîðìå
•••
().
δδ
σ
δ
−−
⎛
⎝⎜⎞
⎠⎟ −−=
2
2
10
7
2
ia
fa
(7.80)
Îáùåå ðåøåíèå ýòîãî óðàâíåíèÿ èìååò âèä
329
δ
λλ
=+
Ce Ce
tt
12
12
,
(7.81)
ãäå Ñ1 è Ñ2 – ïîñòîÿííûå êîýôôèöèåíòû, çàâèñÿùèå îò íà÷àëüíûõ
óñëîâèé;
λσ
σσ
12
77
2
7
2
1
1
2
2
2
,
=−±
−
⎛
⎝⎜⎞
⎠⎟+ ⎛
⎝⎜⎞
⎠⎟
⎡
⎣
⎢
⎢
⎤
⎦
ia
fia
f
a
i
f
a
⎥
⎥
12
/
(7.82)
–
êîðíè õàðàêòåðèñòè÷åñêîãî óðàâíåíèÿ λ
2
−
(2ia − f7)λ−a
2
(1 −σ)=0.
Ó÷èòûâàÿ, ÷òî f7/(2a) – âåëè÷èíà, ìàëàÿ ïî ñðàâíåíèþ ñ åäèíèöåé,
âûðàæåíèå äëÿ λi ìîæíî çàìåíèòü ïðèáëèæåííûì, ïîëàãàÿ
1
1
2
2
2
1
2
2
7
2
7
12
7
−
⎛
⎝⎜⎞
⎠⎟+ ⎛
⎝⎜⎞
⎠⎟
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
≈+
σσ
σ
f
a
i
f
a
i
f
a
/
⎛
⎝⎜⎞
⎠⎟
⎡
⎣⎢
⎤
⎦⎥≈
≈+
⎛
⎝⎜⎞
⎠⎟
⎡
⎣⎢
⎤
⎦⎥
12
7
12
1
1
2
/
/
.
i
f
a
σ
Ñ ó÷åòîì (7.83) çàïèøåì âûðàæåíèÿ äëÿ λi:
λσ
σ
λσ
σ
1
7
2
7
1
2
1
1
1
2
1
1
=+− +
⎛
⎝⎜⎞
⎠⎟
=−− −
⎛
⎝⎜⎞
⎠⎟
ia
f
ia
f
()
;
()
.
(7.84)
Ïîëàãàÿ Cr
e
i
11
1
=
ε
,Cr
e
i
22
2
=
ε
, îáùåå ðåøåíèå (7.81) ïðåäñòàâèì â âèäå
δρ
ρ
ωε
ωε
=+
++
12
11
22
ee
it
it
() ()
,
(7.85)
ãäå ωσ
1
1
=+
a()
;
ωσ
2
1
=−
a()
;
ρρ
σ
σ
σ
σ
11
2
1
22
2
1
77
==
−
+
⎛
⎝⎜⎞
⎠⎟
−
−
⎛
⎝⎜⎞
⎠⎟
re
re
ff
;.
Âåëè÷èíû ρ1 è ρ2 ïðåäñòàâëÿþò ñîáîé àìïëèòóäó áûñòðîãî è ìåä-
ëåííîãî äâèæåíèÿ îñè ñíàðÿäà (ðèñ. 7 .7). Òàêèì îáðàçîì, ðàäèóñ
ìåäëåííîãî êîíè÷åñêîãî äâèæåíèÿ ρ2 âîçðàñòàåò ñî âðåìåíåì, à ðà-
äèóñ áûñòðûõ äâèæåíèé îñè ñíàðÿäà ρ1 – óáûâàåò. Ñëåäîâàòåëüíî,
âëèÿíèå ýêâàòîðèàëüíîãî äåìïôèðóþùåãî ìîìåíòà ïðîÿâëÿåòñÿ
330
(7.83)
ïðåæäå âñåãî â äåìïôèðîâàíèè
àìïëèòóäû áûñòðûõ è íàðàñòà-
íèè àìïëèòóäû ìåäëåííûõ äâè-
æåíèé. Àñèìïòîòè÷åñêîå ïîâå-
äåíèå ðåøåíèé ñèñòåìû (7.79)
êà÷åñòâåííî ïîäòâåðæäàåòñÿ ïî-
ëó÷åííûì ïðèáëèæåííûì ðå-
øåíèåì.
Ðàññìîòðèì òåïåðü îáùèé
ñëó÷àé, êîãäà íà ñíàðÿä äåéñò-
âóþò ëèíåéíûå ïîòåíöèàëüíûå,
äèññèïàòèâíûå, ãèðîñêîïè÷å-
ñêèå è íåêîíñåðâàòèâíûå ïîçè-
öèîííûå ñèëû. Çàìåòèì, ÷òî
ïîñëåäíèå îáóñëîâëåíû ìîìåí-
òîì Ìàãíóñà è ñîâìåñòíûì
âëèÿíèåì çàêðóòêè ñíàðÿäà è
íîðìàëüíîé àýðîäèíàìè÷åñêîé
ñèëû (( )
.
pa
V
mc
N
=−
2
Ma
Õàðàê-
òåðèñòè÷åñêîå óðàâíåíèå ñèñòåìû (7.64) áóäåò èìåòü âèä
λλ
λ
λ
43
2
22
2
2
22 20
+++
++−
⋅+
+
=
bgbc c
b
g
pcp
()
(
).
(7.86)
Êîðíè õàðàêòåðèñòè÷åñêîãî óðàâíåíèÿ áóäóò èìåòü îòðèöàòåëüíûå
âåùåñòâåííûå ÷àñòè, åñëè áóäóò âûïîëíåíû óñëîâèÿ òåîðåìû
Ãóðâèöà, êîòîðûå â äàííîì ñëó÷àå ìîãóò áûòü çàïèñàíû â âèäå
20
20
0
0
22
22
22
22
22
bgbcc
b
g
pcp
bgbccp
>+
+
>−
>+
>
++
+
;;
;
;
()
()
()().
−−
−
+>
cb gp
bcp
22
22
40
(7.87)
Ó÷èòûâàÿ, ÷òî bVc m
ND
=+>
()
;
0 gac
=+>
21
0
();
Ma
c= −+
(42
acMa
+<
VmM
2
0
),
âèäèì, ÷òî ïåðâîå è ÷åòâåðòîå íåðàâåíñòâà ñèñòåìû
(7.87), åñòåñòâåííî, âûïîëíÿþòñÿ, à òðåòüå, êîòîðîå ìîæåò áûòü
çàïèñàíî â ôîðìå
−−
>
||
,
cbgp0
331
Ðèñ. 7.7 . Àìïëèòóäû áûñòðîãî è ìåäëåí-
íîãî äâèæåíèÿ áûñòðîâðàùàþùåãîñÿ
ñíàðÿäà
ìîæåò âûïîëíÿòüñÿ òîëüêî â òîì ñëó÷àå, åñëè pa
V
mc
N
=−
<
20
()
.
Ma
Ýòî â ñâîþ î÷åðåäü âîçìîæíî (ïðè ïðàâîé íàðåçêå), åñëè mc
N
Ma<
,â
òîì ñëó÷àå, êîãäà mMa > 0 (òî÷êà ïðèëîæåíèÿ ñèëû Ìàãíóñà ëåæèò
ìåæäó öåíòðîì ìàññ è âåðøèíîé ñíàðÿäà) ëèáî êîãäà mMa < 0 (òî÷êà
ïðèëîæåíèÿ ñèëû Ìàãíóñà ëåæèò äàëüøå îò íîñêà ñíàðÿäà, ÷åì
öåíòð ìàññ).
Ìîìåíò Ìàãíóñà, ÿâëÿÿñü ôèçè÷åñêîé ïðåäïîñûëêîé íàëè÷èÿ
â ñèñòåìå (7.64) íåêîíñåðâàòèâíûõ ïîçèöèîííûõ ñèë, ìîæåò ïðè
óêàçàííûõ âûøå óñëîâèÿõ ñïîñîáñòâîâàòü îáåñïå÷åíèþ óñòîé÷è-
âîñòè ïîëîæåíèÿ ðàâíîâåñèÿ (7.73). Åñëè æå ýòè óñëîâèÿ íå âû-
ïîëíÿþòñÿ, òî ìîìåíò Ìàãíóñà ñïîñîáñòâóåò ðàçðóøåíèþ óñòîé-
÷èâîñòè ðàâíîâåñèÿ ñèñòåìû. Ñèñòåìà (7.64) äîïóñêàåò ïîñòðîå-
íèå ôóíêöèè Ëÿïóíîâà, êîòîðàÿ ìîæåò áûòü èñïîëüçîâàíà äëÿ
äîêàçàòåëüñòâà óñòîé÷èâîñòè äâèæåíèÿ (7.73) è îïðåäåëåíèÿ íà-
êëàäûâàåìûõ íà ïàðàìåòðû ñèñòåìû óñëîâèé, ïðè êîòîðûõ ýòî
äâèæåíèå óñòîé÷èâî [3].
7.2 . ÄÂÈÆÅÍÈÅ ÎÒÍÎÑÈÒÅËÜÍÎ ÖÅÍÒÐÀ ÌÀÑÑ
ÎÏÅÐÅÍÍÛÕ ÑÍÀÐßÄÎÂ È ÌÈÍ
7.2.1. ÓÃËÎÂÎÅ ÄÂÈÆÅÍÈÅ ÎÏÅÐÅÍÍÛÕ ÂÐÀÙÀÞÙÈÕÑß ÑÍÀÐßÄÎÂ
Âðàùåíèå âîêðóã ïðîäîëüíîé îñè ÷àñòî ïðèäàþò îïåðåííîìó
ñíàðÿäó èëè íåóïðàâëÿåìîé ðàêåòå ñ öåëüþ óìåíüøåíèÿ âëèÿíèÿ
àñèììåòðèé ôîðìû è ýêñöåíòðèñèòåòîâ òÿãè íà äâèæåíèå öåíòðà
ìàññ, ò.å . äëÿ óìåíüøåíèÿ ðàññåèâàíèÿ òðàåêòîðèé, âûçâàííîãî ýòè-
ìè ôàêòîðàìè. Ðàêåòû è ñíàðÿäû ñ òàêèì âðàùåíèåì íàçûâàþò ïðî-
âîðà÷èâàþùèìèñÿ.
Óðàâíåíèÿ äâèæåíèÿ îïåðåííîãî âðàùàþùåãîñÿ ñíàðÿäà îòíî-
ñèòåëüíî öåíòðà ìàññ èäåíòè÷íû ïî ñòðóêòóðå óðàâíåíèÿì äâèæå-
íèÿ ñíàðÿäà, ñòàáèëèçèðóåìîãî âðàùåíèåì. Äîñòàòî÷íî çàìåíèòü
îïðîêèäûâàþùèé àýðîäèíàìè÷åñêèé ìîìåíò ñòàáèëèçèðóþùèì,
èçìåíèâ çíàêè ñîîòâåòñòâóþùèõ ÷ëåíîâ:
••
()
•
()
•
()
δδδ
δ
112
22
1
21
4
2
++ −+
−
−
+
+
Vcm
ac
ac Vm
aV
ND
M
Ma
Ma
()c
o
s
;
••
()
•
()
•
mc
a
Vg
Vcm
ac
N
ND
Ma
Ma
−=
−
++ ++
−
δθ
δδ
2
1
22
2
21 δδ
δθ
1
22
2
1
2
4
2
−−
−
−−
=
=
()
()c
o
s
;
•
ac Vm
aVm
c
mg
aVm
M
ND
Ma
Ma
îï
− Vma
Ã.
(7.88)
332
 ïîñëåäíåå
óðàâíåíèå
(7.88) äîáàâëåíî
ñëàãàåìîå
Vm
dl
cg
VHym
ON
2
2
2
2
îï
îï
Ï
=
π
() , õàðàêòåðèçóþùåå ìîìåíò îò êîñî
ïîñòàâëåííîãî îïåðåíèÿ. Ñëåäóåò ó÷èòûâàòü, ÷òî óãîë "íàáåãàíèÿ"
ïîòîêà íà îòäåëüíîå ïåðî ñòàáèëèçàòîðà è ñîçäàâàåìûé èì ìîìåíò
çàâèñÿò êàê îò ñêîðîñòè ïîñòóïàòåëüíîãî äâèæåíèÿ ñíàðÿäà, òàê è îò
åãî óãëîâîé ñêîðîñòè âðàùåíèÿ âîêðóã ïðîäîëüíîé îñè. Êðîìå òîãî,
ïðè íàëè÷èè ïðîñòðàíñòâåííîãî óãëà àòàêè âîçìîæíî ïîÿâëåíèå
íåñèììåòðèè (íåîäèíàêîâîñòè) ìîìåíòîâ, ñîçäàâàåìûõ "íàâåòðåííûì"
è "ïîäâåòðåííûì" ïåðüÿìè ñòàáèëèçàòîðà. Ïðè äåòàëüíîì àíàëèçå
óãëîâîãî äâèæåíèÿ êîñîîïåðåííûõ ñíàðÿäîâ ýòè ôàêòîðû íåîáõîäèìî
ó÷èòûâàòü.
Ðàññìîòðèì äâèæåíèå âðàùàþùåãîñÿ ñíàðÿäà ïðè íàëè÷èè òîëü-
êî ñòàáèëèçèðóþùåãî ìîìåíòà. Ïåðâûå äâà óðàâíåíèÿ ñèñòåìû
(7.88) áóäóò èìåòü âèä
•
••
;•••
,
δδδ δδδ
12
4
121
4
2
20
20
−+=++=
af
af
(7.89)
ãäå fVm
M
4
2
=
. Ðåøàÿ ýòó ñèñòåìó òàê æå, êàê è (7.11), íàéäåì
δρωερ ωε
δρ ωερ
11 112
22
21 11
=+
+
−
+
=+
+
sin(
) sin(
);
cos(
)
tt
t
22
2
cos(
),
−+
ωε
t
(7.90)
ãäå ωσ
10
1
=+
a()
;
ωσ
20
1
=−
a()
;
σ0 =1+f4/a
2
.
Ïîñòîÿííûå
èíòåãðèðîâàíèÿ ρ1, ρ2, ε1, ε2 îïðåäåëÿþòñÿ íà÷àëüíûìè óñëîâèÿìè è â
îáùåì ñëó÷àå ïðè t = 0, êîãäà δ1 = δ10;
••
;
δδ
11
0
=
δ2 = δ20;
••
,
δδ
22
0
=
íàõîäÿòñÿ èç âûðàæåíèé
ρ
σ
δω
δδω
δ
ρ
σ
δ
1
0
20
210
2
10
220
2
2
0
20
1
2
1
2
=−
+
+
=+
a
a
(•
)(
•
);
(•
ωδ
δωδ
ε
δω
δ
δω
δ
110
2
10
120
2
1
20
210
10
220
)(
•
);
•
•
;
−−
=−
−
+
tg
tgε
δω
δ
δω
δ
2
20
110
10
120
=−
+
−
•
•
.
Äâèæåíèå îñè ñíàðÿäà ïðåäñòàâëÿåò ñîáîé ïîëîæåíèå äâóõ
êîíè÷åñêèõ äâèæåíèé (ðèñ. 7.8): ìåäëåííîãî ñ óãëîâîé ñêîðîñòüþ
(−ω2) è ðàäèóñîì ρ2 è áûñòðîãî ñ óãëîâîé ñêîðîñòüþ ω1 è ðàäèóñîì ρ1,
333
êîòîðûå
íà
êîîðäèíàòíîé
ïëîñêîñòè èìåþò ïðîòèâîïî-
ëîæíûå íàïðàâëåíèÿ âðàùåíèÿ.
Îñü ñíàðÿäà â ðåçóëüòàòå íàëî-
æåíèÿ ýòèõ äâèæåíèé îïèñûâàåò
ãèïîöèêëîèäó. Â çàâèñèìîñòè îò
íà÷àëüíûõ óñëîâèé ìîãóò ïîëó-
÷àòüñÿ ãèïîöèêëîèäû ðàçëè÷íîé
ôîðìû (ðèñ. 7.9).
Ïðè ó÷åòå ýêâàòîðèàëüíîãî
äåìïôèðóþùåãî ìîìåíòà ñèñòå-
ìà óðàâíåíèé äâèæåíèÿ ñâîäèò-
ñÿ ê êîìïëåêñíîìó óðàâíåíèþ
δδ δδ
+− +=
fi
a
f
74
20
••
,
(7.91)
èíòåãðèðóÿ êîòîðîå òàê æå, êàê
óðàâíåíèå (7.80), ìîæíî ïîëó-
÷èòü îáùåå ðåøåíèå, èç êîòîðîãî âèäíî, ÷òî àìïëèòóäû áûñòðîãî è
ìåäëåííîãî äâèæåíèé ñî âðåìåíåì óìåíüøàþòñÿ. Êðèâàÿ, îïèñû-
âàåìàÿ èçîáðàæàþùåé
òî÷êîé íà ïëîñêîñòè
δ2Oδ1, áóäåò ãèïîöèêëî-
èäíîãî
òèïà
(ñì.
ðèñ. 7 .9). Îòíîøåíèå ðà-
äèóñîâ
ρ2/ρ1
=
=
⎛
⎝⎜⎞
⎠⎟
(/)exp
rr
ft
21
7
0
σ
ìî-
íîòîííî âîçðàñòàåò ñî
âðåìåíåì. Äëÿ àíàëèçà
âëèÿíèÿ äðóãèõ âîçìó-
ùàþùèõ ñèë íà óñòîé-
÷èâîñòü äâèæåíèÿ îïå-
ðåííîãî ñíàðÿäà ïåðâûå
äâà óðàâíåíèÿ ñèñòåìû
(7.88) ìîãóò áûòü ïðè-
âåäåíû ê âèäó (7.64),
ïðè÷åì âûðàæåíèÿ ýëå-
ìåíòîâ ìàòðèö Â, G è P
ñîõðàíÿþòñÿ, à ýëåìåí-
òàìè ìàòðèöû Ñ áóäóò
âåëè÷èíû
334
Ðèñ. 7.8 . Äâèæåíèå îñè îïåðåííîãî âðà-
ùàþùåãîñÿ ñíàðÿäà íà êàðòèííîé ïëîñ-
êîñòè
Ðèñ. 7.9. Âîçìîæíûå òðàåêòîðèè èçîáðàæàþùåé
òî÷êè ïëîñêîñòè äëÿ ðàçëè÷íûõ íà÷àëüíûõ óñëîâèé
áåç ó÷åòà ýêâàòîðèàëüíîãî äåìïôèðóþùåãî ìîìåí-
òà è ñ ó÷åòîì
ca
c
V
m
M
=−
−
()
,
422
Ma
(7.92)
ò.å. íà îïåðåííûé âðàùàþùèéñÿ ñíàðÿä, òàê æå êàê è íà íåî-
ïåðåííûé, äåéñòâóþò ïîòåíöèàëüíûå, ãèðîñêîïè÷åñêèå, äèññèïà-
òèâíûå è íåêîíñåðâàòèâíûå ïîçèöèîííûå ñèëû. Äâèæåíèå ñíàðÿäà
ïîä äåéñòâèåì îäíèõ ïîòåíöèàëüíûõ ñèë áóäåò óñòîé÷èâûì.
Îòâåò íà âîïðîñ î âëèÿíèè ãèðîñêîïè÷åñêèõ è äèññèïàòèâíûõ
ñèë íà óñòîé÷èâîñòü ïîëîæåíèÿ ðàâíîâåñèÿ (7.73) äàþò âòîðàÿ è òðå-
òüÿ òåîðåìû Òîìñîíà–Òåéòà–×åòàåâà [85]: åñëè èçîëèðîâàííîå ïî-
ëîæåíèå ðàâíîâåñèÿ ñèñòåìû óñòîé÷èâî ïðè îäíèõ ïîòåíöèàëüíûõ
ñèëàõ, òî ïðè äîáàâëåíèè ïðîèçâîëüíûõ ãèðîñêîïè÷åñêèõ è äèññè-
ïàòèâíûõ ñèë óñòîé÷èâîñòü ðàâíîâåñèÿ ñîõðàíèòñÿ; åñëè èçîëèðî-
âàííîå ïîëîæåíèå ðàâíîâåñèÿ ñèñòåìû óñòîé÷èâî ïðè îäíèõ ïîòåí-
öèàëüíûõ ñèëàõ, òî îíî ñòàíîâèòñÿ àñèìïòîòè÷åñêè óñòîé÷èâûì
ïðè äîáàâëåíèè ïðîèçâîëüíûõ ãèðîñêîïè÷åñêèõ ñèë è ñèë ñîïðî-
òèâëåíèÿ ñ ïîëíîé äèññèïàöèåé.
Òàêèì îáðàçîì, äëÿ ñòàòè÷åñêè óñòîé÷èâîãî ñíàðÿäà çàäàíèå
âðàùåíèÿ âîêðóã ïðîäîëüíîé îñè â îïðåäåëåííîì ñìûñëå ñïîñîáñò-
âóåò åãî ñòàáèëèçàöèè. Èñêëþ÷åíèå ñîñòàâëÿåò ñëó÷àé ðåçîíàíñà,
êîòîðûé áóäåò ðàññìîòðåí íèæå. Âëèÿíèå íåêîíñåðâàòèâíûõ ïîçè-
öèîííûõ ñèë, ïîÿâëåíèå êîòîðûõ îáóñëîâëåíî äåéñòâèåì íà îïå-
ðåííûé âðàùàþùèéñÿ ñíàðÿä ìîìåíòà Ìàãíóñà è ñîâìåñòíûì
âëèÿíèåì åãî çàêðóòêè è ïîäúåìíîé ñèëû, íàïðàâëåíî íà ðàçðóøå-
íèå óñòîé÷èâîñòè óãëîâîãî äâèæåíèÿ ñíàðÿäà. Ýòî ñâÿçàíî ñ ðàâåí-
ñòâîì êîýôôèöèåíòîâ ìàòðèöû Ñ (ñ1 = ñ2 = ñ, ñì. (7.72)) [85] â ðàñ-
ñìàòðèâàåìîì íàìè ñëó÷àå îñåñèììåòðè÷íîãî ñíàðÿäà.
7.2.2 . ÓÃËÎÂÎÅ ÄÂÈÆÅÍÈÅ ÎÏÅÐÅÍÍÛÕ ÍÅÂÐÀÙÀÞÙÈÕÑß
ÑÍÀÐßÄÎÂ
Îïåðåííûå íåóïðàâëÿåìûå ñíàðÿäû ïîñòîÿííîé è ïåðåìåííîé
ìàññû (ìèíû, àâèàáîìáû, ðàêåòû è äð.) ñ öåëüþ îáåñïå÷åíèÿ óãëî-
âîé ñòàáèëèçàöèè äîëæíû îáëàäàòü íåîáõîäèìûì çàïàñîì óñòîé÷è-
âîñòè.
Óðàâíåíèÿ óãëîâîãî äâèæåíèÿ îïåðåííûõ ñíàðÿäîâ ìîãóò áûòü
ïîëó÷åíû èç îáùèõ óðàâíåíèé ïðîñòðàíñòâåííîãî äâèæåíèÿ. Ïðè
ýòîì íåîáõîäèìî ó÷åñòü âîçìîæíîñòü äâèæåíèÿ îïåðåííîãî ñíàðÿäà
(ìèíû) ïî íàâåñíûì òðàåêòîðèÿì, äëÿ êîòîðûõ èçìåíåíèå
•
()
θt ìî-
æåò áûòü çíà÷èòåëüíûì:
335
•••
;
•••
•
••
δδδ
δδ δθθ
11
2
1
22
2
2
0
++=
++=
−
−
Vm Vm
Vm Vm
mV
DM
DM
D
.
(7.93)
 ñëó÷àå êîíñòðóêòèâíî ðàçâèòîãî îïåðåíèÿ ïðè îïðåäåëåíèè
•
θè
••
θ
áóäåì ó÷èòûâàòü âëèÿíèå ïîäúåìíîé ñèëû:
•
cos
;
••
sin
•
cos
•
θθ
δ
θθ
θθδ
=−
+
=++
−
−−
gV
Vc
gV
gV
VVc
N
N
1
2
12
2 +VcN
•
.
δ2
(7.94)
Òàê êàê
•
sin ,
Vc
Vg
=−
−
ò
2
θ ïîñëå ïîäñòàíîâêè (7.94) âî âòîðîå
óðàâíåíèå (7.93) è ïðåîáðàçîâàíèé ïîëó÷èì
•
•
()
•
[()
]
cos (
δδ
δ
θ
22
2
2
2
+++−−
=
=+
+
mc
VVmccm
gmc
DN
MN
D
D
ò
ò
gV −2
sin ).
θ
(7.95)
Ñëàãàåìîå cc m
ND
()
ò
−
íå ïðåâûøàåò, êàê ïðàâèëî, 1 % îò mM , è åãî
ìîæíî íå ó÷èòûâàòü:
••
()
•
cos (
sin ).
δδ
δ
θ
θ
22
2
2
2
2
+++
=
++
−
mc
VV
mgmcg
V
DN
M
Dò
(7.96)
Êîëåáàíèÿ ïðîäîëüíîé îñè îïåðåííîãî ñíàðÿäà íà êðèâîëèíåéíîì
ó÷àñòêå òðàåêòîðèè ïðîèñõîäÿò îòíîñèòåëüíî äèíàìè÷åñêîé îñè
ðàâíîâåñèÿ, ïîëîæåíèå êîòîðîé îïðå-
äåëÿåòñÿ ÷àñòíûì ðåøåíèåì óðàâíåíèÿ
(7.96)
δθ
θ
2
21
2
2
pò
=+
+
+
−
−
gmV
mc
gV
MD
()
c
o
s
(
sin ).
(7.97)
Íà íà÷àëüíîì ó÷àñòêå òðàåêòîðèè óãîë
δ2ð áëèçîê ê íóëþ, à íàèáîëüøåå
çíà÷åíèå îí áóäåò èìåòü â ðàéîíå
âåðøèíû ó íàâåñíûõ òðàåêòîðèé.
Õàðàêòåð èçìåíåíèÿ óãëîâ δ1 è δ2
ïîêàçàí íà ðèñ. 7.10. Ìàêñèìàëüíûå
àìïëèòóäû óãëîâ δ1 è δ2 îïðåäåëÿþòñÿ
336
Ðèñ. 7.10. Çàâèñèìîñòü δ2 = f(δ1)
äëÿ îïåðåííîãî ñíàðÿäà
íà÷àëüíûìè óñëîâèÿìè, äèíàìè÷åñêèìè è àýðîäèíàìè÷åñêèìè
ïàðàìåòðàìè ñíàðÿäà. Èõ âåëè÷èíà íå äîëæíà ïðåâîñõîäèòü
ìàêñèìàëüíî äîïóñòèìûõ çíà÷åíèé óãëîâ δ1max è δ2max, óñòàíàâëè-
âàåìûõ èç îïûòà ïî èçâåñòíûì îáðàçöàì:
AA
11 22
<<
δδ
max
max
;.
(7.98)
Ýòè íåðàâåíñòâà íîñÿò íàçâàíèå óñëîâèé îãðàíè÷åííîñòè àìïëèòóäû
íà íà÷àëüíîì ó÷àñòêå òðàåêòîðèè.
7.3 . ÐÅÇÎÍÀÍÑ ÂÐÀÙÀÞÙÈÕÑß ÎÏÅÐÅÍÍÛÕ
ÑÍÀÐßÄÎÂ
7.3 .1. ÂËÈßÍÈÅ ÌÀËÛÕ ÀÑÈÌÌÅÒÐÈÉ ÔÎÐÌÛ, ÌÀÑÑÛ
È ÝÊÑÖÅÍÒÐÈÑÈÒÅÒÀ ÒßÃÈ ÍÀ ÓÃËÎÂÎÅ ÄÂÈÆÅÍÈÅ ÎÏÅÐÅÍÍÛÕ
ÂÐÀÙÀÞÙÈÕÑß ÑÍÀÐßÄÎÂ
Ïðè ðàññìîòðåíèè âîïðîñîâ óñòîé÷èâîñòè âðàùàþùèõñÿ (ïðî-
âîðà÷èâàþùèõñÿ) îïåðåííûõ ñíàðÿäîâ ñëåäóåò èìåòü â âèäó, ÷òî
äàæå èõ ìàëàÿ àñèììåòðèÿ, âûçûâàåìàÿ òåõíîëîãè÷åñêèìè ïîãðåø-
íîñòÿìè èçãîòîâëåíèÿ, ìîæåò ïðèâåñòè ê ðåçîíàíñíîìó âîçðàñòà-
íèþ óãëîâ àòàêè è ñêîëüæåíèÿ è ñòàòè÷åñêè óñòîé÷èâûé ñíàðÿä ìî-
æåò îêàçàòüñÿ äèíàìè÷åñêè íåóñòîé÷èâûì. Ìàëàÿ àñèììåòðèÿ â
ðàñïðåäåëåíèè ìàññû ñíàðÿäà, åãî ôîðìû è/èëè ýêñöåíòðèñèòåòû
òÿãè âûçûâàþò ïîÿâëåíèå ìàëûõ äîïîëíèòåëüíûõ ìîìåíòîâ, êîòî-
ðûå èçìåíÿþò ïîëîæåíèå îñè äèíàìè÷åñêîãî ðàâíîâåñèÿ ïî ñðàâíå-
íèþ ñ ïîëîæåíèåì îñè, ñîîòâåòñòâóþùèì èäåàëüíî âûïîëíåííîìó
ñíàðÿäó [19, 59, 80, 134, 136, 137, 141].
Ýôôåêò ðåçîíàíñíîãî âîçðàñòàíèÿ óãëîâ àòàêè è ñêîëüæåíèÿ
ïðîÿâëÿåòñÿ ïðè îïðåäåëåííîì ñîîòíîøåíèè ÷àñòîòû êîëåáàíèé
ñíàðÿäà îòíîñèòåëüíî åãî ýêâàòîðèàëüíîé îñè è ÷àñòîòû âðàùåíèÿ
ñíàðÿäà âîêðóã ïðîäîëüíîé îñè.
Äëÿ èññëåäîâàíèÿ ÿâëåíèÿ ðåçîíàíñà óäîáíî âîñïîëüçîâàòüñÿ
ñâÿçàííîé ñèñòåìîé êîîðäèíàò, òàê êàê â íåé ïðîñòî îïðåäåëÿåòñÿ
îðèåíòàöèÿ àñèììåòðèé. Íà÷àëî ñâÿçàííîé ñèñòåìû êîîðäèíàò ïî-
ìåñòèì â öåíòð ìàññ, à îñè OY è OZ íàïðàâèì òàê, ÷òîáû ñîáëþäà-
ëîñü ðàâåíñòâî Iyz = 0. Ñîñòàâëÿþùèå òåíçîðà èíåðöèè Ixy ≠ 0, I xz ≠ 0
ïîçâîëÿò ó÷åñòü äèíàìè÷åñêóþ íåóðàâíîâåøåííîñòü ñíàðÿäà. Ïðè
çàïèñè óðàâíåíèé âðàùàòåëüíîãî äâèæåíèÿ áóäåì ó÷èòûâàòü ñëå-
äóþùèå ñèëû è ìîìåíòû: òÿãó Ð â ôóíêöèè ëèíåéíîãî è óãëîâîãî
ýêñöåíòðèñèòåòîâ; îñåâóþ, íîðìàëüíóþ è áîêîâóþ àýðîäèíàìè÷å-
ñêèå ñèëû; àýðîäèíàìè÷åñêèé ñòàáèëèçèðóþùèé ìîìåíò Ì; àýðî-
337
äèíàìè÷åñêèé äåìïôèðóþùèé ìîìåíò ÌD; ìîìåíò ñèëû Ìàãíóñà
ÌÌà; ìîìåíò Ì∆, âûçâàííûé ñìåùåíèåì öåíòðà äàâëåíèÿ ñ îñè OX
ñâÿçàííîé ñèñòåìû êîîðäèíàò; ìîìåíò àýðîäèíàìè÷åñêîé íåñèì-
ìåòðèè Ì0, îïðåäåëÿåìûé ïîâîðîòîì îñè àýðîäèíàìè÷åñêîé ñèì-
ìåòðèè (îñè "íóëåâîé ïîäúåìíîé ñèëû") íà óãëû αa, βa â ñâÿçàííîé
ñèñòåìå êîîðäèíàò; ìîìåíò Ìå ýêñöåíòðèñèòåòà òÿãè.
Óðàâíåíèÿ äâèæåíèÿ öåíòðà ìàññ ñíàðÿäà (2.48) â ïðàâîé ÷àñòè
áóäóò èìåòü ñîñòàâëÿþùèå
ΣFRP
=+=
−
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
+
qSc
qSc
qSc
P
P
x
y
z
α
β
α
β
ε
εφ
cos
sin cos 1
1
P sin sin
,
εφ
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
(7.99)
ãäå ε (óãëîâîé ýêñöåíòðèñèòåò (sinε≈ε; cosε≈ 1)) è φ1 îïðåäåëÿþò
îðèåíòàöèþ âåêòîðà Ð â ñâÿçàííîé ñèñòåìå êîîðäèíàò.
Óðàâíåíèÿ äâèæåíèÿ ñíàðÿäà îòíîñèòåëüíî öåíòðà ìàññ (2.55) â
íàøåì ñëó÷àå ïîñëå îòáðàñûâàíèÿ ââèäó ìàëîñòè ÷ëåíîâ, ñîäåðæà-
ùèõ êâàäðàòû è ïðîèçâåäåíèÿ ïîïåðå÷íûõ (ωy; ωz) óãëîâûõ ñêîðî-
ñòåé, áóäóò èìåòü âèä
II
I
M
II
I
xx
x
yy xz
x
zz
xy
R
x
yx
•
(•
)(
•
);
•
()
ωω
ω
ωω
ω
ω
ω
−−
−
+=
−−
Σ
ωω
ω
ω
ωω
ω
β
α
x
z
xx
xxR
y
zx
x
y
IIh IIh M
II
I
−−
+−
=
+−
−
()
•
()
;
•
()
2
Σ
()
•
()
,
IIh IIh M
xx
xxR
z
−−
−=
α
β
ωω
2
Σ
(7.100)
ãäå hα = Ixz/(I − Ix), hβ = Ixy/(I − Ix) îïðåäåëÿþò ïîëîæåíèå ãëàâíîé
öåíòðàëüíîé îñè â ñâÿçàííîé ñèñòåìå êîîðäèíàò.
 ïðàâîé ÷àñòè óðàâíåíèé (7.100) èìååì ñîñòàâëÿþùèå
Σ
∆
MMMM MMM
RD
e
y
z
qSl m
qSl m
qSl
=++
+++=
=−
−
+
−
Ma
0
2
0
||
||
β
α
β
α
Vm
qSlV m
qSlV m
qSlV m
xx
yy
zz
−
−
−
−
−
−
+
1
21
21
21
0
||
||
||
ω
ω
ω
ω
ω
ω
Ma
Ma
α
β
α
α
β
αβ
qSlV m
qSc z
y
qSc z
qSc y
qSlm
y
x
z
21
−
+
+
+
−
+
()
∆∆
∆
∆
x
y
z
A
qSlm
qSlm
Pd
Pd
Px
Pd
0
0
0
12
21
+
−+
+
−
εφ
φ
φεφ
cos(
)
sin
sin
cos
cos
,
φεφ
21
−
PxA
(7.101)
ãäå d è φ2 îïðåäåëÿþò ñîîòâåòñòâåííî ëèíåéíûé ýêñöåíòðèñèòåò òÿãè
è åãî îðèåíòàöèþ â ñâÿçàííîé ñèñòåìå êîîðäèíàò; xA – ðàññòîÿíèå îò
338
ïëîñêîñòè YOZ ñâÿçàííîé ñèñòåìû êîîðäèíàò äî òî÷êè ïðèëîæåíèÿ
âåêòîðà Ð. Ñîñòàâëÿþùàÿ qSlmx0 ìîìåíòà Ì0 ïî îñè OX ïîçâîëÿåò
ó÷èòûâàòü êàê ñëó÷àéíóþ, òàê è ïðåäíàìåðåííî ñîçäàâàåìóþ
àñèììåòðèþ ôîðìû, íàïðèìåð, çà ñ÷åò êîñîïîñòàâëåííîãî îïåðåíèÿ.
Ïîëàãàÿ cc
yz
αβ
=
,mm
yz
αβ
=
,mm
yz
ωω
=
,mm
Ma
Ma
αβ
=
, ââåäåì êîìïëåêñ-
íûåïåðåìåííûåδ=β+iα;ω=ωy+iωz;h=hβ+ihα.Ñêëàäûâàÿâòî-
ðîå è òðåòüå óðàâíåíèÿ ñèñòåìû (7.100), ïåðåéäåì ê êîìïëåêñíîìó
óðàâíåíèþ
••
ωω
ω
ω
ω
=−
−
⎛
⎝⎜⎞
⎠⎟ +−
⎛
⎝⎜⎞
⎠⎟+
+−
⎛
⎝⎜⎞
⎠⎟
i
I
I
I
I
h
i
I
I
x
x
x
x
x
11
1
x
i
A
i
yzz
hi
P
I
de
xe
qSlI m im
m
l
V
m
2
1
00
21
−+
+
++
−
−
−
()
|||
φφ
α
ε
δ
zx
x
l
V
mc
lz
i
y
ωβ
ωωδ
|(
)
.
++
−
⎡
⎣⎢
⎤
⎦⎥
−
Ma
1
∆∆
(7.102)
Ñ÷èòàÿ α = −Vy/Vx, β = Vz/Vx, ïîñëå äèôôåðåíöèðîâàíèÿ ïîëó÷èì
•
/
•
(•/)
;•/
•
(•/)
.
VV
VV VV
VV
yx
xx zx
xx
=−−
=
+
αα
ββ
(7.103)
Ïîäñòàâëÿÿ â (7.103) âûðàæåíèå
•
/
VV
xx
= −ωyβ−ωzα−qScx(mVx)
−1
+
+ P(mVx)
−1
, íàéäåííîå èç ïåðâîãî óðàâíåíèÿ ñèñòåìû (2.48), ïîëó÷èì
•
•
;
•
•
V
V
qS
mV
c
P
mV
V
V
y
x
yz
x
x
x
z
x
=−−−
−
−
+
⎛
⎝⎜
⎞
⎠⎟
=+−
αω
βω
α
α
βω
yz
x
x
x
qS
mV
c
P
mV
βωα
β
−−
+
⎛
⎝⎜
⎞
⎠⎟.
(7.104)
Ðàçäåëèâ âòîðîå è òðåòüå óðàâíåíèÿ ñèñòåìû (2.48) íà Vx, ñ ó÷åòîì
(7.104) ïîñëå ïðåîáðàçîâàíèé, ïðåíåáðåãàÿ ÷ëåíàìè ïîðÿäêà α2
, αβ,
β2 è ïðèíèìàÿ Vx ≈ V, áóäåì èìåòü
ωβω
α
βε
φ
ωα
+
β
yx
z
x
z
qS
mV
cc
P
mV
P
mV
=−
+
−
+
⎡
⎣⎢
⎤
⎦⎥−
=
•
()
s
i
n
;
•
1
ωβ
α+
ε
φ
α
xy
x
qS
mV
cc
P
mV
P
mV
+−
+
⎡
⎣⎢
⎤
⎦⎥
()
c
o
s
.
1
(7.105)
Ïåðåéäåì îò (7.105) ê êîìïëåêñíîìó óðàâíåíèþ
339
ωδ ωδ
δ
ε
α
φ
=+
+
+
−
+
⎡
⎣⎢
⎤
⎦⎥
•
().
i
P
mV
qS
mV
cci
P
mV
e
xy
x
i1
(7.106)
Äèôôåðåíöèðóÿ ïî âðåìåíè (7.106) è ïîäñòàâëÿÿ ðåçóëüòàò â (7.102),
ïîëó÷èì óðàâíåíèå, îïèñûâàþùåå óãëîâûå êîëåáàíèÿ ñíàðÿäà:
•••
,
δδδ
++=
kkk
123
(7.107)
ãäå
kPq
S
ccm
Vq
S
l
I
Vmi
I
I
yx
z
x
1
11
2
=+
−
+
+−
⎛
⎝⎜⎞
⎠
−−
[()
]
(
)(
)
|
|
αω
⎟
=−
++
=+
−
+
+
ω
ωλλμ
λ
ωββλ ν
α
β
x
c
cp
ki
kh
h
;
[(
)];
[(
)
2
22
3
2
0
2
1
∆
ih
h
l
V
m
m
P
mV
qS
mV
cc
p
z
z
yx
()
]
;
||
||
()
ααλ ν
λ
β
α
ω
α
α
0
2
+++
=+
−
∆
⎡
⎣⎢
⎤
⎦⎥ ++
−
⎡
⎣⎢
⎤
⎦⎥
=
+
1
2
ω
μω
α
ω
c
yx
z
d
dt
P
mV
qS
mV
cc
l
V
m
()
;
||
êð
||
||
()
•
m
m
P
mV
qS
mV
cc
z
yx
x
Ma
êð
β
α
α
ω
ω
ω
++−
⎡
⎣⎢
⎤
⎦⎥
⎧
⎨
⎩
⎫
⎬
⎭
+
1
2
c
x
22
;
•
;
ν
ω
ω
=
êð
(7.108)
αα
β
αα
0
0
1
0
0
1
=
−
=−
−
=
+
−
−
mcy
l
m
cy
ml
mc
z
l
zx
z
a
x
z
yx
∆
∆
∆
||
||;
|m
cz
ml
P
I
dx
P
mV
z
a
x
z
p
c
A
αα
β
α
ω
φεφ
ω
||
|
;
(si
n
s
in)
=−
+
=+
+
∆
2
21
ω
ω
φφ
ε
ω
ω
α
x
z
z
c
l
V
m
m
d
dt
P
mV
êð
2
11
2
cos
||
||sin
+
⎛
⎝⎜
⎞
⎠⎟−
−
⎛
⎝⎜⎞
⎠⎟
=
−
++
cos ;
(cos
c
o
s)
s
in
φ
β
ω
φεφ
εω
ω
φ
1
2
212
p
c
A
x
P
I
dx
P
mV
êð
11
2
1
−
⎛
⎝⎜
⎞
⎠⎟−
−
⎛
⎝⎜⎞
⎠⎟
l
V
m
m
d
dt
P
mV
z
z
c
||
||cos
sin .
ω
α
φ
ε
ω
φ
 âûðàæåíèÿ äëÿ êîýôôèöèåíòîâ k2 è k3 âõîäèò ïàðàìåòð λ =
= ωx/ωêð, ãäå
340
ω
ω
ω
α
êð
=
−
=
c
x
c
z
II
qSl m
I
1/
;
||.
(7.109)
Âåëè÷èíó ωc ÷àñòî íàçûâàþò ñîáñòâåííîé ÷àñòîòîé êîëåáàíèé
ñíàðÿäà ïî óãëàì òàíãàæà è ðûñêàíèÿ. Âåëè÷èíó ωêð íàçûâàþò êðè-
òè÷åñêîé óãëîâîé ñêîðîñòüþ. Îáû÷íî ó ñíàðÿäîâ è ðàêåò Ix/I << 1,
ïîýòîìó çíà÷åíèÿ ωc è ωêð áëèçêè.
7.3 .2. ÈÑÑËÅÄÎÂÀÍÈÅ ÓÑÒÀÍÎÂÈÂØÅÃÎÑß ÐÅÇÎÍÀÍÑÍÎÃÎ
ÂÐÀÙÅÍÈß
Óðàâíåíèå (7.107), ëèíåéíîå, íåîäíîðîäíîå, ñ ïåðåìåííûìè
êîìïëåêñíûìè êîýôôèöèåíòàìè, îïèñûâàåò èçìåíåíèå ïðîñòðàí-
ñòâåííîãî óãëà àòàêè δ â ñâÿçàííîé ñèñòåìå êîîðäèíàò. Äëÿ êà÷åñò-
âåííîãî àíàëèçà óñòàíîâèâøèõñÿ ðåøåíèé ýòîãî óðàâíåíèÿ ïðè-
ìåì, ÷òî åãî êîýôôèöèåíòû ìàëî èçìåíÿþòñÿ íà èññëåäóåìîì èí-
òåðâàëå âðåìåíè è ïîòîìó ñ÷èòàþòñÿ ïîñòîÿííûìè. Îáùåå ðåøåíèå
áóäåò èìåòü âèä
δρρδ
λλ
=++
12
12
ee
tt
á,
(7.110)
ãäå ρ1, ρ2 – êîìïëåêñíûå ïîñòîÿííûå, çàâèñÿùèå îò íà÷àëüíûõ
óñëîâèé;
λ12
1
1
2
2
2
1
2
4
,
=−
±
−
k
kk
(7.111)
–
êîðíè õàðàêòåðèñòè÷åñêîãî óðàâíåíèÿ; δá – áàëàíñèðîâî÷íîå
óñòàíîâèâøååñÿ çíà÷åíèå ïðîñòðàíñòâåííîãî óãëà àòàêè: δá = k3/k2.
Òàê êàê δá = βá + iαá, ñ ó÷åòîì (7.108) èìååì
δ
ββλν ααλν
λλμ
λ
α
ββ
α
á=
+−+++++
−+
+
()
()
()
0
2
0
2
2
1
pp
hhi
hh
i
∆
;
()
(
)
(
α
ααλνλλ
)−
μ
λ
(
ββλ ν
β
α0
α
β
á=
+++−+
+−+
0
22
2
1
1
pp
hh
hh
∆
−+
+
=
+−+
−+
++
λλμ
λ
βββλνλλμ
λαα
α
β
22
2
2
0
22
0
1
∆
∆
)
;
()
(
)
(
á
p
hh
p
hh
++
−+
+
λν
λλμ
λ
β
α
2
22
2
1
)
()
.
∆
(7.112)
Ìîäóëü êîìïëåêñíîãî óãëà àòàêè ðàâåí
341
||
()
()
(
δβαββλ ν
λλ
α
α
β
áá
2
á
2
=+
=
+−++
−+
+
→
→
+
0
22
22
0
1
p
hh
∆
L
L
αλν
μλ
β
α
p
hh
++
+
22
22
).
(7.113)
Óãëû àòàêè è ñêîëüæåíèÿ çàâèñÿò îò âåëè÷èíû λ, ò.å. îò îòíîøåíèÿ
óãëîâîé ñêîðîñòè âðàùåíèÿ ñíàðÿäà âîêðóã ïðîäîëüíîé îñè ê
êðèòè÷åñêîé ñêîðîñòè. Õàðàêòåð èçìåíåíèÿ |δá| â çàâèñèìîñòè îò
ïàðàìåòðà λ ïðåäñòàâëåí íà ðèñ. 7.11. Ìîæíî ïîêàçàòü, ÷òî ìàêñèìóì
ôóíêöèè δá(λ) ñîîòâåòñòâóåò λλ
=±+
1 ∆ .Òàêêàê∆λ<1,òîâåðøèíà
ðåçîíàíñíîãî ïèêà ñîîòâåòñòâóåò óñëîâèþ λ ±1, ò.å . ωx ≈±ωêð.Â
÷àñòíûõ ñëó÷àÿõ íàëè÷èÿ ó ñíàðÿäà òîëüêî àýðîäèíàìè÷åñêîé
íåñèììåòðèè (Ixy = Ixz = ε = d =0)
||
,
max
δ
αβ
μλ
μ
λλ
μ
á
ïðè
=
+
+−
=±+−
0
2
0
2
2
2
1
4
1
2
∆
∆
òîëüêî äèíàìè÷åñêîé íåóðàâíîâåøåííîñòè (α0 = β0 = ε = d =0)
|| ()
.
max
δ
λ
μλ
μ
λ
λ
λμ
α
β
á
ïðè
=
++
+−
=±
+
+−
1
1
4
1
1
2
22
22
∆
∆
∆
∆
hh
Ó÷èòûâàÿ, ÷òî îáû÷íî μ << 1, äëÿ ýòèõ ñëó÷àåâ ìîæíî èñïîëüçîâàòü
ïðèáëèæåííûå ñîîòíîøåíèÿ:
342
Ðèñ. 7.11 . Èçìåíåíèå áà-
ëàíñèðîâî÷íîãî
óãëà
àòàêè δσ(λ):
1 – ïðè àýðîäèíàìè÷å-
ñêîé è ìàññîâîé àñèì-
ìåòðèè; 2 – ïðè äèíà-
ìè÷åñêîé íåóðàâíîâå-
øåííîñòè
||~
||
max
max
δ
δ
μλ
δ
μ
λ
áá
è
−
+
≈+
00
1
1
∆
∆
h
ïðè λλ
=±+
1 ∆,ãäåhhh
0
22
00
2
0
2
=+
=+
α
β δαβ
;.
Ìàêñèìàëüíîå çíà÷åíèå |δá| ïðîïîðöèîíàëüíî âåëè÷èíå 1/μ.Âå-
ëè÷èíà μ çàâèñèò, â ÷àñòíîñòè, îò êîýôôèöèåíòà äåìïôèðóþùåãî
ìîìåíòà ñíàðÿäà ||
.
mz
ω
Åñëè || ,
mz
ω
→ 0 òî |δá|max ≈δ0/μ→∞. Òàê êàê âå-
ëè÷èíà μ îáû÷íî ìàëà, òî çíà÷åíèå |δá|max ìîæåò íà ïîðÿäîê è áîëåå
ïðåâîñõîäèòü çíà÷åíèå ìàëîé àñèììåòðèè (δ0 èëè h0), åå âûçûâàþ-
ùåé. Ïîýòîìó òàêîé ðåæèì ïîëó÷èë â ëèòåðàòóðå íàçâàíèå ðåçî-
íàíñíîãî ðåæèìà âðàùåíèÿ.
Ïðè ïîïàäàíèè â ðåçîíàíñíûé ðåæèì âðàùåíèÿ èçìåíÿåòñÿ íå
òîëüêî âåëè÷èíà áàëàíñèðîâî÷íûõ óãëîâ àòàêè è ñêîëüæåíèÿ, íî è
õàðàêòåð óãëîâîãî äâèæåíèÿ. Äëÿ êà÷åñòâåííîãî àíàëèçà óïðîñòèì
âûðàæåíèÿ äëÿ êîýôôèöèåíòîâ k1 è k2 (7.108), ïðåíåáðåãàÿ âëèÿíè-
åì ïîäúåìíîé ñèëû, äåìïôèðóþùåãî ìîìåíòà, ìîìåíòà Ìàãíóñà è
ðàññìàòðèâàÿ ïàññèâíûé ó÷àñòîê òðàåêòîðèè. Êîðíè õàðàêòåðèñòè-
÷åñêîãî óðàâíåíèÿ ïðèìóò âèä
λω
ωω
λ
12
2
22
1
2
2
1
2
24
1
,
(
=−
−
⎛
⎝⎜⎞
⎠⎟ ±−
−
⎛
⎝⎜⎞
⎠⎟ −−
i
I
I
I
I
x
xx
x
c
),
ãäå ωωω
cc
x
=
/.
Ïðè óñëîâèè λ = ωx/ωêð < 1 ("äîðåçîíàíñíîå âðàùåíèå")
λω
ωλ
1
2
22
1
2
24
1
1
2
2
=−
⎛
⎝⎜⎞
⎠⎟ +−
−
−
⎛
⎝⎜⎞
⎠⎟
⎡
⎣
⎢
⎢
⎤
i
I
I
I
I
x
x
c
x
()
⎦
⎥
⎥
=
=−
⎛
⎝⎜⎞
⎠⎟ +−
+−
⎛
i
i
I
I
I
I
x
x
c
x
||;
()
λ
λω
ωλ
1
2
2
22
1
2
24
1
1
2
2
⎝⎜⎞
⎠⎟
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
=−
i||
.
λ2
Èç ýòèõ âûðàæåíèé âèäíî, ÷òî |λ2|>|λ1|, à ðàçíûå çíàêè ïðè ìíèìîé
÷àñòè êîðíåé îçíà÷àþò, ÷òî âûñîêî÷àñòîòíàÿ ρ
λ
2
2
e
t
è íèçêî÷àñòîòíàÿ
ρλ
1
1
e
t
ñîñòàâëÿþùèå ïðîñòðàíñòâåííîãî óãëà àòàêè èìåþò íà
êîîðäèíàòíîé ïëîñêîñòè (ðèñ. 7.12) ïðîòèâîïîëîæíûå íàïðàâëåíèÿ
âðàùåíèÿ.
Ïðè óñëîâèè λ = ωx/ωêð ≈ 1 (ðåçîíàíñíîå âðàùåíèå) èìååì λ1 =0;
λω
2
2
=−
−
⎛
⎝⎜⎞
⎠⎟
i
I
I
x
x
, ñëåäîâàòåëüíî, δ = ρ+ρ
δ
λ
12
2
e
t
+ á, è, çíà÷èò, ïðè
343
ðåçîíàíñíîì âðàùåíèè èç-
ìåíåíèÿ óãëà δ ïðåäñòàâëÿ-
þò ñîáîé îäíî÷àñòîòíûå
êîëåáàíèÿ ñ ÷àñòîòîé |λ2|
(ñì. ðèñ. 7.12). Ïîëîæåíèå
âåêòîðà ñêîðîñòè (òî÷êà Ì)
è, ñëåäîâàòåëüíî, ïëîñêîñòè
ñîïðîòèâëåíèÿ â ñâÿçàííîé
ñèñòåìå êîîðäèíàò êàê áû
ôèêñèðóåòñÿ (ñ òî÷íîñòüþ
äî àìïëèòóäû ρ2). Ó ËÀ,
âõîäÿùèõ â àòìîñôåðó [39,
134], òàêîé ðåæèì âðàùå-
íèÿ ïðèâîäèò ê ðåãóëÿðíî-
ìó îäíîñòîðîííåìó îáãàðó.
Ïðè óñëîâèè λ =w
x/ωêð >
>1 ("ñâåðõðåçîíàíñíîå" âðà-
ùåíèå)
λω
λ
12
22
2
1
2
2
1
2
41
2
,
()
=−
−
⎛
⎝⎜⎞
⎠⎟ ±−
−
−
⎛
⎝⎜⎞
⎠⎟
⎡
⎣
⎢
⎢
i
I
I
I
I
x
c
x
⎤
⎦
⎥
⎥
ωx.
Õàðàêòåð óãëîâîãî äâèæåíèÿ ïîêàçàí íà ðèñ. 7.12 .
7.3.3. ÓÑÒÎÉ×ÈÂÎÑÒÜ ÐÅÇÎÍÀÍÑÍÛÕ ÐÅÆÈÌΠÂÐÀÙÅÍÈß
Ðåçîíàíñ ìîæåò âîçíèêàòü íà ðàçíûõ ó÷àñòêàõ ïîëåòà. Íàïðèìåð,
ïðè ðàñêðóòêå ñíàðÿäà ñ ïîìîùüþ êîñî ïîñòàâëåííîãî îïåðåíèÿ
èëè êàêèì-ëèáî èíûì ñïîñîáîì óãëîâàÿ ñêîðîñòü äâèæåíèÿ âîêðóã
ïðîäîëüíîé îñè, ïîñëåäîâàòåëüíî ïðîõîäÿ çíà÷åíèÿ îò íóëåâîãî äî
íåêîòîðîãî óñòàíîâèâøåãîñÿ, ìîæåò ïðîéòè ÷åðåç êðèòè÷åñêîå.
Ïðè ýòîì âîçìîæíî ïîÿâëåíèå áîëüøèõ óãëîâ àòàêè, íàðóøåíèå ðå-
æèìîâ îáòåêàíèÿ ñíàðÿäà (âïëîòü äî ïîòåðè èì óñòîé÷èâîñòè).
Âìåñòå ñ òåì èçìåíåíèå ïàðàìåòðîâ óðàâíåíèé äâèæåíèÿ ìîæåò
áûòü òàêèì, ÷òî ðåçîíàíñíîå ñîâïàäåíèå ÷àñòîò áóäåò êðàòêîâðå-
ìåííûì è íå ïðèâåäåò ê âîçíèêíîâåíèþ áîëüøèõ áàëàíñèðîâî÷íûõ
óãëîâ àòàêè, ò.å . óñëîâèå ωx ≈ωêð ñëóæèò íåîáõîäèìûì, íî íå äîñòà-
òî÷íûì äëÿ ðàçâèòèÿ ðåçîíàíñíûõ ÿâëåíèé. Íàèáîëåå îïàñíî âîç-
íèêíîâåíèå ðåæèìà ðåçîíàíñíîé àâòîðîòàöèè, ïðè êîòîðîì ñîâïà-
344
Ðèñ. 7 .12. Èçìåíåíèå óãëîâ àòàêè è ñêîëüæå-
íèÿ àñèììåòðè÷íîãî îïåðåííîãî âðàùàþùåãî-
ñÿ ñíàðÿäà:
1 – ïðè "äîðåçîíàíñíîì" âðàùåíèè (λ < 1);
2 – ïðè ðåçîíàíñå (λ≈1); 3 – ïðè "ñâåðõðåçî-
íàíñíîì" âðàùåíèè
äåíèå ÷àñòîò "ñàìîïîääåðæèâàåòñÿ" íà áîëüøîì èíòåðâàëå âðåìåíè.
 ýòîì ñëó÷àå ìîæíî ãîâîðèòü îá óñòîé÷èâîì ðåçîíàíñíîì âðàùå-
íèè. Âàæíî îïðåäåëèòü óñëîâèÿ, ïðè êîòîðûõ ïðîèñõîäèò "çàõâàò"
âðàùåíèÿ ïðè ðåçîíàíñå è óñòàíàâëèâàåòñÿ ðåæèì óñòîé÷èâîé ðåçî-
íàíñíîé àâòîðîòàöèè.
Óïðîùåííàÿ ôèçè÷åñêàÿ êàðòèíà, ïîÿñíÿþùàÿ ïîòåðþ óñòîé÷è-
âîñòè ïðè ðåçîíàíñå ñòàòè÷åñêè óñòîé÷èâûì ËÀ, çàêëþ÷àåòñÿ â ñëå-
äóþùåì (ñì. [19]). Ïðè âðàùåíèè àïïàðàòà îòíîñèòåëüíî îñè, íå
ñîâïàäàþùåé ñ ãëàâíîé îñüþ èíåðöèè è ñîñòàâëÿþùåé íåêîòîðûé
óãîë ñ âåêòîðîì ñêîðîñòè V, íà íåãî áóäåò äåéñòâîâàòü êðîìå àýðî-
äèíàìè÷åñêîãî ñòàáèëèçèðóþùåãî ìîìåíòà èíåðöèîííûé ìîìåíò
îò öåíòðîáåæíûõ ñèë My èí ≈ (I − I x)ω2β (ðèñ. 7 .13). Ýòîò ìîìåíò (è
àíàëîãè÷íûé åìó Mz èí), ïðîïîðöèîíàëüíûé óãëó îòêëîíåíèÿ β,
ñòðåìèòñÿ óâåëè÷èòü åãî.
Òàêèì îáðàçîì, ïðè âðàùåíèè ñíàðÿäà ñ ïîñòîÿííîé óãëîâîé
ñêîðîñòüþ êðåíà ω = ωx = const íà íåãî êðîìå àýðîäèíàìè÷åñêîãî
ñòàáèëèçèðóþùåãî ìîìåíòà äåéñòâóåò äîïîëíèòåëüíûé äåñòàáèëè-
çèðóþùèé ìîìåíò, ïðîïîðöèîíàëüíûé êâàäðàòó óãëîâîé ñêîðîñòè
êðåíà, óìåíüøàþùèé "ýôôåêòèâíóþ" ñòåïåíü ñòàòè÷åñêîé óñòîé÷è-
âîñòè. Óñëîâèå íåéòðàëüíîé óñòîé÷èâîñòè èìååò âèä
d
d
MM
I
Iq
S
l
m
yy
x
y
β
ω
β
(
),() ||,
èí
èëè
+=
−
−
=
00
2
îòêóäà ñëåäóåò ïðèáëèæåííàÿ ôîðìóëà äëÿ êðèòè÷åñêîé ñêîðîñòè
âðàùåíèÿ ïî êðåíó (7.109).
Ñóòü ÿâëåíèÿ âðàùàòåëüíîãî ðåçîíàíñà ñîñòîèò âî âçàèìîäåéñò-
âèè äâèæåíèé ïî óãëàì òàíãàæà, êóðñà è êðåíà. Ïîýòîìó íåîáõîäè-
ìî àíàëèçèðîâàòü âðàùàòåëüíîå äâèæåíèå ñíàðÿäà ïðè ðåçîíàíñå
êàê äâèæåíèå íåëèíåéíîé äèíàìè÷åñêîé ñèñòåìû.
345
Ðèñ. 7.13 . Ïîòåðÿ
óñòîé÷èâîñòè ïðè
ðåçîíàíñå îïåðåí-
íûõ âðàùàþùèõñÿ
ñíàðÿäîâ
Ðàññìîòðèì äâèæåíèå íà ïàññèâíîì ó÷àñòêå òðàåêòîðèè ïðè íà-
ëè÷èè òîëüêî àýðîäèíàìè÷åñêîé íåñèììåòðèè. Óðàâíåíèå äâèæå-
íèÿ (7.107) è ïåðâîå óðàâíåíèå ñèñòåìû (7.100) çàïèøåì äëÿ ýòîãî
ñëó÷àÿ â âèäå
•
••
()•
βωνβω λλβ
ωλ
αωμ
λα
+++
−
−
−
⎛
⎝⎜⎞
⎠⎟
−
cc
x
c
I
I
2
1
22
2
12
∆
êð
=
+++
−
+
+−
⎛
⎝⎜⎞
⎠⎟
ωβ
αων
αω
λλα
ωλ
c
cc
x
I
I
2
0
2
1
22
1
2
;
•
••
()
•
∆
êð βωμλβ ωα
λλ
ω
αβ
ωα
α
+=
+=++
−
cc
xx
y
y
mm
c
z
c
y
22
0
1
;
•
()
.
êð
∆∆
(7.114)
 ýòèõ óðàâíåíèÿõ ñäåëàí ïåðåõîä îò ïåðåìåííîé ωx ê ïåðå-
ìåííîé λ = ωx/ωêð è èñïîëüçîâàíû îáîçíà÷åíèÿ: νω
11
2
=k
c
/;
mq
S
lI
Vm
xx
x
ωω
=
−
21
()||
;
mq
S
l
Im
xx
x
=
−1
0; cq
S
l
c
yx
y
αα
=
−1
.
Ñèñòåìà (7.114) ïÿòîãî ïîðÿäêà îòíîñèòåëüíî ôàçîâûõ êîîð-
äèíàò β ,
•
,
βα,
•
,
α λ – íåëèíåéíàÿ, ñ ïåðåìåííûìè êîýôôèöèåíòà-
ìè. Ïðèìåì, ÷òî çà âðåìÿ ðàçâèòèÿ ðåçîíàíñíûõ ÿâëåíèé êîýô-
ôèöèåíòû ñèñòåìû èçìåíÿþòñÿ ìàëî è èõ ìîæíî ñ÷èòàòü ïîñòî-
ÿííûìè.  ýòîì ñëó÷àå äèíàìè÷åñêàÿ ñèñòåìà, çàäàâàåìàÿ
óðàâíåíèÿìè (7.114), îòíîñèòñÿ ê êëàññó ñèñòåì Ìîðñà–Ñìåéëà
[6, 8, 89] è ñòðóêòóðà ðàçáèåíèÿ åå ôàçîâîãî ïðîñòðàíñòâà íà òðà-
åêòîðèè îïðåäåëÿåòñÿ ÷èñëîì, ïîëîæåíèåì è òèïîì îñîáûõ òî-
÷åê, êîòîðûå ìîãóò áûòü íàéäåíû èç ðåøåíèÿ àëãåáðàè÷åñêèõ
óðàâíåíèé, îïèñûâàþùèõ óñòàíîâèâøèåñÿ äâèæåíèÿ (áàëàíñè-
ðîâî÷íûé ðåæèì) ýòîé ñèñòåìû:
();
();
(
1
1
2
0
2
0
1
+−− =
+−+=
=+
−
∆
∆
λλβμ
λαβ
λλαμ
λ
βα
λω
ω
mm
xx
êð
cz cy
yy
αα
αβ
∆∆
+
).
(7.115)
Ðàññìîòðèì äëÿ îïðåäåëåííîñòè êîìïëàíàðíóþ
àñèììåòðèþ:
∆y = α0 =0;βa ≠ 0; ∆z ≠ 0 (ðèñ. 7.14). Ðåøàÿ (7.115) îòíîñèòåëüíî α è β,
ïîëó÷èì
346
β=
λλβ
λλ μλ
α
μλβ
λλ μλ
()
()
;
()
1
1
1
2
0
22
22
0
22
2
+−
+−+
=
−
+−+
∆
∆
∆
2
1
2
=
=−
=
F
m
ñz
m
cz
F
x
y
x
y
();
().
λ
α
ω
λλ
ω
αα
êð
∆∆
(7.116)
Îñîáûå òî÷êè ñèñòåìû (7.114) íàéäåì, ðåøèâ îòíîñèòåëüíî λ
óðàâíåíèå F1(λ)=F2(λ):
m
ñz
m
cz
x
y
x
y
ω
αα
ω
λ
μλβ
λλμλ
êð
∆∆∆
−=
−
+−
0
2222
1()
(7.117)
è ïîäñòàâèâ ïîëó÷åííûå âåùåñòâåííûå êîðíè λ* â âûðàæåíèÿ äëÿ α è
β.
Óðàâíåíèå (7.117) ïðåäñòàâëÿåò ñîáîé îòíîñèòåëüíî λ ïîëèíîì
ïÿòîé ñòåïåíè, êîòîðûé ìîæåò èìåòü â çàâèñèìîñòè îò ïàðàìåòðîâ
îò îäíîãî äî ïÿòè äåéñòâèòåëüíûõ êîðíåé. Ñîîòâåòñòâåííî èçìåíÿ-
åòñÿ ÷èñëî îñîáûõ òî÷åê ñèñòåìû (7.114). Íà ðèñ. 7.15 ïîêàçàí ñëó-
÷àé ñóùåñòâîâàíèÿ òðåõ îñîáûõ òî÷åê â ýòîé ñèñòåìå. Ôóíêöèþ
F2(λ) ìîæíî ðàññìàòðèâàòü êàê çàâèñÿùåå îò ïàðàìåòðà àñèììåòðèè
∆z îäíîïàðàìåòðè÷åñêîå ñåìåéñòâî ïðÿìûõ (ðèñ. 7.15, à), íàêëîí
êîòîðûõ èçìåíÿåòñÿ ïðè èçìåíåíèè ∆z. Ëîêàëüíàÿ ñòðóêòóðà ôàçî-
âîãî ïðîñòðàíñòâà è õàðàêòåð ïîâåäåíèÿ ôàçîâûõ òðàåêòîðèé â îê-
ðåñòíîñòè êàæäîé èç îñîáûõ òî÷åê çàâèñÿò îò èõ òèïà.
Ðàñïðåäåëåíèå êîðíåé ëèíåàðèçîâàííîé â îêðåñòíîñòè êàæäîé
èç îñîáûõ òî÷åê ñèñòåìû è íàïðàâëåíèå èõ ïåðåìåùåíèÿ â ïëîñêî-
ñòè (Re – Im) ïðè óìåíüøåíèè ∆z ïîêàçàíû íà ðèñ. 7.15 . Ïîñêîëüêó
347
Ðèñ. 7 .14. Ñõåìà
îðèåíòàöèè îñåé
êîîðäèíàò â ñëó-
÷àå êîìïëàíàð-
íîé àýðîäèíàìè-
÷åñêîé àñèììåò-
ðèè
ðàçìåðíîñòü ôàçîâîãî ïðîñòðàíñòâà è ïîðÿäîê äèíàìè÷åñêîé ñèñòå-
ìû ðàâíû ïÿòè, èçîáðàçèòü ïîâåäåíèå ôàçîâûõ òðàåêòîðèé â îêðå-
ñòíîñòè îñîáûõ òî÷åê çàòðóäíèòåëüíî. Íà ðèñ. 7.15 ïîêàçàí ïðàêòè-
÷åñêè ðåàëèçóåìûé ñëó÷àé, êîãäà çíà÷åíèÿ ïàðàìåòðîâ ñèñòåìû òà-
êîâû, ÷òî èç òðåõ îñîáûõ òî÷åê ïåðâàÿ è òðåòüÿ ïðåäñòàâëÿþò ñîáîé
îáîáùåííûé ôîêóñ, à âòîðàÿ, ëåæàùàÿ íà âíåøíåì ñêëîíå ðåçî-
íàíñíîãî ïèêà, íåóñòîé÷èâà è â ñîîòâåòñòâèè ñ êëàññèôèêàöèåé
îñîáûõ òî÷åê ìíîãîìåðíûõ ñèñòåì (ñì. [90]) ïðåäñòàâëÿåò ñîáîé
îáîáùåííîå ñåäëî.
Ïîêàçàííàÿ ñòðóêòóðà ñîîòâåòñòâóåò çíà÷åíèþ ïàðàìåòðà, ëåæà-
ùåìó â ïðåäåëàõ ∆z2 < ∆z < ∆z1, ãäå ∆z1 è ∆z2 ÿâëÿþòñÿ áèôóðêàöèîí-
íûìè çíà÷åíèÿìè ïàðàìåòðà ∆z è ñîîòâåòñòâóþò ñëó÷àþ êàñàíèÿ
ïðÿìîé F2(λ) ðåçîíàíñíîãî ïèêà çàâèñèìîñòè F1(λ) (ñì. ðèñ. 7.15, à).
Ðåæèì óñòîé÷èâîé ðåçîíàíñíîé àâòîðîòàöèè îïðåäåëÿåò óñòîé÷è-
âàÿ îñîáàÿ òî÷êà 1, ëåæàùàÿ íà âíóòðåííåì ñêëîíå ðåçîíàíñíîãî
ïèêà (ðèñ. 7.15, à).
Ðèñ. 7 .16 èëëþñòðèðóåò ýôôåêò "çàõâàòà" îïåðåííîãî àñèììåò-
ðè÷íîãî ñíàðÿäà â ðåæèì óñòîé÷èâîé ðåçîíàíñíîé àâòîðîòàöèè íà
ïàññèâíîì ó÷àñòêå ïðè åãî ðàñêðóòêå âîêðóã ïðîäîëüíîé îñè çà ñ÷åò
êîñî ïîñòàâëåííîãî îïåðåíèÿ. Åñëè áû íå áûëî âçàèìîäåéñòâèÿ
âðàùåíèÿ ñíàðÿäà ïî êðåíó ñ äâèæåíèÿìè ïî òàíãàæó è êóðñó, óñòà-
íîâèâøååñÿ çíà÷åíèå ωx (êðèâàÿ I, ðèñ. 7 .16) ñóùåñòâåííî ïðåâûøà-
ëî áû ωêð.
348
Ðèñ. 7 .15. Õàðàêòåð ïîâåäåíèÿ ôàçîâûõ òðàåêòîðèé â îêðåñòíîñòè îñîáûõ òî÷åê ñèñ-
òåìû (7.114):
à – â ñëó÷àå ñóùåñòâîâàíèÿ 3 îñîáûõ òî÷åê; á – â îêðåñòíîñòè îñîáîé òî÷êè 1; â –
â îêðåñòíîñòè îñîáîé òî÷êè 2, îïðåäåëÿþùåé ðåçîíàíñ; ã – â îêðåñòíîñòè îñî-
áîé òî÷êè 3
Âñëåäñòâèå ïåðåêðåñòíîé ñâÿçè äâèæåíèé ïðîèñõîäèò ñëåäóþ-
ùåå: ïðè äîñòèæåíèè ωx êðèòè÷åñêèõ çíà÷åíèé ïîä äåéñòâèåì ìî-
ìåíòîâ àñèììåòðèé íàáëþäàåòñÿ ðåçîíàíñíîå âîçðàñòàíèå óãëîâ
àòàêè è ñêîëüæåíèÿ. Ïîÿâëÿåòñÿ äîïîëíèòåëüíûé ìîìåíò ïî êðåíó
Ì∆=Ic z
xy
α
α∆ (ñì. ðèñ. 7.16), êîòîðûé íàïðàâëåí â ñòîðîíó, ïðîòèâî-
ïîëîæíóþ ìîìåíòó Ìx = Im
xx
îò êîñî ïîñòàâëåííîãî îïåðåíèÿ
(αá < 0) (ñì. ðèñ. 7.15, à), è êîòîðûé óìåíüøàåò óãëîâóþ ñêîðîñòü ïî
êðåíó (ó÷àñòîê 1, ðèñ. 7.16).
Ïðè óäàëåíèè ωx îò êðèòè÷åñêèõ çíà÷åíèé (ó÷àñòîê 2, ðèñ. 7.16)
óãëû àòàêè óìåíüøàþòñÿ è ìîìåíò îò êîñî ïîñòàâëåííîãî îïåðåíèÿ
íà÷èíàåò óâåëè÷èâàòü óãëîâóþ ñêîðîñòü ïî êðåíó ωx äî äîñòèæåíèÿ
êðèòè÷åñêèõ çíà÷åíèé. Äàëåå âñå ïîâòîðÿåòñÿ.
Òàêèì îáðàçîì, ïåðåêðåñòíàÿ ñâÿçü äâèæåíèé ïî òàíãàæó, êóðñó
è êðåíó ïðè äåéñòâèè ìàëûõ ìîìåíòîâ àñèììåòðèè ïðèâîäèò ê
òîìó, ÷òî ðåçîíàíñíûå óñëîâèÿ "ñàìîïîääåðæèâàþòñÿ" íà áîëüøîì
èíòåðâàëå âðåìåíè. Äàííûé ðåæèì óñòîé÷èâîé ðåçîíàíñíîé àâòî-
ðîòàöèè (êðèâàÿ II, ðèñ. 7.16) îçíà÷àåò, ÷òî ôàçîâàÿ òðàåêòîðèÿ ïî-
ïàëà â îáëàñòü ïðèòÿæåíèÿ óñòîé÷èâîé îñîáîé òî÷êè, îïðåäåëÿþ-
ùåé ðåçîíàíñ.
Ðåæèì óñòîé÷èâîãî ðåçîíàíñíîãî âðàùåíèÿ ðåàëèçóåòñÿ â òåõ
ñëó÷àÿõ, êîãäà, âî-ïåðâûõ, ñî÷åòàíèå ïàðàìåòðîâ ñíàðÿäà mx
ω
,m
x
,cy
α
,
μ, ∆λ è àñèììåòðèé βa è ∆z òàêîâî, ÷òî ñóùåñòâóåò óñòîé÷èâàÿ îñîáàÿ
òî÷êà íà ñêëîíå ðåçîíàíñíîãî ïèêà (ñì. ðèñ. 7.15). Òàê, íàïðèìåð,
åñëè ∆z > ∆z1 èëè ∆z < ∆z2, òî â ñèñòåìå ãàðàíòèðóåòñÿ îòñóòñòâèå ðå-
çîíàíñà. Âî-âòîðûõ, íà÷àëüíûå óñëîâèÿ äâèæåíèÿ (β0,
•
,
β0 α0,
•
,
α0 λ0)
äîëæíû áûòü òàêèìè, ÷òîáû ôàçîâàÿ òðàåêòîðèÿ ïîïàëà â îáëàñòü
349
Ðèñ. 7 .16 . Çàõâàò
îïåðåííîãî ñíàðÿ-
äà â ðåçîíàíñ ïðè
ðàñêðóòêå
êîñî
ïîñòàâëåííûì îïå-
ðåíèåì
ïðèòÿæåíèÿ óñòîé÷èâîé òî÷êè, îïðåäåëÿþùåé ðåçîíàíñ. Ïðè
óìåíüøåíèè çíà÷åíèÿ ïàðàìåòðà ∆z è ïðèáëèæåíèè ê áèôóðêàöè-
îííîìó çíà÷åíèþ óñòîé÷èâàÿ è íåóñòîé÷èâàÿ îñîáûå òî÷êè ïðèáëè-
æàþòñÿ ê âåðøèíå ðåçîíàíñíîãî òèïà, ïðè÷åì îáîáùåííûé ôîêóñ
(ðèñ. 7 .17, à) äåôîðìèðóåòñÿ â âûðîæäåííûé óçåë (ðèñ. 7 .17, á),àçà-
òåì ïðîñòî â óçåë (ðèñ. 7.17 . â). Óñòîé÷èâûé ôîêóñ è óñòîé÷èâûé
óçåë òîïîëîãè÷åñêè ýêâèâàëåíòíû. Ïðè ∆z = ∆z1 îñîáûå òî÷êè ñëè-
âàþòñÿ, îáðàçóÿ ñëîæíóþ îñîáóþ òî÷êó òèïà "ñåäëî-óçåë"
(ðèñ. 7 .17, ã). Ýòî âûðîæäåííàÿ îñîáàÿ òî÷êà. Ñèñòåìà îêàçûâàåòñÿ
ñòðóêòóðíî íåóñòîé÷èâîé. Ïðè óìåíüøåíèè ïàðàìåòðà ∆z îñîáåí-
íîñòü èñ÷åçàåò è âåêòîðíîå ïîëå âûïðÿìëÿåòñÿ (ðèñ. 7.17, ä).
7.4 . ÑÂÎÁÎÄÍÛÉ ÏÎËÅÒ ÏÎ ÍÈÑÕÎÄßÙÅÉ ÂÅÒÂÈ
ÒÐÀÅÊÒÎÐÈÈ
7.4.1. ÄÂÈÆÅÍÈÅ ËÀ ÏÐÈ ÂÕÎÄÅ Â ÀÒÌÎÑÔÅÐÓ
Äâèæåíèå íåóïðàâëÿåìîãî ËÀ íà íèñõîäÿùåé âåòâè òðàåêòîðèè
ìîæåò áûòü â êàêîé-òî ïåðèîä âðåìåíè íåîðãàíèçîâàííûì. Ýòî îá-
ñòîÿòåëüñòâî, òàê æå êàê è âîçìîæíûå äîñòàòî÷íî ñèëüíûå âîçìó-
350
Ðèñ. 7 .17. Ïåðåñòðîéêà ñòðóêòóðû ðàçáèåíèÿ ôàçîâîãî ïðîñòðàíñòâà ñèñòåìû ïðè
èçìåíåíèè ïàðàìåòðà àñèììåòðèè ∆z
ùåíèÿ, ïðèâîäèò ê íåîáõîäèìîñòè ðàññìàòðèâàòü çàäà÷ó î äâèæå-
íèè ËÀ ñ ðàçíîîáðàçíûìè, íàïåðåä íåèçâåñòíûìè íà÷àëüíûìè óñ-
ëîâèÿìè.
Ñíèæåíèå ËÀ áóäåò ïðîèñõîäèòü ñ ñóùåñòâåííûìè èçìåíåíèÿìè
óãëîâ àòàêè è ñêîëüæåíèÿ è õàðàêòåðèñòèê äâèæåíèÿ öåíòðà ìàññ
ËÀ. Âðàùåíèå îòíîñèòåëüíî öåíòðà ìàññ ñòàòè÷åñêè óñòîé÷èâîãî
ËÀ ïðè äâèæåíèè â ïëîòíûõ ñëîÿõ àòìîñôåðû áóäåò ïîñòåïåííî ïå-
ðåõîäèòü â êîëåáàíèå ñ óìåíüøåíèåì óãëîâ àòàêè è ñêîëüæåíèÿ.
Ïîëíàÿ ñèñòåìà óðàâíåíèé â âåêòîðíîé ôîðìå, îïèñûâàþùàÿ
äâèæåíèÿ ËÀ, èìååò âèä
d
dt
d
dt
d
dt
K
M
QF
r
V
==
=
;;. (7.118)
Çäåñü, òàê æå êàê è â ãë. 1, Q – âåêòîð êîëè÷åñòâà äâèæåíèÿ; K –
âåêòîð êèíåòè÷åñêîãî ìîìåíòà; r – ðàäèóñ-âåêòîð.
Õàðàêòåðíûå ïðîìåæóòêè âðåìåíè äëÿ âðàùàòåëüíîãî è ïîñòóïà-
òåëüíîãî äâèæåíèé îïðåäåëÿþòñÿ ôîðìóëàìè
tt
r
V
aV
==
1/;
/,
Ω∆
(7.119)
ãäå Ω – õàðàêòåðíàÿ óãëîâàÿ ñêîðîñòü ËÀ îòíîñèòåëüíî öåíòðà ìàññ.
Îáîçíà÷èì ÷åðåç ∆r è ∆V õàðàêòåðíûå èçìåíåíèÿ ðàäèóñ-âåêòîðà
è ñêîðîñòè äâèæåíèÿ öåíòðà ìàññ ËÀ çà ïðîìåæóòîê âðåìåíè tV è
ââåäåì áåçðàçìåðíûå ïåðåìåííûå â (7.118):
QQ
KK
r
r
MM
F
F
V
V
===
==
=
⋅
mV
mli
r
ml
F
F
V
z
z
cn
∆Ω
∆
~
;
~
;
~
||~
;
~
;
~
2
,
(7.120)
ãäå
~
,
K~
,
Q~
,
r
~
,
M~Fè
~
–
V áåçðàçìåðíûå ïåðåìåííûå; iz – áåçðàçìåðíûé
ìîìåíò èíåðöèè; m – ìàññà ËÀ; mz
cn
–
çàïàñ óñòîé÷èâîñòè ËÀ; l –
õàðàêòåðíàÿ äëèíà ËÀ; F – ìîäóëü ãëàâíîãî âåêòîðà ñèñòåìû ñèë.
Ïðè ñâîáîäíîì ïîëåòå â àòìîñôåðå, êîãäà äåéñòâèå àýðîäèíàìè-
÷åñêèõ ñèë ïðåâîñõîäèò äåéñòâèå âñåõ îñòàëüíûõ, ìîæíî íàïèñàòü
Fm
V
Vr
=()
/
.
∆∆
(7.121)
Ïðè èçó÷åíèè äâèæåíèÿ ËÀ îòíîñèòåëüíî öåíòðà ìàññ â êà÷åñòâå
ìàñøòàáà âðåìåíè âûáèðàåòñÿ ta, òîãäà áåçðàçìåðíîå âðåìÿ îïðåäå-
ëèòñÿ îòíîøåíèåì
~
/.
ttt
a
=
Ââîäÿ áåçðàçìåðíîå âðåìÿ â (7.118) è èñïîëüçóÿ (7.119), ïåðåïè-
øåì (7.118) â ñëåäóþùåé áåçðàçìåðíîé ôîðìå:
351
d
dt
V
r
m
i
V
V
r
l
d
dt
V
r
z
c
z
n
~
~
;
~
~
K
M
Q
F
=
⎛
⎝⎜⎞
⎠⎟
=
⎛
⎝⎜⎞
⎠⎟
Ω∆
∆∆
Ω∆
2
;
~
~
~
.
d
dt
V
r
r
V
=
⎛
⎝⎜⎞
⎠⎟
Ω∆
(7.122)
Ñðàâíèâàÿ (7.122) è (7.119), ìîæíî íàïèñàòü
Vr
t
t
aV
/()/.
Ω∆=
Àíàëèç ÷èñëåííûõ çíà÷åíèé êîýôôèöèåíòîâ ïðè
~
,
M
~
Fè
~
Vâ
óðàâíåíèÿõ (7.122) ïîêàçûâàåò, ÷òî äëÿ ó÷àñòêà òðàåêòîðèè ñíèæåíèÿ
ËÀ â àòìîñôåðå êîýôôèöèåíò ïðè
~
M èìååò ïîðÿäîê åäèíèöû, à
êîýôôèöèåíòû ïðè
~
Fè
~
–
V ïîðÿäîê ε = ta/tV, ñóùåñòâåííî ìåíüøèé
åäèíèöû. Ýòî îçíà÷àåò, ÷òî íà èíòåðâàëàõ âðåìåíè, õàðàêòåðíûõ äëÿ
äâèæåíèÿ ËÀ îòíîñèòåëüíî öåíòðà ìàññ ta, ïàðàìåòðû äâèæåíèÿ
ñàìîãî öåíòðà ìàññ èçìåíÿþòñÿ íà âåëè÷èíû ïîðÿäêà ε.
Ïðèâåäåííûå ðåçóëüòàòû ïîçâîëÿþò çàïèñàòü óðàâíåíèÿ (7.122) â
âèäå
d
dt
d
dt
d
dt
K
M
QF
r
V
===
;;,
εε
(7.123)
ãäå ε – ìàëûé ïàðàìåòð, è èñïîëüçîâàòü äëÿ èõ èññëåäîâàíèÿ
àñèìïòîòè÷åñêèå ìåòîäû [43, 67, 136]. Çäåñü è äàëåå çíà÷îê
áåçðàçìåðíîñòè ∼ îïóùåí.
Äëÿ òîãî ÷òîáû ñèñòåìà óðàâíåíèé (7.118) ìîãëà áûòü çàïèñàíà â
âèäå (7.123), íåîáõîäèìî âûïîëíåíèå íåðàâåíñòâà
V
r
Ω∆
<< 1.
Õàðàêòåðèñòèêè äâèæåíèÿ, îïðåäåëÿåìûå (7.123), ìîãóò áûòü
ïðåäñòàâëåíû â âèäå
VV Vt
t
=+
=+
01
01
() (,); () (,),
τετ θθτε
θτ
(7.124)
ãäå τ = εt – òàê íàçûâàåìîå ìåäëåííîå âðåìÿ; ôóíêöèè V0(τ)èθ0(τ)è
ò.ä.
–
ïàðàìåòðû òðàåêòîðèè öåíòðà ìàññ, îïðåäåëÿåìûå áåç ó÷åòà
âëèÿíèÿ âðàùàòåëüíîãî äâèæåíèÿ ËÀ îòíîñèòåëüíî åãî öåíòðà ìàññ;
V1(τ, t), θ1(τ, t) è ò.ä .
–
÷ëåíû, îïðåäåëÿåìûå äâèæåíèåì ËÀ
îòíîñèòåëüíî öåíòðà ìàññ. Â ðåçóëüòàòå ðÿäà ïðåîáðàçîâàíèé è
óïðîùåíèé óðàâíåíèÿ âîçìóùåííîãî äâèæåíèÿ ËÀ îòíîñèòåëüíî
352
öåíòðà ìàññ ìîãóò áûòü ïðèâåäåíû ê âèäó, áëèçêîìó ê âèäó
óðàâíåíèÿ, îïèñûâàþùåãî èçìåíåíèå óãëà àòàêè ËÀ:
d
dt
Mxx
fxx
d
dt
dx
dt
X
z
i
2
2
12
12
0
α
αε
α
α
ε
++=
+
Σ (,,,) (,,,)
;
KK
ixx
i
(,,,) (
,, ,)
,
12
01
2
6
KK
α=
=
(7.125)
ãäå xG
KK
I
xy
z
1==
−
cos
sin
;
αα
KI KI
xx
xyy
y
==
ωω
;
–
ïðîåêöèè êèíåòè÷åñêîãî ìîìåíòà íà ñîîòâåòñòâóþùèå îñè
êîîðäèíàò;x2=r;x3=V;x4=θ;x5=H(âûñîòàïîëåòà);x6=LÇ
(äàëüíîñòü ïîëåòà, èçìåðÿåìàÿ ïî ïîâåðõíîñòè Çåìëè);
•
(,) [(,) (,)]cos (,)sin
xfGff
Y
mV
yx
y
a
1 =+−
−
⎧⎨
τα
τα
τα
α
τα
α
⎩
⎫⎬⎭
==
+
=
r
xfr
x
cq
S
m
g
x
g
x
xa
;
•
(, );•
()
sin ;
•
cos
23
4
τα
α
θ
θ
ò
ò
V
V
Rg
xV
x
R
RH
V
1
2
5
6
−
⎛
⎝⎜
⎞
⎠⎟ =−
=−
+
Çò
Ç
Ç
;•
sin ;
•
cos .
θ
θ
Ðåøåíèå óðàâíåíèé (7.125) çàïèñûâàåòñÿ â âèäå ôóíêöèè äâóõ
ïåðåìåííûõ – ìåäëåííîãî âðåìåíè τ è ôàçû êîëåáàíèé φ.
Ïîðîæäàþùåå óðàâíåíèå èìååò âèä
ωτ
α
φ
ττα
2
2
0
2
10
20
0
0
()
[(),(,), ,]
,
d
d
Mxx
+=
Σ
K
(7.126)
ãäå ω(τ)=dφ/dt è xi0(τ) – ïðîèçâîëüíûå ôóíêöèè, ïîäëåæàùèå
îïðåäåëåíèþ. Ïåðåìåííûå τ è φ â (7.126) ìîãóò ñ÷èòàòüñÿ
íåçàâèñèìûìè. Ïðåäïîëàãàåòñÿ, ÷òî ôóíêöèÿ α0(τ, φ), îïðåäåëåííàÿ
èç óðàâíåíèÿ (7.126), îáëàäàåò ñâîéñòâîì
353
ατφ
ατφ
π
φ
00
0
2
(,)(,)
,
+=
+
⎧
⎨
⎩
T
ãäå Tφ – "ïåðèîä" ôóíêöèè α0(τ, φ)ïîφ. Ïðè äîáàâëåíèè íóëÿ ê
ïðàâîé ÷àñòè ðåøåíèå ñîîòâåòñòâóåò êîëåáàòåëüíîìó äâèæåíèþ ËÀ
îòíîñèòåëüíî ïîïåðå÷íîé îñè; ïðè äîáàâëåíèè 2π – âðàùåíèþ ËÀ
îòíîñèòåëüíî òîé æå îñè. Óðàâíåíèå (7.126) íàçûâàåòñÿ ýòàëîííûì
óðàâíåíèåì [67].
Äëÿ ïðîñòîãî ñëó÷àÿ ïëîñêîãî äâèæåíèÿ ËÀ, ïðèíèìàÿ r = G =0,
óðàâíåíèå, îïðåäåëÿþùåå èçìåíåíèå óãëà àòàêè, ìîæíî çàïèñàòü
òàê:
d
dt
ft
d
dt
Mt
z
2
2
0
α
α
α
α
++
=
(,)
(,)
.
(7.127)
Åñëè ïðèíÿòü äëÿ àýðîäèíàìè÷åñêèõ õàðàêòåðèñòèê â ïðåäåëàõ
èçìåíåíèÿ óãëîâ àòàêè îò 0 äî 360° òðèãîíîìåòðè÷åñêèå çàâèñèìîñòè
è îáû÷íóþ ïðîïîðöèîíàëüíîñòü ñêîðîñòíîìó íàïîðó, ïëîùàäè
ìèäåëÿ è õàðàêòåðíîé äëèíå ËÀ:
Mt qSlm
Yt qSc
Xt
zz
ay
a
(,) ()sin;
(,) ()sin;
(,
αα
αα
α
α
α
=
=
0
0
2
)(s
i
n
)
;
(,)
(),
=+
=
qSc
c
MtS
lVm
xy
zz
aa
zz
0
2
0
2
0
α
ωω
α
αρ
(7.128)
òî óðàâíåíèå (7.127) áóäåò èìåòü âèä
d
dt
ft
d
dt
gt
z
2
2
0
α
α
α
α
++=
(, ) ()sin
,
(7.129)
ãäå
gt
qSl
I
mf
t
S
m
Vc
m
i
z
zz
y
z
z
a
z
() ();(,)
( )cos
==−
⎡
αα
ω
α
ρ
α
0
0
0
2
⎣
⎢
⎢
⎤
⎦
⎥
⎥
=
;
.
i
I
ml
z
z
0
2
354
7.4.2. ÊÀ×ÅÑÒÂÅÍÍÛÉ ÀÍÀËÈÇ ÓÃËÎÂÎÃÎ ÄÂÈÆÅÍÈß ËÀ ÏÐÈ ÂÕÎÄÅ
 ÀÒÌÎÑÔÅÐÓ
Íåëèíåéíîå óðàâíåíèå (7.129) ïðåäñòàâëÿåò ñîáîé óðàâíåíèå ñ ïåðåìåí-
íûìè êîýôôèöèåíòàìè è â êîíå÷íîì âèäå íå èíòåãðèðóåòñÿ.
Ïðåäïîëàãàÿ, ÷òî õàðàêòåðíîå âðåìÿ äâèæåíèÿ ËÀ îòíîñèòåëüíî öåíòðà
ìàññ çíà÷èòåëüíî ìåíüøå õàðàêòåðíîãî âðåìåíè äâèæåíèÿ öåíòðà ìàññ, çà-
ïèøåì óðàâíåíèå (7.129) â ôîðìå, ñîäåðæàùåé ìàëûé ïàðàìåòð:
d
dt
fd
dt
M
z
2
2
0
α
ετα
α
τα
++
=
(,)
(,)
.
(7.130)
Ýòàëîííîå óðàâíåíèå ïðè r0 = G0 = 0 áóäåò èìåòü âèä
ωτ
∂α
∂φ
τα
2
2
0
2
0
0
()
(,)
.
+=
M
(7.131)
Óñëîâèå ïåðèîäè÷íîñòè çàïèñûâàåòñÿ òàê [67, 136]:
d
d
df
d
z
T
τ
ωτ
∂α
∂φ
φτ
α
ω
τ
∂α
∂φ
φ
()
(, )()
0
2
0
0
2
0
⎛
⎝⎜⎞
⎠⎟+
⎛
⎝⎜⎞
⎠⎟
φ
φ
/
/
.
2
0
2
0
∫
∫
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
=
T
(7.132)
Ýòî óðàâíåíèå óïðîñòèòñÿ, åñëè ââåñòè îñðåäíåííîå çíà÷åíèå ôóíêöèè
fz(, )
τα â èíòåðâàëå èçìåíåíèÿ óãëà àòàêè 0 ≤α≤αmax:
ωτ
∂α
∂φ
φ
ττ
τ
τ
φ
()
,
()
/
0
2
0
2
0
⎛
⎝⎜⎞
⎠⎟=
∫−
∫dD
e
fd
T
z
(7.133)
ãäå
f
fd
d
z
z
T
T
()
(,)
/
τ
τα
∂α
∂φ
φ
∂α
∂φ
φ
φ
=
⎛
⎝⎜⎞
⎠⎟
⎛
⎝⎜⎞
⎠⎟
∫002
0
2
0
2
0
φ/
;
2
∫
(7.134)
D – êîíñòàíòà.
Ïðè ñèíóñîèäàëüíîé çàâèñèìîñòè äëÿ ìîìåíòà ýòàëîííîå óðàâíåíèå
èìååò âèä
ωτ
∂α
∂φ
τα
2
2
0
2
0
()
()sin
.
+=
g
(7.135)
Ýòî óðàâíåíèå ÿâëÿåòñÿ èçâåñòíûì óðàâíåíèåì ìàòåìàòè÷åñêîãî ìàÿò-
íèêà, è åãî ðåøåíèå ïîëó÷àåòñÿ â âèäå ýëëèïòè÷åñêèõ ôóíêöèé ßêîáè.
Îäèí èç âàðèàíòîâ ôàçîâîé ïëîñêîñòè óðàâíåíèÿ (7.135) îò 0 äî −π ïîêàçàí
355
íà ðèñ. 7.18. Ïåðåñåêàþùèåñÿ â òî÷êàõ −π è π êðèâûå îáðàçóþò ñåïàðàòðèñó,
êîòîðàÿ îòäåëÿåò îáëàñòü ÂÄ (âðàùàòåëüíîå äâèæåíèå), ñîîòâåòñòâóþùóþ
âðàùåíèþ ËÀ, îò îáëàñòè ÊÄ (êîëåáàòåëüíîå äâèæåíèå), ñîîòâåòñòâóþùåé
êîëåáàíèÿì ËÀ. Ðåøåíèå óðàâíåíèÿ (7.135) äëÿ îáëàñòè ÂÄ èìååò âèä [67,
136]
ατφ
ντφντ
(,)
[[()],()],
=±2am K
(7.136)
ãäå
K
d
()
()
()
ν
ξ
ξν
ξ
=
−−
∫11
0
1
(7.137)
–
ïîëíûé ýëëèïòè÷åñêèé èíòåãðàë ïåðâîãî ðîäà; am[K(ν), φ, ν] – àìïëèòóäà
ßêîáè; ν – êâàäðàò ìîäóëÿ.
Ïðîèçâîëüíàÿ ôóíêöèÿ ω(τ) îïðåäåëÿåòñÿ èç óðàâíåíèÿ
ωτ
ντ
τ
ντ
()
[()]
()
()
,
=
1
K
g
(7.138)
à ôóíêöèÿ ν(τ) – èç óðàâíåíèÿ
ντ
ντ
τ
βτ
ττ
τ
τ
()
(())
()
().
()
4
0
E
g
D
e
fd
z
=
∫
=
(7.139)
Ïîñëåäíåå óðàâíåíèå ðåøàåòñÿ ãðàôè÷åñêè, ôóíêöèÿ E(ν) ïðåäñòàâëÿåò
ñîáîé ïîëíûé ýëëèïòè÷åñêèé èíòåãðàë âòîðîãî ðîäà. Àíàëèç ïðèâåäåííûõ
ôîðìóë ïîêàçûâàåò, ÷òî íåðàâåíñòâî ν(τ) < 1 ÿâëÿåòñÿ óñëîâèåì ñóùåñòâîâà-
íèÿ âðàùàòåëüíîãî äâèæåíèÿ. Ïðè ñòðåìëåíèè ν(τ) ê åäèíèöå èçîáðàæàþ-
ùàÿ òî÷êà íà ôàçîâîé ïëîñêîñòè (dα/dt; α) ñòðåìèòñÿ ê ñåïàðàòðèñå
(ðèñ. 7.19). Òàê êàê ñåïàðàòðèñà ïðîõîäèò ÷åðåç òî÷êó α = π, dα/dt =0,òîåå
óðàâíåíèå èìååò âèä
356
Ðèñ. 7.18 . Ôàçîâûé ïîðòðåò ñèñòåìû (îáëàñòü ÂÄ ñîîòâåòñòâó-
åò âðàùåíèþ ËÀ, îáëàñòü ÊÄ – êîëåáàíèÿì ËÀ)
1
2
2
2
2
2
2
d
dt
gg
α
τ
α
τ
⎛
⎝⎜⎞
⎠⎟ +=
()sin
(). (7.140)
Ñ óâåëè÷åíèåì ïëîòíîñòè àòìîñôå-
ðû óâåëè÷èâàþòñÿ ðàçìåðû îáëàñòè
ÊÄ (ñì. ðèñ. 7 .18) è âðàùàòåëüíîå äâè-
æåíèå áóäåò ïðîäîëæàòüñÿ òîëüêî äî
ìîìåíòà âðåìåíè t *
, îïðåäåëÿåìîãî
óðàâíåíèåì β ()
*
t = 1/4. Äëÿ ñëó÷àÿ
ν0 << 1 ýòî óðàâíåíèå ïðåîáðàçóåòñÿ
òàê:
π
ωτ
ττ
τ
τ
40
0
||() .
*
()
*
z
fd
ge
z
=
∫
(7.141)
Ïåðåõîä âðàùàòåëüíîãî äâèæåíèÿ â êîëåáàòåëüíîå íàãëÿäíî èëëþñòðèðóåòñÿ
ãðàôèêîì íà ðèñ. 7 .19.
Ïðè èññëåäîâàíèè îáëàñòè ÊÄ (ñì. ðèñ. 7.18), ò.å . êîëåáàòåëüíîãî äâè-
æåíèÿ, ðåøåíèå ýòàëîííîãî óðàâíåíèÿ (7.135) íàõîäèòñÿ â âèäå
ατφ
ντ
ντφντ
(, ) arcsin{ () [ [()], ()]}.
=2s
n
K
(7.142)
Êîýôôèöèåíò ïðè φ âûáðàí òàêèì îáðàçîì, ÷òî ïåðèîä K [ν(τ)] íå çàâèñèò îò
ν. Ïðîèçâîëüíûå ôóíêöèè ω(τ)èν(τ) îïðåäåëÿþòñÿ èç óðàâíåíèé
41
1
0
[() ( )()]
() ()
;
()(
()
EK
De
g
g
fd
z
νν
ν
τ
βτ
ωτ
τ
ττ
τ
τ
−−
=
∫
=
=
)/( [()]).
Kντ
(7.143)
Ïðè ñíèæåíèè ËÀ âåëè÷èíà g(τ) ðàñòåò çà ñ÷åò óâåëè÷åíèÿ ïëîòíîñòè àò-
ìîñôåðû ρ, ïðè äîñòèæåíèè ïëîòíûõ ñëîåâ ñòàíîâèòñÿ ìàêñèìàëüíîé, à çà-
òåì íà÷èíàåò ïàäàòü âñëåäñòâèå óìåíüøåíèÿ ñêîðîñòè ËÀ. Ïîýòîìó ïðè
äâèæåíèè â ïëîòíûõ ñëîÿõ àòìîñôåðû αmax(τ) íå ïðåâîñõîäèò îäíîãî ðàäèà-
íà è ìîæíî èñïîëüçîâàòü ïðèáëèæåííûå ôîðìóëû
KE
()
;()
;
max
ν
πν
ν
πν
ν
α
≈+
⎛
⎝⎜⎞
⎠⎟
≈−
⎛
⎝⎜⎞
⎠⎟ =⎛
⎝⎜⎞
⎠⎟
2
1
42
1
42
2
.
(7.144)
 ðåçóëüòàòå ïîëó÷èì ðàñ÷åòíûå ñîîòíîøåíèÿ â âèäå
ατ
τ
π
ττ
τ
τ
max
()
()
()
;
=
∫−
e
g
D
fd
z
1
2
0
4
(7.145)
357
Ðèñ. 7 .19. Ñõåìà ïåðåõîäà âðàùàòåëü-
íîãî äâèæåíèÿ â êîëåáàòåëüíîå
αττ
αττ
π
τ
φ
max
()
max
() () ();()
()
,
==
gT
g
2
(7.146)
ãäå T(τ) – ìãíîâåííûé ïåðèîä êîëåáàíèé.
Åñëè ïðè òîðìîæåíèè ËÀ åãî ñêîðîñòü èçìåíèòñÿ îò ñâåðõçâóêîâîé äî
äîçâóêîâîé, òî ïðè ÷èñëå Ì ≈ 1 ó àýðîäèíàìè÷åñêèõ õàðàêòåðèñòèê ËÀ
ïîÿâèòñÿ íåëèíåéíîñòü, ðåçêî óâåëè÷èâàþùàÿ äåñòàáèëèçèðóþùåå âëèÿíèå
íåñòàöèîíàðíîãî ðåæèìà ïîëåòà, ÷òî ìîæåò ïðèâåñòè ê îïðîêèäûâàíèþ ËÀ.
Ïðèìåðîì íåëèíåéíîñòè òàêîãî ðîäà â óðàâíåíèè (7.130) ìîæåò ñëóæèòü çà-
âèñèìîñòü
Mgb
(,)()(),
τα
τα τα
=−
3
(7.147)
ãäå g(τ)>0;b(τ) ≥ 0.
Ñ ó÷åòîì (7.147) çàïèøåì ýòàëîííîå óðàâíåíèå (7.131) â âèäå
ωτ
∂α
∂φ
τα τα=
2
2
2
3
0
()
() ()
.
+−
gb
(7.148)
Åãî ðåøåíèå óäîáíî èñêàòü â ôîðìå
ατφατ
ντ φντ
(,)
() {[()],()}.
max
=
snK
(7.149)
Îíî çàâèñèò îò òðåõ ïðîèçâîëüíûõ ôóíêöèé αmax(τ), ν(τ)èω(τ), êîòîðûå
îïðåäåëÿþòñÿ èç ñîîòíîøåíèé
4
1
1
22
3
22
3
2
0
νν
ν
τ
τ
ντ
ωτ
ττ
τ
LD
b
g
e
fd
z
()
()
()
()
();
(
()
+
=
∫
=
−
)
()
()
;
()
()()
;
max
()
=
+
=
∫
+
−
K
g
e
D
gL
fd
z
ν
ν
τ
ατ
ν
τν
ττ
τ
1
1
1
20
(7.150)
L
EK
Dg
()( )()( )();
,
max
τ
νν νν
ν
π
α
=
+−
−
=
11
3
4
2
(7.151)
ãäå íà÷àëüíûå çíà÷åíèÿ ôóíêöèé g0 è αmax0 äîëæíû áûòü èçâåñòíû.
Àíàëèç ïîêàçûâàåò, ÷òî óâåëè÷åíèå b(τ) è óìåíüøåíèå g(τ) â âûðàæåíèè
(7.148) ïðèâåäåò ê óâåëè÷åíèþ àìïëèòóäû êîëåáàíèé, ÷òî ìîæåò âûçâàòü
îïðîêèäûâàíèå ËÀ.
358
Âûðàæåíèå äëÿ ìàêñèìàëüíî äîïóñòèìîé âåëè÷èíû íà÷àëüíîé àìïëèòó-
äû, ïðè êîòîðîé åùå íå ïðîèñõîäèò îïðîêèäûâàíèå è ËÀ óñòîé÷èâ â îêðåñò-
íîñòè α = 0, áóäåò ñëåäóþùèì:
max
min
() ()
()
max
()
α
π
ττ
τ
ττ
τ
0
1
2
0
4
42
3
0
=
∫⎡
⎣
⎢
⎢
⎢
⎤
e
g
g
g
b
fd
z
⎦
⎥
⎥
⎥
.
(7.152)
Àíàëèç ïîñëåäíåãî âûðàæåíèÿ ïîêàçûâàåò, ÷òî äåìïôèðîâàíèå, ó÷èòû-
âàåìîå ýêñïîíåíöèàëüíûì ÷ëåíîì, ñóùåñòâåííî ñïîñîáñòâóåò çàòóõàíèþ
êîëåáàíèé è çíà÷èòåëüíî óâåëè÷èâàåò äîïóñòèìûå αmax0.
Êîíòðîëüíûå âîïðîñû
1. Èçëîæèòå ñóùíîñòü ïàññèâíûõ ñïîñîáîâ ñòàáèëèçàöèè íåóïðàâëÿå-
ìûõ ðàêåò è ñíàðÿäîâ. Íàðèñóéòå ñõåìó äåéñòâèÿ àýðîäèíàìè÷åñêîãî ìî-
ìåíòà íà îïåðåííóþ ðàêåòó è âðàùàþùèéñÿ àðòèëëåðèéñêèé ñíàðÿä. Îöå-
íèòå âëèÿíèå âçàèìíîãî ðàñïîëîæåíèÿ öåíòðà ñîïðîòèâëåíèÿ è öåíòðà ìàññ
íà èçìåíåíèå óãëà àòàêè è óñòîé÷èâîñòü ËÀ. Ðàçúÿñíèòå ïîíÿòèå "ñòàòè÷å-
ñêàÿ óñòîé÷èâîñòü". Ñôîðìóëèðóéòå íåîáõîäèìîå óñëîâèå óñòîé÷èâîñòè ïî
Ëÿïóíîâó ïðàâèëüíîãî óãëîâîãî äâèæåíèÿ áûñòðîâðàùàþùåãîñÿ ñíàðÿäà íà
ïðÿìîëèíåéíîì ó÷àñòêå òðàåêòîðèè. Èñïîëüçóÿ (3.161), ïîëó÷èòå âûðàæå-
íèÿ ïåðâûõ èíòåãðàëîâ óðàâíåíèé äâèæåíèÿ ñíàðÿäà îòíîñèòåëüíî öåíòðà
ìàññ íà íà÷àëüíîì ó÷àñòêå òðàåêòîðèè (4.60) â ïåðåìåííûõ δ1, δ2. Îáúÿñíèòå
ñ ôèçè÷åñêîé òî÷êè çðåíèÿ íåóñòîé÷èâîñòü ïî Ëÿïóíîâó èäåàëüíî ïðàâèëü-
íîãî ïîëåòà áûñòðîâðàùàþùåãîñÿ ñíàðÿäà ïðè ó÷åòå ïîëíîé ñèñòåìû äåéñò-
âóþùèõ ñèë è ìîìåíòîâ.
2. Íàçîâèòå îñíîâíûå ïðèíöèïû âûáîðà øàãà ÷èñëåííîãî èíòåãðèðîâà-
íèÿ íà ÖÂÌ óðàâíåíèé âíåøíåé áàëëèñòèêè. Ïðèâåäèòå ïðèìåðû àïïðîê-
ñèìàöèè àýðîäèíàìè÷åñêèõ õàðàêòåðèñòèê, èñïîëüçóåìûõ ïðè ðåøåíèè
áàëëèñòè÷åñêèõ çàäà÷.
3. Êàêèå äîïóùåíèÿ (óïðîùåíèÿ) èñïîëüçóþòñÿ ïðè àíàëèòè÷åñêèõ ìå-
òîäàõ ðåøåíèÿ çàäà÷ âíåøíåé áàëëèñòèêè?  êàêîé òî÷êå ýëëèïòè÷åñêîé
îðáèòû òðàíñâåðñàëüíàÿ ñîñòàâëÿþùàÿ ñêîðîñòè äîñòèãàåò ìàêñèìóìà?
Ñðàâíèòå äîñòîèíñòâà è íåäîñòàòêè àíàëèòè÷åñêèõ è ÷èñëåííûõ ìåòîäîâ
ðåøåíèÿ óðàâíåíèé äâèæåíèÿ.
4. ×åì îòëè÷àåòñÿ ïîñòàíîâêà êðàåâîé çàäà÷è áàëëèñòèêè îò ïîñòàíîâêè
çàäà÷è Êîøè? Êàêîâà öåëü ïîñòàíîâêè è ðåøåíèÿ îáðàòíûõ çàäà÷ áàëëèñòè-
êè? Äàéòå ìàòåìàòè÷åñêóþ ôîðìóëèðîâêó âàðèàöèîííîé çàäà÷è ïðîãðàì-
ìèðîâàíèÿ îïîðíîé òðàåêòîðèè â îáùåì âèäå.  ÷åì óñìàòðèâàåòñÿ ðàçëè-
÷èå â ïîñòàíîâêå çàäà÷ Ëàãðàíæà, Ìàéåðà è Áîëüöà ïðè ðåøåíèè áàëëèñòè-
÷åñêèõ çàäà÷? Ñôîðìóëèðóéòå ïðèíöèï îïòèìàëüíîñòè Áåëëìàíà.
Ïðèâåäèòå îïðåäåëåíèå óñëîâíî îïòèìàëüíîãî óïðàâëåíèÿ.
5.  ÷åì çàêëþ÷àåòñÿ ïðîòèâîðå÷èâîñòü óñëîâèé îãðàíè÷åííîñòè óãëîâ
íóòàöèè áûñòðîâðàùàþùåãîñÿ ñíàðÿäà íà íà÷àëüíîì ó÷àñòêå è â âåðøèíå
òðàåêòîðèè? Îáúÿñíèòå ôèçè÷åñêóþ ñóùíîñòü äåðèâàöèè áûñòðîâðàùàþ-
ùèõñÿ àðòèëëåðèéñêèõ ñíàðÿäîâ. Êàêèå àýðîäèíàìè÷åñêèå ñèëû è ìîìåíòû
îáóñëîâëèâàþò íàëè÷èå â óðàâíåíèÿõ âðàùàòåëüíîãî äâèæåíèÿ ñíàðÿäà
äèññèïàòèâíûõ è íåêîíñåðâàòèâíûõ ïîçèöèîííûõ îáîáùåííûõ ñèë? Ê ÷åìó
359
ïðèâîäèò (ñ òî÷êè çðåíèÿ óñòîé÷èâîñòè) ó÷åò äèññèïàòèâíûõ è íåêîíñåðâà-
òèâíûõ ïîçèöèîííûõ ñèë â óðàâíåíèÿõ óãëîâîãî äâèæåíèÿ íåîïåðåííîãî è
îïåðåííîãî ñíàðÿäîâ.
6. Îáúÿñíèòå ïðè÷èíû äèíàìè÷åñêîé íåóñòîé÷èâîñòè ñòàòè÷åñêè óñòîé-
÷èâîãî ïðîâîðà÷èâàþùåãîñÿ ñíàðÿäà â óñëîâèÿõ ðåçîíàíñíîãî âðàùåíèÿ.
Êàê ïðîÿâëÿåòñÿ â óñëîâèÿõ ðåçîíàíñà àýðîäèíàìè÷åñêàÿ íåñèììåòðèÿ è
äèíàìè÷åñêàÿ íåóðàâíîâåøåííîñòü ñíàðÿäà? Îò êàêèõ ôàêòîðîâ çàâèñèò
ìàêñèìàëüíîå çíà÷åíèå áàëàíñèðîâî÷íûõ óãëîâ àòàêè ïðè ðåçîíàíñå?
ÐÀÇÄÅË III
ÂÎÇÌÓÙÅÍÍÎÅ ÄÂÈÆÅÍÈÅ
ËÅÒÀÒÅËÜÍÛÕ ÀÏÏÀÐÀÒÎÂ
È ÎÏÐÅÄÅËÅÍÈÅ ÕÀÐÀÊÒÅÐÈÑÒÈÊ
ÐÀÑÑÅÈÂÀÍÈß
Ãëàâà 8
ÏÎÏÐÀÂÎ×ÍÛÅ ÔÎÐÌÓËÛ ÂÍÅØÍÅÉ
ÁÀËËÈÑÒÈÊÈ È ÐÀÑ×ÅÒ ÂÎÇÌÓÙÅÍÍÛÕ
ÒÐÀÅÊÒÎÐÈÉ
Òðàåêòîðèþ, ðàññ÷èòàííóþ ïðè "íîðìàëüíûõ" çíà÷åíèÿõ îïðåäåëÿþùèõ åå
ôàêòîðîâ, íàçûâàþò îïîðíîé èëè íåâîçìóùåííîé.
Äëÿ îöåíêè âëèÿíèÿ íà òðàåêòîðèþ êàêîãî-ëèáî ôàêòîðà, ðàíåå íå ðàñ-
ñìàòðèâàåìîãî, íåîáõîäèìî ñîñòàâèòü íîâóþ ñèñòåìó äèôôåðåíöèàëüíûõ
óðàâíåíèé, âêëþ÷àþùóþ èíòåðåñóþùóþ íàñ âåëè÷èíó. Âî ìíîãèõ ñëó÷àÿõ âëèÿ-
íèå âîçìóùàþùèõ ôàêòîðîâ ìîæíî ó÷èòûâàòü, íå ñîñòàâëÿÿ íîâûå äèôôåðåí-
öèàëüíûå óðàâíåíèÿ. Ïðîùå âñåãî ýòî ìîæíî ñäåëàòü òîãäà, êîãäà èíòåðåñóþ-
ùèé íàñ ôàêòîð óæå ó÷òåí â îñíîâíûõ äèôôåðåíöèàëüíûõ óðàâíåíèÿõ è íåîáõî-
äèìî óñòàíîâèòü âëèÿíèå åãî èçìåíåíèÿ íà ðåçóëüòàòû ñòðåëüáû. Åñëè
èññëåäóåìûé ïàðàìåòð èçìåíÿåòñÿ ñóùåñòâåííî, òî âëèÿíèå ýòîãî èçìåíåíèÿ
ñëåäóåò íàõîäèòü, ðåøàÿ îñíîâíóþ ñèñòåìó äèôôåðåíöèàëüíûõ óðàâíåíèé ïðè
íîâûõ, èçìåíåííûõ äàííûõ. Ñðàâíåíèå ðåçóëüòàòîâ ðåøåíèé, ïîëó÷åííûõ ïðè
èçìåíåííûõ è "íîðìàëüíûõ" äàííûõ, äàåò çíà÷åíèå èñêîìîãî îòêëîíåíèÿ.
 íåêîòîðûõ ñëó÷àÿõ îêàçûâàåòñÿ âîçìîæíûì âíåñòè â ðåçóëüòàòû ðåøå-
íèÿ ïîïðàâêè íà âëèÿíèå ôàêòîðîâ, íå ñîäåðæàùèõñÿ â îñíîâíîé ñèñòåìå äèô-
ôåðåíöèàëüíûõ óðàâíåíèé, íå ñîñòàâëÿÿ íîâóþ ñèñòåìó óðàâíåíèé, âêëþ÷àþ-
ùóþ èíòåðåñóþùóþ íàñ âåëè÷èíó.
 ïðàêòèêå, êàê ïðàâèëî, ïðèõîäèòñÿ âñòðå÷àòüñÿ ñ íåáîëüøèìè îòêëîíå-
íèÿìè îïðåäåëÿþùèõ ïàðàìåòðîâ îò èõ íîðìàëüíûõ çíà÷åíèé.  áîëüøèíñòâå
ñëó÷àåâ ìàëûå îòêëîíåíèÿ ïàðàìåòðîâ ïðèâîäÿò ê ìàëûì èçìåíåíèÿì ýëåìåí-
òîâ òðàåêòîðèè, ÷òî ïîçâîëÿåò óñòàíàâëèâàòü âëèÿíèå âîçìóùàþùèõ ôàêòî-
ðîâ íà õàðàêòåðèñòèêè íåâîçìóùåííîé òðàåêòîðèè ñ ïîìîùüþ ðàçëè÷íûõ óï-
ðîùåííûõ ìåòîäîâ è çàâèñèìîñòåé.
361
8.1. ÎÑÍÎÂÍÛÅ ÏÎËÎÆÅÍÈß ÒÅÎÐÈÈ ÏÎÏÐÀÂÎÊ
8.1.1. ÏÎÍßÒÈÅ ÏÎÏÐÀÂÊÈ
Ïîïðàâêàìè íàçûâàþò âçÿòûå ñ îáðàòíûì çíàêîì èçìåíåíèÿ ïà-
ðàìåòðîâ äâèæåíèÿ èëè ýëåìåíòîâ òðàåêòîðèè, ñîîòâåòñòâóþùèå
îòêëîíåíèÿì îïðåäåëÿþùèõ åå ôàêòîðîâ. Ïîïðàâêè, êàê ïðàâèëî,
ââîäÿò â ïàðàìåòðû äâèæåíèÿ öåíòðà ìàññ ðàêåòû èëè ñíàðÿäà äëÿ
ëþáîé ôèêñèðîâàííîé òî÷êè òðàåêòîðèè.
Íà ðèñ. 8 .1 ïîêàçàíû àêòèâíûå ó÷àñòêè íåâîçìóùåííîé 1 è âîç-
ìóùåííîé 2 òðàåêòîðèé íåóïðàâëÿåìîé ðàêåòû. Èçìåíåíèÿ ïàðà-
ìåòðîâ, ñîîòâåòñòâóþùèå ìîìåíòó êîíöà ðàáîòû äâèãàòåëÿ, îáó-
ñëîâëåííûå îòêëîíåíèåì êàêîãî-ëèáî îïðåäåëÿþùåãî ôàêòîðà èëè
ãðóïïû ôàêòîðîâ: δxê – èçìåíåíèå êîîðäèíàòû xê, âûçâàííîå ðåàëü-
íûìè óñëîâèÿìè; δyê – èçìåíåíèå êîîðäèíàòû yê; δVê – èçìåíåíèå
ñêîðîñòè äâèæåíèÿ öåíòðà ìàññ ñíàðÿäà; δtê – èçìåíåíèå âðåìåíè
ðàáîòû äâèãàòåëÿ è ò.ä .
Èçìåíåíèÿ ïàðàìåòðîâ ìîãóò òàêæå îïðåäåëÿòüñÿ äëÿ òî÷êè, çà-
äàííîé êàêîé-ëèáî õàðàêòåðèñòèêîé äâèæåíèÿ (âðåìåíåì, ñêîðî-
ñòüþ, àáñöèññîé, îðäèíàòîé è ïð.), îäèíàêîâîé äëÿ îñíîâíîé è âîç-
ìóùåííîé òðàåêòîðèé. Íàïðè-
ìåð, òî÷êå b íåâîçìóùåííîé
òðàåêòîðèè áóäåò ñîîòâåòñòâî-
âàòü òî÷êà å òðàåêòîðèè âîçìó-
ùåííîãî äâèæåíèÿ, âçÿòàÿ äëÿ
òîãî æå ìîìåíòà âðåìåíè t, ÷òî è
òî÷êà b; ïðè ýòîì âîçìóùåíèÿìè
äëÿ òðàåêòîðèè â òî÷êå b áóäóò
âåëè÷èíû δxt, δyt, δVt è ò.ä . Ïðè
çàäàíèè óñëîâèÿ y = const òî÷êå
à ñîîòâåòñòâóåò òî÷êà ñ, è äëÿ
òðàåêòîðèè â òî÷êå à ïîëó÷èì
âîçìóùåíèÿ δxy, δVy, δθy.
Åñëè ïðèíÿòü óñëîâèå x =
= const, òî òî÷êå à áóäåò ñîîò-
âåòñòâîâàòü òî÷êà d, ïðè÷åì èç-
ìåíåíèÿ ýëåìåíòîâ òðàåêòîðèè
â òî÷êå à ðàâíû δyx, δVx, δtx è ò.ä.
Ïðè ïîäãîòîâêå ñòðåëüáû ïî-
ïðàâêè âíîñÿò â íà÷àëüíûå çíà-
÷åíèÿ, ðàññ÷èòàííûå ïðè íîð-
ìàëüíûõ óñëîâèÿõ. Ïðè îáðà-
áîòêå ðåçóëüòàòîâ
ñòðåëüá,
ïîëó÷åííûõ â äåéñòâèòåëüíûõ
362
Ðèñ. 8.1 . Ãðàôèêè èçìåíåíèÿ òðàåêòîðèè
äâèæåíèÿ öåíòðà ìàññ ðàêåòû â çàâèñè-
ìîñòè îò èçìåíåíèÿ îïðåäåëÿþùåãî ïà-
ðàìåòðà:
1 – íåâîçìóùåííàÿ; 2 – âîçìóùåííàÿ
òðàåêòîðèè
óñëîâèÿõ, ïîïðàâêè âíîñÿòñÿ â îïûòíûå äàííûå ñ òåì, ÷òîáû ïðè-
âåñòè èõ ê íîðìàëüíûì óñëîâèÿì. Îòäåëüíîå ìåñòî çàíèìàþò ïî-
ïðàâêè, ââîäèìûå âî âðåìåíà ïîëåòà, ñâÿçàííûå ñ èñïîëüçîâàíèåì
ðàçëè÷íîãî ðîäà äèñòàíöèîííûõ óñòðîéñòâ (íàïðèìåð, âçðûâàòå-
ëåé).
8.1.2. ÎÑÍÎÂÍÀß ÔÎÐÌÓËÀ ÒÅÎÐÈÈ ÏÎÏÐÀÂÎÊ
 îáùåì âèäå äëÿ ýëåìåíòà òðàåêòîðèè èëè õàðàêòåðèñòèêè äâè-
æåíèÿ À ìîæíî íàïèñàòü
Af
n
=
(,,,)
,
ξξξ
12
K
(8.1)
ãäå ξi – îïðåäåëÿþùèé ïàðàìåòð.
 ñîîòâåòñòâèè ñ îáùåé òåîðèåé ðàçëîæåíèÿ ôóíêöèè â ðÿä Òåé-
ëîðà èçìåíåíèå ýëåìåíòà îïðåäåëÿåòñÿ ôîðìóëîé (2.68), ÷èñëî ÷ëå-
íîâ êîòîðîé çàâèñèò îò òðåáóåìîé òî÷íîñòè ðàñ÷åòà. ×àùå âñåãî ïðè
ðåøåíèè ïðàêòè÷åñêèõ çàäà÷ òåîðèè ïîïðàâîê óäåðæèâàþò ëèíåé-
íûå ÷ëåíû ðàçëîæåíèÿ. Ïîëó÷åííàÿ ïðè ýòîì ôîðìóëà ñîîòâåòñòâó-
åò ôîðìóëå ïîëíîãî äèôôåðåíöèàëà ôóíêöèîíàëüíîé çàâèñèìîñòè
(8.1). Åñëè ïðåäïîëîæèòü, ÷òî ïàðàìåòðû, îáúåäèíåííûå ôóíêöèî-
íàëüíîé çàâèñèìîñòüþ (8.1), íå çàâèñÿò äðóã îò äðóãà, ò.å . óäîâëåòâî-
ðÿþò ïðèíöèïó ñóïåðïîçèöèè, è â ôîðìóëå ïîëíîãî äèôôåðåíöèà-
ëà áåñêîíå÷íî ìàëûå ïðèðàùåíèÿ çàìåíèòü êîíå÷íî ìàëûìè, òî
ìîæíî ïîëó÷èòü
δ
∂
∂ξ
δξ
∂
∂ξ
δξ
∂
∂ξ
δξ
A
fff
n
n
=++
+
1
1
2
2K
.
(8.2)
 ïîñëåäíåé ôîðìóëå, íàçûâàåìîé îñíîâíîé ôîðìóëîé òåîðèè ïî-
ïðàâîê, íå ó÷èòûâàþòñÿ ÷ëåíû ðàçëîæåíèÿ áîëåå âûñîêèõ ïîðÿäêîâ,
÷åì ïåðâûé.  ñâÿçè ñ óâåëè÷åíèåì äàëüíîñòåé ñòðåëüáû â ðÿäå ñëó-
÷àåâ (ïðèìåíèòåëüíî ê ðàêåòíûì ñèñòåìàì çàëïîâîãî îãíÿ, ÎÒÐ è
äð.) ïðèõîäèòñÿ ó÷èòûâàòü ïîïðàâêè íå òîëüêî ëèíåéíîãî, íî è íå-
ëèíåéíîãî õàðàêòåðà. Ïðèìåðîì ìîæåò ñëóæèòü ó÷åò âòîðîé ïðîèç-
âîäíîé ïî òåìïåðàòóðå âîçäóõà è ñìåøàííîé – ïî òåìïåðàòóðå è
äàâëåíèþ.
Ïîïðàâî÷íûå ôîðìóëû òèïà (8.2) íàçûâàþòñÿ äèôôåðåíöèàëüíû-
ìè, à îïðåäåëåííûå ïî íèì çíà÷åíèÿ δA – èçìåíåíèÿìè ýëåìåíòîâ
òðàåêòîðèè, âû÷èñëåííûìè ïî ìåòîäó äèôôåðåíöèàëîâ. Áàëëèñòè-
÷åñêèå ïðîèçâîäíûå ∂f/∂ξi = ∂A/∂ξi â òåîðèè ïîïðàâîê íàçûâàþòñÿ ïî-
ïðàâî÷íûìè êîýôôèöèåíòàìè äëÿ ýëåìåíòà À òðàåêòîðèè íà îòêëî-
363
íåíèå ïàðàìåòðà ξi. Ïîïðàâî÷íûé êîýôôèöèåíò (áàëëèñòè÷åñêàÿ
ïðîèçâîäíàÿ) ÷èñëåííî ðàâåí èçìåíåíèþ ðàññìàòðèâàåìîãî ýëå-
ìåíòà òðàåêòîðèè ïðè óâåëè÷åíèè ñîîòâåòñòâóþùåãî îïðåäåëÿþùå-
ãî ïàðàìåòðà íà ïðèíÿòóþ åäèíèöó åãî èçìåðåíèÿ. Â òåîðèè ïîïðà-
âîê ïîëåâîé àðòèëëåðèè ïîïðàâî÷íûå êîýôôèöèåíòû, õàðàêòåðè-
çóþùèå èçìåíåíèÿ äàëüíîñòè ïðè îòêëîíåíèÿõ áàëëèñòè÷åñêîãî
êîýôôèöèåíòà ∂xc/∂c, íà÷àëüíîé ñêîðîñòè ∂xc/∂V0 è óãëà áðîñàíèÿ
∂xc/∂θ0, ïðèíÿòî íàçûâàòü îñíîâíûìè ïîïðàâî÷íûìè êîýôôèöèåíòà-
ìè.
 êà÷åñòâå ïðèìåðà ðàññìîòðèì ïîëó÷åíèå ïîïðàâî÷íûõ ôîðìóë
äëÿ ïîëíîé ãîðèçîíòàëüíîé äàëüíîñòè ñòðåëüáû èç àðòèëëåðèéñêîé
ñèñòåìû â óñëîâèÿõ áåçâîçäóøíîãî ïðîñòðàíñòâà. Çäåñü ïîëíàÿ
äàëüíîñòü îïðåäåëèòñÿ çàâèñèìîñòüþ xc = Vg
0
2
0
2
sin /
θ=
f(V0, θ0).
Ïîëó÷èì ïîïðàâî÷íóþ ôîðìóëó ñ ó÷åòîì ÷ëåíîâ ðàçëîæåíèÿ
ïåðâîãî è âòîðîãî ïîðÿäêà. Ïîñêîëüêó â ïîñëåäíåé ôîðìóëå òîëüêî
äâà àðãóìåíòà V0 è θ0, â îáùèõ îáîçíà÷åíèÿõ ñîãëàñíî (2.68) áóäåì
èìåòü
δ
∂
∂ξ
δξ∂
∂ξ
δξ ξξ
∂
∂ξ
δξ
xf
c
=+
⎛
⎝⎜
⎞
⎠⎟
+
+
1
1
1
2
1
1
2
21
2
2
1
2
1
!
()
!
()(
)
(
)
.
2
2
12
12
2
2
2
2
2
12
2
++
⎡
⎣⎢
⎤
⎦⎥
∂
∂ξ ∂ξ
δξ δξ
∂
∂ξ
δξ
ξξ
f
(8.3)
 îáîçíà÷åíèÿõ ôîðìóëû, îïðåäåëÿþùåé ïîëíóþ äàëüíîñòü
ñòðåëüáû â ïàðàáîëè÷åñêîé òåîðèè, ïîëó÷èì
δ
∂
∂
δ
∂
∂θ
δθ
∂
∂
δ
∂
∂∂
x
x
V
V
x
x
V
V
x
V
c
cc
cc
=+
+
++
0
0
0
0
2
0
2
0
2
2
1
2
2
()
θ
δδθ
∂
∂θ
δθ
0
00
2
0
2
0
2
V
xc
+
⎡
⎣⎢
⎤
⎦⎥
().
Ðàñêðûâàÿ çíà÷åíèÿ ÷àñòíûõ ïðîèçâîäíûõ, áóäåì èìåòü
δ
θ
δ
θ
δθ
θ
δ
x
V
g
V
V
gg
V
V
c
=++
+
+
22 22
2
4
00
0
0
2
0
0
0
0
2
sin
cos
sin
()
00
00
00
0
2
22
2
cos
sin
().
θ
δδθ
θ
δθ
g
V
V
g
−
(8.4)
Ïîñëåäíèå òðè ñëàãàåìûõ (êâàäðàòíûå ÷ëåíû ðàçëîæåíèÿ) ÿâëÿþòñÿ
âåëè÷èíàìè áîëåå âûñîêîãî ïîðÿäêà ìàëîñòè, ÷åì äâà ïåðâûõ,
364
îïðåäåëÿåìûå ëèíåéíûìè ÷ëåíàìè ðàçëîæåíèÿ.  áîëüøèíñòâå
ñëó÷àåâ èñïîëüçóþò òîëüêî ëèíåéíûå ÷ëåíû è èçìåíåíèå äàëüíîñòè
îïðåäåëÿåòñÿ ïî ôîðìóëå
δ
θ
δ
θ
δθ
x
V
g
V
V
g
c
=+
22 22
00
0
0
2
0
0
sin
cos
,
(8.5)
ãäå áàëëèñòè÷åñêèå ïðîèçâîäíûå (ïîïðàâî÷íûå êîýôôèöèåíòû)
ðàâíû
∂
∂
θ∂
∂θ
θ
x
V
V
g
xV
g
cc
0
00
0
0
2
0
22 22
==
sin
;
cos
.
(8.6)
Èìåÿ âåëè÷èíó ïîïðàâî÷íîãî êîýôôèöèåíòà, ëåãêî íàéòè èçìå-
íåíèå ñîîòâåòñòâóþùåãî ýëåìåíòà òðàåêòîðèè
δ∂
∂ξ
δξ
A
A
i
i
i
i
=
.
(8.7)
Åñëè ïðåäïîëîæèòü, ÷òî èçìåíÿåòñÿ òîëüêî íà÷àëüíàÿ ñêîðîñòü,
òî
δ
∂
∂
δ
x
x
V
V
cV
c
=
0
0.
(8.8)
Èñïîëüçóÿ ôîðìóëó ïîëíîé äàëüíîñòè è ïåðâóþ ôîðìóëó (8.6),
ïîëó÷èì
δδ
xx VV
cV
c
//
,
=200
ò.å. ïðè äîïóùåíèÿõ, ñîîòâåòñòâóþùèõ ïàðàáîëè÷åñêîé òåîðèè,
ìàëîå îòíîñèòåëüíîå îòêëîíåíèå íà÷àëüíîé ñêîðîñòè âûçûâàåò
óäâîåííîå îòíîñèòåëüíîå èçìåíåíèå äàëüíîñòè. Ïîñòóïàÿ ïîäîáíûì
îáðàçîì, ìîæíî ïîëó÷èòü ïîïðàâî÷íûå ôîðìóëû è äëÿ äðóãèõ
ýëåìåíòîâ òðàåêòîðèè.
Âûâîä ïîïðàâî÷íûõ ôîðìóë è ôîðìóë áàëëèñòè÷åñêèõ ïðîèç-
âîäíûõ äëÿ òðàåêòîðèé ðàçëè÷íûõ òèïîâ ðàêåò è ñíàðÿäîâ çíà÷è-
òåëüíî ñëîæíåå, ÷åì â ïîêàçàííîì ïðîñòîì ïðèìåðå, è òðåáóåò ïðè-
ìåíåíèÿ ñïåöèàëüíûõ ìåòîäîâ.
365
8.1.3 . ÊÀ×ÅÑÒÂÅÍÍÎÅ ÂËÈßÍÈÅ ÎÏÐÅÄÅËßÞÙÈÕ ÏÀÐÀÌÅÒÐÎÂ
È ÇÍÀÊÈ ÁÀËËÈÑÒÈ×ÅÑÊÈÕ ÏÐÎÈÇÂÎÄÍÛÕ
Çíàê áàëëèñòè÷åñêîé ïðîèçâîäíîé (ïîïðàâî÷íîãî êîýôôèöèåí-
òà) äëÿ ïîëíîé ïîëåòíîé äàëüíîñòè ñíàðÿäîâ ðàêåòíûõ è àðòèëëå-
ðèéñêèõ ñèñòåì óñòàíàâëèâàåòñÿ â çàâèñèìîñòè îò âîçäåéñòâèÿ óâå-
ëè÷åíèÿ îïðåäåëÿþùåãî ïàðàìåòðà íà äàëüíîñòü ñòðåëüáû. Åñëè
óâåëè÷åíèå ïàðàìåòðà ïðèâîäèò ê óâåëè÷åíèþ äàëüíîñòè ñòðåëüáû,
òî ïîïðàâî÷íûé êîýôôèöèåíò èìååò ïîëîæèòåëüíîå çíà÷åíèå; åñëè
äàëüíîñòü ñòðåëüáû óìåíüøàåòñÿ ñ ðîñòîì îïðåäåëÿþùåãî ïàðàìåò-
ðà, òî – îòðèöàòåëüíîå çíà÷åíèå. Âî ìíîãèõ ñëó÷àÿõ çíàê ïîïðàâî÷-
íîãî êîýôôèöèåíòà ìîæíî óñòàíîâèòü èñõîäÿ èç êà÷åñòâåííîãî
âëèÿíèÿ ïàðàìåòðà íà äàëüíîñòü äî âûïîëíåíèÿ ðàñ÷åòîâ ïî åãî îï-
ðåäåëåíèþ.
Ïðîâåäåì êà÷åñòâåííûé àíàëèç ïî îïðåäåëåíèþ çíàêîâ îñíîâ-
íûõ ïîïðàâî÷íûõ êîýôôèöèåíòîâ. Íà÷àëüíàÿ ñêîðîñòü íåóïðàâëÿå-
ìîãî ñíàðÿäà ïîñòîÿííîé ìàññû (àðòèëëåðèéñêîãî ñíàðÿäà) V0 è
ñêîðîñòü ãîëîâíîé ÷àñòè ðàêåòû â íà÷àëå ïàññèâíîãî ó÷àñòêà òðàåê-
òîðèè Vê ÿâëÿþòñÿ îäíèìè èç îñíîâíûõ ïàðàìåòðîâ, îïðåäåëÿþùèõ
äàëüíîñòü ñòðåëüáû. Ñ óâåëè÷åíèåì íà÷àëüíîé ñêîðîñòè äàëüíîñòü
ðàñòåò, ïîýòîìó ïîïðàâî÷íûé êîýôôèöèåíò èìååò ïîëîæèòåëüíîå
çíà÷åíèå. Äëÿ ðàêåò ïðè íàêëîííîì ñòàðòå ñêîðîñòü ñõîäà ñ ïóñêî-
âîãî óñòðîéñòâà (íà÷àëüíàÿ ñêîðîñòü) ñîñòàâëÿåò, êàê ïðàâèëî, íå-
áîëüøóþ ÷àñòü îò ñêîðîñòè öåíòðà ìàññ ñíàðÿäà â êîíöå àêòèâíîãî
ó÷àñòêà òðàåêòîðèè Vê. Óâåëè÷åíèå ñêîðîñòè ñõîäà ñ íàïðàâëÿþùèõ
ïðèâîäèò ê óâåëè÷åíèþ îðäèíàò âñåé òðàåêòîðèè è ðîñòó Vê. Òàêèì
îáðàçîì, ïðè ïðî÷èõ ðàâíûõ óñëîâèÿõ óâåëè÷åíèå íà÷àëüíîé ñêî-
ðîñòè ïðèâîäèò ê óâåëè÷åíèþ äàëüíîñòè ñòðåëüáû, ñëåäîâàòåëüíî,
∂xc /∂V0> 0. Àíàëîãè÷íî ∂xc /∂Vê >0.
Àýðîäèíàìè÷åñêèå ñâîéñòâà ñíàðÿäà âëèÿþò íà äàëüíîñòü
ñòðåëüáû ÷åðåç õàðàêòåðíóþ ïëîùàäü S è êîýôôèöèåíò ëîáîâîãî
ñîïðîòèâëåíèÿ cx a
().
M Óâåëè÷åíèå õàðàêòåðíîé ïëîùàäè è ñðåäíåãî
çíà÷åíèÿ êîýôôèöèåíòà ëîáîâîãî ñîïðîòèâëåíèÿ cx a ñð
M
()çà âðåìÿ
äâèæåíèÿ ïî òðàåêòîðèè ïðèâåäåò ê óìåíüøåíèþ äàëüíîñòè ñòðåëü-
áû.
Î÷åâèäíî, ÷òî ∂xc /∂S <0è∂∂
xc
cx
a
/.
ñð
< 0 Åñëè ïîäñòàâèòü (1.126)
â óðàâíåíèå dV/dt = −Xa/m − g sinθ, òî ïîëó÷èì
dV dt
cHyFV g
/
()() sin.
=−
−
θ
Îáîçíà÷àÿ ÷åðåç Íñð(y)èFñð(V ) ñðåäíèå çíà÷åíèÿ ýòèõ õàðàêòå-
ðèñòèê çà âðåìÿ äâèæåíèÿ ñíàðÿäà ïî òðàåêòîðèè, áóäåì èìåòü
∂xc /[∂Hñð(y)]<0è∂xc/[∂Fñð(V )] < 0. Äëÿ ñíàðÿäîâ ïîñòîÿííîé ìàññû
îäèí èç îñíîâíûõ ïîïðàâî÷íûõ êîýôôèöèåíòîâ ∂xc /∂c <0.
366
Äëÿ íåóïðàâëÿåìûõ ñíàðÿ-
äîâ ïåðåìåííîé è ïîñòîÿííîé
ìàññû óãîë áðîñàíèÿ ÿâëÿåòñÿ
îäíèì èç ãëàâíûõ îïðåäåëÿþ-
ùèõ ïàðàìåòðîâ. Óãîë íàêëîíà
êàñàòåëüíîé ê òðàåêòîðèè â íà-
÷àëå ïàññèâíîãî ó÷àñòêà òðàåê-
òîðèè íåóïðàâëÿåìîãî ïîëåòà
ðàêåòû òàêæå ñóùåñòâåííî
âëèÿåò íà äàëüíîñòü ñòðåëüáû.
Íà ðèñ. 8 .2 ïîêàçàíà çàâèñè-
ìîñòü ïîëíîé äàëüíîñòè xc èïî-
ïðàâî÷íîãî
êîýôôèöèåíòà
∂xc/∂θí îò óãëà áðîñàíèÿ θí. Äëÿ
àðòèëëåðèéñêèõ ñèñòåì è íå-
óïðàâëÿåìûõ ðàêåò θí = θ0. Äëÿ
ïàññèâíûõ ó÷àñòêîâ òðàåêòîðèé óïðàâëÿåìûõ è íåóïðàâëÿåìûõ ðà-
êåò θí = θê. Çíàê ïîïðàâî÷íîãî êîýôôèöèåíòà èçìåíÿåòñÿ â çàâèñè-
ìîñòè îò ñîîòíîøåíèÿ θí è óãëà íàèáîëüøåé äàëüíîñòè θí max. Åñëè
θí ìåíüøå óãëà íàèáîëüøåé äàëüíîñòè, òî ïîïðàâî÷íûé êîýôôèöè-
åíò ∂xc/∂θí > 0; åñëè θí áîëüøå óãëà θí max,òî∂xc /∂θí < 0. Â îáùåì
âèäå ìîæíî çàïèñàòü ∂xc /∂θí ¤ 0.
Ïðè ôèêñèðîâàííîé íà÷àëüíîé ñêîðîñòè Ví ïîïðàâî÷íûé êîýô-
ôèöèåíò ∂xc/∂θí = 0 ñîîòâåòñòâóåò ìàêñèìàëüíîé äàëüíîñòè è óãëó
áðîñàíèÿ, ïðè êîòîðîì ýòà äàëüíîñòü ïîëó÷åíà. Ïðè ñòðåëüáå ñ óã-
ëàìè, áëèçêèìè ê óãëó ìàêñèìàëüíîé äàëüíîñòè, ìàëûå èçìåíåíèÿ
óãëà θí ïî÷òè íå âëèÿþò íà äàëüíîñòü ñòðåëüáû.
Ýëåìåíòû êîíöà àêòèâíîãî ó÷àñòêà òðàåêòîðèè xê, yê, Vê è θê ìî-
ãóò áûòü ïðèíÿòû çà ñàìîñòîÿòåëüíûå ïàðàìåòðû, îïðåäåëÿþùèå
äàëüíîñòü ñòðåëüáû. Âëèÿíèå Vê è θê íà äàëüíîñòü ñòðåëüáû ñíàðÿäà-
ìè ïîñòîÿííîé ìàññû ðàññìîòðåíî âûøå. Óâåëè÷åíèå àáñöèññû àê-
òèâíîãî ó÷àñòêà òðàåêòîðèè xê ïðè yê = const ñìåùàåò òðàåêòîðèþ
âïðàâî; ïðè ýòîì óâåëè÷åíèå xê è óâåëè÷åíèå äàëüíîñòè ñòðåëüáû xc
îäèíàêîâî, ò.å . ∂xc/∂yê =1
.
Óâåëè÷åíèå îðäèíàòû yê ïðèâîäèò ê óâåëè÷åíèþ äàëüíîñòè
âñëåäñòâèå äâèæåíèÿ ðàêåòû â áîëåå âûñîêèõ è ìåíåå ïëîòíûõ ñëî-
ÿõ àòìîñôåðû è íåêîòîðîãî óäëèíåíèÿ êîíå÷íîãî ó÷àñòêà òðàåêòî-
ðèè. Ïîïðàâî÷íûé êîýôôèöèåíò ∂xc/∂yê > 0. Èçìåíåíèå ìàññû ñíà-
ðÿäà âëèÿåò ðàçëè÷íûì îáðàçîì íà äàëüíîñòü ñòðåëüáû. Äëÿ ñíàðÿ-
367
Ðèñ. 8 .2. Ãðàôèêè èçìåíåíèÿ ïîëíîé
äàëüíîñòè xc è ïîïðàâî÷íîãî êîýôôèöè-
åíòà ∂xc/∂θí â çàâèñèìîñòè îò óãëà áðî-
ñàíèÿ θí
äîâ ïîñòîÿííîé ìàññû èç óðàâíåíèÿ
•
sin
V
X
m
g
a
=−
−
θâèäíî, ÷òî ñ
óâåëè÷åíèåì ìàññû óìåíüøàåòñÿ óñêîðåíèå ñíàðÿäà îò ñèëû ñîïðî-
òèâëåíèÿ âîçäóõà Xa/m, ñêîðîñòü ñíàðÿäà óìåíüøàåòñÿ ìåäëåííåå è
äàëüíîñòü ñòðåëüáû óâåëè÷èâàåòñÿ, ñëåäîâàòåëüíî, ∂xc/∂m >0.
Àðòèëëåðèéñêèé ñíàðÿä ìåíüøåãî âåñà ïðè òåõ æå óñëîâèÿõ ìå-
òàíèÿ (îäèíàêîâîì çàðÿäå) èç îðóäèÿ ïîëó÷àåò áËëüøóþ íà÷àëü-
íóþ ñêîðîñòü V0. Îäíàêî â ïîëåòå ëåãêèé ñíàðÿä áûñòðåå òåðÿåò
ñâîþ ñêîðîñòü, ÷åì òàêîé æå ïî ôîðìå òÿæåëûé ñíàðÿä. Ñóììàð-
íîå âëèÿíèå èçìåíåíèÿ ìàññû (âåñà) ñíàðÿäà íà äàëüíîñòü ñòðåëü-
áû èç àðòèëëåðèéñêîãî îðóäèÿ óñòàíàâëèâàåòñÿ ñïåöèàëüíîé ïî-
ïðàâî÷íîé ôîðìóëîé (ñì. äàëåå). Äëÿ ðàêåò íà àêòèâíîì ó÷àñòêå
òðàåêòîðèè
•
sin ,
V
PX
m
g
a
=
−
−θ
ïðè P > Xa ñ óâåëè÷åíèåì ìàññû óñêîðåíèå óìåíüøàåòñÿ, ÷òî ïðè
ïðî÷èõ ðàâíûõ óñëîâèÿõ ïðèâåäåò ê ìåíüøåé ñêîðîñòè Vê,à
ñëåäîâàòåëüíî, è ê ìåíüøåé äàëüíîñòè. Òàêèì îáðàçîì, çíàê
ïîïðàâî÷íîãî êîýôôèöèåíòà äîëæåí îïðåäåëÿòüñÿ ïðè ðàñ÷åòå ïî
êîíêðåòíûì äàííûì.
Èçìåíåíèå ìåòåîôàêòîðîâ âëå÷åò çà ñîáîé èçìåíåíèå ñèëû ñî-
ïðîòèâëåíèÿ âîçäóõà. Ñ óâåëè÷åíèåì ïëîòíîñòè âîçäóõà óâåëè÷è-
âàåòñÿ ñêîðîñòíîé íàïîð, ñèëà ëîáîâîãî ñîïðîòèâëåíèÿ è óìåíü-
øàåòñÿ äàëüíîñòü ñòðåëüáû, ñëåäîâàòåëüíî, ∂xc/∂ρ <0.
Ðîñò áàðîìåòðè÷åñêîãî äàâëåíèÿ â òî÷êå ïóñêà è íà òðàåêòîðèè
ïðèâîäèò â ñîîòâåòñòâèè ñ (1.79) ê óâåëè÷åíèþ ïëîòíîñòè âîçäóõà,
ñëåäîâàòåëüíî, ∂xc/∂h0 <0è∂xc/∂hê <0.
Ñëîæíûì îêàçûâàåòñÿ âëèÿíèå òåìïåðàòóðû âîçäóõà íà äàëü-
íîñòü ñòðåëüáû.  ñîîòâåòñòâèè ñ (1.79) óâåëè÷åíèå òåìïåðàòó-
ðû τ ïðèâîäèò ê óìåíüøåíèþ ïëîòíîñòè âîçäóõà è îäíîâðåìåí-
íî ê óâåëè÷åíèþ ñêîðîñòè çâóêà â âîçäóõå è óìåíüøåíèþ ÷èñëà
Ì. Óìåíüøåíèå æå ÷èñëà Ì ìîæåò âûçâàòü óìåíüøåíèå ôóíê-
öèè cxa
()
M â îáëàñòè âîçðàñòàíèÿ êðèâîé cx a
()
M è óâåëè÷åíèå
cxa
()
M äëÿ íèñõîäÿùåé âåòâè êðèâîé cx a
().
M Çíà÷åíèå ïîïðàâî÷-
íîãî êîýôôèöèåíòà, õàðàêòåðèçóþùåãî âëèÿíèå òåìïåðàòóðû
âîçäóõà íà äàëüíîñòü ñòðåëüáû, óñòàíàâëèâàåòñÿ äëÿ àðòèëëå-
ðèéñêèõ ñíàðÿäîâ ïîñòîÿííîé ìàññû ïî ïîïðàâî÷íûì ôîðìó-
ëàì è ñïåöèàëüíûì òàáëèöàì äëÿ ðàêåò îäíèì èç ìåòîäîâ, èçëî-
æåííûõ íèæå.
368
8.1 .4. ÈÇÌÅÍÅÍÈÅ ÄÀËÜÍÎÑÒÈ ÑÒÐÅËÜÁÛ ÀÐÒÈËËÅÐÈÉÑÊÈÌÈ
ÑÍÀÐßÄÀÌÈ ÏÐÈ ÈÇÌÅÍÅÍÈÈ ÈÕ ÍÀ×ÀËÜÍÎÉ ÌÀÑÑÛ
Êàê áûëî óñòàíîâëåíî ïðè êà÷åñòâåííîì àíàëèçå âëèÿíèÿ èçìå-
íåíèÿ ìàññû ñíàðÿäà íà äàëüíîñòü åãî ïîëåòà, õàðàêòåð âîçäåéñòâèÿ
äàííîãî ôàêòîðà íå ÿâëÿåòñÿ îäíîçíà÷íûì. Ó÷èòûâàÿ, ÷òî ñóììàð-
íîå èçìåíåíèå ìàññû (âåñà) ñóùåñòâåííûì îáðàçîì ñêàçûâàåòñÿ íà
ïðîòÿæåííîñòè òðàåêòîðèè, îáñóäèì âîïðîñ áîëåå îáñòîÿòåëüíî.
Ïðåæäå âñåãî îòìåòèì, ÷òî ñíàðÿäû ïî èõ ìàññå ðàçäåëÿþòñÿ íà
äåâÿòü âåñîâûõ ãðóïï, ÷òî îòðàæåíî â òàáë. 8.1.
369
Òàáëèöà 8.1
Âåñîâûå ãðóïïû ñíàðÿäîâ ñòâîëüíîé àðòèëëåðèè
Âåñîâûå çíàêè
Îòêëîíåíèå ìàññû ñíàðÿäîâ îò òàáëè÷íûõ çíà÷åíèé,
%
îò
äî
––––
−2
1
3
−3
–––
−1
2
3
−2
1
3
––
−1
−1
2
3
–
−
1
3
−1
N
−
1
3
+
1
3
+
+
1
3
+1
++
+1
+1
2
3
+++
+1
2
3
+2
1
3
++++
+2
1
3
+3
Ðàçëè÷èå ìàññ øòàòíûõ ñíàðÿäîâ ÿâëÿåòñÿ îáúåêòèâíîé ðåàëüíî-
ñòüþ, îáóñëîâëåííîé èõ ïðîèçâîäñòâîì. Èç òðåõ âåëè÷èí, õàðàêòå-
ðèçóþùèõ äàëüíîñòü ñòðåëüáû (V0, θ0 è c), èçìåíåíèå ìàññû ñíàðÿ-
äà, îïðåäåëÿåìîå èçìåíåíèåì ñ, îêàçûâàåò ïðåâàëèðóþùåå âîçäåé-
ñòâèå íà äâå ïåðâûå. Ñëåäîâàòåëüíî, ïðè çàôèêñèðîâàííîì óãëå
áðîñàíèÿ θ0 ìîæíî çàïèñàòü xc = f(V0, c).
Ñäåëàåì äîïóùåíèå î íåçàâèñèìîñòè äåéñòâèé V0 è c íà äàëü-
íîñòü ñòðåëüáû è âîñïîëüçóåìñÿ äèôôåðåíöèàëüíîé ïîïðàâî÷íîé
ôîðìóëîé
δ
∂
∂
δ
∂
∂
δ
x
x
V
V
x
c
c
cQ
cc
=+
0
0
.
(8.9)
Çàâèñèìîñòü íà÷àëüíîé ñêîðîñòè îò âåñà ñíàðÿäà ïîëó÷èì ïî
ïîïðàâî÷íîé ôîðìóëå, èçâåñòíîé èç âíóòðåííåé áàëëèñòèêè:
δ
δ
Vl
V
Q
Q
Q
00
=−
,
ãäå lQ – ïîïðàâî÷íûé êîýôôèöèåíò.
Èç ôîðìóëû äëÿ áàëëèñòè÷åñêîãî êîýôôèöèåíòà c = id 2⋅103/Q,
ïðèíèìàÿ ïðîèçâåäåíèå id 2 ïîñòîÿííûì, ëîãàðèôìèðóÿ, äèôôå-
ðåíöèðóÿ è çàìåíÿÿ áåñêîíå÷íî ìàëûå ïðèðàùåíèÿ êîíå÷íî ìàëû-
ìè, íàéäåì δ
δ
cc
Q
Q
=−
. Ïîäñòàâëÿÿ δV0 è δc â (8.9), áóäåì èìåòü
δ
∂
∂
δ∂
∂
δ
x
x
V
Vl
Q
Q
x
c
c
Q
Q
cQ
c
Q
c
=−
−
0
0
.
(8.10)
Òàê êàê ïîïðàâî÷íûé êîýôôèöèåíò ∂xc/∂c – âåëè÷èíà
îòðèöàòåëüíàÿ, óäîáíî âçÿòü åãî àáñîëþòíîå çíà÷åíèå, è òîãäà
δ
∂
∂
∂
∂
δ
x
x
c
clV
x
V
Q
Q
cQ
c
Q
c
=−
⎡
⎣⎢
⎤
⎦⎥
0
0
,
(8.11)
îòêóäà ïîïðàâî÷íûé êîýôôèöèåíò â äàëüíîñòü íåïîñðåäñòâåííî íà
âåñ ñíàðÿäà áóäåò èìåòü âèä
∂
∂
∂
∂
∂
∂
x
QQ
x
c
clV
x
V
cc
Q
c
=−
⎡
⎣⎢
⎤
⎦⎥
1
0
0
.
(8.12)
370
Ñ ó÷åòîì ýòîãî îáîçíà÷åíèÿ ïîëó÷èì
δ
∂
∂
δ
x
x
Q
Q
cQ
c
=−
.
 çàâèñèìîñòè îò êîíêðåòíûõ óñëîâèé ïîïðàâî÷íûé êîýôôèöè-
åíò â äàëüíîñòü íà îòêëîíåíèå âåñà ñíàðÿäà ìîæåò èìåòü ðàçëè÷íûå
çíàêè.
8.2 . ÌÅÒÎÄÛ ÂÛ×ÈÑËÅÍÈß ÈÇÌÅÍÅÍÈÉ ÝËÅÌÅÍÒÎÂ
ÒÐÀÅÊÒÎÐÈÉ È ÁÀËËÈÑÒÈ×ÅÑÊÈÕ ÏÐÎÈÇÂÎÄÍÛÕ
8.2.1. ÎÏÐÅÄÅËÅÍÈÅ ÈÇÌÅÍÅÍÈÉ ÝËÅÌÅÍÒÎÂ ÒÐÀÅÊÒÎÐÈÉ
È ÏÎÏÐÀÂÎ×ÍÛÕ ÊÎÝÔÔÈÖÈÅÍÒΠÈÍÒÅÃÐÈÐÎÂÀÍÈÅÌ ÑÈÑÒÅÌ
ÓÐÀÂÍÅÍÈÉ ÄÂÈÆÅÍÈß
Ìåòîä ïðèìåíÿåòñÿ ïðè ñóùåñòâåííîì èçìåíåíèè ïàðàìåòðà,
îïðåäåëÿþùåãî èññëåäóåìûé ýëåìåíò òðàåêòîðèè, èëè ïðè íåîáõî-
äèìîñòè îòûñêàíèÿ èçìåíåíèÿ ýëåìåíòà âñëåäñòâèå îòêëîíåíèÿ ïà-
ðàìåòðà, íå ñîäåðæàùåãîñÿ â îñíîâíîé ñèñòåìå óðàâíåíèé, ñîñòàâ-
ëåííîé äëÿ íåâîçìóùåííîé òðàåêòîðèè.
 ïåðâîì ñëó÷àå îñíîâíàÿ ñèñòåìà ðåøàåòñÿ ïðè n äèñêðåòíûõ
çíà÷åíèÿõ îïðåäåëÿþùåãî ïàðàìåòðà èëè ïðè n ôóíêöèîíàëüíûõ
çàâèñèìîñòÿõ, âëèÿíèå èçìåíåíèÿ êîòîðûõ ïðåäïîëàãàåòñÿ íàéòè.
Ïóñòü, íàïðèìåð, â ðåçóëüòàòå êîíñòðóêòèâíûõ èçìåíåíèé âíåøíåé
ôîðìû ðàêåòû èëè åå óïðàâëÿþùèõ îðãàíîâ èçìåíèòñÿ ôîðìà ãðà-
ôèêîâ êîýôôèöèåíòà ëîáîâîãî ñîïðîòèâëåíèÿ. Îáîçíà÷èì ôóíê-
öèîíàëüíóþ çàâèñèìîñòü äëÿ íåâîçìóùåííîé òðàåêòîðèè ÷åðåç
cxa
(,R
e
),
M
à äëÿ òðàåêòîðèè ðàêåòû èçìåíåííîé ôîðìû – ÷åðåç
cxi
a
(,R
e
).
M
Äëÿ îïðåäåëåíèÿ âëèÿíèÿ èçìåíåíèÿ ôîðìû ðàêåòû íà
ýëåìåíòû êîíöà àêòèâíîãî ó÷àñòêà òðàåêòîðèè âîñïîëüçóåìñÿ ñòàí-
äàðòíîé ñèñòåìîé óðàâíåíèé, ïðèíÿâ, ÷òî òÿãà íàïðàâëåíà ïî îñè
ðàêåòû, è îïóñòèâ óïðàâëÿþùèå ñèëû. Äëÿ íåâîçìóùåííîé òðàåêòî-
ðèè ñèñòåìà ìîæåò ðåøàòüñÿ ïðè çíà÷åíèÿõ
X qSc
Y qSc
ax
ay
aa
==
(,R
e
);
(,R
e
),
MM
α
α
à äëÿ ðàêåòû, ôîðìà êîòîðîé èçìåíèëàñü, – ïðè çíà÷åíèÿõ
X qSc
Y qSc
ai
xi
ai
yi
aa
==
(,R
e
);
(,R
e
),
MM
α
α
è ñèñòåìà óðàâíåíèé áóäåò èìåòü âèä
371
•
sin ;
•
cos ;
•
sin;•
c
V
PX
m
g
PY
mV
g
V
yV xV
ai
ai
=
−
−=
+
−
==
θθ
α
θ
θ
α
os;
();
().
θα
θ
θ
mm
t
t
==
−
ïð
Åñëè ïðè èçìåíåíèè ôîðìû ðàêåòû (èëè êîíñòðóêöèè óïðàâëÿþ-
ùèõ îðãàíîâ) êðîìå Xa è Ya èçìåíèòñÿ åùå è îñåâàÿ ñîñòàâëÿþùàÿ
òÿãè äâèãàòåëÿ, òî ïðè ðåøåíèè ïîñëåäíåé ñèñòåìû ñëåäóåò ïîëüçî-
âàòüñÿ èçìåíåííîé çàâèñèìîñòüþ Pi. Ñðàâíåíèå ðåçóëüòàòîâ ðåøå-
íèé äëÿ íåâîçìóùåííîé è âîçìóùåííîé òðàåêòîðèé äàñò âåëè÷èíû
èçìåíåíèé ýëåìåíòîâ òðàåêòîðèè â çàâèñèìîñòè îò èçìåíåíèÿ ôîð-
ìû ðàêåòû (åå àýðîäèíàìè÷åñêèõ õàðàêòåðèñòèê).
Âîçìîæíû ñëó÷àè, êîãäà ïàðàìåòð, îïðåäåëÿþùèé õàðàêòåðè-
ñòèêè äâèæåíèÿ ðàêåòû, íå âûçûâàåò èçìåíåíèÿ äðóãèõ íà÷àëüíûõ
óñëîâèé îñíîâíîé ñèñòåìû óðàâíåíèé. Íàïðèìåð, ïóñòü ïðè ñòðåëü-
áå íåóïðàâëÿåìîé ðàêåòîé èçìåíÿåòñÿ óãîë áðîñàíèÿ θ0. Â ýòîì ñëó-
÷àå ñîîòâåòñòâóþùàÿ ñèñòåìà óðàâíåíèé, íàïðèìåð (3.75) èëè
(3.122), ðåøàåòñÿ íåîáõîäèìîå ÷èñëî ðàç ïðè èçìåíåííûõ çíà÷åíè-
ÿõ θ0i. Êîëè÷åñòâî ðåøåíèé îïðåäåëÿåòñÿ ãðàíèöàìè èçìåíåíèÿ è õà-
ðàêòåðîì èçìåíåíèÿ èññëåäóåìîé âåëè÷èíû â çàâèñèìîñòè îò θ0.
Åñëè, íàïðèìåð, xc = f(θ0) èçìåíÿåòñÿ ïëàâíî è â ïðåäåëàõ èññëåäóå-
ìîãî ó÷àñòêà îò θ0i äî θ0(i+1) ýòó çàâèñèìîñòü ìîæíî ïðèíÿòü çà ëèíåé-
íóþ, äîñòàòî÷íî äâóõ ðåøåíèé ïðè êðàéíèõ çíà÷åíèÿõ θ0. Åñëè
òðåòüå ðåøåíèå, ñîîòâåòñòâóþùåå ïðèìåðíî ñåðåäèíå èíòåðâàëà θ0,
äàñò çàìåòíîå îòêëîíåíèå îò ïðÿìîé, òî ÷èñëî ðåøåíèé íåîáõîäèìî
óâåëè÷èòü. Ïîñòðîåííûå ïî ðåçóëüòàòàì ðåøåíèé ãðàôèê èëè ñãëà-
æåííàÿ òàáëè÷íàÿ çàâèñèìîñòü xc = f(θ0) ïîçâîëÿò îïðåäåëèòü èçìå-
íåíèå äàëüíîñòè δxc, ñîîòâåòñòâóþùåå îòêëîíåíèþ óãëà áðîñàíèÿ δθ0.
Äîñòîèíñòâîì îïèñàííîãî ìåòîäà âû÷èñëåíèÿ èçìåíåíèé ýëå-
ìåíòîâ òðàåêòîðèè ÿâëÿåòñÿ âîçìîæíîñòü ó÷åòà âçàèìíîãî è êîñâåí-
íîãî âëèÿíèÿ íà íèõ èçìåíåíèÿ âåëè÷èí, çàâèñÿùèõ îò îòêëîíåíèÿ
îñíîâíîãî ïàðàìåòðà è ïðåäñòàâëåííûõ â îñíîâíîé ñèñòåìå äèôôå-
ðåíöèàëüíûõ óðàâíåíèé. Êðîìå òîãî, ìåòîä ïîçâîëÿåò îïðåäåëÿòü
èçìåíåíèÿ êàæäîé âû÷èñëÿåìîé õàðàêòåðèñòèêè äâèæåíèÿ â ëþáîé
çàäàííîé òî÷êå òðàåêòîðèè.
Îòûñêàíèå ïîïðàâî÷íûõ êîýôôèöèåíòîâ ïî ðåçóëüòàòàì ðåøå-
íèÿ äèôôåðåíöèàëüíûõ óðàâíåíèé äâèæåíèÿ öåíòðà ìàññ ËÀ öåëå-
ñîîáðàçíî òîãäà, êîãäà çàâèñèìîñòü èññëåäóåìîé âåëè÷èíû îò îïðå-
äåëÿþùåãî ïàðàìåòðà ìîæåò áûòü ïðèíÿòà çà ëèíåéíóþ â ïðåäåëàõ
îæèäàåìîãî èçìåíåíèÿ ïîñëåäíåãî.  ýòîì ñëó÷àå âíà÷àëå ñèñòåìà
óðàâíåíèé èíòåãðèðóåòñÿ ïðè íîðìàëüíûõ óñëîâèÿõ, à çàòåì âòî-
ðè÷íî ïðè áëèçêîì èçìåíåííîì çíà÷åíèè ïàðàìåòðà, âëèÿíèå êîòî-
ðîãî èññëåäóåòñÿ. Ïîñëå ýòîãî ïîäñ÷èòûâàåòñÿ èñêîìûé ïîïðàâî÷-
íûé êîýôôèöèåíò. Íàïðèìåð, äëÿ îïðåäåëåíèÿ ïîïðàâî÷íîãî êî-
372
ýôôèöèåíòà â äàëüíîñòü ñòðåëüáû ñòâîëüíîé ñèñòåìû íà
îòêëîíåíèå íà÷àëüíîé ñêîðîñòè ñëåäóåò èç ðåøåíèÿ ñîîòâåòñòâóþ-
ùåé ñèñòåìû óðàâíåíèé íàéòè äàëüíîñòü ñòðåëüáû ïðè çíà÷åíèè V0,
ïðèíÿòîì çà íîìèíàëüíîå, è ïðè V01 = V0 + δV0:
∂
∂
δ
δδ
x
V
x
V
xx
V
cccV
cV
00
0
01
0
≈=
−
.
(8.13)
Ïðè ðàñ÷åòàõ ìîæíî ïðèíÿòü ∆V0 >0è∆V0 < 0. Ýòîò ìåòîä òðåáóåò
ïðîâåäåíèÿ ðàñ÷åòîâ ñ áîëüøîé òî÷íîñòüþ (ò.å . îáåñïå÷åíèÿ
áîëüøîãî êîëè÷åñòâà âåðíûõ çíà÷àùèõ öèôð), òàê êàê ïðè ìàëîì δV0
âîçìîæíû áîëüøèå îøèáêè â îïðåäåëåíèè ðàçíîñòè xx
cV
cV
01
0
−
è,
ñëåäîâàòåëüíî, ïîïðàâî÷íîãî êîýôôèöèåíòà.
Íà ðèñ. 8.3 äàíû ïðèìåðû çàâèñèìîñòåé ∂xc/∂V0 îò V0 äëÿ ñòâîëü-
íîé ñèñòåìû. Èç ãðàôèêîâ âèäíî, ÷òî âåëè÷èíà ïîïðàâî÷íîãî êî-
ýôôèöèåíòà ìîæåò ñóùåñòâåííî çàâèñåòü îò îïðåäåëÿþùåãî ïàðà-
ìåòðà, ïîýòîìó èñïîëüçîâàíèå äèñêðåòíûõ çíà÷åíèé ïîïðàâî÷íûõ
êîýôôèöèåíòîâ äîïóñòèìî ëèøü â óçêîì ïðåäåëå èçìåíåíèÿ îïðå-
äåëÿþùèõ ïàðàìåòðîâ.
Ñèñòåìà óðàâíåíèé, îïèñûâàþùàÿ íåâîçìóùåííîå äâèæåíèå, è
ñèñòåìà óðàâíåíèé, íàïèñàííàÿ ñ ó÷åòîì âîçìóùàþùèõ ôàêòîðîâ,
äîëæíû áûòü ñîñòàâëåíû â çàâèñèìîñòè îò êîíêðåòíîé çàäà÷è. Ñèñ-
òåìû óðàâíåíèé, ñîñòàâëåííûå ïðè ÷àñòî èñïîëüçóåìûõ äîïóùåíè-
ÿõ, ïîëó÷åíû â ãë. 3. Âîçìóùàþùèå ôàêòîðû ìîãóò áûòü âûðàæåíû
â âèäå äîáàâî÷íûõ óñêîðåíèé ïî îñÿì êîîðäèíàò, â êîòîðûõ ñîñòàâ-
ëåíà îñíîâíàÿ ñèñòåìà óðàâíåíèé. Äëÿ ïàññèâíûõ ó÷àñòêîâ òðàåêòî-
ðèé íåóïðàâëÿåìûõ ðàêåò è òðàåêòîðèé àðòèëëåðèéñêèõ ñíàðÿäîâ
ïðè íåçàâèñèìîì ïåðåìåííîì t (âðåìÿ) â êà÷åñòâå ñèñòåìû óðàâíå-
íèé, îïèñûâàþùåé íåâîçìóùåííûé ïîëåò, ìîæåò áûòü âçÿòà ñèñòå-
ìà (3.127), äîïîëíåííàÿ îäíèì óðàâíåíèåì, îïèñûâàþùèì äâèæå-
íèå â áîêîâîì íàïðàâëåíèè ïî îñè êîîðäèíàò Z:
373
Ðèñ. 8.3 . Ãðàôèê çàâèñèìîñòè
∂xc/∂V0 = f(V0) äëÿ àðòèëëå-
ðèéñêîé ñèñòåìû, ñíàðÿä êî-
òîðîé èìååò áàëëèñòè÷åñêèé
êîýôôèöèåíò ñ ≈ 0,2:
1–θ0=25°;2–55°
•••
; •••;
•••
.
x
Exy
Eygz
Ez
=−
=−
−
=−
Äîáàâî÷íûå óñêîðåíèÿ ïî ñîîòâåòñòâóþùèì îñÿì, âûçâàííûå
âîçäåéñòâèåì âîçìóùàþùåãî ôàêòîðà, îáîçíà÷èì ñîîòâåòñòâåííî εx,
εy è εz. Óñêîðåíèÿ, îïðåäåëÿåìûå âðàùåíèåì Çåìëè, íàéäåì,
âîñïîëüçîâàâøèñü óðàâíåíèåì (2.43). Óñêîðåíèå ñíàðÿäà â
ïåðåíîñíîì äâèæåíèè àïåð îáúåäèíèì ñ óñêîðåíèåì çåìíîãî
ïðèòÿæåíèÿ â îáùåå óñêîðåíèå ñâîáîäíîãî ïàäåíèÿ g (ôîðìóëà
(1.50)).
Òîãäà óñêîðåíèå ñíàðÿäà â îòíîñèòåëüíîì äâèæåíèè çàïèøåì
òàê:
aag
a
îòí
â
êîð
=+
−
,
ãäå àâ – âåêòîð óñêîðåíèÿ ñíàðÿäà îò äåéñòâèÿ ñèëû ñîïðîòèâëåíèÿ
âîçäóõà; −àêîð = ε – âåêòîð äîáàâî÷íîãî (êîðèîëèñîâà) óñêîðåíèÿ,
êîòîðîå â èñõîäíîé ñèñòåìå íå ó÷èòûâàëîñü.
Îñü OXg(OX) íîðìàëüíîé ñèñòåìû êîîðäèíàò íàïðàâèì íà ñåâåð
ïî ìåðèäèàíó, à îñü OXê òðàåêòîðíîé ñèñòåìû êîîðäèíàò – ïîä óã-
ëîì À ê íåìó. Ïðîåêöèè âåêòîðà óãëîâîé ñêîðîñòè Çåìëè Ω íà òðà-
åêòîðíûå îñè êîîðäèíàò ïðåäñòàâèì êàê
ΩΩ
ΩΩ ΩΩ
xy
z
AA
êê
ê
ãö
ãö
ãö
==
=
cos
cos ;
sin ;
cos
sin .
φφ
φ
Ïðîåêöèè êîðèîëèñîâà óñêîðåíèÿ íà òå æå îñè:
ε
ε
xxy
z
yyz
az
y
ax
êêê
ê
êêê
êîð
êîð
=−
=−
−
=−
=−
−
2
2
(••
);
(•
ΩΩ
ΩΩ
x
zzx
y
z
ay
x
ê
êêê
ê
êîð
•
);
(••
).
ε=
−
=
−
−
2ΩΩ
Òîãäà ñèñòåìà óðàâíåíèé, íàïèñàííàÿ â îáùåì âèäå ñ ó÷åòîì
âîçìóùàþùåãî ôàêòîðà, áóäåò èìåòü âèä
•••
•
(••
);
•••
•
xE
x
E
x
zy
yE
ygE
y
xy
z
y
=−
+=−
−
−
=−
−
−
=−
ε
ε
2ΩΩ
êê
−−
−
=−
+=−
−
−
gx
z
zE
z
E
zyx
zx
zx
y
2
2
(••
);
•••
•
(••
).
ΩΩ
ΩΩ
êê
êê
ε
(8.14)
 ñèñòåìàõ, â ëåâîé ÷àñòè óðàâíåíèé êîòîðûõ íå ñòîÿò íåïîñðåä-
ñòâåííî óñêîðåíèÿ, ÷ëåíû, ó÷èòûâàþùèå âîçìóùàþùèå ôàêòîðû,
îòëè÷íû îò εx, εy è εz. Íàïðèìåð, ïðè íåçàâèñèìîì ïåðåìåííîì õ â
374
êà÷åñòâå ñèñòåìû óðàâíåíèé, îïèñûâàþùåé íåâîçìóùåííûé ïîëåò,
âîçüìåì ñèñòåìó óðàâíåíèé (3.129)
′=−
′=−
′=
′=
−
uE
pg
u
yp
tu
xx
x
x
;/
;;.
21
Ýòà æå ñèñòåìà óðàâíåíèé, íàïèñàííàÿ ñ ó÷åòîì âîçìóùàþùèõ
ôàêòîðîâ, áóäåò èìåòü âèä
′=−
+
′=−
+
′=
′=
−
uE pg
u
yp
tu
xu
x
p
xx
εε
;/;
;.
2
1
(8.15)
Ïðåîáðàçóåì âåëè÷èíû ′u
x
è′p
x
, èìåÿ â âèäó (8.14):
′=
′==
−
+
′=
′=
⎛
⎝⎜⎞
⎠⎟
−
ux
t
x
u
Eu
pp
t
d
dt
y
x
dt
d
xx
x
xx
••
••
;
•
•
ε
1
x
yx xy
x
=
−
•••
•
•
.
3
Ïîìíÿ, ÷òî
•
,
xu
=
è èñïîëüçóÿ ïåðâûå äâà óðàâíåíèÿ ñèñòåìû (8.14),
ïîëó÷èì
′=−
+
−
p
g
uu
p
xy
x
22
1
()
.
εε
Òàêèì îáðàçîì, ñðàâíèâàÿ ïîëó÷åííûå óðàâíåíèÿ ñ (8.15), èìååì
ε
ε
εε
ε
u
x
py
x
uu
p
==
−
;()
.
1
2
(8.16)
Íàïðèìåð, äëÿ ñôåðè÷åñêîé ìîäåëè Çåìëè è ïëîñêîé òðàåêòîðèè
÷ëåíû, ó÷èòûâàþùèå âëèÿíèå èçìåíåíèÿ âåëè÷èíû è íàïðàâëåíèÿ
óñêîðåíèÿ ñâîáîäíîãî ïàäåíèÿ íà èçìåíåíèå ýëåìåíòîâ òðàåêòîðèè,
â ñîîòâåòñòâèè ñ [22] ïðèáëèæåííî ðàâíû
εε
up
g
u
x
RR
yx
p
g
u
≈−
≈
+
ÇÇ
;()
.
1
2
2
(8.17)
8.2.2. ÎÏÐÅÄÅËÅÍÈÅ ÏÎÏÐÀÂÎ×ÍÛÕ ÊÎÝÔÔÈÖÈÅÍÒÎÂ
ÈÍÒÅÃÐÈÐÎÂÀÍÈÅÌ ÄÈÔÔÅÐÅÍÖÈÀËÜÍÛÕ ÓÐÀÂÍÅÍÈÉ
 ÎÒÊËÎÍÅÍÈßÕ
 ñëó÷àå ìàëûõ îòêëîíåíèé îïðåäåëÿþùèõ ïàðàìåòðîâ ïîïðà-
âî÷íûå êîýôôèöèåíòû ìîãóò áûòü íàéäåíû ïðè ðåøåíèè äèôôå-
ðåíöèàëüíûõ óðàâíåíèé äâèæåíèÿ â îòêëîíåíèÿõ. Äëÿ ñîñòàâëåíèÿ
375
óðàâíåíèé âîñïîëüçóåìñÿ îáùèì ìåòîäîì ëèíåàðèçàöèè äèôôåðåí-
öèàëüíûõ óðàâíåíèé, îïèñûâàþùèõ äâèæåíèå öåíòðà ìàññ ðàêåòû
èëè ñíàðÿäà. Îáû÷íî ó÷èòûâàþò òîëüêî ïåðâûå ÷ëåíû ðàçëîæåíèÿ â
ðÿä Òåéëîðà. Îñíîâíàÿ ñèñòåìà äèôôåðåíöèàëüíûõ óðàâíåíèé âû-
áèðàåòñÿ â çàâèñèìîñòè îò êîíêðåòíîé çàäà÷è.  êà÷åñòâå ïðèìåðà
ïîëó÷èì äèôôåðåíöèàëüíûå óðàâíåíèÿ â îòêëîíåíèÿõ äëÿ àêòèâíî-
ãî ó÷àñòêà òðàåêòîðèè íåóïðàâëÿåìîé ðàêåòû, èñïîëüçóÿ êàê îñíîâ-
íóþ ñèñòåìó óðàâíåíèé (3.75):
•
sin ;
•
cos
;•
sin;•
cos .
V
PX
m
g
g
V
yV xV
a
=
−
−=
−
==
θθ
θ
θθ
Îáîçíà÷èì ïðàâóþ ÷àñòü ïåðâîãî óðàâíåíèÿ ÷åðåç aV è ðàñêðîåì
âõîäÿùèå â íåå âåëè÷èíû. Áóäåì ñ÷èòàòü, ÷òî êîýôôèöèåíò ëîáîâîãî
ñîïðîòèâëåíèÿ çàâèñèò òîëüêî îò ÷èñëà Ì è íå èçìåíÿåòñÿ ñ
âûñîòîé. Áóäåì òàêæå ïîëàãàòü, ÷òî äëÿ äàííîé ðàñ÷åòíîé òî÷êè
òðàåêòîðèè èçìåíåíèå òÿãè Ð íå çàâèñèò îò èçìåíåíèÿ âûñîòû y :
aV
mm
t
mJg
SV
cg
xa
=
−
−
⎡
⎣⎢
⎤
⎦⎥−
1
2
0
1
2
|•| |
•
|(
s
i
n
.
ρ
θ
M)
(8.18)
Ýòî ðàâåíñòâî ìîæåò áûòü ïåðåïèñàíî â âèäå ôóíêöèîíàëüíîé
çàâèñèìîñòè aV = f1(V, θ, y, J1, S, ρ, cm
xa
(,
•
).
Ì), 0
m
Îáîçíà÷àÿ ïðàâóþ ÷àñòü âòîðîãî óðàâíåíèÿ ñèñòåìû ÷åðåç aθ,çà-
ïèøåì ôóíêöèîíàëüíóþ çàâèñèìîñòü aθ = f2(V, θ).
Ïîñòóïàÿ ïîäîáíûì æå îáðàçîì, ìîæåì íàïèñàòü äëÿ òðåòüåãî è
÷åòâåðòîãî óðàâíåíèé: ay = f3(V, θ)èax = f4(V, θ).
Èñïîëüçóÿ ôîðìóëû ëèíåàðèçàöèè (2.72), ïîëó÷èì ñèñòåìó äèô-
ôåðåíöèàëüíûõ óðàâíåíèé â îòêëîíåíèÿõ
d
dt
V
a
V
V
aa
y
y
a
J
J
a
VVVV
V
()
δ
∂
∂
δ∂
∂θ
δθ∂
∂
δ∂
∂
δ
∂
∂ρ
δρ
=+
+++
+
1
1
+++
=
∂
∂
δ
∂
∂
δ
∂
∂
δ
δθ
∂
∂
θ
a
c
c
a
m
m
a
m
m
d
dt
a
V
V
x
x
VV
a
a
0
0
|•| |
•
|;
()δ∂
∂θ
δθ
δ
∂
∂
δ
∂
∂θ
δθ
δ∂
∂
δ
θ
V
a
d
dt
y
a
V
V
a
d
dt
x
a
V
V
yy
x
+
=+
=
;
()
;
()
+
∂
∂θ
δθ.
ax
(8.19)
376
Íàõîæäåíèå áàëëèñòè÷åñêèõ ïðîèçâîäíûõ ∂ai/∂j âî ìíîãèõ ñëó-
÷àÿõ ïðåäñòàâëÿåò, õîòÿ è íå ñëîæíóþ, íî òðóäîåìêóþ çàäà÷ó. Äëÿ
ïðèíÿòîé íàìè ñèñòåìû ïîëó÷èì
1
2
2
)(
)
(),
)
a
a
V
SV
m
c
c
a
a
VV
V
x
x
V
a
a
==
−
+
⎡
⎣⎢
⎤
⎦⎥
=
∂
∂
ρ
∂
∂
∂
θ
M
M
M
M
V
Vy
y
x
VJ
g
a
a
ym
S
V
c
y
a
a
a
∂θ
θ
∂
∂
∂ρ
∂
∂
=−
==
−
=
cos ,
)(
)
,
)
3
1
2
4
2
1
M
V
V
Va
Vc
x
a
J
P
mJ
a
aX
m
a
a
c
X
m
xa
a
∂
∂
∂ρ
ρ
∂
∂
ρ
11
1
5
1
6
=
==
−
==
−
,
),
)
V
1
7
1
8
1
0
0
c
a
a
m
PX
mm
a
a
m
x
Vm
Va
Vm
V
a
()
,
),
)
|•|
|•|
M
==
−
−
==
∂
∂
∂
∂
|•|
|•|
,
)
cos
m
P
m
mt
m
PX
m
a
a
V
g
V
a
V
+
−
⎛
⎝⎜⎞
⎠⎟
⎡
⎣⎢
⎤
⎦⎥
==
9
2
θ
θ
∂
∂
θ
,
(8.20)
10
11
12
)
sin
,
)s
i
n
,
)
a
a
g
V
a
a
V
a
a
yV
y
y
y
θθ
θ
θ
∂
∂θ
θ
∂
∂
θ
∂
∂θ
==
==
=
=
==
==
−
V
a
a
V
a
a
V
xV
x
x
x
cos ,
)c
o
s
,
)s
i
n
.
θ
∂
∂
θ
∂
∂θ
θ
θ
13
14
Ïîñëå ýòîãî ñèñòåìó äèôôåðåíöèàëüíûõ óðàâíåíèé â îòêëîíå-
íèÿõ çàïèøåì â òàêîì âèäå:
377
d
dt
VaVa ayaJ
aca
VV
V
Vy
VJ
Vc
x
Vm
xa
a
()
δδδ
θ
δδ
δδ
θ
=+
+++
++
1
0
1
mam
d
dt
aVa
d
dt
yaVa
Vm
V
yV
0+
=+
=+
|•| | •|;
()
;
()
δ
δθ
δ
δθ
δδ
θθ
θ
y
xV
x
d
dt
xaVa
θ
θ
δθ
δδδ
θ
.
;
()=+
(8.21)
Ñèñòåìó óðàâíåíèé â îòêëîíåíèÿõ ïðè íåçàâèñèìîé ïåðåìåííîé
t, ïðèãîäíóþ äëÿ ðàñ÷åòà èçìåíåíèÿ ýëåìåíòîâ äâèæåíèÿ è ïîïðà-
âî÷íûõ êîýôôèöèåíòîâ íà ïàññèâíûõ ó÷àñòêàõ òðàåêòîðèé íåóïðàâ-
ëÿåìûõ ðàêåò è òðàåêòîðèé ñíàðÿäîâ àðòèëëåðèéñêèõ ñèñòåì, ïîëó-
÷èì èç ñèñòåìû óðàâíåíèé (8.21).  ýòîì ñëó÷àå ìàññà ðàêåòû (ñíà-
ðÿäà) ïîñòîÿííà, P, J1, |
•
|m ðàâíû íóëþ è ïåðâîå óðàâíåíèå ñèñòåìû
(8.19) ìîæíî íàïèñàòü (äëÿ ñíàðÿäîâ) â ñëåäóþùåé ôîðìå:
d
dt
V
a
V
V
aaa
c
c
a
m
VVVV
x
x
V
a
a
()
δ
∂
∂
δ
∂
∂θ
δθ
∂
∂ρ
δρ
∂
∂
δ
∂
∂
= +++
+
0
δm0.
Ñîîòâåòñòâåííî â ôîðìóëàõ êîýôôèöèåíòîâ (8.20) íàäî ïðèíÿòü
aXm
Vm
a
0
0
2
=
/,â ïåðâîé, òðåòüåé, ïÿòîé è øåñòîé ôîðìóëàõ –
ïîëîæèòü m = m0. Äëÿ ðàêåò â òåõ æå óðàâíåíèÿõ è ôîðìóëàõ ñëåäóåò
îñóùåñòâèòü çàìåíû m = mï. Ñèñòåìà äèôôåðåíöèàëüíûõ óðàâíåíèé
ñ ó÷åòîì ýòîãî áóäåò èìåòü âèä
d
dt
VaVa aya acam
VV
V
Vy
V
Vc
x
Vm
xa
a
()
;
δδδ
θ
δδ
ρδδ
θρ
=+
+++ +
0
0
d
dt
aVa
d
dt
yaVa
d
dt
xa
V
yV
y
x
()
;
()
;
()
δθ
δ
δθ
δδδ
θ
δ
θθ
θ
θ
=+
=+
=
Vx
Va
δδ
θ
θ
+
.
(8.22)
Ïîëó÷èì ñèñòåìó óðàâíåíèé â îòêëîíåíèÿõ, ïðèãîäíóþ äëÿ îï-
ðåäåëåíèÿ èçìåíåíèé ýëåìåíòîâ òðàåêòîðèé ñíàðÿäîâ ïîñòîÿííîé
ìàññû ïðè íåçàâèñèìîé ïåðåìåííîé õ. Çà îñíîâíóþ ñèñòåìó âîçü-
ìåì ñèñòåìó (3.129), îïèñûâàþùóþ äâèæåíèå öåíòðà ìàññ àðòèëëå-
378
ðèéñêîãî ñíàðÿäà èëè íåóïðàâëÿåìîé ðàêåòû íà ïàññèâíîì ó÷àñòêå
òðàåêòîðèè â ïëîòíûõ ñëîÿõ àòìîñôåðû:
′=−
′=−
′=
′=
−
uE
pg
u
yp
tu
xx
x
x
;/
;;.
21
Âñïîìíèì, ÷òî E = cHτ(y)G(Vτ), ãäå Vu pON
τ
ττ
=+
12
/.Òàê êàê
Hτ = f(y)èτ = f1(y), òî E = f(u, p, y). Îáîçíà÷èì
af
u
p
yaf
u
afpaf
u
up
y
t
==
=
=
12
3
4
(,, );
(); (); (),
èòîãäà ′ =
ua
xu
;′=
pa
xp
;′=
ya
xy
;′=
ta
xt
.
Âûïîëíèâ ëèíåàðèçàöèþ óðàâíåíèé ñèñòåìû, ïðèíÿòîé íàìè çà
îñíîâíóþ, ïîëó÷èì ñèñòåìó äèôôåðåíöèàëüíûõ óðàâíåíèé â îòêëî-
íåíèÿõ
d
dx
uauapay
d
dt
au
d
dx
ya
uu
up
uy
pu
y
()
;
() ;()
δδδδ
δρ
δ
δ
=++
==
p
tu
p
d
dx
tau
δ
δδ
;
().
=
(8.23)
Ïðåäâàðèòåëüíî çàïèøåì çíà÷åíèÿ êîýôôèöèåíòîâ aij, âõîäÿ-
ùèõ â ïåðâîå óðàâíåíèå ñèñòåìû (8.23):
a
a
u
E
u
a
a
p
E
p
a
a
y
E
y
uu
u
up
u
uy
u
==
−
==
−
==
−
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
;;.
Çíà÷åíèÿ áàëëèñòè÷åñêèõ ïðîèçâîäíûõ íàéäåì, èñïîëüçóÿ (3.126) è
(8.23). Äèôôåðåíöèðóÿ Å ïî u, èç (3.126) ïîëó÷èì
∂
∂
∂∂
∂∂
τ
τ
τ
τ
ττ
E
u
EV
Vu
cHyGV
pON
==′
+
−
()()()
.
12
1
(8.24)
Óìíîæàÿ ÷èñëèòåëü è çíàìåíàòåëü íà uG(Vτ) è îáîçíà÷àÿ
′
=
−
GVGVV fV
() () (),
ττ
ττ
1
(8.25)
íàéäåì
a
E
u
fV
uu
=−
().
τ
(8.26)
379
Äèôôåðåíöèðóÿ Å ïî ð, ïîëó÷èì
∂
∂
∂∂
∂∂
τ
τ
τ
τ
ττ
E
p
EV
Vp
cHyGVu
p
p
ON
==′
+
()()
.
12
Óìíîæèâ ÷èñëèòåëü è çíàìåíàòåëü íà GV
p
(),
τ
12
+
ïðåäñòàâèì
a
Ep
p
fV
up
=−
+
12()
.
τ
(8.27)
Áîëåå òðóäîåìêèì îêàçûâàåòñÿ îïðåäåëåíèå auy, òàê êàê Å çàâè-
ñèò îò âåëè÷èíû y, ÿâëÿþùåéñÿ â ñâîþ î÷åðåäü ôóíêöèåé Hτ(y)è
Vτ = f(y):
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
τ
τ
τ
τ
E
y
E
Hy
Hy
y
E
V
V
y
=+
[()]
[()
]
.
Èç çàâèñèìîñòè äëÿ Å áóäåì èìåòü ∂E/∂[Hτ(y)] = cG(Vτ)=
=E/[Hτ(y)].
Äëÿ îïðåäåëåíèÿ ∂[Hτ(y)]/∂y âîñïîëüçóåìñÿ ôîðìóëîé (1.88),
ïîäñòàâèâ åå â âûðàæåíèå äëÿ Hτ(y):
Hy
e
ON
R
dy
y
τ
τ
τ
τ
()
.
=
∫−1
0
(8.28)
Ïðîëîãàðèôìèðóåì âûðàæåíèå (8.28):
ln()ln
ln
.
Hy
R
dy
ON
y
τ
ττ
τ
=−
−
∫
1
2
1
2
1
0
Äèôôåðåíöèðóÿ ïî y è ïðåîáðàçóÿ, ïîëó÷èì
∂
∂
τ
ττ
τ
τ
[()
]()
;
Hy
y
Hy
R
y
=−
′
+
⎛
⎝⎜
⎞
⎠⎟
2
1
(8.29)
êðîìå òîãî,
∂
∂τ
ττ
τ
τ
E
V
cHyGV
E
V
fV
=
′
=
()()
();
(8.30)
380
∂
∂
ττ
ττ
τ
τ
τ
τ
V
y
up
V
yO
N
y
=+
−
′
⎛
⎝
⎜
⎞
⎠
⎟=−
′
1
2
2
2
.
(8.31)
Ïîäñòàâëÿÿ çíà÷åíèÿ ÷àñòíûõ ïðîèçâîäíûõ, ïîëó÷èì ïîñëå
ïðåîáðàçîâàíèé
a
E
y
EfV
R
uy
y
=−
=
+
′+
⎛
⎝⎜
⎞
⎠⎟
∂
∂τ
τ
τ
()
.
1
2
1
(8.32)
Êîýôôèöèåíòû ïîñëåäíèõ òðåõ óðàâíåíèé ñèñòåìû (8.23) ðàâíû
a
g
u
aa
u
pu
yp
tu
==
=
−
2
1
1
32
;;.
(8.33)
Èíòåãðèðîâàíèå óðàâíåíèé â îòêëîíåíèÿõ ïîçâîëÿåò ïîëó÷èòü
ïîïðàâî÷íûå êîýôôèöèåíòû è èçìåíåíèÿ õàðàêòåðèñòèê äâèæåíèÿ,
ïðåäñòàâëåííûõ â ëåâûõ ÷àñòÿõ óðàâíåíèé, äëÿ ëþáîé ôèêñèðîâàí-
íîé òî÷êè òðàåêòîðèè. Áåç äîïîëíèòåëüíûõ óïðîùåíèé ñèñòåìà
óðàâíåíèé â îáùåì ñëó÷àå ðåøàåòñÿ òîëüêî ÷èñëåííûì èíòåãðèðî-
âàíèåì íà ÖÂÌ. Êîýôôèöèåíòû aij âû÷èñëÿþòñÿ ïî äàííûì íåâîç-
ìóùåííîé òðàåêòîðèè.
8.2.3. ÑÎÏÐßÆÅÍÍÀß ÑÈÑÒÅÌÀ ÓÐÀÂÍÅÍÈÉ Â ÎÒÊËÎÍÅÍÈßÕ
È ÅÅ ÐÅØÅÍÈÅ
Ñèñòåìà íåîäíîðîäíûõ ëèíåéíûõ äèôôåðåíöèàëüíûõ óðàâíå-
íèé, îòíîñÿùàÿñÿ ê ñèñòåìàì äèôôåðåíöèàëüíûõ óðàâíåíèé â îò-
êëîíåíèÿõ, ìîæåò èìåòü ñîïðÿæåííóþ ñèñòåìó ëèíåéíûõ óðàâíå-
íèé. ×èñëî ïåðåìåííûõ ñîïðÿæåííîé è îñíîâíîé ñèñòåì îäíî è òî
æå. Ïî ïðàâèëó ñîñòàâëåíèÿ ñîïðÿæåííîé ñèñòåìû ëèíåéíûõ îäíî-
ðîäíûõ óðàâíåíèé êîýôôèöèåíòû ïåðâîãî óðàâíåíèÿ áåðóòñÿ ðàâ-
íûìè êîýôôèöèåíòàì ïåðâûõ ÷ëåíîâ îñíîâíîé ñèñòåìû óðàâíå-
íèé, êîýôôèöèåíòû âòîðîãî óðàâíåíèÿ – âòîðûõ ÷ëåíîâ îñíîâíûõ
óðàâíåíèé è ò.ä . Â íîâîé ñèñòåìå âñå êîýôôèöèåíòû áåðóòñÿ ñ îá-
ðàòíûìè çíàêàìè ïî îòíîøåíèþ ê îñíîâíîé. Èñõîäÿ èç îïðåäåëå-
íèÿ îäíîðîäíûõ äèôôåðåíöèàëüíûõ óðàâíåíèé â ñîïðÿæåííîé ñèñ-
òåìå îïóñòèì ñâîáîäíûå ÷ëåíû, èìåþùèåñÿ â îñíîâíîé. Äëÿ ïîÿñ-
íåíèÿ ðàññìîòðèì ñèñòåìó äèôôåðåíöèàëüíûõ óðàâíåíèé (8.23) è
ïåðåïèøåì òðè ïåðâûõ ñîâîêóïíûõ óðàâíåíèÿ, ââåäÿ ÷ëåíû εu è εp,
ó÷èòûâàþùèå âîçìóùåíèÿ. Äëÿ îáùíîñòè çàïèøåì ÷ëåíû, èìåþ-
ùèå íóëåâûå êîýôôèöèåíòû; êîýôôèöèåíòû aij ïðåäñòàâèì àáñî-
ëþòíûìè çíà÷åíèÿìè, óêàçàâ â óðàâíåíèÿõ çíàêè â ÿâíîì âèäå:
381
d
dx
ua
u
a
p
a
y
d
dx
pau p
uu
up
uy
u
pu
()
;
()
δδδ
δ
ε
δδδ
δ
=−
−
+
+
=+
+
00
y
d
dx
yu
a
py
p
yp
+
=++
ε
δδ δδ
;
()
.
00
(8.34)
Ïðèìåì ñèñòåìó (8.34), çàâèñèìûìè ïåðåìåííûìè â êîòîðîé ÿâ-
ëÿþòñÿ δu, δp è δy, çà îñíîâíóþ. Íàïèøåì ñîïðÿæåííóþ ñ (8.34)
ñèñòåìó óðàâíåíèé, îáîçíà÷èâ ïåðåìåííûå ÷åðåç λ1, λ2 è λ3:
d
dx
aa
d
dx
aa
d
dx
uu
pu
up
up
λ
λλλ
λ
λλλ
λ
1
12
3
2
123
3
0
0
=−−
=−
−
=
;
;
−−
−
auyλλλ
123
00
.
(8.35)
 îáùåì ñëó÷àå ôèçè÷åñêèé ñìûñë ïåðåìåííûõ λi çàâèñèò îò ôè-
çè÷åñêîãî ñìûñëà êîýôôèöèåíòîâ îñíîâíîãî óðàâíåíèÿ aij è ñëàãàå-
ìûõ εu è εp. Óñòàíîâèì ñâÿçü ìåæäó ïåðåìåííûìè îñíîâíîé è ñîïðÿ-
æåííîé ñèñòåì óðàâíåíèé äëÿ íàøåãî ñëó÷àÿ. Óìíîæèì óðàâíåíèÿ
îñíîâíîé ñèñòåìû ñîîòâåòñòâåííî íà λ1, λ2 è λ3, à óðàâíåíèÿ ñîïðÿ-
æåííîé ñèñòåìû – íà δu, δp è δy è ñëîæèì èõ. Ïîñëå ïðåîáðàçîâà-
íèé áóäåì èìåòü
λδλδλδ
δ
λδλ
δ
123
12
d
dx
u
d
dx
p
d
dx
y
u
d
dx
p
d
dx
y
d
()()()
+++
+++
λλελε
3
12
dx
up
=+
è äàëåå
d
dx
upy up
()
.
λδλδλδλελε
123 13
++ =+
(8.36)
Ïðîèíòåãðèðóåì ïðàâóþ è ëåâóþ ÷àñòè ïîñëåäíåãî óðàâíåíèÿ îò õ1 äî
õ2. Òîãäà
λδλδλδλδλδ
λδ
λελ
122
222
322
111
211
311
1
upyup
y
u
++ −−−
−=+
(
2
1
2
εp).
dx
x
x
∫
(8.37)
382
Ïîëó÷åííîå óðàâíåíèå ÿâëÿåòñÿ îáùèì
è ñïðàâåäëèâî ïðè ëþáûõ íà÷àëüíûõ
óñëîâèÿõ. Äëÿ ðàññìàòðèâàåìîé îñíîâ-
íîé òðàåêòîðèè ïðåäåëû èíòåãðèðîâàíèÿ
ñîïðÿæåííîé ñèñòåìû ìîãóò áûòü âû-
áðàíû òàê, êàê ýòî óäîáíî äëÿ ðåøåíèÿ
êîíêðåòíîé çàäà÷è òåîðèè ïîïðàâîê. Âî
ìíîãèõ ñëó÷àÿõ îêàçûâàåòñÿ öåëåñî-
îáðàçíûì èíòåãðèðîâàòü ñîïðÿæåííóþ
ñèñòåìó äèôôåðåíöèàëüíûõ óðàâíå-
íèé íà÷èíàÿ ñ êîíå÷íîé òî÷êè òðàåê-
òîðèè.
Íàïðèìåð, ïðè îïðåäåëåíèè èç-
ìåíåíèÿ ýëåìåíòîâ ïàññèâíûõ ó÷à-
ñòêîâ òðàåêòîðèé íåóïðàâëÿåìûõ ðàêåò êëàññà "ïîâåðõíîñòü – ïî -
âåðõíîñòü" è òðàåêòîðèé ñíàðÿäîâ íàçåìíîé àðòèëëåðèè ñîïðÿæåí-
íàÿ ñèñòåìà (8.35) èíòåãðèðóåòñÿ îò òî÷êè ïàäåíèÿ ñíàðÿäà äî
íà÷àëà ðàññìàòðèâàåìîãî ó÷àñòêà òðàåêòîðèè. Íàïèøåì óðàâíåíèå
(8.37) äëÿ ïàññèâíîãî ó÷àñòêà òðàåêòîðèè ðàêåòû
λδλδλδλδλδ
λδ
λελ
1231 2
31
cc
cc
cc
u
upyup
y
++−−−
−=+
êê
êê
êê
(
2εp
x
x
dx
c
).
ê
∫
(8.38)
×òîáû ïîëó÷èòü èç (8.38) ôîðìóëó, îïðåäåëÿþùóþ èçìåíåíèå
äàëüíîñòè, íåîáõîäèìî âûáðàòü îäèí èç êîýôôèöèåíòîâ λic òàê,
÷òîáû îí ñîäåðæàë δxc, îñòàëüíûå êîýôôèöèåíòû ñîïðÿæåííîé ñèñ-
òåìû áåðóòñÿ ðàâíûìè íóëþ. Äëÿ òî÷êè ïàäåíèÿ (ðèñ. 8 .4) ìîæíî
âçÿòü δxc = δyc/|pc|, ïîñëå ñðàâíåíèÿ ñ òðåòüèì ÷ëåíîì óðàâíåíèÿ
(8.38) ïîëó÷èì λ3c = 1/|pc|. Êðîìå òîãî, λ1c =0;λ2c = 0. Èç (8.38) áóäåì
èìåòü
δλ
δλ
δλ
δλ
ελ
ε
xupy
d
x
cu
x
xc
=+++ +
∫
123 1
2
êê
êê
êê
ð
ê
()
.
(8.39)
Ôèçè÷åñêèé ñìûñë âåëè÷èí λ1ê, λ2ê è λ3ê âûÿñíèì, ïðèðàâíÿâ ê
íóëþ εu è εp è ïîïàðíî äðóã ê äðóãó îòêëîíåíèÿ δuê, δpê, δyê. Íàïðè-
ìåð, ïðèíÿâ δpê =0,δyê =0èδuê = 1, íàéäåì λ1ê = ∂xc/∂uê. Ïîäîá-
íûì îáðàçîì ïîëó÷èì
λ∂∂λ ∂∂
23
êê
êê
==
xp
è
xy
cc
//
.
383
Ðèñ. 8 .4 . Îòðåçêè òðàåêòîðèé, ïðèëå-
ãàþùèå ê òî÷êå ïàäåíèÿ
Òåêóùèå çíà÷åíèÿ λ1, λ2, λ3 â ôóíêöèè îò õ ïîëó÷àþòñÿ ÷èñ-
ëåííûì èíòåãðèðîâàíèåì (íà ÝÂÌ èëè ïðè ðó÷íîì ñ÷åòå) ñî-
ïðÿæåííîé ñèñòåìû (8.35) ïðè íà÷àëüíûõ óñëîâèÿõ λ1c =0;λ2c =0;
λ3c = 1/|pc|. Øàã èíòåãðèðîâàíèÿ ïî õ áåðåòñÿ ñî çíàêîì ìèíóñ, òàê
êàê èíòåãðèðîâàíèå îñóùåñòâëÿåòñÿ îò xc äî õê.
Ïðè èñïîëüçîâàíèè ôîðìóëû (8.39) çíà÷åíèÿ δuê, δpê è δyê äîëæ-
íû îïðåäåëÿòüñÿ â ðåçóëüòàòå èññëåäîâàíèÿ ïðåäûäóùåãî ó÷àñòêà
òðàåêòîðèè èëè çàäàâàòüñÿ çàðàíåå. Åñëè ïîëîæèòü δuê = δpê = δyê =
=0
,ò
î
δλ
ε
λ
ε
xd
x
cu
x
xc
=+
∫()
.
12
p
ê
(8.40)
Ïîñëåäíÿÿ ôîðìóëà ïîçâîëÿåò îïðåäåëèòü èçìåíåíèå äàëüíîñòè,
âûçâàííîå ôàêòîðàìè, âëèÿíèå êîòîðûõ ó÷èòûâàåòñÿ ÷åðåç εu è εð
(âëèÿíèå âðàùåíèÿ Çåìëè, èçìåíåíèÿ ìåòåîðîëîãè÷åñêèõ óñëîâèé
è ò.ä.) .
Ïðè îïðåäåëåíèè δxc äëÿ òðàåêòîðèé ñíàðÿäîâ ïîëåâîé àðòèëëå-
ðèè èíòåãðèðîâàíèå ñîïðÿæåííîé ñèñòåìû (8.35) ñëåäóåò ïðîâîäèòü
îò xc äî x = 0. Êðîìå òîãî, äëÿ òî÷êè âûëåòà ìîæíî ïðèíÿòü δy0 =0,è
òîãäà èç (8.39) ïîëó÷èì
δλ
δλ
δλ
ελ
ε
xup
d
x
cu
xc
=++ +
∫
100
200
1
2
0
()
.
ð
(8.41)
Äàííàÿ ôîðìóëà ÿâëÿåòñÿ îáùåé ïîïðàâî÷íîé äëÿ ïîëíîé
ãîðèçîíòàëüíîé äàëüíîñòè ñòðåëüáû ïîëåâîé àðòèëëåðèéñêîé
ñèñòåìû.
8.2.4. ÎÏÐÅÄÅËÅÍÈÅ ÏÎÏÐÀÂÎ×ÍÛÕ ÊÎÝÔÔÈÖÈÅÍÒΠÈÇ ÓÑËÎÂÈß
ÏÎÄÎÁÈß ÒÐÀÅÊÒÎÐÈÉ
×òîáû âû÷èñëèòü èçìåíåíèå ýëåìåíòîâ òðàåêòîðèé ñíàðÿäîâ ïî-
ñòîÿííîé ìàññû, ÷àñòî èñïîëüçóþò çàâèñèìîñòè, ïîëó÷àåìûå èç óñ-
ëîâèÿ ïîäîáèÿ òðàåêòîðèé.
Âîçüìåì ïåðâîå óðàâíåíèå ñèñòåìû (5.93) è îïðåäåëèì ïîïðà-
âî÷íûå êîýôôèöèåíòû äëÿ ïîëíîé äàëüíîñòè íà èçìåíåíèå äàâëå-
íèÿ è òåìïåðàòóðû âîçäóõà â òî÷êå âûëåòà (è äàëåå ïî òðàåêòîðèè).
Åñëè ïîëîæèòü τê = τON,òîVτ0 = V0 è
xV
c
c
=Φ10 0
(,,)
.
*
θ
(8.42)
384
Âñïîìèíàÿ, ÷òî ñ
*
= ch0/hON, è ñ÷èòàÿ V0 è θ0 â (8.42) íåèçìåííûìè,
íàéäåì ïîî÷åðåäíî ïðîèçâîäíûå îò xc ïî ñ èïîh0:
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
x
cc
c
cc
h
h
x
hc
c
h
c
ON
c
==
==
ΦΦ
Φ
11
0
0
1
0
*
*
*
*
*
;
∂
∂
Φ1
c
c
hON
*
.
Ñðàâíèâàÿ äâà ïîñëåäíèõ ðàâåíñòâà, ïîëó÷èì
∂
∂
∂
∂
x
h
x
c
c
h
cc
00
=
.
(8.43)
Åñëè ïðèíÿòü h0 = hON, τ0 ≈τON, òî ïåðâîå óðàâíåíèå ñèñòåìû
(5.93) ïðèìåò âèä
xV
c
c
ON
=
τ
τ
θ
τ
0
10
0
Φ (,,)
.
(8.44)
Ïðèíèìàÿ â ïîñëåäíåì ðàâåíñòâå θ0 íåèçìåííûì è äèôôåðåíöèðóÿ
ïîî÷åðåäíî ïî V0 è τ0, ïîëó÷èì ïîñëå ïðåîáðàçîâàíèé
∂
∂ττ
∂
∂
x
xV
x
V
c
c
c
00
0
0
11
2
=−
⎛
⎝⎜
⎞
⎠⎟.
(8.45)
Èç (8.43) è (8.45) âèäíî, ÷òî ïîïðàâî÷íûå êîýôôèöèåíòû,
ó÷èòûâàþùèå âëèÿíèå íà äàëüíîñòü ñòðåëüáû îòêëîíåíèÿ
áàðîìåòðè÷åñêîãî äàâëåíèÿ è òåìïåðàòóðû âîçäóõà â òî÷êå áðîñàíèÿ
(è äàëåå ïî òðàåêòîðèè) îò äàííûõ íîðìàëüíîé àòìîñôåðû, ìîãóò
áûòü âûðàæåíû ÷åðåç îñíîâíûå ïîïðàâî÷íûå êîýôôèöèåíòû íà
îòêëîíåíèÿ áàëëèñòè÷åñêîãî êîýôôèöèåíòà è íà÷àëüíîé ñêîðîñòè.
8.2.5. ÀÍÀËÈÒÈ×ÅÑÊÈÅ ÌÅÒÎÄÛ ÏÎËÓ×ÅÍÈß ÁÀËËÈÑÒÈ×ÅÑÊÈÕ
ÏÐÎÈÇÂÎÄÍÛÕ
Àíàëèòè÷åñêèå ìåòîäû ìîãóò ïðèìåíÿòüñÿ â ñëó÷àå, êîãäà îñíîâ-
íàÿ èññëåäóåìàÿ âåëè÷èíà îïðåäåëÿåòñÿ ôóíêöèåé, äîïóñêàþùåé
ïîëó÷åíèå ïðîèçâîäíûõ â àíàëèòè÷åñêîì âèäå. Ìåòîä èñïîëüçóåòñÿ
ïðè èññëåäîâàíèè òðàåêòîðèé ñíàðÿäîâ ïîñòîÿííîé ìàññû. Åñëè
ïðåäïîëîæèòü, ÷òî ýëëèïòè÷åñêàÿ òðàåêòîðèÿ ñèììåòðè÷íà è íà÷è-
íàåòñÿ ó ïîâåðõíîñòè ñôåðè÷åñêîé ìîäåëè Çåìëè ïðè íà÷àëüíûõ
385
çíà÷åíèÿõ ñêîðîñòè V0 è óãëà áðîñàíèÿ θ0, òî èçìåíåíèå ëèíåéíîé
êðóãîâîé äàëüíîñòè ñ ó÷åòîì òîëüêî ëèíåéíûõ ÷ëåíîâ ðàçëîæåíèÿ
èìååò âèä
δ
∂
∂
δ
∂
∂θ
δθ
L
L
V
V
L
=+
0
0
0
0.
(8.46)
Áàëëèñòè÷åñêèå ïðîèçâîäíûå, ïîëó÷åííûå äèôôåðåíöèðîâàíèåì
ðàçâåðíóòîãî óðàâíåíèÿ ýëëèïòè÷åñêîé òðàåêòîðèè, çàïèøóòñÿ â
ôîðìå
∂
∂
ψθψ
L
V
R
V
00
0
22 12
=+
−
Ç
ctg
[sin
( cos )],
(8.47)
ãäå 2ψ – óãëîâàÿ äàëüíîñòü;
∂
∂θ
θψ
θ
L
R
=
+
−
⎡
⎣⎢
⎤
⎦⎥
2
2
1
0
Ç
0
sin2(
)
sin
.
(8.48)
Íà ðèñ. 8.5 äàíû ãðàôèêè ∂L/∂V0 = fV 0 0
()
θ ïðè ðàçëè÷íûõ ψ.
Èç ãðàôèêîâ âèäíî, ÷òî âî âñåõ ñëó÷àÿõ áàëëèñòè÷åñêàÿ ïðîèç-
âîäíàÿ ∂L/∂V0 èìååò ïîëîæèòåëüíîå çíà÷åíèå. Ïðè ôèêñèðîâàííîé
óãëîâîé äàëüíîñòè ñòðåëüáû îíà óìåíüøàåòñÿ ñ óâåëè÷åíèåì óãëà
íàêëîíà òðàåêòîðèè â íà÷àëå ïàññèâíîãî ýëëèïòè÷åñêîãî ó÷àñòêà.
386
Ðèñ. 8 .5. Ãðàôèêè èçìåíåíèÿ áàë-
ëèñòè÷åñêèõ ïðîèçâîäíûõ ∂L/∂V0
â ôóíêöèè óãëà áðîñàíèÿ θí = θ0
ïðè ðàçëè÷íûõ çíà÷åíèÿõ óãëîâîé
äàëüíîñòè 2ψ
Çàâèñèìîñòü ∂L/∂θ0 = fθ0(θ0) ïðèâåäåíà íà ðèñ. 8 .6 . Ñ óâåëè÷åíèåì
óãëà áðîñàíèÿ áàëëèñòè÷åñêàÿ ïðîèçâîäíàÿ ∂L/∂θ0 óìåíüøàåòñÿ, ïå-
ðåõîäÿ îò ïîëîæèòåëüíûõ çíà÷åíèé ê îòðèöàòåëüíûì. Íóëåâîå çíà-
÷åíèå ïðîèçâîäíûõ ñîîòâåòñòâóåò îïòèìàëüíûì óãëàì íàêëîíà òðà-
åêòîðèè â íà÷àëå ïàññèâíîãî ó÷àñòêà. Ïðè çàäàííîé äàëüíîñòè ïî-
ëåòà íóëåâîå çíà÷åíèå ïðîèçâîäíîé îòâå÷àåò òðàåêòîðèè,
ïîëó÷åííîé ïðè ìèíèìàëüíîé íà÷àëüíîé ñêîðîñòè V0.
Àíàëèòè÷åñêèé ìåòîä îòûñêàíèÿ ïîïðàâî÷íûõ êîýôôèöèåíòîâ
ìîæåò áûòü òàêæå èñïîëüçîâàí ïðè ðåøåíèè ðàçëè÷íûõ ïðèáëèæåí-
íûõ çàäà÷ âíåøíåé áàëëèñòèêè ñíàðÿäîâ ïîñòîÿííîé ìàññû, äâèæó-
ùèõñÿ â ïëîòíûõ ñëîÿõ àòìîñôåðû, íàïðèìåð ïðè ðåøåíèè çàäà÷ ìå-
òîäîì ïñåâäîñêîðîñòè [22, 130]. Àíàëèòè÷åñêèé ìåòîä èíîãäà ïðè-
ìåíÿþò äëÿ îïðåäåëåíèÿ áàëëèñòè÷åñêèõ ïðîèçâîäíûõ è áîëåå
âûñîêèõ ïîðÿäêîâ, ÷åì ïåðâûé.  ðàìêàõ ïàðàáîëè÷åñêîé òåîðèè
ðàñ÷åòà òðàåêòîðèé áàëëèñòè÷åñêèå ïðîèçâîäíûå, õàðàêòåðèçóþùèå
ãëàâíóþ ÷àñòü èçìåíåíèÿ äàëüíîñòè, âû÷èñëÿþòñÿ ïî ôîðìóëàì
(8.6). Óòî÷íåíèå ýòîãî èçìåíåíèÿ îïðåäåëÿþò òðè ïîñëåäíèõ ñëàãàå-
ìûõ ôîðìóëû (8.4), êîòîðûå ïîëó÷åíû ñ ó÷åòîì âòîðûõ ïðîèçâîä-
íûõ:
∂
∂
θ∂
∂θ
θ∂
∂∂θ
2
0
2
0
2
0
2
0
2
0
2
00
2
2
4
2
x
Vg
xV
g
x
V
cc
c
==
−
sin
;
sin
;
=4
2
00
V
g
cos
.
θ
(8.49)
Íà îñíîâå ýëëèïòè÷åñêîé òåîðèè ìîãóò áûòü ïîëó÷åíû òàêæå
ïðîèçâîäíûå ∂∂
22
LV
/,
í
∂∂
θ
22
L/,
í
∂∂∂
θ
2
LV
/ ííè äð.
387
Ðèñ. 8 .6 . Ãðàôèêè èçìåíåíèÿ
áàëëèñòè÷åñêèõ ïðîèçâîäíûõ
∂L/∂V0 â ôóíêöèè óãëà áðîñà-
íèÿ θí = θ0 ïðè ðàçëè÷íûõ
çíà÷åíèÿõ óãëîâîé äàëüíî-
ñòè 2ψ
Îäíàêî ìàòåìàòè÷åñêèå ñëîæíîñòè ïîëó÷åíèÿ âòîðûõ ïðîèçâîä-
íûõ (ïðè áîëåå ñëîæíûõ ìîäåëÿõ äâèæåíèÿ), ìàëîñòü âåëè÷èí δV í
2
,
δθí
2
,δδ
θ
V ííè êàê ñëåäñòâèå íåçíà÷èòåëüíîñòü óòî÷íåíèÿ, äàâàåìîãî
ýòèìè ÷ëåíàìè, ïðèâîäÿò ê òîìó, ÷òî ïðè ïðàêòè÷åñêèõ ðàñ÷åòàõ èç-
ìåíåíèé ýëåìåíòîâ òðàåêòîðèé ó÷èòûâàþò îáû÷íî òîëüêî ëèíåé-
íûå ÷ëåíû ðàçëîæåíèÿ.
8.2.6 . ÒÀÁËÈ×ÍÛÅ ÌÅÒÎÄÛ ÐÀÑ×ÅÒÀ ÇÍÀ×ÅÍÈÉ ÏÎÏÐÀÂÎ×ÍÛÕ
ÊÎÝÔÔÈÖÈÅÍÒÎÂ
Ïîä òàáëè÷íûìè ìåòîäàìè áóäåì ïîíèìàòü ìåòîäû îïðåäåëåíèÿ
ïîïðàâî÷íûõ êîýôôèöèåíòîâ ñ ïîìîùüþ ðàçëè÷íîãî ðîäà çàðàíåå
âû÷èñëåííûõ òàáëèö. Ïðèìåíåíèå òàáëèö ïîëó÷èëî ðàñïðîñòðàíå-
íèå ïðè ðàñ÷åòå èçìåíåíèé ýëåìåíòîâ òðàåêòîðèé ñíàðÿäîâ ñòâîëü-
íîé àðòèëëåðèè. Äëÿ âû÷èñëåíèÿ ïîïðàâî÷íûõ êîýôôèöèåíòîâ ïî
ìåòîäó ðàçíîñòåé ìîãóò áûòü èñïîëüçîâàíû áàëëèñòè÷åñêèå ñáîðíè-
êè (áàëëèñòè÷åñêèå òàáëèöû) ëèáî òàáëèöû ïîïðàâî÷íûõ êîýôôè-
öèåíòîâ. Áîëüøèíñòâî áàëëèñòè÷åñêèõ ñáîðíèêîâ ñîäåðæèò ýëå-
ìåíòû õàðàêòåðíûõ òî÷åê òðàåêòîðèè äëÿ íîðìàëüíûõ ìåòåîðîëîãè-
÷åñêèõ óñëîâèé â çàâèñèìîñòè îò îïðåäåëÿþùèõ ïàðàìåòðîâ c, V0 è
θ0. Äëÿ çåíèòíûõ òðàåêòîðèé ê ÷èñëó îïðåäåëÿþùèõ ïàðàìåòðîâ îò-
íîñèòñÿ è âðåìÿ t.
Òàáëèöû ñîñòàâëåíû, êàê ïðàâèëî, ïðè ïîñòîÿííîì øàãå îïðåäå-
ëÿþùèõ ïàðàìåòðîâ, è ýòî ïîçâîëÿåò èñïîëüçîâàòü äëÿ ðàñ÷åòà ïî-
ïðàâî÷íûõ êîýôôèöèåíòîâ èçâåñòíóþ ôîðìóëó ÷èñëåííîãî äèô-
ôåðåíöèðîâàíèÿ
′=
−
+−
y
yy
h
x
nn
x
11
2
.
(8.50)
Íàïðèìåð, ïðèìåíèòåëüíî ê ïîëåâûì àðòèëëåðèéñêèì ñèñòåìàì,
ïîïåðåìåííî ïîäñòàâëÿÿ â ÷èñëèòåëü (8.50) äàëüíîñòü ñòðåëüáû,
âçÿòóþ â çàâèñèìîñòè îò èçìåíåíèÿ îïðåäåëÿþùåãî ïàðàìåòðà, à â
çíàìåíàòåëü – òàáëè÷íûé èíòåðâàë (øàã) îïðåäåëÿþùåãî ïàðàìåòðà,
ìîæíî ïîëó÷èòü ôîðìóëû îñíîâíûõ ïîïðàâî÷íûõ êîýôôèöèåíòîâ
äëÿ ðàñ÷åòà èçìåíåíèé äàëüíîñòè
∂
∂
x
c
xch xch
h
ccccc
c
=
+−−
()()
;
2
(8.51)
∂
∂
x
V
xVh
xVh
h
c
cV
cV
V
0
00
00
0
2
=
+−−
()()
;
(8.52)
∂
∂θ
θθ
θθ
θ
x
xhxh
h
c
cc
0
00
00
0
2
=
+−−
()()
.
(8.53)
388
Ïîñëåäíèé ïîïðàâî÷íûé êîýôôèöèåíò â ðÿäå ñëó÷àåâ íåîáõîäèìî
âû÷èñëÿòü ïðè çíà÷åíèè hθ 0
, âçÿòîì â ðàäèàíàõ.
Òàáëèöû ïîïðàâî÷íûõ êîýôôèöèåíòîâ ìîãóò áûòü âû÷èñëåíû
îäíèì èç îïèñàííûõ âûøå ñïîñîáîâ. Ïîñêîëüêó òðàåêòîðèÿ îïðåäå-
ëÿåòñÿ ïàðàìåòðàìè c, V0 è θ0, òî è òàáëèöû ïîïðàâî÷íûõ êîýôôè-
öèåíòîâ èìåþò òå æå âõîäû. Èçâåñòíû òàáëèöû ïîïðàâîê Àðòèëëå-
ðèéñêîé àêàäåìèè, ñîñòàâëåííûå íà îñíîâå ìåòîäà ÷èñëåííîãî èí-
òåãðèðîâàíèÿ äèôôåðåíöèàëüíûõ óðàâíåíèé ïîïðàâîê [21, ÷. III].
Ïðàêòè÷åñêàÿ ðàáîòà ïî òàáëèöàì ñâîäèòñÿ ê ëèíåéíîìó èíòåðïî-
ëèðîâàíèþ ïî çàäàííûì âõîäíûì çíà÷åíèÿì c, V0 è θ0.
8.2.7. ÏÎÍßÒÈÅ È ÌÅÒÎÄÛ ÎÏÐÅÄÅËÅÍÈß ÏÎËÍÛÕ
(ÈÇÎÔÓÍÊÖÈÎÍÀËÜÍÛÕ) ÎÒÊËÎÍÅÍÈÉ ÏÀÐÀÌÅÒÐÎÂ ÄÂÈÆÅÍÈß
Ïîñêîëüêó â óðàâíåíèÿõ ìàëûõ îòêëîíåíèé ïàðàìåòðîâ äâèæåíèÿ
ËÀ â êà÷åñòâå àðãóìåíòà íà àêòèâíîì ó÷àñòêå òðàåêòîðèè ïðèíèìàåòñÿ
âðåìÿ, îïðåäåëÿåìûå ðåøåíèåì ýòèõ óðàâíåíèé îòêëîíåíèÿ áóäóò ñî-
îòâåòñòâîâàòü êîíêðåòíûì ìîìåíòàì ïîëåòíîãî âðåìåíè. Îòêëîíåíèÿ
ïàðàìåòðîâ äâèæåíèÿ, îòíåñåííûå ê ôèêñèðîâàííûì ìîìåíòàì âðåìå-
íè, ïðèíÿòî íàçûâàòü èçîõðîííûìè ëèíåéíûìè îòêëîíåíèÿìè [36].
Âìåñòå ñ òåì ñëåäóåò èìåòü â âèäó, ÷òî ìíîãèå îïåðàöèè, ñâÿçàí-
íûå, íàïðèìåð, ñ "îáíóëåíèåì" òÿãè äâèãàòåëÿ óïðàâëÿåìûõ áàëëè-
ñòè÷åñêèõ ËÀ, âûïîëíÿþòñÿ â ïîëåòå íå ïî çàäàííîìó çíà÷åíèþ
âðåìåíè, à ïî äîñòèæåíèþ íåêîòîðîé óïðàâëÿþùåé ôóíêöèåé òðå-
áóåìîãî çíà÷åíèÿ [36].  ýòîì ñëó÷àå âðåìÿ, îòâå÷àþùåå äåéñòâè-
òåëüíîìó ìîìåíòó âûêëþ÷åíèÿ äâèãàòåëüíîé óñòàíîâêè, çà ñ÷åò
äåéñòâèÿ âîçìóùåíèé íå áóäåò ñîâïàäàòü ñ ðàñ÷åòíûì âðåìåíåì.
Ðàçíîñòü ìåæäó çíà÷åíèÿìè êàêîãî-ëèáî ïàðàìåòðà äâèæå-
íèÿ, âçÿòîãî â äåéñòâèòåëüíûé ìîìåíò îêîí÷àíèÿ àêòèâíîãî
ó÷àñòêà, è òðåáóåìûì íîìèíàëüíûì çíà÷åíèåì òîãî æå ïàðàìåò-
ðà, ñîîòâåòñòâóþùèì íîìèíàëüíîìó âðåìåíè, íàçûâàåòñÿ ïîë-
íûì èëè èçîôóíêöèîíàëüíûì îòêëîíåíèåì. Èçîôóíêöèîíàëüíûå
âàðèàöèè, òàê æå êàê è èçîõðîííûå âàðèàöèè, ïðåäñòàâëÿþò ñî-
áîé ìàëûå èçìåíåíèÿ ïàðàìåòðîâ äâèæåíèÿ ËÀ, íî óæå îáóñëîâ-
ëåííûå íå òîëüêî ïåðåõîäîì â ôèêñèðîâàííûé ìîìåíò âðåìåíè
îò òðåáóåìîé ê âîçìóùåííîé òðàåêòîðèè, íî è èçìåíåíèåì âðå-
ìåíè ïîëåòà ïî âîçìóùåííîé òðàåêòîðèè íà âåëè÷èíó δtê . Íåîá-
õîäèìîñòü îïðåäåëåíèÿ ïîïðàâêè íà ïîëåòíîå âðåìÿ äèêòóåòñÿ
òàêæå óñëîâèÿìè ðåãóëÿðíîãî (ïðàâèëüíîãî) ôóíêöèîíèðîâàíèÿ
ðàçëè÷íîãî ðîäà äèñòàíöèîííî âçâîäèìûõ óñòðîéñòâ, ðàçìåùàå-
ìûõ íà áîðòó ËÀ.
Çíà÷åíèÿ ïîëíûõ îòêëîíåíèé ïàðàìåòðîâ äâèæåíèÿ ËÀ îïðåäå-
ëÿþòñÿ íà îñíîâå òðåõ ñëåäóþùèõ ìåòîäîâ:
ìåòîäà èíòåãðèðîâàíèÿ óðàâíåíèÿ âîçìóùåííîãî äâèæåíèÿ ËÀ;
389
ìåòîäà, áàçèðóþùåãîñÿ íà èñïîëüçîâàíèè ñòåïåííûõ ðàçëîæå-
íèé çàâèñèìîñòåé ïàðàìåòðîâ äâèæåíèÿ ËÀ îò âîçìóùàþùèõ ôàê-
òîðîâ;
ìåòîäà ïåðåñ÷åòà èçîõðîííûõ îòêëîíåíèé â ïîëíûå.
Ïðè èñïîëüçîâàíèè ïåðâîãî ìåòîäà, òàê æå êàê è ïðè îïðåäåëå-
íèè èçîõðîííûõ îòêëîíåíèé, èñõîäíàÿ ñèñòåìà äèôôåðåíöèàëüíûõ
óðàâíåíèé äâèæåíèÿ, ñîäåðæàùàÿ âîçìóùàþùèå ôàêòîðû, èíòåãðè-
ðóåòñÿ ïî âðåìåíè. Íî ìîìåíò îêîí÷àíèÿ ïðîöåññà èíòåãðèðîâàíèÿ
âîçìóùåííîãî äâèæåíèÿ çàäàåòñÿ íå ïî íîìèíàëüíîìó çíà÷åíèþ
êîíöà àêòèâíîãî ó÷àñòêà, à ïî ìîìåíòó ôàêòè÷åñêîãî âûêëþ÷åíèÿ
äâèãàòåëÿ, îïðåäåëÿåìîìó, íàïðèìåð, òðåáóåìûì çíà÷åíèåì êàæó-
ùåéñÿ ñêîðîñòè, ðàññ÷èòàííûì äëÿ íîìèíàëüíîãî âðåìåíè êîíöà àê-
òèâíîãî ó÷àñòêà. Ýòî ïðèâîäèò ê íåîáõîäèìîñòè äîïîëíèòåëüíîãî
âû÷èñëåíèÿ íà êàæäîì øàãå ÷èñëåííîãî èíòåãðèðîâàíèÿ òåêóùåãî
çíà÷åíèÿ êàæóùåéñÿ ñêîðîñòè è ñðàâíåíèÿ åãî ñ çàäàííûì.  ìîìåíò
èõ ñîâïàäåíèÿ ðàñ÷åò âîçìóùåííîé òðàåêòîðèè çàêàí÷èâàåòñÿ. Ïîë-
íûå îòêëîíåíèÿ ïîëó÷àþòñÿ â ðåçóëüòàòå âû÷èòàíèÿ èç âû÷èñëåííûõ
çíà÷åíèé ïàðàìåòðîâ äâèæåíèÿ ËÀ èõ òðåáóåìûõ çíà÷åíèé.
Îñîáåííîñòüþ âòîðîãî ìåòîäà ÿâëÿåòñÿ òî, ÷òî îïðåäåëÿåìûå ïî
íåìó ïîëíûå îòêëîíåíèÿ çàïèñûâàþòñÿ â âèäå ñóììû ïàðíûõ ïðî-
èçâåäåíèé èçîôóíêöèîíàëüíûõ ÷àñòíûõ ïðîèçâîäíûõ íà îòêëîíå-
íèÿ âîçìóùàþùèõ ôàêòîðîâ. Ïðè ýòîì ÷àñòíûå ïðîèçâîäíûå îïðå-
äåëÿþòñÿ ñ ó÷åòîì âîçìîæíîãî èçìåíåíèÿ âðåìåíè îêîí÷àíèÿ àê-
òèâíîãî ó÷àñòêà.
Íàèáîëåå ïðîñòûì è íàèìåíåå òðóäîåìêèì ïðåäñòàâëÿåòñÿ òðå-
òèé ìåòîä. Íî åãî ïðèìåíåíèå òðåáóåò çíàíèÿ ñîîòâåòñòâóþùèõ
èçîõðîííûõ îòêëîíåíèé ïàðàìåòðîâ äâèæåíèÿ è âèäà óïðàâëÿþùåé
ôóíêöèè, ïî êîòîðîé îïðåäåëÿåòñÿ ìîìåíò îêîí÷àíèÿ àêòèâíîãî
ó÷àñòêà ïîëåòà ËÀ.
8.3 . Ó×ÅÒ ÂËÈßÍÈß ÏÀÐÀÌÅÒÐΠÀÒÌÎÑÔÅÐÛ
ÍÀ ÏÎËÅÒ ÐÀÊÅÒ È ÀÐÒÈËËÅÐÈÉÑÊÈÕ ÑÍÀÐßÄÎÂ
8.3.1. ÑÏÎÑÎÁÛ Ó×ÅÒÀ ÂËÈßÍÈß ÎÒÊËÎÍÅÍÈÉ ÌÅÒÅÎÔÀÊÒÎÐÎÂ
ÍÀ ÄÂÈÆÅÍÈÅ ËÀ
Òåîðåòè÷åñêèå èññëåäîâàíèÿ è ñòðåëüáû ïîäòâåðæäàþò ñóùåñò-
âåííîå âëèÿíèå îòêëîíåíèé ìåòåîôàêòîðîâ îò èõ íîðìàëüíûõ çíà-
÷åíèé íà ïîëåò ðàêåò è ñíàðÿäîâ. Èçìåíåíèå ìåòåîôàêòîðîâ ó÷èòû-
âàþò ïðè îïðåäåëåíèè õàðàêòåðèñòèê äâèæåíèÿ, ïðè ðàñ÷åòå ðàñ-
ñåèâàíèÿ òðàåêòîðèé è îïðåäåëåíèè òî÷íîñòè ñòðåëüáû, â ðàñ÷åòàõ
óñòîé÷èâîñòè äâèæåíèÿ ËÀ, à òàêæå â ïðî÷íîñòíûõ ðàñ÷åòàõ.
390
 áàëëèñòèêå âëèÿíèå îòêëîíåíèé ïàðàìåòðîâ àòìîñôåðû íà ïî-
ëåò ðàêåò è ñíàðÿäîâ ìîæåò áûòü ó÷òåíî òðåìÿ ñïîñîáàìè.
Ïåðâûé ñïîñîá – ðàñ÷åò èçìåíåíèé ýëåìåíòîâ òðàåêòîðèè ïî íå-
èçìåííûì îòêëîíåíèÿì äàâëåíèÿ, âëàæíîñòè è òåìïåðàòóðû îò
íîðìàëüíûõ â ïðåäïîëîæåíèè ñïðàâåäëèâîñòè ãèïîòåçû î âåðòè-
êàëüíîì ðàâíîâåñèè àòìîñôåðû è ñîõðàíåíèÿ õàðàêòåðà èçìåíåíèÿ
òåìïåðàòóðû ñ âûñîòîé ñîîòâåòñòâóþùåãî âèäà ôóíêöèè τ(y), ïðè-
íÿòîé â íîðìàëüíîé àòìîñôåðå. Ïðèìåð ïîëó÷åíèÿ ïîïðàâî÷íûõ
êîýôôèöèåíòîâ äëÿ äàëüíîñòè íà îòêëîíåíèå íàçåìíîãî áàðîìåò-
ðè÷åñêîãî äàâëåíèÿ è âèðòóàëüíîé òåìïåðàòóðû ðàññìîòðåí ðàíåå
(ôîðìóëû (8.34) è (8.45)).
Âòîðîé ñïîñîá çàêëþ÷àåòñÿ â îïðåäåëåíèè è èñïîëüçîâàíèè áàë-
ëèñòè÷åñêèõ ñðåäíèõ îòêëîíåíèé ìåòåîôàêòîðîâ – ñðåäíåãî, óñëîâ-
íî ïîñòîÿííîãî ïî âñåé òðàåêòîðèè îòêëîíåíèÿ âèðòóàëüíîé òåìïå-
ðàòóðû îò íîðìàëüíîãî çíà÷åíèÿ è óñëîâíî ïîñòîÿííîãî ñðåäíåãî
âåòðà. Ïåðâûé è âòîðîé ìåòîäû ïðèìåíÿþòñÿ ÷àùå âñåãî â ïðàêòè-
÷åñêîé ðàáîòå ïðè ïîäãîòîâêå è âåäåíèè ñòðåëüá.
Òåîðåòè÷åñêè áîëåå ñòðîãèì ÿâëÿåòñÿ òðåòèé ìåòîä, â ñîîòâåò-
ñòâèè ñ êîòîðûì â ñèñòåìû äèôôåðåíöèàëüíûõ óðàâíåíèé äâèæå-
íèÿ ââîäÿò óðàâíåíèÿ, íåïîñðåäñòâåííî îïðåäåëÿþùèå èçìåíåíèå
ìåòåîôàêòîðîâ â ôóíêöèè êàêîé-ëèáî êîîðäèíàòû (÷àùå âñåãî âû-
ñîòû) èëè â ôóíêöèè âðåìåíè. Ïðè ñòðîãîì ó÷åòå âëèÿíèÿ èçìåíå-
íèÿ ïàðàìåòðîâ àòìîñôåðû íà ïîëåò ðàêåò è àðòèëëåðèéñêèõ ñíàðÿ-
äîâ â ðàñ÷åòå äîëæíû èñïîëüçîâàòüñÿ êîíêðåòíûå (îïûòíûå) ôóíê-
öèè, ïîëó÷åííûå ïî ðåçóëüòàòàì çîíäèðîâàíèÿ àòìîñôåðû.
Ïðè ïðîãíîçèðîâàíèè èçìåíåíèÿ ìåòåîôàêòîðîâ èñïîëüçóþòñÿ
ñòàòèñòè÷åñêèå îáðàáîòêè ðåçóëüòàòîâ ìåòåîðîëîãè÷åñêèõ èññëåäî-
âàíèé. Ðåçóëüòàòû ñòàòèñòè÷åñêîé îáðàáîòêè ìîãóò ïðåäñòàâëÿòüñÿ
â âèäå ñëó÷àéíîãî ïîëÿ (ñëó÷àéíûõ ôóíêöèé ìíîãèõ ïåðåìåííûõ,
ñîñòàâëåííûõ ïî êîîðäèíàòàì è ïî âðåìåíè). Ñòàòèñòè÷åñêàÿ îáðà-
áîòêà ïî êîîðäèíàòàì ïðèìåíÿåòñÿ îáû÷íî â áàëëèñòè÷åñêèõ ðàñ÷å-
òàõ, ñòàòèñòè÷åñêàÿ îáðàáîòêà ïî âðåìåíè – ïðåèìóùåñòâåííî ïðè
óñòàíîâëåíèè âåòðîâîé íàãðóçêè íà ËÀ â ðàñ÷åòàõ íà ïðî÷íîñòü, â
ðàñ÷åòàõ óñòîé÷èâîñòè äâèæåíèÿ è äèíàìèêè ïîëåòà â íåñïîêîéíîé
àòìîñôåðå.
8.3.2 . Ó×ÅÒ ÈÇÌÅÍÅÍÈß ÁÀÐÎÌÅÒÐÈ×ÅÑÊÎÃÎ ÄÀÂËÅÍÈß
È ÒÅÌÏÅÐÀÒÓÐÛ
Èçìåíåíèå áàðîìåòðè÷åñêîãî äàâëåíèÿ è òåìïåðàòóðû ïî âûñîòå
äëÿ íîðìàëüíîé àòìîñôåðû ðàññìîòðåíî â ãë. 1 . Ïðè æåëàíèè
ó÷åñòü â áàëëèñòè÷åñêèõ ðàñ÷åòàõ êîíêðåòíóþ ðåàëèçàöèþ, îïûò-
íóþ èëè ðàñ÷åòíóþ, íåîáõîäèìî èìåòü äàííûå îá èçìåíåíèè áàðî-
ìåòðè÷åñêîãî äàâëåíèÿ, âëàæíîñòè è òåìïåðàòóðû âîçäóõà ïî âûñî-
391
òå, ïðåäñòàâëåííûå â âèäå ôîðìóë, òàáëèö èëè ãðàôèêîâ. Âëàæíîñòü
âîçäóõà ëåãêî ó÷èòûâàåòñÿ ÷åðåç âèðòóàëüíóþ òåìïåðàòóðó ïî ôîð-
ìóëå (1.83). Äàâëåíèå è òåìïåðàòóðà ââîäÿòñÿ â ðàñ÷åò ïî ôîðìóëàì
äëÿ ïëîòíîñòè âîçäóõà, íàïðèìåð ïî (1.85); òåìïåðàòóðà ó÷èòûâàåò-
ñÿ òàêæå è â ôîðìóëå äëÿ ñêîðîñòè çâóêà. Ïðè èñïîëüçîâàíèè ãðà-
ôèêà cx a
(),
M ñîñòàâëåííîãî äëÿ íàçåìíûõ íîðìàëüíûõ óñëîâèé,
âëèÿíèå èçìåíåíèÿ ñêîðîñòè çâóêà ïî âûñîòå íà ëîáîâîå ñîïðîòèâ-
ëåíèå ìîæíî ó÷èòûâàòü ñ ïîìîùüþ ôîðìóëû (1.141). Èçìåíåíèå
òÿãè ïî âûñîòå äîëæíî áûòü âû÷èñëåíî äëÿ êîíêðåòíîé ìåòåîðîëî-
ãè÷åñêîé ðåàëèçàöèè ïî îáùåìó óðàâíåíèþ (1.148).
Î÷åâèäíî, êàæäàÿ ðåàëèçàöèÿ èçìåíåííûõ ìåòåîðîëîãè÷åñêèõ
ýëåìåíòîâ ïî âûñîòå òðåáóåò ñàìîñòîÿòåëüíîãî ðåøåíèÿ âûáðàííîé
ñèñòåìû óðàâíåíèé.
8.3.3. ÓÐÀÂÍÅÍÈß ÄÂÈÆÅÍÈß ÑÍÀÐßÄÀ ÏÎÑÒÎßÍÍÎÉ ÌÀÑÑÛ
ÏÐÈ Ó×ÅÒÅ ÈÇÌÅÍÅÍÈß ÁÀÐÎÌÅÒÐÈ×ÅÑÊÎÃÎ ÄÀÂËÅÍÈß
È ÒÅÌÏÅÐÀÒÓÐÛ
Ïðè îïðåäåëåíèè ëîáîâîãî ñîïðîòèâëåíèÿ âîçäóõà ñ ïîìîùüþ
êîýôôèöèåíòà cx a
()
M ó÷åò èçìåíåíèÿ äàâëåíèÿ è òåìïåðàòóðû ïðî-
âîäèòñÿ òàê æå, êàê îïèñàíî â ïðåäûäóùåì ïîäðàçäåëå äëÿ ñíàðÿäîâ
ïåðåìåííîé ìàññû. Åñëè äëÿ îïðåäåëåíèÿ ëîáîâîãî ñîïðîòèâëåíèÿ
âîñïîëüçîâàòüñÿ âåëè÷èíîé E èç ôîðìóëû (3.126), òî ñèñòåìà äèô-
ôåðåíöèàëüíûõ óðàâíåíèé, îïèñûâàþùàÿ äâèæåíèå ñíàðÿäà ïîñòî-
ÿííîé ìàññû ñ ó÷åòîì èçìåíåíèÿ äàâëåíèÿ è òåìïåðàòóðû, ìîæåò
áûòü ïðèâåäåíà ê îáùåìó âèäó óðàâíåíèé (8.14). Âîçüìåì èçìåíåí-
íóþ âåëè÷èíó (Å + δE), òîãäà áóäåì èìåòü
•••
•
;
xE
x
E
E
Ex
=−
−
δ
(8.54)
•
••
•
.
yE
yg
E
E
Ey
=−
−
−
δ
(8.55)
 ñîîòâåòñòâèè ñ (3.126) ìîæíî ïðåäñòàâèòü E = f(c, h, τ) è ïîëó-
÷èòü [22]
δδδ
δ
τ
τ
τ
E
E
c
c
h
h
fV
=+−
+
().
1
2
(8.56)
Âåëè÷èíà f(Vτ) îïðåäåëÿåòñÿ ïî ôîðìóëå (8.25).
Ïðè èçìåíåíèè òîëüêî áàëëèñòè÷åñêîãî êîýôôèöèåíòà â ñîîò-
âåòñòâèè ñ (8.54)...(8.56) ïîëó÷èì ñëåäóþùóþ ñèñòåìó äèôôåðåíöè-
àëüíûõ óðàâíåíèé:
392
•••
•
;
xE
x
c
c
Ex
=−
−
δ
(8.57)
•••
•
.
yE
yg
c
c
Ey
=−
−
−
δ
(8.58)
Ïðè ïîñòîÿííîì áàëëèñòè÷åñêîì êîýôôèöèåíòå
•
••
() •;
•
••
xE
x
h
h
fV
Ex
yE
yg
h
h
f
=−
−
−
+
⎛
⎝⎜
⎞
⎠⎟
=−
−
−
−
δδ
τ
τ
δ
τ
1
2
()
•
.
V
Ey
τ
δτ
τ
+
⎛
⎝⎜
⎞
⎠⎟
1
2
(8.59)
Ïîñëå èíòåãðèðîâàíèÿ ìîãóò áûòü ïîëó÷åíû õàðàêòåðèñòèêè
äâèæåíèÿ ñíàðÿäà ïîñòîÿííîé ìàññû ïðè îòêëîíåíèÿõ äàâëåíèÿ δh
è âèðòóàëüíîé òåìïåðàòóðû δτ îò âåëè÷èí, îïðåäåëÿåìûõ ñòàíäàðò-
íîé àòìîñôåðîé. Åñëè âîñïîëüçîâàòüñÿ ãèïîòåçîé î âåðòèêàëüíîì
ðàâíîâåñèè àòìîñôåðû, òî èçìåíåííûå õàðàêòåðèñòèêè äâèæåíèÿ
ìîãóò áûòü ïîëó÷åíû â çàâèñèìîñòè îò íàçåìíîãî äàâëåíèÿ è ôóíê-
öèè èçìåíåíèÿ òåìïåðàòóðû ñ âûñîòîé [22].
Ëîãàðèôìèðóÿ è äèôôåðåíöèðóÿ óðàâíåíèå äëÿ h (áàðîìåòðè÷å-
ñêóþ ôóíêöèþ π(y)) è ïåðåõîäÿ îò áåñêîíå÷íî ìàëûõ ê êîíå÷íûì
ïðèðàùåíèÿì, ïîëó÷èì
δ∂
δ
τ
h
h
h
hR
dy
y
=−
⎛
⎝⎜⎞
⎠⎟
∫
0
0
0
1
.
Äèôôåðåíöèðóÿ âòîðîå ñëàãàåìîå ïî τ, áóäåì èìåòü
δ∂
τ
τ
h
h
h
hR
d
dy
y
=+∫
0
0
2
0
1
.
(8.60)
Ââîäÿ çàìåíó â (8.59), ïîëó÷èì
•
••
() •;
•
•
xE
x
h
hR
d
dy
fV
Ex
y
=−
−
+
−
+
⎛
⎝⎜
⎞
⎠⎟
∫
∂τ
τ
δτ
τ
τ
0
0
2
0
11
2
yE
yg
h
hR
d
dy
fV
Ey
y
=−
−
−
+
−
+
⎛
⎝⎜
⎞
⎠⎟
∫
•
()
•
.
∂τ
τ
δτ
τ
τ
0
0
2
0
11
2
(8.61)
393
Ïîñëåäíÿÿ ñèñòåìà óðàâíåíèé íå òðåáóåò äëÿ ñâîåãî ðåøåíèÿ
çíàíèÿ ôóíêöèè èçìåíåíèÿ áàðîìåòðè÷åñêîãî äàâëåíèÿ ñ âûñîòîé
è óäîáíà äëÿ òåîðåòè÷åñêèõ èññëåäîâàíèé.
8.3 .4. Ó×ÅÒ ÂËÈßÍÈß ÂÅÒÐÀ ÍÀ ÏÎËÅÒ ÍÅÓÏÐÀÂËßÅÌÛÕ ÐÀÊÅÒ
È ÀÐÒÈËËÅÐÈÉÑÊÈÕ ÑÍÀÐßÄÎÂ
Îñíîâíûìè çàäà÷àìè ïðè èçó÷åíèè äåéñòâèÿ âåòðà íà ïîëåò ðà-
êåò è àðòèëëåðèéñêèõ ñíàðÿäîâ ÿâëÿþòñÿ çàäà÷è, ñâÿçàííûå ñ óñòà-
íîâëåíèåì ìåõàíèçìà íåïîñðåäñòâåííîãî äåéñòâèÿ âåòðà íà äâèæó-
ùèéñÿ ËÀ, ïîëó÷åíèåì ðàñ÷åòíûõ ñõåì äâèæåíèÿ ìàññ âîçäóõà è äî-
êàçàòåëüñòâîì ïðàâîìåðíîñòè ïðèíÿòîé ñõåìû ïðè ðåøåíèè òîé
èëè èíîé çàäà÷è.
Ïåðåìåùåíèÿ âîçäóøíûõ ìàññ, ïðîèñõîäÿùèå â àòìîñôåðå, ïðè-
íÿòî íàçûâàòü âåòðîì.
Âåòåð ÿâëÿåòñÿ âåëè÷èíîé âåêòîðíîé. Êàê âåêòîðíàÿ âåëè÷èíà
îí õàðàêòåðèçóåòñÿ íàïðàâëåíèåì è ñêîðîñòüþ. Íàïðàâëåíèå âåòðà –
àçèìóò òî÷êè ãîðèçîíòà ÀW, îòêóäà äóåò âåòåð, – èçìåðÿåòñÿ â ãðàäó-
ñàõ. Ñêîðîñòü âåòðà W èçìåðÿåòñÿ â ìåòðàõ â ñåêóíäó. Âåêòîð ñêîðî-
ñòè âåòðà îáû÷íî ïðåäñòàâëÿþò ÷åðåç åãî ñîñòàâëÿþùèå Wx, Wy è
Wz. Ñêîðîñòè âîñõîäÿùèõ è íèñõîäÿùèõ ïîòîêîâ â áîëüøèíñòâå
ñëó÷àåâ íåâåëèêè. Îíè íà ïîðÿäîê, à èíîãäà è íà äâà ìåíüøå ãîðè-
çîíòàëüíûõ ïîòîêîâ. Ýòî äàåò îñíîâàíèå ïðè ïîäãîòîâêå äàííûõ
äëÿ ñòðåëüáû ïðèíÿòü îïðàâäàííîå äîïóùåíèå, ÷òî èçìåíåíèå ñêî-
ðîñòè âåòðà ïî âûñîòå îñòàåòñÿ ïîñòîÿííûì â ïðåäåëàõ âñåé ðàñ-
ñìàòðèâàåìîé òðàåêòîðèè.
Õàîòè÷åñêîå (íåóïîðÿäî÷åííîå, òóðáóëåíòíîå) äâèæåíèå âîçäóõà
íàêëàäûâàåòñÿ íà îòíîñèòåëüíî ñïîêîéíîå ãîðèçîíòàëüíîå ïåðåìå-
ùåíèå âîçäóøíûõ ìàññ (ðèñ. 8 .7). Ýòî ïðèâîäèò ê íåóñòîé÷èâîñòè
394
Ðèñ. 8 .7 . Âàðèàöèè ñêîðîñòè âåòðà â ãîðèçîíòàëüíîì íàïðàâëåíèè
(èçìåí÷èâîñòè) âåòðà, îñîáåííî ðåçêî ïðîÿâëÿþùåéñÿ âáëèçè ïî-
âåðõíîñòè çåìëè. Ïðèíÿòî ðàçëè÷àòü äèíàìè÷åñêóþ è òåðìè÷åñêóþ
òóðáóëåíòíîñòè. Äèíàìè÷åñêàÿ òóðáóëåíòíîñòü â ðàâíèííûõ óñëîâè-
ÿõ ðàñïðîñòðàíÿåòñÿ îáû÷íî äî âûñîò 1000...15000 ì, à íàä ìîðåì åå
ãðàíèöû åùå íèæå. Èíòåíñèâíîñòü òóðáóëåíòíîñòè çàâèñèò ãëàâ-
íûì îáðàçîì îò ñêîðîñòè âåòðà, øåðîõîâàòîñòè ïîâåðõíîñòè è óñ-
òîé÷èâîñòè ïåðåìåùåíèÿ âîçäóøíûõ ìàññ. Îíà ñèëüíåå íàä ïåðåñå-
÷åííîé ìåñòíîñòüþ è ñëàáåå íàä ðàâíèíîé è ìîðåì. Òåðìè÷åñêàÿ
òóðáóëåíòíîñòü ìîæåò ðàñïðîñòðàíÿòüñÿ äî äîñòàòî÷íî áîëüøèõ âû-
ñîò, îñîáåííî â óñëîâèÿõ íåóñòîé÷èâîñòè äâèæåíèÿ çíà÷èòåëüíûõ
ïî îáúåìó ìàññ âîçäóõà è îáðàçîâàíèÿ êó÷åâûõ îáëàêîâ. Åå èíòåí-
ñèâíîñòü çàâèñèò îò âûñîòû ñòîÿíèÿ Ñîëíöà, âðåìåíè ãîäà, õàðàêòå-
ðà ïîäñòèëàþùåé ïîâåðõíîñòè, âëàæíîñòè ñðåäû è ò.ä .
Ïðè íåîáõîäèìîñòè ó÷åòà íåñêîëüêèõ (íå ìåíåå äâóõ) ñîñòàâëÿþ-
ùèõ âåêòîðà W åãî àðãóìåíòû (êîîðäèíàòû è âðåìÿ) äàþò îñíîâàíèå
ðàññìàòðèâàòü âîçäóøíóþ ñðåäó, â êîòîðîé ïðîèñõîäèò ïîëåò, êàê
âåêòîðíîå (â îáùåì ñëó÷àå ïðîñòðàíñòâåííî-âðåìåííîå) ïîëå. Âðå-
ìåííàÿ ñîñòàâëÿþùàÿ äîëæíà ó÷èòûâàòüñÿ ãëàâíûì îáðàçîì ïðèìå-
íèòåëüíî ê âîçìóùåííîìó äâèæåíèþ ìàëîñêîðîñòíûõ ËÀ. Äëÿ
áîëüøèíñòâà îáúåêòîâ äîïóñòèìî ïîëàãàòü, ÷òî âåêòîðíîå ïðî-
ñòðàíñòâåííîå ïîëå òóðáóëåíòíîñòè ÿâëÿåòñÿ èçîòðîïíûì â ïðåäå-
ëàõ òîé îáëàñòè ïðîñòðàíñòâà, â êîòîðîé èññëåäóåòñÿ äâèæåíèå ðà-
êåò è ñíàðÿäîâ.
Âåòåð è òóðáóëåíòíîñòü – ñëó÷àéíûå ôàêòîðû, è ïðè àíàëèçå
äâèæåíèÿ ËÀ îíè äîëæíû ó÷èòûâàòüñÿ ñòàòèñòè÷åñêè, ÷òî è áóäåò
ñäåëàíî â ãë. 10. Çäåñü æå îãðàíè÷èìñÿ äåòåðìèíèðîâàííîé ïîñòà-
íîâêîé, ïðèíèìàÿ, ÷òî âåêòîð ñêîðîñòè âåòðà
WWW
() () (),
yyy
=+
0ò
(8.62)
îòðàæàþùèé ñóììàðíîå ïåðåìåùåíèå âîçäóøíûõ ìàññ, íå ÿâëÿåòñÿ
ñëó÷àéíûì.  âûðàæåíèè (8.62) W0(y) – ïîñòîÿííàÿ ñîñòàâëÿþùàÿ
âåòðà íà âûñîòå y – õàðàêòåðèçóåò ñïëîøíîå ðàâíîìåðíîå ïåðå-
ìåùåíèå ìàññ âîçäóõà; Wò(y) – òóðáóëåíòíàÿ ñîñòàâëÿþùàÿ âåòðà íà
âûñîòå y.
Îñîáåííîñòü äâèæåíèÿ ËÀ â ïåðåìåùàþùåéñÿ àòìîñôåðå çà-
êëþ÷àåòñÿ â òîì, ÷òî åãî ñêîðîñòü îòíîñèòåëüíî Çåìëè è îòíîñè-
òåëüíî äâèæóùèõñÿ ìàññ âîçäóõà ðàçëè÷íà. Ñêîðîñòü ËÀ (ñàìîëå-
òà, ðàêåòû, ñíàðÿäà) îòíîñèòåëüíî Çåìëè ïðèíÿòî íàçûâàòü çåì-
íîé ñêîðîñòüþ, ñêîðîñòü îòíîñèòåëüíî àòìîñôåðû – âîçäóøíîé.
Åñëè çåìíóþ ñêîðîñòü ñíàðÿäà (àáñîëþòíóþ) îáîçíà÷èòü âåêòîðîì
Vê, ñêîðîñòü äâèæåíèÿ àòìîñôåðû îòíîñèòåëüíî Çåìëè (ñêîðîñòü
ïåðåíîñíîãî äâèæåíèÿ – ñêîðîñòü âåòðà) – âåêòîðîì W è âîç-
äóøíóþ ñêîðîñòü ñíàðÿäà (îòíîñèòåëüíóþ) – âåêòîðîì V,ò
î
395
VVW
ê=+
(8.63)
è ñêîðîñòü ñíàðÿäà â äâèæåíèè îòíîñèòåëüíî àòìîñôåðû áóäåò ðàâíà
VVW
=−
ê
.
(8.64)
 ïðîåêöèÿõ íà îñè íîðìàëüíîé ñèñòåìû êîîðäèíàò OXgYgZg
âåêòîðíîå ðàâåíñòâî (8.64) áóäåò èìåòü âèä
V
V
V
VW
VW
VW
x
y
z
xx
yy
zz
g
g
g
gg
gg
gg
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
=
−
−
−
⎡
⎣
⎢
⎢
ê
ê
ê
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
.
(8.65)
Ïðè ïîñòîÿííîì âåòðå èç ïîñëåäíåãî ðàâåíñòâà è ðèñ. 8.8 ïîëó÷èì
VVWVWVW
xx
yy zz
gg
gg
gg
=−
+−+
−
()
()
()
.
êêê
222
(8.66)
Ïðè ó÷åòå òîëüêî ãîðèçîíòàëüíûõ ñîñòàâëÿþùèõ âåòðà
VVWVVW
xx yzz
gg ggg
=−
+
+−
()()
.
êê
ê
22
(8.67)
Íà ðèñ. 8.8 u è uê îáîçíà÷àþò ïðîåêöèè âîçäóøíîé è çåìíîé
ñêîðîñòè ñíàðÿäà íà ãîðèçîíòàëüíóþ ïëîñêîñòü OXgZg. Ïîëüçóÿñü
ðèñ. 8.8, ðàñêðîåì çíà÷åíèÿ ñëàãàåìûõ â ðàâåíñòâå (8.65):
396
Ðèñ. 8.8 . Ñõåìà
âçàèìíîãî ðàñïî-
ëîæåíèÿ âåêòîðîâ
çåìíîé ñêîðîñòè
Vê è ñêîðîñòè âåò-
ðàW
VVW
VVW
V
x
y
g
g
cos cos
cos cos
;
sin
sin
;
cos
θψ
θ
θθ
aa
ê
aê
=−
=−
−
Ψ
θψ
θ
aaê
sin
cos sin
=−
−
VW
zg
Ψ
(8.68)
è íàéäåì ìîäóëü âîçäóøíîé ñêîðîñòè
VV
WVW
VW
xy
z
gg
=−
+
−
+
++
[( cos cos
)(sin
)
(coss
i
n
êê
ê
θθ
θ
Ψ
Ψ
22
g
)].
/
212
(8.69)
Ñîîòâåòñòâåííî
sin
sin
;
cos sin
cos cos
θ
θ
ψ
θ
θ
a
ê
a
ê
ê
tg
=
−
=
+
−
VW
V
VW
VW
yz
x
gg
Ψ
Ψ
g
.
(8.70)
Ìåõàíèçì âîçäåéñòâèÿ âåòðà íà äâèæåíèå ËÀ â îáùåì ñëó÷àå ðå-
øåíèÿ ïðîñòðàíñòâåííîé çàäà÷è ñ ó÷åòîì óãëîâ àòàêè è ñêîëüæå-
íèÿ, îïðåäåëÿåìûõ ïî îòíîøåíèþ ê âîçäóøíîé ñêîðîñòè, âåñüìà
ñëîæåí. Ïîýòîìó â ïðàêòè÷å-
ñêîé ðàáîòå ÷àñòî ðàññìàòðè-
âàþò äåéñòâèå ïðîäîëüíîãî è
áîêîâîãî âåòðà îòäåëüíî.
Ïðè îïðåäåëåíèè íàïðàâ-
ëåíèÿ áîêîâîãî äâèæåíèÿ ðà-
êåòû íà àêòèâíîì ó÷àñòêå òðà-
åêòîðèè èìååò çíà÷åíèå âçà-
èìíîå ðàñïîëîæåíèå öåíòðà
ìàññ è öåíòðà äàâëåíèÿ ðàêå-
òû. Âîçäåéñòâèå áîêîâîãî âåò-
ðà Wz íà ðàêåòó ñîçäàåò äîïîë-
íèòåëüíóþ àýðîäèíàìè÷åñêóþ
ñèëó Râ, ïðèëîæåííóþ â öåí-
òðå äàâëåíèÿ (ðèñ. 8.9). Ó îïå-
ðåííîé ñòàòè÷åñêè óñòîé÷è-
âîé ðàêåòû öåíòð äàâëåíèÿ
ðàñïîëîæåí çà öåíòðîì ìàññ,
áëèæå ê îïåðåíèþ, ïîýòîìó
ïîä äåéñòâèåì ìîìåíòà îò
ñèëû Râ ðàêåòà ïîâåðíåòñÿ ãî-
ëîâíîé ÷àñòüþ íàâñòðå÷ó âåò-
ðó òàê, ÷òî åå ïðîäîëüíàÿ îñü
ñîâïàäåò ñ âåêòîðîì âîçäóø-
397
Ðèñ. 8 .9 . Ñõåìà ïîâîðîòà íåóïðàâëÿåìîé ðà-
êåòû ïðîòèâ âåòðà ("ýôôåêò ôëþãåðà")
íîé ñêîðîñòè. Ïðè ýòîì ïîÿâèòñÿ áîêîâàÿ ñîñòàâëÿþùàÿ òÿãè Ðá,
íàïðàâëåííàÿ ïðîòèâ âåòðà, è ïðè Ðá > Râ ðàêåòà áóäåò ïåðåìåùàòü-
ñÿ òàêæå ïðîòèâ âåòðà. Òóðáîðåàêòèâíûå ñíàðÿäû â ðåçóëüòàòå äåðè-
âàöèè, êîìïëåêñíîãî äåéñòâèÿ ñèëû Ìàãíóñà è áîêîâîãî âåòðà ìî-
ãóò ïåðåìåùàòüñÿ íà àêòèâíîì ó÷àñòêå òðàåêòîðèè â íàïðàâëåíèè
âåòðà. Íà ïàññèâíîì ó÷àñòêå òðàåêòîðèè ïðè Ð = 0 ðàêåòà òàê æå,
êàê è àðòèëëåðèéñêèé ñíàðÿä, áóäåò ïåðåìåùàòüñÿ â íàïðàâëåíèè
áîêîâîãî âåòðà. Íà ðèñ. 8.10 ïðåäñòàâëåíà ñõåìà áîêîâîãî äâèæåíèÿ
ïðîòèâ âåòðà ñòàòè÷åñêè óñòîé÷èâîé îïåðåííîé ðàêåòû íà àêòèâíîì
ó÷àñòêå òðàåêòîðèè ïðè äîïóùåíèè, ÷òî ðàêåòà áåçûíåðöèîííà.
Îáîçíà÷èì ãîðèçîíòàëüíóþ ïðîåêöèþ ñêîðîñòè öåíòðà ìàññ â ñòàð-
òîâîé ñèñòåìå êîîðäèíàò ÷åðåç uê = Vê cosθ, ãîðèçîíòàëüíóþ ïðîåê-
öèþ ñêîðîñòè â îòíîñèòåëüíîì äâèæåíèè – ÷åðåç ur. Ñîãëàñíî
ðèñ. 8.10
398
Ðèñ. 8.10. Ñõåìà ïîñòðîåíèÿ óãëîâ ñêîëüæåíèÿ ïðè áîêîâîì äâèæåíèè ðàêåòû ïðî-
òèâ âåòðà
uu
Wu
W
rz
z
=++
êê
22
2s
i
n
;
Ψ
(8.71)
cos
cos cos
;
Ψ
Ψ
r
r
V
u
=
ê
θ
(8.72)
äîïîëíèòåëüíûå ñîîòíîøåíèÿ äëÿ îïðåäåëåíèÿ óãëà ñêîëüæåíèÿ â
îòíîñèòåëüíîì áîêîâîì äâèæåíèè:
βψββθ
rr
r
r
rr
=−
=
Ψ;c
o
s
.
(8.73)
Íà ðèñ. 8 .11 ïðåäñòàâëåíà ñõåìà áîêîâîãî äâèæåíèÿ ñòàáèëèçè-
ðóåìîé âðàùåíèåì ðàêåòû (ñíàðÿäà) íà àêòèâíîì ó÷àñòêå òðàåêòî-
ðèè â ñëó÷àå, êîãäà áîêîâàÿ ñîñòàâëÿþùàÿ òÿãè äåéñòâóåò â íàïðàâ-
ëåíèè âåòðà. Ñîãëàñíî ðèñ. 8 .11
399
Ðèñ. 8 .11 . Ñõåìà ïîñòðîåíèÿ óãëîâ ñêîëüæåíèÿ ïðè áîêîâîì äâèæåíèè ðàêåòû â íà-
ïðàâëåíèè âåòðà
uu
Wu
W
rz
z
=+−
êê
22
2s
i
n
.
Ψ
(8.74)
Èç (8.68), ïîëîæèâ WW
yx
gg
==
0, ïîëó÷èì
cos
cos cos
ΨΨ
rr
uV
=
−1
ê
θ
(8.75)
è äîïîëíèòåëüíîå óðàâíåíèå
βψ
θ
rr
=−
()
c
o
s
.
Ψ
(8.76)
Ðàññìàòðèâàÿ óñòîé÷èâóþ ðàêåòó êàê ìàòåðèàëüíóþ òî÷êó ïåðå-
ìåííîé ìàññû è ó÷èòûâàÿ, ÷òî ïðè âåòðå âåêòîð òÿãè ñîâïàäàåò ñ
âåêòîðîì âîçäóøíîé ñêîðîñòè öåíòðà ìàññ, ïîëó÷èì êîñèíóñû óã-
ëîâ ìåæäó íàïðàâëåíèåì âîçäóøíîé ñêîðîñòè è ñîîòâåòñòâóþùèìè
îñÿìè ñòàðòîâîé ñèñòåìû êîîðäèíàò
V
V
VW
V
V
V
VW
V
V
V
VW
rx
r
xx
r
ry
r
yy
r
rz
r
zz
cc
c
cc
c
cc
=
−
=
−
=
−
êêê
;;c
Vr
.
(8.77)
Åñëè îïðåäåëèòü ëîáîâîå ñîïðîòèâëåíèå ÷åðåç áàëëèñòè÷åñêèé
êîýôôèöèåíò ñ è ôóíêöèþ G(Vτ), òî âåëè÷èíà Å èç ôîðìóëû (3.126)
ìîæåò áûòü âû÷èñëåíà ÷åðåç ñêîðîñòü Vr τ :
Ec
Hy
G
V
rr
=
ττ
()( ).
(8.78)
Äëÿ ñíàðÿäà ïîñòîÿííîé ìàññû ñèñòåìó óðàâíåíèé, ó÷èòûâàþ-
ùóþ âëèÿíèå âåòðà, ìîæíî íàïèñàòü â âèäå îáùåé ñèñòåìû (8.14):
••
(• ); •••
;
••
(• ).
xE
x
WyE
yg
zE
z
W
rx
r
rz
=−
−
=−
−
=−
−
(8.79)
Ïîëüçóÿñü (8.67), ìîæíî ïîëó÷èòü
VV
W
V
xW
V
zW
V
r
x
z
=−
−
ê
êê
2
ê
2
1+
2
2
2
2
•
•
,
(8.80)
ãäå WWW
xz
=+
22
è Vxyz
ê
=+
+
•••
.
222
Ñêîðîñòü ñíàðÿäîâ ïîñòîÿííîé ìàññû, êàê ïðàâèëî, çíà÷èòåëüíî
áîëüøå ñêîðîñòè âåòðà. Îòáðàñûâàÿ â (8.80) ÷ëåíû WV
2
/ê
2
è
400
2• /,
zWV
z
ê
2
ìàëûå ïî ñðàâíåíèþ ñ åäèíèöåé, à òàêæå ðàçëàãàÿ óïðî-
ùåííóþ ôóíêöèþ (8.80) â áèíîìèàëüíûé ðÿä è ïðåíåáðåãàÿ â íåì
÷ëåíàìè, ñîäåðæàùèìè îòíîøåíèå ïðîåêöèè ñêîðîñòè âåòðà Wx ê
ñêîðîñòè Vê â áîëüøåé, ÷åì ïåðâîé, ñòåïåíè, ìîæíî, ñëåäóÿ [22],
ïîëó÷èòü
VVWx
V
rx
=−
êê
-1
•
;
(8.81)
GV GV
WVfVx
rx
() ()[
( )•];
ττ
τ
=−
êê
-2
ê
1
(8.82)
EEW
Vf
Vx
rx
=−
[(
)
•
],
1
ê
-2
êτ
(8.83)
ãäå f(Vêτ) îïðåäåëÿåòñÿ ïî (8.25).
Ïîäñòàâëÿÿ Er â (8.79) è ïðåíåáðåãàÿ âåëè÷èíàìè âòîðîãî ïîðÿä-
êà ìàëîñòè, ìîæíî ïîëó÷èòü
•••
[(
)
•
];
•••
()
xE
x
EVf
Vx
W
yE
yE
V
f
V
x
=−
+
+
=−
+
1
2
ê
-2
ê
ê
-2
ê
τ
τ
••
;
••
(• ).
xyW g
zE
z
W
x
z
−
=−
−
(8.84)
8.3.5. ÁÀËËÈÑÒÈ×ÅÑÊÈÉ ÑÐÅÄÍÈÉ ÂÅÒÅÐ È ÁÀËËÈÑÒÈ×ÅÑÊÎÅ
ÎÒÊËÎÍÅÍÈÅ ÒÅÌÏÅÐÀÒÓÐÛ
Ââåäåíèå â áàëëèñòè÷åñêèé ðàñ÷åò êîíêðåòíûõ ôóíêöèé èçìå-
íåíèÿ òåìïåðàòóðû è âåòðà ïî âûñîòå ÿâëÿåòñÿ òðóäîåìêîé çàäà-
÷åé. Çíà÷èòåëüíî ïðîùå ïðèáëèæåííûé ìåòîä, çàêëþ÷àþùèéñÿ â
îïðåäåëåíèè èçìåíåíèé ýëåìåíòîâ òðàåêòîðèè ïî äèôôåðåíöè-
àëüíûì ïîïðàâî÷íûì ôîðìóëàì. Ïðèìåíåíèå äèôôåðåíöèàëü-
íûõ ïîïðàâî÷íûõ ôîðìóë äëÿ îïðåäåëåíèÿ âëèÿíèÿ âåòðà è îò-
êëîíåíèÿ òåìïåðàòóðû âîçäóõà îò íîðìàëüíîé ôóíêöèè τ(y) îêà-
çûâàåòñÿ âîçìîæíûì, åñëè ââîäèòü â ðàñ÷åò ñðåäíèé ïîñòîÿííûé
ïî âñåé òðàåêòîðèè âåòåð è ïîñòîÿííîå îòêëîíåíèå òåìïåðàòóðû.
Ýòè ïîñòîÿííûå ïîëó÷èëè íàçâàíèå áàëëèñòè÷åñêèõ ñðåäíèõ. Áàë-
ëèñòè÷åñêèé âåòåð W á è áàëëèñòè÷åñêîå îòêëîíåíèå òåìïåðàòóðû δτá
îïðåäåëÿþòñÿ èç óñëîâèÿ, ÷òî âûçâàííûå èõ äåéñòâèåì îòêëîíå-
íèÿ òî÷êè ïàäåíèÿ áóäóò òàêèìè æå, êàê è ïðè êîíêðåòíîé ðåà-
ëèçàöèè èçìåíåíèÿ âåòðà è òåìïåðàòóðû ïî âûñîòå. Åñëè èçâåñò-
íû áàëëèñòè÷åñêèå ñðåäíèå, òî îòêëîíåíèÿ êîîðäèíàò òî÷êè ïà-
äåíèÿ îò ðàññ÷èòàííûõ ïðè íîðìàëüíûõ ìåòåîðîëîãè÷åñêèõ
óñëîâèÿõ îïðåäåëÿòñÿ ïî ïðîñòûì ôîðìóëàì. Èçìåíåíèå äàëü-
íîñòè, âûçâàííîå áàëëèñòè÷åñêèì îòêëîíåíèåì òåìïåðàòóðû:
401
δ
∂
∂τ
δτ
τ
x
x
c
c
=
á.
(8.85)
Èçìåíåíèå äàëüíîñòè,
âûçâàííîå
äåéñòâèåì
ïðîäîëüíîé
ñîñòàâëÿþùåé áàëëèñòè÷åñêîãî âåòðà:
δ
∂
∂
x
x
W
W
cW
c
x
x
x
=
á.
(8.86)
Áîêîâîå îòêëîíåíèå òî÷êè ïàäåíèÿ îò äåéñòâèÿ áîêîâîé
ñîñòàâëÿþùåé âåòðà:
z
z
W
W
cW
c
z
z
z
=
∂
∂
á.
(8.87)
Íàèáîëåå òåîðåòè÷åñêè îáîñíîâàííûé ìåòîä âû÷èñëåíèÿ áàëëè-
ñòè÷åñêèõ ñðåäíèõ, ïðèãîäíûé äëÿ íàó÷íî-èññëåäîâàòåëüñêèõ ðàáîò
è êîíòðîëÿ ïðèáëèæåííûõ ìåòîäîâ, âûòåêàåò èç óêàçàííîãî âûøå
óñëîâèÿ èõ îïðåäåëåíèÿ.  êà÷åñòâå ïðèìåðà ðàññìîòðèì ìåòîäèêó
ðàñ÷åòà ïðîäîëüíîé ñîñòàâëÿþùåé áàëëèñòè÷åñêîãî âåòðà. Ïî äàí-
íûì íåâîçìóùåííîé íîìèíàëüíîé òðàåêòîðèè îïðåäåëÿåì äàëü-
íîñòü ñòðåëüáû xc è ïîïðàâî÷íûé êîýôôèöèåíò íà ïîñòîÿííûé ïî
âñåé òðàåêòîðèè âåòåð ∂xc/∂Wx. Ïîïðàâî÷íûé êîýôôèöèåíò íàõî-
äèì îäíèì èç òî÷íûõ ìåòîäîâ, íàïðèìåð ðåøåíèåì ñèñòåìû óðàâ-
íåíèé, âêëþ÷àþùåé ïîñòîÿííûé âåòåð.
Ðàñ÷åò òðàåêòîðèè ïîâòîðÿåòñÿ ïðè ïðàêòè÷åñêîé ðåàëèçàöèè
èçìåíåíèÿ ñîñòàâëÿþùåé âåòðà ïî âûñîòå: îïðåäåëÿåòñÿ x cW x
èèç-
ìåíåíèå äàëüíîñòè
δxxx
cW
cW
c
xx
=−
.
(8.88)
Ïðîäîëüíàÿ ñîñòàâëÿþùàÿ áàëëèñòè÷åñêîãî âåòðà äëÿ êîíêðåòíîé
òðàåêòîðèè è êîíêðåòíîé âåòðîâîé ôóíêöèè òàêîâà:
W
x
xW
x
cW
cx
x
á=
δ
∂∂
/
.
(8.89)
Ïîäîáíûé ìåòîä ìîæåò áûòü èñïîëüçîâàí ïðè îïðåäåëåíèè áîêîâîé
ñîñòàâëÿþùåé áàëëèñòè÷åñêîãî âåòðà Wzá è áàëëèñòè÷åñêîãî
îòêëîíåíèÿ òåìïåðàòóðû δτá.
Äëÿ ïðàêòè÷åñêîé ðàáîòû ïðèìåíÿþò áîëåå ïðîñòîé, íî ìåíåå
òî÷íûé ìåòîä, ñâÿçàííûé ñ îïðåäåëåíèåì "âåñîâ ñëîåâ". ×òîáû îï-
ðåäåëèòü âåñà ñëîåâ è áàëëèñòè÷åñêèõ ñðåäíèõ, òðàåêòîðèþ ðàçäåëÿ-
402
þò ïî âûñîòå íà ðÿä ñëîåâ (îáû÷íî ðàâíîé òîëùèíû). Òîëùèíà
êàæäîãî ñëîÿ áåðåòñÿ â çàâèñèìîñòè îò âûñîòû òðàåêòîðèè îò 200 äî
800 ì òàê, ÷òîáû îíà áûëà êðàòíà 100 ì. Äëÿ êàæäîãî èç ñëîåâ âû-
÷èñëÿþòñÿ ïîïðàâî÷íûå êîýôôèöèåíòû (∂xc/∂τ)i;(
∂xc/∂Wx)i;
(∂zc/∂Wz)i. Ïåðâûå äâà îïðåäåëÿþò èçìåíåíèå ïîëíîé äàëüíîñòè ïðè
óâåëè÷åíèè òåìïåðàòóðû íà 1 Ê è ñêîðîñòè âåòðà íà 1 ì/ñ òîëüêî â
i-ì ñëîå . Òðåòèé ïîïðàâî÷íûé êîýôôèöèåíò îïðåäåëÿåò áîêîâîå îò-
êëîíåíèå òî÷êè ïàäåíèÿ ñíàðÿäà ïðè áîêîâîì âåòðå 1 ì/ñ òîëüêî â
i-ì ñëîå. Âû÷èñëåíèå êàæäîãî ïîïðàâî÷íîãî êîýôôèöèåíòà äëÿ i-ãî
ñëîÿ âåäåòñÿ ñàìîñòîÿòåëüíî; åñëè èçìåíÿåòñÿ òåìïåðàòóðà èëè ó÷è-
òûâàåòñÿ âåòåð â i-ì ñëîå, òî â îñòàëüíûõ ñëîÿõ ïðåäïîëàãàåòñÿ íîð-
ìàëüíîå èçìåíåíèå τ(y) è áåçâåòðèå. Äëÿ êàæäîé òðàåêòîðèè òðåáó-
åòñÿ ïðîâåñòè n ðàñ÷åòîâ (n – ìèíèìàëüíîå ÷èñëî öåëûõ ñëîåâ, â
ñóììó âûñîò êîòîðûõ óêëàäûâàåòñÿ âûñîòà òðàåêòîðèè). Áàëëèñòè-
÷åñêîå îòêëîíåíèå òåìïåðàòóðû íàõîäèòñÿ èç ðàâåíñòâà
∂
∂τ
δτ
∂
∂τ
δτ
∂
∂τ
δτ
xx
x
cc
c
n
n
⎛
⎝⎜⎞
⎠⎟ +⎛
⎝⎜⎞
⎠⎟ ++⎛
⎝⎜⎞
⎠⎟=
1
1
2
2K
∂
∂τ
δτ
xc
á,
(8.90)
ãäå δτi – îòêëîíåíèå êîíêðåòíîé ñðåäíåé òåìïåðàòóðû â i-ì ñëîå îò
ñðåäíåé òåìïåðàòóðû â i-ì ñëîå, îïðåäåëÿåìîé ïî íîðìàëüíîìó
èçìåíåíèþ òåìïåðàòóðû ïî âûñîòå, îòêóäà
δτ
∂
∂τ
δτ
∂δ
τ
á=
⎛
⎝⎜⎞
⎠⎟
∑x
x
c
i
i
i
n
c
/
.
(8.91)
Îòíîøåíèå
q
x
x
i
ci
c
τ
∂∂
τ
∂∂
τ
=
(/)
/
(8.92)
íàçûâàåòñÿ âåñîì i-ãî ñëîÿ ïî òåìïåðàòóðå. Ñëåäîâàòåëüíî,
δτ
δτ
τ
á=∑qii
i
n
.
(8.93)
Âû÷èñëåíèå âåñîâ ñëîåâ áàëëèñòè÷åñêîãî âåòðà çàòðóäíåíî òåì,
÷òî âåòåð ÿâëÿåòñÿ âåêòîðíîé âåëè÷èíîé è ìîæåò èçìåíÿòü ìîäóëü è
íàïðàâëåíèå â çàâèñèìîñòè îò íîìåðà ñëîÿ. Êðîìå òîãî, äëÿ îäíî-
òèïíûõ ðàêåòíûõ è àðòèëëåðèéñêèõ ñèñòåì, èìåþùèõ îäèíàêîâûå
403
âåñà ñëîåâ, áàëëèñòè÷åñêèé âåòåð áóäåò ðàçíûì â çàâèñèìîñòè îò íà-
ïðàâëåíèÿ ñòðåëüáû. Âñëåäñòâèå ýòîãî ðàñ÷åò áàëëèñòè÷åñêîãî âåòðà
âåäåòñÿ äëÿ óñëîâíîãî íàïðàâëåíèÿ ñòðåëüáû ïðè íóëåâîì àçèìóòå,
ò.å . äëÿ íàïðàâëåíèÿ íà ñåâåð, ñ ïîñëåäóþùèì ïåðåñ÷åòîì íà äåéñò-
âèòåëüíîå íàïðàâëåíèå ñòðåëüáû. Íàïðàâëåíèå ñòðåëüáû îïðåäåëÿ-
åòñÿ àçèìóòîì ñòðåëüáû Àñò – óãëîì, îòñ÷èòûâàåìûì ïî ÷àñîâîé
ñòðåëêå îò íàïðàâëåíèÿ íà ñåâåð äî íàïðàâëåíèÿ íà öåëü. Àçèìóò
âåòðà ÀW – óãîë, îòñ÷èòûâàåìûé òàêæå ïî ÷àñîâîé ñòðåëêå îò íà-
ïðàâëåíèÿ íà ñåâåð äî íàïðàâëåíèÿ íà òî÷êó, îòêóäà äóåò âåòåð
(ðèñ. 8 .12). Çíàê "ïëþñ" èìåþò ïðîäîëüíûé âåòåð, íàïðàâëåííûé íà
öåëü (ò.å. ïîïóòíûé âåòåð), è áîêîâîé, äóþùèé âïðàâî îò íàïðàâëå-
íèÿ ñòðåëüáû. Ñîãëàñíî îïðåäåëåíèþ, äëÿ ïîïóòíîãî áàëëèñòè÷å-
ñêîãî âåòðà, íàïðàâëåííîãî ñ ñåâåðà íà þã, ìîæíî íàïèñàòü ðàâåí-
ñòâî
δ
∂
∂
∂
∂
x
x
W
W
x
W
W
cW
c
xi
i
i
n
c
x
x
=
⎛
⎝⎜⎞
⎠⎟
=
∑
(
,
ñ-þ)
á(ñ-þ)
îòêóäà ïîëó÷èì âûðàæåíèå äëÿ ïðîäîëüíîé ñîñòàâëÿþùåé
áàëëèñòè÷åñêîãî âåòðà
Wq
W
Wi
i
i
n
x
á(ñ- þ)
c-þ)
=
=
∑(,
1
(8.94)
ãäå
404
Ðèñ. 8.12. Àçèìóò ñòðåëü-
áû Àñò è àçèìóò âåòðà ÀW
q
x
W
x
W
Wi
c
xi
c
x
x
=
⎛
⎝⎜⎞
⎠⎟
∂
∂
∂
∂
/
(8.95)
–
âåñ ñëîÿ ïî ïðîäîëüíîé ñîñòàâëÿþùåé áàëëèñòè÷åñêîãî âåòðà.
Áîêîâîå îòêëîíåíèå ñíàðÿäà ïîä äåéñòâèåì ñîñòàâëÿþùåé âåòðà,
äóþùåãî ñ âîñòîêà íà çàïàä, ðàâíî
z
z
W
W
z
W
W
cW
c
zi
i
i
n
c
z
z
=
⎛
⎝⎜⎞
⎠⎟
=
=
∑∂
∂
∂
∂
(
.
â-ç)
á(â-ç)
1
Îòñþäà áîêîâàÿ ñîñòàâëÿþùàÿ ñêîðîñòè áàëëèñòè÷åñêîãî âåòðà
èìååò âèä
Wq
W
Wi
i
i
n
z
á(â- ç)
â- ç)
=
=
∑(,
1
(8.96)
ãäå
q
z
W
z
W
Wi
c
zi
c
z
z
=
⎛
⎝⎜⎞
⎠⎟
∂
∂
∂
∂
/
–
âåñ ñëîÿ ïî áîêîâîé ñîñòàâëÿþùåé ñêîðîñòè âåòðà.
Íàïðàâëåíèå äåéñòâèÿ áàëëèñòè÷åñêîãî âåòðà îïðåäåëÿåòñÿ ïî
óãëó âåòðà
ΨW
W
W
á
arctg á(â- ç)
á(ñ-þ)
=
.
(8.97)
Åñëè áàëëèñòè÷åñêèé âåòåð íàïðàâëåí íà îãíåâóþ ïîçèöèþ èç
ïåðâîé ÷åòâåðòè, òî A áá
WW
=Ψ ,åñëèèçâòîðîé,òîA áá
WW
=°
−
360Ψ,
åñëè èç òðåòüåé ÷åòâåðòè, òî A áá
WW
=°
+
180 Ψ , è åñëè èç ÷åòâåðòîé,
êàê ïîêàçàíî íà ðèñ. 8.12, òî A áá
WW
=°
−
180Ψ.
Ìîäóëü ñêîðîñòè áàëëèñòè÷åñêîãî âåòðà
WWW
á
á(c þ
á(â ç
=+
−−
))
.
22
(8.98)
Äëÿ äåéñòâèòåëüíîãî íàïðàâëåíèÿ ñòðåëüáû ïðîäîëüíàÿ è áîêî-
âàÿ ñîñòàâëÿþùèå áàëëèñòè÷åñêîãî âåòðà îïðåäåëÿþòñÿ ïî ôîðìó-
ëàì
405
WW
WW
xW
zW
c
c
áá
ñ
ò
ááñ
ò
AA
AA
á
á
=−
−
=−
cos(
);
sin(
).
(8.99)
Âåñà ñëîåâ qτi, qW xi
, qWzi
äëÿ îäíîãî è òîãî æå ñëîÿ ðàçëè÷íû ïî âå-
ëè÷èíå è èçìåíÿþòñÿ ïðè ïåðåõîäå îò ñëîÿ ê ñëîþ. Åñëè â ôîðìóëå
(8.90) ïîëîæèòü δτ1 = δτ2 = ... = δτn = δτá,òîqq q
n
ττ
τ
12
1
+++=
K
; àíà-
ëîãè÷íî qWi
i
n
x
=
=
∑1
1
è
qWi
i
n
z
=
=
∑1
1
. Ðàâåíñòâî åäèíèöå ñóììû âåñîâ ñëîåâ
ÿâëÿåòñÿ ïðîâåðêîé ïðàâèëüíîñòè èõ âû÷èñëåíèÿ.
Äëÿ ðàçëè÷íûõ ñèñòåì è òðàåêòîðèé îäíîé ñèñòåìû âåñà ñëîåâ
ðàçëè÷íû è äîëæíû áûòü âû÷èñëåíû çàðàíåå. Ïðè ïîäãîòîâêå êîí-
êðåòíûõ ñòðåëüá ïî äàííûì ìåòåîáþëëåòåíÿ âû÷èñëÿþòñÿ ïî ñëîÿì
îòêëîíåíèÿ δτi, W(c−þ)i, W(â−ç)i, ïîñëå ÷åãî âû÷èñëÿþòñÿ áàëëèñòè÷å-
ñêîå îòêëîíåíèå òåìïåðàòóðû è áàëëèñòè÷åñêèé âåòåð.
8.3.6. ÏÐÈÁËÈÆÅÍÍÛÅ ÏÎÏÐÀÂÎ×ÍÛÅ ÔÎÐÌÓËÛ ÍÀ ÏÎÑÒÎßÍÍÛÉ
ÏÐÎÄÎËÜÍÛÉ È ÁÎÊÎÂÎÉ ÂÅÒÅÐ
Èçëàãàåìûé ìåòîä ðàçðàáîòàí äëÿ ó÷åòà ðàçäåëüíîãî âëèÿíèÿ ïî-
ñòîÿííîãî ïðîäîëüíîãî è áîêîâîãî âåòðà íà äâèæåíèå öåíòðà ìàññ
àðòèëëåðèéñêîãî ñíàðÿäà. Âåðòèêàëüíàÿ ñîñòàâëÿþùàÿ ñêîðîñòè
âåòðà íå ó÷èòûâàåòñÿ.
Ðàññìîòðèì ñíà÷àëà òîëüêî ïðîäîëüíîå äâèæåíèå. Îñîáåííîñòü
ìåòîäà çàêëþ÷àåòñÿ â òîì, ÷òî îòíîñèòåëüíîå äâèæåíèå öåíòðà ìàññ
ñíàðÿäà ðàññìàòðèâàåòñÿ â ñèñòåìå êîîðäèíàò, ñîâåðøàþùåé ïåðå-
íîñíîå äâèæåíèå îòíîñèòåëüíî Çåìëè â íàïðàâëåíèè âåòðà ñ åãî
ñêîðîñòüþ. Ïîëíàÿ äàëüíîñòü ñòðåëüáû îòíîñèòåëüíî Çåìëè (â àá-
ñîëþòíîì äâèæåíèè) ïðè ïðîäîëüíîì ïîïóòíîì âåòðå ðàâíà
xx
W
t
cW
cr
xc
x
=+,
(8.100)
ãäå xcr – äàëüíîñòü â îòíîñèòåëüíîì äâèæåíèè; tc – ïîëíîå âðåìÿ
ïîëåòà, îäèíàêîâîå äëÿ îòíîñèòåëüíîãî è àáñîëþòíîãî äâèæåíèÿ.
Îáîçíà÷àÿ ÷åðåç õñ äàëüíîñòü â àáñîëþòíîì äâèæåíèè ïðè áåç-
âåòðèè, ïîëó÷èì èçìåíåíèå äàëüíîñòè îò ïðîäîëüíîãî âåòðà
δ
δ
xxx
xx
x
W
t
cW
cW
c
cW
cr
c
xc
xx
x
=−
=−+
,
.
èëè
(8.101)
Ðàçíîñòü xcr − xc îáû÷íî íåâåëèêà, è äëÿ åå îïðåäåëåíèÿ ìîæíî âîñ-
ïîëüçîâàòüñÿ äèôôåðåíöèàëüíîé ïîïðàâî÷íîé ôîðìóëîé, èìåÿ
406
â âèäó, ÷òî òðàåêòîðèÿ ñíàðÿäà ïîñòîÿííîé ìàññû ïðè áåçâåòðèè
çàäàåòñÿ âåëè÷èíàìè c, V0 è θ0:
δ
∂
∂
δ
∂
∂θ
δθ
∂
∂
δ
x
x
V
V
xx
c
cWt
cW
ccc
xc
x
=+
+
+
0
0
0
0
.
(8.102)
Ðàçíîñòè íà÷àëüíûõ ñêîðîñòåé è óãëîâ áðîñàíèÿ â àáñîëþòíîì è
îòíîñèòåëüíîì äâèæåíèÿõ ñîîòâåòñòâåííî ðàâíû
δδ
θ
θ
θ
VVV
rr
00 0000
=−
=−
;. (8.103)
Ðàçíîñòü áàëëèñòè÷åñêèõ êîýôôèöèåíòîâ δc =0.
Îòíîñèòåëüíóþ íà÷àëüíóþ ñêîðîñòü â ïðîäîëüíîì äâèæåíèè è
óãîë áðîñàíèÿ, ñîãëàñíî ðèñ. 8 .13, ìîæíî çàïèñàòü òàê:
VVWV
W
V
VW
rx
x
x
00
22
00
0
00
00
2
=+
−
=
−
cos ;
sin
cos
.
θ
θ
θ
θ
tg
(8.104)
Ïîñëå òîãî êàê îïðåäåëåíû îñíîâíûå ïîïðàâî÷íûå êîýôôèöè-
åíòû ∂xc/∂V0; ∂xc/∂θ0 è âðåìÿ äâèæåíèÿ tc, ïî äàííûì íîìèíàëüíîé
òðàåêòîðèè íåîáõîäèìî ðàññ÷èòàòü V0r, θ0r, δV0, δθ0.
Èçìåíåíèå äàëüíîñòè îò ïðîäîëüíîãî âåòðà îïðåäåëÿåòñÿ ïî
ôîðìóëå (8.102). Äëÿ áîëüøèõ íà÷àëüíûõ ñêîðîñòåé ìîæíî âîñïîëü-
çîâàòüñÿ ôîðìóëîé (8.81), çàìåíèâ â íåé • /
xV
ê
íà cosθ0, òîãäà
δθ
VVV W
rx
000
0
=−=
−
cos .
(8.105)
Ïðåäñòàâèì (8.104) â âèäå tgθ0r =tgθ0(1 − Wx/V0 cosθ0)
−1
. Ðàñêëàäûâàÿ
âåëè÷èíó, çàêëþ÷åííóþ â ñêîáêè, â áèíîìèàëüíûé ðÿä è îïóñêàÿ
÷ëåíû âòîðîãî è âûøå ïîðÿäêîâ ìàëîñòè, áóäåì èìåòü
407
Ðèñ. 8 .13 . Ñõåìà îïðåäåëåíèÿ íà÷àëü-
íîé ñêîðîñòè è óãëà áðîñàíèÿ â îòíîñè-
òåëüíîì ïëîñêîì äâèæåíèè ïðè äåéñò-
âèè ïîñòîÿííîãî ïîïóòíîãî âåòðà
tg
tg0
θθθ
θ
00
0
2
0
rx
WV
−=sin /( cos ).
Ñ÷èòàÿ ïðèáëèæåííî δ(tgθ0)=tgθ0r − tgθ0 ≈δθ0/(cos
2
θ0), ïîëó÷èì
δθ
θ
0
0
0
=
W
V
x
sin .
(8.106)
Ïîäñòàâèì (8.105) è (8.106) â (8.102) è ïîñëå ïðåîáðàçîâàíèé
ïîëó÷èì ïðèáëèæåííóþ ïîïðàâî÷íóþ ôîðìóëó
δ
∂
∂
θ
∂θ
∂θ
xW
t
x
V
x
V
cW
x
c
cc
x
=−
+
⎛
⎝⎜
⎞
⎠⎟
0
0
0
00
cos
sin
,
(8.107)
ãäå ∂xc/∂θ0 áåðåòñÿ â ì/ðàä.
Áîêîâîå îòêëîíåíèå öåíòðà ìàññ ñíàðÿäà ïîä äåéñòâèåì ïîñòî-
ÿííîãî áîêîâîãî âåòðà â àáñîëþòíîì äâèæåíèè ðàâíî
zz
W
t
Wrz
z
=+.
(8.108)
408
Ðèñ. 8.14. Ñõåìà îïðåäåëåíèÿ íà÷àëüíîé ñêîðîñòè è óãëà áðîñàíèÿ â îòíîñèòåëüíîì
áîêîâîì äâèæåíèè ïðè äåéñòâèè ïîñòîÿííîãî áîêîâîãî âåòðà
 ñèñòåìå êîîðäèíàò OrXrYrZr, äâèæóùåéñÿ ñî ñêîðîñòüþ áîêîâîãî
âåòðà â íàïðàâëåíèè åãî äåéñòâèÿ, ñêîðîñòü öåíòðà ìàññ ñíàðÿäà
ðàâíàV0r= V0−Wz.
Ñîãëàñíî ðèñ. 8.14
VVW
rz
00
22
=+
,
(8.109)
èëè
VV WV
rz
00
0
2
1
=+
(/).
(8.110)
Äëÿ áîëüøèõ íà÷àëüíûõ ñêîðîñòåé (Wz/V0)2 << 1, ïîýòîìó δV0 ≈ 0
èV0r≈V0.
Èç òîãî æå ðèñóíêà èìååì
tg
tg
0
0
θ
θ
θ
θ
θ
r
xz
V
VWW
V
=
+
=
+
−
00
0
22
0
22
00
2
1
sin
cos
(cos)
.
(8.111)
Äëÿ îòíîñèòåëüíî ìàëûõ óãëîâ áðîñàíèÿ è áîëüøèõ V0 ìîæíî
ñ÷èòàòü tgθ0r ≈ tgθ0 è δθ0 = 0. Ïðè ïðèíÿòûõ äîïóùåíèÿõ áîêîâîå îò-
êëîíåíèå zr îïðåäåëÿåòñÿ ïîâîðîòîì ïëîñêîñòè òðàåêòîðèè îòíîñè-
òåëüíîãî äâèæåíèÿ â ñèñòåìå êîîðäèíàò Or Xr Yr Zr âîêðóã îñè Yr íà
óãîë ΨW z
, è òîãäà äëÿ òî÷êè ïàäåíèÿ áóäåì èìåòü
zx
Wx
V
cr
c
W
zc
z
=−
=−
tgΨ
00
cos
.
θ
(8.112)
Áîêîâîå îòêëîíåíèå ñíàðÿäà îòíîñèòåëüíî çåìíûõ ñòàðòîâûõ
êîîðäèíàò äëÿ òåêóùåé òî÷êè òðàåêòîðèè ñîãëàñíî (8.108) ðàâíî
zW
t
Wx
V
Wz
zc
z
=−
00
cos
,
θ
(8.113)
è äëÿ òî÷êè ïàäåíèÿ èìååì
zW
t
x
V
cW
zc
c
z
=−
⎛
⎝⎜
⎞
⎠⎟
00
cos
.
θ
(8.114)
409
Çàìåòèì, ÷òî âåëè÷èíà tg ΨW
z
z
W
V
=
00
cos θ
ïîëó÷åíà áåç ó÷åòà ïðî-
äîëüíîé ñîñòàâëÿþùåé ñêîðîñòè âåòðà. Åñëè ó÷åñòü ïðîäîëüíóþ ñî-
ñòàâëÿþùóþ âåòðà, òî
tg ΨW
z
x
z
W
VW
=
−
00
cos
.
θ
(8.115)
 ðåçóëüòàòå ñäåëàííûõ óïðîùåíèé ôîðìóëû (8.107) è (8.114)
äàþò çàìåòíûå îøèáêè ïðè ìàëûõ íà÷àëüíûõ ñêîðîñòÿõ è áîëüøèõ
óãëàõ áðîñàíèÿ. Ïðèåìëåìûå ðåçóëüòàòû ïî ýòèì ôîðìóëàì ìîæíî
ïîëó÷èòü ïðè V0 > 250 ì/ñ è θ0 < 45°.
8.3.7 . ÌÅÒÅÎÐÎËÎÃÈ×ÅÑÊÀß ÏÎÄÃÎÒÎÂÊÀ ÑÒÐÅËÜÁÛ
Èìåÿ â âèäó èçëîæåííûå âûøå îáùåòåîðåòè÷åñêèå ïîëîæåíèÿ, ðàññìîò-
ðèì êðàòêî âîïðîñû ïðàêòèêè ìåòåîðîëîãè÷åñêîé ïîäãîòîâêè ïðè âåäåíèè
áîåâûõ ñòðåëüá èç àðòèëëåðèéñêèõ àâòîìàòè÷åñêèõ ñèñòåì è îðóäèé íàçåì-
íîé àðòèëëåðèè.
Ìåòåîðîëîãè÷åñêàÿ ïîäãîòîâêà ñòðåëüáû çàêëþ÷àåòñÿ â îïðåäåëåíèè è
ó÷åòå ïóòåì ââåäåíèÿ â ïðèáîðû óïðàâëåíèÿ ñòðåëüáîé (ÏÓÑ) çíà÷åíèé îò-
êëîíåíèÿ äàâëåíèÿ ∆h èëè ïëîòíîñòè âîçäóõà ∆Ï, à òàêæå íàïðàâëåíèÿ A á
W
è ñêîðîñòè Wá áàëëèñòè÷åñêîãî âåòðà. ÏÓÑ ïðåäñòàâëÿþò ñîáîé ñëîæíîå
ñî÷åòàíèå ïðèáîðîâ è ñ÷åòíî-ðåøàþùèõ óñòðîéñòâ, ïðåäíàçíà÷åííûõ äëÿ
âûïîëíåíèÿ çàäà÷è óïðàâëåíèÿ îãíåì. Îíè îáåñïå÷èâàþò: ïðèåì öåëåóêàçà-
íèÿ; ñîïðîâîæäåíèå öåëè, ò.å . íåïðåðûâíîå è òî÷íîå îïðåäåëåíèå åå òåêó-
ùèõ êîîðäèíàò; îïðåäåëåíèå ïàðàìåòðîâ äâèæåíèÿ öåëè; ðåøåíèå çàäà÷è
âñòðå÷è ñíàðÿäà ñ öåëüþ; íåïðåðûâíóþ âûðàáîòêó óãëîâ íàâåäåíèÿ è íàâîä-
êó îðóäèé ïî íèì.
Ïðè íåâîçìîæíîñòè ïîëó÷åíèÿ çíà÷åíèé ïëîòíîñòè âîçäóõà íà çàäàííîé
âûñîòå, à òàêæå íàïðàâëåíèÿ è ñêîðîñòè áàëëèñòè÷åñêîãî âåòðà èñïîëüçóþò
èõ íàçåìíûå çíà÷åíèÿ.
Âëèÿíèå íà äâèæåíèå ËÀ îòêëîíåíèé äàâëåíèÿ è òåìïåðàòóðû âîçäóõà
îò íîðìàëüíûõ óñëîâèé ÿâëÿåòñÿ ñóùåñòâåííûì. Âëèÿíèå èçìåíåíèé îòíî-
ñèòåëüíîé âëàæíîñòè íà ïëîòíîñòü âîçäóõà ìåíåå ñóùåñòâåííî. Îíî ó÷èòû-
âàåòñÿ çà ñ÷åò èñïîëüçîâàíèÿ ïîíÿòèÿ âèðòóàëüíîé òåìïåðàòóðû.
Ó÷åò èçìåíåíèÿ ïàðàìåòðîâ àòìîñôåðû (ìåòåîðîëîãè÷åñêèõ óñëîâèé) ïî
âûñîòå ïîëåòà ñíàðÿäà îñóùåñòâëÿåòñÿ ïóòåì îïðåäåëåíèÿ, ðàñ÷åòà è ó÷åòà
óñðåäíåííûõ (áàëëèñòè÷åñêèõ) çíà÷åíèé ìåòåîðîëîãè÷åñêèõ ôàêòîðîâ (áàë-
ëèñòè÷åñêèõ îòêëîíåíèé).
Îïðåäåëåíèå áàëëèñòè÷åñêèõ îòêëîíåíèé âåäåòñÿ ñïåöèàëüíîé ñëóæáîé
(â ÷àñòíîñòè, íà ôëîòå îíî îñóùåñòâëÿåòñÿ ñïåöèàëüíûìè ñòàíöèÿìè ãèä-
ðîìåòåîðîëîãè÷åñêîé ñëóæáû ôëîòà). Ñîîòâåòñòâóþùàÿ èíôîðìàöèÿ ïî çà-
ÿâêàì ïåðåäàåòñÿ â âèäå áþëëåòåíåé â ïîäðàçäåëåíèÿ (íà êîðàáëè). Äëÿ ïîä-
ãîòîâêè ñòðåëüáû íàçåìíîé àðòèëëåðèè ïî áåðåãîâûì è ìîðñêèì öåëÿì èñ-
ïîëüçóåòñÿ áþëëåòåíü "Ìåòåîñðåäíèé",
ñðîê ãîäíîñòè êîòîðîãî ïðè
410
411
Òàáëèöà 8.2
Ïîïðàâêè äëÿ áþëëåòåíÿ "Ìåòåîñðåäíèé"
Âûñîòà ÎÏ Òàáëè÷íàÿ âûñîòà ÎÏ,
ìì
Ïîïðàâêè ê îòêëîíåíèþ çåìíîãî äàâ-
ëåíèÿ, ìì ðò. ñò.
Ïðè èñïîëüçîâàíèè ãîðíûõ òàáëèö ñòðåëüáû
äî 250
0
0
250...750
500
45
750...1250
1000
85
1250...1750
1500
125
1750...2250
2000
160
2250...2750
2500
195
áîëåå 2750
3000
230
Ïðè èñïîëüçîâàíèè îáû÷íûõ òàáëèö ñòðåëüáû
ëþáàÿ
0
0
Âûñîòà ÎÏ Ïîïðàâêè ê îòêëîíåíèþ òåìïåðàòóðû âîçäóõà (°Ñ) ïðè ïðåâûøå-
íèè ÀÌÑ íàä ÎÏ
+1000
+500
0
−500
−1000
Ïðè èñïîëüçîâàíèè ãîðíûõ òàáëèö ñòðåëüáû
äî 250
6
3
0
−3
−
250...750
9630−3
750...1250
1
29630
1250...1750
16
13
10
7
4
1750...2250
19
16
13
10
7
2250...2750
22
19
16
13
10
áîëåå 2750
25
22
19
16
13
Ïðè èñïîëüçîâàíèè îáû÷íûõ òàáëèö ñòðåëüáû
ëþáàÿ
6
3
0
−3
−6
íåóñòîé÷èâîé ïîãîäå íåçàâèñèìî îò âûñîòû òðàåêòîðèè – íå áîëåå 2 ÷. Ïðè
óñòîé÷èâîé ïîãîäå íà âûñîòå òðàåêòîðèè äî 800 ì ñðîê ãîäíîñòè áþëëåòåíÿ
ìîæåò áûòü ïðîäëåí äî 3 ÷, à íà âûñîòàõ îò 800 äî 1600ì–äî6÷.
Îòêëîíåíèå äàâëåíèÿ àòìîñôåðû, ïîìåùåííîå â áþëëåòåíå (4-ÿ ãðóïïà
öèôð), ïåðåñ÷èòûâàþò ê óðîâíþ îãíåâîé ïîçèöèè (ÎÏ). Åñëè ðàçíîñòü âû-
ñîò ÎÏ è àðòèëëåðèéñêîé ìåòåîðîëîãè÷åñêîé ñòàíöèè (ÀÌÑ) áîëüøå 100 ì,
òî äëÿ ïðèâåäåíèÿ òðàåêòîðèé ÀÌÑ ê òðàåêòîðèÿì áàòàðåè íåîáõîäèìî ýòó
ðàçíîñòü óìíîæèòü åùå íà 1,5.  ñëó÷àå êîãäà ðàçíèöà óðîâíåé ÀÌÑ è áàòà-
ðåè íå ïðåâûøàåò 200 ì, íà êàæäûå 10 ì ðàçíèöû ââîäÿò ïîïðàâêóâ1ìì
ðò. ñò . ñî çíàêîì "+", åñëè ÎÏ íèæå ÀÌÑ, è ñî çíàêîì "−", åñëè âûøå.
Áàëëèñòè÷åñêîå îòêëîíåíèå òåìïåðàòóðû âîçäóõà, íàïðàâëåíèå è ñêî-
ðîñòü áàëëèñòè÷åñêîãî âåòðà îïðåäåëÿþò ïî âûñîòå âõîäà â áþëëåòåíü (óñ-
ëîâíàÿ âûñîòà Yáþë), êîòîðóþ áåðóò ïî òàáëèöàì ñòðåëüáû èëè, åñëè Yáþë â
òàáëèöàõ íå óêàçàíà, ïî ñïåöèàëüíûì íîìîãðàììàì. Áàëëèñòè÷åñêèé âåòåð
ðàñêëàäûâàþò íà ïðîäîëüíóþ è áîêîâóþ ñîñòàâëÿþùèå. Äëÿ ýòîãî íàõîäÿò
óãîë âåòðà (ñ îêðóãëåíèåì äî 1...00) ïóòåì âû÷èòàíèÿ èç äèðåêöèîííîãî óãëà
íàïðàâëåíèÿ ñòðåëüáû äèðåêöèîííîãî óãëà áàëëèñòè÷åñêîãî âåòðà è ïî óãëó
âåòðà è ìîäóëþ åãî ñêîðîñòè "âõîäÿò" â ñïåöèàëüíûå òàáëèöû. Ïðè ðåçêî
âûðàæåííîì ãîðíîì ðåëüåôå â áþëëåòåíü "Ìåòåîñðåäíèé" âíîñÿòñÿ [72]
ñëåäóþùèå èñïðàâëåíèÿ:
ê îòêëîíåíèþ íàçåìíîãî äàâëåíèÿ ïðèáàâëÿþò ïîïðàâêó δhτ (òàáë. 8.2)
ïî çíà÷åíèþ òàáëè÷íîé âûñîòû ÎÏ yτ , ïðèíÿòîé äëÿ âõîäà â òàáëèöó óñòà-
íîâîê ïðèöåëà ïðè îïðåäåëåíèè óãëîâ ïðèöåëèâàíèÿ;
ê îòêëîíåíèÿì òåìïåðàòóðû âîçäóõà äëÿ âñåõ ñòàíäàðòíûõ âûñîò ïðèáàâ-
ëÿþò ïîïðàâêó δτ (ñì. òàáë. 8.2) ñ òî÷íîñòüþ äî 1 °Ñ ïî âûñîòå yτ è ðàçíèöå
âûñîò ÀÌÑ è ÎÏ ∆yÀÌÑ = yÀÌÑ − yÎÏ;
êî âñåì ñòàíäàðòíûì âûñîòàì áþëëåòåíÿ ïðèáàâëÿþò (ñ ó÷åòîì çíàêà)
ïîïðàâêó ∆yñò =2∆yÀÌÑ (ñ îêðóãëåíèåì äî ñîòåí ìåòðîâ);
ïîïðàâêó ïðèíèìàþò ðàâíîé íóëþ, åñëè |∆yÀÌÑ| < 200 ì.
Èñïðàâëåííûì áþëëåòåíåì ïîëüçóþòñÿ òàê æå, êàê è áþëëåòåíåì "Ìå-
òåîñðåäíèé" íà ðàâíèííîé ìåñòíîñòè, ïðè÷åì åñëè âûñîòà âõîäà â áþëëå-
òåíü ìåíüøå íàèìåíüøåé èñïðàâëåííîé ñòàíäàðòíîé âûñîòû, òî äàííûå îá
îòêëîíåíèè òåìïåðàòóðû è âåòðà îïðåäåëÿþò ïî ýòîé íàèìåíüøåé âûñîòå.
8.4 . ÓÐÀÂÍÅÍÈß ÂÎÇÌÓÙÅÍÍÎÃÎ
ÏÐÎÑÒÐÀÍÑÒÂÅÍÍÎÃÎ ÄÂÈÆÅÍÈß ÍÅÓÏÐÀÂËßÅÌÎÉ
ÐÀÊÅÒÛ
8.4.1. Ó×ÅÒ ÂËÈßÍÈß ÝÊÑÖÅÍÒÐÈÑÈÒÅÒÀ ÒßÃÈ
Ê ÷èñëó îñíîâíûõ âîçìóùàþùèõ ôàêòîðîâ, óõóäøàþùèõ òî÷-
íîñòü ñòðåëüáû íåóïðàâëÿåìûìè ðàêåòàìè, ïîìèìî ìåòåîðîëîãè÷å-
ñêèõ ôàêòîðîâ (è ïðåæäå âñåãî âåòðà) îòíîñÿò ýêñöåíòðèñèòåò òÿãè.
Ýêñöåíòðèñèòåò òÿãè îïðåäåëÿåòñÿ âåëè÷èíîé ëèíåéíîãî ñìåùå-
íèÿ òî÷êè ïåðåñå÷åíèÿ âåêòîðà òÿãè ñ ïëîñêîñòüþ âûõîäíîãî ñå÷å-
412
íèÿ ñîïëà îòíîñèòåëüíî ïðîäîëüíîé îñè ðàêåòû è óãëîì îòêëîíå-
íèÿ âåêòîðà òÿãè îò ïðîäîëüíîé îñè [37].
Äëÿ ó÷åòà âëèÿíèÿ âîçìóùåíèÿ òðàåêòîðèè, âûçâàííîãî ýêñöåí-
òðèñèòåòîì òÿãè, â îáùèå óðàâíåíèÿ ïðîñòðàíñòâåííîãî äâèæåíèÿ
öåíòðà ìàññ ðàêåòû ââåäåì ñëàãàåìûå òÿãè, îáóñëîâëåííûå íåïàðàë-
ëåëüíîñòüþ âåêòîðà òÿãè ïðîäîëüíîé îñè ðàêåòû.
Óãîë φ1 îïðåäåëÿåò â ñâÿçàííîé ñèñòåìå êîîðäèíàò ïîëîæåíèå
ïëîñêîñòè äåéñòâèÿ ñîñòàâëÿþùåé òÿãè, íîðìàëüíîé ê îñè ñíàðÿäà
Ðn; óãîë φ2 – ïîëîæåíèå ïëîñêîñòè äåéñòâèÿ ìîìåíòà òÿãè îò ëèíåé-
íîãî ýêñöåíòðèñèòåòà; ðàçìåð xò âäîëü ïðîäîëüíîé îñè – ðàññòîÿíèå
îò öåíòðà ìàññ ñíàðÿäà äî ïëîñêîñòè, âêëþ÷àþùåé òî÷êó ïðèëîæå-
íèÿ òÿãè. Ñîñòàâëÿþùèå òÿãè ïî îñÿì ñâÿçàííîé ñèñòåìû êîîðäè-
íàò áóäóò èìåòü âèä
PP PP
PP
xy
z
==
=
cos ;
sin cos ;
sin sin .
εε
φε
φ
11
(8.116)
Ââåäÿ ñèñòåìó êîîðäèíàò OX Y Z
′′′
, íå ó÷àñòâóþùóþ â ñîáñòâåííîì
âðàùåíèè ñíàðÿäà (íà ðèñ. 8.15 γ
–
óãîë ñîáñòâåííîãî âðàùåíèÿ),
íàéäåì ïðîåêöèè òÿãè íà îñè ýòîé ñèñòåìû:
P
P
P
x
y
z
′
′
′
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
100
0
0
cos
sin
sin
cos
γγ
γγ
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
P
P
P
x
y
z
.
(8.117)
413
Ðèñ. 8.15. Ñõåìà îðèåíòàöèè âåêòîðà òÿãè ïðè ëèíåéíîì ýêñöåíòðèñèòåòå d è óãëå
ïîâîðîòà ξ
Çàïèñûâàÿ ïîýëåìåíòíî, íàéäåì
PP
PP
P
P
x
y
′
′
=
=−=
=
cos ;
sin cos cos
sin sin sin
sin
ε
εφγ
εφγ
ε
11
cos(
);
sin cos sin
sin sin cos
sin
φγ
εφγ
εφγ
ε
1
11
+
=+=
=
′
PP
P
P
z
sin(
).
φγ
1+
(8.118)
Èñïîëüçóÿ ìàòðèöó ïåðåõîäà îò OX Y Z
′′ ′ê òðàåêòîðíîé ñèñòåìå
êîîðäèíàò, íàéäåì ïðîåêöèþ òÿãè íà îñè ïîñëåäíåé:
P
P
P
x
y
z
ê
ê
ê
êê
êêê
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
−
cos cos
sin cos
sin
sin
αβ
αββ
αêê
êê
êê
ê
cos
cos sin
sin
sin
cos
α
αβαββ
0
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
′
′
P
P
P
x
y
′
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥z
,
(8.119)
ãäå óãëû αê è βê îïðåäåëÿþò îðèåíòàöèþ çåìíîé ñêîðîñòè Vê
îòíîñèòåëüíî ñèñòåìû êîîðäèíàò OX Y Z
′′′
. Çàïèñûâàÿ ïîýëåìåíòíî,
ïîëó÷èì
PP
P
P
xê
êê
êê
=−
+
++
cos cos cos
sin cos(
) sin cos
sin
εαβ
εφ
γαβ
1
εφγ β
εα
εφγα
sin(
)sin ;
cos sin
sin cos(
) cos
1
1
+
=++
ê
êê
ê
PP
P
y
;
cos cos sin
sin cos(
)sin sin
s
PP
P
P
zê
êê
êê
=−
+
+
++
εαβ
εφ
γαβ
1
in sin(
)cos .
εφγ β
1+
ê
8.4 .2. ÌÀÒÅÌÀÒÈ×ÅÑÊÀß ÌÎÄÅËÜ ÏÐÎÑÒÐÀÍÑÒÂÅÍÍÎÃÎ
ÂÎÇÌÓÙÅÍÍÎÃÎ ÄÂÈÆÅÍÈß ÍÅÓÏÐÀÂËßÅÌÎÉ ÐÀÊÅÒÛ
Ñ öåëüþ óïðîùåíèÿ îáùåé ñèñòåìû óðàâíåíèé ïðåäïîëîæèì,
÷òî âðàùåíèå îñåñèììåòðè÷íîãî ËÀ âîêðóã ñîáñòâåííîé ïðîäîëü-
íîé îñè íå èçìåíÿåò îðèåíòàöèþ â ïðîñòðàíñòâå àýðîäèíàìè÷åñêèõ
ñèë è ìîìåíòîâ; ïðè ýòîì ìîæíî ïðèíÿòü γa = 0. Êðîìå òîãî, ïðè çà-
ïèñè óðàâíåíèé âðàùàòåëüíîãî äâèæåíèÿ îñåñèììåòðè÷íîãî ËÀ öå-
ëåñîîáðàçíî èñïîëüçîâàòü ñèñòåìó êîîðäèíàò OX Y Z
′′′
, îñüOX′ êî-
òîðîé ñîâïàäàåò ñ ïðîäîëüíîé îñüþ ËÀ è êîòîðàÿ íå ó÷àñòâóåò âî
âðàùåíèè îòíîñèòåëüíî ïðîäîëüíîé îñè (ïîëóñâÿçàííóþ ñèñòåìó).
Ââåäåíèå ïîäîáíîé ñèñòåìû íåñêîëüêî óïðîùàåò êèíåìàòè÷åñêèå è
äèíàìè÷åñêèå óðàâíåíèÿ âðàùàòåëüíîãî äâèæåíèÿ.
Âåêòîð óãëîâîé ñêîðîñòè ñíàðÿäà ω ðàñêëàäûâàåòñÿ ïî îñÿì ýòèõ
ñèñòåì êîîðäèíàò ñëåäóþùèì îáðàçîì:
414
ωωωωω ω ω
=++=++
′′′
xyzxyz
.
(8.120)
 ïðîåêöèÿõ íà îñè ñâÿçàííîé ñèñòåìû êîîðäèíàò äèíàìè÷åñêèå
óðàâíåíèÿ âðàùàòåëüíîãî äâèæåíèÿ èìåþò âèä
II
I
M
II
I
M
xx
zyyz
x
i
i
n
yy
x
zxz
y
i
i
•
()
;
•
()
;
ωω
ω
ωω
ω
+−
=
+−
=
=
∑1
=
=
∑
∑
+−
=
1
1
n
zz
yxyx
z
i
i
n
II
I
M
•
()
.
ωω
ω
 ïðèâåäåííûõ óðàâíåíèÿõ ñäåëàåì ïîäñòàíîâêó
ωωγωγ
γ
γ
yy
z
y
i
y
i
i
n
i
n
zi
MM
M
=−
=
+
′′
′
=
=
′
∑
∑
cos
sin ;
cos
sin
1
1
;
cos
sin ;
cos
i
n
zz
y
z
i
z
i
i
n
i
n
MM
M
=
′′
′
=
=
′
∑
∑
∑
=−
=
−
1
1
1
ωωγωγ
γyi
i
n
sin ,γ
=
∑1
(8.121)
ïîñëå ÷åãî, ó÷èòûâàÿ, ÷òî äëÿ îñåñèììåòðè÷íûõ ñíàðÿäîâ Iy = Iz = A,
Ix = C, ïîëó÷èì
CM
AC
M
xx
i
i
n
yx
z
x
zy
i
i
n
•
;
[•(
•
)]
;
ω
ωγ
ω
ωω
ω
=
+−
′
+=
=
′′
′
′
=
∑1
1
∑
∑
′′
′
′
=
+−′
−=
AC
M
zxyx
y
z
i
i
n
[•(
•
)]
.
ωωγ
ωω
ω
1
(8.122)
Êèíåìàòè÷åñêèå óðàâíåíèÿ èìåþò âèä
ωγψθ
ω ωγψθ
ωψθ
ωθ
xx
x
yz
=+
=−=
==
′
′′
••
sin (
••
sin );
•
cos ;
•
.
(8.123)
Ïîäñòàâëÿÿ êèíåìàòè÷åñêèå ñîîòíîøåíèÿ â äèíàìè÷åñêèå óðàâ-
íåíèÿ, ïîëó÷èì
415
CM
AACM
xx
i
i
n
xy
i
i
n
•
;
••
cos
•
•
sin
•
;
ω
ψθψ
θθω
θ
=
−+
=
=
′
=
∑
∑
1
1
2
AA
C
M
xz
i
i
n
••
•
sin cos
•
cos
.
θψ θθω
ψθ
+−
=
′
=
∑
2
1
(8.124)
Ïðè çàïèñè óðàâíåíèé âðàùàòåëüíîãî äâèæåíèÿ â ïðàâûå ÷àñòè
âîéäóò ïðîåêöèè ìîìåíòà òÿãè, âûçâàííîãî ëèíåéíûì è óãëîâûì
ýêñöåíòðèñèòåòîì Ìý. Îïðåäåëèì íåîáõîäèìûå ïðîåêöèè ýòîãî ìî-
ìåíòà Ìýõ, Ìýy, Ìýz. Èç ðèñ. 8 .15 íàéäåì ñîñòàâëÿþùèå ìîìåíòû
ýêñöåíòðèñèòåòà ïî îñÿì ñâÿçàííîé ñèñòåìû êîîðäèíàò OXYZ:
MP
dP
d
MP
dP
x
MP
d
xy
z
yx
z
a
zx
ý
ý
ý
=−
+
=+
=−
cos
sin ;
sin
;
c
φφ
φ
22
2
os
.
φ2−Px
ya
(8.125)
Ïðîåêöèè ìîìåíòîâ M yý ′ è M xý ′ íà ïîëóñâÿçàííûå îñè íàéäåì,
îñóùåñòâèâ ïåðåõîä îò ñâÿçàííîé ñèñòåìû êîîðäèíàò ê
ïîëóñâÿçàííîé:
MMM
MMM
yy
z
zy
z
ýý
ý
ýý
ý
′
′
=−
=+
cos
sin ;
sin
cos .
γγ
γγ
(8.126)
Ïîäñòàâëÿÿ ñþäà âûðàæåíèÿ äëÿ Mýy è Mýz, ïîëó÷èì
MP
d
P
xP
d
Px
yx
z
x
y
ýò
ò
′
=+
++
+=
sin cos
cos
cos sin
sin
φγ
γ
φγ
γ
22
Pd
xP
P
MP
d
P
xz
y
z
x
sin(
)(cos
sin );
sin sin
φγ
γ
γ
φγ
2
2
++
+
=+
′
ò
ý
zx
yx
z
xP
d
Px
Pd
xP
ò
òò
sin
cos cos
cos
cos(
)(
γφ
γ
γφ
γ
−−
−=
−
+
+
2
2
sin
cos ).
γγ
−
Py
(8.127)
Ïîäñòàâëÿÿ â ïîñëåäíèå âûðàæåíèÿ ñîîòíîøåíèÿ (8.116), ïîëó÷èì
MP
d
P
d
Pd
x
ý
=−
+
=
=−
sin cos cos
sin sin sin
sin cos
εφφ
εφφ
ε
12
12
()
;
cos sin(
)
sin sin(
);
φφ
εφγ
εφγ
12
21
+
=+
++
′
′
MP
d
P
x
M
y
z
ýò
ý
=−
+−
+
Pd
Px
cos cos(
)
sin cos(
).
εφγ
εφγ
21
ò
(8.128)
416
Ïîäñòàâëÿÿ â óðàâíåíèÿ ïîñòóïàòåëüíîãî è âðàùàòåëüíîãî äâèæåíèé
íàéäåííûå ïðîåêöèè ñèë è ìîìåíòîâ, ïîëó÷èì ñëåäóþùóþ ñèñòåìó
óðàâíåíèé â âèäå, óäîáíîì äëÿ ðåøåíèÿ íà ÝÂÌ:
1
1
1
)
[ cos cos cos
sin cos(
)
sin co
dV
dtm
PP
ê
êê
ê
=−
+
×
×
εαβ
εφγ
α
s
sin sin(
) sin
{cos cos [cos(
βε
φ
γ
βρ
θθ
êê
++
−
×
×
Pc
V
S
x
a
a
1
2
2
Ψ −−+
×
×−
−
+
−
ψ
ρ
θθ
ψ
θθ
ay
aa
c
V
S
a
)]}
{cos sin [ cos(
)] sin(
1
2
1
2
Ψ
a
za
c
V
Sg
a
)}
cos sin(
)] sin;
+
+−
−
ρ
θψ
θ
2
2
Ψ
2
1
1
2
)
( cos sin
sin cos(
) cos
d
dt mV
PP
c
V
xa
θ
εα
εφγα
ρ
=+
+
−
−
ê
êê
2
1
2
2
S
c
V
S
aa
a
ya
{sin cos [ cos(
)] sin(
)}
{sin
θθ
ψθθ
ρ
−−
+−
+
+
Ψ
θθ
ψ
θθ
ρ
θ
sin [cos(
)]cos(
)}
sin sin(
aa
a
x
c
V
S
a
Ψ
Ψ
−−
+−+
+−
1
2
2
ψθ
a
g
V
)) cos;
−
ê
3
1
1
)
cos
[c
o
sc
o
ss
i
n
sin cos(
)s
d
dt
mV
P
P
Ψ
=−
−
+
++
ê
êê
θ
εαβ
εφγ
in sin
sin sin(
) cos
cos
sin(
αβ
εφγβ
ρ
θ
êê
ê
++
−
−−
P
c
V
S
xa
a
1
2
2
Ψψ
ρ
θ
ψ
ρ
ψ
ay
a
ax
a
c
V
S
c
V
S
a
a
)s
i
n
sin(
)
cos(
)];
)
+×
×−
+
−
2
2
2
2
4
ΨΨ
d
dt
d
dt
C
A
m
V
A
Sl
xz
θ
ω
ω
ωθθω
ωθ
ρ
α
=
=−
+
+
1
1
2
2
2
2
5
2
;
)s
i
n
c
o
sc
o
sα+
417
+−+
−
+
m
V
Sl
Pd
A
Px
A
z
z
ωρ
ωε
φ
γε
φ
γ
2
6
2
12
1
cos cos(
)
sin cos(
);
ò
);
d
dt
ψ
ω
=
2
72
2
2
12
1
2
)
cos
cos
d
dt
C
A
m
VS
A
l
m
V
x
y
y
ω
ωωθ
ωω
θ
ρ
θ
β
ρ
β
β
=−
+
+
+
tg
S
A
l
Pd
A
Px
A
ω
θ
εφγ
θ
εφγ
22
1
8
++
++
cos
cos sin(
) cos sin sin(
);
ò
)s
i
n
;
)s
d
dt
d
dt
m
V
C
Slm
V
C
Sl
Pd
x
x
xx
x
x
γ
ωωθ
ωρ
ρ
ω
ω
=−
=+
−
2
2
2
9
2
in cos(
);
εφφ
12
+
10
11
12
)c
o
s
c
o
s
;
)s
i
n
;
)c
o
dx
dt
V
dy
dt
V
dz
dt
V
c
c
c
=
=
=−
ê
ê
ê
θ
θ
Ψ
ss
in;
) cos cos cos cos cos cos sin cos sin
θ
θψθ
αβθ
α
Ψ
ΨΨ
13
=−
êê
ê
êê
−
−
sin cos sin ;
Ψαβ
14
15
) sin
sin cos cos
cos sin ;
) cos cos cos
θθ
αβθ
α
θψθ
=+
=
êê
ê
a
cos cos cos
sin
cos
sin
sin
cos sin ;
)sin
ψαβ θψα
ψαβ
aa
a
a
−−
−
16
θθα
βθα
=+
sin
cos cos
cos
sin ;
aa
17
22
)(
c
o
s
c
o
s)
(
s
i
n)
(coss
i
n
VV
WVW
V
xy
gg
=−
+
−
+
++
êê
ê
θθ
θ
Ψ
ΨW
VV
W
V
z
ay
a
g
g
);
) arcsin[ ( sin
)];
)
c
2
1
18
19
θθ
ψ
=−
=
−
ê
ê
arctg
os sin
cos cos
;
θ
θ
Ψ
Ψ
+
−
⎛
⎝
⎜⎜
⎞
⎠
⎟⎟
W
VW
z
x
g
g
ê
418
20
21
22
0
0
0
)|
•
|;
)|
•
|;
)|
•
mm md
t
AA Ad
t
CC
t
t
t
t
=−
=−
=−
∫
∫
í
ê
í
ê
Cdt
t
t
|,
í
ê
∫
ãäå tí, tê – çíà÷åíèÿ âðåìåíè äëÿ ìîìåíòîâ âêëþ÷åíèÿ è âûêëþ÷åíèÿ
äâèãàòåëÿ.
Ïðèâåäåííàÿ ñèñòåìà óðàâíåíèé äàåò âîçìîæíîñòü àíàëèçèðî-
âàòü âîçìóùåííîå äâèæåíèå îñåñèììåòðè÷íûõ ñíàðÿäîâ è ðàêåò
ïðè âîçäåéñòâèè ñèñòåìàòè÷åñêîé ñîñòàâëÿþùåé âåòðà, çàäàâàåìîé
òðåìÿ êîìïîíåíòàìè ïî îñÿì ñèñòåìû êîîðäèíàò O0XgYgZg. Ìîäåëè-
ðîâàíèå ïîëåòà ñíàðÿäà íà ÖÂÌ ïî ïðèâåäåííîé ñèñòåìå ïîçâîëÿåò
ïðèáëèæåííî îöåíèâàòü òàêèå îñîáåííîñòè âåòðîâîãî âîçäåéñòâèÿ,
êàê íåëèíåéíóþ çàâèñèìîñòü âåòðîâûõ îòêëîíåíèé âîçìóùåííûõ
òðàåêòîðèé îò íîìèíàëüíîé, ïåðåêðåñòíîå âëèÿíèå ñîñòàâëÿþùèõ
âåòðà íà äâèæåíèå ñíàðÿäà â ïðîäîëüíîé è áîêîâîé ïëîñêîñòÿõ,
ôîðìèðîâàíèå ñëîæíûõ òðàåêòîðèé.
Ãëàâà 9
ÍÀ×ÀËÜÍÛÅ ÓÑËÎÂÈß ÂÎÇÌÓÙÅÍÍÎÃÎ
ÄÂÈÆÅÍÈß ÐÀÊÅÒ È ÑÍÀÐßÄÎÂ
Òèï è íàçíà÷åíèå ËÀ, èõ àýðîäèíàìè÷åñêèå, áàëëèñòè÷åñêèå è æåñòêîñò-
íûå õàðàêòåðèñòèêè, êîíñòðóêöèè ìåòàòåëüíîé èëè ïóñêîâîé óñòàíîâêè è óñ-
ëîâèÿ, ïðè êîòîðûõ âåäåòñÿ ñòðåëüáà èëè ïóñê ðàêåòû, îïðåäåëÿþò íà÷àëüíûå
óñëîâèÿ âîçìóùåííîãî äâèæåíèÿ ðàêåò è ñíàðÿäîâ. Äëÿ íåóïðàâëÿåìûõ ðàêåò è
ñíàðÿäîâ íà÷àëüíûå óñëîâèÿ îäíîçíà÷íî çàäàþò ôîðìó òðàåêòîðèè. Êîëè÷åñò-
âî ïàðàìåòðîâ, êîòîðûå äîëæíû áûòü çàôèêñèðîâàíû â êà÷åñòâå íà÷àëüíûõ
óñëîâèé, îïðåäåëÿåòñÿ âèäîì ìàòåìàòè÷åñêîé ìîäåëè, òî÷íåå, êîëè÷åñòâîì
ôàçîâûõ êîîðäèíàò, îïðåäåëÿþùèõ ñîñòîÿíèå ËÀ â ðàìêàõ ðàññìàòðèâàåìîé
ïîñòàíîâêè çàäà÷è. Ñ òî÷êè çðåíèÿ ðåøåíèÿ çàäà÷ âíåøíåé áàëëèñòèêè íà÷àëü-
íûå óñëîâèÿ äîëæíû áûòü óñòàíîâëåíû äëÿ ìîìåíòà ïîòåðè ñèëîâîé ñâÿçè íå-
óïðàâëÿåìîé ðàêåòû ñ ïóñêîâîé óñòàíîâêîé ëèáî äëÿ ìîìåíòà ïðåêðàùåíèÿ ñè-
ëîâîãî âîçäåéñòâèÿ èñòåêàþùèõ èç êàíàëà ñòâîëà ãàçîâ íà ïîêèäàþùèé åãî àð-
òèëëåðèéñêèé ñíàðÿä.
419
9.1. ÂËÈßÍÈÅ ÄÂÈÆÅÍÈß ÍÎÑÈÒÅËß ÂÎÎÐÓÆÅÍÈß
ÍÀ ÍÀ×ÀËÜÍÛÅ ÓÑËÎÂÈß ÂÛÑÒÐÅËÀ
9.1.1. ÎÏÐÅÄÅËÅÍÈÅ ÑÓÌÌÀÐÍÎÉ ÍÀ×ÀËÜÍÎÉ ÑÊÎÐÎÑÒÈ
Äâèæåíèå íîñèòåëÿ âîîðóæåíèÿ êàê òâåðäîãî òåëà ìîæíî ðàçäåëèòü
íà ïåðåìåùåíèå åãî öåíòðà ìàññ è êîëåáàíèå îòíîñèòåëüíî öåíòðà
ìàññ. Ïåðåìåùåíèå öåíòðà ìàññ îïðåäåëÿåòñÿ äâóìÿ äâèæåíèÿìè – îñ -
íîâíûì äâèæåíèåì íîñèòåëÿ âîîðóæåíèÿ ïîä äåéñòâèåì äâèæèòåëåé è
êîëåáàòåëüíûì äâèæåíèåì öåíòðà ìàññ ïîä âîçäåéñòâèåì âîçìóùåííîé
ñðåäû (íàïðèìåð, êà÷êè êîðàáëÿ, âûçûâàåìîé âîëíåíèÿìè ìîðÿ).
Ñóììàðíàÿ íà÷àëüíàÿ ñêîðîñòü ñíàðÿäà â çåìíîé ñèñòåìå êîîð-
äèíàò áåç ó÷åòà âëèÿíèÿ âðàùåíèÿ Çåìëè ðàâíà
VV VV
00
=++
r
íä
,
(9.1)
ãäå V0r – ñêîðîñòü ñíàðÿäà îòíîñèòåëüíî ìåòàòåëüíîé óñòàíîâêè â
ìîìåíò ïîòåðè ñèëîâîé ñâÿçè ñ íàïðàâëÿþùèìè ïîñëåäíåé (äëÿ
ñíàðÿäà àðòèëëåðèéñêîãî îðóäèÿ – äóëüíàÿ ñêîðîñòü); Ví – ñêîðîñòü
õîäà íîñèòåëÿ âîîðóæåíèÿ (êîðàáëÿ, òàíêà, ñàìîëåòà); Vä – äîïîëíè-
òåëüíàÿ íà÷àëüíàÿ ñêîðîñòü, âûçâàííàÿ âîçìóùåíèåì ñðåäû, â êîòî-
ðîé äâèæåòñÿ íîñèòåëü (íàïðèìåð, êà÷êà êîðàáëÿ-ðàêåòîíîñèòåëÿ).
Íàèáîëüøèå òðóäíîñòè âñòðå÷àþòñÿ ïðè îïðåäåëåíèè Vä. Åñëè
íå ó÷èòûâàòü âëèÿíèå ñðåäû è ñ÷èòàòü Vä = 0, òî çíà÷åíèå ñêîðîñòè
ðàêåòû (ñíàðÿäà) ïî ìîäóëþ è íàïðàâëåíèþ â çåìíîé ñèñòåìå êîîð-
äèíàò îïðåäåëÿåòñÿ ñëåäóþùèì îáðàçîì. Ñîâìåñòèì íà÷àëî çåìíîé
ñèñòåìû êîîðäèíàò ñ öåíòðîì ìàññ íîñèòåëÿ è íàïðàâèì îñü Î0Xg
òàê, ÷òîáû îíà ñîâïàëà ñ âåêòîðîì ñêîðîñòè Ví (ðèñ. 9 .1). Íàïðàâëå-
420
Ðèñ. 9 .1. Êóðñîâîé óãîë,
íà÷àëüíàÿ ñêîðîñòü è óãîë
áðîñàíèÿ, ïîëó÷åííûå ñ
ó÷åòîì ñêîðîñòè íîñèòåëÿ
íèå âåêòîðà ñêîðîñòè äâèæåíèÿ öåíòðà ìàññ ñíàðÿäà ïî îòíîøåíèþ
ê íîñèòåëþ V0r çàäàäèì óãëîì áðîñàíèÿ â îòíîñèòåëüíîì äâèæåíèè
θ0r è êóðñîâûì óãëîì ñòðåëüáû qr c [79]. Òîãäà, èìåÿ â âèäó, ÷òî Ví –
ñêîðîñòü ïåðåíîñíîãî äâèæåíèÿ, ïîëó÷èì äëÿ ïðîåêöèé ñêîðîñòè
ñíàðÿäà íà îñè çåìíîé ñèñòåìû êîîðäèíàò âûðàæåíèÿ
VV
qV
VV VV
xrrr
yrr
zr
g
gg
000
000
00
=+
==
−
cos cos
;
sin ;
co
θ
θ
cí
ss
i
n.
θ0rr
qc
(9.2)
Ìîäóëü ñêîðîñòè ñíàðÿäà â àáñîëþòíîì äâèæåíèè ðàâåí
VVVV
xyz
ggg
00
2
0
2
0
2
=+
+
.
Ïîäñòàâëÿÿ ñþäà ðàâåíñòâà (9.2), ïîëó÷èì ïîñëå ïðåîáðàçîâàíèé
VVV
V
qVV
rr
r
r
r
00
0
1
0
2
0
2
12
=+
+
−−
íc
í
cos cos
.
θ
(9.3)
Êóðñîâîé óãîë ñòðåëüáû â àáñîëþòíîì äâèæåíèè
q
Vq
Vq
V
rrr
rrr
c
c
cí
arctg
=
+
⎛
⎝⎜
⎞
⎠⎟
00
00
cos
sin
cos cos
.
θ
θ
(9.4)
Óãîë áðîñàíèÿ â àáñîëþòíîì äâèæåíèè
θ
θ
0
00
0
=
+
⎛
⎝⎜
⎞
⎠⎟
arccos
cos cos
cos
.
Vq
V
Vq
rrr
cí
c
(9.5)
Òðè ïîñëåäíèå ôîðìóëû ïîëó÷åíû â ïðåäïîëîæåíèè, ÷òî ñíà-
ðÿä – ìàòåðèàëüíàÿ òî÷êà.
9.1 .2. ÂËÈßÍÈÅ ÊÎËÅÁÀÍÈÉ ÍÎÑÈÒÅËß ÍÀ ÔÎÐÌÈÐÎÂÀÍÈÅ
ÍÀ×ÀËÜÍÛÕ ÓÑËÎÂÈÉ ÏÓÑÊÀ ÐÀÊÅÒÛ
Äëÿ îïðåäåëåíèÿ íà÷àëüíîãî ïîëîæåíèÿ ðàêåòû îòíîñèòåëüíî
Çåìëè íåîáõîäèìî ó÷åñòü âëèÿíèå êîëåáàíèé íîñèòåëÿ ðàêåòíî-àð-
òèëëåðèéñêîãî âîîðóæåíèÿ è ïóñêîâîé óñòàíîâêè.
Ðàññìîòðèì âëèÿíèå êîëåáàíèé íîñèòåëÿ îòíîñèòåëüíî öåíòðà
ìàññ íà èçìåíåíèå ïàðàìåòðîâ äâèæåíèÿ ðàêåòû ïðè ñõîäå ñ íà-
ïðàâëÿþùèõ ïóñêîâîé óñòàíîâêè. Èñïîëüçóåì ïÿòü ñèñòåì êîîðäè-
íàò (ðèñ. 9 .2). Êîëåáàíèå íîñèòåëÿ âîîðóæåíèÿ áóäåì ðàññìàòðèâàòü
îòíîñèòåëüíî çåìíîé ñèñòåìû êîîðäèíàò O0XgYgZg. Íà÷àëî ñèñòåìû
421
êîîðäèíàò OíÕíYíZí, æåñòêî ñâÿçàííîé ñ íîñèòåëåì, ïîìåñòèì â
öåíòðå ìàññ íîñèòåëÿ Îí. Ïîâîðîò ñèñòåìû êîîðäèíàò ÎíXíYíZí îò-
íîñèòåëüíî ñèñòåìû O0XgYgZg áóäåì îïðåäåëÿòü òðåìÿ óãëàìè: â ãî-
ðèçîíòàëüíîé ïëîñêîñòè – óãëîì ψí; â âåðòèêàëüíîé ïëîñêîñòè –
óãëîì φí; ïîâîðîò îòíîñèòåëüíî îñè OíÕí – óãëîì γí .  öåíòðå êà÷à-
íèÿ ïóñêîâîé óñòàíîâêè Îï ïîìåñòèì íà÷àëà äâóõ ñèñòåì êîîðäè-
íàò: ñèñòåìû êîîðäèíàò ÎïÕí1Yí1Zí1, æåñòêî ñâÿçàííîé ñ íîñèòåëåì,
è ñèñòåìû êîîðäèíàò, ñâÿçàííîé ñ ïóñêîâîé óñòàíîâêîé.
Îñè êîîðäèíàò ÎïÕí1Yí1Zí1 êîëëèíåàðíû îñÿì ÎíÕíYíZí. Ïîâîðîò
ïóñêîâîé óñòàíîâêè îòíîñèòåëüíî íîñèòåëÿ îïðåäåëÿåòñÿ äâóìÿ óã-
ëàìè: êóðñîâûì óãëîì ñòðåëüáû qr ñ ìåæäó îñÿìè ÎïÕí1 è ÎïÕï1 èóã-
ëîì φï, õàðàêòåðèçóþùèì íàêëîí ïóñêîâîé óñòàíîâêè ê ïëîñêîñòè
îñåé ÎïÕí1 è ÎïÕï1, æåñòêî ñâÿçàííîé ñ íîñèòåëåì. Ïÿòîé ñèñòåìîé
êîîðäèíàò ÿâëÿåòñÿ ñèñòåìà OXYZ, ñâÿçàííàÿ ñ ðàêåòîé; â ìîìåíò
ñõîäà ðàêåòû ñ íàïðàâëÿþùèõ îñü ÎÕ ýòîé ñèñòåìû (ò.å . ïðîäîëüíàÿ
îñü ðàêåòû) ëåæèò â ïëîñêîñòè ñòðåëüáû.
Óãëû òàíãàæà, ðûñêàíèÿ è êðåíà ðàêåòû â ìîìåíò ïîòåðè ñèëî-
âîé ñâÿçè ñ íàïðàâëÿþùèìè íåñòàáèëèçèðîâàííîé ïóñêîâîé óñòà-
íîâêè ìîãóò áûòü íàéäåíû äëÿ äâóõ ïîëîæåíèé íîñèòåëÿ: ïðè íóëå-
âûõ çíà÷åíèÿõ óãëîâ ïîâîðîòà ñèñòåìû êîîðäèíàò ÎíÕíYíZí, ñâÿçàí-
íîé ñ íîñèòåëåì, îòíîñèòåëüíî çåìíîé ñèñòåìû (ψí = φ í = γí =0)è
422
Ðèñ. 9.2. Ñõåìà èñïîëüçóåìûõ ñèñòåì êîîðäèíàò äëÿ ñëó÷àÿ ñòàðòà ðàêåòû ñ íåñòà-
áèëèçèðîâàííîé ïóñêîâîé óñòàíîâêè äâèæóùåãîñÿ íîñèòåëÿ
äëÿ óãëîâ ïîâîðîòà, îòëè÷íûõ îò íóëÿ (ò.å . äëÿ ñëó÷àÿ ψí ≠ 0, φ í ≠ 0è
γí ≠ 0). Ðàçíîñòè çíà÷åíèé óêàçàííûõ óãëîâ áóäóò îïðåäåëÿòü ñòå-
ïåíü âëèÿíèÿ êîëåáàíèÿ íîñèòåëÿ íà óãëîâîå ïîëîæåíèå ðàêåòû îò-
íîñèòåëüíî çåìíîé ñèñòåìû êîîðäèíàò.
Åñëè íå ó÷èòûâàòü óïðóãèõ êîëåáàíèé êîíñòðóêöèé íîñèòåëÿ è
ïóñêîâîé óñòàíîâêè, à òàêæå âîçìóùåíèé ðàêåòû â ìîìåíò åå ñõîäà
ñ íàïðàâëÿþùèõ, òî, ïîëüçóÿñü òàáëèöåé ïåðåõîäíûõ êîñèíóñîâ îò
çåìíîé ñèñòåìû êîîðäèíàò ê ñèñòåìå êîîðäèíàò, ñâÿçàííîé ñ íîñè-
òåëåì, ïîëó÷èì óðàâíåíèÿ äëÿ îïðåäåëåíèÿ îòêëîíåíèé óãëîâ òàí-
ãàæà, ðûñêàíèÿ è êðåíà ðàêåòû â ìîìåíò ñòàðòà â çàâèñèìîñòè îò óã-
ëîâ êîëåáàíèÿ íîñèòåëÿ.
Äëÿ ñëó÷àÿ ψí = φí = γí = 0 è ïðèíÿòûõ äîïóùåíèé â ìîìåíò ñõî-
äà ðàêåòû ñ íàïðàâëÿþùèõ áóäåì, î÷åâèäíî, èìåòü θ0 = φ ï, ψ0 = qr c
(îò íàïðàâëåíèÿ ÎïÕí)èγ =0
.
 äðóãîì ñëó÷àå, ïðè ψí ≠ 0; φí ≠ 0èγí ≠ 0, ðàêåòà ñîéäåò ñ íàïðàâ-
ëÿþùèõ ïîä óãëàìè ψ, θ è γ. Ñðàâíèâàÿ, ñëåäóÿ [33], ýëåìåíòû ïåðå-
õîäà â ìîìåíò ñòàðòà ðàêåòû îò ñèñòåìû êîîðäèíàò O0XgYgZg ê ñèñòå-
ìå OXYZ ïî óãëàì ψí, φí, γí, φï è qr c è ýëåìåíòû ïåðåõîäà íåïîñðåä-
ñòâåííî îò çåìíîé ñèñòåìû O0XgYgZg ê ñèñòåìå OXYZ ïî óãëàì θ, ψ è
γ, ïîëó÷èì óðàâíåíèÿ äëÿ îïðåäåëåíèÿ îòêëîíåíèé óãëîâ òàíãàæà,
ðûñêàíèÿ è êðåíà ðàêåòû â çàâèñèìîñòè îò óãëîâ êîëåáàíèÿ íîñèòå-
ëÿ [33]. Ïðèíèìàÿ âñëåäñòâèå ìàëîñòè óãëîâ sinψí ≈ψí,
sin
, sin
, cos
cos
cos
,
φφγγψφγ
íí íí
í
í
í
≈≈≈
≈
≈
1
ïîëó÷èì
∆ψ
ψγ
φ
φφψ
=
−+
+
−+
arctg
tg
tg
íc
í
í
c
cíí í
cos
sin
cos
sin
qq
q
rr
r
q
q
r
r
c
c
⎛
⎝⎜
⎞
⎠⎟− ;
(9.6)
∆θ
φ
φ
φγ
φ
φ
=+
−
−
arcsin( cos
cos
sin
cossin);
ícï ï
íïc
ï
qq
rr
(9.7)
∆γ
φγ
φφφ
γφ
=
+
−−
−
arctg
tg
tg
ící
íï
ï
c
íï
q
qq
r
r
sin
cos
cos
sin
1
rc
⎛
⎝⎜
⎞
⎠⎟. (9.8)
Ïðîåêöèè âåêòîðà óãëîâîé ñêîðîñòè íîñèòåëÿ îòíîñèòåëüíî çåì-
íîé ñèñòåìû êîîðäèíàò íà ñâÿçàííûå ñ íèì êîîðäèíàòíûå îñè çà-
ïèøåì â âèäå
ωψ φγ
ωψφγφγ
ω
x
y
z
í
í
í
íí
í
ííí
íí
=+
=+
=−
•
sin
•
;
•
cos cos
•
sin ;
•
ψφγφγ
ííí
íí
cos sin
•
cos .
+
(9.9)
423
Òàê êàê ìû ðàññìàòðèâàåì íîñèòåëü è ïóñêîâóþ óñòàíîâêó êàê
æåñòêèå è æåñòêî ñâÿçàííûå òåëà, òî âåêòîð ìãíîâåííîé óãëîâîé
ñêîðîñòè íàïðàâëÿþùèõ ïóñêîâîé óñòàíîâêè áóäåò ñîâïàäàòü ñ âåê-
òîðîì ìãíîâåííîé óãëîâîé ñêîðîñòè íîñèòåëÿ.
Åñëè ââåñòè äîïóùåíèå, ÷òî ðàêåòà ïðè äâèæåíèè ïî íàïðàâëÿþ-
ùèì ïóñêîâîé óñòàíîâêè ïîëíîñòüþ âîñïðèíèìàåò óãëîâûå ïåðåìå-
ùåíèÿ íàïðàâëÿþùèõ, ÷òî ñîîòâåòñòâóåò æåñòêîé ñâÿçè ìåæäó
íèìè, òî âåêòîð ìãíîâåííîé óãëîâîé ñêîðîñòè ðàêåòû áóäåò ðàâåí
âåêòîðó ìãíîâåííîé óãëîâîé ñêîðîñòè íàïðàâëÿþùèõ. Èñõîäÿ èç
ñêàçàííîãî, ìîæíî ëåãêî íàéòè ïðîåêöèè âåêòîðà ìãíîâåííîé óãëî-
âîé ñêîðîñòè ðàêåòû, îáóñëîâëåííîé äâèæåíèåì íîñèòåëÿ, íà îñè
ñâÿçàííîé ñ ðàêåòîé ñèñòåìû êîîðäèíàò OXYZ. Ó÷èòûâàÿ çàâèñèìî-
ñòè (9.9), à òàêæå íàïðàâëÿþùèå êîñèíóñû ïåðåõîäà îò ñèñòåìû êî-
îðäèíàò ÎíÕíYíZí ê ñèñòåìå êîîðäèíàò OXYZ, áóäåì èìåòü
ωω
ωφωφ
ωω
xx
ry
z
r
yx
qq
q
=+
+
=−
íí
í
í
ïc
ï
ïc
cos cos
sin
cos sin ;
sin cos
cos
sin
sin ;
sin
φω
φ
ω
φ
ωω
ω
ïc
ï
ïc
ñ
íí
í
qq
q
ry
z
r
zxr
+−
=−
+zr
q
í
c
cos .
(9.10)
Ïîëó÷åííûå óðàâíåíèÿ ïîçâîëÿþò îïðåäåëèòü óãëîâûå ñêîðîñòè
ðàêåòû â ìîìåíò ñòàðòà ñ íåñòàáèëèçèðîâàííîé ïóñêîâîé óñòàíîâ-
êè, êîëåáëþùåéñÿ âìåñòå ñ íîñèòåëåì (áåç ó÷åòà âîçìóùåíèé ïðè
ñõîäå).
Ðàññìîòðèì âîçìóùåíèÿ ðàêåòû ïðè ñõîäå ñ íàïðàâëÿþùèõ ñòà-
áèëèçèðîâàííîé ïóñêîâîé óñòàíîâêè, îáóñëîâëåííûå òîëüêî äâè-
æåíèåì íîñèòåëÿ. Àâòîìàò óãëîâîé ñòàáèëèçàöèè ïóñêîâîé óñòàíîâ-
êè îáåñïå÷èâàåò ïîñòîÿíñòâî óãëîâîãî ïîëîæåíèÿ íàïðàâëÿþùèõ ñ
ðàêåòîé â ïðîñòðàíñòâå. Îäíàêî ðàêåòà áóäåò èìåòü íà÷àëüíûå âîç-
ìóùåíèÿ ïî ïîëîæåíèþ öåíòðà ìàññ è ñêîðîñòè äâèæåíèÿ ïðè ñòàð-
òå, îïðåäåëÿåìûå äâèæåíèåì íîñèòåëÿ, íåðàâíîìåðíîñòüþ õîäà,
ïðîñòðàíñòâåííûìè ïåðåìåùåíèÿìè åãî öåíòðà ìàññ è êîëåáàíèåì
íîñèòåëÿ îòíîñèòåëüíî öåíòðà ìàññ. Íåîáõîäèìûå ñèñòåìû êîîðäè-
íàò ïîêàçàíû íà ðèñ. 9.3 . Íåïîäâèæíûå (çåìíûå) êîîðäèíàòû îáî-
çíà÷èì Î0XgYgZg è íàïðàâèì îñü Î0Xg êîëëèíåàðíî âåêòîðó ñêîðîñòè
íîñèòåëÿ Ví; êîîðäèíàòû, æåñòêî ñâÿçàííûå ñ íîñèòåëåì, îáîçíà-
÷èì ïî-ïðåæíåìó ÎíÕíY íZí . Ââåäåì òðè âñïîìîãàòåëüíûå ñèñòåìû
êîîðäèíàò OíÕg1Yg1Zg1, ÎïXg2Yg2Zg2 è OXg3Yg3Zg3, îñè êîòîðûõ íàïðà-
âèì êîëëèíåàðíî ñîîòâåòñòâóþùèì îñÿì îñíîâíîé çåìíîé ñèñòåìû
êîîðäèíàò, à íà÷àëà ïîìåñòèì: Îí – â öåíòð ìàññ íîñèòåëÿ; Îï –â
óñëîâíûé öåíòð êà÷àíèÿ ïóñêîâîé óñòàíîâêè; Î – â òî÷êó, ñîâïà-
äàþùóþ ñ öåíòðîì ìàññ ðàêåòû â ìîìåíò åå ñõîäà ñ íàïðàâëÿþùèõ
ïóñêîâîé óñòàíîâêè.
424
Îñè ñèñòåìû êîîðäèíàò ÎíÕíYíZí ïîâåðíóòû îòíîñèòåëüíî ñèñ-
òåìû êîîðäèíàò OíÕg1Yg1Zg1 íà óãëû φí, ψí è γí , îïðåäåëÿþùèå êîëå-
áàíèÿ íîñèòåëÿ âîîðóæåíèÿ îòíîñèòåëüíî öåíòðà ìàññ. Ââåäåì åùå
ñèñòåìó êîîðäèíàò OXYZ, íà÷àëî êîòîðîé ïîìåñòèì â òî÷êó Î. Îñü
ÎÕ íàïðàâèì ïî ïðîäîëüíîé îñè ðàêåòû, îñü OY ðàñïîëîæèì â
ïëîñêîñòè ñòðåëüáû, à îñü OZ áóäåò äîïîëíÿòü ñèñòåìó äî ïðàâîé.
Òàê êàê ïóñêîâàÿ óñòàíîâêà ñòàáèëèçèðîâàíà, òî ïðè ïðèíÿòîì äî-
ïóùåíèè íàïðàâëåíèå îñåé ñèñòåìû êîîðäèíàò OXYZ íåèçìåííî â
ïðîñòðàíñòâå è ïëîñêîñòü ñòðåëüáû ñîâïàäàåò ñ êîîðäèíàòíîé ïëîñ-
êîñòüþ OXY. Óãîë íàïðàâëåíèÿ ñòðåëüáû è óãîë âîçâûøåíèÿ íà-
ïðàâëÿþùèõ ïóñêîâîé óñòàíîâêè îáîçíà÷èì ÷åðåç ψ0 è φ0 (ñì.
ðèñ. 9 .3). Íå ðàññìàòðèâàÿ âîçìóùåíèÿ ðàêåòû ïðè ñõîäå ñ íàïðàâ-
ëÿþùèõ, áóäåì ñ÷èòàòü, ÷òî íà÷àëüíûé óãîë òàíãàæà θ0 = φ0. Äëÿ
óäîáñòâà ââåäåì åùå îäíó âñïîìîãàòåëüíóþ ñèñòåìó êîîðäèíàò
Î0XYZ, îñè êîòîðîé êîëëèíåàðíû ñîîòâåòñòâóþùèì îñÿì ñèñòåìû
êîîðäèíàò OXYZ, è ðàäèóñ-âåêòîðû: rí, ïðîâåäåííûé èç íà÷àëà çåì-
íîé ñèñòåìû êîîðäèíàò â öåíòð ìàññ íîñèòåëÿ; rï, ïðîâåäåííûé èç
öåíòðà ìàññ íîñèòåëÿ â óñëîâíûé öåíòð êà÷àíèÿ ïóñêîâîé óñòàíîâ-
êè; rð, ïðîâåäåííûé èç öåíòðà êà÷àíèÿ ïóñêîâîé óñòàíîâêè â òî÷êó,
çàíèìàåìóþ öåíòðîì ìàññ ðàêåòû â ìîìåíò åå ñõîäà ñ íàïðàâëÿþ-
ùèõ. Â ïðîöåññå äâèæåíèÿ íîñèòåëÿ âîîðóæåíèÿ rí èçìåíÿåòñÿ ïî
425
Ðèñ. 9.3 . Ñèñòåìà âçàèìíîãî ðàñïîëîæåíèÿ ñèñòåì êîîðäèíàò äëÿ ñëó÷àÿ ñòàðòà ðà-
êåòû ñî ñòàáèëèçèðîâàííîé ïóñêîâîé óñòàíîâêè
ìîäóëþ è íàïðàâëåíèþ, rï èçìåíÿåòñÿ òîëüêî ïî íàïðàâëåíèþ; rð
ïîñòîÿíåí ïî âåëè÷èíå (åñëè íå ó÷èòûâàòü ðàçáðîñ âðåìåíè äâèæå-
íèÿ ðàêåòû ïî íàïðàâëÿþùèì äî ïîòåðè ñ íèìè ñèëîâîãî âçàèìî-
äåéñòâèÿ) è íå èçìåíÿåò ñâîåãî íàïðàâëåíèÿ â ïðîñòðàíñòâå.
Îáîçíà÷èì ÷åðåç V0
*
è V0 âåêòîðû ñêîðîñòè äâèæåíèÿ öåíòðà
ìàññ ðàêåòû (îòíîñèòåëüíî Çåìëè) â ìîìåíò åå ñõîäà ñ íàïðàâëÿþ-
ùèõ ñîîòâåòñòâåííî ïðè äâèæóùåìñÿ è ïðè íåïîäâèæíîì íîñèòå-
ëÿõ; Vx 0
*
, Vy0
*
, Vz0
*
–
ïðîåêöèè V0
*
íà îñè ñèñòåìû êîîðäèíàò Î0XYZ.
Îòêëîíåíèÿ ñêîðîñòè ðàêåòû, îïðåäåëÿåìûå äâèæåíèåì íîñèòå-
ëÿ, ðàâíû
∆∆
∆
VVVVV VV
xx
yy zz
000 00 00
=−
=
=
**
*
;;.(9.11)
Ó÷èòûâàÿ ðèñ. 9.3 è îãîâîðåííûå óñëîâèÿ, èìååì
VVV
rrV
00
*
()
[
()
]
.
=+ +×++
ííí
ï
p
∆ω
(9.12)
Çäåñü Ví – âåêòîð ñêîðîñòè íåâîçìóùåííîãî äâèæåíèÿ öåíòðà ìàññ
íîñèòåëÿ; ∆Ví – âåêòîð äîáàâî÷íîé ñêîðîñòè ïîñòóïàòåëüíîãî
äâèæåíèÿ öåíòðà ìàññ íîñèòåëÿ, âûçâàííîé íåðàâíîìåðíîñòüþ åãî
äâèæåíèÿ; ωí – âåêòîð óãëîâîé ñêîðîñòè íîñèòåëÿ îòíîñèòåëüíî
öåíòðà ìàññ.
Ðàäèóñ-âåêòîð rð êàê âåëè÷èíó, ìàëóþ ïî ñðàâíåíèþ ñ ðàäèóñîì
rï, â äàëüíåéøåì ó÷èòûâàòü íå áóäåì.
Ïðåäñòàâèì âåêòîð ñêîðîñòè Ví êàê VV
x
íí
=
g
o
, à äîáàâî÷íóþ ñêî-
ðîñòü – êàê ∆Vxyz
í
=++
•••
,
xyz
ggg
ooo
ãäå ÷åðåç •
,
x•
,
y •z îáîçíà÷åíû ïðî-
åêöèè âåêòîðà ∆Ví íà îñè çåìíîé ñèñòåìû êîîðäèíàò O0XgYgZg.
Çàïèøåì (9.12) â ðàçâåðíóòîé ôîðìå:
Vx
y
z
xyz
0
*
(•)
••
=+ +++
Vxyz
x
ggg xyz
í
ííí
ííí
ï
ííí
ooo
ooo
ωωω
.í
ï.í
ï.í
yz
V
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
+0x
o
,
(9.13)
âûðàçèâ âåêòîðû ωí è rí ÷åðåç èõ ïðîåêöèè íà îñè ñèñòåìû êîîðäèíàò
ÎíÕíYíZí.
Èñïîëüçóÿ êîñèíóñû óãëîâ ïåðåõîäà îò îñåé êîîðäèíàò O0XgYgZg ê
ñèñòåìå O0XYZ, à òàêæå êîñèíóñû óãëîâ ïåðåõîäà îò îñåé ñèñòåìû
êîîðäèíàò ÎíÕíY íZí ê ñèñòåìå êîîðäèíàò Î0XYZ, íåòðóäíî ïîëó÷èòü
[33] ïðîåêöèè âåêòîðíîãî ðàâåíñòâà (9.13) íà îñè êîîðäèíàò Î0XYZ.
Äëÿ îòûñêàíèÿ ôîðìóë, îïðåäåëÿþùèõ èçìåíåíèÿ ìîäóëÿ ñêî-
ðîñòè, óãëîâ àòàêè è ñêîëüæåíèÿ, õàðàêòåðèçóåìûõ äâèæåíèåì íî-
ñèòåëÿ â ìîìåíò ñõîäà ðàêåòû ñ íàïðàâëÿþùèõ ñòàáèëèçèðîâàííîé
426
ïóñêîâîé óñòàíîâêè, áóäåì ñ÷èòàòü, ÷òî ñòðåëüáà ïðîèçâîäèòñÿ ïðè
áåçâåòðèè; â ìîìåíò ñõîäà ðàêåòû ñ íàïðàâëÿþùèõ ïëîñêîñòü åå
ñèììåòðèè Ñ âåðòèêàëüíà è ñîâïàäàåò ñ ïëîñêîñòüþ ñèñòåìû êîîð-
äèíàò Î0XY. Ïðè äâèæåíèè íîñèòåëÿ ïðîäîëüíàÿ îñü ÎÕ ðàêåòû â
ìîìåíò ñõîäà ñ íàïðàâëÿþùèõ áóäåò ñîâïàäàòü ïî íàïðàâëåíèþ ñ
îñüþ Î0Õ, à âåêòîð ñóììàðíîé ñêîðîñòè ðàêåòû V0
*
áóäåò îòêëîíåí îò
îñè ðàêåòû íà óãëû ∆α0 è ∆β0 (ðèñ. 9 .4). Óãîë ∆α0 îïðåäåëÿåì êàê óãîë
ìåæäó ïðîåêöèåé âåêòîðà ñêîðîñòè íà ïëîñêîñòü ñèììåòðèè ðàêåòû
V0( )
*
c
è îñüþ ðàêåòû ÎÕ, óãîë ∆β0 – êàê óãîë ìåæäó âåêòîðîì ñêîðîñòè
V0
*
è åãî ïðîåêöèåé V0( )
*
c
íà ïëîñêîñòü ñèììåòðèè. Ïî ðèñ. 9 .4 ïðè ïî-
ëîæèòåëüíûõ çíà÷åíèÿõ ñîñòàâëÿþùèõ ñêîðîñòè ∆Vx0, ∆Vy0, ∆Vz0 ïî-
ëó÷èì ïîëîæèòåëüíîå çíà÷åíèå èçìåíåíèÿ óãëà ñêîëüæåíèÿ ∆β0 è
îòðèöàòåëüíîå çíà÷åíèå èçìåíåíèÿ óãëà àòàêè ∆α0.  ñîîòâåòñòâèè ñ
ðèñ. 9.4 èìååì
sin( )
/||,()
,
*
∆∆
∆
∆
∆
βα
00
00
0
00
==
−
+
VV
V
VV
z
y
x
tg
(9.14)
èëè
∆
∆
∆∆∆
∆
∆
β
α
0
0
00
2
0
2
0
2
0
=
+++
=−
arcsin
()
,
V
VV VV
V
z
xy
z
y
arctg
0
00
VV
x
+
⎛
⎝⎜
⎞
⎠⎟
∆
.
(9.15)
Èçìåíåíèå ìîäóëÿ ñêîðîñòè ðàêåòû â ìîìåíò ñõîäà ñ íàïðàâëÿþ-
ùèõ, âûçâàííîå äâèæåíèåì íîñèòåëÿ, îïðåäåëèì èç çàâèñèìîñòè
∆∆
∆
∆
VVVVVVVV
xy
z
00000
2
0
2
0
2
0
=
−
=+ ++−
*
()
.
(9.16)
427
Ðèñ. 9 .4. Èçìåíåíèå ïî âðåìåíè óã-
ëîâ àòàêè è ñêîëüæåíèÿ, îïðåäåëÿå-
ìîå äâèæåíèåì íîñèòåëÿ
9.2 . ÄÂÈÆÅÍÈÅ ÐÀÊÅÒ ÏÐÈ ÏÓÑÊÅ
9.2.1. ÎÑÎÁÅÍÍÎÑÒÈ ÑÒÀÐÒÎÂÎÃÎ ÄÂÈÆÅÍÈß ÐÀÊÅÒ
Ïóñê ðàêåò ëþáîãî êëàññà îñóùåñòâëÿåòñÿ ñ èñïîëüçîâàíèåì ïóñ-
êîâîãî óñòðîéñòâà (ÏÓ). Êîíñòðóêöèÿ ÏÓ âî ìíîãîì îïðåäåëÿåòñÿ
òèïîì ËÀ è óñëîâèåì çàïóñêà.
ÏÓ íåóïðàâëÿåìûõ ðàêåò – íàèáîëåå ïðîñòûå; ýòî òðóá÷àòûå íà-
ïðàâëÿþùèå, ëåãêèå ôåðìû äëÿ ïîäâåñêè ðàêåò è ò.ä .
Ðàêåòà, íàõîäÿùàÿñÿ íà íàïðàâëÿþùèõ ÏÓ, îáû÷íî èìååò ïå-
ðåäíèå è çàäíèå âåäóùèå ýëåìåíòû (áóãåëè), ñêîëüçÿùèå â ïàçàõ,
âûïîëíåííûõ â íàïðàâëÿþùèõ. Ïðè ýòîì âîçìîæíû äâà òèïà
íàïðàâëÿþùèõ, êâàëèôèöèðóåìûõ ïî ñõåìå ñõîäà ðàêåòû ñ ÏÓ:
íàïðàâëÿþùèå ïåðâîãî ðîäà, êîãäà è ïåðåäíèé è çàäíèé ýëåìåí-
òû îäíîâðåìåííî ñõîäÿò ñ íàïðàâëÿþùèõ ("îäíîâðåìåííûé" è
"íóëåâîé ñòàðò"), è íàïðàâëÿþùèå âòîðîãî ðîäà, êîãäà ñõîä âåäó-
ùèõ ýëåìåíòîâ ÿâëÿåòñÿ íåîäíîâðåìåííûì ("ðàâíîìåðíûé
ñòàðò").  ðÿäå èñòî÷íèêîâ [108] "íóëåâîé ñòàðò", ñîîòâåòñòâóþ-
ùèé ñòàðòó ËÀ, ïðè êîòîðîì åãî ñâÿçü ñ ÏÓ òåðÿåòñÿ â ìîìåíò
íà÷àëà îòíîñèòåëüíîãî äâèæåíèÿ àïïàðàòà, âûäåëÿåòñÿ â ñàìî-
ñòîÿòåëüíûé òèï ñòàðòà.
9.2.2 . ÄÂÈÆÅÍÈÅ ÐÀÊÅÒ ÏÎ ÍÀÏÐÀÂËßÞÙÅÉ ÏÓÑÊÎÂÎÉ ÓÑÒÀÍÎÂÊÈ
Îäíîé èç íàèáîëåå ðàñïðîñòðàíåííûõ ñõåì ïóñêà ðàêåò ìàëîé è
ñðåäíåé äàëüíîñòè ÿâëÿåòñÿ ñõåìà ñòàðòà ðàêåòû ñ íàêëîííûõ íà-
ïðàâëÿþùèõ ïóñêîâîé óñòàíîâêè.
Îñíîâíûå ñèëû è ìîìåíòû, äåéñòâóþùèå íà ðàêåòó ïðè åå
äâèæåíèè ïî íàïðàâëÿþùèì ñ îäíîâðåìåííûì ñõîäîì áóãåëåé,
ïîêàçàíû íà ðèñ. 9 .5 . Íà ðàêåòó äåéñòâóþò òÿãà Ð, ïðîäîëüíàÿ Õ
è íîðìàëüíàÿ Y àýðîäèíàìè÷åñêèå ñèëû, ïðîäîëüíàÿ Õã è íîð-
ìàëüíàÿ Yã ãàçîäèíàìè÷åñêèå ñèëû, ñèëà òÿæåñòè mg, íîðìàëü-
íûå ðåàêöèè FN1, FN2 è ñèëû òðåíèÿ Fò1, Fò2 â êîíòàêòíûõ ýëå-
ìåíòàõ. Íà ðèñ. 9 .5 òàêæå ïîêàçàíû ñòàðòîâàÿ ñèñòåìà êîîðäèíàò
Î0ÕñYñ è ñèñòåìà êîîðäèíàò ÎïÕïYï, íà÷àëî êîòîðîé Îï ñîâïàäàåò
ñ íà÷àëüíûì ïîëîæåíèåì öåíòðà ìàññ ðàêåòû Î0. Îñü ÎïÕï ñîâ-
ïàäàåò ñ ïðîäîëüíîé îñüþ ðàêåòû è ïàðàëëåëüíà íàïðàâëÿþùèì;
îñü ÎïY ï ïåðïåíäèêóëÿðíà îñè ÎïÕï è ëåæèò â ïðîäîëüíîé ïëîñ-
êîñòè ñèììåòðèè ðàêåòû.
Çàïèøåì óðàâíåíèÿ äâèæåíèÿ ðàêåòû ïî íàïðàâëÿþùèì â ñèñ-
òåìå êîîðäèíàò ÎïÕïYï, êîòîðóþ áóäåì ñ÷èòàòü íåïîäâèæíîé. Áóäåì
ðàññìàòðèâàòü ÏÓ êàê àáñîëþòíî æåñòêîå òåëî ñ ïðÿìîëèíåéíûìè
íàïðàâëÿþùèìè. Òîãäà
428
m
dx
dt
PXXFFm
g
m
dy
dt
YYF
N
2
2
12
0
2
2
1
ï
ãòò
ï
ã
=−+
−
−
−
=++ +
sin ;
θ
Fm
g
I
d
dt
MM FlFlF
d
F
N
z
z
zz
NN
20
11
22
1
2
0
2
−=
=++−
−
−
cos
;
θ
ω
ãò
ò
d
2
0
=
.
(9.17)
Ðàâåíñòâî íóëþ ïðàâûõ ÷àñòåé âòîðîãî è òðåòüåãî óðàâíåíèé ñèñ-
òåìû (9.17) îáóñëîâëåíî ââåäåííûìè äîïóùåíèÿìè.
Ðàññìîòðèì äâèæåíèå ðàêåòû ïî íàïðàâëÿþùèì ñ íåîäíîâðå-
ìåííûì ñõîäîì êîíòàêòíûõ ýëåìåíòîâ.  ýòîì ñëó÷àå íåîáõîäèìî
ðàçëè÷àòü äâà ó÷àñòêà äâèæåíèÿ. Ïåðâûé ó÷àñòîê – äâèæåíèå ðàêå-
òû äî ìîìåíòà ñõîäà ïåðâîãî áóãåëÿ ñ íàïðàâëÿþùèõ. Äâèæåíèå ðà-
êåòû íà ýòîì ó÷àñòêå íè÷åì íå îòëè÷àåòñÿ îò äâèæåíèÿ ðàêåòû â
ñëó÷àå îäíîâðåìåííîãî ñõîäà ðàêåòû ñ íàïðàâëÿþùèõ. Ïîýòîìó
óðàâíåíèÿ, ïîëó÷åííûå âûøå, âïîëíå ïðèãîäíû äëÿ ðàñ÷åòà ïåðâî-
ãî ó÷àñòêà. Âðåìÿ äâèæåíèÿ ðàêåòû ïî íàïðàâëÿþùèì äî ñõîäà ïåð-
âîãî áóãåëÿ îáîçíà÷èì t1. Âòîðîé ó÷àñòîê äâèæåíèÿ (èíîãäà åãî íà-
çûâàþò ó÷àñòêîì âûõîäà) íà÷èíàåòñÿ â ìîìåíò âðåìåíè t1 è îêàí÷è-
âàåòñÿ â ìîìåíò ñõîäà âòîðîãî áóãåëÿ ðàêåòû ñ íàïðàâëÿþùèõ. Äëÿ
ýòîãî ó÷àñòêà õàðàêòåðíî òî, ÷òî ðàêåòà ïîëó÷àåò äîïîëíèòåëüíûå
ñòåïåíè ñâîáîäû, à èìåííî âîçìîæíîñòü ïîâîðà÷èâàòüñÿ âîêðóã
çàäíåãî áóãåëÿ.
Îñíîâíûå ñèëû è ìîìåíòû, äåéñòâóþùèå íà ðàêåòó íà âòîðîì
ó÷àñòêå åå äâèæåíèÿ ïî íàïðàâëÿþùèì (äëÿ óñëîâíîãî ïîâîðîòà
429
Ðèñ. 9 .5 . Ñõåìà ñèë, äåéñòâóþùèõ íà ðàêåòó ïðè åå äâèæåíèè ïî íàïðàâëÿþùèì
ïðîòèâ ÷àñîâîé ñòðåëêè), ïîêàçàíû íà ðèñ. 9.6. Ñîñòàâèì óðàâíåíèÿ
äâèæåíèÿ ðàêåòû îòíîñèòåëüíî îñåé ñèñòåìû êîîðäèíàò ÎïÕïYï,
ïðè ýòîì áóäåì ñ÷èòàòü íàïðàâëÿþùèå íåïîäâèæíûì æåñòêèì òå-
ëîì. Ïðèìåì òàêæå, ÷òî Ð = Ð0. Òîãäà
mx
P
X
Y
Fmg
myP
••
cos
cos
sin
sin ;
••
si
ïò
2
ï
=−−−
−
=
0
0
0
∆∆∆
θθθ θ
ns
i
nc
o
s
c
o
s
;
cos
∆∆∆
∆
θθθ
θ
ω
−+
+
−
=−
XYF
m
g
I
d
dt
MFl
N
z
z
zN
20
22
θθ
θθ
−+
+−
F
d
F
d
Fl
N
ò2
ò2
2
2
22
cos
sin
sin .
∆
∆∆
(9.18)
Ê ýòèì óðàâíåíèÿì íåîáõîäèìî äîáàâèòü óðàâíåíèå ñâÿçè,
îáóñëîâëåííîå ïåðåìåùåíèåì öåíòðà ìàññ ðàêåòû ïðè åå
ïîâîðà÷èâàíèè íà âòîðîì êîíòàêòíîì ýëåìåíòå:
yl
ï
=
2∆θ.
(9.19)
Èññëåäîâàíèÿ äâèæåíèÿ ðàêåòû íà ó÷àñòêå âûõîäà ïîêàçàëè, ÷òî
çà âñå âðåìÿ äâèæåíèÿ óãîë ∆θ íå ïðåâûøàåò äåñÿòêà óãëîâûõ ìè-
íóò. Ïîýòîìó äëÿ òðèãîíîìåòðè÷åñêèõ ôóíêöèé ìîæíî ïðèíÿòü
ñëåäóþùèå çíà÷åíèÿ: cos∆θ =1;sin∆θ = ∆θ.
Óïðîñòèì òðåòüå óðàâíåíèå ñèñòåìû (9.18), èñõîäÿ èç òîãî, ÷òî
óãîë ∆θ ìàë; äëÿ ðàêåò îáû÷íî l2 =10d è Fò2 = fFN2, ãäå êîýôôèöèåíò
òðåíèÿ ñòàëè ïî ñòàëè f = 0,2. Ïîëó÷èì
430
Ðèñ. 9.6 . Ñõåìà ñèë, äåéñòâóþùèõ íà ðàêåòó íà ó÷àñòêå ñõîäà ñ íàïðàâëÿþùèõ
I
d
dt
MFl
d
fd fl
MFl
z
z
zN
zN
ω
θθ
=−
−
++
⎡
⎣⎢
⎤
⎦⎥ =−
22
2
22
22
∆∆ ; (9.20)
òàê êàê òðè ïîñëåäíèõ ñëàãàåìûõ â ñêîáêàõ äëÿ óêàçàííûõ çíà÷åíèé f,
d è ∆θ îêàçûâàþòñÿ âåëè÷èíàìè ìàëûìè ïî ñðàâíåíèþ ñ l2, èìè
ìîæíî ïðåíåáðå÷ü. Ñêîðîñòü äâèæåíèÿ ðàêåòû ïî íàïðàâëÿþùèì
îáû÷íî íå ïðåâûøàåò 70 ì/ñ.  ýòîì ñëó÷àå àýðîäèíàìè÷åñêèå ñèëû
è ìîìåíòû ïîëó÷àþòñÿ äîñòàòî÷íî ìàëûìè è â óðàâíåíèÿõ (9.18) èìè
ìîæíî ïðåíåáðå÷ü.
Ñ ó÷åòîì ñêàçàííîãî âûøå ñèñòåìà óðàâíåíèé (9.18) ïðèâîäèòñÿ
ê ñëåäóþùåìó óïðîùåííîìó âèäó:
mx
Pmg
myPmg
F
Il
F
N
zN
••
sin ;
••
cos
;
••
ï
ï
=−
=−
+
=−
00
00
2
2
θ
φθ
φ
2.
(9.21)
Çäåñü äëÿ óäîáñòâà çàïèñè îáîçíà÷åíî ∆θ = φ.  ïîëó÷åííîé ñèñ-
òåìå óðàâíåíèé ïåðâîå óðàâíåíèå íå ñâÿçàíî ñî âòîðûì è òðåòüèì.
Ñëåäîâàòåëüíî, åãî ìîæíî ïðîèíòåãðèðîâàòü îòäåëüíî, ÷òî äàñò
ñêîðîñòü äâèæåíèÿ öåíòðà ìàññ ðàêåòû ïî íàïðàâëÿþùèì â ôóíê-
öèè âðåìåíè. Ôèçè÷åñêèé ñìûñë âîçìîæíîñòè èíòåãðèðîâàíèÿ îò-
äåëüíî ïåðâîãî óðàâíåíèÿ ñèñòåìû (9.21) çàêëþ÷àåòñÿ â òîì, ÷òî áî-
êîâûå âîçìóùåíèÿ ìàëî âëèÿþò íà âåëè÷èíó ñêîðîñòè äâèæåíèÿ.
Íàñ èíòåðåñóåò ïîâîðîò ðàêåòû ïðè åå äâèæåíèè íà ó÷àñòêå âû-
õîäà. Ïîýòîìó ðàññìîòðèì âòîðîå è òðåòüå óðàâíåíèÿ ñèñòåìû
(9.21). Ââåäåì çàìåíó yï = l2φ, ïåðåãðóïïèðóåì âòîðîå óðàâíåíèå
ñèñòåìû îòíîñèòåëüíî FN2 è ïîäñòàâèì ïîëó÷åííîå çíà÷åíèå â
òðåòüå óðàâíåíèå. Ñ ó÷åòîì óðàâíåíèÿ ñâÿçè (9.19) ïîëó÷èì
()
••
cos .
Im
lP
lm
g
l
z+=
−
2
2
02
2
0
φφθ
(9.22)
Ââåäåì îáîçíà÷åíèÿ ′ =+
IIm
l
zz2
2
;PlIa
z
02
1
/.
′=
Ïîäñòàâèì íîâûå
óðàâíåíèÿ â óðàâíåíèå (9.22) è ïîñëå ïðåîáðàçîâàíèÿ ïîëó÷èì
•
•
cos
.
φφ
θ
−=
−
′
a
mgl
Iz
1
20
(9.23)
Ïðè èíòåãðèðîâàíèè óðàâíåíèÿ (9.23) íà ó÷àñòêå âûõîäà ìîæíî
áðàòü ñðåäíèå çíà÷åíèÿ ìàññû ðàêåòû.  ýòîì ñëó÷àå ïðàâàÿ ÷àñòü
óðàâíåíèÿ (9.23) ÿâëÿåòñÿ ïîñòîÿííîé âåëè÷èíîé, à ñàìî óðàâíå-
íèå – ëèíåéíûì íåîäíîðîäíûì ñ ïîñòîÿííûìè êîýôôèöèåíòàìè.
Ðåøåíèå òàêîãî óðàâíåíèÿ ìîæíî ïîëó÷èòü â àíàëèòè÷åñêîì âèäå.
431
Íå ïðèâîäÿ ïðîìåæóòî÷íûõ âûêëàäîê, çàïèøåì ðåçóëüòàòû èíòåã-
ðèðîâàíèÿ
∆θφ
θ
00
0
0
2
2
121
121
==
−
+
−
−−
−
mg
P
ee
att
att
ñð cos
[]
;
()
()
(9.24)
•
•
cos
[]
()
()
θφ
θ
00
0
2
0
2
121
121
==
−
′
−
−−
−
mg
l
PI
ee
z
att
att
ñð
,
(9.25)
ãäå t2 – âðåìÿ ñõîäà âòîðîãî áóãåëÿ ñ íàïðàâëÿþùèõ ïóñêîâîé
óñòàíîâêè; ∆θ0 – óãîë ïîâîðîòà îñè ðàêåòû â êîíöå ó÷àñòêà âûõîäà;
ƥ
–
θ 0 óãëîâàÿ ñêîðîñòü îñè ðàêåòû â êîíöå ó÷àñòêà âûõîäà.
9.3 . ÔÎÐÌÈÐÎÂÀÍÈÅ ÍÀ×ÀËÜÍÛÕ ÓÑËÎÂÈÉ
ÂÎÇÌÓÙÅÍÍÎÃÎ ÄÂÈÆÅÍÈß ÑÍÀÐßÄÀ
9.3 .1. ÍÀ×ÀËÜÍÎÅ ÏÐÅÖÅÑÑÈÎÍÍÎÅ ÄÂÈÆÅÍÈÅ
Áóäåì ïðåäâàðèòåëüíî ñ÷èòàòü, ÷òî êàíàë ñòâîëà, èç êîòîðîãî
ïðîèçâîäèòñÿ âûñòðåë, è ñíàðÿä îáëàäàþò àáñîëþòíîé îñåâîé ñèì-
ìåòðèåé. Òîãäà, çàäàâ óãîë γ íàêëîíà íàðåçîâ ê îñè êàíàëà ñòâîëà è
îáîçíà÷èâ ÷åðåç η äëèíó õîäà íàðåçîâ â êàëèáðàõ, ïîëó÷èì
vt
g
îêð
==
VV
rr
00
γ
π
η
.
(9.26)
Íî, ñ äðóãîé ñòîðîíû,
vîêð=05 0
,
•
,
dφ
(9.27)
ïîýòîìó
•
.
φ
π
η
00
2
=
d
Vr
(9.28)
Ðàíåå áûëî ïîëó÷åíî (ñì. ãë. 7) âûðàæåíèå äëÿ ñêîðîñòè ïðåöåññèè •
,
ν
êîòîðîå ïðè δ0 = 0 ñ ó÷åòîì (9.28) ïðåîáðàçóåì ê âèäó
•
ν
π
η
==
=
C
Ad
Va
r
0
const.
(9.29)
432
Ïðè îòñóòñòâèè äâèæåíèÿ ñòâîëà îòíîñèòåëüíî àòìîñôåðû åäèíñòâåííûì
èñòî÷íèêîì âîçíèêíîâåíèÿ ïðåöåññèîííûõ äâèæåíèé áóäåò ñèëà
òÿæåñòè, ïðèâîäÿùàÿ ê èñêðèâëåíèþ òðàåêòîðèè. Èçâåñòíî, ÷òî ïîä
äåéñòâèåì ñèëû òÿæåñòè äèíàìè÷åñêàÿ îñü ðàâíîâåñèÿ, îêîëî êîòîðîé
ïðîèñõîäèò ïðåöåññèîííîå äâèæåíèå, îòêëîíÿåòñÿ îò âåêòîðà ñêîðîñòè
âïðàâî íà óãîë
δθ
ð0
0
40
2
=− af
•
/,
(9.30)
ãäå
fdh
gA
HyV K
V
a
rM
ON
40
2
0
2
0
1000
=⋅⋅
⎛
⎝⎜⎞
⎠⎟
()
.
(9.31)
Çíà÷åíèå
•
θ0 â ôîðìóëå (9.30) îïðåäåëÿåòñÿ èç î÷åâèäíîãî
ñîîòíîøåíèÿ
•
cos /
.
θθ
00
0
=−gV
r
(9.32)
Ïîäñòàâëÿÿ (9.32) è (9.29) â (9.30), ïîëó÷èì îêîí÷àòåëüíî
δ
πθ
η
p0
0
40
1
21
=
⎛
⎝⎜⎞
⎠⎟
−
g
df
A
C
cos
.
(9.33)
Âû÷èñëèì δp0 äëÿ ñíàðÿäà êàëèáðà d = 100 ìì ïðè V0r = 1000 ì/ñ è
η = 30. Ïðèìåíèòåëüíî ê àðòèëëåðèéñêîìó ñíàðÿäó óêàçàííîãî
êàëèáðà îòíîøåíèå ýêâàòîðèàëüíîãî ìîìåíòà èíåðöèè ê ìîìåíòó
èíåðöèè ñíàðÿäà îòíîñèòåëüíî ïðîäîëüíîé îñè ñîñòàâëÿåò
A
C
=
⋅
⋅
=
−
−
225910
0 2115 10
10 68
2
2
,
,
,.
Îïðåäåëèâ èç òàáëèö K
V
a
M
ON
0
3
090 10
⎛
⎝⎜⎞
⎠⎟ =⋅
−
,
è
âû÷èñëèâ ïëå÷î îïðîêèäûâàþùåé ïàðû h = 1,6d, íàéäåì
f40
22
3
01 0161000 11000 090 10
981 225910
=
⋅⋅⋅
⋅
⋅⋅
⋅⋅
−
−
,,
,
,,
2
2
6420
≈
−
ñ.
Ïðèíÿâ cosθ0 = 1, îêîí÷àòåëüíî ïîëó÷èì
δp0
3
2314 9811
40 100 10
1
6420
1
10 68
225 10
=
⋅⋅⋅
⋅⋅
⋅⋅ =⋅
−
−
,,
,
,
4
0013
š
,.
433
Äàííûå ðàñ÷åòà ñâèäåòåëüñòâóþò, ÷òî âåëè÷èíà δp0 ÿâëÿåòñÿ
îòíîñèòåëüíî ìàëîé è ê òîìó æå, áóäó÷è ïîñòîÿííîé âåëè÷èíîé, îíà
ìîæåò áûòü ëåãêî ó÷òåíà êàê ñèñòåìàòè÷åñêîå îòêëîíåíèå.
9.3.2. ÍÀ×ÀËÜÍÛÅ ÓÃËÎÂÀß ÑÊÎÐÎÑÒÜ È ÓÃÎË ÍÓÒÀÖÈÈ,
ÎÁÓÑËÎÂËÅÍÍÛÅ ÍÅÓÐÀÂÍÎÂÅØÅÍÍÎÑÒÜÞ ÑÍÀÐßÄÀ
 îáùåì ñëó÷àå ââåäåííîå ðàíåå ïðåäïîëîæåíèå îá àáñîëþòíîé
îñåâîé ñèììåòðèè êàíàëà ñòâîëà è ñíàðÿäà íå âûïîëíÿåòñÿ. Èç-çà
ïîãðåøíîñòåé èçãîòîâëåíèÿ äâèæåíèå ñíàðÿäà â êàíàëå ñòâîëà ïðî-
èñõîäèò ïðè íåñîâïàäåíèè ñîîòâåòñòâóþùèõ îñåé. Âåäóùèé ïîÿñîê,
ðàñïîëîæåííûé â çàäíåé (êîðìîâîé) ÷àñòè êîðïóñà ñíàðÿäà, ïðåä-
íàçíà÷åí äëÿ ñîçäàíèÿ îäíîé èç êîíòàêòíûõ ïàð è îáåñïå÷åíèÿ íó-
ëåâîãî çàçîðà ñçàäè. Äðóãèì ìåñòîì îïîðû ñíàðÿäà ñëóæèò ïåðåäíåå
öåíòðèðóþùåå óòîëùåíèå. Íàëè÷èå çàçîðà ∆1 (ðèñ. 9.7) ó ïåðåäíåãî
öåíòðèðóþùåãî óòîëùåíèÿ îáû÷íî íåìåäëåííî îòðàæàåòñÿ íà óãëå
íóòàöèè ñíàðÿäà. Âîçíèêíîâåíèå çàçîðà, êàê ïðàâèëî, îáóñëîâëèâà-
åòñÿ íåñèììåòðè÷íûì âðåçàíèåì öåíòðèðóþùåãî óòîëùåíèÿ â íà-
ðåçû.  ñâîþ î÷åðåäü ýòî ìîæåò âûçâàòü ñìåùåíèå öåíòðà ìàññ äàæå
èäåàëüíî ñáàëàíñèðîâàííîãî ñíàðÿäà ñ îñè êàíàëà ñòâîëà ε2. Ïðè
íàëè÷èè ðàâíîäåéñòâóþùåé ñèëû äàâëåíèÿ ïîðîõîâûõ ãàçîâ Ðêí íà
äíî ñíàðÿäà, íàïðàâëåííîé âäîëü êàíàëà ñòâîëà, ýòî ïðèâåäåò ê ïî-
ÿâëåíèþ âðàùàòåëüíîãî ìîìåíòà, èìåþùåãî òåíäåíöèþ óâåëè÷è-
âàòü óêàçàííîå ñìåùåíèå. Âåëè÷èíà çàçîðà è âûçûâàåìîãî èì
ýôôåêòà áóäåò òåì áîëüøå, ÷åì áîëüøå èçíîñ è íàãðåâ ñòâîëà.
Äðóãîé âàæíîé ïðè÷èíîé âîçíèêíîâåíèÿ íà÷àëüíûõ óãëîâîé
ñêîðîñòè è óãëà íóòàöèè ÿâëÿåòñÿ ýêñöåíòðèñèòåò ìàññû ñíàðÿäà.
Çäåñü ñëåäóåò ðàçëè÷àòü äâà âèäà íåóðàâíîâåøåííîñòè. Ïåðâûé, íà-
çûâàåìûé ñòàòè÷åñêîé íåóðàâíîâåøåííîñòüþ, çàêëþ÷àåòñÿ â òîì, ÷òî
â ñèëó òåõíîëîãè÷åñêèõ ïîãðåøíîñòåé èçãîòîâëåíèÿ êîðïóñà è îñî-
áåííîñòåé åãî íàïîëíåíèÿ öåíòð ìàññ ñíàðÿäà îêàçûâàåòñÿ ñìåùåí-
íûì íà íåêîòîðîå ðàññòîÿíèå ∆2 îòíîñèòåëüíî ïðîäîëüíîé îñè ñíà-
434
Ðèñ. 9 .7. Äâèæåíèå
ñíàðÿäà â êàíàëå
ñòâîëà
ðÿäà. Âòîðîé – äèíàìè÷åñêàÿ íå-
óðàâíîâåøåííîñòü – ñâÿçàí ñ íåñîâ-
ïàäåíèåì ãåîìåòðè÷åñêîé îñè ñèì-
ìåòðèè ñíàðÿäà è åãî ãëàâíîé öåí-
òðàëüíîé ïîëÿðíîé îñè èíåðöèè.
Âåëè÷èíà äèíàìè÷åñêîãî ýêñöåí-
òðèñèòåòà îïðåäåëÿåòñÿ óãëîì ε1
(ñì. ðèñ. 9 .7). Ó÷èòûâàÿ ìàëîñòü óã-
ëîâ ε1 è ε2, â ïåðâîì ïðèáëèæåíèè
áóäåì ñ÷èòàòü, ÷òî ε1 + ε2 = ε,àóã-
ëîâàÿ ñêîðîñòü ïðåöåññèîííîãî
äâèæåíèÿ ñíàðÿäà â êàíàëå ñòâîëà
••
.
νφ
=
Òîãäà â ìîìåíò ïðîõîæäåíèÿ
ñíàðÿäîì äóëüíîãî ñðåçà
•
•
,
δφ
ε
00
=
ãäå ε = δ0 – íà÷àëüíûé óãîë íóòà-
öèè. Ïðåäïîëîæèì, ÷òî ê ìîìåíòó ïðåêðàùåíèÿ ìåõàíè÷åñêîé ñâÿ-
çè ñíàðÿäà ñî ñòâîëîì ïëîñêîñòü ñîïðîòèâëåíèÿ, îáðàçîâàííàÿ â
ðàññìàòðèâàåìîì ñëó÷àå ãåîìåòðè÷åñêîé îñüþ êàíàëà ñòâîëà è ãëàâ-
íîé ïîëÿðíîé îñüþ èíåðöèè ñíàðÿäà, ñîñòàâëÿåò ñ ïëîñêîñòüþ áðî-
ñàíèÿ íà÷àëüíûé óãîë ïðåöåññèè ν0. Òîãäà ñîñòàâëÿþùèå íà÷àëüíûõ
ïàðàìåòðîâ íóòàöèîííîãî äâèæåíèÿ â êîîðäèíàòàõ Êðûëîâà
(ðèñ. 9.8) áóäóò îïðåäåëÿòüñÿ ñëåäóþùèì îáðàçîì:
δενδεν
δφ
ενδφ
εν
20
010
0
20
0
010
0
==
==
cos ;
sin ;
•
•
cos ;
•
•
sin 0.
(9.34)
Èìåÿ â âèäó ñâÿçü ìåæäó ðåøåíèÿìè èñõîäíîé ñèñòåìû óãëîâîãî
äâèæåíèÿ ñíàðÿäà â êîîðäèíàòàõ Ýéëåðà è Êðûëîâà, âûðàæåíèå
ñóììàðíîãî ìàêñèìàëüíîãî óãëà íóòàöèè îïðåäåëèì ñëåäóþùèì
îáðàçîì.
Çíà÷åíèå óãëà δê ìîæåò áûòü ïðåäñòàâëåíî êàê
δδδ ρρρ
ρσχ
ê
=+
=+
−
+
10
2
20
2
1
2
2
2
12
22
cos(
),
at
(9.35)
ãäå
ρ
σ
δω
δδω
δ
12
0
2
1
0
2
10
220
2
1
2
=+
+
−
a
(•
)(
•
);
(9.36)
435
Ðèñ. 9.8 . Îïðåäåëåíèå ìàêñèìàëüíî-
ãî ñóììàðíîãî óãëà íóòàöèè ïðè âû-
ñòðåëå
ρ
σ
δω
δδω
δ
22
0
1
1
0
2
10
120
2
1
2
=+
+
−
a
(•
)(
•
);
(9.37)
χ
δω
δ
δω
δ
δω
δ
δω
=−
+
−
+
+
−
arctg
arctg
•
•
•
•
10
210
20
220
10
210
20
120
δ
;
(9.38)
ωσ
12
1
=±
a()
.
Çíà÷åíèå δ =1− f4a−2
.
Àíàëèçèðóÿ õàðàêòåð âûðàæåíèÿ (9.35),
ïðèõîäèì ê âûâîäó, ÷òî δ áóäåò ïðèíèìàòü ìàêñèìàëüíîå çíà÷åíèå
ïðè cos(
),
21
at
σχ
+=
−
ò.å .
δρρ
max
.
=+
12
(9.39)
Ïðè ôèêñèðîâàííîì çíà÷åíèè ε è ν0, èìåÿ â âèäó (9.34), ïîëó÷èì èç
(9.36) è (9.37)
ρ
φε
σ
ω
φ
1
02
2
0
2
2
1
=+
•
•
;
a
(9.40)
ρ
φε
σ
ω
φ
2
01
2
0
2
2
1
=+
•
•
.
a
(9.41)
Ïîëàãàÿ ωφ ωφ
2
2
0
2
1
2
0
2
0
/•
/•
,
≈=
íàéäåì îêîí÷àòåëüíî
δ
φε
σ
ε
σ
max
•
.
==
0
2
a
A
C
(9.42)
Ó÷èòûâàÿ, ÷òî ÀÑ
−1
èìååò ïîðÿäîê äåñÿòè, à σ ëåæèò â ïðåäåëàõ
0,45...0,70, çàïèøåì ñëåäóþùåå ïðèáëèæåííîå ñîîòíîøåíèå:
δε
max
()
.
≈30
45
K
(9.43)
Ïîëó÷åííîå ñîîòíîøåíèå ñâèäåòåëüñòâóåò, ÷òî ε îêàçûâàåò
ñóùåñòâåííîå âëèÿíèå íà âåëè÷èíó íóòàöèîííûõ êîëåáàíèé ñíàðÿäà.
9.3 .3. ÂËÈßÍÈÅ ÐÀÄÈÀËÜÍÎÃÎ ÝÊÑÖÅÍÒÐÈÑÈÒÅÒÀ ÖÅÍÒÐÀ ÌÀÑÑ
ÑÍÀÐßÄÀ ÍÀ ÎÒÊËÎÍÅÍÈÅ ÂÅÊÒÎÐÀ ÍÀ×ÀËÜÍÎÉ ÑÊÎÐÎÑÒÈ
Ïðè íåñîâïàäåíèè öåíòðà ìàññ ñíàðÿäà ñ îñüþ åãî âðàùåíèÿ â
êàíàëå ñòâîëà (ñì. ðèñ. 9.8) â ìîìåíò ïðîõîæäåíèÿ äóëüíîãî ñðåçà
436
öåíòð ìàññ ñíàðÿäà áóäåò èìåòü îêðóæíóþ ñêîðîñòü, îïðåäåëÿåìóþ
êàê
v îêð
=
•
.
φ02
∆
(9.44)
Èìåÿ â âèäó ïðèâåäåííîå ðàíåå ñîîòíîøåíèå (9.28), çàïèøåì
v îêð
=
20
2
π
η
V
d
r
∆.
(9.45)
Íàëè÷èå ñîñòàâëÿþùåé vîêð ïðèâåäåò ê îòêëîíåíèþ âåêòîðà
íà÷àëüíîé ñêîðîñòè ñíàðÿäà íà óãîë
γ
π
η
∆
∆
2
0
2
2
=≈
arctg
vîêð
Vd
r
.
(9.46)
Ñ öåëüþ îöåíêè âëèÿíèÿ γ ∆ 2
ïðèìåì äëÿ ñíàðÿäà êàëèáðà 100 ìì
∆2 = 0,1 ìì; η = 30. Äëÿ óêàçàííûõ çíà÷åíèé γ ∆ 2
0 0002
=
,.
Ïðè
ñòðåëüáå íà äàëüíîñòü â 10 êì òîëüêî ýêñöåíòðèñèòåò öåíòðà ìàññ
ñíàðÿäà êàëèáðà 100 ìì, ðàâíûé 0,1 ìì, âûçûâàåò îòêëîíåíèå òî÷êè
ïàäåíèÿ îò ðàñ÷åòíîé, ðàâíîå 2 ì.
9.3.4 . ÂÎÇÄÅÉÑÒÂÈÅ ÍÀ ÑÍÀÐßÄ ÄÓËÜÍÎÉ ÂÎËÍÛ Â ÏÅÐÈÎÄ
ÏÎÑËÅÄÅÉÑÒÂÈß
Ïîñëå âûëåòà ñíàðÿäà èç êàíàëà ñòâîëà íà÷èíàåòñÿ èñòå÷åíèå ïî-
ðîõîâûõ ãàçîâ, ïðîäîëæàþùèõ âîçäåéñòâîâàòü íà ñíàðÿä. Ýòîò ïðî-
öåññ íîñèò íàçâàíèå ïåðèîäà ïîñëåäåéñòâèÿ ãàçîâ íà ñíàðÿä. Åãî ïðî-
äîëæèòåëüíîñòü âåñüìà íåâåëèêà. Ïîýòîìó ïðè ïðîâåäåíèè îöåíî÷-
íîãî àíàëèçà âîçäåéñòâèÿ äóëüíîé âîëíû (âîëíîîáðàçíûõ
êîëåáàíèé ïîðîõîâûõ ãàçîâ) ïîñëå âûõîäà âåäóùåãî ïîÿñêà ñíàðÿäà
èç êàíàëà ñòâîëà ïðåäñòàâëÿåòñÿ ïðàâîìåðíûì ðàññìàòðèâàòü äàí-
íîå ÿâëåíèå êàê èìïóëüñíîå âîçäåéñòâèå. Ïðè òàêîì ïðåäïîëîæå-
íèè, ñâîäÿùåìñÿ ê ìãíîâåííîé ïåðåäà÷å ìîìåíòà êîëè÷åñòâà äâè-
æåíèÿ ãàçîâ ñíàðÿäó, óêàçàííîå âîçäåéñòâèå íå çàâèñèò îò óãëîâîé
ñêîðîñòè ñíàðÿäà, à îïðåäåëÿåòñÿ òîëüêî åãî ïîëîæåíèåì. Åñëè ïðè
ïîòåðå ìåõàíè÷åñêîé ñâÿçè ñíàðÿäà ñî ñòâîëîì óãîë íóòàöèè – íó-
ëåâîé, òî áóäåò èìåòü ìåñòî "öåíòðàëüíîå" ñèëîâîå âîçäåéñòâèå (ò.å .
âîçäåéñòâèå â íàïðàâëåíèè îñè ñíàðÿäà). Ýêñïåðèìåíòàëüíûå èñ-
ñëåäîâàíèÿ ñâèäåòåëüñòâóþò, ÷òî ïðèðîñò ñêîðîñòè ïðè òàêîì âîç-
äåéñòâèè ìîæåò ñîñòàâèòü äî1%îòäóëüíîé (íà÷àëüíîé) ñêîðîñòè
ñíàðÿäà. Åñëè æå ñíàðÿä ïîêèäàåò ñòâîë ñ íåíóëåâûì óãëîì íóòà-
437
öèè, âîçíèêàþùèé ìîìåíò ìîæåò îêàçàòü çàìåòíîå îòðèöàòåëüíîå
âîçäåéñòâèå íà äèíàìèêó óãëîâîãî äâèæåíèÿ ñíàðÿäà, êîòîðîå ïîä-
äàåòñÿ èçó÷åíèþ ïðàêòè÷åñêè òîëüêî ýêñïåðèìåíòàëüíûìè ìåòîäà-
ìè.
Ãëàâà 10
ÌÅÒÎÄÛ ÑÒÀÒÈÑÒÈ×ÅÑÊÎÉ ÄÈÍÀÌÈÊÈ
ÏÎËÅÒÀ, ÐÀÑÑÅÈÂÀÍÈÅ ÐÀÊÅÒ
È ÑÍÀÐßÄΠÏÐÈ ÑÒÐÅËÜÁÅ
Âîçìóùàþùèå ôàêòîðû, ïîä äåéñòâèåì êîòîðûõ ôîðìèðóåòñÿ òðàåêòîðèÿ
ËÀ, â ñâîåì ïîäàâëÿþùåì áîëüøèíñòâå íîñÿò ñëó÷àéíûé õàðàêòåð. Èõ, à òàê-
æå ïàðàìåòðû äâèæåíèÿ ìîæíî îòíåñòè ê îäíîé èç ñëåäóþùèõ ãðóïï:
ïðîöåññû, ÿâëÿþùèåñÿ ôóíêöèåé âðåìåíè, ìåíÿþùèåñÿ îò ðåàëèçàöèè ê ðåà-
ëèçàöèè;
ïîëÿ, èçìåíÿþùèåñÿ â êàæäîé ðåàëèçàöèè â ôóíêöèè ìíîãèõ íåçàâèñèìûõ
ïåðåìåííûõ;
âåëè÷èíû, ïîñòîÿííûå â êàæäîé îòäåëüíîé ðåàëèçàöèè, íî ìåíÿþùèåñÿ ñëó-
÷àéíûì îáðàçîì îò îäíîé ðåàëèçàöèè ê äðóãîé;
ñîáûòèÿ, êîòîðûå â êàæäîé îòäåëüíîé ðåàëèçàöèè ìîãóò ëèáî ïðîèçîéòè,
ëèáî íå ïðîèçîéòè.
Ôàêòîðû, ñîñòàâëÿþùèå ïåðâóþ èç íàçâàííûõ ãðóïï, ÿâëÿþòñÿ íàèáîëåå
ðàñïðîñòðàíåííûìè è, ïîæàëóé, ãëàâíûìè ïðè èññëåäîâàíèè ñòàòèñòè÷åñêîé
äèíàìèêè ïîëåòà. Ê èõ ÷èñëó îòíîñÿòñÿ âîçìóùàþùèå ñèëû è ìîìåíòû, äåéñò-
âóþùèå íà ËÀ â ïîëåòå, à òàêæå ïàðàìåòðû (ôàçîâûå êîîðäèíàòû), õàðàêòå-
ðèçóþùèå åãî òåêóùåå ñîñòîÿíèå. Òèïè÷íûì ïðèìåðîì "ïîëåé" ñëóæèò ñëó÷àé-
íîå äâèæåíèå (òóðáóëåíòíîñòü) àòìîñôåðû, â êîòîðîé ïðîèñõîäèò èññëåäóå-
ìûé ïîëåò. Ê ñëó÷àéíûì âåëè÷èíàì, ìåíÿþùèìñÿ îò ðåàëèçàöèè ê ðåàëèçàöèè,
îòíîñÿò îøèáêè îïðåäåëåíèÿ íà÷àëüíûõ óñëîâèé äâèæåíèÿ, îòêëîíåíèÿ êîíñò-
ðóêòèâíûõ, ìàññîâî-èíåðöèîííûõ è äðóãèõ õàðàêòåðèñòèê ËÀ. Íàêîíåö, ñðåäè
ñëó÷àéíûõ ñîáûòèé, êîòîðûå â êàæäîé îòäåëüíîé ðåàëèçàöèè ìîãóò ïðîèçîéòè
ëèáî íå ïðîèçîéòè, óêàæåì ïåðåêîñ èëè èçëîì ðàñêðûâàþùåãîñÿ ïåðüåâîãî ñòà-
áèëèçàòîðà, äðóãèå îòêàçû ýëåìåíòîâ êîíñòðóêöèè.
Ñëåäñòâèåì ðàçëè÷íîãî ðîäà îòêëîíåíèé ðåàëüíûõ óñëîâèé âûñòðåëà èëè
ïóñêà ðàêåò îò íîìèíàëüíûõ ÿâëÿþòñÿ îøèáêè ñòðåëüáû. Ñëó÷àéíûå îøèáêè
ïðèâîäÿò ê òîìó, ÷òî ïðè ñòðåëüáå ðàêåòàìè, èçãîòîâëåííûìè ïî îäíèì ÷åð-
òåæàì è òåõíè÷åñêèì óñëîâèÿì, ñ íàïðàâëÿþùèõ îäíîé è òîé æå ïóñêîâîé óñ-
òàíîâêè, ñ îäíîé ñòàðòîâîé ïîçèöèè, ïðè îäíèõ è òåõ æå óñòàíîâêàõ ïðèöåëü-
íûõ ïðèñïîñîáëåíèé òðàåêòîðèè ýòèõ ðàêåò íå ñîâïàäàþò äðóã ñ äðóãîì. Ïðè
ñòðåëüáå îäèíàêîâûìè ñíàðÿäàìè èç ñòâîëüíîé àðòèëëåðèéñêîé ñèñòåìû ïðè
îäèíàêîâûõ çàðÿäàõ è óñòàíîâêàõ ïðèöåëîâ òðàåêòîðèè îòäåëüíûõ ñíàðÿäîâ
òàêæå íå ñîâïàäàþò. Îòìå÷åííîå ÿâëåíèå íàçûâàþò ðàññåèâàíèåì òðàåêòî-
ðèé.
438
Ïîëåò ðàêåòû èëè ñíàðÿäà, ðàññìàòðèâàåìûé ñ ó÷åòîì äåéñòâèÿ ñëó÷àé-
íûõ ôàêòîðîâ, äîëæåí èññëåäîâàòüñÿ êàê ñòîõàñòè÷åñêèé (ñëó÷àéíûé) ïðî-
öåññ. Èçó÷åíèå òàêîãî ðîäà ïðîöåññîâ îñíîâûâàåòñÿ íà ïðèìåíåíèè àïïàðàòà è
ìåòîäîâ ñïåöèàëüíîãî ðàçäåëà òåîðèè âåðîÿòíîñòåé – òåîðèè ñëó÷àéíûõ ôóíê-
öèé [23, 101, 102]. Îáëàñòü èññëåäîâàíèÿ ñòàòèñòè÷åñêîé äèíàìèêè ïîëåòà
÷ðåçâû÷àéíî îáøèðíà [114]. Ïðèìåíèòåëüíî ê âíåøíåé áàëëèñòèêå ðàêåò è ñíà-
ðÿäîâ ñòîõàñòè÷åñêèå çàäà÷è ìîãóò áûòü óñëîâíî ðàçäåëåíû íà äâà áîëüøèõ
êëàññà.
Ïåðâûé êëàññ çàäà÷ èñïîëüçóåòñÿ íà ýòàïàõ ïðîåêòèðîâàíèÿ ñðåäñòâ
âîîðóæåíèÿ, èõ îòðàáîòêè è èñïûòàíèÿ. Äàííîìó êëàññó ñîîòâåòñòâóþò
òàê íàçûâàåìûå ìåòîäû àïðèîðíîãî ñòàòèñòè÷åñêîãî àíàëèçà äâèæåíèÿ
ËÀ.
Âòîðîé êëàññ îõâàòûâàåò çàäà÷è, ñâÿçàííûå íåïîñðåäñòâåííî ñ èñïîëüçîâà-
íèåì óæå èìåþùèõñÿ ñðåäñòâ âîîðóæåíèÿ. Ýòîìó êëàññó çàäà÷ îòâå÷àþò ìå-
òîäû àïîñòåðèîðíîé îáðàáîòêè ñòàòèñòè÷åñêîé èíôîðìàöèè, ïîëó÷åííîé ïî
ðåçóëüòàòàì îïûòíûõ è (èëè) áîåâûõ ñòðåëüá.
10.1. ÌÅÒÎÄÛ ÀÏÐÈÎÐÍÎÃÎ ÑÒÀÒÈÑÒÈ×ÅÑÊÎÃÎ
ÀÍÀËÈÇÀ ÄÂÈÆÅÍÈß ÐÀÊÅÒ È ÑÍÀÐßÄÎÂ
10.1 .1. ×ÈÑËÎÂÛÅ ÕÀÐÀÊÒÅÐÈÑÒÈÊÈ, ÈÑÏÎËÜÇÓÅÌÛÅ
ÏÐÈ ÑÒÀÒÈÑÒÈ×ÅÑÊÎÌ ÀÍÀËÈÇÅ ÄÂÈÆÅÍÈß ËÀ
 ðåçóëüòàòå ðàññåèâàíèÿ òðàåêòîðèé èõ ìíîæåñòâåííàÿ ñîâî-
êóïíîñòü, îòâå÷àþùàÿ èäåíòè÷íûì íà÷àëüíûì óñëîâèÿì, çàéìåò
íåêîòîðóþ îáëàñòü â ïðîñòðàíñòâå, íàçûâàåìóþ òðóáêîé èëè ïó÷êîì
(ñíîïîì) òðàåêòîðèé. Ïîñëåäíèå òåðìèíû èñïîëüçóþò ãëàâíûì îá-
ðàçîì ïðèìåíèòåëüíî ê àðòèëëåðèéñêèì ñíàðÿäàì. Òðóáêà òðàåêòî-
ðèé ñ ìàòåìàòè÷åñêîé òî÷êè çðåíèÿ ïðåäñòàâëÿåò ñîáîé îáëàñòü
ïðîñòðàíñòâà, âåðîÿòíîñòü âûõîäà òðàåêòîðèè çà ïðåäåëû êîòîðîé
íå ïðåâîñõîäèò íàïåðåä çàäàííîé ìàëîé (â ÷àñòíîì ñëó÷àå – íóëå-
âîé) âåëè÷èíû.
Îñü òðóáêè îïðåäåëÿåò ñðåäíþþ òðàåêòîðèþ â íåé, ñîâïàäàþ-
ùóþ ñ íîìèíàëüíîé.
Ñå÷åíèåì òðóáêè òðàåêòîðèé ïîâåðõíîñòüþ Çåìëè îïðåäåëÿåòñÿ
ýëëèïñ (ëèáî êðóã) ðàññåèâàíèÿ, à ïåðåñå÷åíèå òðàåêòîðèè ñ ïîâåðõ-
íîñòüþ äàåò òî÷êó, íàçûâàåìóþ öåíòðîì ãðóïïèðîâàíèÿ (ðàññåèâà-
íèÿ).
Î÷åâèäíî, ÷òî ýôôåêòèâíîå ðåøåíèå çàäà÷è ïðèöåëüíîé ñòðåëü-
áû òðåáóåò ââåäåíèÿ â ðàññìîòðåíèå õàðàêòåðèñòèê òî÷íîñòè äâèæå-
íèÿ ËÀ â ïðîöåññå ðåàëüíîãî âîçìóùåííîãî ïîëåòà.  îáùåì ñëó÷àå
òî÷íîñòü ñòðåëüáû îïðåäåëÿåòñÿ:
ïîëîæåíèåì îñè òðóáêè òðàåêòîðèé â ïðîñòðàíñòâå;
ðàçìåðàìè è ôîðìîé òðóáêè òðàåêòîðèé;
439
ðàñïîëîæåíèåì îòäåëüíûõ òðàåêòîðèé âíóòðè òðóáêè.
Óêàçàííîå îáñòîÿòåëüñòâî ïðåäîïðåäåëÿåò ïåðå÷åíü ÷èñëîâûõ
õàðàêòåðèñòèê, èñïîëüçóåìûõ ïðè ñòàòèñòè÷åñêîì àíàëèçå äâèæå-
íèÿ ËÀ.
Ðàññìàòðèâàÿ òðàåêòîðèþ êàê ñëó÷àéíóþ ôóíêöèþ, íàïîìíèì,
÷òî ñëó÷àéíîé ôóíêöèåé X(t) íàçûâàåòñÿ òàêàÿ ôóíêöèÿ ñâîåãî àðãó-
ìåíòà, êîòîðàÿ ÿâëÿåòñÿ ñëó÷àéíîé âåëè÷èíîé ïðè ëþáîì íåñëó÷àé-
íîì t ∈T. Ïðè ýòîì ïðèíÿòî ðàçëè÷àòü äâà ñëó÷àÿ:
à) àðãóìåíò ñëó÷àéíîé ôóíêöèè t ìîæåò ïðèíèìàòü ëþáûå çíà÷å-
íèÿ â çàäàííîì èíòåðâàëå (êîíå÷íîì èëè áåñêîíå÷íîì);
á) àðãóìåíò ñëó÷àéíîé ôóíêöèè ìîæåò ïðèíèìàòü òîëüêî îïðå-
äåëåííûå äèñêðåòíûå çíà÷åíèÿ.
 ïåðâîì ñëó÷àå X(t) îáû÷íî íàçûâàþò ñëó÷àéíûì ïðîöåññîì, âî
âòîðîì – ñëó÷àéíîé ïîñëåäîâàòåëüíîñòüþ. Åñëè äëÿ îïðåäåëåíèÿ
X(t) ïðîâåñòè n íåçàâèñèìûõ îïûòîâ, òî èõ èòîãîì áóäóò îïðåäåëåí-
íûå ôóíêöèîíàëüíûå çàâèñèìîñòè xi(t)(i =1
,
... , n), íàçûâàåìûå
äèñêðåòíûìè ðåàëèçàöèÿìè ñëó÷àéíîé ôóíêöèè X(t). Èñ÷åðïûâàþ-
ùåé õàðàêòåðèñòèêîé ñëó÷àéíîãî ïðîöåññà ñëóæàò ñîîòâåòñòâóþùèå
åìó ôóíêöèÿ ðàñïðåäåëåíèÿ è ïëîòíîñòü ðàñïðåäåëåíèÿ âåðîÿòíî-
ñòè
F
xx
ttP
X
txX
tx
kk
k
k
(,,;,,) [() ,,() ];
11
1
1
KK
K
=<
< (10.1)
fxxtt
Fxxtt
xxx
kk
k
kk
k
(,,;, ,)
(,,;, ,)
,
11
11
12
KK
KK
K
=
∂
∂∂∂
(10.2)
ãäå 0 ≤ P ≤ 1 – âåðîÿòíîñòü ñîáûòèÿ, õàðàêòåðèçóþùàÿ ñòåïåíü
âîçìîæíîñòè åãî ïîÿâëåíèÿ.
Òàêèì îáðàçîì, ôóíêöèÿ ïëîòíîñòè ðàñïðåäåëåíèÿ âåðîÿòíîñòè
(èëè ïðîñòî ïëîòíîñòü ðàñïðåäåëåíèÿ) ñëó÷àéíîãî ïðîöåññà Õ(t)îï-
ðåäåëÿåò âåðîÿòíîñòü òîãî, ÷òî äàííûé ïðîöåññ â ìîìåíò âðåìåíè t1
íàõîäèòñÿ â äèàïàçîíå x1 < X(t1)<x1 + dx1, â ìîìåíò t2 – â äèàïàçîíå
x2 < X(t2)<x2 + dx2 è ò.ä . Åñòåñòâåííî, ÷åì áîëüøå ÷èñëî k, òåì ïîë-
íåå îïèñûâàþòñÿ ñòàòèñòè÷åñêèå ñâîéñòâà ñëó÷àéíîãî ïðîöåññà.
Âåëè÷èíó ñëó÷àéíîé ôóíêöèè õàðàêòåðèçóåò ïðåæäå âñåãî ìàòå-
ìàòè÷åñêîå îæèäàíèå (ÌÎ) mx(t), ò.å . íåêîòîðàÿ íåñëó÷àéíàÿ ïðè
áåñêîíå÷íî áîëüøîì ÷èñëå èñïûòàíèé ôóíêöèÿ, îòíîñèòåëüíî êî-
òîðîé ãðóïïèðóþòñÿ êîíêðåòíûå ðåàëèçàöèè ñëó÷àéíîé ôóíêöèè
(âîçìóùåííûå òðàåêòîðèè). Îïðåäåëÿÿ îñü òðóáêè, ÌÎ çàäàåò ñðåä-
íþþ òðàåêòîðèþ â íåé è ïîëîæåíèå öåíòðà ãðóïïèðîâàíèÿ â ýëëèï-
ñå ðàññåèâàíèÿ. Îòêëîíåíèå êîíêðåòíûõ ðåàëèçàöèé (òðàåêòîðèé â
òðóáêå è òî÷åê ïàäåíèÿ â ýëëèïñå) îò ÌÎ õàðàêòåðèçóåò ñîáñòâåííî
âåëè÷èíó ðàññåèâàíèÿ. Îöåíêà ýòîé âåëè÷èíû ïîçâîëÿåò óñòàíî-
440
âèòü ñ çàäàííîé âåðîÿòíîñòüþ îáëàñòü, â êîòîðîé ìîãóò ðàñïîëà-
ãàòüñÿ òðàåêòîðèè, à ñëåäîâàòåëüíî, ðàçìåðû òðóáêè è ýëëèïñà ðàñ-
ñåèâàíèÿ. Íàèáîëåå óíèâåðñàëüíîé ÷èñëîâîé õàðàêòåðèñòèêîé, îï-
ðåäåëÿþùåé ðàññåèâàíèå, ÿâëÿåòñÿ ìîìåíò öåíòðèðîâàííîé
ñëó÷àéíîé âåëè÷èíû âòîðîãî ïîðÿäêà, íàçûâàåìîé äèñïåðñèåé Äõ(t).
Îäíàêî ïðàêòè÷åñêîå ïðèìåíåíèå äèñïåðñèè ñâÿçàíî ñ îïðåäåëåí-
íûì íåóäîáñòâîì, îáóñëîâëåííûì òåì, ÷òî äèñïåðñèÿ èìååò ðàçìåð-
íîñòü êâàäðàòà ìåðíîé âåëè÷èíû. Ïîýòîìó îò äèñïåðñèé ïåðåõîäÿò
ê ñðåäíèì êâàäðàòè÷íûì îòêëîíåíèÿì (ÑÊÎ) σx(t)= Ä
x
t().Îòìå-
òèì, ÷òî ÌÎ è ÑÊÎ ÿâëÿþòñÿ õàðàêòåðèñòèêàìè ëþáîãî çàêîíà ðàñ-
ïðåäåëåíèÿ, íî â ñëó÷àå íîðìàëüíîãî (ãàóññîâñêîãî) çàêîíà ýòè äâå
õàðàêòåðèñòèêè ÿâëÿþòñÿ èñ÷åðïûâàþùèìè. Ïðèìåíèòåëüíî ê äðó-
ãèì çàêîíàì ðàñïðåäåëåíèÿ, ïîìèìî íèõ äëÿ ïîñòðîåíèÿ ãðàôè÷å-
ñêîãî èçîáðàæåíèÿ çàêîíà ðàñïðåäåëåíèÿ íåîáõîäèìî îïðåäåëèòü
ìîìåíòû òðåòüåãî è áîëåå âûñîêèõ ïîðÿäêîâ.
Õîòÿ äèñïåðñèÿ è ÑÊÎ – óíèâåðñàëüíûå ÷èñëîâûå õàðàêòåðè-
ñòèêè, ïðè îöåíêå òî÷íîñòè ñòðåëüáû ïðåäïî÷òåíèå îòäàåòñÿ íå èì,
à äðóãîé, ìåíåå óíèâåðñàëüíîé õàðàêòåðèñòèêå, íàçûâàåìîé ñðåäèí-
íûì èëè âåðîÿòíûì îòêëîíåíèåì Å. Îáëàñòü ïðèìåíåíèÿ äàííîé
÷èñëîâîé õàðàêòåðèñòèêè îãðàíè÷èâàåòñÿ ñëó÷àéíûìè ïðîöåññàìè
(âåëè÷èíàìè), ïîä÷èíÿþùèìèñÿ òîëüêî íîðìàëüíîìó çàêîíó ðàñ-
ïðåäåëåíèÿ. Åñòåñòâåííî, âîçíèêàåò âîïðîñ, ÷åì æå ìîæíî îáúÿñ-
íèòü äàííîå îáñòîÿòåëüñòâî. Äåëî çàêëþ÷àåòñÿ â òîì, ÷òî â îáùåì
ñëó÷àå ïðîâåäåíèÿ ñòðåëüá èìååòñÿ äîñòàòî÷íî âåñêîå îñíîâàíèå
àïðèîðè ñ÷èòàòü äàííûé ïðîöåññ ãàóññîâñêèì. Ýòèì îñíîâàíèåì
ñëóæèò òàê íàçûâàåìàÿ öåíòðàëüíàÿ ïðåäåëüíàÿ òåîðåìà òåîðèè âåðî-
ÿòíîñòåé. Äåéñòâèòåëüíî, êàê ñâèäåòåëüñòâóåò îïûò, ïðè äîñòàòî÷íî
áîëüøîì êîëè÷åñòâå ñëó÷àéíûõ ôàêòîðîâ, îêàçûâàþùèõ âëèÿíèå
íà äâèæåíèå ËÀ, íè îäèí èç íèõ íå ÿâëÿåòñÿ ïðåâàëèðóþùèì. Â
ýòîé ñèòóàöèè, ñîãëàñíî íàçâàííîé òåîðåìå, ìîæíî ïîëàãàòü, ÷òî
âíå çàâèñèìîñòè îò òîãî, êàêèìè ÿâëÿþòñÿ ðàñïðåäåëåíèÿ êàæäîãî
èç âîçìóùàþùèõ ñëó÷àéíûõ ôàêòîðîâ, ïîðîæäàåìûé èìè ïðîöåññ
äâèæåíèÿ ËÀ áóäåò àñèìïòîòè÷åñêè íîðìàëüíûì. Ñ äðóãîé ñòîðî-
íû, ïðèìåíåíèå äëÿ îöåíêè ðàññåèâàíèÿ ñðåäèííîãî îòêëîíåíèÿ
óäîáíî òåì, ÷òî ìîæíî ëåãêî óñòàíîâèòü âåðîÿòíîñòü ïîïàäàíèÿ
ñëó÷àéíîé âåëè÷èíû â ïðåäåëû, âûðàæåííûå â åãî äîëÿõ.
Ïî îïðåäåëåíèþ âåðîÿòíûì (ñðåäèííûì) îòêëîíåíèåì íàçûâà-
åòñÿ ïîëîâèíà øèðèíû ïîëîñû (ó÷àñòêà), êîòîðàÿ ñèììåòðè÷íà îò-
íîñèòåëüíî îñè, ïðîâåäåíà ÷åðåç öåíòð ãðóïïèðîâàíèÿ, ïåðïåíäè-
êóëÿðíà íàïðàâëåíèþ ñòðåëüáû è âåðîÿòíîñòü ïîïàäàíèÿ â êîòîðóþ
ðàâíà 0,5 (ðèñ. 10.1). Óêàçàííûå íà ðèñ. 10.1 âåðîÿòíîñòè ïîÿâëåíèÿ
ñëó÷àéíûõ âåëè÷èí, ñîîòâåòñòâóþùèå ïðåäåëàì 0...Å; Å...2Å;
2Å...3Å è3Å...4Å, ÿâëÿþòñÿ ïðèáëèæåííûìè. Íà ñàìîì äåëå òî÷íûå
441
çíà÷åíèÿ èõ ðàâíû 0,2500; 0,1611; 0,0674; 0,0180. Òàêèì îáðàçîì, â
ïðåäåëàõ îò −4Å äî +4Å ñóììàðíîå çíà÷åíèå âåðîÿòíîñòè ðàâíî
0,993, ò.å . âåðîÿòíîñòü âûõîäà ñëó÷àéíîé âåëè÷èíû çà ïðåäåëû ýë-
ëèïñà, îïðåäåëÿåìîãî "çàêîíîì ±4Å ", ñîñòàâëÿåò âñåãî 0,7 %. Â ïî-
äàâëÿþùåì áîëüøèíñòâå ñëó÷àåâ ýòîé âåðîÿòíîñòüþ ìîæíî ïðå-
íåáðå÷ü, ñ÷èòàÿ âåðîÿòíîñòü ñòîïðîöåíòíîé.
Âåëè÷èíà âåðîÿòíîãî îòêëîíåíèÿ Å ñâÿçàíà ñ âåëè÷èíîé Ð ñëå-
äóþùèì óðàâíåíèåì:
Pxm E
x
(|
|)/,
−<=
12
(10.3)
èëè
2
2
1
2
2
2
2
0
σπ
σ
x
x
E
ed
x
x
−
∫=
()
,
o
o
(10.4)
ãäå xxm
ix
o
=− – öåíòðèðîâàííàÿ ñëó÷àéíàÿ âåëè÷èíà. Óðàâíåíèå
(10.4) ïîçâîëÿåò ïîëó÷èòü âûðàæåíèå äëÿ Å â âèäå E
x
=ρσ
2 èëè,
ó÷èòûâàÿ, ÷òî ρ = 0,4770, â âèäå Å = 0,6745σõ.
×òîáû áîëåå ïîëíî îõàðàêòåðèçîâàòü ïðîöåññ ñòðåëüáû êàê
ñëó÷àéíûé ïðîöåññ, ñëåäóåò
óñòàíîâèòü çàâèñèìîñòü èëè,
èíà÷å, ñòåïåíü ñòîõàñòè÷åñêîé
âçàèìîñâÿçè ìåæäó çíà÷åíèÿ-
ìè, õàðàêòåðèçóþùèìè îò-
äåëüíûå ðåàëèçàöèè (òðàåêòî-
ðèè) â ðàçëè÷íûå ìîìåíòû
âðåìåíè. ×èñëîâîé õàðàêòåðè-
ñòèêîé, "îòâå÷àþùåé" çà êîëè-
÷åñòâåííóþ îöåíêó âíóòðåí-
íåé ñòðóêòóðû òðóáêè òðàåêòî-
ðèé è ñîîòâåòñòâåííî îðèåí-
òàöèþ îñåé ýëëèïñà ðàññåèâà-
íèÿ, ñëóæèò êîððåëÿöèîííàÿ
ôóíêöèÿ Kx(t).
Ïðè èññëåäîâàíèè ñòàòè-
ñòè÷åñêîé äèíàìèêè ïîëåòà
ñîîòâåòñòâóþùèå ÷èñëîâûå õà-
ðàêòåðèñòèêè (ÌÎ, äèñïåðñèÿ,
ÑÊÎ) äîëæíû áûòü îïðåäåëå-
442
Ðèñ. 10 .1. Îïðåäåëåíèå ïîíÿòèÿ âåðîÿò-
íîãî îòêëîíåíèÿ
íû äëÿ âñåõ êîìïîíåíòîâ âåêòîðà ñîñòîÿíèÿ ËÀ ïðèìåíèòåëüíî ê
ëþáîìó (â òîì ÷èñëå è êîíå÷íîìó) ìîìåíòó âðåìåíè. Ïðè ýòîì ðàç-
ìåðíîñòü ïîäëåæàùåãî îöåíèâàíèþ ñòîõàñòè÷åñêîãî âåêòîðà ôàçî-
âîãî ñîñòîÿíèÿ îïðåäåëÿåòñÿ ðàçìåðíîñòüþ êîððåëÿöèîííîé ìàò-
ðèöû. Ïîä ïîñëåäíåé ïîíèìàåòñÿ ìàòðèöà Kõ ðàçìåðîì n×n,ñî-
ñòàâëåííàÿ èç êîððåëÿöèîííûõ ìîìåíòîâ kij, i, j =1,..., n, i ≠ j,è
äèñïåðñèé Äi = kii, i =1,2,..., n, êîìïîíåíòîâ n-ìåðíîãî âåêòîðà
x(t):
KxK
xx
x
t{}
{},
==
Mò
oo
(10.5)
ïðè÷åì, åñëè kij = kji, ìàòðèöà Kt{x} áóäåò ñèììåòðè÷åñêîé.
Ñèììåòðè÷åñêóþ êîððåëÿöèîííóþ (n×n) ìàòðèöó íàçûâàþò èíîãäà
êîâàðèàöèîííîé ìàòðèöåé èëè ìàòðèöåé êîâàðèàöèé.
Îòìåòèì òàêæå, ÷òî ïðè îäèíàêîâûõ çíà÷åíèÿõ àðãóìåíòîâ
ôóíêöèé êîâàðèàöèîííàÿ ìàòðèöà èìååò ñïåöèàëüíîå íàçâàíèå
ìàòðèöû äèñïåðñèé èëè äèñïåðñèîííîé ìàòðèöû. Åñëè ñîñòàâëÿþùèå
ñëó÷àéíîãî âåêòîðà x(t) âçàèìíî íåêîððåëèðîâàíû, ìàòðèöà áóäåò
äèàãîíàëüíîé, ò.å . âñå åå âíåäèàãîíàëüíûå ýëåìåíòû ðàâíû íóëþ.
 ðÿäå ñëó÷àåâ îêàçûâàåòñÿ âûãîäíûì îñóùåñòâèòü íîðìèðîâàíèå
êîððåëÿöèîííîé ìàòðèöû, ïåðåéäÿ îò kij ê êîýôôèöèåíòàì êîððåëÿ-
öèè rij = kij/σξi σξj.
Ïðè ñòðåëüáå ïî ìåñòíîñòè, à òàêæå ïðè îáðàáîòêå ðåçóëüòàòîâ
îïûòíûõ ñòðåëüá ïî ùèòàì çà÷àñòóþ îêàçûâàåòñÿ äîñòàòî÷íûì
ëèøü îñóùåñòâèòü ñòàòèñòè÷åñêóþ îáðàáîòêó òî÷åê ïàäåíèÿ ñíàðÿ-
äîâ èëè ïðîáîèí â ùèòå.  ýòîì ïðîñòåéøåì ñëó÷àå óæå íåò íåîáõî-
äèìîñòè èìåòü äåëî ñî ñëó÷àéíûìè ôóíêöèÿìè. Äîñòàòî÷íî îãðà-
íè÷èòüñÿ ïðîâåäåíèåì èññëåäîâàíèÿ íà óðîâíå ðàññìàòðèâàíèÿ
ñëó÷àéíûõ âåëè÷èí, îòðàæàþùèõ ïàðàìåòðû ïðîöåññà â îäíîì, êàê
ïðàâèëî íàèáîëåå âàæíîì, åãî ñå÷åíèè.
10.1.2 . ÌÅÒÎÄ ÌÀÒÐÈÖÛ ÂËÈßÍÈß
Äîñòàòî÷íî ïðîñòûì è ýôôåêòèâíûì ìåòîäîì ñòàòèñòè÷åñêîãî
àíàëèçà âîçìóùåííîãî äâèæåíèÿ ËÀ â îêðåñòíîñòè íîìèíàëüíîé
áàëëèñòè÷åñêîé òðàåêòîðèè ÿâëÿåòñÿ ìåòîä ìàòðèöû âëèÿíèÿ.Îá
-
ñóæäàåìîìó âèäó äâèæåíèÿ îòâå÷àåò [36] ñëåäóþùàÿ ìîäåëü ëèíåà-
ðèçîâàííîãî äâèæåíèÿ:
d
dt
tt
tt
xA
xxx
() ()(), ()
.
==
00
(10.6)
443
Ïðåäïîëîæèì, ÷òî äëÿ ñïåöèàëüíî âûáðàííûõ íà÷àëüíûõ óñëîâèé
x0
1
100 0
() [,,, ,];
=
K
ò
xx
0
2
0
010 0
000 1
()
()
[,,, ,], , [,,, ,]
==
KK
K
òò
n
ïîëó÷åíî n
(ïî ÷èñëó êîìïîíåíòîâ âåêòîðà ñîñòîÿíèÿ) ðåøåíèé çàäà÷è Êîøè
äëÿ óðàâíåíèÿ (10.6). Ñîáèðàÿ ýòè ðåøåíèÿ â ìàòðèöó ðàçìåðîì n×n,
ïîëó÷èì
xt xt
xt
xt xt
xt
x
n
n
n
1
1
1
2
1
2
1
2
2
2
()
()
()
()
(
() ()
()
() ()
()
K
K
M
12
11
1
1
)(
)
() ()
()
txt
xt
ff
ff
nn
n
n
nn
n
K
K
MM
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=Φ()
t
–
ìàòðèöó, ñîñòàâëåííóþ èç ôóíäàìåíòàëüíîé ñèñòåìû ðåøåíèé,
óäîâëåòâîðÿþùóþ ëèíåéíîìó îäíîðîäíîìó óðàâíåíèþ (10.6):
d
dt
tt
t
ΦΦ
() () ().
=A
(10.7)
Ïîëó÷åííàÿ ìàòðèöà, ÿâëÿþùàÿñÿ íåîñîáåííîé ïðè ëþáîì t,
íàçûâàåòñÿ èíòåãðàëüíîé (ôóíäàìåíòàëüíîé) ìàòðèöåé ðåøåíèé
óðàâíåíèÿ (10.7).  îòëè÷èå îò èíòåãðàëüíîé ìàòðèöà âèäà
ΦΦ ΦΦ
t
t
tt
tt
0
0
1
0
==
−
(,) ()()
(10.8)
íàçûâàåòñÿ íîðìèðîâàííîé èíòåãðàëüíîé ìàòðèöåé èëè ïåðåõîäíîé
ìàòðèöåé ôàçîâûõ ñîñòîÿíèé. Ïðè t = t0 ìàòðèöà Φ(t, t0)=Φ(t0, t0)=
=E,ãäå
E=
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
10
0
01
0
00
1
......
MM
M
ïðåäñòàâëÿåò ñîáîé åäèíè÷íóþ ìàòðèöó ðàçìåðîì (n×n). Åñëè äëÿ
ñèñòåìû (10.6) èçâåñòíà ïåðåõîäíàÿ ìàòðèöà ôàçîâûõ ñîåäèíåíèé, òî
îáùåå ðåøåíèå (10.6) çàïèñûâàåòñÿ â âèäå
xx
() (,)().
tt
t
t
=Φ 00
(10.9)
Ðàññìàòðèâàÿ âåêòîð x(t) êàê ñëó÷àéíûé, ïîíèìàÿ ïîä íèì
xx
x
x
()()()(),
tt tt
i
=−=
M
o
(10.10)
444
ãäå Ìx(t) îïðåäåëÿåò íîìèíàëüíîå áàëëèñòè÷åñêîå äâèæåíèå,
ïîëó÷èì
xx
oo
() (,)().
tt
tt
=Φ 00
(10.11)
Ñ ó÷åòîì òîãî ÷òî xx
òò
ò
() ()(,),
ttt
t
o
o
=
00
Φ
èç (10.5) ñëåäóåò
KK
xx
() (,)()(,).
tt
ttt
t
=Φ
Φ
000
ò
(10.12)
Åñëè âîçìóùåííîå äâèæåíèå â îêðåñòíîñòè íîìèíàëüíîé
áàëëèñòè÷åñêîé òðàåêòîðèè îáóñëîâëåíî íå òîëüêî âîçìóùåíèÿìè,
îïðåäåëÿåìûìè íà÷àëüíûìè óñëîâèÿìè äâèæåíèÿ x(t0), íî è
íåïðåðûâíî äåéñòâóþùèì âäîëü òðàåêòîðèè âîçìóùåíèåì, òî,
ïåðåõîäÿ ê ñòîõàñòè÷åñêîìó óðàâíåíèþ (ñì. (2.14)) âèäà
dt
d
t
d
t
xAx
=+
()
(),
η
çàïèøåì [36] åãî ðåøåíèå â ôîðìå
xx
() (,)() (,)().
tt
ttt
d
t
t
=+
∫
ΦΦ
00
0
τητ
(10.13)
Èíòåãðàë â ïðàâîé ÷àñòè (10.13) èç-çà íàëè÷èÿ äèôôåðåíöèàëà
íåëüçÿ èíòåðïðåòèðîâàòü êàê îáû÷íûå èíòåãðàëû Ðèìàíà èëè
Ñòèëòüåñà [35]. Èíòåãðàë ìîæåò áûòü âû÷èñëåí ïî ÷àñòÿì òîëüêî â
òîì ñëó÷àå, êîãäà Φ(t, τ) – ãëàäêàÿ ôóíêöèÿ.
 ðåçóëüòàòå èíòåãðèðîâàíèÿ ïîëó÷èì
ΦΦΦ
(,)() () (,)() ()(,).
td
t ttt
dt
t
t
t
t
τητ η
η
ηττ
=−
−
∫
E
00
0
0
∫
(10.14)
Òàêèì îáðàçîì, ñòàòèñòè÷åñêèé àíàëèç ïðîöåññà äâèæåíèÿ ËÀ,
óäîâëåòâîðÿþùåãî ìîäåëè (2.14), ïî ñóùåñòâó ñâîäèòñÿ ê àíàëèçó
ñòîõàñòè÷åñêîãî èíòåãðàëà ητ
() (,),
tdt
t
t
Φ
0
∫
íàçûâàåìîãî èíòåãðàëîì Èòî
[35, 36].
 çàäà÷àõ îöåíêè òî÷íîñòè ñòðåëüáû èíòåðåñ ïðåäñòàâëÿåò ñëó-
÷àé, îòâå÷àþùèé t = tc = Ò. Ïðè ýòîì ïîä t0 ìîæåò ïîíèìàòüñÿ ëèáî
êàêîé-òî ôèêñèðîâàííûé íà÷àëüíûé ìîìåíò âðåìåíè (íàïðèìåð,
ìîìåíò ïðîõîæäåíèÿ àðòèëëåðèéñêèì ñíàðÿäîì äóëüíîãî ñðåçà,
445
âðåìÿ îêîí÷àíèÿ êîíöà àêòèâíîãî ó÷àñòêà), ëèáî ëþáîé ïðîèçâîëü-
íûé ìîìåíò âðåìåíè äâèæåíèÿ ËÀ.
Îòâå÷àþùàÿ ýòîìó ñëó÷àþ ìàòðèöà
ΦΦ
Φ
(,)
()
tt
ct
t
t
t
c
c
==
−1
(10.15)
íàçûâàåòñÿ ìàòðèöåé âëèÿíèÿ.
 ñèëó íåâûðîæäåííîñòè ïåðåõîäíîé ìàòðèöû, à ñëåäîâàòåëüíî,
è ìàòðèöû âëèÿíèÿ
ΦΦ
−
=
1
(,) (,)
,
tt
tt
cc
c
ò
(10.16)
ãäå Φcc
tt
ò
(,)–ìàòðèöà âëèÿíèÿ ñîïðÿæåííîé ñèñòåìû.
Èñêîìàÿ ìàòðèöà Φt
tc
ìîæåò áûòü íàéäåíà îäíîêðàòíûì èíòåãðè-
ðîâàíèåì â "îáðàòíîì" âðåìåíè îò tc = T äî t ñîïðÿæåííîé ñèñòåìû
d
dt
tt
t
ΦΦ
() ()()
=−A
(10.17)
ïðè î÷åâèäíîì ãðàíè÷íîì óñëîâèè Φ(tc)=E. Äåéñòâèòåëüíî,
ïîëó÷åííàÿ â ðåçóëüòàòå ðåøåíèÿ (10.17) ìàòðèöà ()
Φt
t
c
c
ñâÿçàíà ñ
ìàòðèöåé Φt
t
k
ñîîòíîøåíèåì òèïà (10.16), è ïîýòîìó
ΦΦ
t
t
cc
c
tt
=
ò
(, ).
(10.18)
Ïî ñâîåé ñóòè ìàòðèöà âëèÿíèÿ ïðåäñòàâëÿåò ñîáîé ìàòðèöó
÷àñòíûõ ïðîèçâîäíûõ êîìïîíåíòîâ âåêòîðà ñîñòîÿíèÿ ËÀ â òî÷êå
ïàäåíèÿ ïî òåêóùèì êîìïîíåíòàì äàííîãî âåêòîðà, ÿâëÿþùèìñÿ
ôóíêöèåé âðåìåíè äëÿ ëþáîãî ïðîèçâîëüíîãî ìîìåíòà âîçìóùåí-
íîãî äâèæåíèÿ, ò.å .
Φt
t
c
c
t
t
=
∂
∂
x
x
()
().
(10.19)
Çíàÿ Φt
tc
, ïîëó÷èòü õàðàêòåðèñòèêè òî÷íîñòè ñòðåëüáû, îïðåäåëÿåìûå
äèñïåðñèîííîé ìàòðèöåé Kx(tc), äëÿ âñåõ èíòåðåñóþùèõ ôàçîâûõ
êîîðäèíàò óæå íå ñîñòàâëÿåò íèêàêèõ òðóäíîñòåé:
KK
xx
()()()().
tt
ct
t
t
t
cc
=Φ
Φò
(10.20)
Ïîä÷åðêíåì, ÷òî äåéñòâóþùèå âîçìóùåíèÿ òðàêòóþòñÿ çäåñü êàê
ñëó÷àéíûå ôóíêöèè. Åñëè æå òåïåðü çàôèêñèðîâàòü t, ïðèíÿâ, íà-
446
ïðèìåð, åãî ðàâíûì t = tê, ãäå tê – âðåìÿ êîíöà àêòèâíîãî ó÷àñòêà
òðàåêòîðèè, â ðàññìîòðåíèè âîçìóùåíèé êàê ñëó÷àéíûõ ôóíêöèé
íåîáõîäèìîñòè íå áóäåò.  ýòîì ñëó÷àå ïðåäñòàâëÿåòñÿ âîçìîæíûì
ïåðåéòè ê ïðåäñòàâëåíèþ âîçìóùåíèé â ôîðìå ñëó÷àéíûõ âåëè÷èí:
KK
xx
()
()( ).
tt
ct
t
t
t
cc
=Φ
Φ
êê
ê
ò
(10.21)
Çäåñü óæå Kx(tê) – äèñïåðñèîííàÿ ìàòðèöà, õàðàêòåðèçóþùàÿ
ðàññåèâàíèå ýëåìåíòîâ òðàåêòîðèè â êîíöå àêòèâíîãî ó÷àñòêà; Φt
tc
ê
–
ìàòðèöà, ýëåìåíòû êîòîðîé ñóòü ïîïðàâî÷íûå êîýôôèöèåíòû,
ðàññìîòðåííûå â ãë. 8.
Ïóñòü, íàïðèìåð, òðåáóåòñÿ îïðåäåëèòü â òî÷êå ïàäåíèÿ ðàññåè-
âàíèå ïðîäîëüíîé äàëüíîñòè õñ, ñêîðîñòè Vc è óãëà θc ïðè çàäàííûõ
ÑÊÎ óêàçàííûõ ýëåìåíòîâ â êîíöå àêòèâíîãî ó÷àñòêà òðàåêòîðèè.
Äëÿ ïðîñòîòû ñíà÷àëà áóäåì ñ÷èòàòü, ÷òî óêàçàííûå ñëó÷àéíûå âå-
ëè÷èíû âçàèìíî íåêîððåëèðîâàíû (kij = kji = 0). Òîãäà
σ
σ
σ
∂
∂
∂
∂
∂
θ
x
V
c
k
c
k
c
c
c
x
x
x
y
2
2
2
22
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
⎛
⎝⎜⎞
⎠⎟⎛
⎝⎜⎞
⎠⎟x
V
x
V
x
V
y
c
k
c
k
c
k
c
k
∂
∂
∂θ
∂
∂
∂
∂
⎛
⎝⎜⎞
⎠⎟⎛
⎝⎜⎞
⎠⎟
⎛
⎝⎜⎞
⎠⎟⎛
⎝⎜⎞
⎠⎟
22
2
222
2
∂
∂
∂
∂θ
∂θ
∂
∂θ
∂
V
V
V
xy
c
k
c
k
c
k
c
k
⎛
⎝⎜⎞
⎠⎟⎛
⎝⎜⎞
⎠⎟
⎛
⎝⎜⎞
⎠⎟⎛
⎝⎜⎞
⎠⎟⎛
⎝⎜⎞
⎠⎟⎛
⎝⎜⎞
⎠⎟
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
222
∂θ
∂
∂θ
∂θ
c
k
c
k
V
⎥
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
σ
σ
σ
σθ
x
y
V
k
k
k
k
2
2
2
2
,
÷òî ýêâèâàëåíòíî ïðè èñïîëüçîâàíèè îáîáùåííîé ôîðìû çàïèñè
ñîîòíîøåíèþ âèäà
σ
∂
∂ξ
σξ
A
j
im
i
n
j
ij
A
2
2
2
1
=
⎛
⎝⎜⎞
⎠⎟
=
∑
.
(10.22)
Åñëè öåëüþ èññëåäîâàíèÿ ÿâëÿåòñÿ îïðåäåëåíèå òîëüêî ïðîäîëüíîãî
ðàññåèâàíèÿ òî÷åê ïàäåíèÿ ðàêåòû, òî
σ
∂
∂
∂
∂
∂
∂
∂
∂θ
x
c
k
c
k
c
k
c
k
c
x
x
x
y
x
V
x
2
222
=
⎛
⎝⎜⎞
⎠⎟⎛
⎝⎜⎞
⎠⎟⎛
⎝⎜⎞
⎠⎟⎛
⎝⎜⎞
⎠⎟
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
2
2
2
2
2
σ
σ
σ
σθ
x
y
V
k
k
k
k
.
447
Ïîëàãàÿ àïðèîðè, ÷òî ïðîöåññ ïîä÷èíÿåòñÿ íîðìàëüíîìó çàêîíó
ðàñïðåäåëåíèÿ, è èñïîëüçóÿ èçâåñòíîå ñîîòíîøåíèå Å = 0,6745σx,
ïåðåéäåì ê âåðîÿòíûì îòêëîíåíèÿì. Ïðè ýòîì âåðîÿòíûå
îòêëîíåíèÿ xk, yk, Vk è θk îáîçíà÷èì ñîîòâåòñòâåííî ÷åðåç rx k
, ryk
, rVk
è
rk
θ . Òîãäà
E
x
x
r
x
y
r
x
V
r
x
c
k
x
c
k
y
c
k
V
ckk
k
=
⎛
⎝⎜⎞
⎠⎟ +⎛
⎝⎜⎞
⎠⎟+⎛
⎝⎜
∂
∂
∂
∂
∂
∂
22
⎞
⎠⎟ +⎛
⎝⎜⎞
⎠⎟
22
∂
∂θθ
x
r
c
k
k
,
èëè â îáùåì âèäå
E
A
r
A
j
i
i
i
n
j
=
⎛
⎝⎜⎞
⎠⎟
=
∑∂
∂ξ
2
1
.
(10.23)
Åñëè óñëîâíî îáîçíà÷èòü
∂
∂ξ
A
rE
j
i
iA
i
⎛
⎝⎜⎞
⎠⎟=
,òî
EEE E
AA
AA
jn
=+
+
+
12
222
K
.
(10.24)
 ÷àñòíîñòè, äëÿ àðòèëëåðèéñêîé ñèñòåìû xc = f(V0, θ0, c), ïîýòî-
ìó, ñ÷èòàÿ óêàçàííûå àðãóìåíòû íåçàâèñèìûìè ñëó÷àéíûìè âåëè-
÷èíàìè, ïîëó÷èì
EB rrr
xx
x
x
cVc
==
++
ä
00
222
θ
,
(10.25)
ãäå rr
V
Q
xVV
V0
00
0
100
=
–
âåðîÿòíîå îòêëîíåíèå, õàðàêòåðèçóþùåå ðàñ-
ñåèâàíèå ñíàðÿäîâ ïî äàëüíîñòè âñëåäñòâèå ðàçáðîñà çíà÷åíèé
íà÷àëüíîé ñêîðîñòè; rrQ
xθ
θθ
θ
0
00
0
60
=
–
âåðîÿòíîå îòêëîíåíèå, õàðàê-
òåðèçóþùåå ðàññåèâàíèå äàëüíîñòè âñëåäñòâèå ðàçáðîñà çíà÷åíèé
óãëà áðîñàíèÿ; rr
Q
xc
c
c
c
=
δ – âåðîÿòíîå îòêëîíåíèå, õàðàêòåðèçóþùåå
ðàññåèâàíèå ïî äàëüíîñòè âñëåäñòâèå ðàçáðîñà çíà÷åíèé áàëëèñ-
òè÷åñêîãî êîýôôèöèåíòà. Ñîîòâåòñòâåííî rV 0
, rθ0
è rc – âåðîÿòíûå
îòêëîíåíèÿ íà÷àëüíîé ñêîðîñòè (â ïðîöåíòàõ), óãëà áðîñàíèÿ
(â óãëîâûõ ìèíóòàõ) è áàëëèñòè÷åñêîãî êîýôôèöèåíòà (â ïðîöåíòàõ),
à QV0
,Qθ0
èQc
c
δ – òàáëè÷íûå îñíîâíûå ïîïðàâî÷íûå êîýôôèöèåíòû,
448
âûðàæàþùèå èçìåíåíèå ïîëíîé äàëüíîñòè ñòðåëüáû ïðè åäèíè÷íûõ
èçìåíåíèÿõ ñêîðîñòè, óãëà áðîñàíèÿ è áàëëèñòè÷åñêîãî êîýô-
ôèöèåíòà. Åñëè ýëåìåíòû êîâàðèàöèîííîé ìàòðèöû Kij ≠ 0, òî
âûðàæåíèå äëÿ îïðåäåëåíèÿ ðàññåèâàíèÿ òî÷åê ïàäåíèÿ ðàêåò â
ïðåäïîëîæåíèè, ÷òî
xf
Vxy
c
kkkk
=
(,,,)
,
θ
áóäåò èìåòü âèä
σ
∂
∂
σ
∂
∂θ
σ
∂
∂
σ
θ
x
c
k
V
c
k
c
k
x
c kkk
x
V
xx
x
=
⎛
⎝⎜
⎞
⎠⎟ +⎛
⎝⎜⎞
⎠⎟ +⎛
⎝⎜
22
⎞
⎠⎟+
⎧
⎨⎪
⎩⎪
⎛
⎝⎜⎞
⎠⎟+
+
22
2
∂
∂
σ
∂
∂
∂
∂θ
σσ
θ
x
y
x
V
x
r
c
k
y
c
k
c
k
VV
k
kk kθ
θ
∂
∂
∂
∂
σσ
∂
∂
∂
∂
σ
kk
k
k
k
kkk
x
V
x
y
r
x
V
x
x
r
c
k
c
k
VyVy
c
k
c
k
VV
++
+
2
2
σ
∂
∂θ
∂
∂
σσ
∂
∂θ
∂
∂
σ
θθ
θθ
x
c
k
c
k
xx
c
k
c
k
y
kk
k
k
k
kk
xx
x
r
xx
y
r
++
+
2
2
kk
k
kkk
y
c
k
c
k
yxyx
x
y
x
x
r
δ
∂
∂
∂
∂
σσ
+
⎫
⎬
⎭
2
12
/
.
Ýêâèâàëåíòíûé ðåçóëüòàò ìîæåò áûòü ïîëó÷åí è ïðè èñïîëü-
çîâàíèè íåñêîëüêî èíîãî ïîäõîäà ê ðåøåíèþ ðàññìàòðèâàåìîé
çàäà÷è, à èìåííî íà îñíîâå ðàçëîæåíèÿ ôóíêöèè ñëó÷àéíûõ àð-
ãóìåíòîâ â ñòåïåííîé ðÿä â îêðåñòíîñòè çíà÷åíèÿ ôóíêöèè, îò-
âå÷àþùåãî âûáðàííîìó âðåìåííîìó ñå÷åíèþ (íàïðèìåð, êîíöó
àêòèâíîãî ó÷àñòêà) è ñîîòâåòñòâóþùåãî ìàòåìàòè÷åñêèì îæèäà-
íèÿì àðãóìåíòîâ ðàññìàòðèâàåìîé ôóíêöèè. Ïðè ýòîì â ðàçëî-
æåíèè îáû÷íî ðåêîìåíäóåòñÿ ñîõðàíÿòü ÷ëåíû íå âûøå âòîðîãî
ïîðÿäêà.
Âûðàæåíèå äëÿ îïðåäåëåíèÿ ñðåäíåãî êâàäðàòè÷åñêîãî îòêëîíå-
íèÿ íåêîòîðîé ñëó÷àéíîé ôóíêöèè À = f(ξ1, ξ2,..., ξn) äëÿ äàííîãî
ñëó÷àÿ áóäåò èìåòü âèä
σ
∂
∂ξ
σ
∂
∂ξ
∂
∂ξ
ξ
A
im
i
n
im
j
ff
f
i
i
i
2
2
2
1
2
=
⎛
⎝⎜⎞
⎠⎟+⎛
⎝⎜⎞
⎠⎟⎛
⎝⎜
=
∑
⎞
⎠⎟
<
∑
m
ij
ij
j
ij
rσσ
ξξ,
(10.27)
ãäå rij – êîýôôèöèåíò êîððåëÿöèè ñëó÷àéíûõ âåëè÷èí ξi è ξj.
449
(10.26)
Îäíàêî èìååò ñìûñë ïîä÷åðêíóòü, ÷òî èçëîæåííûé ïîäõîä ÿâëÿ-
åòñÿ âñå æå ÷àñòíûì ïî îòíîøåíèþ ê ðàññìîòðåííîìó îáùåìó ìåòî-
äó (ìåòîäó ìàòðèöû âëèÿíèÿ).
Ïðè ïðèìåíåíèè ìåòîäà ñòåïåííûõ ðàçëîæåíèé ôóíêöèè ñëó-
÷àéíûõ àðãóìåíòîâ íåîáõîäèìî èìåòü â âèäó, ÷òî ÷àñòíûå ïðîèç-
âîäíûå ∂f/∂ξi (ñóùåñòâîâàíèå êîòîðûõ äîëæíî ãàðàíòèðîâàòüñÿ òè-
ïîì ôóíêöèè f, ÷òî ÿâëÿåòñÿ îáùèì òðåáîâàíèåì) áåðóòñÿ â òî÷êå
{mi}, i =1,..., n, ñîîòâåòñòâóþùåé ìàòåìàòè÷åñêîìó îæèäàíèþ àðãó-
ìåíòîâ.
10.1.3. ÏÐÈÌÅÍÅÍÈÅ ÒÅÎÐÈÈ ÌÀÐÊÎÂÑÊÈÕ ÏÐÎÖÅÑÑÎÂ
ÏÐÈ ÎÏÐÅÄÅËÅÍÈÈ ÕÀÐÀÊÒÅÐÈÑÒÈÊ ÐÀÑÑÅÈÂÀÍÈß ÒÐÀÅÊÒÎÐÈÉ ËÀ
 ïîñëåäíèå ãîäû â êà÷åñòâå ìåòîäîâ àïðèîðíîãî ñòàòèñòè÷åñêî-
ãî àíàëèçà äâèæåíèÿ ËÀ âñå áîëåå øèðîêîå ïðèìåíåíèå íàõîäÿò ìå-
òîäû, áàçèðóþùèåñÿ íà òåîðèè ìàðêîâñêèõ ïðîöåññîâ.
Ïðåæäå ÷åì ïåðåéòè ê ðàññìîòðåíèþ ýòèõ ìåòîäîâ, ââåäåì íå-
ñêîëüêî îáùèõ ïîíÿòèé, ñâÿçàííûõ ñ ìîäåëèðîâàíèåì ñëó÷àéíûõ
âåëè÷èí è ïðîöåññîâ, îïðåäåëÿþùèõ ñòàòèñòè÷åñêóþ äèíàìèêó ËÀ.
Ñðåäè ýòèõ ïîíÿòèé âàæíóþ ðîëü èãðàþò òàê íàçûâàåìûå ñòàöèî-
íàðíûå ñëó÷àéíûå ïðîöåññû. Ñëó÷àéíûé ñêàëÿðíûé èëè âåêòîðíûé
ïðîöåññ X(t) íàçûâàåòñÿ ñòàöèîíàðíûì â øèðîêîì ñìûñëå, åñëè åãî
ìàòåìàòè÷åñêîå îæèäàíèå åñòü âåëè÷èíà ïîñòîÿííàÿ (mx = const) è
êîððåëÿöèîííàÿ ôóíêöèÿ Kx(t1, t2) íå çàâèñèò îò çíà÷åíèé àðãóìåí-
òîâ t1 è t2, à îïðåäåëÿåòñÿ èõ ðàçíîñòüþ τ = t2 − t1. Ïðè τ = 0 êîððå-
ëÿöèîííàÿ ôóíêöèÿ ñêàëÿðíîãî ñòàöèîíàðíîãî ïðîöåññà Kx(τ)=
= Kx(0)=σ
x
2
= const.
Êâàçèïåðèîäè÷åñêèé õàðàêòåð ïî âðåìåíè âåðîÿòíîñòíûõ õàðàê-
òåðèñòèê ñòàöèîíàðíûõ ñëó÷àéíûõ ïðîöåññîâ ïîçâîëÿåò çàìåíèòü
èññëåäîâàíèå ñòàöèîíàðíîé ñëó÷àéíîé ôóíêöèè âðåìåíè èññëåäî-
âàíèåì ñëó÷àéíîé ôóíêöèè íåêîòîðîé âñïîìîãàòåëüíîé ïåðåìåí-
íîé.  ÷àñòíîñòè, ïðèåìëåìûå ðåçóëüòàòû ìîãóò áûòü ïîëó÷åíû ïðè
àïïðîêñèìàöèè ñòàöèîíàðíîé ñëó÷àéíîé ôóíêöèè X(t) ñóììîé ãàð-
ìîíè÷åñêèõ ïðîöåññîâ ñ ðàçëè÷íûìè êîìïëåêñíûìè àìïëèòóäàìè,
êîòîðûå âûðàæàþòñÿ â âèäå ïðîèçâåäåíèÿ èõ ìîäóëåé (âåùåñòâåí-
íûõ àìïëèòóä) íà ýêñïîíåíöèàëüíûé ìíîæèòåëü, ó÷èòûâàþùèé
ôàçó ãàðìîíèêè. Äàííîå îáñòîÿòåëüñòâî äàåò îñíîâàíèå ñâÿçàòü
Kx(τ) ñî ñïåêòðàëüíîé ïëîòíîñòüþ ïðîöåññà Sx(ω) ñîîòíîøåíèåì
âèäà
Se
K
d
x
j
x
()
().
ω
π
ττ
ωτ
=
−
−∞
∞
∫1
2
(10.28)
450
Îáðàòíîå ïðåîáðàçîâàíèå Ôóðüå ïîçâîëÿåò íàéòè
KS
e
d
xx
j
()().
τω
ω
ωτ
=
−∞
∞
∫
(10.29)
×àñòíûì ñëó÷àåì äàííîé ôîðìóëû (τ = 0) ÿâëÿåòñÿ âûðàæåíèå,
ïðåäñòàâëÿþùåå äèñïåðñèþ ñëó÷àéíîãî ïðîöåññà ÷åðåç ñïåê-
òðàëüíóþ ïëîòíîñòü:
KS
d
xxx
()
().
02
==
−∞
∞
∫
σω
ω
(10.30)
Ñòàöèîíàðíûé ñëó÷àéíûé ïðîöåññ, èìåþùèé ïîñòîÿííóþ ñïåê-
òðàëüíóþ ïëîòíîñòü Sx(ω)=c = const, íîñèò íàçâàíèå áåëîãî øóìà.
Çíà÷åíèå ñ õàðàêòåðèçóåò âåëè÷èíó èíòåíñèâíîñòè áåëîãî øóìà:
c
x
=
−
σπ
α
21
(),
(10.31)
ãäå êîýôôèöèåíò α > 0 èìååò ðàçìåðíîñòü, îáðàòíóþ ðàçìåðíîñòè
âðåìåíè.
Ôîðìàëüíî âûðàæåíèå êîððåëÿöèîííîé ôóíêöèè áåëîãî øóìà
ìîæíî ïðåäñòàâèòü â âèäå
Kc
Q
x()
() (),
τ
πδτ δτ
==
2
(10.32)
ãäå δ(τ) – äåëüòà-ôóíêöèÿ; Q – èíòåíñèâíîñòü áåëîãî øóìà.
Ôèçè÷åñêèé ñìûñë ïîëó÷åííîãî ðåçóëüòàòà ñîñòîèò â òîì, ÷òî
îðäèíàòû áåëîãî øóìà, âçÿòûå äëÿ ëþáûõ ðàçëè÷íûõ ìîìåíòîâ âðå-
ìåíè, ÿâëÿþòñÿ íåêîððåëèðîâàííûìè, à åãî äèñïåðñèÿ ðàâíà áåñêî-
íå÷íîñòè.
 äîïîëíåíèå ê èñïîëüçîâàííîìó ðàíåå ïîíÿòèþ áåçóñëîâíîé
ïëîòíîñòè ðàñïðåäåëåíèÿ âåðîÿòíîñòè, îòâå÷àþùåé (10.2), ââåäåì â
ðàññìîòðåíèå ïîíÿòèå óñëîâíîé (ïåðåõîäíîé) ïëîòíîñòè ðàñïðåäåëå-
íèÿ âåðîÿòíîñòè f(xk, tk |x1, t1; x2, t2; ...; xk−1, tk−1), ãäå âåðòèêàëüíàÿ ÷åð-
òà îçíà÷àåò "äëÿ äàííîãî" èëè "ïðè óñëîâèè, ÷òî". Åñëè áåçóñëîâíàÿ
ïëîòíîñòü ðàñïðåäåëåíèÿ îïðåäåëÿëà âåðîÿòíîñòü ïîñëåäîâàòåëüíî-
ãî ïðîõîæäåíèÿ îäíèõ è òåõ æå ðåàëèçàöèé ïðîöåññà X(t) ÷åðåç çà-
äàííûå èíòåðâàëû ñîîòâåòñòâåííî â ìîìåíòû t1, t2,..., tk, òî óñëîâíàÿ
ïëîòíîñòü õàðàêòåðèçóåò ðàñïðåäåëåíèå âåðîÿòíîñòåé ðåàëèçàöèè
ïðîöåññà X(t) ïðè óñëîâèè, ÷òî çíà÷åíèÿ îðäèíàò ñëó÷àéíîãî ïðî-
öåññà â ïðåäøåñòâóþùèå ìîìåíòû âðåìåíè t1, t2,..., tk−1 èçâåñòíû.
451
Ïðîöåññ X(t) íàçûâàåòñÿ àáñîëþòíî ñëó÷àéíûì, åñëè ñëó÷àéíûå
âåëè÷èíû x(ti)èx(tj) íåçàâèñèìû ïðè ñêîëü óãîäíî ìàëîì ∆t = tj − ti.
Èìåÿ â âèäó, ÷òî ïëîòíîñòü ðàñïðåäåëåíèÿ âåêòîðà ñî âçàèìíî íåçà-
âèñèìûìè êîìïîíåíòàìè ìîæåò áûòü ïðåäñòàâëåíà â âèäå
fxxtt
fxt
kk
i
i
i
k
(,,;, ,)
(,)
,
11
1
KK
=
=
∏
(10.33)
àáñîëþòíî ñëó÷àéíûé ïðîöåññ áóäåò ïîëíîñòüþ õàðàêòåðèçîâàòüñÿ
îäíîìåðíûì ðàñïðåäåëåíèåì ñ ïëîòíîñòüþ f(x, t). Áåëûé øóì, òàêèì
îáðàçîì, ïðåäñòàâëÿåò ñîáîé íå ÷òî èíîå, êàê àáñîëþòíî ñëó÷àéíûé
ïðîöåññ X(t) ñ íîðìàëüíîé îäíîìåðíîé ïëîòíîñòüþ. Äëÿ ìàòåìà-
òè÷åñêîé ôîðìóëèðîâêè îñíîâíîãî ñâîéñòâà ìàðêîâñêîãî ïðîöåññà
íåîáõîäèìî ðàññìîòðåòü óñëîâíóþ ïëîòíîñòü ðàñïðåäåëåíèÿ. Â îáùåì
ñëó÷àå ýòà ïëîòíîñòü çàâèñèò îò çíà÷åíèé x1, x2,..., xk−1 îðäèíàò
ñëó÷àéíîãî ïðîöåññà â ìîìåíòû âðåìåíè t1, t2,..., tk−1
.
Îäíàêî äëÿ
ìàðêîâñêèõ ïðîöåññîâ ñóùåñòâåííûì ÿâëÿåòñÿ òîëüêî çíàíèå îðäè-
íàòû ïðîöåññà â ìîìåíò âðåìåíè, áëèæàéøèé ê ðàññìàòðèâàåìîìó
ìîìåíòó âðåìåíè tk. Ïîýòîìó â êà÷åñòâå îïðåäåëåíèÿ ìàðêîâñêîãî
ïðîöåññà ìîæíî çàïèñàòü ñëåäóþùåå óñëîâèå: åñëè äëÿ ëþáûõ
ìîìåíòîââðåìåíèt1<t2<...<tk−1<tk
fxxx fxx
kkk
k
(|,,)(|)
,
11
1
K
−−
=
(10.34)
ò.å. åñëè ïëîòíîñòü ðàñïðåäåëåíèÿ f(xk, tk) çàâèñèò òîëüêî îò îð-
äèíàò ïðîöåññà â ìîìåíò âðåìåíè tk−1 è ñîâåðøåííî íå çàâèñèò
îò èõ çíà÷åíèé â ïðîøëîì, òî òàêîé ïðîöåññ íàçûâàåòñÿ ìàðêîâ-
ñêèì. Èìåííî â ýòîì ñìûñëå ìàðêîâñêèé ïðîöåññ èíîãäà íàçûâà-
þò "ïðîöåññîì áåç ïîñëåäåéñòâèÿ". Åãî èñ÷åðïûâàþùèìè õàðàê-
òåðèñòèêàìè ÿâëÿþòñÿ íà÷àëüíàÿ îäíîìåðíàÿ ïëîòíîñòü (ïëîò-
íîñòü âåðîÿòíîñòè ïåðâîé îðäèíàòû) f(x1)èïåðåõîäíàÿ ïëîòíîñòü
f(xk | xk−1). Ìàðêîâñêèé ïðîöåññ ñ íåçàâèñèìûìè ïðèðàùåíèÿìè
X(t), ó êîòîðîãî ïåðåõîäíàÿ ïëîòíîñòü ãàóññîâñêàÿ, íàçûâàåòñÿ
âèíåðîâñêèì ñëó÷àéíûì ïðîöåññîì (ïðîöåññîì ñëó÷àéíîãî áëóæäà-
íèÿ). Ñ òî÷êè çðåíèÿ ñâîéñòâ ñîâìåñòíîé ïëîòíîñòè ðàñïðåäåëå-
íèÿ ñòàöèîíàðíûå ïðîöåññû ñëåäóåò òðàêòîâàòü êàê ïðîöåññû, ó
êîòîðûõ ïëîòíîñòü ðàñïðåäåëåíèÿ âåðîÿòíîñòåé èíâàðèàíòíà ê
âðåìåííîìó ñäâèãó.
Åñëè òåïåðü âñïîìíèòü, êàêèå òðåáîâàíèÿ áûëè ïðåäúÿâëåíû ê
ñâîéñòâàì ââåäåííûõ â ðàññìîòðåíèå â ãë. 2 ñòîõàñòè÷åñêèõ äèôôå-
ðåíöèàëüíûõ óðàâíåíèé, íåòðóäíî óñòàíîâèòü, ÷òî ïðîöåññû, îïðå-
452
äåëÿåìûå òàêèìè óðàâíåíèÿìè, îòíîñÿòñÿ ê ÷èñëó ìàðêîâñêèõ. Äîñ-
òîèíñòâîì ïîäõîäà, áàçèðóþùåãîñÿ íà òåîðèè ìàðêîâñêèõ ïðîöåñ-
ñîâ, ÿâëÿåòñÿ òî, ÷òî â îòëè÷èå îò ñëó÷àéíûõ ïðîöåññîâ îáùåãî âèäà
èõ èñïîëüçîâàíèå ïðèâîäèò ê ñóùåñòâåííîìó óïðîùåíèþ ìåòîäîâ
àíàëèçà ïðîöåññîâ è äèíàìèêè ñòîõàñòè÷åñêèõ ñèñòåì, äëÿ èññëåäî-
âàíèÿ êîòîðûõ àïïàðàò êîððåëÿöèîííîé òåîðèè, ò.å . òåîðèè, îïåðè-
ðóþùåé ìîìåíòàìè íå âûøå âòîðîãî ïîðÿäêà, îêàçûâàåòñÿ íåäîñòà-
òî÷íûì.
 îòëè÷èå îò ëèíåéíûõ ñòîõàñòè÷åñêèõ äèôôåðåíöèàëüíûõ óðàâ-
íåíèé, äëÿ êîòîðûõ óñëîâíàÿ ïëîòíîñòü ðàñïðåäåëåíèÿ ïðè çàäàí-
íîì íîðìàëüíîì ïðåäøåñòâóþùåì ñîñòîÿíèè îòâå÷àåò ãàóññîâñêî-
ìó ðàñïðåäåëåíèþ, â íåëèíåéíûõ ñèñòåìàõ äàííîå óñëîâèå â îáùåì
ñëó÷àå íå âûïîëíÿåòñÿ. Äëÿ îòûñêàíèÿ ñîîòâåòñòâóþùèõ óñëîâíûõ
ïëîòíîñòåé ðàñïðåäåëåíèÿ èñïîëüçóþò äèôôåðåíöèàëüíûå óðàâíå-
íèÿ â ÷àñòíûõ ïðîèçâîäíûõ ïàðàáîëè÷åñêîãî òèïà, ïîëó÷èâøèå íà-
çâàíèÿ ïðÿìîãî è îáðàòíîãî óðàâíåíèé À.Í. Êîëìîãîðîâà. Ïðÿìîå
óðàâíåíèå åùå äî òîãî, êàê îíî áûëî ñòðîãî âûâåäåíî À.Í. Êîëìî-
ãîðîâûì, áûëî èñïîëüçîâàíî Ï. Ôîêêåðîì è Ì. Ïëàíêîì ïðè èñ-
ñëåäîâàíèè äèôôóçèîííûõ ïðîöåññîâ, ïîýòîìó åãî òàêæå íàçûâàþò
óðàâíåíèåì Ôîêêåðà – Ïëàíêà – Êîëìîãîðîâà. Ïðèìåíèòåëüíî ê
ìíîãîìåðíîìó äèôôóçèîííîìó ïðîöåññó, îïèñûâàåìîìó âåêòîð-
íûì ñòîõàñòè÷åñêèì äèôôåðåíöèàëüíûì óðàâíåíèåì (2.14), ïðè
îáåñïå÷åíèè óñëîâèé ãëàäêîñòè ïåðåõîäíàÿ ïëîòíîñòü ðàñïðåäåëå-
íèÿ f (ïîä êîòîðîé, êàê ñëåäóåò èç îïðåäåëåíèÿ, ïîíèìàåòñÿ ïëîò-
íîñòü âåðîÿòíîñòè ñîñòîÿíèÿ x(t) ïðè óñëîâèè, ÷òî â ïðåäøåñòâóþ-
ùèé ìîìåíò t0, ïðèíèìàåìûé çà íà÷àëüíûé, ïðîöåññ õàðàêòåðèçóåò-
ñÿ ñîñòîÿíèåì x0) áóäåò óäîâëåòâîðÿòü îáðàòíîìó óðàâíåíèþ
Êîëìîãîðîâà
∂
∂
∂
∂
σσ
∂
∂∂
f
t
F
f
x
f
xx
i
i
ik jk
ij
ijk
n
i
n
=−
−
=
=
∑
∑
1
2
2
1
1,
,
(10.35)
ñ íà÷àëüíûì óñëîâèåì
ftt
(,|,)()
.
xx
xx
00
0
=−
δ
 ôóíêöèè àðãóìåíòîâ τ(τ > t)èx(τ) èçìåíåíèå ïåðåõîäíîé
ïëîòíîñòè îïèñûâàåòñÿ ïðÿìûì óðàâíåíèåì Êîëìîãîðîâà
∂
∂τ
∂
∂
∂
∂∂
σσ
τ
τ
ττ
τ
f
x
fF
xx
f
i
i
ij
ik jk
ijk
n
i
=−
+
=
∑
()
()
,,
1
2
2
1
=
∑1
n
(10.36)
ïðè ýòîì æå íà÷àëüíîì óñëîâèè.
453
Ïåðåõîäÿ îò (2.14) ê ñòîõàñòè÷åñêîìó íåëèíåéíîìó óðàâíåíèþ
ïåðâîãî ïîðÿäêà, çàïèøåì
dx F xtdt xtd
=+
(,) (,) .
ση
(10.37)
Îòíîñèòåëüíàÿ áåçóñëîâíàÿ ïëîòíîñòü ðàñïðåäåëåíèÿ f(x, t) äëÿ íåãî,
ïîëó÷àåìàÿ èç óðàâíåíèÿ Ôîêêåðà – Ïëàíêà – Êîëìîãîðîâà, áóäåò
èìåòü âèä
∂
∂
∂
∂
∂
∂
σ
fxt
tx
Fxtf xt
x
xtfxt
(,)
[(,)( ,)]
[(,)( ,)
=−
+
1
2
2
2
2
]. (10.38)
Èç ýòîãî óðàâíåíèÿ ìîãóò áûòü ïîëó÷åíû [36, 114] óðàâíåíèÿ,
õàðàêòåðèçóþùèå èçìåíåíèå ìàòåìàòè÷åñêîãî îæèäàíèÿ è
äèñïåðñèè ïðîöåññà x(t) â ôóíêöèè âðåìåíè:
d
dt
mt Fxtfxtdx
x
() (,)(,);
=
−∞
∞
∫
(10.39)
d
dt
tx
m
F
x
t
f
x
t
d
x
xtfxtd
xx
Ä() ( )(,)(,)
(,)(,)
=−
+
+
−∞
∞
∫2
2
σ
x.
−∞
∞
∫
(10.40)
 îáùåì ñëó÷àå íåëèíåéíîé ñèñòåìû ïðèâåäåííûå ñîîòíîøåíèÿ
ÿâëÿþòñÿ íåçàìêíóòûìè, òàê êàê âõîäÿùàÿ ïîä çíàêè èíòåãðàëîâ
ïëîòíîñòü f(x, t) äèôôóçèîííîãî ïðîöåññà x(t) íåèçâåñòíà.
Äëÿ ëèíåéíîé ñèñòåìû îíè ïðåâðàùàþòñÿ â óðàâíåíèÿ îòíîñè-
òåëüíî mx(t)èÄõ(t) è ñòàíîâÿòñÿ çàìêíóòûìè. Äåéñòâèòåëüíî, äëÿ
ëèíåéíîé îäíîìåðíîé ñèñòåìû
Fxtf xtdx atm t bt
xmFxtfx
x
x
(,)( ,) ()() ();
()
(
,
)
(
,
=+
−
−∞
∞
∫
tdxatt
xt f xtdx
t
x
)(
)
(
)
;
(,)(,) ()
,
=
=
−∞
∞
−∞
∞
∫
∫
Ä
σσ
22
ïîýòîìó
454
d
dt
mt atmt bt
xx
()()()();
=+
(10.41)
d
dt
ta
ttt
xx
ÄÄ
() ()()().
=+
2
2
σ
(10.42)
Èíòåãðèðîâàíèå ïîëó÷åííûõ äèôôåðåíöèàëüíûõ óðàâíåíèé ïðè
çàäàííûõ íà÷àëüíûõ óñëîâèÿõ mx(t0)èÄx(t0) ïðèâîäèò ê îòûñêàíèþ
ðàñ÷åòíûõ çàâèñèìîñòåé èçìåíåíèé ìàòåìàòè÷åñêîãî îæèäàíèÿ è
äèñïåðñèè â ôóíêöèè âðåìåíè. Ðàñïðîñòðàíåíèå çàâèñèìîñòåé
(10.41) è (10.42) íà ìíîãîìåðíóþ ëèíåéíóþ ìàðêîâñêóþ ñèñòåìó,
îòâå÷àþùóþ âåêòîðíîìó óðàâíåíèþ (2.14), äàåò
d
dt
tttt
mA
mb
xx
()()()();
=+
(10.43)
d
dt
ttt ttt
t
t
KA
KK
AG
xx
x
() ()() ()() ()()(),
=++
òò
σσ
(10.44)
ãäå G(t) – èíòåíñèâíîñòü âõîäíîãî âîçìóùàþùåãî âîçäåéñòâèÿ,
àïïðîêñèìèðóåìîãî, â ÷àñòíîñòè, áåëûì øóìîì.  ñîâîêóïíîñòè
óðàâíåíèÿ (10.43) è (10.44) ñîñòàâëÿþò êîððåëÿöèîííóþ ñèñòåìó
óðàâíåíèé. Áóäó÷è íåçàâèñèìûìè, îíè ìîãóò èíòåãðèðîâàòüñÿ
ðàçäåëüíî.
Ìåòîäèêó ïðàêòè÷åñêîãî èñïîëüçîâàíèÿ êîððåëÿöèîííîé ñèñòå-
ìû óðàâíåíèé ðàññìîòðèì íà ïðèìåðå âû÷èñëåíèÿ õàðàêòåðèñòèê
ðàññåèâàíèÿ íèñõîäÿùèõ ïàññèâíûõ ó÷àñòêîâ òðàåêòîðèé ïîëåòà ðà-
êåò è ñíàðÿäîâ ìàëîé äàëüíîñòè.  êà÷åñòâå èñõîäíîé ìîäåëè âîñ-
ïîëüçóåìñÿ ìîäåëüþ äâèæåíèÿ ËÀ êàê ìàòåðèàëüíîé òî÷êè:
m
dV
dt
Xm
g
mV
d
dt
mg
dy
dt
V
dx
dt
V
a
=−
−
=−
=
=
sin ;
cos ;
sin ;
c
θ
θ
θ
θ
os.
θ
Áóäåì ñ÷èòàòü, ÷òî â ìîìåíò âðåìåíè t = t0, ïðèíÿòûé çà íà÷àëüíûé,
èçâåñòíû çíà÷åíèÿ ïîñòîÿííûõ m, g, S. Çíà÷åíèÿ V, θ, x, y, c
xa
(),
Mà
455
òàêæå ρ(y) ðàññìàòðèâàþòñÿ êàê ñëó÷àéíûå ïåðåìåííûå ñ
çàäàííûìè íà÷àëüíûìè ñòàòèñòè÷åñêèìè õàðàêòåðèñòèêàìè.
Îáîçíà÷èì V = x1; θ = x2; y = x3; x = x4. Òîãäà âåêòîð ñîñòîÿíèÿ
èìååò âèä x(t)=[x1, x2, x3, x4]
ò
, à íåëèíåéíàÿ ïðàâàÿ ÷àñòü èñõîäíîé
íåëèíåéíîé ìîäåëè – âèä
d
dt
xt fxt
fxt ffff
() (,);
(,) [,,,]
,
=
=
1234
ò
ãäå
fcxxxxSmgx
fg
xx
xa
11
3
3
1
21
2
21
1
2
=−
−
=−
−
−
(,)() ()
s
in;
cos
ρ
2
312
412
;
sin ;
cos .
fxx
fxx
=
=
Ïðåäñòàâèì âåêòîð ñîñòîÿíèÿ ËÀ â âèäå ñóììû: x(t)=mx(t)+∆x(t).
Äàëåå, èñïîëüçóÿ ðàññìîòðåííûå ðàíåå ïðàâèëà ëèíåàðèçàöèè
äèôôåðåíöèàëüíûõ óðàâíåíèé äâèæåíèÿ, ëèíåàðèçóåì âåê-
òîð-ôóíêöèþ f(x, t) â îêðåñòíîñòè x(t)=mx(t).  ðåçóëüòàòå ïîëó÷èì
fxfmAm
x
xx
(,)( ,)( ,)()
,
ttt
t
≈+∆
ãäå A(mx, t)=[(,)/ ] –
∂∂
fx xxm
x
t
−
êâàäðàòíàÿ (4×4)-ìàòðèöà ÷àñòíûõ
ïðîèçâîäíûõ (ÿêîáèàí) âåêòîð-ôóíêöèè f(x, t) ïî ñîñòàâëÿþùèì x(t).
Òîãäà
d
dt
tt
t
()
(
,
)
(
,
)
(
)
,
mxf
mA
mx
xx
x
+=
+
∆∆
îòêóäà â ðåçóëüòàòå óñðåäíåíèÿ íåïîñðåäñòâåííî íàõîäèì
d
dt
tt
mf
m
xx
()(,).
=
Îïðåäåëèâ çíà÷åíèÿ ìàòåìàòè÷åñêèõ îæèäàíèé äëÿ îïîðíîãî
äâèæåíèÿ, ïåðåéäåì ê óðàâíåíèþ âîçìóùåííîãî äâèæåíèÿ â
îêðåñòíîñòè "ñðåäíåé" òðàåêòîðèè
456
d
dt
tt
t
∆∆
xA
mx
x
()(,)(),
=
íà îñíîâå êîòîðîãî ñîñòàâëÿåì óðàâíåíèå äëÿ ðàñ÷åòà
êîððåëÿöèîííîé ìàòðèöû âåêòîðà ñîñòîÿíèÿ x(t):
d
dt
tt
t
tt
KA
m
KK
A
m
xx
x
x
x
()(,)() ()(
,).
=+
ò
Ïðè çàäàííûõ íà÷àëüíûõ óñëîâèÿõ mx(t0), Kx(t0) ñîâìåñòíîå
èíòåãðèðîâàíèå êîððåëÿöèîííîé ñèñòåìû óðàâíåíèé ïîçâîëÿåò
ïîëó÷èòü mx(t)èKx(t) äëÿ ëþáîãî òåêóùåãî ìîìåíòà âðåìåíè, à òàêæå
äëÿ ìîìåíòà t = tc, ñîîòâåòñòâóþùåãî òî÷êå ïàäåíèÿ.
Åñëè ËÀ â ïðîöåññå ïîëåòà íàõîäèòñÿ ïîä âîçäåéñòâèåì ñëó÷àé-
íûõ âîçìóùåíèé, êîòîðûå ïî ñâîåé ïðèðîäå ñóùåñòâåííî îòëè÷à-
þòñÿ îò ïðîöåññîâ òèïà áåëîãî øóìà, èõ àïïðîêñèìàöèÿ ñòàöèîíàð-
íûì ñëó÷àéíûì ïðîöåññîì ñ ïîñòîÿííîé ñïåêòðàëüíîé ïëîòíîñòüþ
ïðèâîäèò ê ñëèøêîì áîëüøîé îøèáêå. Äàííîå îáñòîÿòåëüñòâî âû-
äâèãàåò çàäà÷ó ðàçðàáîòêè àëãîðèòìà, ïîçâîëÿþùåãî ïðåîáðàçîâàòü
ïðîöåññ òèïà áåëîãî øóìà â ñëó÷àéíûé ïðîöåññ ξ(t) ñ çàäàííûìè
ñòàòèñòè÷åñêèìè õàðàêòåðèñòèêàìè, êîòîðàÿ èçâåñòíà êàê çàäà÷à
ïîñòðîåíèÿ ôîðìèðóþùåãî ôèëüòðà. Ñóùíîñòü ýòîé çàäà÷è ñâîäèòñÿ
ê ñëåäóþùåìó. Åñëè âîçíèêàåò íåîáõîäèìîñòü ñôîðìèðîâàòü íåêî-
òîðûé êîððåëèðîâàííûé ïî âðåìåíè ñëó÷àéíûé ïðîöåññ ξ(t)ñçà-
äàííûìè õàðàêòåðèñòèêàìè (ìàòåìàòè÷åñêèì îæèäàíèåì, êîððåëÿ-
öèîííîé ôóíêöèåé èëè ñïåêòðàëüíîé ïëîòíîñòüþ), âîçäåéñòâóþ-
ùèé íà äèíàìè÷åñêóþ ñèñòåìó, óäîâëåòâîðÿþùóþ ìîäåëè âèäà
d
dt
tt
tt
xA
x
() ()() (),
=+
ξ
(10.45)
òî ñëåäóåò âîñïîëüçîâàòüñÿ íåêîòîðîé äîïîëíèòåëüíîé ìîäåëüþ,
îòâå÷àþùåé äèôôåðåíöèàëüíîìó óðàâíåíèþ
d
dt
ttt
ξξ
ξ
() () ().
=+
KB
q
q
(10.46)
Äèíàìè÷åñêàÿ ñèñòåìà, ñîñòîÿíèå êîòîðîé îïèñûâàåòñÿ óðàâíåíèåì
(10.46), íàçûâàåòñÿ ôîðìèðóþùèì ôèëüòðîì. Â óðàâíåíèè (10.46)
ïðèíÿòû ñëåäóþùèå îáîçíà÷åíèÿ: Kξ – ìàòðèöà êîýôôèöèåíòîâ
óñèëåíèÿ ôîðìèðóþùåãî ôèëüòðà; q(t) – âîçáóæäàþùèé (ïîðîæ-
äàþùèé) ïðîöåññ ξ(t) áåëûé øóì. Îáúåäèíåíèå âåêòîðîâ x(t)èξ(t)â
457
âåêòîð xp(t)=[x(t); ξ(t)]ò ïðèâåäåò ê ïîëó÷åíèþ ðàñøèðåííîãî âåêòîðà
ñîñòîÿíèÿ [35], äëÿ êîòîðîãî óæå áóäóò ñïðàâåäëèâû óðàâíåíèÿ (10.43)
è (10.44), ñîäåðæàùèå â êà÷åñòâå âõîäíîãî ñëó÷àéíîãî âîçäåéñòâèÿ áå-
ëûé øóì ïðè äåéñòâèè ðåàëüíûõ âîçìóùåíèé, îòëè÷àþùèõñÿ îò ïðî-
öåññà òèïà áåëîãî øóìà. Ôóíêöèîíàëüíûé àíàëîã ìàòåìàòè÷åñêîé ìî-
äåëè ñèñòåìû, èçîáðàæåííîé íà ðèñ. 10 .2, ïðèâåäåí íà ðèñ. 10.3.
Íàèáîëåå ïîëíî è íàãëÿäíî äîñòîèíñòâà ìåòîäà ôîðìèðóþùåãî
ôèëüòðà ïðîÿâëÿþòñÿ ïðè àíàëèçå äâèæåíèÿ ËÀ â òóðáóëåíòíîé àò-
ìîñôåðå.
Ïðè ðåøåíèè ïîäàâëÿþùåãî áîëüøèíñòâà áàëëèñòè÷åñêèõ çàäà÷
ìîæíî ïðèíÿòü, ÷òî â ïðåäåëàõ îáëàñòè ïðîñòðàíñòâà, â êîòîðîé
ðàññìàòðèâàåòñÿ äâèæåíèå ËÀ, ïîëå òóðáóëåíòíîñòè ÿâëÿåòñÿ èçî-
òðîïíûì (ñì. ãë. 8).  ðàìêàõ êîððåëÿöèîííîé òåîðèè èñ÷åðïûâàþ-
ùåé õàðàêòåðèñòèêîé èçîòðîïíîãî ïîëÿ ÿâëÿþòñÿ êîððåëÿöèîííûå
ôóíêöèè ïîïåðå÷íîãî (áîêîâîãî) è ïðîäîëüíîãî ïåðåìåùåíèé Kz(τ)
è Kx(τ). Èõ âûðàæåíèÿ èìåþò âèä [42, 129]
KT
x
() exp(|| );
τσ
τ
=−
−
ò
21
(10.47)
KT
T
z() [ ||( )]exp(|| ),
τστ
τ
=−
−
−−
ò
211
12
(10.48)
ãäå σò
2
õàðàêòåðèçóåò èíòåíñèâíîñòü òóðáóëåíòíîñòè; Ò = LV
−1
–
âðåìÿ ïðîõîæäåíèÿ ËÀ ìàñøòàáà òóðáóëåíòíîñòè L.
458
Ðèñ. 10.2 . Ìàòåìàòè÷åñêèé
àíàëîã ñèñòåìû ñ ôîðìèðóþ-
ùèì ôèëüòðîì:
1 – ôîðìèðóþùèé ôèëüòð;
2 – ñèñòåìà, îòâå÷àþùàÿ
óðàâíåíèþ ñîñòîÿíèÿ (10.45)
Ðèñ. 10.3 . Ñõåìà ïðåîáðàçîâàíèÿ áåëîãî øóìà â êîððåëèðîâàííûé ïî âðåìåíè ("îê-
ðàøåííûé") øóì ñ ïîìîùüþ ôîðìèðóþùåãî ôèëüòðà
Ìàñøòàáîì òóðáóëåíòíîñòè îïðåäåëÿåòñÿ óðîâåíü êîððåëÿöèè
ìåæäó âîçäóøíûìè ïîðûâàìè â ðàçëè÷íûõ òî÷êàõ ïðîñòðàíñòâåí-
íîãî ïîëÿ òóðáóëåíòíîñòè. Äî âûñîò ïîëåòà Í ≈ 500 ì âåëè÷èíà L ≈
H ïðè ïîëåòå íàä ðàâíèíîé è L ≈ 2H ïðè ïîëåòå íàä õîëìèñòîé
ìåñòíîñòüþ è ãîðàìè. Ïðè äâèæåíèè ËÀ íà áîëüøèõ âûñîòàõ ïàðà-
ìåòð L îêàçûâàåòñÿ ñóùåñòâåííî çàâèñÿùèì îò êëèìàòà è ìåòåîðî-
ëîãè÷åñêèõ óñëîâèé â ðàññìàòðèâàåìîé îáëàñòè âîçäóøíîãî ïðî-
ñòðàíñòâà íàä çåìíîé ïîâåðõíîñòüþ. Ïðèíÿòî ñ÷èòàòü [42], ÷òî ïðè
σò < 0,5 ì/ñ òóðáóëåíòíîñòü ÿâëÿåòñÿ ñëàáîé, à ïðè σò > 2,5 ì/ñ –
ñèëüíîé.
Ñîîòíîøåíèÿì (10.47) è (10.48) îòâå÷àþò âûðàæåíèÿ äëÿ ñïåê-
òðàëüíûõ ïëîòíîñòåé ïðîäîëüíîé è ïîïåðå÷íîé ñîñòàâëÿþùèõ òóð-
áóëåíòíîñòè
S
T
T
x
() ()
;
ω
σ
πω
=
+
ò
2
22
1
(10.49)
S
TT
T
z()
()
()
,
ω
σω
πω
=
+
+
ò
22
2
222
13
21
(10.50)
ãäå ω – ÷àñòîòà, èìåþùàÿ ðàçìåðíîñòü ñ
−1
.
Ñîîòâåòñòâóþùèå
óðàâíåíèÿ ôîðìèðóþùåãî ôèëüòðà, ìîäåëèðóþùåãî ïîëå òóðáó-
ëåíòíîñòè àòìîñôåðû, îòâå÷àþùèå (10.49) è (10.50), áóäóò èìåòü âèä:
äëÿ ïðîäîëüíîé ñîñòàâëÿþùåé
xt
t
xt xt Kxt bqt
1
21
11
1
() ();
() •()
() (),
=
==
+
ξ
ξ
(10.51)
ãäå KTb T
ξ
σ
1
1
1
1
2
=−
=
−−
;;
ò
äëÿ ïîïåðå÷íîé (áîêîâîé) ñîñòàâëÿþùåé
xt
t
xtxbqt
xtKxKxbq
1
12
1
21
2
2
12
() ();
•
()
();
•
()
=
=+
=++
ξ
ξξ (),
t
(10.52)
ãäåKTKTb Ò
ξξσ
12
21
1
1
23
=−
=−
=
−−−
;;;
ò
bT
2
32
123
=−
−
().
/
σò
459
Ñóùåñòâåííûå âûãîäû ïðèìåíåíèÿ ìåòîäà ôîðìèðóþùåãî ôèëüòðà
îñîáåííî ïðîÿâëÿþòñÿ ïðè åãî ðåàëèçàöèè íà ÝÂÌ, è â ÷àñòíîñòè
ïðè îïðåäåëåíèè õàðàêòåðèñòèê ðàññåèâàíèÿ íà îñíîâå ìåòîäà
ñòàòèñòè÷åñêèõ èñïûòàíèé. Âìåñòå ñ òåì ñëåäóåò ïîä÷åðêíóòü, ÷òî
îáñóæäàåìûé ìåòîä îòíîñèòñÿ ê ÷èñëó ïðèáëèæåííûõ ìåòîäîâ
ìîäåëèðîâàíèÿ ñëó÷àéíûõ ïðîöåññîâ. Íàèáîëåå íàäåæíûì ñïîñîáîì
êîíòðîëÿ òî÷íîñòè ìîäåëèðîâàíèÿ ñëó÷àéíîãî ïðîöåññà íà îñíîâå
àëãîðèòìà ôîðìèðóþùåãî ôèëüòðà ñ÷èòàåòñÿ ñïîñîá ñòàòèñòè÷åñêîé
îáðàáîòêè ìîäåëèðóåìûõ ðåàëèçàöèé [129].
10.1.4. ÎÏÐÅÄÅËÅÍÈÅ ÕÀÐÀÊÒÅÐÈÑÒÈÊ ÐÀÑÑÅÈÂÀÍÈß ÌÅÒÎÄÎÌ
ÑÒÀÒÈÑÒÈ×ÅÑÊÈÕ ÈÑÏÛÒÀÍÈÉ
Ìåòîä ñòàòèñòè÷åñêèõ èñïûòàíèé (ìåòîä Ìîíòå-Êàðëî), íàçû-
âàåìûé â ëèòåðàòóðå òàêæå ìåòîäîì ñòàòèñòè÷åñêîãî ìîäåëèðîâà-
íèÿ, ÿâëÿåòñÿ íàèáîëåå óíèâåðñàëüíûì ìåòîäîì âåðîÿòíîñòíîãî
àíàëèçà äèíàìè÷åñêèõ ñèñòåì âîîáùå è îïðåäåëåíèÿ õàðàêòåðè-
ñòèê ðàññåèâàíèÿ ËÀ â ÷àñòíîñòè. Ìåòîä îñíîâûâàåòñÿ íà òàê
íàçûâàåìîì çàêîíå áîëüøèõ ÷èñåë, óòâåðæäàþùåì, ÷òî ðåçóëüòàò
óñðåäíåíèÿ, âû÷èñëåííûé ïî n ðåàëèçàöèÿì ñëó÷àéíîãî ïðîöåñ-
ñàïðèn→∞
, ïåðåñòàåò áûòü ñëó÷àéíûì è ìîæåò ðàññìàòðè-
âàòüñÿ â êà÷åñòâå îöåíêè ñîîòâåòñòâóþùåé ÷èñëîâîé õàðàêòåðè-
ñòèêè èññëåäóåìîãî ïðîöåññà. Åñòåñòâåííî, ðåàëèçîâàòü íà ïðàê-
òèêå "áåñêîíå÷íî áîëüøîå" ÷èñëî èñïûòàíèé íå óäàåòñÿ. Îäíàêî
â ýòîì îáû÷íî è íå âîçíèêàåò íåîáõîäèìîñòè. Äîñòàòî÷íî îáåñ-
ïå÷èòü îòíîñèòåëüíî áîëüøîå ÷èñëî ðåàëèçàöèé. Ïðè ýòîì ÷àñ-
òîòà ñëó÷àéíîãî ñîáûòèÿ áóäåò ïðèáëèæàòüñÿ ê âåðîÿòíîñòè ýòî-
ãî ñîáûòèÿ, à "ñòåïåíü ïðèáëèæåíèÿ" áóäåò çàâèñåòü îò êîëè÷å-
ñòâà ðåàëèçàöèé (îïûòîâ).
×òî êàñàåòñÿ çàäà÷ âíåøíåé áàëëèñòèêè, ðåøàåìûõ â ðàìêàõ àï-
ðèîðíîãî ñòàòèñòè÷åñêîãî àíàëèçà, òî ðàññìàòðèâàåìûé ìåòîä çà-
êëþ÷àåòñÿ â ïðîâåäåíèè ñ èñïîëüçîâàíèåì ñðåäñòâ âû÷èñëèòåëüíîé
òåõíèêè ñòàòèñòè÷åñêèõ ýêñïåðèìåíòîâ, èìèòèðóþùèõ äâèæåíèå
èññëåäóåìîãî ËÀ ïðè äåéñòâèè ñëó÷àéíûõ ôàêòîðîâ, è â ïîñëåäóþ-
ùåé îáðàáîòêå ïîëó÷åííûõ ðåçóëüòàòîâ ñ ïîìîùüþ ìåòîäîâ ìàòåìà-
òè÷åñêîé ñòàòèñòèêè.
Ïðèìåíåíèå äàííîãî ìåòîäà òðåáóåò:
âûÿâèòü âñþ ñîâîêóïíîñòü ñëó÷àéíûõ ôàêòîðîâ, âëèÿþùèõ íà
äâèæåíèå ËÀ;
óñòàíîâèòü (íàñêîëüêî ýòî âîçìîæíî) çàêîíû ðàñïðåäåëåíèÿ
ýòèõ ôàêòîðîâ;
460
ñîñòàâèòü íàèáîëåå ïîëíóþ ìàòåìàòè÷åñêóþ ìîäåëü äâèæåíèÿ
ËÀ, êîððåêòíî îòðàæàþùóþ âîçäåéñòâèå íà ïðîöåññ âûÿâëåííûõ
ôàêòîðîâ.
Åñëè íåâîçìîæíî ïîëíîå àäåêâàòíîå ìàòåìàòè÷åñêîå îïèñàíèå
ôóíêöèîíèðîâàíèÿ îòäåëüíûõ ýëåìåíòîâ ñèñòåì ËÀ (íàïðèìåð, èñ-
ïîëíèòåëüíûõ îðãàíîâ ñèñòåìû óïðàâëåíèÿ êîððåêòèðóåìîãî àð-
òèëëåðèéñêîãî ñíàðÿäà), òî ñòàòèñòè÷åñêèì èñïûòàíèÿì ìîæåò
áûòü ïîäâåðãíóòà ïîëóíàòóðíàÿ ìîäåëü, ò.å . ìîäåëü, ñîäåðæàùàÿ íà-
ðÿäó ñ ìàòåìàòè÷åñêèìè ñîîòíîøåíèÿìè, ðåàëèçóåìûìè, êàê ïðà-
âèëî, íà àíàëîãîâûõ âû÷èñëèòåëüíûõ ìàøèíàõ (ÀÂÌ), îáðàçöû
êîíêðåòíûõ ïðèáîðîâ è óñòðîéñòâ, âêëþ÷åííûõ â ðàñ÷åòíóþ ñõåìó.
Ðåàëèçàöèÿ ìåòîäà ñòàòèñòè÷åñêèõ èñïûòàíèé âîçìîæíà êàê â
íåïðåðûâíîì, òàê è â äèñêðåòíîì âàðèàíòàõ. Äèñêðåòíûé âàðèàíò
ìåòîäà ñâîäèòñÿ ê ïðîâåäåíèþ íà ÝÂÌ ìíîãîêðàòíî ïîâòîðÿåìûõ
âû÷èñëåíèé ïàðàìåòðîâ ìîäåëèðóåìîãî ñëó÷àéíîãî ïðîöåññà. Ìî-
äåëèðîâàíèå ïðîöåññà äâèæåíèÿ ËÀ, ïðîèñõîäÿùåãî ïðè äåéñòâèè
ñëó÷àéíûõ ôàêòîðîâ, òðåáóåò ôîðìèðîâàíèÿ ôèçè÷åñêèìè èëè ïðî-
ãðàììíûìè ìåòîäàìè ðåàëèçàöèè ñëó÷àéíûõ âåëè÷èí (ôóíêöèé) ñ
çàäàííûì ðàñïðåäåëåíèåì. Ôèçè÷åñêèå äàò÷èêè ñëó÷àéíûõ ïîñëåäî-
âàòåëüíîñòåé (ãåíåðàòîðû ñëó÷àéíûõ øóìîâ), êàê ïðàâèëî, ïðèìå-
íÿþòñÿ ïðè ïðîâåäåíèè èññëåäîâàíèé ñëó÷àéíûõ ïðîöåññîâ è ïðè
ðåøåíèè ñòàòèñòè÷åñêèõ çàäà÷ íà àíàëîãîâûõ è ãèáðèäíûõ àíàëî-
ãî-öèôðîâûõ âû÷èñëèòåëüíûõ ìàøèíàõ.
Ïðè ìîäåëèðîâàíèè ðåàëèçàöèè ñëó÷àéíûõ âåëè÷èí íà óíèâåð-
ñàëüíûõ ÝÂÌ ïðåäïî÷òåíèå îòäàåòñÿ ïðîãðàììíûì ìåòîäàì ôîð-
ìèðîâàíèÿ ñëó÷àéíûõ ïîñëåäîâàòåëüíîñòåé. Ñ íåêîòîðîé äîëåé óñ-
ëîâíîñòè ñîîòâåòñòâóþùèå ñòàíäàðòíûå ïîäïðîãðàììû íàçûâàþò
ïðîãðàììíûìè äàò÷èêàìè ïñåâäîñëó÷àéíûõ ÷èñåë. "Ïñåâäîñëó÷àé-
íîñòü" ôîðìèðóåìîé èìè ïîñëåäîâàòåëüíîñòè çäåñü îáóñëîâëåíà
òåì, ÷òî â "äàò÷èêå" êàæäîå ïîñëåäóþùåå "ñëó÷àéíîå" çíà÷åíèå âû-
÷èñëÿåòñÿ ñ ïîìîùüþ ðåêóððåíòíîé çàâèñèìîñòè ïðè èñïîëüçîâà-
íèè â êà÷åñòâå àðãóìåíòà íåñêîëüêèõ ÷èñåë, ïîëó÷åííûõ â ïðîöåññå
ïðåäûäóùèõ îáðàùåíèé ê ïîäïðîãðàììå. Êîëè÷åñòâî âû÷èñëèòåëü-
íûõ ðåàëèçàöèé ïðè ñòàòèñòè÷åñêîì ìîäåëèðîâàíèè îïðåäåëÿåòñÿ
õàðàêòåðîì ðåøàåìîé çàäà÷è, òðåáóåìîé òî÷íîñòüþ è íàäåæíîñòüþ
ïîëó÷åíèÿ îöåíîê ÷èñëîâûõ õàðàêòåðèñòèê. Äîñòîèíñòâàìè ìåòîäà
ÿâëÿþòñÿ åãî óíèâåðñàëüíîñòü è âûñîêàÿ òî÷íîñòü, íåäîñòàòêîì –
ãðîìîçäêîñòü è òðóäîåìêîñòü.
Êðàòêî ðàññìîòðèì îñíîâíûå ýëåìåíòû ìåòîäèêè ñòàòèñòè÷å-
ñêîãî ìîäåëèðîâàíèÿ ïðè ïðîâåäåíèè áàëëèñòè÷åñêèõ ðàñ÷åòîâ.
Ñóùåñòâåííûì çäåñü ÿâëÿåòñÿ ôîðìà çàäàíèÿ ñëó÷àéíûõ ôóíê-
öèé.  òîì ñëó÷àå, êîãäà î äåéñòâóþùèõ âîçìóùåíèÿõ èìååòñÿ
äîñòàòî÷íî ïîëíàÿ èíôîðìàöèÿ, èõ ïðåäñòàâëåíèå ìîæåò áûòü
îñóùåñòâëåíî ëèáî â âèäå îïûòíûõ êîíêðåòíûõ ðåàëèçàöèé, ïî-
461
ëó÷åííûõ ïðè èñïûòàíèÿõ, ëèáî â âèäå ðåàëèçàöèé, ïîëó÷åííûõ
ïðè êàíîíè÷åñêîì ðàçëîæåíèè ñëó÷àéíûõ ôóíêöèé, îïèñûâàþ-
ùèõ èçìåíåíèå êàæäîé èç õàðàêòåðèñòèê. Îäíàêî íåðåäêè ñèòóà-
öèè, êîãäà èññëåäîâàòåëü íå îáëàäàåò òàêîé èíôîðìàöèåé è ïî-
ýòîìó íå èìååò âîçìîæíîñòè ïðåäñòàâèòü ìîäåëèðóåìûé ñëó÷àé-
íûé ïðîöåññ â âèäå ñóììû ñëó÷àéíûõ ïðîöåññîâ áîëåå ïðîñòîãî
âèäà. Ýòî îáñòîÿòåëüñòâî âûíóæäàåò ïðèáåãàòü ê ðàçëè÷íîãî ðîäà
àïïðîêñèìàöèÿì, áàçèðóþùèìñÿ íà ïðèíÿòèè íåêîòîðûõ ãèïîòåç
â îòíîøåíèè ñòàòèñòè÷åñêèõ õàðàêòåðèñòèê àïïðîêñèìèðóþùåãî
ïðîöåññà.  êà÷åñòâå ïîñëåäíåãî, â ÷àñòíîñòè, ìîãóò âûñòóïàòü
ïðîöåññû òèïà áåëîãî èëè îêðàøåííîãî øóìà.
Ïðåäâàðèòåëüíî îáñóäèì âàðèàíò èñïîëüçîâàíèÿ ìåòîäà êàíîíè-
÷åñêîãî ðàçëîæåíèÿ. Ñóùíîñòü ýòîãî ìåòîäà ñîñòîèò â òîì, ÷òî ñëó-
÷àéíàÿ ôóíêöèÿ X(t) çàìåíÿåòñÿ íåêîòîðîé ëèíåéíîé êîìáèíàöèåé
íåñëó÷àéíûõ (êîîðäèíàòíûõ) ôóíêöèé φj(t), êîýôôèöèåíòàìè êîòî-
ðûõ ñëóæàò ñëó÷àéíûå âåëè÷èíû Vj, âçàèìíî íåêîððåëèðîâàííûå
ìåæäó ñîáîé è îáëàäàþùèå íóëåâûì ìàòåìàòè÷åñêèì îæèäàíèåì,
ò.å . óäîâëåòâîðÿþùèå ñîîòíîøåíèÿì
MM
[];[] (,,,)
,
VV
Vj
k
jj
k
j
k
==
=
01
2
δ
K
(10.53)
ãäå δjk – ñèìâîë Êðîíåêåðà, îïðåäåëÿåìûé óñëîâèåì
δjk
jk
jk
=
=
≠
⎧
⎨
⎩
1
0
,;
,.
åñëè
åñëè
(10.54)
Äîêàçàòåëüñòâî ïðàâîìåðíîñòè óêàçàííîé çàìåíû îñíîâûâàåòñÿ íà
òåîðåìå, ñîãëàñíî êîòîðîé äëÿ ëþáîé íåïðåðûâíîé ñëó÷àéíîé
ôóíêöèè X(t) ñïðàâåäëèâî ðàçëîæåíèå
Xt
Xt
V
t
j
j
j
j
() [()]
(),
=+
=
∞
∑
M
φ
λ
1
(10.55)
ãäå λj è φj(t) – ñîáñòâåííûå ÷èñëà è ñîáñòâåííûå ôóíêöèè
èíòåãðàëüíîãî óðàâíåíèÿ
φλτ
φ
τ
τ
()
(,)() .
tK
td
x
t
t
=
∫1
2
(10.56)
Ðÿä (10.55) ÿâëÿåòñÿ áåñêîíå÷íûì. Åñëè ïðîèçâåñòè åãî óñå÷åíèå,
îãðàíè÷èâ êîíå÷íûì (íåáîëüøèì) ÷èñëîì ñëàãàåìûõ, òî çàäà÷ó
462
ìàòåìàòè÷åñêîãî ìîäåëèðîâàíèÿ X(t) ìîæíî ñâåñòè ê çàìåíå åãî
èñòèííîãî çíà÷åíèÿ ñèñòåìîé ñëó÷àéíûõ âåëè÷èí Vj. Åñòåñòâåííî,
÷òî ñòåïåíü ïðèáëèæåíèÿ ìîäåëè ê äåéñòâèòåëüíîìó ïðîöåññó áóäåò
îïðåäåëÿòüñÿ ÷èñëîì ó÷èòûâàåìûõ ÷ëåíîâ ðàçëîæåíèÿ. Ñëåäóåò
çàìåòèòü ïðè ýòîì, ÷òî äëÿ íàõîæäåíèÿ êàíîíè÷åñêîãî ðàçëîæåíèÿ
(10.55) íå îáÿçàòåëüíî ðåøàòü èíòåãðàëüíîå óðàâíåíèå (10.56). Äëÿ
ýòîãî ìîæíî âîñïîëüçîâàòüñÿ ðàçëè÷íûìè ïðèáëèæåííûìè
ñïîñîáàìè. Çàìåíèì, â ÷àñòíîñòè, ñëó÷àéíóþ ôóíêöèþ X(t)
ëèíåéíîé êîìáèíàöèåé ïðîèçâåäåíèé íåñëó÷àéíûõ ôóíêöèé φj(t)íà
ñëó÷àéíûå êîýôôèöèåíòû Aj, âûáèðàåìûå òàêèì îáðàçîì, ÷òîáû
èìåëî ìåñòî íàèëó÷øåå (íàïðèìåð, â ñìûñëå ñðåäíåãî
êâàäðàòè÷íîãî) ïðèáëèæåíèå àïïðîêñèìèðóþùåé çàâèñèìîñòè ê
X(t). Îäíàêî âûðàæåíèå
XtAt
jj
()
()
≈Σφ
(10.57)
åùå íå áóäåò õàðàêòåðèçîâàòü êàíîíè÷åñêîå ðàçëîæåíèå, ïîñêîëüêó
ïðè âûáðàííîì ñïîñîáå àïïðîêñèìàöèè ñëó÷àéíûå êîýôôèöèåíòû
Aj íå ÿâëÿþòñÿ íåêîððåëèðîâàííûìè ñëó÷àéíûìè âåëè÷èíàìè, à
èìåþò êîâàðèàöèîííóþ ìàòðèöó, îïðåäåëÿåìóþ âèäîì Kx(t1, t2)è
ñïîñîáîì àïïðîêñèìàöèè. Äëÿ òîãî ÷òîáû ïåðåéòè îò (10.57) ê
êàíîíè÷åñêîìó ðàçëîæåíèþ, íåîáõîäèìî ïðåäñòàâèòü Aj â âèäå
ëèíåéíîé êîìáèíàöèè íîâûõ ñëó÷àéíûõ âåëè÷èí Vk, îáåñïå÷åíèå
óñëîâèÿ íåêîððåëèðîâàííîñòè êîòîðûõ îñóùåñòâëÿåòñÿ â ðåçóëüòàòå
ñîîòâåòñòâóþùåãî âûáîðà êîýôôèöèåíòîâ ajk ïðè óêàçàííûõ
çíà÷åíèÿõ ñëó÷àéíûõ âåëè÷èí, ò.å .
Xt
aVt
jkkj
k
n
j
n
()
().
=
=
=
∑
∑φ
1
1
(10.58)
 êà÷åñòâå ÷àñòíûõ ïðèìåðîâ âîçìóùàþùèõ âîçäåéñòâèé ðàñ-
ñìîòðèì âëèÿíèå íà ïîëåò ËÀ àòìîñôåðíûõ âîçìóùåíèé òèïà ïî-
ðûâîâ âåòðà W è îòêëîíåíèÿ ïëîòíîñòè àòìîñôåðû îò ñòàíäàðòíîé
∆ρ(H).
Êàê íåñòàöèîíàðíûå ñòîõàñòè÷åñêèå ïðîöåññû ýòè âåëè÷èíû
ìîæíî ïðåäñòàâèòü, èñïîëüçóÿ êàíîíè÷åñêîå ðàçëîæåíèå, â âèäå
WVH
W
i
n
W
ii
=
=
∑1
φ ();
(10.59)
∆
∆∆
ρφ
ρρ
()
().
HVH
ii
i
n
=
=
∑1
(10.60)
463
Äàííûì ðàçëîæåíèÿì ñîîòâåòñòâóþò êîððåëÿöèîííûå ôóíêöèè âèäà
KHH
HH
WW
W
i
n
ii
(,) () ()
;
12
1
1
2
=
=
∑φφ
(10.61)
KHH
HH
ii
i
n
∆∆
∆
ρρ
ρ
φφ
(,)
() ().
12
1
1
2
=
=
∑
(10.62)
Õàðàêòåð èçìåíåíèÿ êîððåëÿöèîííûõ ôóíêöèé, ïîëó÷åííûõ â
ðåçóëüòàòå ñòàòèñòè÷åñêîé îáðàáîòêè ïðîöåññîâ çîíäèðîâàíèÿ
àòìîñôåðû, ïðèâåäåí, íàïðèìåð, â ðàáîòå [138].
Ñëó÷àéíóþ ôóíêöèþ äëÿ âåòðà ïî ñîîáðàæåíèÿì, èçëîæåííûì â
ãë. 8, öåëåñîîáðàçíî ïðåäñòàâèòü â âèäå äâóõ ôóíêöèé [33]:
â íàïðàâëåíèè ñåâåð – þã
WHWH V
H
WiWi
i
m
cþ
cþ
ñþ
ñþ
−−
=
=+
−−
∑
()~()
();
φ
1
â íàïðàâëåíèè âîñòîê – çàïàä
WHWH V
H
WiWi
i
m
âç
âç
âç
âç
−−
=
=+
−−
∑
()~()
().
φ
1
Çäåñü
~
()
WH
ñþ
−
è
~
()–
WH
âç
−
èçìåíåíèÿ ïî âûñîòå ñðåäíèõ çíà÷å-
íèé ïðîåêöèé ñêîðîñòè âåòðà; VWi
ñþ
−
, VWi
âç
−
–
ñëó÷àéíûå âåëè÷èíû;
φWiH
ñþ
−
(),φ WiH
âç
−
()–êîîðäèíàòíûå ôóíêöèè, îïðåäåëÿþùèå ñëó-
÷àéíûå ñîñòàâëÿþùèå ñêîðîñòè âåòðà â ñîîòâåòñòâóþùåì íàïðàâëå-
íèè ïî âûñîòå.
 êàæäîì êîíêðåòíîì ðàñ÷åòå òðàåêòîðèè èñïîëüçóåòñÿ ïî îäíîé
èç ðåàëèçàöèé ñëó÷àéíûõ ôóíêöèé Wc−þ(H)èWâ−ç(H). Ñëó÷àéíûå
âåëè÷èíû è êîîðäèíàòíûå ôóíêöèè îïðåäåëÿþòñÿ â ðåçóëüòàòå
âåñüìà òðóäîåìêîãî âåðîÿòíîñòíîãî àíàëèçà áîëüøîãî êîëè÷åñòâà
îïûòíûõ äàííûõ, ïîëó÷åííûõ ïðè ìåòåîðîëîãè÷åñêîì çîíäèðîâà-
íèè àòìîñôåðû. Ïðè áàëëèñòè÷åñêèõ ðàñ÷åòàõ ÷èñëî ñëàãàåìûõ â
ïðàâûõ ÷àñòÿõ ðàçëîæåíèé ñëó÷àéíûõ ôóíêöèé îïðåäåëÿåòñÿ ðàñïî-
ëàãàåìûìè îïûòíûìè äàííûìè, èõ äîñòîâåðíîñòüþ è êîëè÷åñòâîì.
 áîëüøèíñòâå ñëó÷àåâ îêàçûâàåòñÿ âîçìîæíûì âçÿòü 10...15 ÷ëåíîâ
ðàçëîæåíèÿ.
Ðàññìîòðèì ïðèìåðíûé ïîðÿäîê èñïîëüçîâàíèÿ ðàçëîæåíèé ïðè
ðàñ÷åòå õàðàêòåðèñòèê ðàññåèâàíèÿ ðàêåò. Õàðàêòåðèñòèêè ñëó÷àé-
íûõ âåëè÷èí Vi è êîîðäèíàòíûå ôóíêöèè φi ñ÷èòàþòñÿ èçâåñòíûìè.
Ïðåäïîëîæèì, ÷òî èìååòñÿ ïî n êîîðäèíàòíûõ ôóíêöèé äëÿ îïðå-
464
äåëåíèÿ Wc−þ è Wâ−ç èïîn òàáëèö ñëó÷àéíûõ êîýôôèöèåíòîâ. Âçÿâ
ïî îäíîìó ñëó÷àéíîìó ÷èñëó Vi èç êàæäîé òàáëèöû, óìíîæèâ êàæ-
äîå èç íèõ íà ñâîþ (ñîâïàäàþùóþ ïî íîìåðó) êîîðäèíàòíóþ ôóíê-
öèþ è ïðîñóììèðîâàâ ïîëó÷åííûå ÷ëåíû, íàõîäÿò êîíêðåòíóþ êðè-
âóþ (ðåàëèçàöèþ), êîòîðàÿ â çàâèñèìîñòè îò âûñîòû çàäàåò çàêîí
èçìåíåíèÿ ñêîðîñòè âåòðà, õàðàêòåðèçóåìûé ôóíêöèÿìè Wñ− þ(Í)è
Wâ−ç(Í). ×òîáû îáëåã÷èòü ðàñ÷åòû, ïðîåêòèðóþò âåêòîð ñêîðîñòè
âåòðà íà íàïðàâëåíèå ñòðåëüáû è áîêîâîå íàïðàâëåíèå, â ðåçóëüòàòå
÷åãî ïîëó÷àþò ðåàëèçàöèè Wx(H)èWz(H), êîòîðûå èñïîëüçóþò ïðè
ðåøåíèè ñèñòåìû óðàâíåíèé äâèæåíèÿ ðàêåòû äëÿ ïåðâîãî "ïóñêà".
Ñîâåðøåííî òàê æå âû÷èñëÿþòñÿ ðåàëèçàöèè Wx(H)èWz(H) äëÿ
âòîðîãî, òðåòüåãî è ò.ä . "ïóñêîâ".
Èìåÿ ïîëó÷åííûå çíà÷åíèÿ ñëó÷àéíûõ ïàðàìåòðîâ è ñëó÷àéíûõ
ôóíêöèé, ïðîâîäÿò ðàñ÷åòû òðàåêòîðèé ("îïûòû") íà ÝÂÌ èëè
ÀÂÌ. Àíàëîãîâûå âû÷èñëèòåëüíûå ìàøèíû äàþò ðåçóëüòàòû ñ
áîëüøèìè îøèáêàìè, îäíàêî èõ èñïîëüçîâàíèå öåëåñîîáðàçíî â òåõ
ñëó÷àÿõ, êîãäà îïèñàòü ìàòåìàòè÷åñêè ÿâëåíèå ïîëíîñòüþ íå ïðåä-
ñòàâëÿåòñÿ âîçìîæíûì è ïðèõîäèòñÿ âêëþ÷àòü â ýëåêòðè÷åñêóþ âû-
÷èñëèòåëüíóþ ñõåìó ìàøèíû ðåàëüíûå óçëû èçäåëèÿ.
Ðåçóëüòàòû ðàñ÷åòà, ïîëó÷åííûå â ïåðâîì "èñïûòàíèè", âíîñÿòñÿ
â òàáëèöó. Çàòåì òàê æå ïðîèçâîäèòñÿ âòîðîå èñïûòàíèå, òðåòüå è
òàê âïëîòü äî ïîñëåäíåãî. Êîãäà ïðîâåäåíû âñå "îïûòû", èç òàáëèöû
âûïèñûâàåòñÿ èíòåðåñóþùàÿ íàñ âåëè÷èíà (íàïðèìåð, äàëüíîñòü,
âûñîòà ïîëåòà è äð.), óñòàíàâëèâàþòñÿ çàêîí åå ðàñïðåäåëåíèÿ è ÷è-
ñëîâûå õàðàêòåðèñòèêè çàêîíà. Òàêèì îáðàçîì, â ðåçóëüòàòå èñïû-
òàíèé ïîëó÷àåòñÿ ïîëíîå îïèñàíèå èññëåäóåìîé âåëè÷èíû ñ âåðîÿò-
íîñòíîé òî÷êè çðåíèÿ.
Ïðè ìîäåëèðîâàíèè íà ÝÂÌ óðàâíåíèé ôîðìèðóþùåãî ôèëüòðà
ïðèõîäèòñÿ ñòàëêèâàòüñÿ ñ äâóìÿ ïðîáëåìàìè:
ïîëó÷åíèåì äèñêðåòíîãî áåëîãî øóìà ñ åäèíè÷íîé ñïåêòðàëüíîé
ïëîòíîñòüþ èç ïîñëåäîâàòåëüíîñòè ïñåâäîñëó÷àéíûõ ÷èñåë, âûðà-
áàòûâàåìûõ ñòàíäàðòíîé ïîäïðîãðàììîé, âõîäÿùåé â ñîñòàâ ìàòå-
ìàòè÷åñêîãî îáåñïå÷åíèÿ;
âûáîðîì îïòèìàëüíîãî øàãà èíòåãðèðîâàíèÿ äèôôåðåíöèàëüíî-
ãî óðàâíåíèÿ ôîðìèðóþùåãî ôèëüòðà.
Äèñêðåòíûé áåëûé øóì ñ ìàòðèöåé êîâàðèàöèé
Mò
[]
qqQ
ij
ii
j
=δ
(10.63)
ÿâëÿåòñÿ ìàòåìàòè÷åñêîé àáñòðàêöèåé.  (10.63) ÷åðåç δij îáîçíà÷åíà
ôóíêöèÿ Êðîíåêåðà (ñì. (10.54)). Ñ öåëüþ ïîëó÷åíèÿ äèñêðåòíîãî
áåëîãî øóìà íà ÝÂÌ èñïîëüçóåòñÿ ïîäïðîãðàììà ôîðìèðîâàíèÿ
íîðìàëüíî ðàñïðåäåëåííûõ ïñåâäîñëó÷àéíûõ ÷èñåë ñ íóëåâûì
465
ìàòåìàòè÷åñêèì îæèäàíèåì è åäèíè÷íîé äèñïåðñèåé. Èíòåíñèâíîñòü
øóìà, ñíèìàåìîãî ñ òàêîãî ïðîãðàììíîãî äàò÷èêà, ðàâíà G =Äq/ht, ãäå
Äq – äèñïåðñèÿ ñëó÷àéíûõ âåëè÷èí, ôîðìèðóåìûõ ïðîãðàììîé; ht –
øàã ïî âðåìåíè îáðàùåíèÿ ê ïðîãðàììå. Ñïåêòðàëüíàÿ ïëîòíîñòü è
èíòåíñèâíîñòü áåëîãî øóìà â ñîîòâåòñòâèè ñ (10.32) ñâÿçàíû ìåæäó
ñîáîé ñîîòíîøåíèåì 2πc = Q, ãäå c = const. ×òîáû ñôîðìèðîâàòü
áåëûé øóì ñ åäèíè÷íîé ñïåêòðàëüíîé ïëîòíîñòüþ èç ïîñëå-
äîâàòåëüíîñòè ïñåâäîñëó÷àéíûõ ÷èñåë, âûðàáàòûâàåìûõ ïðîãðàì-
ìîé, íåîáõîäèìî äîïîëíèòåëüíî ïîäâåðãíóòü ýòó ïîñëåäîâàòåëüíîñòü
ïðåîáðàçîâàíèþ, ïðîïóñòèâ ÷åðåç çâåíî ñ êîýôôèöèåíòîì ïåðåäà÷è
kh
qt
=
2π/( ).
Ä Ó÷èòûâàÿ, ÷òî Äq ÷èñëåííî ðàâíà åäèíèöå, îêîí-
÷àòåëüíî èìååì kh
t
=
2π /.
Âûáîð øàãà èíòåãðèðîâàíèÿ óðàâíåíèé ôîðìèðóþùåãî ôèëüòðà
îïðåäåëÿåòñÿ èç óñëîâèé îáåñïå÷åíèÿ çàäàííîé òî÷íîñòè âîñïðîèç-
âåäåíèÿ ñïåêòðàëüíîé ïëîòíîñòè ïðîöåññà â óñòàíîâëåííîì äèàïà-
çîíå ÷àñòîò.
Ïðè ht → 0 è ôèêñèðîâàííîì äèàïàçîíå ÷àñòîò ω∈[0, ω0] ôóíê-
öèÿ Sh(ω) ñòðåìèòñÿ ê ïîñòîÿííîé ñïåêòðàëüíîé ïëîòíîñòè, ïðè÷åì
ìàêñèìàëüíîå ïî ω îòêëîíåíèå äîñòèãàåòñÿ íà êîíöå ïðîìåæóòêà
ïðè ω = ω0. Îòíîñèòåëüíàÿ ïîãðåøíîñòü â èìèòàöèè ïðîöåññîì
òèïà äèñêðåòíîãî áåëîãî øóìà ñâîéñòâ íåïðåðûâíîãî áåëîãî øóìà
õàðàêòåðèçóåòñÿ âåëè÷èíîé
|() ()|
()
,
*
SS
S
hh
h
0
0
0
−
≤
ω
ε
(10.64)
ãäå ε
*
–
íàïåðåä çàäàííàÿ âåëè÷èíà ïðåäåëüíîé ïîãðåøíîñòè. Èç íå-
ðàâåíñòâà (10.64) èìååì [129] íåðàâåíñòâî äëÿ âûáîðà øàãà ht:
hh
t≤≤
−
*
*
.
230
1
εω
(10.65)
Ïðèìåíèòåëüíî ê óðàâíåíèÿì ôîðìèðóþùèõ ôèëüòðîâ (10.51) è
(10.52) çíà÷åíèÿ h
*
äîëæíû áûòü âçÿòû [129] ñîîòâåòñòâåííî ðàâ-
íûìè0,1Òè0,66Ò.
Êðîìå òîãî, ïðè ïðîãðàììíîé ðåàëèçàöèè ôîðìèðóþùèõ ôèëüò-
ðîâ ñëåäóåò èìåòü â âèäó, ÷òî òðåáóåìûé ñëó÷àéíûé ïðîöåññ íà âû-
õîäå ôèëüòðà ìîæíî ïîëó÷èòü ñ òðåáóåìîé òî÷íîñòüþ òîëüêî ïîñëå
çàòóõàíèÿ ïåðåõîäíîãî ïðîöåññà. Ïîýòîìó äèôôåðåíöèàëüíûå óðàâ-
íåíèÿ ôèëüòðà íåîáõîäèìî èíòåãðèðîâàòü ðàíüøå, ÷åì óðàâíåíèÿ
äèíàìèêè ïîëåòà ËÀ, ñ öåëüþ èñêëþ÷åíèÿ âëèÿíèÿ ïåðåõîäíûõ
466
ïðîöåññîâ ôèëüòðà íà òî÷íîñòü ðàñ÷åòà õàðàêòåðèñòèê ðàññåèâàíèÿ.
Ñõåìà ôîðìèðîâàíèÿ ìîäåëåé ñëó÷àéíûõ ïðîöåññîâ íà îñíîâå ôîð-
ìèðóþùåãî ôèëüòðà ïðèâåäåíà íà ðèñ. 10 .4 .
Ïóñòü â ðàìêàõ ðåøåíèÿ çàäà÷è áîêîâîé ñòàáèëèçàöèè ïîëåòà
ËÀ, ñîîòâåòñòâóþùåé ìîäåëè âèäà (3.98), òðåáóåòñÿ îïðåäåëèòü òî÷-
íîñòíûå õàðàêòåðèñòèêè ïðîöåññà ïðè ó÷åòå ïîïåðå÷íîé ñîñòàâ-
ëÿþùåé òóðáóëåíòíîñòè àòìîñôåðû.
Âåêòîð ñîñòîÿíèÿ ñèñòåìû â ðàññìàòðèâàåìîì ñëó÷àå:
x() [,
•
,, ,]
.
tz
zy
=ψ
ω
β
ò
Ëèíåàðèçîâàííàÿ ìîäåëü âîçìóùåííîãî óïðàâëÿåìîãî äâèæåíèÿ ËÀ
äëÿ îáñóæäàåìîãî ñëó÷àÿ áóäåò èìåòü âèä
dz
dt
z
dz
dt
aza b
d
dt
d
dt
a
y
y
y
=
=−+
=
=+
•
;
•
•
;
•
;
22
25
2
44
βδ
ψ
ψ
ω
ω
aba
yW
45
4
45
βδβ
++;
d
dt
aba
WtV
T
yW
wz
yy
β ψβδβ
β
δσδ
=+
++
=
=−
−
−
•
;
();
•
()
55
5
55
1
1
1
;
•
,
•
•
σψ
ω
ψ
ψ
=++ +
kzkzk k
zz
y
ãäå Ò1 – ïîñòîÿííàÿ âðåìåíè ñèñòåìû.
467
Ðèñ. 10.4 . Ñõåìà ìîäåëèðîâàíèÿ ïðîöåññà ïðè ôîðìèðîâàíèè ñëó÷àéíîãî âîçäåéñò-
âèÿ ñ çàäàííûìè ñâîéñòâàìè
Äàííóþ ìîäåëü íåîáõîäèìî äîïîëíèòü óðàâíåíèÿìè ôîðìèðóþ-
ùåãî ôèëüòðà, çàäàííûìè â ôîðìå (10.52). Ðàñøèðÿÿ âåêòîð ñîñòîÿ-
íèÿ:
xp
ò
() [,
•
,,
•
,,,, ]
,
tz
z
x
x
y
=
ψψβδ 12
ïåðåõîäèì ê äèñêðåòíîé ìîäåëè âèäà
xA
x
B
q
pp
()()()()
()
,
kk
k
k
k
+=
+++
11
1
â êîòîðîé A(k)èB(k + 1) – ìàòðèöû ðàçìåðíîñòè (8×8); q(k +1)–
íîðìàëüíî ðàñïðåäåëåííàÿ ïñåâäîñëó÷àéíàÿ ïîñëåäîâàòåëüíîñòü ñ
íóëåâûì ìàòåìàòè÷åñêèì îæèäàíèåì è åäèíè÷íîé äèñïåðñèåé,
âûðàáàòûâàåìàÿ ñîîòâåòñòâóþùåé ñòàíäàðòíîé ïîäïðîãðàììîé.
Ñòàòèñòè÷åñêàÿ îáðàáîòêà ïîëó÷àåìûõ ñëó÷àéíûõ ðåàëèçàöèé
ïîçâîëÿåò îïðåäåëèòü çíà÷åíèÿ êîððåëÿöèîííîé ôóíêöèè (ìàòðèöû)
õàðàêòåðèñòèê ïðîöåññà ñòàáèëèçàöèè ñ ó÷åòîì áîêîâûõ
(ïîïåðå÷íûõ) ôëþêòóàöèé àòìîñôåðû.
Äîñòîâåðíîñòü ðåçóëüòàòîâ ïðè ïðèìåíåíèè ìåòîäà ñòàòèñòè-
÷åñêèõ èñïûòàíèé â çíà÷èòåëüíîé ìåðå çàâèñèò îò ÷èñëà ïðîâå-
äåííûõ "îïûòîâ" è îò êîððåêòíîñòè ìàòåìàòè÷åñêîãî îïèñàíèÿ
èññëåäóåìîãî ïðîöåññà. Íåîáõîäèìîå ÷èñëî ðåàëèçàöèé n, îáåñ-
ïå÷èâàþùåå çàäàííóþ òî÷íîñòü è íàäåæíîñòü ðåçóëüòàòà, îïðåäå-
ëÿåòñÿ ïî èçâåñòíûì [113] ôîðìóëàì, óñòàíàâëèâàþùèì çàâèñè-
ìîñòü ìåæäó èñêîìûì çíà÷åíèåì, äîâåðèòåëüíîé âåðîÿòíîñòüþ è
äîâåðèòåëüíûì èíòåðâàëîì. Äëÿ ïðèáëèæåííîãî âû÷èñëåíèÿ
÷èñëà n ïðè îïðåäåëåíèè êîððåëÿöèîííîé ìàòðèöû íîðìàëüíî
ðàñïðåäåëåííûõ ñëó÷àéíûõ âåëè÷èí ìîæåò áûòü ðåêîìåíäîâàíî
ñîîòíîøåíèå
nt
xa
=
−
241
σε
σ,
(10.66)
ãäå εσ – âåëè÷èíà, õàðàêòåðèçóþùàÿ çíà÷åíèå äîâåðèòåëüíîãî
èíòåðâàëà; ta – ïàðàìåòð ðàñïðåäåëåíèÿ Ñòüþäåíòà, çíà÷åíèÿ êîòî-
ðîãî â çàâèñèìîñòè îò ÷èñëà ñòåïåíåé ñâîáîäû è äîâåðèòåëüíîé
âåðîÿòíîñòè ïðèâåäåíû â ñïåöèàëüíûõ òàáëèöàõ, èìåþùèõñÿ â
ëèòåðàòóðå ïî òåîðèè âåðîÿòíîñòåé.
468
10.2 . ÑÒÀÒÈÑÒÈ×ÅÑÊÀß ÎÁÐÀÁÎÒÊÀ ÐÅÇÓËÜÒÀÒÎÂ
ÑÒÐÅËÜÁ
10.2.1. ÎÏÐÅÄÅËÅÍÈÅ ÕÀÐÀÊÒÅÐÈÑÒÈÊ ÐÀÑÑÅÈÂÀÍÈß
ÏÎ ÐÅÇÓËÜÒÀÒÀÌ ÎÏÛÒÍÛÕ ÑÒÐÅËÜÁ
Ïðÿìîé îïûò (ñòðåëüáà) äàåò âîçìîæíîñòü íàèáîëåå ïðàâèëüíî
îöåíèâàòü õàðàêòåðèñòèêè ðàññåèâàíèÿ. Ñòðåëüáà âûïîëíÿåòñÿ íà
çàêëþ÷èòåëüíûõ ýòàïàõ îòðàáîòêè ðàêåòíîãî èëè àðòèëëåðèéñêîãî
êîìïëåêñà. Ñ óâåëè÷åíèåì ñòîèìîñòè ðàêåò (ñíàðÿäîâ), åñòåñòâåí-
íî, ñíèæàþòñÿ âîçìîæíîñòè ïîëó÷åíèÿ äîñòàòî÷íîãî ñòàòèñòè÷å-
ñêîãî ìàòåðèàëà ïóòåì ïðîâåäåíèÿ ñòðåëüá. Ïîýòîìó ðåçóëüòàòû
ñòðåëüáû âñåãäà îöåíèâàþòñÿ â ñî÷åòàíèè ñ òåîðåòè÷åñêèìè ðàñ÷å-
òàìè. Îñíîâíàÿ òðóäíîñòü ðåøåíèÿ ýòîé çàäà÷è ïðè ðàêåòíûõ
ñòðåëüáàõ çàêëþ÷àåòñÿ â îãðàíè÷åííîñòè ñòàòèñòè÷åñêîãî ìàòåðèà-
ëà èëè, äðóãèìè ñëîâàìè, â ìàëîì ÷èñëå ïóñêîâ ðàêåò, à òàêæå â
òîì, ÷òî çàðàíåå íåèçâåñòåí çàêîí ðàñïðåäåëåíèÿ îáðàáàòûâàåìûõ
âåëè÷èí.  ñâÿçè ñ ýòèì â ïðîöåññå ðàñ÷åòà ÷èñëîâûõ õàðàêòåðè-
ñòèê ïî ðåçóëüòàòàì îïûòà ïðèõîäèòñÿ èìåòü äåëî íå ñ èõ òî÷íûìè
çíà÷åíèÿìè, à ëèøü ñî ñðåäíèìè ñòàòèñòè÷åñêèìè çíà÷åíèÿìè.
Ñðåäíèå ñòàòèñòè÷åñêèå çíà÷åíèÿ ÷èñëîâûõ õàðàêòåðèñòèê îáû÷íî
îòìå÷àþòñÿ ÷åðòî÷êîé íàâåðõó.
Íàïðèìåð, mx m
x
[]–
=
ñðåäíåå
ñòàòèñòè÷åñêîå ìàòåìàòè÷åñêîå
îæèäàíèå ñëó÷àéíîé âåëè÷è-
íû; ÄÄ
[]–
x
x
=
ñðåäíÿÿ ñòàòè-
ñòè÷åñêàÿ äèñïåðñèÿ ñëó÷àé-
íîé âåëè÷èíû è ò.ä. Óêàçàííûå
çíà÷åíèÿ íàçûâàþò îöåíêàìè
ñîîòâåòñòâóþùèõ ÷èñëîâûõ õà-
ðàêòåðèñòèê.
Ðàññìîòðèì îñíîâíûå ýòàïû
îáðàáîòêè ðåçóëüòàòîâ ñòðåëü-
áû. Äîïóñòèì, ÷òî ïðè n ïóñêàõ
ðàêåò ìû èìååì n òî÷åê èõ ïàäå-
íèÿ
íà
ïëîñêîñòè
OXZ
(ðèñ. 10.5). Êîîðäèíàòû òî÷åê
ïàäåíèÿ íàèáîëåå öåëåñîîáðàç-
íî îïðåäåëÿòü â ñòàðòîâîé ñèñ-
òåìå êîîðäèíàò (äëÿ áàëëèñòè-
÷åñêèõ ðàêåò áîëüøîé äàëüíî-
ñòè – â ãåîöåíòðè÷åñêîé ÑÊ).
469
Ðèñ. 10 .5 . Ñõåìà ðàññåèâàíèÿ êîîðäèíàò
òî÷åê ïàäåíèÿ ñíàðÿäîâ íà ìåñòíîñòè
Ïðåæäå âñåãî âûïèñûâàþò ïîñëåäîâàòåëüíî êîîðäèíàòû x, z êàæäîé
òî÷êè ïàäåíèÿ. Çàòåì îïðåäåëÿþò âåëè÷èíû ñðåäíèõ ñòàòèñòè÷å-
ñêèõ ìàòåìàòè÷åñêèõ îæèäàíèé ïî êîîðäèíàòàì x è z
m
n
x
xi
i
n
=
=
∑
1
1
;
(10.67)
m
n
z
zi
i
n
=
=
∑
1
1
(10.68)
è ñðåäíèõ ñòàòèñòè÷åñêèõ äèñïåðñèé ÄÄ
xz
,
è êîððåëÿöèîííîãî
ìîìåíòà K xz :
Äxi
x
i
n
n
xm
=
−
−
=
∑
1
1
2
1
()
;
(10.69)
Äzi
z
i
n
n
zm
=
−
−
=
∑
1
1
2
1
()
;
(10.70)
K
n
xmz m
x
z
ixiz
i
n
=
−
−−
=
∑
1
11
()
()
.
(10.71)
Äàëåå ðàññ÷èòûâàþò ñðåäíèå ñòàòèñòè÷åñêèå çíà÷åíèÿ ñðåäíèõ
êâàäðàòè÷åñêèõ îòêëîíåíèé σσ
xz
,
è êîýôôèöèåíòà êîððåëÿöèè rxz :
σxx
=
Ä;
(10.72)
σzz
=
Ä;
(10.73)
rK
xz
xz
zx
=
−
().
σσ
1
(10.74)
×òîáû îöåíèòü íàäåæíîñòü ïîëó÷åííûõ ñðåäíèõ ñòàòèñòè÷åñêèõ
çíà÷åíèé ÷èñëîâûõ õàðàêòåðèñòèê, äëÿ íèõ ðàññ÷èòûâàþò äîâåðè-
òåëüíûå èíòåðâàëû.
Ïóñòü â ðåçóëüòàòå îáðàáîòêè äàííûõ ñòðåëüáû ìû ïîëó÷èëè mx è
íåîáõîäèìî îöåíèòü îøèáêó mm
xx
−
, ãäå mx – òî÷íîå çíà÷åíèå ìàòå-
ìàòè÷åñêîãî îæèäàíèÿ ñëó÷àéíîé âåëè÷èíû õ. Íàçíà÷èì íåêîòîðóþ
äîñòàòî÷íî áîëüøóþ âåðîÿòíîñòü β (íàïðèìåð, β = 0,9 èëè äàæå β =
= 0,999), òàêóþ, ÷òî ñîáûòèå ñ âåðîÿòíîñòüþ β ìîæíî ñ÷èòàòü ïðàê-
òè÷åñêè äîñòîâåðíûì, è íàéäåì òàêîå çíà÷åíèå ε, äëÿ êîòîðîãî
470
Pmm
xx
(|
|).
−<=
εβ (10.75)
Òîãäà äèàïàçîí ïðàêòè÷åñêè
âîçìîæíûõ îøèáîê, âîçíèêà-
þùèõ ïðè çàìåíå mx íà mx ,
áóäåò ñîñòàâëÿòü ±ε. Áîëüøèå
ïî
àáñîëþòíîé
âåëè÷èíå
îøèáêè áóäóò ïîÿâëÿòüñÿ ñ ìàëîé âåðîÿòíîñòüþ
a=−
1β.
(10.76)
Ïåðåïèøåì ðàâåíñòâî (10.75) â òàêîì âèäå:
Pm
mm
xx
x
()
.
−<
<+=
εε
β (10.77)
Ðàâåíñòâî (10.77) îçíà÷àåò, ÷òî ñ âåðîÿòíîñòüþ β íåèçâåñòíîå òî÷íîå
çíà÷åíèå mx ïîïàäàåò â ñëåäóþùèé èíòåðâàë (ðèñ. 10.6):
Jmm
xx
β
εε
=−
+
(;)
.
(10.78)
Âåëè÷èíà Jβ íîñèò íàçâàíèå äîâåðèòåëüíîãî èíòåðâàëà,àβ – äîâå-
ðèòåëüíîé âåðîÿòíîñòè.  íàøåì ñëó÷àå β – âåðîÿòíîñòü òîãî, ÷òî
äîâåðèòåëüíûé èíòåðâàë Jβ "íàêðîåò" âåëè÷èíó mx.
Îïðåäåëèì äîâåðèòåëüíûå èíòåðâàëû äëÿ ñðåäíèõ ñòàòèñòè÷å-
ñêèõ ìàòåìàòè÷åñêèõ îæèäàíèé ñëó÷àéíûõ âåëè÷èí êîîðäèíàò x è z.
Äëÿ ýòîãî çàäàäèìñÿ âåëè÷èíîé β, ïî êîòîðîé íàéäåì tβ. Îòíîñè-
òåëüíûå ãðàíèöû äîâåðèòåëüíûõ èíòåðâàëîâ îïðåäåëèì ïî ôîðìó-
ëàì
()
;
ε
β
mx
x
t
n
=
1
Ä
(10.79)
()
.
ε
β
mz
z
t
n
=
1
Ä
(10.80)
Ñëåäîâàòåëüíî, ìû èìååì òàêèå äîâåðèòåëüíûå èíòåðâàëû äëÿ
ñðåäíèõ ñòàòèñòè÷åñêèõ ìàòåìàòè÷åñêèõ îæèäàíèé:
() [ (); ()];
Jmm
mxm
xm
xx
x
β
εε
=−
+
(10.81)
() [ (); ()].
Jmm
mzm
zm
zz
z
β
εε
=−
+
(10.82)
471
Ðèñ. 10 .6. Îïðåäåëåíèå ïîíÿòèÿ äîâåðèòåëü-
íîãî èíòåðâàëà
Îòíîñèòåëüíûå ãðàíèöû äîâåðèòåëüíûõ èíòåðâàëîâ äëÿ ñðåäíèõ
ñòàòèñòè÷åñêèõ äèñïåðñèé ñëó÷àéíûõ âåëè÷èí x è z ìîæíî îïðåäå-
ëèòü ïî ñëåäóþùèì ôîðìóëàì:
()
;
ε
β
Ä
Ä
x
t
n
x
=
−
2
1
(10.83)
()
,
ε
β
Ä
Ä
z
t
n
z
=
−
2
1
(10.84)
è ìû èìååì ñëåäóþùèå äîâåðèòåëüíûå èíòåðâàëû ñðåäíèõ
ñòàòèñòè÷åñêèõ äèñïåðñèé:
() [ (); ()];
J xxx
xx
β
εε
ÄÄÄ
ÄÄ
=−
+
(10.85)
() [ (); ()].
J zzz
zz
β
εε
ÄÄÄ
ÄÄ
=−
+
(10.86)
Åñëè ìû îáîçíà÷èì
σε
σε
1
2
xx
xx
x
x
=−
=+
Ä
Ä
Ä
Ä
();
(),
òî ìîæíî ïîëó÷èòü äîâåðèòåëüíûå èíòåðâàëû äëÿ ñðåäíèõ
ñòàòèñòè÷åñêèõ êâàäðàòè÷åñêèõ îòêëîíåíèé
()(;);
Jx
xx
βσ
σσ
=
12
(10.87)
()(;).
Jz
zz
βσ
σσ
=
12
(10.88)
Ñëåäóþùèì ýòàïîì îáðàáîòêè ñòðåëüá ÿâëÿåòñÿ ïîñòðîåíèå ãèñ-
òîãðàììû, ôîðìà êîòîðîé äàåò îñíîâàíèå äëÿ ïðèíÿòèÿ ãèïîòåçû î
âîçìîæíîì õàðàêòåðå çàêîíà ðàñïðåäåëåíèÿ. Äëÿ ïîñòðîåíèÿ ãèñòî-
ãðàììû ïðîâîäÿò ñëåäóþùèå îïåðàöèè. Äåëÿò âåñü äèàïàçîí ïîëó-
÷åííûõ õ è z íà ðàçðÿäû (èíòåðâàëû), îãðàíè÷åííûå çíà÷åíèÿìè xi,
xi+1 è zi, zi+1 (äëÿ i-ãî èíòåðâàëà), è ïîäñ÷èòûâàþò ÷èñëî çíà÷åíèé
ñëó÷àéíîé âåëè÷èíû mi, ïðèõîäÿùååñÿ íà êàæäûé i-é ðàçðÿä. Äëÿ
óäîáñòâà ïîñòðîåíèÿ ãèñòîãðàììû áåðóò íå èñòèííûå çíà÷åíèÿ xi è
zi, à èõ îòêëîíåíèÿ îò ñîîòâåòñòâóþùèõ ìàòåìàòè÷åñêèõ îæèäàíèé
xi
o
èzi
o
. Îáû÷íî ÷èñëî ðàçðÿäîâ ðàâíî øåñòè èëè âîñüìè è ðåæå – äå-
ñÿòè. Âîîáùå êîëè÷åñòâî ðàçðÿäîâ k çàâèñèò îò ÷èñëà ïðîâåäåííûõ
îïûòîâ. ×åì áîëüøå îïûòîâ (n), òåì áîëüøåå ÷èñëî ðàçðÿäîâ ìîæíî
472
áðàòü. Äëèíó ðàçðÿäà óäîáíî ïðè-
íÿòü ðàâíîé ñðåäíåìó êâàäðàòè÷å-
ñêîìó îòêëîíåíèþ.
Ïî ïîëó÷åííûì äàííûì ñòðîÿò
ãèñòîãðàììû êàê äëÿ ñëó÷àéíîé âå-
ëè÷èíû õ, òàê è äëÿ ñëó÷àéíîé âå-
ëè÷èíû z, îòêëàäûâàÿ ïî îñÿì àáñ-
öèññ ðàçðÿäû, à ïî îñÿì îðäèíàò –
ñîîòâåòñòâóþùèå èì çíà÷åíèÿ mi
ñëó÷àéíûõ âåëè÷èí.
Àíàëèçèðóÿ ïîëó÷åííûå ãèñòî-
ãðàììû, ïðèíèìàþò ãèïîòåçó î âîç-
ìîæíîì õàðàêòåðå çàêîíà ðàñïðåäå-
ëåíèÿ äàííîé ñëó÷àéíîé âåëè÷èíû.
Íàïðèìåð, ïî ãèñòîãðàììå, ïðåä-
ñòàâëåííîé íà ðèñ. 10 .7, ìîæíî
ïðèíÿòü ãèïîòåçó î íîðìàëüíîì çàêîíå ðàñïðåäåëåíèÿ ñëó÷àéíîé
âåëè÷èíû õ.
Ïðèíÿòóþ ãèïîòåçó î çàêîíå ðàñïðåäåëåíèÿ äàííîé ñëó÷àéíîé
âåëè÷èíû íåîáõîäèìî ïðîâåðÿòü ïî êðèòåðèþ ñîãëàñèÿ. ×àùå âñåãî
äëÿ ýòîãî ïðèìåíÿþò êðèòåðèé χ2 Ïèðñîíà, êîòîðûé äàåò âîçìîæ-
íîñòü îöåíèòü ñòåïåíü ñîãëàñîâàííîñòè ââåäåííîãî òåîðåòè÷åñêîãî
è ñòàòèñòè÷åñêîãî çàêîíîâ ðàñïðåäåëåíèÿ.
Âåëè÷èíó χ2 îïðåäåëÿþò ïî çàâèñèìîñòè
χ2
2
1
=
−
=
∑()
,
mn
p
np
ii
i
i
k
(10.89)
ãäå pi – âåðîÿòíîñòü ïîïàäàíèÿ â i-é ðàçðÿä, ðàññ÷èòàííàÿ ïî
ââåäåííîìó òåîðåòè÷åñêîìó çàêîíó ðàñïðåäåëåíèÿ.
Íàïðèìåð, äëÿ íîðìàëüíîãî çàêîíà ðàñïðåäåëåíèÿ âåðîÿòíîñòü
ïîïàäàíèÿ ñëó÷àéíîé âåëè÷èíû õ â äàííûé ðàçðÿä ïîäñ÷èòûâàåòñÿ
ïî ôîðìóëå
p
x
x
i
i
x
i
x
=−
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
+
1
2
22
1
^^
,
ΦΦ
o
o
ρσ ρσ
(10.90)
ãäå xx
i
i
oo
,–
+1
ãðàíè÷íûå çíà÷åíèÿ i-ãî ðàçðÿäà; ρ 2 0 6745
=
,;
σx–
ñðåäíåå êâàäðàòè÷åñêîå çíà÷åíèå äàííîé ñëó÷àéíîé âåëè÷èíû, íàé-
473
Ðèñ. 10 .7. Ïîñòðîåíèå ãèñòîãðàììû
äåííîå ðàíåå ïî îïûòíûì äàííûì; ^
–
Φ
xi
x
o
ρσ
2
çíà÷åíèå ïðèâåäåí-
íîé ôóíêöèè Ëàïëàñà.
Äàëåå îïðåäåëÿåòñÿ ÷èñëî ñòåïåíåé ñâîáîäû r êàê ðàçíîñòü ÷èñëà
ðàçðÿäîâ k è ÷èñëà óñëîâèé (ñâÿçåé) S, íàëîæåííûõ íà ïðèíÿòûé
òåîðåòè÷åñêèé çàêîí ðàñïðåäåëåíèÿ:
rkS
=−
.
(10.91)
 íàøåì ñëó÷àå ÷èñëî íàëîæåííûõ óñëîâèé (ñâÿçåé) S ðàâíî
òðåì, òàê êàê íåîáõîäèìî, ÷òîáû:
1) ñóììà ÷àñòîò ðàâíÿëàñü åäèíèöå;
2) ñîâïàäàëè òåîðåòè÷åñêèå è ñðåäíèå ñòàòèñòè÷åñêèå ìàòåìàòè-
÷åñêèå îæèäàíèÿ;
3) ñîâïàäàëè òåîðåòè÷åñêèå è ñðåäíèå ñòàòèñòè÷åñêèå äèñïåð-
ñèè.
Äàëåå ïî íàéäåííûì χ2 è r îïðåäåëÿþò âåðîÿòíîñòü ð òîãî, ÷òî
ïðèíÿòûé çàêîí ðàñïðåäåëåíèÿ íå ïðîòèâîðå÷èò îïûòíûì äàííûì
[23]. Åñëè âåðîÿòíîñòü ð ìàëà, òî ãèïîòåçà î ââåäåííîì çàêîíå ðàñ-
ïðåäåëåíèÿ îòáðàñûâàåòñÿ êàê íåïðàâäîïîäîáíàÿ. Åñëè æå íàéäåí-
íàÿ âåðîÿòíîñòü îòíîñèòåëüíî âåëèêà, òî ãèïîòåçó ìîæíî ïðèçíàòü
íå ïðîòèâîðå÷àùåé îïûòíûì äàííûì.
Íàñêîëüêî ìàëà äîëæíà áûòü âåðîÿòíîñòü ð äëÿ òîãî, ÷òîáû îò-
áðîñèòü ãèïîòåçó î ââåäåííîì çàêîíå ðàñïðåäåëåíèÿ, – âîïðîñ íå-
îïðåäåëåííûé. Îí íå ìîæåò áûòü ðàçðåøåí èç ìàòåìàòè÷åñêèõ ñî-
îáðàæåíèé. Íà ïðàêòèêå, åñëè ð < 0,1, òî íåîáõîäèìî ýêñïåðèìåíò
ïîâòîðèòü ëèáî ïîïûòàòüñÿ íàéòè áîëåå ïîäõîäÿùèé çàêîí ðàñïðå-
äåëåíèÿ.
Êðîìå êðèòåðèÿ χ2 ÷àñòî èñïîëüçóåòñÿ êðèòåðèé ñîãëàñèÿ Êîëìî-
ãîðîâà.  êà÷åñòâå ìåðû ðàñõîæäåíèÿ ìåæäó òåîðåòè÷åñêèì è ñòàòè-
÷åñêèì ðàñïðåäåëåíèÿìè À.Í. Êîëìîãîðîâ ïðåäëîæèë ðàññìàòðè-
âàòü ìàêñèìàëüíîå çíà÷åíèå ìîäóëÿ ðàçíîñòè ìåæäó ñòàòèñòè÷å-
ñêîé è ïðèíÿòîé òåîðåòè÷åñêîé ôóíêöèÿìè ðàñïðåäåëåíèÿ [23].
Ñëåäóåò îòìåòèòü, ÷òî ñ ïîìîùüþ êðèòåðèÿ Êîëìîãîðîâà, òàê æå
êàê è êðèòåðèÿ ñîãëàñèÿ χ2, ïðè äîñòàòî÷íî áîëüøèõ çíà÷åíèÿõ âå-
ðîÿòíîñòè ð ìîæíî òîëüêî óñòàíîâèòü, ÷òî ïðèíÿòàÿ ãèïîòåçà î çà-
êîíå ðàñïðåäåëåíèÿ íå ïðîòèâîðå÷èò îïûòíûì äàííûì.
Îïûòíûå õàðàêòåðèñòèêè ðàññåèâàíèÿ ñðàâíèâàþòñÿ ñ ðàñ÷åò-
íûìè è îöåíèâàþòñÿ ñîâìåñòíî. Ïðè íåîáõîäèìîñòè ââîäÿò êîð-
ðåêòèâû â ðàñ÷åòíûé çàêîí ðàñïðåäåëåíèÿ è õàðàêòåðèñòèêè ðàñ-
ñåèâàíèÿ.
474
Ðàññåèâàíèå òî÷åê ïàäåíèÿ àðòèëëå-
ðèéñêèõ ñíàðÿäîâ è íåóïðàâëÿåìûõ ðà-
êåò ïîä÷èíÿåòñÿ íîðìàëüíîìó çàêîíó
ðàñïðåäåëåíèÿ; ïðè ýòîì òî÷êè ïàäåíèÿ
ðàñïîëàãàþòñÿ íà ïëîñêîñòè â ïðåäåëàõ
ýëëèïñà ðàññåèâàíèÿ. Öåíòð ýëëèïñà
ñîâïàäàåò ñ öåíòðîì ðàññåèâàíèÿ (èëè
öåíòðîì ãðóïïèðîâàíèÿ). Ïðè ñòðåëüáå
àðòèëëåðèéñêèìè âðàùàþùèìèñÿ ñíà-
ðÿäàìè âñëåäñòâèå ïðàâîé äåðèâàöèè
öåíòð ýëëèïñà ðàññåèâàíèÿ ñìåùàåòñÿ
âïðàâî îò ïëîñêîñòè ñòðåëüáû. Ïðè
ñòðåëüáå òàêèìè ñíàðÿäàìè ïî ìåñòíî-
ñòè â ñëó÷àå rxz = 0 ïðîäîëüíàÿ îñü ýë-
ëèïñà ðàâíà 8Âä, áîêîâàÿ – 8Âá, ïðè÷åì
îáû÷íî Âä > Âá.
Ïðè ñòðåëüáå ïî ìåñòíîñòè íåóïðàâ-
ëÿåìûìè îïåðåííûìè ñíàðÿäàìè ïîä
ìàëûìè óãëàìè âîçâûøåíèÿ, òàê æå êàê
è ïðè ñòðåëüáå àðòèëëåðèéñêèìè ñíàðÿ-
äàìè, Âä > Âá (ðèñ. 10.8, á); ïðè ñòðåëüáå
ïîä óãëàìè, áëèçêèìè ê óãëàì íàèáîëü-
øåé äàëüíîñòè, Âá > Âä è áîëüøàÿ îñü ýë-
ëèïñà íàïðàâëåíà ïåðïåíäèêóëÿðíî ê
íàïðàâëåíèþ ñòðåëüáû (ðèñ. 10 .8, à).
Ïðè íåêîòîðîì ñî÷åòàíèè äåéñòâóþ-
ùèõ ñëó÷àéíûõ ôàêòîðîâ, îïðåäåëÿþ-
ùèõ ïîëíîå ðàññåèâàíèå, ïðîäîëüíàÿ îñü ýëëèïñà ìîæåò íå ñîâïà-
äàòü ñ íàïðàâëåíèåì ñòðåëüáû (rxz ≠ 0). Ïðè ñòðåëüáå ïî ùèòó ñíàðÿ-
äàìè, èìåþùèìè íàñòèëüíóþ òðàåêòîðèþ, ýëëèïñ ðàññåèâàíèÿ
ïðèáëèæàåòñÿ ê îêðóæíîñòè. Åãî îñè ðàâíû 8Âá è8Ââ, ãäå Ââ – âåðî-
ÿòíîå (ñðåäèííîå) îòêëîíåíèå ïî âûñîòå.
Ïî õàðàêòåðèñòèêàì ïîëíîãî ðàññåèâàíèÿ ìîæíî âû÷èñëèòü õà-
ðàêòåðèñòèêó ðàññåèâàíèÿ îäíîé èç îïðåäåëÿþùèõ âåëè÷èí. Íà-
ïðèìåð, åñëè ñòðåëÿòü èç àðòèëëåðèéñêîé ñèñòåìû ïðè óãëå âîçâû-
øåíèÿ, áëèçêîì ê óãëó íàèáîëüøåé äàëüíîñòè, è îïðåäåëèòü îïûò-
íûå Âä, òî, çíàÿ, ÷òî ïðè òàêèõ óãëàõ ∂õñ/∂θ0 ≈ 0, èç ôîðìóëû (10.25)
ìîæíî íàéòè
r
c
x
B
x
V
r
c
c
c
V
=−
⎛
⎝⎜⎞
⎠⎟
∂
∂
∂
∂
ä
2
0
2
0
.
475
Ðèñ. 10.8 . Ýëëèïñû ðàññåèâà-
íèÿ â ñëó÷àå ñòðåëüáû íå-
óïðàâëÿåìûìè ðåàêòèâíûìè
ñíàðÿäàìè ïðè ðàçëè÷íûõ óã-
ëàõ âîçâûøåíèÿ
Âåëè÷èíà rV 0
îïðåäåëÿåòñÿ ïî ðåçóëüòàòàì áàëëèñòè÷åñêèõ
ñòðåëüá ñ èñïîëüçîâàíèåì ôîðìóëû
r
n
V
Vi
i
n
0
06745
1
1
2
1
=
−
=
∑
,(
)
,
δ
(10.92)
ãäå δVi = Vi − Vñð – îòêëîíåíèå íà÷àëüíîé ñêîðîñòè ïðè îòäåëüíûõ
âûñòðåëàõ Vi îò ñðåäíåé àðèôìåòè÷åñêîé ñêîðîñòè â ãðóïïå Vñð =
=
⎛
⎝⎜⎞
⎠⎟
=
∑Vn
i
i
n
1
/.
 òåõ ñëó÷àÿõ, êîãäà ïðè ñòðåëüáå ïî ìåñòíîñòè èëè ïî âåðòè-
êàëüíîé ïðåãðàäå âåðîÿòíûå îòêëîíåíèÿ â ðàçëè÷íûõ íàïðàâëåíèÿõ
îäèíàêîâû, ââîäÿò â ðàññìîòðåíèå âåðîÿòíîå êðóãîâîå îòêëîíåíèå,
÷àñòî íàçûâàÿ åãî ïðîñòî êðóãîâûì îòêëîíåíèåì èëè êðóãîâîé îøèá-
êîé.
Êðóãîâûì âåðîÿòíûì îòêëîíåíèåì íàçûâàþò ðàäèóñ êðóãà ñ
öåíòðîì â òî÷êå ãðóïïèðîâàíèÿ, âåðîÿòíîñòü ïîïàäàíèÿ â êîòîðûé
ðàâíà 0,5. Î÷åâèäíî, êðóãîâàÿ îøèáêà áóäåò áîëüøå ñîîòâåòñòâóþ-
ùèõ îòêëîíåíèé ïî íàïðàâëåíèþ. Çàâèñèìîñòü ìåæäó âåðîÿòíûì
êðóãîâûì îòêëîíåíèåì Åêð (êðóãîâîé îøèáêîé) è âåðîÿòíûì îòêëî-
íåíèåì ïî íàïðàâëåíèþ èìååò âèä
EE
êð
≈ 175
,
(10.93)
èëè ïðèìåíèòåëüíî ê ñòðåëüáå ïî ìåñòíîñòè èëè ïî ùèòó
rBB
êð
ä
á
==
175 175
,,
.
Î÷åâèäíî, ïðè Âä ≈ Âá ≈ Ââ ìîæíî ââåñòè â ðàññìîòðåíèå ñôåðó
ðàññåèâàíèÿ è äëÿ åå õàðàêòåðèñòèêè – ñôåðè÷åñêîå âåðîÿòíîå îò-
êëîíåíèå. Ïîä ñôåðè÷åñêèì âåðîÿòíûì îòêëîíåíèåì ïîíèìàåòñÿ
ðàäèóñ ñôåðû, âåðîÿòíîñòü ïîïàäàíèÿ òî÷êè ðàçðûâà â êîòîðóþ ðàâ-
íà 0,5. Ñôåðè÷åñêîå âåðîÿòíîå îòêëîíåíèå ìîæíî îïðåäåëèòü ÷åðåç
îäíî èç âåðîÿòíûõ îòêëîíåíèé ïî íàïðàâëåíèþ èç ôîðìóëû
EE
ñô
≈ 228
,.
(10.94)
10.2.2 . ÎÁÐÀÁÎÒÊÀ ÄÀÍÍÛÕ ÏÐÈÑÒÐÅËÊÈ È ÁÎÅÂÛÕ
ÀÐÒÈËËÅÐÈÉÑÊÈÕ ÑÒÐÅËÜÁ
Çàäà÷åé áîåâûõ àðòèëëåðèéñêèõ ñòðåëüá ÿâëÿåòñÿ íàíåñåíèå ïðîòèâíèêó
óùåðáà, ñíèæàþùåãî åãî áîåâûå âîçìîæíîñòè. Âåäåíèå áîåâîé ñòðåëüáû
îñóùåñòâëÿåòñÿ íà îñíîâå óñòàíîâîê, îïðåäåëÿåìûõ ñëåäóþùèìè ñïîñîáà-
ìè: ïîëíîé ïîäãîòîâêîé; ïåðåíîñîì îãíÿ îò ðåïåðà (öåëè); èñïîëüçîâàíèåì
476
äàííûõ ïðèñòðåëî÷íîãî îðóäèÿ (ÏÎÐ); ïðèñòðåëêîé öåëè ñ ïîìîùüþ òåõ-
íè÷åñêèõ ñðåäñòâ (ðàäèîëîêàöèîííûõ ñòàíöèé (ÐËÑ), âåðòîëåòà), à òàêæå
ïîäðàçäåëåíèé çâóêîâîé ðàçâåäêè.
Êàê ïðàâèëî, óñòàíîâêè îïðåäåëÿþò ïðèñòðåëêîé. Ñòðåëüáó íà ïîðàæå-
íèå áåç ïðèñòðåëêè ïðè îïðåäåëåíèè óñòàíîâîê ñïîñîáîì ïîëíîé ïîäãîòîâ-
êè, èñïîëüçîâàíèÿ äàííûõ ÏÎÐ è ïåðåíîñà îãíÿ îò ðåïåðà ðàçðåøàåòñÿ âåñ-
òè ïî îãðàíè÷åííîìó ÷èñëó öåëåé ïðè ãàðàíòèðîâàííîì îáåñïå÷åíèè áåçî-
ïàñíîñòè ñâîèõ ñèë.
Çàäà÷à ïðèñòðåëêè – ïðèâåäåíèå ê öåëè ìåòîäîì ïîñëåäîâàòåëüíûõ ïðè-
áëèæåíèé ñðåäíåé òðàåêòîðèè çàëïà ïóòåì îïðåäåëåíèÿ çíà÷åíèÿ îòêëîíå-
íèé òî÷åê ïàäåíèÿ îò öåëè. Ââåäåíèå êîððåêòóðû âîçìîæíî ïî ñðåäíåé âå-
ëè÷èíå îòêëîíåíèÿ ãðóïïû ðàçðûâîâ (íå ìåíåå òðåõ) èëè çàëïà.
Ðåøåíèå óêàçàííîé çàäà÷è äåëàåò íåîáõîäèìûì íàáëþäåíèå çà ñòðåëü-
áîé, â ñâÿçè ñ ÷åì ñòðåëüáó ïðèíÿòî ïîäðàçäåëÿòü: ïî íàáëþäåíèþ çíàêîâ
ïàäåíèÿ; ïî èçìåðåííûì îòêëîíåíèÿì; ïî èçìåðåííûì äàëüíîñòÿì.
Íàèáîëåå ïðîñòûì ñïîñîáîì äèñòàíöèîííîãî îïðåäåëåíèÿ ðåçóëüòàòîâ
ñòðåëüáû ÿâëÿåòñÿ íàáëþäåíèå ïî çíàêàì ïàäåíèÿ. Íåäîëåòíûì ïàäåíèÿì
ïðèñâîåí çíàê "ìèíóñ", ïåðåëåòíûì – "ïëþñ". Íàáëþäàòü çíàê ïàäåíèÿ âîç-
ìîæíî òîëüêî â ñëó÷àå ïàäåíèÿ ñíàðÿäà âäîëü ëèíèè íàáëþäåíèÿ "íàáëþäà-
òåëüíûé ïóíêò – öåëü". Îñíîâíûì âèäîì íàáëþäåíèé ÿâëÿåòñÿ âèçóàëüíûé,
ñ ïðèìåíåíèåì îïòè÷åñêèõ ñðåäñòâ.  ðÿäå ñëó÷àåâ (íàïðèìåð, ïðè ñòðåëüáå
ïî ìîðñêèì öåëÿì) ïðè îòñóòñòâèè âèçóàëüíîé âèäèìîñòè âñïëåñê îò óïàâ-
øåãî â âîäó ñíàðÿäà ìîæíî íàáëþäàòü íà èíäèêàòîðå àðòèëëåðèéñêîé ðà-
äèîëîêàöèîííîé ñòàíöèè (ÀÐËÑ).
Äâà äðóãèõ ñïîñîáà íàáëþäåíèÿ ñóùåñòâåííî áîëåå òðóäîåìêè ïî îðãà-
íèçàöèè, òðåáóþò äîâîëüíî ñëîæíîãî îáîðóäîâàíèÿ, íî îáåñïå÷èâàþò çà
ìåíüøåå âðåìÿ óòî÷íåíèå ìåñòà öåëè, ÷åì ïðè íàáëþäåíèè ïî çíàêàì ïàäå-
íèÿ. Ñóùíîñòü ïðèñòðåëêè ïî èçìåðåííûì îòêëîíåíèÿì çàêëþ÷àåòñÿ â îï-
ðåäåëåíèè îòêëîíåíèÿ ðàçðûâà îäèíî÷íîãî ñíàðÿäà èëè çàëïà â áîêîâîì
íàïðàâëåíèè ñ ïîìîùüþ âèçèðà, ïî äàëüíîñòè – ñ ïîìîùüþ äàëüíîìåðîâ,
ïóíêòîâ ñîïðÿæåííîãî íàáëþäåíèÿ áàòàðåè (ÑÍÁ), à òàêæå ÀÐËÑ. Ïðè
ñòðåëüáå íàçåìíîé àðòèëëåðèåé ïðèñòðåëêó íà÷èíàþò îäèíî÷íûì âûñòðå-
ëîì íà èñ÷èñëåííûõ óñòàíîâêàõ. Åñëè èçìåðåííîå îòêëîíåíèå ðàçðûâà îò
öåëè ïî äàëüíîñòè íå ïðåâûøàåò 100 ì, à ïî íàïðàâëåíèþ ñîñòàâëÿåò 0...20
äåëåíèé óãëîìåðà, òî íà èñïðàâëåííûõ óñòàíîâêàõ ïåðåõîäÿò ê ñòðåëüáå íà
ïîðàæåíèå, à â îñòàëüíûõ ñëó÷àÿõ íàçíà÷àþò âòîðîé âûñòðåë. Ïî èçìåðåí-
íûì îòêëîíåíèÿì âòîðîãî ðàçðûâà îò öåëè ââîäÿò êîððåêòóðû è ïåðåõîäÿò ê
ñòðåëüáå íà ïîðàæåíèå.
Ïðè çàëïîâîé ñòðåëüáå ïî ìîðñêèì öåëÿì ïðèñòðåëêó ïðîèçâîäÿò, êàê
ïðàâèëî, î÷åðåäüþ íà òðåõ ïðèöåëàõ ñ øèðîêèì øàãîì ïðèöåëà (ØÏ) 4Âä.
Àíàëîãè÷íî ïðîâîäèòñÿ è ïðèñòðåëêà ïî èçìåðåííûì äàëüíîñòÿì. Îäíàêî
çäåñü âûïîëíåíèå î÷åðåäè íà÷èíàþò ñ äàëüíåãî ïðåäåëà. Ïîïðàâêó äàëüíî-
ñòè îïðåäåëÿþò êàê ñðåäíþþ èç ïîïðàâîê êî âñåì çàëïàì ïðèñòðåëî÷íîé
î÷åðåäè ñ ó÷åòîì øàãà ïðèöåëà. Ïîñëå ïðîâåäåíèÿ âñåõ çàëïîâ ïðèñòðåëî÷-
íîé î÷åðåäè êîððåêòèðóþò ñíà÷àëà öåëèê íà âåëè÷èíó èçìåðåííîãî îòêëî-
íåíèÿ. Äàëüíîñòü äî òî÷åê ïàäåíèÿ êàæäîãî ñíàðÿäà â çàëïå ïðèñòðåëî÷íîé
î÷åðåäè ïåðåäàþò â öåíòðàëüíûé àâòîìàò ñòðåëüáû (ÖÀÑ), ãäå ÷èñëî è çíàê
îòêëîíåíèé çàëïîâ ïî äàëüíîñòè îïðåäåëÿþòñÿ êàê ðàçíîñòü àâòîìàòíîé
äàëüíîñòè äî öåëè è äàëüíîñòè äî òî÷åê ïàäåíèÿ êàæäîãî çàëïà ïðèñòðåëî÷-
477
íîé î÷åðåäè. Ñðåäíåå îòêëîíåíèå ïî òðåì çàëïàì ðàññ÷èòûâàåòñÿ êàê ñóììà
òðåõ èçìåðåííûõ îòêëîíåíèé, äåëåííàÿ íà ÷èñëî èçìåðåíèé áåç ó÷åòà øàãà
î÷åðåäè.
Îøèáêè ïðèñòðåëêè, âûïîëíÿåìîé èíñòðóìåíòàëüíûìè ñïîñîáàìè,
îáû÷íî ïðèíèìàþòñÿ ïîä÷èíÿþùèìèñÿ íîðìàëüíîìó çàêîíó ðàñïðåäåëå-
íèÿ, ÷òî äîïóñòèìî â ïåðâîì ïðèáëèæåíèè, åñëè øàã î÷åðåäè íå ïðåâûøàåò
ØÏ=8Âä [112]. Èõ âåëè÷èíà çàâèñèò îò òî÷íîñòè ïðèìåíÿåìûõ èçìåðè-
òåëüíûõ ïðèáîðîâ, óñëîâèé íàáëþäåíèÿ, ñïîñîáà îöåíêè îòêëîíåíèé ñðåä-
íåé òðàåêòîðèè îò öåëè è òåõíè÷åñêîãî ðàññåèâàíèÿ ñíàðÿäîâ.
Äèñòàíöèîííîå îïðåäåëåíèå ðåçóëüòàòîâ ïðèñòðåëêè, à òàêæå ñòðåëüáû
íà ïîðàæåíèå öåëè âíîñèò îñîáåííîñòè â èñïîëüçóåìûå ìåòîäû ñòàòèñòè÷å-
ñêîé îáðàáîòêè äàííûõ ñòðåëüáû.
 ÷àñòíîñòè, ñðåäèííàÿ, èëè âåðîÿòíàÿ, îøèáêà ïðèñòðåëêè (â ìåòðàõ)
ïî èçìåðåííûì äàëüíîñòÿì îïðåäåëÿåòñÿ êàê
EE
t
x
=+
èçì
âèð
í
22
2
183
()
,
τ
(10.95)
ãäå Åèçì – âåðîÿòíàÿ îøèáêà îïðåäåëåíèÿ ïîëîæåíèÿ ñðåäíåé òðàåêòîðèè
îòíîñèòåëüíî öåëè, ì; τâèð – âåðîÿòíàÿ îøèáêà âåëè÷èíû èçìåðåíèÿ
ðàññòîÿíèÿ çà 1 ìèí (ÂÈÐ = 1/6V cos q, V – ñêîðîñòü öåëè, q – êóðñîâîé
óãîë); tí – âðåìÿ íàêîïëåíèÿ îøèáêè ó÷åòà ïåðåìåùåíèÿ öåëè îò ìîìåíòà
èçìåðåíèÿ îòêëîíåíèÿ è äî ìîìåíòà ïàäåíèÿ ñíàðÿäîâ çàëïà (î÷åðåäè),
ïðîèçâåäåííîãî ïîñëå ââåäåíèÿ êîððåêòóðû.
 ñëó÷àå ïðèíÿòèÿ îòêëîíåíèÿ ñðåäíåé òðàåêòîðèè ðàâíûì ðàçíîñòè
äàëüíîñòåé äî öåíòðà ãðóïïèðîâàíèÿ ñíàðÿäîâ çàëïà è äî öåëè
E
mBB
m
èçì
èçì
ä
2
32
1
=
++
(),
∆
(10.96)
ãäå ∆Bèçì – âåðîÿòíàÿ îøèáêà èçìåðåíèé äàëüíîñòè äî öåëè è äî òî÷êè
ïàäåíèÿ, ì; Âä – âåðîÿòíîå îòêëîíåíèå ïî äàëüíîñòè; m – ÷èñëî íàáëþ-
äàåìûõ òî÷åê ïàäåíèÿ.
Èìåÿ â âèäó åñòåñòâåííûé äåôèöèò âðåìåíè, âîçíèêàþùèé ïðè ïðîâå-
äåíèè áîåâûõ ñòðåëüá, ñëåäóåò ñ÷èòàòü îïðàâäàííûì ìàêñèìàëüíîå óïðîùå-
íèå ïðîöåäóðû îáðàáîòêè èõ ðåçóëüòàòîâ â áîåâûõ óñëîâèÿõ. Ñ öåëüþ óïðî-
ùåíèÿ ðàñ÷åòîâ ýôôåêòèâíîñòè ñòðåëüáû ñîïðîâîæäàþùèå åå îøèáêè ðå-
êîìåíäóåòñÿ [112] ïðèáëèæåííî ñâîäèòü ê äâóì ãðóïïàì: ïîâòîðÿþùèìñÿ è
íåïîâòîðÿþùèìñÿ. Âåðîÿòíûå îòêëîíåíèÿ óêàçàííûõ ãðóïï îïðåäåëÿþòñÿ
êàê
EEr
xx
äâ
0
0
=
;
(10.97)
BEE
xx
äâ
2
00
2
=−
.
(10.98)
Çäåñü
478
r
nn
r
xx
ji
ij
0
1
1
2
=
−
≠
∑
()
,
(10.99)
ãäå rx ij
–
êîýôôèöèåíò êîððåëÿöèè i-ãî è j-ãî âûñòðåëîâ; Åxâ – âåðîÿòíàÿ
îøèáêà âûñòðåëà, ïðè÷åì rE
E
xx
x
ij
ij
=
−
22
â
; n – ÷èñëî âûñòðåëîâ.
Àíàëîãè÷íûì ñïîñîáîì ñâîäÿòñÿ ê äâóì ãðóïïàì îøèáêè ñòðåëüáû â áî-
êîâîì íàïðàâëåíèè.
Ãëàâà 11
ÁÀËËÈÑÒÈÊÀ ÊÎÐÐÅÊÒÈÐÓÅÌÛÕ
ÀÐÒÈËËÅÐÈÉÑÊÈÕ ÑÍÀÐßÄÎÂ,
ÑÓÁÁÎÅÏÐÈÏÀÑÎÂ È ÁÎÅÂÛÕ
ÏÎÐÀÆÀÞÙÈÕ ÝËÅÌÅÍÒÎÂ
ÑËÎÆÍÎÉ ÔÎÐÌÛ
Îäíèì èç ñïîñîáîâ ïîâûøåíèÿ òî÷íîñòè ñòðåëüáû ÿâëÿåòñÿ êîððåê-
öèÿ òðàåêòîðèè äâèæåíèÿ áîåïðèïàñà ñ öåëüþ ïàðèðîâàíèÿ äåéñòâóþ-
ùèõ íà íåãî âîçìóùàþùèõ ôàêòîðîâ è, ñëåäîâàòåëüíî, êîìïåíñàöèè
âîçíèêàþùèõ ïðîìàõîâ.
Äèíàìèêà óãëîâîãî äâèæåíèÿ, îðãàíèçàöèÿ òðåáóåìîãî âèäà äâè-
æåíèÿ ñíàðÿäà îòíîñèòåëüíî öåíòðà ìàññ, îáåñïå÷åíèå óñòîé÷èâî-
ñòè äâèæåíèÿ ïðè êîððåêöèÿõ ÿâëÿþòñÿ âàæíåéøèìè âîïðîñàìè, ðå-
øàåìûìè ïðè ïðîåêòèðîâàíèè òàêîãî òèïà áîåïðèïàñîâ.
Ðàçðàáîòêà è ñîçäàíèå ñóááîåïðèïàñîâ è ïîðàæàþùèõ ýëåìåíòîâ
êàññåòíûõ áîåâûõ ÷àñòåé ïðèâîäÿò ê íåîáõîäèìîñòè ó÷åòà ñïåöèôèêè
èõ êîíñòðóêöèè ïðè ðåøåíèè áàëëèñòè÷åñêèõ çàäà÷. Îñîáåííîñòÿìè
êîíñòðóêöèè ÿâëÿþòñÿ ìàëûå óäëèíåíèÿ, â ðÿäå ñëó÷àåâ íåäîîáòåêàå-
ìûå ôîðìû, ñëó÷àéíî èëè ïðåäíàìåðåííî ñîçäàâàåìûå àñèììåòðèè
ôîðìû è ìàññû [48, 140, 143]. Âûÿâëåíèå ôèçè÷åñêîé êàðòèíû è ïî-
ñòðîåíèå àäåêâàòíîé ìàòåìàòè÷åñêîé ìîäåëè, îòðàæàþùåé äèíàìè-
êó ïðîñòðàíñòâåííîãî äâèæåíèÿ òàêîãî ðîäà îáúåêòîâ, ÷àñòî îêàçû-
âàåòñÿ äîñòàòî÷íî ñëîæíîé çàäà÷åé, òðåáóþùåé ïðèìåíåíèÿ ñïåöè-
àëüíî ðàçðàáîòàííûõ ïîäõîäîâ è ìåòîäîâ èññëåäîâàíèÿ.
479
11.1 . ÎÑÎÁÅÍÍÎÑÒÈ ÈÑÑËÅÄÎÂÀÍÈß ÄÈÍÀÌÈÊÈ
ÏÐÎÑÒÐÀÍÑÒÂÅÍÍÎÃÎ ÄÂÈÆÅÍÈß ÊÎÐÐÅÊÒÈÐÓÅÌÛÕ
ÁÎÅÏÐÈÏÀÑÎÂ*
11.1.1 . ÏÎÑÒÀÍÎÂÊÀ ÇÀÄÀ×È ÊÎÐÐÅÊÖÈÈ ÄÂÈÆÅÍÈß ÑÍÀÐßÄÀ
Òðàåêòîðèÿ êîððåêòèðóåìîãî áîåïðèïàñà ìîæåò ñîñòîÿòü èç îä-
íîãî èëè íåñêîëüêèõ áàëëèñòè÷åñêèõ ó÷àñòêîâ è ñîîòâåòñòâåííî îä-
íîãî èëè íåñêîëüêèõ ó÷àñòêîâ êîððåêöèè [88]. Âûáîð ìåñòà ïðîâå-
äåíèÿ êîððåêöèè ñâÿçàí ñ îöåíêîé âêëàäà ðàçëè÷íûõ âîçìóùåíèé,
äåéñòâóþùèõ íà ñíàðÿä â ïîëåòå. Íàïðèìåð, åñëè ïðîìàõ àðòèëëå-
ðèéñêîãî ñíàðÿäà âîçíèêàåò èç-çà äåéñòâèÿ âîçìóùàþùèõ ôàêòîðîâ
ïðè äâèæåíèè íà ïàññèâíîì ó÷àñòêå òðàåêòîðèè, òî è ïàðèðîâàòü
åãî íåîáõîäèìî â ïðîöåññå ôîðìèðîâàíèÿ âîçìóùåíèé ëèáî â îê-
ðåñòíîñòè öåëè íà êîíå÷íîì ó÷àñòêå òðàåêòîðèè.
Åñëè æå ðàññìàòðèâàåòñÿ äâèæåíèå ðåàêòèâíîãî ñíàðÿäà ëèáî
óïðàâëÿåìîãî ËÀ, ó êîòîðîãî çíà÷èòåëüíàÿ ÷àñòü êîíå÷íîãî ïðîìàõà
ôîðìèðóåòñÿ çà ñ÷åò âîçìóùåíèé àêòèâíîãî ó÷àñòêà òðàåêòîðèè, òî
ïðèíöèïèàëüíî âîçìîæíî ïàðèðîâàíèå âëèÿíèÿ ýòèõ âîçìóùåíèé
è ñîîòâåòñòâåííî ïðîâåäåíèå êîððåêöèè (óïðàâëåíèÿ) íà íà÷àëüíîì
ó÷àñòêå.
Îáåñïå÷èòü ñòàáèëèçàöèþ óãëîâîãî äâèæåíèÿ êîððåêòèðóåìûõ
áîåïðèïàñîâ ìîæíî è áëàãîäàðÿ èñïîëüçîâàíèþ ýôôåêòà ãèðîñêî-
ïè÷åñêîé ñòàáèëèçàöèè [142], è ñ ïîìîùüþ îïåðåíèÿ [88], ïðè÷åì
êàê ðàñêðûâàþùåãîñÿ ïîñëå ïðîõîæäåíèÿ äóëüíîãî ñðåçà ñòâîëà,
òàê è ïîäêàëèáåðíîãî.
Ñèñòåìû ñ êîððåêöèåé äâèæåíèÿ íà êîíå÷íîì ó÷àñòêå òðàåêòî-
ðèè ïðåäñòàâëÿþò ñîáîé îñîáûå ñèñòåìû àâòîìàòè÷åñêîãî óïðàâëå-
íèÿ, êîòîðûå ðàáîòàþò òîëüêî íà÷èíàÿ ñ íåêîòîðîãî ìîìåíòà âðå-
ìåíè ïîëåòà áîåïðèïàñà è òîëüêî â òîì ñëó÷àå, åñëè îòêëîíåíèå ïî-
ïàäàþùåé òðàåêòîðèè îò öåëè îêàçûâàåòñÿ áîëüøå äîïóñòèìîãî.
Ïðè ýòîì èñïîëüçóåòñÿ îãðàíè÷åííîå ÷èñëî êîððåêòèðóþùèõ èì-
ïóëüñîâ, òðåáóåìîå äëÿ óñòðàíåíèÿ èìåþùåãîñÿ îòêëîíåíèÿ. Âñå
ñî÷åòàíèÿ óñëîâèé, ïðèâîäÿùèõ ê ñðàáàòûâàíèþ ñèñòåìû, ñëó÷àé-
íû è íå ìîãóò áûòü ïîâòîðåíû ïðè ñëåäóþùåì åå ïðèìåíåíèè â ðå-
àëüíûõ ïîëåòíûõ óñëîâèÿõ.
Íî íåçàâèñèìî îò óñëîâèé ðàáîòû êîíêðåòíûå ñèñòåìû èìåþò îá-
ùóþ öèêëîãðàììó ïîñëåäîâàòåëüíîñòè ïðîèñõîäÿùèõ â íåé îïå-
480
*
Ïàðàãðàô íàïèñàí ê.ò .í ., äîöåíòîì Â. . Ãðàáèíûì.
ðàöèé. Âèä òàêîé öèêëîãðàììû ïðåäñòàâëåí íà ðèñ. 11.1 . Íà íåé
óêðóïíåííî âûäåëåíî 5 ýòàïîâ.
Ïåðâûé ýòàï íà÷èíàåòñÿ â ìîìåíò âðåìåíè (t – 0), êîãäà ñíàðÿä
òåðÿåò ìåõàíè÷åñêóþ ñâÿçü ñ íàïðàâëÿþùåé. Äëÿ ýòîãî ìîìåíòà
âðåìåíè ðåàëèçóþòñÿ ïàðàìåòðû òðàåêòîðèè, îïðåäåëÿåìûå ïðîöåñ-
ñàìè äâèæåíèÿ ñíàðÿäà ïî íàïðàâëÿþùåé íà îòðåçêå âðåìåíè, êî-
ãäà ãîëîâíîé öåíòðóþùèé ïîÿñîê êîðïóñà óæå îêàçàëñÿ âíå íåå.
Ïðè ýòîì ñàìà íàïðàâëÿþùàÿ ïîëó÷àåò íåêîòîðûå óãëîâûå ñêîðî-
ñòè è îãðàíè÷åííûå óãëû ïîâîðîòà îòíîñèòåëüíî íåïîäâèæíîé çåì-
íîé ñèñòåìû êîîðäèíàò, â êîòîðîé çàòåì ïðîèñõîäèò ñâîáîäíîå
äâèæåíèå ñíàðÿäà. Ñ ýòîãî ìîìåíòà íà÷èíàåòñÿ ðàñêðûòèå îïåðå-
íèÿ ñòàáèëèçàòîðà.
Ïî ìåðå ðàñêðûòèÿ îïåðåíèÿ âîçðàñòàåò óãëîâàÿ ñêîðîñòü âðàùå-
íèÿ ñíàðÿäà âîêðóã åãî ïðîäîëüíîé îñè ïîä äåéñòâèåì àýðîäèíàìè-
÷åñêîãî âðàùàþùåãî ìîìåíòà, ñîçäàâàåìîãî êîñî ïîñòàâëåííûì
ñòàáèëèçèðóþùèì îïåðåíèåì, è íà÷èíàþòñÿ ïåðåõîäíûå ïðîöåññû
â äèíàìèêå óãëîâîãî äâèæåíèÿ ïîä âîçäåéñòâèåì óñêîðåíèÿ ñèëû
òÿæåñòè.
Ýòè ïðîöåññû èìåþò ìåñòî è ïðè äâèæåíèè ñíàðÿäà ñ ïîäêàëè-
áåðíûì îïåðåíèåì. Ïðè îòñóòñòâèè ðàñêðûòèÿ îïåðåíèÿ ïðîèñõî-
äèò îáû÷íîå ïàðèðîâàíèå íà÷àëüíûõ âîçìóùåíèé è äåéñòâèå óñêî-
ðåíèÿ ñèëû òÿæåñòè, õàðàêòåðíîå äëÿ ñòàòè÷åñêè óñòîé÷èâîãî ñíà-
ðÿäà.
481
Ðèñ. 11.1 . Öèêëîãðàììà ôóíêöèîíèðîâàíèÿ êîððåêòèðóåìîãî àðòèëëåðèéñêîãî ñíà-
ðÿäà
 ðåçóëüòàòå ÷åðåç äîñòàòî÷íî êîðîòêèé èíòåðâàë âðåìåíè êîëå-
áàíèÿ ïðîäîëüíîé îñè ñíàðÿäà îòíîñèòåëüíî âåêòîðà ñêîðîñòè çàòó-
õàþò è óãëîâàÿ ñêîðîñòü åãî âðàùåíèÿ îòíîñèòåëüíî ïðîäîëüíîé
îñè ïðèîáðåòàåò êâàçèñòàöèîíàðíîå çíà÷åíèå. Ìîìåíò, êîãäà äîñ-
òèãàåòñÿ ýòà âåëè÷èíà óãëîâîé ñêîðîñòè âðàùåíèÿ âîêðóã ïðîäîëü-
íîé îñè, à çíà÷åíèÿ óãëîâ àòàêè è ñêîëüæåíèÿ ñòàíîâÿòñÿ äîïóñòè-
ìî ìàëûìè (ïîðÿäêà 0,5...1 ãðàäóñà), ìîæíî ñ÷èòàòü ìîìåíòîì
îêîí÷àíèÿ ïåðâîãî ýòàïà äâèæåíèÿ êîððåêòèðóåìîãî àðòèëëåðèé-
ñêîãî ñíàðÿäà.
Äàëüíåéøåå äâèæåíèå (âòîðîé ýòàï) ïðîèñõîäèò ñ ìàëûìè óãëà-
ìè àòàêè è ñêîëüæåíèÿ êàê ñâîáîäíûé ïîëåò ïîä äåéñòâèåì àýðîäè-
íàìè÷åñêèõ ñèë è ìîìåíòîâ, à òàêæå ñèëû òÿæåñòè.
Òðåòèé ýòàï äâèæåíèÿ (ïîäãîòîâêà ê íà÷àëó êîððåêöèè) íà÷èíà-
åòñÿ çà íåñêîëüêî ñåêóíä äî ìîìåíòà âñòðå÷è ñíàðÿäà ñ öåëüþ.  ýòîò
ìîìåíò ïðèâîäèòñÿ â äåéñòâèå, êàê ïðàâèëî, ôëþãåðíûé áîðòîâîé
êîîðäèíàòîð öåëè (ÁÊÖ) è âûäàåòñÿ êîìàíäà íà ñáðîñ îáòåêàòåëÿ.
Ñáðîñ îáòåêàòåëÿ ÿâëÿåòñÿ ñëîæíûì äèíàìè÷åñêèì ïðîöåññîì,
çàíèìàþùèì äîñòàòî÷íî ìàëîå, íî êîíå÷íîå âðåìÿ. Èññëåäîâàíèå
òàêèõ ïðîöåññîâ â ïëîòíûõ ñëîÿõ àòìîñôåðû ïðåäñòàâëÿåò ñîáîé ñà-
ìîñòîÿòåëüíóþ çàäà÷ó, ðåøåíèå êîòîðîé òðåáóåò áîëüøîãî îáúåìà
ñïåöèàëüíîé èíôîðìàöèè î ñâîéñòâàõ è ïàðàìåòðàõ ïðîöåññà ðàçäå-
ëåíèÿ.  ÷àñòíîñòè, äëÿ òî÷íîãî ðàñ÷åòà äèíàìèêè ýòîãî ïðîöåññà
íåîáõîäèìî çíàíèå àýðîäèíàìè÷åñêèõ õàðàêòåðèñòèê íå òîëüêî
ñíàðÿäà è îáòåêàòåëÿ â îòäåëüíîñòè, íî è ïðîìåæóòî÷íîé ñèñòåìû,
ïðåäñòàâëÿþùåé ñîáîé ñîâîêóïíîñòü êîðïóñà ñíàðÿäà è ïîòåðÿâøå-
ãî ñ íèì ìåõàíè÷åñêóþ ñâÿçü îáòåêàòåëÿ ïðè ìàëûõ îòíîñèòåëüíûõ
ðàññòîÿíèÿõ ìåæäó íèìè è ïðè ðàçëè÷íîé îòíîñèòåëüíîé óãëîâîé
îðèåíòàöèè.
Äàëåå, äëÿ ÷åòâåðòîãî ó÷àñòêà òðàåêòîðèè îáû÷íî ïðèíèìàåòñÿ,
÷òî îáòåêàòåëü ñðàçó óäàëÿåòñÿ èç ïîëÿ çðåíèÿ êîîðäèíàòîðà è íå
âëèÿåò íà åãî ðàáîòó, ÷òî ðàìêè êîîðäèíàòîðà ðàçàððåòèðîâàíû, à
åãî îïòîýëåêòðîííàÿ ÷àñòü ïîëíîñòüþ ãîòîâà ê ðàáîòå.
Ïðè îòäåëåíèè îáòåêàòåëÿ ïðàêòè÷åñêè ñêà÷êîì èçìåíÿþòñÿ íå
òîëüêî ìàññîâî-èíåðöèîííûå, íî è àýðîäèíàìè÷åñêèå õàðàêòåðè-
ñòèêè áîåïðèïàñà.
Íîâûå óñëîâèÿ äâèæåíèÿ â íà÷àëå ÷åòâåðòîãî ó÷àñòêà îïðåäåëÿ-
þòñÿ ïðèïàñîâûâàíèåì êîíå÷íûõ çíà÷åíèé ïàðàìåòðîâ òðàåêòîðèè
ñíàðÿäà â ìîìåíò îêîí÷àíèÿ ïðîöåññà îòäåëåíèÿ îáòåêàòåëÿ ê íà÷à-
ëó ó÷àñòêà âîçìîæíîé êîððåêöèè.
Íà ÷åòâåðòîì ýòàïå ðàáîòû â ñèñòåìå ìîãóò ïðîèñõîäèòü î÷åíü
âàæíûå è ñëîæíûå ïðîöåññû ñîáñòâåííî êîððåêöèè òðàåêòîðèè ïî-
ëåòà.  íåêîòîðûé ñëó÷àéíûé ïî ñâîåé ïðèðîäå ìîìåíò âðåìåíè â
ïîëå çðåíèÿ êîîðäèíàòîðà ïîïàäàåò èçîáðàæåíèå ïÿòíà ÷àñòîò-
íî-ìîäóëèðîâàííîãî ñèãíàëà ïîäñâåòêè, îòðàæåííîãî îò öåëè. Åñëè
482
óðîâåíü ïîëó÷åííîãî ñèãíàëà ðàâåí èëè ïðåâîñõîäèò ïîðîã ÷óâñòâè-
òåëüíîñòè îïòîýëåêòðîííîé ñèñòåìû êîîðäèíàòîðà, íà åãî âûõîäå
ïîÿâëÿåòñÿ "ñïóñêîâîé" ñèãíàë, ðàçðåøàþùèé âêëþ÷åíèå ñîîòâåò-
ñòâóþùåãî êîððåêòèðóþùåãî äâèãàòåëÿ. Êîãäà ýòîò äâèãàòåëü îêà-
çûâàåòñÿ â ïëîñêîñòè êîððåêöèè, ïðîèñõîäèò âîñïëàìåíåíèå òâåð-
äîãî òîïëèâà è ñîçäàåòñÿ êîððåêòèðóþùàÿ ñèëà òÿãè. Íà÷èíàåòñÿ
ïåðâûé ýïèçîä êîððåêöèè ïîëåòà. Îí çàêàí÷èâàåòñÿ, êîãäà â äâèãà-
òåëå âûãîðàåò âñå òîïëèâî è îí ïðåêðàùàåò ðàáîòàòü. Åñëè ïåðâàÿ
êîððåêöèÿ îêàçàëàñü íåäîñòàòî÷íîé, òî ìîãóò ïðîèñõîäèòü âòîðàÿ,
òðåòüÿ è ïîñëåäóþùèå êîððåêöèè äî òåõ ïîð, ïîêà íå ñðàáîòàþò âñå
èìåþùèåñÿ êîððåêòèðóþùèå äâèãàòåëè.
Ïîñëå òîãî êàê ïðîâåäåíà êîððåêöèÿ ëèáî äîñòèãíóòà îòíîñè-
òåëüíàÿ äàëüíîñòü, ñîîòâåòñòâóþùàÿ ìîìåíòó "íàñûùåíèÿ" èëè "îñ-
ëåïëåíèÿ" ÁÊÖ, íà÷èíàåòñÿ ïîñëåäíèé, ïÿòûé, ýòàï ïîëåòà, ïðåä-
ñòàâëÿþùèé ñîáîé ñâîáîäíîå äâèæåíèå â àòìîñôåðå äî ìîìåíòà
âñòðå÷è ñ öåëüþ ëèáî äî ìîìåíòà ïàäåíèÿ íà ïîâåðõíîñòü çåìëè â
ñëó÷àå ïðîìàõà ïî öåëè.
11.1.2. ÌÀÒÅÌÀÒÈ×ÅÑÊÎÅ ÌÎÄÅËÈÐÎÂÀÍÈÅ ÏÐÎÑÒÐÀÍÑÒÂÅÍÍÎÃÎ
ÄÂÈÆÅÍÈß ÈÌÏÓËÜÑÍÎ-ÊÎÐÐÅÊÒÈÐÓÅÌÎÃÎ ÑÍÀÐßÄÀ
Ñ ó÷åòîì ïðèâåäåííîé öèêëîãðàììû ðàçðàáàòûâàåìûå ìàòåìà-
òè÷åñêèå ìîäåëè äâèæåíèÿ è ôóíêöèîíèðîâàíèÿ èìïóëüñíî-êîð-
ðåêòèðóåìûõ ñíàðÿäîâ äîëæíû àäåêâàòíî îòðàæàòü îñíîâíûå äèíà-
ìè÷åñêèå ïðîöåññû êîððåêòèðóåìîãî ïîëåòà, ãàðàíòèðóÿ "ñòûêîâêó"
äèíàìè÷åñêèõ ãðàíè÷íûõ óñëîâèé êàæäîãî èç ýëåìåíòîâ öèêëî-
ãðàììû.
Ïðè ðàçðàáîòêå ñîîòâåòñòâóþùèõ ìîäåëåé îáû÷íî ïðèíèìàþò,
÷òî âðåìÿ ñèëîâîãî âîçäåéñòâèÿ èñïîëíèòåëüíûõ îðãàíîâ ìàëî ïî
ñðàâíåíèþ ñî âðåìåíåì íàâåäåíèÿ. Ýòî ïîçâîëÿåò ââåñòè ïîíÿòèå
ñèëîâîãî êîððåêòèðóþùåãî èìïóëüñà, ïîä êîòîðûì áóäåì ïîíèìàòü
èìïóëüñ ñèëû, ñîçäàâàåìîé èñïîëíèòåëüíûì îðãàíîì ñèñòåìû êîð-
ðåêöèè: IF
d
t
kk
t
t
=
∫,
1
2
ãäå Ik – ñèëîâîé êîððåêòèðóþùèé èìïóëüñ,
èìåþùèé ðàçìåðíîñòü [êã⋅ñ]; ti, ti+1 – ìîìåíòû âðåìåíè, îïðåäåëÿþ-
ùèå íà÷àëî è êîíåö ïðèëîæåíèÿ êîððåêòèðóþùåé ñèëû.
Åñëè ïðåíåáðå÷ü èçìåíåíèåì ìàññû ñíàðÿäà ïðè ðàáîòå èñïîë-
íèòåëüíîãî îðãàíà, òî, çíàÿ âåëè÷èíó èìïóëüñà êîððåêöèè, ìîæíî
îöåíèòü èçìåíåíèå âåêòîðà ñêîðîñòè ñíàðÿäà ∆V ïðè èìïóëüñíîì
ñèëîâîì âîçäåéñòâèè: ∆V = Ik/m. Ïðè ýòîì ïðåäïîëàãàåòñÿ, ÷òî
âëèÿíèå äðóãèõ ñèë âî âðåìÿ êîððåêöèè ïðåíåáðåæèìî ìàëî. Äîïó-
ùåíèå î ìãíîâåííîñòè ñðàáàòûâàíèÿ êîððåêòèðóþùåãî èìïóëüñà
ñëåäóåò îáîñíîâûâàòü â êàæäîì êîíêðåòíîì ñëó÷àå, òàê êàê íåó÷åò
483
"êîíå÷íîñòè" âðåìåííûõ èíòåðâàëîâ âîçäåéñòâèÿ êîððåêòèðóþùåé
ñèëû ìîæåò îòðàçèòüñÿ íà òî÷íîñòè ðàñ÷åòà òðàåêòîðèé ñíàðÿäà ïî-
ñëå êîððåêöèè.
Èçìåíåíèå òðàåêòîðèè ïðè ïðîâåäåíèè êîððåêöèè çàâèñèò îò
ñïîñîáà ôîðìèðîâàíèÿ, âåëè÷èíû, íàïðàâëåíèÿ êîððåêòèðóþùåé
ñèëû è ìåñòà åå ïðèëîæåíèÿ íà ñíàðÿäå. Ýòè ôàêòîðû îïðåäåëÿ-
þò äèíàìèêó ïðîöåññà êîððåêöèè ñíàðÿäà è îêàçûâàþò âëèÿíèå
íà êèíåìàòè÷åñêèå ïàðàìåòðû òðàåêòîðèè ïîñëå ñíÿòèÿ êîððåê-
òèðóþùåãî âîçäåéñòâèÿ ïðè "ñâîáîäíîì" äâèæåíèè ïî ñêîððåê-
òèðîâàííîé òðàåêòîðèè. Ïðè êîððåêöèè òðàåêòîðèè áûñòðîâðà-
ùàþùåãîñÿ (îáëàäàþùåãî ãèðîñêîïè÷åñêîé óñòîé÷èâîñòüþ) ñíà-
ðÿäà ìåñòî ïðèëîæåíèÿ, âåëè÷èíà è íàïðàâëåíèå êîððåê-
òèðóþùåé ñèëû îñîáåííî îòðàæàþòñÿ íà õàðàêòåðèñòèêàõ åãî
âðàùàòåëüíîãî äâèæåíèÿ. Âîçìîæíîñòü ïîÿâëåíèÿ èíòåíñèâíûõ
äâèæåíèé âîêðóã öåíòðà ìàññ ïîñëå êîððåêöèè äîëæíà ó÷èòû-
âàòüñÿ ïðè àíàëèçå óñòîé÷èâîñòè äâèæåíèÿ êîððåêòèðóåìîãî
ñíàðÿäà ëþáîãî òèïà è ïðè îöåíêå òî÷íîñòè ñòðåëüáû. Âûáîð
âåëè÷èíû êîððåêòèðóþùåãî èìïóëüñà ïðåäñòàâëÿåò ñîáîé àêòó-
àëüíóþ ñàìîñòîÿòåëüíóþ çàäà÷ó, êîòîðàÿ íåïîñðåäñòâåííî ñâÿçà-
íà ñ îáùåé çàäà÷åé îïòèìèçàöèè ïàðàìåòðîâ êîíñòðóêöèè ñíà-
ðÿäà è ñèñòåìû êîððåêöèè â öåëîì.
Íå îñòàíàâëèâàÿñü íà ðàññìîòðåíèè ìåòîäîâ èññëåäîâàíèÿ
ïîëåòà ñíàðÿäà íà ïðåäøåñòâóþùèõ ýòàïó êîððåêöèè ó÷àñòêàõ
òðàåêòîðèè, áàçèðóþùèõñÿ íà ñòàíäàðòíûõ ïîäõîäàõ, ïåðåéäåì
íåïîñðåäñòâåííî ê îáñóæäåíèþ ïðîáëåì äèíàìèêè äâèæåíèÿ
ñíàðÿäà ïîñëå çàõâàòà öåëè åãî áîðòîâûì êîîðäèíàòîðîì.
Ïðåäâàðèòåëüíî îáñóäèì ýòó ïðîáëåìó äëÿ ñòàòè÷åñêè óñòîé÷è-
âîãî îïåðåííîãî ñíàðÿäà.
Àëãîðèòì ôîðìèðîâàíèÿ èìïóëüñíûõ êîððåêòèðóþùèõ âîçäåé-
ñòâèé, èñïîëüçóåìûé ïðè ñèíòåçå ìàòåìàòè÷åñêîé ìîäåëè, îáû÷íî
ñîñòîèò èç äâóõ ÷àñòåé.
Ïåðâàÿ ÷àñòü èñïîëüçóåòñÿ äëÿ îïðåäåëåíèÿ âåëè÷èíû è çíàêà
óãëîâîé îøèáêè ñèñòåìû êîððåêöèè, â ñîîòâåòñòâèè ñ êîòîðîé ïðî-
èñõîäèò ôîðìèðîâàíèå ñèãíàëà íà ðàçðåøåíèå âêëþ÷åíèÿ êîððåê-
òèðóþùåãî äâèãàòåëÿ. Âòîðàÿ ÷àñòü ïðåäíàçíà÷åíà äëÿ îïðåäåëåíèÿ
òîãî êîððåêòèðóþùåãî äâèãàòåëÿ, êîòîðûé äîëæåí âûïîëíèòü êîð-
ðåêöèþ òðàåêòîðèè â íóæíîì íàïðàâëåíèè.
Óãëîâàÿ îøèáêà ñèñòåìû êîððåêöèè îïðåäåëÿåòñÿ â èçìåðèòåëü-
íîé ñèñòåìå êîîðäèíàò. Äëÿ ïåðåõîäà îò ñâÿçàííîé ê èçìåðèòåëü-
íîé ñèñòåìå êîîðäèíàò â ìîäåëè èñïîëüçóåòñÿ ìàòðèöà D ñ ýëåìåí-
òàìè
484
ddd
dd
11
12
13
13
22
===
−
=−
=
cos cos ;
cos sin ;
sin ;
sin ;
νμ
νμ
ν
ν
cos ;
;
sin cos ;
sin sin ;
cos .
μ
νμ
νμ
ν
d
ddd
23
31
32
33
0
=
===
−
Çäåñü ν è μ ïðåäñòàâëÿþò ñîáîé òåêóùèå çíà÷åíèÿ ïàðàìåòðîâ
Ðîäðèãî–Ãàìèëüòîíà ρÐÃ, λÐÃ, νÐÃ, μÐÃ, îïðåäåëÿåìûå ñ ïîìîùüþ
ñîîòíîøåíèé
•
()
;
•
(
ρω
λ
ω
μ
ω
ν
λω
ρ
ω
ν
ω
ÐÃ
ÐÃ
ÐÃ
ÐÃ
ÐÃ
ÐÃ
ÐÃ
=−
+
+
=+
+
1
2
1
2
xyz
xyz
μ
μω
ν
ω
ρ
ω
λ
νω
μ
ω
λ
ÐÃ
ÐÃ
ÐÃ
ÐÃ
ÐÃ
ÐÃ
ÐÃ
);
•
()
;
•
(
=+
−
=−
+
1
2
1
2
xyz
xy
ÐÃ
ÐÃ
+ωρ
z
).
Ïðè ýòîì
θρ
ν
λ
μ
ψ
ρμ λν
ρ
=+
=
−
arcsin (
);
()
2
2
ÐÃ ÐÃ
ÐÃ ÐÃ
ÐÃ ÐÃ
ÐÃ ÐÃ
Ð
arctg
Ã
2
ÐÃ
2
ÐÃ
2
ÐÃ
2
ÐÃ ÐÃ
ÐÃ ÐÃ
ÐÃ
2
ÐÃ
2
arctg
2(
+−−
=
−
+
λμν
γ
ρλ νμ
ρμ
;
)
−−
νλ
ÐÃ
2
ÐÃ
2.
Èñïîëüçîâàíèå ìåòîäà îòûñêàíèÿ óãëîâûõ êîîðäèíàò âðàùàþ-
ùåãîñÿ êîððåêòèðóåìîãî ñíàðÿäà ñ ïîìîùüþ ñîîòíîøåíèé Ðîäðè-
ãî–Ãàìèëüòîíà îáóñëîâëèâàåòñÿ íåîáõîäèìîñòüþ óñòðàíåíèÿ îñî-
áûõ òî÷åê ïî óãëó êðåíà, êîòîðûé ìåíÿåòñÿ â ïðîöåññå ïîëåòà â øè-
ðîêèõ ïðåäåëàõ.
 èçìåðèòåëüíîé ñèñòåìå êîîðäèíàò "ñòðîÿòñÿ" äâà ïëîñêèõ êî-
îðäèíàòíûõ óãëà, çàäàþùèå ïîëîæåíèå òî÷å÷íîé öåëè â ýòîé ñèñòå-
ìå:
ζ – óãîë ïåëåíãà öåëè, ò.å . óãîë îòêëîíåíèÿ öåëè îò ïðîäîëüíîé
îñè ÁÊÖ â ìãíîâåííîé ïëîñêîñòè îøèáêè;
χ – óãîë ïîâîðîòà (êðåíà) ýòîé ïëîñêîñòè îòíîñèòåëüíî íà÷àëà
îòñ÷åòà óãëîâ "êðåíà" èçîáðàæåíèÿ öåëè â ïëîñêîñòè OèYèZè.
Êîíñòðóêòèâíî íà÷àëî îòñ÷åòà óãëîâ χ æåñòêî ñâÿçàíî ñ íà÷àëîì
îòñ÷åòà ïî óãëó êðåíà ïîëîæåíèÿ êîððåêòèðóþùèõ äâèãàòåëåé â ýê-
âàòîðèàëüíîì ñå÷åíèè ñíàðÿäà. Ýòî ïîçâîëÿåò îäíîçíà÷íî âêëþ÷àòü
485
ñîîòâåòñòâóþùèé êîððåêòèðóþùèé äâèãàòåëü ïðè ñîâïàäåíèè åãî
óãëà êðåíà ñ óãëîì χi.
Äëÿ óäîáñòâà çàäàíèÿ â ìàòåìàòè÷åñêîé ìîäåëè íàïðàâëåíèÿ íà
öåëü èñïîëüçóþòñÿ äâà âåêòîðà bè è bg, íîìèíàëüíî ñîâïàäàþùèå
äðóã ñ äðóãîì.
Ââåäåì åùå îäèí ðàäèóñ-âåêòîð, êîòîðûé ñîåäèíÿåò íà÷àëî íîð-
ìàëüíîé çåìíîé ñèñòåìû êîîðäèíàò ñ íà÷àëîì èçìåðèòåëüíîé ñèñ-
òåìû êîîðäèíàò. Ýòîò âåêòîð ìîæåò áûòü ïðåäñòàâëåí ñóììîé äâóõ
âåêòîðîâ:
SRAL
gg
=+
⋅
,
(11.1)
èëè â ìàòðè÷íîé ôîðìå
SA
g
g
g
g
g
x
y
z
l
=+
⋅
0
0
,
ãäå L – ðàäèóñ-âåêòîð, ñâÿçûâàþùèé öåíòð ìàññ ñíàðÿäà ñ íà÷àëîì
èçìåðèòåëüíîé ñèñòåìû êîîðäèíàò è ïîçâîëÿþùèé ó÷èòûâàòü
ñìåùåíèå ôîêàëüíîé ïëîñêîñòè ÁÊÖ îòíîñèòåëüíî åãî öåíòðà ìàññ.
Ïîëîæåíèå öåëè ìîæåò áûòü îïðåäåëåíî ðàäèóñ-âåêòîðîì, ñâÿ-
çûâàþùèì òî÷êó, îïðåäåëÿþùóþ â ìàòåìàòè÷åñêîé ìîäåëè öåíòð
öåëè, ñ íà÷àëîì êîîðäèíàò íîðìàëüíîé çåìíîé ñèñòåìû êîîðäèíàò
Rgö.
Ñ ó÷åòîì ïðèíÿòûõ îáîçíà÷åíèé ðàäèóñ-âåêòîð, ñîåäèíÿþùèé
íà÷àëî èçìåðèòåëüíîé ñèñòåìû êîîðäèíàò ñ öåëüþ, ìîæåò áûòü çà-
ïèñàí êàê
bRS
ggg
=−
ö
.
(11.2)
Ïðîåêöèè ýòîãî âåêòîðà íà îñè íîðìàëüíîé çåìíîé ñèñòåìû êî-
îðäèíàò çàäàþòñÿ â âèäå
bXs
bYs
bZs
gx
g
xg
gy
g
yg
gz
g
zg
=−
=−
=−
ö
ö
ö
;
;
.
Âåêòîð bè â ñâîþ î÷åðåäü ìîæåò áûòü ïðåäñòàâëåí êàê âåêòîðíîå
ïðîèçâåäåíèå:
bDAb
è
ò
=⋅⋅
g.
(11.3)
486
Èñïîëüçóÿ ïðèâåäåííûå âûøå ñîîòíîøåíèÿ, íåòðóäíî îïðåäå-
ëèòü óãîë ïåëåíãà öåëè:
ζ=
+
arcsin
||.
bb
yz
èè
è
22
b
(11.4)
Çäåñü
||
.
bèèèè
=+
+
bbb
xyz
222
Ñîîòâåòñòâåííî îïðåäåëÿåòñÿ è óãîë χ:
χ=arctg è
è
b
b
z
y
.
(11.5)
Âòîðîé áëîê, ôîðìèðóþùèé ìîìåíò âêëþ÷åíèÿ è íàïðàâëåíèå
äåéñòâèÿ êàæäîé êîððåêòèðóþùèé ñèëû, áàçèðóåòñÿ íà èñïîëüçîâà-
íèè èñïîëíèòåëüíîé ñèñòåìû êîîðäèíàò.
Ìîìåíò âêëþ÷åíèÿ ñîîòâåòñòâóþùåãî i-ãî êîððåêòèðóþùåãî
äâèãàòåëÿ îïðåäåëÿåòñÿ óãëîì ïîâîðîòà ñíàðÿäà îòíîñèòåëüíî âû-
áðàííîãî íà÷àëà îòñ÷åòà óãëîâ êðåíà äâèãàòåëåé
∆∆
γγ
π
i
i
N
=+
−
0
1
2
()
(11.6)
ïðè ∆γi ≤πè
∆∆
γγπ
i
i
N
=+
−
−
⎛
⎝⎜
⎞
⎠⎟
02
1
1
(11.7)
ïðè ∆γi >π.
Çà íà÷àëî îòñ÷åòà óãëîâ ñìåùåíèÿ äâèãàòåëåé ïî óãëó êðåíà ïðè-
íèìàåòñÿ ïîëîæåíèå îñè OY ñâÿçàííîé ñèñòåìû êîîðäèíàò.
Ôîðìèðîâàíèå íàïðàâëåíèÿ äåéñòâèÿ ñèëû i-ãî êîððåêòèðóþùå-
ãî äâèãàòåëÿ ïðîèçâîäèòñÿ â èñïîëíèòåëüíîé ñèñòåìå êîîðäèíàò, à
çàòåì ýòà ñèëà ïðîåöèðóåòñÿ íà îñè ñâÿçàííîé ñèñòåìû êîîðäèíàò.
Äëÿ ïåðåõîäà îò èñïîëíèòåëüíîé ê ñâÿçàííîé ñèñòåìå êîîðäèíàò
èñïîëüçóåòñÿ ìàòðèöà
Si
iii
iii
iii
sss
sss
sss
=
11
12
13
21
22
23
31
32
33
,
487
ãäå s
ii
i
11=cos
cos ;
εφ
äâ
äâs
ii
i
12 =−sin
cos ;
εφ
äâ
äâs
ii
13=sin ;
φäâ s
ii
21=sin ;
εäâ
s
ii
22=cos ;
εäâ s
i
230
=
;s
ii
i
31=cos
sin ;
εφ
äâ
äâs
ii
i
32=sin
sin ;
εφ
äâ
äâs
ii
33=cos ;
φäâ
εäâ
i
–
óãîë îòêëîíåíèÿ ëèíèè ðàñïîëîæåíèÿ i-ãî êîððåêòèðóþùåãî
äâèãàòåëÿ îò ñëåäà ïëîñêîñòè îøèáêè êîððåêöèè, â êîòîðîé ëåæàò
öåëü è îñü àáñöèññ èçìåðèòåëüíîé ñèñòåìû êîîðäèíàò; φ äâ
i
–
óãîë
íàêëîíà ïëîñêîñòè ðàçìåùåíèÿ êîððåêòèðóþùèõ äâèãàòåëåé îòíî-
ñèòåëüíî ïðîäîëüíîé îñè ñíàðÿäà.
Äëÿ îïðåäåëåíèÿ óãëà ε äâ
i
èñïîëüçóåòñÿ ñëåäóþùèé ïðèíöèï îò-
ñ÷åòà. Ââîäèòñÿ ïîíÿòèå óãëîâîãî ñäâèãà (óãëîâîãî ðàññòîÿíèÿ) ìå-
æäó ñîñåäíèìè êîððåêòèðóþùèìè äâèãàòåëÿìè ∆=
°
360
Q
,ãäåQ–
÷èñëî êîððåêòèðóþùèõ äâèãàòåëåé, óñòàíîâëåííûõ â îäèí ðÿä ïî
îêðóæíîñòè êîðïóñà. Îïðåäåëÿåòñÿ ñäâèã (óãëîâîé "îòñòóï") ïîñëåä-
íåãî êîððåêòèðóþùåãî äâèãàòåëÿ (åìó ïðèñâàèâàåòñÿ íîìåð "0") îò-
íîñèòåëüíî íà÷àëà îòñ÷åòà
ε
t
=°
−
90 ∆.
Îïðåäåëÿþòñÿ óãëîâûå êîîðäèíàòû ðàñïîëîæåíèÿ âñåõ Q êîððåê-
òèðóþùèõ äâèãàòåëåé
εε
äâ
it
i
=++
().
1∆
(11.8)
×òîáû ïðàâèëüíî îðãàíèçîâàòü âûáîð òðåáóåìîãî äëÿ âêëþ÷åíèÿ
â äàííûé ìîìåíò êîððåêòèðóþùåãî äâèãàòåëÿ, â ìàòåìàòè÷åñêóþ
ìîäåëü ââîäèòñÿ óãîë χ äâ
t
i
=⋅
∆.
Ñ öåëüþ îïðåäåëåíèÿ ìîìåíòà âêëþ÷åíèÿ äàííîãî êîððåêòèðóþ-
ùåãî äâèãàòåëÿ â ìàòåìàòè÷åñêîé ìîäåëè èñïîëüçóåòñÿ ïðèíöèï
ïðèîðèòåòîâ, ñóòü êîòîðîãî ñîñòîèò â ñëåäóþùåì. Ââîäèòñÿ â ðàñ-
ñìîòðåíèå íåñêîëüêî ñîáûòèé, ÷èñëî êîòîðûõ â îáùåì ñëó÷àå íå îã-
ðàíè÷åíî. Êàæäîå èç ýòèõ ñîáûòèé ìîæåò ñîñòîÿòüñÿ, à ìîæåò è íå
ñîñòîÿòüñÿ ê òîìó ìîìåíòó âðåìåíè, êîãäà äàííûé êîððåêòèðóþ-
ùèé äâèãàòåëü îêàæåòñÿ íà ëèíèè âêëþ÷åíèÿ. Ýòè ñîáûòèÿ îáîçíà-
÷àþòñÿ δij. Êàæäîå èç ýòèõ ñîáûòèé èìååò ñâîé ïðèîðèòåò, îïðåäå-
ëÿåìûé êàê åãî ñîñòîÿíèå, ðàâíîå 1, åñëè ýòî ñîáûòèå ñîñòîÿëîñü,
èëè 0, åñëè îíî íå ñîñòîÿëîñü.
Èòîãîâîå ñîáûòèå – âêëþ÷åíèå äàííîãî êîððåêòèðóþùåãî äâè-
ãàòåëÿ – ñîñòîèòñÿ òîëüêî â òîì ñëó÷àå, åñëè åãî ïðèîðèòåò, îïðåäå-
ëÿåìûé ïðîèçâåäåíèåì δij, áóäåò ðàâåí 1. Ýòî îçíà÷àåò, ÷òî åñëè íå
âûïîëíåíî õîòÿ áû îäíî óñëîâèå âêëþ÷åíèÿ, òî îíî íå ñîñòîèòñÿ.
Ïîñëå ñáðîñà îáòåêàòåëÿ ÷åðåç óñòàíîâëåííûé èíòåðâàë âðåìåíè
âîçìîæíî âêëþ÷åíèå êàêîãî-ëèáî êîððåêòèðóþùåãî äâèãàòåëÿ. Ïî-
ýòîìó ê ýòîìó ìîìåíòó äîëæíî âûïîëíÿòüñÿ óñëîâèå
488
δδδδ
i
i
it
iQ
01
1
===== =
KK
.
 ñëó÷àå ñïðàâåäëèâîñòè ýòîãî óñëîâèÿ íà êàæäîì øàãå ÷èñëåí-
íîãî èíòåãðèðîâàíèÿ äîëæíà âåñòèñü ïðîâåðêà âûïîëíåíèÿ ñëåäóþ-
ùèõ óñëîâèé.
I. Óñëîâèå
0
0 0001
≤−≤
χχ
êîð
äâ
i
,
ïðè âðàùåíèè ñíàðÿäà âîêðóã ñâîåé ïðîäîëüíîé îñè ïî ÷àñîâîé
ñòðåëêå. Çäåñü χêîð – óãîë ìåñòîïîëîæåíèÿ èñòèííîé ëèíèè
êîððåêöèè â ôîêàëüíîé ïëîñêîñòè ÁÊÖ. Ïðè ýòîì
χχπ
χ
êîð
í
óïð
=+
+,
ãäå χóïð – ñïåöèàëüíî ââîäèìîå óãëîâîå óïðåæäåíèå ïî ôàçå èëè
ìîìåíòó âêëþ÷åíèÿ êîððåêòèðóþùåãî äâèãàòåëÿ.
Äàëåå ïðîâîäèòñÿ àíàëèç âåëè÷èíû óãëà êîððåêöèè. Åñëè χóïð >
> 360°, òî óãîë âêëþ÷åíèÿ êîððåêòèðóþùåãî äâèãàòåëÿ âû÷èñëÿåòñÿ
ïî ôîðìóëå
χχπ
χ
êîð
í
óïð
=−
+.
II. Óñëîâèå
ζζζ
min
max
.
≤≤
III. Óñëîâèå δχi = δζi = 1. Åñëè ïðè ýòîì δτi = 0, òî ìîæåò ïðîèçîé-
òè âêëþ÷åíèå êîððåêòèðóþùåãî äâèãàòåëÿ.
Îäíîâðåìåííî ôîðìèðóåòñÿ óñëîâèå δτi = 1. Îíî ñîõðàíÿåòñÿ äî
òåõ ïîð, ïîêà íå çàêîí÷èòñÿ ðàáîòà äàííîãî äâèãàòåëÿ. Ìîìåíò
îêîí÷àíèÿ ðàáîòû äâèãàòåëÿ Tend îïðåäåëÿåòñÿ èç óñëîâèÿ
Tt
end
=+
τ
,
ãäå t – òåêóùåå âðåìÿ; τ – èíòåðâàë âðåìåíè ðàáîòû êîððåê-
òèðóþùåãî äâèãàòåëÿ.
 ïðåäåëàõ èíòåðâàëà âðåìåíè ðàáîòû êîððåêòèðóþùåãî äâèãà-
òåëÿ ñîõðàíÿåòñÿ óñëîâèå δτi =1
.
Äàëåå, åñëè δτi =1èt ≥ Tend, ïðîèñõîäèò ïåðåêëþ÷åíèå δτi =1íà
δτi = 0. Â ðåçóëüòàòå ñèëà òÿãè äàííîãî êîððåêòèðóþùåãî äâèãàòåëÿ
îáíóëÿåòñÿ.
IV. Óñëîâèå
489
δδδδ
ζχτ
mi
i
i
i
=⋅⋅=
1.
 ýòîì ñëó÷àå ïðîèñõîäèò âêëþ÷åíèå êîððåêòèðóþùåãî äâèãàòå-
ëÿ. Ñèëà òÿãè êîððåêòèðóþùåãî äâèãàòåëÿ ïðè ýòîì äîëæíà îïðåäå-
ëÿòüñÿ ïî ôîðìóëå
PPS
pyee
ia
O
N
tt
jj
=+
−
−
−−
−−
+
[(
(
)
)
]
(
)
,
()( )
0
11
1
π
ττ
(11.9)
ïîñêîëüêó íåó÷åò âðåìåíè ñðàáàòûâàíèÿ çäåñü íåäîïóñòèì.
 ôîðìóëå (11.9) ïðèíÿòû ñëåäóþùèå îáîçíà÷åíèÿ:
Pm
W
e
0=|
•
|;
|•|–
m
âåëè÷èíà ñåêóíäíîãî ìàññîâîãî ðàñõîäà äâèãàòåëÿ;
We – ýôôåêòèâíàÿ ñêîðîñòü èñòå÷åíèÿ ðàáî÷åãî òåëà èç ñîïëà
êîððåêòèðóþùåãî äâèãàòåëÿ;
pON – äàâëåíèå íà ïîâåðõíîñòè Çåìëè ïðè íîðìàëüíûõ óñëîâèÿõ;
Sa – ïëîùàäü âûõîäíîãî ñå÷åíèÿ ñîïëà êîððåêòèðóþùåãî äâèãà-
òåëÿ;
π(y) – ôóíêöèÿ èçìåíåíèÿ äàâëåíèÿ ñ âûñîòîé;
τj – èíòåðâàë âðåìåíè, â ïðåäåëàõ êîòîðîãî ïðîèñõîäèò íàðàñòà-
íèå ñèëû òÿãè êîððåêòèðóþùåãî äâèãàòåëÿ äî óñòàíîâèâøåéñÿ âå-
ëè÷èíû;
τj+1 – èíòåðâàë âðåìåíè ñïàäà ñèëû òÿãè äâèãàòåëÿ äî íóëÿ.
 ðàñ÷åòíóþ çàâèñèìîñòü äëÿ îïðåäåëåíèÿ ñèëû òÿãè êîððåêòè-
ðóþùåãî äâèãàòåëÿ ââåäåí ÷ëåí, ó÷èòûâàþùèé âûñîòó òî÷êè êîð-
ðåêöèè íàä ãîðèçîíòîì, ÷òî ñâÿçàíî ñ âîçìîæíîñòüþ èñïîëüçîâàíèÿ
ñíàðÿäà íà ðàçíûõ âûñîòàõ, â òîì ÷èñëå è â ãîðàõ.
Òàê êàê èíòåðâàë âðåìåíè ðàáîòû êîððåêòèðóþùèõ äâèãàòåëåé
äîñòàòî÷íî âåëèê, à óãëîâàÿ ñêîðîñòü âðàùåíèÿ ñíàðÿäà âîêðóã ñâî-
åé ïðîäîëüíîé îñè îòíîñèòåëüíî ìàëà, òî íà èíòåðâàëå âðåìåíè ðà-
áîòû îäíîãî äâèãàòåëÿ âîçìîæíî âêëþ÷åíèå äðóãèõ äâèãàòåëåé.
Åñëè èñïîëüçóåòñÿ îäíîðÿäíàÿ ñõåìà ðàçìåùåíèÿ áîëüøîãî ÷èñëà
êîððåêòèðóþùèõ äâèãàòåëåé, â ðàñ÷åò ââîäèòñÿ ñóììàðíàÿ êîððåê-
òèðóþùàÿ ñèëà
FF
i
i
Q
Σ êîðð
êîðð
=
=
∑.
0
(11.10)
Ñèëà òÿãè êîððåêòèðóþùåãî äâèãàòåëÿ ìîæåò ñîçäàâàòü ìîìåíòû
îòíîñèòåëüíî öåíòðà ìàññ ñíàðÿäà ïî âñåì òðåì îñÿì ñâÿçàííîé
490
ñèñòåìû êîîðäèíàò. Â îáùåì âèäå ìîìåíò îò êîððåêòèðóþùåé ñèëû
i-ãî äâèãàòåëÿ ìîæíî çàïèñàòü êàê
nR
F
êîðð
êîðð
iii
=×
.
(11.11)
491
Ðèñ. 11.2 . Õàðàêòåð èçìåíåíèÿ êîððåêòèðóþùèõ ñèë è êîððåêòèðóåìûõ ïàðàìåòðîâ
äâèæåíèÿ íà âðåìåííîì èíòåðâàëå êîððåêöèè ïîëåòà àðòèëëåðèéñêîãî ñíàðÿäà:
à – ñîñòàâëÿþùèå êîððåêòèðóþùèõ ñèë íà îñè áàçîâîé ñèñòåìû êîîðäèíàò; á –
ïðîåêöèè âåêòîðà ñêîðîñòè íà îñè òîé æå ñèñòåìû êîîðäèíàò; â – çàâèñèìîñòü
θ(t); ã – çàâèñèìîñòü Ψ(t); ä – èçìåíåíèå ñêîðîñòè âðàùåíèÿ ñíàðÿäà îòíîñè-
òåëüíî ïðîäîëüíîé îñè â ôóíêöèè âðåìåíè
 êà÷åñòâå ïðèìåðà íà ðèñ. 11.2 ïðèâåäåíû ðåçóëüòàòû ðàñ÷åòîâ,
èëëþñòðèðóþùèå äèíàìèêó äâèæåíèÿ ãèïîòåòè÷åñêîãî êîððåêòè-
ðóåìîãî îïåðåííîãî àðòèëëåðèéñêîãî ñíàðÿäà êàëèáðà 110 ìì (íà-
÷àëüíàÿ ñêîðîñòü 440 ì/ñ, ìàññà áåç îáòåêàòåëÿ 19 êã, ñðåäíÿÿ äàëü-
íîñòü ñòðåëüáû 6500 ì, óãîë áðîñàíèÿ ∼70°), äàþùèå äîñòàòî÷íî
ïîëíîå ïðåäñòàâëåíèå î êà÷åñòâåííîé ñòîðîíå ðàññìàòðèâàåìîãî
ïðîöåññà.
Íà ðèñ. 11.2, à ïîêàçàíû ñîñòàâëÿþùèå ñèë, äåéñòâóþùèõ íà
ñíàðÿä âî âðåìÿ êîððåêöèè, â ïðîåêöèÿõ íà îñè çåìíîé ñèñòåìû êî-
îðäèíàò. ×åòêî ïðîñëåæèâàþòñÿ òðè êîððåêòèðóþùèõ èìïóëüñà,
492
Ðèñ. 11.2 (ïðîäîëæåíèå)
ðàñïîëîæåííûå âäîëü âåðòèêàëüíîé îñè è îñè äàëüíîñòè. Âèäíî,
÷òî ïîëîæèòåëüíîå (îïåðåæàþùåå) ñìåùåíèå ìîìåíòà âêëþ÷åíèÿ
íà ñåðåäèíó èíòåðâàëà äåéñòâèÿ êîððåêòèðóþùåé ñèëû ïðàêòè÷å-
ñêè îáíóëÿåò ýôôåêò ïàðàçèòíîãî (áîêîâîãî) ñèëîâîãî âîçäåéñòâèÿ
íà ñíàðÿä, îáóñëîâëåííîãî "ðàçìàçûâàíèåì" èìïóëüñà ïî âðåìåíè,
âûçâàííûì âðàùàòåëüíûì äâèæåíèåì ñíàðÿäà îòíîñèòåëüíî åãî
ïðîäîëüíîé îñè.
Íà ðèñ. 11.2, á äàþòñÿ ïðîåêöèè âåêòîðà ñêîðîñòè íà òå æå êîîð-
äèíàòíûå îñè. Ïðè ýòîì ïîñëåäíåå ñòóïåí÷àòîå èçìåíåíèå ïðîåê-
öèé ïðîèñõîäèò â íåïîñðåäñòâåííîé áëèçîñòè îò öåëè.
493
Ðèñ. 11.2 (îêîí÷àíèå)
Íà ðèñ. 11 .2, â ïîêàçàíà çàâèñèìîñòü óãëà θ îò âðåìåíè ïîëåòà íà
ó÷àñòêå êîððåêöèè, à íà 11.2, ã – àíàëîãè÷íàÿ çàâèñèìîñòü Ψ(t).
Çäåñü òàêæå õîðîøî ïðîñìàòðèâàåòñÿ ÷åòêèé ñòóïåí÷àòûé õàðàêòåð
èçìåíåíèÿ ïàðàìåòðîâ.
Íà ðèñ. 11.2, ä ïðèâåäåíà çàâèñèìîñòü îò âðåìåíè èçìåíåíèÿ óã-
ëîâîé ñêîðîñòè âðàùåíèÿ ñíàðÿäà âîêðóã åãî ïðîäîëüíîé îñè íà
ó÷àñòêå êîððåêöèè. Íåòðóäíî çàìåòèòü, ÷òî, íåñìîòðÿ íà êîëåáà-
òåëüíûé õàðàêòåð çíà÷åíèÿ ýòîé âåëè÷èíû â ïðîöåññå ñáðîñà îáòå-
êàòåëÿ (íà÷àëî ãðàôèêà) è â ïðîöåññå êîððåêöèè, îíà ìåíÿåòñÿ íå-
çíà÷èòåëüíî, ÷òî îáåñïå÷èâàåò íîðìàëüíûå óñëîâèÿ ïðîâåäåíèÿ
êîððåêöèè.
11.1 .3. ÓÃËÎÂÎÅ ÄÂÈÆÅÍÈÅ ÃÈÐÎÑÊÎÏÈ×ÅÑÊÈ ÓÑÒÎÉ×ÈÂÛÕ
 ÏÎËÅÒÅ ÑÍÀÐßÄΠÏÐÈ ÂÎÇÄÅÉÑÒÂÈÈ ÓÄÀÐÍÛÕ ÌÎÌÅÍÒÎÂ
Ðàññìîòðèì äâèæåíèå ãèðîñêîïè÷åñêè óñòîé÷èâîãî ñíàðÿäà ïðè âîçäåé-
ñòâèè íà íåãî êðàòêîâðåìåííûõ óäàðíûõ ìîìåíòîâ [38]. Áóäåì ñ÷èòàòü, ÷òî
âðåìÿ óäàðà ìàëî ïî ñðàâíåíèþ ñ ïðîäîëæèòåëüíîñòüþ îäíîãî îáîðîòà Tx =
=2π/ωx. Îáñóæäåíèå îãðàíè÷èì àíàëèçîì äâèæåíèÿ ñíàðÿäà íà êîðîòêîì
èíòåðâàëå âðåìåíè äåéñòâèÿ êîíå÷íîãî ÷èñëà óäàðíûõ âîçäåéñòâèé. Áóäåì
ïîëàãàòü, ÷òî âåëè÷èíà àýðîäèíàìè÷åñêèõ ìîìåíòîâ ìàëà ïî ñðàâíåíèþ ñ
óäàðíûìè ìîìåíòàìè, òàê ÷òî ïåðâûìè ìîæíî ïðåíåáðå÷ü. Òîãäà â îáùåì
ñëó÷àå èìååì
CM
t
AA
CM
t
AA
CM
xk
x
yx
z
k
y
zx
y
•
();
•
()(
)
;
•
()
ω
ωω
ω
ωω
ω
=
−−
=
+−
=
kz t(),
(11.12)
ãäå A = Iy = Iz – ýêâàòîðèàëüíûé ìîìåíò èíåðöèè ñíàðÿäà; C = Ix – îñåâîé
(àêñèàëüíûé) ìîìåíò èíåðöèè.
Ïðåäïîëîæèì [38], ÷òî ñîñòàâëÿþùàÿ ïî îñè ñèììåòðèè îòñóòñòâóåò:
Mkx(t) = 0. Èç ïåðâîãî óðàâíåíèÿ (11.12) ïîëó÷èì ωx = ωx0 = const. Ââîäÿ íî-
âóþ ïåðåìåííóþ
dd
t
x
φω
=
,
(11.13)
ìîæíî ïðåîáðàçîâàòü âòîðîå è òðåòüå óðàâíåíèÿ, èìåÿ â âèäó, ÷òî
•
(,
)
,
ω
ωω
φ
φωω
j
jj
jx
d
dt
d
d
d
dt
jyz
==
=
′
≈
(11.14)
ãäå øòðèõîì îáîçíà÷åíà ïðîèçâîäíàÿ ïî ïåðåìåííîé φ. Ñ ó÷åòîì (11.14)
âòîðîå è òðåòüå óðàâíåíèÿ (11.12) ïðèâîäÿòñÿ ê âèäó
494
′−=
′+=
ωμ
ω
ωμ
ω
yzk
y
zyk
z
m
m
;
,
(11.15)
ãäå
μ
ωω
=−
=
=
1C
A
m
M
A
m
M
A
ky
ky
x
kz
kz
x
;;.
Ââîäÿ êîìïëåêñíûå âåëè÷èíû ωy + iωz = ω; mky + imkz = mk, ïðåîáðàçóåì [38]
óðàâíåíèå (11.15) ê âèäó
′+=
ωμ
ω
im
k.
(11.16)
Ñ ó÷åòîì ïîäñòàíîâêè (11.13) êîìïëåêñíîå âîçäåéñòâèå mk = mk(t) ìîæíî
ïðåäñòàâèòü êàê ôóíêöèþ íîâîé ïåðåìåííîé φ. Îáùåå ðåøåíèå óðàâíåíèÿ
(11.16) èìååò âèä
ωωψ
ψ
μφ
μψ
φ
=+
⎛
⎝
⎜
⎞
⎠
⎟
−
∫
em
e
d
i
k
i
0
0
(),
(11.17)
ãäå ω0 = ω(0) – ïðîèçâîëüíàÿ ïîñòîÿííàÿ, èëè â âåùåñòâåííîé ôîðìå
ωωμ
φωμ
φ
μφψ
μφψ
yy
z
ky
kz
mm
d
=++
+−
+
−
00
cos
sin
[c
o
s
()s
i
n
()
]ψ
ωωμ
φωμ
φ
μφψ
μφ
φ
;
cos
sin
[c
o
s
()s
i
n
(
0
00
∫
=−+
+−
−
zz
y
kz
ky
mm
−
∫
ψψ
φ
)].
d
0
(11.18)
Ïîñëåäîâàòåëüíîñòü êðàòêîâðåìåííûõ óäàðíûõ ìîìåíòîâ ìîæíî ïðåäñòàâèòü
ñ ïîìîùüþ ôóíêöèè Äèðàêà δ(t):
Mt Mtt
kk
j
j
j
()
(),
=−
∑δ
(11.9)
ãäå tj – âðåìÿ j-ãî óäàðà; Mkj – ìåðà âåëè÷èíû j-ãî óäàðà. Ñîîòâåòñòâåííî
(11.19) îïðåäåëÿåòñÿ ÷åðåç êîìïëåêñíîå âîçäåéñòâèå mk(t). Îáùåå ðåøåíèå
(11.17) ìîæåò áûòü çàïèñàíî â âèäå
ωω
ω
δττ
μω
μω
τ
=+
−
−
−−
∫
∑
00
0
0
eem
t
d
it
x
it
t
kj
y
j
xx
()
(). (11.20)
Êàæäûé îòäåëüíûé óäàð ïðèâîäèò ê ñêà÷êîîáðàçíîìó èçìåíåíèþ
ìãíîâåííîé óãëîâîé ñêîðîñòè
495
∆ωω
δτ
τ
ε
ε
jx
k
j
j
t
t
mt
d
j
j
=−
−
+
∫
0
().
(11.21)
Ââîäÿ åäèíè÷íóþ ñòóïåí÷àòóþ ôóíêöèþ
1
0
1
0
() ()
,
,
tt
td
tt
tt
jj
j
j
t
−=
−
=
<
>
⎧
⎨
⎩
∫δτ τ
ïðè
ïðè
(11.22)
îáùåå ðåøåíèå (11.20) ïðèâîäèì ê âèäó
ωω
ω
μω
μω
=+
−
−
−−
∑
00
0
0
1
em
t
t
e
it
xk
jj
it
t
j
x
xj
().
()
(11.23)
Ýòî ðåøåíèå [38] ïðåäñòàâëÿåò ñîáîé âçàèìíîå íàëîæåíèå ñîáñòâåííûõ
êîëåáàíèé îñè ñíàðÿäà, âîçáóæäàåìûõ îòäåëüíûìè óäàðíûìè ìîìåíòàìè.
11.1 .4. ÓÑÒÎÉ×ÈÂÎÑÒÜ ÓÃËÎÂÎÃÎ ÄÂÈÆÅÍÈß
ÈÌÏÓËÜÑÍÎ-ÊÎÐÐÅÊÒÈÐÓÅÌÎÃÎ ÃÈÐÎÑÊÎÏÈ×ÅÑÊÈ
ÑÒÀÁÈËÈÇÈÐÓÅÌÎÃÎ ÑÍÀÐßÄÀ*
Ïðè âûáîðå çíà÷åíèÿ ñèëîâîãî èìïóëüñà äëÿ êîððåêöèè òðàåêòîðèè ãè-
ðîñêîïè÷åñêè óñòîé÷èâîãî àðòèëëåðèéñêîãî ñíàðÿäà íåîáõîäèìî ó÷èòû-
âàòü, ïî êðàéíåé ìåðå, äâà îãðàíè÷åíèÿ [38]. Ïåðâîå îïðåäåëÿåò ïðåäåëüíûå
çíà÷åíèÿ ñèëîâûõ óäàðíûõ íàãðóçîê ñ òî÷êè çðåíèÿ ïðî÷íîñòíûõ õàðàêòå-
ðèñòèê êîíñòðóêöèè, âòîðîå ñâÿçàíî ñ îáåñïå÷åíèåì óñòîé÷èâîñòè óãëîâîãî
äâèæåíèÿ ñíàðÿäà ïîñëå ïðîâåäåíèÿ èìïóëüñíîé êîððåêöèè. Åñëè êîððåê-
òèðóþùèé èìïóëüñ ñëèøêîì âåëèê, ñíàðÿä ìîæåò ïîòåðÿòü óñòîé÷èâîñòü, à
óãëû íóòàöèè âîçðàñòè âïëîòü äî "îïðîêèäûâàíèÿ" ñíàðÿäà, ò.å . âðàùåíèÿ
âîêðóã ýêâàòîðèàëüíîé îñè. Äëÿ òîãî ÷òîáû îöåíèòü ïðåäåëüíûå çíà÷åíèÿ
êîððåêòèðóþùèõ èìïóëüñîâ, ïðè êîòîðûõ âîçìîæíî ïîÿâëåíèå òàêèõ ðåæè-
ìîâ äâèæåíèÿ âîêðóã öåíòðà ìàññ, íåîáõîäèìî çíàòü çàâèñèìîñòü àýðîäèíà-
ìè÷åñêèõ õàðàêòåðèñòèê, è ïðåæäå âñåãî îïðîêèäûâàþùåãî ìîìåíòà, îò
óãëà íóòàöèè ïðè åãî èçìåíåíèè â èíòåðâàëå −π < δ < π.
Àêòóàëüíîé ïðåäñòàâëÿåòñÿ ñëåäóþùàÿ çàäà÷à: çíàÿ çíà÷åíèÿ óãëîâûõ
êîîðäèíàò è ñêîðîñòåé äî ïðîâåäåíèÿ èìïóëüñíîé êîððåêöèè, îïðåäå-
ëèòü ïðåäåëüíîå çíà÷åíèå ñèëîâîãî êîððåêòèðóþùåãî èìïóëüñà, ïðè êî-
òîðîì óãëû íóòàöèè â ïîñëåäóþùåì ïîñëå êîððåêöèè äâèæåíèè íå
ïðåâûñÿò çàäàííîãî ïðåäåëüíî äîïóñòèìîãî çíà÷åíèÿ δämax (δ < δämax ïðè
t > tk, ãäå tk – ìîìåíò ïðîâåäåíèÿ êîððåêöèè).
Çàìåòèì, ÷òî èñïîëüçîâàíèå ïðè ðåøåíèè ýòîé çàäà÷è ìàòåìàòè÷åñêèõ
ìîäåëåé, ïîëó÷åííûõ â ïðåäïîëîæåíèè ìàëîñòè óãëîâ íóòàöèè, â îáùåì
ñëó÷àå íåîáîñíîâàííî. Äîïóñòèìîñòü ïðèìåíåíèÿ òàêèõ ìîäåëåé äîëæíà
496
*
Ïðè ïîäãîòîâêå ìàòåðèàëà èñïîëüçîâàëèñü ðåçóëüòàòû, ïîëó÷åííûå
ê.ò .í ., ñíñ Ñ.Ñ . Áîãîäèñòîâûì ïðè íàïèñàíèè 3-ãî èçäàíèÿ ó÷åáíèêà.
áûòü îáåñïå÷åíà òåõíè÷åñêîé ïîñòàíîâêîé çàäà÷è. Ðàññìîòðèì âîçìîæíûé
ïîäõîä ê åå ðåøåíèþ áåç ïîäîáíûõ îãðàíè÷åíèé.
Ïðåäïîëîæèì, ÷òî âðåìÿ ñèëîâîãî âîçäåéñòâèÿ íà ñíàðÿä ìàëî ïî ñðàâ-
íåíèþ ñ ïåðèîäîì åãî îáîðîòà âîêðóã ïðîäîëüíîé îñè Tx =2π/ωx. Òîãäà
ìîæíî ñ÷èòàòü, ÷òî â ìîìåíò ïðîâåäåíèÿ èìïóëüñíîé êîððåêöèè ìãíîâåííî
èçìåíÿþòñÿ óãëîâûå êîîðäèíàòû è óãëîâûå ñêîðîñòè ñíàðÿäà, ò.å. ïðè
t=tk−0
δδδδν νν ν
=====
kkkk
k
rr
,
••
,,
••
,
(11.24)
–
èçâåñòíûå çíà÷åíèÿ ôàçîâûõ êîîðäèíàò äî ïðîâåäåíèÿ êîððåêöèè; ïðè
t=tk+0
δδδδν νν ν
=== ==
00000
,
••
,,
••
,rr
(11.25)
–
çíà÷åíèÿ ôàçîâûõ êîîðäèíàò ïîñëå ïðèëîæåíèÿ êîððåêòèðóþùåãî
èìïóëüñà. Èçìåíåíèå óãëîâûõ êîîðäèíàò è èõ ïðîèçâîäíûõ (∆δ = δ0 −δk,
∆•• •
,
δδδ
=−
0
k ∆ν=ν0
−ν
k,∆
•••
,
ννν
=−
0
k ∆r = r0 − rk) çàâèñèò êàê îò âåëè÷èíû
êîððåêòèðóþùåãî èìïóëüñà, òàê è îò òî÷êè åãî ïðèëîæåíèÿ íà ñíàðÿäå. Äëÿ
êàæäîé êîíêðåòíîé ñõåìû ðåàëèçàöèè ñèëîâîãî êîððåêòèðóþùåãî èìïóëüñà,
çíàÿ åãî îðèåíòàöèþ â ñâÿçàííîé ñî ñíàðÿäîì ñèñòåìå êîîðäèíàò, ìîæíî
îïðåäåëèòü èçìåíåíèå ôàçîâûõ êîîðäèíàò.
Åñëè êîððåêòèðóþùèé èìïóëüñ ïðèêëàäûâàåòñÿ òî÷íî ïî ëèíèè, ïðîõî-
äÿùåé ÷åðåç öåíòð ìàññ ñíàðÿäà, òî èçìåíÿþòñÿ òîëüêî óãëîâûå êîîðäèíàòû
(δ, ν), òàê êàê ïðè ïðèíÿòîì âûøå äîïóùåíèè ìãíîâåííî èçìåíÿåòñÿ âåëè-
÷èíà âåêòîðà ñêîðîñòè VV I
0
1
=+
kk
m
, ãäå Vk – âåêòîð ñêîðîñòè ñíàðÿäà äî
ïðèëîæåíèÿ ñèëîâîãî âîçäåéñòâèÿ (t = tk − 0) è ïîñëå êîððåêöèè (t = tk + 0).
 îáùåì ñëó÷àå, êîãäà ñèëîâîé èìïóëüñ ïðèëîæåí íå ïî öåíòðó ìàññ, íà
ñíàðÿä áóäåò äåéñòâîâàòü åùå è óäàðíûé ìîìåíò, èçìåíÿþùèé âåëè÷èíó è
íàïðàâëåíèå âåêòîðà óãëîâîé ñêîðîñòè. Ïðè ýòîì êðîìå óãëîâ δ è ν èçìåíÿ-
þòñÿ è èõ ïðîèçâîäíûå
•
,
•
,
δν à òàêæå r.
 ñëó÷àå, êîãäà êîððåêòèðóþùåå âîçäåéñòâèå ðåàëèçóåòñÿ ïàðîé ïðîòè-
âîïîëîæíî íàïðàâëåííûõ ñèëîâûõ èìïóëüñîâ, òî÷êè ïðèëîæåíèÿ êîòîðûõ
ñèììåòðè÷íû îòíîñèòåëüíî öåíòðà ìàññ, íà ñíàðÿä áóäåò äåéñòâîâàòü óäàð-
íûé ìîìåíò, ÷òî ïðèâåäåò ê èçìåíåíèþ òîëüêî ñîñòàâëÿþùèõ óãëîâîé ñêî-
ðîñòè
•
,
•
,
δνr. Åñëè ëèíèÿ äåéñòâèÿ ñèëîâîãî èìïóëüñà ïåðåñåêàåò ïðîäîëüíóþ
îñü ñíàðÿäà, òî çíà÷åíèå r â ðåçóëüòàòå êîððåêöèè íå èçìåíèòñÿ. Òàêèì îá-
ðàçîì, çíàÿ âåëè÷èíó è íàïðàâëåíèå Ik â ñâÿçàííîé ñèñòåìå êîîðäèíàò,
ìîæíî îïðåäåëèòü íà÷àëüíûå óãëîâûå âîçìóùåíèÿ (δ0,
•
,
δ0 ν0,
•
,
ν0 r0) ñíàðÿäà
äëÿ ïîñëåäóþùåãî äâèæåíèÿ ïîñëå êîððåêöèè. Òîãäà äëÿ îöåíêè ïðåäåëü-
íûõ çíà÷åíèé óãëîâ íóòàöèè ìîæíî èñïîëüçîâàòü ìåòîä Í.à . ×åòàåâà. Áóäåì
ñ÷èòàòü, ÷òî òðàåêòîðèÿ ñíàðÿäà ïîñëå ïðîâåäåíèÿ èìïóëüñíîé êîððåêöèè
áëèçêà ê ïðÿìîëèíåéíîé, ñêîðîñòü öåíòðà ìàññ ÿâëÿåòñÿ èçâåñòíîé ôóíê-
öèåé âðåìåíè, à âðàùàòåëüíîå äâèæåíèå ïðîèñõîäèò ïîä äåéñòâèåì îïðîêè-
äûâàþùåãî ìîìåíòà è ìîìåíòà ïîâåðõíîñòíîãî òðåíèÿ. Óðàâíåíèÿ âðàùà-
òåëüíîãî äâèæåíèÿ ñíàðÿäà äëÿ ýòîãî ñëó÷àÿ ìîãóò áûòü ïîëó÷åíû èç ñèñòå-
497
ìû óðàâíåíèé ïðîñòðàíñòâåííîãî äâèæåíèÿ àðòèëëåðèéñêîãî ñíàðÿäà â
ôîðìå Â.Ñ . Ïóãà÷åâà, çàïèñûâàåìîé â âèäå (3.157).
Ïîëîæèì â óêàçàííîé ñèñòåìå
ffff
235700
====
==
;••
•
.
θθ
(11.26)
Òîãäà óðàâíåíèÿ âðàùàòåëüíîãî äâèæåíèÿ ñíàðÿäà ïðèìóò âèä
z
zz
za
zf
zzzz
zzz
31 31
2
431
2
2
2
3
2
12
21
•
••
••
;;
•
••
•
−+=
−
++=
−
12
3
42
6
2
za
zf
zaf
a
+==
−
•
;•
,
(11.27)
ãäå ÷åðåç à îáîçíà÷åíî îòíîøåíèå a Cr
A
=
2
.
 ñèñòåìå (11.27) f4 = f4(t). Èñïîëüçóÿ ñòàíäàðòíûå ïðåîáðàçîâàíèÿ, ïðè-
ìåíÿåìûå â ïåðâîì ìåòîäå Ëÿïóíîâà, ìîæíî ïîêàçàòü, ÷òî âûðàæåíèÿ äâóõ
ïåðâûõ èíòåãðàëîâ óðàâíåíèé äâèæåíèÿ
−+
+=
−+
++=
zzzzazh
zzz f
zh
z
32 23
11
1
2
2
2
3
2
412
2
1
2
••
;
(•••);
1
2
2
2
3
2
03
1
++= ==
zz aah
;
(11.28)
â äàííîì ñëó÷àå ìîãóò áûòü ïðåäñòàâëåíû â âèäå
zzzzhaz
fazdt
zzz h
t
23 32
1
1
61
0
1
2
2
2
3
2
2
22
2
••
;
•••
−=
−−
++=
∫
−+
∫
22
41
4
0
1
fz
df
dt
zdt
t
,
(11.29)
ãäå ìîìåíò ïðîâåäåíèÿ êîððåêöèè ïðèíÿò â êà÷åñòâå íà÷àëüíîãî íóëåâîãî
ìîìåíòà âðåìåíè. Èñêëþ÷àÿ íà îñíîâå ïîäõîäà, ïðèìåíÿåìîãî â ìåòîäå
Í.Ã. ×åòàåâà, â âûðàæåíèÿõ (11.29) ïåðåìåííûå z2, z3, • ,
•
,
zz
23ìîæíî ïîëó÷èòü
âûðàæåíèå äëÿ ïåðåìåííîé z1 = cos δ:
•
()
zhf
z
df
dt
zdt
z
t
1
2
24
1
4
1
0
1
2
222
1
=−+
⎛
⎝⎜
⎞
⎠⎟ −−
∫
−−
−
⎛
⎝⎜
⎞
⎠⎟=
∫
haz
fazdt
fz
t
216 1
0
2
1
22
(
)
.
(11.30)
Áóäåì ñ÷èòàòü, ÷òî äî âîçäåéñòâèÿ ñèëîâîãî èìïóëüñà êîððåêöèè ñíàðÿä èìåë
íàèìåíüøèé óãîë íóòàöèè (â èäåàëüíîì ñëó÷àå z1 = cosδ = 1). Òîãäà ñ ó÷åòîì
498
òîãî, ÷òî ñíàðÿä äâèæåòñÿ ñ óìåíüøàþùåéñÿ ñêîðîñòüþ â ïîñòóïàòåëüíîì
äâèæåíèè
df
dt
4
0
<
⎛
⎝⎜⎞
⎠⎟ , ìîæíî óòâåðæäàòü, ÷òî
222
22
2
24
1
4
12
4
1
14
4
0
0
hf
z
df
dt
zdthfzzff
h
t
−+
<−+
−
∫
min ()
;
116 11
0
222
1
−−
>−
∫
az
fazdt a
z
t
()
.
(11.31)
Ñëåäîâàòåëüíî,
fzzhfzzff
z
a
() ()(
())()
min
112
4
1
1
2
44
0
1
2
22
2
1
4
<=
−+
−
−
−
−
φ
2
1
2
1()
.
−
z
(11.32)
 ñîîòâåòñòâèè ñ âûðàæåíèåì •
()
zf
z
1
2
1
=
(ñì. (10.30)) ðåàëüíûì âðàùàòåëüíûì
äâèæåíèÿì ñíàðÿäà áóäåò îòâå÷àòü òîò îòðåçîê èíòåðâàëà èçìåíåíèÿ
ïåðåìåííîé z1(z1 ∈ [−1; 1]), íà êîòîðîì ôóíêöèÿ f(z1) ïîëîæèòåëüíà. Òîãäà
0
11
<<
fzz
() ().
φ
(11.33)
Çíà÷èò, äëÿ ëþáîãî ìîìåíòà âðåìåíè t â ïîñëåäóþùåì ïîñëå ïðîâåäåíèÿ
êîððåêöèè äâèæåíèè äåéñòâèòåëüíûå çíà÷åíèÿ z1 äîëæíû íàõîäèòüñÿ íà
îòðåçêå èíòåðâàëà [−1; 1], ãäå ïîëèíîì φ(z1) ïîëîæèòåëåí. Ïîäñòàâëÿÿ z1 = ±1
â (11.32), ìîæíî ïîêàçàòü, ÷òî φ(−1)<0,φ(+1)=0èφ(z1) > 0 ïðè |z1|>1.Äëÿ
ôèêñèðîâàííîãî çíà÷åíèÿ t ïîëèíîì φ(z1) èìååò îäèí êîðåíü z11 âíóòðè
èíòåðâàëà [−1; 1] (ðèñ. 11 .3). Íà èçìåíÿþùåìñÿ ñ òå÷åíèåì âðåìåíè
èíòåðâàëå [z11;1](z11 = z11(t)) ìîæåò íàõîäèòüñÿ îòâå÷àþùåå ðåàëüíîìó
äâèæåíèþ ñíàðÿäà çíà÷åíèå ïåðåìåííîé z1:
zz
11
11
<<.
(11.34)
Ñëåäîâàòåëüíî, óãîë íóòàöèè δ áóäåò èìåòü òåì ìåíüøåå îòêëîíåíèå îò 0, ÷åì
áëèæå ê +1 áóäåò ëåæàòü êîðåíü z11 = cosδmax â òå÷åíèå âñåãî îãðàíè÷åííîãî
âðåìåíè ïîëåòà ñíàðÿäà ïîñëå êîððåêöèè. Îòñþäà ìîæíî óñòàíîâèòü
óñëîâèÿ, ïðè êîòîðûõ âñå êîðíè ïîëèíîìà φ(z1) (ñì. ðèñ. 11 .3) äëÿ âñåãî
âðåìåíè ïîëåòà áóäóò áîëüøå, ÷åì (1 −∆), ãäå ∆ – ìàëàÿ, ïîëîæèòåëüíàÿ
âåëè÷èíà, îïðåäåëÿþùàÿ ìàêñèìàëüíî
äîïóñòèìûå çíà÷åíèÿ óãëîâ íóòàöèè:
zz
11
1
min
max
min
;
arccos
.
=−
=
∆δä
(11.35)
Óñëîâèå δ < δämax ðàâíîñèëüíî óñëîâèþ
cosδ = z1 > z1min =1−∆, êîòîðîå áóäåò
âûïîëíÿòüñÿ, åñëè 1 −∆ −z1 < 0 èëè
åñëè
îòðèöàòåëüíû
âñå
êîðíè
ïîëèíîìà
499
Ðèñ. 11 .3. Ãðàôèê ïîëèíîìà φ(z1)
F
x
xf
xa
xa
xa
()(
)
,
=−
−
−
=
+
++
φ12
4
3
1
2
23
∆
(11.36)
ãäå
aaf hf ff
ah
f
1
2
42
4
0
2
40
4
22
4
0
42
2
42
=−
+−+ +
=−
−
+
()()( )
;
()
∆
∆[(
(
))
()
]()
;
(
42
22
2
4
2
44
0
24
0
2
44
0
3
aff
hf
ff
ah
−++
+−+ +
=−
∆
∆24
0
22
40
2
40
40
3
422
−+
−+
−
+
fa
fh
ff
)[
()()
].
∆∆
(11.37)
Óñëîâèå îòðèöàòåëüíîñòè êîðíåé ïîëèíîìà F(x) íàõîäèòñÿ, ñîãëàñíî òåîðåìå
Ãóðâèöà, â âèäå íåðàâåíñòâ
àa
af
aa
11
2
4
33
0200
>−>>
;;
,
èëè ïîñëå ïîäñòàíîâêè çíà÷åíèé ai (i = 1, 2, 3) – â âèäå íåðàâåíñòâ
422
4
0
44
2
4
2
40
40
4
24
0
2
()()( );
()
[
(
afhfff
hf af
−+
−
++>
−−
−
∆
42
4
0
2
42
4
0
2
40
2
24
2
4
)()
]
[((
)(
))( (
)
+−+
+−
+
−
−
+
+
hf
afhfaf
∆
24
4
2
3
244
0
24
0
22
24
0
40
4
()( )
][()
()
hf fhf
ahf
ff
−−
−
+ +−−
−+
∆
](
)(
);
()[
()
880
44
40
4
3
44
0
2
24
0
22
40
ff ff
hf
af
−+
+>
−−
+−
∆
∆∆+
−
+
>
22
0
24
0
4
0
3
()
].
hf f∆
(11.38)
Ðàññìîòðèì äâà ÷àñòíûõ ñëó÷àÿ.
Ïóñòü íà ñíàðÿä â ìîìåíò êîððåêöèè äåéñòâóåò òîëüêî óäàðíûé ìîìåíò
òàê,÷òîïðèt=tk+0áóäåìèìåòüδ0=ν0
=0;••
.
δδ
=
0 Òîãäà, ïåðåõîäÿ â (10.29)
îò ïåðåìåííûõ z11, zi (i = 1, 2, 3) ê óãëîâûì êîîðäèíàòàì δ è ν, ïîëó÷èì âû-
ðàæåíèå äëÿ h2:
22
2
2
22
4
4
0
hf
df
dt
dt
t
=+
+
−
∫
•
•
sin
cos
cos ,
δνδ
δ
δ
(11.39)
èç êîòîðîãî äëÿ íà÷àëüíîãî ìîìåíòà âðåìåíè (tk = 0) ñëåäóåò
22
240
hf
−=
•
.
δ
(11.40)
Äëÿ ðàññìàòðèâàåìûõ íà÷àëüíûõ óñëîâèé äâèæåíèÿ ïîñëå êîððåêöèè ñ
ó÷åòîì (11.40) íåðàâåíñòâà (11.37) ïðèìóò âèä
42
0
24
2
40
22
40
4
0
22
40
2
()
•
()
;
•
[( )•]
af
ff
af
−+
++>
−−
+
+
δ
δδ
∆
∆[(( )
•
)((
)•)
•
]
24
422
2
2
4
0
22
40
4
0
2
400
2
af
aff
f
−+
+−
+
+
−
δδ
δ
+
+−
+++
+
++>
∆
∆
22
40
4
0
2
40
4
3
44
0
2
43
8
80
[()
•
](
)
();
aff
ff
ff
δ
−+
−
++>
24
20
0
222
40
0
2
40
3
•
[(
)•].
δδ
∆∆
af
f
(11.41)
500
Ïåðâîå èç íåðàâåíñòâ (11.41) áóäåò óäîâëåòâîðÿòüñÿ íåçàâèñèìî îò ∆, åñëè
40
2
40
2
()
•
.
af
−+>
δ
(11.42)
Ñîãëàñíî (11.42) èç íåðàâåíñòâà (11.41) ñëåäóåò, ÷òî ìàëûå óãëû íóòàöèè
âîçìîæíû â ñëó÷àå
40
2
40
0
2
()
•
.
af
−+>
δ
(11.43)
Òîãäà òðåòüå íåðàâåíñòâî áóäåò âûïîëíÿòüñÿ, åñëè
−+
−
+>
244 0
0
22
40
0
2
•
(
•
).
δδ
∆af
Ñ ó÷åòîì òîãî, ÷òî 2f40∆3 > 0, ãðàíè÷íîå çíà÷åíèå ∆ â ïåðâîì ïðèáëèæåíèè
ìîæíî îöåíèòü ñëåäóþùèì îáðàçîì:
∆<
−+
2
4
0
2
2
40
0
2
•
()
•
.
δ
δ
af
Âòîðîå íåðàâåíñòâî (11.41) áóäåò âûïîëíåíî, åñëè
(( )•)( (
)•)
•
44
2
2
2
0
2
4
22
40
4
0
2
400
2
af
aff
f
−+
−
++− >
δδ
δ
è, êðîìå òîãî, ∆(4a2 +
•
δ0
2
−
(2f40 +2f4)) > 2 0
2
•
.
δ Êîýôôèöèåíòû ïðè ∆2 è ∆3 áóäóò
ïîëîæèòåëüíû, è ãðàíè÷íîå çíà÷åíèå ñîãëàñíî âòîðîìó èç íåðàâåíñòâ
ïðèîáðåòåò âèä
∆<
+−+
2
42
2
0
2
2
0
2
40
4
•
•
()
.
δ
δ
af
f
(11.44)
Äëÿ íåáîëüøèõ âðåìåí ïîëåòà ñíàðÿäà ïîñëå êîððåêöèè (f4 ≈ f40) ìîæíî
ïðèíÿòü, ÷òî âñå òðè íåðàâåíñòâà áóäóò óäîâëåòâîðåíû, åñëè
∆<
−+
2
4
0
2
2
40
0
2
•
()
•
.
δ
δ
af
(11.45)
Çàìåòèì, ÷òî óñëîâèå a2 − f40 > 0 ïðåäñòàâëÿåò ñîáîé óñëîâèå óñòîé÷èâîñòè
Ìàèåâñêîãî. Íåðàâåíñòâî (11.45), ïîëó÷åííîå Ñ.Ñ. Áîãîäèñòîâûì, ñ
ïîìîùüþ çíà÷åíèÿ
•
,
δ0 îïðåäåëÿåìîãî âåëè÷èíîé ñèëîâîãî êîððåêòèðóþùåãî
èìïóëüñà, ïîçâîëÿåò îöåíèòü ñîãëàñíî (11.35) ìàêñèìàëüíûå çíà÷åíèÿ óãëîâ
íóòàöèè, è íàîáîðîò.
Ðàññìîòðèì âòîðîé ÷àñòíûé ñëó÷àé, êîãäà íà ñíàðÿä äåéñòâóåò ñèëîâîé
êîððåêòèðóþùèé èìïóëüñ, ïðèëîæåííûé òàê, ÷òî ïðè t = tk + 0 áóäåì èìåòü
•
;
ν=0
•
;
δ=0 δ = δ0. Òîãäà â íà÷àëüíûé ìîìåíò âðåìåíè ñîãëàñíî (11.39) èìå-
åì 2h2 =2f40cosδ0.
501
Îáîçíà÷èâ ∆0 =1− cosδ0; s = a2 − f4; s0 = a2 − f40, ñèñòåìó íåðàâåíñòâ
(11.37) ìîæíî ïðèâåñòè ê âèäó
42220
42
8
2
400
40
4
400
2
400
sf
ff
fsf
s
f
−+ +>
−+
−
∆∆
∆∆
∆
()
;
()
[
(
400
0
400
40
4
40
2
0
2
40
4
2
48
4
∆
∆∆
∆
)(
)](
)[
s
ffff f
fs
−
−+
+−++
+−
28
0
44
2
400
40
4
3
44
0
2
400
40
fff f
f
fs
f
∆∆
∆∆∆
−−+
+>
+−
()
]( );
[(∆∆
04
0
2
20
)]
.
+>
f
(11.46)
Åñëè çàäàíî çíà÷åíèå êîððåêòèðóþùåãî èìïóëüñà è ñîîòâåòñòâåííî çíà÷åíèå
∆0, òî ñèñòåìó (11.46) ðåøàåì îòíîñèòåëüíî ∆, íàõîäÿ ïðåäåëüíûå óãëû
íóòàöèé ïîñëå êîððåêöèè. Åñëè çàäàíû ïðåäåëüíî äîïóñòèìûå çíà÷åíèÿ
óãëîâ íóòàöèè, ò.å. ∆, òî ñèñòåìó ðåøàåì îòíîñèòåëüíî ∆0, ò.å. óñòàíàâëèâàÿ
ïðåäåëüíî äîïóñòèìûé ñèëîâîé êîððåêòèðóþùèé èìïóëüñ.  îáùåì ñëó÷àå
íà÷àëüíûõ óñëîâèé íåîáõîäèìî íåïîñðåäñòâåííî ðåøàòü ñèñòåìó (11.37).
11.2 . ÄÂÈÆÅÍÈÅ ÑÓÁÁÎÅÏÐÈÏÀÑÎÂ È ÁÎÅÂÛÕ
ÏÎÐÀÆÀÞÙÈÕ ÝËÅÌÅÍÒÎÂ ÑËÎÆÍÎÉ ÔÎÐÌÛ*
11.2.1. Ó×ÅÒ ÑÊÀ×ÊÎÎÁÐÀÇÍÎÃÎ ÈÇÌÅÍÅÍÈß ÁÀËËÈÑÒÈ×ÅÑÊÎÃÎ
ÊÎÝÔÔÈÖÈÅÍÒÀ ÑÓÁÁÎÅÏÐÈÏÀÑΠÊÀÑÑÅÒÍÛÕ ÑÍÀÐßÄÎÂ
Ïðè ðàñ÷åòå òðàåêòîðèé áîåâûõ ýëåìåíòîâ èëè ñóááîåïðèïàñîâ
êàññåòíûõ ñíàðÿäîâ, èìåþùèõ ïî ñðàâíåíèþ ñî ñíàðÿäîì-íîñèòå -
ëåì óâåëè÷åííûé áàëëèñòè÷åñêèé êîýôôèöèåíò [48, 145], ïîëó÷àþò
òðàåêòîðèþ, ñîñòîÿùóþ èç äâóõ ó÷àñòêîâ: ïåðâûé ñîîòâåòñòâóåò
äâèæåíèþ ñíàðÿäà-íîñèòåëÿ, à âòîðîé – äâèæåíèþ ñóááîåïðèïàñà
ïîñëå îòäåëåíèÿ îò íîñèòåëÿ. Ïðè ýòîì íà÷àëüíûå óñëîâèÿ äëÿ ðàñ-
÷åòà òðàåêòîðèè ñóááîåïðèïàñà îïðåäåëÿþòñÿ ïî çíà÷åíèÿì ôàçî-
âûõ êîîðäèíàò íîñèòåëÿ â ìîìåíò âñêðûòèÿ êàññåòû ñ ó÷åòîì âîçìó-
ùåíèé ïðè âûáðîñå è ñêà÷êîîáðàçíîãî èçìåíåíèÿ áàëëèñòè÷åñêîãî
êîýôôèöèåíòà. Áàëëèñòè÷åñêèé êîýôôèöèåíò ñóááîåïðèïàñà, êàê
ïðàâèëî, ñóùåñòâåííî áîëüøå áàëëèñòè÷åñêîãî êîýôôèöèåíòà ñíà-
ðÿäà-íîñèòåëÿ è ìîæåò ïðåâûøàòü ïîñëåäíèé áîëåå ÷åì íà ïîðÿäîê.
Òàêèì îáðàçîì, ïðèõîäèì ê ñõåìå ðàñ÷åòà òðàåêòîðèè ñ îäíî-
êðàòíûì èçìåíåíèåì áàëëèñòè÷åñêîãî êîýôôèöèåíòà. Àíàëîãè÷-
502
*
Ìàòåðèàë, â íàïèñàíèè êîòîðîãî ïðèíèìàë ó÷àñòèå Ñ.Ñ . Áîãîäèñòîâ,
äàåòñÿ â ðåäàêöèè 3-ãî èçäàíèÿ ó÷åáíèêà.
íàÿ ñõåìà èçìåíåíèÿ äàëüíîñòè ïîëåòà [48, 140, 143] ìîæåò èñ-
ïîëüçîâàòüñÿ ïðè ðàñ÷åòå òðàåêòîðèé ñíàðÿäîâ èëè ðàêåò, ñíàá-
æåííûõ òîðìîçíûìè óñòðîéñòâàìè, ðàáîòàþùèìè íà êîíå÷íîì
ó÷àñòêå äâèæåíèÿ (íàïðèìåð, ïàðàøþò, òîðìîçíûå ùèòêè).
Îäíîé èç çàäà÷, ðåøàåìûõ ïðè ïðîåêòèðîâàíèè êàññåòíûõ ñíà-
ðÿäîâ, ÿâëÿåòñÿ çàäà÷à âûáîðà ìîìåíòà âñêðûòèÿ êàññåòû è îïðåäå-
ëåíèÿ çàâèñèìîñòè õàðàêòåðèñòèê ðàññåèâàíèÿ áîåâûõ ýëåìåíòîâ îò
ïàðàìåòðîâ òðàåêòîðèè â òî÷êå âñêðûòèÿ è âîçìóùåíèé ïðè îòäåëå-
íèè áîåâûõ ýëåìåíòîâ íîñèòåëÿ. Ýòà çàäà÷à ðåøàåòñÿ èçâåñòíûìè
ñïîñîáàìè, èçëîæåííûìè â ãë. 8. Èñïîëüçóÿ êà÷åñòâåííûå ðåçóëüòà-
òû àíàëèçà ïîñòóïàòåëüíîãî äâèæåíèÿ öåíòðà ìàññ ñíàðÿäà, äàäèì
ãåîìåòðè÷åñêóþ èëëþñòðàöèþ çàäà÷è ðàñ÷åòà ðàññåèâàíèÿ òðàåêòî-
ðèé ñî ñêà÷êîîáðàçíûì èçìåíåíèåì áàëëèñòè÷åñêîãî êîýôôèöèåí-
òà.
Ðàññìîòðèì ïðîäîëüíîå äâèæåíèå ËÀ ïðè äåéñòâèè ñèëû òÿæå-
ñòè, ñèëû ëîáîâîãî ñîïðîòèâëåíèÿ è àýðîäèíàìè÷åñêîé ïîäúåìíîé
ñèëû.  òàêîé ïîñòàíîâêå ýòà çàäà÷à èçâåñòíà êàê çàäà÷à Æóêîâñêî-
ãî î ïîëåòå ïëàíåðà [3]. Óðàâíåíèÿ äâèæåíèÿ öåíòðà ìàññ ËÀ ïðè
óêàçàííûõ äîïóùåíèÿõ ìîæíî ïîëó÷èòü èç ñèñòåìû (3.68), ïîëàãàÿ
Px=Py=Xp=Yp=0:
13
24
2
)•
sin ;
)•
sin ;
)•
cos ;
)•
Vc
Vg
yV
cV
g
V
xV
x
y
=−
−
=
=−
=
θθ
θθcos,
θ
(11.47)
ãäå c
S
m
c
xx
=
ρ
2
;c
S
m
c
yy
=
ρ
2
.
Ðàññìîòðèì ïåðâûå äâà óðàâíåíèÿ ñèñòåìû (11.47). Ïîëàãàÿ
cx
= const, ρ(y) ≈ρ(yñð) = const, ìîæíî ñ÷èòàòü èõ íåçàâèñèìûìè îò
îñòàëüíûõ óðàâíåíèé:
•
sin ;
•
cos .
Vc
Vg
c
V
g
V
xy
=−
−
=
−
2
θθ
θ
(11.48)
Îñîáûå òî÷êè ñèñòåìû (11.48) íàéäåì, ðåøàÿ îòíîñèòåëüíî V è θ
óðàâíåíèÿ
cVg
cV
g
V
xy
2
00
+=−=
sin
;
cos
.
θθ
503
 ðåçóëüòàòå ïîëó÷èì, ÷òî ñèñòåìà (11.48) èìååò òðè îñîáûå òî÷êè ñ
êîîðäèíàòàìè (;)
,
**
Vii
θ i =1,2,3:
VVV
g
cc
xy
*
*
*
*
*
;
;
;
;
1
1
2
2
3
2
22
0
2
0
2
=
=
⎧
⎨⎪
⎩⎪
=
=−
⎧
⎨⎪
⎩⎪
=
+
θ
π
θ
π
4
3
θ*
(/)
.
=−
⎧
⎨⎪
⎩
⎪ arcctg cc
yx
(11.49)
Òèï îñîáîé òî÷êè è ñîîòâåòñòâåííî õàðàêòåð ïîâåäåíèÿ ôàçîâûõ
êðèâûõ â åå îêðåñòíîñòè îïðåäåëèì, ëèíåàðèçóÿ (11.49) â
îêðåñòíîñòè êàæäîé èç íèõ è íàõîäÿ êîðíè õàðàêòåðèñòè÷åñêîãî
óðàâíåíèÿ ëèíåàðèçîâàííîé ñèñòåìû
dV
dt
aa
V
d
dt
aa
V
VV
V
V
δ
δθ
δ
δθ
δθ
δ
θ
θθ
θ
=+
=+
;
,
(11.50)
ãäå
ag ac
V
a
g
V
a
g
V
VV
V
x
V
θθ
θ
θ
θθ
θ
=−
=−
=
=
cos ;
;
sin ;
cos
;
**
*
*
*
*
2
2
δδ
θ
θ
θ
VVV
=−
=
−
**
;.
Õàðàêòåðèñòè÷åñêîå óðàâíåíèå ñèñòåìû (11.50) áóäåò èìåòü âèä
aaa a
VV
V
V
θθ
θ
θ
λλ
+−− =
().
2
0
(11.51)
 çàâèñèìîñòè îò çíàêà âåëè÷èíû
()
()
*
aaa
aV
cc
VV
VV
x
y
−+
=−
θθ
θ
θ
22
2
2
44
¤0
(11.52)
áóäåì ïîëó÷àòü ðàçëè÷íûå êîðíè óðàâíåíèÿ (11.51) è ñîîòâåòñòâåííî
êà÷åñòâåííî ðàçëè÷íóþ êàðòèíó ïîâåäåíèÿ èíòåãðàëüíûõ êðèâûõ â
îêðåñòíîñòè äàííîé îñîáîé òî÷êè. Ïîäñòàâëÿÿ V i* è θ* i ñîãëàñíî
(11.49) â âûðàæåíèÿ äëÿ êîýôôèöèåíòîâ aVθ, aVV, aθθ è aθV, íàéäåì
êîðíè õàðàêòåðèñòè÷åñêîãî óðàâíåíèÿ (11.51) äëÿ êàæäîé èç òðåõ
îñîáûõ òî÷åê.  ðåçóëüòàòå ìîæíî ïîêàçàòü, ÷òî ïåðâûå äâå îñîáûå
òî÷êè ÿâëÿþòñÿ ñåäëîâûìè (êîðíè âåùåñòâåííû è ïðîòèâîïîëîæíûõ
çíàêîâ). Èõ ïîëîæåíèå â ôàçîâîì ïðîñòðàíñòâå íå çàâèñèò îò
504
ïàðàìåòðîâ ñx è c y è, ñëåäîâàòåëüíî, íå èçìåíÿåòñÿ ïðè èçìåíåíèè
ýòèõ ïàðàìåòðîâ. Âèä òðåòüåé òî÷êè (; )
,
**
V33
θ åå ïîëîæåíèå â ôàçîâîì
ïðîñòðàíñòâå è õàðàêòåð ïîâåäåíèÿ ôàçîâûõ êðèâûõ â åå îêðåñòíîñòè
ñóùåñòâåííî çàâèñÿò îò çíà÷åíèé ïàðàìåòðîâ ñx è cy .
Àíàëèçèðóÿ âûðàæåíèå (11.52), âèäèì, ÷òî ïëîñêîñòü ïàðàìåòðîâ
()
cc
xy ðàçäåëÿåòñÿ íà äâå îáëàñòè ëîìàíîé, îïðåäåëÿåìîé óðàâíåíè-
åì||||
.
cc
xy
=2
Åñëè cc
xy
22
4
>
, òî êîðíè óðàâíåíèÿ (11.51) äåéñòâèòåëü-
íûå è ðàçëè÷íûå, à îñîáàÿ òî÷êà (; )
**
V33
θ ïðåäñòàâëÿåò ñîáîé óçåë;
åñëè cc
xy
22
4
=
, òî îñîáàÿ òî÷êà – âûðîæäåííûé óçåë; åñëè cc
xy
22
4
<
,òî
òðåòüÿ îñîáàÿ òî÷êà ïðåäñòàâëÿåò ñîáîé ôîêóñ.  ñëó÷àå êîãäà cx
=0,
òðåòüÿ îñîáàÿ òî÷êà ïðåäñòàâëÿåò ñîáîé öåíòð.
Íà ðèñ. 11 .4 ïîêàçàíà ñòðóêòóðà ðàçáèåíèÿ ôàçîâîãî ïðîñòðàíñò-
âà ñèñòåìû ïðè ðàçëè÷íûõ ïàðàìåòðàõ cx è c y . Èç äåâÿòè âîçìîæíûõ
ôàçîâûõ ïîðòðåòîâ âàðèàíòû 6...9 ÿâëÿþòñÿ çåðêàëüíûì îòðàæåíè-
åì âàðèàíòîâ 1...4 ñîîòâåòñòâåííî. Íà ïðàêòèêå ýòî îçíà÷àåò èçìå-
íåíèå íàïðàâëåíèÿ äåéñòâèÿ ïîäúåìíîé ñèëû (èëè çíàêà óãëà àòàêè
ËÀ). Ïðàâûå ÷àñòè ñèñòåìû (11.48) ïðåäñòàâëÿþò ñîáîé àïåðèîäè÷å-
ñêèå ôóíêöèè θ. Ýòî ãîâîðèò î òîì, ÷òî çíà÷åíèÿ (V; θ)è(V; θ +2π)
ñîîòâåòñòâóþò îäíîìó è òîìó æå ñîñòîÿíèþ äèíàìè÷åñêîé ñèñòåìû.
Ïîýòîìó â êà÷åñòâå ôàçîâîãî ïðîñòðàíñòâà òàêîé ñèñòåìû óäîáíî
505
Ðèñ. 11 .4 . Âîçìîæíûå ñòðóêòóðû ðàçáèåíèÿ ôàçîâîãî ïðîñòðàíñòâà ñèñòåìû (11.47)
ïðè èçìåíåíèè ïàðàìåòðîâ c x è ñ y
âçÿòü ïîâåðõíîñòü öèëèíäðà, íà êîòî-
ðîì âäîëü îáðàçóþùåé îòëîæåíà âå-
ëè÷èíà V, à âäîëü íàïðàâëÿþùåé –
óãîë θ.  ýòîì ñëó÷àå ôàçîâûå ïîðòðå-
òû íà ðèñ. 11.4 ïðåäñòàâëÿþò ñîáîé
ðàçâåðòêó öèëèíäðà ñ èçìåíåíèåì
óãëà θ â ïðåäåëàõ – π≤θ≤π. Òàêèå äè-
íàìè÷åñêèå ñèñòåìû íàçûâàþò ñèñòå-
ìàìè ñ öèëèíäðè÷åñêîé ôàçîâîé ïî-
âåðõíîñòüþ. Ðàçáèåíèå ôàçîâîãî öè-
ëèíäðà íà òðàåêòîðèè äëÿ ñëó÷àÿ
cy=0,
ñîîòâåòñòâóþùåãî
ïîëåòó
îáû÷íîãî àðòèëëåðèéñêîãî ñíàðÿäà,
ïîêàçàíî íà ðèñ. 11.5.
Åñëè ââåñòè â ðàññìîòðåíèå òðåòüå
è ÷åòâåðòîå óðàâíåíèÿ ñèñòåìû
(11.47), òî ìîæíî èçîáðàçèòü â òðåõ-
ìåðíûõ ôàçîâûõ ïðîñòðàíñòâàõ (V; θ;
y)è(V; θ; x) ôàçîâûå òðàåêòîðèè ïðè
ôèêñèðîâàííîé íà÷àëüíîé ñêîðîñòè
V = V0 è êîîðäèíàòàõ x0 = y0 =0.Äëÿ
ðàçëè÷íûõ óãëîâ áðîñàíèÿ 0
2
0
≤≤
θ
π
íà ðèñ. 11.6 ïîêàçàíû ïîëó÷àþùèåñÿ
ïðè ýòîì ïîâåðõíîñòè â òðåõìåðíûõ
ôàçîâûõ ïðîñòðàíñòâàõ.
Ôàçîâàÿ òðàåêòîðèÿ, êîòîðàÿ çàêàí÷èâàåòñÿ â âåðøèíå "õîëìà"
(ðèñ. 11.6, á), ñîîòâåòñòâóåò òðàåêòîðèè ñ ìàêñèìàëüíîé äàëüíîñòüþ
ïîëåòà Xmax, à åå íà÷àëüíàÿ òî÷êà îïðåäåëÿåò óãîë áðîñàíèÿ êàê óãîë
ìàêñèìàëüíîé äàëüíîñòè ñòðåëüáû ïðè äàííîé íà÷àëüíîé ñêîðîñòè
V = V0. Äâèæåíèå öåíòðà ìàññ ñíàðÿäà-íîñèòåëÿ è ñóááîåïðèïàñà
îïðåäåëÿåòñÿ ñèñòåìîé óðàâíåíèé (11.47). Îáùèé ôàçîâûé ïîðòðåò,
èçîáðàæàþùèé äâèæåíèå ñóááîåïðèïàñà "â íîñèòåëå" è ïîñëå îòäå-
ëåíèÿ îò íåãî, õàðàêòåðèçóåòñÿ íàëîæåíèåì ôàçîâûõ ïîðòðåòîâ ñî-
îòâåòñòâóþùèõ ñèñòåì (ðèñ. 11.7). Çíà÷åíèå ôàçîâûõ êîîðäèíàò
ñóááîåïðèïàñà â ìîìåíò âûáðîñà åãî èç êàññåòû îïðåäåëÿåòñÿ çíà-
÷åíèåì ôàçîâûõ êîîðäèíàò íîñèòåëÿ. Áåç ïîòåðè îáùíîñòè ìîæíî
ñ÷èòàòü, íàïðèìåð, ÷òî îòäåëåíèå ïðîèñõîäèò ñ íóëåâîé îòíîñè-
òåëüíîé ñêîðîñòüþ. Òîãäà äî ìîìåíòà âñêðûòèÿ èçîáðàæàþùàÿ òî÷-
êà íàõîäèòñÿ â îáëàñòè ïðèòÿæåíèÿ óñòîé÷èâîãî óçëà (, )
,
**
V33
íí
θ îï-
ðåäåëÿåìîãî äèíàìè÷åñêèìè ïàðàìåòðàìè íîñèòåëÿ, à ïîñëå îòäåëå-
íèÿ åå äâèæåíèå îïðåäåëÿåòñÿ óñòîé÷èâîé îñîáîé òî÷êîé
(,)
.
**
V33
ñóá
ñóá
θ
Ïîëîæåíèå ýòèõ îñîáûõ òî÷åê â ñîîòâåòñòâèè ñ (11.49)
506
Ðèñ. 11.5 . Ôàçîâûé ïîðòðåò íà
öèëèíäðè÷åñêîé ôàçîâîé ïîâåðõ-
íîñòè
áóäåò îïðåäåëÿòüñÿ âûðàæåíèåì Vg
c
x
*
/,
3=
ãäå c
S
m
c
xx
=
ρ
2
, ïðè÷åì
äëÿ ñóááîåïðèïàñà è íîñèòåëÿ VV
**
,
33
ñóá
í
<
òàê êàê cc
xx
ñóá
í
>
.
Ðàññåèâàíèå òî÷åê ïàäåíèÿ áîåâûõ ýëåìåíòîâ áóäåò çàâèñåòü îò
ðàçáðîñà íà÷àëüíûõ çíà÷åíèé V0í è θ0í íîñèòåëÿ è ðàçáðîñà åãî áàë-
ëèñòè÷åñêîãî êîýôôèöèåíòà. Ìàëûå îòêëîíåíèÿ áàëëèñòè÷åñêîãî
êîýôôèöèåíòà îò íîìèíàëüíîãî çíà÷åíèÿ ñîîòâåòñòâóþò ìàëûì ïå-
ðåìåùåíèÿì îñîáîé òî÷êè (, )
**
V33
íí
θ âäîëü ïðÿìîé θ = −π/2 (ñì.
ðèñ. 11 .7). Ñóùåñòâåííûé âêëàä â ðàññåèâàíèå òðàåêòîðèè íîñèòåëÿ
äàþò ðàçáðîñû çíà÷åíèé V0 è θ0. Ïðåäïîëîæèì, ÷òî â ìîìåíò âû-
ñòðåëà êîîðäèíàòû íîñèòåëÿ x0 è y0 èçâåñòíû òî÷íî.  ïëîñêîñòè
(V −θ) (ñì. ðèñ. 11 .7) âîçüìåì â îêðåñòíîñòè òî÷êè (V0; θ0) ïëîùàäêó
Ï0, ðàçìåðû êîòîðîé õàðàêòåðèçóþò âîçìîæíûå îòêëîíåíèÿ íà÷àëü-
íûõ óñëîâèé îò ðàñ÷åòíûõ çíà÷åíèé: (; )
VV
VV
00
33
00
−+
σσ
è
(;)
.
θσθσ
θθ
033
00
− +Êàæäàÿ òî÷êà ïëîùàäêè Ï0 äâèæåòñÿ ïî ñâîåé
ôàçîâîé êðèâîé äî ìîìåíòà âðåìåíè t1, ñîîòâåòñòâóþùåãî âñêðû-
òèþ êàññåòû. Ñîâîêóïíîñòü ôàçîâûõ òðàåêòîðèé ñîîòâåòñòâóåò ôà-
çîâîìó ïîòîêó ñèñòåìû è îïðåäåëÿåò ïðåîáðàçîâàíèå Ï0 â ïîâåðõ-
íîñòü Ï1 (ñì. ðèñ. 11 .7) ïðè t = t1. Çà âðåìÿ ïîëåòà ñóááîåïðèïàñà ïîc-
507
Ðèñ. 11 .6. Ôàçîâûå òðàåêòîðèè ñèñòåìû (11.47) â òðåõìåðíîì ôàçîâîì ïðîñòðàíñò-
âå:
à – â êîîðäèíàòàõ (V, θ, y); á – â êîîðäèíàòàõ (V, θ, x)
ëå îòäåëåíèÿ ôàçîâûé ïîòîê ñèñòåìû, çàäàþùåé äâèæåíèå ñàìîãî
ñóááîåïðèïàñà, ïðåîáðàçóåò ïîâåðõíîñòü Ï1 â ïîâåðõíîñòü Ï2.
Êàê äî îòäåëåíèÿ ñóááîåïðèïàñà îò íîñèòåëÿ, òàê è ïîñëå íåãî
õàðàêòåð èçìåíåíèÿ V è θ îïðåäåëÿåòñÿ óñòîé÷èâûìè óçëàìè
(;)
**
V33
íí
θ è(;)
.
**
V33
ñóá
ñóá
θ
Ñëåäîâàòåëüíî, ôàçîâûé ïîòîê âñåé ñèñòå-
ìû â öåëîì ïðåäñòàâëÿåò ñîáîé ñæàòèå âäîëü îñåé V è θ (ñì.
ðèñ. 11.7) è ðàñòÿæåíèå âäîëü îñè Õ. Î÷åâèäíî, ìèíèìàëüíîìó ðàñ-
ñåèâàíèþ áóäåò ñîîòâåòñòâîâàòü ìèíèìàëüíîå ðàñòÿæåíèå Ï0 âäîëü
îñè õ, õàðàêòåðèçóåìîå âåëè÷èíîé ∆x. Òàêèì îáðàçîì, ìîæíî ïîñòà-
âèòü çàäà÷ó âûáîðà òàêîãî ìîìåíòà âñêðûòèÿ êàññåòû, ïðè êîòîðîì
äëÿ òðåáóåìîé äàëüíîñòè ïîëåòà ñóááîåïðèïàñîâ îáåñïå÷èâàåòñÿ
ìèíèìóì âåëè÷èíû ∆x, ÷åãî ìîæíî äîáèòüñÿ çà ñ÷åò èçìåíåíèÿ äâóõ
ïàðàìåòðîâ – áàëëèñòè÷åñêîãî êîýôôèöèåíòà ñóááîåïðèïàñà (îïðå-
äåëÿþùåãî ïîëîæåíèå îñîáîé òî÷êè (; )
**
V33
ñóá
ñóá
θ ) è âðåìåíè âñêðû-
òèÿ êàññåòû.
11.2.2. ÎÏÐÅÄÅËÅÍÈÅ ÒÐÀÅÊÒÎÐÈÉ ÂÛÑÎÊÎÑÊÎÐÎÑÒÍÛÕ
ÀÑÈÌÌÅÒÐÈ×ÍÛÕ ÁÎÅÂÛÕ ÏÎÐÀÆÀÞÙÈÕ ÝËÅÌÅÍÒÎÂ
Âûñîêîýíåðãåòè÷åñêèå ñïîñîáû ìåòàíèÿ ïîðàæàþùèõ ýëåìåíòîâ [48,
143] ìîãóò ïðèâîäèòü ê äåôîðìàöèè èõ ôîðìû. Ïîýòîìó òðàåêòîðèè òàêèõ
ýëåìåíòîâ íåîáõîäèìî ðàññ÷èòûâàòü ñ ó÷åòîì âîçíèêíîâåíèÿ ñîîòâåòñòâóþ-
ùèõ àñèììåòðèé.
508
Ðèñ. 11 .7. Õàðàêòåð ôàçîâûõ òðàåêòîðèé ïðè äâèæåíèè ñ èçìåíåíèåì áàëëèñòè÷å-
ñêîãî êîýôôèöèåíòà
Ïðè âûñîêèõ ñêîðîñòÿõ ïîëåòà ïîðàæàþùèõ ýëåìåíòîâ ïðàêòè÷åñêèé
èíòåðåñ ìîãóò ïðåäñòàâëÿòü ó÷àñòêè òðàåêòîðèé, âðåìÿ ïîëåòà ïî êîòîðûì
ìåíüøå ïåðèîäà ñîáñòâåííûõ êîëåáàíèé ýëåìåíòà îòíîñèòåëüíî ýêâàòîðè-
àëüíûõ îñåé, ïðè÷åì ðàññìàòðèâàåìûå ïîðàæàþùèå ýëåìåíòû ìîãóò áûòü
êàê ñòàòè÷åñêè óñòîé÷èâûìè, òàê è íåóñòîé÷èâûìè.
 ïðîöåññå äâèæåíèÿ èñêàæåíèå ôîðìû âûçûâàåò íåñîâïàäåíèå àýðîäè-
íàìè÷åñêîé îñè ñèììåòðèè ýëåìåíòà è âåêòîðà ñêîðîñòè â íà÷àëüíûé ìî-
ìåíò âðåìåíè ïîëåòà. Ïîýòîìó ïðè ðàñ÷åòå òðàåêòîðèè åãî äâèæåíèÿ âîçíè-
êàåò íåîáõîäèìîñòü â ó÷åòå íåíóëåâîãî ýêâèâàëåíòíîãî óãëà àòàêè è ñîîò-
âåòñòâåííî ïîäúåìíîé ñèëû.
Äâèæåíèå öåíòðà ìàññ ýëåìåíòà â ýòîì ñëó÷àå ìîæåò áûòü îïèñàíî ñèñ-
òåìîé äèôôåðåíöèàëüíûõ óðàâíåíèé âèäà (11.47), ãäå, êàê è ðàíåå,
c
S
m
c
xx
=
ρ
2
;c
S
m
c
yy
=
ρ
2
.
Ââåäåì áåçðàçìåðíûå ïåðåìåííûå
~
/;~
/;~
/;~ /,
VVVx xly ylt t
==
=
=
0
τ
(11.53)
ãäå τ = l/V0; l =2m/cx ρS. Òîãäà, ïåðåõîäÿ ê áåçðàçìåðíîìó âèäó (îïóñêàÿ â
äàëüíåéøèõ âûêëàäêàõ çíàêè áåçðàçìåðíîñòè ∼), ïîëó÷èì
•
sin;•
cos ;
•
cos ;•
sin .
VV
xV
kV
yV
+=
−
=
−=
−
=
2
εθ
θ
θε
θθ
(11.54)
Çäåñü k = cy/cx; ε
ρ
==
⎛
⎝⎜
⎞
⎠⎟
GXmgc
VS
x
/()
–
0
0
2
2
îòíîøåíèå âåñà ýëåìåíòà ê
ñèëå ëîáîâîãî ñîïðîòèâëåíèÿ â íà÷àëüíûé ìîìåíò âðåìåíè. Ó÷èòûâàÿ
âûñîêèå ñêîðîñòè äâèæåíèÿ ïîðàæàþùåãî ýëåìåíòà, ïîëó÷èì, ÷òî ε ÿâëÿåòñÿ
ìàëûì ïàðàìåòðîì. Ýòî ïîçâîëÿåò èñïîëüçîâàòü àñèìïòîòè÷åñêèå ìåòîäû
ìàëîãî ïàðàìåòðà äëÿ ðåøåíèÿ ñèñòåìû (11.54).
Èñêîìûå ôóíêöèè V(t, ε), θ(t, ε), x(t, ε), y(t, ε) ìîãóò áûòü ïðåäñòàâëåíû â
âèäå ðàçëîæåíèé ïî ñòåïåíÿì ìàëîãî ïàðàìåòðà ε:
VtVtVt
ttt
xt
(,)()();
(,)()();
(,)
εε
θεθ ε
θ
ε
=++
=++
12
12
K
K
=++
=++
xt
xt
yt
yt yt
12
12
()();
(,) () ()
.
ε
εε
K
K
(11.55)
Ðàññìîòðèì ïåðâûå äâà óðàâíåíèÿ ñèñòåìû (11.54). Ðàçëîæèì èõ ïðàâûå
÷àñòè â ðÿä Òåéëîðà, à â ëåâûå ïîäñòàâèì ñîîòâåòñòâóþùèå ðàçëîæåíèÿ
(11.55). Òîãäà, ïðèðàâíèâàÿ ÷ëåíû ñ îäèíàêîâûìè ñòåïåíÿìè ε, ïîëó÷èì äâå
ñèñòåìû óðàâíåíèé äëÿ îïðåäåëåíèÿ V1, V2, θ1 è θ2:
509
•
,
•
;
VV
kV
11
2
11
0
0
+=
−=
θ
(11.56)
•
sin
cos
cos ,
•
cos
VV
V
kV
21
2
00010
22
00
2
+=
−+
−
−=
−
−
θθθθθ
θθ
θ
sin
sin .
θθθ
010
+
(11.57)
Èíòåãðèðóÿ (11.56) ïðè íà÷àëüíûõ óñëîâèÿõ t =0:V1 =1;θ1 = θ0, ïîëó÷èì
V
t
kt
11
0
1
1
1
=
+
=+
+
;l
n
(
)
.
θθ
(11.58)
Ñ ó÷åòîì (11.58) ïåðâîå óðàâíåíèå ñèñòåìû (11.57) ïðèìåò âèä
•
cos ln( )
sin .
V
t
Vk
t
220
0
2
1
1
+
+
++
=
−
θθ(11.59)
Îáùåå ðåøåíèå ýòîãî óðàâíåíèÿ ìîæíî çàïèñàòü êàê
Ve
k
ted
tC
e
t
dt
t
dt
2
2
1
00
2
1
2
1
=
∫−−
+
∫
+
−
++
−
∫ [sin
cos ln( )]
θθ
1+
∫t
dt
.
(11.60)
Èíòåãðèðóÿ è îïðåäåëÿÿ ïîñòîÿííóþ Ñ èç íà÷àëüíûõ óñëîâèé t =0:V2 =0,
îêîí÷àòåëüíî íàéäåì
V
k
t
t
k
200
2
1
33
1
1
1
3
=−
⎛
⎝⎜
⎞
⎠⎟+
−+
⎡
⎣⎢
⎤
⎦⎥−
−
sin
cos
()
()
cos
θθ
θ0 11
()
l
n
()
.
++
tt
(11.61)
Àíàëîãè÷íî ðåøàÿ âòîðîå óðàâíåíèå (11.57), ïîëó÷èì
θθθθ
θθ
20
2
00
00
3
33
=−
+
−
⎛
⎝⎜
⎞
⎠⎟+
+−
cos
cos
sin
(sin
cos
k
kt
kk1
1
1
3
11
1
2
0
2
0
+
−+
⎡
⎣⎢
⎤
⎦⎥−
−+
+
+
t
t
k
tt
k
ln( )
cos (
)ln( )
sin (
θθ
+
+
tt
)ln( ).
1
(11.62)
Ðàññìîòðèì òðåòüå è ÷åòâåðòîå óðàâíåíèÿ ñèñòåìû (11.54). Ðàñêëàäûâàÿ
òðèãîíîìåòðè÷åñêèå ôóíêöèè â ïðàâûõ ÷àñòÿõ â ðÿä Òåéëîðà ñ ó÷åòîì
(11.55) òàê æå, êàê è âûøå, ïîëó÷èì äâå ñèñòåìû óðàâíåíèé äëÿ îïðåäåëå-
íèÿ íåèçâåñòíûõ x1, x2, y1, y2:
•
,
•
;
xa
Vb
V
yc
Vd
V
111
1
111
1
=+
=+
θ
θ
(11.63)
510
•
,
•
,
xa
Vb
Vb
V
yc
VVd
V
221
22
1
22
1
22
1
=−−
=++
θθ
θθ
(11.64)
ãäå
ab
cd
=+
=
=−
=
cos
sin ;
sin ;
sin
cos ;
cos .
θθθ
θ
θθθ
θ
000
0
000
0
Èíòåãðèðóÿ (11.63) ñ ó÷åòîì (11.58) ïðè íà÷àëüíûõ óñëîâèÿõ t =0;x1 =0;
y1 = y0 (ñ÷èòàåì, ÷òî îòñ÷åò äàëüíîñòè ïîëåòà ïîðàæàþùåãî ýëåìåíòà
íà÷èíàåòñÿ íà íåêîòîðîé âûñîòå y0 ≠ 0), ïîëó÷èì [38]
xt
k
t
10
0
2
1
2
1
=+
−
+
c
o
sl
n
()s
i
nl
n
()
;
θθ
(11.65)
yy
t
k
t
100
0
2
1
2
1
=+
++
+
sin ln( )
cos ln( ).
θθ
(11.66)
Îáùåå ðåøåíèå óðàâíåíèÿ (11.64) èìååò âèä
xa
Itb
Itb
It
2123
=−−
() () ();
(11.67)
yc
I
tI
td
It
2123
=++
() () (),
(11.68)
ãäå
It Vtdt
It Vt tdt
It Vt
t
t
12
0
21
2
0
32
() ();
() ()();
() ()
=
=
=
∫
∫θ
θ1
0
().
tdt
t
∫
Ïðèâåäåííûå èíòåãðàëû I1, I2, I3 îïðåäåëÿþòñÿ ñîîòâåòñòâåííî âûðàæåíèÿìè
It
kt
t
t
k
10
0
2
0
1
63
3
1
3
1
()
sin
cos
()
cos [(
=−
−
⎛
⎝⎜
⎞
⎠⎟+
+
−
−
θθ
θ++
−
=−
−
⎛
⎝⎜
⎞
⎠⎟
tt
t
Itk
kt
)ln( ) ],
()coscossin[
2
2
2
000
1
3
θθθ
−
+
+
ln( )]
1t
511
+−
⎛
⎝⎜
⎞
⎠⎟ +−
+
−
⎡
⎣⎢
−+
⎤
kkt
t
t
t
33
1
1
1
2
1
00
2
sin
cos
ln( )
ln( )
θθ
⎦⎥ −+
+
−
+
++
+
−
k
tt
t
kt
t
2
0
2
0
3
11
11
c
o
s
[
()l
n
()]
s
i
n
[
()
l
n
()
θ
θ
t
It
kt
t
t
k
];
()
sin
cos
()
c
30
00
2
0
1
63
3
1
3
=−
−
⎛
⎝⎜
⎞
⎠⎟+
+
−
−
θθθ
θos[()ln()]
sin
cos
(
θ
θθ
0
2
00
11
331
++
−
−
−−
⎛
⎝⎜
⎞
⎠⎟+
tt
t
kkt
t
t−+
−
⎡
⎣⎢
−+
++−
×
×+
ln( ))
()l
n
()] c
o
s
()
(
1
11
3
1
2
1
2
2
0
2
t
tt
t
k
t
θ
ln()ln())
.
2
11
++ ++
⎡
⎣⎢
⎤
⎦⎥
tt
t
Òàêèì îáðàçîì, åñëè îãðàíè÷èòüñÿ äâóìÿ ïåðâûìè ÷ëåíàìè ðàçëîæåíèé
(11.55), òî ïàðàìåòðû òðàåêòîðèè ïîðàæàþùåãî ýëåìåíòà áóäóò îïðåäåëÿòüñÿ
ñëåäóþùèìè ñîîòíîøåíèÿìè:
Vt
t
k
t
t
(,)
sin
cos
()
()
εε
θθ
=
+
+−
⎛
⎝⎜
⎞
⎠⎟+
−+
⎡
⎣⎢
1
1
1
33
1
1
1
002
⎤
⎦⎥−
−+
+
=+
++
εθ
θεθ
ε
k
tt
tk
t
k
3
11
1
3
0
0
2
cos (
)ln( );
(,)
ln( )
cos
cos
sin
sin
cos
θθθ
θθ
ε
000
00
331
−−
⎛
⎝⎜
⎞
⎠⎟+
+−
⎛
⎝⎜
⎞
⎠⎟
kt
kkt
+
−+
⎡
⎣⎢
⎤
⎦⎥−
−+
+
+
t
t
k
tt
k
ln( )
cos (
)ln( )
sin (
1
3
11
1
2
0
2
0
εθ
ε
θ
++
=+
−
+
+
tt
xt
t
k
ta
)ln( );
(
,
)c
o
sl
n
()s
i
nl
n
()(
1
1
2
1
00
2
εθ
θ
ε
IIb
I
yt
y
t
k
t
123
00
0
2
1
2
1
−−
=+
++
++
);
(,)
sin ln( )
cos ln( )
εθ
θε
()
.
cI
IdI
123
++
(11.69)
Ïîëó÷åííîå ðåøåíèå äîñòàòî÷íî òî÷íî îïèñûâàåò ñîñòîÿíèå îáúåêòà,
óäîâëåòâîðÿþùåå ñèñòåìå (11.54) íà èíòåðâàëå âðåìåíè 0 < t <1/ε.Îò
áåçðàçìåðíûõ ïåðåìåííûõ, äëÿ êîòîðûõ âûâåäåíû óðàâíåíèÿ (11.69),
ïðèìåíÿÿ (11.53), ìîæíî ïåðåéòè ê ðàçìåðíûì ôàçîâûì êîîðäèíàòàì.
512
×èñëåííîå ðåøåíèå ñèñòåìû (11.54) äîñòàòî÷íî ïðîñòî ìîæåò áûòü ïî-
ëó÷åíî ñ èñïîëüçîâàíèåì ÝÂÌ. Îäíàêî ñ òî÷êè çðåíèÿ àíàëèçà ïðåäåëüíûõ
îòêëîíåíèé ïàäåíèÿ àñèììåòðè÷íûõ ýëåìåíòîâ îïðåäåëåíèå âëèÿíèÿ îò-
äåëüíûõ äèíàìè÷åñêèõ è àýðîäèíàìè÷åñêèõ ïàðàìåòðîâ íà îòêëîíåíèå òðà-
åêòîðèé îò íîìèíàëüíûõ çíà÷åíèé ïóòåì èñïîëüçîâàíèÿ ðåøåíèÿ (11.69)
ÿâëÿåòñÿ ïðåäïî÷òèòåëüíûì.
11.2 .3. ÎÑÎÁÛÅ È ÐÅÇÎÍÀÍÑÍÛÅ ÐÅÆÈÌÛ ÏÎËÅÒÀ
ÀÑÈÌÌÅÒÐÈ×ÍÛÕ ÑÓÁÁÎÅÏÐÈÏÀÑÎÂ
Ðàññìîòðèì äâèæåíèå íåâðàùàþùåãîñÿ ñòàòè÷åñêè óñòîé÷èâîãî
ñóááîåïðèïàñà ïîñëå òîãî, êàê åãî âûáðîñèëè èç êàññåòû. Åñëè ñèì-
ìåòðè÷íûé ñóááîåïðèïàñ äâèæåòñÿ â âîçäóõå ïðè íóëåâîì óãëå íóòà-
öèè, òî ðåçóëüòèðóþùàÿ ñèëà ñîïðîòèâëåíèÿ âîçäóõà íàïðàâëåíà ïî
åãî ãåîìåòðè÷åñêîé îñè âäîëü ïðîäîëüíîé îñè ñâÿçàííîé ñèñòåìû
êîîðäèíàò. Ïðè íàëè÷èè àñèììåòðèè ôîðìû, îáóñëîâëåííîé íå-
ñèììåòðèåé êîðïóñà è ñòàáèëèçàòîðîâ, ðåçóëüòèðóþùàÿ ñèëà ñî-
ïðîòèâëåíèÿ âîçäóõà áóäåò íàïðàâëåíà ïî àýðîäèíàìè÷åñêîé îñè,
íå ñîâïàäàþùåé â îáùåì ñëó÷àå ñ ïðîäîëüíîé îñüþ. Òàêèì îáðà-
çîì, óãîë íóòàöèè, âûçâàííûé àñèììåòðèåé, ïðèâîäèò ê ïîÿâëåíèþ
íîðìàëüíîé ñîñòàâëÿþùåé ñèëû ñîïðîòèâëåíèÿ âîçäóøíîé ñðåäû.
Ñ÷èòàÿ, ÷òî äâèæåíèå îòíîñèòåëüíî öåíòðà ìàññ óñòàíîâèëîñü è áà-
ëàíñèðîâî÷íûå çíà÷åíèÿ óãëîâ δ1a è δ2a îïðåäåëÿþòñÿ çíà÷åíèÿìè
àñèììåòðèé, óðàâíåíèÿ äâèæåíèÿ öåíòðà ìàññ ìîæíî çàïèñàòü, èñ-
ïîëüçóÿ ñèñòåìó óðàâíåíèé â ôîðìå Â.Ñ. Ïóãà÷åâà (3.166), â âèäå
•
sin
(
);
•
cos
;
•
VgV
ck
gV
Vc
Vc
a
Na
=−
−
+
−+
=
−
θδ
θθ
δ
2
0
2
1
2
1
ò
í
=
Ψ
Na
δ1,
(11.70)
ãäå δδδ
aa
a
=+
1
2
2
2
; k – êîýôôèöèåíò, îïðåäåëÿþùèé èíäóêòèâíóþ
ñîñòàâëÿþùóþ ñèëû ëîáîâîãî ñîïðîòèâëåíèÿ; cò0
–
êîýôôèöèåíò
ëîáîâîãî
ñîïðîòèâëåíèÿ
ïðè
íóëåâîì óãëå
íóòàöèè;
c
d
mg
Hyc
V
a
N
ON
N
=
⎛
⎝⎜⎞
⎠⎟
πÏ
8
2
() ,à cN – ýêâèâàëåíò òèïîâîé ôóíêöèè
ñîïðîòèâëåíèÿ, ïîëó÷åííîé â ïðåäïîëîæåíèè ìàëîñòè óãëà íóòàöèè.
Ïðè ìàëûõ óãëàõ δa êîýôôèöèåíò ëîáîâîãî ñîïðîòèâëåíèÿ ðàñòåò
íåçíà÷èòåëüíî è âëèÿíèå àýðîäèíàìè÷åñêîé àñèììåòðèè íà èçìå-
íåíèå âåëè÷èíû ñêîðîñòè íåâåëèêî. Îòíîñèòåëüíîå âëèÿíèå àýðî-
äèíàìè÷åñêîé ñèëû íà èçìåíåíèå íàïðàâëåíèÿ âåêòîðà ñêîðîñòè
ìîæíî îöåíèòü, ñîïîñòàâëÿÿ â ïðàâîé ÷àñòè âòîðîãî óðàâíåíèÿ
(11.70) ïåðâûé è âòîðîé ÷ëåíû, à èìåííî
513
Vc
gV
V
mg
S
c
V
a
Na
Na
δ
θ
ρ
θ
δ
2
1
2
2
−
=
⎛
⎝⎜⎞
⎠⎟
cos
cos
.
Îòíîñèòåëüíîå âëèÿíèå àñèììåòðèè ïðîïîðöèîíàëüíî êâàäðàòó
ñêîðîñòè è òåì áîëüøå, ÷åì áîëüøå âåëè÷èíà êîýôôèöèåíòà
ccc
NNy
a
()
.
≈
α
Îòíîñèòåëüíîå âëèÿíèå àýðîäèíàìè÷åñêîé àñèììåòðèè
òåì ìåíüøå, ÷åì áîëüøå ìàññà ñóááîåïðèïàñà.
Äâèæåíèå ñóááîåïðèïàñà îòíîñèòåëüíî öåíòðà ìàññ çàâèñèò îò
èíòåíñèâíîñòè óãëîâûõ âîçìóùåíèé ïðè âûáðîñå åãî èç êàññåòû. Ñî
âðåìåíåì âðàùàòåëüíîå äâèæåíèå îòíîñèòåëüíî ýêâàòîðèàëüíîé
îñè òðàíñôîðìèðóåòñÿ ïðè íàëè÷èè ñèíóñîèäàëüíîé çàâèñèìîñòè
ñòàòè÷åñêîãî ìîìåíòà îò óãëà àòàêè (íóòàöèè) â êîëåáàòåëüíîå äâè-
æåíèå. Íà ïðàêòèêå ïðè ìàëûõ óäëèíåíèÿõ ñóááîåïðèïàñîâ íàáëþ-
äàþòñÿ ñëó÷àè èõ ñòàáèëèçàöèè â ïîëåòå "õâîñòîì âïåðåä". Äëÿ íå-
âðàùàþùåãîñÿ âîêðóã ïðîäîëüíîé îñè ñóááîåïðèïàñà ýòî âîçìîæíî
ïðè îïðåäåëåííîé çàâèñèìîñòè ñòàòè÷åñêîãî ìîìåíòà îò óãëà àòàêè,
ïðè êîòîðîé â íåêîòîðîé îêðåñòíîñòè óãëà α – π îí îêàçûâàåòñÿ ñòà -
òè÷åñêè óñòîé÷èâûì.
 êà÷åñòâå ïðèìåðà ðàññìîòðèì çàâèñèìîñòü êîýôôèöèåíòà ñòà-
òè÷åñêîãî ìîìåíòà mz(α) èëè my(β), èçîáðàæåííóþ íà ðèñ. 11 .8. Ñî-
îòâåòñòâóþùèé ôàçîâûé ïîðòðåò ñèñòåìû ñ ó÷åòîì åñòåñòâåííîãî
äåìïôèðîâàíèÿ ïîêàçàí íà ðèñ. 11 .8, á.  ýòîì ñëó÷àå α = π, α =0
îïðåäåëÿþò îñîáóþ òî÷êó òèïà óñòîé÷èâîãî ôîêóñà. Ïðè ýòîì îá-
ëàñòü ôàçîâîãî ïðîñòðàíñòâà, ñîîòâåòñòâóþùàÿ îáëàñòè ïðèòÿæåíèÿ
óñòîé÷èâûõ îñîáûõ òî÷åê •
;()
;
αα
π
==
+
01
2
n n =0,±1,..., îïðåäå-
ëÿþùèõ äâèæåíèå ñóááîåïðèïàñà "õâîñòîì âïåðåä", îêàçûâàåòñÿ ñó-
ùåñòâåííî ìåíüøå, ÷åì îáëàñòü ôàçîâîãî ïðîñòðàíñòâà, îïðåäåëÿå-
514
Ðèñ. 11.8 . Âîçìîæíîñòü ñòàáèëèçàöèè òåëà â ïîëåòå "õâîñòîì âïåðåä":
à – âîçìîæíàÿ çàâèñèìîñòü mz(α); á – ôàçîâûé ïîðòðåò ñèñòåìû
ìàÿ ïðèòÿæåíèåì óñòîé÷èâûõ òî÷åê (• ;;
ααπ
==
02
n n =0,±1,...), ñî-
îòâåòñòâóþùèõ ïðàâèëüíîìó ïîëåòó ñóááîåïðèïàñà. Ïîýòîìó äëÿ
áîëüøèíñòâà íà÷àëüíûõ óñëîâèé ñóááîåïðèïàñ ñòàáèëèçèðóåòñÿ
ïðàâèëüíî, è òîëüêî â îòäåëüíûõ ñëó÷àÿõ íà÷àëüíûå óñëîâèÿ äâèæå-
íèÿ îêàçûâàþòñÿ òàêèìè, ÷òî ñóááîåïðèïàñ äâèæåòñÿ "õâîñòîì âïå-
ðåä".
Òåõíîëîãè÷åñêèå ïîãðåøíîñòè èçãîòîâëåíèÿ, à òàêæå äåôîðìà-
öèè êîðïóñà è ñòàáèëèçàòîðîâ ïðè âûáðîñå ñóááîåïðèïàñîâ ìîãóò
ïðèâåñòè ê ïîÿâëåíèþ àýðîäèíàìè÷åñêîé àñèììåòðèè.  ýòîì ñëó-
÷àå ïîëîæåíèå óñòîé÷èâîãî ôîêóñà ïðè α = π ìîæåò íåìíîãî ñìå-
ñòèòüñÿ, òàê ÷òî óñòîé÷èâîé îêàæåòñÿ áàëàíñèðîâêà, íàïðèìåð, ïðè
α=αa<0èααπ
=<
*
. Ïðè ýòîì êà÷åñòâåííî ôàçîâûé ïîðòðåò íå
èçìåíèòñÿ.
Àñèììåòðèÿ ôîðìû èëè ìàññû ñóááîåïðèïàñà ìîæåò ñîçäàâàòüñÿ
ïðåäíàìåðåííî ñ öåëüþ îðãàíèçàöèè îïðåäåëåííîãî âèäà åãî óãëî-
âîãî äâèæåíèÿ íà òðàåêòîðèè. Óãëû àòàêè è ñêîëüæåíèÿ ïðè ýòîì
ìîãóò áûòü äîñòàòî÷íî áîëüøèìè è êàê ñëåäñòâèå ïðèâåñòè ê ñóùå-
ñòâåííîìó èçìåíåíèþ õàðàêòåðà äâèæåíèÿ öåíòðà ìàññ.
 íåêîòîðûõ ñëó÷àÿõ òðåáóåòñÿ îðãàíèçîâàòü îïðåäåëåííûé âèä
äâèæåíèÿ ïðîäîëüíîé îñè ñóááîåïðèïàñà îòíîñèòåëüíî âåêòîðà
ñêîðîñòè, íàïðèìåð äëÿ ñêàíèðîâàíèÿ ìåñòíîñòè â ðàéîíå öåëè
æåñòêîçàêðåïëåííûì êîîðäèíàòîðîì. Ðàññìîòðèì îñîáåííîñòè èñ-
ïîëüçîâàíèÿ äëÿ ýòîãî óñòîé÷èâûõ ðåçîíàíñíûõ ðåæèìîâ âðàùåíèÿ
àñèììåòðè÷íûõ ñóááîåïðèïàñîâ.
Äëÿ òîãî ÷òîáû äîáèòüñÿ ðåçî-
íàíñíîãî âðàùåíèÿ ñóááîåïðèïà-
ñà ñ áîëüøèìè óãëàìè àòàêè è
ñêîëüæåíèÿ, íåîáõîäèìî îáåñïå-
÷èòü òàêîå ñîîòíîøåíèå ìåæäó
äèíàìè÷åñêèìè è àýðîäèíàìè÷å-
ñêèìè ïàðàìåòðàìè ñóááîåïðèïàñà
(,,,)
mmcm
xxy z
ωαα
è çíà÷åíèÿìè àñèì-
ìåòðèé (αa, βa, ∆y, ∆z), ÷òîáû ñóùåñò-
âîâàëà óñòîé÷èâàÿ îñîáàÿ òî÷êà, ëå-
æàùàÿ íà ñêëîíå ðåçîíàíñíîãî ïèêà,
ãàðàíòèðóþùàÿ óñòîé÷èâîå ðåçîíàíñ-
íîå âðàùåíèå.
Ïðè ýòîì âîçíèêàåò òàê íàçû-
âàåìîå "ëóííîå äâèæåíèå", ïðè
êîòîðîì ïîëîæåíèå ïëîñêîñòè ñî-
ïðîòèâëåíèÿ ôèêñèðóåòñÿ â ñâÿ-
çàííîé ñèñòåìå êîîðäèíàò. Òàê
êàê ñàìà ñâÿçàííàÿ ñèñòåìà êîîð-
515
Ðèñ. 11.9 . Óãëîâîå äâèæåíèå àñèì-
ìåòðè÷íîãî ýëåìåíòà â ðåæèìå ðåçî-
íàíñíîãî âðàùåíèÿ
äèíàò âðàùàåòñÿ ñ óãëîâîé ñêîðîñòüþ ωõ, òî â òðàåêòîðíîé ñèñòåìå
êîîðäèíàò òàêîé âèä äâèæåíèÿ áóäåò ñîîòâåòñòâîâàòü òîìó, ÷òî ïðî-
äîëüíàÿ îñü ñóááîåïðèïàñà ñîâåðøàåò âîêðóã âåêòîðà ñêîðîñòè êî-
íè÷åñêîå äâèæåíèå (ðèñ. 11.9).
Ïðè äâèæåíèè öåíòðà ìàññ ñóááîåïðèïàñà ïî òðàåêòîðèè, áëèç-
êîé ê òðàåêòîðèè âåðòèêàëüíîãî ïàäåíèÿ, ïðîäîëüíàÿ îñü áóäåò ñî-
âåðøàòü òðåáóåìîå óãëîâîå äâèæåíèå (ñì. ðèñ. 11.9).
Åñëè ìîìåíòû èíåðöèè ñóááîåïðèïàñà îòíîñèòåëüíî ïðîäîëü-
íîé è ýêâàòîðèàëüíîé îñåé áëèçêè, òî êðèòè÷åñêîå çíà÷åíèå óãëî-
âîé ñêîðîñòè êðåíà ωêð áóäåò îòëè÷àòüñÿ îò ÷àñòîòû ñîáñòâåííûõ êî-
ëåáàíèé ñóááîåïðèïàñà ïî óãëàì òàíãàæà è êóðñà ωc, êîòîðàÿ, êàê
èçâåñòíî, îïðåäåëÿåòñÿ, íàïðèìåð, äëÿ òàíãàæíîãî äâèæåíèÿ ñîîò-
íîøåíèåì
ω
α
c
z
qSl m
I
=
||,
(11.71)
ãäåI=Iy≅Iz=const.
Ñîîòâåòñòâåííî áóäåò èìåòü ìåñòî ñîîòíîøåíèå
ωω
α
êð =−
⎛
⎝⎜⎞
⎠⎟=
−
⎛
⎝⎜
⎞
⎠⎟
−
c
x
z
x
I
I
qSl m
II
1
1
2
1
2
||.
(11.72)
 ñëó÷àå êîãäà çíà÷åíèÿ I è Ix áëèçêè, ωêð ñóùåñòâåííî áîëüøå
ωc.
 ëèíåéíîì ïðèáëèæåíèè äëÿ óñëîâèé äâèæåíèÿ ñóááîåïðèïàñà
ñ ïîñòîÿííîé (èëè áëèçêîé ê íåé) ñêîðîñòüþ è ïîñòîÿííûì óãëîì
íàêëîíà âåêòîðà ñêîðîñòè ê ìåñòíîìó ãîðèçîíòó ìîæíî ïîëó÷èòü
çàâèñèìîñòü ìåæäó ìàêñèìàëüíûì çíà÷åíèåì ïðîñòðàíñòâåííîãî
óãëà àòàêè è êîìïëåêñîì àñèììåòðèé, ïðèâîäÿùèì ê ÿâëåíèþ ïàðà-
ìåòðè÷åñêîãî ðåçîíàíñà:
α
βα
Ïmax
|| ||
=+
−
−
⎛
⎝⎜
⎞
⎠⎟+
⎡
⎣
⎢
⎢
+
k
m
m
Cz
lm
I
II
m
y
y
x
z
xz
x
z
1
2
0
∆
0
212
|| ||
,
/
m
Cy
lm
I
II
z
x
y
xy
x
αβ
−+
−
⎛
⎝⎜
⎞
⎠⎟
⎤
⎦
⎥
⎥
∆
(11.73)
516
ãäå k1 – êîýôôèöèåíò óñèëåíèÿ âëèÿíèÿ àñèììåòðèé; S, l – ïëîùàäü
ìèäåëåâîãî ñå÷åíèÿ è äëèíà ñóááîåïðèïàñà; ||
,
mz
α
||–
my
β
ìîäóëè
ïðîèçâîäíîé îò àýðîäèíàìè÷åñêîãî êîýôôèöèåíòà ìîìåíòà ïî óãëó
àòàêè; ∆y è ∆z – áîêîâûå îòêëîíåíèÿ ïîëîæåíèÿ öåíòðà ìàññ
îòíîñèòåëüíî ïðîäîëüíîé îñè; mm
yy
a
00
=−||,
β
δ
βmm
zz
a
00
=−||
–
α
δ
α
âåëè÷èíû àýðîäèíàìè÷åñêèõ êîýôôèöèåíòîâ àñèììåòðèé âíåøíåé
ôîðìû; αδa
è βδa
–
áàëàíñèðîâî÷íûå óãëû àòàêè è ñêîëüæåíèÿ,
îáóñëîâëåííûå àñèììåòðèåé âíåøíåé ôîðìû.
Êîíòðîëüíûå âîïðîñû
1. Ïåðå÷èñëèòå ïðè÷èíû, ïðèâîäÿùèå ê ïîÿâëåíèþ âîçìóùåíèé â ðå-
àëüíîì ïîëåòå ñíàðÿäà, ðàêåòû. Êàêèå ïðåäïîñûëêè ëåæàò â îñíîâå ìåòîäà
"ìàëûõ âîçìóùåíèé"? ×òî õàðàêòåðèçóåò (÷åìó ÷èñëåííî ðàâíî) èçìåíåíèå
ïîïðàâî÷íîãî êîýôôèöèåíòà (áàëëèñòè÷åñêîé ïðîèçâîäíîé)? Ïî÷åìó áàë-
ëèñòè÷åñêèå ïðîèçâîäíûå ðàññ÷èòûâàþòñÿ ïî ïàðàìåòðàì òðåáóåìîãî, à íå
âîçìóùåííîãî äâèæåíèÿ? Îïðåäåëèòå çíàêè ïîïðàâî÷íûõ êîýôôèöèåíòîâ
âèäà
∂
∂θ
xc;
∂
∂
x
m
c
;
∂
∂
x
h
i
0
;
∂
∂
x
W
i
x
.  ÷åì ñîñòîèò ñõîäñòâî è ðàçëè÷èå ìåæäó èçîõðîí-
íûìè è ïîëíûìè âàðèàöèÿìè? Ïåðå÷èñëèòå îñíîâíûå ìåòîäû îïðåäåëåíèÿ
áàëëèñòè÷åñêèõ ïðîèçâîäíûõ.
2. Ïîÿñíèòå, êàê âëèÿåò âåòåð íà ïîëåò íåóïðàâëÿåìûõ ðàêåò è àðòèëëå-
ðèéñêèõ ñíàðÿäîâ. Äàéòå îïðåäåëåíèå "áàëëèñòè÷åñêèõ ñðåäíèõ".
3. ×åðåç êàêèå ôàêòîðû è ïàðàìåòðû ïðîÿâëÿåòñÿ âëèÿíèå äâèæåíèÿ ðà-
êåòû-íîñèòåëÿ íà ïîëåò ðàêåò è ñíàðÿäîâ? Çàïèøèòå äèíàìè÷åñêèå óðàâíå-
íèÿ äâèæåíèÿ ðàêåòû îòíîñèòåëüíî ñèñòåìû êîîðäèíàò, ñâÿçàííîé ñ ïóñêî-
âîé óñòàíîâêîé áåç ó÷åòà äåéñòâèÿ àýðîäèíàìè÷åñêèõ ñèë. Ïðèâåäèòå òðàê-
òîâêó ïîíÿòèé ñòàòè÷åñêîé è äèíàìè÷åñêîé íåóðàâíîâåøåííîñòè
àðòèëëåðèéñêîãî ñíàðÿäà. Êàê âëèÿåò ðàäèàëüíûé ýêñöåíòðèñèòåò öåíòðà
ìàññ ñíàðÿäà íà îòêëîíåíèå íà÷àëüíîé ñêîðîñòè?
4. Èçîáðàçèòå òðóáêó (ñíîï) òðàåêòîðèé è ýëëèïñ ðàññåèâàíèÿ. Ïîêàæè-
òå ïîëîæåíèå ñðåäíåé òðàåêòîðèè è öåíòðà ãðóïïèðîâàíèÿ. Êàêèå ÷èñëîâûå
õàðàêòåðèñòèêè îïðåäåëÿþò âåëè÷èíó ðàññåèâàíèÿ. Êàêèå èç íèõ ÿâëÿþòñÿ
áîëåå óíèâåðñàëüíûìè?
5. Äëÿ ÷åãî ñëóæèò è â ÷åì çàêëþ÷àåòñÿ ñóùíîñòü ìåòîäà "ìàòðèöû âëèÿ-
íèÿ"? Çàïèøèòå óðàâíåíèÿ ôîðìèðóþùåãî ôèëüòðà, ìîäåëèðóþùåãî ïîëå
òóðáóëåíòíîñòè àòìîñôåðû äëÿ ïðîäîëüíîé ñîñòàâëÿþùåé òóðáóëåíòíîñòè.
6. Ïðåäñòàâüòå â âèäå ãðàôè÷åñêîé ïîñëåäîâàòåëüíîñòè âû÷èñëèòåëüíûé
àëãîðèòì îïðåäåëåíèÿ õàðàêòåðèñòèê ðàññåèâàíèÿ ïî ðåçóëüòàòàì îïûòíûõ
ñòðåëüá.
7. Äàéòå îïðåäåëåíèå öåëè ïðèñòðåëêè. Ê êàêèì ãðóïïàì ðåêîìåíäóåòñÿ
ñâîäèòü îøèáêè ñòðåëüáû ïðè ïðèñòðåëêå? Ñ ÷åì ýòî ñâÿçàíî?
8. Íàïèøèòå äèíàìè÷åñêèå óðàâíåíèÿ, îïèñûâàþùèå äâèæåíèå öåíòðà
ìàññ ñíàðÿäà íà ó÷àñòêå êîððåêöèè ïðè äåéñòâèè ñèëîâîãî êîððåêòèðóþùå-
ãî èìïóëüñà. Ïåðå÷èñëèòå îñíîâíûå ôàêòîðû, îïðåäåëÿþùèå ðàññåèâàíèå
ñóááîåïðèïàñîâ êàññåòíûõ àðòèëëåðèéñêèõ ñíàðÿäîâ. Äàéòå êà÷åñòâåííóþ
õàðàêòåðèñòèêó âëèÿíèÿ àñèììåòðèé ôîðìû ËÀ íà òðàåêòîðèþ öåíòðà ìàññ.
517
ÐÀÇÄÅË IV
ÒÅÎÐÅÒÈ×ÅÑÊÈÅ ÎÑÍÎÂÛ
ÝÊÑÏÅÐÈÌÅÍÒÀËÜÍÎÉ ÂÍÅØÍÅÉ
ÁÀËËÈÑÒÈÊÈ È ËÅÒÍÛÕ ÈÑÏÛÒÀÍÈÉ
ÐÀÊÅÒ. ÏÎÍßÒÈß Î ÑÎÑÒÀÂËÅÍÈÈ
ÒÀÁËÈÖ ÑÒÐÅËÜÁÛ
Ãëàâà 12
ÔÎÐÌÓËÈÐÎÂÊÀ ÇÀÄÀ× ÝÊÑÏÅÐÈÌÅÍÒÀËÜÍÎÉ
ÁÀËËÈÑÒÈÊÈ, ÝËÅÌÅÍÒÛ ÏËÀÍÈÐÎÂÀÍÈß
È ÎÁÐÀÁÎÒÊÀ ÐÅÇÓËÜÒÀÒÎÂ ËÅÒÍÛÕ
ÈÑÏÛÒÀÍÈÉ
Ìåòîäû ýêñïåðèìåíòàëüíîé áàëëèñòèêè è ëåòíûõ èñïûòàíèé ðàêåò, èõ
îðãàíèçàöèÿ, èñïîëüçóåìàÿ èçìåðèòåëüíàÿ àïïàðàòóðà, à òàêæå ïðèìåíÿåìûå
àëãîðèòìû îáðàáîòêè ïîëó÷àåìûõ ðåçóëüòàòîâ çàâèñÿò îò êîíêðåòíîãî òèïà
èñïûòóåìîãî ËÀ è íàçíà÷åíèÿ èñïûòàíèé [135].
Áàëëèñòè÷åñêèå èñïûòàíèÿ ïðèíÿòî ïîäðàçäåëÿòü íà äâå áîëüøèå ãðóïïû –
ëàáîðàòîðíûå, ïðîâîäèìûå, êàê ïðàâèëî, ïðè ñòðåëüáå èç ñïåöèàëüíûõ ìåòà-
òåëüíûõ óñòàíîâîê â ñïåöèàëüíî îáîðóäîâàííûõ òèðàõ, íà îòêðûòûõ èëè çà-
êðûòûõ áàëëèñòè÷åñêèõ òðàññàõ, è ïîëèãîííûå, îñíîâíûìè ýëåìåíòàìè êîòî-
ðûõ ÿâëÿþòñÿ îòëàäî÷íûå, áîåâûå (âîéñêîâûå), ïðèåìíûå (ñîâìåñòíûå) èñïû-
òàíèÿ, à òàêæå "òàáëè÷íûå ñòðåëüáû".
 ïðîöåññå ñîçäàíèÿ è îòðàáîòêè íîâûõ îáðàçöîâ ðàêåò, êîððåêòèðóåìûõ
áîåïðèïàñîâ è íåêîòîðûõ äðóãèõ âèäîâ ËÀ çàêëþ÷èòåëüíûì ýòàïîì ÿâëÿåòñÿ
ïðîâåäåíèå ëåòíûõ èñïûòàíèé. Îíè ñëóæàò äëÿ ïîëó÷åíèÿ íàèáîëåå ïîëíîé èí-
ôîðìàöèè î ôóíêöèîíèðîâàíèè êàê êîìïëåêñà âîîðóæåíèÿ â öåëîì, òàê è åãî
îòäåëüíûõ ýëåìåíòîâ.
Îòëàäî÷íûå èñïûòàíèÿ ñòàâÿò öåëüþ ïðîâåðêó ðàáîòû ðàçëè÷íûõ ñèñòåì,
ðàçìåùåííûõ íà áîðòó ËÀ, è åãî ëåòíûõ êà÷åñòâ.
Áîåâûå èñïûòàíèÿ ïðåäíàçíà÷åíû äëÿ ïðîâåðêè áîåâûõ ñâîéñòâ îáðàçöà âîî-
ðóæåíèÿ. Îíè ïðîâîäÿòñÿ äëÿ îöåíêè ýôôåêòèâíîñòè åãî äåéñòâèÿ ïî öåëÿì â
îáñòàíîâêå, ìàêñèìàëüíî ïðèáëèæåííîé ê áîåâîé.
Ïðèåìíûå èñïûòàíèÿ ïðåæäå âñåãî äîëæíû äàòü îòâåò î ñîîòâåòñòâèè
õàðàêòåðèñòèê ñîçäàííîãî êîìïëåêñà (ëèáî îáðàçöà âîîðóæåíèÿ) òðåáîâàíèÿì
òàêòèêî-òåõíè÷åñêîãî çàäàíèÿ.
Òàáëè÷íûå ñòðåëüáû ÿâëÿþòñÿ ñïåöèôè÷åñêèì è âåñüìà âàæíûì ýëåìåíòîì
âíåøíåáàëëèñòè÷åñêèõ èñïûòàíèé. Äåëî çàêëþ÷àåòñÿ â òîì, ÷òî îñíîâíûì ìå-
òîäîì ñîñòàâëåíèÿ òàáëèö ñòðåëüáû ÿâëÿåòñÿ (ñì. íèæå) òàê íàçûâàåìûé
518
îïûòíî-òåîðåòè÷åñêèé ìåòîä. ×èñòî îïûòíûé ìåòîä íåïðèìåíèì äëÿ ýòèõ
öåëåé â ñèëó íåâûñîêîé íàäåæíîñòè ïîëó÷àåìîé èíôîðìàöèè è áîëüøîãî ðàñõî-
äà áîåïðèïàñîâ. Ñ äðóãîé ñòîðîíû, òåîðåòè÷åñêèé ìåòîä, íåñìîòðÿ íà âñþ åãî
ïðèâëåêàòåëüíîñòü, íå ìîæåò áûòü èñïîëüçîâàí â "÷èñòîì" âèäå, ïîñêîëüêó
òðåáóåò ïðèâëå÷åíèÿ ñëèøêîì áîëüøîãî îáúåìà àïðèîðè çàäàâàåìîé äîñòîâåð-
íîé èíôîðìàöèè, êîòîðàÿ îáúåêòèâíî îòñóòñòâóåò.
 ñëó÷àå òåîðåòè÷åñêîãî îïðåäåëåíèÿ (áåç ïðîâåäåíèÿ ñòðåëüáû) íà÷àëüíîé
(äóëüíîé) ñêîðîñòè ñíàðÿäà ëèáî ñêîðîñòè ðàêåòû â êîíöå àêòèâíîãî ó÷àñòêà
òðàåêòîðèè, óãëîâ âûëåòà, íà÷àëüíûõ óãëîâ è óãëîâûõ ñêîðîñòåé íóòàöèè è
ïðåöåññèè (òàíãàæà, ðûñêàíèÿ è êðåíà) íåîáõîäèìî çíàòü òàêîå êîëè÷åñòâî
ôàêòîðîâ è âûçûâàþùèõ èõ ïîÿâëåíèå ïðè÷èí, ÷òî äàæå ïðîñòîå óñòàíîâëåíèå
íàëè÷èÿ ýòèõ ôàêòîðîâ, íå ãîâîðÿ óæå î òî÷íûõ êîëè÷åñòâåííûõ îöåíêàõ õà-
ðàêòåðèçóþùèõ èõ ïàðàìåòðîâ, ÿâëÿåòñÿ ïðîáëåìàòè÷íûì.
Äåéñòâèòåëüíî, â íàñòîÿùåå âðåìÿ ðåàëüíûå îøèáêè ðàñ÷åòíîãî îïðåäåëå-
íèÿ òðàåêòîðíûõ ôóíêöèé, ãëàâíûì îáðàçîì àýðîäèíàìè÷åñêèõ, ñîñòàâëÿþò
åäèíèöû, à èíîãäà è äåñÿòêè ïðîöåíòîâ. Â òî æå âðåìÿ òðåáóåìàÿ äëÿ ñîñòàâ-
ëåíèÿ òàáëèö ñòðåëüáû òî÷íîñòü îïðåäåëåíèÿ, â ÷àñòíîñòè, ñèëû ëîáîâîãî ñî-
ïðîòèâëåíèÿ ñðåäû äîëæíà õàðàêòåðèçîâàòüñÿ ñðåäèííîé îøèáêîé, íå ïðåâû-
øàþùåé äâóõ-òðåõ äåñÿòûõ äîëåé ïðîöåíòà.
Îòñþäà ñëåäóåò, ÷òî ïðàêòè÷åñêè åäèíñòâåííûì ìåòîäîì ðåøåíèÿ çàäà÷è
ñîñòàâëåíèÿ òàáëèö ñòðåëüáû ÿâëÿåòñÿ ìåòîä, â êîòîðîì êîððåêòíûå ìàòå-
ìàòè÷åñêèå ðàñ÷åòû, îñóùåñòâëÿåìûå ñ èñïîëüçîâàíèåì ìàêñèìàëüíîãî îáúåìà
äîïóñòèìîé îïûòíîé èíôîðìàöèè, êîìïëåêñèðóþòñÿ äàííûìè ïðîâîäèìûõ ïî
ñïåöèàëüíî ðàçðàáîòàííûì ìåòîäèêàì òàáëè÷íûõ ñòðåëüá, íîñÿùèõ ïðîâåðî÷-
íûé õàðàêòåð. Î÷åâèäíî, ÷òî âíå çàâèñèìîñòè îò òèïà èñïûòàíèé îäíîé èç
ïðèîðèòåòíûõ ñîñòàâëÿþùèõ áàëëèñòè÷åñêîãî ýêñïåðèìåíòà ÿâëÿåòñÿ îáðà-
áîòêà ðåçóëüòàòîâ èçìåðåíèé äëÿ ïîëó÷åíèÿ íåîáõîäèìûõ äîñòîâåðíûõ ñâåäå-
íèé î õàðàêòåðèñòèêàõ îòðàáàòûâàåìûõ îáðàçöîâ.
Áîëüøèå ïîòîêè èçìåðèòåëüíîé èíôîðìàöèè, âûñîêèå òðåáîâàíèÿ ïî êà÷å-
ñòâó åå îáðàáîòêè, ìàëûå èíòåðâàëû âðåìåíè, îòâîäèìûå íà ïðèíÿòèå îïåðà-
òèâíûõ ðåøåíèé, – âñå ýòî òðåáóåò øèðîêîãî èñïîëüçîâàíèÿ ñîâðåìåííîé âû-
÷èñëèòåëüíîé òåõíèêè.
Îñîáåííî ýòî àêòóàëüíî ïðèìåíèòåëüíî ê ïðîâåäåíèþ ëåòíûõ èñïûòàíèé
ðàêåò, îðãàíèçàöèÿ êîòîðûõ ïðåäïîëàãàåò íåîáõîäèìîñòü ñîçäàíèÿ íå òîëüêî
âçàèìîñâÿçàííûõ ñèñòåì âíåøíåòðàåêòîðíûõ è áîðòîâûõ òåëåìåòðè÷åñêèõ
èçìåðåíèé, íî è áûñòðîäåéñòâóþùèõ àâòîìàòèçèðîâàííûõ ñèñòåì óïðàâëåíèÿ
ëåòíûì ýêñïåðèìåíòîì.
Âûñîêàÿ ñòîèìîñòü ïðîâåäåíèÿ èñïûòàíèé (îñîáåííî ëåòíûõ) âûäâèãàåò
òðåáîâàíèå èõ ïðåäâàðèòåëüíîãî îïòèìàëüíîãî ïëàíèðîâàíèÿ. Ïëàíèðîâàíèå
äîëæíî áûòü îðèåíòèðîâàíî íà îáåñïå÷åíèå êîìïëåêñíîñòè âñåãî öèêëà îòðà-
áîòêè èçäåëèÿ ñ ó÷åòîì åãî íàçíà÷åíèÿ, ýôôåêòèâíîñòè èñïîëüçóåìîãî èçìåðè-
òåëüíîãî îáîðóäîâàíèÿ è ðÿäà äðóãèõ ôàêòîðîâ.
Ýêñïåðèìåíòàëüíàÿ áàëëèñòèêà, à òåì áîëåå ëåòíûå èñïûòàíèÿ ðàêåò,
êàê ýòî áûëî îòìå÷åíî âî ââåäåíèè ê äàííîìó ó÷åáíèêó, ÿâëÿþòñÿ â äîñòàòî÷-
íîé ñòåïåíè ñàìîñòîÿòåëüíûì íàïðàâëåíèåì è íå âõîäÿò íåïîñðåäñòâåííî â
÷èñëî âîïðîñîâ, ñîñòàâëÿþùèõ ñîäåðæàíèå ñîâðåìåííîé âíåøíåé áàëëèñòèêè
êàê íàóêè. Òåì íå ìåíåå èç èçëîæåííîãî âûøå ñëåäóåò, ÷òî ïî ìíîãèì àñïåê-
òàì îíè ñòîëü òåñíî âçàèìîñâÿçàíû (îñîáåííî â ÷àñòè àëãîðèòìè÷åñêîãî îáåñ-
ïå÷åíèÿ ýêñïåðèìåíòà, ïðîâåäåíèÿ òàáëè÷íûõ ñòðåëüá, îáðàáîòêè ðåçóëüòà-
519
òîâ îïûòíûõ ñòðåëüá), ÷òî èñêëþ÷åíèå èõ èç ÷èñëà çäåñü îáñóæäàåìûõ ñî âñåé
î÷åâèäíîñòüþ ïðèâåäåò ê ñíèæåíèþ êà÷åñòâà ïîäãîòîâêè ñïåöèàëèñòà.
Ñ äðóãîé ñòîðîíû, ýêñïåðèìåíòàëüíàÿ áàëëèñòèêà ÿâëÿåòñÿ íàèìåíåå ñòà-
áèëüíûì ðàçäåëîì áàëëèñòèêè, ïîäâåðæåííûì ñóùåñòâåííûì èçìåíåíèÿì, îáó-
ñëîâëåííûì îïåðåæàþùèì áàëëèñòè÷åñêóþ òåîðèþ ñîâåðøåíñòâîâàíèåì òåõ-
íè÷åñêèõ ñðåäñòâ, ïðèìåíÿåìûõ ïðè ïðîâåäåíèè ýêñïåðèìåíòîâ. Îòñëåæèâàíèå
äèíàìèêè ðàçâèòèÿ òàêèõ ñðåäñòâ, à ñîîòâåòñòâåííî è êîíêðåòíûõ, áàçèðóþ-
ùèõñÿ íà íèõ ìåòîäèê âðÿä ëè öåëåñîîáðàçíî â äîñòàòî÷íî ñòàáèëüíîì ó÷åáíè-
êå è âñåãäà ñîïðÿæåíî ñ åãî ïðåæäåâðåìåííûì "ñòàðåíèåì".
Ó÷èòûâàÿ äàííîå îáñòîÿòåëüñòâî, îãðàíè÷èìñÿ çäåñü èçëîæåíèåì îáùå-
òåîðåòè÷åñêèõ îñíîâ ýêñïåðèìåíòàëüíîé âíåøíåé áàëëèñòèêè è ëåòíûõ èñïû-
òàíèé ðàêåò, íå îñòàíàâëèâàÿñü íà êîíêðåòíûõ ñðåäñòâàõ ðåàëèçàöèè ñîîò-
âåòñòâóþùèõ ìåòîäèê è àëãîðèòìîâ.
12.1 . ÎÏÐÅÄÅËÅÍÈÅ ÏÀÐÀÌÅÒÐÎÂ ÄÂÈÆÅÍÈß
È ÎÑÍÎÂÍÛÕ ÕÀÐÀÊÒÅÐÈÑÒÈÊ ËÀ ÏÎ ÐÅÇÓËÜÒÀÒÀÌ
ÈÑÏÛÒÀÍÈÉ
12.1.1. ÎÁÙÀß ÕÀÐÀÊÒÅÐÈÑÒÈÊÀ ÁÀËËÈÑÒÈ×ÅÑÊÈÕ ÒÐÀÑÑ,
ÈÑÏÎËÜÇÓÅÌÛÕ ÏÐÈ ÏÐÎÂÅÄÅÍÈÈ ËÀÁÎÐÀÒÎÐÍÛÕ ÈÑÏÛÒÀÍÈÉ
Ïîä áàëëèñòè÷åñêîé òðàññîé îáû÷íî ïîíèìàþò ñïåöèàëüíî îáî-
ðóäîâàííûé èçìåðèòåëüíûé êîìïëåêñ, ïðåäíàçíà÷åííûé äëÿ ýêñ-
ïåðèìåíòàëüíîãî îïðåäåëåíèÿ äèíàìè÷åñêèõ õàðàêòåðèñòèê íàòóð-
íûõ è ìîäåëüíûõ, ñâîáîäíî äâèæóùèõñÿ òåë (ïóëü, àðòèëëåðèéñêèõ
ñíàðÿäîâ, ìîäåëåé ðàêåò è ò.ä .) .
Ïðèíÿòî ðàçëè÷àòü àýðîáàëëèñòè÷åñêèå, ãèäðîáàëëèñòè÷åñêèå è
òåððîáàëëèñòè÷åñêèå òðàññû. Ðàçëè÷èÿ óêàçàííûõ òðàññ îïðåäåëÿ-
þòñÿ ñîçäàâàåìîé â íèõ ñðåäîé.
 àýðîáàëëèñòè÷åñêîé òðàññå (ÀÁÒ) âîçäóøíàÿ ñðåäà ìîæåò èìåòü
ïîñòîÿííóþ (îòêðûòûå ÀÁÒ) èëè ïåðåìåííóþ (áàðîâàêóóìíûå
ÀÁÒ) ïëîòíîñòü.  òîì ñëó÷àå, êîãäà àýðîáàëëèñòè÷åñêèé êîìïëåêñ
îáîðóäóåòñÿ äîïîëíèòåëüíûìè ñðåäñòâàìè äëÿ ñîçäàíèÿ äâèæóùå-
ãîñÿ íàâñòðå÷ó ìåòàåìîìó ËÀ èëè åãî ìîäåëè ïîòîêà ñðåäû ñ çàðàíåå
çàäàííûìè õàðàêòåðèñòèêàìè, åãî íàçûâàþò àýðîáàëëèñòè÷åñêîé
òðóáîé. Ãèäðîáàëëèñòè÷åñêèå òðàññû (ÃÁÒ) ïðåäñòàâëÿþò ñîáîé
êîìïëåêñû, â êîòîðûõ ìåòàåìîå òåëî ñâîáîäíî äâèæåòñÿ â ãèäðîñðå-
äå. Êîíñòðóêòèâíî ÃÁÒ âûïîëíÿåòñÿ ëèáî â âèäå ãèäðîáàëëèñòè÷å-
ñêèõ êîëîäöåâ, ëèáî â âèäå ãèäðîáàëëèñòè÷åñêèõ ëîòêîâ. Ïåðâûå èç
íàçâàííûõ óñòðîéñòâ ïðåäíàçíà÷àþòñÿ äëÿ èññëåäîâàíèÿ äâèæåíèÿ
ìåòàåìûõ òåë, ðåàëèçóþùèõ îòâåñíûå èëè î÷åíü êðóòûå òðàåêòîðèè,
âòîðûå – ïîëîãèå òðàåêòîðèè. Òåððîáàëëèñòè÷åñêèå òðàññû (ÒÁÒ)
520
ñîäåðæàò çàêëþ÷åííóþ â ñïåöèàëüíûå êîíòåéíåðû ñðåäó ñî ñòðóê-
òóðîé è ñîñòàâîì, ìîäåëèðóþùóþ "ïðåãðàäó", ò.å. ñðåäó ïðîíèêíî-
âåíèÿ ñíàðÿäà (ïåñîê, ìåòàëë è äð.) . Ïî êîëè÷åñòâó ñîñòàâëÿþùèõ
êîìïîíåíòîâ ñðåä ðàçëè÷àþò ìîíîñðåäó (îäíîêîìïîíåíòíóþ) è ïî-
ëèñðåäó (ìíîãîêîìïîíåíòíóþ).
Âíå çàâèñèìîñòè îò êîíñòðóêòèâíûõ îñîáåííîñòåé ê ÷èñëó îá-
ùèõ îáÿçàòåëüíûõ ôóíêöèîíàëüíûõ ýëåìåíòîâ òðàññ îòíîñÿò: ìåòà-
òåëüíîå óñòðîéñòâî, ñèñòåìó ðåãèñòðàöèè (èçìåðåíèé), ñèñòåìó àâ-
òîìàòèçèðîâàííîé îáðàáîòêè ðåçóëüòàòîâ èçìåðåíèé è ïðèåìíîå
óñòðîéñòâî ìîäåëè èëè ñíàðÿäà (óëàâëèâàòåëü ìåòàåìîãî òåëà).
Íàèáîëåå ðàñïðîñòðàíåííûìè çàäà÷àìè, ðåøàåìûìè ñ èñïîëü-
çîâàíèåì áàëëèñòè÷åñêèõ òðàññ, ÿâëÿþòñÿ ñëåäóþùèå çàäà÷è ýêñïå-
ðèìåíòàëüíîé âíåøíåé áàëëèñòèêè:
îïðåäåëåíèå ñêîðîñòè è äðóãèõ ïàðàìåòðîâ ïîñòóïàòåëüíîãî è
âðàùàòåëüíîãî äâèæåíèé âûñòðåëèâàåìîãî èç ìåòàòåëüíîé óñòàíîâ-
êè îáúåêòà;
íàõîæäåíèå çíà÷åíèé àýðîäèíàìè÷åñêèõ êîýôôèöèåíòîâ ñèë è
ìîìåíòîâ, äåéñòâóþùèõ íà ËÀ â ïîëåòå;
èññëåäîâàíèå óñòîé÷èâîñòè äâèæåíèÿ ËÀ;
àíàëèç âëèÿíèÿ âîçìóùàþùèõ ôàêòîðîâ (íà÷àëüíûõ óñëîâèé)
âûñòðåëà, ðàçäåëåíèÿ ñòóïåíåé, ðàñêðûòèÿ îïåðåíèÿ è ò.ä . íà èçìå -
íåíèå ïàðàìåòðîâ äâèæåíèÿ ËÀ;
"íàáîð ñòàòèñòèêè" â ðàìêàõ ðåøåíèÿ ïåðå÷èñëåííûõ âûøå çà-
äà÷.
Ïîä÷åðêíåì, ÷òî óêàçàííûé ïåðå÷åíü íå èñ÷åðïûâàåò âñå âîç-
ìîæíûå âèäû ýêñïåðèìåíòàëüíûõ èññëåäîâàíèé, ïðîâîäèìûõ íà
òðàññàõ.  íåãî íå âîøëè ìíîãèå ñïåöèàëüíûå çàäà÷è òèïà èçó÷åíèÿ
àýðîäèíàìèêè ãðóïïîâîãî äâèæåíèÿ òåë, äâèæåíèÿ òåëà â ñïóòíîì
ñëåäå ëèäèðóþùåãî îáúåêòà è ìíîãèå äðóãèå, òðåáóþùèå ïîñòàíîâ-
êè è ïðîâåäåíèÿ èñêëþ÷èòåëüíî ñëîæíîãî è "òîíêîãî" ýêñïåðèìåí-
òà.
Ê ÷èñëó íåñîìíåííûõ äîñòîèíñòâ òðàññîâûõ èñïûòàíèé ñëåäóåò
îòíåñòè:
ïðîñòîòó êîíòðîëÿ ïàðàìåòðîâ ñðåäû, â êîòîðîé ïðîâîäèòñÿ ýêñ-
ïåðèìåíò;
âûñîêóþ òî÷íîñòü ïðîâîäèìûõ èçìåðåíèé;
âîçìîæíîñòü âûïîëíåíèÿ èçìåðåíèé è íàáëþäåíèé çà îáúåêòîì
íà ñðàâíèòåëüíî ìàëûõ ìåðíûõ áàçàõ;
äîïóñòèìîñòü âàðüèðîâàíèÿ â øèðîêèõ ïðåäåëàõ ïàðàìåòðîâ ñðå-
äû è õàðàêòåðèñòèê èñïûòóåìîãî îáúåêòà (èëè åãî ìîäåëè);
îòíîñèòåëüíî ìàëóþ ñòîèìîñòü ïðîâåäåíèÿ èñïûòàíèé.
Âìåñòå ñ òåì ñëåäóåò îòäàâàòü ñåáå îò÷åò â òîì, ÷òî èñïûòàíèÿ ñ
èñïîëüçîâàíèåì áàëëèñòè÷åñêèõ òðàññ èìåþò è äîñòàòî÷íî ñåðüåç-
íûå íåäîñòàòêè, ê êîòîðûì ïðåæäå âñåãî ñëåäóåò îòíåñòè:
521
ìàëûé ìàñøòàá ìîäåëåé èñïûòóåìîãî ËÀ;
íåâîçìîæíîñòü â ðÿäå ñëó÷àåâ ïîëíîãî ìîäåëèðîâàíèÿ ðåàëüíûõ
óñëîâèé äâèæåíèÿ ËÀ;
âëèÿíèå îòäåëüíûõ òåõíè÷åñêèõ ñèñòåì, èñïîëüçóåìûõ ïðè èñ-
ïûòàíèÿõ, íà ìîäåëüíîå äâèæåíèå íà òðàññå;
ìàëûé èíòåðâàë âðåìåíè ïðîâåäåíèÿ îäíîãî èñïûòàíèÿ è äëè-
òåëüíîñòü åãî ïîäãîòîâêè.
Îòìå÷åííûå íåäîñòàòêè, ïðèâîäÿùèå ê "ìàñøòàáíûì ýôôåê-
òàì" (ïîãðåøíîñòÿì ìîäåëèðîâàíèÿ), âîçíèêíîâåíèå íåîïðåäå-
ëåííîñòè â âûÿâëåíèè ôàêòîðîâ âçàèìîäåéñòâèÿ ËÀ ñî ñðåäîé è
îòäåëüíûìè èñïîëüçóåìûìè òåõíè÷åñêèìè ñðåäñòâàìè âûíóæäà-
þò ïðîåêòèðîâàòü ËÀ ñî çíà÷èòåëüíûìè çàïàñàìè ïî ïðî÷íîñò-
íûì è äðóãèì õàðàêòåðèñòèêàì. Â ñâÿçè ñ ýòèì èñïûòàíèÿ íà
áàëëèñòè÷åñêèõ òðàññàõ íå èñêëþ÷àþò íåîáõîäèìîñòè ïðîâåäå-
íèÿ ïîëèãîííûõ ñòðåëüá è ëåòíûõ èñïûòàíèé êàê ñóùåñòâåííûõ
ïî çíà÷èìîñòè ýòàïîâ ñîçäàíèÿ, îòðàáîòêè è ñäà÷è ïðîåêòèðóå-
ìûõ îáðàçöîâ âîîðóæåíèÿ.
12.1 .2. ÀËÃÎÐÈÒÌÈ×ÅÑÊÈÅ ÎÑÍÎÂÛ ÎÏÐÅÄÅËÅÍÈß ÑÊÎÐÎÑÒÈ
ÄÂÈÆÅÍÈß ÑÍÀÐßÄÀ È ÅÅ ÏÐÈÂÅÄÅÍÈß Ê ÄÓËÜÍÎÌÓ ÑÐÅÇÓ ÑÒÂÎËÀ
Ñóùåñòâóåò íåñêîëüêî ìåòîäîâ îïðåäåëåíèÿ ñêîðîñòè äâèæåíèÿ
òåëà ïî òðàåêòîðèè: îò íàèáîëåå ñòàðîãî, øèðîêî èñïîëüçóåìîãî íà
çàðå âîçíèêíîâåíèÿ ýêñïåðèìåíòàëüíîé áàëëèñòèêè, ñâÿçàííîãî ñ
èçìåðåíèåì âðåìåíè t ïðîõîæäåíèÿ òåëîì ó÷àñòêà òðàññû îïðåäå-
ëåííîé äëèíû l (ìåðíîé áàçû), äî ñîâðåìåííûõ ìåòîäîâ, áàçèðóþ-
ùèõñÿ íà ðåíòãåíîìåòðè÷åñêèõ, ðàäèî- è ëàçåðîëîêàöèîííûõ ñïî-
ñîáàõ.
Âíå çàâèñèìîñòè îò èñïîëüçóåìûõ òåõíè÷åñêèõ ñðåäñòâ íàéäåí-
íîå çíà÷åíèå ñêîðîñòè V (èçìåðÿåìîå â ì/ñ) áóäåò îòíîñèòüñÿ ê íå-
êîòîðîé òî÷êå òðàåêòîðèè (â áîëüøèíñòâå ñëó÷àåâ ñîâïàäàþùåé ñ
ñåðåäèíîé èçìåðèòåëüíîãî ó÷àñòêà), îòñòîÿùåé îò äóëüíîãî ñðåçà
ìåòàòåëüíîé óñòàíîâêè.
Äëÿ ïðèâåäåíèÿ ñêîðîñòè ê äóëüíîìó ñðåçó, ò.å . äëÿ îïðåäåëåíèÿ
íà÷àëüíîé ñêîðîñòè V0, ïîëüçóþòñÿ ôîðìóëîé, ïîëó÷åííîé â àíàëè-
òè÷åñêîì ìåòîäå ïñåâäîñêîðîñòè ïðèìåíèòåëüíî ê êîðîòêèì íà-
ñòèëüíûì òðàåêòîðèÿì:
DVDVcx
()().
−=
0
(12.1)
Ïðèíèìàÿ äëÿ ðàññìàòðèâàåìîãî ÷àñòíîãî ñëó÷àÿ ëèíåéíóþ
çàâèñèìîñòü ìåæäó èçìåíåíèåì ñêîðîñòè è èçìåíåíèåì ôóíêöèè
D(V ), ìîæíî ñîñòàâèòü ïðîïîðöèþ
522
DV DV
VV
DV
() () (),
−
−
=
0
0
10
∆
(12.2)
ãäå ∆D(V ) – èçìåíåíèå ôóíêöèè D(V ), îòâå÷àþùåå èçìåíåíèþ
àðãóìåíòà V íà 10 ì/ñ.
Îáîçíà÷àÿ V − V0 = ∆V è ñðàâíèâàÿ (12.1) è (12.2), ïîëó÷èì
∆
∆
DV
Vc
x
()
.
10
=
Ðàñêðûâàÿ çíà÷åíèå áàëëèñòè÷åñêîãî êîýôôèöèåíòà ñ, íàéäåì
ïîïðàâêó íà ïðèâåäåíèå ñêîðîñòè ê äóëüíîìó ñðåçó
∆
∆
V
id
Q
x
DV
=⋅
2
4
10
()
,
(12.3)
ãäå õ – ðàññòîÿíèå ìåæäó äóëüíûì ñðåçîì è ñåðåäèíîé ìåðíîãî
ó÷àñòêà òðàåêòîðèè; i – îïûòíûé êîýôôèöèåíò ôîðìû ñíàðÿäà
(ïóëè).
Çíà÷åíèÿ ∆D(V ) ïðèìåíèòåëüíî ê ôóíêöèè ñîïðîòèâëåíèÿ âîç-
äóõà Ñèà÷÷è ìîæíî áðàòü ïî òàáë. 3 .1, ïðèâåäåííîé â ðàáîòå [130].
Áîëåå òî÷íûå ðåçóëüòàòû äàåò èñïîëüçîâàíèå "ýòàëîííîé ôóíêöèè
1943 ã." . Â íàøåäøèõ øèðîêîå ðàñïðîñòðàíåíèå àðòèëëåðèéñêèõ
áàëëèñòè÷åñêèõ ñòàíöèÿõ (ÀÁÑ) âî èçáåæàíèå èñïîëüçîâàíèÿ òàá-
ëè÷íîé ôóíêöèè ∆D(V) ïðèìåíÿåòñÿ óïðîùåííûé ìåòîä ïðèâåäå-
íèÿ íà îñíîâå äîïëåðîâñêèõ èçìåðåíèé â äâóõ òî÷êàõ òðàåêòîðèè.
Ïðè ýòîì äîñòèãàåòñÿ ïðàêòè÷åñêè àáñîëþòíàÿ òî÷íîñòü (ïîãðåø-
íîñòü << 0,1%).
 ýêñïåðèìåíòàëüíûõ ðàáîòàõ ïî èçó÷åíèþ âûñîêîñêîðîñòíîãî
äâèæåíèÿ òåë íà áàëëèñòè÷åñêèõ òðàññàõ ÷àñòî ïðèìåíÿþò ìåòîä
ôîòîðåãèñòðàöèè. Ôîòîðåãèñòðàöèþ îñóùåñòâëÿþò íà ÀÁÒ ñ ïîìî-
ùüþ ñïåöèàëüíîé àïïàðàòóðû, êîòîðàÿ ÷åðåç ñòðîãî îïðåäåëåííûå
èíòåðâàëû âðåìåíè ôîòîãðàôèðóåò ñ ìàëîé ýêñïîçèöèåé äâèæóùåå-
ñÿ òåëî íà ôîíå ðåïåðíîé ñèñòåìû îòñ÷åòà (ò.å . êîîðäèíàòíûõ ñå-
òîê).
Èçìåðÿÿ ïðîñòðàíñòâåííûå êîîðäèíàòû òåëà ïî íåãàòèâàì ôîòî-
ãðàôèé (ôîòîïëàñòèíêàì) è çíàÿ, êàêîìó âðåìåíè îíè ñîîòâåòñòâó-
þò (ñ òî÷íîñòüþ äî ìèêðîñåêóíä), âû÷èñëÿþò ñêîðîñòü äâèæåíèÿ ñ
òî÷íîñòüþ äî ñîòûõ äîëåé ïðîöåíòà.
Íàðÿäó ñ ýòèì ôîòîãðàôèðîâàíèå òåë, äâèæóùèõñÿ ñî ñâåðõçâó-
êîâûìè ñêîðîñòÿìè, îáåñïå÷èâàåò ïîëó÷åíèå ñïåêòðîâ îáòåêàíèÿ.
Ôîðìà óäàðíîé âîëíû, ïîëîæåíèå òî÷åê îòõîäà çâóêîâûõ âîëí íà
ïîâåðõíîñòè òåëà è äð. äàþò âîçìîæíîñòü ñóäèòü î ñêîðîñòè äâèæå-
íèÿ òåëà, åñëè äëÿ åå îòûñêàíèÿ íå áûëè ïðîâåäåíû ñïåöèàëüíûå
523
èçìåðåíèÿ. Òî÷íîñòü îöåíêè ñêîðîñòè
ïðè ýòîì, ïðàâäà, ñóùåñòâåííî íèæå,
÷åì â ïðÿìûõ èçìåðåíèÿõ.
Ïðè äâèæåíèè òåëà ñî ñâåðõçâó-
êîâîé ñêîðîñòüþ ïåðåä íèì îáðàçó-
åòñÿ â îáùåì ñëó÷àå êðèâîëèíåéíàÿ
óäàðíàÿ âîëíà, êîòîðàÿ âäàëè îò òåëà
âûðîæäàåòñÿ â ñëàáóþ (çâóêîâóþ)
âîëíó âîçìóùåíèÿ, íàêëîíåííóþ ê
íàïðàâëåíèþ äâèæåíèÿ òåëà ïîä óã-
ëîì
μ=arcsin ,
1
M
(12.4)
ãäå Ì – ÷èñëî Ìàõà.
Ôîðìà óäàðíîé âîëíû â íåïîñðåäñò-
âåííîé áëèçîñòè îò äâèæóùåãîñÿ òåëà
çàâèñèò îò ôîðìû òåëà, ÷èñëà Ì è ñîîòíîøåíèÿ óäåëüíûõ òåïëîåì-
êîñòåé ãàçà k = Cp/CV.
Îäíàêî çàâèñèìîñòè, ñâÿçûâàþùèå çíà÷åíèå Ì (èëè V) ñ ãåîìåò-
ðè÷åñêèìè õàðàêòåðèñòèêàìè óäàðíîé âîëíû, â àíàëèòè÷åñêîì âèäå
ìîãóò áûòü ïîëó÷åíû òîëüêî äëÿ òåë ïðîñòûõ ãåîìåòðè÷åñêèõ
ôîðì – êëèíà, êîíóñà è ò.ï.
Íà ðèñ. 12 .1 ïîêàçàíà ôîðìà óäàðíîé âîëíû ïðè îáòåêàíèè
òåëà êîíè÷åñêîé ôîðìû. Óäàðíàÿ âîëíà çäåñü èìååò ôîðìó êî-
íóñà ñ óãëîì íàêëîíà êîñîãî ñêà÷êà, ðàâíûì θc. Óãîë θc ìîæåò
áûòü îïðåäåëåí ïðè îáðàáîòêå ôîòîñíèìêà ñïåêòðà îáòåêàíèÿ
êîíóñà.
Äëÿ ðàñ÷åòà ñêîðîñòè äâèæåíèÿ êîíè÷åñêîãî òåëà ïî èçâåñòíîìó
óãëó íàêëîíà ñêà÷êà ìîæíî èñïîëüçîâàòü ïðèáëèæåííóþ çàâèñè-
ìîñòü
MM
êê
sin
cos
sin
,
θβ
β
c
k
=−
++
−
⎧⎨⎩
⎫⎬⎭
11
1
2
22
1
2
(12.5)
ãäå βê – óãîë ïîëóðàñòâîðà êîíóñà.
Âû÷èñëåíèÿ ïî ýòîé çàâèñèìîñòè â äîñòàòî÷íî øèðîêîì äèàïà-
çîíå ÷èñåë Ì è βê äàþò îøèáêó â âåëè÷èíå V äî 5 %.
Ïðèìåðíî òàêóþ æå òî÷íîñòü äàåò ôîðìóëà
M
c
=−
−
(sin
,sin),
/
22
1
2
12
θβ
ê
(12.6)
ïðèãîäíàÿ äëÿ k = 1,4, ò.å . äëÿ âîçäóõà.
524
Ðèñ. 12 .1 . Ôîðìà óäàðíîé âîë-
íû ïðè îáòåêàíèè êîíè÷åñêîãî
òåëà
Èñïîëüçîâàíèå áîëåå ñëîæíûõ ìåòîäîâ àíàëèçà ïîçâîëÿåò íàõî-
äèòü ïî óãëó íàêëîíà ñêîðîñòü äâèæåíèÿ êîíóñà ïðè îáòåêàíèè åãî
ïîòîêîì ïîä óãëîì. Íî òî÷íîñòü òàêîé ìåòîäèêè íåâûñîêà, à ñëîæ-
íîñòü çíà÷èòåëüíà.
Ïðè äâèæåíèè çàòóïëåííîãî òåëà ëþáîé ôîðìû ñî ñâåðõçâóêî-
âîé ñêîðîñòüþ îáðàçóþùàÿñÿ ãîëîâíàÿ óäàðíàÿ âîëíà îòõîäèò îò
íåãî íà íåêîòîðîå ðàññòîÿíèå.  ïðîñòåéøåì ñëó÷àå ðàññòîÿíèå ìå-
æäó ïåðåäíåé êðîìêîé òåëà è ôðîíòîì óäàðíîé âîëíû îïðåäåëÿåò-
ñÿ, êàê è ôîðìà âîëíû, ôîðìîé ãîëîâíîé ÷àñòè òåëà, ÷èñëîì Ì è
îòíîøåíèåì óäåëüíûõ òåïëîåìêîñòåé ãàçà k = Cp/CV.
Ñëåäîâàòåëüíî, ïî èçìåðåííîìó íà ôîòîãðàôèè îòõîäó óäàðíîé
âîëíû òàêæå ìîæíî îïðåäåëèòü ñêîðîñòü äâèæåíèÿ òåëà.  êà÷åñòâå
çàòóïëåííûõ òåë, äëÿ êîòîðûõ ïðîâîäÿòñÿ èññëåäîâàíèÿ ïî îòõîäó
óäàðíîé âîëíû, îáû÷íî âûáèðàþòñÿ ñôåðà, ïîëóñôåðà, ýëëèïñîèä.
Ïðîèëëþñòðèðóåì ìåòîä íà ïðèìåðå îïðåäåëåíèÿ ñêîðîñòè òåëà
ñôåðè÷åñêîé ôîðìû.
Èçâåñòíî, ÷òî îòõîä ãîëîâíîé óäàðíîé âîëíû, èçìåðÿåìîé â òî÷-
êå, ãäå θc = 90°, ìîæåò áûòü âûðàæåí ÷åðåç îòíîñèòåëüíîå óïëîòíå-
íèå ãàçà íà íîðìàëüíîì ó÷àñòêå âîëíû, ò.å . íà ôðîíòå ïðÿìîãî ñêà÷-
êà óïëîòíåíèÿ.
Íàèáîëåå èçâåñòíû ñîîòíîøåíèÿ, ïðåäëîæåííûå Ñåðáèíûì:
∆=
−
−
2
3
11
(),
ρ
(12.7)
Ñåéôîì:
∆=
−
078 1
,,
ρ
(12.8)
Àìáðîçèî è Óîðòìàíîì:
∆=
−
−
052 1 0861
,(
).
,
ρ
(12.9)
Çäåñü ∆∆
=
/–
ρ îòíîñèòåëüíûé îòõîä âîëíû, èçìåðÿåìûé â äî-
ëÿõ ðàäèóñà ñôåðû r, ρρρ
=
∞
/–
îòíîñèòåëüíîå èçìåíåíèå ïëîòíî-
ñòè ãàçà íà ñêà÷êå.
Ýòè ñîîòíîøåíèÿ ñïðàâåäëèâû â øèðîêîì äèàïàçîíå èçìåíåíèÿ
âåëè÷èí k è ρ. Íàèáîëåå óíèâåðñàëüíûì ÿâëÿåòñÿ ïîñëåäíåå ñîîòíî-
øåíèå, ïðèãîäíîå äëÿ áîëüøîãî äèàïàçîíà èçìåíåíèé ÷èñëà Ìàõà.
Äëÿ k = 1,4 ðàñõîæäåíèÿ áîëåå 4 % íàáëþäàþòñÿ ëèøü ïðè Ì < 1,1.
Òàêèì îáðàçîì, çíàÿ ðàäèóñ ñôåðû r è îòõîä âîëíû ∆, èçìåðåí-
íûé ïî ôîòîãðàôèè, ìîæíî, èñïîëüçóÿ ñîîòíîøåíèÿ (12.7)...(12.9),
âû÷èñëèòü âåëè÷èíó ρ.  ñâîþ î÷åðåäü ρ äëÿ ïðÿìîãî ñêà÷êà óïëîò-
íåíèÿ îäíîçíà÷íî ñâÿçûâàåòñÿ ñ ÷èñëîì Ìàõà ñîîòíîøåíèåì
525
ρ=
+
65
22
MM
/( ).
Èñïîëüçóÿ äàííûå ðàñ÷åòà ïî ýòîé ìåòîäèêå, à òàêæå äðóãèå òåî-
ðåòè÷åñêèå è ýêñïåðèìåíòàëüíûå äàííûå, ìîæíî ïîñòðîèòü ãðàôèê
∆()
M (ðèñ. 12 .2), ïîçâîëÿþùèé ïî âåëè÷èíå îòíîñèòåëüíîãî îòõîäà
óäàðíîé âîëíû ∆ îïðåäåëÿòü ÷èñëî Ì è äàëåå ñêîðîñòü V äâèæåíèÿ
òåëà.
Àíàëîãè÷íî ìîãóò áûòü ïîñòðîåíû ãðàôèêè äëÿ ïîëóñôåðû è ýë-
ëèïñîèäà ñ ðàçëè÷íûìè ñîîòíîøåíèÿìè ïîëóîñåé.
12.1 .3. ÝÊÑÏÅÐÈÌÅÍÒÀËÜÍÎÅ ÎÏÐÅÄÅËÅÍÈÅ ÊÎÝÔÔÈÖÈÅÍÒÀ
ËÎÁÎÂÎÃÎ ÑÎÏÐÎÒÈÂËÅÍÈß ÑÐÅÄÛ ÁÀËËÈÑÒÈ×ÅÑÊÈÌÈ
ÌÅÒÎÄÀÌÈ
Îáû÷íî ñòðåëüáû äëÿ îïðåäåëåíèÿ cx a
()
Ì íà áàëëèñòè÷åñêîé
òðàññå îðãàíèçóþòñÿ òàê, ÷òîáû èçìåðÿåìûé ó÷àñòîê òðàåêòîðèè
îêàçàëñÿ ãîðèçîíòàëüíûì ñ öåëüþ èñêëþ÷åíèÿ ðàáîòû ñèëû òÿæå-
ñòè. Òîãäà íà îñíîâå çàêîíà èçìåíåíèÿ êèíåìàòè÷åñêîé ýíåðãèè
ñíàðÿäà ïîëó÷èì
m
VV Xd
S
a
S
S
21
2
2
2
1
2
(),
−=
∫
(12.10)
ãäå S2 − S1 = L õàðàêòåðèçóåò äëèíó ìåðíîãî ó÷àñòêà, íà êîòîðîì
îïðåäåëÿåòñÿ ñðåäíåå çíà÷åíèå ñèëû ëîáîâîãî ñîïðîòèâëåíèÿ X a ñð
,
ïðèíèìàåìîé ïîñòîÿííîé. Òîãäà
X
mVV
L
añð
=
−
2
1
2
2
2
.
(12.11)
526
Ðèñ. 12.2 . Ãðàôèê ∆/r â ôóíêöèè ÷èñëà Ìàõà
Ïîëó÷åííîå ïî äàííûì ýêñïåðèìåíòà çíà÷åíèå X a ñð
äîëæíî áûòü
îòíåñåíî ê îïðåäåëåííîìó çíà÷åíèþ ñêîðîñòè èñïûòûâàåìîãî
îáúåêòà, çà êîòîðóþ ïðèíèìàþò ñðåäíþþ ñêîðîñòü VV
V
ñð
=−
1
21
2
2
2
()
.
Äëÿ ïåðåõîäà îò ñèëû ëîáîâîãî ñîïðîòèâëåíèÿ X a ñð
ê
àýðîäèíàìè÷åñêîìó êîýôôèöèåíòó cx a
()
Ì èñïîëüçóåòñÿ çàâèñèìîñòü
XS
V
ñ
V
a
ax
a
ñð
ñð
ñð
=
⎛
⎝⎜⎞
⎠⎟
ρ2
2
,
(12.12)
ãäå ρ è à – ñîîòâåòñòâåííî ìàññîâàÿ ïëîòíîñòü âîçäóõà è ñêîðîñòü
çâóêà â âîçäóõå â ìîìåíò ïðîâåäåíèÿ ýêñïåðèìåíòà; S – õàðàêòåðíàÿ
ïëîùàäü òåëà.
Èç ñîïîñòàâëåíèÿ âûðàæåíèé (12.11) è (12.12) äëÿ X a ñð
ñëåäóåò
mVV
L
S
VV
c
V
a
xa
22
2
1
2
2
2
1
2
2
22
−
⎛
⎝⎜
⎞
⎠⎟=
−
⎛
⎝⎜
⎞
⎠⎟⎛
⎝⎜⎞
⎠⎟
ρ
ñð
.
Îòñþäà èñêîìîå çíà÷åíèå cx a
()
M ðàâíî
c
V
a
m
SL
VV
VV
x
ñð
a
⎛
⎝⎜⎞
⎠⎟=
−
+
412
12
ρ
.
(12.13)
Îêîí÷àòåëüíàÿ ðàñ÷åòíàÿ çàâèñèìîñòü ïîñëå îáúåäèíåíèÿ âñåõ
ïîñòîÿííûõ âåëè÷èí è ìàñøòàáíûõ êîýôôèöèåíòîâ èìååò âèä
c
V
a
Q
dL
VV
VV
xa
ñð
Ï
⎛
⎝⎜⎞
⎠⎟ =⋅
−
+
509 2
12
12
,,
(12.14)
ãäå d – äèàìåòð õàðàêòåðíîé ïëîùàäè òåëà; Ï – óäåëüíûé âåñ
âîçäóõà.
Ïðè ðàñ÷åòå âõîäÿùèå â ôîðìóëó âåëè÷èíû äîëæíû èìåòü ñëå-
äóþùèå ðàçìåðíîñòè: Q (H); d (ìì); L (ì); Ï (Í/ì3); V (ì/ñ). Çíà÷å-
íèÿ óäåëüíîãî âåñà âîçäóõà Ï äëÿ ðàçëè÷íûõ çíà÷åíèé áàðîìåòðè÷å-
ñêîãî äàâëåíèÿ h (ìì ðò. ñò .) è òåìïåðàòóðû âîçäóõà t (°C) îïðåäåëÿ-
þòñÿ ïî ñîîòâåòñòâóþùèì òàáëèöàì, ãäå Ï çàäàíî ÷åðåç çíà÷åíèÿ ñ
ðàçìåðíîñòüþ êã/ì3.
Äëèíà áàçû L äëÿ èçìåðåíèÿ cx a
äîëæíà âûáèðàòüñÿ òàê, ÷òîáû
îïðàâäûâàëîñü îñðåäíåíèå âåëè÷èíû Xa è âìåñòå ñ òåì îáåñïå÷èâà-
ëîñü çàìåòíîå ïàäåíèå ñêîðîñòè òåëà, íåîáõîäèìîå äëÿ ïîëó÷åíèÿ
òðåáóåìîé òî÷íîñòè ðàñ÷åòà.
527
 ïðàêòèêå èñïûòàíèé, îäíàêî, âîçíèêàþò ñèòóàöèè, êîãäà
ìåòàòåëüíàÿ óñòàíîâêà (íàïðèìåð, ïóøêà-ãàóáèöà èëè ìèíîìåò)
íå îáåñïå÷èâàåò ãîðèçîíòàëüíóþ òðàåêòîðèþ. Äàííîå îáñòîÿòåëü-
ñòâî â ñî÷åòàíèè ñ äîñòàòî÷íî ïðîòÿæåííûìè ìåðíûìè áàçàìè
(200...400 ì), ðåàëèçóåìûìè íà ïîëèãîíàõ, òðåáóåò ó÷åòà âëèÿíèÿ
ñèëû òÿæåñòè ïðè îïðåäåëåíèè cx a
ìåòîäîì áàëëèñòè÷åñêèõ
ñòðåëüá. Äàííàÿ ïðîáëåìà íå âîçíèêàåò ïðè èçìåðåíèè ñêîðîñòè
ñ èñïîëüçîâàíèåì èçìåðèòåëåé äîïëåðîâñêîãî òèïà.
Äëÿ ñëó÷àÿ, òðåáóþùåãî ó÷åòà âëèÿíèÿ ñèëû òÿæåñòè, âûðàæåíèå
(12.10) ïðèîáðåòàåò âèä
mV
mV
Xd
S
m
g
aa
S
S
2
2
1
2
221
2
−=
⎛
⎝⎜⎞
⎠⎟+
⎛
⎝⎜⎞
⎠⎟
∧
∧
∫ cos
cos
XS
gy
y
y
dy
1
2
∫
.
(12.15)
Ó÷èòûâàÿ, ÷òî cos
cos
,
XS
a
∧
⎛
⎝⎜⎞
⎠⎟ =°
=
−
180 1 ïîëó÷èì
m
VVm
g
yy Xd
S
a
S
S
21
2
2
2
21
1
2
()() .
−−
−
=
∫
(12.16)
Èñïîëüçóÿ
ïîíÿòèå
"ñðåäíåãî
çíà÷åíèÿ"
ñèëû
ëîáîâîãî
ñîïðîòèâëåíèÿ äëÿ ìåðíîãî ó÷àñòêà òðàåêòîðèè, íàéäåì
X
mVV
gyy
SS
añð
=
−−
−
−
2
2
1
2
2
2
21
21
()
.
(12.17)
Ó÷èòûâàÿ âûðàæåíèå (12.12), îêîí÷àòåëüíî ïîëó÷èì
c
V
a
m
SSS
VVg
yy
VV
xa
ñð
Ì
⎛
⎝⎜⎞
⎠⎟=
−
−−
−
+
42
21
1
2
2
2
21
12
()
()
()
ρ
2
.
(12.18)
Íåäîñòàòêîì äàííîãî ïîäõîäà, âïðî÷åì, êàê è ðàññìîòðåííîãî ðàíåå
ìåòîäà îïðåäåëåíèÿ cx a
íà ÀÁÒ, ÿâëÿåòñÿ òî, ÷òî îí äàåò òî÷å÷íóþ
îöåíêó èñêîìîãî êîýôôèöèåíòà, îòíåñåííóþ ê ñðåäíåé ñêîðîñòè,
ïîëó÷åííîé äëÿ ôèêñèðîâàííîãî ìåðíîãî ó÷àñòêà.
 ýòîì ñìûñëå áîëåå ïåðñïåêòèâíûì ÿâëÿåòñÿ ñïîñîá, îñíîâàí-
íûé íà îïðåäåëåíèè ñêîðîñòè äâèæåíèÿ òåëà â èñêîìîé òî÷êå ïî
èçìåðåíèÿì âðåìåíè ïðîõîæäåíèÿ èì íåñêîëüêèõ ìåðíûõ áàç. Â
ýòîì ñïîñîáå ôèêñèðóþò âðåìÿ ïîëåòà òåëà îò äóëüíîãî ñðåçà äî
ðàâíîîòñòîÿùèõ íà ðàññòîÿíèè h äðóã îò äðóãà òî÷åê òðàåêòîðèè. Ïî
ðåçóëüòàòàì çàìåðîâ âðåìåíè îïðåäåëÿþò çíà÷åíèÿ
528
∆ttt
nn
n
−−
=−
11
.
Äàëåå â ðåçóëüòàòå ÷èñëåííîãî äèôôåðåíöèðîâàíèÿ çàâèñèìîñòè
∆t = f1(S) îïðåäåëÿþò ôóíêöèþ f2(S)=dt/dS, à çàòåì âû÷èñëÿþò
V = dS/dt = f3(S). Èìåÿ çíà÷åíèÿ ôóíêöèè dV/dS = f4(S), ìîæíî íàéòè
cf
S
xa
=
5().Äëÿ èñêîìîé k-é òî÷êè òðàåêòîðèè
||
s
i
n,
c
m
SV
dV
dt
g
xk
k
k
a
=+
⎛
⎝⎜
⎞
⎠⎟
2
2
ρ
θ
Ì
ó÷èòûâàÿ, ÷òî
ïîëó÷èì îêîí÷àòåë
dV
dt
dV
dS
dS
dt
dV
dS
V
==
,ü
í
î
||
s
i
n.
c
m
SV
dV
dS
Q
SV
xk
k
k
k
k
a
=
⎛
⎝⎜⎞
⎠⎟+
21
2
2
ρρ
θ
MM
(12.19)
Äîñòîèíñòâîì ðàññìîòðåííîãî ñïîñîáà ÿâëÿåòñÿ òî, ÷òî â îäíîì
ýêñïåðèìåíòå ìîæåò áûòü îäíîâðåìåííî ïîëó÷åíî íåñêîëüêî
çíà÷åíèé cx a
, ñîîòâåòñòâóþùèõ îïðåäåëÿåìûì çíà÷åíèÿì ñêîðîñòè.
Ñóùåñòâåííûé íåäîñòàòîê çàêëþ÷àåòñÿ â ñëîæíîñòè è íåîá-
õîäèìîñòè âûïîëíåíèÿ ÷èñëåííîãî äèôôåðåíöèðîâàíèÿ òàáëè÷íûõ
ôóíêöèé, ñîïðîâîæäàþùåãîñÿ, êàê èçâåñòíî, âîçíèêíîâåíèåì
îøèáîê.
12.1 .4. ÎÏÐÅÄÅËÅÍÈÅ ÀÝÐÎÄÈÍÀÌÈ×ÅÑÊÈÕ ÊÎÝÔÔÈÖÈÅÍÒÎÂ
ÍÎÐÌÀËÜÍÎÉ ÑÈËÛ È ÎÏÐÎÊÈÄÛÂÀÞÙÅÃÎ ÌÎÌÅÍÒÀ
Àýðîäèíàìè÷åñêèå ôóíêöèè ïðè îïðîêèäûâàþùåì ìîìåíòå
KÌ(V/a) è ïðè ïîäúåìíîé ñèëå KN(V/a) òàêæå ìîãóò áûòü îïðåäåëå-
íû ïî ðåçóëüòàòàì ñòðåëüáû. Äëÿ ýòîãî â îïûòå èçìåðÿþòñÿ ýëåìåí-
òû âðàùàòåëüíîãî äâèæåíèÿ ñíàðÿäà δ,
•
,
δν,
•
,
ν r, ïîñëå ÷åãî íàçâàí-
íûå êîýôôèöèåíòû íàõîäÿòñÿ èç ñîîòâåòñòâóþùèõ ðàñ÷åòíûõ ôîð-
ìóë.
Ïðèìåíèòåëüíî ê ñëó÷àþ äâèæåíèÿ ãèðîñêîïè÷åñêè ñòàáèëèçè-
ðîâàííîãî ñíàðÿäà íà íà÷àëüíîì ó÷àñòêå òðàåêòîðèè ñ ìàëûìè óãëà-
ìè íóòàöèè (äî 10...15 °), êàê áûëî ïîêàçàíî ðàíåå (ñì. ãë . 7), óðàâ-
íåíèå íóòàöèîííûõ êîëåáàíèé èìååò âèä
δδσ
σ
=
−
•
()s
i
n,
0
1
at
529
ãäå óãëîâàÿ ñêîðîñòü ïðåöåññèè à ìîæåò áûòü ïðèíÿòà ïîñòîÿííîé
âåëè÷èíîé, ðàâíîé aA
C
=
−
1
2
1
0
•
,
φ à êîýôôèöèåíò ãèðîñêîïè÷åñêîé
óñòîé÷èâîñòè ïðè äâèæåíèè ñíàðÿäà ïî òðàññå – ðàâíûì åãî
ñðåäíåìó çíà÷åíèþ σ = σñð.
Òîãäà èç óðàâíåíèÿ íóòàöèîííûõ êîëåáàíèé íåòðóäíî îïðåäå-
ëèòü èõ ïîëóïåðèîä
T
a
δ
π
σ
2
=
.
(12.20)
Èç (12.20) èìååì
σ
π
δ
=
42
22
aT
.
Ó÷èòûâàÿ äàëåå, ÷òî a
2
(1 −σ)=β, ïîëó÷èì
β
π
δ
=−
⎛
⎝⎜
⎞
⎠⎟
a
aT
2
2
22
1
4
.
(12.21)
Ïîäñòàâëÿÿ â (12.21) âûðàæåíèÿ, âõîäÿùèå â çàâèñèìîñòü
ïàðàìåòðîâ, íàéäåì
dh
gA
HyV K
V
a
cV
AdT
2
32
22
0
2
222
2
10
4
⋅
⎛
⎝⎜⎞
⎠⎟ =−
()ñð M
ñð
ñð
π
η
π
δ
2.
Ïðè ñòðåëüáå íà ÀÁÒ ñ÷èòàþò, ÷òî H(y) = 1. Òîãäà íà ó÷àñòêå
ðåãèñòðàöèè ïðè V = Vñð èìååì
K
V
a
g
dhV
cV
Ad
A
T
M
ñð
ñð
⎛
⎝⎜⎞
⎠⎟=
⋅
−
⎛
⎝⎜
⎞
⎠⎟
π
η
δ
2
223
2
0
2
22
2
10
4
.
(12.22)
Çíà÷åíèå Òδ, âõîäÿùåå â çàâèñèìîñòü (12.22), áåðóò èç
ýêñïåðèìåíòàëüíîãî ãðàôèêà. Çíà÷åíèå h ïðèíèìàåòñÿ ïîñòîÿííûì.
Îíî ìîæåò áûòü âû÷èñëåíî ïî ýìïèðè÷åñêèì ôîðìóëàì. Íàèáîëåå
ïðîñòîé èç íèõ ÿâëÿåòñÿ çàâèñèìîñòü òèïà óïðîùåííîãî âàðèàíòà
ôîðìóëû Ãîáàðà (ñì. ãë. 1)
530
hhh
=+
1
1
3ã,
ãäå h1 – ðàññòîÿíèå îò öåíòðà ìàññ ñíàðÿäà äî íà÷àëà îæèâàëüíîé
÷àñòè; hã – äëèíà îæèâàëüíîé ÷àñòè.
Áîëåå ñëîæíîé, íî è áîëåå ïîëíî õàðàêòåðèçóþùåé ïàðàìåòðû
ñíàðÿäà è îáåñïå÷èâàþùåé ëó÷øåå ñîãëàñîâàíèå äàííûõ ýêñïåðè-
ìåíòà äëÿ ðàçëè÷íûõ âèäîâ ñíàðÿäîâ ñëåäóåò ñ÷èòàòü çàâèñèìîñòü
hWSld
=−
−
()
,
ÄÖ
2
â êîòîðîé SÄ – ïëîùàäü äîííîé ÷àñòè ñíàðÿäà; lÖ – ðàññòîÿíèå îò
äîííîãî ñðåçà äî öåíòðà ìàññ; W – îáúåì; d – êàëèáð.
Òàáëèöû çíà÷åíèé ôóíêöèè K
V
a
Ì
⎛
⎝⎜⎞
⎠⎟ ñîñòàâëÿþòñÿ äëÿ âïîëíå
îïðåäåëåííîãî ñïîñîáà íàõîæäåíèÿ âåëè÷èíû h, ÷òî äîëæíî áûòü
ñïåöèàëüíî îãîâîðåíî (ñì. ãë . 1).
Îïðåäåëåíèå àýðîäèíàìè÷åñêîãî êîýôôèöèåíòà íîðìàëüíîé
ñèëû ïðè ñòðåëüáå íà áàëëèñòè÷åñêîé òðàññå ìîæåò áûòü îñóùåñòâ-
ëåíî äâóìÿ ñïîñîáàìè:
ïåðâûé òðåáóåò ïðîâåäåíèÿ äâóêðàòíûõ ñòðåëüá ïðè ñìåùåíèè
âî âòîðîì âûñòðåëå öåíòðà ìàññ ñíàðÿäà ïî ïðîäîëüíîé îñè íà çà-
äàííóþ âåëè÷èíó áåç èçìåíåíèÿ åãî ãåîìåòðè÷åñêîé ôîðìû;
âòîðîé áàçèðóåòñÿ íà âûäåëåíèè ïåðèîäè÷åñêîé ñîñòàâëÿþùåé,
íåñóùåé èíôîðìàöèþ î âåëè÷èíå KN ïî ðåçóëüòàòàì ðåãèñòðàöèè
ïðîñòðàíñòâåííîãî äâèæåíèÿ öåíòðà ìàññ èññëåäóåìîãî òåëà.
Çäåñü ìû îãðàíè÷èìñÿ ðàññìîòðåíèåì îñíîâ âòîðîãî ñïîñîáà êàê
áîëåå ïðîñòîãî.
Ëèíåéíûå ïåðåìåùåíèÿ öåíòðà ìàññ ñíàðÿäà â âåðòèêàëüíîé è
áîêîâîé ïëîñêîñòÿõ ïîä äåéñòâèåì íîðìàëüíîé ñèëû îïèñûâàþòñÿ
çàâèñèìîñòÿìè
y
m
at
t
t
z
m
N
N
1
2
1
1
1
2
1
2
2
=−
−
+
⎛
⎝⎜
⎞
⎠⎟
=
δ
β
σ
ω
ω
ω
ω
ω
ω2
max
sin
sin ;
δ
β
ω
ω
ω
ω
ω
ω
max
cos
cos
.
2
11
2
1
1
1
2
2
tt
−
⎛
⎝⎜
⎞
⎠⎟ −−
⎛
⎝⎜
⎞
⎠⎟
⎡
⎣
⎢
⎤
⎦
⎥
(12.23)
Àíàëèç ñîîòíîøåíèé (12.23) äàåò îñíîâàíèå ñäåëàòü âûâîä, ÷òî öåíòð
ìàññ òåëà ñîâåðøàåò ñëîæíîå äâèæåíèå, ñîñòîÿùåå èç
íåïåðèîäè÷åñêîãî è äâóõ êðóãîâûõ ïåðèîäè÷åñêèõ ñ óãëîâûìè
ñêîðîñòÿìè ω1 è ω2. Àìïëèòóäà ïåðèîäè÷åñêîãî äâèæåíèÿ ñ óãëîâîé
531
ñêîðîñòüþ ω1 ìàëà ïî ñðàâíåíèþ ñ àìïëèòóäîé êðóãîâîãî äâèæåíèÿ ñ
óãëîâîé ñêîðîñòüþ ω2 , è ïðàêòè÷åñêè îíî íå îêàçûâàåò âëèÿíèÿ íà
äâèæåíèå öåíòðà ìàññ.
Ñ äðóãîé ñòîðîíû, ïðè ðåãèñòðàöèè äâèæåíèÿ öåíòðà ìàññ â
ïëîñêîñòè íåïîäâèæíîé ñèñòåìû êîîðäèíàò ÎèçìYèçìZèçì (ðèñ. 12 .3)
ïðåäñòàâëÿåòñÿ âîçìîæíûì âûäåëèòü ïåðèîäè÷åñêóþ ñîñòàâëÿþ-
ùóþ
2
1
2
r
m
m
N
=
δ
β
ω
ω
max
.
Òîãäà
K
ra
dlV
N
m
=
−
⋅
21
10
22
32
σσ
δ
().
max
(12.24)
Ïîãðåøíîñòè âû÷èñëåíèÿ KN ïî äàííîé ôîðìóëå â îñíîâíîì
îïðåäåëÿþòñÿ ïîãðåøíîñòÿìè èçìåðåíèÿ ïàðàìåòðîâ rm è δmax.
Ïðè ïðîâåäåíèè ïîëèãîííûõ èñïûòàíèé ðåãèñòðàöèÿ óãëîâîãî
ïîëîæåíèÿ îáúåêòà íà ôîíå ðåïåðíîé ñèñòåìû îòñ÷åòà â ïîäàâëÿþ-
ùåì áîëüøèíñòâå ñèòóàöèé ïðàêòè÷åñêè íåâîçìîæíà.  ýòîì ñëó÷àå
ïðè íåîáõîäèìîñòè ïîëó÷åíèÿ èíôîðìàöèè î ïàðàìåòðàõ óãëîâîãî
äâèæåíèÿ äîëæíû áûòü èñïîëüçîâàíû ëèáî ñïåöèàëüíî ñîçäàííûå,
ëèáî ïðèåìëåìûå äëÿ ýòèõ öåëåé ñóùåñòâóþùèå ñèñòåìû è ïðèáî-
ðû. Óêàçàííûå ñèñòåìû ïðåäñòàâëÿþò ñîáîé êîìïëåêñû èçìåðèòå-
ëåé (äàò÷èêîâ) óãëîâîé ñêîðîñòè è óãëîâîãî ïîëîæåíèÿ îáúåêòà â
532
Ðèñ. 12.3 . Ýêñïåðèìåíòàëüíàÿ çàïèñü äâèæåíèÿ öåíòðà ìàññ òåëà â ïëîñêîñòè, ïåð-
ïåíäèêóëÿðíîé ê âåêòîðó ñêîðîñòè:
* – ýêñïåðèìåíòàëüíûå òî÷êè
ñîîòâåòñòâóþùåé ñèñòåìå êîîðäèíàò. Íàèáîëåå ðàñïðîñòðàíåííû-
ìè ñèñòåìàìè òàêîãî òèïà ÿâëÿþòñÿ ãèðîñêîïè÷åñêèå. Îäíàêî äîñ-
òèãíóòûå ê íàñòîÿùåìó ïåðèîäó ðàçâèòèÿ èçìåðèòåëüíîé òåõíèêè
ãàáàðèòû òàêîãî ðîäà ñèñòåì çà÷àñòóþ èñêëþ÷àþò âîçìîæíîñòü èõ
èñïîëüçîâàíèÿ äëÿ îïðåäåëåíèÿ óãëîâîãî ïîëîæåíèÿ ìåòàåìûõ îáú-
åêòîâ ìàëûõ ãàáàðèòîâ. Äðóãèì ñóùåñòâåííûì íåäîñòàòêîì ÿâëÿåò-
ñÿ ñëàáàÿ çàùèùåííîñòü îò äåéñòâèÿ âûñîêèõ ïåðåãðóçîê, èñïûòû-
âàåìûõ ñíàðÿäîì â êàíàëå ñòâîëà àðòèëëåðèéñêîãî îðóäèÿ. Îòìå-
÷åííûå îáñòîÿòåëüñòâà âûíóæäàþò èñïîëüçîâàòü ñîîòâåòñòâóþùèå
èçìåðèòåëüíûå ñèñòåìû, ñâîáîäíûå îò óêàçàííûõ íåäîñòàòêîâ. Ê èõ
÷èñëó îòíîñÿòñÿ, â ÷àñòíîñòè, ìàãíèòîìåòðè÷åñêèå ñèñòåìû, ïî-
ñòðîåííûå íà îñíîâå ôåððîçîíäíûõ ìàãíèòîìåòðîâ (ÔÇÌ). Ïðèí-
öèï äåéñòâèÿ ìàãíèòîìåòðà îñíîâàí íà ïðåîáðàçîâàíèè íàïðÿæåí-
íîñòè èçìåðÿåìîãî ìàãíèòíîãî ïîëÿ â ïðîïîðöèîíàëüíûé ýëåêòðè-
÷åñêèé ñèãíàë. Îäíîêîìïîíåíòíûé ìàãíèòîìåòð ïîçâîëÿåò
èçìåðèòü òîëüêî îäíó ñîñòàâëÿþùóþ âåêòîðà íàïðÿæåííîñòè ìàã-
íèòíîãî ïîëÿ (Â). ×òîáû îïðåäåëèòü ïîëíûé âåêòîð, íåîáõîäèìî
èñïîëüçîâàòü òðè îðòîãîíàëüíî ðàçìåùåííûõ îäíîêîìïîíåíòíûõ
ìàãíèòîìåòðà. Èìåþòñÿ è ìíîãîêîìïîíåíòíûå ÔÇÌ, îäíîâðåìåí-
íî èçìåðÿþùèå òðåáóåìîå ÷èñëî ñîñòàâëÿþùèõ âåêòîðà Â. Ïðè èñ-
ïîëüçîâàíèè îäíîêîìïîíåíòíîãî ìàãíèòîìåòðà âûõîäíîé ñèãíàë
ÔÇÌ ìîæåò áûòü ïðåäñòàâëåí â âèäå ñêàëÿðíîãî ïðîèçâåäåíèÿ
U=°
BU,
ãäå U° – îðò íàïðàâëåíèÿ îñè ÷óâñòâèòåëüíîñòè ïðèáîðà. Òàêèì
îáðàçîì, ìàãíèòîìåòð ïîçâîëÿåò èçìåðèòü êîìïîíåíòó âåêòîðà B êàê
åãî ïðîåêöèþ íà îñü ÷óâñòâèòåëüíîñòè ïðèáîðà. Äëÿ òîãî ÷òîáû
óñòàíîâèòü ñâÿçü ìåæäó îðèåíòàöèåé ñíàðÿäà è âûõîäíûì ñèãíàëîì
ïðèáîðà, íåîáõîäèìî çàäàòü âåêòîð Â è âåêòîð U° (ïîëîæåíèå îñè
÷óâñòâèòåëüíîñòè) â îñÿõ îäíîãî è òîãî æå êîîðäèíàòíîãî áàçèñà.
Âûáîð â êà÷åñòâå ïîñëåäíåãî ñâÿçàííîé ñèñòåìû êîîðäèíàò äëÿ
çàäàíèÿ îáñóæäàåìûõ âåêòîðîâ äàåò âîçìîæíîñòü ïðèìåíÿòü
âûñòàâëåííûå îòíîñèòåëüíî îñåé ñèñòåìû ìàãíèòîìåòðû äëÿ
íåïîñðåäñòâåííîãî èçìåðåíèÿ îðèåíòàöèè ËÀ â ïðîöåññå ïîëåòà.
Ëîêàëüíûé âåêòîð íàïðÿæåííîñòè ìàãíèòíîãî ïîëÿ äîëæåí áûòü
èçâåñòåí ñ äîñòàòî÷íî âûñîêîé ñòåïåíüþ òî÷íîñòè, ïîñêîëüêó ïî-
ãðåøíîñòü â âû÷èñëåíèè óãëà ìåæäó  è U° íåïîñðåäñòâåííî çàâè-
ñèò îò òî÷íîñòè çíàíèÿ êàê íàïðàâëåíèÿ, òàê è ìîäóëÿ Â:
κ=
°
∧
−
arccos[( ) ].
BU B1
(12.25)
533
 èñõîäíîì âûðàæåíèè óêàçàííûé âåêòîð îáû÷íî çàäàåòñÿ â
ãåîäåçè÷åñêîé ñèñòåìå êîîðäèíàò òðåìÿ îðòîãîíàëüíûìè ïðîåê-
öèÿìè. Ïðè ýòîì äëÿ èõ îïèñàíèÿ ïðèìåíèòåëüíî ê ëîêàëüíûì
ðàéîíàì Çåìëè øèðîêî èñïîëüçóþòñÿ ôóíêöèîíàëüíûå ðÿäû: Òåé-
ëîðà, äâîéíîé ðÿä Ôóðüå, ðàçëîæåíèÿ ïî ñôåðè÷åñêèì ôóíêöèÿì,
ïîëèíîìû ×åáûøåâà è ò.ä.
Îïðåäåëåíèå óãëà ðàñòâîðà êîíóñà ðåãóëÿðíîé ïðåöåññèè, ñêîðî-
ñòè ïðåöåññèè è äðóãèõ ïàðàìåòðîâ äâèæåíèÿ âðàùàþùåãîñÿ îáúåê-
òà ìîæåò áûòü îñóùåñòâëåíî, åñëè èçâåñòåí âåêòîð êèíåòè÷åñêîãî
ìîìåíòà ñíàðÿäà K. Îðèåíòàöèÿ K â èíåðöèàëüíîì ïðîñòðàíñòâå
îäíîçíà÷íî îïðåäåëÿåòñÿ íà îñíîâå ìàãíèòîìåòðè÷åñêèõ èçìåðå-
íèé òîëüêî â òîì ñëó÷àå, êîãäà íà èíòåðâàëå èçìåðåíèé îðèåíòàöèÿ
âåêòîðà B íå îñòàåòñÿ íåèçìåííîé. Ïðè ýòîì íåîáõîäèìî èìåòü, êàê
ìèíèìóì, òðè íåêîìïëàíàðíûå ñîñòàâëÿþùèå âåêòîðà íàïðÿæåí-
íîñòè ìàãíèòíîãî ïîëÿ, ÷òî âûäâèãàåò ñîîòâåòñòâóþùèå òðåáîâàíèÿ
ê âûáîðó ïðîòÿæåííîñòè ìåðíîé áàçû.
Îöåíèâàÿ â öåëîì âîçìîæíîñòè îáñóæäàåìîãî ñïîñîáà, ñëåäóåò
ïîä÷åðêíóòü, ÷òî îí ïðèíöèïèàëüíî íå ìîæåò îáåñïå÷èòü âûñîêîé
òî÷íîñòè èçìåðåíèé, ñîïîñòàâèìîé ñ òî÷íîñòíûìè õàðàêòåðèñòèêà-
ìè, äîñòèãàåìûìè ñ èñïîëüçîâàíèåì ãèðîñêîïè÷åñêèõ èçìåðèòå-
ëåé, îñîáåííî ïðè îïðåäåëåíèè çíà÷åíèé ìàëûõ óãëîâ. Íåâûñîêàÿ
òî÷íîñòü îáúÿñíÿåòñÿ ïîãðåøíîñòÿìè, ñâÿçàííûìè ñ íåîïðåäåëåí-
íîñòüþ çíàíèÿ ïàðàìåòðîâ ìàãíèòíîãî ïîëÿ, ìåòîäè÷åñêèìè ïî-
ãðåøíîñòÿìè èõ ïðåäñòàâëåíèÿ, íàëè÷èåì âíóòðåííèõ øóìîâ òåëå-
ìåòðè÷åñêîé ñèñòåìû, ïåðåäàþùåé èíôîðìàöèþ ñ áîðòà èñïûòû-
âàåìîãî îáúåêòà íà Çåìëþ, à òàêæå èíñòðóìåíòàëüíûìè
ïîãðåøíîñòÿìè ñàìîãî ïðèáîðà.
Äîñòîèíñòâà ìàãíèòîìåòðè÷åñêèõ èçìåðèòåëåé – â íåâûñîêîé
ñòîèìîñòè, ìàëîé ìàññå è âûñîêîé íàäåæíîñòè ïðè äåéñòâèè âûñî-
êèõ ïåðåãðóçîê íà êîðïóñ ñíàðÿäà.
12.1.5. ÎÑÍÎÂÛ ÈÄÅÍÒÈÔÈÊÀÖÈÈ ÌÎÄÅËÜÍÎÃÎ ÄÂÈÆÅÍÈß ËÀ
Àíàëèç ðàññìîòðåííûõ âûøå çàäà÷, ðåøàåìûõ â ðàìêàõ ýêñ-
ïåðèìåíòàëüíûõ ïîëèãîííûõ èñïûòàíèé, äàåò îñíîâàíèå ñäåëàòü
âûâîä, ÷òî â ïîäàâëÿþùåì áîëüøèíñòâå ñëó÷àåâ íå ïðåäñòàâëÿ-
åòñÿ âîçìîæíûì ïî ðåçóëüòàòàì ïðÿìûõ èçìåðåíèé íåïîñðåäñò-
âåííî óñòàíîâèòü òðåáóåìóþ ñîâîêóïíîñòü ïàðàìåòðîâ, õàðàêòå-
ðèçóþùèõ ñîñòîÿíèå èñïûòóåìîãî îáúåêòà è åãî âçàèìîäåéñòâèå
ñ âíåøíåé ñðåäîé. Â ñâÿçè ñ ýòèì âîçíèêàåò íåîáõîäèìîñòü â
ïîñòàíîâêå è ðåøåíèè çàäà÷è èäåíòèôèêàöèè äèíàìè÷åñêîé ñèñ-
òåìû. Ïðèíÿòî ðàçëè÷àòü èäåíòèôèêàöèþ â øèðîêîì è óçêîì
ñìûñëå. Ïîä èäåíòèôèêàöèåé â øèðîêîì ñìûñëå îáû÷íî ïîíè-
534
ìàþò îïðåäåëåíèå ôîðìû îïòèìàëüíîãî ìàòåìàòè÷åñêîãî îïèñà-
íèÿ îáúåêòà è åãî ïàðàìåòðîâ, ñòåïåíè èçîìîðôíîñòè, ëèíåéíî-
ñòè, ñòàöèîíàðíîñòè è äðóãèõ ôóíäàìåíòàëüíûõ ñâîéñòâ, õàðàê-
òåðèçóþùèõ óðîâåíü îòîáðàæåíèÿ çàêîíîìåðíîñòåé, ïðèñóùèõ
îáúåêòó-îðèãèíàëó.  äàííîì ó÷åáíèêå èäåíòèôèêàöèÿ ðàññìàò-
ðèâàåòñÿ â óçêîì ñìûñëå êàê ïðîöåäóðà îïðåäåëåíèÿ íåïîñðåäñò-
âåííî íåèçìåðÿåìûõ ïàðàìåòðîâ äâèæåíèÿ, õàðàêòåðèñòèê îáúåê-
òà è ïàðàìåòðîâ ïðîöåññà åãî âçàèìîäåéñòâèÿ ñ âíåøíåé ñðåäîé
ïî èçìåðåíèÿì ïðîñòðàíñòâåííî-âðåìåííûõ õàðàêòåðèñòèê äâè-
æåíèÿ è íà îñíîâå èñïîëüçîâàíèÿ àïðèîðíûõ (äîîïûòíûõ) ìîäå-
ëåé ñèñòåìû (îáúåêòà) è (èëè) ñîîòâåòñòâóþùåãî èññëåäóåìîãî
ïðîöåññà. Ïðè ýòîì èñõîäíàÿ ïîñòàíîâêà çàäà÷è ïðåäïîëàãàåò
âîçìîæíîñòü ïîëó÷åíèÿ ðåçóëüòàòà äëÿ ïîëíîðàçìåðíîãî (íàòóð-
íîãî) ïðîöåññà ïî äàííûì ìîäåëüíûõ èñïûòàíèé.
Ó÷èòûâàÿ ñëîæíîñòü äàííîé çàäà÷è, èìåþùåé ñàìîñòîÿòåëüíîå
çíà÷åíèå, ìû îãðàíè÷èìñÿ ëèøü åå îáùåé ìàòåìàòè÷åñêîé ôîðìó-
ëèðîâêîé.
Ïóñòü çàäàíà àïðèîðíàÿ ìàòåìàòè÷åñêàÿ ìîäåëü ñîñòîÿíèÿ èñ-
ïûòóåìîãî îáúåêòà, ïðåäñòàâëÿþùåãî ñîáîé ìàñøòàáíóþ èëè ôèçè-
÷åñêóþ ìîäåëü ðåàëüíîãî (íàòóðíîãî) ËÀ:
d
dt
tt
tt
xF
x
xx
() [, (), ()], ()
,
==
λ
00
(12.26)
ãäå õ(t)–n -ìåðíûé âåêòîð-ñòîëáåö ïàðàìåòðîâ äâèæåíèÿ (ôàçîâûõ
êîîðäèíàò); x(0) = x0 – ïîäëåæàùèé îïðåäåëåíèþ âåêòîð íà÷àëüíûõ
óñëîâèé (t = 0) äëÿ ñèñòåìû (12.26); λ(t)–m -ìåðíûé âåêòîð-ñòîëáåö
îöåíèâàåìûõ (èäåíòèôèöèðóåìûõ) ïàðàìåòðîâ îáúåêòà, âíåøíåé
ñðåäû è ò.ä.; F –n
-ì åðíàÿ âåêòîð-ôóíêöèÿ, õàðàêòåðèçóþùàÿ
ñòðóêòóðó ïðàâûõ ÷àñòåé äèôôåðåíöèàëüíûõ óðàâíåíèé ñîñòîÿíèÿ,
îòâå÷àþùèõ âåêòîðíîìó óðàâíåíèþ (12.26).
Áóäåì ñ÷èòàòü òàêæå, ÷òî èçâåñòíà çàâèñèìîñòü, ñâÿçûâàþùàÿ
âåêòîð èçìåðÿåìûõ ïàðàìåòðîâ y(t) ñ âåêòîðîì ïàðàìåòðîâ äâèæå-
íèÿ îáúåêòà:
yCxN
x
() [; (), (; ())],
tt
tt
t
=
(12.27)
ãäå Ñ – p -ìåðíàÿ âåêòîð-ôóíêöèÿ, çàäàþùàÿ âèä ñêàëÿðíûõ
óðàâíåíèé, îòâå÷àþùèõ (12.27), íàçûâàåìûõ óðàâíåíèÿìè èçìå-
ðåíèé; N(t; x(t)) – âåêòîð ñîñòàâëÿþùèõ øóìîâ èçìåðåíèé ñ çàðàíåå
çàäàííûìè õàðàêòåðèñòèêàìè (ñòàòèñòè÷åñêèìè èëè äåòåðìè-
íèðîâàííûìè).
535
Çàäà÷à ïîëó÷åíèÿ íàèëó÷øèõ (â îïðåäåëåííîì ñìûñëå) îöåíîê
âåêòîðà x(t) ïî ðåçóëüòàòàì èçìåðåíèé âåêòîðà y(t) â ïðèñóòñòâèè
øóìîâ ñâîäèòñÿ ê çàäà÷å äèíàìè÷åñêîé ôèëüòðàöèè. Õîòÿ íàçâàí-
íàÿ çàäà÷à áëèçêî ñîïðèêàñàåòñÿ [35, 77] ñ çàäà÷åé èäåíòèôèêàöèè,
â ïîñëåäíþþ âñå æå âêëàäûâàþò íåñêîëüêî èíîé ñìûñë.
Ïðåäïîëîæèì, ÷òî øóì èçìåðåíèé îòñóòñòâóåò, ò.å . N(t; x(t))=0.
Òîãäà C[t; x(t)] áóäåò ïðåäñòàâëÿòü ñîáîé âåêòîð, êîòîðûé ïðè àáñî-
ëþòíî òî÷íûõ èçìåðåíèÿõ òîæäåñòâåííî ðàâåí ïîëíîìó (ð = n) ëèáî
óñå÷åííîìó (p < n) âåêòîðó èçìåðÿåìûõ ïàðàìåòðîâ.
Èìåÿ â âèäó (12.26), ïîäëåæàùèé èäåíòèôèêàöèè âåêòîð ïðåä-
ñòàâèì êàê
Φ=
=
=+
[,,][,,;,,];
.
ff xx
qnm
qn
m
11
0
0
1
KK
K
òò
λλ
(12.28)
Êàê ïðàâèëî, èçìåðåíèå õàðàêòåðèñòèê äâèæåíèÿ îñóùåñòâëÿåò-
ñÿ â äèñêðåòíûå ìîìåíòû âðåìåíè ti (i =0,1,..., k), ïðè÷åì îáû÷íî
ñïðàâåäëèâî íåðàâåíñòâî k > n.
Îòûñêàíèå îöåíêè âåêòîðà Φ òðåáóåò ââåäåíèÿ íåêîòîðîãî êðè-
òåðèÿ êà÷åñòâà
JJ
k
tt
ii
()y
C
ΦΦ
=
[; (; ), ()],
(12.29)
ãäå y(ti; Φ) – ðàñ÷åòíîå çíà÷åíèå èçìåðÿåìîãî âåêòîðà yi â ìîìåíò
âðåìåíè ti, ò.å. âåêòîð C(ti)|N=0; C(ti) – âåñîâàÿ ìàòðèöà èçìåðåíèé.
Âûáîð âèäà êðèòåðèÿ (ôóíêöèè) êà÷åñòâà (12.29) ñóáúåêòèâåí.
Îäíàêî åãî ñòðóêòóðà äîëæíà îòðàæàòü òðåáîâàíèå "áëèçîñòè" ïîëó-
÷àåìîé îöåíêè èñòèííîìó çíà÷åíèþ îïðåäåëÿåìîé âåëè÷èíû.  êà-
÷åñòâå óñëîâèÿ îïòèìàëüíîñòè ìîæåò âûñòóïèòü ðàâåíñòâî
∂∂
J()
ΦΦ
/=0
(12.30)
ëèáî
JJ
()
()
^
min
,
ΦΦ
=
(12.31)
ãäå Φ
∧
–
îöåíêà âåêòîðà Φ.
 ðàññìîòðåííîé ïîñòàíîâêå îáñóæäàåìàÿ çàäà÷à ïðåäñòàâëÿåò
ñîáîé â îáùåì ñëó÷àå çàäà÷ó ïàðàìåòðè÷åñêîé íåëèíåéíîé èäåíòèôè-
êàöèè. Åå ðåøåíèå ìîæåò áûòü ïîëó÷åíî íà îñíîâå ïðèìåíåíèÿ ðàç-
ëè÷íûõ ÷èñëåííûõ ìåòîäîâ.
536
 ðàìêàõ ñòîõàñòè÷åñêîé ïîñòàíîâêè çàäà÷è ïîëó÷åíèå ñîîòâåò-
ñòâóþùèõ îöåíîê ïðåäïîëàãàåò íàõîæäåíèå êîâàðèàöèîííîé ìàò-
ðèöû
KK
y
x
ΦΦ
=
⎛
⎝⎜⎞
⎠⎟
∂
∂
,,
*
p
(12.32)
ãäå pi
*
–
íàïåðåä çàäàííàÿ âåðîÿòíîñòü, çíà÷åíèå êîòîðîé îïðåäå-
ëÿåòñÿ õàðàêòåðîì ðåøàåìîé çàäà÷è è òðåáóåìîé ãàðàíòèðîâàííîé
íàäåæíîñòüþ ïîëó÷àåìîãî ðåçóëüòàòà.
Èçëîæåííîå âûøå ñïðàâåäëèâî äëÿ ðåøåíèÿ çàäà÷ èäåíòèôèêà-
öèè ëþáîãî äèíàìè÷åñêîãî ïðîöåññà íåçàâèñèìî îò òîãî, èäåò ëè
ðå÷ü î íàòóðíîì èëè ìîäåëüíîì ýêñïåðèìåíòå. Ïðèìåíèòåëüíî ê
ïîñëåäíåìó ñëó÷àþ, êîãäà ñòàâèòñÿ çàäà÷à íàõîæäåíèÿ ïî äàííûì
ìîäåëüíîãî ýêñïåðèìåíòà õàðàêòåðèñòèê äâèæåíèÿ ïîëíîðàçìåðíî-
ãî ËÀ, âåêòîð Φ
∧
äîëæåí áûòü ïîäâåðãíóò êîððåêöèè. Ïðåîáðàçîâà-
íèå âåêòîðà Φ
∧
â âåêòîð ′
∧
Φ îñóùåñòâëÿåòñÿ íà îñíîâå ðàçðàáîòàííûõ
ìåòîäîâ ìîäåëèðîâàíèÿ è òåîðèè ïîäîáèÿ äèíàìè÷åñêèõ ïðîöåñ-
ñîâ, ïðîèñõîäÿùèõ ïðè âçàèìîäåéñòâèè äâèæóùåãîñÿ ËÀ ñ âíåøíåé
ñðåäîé [110].
Ðåøåíèå î ñîñòîÿíèè íàòóðíîãî ËÀ ïî ðåçóëüòàòàì èäåíòèôèêà-
öèè ïàðàìåòðîâ äâèæåíèÿ ìîäåëüíîãî îáúåêòà ïðèíèìàåòñÿ íà îñ-
íîâå ïðîâåðêè âûïîëíåíèÿ íåðàâåíñòâ òèïà (12.32), çàïèñàííûõ äëÿ
ïîëíîðàçìåðíîãî ËÀ.
12.2 . ÁÀËËÈÑÒÈ×ÅÑÊÈÅ ÑÒÐÅËÜÁÛ
12.2.1 . ÑÒÐÅËÜÁÛ ÍÀ ÎÏÐÅÄÅËÅÍÈÅ ÓÃËÀ ÂÛËÅÒÀ
Ïîä óãëîì âûëåòà ïðèíÿòî ïîíèìàòü óãîë ìåæäó âåêòîðîì ñêîðî-
ñòè ñíàðÿäà â ìîìåíò ïðîõîæäåíèÿ èì äóëüíîãî ñðåçà è îñüþ êàíàëà
ñòâîëà îðóäèÿ äî ïðîèçâîäñòâà âûñòðåëà. Íåîáõîäèìîñòü îïûòíîãî
îïðåäåëåíèÿ óãëà âûëåòà îáóñëîâëåíà ãëàâíûì îáðàçîì òðåáîâàíè-
åì óòî÷íåíèÿ óãëà áðîñàíèÿ, à òàêæå îò÷àñòè åãî âçàèìîñâÿçüþ ñ âå-
ëè÷èíîé êîýôôèöèåíòà ôîðìû ñíàðÿäà, à ñëåäîâàòåëüíî, è åãî áàë-
ëèñòè÷åñêîãî êîýôôèöèåíòà. Íàõîæäåíèå ïîñëåäíåãî îñóùåñòâëÿ-
åòñÿ àïðèîðè ñ îòíîñèòåëüíîé ïîãðåøíîñòüþ, êàê ïðàâèëî, íå
ïðåâûøàþùåé 20 % îò ñðåäíåãî çíà÷åíèÿ âû÷èñëåííîãî áàëëèñòè-
÷åñêîãî êîýôôèöèåíòà. Õîòÿ çíà÷åíèå ñîîòâåòñòâóþùåé îøèáêè è
íåâåëèêî, îíî ìîæåò îêàçàòü âëèÿíèå íà èñòèííîå çíà÷åíèå óãëà
537
áðîñàíèÿ. Ïðè ýòîì îøèáêà áóäåò òåì ìåíüøå, ÷åì áîëüøå êàëèáð
îðóäèÿ è íà÷àëüíàÿ ñêîðîñòü ñíàðÿäà è ìåíüøå çàäàííàÿ äàëüíîñòü
ñòðåëüáû.
 àðòèëëåðèéñêîé ïðàêòèêå ïî ðåçóëüòàòàì áàëëèñòè÷åñêèõ
ñòðåëüá îáû÷íî ðàçäåëüíî îïðåäåëÿþò óãîë âûëåòà â âåðòèêàëüíîé è
ãîðèçîíòàëüíîé ïëîñêîñòÿõ. Äëÿ ýòîãî îñóùåñòâëÿþòñÿ ñòðåëüáû
ïî ùèòó, óñòàíîâëåííîìó íà ôèêñèðîâàííîì ðàññòîÿíèè (ïîðÿäêà
100 ì) îò îðóäèÿ.
Âåëè÷èíà óãëà âûëåòà íàõîäèòñÿ êàê ðàçíîñòü óãëîâ
γθφ
=−
0
,
(12.33)
ãäå θ0 – âû÷èñëåííûé óãîë áðîñàíèÿ; φ – ýêñïåðèìåíòàëüíî
îïðåäåëåííûé ïðè ñòðåëüáå óãîë âîçâûøåíèÿ.
Èçìåðåíèå óãëà φ âåäåòñÿ ïî ïîêàçàíèÿì êâàäðàíòà. Ïðè ñîîò-
âåòñòâóþùèõ âûâåðêàõ êâàäðàíòà è êîíòðîëüíîé ïëîùàäêè ìîæåò
áûòü îáåñïå÷åíà òî÷íîñòü èçìåðåíèé, õàðàêòåðèçóåìàÿ ìàêñèìàëü-
íîé ïðåäåëüíîé îøèáêîé, íå ïðåâûøàþùåé 1′.
Âåðòèêàëüíîå ïðåâûøåíèå ñðåäíåé òî÷êè ïîïàäàíèÿ ñíàðÿäîâ â
ùèò îòíîñèòåëüíî öåíòðà ìèøåíè, îòíåñåííîå ê ðàññòîÿíèþ äî
ùèòà õ, äàåò âåëè÷èíó òàíãåíñà óãëîâîãî ñìåùåíèÿ φñì. Òîãäà ïðè-
ìåíèòåëüíî ê èçâåñòíûì çíà÷åíèÿì φîï è ε (ïîä ε ïîíèìàåòñÿ óãîë
ìåñòà ãåîìåòðè÷åñêîãî öåíòðà ìèøåíè îòíîñèòåëüíî ãîðèçîíòà îðó-
äèÿ) èìååì
φφ εφ
=−
−
îï
ñì
.
(12.34)
Çíà÷åíèå óãëà θ0 âû÷èñëÿåòñÿ ïî ôîðìóëàì (ñì. ãë . 5)
cxDVDV
*
() ();
=−
0
(12.35)
sin
()()()
**
2
1
0
0
θ=
−
−
⎡
⎣⎢
⎤
⎦⎥
c
AV AV
cx
JV
(12.36)
ñ îøèáêîé, íå ïðåâîñõîäÿùåé 0,1 òûñÿ÷íîé, ñîîòâåòñòâóþùåé
óïîìÿíóòîìó âûøå çíà÷åíèþ ïðåäåëüíîé îòíîñèòåëüíîé îøèáêè
àïðèîðíîãî îïðåäåëåíèÿ áàëëèñòè÷åñêîãî êîýôôèöèåíòà. Ñêîðîñòü
V0 íàõîäèòñÿ ïî ìåòîäèêå, èçëîæåííîé â ï. 12.1.2. Âåëè÷èíà
ïðèâåäåííîãî áàëëèñòè÷åñêîãî êîýôôèöèåíòà äëÿ íîðìàëüíîé
ïëîòíîñòè âîçäóõà îïðåäåëÿåòñÿ êàê ñ* = cH(y).
Çäåñü æå îòìåòèì, ÷òî óãîë âûëåòà ìîæåò áûòü íàéäåí, îñîáåííî
äëÿ îðóäèé íåáîëüøèõ êàëèáðîâ, è â ïðîöåññå îïðåäåëåíèÿ íà÷àëü-
538
íîé ñêîðîñòè V0 ñòðåëüáîé íà ÀÁÒ. Äëÿ ýòèõ öåëåé â ïëîñêîñòè âòî-
ðîãî áëîêèðóþùåãî óñòðîéñòâà äîëæåí áûòü ðàçìåùåí ùèò ñ ðàçìå-
÷åííûìè íà íåì òî÷êàìè íàâîäêè (ïî ÷èñëó ïðîèçâîäèìûõ âûñòðå-
ëîâ). Îðóäèéíàÿ óñòàíîâêà â ýòîì ñëó÷àå ïåðåä êàæäûì âûñòðåëîì
ïî ïåðåêðåñòüÿì íà äóëüíîì è êàçåííîì ñðåçàõ íàâîäèòñÿ íà ðàçìå-
÷åííûå òî÷êè (êðåñòû). Ñíàðÿä â ñèëó íàëè÷èÿ óãëà âûëåòà è åãî ïî-
íèæåíèÿ ïîä âëèÿíèåì ñèëû òÿæåñòè ïîïàäàåò â ùèò, îñòàâëÿÿ ïðî-
áîèíó íà îïðåäåëåííîì ðàññòîÿíèè äî òî÷êè íàâîäêè.
Óãîë γ â ýòîì ñëó÷àå âû÷èñëÿåòñÿ íåïîñðåäñòâåííî ïî çàâèñèìî-
ñòè
tgγ= +
y
x
gx
V20
2,
(12.37)
ãäå y – âåðòèêàëüíàÿ ñîñòàâëÿþùàÿ îòêëîíåíèÿ.
Çíàê òðèãîíîìåòðè÷åñêîé ôóíêöèè áóäåò îïðåäåëÿòü è çíàê ñà-
ìîãî óãëà âûëåòà.
12.2.2 . ÑÒÐÅËÜÁÛ ÍÀ ÄÀËÜÍÎÑÒÜ È ÊÓ×ÍÎÑÒÜ
Öåëüþ ïðîâåäåíèÿ ñòðåëüá íà äàëüíîñòü è êó÷íîñòü ÿâëÿåòñÿ:
íàõîæäåíèå ýêñïåðèìåíòàëüíîé çàâèñèìîñòè ìåæäó óãëàìè áðî-
ñàíèÿ è äàëüíîñòÿìè ïîëåòà ñíàðÿäà ïðè îïðåäåëåííûõ ìåòåîáàëëè-
ñòè÷åñêèõ óñëîâèÿõ;
îöåíêà êîìïëåêñíîé õàðàêòåðèñòèêè äàííîé ïàðòèè ñíàðÿäîâ è
îáðàçöà âîîðóæåíèÿ â öåëîì ïðè èõ ïðèíÿòèè íà âîîðóæåíèå.
Ñòðåëüáû ïðè ýòîì ïðîèçâîäÿòñÿ äëÿ ôèêñèðîâàííûõ óãëîâ áðî-
ñàíèÿ ãðóïïàìè âûñòðåëîâ. Îäíîâðåìåííî ñî ñòðåëüáîé îñóùåñòâ-
ëÿåòñÿ ìåòåîïîäãîòîâêà. Ìåòåîèçìåðåíèÿ âåäóòñÿ íà âûñîòàõ, ïðå-
äåëüíûå çíà÷åíèÿ êîòîðûõ äëÿ êàæäîãî óãëà áðîñàíèÿ âû÷èñëÿþòñÿ
çàðàíåå ïî òàáëèöàì âíåøíåé áàëëèñòèêè ïðè ïðèáëèæåííîì çàäà-
íèè êîýôôèöèåíòà ôîðìû ñíàðÿäà.
Èçìåðåíèÿ äàëüíîñòè ïðîâîäÿò ñ òî÷íîñòüþ 1 ì, ôèêñèðóÿ ïðè
ýòîì çíà÷åíèÿ íà÷àëüíûõ (äóëüíûõ) ñêîðîñòåé ñíàðÿäà. Çàâèñèìî-
ñòè xc = f(θ0) äëÿ çàôèêñèðîâàííûõ V0 è ñ ñîñòàâëÿþò îñíîâó äëÿ òàá-
ëèö ñòðåëüáû. Â çàâèñèìîñòÿõ xc = f(V0, θ0, c) ôóíêöèîíàëüíàÿ ñâÿçü
xc = f(c), õîòÿ è ÿâëÿåòñÿ ìåíåå çíà÷èìîé, íî îêàçûâàåò íà òî÷íîñòü
îïðåäåëåíèÿ xc ñóùåñòâåííîå âëèÿíèå. Äåëî çàêëþ÷àåòñÿ â òîì, ÷òî
õàðàêòåð âðàùàòåëüíîãî äâèæåíèÿ ñíàðÿäà çàâèñèò îò óãëà áðîñà-
íèÿ, ñëåäîâàòåëüíî, ïðè ïîñòîÿííîé ñêîðîñòè áðîñàíèÿ è ñ = f(θ0).
Êðîìå òîãî, âåëè÷èíà ñ çàâèñèò è îò çíà÷åíèÿ ôóíêöèè ñîïðîòèâëå-
íèÿ âîçäóõà, ïðè ïîìîùè êîòîðîé óñòàíàâëèâàåòñÿ çàêîíîìåðíîñòü
èçìåíåíèÿ áàëëèñòè÷åñêèõ êîýôôèöèåíòîâ îò óãëîâ áðîñàíèÿ è íà-
539
÷àëüíûõ ñêîðîñòåé ýêñïåðèìåíòàëüíûì ïóòåì, ïîñêîëüêó äåéñòâè-
òåëüíûé ("èíäèâèäóàëüíûé") êîýôôèöèåíò ëîáîâîãî ñîïðîòèâëå-
íèÿ íåïðîïîðöèîíàëåí ýòàëîííîìó êîýôôèöèåíòó âî âñåì ðàáî÷åì
èíòåðâàëå ÷èñåë Ì. Ïðàêòèêà áàëëèñòè÷åñêèõ èñïûòàíèé ñâèäå-
òåëüñòâóåò, ÷òî íàèáîëüøàÿ òî÷íîñòü îïðåäåëåíèÿ áàëëèñòè÷åñêîãî
êîýôôèöèåíòà äîñòèãàåòñÿ ïðè óãëàõ áðîñàíèÿ â äèàïàçîíå îò 25 äî
50° . Ïðè ýòîì ÷òîáû ïîëó÷àòü çíà÷åíèÿ áàëëèñòè÷åñêîãî êîýôôè-
öèåíòà ñ îäíîé è òîé æå òî÷íîñòüþ, íåîáõîäèìî, ÷òîáû îòíîøåíèå
÷èñåë ïîâòîðåíèé èñïûòàíèé ïðè ðàçíûõ θ0 áûëî ðàâíî îòíîøåíèþ
êâàäðàòîâ ñðåäèííûõ îøèáîê ïîëó÷åíèÿ áàëëèñòè÷åñêîãî êîýôôè-
öèåíòà ïðè ðàññìàòðèâàåìûõ óãëàõ áðîñàíèÿ.
Ñòðåëüáû íà êó÷íîñòü êàê ñàìîñòîÿòåëüíûé âèä èñïûòàíèé ïðî-
âîäÿò ïðè ïðèíÿòèè îò ïðîìûøëåííîñòè îáðàçöà èëè âàëîâîé ïàð-
òèè áîåïðèïàñîâ íà âîîðóæåíèå. Äàæå â òîì ñëó÷àå, åñëè î÷åðåäíàÿ
ïàðòèÿ ñíàðÿäîâ íå ÿâëÿåòñÿ íîâîé è, ïî äàííûì ïðîèçâîäñòâà,
èìåþòñÿ ñâåäåíèÿ, ïîçâîëÿþùèå óòî÷íèòü èñêîìûå õàðàêòåðèñòèêè
êó÷íîñòè, àðòèëëåðèéñêàÿ ïðàêòèêà ñâèäåòåëüñòâóåò î öåëåñîîáðàç-
íîñòè ïðîâåäåíèÿ îáñóæäàåìîãî òèïà èñïûòàíèé. Ðàññìîòðèì îñ-
íîâíûå ïðàâèëà åãî ïðîâåäåíèÿ. Ïðåæäå âñåãî îáñóäèì ñàìî ïîíÿ-
òèå êó÷íîñòè ñòðåëüáû. Ïðè âûïîëíåíèè ëþáûõ ñòðåëüá íà äàëü-
íîñòü âû÷èñëÿþò âåëè÷èíû ñðåäèííûõ îòêëîíåíèé Âä è Âá. Ââèäó
òîãî ÷òî ïðè áàëëèñòè÷åñêèõ ñòðåëüáàõ çíà÷åíèå Âä â ñðåäíåì íà ïî-
ðÿäîê ïðåâîñõîäèò Âá, íà ïðàêòèêå êîíòðîëèðóþò ãëàâíûì îáðàçîì
ðàññåèâàíèå ñíàðÿäîâ ïî äàëüíîñòè. Áåçîòíîñèòåëüíî ê äàëüíîñòè è
óñëîâèÿì ïðîâåäåíèÿ ñòðåëüáû ñàìà ïî ñåáå âåëè÷èíà Âä íå ìîæåò
ñëóæèòü èíôîðìàòèâíûì êðèòåðèåì. Ïîýòîìó ñðåäèííûå îòêëîíå-
íèÿ, õàðàêòåðèçóþùèå ðàññåèâàíèå, îòíîñÿò ê äàëüíîñòè. Ýòè îòíî-
øåíèÿ è íàçûâàþòñÿ êó÷íîñòüþ. Ñòðîãî ãîâîðÿ, çäåñü ðå÷ü èäåò îá
îòíîñèòåëüíûõ õàðàêòåðèñòèêàõ êó÷íîñòè, êîòîðûå îáû÷íî óêàçû-
âàþòñÿ äðîáíûì ÷èñëîì, íàïðèìåð Bx
c
ä//
.
=1
240 Îñòàâëÿÿ â ñòî-
ðîíå óñëîâèÿ ïðîâåäåíèÿ èñïûòàíèé, ìîæíî óòâåðæäàòü, ÷òî ïðè
ñòðåëüáå ïîä óãëàìè áðîñàíèÿ, áëèçêèìè ê óãëó íàèáîëüøåé äàëü-
íîñòè, âåëè÷èíà êó÷íîñòè äëÿ çàäàííîé äàëüíîñòè ñòðåëüáû áóäåò
îïðåäåëÿòüñÿ òîëüêî ðàññåèâàíèåì áàëëèñòè÷åñêèõ êîýôôèöèåíòîâ
è ðàññåèâàíèåì íà÷àëüíûõ ñêîðîñòåé. Íà ïåðâûé âçãëÿä ìîæåò
ïðåäñòàâèòüñÿ öåëåñîîáðàçíûì ñ öåëüþ ïîâûøåíèÿ òî÷íîñòè è íà-
äåæíîñòè âû÷èñëåíèé ñîîòâåòñòâóþùèõ ñðåäèííûõ îòêëîíåíèé
ïîéòè ïî ïóòè ïîâûøåíèÿ êîëè÷åñòâà âûñòðåëîâ. Ïðåèìóùåñòâà òà-
êîãî ïóòè, îäíàêî, ÿâëÿþòñÿ êàæóùèìèñÿ. Äåëî çàêëþ÷àåòñÿ â òîì,
÷òî ïðè óâåëè÷åíèè ÷èñëà âûñòðåëîâ â ãðóïïå óâåëè÷èâàåòñÿ è âðå-
ìÿ îòñòðåëà ñíàðÿäîâ äàííîé ãðóïïû. Ýòî â ñâîþ î÷åðåäü ïðèâîäèò
ê óâåëè÷åíèþ âåðîÿòíîñòè èçìåíåíèÿ óñëîâèé ñòðåëüáû (ïðåæäå
âñåãî ïîãîäíûõ), à òàêæå ê èçìåíåíèþ áàëëèñòè÷åñêèõ õàðàêòåðè-
540
ñòèê ñòâîëà âñëåäñòâèå ðàçîãðåâà è èçíîñà. Ïðàêòèêà áàëëèñòè÷å-
ñêèõ ñòðåëüá ïîêàçàëà, ÷òî îïòèìàëüíûì ÷èñëîì âûñòðåëîâ â ãðóïïå
ñëåäóåò ñ÷èòàòü 7...10 âûñòðåëîâ. Îäíîêðàòíàÿ ñòðåëüáà óêàçàííûì
÷èñëîì âûñòðåëîâ â ãðóïïå ïîçâîëÿåò îïðåäåëèòü çíà÷åíèå Âä/õ ñ
îòíîñèòåëüíîé ñðåäèííîé îøèáêîé, íå ïðåâîñõîäÿùåé 20 % åãî
ñðåäíåãî çíà÷åíèÿ. Äëÿ ïîâûøåíèÿ òî÷íîñòè íåîáõîäèìû ìíîãî-
êðàòíûå ïîâòîðåíèÿ èñïûòàíèé.
12.2.3. ÎÏÐÅÄÅËÅÍÈÅ ÄÅÐÈÂÀÖÈÈ
Ñòðåëüáû íà îïðåäåëåíèå äåðèâàöèè, ò.å. áîêîâîãî îòêëîíåíèÿ
ñíàðÿäà âïðàâî ïðè ïðàâîé íàðåçêå îðóäèÿ (èëè âëåâî ïðè ëåâîé íà-
ðåçêå), ïðåäíàçíà÷åíû äëÿ óñòàíîâëåíèÿ îïûòíûõ çíà÷åíèé, íà îñ-
íîâå êîòîðûõ âîçìîæíî âû÷èñëåíèå òàáëè÷íûõ õàðàêòåðèñòèê äå-
ðèâàöèè. Ïðèíöèïèàëüíî äåðèâàöèÿ ìîæåò áûòü îïðåäåëåíà ïðè
ñòðåëüáàõ íà äàëüíîñòü è êó÷íîñòü,
ïðè âñòðå÷íûõ ñòðåëüáàõ è ïðè
ñòðåëüáå èç äâóõ îäíîòèïíûõ îðóäèé,
ñòâîëû êîòîðûõ íàðåçàíû â ïðîòèâî-
ïîëîæíûõ íàïðàâëåíèÿõ.
Èç âñåõ ïåðå÷èñëåííûõ ñïîñîáîâ
íàèáîëåå ïðîñòî òåõíè÷åñêè ðåàëèçóå-
ìûì è, ïîæàëóé, íàèáîëåå ýôôåêò-
íûì ñ òåîðåòè÷åñêîé òî÷êè çðåíèÿ ÿâ-
ëÿåòñÿ ñïîñîá âñòðå÷íûõ ñòðåëüá.
Ñóùíîñòü ýòîãî ñïîñîáà çàêëþ÷àåòñÿ
â ñëåäóþùåì. Ïîäáèðàþòñÿ äâà îðó-
äèÿ ïî âîçìîæíîñòè èäåíòè÷íûõ áàë-
ëèñòè÷åñêèõ êà÷åñòâ. Îðóäèÿ óñòàíàâ-
ëèâàþòñÿ íà åäèíîé ëèíèè áðîñàíèÿ
(ðèñ. 12 .4) äðóã ïðîòèâ äðóãà íà äèñ-
òàíöèè, ãàðàíòèðîâàííî îáåñïå÷è-
âàþùåé áåçîïàñíîñòü ïðîâåäåíèÿ
ñòðåëüá. Íàâîäêà îðóäèé îñóùåñòâëÿ-
åòñÿ òàê, ÷òîáû èõ ïëîñêîñòè áðîñà-
íèÿ ñîâïàäàëè.  êðàéíåì ñëó÷àå äî-
ïóñêàåòñÿ íåáîëüøîå ïàðàëëàêñíîå
ñìåùåíèå òî÷åê óñòàíîâêè îðóäèé
ïðè îáåñïå÷åíèè ñòðîãîé ïàðàëëåëü-
íîñòè ïëîñêîñòåé áðîñàíèÿ. Ñòðåëüáà
èç îðóäèé âåäåòñÿ ïî âîçìîæíîñòè îä-
íîâðåìåííî, ÷òî îáåñïå÷èâàåò îäèíà-
êîâîå âîçäåéñòâèå íà òðàåêòîðèè
âíåøíèõ ôàêòîðîâ, â ÷àñòíîñòè âåòðà.
541
Ðèñ. 12 .4. Îïðåäåëåíèå äåðèâà-
öèè ïðè âñòðå÷íûõ ñòðåëüáàõ â
ïðèñóòñòâèè âåòðà
Ïðè íàëè÷èè áîêîâîé ñîñòàâëÿþùåé ñêîðîñòè âåòðà (Wz) áîêîâîå
îòêëîíåíèå òî÷åê ïàäåíèÿ ïåðâîãî îðóäèÿ óìåíüøèòñÿ, à âòîðîãî –
óâåëè÷èòñÿ íà îäíó è òó æå âåëè÷èíó z W z
.
Ñóììà ïîëó÷åííûõ ïðè ñòðåëüáå áîêîâûõ îòêëîíåíèé áóäåò ðàâ-
íà âåëè÷èíå óäâîåííîé äåðèâàöèè:
zzzz z
WW
zz
äää
−+
+=
2.
(12.38)
Áîëåå ðàñïðîñòðàíåííûì, îäíàêî, ÿâëÿåòñÿ îïðåäåëåíèå äåðèâà-
öèè ïî âåëè÷èíå áîêîâîãî îòêëîíåíèÿ, èñïðàâëåííîãî íà âåòåð è
áîêîâîé óãîë âûëåòà, ñîãëàñîâàííîãî ñî ñïåöèàëüíîé "ôóíêöèåé äå-
ðèâàöèè" (ñì. ÃÎÑÒ 24288 -80).
12.2 .4. ÑÎÑÒÐÅË ÄÀËÜÍÎÑÒÅÉ È ÍÀ×ÀËÜÍÛÕ ÑÊÎÐÎÑÒÅÉ
ÏÐÈ ÈÇÌÅÍÅÍÈÈ ÊÎÍÑÒÐÓÊÒÈÂÍÛÕ ÝËÅÌÅÍÒÎÂ ÁÎÅÏÐÈÏÀÑÀ
Äàæå ìèíèìàëüíûå êîíñòðóêòèâíûå è òåõíîëîãè÷åñêèå èçìåíå-
íèÿ ïðè ïðîèçâîäñòâå áîåïðèïàñîâ ïðèâîäÿò ê çàìåòíûì èçìåíåíè-
ÿì èõ áàëëèñòè÷åñêèõ ñâîéñòâ. Íàïðèìåð, îêðàøåííûé è íåîêðà-
øåííûé ñíàðÿäû ïðè ïðî÷èõ èäåíòè÷íûõ õàðàêòåðèñòèêàõ èìåþò
ðàçëè÷íóþ äàëüíîñòü ïîëåòà.  ñèëó îòìå÷åííîãî îáñòîÿòåëüñòâà
ïðè ñîñòàâëåíèè òàáëèö ñòðåëüáû âîçíèêàåò íåîáõîäèìîñòü â îïðå-
äåëåíèè äàëüíîñòè ïîëåòà ïðè èçìåíåíèè êàêîãî-ëèáî ýëåìåíòà áîå-
ïðèïàñà. Ðåøåíèå òàêîé çàäà÷è òðåáóåò ïðîâåäåíèÿ ñòðåëüá ïðè
âîçìîæíî îäíîîáðàçíûõ óñëîâèÿõ îïûòà. Ïðè ýòîì âàðüèðóåìûå âà-
ðèàíòû âûñòðåëà ÷åðåäóþò ìåæäó ñîáîé. Òàêîé ñïîñîá ïðîâåäåíèÿ
ñòðåëüá íàçûâàþò ñîñòðåëîì.
×åðåäîâàíèå èñïûòóåìûõ âûñòðåëîâ ïðè ñîñòðåëàõ äàëüíîñòåé
ïðèâîäèò ê òîìó, ÷òî îøèáêè ïîëíîé ïîäãîòîâêè ñòðåëüáû äëÿ ðàç-
ëè÷íûõ ãðóïï âûñòðåëîâ îêàçûâàþòñÿ ïðàêòè÷åñêè îäèíàêîâûìè. Â
ðåçóëüòàòå èõ äåéñòâèå ñâåäåòñÿ ê òîìó, ÷òî öåíòðû ãðóïïèðîâàíèÿ
îòñòðåëÿííûõ ãðóïï ñìåñòÿòñÿ â êàêóþ-ëèáî îäíó ñòîðîíó, à âåëè-
÷èíà δxc ïî ñóùåñòâó íå èçìåíèòñÿ. Òî÷íîñòü îïðåäåëåíèÿ ðàçíîñòè
äàëüíîñòåé òåîðåòè÷åñêè íå çàâèñèò îò òîãî, èçðàñõîäîâàí ëè áîåçà-
ïàñ, ïðåäíàçíà÷åííûé äëÿ ïðîâåäåíèÿ èñïûòàíèé, ñðàçó ëèáî ïðè
ïîâòîðåíèè îïûòà íåñêîëüêî ðàç â ñëó÷àå ñîõðàíåíèÿ ñóììàðíîãî
÷èñëà âûñòðåëîâ â ãðóïïàõ. Îäíàêî ïðàêòè÷åñêè, êàê è ïðè ñòðåëü-
áàõ íà êó÷íîñòü, óâåëè÷åíèå êîëè÷åñòâà âûñòðåëîâ â ãðóïïå íå ðåêî-
ìåíäóåòñÿ.
Ñîñòðåëû íà÷àëüíûõ ñêîðîñòåé ïðîâîäÿòñÿ ñ öåëüþ îïðåäåëåíèÿ
èõ òàáëè÷íûõ çíà÷åíèé äëÿ îïûòíûõ ñòâîëîâ è ñíàðÿäîâ, à òàêæå
ïðè óñòàíîâëåíèè áàëëèñòè÷åñêèõ õàðàêòåðèñòèê çàðÿäîâ äàííîé
ïàðòèè ïî îòíîøåíèþ ê îáðàçöîâûì çàðÿäàì.
542
12.3 . ÎÑÍÎÂÛ ÒÅÎÐÈÈ ËÅÒÍÛÕ ÈÑÏÛÒÀÍÈÉ ÐÀÊÅÒ
È ÓÏÐÀÂËßÅÌÛÕ ÑÍÀÐßÄÎÂ
12.3 .1. ÝËÅÌÅÍÒÛ ÏËÀÍÈÐÎÂÀÍÈß ËÅÒÍÎÃÎ ÁÀËËÈÑÒÈ×ÅÑÊÎÃÎ
ÝÊÑÏÅÐÈÌÅÍÒÀ
Çàäà÷à ïëàíèðîâàíèÿ ëåòíîãî áàëëèñòè÷åñêîãî ýêñïåðèìåíòà (ËÁÝ)
ôîðìóëèðóåòñÿ ñëåäóþùèì îáðàçîì: òðåáóåòñÿ âûáðàòü ïðèåìëå-
ìóþ ìîäåëü ñîñòîÿíèÿ ËÀ, óñòàíîâèòü ñîñòàâ èçìåðÿåìûõ ïàðàìåò-
ðîâ, ñîãëàñîâàííûõ ñ âûáðàííîé ìîäåëüþ è äîïóñêàþùèõ èõ òåõíè-
÷åñêîå îñóùåñòâëåíèå, à òàêæå ðàçðàáîòàòü ïðîãðàììó èçìåðåíèé è
ñõåìó îáðàáîòêè èõ ðåçóëüòàòîâ ñ öåëüþ îïðåäåëåíèÿ è àíàëèçà ñ
òðåáóåìîé òî÷íîñòüþ è ìèíèìàëüíûìè çàòðàòàìè äåéñòâèòåëüíîãî
äâèæåíèÿ è (èëè) èñêîìûõ ëåòíî-êîíñòðóêòîðñêèõ õàðàêòåðèñòèê
(ìàññîâûõ, èíåðöèîííûõ, àýðîäèíàìè÷åñêèõ è ò.ä .) èñïûòóåìîãî
ËÀ.
Ñôîðìóëèðîâàííàÿ ïîñòàíîâêà çàäà÷è ïðåäîïðåäåëÿåò ðàññìîò-
ðåíèå ñàìîãî ïðîöåññà ëåòíûõ èñïûòàíèé êàê îáúåêòà èññëåäîâà-
íèÿ. Åñëè ïðè ïîëèãîííûõ àðòèëëåðèéñêèõ ñòðåëüáàõ íåîáõîäè-
ìîñòü îáðàùåíèÿ ê òåîðèè âîçíèêàåò ó ýêñïåðèìåíòàòîðîâ ëèøü íà
ïîñëåäíåì ýòàïå – ïðè îáðàáîòêå ðåçóëüòàòîâ èçìåðåíèé çàêîí÷åí-
íîãî îïûòà (ñòðåëüáû), òî â îòíîøåíèè ëåòíûõ èñïûòàíèé ðàêåò è
óïðàâëÿåìûõ ñíàðÿäîâ ïîëîæåíèå ðåçêî ìåíÿåòñÿ.
Çàòðàòû âðåìåíè, äåíåæíûõ èëè èíûõ ìàòåðèàëüíûõ ñðåäñòâ íà
ëåòíóþ îòðàáîòêó ñîâðåìåííûõ îáðàçöîâ (ïðè÷åì äàæå ïðîñòåéøèõ
íåóïðàâëÿåìûõ ðàêåò, íå ãîâîðÿ óæå îá óïðàâëÿåìûõ ðàêåòàõ è ñíà-
ðÿäàõ) âîçðàñòàþò íàñòîëüêî, ÷òî òðåáîâàíèå ïîâûøåíèÿ ýôôåêòèâ-
íîñòè ýêñïåðèìåíòà çà ñ÷åò åãî ïðåäâàðèòåëüíîãî îïòèìàëüíîãî
ïëàíèðîâàíèÿ ïåðåõîäèò èç ðàçðÿäà æåëàòåëüíîãî â ðàçðÿä îáÿçà-
òåëüíîãî. Ïëàíèðîâàíèå ýêñïåðèìåíòà ñòàâèò ñâîåé öåëüþ ðàçðàáî-
òàòü ÷åòêóþ ëîãè÷åñêóþ ñõåìó ïðîâåäåíèÿ ËÁÝ, äàòü íàó÷íî îáîñ-
íîâàííóþ ìåòîäèêó ðåøåíèÿ çàäà÷, âîçíèêàþùèõ â ïðîöåññå åãî
âûïîëíåíèÿ.
Ïëàíèðîâàíèå ËÁÝ äîëæíî íà÷èíàòüñÿ ñ èçó÷åíèÿ íåîïðåäåëåí-
íîñòåé è íåòî÷íîñòåé îòäåëüíûõ èçìåðåíèé è èõ êîìáèíàöèé, âîç-
íèêàþùèõ èç-çà èçìåðèòåëüíîé àïïàðàòóðû, êîòîðàÿ ìîæåò áûòü
èñïîëüçîâàíà ïðè ïðîâåäåíèè ëåòíûõ èñïûòàíèé íà äàííîì ïîëè-
ãîíå. Ñëåäóåò îòäàâàòü ñåáå îò÷åò â òîì, ÷òî, åñëè ïîòåíöèàëüíûå
òî÷íîñòíûå õàðàêòåðèñòèêè èçìåðèòåëüíûõ ñèñòåì ÷ðåçìåðíî íèç-
êè, íèêàêîé îïòèìàëüíûé ïëàí íå ñïàñåò ïîëîæåíèÿ. Îäíàêî, åñëè
àíàëèç íåîïðåäåëåííîñòåé äàåò îñíîâàíèå ñ÷èòàòü, ÷òî ïîãðåøíî-
ñòè ðàñïîëàãàåìîé èçìåðèòåëüíîé àïïàðàòóðû íàõîäÿòñÿ â ïðåäåëàõ
äîïóñêà, ó ýêñïåðèìåíòàòîðîâ ïîÿâëÿåòñÿ äîâîä äëÿ îáðàùåíèÿ ê
áîëåå òîíêèì àñïåêòàì ïëàíèðîâàíèÿ.
543
Ïðè îïðåäåëåíèè îïòèìàëüíîãî ïëàíà íàèáîëåå åñòåñòâåííûì
ïðåäñòàâëÿåòñÿ èñõîäèòü èç ïðèíöèïà îïòèìèçàöèè êàæäîãî ýòà-
ïà ïîäãîòîâêè è ïðîâåäåíèÿ ëåòíûõ èñïûòàíèé ñ òî÷êè çðåíèÿ
åäèíîãî êðèòåðèÿ, ÿâëÿþùåãîñÿ âàæíåéøèì ïîêàçàòåëåì ýêñïå-
ðèìåíòà.
Òàêèì îáîáùåííûì ïîêàçàòåëåì ñëóæèò ìàêñèìàëüíûé îáúåì
äîñòîâåðíûõ äàííûõ, ïîëó÷åííûõ â õîäå èñïûòàíèé ïðè ìèíèìàëü-
íûõ çàòðàòàõ. Åñòåñòâåííî, êîíêðåòíîå ìàòåìàòè÷åñêè ôîðìàëèçî-
âàííîå ïðåäñòàâëåíèå óêàçàííîãî îáîáùåííîãî êðèòåðèÿ ìîæåò
áûòü ðàçëè÷íûì.
Ïóñòü èìååòñÿ íåêîòîðàÿ îöåíî÷íàÿ ôóíêöèÿ φ(q), çàâèñÿùàÿ îò
âåêòîðà ïàðàìåòðîâ q =[q1, q2,..., qr]
ò
, íåñóùèõ èíôîðìàöèþ îá èñ-
ïûòûâàåìîì îáúåêòå. Ïðè ýòîì âåêòîð q ìîæåò âêëþ÷àòü â ñåáÿ ïî-
ìèìî ðåçóëüòàòîâ èçìåðåíèé ïîëíóþ èëè íåïîëíóþ àïðèîðíóþ èí-
ôîðìàöèþ. Ïóñòü, íàïðèìåð,
qm
K
qq
∈Q(,)
,
(12.39)
ãäå mq – ìàòåìàòè÷åñêîå îæèäàíèå âåêòîðà q; Kq – åãî
êîððåëÿöèîííàÿ ìàòðèöà.
Âñÿ èíôîðìàöèÿ î âåêòîðå q ïîñëå ïðîâåäåíèÿ ýêñïåðèìåíòà áó-
äåò çàêëþ÷åíà â ïëîòíîñòè âåðîÿòíîñòåé åãî îöåíêè p(),
q
∧
îïðåäåëÿå-
ìîé êàê
p
r
()() exp (
)()
qKq
m
K
q
m
q
qq
q
∧
−
−
∧
−
∧
=−
−
−
⎧⎨⎩
⎫
∧∧
∧
2
1
2
2
1
2
1
π
ò
⎬⎭
.
(12.40)
Ïëîòíîñòü âåðîÿòíîñòåé p (),
q
∧
åñòåñòâåííî, áóäåò çàâèñåòü îò óñ-
ëîâèé ïðîâåäåíèÿ ýêñïåðèìåíòà, îïðåäåëÿþùèõ ìíîæåñòâî {Q}, ò.å .
îò âûáîðà ìîäåëè äâèæåíèÿ Õ èç çàäàííîãî ìíîæåñòâà {X}, âûáîðà
ñîñòàâà èçìåðÿåìûõ ôóíêöèé Y ∈ {Y}, ïðîãðàììû èçìåðåíèé U ∈ {U}
è, íàêîíåö, ìåòîäà îáðàáîòêè ðåçóëüòàòîâ èçìåðåíèé W ∈ {W}. Òî-
ãäà ïðè àïðèîðè íåèçâåñòíîì çàêîíå ðàñïðåäåëåíèÿ q â êà÷åñòâå
êðèòåðèÿ îïòèìàëüíîñòè ýêñïåðèìåíòà ìîæåò áûòü ïðèíÿòà [17] âå-
ðîÿòíîñòü íàõîæäåíèÿ îöåíêè â çàäàííûõ ïðåäåëàõ
JQ pQ
(){||},
=−
<
∧
qqε
ãäå ε – íàïåðåä çàäàííàÿ ìàëàÿ âåëè÷èíà.
544
Ïðè ýòîì ïëàí ýêñïåðèìåíòà Q, ïðèíàäëåæàùèé ìíîæåñòâó {Q}
({}
)
,
QQ
∧
∈
îïðåäåëåííîìó êàê ïðÿìîå ïðîèçâåäåíèå ìíîæåñòâ {X} ×
×{Y} × {U} × {W}, áóäåò îïòèìàëüíûì ïî âåðîÿòíîñòè, åñëè
JQ
JQ
Q
() max ().
{}
∧
=
(12.41)
Åñëè çàêîí ðàñïðåäåëåíèÿ q ìîæíî ñ äîñòàòî÷íûìè íà òî
îñíîâàíèÿìè çàðàíåå ñ÷èòàòü íîðìàëüíûì (ãàóññîâñêèì), òî÷íîñòü
îïðåäåëåíèÿ âåêòîðà îöåíêè áóäåò îäíîçíà÷íî õàðàêòåðèçîâàòüñÿ
êîððåëÿöèîííîé ìàòðèöåé
K(
q
)
q
∧ =||
.
kij
(12.42)
 ïîñëåäíåì ñëó÷àå â êà÷åñòâå êðèòåðèåâ îïòèìàëüíîãî
ïëàíèðîâàíèÿ ýêñïåðèìåíòà ìîãóò áûòü èñïîëüçîâàíû [119]
ðàçëè÷íûå ñêàëÿðíûå õàðàêòåðèñòèêè óêàçàííîé ìàòðèöû, ïðè÷åì çà
ìíîãèìè èç íèõ â ëèòåðàòóðå çàêðåïèëèñü ñîáñòâåííûå íàçâàíèÿ.
Ïëàí íàçûâàåòñÿ À-îïòèìàëüíûì, åñëè êîððåëÿöèîííàÿ ìàòðèöà
èìååò íàèìåíüøèé ñëåä (øïóð)
min
.
{}
Q
SpK
q
∧
(12.43)
Êàê èçâåñòíî, ïîä ñëåäîì Sp (øïóðîì) ìàòðèöû K ïîíèìàþò ñóììó
äèàãîíàëüíûõ ýëåìåíòîâ k ii
i
m
.
=
∑1
Ó÷èòûâàÿ, ÷òî íà ãëàâíîé äèàãîíàëè
êîððåëÿöèîííîé ìàòðèöû ðàñïîëàãàþòñÿ äèñïåðñèè, À-îïòè-
ìàëüíûé ïëàí ìèíèìèçèðóåò ñðåäíþþ äèñïåðñèþ îöåíîê ïàðà-
ìåòðîâ. Ôèçè÷åñêèé ñìûñë äàííîãî è ïîñëåäóþùèõ êðèòåðèåâ
íàèáîëåå ïðîñòî ïîÿñíèòü ïðè èñïîëüçîâàíèè ãåîìåòðè÷åñêîé
èíòåðïðåòàöèè êîððåëÿöèîííîé ìàòðèöû îöåíîê èñêîìûõ ïàðà-
ìåòðîâ (ðèñ. 12.5). Ïðè íîðìàëüíîì çàêîíå ðàñïðåäåëåíèÿ ðåçóëü-
òàòîâ íàáëþäåíèé ïîâåðõíîñòÿìè ïîñòîÿííûõ çíà÷åíèé ôóíêöèè
ïëîòíîñòè ðàñïðåäåëåíèÿ ÿâëÿþòñÿ ýëëèïñîèäû, õàðàêòåðèñòèêè
êîòîðûõ ïîëíîñòüþ îïðåäåëÿþòñÿ ýëåìåíòàìè ìàòðèöû K
q
∧.
Äëÿ
óïðîùåíèÿ íà ðèñ. 12.5 ïðåäñòàâëåí ýëëèïñ äëÿ äâóìåðíîãî ñëó÷àÿ
(m = 2). Èç ðèñóíêà ñëåäóåò, ÷òî À-îïòèìàëüíûé ïëàí ìèíèìèçèðóåò
âåëè÷èíó äèàãîíàëè ïðÿìîóãîëüíîãî ïàðàëëåëåïèïåäà, â êîòîðûé
âïèñûâàåòñÿ êîððåëÿöèîííûé ýëëèïñîèä (ýëëèïñ äëÿ ðàññìàò-
ðèâàåìîãî ñëó÷àÿ).
545
Ïëàí íàçûâàåòñÿ D-îïòèìàëüíûì, åñëè åìó ñîîòâåòñòâóåò êîððå-
ëÿöèîííàÿ ìàòðèöà ñ íàèìåíüøèì çíà÷åíèåì îïðåäåëèòåëÿ
min det .
{}
Q
Kq
∧
(12.44)
Íàïîìíèì, ÷òî îïðåäåëèòåëåì êâàäðàòíîé ìàòðèöû K ïîðÿäêà m
íàçûâàåòñÿ ÷èñëî, ïîëó÷åííîå èç ýëåìåíòîâ ýòîé ìàòðèöû ïî
ôîðìóëå |K|=|| ()
,
KK
K
K
ik
mk
kkm
k
m
11
2
112
=−
Σ
K
ãäåKi(i=1
,2
,..., n)
ïðèíèìàþò âñå âîçìîæíûå çíà÷åíèÿ m! ïåðåñòàíîâîê èç ÷èñåë 1,
2, ..., m; k – ÷èñëî èíâåðñèé â êàæäîé ïåðåñòàíîâêå. Äàííûé ïëàí
ìèíèìèçèðóåò îáîáùåííóþ äèñïåðñèþ îöåíîê ïàðàìåòðîâ èëè
îáúåì êîððåëÿöèîííîãî ýëëèïñîèäà.
Íàêîíåö, ïëàí íàçûâàåòñÿ Å-îïòèìàëüíûì, åñëè ìàêñèìàëüíîå
õàðàêòåðèñòè÷åñêîå ÷èñëî ñîîòâåòñòâóþùåé åìó êîððåëÿöèîííîé
ìàòðèöû ìèíèìàëüíî:
min().
{} max
Q
λKq
∧
(12.45)
Ïîä õàðàêòåðèñòè÷åñêèìè ÷èñëàìè ìàòðèöû K ïîíèìàþò êîðíè λi
(i =1,2,..., m) óðàâíåíèÿ |λE − K| = 0, ãäå îïðåäåëèòåëü ìàòðèöû λE −
– K íàçûâàåòñÿ õàðàêòåðèñòè÷åñêèì ìíîãî÷ëåíîì ìàòðèöû K.
Îáñóæäàåìûé ïëàí ìèíèìèçèðóåò ìàêñèìàëüíóþ îñü êîððåëÿ-
öèîííîãî ýëëèïñîèäà. Îòìåòèì, ÷òî â îáùåì ñëó÷àå îäèí èç ïëàíîâ
ìîæåò îêàçàòüñÿ áîëåå ïðåäïî÷òèòåëüíûì ïî ñðàâíåíèþ ñ äðóãèì â
ñìûñëå îäíîãî èëè íåñêîëüêèõ êðèòåðèåâ, â òî âðåìÿ êàê ñ òî÷êè
çðåíèÿ äðóãîé ãðóïïû êðèòåðèåâ ïðåäïî÷òèòåëüíûì ìîæåò îêàçàòü-
ñÿ âòîðîé ïëàí ýêñïåðèìåíòà, ïðèçíàííûé íà îñíîâå ïåðâîé ãðóï-
ïû êðèòåðèåâ íåîïòèìàëüíûì [119].
546
Ðèñ. 12.5 . Ãåîìåòðè÷åñêàÿ èí-
òåðïðåòàöèÿ
êîððåëÿöèîííîé
ìàòðèöû îöåíîê èñêîìûõ ïàðà-
ìåòðîâ
Ïîêàæåì ýòî íà ñëåäóþùåì ïðîñòîì ïðèìåðå. Ïðåäïîëîæèì,
÷òî ïðîâåäåíû äâà îäíîòèïíûõ ýêñïåðèìåíòà ïðè îäèíàêîâîì ÷èñ-
ëå èçìåðåíèé n = 12.  ðåçóëüòàòå ïîëó÷åíû êîððåëÿöèîííûå ìàò-
ðèöû âèäà
KK
qq
1
2
1
12
303
015 0
3045
1
12
202
020
∧∧
=
−
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
−
−
,
,
;
204
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
.
Äëÿ íèõ èìååì |K1q| = 6,75⋅12
−3
;|K2q|=8
⋅12
-3
; SpKq1
34
∧=
/;
SpK q
2
23
∧=
/. Òàêèì îáðàçîì, â ñîîòâåòñòâèè ñ êðèòåðèåì
À-îïòèìàëüíîñòè ïðåäïî÷òåíèå äîëæíî áûòü îòäàíî âòîðîìó ïëàíó,
à ïî êðèòåðèþ D-îïòèìàëüíîñòè
–
ïåðâîìó.
Âûáîð òîãî èëè èíîãî êðèòåðèÿ, "îòâå÷àþùåãî" çà òî÷íîñòíûå
õàðàêòåðèñòèêè ïàðàìåòðîâ, îöåíèâàåìûõ ïî ðåçóëüòàòàì ýêñïåðè-
ìåíòà, îïðåäåëÿåòñÿ èñõîäÿ èç ôèçè÷åñêèõ îñîáåííîñòåé, ñâîéñò-
âåííûõ êîíêðåòíîìó ËÁÝ.
Ñðàâíåíèå îïòèìàëüíîñòè ïëàíîâ ýêñïåðèìåíòà òîëüêî ïî êî-
íå÷íûì òî÷íîñòíûì ðåçóëüòàòàì íå ó÷èòûâàåò çàòðàò, ïðè êîòîðûõ
áûë äîñòèãíóò òîò èëè èíîé ðåçóëüòàò. Èíîãäà æå ýêñïåðèìåíò ñ íå-
ñêîëüêî õóäøèìè (â ñìûñëå ðàññìîòðåííûõ âûøå êðèòåðèåâ) ïîêà-
çàòåëÿìè ìîæåò îêàçàòüñÿ áîëåå âûãîäíûì, åñëè çàòðàòû íà íåãî
îêàçûâàþòñÿ ñóùåñòâåííî ìåíüøèìè, ÷åì íà ïðîâåäåíèå ýêñïåðè-
ìåíòà ïî A-, D- èëè Å-îïòèìàëüíîìó ïëàíó.
Ïîýòîìó áîëåå óíèâåðñàëüíûì êðèòåðèåì îïòèìèçàöèè ïëàíà
ËÁÝ ñëåäóåò ñ÷èòàòü ôóíêöèþ âèäà
JQCkL
()
[],
=+
∧
Kq
(12.46)
ãäå k – ïîñòîÿííûé íîðìèðóþùèé ìíîæèòåëü; L[]–
Kq
∧
ôóíêöèîíàë,
îòâå÷àþùèé çà òî÷íîñòü îöåíèâàíèÿ è îïðåäåëÿåìûé òåì ìåòîäîì
ñðàâíåíèÿ ïëàíîâ, êîòîðûé íàèëó÷øèì îáðàçîì ñîîòâåòñòâóåò
äàííîé ýêñïåðèìåíòàëüíîé ñèòóàöèè; Ñ – ñóììàðíûå çàòðàòû íà
ïðîâåäåíèå ýêñïåðèìåíòà.
Ôóíêöèÿ J(Q) íàçûâàåòñÿ ôóíêöèåé ïîòåðü ýêñïåðèìåíòà Q. Êàê
è â ðàññìîòðåííûõ âûøå ÷àñòíûõ ñëó÷àÿõ çàäàíèÿ êðèòåðèÿ, äëÿ åãî
âûðàæåíèÿ, ñîîòâåòñòâóþùåãî (12.46), ïëàí ïðîâåäåíèÿ ýêñïåðè-
ìåíòà áóäåò îïòèìàëüíûì, åñëè ôóíêöèÿ ïîòåðü ïðèíèìàåò ìèíè-
ìàëüíîå çíà÷åíèå.
 ïîäàâëÿþùåì áîëüøèíñòâå ëåòíûõ ýêñïåðèìåíòîâ ñîñòàâ
íåïîñðåäñòâåííî èçìåðÿåìûõ ïàðàìåòðîâ îêàçûâàåòñÿ ñóùåñòâåí-
547
íî ìåíüøå ÷èñëà ïàðàìåòðîâ, ïîäëåæàùèõ îïðåäåëåíèþ. Ýòî âû-
íóæäàåò ïðèâëåêàòü äîïîëíèòåëüíóþ àïðèîðíóþ èíôîðìàöèþ â
âèäå ìàòåìàòè÷åñêîé ìîäåëè ñîñòîÿíèÿ èñïûòûâàåìîãî ËÀ. Î÷å-
âèäíî, ÷òî ïðè ýòîì ìîãóò áûòü èñïîëüçîâàíû ðàçëè÷íûå ìîäå-
ëè, â ÷àñòíîñòè è èç ÷èñëà òåõ, êîòîðûå áûëè ðàññìîòðåíû â
ãë. 3 . Ñîñòàâ èçìåðÿåìûõ ïàðàìåòðîâ òàêæå ìîæåò áûòü ðàçíîîá-
ðàçíûì. Ïîíÿòíî, ÷òî äàëåêî íå ïðè âñÿêîì ñî÷åòàíèè ìîäåëåé
Xi è Yj âîçìîæíî ïîëó÷åíèå òðåáóåìîãî ðåçóëüòàòà ìåòîäîì êîñ-
âåííûõ èçìåðåíèé. Ïîýòîìó ïðåæäå ÷åì ïåðåõîäèòü ê îïòèìàëü-
íîìó âûáîðó ìîäåëåé èç ìíîæåñòâà, îáðàçîâàííîãî ïðÿìûì ïðî-
èçâåäåíèåì ìíîæåñòâ {X} × {Y}, íåîáõîäèìî ïîëó÷èòü îòâåò íà
âîïðîñ î ñóùåñòâîâàíèè è åäèíñòâåííîñòè ðåøåíèÿ çàäà÷è îïðå-
äåëåíèÿ âåêòîðà îöåíèâàåìûõ ïàðàìåòðîâ ïî âåêòîðó èçìåðÿå-
ìûõ ïàðàìåòðîâ. Ïðè îïðåäåëåíèè äâèæåíèÿ ËÀ ïî äàííûì
âíåøíåòðàåêòîðíûõ èçìåðåíèé (ÂÒÈ) íàèáîëåå õàðàêòåðíûì ÿâëÿ-
åòñÿ îöåíèâàíèå íà÷àëüíûõ óñëîâèé äâèæåíèÿ. Íàïîìíèì [17,
35], ÷òî âîçìîæíîñòü âîññòàíîâëåíèÿ íà÷àëüíîãî ñîñòîÿíèÿ äè-
íàìè÷åñêîé ñèñòåìû ïî èçìåðåíèÿì åå âûõîäà òðàêòóåòñÿ êàê
ñâîéñòâî íàáëþäàåìîñòè äèíàìè÷åñêîé ñèñòåìû.
Óáåäèâøèñü, ÷òî îòîáðàííûå äëÿ ðàññìîòðåíèÿ ìîäåëè ïàð
X ↔ Y èç ìíîæåñòâà {X ↔ Y} óäîâëåòâîðÿþò óñëîâèþ íàáëþäàåìî-
ñòè, ìîæíî ïåðåéòè ê âûáîðó íàèëó÷øåé (â ñìûñëå ïðèíÿòîãî êðè-
òåðèÿ) ïàðû èç èõ âîçìîæíûõ ñîâîêóïíîñòåé. Äëÿ êàæäîé èç óêà-
çàííûõ ïàð ìîæåò áûòü íàéäåíà ñâîÿ êîððåëÿöèîííàÿ ìàòðèöà, îï-
ðåäåëÿåìàÿ êàê
K
x
q
y
x
K
y
x
x
q
q
n
∧=
⎡
⎣⎢
⎤
⎦⎥
⎡
⎣⎢
⎤
⎦⎥
⎡
⎣⎢
⎤
⎦⎥
⎡
⎣⎢
⎤
⎦⎥
−
∂
∂
∂
∂
∂
∂
∂
∂
1
ò
ò
⎧
⎨⎪
⎩⎪
⎫
⎬⎪
⎭⎪ä=mq
.
(12.47)
Çäåñü ìàòðèöà
R
y
x
K
y
x
n
()
,
Y=⎡
⎣⎢
⎤
⎦⎥
⎡
⎣⎢
⎤
⎦⎥
−
∂
∂
∂
∂
1
ò
ãäå Kn
–
êîððåëÿöèîííàÿ ìàòðèöà èçìåðèòåëüíûõ øóìîâ,
õàðàêòåðèçóþùàÿ ìîäåëü èçìåðåíèé, à ìàòðèöà
G
x
q
()
X=
⎡
⎣⎢
⎤
⎦⎥
∂
∂
–
ìîäåëü äâèæåíèÿ.
548
Âîñïîëüçîâàâøèñü îäíèì èç êðèòåðèåâ îïòèìàëüíîãî ïëàíèðî-
âàíèÿ, íàïðèìåð êðèòåðèåì D-îïòèìàëüíîñòè, óñëîâèå îïòèìàëüíî-
ñòè âûáðàííîé ïàðû X ↔ Y ïðåäñòàâèì â âèäå
min det{
( )}.
{}
XY
GXRYGX
↔
()() ò
(12.48)
Ïðîöåäóðó ïîèñêà îïòèìàëüíîãî ðåøåíèÿ, îòâå÷àþùåãî (12.48),
ðàññìîòðèì íà ïðîñòåéøåì ñëó÷àå ïåðåáîðà âàðèàíòîâ, êîãäà êàæäîå
èç ìíîæåñòâ {X}è{Y} âêëþ÷àåò â ñåáÿ ïî äâå ìîäåëè.
Î÷åâèäíî, ÷òî, êîìáèíèðóÿ ðàçëè÷íûå ìîäåëè äâèæåíèÿ èç ìíî-
æåñòâà {X} ñ ðàçëè÷íûìè óðàâíåíèÿìè èçìåðåíèÿ èç ìíîæåñòâà {Y},
ìîæíî ïîëó÷èòü ÷åòûðå ðàçëè÷íûõ âàðèàíòà êîððåëÿöèîííûõ ìàò-
ðèö îöåíîê âåêòîðà q. Äëÿ êàæäîé èç ýòèõ ìàòðèö íåîáõîäèìî âû-
÷èñëèòü çíà÷åíèå åå îïðåäåëèòåëÿ. Íàèáîëüøåå çíà÷åíèå îïðåäåëè-
òåëÿ, íàïðèìåð ||,
Kq
∧
21 óêàæåò íà îïòèìàëüíûé âàðèàíò ñîãëàñîâàí-
íûõ ìîäåëåé. Äëÿ íàøåãî ñëó÷àÿ – âòîðîé ìîäåëè äâèæåíèÿ è
ïåðâîé ìîäåëè èçìåðåíèÿ. Ñëåäóåò îòìåòèòü, ÷òî ðàññìîòðåííûé
âûáîð îïòèìàëüíîé ñîãëàñîâàííîé ïàðû X ↔ Y â ðàìêàõ äàííîé ïî-
ñòàíîâêè çàäà÷è îñóùåñòâëÿåòñÿ äëÿ ôèêñèðîâàííîé ïðîãðàììû èç-
ìåðåíèé U ∈ {U}. Âàðüèðóÿ ïîñëåäîâàòåëüíîñòü èçìåðåíèé uy, îïðå-
äåëÿþùóþ ïðîãðàììó, ìîæíî ïðèéòè ê áîëåå îïòèìàëüíîìó âàðè-
àíòó. Åãî ïîèñê â ðàìêàõ D-îïòèìàëüíîãî ïëàíèðîâàíèÿ ñâîäèòñÿ ê
ðåøåíèþ ñèñòåìû ýêñòðåìàëüíûõ óðàâíåíèé
∂∂ ∂∂
Ku
K
q
y
q
∧∧
==
/;/.
00
t
(12.49)
Ïðè ñîâìåñòíîì ðàññìîòðåíèè ìîäåëè äâèæåíèÿ ËÀ è ìîäåëè
èçìåðåíèÿ, ñ îäíîé ñòîðîíû, è ðåàëüíûõ óñëîâèé èçìåðåíèÿ – ñ
äðóãîé, âîçíèêàåò âîïðîñ òîæäåñòâåííîñòè ìàòåìàòè÷åñêîé ìîäåëè
X ↔ Y äåéñòâèòåëüíîìó ïðîöåññó ëåòíûõ èñïûòàíèé. Èñ÷åðïûâàþ-
ùåé èíôîðìàöèåé î ôàêòè÷åñêîì ñîñòîÿíèè ËÀ êàê äèíàìè÷åñêîé
ñèñòåìû ÿâëÿåòñÿ èçìåðèòåëüíàÿ èíôîðìàöèÿ, ïîëó÷àåìàÿ âî âðåìÿ
ïðîâåäåíèÿ ËÁÝ. Ïîýòîìó âîïðîñ òîæäåñòâåííîñòè ìàòåìàòè÷åñêîé
ìîäåëè ïðîöåññà ðåàëüíîìó ýêñïåðèìåíòó ìîæíî ðàññìàòðèâàòü êàê
âîïðîñ ñîîòâåòñòâèÿ ìîäåëè ïðîöåññà óñëîâèÿì èçìåðåíèé. Óñëî-
âèå, ïðè êîòîðîì ìîäåëü ïðîöåññà îïðåäåëåíèÿ è àíàëèçà äâèæåíèÿ
ñîîòâåòñòâóåò óñëîâèÿì èçìåðåíèé, íàçûâàåòñÿ óñëîâèåì àäåêâàòíî-
ñòè [17]. Ñîãëàñîâàííàÿ ìîäåëü äâèæåíèÿ è èçìåðåíèÿ X ↔ Y íà èí-
òåðâàëå [0, T] íàçûâàåòñÿ àäåêâàòíîé äåéñòâèòåëüíîìó äâèæåíèþ,
åñëè ñïðàâåäëèâà ãèïîòåçà î ïðèíàäëåæíîñòè îöåíîê âåêòîðà îøè-
áîê ñ çàäàííîé äîâåðèòåëüíîé âåðîÿòíîñòüþ, îïðåäåëÿþùåé íàäåæ-
íîñòü ðåçóëüòàòà, óñòàíîâëåííîìó äëÿ óñëîâèé ïðîâåäåíèÿ èçìåðå-
íèé çàêîíó ðàñïðåäåëåíèÿ ñ òðåáóåìûì (â ÷àñòíîñòè, íóëåâûì) çíà-
549
÷åíèåì ìàòåìàòè÷åñêîãî îæèäàíèÿ è ñðåäíèìè êâàäðàòè÷åñêèìè
îòêëîíåíèÿìè, íå ïðåâîñõîäÿùèìè äîïóñòèìûõ ïðåäåëîâ.
Çàìåòèì, ÷òî àäåêâàòíîñòü ÿâëÿåòñÿ íåîáõîäèìûì, íî íå äîñòà-
òî÷íûì óñëîâèåì ïðàâèëüíîñòè (ðåãóëÿðíîñòè) ïîñòàíîâêè çàäà÷è.
Ìîæåò ñóùåñòâîâàòü [17] òàêàÿ êîìáèíàöèÿ ïîãðåøíîñòåé â ìîäåëè
äâèæåíèÿ è óñëîâèÿõ ïðîâåäåíèÿ èçìåðåíèé, ÷òî îöåíêè íà÷àëüíûõ
è òåêóùèõ ïàðàìåòðîâ äâèæåíèÿ (ôàçîâûõ êîîðäèíàò) x 0
∧
èx
∧
(),
tà
òàêæå èäåíòèôèöèðóåìûõ ïàðàìåòðîâ ËÀ λ
∧
()t áóäóò â áîëüøîé ñòå-
ïåíè îòëè÷àòüñÿ îò ñâîèõ äåéñòâèòåëüíûõ çíà÷åíèé, â òî âðåìÿ êàê
óñëîâèå àäåêâàòíîñòè áóäåò âûïîëíåíî. Ïðîâåðêà àäåêâàòíîñòè åùå
íå äàåò îñíîâàíèé äëÿ âûÿâëåíèÿ ñàìîé ïîãðåøíîñòè, à ñâèäåòåëü-
ñòâóåò òîëüêî î åå âîçìîæíîì ïðèñóòñòâèè.
12.3.2. ÊÐÀÒÊÀß ÕÀÐÀÊÒÅÐÈÑÒÈÊÀ ÌÅÒÎÄÎÂ ÎÁÐÀÁÎÒÊÈ
ÐÅÇÓËÜÒÀÒÎÂ ÈÇÌÅÐÅÍÈÉ
Ïðîöåññ èçìåðåíèé îáúåêòèâíî ñâÿçàí ñ íàëè÷èåì òåõ èëè èíûõ
ïîãðåøíîñòåé èçìåðåíèé, ÷òî îáóñëîâëåíî âîçäåéñòâèåì íà íåãî
íåó÷èòûâàåìûõ ôàêòîðîâ. Ïîýòîìó ôàêòè÷åñêèé ðåçóëüòàò èçìåðå-
íèé âñåãäà ÿâëÿåòñÿ ñëó÷àéíîé ðåàëèçàöèåé. Ðàçëè÷àþò ïîãðåøíî-
ñòè òðåõ âèäîâ: ñèñòåìàòè÷åñêèå, ñëó÷àéíûå (ðåãóëÿðíûå) è ãðóáûå.
Ïîãðåøíîñòè âñåõ òðåõ âèäîâ ÿâëÿþòñÿ ñëó÷àéíûìè. Òàê, ñèñòåìà-
òè÷åñêàÿ ïîãðåøíîñòü ñëó÷àéíà â ñåðèè ñåàíñîâ èçìåðåíèé. Ñëó-
÷àéíû ïî ñâîåé ïðèðîäå è äâà äðóãèõ âèäà ïîãðåøíîñòåé.
Ñ öåëüþ óìåíüøåíèÿ âëèÿíèÿ ïîãðåøíîñòåé èçìåðåíèé íà òî÷-
íîñòü îïðåäåëåíèÿ èñêîìûõ ïàðàìåòðîâ ïðîâîäÿò ìíîãîêðàòíûå èç-
ìåðåíèÿ.  ýòîì ñëó÷àå ïðèìåíÿåòñÿ ñòàòèñòè÷åñêàÿ ìåòîäèêà ðå-
øåíèÿ, ïîçâîëÿþùàÿ çà ñ÷åò èçáûòî÷íîñòè èñõîäíîé èíôîðìàöèè
ñãëàæèâàòü ôóíêöèîíàëüíûå çàâèñèìîñòè, íàéäåííûå ïðè íàëè÷èè
ñëó÷àéíûõ ïîãðåøíîñòåé èçìåðåíèé [76].
Ðàññìîòðèì ãëàâíûå ïîëîæåíèÿ, ëåæàùèå â îñíîâå ñòàòèñòè÷å-
ñêîãî ïîäõîäà ê ðåøåíèþ çàäà÷ îáðàáîòêè èçìåðèòåëüíîé èíôîðìà-
öèè. Ïðèíÿòî ñ÷èòàòü, ÷òî îñíîâíûì èñòî÷íèêîì ýêñïåðèìåíòàëü-
íî ïîëó÷àåìîé èíôîðìàöèè ÿâëÿþòñÿ ðåçóëüòàòû èçìåðåíèé (àïî-
ñòåðèîðíàÿ èíôîðìàöèÿ), ïðè÷åì äëÿ íåêîòîðîé ÷àñòè ïîëó÷åííûõ
äàííûõ õàðàêòåðíà èõ êîððåëÿöèîííàÿ âçàèìîñâÿçü. Ïðè ïðîâåäå-
íèè àíàëèçà èñïîëüçóåòñÿ òàêæå è àïðèîðíàÿ èíôîðìàöèÿ (ïîëó÷åí-
íàÿ äî ïðîâåäåíèÿ òåêóùåé ñåðèè èçìåðåíèé) â âèäå ìàòåìàòè÷å-
ñêîé ìîäåëè, ïîçâîëÿþùåé óñòàíîâèòü îæèäàåìûå çíà÷åíèÿ ïàðà-
ìåòðîâ äâèæåíèÿ ËÀ. Ñ÷èòàþòñÿ èçâåñòíûìè òàêæå ñîîòâåò-
ñòâóþùèå âåðîÿòíîñòíûå õàðàêòåðèñòèêè âîçìîæíûõ ïîãðåøíî-
ñòåé.  ðåçóëüòàòå ïðîâåäåíèÿ ñòàòèñòè÷åñêîé îáðàáîòêè èçìåðåíèé
550
äîëæíà áûòü íàéäåíà òàêàÿ ñîâîêóïíîñòü èñêîìûõ âåëè÷èí, êîòî-
ðàÿ íàèëó÷øèì îáðàçîì ñîãëàñóåòñÿ ñ ðåçóëüòàòàìè èçìåðåíèé. Ïðè
ýòîì îïòèìèçàöèÿ ìîæåò áûòü îñóùåñòâëåíà ïî ðàçëè÷íûì êðèòå-
ðèÿì, îäíàêî íàèáîëüøåå ðàñïðîñòðàíåíèå ïîëó÷èë êðèòåðèé ìèíè-
ìóìà äèñïåðñèè îïðåäåëÿåìûõ ïàðàìåòðîâ äâèæåíèÿ. Óäîâëåòâîðÿþ-
ùèå ýòîìó êðèòåðèþ ñòàòèñòè÷åñêèå ìåòîäû ðàçäåëÿþòñÿ íà äâå
ãðóïïû: ìåòîäû èíòåðâàëüíîé è òî÷å÷íîé îáðàáîòêè. Ìåòîäû èíòåð-
âàëüíîé îáðàáîòêè, ê êîòîðûì îòíîñÿòñÿ ìåòîä ìàêñèìàëüíîãî ïðàâ-
äîïîäîáèÿ è ìåòîä íàèìåíüøèõ êâàäðàòîâ, òðåáóþò äëÿ ñâîåãî ïðèìå-
íåíèÿ ïîëíîãî îáúåìà èíôîðìàöèè, íàêàïëèâàåìîé (ñîáèðàåìîé) â
òå÷åíèå ïðîâîäèìûõ ñåàíñîâ èçìåðåíèé. Ê ìåòîäàì òî÷å÷íîé îáðà-
áîòêè îòíîñÿòñÿ ðåêóððåíòíûå âû÷èñëèòåëüíûå ñõåìû (â òîì ÷èñëå è
ñõåìà äèíàìè÷åñêîé ôèëüòðàöèè Êàëìàíà), èñïîëüçóþùèå íå ïîë-
íûé îáúåì èíôîðìàöèè, à ïîñëåäîâàòåëüíî íàêàïëèâàåìûé (ïî
ìåðå óâåëè÷åíèÿ êîëè÷åñòâà ïðîâîäèìûõ èçìåðèòåëüíûõ ñåàíñîâ).
Íå ðàññìàòðèâàÿ ñóùåñòâà óêàçàííûõ ìåòîäîâ, êîòîðûå äîñòà-
òî÷íî ïîëíî îïèñàíû, íàïðèìåð, â ó÷åáíèêàõ [36, 77, 135], à òàêæå â
ñïåöèàëüíîé ëèòåðàòóðå [17, 35, 76, 78, 121] è äð., êðàòêî îõàðàêòå-
ðèçóåì çäåñü äîñòîèíñòâà è íåäîñòàòêè, à òàêæå îáëàñòè ïðèìåíå-
íèÿ îáñóæäàåìûõ ìåòîäîâ.
Ìåòîä ìàêñèìàëüíîãî ïðàâäîïîäîáèÿ (ÌÌÏ) ÿâëÿåòñÿ íàèáî-
ëåå óíèâåðñàëüíûì è ýôôåêòèâíûì ìåòîäîì. Åãî ïðèìåíåíèå
îñîáåííî îïðàâäàííî, êîãäà çàêîí ðàñïðåäåëåíèÿ àïðèîðè íåèç-
âåñòåí, à â ñîñòàâå îáðàáàòûâàåìîé èíôîðìàöèè èìåþòñÿ êàê
íåêîððåëèðîâàííûå, òàê è êîððåëèðîâàííûå èçìåðåíèÿ. Îáðà-
áîòêà èçìåðåíèé ïî ìåòîäó íàèìåíüøèõ êâàäðàòîâ (ÌÍÊ) ïðåä-
ñòàâëÿåò ñîáîé ÷àñòíûé ñëó÷àé ìåòîäà ìàêñèìàëüíîãî ïðàâäîïî-
äîáèÿ. Ïðèìåíåíèå ÌÍÊ ïðåäñòàâëÿåòñÿ ïðåäïî÷òèòåëüíûì, êî-
ãäà ïðîâîäèìûå èçìåðåíèÿ ÿâëÿþòñÿ íåçàâèñèìûìè è íîðìàëüíî
ðàñïðåäåëåííûìè.  ýòîì ñëó÷àå ïîëó÷àåìûå ñ åãî ïîìîùüþ ðå-
çóëüòàòû íå óñòóïàþò ïî òî÷íîñòè è äîñòîâåðíîñòè ÌÌÏ, à ñ
òî÷êè çðåíèÿ ðåàëèçóåìîé âû÷èñëèòåëüíîé ñõåìû îí îêàçûâàåò-
ñÿ ñóùåñòâåííî áîëåå ïðîñòûì. Îäíàêî ïðè íàëè÷èè è íåó÷åòå
ñóùåñòâåííûõ êîððåëÿöèîííûõ ñâÿçåé ìåæäó èçìåðÿåìûìè ïàðà-
ìåòðàìè åãî ïðèìåíåíèå ìîæåò ïðèâåñòè ê çíà÷èòåëüíûì îøèá-
êàì. Ïðè îáðàáîòêå èçìåðèòåëüíîé èíôîðìàöèè ïî ÌÍÊ ïðåä-
âàðèòåëüíî òðåáóåòñÿ ïîëó÷èòü âûáîðêó èçìåðåíèé äîñòàòî÷íîãî
îáúåìà. Âñëåäñòâèå ýòîãî ïîëó÷åíèå îöåíîê áóäåò îñóùåñòâëÿòü-
ñÿ ìåäëåííåå, ÷åì ïîñòóïëåíèå èçìåðèòåëüíîé èíôîðìàöèè â
îáðàáîòêó. Êðîìå òîãî, ïðè âûïîëíåíèè êàæäîãî ïîñëåäóþùåãî
ýòàïà ðàñ÷åòà íå âñÿ àïðèîðíàÿ èíôîðìàöèÿ áóäåò ó÷àñòâîâàòü â
îáðàáîòêå (ò.å . ó÷èòûâàþòñÿ òîëüêî ïðèáëèæåíèÿ ïàðàìåòðîâ
äâèæåíèÿ, îòíîñÿùèåñÿ ê ïðåäûäóùèì ýòàïàì). Óêàçàííûõ íå-
551
äîñòàòêîâ ëèøåíû ìåòîäû âòîðîé ãðóïïû, îñóùåñòâëÿþùèå îá-
ðàáîòêó íàðàñòàþùåãî îáúåìà èçìåðåíèé. Âàæíîé îñîáåííîñòüþ
ýòèõ ìåòîäîâ ÿâëÿåòñÿ âîçìîæíîñòü äîáàâëÿòü èçìåðèòåëüíóþ
èíôîðìàöèþ ëþáûìè ïîðöèÿìè, âïëîòü äî åäèíè÷íûõ èçìåðå-
íèé. Ïðè ýòîì äëÿ ïðîâåäåíèÿ ðàñ÷åòîâ èñïîëüçóþòñÿ ðåêóð-
ðåíòíûå çàâèñèìîñòè, ñâÿçûâàþùèå îöåíêó íà (i + 1)-ì øàãå
ñ÷åòà ñ îöåíêàìè è ïàðàìåòðàìè, ïîëó÷åííûìè íà ïðåäûäóùåì
i-ì øàãå . Ýòî îáñòîÿòåëüñòâî ïîçâîëÿåò îáåñïå÷èòü íàõîæäåíèå
íîâûõ óòî÷íåííûõ îöåíîê â ëþáîé ìîìåíò âðåìåíè (äëÿ ëþáîé
ôèêñèðîâàííîé òî÷êè) ñ ó÷åòîì íàêîïèâøåéñÿ ê ýòîìó ìîìåíòó
ñîâîêóïíîñòè èçìåðåíèé. Íàèáîëåå ýôôåêòèâíî ïðèìåíåíèå ìå-
òîäîâ îáðàáîòêè ïî íàðàñòàþùåìó îáúåìó èçìåðåíèé â òåõ ñëó-
÷àÿõ, êîãäà èçìåðåíèÿ ðàññðåäîòî÷åíû ïî âðåìåíè, ïîñòóïàþò â
ðàâíîìåðíîì òåìïå è íåîáõîäèìî îïåðàòèâíîå ïðèíÿòèå ðåøå-
íèé (ïî ðåæèìó ñëåæåíèÿ çà ËÀ); êîãäà íàêîïëåíèå áîëüøîãî
êîëè÷åñòâà èíôîðìàöèè íåâûãîäíî èëè íå ïðåäñòàâëÿåòñÿ âîç-
ìîæíûì. Äàííûå ìåòîäû íå ñâîáîäíû îò ñóùåñòâåííûõ íåäîñ-
òàòêîâ. Îòìåòèì ïðåæäå âñåãî âûñîêóþ ÷óâñòâèòåëüíîñòü ðåêóð-
ðåíòíûõ ìåòîäîâ îáðàáîòêè ê óðîâíþ äîñòîâåðíîñòè ïðèâëåêàå-
ìîé àïðèîðíîé èíôîðìàöèè, îáúåì êîòîðîé çíà÷èòåëüíî
ïðåâîñõîäèò ñîîòâåòñòâóþùèé îáúåì èíôîðìàöèè ìåòîäîâ ïåð-
âîé ãðóïïû.
12.3.3 . ÈÄÅÍÒÈÔÈÊÀÖÈß ÏÀÐÀÌÅÒÐΠËÀ ÊÀÊ ÄÈÍÀÌÈ×ÅÑÊÈÕ
ÑÈÑÒÅÌ Â ÇÀÄÀ×ÀÕ ÎÁÐÀÁÎÒÊÈ ÐÅÇÓËÜÒÀÒΠËÅÒÍÛÕ ÈÑÏÛÒÀÍÈÉ
Ñîäåðæàòåëüíîå îïðåäåëåíèå è îáùàÿ ìàòåìàòè÷åñêàÿ ôîðìóëè-
ðîâêà çàäà÷è èäåíòèôèêàöèè, â ñóùíîñòè, óæå áûëà äàíà â ïîä-
ðàçä. 12.1 .5. Çäåñü ìû åå êîíêðåòèçèðóåì â ÷àñòè òðàêòîâêè è ïðèìå-
íÿåìûõ ìåòîäîâ ðåøåíèÿ â ðàìêàõ ïðîöåññà îáðàáîòêè ðåçóëüòàòîâ
ëåòíûõ èñïûòàíèé. Ðàññìàòðèâàÿ çàäà÷ó èäåíòèôèêàöèè â óçêîì
ñìûñëå, áóäåì ïðåäïîëàãàòü, ÷òî íà èññëåäóåìîì èíòåðâàëå äâèæå-
íèÿ ïî ðåçóëüòàòàì ëåòíûõ èñïûòàíèé ïîëó÷åíà èíôîðìàöèÿ î
"âõîäàõ" è "âûõîäàõ" ñèñòåìû è òðåáóåòñÿ îïðåäåëèòü åå íåèçâåñò-
íûå (íåèçìåðÿåìûå íåïîñðåäñòâåííî) ïàðàìåòðû. Ïðè ýòîì ìû áó-
äåì ïðåäïîëàãàòü, ÷òî ìàòåìàòè÷åñêàÿ ìîäåëü ïðîöåññà äâèæåíèÿ
ËÀ çàäàíà è óäîâëåòâîðÿåò ðàññìîòðåííîìó âûøå óñëîâèþ àäåêâàò-
íîñòè. Ýòî ïîçâîëèò îòîæäåñòâèòü çàäà÷ó èäåíòèôèêàöèè ïàðàìåò-
ðîâ ðåàëüíîãî ïðîöåññà äâèæåíèÿ ñ çàäà÷åé èäåíòèôèêàöèè ïàðà-
ìåòðîâ åãî ìàòåìàòè÷åñêîé ìîäåëè. Âõîäíûìè âîçäåéñòâèÿìè â ðå-
øàåìîé çàäà÷å áóäóò ïàðàìåòðû, õàðàêòåðèçóþùèå ñîñòîÿíèå
àòìîñôåðû, îïðåäåëÿåìûå ïî ðåçóëüòàòàì ìåòåîïîäãîòîâêè, ïðåä-
øåñòâóþùåé ëåòíûì èñïûòàíèÿì èëè ïðîâîäèìîé ïàðàëëåëüíî èì,
552
à òàêæå çàäàííàÿ (äëÿ óïðàâëÿåìûõ ËÀ) ïðîãðàììà ôîðìèðîâàíèÿ
óïðàâëÿþùèõ âîçäåéñòâèé. Ïîñëåäíÿÿ ìîæåò áûòü çàðàíåå çàëîæå-
íà íà áîðò ëèáî ìîæåò ôèêñèðîâàòüñÿ ñ ïîìîùüþ òåëåìåòðèè ïðè
åñòåñòâåííîé îòðàáîòêå êîìàíä ðóëÿìè â ïðîöåññå íàâåäåíèÿ
(óïðàâëåíèÿ äâèæåíèåì). Èçìåðÿåìûìè âûõîäíûìè ïåðåìåííûìè
ÿâëÿþòñÿ êîìïîíåíòû âåêòîðà ñîñòîÿíèÿ ËÀ, íàïðèìåð ñêîðîñòü,
ëèíåéíûå êîîðäèíàòû, óãëîâûå ñêîðîñòè, óãëû, îïðåäåëÿþùèå îðè-
åíòàöèþ àïïàðàòà â ïðîñòðàíñòâå, è ò.ä .  êà÷åñòâå èäåíòèôèöèðóå-
ìûõ ïåðåìåííûõ ìîãóò ðàññìàòðèâàòüñÿ: íåïîñðåäñòâåííî íåèçìå-
ðÿåìûå çíà÷åíèÿ êîìïîíåíòîâ âåêòîðà íà÷àëüíîãî ôàçîâîãî ñîñòîÿ-
íèÿ x(t0), ýëåìåíòîâ ìàòðèöû ñîñòîÿíèÿ A(t), àýðîäèíàìè÷åñêèõ
êîýôôèöèåíòîâ (, ,
ccm
xyz
aaa
è ò.ä.), èçìåíÿþùèõñÿ â ïðîöåññå ïîëåòà
ìîìåíòîâ èíåðöèè ËÀ (Ix, Iy, Iz) è äð.
Ïîä÷åðêíåì, ÷òî ðàññìàòðèâàåìàÿ çàäà÷à èäåíòèôèêàöèè àêòó-
àëüíà êàê äëÿ óïðàâëÿåìûõ, òàê è íåóïðàâëÿåìûõ ËÀ.  ÷àñòíîñòè,
äëÿ ïîñëåäíèõ â ïðîöåññå ëåòíûõ èñïûòàíèé âàæíî óñòàíîâèòü ôàê-
òè÷åñêèå çíà÷åíèÿ çàïàñîâ ïðîäîëüíîé è áîêîâîé ñòàòè÷åñêîé óñ-
òîé÷èâîñòè íà àêòèâíîì ó÷àñòêå òðàåêòîðèè ïðè ðàçëè÷íûõ óñëîâè-
ÿõ ïóñêà, çíà÷åíèÿ àýðîäèíàìè÷åñêèõ êîýôôèöèåíòîâ ïðè âûñîêî-
ñêîðîñòíîì äâèæåíèè â àòìîñôåðå àñèììåòðè÷íûõ áàëëèñòè÷åñêèõ
àïïàðàòîâ [59] è ò.ä . Äëÿ óïðàâëÿåìûõ ËÀ åå ðåøåíèå ÿâëÿåòñÿ îï-
ðåäåëÿþùèì ïðè îöåíêå äèíàìè÷åñêîé óñòîé÷èâîñòè, óïðàâëÿåìî-
ñòè è äðóãèõ õàðàêòåðèñòèê îáúåêòà ðåãóëèðîâàíèÿ â ïðîöåññå åãî
ëåòíîé îòðàáîòêè.
Íåòðóäíî çàìåòèòü, ÷òî â ðàññìàòðèâàåìîé ïîñòàíîâêå çàäà÷à
èäåíòèôèêàöèè, ïî êðàéíåé ìåðå äëÿ óïðàâëÿåìîãî ËÀ, âåñüìà
ñõîäíà ñ çàäà÷åé îïðåäåëåíèÿ ÷àñòîòíûõ õàðàêòåðèñòèê ñèñòåìû íà
îñíîâå èñïîëüçîâàíèÿ "ïðîáíûõ âîçäåéñòâèé". Êàçàëîñü áû, ýòî
äåéñòâèòåëüíî òàê. Îïðåäåëåíèå ïî ðåçóëüòàòàì èçìåðåíèé "âõîäà"
è "âûõîäà" ñèñòåìû åå ÷àñòîòíîé õàðàêòåðèñòèêè, ñâÿçàííîé â ñâîþ
î÷åðåäü ñ õàðàêòåðèñòè÷åñêèì óðàâíåíèåì è åãî êîðíÿìè, â ïðèí-
öèïå ïîçâîëÿåò íàéòè ïàðàìåòðû åå ìîäåëè. Îäíàêî ñõîäñòâî çäåñü
êàæóùååñÿ. Íå ãîâîðÿ óæå î òîì, ÷òî óêàçàííûé ïîäõîä â ïîäàâëÿþ-
ùåì áîëüøèíñòâå ñëó÷àåâ ðàñïðîñòðàíÿåòñÿ ëèøü íà äîñòàòî÷íî óç-
êèé êëàññ ñòàöèîíàðíûõ ñèñòåì, èìååòñÿ è áîëåå ãëóáîêîå ðàçëè-
÷èå. Èñïîëüçîâàíèå "ïðîáíûõ âîçäåéñòâèé" (ñòóïåí÷àòûõ, èìïóëüñ-
íûõ èëè ñèíóñîèäàëüíûõ ñ ðàçëè÷íûìè ÷àñòîòàìè) ïðèâîäèò ê
ïîëó÷åíèþ ðåøåíèÿ çàäà÷è èäåíòèôèêàöèè "âíå äèíàìè÷åñêîãî
ïðîöåññà". Ïîýòîìó ôèêñèðóåìûå ïðè ýòîì ðåçóëüòàòû áóäóò ñïðà-
âåäëèâû òîëüêî äëÿ óñëîâèé, ïðèìåíèòåëüíî ê êîòîðûì îòíîøåíèÿ
âõîä/âûõîä, ïîëó÷åííûå äëÿ îäíîãî òèïà âõîäíûõ âîçäåéñòâèé, ñî-
õðàíÿþòñÿ è äëÿ âñåõ äðóãèõ òèïîâ âõîäíûõ âîçäåéñòâèé.
Çàäà÷à ìíîãîìåðíîé äèíàìè÷åñêîé èäåíòèôèêàöèè (â ñìûñëå
îöåíèâàíèÿ ïàðàìåòðîâ ñèñòåìû ïî ðåçóëüòàòàì ëåòíûõ èñïûòà-
553
íèé), òàê æå êàê è çàäà÷à äèíàìè÷åñêîé ôèëüòðàöèè (îïðåäåëåíèÿ
"íàèëó÷øèõ" îöåíîê ïåðåìåííûõ ñîñòîÿíèÿ ËÀ), äîëæíà ðàññìàò-
ðèâàòüñÿ â äâóõ àñïåêòàõ – âåðîÿòíîñòíîì è îïòèìàëüíîì. Çäåñü,
êàê è â ðàññìîòðåííîì âûøå ñëó÷àå (ñì. ï. 12 .3.1), âûáðàííîé
ôóíêöèè ïîòåðü ïðèäàåòñÿ âåðîÿòíîñòíàÿ èíòåðïðåòàöèÿ èëè æå
îíà èçíà÷àëüíî îïðåäåëÿåòñÿ èç âåðîÿòíîñòíûõ ñîîáðàæåíèé ïðè
ïîñëåäóþùåì ñâåäåíèè çàäà÷è îöåíèâàíèÿ ê çàäà÷å îïòèìèçàöèè.
Ôóíêöèè ïîòåðü, ñâÿçàííûå ñ íåäîñòèæåíèåì àáñîëþòíî òî÷íîé
èäåíòèôèêàöèè, íàçûâàþòñÿ ôóíêöèÿìè øòðàôà.  êà÷åñòâå ôóíê-
öèè øòðàôà ìîæåò âûñòóïàòü ÷àñòíîå çíà÷åíèå êâàäðàòà îòêëîíå-
íèÿ îöåíêè èäåíòèôèöèðóåìîãî ïàðàìåòðà îò åãî èñòèííîãî çíà÷å-
íèÿ. Ïîñêîëüêó ïîñëåäíåå çàðàíåå íåèçâåñòíî (÷òî è ñëóæèò ïðè÷è-
íîé ïîñòàíîâêè çàäà÷è èäåíòèôèêàöèè), ïðåäïî÷òèòåëüíûì
ÿâëÿåòñÿ èñïîëüçîâàíèå ñòàòèñòè÷åñêèõ õàðàêòåðèñòèê îòêëîíåíèÿ,
çàïèñûâàåìûõ â âèäå óñëîâíîãî ìàòåìàòè÷åñêîãî îæèäàíèÿ øòðàôà
çà îøèáêó â îöåíêå èñêîìîãî çíà÷åíèÿ ïàðàìåòðà.
Ìåòîäû èäåíòèôèêàöèè, îñíîâàííûå íà ðåãðåññèîííûõ ïðîöå-
äóðàõ, áàçèðóþùèõñÿ íà ÌÍÊ, ïðèìåíèìû êàê ê ëèíåéíûì, òàê è
íåëèíåéíûì ìíîãîìåðíûì ñèñòåìàì. Çäåñü òðåáîâàíèå ñòàöèîíàð-
íîñòè ðàñïðîñòðàíÿåòñÿ òîëüêî íà èíòåðâàë, â òå÷åíèå êîòîðîãî íà-
êàïëèâàåòñÿ èíôîðìàöèÿ äëÿ ðåãðåññèîííîé èäåíòèôèêàöèè. Îò-
ìåòèì, ÷òî ïðè èäåíòèôèêàöèè ìíîãîìåðíûõ ñèñòåì äëÿ ïîëó÷åíèÿ
ïàðàìåòðîâ ðåãðåññèè òðåáóåòñÿ îáðàùåíèå ìàòðèö. Îäíàêî óêàçàí-
íóþ, íåïðîñòóþ â âû÷èñëèòåëüíîì îòíîøåíèè îïåðàöèþ ìîæíî èñ-
êëþ÷èòü, åñëè èñïîëüçîâàòü ðåêóððåíòíûé õàðàêòåð ðåãðåññèîííûõ
ìåòîäîâ è ïåðåéòè ê òàê íàçûâàåìûì ïîñëåäîâàòåëüíûì ðåãðåññè-
îííûì ìåòîäàì èäåíòèôèêàöèè. Äëÿ ïðîöåäóðû ìèíèìèçàöèè
ôóíêöèè øòðàôà íåîáõîäèìî ÷èñëåííîå îïðåäåëåíèå ïåðâûõ
(à èíîãäà è âòîðûõ) ïðîèçâîäíûõ. Äëÿ ýòîãî ìîãóò áûòü ïðèìåíåíû
ðàçëè÷íûå ÷èñëåííûå ìåòîäû îïòèìèçàöèè, îñíîâàííûå íà èñïîëü-
çîâàíèè ëèíåàðèçîâàííûõ ìîäåëåé: ãðàäèåíòíûé ìåòîä, ìåòîä Ãà-
óññà–Íüþòîíà (Íüþòîíà–Ðàôñîíà), ìåòîä ïîãðóæåíèÿ (âîçîáíîâ-
ëåíèÿ) è äð. Íàèáîëåå ïðèãîäíûì äëÿ îáñóæäàåìûõ çàäà÷ ïðèíÿòî
ñ÷èòàòü ìåòîä Ãàóññà–Íüþòîíà è åãî ìîäèôèêàöèè. Ðàçðàáîòêà ñî-
îòâåòñòâóþùèõ "ìîäèôèêàöèé" îáóñëîâëåíà ñëåäóþùèì: ìåòîä Ãà-
óññà–Íüþòîíà õàðàêòåðèçóåòñÿ ìàêñèìàëüíîé (ïî ñðàâíåíèþ ñ äðó-
ãèìè ìåòîäàìè) ñõîäèìîñòüþ ïðè ðåøåíèè çàäà÷ èäåíòèôèêàöèè ñ
âûïóêëûìè ôóíêöèÿìè êà÷åñòâà (ôóíêöèÿìè øòðàôà). Îäíàêî âû-
ñîêàÿ ñêîðîñòü ïðèáëèæåíèÿ ê ýêñòðåìóìó äîñòèãàåòñÿ â íåì òîëüêî
â òîì ñëó÷àå, åñëè íóëåâîå ïðèáëèæåíèå îöåíêè íàõîäèòñÿ â ïðåäå-
ëàõ îáëàñòè "ïðèòÿæåíèÿ". Åñëè íóëåâîå ïðèáëèæåíèå îöåíêè ïàðà-
ìåòðîâ íàõîäèòñÿ âíå îáëàñòè "ïðèòÿæåíèÿ" èñòèííûõ çíà÷åíèé
ýòèõ ïàðàìåòðîâ, ðàññìàòðèâàåìûé ìåòîä ïðîèãðûâàåò ïî ñêîðîñòè
ñõîäèìîñòè äðóãèì ìåòîäàì, â ÷àñòíîñòè ìåòîäó ïîãðóæåíèÿ, îáëà-
554
äàþùåìó óñòîé÷èâîé (íî ìåäëåííîé) ñõîäèìîñòüþ äàæå ïðè î÷åíü
íåòî÷íîì íà÷àëüíîì ïðèáëèæåíèè. Äëÿ óñòðàíåíèÿ îòìå÷åííîãî
íåäîñòàòêà ìåòîäà Ãàóññà–Íüþòîíà è ðàçðàáàòûâàþòñÿ åãî ðàçëè÷-
íûå ìîäèôèêàöèè íà îñíîâå ñîåäèíåíèÿ âû÷èñëèòåëüíûõ ïðîöåäóð
îáñóæäàåìîãî ìåòîäà è ìåòîäà ïîãðóæåíèÿ. Ñëîæíîñòü è òðóäîåì-
êîñòü ðåàëèçàöèè àëãîðèòìîâ èäåíòèôèêàöèè ïðèâîäÿò ê íåîáõîäè-
ìîñòè ïîèñêà ïóòåé ðàçäåëåíèÿ çàäà÷è íà ñîâîêóïíîñòü ÷àñòè÷íî
èëè ïîëíîñòüþ íåçàâèñèìûõ ïîäçàäà÷, ðåøàåìûõ ïàðàëëåëüíî. Òà-
êîå ýêâèâàëåíòíîå ïðåîáðàçîâàíèå èñõîäíîé ìîäåëè, â ïîëíîé ìåðå
ó÷èòûâàþùåé íàëè÷èå ïåðåêðåñòíûõ ñâÿçåé (àýðîäèíàìè÷åñêèõ, ãà-
çîäèíàìè÷åñêèõ, êàíàëîâ óïðàâëåíèÿ), ìîæåò áûòü îñóùåñòâëåíî
íà îñíîâå âûïîëíåíèÿ óñëîâèÿ äåêîìïîçèðóåìîñòè ìíîãîìåðíûõ ñèñ-
òåì ñ ïîìîùüþ îáðàòíîé ñâÿçè ïî âûõîäó. Ñòðóêòóðíîå ñâîéñòâî äå-
êîìïîçèðóåìîñòè íåïîñðåäñòâåííî âûòåêàåò èç âîçìîæíîñòè ïî-
ñòðîåíèÿ ðåäóöèðîâàííûõ ìîäåëåé ñîñòîÿíèÿ, îïèñûâàþùèõ ýâîëþ-
öèè íå ïîëíîãî âåêòîðà ñîñòîÿíèÿ, à òîëüêî îòäåëüíûõ,
èíòåðåñóþùèõ èññëåäîâàòåëÿ åãî êîìïîíåíòîâ.
Ñðåäè âîçìîæíûõ òèïîâ ëèíåéíûõ ïðåîáðàçîâàíèé èñõîäíîé
ìîäåëè ñîñòîÿíèÿ, ñòàâÿùèõ öåëüþ ïðîâåäåíèå åå äåêîìïîçèöèè
(ðàñ÷ëåíåíèÿ), îñîáóþ ðîëü èãðàåò êàíîíè÷åñêîå ïðåîáðàçîâàíèå
[11]. Ýòî ïðåîáðàçîâàíèå îñóùåñòâëÿåòñÿ ñ ïîìîùüþ ñïåöèàëü-
íîé ìàòðèöû V, ñòîëáöàìè êîòîðîé ñëóæàò ñîáñòâåííûå âåêòîðû
Vi èñõîäíîé ñèñòåìû. Óêàçàííûå ñîáñòâåííûå âåêòîðû, à ñëåäî-
âàòåëüíî, è ìàòðèöà V îïðåäåëÿþòñÿ íà îñíîâå ðåøåíèÿ îäíî-
ðîäíîãî óðàâíåíèÿ, êîòîðîå ìîæåò áûòü ïðåäñòàâëåíî â ñëåäóþ-
ùåé ôîðìå:
xV
() exp( ).
tt
=λ
(12.50)
Ïðîäèôôåðåíöèðîâàâ (12.50), ïîëó÷èì
d
dt
te
e
t
nn
tn
xV
V
()
.
=+
+
λλ
λλ
11
1
K
(12.51)
Ñ äðóãîé ñòîðîíû,
d
dt
tee
t
n
tn
xA
V
V
()[
].
=+
+
1
1
λλ
K
(12.52)
Òîãäà, ïðèðàâíèâàÿ ïðàâûå ÷àñòè (12.51) è (12.52), ïðèõîäèì ê
óðàâíåíèÿì
λiiiin
VA
V
==
,,
,
,
1K
(12.53)
555
èç ðåøåíèÿ êîòîðûõ îòíîñèòåëüíî Vi ìîãóò áûòü ïîëó÷åíû èñêîìûå
ñîáñòâåííûå âåêòîðû. Äëÿ ïðèäàíèÿ èì îäíîçíà÷íîñòè â êàæäîì èç
íèõ ïåðâûé ýëåìåíò ïðèíèìàþò ðàâíûì åäèíèöå.
Âûïîëíåíèå êàíîíè÷åñêîãî ïðåîáðàçîâàíèÿ ïîçâîëÿåò îñóùåñò-
âèòü ïðîöåäóðó äèàãîíàëèçàöèè ñèñòåìû, çàêëþ÷àþùóþñÿ â ñëåäóþ-
ùåì.
Ïóñòü ìàòðèöà λ – äèàãîíàëüíàÿ ìàòðèöà, òîãäà
VVV
λλλ
=(
1
1,,)
.
K
nn
(12.54)
Èìåÿ â âèäó (12.53), ïîëó÷èì
(,, )(,
,)
.
λλ
11
1
V
V
AV
AV
KK
nn
n
=
(12.55)
Ïîñëåäíèå äâå çàâèñèìîñòè ïðèâîäÿò ê ðàâåíñòâó
VA
V
λ=
,
(12.56)
èç êîòîðîãî ñëåäóåò
AV
A
V
*
.
==
−
λ
1
(12.57)
Ïðèìåíåíèå ìàòðèöû V â êà÷åñòâå ïðåîáðàçóþùåé ïîçâîëÿåò
ïîëó÷èòü êàíîíè÷åñêóþ ñèñòåìó
d
dt
ttT
xA
xB
u
**
**
()
() (),
=+
(12.58)
ãäå
BVB
*
,
=
−1
(12.59)
â êîòîðîé ñâÿçü ìåæäó ñêàëÿðíûìè óðàâíåíèÿìè ïî ïåðåìåííûì
ñîñòîÿíèÿ îòñóòñòâóåò.
Ïðîèëëþñòðèðóåì ïðîöåäóðó äèàãîíàëèçàöèè èñõîäíîé ñèñòåìû íà ñëå-
äóþùåì ÷àñòíîì ïðèìåðå.
Ïðèìåð. Ïðåäïîëîæèì, òðåáóåòñÿ ïðèâåñòè ê äèàãîíàëüíîé ôîðìå ìî-
äåëü äâèæåíèÿ ËÀ, îòâå÷àþùóþ ñëó÷àþ ãîðèçîíòàëüíîãî, ñòàáèëèçèðîâàí-
íîãî â ïëîñêîñòè ñòðåëüáû ïîëåòà (ïðè êîìïåíñàöèè îòêëîíåíèé â áîêîâîé
ïëîñêîñòè) íà ïàññèâíîì ó÷àñòêå òðàåêòîðèè ïðè •
.
ψω
==
y
0
Ñîãëàñíî ñîîòíîøåíèÿì (3.87), (3.90) è (3.95) äàííàÿ ìîäåëü áóäåò èìåòü
ñëåäóþùèé âèä:
556
dz
dt
X
mV
z
Z
m
Z
m
aaa
•
•
;
=−
+
+
ββ
βδ
(12.60)
d
dt
X
mV
z
Z
mV
Z
mV
aaa
β
βδ
ββ
=−
+
+
2
•
.
(12.61)
Îáîçíà÷èâ •
;
zx
=
1 β = x2; δ = u, ïðåäñòàâèì (12.60) è (12.61) â ñëåäóþùåé
ôîðìå:
d
dt
x
x
X
mV
Z
m
X
mV
Z
mV
x
x
aa
aa
1
2
2
1
2
⎡
⎣⎢
⎤
⎦⎥=
−
−
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
β
β
⎡
⎣⎢
⎤
⎦⎥+
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
Z
m
Z
mV
u
a
a
β
β
.
(12.62)
Ïðè îïðåäåëåíèè ïîðÿäêîâ âåëè÷èí, âõîäÿùèõ â ìàòðèöû ñîñòîÿíèÿ è
óïðàâëåíèÿ, áóäåì ñ÷èòàòü, ÷òî äëÿ ðåàëüíûõ óñëîâèé ïîëåòà çíà÷åíèå
Zm
V
a
β
/ èìååò ïîðÿäîê òûñÿ÷íûõ ñ ðàçìåðíîñòüþ ñ−1
.
Ñ öåëüþ ïðèäàíèÿ
íàãëÿäíîñòè è óïðîùåíèÿ âû÷èñëåíèé â äàííîì ïðèìåðå èçìåíèì ïîðÿäîê
ìàñøòàáîâ, ïðèâåäÿ çíà÷åíèÿ êîýôôèöèåíòîâ ê öåëûì ÷èñëàì. Òîãäà,
ïîëàãàÿ, ÷òî ýëåìåíòû ðàññìàòðèâàåìûõ ìàòðèö íà èíòåðâàëå èçìåðåíèé
îñòàþòñÿ ïîñòîÿííûìè, ìîäåëü ñîñòîÿíèÿ íåêîòîðîãî ãèïîòåòè÷åñêîãî ËÀ
ïðåäñòàâèì â âèäå
d
dt
x
x
x
x
u
1
2
1
2
67
12
7
2
⎡
⎣⎢
⎤
⎦⎥=
−
−
⎡
⎣⎢
⎤
⎦⎥
⎡
⎣⎢
⎤
⎦⎥+⎡
⎣⎢
⎤
⎦⎥.
Ñîáñòâåííûìè çíà÷åíèÿìè ðàññìàòðèâàåìîé ñèñòåìû ÿâëÿþòñÿ êîðíè
óðàâíåíèÿ
det
.
−
−
⎡
⎣⎢
⎤
⎦⎥− ⎡
⎣⎢
⎤
⎦⎥
⎧
⎨
⎩
⎫
⎬
⎭
=
67
12
10
01
0
λ
(12.63)
Ðàñêðûâàÿ îïðåäåëèòåëü
det
,
−−
−−
⎡
⎣⎢
⎤
⎦⎥
67
12
λ
λ
çàïèøåì óðàâíåíèå (12.63) â âèäå
λλ
2
450
+−
=
.
Îòñþäà ïîëó÷èì èñêîìûå ñîáñòâåííûå çíà÷åíèÿ
λλ
12
15
==
−
;.
557
Äëÿ îòûñêàíèÿ ñîáñòâåííûõ âåêòîðîâ çàïèøåì ñëåäóþùèå óðàâíåíèÿ:
v
v
v
v
11
12
11
12
67
12
⎡
⎣⎢
⎤
⎦⎥=
−
−
⎡
⎣⎢
⎤
⎦⎥
⎡
⎣⎢
⎤
⎦⎥;
(12.64)
()
.
−
⎡
⎣⎢
⎤
⎦⎥=
−
−
⎡
⎣⎢
⎤
⎦⎥
⎡
⎣⎢
⎤
⎦⎥
5
67
12
21
22
21
22
v
v
v
v
(12.65)
Ïåðåõîäÿ îò ìàòðè÷íîé ôîðìû ïðåäñòàâëåíèÿ óðàâíåíèé (12.64), (12.65) ê
ïîýëåìåíòíîé çàïèñè, ïîëó÷èì
vvv v
vv vv
11
12
21
22
12
11
22
21
7
7
==
−=
−
−
=
−
;;
;.
Ïîëàãàÿ ïåðâûå ýëåìåíòû ïîäìàòðèö ðàâíûìè åäèíèöå (v11 =v22 = 1),
íàéäåì
VV
1
11
12
2
21
22
1
1
1
17
=
⎡
⎣⎢
⎤
⎦⎥=⎡
⎣⎢
⎤
⎦⎥ =⎡
⎣⎢
⎤
⎦⎥=⎡
⎣⎢
⎤
⎦
v
v
v
v
;
/⎥.
Ñëåäîâàòåëüíî, ìàòðèöà V, ïðåîáðàçóþùàÿ èñõîäíóþ ñèñòåìó ê
äèàãîíàëüíîé ôîðìå, áóäåò èìåòü âèä
VVV
==
⎡
⎣⎢
⎤
⎦⎥
[,]
/
.
12
11
117
Âû÷èñëèì îáðàòíóþ ìàòðèöó:
V−
=
−
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1
1
6
7
6
7
6
7
6
,
èñïîëüçóÿ êîòîðóþ, íàõîäèì ýëåìåíòû ìàòðèö À* è Â*:
AVA
V
*
/
==
−
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
−
−
⎡
⎣⎢
⎤
⎦⎥
⎡
⎣⎢
−1
1
6
7
6
7
6
7
6
67
12
11
117
⎤
⎦⎥=
−
⎡
⎣⎢
⎤
⎦⎥
==
−
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎡
⎣⎢
⎤
−
10
05
1
6
7
6
7
6
7
6
7
2
1
;
*
BVB
⎦⎥=⎡
⎣⎢
⎤
⎦⎥
76
356
/
/
.
 ðåçóëüòàòå ïðèõîäèì ê äèàãîíàëèçèðîâàííîé ñèñòåìå
558
d
dt
tx
t
u
t
x
**
()
()
(),
=
−
⎡
⎣⎢
⎤
⎦⎥+
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
10
05
7
6
35
6
ãäå
x
*
() [•(), ()]; () ().
tz
ttu
tt
==
βδ
ò
Èòàê, ñîãëàñíî (12.58), ñèñòåìà óðàâíåíèé ñîñòîÿíèÿ â ñêàëÿð-
íîé ôîðìå ïðè m-ìåðíîì âåêòîðå óïðàâëåíèé áóäåò èìåòü âèä
d
dt
xtaxtbu bu
ii
i
iii
j
j
**
**
*
() ()
=+
+
+
11K
(12.66)
ïðèi=1,..., n èj=1,..., m.
Åñëè òåïåðü ïåðåéòè ê äèñêðåòíîé ôîðìå ïðåäñòàâëåíèÿ (12.66)
è ââåñòè â ðàññìîòðåíèå ðàñøèðåííûé (n + m) âåêòîð
wkk n
k
km
k
xx
uu
Ò
= [,,; ,,]
,
11
KK
(12.67)
à òàêæå ðàñøèðåííóþ ìàòðèöó
Φ=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
ab
b
abb
m
nn
n
nm
11
11
1
1
0
0
**
*
***
;
;
,
KK
M
KK
(12.68)
òî óðàâíåíèå (12.68) ìîæåò áûòü ïðåîáðàçîâàíî ê ñëåäóþùåìó âèäó:
xw
kk
+=
1Φ.
(12.69)
 óðàâíåíèè (12.69) k = tT −1
, ãäå Ò – ïåðèîä äèñêðåòèçàöèè, â äàííîì
ñëó÷àå – èíòåðâàë âðåìåíè, ÷åðåç êîòîðûé ïðîèçâîäÿòñÿ èçìåðåíèÿ
âõîäíûõ è âûõîäíûõ âåëè÷èí. Çàäà÷à èäåíòèôèêàöèè áóäåò
çàêëþ÷àòüñÿ â îïðåäåëåíèè îöåíîê ýëåìåíòîâ ìàòðèöû Φ
∧
ñ ïîìîùüþ
ÌÍÊ èëè ÌÌÏ ïðè ìíîãîêðàòíûõ èçìåðåíèÿõ âåêòîðà âûõîäíûõ
ïåðåìåííûõ
yC
xn
kk
k
=+
,
(12.70)
ãäå nk – äèñêðåòíûé øóì èçìåðåíèé.
Ôóíêöèþ øòðàôà ïðåäñòàâèì â ôîðìå
559
J
r
k
kk
k
r
kk
=
−
−−
+
∧
=
−
+
∧
∑
1
1
1
1
1
1
[]
(
)
[]
,
yw
Kyw
n
ΦΦ
ò
(12.71)
ãäå r – ÷èñëî âðåìåííÏõ òî÷åê (òî÷åê èçìåðåíèÿ); Kn
–
êîððåëÿöèîííàÿ ìàòðèöà îøèáîê èçìåðåíèé.
Íàõîæäåíèå îïòèìàëüíûõ â ñìûñëå minJ îöåíîê ìàòðèöû Φ
äîëæíî îñóùåñòâëÿòüñÿ èç óñëîâèÿ ìèíèìèçàöèè J íà êàæäîé èç i-é
ñòðîê ìàòðèöû Φ.
×òîáû íàéòè êîíå÷íîå âûðàæåíèå Φ
∧
i , ïðåäâàðèòåëüíî îáñóäèì
ðåøåíèå ðàññìàòðèâàåìîé çàäà÷è â óïðîùåííîé ïîñòàíîâêå äëÿ
ñòàòè÷åñêîé ñèñòåìû ñî ñêàëÿðíûì âûõîäîì è âåêòîðíûì âõîäîì.
Òàêàÿ ñèñòåìà îïèñûâàåòñÿ óðàâíåíèåì
xaa
ua
u
a
u
mm
**
**
.
=+
+++
01
12
2K
(12.72)
Ïðåäïîëîæèì, ïðîèçâåäåíî ν èçìåðåíèé âåëè÷èí õ
*
èuj
*
(j =0,1,...
... , m). Ïî ðåçóëüòàòàì ýòèõ èçìåðåíèé ìîãóò áûòü âû÷èñëåíû
ñðåäíèå çíà÷åíèÿ x ñð
*
è ujñð
*
, ãäå ujñð
*
–
ñðåäíåå çíà÷åíèå u j
*
â äàííîì
ðÿäó èçìåðåíèé.
Ââîäÿ â ðàññìîòðåíèå ðàçíîñòè
xxxuuu
jjj
()()();()() (),
**
**
νννννν
=−
=−
ñð
ñð
óðàâíåíèå (12.72), îñðåäíåííîå ïî ðÿäó ν èçìåðåíèé, ïðåäñòàâèì êàê
xa
ua
u
a
u
mm
()()()
(),
ννν
ν
=++
+
11
22
K
(12.73)
ãäå x(ν)èuj(ν) – îòêëîíåíèÿ ñðåäíèõ çíà÷åíèé äëÿ ðÿäà èçìåðåíèé.
Ñîâîêóïíîñòè r èçìåðåíèé äàþò
xua
() ()(), ,,,.
νν
ν
ν
==
ò
12K r
(12.74)
Çäåñü
uU
u
u
ò
ò
ò
()
()
()
() ..... ()
(
ν==
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
111
1
1
MM
r
uu
ur
m
)..... ()
,
ur
m
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
560
à x(ν)èa(ν) – âåêòîð-ñòîëáöû, ðàçìåðíîñòü êîòîðûõ îïðåäåëÿåòñÿ
÷èñëîì ïðîâåäåííûõ èçìåðåíèé (ν =1
,2
,..., r). Ìèíèìèçèðóÿ
êðèòåðèé
J=−
−
−
()()
xU
aKxU
à
n
ò1
(12.75)
ïî à, èìåÿ â âèäó î÷åâèäíîå óñëîâèå
∂
∂
J
a
=0,
(12.76)
ïîëó÷èì
aU
KUU
Kx
nn
∧
−−
−
=().
òò
111
(12.77)
Çäåñü aaa a
∧∧
∧
∧
= [,,,]
.
1
2K
m
ò
Âîçâðàùàÿñü òåïåðü ê (12.69), ïî àíàëîãèè ñ (12.77) çàïèøåì âû-
ðàæåíèå äëÿ îïðåäåëåíèÿ íàèëó÷øåé (â ñìûñëå ìèíèìóìà êðèòåðèÿ
(12.71)) îöåíêè Φ
∧
i , ò.å. i -é ñòðîêè ìàòðèöû Φi
ò
(i =1,2,..., n), â âèäå
Φik kk
i
k
kk
òò
ò
∧
−−
−
+
=[(
)](
),
,
wK
wwK
x
nn
111
1
(12.78)
ãäå
w
ww
wr
wr
k
kn
m
k
kn
m
k
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
+
+
1
1
11
(), ,
()
(), ,
()
,
,
K
MM
K
⎥
=
=
−+
−+
xt
xt
xr Tt
xr Tt
n
n
10
0
10
0
11
(),
,
(),
[()],,[()
KK
MM
K
],
,(
)
,,
(
)
,[
()]
,,[
K
KK
MM
KK
⎡
⎣
⎢
⎢
⎢
+
−+
ut
uTt
ur Tt
u
m
m
10
0
10
1(
)
]
;
rTt
−+
⎤
⎦
⎥
⎥
⎥
1
0
(12.79)
xik
i
i
xTt
xrT t
,
[( ),,( )].
+=+
+
10
0
K
(12.80)
561
Êàê ñëåäóåò èç ýòèõ çàâèñèìîñòåé, òðåáóåìûé èíòåðâàë âðåìåíè íà
ïðîâåäåíèå
èçìåðåíèé,
íåîáõîäèìûõ äëÿ
îñóùåñòâëåíèÿ
èäåíòèôèêàöèè ïàðàìåòðîâ ñèñòåìû, ñîñòàâëÿåò íå ìåíåå rT, ãäå
r ≥ n + m + 1. Íàèáîëåå ïðîñòî ïðîöåññ èäåíòèôèêàöèè îñó-
ùåñòâëÿåòñÿ äëÿ äèàãîíàëèçèðîâàííîé ìîäåëè ñèñòåìû ñî
ñêàëÿðíûì âõîäîì (îäíîìåðíûì óïðàâëåíèåì), ò.å . òîãäà, êîãäà
Φii
i
i
ab
ò
∧
∧∧
= [,]
.
**
(12.81)
Çäåñü èíäåêñ i ó ìàòðèöû Φ è ó ïàðàìåòðîâ aii
*
èbi
*
(i =1,2,..., n)
îïðåäåëÿåò íîìåð ñòðîêè, ñîîòâåòñòâóþùåé íàêîïëåííîìó ðÿäó
èçìåðåíèé âåêòîðîâ âõîäà è âûõîäà.
Îòìåòèì, ÷òî îñóùåñòâëåíèå äèàãîíàëèçàöèè èñõîäíîé ñèñòåìû
ïî ðàññìîòðåííîé êàíîíè÷åñêîé ñõåìå, çíà÷èòåëüíî óïðîùàþùåé
ïðîöåäóðó èäåíòèôèêàöèè, ïðèâîäèò ê îöåíèâàíèþ "îáîáùåííûõ"
ïàðàìåòðîâ ñèñòåìû (ýëåìåíòîâ ìàòðèö A* è Â*), èñêëþ÷àþùèõ ïî-
ñëåäóþùóþ äåòàëüíóþ îöåíêó èõ ñîñòàâëÿþùèõ (ìàññîâî-èíåðöè-
îííûõ, àýðîäèíàìè÷åñêèõ õàðàêòåðèñòèê è ò.ä .) .
Êîãäà ïðè ðåøåíèè çàäà÷è èäåíòèôèêàöèè ñòàâèòñÿ öåëü ïîëó-
÷åíèÿ îöåíîê íåèçìåðÿåìûõ êîìïîíåíòîâ íà÷àëüíîãî âåêòîðà ñî-
ñòîÿíèÿ, îöåíèâàíèå ýëåìåíòîâ ìàòðèöû ñîñòîÿíèÿ (è ìàòðèöû
óïðàâëåíèÿ äëÿ óïðàâëÿåìûõ ËÀ) èãðàåò âñïîìîãàòåëüíóþ ðîëü.
Çäåñü àïîñòåðèîðíîå îöåíèâàíèå ýëåìåíòîâ ìàòðèö À*(t)èB*(t) òðå-
áóåòñÿ äëÿ äîñòèæåíèÿ áîëåå âûñîêîé òî÷íîñòè îöåíèâàíèÿ âåêòîðà
x(t0) è íå áîëåå òîãî. Ïîýòîìó êàíîíè÷åñêàÿ äèàãîíàëèçàöèÿ ìàòðè-
öû À(t) çäåñü ïðåäñòàâëÿåòñÿ íå òîëüêî äîïóñòèìîé, íî è öåëåñîîá-
ðàçíîé.
Åñëè æå "öåíòð òÿæåñòè" çàäà÷è ïåðåíåñòè íà èäåíòèôèêàöèþ
àýðîäèíàìè÷åñêèõ è èíåðöèîííûõ õàðàêòåðèñòèê ËÀ ïî ðåçóëüòà-
òàì ëåòíûõ èñïûòàíèé, ò.å. ïàðàìåòðè÷åñêóþ èäåíòèôèêàöèþ, òî
äàííûé ïîäõîä â ïîäàâëÿþùåì áîëüøèíñòâå ñëó÷àåâ íåïðèìåíèì.
Ïðîâåäåíèå èäåíòèôèêàöèè ïàðàìåòðîâ ìàòðèö ñîñòîÿíèÿ è
óïðàâëåíèÿ íåäèàãîíàëèçèðîâàííîé ñèñòåìû, ÷òî ñîîòâåòñòâóåò
ïðåäñòàâëåíèþ
Φii i
n
ii
m
aa
bb
ò
∧
∧∧
∧∧
=[,,,,,]
,
11
KK
(12.82)
ñîïðÿæåíî ñî çíà÷èòåëüíûìè âû÷èñëèòåëüíûìè òðóäíîñòÿìè,
îñîáåííî äëÿ ìîäåëåé áîëüøîé ðàçìåðíîñòè [80]. Ïðè ýòîì íàäî
èìåòü òàêæå â âèäó, ÷òî â îáùåì ñëó÷àå ýëåìåíòû ìàòðèö ñîñòîÿíèÿ è
óïðàâëåíèÿ ïåðåìåííû ïî âðåìåíè. Äàííîå îáñòîÿòåëüñòâî ïðèâîäèò
562
ê íåîáõîäèìîñòè ìíîãîêðàòíîãî ïîâòîðåíèÿ ïðîöåññîâ èäåí-
òèôèêàöèè ïðè ìèíèìàëüíûõ ïî ïðîäîëæèòåëüíîñòè (ñ öåëüþ
ïîâûøåíèÿ òî÷íîñòè) ïåðèîäàõ äèñêðåòèçàöèè.
Êðîìå òîãî, ïðè èäåíòèôèêàöèè ïî äàííûì ëåòíûõ èñïûòàíèé
êîíêðåòíûõ àýðîäèíàìè÷åñêèõ è ìàññîâî-èíåðöèîííûõ õàðàêòåðè-
ñòèê ËÀ óðàâíåíèå (12.69) ÷àñòî îêàçûâàåòñÿ íåëèíåéíûì îòíîñè-
òåëüíî îïðåäåëÿåìûõ âåëè÷èí, âõîäÿùèõ â íåãî â âèäå ïðîèçâåäå-
íèé ôàçîâûõ êîîðäèíàò è íåèçâåñòíûõ êîýôôèöèåíòîâ. Äëÿ îáñóæ-
äàåìîãî ñëó÷àÿ èçìåðÿåìûé âåêòîð âûõîäíûõ ïåðåìåííûõ yk áóäåò
ïðåäñòàâëÿòü ñîáîé íåëèíåéíóþ ôóíêöèþ y(Φ, w) êîìïîíåíò âåêòî-
ðà xk è èäåíòèôèöèðóåìûõ ïàðàìåòðîâ ìàòðèöû
Φ
Φ
Φ
=
⎡
⎣⎢
⎤
⎦⎥=⎡
⎣
⎢
⎤
aa bb
aabb
nm
nn
n
nn
m
11
1
11
1
11
KK
KK
;
;
I
ò
II
ò
⎦
⎥.
Ïðè ýòîì çíà÷åíèÿ èäåíòèôèöèðóåìûõ ýëåìåíòîâ ìàòðèöû Φ áóäóò
ëåæàòü â îáëàñòè
Φ∆
ΦΦΦ ∆
Φ
èñò
èñò
−≤
≤+,
(12.83)
ãäå Φèñò
–
èñòèííîå çíà÷åíèå ìàòðèöû èäåíòèôèöèðóåìûõ
ïåðåìåííûõ; ∆Φ – äîïóñòèìûé ðàçáðîñ åå çíà÷åíèé.
Äëÿ ËÀ, ñîâåðøàþùèõ ïîëåò ïðè ÷èñëàõ Ìàõà Ì ≥ 1,5 è ïðè èç-
ìåíåíèè
ïðîñòðàíñòâåííîãî
(ïîëíîãî)
óãëà
àòàêè
αï
=+
arcsin (
)/
VVV
yz
222
â äèàïàçîíå 0 ≤αï ≤ 25°, ïðåäñòàâëåíèå
èäåíòèôèöèðóåìûõ àýðîäèíàìè÷åñêèõ êîýôôèöèåíòîâ ðåêîìåíäó-
åòñÿ [59] â âèäå ñëåäóþùèõ àïïðîêñèìèðóþùèõ ïîëèíîìîâ:
êîýôôèöèåíòà ñèëû ëîáîâîãî ñîïðîòèâëåíèÿ
cc
c
A
c
xx
x
y
aa
(,)
Mïï
ïï
αα
αα
=+
+
0
22
(12.84)
(,
–
cc
xx
0
αα
ïï
èäåíòèôèöèðóåìûå ïîñòîÿííûå; êîýôôèöèåíò cx
αα
ïï
ïðèíèìàåòñÿ íåçàâèñèìûì îò ÷èñëà Ì è óãëà àòàêè);
êîýôôèöèåíòà ïîäúåìíîé ñèëû
cc
yy
a
(,)
Mïï
ï
αα
α
=
(12.85)
(–
cy
αï
èäåíòèôèöèðóåìûé ïàðàìåòð, êîòîðûé ìîæíî ñ÷èòàòü
êîíñòàíòîé â ñèëó åãî ñëàáîé çàâèñèìîñòè îò ÷èñëà Ì è
ïðàêòè÷åñêîé íåçàâèñèìîñòè ïðè αï ≤ 25° îò óãëà àòàêè);
êîýôôèöèåíòà öåíòðà äàâëåíèÿ
563
cñ
c
dd
d
(,)
MÌ
ï
Ì
α=+
00
(12.86)
(cd 0
è cd0
Ì
–
èäåíòèôèöèðóåìûå êîíñòàíòû);
êîýôôèöèåíòà äåìïôèðóþùåãî ìîìåíòà
mm
m
m
zz
z
z
yz
z
z
ωω
ω
ω
α
α
αα
α
(,)
()
MM
M
,
ï
M
ïï
2
ïï
=+
+
0
(12.87)
(,
mm
zz
zz
0
ωω
M
èmz
z
ωαα
ïï
–
èäåíòèôèöèðóåìûå êîíñòàíòû).
Òàê êàê â ðàññìàòðèâàåìîì ñëó÷àå ôóíêöèÿ y(Φi, w) ÿâëÿåòñÿ íå-
ëèíåéíîé ôóíêöèåé ïàðàìåòðîâ, òî óñëîâèå ìèíèìóìà ôóíêöèîíà-
ëà (12.71), çàïèñàííîãî äëÿ íåïðåðûâíîãî âðåìåíè, ïðèìåò ñëåäóþ-
ùèé âèä:
∂
∂
∂
∂
J
t
i
i
i
i
Φ
Φ
Φ
Φ
=−
=
∧
−
∧
yyy wK
yw
n
[(,)
](
)().
ò
,
1
0
(12.88)
Ñ öåëüþ ïîëó÷åíèÿ åäèíñòâåííîãî ðåøåíèÿ îòíîñèòåëüíî Φi
∧
(i =1,
2, ..., n) íåîáõîäèìî ïðîèçâåñòè ëèíåàðèçàöèþ ñèñòåìû (12.88),
íàçûâàåìîé ñèñòåìîé íîðìàëüíûõ óðàâíåíèé [74]. Äëÿ ýòîãî ðàçëîæèì
ôóíêöèè, âõîäÿùèå â ñîñòàâ ñèñòåìû, â ñòåïåííîé ðÿä (â ÷àñòíîñòè,
ðÿä Òåéëîðà) îòíîñèòåëüíî íåêîòîðûõ àïðèîðíûõ çíà÷åíèé
ýëåìåíòîâ ñòðîêè Φ0i ìàòðèöû Φ0, óäîâëåòâîðÿþùåé óñëîâèþ (12.83).
 ðåçóëüòàòå ðàçëîæåíèÿ ïîëó÷èì
yyw
yw
Kn
−×
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
∧
∧
=
∧
−
(,)(,)
(
Φ
Φ
Φ
∆Φ
ΦΦ
i
i
i
i
ii
t
∂
∂
0
1
ò
)
(,)
(,)
×
×+
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
∧
=
∧
=
∂
∂
∂
∂
yw
yw
Φ
Φ
Φ
Φ
ΦΦ
ΦΦ
i
i
i
i
ii
ii
00
2
2
⎥
⎥
=0,
ãäå
∂
∂
∂
∂
∂
∂∂
2
2
2
0
1
2
2
1
yw
yw yw
(,)
(,)
()
(,)
Φ
Φ
Φ
Φ
Φ
ΦΦ
i
i
i
i
i
i
∧
∧∧
=
K
ik
i
ik
i
i
ik
∂
∂∂
∂
∂
2
1
2
2
yw yw
(,) (,)
()
Φ
ΦΦ
Φ
Φ
∧∧
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
K
⎥
⎥
=
=
ΦΦ
Φ
ii
i
0
0
M(,),
w
(12.89)
564
ïðè÷åì êàæäûé ýëåìåíò ìàòðèöû [(,)]/( )
∂∂
22
yw
ΦΦ
ii
k
∧
ïðåäñòàâëÿåò
ñîáîé n-ìåðíûé âåêòîð.
Ââåäåì òàêæå ñëåäóþùèå îáîçíà÷åíèÿ:
∂
∂
2
yw
Nw
yyw y
(,)
(,)
;
()(,)(
Φ
Φ
Φ
Φ∆
ΦΦ
i
i
i
i
ii
t
∧
=
∧
=
−=
èñò
èñò
t).
(12.90)
Òîãäà, ðàñêðûâàÿ ñêîáêè â âûðàæåíèè (12.89), ïåðåéäåì ñ ó÷åòîì
ïðèíÿòûõ îáîçíà÷åíèé ê ñëåäóþùåé ñèñòåìå ëèíåéíûõ íîðìàëüíûõ
óðàâíåíèé:
[(,)( ,)(,)()]
(
Nw
K
Nw
Mw
K
y
N
nn
ò
èñò
èñò
ò
ΦΦΦ
∆
∆
Φ
iii
i
t
−=
=
∧
0
Φ∆
i
t
èñò
,)
(),
wKy
n
(12.91)
îòêóäà, îïóñêàÿ ñ öåëüþ óïðîùåíèÿ çàïèñè àðãóìåíòû ó ìàòðèö N è
M, íàéäåì
∆Φ
∆
∆
i
tt
∧
−
=−
(
())(
( )).
NKNMKy NKy
nn
n
òò
1
(12.92)
Ñëàãàåìîå MKn∆y(t) â âûðàæåíèè (12.92) èìååò òåì áîëüøèé "âåñ",
÷åì áîëüøå ðàññîãëàñîâàíèå ìåæäó èçìåðåíèÿìè è àïðèîðíîé
ìîäåëüþ.
Äëÿ ïîñòðîåíèÿ âû÷èñëèòåëüíîãî àëãîðèòìà òåïåðü ìîæíî âîñ-
ïîëüçîâàòüñÿ òåì îáñòîÿòåëüñòâîì, ÷òî ïðè äîñòàòî÷íî ãëàäêîé
ôóíêöèè y(Φi, w), èìåþùåé íåïðåðûâíûå ïåðâûå è âòîðûå ïðîèç-
âîäíûå ïî Φi(t) â çàìêíóòîé îáëàñòè, ñîäåðæàùåé òî÷êó Φèñò, ìàòðè-
öà Φi (i =1,2,..., n) äîëæíà ñòðåìèòüñÿ ê Φi èñò ïðè ðåàëèçàöèè èòå-
ðàöèîííîé âû÷èñëèòåëüíîé ïðîöåäóðû âèäà
∆ΦΦ
∆Φ
ik
i
i
kk
∧∧
∧
=−
+−
(1
1
)()
,
(12.93)
ãäå ∆Φi
∧
îïðåäåëÿåòñÿ ïî ôîðìóëå (12.92), k – íîìåð èòåðàöèè.
Òàê êàê èñòèííîå çíà÷åíèå Φi íåèçâåñòíî, â êà÷åñòâå íà÷àëüíîãî
ïðèáëèæåíèÿ âûáèðàåòñÿ åãî ëþáîå ïðåäïîëàãàåìîå çíà÷åíèå èç
îáëàñòè (12.83). Ñõîäèìîñòü èñêîìûõ îöåíîê ïðè ýòîì áóäåò çàâè-
ñåòü îò ñòåïåíè áëèçîñòè íà÷àëüíîãî ïðèáëèæåíèÿ èñòèííîìó çíà-
565
÷åíèþ, òèïà ðåàëèçóåìîãî ÷èñëåííîãî ìåòîäà (óæå îòìå÷àëîñü, ÷òî
ïðåäïî÷òåíèå ñëåäóåò îòäàòü ìîäèôèöèðîâàííûì ìåòîäàì Ãàóñ-
ñà–Íüþòîíà), õàðàêòåðà ðåøàåìîé çàäà÷è. Òî÷íîñòü îöåíîê Φik
,
+
∧
1
(i =1,2,..., n) ïðè k →∞áóäåò îïðåäåëÿòüñÿ äèñïåðñèîííîé ìàòðè-
öåé
KN
K
N
M
K
y
nn
Φ
∆
∧
→∞
=−
−
=
()(
()) .
k
r
k
ò
ν
ν
1
Íà ïðàêòèêå ÷èñëî èòåðàöèé k íå ìîæåò áûòü áåñêîíå÷íî áîëüøèì.
Åãî îãðàíè÷èâàþò çíà÷åíèåì, ïðè êîòîðîì ïîñëåäóþùèå èòåðàöèè
íå ïðèâîäÿò ê çàìåòíîìó óâåëè÷åíèþ òî÷íîñòè èñêîìûõ
èäåíòèôèöèðóåìûõ ïàðàìåòðîâ.
Íà îñíîâàíèè èçëîæåííîãî ïåðåéäåì ê ðàññìîòðåíèþ ñëåäóþ-
ùåé çàäà÷è. Áóäåì ñ÷èòàòü, ÷òî â ïðîöåññå ëåòíîãî ýêñïåðèìåíòà
ïîëó÷åíû äàííûå î ñîñòàâëÿþùèõ âåêòîðà ïåðåãðóçêè n, èñïûòû-
âàåìîé ËÀ, î ñîñòàâëÿþùèõ óãëîâîé ñêîðîñòè ωx, ωy è ωz, âûñîòå è
ñêîðîñòè íåóïðàâëÿåìîãî ïîëåòà w(t)=X(t) íà ìåðíîì ó÷àñòêå áàë-
ëèñòè÷åñêîé òðàåêòîðèè. Ïî äàííûì ìåòåîïîäãîòîâêè ïîëó÷åíû
òàêæå ñâåäåíèÿ î ñîñòîÿíèè àòìîñôåðû. Èçâåñòíû îñíîâíûå ãåî-
ìåòðè÷åñêèå (õàðàêòåðíàÿ ïëîùàäü S, äëèíà l, êîîðäèíàòà öåíòðà
ìàññ lö.ì) è ìàññîâûå õàðàêòåðèñòèêè àïïàðàòà (mg, Ix, Iy, I z è äð.) .
Òðåáóåòñÿ ïî ðåçóëüòàòàì ëåòíûõ èñïûòàíèé èäåíòèôèöèðîâàòü
áåçðàçìåðíóþ êîîðäèíàòó öåíòðà äàâëåíèÿ ÑÑ
l
ö.ä
ö.ä
=
−1
, à òàêæå êî-
ýôôèöèåíòû ñîñòàâëÿþùèõ ìîìåíòà äåìïôèðîâàíèÿ my
y
ω
èmz
z
ω
.
Â
êà÷åñòâå èñõîäíîé ìîäåëè èñïîëüçóåì óðàâíåíèÿ âðàùàòåëüíîãî
äâèæåíèÿ ËÀ îòíîñèòåëüíî åãî öåíòðà ìàññ (2.56), çàïèñàííûå â
îñÿõ ñâÿçàííîé ñèñòåìû êîîðäèíàò.
Òîãäà âûðàæåíèå âåêòîðà y(t) â (12.88) ïðèìåò âèä
y()
()
()
()
t
yt
yt
yt
III
III
xx
yx
z
yx
y
y
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
−−
−−
1
2
3
z
zx
zy
z
x
y
z
zyx
y
III
III
−−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
+
+
−
•
•
•
ω
ω
ω
−
−−
−−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
I
IIII
II
I
I
xz
xy
x
z
yz
xz
yz
y
x
yz
xz
xy
ωω
ωω
ωω
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
+
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
−
−
I
I
I
yz
xz
xy
zy
x
00
00
00
22
2
()
(
ωω
ωω
ωω
z
yx
2
22
)
()
.
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
Èìåÿ â âèäó îãîâîðåííóþ ñîâîêóïíîñòü èäåíòèôèöèðóåìûõ è
èçìåðÿåìûõ ïàðàìåòðîâ, âûðàæåíèå y(Φ, X) ïðåäñòàâèì â ôîðìå
566
yX
(,)
(
Φ=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
+−
−
ρV
Sl
m
m
m
mg
CC
x
y
z
2
2
00
0
00
0
0
0
ö.ì
ö.ä
ö.ì
ö.ä
)
()
l
CÑl
n
n
n
VSl
x
y
z
00
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
×
×
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
+
ρ2
2
000
00
00
m
m
y
z
x
y
z
y
z
ω
ω
ω
ω
ω
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
.
Çäåñü öåëåñîîáðàçíî íåñêîëüêî çàäåðæàòü âíèìàíèå íà ôîð-
ìå çàïèñè y(t). Îáùèì òðåáîâàíèåì ïðåäñòàâëåíèÿ ñîîòíîøå-
íèé y(t)èyw
(,)
,
Φi
∧
ðàçíîñòü êîòîðûõ ∆y(t) íàçûâàåòñÿ íåâÿçêîé,
ÿâëÿåòñÿ òðåáîâàíèå îáåñïå÷åíèÿ óñëîâèé ñîïîñòàâëåíèÿ àïðè-
îðíîé èíôîðìàöèè ñ àïîñòåðèîðíîé (ò.å . ïîëó÷àåìîé â ïðîöåñ-
ñå ýêñïåðèìåíòà) èíôîðìàöèåé òîãî æå òèïà. Â ïðèâåäåííûõ
âûðàæåíèÿõ ýòîò ïðèíöèï, âîîáùå ãîâîðÿ, íàðóøåí. Äåéñòâè-
òåëüíî, âûðàæåíèå y(t) âêëþ÷àåò â ñåáÿ íå òîëüêî àïðèîðíóþ,
íî è àïîñòåðèîðíóþ èíôîðìàöèþ â âèäå èçìåðÿåìûõ ñîñòàâ-
ëÿþùèõ âåêòîðà óãëîâîé ñêîðîñòè ËÀ. Â ðåçóëüòàòå, åñëè íå
ïðèíÿòü ñïåöèàëüíûõ ìåð, ýòî ìîæåò ïðèâåñòè ê äîïîëíèòåëü-
íîé ïîãðåøíîñòè â îïðåäåëåíèè èäåíòèôèöèðóåìûõ ïàðàìåò-
ðîâ. Ñëåäóåò îòìåòèòü, ÷òî â ñïåöèàëüíîé ëèòåðàòóðå [17] ñî-
äåðæàòñÿ ñâåäåíèÿ î íàëè÷èè ìåòîäîâ, ïîçâîëÿþùèõ èñêëþ÷èòü
òàêîãî ðîäà ïîãðåøíîñòè. Ó÷èòûâàÿ ó÷åáíûé õàðàêòåð ðàññìàò-
ðèâàåìîãî ïðèìåðà, îáñóæäàòü çäåñü óïîìÿíóòûå ìåòîäû íå
ïðåäñòàâëÿåòñÿ âîçìîæíûì.
Èñïîëüçóÿ ïðèâåäåííûå âûðàæåíèÿ, ïîëó÷èì òåïåðü íîðìàëü-
íóþ ñèñòåìó óðàâíåíèé, ñîîòâåòñòâóþùóþ (12.83) ïðè Kn = Å (ñëó-
÷àé, îòâå÷àþùèé äåòåðìèíèðîâàííûì èçìåðåíèÿì ïðè îòñóòñòâèè
øóìîâ), ò.å . íàéäåì óðàâíåíèÿ, óäîâëåòâîðÿþùèå óñëîâèþ
∂
∂
J
Φ
=0,
(12.94)
ãäå Φ äëÿ îáñóæäàåìîé çàäà÷è ïðèíèìàåò âèä âåêòîð-ñòîëáöà
èäåíòèôèöèðóåìûõ êîýôôèöèåíòîâ Φ=[, , ]
.
Cmm
yz
yz
ö.ä
ò
ωω
 ðàìêàõ
èçëîæåííîé ïîñòàíîâêè è ïðèíÿòîé ê ðàññìîòðåíèþ ìîäåëè ñèñòåìà
(12.94) áóäåò ëèíåéíîé ïî îòíîøåíèþ ê îïðåäåëÿåìûì ïàðàìåòðàì.
Ýòî äàåò îñíîâàíèå âîñïîëüçîâàòüñÿ äëÿ íàõîæäåíèÿ ðåøåíèÿ
ñîîòíîøåíèåì òèïà (12.78), êîòîðîå ïðè Kn = E è
567
wX
kk
xT
t
xT
t
xT
t
==
−+
−+
−+
()
[()][()][()
ν
ννν
11
0
12
0
13
0
111
]
[()][()][()]
[(
xT
t
xT
t
xT
t
x
21
0
22
0
23
0
31
111
ννν
ν
−+
−+
−+
− 111
03
2
03
3
0
)][
()][
()]
Ttx
Ttx
Tt
+−
+−
+
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
νν
ñâîäèòñÿ ê óðàâíåíèþ âèäà
Φ
∧
−
+
==
Xx
kk
r
1
1
1
(),,,,
νν
K
(12.95)
ãäå ýëåìåíòû ìàòðèöû X(ν) è âåêòîð-ñòîëáöà xk+1 îïðåäåëÿþòñÿ ïî
ñëåäóþùèì ñîîòíîøåíèÿì, îáðàçóþùèì ñèñòåìó ëèíåéíûõ
àëãåáðàè÷åñêèõ óðàâíåíèé:
xnn
m
g
l
xxl
V
kz
ky
k
kk
k
y
11
222
2
12
21
3
05
,,
,
,,
,
[]
(
)
;
,[
=+
==
ω
kzk
k
kk
k
z
k
y
kk
nm
gS
xxl
Vn
m
g
,
,,
,
,
() ];
,[
()
2
13
31
22
05
ρ
ωρ
==
S
xl
VS
xl
VS
kk
y
k
k
kk
z
k
k
];
,[
];
,[
]
,,
,,
22
32
33
22
05
05
=
=
ωρ
ωρ;
;
[
,,
,,
,
,
,
xx
xy
n
n
m
g
C
l
y
n
kk
k
kzk
zk
k
23
32
112
2
3
0
==
=+
−
+
ö.ì
yk
yk
kk
z
k
nm
gC lmgl
xy
n
m
g
C
l
,,
,,
,
]( );
,[
+
=+
+
2
21
2
05
ö.ì
ö.ì
];
,[
]
,
,,
,
,
ρω
ρω
kk yk
kk
y
kk
k
z
k
VS
l
xy
n
m
g
C
l
V
S
l
31
3
05
+=−
ö.ì
.
Çäåñü ïîä xij,k è xi,k+1 ñëåäóåò ïîíèìàòü ñèìâîëè÷åñêóþ ôîðìó çàïèñè
îáîçíà÷åíèé ýëåìåíòîâ, ñîîòâåòñòâóþùèõ íå k-ìó è (k + 1)-ìó
ìîìåíòàì âðåìåíè, à ñäâèíóòûì íà ïåðèîä Ò ïîñëåäîâàòåëüíîñòÿì
ìîìåíòîâ (ν−1)T + t0 è νT + t0 ïðè ν =1,2,..., r.
Îòìåòèì, ÷òî ïðè íåçíà÷èòåëüíîì ðàñøèðåíèè ñîñòàâà èçìåðÿå-
ìûõ ïàðàìåòðîâ çà ñ÷åò äîïîëíèòåëüíîãî îïðåäåëåíèÿ òåêóùåãî óã-
ëîâîãî ïîëîæåíèÿ (θ, ψ, γ) ïðåäñòàâëÿåòñÿ âîçìîæíûì íàéòè òàêæå
è çíà÷åíèÿ áàëàíñèðîâî÷íûõ óãëîâ àòàêè (αá) è ñêîëüæåíèÿ (βá)
âðàùàþùåãîñÿ (ωx ≠ 0) ëèáî ñòàáèëèçèðîâàííîãî ïî êðåíó (ωx =0)
àïïàðàòà, èìåþùåãî àýðîäèíàìè÷åñêóþ àñèììåòðèþ ïðè íåñòàöèî-
íàðíûõ íà èíòåðâàëå [0, tν] àýðîäèíàìè÷åñêèõ õàðàêòåðèñòèêàõ [80].
Íåñòàöèîíàðíîñòü óêàçàííûõ õàðàêòåðèñòèê ìîæåò áûòü îáóñëîâëå-
íà íåñèììåòðè÷íûì îáãàðîì êîðïóñà àïïàðàòà ïðè åãî âûñîêîñêî-
ðîñòíîì äâèæåíèè â ïëîòíûõ ñëîÿõ àòìîñôåðû, ðàñêðûòèåì òîð-
ìîçíûõ ùèòêîâ è ò.ä.
568
Ïóñòü ê íåêîòîðîìó ìîìåíòó âðåìåíè, ïðèíÿòîìó çà íà÷àëüíûé
(t0 = 0), äîñòèãíóòî êâàçèóñòàíîâèâøååñÿ èçìåíåíèå ïàðàìåòðîâ êî-
ëåáàòåëüíî-âðàùàòåëüíîãî äâèæåíèÿ. Ýòîìó ìîìåíòó áóäóò îòâå-
÷àòü (ïðè ωx ≠ 0) íà÷àëüíûå áàëàíñèðîâî÷íûå çíà÷åíèÿ óãëîâ àòàêè
è ñêîëüæåíèÿ
αω
ω
βωω
00
0
0
1
00
0
0
0
0
á
á
=−
⎛
⎝⎜
⎞
⎠⎟
=+
⎛
⎝⎜
⎞
⎠⎟
−
−
y
z
x
z
y
x
gn
V
gn
V
;
1
.
(12.96)
Çàâèñèìîñòè (12.96) ïîëó÷åíû èç âòîðîãî è òðåòüåãî óðàâíåíèé
ñèñòåìû (2.49) ïðè ïðèíÿòèè ïðåäïîëîæåíèÿ î ìàëîñòè
ãðàâèòàöèîííîãî óñêîðåíèÿ ïî îòíîøåíèþ ê óñêîðåíèþ îò ñèëû
ëîáîâîãî ñîïðîòèâëåíèÿ ñ ó÷åòîì òîãî, ÷òî ïðè ìàëûõ óãëàõ àòàêè è
ñêîëüæåíèÿ α = VyV
−1
èβ=VzV
−1
.
Êàê ñëåäóåò èç ïðèâåäåííûõ
ñîîòíîøåíèé (12.96), ïðè áëèçêèõ ê íóëþ çíà÷åíèÿõ ωx ñîñòàâëÿþùèå
ïîëíîãî óãëà àòàêè äëÿ êâàçèóñòàíîâèâøèõñÿ èçìåíåíèé ïàðàìåòðîâ
óãëîâîãî äâèæåíèÿ îêàçûâàþòñÿ íåîïðåäåëåííûìè. Èõ ïðèáëèæåííîå
âû÷èñëåíèå â ýòîì ñëó÷àå îñíîâûâàåòñÿ íà èññëåäîâàíèè òàê
íàçûâàåìîãî êîýôôèöèåíòà óñèëåíèÿ ïîëíîãî óãëà àòàêè [59],
ñâÿçûâàþùåãî
αα
ββ
ω
α
ω
ω
α
ω
0
0
1
0
0
0
0
1
0
0
áá
áá
ï
ï
xx
xx
K
K
=
−
≠
=
−
≠
=
=
*
*
,
,
(12.97)
ãäå êîýôôèöèåíò óñèëåíèÿ ïîëíîãî óãëà àòàêè
K
ñCCVS
l
II
y
x
a
α
α
ρ
ï
ï
ñ.ä
ö.ì
*
()
()
≈
−
−
⎛
⎝
⎜⎜
⎞
⎠
⎟⎟
−
2
1
2
(12.98)
ïðèI=Iy=Iz.
Ïîëàãàÿ òåïåðü, ÷òî ñ ìîìåíòà t0 äî ìîìåíòà tv àýðîäèíàìè÷åñêèå
õàðàêòåðèñòèêè àïïàðàòà íåïðåðûâíî èçìåíÿþòñÿ, ïðèâîäÿ ê èçìå-
íåíèþ ïàðàìåòðîâ åãî äâèæåíèÿ, íå âûõîäÿùèõ çà ïðåäåëû ìàëûõ
îòêëîíåíèé ïî îòíîøåíèþ ê íîìèíàëüíîìó äâèæåíèþ, îòâå÷àþùå-
ìó α0
á
èβ0
á
, ïîëó÷èì
569
ααω
θθγ
áá
v
=±
−
−
⎡
⎣⎢
⎤
⎦⎥
∫00
z
y
t
ng
V
g
V
dt
sin cos
.
(12.99)
Âû÷èñëèâ òåêóùåå áàëàíñèðîâî÷íîå çíà÷åíèå óãëà àòàêè, íåòðóäíî
îïðåäåëèòü è çíà÷åíèå
β
βω
α
ω
α
γ
θ
γ
á
áá
á
0
=
=±
+
−
−
⎡
⎣⎢
⎤
⎦⎥
−
0
1
ng
V
gV
z
xy
t
sin
cos
cos cos
v
∫
dt.
(12.100)
Çíàê "ìèíóñ" â (12.99) è (12.100) ñîîòâåòñòâóåò óìåíüøåíèþ
àýðîäèíàìè÷åñêîé àñèììåòðèè, "ïëþñ" – óâåëè÷åíèþ.
Ïðè íàëè÷èè èíôîðìàöèè î αá è βá ìîæåò áûòü íàéäåíî çíà÷å-
íèå ïðîèçâîäíîé
cm
g
n
n
V
S
yy
z
a
α
ρ
αβ
ï
áá
=+
+
⎛
⎝⎜
⎞
⎠⎟
−
()(
)
(
)
,
22
2
22
1
2
(12.101)
à çàòåì ìîæíî âû÷èñëèòü â ïåðâîì ïðèáëèæåíèè ñîñòàâëÿþùèå
êîýôôèöèåíòà àýðîäèíàìè÷åñêîãî ìîìåíòà my 0
è mz0
, îáóñëîâëåííîãî
àýðîäèíàìè÷åñêîé àñèììåòðèåé ËÀ:
mcÑÑ
yy
a
0
=−
∧
α
β
ï
ö.ä
ö.ì
á
()
;
(12.102)
mcÑÑ
zy
a
0
=−
∧
α
α
ï
ö.ä
ö.ì
á
()
,
(12.103)
ãäå Ñö.ä
∧
–
èäåíòèôèöèðóåìîå çíà÷åíèå áåçðàçìåðíîé êîîðäèíàòû
öåíòðà äàâëåíèÿ.
Âåëè÷èíà (Ñö.ä
−
Ñö.ì), êàê èçâåñòíî, îïðåäåëÿåò çàïàñ ñòàòè÷å-
ñêîé óñòîé÷èâîñòè ËÀ. Êîýôôèöèåíò ñèëû ëîáîâîãî ñîïðîòèâëå-
íèÿ ñõ (êîýôôèöèåíò îñåâîé ñèëû ñîïðîòèâëåíèÿ) äîñòàòî÷íî òî÷íî
âû÷èñëÿåòñÿ ïðè íàëè÷èè ïîêàçàíèé îñåâîãî àêñåëåðîìåòðà ïî
ôîðìóëå
cn
m
g
V
S
xx
=
−−
−
2
121
ρ
ì
.
(12.104)
Ïðè èñïîëüçîâàíèè â êà÷åñòâå èñõîäíîé ìîäåëè ñèñòåìû óðàâ-
íåíèé ïðîñòðàíñòâåííîãî äâèæåíèÿ ËÀ ñ 12-ìåðíûì âåêòîðîì ñî-
ñòîÿíèÿ x(t)=[V, θ, Ψ, x, y, z, ωx, ωy, ωz, ψ, θ, γ]ò
, 6-ìåðíûì âåêòîðîì
570
èçìåðÿåìûõ ïàðàìåòðîâ y(t, Φ)=[x(t, Φ); y(t, Φ); z(t, Φ); ψ(t, Φ); θ(t,
Φ); γ(t, Φ)]T
è 16-ìåðíûì âåêòîðîì èäåíòèôèöèðóåìûõ ïàðàìåòðîâ
Φ=Φi=[V0,θ0,Ψ0,x0,y0,z0,ω
x0
, ωy0
, ωz0
,ψ0,θ0,γ0,cx,cy
αï
, Ñö.ä, mz
z
ω
]ò
íîðìàëüíàÿ ñèñòåìà óðàâíåíèé áóäåò âêëþ÷àòü â ñåáÿ 192 íåëèíåé-
íûõ äèôôåðåíöèàëüíûõ óðàâíåíèÿ. Ïðè ýòîì ðàññìîòðåííûé âûøå
ïîäõîä îêàçûâàåòñÿ íåðåàëèçóåìûì. Ðåøåíèå ìîæåò áûòü ïîëó÷åíî
òîëüêî íà îñíîâå ïðèìåíåíèÿ èòåðàöèîííîé âû÷èñëèòåëüíîé ïðî-
öåäóðû ñ èñïîëüçîâàíèåì ìåòîäà Ãàóññà–Íüþòîíà (ëèáî àíàëîãè÷-
íîãî åìó). Çíà÷åíèå âåêòîðà îöåíèâàåìûõ ïàðàìåòðîâ Φ íà k-ì øàãå
èòåðàöèè îïðåäåëÿåòñÿ ïî ôîðìóëå (12.93). Ïðåêðàùåíèå èòåðàöè-
îííîãî ïðîöåññà äîëæíî îñóùåñòâëÿòüñÿ ïî óñëîâèþ
[]
[
]
,
ΦΦ∆
Φ
kk
∧
−
∧
−≤
1ä
(12.105)
ãäå ∆Φä – äîïóñòèìîå çíà÷åíèå ðàçíîñòè îöåíèâàåìûõ âåêòîðîâ,
ïîëó÷åííûõ íà ïîñëåäóþùåé è ïðåäûäóùåé èòåðàöèÿõ. Ïðè
ïðèìåíåíèè
ìîäèôèöèðîâàííîãî
ìåòîäà Ãàóññà–Íüþòîíà,
ïðåäóñìàòðèâàþùåãî âû÷èñëåíèå ïåðâîãî è âòîðîãî ãðàäèåíòà
(ïåðâîé è âòîðîé ÷àñòíîé ïðîèçâîäíîé) J ïî âåêòîðó îöåíèâàåìûõ
ïåðåìåííûõ ïðè ÷èñëå èòåðàöèé, íå ïðåâîñõîäÿùåì ïÿòè è
ñóùåñòâåííî ìåíüøåì, ÷åì óêàçàííîå âûøå ÷èñëî îöåíèâàåìûõ
âåëè÷èí, âðåìÿ ðåøåíèÿ îáñóæäàåìîé çàäà÷è íà ÝÂÌ, îáëàäàþùåé
áûñòðîäåéñòâèåì ïîðÿäêà 400000 îïåðàö/ñ, ñîñòàâëÿåò íåñêîëüêî
÷àñîâ. Ïîñêîëüêó ñêîðîñòü ñõîäèìîñòè â çíà÷èòåëüíîé ñòåïåíè
çàâèñèò îò ñòåïåíè áëèçîñòè íà÷àëüíîãî ïðèáëèæåíèÿ èñòèííîìó
çíà÷åíèþ, ÷èñëî èòåðàöèé, à ñëåäîâàòåëüíî, è âðåìÿ ñ÷åòà ìîæåò
ñóùåñòâåííî óâåëè÷èâàòüñÿ.  êà÷åñòâå ïðèìåðà çàâèñèìîñòè ÷èñëà
èòåðàöèé îò âåëè÷èíû îòêëîíåíèÿ àïðèîðíûõ íà÷àëüíûõ çíà÷åíèé
(10 % – êðèâàÿ 1, 20 % – êðèâàÿ 2) êîýôôèöèåíòà mz
ω
ïðèâåäåì
ñîîòâåòñòâóþùèé ãðàôèê (ðèñ. 12.6), çàèìñòâîâàííûé èç [60],
ïîëó÷åííûé ïðè ïðèìåíåíèè êëàññè÷åñêîãî ìåòîäà Ãàóññà–Íüþòîíà.
 ðàáîòå [60] îòìå÷àåòñÿ, ÷òî ïðè èäåíòèôèêàöèè ñ 30-ïðîöåíòíûì
îòêëîíåíèåì íà÷àëüíîãî çíà÷åíèÿ ïîëó÷èòü ñõîäÿùèéñÿ ïðîöåññ
îêàçàëîñü íåâîçìîæíûì.
Èçëîæåííîå íàãëÿäíî ïîêàçûâàåò, ñêîëü âàæíûìè è îòâåòñòâåí-
íûìè ÿâëÿþòñÿ ýòàïû ïëàíèðîâàíèÿ ýêñïåðèìåíòà, ñâÿçàííûå ñ
âûáîðîì è ñîãëàñîâàíèåì ìîäåëåé ñîñòîÿíèÿ è èçìåðåíèÿ, ò.å . ìî -
äåëè ïàðû Õ ↔ Y. Ýòî îáñòîÿòåëüñòâî äàåò îñíîâàíèå åùå ðàç âåð-
íóòüñÿ, òåïåðü óæå íà íîâîì óðîâíå ïðåäñòàâëåíèé, ê âîïðîñó äî-
ïóñòèìîñòè óïðîùåíèÿ èñõîäíîé ìîäåëè ïðîöåññà. Îòìå÷åííàÿ
571
âûøå íåâîçìîæíîñòü ïðàêòè÷åñêîãî èñïîëüçîâàíèÿ êàíîíè÷åñêîé
ñõåìû äèàãîíàëèçàöèè ìàòðèöû ñîñòîÿíèÿ â çàäà÷àõ èäåíòèôèêàöèè
ìàññîâî-èíåðöèîííûõ è àýðîäèíàìè÷åñêèõ õàðàêòåðèñòèê ËÀ íà îñ-
íîâå ëåòíûõ èñïûòàíèé äåëàåò íåîáõîäèìûì ïîèñê èíûõ ïîäõîäîâ è
ìåòîäîâ. Ê èõ ÷èñëó îòíîñèòñÿ, â ÷àñòíîñòè, ìåòîä äèàãîíàëèçàöèè
ìàòðèöû, áàçèðóþùèéñÿ íà ýâðèñòè÷åñêîé äåêîìïîçèöèè ñèñòåìû.
Ýòîò ìåòîä ÿâëÿåòñÿ íàèáîëåå ýôôåêòèâíûì è ïðàêòè÷åñêè åäèíñò-
âåííî âîçìîæíûì ìåòîäîì óïðîùåíèÿ èñõîäíîé ìíîãîìåðíîé ïðî-
ñòðàíñòâåííîé ìîäåëè ñîñòîÿíèÿ óïðàâëÿåìîãî ËÀ. Îí çàêëþ÷àåòñÿ
â àíàëèçå óðîâíÿ "ãðóáîñòè" óïðàâëÿåìîé ñèñòåìû, ò.å . â îöåíêå
ïðàâîìåðíîñòè ïðèíÿòèÿ äîïóùåíèÿ î ìàëîñòè îòêëîíåíèé ïàðà-
ìåòðîâ ïðîöåññà óïðàâëÿåìîãî äâèæåíèÿ ïðè íàëè÷èè ìàëûõ âàðèà-
öèé, çàâèñÿùèõ îò ñòàòè÷åñêèõ îòêëîíåíèé êîýôôèöèåíòîâ óñèëå-
íèÿ ïåðåêðåñòíûõ ñâÿçåé ñèñòåìû óðàâíåíèÿ [68].
Ãëàâà 13
ÁÀËËÈÑÒÈ×ÅÑÊÈÅ ÀÑÏÅÊÒÛ
ÑÎÑÒÀÂËÅÍÈß ÒÀÁËÈÖ ÑÒÐÅËÜÁÛ
Òàáëèöû ñòðåëüáû äîëæíû ñîäåðæàòü âñå ñâåäåíèÿ, íåîáõîäèìûå ñòðåëÿþ-
ùåìó äëÿ ðåøåíèÿ çàäà÷è îïðåäåëåíèÿ äàííûõ, îáåñïå÷èâàþùèõ ïðîõîæäåíèå
òðàåêòîðèè ðàêåòû èëè ñíàðÿäà ÷åðåç öåëü.
 îáùåì ñëó÷àå ýòè ñâåäåíèÿ âêëþ÷àþò â ñåáÿ: îñíîâíûå ýëåìåíòû ïîïà-
äàþùåé òðàåêòîðèè, äîñòàòî÷íûå äëÿ ôîðìèðîâàíèÿ ïðèöåëüíûõ óñòàíîâîê
ïðè âåäåíèè ñòðåëüáû ïî êîíêðåòíîé öåëè; ïîïðàâêè â êîîðäèíàòû òî÷åê ïàäå-
íèÿ, â óñòàíîâêè ïðèöåëüíûõ óñòðîéñòâ è âçðûâàòåëåé, ó÷èòûâàþùèå èçìåíå-
íèå ðàçëè÷íûõ ôàêòîðîâ ñòðåëüáû; âåëè÷èíû, õàðàêòåðèçóþùèå ðàññåèâàíèå
ñíàðÿäîâ è ðàêåò. Ïðèìåíèòåëüíî ê àðòèëëåðèéñêèì ñèñòåìàì ïðîõîäÿùàÿ ÷å-
ðåç êîîðäèíàòû òî÷êè öåëè òðàåêòîðèÿ ñíàðÿäà ìîæåò áûòü îïðåäåëåíà ïðè
çàäàíèè àçèìóòà, íà÷àëüíîé ñêîðîñòè, óãëà áðîñàíèÿ è áàëëèñòè÷åñêîãî êîýô-
572
Ðèñ. 12.6 . Çàâèñèìîñòü ÷èñëà èòåðà-
öèé îò âåëè÷èíû îòêëîíåíèÿ àïðè-
îðíûõ íà÷àëüíûõ çíà÷åíèé êîýôôè-
öèåíòà m z
ω
ôèöèåíòà. Ñòîëü íåáîëüøîå ÷èñëî îïðåäåëÿþùèõ (âõîäíûõ è âûõîäíûõ) ïàðà-
ìåòðîâ ïðèâîäèò ê äîñòàòî÷íî ïðîñòîé ñòðóêòóðå àðòèëëåðèéñêèõ òàáëèö
ñòðåëüáû. Ðàçðàáîòêà òàáëèö ñòðåëüáû äëÿ ðàêåò ñâÿçàíà ñ èõ áîëåå ñëîæíûì,
÷åì àðòèëëåðèéñêèå òàáëèöû, ïîñòðîåíèåì. Äåëî â òîì, ÷òî ÷èñëî ôàêòîðîâ,
õàðàêòåðèçóþùèõ òðàåêòîðèþ ðàêåòû, îêàçûâàåòñÿ ñóùåñòâåííî áîëüøå, ÷åì
äëÿ àðòèëëåðèéñêîãî ñíàðÿäà.
Îñîáåííîñòè áàëëèñòèêè ðàçëè÷íûõ òèïîâ áîåïðèïàñîâ ïðèâîäÿò ê íåîáõî-
äèìîñòè ñîçäàíèÿ íåñêîëüêèõ ãðóïï òàáëèö ñòðåëüáû. Êà÷åñòâåííîå ðàçëè÷èå
èìååò ìåñòî ìåæäó òàêèìè ãðóïïàìè òàáëèö ñòðåëüáû, êàê äëÿ íåóïðàâëÿå-
ìûõ (êðîìå çåíèòíûõ), óïðàâëÿåìûõ è çåíèòíûõ áîåïðèïàñîâ, ïðè÷åì òàáëèöû
ñòðåëüáû äëÿ çåíèòíûõ ñíàðÿäîâ â áîåâîé îáñòàíîâêå íå èñïîëüçóþòñÿ, à ñëó-
æàò òîëüêî äëÿ ñîçäàíèÿ ïðîãðàììíî-àëãîðèòìè÷åñêîãî îáåñïå÷åíèÿ ñ÷åò-
íî-ðåøàþùèõ ïðèáîðîâ ðàçëè÷íîãî òèïà.
Ñîñòàâëåíèå òàáëèö ñòðåëüáû îñíîâûâàåòñÿ íà èñïîëüçîâàíèè íîðìàëüíîé
àðòèëëåðèéñêîé àòìîñôåðû, îïðåäåëÿåìîé íîðìàëüíûìè ìåòåîðîëîãè÷åñêèìè
óñëîâèÿìè ó ïîâåðõíîñòè Çåìëè, ãèïîòåçîé î âåðòèêàëüíîì ðàâíîâåñèè àòìî-
ñôåðû è ïðèíÿòûì çàêîíîì èçìåíåíèÿ òåìïåðàòóðû ñ âûñîòîé. Ïðè ïðîâåäå-
íèè áàëëèñòè÷åñêèõ ðàñ÷åòîâ ó÷èòûâàþò âèðòóàëüíóþ òåìïåðàòóðó (ñì.
ãë. 1, ï. 1.3).
Ñîñòàâëåíèå òàáëèö îñóùåñòâëÿåòñÿ íà îñíîâå ñïåöèàëüíûõ ðàñ÷åòîâ è
ñòðåëüá, íàçûâàåìûõ "îòñòðåëîì òàáëèö ñòðåëüáû" ëèáî "òàáëè÷íûìè ñòðåëü-
áàìè". Òðåáîâàíèÿ ê òî÷íîñòè òàáëèö íå îñòàþòñÿ ïîñòîÿííûìè. Îíè ïîñòå-
ïåííî âîçðàñòàþò â ôóíêöèè óâåëè÷åíèÿ òî÷íîñòè ïîäãîòîâêè ñàìèõ ñòðåëüá â
áîåâûõ óñëîâèÿõ è òî÷íîñòè ñàìîé ñòðåëüáû.
13.1. ÌÅÒÎÄÎËÎÃÈ×ÅÑÊÈÅ ÎÑÍÎÂÛ ÑÎÑÒÀÂËÅÍÈß
ÒÀÁËÈÖ ÑÒÐÅËÜÁÛ ÀÐÒÈËËÅÐÈÉÑÊÈÌÈ ÑÍÀÐßÄÀÌÈ
13.1.1. ÏÎÄÃÎÒÎÂÊÀ Ê ÎÒÑÒÐÅËÓ ÒÀÁËÈÖ
Ïðîâåäåíèå ñòðåëüá ñ öåëüþ ïîëó÷åíèÿ ýêñïåðèìåíòàëüíûõ äàí-
íûõ äëÿ ñîñòàâëåíèÿ òàáëèö ñòðåëüáû òðåáóåò ïðåäâàðèòåëüíîãî âû-
ïîëíåíèÿ êîìïëåêñà ìåðîïðèÿòèé, íàïðàâëåííûõ íà ïîëó÷åíèå
äîñòîâåðíûõ è â äîñòàòî÷íîé ìåðå îáîáùåííûõ ðåçóëüòàòîâ. Óêà-
çàííûé êîìïëåêñ ìåðîïðèÿòèé âêëþ÷àåò: ïîäãîòîâêó îðóæèÿ (îðó-
äèÿ è áîåïðèïàñîâ) ê ïðîâåäåíèþ ñòðåëüá; ìåòåîðîëîãè÷åñêóþ ïîä-
ãîòîâêó ñòðåëüáû; òîïîãðàôè÷åñêóþ ïîäãîòîâêó.
Îòñòðåë òàáëèö ñòðåëüáû äîëæåí ïðîèçâîäèòüñÿ èç ñïåöèàëüíî
ïîäãîòîâëåííîãî ìàëîèçíîøåííîãî îðóäèÿ, èìåþùåãî ìèíèìàëü-
íîå çíà÷åíèå äóëüíîé êðèâèçíû, ñíàðÿäàìè îäíîé ïàðòèè ïî êîð-
ïóñàì è ñíàðÿæåíèþ, ò.å . èçãîòîâëåííûìè ïî îäíèì ÷åðòåæàì è ïî
åäèíîé òåõíîëîãèè. Ìàëîèçíîøåííûì îðóäèåì ïðèíÿòî ñ÷èòàòü
[34] îðóäèå, ó êîòîðîãî ïàäåíèå íà÷àëüíîé ñêîðîñòè íå ïðåâîñõîäèò
3%.Ïðèïîäãîòîâêå îðóäèÿ ê ñòðåëüáå íåîáõîäèìî óáåäèòüñÿ â òîì,
÷òî îáåñïå÷èâàåòñÿ óñëîâèå ïàðàëëåëüíîñòè êîíòðîëüíîé ïëîùàäêè
îðóäèÿ îñè êàíàëà ñòâîëà. Äàííàÿ ïðîâåðêà ïðîèçâîäèòñÿ ñ ïîìî-
573
ùüþ òåîäîëèòà. Îí ïðèìåíÿåòñÿ òàêæå äëÿ îïðåäåëåíèÿ è ïîñëå-
äóþùåãî ó÷åòà âëèÿíèÿ íàêëîíà îñè öàïô îðóäèÿ íà íàïðàâëåíèå
ïëîñêîñòè ñòðåëüáû, ò.å . îïðåäåëåíèÿ "ãîðèçîíòà îðóäèÿ". Ó÷åò
âëèÿíèÿ íàêëîíà îñè öàïô íà èçìåíåíèå íàïðàâëåíèÿ ïëîñêîñòè
ñòðåëüáû äîëæåí áûòü ïðîèçâåäåí äëÿ êàæäîãî óãëà áðîñàíèÿ. Ïðè
îòñòðåëå òàáëèö ñòðåëüáû äëÿ îðóäèé, èìåþùèõ îòíîñèòåëüíóþ
äëèíó ñòâîëîâ, ïðåâûøàþùóþ 45 êàëèáðîâ, çà÷àñòóþ íå óäàåòñÿ ïî-
äîáðàòü îðóäèå ñ àáñîëþòíî ïðÿìîëèíåéíûì ñòâîëîì. Ýòî ïðèâî-
äèò ê íåîáõîäèìîñòè èçìåðåíèÿ äóëüíîé êðèâèçíû è ââåäåíèÿ ïî-
ïðàâêè â îïûòíûå çíà÷åíèÿ óãëîâ âûëåòà. Êîíòðîëü êðèâèçíû êàíà-
ëà ñòâîëà ïðîèçâîäèòñÿ ïåðèîäè÷åñêè ïðè êàæäîé âûâåðêå
ïðèöåëüíûõ ïðèñïîñîáëåíèé.
Ïîäãîòîâêà áîåïðèïàñîâ ê ñòðåëüáå ñîñòîèò â îïðåäåëåíèè ñîîò-
âåòñòâèÿ òàáëè÷íûì õàðàêòåðèñòèêàì îòîáðàííûõ íà ñòðåëüáó áîå-
ïðèïàñîâ ïî êëåéìåíèþ, à òàêæå âî âçâåøèâàíèè ñíàðÿäîâ è îïðå-
äåëåíèè òåìïåðàòóðû çàðÿäîâ. Îòñòðåë òàáëèö îáû÷íî ïðîèçâîäèò-
ñÿ îêðàøåííûìè ñíàðÿäàìè. Îäíàêî ñ öåëüþ îïðåäåëåíèÿ
âåëè÷èíû ïîïðàâêè â äàëüíîñòü íà îêðàñêó íàðÿäó ñ îêðàøåííûìè
ñíàðÿäàìè îñóùåñòâëÿåòñÿ îòñòðåë è íåîêðàøåííûõ ñíàðÿäîâ òîé
æå ïàðòèè ïî êîðïóñàì è ñíàðÿæåíèþ, ÷òî è îêðàøåííûå. Ñòðåëüáà
ïðîèçâîäèòñÿ ñíàðÿäàìè øòàòíîãî ñíàðÿæåíèÿ. Âåñ çàðÿäîâ íå äîë-
æåí îòêëîíÿòüñÿ îò òàáëè÷íûõ çà ïðåäåëû äâóõ âåñîâûõ (ìàññîâûõ)
çíàêîâ, ñíàðÿäû îäíîé ãðóïïû âûñòðåëîâ äîëæíû áûòü îäíîãî âåñî-
âîãî (ìàññîâîãî) çíàêà. Íà ñòðåëüáó çàðÿäû ïîäàþòñÿ ïåðåä ñàìûì
âûñòðåëîì â òåðìîèçîëÿöèîííûõ ÷åõëàõ.
Ñóùåñòâåííûì ìîìåíòîì ïîäãîòîâêè ê îòñòðåëó òàáëèö ñòðåëü-
áû ÿâëÿåòñÿ ìåòåîðîëîãè÷åñêàÿ ïîäãîòîâêà. Î÷åâèäíî, ÷òî ðåçóëü-
òàòû îòñòðåëà áóäóò óäîâëåòâîðÿòü ñôîðìóëèðîâàííîìó âûøå óñ-
ëîâèþ îáùíîñòè òîëüêî â òîì ñëó÷àå, åñëè áóäåò èçâåñòíî, ïðè
êàêèõ ìåòåîðîëîãè÷åñêèõ óñëîâèÿõ îíè ïîëó÷åíû. Èçìåðåíèÿ ïà-
ðàìåòðîâ, õàðàêòåðèçóþùèõ ñîñòîÿíèå àòìîñôåðû, îñóùåñòâëÿþò-
ñÿ ó ïîâåðõíîñòè Çåìëè è â çàäàííîì äèàïàçîíå âûñîò, äëÿ êîòî-
ðîãî òðåáóåòñÿ îïðåäåëèòü èõ ðàñïðåäåëåíèå. Ó÷èòûâàÿ òî îáñòîÿ-
òåëüñòâî, ÷òî ìåòåîðîëîãè÷åñêîå ñîñòîÿíèå àòìîñôåðû ÿâëÿåòñÿ
ôóíêöèåé âðåìåíè è ðàññòîÿíèÿ îò ïóíêòà íàáëþäåíèÿ, ñëåäóåò
ñòðåìèòüñÿ ê ñîêðàùåíèþ ñîîòâåòñòâóþùèõ èíòåðâàëîâ.  ÷àñòíî-
ñòè, äëÿ ìåòåîðîëîãè÷åñêîãî îáåñïå÷åíèÿ ñòðåëüá â óñëîâèÿõ ïî-
ëèãîíà ðåêîìåíäóåòñÿ îñóùåñòâëÿòü âåòðîâîå çîíäèðîâàíèå ñ èí-
òåðâàëîì, íå ïðåâûøàþùèì ïîëó÷àñîâîé, òåìïåðàòóðíîå – íå áî-
ëåå ÷åì ñ äâóõ÷àñîâûì èíòåðâàëîì.
Íåîáõîäèìîñòü òîïîãðàôè÷åñêîé ïîäãîòîâêè îáóñëîâëåíà òåì, ÷òî
â ïðèðîäå íå ñóùåñòâóåò èäåàëüíî ðîâíûõ ïîëèãîíîâ ñ çàðàíåå ðàç-
ìå÷åííûìè ñ âûñîêîé òî÷íîñòüþ êîîðäèíàòàìè òî÷åê ïîâåðõíîñòè
574
îòíîñèòåëüíî âûáðàííîé îãíåâîé ïîçèöèè. Äëÿ èçìåðåíèÿ êîîðäè-
íàò òî÷åê ïàäåíèÿ è ðàçðûâîâ ñíàðÿäîâ íà ìàëîïåðåñå÷åííîé ìåñò-
íîñòè ïîëèãîíà ðàçìå÷àåòñÿ äèðåêòðèñà. Äèðåêòðèñà îïðåäåëÿåòñÿ
ãåîäåçè÷åñêèì ïóòåì. Ïðè ýòîì ñ âîçìîæíî áîëåå âûñîêîé òî÷íî-
ñòüþ ïðîèçâîäèòñÿ êèëîìåòðîâàÿ ðàçìåòêà ñ ïîìîùüþ òàê íàçûâàå-
ìûõ ãåîäåçè÷åñêèõ öåíòðîâ, à çàòåì è äåñÿòèìåòðîâàÿ ðàçìåòêà. Ïà-
ðàëëåëüíî äèðåêòðèñå íà áåçîïàñíîì îò íåå ðàññòîÿíèè ðàçìåùàþò
íàáëþäàòåëüíûå âûøêè ñ óñòàíîâëåííûìè íà íèõ óãëîìåðíûìè ïðè-
áîðàìè äëÿ çàñå÷êè ðàçðûâîâ. Ðàñïîëîæåíèå âûøåê êîîðäèíèðóåòñÿ
ñ âûñîêîé òî÷íîñòüþ. Êîîðäèíàòû ãåîìåòðè÷åñêîãî öåíòðà ïîçèöèè
ôèêñèðóþòñÿ îòíîñèòåëüíî íà÷àëà äèðåêòðèñû ñ ïðåäåëüíîé îøèá-
êîé ïîðÿäêà 0,1 ì. Êîîðäèíàòû òî÷åê ðàçðûâîâ, îïðåäåëÿåìûå, êàê
ìèíèìóì, ñ òðåõ íàáëþäàòåëüíûõ âûøåê, ïåðåñ÷èòûâàþòñÿ â êîîð-
äèíàòû, çàäàííûå îòíîñèòåëüíî îðóäèÿ. Ïîñëå òîãî êàê îïðåäåëåíà
îïûòíàÿ äàëüíîñòü, ïðèâîäÿòñÿ ê ãîðèçîíòó òî÷êè âûëåòà ñíàðÿäà.
Äëÿ ýòîãî âû÷èñëÿþò ïðåâûøåíèå ìåñòà ïàäåíèÿ ñíàðÿäîâ íàä öåí-
òðîì äóëüíîãî ñðåçà ñòâîëà, íàâåäåííîãî ïîä óãëîì âîçâûøåíèÿ.
Ïðè ïðîâåäåíèè ñòðåëüá íà ìàëûå äàëüíîñòè ìîæåò áûòü èñ-
ïîëüçîâàí ñïîñîá ñòðåëüáû ïî ùèòàì, êîòîðûé ÿâëÿåòñÿ îáÿçàòåëü-
íûì ñðåäñòâîì îòñòðåëà òàáëèö âñåõ îðóäèé (â òîì ÷èñëå çåíèòíûõ),
ñ ó÷åòîì âîçìîæíîñòè îñóùåñòâëåíèÿ ñòðåëüá ïðÿìîé íàâîäêîé. Â
ýòîì ñëó÷àå èçìåðÿþò ðàññòîÿíèÿ äî ùèòà è ïðåâûøåíèå öåíòðà
ùèòà ("ÿáëîêà"), ïðèíèìàåìîãî çà íà÷àëî ñèñòåìû ïðÿìîóãîëüíûõ
êîîðäèíàò, íàä öåíòðîì äóëüíîãî ñðåçà. Êîîðäèíàòû ïðîáîèí íà
ùèòå ôèêñèðóþòñÿ îòíîñèòåëüíî öåíòðà "ÿáëîêà".
13.1.2. ÏÐÈÂÅÄÅÍÈÅ ÐÅÇÓËÜÒÀÒÎÂ ÑÒÐÅËÜÁ Ê ÍÎÐÌÀËÜÍÛÌ
È ÒÀÁËÈ×ÍÛÌ ÓÑËÎÂÈßÌ
Óäîâëåòâîðåíèå óñëîâèÿ îáùíîñòè ðåçóëüòàòîâ ïðè âûïîëíåíèè
ñòðåëüá íà ñîñòàâëåíèå òàáëèö äèêòóåòñÿ òðåáîâàíèåì âîçìîæíîñòè
èõ ñðàâíåíèÿ â ñëó÷àå ïðîâåäåíèÿ îòñòðåëîâ â íåñîïîñòàâèìûõ óñ-
ëîâèÿõ. Äîñòèæåíèå óêàçàííîé îáùíîñòè ñòàíîâèòñÿ ðåàëüíûì ïðè
ïðèâåäåíèè ðåçóëüòàòîâ ñòðåëüá ê íîðìàëüíûì è òàáëè÷íûì óñëî-
âèÿì. Íåîáõîäèìî îòìåòèòü, ÷òî ýòà ïðîöåäóðà ñîïðîâîæäàåòñÿ
îøèáêàìè, ìåíÿþùèìèñÿ îò ñòðåëüáû ê ñòðåëüáå.
Ñðåäèííàÿ îøèáêà îïðåäåëåíèÿ íîðìàëüíûõ äàëüíîñòåé îòäåëü-
íûõ ãðóïï âûñòðåëîâ, ïðîâåäåííûõ ïðè ïîëíîé ïîäãîòîâêå ñòðåëüá,
ìîæåò áûòü âû÷èñëåíà ïî ôîðìóëå
E
B
n
E
xx
ñc
ä
=+
2
2*
,
(13.1)
575
ãäå Bn
ä/–
ñðåäèííàÿ îøèáêà îïðåäåëåíèÿ ñðåäíåé äàëüíîñòè ïî
äàííîé ãðóïïå n âûñòðåëîâ; Ex c
*
–
ñðåäèííàÿ îøèáêà ïðèâåäåíèÿ
ðåçóëüòàòîâ ñòðåëüá ê íîðìàëüíûì è òàáëè÷íûì óñëîâèÿì,
îáóñëîâëåííàÿ ñóììàðíûì âîçäåéñòâèåì îøèáîê, âëèÿþùèõ íà
ðàññåèâàíèå ñðåäíèõ òðàåêòîðèé ãðóïï âûñòðåëîâ.
 èõ ÷èñëî âõîäÿò îøèáêè îïðåäåëåíèÿ íà÷àëüíîé ñêîðîñòè óãëà
áðîñàíèÿ è áàëëèñòè÷åñêîãî êîýôôèöèåíòà ñíàðÿäà, à òàêæå íåòî÷-
íîñòè îïðåäåëåíèÿ ïàðàìåòðîâ, õàðàêòåðèçóþùèõ ñîñòîÿíèå àòìî-
ñôåðû â ïðîöåññå ïðîèçâîäñòâà ãðóïïû âûñòðåëîâ.
Èç ðàññìîòðåíèÿ çàâèñèìîñòè (13.1) ñëåäóåò, ÷òî äëÿ ïîâûøåíèÿ
òî÷íîñòè îïðåäåëåíèÿ íîðìàëüíîé äàëüíîñòè öåëåñîîáðàçíî ïîâòî-
ðÿòü ñòðåëüáû ïðè îäíèõ è òåõ æå íà÷àëüíûõ óñëîâèÿõ N ðàç. Ïðè
ýòîì ìîæåò áûòü äîñòèãíóòî óìåíüøåíèå ñðåäèííîé îøèáêè îïðå-
äåëåíèÿ ñðåäíåãî ðåçóëüòàòà íîðìàëüíûõ äàëüíîñòåé â N ðàç, ò.å .
ïîëó÷åíî
~
/.
EEN
xx
cc
=
(13.2)
Èìåÿ â âèäó (13.1), îêîí÷àòåëüíî çàïèøåì
~
.
*
E
B
nN
E
N
x
xc
c
ä
2
=+
2
(13.3)
Çàâèñèìîñòü (13.3) ñâèäåòåëüñòâóåò, ÷òî îäíà è òà æå òî÷íîñòü
çíà÷åíèé íîðìàëüíîé äàëüíîñòè ìîæåò áûòü äîñòèãíóòà ïðè
ðàçëè÷íîì ñî÷åòàíèè ÷èñåë n âûñòðåëîâ â ãðóïïå è ÷èñëå ïîâòîðåíèÿ
ãðóïï èñïûòàíèé N. Îäíàêî îäíîçíà÷íûé âûâîä îá îïòèìàëüíîñòè
òîãî èëè èíîãî âàðèàíòà çäåñü íåâîçìîæåí. Äåéñòâèòåëüíî, ñ îäíîé
ñòîðîíû, ïðåäïî÷òèòåëüíûì ñëåäóåò ñ÷èòàòü âàðèàíò, â êîòîðîì
÷èñëî n ìèíèìàëüíî. Ìåíüøåå ÷èñëî âûñòðåëîâ ïðîèçâîäèòñÿ çà
ìåíüøåå âðåìÿ, çíà÷èò, ïðè ìåíüøåé âåðîÿòíîñòè èçìåíåíèÿ
ìåòåîðîëîãè÷åñêèõ óñëîâèé. Ïðè ýòîì èìååò ìåñòî è ìåíüøåå
èçìåíåíèå áàëëèñòè÷åñêèõ õàðàêòåðèñòèê ñòâîëà. Íî, ñ äðóãîé
ñòîðîíû, ïðè ìàëîì ÷èñëå ðåàëèçàöèé (èñïûòàíèé) ìàëà íàäåæíîñòü
è òî÷íîñòü ïîëó÷åíèÿ îöåíêè ñðåäèííîé (âåðîÿòíîé) îøèáêè. Â
ïðàêòèêå ïîëèãîííûõ àðòèëëåðèéñêèõ ñòðåëüá ÷èñëî âûñòðåëîâ â
ãðóïïå ðåêîìåíäóåòñÿ ïðèíèìàòü ðàâíûì n ≥ 5...10 â çàâèñèìîñòè îò
êàëèáðà, ïðè÷åì öåëåñîîáðàçíûì ñ÷èòàåòñÿ n = 7. Åñëè ñ÷èòàòü
âåëè÷èíó Ex c
*
àïðèîðè çàäàííîé (åå çíà÷åíèå ïîäòâåðæäàåòñÿ
áîëüøèì ñòàòèñòè÷åñêèì ìàòåðèàëîì ïðîâåäåíèÿ ïîëèãîííûõ
576
ñòðåëüá), ÷èñëî N ïîâòîðåíèé èñïûòàíèé äëÿ îáåñïå÷åíèÿ
ãàðàíòèðîâàííîé òî÷íîñòè, ñ êîòîðîé äîëæíû áûòü ïîëó÷åíû
ñðåäíèå íîðìàëüíûå äàëüíîñòè ïðè îãîâàðèâàåìîé ñðåäèííîé
îøèáêå îòäåëüíîé ñòðåëüáû, ìîæåò áûòü îïðåäåëåíî ñëåäóþùèì
îáðàçîì.
Èç ôîðìóëû (13.2) ñëåäóåò, ÷òî
NEE
xx
=
−
cc
22
~
.
(13.4)
Ïóñòü δ – âûðàæåííàÿ â ïðîöåíòàõ âåëè÷èíà îøèáêè, ñ êîòîðîé
äîïóñêàåòñÿ óâåëè÷åíèå ñðåäèííîé îøèáêè îòäåëüíîé ñòðåëüáû ïðè
ïðîâåäåíèè ïîëíîé ïîäãîòîâêè. Òîãäà
[(,)]
~
.
1001 22 2
+=
+
δ EEE
xx
x
cc
c
(13.5)
Îïðåäåëèâ èç (13.5) âûðàæåíèå
~
Exc
2
è ïîäñòàâèâ â (13.4), ïîëó÷èì
N=
+
100
2001
δδ
(,)
.
(13.6)
Èñõîäÿ èç ðåàëüíî ïðèåìëåìûõ çíà÷åíèé δ âòîðîå ñëàãàåìîå â
çíàìåíàòåëå (13.6) áóäåò èìåòü âòîðîé ïîðÿäîê ìàëîñòè, ïîýòîìó
N≈50/.δ
(13.7)
Íàïðèìåð, ïðè n = 7 ñðåäèííàÿ îøèáêà â íîðìàëüíîé äàëüíîñòè,
ñîîòâåòñòâóþùåé δ = 10 %, áóäåò ãàðàíòèðîâàííî îáåñïå÷åíà ïðè
÷èñëå ïîâòîðåíèé èñïûòàíèé N =5.
Ðåçåðâû â ïîâûøåíèè òî÷íîñòè íàõîæäåíèÿ íîðìàëüíûõ äàëü-
íîñòåé â ïîëèãîííûõ óñëîâèÿõ, à â êîíå÷íîì èòîãå è òî÷íîñòè òàá-
ëèö ñòðåëüáû ñëåäóåò èñêàòü ãëàâíûì îáðàçîì íà ïóòÿõ ïîâûøåíèÿ
òî÷íîñòè ìåòåîáàëëèñòè÷åñêîé ïîäãîòîâêè.
13.1.3. ÂÛ×ÈÑËÅÍÈÅ ÏÎÏÐÀÂÎÊ, ÎÑÍÎÂÍÛÕ ÝËÅÌÅÍÒÎÂ
ÒÐÀÅÊÒÎÐÈÈ È ÎÏÛÒÍÎÉ ÇÀÂÈÑÈÌÎÑÒÈ ÁÀËËÈÑÒÈ×ÅÑÊÎÃÎ
ÊÎÝÔÔÈÖÈÅÍÒÀ ÎÒ ÓÃËÀ ÁÐÎÑÀÍÈß
Ïîëó÷èâ íîðìàëüíûå äàëüíîñòè, ñîîòâåòñòâóþùèå òàáëè÷íîé
íà÷àëüíîé ñêîðîñòè, ïåðåõîäÿò ê âû÷èñëåíèþ áàëëèñòè÷åñêîãî êî-
ýôôèöèåíòà ïðèìåíèòåëüíî ê êàæäîìó óãëó áðîñàíèÿ äëÿ êàæäîãî
äíÿ ñòðåëüáû îòäåëüíî. Ðàñ÷åò ñëåäóåò ïðîèçâîäèòü, èñïîëüçóÿ òó æå
577
ýòàëîííóþ ôóíêöèþ ñîïðîòèâëåíèÿ è òîò æå ìåòîä, êîòîðûì ïðåä-
ïîëàãàåòñÿ âåñòè âû÷èñëåíèå òàáëè÷íûõ äàííûõ. Ïîëó÷åíèå íîðìà-
ëèçîâàííûõ äàëüíîñòåé îñóùåñòâëÿåòñÿ ñ ïðèìåíåíèåì èòåðàöèîí-
íûõ ïðîöåäóð. Äëÿ íåêîòîðîãî çíà÷åíèÿ êîýôôèöèåíòà ôîðìû i
(íàïðèìåð, i =1) íàõîäÿò âñå ïîïðàâêè, èñïðàâëÿþò îïûòíóþ äàëü-
íîñòü, ñðàâíèâàþò ñ ðàñ÷åòíîé, íàõîäÿò î÷åðåäíîå çíà÷åíèå i è
ò.ä ., ïîêà íå áóäåò äîñòèãíóòà ñòàáèëèçàöèÿ îïðåäåëÿåìîãî çíà÷å-
íèÿ i. Ïðè âû÷èñëåíèè áàëëèñòè÷åñêèõ êîýôôèöèåíòîâ íà îñíîâà-
íèè ðåçóëüòàòîâ ñòðåëüá ïî ùèòàì èñïîëüçóþò ñëåäóþùèå èñõîäíûå
äàííûå: ðàññòîÿíèå è âðåìÿ ïîëåòà ñíàðÿäà äî ùèòà, íà÷àëüíóþ
ñêîðîñòü è óãîë áðîñàíèÿ, ïðèâåäåííûå ê íîðìàëüíûì ìåòåîóñëî-
âèÿì è òàáëè÷íîìó âåñó ñíàðÿäà.
Ïî ïîëó÷åííûì äëÿ îïîðíûõ óãëîâ áðîñàíèÿ ãðàôè÷åñêèì èëè
àíàëèòè÷åñêèì èíòåðïîëèðîâàíèåì áàëëèñòè÷åñêèì êîýôôèöèåí-
òàì è òàáëè÷íûì çíà÷åíèÿì V0 òåïåðü ìîãóò áûòü îïðåäåëåíû îñ-
íîâíûå ýëåìåíòû òðàåêòîðèè. Óñòàíîâèâ ýêñïåðèìåíòàëüíî äëÿ îò-
ñòðåëèâàåìîãî îðóäèÿ óãîë âûëåòà, ïðèìåíèòåëüíî ê çàôèêñèðîâàí-
íîìó íàáîðó îñíîâíûõ ýëåìåíòîâ òðàåêòîðèè íàõîäÿò ðàçíîñòü
óãëîâ θ0 è âûëåòà, ò.å . óãîë ïðèöåëèâàíèÿ. Äàëåå íåîáõîäèìî îñóùå-
ñòâèòü âû÷èñëåíèå ïîïðàâîê. Ðàçëè÷àþò ïîïðàâêè äëÿ óãëà ïðèöå-
ëèâàíèÿ íà óãîë ìåñòà öåëè, ïîïðàâêè íà íàêëîí îñè öàïô îðóäèÿ,
íàêîíåö, ïîïðàâêè â äàëüíîñòü è íàïðàâëåíèå ñòðåëüáû.
Ïîïðàâêè ê óãëó ïðèöåëèâàíèÿ íà óãîë ìåñòà öåëè âû÷èñëÿþòñÿ
äëÿ çàäàííîé ãîðèçîíòàëüíîé ëèáî íàêëîííîé äàëüíîñòè. Ïîñêîëü-
êó ïðè òîïîãðàôè÷åñêîé ïîäãîòîâêå ñòðåëüáû íåïîñðåäñòâåííî îï-
ðåäåëÿåòñÿ ãîðèçîíòàëüíàÿ äàëüíîñòü, èñïîëüçîâàíèå ïîñëåäíåé ÿâ-
ëÿåòñÿ ïðåäïî÷òèòåëüíûì. Ðàñ÷åò ïðîâîäèòñÿ ïî ñïåöèàëüíîé ìåòî-
äèêå.
Âû÷èñëåíèå ïîïðàâîê íà íàêëîí îñè öàïô ñâîäèòñÿ ê îïðåäå-
ëåíèþ ïðèðàùåíèé ìàëûõ óãëîâ ñ èñïîëüçîâàíèåì ôîðìóë ñôå-
ðè÷åñêîé òðèãîíîìåòðèè. Ïîïðàâêè â äàëüíîñòü è íàïðàâëåíèå
ñòðåëüáû èíîãäà ïîäðàçäåëÿþò íà äâå ãðóïïû. Ïåðâóþ ñîñòàâëÿ-
þò ïîïðàâêè, îáóñëîâëåííûå îòêëîíåíèåì îò íîðìàëüíûõ óñëî-
âèé äàâëåíèÿ è òåìïåðàòóðû âîçäóõà, íà÷àëüíîé ñêîðîñòè è âåñà
ñíàðÿäà, à òàêæå òåìïåðàòóðû çàðÿäà; âòîðóþ – ïîïðàâêè íà
ïðîäîëüíûé, áîêîâîé âåòåð è äåðèâàöèþ. Ñàìîñòîÿòåëüíîå ìåñòî
çàíèìàþò ïîïðàâêè íà âðàùåíèå Çåìëè. Óêàçàííûå ïîïðàâêè
âû÷èñëÿþòñÿ â òîì ñëó÷àå, êîãäà äàëüíîñòü ñòðåëüáû ïðåâûøàåò
10...15 êì.
578
13.1.4. ÀËÃÎÐÈÒÌ ÑÎÑÒÀÂËÅÍÈß ÀÐÒÈËËÅÐÈÉÑÊÈÕ ÒÀÁËÈÖ
ÑÒÐÅËÜÁÛ
Ïðèâåäåì â êðàòêîé êîíñïåêòèâíîé ôîðìå ñîâîêóïíîñòü îñíîâ-
íûõ êîìïîíåíòîâ ïðîöåññà ñîñòàâëåíèÿ òàáëèö ñòðåëüáû äëÿ
ñòâîëüíîé àðòèëëåðèè.
Êàê ñëåäóåò èç èçëîæåííîãî âûøå, óêàçàííûé ïðîöåññ ìîæåò
áûòü óñëîâíî ïîäðàçäåëåí íà ÷åòûðå ýòàïà:
1) ïîäãîòîâêó ê îòñòðåëó òàáëèö,
2) ñîáñòâåííî îòñòðåë òàáëèö,
3) îáðàáîòêó ðåçóëüòàòîâ ñòðåëüá,
4) îôîðìëåíèå áëàíêà òàáëèö ñòðåëüáû.
 ñâîþ î÷åðåäü êàæäûé èç ïåðå÷èñëåííûõ ýòàïîâ âêëþ÷àåò â
ñåáÿ ðÿä ýëåìåíòîâ, îïèñàíèå êîòîðûõ ñîïðîâîäèì ñëåäóþùåé íó-
ìåðàöèåé: ïåðâàÿ öèôðà ñîîòâåòñòâóåò íîìåðó ýòàïà, âòîðàÿ, ïðî-
ñòàâëÿåìàÿ ÷åðåç òî÷êó, – ïîðÿäêîâîìó íîìåðó âûïîëíÿåìîé îïå-
ðàöèè â îáùåì ïîðÿäêå ðàáîò ïðè ñîñòàâëåíèè òàáëèö.
1.1. Òîïîãðàôè÷åñêàÿ ïîäãîòîâêà ïîëèãîíà ê îòñòðåëó òàáëèö.
1.2. Ïîäãîòîâêà îðóäèÿ ê ñòðåëüáå.
1.3. Ïîäãîòîâêà áîåïðèïàñîâ ê ñòðåëüáå.
1.4. Ìåòåîðîëîãè÷åñêàÿ ïîäãîòîâêà.
2.5 . Ñòðåëüáà íà äàëüíîñòü è êó÷íîñòü äëÿ ôèêñèðîâàííûõ óãëîâ
áðîñàíèÿ ïðè îäíîì çàðÿäå.
2.6 . Ñòðåëüáû íà îïðåäåëåíèå äåðèâàöèè (ìîãóò áûòü ñîâìåùåíû
ñ ïðåäûäóùèì ïóíêòîì).
2.7 . Ñòðåëüáû íà îïðåäåëåíèå íà÷àëüíûõ ñêîðîñòåé (ìîãóò áûòü
ñîâìåùåíû ñ ï. 2 .5).
2.8 . Ñòðåëüáû íà îïðåäåëåíèå óãëà âûëåòà.
2.9 . Ïîâòîðåíèå ñòðåëüá (ñòðåëüáû, óêàçàííûå â ï. 2.5...2 .8, ïî-
âòîðÿþòñÿ íå ìåíåå ÷åì òðè ðàçà).
3.10. Îïðåäåëåíèå îïûòíûõ äàëüíîñòåé è áîêîâûõ îòêëîíåíèé
ñíàðÿäà, à òàêæå èõ ñðåäèííûõ îòêëîíåíèé íà îñíîâå îáðàáîòêè
ñòðåëüá ïî ï. 2.5.
3.11. Îáðàáîòêà ðåçóëüòàòîâ ñòðåëüá ïî ï. 2 .7 è 2.8 ñ öåëüþ óñòà-
íîâëåíèÿ çíà÷åíèé íà÷àëüíûõ ñêîðîñòåé è óãëîâ âûëåòà, à òàêæå
ñðåäèííûõ îòêëîíåíèé íà÷àëüíûõ ñêîðîñòåé, óãëîâ áðîñàíèÿ è ãî-
ðèçîíòàëüíûõ óãëîâ.
3.12. Ïðèâåäåíèå ñòðåëüá ê íîðìàëüíûì óñëîâèÿì, ðåçóëüòàòîì
÷åãî ÿâëÿåòñÿ íàõîæäåíèå äëÿ êàæäîãî óãëà áðîñàíèÿ íîðìàëüíûõ
äàëüíîñòåé, ñîîòâåòñòâóþùèõ òàáëè÷íîìó çíà÷åíèþ íà÷àëüíîé ñêî-
ðîñòè, è âåëè÷èíû äåðèâàöèè (îñóùåñòâëÿåòñÿ ìåòîäîì èòåðàöèé).
3.13. Ñîñòàâëåíèå òàáëèö èñõîäíûõ äàííûõ êàê îñíîâû ïîñëå-
äóþùåé ðàçðàáîòêè òàáëèö ñòðåëüáû.
3.14. Âû÷èñëåíèå êîýôôèöèåíòà ôîðìû.
579
580
Ò
à
á
ë
è
ö
à
1
3
.
1
Â
î
ç
ì
î
æ
í
û
é
â
à
ð
è
à
í
ò
á
ë
à
í
ê
à
î
ñ
í
î
â
í
û
õ
ò
à
á
ë
è
ö
ñ
ò
ð
å
ë
ü
á
û
Ñ
í
à
ð
ÿ
ä
Ç
à
ð
ÿ
ä
Í
à
÷
à
ë
ü
í
à
ÿ
ñ
ê
î
ð
î
ñ
ò
ü
Ø
ê
à
ë
à
ï
ð
è
ö
å
ë
à
È
ç
ì
å
í
å
í
è
å
ó
ñ
ò
à
í
î
â
ê
è
â
ç
ð
û
â
à
ò
å
ë
ÿ
Ä
à
ë
ü
-
í
î
ñ
ò
ü
õ
ñ
Ó
ñ
ò
à
í
î
â
ê
à
ï
ð
è
ö
å
ë
à
Â
û
ñ
î
ò
à
ò
ð
à
å
ê
ò
î
-
ð
è
è
y
s
Ï
î
ï
ð
à
â
ê
è
Ï
î
í
à
ï
ð
à
â
ë
å
í
è
þ
Ï
î
ä
à
ë
ü
í
î
ñ
ò
è
ä
ë
ÿ
ñ
í
à
ð
ÿ
-
ä
î
â
ñ
ï
å
ö
è
-
à
ë
ü
í
î
-
ã
î
í
à
ç
í
à
-
÷
å
í
è
ÿ
í
à
ê
î
ë
ï
à
-
÷
î
ê
â
ç
ð
û
-
â
à
ò
å
ë
ÿ
í
à
ï
ð
î
-
ä
î
ë
ü
-
í
û
é
â
å
ò
å
ð
W
x
=
1
0
ì
/
ñ
Í
à
è
ç
ì
å
í
å
í
è
å
í
à
ä
å
ð
è
-
â
à
ö
è
þ
í
à
á
î
ê
î
-
â
î
é
â
å
ò
å
ð
W
z
=
=
1
0
ì
/
ñ
á
à
ð
î
ì
å
-
ò
ð
è
÷
å
ñ
-
ê
î
ã
î
ä
à
â
ë
å
-
í
è
ÿ
í
à
1
0
ì
/
ñ
ò
å
ì
ï
å
-
ð
à
ò
ó
ð
û
â
î
ç
ä
ó
-
õ
à
í
à
1
0
°
Ñ
í
à
÷
à
ë
ü
-
í
î
é
ñ
ê
î
ð
î
-
ñ
ò
è
í
à
1
%
ò
å
ì
ï
å
-
ð
à
ò
ó
ð
û
ç
à
ð
ÿ
ä
à
í
à
1
0
°
Ñ
ì
à
ñ
ñ
û
ñ
í
à
ð
ÿ
-
ä
î
â
í
à
î
ä
è
í
â
å
ñ
î
-
â
î
é
ç
í
à
ê
ì
ä
å
ë
å
-
í
è
ÿ
ò
û
ñ
ÿ
÷
í
û
å
ì
ò
û
ñ
ÿ
÷
-
í
û
å
ò
û
ñ
ÿ
÷
-
í
û
å
ì
ì
ì
ì
ì
ì
ì
ì
È
ç
ì
å
í
å
í
è
å
ä
à
ë
ü
í
î
ñ
ò
è
ï
ð
è
è
ç
ì
å
í
å
í
è
è
ó
ã
ë
à
ï
ð
è
ö
å
ë
è
â
à
í
è
ÿ
í
à
0
,
0
0
1
Ð
à
ç
ì
å
ð
û
ý
ë
ë
è
ï
ñ
à
ð
à
ñ
ñ
å
è
â
à
-
í
è
ÿ
ï
î
ä
à
ë
ü
í
î
ñ
ò
è
ä
ë
ÿ
"
ó
ç
ê
î
é
"
â
è
ë
ê
è
(
4
Â
ä
)
Ó
ã
î
ë
ï
ð
è
ö
å
ë
è
-
â
à
í
è
ÿ
Ó
ã
î
ë
í
à
ê
ë
î
í
à
â
å
ê
ò
î
ð
à
ñ
ê
î
ð
î
ñ
ò
è
ê
ì
å
ñ
ò
í
î
ì
ó
ã
î
ð
è
ç
î
í
ò
ó
â
ò
î
÷
ê
å
ï
à
ä
å
í
è
ÿ
θ
ñ
Ê
î
í
å
÷
í
à
ÿ
ñ
ê
î
ð
î
ñ
ò
ü
V
c
Ï
î
ë
í
î
å
â
ð
å
ì
ÿ
ï
î
ë
å
ò
à
t
c
Ñ
ð
å
ä
è
í
í
û
å
î
ò
ê
ë
î
í
å
í
è
ÿ
Ä
à
ë
ü
-
í
î
ñ
ò
ü
õ
ñ
ï
î
ä
à
ë
ü
-
í
î
ñ
ò
è
Â
ä
ï
î
â
û
ñ
î
ò
å
Â
â
á
î
ê
î
-
â
û
å
Â
á
ì
ò
û
ñ
ÿ
÷
í
û
å
ã
ð
à
ä
ó
ñ
(
ì
è
í
)
ã
ð
à
ä
ó
ñ
ì
/
ñ
ñ
ì
ì
ì
ì
3.15. Âû÷èñëåíèå è ãðàôè÷åñêîå ïðåäñòàâëåíèå îñíîâíûõ ýëå-
ìåíòîâ òðàåêòîðèè â ôóíêöèè äàëüíîñòè ïðè ôèêñèðîâàííûõ (äëÿ
âûáðàííîãî øàãà èçìåíåíèÿ àðãóìåíòà) óãëàõ áðîñàíèÿ.
3.16. Âû÷èñëåíèå óãëîâ ïðèöåëèâàíèÿ.
3.17. Âû÷èñëåíèå ïîïðàâî÷íûõ êîýôôèöèåíòîâ è âåëè÷èí òàá-
ëè÷íûõ ïîïðàâîê â äàëüíîñòü è íàïðàâëåíèå ñòðåëüáû. Èõ ãðàôè÷å-
ñêîå ïðåäñòàâëåíèå.
3.18. Âû÷èñëåíèå ñðåäèííûõ îòêëîíåíèé áàëëèñòè÷åñêîãî êîýô-
ôèöèåíòà è êîýôôèöèåíòà äåðèâàöèè, à òàêæå ñðåäíèõ çíà÷åíèé
ïàðàìåòðîâ ðàññåèâàíèÿ.
3.19. Âû÷èñëåíèå òàáëè÷íûõ õàðàêòåðèñòèê ðàññåèâàíèÿ ñíàðÿ-
äîâ è èõ ãðàôè÷åñêîå ïðåäñòàâëåíèå â ôóíêöèè äàëüíîñòè.
3.20. Âû÷èñëåíèå èçìåíåíèé äàëüíîñòè è âûñîòû ïîëåòà ñíàðÿ-
äîâ ïðè èçìåíåíèè óãëà ïðèöåëèâàíèÿ íà îäíó òûñÿ÷íóþ (0°3,6′)
èëè ïðèöåëà íà îäíî äåëåíèå.
4.21. Ðàçðàáîòêà áëàíêà òàáëèö ñòðåëüáû è çàïîëíåíèå åãî ãðàô.
Îäèí èç âîçìîæíûõ [72] âàðèàíòîâ ñòðóêòóðû áëàíêà îñíîâíûõ
òàáëèö ñòðåëüáû äëÿ àðòèëëåðèéñêèõ ñèñòåì ïðåäñòàâëåí òàáë. 13.1 .
 ñâÿçè ñ ïðèíÿòèåì íà âîîðóæåíèå ÀÁÑ ïîïðàâêó íà òåìïåðàòó-
ðó çàðÿäà ââîäÿò îòäåëüíî â îòêëîíåíèå íà÷àëüíîé ñêîðîñòè, à óæå
ïîëó÷åííîå îáùåå ("ñóììàðíîå") îòêëîíåíèå íà÷àëüíîé ñêîðîñòè
ó÷èòûâàþò ââåäåíèåì ïîïðàâêè â äàëüíîñòü íà ñóììàðíîå îòêëîíå-
íèå V0.
13.2 . ÎÑÎÁÅÍÍÎÑÒÈ ÑÎÑÒÀÂËÅÍÈß ÒÀÁËÈÖ ÑÒÐÅËÜÁÛ
ÄËß ÐÀÊÅÒÍÛÕ ÑÈÑÒÅÌ
13.2.1 . ÒÀÁËÈ×ÍÛÅ È ÄÅÉÑÒÂÈÒÅËÜÍÛÅ ÓÑËÎÂÈß ÏÓÑÊÀ ÐÀÊÅÒ
Ïðèíöèï ñîñòàâëåíèÿ òàáëèö ñòðåëüáû äëÿ ðàêåò [4, 33, 71] òàê-
æå áàçèðóåòñÿ íà îïûòíî-òåîðåòè÷åñêîì ìåòîäå è ïðàêòè÷åñêè îñòà-
åòñÿ òàêèì æå, êàê è äëÿ àðòèëëåðèéñêèõ ñèñòåì. Ïðåäâàðèòåëüíî
óñòàíàâëèâàþòñÿ òàáëè÷íûå äàííûå äëÿ íîðìàëüíûõ óñëîâèé, îïðå-
äåëåíèå êîòîðûõ íå âûçûâàåò îñîáûõ òðóäíîñòåé â ñèëó òîãî, ÷òî
îíè îòðàæàþò ëèøü íîìèíàëüíîå äâèæåíèå. Çàòåì äîëæíû áûòü
íàéäåíû ïîïðàâêè, ó÷èòûâàþùèå îòëè÷èÿ äåéñòâèòåëüíûõ óñëîâèé
ïóñêà îò íîðìàëüíûõ óñëîâèé.
Äëÿ íåóïðàâëÿåìûõ ðàêåò, èìåþùèõ, êàê ïðàâèëî, ìàëóþ äàëü-
íîñòü ñòðåëüáû, îñíîâíûìè ôàêòîðàìè, îïðåäåëÿþùèìè ðàçëè÷èÿ
ìåæäó äåéñòâèòåëüíûìè óñëîâèÿìè ïóñêà è íîðìàëüíûìè, ÿâëÿþò-
ñÿ:
îòêëîíåíèÿ ìåòåîôàêòîðîâ îò íîðìàëüíûõ çíà÷åíèé;
581
îòëè÷èÿ ïàðàìåòðîâ ðàêåòû (ìàññû è ðàçìåðîâ ðàêåòû, ìàññû è
õàðàêòåðèñòèê òîïëèâà) îò ïðèíÿòûõ ïðè ðàñ÷åòå.
Îòìåòèì, ÷òî óêàçàííûå îòëè÷èÿ îáúÿñíÿþòñÿ, êàê è â ñëó÷àå àð-
òèëëåðèéñêèõ ñíàðÿäîâ, íå ðàçáðîñîì â ïðåäåëàõ ïîëÿ äîïóñêà, à
ñìåùåíèåì ìàòåìàòè÷åñêîãî îæèäàíèÿ, ò.å . ñðåäíåå çíà÷åíèå òîãî
èëè èíîãî ïàðàìåòðà â äàííîé ãðóïïå ðàêåò íå ñîîòâåòñòâóåò ðàñ÷åò-
íîé âåëè÷èíå.
Ó óïðàâëÿåìûõ àêòèâíî-ðåàêòèâíûõ ñíàðÿäîâ è áàëëèñòè÷åñêèõ
ðàêåò, îáëàäàþùèõ ïîâûøåííîé äàëüíîñòüþ äåéñòâèÿ, îáñóæäàå-
ìûå ôàêòîðû èìåþò íåñêîëüêî èíóþ ïðèðîäó. Íàçíà÷åíèåì èõ ñèñ-
òåì óïðàâëåíèÿ ÿâëÿåòñÿ êîìïåíñàöèÿ âîçìîæíûõ îòêëîíåíèé äåé-
ñòâèòåëüíûõ óñëîâèé ïóñêà îò íîðìàëüíûõ óñëîâèé. Îäíàêî ëþáàÿ
ñèñòåìà óïðàâëåíèÿ õàðàêòåðèçóåòñÿ ìåòîäè÷åñêèìè ïîãðåøíîñòÿ-
ìè, çàâèñÿùèìè îò âåëè÷èíû äåéñòâóþùèõ âîçìóùåíèé, è äàëåêî
íå âñå âîçìóùàþùèå ôàêòîðû ìîãóò áûòü åþ àâòîìàòè÷åñêè ñêîì-
ïåíñèðîâàíû. Êîìïåíñàöèÿ òàêîãî ðîäà ôàêòîðîâ öåëåñîîáðàçíà ñ
èñïîëüçîâàíèåì ïîïðàâîê, ââîäèìûõ â îñíîâíûå óñòàíîâêè ïðàêòè-
÷åñêè ïî òîé æå ñõåìå, êîòîðàÿ ðåàëèçóåòñÿ ïðèìåíèòåëüíî ê íå-
óïðàâëÿåìûì áîåïðèïàñàì. Âàæíåéøèìè èç òàêèõ ôàêòîðîâ ÿâëÿ-
þòñÿ ãåîôèçè÷åñêèå óñëîâèÿ ïóñêà ðàêåò.
13.2.2. ÏÐÈÂÅÄÅÍÈÅ ÐÅÇÓËÜÒÀÒΠÒÀÁËÈ×ÍÛÕ ÑÒÐÅËÜÁ
Ê ÍÎÐÌÀËÜÍÛÌ ÓÑËÎÂÈßÌ È ÑÎÑÒÀÂËÅÍÈÅ ÒÀÁËÈÖ ÑÒÐÅËÜÁÛ
ÄËß ÍÅÓÏÐÀÂËßÅÌÛÕ ÐÀÊÅÒ
Ïðèâåäåíèå ðåçóëüòàòîâ òàáëè÷íûõ ñòðåëüá ê íîðìàëüíûì óñëî-
âèÿì îñóùåñòâëÿåòñÿ [33] ïî ñëåäóþùåé ñõåìå.
1. Îïðåäåëÿåòñÿ ñðåäíåå ïî ãðóïïå çíà÷åíèå ýëåìåíòà òðàåêòî-
ðèè Àñð (ïîëíîé äàëüíîñòè è áîêîâîãî îòêëîíåíèÿ òî÷êè ïàäåíèÿ),
êîòîðîå òðåáóåòñÿ ïðèâåñòè ê íîðìàëüíûì óñëîâèÿì.
2. Óñòàíàâëèâàþòñÿ ñðåäíèå çíà÷åíèÿ ïàðàìåòðîâ ðàêåòû ξj,ñðïðè
ñòðåëüáå äàííîé ãðóïïû è îïðåäåëÿþòñÿ îòêëîíåíèÿ ïàðàìåòðîâ δξj
îò ðàñ÷åòíûõ:
δξξ
ξ
jjj
=−
,
.
ñð
(13.8)
3. Âû÷èñëÿåòñÿ èçìåíåíèå ñðåäíåãî çíà÷åíèÿ ðàññìàòðèâàåìîãî
ýëåìåíòà òðàåêòîðèè âñëåäñòâèå îòêëîíåíèé ïàðàìåòðîâ ðàêåòû è
ïàðàìåòðîâ àòìîñôåðû:
δ
∂
∂ξ
δξ
∂
∂
δ
∂
∂
δ
∂
∂
A
AA
h
h
A
T
T
A
W
W
j
j
i
i
=+
+
⎛
⎝⎜⎞
⎠⎟+⎛
⎝⎜⎞
⎠⎟
0
0
ê
ê
,
k
p
i
n
j
m
=
=
=
∑
∑
∑
1
1
1
(13.9)
582
ãäå m – ÷èñëî ïàðàìåòðîâ, äëÿ êîòîðûõ èìåëî ìåñòî îòëè÷èå
èçìåðåííûõ çíà÷åíèé îò ðàñ÷åòíûõ; n è p – ÷èñëî ñëîåâ ïðè ó÷åòå
âëèÿíèÿ îòêëîíåíèÿ òåìïåðàòóðû âîçäóõà è âåòðà.
4. Âû÷èñëÿåòñÿ ýëåìåíò òðàåêòîðèè AN ïðè ðàñ÷åòíûõ çíà÷åíèÿõ
ïàðàìåòðîâ è ñòðåëüáå â àòìîñôåðå, ïðèâåäåííîé ê ñòàíäàðòíîé:
AAA
N=−
ñð
δ.
(13.10)
Íà îñíîâå äàííîé ìåòîäèêè ìîæåò áûòü ïîëó÷åíî çíà÷åíèå ëþáîãî
ýëåìåíòà òðàåêòîðèè ïðè íîðìàëüíûõ óñëîâèÿõ.
Ïðè ñîñòàâëåíèè òàáëèö ñòðåëüáû âûäåëÿåòñÿ ðÿä òðàåêòîðèé,
íàçûâàåìûõ îïîðíûìè, ñ òàêèì ðàñ÷åòîì, ÷òîáû îíè îõâàòûâàëè
âåñü äèàïàçîí èçìåíåíèÿ íóæíîãî ýëåìåíòà òðàåêòîðèè. Âû÷èñëå-
íèå ýëåìåíòîâ îïîðíûõ òðàåêòîðèé âåäåòñÿ èíòåãðèðîâàíèåì íàè-
áîëåå ïîëíîé ñèñòåìû óðàâíåíèé äâèæåíèÿ ñ âûñîêîé òî÷íîñòüþ.
Òî÷íîñòü ðàñ÷åòîâ ïðè ýòîì îïðåäåëÿåòñÿ òî÷íîñòüþ çàäàíèÿ îñ-
íîâíûõ ïàðàìåòðîâ ðàêåòû.
Ðàññ÷èòàííûå îïîðíûå òðàåêòîðèè êîððåêòèðóþòñÿ ïî ðåçóëüòà-
òàì òàáëè÷íûõ ñòðåëüá, ïîçâîëÿþùèõ óòî÷íèòü âëèÿíèå îòäåëüíûõ
ïàðàìåòðîâ.
Ïîñëå òîãî êàê îïðåäåëåíû ýëåìåíòû îïîðíûõ òðàåêòîðèé, âçÿ-
òûå â îòíîñèòåëüíî íåáîëüøîì êîëè÷åñòâå, íà îñíîâå ìåòîäîâ èí-
òåðïîëèðîâàíèÿ íàõîäÿòñÿ ýëåìåíòû ïðîìåæóòî÷íûõ òðàåêòîðèé è
ñîñòàâëÿþòñÿ ñàìè òàáëèöû.
Äëÿ ïðîâåäåíèÿ ñòðåëüá íåîáõîäèìî çíàòü óãîë áðîñàíèÿ, îò-
âå÷àþùèé çàäàííîé äàëüíîñòè ïîëåòà. Ïîýòîìó â òàáëèöàõ â êà-
÷åñòâå âõîäíîãî ýëåìåíòà âûáèðàåòñÿ ïîëíàÿ äàëüíîñòü õñ, èçìå-
íÿþùàÿñÿ ñ äîñòàòî÷íî ìàëûì øàãîì (ïîðÿäêà 200 ì), äîïóñ-
êàþùèì ëèíåéíóþ èíòåðïîëÿöèþ.  ðåçóëüòàòå ðàñ÷åòîâ
ïîëó÷àþò çàâèñèìîñòü θ0
0
= fxc
(),à òàêæå çíà÷åíèÿ äðóãèõ ýëå-
ìåíòîâ òðàåêòîðèè (âðåìåíè ïîëåòà, âûñîòû òðàåêòîðèè è óãëà
ïàäåíèÿ) äëÿ êàæäîé äàëüíîñòè.
 òàáëèöàõ, êðîìå òîãî, äîëæíû áûòü çàäàíû ïîïðàâî÷íûå êîýô-
ôèöèåíòû äëÿ äàëüíîñòè ïîëåòà è áîêîâîãî îòêëîíåíèÿ òî÷êè ïàäå-
íèÿ íà îòêëîíåíèÿ ïàðàìåòðîâ ðàêåòû îò ðàñ÷åòíûõ (ïðåæäå âñåãî
òåìïåðàòóðû è ìàññû òîïëèâà, à òàêæå ìàññû ðàêåòû) è íà îòêëîíå-
íèÿ ïàðàìåòðîâ àòìîñôåðû (äàâëåíèå, òåìïåðàòóðà è âåòåð) îò ñòàí-
äàðòíîé. Â òàáëèöû âíîñÿò òàêæå ïîïðàâêè äëÿ óñòàíîâîê ïðèöåëà â
ñëó÷àå ðàñïîëîæåíèÿ öåëè âûøå èëè íèæå óðîâíÿ ïóñêîâîé óñòà-
íîâêè.
583
13.3. ÁÀËËÈÑÒÈ×ÅÑÊÈÅ ÀËÃÎÐÈÒÌÛ ÐÀÑ×ÅÒÀ
ÓÑÒÀÍÎÂÎÊ ÄËß ÑÒÐÅËÜÁÛ ÀÐÒÈËËÅÐÈÈ È ÏÓÑÊÎÂ
ÐÀÊÅÒ
13.3.1 . ÏÎÍßÒÈÅ ÁÀËËÈÑÒÈ×ÅÑÊÎÃÎ ÀËÃÎÐÈÒÌÀ
È ÏÐÅÄÚßÂËßÅÌÛÅ Ê ÍÅÌÓ ÒÐÅÁÎÂÀÍÈß
Äî îòíîñèòåëüíî íåäàâíåãî âðåìåíè ïðè íåïîñðåäñòâåííîì îï-
ðåäåëåíèè èñêîìûõ óñòàíîâîê ïðèöåëüíûõ ïðèñïîñîáëåíèé äëÿ âå-
äåíèÿ àðòèëëåðèéñêèõ ñòðåëüá è ïóñêîâ ðàêåò â âîéñêàõ èñïîëüçîâà-
ëèñü èñêëþ÷èòåëüíî òàáëèöû ñòðåëüáû è ðàçëè÷íûå âñïîìîãàòåëü-
íûå ñðåäñòâà òèïà íîìîãðàìì, ãðàôèêîâ, ñïåöèàëüíûõ áëàíêîâ è
ò.ä ., â îñíîâå êîòîðûõ ëåæàëè âñå òå æå òàáëèöû ñòðåëüáû.
Âìåñòå ñ òåì ïðîöåññ îïðåäåëåíèÿ óñòàíîâîê äëÿ ñòðåëüáû, êàê
áûëî ïîêàçàíî â ãë. 6, èìååò âïîëíå ñòðîãóþ ìàòåìàòè÷åñêóþ îñíî-
âó, áàçèðóþùóþñÿ íà ðåøåíèè îáðàòíûõ (ðåæå ïðÿìûõ) çàäà÷ áàë-
ëèñòèêè.
Ýòî ðåøåíèå ïîääàåòñÿ êîððåêòíîé àëãîðèòìèçàöèè, ò.å . ñîñòàâ-
ëåíèþ ñîâîêóïíîñòè ìàòåìàòè÷åñêèõ îïåðàöèé è ïðîâåðÿåìûõ óñ-
ëîâèé, âûïîëíÿåìûõ ïî îïðåäåëåííûì ïðàâèëàì, ñëåäîâàíèå êîòî-
ðûì ïîñëå êîíå÷íîãî ÷èñëà øàãîâ îáÿçàòåëüíî ïðèâîäèò ê ðåøåíèþ
ïîñòàâëåííîé çàäà÷è [14].
Ïîä áàëëèñòè÷åñêèì àëãîðèòìîì, òàêèì îáðàçîì, ïðèíÿòî ïîíè-
ìàòü ñîâîêóïíîñòü ìàòåìàòè÷åñêèõ è ëîãè÷åñêèõ äåéñòâèé, âûïîë-
íÿåìûõ ñ ïîìîùüþ ñðåäñòâ âûñîêîïðîèçâîäèòåëüíîé âû÷èñëèòåëü-
íîé òåõíèêè è íàïðàâëåííûõ íà îïðåäåëåíèå íà÷àëüíûõ óñëîâèé,
ïðè êîòîðûõ ñíàðÿä èëè ðàêåòà â çàäàííûõ óñëîâèÿõ ïîëåòà îïèøåò
òðàåêòîðèþ, ïðîõîäÿùóþ ÷åðåç òî÷êó íà ïîâåðõíîñòè Çåìëè, îòîæ-
äåñòâëÿåìóþ ñ öåëüþ ("òî÷êó ïðèöåëèâàíèÿ").
Òðåáîâàíèÿ, ïðåäúÿâëÿåìûå ê áàëëèñòè÷åñêèì àëãîðèòìàì, ïîä-
ðàçäåëÿþòñÿ íà äâå ãðóïïû:
1) òðåáîâàíèÿ, âûòåêàþùèå èç óñëîâèé áîåâîãî ïðèìåíåíèÿ ðà-
êåòíî-àðòèëëåðèéñêîãî âîîðóæåíèÿ;
2) òåõíè÷åñêèå òðåáîâàíèÿ, îïðåäåëÿåìûå âîçìîæíîñòÿìè âîé-
ñêîâûõ ñïåöèàëèçèðîâàííûõ ÝÂÌ, èñïîëüçóåìûõ äëÿ ðàñ÷åòà óñòà-
íîâîê.
Ìû îãðàíè÷èìñÿ çäåñü êðàòêèì îáñóæäåíèåì êîíöåïòóàëüíûõ
îñíîâ ôîðìóëèðîâàíèÿ òðåáîâàíèé ê áàëëèñòè÷åñêèì àëãîðèòìàì,
ñâÿçàííûõ ñ îñîáåííîñòÿìè ðàêåòíî-àðòèëëåðèéñêîãî âîîðóæåíèÿ
è åãî áîåâîãî ïðèìåíåíèÿ. Äàííàÿ ãðóïïà òðåáîâàíèé îòíîñèòñÿ ê
÷èñëó îïðåäåëÿþùèõ. Óêðóïíåííî îíè ìîãóò áûòü ñôîðìóëèðîâàíû
êàê òðåáîâàíèÿ óíèâåðñàëüíîñòè, ãàðàíòèðîâàííîé òî÷íîñòè è âûñî-
êîãî áûñòðîäåéñòâèÿ.
Ðàñêðîåì ñóùíîñòü ýòèõ îáîáùåííûõ òðåáîâàíèé.
584
Ïðåæäå âñåãî îòìåòèì, ÷òî áàëëèñòè÷åñêèé àëãîðèòì (ÁÀ) äîë-
æåí îõâàòûâàòü äîñòàòî÷íî áîëüøóþ ãðóïïó îáðàçöîâ àðòèëëåðèé-
ñêîé è/èëè ñîîòâåòñòâåííî ðàêåòíîé òåõíèêè.
 àðòèëëåðèè èìåþòñÿ ñèñòåìû îäíîãî è òîãî æå êàëèáðà
(ïóøêè, ãàóáèöû, ìèíîìåòû è äð.) . Áîåêîìïëåêò êàæäîé èç ñèñ-
òåì âêëþ÷àåò ðàçíûå ñíàðÿäû, à êàæäûé ñíàðÿä ìîæåò èñïîëüçî-
âàòüñÿ ñ íåñêîëüêèìè çàðÿäàìè. Ó ðàêåò îäíîãî öåëåâîãî íàçíà-
÷åíèÿ ìîãóò áûòü ðàçëè÷íûå äâèãàòåëè, ìîãóò èñïîëüçîâàòüñÿ
ðàçëè÷íûå ïðèíöèïû è òåõíè÷åñêèå ðåøåíèÿ îáåñïå÷åíèÿ ñòàáè-
ëèçàöèè â ïîëåòå è ò.ä .
Íåñìîòðÿ íà ýòî îáñòîÿòåëüñòâî, ÁÀ äîëæåí áûòü ïðèñïîñîáëåí
ê ðàñ÷åòó óñòàíîâîê äëÿ âåäåíèÿ îãíÿ èç ìíîãèõ îáðàçöîâ ðàêåò-
íî-àðòèëëåðèéñêîé òåõíèêè â ëþáûõ óñëîâèÿõ áîåâîãî ïðèìåíåíèÿ
(ëþáîå âðåìÿ ãîäà, ëþáûå ãåîãðàôè÷åñêèå øèðîòû, ëþáàÿ âûñîòà
íàä óðîâíåì ìèðîâîãî îêåàíà).
Ñ áàëëèñòè÷åñêîé òî÷êè çðåíèÿ íè îäèí èç îáðàçöîâ âîîðóæå-
íèÿ íå ÿâëÿåòñÿ àáñîëþòíî ñòàáèëüíûì âî âðåìåíè. Â ïðîöåññå
ïðîèçâîäñòâà è ýêñïëóàòàöèè â âîéñêàõ îáðàçåö êîíñòðóêòèâíî
èëè òåõíîëîãè÷åñêè ñîâåðøåíñòâóåòñÿ, ïîäâåðãàåòñÿ ïëàíîâîé ìî-
äåðíèçàöèè, èñõîäÿ èç ïðîãíîçíûõ õàðàêòåðèñòèê ðàçâèòèÿ ñîîò-
âåòñòâóþùåãî âèäà âîîðóæåíèÿ. Ýòî âëå÷åò çà ñîáîé íåîáõîäè-
ìîñòü îïåðàòèâíîé àäàïòàöèè áàëëèñòè÷åñêîãî è ïðîãðàììíîãî
îáåñïå÷åíèÿ ðàñ÷åòà óñòàíîâîê íå òîëüêî äëÿ ñòàðûõ, îñòàþùèõñÿ
íà âîîðóæåíèè îáðàçöîâ, íî è äëÿ íîâûõ, ìîäåðíèçèðîâàííûõ.
Âñå ýòî ïîäïàäàåò ïîä îïðåäåëåíèå óíèâåðñàëüíîñòè ÁÀ.
Äàëåå íàïîìíèì, ÷òî òî÷íîñòü ñòðåëüáû èç àðòèëëåðèéñêèõ è ðà-
êåòíûõ ñèñòåì â îñíîâíîì îïðåäåëÿåòñÿ êó÷íîñòüþ ñòðåëüáû (òåõ-
íè÷åñêèì ðàññåèâàíèåì), òî÷íîñòüþ ïîäãîòîâêè èñõîäíûõ äàííûõ
è ïðîãðàììíûõ óñòàíîâîê (ìåòîäè÷åñêèìè îøèáêàìè).
Ïîãðåøíîñòè îïðåäåëåíèÿ óñòàíîâîê, òàêèì îáðàçîì, âõîäÿò ñî-
ñòàâíîé ÷àñòüþ â îøèáêè ïîëíîé ïîäãîòîâêè ñòðåëüáû.
 ñâÿçè ñ ýòèì ê àëãîðèòìàì ðàñ÷åòà óñòàíîâîê ïðåäúÿâëÿþòñÿ
ïîâûøåííûå òðåáîâàíèÿ ïî òî÷íîñòè. Îáû÷íî ñ÷èòàåòñÿ íåîáõîäè-
ìûì [14] äîñòèæåíèå òàêîé òî÷íîñòè, ïðè êîòîðîé îøèáêè ðåçóëü-
òàòîâ ïðåíåáðåæèìî ìàëû äàæå ïî ñðàâíåíèþ ñ õàðàêòåðèñòèêàìè
êó÷íîñòè.
Êîëè÷åñòâåííî äëÿ àðòèëëåðèéñêèõ ñèñòåì ýòî ñîîòâåòñòâóåò
îøèáêå ïî äàëüíîñòè 5...20 ì (â çàâèñèìîñòè îò ñàìîé äàëüíîñòè), à
ïî íàïðàâëåíèþ – â ïðåäåëàõ 5...10 ì, ÷òî ïðåâûøàåò òðåáîâàíèÿ,
ïðåäúÿâëÿåìûå ïî òî÷íîñòè ê òàáëèöàì ñòðåëüáû.
Íàêîíåö, ñëåäóåò èìåòü â âèäó, ÷òî àðòèëëåðèÿ, îñîáåííî ñàìî-
õîäíàÿ, è ðàêåòíûå ñèñòåìû çàëïîâîãî îãíÿ, âïðî÷åì, êàê îò÷àñòè è
ïîäâèæíûå ðàêåòíûå êîìïëåêñû îïåðàòèâíîãî íàçíà÷åíèÿ, îòíî-
585
ñÿòñÿ ê ÷èñëó äîñòàòî÷íî ìîáèëüíûõ âèäîâ âîîðóæåíèÿ. Ïîýòîìó
çàòðà÷èâàåìîå íà ðåøåíèå çàäà÷ ïîäãîòîâêè ñòðåëüáû âðåìÿ äîëæíî
áûòü äîñòàòî÷íî ìàëî. Òîëüêî ïðè ýòîì óñëîâèè ìîæåò áûòü îáåñïå-
÷åíî óïðåæäåíèå ïðîòèâíèêà â îòêðûòèè îãíÿ. Òåì áîëåå âûïîëíå-
íèå òðåáîâàíèÿ îïåðàòèâíîñòè êðàéíå âàæíî â ñëó÷àå, êîãäà ðå÷ü
èäåò î ïîðàæåíèè äâèæóùèõñÿ öåëåé.
Ïðè ýòîì íåîáõîäèìî ó÷èòûâàòü, ÷òî êðîìå ñîáñòâåííî âðå-
ìåíè, çàòðà÷èâàåìîãî íà ïðîâåäåíèå âû÷èñëåíèé ïî ÁÀ, òðåáóåò-
ñÿ íåêîòîðîå âðåìÿ íà ââîä íà÷àëüíûõ äàííûõ äëÿ âûïîëíåíèÿ
ðàñ÷åòîâ.
 ïåðâîì ïðèáëèæåíèè ìîæíî ñ÷èòàòü [14], ÷òî ïîëíîå âðåìÿ,
îòñ÷èòûâàåìîå ñ ìîìåíòà ïîñòóïëåíèÿ íà÷àëüíûõ óñëîâèé (äàííûõ
ðàçâåäêè ïî îïðåäåëåíèþ êîîðäèíàò öåëåé, òîïîãðàôè÷åñêîé, ìå-
òåîðîëîãè÷åñêîé è òåõíè÷åñêîé ïîäãîòîâêè) äî ïîëó÷åíèÿ ðåçóëüòà-
òîâ ðåøåíèÿ çàäà÷è ïî ÁÀ, íå äîëæíî ïðåâûøàòü 10 ñ, ÷òî ñîñòàâëÿ-
åò ïðèìåðíî ïîëîâèíó âðåìåíè, îòâîäèìîãî íà ðåøåíèå çàäà÷è ïîä-
ãîòîâêè ñòðåëüáû. Âïðî÷åì, âîçìîæíîñòè ñîâðåìåííîé âû÷èñ-
ëèòåëüíîé òåõíèêè ïðàêòè÷åñêè íå ðåãëàìåíòèðóþò ïðîäîëæèòåëü-
íîñòü ñîáñòâåííî âû÷èñëèòåëüíîãî ïðîöåññà ïî ÁÀ, êîòîðàÿ ñåãî-
äíÿ âïîëíå ìîæåò áûòü óìåíüøåíà äî 3...5ñ.
13.3.2. ÂÈÄÛ ÁÀËËÈÑÒÈ×ÅÑÊÈÕ ÀËÃÎÐÈÒÌÎÂ
Ñóùåñòâóþùèå âèäû áàëëèñòè÷åñêèõ àëãîðèòìîâ ïðèíÿòî ïîä-
ðàçäåëÿòü íà:
àëãîðèòìû, îñíîâàííûå íà ãîòîâûõ ðåøåíèÿõ áàëëèñòè÷åñêîé
çàäà÷è, èëè "òàáëè÷íûå àëãîðèòìû";
àëãîðèòìû, îñíîâàííûå íà èíòåãðèðîâàíèè ñèñòåì äèôôåðåíöè-
àëüíûõ óðàâíåíèé äâèæåíèÿ ñíàðÿäîâ è ðàêåò ("èíòåãðèðóþùèå àë-
ãîðèòìû").
Òàáëè÷íûå àëãîðèòìû õàðàêòåðèçóþòñÿ òåì, ÷òî â òîé èëè èíîé
ñòåïåíè îíè îáÿçàòåëüíî èñïîëüçóþò ñîâîêóïíîñòü çàðàíåå ïîëó-
÷åííûõ ðåøåíèé áàëëèñòè÷åñêîé çàäà÷è äëÿ àðòèëëåðèéñêèõ ñèñòåì
â ÷àñòè âîçìîæíûõ çíà÷åíèé îñíîâíûõ (äàëüíîñòü, íà÷àëüíàÿ ñêî-
ðîñòü) è âñïîìîãàòåëüíûõ (ìåòåîðîëîãè÷åñêèå, ãåîôèçè÷åñêèå è
äðóãèå ïàðàìåòðû, îïðåäåëÿþùèå óñëîâèÿ ñòðåëüáû) àðãóìåíòîâ.
Ïðè ýòîì, â ïðèíöèïå, ìîãóò áûòü èñïîëüçîâàíû ëèáî òàáëèöû
âíåøíåé áàëëèñòèêè, ëèáî òàáëèöû ñòðåëüáû. Ïðèìåíåíèå ïîñëåä-
íèõ ñ÷èòàåòñÿ áîëåå ïðåäïî÷òèòåëüíûì.
Ïîäõîä, èñïîëüçóåìûé ïðè ðåàëèçàöèè òàáëè÷íûõ àëãîðèòìîâ,
íà ïåðâûé âçãëÿä ïðåäñòàâëÿåòñÿ î÷åâèäíûì.  çàïîìèíàþùèõ óñò-
ðîéñòâàõ âîéñêîâûõ ñïåöèàëèçèðîâàííûõ ÝÂÌ äîëæíû ñîäåðæàòü-
ñÿ ãîòîâûå ðåøåíèÿ ïðÿìîé èëè îáðàòíîé çàäà÷è âíåøíåé áàëëè-
ñòèêè è äîëæíà áûòü ïðåäóñìîòðåíà âîçìîæíîñòü âûáîðà êîíêðåò-
586
íîãî ãîòîâîãî ðåøåíèÿ, ñîîòâåòñòâóþùåãî çàäàííûì çíà÷åíèÿì
àðãóìåíòà.
Îäíàêî íå âñå òàê ïðîñòî. Äåëî çàêëþ÷àåòñÿ â òîì, ÷òî ðåàëüíûå
çíà÷åíèÿ âûáðàííûõ çíà÷åíèé àðãóìåíòîâ (äàëüíîñòü, îòêëîíåíèÿ
ìåòåîôàêòîðîâ îò íîðìàëüíûõ è äð.) ïðàêòè÷åñêè íèêîãäà íå ñîâïà-
äàþò ñ òåìè äèñêðåòíûìè çíà÷åíèÿìè òàáëè÷íûõ çíà÷åíèé, êîòî-
ðûå "çàïîìíèëà" ÝÂÌ. Íàèáîëåå ïðîñòûì ïîäõîäîì â ïîäîáíîé ñè-
òóàöèè ïðåäñòàâëÿåòñÿ ïîäõîä, ñâÿçàííûé ñ âûáîðîì ìåòîäîâ ëè-
íåéíîé èíòåðïîëÿöèè, èñïîëüçóåìûé ïðè ðó÷íîì ïðèìåíåíèè
òàáëèö ñòðåëüáû. Äëÿ òîãî ÷òîáû îáåñïå÷èòü òðåáóåìóþ òî÷íîñòü,
âûáîðêó ïðè ýòîì ñëåäóåò ïðîèçâîäèòü èç ïîëíîãî íàáîðà ðåøåíèé,
ò.å . çàïîìèíàòüñÿ äîëæåí âåñü îáúåì ÷èñëîâîé èíôîðìàöèè ñîîò-
âåòñòâóþùåãî òèïà òàáëèö ñòðåëüáû. Àëüòåðíàòèâîé, âïîëíå ïðèåì-
ëåìîé ïðè ïðèìåíåíèè ÝÂÌ, ìîæåò ñëóæèòü êîìáèíàöèÿ ñîêðà-
ùåííîãî îáúåìà çàïîìíåííîé èíôîðìàöèè èç òàáëèö ñòðåëüáû ñ
ìåòîäàìè íåëèíåéíîé èíòåðïîëÿöèè.
Îáà ïîäõîäà, îäíàêî, ñòðàäàþò ñóùåñòâåííûì íåäîñòàòêîì, ñâÿ-
çàííûì ñ íåâîçìîæíîñòüþ äîñòèæåíèÿ òðåáóåìîãî óðîâíÿ óíèâåð-
ñàëüíîñòè. Ê òîìó æå àëãîðèòìû ñ èíòåðïîëÿöèåé òàáëè÷íîãî ìàòå-
ðèàëà íå óäîâëåòâîðÿþò ñåãîäíÿ òðåáóåìîé òî÷íîñòè è ýôôåêòèâíî-
ñòè ïðåæäå âñåãî èç-çà ïðàêòè÷åñêîé íåðåàëèçóåìîñòè ïðèìåíåíèÿ
ôóíêöèé íåñêîëüêèõ ïåðåìåííûõ.
Áîëåå ïðèåìëåìûìè â ýòîì ñìûñëå ñ÷èòàþòñÿ òàê íàçûâàåìûå
òàáëè÷íûå ïîëèíîìíûå àëãîðèòìû, â êîòîðûõ òàáëèöû ñòðåëüáû èñ-
ïîëüçóþòñÿ îïîñðåäîâàííî ïóòåì èõ ïðåäâàðèòåëüíîé àïïðîêñèìà-
öèè ïîëèíîìàìè òîé èëè èíîé ñòåïåíè îò îäíîãî èëè íåñêîëüêèõ
àðãóìåíòîâ.
 ÝÂÌ ïðè ýòîì çàïèñûâàþòñÿ íå òàáëèöû ñòðåëüáû, à êîýôôè-
öèåíòû óêàçàííûõ ïîëèíîìîâ. Òðåáóåìîå ðåøåíèå áàëëèñòè÷åñêîé
çàäà÷è íàõîäèòñÿ ïóòåì ïîäñòàíîâêè â ýòè ïîëèíîìû çàäàííûõ çíà-
÷åíèé àðãóìåíòîâ.
"Ñâåðòûâàíèå" àðòèëëåðèéñêèõ òàáëèö ñòðåëüáû íàèáîëåå öåëå-
ñîîáðàçíî îñóùåñòâëÿòü, èñïîëüçóÿ ôóíêöèè íåñêîëüêèõ ïåðåìåí-
íûõ òèïà f(xc, V0, p0), à èíîãäà è áîëüøåãî ÷èñëà àðãóìåíòîâ. Çäåñü
õñ – äàëüíîñòü, çàäàííàÿ äèñêðåòíûìè çíà÷åíèÿìè; V0 – íà÷àëüíàÿ
ñêîðîñòü ñíàðÿäà; p0 – àòìîñôåðíîå äàâëåíèå íà âûñîòå îãíåâîé
(ñòàðòîâîé) ïîçèöèè, êîòîðîå îñîáåííî âàæíî ó÷èòûâàòü â ãîðíûõ
óñëîâèÿõ (â ñèëó ýòîãî îáñòîÿòåëüñòâà âñå òàáëè÷íûå àëãîðèòìû
äîëæíû áûòü "ãîðíûìè" [14]).
Ñóòü îáñóæäàåìîãî ìåòîäà ñâîäèòñÿ ê ïîäáîðó òàêîãî ïîëèíîìà,
êîòîðûé â îïðåäåëåííîì ñìûñëå áóäåò íàèáîëåå áëèçîê ê çàäàííîé
òàáëèöàìè ñòðåëüáû ìíîãîàðãóìåíòíîé ôóíêöèè.
Ïóñòü òàêîé ïîëèíîì èìååò âèä
587
FFxVp
kk
c
=
(, ,)
,
00
(13.11)
à â ðàçâåðíóòîé ôîðìå ïðè ñîõðàíåíèè ÷ëåíîâ íå âûøå âòîðîãî
ïîðÿäêà – âèä
FxVpa axaVapax
kc
k
kck
k
kc
(, ,)
00
000
100
010 0
001 0
200
=+
+++2
020 0
2
002 0
2
110
0
101
0
01100
+
+++++
aV apaxV axpaVp
kkk
c
k
c
k
.
(13.12)
Êàê ñëåäóåò èç (13.12), ïîëó÷àåìûé ïîëèíîì äàæå äëÿ ïðîñòåé-
øåãî ñëó÷àÿ ôóíêöèè òðåõ àðãóìåíòîâ èìååò äîñòàòî÷íî ãðîìîçäêîå
âûðàæåíèå.
Õîòÿ äëÿ ñîâðåìåííûõ ÝÂÌ ýòî íå ñòîëü óæ ñóùåñòâåííûé ôàê-
òîð, ñëåäóåò ó÷èòûâàòü, ÷òî çíà÷èòåëüíîå óâåëè÷åíèå ÷èñëà àðãó-
ìåíòîâ (÷òî, êàê áûëî óêàçàíî âûøå, ÿâëÿåòñÿ îáúåêòèâíîé îñîáåí-
íîñòüþ ðàêåòíûõ òàáëèö ñòðåëüáû) ïðèâåäåò ê çíà÷èòåëüíîìó ñíè-
æåíèþ áûñòðîäåéñòâèÿ è íåîáõîäèìîñòè "çàïîìèíàíèÿ" îãðîìíûõ
ìàññèâîâ êîýôôèöèåíòîâ ak000, ak100, ... äëÿ âñåõ áàëëèñòè÷åñêèõ
ôóíêöèé, ò.å . äëÿ âñåõ èíäåêñîâ k.
Äàííîå îáñòîÿòåëüñòâî äåëàåò íåöåëåñîîáðàçíîé âîçìîæíîñòü
ðåêîìåíäàöèé òàáëè÷íûõ ïîëèíîìíûõ àëãîðèòìîâ ïðè ïîäãîòîâêå
ïóñêîâ ðàêåò.
Îäíàêî ïðåæäå ÷åì ïåðåéòè ê ðàññìîòðåíèþ áîëåå ïðåäïî÷òè-
òåëüíûõ â ýòîì ñìûñëå èíòåãðèðóþùèõ àëãîðèòìîâ ðàñ÷åòà óñòàíî-
âîê, óäåëèì åùå íåêîòîðîå âíèìàíèå îðãàíèçàöèè âû÷èñëèòåëüíîé
ðàáîòû ñ òàáëè÷íûìè ïîëèíîìíûìè àëãîðèòìàìè.
Ïðè ïîñòóïëåíèè èñõîäíûõ äàííûõ xc, V0 è ð0 (èëè äðóãèõ âåëè-
÷èí, õàðàêòåðíûõ äëÿ êîíêðåòíîãî îáðàçöà âîîðóæåíèÿ) ÝÂÌ ïî
ñîîòâåòñòâóþùåé ïðîãðàììå îòûñêèâàåò â ìàññèâå ÷èñëåííûõ äàí-
íûõ ïîñëåäîâàòåëüíî äëÿ êàæäîé k-é ôóíêöèè (îñíîâíîé, ïîïðà-
âî÷íîé èëè âñïîìîãàòåëüíîé) çíà÷åíèÿ êîýôôèöèåíòîâ ïîëèíîìîâ
è âû÷èñëÿåò çíà÷åíèÿ ïîëèíîìîâ òèïà (13.11), ïðèíèìàåìûõ çà çíà-
÷åíèÿ èñêîìûõ òàáëè÷íûõ ôóíêöèé.
Äàëåå, ñ ïîìîùüþ íàéäåííûõ çíà÷åíèé Fk ðàññ÷èòûâàþòñÿ èñ-
÷èñëåííûå äàëüíîñòè ïåðâîãî, âòîðîãî è ïîñëåäóþùèõ ïðèáëèæå-
íèé.
Åñëè îáîçíà÷èòü ïîïðàâî÷íûå ïîëèíîìû ÷åðåç Fl (èç îáùåãî
÷èñëà Fk), òî ïðè îòûñêàíèè l-é ïîïðàâêè ∆x c l
()1
ïåðâîãî ïðèáëèæå-
íèÿ áóäåì èìåòü
∆∆
xF
x
V
pl
cl
c
l
()
(,,),
1
00
=
ã
(13.13)
ãäå xcã
–
ãåîôèçè÷åñêàÿ èëè òîïîãðàôè÷åñêàÿ äàëüíîñòü äî öåëè; ∆l –
îòêëîíåíèå l-ãî óñëîâèÿ ñòðåëüáû îò íîðìàëüíîãî; Fx V p
lc
(,,)
–
ã
00
çíà÷åíèå l-ãî ïîïðàâî÷íîãî êîýôôèöèåíòà. Òîãäà èñ÷èñëåííàÿ
äàëüíîñòü ïåðâîãî ïðèáëèæåíèÿ áóäåò îïðåäåëÿòüñÿ êàê
588
xxx
ñc
c
l
n
l
èã
()
().
11
1
=+
=
∑∆
(13.14)
Âñå èñ÷èñëåííûå äàëüíîñòè ïîñëåäóþùèõ ïðèáëèæåíèé îïðåäå-
ëÿþòñÿ àíàëîãè÷íûì îáðàçîì ïóòåì ïîäñòàíîâêè â ïîëèíîìû Fl
ïðåäûäóùèõ èñ÷èñëåííûõ äàëüíîñòåé.
Ïðîöåññ ïîñëåäîâàòåëüíûõ óòî÷íåíèé ïðîäîëæàåòñÿ äî òåõ ïîð,
ïîêà íà r-ì ïðèáëèæåíèè íå áóäåò âûïîëíåíî óñëîâèå
xx
c
r
c
r
èè
()(),
−≤
−1
ε
(13.15)
ãäå ε – çàðàíåå çàäàííàÿ ìàëàÿ ïîëîæèòåëüíàÿ âåëè÷èíà,
îïðåäåëÿåìàÿ òðåáóåìîé òî÷íîñòüþ ðàñ÷åòîâ. Êàê ïðàâèëî, ïîëíîå
÷èñëî ïðèáëèæåíèé äîñòèãàåòñÿ ïðè r ≤ 3...4. Ïîñëå òîãî êàê
íåðàâåíñòâî (13.15) âûïîëíåíî, àëãîðèòì ïðåäóñìàòðèâàåò
íàõîæäåíèå èñêîìîé óñòàíîâêè Óèñê ñ èñïîëüçîâàíèåì âñå òîãî æå
ïîëèíîìà (13.11), ò.å .
Ó èñê
ó
è
= FxVp
c
r
(,,)
.
()
00
(13.16)
Ïàðàëëåëüíî ïî ñâîèì ïîëèíîìàì îïðåäåëÿþò ïîïðàâêè äëÿ
íàïðàâëåíèÿ ñòðåëüáû (íà áîêîâóþ ñîñòàâëÿþùóþ ñêîðîñòè âåòðà,
äåðèâàöèþ, âðàùåíèå Çåìëè), à çàòåì èõ ñóììèðóþò.
 öåëîì ìåòîä ïîëèíîìíîé ìíîãîìåðíîé (ìíîãîàðãóìåíòíîé)
àïïðîêñèìàöèè ÿâëÿåòñÿ äîñòàòî÷íî ïðîäóêòèâíûì (ïðåæäå âñåãî
äëÿ ñòâîëüíûõ ñèñòåì), îäíàêî åãî ýôôåêòèâíîñòü â çíà÷èòåëüíîé
ñòåïåíè çàâèñèò îò ñòåïåíè ðàöèîíàëüíîñòè àïïðîêñèìàöèè òàá-
ëè÷íûõ çàâèñèìîñòåé îïèñàííûìè ïîëèíîìàìè.
Çàèíòåðåñîâàííûé ÷èòàòåëü ìîæåò áûòü àäðåñîâàí ê ðàáîòå [14],
â êîòîðîé äàíî ïîäðîáíîå èçëîæåíèå âîçìîæíûõ ïîäõîäîâ ê ðåøå-
íèþ ñîîòâåòñòâóþùåé çàäà÷è.
Ïåðåéäåì òåïåðü ê êðàòêîìó ðàññìîòðåíèþ ïðèíöèïèàëüíî äðó-
ãîãî òèïà áàëëèñòè÷åñêèõ àëãîðèòìîâ, à èìåííî èíòåãðèðóþùèõ àë-
ãîðèòìîâ.
Êîíöåïòóàëüíûå âîïðîñû èõ ïîñòðîåíèÿ óæå îáñóæäàëèñü ðàíåå
â ãë. 6. Çäåñü æå îñòàíîâèìñÿ íà ñïåöèôèêå èõ ïîñòðîåíèÿ è ïðè-
ñïîñîáëåíèÿ ê òðåáîâàíèÿì, èçëîæåííûì â ï. 13.3.1 .
Êàê óæå îòìå÷àëîñü, äàííûé âèä àëãîðèòìà ïðåäíàçíà÷åí äëÿ
îïðåäåëåíèÿ óñòàíîâîê íà ïðîâåäåíèå ñòðåëüá èëè ïóñêîâ ðàêåò ïî-
ñðåäñòâîì ðåøåíèÿ (èíòåãðèðîâàíèÿ) ñèñòåìû äèôôåðåíöèàëüíûõ
óðàâíåíèé, îïèñûâàþùèõ äâèæåíèå ËÀ (ñíàðÿäà, ìèíû, ðàêåòû).
589
Ïîýòîìó ïåðâûì è, ïîæàëóé, îïðåäåëÿþùèì ÿâëÿåòñÿ âîïðîñ
âûáîðà ðàöèîíàëüíîé ñèñòåìû äèôôåðåíöèàëüíûõ óðàâíåíèé äâè-
æåíèÿ. Åäèíîãî ðåöåïòà çäåñü íå ìîæåò áûòü.  çíà÷èòåëüíîé ñòåïå-
íè ýòîò âûáîð çàâèñèò îò êîíêðåòíîãî òèïà ËÀ, ÷òî ïîä÷åðêèâàëîñü
ðàíåå (ñì. ï. 6.1.2). Âìåñòå ñ òåì ñóùåñòâóþò íåêîòîðûå îáùèå ïî-
ëîæåíèÿ, êîòîðûõ íåîáõîäèìî ïðèäåðæèâàòüñÿ. Îíè ñâîäÿòñÿ ê
ñëåäóþùåìó.
1. Âûáèðàåìàÿ ÌÌÄ äîëæíà îòðàæàòü îñîáåííîñòè óñòðîéñòâà è
ôóíêöèîíèðîâàíèÿ âñåãî ðàçíîîáðàçèÿ ËÀ ðàññìàòðèâàåìîãî òèïà,
äëÿ êîòîðûõ ïðåäíàçíà÷àåòñÿ ðàçðàáàòûâàåìûé àëãîðèòì, ò.å . îíà
äîëæíà óäîâëåòâîðÿòü óñëîâèþ óíèâåðñàëüíîñòè.
2. Ñòðóêòóðà è ñòåïåíü äåòàëèçàöèè ÌÌÄ äîëæíû áûòü òàêèìè,
÷òîáû â íåé ñîäåðæàëèñü â ÿâíîì âèäå ïàðàìåòðû, îòðàæàþùèå âñå
óñëîâèÿ ñòðåëüáû: ìåòåîðîëîãè÷åñêèå, áàëëèñòè÷åñêèå, ãåîôèçè÷å-
ñêèå è äðóãèå ïàðàìåòðû, îïðåäåëÿþùèå äâèæåíèå ËÀ è äîïóñêàþ-
ùèå âîçìîæíîñòü èõ èçìåðåíèÿ.
3. Óðîâåíü àäåêâàòíîñòè ÌÌÄ ðåàëüíîìó ïðîöåññó äîëæåí áûòü
òàêèì, ÷òîáû íåñîîòâåòñòâèå ìîäåëè èñòèííîìó õàðàêòåðó äâèæå-
íèÿ äîïóñêàëîñü ëèøü â ïðåäåëàõ, íåñóùåñòâåííî âëèÿþùèõ íà îï-
ðåäåëÿåìûå ýëåìåíòû.
4. Ôàêòîðû, èçìåíÿþùèåñÿ îò âûñòðåëà ê âûñòðåëó (îò ïóñêà ê
ïóñêó ðàêåò) èëè â ïðîöåññå ïîëåòà íåîïðåäåëåííî è ñëó÷àéíûì îá-
ðàçîì, â ÌÌÄ íå äîëæíû ó÷èòûâàòüñÿ è âîîáùå íå äîëæíû ðàñ-
ñìàòðèâàòüñÿ.
Ðàíåå (ñì. ãë. 6) îòìå÷àëîñü òàêæå, ÷òî îïðåäåëåíèå óñòàíîâîê
äëÿ ïðîâåäåíèÿ ñòðåëüá (ïóñêîâ ðàêåò) îòíîñèòñÿ ãëàâíûì îáðàçîì
ê ÷èñëó îáðàòíûõ çàäà÷ áàëëèñòèêè. Èç âñåõ ñóùåñòâóþùèõ ìåòîäîâ
ðåøåíèÿ îáðàòíûõ çàäà÷ ïðàêòè÷åñêè íàèáîëåå ïðèåìëåìûì ÿâëÿ-
åòñÿ èòåðàöèîííûé. Îäíàêî èòåðàöèîííàÿ ïðîöåäóðà äîïóñêàåò
ìíîæåñòâî ñïîñîáîâ åå ïîñòðîåíèÿ. Îò âûáîðà ðàöèîíàëüíîé (èëè
íåðàöèîíàëüíîé) ñõåìû ïîñòðîåíèÿ èòåðàöèîííîãî ïðîöåññà çàâè-
ñèò ñòåïåíü åãî ñõîäèìîñòè, ò.å. íåîáõîäèìîå ÷èñëî ïðèáëèæåíèé
äî ïîëó÷åíèÿ òðåáóåìîãî ðåçóëüòàòà.
Ïîýòîìó âòîðûì (ïîñëå âûáîðà ÌÌÄ) ïî âàæíîñòè âîïðîñîì
ðàçðàáîòêè èíòåãðèðóþùåãî àëãîðèòìà ÿâëÿåòñÿ ðàöèîíàëüíàÿ îð-
ãàíèçàöèÿ èòåðàöèîííîãî ïðîöåññà. Ïðè ýòîì ñîîòâåòñòâóþùèå
êðèòåðèè âûòåêàþò èç îáùèõ òðåáîâàíèé, ïðåäúÿâëÿåìûõ ê áàëëè-
ñòè÷åñêèì àëãîðèòìàì:
óíèâåðñàëüíîñòü ïî îòíîøåíèþ êî âñåì âèäàì ñíàðÿäîâ è ðàêåò
ñîîòâåòñòâóþùåãî òèïà;
ìèíèìàëüíûé îáúåì ñîáñòâåííîé ïåðâîíà÷àëüíîé èíôîðìàöèè,
îáåñïå÷èâàþùåé íà÷àëî è íîðìàëüíûé õîä ïðîöåññà ñáëèæåíèÿ;
íàèëó÷øåå íóëåâîå ïðèáëèæåíèå;
áûñòðîòà ñõîäèìîñòè íà òåêóùèõ øàãàõ;
590
óñòîé÷èâàÿ ðàáîòà àëãîðèòìà èòåðàöèé ïðè âñåõ âîçìîæíûõ óñ-
ëîâèÿõ (ïðè ïîëíîì èñêëþ÷åíèè íåïðåäâèäåííîé îñòàíîâêè ïðî-
öåññà èëè, íàîáîðîò, åãî áåñêîíå÷íîì ïðîäîëæåíèè ïðè âîçíèêíî-
âåíèè ñëó÷àåâ äåëåíèÿ íà íîëü);
ïðèåìëåìûå äëèíû ÷èñåë, ó÷àñòâóþùèõ â èòåðàöèÿõ.
Ñõåìû ïîñòðîåíèÿ èòåðàöèîííûõ ïðîöåäóð, óäîâëåòâîðÿþùèõ
óêàçàííûì êðèòåðèÿì äëÿ ðàçëè÷íûõ èíòåãðèðóþùèõ àëãîðèòìîâ è
òèïîâ ÌÌÄ, ìîãóò ñóùåñòâåííî ðàçëè÷àòüñÿ. Íàïðèìåð, äëÿ
ñòâîëüíûõ ñèñòåì îäíîé èç íàèáîëåå ðàöèîíàëüíûõ ñ÷èòàåòñÿ ñõåìà
îðãàíèçàöèè èòåðàöèîííîãî ïðîöåññà ïî "ýòàëîííîé êðèâîé" [14],
íî îíà ïðàêòè÷åñêè íåïðèåìëåìà äëÿ ÁÐ.
Îäíàêî ýòîò âîïðîñ óæå âûõîäèò çà ðàìêè ïðîáëåì, ÿâëÿþùèõñÿ
ïðåäìåòîì ðàññìîòðåíèÿ íàñòîÿùåãî ó÷åáíèêà.
Êîíòðîëüíûå âîïðîñû
1. Ïåðå÷èñëèòå äîñòîèíñòâà è íåäîñòàòêè èñïûòàíèé, ïðîâîäèìûõ íà
áàëëèñòè÷åñêèõ òðàññàõ. Óêàæèòå îñíîâíûå ñïîñîáû îïðåäåëåíèÿ àýðîäè-
íàìè÷åñêîãî êîýôôèöèåíòà íîðìàëüíîé ñèëû ïðè ñòðåëüáå íà áàëëèñòè÷å-
ñêîé òðàññå. Êàêîé ïðèíöèï ïîëîæåí â îñíîâó ìàãíèòîìåòðè÷åñêîãî ñïîñî-
áà îïðåäåëåíèÿ óãëîâîãî äâèæåíèÿ ËÀ?
2. ×òî òàêîå óãîë âûëåòà? Îïðåäåëèòå ïîíÿòèå êó÷íîñòè ñòðåëüáû. ×òî
ïîíèìàåòñÿ ïîä ñîñòðåëîì äàëüíîñòåé è íà÷àëüíûõ ñêîðîñòåé?
3. Ïåðå÷èñëèòå ñêàëÿðíûå êðèòåðèè îïòèìàëüíîñòè ïëàíà áàëëèñòè÷å-
ñêîãî ýêñïåðèìåíòà è äàéòå èõ ôèçè÷åñêóþ òðàêòîâêó. Íàçîâèòå ìåòîäû îá-
ðàáîòêè ðåçóëüòàòîâ èçìåðåíèé è äàéòå èõ êðàòêóþ õàðàêòåðèñòèêó.  ÷åì
çàêëþ÷àåòñÿ ñóùíîñòü çàäà÷è ïàðàìåòðè÷åñêîé èäåíòèôèêàöèè ËÀ ïî ðå-
çóëüòàòàì ëåòíûõ èñïûòàíèé? ×òî ïîíèìàåòñÿ ïîä íåâÿçêîé?
4. Äàéòå òðàêòîâêó ïîíÿòèÿ è îáîñíóéòå íåîáõîäèìîñòü îòñòðåëà òàáëèö
ñòðåëüáû. Çà ñ÷åò ÷åãî äîñòèãàåòñÿ óíèâåðñàëèçàöèÿ äàííûõ, ïîëó÷åííûõ
ïðè ïðîâåäåíèè òàáëè÷íûõ ñòðåëüá â êîíêðåòíûõ ìåòåîðîëîãè÷åñêèõ óñëî-
âèÿõ, êîòîðàÿ âûðàæàåòñÿ â âîçìîæíîñòè èñïîëüçîâàíèÿ òàáëèö ñòðåëüáû
ïðèìåíèòåëüíî ê ëþáûì ìåòåîðîëîãè÷åñêèì óñëîâèÿì?
5. Ñôîðìóëèðóéòå ïîíÿòèå áàëëèñòè÷åñêîãî àëãîðèòìà, ïåðå÷èñëèòå îñ-
íîâíûå òðåáîâàíèÿ, ïðåäúÿâëÿåìûå ê áàëëèñòè÷åñêèì àëãîðèòìàì, è ðàñ-
êðîéòå èõ ñóùíîñòü. Íà êàêèå âèäû ïîäðàçäåëÿþòñÿ áàëëèñòè÷åñêèå àëãî-
ðèòìû?
6.  ÷åì ñîñòîèò îñîáåííîñòü òàáëè÷íûõ àëãîðèòìîâ? Äàéòå îïðåäåëåíèå
òàáëè÷íûõ ïîëèíîìíûõ àëãîðèòìîâ. Êàê îñóùåñòâëÿåòñÿ "ñâåðòûâàíèå" àð-
òèëëåðèéñêèõ òàáëèö ñòðåëüáû ñ èñïîëüçîâàíèåì ôóíêöèé íåñêîëüêèõ ïå-
ðåìåííûõ?  ÷åì çàêëþ÷àåòñÿ ñóùíîñòü ïðèìåíåíèÿ èíòåãðèðóþùèõ àëãî-
ðèòìîâ? Ïî÷åìó èíòåãðèðóþùèå àëãîðèòìû ÿâëÿþòñÿ áîëåå ïðåäïî÷òèòåëü-
íûìè ïðè îïðåäåëåíèè óñòàíîâîê íà ïóñê ðàêåò, ÷åì òàáëè÷íûå
ïîëèíîìíûå àëãîðèòìû?
Ïåðå÷èñëèòå êðèòåðèè, êîòîðûìè ñëåäóåò ðóêîâîäñòâîâàòüñÿ ïðè îòäà-
íèè ïðåäïî÷òåíèÿ òîé èëè èíîé ñõåìå îðãàíèçàöèè èòåðàöèîííîãî ïðîöåñ-
ñà ïðè ðåøåíèè çàäà÷ ïîäãîòîâêè äàííûõ íà ïóñê ðàêåò íà îñíîâå èíòåãðè-
ðóþùèõ àëãîðèòìîâ.
591
ËÈÒÅÐÀÒÓÐÀ
1. Àáãàðÿí Ê.À ., Ðàïîïîðò È.Ì. Äèíàìèêà ðàêåò. Ì .: Ìàøèíîñòðîåíèå,
1969.
2. Àáãàðÿí Ê.À . Óñòîé÷èâîñòü äâèæåíèÿ íà êîíå÷íîì èíòåðâàëå // Èòîãè
íàóêè è òåõíèêè. Îáùàÿ ìåõàíèêà. Ò. 3 . Ì .: ÂÈÍÈÒÈ, 1976. Ñ . 43–124.
3. Àíäðîíîâ Ð.Ô., Âèòò À.À., Õàéêèí Ñ.Ý . Òåîðèÿ êîëåáàíèé. Ì .:
ÃÈÔÌË, 1959.
4. Àïïàçîâ Ð.Ô ., Ëàâðîâ Ñ.Ñ., Ìèøèí Â.Ï. Áàëëèñòèêà óïðàâëÿåìûõ ðà-
êåò äàëüíåãî äåéñòâèÿ. Ì .: Íàóêà, 1966.
5. Àïïàçîâ Ð.Ô ., Ñûòèí Î.Ã . Ìåòîäû ïðîåêòèðîâàíèÿ òðàåêòîðèé íîñè-
òåëåé è ñïóòíèêîâ Çåìëè. Ì .: Íàóêà, 1987.
6. Àðíîëüä Â.È . Äîïîëíèòåëüíûå ãëàâû òåîðèè îáûêíîâåííûõ äèôôå-
ðåíöèàëüíûõ óðàâíåíèé. Ì .: Íàóêà, 1978.
7. Àðíîëüä Â.È. Îáûêíîâåííûå äèôôåðåíöèàëüíûå óðàâíåíèÿ. 3-å èçä.
Ì.: Íàóêà, 1984.
8. Àðíîëüä Â.È., Èëüÿøåíêî Þ.Ñ . Îáûêíîâåííûå äèôôåðåíöèàëüíûå
óðàâíåíèÿ // Èòîãè íàóêè è òåõíèêè. Ñîâðåìåííûå ïðîáëåìû ìàòåìàòèêè.
Ò. 1. Äèíàìè÷åñêèå ñèñòåìû. Ì .: ÂÈÍÈÒÈ, 1985.
9. Àýðîäèíàìèêà ðàêåò / Ïîä ðåä. Í .Ô . Êðàñíîâà. Ì .: Âûñøàÿ øêîëà,
1968*
.
10. Àýðîìåõàíèêà ñàìîëåòà (äèíàìèêà ïîëåòà): Ó÷åáíèê äëÿ àâèàöèîííûõ
âóçîâ / À.Ô . Áî÷êàðåâ, Â. . Àíäðååâñêèé, Â.Ì . Áåëîêîíîâ è äð. 2-å èçä., ïå-
ðåðàá. è äîï. Ì .: Ìàøèíîñòðîåíèå, 1985.
11. Áàóòèí Í.Í., Ëåîíòîâè÷ Å.À . Ìåòîäû è ïðèåìû êà÷åñòâåííîãî èññëå-
äîâàíèÿ äèíàìè÷åñêèõ ñèñòåì íà ïëîñêîñòè. Ì .: Íàóêà, 1976.
12. Áåëëìàí Ð. Ââåäåíèå â òåîðèþ ìàòðèö. Ì .: Íàóêà, 1969.
13. Áåëÿåâà Ñ.Ä . Èññëåäîâàíèå óñòîé÷èâîñòè íåâîçìóùåííîãî äâèæåíèÿ
îäíîãî òâåðäîãî òåëà â ñëó÷àå ïðîñòðàíñòâåííîãî äâèæåíèÿ â âîçäóõå åãî
öåíòðà ìàññ // Ïðèêëàäíàÿ ìàòåìàòèêà è ìåõàíèêà. 1978. Ò. 42, âûï. 2.
Ñ. 46–53.
14. Áåëÿåâà Ñ.Ä., Ìîí÷åíêî Í.Ì., Ïàðøèí Æ.Ï. Âíåøíÿÿ áàëëèñòèêà.
×. II: Óñòîé÷èâîñòü äâèæåíèÿ ñíàðÿäîâ. Ì .: Èçä-âî ÌÎ ÑÑÑÐ, 1988; ×. III:
Ïðàêòè÷åñêèå ïðèëîæåíèÿ òåîðèè äâèæåíèÿ ñíàðÿäà îòíîñèòåëüíî öåíòðà
ìàññ, 1989.
15. Áåññìåðòíûõ Ã.À. Î ñóùåñòâîâàíèè è åäèíñòâåííîñòè ðåøåíèÿ ìíî-
ãîòî÷å÷íîé çàäà÷è Âàëëå-Ïóññåíà äëÿ íåëèíåéíûõ äèôôåðåíöèàëüíûõ
óðàâíåíèé // Äèôôåðåíöèàëüíûå óðàâíåíèÿ. Ò. VI, 1 2. Ìèíñê: Íàóêà è
òåõíèêà, 1970. Ñ . 298–310 .
16. Áîäíåð Â.À . Ñèñòåìû óïðàâëåíèÿ ëåòàòåëüíûìè àïïàðàòàìè. Ì .: Ìà-
øèíîñòðîåíèå, 1973.
17. Áðàíäèí Â.Í., Âàñèëüåâ À.À., Õóäÿêîâ Ñ.Ò . Îñíîâû ýêñïåðèìåíòàëü-
íîé êîñìè÷åñêîé áàëëèñòèêè / Ïîä ðåä. Ä .À . Ïîãîðåëîâà. Ì .: Ìàøèíî-
ñòðîåíèå, 1974.
592
18. Áþøãåíñ Ã.Ñ., Ñòóäíåâ Ð. . Äèíàìèêà ïðîñòðàíñòâåííîãî äâèæåíèÿ
ñàìîëåòà. Ì .: Ìàøèíîñòðîåíèå, 1967.
19. Áþøãåíñ Ã.Ñ ., Ñòóäíåâ Ð. . Äèíàìèêà ïðîñòðàíñòâåííîãî äâèæåíèÿ
ñàìîëåòà. 2-å èçä., ïåðåðàá. è äîï. Ì .: Ìàøèíîñòðîåíèå, 1983.
20. Áóñëåíêî Í.Ï. Ìåòîä ñòàòèñòè÷åñêèõ èñïûòàíèé. Ì .: Ôèçìàòãèç,
1962.
21. Âåíòöåëü Ä.À., Îêóíåâ Á.Í., Øàïèðî ß.Ì. Âíåøíÿÿ áàëëèñòèêà. Ì .;
Ë.: ÂÀÀ èì. Ô.Ý. Äçåðæèíñêîãî. 1933. Ò . I, III; 1934. Ò . II.
22. Âåíòöåëü Ä.À., Øàïèðî ß.Ì. Âíåøíÿÿ áàëëèñòèêà. Ì .: Îáîðîíãèç,
1939.
23. Âåíòöåëü Å.Ñ . Òåîðèÿ âåðîÿòíîñòåé. Ì .: Íàóêà, 1964.
24. Âåðåùàãèí È.Ô . Ìåòîäû èññëåäîâàíèÿ ðåæèìîâ ïîëåòà àïïàðàòà ïå-
ðåìåííîé ìàññû. × . II: Ìåõàíèêà ïðîãðàììíîãî äâèæåíèÿ àïïàðàòà. Ïåðìü:
Èçä-âî ÏÃÓ èì. À .Ì . Ãîðüêîãî, 1972.
25. Âîðîáüåâ Ë.Ì. Ê òåîðèè ïîëåòà ðàêåò. Ì .: Ìàøèíîñòðîåíèå, 1970.
26. Ãàíòìàõåð Ô.Ð., Ëåâèí Ë.Ì. Òåîðèÿ ïîëåòà íåóïðàâëÿåìûõ ðàêåò. Ì .:
Ôèçìàòãèç, 1959.
27. Ãàíòìàõåð Ô.Ð . Òåîðèÿ ìàòðèö. 3-å èçä. Ì .: Íàóêà, 1967.
28. Ãîðáàòåíêî Ñ.À . è äð. Ìåõàíèêà ïîëåòà (èíæåíåðíûé ñïðàâî÷íèê).
Ì.: Ìàøèíîñòðîåíèå, 1969.
29. Ãîðáàòåíêî Ñ.À . è äð. Ðàñ÷åò è àíàëèç äâèæåíèÿ ëåòàòåëüíûõ àïïàðà-
òîâ. Ì .: Ìàøèíîñòðîåíèå, 1971.
30. Ãðóøèíñêèé È.Ï . Òåîðèÿ ôèãóðû Çåìëè. Ì .: Ôèçìàòãèç, 1963.
31. Ãóòêèí Ë.Ñ . Ïðèíöèïû ðàäèîóïðàâëåíèÿ áåñïèëîòíûìè îáúåêòàìè.
Ì.: Ñîâåòñêîå ðàäèî, 1959.
32. Ãóòêèí Ë.Ñ . è äð. Ðàäèîóïðàâëåíèå ðåàêòèâíûìè ñíàðÿäàìè è êîñìè-
÷åñêèìè àïïàðàòàìè. Ì .: Ñîâåòñêîå ðàäèî, 1963.
33. Äâèæåíèå ðàêåò (Ââåäåíèå â òåîðèþ ïîëåòà ðàêåò) / Ïîä ðåä.
À.À . Äìèòðèåâñêîãî / À.À . Äìèòðèåâñêèé, Â.Ï. Êàçàêîâöåâ, Ë.Í. Ëûñåíêî è
äð.; Ì.: Âîåíèçäàò, 1968.
34. Äìèòðèåâñêèé À.À . Âíåøíÿÿ áàëëèñòèêà. Ì .: Ìàøèíîñòðîåíèå, 1972.
35. Äìèòðèåâñêèé À.À ., Ëûñåíêî Ë.Í . Ïðèêëàäíûå çàäà÷è òåîðèè îïòè-
ìàëüíîãî óïðàâëåíèÿ äâèæåíèåì áåñïèëîòíûõ ëåòàòåëüíûõ àïïàðàòîâ. Ì .:
Ìàøèíîñòðîåíèå, 1978.
36. Äìèòðèåâñêèé À.À., Ëûñåíêî Ë.Í., Èâàíîâ Í.Ì. Áàëëèñòèêà è íàâèãà-
öèÿ ðàêåò. Ì .: Ìàøèíîñòðîåíèå, 1985*
.
37. Äìèòðèåâñêèé À.À . Âíåøíÿÿ áàëëèñòèêà: Ó÷åáíèê äëÿ âòóçîâ. 2-å èçä.
Ì.: Ìàøèíîñòðîåíèå, 1979.
38. Äìèòðèåâñêèé À.À ., Ëûñåíêî Ë.Í., Áîãîäèñòîâ Ñ.Ñ. Âíåøíÿÿ áàëëè-
ñòèêà. 3 -å èçä., ïåðåðàá. è äîï. Ì .: Ìàøèíîñòðîåíèå, 1985*
.
39. Äìèòðèåâñêèé À.À ., Áîãîäèñòîâ Ñ.Ñ . Ê àíàëèçó óñòîé÷èâîñòè âðàùà-
òåëüíîãî äâèæåíèÿ àñèììåòðè÷íîãî àïïàðàòà, âõîäÿùåãî â àòìîñôåðó //
Òð. V íàó÷íûõ ÷òåíèé ïî êîñìîíàâòèêå. Ì .: ÀÍ ÑÑÑÐ, 1981. Ñ . 81 –88.
40. Äìèòðèåâñêèé À.À ., Æèëåéêèí Â.Ä. Ìåòîäèêà ðåøåíèÿ çàäà÷ äâèæå-
íèÿ ëåòàòåëüíûõ àïïàðàòîâ íà ÝÂÌ: Ó÷åá. ïîñîáèå. Ì .: ÌÂÒÓ èì. Í.Ý. Áàó-
ìàíà, 1986.
41. Äìèòðèåâñêèé À.À., Êîøåâîé Â.Í. Îñíîâû òåîðèè ïîëåòà ðàêåò. Ì .:
Âîåíèçäàò, 1968.
593
42. Äîáðîëåíñêèé Þ.Ï . Äèíàìèêà ïîëåòà â íåñïîêîéíîé àòìîñôåðå. Ì .:
Ìàøèíîñòðîåíèå, 1969.
43. Äîðîäíèöèí À.À . Àñèìïòîòè÷åñêèå çàêîíû ðàñïðåäåëåíèÿ ñîáñòâåí-
íûõ çíà÷åíèé äëÿ íåêîòîðûõ îñîáûõ âèäîâ äèôôåðåíöèàëüíûõ óðàâíåíèé
âòîðîãî ïîðÿäêà // Èçâ. âóçîâ. Óñïåõè ìàòåìàòè÷åñêèõ íàóê. 1952. Ò . 3, 1 6.
Ñ. 32 –48.
44. Äýâèñ Ë. è äð. Âíåøíÿÿ áàëëèñòèêà ðàêåò. Ì .: Âîåíèçäàò, 1962.
45. Åðìîëàåâ Ñ.È., Êîìàðîâ Ë.Á ., ×óðáàíîâ Å. . Âíåøíÿÿ áàëëèñòèêà. Ë.:
Èçä-âî ÂÌÀ èì. À .Í. Êðûëîâà, 1958.
46. Æàêîâ À.Ì., Ïèãóëåâñêèé Ô.À . Óïðàâëåíèå áàëëèñòè÷åñêèìè ðàêåòà-
ìè. Ì .: Âîåíèçäàò, 1965.
47. Æàíãîëîâè÷ È.Ä . Ïîòåíöèàë çåìíîãî òÿãîòåíèÿ / Áþëëåòåíü Èíñòè-
òóòà òåîðåòè÷åñêîé àñòðîíîìèè ÀÍ ÑÑÑÐ. 1957. Ò . 6, 1 8. Ñ . 29–37.
48. Çàðóáåæíîå âîåííîå îáîçðåíèå. 1981. 1 11. Ñ . 41–42; 1982. 1 12.
Ñ. 68–72; 1983. 1 11. Ñ. 37–39; 1983. 1 12. Ñ. 36–41.
49. Çóáîâ Â.È. Óñòîé÷èâîñòü äâèæåíèÿ. Ì .: Âûñøàÿ øêîëà, 1973.
50. Èâàíîâ Â.À ., ×åìîäàíîâ Á.Ê., Ìåäâåäåâ Â.Ñ . Ìàòåìàòè÷åñêèå îñíîâû
òåîðèè àâòîìàòè÷åñêîãî ðåãóëèðîâàíèÿ / Ïîä ðåä. Á.Ê. ×åìîäàíîâà. Ì .:
Âûñøàÿ øêîëà, 1971.
51. Èâàíîâ Í.Ì ., Ìàðòûíîâ À.È. Äâèæåíèå êîñìè÷åñêèõ ëåòàòåëüíûõ
àïïàðàòîâ â àòìîñôåðàõ ïëàíåò. Ì .: Íàóêà, 1985.
52. Èîôôå À.Ä ., Òèõîìèðîâ Â.Ì . Òåîðèÿ ýêñòðåìàëüíûõ çàäà÷. Ì.: Íàó-
êà, 1974.
53. Èøëèíñêèé À.Þ. Èíåðöèàëüíîå óïðàâëåíèå áàëëèñòè÷åñêèìè ðàêå-
òàìè. Ì .: Íàóêà, 1968.
54. Èññëåäîâàíèå îïòèìàëüíûõ ðåæèìîâ äâèæåíèÿ ðàêåò // Ñá. ïåðåâîä-
íûõ ñòàòåé. Ì .: Îáîðîíãèç, 1959.
55. Êàðàãîäèí Â.Ì. Òåîðåòè÷åñêèå îñíîâû ìåõàíèêè òåëà ïåðåìåííîãî
ñîñòàâà. Ì .: Îáîðîíãèç, 1963.
56. Êèðè÷åíêî Â.Ä. Áàëëèñòèêà. Ë .: Èçä-âî Âûñøåãî àðòèëëåðèéñêîãî
èíæåíåðíîãî ó÷èëèùà, 1957.
57. Êîîé È., Þòåíáîãàðò È. Äèíàìèêà ðàêåò. Ì .: Îáîðîíãèç, 1964.
58. Êîñìîäåìüÿíñêèé À.À. Êóðñ òåîðåòè÷åñêîé ìåõàíèêè. ×. II. Ì .: Ïðî-
ñâåùåíèå, 1966.
59. Êîñòðîâ À. . Äâèæåíèå àñèììåòðè÷íûõ áàëëèñòè÷åñêèõ àïïàðàòîâ.
Ì.: Ìàøèíîñòðîåíèå, 1984.
60. Êîñòðîâ À. ., Ãóêîâ Â. . Èòåðàöèîííûé ñèíòåç – ìåòîä èäåíòèôèêà-
öèè àýðîäèíàìè÷åñêèõ õàðàêòåðèñòèê ÊÀ ïî èçìåðåíèÿì åãî äâèæåíèÿ //
Êîñìè÷åñêèå èññëåäîâàíèÿ. 1986. Ò. XXIV, âûï. 5. Ñ. 680–694.
61. Êîëåñíèêîâ Ê.Ñ. Äèíàìèêà ðàêåò: Ó÷åáíèê äëÿ âòóçîâ. 2-å èçä. Ì .:
Ìàøèíîñòðîåíèå, 2003.
62. Êðàñíîâ Í.Ô ., Êîøåâîé Â.Í. Óïðàâëåíèå è ñòàáèëèçàöèÿ â àýðîäèíà-
ìèêå. Ì .: Âûñøàÿ øêîëà, 1978.
63. Êðóòüêî Ï.Ä . Îáðàòíûå çàäà÷è äèíàìèêè óïðàâëÿåìûõ ñèñòåì (Ëè-
íåéíûå ìîäåëè). Ì .: Íàóêà, 1987.
64. Êðûëîâ À.Í. Î âðàùàòåëüíîì äâèæåíèè ïðîäîëãîâàòîãî ñíàðÿäà âî
âðåìÿ ïîëåòà // Ïîëí. ñîáð. ñî÷ . Ò. 4. Ì .; Ë., 1937. Ñ . 1–32.
594
65. Êóäèí Ã.È., Íàñîíîâ Â.Ï., Ðÿïîëîâ Ñ.È. è äð. Òåîðèÿ ïîëåòà ðà-
êåò-íîñèòåëåé. Ñ . -Ïá.: ÌÎ ÐÔ, 1994.
66. Êóçíåöîâ À.À . Îïðåäåëåíèå íà÷àëüíûõ óñëîâèé ïðè ñòàðòå ëåòàòåëü-
íîãî àïïàðàòà ñ ïîäâèæíîé ïëàòôîðìû // Èññëåäîâàíèÿ ïî äèíàìèêå ïîëå-
òà / Ïîä ðåä. ïðîô. È . . Îñòîñëàâñêîãî. Âûï. 1 . Ì .: Ìàøèíîñòðîåíèå, 1965.
Ñ. 257–282.
67. Êóçìàê Ã.Å . Äèíàìèêà íåóïðàâëÿåìîãî äâèæåíèÿ ëåòàòåëüíûõ àïïà-
ðàòîâ ïðè âõîäå â àòìîñôåðó. Ì .: Íàóêà, 1970.
68. Êóçîâêîâ Í.Ò. Ñèñòåìû ñòàáèëèçàöèè ëåòàòåëüíûõ àïïàðàòîâ (áàëëè-
ñòè÷åñêèõ è çåíèòíûõ ðàêåò). Ì .: Âûñøàÿ øêîëà, 1976.
69. Ëàõòèí Ë.Ì. Ñâîáîäíîå äâèæåíèå â ïîëå çåìíîãî ñôåðîèäà. Ì .: Ôèç-
ìàòãèç, 1963.
70. Ëåáåäåâ À.À ., ×åðíîáðîâêèí Ë.Ñ. Äèíàìèêà ïîëåòà áåñïèëîòíûõ ëåòà-
òåëüíûõ àïïàðàòîâ. Ì .: Ìàøèíîñòðîåíèå, 1973*
.
71. Ëåáåäåâ À.À., Ãåðàñþòà Í.Ô . Áàëëèñòèêà ðàêåò. Íåêîòîðûå çàäà÷è
áàëëèñòèêè ðàêåò äàëüíåãî äåéñòâèÿ. Ì .: Ìàøèíîñòðîåíèå, 1970.
72. Ëåáåäåâ Â.ß. Ñïðàâî÷íèê îôèöåðà íàçåìíîé àðòèëëåðèè. 2-å èçä.,
ïåðåðàá. è äîï. Ì .: Âîåíèçäàò, 1984.
73. Ëåéòìàí Äæ. Ââåäåíèå â òåîðèþ îïòèìàëüíîãî óïðàâëåíèÿ. Ì .: Íàó-
êà, 1968.
74. Ëåòíûå èñïûòàíèÿ ðàêåò è êîñìè÷åñêèõ àïïàðàòîâ: Ó÷åá. ïîñîáèå äëÿ
âòóçîâ / Å.È . Êðèíåöêèé, Ë.Í . Àëåêñàíäðîâñêàÿ, À. . Øàðîíîâ è äð.; Ïîä
ðåä. Å.È. Êðèíåöêîãî. Ì .: Ìàøèíîñòðîåíèå, 1979.
75. Ëåòîâ À.Ì. Äèíàìèêà ïîëåòà è óïðàâëåíèå. Ì .: Íàóêà, 1969.
76. Ëèííèê Þ. . Ìåòîä íàèìåíüøèõ êâàäðàòîâ è îñíîâû òåîðèè îáðà-
áîòêè íàáëþäåíèé. 2-å èçä. Ì .: Ôèçìàòãèç, 1962.
77. Ëûñåíêî Ë.Í., Ïàíêðàòîâ È.À. Îáðàáîòêà ðåçóëüòàòîâ èçìåðåíèé â
çàäà÷àõ óïðàâëåíèÿ äâèæåíèåì: Ó÷åá. ïîñîáèå / Ïîä ðåä. ïðîô. Ë.Í. Ëûñåí-
êî. Ì .: Èçä-âî ÌÂÒÓ èì. Í.Ý. Áàóìàíà, 1980.
78. Ëûñåíêî Ë.Í. Ïðîáëåìû àëãîðèòìèçàöèè îïòèìàëüíûõ ñòðàòåãèé
ñòîõàñòè÷åñêîãî óïðàâëåíèÿ ñïóñêàåìûì àïïàðàòîì // Îáîðîííàÿ òåõíèêà.
1994. 1 1. Ñ. 10–15 .
79. Ëûñåíêî Ë.Í., Ïàíêîâ À.À . Ïðèìåíåíèå ìåòîäîâ ðåêêóðåíòíîãî îöå-
íèâàíèÿ ïðè ñèíòåçå àëãîðèòìîâ óïðàâëåíèÿ îãíåì êîðàáåëüíûõ çåíèòíûõ
àðòèëëåðèéñêèõ óñòàíîâîê // Îáîðîííàÿ òåõíèêà. 2000 . 1 1–2. Ñ. 75–79.
80. Ëûñåíêî Ë.Í., Àëüõàô Íàäåð. Ìîäèôèöèðîâàííûé ôèëüòð Êàëìàíà
äëÿ îöåíèâàíèÿ äâèæåíèÿ áîåïðèïàñîâ â óñëîâèÿõ ïðîãíîçèðóåìîãî ÿâëå-
íèÿ ïàðàìåòðè÷åñêîãî ðåçîíàíñà // Èçâ. Ðîññèéñêîé Àêàäåìèè ðàêåòíûõ è
àðòèëëåðèéñêèõ íàóê. 2004 . Âûï. 1 (38). Ñ . 13 –21.
81. Ìàèåâñêèé Í. . Êóðñ âíåøíåé áàëëèñòèêè. Ñàíêò-Ïåòåðáóðã, 1870.
82. Ìàèåâñêèé Í. . Î âëèÿíèè âðàùàòåëüíîãî äâèæåíèÿ íà ïîëåò ïðî-
äîëãîâàòûõ ñíàðÿäîâ â âîçäóõå // Àðòæóðíàë. 1865. 1 3. Ñ . 1 –18.
83. Ìàìîí Ï.À ., Ïîëîâíèêîâ Â.È., Ñëåçêèíñêèé Ñ.Ê . Áàëëèñòè÷åñêîå
îáåñïå÷åíèå êîñìè÷åñêèõ ïîëåòîâ. Ë .: ÂÈÊÈ, 1990.
84. Ìàòåìàòè÷åñêàÿ òåîðèÿ îïòèìàëüíûõ ïðîöåññîâ / Ë.Ñ . Ïîíòðÿãèí,
Â.à . Áîëòÿíñêèé, Ð. . Ãàìêðåëèäçå è äð. 2-å èçä. Ì .: Íàóêà, 1969.
85. Ìàðêèí Ä.Ð. Ââåäåíèå â òåîðèþ óñòîé÷èâîñòè äâèæåíèÿ. Ì .: Íàóêà,
1976.
595
86. Ìåùåðñêèé È. . Ðàáîòû ïî ìåõàíèêå òåë ïåðåìåííîé ìàññû. Ì .: Ãîñ-
òåõèçäàò, 1952.
87. Ìîèñååâ Í.Í. Àñèìïòîòè÷åñêèå ìåòîäû íåëèíåéíîé ìåõàíèêè. Ì .:
Íàóêà, 1969.
88. Ìîððèñîí Ô.Ê., Ýìáåðòñîí Ä.Ñ . Ñèñòåìà íàâåäåíèÿ âûñòðåëèâàåìîãî
èç ïóøêè óïðàâëÿåìîãî ñíàðÿäà // Ðàêåòíàÿ òåõíèêà è êîñìîíàâòèêà. 1978.
Ò. 16, 1 2. Ñ. 184–193.
89. Íåéìàðê Þ.È. Äèíàìè÷åñêèå ñèñòåìû è óïðàâëÿåìûå ïðîöåññû. Ì .:
Íàóêà, 1978.
90. Íåìûöêèé Â. ., Ñòåïàíîâ Â. . Êà÷åñòâåííàÿ òåîðèÿ äèôôåðåíöèàëü-
íûõ óðàâíåíèé. Ì .; Ë.: ÎÃÈÇ. Ãîñòåõèçäàò, 1947.
91. Îêóíåâ Á.Í. Îñíîâû áàëëèñòèêè. Ò . I, êí. 1 è 2. Ì .: Âîåíèçäàò, 1943.
92. Îñòîñëàâñêèé È. ., Ñòðàæåâà È. . Äèíàìèêà ïîëåòà. Ì .: Ìàøèíî-
ñòðîåíèå, 1969.
93. Îõîöèìñêèé Ä.Å . Ê òåîðèè äâèæåíèÿ ðàêåò // Ïðèêëàäíàÿ ìåõàíèêà
è ìàòåìàòèêà. 1946. Ò . 10, âûï. 2 . Ñ . 251–273.
94. Îõîöèìñêèé Ä.Å ., Ýíååâ Ò.Ì. Íåêîòîðûå âàðèàöèîííûå çàäà÷è, ñâÿ-
çàííûå ñ çàïóñêîì èñêóññòâåííîãî ñïóòíèêà Çåìëè // Èçâ. âóçîâ. Óñïåõè
ôèçè÷åñêèõ íàóê. 1957. Ò. 63, âûï. 1à. Ñ. 5–32.
95. Ïàðøèí Æ.Ï ., ×óíàåâ Í.È., Ëîãâèí À.Ì . Âíåøíÿÿ áàëëèñòèêà. × . I.
Ì.: Èçä-âî ÌÎ ÑÑÑÐ, 1984.
96. Ïîãîðåëîâ Ä.À. Òåîðèÿ êåïëåðîâñêèõ äâèæåíèé ëåòàòåëüíûõ àïïàðà-
òîâ. Ì .: Ôèçìàòãèç, 1961.
97. Ïîñòíèêîâ À.Ã ., ×óéêî Â.Ñ. Âíåøíÿÿ áàëëèñòèêà íåóïðàâëÿåìûõ
àâèàöèîííûõ ðàêåò è ñíàðÿäîâ. Ì .: Ìàøèíîñòðîåíèå, 1985.
98. Ïóãà÷åâ Â.Ñ. Îáùàÿ çàäà÷à î äâèæåíèè âðàùàþùåãîñÿ àðòèëëåðèé-
ñêîãî ñíàðÿäà â âîçäóõå // Òð. ÂÂÈÀ èì. Í.Å. Æóêîâñêîãî. 1940. Âûï. 70.
Ñ. 1–89.
99. Ïóãà÷åâ Â.Ñ . Î êîëåáàíèÿõ îïåðåííûõ ñíàðÿäîâ. Î äâèæåíèè âðà-
ùàþùåãîñÿ îïåðåííîãî ñíàðÿäà // Òð. ÂÂÈÀ èì. Í .Å . Æóêîâñêîãî. 1940.
Âûï. 74. Ñ. 1–55.
100. Ïóãà÷åâ Â.Ñ. Îáùàÿ òåîðèÿ êîððåëÿöèîííûõ ñëó÷àéíûõ ôóíêöèé //
Èçâ. ÀÍ ÑÑÑÐ . Ñåð. ìàòåìàòè÷åñêàÿ . 1953. Ò. 17, 1 5. Ñ . 401–420.
101. Ïóãà÷åâ Â.Ñ ., Ñèíèöûí È.Í. Ñòîõàñòè÷åñêèå äèôôåðåíöèàëüíûå
ñèñòåìû. Ì .: Íàóêà, 1985.
102. Ïóãà÷åâ Â.Ñ . Òåîðèÿ ñëó÷àéíûõ ôóíêöèé è åå ïðèìåíåíèå ê çàäà÷àì
àâòîìàòè÷åñêîãî óïðàâëåíèÿ. Ì .: Ôèçìàòãèç, 1962.
103. Ïðàâäèí Â.Ì., Øàíèí À.Ï . Áàëëèñòèêà íåóïðàâëÿåìûõ ëåòàòåëüíûõ
àïïàðàòîâ. Ñíåæèíñê: Èçä-âî ÐÔßÖ – ÂÍÈÈÒÔ, 1999.
104. Ïðîåêòèðîâàíèå è èñïûòàíèÿ áàëëèñòè÷åñêèõ ðàêåò / Ïîä ðåä.
Â.È . Âàðôîëîìååâà, Í.È . Êîïûòîâà. Ì .: Âîåíèçäàò, 1970.
105. Ðàáèíîâè÷ Á.È . Âàðèàöèîííûå ðåæèìû ïîëåòà êðûëàòûõ ëåòàòåëü-
íûõ àïïàðàòîâ. Ì .: Ìàøèíîñòðîåíèå, 1966.
106. Ðàçóìååâ Â.Ô ., Êîâàëåâ Á.Ê . Îñíîâû ïðîåêòèðîâàíèÿ áàëëèñòè÷å-
ñêèõ ðàêåò íà òâåðäîì òîïëèâå. Ì .: Ìàøèíîñòðîåíèå, 1976.
107. Ðóìÿíöåâ Â. . Ìåòîä ôóíêöèé Ëÿïóíîâà â òåîðèè óñòîé÷èâîñòè
äâèæåíèÿ // Ìåõàíèêà â ÑÑÑÐ çà 50 ëåò. Ò . I: Îáùàÿ ïðèêëàäíàÿ ìåõàíèêà.
Ì.: Íàóêà, 1968. Ñ. 7–65.
596
108. Ñâåòëèöêèé Â.À . Äèíàìèêà ñòàðòà ëåòàòåëüíûõ àïïàðàòîâ. Ì .: Íàó-
êà, 1986.
109. Ñâÿòîäóõ Â.Ê . Äèíàìèêà ïðîñòðàíñòâåííîãî äâèæåíèÿ óïðàâëÿåìûõ
ðàêåò. Ì .: Ìàøèíîñòðîåíèå, 1969.
110. Ñåäîâ Ë.È. Ìåòîäû ïîäîáèÿ è ðàçìåðíîñòè â ìåõàíèêå. Ì .: Íàóêà,
1965.
111. Ñèõàðóëèäçå Þ.Ã . Áàëëèñòèêà ëåòàòåëüíûõ àïïàðàòîâ. Ì .: Íàóêà,
1982.
112. Ñïðàâî÷íèê ïî ñòðåëüáå áåðåãîâîé àðòèëëåðèè ÂÌÔ / Ï.À . Ëîñü,
Á.È . Þðêåâè÷, Ë.Ë. Íîãà è äð. Ì .: Âîåíèçäàò, 1977.
113. Ñïðàâî÷íèê ïî èññëåäîâàíèþ îïåðàöèé / Ïîä îáù. ðåä. Ô .À . Ìàòâåé-
÷óêà. Ì .: Âîåíèçäàò, 1979.
114. Ñòàòèñòè÷åñêàÿ äèíàìèêà è îïòèìèçàöèÿ óïðàâëåíèÿ ëåòàòåëüíûõ àï-
ïàðàòîâ: Ó÷åá. ïîñîáèå äëÿ âóçîâ / À.À . Ëåáåäåâ, Â.Ò . Áîáðîííèêîâ,
Ì.Í. Êðàñèëüùèêîâ, Â.Â. Ìàëûøåâ. Ì .: Ìàøèíîñòðîåíèå, 1985.
115. Òàðàñîâ Å. . Îïòèìàëüíûå ðåæèìû ïîëåòà ëåòàòåëüíûõ àïïàðàòîâ.
Ì.: Ìàøèíîñòðîåíèå, 1969.
116. Òåîðèÿ ïîëåòà ðàêåò-íîñèòåëåé: Ó÷åá. äëÿ âóçîâ / Ã.È . Êóäèí,
Â.Ï . Íàñîíîâ, Ñ.Ê. Ñëåçêèíñêèé è äð. Ì .: ÌÎ ÐÔ, 1994.
117. Óñòèíîâ Â.Ô ., Êîëüöîâ Þ.Ô ., Ñìèðíîâ Í.Í. Îïðåäåëåíèå ñêîðîñòè
äâèæåíèÿ òåë: Ó÷åá. ïîñîáèå. Ì .: ÌÂÒÓ èì. Í .Ý . Áàóìàíà, 1983.
118. Óñòèíîâ Â.Ô . Îïòèìàëüíûå ðåæèìû ïëàíèðóþùåãî ïîëåòà // Îïòè-
ìàëüíîå óïðàâëåíèå è îïðåäåëåíèå ïåðåìåííûõ ñîñòîÿíèÿ ñèñòåì / Ïîä
ðåä. ïðîô. Ë.Í. Ëûñåíêî. Ì .: ÌÂÒÓ èì. Í.Ý. Áàóìàíà, 1985. Ñ . 51–58.
119. Ôåäîðîâ Â. . Òåîðèÿ îïòèìàëüíîãî ýêñïåðèìåíòà. Ì .: Íàóêà, 1971.
120. Ôåîäîñüåâ Â.È., Ñèíÿðåâ Ã.Á. Ââåäåíèå â ðàêåòíóþ òåõíèêó. Ì .:
Îáîðîíãèç, 1960.
121. Ôîìèí Â.Í. Ðåêóððåíòíîå îöåíèâàíèå è àäàïòèâíàÿ ôèëüòðàöèÿ.
Ì.: Íàóêà, 1984.
122. Öèîëêîâñêèé Ê.Ý . Òðóäû ïî ðàêåòíîé òåõíèêå. Ì .: Îáîðîíãèç, 1947.
123. Öëàô Ë.ß. Âàðèàöèîííîå èñ÷èñëåíèå è èíòåãðàëüíûå óðàâíåíèÿ.
Ì.: Íàóêà, 1970.
124. ×åáîòàðåâ Ã.À . Àíàëèòè÷åñêèå è ÷èñëåííûå ìåòîäû íåáåñíîé ìåõà-
íèêè. Ì .: Íàóêà, 1965.
125. ×åðíîçóáîâ À.Ä ., Êèðè÷åíêî Â.Ä ., Ðàçèí È.È ., Ìèõàéëîâ Ê. . Âíåø-
íÿÿ áàëëèñòèêà. ×. I, II, III. Ì .: Èçä-âî Àðòàêàäåìèè èì. Ô .Ý . Äçåðæèíñêî-
ãî, 1954.
126. ×åòàåâ Í.à . Î äîñòàòî÷íûõ óñëîâèÿõ óñòîé÷èâîñòè âðàùàòåëüíîãî
äâèæåíèÿ ñíàðÿäà // Ïðèêëàäíàÿ ìàòåìàòèêà è ìåõàíèêà. 1943. Ò . 7, âûï. 2.
Ñ. 81 –96.
127. ×åòàåâ Í.Ã. Îá óñòîé÷èâîñòè âðàùàòåëüíûõ äâèæåíèé ñíàðÿäîâ //
Ïðèêëàäíàÿ ìàòåìàòèêà è ìåõàíèêà. 1946. Ò . 10, âûï. 1 . Ñ . 135–138.
128. ×óåâ Þ. . è äð. Îñíîâû èññëåäîâàíèÿ îïåðàöèé â âîåííîé òåõíèêå.
Ì.: Ñîâåòñêîå ðàäèî, 1965.
129. Øàëûãèí À.Ñ ., Ïàëàãèí Þ.È. Ïðèêëàäíûå ìåòîäû ñòàòèñòè÷åñêîãî
ìîäåëèðîâàíèÿ. Ë .: Ìàøèíîñòðîåíèå, 1986.
130. Øàïèðî ß.Ì. Âíåøíÿÿ áàëëèñòèêà. Ì .: Îáîðîíãèç, 1946.
597
131. Øàïèðî ß.Ì. è äð. Îñíîâû ïðîåêòèðîâàíèÿ ðàêåò íà òâåðäîì òîï-
ëèâå. Ì .: Âîåíèçäàò, 1968.
132. Øàðîíîâà È.Ì. Ïðèìåíåíèå ìåòîäà äèíàìè÷åñêîãî ïðîãðàììèðî-
âàíèÿ ê ðåøåíèþ âàðèàöèîííûõ çàäà÷ äèíàìèêè ëåòàòåëüíûõ àïïàðàòîâ //
Èññëåäîâàíèÿ ïî äèíàìèêå ïîëåòà / Ïîä ðåä. ïðîô. È . . Îñòîñëàâñêîãî;
Âûï. 1. Ì .: Ìàøèíîñòðîåíèå, 1965. Ñ . 338–354.
133. Øèãîëåâ Á.Ì. Ìàòåìàòè÷åñêàÿ îáðàáîòêà íàáëþäåíèé. 3-å èçä. Ì .:
Íàóêà, 1969.
134. Øèëîâ À.À ., Ãîìàí Ì.Ã. Ðåçîíàíñíûå ðåæèìû ïðîñòðàíñòâåííîãî
íåóïðàâëÿåìîãî äâèæåíèÿ àïïàðàòîâ íà ó÷àñòêå âõîäà â àòìîñôåðó // Òð.
ÖÀÃÈ. 1985. Âûï. 1624. Ñ . 1–44 .
135. Ýêñïåðèìåíòàëüíàÿ áàëëèñòèêà ðàêåòíî-êîñìè÷åñêèõ ñðåäñòâ: Ó÷åá.
äëÿ ââóçîâ / Ïîä ðåä. Ë .Í . Ëûñåíêî, Â. . Áåòàíîâà, È.Â. Ëûñåíêî. Ì .: ÂÀ
ÐÂÑÍ èì. Ïåòðà Âåëèêîãî, 2000.
136. ßðîøåâñêèé Â.À. Äâèæåíèå íåóïðàâëÿåìîãî òåëà â àòìîñôåðå. Ì .:
Ìàøèíîñòðîåíèå, 1978.
137. Barbera J., Frank J. An analytical technique for studing the anomalies roll
behavior of ballistic re-entry vehicles // J. Spacecraft and Rockets. 1969. V . 6,
N 11. P. 131–139.
138. Bieber R.E . Missile structural loads by non-stationary statistical
methods // J. Aerospace Sci. 1961. V. 28. P . 284 –294.
139. Gilbert E.G. The decoupling of multivariable systems by state jeedback //
SIAM J. Contr. 1969. V. 7, N 1. P. 50–61.
140. Hewish M. The Assault Breaker Program, US stand-off weapon
technology of the future // International Defense Review 1982. Sept. V . 15.
P. 1207–1211.
141. Nicolaides J. JAS Preprint (Institute of Aeronautical Sciences). 1953.
N 395. P. 1–32.
142. Pegan F., Smith J. Aeroballistics of terminally corrected spinning
projectile (TCSP) // J. Spacecraft and Rockets. 1975. V. 12. P . 733 –738.
143. Swictak R.R. Assault breaker breaks out // Aeronaut. and Astronaut. 1983.
Febr. V. 21, N 2. P. 38–41.
144. Tomson W., Tait P. Threatise on Natural Philosophy. Cambridge
University Press, 1886.
599
ÏÐÅÄÌÅÒÍÛÉ ÓÊÀÇÀÒÅËÜ
Àçèìóò 19
–
ïóñêà ðàêåòû 19
–
ñòðåëüáû 19, 44, 404
Àëãîðèòì
–
áàëëèñòè÷åñêèé 584
–
èíòåãðèðóþùèé 586, 589
–
òàáëè÷íûé 586
Àòìîñôåðà Çåìëè 49
–
ñòàíäàðòíàÿ 51
Áàëëèñòèêà 12
–
âíåøíÿÿ 4, 13
–
óïðàâëÿåìûõ è êîððåêòèðóå-
ìûõ ñíàðÿäîâ 13, 479
–
ýêñïåðèìåíòàëüíàÿ 13
Áàëëèñòè÷åñêèå ñðåäíèå 401
Âàðèàöèè ïàðàìåòðîâ 179
Âåðøèíà òðàåêòîðèè 228
Âåòâü òðàåêòîðèè 147
–
âîñõîäÿùàÿ 147
–
íèñõîäÿùàÿ 147
Âû÷èñëåííûå óñòàíîâêè 259, 584
Ãåîèä 32
Ãîðèçîíò îðóäèÿ 574
Äàííûå óñòàíîâî÷íûå 259
Äâèæåíèå
–
áîêîâîå 128
–
âîçìóùåííîå 172
–
íåâîçìóùåííîå 172
–
ïðîäîëüíîå 128, 148
–
ñâîáîäíîå 13
–
óïðàâëÿåìîå 141, 292
Äåëåíèå óãëîìåðà 477
Äåðèâàöèÿ 317, 541
Çàäà÷à áàëëèñòèêè 15
–
êðàåâàÿ 257
–
îñíîâíàÿ (ïðÿìàÿ) 15, 221, 256
–
îáðàòíàÿ 15, 256, 267
Çàäà÷à îïòèìèçàöèè 254
–
Áîëüöà 281
–
Ëàãðàíæà 281
–
Ìàéåðà 281, 288
Çàñå÷êà
–
ïî èçìåðåííûì ðàññòîÿíè-
ÿì 477
–
ïî çíàêàì ïàäåíèÿ 477
Èäåíòèôèêàöèÿ 534
Êîýôôèöèåíò
–
àýðîäèíàìè÷åñêèé 60
–
áàëëèñòè÷åñêèé 67
–
ôîðìû 66
Êó÷íîñòü ñòðåëüáû 540
Ëèíåàðèçàöèÿ 84, 105
Ëèíèÿ áðîñàíèÿ 541
Ìåòîä
–
Ìîíòå-Êàðëî 460
–
ïñåâäîñêîðîñòè 247
–
òàáëè÷íûé 252
Ìîäåëü äâèæåíèÿ 80, 260
–
äåòåðìèíèðîâàííàÿ 83
–
äèñêðåòíàÿ 83
–
ëèíåàðèçîâàííàÿ 84
–
ëèíåéíàÿ 83
–
íåëèíåéíàÿ 82
–
íåïðåðûâíàÿ 83
–
ñìåøàííàÿ 82
–
ñòîõàñòè÷åñêàÿ 83, 87
Íàïðàâëåíèå
ñòðåëüáû 19, 404
Íà÷àëüíûå óñëîâèÿ 419
–
âûñòðåëà 432, 434
–
äâèæåíèÿ 420, 421
Íåóðàâíîâåøåííîñòü
–
äèíàìè÷åñêàÿ 435
–
ñòàòè÷åñêàÿ 434
Îáåñïå÷åíèå
áàëëèñòè÷åñêîå 16, 256
Îáðàáîòêà äàííûõ
ñòðåëüáû 469
–
ïîëíàÿ 469
–
÷àñòè÷íàÿ 478
Îòêëîíåíèÿ 362
–
èçîôóíêöèîíàëüíûå 389
–
èçîõðîííûå 389
–
ìåòåîôàêòîðîâ 390
Ïàðàìåòðû äâèæåíèÿ 115, 147,
260
Ïåðåãðóçêà 141
Ïëàíèðîâàíèå áàëëèñòè÷åñêèõ
ýêñïåðèìåíòîâ 543
Ïëîñêîñòü ñòðåëüáû
600
(áðîñàíèÿ) 19, 541
Ïîäãîòîâêà ñòðåëüáû 573
–
áàëëèñòè÷åñêàÿ 573
–
áîåïðèïàñîâ ê ñòðåëüáå 574
–
ìåòåîðîëîãè÷åñêàÿ 410, 574
–
ïîëíàÿ 476
–
òîïîãðàôè÷åñêàÿ (òîïîãåîäåçè-
÷åñêàÿ) 574
Ïîïðàâêè áàëëèñòè÷åñêèå 362
–
â äàëüíîñòü 578
–
ê óãëó ïðèöåëèâàíèÿ 578
–
íà íàêëîí îñè öàïô 578
–
â íàïðàâëåíèå ñòðåëüáû 578
–
ìåòåîðîëîãè÷åñêèå 391
Ïîòåíöèàë Çåìëè 31, 38
–
íîðìàëüíûé 35
–
ïîëÿ òÿãîòåíèÿ 31, 33
Ïðèíöèï
–
çàòâåðäåâàíèÿ 90
–
ìàêñèìóìà 281
–
îïòèìàëüíîñòè Áåëëìàíà 282
–
ñóïåðïîçèöèè 363
Ðàññåèâàíèå 439
–
ïðè ñòðåëüáå 469
–
ñíàðÿäîâ 475
–
òðàåêòîðèé 438, 507
Ðåçîíàíñ
–
âðàùàòåëüíûé 343, 515
–
ïàðàìåòðè÷åñêèé 337, 516
Ñèñòåìà êîîðäèíàò 18
–
àýðîäèíàìè÷åñêàÿ 20
–
ãåîöåíòðè÷åñêàÿ 18
–
íîðìàëüíàÿ 19
–
ñâÿçàííàÿ 20
–
ñòàðòîâàÿ 19
–
òðàåêòîðíàÿ 21
Ñòðåëüáà áîåâàÿ 476
–
íà äàëüíîñòü è êó÷íîñòü 539
–
ïî èçìåðåííûì äàëüíîñ-
òÿì 477
–
ïî îòêëîíåíèÿì 477
–
ïî íàáëþäåíèþ çíàêîâ
ïàäåíèé 477
–
òàáëè÷íàÿ 573
Ñíàðÿä 14
Ñóááîåïðèïàñû 479, 513
Òàáëèöû
–
áàëëèñòè÷åñêèå 252
–
ïîïðàâîê 247, 411
–
ñòðåëüáû 572, 579, 580, 581
Òåîðèÿ
–
ïàðàáîëè÷åñêàÿ 227
–
ýëëèïòè÷åñêàÿ 229
Òî÷êè ïîïàäàíèÿ 538
–
íàâîäêè 539
Òðàåêòîðèÿ 80
–
âîçìóùåííàÿ 172, 362
–
íîìèíàëüíàÿ 172
–
îïòèìàëüíàÿ 274, 283
–
ïîïàäàþùàÿ 256, 259
Òðàññà áàëëèñòè÷åñêàÿ 520
Òóðáóëåíòíîñòü àòìîñôåðíàÿ 458
–
äèíàìè÷åñêàÿ 395
–
òåðìè÷åñêàÿ 395
Òÿãà 74
–
ñòåíäîâàÿ 75
–
ýôôåêòèâíàÿ 74
Óãîë
–
áðîñàíèÿ 45, 228
–
âåòðà 24
–
âîçâûøåíèÿ 23
–
êðåíà 23
–
ìåñòà öåëè 19
–
íóòàöèè 70, 72, 165
–
ïàäåíèÿ 228, 271
–
ïðåöåññèè 165
–
ðûñêàíèÿ 21
Óïðàâëåíèå îãíåì 255
Óñòàíîâêè äëÿ ñòðåëüáû 255, 257
Ó÷àñòîê òðàåêòîðèè 14
–
àêòèâíûé 14
–
ïàññèâíûé 14
Óñòîé÷èâîñòü äâèæåíèÿ 171
–
ïî Ëÿïóíîâó 172
–
òåõíè÷åñêàÿ 172
Ôàçîâûå êîîðäèíàòû 81
Ôèëüòð ôîðìèðóþùèé 457
Ôóíêöèÿ
–
áàëàíñèðîâî÷íàÿ 115
–
âñïîìîãàòåëüíàÿ Ñèà÷÷è 250
–
Íüþòîíà 257
Øàã
–
ïðèöåëà 477
–
èíòåãðèðîâàíèÿ 212, 220
Øèðîòà 38
–
ãåîãðàôè÷åñêàÿ 38
–
ãåîöåíòðè÷åñêàÿ 38
Ýëëèïñîèä 33
–
çåìíîé Êðàñîâñêîãî 33
–
òðåõîñíûé 33
ÎÃËÀÂËÅÍÈÅ
Èç ïðåäèñëîâèÿ ê ïåðâîìó èçäàíèþ .....................3
Ïðåäèñëîâèå ê ÷åòâåðòîìó èçäàíèþ .....................5
Îñíîâíûå îáîçíà÷åíèÿ .............................9
Ââåäåíèå ......................................12
Ðàçäåë I. ÓÑËÎÂÈß ÏÎËÅÒÀ ÐÀÊÅÒ È ÑÍÀÐßÄÎÂ,
ÌÀÒÅÌÀÒÈ×ÅÑÊÈÅ ÌÎÄÅËÈ ÈÕ ÄÂÈÆÅÍÈß .....17
Ãëàâà 1. Ñèëû è ìîìåíòû, äåéñòâóþùèå íà ËÀ â ïîëåòå ........17
1.1. Ñèñòåìû êîîðäèíàò è óãëû, îïðåäåëÿþùèå
ïîëîæåíèå ËÀ â ïðîñòðàíñòâå ...................18
1.1.1 . Îáùàÿ õàðàêòåðèñòèêà ñèñòåì êîîðäèíàò ......18
1.1.2 . Îïðåäåëåíèå âçàèìíîé îðèåíòàöèè
ñèñòåì êîîðäèíàò ........................21
1.1.3 . Êîîðäèíàòíûå ïðåîáðàçîâàíèÿ ñ ïîìîùüþ
ìàòðèö íàïðàâëÿþùèõ êîñèíóñîâ ..............25
1.2. Âëèÿíèå ïîëÿ òÿãîòåíèÿ Çåìëè è åå âðàùåíèÿ
íà ïîëåò ðàêåò è ñíàðÿäîâ .....................31
1.2.1 . Ïîòåíöèàë ñèëû çåìíîãî òÿãîòåíèÿ,
ôîðìà è ðàçìåðû Çåìëè ....................31
1.2.2. Ñèëà òÿæåñòè è åå ïîòåíöèàë .............38
1.2.3. Âëèÿíèå âðàùåíèÿ Çåìëè íà ïîëåò ðàêåò
è ñíàðÿäîâ ............................42
1.3. Çåìíàÿ àòìîñôåðà è åå ñâîéñòâà ..............49
1.3.1 . Ñòðóêòóðà àòìîñôåðû ..................49
1.3.2. Ñòàíäàðòíûå àòìîñôåðû ................51
1.4. Àýðîäèíàìè÷åñêèå ñèëû è èõ ìîìåíòû ...........58
1.4.1 . Âåêòîð àýðîäèíàìè÷åñêîãî ñîïðîòèâëåíèÿ
è îáóñëîâëåííûé èì ìîìåíò .................58
1.4.2. Ñîñòàâëÿþùèå ïîëíîé àýðîäèíàìè÷åñêîé
ñèëû è ïîëíîãî àýðîäèíàìè÷åñêîãî ìîìåíòà .......59
1.4.3. Ïðèâåäåíèå àýðîäèíàìè÷åñêèõ ñèë è
ìîìåíòîâ ê ýòàëîííûì ôóíêöèÿì ñîïðîòèâëåíèÿ ....66
1.5. Òÿãà ðàêåòíîãî äâèãàòåëÿ ...................74
1.6. Äîïîëíèòåëüíûå è óïðàâëÿþùèå ñèëû
è ìîìåíòû ..............................77
1.6.1 . Äîïîëíèòåëüíûå ñèëû è ìîìåíòû ..........77
1.6.2. Óïðàâëÿþùèå ñèëû è ìîìåíòû ............78
Ãëàâà 2. Òåîðåòè÷åñêèå îñíîâû ñîñòàâëåíèÿ ìàòåìàòè÷åñêèõ
ìîäåëåé äâèæåíèÿ ËÀ ........................80
2.1. Êëàññèôèêàöèÿ è ôîðìû ïðåäñòàâëåíèÿ
ìàòåìàòè÷åñêèõ ìîäåëåé ......................80
2.1.1 . ËÀ êàê äèíàìè÷åñêàÿ ñèñòåìà ............80
2.1.2. Âîçìîæíûå âèäû ìàòåìàòè÷åñêèõ ìîäåëåé .....82
2.2. Ïðèíöèïû ñîñòàâëåíèÿ óðàâíåíèé äâèæåíèÿ ËÀ .....87
2.2.1. Óðàâíåíèÿ È. . Ìåùåðñêîãî .............87
601
2.2.2. Îñíîâíûå òåîðåìû äèíàìèêè òåë ïåðåìåííîé
è ïîñòîÿííîé ìàññ, ïðèíöèï çàòâåðäåâàíèÿ ........90
2.2.3. Âåêòîðíûå óðàâíåíèÿ ïîñòóïàòåëüíîãî äâèæåíèÿ
ËÀ êàê òåëà ïåðåìåííîé ìàññû ...............95
2.2.4. Óðàâíåíèÿ âðàùàòåëüíîãî äâèæåíèÿ ËÀ ......99
2.2.5. Ïðîåêöèè âåêòîðíûõ óðàâíåíèé íà íîðìàëü
è êàñàòåëüíóþ ê òðàåêòîðèè .................102
2.2.6. Ëèíåàðèçàöèÿ óðàâíåíèé äâèæåíèÿ ðàêåò è ñíà-
ðÿäîâ ................................105
Ãëàâà 3. Ñîñòàâëåíèå äèôôåðåíöèàëüíûõ óðàâíåíèé äâèæåíèÿ ðàêåò
è ñíàðÿäîâ ...............................110
3.1. Óðàâíåíèÿ ïðîñòðàíñòâåííîãî äâèæåíèÿ ðàêåò
íà àêòèâíîì ó÷àñòêå òðàåêòîðèè .................110
3.1.1 . Èñõîäíàÿ ñèñòåìà óðàâíåíèé ïðîñòðàíñòâåííîãî
äâèæåíèÿ ðàêåòû .........................110
3.1.2. Óïðîùåííûå ñèñòåìû óðàâíåíèé,
îïèñûâàþùèå ïðîñòðàíñòâåííîå äâèæåíèå ðàêåò
â ïëîòíûõ ñëîÿõ àòìîñôåðû îòíîñèòåëüíî
íîðìàëüíîé çåìíîé ñèñòåìû êîîðäèíàò ..........115
3.1.3. Ñèñòåìû óðàâíåíèé äâèæåíèÿ öåíòðà
ìàññ ðàêåòû ñ ó÷åòîì âðàùåíèÿ Çåìëè ...........121
3.2. Óïðîùåííûå ñèñòåìû óðàâíåíèé ïðîäîëüíîãî
è áîêîâîãî äâèæåíèé ËÀ íà àêòèâíîì ó÷àñòêå
òðàåêòîðèè ..............................128
3.2 .1 . Ðàçäåëåíèå äâèæåíèÿ íà ïðîäîëüíîå è áîêîâîå ...128
3.2.2. Óðàâíåíèÿ ïðîäîëüíîãî äâèæåíèÿ óïðàâëÿåìîé
ðàêåòû â öåíòðàëüíîì ãðàâèòàöèîííîì ïîëå .......131
3.2.3. Óðàâíåíèÿ ïðîäîëüíîãî äâèæåíèÿ ðàêåòû
â ïëîñêîïàðàëëåëüíîì ãðàâèòàöèîííîì ïîëå .......132
3.2.4. Ëèíåéíûå óðàâíåíèÿ áîêîâîãî è ïðîäîëüíîãî
ñòàáèëèçèðóåìûõ äâèæåíèé â íîðìàëüíîé ôîðìå ....134
3.2.5. Ñèñòåìû óðàâíåíèé ïðè îòíîñèòåëüíûõ
áåçðàçìåðíûõ àðãóìåíòàõ ....................139
3.2.6. Óðàâíåíèÿ äâèæåíèÿ â ïåðåãðóçêàõ .........141
3.3. Ìîäåëè äâèæåíèÿ óïðàâëÿåìûõ
è íåóïðàâëÿåìûõ ðàêåò íà ïàññèâíîì ó÷àñòêå
òðàåêòîðèè ..............................146
3.3.1. Óðàâíåíèÿ ñâîáîäíîãî äâèæåíèÿ ËÀ ïîñòîÿííîé
ìàññû â ïëîòíûõ ñëîÿõ àòìîñôåðû .............146
3.3.2. Óïðîùåííûå óðàâíåíèÿ ïðîäîëüíîãî
äâèæåíèÿ öåíòðà ìàññ ËÀ â àòìîñôåðå ..........148
3.3.3. Óðàâíåíèÿ, îïèñûâàþùèå ñâîáîäíîå äâèæåíèå
öåíòðà ìàññ ËÀ áåç ó÷åòà ñîïðîòèâëåíèÿ
âíåøíåé ñðåäû ..........................152
3.4. Ñâîáîäíûé ïîëåò àðòèëëåðèéñêèõ ñíàðÿäîâ ........155
3.4.1. Óðàâíåíèÿ äâèæåíèÿ ñíàðÿäà â âåêòîðíîé ôîðìå 155
3.4.2. Óðàâíåíèÿ äâèæåíèÿ àðòèëëåðèéñêîãî ñíàðÿäà
â ôîðìå Â.Ñ . Ïóãà÷åâà .....................160
602
3.4.3. Óðàâíåíèÿ ïðîñòðàíñòâåííîãî äâèæåíèÿ àðòèëëå-
ðèéñêîãî ñíàðÿäà ïðè ìàëûõ óãëàõ íóòàöèè ........166
Êîíòðîëüíûå âîïðîñû ......................169
Ðàçäåë II. ÈÑÑËÅÄÎÂÀÍÈÅ ÌÀÒÅÌÀÒÈ×ÅÑÊÈÕ ÌÎÄÅËÅÉ
ÄÂÈÆÅÍÈß ËÅÒÀÒÅËÜÍÛÕ ÀÏÏÀÐÀÒÎÂ È ÌÅÒÎÄÛ
ÐÅØÅÍÈß ÇÀÄÀ× ÂÍÅØÍÅÉ ÁÀËËÈÑÒÈÊÈ ......170
Ãëàâà 4. Óñòîé÷èâîñòü äâèæåíèÿ ðàêåò è ñíàðÿäîâ ............170
4.1. Îáîáùåíèå ïîíÿòèÿ îá óñòîé÷èâîñòè äâèæåíèÿ
è ñòàáèëèçàöèè ðàêåò è ñíàðÿäîâ .................171
4.1.1 . Óñòîé÷èâîñòü òðàåêòîðèé ðàêåò è ñíàðÿäîâ ....171
4.1.2. Ñïîñîáû ñòàáèëèçàöèè íåóïðàâëÿåìûõ ðàêåò
è ñíàðÿäîâ ............................173
4.2. Óñòîé÷èâîñòü äâèæåíèÿ ïî Ëÿïóíîâó ............178
4.2.1. Îïðåäåëåíèå óñòîé÷èâîñòè ïî Ëÿïóíîâó ......178
4.2.2. Ïåðâûé ìåòîä Ëÿïóíîâà.
Óñòîé÷èâîñòü ïî ïåðâîìó ïðèáëèæåíèþ ..........182
4.2.3. Âòîðîé ìåòîä Ëÿïóíîâà .................185
4.3. Óñòîé÷èâîñòü äâèæåíèÿ
áûñòðîâðàùàþùåãîñÿ ñíàðÿäà ..................191
4.3.1. Ïåðâûå èíòåãðàëû óðàâíåíèé äâèæåíèÿ
ñíàðÿäà îòíîñèòåëüíî öåíòðà ìàññ
íà íà÷àëüíîì ó÷àñòêå òðàåêòîðèè ..............191
4.3.2. Íåîáõîäèìîå óñëîâèå óñòîé÷èâîñòè
óãëîâîãî äâèæåíèÿ àðòèëëåðèéñêîãî ñíàðÿäà .......193
4.3.3. Òðàêòîâêà ïîíÿòèÿ íåóñòîé÷èâîñòè äâèæåíèÿ
àðòèëëåðèéñêîãî ñíàðÿäà ïî Ëÿïóíîâó ...........204
Ãëàâà 5. ×èñëåííîå èíòåãðèðîâàíèå óðàâíåíèé äâèæåíèÿ ËÀ è ïðèáëè-
æåííûå ìåòîäû ðåøåíèÿ çàäà÷ âíåøíåé áàëëèñòèêè ......209
5.1. Ïîøàãîâûå ìåòîäû èíòåãðèðîâàíèÿ
è ïðàêòèêà èõ ïðèìåíåíèÿ .....................210
5.1 .1. ×èñëåííîå èíòåãðèðîâàíèå ðàçíîñòíûì ìåòîäîì ...210
5.1.2. Òî÷íîñòü ðàñ÷åòîâ è âûáîð øàãà èíòåãðèðîâàíèÿ 219
5.1.3. Ðåøåíèå îñíîâíîé (ïåðâîé) çàäà÷è âíåøíåé
áàëëèñòèêè íà ÝÂÌ ......................221
5.1.4. Ñîñòàâëåíèå ïðîãðàììû èíòåãðèðîâàíèÿ óðàâíåíèé
äâèæåíèÿ ËÀ íà ÝÂÌ .....................223
5.2. Ïðèáëèæåííûå àíàëèòè÷åñêèå
è òàáëè÷íûå ìåòîäû .........................227
5.2.1. Ïàðàáîëè÷åñêàÿ òåîðèÿ .................227
5.2.2. Ýëëèïòè÷åñêàÿ òåîðèÿ ..................229
5.2.3. Ôîðìóëà Ê.Ý . Öèîëêîâñêîãî äëÿ ðàñ÷åòà
ìàêñèìàëüíîé ñêîðîñòè ïîëåòà ðàêåòû ...........239
5.2.4. Ïðèáëèæåííûå ìåòîäû ðàñ÷åòà òðàåêòîðèé ñíà-
ðÿäîâ ïîñòîÿííîé ìàññû ....................240
5.2.5. Ïîäîáèå òðàåêòîðèé
è òàáëè÷íûå ìåòîäû ðåøåíèÿ ................252
Ãëàâà 6. Ðåøåíèå îïòèìèçàöèîííûõ çàäà÷ áàëëèñòèêè ..........254
603
6.1. Êðàåâûå çàäà÷è áàëëèñòèêè .................255
6.1.1 . Îáùàÿ õàðàêòåðèñòèêà êðàåâûõ çàäà÷ áàëëèñòèêè
è ìåòîäîâ èõ ðåøåíèÿ .....................255
6.1.2. Îñîáåííîñòè ïîñòàíîâêè è ðåøåíèÿ êðàåâûõ çàäà÷
ðàñ÷åòà óñòàíîâî÷íûõ äàííûõ áàëëèñòè÷åñêèõ ðàêåò ...259
6.1.3. Äâóõòî÷å÷íûå êðàåâûå çàäà÷è âíåøíåé
áàëëèñòèêè ............................263
6.1.4. Ïîñòàíîâêà çàäà÷è îïðåäåëåíèÿ ìíîãîòî÷å÷íîé
êðèâîé â êðàåâûõ çàäà÷àõ óïðàâëÿåìîãî ïîëåòà .....266
6.2. Îáðàòíûå çàäà÷è äèíàìèêè ïîëåòà .............267
6.2.1. Êîíöåïöèÿ îáðàòíûõ çàäà÷ äèíàìèêè ïîëåòà ...267
6.2.2. Ðåøåíèå êðàåâûõ çàäà÷ äèíàìèêè óïðàâëÿåìîãî
ïîëåòà íà îñíîâå êîíöåïöèè îáðàòíûõ çàäà÷ .......268
6.2.3. Ïðèáëèæåííîå îïðåäåëåíèå ïàðàìåòðè÷åñêîãî óï-
ðàâëåíèÿ äàëüíîñòüþ ñòðåëüáû ïðè ðåøåíèè îáðàòíûõ
çàäà÷ âíåøíåé áàëëèñòèêè äëÿ ñòâîëüíûõ ñèñòåì ....271
6.3. Ïðîñòåéøèå ýêñòðåìàëüíûå çàäà÷è ïðîãðàììèðîâàíèÿ
îïîðíîãî äâèæåíèÿ .........................274
6.3.1. Îïðåäåëåíèå îïòèìàëüíîãî óãëà áðîñàíèÿ
äëÿ áàëëèñòè÷åñêèõ òðàåêòîðèé ................274
6.3.2. Ìàêñèìàëüíàÿ äàëüíîñòü ãîðèçîíòàëüíîãî ïëàíè-
ðóþùåãî ïîëåòà îïåðåííîãî óïðàâëÿåìîãî ñíàðÿäà ...277
6.4. Âàðèàöèîííûå çàäà÷è ðàêåòîäèíàìèêè
è áàëëèñòèêè .............................279
6.4.1. Ïîñòàíîâêà è êëàññèôèêàöèÿ çàäà÷ âàðèàöèîí-
íîãî èñ÷èñëåíèÿ è îïòèìàëüíîãî óïðàâëåíèÿ .......279
6.4.2. Îïòèìàëüíîå ïðîãðàììèðîâàíèå îïîðíîãî
äâèæåíèÿ íà îñíîâå ìåòîäîâ êëàññè÷åñêîãî
âàðèàöèîííîãî èñ÷èñëåíèÿ ..................283
6.4.3. Îïðåäåëåíèå îïòèìàëüíîãî óïðàâëåíèÿ äâèæåíèåì
ËÀ íà îñíîâå ïðèíöèïà ìàêñèìóìà .............292
6.4.4. Ðàñ÷åò òðàåêòîðèè íàêëîííîé ìàêñèìàëüíîé
äàëüíîñòè ïîëåòà ïëàíèðóþùåãî ËÀ ìåòîäîì
äèíàìè÷åñêîãî ïðîãðàììèðîâàíèÿ ..............299
Ãëàâà 7. Èññëåäîâàíèå óãëîâîãî äâèæåíèÿ ðàêåò è ñíàðÿäîâ .......306
7.1. Äâèæåíèå îòíîñèòåëüíî öåíòðà ìàññ ñíàðÿäîâ,
ñòàáèëèçèðîâàííûõ âðàùåíèåì ...................306
7.1 .1. Óãëîâîå äâèæåíèå âðàùàþùåãîñÿ ñíàðÿäà
ïîä äåéñòâèåì òîëüêî îïðîêèäûâàþùåãî ìîìåíòà ....306
7.1 .2. Äîñòàòî÷íûå óñëîâèÿ óñòîé÷èâîñòè óãëîâîãî
äâèæåíèÿ ñíàðÿäà ........................319
7.1 .3. Âëèÿíèå ñòðóêòóðû äåéñòâóþùèõ ñèë íà óñòîé÷è-
âîñòü äâèæåíèÿ ñíàðÿäîâ, ñòàáèëèçèðóåìûõ
âðàùåíèåì .............................325
7.2. Äâèæåíèå îòíîñèòåëüíî öåíòðà ìàññ îïåðåííûõ
ñíàðÿäîâ è ìèí ............................332
7.2 .1. Óãëîâîå äâèæåíèå îïåðåííûõ âðàùàþùèõñÿ
ñíàðÿäîâ ..............................332
604
7.2 .2. Óãëîâîå äâèæåíèå îïåðåííûõ íåâðàùàþùèõñÿ
ñíàðÿäîâ ..............................335
7.3. Ðåçîíàíñ âðàùàþùèõñÿ îïåðåííûõ ñíàðÿäîâ .......337
7.3 .1. Âëèÿíèå ìàëûõ àñèììåòðèé ôîðìû, ìàññû è
ýêñöåíòðèñèòåòà òÿãè íà óãëîâîå äâèæåíèå îïåðåííûõ
âðàùàþùèõñÿ ñíàðÿäîâ .....................337
7.3 .2. Èññëåäîâàíèå óñòàíîâèâøåãîñÿ ðåçîíàíñíîãî
âðàùåíèÿ .............................341
7.3 .3. Óñòîé÷èâîñòü ðåçîíàíñíûõ ðåæèìîâ âðàùåíèÿ . . 344
7.4. Ñâîáîäíûé ïîëåò ïî íèñõîäÿùåé âåòâè òðàåêòîðèè ...350
7.4 .1. Äâèæåíèå ËÀ ïðè âõîäå â àòìîñôåðó ........350
7.4 .2. Êà÷åñòâåííûé àíàëèç óãëîâîãî äâèæåíèÿ ËÀ
ïðè âõîäå â àòìîñôåðó ....................355
Êîíòðîëüíûå âîïðîñû ......................359
Ðàçäåë III. ÂÎÇÌÓÙÅÍÍÎÅ ÄÂÈÆÅÍÈÅ ËÅÒÀÒÅËÜÍÛÕ ÀÏÏÀ-
ÐÀÒÎÂ È ÎÏÐÅÄÅËÅÍÈÅ ÕÀÐÀÊÒÅÐÈÑÒÈÊ
ÐÀÑÑÅÈÂÀÍÈß ..........................361
Ãëàâà 8. Ïîïðàâî÷íûå ôîðìóëû âíåøíåé áàëëèñòèêè è ðàñ÷åò
âîçìóùåííûõ òðàåêòîðèé ......................361
8.1. Îñíîâíûå ïîëîæåíèÿ òåîðèè ïîïðàâîê ...........362
8.1 .1. Ïîíÿòèå ïîïðàâêè ....................362
8.1 .2. Îñíîâíàÿ ôîðìóëà òåîðèè ïîïðàâîê .........363
8.1 .3. Êà÷åñòâåííîå âëèÿíèå îïðåäåëÿþùèõ ïàðàìåòðîâ
è çíàêè áàëëèñòè÷åñêèõ ïðîèçâîäíûõ ............366
8.1 .4. Èçìåíåíèå äàëüíîñòè ñòðåëüáû àðòèëëåðèéñêèìè
ñíàðÿäàìè ïðè èçìåíåíèè èõ íà÷àëüíîé ìàññû .....369
8.2. Ìåòîäû âû÷èñëåíèÿ èçìåíåíèé ýëåìåíòîâ òðàåêòîðèé
è áàëëèñòè÷åñêèõ ïðîèçâîäíûõ ..................371
8.2 .1. Îïðåäåëåíèå èçìåíåíèé ýëåìåíòîâ òðàåêòîðèé
è ïîïðàâî÷íûõ êîýôôèöèåíòîâ èíòåãðèðîâàíèåì
ñèñòåì óðàâíåíèé äâèæåíèÿ ..................371
8.2 .2. Îïðåäåëåíèå ïîïðàâî÷íûõ êîýôôèöèåíòîâ
èíòåãðèðîâàíèåì äèôôåðåíöèàëüíûõ óðàâíåíèé
â îòêëîíåíèÿõ ..........................375
8.2 .3. Ñîïðÿæåííàÿ ñèñòåìà óðàâíåíèé â îòêëîíåíèÿõ
è åå ðåøåíèå ...........................381
8.2 .4. Îïðåäåëåíèå ïîïðàâî÷íûõ êîýôôèöèåíòîâ èç óñ-
ëîâèÿ ïîäîáèÿ òðàåêòîðèé ...................384
8.2 .5. Àíàëèòè÷åñêèå ìåòîäû ïîëó÷åíèÿ áàëëèñòè÷åñêèõ
ïðîèçâîäíûõ ...........................385
8.2 .6. Òàáëè÷íûå ìåòîäû ðàñ÷åòà çíà÷åíèé
ïîïðàâî÷íûõ êîýôôèöèåíòîâ .................388
8.2 .7. Ïîíÿòèå è ìåòîäû îïðåäåëåíèÿ ïîëíûõ (èçî-
ôóíêöèîíàëüíûõ) îòêëîíåíèé ïàðàìåòðîâ äâèæåíèÿ . . 389
8.3. Ó÷åò âëèÿíèÿ ïàðàìåòðîâ àòìîñôåðû
íà ïîëåò ðàêåò è àðòèëëåðèéñêèõ ñíàðÿäîâ ...........390
8.3 .1. Ñïîñîáû ó÷åòà âëèÿíèÿ îòêëîíåíèé ìåòåîôàê-
òîðîâ íà äâèæåíèå ËÀ .....................390
605
8.3 .2. Ó÷åò èçìåíåíèÿ áàðîìåòðè÷åñêîãî äàâëåíèÿ
è òåìïåðàòóðû ..........................391
8.3 .3. Óðàâíåíèÿ äâèæåíèÿ ñíàðÿäà ïîñòîÿííîé ìàññû
ïðè ó÷åòå èçìåíåíèÿ áàðîìåòðè÷åñêîãî äàâëåíèÿ
è òåìïåðàòóðû ..........................392
8.3 .4. Ó÷åò âëèÿíèÿ âåòðà íà ïîëåò íåóïðàâëÿåìûõ
ðàêåò è àðòèëëåðèéñêèõ ñíàðÿäîâ ..............394
8.3 .5. Áàëëèñòè÷åñêèé ñðåäíèé âåòåð è áàëëèñòè÷åñêîå
îòêëîíåíèå òåìïåðàòóðû ....................401
8.3 .6. Ïðèáëèæåííûå ïîïðàâî÷íûå ôîðìóëû
íà ïîñòîÿííûé ïðîäîëüíûé è áîêîâîé âåòåð .......406
8.3 .7. Ìåòåîðîëîãè÷åñêàÿ ïîäãîòîâêà ñòðåëüáû ......410
8.4. Óðàâíåíèÿ âîçìóùåííîãî ïðîñòðàíñòâåííîãî äâèæåíèÿ
íåóïðàâëÿåìîé ðàêåòû ........................412
8.4 .1. Ó÷åò âëèÿíèÿ ýêñöåíòðèñèòåòà òÿãè .........412
8.4 .2. Ìàòåìàòè÷åñêàÿ ìîäåëü ïðîñòðàíñòâåííîãî âîç-
ìóùåííîãî äâèæåíèÿ íåóïðàâëÿåìîé ðàêåòû .......414
Ãëàâà 9. Íà÷àëüíûå óñëîâèÿ âîçìóùåííîãî äâèæåíèÿ ðàêåò è ñíàðÿäîâ ...419
9.1. Âëèÿíèå äâèæåíèÿ íîñèòåëÿ âîîðóæåíèÿ
íà íà÷àëüíûå óñëîâèÿ âûñòðåëà ..................420
9.1.1 . Îïðåäåëåíèå ñóììàðíîé íà÷àëüíîé ñêîðîñòè ...420
9.1.2. Âëèÿíèå êîëåáàíèé íîñèòåëÿ íà ôîðìèðîâàíèå
íà÷àëüíûõ óñëîâèé ïóñêà ðàêåòû ..............421
9.2. Äâèæåíèå ðàêåò ïðè ïóñêå ..................428
9.2.1. Îñîáåííîñòè ñòàðòîâîãî äâèæåíèÿ ðàêåò ......428
9.2.2. Äâèæåíèå ðàêåò ïî íàïðàâëÿþùåé ïóñêîâîé óñòà-
íîâêè ................................428
9.3. Ôîðìèðîâàíèå íà÷àëüíûõ óñëîâèé âîçìóùåííîãî äâè-
æåíèÿ ñíàðÿäà ............................432
9.3.1. Íà÷àëüíîå ïðåöåññèîííîå äâèæåíèå .........432
9.3.2. Íà÷àëüíûå óãëîâàÿ ñêîðîñòü è óãîë íóòàöèè,
îáóñëîâëåííûå íåóðàâíîâåøåííîñòüþ ñíàðÿäà ......434
9.3.3. Âëèÿíèå ðàäèàëüíîãî ýêñöåíòðèñèòåòà öåíòðà
ìàññ ñíàðÿäà íà îòêëîíåíèå âåêòîðà íà÷àëüíîé
ñêîðîñòè ..............................436
9.3.4. Âîçäåéñòâèå íà ñíàðÿä äóëüíîé âîëíû â ïåðèîä
ïîñëåäåéñòâèÿ ..........................437
Ãëàâà 10. Ìåòîäû ñòàòèñòè÷åñêîé äèíàìèêè ïîëåòà, ðàññåèâàíèå ðàêåò
è ñíàðÿäîâ ïðè ñòðåëüáå .......................438
10.1 . Ìåòîäû àïðèîðíîãî ñòàòèñòè÷åñêîãî àíàëèçà äâèæåíèÿ
ðàêåò è ñíàðÿäîâ ...........................439
10.1.1 . ×èñëîâûå õàðàêòåðèñòèêè, èñïîëüçóåìûå
ïðè ñòàòèñòè÷åñêîì àíàëèçå äâèæåíèÿ ËÀ .........439
10.1.2 . Ìåòîä ìàòðèöû âëèÿíèÿ ...............443
10.1.3 . Ïðèìåíåíèå òåîðèè ìàðêîâñêèõ ïðîöåññîâ
ïðè îïðåäåëåíèè õàðàêòåðèñòèê ðàññåèâàíèÿ òðàåêòî-
ðèéËÀ ...............................450
606
10.1.4 . Îïðåäåëåíèå õàðàêòåðèñòèê ðàññåèâàíèÿ ìåòîäîì
ñòàòèñòè÷åñêèõ èñïûòàíèé ...................460
10.2 . Ñòàòèñòè÷åñêàÿ îáðàáîòêà ðåçóëüòàòîâ ñòðåëüá .....469
10.2.1 . Îïðåäåëåíèå õàðàêòåðèñòèê ðàññåèâàíèÿ
ïî ðåçóëüòàòàì îïûòíûõ ñòðåëüá ...............469
10.2.2 . Îáðàáîòêà äàííûõ ïðèñòðåëêè è áîåâûõ àðòèëëå-
ðèéñêèõ ñòðåëüá .........................476
Ãëàâà 11. Áàëëèñòèêà êîððåêòèðóåìûõ àðòèëëåðèéñêèõ ñíàðÿäîâ, ñóááîå-
ïðèïàñîâ è áîåâûõ ïîðàæàþùèõ ýëåìåíòîâ ñëîæíîé ôîðìû ...479
11.1 . Îñîáåííîñòè èññëåäîâàíèÿ äèíàìèêè ïðîñòðàíñòâåííîãî
äâèæåíèÿ êîððåêòèðóåìûõ áîåïðèïàñîâ
*
.............4
80
11.1.1. Ïîñòàíîâêà çàäà÷è êîððåêöèè äâèæåíèÿ
ñíàðÿäà ...............................480
11.1.2. Ìàòåìàòè÷åñêîå ìîäåëèðîâàíèå ïðîñòðàí-
ñòâåííîãî äâèæåíèÿ èìïóëüñíî-êîððåêòèðóåìîãî
ñíàðÿäà ...............................483
11.1.3. Óãëîâîå äâèæåíèå ãèðîñêîïè÷åñêè óñòîé÷èâûõ
â ïîëåòå ñíàðÿäîâ ïðè âîçäåéñòâèè óäàðíûõ ìîìåíòîâ . 494
11.1.4. Óñòîé÷èâîñòü óãëîâîãî äâèæåíèÿ èìïóëüñíî-
êîððåêòèðóåìîãî ãèðîñêîïè÷åñêè ñòàáèëèçèðóåìîãî
ñíàðÿäà
*
..............................496
11.2 . Äâèæåíèå ñóááîåïðèïàñîâ è áîåâûõ ïîðàæàþùèõ ýëå-
ìåíòîâ ñëîæíîé ôîðìû
*
.......................5
02
11.2.1. Ó÷åò ñêà÷êîîáðàçíîãî èçìåíåíèÿ áàëëèñòè÷åñêîãî
êîýôôèöèåíòà ñóááîåïðèïàñîâ êàññåòíûõ ñíàðÿäîâ ...502
11.2.2. Îïðåäåëåíèå òðàåêòîðèé âûñîêîñêîðîñòíûõ
àñèììåòðè÷íûõ áîåâûõ ïîðàæàþùèõ ýëåìåíòîâ .....508
11.2.3. Îñîáûå è ðåçîíàíñíûå ðåæèìû ïîëåòà
àñèììåòðè÷íûõ ñóááîåïðèïàñîâ ...............513
Êîíòðîëüíûå âîïðîñû ......................517
Ðàçäåë IV. ÒÅÎÐÅÒÈ×ÅÑÊÈÅ ÎÑÍÎÂÛ ÝÊÑÏÅÐÈÌÅÍÒÀËÜÍÎÉ
ÂÍÅØÍÅÉ ÁÀËËÈÑÒÈÊÈ È ËÅÒÍÛÕ ÈÑÏÛÒÀÍÈÉ
ÐÀÊÅÒ. ÏÎÍßÒÈß Î ÑÎÑÒÀÂËÅÍÈÈ ÒÀÁËÈÖ
ÑÒÐÅËÜÁÛ .............................518
Ãëàâà 12. Ôîðìóëèðîâêà çàäà÷ ýêñïåðèìåíòàëüíîé áàëëèñòèêè, ýëåìåíòû
ïëàíèðîâàíèÿ è îáðàáîòêà ðåçóëüòàòîâ ëåòíûõ èñïûòàíèé . . 518
12.1 . Îïðåäåëåíèå ïàðàìåòðîâ äâèæåíèÿ è îñíîâíûõ
õàðàêòåðèñòèê ËÀ ïî ðåçóëüòàòàì èñïûòàíèé .........520
12.1.1. Îáùàÿ õàðàêòåðèñòèêà áàëëèñòè÷åñêèõ òðàññ,
èñïîëüçóåìûõ ïðè ïðîâåäåíèè ëàáîðàòîðíûõ èñïû-
òàíèé ................................520
12.1.2. Àëãîðèòìè÷åñêèå îñíîâû îïðåäåëåíèÿ ñêîðîñòè
äâèæåíèÿ ñíàðÿäà è åå ïðèâåäåíèÿ ê äóëüíîìó ñðåçó
ñòâîëà ...............................522
12.1.3. Ýêñïåðèìåíòàëüíîå îïðåäåëåíèå êîýôôèöèåíòà
ëîáîâîãî ñîïðîòèâëåíèÿ ñðåäû áàëëèñòè÷åñêèìè
ìåòîäàìè ..............................526
607
12.1.4. Îïðåäåëåíèå àýðîäèíàìè÷åñêèõ êîýôôèöèåíòîâ
íîðìàëüíîé ñèëû è îïðîêèäûâàþùåãî ìîìåíòà .....529
12.1.5. Îñíîâû èäåíòèôèêàöèè ìîäåëüíîãî äâèæåíèÿ
ËÀ .................................534
12.2 . Áàëëèñòè÷åñêèå ñòðåëüáû ..................537
12.2.1 . Ñòðåëüáû íà îïðåäåëåíèå óãëà âûëåòà .......537
12.2.2 . Ñòðåëüáû íà äàëüíîñòü è êó÷íîñòü .........539
12.2.3 . Îïðåäåëåíèå äåðèâàöèè ................541
12.2.4. Ñîñòðåë äàëüíîñòåé è íà÷àëüíûõ ñêîðîñòåé
ïðè èçìåíåíèè êîíñòðóêòèâíûõ ýëåìåíòîâ áîåïðèïàñà ...542
12.3 . Îñíîâû òåîðèè ëåòíûõ èñïûòàíèé ðàêåò
è óïðàâëÿåìûõ ñíàðÿäîâ ......................543
12.3.1 . Ýëåìåíòû ïëàíèðîâàíèÿ ëåòíîãî áàëëèñòè÷åñêîãî
ýêñïåðèìåíòà ...........................543
12.3.2 . Êðàòêàÿ õàðàêòåðèñòèêà ìåòîäîâ îáðàáîòêè ðå-
çóëüòàòîâ èçìåðåíèé ......................550
12.3.3 . Èäåíòèôèêàöèÿ ïàðàìåòðîâ ËÀ êàê äèíàìè÷åñêèõ
ñèñòåì â çàäà÷àõ îáðàáîòêè ðåçóëüòàòîâ ëåòíûõ
èñïûòàíèé .............................552
Ãëàâà 13. Áàëëèñòè÷åñêèå àñïåêòû ñîñòàâëåíèÿ òàáëèö ñòðåëüáû ....572
13.1 . Ìåòîäîëîãè÷åñêèå îñíîâû ñîñòàâëåíèÿ òàáëèö ñòðåëüáû
àðòèëëåðèéñêèìè ñíàðÿäàìè ....................573
13.1.1. Ïîäãîòîâêà ê îòñòðåëó òàáëèö ............573
13.1.2. Ïðèâåäåíèå ðåçóëüòàòîâ ñòðåëüá ê íîðìàëüíûì
è òàáëè÷íûì óñëîâèÿì .....................575
13.1.3. Âû÷èñëåíèå ïîïðàâîê, îñíîâíûõ ýëåìåíòîâ
òðàåêòîðèè è îïûòíîé çàâèñèìîñòè áàëëèñòè÷åñêîãî
êîýôôèöèåíòà îò óãëà áðîñàíèÿ ...............577
13.1.4. Àëãîðèòì ñîñòàâëåíèÿ àðòèëëåðèéñêèõ òàáëèö
ñòðåëüáû ..............................579
13.2 . Îñîáåííîñòè ñîñòàâëåíèÿ òàáëèö ñòðåëüáû
äëÿ ðàêåòíûõ ñèñòåì ........................581
13.2.1 . Òàáëè÷íûå è äåéñòâèòåëüíûå óñëîâèÿ ïóñêà
ðàêåò ................................581
13.2.2 . Ïðèâåäåíèå ðåçóëüòàòîâ òàáëè÷íûõ ñòðåëüá
ê íîðìàëüíûì óñëîâèÿì è ñîñòàâëåíèå òàáëèö ñòðåëüáû
äëÿ íåóïðàâëÿåìûõ ðàêåò ...................582
13.3 . Áàëëèñòè÷åñêèå àëãîðèòìû ðàñ÷åòà óñòàíîâîê
äëÿ ñòðåëüáû àðòèëëåðèè è ïóñêîâ ðàêåò ............584
13.3.1 . Ïîíÿòèå áàëëèñòè÷åñêîãî àëãîðèòìà
è ïðåäúÿâëÿåìûå ê íåìó òðåáîâàíèÿ ............584
13.3.2 . Âèäû áàëëèñòè÷åñêèõ àëãîðèòìîâ ..........586
Êîíòðîëüíûå âîïðîñû ......................591
Ëèòåðàòóðà .....................................592
Ïðåäìåòíûé óêàçàòåëü ..............................599