Text
ОСНОВЫ СТРОИТЕЛЬНОЙ МЕХАНИКИ РАКЕТ
ш
основы строительной механики
Л. И. БАЛАБУХ, К. С. КОЛЕСНИКОВ
В. С. ЗАРУБИН, Н. А. АЛФУТОВ,
В. И. УСЮКИН, В. Ф. ЧИЖОВ
Допущено Министерством высшего и
среднего специального образования СССР
в качестве учебного пособия для студентов
высших учебных заведений
ИЗДАТЕЛЬСТВО «ВЫСШАЯ ШКОЛА>
МОСКВА—1969
УДК 629.136
0-75
Основы строительной механики ракет. Учеб, пособие длят
студентов высших учебных заведений. М., «Высшая школа»,
1969.
Перед загл. авт.: Балабух Л. И., Колесников К. С., Зару-
бин В. С., Алфутов Н. А., Ускжи'Н В. И., Чижов В. Ф.
Основы строительной механики ракет изложены в виде
комплекса вопросов, связанных с анализом работоспособно-
сти силовых элементов ракетных конструкций. Приведены/
необходимые сведения из прикладной теории упругости и пла-
стичности, теории оболочек, а также основы динамических и
температурных расчетов конструкций ракет и ракетных двига-
телей.
Особое внимание уделено анализу действующих нагрузок
и выбору для конкретных элементов конструкции (баков, от-
секов, головных частей, двигателей) наиболее неблагоприят-
ных расчетных случаев. Способы проведения динамических,,
температурных расчетов и расчетов на прочность иллюстри-
рованы числовыми примерами.
Таблиц 18. Иллюстраций 209. Библиография — 125*.
496 стр. с илл.
Рецензенты:
кафедра динамики и прочности машин Ленинградского-
политехнического института;
проф. Н. И. Безухов
3—2—5
69—69
щ
S
CQ
О
О
s
Щ
a.
E
Развитие ракетной техники в настоящее время
идет настолько быстро и широко, что определяет
прогресс в развитии многих отраслей народного
хозяйства. Успехи ракетной техники отражают до-
стижения во многих смежных областях науки.
Помимо военного назначения, ракеты все боль-
ше и больше используются для изучения космоса и
других планет. Юрий Алексеевич Гагарин 12 апре-
ля 1961 года совершил на советском космическом
корабле «Восток» полет вокруг земного шара.
3 февраля 1966 года советская автоматическая стан-
ция «Луна-9» произвела мягкую посадку на Луну
и передала на Землю изображения лунного ланд-
шафта. 18 октября 1967 года советская автоматиче-
ская межпланетная станция «Венера-4» совершила
посадку на поверхность Венеры. Большое число ис-
кусственных спутников Земли и межпланетных
станций изучают нашу Землю и космическое про-
странство Солнечной системы. Мирное использова-
ние ракетной техники все больше и больше возра-
стает. Недалеко то время, когда осуществится пред-
сказание К. Э. Циолковского и люди будут путеше-
ствовать по Вселенной на больших космических
кораблях.
Каждый этап в развитии ракетной техники, в
изучении космоса — это множество сложных проб-
лем, которые решаются нашей наукой и техникой.
Среди этих проблем важное место занимает проч-
ность ракет.
Решение проблемы прочности современных ра-
кет базируется на достижениях в передовых отрас-
лях нашей промышленности, прежде всего, в судо-
строении и самолетостроении. Фундаментальные
работы в области прочности и строительной меха-
ники связаны с именами выдающихся отечествен-
ных ученых А. Н. Крылова, И. Г. Бубнова, С. П. Ти-
3
мошенко, П. Ф. Папковича, Б. Г. Галеркина, Л. С. Лейбензона,
В. 3. Власова, Ю. А. Шиманского. Вклад этих ученых в развитие оте-
чественной науки и техники далеко выходит за рамки их чисто научных
достижений. Они были одновременно исследователями-теоретиками и
инженерами-практиками. А. Н. Крылова, например, называли инжене-
ром-ученым, инженером-математиком. С его именем связана современная
отечественная школа механиков. Трудно переоценить значение научной
направленности в инженерных исследованиях этих ученых. Научная на-
правленность, присущая советским ученым и инженерам, в значительной
мере определила успехи отечественной техники вообще и ракетной тех-
ники в частности.
К инженеру-специалисту в области прочности ракет предъявляются
очень высокие требования. Он должен знать основы механики деформи-
руемых тел, строительной механики, динамики упругих конструкций,
теплопередачи, а также уметь быстро и уверенно делать как оконча-
тельные, контрольные расчеты, так и предварительные, проектировоч-
ные расчеты в процессе анализа различных вариантов конструкций.
Этот комплекс знаний применительно к баллистическим ракетам
излагается в минимально необходимом объеме в данном учебном посо-
бии, названном «Основы строительной механики ракет». Для чтения
книги достаточно знания обычных курсов сопротивления материалов,
теории механических колебаний и физики.
Включение в строительную механику разделов из механики сплош-
ной среды, динамики, теплопередачи, расчета внешних нагрузок не яв-
ляется обычным. Первые курсы строительной механики были в основ-
ном посвящены расчетам стержневых систем и отражали потребности
строителей мостов и различных промышленных сооружений. С разви-
тием кораблестроения понадобилась другая строительная механика.
В курс строительной механики корабля, созданный П. Ф. Папковичем,
введена, например, теория изгиба и устойчивости пластин. Этот кур-с
можно было бы назвать не строительной механикой, а прикладной тео-
рией упругости. Основной особенностью курса строительной механики
самолета является введение теории тонкостенных стержней.
Совершенно естественно, что курс строительной механики ракет так-
же должен иметь свои специфические особенности, присущие расчетам
на прочность в ракетной технике. Основной из них является взаимосвязь
между проектированием, температурными, динамическими и статиче-
скими расчетами конструкций. Для того чтобы быстро и максимально
точно определить основные размеры элементов конструкции ракеты,
инженер должен обладать комплексом знаний, позволяющим ему само-
му произвести весь цикл этих расчетов. Узкая специализация с разделе-
нием труда в расчетах может привести к потере драгоценного времени.
По этой причине также желательно, чтобы инженеры, занимающиеся
разработкой проектов конструкций, могли сами делать простые, прибли-
женные расчеты на прочность. Эти соображения были положены в ос-
нову построения данного учебного пособия.
Книга разделена на три части.
4
В первой части изложены основы механики деформируемых тел,
теории оболочек вращения, динамических расчетов и расчетов темпера-
турных полей в тонкостенных конструкциях. При написании этой части
авторы хотели в концентрированной форме изложить весь тот теорети-
ческий материал, который лежит в основе всего комплекса расчетов
ракет на прочность. Это как бы тот минимум дополнительных общетео-
ретических знаний, который нужен инженеру, работающему в данной
области. В том случае, когда студентам читаются отдельные курсы по
таким дисциплинам, как теория оболочек, динамика ракет, теплопровод-
ность в тонкостенных конструкциях, соответствующие главы первой
части книги могут служить в качестве дополнительного учебного
пособия.
В первой главе этой части излагаются основные сведения из меха-
ники деформируемых тел. При этом используются понятия и методы
теоретической механики. Так, уравнения равновесия и граничные усло-
вия выводятся на основе принципа возможных перемещений. Это сде-
лано для того, чтобы подготовить читателя к изучению следующей гла-
вы, где приближенные теории оболочек излагаются на основе вариаци-
онных уравнений механики. Большое внимание уделено разъяснению
основных понятий теории пластичности. Назначение параграфа, посвя-
щенного сложным средам, — ознакомить читателя с некоторыми идеями
приближенных теорий таких сред.
Во второй главе выводятся основные дифференциальные уравнения
теории оболочек вращения и даются методы их интегрирования. Много
внимания уделяется разъяснению особенностей работы оболочек при
различных условиях их нагружения и закрепления. Подробно излагают-
ся методы расчета, основанные на выделении безмоментного напряжен-
ного состояния. В последних двух параграфах этой главы рассматри-
вается несущая способность и устойчивость оболочек. Приводятся основ-
ные понятия и зависимости, которые затем используются в других главах
книги при изложении методов приближенных расчетов на устойчивость
и несущую способность элементов конструкций ракет.
Третья глава посвящена динамическим расчетам конструкций. Она
включает методику расчета форм и частот собственных колебаний и
динамических нагрузок для типичных расчетных схем. В качестве рас-
четной схемы для изучения продольных и поперечных колебаний корпуса
ракеты принят прямой неоднородный упругий стержень. Учет колебаний
жидкости в баках проведен в минимальном объеме, необходимом для
определения частот собственных колебаний и динамических нагрузок.
В четвертой главе рассмотрены методы расчета температурных полей
в тонкостенных элементах конструкций, наиболее характерных для
ракетной техники. Здесь приведено краткое описание условий теплооб-
мена конструкции с воздушным потоком и рабочим телом двигателей,
даны уравнения и краевые условия, которые составляют математическое
описание процесса теплопроводности в конструкции, и разобраны спо-
собы решения задач теплопроводности.
По мнению авторов, главы первой части книги будут полезны также
и для тех инженеров конструкторских бюро, которые хотят повысить
5
свою квалификацию. Изучение этих глав позволит инженеру и студен-
ту читать научно-техническую литературу по соответствующим разде-
лам науки и участвовать в обсуждении вопросов, связанных с анализом
работоспособности ракетных конструкций с учетом динамических и теп-
ловых процессов.
Вторая часть книги посвящена практическому расчету ракет на
прочность. Особое внимание уделено простым методам так называемых
проектировочных расчетов, т. е. расчетов в начальной стадии проектиро-
вания. Качество и быстрота выполнения этих расчетов оказывают
решающее влияние на совершенство проектируемых конструкций, тогда
как окончательные, поверочные расчеты по уже выпущенным чертежам
могут только зафиксировать картину весового и прочностного несовер-
шенства ракеты.
Качество проектировочных расчетов в сильной степени зависит от
понимания силовой схемы ракеты. Поэтому все главы второй части
книги начинаются с краткого описания наиболее характерных силовых
схем. Приведенные на рисунках конструктивные схемы должны помочь
студенту научиться смотреть на конструкцию ракет глазами инженера-
специалиста в области прочности.
Пятая глава посвящена описанию силовых схем ракет, расчетным
случаям, нагрузкам и коэффициентам безопасности. Введено понятие
определяющей нагрузки, от которой, в основном, зависит силовая схема
конструкции (для сухого отсека это осевая сжимающая сила, для ба-
ков— осевая сила и гидростатическое давление и т. д.).
В шестой главе рассматриваются различные конструктивные схемы
и нагрузки для баков ракет, а также приводится расчет баков и их эле-
ментов. Прежде всего анализируются различные силовые схемы цилинд-
рических несущих баков. Рассматриваются особенности расчета сфери-
ческих и торовых баков. Приводится расчет баков гладкой конструкции
и рассмотрены особенности расчета баков вафельной конструкции.
В седьмой главе описаны некоторые конструктивные схемы сухих
отсеков. В этой же главе приведены способы расчета стрингерных, лон-
жеронных и гофрированных отсеков, а также переходных и двигатель-
ных ферм и отсеков, работающих на внешнее давление.
В восьмой главе приводятся приближенные расчеты головной части
ракеты на участке входа в атмосферу с учетом нагрева конструкции, в
том числе расчеты на прочность и устойчивость оболочки и стабилизи-
рующей юбки от внешнего давления. В последнем параграфе этой главы
приведены некоторые сведения по расчету и конструктивным формам
обтекателей спутников и космических аппаратов.
Девятая глава посвящена расчету на прочность отдельных элементов
конструкции ракеты — силовых шпангоутов, баллонов высокого давле-
ния, трубопроводов, сильфонов.
Главы второй части книги, по мнению авторов, могут быть полезны-
ми для студентов и инженеров как при проведении расчетов ракет на
прочность, так и при проектировании конструкции.
Третья часть книги посвящена прочности ракетных двигателей.
Характер изложения здесь такой же, как и во второй части.
6
В десятой главе рассмотрены типичные конструктивные схемы камер
ЖРД и действующие на них нагрузки. Изложены способы расчета тем-
пературного и напряженно-деформированного состояний оболочек ЖРД.
В одиннадцатой главе проведен расчет температурных полей в ра-
кетных двигателях твердого топлива и изложены некоторые задачи
расчета на прочность камеры РДТТ. Так же, как и для ЖРД, динами-
ческие явления в камере РДТТ описаны главным образом с качественной
’Стороны.
В книге не рассматривается прочность космических кораблей. Они
имеют свои специфические расчетные схемы и к их прочности предъяв-
ляются несколько иные требования, чем к прочности ракет-носителей.
В конце книги приведена довольно большая библиография, позво-
ляющая читателю найти те работы, где интересующие его вопросы
изложены более полно. Библиография дает также представление о том
цикле работ, который лежит в основе строительной механики ракет.
Это в большой степени освобождает авторов, по их мнению, от подроб-
ного описания вклада различных ученых в развитие тех отраслей науки,
на которых базируются методы статических, динамических и темпера-
турных расчетов конструкций ракет.
Главы I и II книги (кроме параграфов 15 и 16) написаны проф. докт.
техн, наук Л. И. Балабухом; им же написаны параграфы 28 и 37;
глава III и параграфы 53, 59 — проф. докт. техн, наук К. С. Колесни-
ковым; глава IV и параграфы 29, 42, 48—50, 54—56 — канд. техн, наук
В. С. Зарубиным; параграфы 15, 16, 40, 43, 51, 52, 57, 58 — канд. техн,
наук Н. А. Алфутовым; глава VI и параграфы 30, 31, 36, 39, 45, 47 —
канд. техн, наук В. И. Усюкиным; параграфы 27, 38, 41, 44, 46 — канд.
техн, наук В. Ф. Чижовым.
Авторы заранее благодарны читателям, которые выскажут свои за-
мечания и пожелания, и просят направлять их в издательство «Высшая
школа» по адресу: Москва К-51, Неглинная, 29/14.
Авторы выражают свою глубокую признательность В. И. Феодосьеву,
II. И. Безухову, А. И. Лурье и В. А. Пальмову, А. В. Кармишину и его
сотрудникам за ряд замечаний, существенно улучшивших книгу.
ос
-D
rC
О
ОС
<
I
-D
EC
UJ
x
iz
О
co
Ракетная техника относится к числу наиболее
молодых и бурно развивающихся областей челове-
ческой деятельности. Самые яркие и впечатляющие
достижения второй половины 20 века связаны
именно с ракетной техникой и началом освоения
космоса. Эти достижения стали возможны только
на определенной ступени развития знаний и тесно
связаны с такими понятиями, как комплексность
научных исследований и кооперирование промыш-
ленности.
Общая тенденция к взаимной увязке до сих пор
относительно самостоятельных разделов науки на-
ходит свое отражение, в частности, и в вопросах
механики ракет. Если в недавнем прошлом счита-
лось, что прочность конструкции, теория колебаний,
тепловые процессы и аэрогазодинамика могут рас-
сматриваться как самостоятельные дисциплины, то
в настоящее время при решении ряда задач ракет-
ной техники обнаружилось, насколько тесно они
связаны; квалификация инженера-ракетчика стала
определяться не только тем, насколько хорошо он
владеет той или другой из перечисленных дисцип-
лин, но также и тем, насколько правильно он пони-
мает их взаимную связь и свободно мыслит катего-
риями, присущими каждому из перечисленных раз-
делов механики. \
Но дело не только в этом. Весьма важным (нс
только для ракетной техники) является рациональ-
ный образ мышления, позволяющий правильно оце-
нить соответствие аналитического аппарата исход-
ным предпосылкам, с одной стороны, и конечным
целям исследования, — с другой. Каждый инже-
нерный расчет и, вообще, исследование в области
технических наук, включает следующие три этапа:
1. Выбор расчетной схемы. На этом этапе рас-
сматривается реальный объект и выделяются его
особенности, наиболее существенные для рассмат-
риваемой стороны явления.
2. Анализ расчетной схемы. Здесь при помощи
логики, обычно в форме математической символи-
ки, выясняются закономерности расчетной схемы,
отвечающей реальному объекту.
8
3. Обратный переход от расчетной схемы к реальному объекту и
формулировка выводов, ради которых было предпринято исследование.
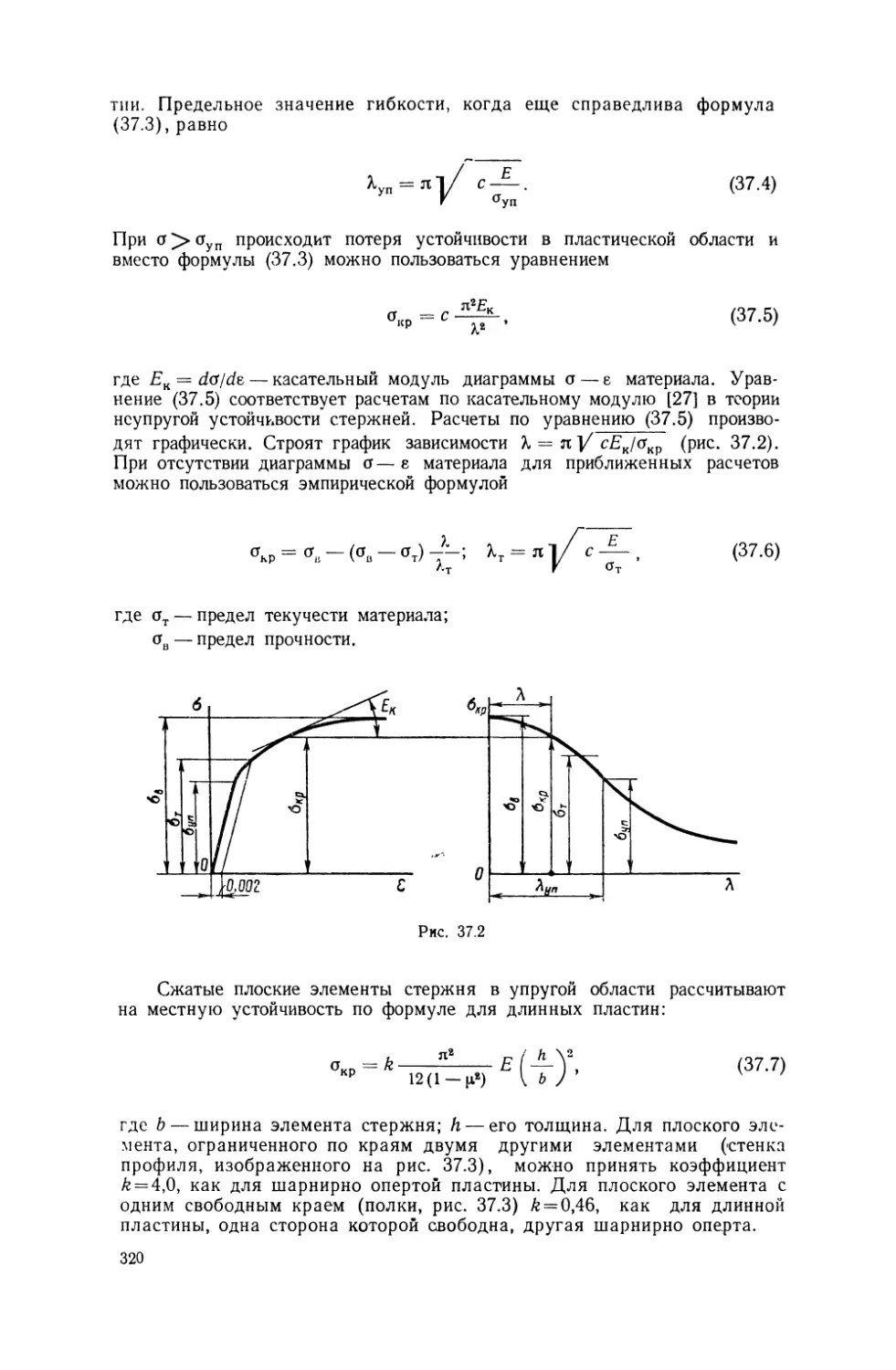
Изложение общих курсов прочностного цикла часто ограничивается
аппаратно-теоретической стороной вопроса (этап 2). Что же касается
выбора расчетной схемы и оценки надежности самой конструкции, то
ответа на эти вопросы в общих курсах обычно не дается. Да это и по-
нятно. Многообразие современных инженерных конструкций настолько
велико, что необходима дифференциация по инженерным направлениям.
Расчетные схемы, выходящие за рамки общетехнических дисциплин
и свойственные только конкретно взятому разделу техники, рассматри-
ваются в курсах, название которых начинается словами «строительная
механика»: строительная механика сооружений, строительная механика
сварных конструкций, строительная механика корабля, самолета и пр.
В этих курсах развиваются эффективные методы анализа специфиче-
ских расчетных схем. Так, в строительной механике самолета рассмат-
риваются вопросы устойчивости пластин, подкрепленных оболочек и
других тонкостенных элементов. В строительной механике сооружений
большое место занимают специальные вопросы раскрытия статической
неопределимости рам и стержневых систем.
Вопросы о выборе расчетной схемы (этап 1) и оценки коэффициентов
безопасности (этап 3) наиболее полно излагаются в курсах, название
которых начинается словом «прочность»: прочность строительных соору-
жений, прочность корабля, прочность самолета и т. д.
Например, для курса прочности самолета естественным является его-
изложение по принципу последовательного рассмотрения типичных
узлов. Рассматривается, например, фюзеляж. Анализируются условия
его работы и основные типы нагрузок, устанавливаются расчетные слу-
чаи. Соответственно каждому случаю выбирается расчетная схема и на
основе ее анализа делается заключение о работоспособности конструк-
ции. Конкретно говоря, решается вопрос об оценке прочности с некото-
рым коэффициентом безопасности, величина которого зависит от типа
летательного аппарата, его конструкции и назначения.
Уместно сказать, что подобные курсы создаются очень редко. Объяс-
няется это прежде всего сложностью вопроса. Курс прочности, в отличие
от курса строительной механики, помимо расчетно-теоретического аппа-
рата рассматривает совокупность вопросов, связанных с особенностями
конструкции, ее технологии и эксплуатации. Изложение этих вопросов в
правильном сочетании предъявляет к труду авторов очень высокие тре-
бования, выполнение которых далеко не всегда под силу даже хорошо
подобранному коллективу.
Большую роль в расчетах на прочность играет элемент ответствен-
ности. Ясно, что общие суждения, связанные с подсчетом напряжений,
с определенными математическими оценками, в частности с пренебреже-
нием теми или иными величинами в промежуточных выкладках, по сути
говоря, ко многому не обязывают. Даже в том случае, когда они сомни-
тельны, их легко оправдать (как это обычно и делается) выражениями:
«положим, что», «можно принять» и т. п. Все погрешности и допущения
в подобном анализе могут быть перекрыты введением запаса прочности,
а наиболее грубые — выявлены на стадии предварительных испытаний
конструкции.
Что же касается выбора величины коэффициента безопасности, то
всякие рекомендации по этому вопросу являются достаточно ответствен-
ными, а главное — очень трудными. Для того чтобы их дать, надо учи-
тывать и современный уровень технологии, и опыт, который накоплен в
области создания подобных конструкций, и те последствия, которые
влечет за собой выход из строя рассматриваемого узла, и многие другие
обстоятельства.
9
Наконец, в вопросах создания курсов прочности большую роль
играет скоротечность тех изменений, которые претерпевают некоторые
области техники. Поэтому курс прочности быстро устаревает, тогда как
курс строительной механики может жить десятилетиями.
Все сказанное выше относится и к вопросам ракетной техники с той
лишь разницей, что здесь перечисленные методические и технические
трудности приобретают наибольшую остроту. Современная баллистиче-
ская ракета представляет собой тонкостенную конструкцию одноразо-
вого действия. К ее элементам далеко не всегда применим расчет по
упругим напряжениям. В ряде случаев допускаются и пластические
деформации, и местная потеря устойчивости. Выбор расчетных схем
тесно связан с вопросами теплопередачи и динамики. Все это в целом
создает комплекс проблем, трудно поддающихся взаимной увязке и си-
стематике.
Если курс по расчету ракет на прочность попытаться построить в
духе традиций строительной механики, то это сузило бы поле зрения
читателя и могло увести его от важнейших вопросов, непосредственно
связанных с практическими расчетами. С другой стороны, форма изло-
жения, свойственная немногим курсам прикладной прочности, также не
может быть признана приемлемой. В этом случае не была бы представ-
лена совершенно необходимая общетеоретическая база. Кроме того,
возникла бы опасность, что при продолжающемся бурном развитии ра-
кетной техники курс устареет, не появившись на свет.
Авторы представленного пособия, хотя и назвали свой труд «Основы
строительной механики ракет», выбрали форму изложения, промежуточ-
ную между строительной механикой и расчетом на прочность. С одной
стороны, изложению предпослана солидная общетеоретическая основа,
с другой, — уделено большое внимание особенностям конструкции, си-
ловым схемам, вопросам выбора расчетной схемы и назначению коэф-
фициента безопасности. Естественно, что это потребовало экскурса в
смежные с ними области температурных и динамических расчетов.
Попытка авторов настоящего пособия не обходить трудных вопросов,
а по мере возможности осветить их заслуживает внимания и обязывает
нас — читателей быть снисходительными к возможным недостаткам
работы. Естественно, что в дальнейшем курс будет развиваться и совер-
шенствоваться. Однако уже в настоящем виде он представляет не толь-
ко методическую ценность учебного пособия, но имеет в своей идейной
основе все данные и для того, чтобы занять почетное место среди книг
(инженера-проектанта и расчетчика.
проф. В. И. Феодосьев
ГЛАВА I
МЕХАНИКА ДЕФОРМИРУЕМЫХ ТЕЛ
§ 1. ОСНОВНЫЕ ПОНЯТИЯ и УРАВНЕНИЯ
Напряжения. Напряжения характеризуют уро-
вень интенсивности внутренних сил в материале
конструкции. Напряжения не обязательно являют-
ся следствием действия приложенных к телу
внешних сил. Они могут быть результатом темпе-
ратурных деформаций или технологических про-
цессов производства. В последнем случае их
называют остаточными напряжениями. Изучение
влияния остаточных напряжений на прочность
конструкций является специальной задачей, которая
в данной книге не затрагивается. С теорией оста-
точных напряжений читатель может ознакомиться
в книге [18]. В дальнейшем предполагается, что
начальные остаточные напряжения в материале
рассматриваемых конструкций отсутствуют, т. е.
что существует такое начальное состояние, когда
напряжения равны нулю. В этом случае можно
считать, что напряжения являются следствием дей-
ствия внешних сил и температурных полей.
По определению, напряжение есть сила, отне-
сенная к единице площади поверхности, разделя-
ющей тело на две части. Если через dS обозначить
площадь элементарной площадки на этой поверх-
ности, а через dR — приложенную к ней силу, то
напряжение
dR
dS
Вектор о зависит не только от положения эле-
ментарной площадки на рассматриваемой поверхно-
сти , но и от ориентации этой площадки в про-
странстве, т. е. от направления вектора нормали п к
—>
площадке dS. Вектор o' можно разложить на две вза-
имно перпендикулярные составляющие: вдоль норма-
ли к площадке и в плоскости этой площадки
(рис. 1,1, а). Эти две составляющие соответствуют
нормальному напряжению ол и тангенциальному т.
Модуль вектора напряжения о= V + т2 .
11
Тангенциальное напряжение, в свою очередь, можно разложить по
любым двум направлениям в плоскости площадки.
Чтобы полностью определить напряженное состояние в точке тела,
достаточно рассмотреть проекции на координатные оси х, у, z векторов
напряжений, действующих на площадках, параллельных координатным
Рис. 1.1
плоскостям. Обозначим через ох, тху, txz нормальную и тангенциальные
составляющие напряжения на площадке х = const (параллельной коор-
динатной плоскости yz, рис. 1.1,5). Первый индекс в записи касательных
Рис. 1.2
напряжений характеризует поло-
жение площадки, в которой лежит
вектор напряжения, второй — на-
правление этого вектора. Для
площадки у = const составляющие
напряжения будут ow, хух, xyz, для
площадки z = const соответственно
oz, tzx, Tzy. Введенные таким об-
разом составляющие напряжения
можно представить в форме мат-
рицы
Хух бу Xyz
Х?Х XZ4 ^Z
(LI)
Вследствие парности касатель-
ных напряжений (хху = хух, х2У =
= ху2* хХ2 = х2Х) матрица (1.1) яв-
ляется симметричной.
Из равновесия бесконечно малой пирамиды, боковые грани которой
параллельны координатным плоскостям, а основанием является пло-
щадка с заданным направлением нормали п (рис. 1.2), можно получить
известные уравнения Коши [15]:
xxyl + oytn + x2yn = Y, (1.2)
хх21 + хугт + в2п = Z.
Здесь I = cos (n, х), т. = cos (п, у), [п = cos (п, z) — направляющие ко-
синусы нормали п к площадке, для которой определяется вектор напря-
жения o', а X, У, Z — проекции этого вектора на оси координат.
+ V = Х’
12
Если для данной точки заданы составляющие напряжений (1.1), то
по формулам (1.2) можно определить компоненты вектора напряже-
ния о для любой площадки, проходящей через эту точку. Модуль векто-
ра напряжения
О’ = /X2 т У2 + Z2.
Нормальное напряжение
о п = XI У/тг Zti.
Абсолютное значение касательного напряжения
т = <т2 — •
Систему уравнений (1.2) можно рассматривать как преобразование
вектора п с компонентами Z, т, п в вектор ст с компонентами X, У, Z при
помощи матрицы То. Матрица, преобразующая один вектор в другой,
называется тензором [49]. Таким образом, матрица (1.1) — симметричный
тензор напряжений.
Главные напряжения определяются как корни кубического уравнения
— о3 + J^2 + J2e + J3 = О,
где J2, J3— инварианты тензора напряжений [15]. Через главные на-
пряжения ох, о2, они выражаются формулами:
*/1 — 0^1 0^2 4“ ^з» *^2 = ^1^2 ^2^3 ^1» *Аз ~ ^1^2^3*
При этом
‘Г + O'z = ^1 + ^2 + П3-
Средним напряжением называется величина
= = + + (1-3)
о о
Тензор напряжений можно
представить в виде суммы двух тензоров
ТО = ТС + DOi
где
ос О О
О ос О
О 0 ос
(1.4)
Do
°х Хху Т
^УХ «у Хуг
Xzy 6 2
(1.5)
Тензор Тс называется тензором всестороннего растяжения, а тензор
Do —девиатором напряжений; последний играет важную роль в теории
пластичности.
Деформации. Предположим, что в начальном, ненапряженном со-
стоянии произвольная точка М тела имела координаты х, уу г. Рассмот-
рим перемещения точки от действия внешних сил или температурного
поля. Пусть и, v, w — проекции полного перемещения точки М на коор-
динатные оси х, у, z (рис. 1.3, а). Очевидно, и, v, w можно рассматри-
13
вать как функции координат х, у, z точки Л4 до деформирования тела.
После деформирования точка М будет иметь координаты
£ = х + и(х, у, z),
П = У + v(x, у, z), (1.6)
C = z + w(x, y, z).
В формулах (1.6) независимые переменные х, у, z играют роль пара-
метров, как бы привязанных к точке М тела. Они позволяют отличать
точку М от других точек тела в процессе всего деформирования. Описа-
ние деформаций сплошной среды с помощью независимых переменных
х, у, z, которые являются координатами точек среды в начальном ее
состоянии, соответствует описанию в так называемых координатах Лаг-
ранжа. (Координаты Лагранжа х, у, z называют еще материальными
координатами.) В теории упругости такой способ описания является
обычным, в отличие от гидродинамики, где чаще пользуются координа-
тами Эйлера, фиксированными в пространстве.
Возьмем теперь другую точку N тела, бесконечно близкую к точке Л4,
с начальными координатами x + dx, y+dy, z + dz. После деформирования
координаты точки N будут (рис. 1.3,6):
£ + = х 4- dx + и (х + dx, у + dy, z + dz),
т) + dx\ = у 4- dy + v (х + dx, у + dy, z + dz), (1.7)
£ + d£ = z + dz + w (x 4- dx, у + dy, z + dz).
Согласно правилам дифференциального исчисления
d£ = (1 + dx + ^-dy+ ^-dz,
\ dx / dy dz
di] = — dx 4- (1 + —A dy -j- dz, (1.8)
dx \ dy J dz k ’
dw , . dw , . / . , dw \ «
=-----dx-\------dy+ 1 H--------]dz.
dx dy \ dz J
Квадрат длины отрезка MN: до деформирования dsl =dxi-\-dyt +dz2, пос-
ле деформирования ds2 = + di]2 -+- d^2. На основании формул (1.8) по-
лучим
14
ds2 = ds20 + 2 (8XV. dx2 + e,yy dy2 4- e„ dz2 + exy dx dy 4- ei,z dy dz 4- егл. dz dx),
(1.9>
где
du । dv t du du l dv dv t dw dw
—j— -j— t
dy dx dx dy dx dy dx dy
(1.10)
Другие аналогичные величины легко получить из формул (1.10) с
dx
помощью круговой перестановки (u, v, w) и (х, у, z). Пусть / = -, т =
ds0
= и п = —---------направляющие косинусы отрезка MN до деформиро-
вав ds0
вания. Из формулы (1.9) следует
•- 2 (&хх12 + Еуут2 4- szzn2 + еху1т 4- eyztnn 4- ezxnl). (1.11)
Считая величины ехх, гуу, ... , е2Х весьма малыми по сравнению с
единицей и пользуясь приближенной формулой 1^1 + а 1 + для ма-
лых а, получим из выражения (1.11)
е = ----1 = ехх12 4- &уут2 + егго2 4- £ху1т 4- e,yzmn 4- ezxnl. (1.12)
ds0
Формула (1.12) определяет относительное удлинение произвольного
отрезка с направляющими косинусами /, т, п через величины ъхх, ь ...
... , е2Х. Поэтому эти величины называют компонентами деформации. Их
выражение существенно упрощается, если считать, что все частные про-
изводные функций u, v, w по х, у, z весьма малы по сравнению с едини-
цей. В этом случае в формулах (1.10) можно отбросить слагаемые с квад-
ратами и произведениями этих производных. Полученные таким образом
линеаризованные выражения для компонентов деформаций обозначим,
чтобы отличать их от выражений (1.10), через ех, е , е2, у , уу2, у2х:
du dv dw
x dx y dy 2 dz
du , dv dv , dw
Уху +
(1.13>
Y zx 4xz ' a? *
dx oz
Это известные выражения для относительных удлинений и сдвигов
в линейной теории упругости. В дальнейшем во всех случаях, когда нег
специальных оговорок, будут рассматриваться линейные уравнения тео-
рии упругости. Это означает, что уравнения равновесия будут состав-
ляться для исходной, начальной геометрии рассматриваемого тела и
выражения для деформаций приниматься в форме (1.13). Читателю, ин-
тересующемуся нелинейной теорией упругости, советуем обратиться к
книге В. В. Новожилова [60].
1 5
Матрица
ех 1 2 Уху 1 2 Yxz
1 2 Уух гу 1
1 2 ^zx 1 2 ег
(1-14)
является симметричным тензором, аналогичным ранее рассмотренному тен-
зору напряжений. Все формулы, справедливые для тензора напряжений,
можно переписать для тензора деформаций путем замены <тА. на ех, на еу,
<тг на е2, хху на -Ь Yw, хуг на -i- ууг, хгх на -Ь у2х. Так, главные удли-
нения определяются из кубического уравнения
— е3 4- + J2e + J3 = О,
(1-15)
где J3 — инварианты тензора деформаций. Первый инвариант J± =
= 61 -г е2 т е3 = + еД е2 равен относительной деформации элемента
объема тела.
Средней деформацией называется величина
ес= V (бх + ^ + е,).
О
(1.16)
Введение этой величины позволяет представить тензор деформаций
в виде суммы двух тензоров подобно тому, как это было сделано для
тензора напряжений.
Девиатор деформаций имеет вид
Уравнения механики деформируемого тела. Деформации 8Х, ер, 82, \ху,
у^2, Угх являются обобщенными перемещениями для напряжений вх, <зу, в2,
тху, xyz, Xzx* Работа, которую необходимо затратить, чтобы сообщить эле-
ментарному параллелепипеду dx, dy, dz, вырезанному из тела, дополни-
тельные деформации 6ех, бе^, ... , бу2Х, равна
(стхЧ + ^6е!/+ ... dxdydz. (1.18)
Пусть на рассматриваемое тело действуют распределенные объемные
нагрузки (силы тяжести, силы инерции) с составляющими по осям коор-
динат рх, ру, pz и поверхностные нагрузки с составляющими Хп, Yn, Zn
(рис. 1.4). Объемные нагрузки относятся к единице объема тела, а по-
верхностные — к единице площади его поверхности. Кроме заданных
внешних нагрузок к поверхности тела или части ее могут быть прило-
жены силы реакций опорных связей. С помощью таких связей тело мо-
жет быть или закреплено в пространстве, или точкам его поверхности
могут быть сообщены какие-либо перемещения ur, vr, wr. Во всех слу-
чаях будем считать связи идеальными, полагая, что силы реакций свя-
зей нс совершают работу на любых возможных перемещениях точек
поверхности тела, к которым приложены эти силы. Идеальные опорные
связи можно представить в виде абсолютно жестких стерженьков, при-
16
крепляющих тело к основанию, внешнему по отношению к рассматри-
ваемому телу. Это основание может быть или неподвижным, или иметь
заданные перемещения.
Внутри рассматриваемого деформируемого тела возможными пере-
мещениями являются любые функции би, 6у, 6су, которые можно рас-
Рис. 1.4 Рис. 1.5
сматривать как малые изменения (вариации) действительных переме-
щений u, v, w (рис. 1.5). Объемные нагрузки рх, ру, pz на возможных
перемещениях би, 6v, 6w совершают работу
6/?r = JJj (pxbu + pyt>v + pzbw)dxdydz. (1.19)
Поверхностные нагрузки Хл, Ул, Zn соответственно совершают работу
б/?2 = С f (Хп би + Yn 6v + Zn 6w) dS, (1.20)
где 6u, 6v, 6w — возможные перемещения точек поверхности тела.
Интегрирование производится по поверхности тела, где приложены
внешние нагрузки Хл, Ул, Zn, так как силы реакций связей не совершают
работу на возможных перемещениях. Возможным перемещениям du, 6v,
соответствуют возможные изменения деформаций, т. е. их вариации
& дби А dbv & dbw , дби
бег =----, бе =-------, ... , оу2Х =------1-----
дх у ду дх дг
(1.21)
В дальнейшем будет часто встречаться термин «вариация». Это не
значит, что читатель должен знать вариационное исчисление. Достаточ-
но помнить, что вариацией называется малое возможное изменение
какой-либо величины или функции. В каком смысле надо понимать
слово «возможное» будет оговорено в каждом конкретном случае. При-
менительно к вариациям би, би, бш функций и, у, w уже было сказано,
что эти вариации надо рассматривать как малые возможные перемеще-
ния, совместные с опорными связями.
Согласно соотношению (1.18), полная работа, затрачиваемая на до-
полнительное деформирование всего объема тела,
бл = Ш + ••• + tzx^zx)dxdydz. (1.22)
На основании принципа возможных перемещений механики, условие
равновесия деформированного тела можно представить в виде одного урав-
нения
б4 = 67?х + б7?2. (1.23)
Уравнение (1.23) должно быть справедливо для любых возможных
перемещений би, би, 6ш.
2 Зак. 96
17
Из уравнения (1.23) можно получить дифференциальные уравнения
равновесия элементарного параллелепипеда, вырезанного из тела, и
граничные условия на поверхности. Для этого надо воспользоваться из-
вестными формулами интегрирования по частям тройных интегралов:
-yL dx dy dz,
dx dy dz = J срфт dS — ф dx dy dz,
УУУ dX(ty dz “ J — jyj ty-^-dxdydz.
(1.24)
В этих формулах тройные интегралы берутся по объему тела, ограничен-
ному поверхностью S, а двойные — по этой поверхности; /, т, п — напра-
вляющие косинусы внешних нормалей к поверхности. При этом IdS = dSyz,
mdS — dSxz, ndS = dSxy—проекции площадки dS поверхности на коор-
динатные плоскости.
Формулы (1.24) позволяют преобразовать выражение (1.22) для 6Л.
Интегрируя по частям интегралы вида
и группируя слагаемые .с одинаковыми множителями, получим подробную
запись уравнения (1.23):
т + хгхп) би + (хху1 + вут + х2уп) bv +
+ Ы + V + «.») ta] 4S - у j [( + ч
j_ ( д^ху । &ау 1 д^У \ I
ду dz J
-^-'\?!w\dxdydz= bRx-\i>R„. (1.25)
dz J J
\ дх
ду
Выражения для 6/?i и б/?2 даны формулами (1.19), <1.20). Так как
вариации би, 6у, 6w внутри объема тела произвольны, то из уравнения
(1.25) следует, что должны быть равны соответствующие множители при
би, 6w и 6w в выражениях, стоящих под знаками тройных интегралов в
левой и правой частях этого уравнения. Следовательно,
д^х I д^ух I ^zx Ip _ о
дх ду dz ’ГРх
+ +Ру = 0,
дх ду dz
d^XZ I &*У2 I d&Z I p Q
dx dy dz z )
(1.26)
Это дифференциальные уравнения равновесия элемента объема тела.
Приравнивая соответствующие множители при би, би, bw в двойных
интегралах, стоящих в левой и правой частях уравнения (1.25), получим
силовые граничные условия на поверхности тела:
<М + Хухт + Х2хп = хп,
xxyl + <зут + x2yti = Yn,
ххг1 + хугт + о/г = Zn. .
(1-27)
18
На участках поверхности тела, где приложены силы реакций непо-
движных опорных связей, могут быть или геометрические граничные
условия u = y = w = 0, если опорные связи полностью запрещают переме-
щения, или смешанные условия, если опорные связи препятствуют
перемещениям только в одном или двух направлениях. В каждом част-
ном случае эти граничные условия легко составить. Всего в каждой
точке поверхности тела должно быть три граничных условия. Если, на-
пример, опорные связи препятствуют только перемещениям в направле-
нии оси г, то соответствующие граничные условия будут
W = 0, ох1 + хухт + хгхп = Хп, хху1 4- <зут 4- ггуп = Yп.
На поверхности или ее части могут быть также заданы перемещения
ur, vr, wr. В этом случае на той же части поверхности 6u = Sy = 6w = 0.
Уравнения вида (1.23) иногда называют вариационными, но точнее
их называть уравнениями в вариациях,, так как в общем случае в таких
уравнениях имеют смысл только величины 64, 6/?! и 6/?2, а не Д, и/?2.
Только при существовании потенциальной энергии деформаций и усло-
вии потенциальности внешних нагрузок рх, ру, pz, Хп, Yn, Zn можно, как
будет видно из дальнейшего, определить сами функции Д, /?2 и
представить уравнение (1.23) в форме вариационного уравнения
6(Д-/?1-/?2)=0.
Между уравнениями в вариациях и вариационными уравнениями су-
ществует такое же различие, как между уравнениями принципа воз-
можных перемещений механики и условием экстремума полной потен-
циальной энергии.
Уравнения в вариациях напряжений. Дадим напряжениям вх, oyt
az, ... , rzx малые приращения (вариации) 6сгх, 6ву, ... , 6т2х и потребуем,
чтобы суммарные напряжения вх + 6ах, ву + бсг^, ... , xzx Д- 6т2х были
статически возможными, т. е. удовлетворяли уравнениям равновесия и
силовым граничным условиям. Это означает, что возможные вариации
напряжений 6ах, Ъвуу . .. , 6т2Х не должны изменять величин внешних сил,
действующих на тело.
Из уравнений равновесия (1.26) следует, что
дЬах • д&Хух , — л 1
. т~ .— . - . в
дх ду dz
д(>Тху дх . дЪау _ ду д&с2у dz = 0, (1-28)
ддтхг 1 1 д6а2 = о,
дх ду dz 1
а из граничных условий (1.27) на части поверхности тела, где заданы
внешние нагрузки,
4- ^ухт 4- 6т2Ал = 0, '
bxxyl + Ьвут 4- Ъхгуп = О,
Ъхх21 4- бт^/п 4- 6сг2п = 0.
(1.29)
Вычислим интеграл, аналогичный интегралу (1.22), но от суммы
произведений компонентов деформаций на вариации напряжений
JjJ>(ex6ox4-ei,6^4- ••• +yzx^zx)dxdydz. (1.30)
Заменяя 8Х, гу,..., у1Х их выражениями через производные от переме-
щений по формулам (1.13) и интегрируя по частям согласно формулам
(1.24), найдем, что тройной интеграл, в силу уравнений равновесия
(1.28), обратится в нуль, а двойной интеграл с учетом соотношений
2* 19
(1.29) не будет равен нулю только на той части поверхности, где зада-
ны перемещения.
Заданные на поверхности перемещения могут осуществляться путем
принудительного перемещения опорных связей, прикрепленных к телу.
Возможность задания этих перемещений не противоречит ранее сделан-
ному предположению об идеальности связей, так как при заданных пе-
ремещениях точек поверхности тела вариации этих перемещений должны
полагаться равными нулю, и, следовательно, силы реакций связей не
будут совершать работу.
Обозначим через ur, vr, wr заданные перемещения на какой-либо ча-
сти поверхности тела и через Хг, Уг, Zr — составляющие соответствую-
щей поверхностной нагрузки реакций связей, с помощью которых осу-
ществляются перемещения ur, vr, wr. С учетом этих обозначений по-
лучим
J У J (ех б®, + + ... + ytxbxzx)dxdydz =
= [ J (ur дХг + vr dYr + wr 6Zr) dS, (1.31)
где 6Xr, bYn 6Zr— приращения составляющих сил реакций связей при
изменении (варьировании) напряжений в теле;
6ХГ = 6вх1 + Ьгухт + дт2Ал, 6УГ = бтХА/ + + Ъг2уп\
6Zr = дтх21 + 6гу2 т + 6а2п.
Если связи прикрепляют рассматриваемое тело к абсолютно жестко-
му основанию, то работа сил реакций таких связей на действительных
перемещениях точек их приложения равна нулю и правая часть урав-
нения (1.31) обратится в нуль. В этом случае
У J J (ех 6of.v + еу ЪОу -Г • • • + угх бтJ dx dy dz = 0. (1.32)
Как будет видно из дальнейшего, уравнение (1.32) позволит полу-
чить уравнения типа уравнений метода сил, рассматриваемых в курсе
сопротивления материалов [94]. Из уравнения (1.32) можно также полу-
чить уравнения совместности деформаций (уравнения Сен-Венана). Под-
робное рассмотрение этого вопроса читатель может найти в работе
Л. С. Лейбензона [54].
§ 2. УПРУГИЕ ТЕЛА. ВАРИАЦИОННЫЕ УРАВНЕНИЯ. ТЕМПЕРАТУРНЫЕ
НАПРЯЖЕНИЯ
Потенциальная энергия упругого тела. До сих пор не делалось каких-
либо предположений о законах деформирования. Полученные в преды-
дущем параграфе уравнения справедливы для случая малых деформа-
ций любого сплошного тела.
Инженеру наиболее часто приходится иметь дело с упругими телами.
Отличительной особенностью упругих тел является обратимость процес-
сов деформирования. Считается, что в упругой области работы мате-
риала полностью отсутствуют остаточные деформации. Это означает, что
работа внешних сил переходит в потенциальную энергию деформаций.
Так как деформации ех, ъу,..., yZx являются обобщенными координатами
для напряжений ох, ву,..., т2Х, то, в соответствии с определением потен-
циальной энергии в механике, назовем удельной потенциальной энергией
деформаций упругого тела функцию F, обладающую тем свойством,
что [54]
„ _ dF , __ dF ~ 3F /су
стх — f cff. — , ... , т_х — е (2.
деу &УгХ
20
Если функция F прямо не зависит от координат х, у, z, то упругое
тело называется однородным. Зависимость напряжений от деформаций
в таком теле будет одинаковой для всех точек тела. Соотношения (2.1)
можно рассматривать как математическую формулировку свойства
упругости. С учетом этих соотношений удельная работа напряжений на
вариациях деформаций будет равна
+ ••• = ••• <2-2>
°1ZX
Назовем вариацией функции F (гх, гу, ... , угл) приращение этой функ-
ции при малых приращениях аргументов на бех, бе^, ... , бу2х, определя-
емое по правилу вычисления полных дифференциалов,
6F = F (ех + бех, гу + Ъгу, ... ,угх + бу„) — F (ех, еу,
dF
дех
деи *
4
дугх 2
• • » Угх)
(2.3)
Следовательно, удельная работа, затрачиваемая на приращения дефор-
маций., определяемая формулой (2.2), равна вариации (приращению)
удельной потенциальной энергии деформаций 6F.
Полная потенциальная энергия деформаций упругого тела будет
Ф = JJJ Fdxdydz. (2.4)
Полная работа, затрачиваемая на дополнительное деформирование тела и
определяемая формулой (1.22), может быть представлена в виде
дЛ = JJ j bFdxdydz = 6Ф. <2.5)
Таким образом, для упругого тела выражение б Л имеет смысл вари-
ации потенциальной энергии Ф. Если при деформациях тела величины
внешних сил ру, р2, Хп, Yni Zn не изменяются, т. е. силы являются
потенциальными, то работа их на возможных перемещениях, задаваемая
формулами (1.19) и (1.20) будет
+ pyv 4- рги-) dx dy dz, (2.6)
б/?2 = б Jj (Х„и + Ynv 4- Znw) dS.
Следовательно, для упругого тела при потенциальных внешних силах
основную формулу (1.23), полученную на основе принципа возможных
перемещений механики, можно представить в форме вариационного урав-
нения
6П = 0, (2.7)
где
П = Ф — j J J (pxii 4- pyv 4- рг&) dx dy dz —
-^(Xnii + Ynv + Znw)dS. (2.8)
Величина П имеет простой физический смысл. Это полная потенци-
альная энергия механической системы, состоящей из упругого тела и
приложенных к нему внешних потенциальных сил. Знак минус перед
интегралами появился потому, что направление внешних сил совпадает
с направлением перемещений u, v, w и, следовательно, при увеличении
перемещений уменьшается потенциальная энергия этих сил.
21
Из формулы (2.7) следует, что в положении равновесия полная энер-
гия системы имеет стационарное (экстремальное) значение. Более под-
робный анализ показывает, что оно соответствует минимуму.
Вариационное уравнение (2.7) называют вариационным
уравнением Лагранжа [54]. В отличие от более общего уравне-
ния (1.23) в вариациях вариационное уравнение Лагранжа справедливо
только для упругого тела, нагруженного потенциальными внешними
силами.
Вариационное уравнение Лагранжа лежит в основе приближенного
метода Ритца. Суть этого метода состоит в том, что выражения для
перемещений задаются в виде рядов с неопределенными коэффициента-
ми, которые затем определяются из условий экстремума полной потен-
циальной энергии П как функции этих коэффициентов. Изложение этого
метода и его различные применения можно найти в книгах [54, 66].
Зависимости между напряжениями и деформациями, определяемые
формулами (2.1), могут быть нелинейными. Такие зависимости будут
рассматриваться в следующем параграфе и при рассмотрении теории
пластичности.
Однако в упругих телах при малых деформациях можно, как прави-
ло, ограничиваться рассмотрением линейных зависимостей между на-
пряжениями и деформациями. Тела, для которых справедлива линейная
связь между напряжениями и деформациями, называются линейно-упру-
гими телами, или телами Гука.
Свойства линейно-упругого тела. Для линейно-упругого тела удель-
ная потенциальная энергия F выражается в форме однородного квадра-
тичного полинома независимых переменных — деформаций ет, еу,..., угг-
В общем виде без учета температурных деформаций удельную по-
тенциальную энергию линейно-упругого тела можно записать в форме:
F = Y (Д11 ех + + а33ег + аиУ2ху + аыЧ2уг + fleeY« + ^12^у +
+ 2ai3exe2 + 2я14еА.уХ{/ + 2a16exYl;2 + 2а1вгхугх + 2агзерег + 2апгууху +
+ 2а25М;/г + 2а2<£уУгх НН 2о34е2у^ + 2a3iezyyz 2a3ee2y2V -1- 2а^ухуууг +
-Н 2a46Yxz/Yz.v + 2аЪйуугугх), (2.9)
где а119 а22, .. . ,а56 —коэффициенты, зависящие от упругих свойств тела.
Для однородного тела это константы. В общем случае число коэффициен-
тов упругости равно 21.
На основании формул (2.1) получим:
= ап^х + <*12^ + ад 4- апуху ~ а^уу2 + а1ву2Х,
~ а22гу т ^23ez “Ь ~~ fl2eYzx> /9
Xzx ^4flYxy "4" ^66Yzx
Симметрия матрицы коэффициентов в формулах (2.10) вытекает
из формы записи выражения (2.9) для потенциальной энергии. Следо-
вательно, для любого линейно-упругого тела связь между напряжениями
и деформациями должна выражаться симметричными формулами или,
точнее, с помощью симметричной матрицы коэффициентов.
Рассмотрим более подробно некоторые общие свойства удельной по-
тенциальной энергии линейно-упругого тела.
Для однородного многочлена второй степени (2.9) справедливо тож-
дество Эйлера
2F _ SL- е, -1L
дех деу
dF
Д уzx
дУгх
(2.U)
22
из которого, на основании соотношения (2.1), следует формула Клапейрона
F = ~~ (вхех + + . .. + ^2XY2x) • (2.12)
Формулу (2.11) легко проверить непосредственно. Удельную потенци-
альную энергию можно выразить или через деформации F = F (ех, е^, ...
... , у2Х), или через напряжения F = F (ох, ву, ... , т2х). Следовательно,
можно получить уравнение
(ех, ... , + F (ох, <sy,..., xzx) = <тЛ + ст^Ц- ... + xzxyzx. (2.13)
Вычислим вариации (приращения) слагаемых в обеих частях уравне-
ния (1.45) при приращении деформаций и напряжений на
6ех, Ъгу, ..., 6уг/, ^х, toy, .... Чх-
Имеем
. „ х dF х । dF А 1 dF *
6F<C- ........ь,) - у- 4+ у; «'. + -г
или с учетом формул (2.1)
6F (ех, еу, , у2х) = охЪгх + <fytey + • • • + (2.14)
6F (ох. чу, ... , тгх) = 6<тх + -%- ^у + • • • + 6г2д. (2.15)
дбх Обу и^2Х
Вариации произведений вхех, вуъу и т. д. определяются по формулам,
аналогичным формулам дифференциального исчисления
6 (gaex) = (ох + 6<тх) (ех + 6вх) — стхех = ох6ех + ех6ох, (2.16)
так как произведение бахбех—величина малая высшего порядка.
Варьируя теперь левую и правую части уравнения (2.13), получим,
с учетом формул (2.14), (2.15) и (2.16),
^-6сгх+^6(Т,+ ... +^_6тгх = ехб<гх+8^+ ... KYZX4X. (2.17)
д(5у dx2X
Так как вариации So'x, дву1 ..., 6х2Х независимы друг от друга, то из
уравнения (2.17) следует, что
dF dF dF
er = ---’ = ---» • • •, Y?r — - •
d(ix do у dxzx
В отличие от формул (2.1) зависимости (2.18) справедливы только
для линейно-упругого тела. Эти зависимости позволяют уравнение (1.32)
в вариациях написать в форме вариационного уравнения
6Ф = 0, (2.19)
где
ф = J J J F ^х’ ау' ' dxdydz (2.20)
есть полная потенциальная энергия, выраженная через напряжения.
Из уравнения (2.19) следует, что полная потенциальная энергия ли-
нейно-упругого тела при истинных напряжениях имеет экстремум. Мож-
но показать, что этот экстремум соответствует минимуму. Другими
словами, истинные напряжения отличаются от статически возможных
тем, что при истинных напряжениях потенциальная энергия тела, выра-
женная через напряжения, имеет минимум. Это положение называется
вариационным принципом Кастилиано, а уравнение (2.19) — вариа-
ционным уравнением Кастилиано. Оно позволяет находить
23
приближенные решения задач теории упругости, задаваясь напряже-
ниями в форме функциональных рядов с неопределенными коэффициен-
тами. Заданные таким образом напряжения должны удовлетворять
дифференциальным уравнениям равновесия и силовым граничным усло-
виям на поверхности тела. Коэффициенты рядов определяются из усло-
вий экстремума потенциальной энергии (2.20) как функции этих коэф-
фициентов [54, 66].
Вместо вариационного уравнения (2.19) для решения задач теории
упругости можно воспользоваться уравнением в вариациях (1.32). Пусть
^(О), а(о), . .. , г— какая-либо статически возможная система напряжений,
удовлетворяющая неоднородным дифференциальным уравнениям равновесия
(1.26) и неоднородным граничным условиям (1.27).
Однородные уравнения (1.26) при рх = ру = рг = 0 и однородные гра-
ничные условия (1.27) при Хп = Yп = Zn = 0 имеют решения, отличные
от тождественного нуля. Обозначим эти решения через crW, ... , т(*],
k = 1, 2, 3 ... В строительной механике стержневых систем им соответ-
ствуют напряжения от единичных значений лишних неизвестных.
Истинные напряжения будем искать в виде
4- 2ХЛА>; = <^0) + °* = oi0)+lx^k}>
k k k
+ Sх.ф s. = Ч? + £W « + sx»4"
k k k
Коэффициенты %i, Л2, A3,... , Aft,... играют роль искомых лишних не-
известных. Так как упругое тело является системой с бесконечным чис-
лом степеней свободы, то число таких неизвестных, вообще говоря,
бесконечно большое. В практических же расчетах ограничиваются отно-
сительно небольшим числом этих неизвестных.
Из линейных зависимостей между напряжениями и деформациями для
каждой группы напряжений можно найти соответствующие им деформа-
ции. Пусть напряжениям о^0), о^0), ... , соответствуют деформации e(v0),
е^0), ... , у^, а напряжениям <yW, — деформации е^, .. .
. ..,у(*). Тогда полные деформации согласно (2.21) будут
= е(0)3+ ъу = Ч0> + : Y- = Y« + ЕХ^- (2.22)
k k k
Напряжения <yW, ... , т^, где i—любое значение индекса k, можно
рассматривать как вариации напряжений, так как они удовлетворяют од-
нородным уравнениям (1.28) и (1.29).
Полагая
• • • - Чх = т1х (2.23)
и учитывая соотношения (2.22), из уравнения (1.32) получим
Х1Дд + X2&i2 + ... + Xk\ik + ... + Д/о = 0. (2.24)
Уравнение (2.24) является записью бесконечной системы уравнений,
так как индекс i принимает все значения от 1 до бесконечности.
Если в суммах (2.21) ограничимся п слагаемыми (k = 1, 2, ... , п и
4 = 1,2, ... , и), то из уравнения (2.24) в развернутом виде получим сис-
тему
Х1Дц + Х2Д12 + ... + Х„Д1п -f- Д1о = 0,
ХхД21 + Х2Д22 4- • •. + Хп\2п + Д20 =0, (2.25)
ХхДп1 + х2дл2 + ... + Хп&пп + Дл0 = о, -
(2.21)
24
где
Alft = JJJ + (T<j>eW + ... + т<^<*>) dxdydz, (2.26)
A,0 = J J j (®(;40) + °y40) + • • • + TM) dxdydz. (2.27)
Из уравнений (2.25) — (2,27) в качестве частных случаев легко получить
уравнение метода сил для стержневых конструкций.
Температурные напряжения. Вызванные неравномерным нагревом и
силами реакций опорных связей, препятствующих температурному рас-
ширению тела, температурные напряжения можно определить путем
сведения температурной задачи к статической, вводя фиктивные объем-
ные и поверхностные нагрузки [86].
Пусть Т — заданное распределение температуры, отсчитываемой от
начальной постоянной температуры То, и а — коэффициент линейного
расширения. Тогда чисто температурные деформации элемента тела, сво-
бодного от напряжений, будут ех = е1/=ez = a(T—То). Мысленно закрепим
в пространстве все точки тела, приняв перемещения u = v = w = 0. Тогда
полные деформации также будут равны нулю. Но деформации склады-
ваются из чисто температурных и от действия напряжений. Приравни-
вая нулю компоненты ех, ev, ez, уху, уу2, у2Х суммарной деформации,
можно определить напряжения, при которых перемещения всех точек
тела равны нулю.
В случае изотропного линейно-упругого тела эти напряжения равны
°х = ^ = О2=— fа , *ху = Хуг = Т2Х = 0, (2.28)
где Е — модуль упругости, ц — коэффициент Пуассона.
Этим напряжениям соответствуют объемные и поверхностные нагруз-
ки — реакции фиктивных связей, закрепляющих точки тела в простран-
стве. Эти нагрузки определяют из дифференциальных уравнений равно-
весия элемента тела (1.26) и силовых граничных условий на поверхно-
сти (1.27).
Из уравнений (1.26) находят фиктивные объемные нагрузки, соответ-
ствующие напряжениям (2.28):
(2.29)
В уравнениях (2.29) величины £, 1—2 ц и а не вынесены из-под знака
производных, так как при неравномерном нагреве они могут быть функ-
циями координат точек тела.
Из уравнений (1.27) определяют фиктивные поверхностные нагрузки
Xn = —Ea^=^-l,Yn = —Ea-^^-m,Zn^ — Ea^^-n. (2.30)
1 — 2р. " 1 - 2ц п 1 — 2ц V
Легко видеть, что эти нагрузки соответствуют фиктивному давлению
на поверхность тела, равному
р = Еа
T — Tq
1 — 2р ’
(2.31)
Пользуясь формулами (1.24) интегрирования по частям, можно до-
казать, что фиктивные объемные нагрузки (2.29) и фиктивные поверхно-
стные нагрузки (2.30) образуют в целом самоуравновешенную систему
сил.
25
Чтобы получить истинные температурные напряжения в рассматри-
ваемом упругом теле, необходимо дополнительно приложить к этому
телу найденные фиктивные объемные и поверхностные нагрузки с об-
ратным знаком, решить соответствующую статическую задачу и полу-
ченные напряжения сложить с напряжениями, определяемыми формула-
ми (2.28). Этот прием соответствует «снятию» фиктивных нагрузок. При
решении статической задачи необходимо, конечно, учитывать силы реак-
ций действительных опорных связей.
Пусть перемещения и напряжения, соответствующие решению стати-
ческой задачи, когда к телу приложены объемные нагрузки — рЛ, — ру>
— pz и поверхностные нагрузки — Хп, —Yn, — Zn, где рх, ру, р2, Хп,
Yn, Zn определены формулами (2.29) и (2.30), будут
й, V, й, —?„.
Тогда искомые перемещения и напряжения для рассматриваемой чисто
температурной задачи определяются формулами:
и = u, и = и, w = w\
а = — Еа —р Э ву — —Еа ——— + o'
А 1 —2|л х у 1 — 2р. у'
az = —Еа т~то. + 3;
2 1 —2р. 2
^ху ^ху* Xyz I'yz' Xzx ^zx‘
(2.32)
Если все точки тела нагреты до постоянной температуры Г, то, со-
гласно формулам (2.29), фиктивные объемные нагрузки рх = Py = Pz = ®,
а поверхностные фиктивные нагрузки Хп, Yn, Zn, согласно формулам
(2.30) и (2.31), соответствуют равномерно распределенному гидроста-
тическому давлению Еа(Т—То)/(1—2 р.). Чтобы снять эту фиктивную
поверхностную нагрузку, надо приложить к поверхности тела гидроста-
тическую нагрузку той же абсолютной величины, но противоположного
знака, т. е.
X = Еа .т~т9. I у = Еа -Г m, Zn = Еа T~Tq п. (2.33)
п 1 — 2|Л п 1 — 2р. rl 1 —2р V 7
Если тело не закреплено в пространстве или закреплено статически
определимым образом, то нагрузке, задаваемой формулами (2.33), бу-
дет соответствовать система напряжений, отвечающая равномерному
всестороннему растяжению:
= оу = 92 = Еа **у = = << = 0-
Суммарные действительные напряжения в теле, определяемые фор-
мулами (2.32), будут
crv = ау = а = — Еа T~~Tq- 4- Еа — ~ Г°- = 0, х = х — х = 0,
l-2u 1 — 2р. ху yz zx
т. е. равномерный нагрев свободного или статически определимым обра-
зом закрепленного тела не вызывает в нем температурных напряжений.
§ 3. ИЗОТРОПНЫЕ, ОРТОТРОПНЫЕ И СОСТАВНЫЕ УПРУГИЕ ТЕЛА
Однородное изотропное нелинейно-упругое тело. Такое тело имеет
одинаковые во всех направлениях упругие свойства. Следовательно,
выражение удельной потенциальной энергии через компоненты деформа-
26
ций ех, E?J,... , Yzx не Должно зависеть от ориентации координатной си-
стемы х, у, z относительно тела. Это означает, что в формулу для
удельной потенциальной энергии изотропного тела должны входить
только инварианты тензора деформаций. В общем случае потенциальная
энергия должна выражаться через три инварианта 1\, J3 или их ком-
бинации. В случае малых деформаций можно считать, что удельная
потенциальная энергия изотропного упругого тела зависит только от
величины квадрата первого инварианта тензора деформаций = (ех+
+ еу + Е2)2 и второго инварианта девиатора деформаций (1.17). В даль-
нейшем вторые инварианты девиаторов напряжений и деформаций будем
обозначать соответственно J (о) и 7(e), причем
J И = А + Д- Л = Д-1 (°х — Су)2 + к — аг)2 + (<Т2 — ох)2 -Г
О о
+ 6К, + ^ + О> (3-1)
J (е) = “б" [ (е* -е^2 + ~6г)2 + (£г — е^2 +
+ v^ + ^ + yL)]- (3-2)
Эти инварианты не зависят от величин среднего напряжения ас =
= — Ji (а) и средней деформации ес = — При равномерном гидро-
3 3
статическом давлении, когда J (а) = J (е) = 0, большинство конструкцион-
ных материалов деформируется как линейно-упругие тела, вплоть до весьма
высоких значений напряжений. Поэтому удельную потенциальную энергию
нелинейно-упругого изотропного тела можно представить в следующей
общей форме:
F = aJf(e)+/[J (в)], (3.3)
где а — константа, а / [J (е) ] — функция аргумента J (е).
. Так как
dJ 1 dj £ dJ j
де х д&у дг2
и
dJ 1 /о v dj 1 ул \
= ех-ес. —(2е^-ег-ех) =е -ес,
dJ 1 . .
dj __ 1 dJ _ 1 dj 1
духу ~ 2 Уху’ дууг ~ТУуг’ ~д^~^У2х
к df
то, обозначая —— =- f , получим:
dj
ох = 2aJi + (8Х — ес) хху = Д- yxyf; '
ау = 2aJj, + (еу — 8С) туг = Д- yyJ’-,
вг = 2aJi J- (ег — 8С) хгх = Д- yzxf.
Здесь, как и раньше,
ес == V (е* + ег) = V
О (J
(3.4)
27
Складывая первые три уравнения (3.4), получим
°* + + °г = 6а (ех 4- е, + ег). (3.5)
Но ех + + е2 есть относительное изменение объема элемента тела. Для
гидростатического давления, когда ах = ву = <jz = — р, из формулы (3.5)-
следует
о Д'7
р -= —2а--.
V
Обозначим через К модуль упругости для объемной деформации. Тогда
„ V д1/
"=-к—
(3.6)
1Z
и a = —. Из уравнения (3.5) получим
ac = tf(ex + ^ + ez) =3tfec. (3.7)
и, следовательно,
2aJi = К (еЛ 4- еу + е2) = <тс.
Теперь уравнения (3.4) можно представить в форме пропорции
&Х -- О'с = Оу _______ ®2 <^С ___ Txt/ __ 'tyz __ Т2Х __ ff (3 8)
ех —ес Су —ес е2 — ес Yxz//2 у^/2 yzx/2
Формулы (3.8) устанавливают подобие девиаторов напряжений и деформа-
ций. Если обозначить
/' = -A=2G(J), (3.9)
уравнения (3.8) можно представить еще в такой форме:
- ffc = 20 GO (6х — ес) - Хху = G (/) Уху,
Оу — <*С = 2G GO &у — ес). ХУ2 = G (J) Ууг’
о2 — ос = 26 (J) (ег — ес), тгл. = 6 (J) угх.
(3.10/
Зависимость G(/) можно определить по результатам испытаний об-
разцов материала на чистый сдвиг путем, например, испытаний на кру-
чение тонкостенных труб.
Зависимости (3.7) и (3.10) являются общими для всех изотропных
материалов, потенциальную энергию которых можно представить в
форме уравнения (3.3). К этим зависимостям мы вернемся при рассмот-
рении теории пластичности.
Однородное изотропное линейно-упругое тело. Для однородного изо-
тропного линейно-упругого тела из формул (3.10) следует, что величи-
на G должна быть постоянной, равной модулю сдвига. Следовательно,
в этом случае
/ (J) - 2GJ.
(3.11)
Согласно уравнению (3.3) удельная потенциальная энергия линейно-упру-
гого тела
F = А (Сл + + ег)2 + 4 Г (8Х - е,)2 +
х о I
+ (8Р - е2)2 4- (е2 - гх? + -|- (y2vy + у2, + у2,) ]. (3.12)
28
Из формул (3.7) и (3.10) следует:
е, + + ег = Зес =(3.13)
Л
Ох ° у 2G (бд. 8 у), Тху @Уху’
^у — Сг = у — 8Z), Ту, = 6уу2;
О2 Од, 2G (вг ех), т2х Gy2X.
(3-14)
Удельная потенциальная энергия (3.12) выражается через напряже-
ния в форме
2
F — —— Н----------------I (°х — tfJ2 + (<7„ — ст,)2 + (ст — ст )2 +
9 /Г 19Г1 ' х У' ' ' У z' ' \ z л/ •
+ 6(т2 4-т2 4-Т2 )].
1 ' ху 1 уг ' ZX' J
(3.15)
Первое слагаемое формулы (3.15) соответствует удельной потенци-
альной энергии изменения объема элемента тела, а второе — удельной
потенциальной энергии изменения формы этого элемента. Из формулы
(3.15), в частности, следует, что второй инвариант девиатора напряже-
ний пропорционален потенциальной энергии изменения формы элемента
линейно-упругого тела.
Зависимости между напряжениями и деформациями для изотропного
линейно-упругого тела (закон Гука) можно представить в различных
вариантах. Кроме зависимостей (3.7) и (3.10), можно получить фор-
мулы:
Ех = у (°* ~ ~ = 2
e</ = 7'(^-lltrz — Наж)> Т^ = 2-^ v; . (3.16)
ez = 4" (°г — Угх = 2 тгх
L L 1
и
= к (ЕХ + ЕУ + Ег) + 2СеЛ;
Оу = Ь (8Х + 8у 4- е2) + 208^;
ст2 = А, (ех + е,у + 8г) + 2Gex.
(3.17)
Здесь X = - , Е — модуль Юнга, р — коэффициент Пуассона,
Е к = Е
2(1 +и) ’ 3(1-гр)’
С учетом температурных деформаций (эффекта температурного расширения
тел) закон Гука для линейно-упругого тела принимает вид
— Н°г) + « (F — Л);
Г,
Ев = -^(^—^ох—]М1х) + а(Г — Т9);
Ez = 4 + а (т — г«) •
(3.18)
29
Здесь TQ — начальная температура, при которой температурные деформации
считаются равными нулю; а — коэффициент линейного расширения. Об-
ратные зависимости:
сг = X (е е + ez) + 2Gev — Еа -Т ,
х \ х У г/ х 1—2,11
= X (8, -j- 8, + ег) + 2G6p - Еа ^2^ ’ > <3-19*
(ех -Г еу + 8г) + 2Gez — Еа
Зависимость среднего напряжения сгс от средней деформации ес и темпе-
ратурного расширения определяется формулой
+ (3.20)
ИЛИ
ас = ЗК [ес — а (Т — То) ]. (3.21)
Влияние нагрева в общем случае учитывается не только через коэф-
фициент линейного расширения а, но и через изменение величин моду-
лей упругости. С увеличением температуры модули упругости Е и G
уменьшаются.
При высоких температурах возникает явление ползучести, которое
кратко будет описано в § 7.
Однородное ортотропное упругое тело. Ортогонально-анизотропным,
или ортотропным, называется тело, упругие свойства которого симмет-
ричны относительно трех взаимно перпендикулярных плоскостей. Это
значит, что если из тела вырезать достаточно малый элемент в форме
параллелепипеда с гранями, параллельными этим плоскостям симмет-
рии, и приложить к этому элементу только симметричные компоненты
тензора напряжений, то они вызовут только симметричные компоненты
тензора деформаций. Кососимметричные же компоненты тензора напря-
жений вызовут только кососимметричные компоненты тензора дефор-
маций.
Пусть координатные оси х, у, z, в которых заданы напряжения и де-
формации в данной точке тела, направлены по линиям пересечения
плоскостей симметрии упругих свойств. Тогда симметричными относи-
тельно координатных плоскостей компонентами тензоров напряжений и
деформаций будут crx, ву, oz; ех, еу, ez, кососимметричными — касатель-
ные напряжения хху, xyz, Xzx и соответствующие им деформации сдвига
Уху, Ууг, Угх- Следовательно, для ортотропного тела при принятой систе-
ме координат в общих формулах (2.10) чдля анизотропного линейно-
упругого тела должны обратиться в нуль коэффициенты, связывающие
нормальные напряжения с деформациями сдвига и касательные напря-
жения с деформациями удлинения.
Кроме того, в силу симметрии упругих свойств тела относительно
координатных плоскостей, должны отсутствовать коэффициенты, связы-
вающие деформации сдвига в одной координатной плоскости с касатель-
ными напряжениями, действующими в других координатных плоско-
стях.
Следовательно, для ортотропного тела закон Гука имеет форму:
<*х = “Г
&у = a21Sx + а22Еу + ^238z,
&z = ^31ех “Ь Я328^ + a33^z,
Хху ““Уху’ ^yz OxbYyz’ ^zx =
(3.22>
30
При этом 021 = 012, 032 = 023, 01з = 0зь Таким образом, закон Гука для ли-
нейно-упругого ортотропного тела содержит девять независимых кон-
стант упругости. Этим константам можно придать другую форму, подоб-
ную форме констант упругости изотропного тела.
Плоскостями, параллельными координатным плоскостям, вырежем
из тела для лабораторных механических испытаний образец в форме
параллелепипеда с поперечным сечением, параллельным плоскости yz.
Ось образца параллельна оси х. В испытательной машине нагрузим об-
разец растягивающим напряжением сгх и запишем диаграммы удлинения
образца и укорочения двух сторон его прямоугольного сечения. Зная
характерные размеры испытуемого образца, из этих диаграмм можно
определить относительное удлинение ех и относительные деформации е7у
и ez укорочения ребер поперечного сечения. Принимая для линейного
участка диаграмм
В у. — , M'ls , 6^ — 1 M'iq •
х Е± у г12 Ех 2 Г13 Ех
определяем модуль упругости Е± и коэффициенты Пуассона р12, р,13.
Аналогично можно вырезать из тела и испытать образец в форме па-
раллелепипеда с осью, параллельной оси у, загрузив его напряжением $у.
В этом случае
G и (Т ц G и
= — Н23-7Г-. .
£^2 ^2 ^2
Соответственно для образца с осью, параллельной оси z,
^z
s2
Qr СТ?
7"» ^ = -Нзх-^. ^ = -Из2-5-.
13 3 23 з £-3
Таким образом, исходя из результатов испытаний, можно определить
модули упругости и коэффициенты Пуассона для зависимостей удлинений
ех, гу, е2 от напряжений сгх, azt заданных в форме
х Et Г21 Ег Г31 Е3
। U ^2
гу-----И12 —----1- —---Нз2~7~>
JC1 £2 £3
(У г (То , (Т?
62= — Н13 7 Н23-7-+
£1 £2 £з
(3.23)
Из условий симметрии коэффициентов упругости получим
Р21 _ Р12 Цз2 __ Ц23 Ц13 Р31
^2 ^з Е"2 Ех Е3
(3.24)
Соотношения (3.24) могут служить контролем правильности опреде-
ления коэффициентов Пуассона. С помощью соотношений (3.24) уравне-
ния (3.23) можно представить в другой форме:
— р12сгу — р13(У2),
*у = -7“ (— И2Л + <*у — р2з(У2),
^2
(3.25)
— ( ИзЛ + az)-
£3 у
31
Коэффициенты а44, л55, а6б, входящие в формулы (3.22), можно опре-
делить по результатам испытаний на сдвиг плоских пластин, вырезан-
ных плоскостями, параллельными плоскостям симметрии упругих
свойств тела. Эти коэффициенты удобно, по аналогии с изотропным те-
лом, назвать модулями сдвига Gi2, G23, G3i. Тогда
Хху = ^12Yx£/» Xyz = ^23Y^Z> Xzx = ^31Yzx* (3.26)
Соответственно
Хух = ^lY^x» Xzy = ^32Yz^, Xxz = ^isYxz
и
G21 = ^12» ^32 = ^23» G13 = ^31-
Составные тела. Составными, или конструктивно-анизотропными, бу-
дем называть тела типа армированных пластиков.
Составное тело, по существу, является неоднородным телом. Однако
если составляющие его элементы чередуются часто и в правильном по-
рядке, то достаточно большой объем такого тела можно рассматривать
«в среднем» как однородный. Здесь можно провести аналогию с рас-
смотрением структуры твердых тел. В объемах, соизмеримых с разме-
рами зерен или кристаллов, твердое тело не является однородным, но
элементарные объемы, рассматриваемые в теории упругости, наделяют-
ся свойствами сплошной однородной среды.
В теории конструктивно-анизотропных тел основным является допу-
щение существования в достаточно больших объемах однородных дефор-
маций, т. е. деформаций, не зависящих от координат точек внутри этих
объемов. Задаваясь различными компонентами деформаций и определяя
силы, необходимые для создания таких деформаций, можно эксперимен-
тально или теоретически определить коэффициенты (модули) упругости.
Наиболее легко определяются приведенные модули упругости при рас-
тяжении и сдвиге.
Корпуса ракет чаще всего представляют собой тонкостенные конст-
рукции. Напряженное состояние в таких тонкостенных конструкциях
обычно близко к плоскому напряженному состоянию. Если ось г распо-
ложить в направлении наименьшего размера тела (толщины стенки), то
при плоском напряженном состоянии oz=t1/z = tzx = 0. Из уравнений
(3.23) и (3.26) для ортотропного тела при плоском напряженном состоя-
нии получим
ех = ”~ Н21 гу ~ ----Н12 Хху = ^12Уху (3.27)
Первые два соотношения можно разрешить относительно напряжений:
ах = -j— ------(ех + P-218J,), оу = —— -----(гу + p12ej. (3.28)
При плоском напряженном состоянии удобно вместо напряжений рас-
сматривать погонные усилия (т. е. усилия на единицу длины):
T1 = (Jxh, 7’2 = <тД S = rxyh,
где h — толщина пластины или оболочки из ортотропного материала. Обоз-
начим
В1 = —, В2 = —B12 = G12h.
1 — ^12^21 1 — Н12Ц21
Тогда из соотношений (3.28) получим:
7\ = Bi (8Х + 7*2 = В2 (&у + Hu8*), S = B12yxyt (3.29)
причем В1Ц21 = В2Ц12. Константы Вь В2, В12, Ц12, p2i представляют собой
жесткостные характеристики ортотропной пластины, подвергающейся
деформациям удлинения и сдвига в своей плоскости.
32
Рассмотрим теперь, как приближенно определяются приведенные
жесткостные характеристики конструктивно-анизотропной пластины при
деформациях в ес плоскости. В качестве примера возьмем стеклопла-
стиковую пластину толщиной h, составленную из слоев стеклянных ни-
тей. Предположим, что в каждом слое стеклянные нити имеют одно
направление. Пусть число слоев будет т + п и нити в п слоях параллель-
ны оси %, а нити в т слоях параллельны оси у (рис. 3.1). Будем также
считать, что в процессе изготовления стеклопластиковой пластины слои
с различным направлением стеклянных волокон чередуются в правиль-
ном порядке и склеиваются свя-
зующим материалом. Упругие
свойства такой пластины при
изотропном связующем будут
симметричны относительно осей
к, у и, следовательно, пластину
можно рассматривать как кон-
структивно ортотропную. Обозна-
чим через f суммарную площадь
сечения стеклянных нитей в по-
лоске слоя единичной ширины.
Если размеры пластины в на-
правлении осей х и у будут соот-
ветственно а и Ь, то площадь
Рис. 3.1
сечения стекла плоскостями хг будет maf, а плоскостями yz — nbf. Пусть
модуль упругости стекла на растяжение Е. Модуль упругости связу-
ющего будем считать пренебрежимо малым по сравнению с модулем
упругости стекла.
Приложим к рассматриваемой стеклопластиковой пластине равно-
мерно распределенное усилие Общая сила, растягивающая пластину
в направлении оси х, будет Т\Ь.
Суммарное напряжение в стеклянных нитях, параллельных оси х,
будет
Л nbf nf
Относительное удлинение
е
х ~~ Е nfE ‘
Относительное поперечное сужение пластины гу при действии нагруз-
ки Г1 зависит от сил взаимодействия слоев с различным направлением
стекловолокон. Эти силы, в свою очередь, определяются местной жест-
костью связующего. Достоверное значение гу и, следовательно, коэффи-
циента Пуассона можно определить только с помощью специально по-
ставленных экспериментов. При отсутствии таких экспериментов в при-
ближенных расчетах можно предположить, что коэффициент поперечно-
го сужения равен нулю.
В этом предположении из первого уравнения (3.29) получим Вх=пЕ^.
Аналогично, рассматривая растяжение пластины равномерно распреде-
ленной нагрузкой Т2 в направлении оси у, получим B2 = mEf, Жесткость
на сдвиг пластины Д2 зависит, в основном, от жесткости на сдвиг свя-
зующего, так как взаимно перпендикулярные сети волокон, не свя-
занные друг с другом, слабо сопротивляются сдвигу. Однако было бы
ошибочным погонную жесткость сдвига В[2 определять по результатам
опытов на сдвиг чистого связующего. Так как объем, занимаемый стек-
лом, того же порядка, что и объем, занимаемый связующим, то жест-
кость пластины на сдвиг будет определяться сложным взаимодействием
стекловолокон и связующего. Практически жесткость стеклопластиковой
3 Зак. 96
33
пластины на сдвиг можно определить экспериментально. Так как стекло-
пластики применяются чаще всего в конструкциях, работающих только
на растяжение (или сжатие) в двух определенных направлениях, на-
пример, в качестве оболочек, нагруженных внутренним давлением, то
величина жесткости стеклопластика на сдвиг не является важной ха-
рактеристикой.
Если стеклопластик сделан из ткани с переплетенными продольными
и поперечными стеклянными волокнами, то растяжение волокон сопро-
вождается их распрямлением и приведенная жесткость стеклопластика
не будет определяться только жесткостью волокон на растяжение. Ана-
логичное замечание можно сделать и в отношении стеклопластиковых
конструкций со сложной технологией намотки стекловолокон. Во всех
подобных случаях особенности деформирования и в том числе жесткост-
ные характеристики лучше всего устанавливать экспериментально.
§ 4. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ПЛАСТИЧНОСТИ
Известно, что большинство конструкционных материалов сохраняет
упругие свойства только до определенного уровня напряжений. При на-
пряжениях выше этого уровня появляются остаточные, пластические
деформации. В теории пластичности изучают два вопроса: как в случае
произвольного напряженного состояния определить ту границу, переход
которой вызывает появление пластических деформаций в материале, и
как за пределами этой границы найти напряжения и деформации. От-
дельно стоит вопрос о поведении материалов при повторных нагруже-
ниях за пределом упругости. Последний вопрос, связанный с еще мало
разработанной теорией эффекта Баушингера, здесь рассматриваться не
будет.
Определение границы упругости материала при сложном напряжен-
ном состоянии в курсах сопротивления материалов рассматривается в
разделе теорий прочности. Это связано с проектированием машин, для
которых недопустимы остаточные деформации. В конструкциях однора-
зового, кратковременного действия типа, например, узлов жидкостного
реактивного двигателя допускаются остаточные деформации и переход
материала за предел упругости не рассматривается как исчерпание
прочности. Граница перехода из упругой области в пластическую являет-
ся, конечно, достаточно условной. Она зависит от той минимальной
величины остаточной деформации, которая в обычных условиях может
быть надежно замерена, и от требуемой степени точности определения
деформаций вообще.
В сопротивлении материалов рассматриваются напряжения, соответ-
ствующие пределу пропорциональности, и напряжения, соответствующие
пределу текучести. Напряжение предела текучести при растяжении
определяется как то напряжение, при котором остаточная относительная
деформация на контрольной длине образца материала не превосходит
0,2%. Это напряжение обозначается сгт или о02- В дальнейшем предел
текучести будет рассматриваться как условная граница, отделяющая
упругую зону работы материала от неупругой, пластической.
Первая задача теории пластичности состоит в определении этой гра-
ницы в общем случае напряженного состояния, если экспериментально
найден предел текучести о*т при одноосном растяжении или тт при чистом
сдвиге. Другими словами, нужно в общем виде установить ограничения
для тензора напряжений, если известны некоторые частные предельные
значения этого тензора. Эта задача решается на основе лабораторных
испытаний. В настоящее время практические расчеты ведут на основе
двух теорий предельного состояния — теории Сен-Венана и теории Ми-
зеса.
34
Теория Сен-Вен ан а связывает наступление предельного со-
стояния с величиной максимального касательного напряжения; переход
в пластическую зону происходит тогда, когда наибольшее из касатель-
ных напряжений достигает предельной величины ±тт. Максимальные
касательные напряжения действуют в площадках, наклоненных под
углом 45° к площадкам главных нормальных напряжений о2, сг3, и
равны
— а2 _ а2 — а3 _______ аз —
П2- ~ > *23“ > *31- 2 •
Следовательно, согласно теории Сен-Венана, предельное состояние в
материале наступит, если в каком-либо из трех условий
|<h—°2|<2гт, | <у2 — <j3 | < 2тт, | <т3 — <Tj |<2тт (4.1)
знак «меньше» перейдет в знак «равно».
В случае одноосного растяжения, когда О2 = о3 = 0, 01 = 0, из условий
(4.1) следует, что от = 2гт. Следовательно, предел текучести при сдвиге
связан с пределом текучести при растяжении зависимостью тт = 0,5 от.
Для мягких материалов эта зависимость экспериментами подтверждает-
ся плохо.
Теория Мизеса связывает наступление предельного состояния
с величиной удельной потенциальной энергии изменения формы элемен-
та тела. Согласно формуле (3.15), она равна
где
J ((Т) = А [(^ _ + + (<тг— + 6 (Т^ + + Т2х)] (4.3)
— второй инвариант девиатора напряжений.
По теории Мизеса переход тела из упругого состояния в пластиче-
ское произойдет тогда, когда удельная потенциальная энергия измене-
ния формы достигнет определенной предельной величины, зависящей
только от физических свойств материала тела. Эту предельную величину
для Рф можно определить или по пределу текучести от при одноосном
растяжении, или по пределу текучести тт при чистом сдвиге. Для одно-
осного растяжения все компоненты напряжений, кроме оЛ = о, равны
нулю и/(а)= — o'2. Для чистого сдвига тХ!/ = т, J (о) =т2.
Значит, условия текучести можно представить или в виде
<ц<о=4<т?- <4-4)
о
т. е.
4 - ^)2 + - ^г)2 + (<Тг - ^)2 + 6 (Т^ 4- Т2г + ?£)] = <%, (4.5)
или в виде
J (*) = 4 (4.6)
Из сравнения формул (4.4) и (4.6) получим
= Зт2, или гт = -4~- <?т. (4.7)
У 6
Формула (4.7) удовлетворительно подтверждается экспериментами
для большинства мягких конструкционных материалов.
3*
35
В дальнейшем мы будем пользоваться критерием Мизеса, так как
соответствующие уравнения теории пластичности при этом имеют более
простой вид, чем по теории Сен-Венана.
Интенсивностью напряжений называется величина
<Т/ = VW) = V - 0/ + -0г)2 + (0г - a J2 + 6 (т2ху + т2 2 + т2х).
(4-8)
При одноосном растяжении (сгх — о) интенсивность напряжений crz = o'
и условие текучести соответствует условию crz = от. При чистом сдвиге
хху = г, oz = У 3 т и условие текучести oz = У Зтт = сгт.
Интенсивностью деформаций называется величина
= (6х — Sj,)2 + 0^— 8г)2 + (ег — ех)2 + -|-(у2г/ + у22 + у2х). (4.9)
Интенсивность деформаций выражается через второй инвариант девиатора
деформаций
^=4^ (4-10>
уз
где
^(е) = У 1(ех — е^)2 + (8^— 8г)2 + (е2 — 8Х)2 + (у2у -|- у2уг + ^х)]. (4.11)
При одноосном растяжении в упругой области
ех = е, е^ = —ре, е2 = — ре, ez =-|-(1 + р) е. (4.12)
Если р = 0,5, то ez = е.
При чистом сдвиге уху = у, 8Z= —
у 3
Легко проверить, что в упругой области справедлива зависимость
oz =3Gez. (4.13)
Уравнение (4.13) вместе с уравнением
0c = 3№c = T^-ec) (4.14)
где, как и раньше,
0С = У + ° у + и 6с = V + еу + Ёг)’
О О
представляют выражение закона Гука для упругой области. Уравнение
(4.14) определяет зависимость среднего напряжения от изменения объема
элемента упругого тела, а уравнение (4.13) связывает напряжения и де-
формации, определяющие изменение формы этого элемента.
Удельная потенциальная энергия изменения формы согласно форму-
лам (4.2), (4.8) и (4.13) будет
и? з
= (4.15)
6G 2 L
С учетом тождеств
(вх -0,)2 + (<т, - а2)3 + (02 - 0J3 = 3 [(0Х -0С)2 + (0,- 0С)2 + (0г - 0С)21.
(4.16)
.(&х — еу)2 -I- (8У — 8г)3 + (б2 — 8Х)2 = 3 [(8, — 8С)2 + (еу — ес)2 + (е2 — ес)2]
(4.17)
36
и е(- можно представить в виде
^ = 1/-у / -- «с)2 + - °е)2 + ~ <*с)2 + 2 (Т2у + г22 + ту,
(4.18)
е/ = тЛ-у 1/"(ех — ес)# + (гу — ес)2 + (е2— ес)2 4- -L (tfxy + .
(4-19)
Идеально пластическим телом называется такое тело,для
которого интенсивность напряжений о; не может превышать предела
текучести от. Диаграмма Ог—&г показана на рис. 4.1, а. При 30ег>от
происходит пластическое течение материала.
а)
б,
б7
О
Рис. 4.1
Теория течения идеально пластических тел является наиболее разра-
ботанной частью математической теории пластичности.
Рост интенсивности напряжений за пределом текучести называется
упрочнением. Соответствующие диаграммы сг2- — называются диа-
граммами для материалов с упрочнением (рис. 4.1, б).
Жестко-пластическим телом называется такое идеализи-
рованное тело, упругими деформациями которого можно пренебречь.
На рис. 4.1,в показана диаграмма Ог—8г- для жестко-пластического тела
без упрочнения (идеальное жестко-пластическое тело), на рис. 4.1, г —
для жестко-пластического тела с линейным упрочнением.
Пластическую деформацию можно определить как разность между
полной деформацией и чисто упругой ее частью. Это необратимая часть
деформации, равная остаточной деформации после снятия напряжений.
Чтобы отличать пластические деформации от полных и упругих, будем их
обозначать через , у^, 8<р). Упругие деформации будем обоз-
начать через 8^, 8^\ ... , 8-е)* Таким образом, ех = е(^ + 8^, 8^ =
= е£> е(Р> и т. д.
Активной деформацией тела называется такой процесс
деформирования, при котором абсолютная величина интенсивности де-
формаций 8i возрастает.
Обратный процесс, при котором абсолютная величина интенсивности
деформаций 8t- уменьшается, называется разгрузкой. На рис. 4.2
направление процессов активной деформации и разгрузки показано со-
ответственно сплошными и пунктирными стрелками.
Один из основных законов теории пластичности гласит, что при раз-
грузке изменение деформаций связано с изменением напряжений линей-
ной зависимостью Acfi = 3G\Ei, т. е. при разгрузке тело ведет себя как
упругое. Этот закон позволяет рассматривать пластические деформации
как необратимые остаточные деформации.
Связь между напряжениями и деформациями в пластической обла-
сти существенно более сложная, чем в упругой. В общем случае зави-
37
симость между напряжениями и деформациями для данного момента
деформирования тела зависит от последовательности деформирования.
Это можно иллюстрировать на простом примере. Пусть абсолютно
жесткая балка АВС прикреплена к неподвижному основанию тремя
стержнями (рис. 4.3, а). Стержни сделаны из идеально пластического
материала с модулем упругости Е и пределом текучести на растяжение
и сжатие ±от. Длина стержней /, площадь поперечного сечения каж-
дого стержня /, расстояние между стержнями а. Пусть окончательное
Рис. 4.3
деформированное состояние системы соответствует поступательному
перемещению балки АВС вниз на величину А = 2 — и повороту, отно-
Е
сительно точки В против часовой стрелки на угол ф = 2 — Рассмот-
а Е
рим два вида последовательности деформирования системы: в первохМ
случае вначале дается перемещение А, затем поворот ф* а во втором —
вначале поворот ср, затем перемещение А. Для обоих случаев деформи-
рования определим усилия в стержнях А, В, С. Для крайнего стержня С
на рис. 4.3,6 показаны пути движения точки на диаграмме о = о(в).
В первом случае стержни А и В в процессе деформирования будут
находиться в условиях активной деформации и окончательные напряже-
ния в них будут равны пределу текучести сгт. Стержень С вначале бу-
дет растянут за пределом текучести (точка а), затем сжат (точка Ь).
Окончательное напряжение в нем будет —от.
Во втором случае деформирования стержни А и В по-прежнему бу-
дут находиться в условиях активной деформации, а стержень С вначале
будет сжат за пределом текучести, а затем растянут до напряжения
+ от. Таким образом, в зависимости от последовательности деформаций
стержень С может оказаться или сжатым, или растянутым.
В рассматриваемой задаче величины усилий в стержнях будут одно-
значными, если в процессе деформирования будет сохраняться неизмен-
ным отношение ср/А, т. е. угол поворота ф будет возрастать пропорцио-
нально перемещению А. В этом случае каждый стержень на протяжении
всего процесса деформирования системы будет находиться в условиях
активной деформации.
Если от этого простого, схематичного примера перейти к рассмотре-
нию особенностей деформирования сплошного тела, то можно выделить
случай, при котором все компоненты девиатора деформаций изменяют-
ся по одному и тому же закону, оставаясь пропорциональными друг
другу. Такое деформирование называется простым. Если при этом
38
знак скорости изменения компонентов девиатора деформаций остается
постоянным (нет разгрузки), то соответствующее деформирование будет
и активным и простым. Эксперименты показывают, что в этом случае
законы, связывающие напряжения с деформациями, будут такими же,
как в нелинейно-упругом теле. При этом пластическое тело отличается
от нелинейно-упругого только процессом разгрузки. Разгрузка нелиней-
но-упругого тела происходит по тем же законам (диаграммам), что и
нагрузка, а разгрузка пластического тела — по законам линейно-упруго-
го тела.
§ 5. ДЕФОРМАЦИОННАЯ ТЕОРИЯ ПЛАСТИЧНОСТИ
Теория пластичности, рассматривающая пластическое тело при
активном деформировании как нелинейно-упругое, называется деформа-
ционной теорией пластичности, или теорией малых упруго-пластических
деформаций. Она была разработана в трудах Генки и А. А. Ильюшина
[38]. Пределы применимости деформационной теории до настоящего
времени обсуждаются в научной литературе. А. А. Ильюшин ввел важ-
ное понятие простого, или пропорционального, нагружения. Это такое
нагружение тела, при котором все составляющие внешних нагрузок (на-
пример, продольная сила и крутящий момент) изменяются в процессе
нагружения пропорционально одному параметру. В терминах строитель-
ной механики это означает, что внешняя нагрузка задается в форме
одной обобщенной силы.
А. А. Ильюшину удалось для частного вида зависимости Oi—ег- дока-
зать эквивалентность простого нагружения и простого деформирования.
Опубликованные результаты экспериментов при простом и сложном
нагружениях различных металлов показывают, что деформационная
теория пластичности лучше всего описывает процессы пластического
деформирования при простом нагружении или нагружении, близком к
простому. В силу своей относительной простоты и универсальности де-
формационная теория пластичности получила широкое распространение
в инженерных расчетах, поэтому на ней мы остановимся наиболее под-
робно. При практических расчетах конструкций за пределом упругости
не следует переоценивать точность теории пластичности. Во всех случаях,
когда в конструкции допускаются пластические деформации, результа-
ты теоретических расчетов крайне желательно проверять и уточнять со-
ответствующими испытаниями.
Уравнения деформационной теории пластичности (теории малых
упруго-пластических деформаций). При активной деформации, как уже
говорилось, рассматриваемая теория пластичности базируется на урав-
нениях нелинейно-упругого тела. Воспользуемся уравнениями теории
нелинейно-упругого тела, выведенными в § 3. Эти уравнения можно
представить в виде
р
ас = 'Ж = _Г^Гес’ М
__°х — ° У ас __ ^ху __ tyz __ _ Q zg 2)
2 (еХ Ес) 2 (Gy Ес) 2 (ег Ес) уХу Уу2 yzx
Величина G является функцией второго инварианта тензора напряжений.
Из пропорций (5.2) можно составить уравнение
V- *с)2 + - М3 -Г (<тг - Пс)2 + 2(т^ + г2г + T2J =
= 2G | / (e.v - ес)2, + - 8С)2 + (ег - 8С)2 + Д- + + уЦ (5.3)
39
или с учетом уравнений (4.18) и (4.19)
<5-4'
Следовательно, уравнения (5.2) можно представить в виде:
Пс — 3 (8х~8с)> Хху — ~7Г~ Ул//’
Oct и8/
ве = Ор (гу 8с)’ Хуг = ~ Yyz> (5.5)
ос/ о8/ *
_, 2(У! / , (Ji I
аг — °C = -7— (8г — ес), хгх = угх.
Зе/ Зе/ )
Уравнения (5.1) и (5.5) являются основными уравнениями деформа-
ционной теории пластичности, или теории малых упруго-пластических
деформаций. Уравнения (5.5) можно представить в форме одного «де-
виаторного» уравнения
Da=^De, (5.6)
Зе/
где О/ и 8/ являются функциями вторых инвариантов девиаторов соот-
ветственно напряжений и деформаций.
В силу инвариантного характера уравнений (5.1) и (5.6) функцию
и = % - можно определить из рассмотрения результатов простых ис-
пытаний образцов (одноосное растяжение, чистый сдвиг). В случае чис-
того сдвига, который можно осуществить путем испытания труб на
кручение,
(Гг = ГЗт, 6, = -^У И =G(y)=—, (5.7)
У 3 Зе/ у
т. е. функция (J//3 8/ играет роль переменного модуля сдвига, зависяще-
го от величины деформации у.
В случае одноосного растяжения ог=(У. Однако ег нельзя определить
через 8 непосредственно из формулы (4.19), если нет эксперименталь-
ных графиков для коэффициента Пуассона в пластической области (та-
кие графики, как правило, не снимаются одновременно с диаграммами
а—е). Поэтому необходимо воспользоваться формулой (5.1), связываю-
щей среднее напряжение <ус со средней деформацией ес. При одноосном
растяжении ос = стЗ и, следовательно,
Из первой формулы уравнений (5.5) для одноосного растяжения при
8V = 8, вх = (У и ос = — (У с учетом формулы (5.8) получим
1 — 2ц
ЗЕ
или
8/ 8 1 — 2ll
а/ о ЗЕ
(5-9)
Формула (5.9) позволяет определить функцию (Ух-/е,- с помощью из-
вестной диаграммы ст — 8.
40
Теперь можно определить коэффициент Пуассона рр в пластической
области. Полагая 8у = — рр8, ву = 0, сгс = — сг, из второй формулы сис-
О
темы (5.5) получим
----— = 2( — ц е— ес),
что с учетом (5.8) и (5.9) дает
Но — есть упругая часть № полной деформации 8. Следовательно,
Е
I 5 Н)
2 2 е V
Так как 8 = 8(е) -J- 8(р), то из формулы (5.11) видно, что с увеличе-
нием пластических деформаций коэффициент Пуассона стремится к 0,5.
При р = 0,3 и 8 = 2е<е) получим рр = 0,4; если 8 =4е<е), то рр = 0,45.
Формулы (5.1), (5.5) и (5.9) позволяют определять напряжения через
деформации, если известна диаграмма о — 8 одноосного растяжения мате-
риала. Полученные формулы удобно преобразовать к другому виду. Обоз-
начим через
Ес £*о) = — (5.12)
е/ е
так называемые секущие модули диаграмм сг£.—et- и о — 8 (рис. 5.1, а).
Будем считать их функциями соответственно o'- и о:
ЕС = ЕС(^), Е^ = Е^(о).
'а) 5)
В упругой области работы материала Е^ = Е и
согласно формуле (5.9)
1 _ J 1 — 2р
Ес Е ЗЕ
(5.13)
При коэффициенте Пуассона р = 0,5, т. е. для несжимаемого мате-
риала в упругой области EQ = Е. В пластической области, как уже отме-
чалось, деформации 8Z и е складываются из упругих деформаций е!е),
и чисто пластических 8(р). Для одноосного растяжения
1 = e(g) + е(р) __ 1 , е(р)
Е^ сг “ Е + CF
(5.14)
4 1
Для дальнейших преобразований обозначим
где Епл — секущий модуль диаграммы т. е. диаграммы, перест-
роенной в координатах и crz. Такую перестройку обычной диаграммы
о —е для одноосного растяжения легко выполнить, откладывая на оси
абсцисс для каждого напряжения сг не полную деформацию е,
g(p) = 8---—•
Е
На рис. 5.1, б показан примерный вид такой диаграммы,
нается не из точки а = е = 0, а из точки 8^ = 0 и ст = сгт.
(5.14) теперь можно представить в форме
11, 1
Е<0’ Е ' Епл‘
Для диаграммы сг.—ez получим с учетом формул (5.9) и (5.15)
е,- _ + ejp) _ 1 _ 1 — 2ц__________1
Qi crt- Е ЗЕ Епл
или
-t- = — —th- + —, (5.18)
(Jf 3 Е EnJl
где
а величину
(5.16)
Она начи-
Уравнение
(5.17)
Таким образом, при переходе от диаграммы сг — 8 к диаграмме сг£- — 8£
«пересчитывается» только упругая часть диаграммы б — 8. Первое уравне-
ние (5.5) представим в таком виде:
или с учетом формулы (5.18)
Ьх = — 4- (ъ — V (5’20)
Е ЕПл \ * /
Аналогично
е„ = — (о„ — tier, — tier) Н—— (а..--— в.---1 crY
£/ £ ' » Г Z г X/ 1 E у у 2 2 2 '
e. = — (о, — art — u.a„) -]-— (в.-— cr,--*- 0„ Y
z e v z г x * У' ' e \ 2 2 х 2*/
Для деформаций сдвига получим
^пл
Аналогичные формулы будут для у^2 и у2Х.
Обозначая Епл/3 = Спл, для чисто пластической части деформации
получим:
42
е(р) —------- 1$---------o’---------(Т \ = ——
х р \ х 9 У 9 2 Хху G
СПЛ \ 2 2. J °пл
»“> - -1- к 1
У Е \ у 2
22 пл \ z
1
ст,,------------а,---------------а
‘ 2 '
,(Р) = -2ML
Уг G
ипл
(5.22)
8<Р) := —
2 Е
'ПЛ
1 1 ’
0 2 о ПЛ 2 6 У
1
2
гх G '
иПЛ )
Структура формул (5.22) аналогична структуре соответствующих
формул в упругой области при ц = 0,5, но с той существенной разницей,
что £Пл является функцией интенсивности напряжений ог-. Для каждого
значения ог-, отождествляя его с напряжением о в диаграмме о—8(р)
одноосного растяжения, можно найти соответствующую величину чисто
пластической деформации и определить модуль £пл- Для жестко-
пластического тела — =0, и формулы (5.20), (5.21) переходят в фор-
мулы (5.22). Для идеально-пластического тела
1
Епл
(5.23)
где 8г- может быть любой величиной, а напряжения ох, оу,... , т2Х связа-
ны между собой уравнением (4.5).
Полные деформации жестко-пластического тела определяются фор-
мулами (5.22). Из этих формул напряжения можно получить, конечно,
только с точностью до величины среднего напряжения вс.
Вычислим работу напряжений ох, av,..., т2Х на вариациях деформа-
ций 6бх, б8у,... , бу2Х. Согласно формулам (5.5)
Ч + <^ Ч + • • • + хгх 6угх =
= (Ч + 4- tej + [2 (ех — ес) 6ел. + ... + бу J.
08/
Из формулы (4.19), учитывая, что вариации определяются по тем же
правилам, что и дифференциалы в дифференциальном исчислении, полу-
чим
2 Ч — ес) tex |- ... + у2х Ьу2х = Зе; бе,-.
Учитывая также, что бех бе^ + бег = Збес, найдем
<*хЧ + ^Ч+ ••• + т~Чх = Засбес+ ^бе,. (5.24)
Формула (5.24) показывает, что интенсивность деформаций е,- явля-
ется обобщенной координатой для интенсивности напряжений <г(-. Так как
ос = 3/(ес и а( = Есе;, то из формулы (5.24) получим
... + т2Х6у2Х = бЛе, (5.25)
где
е/
Лбе + Ес d&t — (5.26)
b
удельная потенциальная энергия, выраженная через деформации.
На первый взгляд, полученный результат может показаться неожи-
данным, так как процесс пластического деформирования является необ-
ратимым. Но, как уже отмечалось, при активном деформировании эле-
мент упруго-пластического тела в деформационной теории пластичности
рассматривается как элемент нелинейно-упругого тела.
43
Аналогично можно вычислить работу, производимую вариациям
напряжений , 6т2Х на деформациях ev, е^, . .. , у2х. Учитывая’
что
°;Ч- = у 1(<ъ— <0 6°х + • • • + 2тгх dtj,
получим
ех 6°л + е</ + • • • + Уг.г бтгл- = Зес 6(Тс + е< 6<Ti • (5-27)
Но
ес 6сгс + е4 --- 6F0, (5.28)
где
9
р = °с (’ d<^
° 2К ' J Ее
о
удельная потенциальная энергия при активном деформировании, выра-
женная через напряжения.
Таким образом, в деформационной теории пластичности упруго-пла-
стическое тело рассматривается
(5.29)
как
х
б.
Рис. 5.2
своеобразное тело, которое являет-
ся нелинейно-упругим при актив-
ном деформировании, когда де-
формации возрастают, и линейно-
упругим— при разгрузке. В каж-
дый момент времени процесса
активного деформирования суще-
ствует однозначная зависимость
напряжений! от деформаций, не
зависящая от последовательности
деформирования.
Наиболее простой вид имеют
уравнения деформационной тео-
рии пластичности при ц = 0,5.
теорию применительно к плоскому на-
Рассмотрим эту приближенную
пряженному состоянию, с которым особенно часто приходится встре-
чаться при расчетах ракетных конструкций (рис. 5.2).
Уравнения для плоского напряженного состояния. При
плоского напряженного состояния
= Хуг = Т2Л. = 0,
ц = 0,5 для
(5.30)
е2 = — (e.v + е;/).
Интенсивность напряжений и деформаций
\ + &у — ^х°у Ч" ^ху *
2 п ГТ ’ i т
6/ = тг у Ех + тУл-
(5.32)
(5.33)
(5.34)
При этом секущий модуль £с равен Ес0), а диаграмма ст, — ez идентична
диаграмме ст — е при одноосном растяжении.
Основные уравнения (5.5) легко преобразуются к виду
~ oi \ у 2 °х)
(5.35)
44
= <5-36)
Щ <JC
где секущий модуль сдвига Gc = Ес/3. Обратные зависимости —
еД ~тех\ x*u=G<^*v- (5-37)
О у / О \ /
В рассматриваемом случае (ц = 0,5) не целесообразно разделять де-
формации на упругие и чисто пластические. Удобно диаграмму сгг-—ег-
рассматривать как единую кривую, полученную при испытаниях образ-
цов на одноосное растяжение. Это особенно удобно для мягких мате-
риалов типа алюминиевых сплавов, где нет явно выраженной площадки
текучести.
Диаграмму аг— е/ можно аппроксимировать какими-либо простыми
аналитическими функциями. Чаще всего применяется степенная аппрок-
симация
1
где Л, В и х определяются из условий наилучшего приближения теоре-
тической кривой к экспериментальной. Обычно х^б. Материал, для ко-
торого с достаточной точностью подтверждается зависимость (5.38),
условно называется материалом со степенным упрочнением. Его можно
рассматривать как материал с пределом текучести от, близким к нулю,
а степенную зависимость (5.38)—как зависимость о*—е* в области
упрочнения 0г>от- Конечно, разгрузка рассматриваемого материала, в
соответствии с основным законом теории пластичности, должна следо-
вать законам линейно-упругого тела. Обычно за модуль упругости Е
в этом случае принимается величина тангенса угла наклона касатель-
ной к экспериментальной кривой диаграммы о—е вблизи начала коор-
динат. Аппроксимирующая формула (5.38) не является, конечно, един-
ственной.
§ 6. ТЕОРИЯ ТЕЧЕНИЯ. ОСОБЕННОСТИ РАЗРУШЕНИЯ
ВЫСОКОПРОЧНЫХ МАТЕРИАЛОВ
Теория течения. Эта теория является другой, более общей, теорией
пластичности. Для случая простого деформирования она преобразуется
в рассмотренную ранее деформационную теорию пластичности. В теории
течения деформации ел-, е?/, ... , yzx в данный момент времени зависят ог
последовательности деформирования. Свой вклад в разработку теории
течения для идеально-пластических тел внесли многие выдающиеся
ученые. Однако для материалов с упрочнением в настоящее время еще
нет общепринятой, экспериментально обоснованной теории течения. Мы
рассмотрим один из простых вариантов теории течения, наиболее близко
стоящий к деформационной теории пластичности.
Основные гипотезы этой теории состоят в следующем:
1) деформации ех, е^, . . . , yzx складываются из упругих е^, е^, .. .
. .. , у<£ и чисто пластических, необратимых е^\ е<р), ... ,
2) пластические деформации нс сопровождаются изменением объема
элемента тела;
3) разгрузка происходит по законам линейно-упругого тела;
4) в процессе деформирования элемента тела за пределом упругости
приращения пластических деформаций пропорциональны девиатору на-
пряжений.
45
Теорию течения отличает от деформационной теории лишь п. 4, т. е.
то, что приращения пластических деформаций (а не сами пластические
деформации) пропорциональны девиатору напряжений. В соответствии
с перечисленными гипотезами уравнения теории течения при активном
деформировании можно представить в форме:
dtx = y (d<sx — ^dcSy — ^ dez) + (csx - <тс) d’K, j
dty = (day — p daz — p dex) + (<r — ac) dX,
lL
d^z = -4— H dox — p dOy) + (<rz — <rc) dX;
£
(6.1)
dyxy = + 2txz/ dX, dyyz = -^- + 2ryz dK,
dyzX = -^~ + ^2XdK. (6.2)
(j
В этих уравнениях dk— коэффициент пропорциональности между
приращениями пластических деформаций и девиатором напряжений.
Удельная работа, совершаемая напряжениями на действительных при-
ращениях деформаций,
(Jxdex +<Jyd£y+ ... + rzxdyZx = dFt^--^- a?dX, (6.3)
О
где Fe — удельная потенциальная энергия упругих деформаций, а сгг-,
как и раньше, интенсивность напряжений. Работа напряжений на при-
ращениях пластических деформаций определяется вторым слагаемым
правой части уравнения (6.3). Если считать, что параметр dk не зависит
от вида напряженного состояния, то, применяя уравнение (6.3) к слу-
чаю простого одноосного растяжения, когда о = ах = сГг, ех = е, получим,
сокращая на о,
1 de 2 „
d& =-------;---стал.
Е 3
(б.4>
Но de--------= de(p) — приращение чисто пластической деформации. Следо-
Е
вательно, из уравнения (6.4) получим
3
dk
(6.5>
а
Пусть известна диаграмма о—е(р), перестроенная из диаграммы о—в
для одноосного растяжения по изложенному в § 5 правилу. Назовем
величину тангенса угла наклона касательной к кривой а — g(r) пласти-
ческим касательным модулем (рис. 5.1, б)
Еплк = (6-6)
При одноосном растяжении модуль Е„„.к есть функция напряжения в. В
Упругой области Епл.к = оо. Так как диаграммы а —е(р) и <т(-—е!р) иден-
тичны, то модуль Епл.к в общем случае будет функцией <г(-. Переходя от
напряжения о к напряжению о, из формулы (6.5) с учетом соотношения
(6.6) получим
46
Следовательно, приращения пластических частей полных деформаций со-
гласно формулам (6.1) будут:
de(₽) __ GX °C dyl$ = 3-^- dot
ut,x " 2 Gi F f ^пл.к E ’ ^пл.к
_ _3_ Gy — gc ' do i dy^= 3^- dOj
“ 2 Gi E ’ ПЛ.К E ’ ПЛ.К
_3_ dOi dy^ = 3 Oi dOj
"" 2 Gi E ’ ^пл.к ^пл.к J
(6.8)
Для идеально пластического материала ог=пт, б/ог = 0, Епл к = 0 п
dX— неопределенная величина. В этом случае из уравнений (6.8) мож-
но определить только отношения приращений деформаций. Упругая со-
ставляющая деформаций определится из уравнений (6.1) при dX = 0,
т. е. из формул закона Гука.
Если в процессе деформирования все составляющие девиатора на-
пряжений изменяются пропорционально, то из уравнений (6.8) следует
„(р)_ 3 ах ас р d&i
х " 2 at J Епл.к *
Но dcrz = Епл.к ^е*₽), следовательно,
Q g(P)
= ^-4-(0х-<тс). (6.9)
о i
Такую же формулу можно получить из соотношений (5.22) для пла-
стической составляющей деформации е**, если учесть, что е(ср) =0. Сле-
довательно, теория течения переходит в деформационную теорию пла-
стичности в случае простого пропорционального деформирования. Одна-
ко в общем случае пластические деформации в теории течения будут
определяться интегрированием уравнений (6.8) и, следовательно, будут
зависеть от истории нагружения.
При разгрузке, когда величина dod^i меньше нуля, в формулах
(6.1) надо положить dX = 0 и определять изменение деформаций из
уравнений линейной теории упругости. Остаточная деформация в каж-
дый момент деформирования определяется как сумма накопленных к
этому моменту пластических деформаций.
При определении модулей ЕПл и ЕПл.к по диаграмме о — полезно
контролировать расчеты, подставляя вычисленные значения этих моду-
лей в тождество
—— =—1----------—/б д0)
£Пл.к £пл Е*л da
Особенности разрушения высокопрочных материалов. Теория разру-
шения твердых тел является наименее разработанным разделом науки
о прочности. В отличие от теорий деформирования теория разрушения
в общем виде не может быть построена на основе механики сплошной
среды. Только в тех случаях, когда разрушение происходит вследствие
потери устойчивости пластического течения больших объемов материа-
ла, можно методами механики сплошной среды искать критические зна-
чения внешних сил. Примером может служить потеря устойчивости
цилиндрической формы растягиваемого образца мягкой стали с образо-
ванием шейки, когда предельное значение растягивающей силы соответ-
ствует началу потери устойчивости.
В реальных конструкциях при сложном неоднородном поле напряже-
ний разрушение наиболее часто является следствием общих или местных
47
разрывов материала. Физические теории разрушения металлов рассмат-
ривают механизм происходящих при этом процессов в микрообъемах
тела. С основами этих теорий читатель может ознакомиться по книге [73].
В практических расчетах конструкций на прочность инженер поль-
зуется выданными ему механическими характеристиками материалов.
Для металлов это обычно величины предела прочности предела те-
кучести сгт, модуля упругости Е, ударной вязкости, остаточного удлине-
ния и остаточного сужения поперечного сечения стандартного образца
материала при испытаниях на разрыв. В некоторых случаях инженер
получает диаграмму о—е. Все перечисленные данные определяются пу-
тем испытаний стандартных образцов материала на разрывных маши-
нах и копрах. Величины остаточного удлинения при разрыве, сужения
поперечного сечения и ударной вязкости косвенно характеризуют пла-
стические свойства материала при статических и ударных нагрузках.
Опыт машиностроения прошлого и начала текущего столетия показывал,
что перечисленные характеристики материалов были достаточны для
правильного проектирования металлических конструкций. Однако это
продолжалось лишь до тех пор, пока не были созданы более легкие и,
следовательно, более напряженные конструкции, применены новые вы-
сокопрочные материалы и новая технология производства. Широко
известны аварии сороковых годов в американском морском флоте, когда
корабли буквально ломались пополам. Описаны случаи, когда огром-
ные резервуары для нефтепродуктов разрывались от верха до низа без
заметной пластической деформации. Эти и многие другие происшествия
и аварии заставили ученых и инженеров заново пересмотреть сложив-
шиеся представления и традиции. Прежде всего изменилось представле-
ние о пластическом и хрупком разрушениях. Раньше эти виды разруше-
ний связывались только с пластическими свойствами тех или других ма-
териалов (имеются в виду металлы и их сплавы). Сейчас хрупкое и
пластическое разрушения рассматриваются как две возможные формы
разрушения конструкций.
Пластическое и хрупкое разрушения перестали быть свойством толь-
ко материала, а стали так же свойством конструкции из данного мате-
риала при данном напряженном состоянии. Это основной практически
важный вывод, который был сделан из современной практики и теории
разрушения конструкций. Конечно, неверно думать, что пластические
свойства материала потеряли свое прежнее значение. При прочих рав-
ных условиях более пластичный материал, как правило, менее подвер-
жен влиянию концентрации напряжений, чем менее пластичный. Но это
нс означает, что пластический характер разрушения образцов материа-
ла при одноосном растяжении гарантирует пластическое разрушение
конструкций из этого материала.
Некоторые свойства материала связаны с развитием трещин при
хрупком разрушении. Их особенность в том, что при испытаниях стан-
дартных гладких образцов на растяжение они полностью нс выявляют*
ся. Проявление таких свойств при разрушении предсказывалось еще
Фёпплем. В статье [112] он пытался найти характеристику материала,
определяющую влияние концентрации напряжений на прочность растя-
гиваемых образцов с надрезами. Эта работа Фёппля в свое время не
получила признания.
Позднее Орован, развивая теорию равновесных трещин Гриффитса
и Ирвина, ввел константу с размерностью энергии на единицу площади,
определяющую рост трещин при хрупком разрушении пластических ма-
териалов. В настоящее время еще нет методов прямого определения
сравнительных величин этой константы для различных материалов. Но
разъяснение возможности хрупкого разрушения пластических материа-
лов (его называют еще квазихрупким) является практически важным
48
достижением современной математической теории трещин. Обзор работ
по этому вопросу содержится в статье [13].
При оценке конструкционных качеств новых материалов наряду со
стандартными механическими испытаниями образцов необходимо свое-
временно производить испытания различных вариантов образцов конст-
рукций в условиях, близких к реальным. При современном состоянии
теории разрушения такие испытания являются практическим методом
проверки работы нового материала в сложных условиях действительно-
го нагружения.
§ 7. ОСОБЕННОСТИ ДЕФОРМИРОВАНИЯ СЛОЖНЫХ СРЕД
При упругом и пластическом деформировании, которое было рас-
смотрено в предыдущих параграфах, величины деформаций или напря-
жений прямо не зависели от времени. Дифференциалы, входящие в фор-
мулы теории пластического течения, не обязательно должны были отно-
ситься к приращению времени как параметра процесса; в качестве таких
параметров могли быть приняты внешние силы или перемещения в за-
висимости от условий задачи.
Однако в реальных материалах могут существовать деформации,
существенно зависящие от времени. ПримерОхМ таких деформаций могут
служить деформации ползучести, возникающие при нагружении сильно
нагретых металлов. При постоянной величине напряжения деформации
ползучести растут со временем; материал как бы ползет.
Существенно зависят от времени также деформации полимерных
материалов. Для полимеров одной из характерных деформаций являет-
ся так называемая деформация упругого последействия.
Среды, величина деформаций которых существенно зависит от време-
ни, принято называть сложными. Характер деформирования реальных
тел часто зависит не только от их свойств, но и от внешних условий,
при которых происходит это деформирование. Так, например, упруго-
пластическое тело при неизотермическом процессе деформирования
должно рассматриваться как сложная среда. В этом параграфе будут
рассмотрены расчетные модели некоторых практически важных сложных
сред. Описание физических явлений, происходящих в сложных телах
при деформировании, читатель может найти в книгах [62, 76].
Неизотермическая пластическая деформация. Примером неизотерми-
ческих деформаций могут служить деформации оболочек жидкостного
ракетного двигателя, когда нагружение сопровождается действием мощ-
ных тепловых потоков. Начиная с некоторого уровня нагрева, механиче-
ские характеристики материалов существенно зависят от температуры.
При повышении температуры, как правило, уменьшаются модуль упру-
гости и предел текучести от. Диаграмма о—е становится более пологой,
со слабо выраженным участком упругости, а коэффициент Пуассона
увеличивается, приближаясь к 0,5.
Полное исследование неизотермической деформации при очень бы-
стром нагреве затруднено тем, что изменение механических характери-
стик материалов строго не следует за изменением температуры. Изме-
нения свойств материала как бы запаздывают по отношению к измене-
ниям температуры. Это явление еще мало изучено и обычно не учиты-
вается в расчетах. Если процесс деформирования происходит достаточно
быстро и температура не слишком высокая, можно также не учитывать
деформацию ползучести материала.
Рассмотрим неизотермическое пластическое деформирование при
простом одноосном напряженном состоянии. Модуль упругости Е будем
считать известной функцией температуры 7, которая является заданной
4 Зак. 96
49
функцией времени t. Температура отсчитывается от условной начальной
температуры Т = То = О-
Полную деформацию еп будем рассматривать как сумму «силовой»
деформации е и чисто температурной деформации и.Т (а — коэффициент
линейного расширения):
8п = е + аТ\ (7.1)
Силовая деформация, в свою очередь, складывается из чисто упругой и
пластической:
е = — + eW. (7.2)
Е
Упругую деформацию и деформацию температурного расширения
будем считать мгновенно обратимыми деформациями. Относительно
пластической деформации сделаем предложение, являющееся естествен-
ным обобщением основного закона теории пластичности, что величина
пластической деформации не уменьшается при понижении напряже-
ния независимо от изменения температуры. Другими словами, разгруз-
Рис. 7.1
ка всегда, вне зависимости от того, повышается или понижается при
этом температура, сопровождается уменьшением только упругой части
силовой деформации. Так, если при постоянном напряжении о происхо-
дит охлаждение тела, то пластическая деформация остается неизмен-
ной, хотя понижение температуры сопровождается увеличением пласти-
ческого секущего модуля ЕПл- Если же при постоянном напряжении
температура возрастает, то пластическая деформация увеличивается в
соответствии с изменением диаграммы о—8. Таким образом, пластиче-
ские деформации рассматриваются как необратимые, накапливающиеся
в процессе активного нагружения или роста температуры. Пусть извест-
ны диаграммы о—8, полученные путем испытаний образцов на растяже-
ние при различных температурах Т (рис. 7,1, а). На основании этих
диаграмм и с учетом принятых свойств пластических деформаций мож-
но решить следующие практически интересные задачи: 1) заданы изме-
нения Г и а во времени, определяется деформация 8П; 2) заданы изме-
нения Т и 8П, определяется о; 3) заданы изменение Т и связь между о
и 8ц, определяются о и 8П. Последняя задача возникает при расчете ста-
тически неопределимых конструкций.
50
Эти задачи можно решить графически на основе экспериментальных
диаграмм о—е при различных температурах Т [37]. Пользуясь тем, что
при разгрузке не изменяется величина пластической деформации, пере-
ход из заданной точки диаграммы о—е, соответствующей одной темпера-
туре Г, в какую-либо точку плоскости о—е можно осуществить в два
этапа: сначала произвести полную разгрузку при модуле упругости, со-
ответствующем первой температуре, а затем нагрузку (или заданное
деформирование) при характеристиках материала, соответствующих
второй температуре. Этот прием графического расчета проследим на
примерах решения трех ранее сформулированных задач.
Рассмотрим подробно первую задачу.
Пусть начальный момент соответствует точке С на диаграмме о—е
при температуре Т3. Затем температура понижается до Т = Т\, а напря-
жение возрастает до значения Найдем положение точки F на плоско-
сти диаграмм о—е (см. рис. 7.1,а). При температуре Т = Т3 произведем
полную разгрузку из точки С в точку Со. После этого при новой темпе-
ратуре Т=Т\ будем нагружать стержень до напряжения oF.
В упругой области этому нагружению будет соответствовать прямая
Со/?,,/, выходящая из точки Со с угловым коэффициентом, равным мо-
дулю упругости материала при температуре Если заданное напря-
жение ниже напряжения ог"',то искомая точка будет лежать на этой
прямой (точка F'). Полная силовая деформация
с 6(р) + 2£1. (7.3)
с Е(7\) v
Если напряжение выше crF"', то точка сначала будет двигаться по
прямой CqF" до пересечения с диаграммой а — е для температуры Тг, а
затем по этой диаграмме до точки F", где напряжение oF" равно задан-
ному напряжению crF. Полная силовая деформация
еЛ, =е(Р)А (7.4)
F E(Ti) v
Полное изменение деформации с учетом температурного расширения
Деп = ef — ес + а(7\—Т3). (7.5)
Рассмотрим графическое решение второй задачи.
Пусть начальная силовая деформация и температура Т снова соот-
ветствуют точке С на диаграмме о—е при Т = Т3. Допустим, что темпе-
ратура повышается до Т = 1\ и окончательная силовая деформация
равна еб = еп—а (Л). Опять переход из точки С в точку D плоскости
диаграмм о—е осуществим в два этапа. Сначала произведем полную
разгрузку по прямой СС0 при температуре Т = Т3 и затем деформирова-
ние до e-=ed при температуре Т = 1\. В упругой области точка (о, е) при
этом деформировании будет двигаться по лучу, соответствующему
модулю упругости материала при температуре Т = Т4. Если точка пере-
сечения D' вертикальной линии e = ed с этим лучом лежит ниже кривой
о—е при Т = 1\, то эта точка будет искомой и соответствующее напря-
жение
^=Е(Т4)(е^-е^)). (7.6)
Если точка пересечения линии e = ed с лучом CqD' лежит выше кри-
вой о—е для 71 = Г4, то деформирование сначала будет происходить по
лучу Со£)///, а затем по диаграмме о—е до точки D". Искомое напряже-
ние будет о'".
Для графического решения третьей задачи на плоскости диаграмм
о—е надо построить две кривые о—е для двух температур — начальной
4* 51
Т3 и конечной Т2 и заданную кривую о = о(е) для температуры
Г2(е = еп—аГ2). Пусть начальная точка состояния материала (до зада-
ния связи о—е) определяется точкой С на диаграмме о—8 при Т = Т3
(рис. 7.1,6). Производим, как и раньше, разгрузку до точки Со по лучу
CCq. После этого из точки Со проводим луч, угловой коэффициент кото-
рого равен модулю упругости материала при Т = Т2. Если заданная кри-
вая о=о(е) расположена в плоскости о—8 так, что этот луч пересекает
ее ниже диаграммы о—г при Т = Т2 (точка Нх на рис. 7.1,6), то точка
пересечения будет искомой. Соответствующие напряжения и силовая
деформация будут о = онх и
(7.7)
О jj
ен, = + ——
С Е(Т2)
Если же эта точка окажется выше кривой о = о(е), то деформирова-
ние из точки Со сначала будет идти по лучу С^Н3 до точки Н3 пересече-
ния с диаграммой о—8 при Т = Т2, а затем по этой диаграмме до точ-
ки Н2 пересечения диаграммы с кривой о = а(е). Соответствующее
напряжение будет вН2 и силовая деформация еН2.
На проведенных построениях мы подробно остановились потому, что
они являются достаточно типичными для графического решения практи-
ческих задач теории деформирования сложных сред.
Изложенную методику расчета неизотермическою деформирования
легко формально распространить на общий случай объемного напряжен-
ного состояния. При высоких температурах можно принять коэффициент
Пуассона ц = 0,5 и диаграммы о—8 одноосного растяжения отождест-
вить с диаграммами (J;—8;.
Определив из условий задачи по диаграммам о—8 расчетные вели-
чины Ог и 8г, можно из общих уравнений (5.5) найти связь между ком-
понентами девиатора деформаций и девиатора напряжений. Неизотер-
мический характер деформирования при таком методе расчета будет
учитываться при нахождении величин Ог и 8г. Дополнительным усло-
вием является равенство нулю силовой объемной деформации. Полная
объемная деформация при ц = 0,5 в этом случае будет равна чисто тем-
пературной: 8с = аГ. Для плоского напряженного состояния из уравне-
ний (5.35) и (5.36) получим
в'- О, (°' 2 +
Q St
Уху ~~ ^ху
(7.8)
Изложенный метод расчета основан на формулах деформационной
теории пластичности. В работе [19] неизотермическое упруго-пластиче-
ское деформирование рассматривается на основе уравнений теории
течения. В настоящее время мало экспериментальных материалов, под-
тверждающих точность той или иной теории неизотермического дефор-
мирования. Это позволяет отдать предпочтение той теории, с помощью
которой можно наиболее просто решить практическую задачу. Конечно,
если заданные внешние условия задачи заведомо соответствуют слож-
ному непропорциональному нагружению, желательно отдать предпоч-
тение теории течения. В ракетных двигателях, где основная нагрузка в
неизотермических задачах определяется давлением горячих газов, на-
гружение близко к простому и целесообразно пользоваться деформаци-
онной теорией пластичности как более простой.
;52
Ползучесть. При испытаниях на ползучесть обычно измеряют вели-
чины относительных удлинений е в функции времени t для образцов
материала, нагретых до определенных температур Т и нагруженных рас-
тягивающими силами до фиксированных значений напряжений.
Варьируя температуры Т и напряжения о, получают серии кривых
зависимостей е от времени t. На рис. 7.2 показаны две такие кривые для
одной температуры Т и разных напряжений cr(oi<cF2). В начальный
момент времени / = 0 деформация
равна «мгновенно» устанавливаю-
щейся упругой или упруго-пластиче-
ской в зависимости от уровня на-
пряжения о. Если о<от для данной
температуры, то мгновенная дефор-
мация при / = 0 будет чисто упругой;
если же о>ат — упруго-пластиче-
ской. Деформация ползучести
е«о = е(/)—е(0). (7.9)
Индекс «(^)», отличающий дефор-
мацию ползучести, соответствует
первой букве английского слова
creep (крип). Крип — другое назва-
ние явления ползучести.
При относительно низком уровне напряжения о = си кривая ползуче-
сти е(с) = е(с)(/) имеет три характерных участка: участок /, соответствую-
щий начальной неустановившейся стадии ползучести, происходящей с
уменьшающейся скоростью; наиболее протяженный участок II устано-
вившейся ползучести, когда скорость ползучести е(с) = const (в дальней-
шем точка над буквой всегда будет обозначать производную по вре-
мени), и участок III с ускоренной ползучестью, предшествующей
разрушению образца.
При высоком уровне напряжения о = о2 второй участок практически
отсутствует и кривая деформации ползучести имеет S-образный вид с
участком перегиба. Разрушение при ползучести определяется двумя
величинами—напряжением о, при котором произошел разрыв образца, и
временем /тах, в течение которого образец находился под напряже-
нием о без разрушения. Чтобы отличить это разрушающее напряжение
от предела прочности сгв, вводится понятие разрушающего напряжения
длительной прочности. Для конструкционных материалов, предназначен-
ных для работы при высоких температурах, приводятся таблицы гаран-
тированных величин разрушающих напряжений длительной прочности
в зависимости от времени /тах до разрушения (длительная прочность
для 30 мин, 1 ч, 10 ч, 100 ч и т. д.) при различных температурах Т. При
приближении температуры Т к точке плавления или размягчения мате-
риала его длительная прочность стремится к нулю.
Теоретические методы расчета конструкций, работающих в условиях
ползучести материала при сложном напряженном состоянии, разрабо-
таны, главным образом, для относительно низких уровней напряжений,
когда основным участком диаграммы ползучести является участок //
с постоянной скоростью ползучести. В конструкциях ракетных двигате-
лей ползучесть материала, если она допускается по условиям работы
теплонапряженных узлов, происходит в течение малых отрезков време-
ни и соответствует, как правило, диаграммам неустановившейся ползу-
чести. В этих условиях наиболее простым методом расчета является
метод, основанный на теории старения. Под «старением» здесь пони-
мается рассмотрение времени как фактора, изменяющего сопротивляе-
мость материала действию напряжения; на /// участке диаграммы эта
53
сопротивляемость резко падает и происходит разрыв образца. Теория
старения позволяет для приближенных расчетов непосредственно поль-
зоваться графиками результатов испытаний образцов на ползучесть, и
в этом ее большое преимущество при расчетах весьма напряженных
элементов ракетных двигателей. Соответствующие расчеты будут тем
точнее, чем медленнее изменяются напряжения [72].
Пусть известны диаграммы ползучести е—t для различных напря-
жений oi, 02, сгз, (рис. 7.3, а). Эти диаграммы легко формально пере-
строить в привычные диаграммы о—е для различных t (рис. 7.3,6). Для
этого надо рассечь диаграммы е—t вертикалями t = const и по соответ-
ствующим точкам построить диаграммы о—г для различных моментов
времени t.
Диаграммы о—8 должны иметь горизонтальные асимптоты, соответ-
ствующие напряжениям длительной прочности для заданных значений
времени t. С помощью диаграмм о—8 можно приближенно решать раз-
личные задачи теории одномерной ползучести. Если задано изменение
напряжения во времени, можно найти соответствующий закон измене-
ния деформации 8. При заданном законе изменения деформации е мож-
но найти соответствующий закон изменения напряжения. При задан-
ных о и 8 можно найти время /, при котором будут реализованы эти
значения напряжения и деформации. Вертикальное сечение диаграмм
о—8 прямой e = const соответствует приближенному решению задачи о
релаксации напряжений. Под релаксацией напряжения понимают умень-
шение с течением времени напряжения при фиксированной величине
деформации. Уменьшение напряжения является следствием того, что в
процессе ползучести уменьшается упругая деформация и растет дефор-
мация ползучести. С опасными следствиями релаксации напряжений
приходится например, сталкиваться при проектировании различных гер-
метических сосудов, работающих в условиях высоких температур. Релак-
сация напряжений в предварительно затянутых болтах крепления кры-
шек может привести к нарушению герметичности этих сосудов.
Диаграммы, подобные диаграммам на рис. 7.3, можно построить и
для практически важных расчетов конструкций, нагрев которых проис-
ходит одновременно с силовым нагружением, т. е. для неизотермической
ползучести. Пусть известен закон изменения температуры по времени
71 = Г(/). Воспроизведя этот закон изменения температуры при испыта-
ниях образцов материала на ползучесть, можно построить соответствую-
щие диаграммы 8—t для разных значений напряжения о. Эти диаграм-
мы только видом кривых 8—t будут отличаться от диаграмм, приведен-
ных на рис. 7.3, а. Перестраивая прежним способом эти диаграммы в
диаграммы о—8, получим серию кривых, подобных изображенным на
54
рис. 7.3, б. Очевидно, каждому значению времени t будет соответство-
вать одна определенная температура Т. На графиках о—8 время t мож-
но заменить температурой Т. Построенные таким образом графики
внешне будут похожи на графики рис. 7.1, а для неизотермического
упруго-пластического деформирования.
Расчет по этим графикам производится так же, как по графикам
ползучести на рис. 7.3,6 для постоянной температуры, т. е. путем дви-
жения по сетке кривых в плоскости о—8 в соответствии с условием
задачи. Этот расчет существенно проще расчета неизотермической
упруго-пластической деформации по графикам рис. 7.1. Это объясняется
тем, что в теории ползучести не вводится понятие, аналогичное понятию
предела текучести от в теории пластичности.
Теория ползучести не предусматривает качественного изменения
законов деформирования при увеличении напряжения выше определен-
ного предела. С другой стороны, принято оговаривать, что начальная
деформация е(0) может быть или чисто упругой, или упруго-пластиче-
ской в зависимости от величины силы, прикладываемой к нагретому
образцу. Начальный момент деформирования наделяется как бы осо-
быми качествами, что противоречит требованию, предъявляемому к фи-
зическим теориям об инвариантности законов относительно выбора
начала отсчета. Следовательно, теорию старения нельзя рассматривать
как универсальную физическую теорию; она является приближенной
инженерной теорией, позволяющей весьма простым способом оценить
величины напряжений и деформаций при ползучести.
Изложенная применительно к одноосному растяжению теория старе-
ния формально легко распространяется на произвольное трехосное
напряженное состояние. При высоких температурах коэффициет Пуас-
сона как для упругих деформаций, так и для деформаций ползучести
приближенно принимается равным 0,5, т. е. соответствующим несжимае-
мому материалу. Принимая, как и в деформационной теории пластич-
ности, что девиатор деформаций пропорционален девиатору напряже-
ний, можно получить формулы, аналогичные формулам (5.5) § 5 при
8с = 0. Зависимость интенсивности деформаций 8г- от интенсивности на-
пряжений сгг- принимается такой же, как зависимость 8 от о при испыта-
ниях на ползучесть растянутых образцов, т. е. диаграммы о—8 для
различных t (см. рис. 7.3,6) рассматриваются как универсальные диа-
граммы (7г-—8t. Более полное и строгое изложение теории старения чита-
тель может найти в книге [68].
Физические теории ползучести не содержат явно время t. В настоя-
щее время существует несколько вариантов физических теорий ползуче-
сти. Они различаются формами связи между девиаторами напряжений,
деформаций и скоростей деформаций. По существу теории ползучести
построены по образу и подобию теорий пластичности. В одном из наи-
более часто встречающихся в теоретических исследованиях варианте
теории ползучести, а именно теории упрочнения, закон деформирования
задается в форме Ф(е(с), 8(с), о, Т) =0. Вид функции Ф определяется путем
испытаний образца и аналитической аппроксимации экспериментальных
кривых. Различные теории ползучести изложены в книге Л. М. Кача-
нова [42].
Деформация полимеров. Вследствие разнообразной структуры поли-
меров их деформации нельзя описать единой универсальной теорией.
Однако существуют некоторые особенности деформаций, присущие
большинству конструкционных полимерных материалов, которые могут
быть описаны в терминах механически сложных сред. При не очень
высоком уровне напряжений такие полимерные материалы могут рас-
сматриваться как упругие с запаздывающей упругостью. Будем назы-
вать соответствующие упругие деформации полимеров высокоэластиче-
55
скими. Суть запаздывающей упругости [73] можно объяснить с помощью
модели, изображенной на рис. 7.4.
Перемещение х точки приложения силы Р складывается из переме
щения Xi поршня А и растяжения пружины k0
х = Х1 + ^~. (7.10)
Поршень А движется в вязкой жидкости и растягивает внутреннюю
пружину Обозначив ц коэффициент, пропорциональный вязкости жид-
кости, и пренебрегая силами инерции, получим
Р =
(7.П)
или
где х — скорость движения поршня, а цХ] — сила вяз-
кого трения. Исключая из формул (7.10) и (7.11) ве-
личину xi, получим
р = k±(X---—А + Т] I х----
(7.12)
Рис. 7.4
При очень медленном процессе нагружения вели-
чины х и Р могут быть сделаны пренебрежимо малыми
и из уравнения (7.12)
1_р __ kg ~i~ р
J Ml
(7.13)
Наоборот, при очень быстром нагружении в уравнении
(7.12) пренебрежимо малыми станут величины Р и х
и тогда
1
/г0
(7.14)
Величина £0 является как бы мгновенным модулем упругости. В пер-
вые моменты быстрого нагружения поршень А практически стоит на месте,
а растягивается только пружина Ао.
Величину —— можно рассматривать как модуль длительной упру-
го 4" ki
гости. В конце процесса нагружения скорость поршня приближается к ну-
лю и внешняя сила Р уравновешивается силами упругости пружин.
Для перехода от [механической модели к полимерному материалу
обозначим х = е; Р = о; X =
П
1 _ 1 1 , 1 _ 1
^0 ^0 Яд
В этих обозначениях уравнение (7.12) примет вид
Л । X । 1 ’
Ле —е =------о -4-----о,
Ед Ем
(7.15)
(7.16)
56
Тело, деформирование которого определяется уравнением (7.11), называет-
ся вязко-упругим [73]. При X = 0 уравнение (7.16) переходит в закон Гука
= (7.17)
При Ем—»оо из уравнения (7.16) получим
о = Еде + -^ё. (7.18)
Первое слагаемое правой части соответствует упругому сопротивлению,
а второе — вязкому сопротивлению, пропорциональному скорости дефор-
мирования.
Положим, что в момент t = /0, когда деформация была равна е = е0,
внешняя сила снимается. Деформация мгновенно уменьшится на величи-
ну (рис. 7.5). Последующее деформирование будет определяться диф-
ференциальным уравнением
= 0 (7.19)
и начальным условием: при t = /0, е = s0--—.
Ем
Решение уравнения (7.19) при этом начальном условии будет
(7.20)
Из формулы (7.20) видно,
что с течением времени деформа-
ция уменьшается и при /->оое->0,
г. е. тело постепенно возвращает-
ся к исходному недеформирован-
ному состоянию (е = 0). Пружина
^1, определяющая запаздываю- г
щую упругость, постепенно (из- kj
за сил вязкости) возвращает
поршень в исходное положение.
Этот пример хорошо иллюстри-
рует явление запаздывающей
упругости.
Положим
Рис. 7.5
е = е(^) 4- е^), (7.21)
где 8(е) — мгновенная упругая деформация, определяемая формулой
(7.17), а — вязко-упругая (высокоэластическая) составляющая пол-
ной деформации. Вязко-упругая, или высокоэластическая, деформация
будет удовлетворять дифференциальному уравнению
е(^) + е(иг)х = Ло, (7.22)
где
л = х(—Y
\ eJ
Уравнения типа (7.17) и (7.22) называются реологическими, а наука,
изучающая такйе уравнения, — реологией [15, 76]. Для линейно-упругого
тела реологическим уравнением является закон Гука. Реологические
законы деформирования устанавливаются на основе опытов и поэтому
называются феноменологическими.
В реологическом уравнении (7.22) параметры X и А для полимерных
материалов надо рассматривать как величины, подлежащие эксперимен-
57
тальному определению. Для каждого полимера должны определяться
свои значения этих параметров.
Однако при постоянных значениях X и А не всегда может получиться
удовлетворительное совпадение решений уравнения (7.22) с экспери-
ментальными кривыми. Уравнение (7.22) было получено для весьма
упрощенной модели с постоянными значениями физических параметров
йо, Й1 и т]. Поэтому для полимеров необходимо уточнить уравнение
(7.22). Такое уточнение естественнее всего выполнить, считая парамет-
ры д п А функциями напряжения о и температуры Т:
% = X (а, Т), А - А (о, Т). (7.23)
Уравнение (7.22) будет иметь вид
е(ие) _|_ х (а, Т) № = А (а, Т) о. (7.24)
При а и 7, не зависящих от времени, уравнение (7.24) будет по-преж-
нему уравнением с постоянными коэффициентами. В этом случае для про-
цесса активной деформации получим
8<W) = (1 — ехр[—%/]). (7.25)
Скорость роста деформации
е(^) = о А (о, Т) exp [ — V]. (7.26)
В формулах (7.25) и (7.26) существенно то, что параметр X зависит от
уровня напряжения а и температуры Т.
При анализе экспериментов параметры А и X можно, например, при-
нять в форме
А = А0 (Т) + а2Д (Т), X = Хо (Т) + (Т) (7.27)
или в форме
A = AQ(T)0n9 b = X0(T)<j",
где п—число, подлежащее определению.
При фиксированной температуре Т с помощью четырех констант Ло,
Д и Хо, Д можно приближенно аппроксимировать экспериментальные
диаграммы о — е полимеров. Если считать, что вязко-упругие высокоэла-
стические деформации происходят без изменения объема (е^)=0), то
уравнения (7.17) и (7.24) можно распространить на случай сложного на-
пряженного состояния в соответствии с деформационной теорией пластич-
ности.
Для этого уравнение (7.24) надо выразить через интенсивности на-
пряжений 0t и интенсивности вязко-упругих деформаций Тогда по-
лучим
ё(Л’ + X (а,., Т) e(“> = A (ait Т) oif U-28)
при этом надо считать, что
(7-29)
Из уравнений (5.22) деформационной теории пластичности получим
е(^) = —— (в---------<у-------оД = —— [0у----------------------
х 01 \ 2 у 2 / у 0i \ 2 z 2 х/
58
е) ' / 1 1 \
8(ve) = _л—7а Lo _La V (7.30)
2 Oi \ 2 2 х 2 у) 7
Зе<ие> Зе<ие) Зе^>
v(ue) _ 1_ т V(ve) = —i т V(ve) _ 1_ х
УХу ^У> Ууг щ ^yv УгХ Tzx«
Уравнения (7.30) взяты из теории идеального нелинейно-упругого тела
без учета вязкости. Поэтому точность их относительно невысокая. Тем
не менее они очень удобны для приближенных инженерных расчетов
ввиду чрезвычайной простоты. Конечно, уравнения (7.30) могут ока-
заться непригодными при сложном нагружении.
Расчет по уравнениям (7.28) и (7.30) производится следующим об-
разом. Вычисляются ог- для различных моментов времени, численно
интегрируется уравнение (7.28), строится график функции
----j---= —-— (7.31)
£пл(0 Ъ
и по формулам (7.30) определяются компоненты деформаций в функ-
ции времени. Такой способ расчета, как уже отмечалось, является весь-
ма приближенным. Более совершенные методы сейчас только начинают
разрабатываться. Читателю, желающему ознакомиться с современным
состоянием механики полимеров, можно рекомендовать книгу [62]. В ней
содержится большой фактический материал по механическим свойствам
армированных пластиков и большой перечень литературы, посвященной
механическим свойствам полимеров.
ГЛАВА II
ОСНОВЫ ТЕОРИИ ОБОЛОЧЕК
ВРАЩЕНИЯ ПОСТОЯННОЙ ТОЛЩИНЫ
§ 8. ГЕОМЕТРИЯ ОБОЛОЧЕК
Основными геометрическими понятиями теории оболочек постоянной
толщины являются понятия средней (срединной) поверхности и слоя
оболочки. Средней, или срединной, поверхностью оболочки называется
5) °4
Рис. 8.1
поверхность, равноудаленная от ее
боковых поверхностей. Средняя по-
верхность делит толщину h оболочки
пополам. Откладывая по внутренним
нормалям средней поверхности обо-
лочки отрезки длиной z и соединяя их
концы, получим новую поверхность,
которую назовем слоем z оболочки.
Поверхность z = h;2 соответствует
внутренней поверхности оболочки, а
поверхность z=—h/2— внешней (рис.
8.1, а). Произвольную точку средней
поверхности вращения определим как
точку пересечения параллели и мери-
диана (рис. 8.1,6). Каждой параллели
будет соответствовать угол 0 между
осью вращения оболочки и нормалью
и; это как бы широта параллели, от-
считываемая от северного полюса. По-
ложение меридиана на средней по-
верхности можно определить углом ф
в плоскости параллели. Система коор-
динат 0, ф и z определяет положение
произвольной точки Л12 внутри тела
оболочки. Это ортогональная криволи-
нейная система координат в простран-
стве. В точке М средней поверхности
можно построить три взаимно ортого-
нальных вектора единичной длины:
вектор касательной к меридиану
вектор касательной к параллели t2 и
вектор нормали п к поверхности. Век-
—> —>
торы t\ и t2 лежат в касательной плос-
кости к средней поверхности. При
движении точки М по поверхно-
сти трехгранник, образованный векторами t\, t2 и м, будет перемещаться
в пространстве, обкатывая плоскостью поверхность. В дифференци-
альной геометрии этот трехгранник называется трехгранником Дарбу.
60
Вместо угловой координаты 0 можно ввести координату s, отсчиты-
ваемую по длине меридиана средней поверхности. Точка пересечения Oi
двух бесконечно близких нормалей в плоскости меридиана будет цент-
ром кривизны меридиана. Кривизна меридиана определяется как вели-
чина, обратная радиусу кривизны
1 =
1?! ds
(8.1)
Если нормалью м, двигаясь по окружности параллели, разрежем
оболочку, то в сечении получим поверхность конуса с длиной образую-
щей Л. Вершина этой конической поверхности будет в точке О2 на оси
вращения оболочки (ось х на рис. 8.1,6). Отрезок МО2 определяет вели-
чину второго радиуса кривизны R2 средней поверхности. Это радиус
кривизны в точке М плоской кривой, образованной пересечением сред-
ней поверхности с нормальной плоскостью nt2, в которой лежит каса-
тельная t2 к параллели в точке М.
Рассмотрим еще одну характерную точку — точку О3 пересечения
касательных к меридианам, проведенных из точек одной параллели.
В силу симметрии точка Оз также будет лежать на оси вращения сред-
ней поверхности. Обозначим радиус параллели средней поверхности че-
рез г и длину отрезка МО3 через а. Отрезки МО3 и МО2 образуют в точ-
ке М. прямой угол. Из рассмотрения треугольников О2МО и О3МО
получим
sin 6
(8.2)
г
cos 6
(8.3)
Пусть x — координата, отсчитываемая по оси вращения средней по-
верхности. Тогда х и г можно рассматривать как декартовы координаты
в плоскости меридиана. Следовательно,
— = sin 0, — = cos0. (8.4)
ds ds
Умножая уравнение (8.2) на sin 0 и дифференцируя по 0, получим
— = — (Я2 sin0) = sin0 4- Rzcos0.'
d0 dQ 4 2 ’ dQ 2
Но, согласно формулам (8.1) и (8.4),
dr dr ds гъ r\
— = —- -— = Ri cos 0.
dQ ds dQ 1
Следовательно,
-^_ = (tfi-fl2)ctg0. (8.5)
au
Уравнение (8.5) является важным соотношением, связывающим радиу-
сы кривизны /?1 и /?2 средней поверхности оболочки.
Пусть две точки М и N соответствуют приращению Ар угловой коор-
динаты <р в плоскости параллели. Длина дуги MN будет равна rdq>.
Угол dty между двумя соседними нормалями МО2 и NO2 определится из
равенства
R2dty = rdq (8.6)
или
dty = dtp = sin 0dq). (8.6')
/?2
61
Угол d% между двумя отрезками О3М и 03N определится соответ-
ственно из равенства
ad% = rdq,
откуда
d% = — Лр = cos 0d(f. (8.7)
Пусть вследствие каких-либо причин оболочка деформировалась.
Обозначим через и, v и w перемещения точки М средней поверхности
соответственно вдоль меридиана, параллели и внешней нормали
(рис. 8.2,а). Перемещения их и иг в направлении оси х и радиуса г будут
(рис. 8.2,6)
их = и sin 6 — w cos 9, (8.8)
ur = ucosO -r ay sin 6. (8.9)
Перемещения и, v, w, ur, ux и их производные будем считать доста-
точно малыми и пренебрегать их квадратами и произведениями. При
этих условиях вычислим деформации элемента средней поверхности.
Рассмотрим на этой поверхности элемент (рис. 8.3), обра-
зованный пересечением двух близких меридианов и параллелей; длины
дуг NNi и MMi равны ds = R}dQ (см. рис. 8.1,6), длина дуги MN равна
rdcp и дуги —(r+dr)d<p. Площадь четырехугольника MMiN^N
равна rdsdq. Будем считать перемещения u, v, w, их и иг функциями не-
зависимых переменных 0 (или s) и ф. От перемещения и элемент
длиной ds получит относительное удлинение (рис. 8.4)
ди _ 1 ди
ds dQ
Перемещения v перпендикулярны к плоскости меридиана и при
принятом предположении об их малости они не вызовут его удлинения.
Относительное удлинение элемента ММ{ от перемещения w можно
найти как относительное удлинение дуги окружности радиуса Оно
равно Полное относительное удлинение элемента MMt, будет
8Х = — (— 4-йД (8.10)
1 /?! \ <эе J v ’
Выражение (8.10) определяет деформацию средней поверхности в
плоскости меридиана. Относительное удлинение элемента Al/V парал-
62
лели легко получить, повторяя соответствующие рассуждения. Так как
малые перемещения их не вызовут удлинений элемента MN, то доста-
точно рассмотреть перемещения только в плоскости параллели.
Поскольку начальная длина элемента MN равна /т/гр, получим для
относительного удлинения 82 выражение
е2 = —+ (8-И)
г \ дф J
или, с учетом формул (8.9) и (8.2),
1 dv , U ъ . W /о 1л\
е2 =-----— Ч------COS0-}- —. (8.12)
Г Зф Г /?2
Формулой (8.12) выражается
деформация средней поверхности
в направлении параллели. Срав-
нительно сложнее вычисляется
деформация сдвига, т. е. измене-
ние первоначального прямого
угла NMMly четырехугольника
Перемещение w при при-
нятом предположении о его ма-
лости не влияет на величину де-
формации сдвига. Поэтому вместо
элемента поверхности MM}N{N
можно рассмотреть его проекцию
на плоскость, проходящую через
точки Му Mh Wi и /V, т. е. трапе-
цию MMiNiN. Точка пересечения Рис. 8.5
касательных к меридианам лежит
в плоскости этой трапеции. Вычислим уменьшение угла NMM} отдельно
от перемещения и и от перемещения v.
Перемещения отрезков 7ИЛ41 и NNX вдоль касательных к меридианам
будут (рис. 8.5) и и и + (/ср. Соответствующее уменьшение угла NMMX
Yi =
ди
и —— dq — и
Оф
г dtp
1 ди
г дф
63
Перемещения отрезков MN и MTNr вдоль касательных к параллелям
будут v и v + df). Но разность этих перемещений уже не будет
00
полностью определять изменение угла так как вращение элемен-
та NMM±N± как твердого тела вокруг точки О3 влияет на величину этой
разности. Без деформации сдвига перемещению v отрезка MN будет соот-
ветствовать перемещение
O4Mi а Ф ds f л х dr \
О3М а \ г )
отрезка Следовательно, сдвиг определится величиной разности
, dv f \ \ dr \ ди dr
tH-----dQ — v( 1 4- --- =----dQ — v------.
dQ \ r J dQ r
Окончательно уменьшение угла NMM± вследствие только перемещений v
будет равно
dv dQ v dr 1 dv v n
y9 =------------------=----------------cos 6.
30 ds r ds dQ r
Суммарное уменьшение угла NMMlf т. e. величина деформации сдвига
элемента средней поверхности оболочки,
. 1 du , 1 dv и Q /о iq\
Y==Y _------COS0. (8.13)
r 0<p Kj 00 r
Если смотреть на касательную плоскость со стороны внешней нор-
мали, то у2 и —Yi будут углами поворота векторов tx и t2 вокруг нор-
мали по часовой стрелке (см. рис. 8.1,6). Формулы (8.10), (8.12) и
(8.13) определяют деформации средней поверхности оболочки в каса-
тельной (тангенциальной) плоскости. Их часто называют тангенциаль-
ными деформациями.
Изгибные деформации средней поверхности оболочки определяются
через углы поворота нормали. В меридиональной плоскости вследствие
перемещений и и w векторы t\ и п повернутся на угол
dw и
ds /?!
(8.14)
по часовой стрелке, если смотреть в
M02N векторы t2 и п повернутся на
направлении вектора /2.
угол
В плоскости
dw v
rdq R2
(8.15)
против часовой стрелки, если смотреть в направлении вектора t\. Углы
Yi, Y2, 'От и 0*2 полностью определяют повороты векторов трехгранника
Дарбу при малых перемещениях и, у, w. При переходе от угловой коор-
динаты 9 к линейной $, отсчитываемой вдоль меридиана от какой-либо
условной параллели, следует пользоваться простой зависимостью
RxdQ = ds.
(8.16)
В случае цилиндрической оболочки с радиусом R средней поверхности
л
= оо; г = R2 = /?; R±dQ == ds = dx и, следовательно,
du 1 / dv , X du . dv
—, = —f------r b Y =--------F-----;
dx R \ 0<p J rdq dx
(8.17)
64
ди ди а
Yi — ’ Y2 — ~Г~ ’ ~
Rdq дх
dw ________ dw v
~дх~’ 2 ~ Rd<f R
(8.18)
Для сферической оболочки г = R sin 0 и /?, = Т?2 = R. Следовательно,
1/1 dv
R \ sin 0 0ф
+ uctgO + w ),
1/1 ди
R \ sin0 дер
ди 1
-------v ctg 0 .
00 & /
(8.19)
Рассмо средней пс вать перем вил и реш трим задачу об изгибе сферической оболочки без деформаций )верхности, т. с. найдем, при каких условиях будут существо- [ещения и, v, w, когда ei = e2 = y = 0. Эту задачу впервые поста- ил Рэлей. Из уравнений (8.19) следует ~ + W = 0, (8.20) —L_2fL + uctg0 + ai = 0, (8.21) Sill 0 0ф -S' — cfg 0 = 0. (8.22) sin 0 дф 00
Исключив из уравнения (8.20) и (8.21) до, получим sine — <_Ч— \ — — =0, (8.23) 00 V sin 0 J sin 0 0ф sinO — f—— — — = 0. (8.24) 00 \ sin 0 J sin 0 0ф
Обозначив и V и\, = V1, sin 0 sin 0
уравнения (8.23) и (8.24) представим в виде sin 6 — = 0, (8.25) 00 0ф sin 0-^1— 1- =0. (8.26) 00 0ф
Будем искать решения этих уравнений в форме (0) cos nep, = f2 (0) sin nep, (8.27)
где п — целое число. Выражения (8.27) удовлетворяют условию периодич-
ности по углу ср. Уравнения (8.25) и (8.26) в частных производных пере-
ходят в обыкновенные дифференциальные уравнения
sin 0—/г/2 = О, sinO-^- — nfi = 0. (8.28)
dB d0
Складывая и вычитая эти уравнения и обозначая
Л(0) /2(0)-У1, /1(0) —/2(в) = Уг,
получим
sin 0 — nth = 0, sin 0 J- пу2 = 0.
Общие интегралы этих уравнений
Уг - Сп tg" 0/2, у2 = Dn ctg- 0/2,
5 Зак. 96
65
где Сп и Dn — произвольные константы интегрирования (и = 1, 2, 3, ...).
Следовательно,
2и = sin 6 [Сл tg" 0/2 4- Dn ctgn 6/2] cos пф, (8.29)
2v = sin 6 [Cn tg" 6/2 — Dn ctgn 6/2] sin шр.
(8.30)
Правые части уравнений (8.29) и (8.30) не имеют особенностей (не
стремятся к бесконечности) в полюсах 9 = 0 и 0 = л только для п=\.
Но решение для п=1, как легко проверить, соответствует движению
всей оболочки как твердого тела и не представляет интереса. Если
исключить движение как твердого тела, то из уравнений (8.29) и (8.30)
следует, что замкнутая сферическая оболочка не может изгибаться без.
растяжений или сдвигов средней поверхности. Этот результат следует
также из известной теоремы геометрии, согласно которой замкнутая
сферическая поверхность не мо-
жет плавно изгибаться без рас-
тяжения. Если же оболочка пред-
ставляет собой сферический пояс
(01^9^02) или сферический
купол (O<Z0^C0о), то она может
быть изогнута без деформаций
средней поверхности. Однако та-
кое деформирование можно сде-
лать невозможным с помощью*
внешних опорных связей. Если,.
например, в торцовых сечениях
0 = 01, и 0 = 02 запретить перемещения и, то константы Сп и Dn будут
равны нулю и перемещения и и v обратятся в нуль. Эти перемещения
также обратятся в нуль, если в одном торцовом сечении 9 = 02 оболочку
закрепить так, что при 0 = 02, u = v = 0.
Из проведенного анализа следует, что незамкнутые сферические
оболочки ведут себя в отношении деформаций без растяжений и сдвигов
средней поверхности подобно кинематически изменяемым системам.
Этот результат можно распространить на достаточно произвольные не-
замкнутые оболочки вращения. Если такие оболочки имеют малую
жесткость на изгиб (пропорциональную, как и в пластинах, произведе-
нию ЕЛ3), то при отсутствии соответствующего закрепления они могут
работать подобно кинематически изменяемым стержневым системам.
Рассмотрим открытый стержневой купол, состоящий из поперечных
ферм, продольных стержней и раскосов (рис. 8.6,а). Поперечные фермы
сделаны как шарнирные правильные многоугольники (рис. 8.6,6). Про-
дольные стержни (стрингеры) и раскосы шарнирно крепятся к узлам
этих поперечных ферм. Пусть в каждом отсеке купола будет п стринге-
ров и п раскосов. Если число отсеков обозначить т, то общее число-
поперечных ферм будет т+1. Общее количество стержней в куполе рав-
но 2пт-}- (т + 1 )п = 3тп + п, а число узлов (т + 1)п=тп+п. В соответ-
ствии с законами строительной механики пространственных ферм число
независимых уравнений равновесия узлов для случая свободного (неза-
крепленного) купола будет 3(mn + n)—6 = 3 тп + 3 п—6. Степень кине-
матической изменяемости рассматриваемой стержневой системы
г= (3 тп + 3 п—6) — (3 тп + п) = 2п—6.
Только при м = 3, когда поперечные фермы становятся геометрически
неизменяемыми треугольниками, г = 0 и купол в целом будет геометри-
чески неизменяемым. В других случаях это 2п— 6 раз кинематически
изменяемая система. При м->оо 2п — 6 параметрам кинематической из-
меняемости соответствуют две группы констант Сп и Dn, входящих в.
уравнения (8.29) и (8.30).
66
Если, например, узлы крайней нижней поперечной фермы жестко
закрепить, то число уравнений равновесия свободных узлов купола
будет Зтп. Число стержней, кроме стержней закрепленной поперечной
фермы, будет также равно 2 пт + тп = 3 тп, т. е. купол становится гео-
метрически неизменяемой статически определимой системой. Соответ-
ствующая оболочка, у которой запрещены перемещения и и v нижнего
торцового шпангоута, будет также геометрически неизменяемой систе-
мой. В следующем параграфе будет показано, что такая безмоментная
оболочка является и статически определимой.
Таким образом, между безмоментной оболочкой вращения и стерж-
невым куполом имеется глубокая аналогия. Эта аналогия может быть
использована при проектировании сложных оболочечных конструкций.
Она позволяет правильно подойти к оценкам различных способов за-
крепления оболочек. Конструктор должен учитывать, что неправильно
закрепленная оболочка может оказаться близкой к геометрически изме-
няемой системе. Это, в частности, нужно учитывать при проектировании
различных обтекателей. По условиям эксплуатации обтекатели могут
крепиться с помощью ограниченного числа замков и важно правильно
задать их число и расположение.
§ 9. БЕЗМОМЕНТНАЯ ТЕОРИЯ ОБОЛОЧЕК
Эту теорию называют и безмоментной теорией оболочек, и теорией
безмоментных оболочек. В эти два названия часто вкладывают различ-
ные понятия, нуждающиеся в разъяснении. Вернемся к стержневому
куполу, рассмотренному в предыдущем параграфе. Предположим, что
стержни купола связаны не шарнирами, а жесткими узлами. В этом
случае в сечениях стержней будут действовать не только осевые силы,
но и изгибающие и крутящие моменты. Такие конструкции иногда назы-
вают фермами с жесткими узлами. Если при замене жестких узлов
шарнирными конструкция не перестает быть геометрически неизменяе-
мой, ее обычно рассчитывают как ферму с шарнирными узлами.
Шарнирный купол можно рассматривать как расчетную модель неко-
торого реального стержневого купола с жесткими узлами. Такая рас-
четная модель будет правильно отражать основные свойства реального
купола, если влияние изгиба и кручения стержней на его деформации и
прочность пренебрежимо мало и если купол закреплен так, что исклю-
чены его кинематически возможные перемещения как шарнирной си-
стемы. Таким образом, купол с шарнирными узлами является расчетной
безмоментной моделью реального купола с жесткими узлами. Замена
реального купола шарнирным в общем случае допустима только при
кинематической неизменяемости закрепленного купола как шарнирной
системы.
Подобным же образом безмоментную оболочку можно
рассматривать как приближенную модель реальной оболочки, если в
последней можно не учитывать изгибающие и скручивающие моменты;
безмоментная теория оболочек есть приближенная теория
расчета без учета изгибающих и скручивающих моментов; замена реаль-
ной оболочки безмоментной не допустима, если ее средняя поверхность
при заданном способе закрепления может изгибаться без растяжений и
сдвигов. Только при действии на оболочку вращения строго осесиммет-
ричной нагрузки допустима кинематическая изменяемость средней по-
верхности.
Уравнения безмоментной теории оболочек вращения. Обозначим
меридиональные напряжения, — кольцевые напряжения и т — напря-
жения сдвига. Вместо этих напряжений, которые в безмоментной тео-
5!
67
рии считаются равномерно распределенными по толщине h оболочки,
удобно рассматривать усилия
Ti = GQh, Т2 = Gqh, S = xh.
Эти усилия можно рассматривать как погонные усилия, действующие
в средней поверхности оболочки. Составим дифференциальные уравне-
ния равновесия элемента AlA/TViAl! средней поверхности, к которой отне-
сены усилия Ti, Т2 и S (рис. 9.1). Пусть внешние нагрузки, действующие
на оболочку, отнесены к единице площади средней поверхности:
qe—тангенциальная нагрузка в направлении касательной к мери-
диану,
—тангенциальная нагрузка в направлении касательной к парал-
лели,
qn — нормальная нагрузка, действующая в направлении внешней
нормали. Площадь элемента MNN{M\ равна rdqds. Внешние силы
q^rdyds, q^rdqds и qnrdqds производят работу на перемещениях u, v и w
соответственно. Для составления уравнений равновесия сил в тангенци-
альной плоскости надо рассмотреть равновесие плоской трапеции
с углом dx между направлениями ММ{ и NNX. Длины сторон
MN, MiNT[ и MMi=NNi трапеции соответственно равны rd(p, (r + dr)dcp
и ds.
Рис. 9.1
Так как cos dx = 1, sin dx = —dx и
d% = — dtp, то, проектируя
a
все силы на ось, перпендикулярную к сторонам ММ и MlN1 трапеции,
получим
dQ^ (г + dr) dep — Тrrdq — T2ds -у dx —
— f + -^-dqAds — dx + (S — dep^ ds — Sds + qtfdqds = 0.
\ 1 d<p J 2 V дф J
Сокращая на dsdcp и полагая, в соответствии с правилами дифференциаль-
ного исчисления, dr 0, dqp -> 0, найдем
'Р 1 r d0 гр d% ; dS __ q
Г 1“Г“ + ”3----1 2 -J-г—г- + rQe —
ds дО ds dф dф
(9.1)
68
Но
dy г dr ex dB 1 /n Пл
= — =----- = COS 6, --- =----. (9.2)
dtp a ds ds Rt
Следовательно, из уравнения (9.1), сократив на г, получим
-^•-^ + (Л-Л) —+ ^ + 7е = 0. (9.3)
/?1 дВ г гдф
Второе уравнение равновесия в тангенциальной плоскости удобнее
всего получить, взяв сумму моментов всех сил относительно точки О3
пересечения сторон ШЛХ и трапеции (см. рис. 8.5)
(?2 + + -^-)ds~T^a + -v)ds +
4* (S + do') (а + ds) (г + dr) dq> — Sardq 4- qvrd<fds (a + = 0.
\ 30 J \ 2 /
Сократив на dsdcp и полагая ds-*O, dtp-» О, найдем
дТ2 ' dS dB . c . c dr . n
—^аЧ-—ar —4-rS + aS—4-r^a = 0. (9.4)
dtp d0 ds ds
Разделив уравнение (9.4) на ar и учитывая тождества (9.2), получим
1 дТ2 1 1 ГdS . q S п । л /л
— • —- Ч-------•-----h 2 — cos 6 -г <7® = 0. (9.5)
г а<р ае г 7Ф v 7
Третье уравнение равновесия получим, составив сумму проекций всех
сил на направление внутренней нормали к поверхности. Силы 7\rdq и
^0^ (г + dr) d(p лежат в плоскости меридиана и угол между
ними d6. С точностью до величин второго порядка малости силы T2ds и
(т2 + -^-dq\ ds лежат в нормальной плоскости M02N и угол между
\ дер у
ними dip (см. рис. 8.1, 6). Сумма проекций всех сил на нормаль с тре-
буемой точностью в отношении порядков малости произведений дифферен-
циалов будет
TtfdqdB + T2dsdty — qnrdqds = 0. (9.6)
Так как, согласно формулам (8.1) и (8.6),
d0 1 dib г
= и —— = ----,
ds-------------------R±-dtp R2
то, разделив уравнение (9.6) на rdqds, получим
(9-7)
Это известное уравнение Лапласа, рассматриваемое в курсах сопротив-
ления материалов.
Три уравнения (9.3), (9.5) и (9.7) являются искомыми уравнениями
равновесия элемента безмоментной оболочки вращения. Усилия Ть Т2
и S связаны законом Гука с деформациями ei, ег, у средней поверхности,
вычисленными в предыдущем параграфе. Для изотропной упругой обо-
лочки с учетом температурного расширения
ei = -l-(7’i-liT2) + a(7’-T0), (9.8)
69
e2 = ^-(T2-T1|i)4-a(T-7’0), (9.9)
Eh
Здесь E и G — модуль Юнга и модуль сдвига материала оболочки, а —
коэффициент линейного расширения и Т—То приращение температуры в
средней поверхности оболочки.
Система уравнений будет полной, если добавить ранее полученные
выражения деформаций через перемещения и, и, w и их производные:
61 = —— + (9-Н)
1 \ dO J v
1 dV . U Л - /Z-Ч 1 o\
e2 =---— H----cos 6(9.12)
r d(p r R2
1 du . 1 dv v __ n /n iq\
y =--------------------008 e- <9-13)
r dq> Ri dQ r
Через перемещение ur вдоль радиуса г удлинение е2 выражается формулой
е2 = — -^ + —• (9-14)
г д(р г
Отличительной чертой полученных уравнений является то, что они
допускают раздельное интегрирование. Интегрируя уравнения (9.3),
(9.5), (9.7), можно найти общие выражения для усилий Tly Т2, S; затем
определить деформации ei, 62, у из выражений (9.8) — (9.10) закона
Гука и, наконец, найти общие выражения для перемещений u, v, w,
интегрируя уравнения (9.11) — (9.13).
Если на торцах оболочки заданы только силовые граничные условия,
т. е. нет ограничений для перемещений, то можно поставить задачу о
нахождении усилий Ть Т2 и S, используя только уравнения равновесия
(9.3), (9.5), (9.7) и силовые граничные условия. В терминах строитель-
ной механики стержневых систем можно сказать, что безмоментная
оболочка обладает внутренней статической определимостью. Статиче-
ская определимость, неопределимость или геометрическая изменяемость
безмоментной оболочки как механической системы зависят от гранич-
ных условий на торцах.
В первых работах, посвященных безмоментным оболочкам вращения,
их расчет сводился к интегрированию уравнений равновесия. При рас-
смотрении граничных условий ставилась обратная задача: найти такие
граничные условия, при которых найденные частные решения для уси-
лий Г] и5 будут справедливыми; перемещения и, и, w не определялись.
Вследствие этого в некоторых книгах по теории оболочек расчет безмо-
ментных оболочек рассматривается только как задача определения уси-
лий Ть Т2 и S для оболочек разной формы при различных нагрузках.
При общей постановке расчета оболочки по безмоментной теории
принципиально важна правильная формулировка граничных условий.
Безмоментная оболочка является расчетной схемой реальной оболочки
и правильно отражает ее главные свойства только при определенных
условиях загружения или закрепления. Рассмотрим допустимые гранич-
ные условия на торцах безмоментной оболочки. Наиболее просто такие
условия получаются из рассмотрения вариаций полной потенциальной
энергии.
Без учета температурных деформаций, которые в данном случае
несущественны, удельная потенциальная энергия безмоментной упру-
гой оболочки, отнесенная к единице средней поверхности, равна
F = ^-(T]ei + 7’2e2 + SY). (9.15)
70
Из уравнений (9.8)—(9.10) имеем
Т1 = -г^-г(81 + 1*82), (9.16)
1 - и2
Т2= _^_(e2 + R1), (9.17)
1 — ц2
S=OftV = ?(^)’- <9J8>
Следовательно,
F ~ + '* + <9-19>
\ 1 [Л f Zf
При приращениях деформации на 6еь бе2, бу приращение (вариация)
удельной потенциальной энергии (вычисляемое по правилам дифференциаль-
ного исчисления) будет
67 = — (fiiftei + е26е2 +- M^i6e2 + P-e2^ei) + Ghyby
1 — |LA2
или с учетом формул (9.16) — (9.18)]
6F = T16e1 + 7*2662 + S6y.
(9.20)
Дадим теперь приращение 6u только перемещению и. Приращение
деформаций согласно уравнениям (9.11)—(9.13) будет
с дди 'дби с би А с 1 дди
ое1 —----=-------, 6е2 —---COS 0, оу =------.
ds R±dQ г г дф
Соответствующее приращение удельной потенциальной энергии
S 77 гр дЬи . гр Ьи _— _ A I Q 1 д&и
Оиг = Т1----н 2---COS 0 + 0 •------.
*4 А 1 & 1 ->
OS Г Г Оф
При приращении v на bv получим
X 77 гр 1 dbv . с / dbv 6v а\
6VF = Т2-------h S —----------cos 6 ).
г дф \ ds г J
Аналогично, при варьировании только по w
V-Л^ + г,^.
(9.21)
(9.22)
(9.23)
Пусть к верхнему торцу оболочки (s = приложены усилия Т\1) и
-S*0, а к нижнему торцу (s = s2) — усилия Т™ и S(2). Работа внешних сил
на вариациях перемещений (>и, Su, f>w будет
= г2 [ [Т^Ьи + S(2)6y]r=r! dq> - g f [Tf’fiw + S(,)6u]f=ridq) +
0 6
+ [ J (<7o6u 4- q^v + qndw) dsrdq. (9.24)
Si 0
Вариация потенциальной энергии всей оболочки
6Ф = J J (6UF + f>vF + 6WF) dsrdy. (9.25)
Si 0
71
Согласно формулам (9.21), (9.22) и (9.23), имеем
s2 2л
s2 2л
г7\ — + Т2Ъи cos 6 + 3 —1 dsdy.
ds dtp J
Si 0 Si 0
Интегрируя по частям, получим
У r7\ ds = — j buds,
Si Si
2л 2л
Js b “ч = j -f- »““v-
0 0
В силу периодичности по переменному ср получим
2л 2л
I s dtp = — ( fiudcp.
J дф J дф
о о
s 2 2 Л
+ 16„<М1р +
rds r rdcp J
Следовательно,
s2 2Л
st 0 St 0
2Л 2Л
+ r2 у (Tj6u)s=s2dcp — rxJ (T^tijs^dq.
0 0
Аналогично вычисляются два других интеграла
s2 2л s2 2л
J J i>vFdsrd<f = j у -------------------S cos® j bvdsrdq +
Si 0 st О
2Л 2Л
+ r2 f (SSv)s=S2dsd<p — ri J (Si>v)s=Sldsd<f,
о о
s2 2Л s2 2л
Sb— HQ
Sj 0 st 0
(9.26)
(9.27)
(9.28)
bwdsrdq.
R2 J
Согласно принципу возможных перемещений для любых вариаций не-
зависимых перемещений
6F = 67?. (9.29)
Полагая dv = dw = 0, из уравнения (9.29) получим
s2 2Л
Ш1 d(rTj) Т2 cos 0 . dS . "I с , , .
----------------------F —------1- </е budsrdq +
г ds г rd<p J
Si О
2л 2Л
+ г2 у((Ti-Ti2)) 6u]s=S2 d<p - rx f КЛ -T?) du]s- S16<p 0. (9.30)
0 0
Подынтегральное выражение в двойном интеграле формулы (9.30)
должно быть равно нулю, так как вариации du произвольны. При этом
72
условии получаем уравнение равновесия элемента оболочки в проекции на
направление перемещения и:
— _3(гГ1)-----T2cose + dS + = 0 (9
г ds г rdq>
Так как
1 д (rTj) _ d7\ cos 0 у,
г ds ds г 1 *
уравнение (9.31) тождественно уравнению (9.3).
Рассмотрим подробнее контурные интегралы при s = s2 и 5 = 5!. Если
перемещение и на нижнем торце (5 = 52) не задано, т. е. нет связей,
определяющих его величину, то, согласно принципу возможных переме-
щений, вариация би при 5 = 52 ’произвольна и, следовательно, из условия
(9.30) ПОЛуЧИМ, ЧТО При 5 = 52
7\ — Т|2) = 0. (9.32)
Это силовое граничное условие, означающее, что на торце 5 = 52
внутреннее усилие 1\ в оболочке равно заданному значению T(i2). Если,
на торце задано перемещение и (ср), то вариация би = 0 и соответствую-
щий контурный интеграл автоматически обращается в нуль. То же будет
и на верхнем торце 5 = 5Ь Приняв би = б^ = 0, аналогично получим диф-
ференциальное уравнение равновесия элемента в проекции на направ-
ление перемещения v и граничные условия на торцах 5 = 5j и 5 = 52.
Согласно выражениям (9.24) и (9.27), эти граничные условия можно
представить в форме:
при 5 = 52
2л
[ (S — S(2)) 6udq> = 0, (9.33)
б
при S =• $!
2л
j (S — S(1>) fiudcp = 0. (9.34)
о
Следовательно, либо усилия S на торцах равны заданным, либо за-
даны перемещения v и 6у = 0. Наконец, приняв би = 6^ = 0, из уравнений
(9.28) и (9.29) получим только одно уравнение — уравнение равновесия
элемента оболочки в проекции на нормаль к средней поверхности. Новых
граничных условий не будет, так как в формулу (9.28) для вариации
потенциальной энергии по перемещению w не входят контурные инте-
гралы. Следовательно, в безмоментной теории оболочек на торцах
можно задавать только тангенциальные граничные условия, в которые
могут входить либо тангенциальные усилия 7\, S, либо тангенциальные
перемещения u, v. На одном торце можно задать только два граничных
условия. В следующих параграфах мы увидим, что граничные условия
для w можно удовлетворить, рассматривая краевой эффект в моментных
оболочках.
Уравнения осесимметричной задачи. Принимая ^ф=0, v = 0, S = 0,
а перемещения u, w и усилия Т2 зависящими только от 9 (или 5),
получаем уравнения равновесия
4- + (Л - т2) + qQ = о, (9.35)
Ki dv г
+ = (9-36)
Л2
73.
выражения деформаций через перемещения
1 du , w — , dd Rl (9.37)
U л . «Г e2 = — cos 6 H = —-, r R2 r (9.38)
где
ur = и cos 9 + sin 6; (9.39)
закон Гука с учетом температурного расширения
ei (Т1 г) + а» (9.40)
е2 = —(Т2 — + аДТ, Eh (9.41)
тде ДТ = Т — То — заданные приращения температуры средней поверхности.
Проинтегрируем систему уравнений (9.35) и (9.36) для усилий 7\ и Т2.
Из уравнения (9.36) находим
A = Rz(qn-^-\ (9.42)
Подставляя в уравнение (9.35) это значение Т2 и учитывая, что 7?^0 = ds, R2 = ctg 6, Г
получаем + + Т1 + - qn ctg 0 = 0. (9.43) ds \ г J
Примем (9.44) 2лг sin 9
где Р = Р (s) —новая искомая функция. Ее смысл будет рассмотрен ниже.
Подставив это выражение 7\ в уравнение (9.43) и учтя тождества
dr А dO 1
= cos 6, = —,
ds-------------ds Ri
получим после умножения на 2nrsin0
dP
— = 2 лг (q cos 0 — sin 0).
ds
Отсюда
P = Po + 2л J r (qncos6 — qe sin6) ds. (9.45)
si
Величина
qn cos 6 — </e sin 6 = qx (9.46)
есть проекция нагрузки на отрицательное направление оси х.
С учетом обозначения (9.46) формулу (9.45) можно представить в
виде
р = ро + 2л J rqxds. (9.47)
74
Все величины, входящие в формулу (9.47), имеют следующий смысл
(рис. 9.2):
Р— продольная сила в рассматриваемом сечении оболочки;
Ро— продольная сила, приложенная в торцовом сечении s = si;
2nrqxds— осевая нагрузка, действующая на элементарное кольцо
оболочки длиной ds. Следовательно, формула (9.47) определяет эпюру
продольных сил, растягивающих оболочку как стержень переменного
сечения.
Меридиональное растягивающее напряже-
ние согласно формуле (9.44) будет
°е=^- = , .Р. й-. (9-48)
h 2nrh sin 0
а кольцевое напряжение
zr 7*2 7*1 /?2 щ ^2
0 — ---- —---------------- - —----------ОД ---
Р h h h Rr h
(9.49)
Рассмотрим подробно практически важный
случай действия только гидростатического давле-
ния. Принимая qQ = 0 и cos Qds = dr из уравне-
ния (9.45), получаем
Р = PQ + 2л J qnrdr. (9.50)
Если замкнутая в вершине оболочка (гх = 0) нагружена внутренним по-
стоянным давлением qn = р = const, то
Р = 2лр j rdr = лг2р.
б
(9.51)
Формулу (9.51) легко получить непосредственно из теоремы Паскаля,
так как яг2—проекция поверхности оболочки на плоскость, перпендику-
лярную к вектору силы Р. В этом случае меридиональное усилие
7\ = pr)2 sin 0. (9.52)
Но r = T?2sin0. Следовательно,
Л - р/?2/2. (9.53)
Кольцевое усилие
Л = pR2-7\ = pR, fl - (9.54)
Для цилиндрической оболочки радиуса г, закрытой на торцах дни -
щами и нагруженной равномерным внутренним давлением,
Л = Л = рг. (9.55)
Для сферической оболочки радиуса г, нагруженной внутренним дав-
лением,
= Т2 = рг/2. (9.56)
По безмоментной теории оболочек перемещения точек средней по-
верхности легко найти из уравнений (9.37), (9.38), (9.40) и (9.41), если
известны усилия 7\ и Т2. Имеем
75
+ w = (Тх - ИТ2) + а^ДТ, (9.57)
d0 Eh
и ctg О w = (Т„ — и7\) + аТ?2ДТ. (9.58)
Eh
Обозначим
7(0)=-§-(Т1-ИТ2)-^-(Т2-ИТ1) + а(Л1-/?2)ДТ. (9.59)
Eh Eh
Вычитая из уравнения (9.57) уравнение (9.58), получаем
uctgO=/(0) (9.60)
at)
ИЛИ
— (—— = (9.61)
dQ \ sin 0 J sin 0
Интегрируя выражение (9.61), находим
u = Csin0 + sinO Г/(0) —. (9.62)
J sin 0
Произвольная константа С соответствует перемещению оболочки как
твердого тела вдоль оси х. Из уравнения (9.58) получим
W = (Т2 — иТ.) 4- аТ?2ДТ— Ccos0 — cos 0 С/(0) —(9.63)
Eh J sin 0
Согласно соотношению (9.39) перемещение в плоскости параллели
иг = ^ (Т2 - нЛ) + аг&Т. (9.64}
Перемещение в направлении оси вращения оболочки определяется
формулой их = wsin0— r^cosO. Отсюда с учетом формул (9.62) и (9.63)
получим
u =C+f/(0)-^-----------cos9 (Т, — u7\) — aT?2cos0 • AT. (9.65)
J sin 0 Eh “
Для цилиндрических и конических оболочек, где неудобно пользо-
ваться независимой переменной 0, можно оперировать формулами (9.37)—
(9.41), принимая ^-»оо и /?xd0 = ds. Получим
— = Tl ~ + аДТ. (9.66)
ds Eh
Отсюда интегрированием определяется перемещение и. Перемещение w
определяется из уравнения (9.58). Для сферической оболочки R±=R2^-R
и из формул (9.59) и (9.62) следует
f (°) = (1ptg) (Л - Л) (9.67)
Lil
и
и = С sin 0 + /?(1 + и) sin 0 С - l~ Тг~ de. (9.68)
Eh J sin 0
Рассмотрим условия сопряжения двух оболочек вращения на основе
безмоментной теории. Пусть две оболочки, нагруженные осесимметрич-
ной нагрузкой, соединяются по параллели радиуса го (рис. 9.3). В место
стыка угол 0 делает скачок на величину Д0 = 02—01 (все величины для
76
верхней оболочки будем снабжать индексом (1), а для нижней — индек-
сом (2). Спроектировав усилия Т\1} и Т{2) вблизи стыка на ось враще-
ния оболочек, получим первое условие сопряжения
TV’sinG^T^sinGj,. (9.69)
Проекция этих же усилий на плоскость параллели даст погонную нагрузку
рг = TV’ cos 0х — Т(,2) cos 02. (9.70)
Эта нагрузка не может быть воспринята безмоментными оболочками.
Стык должен быть усилен достаточно прочным и жестким шпангоутом.
Нагрузка рг будет расчетной сжимающей нагрузкой для этого шпангоута.
Сжимающее усилие в шпангоуте
W = prr0 = (TV’cos 0J — tV’cos 02) г0. (9.71)
Например, для шпангоута в стыке цилиндрической оболочки со сферическим
днищем, нагруженным равномерным гидростатическим давлением р,
Рг = -у- cos 01;
(9.72)
так как в этом случае Т\1}— где R— радиус кривизны днища, а 62 =
2
Наиболее сложной в безмоментной теории оболочек является задача
составления условий сопряжения перемещений. Как уже было показано,
в рамках безмоментной теории можно
альные перемещения. Но в сты-
ке оболочек нормальное пере-
мещение w одной оболочки
проектируется на направление
тангенциального перемещения
другой оболочки. Правильное
решение этой задачи можно
рассматривать только тангенци-
Рис. 9.3
получить, используя вариаци-
онные уравнения. Это наиболее
надежный и прямой путь реше-
ния сложных задач, когда расчетная схема сильно упрощена и не учиты-
вает всех свойств реальной конструкции.
В нашем случае для упрощения задачи не будем также учитывать
деформацию стыкового кольца.
Составив вариацию полной потенциальной энергии двух стыкуемых
оболочек и проинтегрировав по частям входящие в нее интегралы, по-
лучим, подобно тому как это делалось при рассмотрении граничных
условий для безмоментных оболочек, следующее вариационное условие
в стыке оболочек:
tVW» —TfW2» = о,
(9.73)
где buW и Su(2) — вариации меридиональных перемещений и оболочек в се-
чениях выше и ниже стыка соответственно. Но, согласно соотношению
{9.69), усилия и Т\2} в стыке оболочек можно представить в виде
уЮ) = Т 7^(2) = Т
sin 0b ’ sin 02
77
где Т — проекция этих усилий на оси вращения оболочек. Следовательно,
из вариационного условия (9.73) получим
sin02 • Su(O = sin01 • (9.74)
В уравнении (9.74) 6u(1) и би<2) обозначают возможные меридиональ-
ные перемещения и двух оболочек вблизи стыка. Так как истинные пере-
мещения U0) и должны быть также и возможными перемещениями,
то из уравнения (9.74) следует единственное геометрическое условие
сопряжения двух оболочек в рассматриваемом случае
и™
sin 0i sin 02
В месте стыка цилиндрической оболочки ^02 = со сферической
(9.76)
(9.75}
Индекс (1) относится к сферической оболочке, индекс (2)—к цилинд-
рической.
Условие (9.75) не означает, конечно, что перемещения оболочек не
претерпевают разрыва в месте стыка. В силу основного предположения
о безмоментности оболочек, перемещения оЛ1) и не входят в усло-
вия сопряжения. Безмоментная теория оболочек принципиально не поз-
воляет ставить задачу о полном геометрическом сопряжении двух оболо-
чек в месте стыка. Она не позволяет вообще ставить граничные условия
для нормальных перемещений w. Полные граничные условия и условия
сопряжения будут рассмотрены в следующих параграфах применитель-
но к моментным оболочкам.
§ 10. МОМЕНТНАЯ ТЕОРИЯ ОБОЛОЧЕК. КЛАССИФИКАЦИЯ
НАПРЯЖЕННЫХ СОСТОЯНИЙ
Уравнения моментной теории оболочек. Рассмотрим слой оболочки
на расстоянии z от средней поверхности. Произвольной точке М на сред-
ней поверхности (см. рис. 8.1) будет соответствовать точка Mz на слое.
Обе точки лежат на одной нормали к средней поверхности и имеют одни
и те же координаты 0 и ср. Геометрические характеристики поверхности
слоя z в точке Mz будут
z = А _ _£_\ А _
\ *4 / \ ^2 J
гг = Т?2г sin 6 = г (1-— ).
Будем считать, что оболочка достаточно тонкая, т. е.
« 1, — « 1.
'1 /?2
(ЮЛ)
(10.2)
В тех случаях, когда это упрощает окончательные формулы, будем по-
лагать
RXz = Rlf R2z = R2, rz = r. (10.3)
В теории тонких оболочек деформации слоя z определяются при по-
мощи гипотезы прямых нормалей, согласно которой точки, лежавшие
до деформации оболочки на какой-либо нормали к средней поверхности,
будут перемещаться вместе с этой нормалью в процессе деформирова-
ния оболочки. Эта гипотеза устанавливает кинематическую связь между
78
перемещениями и, v, w точки М средней поверхности и перемещениями
п2, vz, wz точки Mz на слое г.
Углы поворота нормали к средней поверхности в точке М согласно
формулам (8.14), (8.15) будут
1 / dw
~R\~dd
(10.4>
й2 = ^ (10.5) Гиф г\2
Следовате л ьн о, согласи о гипотезе прямых нормалей тангенциальные пе-
ремещения точки Mz слоя z будут
u2 = « + z01 = u + — «). (Ю.6)
v2 = V + zO2 = и + г(-^-----(Ю.7)
\ гду /?2 /
и перемещение в направлении нормали
wz = w. (10.8)
Для определения деформаций е12, e2z, yz слоя z воспользуемся фор-
мулами (8.10), (8.12) и (8.13), заменяя в них перемещения u, v переме-
щениями u2, vz и геометрические величины R19 R2, г средней поверхности
геометрическими величинами Rlz, R2z, rz поверхности слоя z. Получим
Подставляя в уравнения (10.9) uz, vz из выражений (10.6), (10.7) и
учитывая, что
— =^— <1-F — \ — (1 + —— (i+—
R12 \ R1 / ^2Z Ri \ R / Г2 Г \ ^2 /
с точностью до первой степени величины z, получаем
£iz = 6, + zxv е2г = е2 + zx2, у2 = у + 2гт, (10.10>
где
1 ( ди X ди , W 1 dv !
Q . ( _L. 7/1, \ - о
с-» — । Ri \ ае J ds » — Ri “ г д(р
+ — соь 0 + W (10.11)
г ^2
ди . 1 dv У л
у = cos 0 —
гду /?! ае г
тангенциальные деформации средней поверхности и
Х1 = 1 . R ае 1 — е1 - Ri i_ a^i (10.12)
~ Ri ае ‘
ая, . х2 = —--I a COS 0 . V, + 1 — е2 - -- + (10.13)
гд^> г Rz гду Г
1 f , 1 д$2 $2 п । 1 ди .
— ( £_
2 \ rdq ' ае Г «2 гдф
79
1 д02 $•> п
------- -COS О
дО-----г
, 1 dv v
H-------------------cos 0
R2{ d0 R2r
параметры изменения кривизн средней поверхности. Формулу (10.14) мож-
но представить в другом виде:
1 / дОт r 1 дй2 Л Y
2 I гдф дО г R2
1 dv 1 dv
RtR2 ~dd ~dQ
(10.15)
В предлагаемых приближенных выражениях (10.12) — (10.14) для
Xi, Х2, т отброшены слагаемые вида 8i//?i, 82^2 как малые по сравнению
с производными от углов Oi, О2 поворота нормали. Это означает, что
при вычислении изменения кривизн допустимо пренебрегать деформа-
циями 81, 82 и поворотами yi, Y2 элемента поверхности оболочки в его
плоскости. Другими словами, параметры изменения кривизн хь Х2 и т
в основном определяются поворотами нормали к средней поверхности
оболочки.
Перейдем к определению погонных усилий и моментов. Слой z обо-
лочки можно считать находящимся в условиях плоского напряженного
состояния. Закон Гука для слоя z изотропной оболочки без учета темпе-
ратурных деформаций можно представить в форме
р
= + (10.16)
1 р
F
+ (10.17)
(10Л8)
Согласно формулам (10.10) напряжения а0, аф и тОф изменяются по
толщине оболочки по линейному закону. Вместо напряжений можно ввести
статически эквивалентные им погонные усилия Tv Т2, S и погонные моменты
Л4Х, М2, Ml2. С учетом допущений (10.3) получим меридиональное погон-
ное усилие
h/2
Л = ’ <fodz = Eh 9 (8, 4- не2), (10.19)
J 1 — р2
-h/2
кольцевое погонное усилие
h/2
iFh
Gqdz =------— (е2 -j - р8х). (10.20)
1 p2
—h/2
погонное усилие сдвига
h/2
S = j T^dz = Ghy = 2(1Е^} y, (10.21)
—h/2
погонный изгибающий момент в меридиональной плоскости
h/2
М± = [ (fyzdz = D (хх + рх2), (10.22)
—h/2
SO
погонный окружной изгибающий момент
Л/2
М2 = j* e^zdz = D (х2 + рх,), (10.23)
—h/2
погонный скручивающий момент
/1/2
f xQ(pZdz=D(\ — р)т. (10.24)
—7i/2
Здесь
D=—______________
12(1 —ц2)
цилиндрическая погонная жесткость оболочки на изгиб. Положитель-
ные направления моментов показаны на рис. 10.1. Моменты изображены
в виде векторов, перпендикулярных к плоскостям их действия; положи-
тельное направление векторов соответствует правилу правого винта.
Рис. 10.1
Рассмотрим уравнения равновесия элемента оболочки. В предыду-
щем параграфе были составлены уравнения равновесия для элемента
безмоментной оболочки, т. е. когда моменты =Af2 = Afi2 = 0. В рассмат-
риваемой моментной оболочке при составлении уравнений равновесия
элемента ATM'/Vi'Af/ средней поверхности, к которой отнесены усилия
71, Т2, S и моменты Mh М2, М12, надо еще учесть погонные перерезываю-
щие усилия Qi и Q2. Это чисто статические факторы, определяемые из
уравнений равновесия элемента M'N'N/М/. На рис. 10.1, чтобы его не
усложнять, показаны только усилия Qi, Q2 и моменты Л4Ь М2, Mi2.
Повторяя те же рассуждения, которые были подробно изложены в
предыдущем параграфе, легко получить уравнения равновесия элемента
моментной оболочки. Из равенства нулю суммы моментов от-
носительно линии M[N\ определяется усилие
Qi = + (Л11 ~ — +-ф4 (10-25)
d0 г rdq
Аналогично из уравнения моментов относительно линии N'N[
Q2 = + 2Л112 (10.26)
rdq г
6 Зак. 96
81
Уравнение равновесия сил в проекции на направление касательной к
меридиану
-^-^L + (T1-7’2) —+ -^--v- + <7e = 0- (Ю.27)
/?! 30 г гду
Аналогично для направления касательной к параллели
+ cos0~-)T + ‘7<p = O- (10-28)
гдср /?1 dO г Ry
Уравнение равновесия в проекции на нормаль
-Z!- + -b_^_L J?!_ + Q qn = 0. (10.29)
7?! R2 Ri dQ r r«9<p
Здесь, как, и в теории безмоментных оболочек, и qn — составляю-
щие внешней нагрузки, отнесенные к единице площади средней поверх-
ности.
Шестое уравнение равновесия элемента M'N'N\Mi—равенство
нулю суммы моментов относительно нормали — должно быть следст-
вием парности касательных напряжений и удовлетворяться автоматиче-
ски при точных выражениях усилий и моментов через деформации и
параметры изменения кривизн.
Для полученных выражений (10.19) — (10.24) это уравнение точно не
удовлетворяется вследствие допущения (10.3). Так как система пяти
уравнений равновесия (10.25) — (10.29) в принципе достаточна для пол-
ного решения задач о деформациях оболочек, шестое уравнение равно-
весия можно не рассматривать.
Классификация напряженных состояний. Из уравнений (10.25) —
(10.29) можно исключить перерезывающие усилия Qb Q2, в оставшиеся
уравнения подставить выражения усилий Т[у Т2, S и моментов Л12,
Л112 через перемещения u, v, w и их производные и получить три диффе-
ренциальных уравнения в частных производных для определения пере-
мещений. Однако практическое решение этих уравнений наталкивается
па большие математические трудности и оказывается возможным только
в некоторых простых частных случаях. В то же время очевидна специ-
фика уравнений моментной теории оболочек: усилия Т2 и S пропор-
циональны первой степени, а моменты Л1Ь М2 и Мх2 — кубу толщины
оболочки. По предположению, толщина оболочки h весьма мала по
сравнению с характерными размерами (например, или /?2) средней
поверхности. Следовательно, до решения уравнений можно поставить
задачу их максимального упрощения с учетом малости толщины обо-
лочки. Развитие теории тонких оболочек за последние 30 лет в значи-
тельной мере определялось поисками этих упрощений. С соответствую-
щими исследованиями можно ознакомиться по книге [61].
Рассмотрим метод упрощения уравнений моментной теории оболочек,
основанный на малости толщины оболочки по сравнению с ее радиусами
кривизны [30].
Средние по толщине оболочки напряжения можно определить из
уравнений (10.19) — (10.21):
« = = -jj (8i + Не2). (<УФ)с = -у- = тДу
(т0ф)с = — = —----- у- (Ю.
°Ф'С h 2(1 +Ц) Г '
Моментные (изгибные) напряжения при z = + h/2 можно определить из
уравнений (10.22) — (10.24):
82
(сге) = 4-6 = +-------—-----(Xj + |ХХ2),
' B/и - л2 - 2(1 -ц2) v 1 г 27
(аф) =4-6 = + ——— (х. -}- p.Xj),
V Ф/и - ft2 2(1 —н2)
(t0 ) = 4- 6-^- = ± ———
v ф7и - Л2 2(14г|1)
(10.31)
г.
)
В формулах (10.31) величина А2/6 есть погонный момент сопротивле-
ния нормальных сечений оболочки. Это момент сопротивления сечения
прямоугольника, высота которого А, а ширина равна единице.
Рассмотрим структуру выражений для деформаций 81, е2, у и пара-
метров изменений кривизн хь х2, т. Возьмем для определенности выра-
жения 82 И Хь
1 dv . и а । w
е2 =-----— Ч-----cos 0-Ь — =
г дф г Т?2
1 д^ 1
Xi =--------— = — ,
д0 00 L
Эти выражения не зависят прямо от толщины оболочки А, а величи-
ны 82 и xi/?i имеют одинаковую размерность. Пусть /?о — какой-либо
характерный размер средней поверхности, например радиус кривизны /?2
торцового сечения оболочки. Введем вместо Xi, х2, т безразмерные вели-
чины Х1=/?0Х1, х2 = /?0Х2, т = /?от. Тогда суммарные напряжения в
ке при z=±h!2, согласно формулам (10.30) и (10.31), будут
----~ ei г Це2 ± —- (хх -г цх2)], ।
Е
1 — |Л2
______Е
Т0<Р“ 2(1 +И) V 2R0 J'
Так как весьма малая величина, то на первый взгляд
мул (10.34) следует парадоксальный вывод, что все слагаемые
метрами изменения кривизн можно отбросить. Но в этом случае напря-
жения будут определяться только деформациями 81, 82, у безмоментного
состояния. Более глубокое рассмотрение показывает, что параметры
Xi, х2, т, а следовательно, и хь х2, т отличаются от 81, 82, у порядками
частных производных от перемещения w. Так, из рассмотрения формул
(10.32) и (10.33) видно, что в выражение для 82 входит только само пе-
ремещение w, а в выражение для xi — вторая производная от этого пе-
ремещения.
Но дифференцирование функции может увеличить порядок ее вели-
чины, т. е. максимальное абсолютное значение производной может быть
существенно больше максимального абсолютного значения самой
функции. Порядок абсолютной величины какой-либо функции можно
обозначить введением фигурных скобок. Например, порядок w обозна-
чается как {^}. Предположим, что решение уравнений моментной тео-
рии оболочек в каком-либо частном случае можно представить в форме
(Z> 1)
1 / 1 ди , 4.^ л ,
— (----------------Н и ctg 6 + w
R2 \ sin 0 дф
д Г 1 / dw \ "i
-------И I .
д0----J \
(10.33)
оболоч-
<Ь =
—
Ге2 + (х. + Н*1)], >
L
(10.34)
из фор-
с пара-
w = Ле-х<0-0о) cos пф.
(10.35)
Тогда
= — ХЛе-х<е“е®>cos /пр, = — пЛе-А<0_0о) sin пф. (10.36)
дО дф
6=
83
Из формул (10.35) и (10.36) следует
{>*
Если К и п — большие числа, то можно сказать, что дифференциро-
вание функции (10.35) по 0 увеличивает ее порядок величины в Z раз,
а дифференцирование по ср — в п раз. Если X или п порядка единицы, то
говорят, что дифференцирование не изменяет порядка величины функ-
ции. В теории оболочек коэффициенты X и п называются коэффициента-
ми изменяемости напряженного или деформированного состояния. Поло-
жим теперь, что k=VRo/h. Тогда xi будет порядка X2w и соответствую-
щими слагаемыми в формулах (10.34) уже нельзя пренебрегать. В этом
случае
= <10-37>
Из этого простого анализа следуют три важных вывода.
1. Если напряженное состояние моментной оболочки описывается
функциями с малой изменяемостью, т. е. функциями, порядок которых
не возрастает при дифференцировании, то это напряженное состояние
можно приближенно найти по безмоментной теории оболочек, полагая
М.\ = Л12 = Л112 = 0.
2. Если средние напряжения от усилий 7\, Т2, S и изгибные напряже-
ния от моментов Л4Ь Л12, М12 имеют один и тот же порядок величины, то
соответствующее напряженное состояние будет напряженным состоя-
нием с большим коэффициентом изменяемости (в одном или двух на-
правлениях). Такое напряженное состояние можно определить из
приближенных уравнений теории оболочек, учитывающих различные
порядки величин производных от перемещений, усилий и моментов.
3. Если изгибные напряжения значительно больше средних напря-
жений от усилий Ть Т2, S, то перемещения и, ц, w для такого напряжен-
ного состояния можно определить из уравнений
= е2 = у = 0. (10.38)
Это напряженное состояние соответствует деформированию оболочки
без растяжения и сдвига средней поверхности.
В общей теории тонких оболочек первое напряженное состояние
называется без мом ентн ы м, второе — смешанным, третье —
моментным [30].
Действительное напряженное состояние конкретной оболочки при
заданных внешних нагрузках и граничных условиях в общем случае не
определяется, конечно, каким-либо одним видом напряженного состоя-
ния, а может складываться из этих характерных напряженных состоя-
ний. Каждое из них является частным интегралом уравнений теории
моментных оболочек.
Другими словами, малость параметра hlZRu позволяет определять
различные частные интегралы дифференциальных уравнений теории
'тонких оболочек из решений соответствующих упрощенных уравнений.
Так как дифференциальные уравнения теории оболочек являются линей-
ными, то общее решение их можно искать в виде суммы частных интег-
ралов, содержащих достаточное число произвольных функций или
констант интегрирования для удовлетворения граничным условиям.
Суммарное напряженное состояние в различных частях оболочки может
быть близким к тому или другому характерному напряженному со-
стоянию.
84
Если оболочка не является пологой и внешние нагрузки 90, q<p и qn
заданы как функции с малой изменяемостью, т. е. их производные по
0 и ф имеют тот же порядок, что и сами функции, то частное решение
общих уравнений можно определять по безмоментной теории. Общее
решение в этом случае будет складываться из этого частного решения и
интегралов упрощенных однородных уравнений. Это основной практиче-
ский вывод из математической теории интегрирования уравнений теории
тонких оболочек. Для пологих оболочек и для оболочек, загруженных
сосредоточенными или разрывными распределенными нагрузками, изло-
женный прием приближенного решения с выделением частного решения
по безмоментной теории не всегда пригоден.
иметь вид:
§ 11. КРАЕВОЙ ЭФФЕКТ В МОМЕНТНОЙ ТЕОРИИ ОБОЛОЧЕК
Уравнения краевого эффекта и их анализ. В общих уравнениях мо-
ментной теории в случае осесимметричной деформации положим =
?ф=0 и все величины не зависящими от угловой координаты ф. В этом
случае y = r = Mi2 = Q2 = 0. Полная система уравнений будет
1 f du . \
8i =- —— + ),
/?! \ de /
е2 = (и ctg 6 -I- w),
^2
(U-2)
fl
(11.3)
__ 1 d Г 1 / dw
Kl ~ Ri de L R1 \ 40
ctg 0 / dw \
R1R2 \ de /
ЛД = D (xx + p,x2),
7W2 = jD(x2 н-цхЛ,
q _L + (Mi — м.)
1 Ri dO v
(И.4)
(П-5)
(Н.6)
(П-7)
— (Т _ 7 ) _ Jk
Ri de v r2
ctg 9
*2
(Н-8)
Ri
Ri ' r2 + Ri de +Q1 r2
ei -= “77“ (^1 e2 ~ “77“ (^2 1) •
Eh Eh
(П-9)
(11.10)
При составлении уравнений (11.1), (11.8) — (11.10) учтено, что r=/?2sin0.
Если нагрузки до и qn меняются вдоль меридиана достаточно плавно,
частное решение уравнений можно, как уже указывалось, найти по фор-
мулам для безмоментной теории оболочек.
Рассмотрим подробно однородные уравнения, когда qe=qn = Q-
Моментное напряженное состояние при осесимметричной деформации
теряет смысл, так как из решения уравнений ei = e2 = 0 получаются пере-
мещения и и w, соответствующие лишь движению оболочки вдоль оси
симметрии как твердого тела. Для приближенного определения смешан-
ного напряженного состояния, которое называется краевым эффек-
том, рассмотрим упрощения исходных уравнений, следующие из усло-
85
вия быстрой изменяемости напряженного состояния вдоль меридиана.
Будем считать, что для всех искомых величин выполняется условие
Фигурные скобки обозначают, как и раньше, порядок соответствующих
величин. Конкретные значения /?о определим позднее.
Будем также считать, что величина ctg0 для любого края оболочки
не слишком велика и радиус кривизны /?1 изменяется вдоль меридиана
достаточно плавно. Эти предположения будут еще обсуждены в даль-
нейшем. Естественно предположить, что порядок величины перемеще-
ния w выше порядка величины перемещения и. Положим, что
Тогда главные значения величин, определенных формулами (11.2 будут — 11.5)
W е2 = , (П-14)
л =_L 1 R1 de ' (11.15)
1 d?w X, = r2 d0* ’ (11.16)
_ ctg 0 dw X? RXR2 de (П-17)
Из уравнений (11.16) и (11.17) следует, что
W > {х2}- (11.18)
Поэтому можно считать, что
•, г, В d-w М, = Ох. = , r2 d02 (11.19)
Л42 = = pMr. (11.20)
Из соотношения (11.8) с той же степенью точности следует
Q D_^_ r3 № (П-21)
Уравнения равновесия (11.9) и (11.10) сразу упростить нельзя, так
как неизвестен относительный порядок величин усилий 7\ и Т2. Исключим
из этих двух уравнений величину Т2. Умножим уравнение (11.10) на ctg О
и сложим его с уравнением (11.9). Так как по условию qn = q$ = 0,
получим
1 dl\ т Ctg 0 , т ctg 0 . ctg е dQt _ „ ctg8 0 = Q
Rt de ' 1 Rt ' 1 Rj. Ri de Rt 41 R2
Это уравнение можно проинтегрировать, учитывая, что
1 dQ п г dr А
---=------, Кп =-------, ----= cos 0.
Ri ds “ sin 0 ds
Умножив его на г sin 0, получим
— (г7\ sin 0 + rQ± cos 0)^0
ds
86
или, интегрируя, найдем
г (7\ sin 0 + Qx cos 0) = С.
Но
2лг (7\ sin 6 4- Qr cos 6) = Р,
где Р — продольная сила в сечении оболочки. При исследовании краевого
эффекта будем считать Р = 0. Частное решение, соответствующее продоль-
ной силе Р, отнесем к безмоментному напряженному состоянию.
Следовательно, для интегралов краевого эффекта
T1=-Q1ctgO. (11.22)
С учетом формулы (11.22) уравнение (11.10) для краевого эффекта будет
ZL-i- _L 4-Q _q
/?» Rt dQ 1 Rz 1 /?х
или, учитывая соотношение (11.21) и условие (11.12),
D d*w _ Q
R4 d№ R2
(11.23)
Уравнение (11.23) — одно из основных уравнений теории краевого
эффекта. Из него следует
т _ DR2 d*w (11.24)
Из уравнений (11.21) и (11.22) получим
7\ = — — — ctgO. R\ d& (11.25)
При принятых предположениях порядок Т2 выше порядка Тх, т. е.
(11.26)
Следовательно, из соотношений (11.12) и (11.14) получим
ш Т2 8о = = —— R2 Eh (11.27)
ИЛИ
То =Eh —. *2 (11.28)
Это второе основное уравнение теории краевого эффекта. Из сравнения
формул (11.24) и (11.28) следует разрешающее уравнение
EhR] W rf04 dr\ = 0. (11.29)
Но D — , следовательно,
1 LJ — , 12 (1 — р=)
-= 12(1 —ц2 DRo h-R^ (11.30)
Обозначим л Rj_ •/" Roh
k = |/3 (1 — н2) - (11.31)
87
Тогда уравнение (11.30) можно написать в виде
+ 4k^w = 0. (11.32)
dO4 v
Аналогичным уравнением описывается изгиб балки, лежащей на упругом
основании [73].
Для сферической оболочки R± = R2 = R и коэффициент
k = ^3(1-/) 1/4
у h
является постоянным большим числом Г при — >100, &> 10
Особенности деформации оболочки в зоне краевого эффекта. При
постоянном k общий интеграл уравнения (11.32) можно представить в виде
w = e~kQ (A cos kft + В sin A0) + ekQ (C cos kQ -k D sin £6), (11.33)
где А, В, С и D — произвольные константы.
Выражение (11.33) обладает тем свойством, что при каждом его
дифференцировании оно «выбрасывает» множитель k, т. е.
= |и т. д
( d0 J 1 \ 1 {
Следовательно, это решение удовлетворяет условию (11.12). За харак-
терный размер Ro для сферической оболочки естественно принять ра-
диус сферы R.
Рассмотрим теперь только одну, затухающую часть выражения
(11.33):
W = e~kQ (Д cos kQ В sin /?0), (11.34)
где cos£0 и sin£0 являются периодическими функциями угловой коор-
динаты 0 с периодом
2л __ 2л Г 1г
k Уз(1 —р.2) V R '
При увеличении 0 на период величина w уменьшается в е2я раз, т. е.
становится пренебрежимо малой величиной. Длина отрезка меридиана,
соответствующая этому периоду,
\s = —R = -.----2я УМ. (11.35)
k /3(1-и2)
При практических расчетах уменьшение амплитуды синусоидальной
функции в ел раз является достаточным, чтобы считать се полностью
затухшей. Другими словами, функцию (11.34) можно считать практиче-
ски полностью затухающей на длине отрезка меридиана сферы
As = - л' VRh. (11.36)
/3(1-/)
При /?/Л= 100, As//? = 0,244, а при /?/А = 400, As//? = 0,122. Отсюда можно
сделать важный вывод, что если на длине As меридиана, отсчитываемой
от торца оболочки, радиусы кривизны /?1 и мало изменяются, то в
дифференциальном уравнении (11.32) коэффициент k можно считать
постоянным и определять его по значениям и R2 в сечении рассматри-
ваемого торца.
88
Пусть оболочка имеет форму пояса с торцами, соответствующими
0 = 0Х и 0 = 02 (рис. 11.1). Длину меридиана между торцами 0 = и
0 = 02 обозначим s0. Радиусы [кривизны средней поверхности оболочки в
сечениях 0 = 0г и 0 = 02 обозначим У?!0, Rz} и /?(2), R^ соответственно.
Для каждого торца оболочки вычислим коэффициент k по формуле (11.31):
4 Я(1) 4 /?(2)
VR^h VR^h
При этих обозначениях краевой эффект вблизи верхнего торца (0 > 0х)
выражается формулой
w = e-k> (о-0*) [Лх cos k± (0 — 0Х) В, sin kv (0 — OJ], (11.37)
а вблизи нижнего торца (0<02)—формулой
w e-k2 (02-0) [Д cos k2 (02 — 0) + sin k2 (02 — 0)]. (11.38)
В некоторых случаях, например для цилиндрических и конических
оболочек, вместо угловой координаты 0 следует ввести линейную коор-
динату s. Тогда формулы (11.37) и (11.38) примут вид:
для краевого эффекта у верхнего торца
w = e-₽i(s-si) [Л1 cos Pi (s — sj + sin Pi (s — sj], (11.39)
для краевого эффекта у нижнего торца
w = e-P»(s2-s) [Л2 cos Р2 (s2 — s) + В2 sin Р2 (s2 — s)J, (11.40)
где
р = — = . (11.41)
Ri / RJi
Величины Pi, р2 вычисляются для
значений радиусов кривизны /?2 сече-
ний оболочки, соответствующих верх-
нему и нижнему торцам. Разделение
общего решения уравнения (11.32) на
два затухающих решения (11.37),
(11.38) или (11.39), (11.40) будет
справедливым при выполнении следу-
ющих двух условий:
а) расстояние между торцами
оболочки s0, отсчитываемое по мери-
диану, больше максимальной из длин
зон затухания краевых эффектов, т. е.
S0> у " V^h, So
/3(1-^)
4/.. я.-—
/3(1-н2)
(11.42)
б) на длинах зон затухания краевых эффектов радиусы кривизн R^} и
с достаточной для расчетов точностью можно считать постоянными вели-
чинами.
Проверим теперь справедливость принятого раньше условия (11.13).
Из формул (11.11) с учетом неравенства (11.26) следует
е — — Т
1 Eh 2‘
Из уравнений (11.1) и (11.28) находим
du , U.R, m Ri
dv Eh Rz
89
или
1 4- |x
R2 J
du
~dd
что и требовалось доказать.
Перемещению w краевого эффекта соответствует угол поворота каса-
тельной к меридиану погонный изгибающий момент м1 = -5- dw dw RidQ ds d2w d2w d& ~ ds2 (11.43) (11.44)
погонное перерезывающее усилие Qx=4 d3w d d№ ~ ds3 » (11.45)
погонное растягивающее меридиональное усилие Л = — Qi ctg 9. Усилия Qi и 7\ дают равнодействующую Qr = Qi sin 6 — 7\ cos 0 = <2i sin 0 (11.46) (П.47)
лежащую в плоскости параллели.
Таким образом, краевой эффект соответствует загружению торцов обо-
лочки погонными изгибающими моментами и погонными усилиями Qr.
Для верхнего торца усилия Qr = Q(r1} действуют в плоскости параллели
0 = 6Х и направлены от центра окружности этой параллели, а для ниж-
него торца усилия Qf = Q(2) действуют в плоскости параллели 0 = 62 и
направлены к центру окружности параллели (рис. 11.2, а). Положитель-
ные моменты и 2И(12) сжимают внешние меридиональные волокна обо-
лочки.
Граничные условия для осесимметричной задачи. В решение краевого
эффекта для какого-либо торца оболочки входят две константы интегри-
рования. Следовательно, на торце оболочки можно задать для опреде-
ления этих констант два граничных условия. В эти граничные условия
90
могут входить только величины w, <h, Mi и Qr. Можно, например, задать
нормальный прогиб w и поворот касательной к меридиану 01 или погон-
ный момент Mi и погонную силу Qr. Можно задать какие-либо две физи-
чески реальные комбинации из этих величин, но нельзя задавать пере-
мещение и или усилие В решении краевого эффекта эти величины
являются вторичными.
С другой стороны, в предыдущем параграфе было показано, что в
безмоментной теории оболочек основными величинами, для которых
можно задавать граничные условия, являются и и 1\. Это предопреде-
ляет разделение граничных условий в общей задаче моментной теории
оболочек вращения. Рассмотрим этот вопрос более строго, основываясь
на уравнениях принципа возможных перемещений применительно к рас-
сматриваемой осесимметричной задаче моментной теории. Для погонных
усилий Т\ и Т2, как было показано в предыдущем параграфе, обобщен-
ными перемещениями являются деформации ei и е2. Аналогично можно
показать, что обобщенными перемещениями для моментов М1 и М2
будут параметры изменения кривизн xi и х2, так как моменты совер-
шают работу на изменении углов поворота сечений, в которых они дей-
ствуют.
Для осесимметричной задачи вариация внутренней потенциальной
энергии оболочки с точностью до множителя 2л будет
S2
6Ф = j (Т^ + Т2де2 4- + M2dx2) rds. (11.48)
S1
Согласно уравнениям (11.1) — (Н.5)
1 ds R! 2 R2 R2
___d2 (6ш) d6u ________ etg 0 d6w ctgO
1 ~ ds2 ~~ Rrds1 2 R2 ds RtR2
Подставляя эти выражения в равенство (11.48) и интегрируя по
частям те слагаемые, в которые входят производные от вариаций би
и 6w, столько раз, сколько нужно, чтобы подынтегральное выражение
содержало би и 6w только в виде множителей, получим
s2
дФ = f ([/] Ьи + [II] dw) rds + Г (т1 — rbu 1s=s’ -ь
J L \ #1 / Js=s1
Гмхг Г ” -1 • (11.50)
L ds Js=S1
Выражения / и //, стоящие в квадратных скобках под знаком интег-
рала, представляют, как и должно быть, левые части дифференциаль-
ных уравнений (11.9) и (11.10) равновесия элемента оболочки, в кото-
рые подставлено выражение для Qi из соотношения (11.8). Рассмотрим
подробнее сумму
^-y«ls=s’ \rM> 4^-]s=S2 - WiMsS: = Hr]i=s:,
. \ R1 J Js=s, L Js=St
где
дГ = f 7\ — дм + М, - Q-дш.
\ Ri ) 1 ds 41
Из уравнения (11.3) следует
_________________________________ dbw би
1 ~ ~ds rT '
91
Отсюда
dbw с л . &и
----- = 0th -------.
ds 1 Ri
Следовательно,
6Г = Т^и + — Q^w.
(11.51>
Уравнение (11.51) имеет простой механический смысл: усилие 1\ со-
вершает работу на вариациях тангенциального перемещения ц, момент
Mi —на вариациях угла поворота касательной к меридиану th и усилие
Qi—на вариациях перемещения w. Выражение (11.51) допускает инте-
ресное преобразование [105]. Из второго уравнения (11.49) имеем
6ш = Т?2 (6е2---• 6ц^ = /?2бе2 — ctg 06ц.
Подставляя в уравнение (11.51), получим
6Г = (7\ + Qx ctg 6) бц + 714,6^ —
Но согласно соотношению (11.47)
sin 0
где Qr — погонное радиальное усилие в плоскости параллели. Следовательно
6Г - (7\ + Qi ctg 0) 6ц + Л^б^ — rQr6e2. (11.52)
Формула (11.52) математически обосновывает разделение граничных
условий в соответствии с разделением общего решения уравнений мо-
ментной теории на безмоментное решение и краевой эффект. Величина
T’l + QictgO, согласно соотношению (11.46), тождественно равна нулю в
решении для краевого эффекта, а величины Л4i и Qr полностью опреде-
ляются краевым эффектом. Таким образом, краевой эффект ведает толь-
ко погонным моментом Mi и погонным усилием Qr.
Граничные условия можно разделить на три группы: 1) в танген-
циальной плоскости для усилия 7"1 или перемещения ц, 2) в меридио-
нальной плоскости для Mi или и 3) в плоскости параллели для Qr
или ге2 = ^г, где иг — радиальное перемещение в плоскости параллели.
Решение краевого эффекта позволяет удовлетворить граничным усло-
виям в меридиональной плоскости и в плоскости параллели. Граничные
условия в тангенциальной плоскости (по Т\ или ц) следует удовлетво-
рять решением по безмоментной теории. Этим полностью определяется
место безмоментной теории в моментной теории оболочек.
Следует подчеркнуть, что усилия 7\ из безмоментного решения и уси-
лия Qr из решения краевого эффекта действуют не по взаимно ортогональ-
ным направлениям. Они ортогональны только в случае цилиндрической
оболочки, когда 9 =-^-. Если, например, к нижнему торцу оболочки при-
ложены внешние усилия р№ и действующие по оси х по радиусу па-
раллели г в направлении к центру, то, раскладывая их по правилу парал-
лелограмма в направлении касательной к меридиану и радиусу параллели,
получим (рис. 11,2, б)
0(2)
Sin 02
Соответственно для верхней параллели при тех же направлениях усилий
pH) и р^ (р0>— ВНИЗ ПО ОСИ X, —к оси оболочки)
й" = pi"ctg
sin 0г
92
Последовательность расчета осесимметрично нагруженной оболочки
вращения по моментной теории с разделением напряженного состояния
на безмоментное и краевой эффект следующая:
1. Определяют по безмоментной теории усилия Тх, Т2 и перемещения
и, w по заданным внешним нагрузкам и граничным условиям для Т{
или и. В выражение для перемещений может входить константа интег-
рирования, соответствующая перемещению оболочки как твердого тела.
2. Находят, решая однородные уравнения краевого эффекта для
каждого торца, общие выражения для е2, 'O'i, Mi и Qr через соответст-
вующие константы интегрирования (по две константы на каждом торце).
3. Составляют граничные условия для каждого торца оболочки. Если
заданы силовые граничные условия, т. е. величины Мх и Qr, то сразу
определяют константы интегрирования уравнений краевого эффекта.
Если заданы геометрические условия, т. е. величины е2 и 'fti, то по вели-
чинам перемещений и и w безмоментного решения определяют величи-
ны е2о и Ою (перемещение оболочки как твердого тела в них не войдет)
и составляют суммарные выражения для е2 и th от безмоментного реше-
ния и краевого эффекта. Константы интегрирования, входящие в эти
выражения, определяют из заданных геометрических граничных условий.
Изложенную последовательность расчета нетрудно обобщить на слу-
чаи, когда заданы смешанные граничные условия или надо удовлетворить
условиям сопряжения двух оболочек. В последнем случае удобно ввести
вспомогательные величины: — удлинение стыковой параллели (обычно
это окружное удлинение шпангоута) и —вращение элементов этой па-
раллели (соответствует деформации симметричного выкручивания шпангоу-
та). Через эти вспомогательные величины определяют значения е2 и для
обеих оболочек в месте стыка и соответствующие им выражения для сил
Qr и моментов Л4Р Сами величины и затем определят из уравне-
ний для стыкового шпангоута. Пример такого расчета будет приведен в
дальнейшем.
До сих пор мы рассматривали участок оболочки, где ctg0 не слиш-
ком велик. Прежде всего оценим предельное значение ctg0, когда еще
можно пользоваться уравнениями краевого эффекта.
Рассмотрим купол оболочки (0^0^01). Чтобы у торца купола при
0 = 0i (5 = sJ были справедливы уравнения краевого эффекта, диффе-
ренцирование по 0 должно увеличивать искомые функции в большее
число раз, чем умножение на ctg0. Это значит, что у торца оболочки
должно удовлетворяться условие
^3(1-Иг) -A^ctgO,. (11.53)
/я2/1
С другой стороны, решение краевого эффекта должно затухнуть, не
дойдя до вершины купола. Согласно неравенствам (11.42) должно вы-
полняться условие
t " VRJi < Si. (11.54)
/ 3(1-И2)
Требования условий (11.53) и (11.54) качественно не противоречат друг
другу. Действительно, из неравенства (11.53) следует
93
При малых углах 0г tg Ох sx. Для практических оценок
применимости приближенных формул можно рекомендовать следующий
критерий:
tg61>2n . (11.55)
#1
Для сферического купола = Т?2 = R и Rih =- 400 получим, например,
tgOx > л/10 и 0Х> 18°.
Из формулы (11.55) следует практически важный вывод, что пре-
дельный минимальный угол 01, при котором еще можно пользоваться
приближенной теорией краевого эффекта, зависит от толщины оболоч-
ки h. Чем меньше толщина оболочки, тем точнее пологий купол можно
рассчитывать по приближенной теории оболочек с разделением напря-
женного состояния на безмоментное и краевой эффект.
В заключение выведем формулы для определения перемещений иг и их
по направлениям радиуса параллели и оси вращения оболочки. Относитель-
ное удлинение параллели е2 = Следовательно, в общем случае
г
ur = re,2 —— (11.56)
Eh
В случае разделения напряженного состояния па безмоментное и краевой
эффект
иг = ~т— (T2q Ч ~ wk.
Eh R2
где Тю, Т20—усилия безмоментного состояния, a wk — нормальное пере-
мещение, определяемое из решения однородного уравнения (11.32)
краевого эффекта.
Для определения осевого перемещения их удобно воспользоваться
следующим тождеством, справедливым для произвольного осесиммет-
ричного напряженного состояния оболочки вращения:
. п п п ( du . w \ а / dw и \ А
eiSinG — (hcosS = i----------sin 0 — (-----------)cos0 =
1 \ ds /?! J \ ds Rt J
= — (u'sinO — ^cos0) =
ds ds
Следовательно,
ux = C + J (fii sin 0 — {^cos0) ds, (11.57)
где C — произвольная константа интегрирования, соответствующая пе-
ремещению оболочки как твердого тела. При разделении напряженного
состояния на безмоментное и краевой эффект полное осевое переме-
щение
Ux = UxO~ ^АСОЬ0.
§ 12. РАСЧЕТ ПОЛОГОЙ СФЕРИЧЕСКОЙ ОБОЛОЧКИ
И ЦИЛИНДРИЧЕСКОГО БАКА СО СФЕРИЧЕСКИМИ ДНИЩАМИ
Пологая сферическая оболочка. Рассмотрим пологую сферическую
оболочку, нагруженную равномерным внутренним давлением р (рис. 12.1).
Будем считать углы 0 малыми и cos0 = 1; sin 0 = tg 0 = 0, ds = RdQ = dr,
ctg0 = - . e ~ = —• В качестве независимой переменной примем радиус г.
Для пологой оболочки можно считать, что угол поворота касательной к
94
меридиану практически не зависит от тангенциального перемещения и.
Тогда согласно уравнению (11.3)
а dw dw
Vi = ----=-------.
ds dr
Соответственно из уравнений (11.4) — (11.7)
d2w 1 dw
1 dr2 2 г dr
d2w ! P- dw
dr2 r dr J ’
dw . d2w \
dr r dr2 J
(12.1)
(12.2)
(12.3)
(12.4)
Л12
Формулы (12.2) — (12.4) совпадают с ана-
логичными формулами в теории осесим-
метричного изгиба круглых пластин.
Перерезывающее усилие согласно со-
отношению (11.8)
q = dMi ^1-^2
1 dr г '
Подставляя сюда выражения для момен-
тов Mf и М2 из формул (12.3) и (12.4),
получим
d?w . 1 d2w 1 dw \
~dr^ г dr2 ~ г2 dr )'
(12.5)
Рис. 12.1
Вместо уравнения (11.9) равновесия элемента оболочки рассмотрим
уравнение равновесия части сферической оболочки с радиусом основания г,
проектируя все силы, действующие на эту часть оболочки, на направление
ее вертикальной оси симметрии. Получим
лг2р = 2лг (7\ sin 0 + Qi cos 0).
Отсюда
(12.6)
Уравнение (11.10) равновесия сил в проекции на нормаль будет
4 (?i + + — = Р- (12-7)
R dr г
С учетом формулы (12.6) получим
T2=-^-—R-^-. (12.8)
Удлинения ех и е2 согласно уравнениям (11.1) и (11.2)
du , w и . w
е1 = -7- + -Б’> е2=-----Н —•
dr R г R
Закон Гука
<12-9»
T + T“’S'<r,_|‘7'l)- (12д0)
95
Вычитая уравнение (12.10) из уравнения (12.9), получим
г~1~(—^-^(Л-Тг). (12.11)
dr \ г J Eh
Но согласно формулам (12.6) и (12.8)
Т Г, --------------QkA=Rr—(-^\ (12.12)
\ dr г / dr \ г J
Подставляя выражение (12.12) в уравнение (12.11) и интегрируя, найдем
(12.13)
Так как г = /?sinG, то константа интегрирования Со соответствует пере-
мещению оболочки как твердого тела в направлении оси симметрии от
центра кривизны. Складывая уравнения (12.9) и (12.10), получим
- Л. {ги) + 2 = Alt (Л + 7\). (12.14)
г dr R Eh,
Но из уравнения (12.7) следует
Tl + T2=pR--^-^-(rQ1),
г dr
а из формулы (12.13)
-L J- (ru) = A _А (rQr) - 2С0 --.
г dr V ’ Eh г dr V ° R
Подставляя это выражение в уравнение (12.14), находим
w = Air pR2 - 4г — 4- С«- (12-15>
2Eh Eh г dr
Здесь константа Со по-прежнему соответствует перемещению оболочки как
твердого тела. Согласно формуле (12.5)
AA_(rQ1) = £>fJA + AAL_ J_Al + _L (12.16)
г dr \ dr* г dr3 г2 dr2 г3 dr J
Для упрощения записи введем дифференциальный оператор
д, = AL + AjL = А-АЛ-АД
dr2 г dr г dr \ dr J
Это оператор Лапласа в полярных координатах для осесимметричных за-
дач. Теперь формула (12.5) примет вид
Q1 = D—^w, (12.17)
dr
а формула (12.16)—вид
-—— (rQl) = D\Arw. (12.18)
г dr
Выражение ДГДГ есть бигармонический оператор от w. Его развернутое
выражение соответствует многочлену в скобках правой части уравнения
(12.16). Дифференциальное уравнение (12.15) теперь можно представить в
форме
Д,Д^ + W = pR* + со. (12.19)
96
Параметр
R2D = R2h2
Eh ~~ 12(1—p2)
имеет размерность ж4.
Введем новый параметр /, имеющий размерность длины:
Параметр I позволяет просто перейти от размерного независимого перемен-
ного г к безразмерному независимому переменному |
г = 1Ъ>. (12.21)
Так как dr = то оператор Лапласа Дг при независимом переменном г
переходит в оператор Лапласа А при независимом переменном £ по правилу
Дг = — Д,
/2
где
(12.22)
(12.23)
Уравнение (12.19) теперь получит более простую форму
ДДш + ® = -Ц^р/?2 + С0.
2E/z
Так как оператор Лапласа (12.22) от постоянной величины равен нулю, то
частное решение уравнения (12.23) будет
= + (12.24)
2Eh
Для этого частного решения из формул (12.3) — (12.6), (12.8) и (12.13)
получим
M1 = M2^Q1 = 0, 7’10 = Т20 = -^, «0 = -С0^. (12.25)
По формулы (12.24) и (12.25) соответствуют решению задачи по безмо-
ментной теории. Следовательно, и в теории пологой сферической обо-
лочки имеется разделение напряженного состояния на безмоментное и
смешанное. Только в этом случае смешанное напряженное состояние
уже нельзя определять по теории краевого эффекта, так как длина уча-
стка затухания напряженного состояния краевого эффекта соизмерима
с длиной меридиана. Край оболочки близок к ее вершине. Смешанное
напряженное состояние определяется решением однородного уравнения
АД^ + w = 0. (12.26)
Общее решение уравнения (12.26) выражается через четыре табулирован-
ные функции фх(£), ф2(£), ф3(£), ф4(£):
w = |- С2ф2 + С3ф3 + С4ф4. (12.27)
Они удовлетворяют системе уравнений
A^i = 42, Д-ф2 = — ip,, Аф3 = Ц>4, Дг|>4 = — if3 (12.28)
7 Зак. 9G
97
Численные значения этих функций даны в книге [89], стр. 542-547.
Согласно формулам (12.7), (12.21) и (12.28)
Qx = — — С2-^ + С3-^- — С4--4'3 Л. (12.29)
1 /3 \ х dg 2 dl 3 dZ 4 dg J v ’
В полюсе (£ = 0) функция ф4 и ее производная стремятся к —оси не-
соответственно.
Следовательно, из условия ограниченности перемещения в полюсе
(£ = 0) получим С4 = 0, а из условия ограниченности перерезывающего
усилия — С3 = 0. Константа С3 не равна нулю только в случае загруже-
ния сферической оболочки сосредоточенной силой в вершине. Этот слу-
чай рассмотрен в книге [89].
Итак, общее решение полного уравнения (12.23) в рассматриваемом
случае будет
PR2 + Со + Схфх + С2ф2; (12.30)
2Eh
перерезывающее усилие
Qt = — (12.31)
1 R2 \ 1 dg " dg J v ’
тангенциальное перемещение
« = ; (12.32)
меридиональное усилие
7\ = -^----— — С2—М ; (12.33)
2 R g k dg 2 dg J к
сумма
T1 + T2=pR + -^- (С^ + С2ф2); (12.34)
перемещение вдоль радиуса г
иг = и cos O + u)sln0 = « + u) — = —— pRr —
r R2Eh
+ 4 f + u + H) Cy - (1 + p) c2 1 ; (12.35)
A L “b “b J
удлинение параллели
e2 = — = — = 1-11 pR + — (Схфх + С2ф2) 4- -L+1L (Cx — C2 •
r /g 2Eh ‘ R V 1T1 2Y2? Rg \ 1 dg 2 dg Г
(12.36)
угол поворота касательной к меридиану
^i=(12-37)
I \ dt, )
погонный изгибающий момент в меридиональной плоскости
M1=D + _!L J?L\ = P_(^w--------) =
\ dr* r dr ) I* \ g dg j
= 4fC^-C2,l’i-+ • (,2-38)
P L € \ dl J \
98
Составляющая усилий 7\ и Qj в направлении оси симметрии оболочки
согласно формулам (12.31) и (12.33)
Л sin 9 + Qi cose = т ' +;q1 = -^- ,
т. е. полностью определяется безмоментным решением. Смешанное на-
пряженное состояние, соответствующее решению (12.27), определяет вели-
чину погонного момента Мх и усилия Qr в плоскости параллели:
о =—9i = QiR .
r sin 0 г
Для смешанного напряженного состояния Qr есть проекция погонных
усилий Т\ и Qx на плоскость параллели. Действительно, при р = 0 Тг =
= — QiCtgQ и
Q. = Qi sin 0 — 7\ cos 0 — Qi (sin 0 + cos 9 ctg 9) = & .
sin 0
Согласно формуле (12.31)
Qr= — С2-^М . (12.39)
k dg dg ) v ’
Таким образом, схема расчета рассматриваемой пологой оболочки
остается в принципе такой же, как и для непологой, только простое
уравнение (11.32) краевого эффекта заменяется более сложным уравне-
нием (12.26) смешанного напряженного состояния.
В обоих случаях тангенциальное перемещение и, соответствующее
решениям однородных уравнений, т. е. смешанному напряженному со-
стоянию, значительно меньше нормального перемещения w. В формулу
(12.32) для этого перемещения входит множитель
I V~h/R L
К V 12(1 — (X2)
Решение для смешанного напряженного состояния позволяет удовлетво-
рить граничным условиям для перемещения иг (или силы Qr) и угла th
(или момента MJ. Рассмотрим подробнее условие пологости оболочки.
Радиус торцовой, опорной параллели средней поверхности обозначим г\
(см. рис. 12.1). Значение безразмерной координаты g = |i, соответствую-
щей этому радиусу, определится из условия отсюда
= ><12(1 —И2) -±=- , (12.40)
у Rh
или, так как
|1 = У12(1-И2)1/’ А 9Р
г Л
Для рассматриваемой оболочки в форме сферического сегмента при-
нятый ранее критерий (11.55) непологости оболочки в зоне краевого
эффекта можно при относительно малом угле 01 представить в форме
01^2л]/ h/R. Следовательно, для непологой сферической оболочки со-
гласно формуле (12.40) должно выполняться неравенство
^>2лУ 12(1 —р.2).
В этом случае решение а» = С1ф] (|) + С2фг(^) при аргументе близ-
ком к |1, должно приближаться к решению типа краевого эффекта. Дей-
7*
99
ствительно, при функции ф1(£) и ф2(£) можно представить в форме
произведений экспоненциальных функций на тригонометрические функ-
ции. Соответствующие асимптотические формулы можно найти в книге
[89], стр. 542—547.
Таким образом, сферическую оболочку с радиусом R средней поверх-
ности, толщиной h и радиусом основания можно рассчитывать по при-
ближенной теории краевого эффекта, если
Параметр
_£1_
/ад
> 2л.
__ 1 /~ _Е_ 0 =__________11______
V Rh V h 1 у 12(1 _ И2)
(12.41)
(12.42)
определяет степень пологости сферического сегмента. Для очень полого-
го сферического сегмента, т. е. для слегка изогнутой по сферической
поверхности круглой пластинки, когда gi<^2, что соответствует углу
раствора сегмента
функции фх (£) и ф2 (£) приближенно равны
64 4
Соответственно
-—-pR2,
2Eh
W
i . g2 _____1
16 ’ g d£ 2
В этом случае нормальное перемещение
64 J 4
угол поворота касательной к меридиану
а у 12(1- ц2) f
1 /ад \
погонный изгибающий момент
Eh?/R Г ci zq । '
М,=
' 32
удлинение параллели
е2 = ——— pR +
а 2Eh
32
С^(3
16 v
-н)^2 .
усилие в плоскости параллели
Cl_____С2
2 16 5 /
Для нахождения констант Ci и С2 надо задать два граничных усло-
вия. Вид этих граничных условий определяется способом закрепления
или загружения оболочки на торцовой параллели £ = На этой парал-
лели можно задать усилие Qr или удлинение е2, момент Aft или
угол поворота fti. Если на торце оболочки известно погонное уси-
100
лие Af, уравновешивающее давление q, то его, как уже указывалось
ранее при рассмотрении непологих оболочек, надо разложить по двум
не взаимно перпендикулярным направлениям: вдоль касательной к мери-
диану и вдоль радиуса опорной параллели, т. е. на направления усилий
Т\ и Qr. Составляющая усилия W вдоль касательной к меридиану равна
усилию Т10 безмоментного напряженного состояния, а составляющая Qr
определит смешанное напряженное состояние.
В любом случае при составлении граничных условий для пологой или
непологой оболочки надо помнить, что погонное меридиональное уси-
лие 1\ соответствует усилию TiQ только безмоментного напряженного
состояния, а погонное усилие Qr и момент Afj соответствуют лишь сме-
шанному напряженному состоянию. Не следует
также забывать, что направления усилий Гю и Qr
не ортогональны. Расчетное для прочности оболоч-
ки усилие Т\ на торце складывается из безмомент-
ного усилия Ло и проекции усилия Qr на касатель-
ную к меридиану. Величины Qr и М на торце обо-
лочки служат для определения констант интегри-
рования однородных уравнений смешанного напря-
женного состояния, когда заданы силовые гранич-
ные условия.
Цилиндрический бак со сферическими дни-
щами. Рассмотрим схему расчета бака, имеющего
форму цилиндрической оболочки со сферическими
днищами, при действии равномерного внутреннего
давления р (рис. 12.2). Стык оболочек усилен
упругим шпангоутом площадью f и моментом
инерции J поперечного сечения относительно оси,
лежащей в плоскости стыка и направленной по радиусу шпангоута.
Радиус средней поверхности цилиндрической оболочки а, сфериче-
ской R. Стыковая параллель сферической оболочки соответствует углу
01, связанному с а и R уравнением
а = R sin 0Х.
Толщина цилиндрической оболочки сферической h2. Оболочки жестко
соединены со стыковым шпангоутом. Для упрощения расчета будем
считать, что осевая линия шпангоута, т. е. линия центров тяжести сече-
ний, совпадает с линией пересечения средних поверхностей оболочек.
В этом случае шпангоут не нагружается эксцентрично приложенными
нагрузками. Относительно размеров резервуара сделаем только предпо-
ложение, что длина цилиндрической оболочки достаточно велика, чтобы
можно было нс учитывать взаимное влияние краевых эффектов на ее
торцах. Сферические днища могут быть как пологими, так и непологими
оболочками.
Обозначим через А радиальное перемещение точек осевой линии
шпангоута в его плоскости, а через б — угол поворота поперечных сече-
ний шпангоута как жестких дисков в их плоскости (рис. 12.3, а). Относи-
тельное удлинение осевой линии шпангоута & = А/а. Поворот сечений на
угол б вызывает в любом кольцевом волокне шпангоута напряжение
<т = Ед -S- ,
а
где у — расстояние от этого кольцевого волокна до плоскости стыка
(плоскости, содержащей осевую окружность шпангоута). Напряжения сг,
вызванные поворотом сечений шпангоута на угол б, статически эквива-
лентны изгибающему моментуМш = EJ-. Вектор этого момента, дейст-
а
101
вующего в сечении шпангоута, направлен по радиусу стыковой парал-
лели (рис. 12.3,6). Рассмотренное явление называется выкручиванием
(выворачиванием) кольца. Для такого выкручивания к шпангоуту надо
приложить погонные равномерно распределенные моменты т.
Рис. 12.3
Из уравнения равновесия элемента кольца, вырезанного двумя мери-
диональными сечениями, следует
или
EJ х
т =------о
а2
(12.43)
где EJ/a2—жесткость шпангоута на выкручивание.
Введем обозначения: индекс (1) над буквой показывает, что соответ-
ствующая величина относится к цилиндрической оболочке, а индекс
(2) — к сферической; добавление индекса «О» снизу букв относится к
величинам безмоментного напряженного состояния, индекса «£» — к ве-
личинам краевого эффекта или смешанного напряженного состояния
(в случае пологого днища).
В этих обозначениях безмоментные решения будут:
Т\о = ра/2, Ло’ = ра, Т® = = рЯ/2;
#<>> = =0, = Л4ю =0, Qfl = = 0;
(12.44)
Перемещения wk напишем в форме
= Л<₽1 (*) + В(р2 (х), (12.45)
Ч2) = СЛ® + <^2®-
(12.46)
Здесь х = s — координата по длине меридиана цилиндической оболочки от-
. t г V 12(1 —ц2)
считываемая от стыка со сферическим днищем, £= — = ——,2— г —
I у Rh,2
безразмерная координата для днища в форме пологой сферической оболоч-
ки и £ = 0 — для днища в форме непологой сферической оболочки. Сог-
ласно формулам (11.39) — (П-41)
(х) = е~$х cos Рх> Фг (х) = е~$х sin Рх, (12.47)
где
в_ 4/3(1-н2)
102
Для непологой сферической оболочки согласно формуле (11.38) при
02 = 01 и k2 = k
фх(0) = e-*(0i-0)cos£(0x — 0), ф2(0) =e-^-0)sin&(01 —0), (12.48)
где
k = ^3(\-^)VRlhz.
В случае пологого днища функции фх (£) и ф2 (£) представляют собой
рассмотренные ранее функции, определяемые формулами (12.28). Для
цилиндрической оболочки в сечении х = 0
где
= Р(-Д + В), eU)
\ dx /x=o
,n / d2u№
\ dx2
/ d3tv<b) \
= dJ-±-} =2D^(A + B),
\ dx3 /x=o
х=0
= -2D^B, QV1^ =QVfe> =
Eh3,
Di =-------!--- •
12(1—Ц2)
Для непологой сферической оболочки в сечении 0 = 0
/ dw^3 \ k
0(2) = (---k— ) =±-(С1- Cz), e<2) =
< RM Je=e, R v 1 2/’ 2k
d2w^? \
—— ) = —2D2 —C2,
/?2d02 >0=0, R1
0=0!
«? = Д-
sin
0=0!
R3 sin 0Х
А_
а
Ci
/? ’
(12.49)
} (12.50)
<> =
где
d2 =—^L_
12(1-H2)
Положительные направления
усилий и моментов, действующих в
месте стыка сферической и цилин-
дрической оболочек, показаны на
рис. 12.4.
Для пологого днища соответст-
вующие величины определятся по
формулам (12.36) — (12.39) при
ё = £ь В дальнейших выкладках для
упрощения формул будем рассмат-
ривать вариант непологой сфериче-
ской оболочки. Обычно днища ба-
ков делаются в форме сферических
оболочек с относительно малой тол-
щиной и с углом раствора 0i> 10°.
Такие днища, как правило, можно
рассчитывать как непологие сфери-
ческие оболочки. Напомним, что как
'было раньше подробно разъяснено,
Рис. 12.4
понятие пологости определяется не только величиной угла Qb но и от-
носительной толщиной оболочки.
103
Геометрические условия сопряжения оболочек между собой и со сты-
ковым шпангоутом будут
&(')= 0(2) = б, (12.51)
e(D = е<2) д/а. (12.52)
С учетом формул (12.44), (12.49) и (12.50) получим
Р(-Л + В) = А(С1_С2) = б,
А
ра
2EhY
(2-и)4- —=
а
^(1-Н) т| = -
2Eh2 R а
Отсюда
Л = А —-2~и ра2, В = — 4-Д — 2~>г ра2,
2Eh± р 2£/ix
с1 = дА_кд'
a 2Eh2
^—^PR2.
—pR2, а = — б — + д —
k • a 2Eh2
Подставляя найденные выражения констант А, В, Съ С2 в формулы
(12.49) и (12.50) и учитывая, что
D1 = = 1 D2 ________(М#)2 =.
Eh,. 12(1 —ц2) ~ 4а2Р4 ’ R*Eh2 ' 12(1 —р)
получаем
<’ = mW = - 2Z\p2 < А + ДА и р ,
\ Р / 4р2
М(12) = AfW = — 2D2 — (— — -ь —\ Al4_
R \ k а / 4/г2
J___
4/г4 ’
(12.53}
(12.54)
Q*1’ = = 2DJ>3 (— 4- 2Д^ — р Alh
4 4 к ₽ J 2р
Q<2’ = qW = 2D2-(-А _ 2Д + _Р^ AzH
R3 sin 0i \ k a J sin 0х 2k
так как
од Ehi 1,4 Eh2R2 п . л
В4 =--, k4 =------ и а = R sin 0Ъ
4^2 4Z)2
ТО
=(4+2Д) ~р (2 ’
2р L ai \ Р ' J
(12.55)
(12.56)
(2)
Qr
1
2k sin 0j
2Д )4-p(l—ц)
Для определения констант 6 и Д рассмотрим уравнения равновесия
элемента шпангоута.
Выкручивающий момент т (см. рис. 12.4), создающий угол поворота
S сечений шпангоута (в сторону положительного направления углов Фу* и
Oil2*), равен
т = Mi1’ — MW. (12.57)
Погонная радиальная нагрузка, сжимающая шпангоут,
рщ =-y-cosOj 4-QW — Qr2)- (12.58>
104
Первое слагаемое формулы (12.58) соответствует нагрузке от состав-
ляющей безмоментного усилия Т1о сферической оболочки; два других
слагаемых соответствуют усилиям Qr в оболочках от напряженного состоя-
ния краевого эффекта,
С учетом формулы (12.43) из уравнения (12.57) получим
mV’ — М(12) = — 6- (12.59)
а2
(12.60)
Нагрузка рш создает в сечении шпангоута сжимающее усилие S = рша.
Радиальное перемещение А шпангоута равно
л -‘\ - 9?:|.
Так как величины M(i0, М(2), Qj0 и Q(r2) выражены через б и А, то
уравнения (12.59) и (12.60) представляют систему двух уравнений для
определения неизвестных б и А. В каждом конкретном случае эта система
решается без труда. Найдя б и А, можно вычислить перемещения w, углы
поворота 'О', погонные изгибающие моменты и напряжения в оболочках и
шпангоуте.
В заключение поясним значение моментной теории симметрично
нагруженных оболочек вращения в расчетах на прочность ракетных
конструкций.
При расчетах на прочность по допускаемым напряжениям роль этой
теории очевидна; чтобы знать запасы прочности по напряжениям, надо
возможно более точно определять величины напряжений от действую-
щих нагрузок. По при расчетах на прочность по разрушающим нагруз-
кам надо знать только величину этих разрушающих нагрузок, т. с. несу-
щую способность рассчитываемой конструкции; сами по себе величины
напряжений при разрушающих или эксплуатационных нагрузках еще
нс дают прямого ответа на вопрос о фактической прочности конструк-
ций. В связи с этим возникает естественный вопрос: нужно ли опреде-
лять напряжения с учетом краевого эффекта? На этот вопрос нельзя
дать общий, универсальный для всех случаев ответ. Напряженное со-
стояние краевого эффекта в конструкциях, работающих на внутреннее
давление, влияет в основном на величины изгибных напряжений и коль-
цевых средних напряжений вблизи торцов или сечений с резким измене-
нием жесткостей.
Напряженное состояние краевого эффекта определяет изгибающие
моменты Л41 и уточняет кольцевые усилия Т2о, найденные расчетом по
безмоментной теории. Как правило, учет краевого эффекта не приводит
к росту максимальных значений этих усилий и, следовательно, не изме-
няются их расчетные значения. Обычно они определяются по безмомент-
ной теории в сечениях бака, удаленных от мест действия краевых
эффектов.
Следовательно, основными факторами, действие которых нужно выяс-
нить, являются изгибающие моменты Afi и М2, величины которых цели-
ком определяются напряженным состоянием краевого эффекта. Величи-
ны напряжений от этих моментов могут быть весьма значительными.
Пусть при каком-нибудь значении внутреннего давления р, меньшем
расчетного разрушающего давления интенсивность напряжений аг-
в точках на внешнем или внутреннем слое оболочки бака в зоне дейст-
вия краевого эффекта достигла предела текучести огт материала. Что
будет происходить при дальнейшем увеличении давления?
Вследствие роста изгибных деформаций будет расти величина интен-
сивности деформаций 8г- в зоне краевого эффекта. В соответствии с диа-
граммой ст/—8> рост напряжений в области пластических деформаций
будет замедляться. Но сама область пластических деформаций будет
105,
увеличиваться, распространяясь в глубь толщины оболочки. Если мате-
риал весьма пластичен и не имеет склонности к хрупкому разрушению,
т. с. допускает пластическое деформирование до больших значений де-
формаций 8г-, существенно (в несколько раз) превосходящих величину
деформации 8Т при напряжении предела текучести, то можно не боять-
ся преждевременного разрушения бака в зоне краевого эффекта. Диа-
грамма зависимости изгибающих моментов от величины давления р
в этом случае будет напоминать пологую диаграмму вг—Ег материала
оболочки; начиная с некоторой величины давления, изгибающие момен-
ты от краевого эффекта перестают увеличиваться. Другими словами, в
случае весьма пластичного материала, не подверженного при сложном
напряженном состоянии опасности хрупкого разрушения или образова-
ния трещин, переход напряжений в зоне краевого эффекта за предел
текучести сопровождается образованием так называемого пластическо-
го шарнира, как бы предохраняющего конструкцию от разрушения
вследствие роста изгибных деформаций. Конструкция бака является
статически неопределимой, но пластические шарниры, образующиеся в
зоне краевого эффекта, как бы превращают ее в статически определш
мую конструкцию, расчет которой можно производить по безмоментной
теории оболочек.
Так обстоит дело в случае весьма пластических «благородных» мате-
риалов. Но такие материалы, как правило, имеют низкую удельную
прочность (отношение временного сопротивления при растяжении к
удельному весу).
Многие современные материалы с высокой удельной прочностью
только в очень небольшой области диаграммы or—8 способны восприни-
мать пластическое деформирование без разрушения и образования недо-
пустимых трещин. Стеклопластиковые материалы при растяжении вдоль
направления стеклянных нитей разрушаются почти без пластических
деформаций. Некоторые высокопрочные алюминиевые сплавы в усло-
виях двухосного растяжения имеют склонность к хрупкому разрушению.
При применении таких материалов для оболочек баков необходимо тща-
тельно изучать напряженные состояния краевого эффекта и принимать
меры для уменьшения величины напряжений изгиба. Анализ краевых
эффектов в оболочках необходим также во всех случаях при проектиро-
вании сложных стыковых узлов.
§ 13. МОМЕНТНАЯ ТЕОРИЯ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
Исходные уравнения. В этом параграфе рассматривается моментная
теория замкнутых круговых цилиндрических оболочек постоянной тол-
щины. Пусть R—радиус средней поверхности оболочки, х, ср — коорди-
наты точек этой поверхности в цилиндрической системе координат. Для
круговой цилиндрической поверхности
— = 0, — = — , cose =0, = dx,
Ri Rt R
деформации элемента средней поверхности
« 1 f dv . \ да . dv /1О
61=—— , е2 = — (--------h^),'Y =-------1----, (13.1)
дх R \ д(р / Ядер дх
углы поворота нормали
#1 = •&2 = — (— • (13.2)
дх R < д<р J V
В формулах (13.1) и (13.2) и — перемещение точек средней поверх-
ности в направлении возрастания координаты х, v — в направлении воз-
растания угла <р и w — в направлении внешней нормали (рис. 13.1).
Согласно формулам (10.12) — (10.15) § 10 параметры изменения кривизн
106
средней поверхности xi, х2, т можно представить различно, сохраняя или
отбрасывая малую величину z/R при определении деформаций слоя z
•оболочки. Если в самом начале определения этих деформаций положить
1+i=al,
где |z|<Л/2 — координата по
d2w
1 дх дх2
dv \
дф /
dv
(13.3)
% =
толщине оболочки, то
д$2 1 / д2ш
Х2 = ---— = ----- -----
Rdq R2 \ дф2
д$2 \ d2w 1 1
дх J дхду R 2R дх
При определении этих же величин с точностью до z/R
d^i d2w dft2 , e2 1 f । „Л
1 dx dx2 Rdq> /? R2 \ дф2 J
— * ( I I 1 du \ ____ 1 d2w
2 \ Rdq dx R2 дф / R dxdq>
ди
Rdq>
dv
дх
(13.4)
Наконец, согласно формуле (10.15)
T = _L / j_ dO2 । у _jJ_
2 \ Доф ‘ rax '(Я R dx
(13.5)
Если в формуле (13.4) для х2 пренебречь слагаемым е2/Т?, а в фор-
муле (13.5) для т — слагаемым y/R, то получим новый вариант записи вы-
ражений хх, х2 и т:
d2w 1 / d2w dv \ гд2до 1 ди /1О
----, х2 =-----------------------), т =------------------------• (13.6)
дх2 R2 \ дф2 дф J Rdydx R дх
Этот последний вариант используется в
книгах С. П. Тимошенко. Так как величина
z/R для реальных оболочек составляет обычно
меньше 1%, то расчет оболочек с применением
того или другого варианта формул дляхьх2, т
должен в итоге привести к практически одним
и тем же результатам. Исключением может
быть случай, когда ^/R и y/R одного порядка
с х2 и т, но, как было показано в § 10, этот
случай соответствует безмоментному напря-
женному состоянию, когда в уравнениях рав-
новесия можно вообще не учитывать моменты
Л4Х, -Л412.
Сопоставление формул (13.3), (13.4) и
(13.6) показывает, что только слагаемые
•с производными от радиального перемещения
Рис. 13.1
w имеют во всех фор-
мулах один и тот же вид. Они играют основную роль в величинах
xi, х2 и т. Следовательно, для приближенной теории цилиндрических
оболочек естественно принять, что
d2w 1 d2w 1 д2ш
Xi =------, Хо =------------, Т =------------
дх2 “ У?2 дф2 R дхдф
(13.7)
Из формул (13.7) следует, что выражение угла поворота нормали в
плоскости поперечного сечения оболочки можно взять в форме
dw
Rdq ’
(13.8)
107
Условие (13.8) выполняется во всех случаях, когда деформация
цилиндрической оболочки сопровождается существенным изгибом ее
поперечного сечения, т. е. когда напряженное состояние оболочки нельзя
считать безмоментным.
Уравнения равновесия элемента цилиндрической оболочки, согласно
формулам (10.25) — (10.29) можно представить в виде
а - дм^ дх . дМ jo (13.9)
<W12 дх (13.10)
д7\ dS дх ' Rdtp + qx = о, (13.11)
дТ2 , dS 4- а — 0 (13.12)
Rdq дх £ -f-
Г2 dQ, -г = я, (13.13)
R дх /?д(р
где Qi, Q2—погонные перерезывающие усилия;
qx, и q — составляющие внешних поверхностных нагрузок в направле-
нии перемещений и, v и w (см. рис. 13.1);
7\, Т2 и S — погонные тангенциальные усилия (рис. 13.2, а)
Л = (вх + нМ. т2 = -^—(82J-nei), S = G/ry; (13.14)
1 — |Х2 1 — р2
Mlf М2, М12 — погонные моменты (рис. 13.2,6);
Mr = D (xt + рс2), М2 = D (х2 + iixj, A412 = Z)(1—р,) т. (13.15)
Рис. 13.2
Приближенные уравнения в перемещениях. Уравнения равновесия
(13.9) — (13.13) точные. Возникает вопрос: можно ли эти уравнения
упростить, сделав их приближенными, в соответствии с приближенными
формулами (13.7) для параметров изменения кривизны? Ответ на этот
вопрос можно получить, если вывести уравнения равновесия заново,
используя вариационные уравнения Лагранжа. На первый взгляд, эта
идея кажется парадоксальной. Казалось бы, какое отношение имеют
уравнения равновесия к выражениям хь х2, т. Но использование кинема-
тических гипотез превращает оболочку в некоторую механическую систе-
му с дополнительными внутренними связями. Уравнения равновесия
такой системы должны строиться с учетом этих связей. Вариационные
уравнения Лагранжа являются как раз теми уравнениями, которые
108
автоматически учитывают влияние связей, наложенных на систему.
Уравнения равновесия, полученные на основе вариационных уравнений
Лагранжа, должны находиться в полном соответствии с принятыми
упрощающими предположениями о характере зависимостей xi, х2 и т
от перемещений средней поверхности и их производных.
Пусть возможными перемещениями 6u, 6v, 6w будут бесконечно
малые приращения истинных перемещений, u, v, w. Приращения (вариа-
ции) деформаций будут
я дЬи е 1 / дои I « \ я 1 дби . ddv /1О
66! = ——, бе2 = — ( —— -гбш), бу = — —- к — • (13.16)
дх R \ дер J R дер дх
Приращения углов ftx, ft2 с учетом соотношения (13.8)
6ft
дЪш я а 1 dbw
-----, Ofto =
дх---R дер
(13.17)
Деформации еь е2, у являются обобщенными перемещениями для уси-
лий T2l S. Моменты совершают работу на изменении углов поворота.
Обобщенными перемещениями для моментов Мь М2 и М12 будут xi,
х2, 2т.
Следовательно, если элементу оболочки площадью Rdqdx сооб-
щить возможные перемещения би, 6у, 6w, то усилия 74, Г2, S и моменты
Мь М2, М12 совершат работу
(Tidei + 726b2 + Sdy 4- M^Xi + М2бх2 4- 2М12бт) Rdydx, (13.18)
где с учетом соотношений (13.7) и (13.8)
dx =^L(6uy), 6х2 = -±- = (13-19)
дх2 R2 дер2 R дхдер
Полная работа внутренних усилий и моментов, равная вариации потен-
циальной энергии упругой оболочки, будет
L 2л
6Ф = J J (TjSej - Г2бе2 2М12бт) dxdq,
и и
(13.20)
где L — длина оболочки.
Подставляя в уравнение (13.20) выражения беь бе2, бу из соотноше-
ний (13.16), a 6xi, бх2, бт — из соотношений (13.19) и интегрируя по
частям слагаемые с производными от вариаций перемещений би, 6у, бш
столько раз, сколько нужно, чтобы под знаком двойного интеграла оста-
лись только слагаемые с множителями би, 6v и бш, получим, учитывая
периодичность по <р всех функций,
6Ф = Я
2Л
О
о
Rdq
L 2Л
о 0
1 dS \
R dtp /
6u —
d2M, 2 d2M12
dx2 Rdepdx
. 1 d2Af2 \ я 'I j j
4-----------— ] bw I dxd®.
R2 dtp2 J J
(13.21)
Значки x = L и x = 0 при квадратных скобках означают, как это при-
нято при интегрировании по частям, разность соответствующих величин,
заключенных внутри скобок, при x = L и х = 0.
109
(13.22)'
следует
Работа поверхностных нагрузок qx, и q на возможных перемеще-
ниях 6u, dv и 6w будет
L 2л
j* [ + q^w) dxdq.
6 6
Вариации 6u, dv и dw в любой точке средней поверхности оболочки про-
извольны, поэтому из сравнения выражений (13.21) и (13.22)
д!\ дх 1-^- + ^=°, Rdep (13.23>
дТ2 1 dS . = 0, (13.24)
Кдф п т ft дх
21 + d2Mi , 2 аш12 1 амт, _ /7 (13.25)-
Так как R дх2 ‘ R дхдер R2 дф2 ч-
dQ, 1 дх R ^2 дф д2Мх 2 дх2 R дМ12 । 1 дхду R2 д^М2 Эф2 (13.26).
то, сопоставляя уравнения (13.23) с (13.1 1), (13.24) с (13.12) и (13.26)
и (13.12).
с (13.13), видим, что различаются только уравнения (13.24)
В уравнении (13.24) отсутствует по сравнению с уравнением (13.12) сла-
гаемое — —. В этом состоит упрощение уравнений равновесия с уче-
R
том упрощений выражений для хь х2 и т.
Из выражения (13.21) для 6Ф можно также получить граничные-
условия на торцах оболочки. На каждом торце при x = L или х = 0 могут
быть заданы четыре граничных условия:
1) либо перемещение и, либо усилие 7\;
2) либо перемещение v, либо усилие S;
3) либо угол -61= —, либо момент All;
дх
4) либо перемещение w, либо величина приведенного перерезываю-
щего усилия
Q = 2 dMi2 = Qi j 1 дМ12
дх R дер R дер
Введем вместо размерной координаты х безразмерную координату
£ = %//?. Тогда развернутые выражения для усилий Ti, Т2, S, моментов
Mi, М2, М12 и перерезывающих усилий Qi, Q2 будут
гр _ Eh Г ди /ди \“]
Л — ~ 2Ч п “Ь и ( з и ,
(1 — p2)R L \ д<Р /J
гр Eh Г dv . . ди 1
Т о =-----------------И W + Н---- ,
и - н*) я L л₽ J
(13.27)
S =
/ди , dv \ Eh
\ лГ "аГ/ 2(ц-
\ О£2 Оф2
\ дф2 dg2 J
R2 д^дф
НО
1 / dMr дМ12 X D д
R\d^ + <э<р 7 ”da
(Аш),
1 /дМг dM12 X
R \ dtp J
D
R3
(Any),
где
A d2w d2w Aw = + ду2 оператор Лапласа в координатах £ и ср от функции ш._
Обозначим
Z) (1 Ц2) h2 _ г*2 /1 о оо\ R*Eh (13'28)
АДш = + 2 + (13,29). да1 да2дф2 дф4 v ’
Теперь уравнения равновесия (13.23) — (13.25) примут вид
д2“ 1/1 „1 д2“ 1 d2v dw (1-р2)Я2 /loom .V г 1 >* as я (13'30>
1 11 ц) 1 d2v 1 'dw - а /1331) д£дф ( да2 дф2 1 дф ’ Eh q*' ( 3’3 ’
р + ш + С2ААш = (1~ (х2) R2 q. (13.32). og дф Eh
Обобщенное перерезывающее усилие, которое нужно вводить только при
составлении граничных условий на торцах оболочки
= (^1 + (2 — р)-^-1. (13.33).
Rd<p R3 д£ L ft? дф2 J '
Другая форма уравнений цилиндрической оболочки. В частном, но
практически наиболее важном случае, когда ?х = ?ф = 0, уравнения ци-
линдрической оболочки можно представить в более простом, компакт-
ном виде. Исходные уравнения (13.23) — (13.25) в этом случае в перемен-
ных g и ф будут иметь вид
-^- + —=0, (13.34)
да дф
-^ + — = 0, (13.35)
дф да v
АЛщ = (13.36)
Уравнения (13.34) и (13.35) тождественно удовлетворятся, если поло-
жить
Тг = ^, S=- дф2 2 dg2 д2Ф (13.37)
agdT ’
где Ф(£, ср) — произвольная функция. Подставив Т2 в уравнение (13.36) получим
д2Ф । D ла п ДЛиу = qR. dg2 R3 4 (13.38)
Второе уравнение, связывающее Ф и w, найдем, кона Гука, связывающие деформации вх, в2, у с используя усилиями уравнения за- Л, Т2, S,
^-^-(Л-рТ,). ^-^(Л-рЛ), у = 2-L±lL S. (13.39)
Eh Eh Eh
111
Подставив выражения Bi, е2> У из формул (13.1) и усилия из формул
(13.37), получим
ди __ R ( д2Ф [а2Ф \
5g “ Т/Г V 5<р2 dg2 J'
dv , R / д2Ф д2ф \
h W ( и ),
дф-------------------------------Eh \ д^2-дф2 /
ди ( dv _ 2 (1 4- И) д2Ф
дф * дс, Eh д^д^
(13.40)
(13.41)
(13.42)
Из уравнений (13.40) — (13.42) легко исключить перемещения и и v.
Для этого надо сложить уравнения (13.40) и (13.41), предварительно
продифференцировав первое из них два раза по <р, а второе — два раза
по g, и вычесть из них уравнение (13.42), предварительно продифферен-
цированное один раз по ф и один раз по g. В результате этой операции
получим
d2w _ R / д4Ф , 2 д4Ф , д4Ф \
д£2 ~~ Eh \ дф4 ' дф2д£2 1 д£* )'
или в сокращенном виде
-^ = -^-ДДФ. (13.43)
5g2 Eh
Уравнения (13.38) и (13.43) являются двумя уравнениями в частных
производных для двух неизвестных функций w и Ф. Исследованию урав-
нений (13.38), (13.43) посвящены работы В. 3. Власова [26]. Продиффе-
ренцировав уравнение (13.38) два раза по £ и исключив с помощью вы-
ражения (13.43) w, получим
д4Ф - —— ДДДДФ = R2Eh dg2 (13.44)
или, так как D = h2 = &
R?Eh 12/?2(1—p2) ~ 1 —p2
и АДДД \ ag2 5<p2;
найдем 5«Ф , д? - Д4Ф = 7?^-. 1 — p2 d^2 (13.45)
Пусть радиальная нагрузка q симметрична относительно вертикаль-
ной плоскости симметрии оболочки. Такую нагрузку можно представить
в форме простого ряда Фурье:
<7 = <7о Ю + <71 (£) cos ф + q2 (I) cos 2q> -j- ...
ИЛИ
oo
<7 = £ <7„ (£) cos пф.
/z—0
Будем искать решение уравнения (13.45) в виде аналогичного ряда
Ф = £ fn (ъ) COS Пф.
72=0
(13.46)
(13.47)
112
Подставив формулы (13.46) и (13.47) в уравнение (13.45) и приравняв
выражения при cosntp, получим
f„(£) = (13.48)
dg4 1 - ц2 к dtf J п di?
Константа C2 = h2/\2R2 является весьма малой величиной порядка
10~5—10“7 для оболочек типичных ракетных конструкций. Следователь-
но, относительно уравнения (13.48) можно повторить часть из того, что
подробно обсуждалось в § 10 и 11 при рассмотрении смешанного напря-
женного состояния и краевого эффекта. Если нагрузка q плавно изме-
няется по окружности поперечного сечения оболочки, что обычно и имеет
место для гидростатических и аэродинамических нагрузок, и ее можно
с достаточной для практических расчетов точностью аппроксимировать,
например, суммой только из четырех слагаемых
q = <7о (У + <71 ft) cos Ф “I Яг ft) <os 2Ф + q3 ft) cos 3(₽> (13.49)
то уравнение (13.48) можно заменить более простым:
С- d*f„ (g) = nd-^(§) {13 5Q)
1—p dg8 ' dg4 dg2 ’ \ )
где n = 0, 1,2 и 3.
Сделаем подстановку
= Rqn ©+ф„ (У.
Тогда для (5) получим уравнение
с2 d^n (g) d^n (g) = _ C2 n d*qn(l) fl3 51)
1 — ji2 dge d£2 1 —p2 (ft* ' \ >
Если нагрузка q изменяется по длине оболочки достаточно плавно, то в
уравнении (13.51) можно пренебречь слагаемыми с малым множителем
С2, и оно будет иметь приближенное частное решение фп(£)=0. Ему
соответствует частное решение уравнения (13.50)
J^~L = ^ft)- (13.52)
ag2
Следовательно, в этих условиях существует приближенное решение
Ti = = $ (q° <71C0S(p + <72cos2<p + q33q>) = Rq. (13.53)
Но это есть безмоментное решение задачи. Однородное уравнение, кото-
рое следует из уравнения (13.50), можно представить в виде
d4 / d*fn ,1 р.2 < \ _„ . о _
W \~^ Ч (13,54)
Полагая /п(£)=е^, для К получаем четыре нулевых корня и четыре
больших корня из решения характеристического уравнения
Ь4 + -Ц^-=°. (13.55)
Легко доказать, что нулевым корням будет соответствовать решение
однородных уравнений безмоментной теории, а четырем корням урав-
нения (13.55) — решение обычного краевого эффекта. Таким образом,
из произведенного анализа следует практически важный вывод: если
радиальная нагрузка q плавно изменяется по координатам £ = — и ср,
8 Зак. 96
ИЗ
то расчет цилиндрической оболочки приближенно сводится: 1) к нахож-
дению безмоментного решения и 2) к решению обыкновенного краевого
эффекта из уравнения
-^Н-4^ш = 0, (13.56)
где
4fe4 = 12 (13.57)
В практических расчетах часто бывает достаточно рассмотреть крае-
вой эффект только для осесимметричной части общего решения. Для
этого нагрузку надо представить в форме
Ч = + (13.58)
где
2Л
о
и с учетом краевого эффекта решить только задачу расчета оболочки,
нагруженной осесимметричной нагрузкой q0. Расчет оболочки на дейст-
вие нагрузки q производится при этом только по безмоментной теории.
Необходимо еще раз подчеркнуть, что изложенный приближенный ме-
тод справедлив только в том случае, когда нагрузка q плавно изменяется
как в окружном, так и в меридиональном направлениях.
Относительно простое строгое решение уравнений (13.38) и (13.43)
можно получить в двойных тригонометрических рядах для частного, но
практически важного случая граничных условий свободного шарнирного
опирания оболочки на торцах. Под свободным шарнирным опиранием
понимают граничные условия w = v = T{ =МХ = 0.
Для случая нагрузки q, симметричной относительно вертикальной
плоскости симметрии оболочки, функции wfa ф) и Ф(£, ф) можно
искать в форме
w = у1 Атп sin тл cos лер, (13.59)
ГП=\ n—Q
Ф = У Brnn sin тл у- cos /др. (13.60)
т=1 п=0
Легко проверить, что на торцах оболочки (£ = 0 и % = L/R) удовлетво-
ряются граничные условия свободного шарнирного опирания. Произволь-
ную нагрузку q можно разложить в двойной ряд Фурье:
<7 = 2 Zj qmn Sin/Wl Y^cos/Mp- (13.61)
m— 1 n—~ 0
Коэффициенты этого ряда в силу ортогональности тригонометрических
функций определяются формулами:
при п = 0 и произвольном т
R/L л
= <7(s, ф) sinmn-y- в- (13.62)
о о
114
при п = 1, 2, 3, ... и произвольном т
R/L л
q = С ( q(Z„ ср) sin /пл — ^cosncp • d£dcp. (13.63)
л/? J J L
о о
Так как при любых тип
АЛ
s R t
sin /пл — g cos nep
sin /ил — g cos nep,
то из уравнений (13.38) и (13.43) получим
» / mnR \2 j D
mn\ L ) 1 R3
/212 . _
I j I mn *'4nw
где, согласно соотношению (13.28), С2 = h2/12R2.
Из формул (13.64) и (13.65) также следует, что если нагрузка q^ ер)
достаточно плавная и в ее разложении в двойной ряд Фурье (13.61) мож-
но ограничиться несколькими первыми членами (/и = 1, 2, 3; и = 0, 1, 2, 3),
то в знаменателе этих формул можно пренебречь слагаемым
С2 Г / rrniR V 2]4
-------- -------- ) + Л
1 — р2 L \ / J
В этом случае приближенные формулы
QmnR2 Г । । / nL \2 2
Eh L ' \ mnR J - *
- qmnR ( mnR }
будут соответствовать расчету по безмоментной теории.
В случае быстро изменяющихся по координатам £ и ер нагрузок вы-
числения по формулам (13.59), (13.60) и (13.64), (13.65) весьма тру-
доемки вследствие медленной сходимости двойных рядов. Эти вычисле-
ния целесообразно проводить с помощью цифровых математических
машин.
Однако во многих случаях оказывается возможным производить рас-
четы на основе приближенных теорий, изложенных в следующем пара-
графе.
§ 14. ПРИБЛИЖЕННЫЕ ТЕОРИИ РАСЧЕТА ЦИЛИНДРИЧЕСКИХ
ОБОЛОЧЕК
Анализ деформаций цилиндрической оболочки. Чтобы пояснить идеи
приближенных теорий расчета цилиндрических оболочек, рассмотрим
деформации шарнирно опертой на обоих торцах цилиндрической обо-
«*
115
лочки, нагруженной распределенной нормальной нагрузкой, которая
является функцией только угла ср и изменяется по закону
<7 = cos 2ср. (14.1)
Эта нагрузка стремится «сплющить» оболочку в вертикальной плоско-
сти (рис. 14.1). Так как нагрузка не изменяется по координате £ = х//?
и сравнительно медленно изменяется по координате <р, то основное на-
пряженное состояние можно найти по безмоментной теории. Пусть длина
оболочки Т = 2/ и начало отсчета координаты g в середине длины обо-
лочки. Ввиду симметрии конструкции и нагрузки в сечении £ = 0
и = О, 5 = 0, (14.2)
Рис. 14.2
Уравнения равновесия безмоментной цилиндрической оболочки в коор-
динатах £ и ср (рис. 14.2), согласно выражениям (13.34) — (13.36), при
0 = 0 + — = 0, (14.3) <Э<р + — = 0, (14.4) 5<р dg V ’ T2 = qR = q0Rcos 2q>. (14.5)
Подставляя Т2 в уравнение (14.4) и интегрируя с учетом граничных
условий (14.2), получим
S = 2?0/?£ sin 2<р.
(14.6)
.116
Из уравнения (14.3) следует
-^- = — 4^cos2<p.
Интегрируя, находим
Л = - 2g0^2cos2<p + f (ср), (14.7)
где /(<р)—произвольная функция интегрирования. Из граничного условия
на торце оболочки 7\ = 0 при £ = 1/R получим
/ (Ч>) = 2<7о 4-cos 2<₽-
К
Следовательно,
7\-2<70fl(-^-B2)cos2cp.
(14-8)
Перейдем к определению перемещений. Согласно формулам (13.39) имеем
-^- = -£-(Л-НЛ), (14-9)
Eh
+а> = -^-(7’2-р7\), (14.10)
дф Eh
ди । dv 2 (1 4~ р>) /? (14 11)
дф ’dg Eh ' V • /
Из уравнения (14.9) с учетом первого условия (14.2) получим
« = ^f2f^T^-^3)-^bos2(₽- (14.12)
Eh L \ Я2 J |
Из выражения (14.11) следует
dv л qQR2 ft/ii И 1 /2 \ £3 1 « п
д£> Eh L \ 2 Я2 J 3 J
Интегрируя, находим перемещение
и = 2^[^(' + ^+^)-v]sin2(p+/1((p)’ (14J3)
где/1(ср)—новая произвольная функция интегрирования. Из уравнения
(14.10) получим
Eh дф
При расчете по безмоментной теории граничные условия можно зада-
вать, как было показано в § 9, только для тангенциальных усилий 7\, S
или тангенциальных перемещений и и v. Следовательно, произвольную
функцию Л (ф) надо определить из граничного условия v = 0 при =
Получим из формулы (14.13)
г / \ о q»R2 Г/ii Р- \ । /4 1 , о
/1 (<Р) = — 2 —— ( 1 + —-------------------sin 2ф.
1 v Еh L \ 2 J R2 6 Я4 J Y
Следовательно,
У = 2^-ГЛ + — lsin2cp
Eh [ \ 2 Дь R2 J \R J 6 6 R* J
(14.15)
117
и
w = Jo^-h + 4 Г JL + A JL _(1 JLV2-I-JLl)cos2(p. (14.16)
Eh I L R2 6 R1 \ R2 J 6 J J '
При В = l/R для шарнирного опирания, строго говоря, должны также
удовлетворяться моментные граничные условия
w = 0 и М, = 0. (14.17)
Но при В = 1/R из формулы (14.16) следует
qaR2 а
w = —— cos 2<р,
Eh
= — A«(2-Hi) ras 2<p
1 3(1- nV0 T
Граничным условиям (14.17) можно строго удовлетворить, добавив
решение уравнения (13.56) краевого эффекта
— 12-^^/?2ш= 0
Л2
в форме
-k{-L
w = е
) j cos 2<р,
где, как обычно, /? = •/" 3(1 — р2) VR/h — большая величина.
Решение краевого эффекта быстро затухает при удалении от торца
оболочки. Оно имеет практическое значение только тогда, когда нагруз-
ка q вызывает значительные относительные удлинения сечений оболочки
вблизи торцов. Это происходит при осесимметричном нагружении обо-
лочки равномерным внутренним давлением. В этом случае кольцевые
удлинения являются основной деформацией оболочки. Но в нашем слу-
чае действия неравномерной нагрузки относительное удлинение е2 Для
достаточно длинной оболочки не является основной деформацией.
Неравномерная нагрузка ^ = ^0cos2q), стремящаяся деформировать в
эллипс первоначально круглое поперечное сечение цилиндрической обо-
лочки, вызывает прежде всего значительные меридиональные усилия Т\
и относительные удлинения 8ь
Погонный изгибающий момент М{ в рассматриваемом случае также
имеет относительно малую величину. Следовательно, краевой эффект в
случае переменной по сечению оболочки нагрузки не играет такой боль-
шой роли, как при осесимметричных деформациях. Поэтому возникает
естественная мысль построить такую приближенную теорию тонких
оболочек, которую не нужно исправлять добавлением напряженного
состояния краевого эффекта.
В общем случае, как было показано в § 11, решение краевого эффек-
та корректирует кольцевое удлинение 82, угол поворота касательной к
меридиану 41 и полностью определяет величину усилия Qi и момента М{.
Поэтому желательно, чтобы в приближенную теорию не входили гранич-
ные условия для 82, -Qi, Qi и Перерезывающее усилие Qi определяет-
ся, согласно уравнению (13.9), формулой
п __ 1 f дМг дМ12 \
У1 R \ * дф Л
Поэтому граничные условия по и Qx отпадут, если в приближенной
теории цилиндрических оболочек положить моменты
М, = Л412 = 0.
(14.18)
118
Граничные условия для е2 также отпадут, если положить
е2 = 0. (14.19)
Предположения (14.18) и (14.19) являются основными допущениями
приближенных теорий цилиндрических оболочек при неосесимметричных
деформациях. Дополнительными упрощающими расчет допущениями
являются пренебрежение усилием Т2 по сравнению с Л в формуле
(14.9) закона Гука и пренебрежение величиной относительного сдвига у
от действия усилия S.
С учетом этих дополнительных условий получим формулы
= (14-20)
Eh
= (14.21)
dtp
При условиях (14.18) — (14.21) закон Гука, связывающий деформации
ех, е2, Y и %2> т с усилиями 7\, Т2, S и моментами Мъ М2, М12 будет
выражаться только двумя формулами: (14.20) и
х2 = ^-. (14.22)
Система уравнений (14.18) — (14.22) в приближенной теории заме-
няет шесть уравнений закона Гука моментной теории оболочек. Усилия
Т2 и S в приближенной теории не выражаются через деформации и яв-
ляются чисто статическими факторами, подобно перерезывающим уси-
лиям Qi и Q2 в моментной теории оболочек.
Условия (14.18) — (14.22) допускают интересную и практически важ-
ную интерпретацию на основе рассмотрения ортотропных оболочек.
Для ортотропной оболочки закон Гука, согласно формулам § 3, мож-
но представить в виде
е1~(Л-нЛ (14-23)
(14.24)
E^h
y^S/G^h, (14.25)
Xi = ^-(Mx-plsAf2), (14.26)
х2 -= — (М2 — й21Л4х), (14.27)
^2
т - М12/О3. (14.28)
Здесь £i, £2, G12 — модули упругости при растяжении и сдвиге; £>ь D2
и — жесткости на изгиб и скручивание; pi2 и — коэффициенты
Пуассона при деформациях в плоскости средней поверхности и |ii2, ц21—
приведенные коэффициенты Пуассона, связывающие изменения кривизн
X], х2 с моментами Л41, М2.
Модули упругости £i, £2, Gi2 и коэффициенты Пуассона pi2 и p2i
определяют по результатам испытаний пластинок, конструктивно подоб-
ных оболочке, при нагружении в их плоскости. Величины жесткостей
D2, D3 и приведенные коэффициенты Пуассона pi2 и ц21 вычисляют
по данным испытаний аналогичных пластинок на изгиб в двух плоскостях
и скручивание.
119
Модули упругости и жесткости Еь Е2, Gl2, Dh D2, D3 могут быть не-
зависимыми величинами, а коэффициенты Пуассона должны удовлетво-
рять условиям
Ц12 _ Р-21
£1 ~ Е2 ’
Ц12 ____ Ц21
D2
(14.29)
(14.30)
Предположим теперь, что в рассматриваемой ортотропной оболочке
и D^D2. Подобные соотношения могут быть, например, у кон-
структивно ортотропных оболочек, усиленных часто расположенными
кольцами. Из условий (14.29) и (14.30) следует, что в этом случае (щг
и Ц12 очень малые величины. В пределе, когда Е2-+оо и Z)i->0, из соотно-
шений (14.23), (14.24), (14.26) и (14.27) получим
= е2 = 0’ М1 = 0’ =
E±h D2
Если еще принять G12—*ос и Z)3—>0, то из формул (14.25) и (14.28) по
лучим у = 0 и Л412 = 0.
Это не означает, что приближенная теория цилиндрических оболочек
соответствует только ортотропным оболочкам. Рассмотрение ортотроп-
ной оболочки только показывает, что приближенная теория оболочек,
определенная уравнениями
е2 = У = М1 = М12 = 0 (14.31)
и
М2 = Г>х2, (14.32)
является в пределе точной теорией для ортотропных оболочек, у которых
Di->0, D3->0, Е2-+оо и Gi2^oo. Практически это означает, что теория,
основанная на гипотезах (14.31), может особенно хорошо описывать
напряженное состояние конструктивно ортотропной цилиндрической
оболочки, состоящей из тонкой обшивки, подкрепленной часто располо-
женными кольцами — шпангоутами.
Действительная область применимости условий (14.31) гораздо шире
и связана в основном с величиной относительной длины оболочки. Для
доказательства этого вернемся к рассмотренной задаче о деформациях
шарнирно опертой цилиндрической оболочки, находящейся под нагруз-
кой g = ^ocos2q).
При гипотезах е2 = у = 0 получим
и = 2 (— I — cos 2<р, (14.33)
Eh \ Л2 3 J v
и = 2-^-(—-------------------- ^sin2cp, (14.34)
Eh \ Я2 6 6 R4 J
л q0R2 ( /2 t2 £4 5 /4 \ п /1лое\
w = —4 —-— (------д2----------------) cos 2ср. (14.35)
Eh \ R2 6 6 Я4 ) т '
Из сравнения формул (14.33) — (14.35) с формулами (14.12), (14.15)
и (14.16) видно, что чем больше отношение ///?, тем ближе перемещения,
вычисленные в предположении е2 = у = 0> к перемещениям, вычисленным
на основе обычных формул закона Гука для безмоментной оболочки.
Можно показать, что если оболочка находится под нагрузкой g = g0cos Пф,
где п>2, то введение условий е2 = у = 0 будет еще более оправданным.
Более детальный анализ показывает, что приближенная теория, основан-
ная на условиях (14.31) и (14.32), описывает напряженное состояние в
120
цилиндрических оболочках со слабой изменяемостью в направлении g„
т. е. напряженное состояние, для которого
I д<Р I I I
(14.36)
Условие (14.36) выполняется тем лучше, чем больше отношение
длины оболочки L к ее диаметру D. Практически гипотезами (14.31) и
(14.32) можно пользоваться при L>2D. Для оболочек, подкрепленных
часто расположенными кольцами, эти гипотезы будут приемлемыми и
при меньшей длине. На основе этих гипотез можно построить две при-
ближенные теории цилиндрических оболочек: приближенную безмомент-
ную теорию, когда в дополнение к уравнениям (14.31) и (14.32) прини-
мают Л42 = 0, и приближенную моментную теорию с учетом моментов М2.
Последняя теория часто называется полубезмоментной теорией цилинд-
рических оболочек. Эта теория весьма полно разработана в книгах
[26, 61].
Приближенная безмоментная теория. При действии произвольных
поверхностных нагрузок qx, q, где q = qn — нагрузка, нормальная к
средней поверхности оболочки, уравнения равновесия элемента безмо-
ментной оболочки, отнесенные к координатам g и ф, будут
-5- + -^ = -^. (14.37)
dg dtp
+ = (14.38)
<э<р ag
Т2 = qR. (14.39)
Из уравнения (14.38) получим
dg dtp
Следовательно, усилие сдвига
5=Ф1(ф)-/?У(<7Ф + -^-)^. (14.40)
о
Здесь Ф1(ф)—произвольная функция интегрирования.
Подставляя найденное значение усилия сдвига в уравнение (14.37),.
получим
«i = _ _ ‘'«’И + Я С + \
dg чх d(p J < дф дф2 /
Интегрируя, найдем
В g л
7\ = Ф2(ф)—£ ^1(ф) -Я|Т + (14.41)
аф J L J \ дф дф2 /
о о
где Ф2 (ф) — вторая произвольная функция интегрирования.
Обозначим
S = + (14.42)
о
£ £ -
Л = -R j qxdt, (14.43)
О о
121.
где S, 7\ —частные решения уравнений (14.37) — (14.39). Это известные
функции, определяемые внешними поверхностными нагрузками. При этих
обозначениях
3=Ф1(<р) + 5, (14.44)
Л = Ф3(ф)-£-^-+Л- (14.45)
дф
Перемещения и, v и w определятся из уравнений
ди __ R р
~ ~Eh Ъ
dv ди dv
--- =------, W --------.
d^ дф дф
Интегрируя, получим
£
« = Ф3(Ф) + -^-[^Ф2(<р)---(14.46)
Eh, L 2 дф J J
о
У _ ф Г™)__£ ^фз (ф)___Г £2 ^ф2 (ф) _
4 дф Eh [ 2 дф
£ s
_ _^ФНф)_ + Г С дТ^_ ^2-| (14.47)
6 дф2 J J дф J v 1
о о
где Ф3(ф), и Ф4(ф)—новые произвольные функции интегрирования.
Обозначим
. R h
(14.48)
Eh J
о
9=— — (14.49)
Eh J J a<p
0 0
С учетом обозначений (14.48), (14.49)
ы = ф3(ф)+-АЬф2(ф)_ JL-M-l+Ji, (14.50)
Eh |_ 2 дф J
. e. <*Ф,(<р) R Г ?2
у = ф4(<р)—£—-------— —
d(p Eh
ЛФг (<p)
2 d(f
^1-H, (14.51)
6 дф2 J
функции и и v имеют смысл частных решений.
Нормальное перемещение
ЛФ4(Ф) . t д2Ф2(Ф) , /? Г £2 д2Ф2 (ф)
дф дф2 Eh L 2 дф2
g6 д3Ф! (ф) 1 dv
6 дф3 J дф ’
(14.52)
Таким образом, общее решение уравнений безмоментной теории со-
держит четыре произвольных функции интегрирования. Они должны
определяться из четырех граничных условий на торцах оболочки. Расчет
по приближенной безмоментной теории цилиндрических оболочек чрез-
вычайно прост и достаточно надежен, если внешние нагрузки изменяют-
ся по координатам g и ф не слишком резко. К таким нагрузкам относят-
ся, как правило, гидростатические и аэродинамические нагрузки. Однако
могут быть случаи, когда на цилиндрическую оболочку действуют на-
122
грузки, приложенные к узким участкам поверхности. Примером таких
нагрузок могут быть нагрузки от реакций опорных ложементов во время
транспортировки ракет в горизонтальном положении.
Наиболее простой приближенной теорией, позволяющей производить
расчеты на действие таких нагрузок с удовлетворительной точностью,
является полубезмоментная теория цилиндрических оболочек.
Полубезмоментная теория цилиндрических оболочек. При Л41=А412 =
= Q, =0 уравнения равновесия элемента оболочки в координатах ^ = x!R
и ср, согласно выражениям (13.9) — (13.13), будут (см. рис. 14.2)
д7\ , dS dg ' dtp (14.53)
dtp dg (14.54)
т2 + -^- = qR, дф (14.55)
Q = Rdq (14.56)
В уравнении (14.53) опущена продольная составляющая нагрузки,
редко встречающаяся в практических расчетах.
Согласно формулам (14.22) и (13.4) получим
(14.57)
Здесь D — погонная жесткость на изгиб оболочки в плоскости параллели
D = EJnor, где Jnor—момент инерции сечения кольца единичной ширины,
вырезанного из оболочки. Для изотропной оболочки D Eh3lV2. Из урав-
нения (14.56) следует
D f d3w । dw \ xi л co\
= (14-58)
R3 \ dtp3 dq> J
а из уравнения (14.55)
= —+ -^М. (14.59)
R3 V дер4 дф2 J
Дифференцируя выражение (14.53) по а выражение (14.54)—по ср и
исключая усилие сдвига S, получим
d27\ d2T2 dQ2 dq
— + — 7?-^- = 0.' (14.60)
d£2 дф2 1 дф дф v '
Подставляя Тг из соотношения (14.59) в уравнение (14.60), приходим к
первому основному уравнению полубезмоментной теории
2^ + 2^ + ^|-7?(Z^- + 2M = 0. (14.61)
dg2 R3 \ дф® дф4 дф2 / \ дф2 дф У
Второе уравнение получим, рассматривая условия е2 = V = 0 и зависимость
“ (14.62)
Здесь В — погонная жесткость оболочки на растяжение в направлении об-
разующих; В = Ehny где йпр — приведенная толщина оболочки с учетом
продольного подкрепления. При отсутствии продольного подкрепления
В = Eh. Из условия у = 0 имеем
—+ —= о. (14.63)
5<Р dg V '
123
Дифференцируя уравнение (14.63) по g и заменяя производную от и по £
через 7\, согласно соотношению (14.62) получим
R д7\ , д2и __ 0
В dtp 1 dg2
Согласно условию е2 = О
dv
--- = — W.
дф
(14.64)
(14.65)
Дифференцируя уравнение (14.64) по
мощью равенства (14.65), получим
ср и исключая перемещения v с по-
д27\В_ д2^
дф2 R dg2
(14.66)
Это второе основное уравнение полубезмоментной теории. Дифференцируя
выражение (14.61) два раза по ср и исключая 7\ с помощью уравнения
(14.66), получим одно уравнение в частных производных для перемещения w:
+ + + = + (14.67)
д%* BR2 <3q>4 \ dq>4 d<p2 ) В \ d<p4 d<p« /
Для изотропной оболочки
A + ^JLf*L+2*L + »')_A('A + 4\ (14.68}
dg* 127?2 дф* k дф* дф2 ) Eh \ дф* дф3 J v 7
Рассмотрим граничные условия на торцах (краях) оболочки (g = 0 и
l = UR).
Поскольку в полубезмоментной теории (так же, как и в приближен-
ной безмоментной теории) условиями A4i = Qi = e2 = 0 исключен краевой
эффект, то на краях оболочки можно ставить граничные условия только
для тангенциальных усилий S или перемещений u, v. Но усилие S и
перемещения u, v прямо не входят в уравнения (14.61) и (14.66). По-
этому необходимо граничные условия выразить через перемещение w п
его производные по g на краях оболочки.
Если на краю оболочки тангенциальное перемещение у = 0, то, со-
гласно равенству (14.65), равно нулю и перемещение w. Из формул
(14.63) и (14.65) следует, что если на краю оболочки и = 0, то равна Ну-
ди ТТ /1 Л
лю величина а следовательно, и —Из уравнения (14.66) сле-
дует, что если на краю оболочки 7\ = 0, то и вторая производная от w
по g равна нулю. Наконец, если на краю оболочки усилие S = 0, то, со-
гласно формуле (14.53), равна нулю производная -Т1 и, следователь-
но, в соответствии с уравнением (14.66) будет равна нулю третья про-
изводная Таким образом, на каждом торце (краю) оболочки в
зависимости от способа закрепления могут быть следующие варианты
однородных граничных условий:
1. Свободное опирание края оболочки. Запрещены радиальные пере-
мещения w и нет продольных усилий 7\. Край оболочки как бы оперт
на катки, свободно перемещающиеся в направлении оси оболочки. Гра-
ничными условиями при g = 0 или g = 1/R будут
d2u> n
w =-----= 0.
dg2
(14.69)
124
2. Неподвижное закрепление края оболочки. В этом случае запреще-
ны все перемещения края оболочки (w = u = 0). Граничными условиями
будут
^, = 2^=0. (14.70)
3. Свободный край оболочки. В этом случае равны нулю усилия 7\
и S. Граничными условиями будут
(14.71)
д^3
В граничных условиях (14.69) — (14.71) можно, конечно, дифферен-
цирование по g заменить дифференцированием по х. Условиями сопря-
жения двух оболочек с различными жесткостями и В2 будут
a,1 = a>2, = в в1^l==b9^i. (14.72)
1 2 дх дх дх2 - дх2 дх* - дх*
Уравнения (14.67) и (14.68) относительно легко решаются в тригоно-
метрических рядах по угловой координате ф. Рассмотрим случай загру-
жения оболочки нагрузками, симметричными относительно вертикаль-
ной плоскости симметрии оболочки. Радиальную нагрузку q и тангенци-
альную нагрузку в этом случае можно представить в форме рядов
Фурье с коэффициентами, зависящими от осевой координаты ^ = xjR\
Я = ?О (У -Г <71 COS ф + £ qn (I) cos лф, (14.73)
п=2
qv = q<f, Bin ф + q(fn sitimp. (14.74)
п=2
Осесимметричная часть нагрузки ^о(£), как и следовало ожидать,
вследствие того, что 62 = 0, не создает перемещения w. На действие на-
грузки до оболочку надо рассчитать отдельно по методике, изложенной
в § И, с учетом краевого эффекта. Нагрузке q^ соответствует кольце-
вое усилие T2 = qoR. Отдельно рассмотрим нагрузки
q = qi (I) cos ф и q^ = q4>1 sin ф. (14.75
Такие нагрузки возникают от сил веса и гидростатического давления. Для
этих нагрузок
S + = 071-<7ч>.)СО5(Р- (14-76)
Оф4 Оф’1
Соответствующее радиальное перемещение будем искать в виде
w = (£) cos ф. (14.77)
Подстановка выражений (14.76) и (14.77) в уравнение (14.67) дает
^^- = -^-(<71-<7ф,). (14.78)
Следовательно, действие нагрузок (14.75) не вызывает изгиба попе-
речного сечения оболочки; оболочка работает на поперечный изгиб как
балка. Действительно, нагрузки (14.75), приложенные к поверхности
оболочки, эквивалентны поперечной нагрузке на оболочку как балку
2л
Р = X [ (Я1 cos2 ф — sin2 ф) cfcp = л (<7i — qVt) R.
о
125
Если теперь через у обозначить прогиб оси оболочки ’как балки, то ра-
диальное перемещение оболочки будет равной
w = у cos ср. (14.79)
Из сравнения выражений (14.77) и (14.79) следует, чтооуД^^у, и урав-
нение (14.78) можно представить в форме
d*y = _pR_
— лВ ’
Но В = Eh, £ = x/R и xR3h = J, где J — момент инерции поперечного се-
чения оболочки. Следовательно, уравнение (14.78) эквивалентно уравнению
EJ^- =р
dx*
для поперечного изгиба оболочки как балки.
Таким образом, от действия нагрузок (14.75) оболочку надо рассчи-
тать на изгиб как балку. Согласно уравнению (14.59) кольцевое усилие от
этих нагрузок
Т2 = Rqt (£) cos ср.
Из этой формулы следует важное заключение, что от действия чисто
гидростатической нагрузки q = qQ + qY cos ф кольцевое усилие в цилиндри-
ческой оболочке
T\ = qR. (14.80)
Рассмотрим теперь нагрузки, изменяющиеся в поперечном сечении по
гармоникам с номерами n>l. Так как системы функций cos шр и sii mp
ортогональные, то достаточно рассмотреть только нагрузки «номера п»:
q = qn cos пф, ?ф = sin Иф.
Для них
п cos n(V-
Обычно тангенциальная нагрузка создается только силами веса в
уф = уф1 sin ф. Поэтому, чтобы не усложнять формул, в дальнейшем при-
мем q^n = 0. Тогда правая часть уравнения (14.67), соответствующая наг-
рузке q = qn cos пф, будет
-^n4<7ncosncp.
Перемещение w будем искать в форме
w = wn (У cos/гф.
(14.81)
Из уравнения в частных производных (14.67) получим обыкновенное
дифференциальное уравнение для функции wn (£):
d*wn , р п4 (п2 — I)2
dg4 BR2
wn = — n*qn
D
Для изотропной оболочки, согласно уравнению (14.68),
d*wn , h2n* (n2 — I)2 R2 .
----— H----------1-------— Wn =-----------n4<7„.
12/?2 n Eh n
(14.82)
(14.83)
126
Если от переменного £ вернуться к переменному х = то уравне-
ния (14.82) е (14.83) будут иметь вид
d4wn dx4 , п п4 п2 - 12 + D 5 W. = BR* п - w <14-84»
d4wn h2n4 (п2 — I)2 _1_ 2 ' 7/1 • n* n /id.
[dx* 1 МЬ/ м 12/?в " EhR2 4”' ( • )
Уравнения (14.84) и (14.85) аналогичны уравнению изгиба балки на-
упругом основании J^ + _Ly= JL dx* EJ EJ (14.86)
Если под EJ для цилиндрической оболочки понимать ее изгибную жест-
кость как балки, т. е. считать EJ = nR3Eh = л/?3В, то из сопоставления
уравнений (14.84) и (14.85) с уравнением (14.86) получим
k -= л —— и4 (п2 — I)2 = лД п р = itRq п**
12/?3 R3 н Чп
Следовательно, жесткость упругого основания и поперечная нагрузка для
условной балки на упругом основании зависят от номера гармоники «/г».
Обозначив
D П<(П2-1)2 =
BR2 п
(14.87)
представим уравнение (14.82) в виде
^- + 4рХ= -^Яп-
d%* ' гп п в
Общее решение этого уравнения можно представить в двух эквива-
лентных формах
wn -= и- A5 (A cos Н- В sin РД) + е~₽«? (С cos РД + Dsin Рл|), (14.88)
wn = w(n + Ci ch 0Л cos ₽л£ + с2 sh РЛ sin р„£ 4-
+ С3 ch р„£ sin рД + С4 sh рД cos РЛ (14.89)
В формулах (14.88) и (14.89) через обозначено частное решение урав-
нения (14.87).
Если нагрузка qn изменяется по закону qn (g) = ап + + сД2 -F dn£,3,
то частное решение уравнения (14.87) будет выражаться простой формулой
^.(0) _±L_ =------______qn,
п 4р4 В D (п2 — 1)
Справедливость этой формулы легко проверить подстановкой в диффе-
ренциальное уравнение.
Константы Л, В, С, Д или Сь С2, С3, С4 следует определять из гра-
ничных условий на краях оболочки. Когда все функции wn(%) найдены,
перемещение w оболочки (за вычетом перемещения от общего изгиба
оболочки как балки) можно определить из формулы
оо
W = Wn COS Пф.
п=2
Зная перемещение w, легко найти и все другие расчетные величины.
Изгибающий момент М2 определится из формулы (14.57), усилие Т2 —
из уравнения (14.59), усилие 7\ — из уравнения (14.66).
127
§ 15. РАСЧЕТ ОБОЛОЧЕК ПО ПРЕДЕЛЬНЫМ НАГРУЗКАМ
Основные понятия предельного анализа конструкций. Методы расче-
та конструкций по предельным нагрузкам в последнее время получают
все большее распространение. Они применимы как к стержневым и ба-
лочным системам, так и к элементам конструкций, выполненным в виде
пластин и оболочек.
При расчете по предельным нагрузкам реальный материал конструк-
ции обычно заменяют схематизированным жестко-пластическим телом,
диаграмма деформирования которого показана на рис. 15.1, а. При од-
нородном одноосном нагружении такое жестко-пластическое тело остает-
ся недеформируемым до тех пор, пока напряжение в нем меньше пре-
дела текучести от; при достижении напряжением значения от тело,
наоборот, деформируется неограниченно. Величину предела текучести
жестко-пластического тела будем в дальнейшем называть предельным
напряжением. Несмотря на такое чрезвычайно сильное упрощение
свойств реальных материалов, использование схемы жестко-пластическо-
го тела позволяет с достаточной точностью и, главное, сравнительно
просто оценить предельные нагрузки (несущую способность) для многих
конструкций.
Значение предельного напряжения от жестко-пластического тела,
схематизирующего реальный материал, следует выбирать исходя каж-
дый раз из конкретного вида диаграммы растяжения этого реального
материала. Если диаграмма растяжения имеет ясно выраженную пло-
щадку текучести, то значение предельного напряжения сгт можно взять
просто равным пределу текучести реального материала (см. рис. 15.1, в).
Если диаграмма растяжения имеет вид, показанный на рис. 15.1, г, то за
величину предельного напряжения от целесообразно взять предел проч-
ности реального материала ов. А для диаграммы растяжения без пло-
щадки текучести, но с четко выраженным участком упрочнения
(рис. 15.1, д) замена реального материала жестко-пластическим телом
делается вообще весьма условной. Но и в этом случае для оценочных
расчетов по несущей способности такая замена возможна, причем мож-
но, например, значение предельного напряжения от жестко-пластическо-
го тела брать равным половине суммы предела прочности и предела
текучести реального материала.
Предельной нагрузкой называется такое значение нагрузки,
действующей на конструкцию, при котором эта конструкция в результате
развития пластических деформаций становится кинематически изменяе-
128
мой, превращается в механизм. Основные приемы определения предель-
ных нагрузок сначала будут рассмотрены на простейших примерах
поперечного изгиба неразрезной балки. На рис. 15.2, а показана трех-
опорная балка прямоугольного поперечного сечения, материал которой
считается работающим по диаграмме жестко-пластического тела. Для
этой балки найдем предельное значение силы Р = Р1Г[). Если, как это
обычно делается в теории изгиба балок, влиянием перерезывающей си-
лы пренебречь, то единственным силовым фактором в сечении останется
изгибающий момент М. Максимально возможное значение момента в
сечении балки, очевидно, равно (рис. 15.1, б)
Л4т = -^-атО. (15.1)
При достижении значения Л4Т в сечении балки образуется так называе-
мый пластический шарнир.
Существуют два основных метода определения предельных нагрузок:
статический и кинематический. При статическом методе рассмат-
риваются различные статически возможные состояния равновесия, при
которых изгибающие моменты в балке нигде не превышают Л1Т, т. е.
Рис. 15.2
когда всюду в балке нагрузку, соответствующую статически
возможному состоянию равновесия, будем обозначать РСт- Можно стро-
го доказать [63, 69, 104], что из всех статически возможных состояний
предельным состоянием будет то, которому соответствует максимальное
значение нагрузки Рст; Другими словами, предельная нагрузка Рпр яв-
ляется максимумом всех статически возможных нагрузок РСт-
Поэтому при приближенном решении сложных задач, когда статически
возможным состоянием равновесия задаются, величина РСт для пре-
дельной нагрузки Рпр дает оценку снизу. Если рассматриваются не-
сколько статически возможных состояний, то лучшее приближение к
точному значению Рпр получается при том статически возможном со-
стоянии, которому соответствует наибольшее значение РС[.
Для упомянутой выше балки статически возможным состоянием рав-
новесия будут соответствовать значения реакций в опорах А и D
(рис. 15.2, б)
Na<^T' Nd<JT- (15-2)
Первое неравенство должно выполняться, поскольку иначе изгибаю-
щий момент над опорой В превысит значение Л4Т. Второе неравенство
9 Зак. 96
129
гарантирует, что в сечении С момент не превышает Мт. Рассмотрев
сумму моментов относительно опоры В, получим
Pl = NA-2l + ND -2/<ЗМт, (15.3)
откуда для максимального значения Рст находим
Рст = 2р1. (15-
Кинематический метод определения предельных нагрузок про-
иллюстрируем на том же примере трехопорной балки (см. рис. 15.2).
В кинематическом методе рассматриваются различные кинематически
возможные варианты превращения в механизм заданной конструкции
при заданном конкретном ее нагружении. В частности, превращение в
механизм рассматриваемой в нашем примере неразрезной балки связа-
но с образованием минимум двух пластических шарниров, как показано
на рис. 15.2, в, г. Значение нагрузки Ркип, соответствующее выбранному
кинематически возможному состоянию, определяют из условия равен-
ства работ внешних и внутренних сил.
В теории предельного анализа конструкций [63, 69, 104] доказывается,
что из всех кинематически возможных состояний истинным предельным
состоянием будет то, которому соответствует наименьшее значение на-
грузки Ркин; другими словами, предельная нагрузка РПр является м и-
нимумом всех возможных значений РКип- Поэтому при приближенном
решении задач кинематическим методом величина РКИ11 для Рпр всегда
дает оценку сверху.
В рассматриваемом примере внешняя сила Р совершает работу на
перемещении wc\ внутренние изгибающие моменты совершают работу
только в пластических шарнирах, равную моменту Л4Т, умноженному на
соответствующий угол излома. Так, например, для кинематически воз-
можного состояния, изображенного на рис. 15.2, в, получим, считая пере-
мещения и углы излома малыми,
или
Pwc = ЛТгСр! + Мтф2 = Л4 Не-
(15.5)
(15.5')
минимальное значение Ркин при lr == I будет
Ркин = • (15.6)
Нетрудно убедиться, что к этому же результату можно прийти, рас-
смотрев кинематически возможное состояние, изображенное на рис.
15.2, г.
Сравнивая выражения (15.4) и (15.6) и учитывая, что
Per < РПр < Ркин- получаем
Р„р = • (15.7)
Путем аналогичных очень несложных рассуждений может быть опре-
делена предельная нагрузка для любого другого случая поперечного
изгиба балки. Интересно отметить, что расчет по предельным нагрузкам
статически неопределимых систем принципиально не сложнее расчета
по предельным нагрузкам статически определимых систем: в расчете по
предельным нагрузкам раскрытие статической неопределимости не про-
изводится, а сразу рассматривается состояние равновесия системы, пре-
вратившейся в механизм.
130
Предельные нагрузки для оболочек. Величины (предельных нагрузок
при поперечном изгибе балок вычисляются так просто потому, что
условие возникновения течения в балке (условие образования пласти-
ческого шарнира) определяется значением одного единственного внут-
реннего силового фактора: изгибающего момента. Для пластин и, осо-
бенно, для оболочек вся техника вычисления предельных нагрузок су-
щественно усложняется, поскольку там условие течения будет опреде-
ляться комбинацией значений нескольких внутренних силовых факторов.
Но сам подход к определению предельных нагрузок и существо стати-
ческого и кинематического методов их определения остаются теми же.
Рассмотрим, например, условия течения для цилиндрической оболоч-
ки из жестко-пластического материала при осесимметричном деформи-
ровании. Основные внутренние силовые факторы для рассматриваемого
случая — это окружные и меридиональные усилия Т2 и 1\ и меридио-
нальные изгибающие моменты Если в сечении оболочки действует
только одно меридиональное усилие Ть то, очевидно, условием текучести
будет равенство
Л = = (15.8)
где h — толщина оболочки, сгт— предел текучести материала. Если в
сечении оболочки имеется только окружное усилие Т2, то получим ана-
логичное условие текучести
T2 = oTh = Tr. (15.9)
Наконец, если в сечении оболочки действует только изгибающий мо-
мент Afi, то условие текучести (аналогичное условию образования пла-
стического шарнира в балке прямоугольного поперечного сечения) бу-
дет
Мх = — aT/i2 = MT. (15.10)
4
В дальнейшем будут использоваться безразмерные величины меридио-
нального и окружного усилия и меридионального изгибающего момента
Л
Тт ’
«1 =
Т2
п2 = —±
Тт
=
Величины /21, /г2, пц в предельном ана-
лизе конструкций носят название обоб-
щенных безразмерных усилий.
Теперь задачу определения условий текуче-
сти можно сформулировать так: для задан-
ного закона текучести (например, условия
Треска или Мизеса, см. § 4) выразить усло-
вие текучести оболочки через обобщенные
усилия П1, /г2, т\. Можно доказать [63], что
в трехмерном пространстве /гь /г2, т\ усло-
вию текучести будет соответствовать невог-
нутая поверхность, так называемая по-
верхность текучести. Для цилиндри-
ческой оболочки такая поверхность текуче-
сти изображена на рис. 15.3. Поскольку пол-
ное построение поверхности текучести свя-
зано с довольно длительными и громоздки-
(15.11)
Мт
Рис. 15.3
ми расчетами [104], то сейчас мы ограничимся построением только трех
сечений этой поверхности координатными плоскостями mi = 0, п2 = 0,
П1=0 для условия текучести Треска
шах (| (^1, | а31, | o’! — сг21) = сгт.
(15.12)
9*
131
Сечение поверхности текучести плоскостью /щ — О очевидно: если из-
гибающий момент равен нулю, то и окружные, и меридиональные на-
пряжения постоянны по толщине оболочки и условия текучести будут
max (| nJ, | п21, | Hi — n2|) = l. (15.13)
Другими словами, нужно, чтобы либо одно из усилий, либо их разность
по абсолютной величине равнялись бы предельному значению усилия Тт.
Рис. 15.4
Сечение поверхности текучести плоскостью п2 = 0 можно построить,
учитывая следующее: если в сечении оболочки окружное усилие равно
нулю, то напряженное состояние в этом сечении одноосно; условием те-
кучести тогда будет |cri | =с>т- Пример такого распределения напряже-
ний, когда наружные волокна сжаты, показан на рис. 15.4, а. В этом
случае
Л/2 Л/2
7\ = j ^^ = ^(2^ —1), Л41 = f a1zdz = 4MT(l-1)1 (15.14)
—Л/2 —Л/2
или
п1 = 2£- 1, т1 = 4£(1 —£). (15.14')
Исключив из соотношений (15.14') параметр £, можно найти связь между
пх и mlt соответствующую условию текучести:
tn1 = 1— п\. (15.15)
Если рассмотреть случай растянутых наружных волокон, то совершен-
но аналогично можно получить
— tnl = 1— п\. (15.15')
Полный вид сечения поверхности текучести плоскостью п2 = 0 показан на
рис. 15.4,6; в приближенных решениях нелинейную зависимость между
и П\ часто заменяют отрезками прямых, показанными пунктиром.
Построение сечения поверхности текучести плоскостью пх =0 начнем
с первого квадранта, где п2 и т,\ положительны. Если т\ = \, то, со-
гласно условию текучести Треска, в оболочке могут существовать рас-
тягивающие окружные напряжения, равные от, причем как
показано на рис. 15.5, а; тогда
т1 = 1, и2 = £, (0 <£< 1/2). (15.16)
Условию (10.16) соответствует отрезок на рис. 15.5, в. Если принять
£>1/2, то это приведет к уменьшению осевого момента (рис. 15.5,6). В
этом случае
/п1 = 4£(1-£), п2 = £, (1/2 <£ < 1). (15.17)
132
Исключая из соотношений (10.17) параметр В, можно найти зависимость
mi = 4п2(1 — п2).
(15.17')
Рассуждая аналогично, можно получить для других квадрантов кри-
вую, показанную сплошной линией на рис. 15.5, в. В приближенных
решениях зависимость между т\ и п2 часто упрощенно заменяют или
квадратом, или шестиугольником, как показано на рис. 15.5, в пунктиром
и штрихпунктиром.
На примере рассмотренного выше случая п2 = 0 (см. рис. 15.4, а) вы-
ясним, как деформируется сечение оболочки, находящееся в состоянии
текучести. Будем считать, что гипотеза прямых нормалей (см. § 10)
Рис. 15.5
справедлива и для пластической области деформации оболочки, по-
скольку эта гипотеза носит чисто геометрический характер. Тогда оче-
видно, что отрезок АВ должен поворачиваться относительно точки С,
как это показано пунктиром на рис. 15.4, а. При этом абсолютные вели-
чины относительного меридионального удлинения 81 и изменения кри-
визны в меридиональном направлении xi остаются неопределенными, но
для каждого конкретного распределения напряжений между ними су-
ществует своя определенная зависимость. Действительно, из простых
геометрических соотношений (см. рис. 15.4, а) можно найти, что при
П\<\ 8i=/z(g—V2)xi, а величины внутренних усилий связаны с парамет-
ром g выражениями (15.14'). При Mi<l, т. е. согласно (15.14') при
£<1, зависимость между 81 и xi однозначна, но при пх = \ эта зависи-
мость перестает быть однозначной. Геометрически это означает, что при
/21 = 1 сечение может деформироваться (поворачиваться) таким образом,
что центр вращения отрезка АВ лежит вне сечения на расстоянии от
точки В, причем значение £ может тогда быть любым в интервале
l^Cg^oo (£ = оо соответствует растяжению сечения без изменения кри-
визны).
Аналогичные рассуждения о деформировании сечений оболочки, на-
ходящихся в состоянии текучести, справедливы и для других случаев
сочетаний внутренних силовых факторов [104], но в общем случае кар-
тина деформирования усложняется двухосностью напряженного состоя-
ния.
Как можно видеть из приведенного примера построения сечений
поверхности текучести, условию текучести могут соответствовать многие
различные комбинации значений внутренних силовых факторов. В соот-
ветствии с этим в предельном анализе конструкций говорят о различных
пластических режимах работы оболочки. В общем случаев
133
предельном состоянии оболочки на разных ее участках могут реализо-
вываться разные пластические режимы, и одной из основных трудностей
решения задач по несущей способности оболочек является правильный
выбор этих пластических режимов. Общих правил по выбору пластиче-
ских режимов не существует: в каждой конкретной задаче приходится
просто «перебирать» разные варианты комбинаций пластических режи-
мов, проверяя при этом выполнение геометрических условий деформи-
рования оболочки.
Примеры определения предельных нагрузок оболочки. В качестве
простейшего примера выберем пластический режим и найдем предель-
ное значение внутреннего давления для шарнирно опертой по краям
цилиндрической оболочки, изображенной на рис. 15.6, а. Сначала решим
Рис. 15.6
пример статическим методом. Поскольку меридиональное усилие в рас-
сматриваемой задаче отсутствует, то для выбора пластического режима
следует воспользоваться кривой текучести, построенной при ti\ =0 (см.
рис. 15.5, в). При осесимметричной деформации уравнение равновесия
цилиндрической оболочки имеет вид (см. § 11)
dx2 \R
(15.18)
Граничные условия рассматриваемой задачи
= 0 при х = 0 и х = I. (15.18')
При значении давления рСт, равном предельному, величины Afi и Т2
связаны между собой кривой текучести, изображенной на рис. 15.5, в
сплошной линией. Таким образом, чтобы найти предельное давление,
нужно проинтегрировать уравнение (15.18) при граничных условиях
(15.18') и при дополнительной связи между М\ и Т2, даваемой условием
текучести. Можно упростить решение, заменив точную кривую текучести
квадратом, изображенным на рис. 15.5, в пунктиром; пластический ре-
жим будем выбирать для этого квадрата. Поскольку в окружном на-
правлении оболочка растянута, то естественно выбрать пластический
режим, соответствующий стороне квадрата D\D^ т. е. такой, при кото-
ром п2=1, а величина гп\ может меняться от +1 до —1. При выбранном
пластическом режиме уравнение (15.18) примет вид
___
dx2 Р R
Интегрируя уравнение (15.19) находим
м, = (р — — + Cj
V к ) 2 1
2*
(15.19)
134
Используя граничные условия (15.18'), получаем
Максимальное значение момента (Afi)max будет при х = 1/2, и, следовательно,
Рст = + 4 <II < Мт)- (15.20)
К I2
Поскольку (Л41)тах не может быть больше Л4Т, то окончательно для мак-
симальной величины рст получаем
рст = ^ + 4м- (15,21)
Теперь определим предельное значение давления кинематическим ме-
тодом. Для этого зададимся механизмом потери несушей способности
(рис. 15.6, б). При этом работа внешних сил (давления) будет равна
ГI
• 2л7? ^pwdx = 2nRp [ш0 (/ —2/х) + 2 • -у . (15.22)
о
Работа внутренних растягивающих окружных усилий на соответствую-
щих удлинениях будет равна (согласно выбранному пластическому режиму
Т2 всюду равно 7\)
i
2«/?jTTydx= — 2/1) + 2--1-^-/1] ’ (15-23)
о
а работа внутренних] моментов Л4Т, образующихся в двух сечениях,
будет
2 -2nWT(p = 4л/?Л4т . (15.24)
Приравнивая работу внешних сил работе внутренних, получим
Рки,.-^ + 2 , (0</х<//2). (15.25)
К II (Z — II)
Как легко проверить, минимальному значению ркин будет соответствовать
= //2; тогда значение для ркин получится то же, что и значение рст,
определяемое формулой (10.21)
Ркин=4l+4Mt==jtl(1+2 • (15-26)
Формулы (15.21) и (15.26) получены в предположении, что меридио-
нальные усилия в оболочке при потере ее несущей способности остают-
ся равными нулю. Другими словами, закрепление краев оболочки
предполагается таким, что оно не препятствует их сближению. Именно
в этом случае величина предельного давления оболочки конечной длины
практически очень мало отличается от величины предельного давления
бесконечно длинной оболочки, для которой, очевидно, Рпр = от h/R.
Если бы при решении статическим методом была использована точ-
ная кривая текучести, то совпадение результатов при решении двумя
методами означало бы, что получено точное значение рПр,’ в нашем же
случае можно только утверждать, что полученное значение рПр = Рст =
= Ркин не меньше точного значения рпр.
В качестве второго примера найдем кинематическим методом пре-
дельную нагрузку для длинной цилиндрической оболочки, изображенной
135
на рис. 15.7, а. Механизм потери несущей способности выбираем, как
показано на рис. 15.7,6. Приравнивая (аналогично тому, как это было
сделано в предыдущем примере) работу внешних сил работе внутрен-
них, получим
(15.27)
Так как кинематический метод дает завышенную оценку для пре-
дельной нагрузки, то величину 1Х в выражении (15.27) нужно подобрать
из условия минимума ^Кин. Дифференцируя выражение (15.27) по 1\ и
приравнивая производную нулю, находим
4-^- = V'Rh, (15.28)
и тогда из выражения (15.27) окончательно получаем
<7кин = 2-^т. (15.29)
Точное значение предельной погонной нагрузки [69]
?пр= 1,82^/^. (15.30)
Полученный результат довольно любопытен: вовлекаемая в дефор-
мацию («выламываемая») зона жестко-пластической оболочки имеет
ширину того же порядка, что и зона упругого краевого эффекта
(СМ. § 11).
В рассмотренных примерах решение было получено так просто пото-
му, что выбор пластических режимов не составлял особого труда. В бо-
лее сложных случаях приходится последовательно рассматривать не-
сколько (иногда десятки!) возможных пластических режимов. Однако
использование ЭЦВМ и современных методов линейного программиро-
вания дают возможность и в этих случаях сравнительно легко находить
значения предельных нагрузок.
§ 16. УСТОЙЧИВОСТЬ ОБОЛОЧЕК
Особенности расчета оболочек на устойчивость. Картина потери
устойчивости тонких упругих оболочек обычно качественно отличается
от картины потери устойчивости упругих стержней и пластинок. Стер-
жень или пластинка идеально правильной формы сохраняют первона-
чальную форму равновесия до тех пор, пока сжимающая сила нс
достигнет критического значения (участок О А на рис. 16.1, а). При
дальнейшем увеличении сжимающей силы первоначальная прямолиней-
136
пая форма равновесия перестает быть устойчивой (участок АС) взамен
ее появляется новая изгибная устойчивая форма равновесия, которую и
принимают стержень или пластинка (кривая ДВ).
При нагрузках, меньших критической, ни стержень, ни пластинка не
имеют никаких других статических форм равновесия, кроме прямоли-
нейной; при критической нагрузке участки устойчивых изгибных форм
равновесия и участки прямолинейных форм равновесия имеют общую
точку А. Другими словами, при определенных значениях нагрузки у
стержня и пластинки возможны устойчивые изгибные формы рановесия.
бесконечно близкие к прямолинейной. Поэтому /три плавном нарастании
нагрузки упругий стержень или пластинка идеально правильной формы
должны переходить от прямолинейной формы равновесия к изгибной
тоже плавно без скачков и хлопков, все время проходя только через
статически устойчивые формы равновесия. Закритическое поведение
пластинки отличается от закритического поведения стержня лишь тем,
что если для стержня потеря устойчивости практически является исчер-
панием его несущей способности, то тонкая упругая пластинка с за-
крепленными краями обычно способна и после потери устойчивости уже
в искривленном состоянии воспринимать нагрузки, значительно превы-
шающие критические.
Стержень или пластинка, имеющие какие-то начальные неправильно-
сти формы, ведут себя при нагружении сжимающими усилиями не-
сколько иначе (кривая OD). Но существенным является то обстоятель-
ство, что малые начальные неправильности стержней и пластинок при
нагрузках, меньших критической, приводит и к малым отклонениям от
прямолинейной формы; только при приближении нагрузки к критиче-
скому значению прогибы начинают быстро увеличиваться.
Для работающих на сжатие упругих стержней и пластинок харак-
терно одно критическое значение нагрузки Р\ Кр, называемое обычно
эйлеровой критической нагрузкой: это значение нагрузки, при превыше-
нии которого перестает быть устойчивой начальная прямолинейная фор-
ма равновесия стержня или пластинки идеально правильной формы.
Если закрепления тонкой упругой оболочки таковы, что допускают
чисто изгибную деформацию оболочки без растяжений и сдвигов сред-
ней поверхности (см. § 8), то оболочка может терять устойчивость ана-
логично сжатому стержню или пластинке. Другими словами, в этом слу-
чае тоже существует только одно критическое значение нагрузки Р\ кр,
при превышении которого оболочка плавно, без хлопков переходит в но-
137
вую изгибную форму равновесия. Но если закрепления краев оболочки
исключают возможность чисто изгибной деформации, то поведение тон-
ких упругих оболочек при потере устойчивости становится качественно
иным.
Во-первых, для оболочки идеально правильной формы еще до дости-
жения нагрузкой эйлерового критического значения Р\ Кр возможны
различные устойчивые и неустойчивые изгибные формы равновесия (на
рис. 16.1,6 показана кривая AED для одной из таких форм; участок АЕ
соответствует неустойчивой форме равновесия, участок ED — устойчи-
вой). Во-вторых, участок устойчивых прямолинейных форм равновесия
ОА и участки устойчивых изгибных форм равновесия (например, кри-
вая ED) обычно не имеют общих точек, т. е., как правило, ни при каких
значениях нагрузок у оболочки нет статически устойчивых изгибных
форм равновесия, бесконечно близких к начальной прямолинейной. По-
этому потеря устойчивости оболочки, т. е. переход от начальной прямо-
линейной формы равновесия к изгибной, происходит хлопком: в новую
форму равновесия оболочка может «проскочить», только проходя через
статически неустойчивые формы равновесия.
Практически важно, что новые формы равновесия, появляющиеся у
•оболочки, отделены от начальной формы равновесия сравнительно не-
большим силовым барьером.
Реальная оболочка в результате геометрических несовершенств и не
строго осесимметричного нагружения сразу начинает отклоняться от
своей начальной формы (кривая OF); затем при некотором значении на-
грузки Рхл оболочка хлопком переходит в новую форму равновесия (из
точки F в точку G).
Итак, для упругих оболочек характерны три значения нагрузок:
Р\ Кр — верхняя (эйлерова) критическая нагрузка, при превышении
которой перестает быть устойчивой начальная форма равно-
весия оболочки идеально правильной формы;
Лгкр — нижняя критическая нагрузка, при превышении которой у
оболочки идеально правильной формы оказываются возмож-
ными отличные от начальной изгибные формы равновесия;
Р^л — нагрузка, при которой происходит хлопок реальной оболочки.
Значение верхней критической нагрузки определяют с помощью ли-
неаризованных дифференциальных уравнений теории оболочек. Решение
этих уравнений в настоящее время не представляет принципиальных
трудностей и практически для всякой оболочки при заданных граничных
условиях величина Р\ кр может быть найдена с любой степенью точно-
сти. Но знания величины верхней критической нагрузки часто оказы-
вается недостаточно для расчета некоторых реальных оболочек, которые
могут терять устойчивость при нагрузках Рхл, в несколько раз меньших
Р1 кр-
При определении нижних критических нагрузок приходится иметь
дело с чрезвычайно сложными дифференциальными уравнениями нели-
нейной теории оболочек. Строго аналитически решить эти уравнения до
сих пор не удается, и все имеющиеся зачастую довольно противоречи-
вые результаты получены тем или иным приближенным способом.
Значение нагрузки Рхл реальной оболочки обычно лежит между
верхним и нижним значениями критической нагрузки оболочки идеально
правильной формы и тем ближе к верхнему значению критической на-
грузки, чем точнее изготовлена оболочка. Очень существенно для
потери устойчивости оболочек то, что значение Рхл чрезвычайно чувст-
вительно к величинам и формам начальных неправильностей. Это, с
одной стороны, приводит к очень большому разбросу экспериментальных
значений Рхл, полученных различными исследователями, а с другой
стороны, возникают принципиальные трудности при теоретическом
определении Рхл реальных оболочек: для определения Рхл данной обо-
138
л очки необходимо с очень большой точностью знать ее начальные
неправильности, что практически обычно неосуществимо. Поэтому чаще
всего теоретически удается предсказать только тот диапазон нагрузок,
где можно ожидать хлопок оболочки (т. е. найти верхнее и нижнее
значения критической нагрузки оболочки идеально правильной формы)
и выяснить, насколько сильно при данном нагружении влияют на РХл тс
или иные формы начальных неправильностей.
На практике во многих случаях бывает целесообразно стремиться к
созданию таких конструкций оболочек, у которых нижнее значение кри-
тических нагрузок возможно меньше отличалось бы от верхнего значе-
ния критических нагрузок. В этом случае устойчивость конструкции не
будет сильно зависеть от таких случайных и трудно контролируемых
факторов, как начальные неправильности. Основные пути создания та-
ких конструкций — это использование каркасированных оболочек
(см. гл. VII).
Линейные уравнения для определения верхних критических нагрузок
упругой цилиндрической оболочки. Пусть тонкостенная цилиндрическая
оболочка нагружена осевой сжимающей силой Р, внешним равномер-
ным давлением р и крутящим моментом М. Устойчивость оболочки ис-
следуем в предположении, что ее напряженно-деформированное докри-
тическое состояние является однородным и безмоментным.
Основная особенность вывода уравнений устойчивости состоит в том,
что условия равновесия составляются для деформированного
(искривленного) элемента оболочки. Поэтому произведения докритиче-
-ских внутренних усилий 7?, S0 на соответствующие изменения кри-
визн X], Х2, т входят в уравнение равновесия в проекции на нормаль к
оболочке в виде фиктивной нормальной нагрузки [27]
qn = Х1Т? 4- и2Т°2 + 2S°T, (16.1)
гдех],Х2, т — определяются зависимостями (13.3) или (13.4).
Из общих уравнений равновесия элемента оболочки (13.9) — (13.13),
положив qx = q^=^ и учитывая фиктивную нормальную нагрузку qn,
можно получить три уравнения:
-^- + ^- = 0,
дх Rd<f
дТ2 । dS___1 ( дМ2 дМ12 \ _л zic
Rd<p ‘ дх R\ Rd<f + дх ) ~ ’ ( )
Г2 , dW, , о 3W12 ,
R дх2 Rdqdx ‘ R2dq2 Ч,г'
Внутренние усилия Ть Т2 и т. д. здесь являются дополнительными
усилиями, возникающими в оболочке при отклонении ее от начальной
докритической формы равновесия. Докритические внутренние усилия
выражаются через внешние нагрузки соотношениями
Т1 =-----— , Т°2 = —pR, 8° ------— . (16.3)
2nR к 2л7?2 '
Для изотропной оболочки, когда внутренние силовые факторы связа-
ны с перемещениями зависимостями (13.14) и (13.15), а выражения для
изменения кривизн взяты в виде (13.3), из уравнений (16.2) можно по-
лучить систему [27]
д2и 1 — р д2и 1 + р d2v р dw __ q
дх2 2 Я2дф2 Ф 2 Rdqdx R дх ~~ ’
d2v 1 — р
R2 дф2 2~
д2У . 1 + р д2и . dw ,
дх2 2 R дф дх R2 дф ‘
139
1 —И d~V \ _ Q
2 dx2 / ’
h2 / d3w
\2R2 \ /?2дф3
d3w . d2v
dx2 dtp R2 дф2
dv . n du
^ + — + —
дф dx
h2 / d*w 2^2 d*w
12Л2 X. dip4 d(f2dx2
+ R*^
dx*
_u dSv Ц- D2 d3v
1 дф3 dx2 дф J
(16.4}
Здесь и, v, w — перемещения, отсчитываемые от докритической формы
равновесия оболочки.
При исследовании устойчивости замкнутой оболочки нужно знать-
граничные условия на ее торцах; в соответствии с порядками получен-
ных уравнений на каждом из торцов должны быть заданы по четыре-
граничных условия: два граничных условия относительно нормального
прогиба w и два граничных условия относительно тангенциальных пере-
мещений и и V. Эти граничные условия относятся к перемещениям, воз-
никающим в связи с потерей устойчивости оболочки, и непосредственно
не связаны с граничными условиями для докритической деформации
оболочки.
Устойчивость изотропной цилиндрической оболочки, сжатой в осевом
направлении. Вначале будет рассмотрена осесимметричная форма поте-
ри устойчивости; в этом случае ^ = 0 и все частные производные по у
тоже равны нулю; поэтому система уравнений (16.4) при М = р = 0 при-
нимает вид
d2u ц dw __ q
dx2 R dx
r dx 12R2 dx4 Eh 2л dx2
(16.5)
Если на обоих торцах заданы граничные условия шарнирного опирания
w = v = M1 = TJ=0 при х = I и х = 0, (16.6)
то решением системы (16.5) будут
r.tnx it I ~тх /к?
w = wQ sin---------, u = wQ —-----------cos -------, (16.7)
/ лт R I
где m—число полуволн, образующихся по длине оболочки I при потере
устойчивости. Тогда из второго уравнения (16.5) определится выражение
для верхнего критического значения
• 9тг Г Eh3 Р1тП\2 ' Eh f 1 ¥1
1КР = 2Я|. 12(1-иТR[~T) J-
(16.8)
Входящее в выражение (16.8) число полуволн т следует подбирать из
условия минимума Рщр-
Выражение (16.8) характерно для задач устойчивости оболочек.
В его правую часть входят два слагаемых, первое из которых пропор-
ционально изгибной жесткости оболочки, а второе — жесткости дефор-
мирования оболочки в ее средней поверхности. С увеличением числа
полуволн т первое слагаемое увеличивается, а второе уменьшается;
потеря устойчивости будет происходить при числе полуволн т\ кр, соот-
ветствующему минимуму Pi Кр-
Для достаточно длинной оболочки, когда потеря устойчивости про-
исходит при большом числе полуволн, минимальное значение Pi кр мож-
но найти, приравняв нулю его производную по т. Тогда
140
Е1кР = —2я . Eh2. (16.9)
кр /3(1- н2)
Любопытно отметить, что Р\ кр зависит от толщины оболочки и упругих
свойств материала, но не зависит от радиуса оболочки.
Чаще критическую нагрузку выражают через осевое критическое на-
пряжение
(ох)1кр = —r Eh,R - 0.605Е — . (16.10)
К Х/1КР ’ R '
Если при тех же граничных условиях (€б) рассмотреть общий слу-
чай неосссимметричной деформации оболочки, то решением системы
(1Б4) будет
w = Л sin—j— sin лер, v = В$\п ——cos/icp, и = Cess —-— sin/icp.
(16.11)
Подставив выражения (16.11) в систему уравнений (16.4), получим
систему трех однородных линейных алгебраических уравнений с неизве-
стными А, В, С. Из условия равенства нулю определителя этой системы
можно найти выражение для критической нагрузки. При большом числе
полуволн т и 2п это выражение приводится к упрощенному виду [27]
где
Лкр 2л
п2 I
12(1 -р2) R П2 J ’
п
тк
(16.12)
(16.13)
Т] = п
тл R
п I
Рассматривая комплекс ц как варьируемый параметр и определяя
условие минимума Р\ кр по этому параметру, очевидно, можно опять по-
лучить формулу (16.10). Таким образом, при большом числе полуволн
т и 2/1 значения верхней критической нагрузки цилиндрической обо-
лочки с граничными условиями (16.6) при осесимметричной и при неосе-
симметричной форме потери устойчивости совпадают:
(^х)1кр
1
/3(1-р2)
Е — 0.605Е — .
R R
Вообще, выражение для верхних критических напряжений можно пред-
ставить в виде
/\
(16.14)
где коэффициент k\ зависит от граничных условий на торцах оболочки.
Так, если на торцах оболочки разрешены перемещения и углы поворо-
та, т. с.
Qi = Mi = Ту = S = 0 при х—-0 и х = /, (16.15)
то из уравнений (16.5) для осесимметричной формы потери устойчиво-
сти можно найти (см., например, [77]) &i^0,3.
При других граничных условиях решение полной системы уравнений
(16.4) резко усложняется, и окончательный результат удается получить
только с помощью ЭЦВМ. Как показали проведенные в последнее время
141
исследования [45], значение коэффициента k\ оказывается равным 0,3 и
при граничных условиях
w = 7\ = Mi =--= S = 0 при х = 0 и х=*1. (16.16)
При других вариантах граничных условий для достаточно длинных
оболочек, теряющих устойчивость с образованием большого числа полу-
волн вдоль образующей, значение коэффициента k\ мало отличается от
0,6 (см., например, [45]).
Величина нижнего критического значения сжимающего напряжения
может быть найдена по формуле
= . (16.17)
К
Многие исследователи различными путями получали приближенные-
выражения для коэффициента k2. Для тонких оболочек при RJh> 180
С. А. Алексеевым было получено [68]
k2 = 2,35 VhiR. (16.17')
Как уже отмечалось выше, реальные оболочки теряют устойчивость
хлопком при нагрузках Рхл, обычно лежащих между кр и Р2кр. Вели-
чину Рх:[ можно подсчитать по формуле
Рхл=кхл2пЕН\ (16.18)
причем kx;[ должно определяться экспериментально. Если отсутствуют
конкретные экспериментальные данные по величинам йхл для оболочек,
изготовленных в условиях данного производства, то в расчетах можно
пользоваться эмпирическими формулами, графиками и таблицами; неко-
торые данные по этому вопросу приведены в § 33.
Величина коэффициента &хл с увеличением радиуса оболочки обычно
падает; поэтому получается весьма любопытный результат: если из ли-
ста заданной толщины h изготовить две цилиндрические оболочки раз-
ных диаметров, то может оказаться, что оболочка с большим диаметром
будет нести меньшую осевую нагрузку, т. е. значение Рхл оболочки с
большим диаметром может быть ниже значения Рхл оболочки с мень-
шим диаметром.
В заключение следует отметить, что потеря устойчивости сжатой в
осевом направлении оболочки практически всегда приводит к ее разру-
шению.
Устойчивость цилиндрической оболочки, нагруженной внешним дав-
лением. Для определения верхнего критического давления р\ кр можно
опять воспользоваться системой (16.4), положив M = P = Q. При гранич-
ных условиях (16.6) решение системы уравнений (16.4) снова получает-
ся в виде (16.11), причем нетрудно установить, что наименьшему значе-
нию критического давления всегда будет соответствовать т=\. Таким
образом,
w = Asin sinncp, v = Bsin у- cosncp, и = Ceos у- sin nep. (16.19)
Подстановка этих функций для w, v, и в уравнения (16.4) приводит
к системе трех однородных алгебраических уравнений; из условия ра-
венства нулю определителя этой системы находят критическое давление.
Отбросив некоторые второстепенные слагаемые, выражение для верхне-
го критического давления можно привести к виду [68]
_ EhW В2 Eh Г J у _1_
Р1кр 12(1 — р2) Bi R \ I J Bi ’
(16.20)
142
где
Bt = п2 Г ( л — ¥ + п2
\ I )
2—п4,
В2 == (л у-¥ + п2 Г — 2/г6 -j- п4.
(16.21)
Как и в предыдущей задаче, выражение для критической нагрузки
состоит из двух слагаемых, первое из которых пропорционально жест-
кости оболочки на изгиб, а второе — жесткости оболочки на растяже-
ние. Входящее в выражения (16.19) число окружных волн п нужно в
каждом конкретном случае подбирать из условия минимума р\ кр.
Для длинных оболочек при Z//?>2]/ R/h зависимость (16.20) резко
упрощается. В этом случае оболочку можно рассматривать как бес-
конечно длинную (Z//?->oo), и тогда
л2 — 1 Eh3 о /1С ооч
Pikd =---------------, ^ikd r z 2- (16.22)
р 12(1 —р2) /?3 кр v
Для оболочек средней длины при ///?< 0,3]//?/Л, если пренебречь
некоторыми малыми слагаемыми и найти минимум р1кр по числу волн пг
то из выражения (16,20) получим формулу П. Ф. Папковича
р =--------------------( Л у2 ~ 0,92Е — (—У 1/'-- (16.23)
кр 9(1 —I \rJ I \ rJ У R
и критическое число волн
Л1КР = л А ><36(1 — н2) « 7,5 -5-1/ А . (16.23')
Наконец, для очень коротких оболочек, начиная примерно с l/R<ZVh/R,
общую формулу (16,20) тоже можно резко упростить. Как показывают
численные расчеты, в этом случае оболочка теряет устойчивость по очень
большому числу волн п, и вторым слагаемым в выражении (16.20) вполне
можно пренебречь. Тогда, учитывая условие п2^>1, можно получить
Р1кр
Eh3/R3 Г/ R \2 32 Eh3/R3 / nR \2 г п/ Ч2
------------ I Л----- 1 "7^1 —-------------{ --- 1 I --- г ----
12(1— р.2)п2 |Д lj J 12(1— р.2) \ I J [ nl nR J
(16.24)
Очевидно, что значение р1кр будет минимальным при п = nR/l. Оконча-
тельно получим (р = 0,3)
Р1кр = 4л2
12(1—ц2) RP
(16.24')
Нетрудно убедиться в том, что эта формула совпадает с формулой
для шарнирно опертой удлиненной прямоугольной пластинки, сжатой в
одном направлении усилием T = pR [27]:
, Я2№/&2 , .
Jkp 12(1 —ра)
(16.25)
при условии, что ширина пластинки b равна длине оболочки Z, а крити-
ческое напряжение сжатия e\^ = pR!h.
Нелинейная задача по определению нижнего критического давления
цилиндрической оболочки. Результаты приближенных решений этой за-
дачи, полученные различными авторами [3, 27, 39], сводятся к тому, что
выражение для нижнего критического давления может быть представле-
но в виде
Р2кр V2Plxp»
(16.26)
143
где V2 — коэффициент, зависящий от параметров оболочки и изменяю-
щийся в пределах от 0,6 до 1,0. На рис. 16.2 приведен график изменения
коэффициента v2 в зависимости от параметра.
0 = V Rh/2l2 (см., например, [39]).
Значение давления рхл, при котором происходит хлопок реальной
оболочки, можно определить из выражения
Рхл ' ^ХЛ^1кр-
(16.26')
Значения vXt4 желательно определять экспериментально для конкрет-
ных технологических условий изготовления оболочек. Если эксперимен-
тальные данные отсутствуют, то можно принять vX3=v2 и пользоваться
для определения рхл графиком рис. 16.2.
Поведение работающей на внешнее давление цилиндрической обо-
лочки после потери устойчивости сильно зависит от способа закрепления
ее торцов в осевом направле-
нии. Если торцы закреплены
жестко (ц = 0), то и после по-
тери устойчивости оболочка
может продолжать восприни-
мать возрастающее давление.
Если же торцы могут беспре-
пятственно сближаться, то вме-
сте с потерей устойчивости ис-
черпывается и несущая способ-
ность оболочки.
Влияние граничных усло-
вий на величину piKp будет по-
казано ниже на примере реше-
ния задачи об устойчивости
полубезмоментной оболочки.
Использование полубезмо-
ментной теории оболочек в за-
дачах устойчивости. В тех слу-
чаях, когда потеря устойчиво-
сти цилиндрической оболочки происходит так, что изменение кривизны
вдоль образующей существенно меньше изменения кривизны в окруж-
ном направлении (т. е. %] существенно меньше х2), простые и доста-
точно точные результаты дает полубезмоментная теория оболочек [26,27].
К таким задачам относится, например, задача о потере устойчивости
при кручении оболочки или при осевом сжатии с образованием длин-
ных волн вдоль образующей [28]. Но, по-видимому, наиболее эффек-
тивно применение полубезмоментной теории в задаче об устойчивости
цилиндрической оболочки, нагруженной внешним давлением. На приме-
ре этой задачи и будет ниже показано использование полубезмоментной
теории оболочек.
Согласно статическим допущениям (14.18) полубезмоментной теории
оболочек равны нулю меридиональные и скручивающие моменты:
Л4;—Л412 = 0. Поэтому в полубезмоментной теории оболочки система
(16.2) принимает вид
д- - ds о,
дх Ядер
дТ2 _ dS __ д2М2 __ 0
Rdcp 1 дх /?2д(р2
д‘2М
Я2д<р2
Т2
R ~ Чп'
(16.27)
144
(16.28)
Исключив из этих уравнений Т2 и S, с учетом (13.4) и того, что для
рассматриваемого случая qn = — pRu2, получим
д4М2 , д2Мо , D3 д27\
Л л ;—гд:—га “тт
дер4 дер2 дх1
Использовав геометрические допущения полубезмоментной теории
(Ь==У==0, см. § 14) и выразив Л42 и 1\ через перемещения согласно
(14.57) и (14.62), можно получить одно основное уравнение относитель-
но нормального прогиба wy аналогичное уравнению (14.67), и четыре
дополнительных соотношения, позволяющих выразить через w переме-
щения и и vy осевое усилие 1\ и сдвигающее усилие S:
d*w . £> d4 / d*w , о d2w , \ pR / d6w , d*w \ п
dg1 BR2 дф4 \ дф4 дф2 J В \ дф6 дф4 /
где £ = x;R,
(16.29)
wdq\ и =
т .; в — —; S -=
dl R
Здесь В и D — жесткости оболочки на растяжение в осевом направле-
нии и на изгиб в окружном направлении (см. § 14).
Для решения уравнения (16.29) должны быть заданы четыре гра-
ничных условия (по два на каждом торце). Поскольку рассматривается
полубезмоментная оболочка, то граничные условия могут быть только
типа (14.69) —(14.71).
Если решение уравнения (16.29) искать в виде
w X sin/др,
где X —функция только координаты то нетрудно получить
XIV — Х4Х -0.
(16.29')
(16.30)
(16.31)
где
X4 - /г4 (/г2
— (п2—1)— .
v BR2 J
(16.32)
v
Уравнение (16.31) полностью совпадает с уравнением для однород-
ной колеблющейся балки [4, 7]. Поэтому при определении собственных
функций X и собственных значений X в конкретных задачах можно вос-
пользоваться готовыми результатами теории колебаний балок.
Выражение для критического значения р\ кр получается из зависимо-
сти (16.32):
(16.33)
Р1кр
1 |/2 1 \ 7)
------------ (п2 — 1)--,
/г4 (п2 - 1) V 7 /?3
где а (л/?//)— наименьшее собственное значение X. Если число волн в
окружном направлении п достаточно велико, чтобы можно было принять
п2^> 1, то условие минимума р1кр по п даст
Р1кр - 4а
(16.34)
Полученные выражения можно использовать не только для изотроп-
ной, но и для ортотропной оболочки (см. § 14); тогда под В и D следует
понимать соответственно жесткость ортотропной оболочки на растяже-
ние в осевом направлении и изгибную жесткость ортотропной оболочки
в окружном направлении.
10 Зак. 96
145
В качестве примера сначала рассмотрим оболочку со свободно опер-
тыми краями, т. е. возьмем граничные условия (14.69)
ш = 0 при х = 0 и х = /.
дх* г
Тогда граничные условия для уравнения (16.31) примут вид
Х = Х" = 0 при g = 0 и g =///?. (16.35)
Они тождественны граничным условиям для шарнирно опертой балки
(наименьшее собственное значение X = TtR/l и а = 1). Из формулы (16.33)
получим
Р1кр =4— Г —-— + (п2 - о—. (16.36)
кр \ I ) Rn4 (п* — 1) ' R3
а формула (11.34) примет вид
(,6-эт>
Для случая изотропной оболочки эта формула совпадает с формулой
П. Ф. Папковича (16.23).
В качестве второго примера рассмотрим оболочку с обоими жестко
закрепленными торцами, т. е. с граничными условиями (14.70). Тогда
граничные условия уравнения (16.31) будут
Х = Х'=0 при £ = 0 и £ = ///?. (16.38)
Это ни что иное, как граничные условия для защемленной балки (наи-
меньшее собственное значение А,=4,73 RI и а =1,5). Таким образом,
жесткое закрепление краев оболочки в осевом направлении (и = 0) су-
щественно сказывается на величине критического давления: из формулы
(16.34) следует
Р1кр = 1.5р^р> (16.39>
где — критическое давление для шарнирно-опертой оболочки, опреде-
ляемое по формуле (16.37).
В качестве последнего примера рассмотрим оболочку с одним сво-
бодным, а другим жестко закрепленным краем, т. е. возьмем граничные
условия: w = u = Q при х = 0; Tt = S = Q при х=1. Соответствующие гранич-
ные условия уравнения (11.31), как и для консольной балки [4, 7],
будут
X = X’ = 0 при £ = 0, (16.40)
Х'' = Х"' = 0 при £=///?.
п
При этом наименьшее собственное значение 1 = 1,87 —. Формула (16.34)
дает
Р1кр = 0,6р°"р. (16.41)
Иначе говоря, при большом числе волн критическое давление кон-
сольной оболочки составляет 60% критического давления оболочки с
обоими свободно опертыми краями.
Все приведенные в этом параграфе зависимости относились к упру-
гим оболочкам и возможность возникновения пластических деформаций
не учитывалась. Как правило, таких зависимостей достаточно для рас-
чета на устойчивость тонкостенных оболочек, поскольку их потеря
устойчивости обычно начинается в упругой области, а пластические де-
формации являются только следствием больших деформаций, возникаю-
щих в результате потери устойчивости. Исключением является случай
оболочки типа несущего бака с наддувом, когда тонкостенная оболочка
может воспринимать сжимающие нагрузки и за пределом упругости
Подробнее этот случай рассмотрен в гл. VI.
ГЛАВА III
ОСНОВЫ ДИНАМИЧЕСКИХ РАСЧЕТОВ
КОНСТРУКЦИЙ
§ 17. ОСОБЕННОСТИ ДИНАМИЧЕСКОГО НАГРУЖЕНИЯ
КОНСТРУКЦИЙ
Продольное и поперечное ускорение ракеты. На рис. 17.1 изображе-
ны внешние силы, действующие на ракету: Рэ — эффективная сила тяги
двигателей, О — вес ракеты, X — аэродинамическая сила лобового со-
противления, Y — аэродинамическая подъемная сила, Ур — управляю-
щая сила.
Рис. 17.1
Аэродинамические силы вычисляют по формулам
Y = ^-Scs, X = -^Sucx,
2 м у 2 м х
где р—плотность воздуха;
v — скорость полета;
SM — площадь миделя;
^ — аэродинамический коэффициент подъемной, силы; ^ — аэродинами-
ческий коэффициент силы лобового сопротивления; коэффициенты су и сх
соответствуют поточной системе координат.
Пусть Х[Оу[ — система координат, связанная с корпусом ракеты.
Проекции абсолютного ускорения центра масс на продольную и попе-
речную оси ракеты определяют из уравнений
х1т = — (Р3 — X cos а + Y sin а — G sin Ф),
т
у1т = — (У ios а + X sin а — Geos# + Ур),
т
(17.1)
10*
147
где т — масса ракеты;
а —угол атаки (угол между вектором скорости v и продольной осью
корпуса в вертикальной плоскости);
д — угол тангажа (угол продольной оси корпуса с горизонтом).
Если в уравнениях (17.1) а, Ф, Ур соответствуют программному по-
лету, то х1т, у1т будут равны программным ускорениям центра масс. В про-
граммном движении угловая скорость и угловое ускорение 4 малы, так
что ускорения х1т и yiT можно отнести к любой точке ракеты, если по-
следнюю считать абсолютно твердой.
Проекции аэродинамических сил X, Y на оси yY связанной систе-
мы координат называются соответственно осевой силой Хг и нормальной
(поперечной) силой Ух
Х3 Xcosa — Y sin a = — S/V1,
J 2 M Ap
Y± = Y ios a + Xsina S cy.
2
где cXi, сУх аэродинамические коэффициенты осевой и нормальной силы.
Эти коэффициенты связаны с коэффициентами лобового сопротивления сх
и подъемной силы су соотношениями
сХ1 cxcos a — су sin a,
сУх = c^cosa + сх sin a.
Коэффициенты продольной и поперечной перегрузки [52, 53]. Зная
абсолютные ускорения x1T, t/iT, можно определить внутренние силы —
силы взаимодействия между элементами конструкций. Пусть, например,
требуется вычислить осевую силу Мг в сечении между головной частью
и корпусом ракеты. Эту силу можно представить в виде трех состав-
ляющих: проекции веса головной части, силы инерции и аэродинамиче-
ской осевой силы:
Nr - — Gr sin # — х1тX]r --- — С,г(sin О А — Х1г,
g \ g /
I де Gr — вес головной части на поверхности Земли;
g— ускорение силы земного тяготения на поверхности Земли
(g = 9,81 м секI 2).
Для удобства расчета сил, действующих на элементы конструкций,
вводят коэффициент продольной (осевой) перегрузки*, с помощью ко-
торого объединяют вес и силы инерции:
Тогда
! sin О
Nr ~ GrnXt—Х1Г.
(17.2)
(17-3)
Аналогично коэффициент поперечной перегрузки будет
* Коэффициент перегрузки иногда называют просто перегрузкой.
Н8
Л//1 = _ (J^-j-costf ). (17.4)
\ g J
С учетом равенств (17.1) та<же получим
/гХ1 —----- (Рэ —Xcosa t Y sin а) —----— (Рэ — XJ,
G G .
(17-5)
/1у, =----У (У cos а X sin а Ур) = —(У1 + УР)-
G G
Можно говорить о суммарном (полном) коэффициенте перегрузки
центра масс как векторе
« “ - —, К = Р3 а- X + У 4- Ур, (17.6)
G
причем /7%1 и /7,Z1 есть проекции вектора п на продольную и поперечную
оси ракеты. Коэффициент перегрузки центра масс представляет собой
отношение геометрической суммы всех внешних сил, действующих на
ракету (без сил тяжести), к весу ракеты.
Ускорение вне поля сил земного тяготения. Коэффициенту перегруз-
ки можно дать и иную трактовку. Умножим равенство (17.6) на ска-
ляр g. Получим
а(_г) = -^ = Л (17.7)
пг
Здесь а(_А>) — вектор ускорения центра масс ракеты вне поля сил земно-
го тяготения.
Коэффициент перегрузки показывает, во сколько раз ускорение раке-
ты вне поля сил земного тяготения больше земного ускорения.
Спроектируем вектор а^} на продольную ось ракеты и представим
равенство (17.3) в виде
хг = — Ох, (-£)/пг — Х1Г, (17.8)
где тг — масса головной части.
Внутренняя сила как бы не зависит от веса. В данном случае она
состоит из двух частей: внешней поверхностной силы XiP и силы инер-
ции, вычисленной вне поля сил земного тяготения. Можно также ска-
зать, что сила инерции вычислена в подвижной системе координат, ко-
торая движется к центру Земли с ускорением g.
Важно заметить, что ускорение а(-Аг), вычисленное в этой подвижной
системе координат, не зависит от величины и направления ускорения g.
Как следует из формул (17.7), ускорение а(-я} пропорционально вектору
внешних сил (без сил тяжести) и не зависит от того, в каком поле тяго-
тения совершается движение, будь то в сфере притяжения Земли, Лу-
ны, Марса, Венеры и т. д.
На основании сказанного можно сформулировать следующее простое
правило: если ускорение ракеты вычислить без учета веса, то при опре-
делении внутренних сил вес учитывать не надо.
Для пояснения приведем два примера. На клеть кирпичей действует
только вес. Под действием этих сил клеть с какой-то высоты падает на
землю с ускорением g. Так как /? = 0, то силы взаимодействия между
кирпичами отсутствуют.
Бак с идеальной жидкостью стоит на столе. Кроме веса на бак, дей-
—>
ствует внешняя сила — реакция со стороны стола Rc. Зеркало свобод-
->
пой поверхности жидкости в баке перпендикулярно к внешней силе /?г.
149
Пусть бак с жидкостью падает на землю (без вращения) под дейст-
—>
вием только веса. Так как /? = 0, то силы взаимодействия между баком
и жидкостью отсутствуют, свободная поверхность может занимать лю-
бое положение.
Если при падении на землю без вращения на бак будет действовать
внешняя вертикальная сила сопротивления воздуха /?в, проходящая
через центр тяжести системы, то зеркало свободной поверхности будет
перпендикулярно к силе а сила давления жидкости на бак направ-
лена вертикально и на основании равенства (17.8) равна
— — тж-----,
т0 +
где mQ— масса бака, — масса жидкости.
Если же при падении на землю без вращения на бак с жидкостью
будет действовать только внешняя горизонтальная сила /?г, проходящая
через центр масс системы, то свободная поверхность жидкости будет
вертикальной, а сила давления жидкости на бак направлена горизон-
тально и равна
N = — тж —.
то “Ь тж
Ракета совершает полет под действием внешней силы R. Если счи-
—>
тать, что линия действия силы R проходит через центр тяжести ракеты
и движение является прямолинейным, то зеркало свободной поверхно-
сти жидкого топлива в баке располагается перпендикулярно к векто-
ру /?, т. е. почти перпендикулярно продольной оси ракеты.
Статические нагрузки. Основными внешними силами, действующими
на ракету на активном участке траектории (при полете с работающими
двигателями), являются сила тяги двигателя и аэродинамические силы.
После выхода двигателя на режим и до конца активного участка сила
тяги изменяется медленно, несколько возрастая с увеличением высоты.
При программном полете в спокойной атмосфере аэродинамические си-
лы, пропорциональные скоростному напору, изменяются также сравни-
тельно медленно. Медленно изменяется и управляющая сила, которая
повертывает ракету для движения по программной траектории.
Под медленным изменением силы понимается такое ее измене-
ние, когда время нарастания или убывания силы значительно
больше периода собственных колебаний конструкции. Действие медлен-
но изменяющихся внешних сил на корпус можно поэтому считать стати-
ческим, а нагрузки, вызываемые этими силами, — статическими нагруз-
ками. В технической литературе такие силы и нагрузки иногда называют
квазистатическими. Для расчета ускорений при действии внешних ста-
тических сил ракета считается абсолютно твердым телом.
Таким образом, статической силой (статической нагрузкой), дейст-
вующей на рассматриваемый элемент конструкции, называется сила,
вычисленная в предположении, что движение ракеты как абсолютно
твердого тела происходит по программной траектории. Расчет статиче-
ских нагрузок основан на формулах (17.3) — (17.8), в которых все вели-
чины нужно считать соответствующими программному полету.
Корпус ракеты представляет собой сложную колебатель-
ную систему. Как упругий стержень он может совершать изгибные,
крутильные и продольные колебания, причем в каждом из трех случаев
он обладает спектром собственных частот.
Однако расчетная схема в виде упругого неоднородного стержня во
многих случаях оказывается слишком упрощенной, чтобы выявить осо-
150
бенности, возникающие в системе. Например, при продольных колеба-
ниях, кроме растяжения-сжатия стенок корпуса, дополнительный прогиб
получают днища баков. Относительно стенок корпуса большая масса
жидкого топлива оказывается как бы упруго подвешенной и поэтому
может перемещаться. Двигатель, подвешенный к корпусу на упругой
раме, относительно корпуса может также иметь дополнительные пере-
мещения. При поперечных колебаниях корпуса могут оказаться сущест-
венными колебания жидкого топлива в баках, изгибные колебания тру-
бопроводов и т. д. Внутри корпуса к панелям, днищам баков, стринге-
рам и шпангоутам подвешивают приборы, различные механизмы, емко-
сти, арматуру. Подвеску таких масс во многих случаях следует считать
упругой, так как основания, к которым крепятся грузы, являются неже-
сткими.
Такие упруго подвешенные массы образуют ряд сравнительно про-
стых колебательных систем с одной или несколькими степенями свобо-
ды. С точки зрения теории колебаний корпус ракеты поэтому можно
считать сложной конструкцией, в которой есть большой набор различно
ориентированных колебательных систем.
Динамические нагрузки. На корпус ракеты или отдельные его эле-
менты могут действовать быстроизменяющиеся силы, такие как нараста-
ние силы тяги при пуске двигателя; спад силы тяги при отсечке двига-
теля; аэродинамические силы от действия ветра; силы, действующие на
столб топлива в трубе при резком открытии или закрытии топливных
клапанов; силы, возникающие при поперечных автоколебаниях, связан-
ных с колебаниями жидкости в баках или изгибными колебаниями кор-
пуса; силы, возникающие при транспортировке; колебания силы тяги
двигателя, связанные с продольными автоколебаниями ракеты; высоко-
частотные колебания давления в камере, вызванные особенностями
внутрикамерных процессов. Частоты изменения этих сил могут быть
близки к собственным частотам корпуса или отдельных его элементов
и поэтому при действии быстроизменяющихся сил в системе возникают
колебания, Быстроизменяющиеся силы называются динамически-
ми силами, а нагрузки, возникающие при их действии, — динами-
ческими нагрузками. Анализ движения ракеты под действием
динамических сил и определение динамических нагрузок производится
с учетом упругих свойств конструкции, а иногда и подвижности жидко-
го топлива в баках.
Движение ракеты, происходящее при действии быстро изменяющих-
ся сил, которые не являются программными, называется возмущен-
ным движением. Поэтому и динамические нагрузки называют
иногда нагрузками возмущенного движения.
По аналогии с коэффициентом статической перегрузки в динамиче-
ских расчетах иногда вводят коэффициент динамической пе-
регрузки, который показывает, во сколько раз ускорение, возникаю-
щее при колебаниях упругой конструкции, больше земного ускорения.
Динамические силы возникают не всегда. Например, в рациональной
системе автоколебаний может не возникнуть, а поэтому не будет и вы-
званных ими сил. Так как динамические нагрузки зависят, главным
образом, от соотношения частот изменения действующих сил и собст-
венных частот системы, то конструктор, там где это возможно, должен
так подбирать жесткости и распределять массы, чтобы эти частоты были
по возможности различными.
Коэффициент динамичности. Для удобства учета динамических на-
грузок в расчетной практике вводится коэффициент динамичности т]д.
Коэффициентом динамичности будем называть отношение силы (стати-
ческой плюс динамической), действующей на рассматриваемый элемент
в данном расчетном случае, к статической силе, т. е. к силе, вычислен-
ной исходя из движения ракеты как твердого тела.
151
В пределах закона Гука между силой и перемещением (прогибом,
удлинением) существует линейная зависимость, поэтому равнозначным
будет также следующее определение: коэффициентом динамичности на-
зывается отношение максимального прогиба (статического плюс дина-
мического) упругого элемента в данном расчетном случае к статическо-
му прогибу. Коэффициентом динамичности, таким образом, учитывается
увеличение нагрузки вследствие колебательного движения упругой кон-
струкции. Если, например, в каком-либо сечении определена статическая
осевая сжимающая сила NCT и найден коэффициент динамичности при
продольных колебаниях, то максимальная сжимающая сила в этом
сечении будет
N - Л^стЛд-
Пусть статический прогиб упругого элемента, поддерживающего
какой-либо груз, равен /Ст- Под действием динамических сил груз совер-
шает вынужденные колебания с амплитудой [д. Тогда коэффициент ди-
намичности будет равен
Если на конструкцию действуют только статические силы, то т)д= 1.
В технической литературе не существует единого определения для
коэффициента динамичности. Например, при расчете строительных кон-
струкций под коэффициентом динамичности понимают отношение мак-
симальной силы к весу. Поэтому приведенное выше определение коэф-
фициента динамичности является условным, но, как нам кажется, удоб-
ным для расчетов на прочность ракетных конструкций.
Некоторые определения. Приведем определения основных видов
колебаний, встречающихся при анализе динамических явлений в раке-
тах. Эти определения в теории колебаний установились в первую оче-
редь на основании вида дифференциальных уравнений. Они характери-
зуют особенности движений и причины, их вызывающие.
Собственными (свободными) называются колебания, про-
исходящие без воздействия внешних сил. Дифференциальные уравнения
собственных колебаний однородны, т. е. без правой части:
X + 2&Х -j (й2Х О,
х e~&t D sin (g)^ а), = У со2 — е2 ,
где е— коэффициент затухания собственных колебаний. Амплитуду
колебаний D и начальную фазу а определяют из начальных условий.
В дифференциальных уравнениях и в их решениях под знаком синуса
или косинуса частота колебаний всегда имеет размерность рад)сек. Эта
частота называется круговой частотой. Частота v, выраженная в герцах,
показывает, какое число колебаний совершается в секунду. Время Т сек
одного колебания называется периодом колебаний,
2л v со1
Вынужденные колебания — это колебания, происходящие под
действием вынуждающей внешней силы. Дифференциальное уравнение
вынужденных колебаний неоднородно, т. с. с правой частью
х + 2ех 4- со2х - q (/).
Если принять <?(/) =- qQ sin pt, то будем иметь
х =e~RtD sin ((1)г/ + a) -J- A sin (pt > ф).
152
Колебания можно представить состоящими как бы из двух частей:
из колебаний с собственной частотой (оь которые из-за наличия сопро-
тивления со временем затухают, и вынужденных колебаний с частотой
вынуждающей силы. Последние существуют до тех пор, пока действует
внешняя сила. А—амплитуда вынужденных колебаний, ср — угол сдви-
га фаз (в радианах) между вынужденным движением системы и дейст-
вием вынуждающей силы. Он равен
. / 2ер \
ср -- arctg (----— .
\ со2 — р2 J
Автоколебаниями называются установившиеся периодические
колебания, происходящие в замкнутых системах за счет источника энер-
гии, не обладающего колебательными свойствами. Автоколебания — это
самовозбуждающиеся колебания, обязательно нелинейные, тогда как в
Рис. 17.2
Рис. 17.3
период самовозбуждения (неустановившийся режим) колебания могут
быть линейными.
Принципиальная замкнутая схема автоколебательной системы пока-
зана на рис. 17.2. Она состоит из колебательной системы, источника
энергии и обратной связи. Простейшим примером автоколебательной
системы может служить маятник с «падающей» характеристикой трения
(рис. 17.3). Колебательной системой является масса на пружине, источ-
ником энергии служит электродвигатель, приводящий в движение с
постоянной скоростью и0 непрерывную ленту. Обратную связь осущест-
вляет сила трения где и — скорость скольжения между грузом и
лентой.
Уравнение малых колебаний массы пг имеет вид
тх -J- (h -г Ь) х kx 0. (17.9)
где h — коэффициент внешнего сопротивления
ь = (-flv
\ ди )uj
tt<j — скорость скольжения при x = const = 0.
Если скорость движения ленты uQ выбрана так, что &<0, и, кроме
того, |b|>/z, то из уравнения (17.9) следует, что движение массы //z
будет неустойчивым, а колебания нарастающими. В этом можно убе-
диться и без анализа уравнений. Действительно, за один полупериод,
когда масса и лента движутся в одном направлении, zz<zz0,
/тр(^) >/Тр(^о), сила трения «помогает» колебаниям. За следующий
полупериод, когда масса и лента движутся в разные стороны, zz>z/.i,
/тр(^) </тр(^о), работа силы трения, отнимающая энергию у маятника,
будет меньше, чем в первый полупериод. Следовательно, за целый пе-
риод лента передает энергию от электродвигателя маятнику и увели-
чивает амплитуду колебаний. От источника энергии, не обладающего
колебательными свойствами, обратная связь отбирает энергию отдель-
ными порциями. Вследствие этого и происходит нарастание амплитуд
колебаний.
15а
По линейным уравнениям типа (17.9) можно установить лишь воз-
можность нарастания колебаний. Но как только колебания достигнут
таких значений, что сила трения будет выходить за пределы линейного
участка, колебания будут определяться нелинейным уравнением. При
некотором значении амплитуды приток энергии в систему Е(+) и рассея-
ние энергии £*(_) будут равны
(рис. 17.4), возрастание колеба-
ний прекратится и в системе уста-
новятся устойчивые периодиче-
ские колебания с амплитудой аи
(автоколебания).
Рис. 17.4 Рис. 17.5
Наиболее популярно и подробно автоколебания изложены в книге
Л. А. Харкевича [102]. С автоколебаниями можно познакомиться также
в книгах [8, 75, 85, 88].
Параметрическими называются колебания, которые обуслов-
лены зависимостью параметров системы от времени. Например, если
каким-либо внешним устройством периодически изменять длину маят-
ника, то можно возбудить его параметрические колебания. Наиболее
благоприятные условия для возбуждения параметрических колебаний
при частоте изменения параметра в два раза больше собственной часто-
ты системы. Уравнения параметрических колебаний имеют вид
х + а (/) х = 0.
Смысл параметрических колебаний поясним на простой маятниковой
модели (рис. 17.5), в которой стержень будем считать жестким и неве-
сомым. Уравнение поперечных движений массы т будет
myl = Роу sin pt— kyl — mgy
или
i/+ co2 (1 — e sinp/) у = 0, e = -^-, co2 = —+ -^-. (17.10)
m/w2 m I
Это уравнение параметрических колебаний, поскольку коэффициент при
координате у зависит от времени. Оно называется уравнением Матье и
хорошо изучено.
Действие внешней силы P(t) здесь сводится к периодическому изме-
нению параметра колебательной системы, в данном случае собственной
частоты. Для такой системы характерно, что внешняя сила совершает
работу не на основных, а на вторичных (меньших по порядку) переме-
щениях. Существенно, что в отличие от обычных вынужденных колеба-
ний внешняя сила не способна сама по себе вызвать отклонение системы
от равновесного положения. Необходимо некоторое внешнее воздейст-
вие, которое сообщит системе хотя бы малое отклонение, после чего уже
может сказаться роль внешней периодической силы P(t).
154
Так как за один период поперечных колебаний масса т дважды до-
стигает наибольшего отклонения в вертикальном направлении, то поло-
жительная работа силы P(t) будет наибольшей в том случае, когда
Ртлх будет совпадать с г/max и р = 2(о. Таким образом, для возникновения
параметрического резонанса наиболее благоприятная частота измене-
ния внешней силы вдвое больше частоты собственных колебаний.
Вместе с тем раскачка системы возможна и в том случае, когда
соотношение частот будет удовлетворять равенствам со = р, <о= 1,5 р,
<о = 2р... Наступление резонансного состояния зависит и от амплитуды
силы P(t).
О параметрических колебаниях можно прочитать в книгах [85, 88].
Нелинейные колебания описываются нелинейными дифференци-
альными уравнениями. Для упругих систем нелинейной может быть
зависимость упругих сил от смещения, сил трения от скорости. Нелиней-
ные колебания могут быть как собственные, так и вынужденные. Урав-
нение собственных колебаний имеет вид
/их + (х) + ф2 (*) = 0.
Характерной особенностью собственных нелинейных колебаний яв-
ляется зависимость собственной частоты от амплитуды. Теория нели-
нейных колебаний изложена в книгах [8, 84, 88].
Механизм возникновения изгибных автоколебаний [44, 100, 101]. Кор-
пус ракеты совместно с автоматом стабилизации образует замкнутую
колебательную систему. Эта система снабжена источниками энергии
(например, усилители, рулевые машины), которые не обладают колеба-
тельными свойствами и, как правило, имеют
нелинейные характеристики. 1/
Автомат стабилизации рассчитывается и ]/
проектируется так, чтобы замкнутая система р/
была устойчива в полете. Однако в силу слож- ур
ности динамических свойств корпуса и автома-
та стабилизации в замкнутой системе в неко- __________ 1 1
торые промежутки времени может возникать //
неустойчивость, причем она, как правило, s'
имеет колебательный характер с частотами,
близкими к собственным частотам изгибных
колебаний корпуса. Рис. пб
Механизм возникновения изгибных авто-
колебаний можно представить следующим об-
разом. Допустим, что на упругий корпус подействовали поперечные силы
(например, от ветра) и корпус начал совершать изгибные колебания.
Чувствительный элемент автомата стабилизации — свободный гироскоп
замеряет теперь не угол тангажа -Опр, а угол Оь который отличается
от Фпр на величину поворота поперечного сечения, вызванного изгиб-
ными колебаниями (рис. 17.6),
'O'l = ^пр + Aft sin со/.
Пропорционально возникшей вариации Aftsinco/ автомат стабилиза-
ции отрабатывает дополнительный угол поворота управляющих орга-
нов и, как следствие, — дополнительную управляющую силу
A/pSin (со/+ф). Эта сила имеет колебательный характер и в зависимости
от фазы ф по отношению к изгибным колебаниям корпуса она будет
усиливать эти колебания или ослаблять их. Если система неустойчива,
то нарастающие колебания из-за наличия нелинейностей переходят в
стационарные колебания с постоянной амплитудой и частотой, называе-
мые автоколебаниями. Частота автоколебаний близка к собственной
частоте изгибных колебаний корпуса.
155
Аналогично возникают поперечные автоколебания ракеты и на часто-
тах, близких к собственным частотам колебаний жидкости в баках.
Изгибные автоколебания, так же как и автоколебания на частотах
жидкости, нежелательны для корпуса, поскольку они вызывают допол-
нительные нагрузки в виде поперечной силы и изгибающего момента.
Однако если для полного устранения автоколебаний нужны очень боль-
шие усложнения автомата стабилизации, то такие колебания с малыми
амплитудами допускают при условии, что от них не возникнет наруше-
ние прочности ракеты.
Амплитуды и частоты автоколебаний можно определить только из
решения уравнений, в которых учтены нелинейные свойства замкнутой
системы. В данном случае это уравнения упругих колебаний корпуса,
колебаний жидкости в баках и уравнения автомата стабилизации. Реше-
ние этих уравнений является довольно сложным и производится, как
правило, с применением моделирующих установок. В дальнейшем будем
считать, что если автоколебания существуют, то их амплитуды и ча-
стоты известны.
В автоколебательном режиме все элементы колебательной системы
совершают движения с одной и той же частотой, но различными ампли-
тудами. Отношение амплитуд колебаний различных элементов системы
называется формой колебаний. Когда форма колебаний детально
неизвестна, автоколебания ракеты можно рассматривать как причину
возбуждения вынужденных колебаний отдельных колебательных систем,
например упруго подвешенных приборов, находящихся в корпусе.
Для примера рассмотрим топливную трубу, идущую от бака к
насосу. Так как форма поперечных колебаний корпуса известна, то,
зная режим автоколебаний, найдем частоту и амплитуду поперечных
колебаний любого сечения корпуса, в частности, днища бака и турбо-
насосного агрегата, к которым присоединена труба. Для трубы прихо-
дим к задаче о вынужденных поперечных колебаниях под действием
гармонического движения концевых сечений. Определив собственные
формы и частоты колебаний трубы, можем найти амплитуду вынужден-
ных колебаний и динамические нагрузки, действующие на трубу при
поперечных автоколебаниях ракеты.
Механизм возникновения продольных автоколебаний [47, 115, 116].
Предположим, что по какой-то причине возникли продольные колеба-
ния корпуса. Совместно с корпусом в направлении продольной оси
совершают колебания и днища баков, вследствие чего возникает вариа-
ция давления топлива. Эта вариация вызывает колебания топлива, в
трубопроводе, соединяющем бак с камерой двигателя. Возникает пуль-
сация топлива при впрыске в камеру и как следствие — колебание силы
тяги двигателя. Колебание силы тяги поддерживает пли ослабляет
(в зависимости от фазовых соотношений) возникшие продольиз’.е
колебания корпуса.
Колебательная система, состоящая из упругого корпуса, топливо-
подающих магистралей и ракетного двигателя, оказывается, таким об-
разом, замкнутой. Она имеет мощный источник энергии — двигатель.
При некоторых соотношениях параметров номинальный режим системы
может стать неустойчивым, в системе возникнут нарастающие колеба-
ния, которые из-за наличия нелинейностей могут перейти в автоколеба-
ния. Это один из нежелательных колебательных режимов, который
вызывает большие динамические нагрузки на корпус и подвески при-
боров.
Может случиться, что разрушение конструкции произойдет раньше,
чем установится автоколебательный режим. Такой случай, естественно,
считается аварийным. Если частота продольных колебаний корпуса
близка или совпадает с собственной частотой колебаний топлива в тру-
бопроводе, то усиление колебаний в системе будет наибольшим.
156
Динамическое нагружение корпуса при старте и отсечке двигателя.
На стартовом столе корпус ракеты нагружен весом, в поперечных сече-
ниях возникают сжимающие силы. После запуска двигателя и выхода
его на режим сжимающие силы в поперечных сечениях корпуса увели-
чиваются в rtKi раз, где nXi — коэффициент статической продольной
перегрузки. Сила тяги при запуске двигателя возрастает сравнительно
быстро и поэтому возникают продольные колебания корпуса, от кото-
рых величина сжимающих сил увеличивается. Это увеличение будет тем
больше, чем меньше отношение времени нарастания силы тяги к пе-
риоду собственных продольных колебаний корпуса (см. § 19).
При продольных колебаниях увеличивается давление жидкого топ-
лива на стенки и дно бака. Так, гидростатическое давление на дно бака,
расположенное на расстоянии И от свободной поверхности топлива,
равно
Рст-=Ро + УНпх>-
Здесь ро — давление наддува в баке, у — удельный вес топлива.
Пусть дно бака совершает гармонические колебания с амплитудой а
и частотой (о рад!сек. Тогда максимальное ускорение дна бака и столба
жидкости будет равно а<о2, коэффициент динамической продольной пере-
грузки
а со2
^Л'1Д- .
g
Максимальное давление с учетом колебаний будет
Ртах = Ро + УН (Пх, + Лх.д). (17.11)
Введя коэффициент динамичности, получим
. уНпу _
Ртах - РстПд, Пд = 1 + (17.12)
р0 + yHnXi
При отсечке двигателя сила тяги быстро уменьшается от номиналь-
ного значения до нуля, возникают продольные колебания корпуса.
Поперечные сечения нагружаются как сжимающими, так и растягиваю-
щими силами. Появление значительных растягивающих сил нежелатель-
но для стыковых соединений.
Так как после отсечки двигателя статическая осевая перегрузка
^х,=0, может появиться возможность отрыва жидкого топлива от днищ
баков. Этот вопрос чрезвычайно важен для высших ступеней многосту-
пенчатых ракет. Обозначим высоту столба топлива в баке через Н.
Тогда на основании формулы (17.9) при nVl=0 придем к заключению,
что при
^х.д>Ро (17.13)
-озможен отрыв топлива от днища бака, даже если зеркало свободной
поверхности останется плоским и перпендикулярным к продольной оси
ракеты («прикрытым крышкой»).
Гидроудар в трубах. Гидроудар в трубах возникает при резком
уменьшении скорости движения жидкости по трубе. Это может быть или
при отсечке двигателя, когда быстро закрывается топливный клапан,
или при запуске двигателя, когда после подрыва мембраны или откры-
тия клапана топливо приобретает большую скорость, а затем тормо-
зится значительным сопротивлением в виде форсунок двигателя. Часть
кинетической энергии топлива переходит в потенциальную энергию рас-
тяжения стенок трубы и сжатия топлива.
157
Дополнительное давление, возникающее при гидроударе, вычисляет-
ся по формулам [34]
Др = рисэ при tr <------,
сз
кр = pvc3-------- при (17.14)
Z сэ
где V — скорость движения жидкости в трубопроводе;
сэ — эквивалентная скорость звука в жидкости, т. е. скорость звука,
определенная с учетом упругости стенок трубы;
р—плотность жидкости;
I — длина трубопровода;
t± — время перекрытия магистрали
§ 18. КОЛЕБАНИЯ УПРУГО ПОДВЕШЕННЫХ МАСС
Двигатель или турбонасосный агрегат, подвешенный на раме к кор-
пусу, топливо, поддерживаемое упругим днищем бака, прибор или
какой-либо агрегат, укрепленный на корпусе, в первом приближении
:льные системы с одной степенью сво-
боды (парциальные колебательные
системы). К нескольким системам
с одной степенью свободы приво-
дятся также и колебания более
сложных конструкций, у которых
масса и жесткость являются рас-
пределенными параметрами.
Вынужденные колебания таких
систем могут возникать как от дей-
ствия периодических внешних сил,
приложенных к массе, так и тогда,
когда внешние силы неизвестны,
а известен закон движения точки
подвеса массы.
Так как «чистых» колебатель-
ных систем с одной степенью сво-
боды в ракете очень мало, то важ-
но уметь правильно выделить в каждом частном случае колебательную
систему и определить ее собственную частоту.
Вынужденные колебания под действием силы, приложенной к массе.
Если отклонение массы tn отсчитывать от положения статического рав-
новесия, то уравнение малых колебаний системы с одной степенью сво-
боды будет иметь вид (рис. 18.1, а)
ту + hy + ky = P(t), (18.1)
где k — коэффициент пропорциональности между силой и смещением в
положении статического равновесия, h — коэффициент пропорциональ-
ности между силой и скоростью (коэффициент вязкого трения). Здесь
не уточняется, какую конструктивную форму имеет упругий элемент
(спиральная пружина; стержень, работающий на растяжение-сжатие;
балка, работающая на изгиб, и т. д.).
Если характеристика упругого элемента линейная, то для вычисления
коэффициента k можно рекомендовать следующее правило. В месте
расположения сосредоточенной массы и в направлении ее движения при
колебаниях к упругому элементу надо приложить единичную силу и
вычислить перемещение в направлении действия этой силы. Величина
обратная перемещению, будет равна коэффициенту k.
158
Например, упругим элементом является работающая на изгиб шар-
нирно опертая балка; сосредоточенная масса расположена по середине
длины балки. Длина балки /, жесткость на изгиб EJ. Тогда
4 = 48—,
48EJ /3
Когда сила изменяется по гармоническому закону Р (f) — PosinpZ,
решение уравнения (18.1) имеет вид
у = e~£t (Д cos со^ + В sin сох/) + fp---------sm(p/ + <p)------,
V — у2)2 -Не2у2
8 = —^—, cOi = ]/ со2— 82 , со = 1/ —, у = —,
2т У т со
е = —, fP = ср = arctg (--------------——Y
(О ' k \ со2 — р2 /
Если выполняется условие
2ер < (со2 — р2),
(18.2)
(18.3)
то вместо формул (18.2) перемещение у можно вычислять из выражения
y=e~Ei (Д cos со^ + В sin со^) + fp . (18.4)
1 — у2
Произвольные постоянные Д и В определяют из начальных условий.
Если предположить, что движение возникло из состояния покоя, то на-
чальными условиями будут
/ = О, у = 0, у = 0.
Для уравнения (18.4) получим
Д-0, B = -fP
Р
<*>i(l -Y2) ’
Таким образом,
у = —(sinpt---— e~Et sin cd^
1 — Y2 \
(18.5)
Колебания массы m происходят с двумя частотами: вынужденной р
и собственной coi, причем, так как е>0, то колебания с частотой coi со
временем затухнут. Вынужденные колебания с частотой р будут суще-
ствовать, пока действует возмущающая сила.
Кроме перемещений при вынужденных колебаниях, масса т имеет
статическое перемещение /ст- Полное перемещение равно сумме этих
перемещений.
Представим максимальное перемещение массы т в виде
f max f стЛд>
причем коэффициент динамичности с учетом выражений (18.2) и (18.3)
соответственно будет
Пд = н- ~ лг-------1 _ , Лд = 1 + Т-Ц-. (18-6)
/ст И (1 — y2)2 + 4e2y2 /ст 1 Y
где fp — статическое перемещение от силы Ро.
159
Коэффициент динамичности зависит от отношения частот у - p/w и
от параметра затухания jTe/cd. Коэффициент т]д имеет максимальное зна-
чение при совпадении частот вынужденных и собственных колебаний (точ-
нее, при у2 1 — 2е2)- В этом случае возникают резонансные колебания-
При у — 0 т)° — 1 +/р//ст. Иначе говоря, при статическом приложе-
нии внешней силы Р полный прогиб равен сумме прогибов от силы тя-
жести /ст и от внешней силы fp. Если у>]/2, то Лд<С'Пд- Когда часто-
та вынужденных колебаний значительно больше собственной частоты, амп-
литуда вынужденных колебаний значительно меньше статического пере-
мещения fp и коэффициент динамичности т]д=^ 1.
В практике инженерных расчетов вопросы динамического нагруже-
ния конструкции и резонанса в особенности занимают одно из первых
мест. При наличии гармонической внешней силы оценка производится,
прежде всего, путем сопоставления собственных и вынужденных частот.
Если эти частоты сильно отличаются друг от друга, то значительных
динамических перемещений не возникнет и условия для работы упругих
элементов будут благоприятными. Изменением параметров системы же-
лательно добиваться такой собственной частоты, чтобы условий, близ-
ких к резонансным, не возникало. Если конструктор в силу обстоятельств
лишен возможности варьировать частотами, то в случае возможности
резонанса практикуется установка специальных устройств для рассеи-
вания энергии при колебаниях — демпферов.
Необходимо отметить следующее.
Если при вынужденных колебаниях начальные условия точно опре-
делены, то максимальное динамическое перемещение следует вычислять
из общего решения (18.2). Максимальное динамическое перемещение
в течение первого периода колебаний может быть больше амплитуды
вынужденных установившихся колебаний в чем нетрудно убедиться из
анализа решения (18.5).
Кратковременное действие гармонической силы в условиях резонанса
не представляет опасности для конструкции. Известно, что при P(t) =
= P0sino)^ и h = 0 решением уравнения (18.1) будет
у ------t cos (о/ = — fp — t cos (о/.
2mco 2
Нужно определенное время, чтобы перемещение у превзошло некоторый
допустимый предел.
Колебания массы, вызванные перемещением точки подвеса. Колеба-
ния приборов, емкостей, арматуры и других сосредоточенных масс, упру-
го подвешенных к корпусу, возникают, как правило, из-за перемещений
стенок корпуса.
Пусть точка подвеса сосредоточенной массы (рис. 18.1,б) переме-
щается в направлении оси пружины по закону u(t). Обозначим через
yi(t) перемещение массы т относительно точки подвеса, причем это пе-
ремещение будем отсчитывать от положения статического равновесия. Со
стороны пружины и демпфера на массу т действует сила (hyx +ky{),
ускорение массы равно У=(У1 + й), так что
m (yt + и) = — (hyt 4- kyj.
Тогда уравнение малых колебаний будет следующим:
/ш/1 + hyt 4 tyi — ти- (18.7)
Это уравнение также справедливо, если упругим элементом служит, на-
пример, балка, работающая на изгиб. В случае гармонических перемещений
и (/) u0 sin pt динамическое удлинение пружины
ух e~£t (Лсозсо^ 4- В sin (о^) + uQ —v sin^pz ' . (18.8)
/(1 — у2)2 + 4e2y2
Обозначим статическое удлинение пружины через
£ т mg
/ст ~~Г ay(—S) 7 Пу •
к R,
Учитывая только вынужденные колебания координаты уъ представим мак-
симальное удлинение пружины в виде
/ Imax / стЛд>
причем коэффициент динамичности применительно к выражениям (18.8) и
(18.3) соответственно будет
Пд = 14
Ир
f ст
__________у!__________
V (1 — у2)2 4- 4в2 у2
Ир Y2
/ст 1 У2
(18.9)
= 1
Для жесткой подвески, когда у<1 (р<^Ссо), коэффициент динамично-
сти мало отличается от единицы (т]д^1). При мягкой подвеске (у> 1)
масса т почти неподвижна и удлинение пружины будет равно
перемещению точки подвеса. Коэффициент динамичности в этом случае
будет т]д= 1+W/ct.
Если сравнить между собой коэффициенты динамичности (18.6) и
(18.9), то можно сделать следующий вывод. Для /р//Ст = Ио//ст и одних
и тех же значений у коэффициент динамичности до резонанса в случае
(18.6) больше чем в случае (18.9). После резонанса соотношение будет
обратным.
Таким образом, если колебания возбуждаются движением точки под-
веса, то жесткий упругий элемент (у < 1, колебания до резонанса) удли-
няется меньше мягкого. Однако заметим, что если, например, для при-
бора надо добиваться уменьшения вибрационных ускорений, то подвеску
надо делать возможно более мягкую, так как при мягкой подвеске
(у>1, колебания после резонанса) амплитуда ускорения массы т при
колебаниях практически равна нулю:
У = + и = ио (- --У* 4- А р2 0.
\ 1 - V2 J
Частные решения уравнений (18.1) и (18.7) зависят от вида функций
Р(/) и л(/). Рассмотрим вынужденные колебания под действием негар-
монических сил. Так как левые части уравнений (18.1) и (18.7) совпа-
дают, то с точностью до постоянного множителя частные решения этих
уравнений будут одинаковыми, если одинаковыми будут функции
Р(/) И й(0/ '
Колебания массы под действием мгновенно приложенной силы. Пусть
на массу /л, находившуюся в равновесии (при / — 0, г/ = 0, у = 0), по-
действовала мгновенная сила Р (t) = PQ. При h = 0
/лу + ky - Ро,
у = A cos со/ + В sin го/ Н—у-.
Определив произвольные постоянные, получим
у = /р(1 — cos©/), fp = (18.10)
k
Гармонические колебания с амплитудой fP происходят около поло-
жения статического равновесия. Наибольшее перемещение массы при
КОЛебаНИЯХ /шах = 2/Р.
Колебания массы под действием произвольной периодической силы.
Любая периодическая сила, заданная в виде некоторой произвольной
И Зак. 96
161
периодической функции от времени P(t) с периодом изменения Г, может
быть, как известно, представлена тригонометрическим рядом вида
оо
Р(0=ао +V + (18.П)
Л=1
причем коэффициенты ряда вычисляют по следующим формулам^ [55]:
т т
a0 = ±§p(t)dt,
Q О
Т
bn=-^P(t)sin^t-dt. (18.12)
6
Действие силы P(t) можно заменить суммарным действием отдель-
ных сил на основании равенства (18.11). В силу принципа суперпозиции
(наложения), справедливого для линейного дифференциального уравне-
ния, частное решение уравнения (18.1) находят как сумму частных ре-
шений от каждого члена ряда. Таким путем может быть найдено сум-
марное вынужденное движение массы tn.
Как и силу Р(/), в тригонометрический ряд можно разложить перио-
дическую функцию движения точки подвеса u(t) и затем найти частные
решения уравнений (18.7) от каждого члена разложения.
Колебания массы под действием импульса силы. Предположим, что
время Л действия силы Р на массу tn настолько мало, что все другие
действующие на массу силы (сила упругости, например) оказывают в
течение этого времени пренебрежимо малое влияние на ее движение.
Тогда по известной теореме механики: приращение количества движения
mv равно импульсу силы найдем скорость г», которую приобретает
масса m за время Л:
n, Pti
mv = Ptlt v = ——.
m
Для определения динамического смещения массы tn надо решить од-
нородное дифференциальное уравнение
у + со2у = О
• Pt
при начальных условиях / = О, у = О, у = v = ——. Получим
ш
Ptx •
у = —— Sin (О/.
ma)
Чтобы найти максимальное смещение, надо к динамическому смещению
добавить статическое /ст, вызванное весом колеблющегося тела. Получим
/шах =/стЛд» ^=1 + -^-^-. (18.13)
I ст та)
Приведенные рассуждения можно применить к решению задачи о
колебаниях массы т под действием неупругого удара. Если массу т,
находящуюся в покое, ударяет масса имеющая скорость то это
равносильно тому, что на массу (т + т^) действует импульс силы, вели-
чина которого равна количеству движения т^. Скорость движения
обеих масс после удара будет
у=.-тл ...
тг + т
162
Амплитуда колебаний массы т
где
m1vl
(rnY + т) со *
(18.14)
Колебания массы под действием силы, возрастающей по линейному
закону. Таким может быть принят в первом приближении закон нара-
стания силы тяги двигателя при запуске. Пусть на массу т, находив-
шуюся в равновесии (при / = 0, у = 0, # = 0), начала действовать сила,
изменение которой по времени показано на рис. 18.2, а. Двум разным
участкам изменения силы будут соответствовать две различные правые
части дифференциального уравнения движения:
ту + ky = PQ —,
т
О < t < т,
(18.15)
(18.16)
ту + ky = PQ,
Рис. 18.2
Общее решение уравнения (18.15)
у — cos <£>t + Bj sin <&t + fp—, © = 1/—, fp = -^--
т у m k
С учетом начальных условий Д = О, Вг — —/Р/сот. Тогда
y = fp(—---------— sinco/\ 0</<т. (18.17)
\ Т (ОТ J
Величины смещения и скорости при t = т
/ I \ . г
у^ = ( 1------sin (от ), ух = _ lp (1 —cos сот)
\ (ОТ J т
будут начальными условиями для определения произвольных постоянных
общего решения уравнения (18.16)
у = Л2 cos со/ + В2 sin со/ + fP, т.
Вычислив А2 и В2, получим
г Г1 Т . лт / . лт \
у = fp \ 1--------sin-----cos ( со/-------)
L лт Т \ Т /
(О
Гармоническое колебание происходит с частотой свободных колеба-
ний около положения статического равновесия, вызванного силой Pq.
Амплитуда колебаний, максимальное смещение массы пг и коэффициент
динамичности будут
11
163
= /тах=/РГ1д,
т]д-1 + —sin^. (18.18)
лт Т
Амплитуда колебаний зависит от отношения времени нарастания
силы т к периоду собственных колебаний Т. При мгновенном приложе-
нии силы т = 0, смещение массы m имеет максимальное значение
fmax = 2/p. С возрастанием отношения т/Т максимальное смещение быстро
уменьшается. Например, при ч/Т = 2,5 fmax~l,12 fP.
Рассмотрим теперь случай, когда сила Р(/), действующая на массу,
убывает по линейному закону (рис. 18.2,6). Таким в первом приближе-
нии может быть принят закон убывания силы тяги при отсечке дви-
гателя.
Будем считать, что к некоторому моменту времени система, нагру-
женная силой Ро = const, находится в положении статического равнове-
сия (iy = PQlk = fP, у = 0). Определим амплитуду колебаний массы после
того, как действие силы P(t) прекратится, т. е. Р(/)=0.
Дифференциальное уравнение движения будет
my + ky = Ро (1----ел 0 < t < т*.
\ т /
Общее решение уравнения
у = cos со/ + Вг sin tot + fP (1-— Y 0 < t < т\
V т* /
Определив произвольные постоянные и В± с учетом начальных условий
t = 0, y — fp, у = О,
найдем
t/ = /pf-r-sino)/+1----^Y (18.19)
\ (ОТ* т* /
Смещение и скорость при t = т*
f . f
Ут* = Sin (ОТ*, (Д* =------- (1 — COS (ОТ*)
будут начальными условиями для определения произвольных постоянных
общего решения
у = А2 cos tot + В2 sin coZ
однородного дифференциального уравнения при t тЛ Вычислив Л2 и В2,
получим
y = fp ^-sin-^j-cos((o/+ (18.20)
После спада силы P(t) происходят свободные колебания около по-
ложения статического равновесия с собственной частотой о). Амплитуда
колебаний и коэффициент динамичности
= Пд=^-81п^. (18.21)
Если считать, что спад силы P(t) произошел мгновенно, то колеба-
ния будут совершаться с амплитудой, равной статическому смещению
]p = PQlk. Если взять другой крайний случай, когда отношение х*/Т будет
164
большим, то а?/~0, т. е. произойдет статическая разгрузка системы и
никаких колебаний не возникнет. Во всех других случаях 0<ay<fP.
Переход от системы с распределенными параметрами к эквивалент-
ным системам с сосредоточенными параметрами. В практических расче-
тах по динамике иногда удобно
систему с распределенными пара-
метрами заменить более простой
эквивалентной системой с сосре-
доточенными параметрами. В за-
висимости от конструкции и целей
расчета такая замена может быть
произведена с различной степенью
точности. Теорию вопроса рас-
смотрим на примере колеба-
ний свободно опертой балки
(рис. 18.3,а).
Рис. 18.3
Известно, что собственные колебания упругой балки могут быть пред
ставлены в виде ряда
У (*.')=£ (18.22)
причем
Яп (0 = Dn <-'OS
Для свободно опертой однородной балки
г , V , ПЛ / ИЛ \2 _ / EJ
(х) = sin —— X, = ( — ) 1/ —.
Z \ I / f mQ
где Шо — масса единицы длины балки.
Функции называются собственными функциями задачи пли
формами собственных колебаний. Функции /?}(х) ортогональны на отрез-
ке [0, /] и поэтому их иногда называют нормальными функциями.
Для составления уравнения колебаний координаты ql2 воспользуемся
уравнением Лагранжа второго рода
= р L = T — и, (18.23)
dt \ dqn J dqn
где Т — кинетическая энергия системы;
U — потенциальная энергия деформации системы;
Рп— обобщенная сила, обусловленная действием приложенных к
системе внешних сил.
Составим выражения кинетической Т и потенциальной U энергий
балки:
I I со оо I
т = ‘ -у j <nxy-dx =- Д j* mx (^fnq„ dx = Д У q2n j* mfndx,
0 I) /2-1 /2—=1 О
I Z ОО oo I
и •-= Д EJ (У")2dx=±^Ej(^ fnqnУ dx = Д £ J ЕJ (fn)>dx.
О О п=\ /2=1 О
Для свободных колебаний балки обобщенные силы Рп — 0.
Примем
i i
mn= \ mj^dx, kn= \EJ dx. (18.24)
6 6
165
Подставляя выражения Т и U в уравнения (18.23) и принимая во вни-
мание обозначения (18.24), получаем
£ mпЯп + £ knqn = о
/1=1 /2=1
или
mnqn + knqn=Q (п = 1, 2, 3, ...). (18.25)
Заметим, что коэффициент kn численно равен удвоенному значению
потенциальной энергии n-го тона колебаний, если принять qn=l, а коэф-
фициент тп численно равен удвоенному значению кинетической энергии
при qn=l.
Каждому тону колебаний балки соответствует уравнение (18.25).
Но каждое из уравнений (18.25) есть уравнение собственных колебаний
сосредоточенной массы тп на невесомой пружине с жесткостью kn
(рис. 18.3,6). Если обозначить через qn смещение массы //гп, то кинети-
ческая и потенциальная энергии системы с сосредоточенными парамет-
рами в любой момент времени будут равны кинетической и потенциаль-
ной энергиям балки при ее колебаниях по n-му тону. Поэтому система
с сосредоточенными параметрами называется э к в и в а л е н т о й, или
приведенной, системой для колебаний балки по n-му тону. Пара-
метры тп, kn называются соответственно приведенной массой и приве-
денной жесткостью.
Пусть в плоскости хОу на балку действует внешняя распределенная
нагрузка q(x, t}=p(x)q(t). Вынужденные колебания балки представим
в виде ряда (18.22) по собственным функциям fn. Тогда по определению
обобщенная сила для n-го тона может быть найдена как частная произ-
водная по обобщенной координате от суммы работ всех внешних сил на
возможных перемещениях
P„ = q(t) \p(x)f„dx. (18.26)
О
Уравнение вынужденных колебаний системы с распределенными пара-
метрами (см. рис. 18.3, а), составленное для координаты qn, будет
^ + <ОЛ\= -Lq(t)(p(x)fndx (п = 1,2,3, ...), (18.27)
тп о
где собственная частота n-го тона колебаний балки
08.28)
Уравнение вынужденных колебаний сосредоточенной массы тп (см.
рис. 18.3, б) будет таким же, как и (18.27), если принять, что внешняя
сила
Рп (0 = я (О j р W fndx-
О
Сила Pn(t) называется приведенной (обобщенной) силой.
Таким образом, если известны формы собственных колебаний fn, то
из выражений (18.24), (18.26), (18.28) могут быть вычислены тп, kn,
Pn(t), юп, а из уравнений (18.27) определены обобщенные координаты
?п(0-
На основании равенства (18.22) можно установить, что обобщенная
координата qn представляет перемещение при п-м тоне колебаний такой
166
точки оси балки, для которой /п = 1- Эта точка называется точкой
приведения. Перемещения остальных точек будут fnqn-
Приведенные масса тп> жесткость kn, сила Рп — не константы систе-
мы, они зависят от масштаба формы собственных колебаний. Частота
собственных колебаний соп не зависит от масштаба формы колебаний и
является константой системы. Перемещение любой точки оси балки
у(х, t) также не зависит от масштаба формы собственных колебаний.
Обратим внимание на то, что иногда можно допустить ошибку, если
реакции опор балки при колебаниях определять по эквивалентной систе-
ме (см. рис. 18.3,6). Предположим, что распределение внешней нагруз-
ки q(x, t)=p(x)q(t) такое, что балка совершает вынужденные колеба-
ния только по нечетным формам (симметричным относительно середи-
ны) и требуется найти дополнительную силу давления балки на опоры.
Примем q(t) =qGs\Y}pt, п= 1, 3, 5, ... Тогда
I I со
Y = | mxydx = ^пх V fnqndx =
0 О /г=1,3, 5,...
Z
со У р (х) fndx I
У ,/°р2— Sin/?/ ------------------------- ( mjndx.
^~Р2 \mxf>dx Jo
О
(18.29)
Эта сила не зависит от масштабов форм собственных колебаний.
В эквивалентной системе (см. рис. 18.3,6) сила давления пружины на
опору зависит от масштабов форм собственных колебаний.
Найдем, каким должен быть масштаб Ьп для форм собственных
колебаний, чтобы сила, передаваемая пружиной эквивалентной системы
на опору, была равна силе давления балки на опоры при любом тоне
колебаний.
Предположим, что формы собственных колебаний fn известны, мас-
штаб их произвольный. Обозначим форму собственных колебаний в но-
вом масштабе через
= bnfn. (18.30)
На основании равенств (18.24), (18.26)
тп = bn j mjndx, Pn = q (t) bn [ p (x) /„dx.
о 6
(18.31)
Из уравнения (18.27) найдем
Qn
<7o sin pt
bn(u2n —
f p (x) fndx
0
I
f mxf2dx
b
(18.32)
Дополнительная сила, передаваемая пружиной эквивалентной системы на
опору, будет
Уп = ^nQn
i
q^bn sin pt [p(x)fndx.
“n-P2 J
167
Приравнивая полученное выражение к /г-му члену ряда (18.29), находим
z
|* mxfndx
Ьп = ±-------. (18.33)
mxf2dx
О
На примере однородной балки (тх = mQ = const) можно показать, что
если для формы колебаний принять масштаб Ьп (18.33), то сумма всех
масс тп будет равна массе балки:
л=1,3,5,... л=1,3,5, ... С . о ПЛХ //=1,3,5,...
I sin2—-— dx
о
Уравнения вынужденных колебаний (18.27) применимы к любой
упругой системе, для которой известны формы собственных колебаний.
Если частоты собственных колебаний определены при расчете форм
собственных колебаний или экспериментально, то потенциальная энер-
гия системы может быть подсчитана по формуле
ОО оо
(18-34)
п=\ п=\
Составим более полное, чем (18.26), выражение для приведенной силы
если на балку действует система внешних сил (рис. 18.4). По определе-
нию обобщенной силы с учетом масштабного коэффициента Ьп получим
Рп (0 = [<7х (О f Р (X) fn dx + q2 (О Р (fn)x=x, +
О
Z
+ Яз (О М + Я* (О J (х) f'n dx].
о
(18.35)
Для круглой осесимметричной пластины, например, нагруженной распре-
деленной нагрузкой q(r)q(f), будем иметь
R
Рп (0 = ЬпЯ (0 j Я (г) fn (г) • 2лг dr, bn
О
R
f т (г) fn (г) г dr
о
R
f т (г) f2 (г) г dr
о
168
Если при вынужденных колебаниях требуется найти только обобщен-
ные координаты q„(t) и не надо определять силу, передаваемую пружи-
ной с жесткостью kn, то следует принять bn = 1.
Высокочастотные перегрузки. На отдельных элементах конструкций
ракет регистрируются перегрузки в несколько сот единиц при частотах
в несколько сот и даже тысяч герц. К оценке влияния таких перегрузок
на динамическую прочность надо подходить осторожно.
Так как при гармонических колебаниях с амплитудой ау и часто-
той о коэффициент динамической перегрузки
то при больших частотах перемещения (прогибы) ау очень малы. Напри-
мер, при /г,/д = 500 (о = 2л-1000 \/сек, я?/ = 0,0125 мм.
Небольшим прогибам, как правило, соответствуют и небольшие на-
пряжения. Но это не всегда так. Малым абсолютным прогибам могут
соответствовать большие напряжения, если эти прогибы вызваны на
небольшой длине. Корпус ракеты представляет собой сложную упругую
конструкцию, которая имеет множество форм и частот собственных
колебаний. Чтобы вычислить напряжения, надо знать не только прогиб
в одной точке, но и ту кривую — форму колебаний (длину волны), кото-
рой соответствует найденный прогиб ау. А ее разыскать для высоких
частот не всегда просто.
При колебаниях возникают знакопеременные напряжения, и поэтому
если элементы конструкции будут длительное время находиться в усло-
виях интенсивных высокочастотных вибраций, то возможно появление
усталостных трещин, особенно в местах концентрации напряжений.
Метод Рэлея [79, 88]. Существуют технические задачи, в которых для
уточнения значения собственной частоты надо учесть массу упругого
элемента, но вместе с тем не требуется точного решения, которое можно
получить, зная собственные формы колебаний. Метод приближенного
определения собственной частоты основного тона колебаний с учетом
массы упругого элемента предложен Рэлеем.
Он основан на том, что конфигурация упругой системы при колеба-
ниях по первому тону мало отличается от конфигурации, которую имеет
система в случае статического нагружения. Сущность метода состоит в
том, что задастся приближенная форма колебаний системы, подсчиты-
ваются приведенные массы тпр и жесткость £Пр и затем по формуле
(18.28) вычисляется значение собственной частоты. Форма основного
тона колебаний принимается такой же, какую имеет система в случае
статического нагружения. Если масса упругого элемента мала по
сравнению с массой груза т, то за форму статического прогиба прини-
мают форму прогиба, вызванную действием только сосредоточенной
силы mg\ в противном случае более точный результат можно получить,
если форму статического прогиба вычислить с учетом веса упругого
элемента.
Например, для груза на невесомой пружине (рнс. 18.5) при f(/i=l.
/ = л7/
/
т«Р = mfm + j "V2 dx = т + , knp = kf2m = k.
о
Здесь m0 — масса единицы длины пружины; k — жесткость пружины на
растяжение-сжатие.
Если груз имеет большие размеры и его поступательное движение
сопровождается вращением, то надо учесть и кинетическую энергию его
169
вращения (рис. 18.6). Приведенная масса и приведенная жесткость в
этом случае будут
«пр = + / т (х) f'dx + / *пр = / W')2 dx.
О о
Принимая балку однородной и форму изогнутой оси ее при колеба-
ниях совпадающей с формой кривой статического изгиба, вызванного
приложенным на конце грузом, получаем
с 1 । 9 I . 33 j 1 q EJ
fm -= 1, mnD = т + —.----------------------tnQl, kno = 3 —— .
'т пр 4 /2 140 и ’Пр /3
Рис. 18.5
Если применить полученный результат к крайнему случаю, когда т =
= I = 0, то
О)2 __ ^пр __ ИО EJ
<опр II/4 т0
Точное решение для этого случая
2 / 1,875 у EJ
со2 = ( —--- ) --- .
\ I J т0
Ошибка приближенного решения составляет около 1,5%. Если предпо-
ложить, что форма колебаний совпадает с кривой изгиба от распреде-
ленной нагрузки, то
2 / 1,872 у EJ
со2 = ( —---) ------ .
\ / / т0
Здесь ошибка приближенного решения составляет всего около 0,5%.
Если упругим элементом является свободно опертая балка, а сосредото-
ченная масса т расположена посередине длины балки, то, приняв за
форму колебаний кривую статического прогиба, вызванного сосредото-
ченной силой, можно найти, что
17 / а EJ
тпр = т -|- —mol, knp = 48 — .
35 г*
Существуют технические задачи, в которых упругая балка, поддер-
живающая груз, опирается на податливые опоры (рис. 18.7). Форму
статического прогиба в подобных случаях можно представить состоящей
из двух частей: fi — перемещения вследствие податливости опор и /2 —
170
перемещения, вызванного изгибом балки. Приведенная масса в этом
случае будет равна
i
«Ч = т (flm + f2m)2 + J tnx (fi + /2)2 dx.
0
Так как приведенная жесткость численно равна удвоенному значению
потенциальной энергии при ^п(/) = 1, получим
Ч = (/2)х=о + k2 (ft)x=l + J EJ (ty dx.
0
Поскольку выбор определен-
ной формы колебаний эквивален-
тен введению некоторых допол-
нительных связей, которые при-
водят заданную систему к систе-
ме с одной степенью свободы и
могут лишь увеличить жесткость
системы, то найденное по методу
Рэлея приближенное значение
частоты несколько выше точного
значения.
Метод Ритца [68]. Приближенный метод Ритца является дальнейшим
развитием метода Рэлея. Им можно определить как частоту основного
тона, так и частоты высших форм колебаний. Сначала перемещение
упругой системы f выражают в виде ряда функций, удовлетворяющих
геометрическим граничным условиям и пригодных для представления f:
f = «hcpi (х) + a2q>2 (х) + а3<р3(х) + .... (18.36)
Затем составляют выражения для приведенной массы и приведенной же-
сткости системы
тпр ^mxPdx, knp = ^FJ (ГУ dx (18.37)
6 6
или
knp = $EF (ГУ dx.
О
Чтобы получить возможно лучшее приближение для функции f,
нужно решить вариационную задачу и выбрать коэффициенты а2,
а3, ... выражения (18.36) так, чтобы обратить собственную частоту
(18.28) в минимум. Получается система уравнений вида
д / ^пр \ __ Q
дйп \ ^пр /
Выполняя дифференцирование и принимая во внимание формулу (18.28),
получаем
-^-(knp-^mnp)=0. (18.38)
Если бы функции ф1(х), фг(^), ••• были собственными функциями
рассматриваемой задачи, то в силу условия ортогональности в выраже-
ния для тпр и йПр входили бы только квадраты коэффициентов ап. Урав-
нения (18.38) были бы в этом случае для каждого индекса п самостоя-
171
тельными. Из каждого уравнения определялась бы частота собственных
колебаний (о?г (точное значение).
В приближенных вычислениях функции cpi(x), <р2(*), ••• нсортогональ-
ны, и в выражениях для /ипр, Апр будут присутствовать произведения
вида апат(п=£т). Выполнив дифференцирование, получим систему
алгебраических однородных относительно коэффициентов ап уравнений,
причем число уравнений равно числу коэффициентов а}, а2> ... в выраже-
нии (18.36). Приравняв к нулю определитель системы, получим частот-
ное уравнение, из которого можно вычислить частоты, соответствующие
различным формам колебаний.
В качестве примера определим методом Ритца частоту собственных
изгибных колебаний однородного консольного стержня длиной I с изгиб-
ной жесткостью EJ и погонной массой т0. Перемещение упругого стерж-
ня выразим степенным рядом
f = atx2 + а2х3 |- а3х4 + ...
— функцией, на первый взгляд, мало пригодной для представления формы
собственных колебаний. Граничные условия в заделке (х = 0, f = f = 0)
выполнены.
Учтя один член ряда, получим
2
а 7 р j р г
тпп = т mJ = ---------mJ, k = k’ --------= 4а~ — ,
пр пр 0 5 О’ пр пр р 1 р ’
<о2=-а2—, а*-20.
1 1 mJ* 1
Если учесть два члена ряда, то
mnp = 4а1 Н- 12а1°2 -Ь 12а?, k' - 4" а! 4 V а*а’ V ai-
h Э о /
Выполнив дифференцирование согласно уравнению (18.38), получим
два однородных алгебраических уравнения относительно аг и а2. Прирав-
няв нулю определитель из коэффициентов при и а2, найдем
а2 = 12,6; а2 = 1217.
Если взять три члена ряда, то, выполнив все действия, получим
«2 = 12,35; а2 = 495; а| = 11 300.
Точные значения коэффициентов равны
а2 = 12,358; а2 _ 483>8; а2 г . 3797.
По методу Ритца получаем хорошее приближение для низших частот
и плохое — для высших частот.
Прием Граммеля [10]. Прием Граммеля позволяет вычислить коэф-
фициент приведенной жесткости через инерционную нагрузку, возникаю-
щую при колебаниях. Если перемещение упругой системы задано выра-
жением (18.36), то инерционная нагрузка будет равна /?гл.До2. Изгибаю-
щий момент в поперечном сечении стержня будет
Мх = <о2 (j j тxf dx + CYx + C2j = <о2Л41х,
о о
причем произвольные постоянные Сх и С2 определяют из граничных
условий. Приведенная жесткость равна
I ^2 1
£nD - С dx = <о4 dx = со4/?. (18.39)
пр J EJ J EJ пр 4
о о
172
Применяя уравнения Ритца (18.38), получаем
(18.40)
Если требуется определить только собственную частоту основного
тона по методу Рэлея, то, вычислив по выражению (18.39), вместо
(формулы 18.28) получим
тпп
, (18.41)
^iip
Одним из преимуществ в практических расчетах выражения (18.39) по
сравнению с (18.37) является отсутствие в нем производных.
Для схемы на рис. 18.7 удвоенное значение потенциальной энергии
деформации численно равно работе сил тяжести. Поэтому коэффициент
приведенной жесткости
i
/гпр =•- ёт (Лт + /2т) + g J тх (fi + /2) dx.
о
Формулу (18.28) для вычисления частоты собственных колебаний по ме-
тоду Рэлея можно представить в виде
со2 = > (18.42)
где Ътр — приведенная масса системы, g'Ztnf— работа сил тяжести,
численно равная удвоенному значению потенциальной энергии системы.
Частота собственных колебаний не зависит от статической
перегрузки. Частота собственных колебаний системы с одной сте-
пенью свободы (массы на пружине) может быть подсчитана по формуле
“Vf
в которой g— ускорение силы земного тяготения, fCT —статический
прогиб, вызванный весом колеблющейся сосредоточенной массы.
Пусть на активном участке траектории существует осевая статиче-
ская перегрузка nXl. Тогда статический прогиб будет fcT = ^xJcr. На
первый взгляд кажется, что увеличение статического прогиба приводит
к уменьшению собственной частоты колебаний. Но это, конечно, не так.
Приведенная формула получена из основной следующим образом:
Если вместо g подставить, например, ускорение aXl(-g), то
aXlt_e} = nXtg, /ст ~ пх/ст.
причем
При различных коэффициентах статической перегрузки разными бу-
дут статические перемещения fCr массы. Собственные колебания линей-
ной системы с частотой
k
т
не зависящей от статической перегрузки, будут совершаться относи-
тельно статического положения массы.
173
§ 19. ПРОДОЛЬНЫЕ КОЛЕБАНИЯ НЕОДНОРОДНЫХ СТЕРЖНЕЙ
Вывод дифференциального уравнения колебаний. Введем следующие
обозначения: тх — масса единицы длины стержня; EFX— жесткость на
растяжение-сжатие; и(х, t) —смещение в направлении продольной оси
стержня того сечения, абсцисса которого равна х; q(x, t) —внешняя
сила, действующая на единицу длины стержня.
Уравнение движения элемента стержня длиной dx (рис. 19.1) будет
тх dx dx+ q (х, t) dx.
х дР дх 7
Так как продольная сила, действующая в поперечном сечении,
N = EFX — ,
х дх
то дифференциальное уравнение продольных колебаний неоднородного
стержня будет иметь вид
/пх—= ——/). (19.1)
х di* дх \ х дх ) 4' '
О
dx
Рис. 19.1
q(x,t)dx
—г—
м dN ,
Расчет собственных колебаний методом последовательных прибли-
жений. Определение форм собственных колебаний.
Решение уравнения (19.1) при q(x, t) =0 ищем в виде ряда
оо
« (Х, t) = Ylfn (*) C0S
Л=1
(19.2)
в котором о)п и fn(x) —частота и форма собственных нормальных коле-
баний n-го тона. Подставляя выражение (19.2) в уравнение (19.1), полу-
чаем для любого п
EFx^ = -^nmxfn (и = 1,2,...). (19.3)
Это обычное дифференциальное уравнение растяжения стержня под дей-
ствием распределенной нагрузки ($2ntnxfni равной силам инерции масс
стержня.
Формы собственных колебаний обладают свойством ортогональности
j mxfnfm dx — о (n 7^ nt), (19.4)
о
где I — длина стержня. Проинтегрировав обе части уравнения (19.3) в
пределах от 0 до х, получим следующее выражение для осевых сил в
сечениях стержня:
Nx = EFx^=-^\{mxfndx + C
(19.5)
174
Обозначим
Nlx = ^mJndx + C, (19.6)
О
где — осевая сила от распределенной нагрузки, равной mxfn. Разде-
лив обе части равенства (19.5) на EFX и проинтегрировав второй раз в
пределах от 0 до х, получим уравнение для определения форм собствен-
ных колебаний
X
= + = ~ ^п- (19-7)
о х
Произвольные постоянные С и D в выражениях (19.5) и (19.7) долж-
ны быть определены из условий закрепления стержня. Например, если
конец стержня закреплен жестко, то для этого конца и(х, /)=0, если
конец стержня свободен, то для него Nx = 0. С учетом выражения (19.2),
(19.6), (19.7) будем иметь для жестко закрепленного конца
7л=0, (19.8)
а для свободного конца
Nlx = 0. (19.9)
Когда условие (19.8) выполняется при х = 0, а условие (19.9) — при
х = /, то на основании выражений (19.6) и (19.7) найдем
i
D 0, С = — j* mxfn dx.
6
Если оба конца стержня свободны, то
I X I
C = 0,D =-----— у тх J dx2, in = ^tnxdx. (19.10)
оох о
Формула (19.10) для D получена из выражения (19.6), которое при
х = I принимает вид
i
J mxfndx = 0. (19.10')
о
Это равенство показывает, что при собственных колебаниях любого
n-го тона (п=1, 2, 3, ...) количество движения свободного стержня равно
нулю, центр масс системы не смещается.
Метод последовательных приближений для разыскания формы соб-
ственных колебаний первого тона состоит в следующем. В качестве
исходной функции принимают любую функцию f и от распределенной
нагрузки mxf вычисляют функцию смещения
Тг^-^dx + D.
J EFX
о
Если отношение f/fi не окажется величиной, неизменной для всех се-
чений стержня, то расчет следует повторить, приняв за новую исходную
функцию f\. Продолжая расчет в том же порядке, можно добиться сколь
угодно малой разницы между функциями двух последовательных при-
ближений и получить функцию с нужной степенью точности. Чем более
175
близкой к разыскиваемой форме собственных колебаний была принята
исходная функция, тем меньшее число приближений потребуется прове-
сти для достижения заданной точности. В большинстве случаев форма
собственных колебаний первого тона наиболее быстро может быть
уточнена, если принять в качестве исходной известную форму собствен-
ных колебаний первого тона соответствующего однородного стержня.
При определении форм собственных колебаний второго и более высо-
ких тонов необходимо дополнительно выполнять условия ортогонально-
сти (19.4).
Рассмотрим сначала порядок расчета формы собственных колебаний
второго тона f2. Примем функцию f2 в виде суммы двух функций
/2 = /° + Д21/1- (19.11)
где /2 — форма собственных колебаний второго тона для однородного
стержня, имеющего те же условия закрепления, что и рассматриваемый
неоднородный стержень, Д2! — неизвестный пока коэффициент, с кото-
рым введена уже известная из предыдущего расчета функция /ь
Подставим выражение (19.11) в условие (19.4) и найдем из него зна-
чение коэффициента
i i
Д>п =------ f mf^dx, mj2.dx. (19.12)
J J
о о
Определенные интегралы, входящие в выражения (19.12), легко
могут быть вычислены численным методом, так как подынтегральные
функции известны. Во многих случаях полученная точность достаточна
для решения практических задач. Однако в случае необходимости най-
денная по выражениям (19.11), (19.12) функция /2 может быть уточнена
таким же способом, какой рекомендован для уточнения нормальной
функции первого тона. Чтобы не нарушалось условие ортогональности
после каждого уточнения, надо вновь ввести поправку согласно выра-
жению (19.11), приняв при вычислении A2i вместо полученную в по-
следнем приближении функцию /2.
Определив с нужной точностью значения функций Д и /2, приступим
к разысканию функции /3, для чего примем ее в виде суммы трех
функций:
/з = f°3 + Л31/1 + Л32/2. (19.13)
где /3 —форма собственных колебаний третьего тона для однородного
стержня с аналогичными условиями закрепления.
Неизвестные коэффициенты Дзь Д32 определяют из условий ортого-
нальности (19.4), которых в данном случае два:
i i
J dx = 0, j т J3/2 dx = 0.
О 6
Подставив в них выражение (19.13), получим
i i i
Д31 =-----— f tnjif^dx, Д32 =---— I tnxf2f^dx, т2= С mxf?2dx. (19.14)
О 0 0
Дальнейшие уточнения функции /3 проводят в том же порядке, как
и функций fi и f2. После каждого уточнения вводят поправки согласно
выражению (19.13).
Значения поправочных коэффициентов, определяемых по формулам
(19.12), (19.14), должны уменьшаться как с увеличением числа прибли-
жений, так и по мере перехода к более высокому тону колебаний.
176
Предположим теперь, что собственное движение незакрепленного
стержня совершается с частотой со = 0. Тогда, интегрируя уравнение
(19.3) при (оп = 0, получаем
EFxfa = А.
Па основании граничного условия (19.9) Л = 0. Дальнейшее интегриро-
вание приводит к решению
fn = /о = c°nst.
которое также удовлетворяет условию (19.9).
Собственное движение с f = fo = const и со = 0 — это движение неза-
крепленного стержня как твердого тела.
Определение частот собственных колебаний. Если
отношение fn/fn есть величина постоянная для всех точек оси стержня,
то на основании уравнения (19.7)
= ftJfrr
Практически невозможно добиться, чтобы указанное отношение было
постоянным для любого значения х, и поэтому пользоваться этой фор-
мулой неудобно. Можно взять среднее отношение fn/ln, однако частоту
собственных колебаний предпочтительнее определять по формуле
= (19.15)
где приведенная масса и приведенная жесткость равны
i
т,г = j mxf*dx,
О
k^EF^dx.
О
(19.16)
С учетом зависимости (19.6) выражение для приведенной жестокости
может быть представлено в другом виде:
/V2 /• /V?
kn = С—x—dx = «A—— dx. (19.16')
“ " J EFx J EFX
о о
Собственная частота теперь может быть определена по формуле
i
f dx
------------------------------------------------• (19Л7)
Л/2
В практических расчетах стержней переменного поперечного сечения
функции тх и EFX обычно задают в виде соответствующих кривых
(эпюр). Поэтому вычисление определенных интегралов как при разыска-
нии нормальных функций /п, так и при определении частот собственных
колебаний приходится проводить с помощью численных методов. Фор-
мула (19.17) для такого вычисления более предпочтительна, чем (19.15)
и (19.16), так как не требуется вычислять производную от функции fn,
заданной численно.
Порядок расчета. Исходными данными для расчета служат
эпюры (таблицы) EFX и тх распределения жесткости и массы по длине
стержня и f°i —форма собственных колебаний первого тона однородного
стержня с аналогичными условиями закрепления.
Для улучшения сходимости к вводят поправку
/1 = /? + ^,
12 Зак. 96
177
которую вычисляют из выражения (19.10')
j (/? + a)dx = 0, а =-----— J mj^dx.
о о
(19.18)
Стержень разбивают на k участков одинаковой длины Лис помощью
таблиц вычисляют интегралы, входящие в выражения (19.5), (19.7),
(19.18). Чем больше число k, тем точнее могут быть вычислены опреде-
ленные интегралы. Для упрощения расчетов жесткости EFX и массы тх
можно выразить в масштабах EFq и m0 и тогда при вычислении опреде-
ленных интегралов пользоваться безразмерными функциями EF =--
= EFx/EFOl т = тх/т0.
Далее с учетом граничных условий определяют произвольные по-
стоянные С и D\ таким образом, первое приближение функции Д будет
найдено. Чтобы привести функцию fi к масштабу, при котором ес зна-
чение в характерном сечении х0 было бы равно единице, надо на осно-
вании выражения (19.7) значения fi в каждом сечении стержня умно-
жить на 'постоянное число, по-
лученное от деления минус еди-
ницы на (f{)x=Xo. Полученную
"} функцию принимают в качестве
_] исходной для второго прибли-
j жения и т. д. Затем вычисляют
- интегралы, входящие в форму-
лу (19.17), и определяют ча-
- стоту собственных колебаний.
При разыскании форм соб-
ственных колебаний второго и
более высоких тонов перед
каждым приближением надо
~п дополнительно вводить поправ-
и ку на ортогональность по фор-
мулам (19.11) —(19.14).
Пример. Разыскать форму и частоту собственных колебаний первого тона сво-
бодного стержня, распределения массы т = тх1т^ и жесткости EF=EFX/EFQ которого
представлены графиком на рис. 19.2; длина стержня /=10 м, 6=10, Д=1,0 м.
Весь расчет сведен в табл. 19.1. В столбцах (2) и (3) помещены исходные дан-
ные— ординаты функций EF и т, взятые из графика для каждого сечения. Если в ка-
ком-либо сечении ордината EF или т имеет два предельных значения, то берут сред-
нюю величину ординаты. Определенные интегралы вычисляют по способу трапеции.
Для удобства счета сумму ординат двух соседних сечений не делят пополам и поэтому
крайние ординаты учитывают по одному разу, а все остальные — по два раза. Чтобы
в последующем учесть масштаб длины, результаты каждого интегрирования надо
умножить на Д1 = Д/2. Таким образом, табличное интегрирование сводится к суммиро-
ванию, при котором используется следующая символика:
I k х N
j’( = ), f( )dx=Ax2( ).
0 0 о
Поправка равна
о
a = -—k—
В столбце (11) представлено распределение осевой силы по сечениям стержня. Па
правом конце (в сечении N = k=lQ) осевая сила должна быть равна нулю. Чтобы д>
178
Таблица 19.1
№ EF т 51 К 2-/? 0 f° + “ f (8) (8);V=0 mfi К 2<10> 0 Л\х=(И)+(12)
1 2 3 4 5 6 7 8 9 10 11 12 13
0 4,0 2,0 1,000 0 2,000 0 0,952 1 2 0 0 0
1 4,5 3,0 0,951 5,0 2,853 4,853 0,903 0,948 2,844 4,844 —0,086 4,758
2 4,0 4,0 0,809 12,0 3,236 10,942 0,861 0,906 3,624 11,312 —0,173 11,139
3 3,0 3,0 0,588 19,0 1,764 15,942 0,540 0,567 1,701 16,637 —0,259 16,378
4 3,0 2,0 0,309 24,0 0,618 18,324 0,261 0,274 0,548 18,886 —0,346 18,540
5 2,0 4,0 0,000 30,0 0,000 18,942 —0,048 —0,050 —0,200 19,234 —0,432 18,802
6 2,0 4,0 —0,309 38,0 — 1,236 17,706 —0,357 —0,375 — 1,500 17,534 —0,518 17,016
7 3,0 2,0 —0,588 44,0 — 1,176 15,294 —0,636 —0,668 — 1,336 14,698 —0,605 14,093
8 3,0 1,0 —0,809 47,0 —0,809 13,309 —0,857 —0,900 —0,900 12,462 —0,691 11,771
9 6,0 3,0 —0,951 51,0 —2,853 9,647 —0,999 — 1,049 —3,147 8,415 —0,778 7,637
10 6,0 4,0 —1,000 58,0 —4,000 2,794 — 1,048 — 1,101 —4,404 0,864 —0,864 0
Продолжение табл. 19.1
Ke N 2<14) 0 (3) (15) К 2<1б> 0 f1=(15)+D >\ f"1 К 2^1 0 w| %
EF EF
14 15 16 17 18 19 20 21 22 23 24 25
0 0 0 0 0 39,961 1 1 1 2 0 0 0
1 1,057 1,057 3,171 3,171 38,904 0,973 0,974 0,974 2,847 4,847 5,378 5,378
2 2,785 4,899 19,596 25,938 35,062 0,887 0,881 0,882 3,112 10,806 32,285 43,041
3 5,471 13,155 39,465 84,999 26,806 0,671 0,681 0,682 1,395 15,313 95,524 170,850
4 6,180 24,806 49,612 174,076 15,155 0,379 0,399 0,395 0,312 17,020 130,244 396,618
5 9,401 40,387 161,548 385,236 — 0,426 —0,011 —0,005 —0,002 0 17,332 211,018 737,880
6 8,508 58,296 233,184 779,968 —18,335 —0,459 —0,463 —0,462 0,852 18,184 174,275 1123,173
7 4,698 71,502 143,004 1156,156 —31,541 —0,789 —0,800 —0,801 1,284 20,320 77,170 1374,618
8 3,924 80,124 80,124 1379,284 —40,163 — 1,005 — 1,015 — 1,019 1,038 22,642 46,185 1504,673
9 1,273 85,321 255,963 1715,361 —45,360 — 1,135 — 1,145 — 1,149 3,960 27,640 11,061 1568,629
10 0 86,594 346,376 2317,700 -46,633 — 1,167 — 1,177 — 1,189 5,576 37,176 0 1579,69
биться этого, введем к столбцу (И) поправку Д^, изменение которой по длине примем
линейным:
k
N \1
д" = _т2?10)-
о
Произвольная постоянная
k
S(i6)
о
k
2m
В столбцах (20) и (21) приведены значения функции полученные во втором и
третьем приближениях (для разыскания второго и последующих приближений столбцы
(4) — (8) не нужны). Условно считаем, что третье приближение удовлетворяет требуе-
мой точности.
Функцию fi—столбец (21) —используем для определения собственной частоты
первого тона. В столбцах (23) и (25) выписаны необходимые выражения. На основа-
нии формулы (19.17) -с учетом введенных масштабов EF0, m0, Д имеем
k __
______________о___________
Л . ,9
(fflpAi)2
EF0 EF
о
2^?
EF0 о EF0 31,176
т0Д? vX ~ m°(0’5)2 1579,19
о
= 0,079-^
т0
1
сек,
где
Дх = Д/2 = 0,5 м.
Расчет собственных колебаний методом начальных параметров.
Укажем другой метод определения форм и частот собственных колеба-
ний, более удобный для машинного счета.
Сущность метода начальных параметров состоит в том, что на одном
из краев, кроме граничных условий, задают начальные параметры, кото-
рые полностью определяют поведение упругой системы. Величины
начальных параметров определяют из граничных условий на другом
краю. Метод начальных параметров применяется в строительной меха-
нике в виде различных модификаций. В рассматриваемой задаче началь-
ным параметром будет собственная частота колебаний о)?/.
Разобьем стержень на k участков, для каждого из которых коэффи-
циенты EFX. и mxi считаются постоянными.
Дифференциальное уравнение (19.3) для /-того участка будет иметь
постоянные коэффициенты
а
difl г"
с2... EF*i
mXi
(а)
(б)
и поэтому может быть проинтегрировано в квадратурах:
fri = Ci sin <*ntxi + Di cos a»txi-
(в)
180
Произвольные постоянные Сг, £\- определяют из условий закрепления и
сопряжения отдельных участков стержня между собой.
Если длину z-того участка обозначить через /г-, а начало отсчета коор-
динаты поместить на одном из концов участка (например, левом), то
условия сопряжения двух соседних участков можно представить так:
Xi = I ni = fni+l , (г)
xi+1 = 0 j (ЕFxfn)i = (EFJn)l+i.
Таким образом, для k участков будет 2k граничных условия. Из выра-
жений (в) и (г) найдем
Ci+1 = (Ci cos an.li — Di sin (д)
Di+1 = Ci sin cLn.li Di cos ал./р
где
P x)i __ V(rnxEPx)j • _ । 2 £ j
(anEFx)i+1 /(mxEFx^+i ’
Зная произвольные постоянные предыдущего участка, по рекуррент-
ным формулам (д) можно определить произвольные постоянные для
последующего участка. Этим способом форму собственных колебаний
любого тона можно разыскивать без предварительного нахождения
форм собственных колебаний других тонов.
Порядок расчета проиллюстрируем на примере свободного стержня.
Стержень разбиваем на k участков так, чтобы коэффициенты с? можно
было считать постоянными. При этом длины участков могут быть совер-
шенно различными.
Задаемся приближенным значением частоты <оп и для всех участков
по формуле (б) вычисляем коэффициенты ani. Определяем произволь-
ные постоянные. На левом свободном конце первого участка осевая сила
равна нулю, поэтому при %i=0 fni = 0. Тогда из выражения (в) следует,
что Ci = 0.
Масштаб для искомой функции fnt выбираем так, чтобы на левом
конце (*1=0) было fnt = 1. Тогда D{ = 1.
Произвольные постоянные второго и всех последующих участков
определяем по формулам (д). После определения всех произвольных
постоянных остается еще одно неиспользованное граничное условие на
правом конце последнего участка. Так как этот конец свободен, то
fnk(lk)=0. (е)
При изложенном методе решения условие (е), как правило, выпол-
няться не будет, поскольку был допущен произвол в выборе значения
собственной частоты соп и, следовательно, значения коэффициентов anf
оказались неверными. Задача состоит в том, чтобы найти такое значе-
ние соп, при котором выполнялось бы и условие (е).
Представим выражение f'n (Ik) в виде функции от частоты соп, разде-
rik
лив предварительно на ank:
Ф К) = Ck cos a„klk — Dk sin (ж)
Проводим расчет при различных значениях <оп и методом проб нахо-
дим такое (оп, при котором равенство ф((оп)=0 выполняется с доста-
точной точностью. В практическом расчете удобно следить за знаком
произведения двух чисел
Ф (®п) Ф (<>„ + л®„),
181
где До)п — малая величина. Как только произведение этих чисел изменит
знак с плюса на минус, нужно уменьшить шаг Дсоп, чтобы с достаточной
точностью выполнить условие ф(соп)^0. Для первых тонов колебаний в
качестве грубого ориентира для начального параметра соп можно при-
нять значения собственных частот однородного стержня.
Используя найденные коэффициенты Сг, £>г, а?ч, по выражениям (в)
вычисляем значения формы собственных колебаний в любом сечении
стержня. Определив число узлов, установим номер тона колебаний. Это-
му номеру и будет соответствовать частота соп, которая обращает функ-
цию (р((оп) в ноль. Чтобы в расчете не пропустить какого-либо тона ко-
лебаний, надо убедиться в том, что полученные формы собственных ко-
лебаний имеют последовательно возрастающее число узлов. Номер тона
соответствует числу узлов п = 1, 2, 3 ...
Расчет вынужденных колебаний. Предположим, что внешнюю силу
q(x, t) в уравнении (19.1) можно представить произведением двух функ-
ций:
9 (х, t) = q (х) q (f).
Решение уравнения (19.1) будем искать в виде ряда, составленного из
произведений форм собственных колебаний fn(x) на неизвестные функ-
ции времени qn (t):
оо
и (х, f) = и0 (0 + £ fn (х) qn (О,
п=\
(19.19)
где «о(/) —смещение центра масс стержня в случае, когда стержень
свободен. Подставив выражение (19.19) в уравнение (19.1), получим
тх («о + £ fn4n ) = (EFx £ <7 W- (19.20)
п=\ п=\
Проинтегрируем это уравнение по х в пределах от 0 до Z
+ £ Яп fafndx = EFX^ f'nqn | + q (/) f q (x) dx.
n=l 0 n=l 0 6
Для свободного стержня при любом тоне колебаний
^mxfndx—0, EFxf'n\=O. (19.21)
6 о
Значит вся внешняя сила уравновешивается силами инерции стержня как
абсолютно твердого тела:
i
tnuQ = q (t) J q (x) dx. (19.22)
о
Этой форме движения (/o=l) соответствует собственная частота со = 0.
Все члены уравнения (19.20) умножим теперь на функцию
причем п — произвольное фиксированное число, и проинтегрируем по х
в пределах от 0 до /. С учетом первого равенства (19.21) и свойств
ортогональности (19.4) в левой части уравнения остается только один
член
I оо I
j* mxfc fn4n) № = qnjmfndx = qnmn.
0 n=\ 0
182
Сумма членов правой части уравнения с учетом равенств (19.3) и (19.4)
может быть представлена выражениями двух видов:
i I
§(EFxfnq„) fndx = — <£?nqn J mxf2ndx = — <o2nqnmn,
о б
Z I
f (EFxfmqm) fndx = — ti?mqm J mxfmfndx = 0 (n #= tn).
6 0
Соберем преобразованные выражения и разделим все члены уравне-
ния на получим обычное уравнение вынужденных колебаний для
обобщенной координаты qn:
i
qn+®nqn== q(t)-!—\q(x)fndx, п= 1,2,3,... (19.23)
о
Изложенный способ, таким образом, состоит в том, что внешние си-
лы и вынужденные колебания стержня раскладываются в ряд по собст-
венным формам. Он привел к такому же уравнению, как и в (18.27),
которое было получено из уравнения Лагранжа второго рода. Структура
дифференциального уравнения для обобщенной координаты qn свобод-
ного стержня такая же, как и для стержня закрепленного.
Структура выражения и(х, t) в виде (19.19) справедлива, конечно, и
для представления собственных колебаний. В этом случае
uQ = 0, uQ (t) = А + В/,
где А — координата и В — скорость движения центра масс, определяе-
мые нз начальных условий. Это собственное движение стержня как
твердого тела с со = 0.
Ускорение и0 создает статическую осевую перегрузку, одинаковую
для всего стержня, ускорения fnqn вызывают динамическую осевую пе-
регрузку, которая зависит от координаты х. Коэффициент динамической
осевой перегрузки будет равен
оо
<19-24)
д g
п=1
где (^п)тах — амплитудные значения ускорений.
Для произвольного закона изменения внешней нагрузки по времени
решение уравнения (19.23) имеет вид
t
qn (/) = A sin й)п/ + В cos + — С q (т) sin [o)n (t — т)] dx. (19.25)
< I
Здесь /1 — время, совпадающее с началом действия внешней нагрузки,
т — переменная интегрирования, меняющаяся от Л до /,
i
ап~ ~~ {q(x)fndx.
тп J
о
Начальные условия при t = ti позволяют найти произвольные посто-
янные А и В. Определив для каждого тона колебаний функцию qn(t),
дважды продифференцировав ее и подставив в формулу (19.24), полу-
чим значение коэффициента динамической осевой перегрузки для любо-
го сечения стержня и для любого момента времени
183
Пример. Определить коэффициент динамической перегрузки для неоднородного
свободного стержня, нагруженного в каком-либо сечении продольной силой, закон из-
менения которой изображен на рис. 18,2, а. Для определенности движение будем счи-
тать горизонтальным.
Смещение любого поперечного сечения стержня по направлению продольной оси
в абсолютной системе координат представим так:
оо
и (X, 0 = «о (0 + 2 fn Яп ’
П=1
(3>
где и0 (/) — смещение центра масс стержня; fn (х) — форма собственных колебаний /2-го
тона, fn (х) qn (/) — вынужденные колебания /г-го тона произвольного поперечного сечения
стержня относительно центра масс.
Кинетическая и потенциальная энергии будут
т = ( тхйЧх = mu 2 +
о
1 V -2
т L
оо I
и = У v2nmnq2, mn=^ mxf2ndx.
п=\ О
Обобщенным координатам «0, qn будут соответствовать следующие обобщенные силы:
Р0 = Р(/), Рл = Р(/)(/л)Хр.
где (fn)Xp — значение формы собственных колебаний в сечении х = хрг где приложена
сосредоточенная сила.
Применяя уравнение Лагранжа (18.23), получаем обыкновенные дифференциальные
уравнения для обобщенных координат
muQ = Р (/),
Qn + to„qn — Р (О (/п)хр • (и)
/Пл р
Рассмотрим момент времени Применив зависимости (18.16) — (18.18) ко вто-
рому уравнению (и), получим
f р = (fn)xp
Wn
Ро Тп . лт / лт \ т 2л
qn = ——T—(fn)xp——sin — COS , Tn^—. (К)
(О^/Пл лт Tn \ Tn J
При статическом нагружении колебания отсутствуют и все сечения стержня имеют
одинаковое ускорение uQ = PQlm. Осевую сжимающую силу, возникающую в сечениях
при движении с ускорением н0, назовем статической силой. Она равна
х х
NCT = и0 \ mxdx = — I mxdx, 0 < х < хр>
J /nJ
о о
I
Р
ДДТ = —— \ mxdx, хр < х < /. ( л>
/nJ
х
Коэффициент динамической осевой перегрузки
00
п=\
184
Динамическая осевая сила в сечении будет
оо х ОО X
= V (<7,,)max \fntnxdx=g^ f nXflmxdx, 0<х<1. (н)
п=1
Коэффициент пХд определим,
ние зависимость (к), получим
о 72=1 о
учитывая только один тон колебаний. Принимая во внима-
44-^4 (о>
Коэффициент д зависит не только от отношения х/ТЛ, но и от значения формы
собственных колебаний ([п)лр в точке приложения внешней силы. Кроме того, он за-
висит от формы собственных колебаний fn(x). Будем считать, что сила P(t) действует на
стержень, эпюры tn и EF которого представлены на рис. 19.2. Пусть сила Р(/) прило-
жена в сечении хР=8,5 м. В табл. 19.1 имеются значения формы первого тона в каж-
дом сечении, там же подсчитана и величина приведенной массы /72] = 18,588. Примем
отношение т/Г1 = 2,5.
Для хр = 8,5 м из табл. 19.1 находим
(Л)хр = у (- 1.019- 1,149) = - 1,084.
Тогда множитель
Tt I лт I (Uxp 1 1,084
—- sin----- ------- =-------• 1 • —’---= 0,0074.
лт | Tt | m1 2,5 18,588
Так как действительная приведенная масса в mQ раз больше, то на основании выражения-
(о) будем иметь
пх = 0,0074— Л (х),
А mog
где Д (х) надо взять из табл. 19.1, столбец (21).
§ 20. ПОПЕРЕЧНЫЕ КОЛЕБАНИЯ НЕОДНОРОДНЫХ ПРЯМЫХ
СТЕРЖНЕЙ
Поперечные колебания прямых неоднородных стержней наиболее
подробно изложены в книге Ю. А. Шиманского [108].
Вывод уравнения. Пренебрегая смещениями в направлении продоль-
ной оси и предполагая, что колебания происходят в плоскости симмет-
I 0
Н'Г
° fadx
dx
рии стержня, составим уравнения движения элемента стержня длиной
dx (рис. 20.1) в направлении оси Оу
т dx dx 4- q (х, t) dx.
х dt2 дх 1 ч \ > /
Пренебрегая инерцией вращения, с точностью до величин первого порядка
малости получаем соотношение
-^-dx = Qdx. (20.1)
дх
185
Кроме того, имеем дифференциальное уравнение кривой изгиба стержня
EJx-^- = —M. (20.2)
После преобразований получим линейное дифференциальное уравнение по-
перечных колебаний стержня
— lEJx + т = q (х, t). (20.3)
дх2 \ х дх2 ) х dt2 ч \ , / к /
Расчет собственных колебаний методом последовательных приближе-
ний. Определение форм собственных колебаний. Сущ-
ность метода изложена в § 19. Отличие состоит лишь в том, что для по-
перечных колебаний дифференциальное уравнение имеет четвертый по-
рядок и поэтому расчет оказывается более громоздким.
Примем
У(х, = cos
п=1
Здесь fn(x) и — форма и частота собственных поперечных колебаний
n-го тона.
Подставляя выражение у(х, t) в уравнение (20.3), получаем для
каждого члена ряда следующее дифференциальное уравнение для опре-
деления форм собственных поперечных колебаний:
— (EJ = <d2mxf„. (20.4)
dx2 \ х dx2 J п х/п ’
Расположим начало координат на одном из концов стержня и дваж-
ды проинтегрируем уравнение по х. Получим
X
+ (20’5)
о
EJx^=“Ki fmxfndx2+С1Х+с0- (20,6)
о о
Обозначим
М1х = J J тXfndx2 + С.х + С2, (20.7)
о о
причем
Ч = «Ж (20.8)
представляет собой изгибающий момент в сечении, расположенном на
расстоянии х от начала координат. Еще раз дважды проинтегрируем
по х\
f'n = dx + D^, (20.9)
о
х х
= J\^dx2 + D1(x-xT)+D2y (20.10)
о о
186
где хт— координата центра масс стержня. Для краткости обозначим
X X
^(x)=№~urdx2’ (2ОЛ1)
0 0 х
7n=^(x) + Dl(x — xT) + Dz. (20.12)
Постоянные интегрирования Сь С2, D2 определяют из граничных
условий. На каждом конце стержня должно быть два граничных усло-
вия.
На свободно опертом конце (неподвижный шарнир, каток) прогиб и
изгибающий момент равны нулю, следовательно,
/п=0, Д = 0. (20.13)
На закрепленном конце (в заделке) равны нулю прогиб и угол наклона
касательной к кривой изгиба, значит
/„ = 0, /; = 0. (20.14)
На свободном конце равны нулю изгибающий момент и перерезываю-
щая сила, так что
fn = 0, (EJxfny=O. (20.15)
Найдем, например, постоянные интегрирования для свободного
стержня. Из уравнений (20.5), (20.6) и условий (20.15) при х = 0 полу-
чаем Ci = C2 = 0. Применим теперь условия (20.15) при х = 1. Из уравне-
ния (20.5) найдем
$mxfndx = 0. (20.16)
о
Подставляя сюда выражение (20.12) и принимая во внимание, что ста-
тический момент массы стержня относительно центра масс равен ну-
лю, т. е.
i
§ mx(x— хт) dx = 0, (20.17)
о
находим
i i
D2 =----— f tnxty (х) dx, m = ( tnxdx. (20.18)
m J J
о о
Здесь tn—масса стержня.
Условие fn (I) = 0 удобнее применять, если правую часть уравнения
(20.6) при х = I представить в виде
i
j mxfn (l — x)dx = 0.
о
На основании равенства (20.16) I здесь можно заменить любой констан-
той, в частности хт. После замены получим
f tnxfn(x-xT)dx = 0. (20.19)
б
187
Подставляя сюда функцию fn (20.12) и учитывая соотношение (20.17).
находим
i i
=---L у (х) (х — хт) dx, I = тх (х — хт)2 dx, (20.20)
о о
где / — массовый момент инерции стержня относительно поперечной
оси, проходящей через центр масс.
Равенства (20.16) и (20.19) справедливы только для свободного
стержня. Их смысл в том, что сумма всех сил инерции, возникающих
при колебаниях по любой собственной форме /г-го тона, и момент этих
сил относительно центра тяжести стержня равны нулю. Иначе говоря,
силы инерции, возникающие при колебаниях по собственным формам,
самоуравновешены. Они не могут вызывать ни смещения центра масс
стержня, ни поворота стержня относительно центра масс.
Как и в случае продольных колебаний, за исходную функцию прини-
мают известную форму собственных колебаний /? первого тона одно-
родного стержня с аналогичными условиями закрепления. Затем по
уравнениям (20.5) — (20.12) с учетом граничных условий вычисляют
функцию смещения /ь Так как отношение не будет величиной,
неизменной для всех сечений стержня, то расчет повторяют, причем за
новую исходную функцию принимают функцию /1, полученную в резуль-
тате первого приближения.
Расчет форм собственных колебаний можно считать законченным,
если разница между функциями двух последовательных приближений
удовлетворяет заданной точности.
Особенности расчета этим методом форм собственных колебаний
высших тонов такие же, как и для продольных колебаний. Поэтому на-
до воспользоваться выражениями (19.11) — (19.14) и комментариями к
ним.
Предположим, что в поперечном направлении незакрепленный стер-
жень совершает движение как твердое тело с частотой со = 0. Тогда,,
интегрируя уравнение (20.4) при соп = 0 и граничных условиях (20.15)
на каждом из концов, получаем форму собственных движений неза-
крепленного стержня с (о = 0 в виде прямой линии
/ = А 4- В (х — хт).
Можно также сказать, что А—собственное движение центра масс и
В(х—хт)—поворот вокруг центра масс происходят с нулевыми часто-
тами.
Определение частот собственных колебаний. Частоту
собственных колебаний можно определять по формуле (19.15), причем
здесь
i i
mn = J mxf„dx, kn = [ EJ(f,y dx. (20.21)
о b
Более предпочтительна для коэффициента приведенной жесткости формула
dx.
188
Частота собственных колебаний теперь может быть определена по форму-
ле, аналогичной (19.17),
i
mxf2dx
= -!!--------- (20.22)
п 1 м2х
Порядок расчета. Исходными данными для расчета служат
эпюры (таблицы) распределения массы тх и жесткости EJX по длине
стержня и f°i —форма собственных колебаний первого тона однород-
ного стержня с аналогичными условиями закрепления. Для улучшения
с0
сходимости к /1 вводят поправку
Л = /?4-а-;-6(х-хт). (20.23)
Коэффициенты а и b определяют из равенств (20.16) и (20.19)
i i
а =----— {tn fidx, b — -—[тх^(х-хТ)йх. (20.24)
т J / J
о ' о
Для удобства расчетов обычно вводят масштабы изгибной жесткости и
массы:
EJX = EJ • £V0, тх = mmQ.
Произвольные постоянные Сь С2, D{, D2 определяют из граничных усло-
вий (20.13) —(20.15), (20.19). Далее расчет ведут в том же порядке, что
и для форм собственных продольных колебаний.
Рис. 20.2
Пример, Рассчитать форму и частоту собственных колебаний первого тона сво-
бодного стержня, погонная масса т и жесткость EJ которого представлены на графике
(рис. 20.2), длина 1= 15 м. Чтобы расчетная таблица не была громоздкой, примем число
участков 10, Д= 1,5 я. _
Весь расчет сведен в табл. 20.1 и 20.2. Исходные данные — ординаты функций т
и EJ — взяты из графика на рис. 20.2 для каждого сечения. Исходные данные вписы-
вают в таблицу и табличное интегрирование проводят по тем же правилам, как было
указано в § 19 для продольных колебаний.
189
№ 1 т mN N 0 j* mN _0 N-N\ (W— -лгт)2 (2)-(7)
2 3 4 5 6 7 8 9 10
0 1 0 0 0 —5,089 25,898 25,90 0,00 1,000
1 2 2 3 2 —4,089 16,720 33,44 59,34 0,537
2 1 2 6 6 —3,089 9,542 9,54 102,32 0,098
3 8 24 15 32 —2,089 4,364 34,91 146,77 —0,272
4 8 32 31 88 — 1,089 1,186 9,49 191,17 -0,520
5 5 25 44 145 —0,089 0,008 0,04 200,70 —0,608
6 2 12 51 182 0,911 0,829 1,66 202,40 —0,520
7 4 28 57 222 1,911 3,652 14,61 218,66 —0,272
8 6 48 67 298 2,911 8,474 50,84 284,12 0,098
9 2 18 75 364 3,911 15,296 30,59 365,55 0,537
10 2 20 79 402 4,911 24,118 48,24 444,38 1,000
Таблица 20.1
N S(9) 0 (6) • (11) A f (13) b b (6) a 4- (15) (17)
11 12 13 14 15 16 17 18
1,000 0,000 —5,089 0,000 0,227 0,408 isqShH* 1,408 1,000
1,074 2,074 —4,392 —9,481 0,182 0,364 0,901 0,640
0,098 3,246 —0,302 -14,175 0,138 0,319 0,417 0,296
—2,176 1,168 4,546 —9,931 0,093 0,275 0,003 0,002
—4,162 -5,170 4,532 -0,853 0,048 0,230 —0,290 —0,206
—3,039 —12,371 0,270 3,949 0,004 0,186 —0,422 -0,300
— 1,040 -16,450 -0,947 3,272 -0,041 0,141 —0,379 —0,269
-1,088 -18,578 —2,079 0,246 —0,085 0,096 —0,175 -0,125
0,587 —19,079 1,709 -0,124 —0,130 0,052 —0,150 0,106
1,074 -17,418 4,200 5,785. — 0,174 0,007 0,544 0,387
2,000 —14,344 9,822 19,807 —0,218 —0,037 0,963 0,684
№ EJ fn infi N _ 0 Л' У (6) 0 ДЛ1 = ( -1-
1 2 1 1 3 1 * 5 1 6 7 1 8 1 !
0 4 1,0 1,000 1,000 0,000 0,000 0,000 0
1 5 2,0 0,640 1,280 2,280 2,280 —0,036 2
2 4 1,0 0,296 0,296 3,856 8,416 —0,073 8
3 2 8,0 0,002 0,015 4,167 16,439 —0,109 16
4 2 8,0 —0,206 — 1,648 2,534 23,140 —0,146 22
5 5 5,0 —0,300 — 1,500 —0,614 25,060 —0,183 24
6 3 2,0 —0,269 —0,538 —2,652 21,795 —0,219 21,
7 3 4,0 —0,125 —0,500 —3,690 15,453 -0,256 15,
8 4 6,0 0,106 0,636 —3,554 8,209 —0,292 7.
9 5 2,0 0,387 0,774 —2,144 2,511 —0,329 2
10 5 2,0 0,684 1,368 —0,002 0,365 -0,365 0,
№ 0(15) d2 fi= = (12)4- +(18)+ +(19) (20) рп mfr
(20)дг_0
18 19 1 1 20 21 22 | 23 | 24
0 503,6 —231,3 272,3 1,000 1,000 1,000 1,000
1 404,7 —231,3 173,8 0,638 0,636 0,636 1,272
2 305,7 —231,3 78,3 0,288 0,285 0,284 0,284
3 206,7 —231,3 —4,5 -0,016 —0,019 —0,019 —0,152
4 107,8 —231,3 —57,3 —0,210 —0,211 —0,210 — 1,680
5 8,8 —231,3 —74,1 —0,272 —0,268 -0,268 — 1,340
6 —90,2 —231,3 —62,2 —0,228 —0,222 —0,221 —0,442
7 — 189,1 —231,3 -25,8 —0,095 —0,090 -0,090 —0,360
8 —288,1 —231,3 29,8 0,109 0,110 0,110 0,660
9 —387,1 —231,3 94,9 0,348 0,342 0,341 0,682
Ю —486,0 —231,3 162,9 0,598 0,584 0,582 1,164
Т а б л и ц а 20.2
г 7) + (8) А|1х EJ N У (10) 0 w = У(н) V (v) N V (13) 0 Лг—Лгр (13)-(15) 2 (ад 0
10 11 12 13 14 15 16 17
,000 0,00 0,00 0,00 0,0 0,0 —5,089 0,0 0,0
,24 0,45 0,45 0,45 0,9 0,9 —4,089 —3,7 —3,7
>34 2,08 2,98 3,88 3,9 5,7 —3,089 — 12,0 — 19,4
,33 8,16 13,22 20,08 160,6 170,2 —2,089 -335,0 —366,9
,99 11,50 32,88 66,18 529,4 860,2 — 1,089 —576,5 — 1278,9
,88 4,98 49,36 148,42 742,1 2131,7 —0,089 —66,0 — 1921,4
,58 7,19 61,53 259,31 518,6 3392,4 0 ,У91 472,5 — 1514,9
>20 5,06 73,78 394,62 1578,5 5489,5 1,911 3016,5 1974,2
>92 1,98 80,82 549,22 3295,3 10363,3 2,911 9592,6 14583,2
>18 0,44 83,24 713,28 1426,6 15085,2 3,911 5579,4 29755,1
,00 0,00 83,68 880,20 1760,4 18272,2 4,911 8645,3 43979,9
Продолжение табл. 20.2
2mf' 0 ю сч Ам =(26)+ (27) Л12 1х Л<2 \х ЁЗ 2(30) 0 fl т /2 0
25 26 | 27 1 28 | 29 30 1 31 32 33 1 34
0,000 0,000 0,000 0,000 0,0 0,0 0,0 1,0000 1,0000 0,0000
2,272 2,272 —0,028 2,244 5,0 1,0 1,0 0,4045 0,8090 1,8090
3,828 8,372 —0,056 8,315 69,1 17,3 19,3 0,0806 0,0806 2,6986
3,960 16,160 —0,085 16,075 258,4 129,2 165,8 0,0004 0,0032 2,7824
2,128 22,248 —0,114 22,134 489,9 244,9 539,9 0,0441 0,3528 3,1384
—0,892 23,484 —0,142 23,342 544,8 109,0 893,8 0,0718 0,3590 3,8502
—2,674 19,918 —0,170 19,748 390,0 130,0 1132,8 0,0488 0,0976 4,3068
—3,476 13,768 —0,199 13,569 184,1 61,4 1324,2 0,0081 0,0324 4,4368
—3,176 7,116 —0,227 6,889 47,4 11,8 1397,4 0,0121 0,0726 4,5418
— 1,834 2,106 —0,256 1,850 3,4 0,7 1409,9 0,1630 0,2326 4,8470
0,012 0,284 —0,284 0,000 0,0 0,0 1410,6 0,3387 0,6774 5,7570
Табл. 20.1 является вспомогательной. В столбцах (3)—(9) определено сечение
в котором расположен центр масс стержня, и вычислен момент инерции в масштабе
Д2Д1гп0
k _
2mN *
7VT = —k------- = 5,089; I (8).
0
0
Поправка к функции согласно формулам (20.23) н (20.24) определена в столбцах
(11)-(17):
/г /г
2(9) 2<13>
0 , °
а = - —7г------’ b- - —------------•
2m 2<8>
о о
В последнем столбце получена исправленная форма собственных колебаний flf кото-
рая вписана в столбец (4) табл. 20.2 в качестве исходной для последующего расчета.
k
Вследствие накопления ошибок значение 2 (6), стоящее в столбце (7) и Л-той строке
о
(У=10—k) отличается от нуля, и для выполнения граничного условия на правом конце
должна быть введена поправка AVf. Эту поправку можно считать линейно зависящей от
длины и определить по формуле
/г
N V
д-=-т1(6)-
о
Она внесена в столбец (8) таблицы.
В столбце (12) получена функция ф(х), представляющая собой кривую изгиба
стержня. Чтобы найти функцию //г, надо вычислить коэффициенты Dv и Z?2. Согласно
формулам (20.18) и (20.20)
V(13)
о
7г
о
1г
£ (16)
о_______
т
В столбце (21) получена приведенная к единице в нулевом сечении форма /ь
На этом заканчивается расчет формы собственных колебании в первом приближе-
нии. Его, как правило, оказывается недостаточно, поскольку полученная функция не-
значительно отличается от исходной. Начиная со столбца (4) таблицы расчет надо
повторить, приняв в качестве исходной функцию, полученную в предыдущем при-
ближении.
В столбцах (22) и (23) приведены значения функции полученные во втором и
третьем приближениях. Считая, условно, третье приближение удовлетворяющим задан-
ной точности, проводим расчет формы изгибающих моментов. Результаты расчета све-
дены в столбец (28) таблицы.
Определяем частоту собственных колебаний первого тона. Согласно формуле
(20.22) с учетом масштабов массы т0, изгибной жесткости EJ0 и длины Л получаем
/г _
™0Д1 mf2t
о
EJ о
0
EJ0
о
2(30)
о
0,0129
£Л 1
т() сек
где Дх = Д/2. В нашем примере А: — 0,75 м.
Расчет собственных колебаний методом начальных параметров.
Стержень разбивают на участки, причем нс обязательно одинаковой
длины. Для каждого участка погонную массу тх и изгибную жесткость
192
EJX принимают постоянными. Для каждого участка стержня уравнение
(20.4) приводят к виду
dx4
(а)
где коэффициент а* для любого i-того участка является постоянным и
равным
Уравнение (а) имеет точное решение
fni = Си sin а„,xz + С2{ cos а„ .х(. + С3. sh а„ + С4 ch а„ у (в)
и его произвольные постоянные можно определить через постоянные
интегрирования предыдущего участка из условий сопряжения при xL = и
xz+1 = 0 (/z — длина i-того участка стержня).
На границе i-того i + 1-го участков имеем условия сопряжения
1)/.,-Лч+1. 2)/;, = /”«• w
3) »(£2/;),+1, 4) (ЕЛ'„), -
Подставив сюда выражения (в) для i-того и i 4- 1-го участков, получим
четыре уравнения с восемью коэффициентами С1(, . ..,С4., Решая
их, находим зависимость постоянных i + 1-го участка от постоянных
i-того участка:
>+1 = у Y. 0 + Y-P.) cosan.lt — C2i (1 + у|Р<) sin a> +
+ C3. (1 — yfp.) ch a„4/,- + C4. (1 — y2p() sh
>+l = у + YfPz) staa„./z + C2< (1 + у2р.) со8ап./( +
+ C3. (1 — y2p.) sh a> + C4< (1 — yfp.) ch
(a)
>+l = у Y< lci( 0 - Y.2P/) cos a> - C2. (1 - y2pt.) sta а„,/г +
C3l (1 + yfp.) cha> + C4. (1 + y2p.) shan//.],
c4i+l = -у 1C1< 0 — Y2p<) sta a„4/(. 4- C2i (1 — y2p.) cos a„./z +
+ C3l (1 + yfPi) sh a„,/,. + C4. (1 + y2p.) ch
причем
Используя два граничных условия на левом конце первого участка
и положив в каком-либо сечении fnr=l, выразим все произвольные по-
стоянные решения (в) для первого участка через какую-либо одну.
Например, если левый конец свободный, то
(/;к=о = о, (/„>.=о = о.
13 Зак. 96
193
Полагая, кроме того, (/Л1)Х1=0 = 1, получим
fn. = Cn (sin antx1 + sh аЛ1Хх) + (cos + ch a^Xj). (ж)
Через эту постоянную по формулам (д) будут выражены, следователь-
но, коэффициенты Сг- для всех участков.
Имеющиеся на правом конце последнего участка еще два гранич-
ных условия используют для определения последней постоянной (в при-
веденном примере Си) и контроля правильности заданной частоты сон.
Если принятая в расчете частота соп является собственной частотой
колебаний стержня, то второе условие на правом конце будет выпол-
нено, и расчет форм упругих колебаний можно считать точным.
Однако поскольку частота соп задается вначале весьма ориентиро-
вочно, одно из граничных условий на правом конце последнего участка
заведомо удовлетворяться не будет. В этом случае расчет повторяют
при нескольких близких значениях соп и находят значение частоты
стержня, для которой производят окончательный расчет формы собст-
венных колебаний.
В первоначальном расчете за частоту <оп можно принять частоту
однородного стержня, который по своим параметрам близок к задан-
ному стержню.
После определения частоты собственных колебаний и всех коэффи-
циентов Ci форму собственных колебаний строят последовательно для
всех участков по уравнениям (в).
В заключение целесообразно проконтролировать правильность рас-
положения форм собственных колебаний fn(x) относительно линии от-
счета. Представим функцию fn(x) уравнением (20.23), полагая здесь
вместо fi форму собственных колебаний, полученную расчетом.
Методом начальных параметров можно рассчитать форму и часто-
ту собственных колебаний любого тона, не определяя предварительно
формы собственных колебаний предыдущих тонов. Однако не всегда
можно наперед сказать, для какого тона определена частота собствен-
ных колебаний. Для этого требуется построить форму собственных ко-
лебаний и найти число узлов. Для свободного стержня, например, номер
тона равен числу узлов без одного. Таким образом можно проконтро-
лировать, не пропущен ли в расчете какой-либо тон колебаний.
Расчет вынужденных колебаний. Предположим, что в уравнении
(20.3) внешние силы q(x, t) можно представить в виде
q(x, t)=q(x)q(t).
Вынужденные колебания стержня представим разложенными в ряд по
формам собственных колебаний fn(x). Так как колебания стержня по
формам fn(x) самоуравновешены (см. формулы (20.16) и (20.19), то
для свободного стержня искомая функция у(х, t) должна содержать
еще слагаемые, выражающие движения стержня с со = 0, т. е. как абсо-
лютно твердого тела. Форма такого движения представляет собой пря-
мую линию. Таким образом,
оо
у (х, 0 = у0 (0 + У1 (0 (х - хт) + У fn (X) qn (t). (20.25)
п=\
Подставив выражение (20.25) в уравнение (20.3), получим
(Е42 £&>)’ + тх [i/o + У1 (х — *т) 4- 2 (0• <20-26)
л=1 п— 1
194
Проинтегрируем это’уравнение по х в пределах от 0 до /. Попереч-
ная (перерезывающая) сила на концах свободного стержня равна ну-
лю. Учитывая, кроме того, равенства (20.16) и (20.19), получаем диф-
ференциальное уравнение движения центра масс стержня
i
myQ = q(t) q (х) dx. (20.27)
b
Умножим все члены уравнения (20.26) на (х—хт) и вновь проин-
тегрируем по х в пределах от 0 до /. Применим к первому члену урав-
нения, содержащего множитель х, правило интегрирования по частям:
{(EJJJx dx = х (EJjy (-EJj; j = 0.
6 0 0
Принимая во внимание равенства (20.17) и (20.19), после интегриро-
вания получаем дифференциальное уравнение вращения абсолютно
жесткого стержня относительно центра масс:
i
Ith = q (/) f q (x) (x — xT) dx. (20.28)
b
В правой части уравнения находится момент внешних сил относитель-
но центра масс, yi— угловое ускорение оси стержня.
Умножим все члены уравнения (20.26) на форму собственных коле-
баний fn, причем п будем считать любым фиксированным числом (п =
= 1, 2, 3, ...), и проинтегрируем по всей длине стержня. Интегрированием
по частям можно найти, что
^EJfmyfndx = 0 (п^т), (20.29)
6
f (EJxfny fn dx= [ EJX (ГпУ dx = kn. (20.30)
6 6
Окончательно получим дифференциальное уравнение для обобщенной
координаты qn в таком же виде, как и уравнение (18.27) для закреп-
ленного стержня
+ k„qn = Рп (/) (п =1,2,3,...), (20.31)
где
i i
тп = f mxfn dx, Рп (0 = q (/) J q (x) fn dx.
b о
Так как частоту собственных колебаний находят одновременно с
определением формы собственных колебаний, то приведенную жесткость
неоднородного стержня удобнее вычислять по формуле
kn =
Когда на стержень действует система поперечных сил, как, напри-
мер, изображено на рис. 18.4, то приведенную внешнюю силу Рп(0
подсчитывают по выражению (18.35), причем масштабный коэффициент
для формы собственных колебаний свободного стержня Ьп=\.
Если стержень закреплен, то в выражение (20.25) надо подставить
y0(t) =yi (/) =0. Инерционные силы при колебаниях не самоуравнове-
13*
195
шены. Они уравновешиваются реакциями опор. Вынужденные колеба-
ния для qn определяют из уравнения (20.31).
Если закон изменения внешней силы q(t) гармонический и, кроме
того, частота изменения силы близка к собственной частоте (оп, то из
уравнения (20.31) получаются неверные результаты из-за того, что в
нем не учтены силы демпфирования, которые всегда существуют. По-
этому если приходится определять координаты qn в зоне резонанса, то
в левой части уравнения (20.31) должны быть учтены силы трения,
которые обычно считают пропорциональными скорости. Разделив все
члены уравнения на тп, получим
qn 4- 2znqn + = — Рп (t). (20.32)
тп
Коэффициент затухания еп определяют, как правило, опытным путем.
Например, можно экспериментально получить график затухающих ко-
лебаний и замерить на нем амплитуды двух последовательных циклов
колебаний. Натуральный логарифм отношения амплитуды предыдущего
цикла к амплитуде последующего обозначим
5 =
Величина б называется логарифмическим декрементом колебаний.
Определив б, найдем е„:
= S/rn,
где Тп — период собственных колебаний.
Опытами различных исследователей [90, 110] установлено, что лога-
рифмический декремент колебаний в большинстве случаев увеличи-
вается с повышением напряжения и почти не зависит от частоты коле-
баний. Для стальных и алюминиевых образцов при средних напряже-
ниях 6 = 0,005-^0,015. Для машиностроительных конструкций, в которых
главную роль играет конструкционное демпфирование, он на порядок
выше, чем для образцов: 6 = 0,03—0,12.
Пример. Рассчитать поперечные силы и изгибающие моменты, возникающие в
сечениях стержня, когда на стержень действует внешняя сосредоточенная сила, изме-
няющаяся по гармоническому закону Р (/) =Posin pt. Будем считать, что эпюры масс т
и изгибных жесткостей EJ имеют вид, показанный на рис. 20.2, сила P(t) приложена
в сечении Хр=13.5 м, /=15,0 м, масштабы эпюр т0 и £/0- Упростим задачу и выберем
такое соотношение частот собственных и вынужденных колебаний y = p/coi = 0,8, чтобы
можно было ограничиться учетом только первого тона колебаний, для которого рассчи-
тана форма и частота собственных колебаний (см. табл. 20.2).
Малые поперечные движения стержня представим в виде суммы трех членов ряда
(20.25)
У (х, t) = yQ (/) + у! (/) (х — хт) + (?! (/) Д (х). (з)
Неизвестные yQ, у^ определим из уравнений (20.27), (20.28), (20.31). Вычислим коэф-
фициенты уравнений, приняв Д = 1,5 м, Д1 = 0,75 м,
l _ k _
т = mQ | т dx = m = 59,25mQ,
о о
z_ k
I = т0 \ т(х — хт)2 dx = т0Д2Дх (8) = т0 • 750 м2,
о о
Ро (хр — хт) = (13,5 — Д Мт) = PQ • 5,87 м,
1 _ k _
Wi = fn0 [ rrif\ dx = = 4,318 m0,
о о
Pi (0 = Pofip sin Pz = po sin PP= 0 Д41Р0 sin pt.
196
Таблица 20.3
№ т .v-.vT fi /Л (3) 7. <7i У о //(v)-- -(5)-M6)-! -r(7) in /ДЛ ) V (9) Q'=(10)+ +(11) TV V (12) V M'=( I3)+ +(14)
1 2 3 4 5 G 1 8 9 10 11 12 13 14 15
0 1,0 —5,089 1,100 -0,0595 —0,1405 0,0169 —0,1831 —0,183 0,000 0,000 0,000 0,000 0,000 0,000
1 2,0 —4,089 0,636 —0,0478 —0,0894 0,0169 —0,1203 —0,241 —0,424 0,000 —0,424 —0,424 —0,023 —0,447
2 1,0 —3,089 0,284 —0,0361 —0,0399 0,0169 —0,0591 —0,059 —0,724 0,000 —0,724 — 1,572 —0,045 -1,617
3 8,0 —2,089 —0,019 —0,0244 0,0027 0,0169 —0,0048 —0,038 —0,821 0,000 -0,821 —3,117 —0,068 —3,185
4 8,0 — 1,089 —0,210 —0,0127 0,0295 0,0169 0,0337 0,270 —0,589 0,001 —0,588 —4,526 —0,091 —4,617
5 5,0 —0,089 —0,268 —0,0010 0,0376 0,0169 0,0535 0,267 —0,052 0,001 —0,051 —5,165 —0,114 —5,279
6 2,0 0,911 | —0,221 1 0,0106 0,0310 0,0169 0,0585 0,117 0,332 0,001 0,333 —4,883 —0,136 —5,019
7 4,0 1,911 —0,090 0,0224 0,0126 0,0169 0,0519 0,208 0,657 0,001 1 0,658 —3,892 —0,159 —4,051
8 6,0 2,911 0,110 0,0340 —0,0155 0,0169 0,0354 0,212 1,077 0,001 1,078 —2.156 —0,182 —2,338
9 2,0 3,911 0,341 0,0457 —0,0479 0,0169 0,0147 0,029 1,318 — 0,015 0,001 1,319 — 0,014 0,241 —0,204 0,037
10 2,0 4,911 0,582 0,0574 —0,0818 0,0169 —0,0075 —0,015 —0,001 0,001 0,000 0,227 —0,227 0,000
Из уравнений (20.27) и (20.28) находим
р р
Уо = —~ sin pt = 0,0169 —— sin pi,
m m0
_ xp xt PQ
уi = Pq-----------sin pt = -----sin pt.
На основании уравнения (20.31) получаем
9 Pi (0 Po
<7i+ wfo = = 0,079 —- ship/,
mi m0
= — 0,079 —5------------sin pt = — 0,1405 — sin pt.
m0 1 — у2 m0
Максимальное поперечное ускорение при sin pt = 1 согласно (з) будет
У W = Уо + У1 (х - *т) + Л (*) ft = — [0,0169 + 0,0078 (х - хт) — 0,1405/1 (х)].
Г72О
Дальнейший расчет поперечных сил и изгибающих моментов сведен в табл. 20.3. Уско-
рения в столбцах (5) — (8) уменьшены в Ро/то раз. Погонная инерционная нагрузка в
столбце (9) уменьшена в Ро раз. После умножения столбца (10) на Л1Р0 получим по-
перечную силу Q в сечениях стержня. Так как в сечении № 9 к стержню приложена
внешняя сила Ро, то эпюра Q в этом месте должна иметь скачок на Pq, а в столбцах
(10) и (12)—скачок на 1/Aj. Этот скачок выражен двумя цифрами: в числителе зна-
чение поперечной силы до сечения, в котором приложена сила Ро, в знаменателе —
после этого сечения. При дальнейшем интегрировании и введении поправок по линей-
ному закону получаем значение изгибающего момента М'. Окончательно находим
Q = Q'AiP0, М = М'А2р0.
Особенности расчета вынужденных колебаний,
вызванных движением опор. Можно указать несколько типич-
ных примеров возбуждения колебаний таким способом. Например, при
транспортировке по железной
(шоссейной) дороге вынужден-
ные колебания корпуса раке-
ты возникают вследствие по-
перечных движений ложементов,
на которых укреплен корпус. По-
перечные движения опор трубо-
проводов вместе с корпусом вы-
зывают вынужденные колебания
трубопроводов. Продольные ко-
лебания корпуса приводят к вынужденным колебаниям днищ баков.
Особенность расчета при указанном способе возбуждения колеба-
ний состоит в том, что неизвестны внешние силы, а поэтому уравне-
нием (20.31) воспользоваться нельзя.
Пусть стержень закреплен на двух опорах (рис. 20.3), формы fn и
частоты соп собственных колебаний стержня известны. Прямая линия,
соединяющая опоры А и В, в абсолютной системе координат хОу дви-
жется по закону y0(t) +r/i(/) (х—а), причем функции y0(t) и у At)
заданы. Перемещение любого сечения стержня в направлении оси Оу
будет
У (х, t) = у0 (0 + У1 (0 (X — а) + 2 Мп-
п=1
Составив выражения кинетической и потенциальной энергий стержня
I оо
Т==^\ тЛУ (Х’ dX' U = Т S т'‘ыпуп
0 п= 1 *
198
и применив уравнения Лагранжа (18.23), получим дифференциальное
уравнение для искомой координаты qn:
Яп + “X = — ао„Уо (!) — aln Ух (/), (20.33)
где
i i
аоп = 4- f mxfn dx, aln = — C tnxfn (x — a) dx.
mn J mn J
о о
Примем движение опор, например, гармоническим
Уо (0 = У о sinp/, ух (/) = Ух sin pt
и получим выражения для вычисления поперечной силы и изгибающего
момента в любом поперечном сечении стержня. Из уравнения (20.33)
найдем
Yn о2
Чп = (У^Оп + У&Хп) ----2- S1M Pt’ Уп ~ -4" •
!-Y„ <>„
Максимальное ускорение в любом сечении
Утах (*) = Р2 ро + У1 (X -а)+^[п (у^Оп + Уха1п) ] • (20-34)
П=1
Силы реакций в опорах УА и возникающие при колебаниях, будут равны
i i
у в = —-----( тхУтж W (х — a) dx, YA + УВ={ пгхутах (х) dx, (20.35)
о — a J J
о О
Учитывая, что погонная нагрузка при колебаниях равна тхутах (х), можно
построить эпюру поперечных динамических сил и изгибающих моментов
ТИд. Чтобы получить полную поперечную силу и изгибающий момент, надо
добавить еще их статические значения QCT и Л4СТ, вызванные весом стержня.
Q^Qct + Сд, м = мст + мл.
Особенности расчета колебаний балок на упругом основании.
К этой задаче приводится также задача об осесимметричных колеба-
ниях замкнутой цилиндрической оболочки.
Допустим, что балка лежит на сплошном упругом основании, мас-
сой которого можно пренебречь. Обозначим коэффициент жесткости
основания (коэффициент постели) через k. Силу реакции упругого
основания на балку отнесем к внешним силам; тогда дифференциаль-
ное уравнение поперечных колебаний однородной балки будет
EJo ~ТГ + "Sr = ~ky-
дх* di2
Принимая
У =
п=1
приходим к уравнению для определения форм собственных колебаний
e W*v + ^n = mo(1)2Zn (20.36)
199
Рассмотрим простейший случай балки со свободно опертыми кон-
цами. Решением уравнения (20.36), удовлетворяющим всем граничныхь
условиям, будет
/„ = sin^x. (20.37)
Подставляя это решение в уравнение (20.36), находим
< = (VУ — + 0)’ 0 = • (20.38)
Вынужденные колебания примем в виде разложения в ряд по формам
собственных колебаний:
оо
у(х, /) = (0sta-y-x.
Л=1
Составив выражения кинетической и потенциальной энергии системы и
воспользовавшись уравнениями (18.23), получим уравнение вынужден-
ных колебаний
mnqn + knqn = Рп (t),
в котором
a Pn(t) определяется из выражения (18.35).
Влияние осевой силы на частоту собственных поперечных колеба-
ний стержней. Если однородный стержень со свободно опертыми кон-
цами подвергается действию осевой растягивающей силы Р, то частоту
собственных поперечных колебаний стержня подсчитывают по форму-
ле [88]
= (^У1/— ]/ 1 ч- . (20.39)
\ J г ^0 г ^кр
где Р1<р = дгл2£7о//2 — эйлерова критическая сила. Если стержень растя-
нут, то Р>0, если сжат, то Р<0.
При сжатии Р = Ркр стержень теряет устойчивость по Эйлеру и, как
следует из формулы (20.39), соп = 0. Формула (20.39) не применима,
если сила Р является следящей, т. е. если вектор силы Р при колеба-
ниях повертывается вместе с осью стержня.
Влияние осевой следящей силы на частоту собственных поперечных
колебаний незакрепленного стержня. Дифференциальное уравнение для
определения форм собственных поперечных колебаний стержня, на од-
ном из концов которого приложена сила Р, имеет вид [43, 96]
{EJfn]" [Nxf'n]' - ЙХЛ = °- (20-4°)
где Nx — нормальная сжимающая сила в сечении с абсциссой х,
£2п(1/сек)—частота собственных колебаний. Функции fn должны отве-
чать граничным условиям (20.15) при х = 0 и х = 1.
В работах [43, 96] решение уравнения (20.40) предлагается искать
в виде степенного ряда
f„(x) = £QA
200
Для однородного стержня EJ0 = const, m0 = const зависимость часто-
ты собственных колебаний от величины силы Р, взятая из цитируемых
работ, показана на рис. 20.4, где
(20.41)
С увеличением следящей силы в некоторых пределах частота соб-
ственных поперечных колебаний первых двух тонов уменьшается почти
по линейному закону. Значениям параметра coi = 22,35 и <о2 = 61,6 соот-
ветствуют собственные частоты первого и второго тонов при Р = 0.
На основании графика, представленного на рис. 20.4, составим при-
ближенную зависимость влияния осевой следящей силы на собственные
частоты первого и второго тонов:
(1 — «Л). ’Р = V7-’ 0 < 'Р < 20-
£</0
(20.42)
где (оп — собственная частота, вычисленная при Р = 0, т. е. без учета
следящей силы. Для первого тона си — 0,14, для второго тона а2-0,20.
Формулой (20.42), по-видимому, можно воспользоваться для при-
ближенной оценки влияния осевой следящей силы на частоту собствен-
ных поперечных колебаний неоднородного стержня. Величину /2/Е/0,
входящую в параметр ф,
можно рекомендовать вы-
числять, разбивая стержень
на k участков с постоянными
жесткостями Е/г:
i -1
(20.43)
Учет влияния деформа-
ции сдвига и инерции вра-
щения при поперечных коле-
баниях стержней [88]. При
выводе уравнения (20.3) не
было учтено влияние дефор-
мации сдвига и инерции Р,ис. 20.4
вращательных перемещений.
С учетом этих факторов Ти-
мошенко получил более полное дифференциальное уравнение поперечных
колебаний стержней. Для однородного стержня уравнение имеет вид:
. yF0 д2у
дх* g dt2
/ У Jо 1 ЕЛ)У \
\ g gk'G J dx2dt2
VJq У
g gk'G
= q (x, t).
dt*
(20.44)
Здесь у — удельный вес материала стержня, Fo — площадь поперечного
сечения, G — модуль сдвига, k'— числовой коэффициент, зависящий от
формы поперечного сечения.
Два дополнительных слагаемых по сравнению с уравнением (20.3)
имеют большое значение при изучении колебаний с высокими часто-
тами, когда колеблющийся стержень подразделяется узловыми попереч-
ными сечениями на сравнительно короткие участки. При уменьшении
расстояния между узловыми сечениями растет кинетическая энергия
201
вращательных перемещений, т. е. приведенная масса, и потенциальная
энергия деформации 'сдвига, т. е. приведенная жесткость стержня.
Применение уравнения (20.44) показано в книгах [88, 108].
При расчете форм и частот собственных колебаний первых тонов
длинных стержней так же, как и корпусов ракет, деформацию сдвига
и инерцию вращения можно не учитывать, поскольку добавки при этом
получаются малыми. Кроме того, заметим, что при учете инерции вра-
щения в погонный момент инерции нет основания включать момент
инерции массы жидкого топлива.
§ 21. КОЛЕБАНИЯ ПЛАСТИН И ОБОЛОЧЕК
Если к статическим уравнениям равновесия элемента упругого тела
добавить даламберовы силы инерции, то получатся уравнения колеба-
ний. Так как собственные колебания любой линейной консервативной
системы всегда гармонические, то принимается, что любая точка систе-
мы совершает колебания по закону cosco/, где со — искомая частота.
Основная трудность состоит в отыскании функций, которые были бы
решением дифференциального уравнения и удовлетворяли заданным
граничным условиям. Для решения практических задач широкое рас-
пространение получили приближенные методы.
Рассмотрим определение собственных частот методом Рэлея—Ритца.
Приведенная масса тп и приведенная жесткость kn пластин и обо-
лочек, как и стержней, представляют соответственно удвоенное значе-
ние кинетической энергии при qn=\ и удвоенное значение потенциаль-
ной энергии при ^п = 1. Интегрирование производится по всей поверх-
ности пластины или оболочки. Например, если форма собственных
колебаний w задана, то приведенная масса для прямоугольной и круг-
лой осесимметричной пластины будет
a b R
тп = f т (х, у) а>2 (х, у) dxdy, тп = рп (г) w2n (г) 2nrdr.
6 6 6
Для круговой цилиндрической оболочки
I 2Л
тп= J т (х, ср) w2n (х, ф) Rdqdx.
6 о
Эта формула получена в предположении, что скорости движения в окруж-
ном направлении малы по сравнению со скоростями в радиальном на-
правлении.
Определение частоты собственных колебаний круглой мембраны.
Предполагается, что мембрана равномерно растянута внешней нагруз-
кой во всех направлениях, причем натяжение настолько велико, что
можно пренебречь его изменениями, вызванными малыми колебаниями.
Обозначим через w(r) форму прогиба любой точки мембраны при коле-
баниях, S — равномерное натяжение на единицу длины контура, т0 —
массу единицы площади мембраны.
Увеличение потенциальной энергии мембраны найдем путем умно-
жения натяжения S на приращение площади поверхности мембраны:
R
U == S 2nrdr.
J 2 \ dr J
о
202
Приведенная жесткость &пр = 2U и приведенная масса тпр будут равны
R R
&пр = 2nS J г^г’ шпр = 2лт0 у w2rdr.
о о
Форму прогиба можно принять в виде ряда
, ч яг . З.лг ,
w (г) = ajCOS— + a2cos —- + ... ,
Z.K ZK
каждый член которого удовлетворяет граничным условиям.
Частоты собственных колебаний определяют из уравнений (18.38).
Взяв только первый член ряда, получим
2,415 , / S
(О = —-----1/ ----.
R V mQ
Точное решение в этом случае отличается менее, чем на
V2%:
2,404
(О = -------
7?
частоты, а так-
болыиее число
Чтобы получить лучшее приближение для основной
же для частот высших форм колебаний, нужно взять
членов ряда. Высшие формы колебаний будут иметь одну, две и более
узловые окружности, на которых при колебаниях перемещения w(r]
равны нулю. Кроме осесимметричных форм, круглая мембрана может
иметь формы колебаний с узловыми диаметрами, вдоль которых ^ = 0.
Если контур мембраны имеет приближенно форму окружности, то низ-
шая частота колебаний такой мембраны близка к частоте колебаний
круговой мембраны, имеющей ту же площадь и то же значение S/mG.
Подробнее о колебаниях мембран можно прочесть в книгах Рэлея и
Тимошенко [79. 88].
Определение частоты собственных колебаний круглой пластины.
В случае осесимметричных колебаний выражения для приведенной
жесткости и приведенной массы имеют вид:
R R
£ПР = D J + “ 'д?У 2nrdr' = /no f w22nrdr,
о о
где D — изгибная жесткость пластины. Точное решение задачи о коле-
баниях круглой пластины выражается через функции Бесселя. Для при-
ближенного решения в случае защемленной по контуру пластины мож-
но взять
... (21.1)
Каждый член ряда удовлетворяет как условиям симметрии, так и гра-
ничным условиям на контуре (w = w' = 0). Взяв только один член ряда,
получим
, 192 n nm0R2
k1 =-------пи, т1 = —5—
9/?2 5
<*>1 =
10,33 /~ D
R2 V т0
(21.2)
Для лучшего приближения надо взять два члена ряда. В результа-
те определения knp и тпр и использования двух уравнений (18.38) при-
ходим к двум алгебраическим однородным уравнениям с неизвестными
203
ах и а2. Приравнивая нулю определитель системы этих уравнений, по-
лучаем квадратное уравнение относительно со2. Разрешив его, найдем
10,21 , Л D 43,04 п Г D
со, =---------1/ --------, (Оо =-----------1/ --------,
R2 У mQ R2 У т0
где col — второе приближение к частоте низшей формы колебаний пла-
стины, а (02 дает грубое приближение к частоте второй формы колеба-
ний, когда колеблющаяся пластина имеет одну узловую окружность.
Определение частоты собственных колебаний прямоугольной пла-
стины. Приведенная жесткость и приведенная масса равны
Оу2
д2ги
-г 2 (1 — |х) ()2] dxdy,
V \дхду / J
"2лр = ^0 f f W2dxdy.
Пусть, например, прямоугольная пластина с размерами а и b свободно
оперта по контуру. Тогда можно принять
ОС оо
w(x, у) = У J\m„sin
т—1 п=\
тлх . ппу
----S1H -
а---b
(21.3)
Каждый член этого ряда удовлетворяет дифференциальному уравнению
и всем граничным условиям, поэтому мы получим точное решение
задачи:
Для любых фиксированных значений т и п частота собственных ко-
лебаний будет
k/nn
^тп
~ Л
Задача о формах собственных колебаний прямоугольной пластины,
защемленной по контуру, оказывается более сложной. В приближенном
решении в качестве форм собственных колебаний принимают обычно
формы собственных колебаний призматической балки с заделанными
концами [88].
Влияние растягивающих усилий в срединной поверхности на часто-
ту собственных колебаний. Если статический прогиб пластины не мал
по сравнению с ее толщиной, то при вычислении собственных частот
нужно учесть растягивающие усилия в срединной поверхности. Нали-
чие этих усилий приводит к увеличению потенциальной энергии и, сле-
довательно, к повышению частоты собственных колебаний. В книге
Тимошенко [88] изложен метод и произведена приближенная оценка
влияния растяжения срединной поверхности вследствие изгиба на час-
тоту первого тона круглой защемленной по контуру пластины. Вместо
зависимости (21.2) получена формула
10,33
R2
1,464-—
h2
(21.4)
204
где fCT — статический прогиб центра пластины. С увеличением отноше-
ния /ст//г частота собственных колебаний возрастает. По этой же при-
чине частота собственных колебаний будет повышаться с увеличением
амплитуды колебаний. Здесь, как и в случае мембраны, мы имеем дело
с нелинейными колебаниями.
Расчет вынужденных колебаний пластин. Методика решения задачи
о вынужденных колебаниях пластин такая же, как и для стержней.
Когда формы собственных колебаний известны, действующую на пла-
стину внешнюю нагрузку надо разложить по ним в ряд, после чего
уравнения вынужденных колебаний для любого тона будут иметь вид
(20.31). Если же формы собственных колебаний неизвестны и собствен-
ные частоты найдены приближенно, то, пользуясь приближенным пред-
ставлением функции прогибов, приведенную силу для основного тона
колебаний можно определить как сумму работ всех внешних сил на
возможных перемещениях. Например, если прямоугольная пластина
нагружена распределенной нагрузкой q(t)q(x, у), а функция прогибов
ее есть w(x, «/), то приведенная сила
Рпр = У (0 J [ У (х, у) W (х, у) dxdy.
Пример. Пусть в центре круглой пластины приложена гармоническая сила
P(t)=PGs\n pt. Белем считать, что вынужденные колебания являются малыми и огра-
ничимся учетом только первого члена ряда (21.1).
Обобщенная сила в этом случае равна произведению внешней силы на значение
формы колебаний з месте приложения силы:
Pnp = Р1 = р (0 (0) = Ри sin at.
Обозначим амплитуду колебаний в центре пластины через Тогда уравнение вы-
пужденных колебаний будет иметь вид
"Mi -b Ч<71 = Р« sin pt,
откуда частное решение
р
41 =-------7-------sin pt («j + р).
mi (<of — р2)
Обозначив амплитуду статического прогиба центра пластины через [Ст> а максимальный
прогиб с учетом колебаний — через wmax, получим
Р Р»
^max — /стЛд» Лд ~ 1 “Ь 2 •
/ст^1 («I — Р2)
Если статический прогиб нельзя считать малым, то надо учесть растяжение срединной
поверхности, Для этого надо положить
kv = ,
причем значение взять из формулы (21.4).
Когда на пластину действует распределенная возмущающая сила интенсивности
q(r, t), обобщенная сила будет равна
R
С / г2 V
Рпр=^4(г, /)^1 — — ) 2nrdr.
о
Пусть теперь вынужденные колебания защемленной по контуру круглой пластины
вызываются дв.ижением z(t) опорного кольца. Тогда к выражению (21.1) надо доба-
вить перемещение пластины совместно с кольцом. Учитывая только первый член ряда
(21.1), получим
/ Г2 \2
w(r, t)-= ( 1- — ) •
\ ° J
205
Выражения потенциальной и кинетической энергий системы будут следующими:
Z7 = y
R
_ 1 С . nR2m0 /. 2 •• 1 -9\
Г = — m0 \ -- ——- ( г2 + — .
к) £ \ о □ /
о
Подставляя выражения U и Т в уравнения Лагранжа, находим
5
+ k^i = — — mYz.
О
Если z (/) = zQ sin pt, то
5z0p2
Pi =-----------sin pt (coj = p).
3(^-P2)
Максимальный прогиб центра пластины с учетом колебаний будет
, _1 5г°р2
^тах — / стЛд » Лд — 1 4“ 0
3/Ст(<о2-Р2)
Расчет частот собственных колебаний замкнутой круговой цилинд-
рической оболочки. Уравнения собственных осесимметричных колеба-
ний имеют вид [29]
h2 d*w .1 — ii2 1 — ц2 d2w
--------------—- w =-------— о ----
12 dx* R2 E dt2
ИЛИ
n d*w . Eh
D------------w =
dx* R2
— mQ —
0 dt-
Это уравнение аналогично уравнению колебаний балки на упругом
основании. Жесткость оболочки на растяжение в окружном направле-
нии является аналогом жесткости упругого основания балки.
При осесимметричных колебаниях оболочка в любом поперечном
сечении остается круглой. Если в выражениях (20.38) примем
то получим формулу для определения собственной частоты осесиммет-
ричных колебаний свободно опертой цилиндрической оболочки:
и2 = +
п \. Z4 Я2Л2 ) т0
Сравним слагаемые в скобках. Первое слагаемое характеризует
потенциальную энергию изгиба образующих, второе — потенциальную
энергию растяжения оболочки в окружном направлении. Для низких
тонов длинных оболочек роль энергии изгиба, как правило, невелика
и поэтому граничные условия мало влияют на частоту колебаний. На-
пример, для п=1 и / = 20у/?/г энергия изгиба составляет всего лишь 2%
от энергии растяжения.
Влияние внутреннего давления и осевых сил на частоты осесиммет-
ричных колебаний может быть оценено довольно просто. Решение
можно свести к поперечным колебаниям балки на упругом основании
и считать, что балка нагружена осевой силой и прижата внутренним
давлением к упругому основанию. Для длинной оболочки влияние гра-
ничных условий на низшие частоты незначительно и поэтому общая
206
осадка упругого основания не оказывает влияния на частоты собствен-
ных колебаний. Растягивающая осевая сила увеличивает, а сжимаю-
щая уменьшает частоту собственных колебаний оболочки.
Значительно более сложной является задача об определении частот
собственных неосесимметричных колебаний оболочки, т. е. таких, когда
в окружном направлении образуются волны. Эти частоты существенно
зависят от внутреннего (внешнего) давления. От внутреннего давления
возникает восстанавливающая сила, стремящаяся придать оболочке
круглую форму. Поэтому при наличии внутреннего давления частота
собственных колебаний по неосесимметричным формам повышается,
низшая частота может соответствовать трем, четырем, пяти и т. д. вол-
нам в окружном направлении, а не двум, как в случае отсутствия внут-
реннего давления. Влияние внутреннего давления на собственные час-
тоты оболочек рассмотрено, например, в монографии О. Д. Ониашвили
[64]. При наличии внешнего давления частота собственных неосесим-
метричных колебаний понижается, причем если внешнее давление рав
но критическому, то низшая собственная частота равна нулю.
Расчет собственных осесимметричных колебаний пологой сфериче-
ской оболочки. Уравнения колебаний имеют вид [113]
4 2
+ — wpoh— =4— (C2+C4lnp), (21.5)
v DR* D 0 dt* DR x * 7
где /?, /г, po — радиус кривизны, толщина и плотность материала обо-
лочки;
г0 — краевой радиус (радиус контура оболочки);
г — расстояние от произвольной точки оболочки до оси симметрии;
(> = rlr0.
Полагая, что колебания совершаются по одной из собственных
форм соДр), из уравнения (21.5) получаем
VX' — k- Wi = 4 (С*2 + с; 1пр),
(21.6)
(21.7)
$
4 9
— Eh(-^^— —
D \ Е
1 \
Я2 /
Для оболочки, защемленной по контуру, граничными условиями будут
р = 1, Wi = 0, Wt = 0, еф = О, (21.8)
где 8Ф —деформация в окружном направлении.
Приведем здесь лишь результаты решения уравнения (21.6) при
условиях (21.8), изложенного в работе [67]. Характеристическое урав-
нение для определения собственных чисел kiy с помощью которых на-
ходят частоты собственных колебаний, имеет вид
R*fi? k]
12г4 (1 -И2)
+ 1 т
+ Г_ (/о {k.) ц (ki) + /о (k.} (k.)} 1 = 0. (21.9)
1 — р L “i j
Здесь /о, h — функции Бесселя первого рода, /0, 1\ — модифицирован-
ные функции Бесселя первого рода.
В случае тонкой с малой степенью пологости оболочки /г/го^1/ЗО,
7У]/2ги^1/10 для основного тона слагаемым
W“^/12r^(l-H2)
207
в уравнении (21.9) можно пренебречь по сравнению с единицей, и это
уравнение упрощается
- Jo fe) Л &•) + /о &) Л W + 4 Л (ki) = 0. (21.10)
Из равенства (21.7) получаем формулу для вычисления частоты соб-
ственных колебаний
Е 1 И2
Ро R2 1 12rJ(l — Р2)
(21.Н)
Уравнение (21.9) имеет один нулевой корень йо = О, которому со-
ответствует низшая безузловая форма колебаний (при колебаниях во
всех точках одновременно увеличивается или уменьшается радиус кри-
визны сферической оболочки). Соответствующая этому корню частота
равна
со2 = £/р0 /?2.
(21.12)
Результаты расчетов показывают, что если Я1/2г0> 1/10, то ошибка
в определении частоты собственных колебаний второго тона по фор-
муле, приведенной в работе [64], не превышает 1 %! по сравнению с фор-
мулами (21.9) и (21.11). Ошибка становится значительной и достигает
20% для сильно пологих оболочек.
На числовом примере оценим роль второго слагаемого в квадрат-
ных скобках формулы (21.11). Примем R = 2 м, А = 3-10-3 м, г0= 1 м,
ц = 0,3. Значение первого ненулевого корня, вычисленного по уравне-
нию (21.9), #1 = 5,9. Этому корню соответствует форма собственных ко-
лебаний с узловой окружностью в заделке, т. е. это основной тон коле-
баний защемленной по контуру оболочки. Получим
R2 12^(1-и2) j [ 4 12.Ь(1-о,О9)
Второе слагаемое, учитывающее в данном случае только краевой
эффект, в 250 раз меньше первого.
На основании приведенного примера можно сделать вывод, что при
определении частоты собственных колебаний основного тона тонкостен-
ных оболочек типа баков ракет краевой эффект можно не учитывать
и считать оболочку безмоментной.
Подробную библиографию по колебаниям пластин и оболочек
можно найти в книге В. С. Гонткевича [29].
§ 22. ПРОДОЛЬНЫЕ КОЛЕБАНИЯ КОРПУСА РАКЕТЫ
Определение частоты собственных осесимметричных колебаний
основного тона бака с жидкостью. Точное решение задачи по опреде-
лению форм и частот собственных колебаний бака с жидкостью является
сложным. Решения для некоторых случаев можно найти в работах
[81, 109]. Приближенное определение частоты собственных колебаний
основного тона проведем для случая, когда обечайка бака выполнена
в виде кругового цилиндра, а днище бака — в виде части сферы с вы-
сотой сегмента значительно меньше диаметра (—— *<0,2).
Примем следующие допущения:
1) обечайка и днище бака — безмоментные тонкостенные осесим-
метричные оболочки постоянной толщины;
208
2) жидкость, заполняющая бак, идеальная несжимаемая;
3) кинетическая энергия радиального движения жидкости мала
по сравнению с кинетической энергией движения вдоль оси цилиндра;
4) скорость частичек жидкости в направлении продольной оси ци-
линдра не зависит от радиуса;
5) волновыми колебаниями на свободной поверхности жидкости
пренебрегаем;
6) кинетическая энергия стенок бака мала по сравнению с кине-
тической энергией жидкости.
Конфигурация бака, характерные размеры и способ закрепления
показаны на рис. 22.1,а. Там же изображены статические смещения в
направлении радиуса обечайки и днища бака, вызванные гидростати-
ческим давлением.
Определение основной частоты методом Рэлея. Вычислим потен-
циальную энергию обечайки и днища бака, соответствующую деформа-
циям от гидростатического давления. Удельная потенциальная энергия
деформации обечайки будет
ил =
2 ’ Ehi ’
где у—удельный вес жидкости. Полная потенциальная энергия обечайки
тС 1 яу*$(Н—Н^
UedV = 2xR1h1 Uedx = Y . (22.1)
J 3Eh~i
г" о
Так как высота сегмента сферического днища мала, то для упрощения
примем, что гидростатическое давление жидкости на любую площадку
сферы одинаково и равно давлению в центре днища. Поэтому на осно-
вании [99] удельная потенциальная
энергия
yHR2
2Eh2
/1 \ ®<>
(1 -н) = v
/\2
Объем части сферической оболочки
V = 2л/?2Я1Й2, Hi = R2 - /Rl -
t/2 = UeV =
nR3 yWHt
2Eh2
(22.2)
(l-H).
14 Зак. 96
209
Найдем потенциальную энергию шпангоута. Вес столба жидкости
уравновешивается меридиональными силами 7\ по контуру днища
л/?? = 2л/?х 7\ sin 0О.
Сила 7\, спроектированная на плоскость кольца, дает радиальную нагруз-
ку на кольцо
<?к = Л cos е0 == Y cos 0О.
2sin 0О
Сжимающая сила в поперечном сечении кольца
S =
потенциальная энергия деформации кольца
у X S2 2лР, _
3 2 EFK 4EFK sin2 0О
Приведенная жесткость системы численно разна удвоенному значению
потенциальной энергии:
knp = 2(Ul + U2 + U3). (22.4)
Вычислим приведенную массу жидкости. Для упрощения предста-
вим столб жидкости состоящим из тонких слоев (дисков). Жидкость,
находящуюся в сферическом сегменте, присоединим к столбу с радиу-
сом Ее приведенная высота
Н[ =-- —— f (27?ох — x2}dx.
o’ ’
Тогда полная высота столба будет
/Г-Я —: Н\.
Смещение любого слоя в направлении оси цилиндра можно пред-
ставить состоящим из двух частей: 1) смещения на величину w2 вместе
с днищем и 2) смещения, вызванного уменьшением толщины слоев
вследствие увеличения диаметра.
Так как радиальное смещение обечайки и уменьшение толщины
слоев от гидростатического давления пропорционально координате х,
то вторая часть смещения слоев жидкости будет такой же. как и у сжи-
маемого столба под действием веса. Иначе говоря, вместо несжимаемой
жидкости и податливой обечайки можно рассматривать абсолютно
жесткую в радиальном направлении обечайку и сжимаемый столб
жидкости с приведенным модулем упругости, который можно опреде-
лить исходя из того, что уменьшение высоты слоя жидкости из-за раз-
дутия обечайки от давления ух должно быть равно уменьшению вы-
соты того же слоя вследствие сжимаемости столба.
Увеличение радиуса обечайки
Уменьшение высоты слоя (начальная высота принята за единицу)
д 2 л __ 2yx/?i
jiR]
210
Вследствие сжимаемости слоя
д____________________________ Y* _ ух
ЕПРЛ^1 £пр
Откуда получаем
Е = Е
ьпр
к
2/?! ’
где Е — модуль упругости материала обечайки бака.
На рис. 22.1,в изображена модель бака с жидкостью для расчета
перемещений слоев жидкости (пружина имитирует упругость днища),
а на рис. 22.1,г представлена эпюра этих перемещений ср(л')
где
. Y^*2
w. =--------- (1 — и), и =---------
ZEhz r/ 2Enp
yH*2 Я,
Ehi
(22.5)
(22.6)
Приведенную массу жидкости вычислим по формуле
Г* Y 2 / \ л 2 4 g
т D = \ ----------<р2 (х) dx =-------------( w2 Ч-----w„u |----------и2 ). (22.7)
.) g g \ 3 ' 15 J
0
Частота собственных колебаний
ю2=2пр_ (22.8)
т пр
Если бак является подвесным и подвеска осуществлена за верхний
силовой шпангоут, то от гидростатического давления напряженное со-
стояние обечайки будет двухосным. Возникает дополнительное смеще-
ние слоев жидкости из-за удлинения обечайки бака. Эти особенности
надо учитывать при определении £Пр и тпр.
Определение основной частоты собственных колебаний методом
Рэлея—Граммеля. В гидродинамике важное значение имеет функция
Ф(х, г/, z,/), называемая потенциалом скоростей. Если потен-
циал скоростей известен, то известен весь процесс движения жидкости,
известно давление в любой точке объема жидкости. Потенциал скоро-
стей определяют из уравнения Лапласа, граничных и начальных условий.
Для приближенного решения задачи зададим потенциал скоростей
жидкости в виде
Ф = Лхсо8(о/, v = (22.9)
дх
где А—произвольная константа. Он удовлетворяет уравнению нераз-
рывности и силовому граничному условию на свободной поверхности
жидкости (рх=о = О). Динамическое давление в жидкости р определим
по формуле
(22.10)
Вычислим потенциальную энергию днища бака без предположения
о равномерном давлении. Меридиональное растягивающее усилие 1\
найдем из суммы проекций всех сил на ось Ох (рис. 22.1,6):
г0
7\ =--------!-----С pr dr.
r0 Sin 0О '
о
14=
211
Применяя формулу Лапласа для определения окружного усилия Т2 и под-
ставляя значение р из формул (22.10), (22.9), получаем
7\ = 7\ =
2
Для двухосного напряженного состояния потенциальная энергия дни-
ща [99]
4А1' г sin ° </о-
Ell 2 J
о
cos е0) + ^(l-cos 290) +
Выполнив интегрирование, получим
Г
2Eh2 [
4---— (1 — cos3 60) sin2 w/, В — Н —
3 j
Потенциальную энергию деформации обечайки бака найдем
жения (22.1), положив давление ух = р,
щ>3А2«м8(Н — Hi)3
-----------------sin2 ®/.
(22.11)
из выра-
3E/ix
Определим потенциальную энергию деформации шпангоута,
ленная нагрузка, действующая со стороны днища на кольцо и
рованная на плоскость кольца,
(22.12)
Распреде-
спроекти-
У1 =
= Т1 cos 60.
Сила, возникающая в поперечном сечении кольца от этой нагрузки,
= <7К^1,
и потенциальная энергия деформации кольца будет
.. _ S3nRi _ ^AWR^RliH — Hj)3 cos* 0q
EFK 4EFK
Полная потенциальная энергия системы
U = + U2 + U3 = со2 ([/; |- U, 4- ^з).
Для вычисления кинетической энергии представим всю жидкость зак-
люченной в два объема: объем в пределах обечайки бака и объем сфери-
ческого сегмента. Тогда
(22.13)
(22.14)
Вычислив, получим
т = A2 cos2 О) t Г/?, (Н - Hi) + —
(22.15)
Из равенства Umax ~ Tmax найдем собственную частоту основного тона
колебаний
(О2 = ---------------- (22. J 6)
(U\ + U2 + £/р,пах
1212
Расчет вынужденных осесимметричных колебаний бака с жид-
костью. Пусть силовой шпангоут, к которому присоединено днище бака,
совершает вместе с корпусом вынужденное движение в направлении оси
бака по закону
и (/) = uQ sin pt.
Требуется найти величину вынужденных колебаний жидкости и дина-
мическую силу давления жидкости на днище бака, учитывая только
основной тон колебаний.
Для решения применим модель, изображенную на рис. 22.1,в, форму
колебаний жидкости относительно шпангоута примем такой же. как и
при статических перемещениях (22.5):
Ч>(Х) = l+afl--£/), а=—. (22.17)
\ Н*2 w2
Полное смещение любого слоя жидкости представим в виде
и (х, t) = u(t) + ф (х) q (t). (22.18)
Кинетическая энергия столба жидкости
н*
Т =- — — f (и 4- фр)2 dx.
2 g J
о
Составив выражение для потенциальной энергии и применив уравнение
Лагранжа (18.23), получим уравнение вынужденных колебаний для
обобщенной координаты р(/):
н*
I* Ф W dx
q с ^q - — bu(t), b = _2__________ (22.19)
( ф2(х)с/х
o'
Частное решение уравнения будет следующим:
р — sin pt (со =£р). (22.20)
со2 — р2
Таким образом, закон вынужденных колебаний любого слоя жидкости
в абсолютной системе координат согласно выражениям (22.18), (22.20)
будет следующим:
и (х, t) = и0 ( 1 + ф ——-sinp/. (22.21)
\ со2 — р2 J
Осевая сила, возникающая в поперечном сечении столба жидко-
сти при колебаниях, равна сумме сил инерции всех слоев, расположен-
ных выше сечения:
л\с
g .)
о
Амплитуда силы
п2 х
Nx = p2u0 ( (1-| ip &р~ ) dx.
g J \ СО2 —р2 7
о
213
С учетом равенства (22.17) получим
Nx = рЧ Я/?|УХ Й + Г14-af 1----— 'Ш. (22.22)
g I 0)2 — р2 L \ ЗН*2 7] f '
Положив х = //*, получим динамическую силу, действующую на дно бака,
¥н.=--рЧ—^Гц--^-(1 + -"-а)1. (22-23)
g L со2 — р2^ 3 J J
Если силу Nx разделим на площадь лТ??, найдем дополнительное дав-
ление жидкости, возникающее при колебаниях в сечении х.
Расчетная схема для корпуса. Для расчета форм и частот собствен-
ных продольных колебаний корпус ракеты принимают в виде прямого
неоднородного стержня. Чтобы учесть продольные движения жидкого
топлива и массы двигателя относительно стенок корпуса в сечениях,
где расположены силовые шпангоуты двигателя, и нижних днищ бакоз,
к стержню осесимметрично подвешивают дополнительные массы на
пружинах (рис. 22.2). Это эквивалентные системы с одной степенью
свободы. В каждом из указанных сечений таких масс может быть под-
вешено несколько. Эквивалентная система является механическим ана-
логом соответствующего тона колебаний распределенной системы, на-
пример жидкости в баке, и имеет одинаковую с ним собственную
частоту. Сумма всех подвешенных в сечении масс равна массе жидко-
сти в баке, а сумма всех подвешенных масс и массы неоднородного
стержня равна массе ракеты. Вопрос о том, какое число масс надо под-
вешивать в сечении, должен быть решен из сравнения частот собствен-
ных колебаний эквивалентных систем и частот собственных колебаний
корпуса, подлежащих определению.
Если требуется учесть не один, а несколько тонов колебаний бака
с топливом, то для определения величин подвешенных масс и их частот
собственных колебаний надо предварительно решить задачу о колеба-
ниях жидкости в упругом сосуде.
Как и для баков с жидкостью, должна быть определена частота
собственных колебаний массы двигателя относительно корпуса ракеты
в направлении продольной оси. Принимая двигатель абсолютно жест-
ким, а подвеску двигателя не имеющей массы, найдем грубое прибли-
жение для основной частоты. При расчете статического прогиба необ-
ходимо учитывать податливость опор подвески. Хорошее приближение
для основной частоты можно получить по методу Рэлея. Расчетная
214
схема зависит от конструкции подвески. Когда двигатель подвешен
к корпусу на поперечных балках, расчетная схема (или ее часть) будет
соответствовать рис. 18.7. Если достаточно учесть только основной тон
колебаний массы двигателя, то за эквивалентную массу надо принять
массу двигателя.
Особенности расчета форм и частот собственных колебаний кор-
пуса по методу последовательных приближений. Отметим лишь допол-
нительные особенности, которые возникают в связи с присоединением
к неоднородному стержню упруго подвешенных масс. Положим, что
достаточно учесть только основные тона колебаний баков и двигателя.
Тогда в расчетной схеме (рис. 22.2) тА, —массы жидкости в баках
А и Б, mj\ —масса двигателя, сод» ^в, <од —частоты собственных ко-
лебаний (они определены в предыдущих расчетах и поэтому считаются
известными).
Отличие расчета от изложенного в § 19 состоит в том, что при вы-
числении осевой силы в сечениях х = хА, х = лБ, х = хд надо добавлять
дополнительные сосредоточенные силы инерции масс тЛ, тБ, /пд. Вы-
ражение (19.6) приобретает вид
Л\л. = j mjndx + £ Nljt (22.24)
О (/)
причем здесь тх — масса единицы длины ракеты без учета массы жидкого
топлива в баках и массы двигателя; = 0, если х<х;-. }=А,Б,Д.
Формулы для вычисления сосредоточенных сил NiA и 7ViB получим из ра-
венства (22.23). Обозначив, например, для х = ху значение формы собст-
венных колебаний корпуса fn^ и приняв р = со/:, найдем:
^ = ^(Ц-Ру), ^-^Г1 +(22.25)
где fnj(\ + Ру)— значение формы собственных колебаний массы а)/2 — час-
тота собственных колебаний корпуса. Коэффициенты bj и а, вычисляют по
формулам (22.6), (22.17), (22.19). При учете только основного тона коле-
баний баков с жидкостью
иг: - —/ = А, Б. (22.26)
S
Отличие величины смещения силового шпангоута fnj от смещения массы
топлива rrij существенно зависит от соотношения между собственной
частотой продольных колебаний корпуса и частотой колебаний бака
с топливом. Чем эти частоты ближе, тем больше динамические нагрузки
на днище и обечайку бака, тем больше разница в указанных сме-
щениях.
Обозначив значение формы собственных колебаний корпуса в сече-
нии, которому передается тяга двигателя, через /пд, будем иметь
2
ЛГ>Д = /ИдЛд (1 + Рд), Рд = —. (22.27)
Равенство (19.10), из которого определяется произвольная постоян-
ная D, из-за наличия сосредоточенных масс несколько видоизменяется:
J tnjndx + £ m.Jnj (1 + р,.) = 0. (22.28)
о щ
215
Обозначим
f ~~dx = (*)•
0
Тогда
fn - - [ф(х) +D], /л.(1 + Р?)^ -<о2[ф,.(1 p,) 'r D]. (22.29)
Подставляя величины fn и fnj в соотношение (22.28), получаем
i
D =--------- mxty (x) dx + m^j (1 |- py) j, (22.30)
0 (/)
где
i
m = J tnxdx -j- mjy j = Л, Б, Д.
о u)
Чтобы вычислить коэффициенты P7, после каждого приближения необ-
ходимо определять частоту собственных колебаний:
О
(О2 -- ----—
П
п
kn---
I
тп = j mxfndx + (1 + Р,)2,
0 (/)
kn = dx + V «фпДр? = k'n^n Г Г dx И' У ^'n>№ I.
J nrx L-' Ы x J
о (j) о (!)
py = G)X J-A 5, Д. (22.31)
Значения Ру в формуле для kn нужно взять из предыдущего приближения.
В остальном порядок расчета не отличается от изложенного
в § 19. Заметим лишь, что при табличном вычислении интегралов с вве-
дением масштабных коэффициентов m0, EFq сосредоточенные массы
тЛ. /7?б, /Ид так же, как и тх, должны быть разделены на масштаб /и0,
а при вычислении Nix в сечениях Xj должны быть добавлены удвоенные
значения сил Nij.
Если интегралы в выражениях (22.31) для тп и как и в § 19,
выразить через результаты табличного интегрирования, то получим
k _ _
тп = m0\l Y/nfn + 2m0 V mfii (1 -I- py)2.
0 (!)
2.5 k ./2
k* = (22.31')
0 (!)
График формы собственных колебаний первого тона показан на
рис. 22.2. Если (о;<(о7г, то масса колеблется в противофазе с точкой
подвеса и поэтому для нее Pj<0.
Особенности расчета собственных колебаний методом начальных
параметров. Сечения x = Xj, j=A, Б, Д выделяют в самостоятельные
участки, для которых EFx = ooy тх = 0. Пусть между участками i и f+1
216
находится сечение x=Xj. Тогда для сопряжения участков i и t+t
должны быть использованы следующие равенства (рис. 22.3):
Xi = li
Xi-f-1 — 0
(EFxf'n)i-^N1^n^(EFxf'n)i+1.
Значение в последнем равенстве и в равенствах (22.25), (22.27) при-
нимается таким же, как и для определения чисел ап. (19, б).
Определение частоты собственных осевых колебаний жидкости в
длинном трубопроводе. Жидкость считаем идеальной сжимаемой. Вме-
сто упругой трубы со сжимаемой жидкостью будем рассматривать жест-
кую трубу со сжимаемым столбом жидкости. Эквивалентный модуль
сжатия жидкости определим из условия, что податли-
вость столба в жесткой трубе равна податливости
жидкости в осевом направлении <в упругой трубе. Кине-
тической энергией, соответствующей радиальной ско-
рости жидкости и скорости стенок трубы, из-за их ма-
лости пренебрегаем. Так как общая податливость
столба жидкости равна сумме податливостей [34], то
^ж^пр___ _ _____ --
Еж + £пр ’ ПР ~ 2/? ’ Рис. 22.3
Здесь Еж — модуль сжатия жидкости, £, Л, R—модуль упругости, тол-
щина стенки и радиус трубы.
Найдем эквивалентную скорость звука в сжимаемом столбе жидкости.
Учитывая, что £ж = р0^, где р0 — плотность жидкости, с0 — скорость зву-
ка в ней, получаем
эк Ро 1 -Г V ’ Eh
Закрытый конец трубы соответствует закрепленному концу стержня,
открытый — свободному. Известно, что если у стержня один конец за-
креплен, а другой свободен, то длина волны для n-го тона колебаний
и длина стержня I связаны соотношением
= 4г , п = 1, 2, 3, ...
2/1—1
Период колебаний Тп - Хп,сэк, частота
2л 2п — 1
~ Тп ~ 2/ Сэк’
Когда оба конца трубы открыты, то
п
= Лу Сэк-
Если в невозмущенном состоянии поток жидкости в трубе имеет скорость
t’o, то собственную частоту со* определяют по формуле [75]
G)' = ( 1 — М2) <£>п, М - О0/Сэк.
Расчет вынужденных продольных колебаний корпуса. Решение за-
дачи о продольных колебаниях, изложенное в § 19 для неоднородных
стержней, справедливо и для корпуса. Более сложная расчетная схема
(см. рис. 22.2) отличается некоторой спецификой форм собственных ко-
лебаний.
217
Пусть сила тяги двигателя Р (t) имеет график, показанный на рис. 18.2, а.
Решение задачи приведено в § 19. Обобщенную координату qn (t) вычис-
ляют по формуле (19, к), причем здесь (/п)хР =/пд (1 + Рд). При />т
амплитуда обобщенной координаты при zi-м тоне колебаний будет
(Umax = —"^+Рд) “ sin I, Тп = -2^. (22.32)
Если продольные колебания корпуса совершаются под действием ва-
риации тяги двигателя, изменяющейся по гармоническому закону Р (/) =
= PQ sin pt, то
(Umax = +У (22 -33)
Амплитуда колебаний днища бака при колебаниях корпуса по л-му
тону будет
^ = /^(l+P>)(?,I)max. (22.34)
По этой же формуле можно определить амплитуду колебаний днища
бака и при отсечке двигателя, если считать, что закон спада силы тяги
соответствует графику на рис. 18.2,6. В этом случае в формулу (22.32)
вместо т надо подставить т*.
Амплитуды колебаний при осесимметричном разделении ступеней
приближенно можно определить по изложенной методике, если известен
закон спада силы, которая действует со стороны отделяемой ступени.
В частности, если этот закон соответствует графику на рис. 18.2,6, то
амплитуду колебаний днища бака определяют из выражения (22.32) с
заменой /пд(1 + Рд) на значение формы колебаний (fn)x=z для остав-
шейся части ракеты (без отделившейся ступени).
Продольные колебания корпуса вызывают вынужденные колебания
всех упруго подвешенных масс. Чтобы эти колебания не были чрез-
мерно большими, надо требовать, чтобы собственные частоты подвесок
этих масс не совпадали с частотой собственных продольных колебаний
корпуса.
Определение динамических сил. Осевая динамическая сила в про-
извольном сечении корпуса при колебаниях по n-му тону равна
^ = (Umax^u,
причем Л;1л. вычисляют по выражению (22.24). Методика определения
коэффициента динамической осевой перегрузки изложена в § 19.
Коэффициент динамичности для днища бака может быть вычислен
по общей формуле (17.12). Неизвестную амплитуду а колебаний днища,
входящую в формулу (17.12) и в неравенство (17.13), определим по
формулам (22.32) — (22.34).
Получим формулу коэффициента динамичности для давления жид-
кости на обечайку бака в случае нарастания или спада силы тяги. Ста-
тическое давление жидкости на обечайку бака на расстоянии х от сво-
бодной поверхности будет
Рет = Ро +
Амплитуду дополнительного давления, возникающего при колебаниях п-го
тона, получим из равенства (22.22)
Рд = «п2 (Umax fni -у [ 1 + ^'_П^ ( 1 + ai ( 1 - ’
218
где (qn)max вычислим по формуле (22.32), а коэффициенты а, и bj — по
формулам (22.6), (22.17), (22.19). Коэффициент динамичности будет равен
1 । PR
В § 18 получены формулы (18.9) коэффициента динамичности для
упруго подвешенных масс, когда колебания вызываются движением
точки подвеса. Амплитуду колебаний точки подвеса при колебаниях
n-го тона корпуса вычисляют по формуле
«0 = / л(<7л)тах- (22-35)
Величину (?п)тах находят или по формуле (22.32) или по формуле
(22.33). Если точка подвеса расположена на нижнем днище бака, то
в выражении (22.35) надо положить fn = fnj(l + ₽;)•
Пример. Произвести расчет формы и частоты первого тона собственных продольных
колебаний корпуса воображаемой одноступенчатой жидкостной ракеты, имеющей два несу-
щих бака, частично заполненных топливом. Верхний бак заполнен горючим (уА=800/сГ/л/3)
на высоту Нд = 2,5 м и имеет размеры = 1 м, R2 = 2m, hi = 3 мм, h2 = 3 мм.
Нижний бак заполнен окислителем (уБ = 1140 кГ/м?) на высоту НБ = 3,7 м. Размеры
нижнего бака Rt, R2, h2 примем одинаковыми с размерами верхнего бака, hY = 4 мм. Ма-
териалы баков будем считать одинаковыми, причем Е = 7-105 кГ/см2, р = 0,3. Пусть /=
= 20 ле, k = 10, Д = 2 м.
Двигатель массой /Ид упруго подвешен к корпусу. Собственную частоту колебаний
двигателя как твердого тела на упругой подвеске примем равной Vд = 25 гц.
Расчетная схема в виде прямого неоднородного стержня с тремя упруго подвешен-
ными массами изображена на рис. 22.2. В массы тА и тБ включена вся масса топлива в
баках (в этом примере не будем делать различия между размерами И и //*);
шА = 625 кГ-сек,2/м, тБ = 1325 кГ-сек2/м.
Расстояния от вершины корпуса до сечений Xj следующие:
Хд = 9 де, хБ = 16,5 м, Хд = 18,2 м.
Примем за единицу погонной массы корпуса т0 = 15 кЕ-сек2/м, за единицу жесткости
EFq = 108 кГ, так что
тх = тт0, EFх — EF • EF0.
В масштабе т0 будет тА ж 42, тБ 89. Примем также = 6.
По формулам (22.1) — (22.8) вычислим вначале собственные частоты основного тона
осесимметричных колебаний баков с жидкостью, причем потенциальную энергию шпангоу-
та учитывать не будем. Для верхнего бака
w2 = 1,33-10~2 см, и = 2,38-10"2 см, /ппр = 5,8-10-3 кГ-сек2-см, Ui = 50 кГ-см,
U2= 45 кГ-см, /гпр = 190 кГ-см, соА = 32 800 {/сек2, vA = 28,8 гц.
Для нижнего бака
w2 — 2,81 • 102 см, и = 5,6-10-2 см, mnp = 61,7-10~3 кГ-см-сек2, Ur = 246 кГ-см,
[/2 = 200 кГ-см, /гпр = 892 кГ-см, о>Б = 14 500 1/седс2, vB= 19,2 гц.
По формулам (22.17) — (22.19) вычисляем параметры
а. = 1,78, ак = 2,0, Ь. =0,43, 6к = 0,43.
А Ь А ’ ’ Ь ’
Дальнейший расчет сведен в табл. 22.1. В столбцах (2) и (3) выписаны ординаты
графиков EF и т, в столбце (5) — значения формы колебаний первого тона, подсчитанные
по табл. 19.1 для заданного стержня при условии, когда массы т}- на стержне жестко
закреплены в сечениях № 4, 8, 9. Частота собственных колебаний первого тона в этом
случае 0)2 = 22 248 {/сек2', ее принимаем в качестве исходной для подсчета коэффициен-
тов по формулам (22.25), (22.27)
шл
₽а = 0,94—-----
“л “л
Рб = ^---Рд= 2 ' 2
ШБ-“л ®Д-">л
219
№ EF m 0 f\+D ft
1 2 3 4 5 6 7 8 9
0 0,5 1,0 1,0 1,000 1,000 0 —0,565 1,000
1 2,0 6,0 8,0 0,988 5,928 6,928 —0,577 1,021
2 1,3 4,0 18,0 0,934 3,736 16,592 -0,631 1,117
3 1,3 0,3 22,3 0,837 0,251 20,579 —0,728 1,288
4 1,3 0,3 22,9 0,658 0,197 21,027 -0,907 1,605
A 42 65,2 —3,051 5,398
5 2,5 4,0 111,2 0,428 1,712 22,936 — 1,137 2,012
6 1,7 0,5 115,7 0,166 0,083 24,730 — 1,399 2,475
7 1,7 0,5 116,7 —0,148 —0,074 24,740 — 1,713 3,031
8 1,7 0,5 117,7 —0,395 —0,198 24,468 -1,960 3,468
Б 89 207,2 3,712 -6,567
9 3,0 3,0 299,2 —0,490 — 1,170 22,800 -2,055 3,636
Д 6,0 308,2 -29,743 52,614
10 3,0 i 3,0 317,2 —0,496 — 1,488 19,842 —2,061 3,646
Таблица 22.1
mfl 0 ^ix~~ =(H)+(12) EF M>(*)= = 2(|4) (3)(15) 2<16> 0
10 11 12 13 14 15 16 17
1,100 0 0 0 0 0 0 0
6,126 7,126 0,237 7,363 3,68 3,68 22,09 22,09
4,468 17,720 0,473 18,193 13,99 21,36 85,44 129,62
0,386 22,574 0,710 23,284 17,91 53,25 15,98 231,04
0,482 23,442 0,947 24,389 18,76 89,92 26,98 274,00
226,72 250,664
8,048 485,412 1,184 486,596 194,64 303,32 1213,34 1514,32
1,238 494,698 1,421 496,119 291,83 789,79 394,90 3122,56
1,516 497,452 1,658 499,110 293,59 1375,21 687,62 4205,08
1,734 500,702 1,894 502,596 295,64 1964,44 982,24 5874,94
—584,463 —82,027
10,908 -655,582 2,131 —653,451 —217,451 2042,26 6126,90 12984,08
315,684 —328,990
10,938 —2,368 2,368 0 0 1824,44 5473,47 24584,45
N° (16)+D 'I __ *2 N 0 2L FF CM 4*
18 19 20 21 22 23 24 25
0 970,93 1,000 1,000 0 0 0 1,000 1,000
1 974,61 1,004 6,048 7,048 27,117 27,11 1,004 6,024
2 992,28 1,022 4,176 17,272 254,63 308,85 1,022 4,088
3 1024,18 1,055 0,334 21,782 417,04 980,52 1,055 0,316
4 1060,85 1,093 0,358 22,474 457,65 1855,12 1,093 0,328
A 3481,69 3,586 540,078 562,910
5 1274,25 1,312 6,884 1109,870 94710,4 97023,1 1,312 5,248
6 1760,72 1,813 1,644 1118,40 144785 336518 1,813 0,936
7 2346,14 2,416 2,918 1122,96 146536 627839 2,416 1,208
8 2935,37 3,023 4,569 1130,45 148590 922965 3,023 1,512
Б —5528,56 —5,694 2885,56 4020,58
9 3013,19 3,103 28,887 6935,02 142330 1213888 3,103 9,309
Д 43277,30 44,572 11920,00 18883,9
10 2795,37 2,879 24,867 30828,8 0 1356221 2,879 8,637
Продолжение тадл, 22.1
\ s * м f" ,1V /v ,VI
2G 28 29 30 31 32 33
0 —3,451 1,000 1,000 1,000 1,000 1,000 1,000
7,024 —3,447 0,999 0,996 0,994 0,993 0,993 0,993
17,136 —3,429 0,991 0,974 0,962 0,961 0,961 0,962
21,540 —3,396 0,984 0,936 0,908 0,904 0,905 0,906
22,184 —3,358 0,973 0,895 0,847 0,840 0,842 0,843
—7,403 2,145 1,252 1,151 1,167 1,175 1,177
27,760 —3,139 0,910 0,771 0,718 0,712 0,714 0,715
33,914 —2,638 0,764 0,571 0,472 0,474 0,476 0,477
36,028 —2,035 0,590 0,201 0,177 0,136 0,189 0,189
38,748 — 1,428 0,414 —0,111 —0,119 -0,103 —0,099 —0,098
4,637 — 1,343 —0,701 —0,653 —0,663 -0,667 —0,668
49,569 — 1,348 0,391 —0,257 —0,272 —0,252 —0,247 —0,247
—6,557 1,900 —0,492 —0,506 —0,484 —0,479 —0,479
67,515 — 1,572 0,456 —0,246 —0,278 —0,256 —0,252 —0,251
Так как после подвешивания масс mj на пружины форма колебаний оказывается не
самоуравновешенной, то требуется ввести смещение оси отсчета на величину D. Для
столбца (8) на основании формулы (22.30) получаем
ю
D=~ [ S(б)+2 Sт/Л/ (1+₽/) ] ’
L О (/)
10
m = £(3) + 2£mz, / = Л,Б,Д.
о (/)
Величины определяем линейным интерполированием:
Ла = (f 4 + 1)м 5 4 1»
Лб ~ (Л)№ 8 + [ (Л)к« 9 (Л)дъ el ’
Лд = (Л)лГо 9 + I ^Л)№ ю “ (Л>№ э1*
В строках №/ (j=A, Б, Д) помещены значения форм колебаний Л/0+0/) для по-
пружиненных масс mj.
Таким образом, в качестве исходной для дальнейшего расчета принимаем форму ко*
лебаний из столона (9).
Поправка равна
ю
№ \1
д№ = --7-2?10)-
о
Произвольную постоянную D для столбца (18) вычислим по формуле (22.30), положив
в ней = причем
4 5 4
^а=£(17)+у [S <17)-S(17)]’
О 0 0
8 9 8
о 'о о
9 10 9
'Гд = Х.(17)-!-^-Г^(17)-^(17) .
0 0 0
Столбец (19) получен из столбца (18) умножением на 1/(18)^=0. Форму /* (столбец 19)
используем для расчета частоты по формулам (22.31).
Для улучшения сходимости найдем дополнительное приближение значений f1}- (1+Р/),
применив для вычисления коэффициентов |Зу только что полученное значение со^. Чтобы
получить самоуравновешенную форму собственных колебаний сместим ось отсчета на ве-
личину D (столбец 27); коэффициент D подсчитываем так же, как и для столбца (8).
Окончательные значения формы колебаний первого приближения внесены в столбец (28).
В расчете второго и всех последующих приближений столбцы (5) — (8) не используются.
• В столбцах (29) — (32) даны значения формы собственных колебаний первого тона,
полученные во втором, третьем, ... , шестом приближениях.
Частота собственных колебаний, соответствующая формам первого—шестого при-
ближений, имеет следующие значения: coi2= 18 904; 11448; 11 000; 11 439; 11546;
11 557 Мсек.
Как и следовало ожидать, частота собственных колебаний системы сказалась ниже
наименьшей собственной парциальной частоты (в данном случае — частоты
В рассмотренном примере квадрат частоты продольных колебаний корпуса с уче-
том радиальной податливости обечаек и днищ баков примерно вдвое меньше квадрата
частоты, вычисленной без учета этих свойств.
222
§ 23. ПОПЕРЕЧНЫЕ КОЛЕБАНИЯ КОРПУСА РАКЕТЫ
Определение поперечных колебаний жесткого цилиндра с жид-
костью. Жидкость, как система с распределенными параметрами, имеет
бесконечный спектр форм и частот собственных колебаний, который
зависит от конфигурации сосуда. При малых поперечных колебаниях
на свободной поверхности жидкости возникают волны. В случае кру-
гового цилиндрического бака форма волны в радиальном направлении
представляется функцией Бессел:
лении форма колебаний изме-
няется по закону функции
sin т] [74].
На рис. 23.1 изображен
бак в виде прямого кругового
цилиндра с плоским дном. Бак
заполнен идеальной несжимае-
мой жидкостью. Частоту соб-
ственных колебаний жидкости
в неподвижном цилиндриче-
ском баке вычисляют по фор-
муле
первого рода. В окружном направ-
(23.1) Рис. 23.1
dJ1
где — корни уравнения--------------= 0, причем ^1 = 1,8412; £2 = 5,3315;
dr
^з = 8,5363,... Частота собственных колебаний не зависит от плотности
жидкости и растет с уменьшением радиуса бака. При HjRz^A частота
не зависит от глубины заполнения цилиндра. С повышением номера
тона собственная частота колебаний жидкости увеличивается.
В полете частота собственных колебаний жидкого топлива в ци-
линдрическом баке ракеты равна
где
(23.2)
£) — Пх£-
Как и для упругой системы, каждой форме собственных колебаний
жидкости соответствует ее приведенная масса тп. Для прямого круго-
вого цилиндра [48, 74]
тп = л^р-------1----th ( Zn 4). <23-3)
где р — плотность жидкости. Для первого тона колебаний т\ — 0,45 л/?3р,
для второго тона она в тридцать раз меньше.
Если на бак, который может перемещаться без трения по горизон-
тальной плоскости, в направлении оси Оу действует сила то
уравнения движения цилиндрического бака с жидкостью в абсолютной
системе координат хОу будут
ту + ^тпЪп = Ру, = — У, (23.4)
п=\
223
Здесь у — смещение оси бака, — обобщенная координата волновых
колебаний жидкости, т — масса бака с жидкостью.
Если положить Py(t) = O, то из уравнений (23.4) можно вычислить
частоты собственных колебаний системы бак — жидкость. При учете
только первого тона колебаний жидкости
= ; M1 Hi = — • (23.5)
/ 1 — Hi т
Частота собственных колебаний жидкости в незакрепленном бакс боль-
ше, чем в закрепленном.
Если задана сила Py(t), то из уравнений (23.4) можно найти сме-
щение бака y(t), обобщенные координаты лп(/), дополнительные силы
давления жидкости на стенку бака, возникающие вследствие вол-
новых колебаний.
Уравнения (23.4) получены для малых колебаний. Они справед-
ливы. когда максимальная амплитуда колебаний свободной поверхно-
сти жидкости в направлении оси бака Хшах^ОД R. При колебаниях
реальных жидкостей существует рассеяние энергии и поэтому, как по-
казывают опыты, даже при резонансе амплитуды колебаний жидкости
ограничены. Можно показать, что амплитуда колебаний жидкости не
может превышать радиуса бака. В самом деле, максимальная ампли-
туда возникает при резонансе, т. е. когда колебания совершаются с соб-
ственной частотой. Максимальное ускорение при этом равно Xmnxo)2.
Как только это ускорение будет больше ускорения ракеты вне поля сил
земного притяжения aX(-g) (см. § 17), частички жидкости будут отры-
ваться от остальной массы жидкости и волна начнет разрушаться. Сле-
довательно,
Хтах^ < •
С учетом формулы (23.2) получим
тах "
Для первого тона колебаний = 1,8412. При H/Ry \ максимальная
амплитуда
Хтах Ъ ”1.84 ’
Для приближенного определения амплитуды колебаний жидкости при
резонансе в уравнение вводится сила сопротивления, пропорциональная
скорости, так что вместо второго уравнения (23.4) используется урав-
нение
Ki + = —у.
(23.6)
Механическая модель волновых колебаний жидкости. Механической
моделью волновых колебаний жидкости может служить маятник (ма-
тематический или на пружине) (рис. 23.1). Каждому тону колебаний
соответствует свой маятник. Масса маятника равна приведенной массе
колеблющейся жидкости (23.3), длина математического маятника и же-
сткость пружины
/„ =-------5. k. = mm2 = 2а^.<-я>я/?2р _ (23.7)
По высоте бака
где находится
Cnth(SnH//?) " £2-1
масса маятника должна располагаться на таком уровне,
равнодействующая сил давления жидкости на стенку,
224
возникающих вследствие волновых колебаний. От невозмущенной сво-
бодной поверхности жидкости в круговом цилиндрическом баке масса
маятника должна отстоять на расстоянии
хп = — — th ( —Y (23.8)
п £п k " 2R J
Остальную массу жидкости можно считать как бы «затвердевшей».
Уравнения движения механической модели такие же, как (23.4).
Формулу (23.5) для собственной частоты колебаний системы мож-
но теперь получить из условия, что центр масс механической модели
при собственных колебаниях не смещается. Механическая модель при-
менима и для сложных форм баков, для которых известны приведенные
массы, частоты собственных колебаний и положение равнодействующей
давления жидкости на стенки при волновых колебаниях.
Расчетные схемы [43]. Для изучения изгибных колебаний ракету
можно представить в виде неоднородного стержня. Область примени-
мости теории стержня в ракетной технике связана с гибкими свойст-
вами корпуса ракеты и непригодна для ракет с малым коэффициентом
удлинения. В таких случаях основными могут быть местные колебания
элементов конструкции, колебания жидкого топлива в баках.
Когда низшая частота собственных изгибных колебаний корпуса
значительно выше первой частоты собственных колебаний жидкости
в баках, поперечные динамические перегрузки, обусловленные изгиб-
ными колебаниями корпуса и колебаниями жидкости, можно подсчи-
тать раздельно по сравнительно простым расчетным схемам: 1) жесткий
корпус с учетом колебаний жидкости, 2) упругий корпус с «затвердев-
шей» жидкостью.
Если же указанные частоты близки, то в качестве расчетной схемы
может быть принят упругий неоднородный стержень с маятниками.
Жесткий корпус с учетом колебаний жидкости.
Корпус в этом случае образует совместно с автоматом стабилизации
замкнутую систему, в которой могут возникать автоколебания на часто-
тах, близких к частотам собственных колебаний жидкости в баках. Если
автоколебания возможны и режим их определен, то поперечные дина-
мические перегрузки, действующие па корпус, вычисляют как для твер-
дого тела.
Упругий корпус с «затвердевшей» жидкостью. Тер-
мин «затвердевшая» жидкость означает только то, что в баке нс возни-
кает волновых колебаний жидкости. «Затвердевшая» жидкость может
свободно проворачиваться относительно стенок бака. Она совершенно
не увеличивает изгибную жесткость бака. Это как бы набор абсолютно
гибких и абсолютно гладких стержней, на которые можно мысленно
разделить столб жидкого топлива в баке. При расчете изгибных коле-
баний погонную массу топлива добавляют к погонной массе баков. При
этом расчетной схемой будет неоднородный упругий 'стержень. Мето-
дика расчета изгибных колебаний неоднородных стержней изложена
в § 20.
Определение собственных изгибных колебаний упругого неоднород-
ного стержня с маятниками. В поперечных сечениях, отстоящих от пе-
возмущенной свободной поверхности жидкости в баках на расстоянии
= ^- th (41 (I = А,Б), (23.9)
Cl V **<1 /
имеются массы (рис. 23.2)
/п, = л₽.?Р(---1----= (23.10)
15 Зак. 96
225
подвешенные на пружинах жесткостью
к. = т.& = t (i = A,B). (23.11)
Эти массы приближенно будут моделировать силовое воздействие ко-
леблющейся жидкости на стенки баков.
Если расстояние от вершины ракеты до невозмущенной свободной
поверхности обозначить через Лг-, то от той же вершины до массы
расстояние будет
х; = L- + Х(. = £г + th (с(-
' 11 1 V 2/?г J
Остальная жидкость считается «затвердевшей».
Рис. 23.2
Рис. 23.3
Для расчета форм и частот собственных колебаний можно приме-
нить или метод последовательных приближений, или метод начальных
параметров, которые изложены в § 20. Отличие состоит только в том,
что в сечениях х* надо учитывать дополнительные сосредоточенные
силы, вызванные смещением масс тг- относительно оси стержня.
Пусть fn(x) — искомая форма собственных поперечных колебаний
корпуса (стержня). Обозначим величины формы собственных колеба-
ний в сечениях, где расположены массы тг-, через fni. Считая попереч-
ные колебания гармоническими с частотой соп, найдем амплитуду сме-
щений массы mi относительно корпуса (рис. 23.3).
<23J2>
(О? — 0)2 mi
Тогда полное смещение массы /и, будет
rni-fni-'rfn^. (23.13)
Инерционная нагрузка от массы mt равна
(fat + fm^i)-
Представим ее в виде двух составляющих. Нагрузку пропор-
циональную форме собственных колебаний стержня, отнесем к погонной
226
нагрузке стержня и на этом основании массу тг- будем считать вклю-
ченной в тх — погонную массу стержня.
Дополнительная сосредоточенная сила в сечении xt- зависит от со-
отношения собственных частот колебаний жидкости со< и изгибных ча-
стот корпуса соп. Она равна
9 Г
i}t = —-------------
- <*п
Особенности метода последовательных приближений.
Уравнения (20.5) и (20.7) принимают вид
X k
1=1 (23.14)
MJx f f tnjndxz + £ т^пЛ (х — х') 4- С±х + С2. |
6 6 4 = 1 )
Здесь k — число баков, имеющих жидкость со свободной поверхностью,
погонная масса корпуса тх включает всю массу жидкости. При х < х*
mL = 0, а при х>х* т^О.
Так как масса mL относительно корпуса смещается на величину /глт].,
то в формулы (20.18) и (20.20) для вычисления коэффициентов D2 и Д
надо ввести дополнительные слагаемые
i k
ЛА + AJb = — j тх^п (х) dx —Vm^n (х*)^,
0 4=1
I k
AiDl + AJb = — J mx^n (x) (x - xT) dx — £ m$n (x*) (x* — xT) T](,
0 4=1
k k k
A = —*т). Л = /п + ^/п(., A3= I+ ^mi(x'~x^,
1=1 i=\ 4 = 1
(23.15)
гдеф(х) представлено выражением (20.11).
В связи с наличием сосредоточенных масс на пружинах несколько
видоизменятся и формулы для вычисления приведенной массы тп и
приведенной жесткости kn. С учетом выражения (23.13) получим
mn = \mxPndx + + 2/,(Zti(),
6 4=1
(23.16)
Для вычисления коэффициентов тп и kn нужно знать частоту собственных
колебаний корпуса — ее берут из последнего приближения.
Особенности метода начальных параметров. Они отно-
сятся лишь к условиям сопряжения участков в местах расположения масс
т(. Здесь возникают дополнительные сосредоточенные поперечные силы
15*
227
Сечения х = х* выделяют в самостоятельные участки, для которых
EJx=^ooy tnx = tn;. Тогда для сопрягаемых участков, расположенных сле-
ва и справа от х*, вместо равенств (20, г) будем иметь:
1) Ли-= Лфч-1), 2) fni = f
3) (EJf^ = (EJf^
4) (EJf^+ni^
В остальном порядок расчета аналогичен изложенному в § 20.
Способ замены колеблющейся жидкости маятниками в случае из-
гибных колебаний дает удовлетворительные результаты, если со; и (оп
не очень близки. В противном случае требуется более тщательный ана-
лиз свойств системы.
Приближенный учет влияния следящей силы тяги двигателей на
частоту изгибных колебаний корпуса рекомендуется проводить по фор-
мулам (20.41) —(20.43).
Определение вынужденных изгибных колебаний корпуса. В полете
вынужденные изгибные колебания корпуса могут быть вызваны или
порывами ветра, или поперечными управляющими силами. Вынужден-
ные колебания корпуса выражаются зависимостью (20.25), причем
обобщенные координаты qn(t) определяют из уравнений (20.32), пра-
вую часть которых при различных внешних силах составляют по общей
формуле (18.35).
Управляющие органы вызывают стационарные изгибные колебания
корпуса в двух случаях:
1. Автоколебания в замкнутой системе, состоящей из упругого кор-
пуса и автомата стабилизации, причем частота соа таких автоколеба-
ний близка к собственной частоте изгибных колебаний корпуса.
Умножив выражения (23.14) — первое на qa и второе на (о^а, где
qa — амплитуда автоколебаний точки приведения корпуса, определим
поперечную силу Q и изгибающий момент М в любом поперечном се-
чении корпуса.
2. Автоколебания в сервоприводе автомата стабилизации — замкну-
той системе, состоящей из органа управления (упруго подвешенной по-
воротной камеры), рулевой машины и контура обратной связи [43]. Ча-
стота Оса таких автоколебаний не зависит от изгибной частоты корпуса.
Она незначительно отличается от собственной частоты колебаний пово-
ротной камеры. Колебания управляющей камеры с частотой соса будут
вызывать вынужденные колебания корпуса ракеты, которые можно
определить из уравнения (20.32), представив силу Р?1(/) в виде
Рп (t) = RpfnPba sin соса/,
где RP — градиент управляющей силы, fnP — значение формы попереч-
ных колебаний в сечении, которому передается управляющая сила,
ба—амплитуда автоколебаний поворотной камеры в сервоприводе.
Так как амплитуда вынужденных колебаний корпуса в этом случае
будет зависеть от соотношения частот юса и о)??, то желательно иметь
частоту собственных колебаний подвески поворотной камеры значи-
тельно отличающейся от частот собственных колебаний первых тонов
изгибных колебаний корпуса.
Изгибные колебания корпуса вызывают, кроме того, вынужденные
колебания трубопроводов и различных упруго подвешенных масс. По-
этому желательно не допускать, чтобы частоты собственных колебаний
упруго подвешенных масс и трубопроводов были близкими к собствен-
ным частотам изгибных колебаний корпуса.
228
ГЛАВА IV
ЗАДАЧИ ТЕПЛОПРОВОДНОСТИ
В ТОНКОСТЕННЫХ КОНСТРУКЦИЯХ
§ 24. УСЛОВИЯ ТЕПЛООБМЕНА КОНСТРУКЦИИ С ОКРУЖАЮЩЕЙ
СРЕДОЙ. ОСНОВНЫЕ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
И КРАЕВЫЕ УСЛОВИЯ
Одна из особенностей ракет состоит в том, что их конструкция в
процессе полета подвергается интенсивному тепловому воздействию со
стороны окружающей среды и рабочего тела двигателей. При проекти-
ровании и создании ракет это приводит к необходимости учитывать
влияние теплового воздействия на работоспособность конструкции.
Влияние теплового воздействия проявляется в следующем [22, 70,80]:
1) снижаются показатели механических свойств материалов с ростом
температуры, из-за чего необходимо применять жаростойкие материалы
и усиливать элементы конструкции; 2) происходит температурная
деформация элементов конструкции, обусловливающая дополнитель-
ные напряжения; 3) появляется ползучесть при высоких температурах
и нагрузках. Для учета влияния этих факторов на работоспособность
конструкции необходимо располагать достаточно достоверными дан-
ными о ее температурном состоянии, что, в свою очередь, требует чет-
кого представления и умения количественно охарактеризовать тепловые
процессы, происходящие в конструкции ракет и ракетных двигателей.
Ранее рассмотрение подобных вопросов не входило в сферу дея-
тельности специалистов в области строительной механики и расчетов
на прочность. Для современных ракетных конструкций вопросы тепло-
вого воздействия и прочности оказываются тесно связанными между
собой. Без их совместного решения трудно представить дальнейшее
совершенствование ракетной техники.
Таким образом, определение температурного состояния теплонапря-
женных элементов конструкции необходимо для суждения о ее работо-
способности, для обоснованного выбора материала и является ступенью
к последующему расчету на прочность. Наряду с экспериментальными
способами исследования теплового режима конструкций в настоящее
время разработаны достаточно надежные методы расчета температур-
ных полей, которые широко внедряются в инженерную практику. В на-
стоящей главе рассматриваются методы расчета температурных полей
в тонкостенных элементах конструкций, наиболее характерных для ра-
кетной техники.
Температурное состояние конструкции определяется как процес-
сами теплопроводности в ее элементах, так и условиями теплообмена
этих элементов с окружающей средой. Ниже дается краткая характе-
ристика наиболее типичных случаев теплообмена в ракетных конструк-
циях, а вопросы теплопроводности более подробно обсуждаются в по-
следующих параграфах настоящей главы.
Условия теплообмена конструкции с воздушным потоком, окружаю-
щим пространством, средой в полости отсеков и баков ракеты и пото-
ком рабочего тела в двигателе определяются двумя основными физи-
чески отличными друг от друга процессами: конвекцией и излучением.
При конвекции тепло передается благодаря перемещению частиц среды
229
относительно поверхности твердого тела. Передача тепла излучением
происходит в виде энергии электромагнитных волн, которые для своего
распространения не требуют промежуточной среды.
Теплообмен конвекцией. Теплообмен конвекцией играет ведущую
роль при аэродинамическом нагреве ракеты на активном участке по-
лета и на участке спуска в плотных слоях атмосферы, а также в теп-
ловых процессах, происходящих в ракетных двигателях [65, 83, 95].
При движении ракеты с высокой скоростью в сравнительно плот-
ных слоях атмосферы часть кинетической энергии потока, обтекающего
поверхность, превращается в тепло. Оно вызывает повышение темпе-
ратуры в прилегающем к поверхности слое потока, называемом погра-
ничным слоем. От пограничного слоя тепло конвекцией передается
к поверхности ракеты и идет на нагрев ее конструкции.
Подобным образом происходит процесс теплообмена при движении
с высокой скоростью продуктов сгорания по соплу ракетного двигателя
(жидкостного — ЖРД или на твердом топливе — РДТТ). Движение га-
зов по камере сгорания двигателя происходит с относительно меньшей
скоростью. Поэтому конвективный теплообмен в камере сгорания в
меньшей мере связан с торможением газа у стенки и переходом кине-
тической энергии потока в тепловую. Здесь высокая температура в по-
граничном слое поддерживается благодаря выделению тепла при хими-
ческих реакциях горения топлива и передаче тепла в пограничный слой
из основного потока продуктов сгорания вследствие перемешивания.
В конструкции камеры сгорания двигателя можно выделить уча-
стки поверхности, относительно которых газ движется под действием
подъемных сил, связанных с различной температурой и плотностью ча-
стиц в разных точках объема газа. Такое движение, называемое сво-
бодной конвекцией, происходит, например, вблизи форсуночной головки
ЖРД и в застойной зоне около переднего днища РДТТ. Теплообмен
при свободной конвекции обычно менее интенсивен, чем при рассмот-
ренных выше случаях так называемой вынужденной конвекции, но
все же может заметно повлиять на температурный режим конструкции.
В РДТТ свободная конвекция воздуха в полости камеры сгорания
влияет также на температурный режим заряда твердого топлива в про-
цессе хранения ракеты.
Кроме камеры сгорания ракетного двигателя, свободная конвекция
и связанный с ней теплообмен происходят в полости сухих отсеков ра-
кеты и незаполненной части баков. Таким же способом передастся тепло
от стенок баков к компонентам топлива в процессе полета, подготовке
к старту или хранения жидкостной ракеты в заправленном состоянии.
В отличие от этого при движении компонентов топлива по трубопро-
водам и охлаждающему тракту ЖРД механизм передачи тепла соот-
ветствует вынужденной конвекции.
Интенсивность конвективного теплообмена характеризуется коэф-
фициентом теплоотдачи а, который служит коэффициентом
пропорциональности в формуле Ньютона
Q = а (Тс — Тп) S. (24.1)
Здесь Q — количество тепла, передаваемое от среды к поверхности тела
в единицу времени, называемое тепловым потоком и измеряемое в еди-
ницах мощности, например в вт; Тс и Гп— температура среды и поверх-
ности; S — площадь поверхности тела. Тепловой поток q, приходящийся
на единицу площади поверхности, называется удельным тепло-
вым потоком и измеряется в вт/м2. Из формулы (24.1) следует, что
<7 = а(Тс-Тп). (24.2)
Коэффициент теплоотдачи а зависит, главным образом, от плотно-
сти среды и скорости ее движения относительно поверхности и изме-
ряется в вт!м2 • град. Возможности строгого аналитического решения
230
задачи конвективного теплообмена ограничены. Это значит, что коэф-
фициент теплоотдачи в общем случае не удается представить в виде
функции всех параметров, от которых он зависит. Можно указать два
основных пути решения задачи конвективного теплообмена.
Первый из них основан на экспериментальном изучении единичных
процессов теплообмена с последующим обобщением и распространением
полученных результатов на основе теории подобия на более широкую
группу процессов [31, 57].
Сущность второго состоит в изучении свойств пограничного слоя,
определении, на основе упрощающих предположений, профилей (рас-
пределения) скорости и температуры в этом
слое и вычислении коэффициента теплоотда- / Qnad
чи по распределению температуры среды у / па #
поверхности тела [1]. При использовании RQnad
методов теории пограничного слоя также Jr
требуется экспериментальная проверка по- AQnad
лученных результатов.
В настоящее время накоплено большое
количество теоретических и эксперименталь- Рис 24 1
ных результатов исследования конвективно-
го теплообмена. Некоторые из них относятся
к процессам теплообмена, характерным для ракетной техники, и будут
использованы ниже при рассмотрении конкретных случаев.
Теплообмен излучением. Наряду с конвективным теплообмен излу-
чением также оказывает заметное влияние на температурное состояние
ракетных конструкций. Передача тепла в космическом пространстве и
в сильно разреженных слоях атмосферы осуществляется посредством
теплового излучения. Температурный режим космических объектов и
головных частей ракет на значительном удалении от поверхности Земли
зависит, главным образом, от способности их материала поглощать и
излучать лучистую энергию.
Излучение играет важную роль в передаче тепла и при движении
ракеты с большой скоростью в сравнительно плотных слоях атмосферы.
Если температуры конструкции и воздушного потока при торможении
у ес поверхности достаточно велики, то количество тепла, передаваемое
излучением, сравнимо с передачей тепла конвекцией. В таких случаях
необходимо также рассматривать теплообмен излучением между от-
дельными элементами конструкции и самооблучение вогнутых поверх-
ностей.
В ракетных двигателях тепловое взаимодействие продуктов сгора-
ния и оболочки камеры наряду с конвекцией в некоторой степени опре-
деляется и излучением. Следует ожидать, что с ростом температуры
рабочего тела в двигателях теплообмен излучением будет играть еще
более значительную роль.
Применяемые в конструкции ракет материалы обычно непрозрачны
для теплового излучения. Поэтому процессы излучения и поглощения
происходят на их поверхности. Падающий на поверхность непрозрач-
ного тела лучистый ПОТОК Спад (рИС. 24.1) частично поглощается (ДСпад),
частично отражается (/?Спад), причем А и /?=1—А—поглощательная
и отражательная способности поверхности по отношению к падающему
лучистому потоку. Отраженный лучистый поток вместе с собственным
излучением образует эффективный лучистый поток
Q’ = Жад + eQ°, <2° = CToT’nS, (24.3)
где в и Тп— степень черноты поверхности и ее температура;
по = 5,77 • 10-8 вт/м2 (°К)4 — коэффициент излучения абсолютно
черного тела.
231
Количество энергии, теряемое телом в единицу времени в процессе
теплообмена излучением, называется результативным лучистым пото-
ком Q. С одной стороны, он равен разнице эффективного излучения и
падающего лучистого потока
Q = Q Спад»
с другой, — разности собственного излучения и поглощенного телом лу-
чистого потока
Q = eQ°- Жад-
Исключая из последних двух равенств величины <2Пад, получаем важ-
ное для расчета теплообмена излучением соотношение
(24.4)
Для абсолютно черного тела (е = Л = 1 и /? = 0) эффективное излу-
чение равно собственному. Такой же результат получается и для нечер-
ного тела, если с другими телами оно находится в состоянии темпе-
ратурного равновесия. Когда температурное равновесие отсутствует,
то Q=£0. Определение величины Q и составляет основную задачу рас-
чета теплообмена излучением.
Расчет теплообмена излучением между нечерными телами имеет
особенности, связанные с различием излучательных и поглощательных
свойств их поверхности. Учет этих особенностей приводит к большим
математическим трудностям. Решение задачи упрощается, если погло-
щательная способность поверхности совпадает со степенью черноты
(Л = е) и не зависит от падающего излучения, что соответствует мо-
дели идеального серого тела. Большинство технических материалов
с шероховатой или окисленной поверхностью по своим свойствам близки
к серому телу. Для расчета теплообмена излучением между элементами
ракетных конструкций с такой поверхностью можно применить методы,
известные в литературе [20, 111].
Основные понятия и уравнения теории теплопроводности. Распро-
странение тепла в элементах конструкции, как во всех твердых телах,
определяется процессами теплопроводности. Поэтому задачи по расчету
распределения температуры в конструкции являются задачами теории
теплопроводности.
Процесс теплопроводности описывается при помощи поля темпера-
туры. Температурное поле может быть одно-, двух- или трехмерным,
если температура зависит соответственно от одной, двух или трех про-
странственных координат. Нестационарное поле изменяется во времени,
стационарное не изменяется.
Геометрическое место точек тела, имеющих в данный момент вре-
мени одинаковую температуру, называют изотермической поверхностью.
Сечение таких поверхностей плоскостью дает семейство изотерм. Наи-
более резко температура меняется в направлении нормали п к изотер-
мической поверхности. Предел отношения
lim (\ = grad Т
дп-»о \ Дп / дп
называют градиентом температуры. Это вектор, направленный по нор-
мали к изотермической поверхности в сторону роста температуры.
Связь между векторами удельного теплового потока q и grad Г уста-
навливается соотношением
q=—KgraAT. (24.5)
232
Коэффициент пропорциональности X называется коэффициентом тепло-
проводности и измеряется в вт1м*град. Он определяется эксперимен-
тально и зависит от рода материала, его структуры и температуры.
К теплофизическим характеристикам материала тела также отно-
сятся удельная теплоемкость с дж/кг -град и плотность р кг/м\ В не-
которых случаях в теле действуют внутренние источники тепла, которые
характеризуются объемной мощностью qv вт/м?.
В общем случае величины Z, с, р и qv могут зависеть от простран-
ственных координат и температуры. Если в ожидаемом диапазоне изме-
нения температуры тела изменениями этих величин можно пренебречь
в сравнении с их средними значениями, а само тело однородно, то ма-
тематическое описание процесса теплопроводности дается дифферен-
циальным уравнением с постоянными коэффициентами:
-- .«vr + i + «L + \ + , (24.6)
dt ср \ дх2 ду2 dz2 J ср
где а = К/ср— коэффициент температуропроводности, м2/сек.
Когда внутренние источники тепла в теле отсутствуют (qv = 0),
выражение (24.6) превращается в уравнение Фурье
— = avT. (24.7)
dt
Если процесс теплопроводности стационарный (дТ/dt = 0) и qv — 0, то
получаем уравнение Лапласа
УТ = О. (24.8)
Выражение для оператора Лапласа v зависит от вида системы коор-
динат, в которой рассматривается процесс теплопроводности.
Краевые условия в задачах теплопроводности. Приведенные выше
дифференциальные уравнения отражают общие черты, свойственные
всем процессам теплопроводности. Особенности конкретного процесса
устанавливаются краевыми условиями, которые делятся на временные
и граничные. Они указывают на особенности протекания процесса во
времени и на границах (поверхностях) тела. Для нестационарных про-
цессов временные условия содержат начальное распределение темпе-
ратуры в теле.
В граничные условия входят условия теплообмена тела с окружаю-
щей средой, определяемые конвекцией и излучением. Если рассматри-
ваемое тело имеет идеальный тепловой контакт с другими твердыми
телами, то на участках контакта передача тепла определяется тепло-
проводностью и граничные условия задаются, исходя из непрерывности
температурного поля при переходе через границу между телами.
Пусть в общем случае рассматриваемое тело имеет произвольную
внешнюю поверхность S' и внутреннюю полость с поверхностью S"
(рис. 24.2,а). К обеим поверхностям подводятся конвективные удельные
тепловые потоки qK = а' (Т'с —Т'пУ, q"K = а" (Т"с — Т") и отводятся удельные
результативные потоки q' — q^', q" = — qn. Параметры,
помеченные штрихом, относятся к внешней поверхности тела, двумя штри-
хами — к внутренней; а — коэффициент теплоотдачи, Тс— температура среды,
Тп и е — температура и степень черноты поверхности. Поглощаемый телом
удельный лучистый поток qJi считается нормальным к поверхности. Вели-
чины а, е, Тс и qn в общем случае могут зависеть от времени, температуры
Тп и положения точки на поверхности. Величина qJl определяется не толь-
ко падающим излучением от источников лучистой энергии, но и теплообме-
ном между отдельными участками поверхности тела.
233.
Граничные условия для произвольной точки поверхности тела имеют
вид (штрихи опущены)
Х17 | п = “ q = а (?с ~ ?п) + ?л ” ’
где п — внешняя нормаль к поверхности. Это соотношение удобно привести
к безразмерному
i I <24-э>
Jo 1 О'/l In
где Bi = a/i/Az, ft=T/Ty n = n/hy N= (eoo/a)T3, T = Tc + (q^/a). За харак-
терный размер здесь принята толщина h (в общем случае переменная)
в направлении, нормальном к срединной поверхности, одинаково уда-
Рис. 24.2
.ленной от внешней и внутренней поверхности тела. Приведенная тем-
пература среды Т позволяет учесть в едином выражении конвективный
и лучистый тепловые потоки, поглощаемые поверхностью тела.
Если в соотношении (24.9) N$n мало в сравнении с 1—то соб-
ственное излучение с поверхности можно не учитывать. В случае нагрева
это можно сделать при jV.^0,05.
Критерий Био Bi в формуле (24.9) является отношением термиче-
ского сопротивления тела к термическому сопротивлению теплоотдачи
от среды к поверхности и характеризует степень неравномерности рас-
пределения температуры по толщине тела. При больших значениях
этого критерия (BiZ> 10) правую часть формулы (24.9) можно прирав-
нять нулю и считать, что на поверхности устанавливается так назы-
ваемая равновесная температура Г, соответствующая равновесию кон-
вективного теплового потока и результативного излучения (^к = ?)- От-
водом тепла внутрь тела вследствие теплопроводности при этом прене-
брегают. Значение равновесной температуры определяют из алгебраи-
ческого уравнения
W + = (24.10)
для решения которого удобно пользоваться графиком (рис. 24.3).
Наоборот, при малых значениях критерия Био (Bi^0,l) перепад
температуры по толщине h незначителен и температуру тела в этом на-
правлении можно считать одинаковой (тонкостенное в тепловом отно-
шении тело). Тогда уравнение теплопроводности объединяется с гра-
ничными условиями, образуя одно выражение. Пусть для оболочки по-
стоянной толщины h (рис. 24.2,6) процесс нестационарной теплопро-
водности описывается уравнением (24.7) в виде
„ дТ . / д2Т . д*Т \
Р dt Н dx2 dz2 ) ’
•234
Интегрированием этого уравнения по z можно получить
Л/2 Л/2
ср— f Tdz = \-— С Tdz + x—I —X—| , (24.11)
к dt J dx* J dz ! г=л/2 dz |г=_л,2 ' ’
—h/2 —h/2
причем
дт 1 дТ I дТ I дТ \
dz \z—h/2 dn" In’ dz \z=—h/2 dn' |n
Так как температура по толщине принимается постоянной, то
h/2
j* Tdz=Th и Тп = Т„ = Т.
—h/2
Подставляя в выражение (24.11) граничные условия (24.9), находим
cph = М + 2а (f — Т) — 2е<г0Т4. (24.12)
здесь
О / । v qp CL Т' -|“ ® Т а / I //
2а = а -г а , Т =-------!, 2е = е + е .
а' а"
Когда тело имеет малое терми-
ческое сопротивление распростране-
нию тепла не только по толщине, но
и в других направлениях, его темпе-
ратуру можно считать одинаковой
по всему объему. Тогда отдельные
участки внутренней поверхности те-
ла (см. рис. 24.2,а) находятся в со-
стоянии температурного равновесия,
т. е. q" = G и = е"а0Т4. Это ра-
венство справедливо, если среда в
полости тела не поглощает лучистую
энергию и отсутствуют внутренние
источники излучения. В этом случае
теплообмен излучением во внутрен-
ней полости тела не оказывает
влияния на его температуру. Участ-
ки произвольной по форме внешней
поверхности тела обмениваются
между собой лучистой энергией. Поэтому тепловые потоки дл и е'ооТ4
можно рассматривать независимо друг от друга только для выпуклой
внешней поверхности.
Для тела с малым термическим сопротивлением можно осреднить
условия теплообмена по его поверхностям:
cpV — = С [а' (?; — Г) + qn — е'^Т4] dS' + С a" (fc — Т) dS" =
dt J J
S' sn
-- lacp (^cp 7*) ecp^0^4] >
(24.13)
где
aCD = — f a' dS’ + -1- f a" dS", eCD = — C e' dS',
p S' ,) S' .) cp S' J
S' S" S'
1
Ctcp5
(a'Tc + qn)dS'
235
Если тело сплошное, т. е. внутренняя полость отсутствует, то в вы-
ражениях для осредненных значений коэффициента теплоотдачи аср и
температуры среды Гср пропадают интегралы по поверхности S".
В случае вогнутой внешней поверхности с постоянной степенью черноты
е' при осреднении можно приближенно считать, что
где Si — минимальная выпуклая поверхность, «обтягивающая» тело (см.
рис. 24.2,а).
В наиболее простом случае, когда поверхность сплошного тела выпукла,
условия теплообмена на ней одинаковые и дл = 0, получается, что аср=а'
и Тср = Тс, а уравнение (24.13) принимает вид
cpV-—== [а/(Тс -Т)-е'о0Г]5'. (24.14)
dt
§ 25. СПОСОБЫ РЕШЕНИЯ ЗАДАЧ ТЕПЛОПРОВОДНОСТИ
Математически сформулированная задача теплопроводности содер-
жит дифференциальное уравнение и необходимые краевые условия.
Среди различных способов решения уравнений, описывающих процесс
Рис. 25.1
теплопроводности, можно выделить
аналитические, численные, графиче-
ские и решение с помощью аналогов.
Аналитические способы решения
делятся на точные и приближенные и
занимают особое место. Получаемые с
их помощью функциональные зависи-
мости позволяют проанализировать
влияние отдельных параметров на тем-
пературное поле в конструкции. Эти
способы удобно использовать при про-
ведении проектировочных расчетов,
связанных с выбором оптимальной гео-
метрии или материалов конструкции.
Определение стационарных температурных полей. Для часто встре-
чающихся одномерных стационарных температурных полей задача сво-
дится к решению обыкновенного дифференциального уравнения. На-
пример, для плоской стенки толщиной h (рис. 25.1, а) с заданными
температурами поверхностей 7\ и Т2 интегрирование одномерного урав-
нения Лапласа (см. § 24)
^- = 0
dx2
дает
Т = Сгх + С2.
Постоянные Cj и С2 определяют из граничных условий на поверхно-
стях стенки: при х = 0 Т = 7\ и при х = h Т = Тг', получают формулу
для распределения температуры по толщине плоской стенки:
Т = Т1-(Т1-Т2)^- .
h
(25.1)
Удельный тепловой поток через стенку с коэффициентом теплопровод-
ности X согласно формуле (24.5) равен
« 1 rrt л dT 7\— Т2
q = — X grad Т = — X----= —-------
dx h/k
(25.2)
236
Величину Л/Х принято называть термическим сопротивлением плоской
стенки.
Процесс стационарной теплопроводности в цилиндрической стенке
(рис. 25.1,6) с заданными температурами поверхностей описывается также
одномерным уравнением Лапласа в форме
d2T 1 dT ___ \ d / dT\ д
dr2 r dr r dr \ dr J
Интегрированием этого уравнения получают
Т = Ci In г + С2.
Постоянные определяют из граничных условий: при г = t\ Т = Т19 при
г г2 Т = Т2. Тогда
Т 7\ — (7\ — Т2) |П(Г/Г1) . (25.3)
1п(г2/Г1)
Если толщина h = r2—цилиндрической стенки мала в сравнении с
радиусом /д, то, разложив логарифм в ряд и ограничившись в нем дву-
мя первыми членами, формулу (25.3) можно представить в виде
г — rY 1
Т = Т1_(Т1-Т2)—~
__fi
h
ri 2 к гх
С точностью до 5% вторыми членами в числителе и знаменателе дроби
можно пренебречь, если Л/гд^ОД. Тогда распределение температуры в
цилиндрической стенке допустимо считать линейным и расчет вести по
формуле (25.1), отсчитывая координату х от внутренней поверхности
цилиндрической стенки. Это упрощение важно иметь в виду для тонко-
стенных оболочек вращения, которые являются типичным элементом
ракетных конструкций.
Стационарная теплопроводность в оболочке толщиной h (см. рис.
24.2,6) описывается уравнением
U—-г2а(Т-Т)=0. (25.4)
dx-
Это уравнение получается из выражения (24.12) при dT!dt = Q и пре-
небрежении влиянием теплообмена излучением. Если коэффициент теп-
лоотдачи а и температура среды Т не зависят от координаты х, то общее
решение уравнения (25.4) будет
Т = Т + Dr exp [К2a/Mi х] + D2 exp [— V2a/Mi x] —
= T + Di sh 2a/kh x) + D2 ch (]/2a/X/z x). (25.5)
Постоянные в решении определяют из граничных условий. Например,
при заданной температуре TQ в начале координат и идеально теплоизоли-
рованном сечении оболочки при х = / получаются два соотношения для
определения Di и О2-
TQ = Т -г D2 и D[ ch g + D2 sh £=0, где £ =]/2a/X/i /. Отсюда D2 = TQ — T и
A = -(T0-f)cth£.
Подставляя выражения для D\ и D2 в решение (25.5), находим
т = Т + (То — Т)
Ч'-т)
ch£
(25.6)
237
Тепловой поток, передаваемый путем теплопроводности через сечение
оболочки при х = 0 в направлении оси х, равен
Qo=-U^-| - ^4(T0-T)th£= 2a/(T0-f) 41 • (25.7}
dx |х=о I £
Для решения многомерных стационарных задач можно использо-
вать приближенную математическую модель, в которой непрерывный
процесс теплопроводности в теле заменяется процессом в дискретной
системе, состоящей из узловых точек, соединенных теплопроводящими
стержнями. На рис. 25.2, а изображена схема такой системы для двух-
мерной задачи. При этом область, в которой решается задача, деляг
Рис. 25.2
взаимно перпендикулярными плоскостями на квадратные в плане уча-
стки со сторонами Дх = Ду. В середине каждого участка помещают узло-
вую точку, в которую сходятся тепловые потоки от соседних точек:
Q2 = x4^(r2-T0), Q3 = ^(T3-T0),
by bx by
Qt=K-^-(Tt-T9).
bx
Сумма этих тепловых потоков при установившемся процессе должна
равняться нулю. Отсюда
4Т0 = 7\ + Т2 + Т3 + 7\. (25.8}
Подобное выражение можно получить, если представить двухмерное
уравнение Лапласа
д*т , &т _ п
дх2 + ду2 ~
в конечных разностях. Возникающая при этом погрешность в случае
Дх = Ду пропорциональна (Дх)4. Она характеризует точность решения
задачи с помощью приближенной математической модели процесса теп-
лопроводности.
Соотношения вида (25.8) можно составить для всех внутренних
узловых точек рассматриваемой области. Вместе с соотношениями для
граничных узловых точек, которые получают с учетом конкретных гра-
ничных условий задачи, они составляют систему алгебраических урав-
нений; решая последние, находят значения температур в узловых точ-
ках.
Рассмотренной математической модели процесса стационарной теп-
лопроводности соответствует электрический аналог (рис. 25.2,6), в ко-
238
тором вместо теплопроводящих стержней узловые • точки соединены'
электрическими сопротивлениями. Величина этих сопротивлений про-
порциональна термическому сопротивлению теплопроводящих стерж-
ней. Распределение электрических потенциалов и в узловых точках
аналога в определенном масштабе соответствует распределению темпе-
ратур в узловых точках математической модели процесса теплопровод-
ности, а тепловому потоку Q соответствует электрический ток I. Про-
цесс решения задачи с помощью аналога сводится к измерению потен-
циалов в узловых точках и последующему переходу к соответствующим
значениям температур.
Определение нестационарных температурных полей. Определение
нестационарного температурного поля обычно связано с преодолением
значительно больших математических и технических трудностей.
В большинстве случаев точные аналитические способы применимы
здесь лишь для решения сравнительно простых задач. Пример точного
решения дифференциального уравнения теплопроводности для двух-
слойной пластины приведен в § 55.
Помимо дифференциального уравнения в частных производных про-
цесс нестационарной теплопроводности в теле можно описать с помо-
щью приближенной математической модели. Эта модель основана на
приближенной замене реальной физической системы с распределенны-
ми параметрами эквивалентной ей системой с сосредоточенными пара-
метрами. При этом утрачивается свойство непрерывности температур-
ного поля. Теперь оно характеризуется отдельными значениями темпе-
ратур в дискретно расположенных точках системы.
Для одномерного процесса теплопроводности в теле такое представ-
ление равносильно условному разбиению его на элементарные объемы
в виде отдельных слоев толщиной Ах (рис. 25.3,а). Полная теплоем-
кость срДх каждого слоя сосредоточивается в его середине. Получив-
шиеся узловые точки соединяют теплопроводящими стержнями с тер-
мическим сопротивлением Ах/Х. Следовательно, распределение темпе-
ратуры между узловыми точками принимается линейным. Таким обра-
зом, свойства реального тела одновременно поглощать тепло и оказы-
вать сопротивление проходящему тепловому потоку приписываются в.
данной модели порознь двум разным элементам.
Изменение температуры f-той узловой точки описывается обыкновен-
ным дифференциальным уравнением
СрДх = + T‘+1-Ti = Т. -1-2Г. + Т,+1 (25 9>
dt Ьх/к kxfk \х/К
Число уравнений такого типа равно числу узловых точек модели. На-
чальным условием для системы уравнений является распределение
температуры в узловых точках в момент времени / = 0.
Уравнение вида (25.9) можно получить также из одномерного урав-
нения Фурье (24.7), если его правую часть представить в конечных
разностях:
д*Т _ Тх -! —2TZ + Tf41
dx2 (Ах)2
Погрешность такого представления оказывается пропорциональной
(Ах)2, что можно установить разложением зависимости Т от х в ряд в
окрестности f-той точки. Поэтому погрешность системы дифференци-
альных уравнений вида (25.9) имеет тот же порядок. С уменьшением
Ах описание процесса теплопроводности рассматриваемой математиче-
ской моделью неограниченно приближается к описанию с помощью
дифференциального уравнения.
239
Аналитическое решение системы уравнений вида (25.9) теряет прак-
тически смысл уже при трех и более узловых точках, так как оно свя-
зано с решением алгебраического уравнения соответствующей степени.
В общем случае эту систему можно решить численным интегрирова-
нием, причем для этого целесообразно использовать электронную циф-
ровую вычислительную машину (ЭЦВМ). Для интегрирования системы
удобно также применить электронные аналоговые вычислительные ма-
шины (ЭАВМ) с усилителями постоянного тока. На рис. 25.3,6 пока-
Рис. 25.3
зана ячейка схемы такой машины. Треугольником обозначен усилитель
постоянного тока с емкостью С и сопротивлением R/2 в цепи обрат-
ной связи. На вход усилителя через сопротивления R подаются напря-
жения, пропорциональные текущим температурам соседних с /-той узло-
вых точек. Температуры этих точек должны быть взяты с обратным
знаком. На выходе из усилителя появляется напряжение, пропорцио-
нальное текущей температуре 7\. Масштабом времени при переходе от
процесса решения задачи на ЭАВМ к процессу нестационарной тепло-
проводности в теле служит отношение (Ax)2/aRC.
Для решения нестационарных задач с помощью приближенной ма-
тематической модели можно воспользоваться тем, что процесс тепло-
проводности в этой модели аналогичен процессу распространения заря-
дов в электрической цепи, составленной из сопротивлений и конденса-
торов. Ячейка такой цепи изображена на рис. 25.3, в. Изменение на-
пряжения щ в /-той точке цепи описывается обыкновенным дифферен-
циальным уравнением
С dill = Щ-1 — ui — Ui ui-l^2uj -I- ^4.1 (ух*
dt R ’’ R R ’ 1 ‘ 7
которое аналогично уравнению (25.9). Из уравнений (25.9) и (25.10)
следует, что термическому сопротивлению кх/К соответствует электри-
ческое сопротивление /?, полной теплоемкости срДх — емкость конден-
сатора С, удельному тепловому потоку — электрический ток, а измене-
ние температуры пропорционально изменению напряжения. При этом
можно считать, что Ax/k = kRR, cpAx = kcC, а произведение коэффициен-
тов пропорциональности kRkc является масштабом времени и показы-
вает, во сколько раз быстрее происходит процесс в электрической цепи
в сравнении с процессом теплопроводности в теле.
Очевидно, что решение задачи для любого из аналогичных процес-
сов математически одинаково трудно. Но процесс в электрической цепи
достаточно просто и точно можно исследовать экспериментально, а за-
тем полученные результаты перенести на рассматриваемый процесс
теплопроводности. В этом состоит главное преимущество использова-
240
ния аналогов в виде электрических цепей для решения задач нестацио-
нарной теплопроводности.
Дальнейшее развитие приближенной модели процесса нестационар-
ной теплопроводности состоит в том, что этот процесс предполагается
дискретным не только в пространстве, но и во времени. Время протека-
ния процесса разбивают на ряд конечных интервалов. В пределах каж-
дого интервала скорость изменения температуры любой узловой точки
считают постоянной, т. е. температура от времени зависит линейно.
Следовательно, производную в левой части уравнения (25.9) в пределах
интервала можно заменить разностным соотношением
dt Atk
где Titk-\ и Ti,k—температуры i-той узловой точки в начале и в конце
й-того интервала времени.
Погрешность такой замены пропорциональна Д6<. Она входит в
уравнения, описывающие рассматриваемую модель. Если скорость изме-
нения температуры узловой точки определяется по условиям в конце
£-того интервала, то получается разностное уравнение
Pk <Ti,k — =-• Ti-\fk — 27^ + Pk = (Лх)2/аЛ^. (25.11)
Таким образом, рассматриваемая модель описывается системой
алгебраических уравнений, число которых соответствует количеству
узловых точек. Решение этой системы позволяет перейти от распреде-
ления температуры в узловых точках в начале интервала времени к
распределению в конце интервала. Повторяя подобную операцию, мож-
но последовательно пройти по всем интервалам, на которые разбито
время процесса теплопроводности.
Разностная схема, соответствующая уравнению (25.11), получила
название неявной. Одним из наиболее эффективных при решении си-
стемы уравнений для одномерной неявной разностной схемы является
метод прогонки [16]. Любое из уравнений вида (25.11) можно в общем
случае представить в форме трехчленного
— 4- BiTi'k — = Df
На границах тела при i = l С] = 0, а при i=n Лп = 0. Первое условие
позволяет все искомые температуры последовательно выразить через
значения температур для соседних узловых точек, имеющих на единицу
больший номер:
Т1Л = Т2.к А- + а_ = тиЕ1 + F,
и вообще
Та=Т^Е^Р^ (25.12)
где
Переходя от одной узловой точки к другой в сторону возрастания
их номера (прямая прогонка), можно последовательно вычислить все
коэффициенты Ei и Гг- вплоть до Fn. При этом Еп = 0, так как Лп = 0.
Следовательно, температура в последней узловой точке Tn,k=Fn. Затем
по формуле (25.12) последовательно вычисляют температуры узловых
точек, имеющих на единицу меньший номер (обратная прогонка). На
следующем интервале времени описанный процесс вычислений повто-
ряют.
16 Зак. 96
241
В случае двухмерных и трехмерных задач нестационарной тепло-
проводности уравнения для неявной разностной схемы содержат, соот-
ветственно, 5 и 7 искомых значений температур узловых точек. Но с
помощью приема, получившего название метода дробных шагов, эти
уравнения также можно свести к трехчленным. Например, для двух-
мерной задачи разностное уравнение
*р ____'Г 'р __С)'Т' I 'Р 'р __<ур । 'р
1 i,j,k 1 __ 1 1 i-'-IJ'k 1 ii— 1Л 1
Ii~k ~a 1'a (Л]Л*
можно заменить двумя одномерными:
Абг
btk
1 /2 Л-И./ Л —1/2
(ЛхГ-
(A//)2
где j — номер ряда узловых точек, отсчитываемый в направлении оси//.
Одномерные уравнения позволяют для решения задачи использовать
метод прогонки, который на каждом интервале времени сначала при-
меняется в направлении оси х для каждого ряда узловых точек с но-
мером /, а затем — в направлении оси у для каждого ряда узловых
точек с номером /. Но даже при использовании метода прогонки реше-
ние многомерных задач нестационарной теплопроводности достаточно
трудоемко.
Рассмотренной разностной схеме соответствует электрический ана-
лог в виде цепочки сопротивлений. На рис. 25.3, г показана ячейка
такого аналога. Используя для узловой точки с напряжением
закон Кирхгофа о равенстве нулю суммы притекающих токов, получим
lli,k - = !,/с р5 13)
~ Ri ’ '
Уравнения (25.11) и (25.13) аналогичны, если Pk = RilR°i. Следователь-
но, ячейка решает разностное уравнение (25.11). Электрическая цепь,
составленная из таких ячеек, является аналогом модели процесса теп-
лопроводности, соответствующей неявной разностной схеме.
Решение задачи с помощью этого аналога известно как метод Либ-
мана и подробно описано в литературе [46]. В процессе решения задачи
величины сопротивлений аналога могут изменяться в связи с измене-
нием длительности интервала времени, теплофизических характеристик
материала тела или условий теплообмена с окружающей средой. На
каждом интервале времени в нижнюю точку каждой ячейки (см. рис.
25.3, г) задают напряжение ft_b пропорциональное значению темпе-
ратуры узловой точки в начале интервала. В верхних точках схемы
измеряются значения иЛЙ, по которым определяются температуры
Л, а в конце fe-того интервала. Решение повторяют для всех последую-
щих интервалов времени.
Точность решения задач теплопроводности с помощью различных
аналогов зависит от ряда факторов. Прежде всего аналогу присущи ге
же погрешности, которые появляются при замене непрерывного процесса
теплопроводности приближенной моделью. Второй источник погреш-
ностей— ограниченная точность установки параметров аналога. Име-
ются также некоторые отклонения в работе реальных элементов от тех
законов, которые закладываются в основу построения аналога (напри-
мер, утечки и нелинейность электрических конденсаторов). Наконец,
ошибки вносятся в процессе решения задачи при измерении искомых
242
величин напряжений и других параметров. Суммарные ошибки могут
достигать нескольких процентов и обычно оцениваются по решению
контрольных задач, для которых имеется точное аналитическое реше-
ние.
§ 26. ОСОБЕННОСТИ РАСЧЕТА ТЕМПЕРАТУРЫ В ТОНКОСТЕННЫХ
конструкциях
Тонкостенными в тепловом отношении называют элементы, темпера-
туру которых в направлении наименьшего измерения можно считать
одинаковой. К ним относятся подкрепленные и неподкрепленные тон-
кие металлические оболочки и обшивка, широко применяемые в кон-
струкции ракет. Для таких элементов изменение температуры по тол-
щине незначительно и сравнимо с ошибкой в расчете из-за недостовер-
ности данных об условиях теплообмена и теплофизических свойствах
материала или же не приводит к заметным деформациям элемента и
изменению его механических характеристик.
Степень неравномерности распределения температуры по толщине
элемента конструкции характеризуется величиной критерия Био
(см. § 24), который связывает между собой интенсивность теплообмена
и термическое сопротивление конструкции. С практически достаточной
точностью перепадом температуры по толщине можно пренебречь, если
Bi<0,l.
Чтобы познакомиться с кругом вопросов, возникающих при опреде-
лении температурного состояния тонкостенных конструкций, достаточно
рассмотреть простейшую расчетную схему тела, которое имеет одина-
ковую по всему объему температуру. К подобной расчетной схеме могут
быть приведены конструкции, которые имеют относительно малое
внутреннее сопротивление распространению тепла во всех направле-
ниях. Цель исследования температурного состояния конструкции в та-
ком случае — установить зависимость ее температуры от времени t.
Скорость изменения теплосодержания тела из формулы (24.13)
равна
CT(T)-^ = Q, (26.1)
at
где
Q = [a (f — Т) — еЦ0Т4] S - (26.2)
тепловой поток, выраженный через осредненные по внешней поверхно-
сти S тела параметры, характеризующие условия теплообмена. Полная
теплоемкость СТ(Г) в общем случае может зависеть от температуры
тела, а коэффициент теплоотдачи а и приведенная температура среды
Т могут изменяться во времени.
В частном случае постоянных условий теплообмена по истечении
достаточно длительного промежутка времени (/->оо) температура тела
перестанет изменяться (dTjdt-^Q) и примет равновесное значение Т.
Оно характеризуется равновесием всех действующих тепловых потоков
на поверхности тела. Значение Т находят из условия Q = 0. Из этого
условия получается алгебраическое уравнение вида (24.10)
W4 + d=l, (26.3)
где
N 73 и$=
а
Для решения уравнения (26.3) можно воспользоваться графиком на
рис. 24.3.
16’
243
Если условия теплообмена изменяются во времени, то температура
тела с пренебрежимо малой полной теплоемкостью (Ст->0) будет при-
нимать так называемые мгновенные равновесные значения T(t), кото-
рые соответствуют текущим значениям а и Т. Изменение температуры
Т реального тела, имеющего полную теплоемкость конечной величины,
в силу его тепловой инерции запаздывает по сравнению с изменением
T(t). Запаздывание тем значительнее, чем больше полная теплоемкость
тела^причем оно нагревается, когда T<T(t), и охлаждается, если
При совпадении значений текущей и равновесной температур
Q = 0 и в данный момент скорость изменения температуры dT/di = Q.
Нестационарный процесс изменения температуры возникает и при
постоянных условиях теплообмена, если в некоторый момент времени,
принимаемый за начальный (/ = 0), температура тела равна и отли-
чается от равновесного значения (Т0=/=Г). В этом частном случае при
Ст = const можно получить точное аналитическое решение уравнения
(26.1). Однако это решение весьма громоздко и не имеет практической
ценности.
Наиболее общим способом решения рассматриваемой нестационар-
ной задачи является численное интегрирование уравнения (26.1) по
конечным интервалам времени \th (индекс k указывает порядковый
номер интервала, &=1, 2, 3, ...). Полное время интегрирования должно
быть разбито на интервалы так, чтобы в пределах каждого из них
параметры, характеризующие условия теплообмена, изменялись во вре-
мени монотонно.
В пределах отдельно взятого интервала Д/Л скорость изменения тем-
пературы приближенно принимают постоянной и заменяют выражением
в конечных разностях
dT _ Tk-Tk i
dt
где ТЛ_.1 и Th — температура тела в начале и в конце fe-того интервала
времени. В действительности dT/dt не остается постоянной в пределах
Д6г, так как изменение температуры тела вызывает изменение теплово-
го потока Q, что видно из формулы (26.2). Это обусловливает погреш-
ность в численном интегрировании уравнения (26.1) по сравнению с
его точным решением.
Если скорость изменения температуры тела определить по условиям
теплообмена в начале интервала, то разностное уравнение,
ствующее дифференциальному уравнению (26.1), примет вид
Tk __ Qfe—1 р
~ Ст(7\_1) ”
где — значение теплового потока Q согласно формуле (26.2)
времени при температуре 7\_f, CT(Tk^)—полная теплоемкость тела
при температуре 7\_ь
Из уравнения (26.4) получаем
соответ-
(26.4)
в момент
Т\ — Тk—\ + Tk—\^tk‘
(26.5)
Температура Tk может быть также представлена рядом по степеням
т + ы + — (—') (AU2 +-rlvr) СЧ)3+---.
к \ dt )k-l 2 \ dP /ft-i * 6 \ dP ]k-\ *
(26.6)
244
причем из уравнения (26.1) следует, что
dT \ = Qfe-i
dt Jk--1 Ст(7\_1)
Тогда вместо формулы (26.6) получим
n = 7V, -I- 7W/» + ; W , (А/.)- + • • <26.7)
Сравнение выражений (26.5) и (26.7) показывает, что погрешность
вычисления Tk из уравнения (26.4) пропорциональна (Д6>)2> т- е- имеет
порядок х = 2.
Если скорость изменения температуры тела определить по условиям
теплообмена в конце интервала, то погрешность получится того же
порядка. Это следует из сопоставления разностного уравнения
с разложением в ряд
тк = + Tk\tk - a М)2 + 4"(Ч)3“• • • (26-9)
Порядок погрешности возрастет, если скорость изменения темпе-
ратуры определить как среднюю за интервал, т. е. воспользоваться
разностным уравнением
Tk-Tk-^ = 0 5 фу (26. 10)
А/*
Действительно, после почленного сложения формул (26.7) и (26.9) получим
7. = П_, + 0,5 (П_, + Т„) i ] (W + •
Так как
f d2T \ / d2T \ / d3T \ * , ,
I --- I — । -- ) — ( --- I Л/ь “Ь • •»
\ dt2 Ц \ dt2 Jk-\ \ dt3 Jk-\ к
то погрешность вычисления Th из уравнения (26.10) оказывается про-
порциональной (Д/*)3, т. е. имеет порядок х = 3.
С уменьшением интервала времени Д/ погрешность расчета сни-
жается, но возрастает его трудоемкость из-за увеличения числа интер-
валов при фиксированном времени протекания нестационарного про-
цесса изменения температуры. Знание порядка погрешности х позво-
ляет установить скорость сходимости приближенного решения к точ-
ному с уменьшением Д/. При этом чем х больше, тем скорость сходи-
мости выше. Пусть для одинаковых моментов времени имеются пары
значений Т' и Т", полученные с помощью одного и того же разностного
уравнения, но с различными интервалами времени Д/' и M'' = kt№'.
По этим данным можно экстраполяцией подойти к уточненным значе-
ниям Т для тех же интервалов времени, если в разложении погреш-
ности в ряд удержать лишь первый член. Тогда получим
'prr rp
T' — T
№ „ T . тчьг-т-
J (*,)»-1
Сопоставлением уточненного значения T с Т' и Т" устанавливают коли-
чественную оценку погрешности:
___ rpt у// _у/
ът = Т' — Т = —- и ЪТ" = Т" -Т = -.
(М*-1 ‘
245
Для постоянных условий теплообмена в случае, если тело нагре-
вается, по формуле (26.4) получается завышенный результат, а по
формуле (26.8)—заниженный. Наиболее близкие к точному решению
результаты дает формула (26.10). Принципиально возможно построить
еще более точные разностные уравнения, но они получаются громозд-
кими и содержат значения Q для моментов времени /Л_2, tk-з и т. д.
Такие уравнения неудобны для практических расчетов и поэтому в даль-
нейшем рассматриваются лишь формулы вида (26.4), (26.8) и (26.10).
Помимо обеспечения необходимой точности расчета на выбор интер-
вала времени А^ оказывают влияние и другие соображения. При уве-
личении интервала Д/Л погрешности, вызванные заменой дифференци-
ального уравнения разностным, могут возрасти настолько, что резуль-
таты расчета потеряют физический смысл. По формуле (26.4) с учетом
принятых при ее выводе допущений получаются результаты, сохраняю-
щие физический смысл [36], если температура Tk в конце интервала
находится в пределах когда тело нагревается {Tk^>
или Tk-i>Tk^Tk-b когда тело охлаждается (Tk_i<Th_i).
Здесь через обозначено мгновенное значение равновесной
температуры тела в начале интервала. Эти неравенства определяют
верхний предел величины Д4 при использовании формулы (26.4).
Предельный по величине интервал времени получают из соотношений
(26.2) и (26.4) при условии Tk = Th_\z
Ст (Т fe-i)/
те - 1 — Тk-i __
Tk-i a*-i + £ao (7*-i + Tk-iTk-i +
(26.11)
интервала.
где a/i-i — значение коэффициента теплоотдачи в начале
Для уравнения (26.8) предельный интервал времени следовало бы
выбирать из
при Л^->оо.
этого уравне-
из
условия Th = Th, но оно реализуется лишь
Поэтому интервал для
ния следует выбирать только исходя
соображений точности расчета.
Уравнение (26.10) можно рассматри-
вать как комбинацию уравнений (26.4) и
(26.8), каждое из которых действует на
половине интервала. Поэтому предельный
интервал времени для уравнения (26.10)
равен удвоенному значению [А/л], вычис-
ленному по формуле (26.11).
Наиболее просто вести расчет по фор-
муле (26.4). Эту формулу можно явно
разрешить относительно искомой темпе-
ратуры Tk в конце интервала. Формулы
(26.8) и (26.10) в общем случае -не удает-
ся явно разрешить относительно Т}{. Эту
температуру приходится искать подбором
или графическим путем. Наиболее сло-
расчет по формуле (26.10), но он может быть сравни-
жен численный
тельно просто представлен геометрически.
Пусть на рис. 26.1 температурное состояние тела в момент времени
tk-i характеризуется точкой Bk-\ с координатами 7\_i и Тл-ь Для пере-
хода к моменту времени tk = tk-i + на графике по формуле
________________ cik(Tk T) — ?в()Т4
k ~z cat) ~~ r 'TX
САЛ
246
где ak и Tk — значения коэффициента теплоотдачи и приведенной темпера-
туры среды в конце интервала времени, строят кривую зависимости Tk(T).
Ордината точки Bk пересечения этой кривой с прямой Bk_\Mk, задаваемой
формулой
Tk^=Tk-\-\-0^(Tk-\ + Л)
определяет значение температуры Тк. При этом
„ тт
tgp, = 0,5^-A/A, (26.12)
mT
где m- градIсек • мм и тт град/мм — масштабы графика по осям f и Т.
При построении прямую Bk~\Mk удобнее заменить ломаной Bk~\OkMk
с точкой излома на оси ординат. Аналогично осуществляют переход от
момента времени tk к моменту tk+\ и т. д., но для каждого момента вре-
мени строят свою кривую зависимости Т(Т). При постоянных во времени
условиях теплообмена эта кривая остается неизменной.
Каждая из кривых зависимости Tk (Т) пересекает ось ординат в точке,
соответствующей мгновенному значению равновесной температуры Tk.
Предельному по величине интервалу времени [A/fe] на графике отвечает
предельный угол наклона прямой
[РА] = arctg 0,5 [Д/J = arctg
тт
К рассмотренной выше расчетной схеме тела с одинаковой по объ-
ему температурой может быть сведена тонкостенная неподкрепленная
обшивка или оболочка бака, если принять, что условия теплообмена
сравнительно слабо изменяются по поверхности и передача тепла вдоль
поверхности несущественна. В этом случае каждый участок обшивки
или оболочки можно считать изолированным от влияния соседних.
Расчет изменения температуры таких участков обшивки в условиях
аэродинамического нагрева на траектории полета ракеты рассматри-
вается более подробно в § 29.
Здесь следует остановиться на особенностях расчета элементов кон-
струкции с существенной неравномерностью распределения условий
теплообмена по поверхности. В таких случаях необходимо учитывать
передачу тепла посредством теплопроводности в направлении измене-
ния условий теплообмена [36].
Характерным примером является неравномерное распределение
температуры вдоль образующей оболочки бака в зоне уровня жидкости
(рис. 26.2, а), так как условия теплообмена при переходе через него
резко изменяются. Сведения о распределении температуры в этой зоне
бывают нужны, например, для выяснения напряженно-деформирован-
ного состояния, которое возникает в оболочке при хранении низкокипя-
щего компонента топлива (сжиженного газа) или заполнении им бака.
Коэффициент теплоотдачи аж, который характеризует интенсивность
теплообмена между оболочкой и жидкостью, обычно превышает коэф-
фициент теплоотдачи аг между оболочкой и газом, находящимся в по-
лости бака над уровнем жидкости. Коэффициент теплоотдачи а между
оболочкой и внешней средой можно считать одинаковым для всей обо-
лочки. Смоченную 1 и несмоченную 2 части оболочки представим как
два тонких стержня, имеющих общее основание и постоянную по сече-
нию температуру. Установившееся распределение температуры по дли-
не этих стержней описывается уравнениями:
247
U _ аж (Л -Тж) - а (Л - Тс) = О,
dx2
Хй — аг (Т2 — Тг) - а (Т2 — Тс) = О,
dx2
(26.13)
где 1 и h — коэффициент теплопроводности и толщина оболочки,
Тс, Тж и Тг — температуры внешней среды, жидкости и газа в полости бака.
На достаточном удалении от уровня жидкости (jq-^oo, х2—>оо) пе-
редача тепла посредством теплопроводности вдоль оболочки становится
ничтожной (dT^dXi = dT2/dx2 = 0), а температура оболочки стремится к
значениям
Л = (“жТж + аЛ;)/а1 и Л = (агтг + аТс)/а2у
где
«1 = аж + а и а2 = аг -| а.
Тогда решения уравнений (26.13) будут иметь вид:
T1=^T1-\-D1 exp [— a^J, = Vo^h/h, xv = xjh.
T2 = T2 + D2 exp [— a2x2], a2 = Va2ft/X, x2 — x2\h.
Постоянные и D2 определяем из условия непрерывности распределе-
ния температуры при хх = х2 -= 0: Т\ Т2 = TQ и
_j_ _^2 __ Q
dxL dx2
В итоге получаем
Л — Л __ exp [— a^i] Т2 — Т2 _ ехр [— a2x2] Т() — 7\ __ 1
Т’г— Т1 l-J-fai/do) 7\— Т2 1 + (а2/а1) Т2 — Т\ 1 + (01/02)
(26.14)
Так как ехр [ — 3] 0,05, то практически можно считать, что нерав-
номерность распределения температуры сказывается лишь в зоне х1<^3/а1
и х2<\3/а2. Характер распределения температуры в этой зоне показан на
рис. 26.2, а. Значение температуры TQ зависит от соотношения между
и а2. Если (теплообмен с внешней средой незначителен), то
ах/а —аж/аг и Т± Тж. Отношение аж/аг обычно велико и значение То
мало отличается от Тж. В таком случае температуру всей смоченной час-
ти оболочки можно принимать равной температуре жидкости.
Нестационарный процесс теплопроводности в оболочке описывается
уравнениями:
1 dT^x^t)
a dt
Э2Л fa,/)
dx2
1 dT2(x2,t) д2Т2(х2, t)
a dt dx%
Г2(*2, О -т2]
л /
(26.15)
с теми же граничными условиями, что и для уравнений (26.13). Здесь
а — коэффициент температуропроводности материала оболочки бака.
Если условия теплообмена изменяются вследствие перемещения уровня
жидкости с постоянной скоростью v в направлении оси х{ (см. рис.
26.2,6), то в уравнениях (26.15) целесообразно перейти к подвижным
координатам |i = %i—vt и ^2 = ^2 + ^/, начало отсчета которых связано
248
с текущим положением уровня жидкости. В результате преобразования
координат вместо уравнений (26.15) получим:
1 dT.g^t)
a dt
1 dT2(^t)
a dt
&T\(^t) v d7\alft) z \2
----ГЛ ‘ Г ( ~Г~ ) 1 Vbi
dgf-----------------------------------а dh-\ h J
&T2(U,t) v dT2(l2,t) f й2 /t
лт-2 Лг ’ ( r. ) H2(b2i
^2 a ^2 \ h J
С течением времени после начала перемещения уровня форма про-
филя распределения температуры вдоль оболочки перестает изменяться
и он будет лишь перемещаться вместе с уровнем жидкости. Наступит
так называемый квазистационар ный режим. Он характери-
зуется тем, что в подвижных координатах распределение температуры
не изменяется во времени, т. е.
дЛ(Е1,0 = dT2(g2, /) _ 0
dt dt
Решение уравнений (26.16) совпадет по форме с выражениями (26.14)
если вместо ах и а2 будут
aj = v + J/%2 + а? и а2 = — и Ч~ ]/^2 + «2,
где v = vh!2a, а вместо Xi и х2— соответственно и £2.
В случае опорожнения бака скорость перемещения уровня жидкости
считают положительной (у>0), а при заполнении — отрицательной
(у<0). Изменение в направлении движения уровня влияет на значе-
ния а/ и а2' и вызывает изменение в характере распределения темпе-
ратуры вдоль оболочки (см. рис. 26.2,6).
При относительно большой скорости опорожнения бака, когда (а2/02« 1,
роль передачи тепла посредством теплопроводности вдоль оболочки незна-
чительна. Тогда ai 2у, а2 а2/2у = а2/сри и a2/ai < 1, где с и р — тепло-
емкость и плотность материала оболочки бака. При этом температура смо-
ченной части оболочки 7\ практически равна Тъ а температуру несмочен-
ной части рассчитывают по формуле
То — Т2 Г a2a
= ехР------г Ч
Т1 — Т2 L cph
249-
где t2 = ^,zlv — время, истекшее после прохождения уровня жидкости через
сечение с координатой |2.
В случае большой скорости заполнения бака Т\ Т\ и
П-Т1
Г2-Л
= ехр
cph J v
Две последние формулы устанавливают крайние возможные распреде-
ления температуры вдоль оболочки бака при движении уровня жидко-
сти (см. рис. 26.2, б).
Неравномерное по поверхности нестационарное распределение тем-
пературы возникает также в подкрепленной обшивке или оболочке в
зоне присоединения к ней элементов силового набора. Это вызывает
различные температурные удлинения обшивки и силового набора, что
Рис. 26.3
приводит к появлению термических напряжений в конструкции, которые
могут повлиять на ее работоспособность. Поэтому расчет распределе-
ния температуры в подкрепленных элементах необходим в процессе
проектирования подобных конструкций.
Если в подкрепленный элемент входит мощный силовой набор и
сравнительно тонкая обшивка (рис. 26.3,а), то полной теплоемкостью
последней можно пренебречь и в процессе расчета аэродинамического
нагрева конструкции в полете учитывать лишь полную теплоемкость Ст
силового набора. Такое допущение приводит к несколько завышенным
по сравнению с действительными значениям температуры.
Повторяющийся участок конструкции, выделенный на рисунке двумя
сечениями (показаны штрих-пунктирными линиями), в тепловом отно-
шении можно свести к системе, содержащей массу с полной теплоем-
костью Ст и два ребра толщиной h и длиной I (рис. 26.3,6), равной по-
ловине шага между элементами силового набора. Величину Ст в дан-
ном случае определяют как произведение удельной теплоемкости мате-
риала подкрепляющего элемента на его погонную массу.
Пусть от внешней среды с температурой Тс к каждому из ребер,
соответствующих участкам обшивки, передается конвективный тепло-
вой поток Q. Принимаем, что теплообмен обшивки со средой в полости
конструкции отсутствует. Согласно принятому допущению, ребра не
поглощают воспринимаемый тепловой поток, а лишь передают его по-
средством теплопроводности к подкрепляющему элементу. Изменение
температуры Т элемента по времени описывается уравнением
Ст— = 2Q. (26.17)
250
В любой момент времени распределение температуры Т' по длине
ребра является стационарным и определяется температурой Т его осно-
вания и условиями теплообмена ребра с внешней средой, т. е. описы-
вается формулой (25.6) в виде
Т'= Тс — (Тс— Т) chm(z~x) , ш = ]/аЖ
ch ml
где а — коэффициент теплоотдачи от внешней среды к обшивке, X —
коэффициент теплопроводности материала обшивки. Характер распре-
деления температуры показан на рис. 26.3, в. Тепловой поток, переда-
ваемый от обшивки подкрепляющему элементу, согласно формуле
(25.7) будет
Q=-X/i—I = (Т — T)Vdkh th 1/ — I. (26.18)
dx |x=o V hh
При постоянных во времени условиях теплообмена уравнение (26.17)
с учетом формулы (26.18) легко решить аналитически. Если условия
теплообмена переменны, то для решения этого уравнения можно ис-
пользовать способы, рассмотренные выше в применении к телу с одно-
родной по объему температурой.
В случае когда элементы силового набора выполнены из листового
материала или тонкостенных профилей, полные теплоемкости обшивки
и подкрепления сравнимы по величине. Тогда расчетная схема задачи
определения температурного состояния в подобной конструкции замет-
но усложняется.
В некоторых простых частных случаях эта задача поддается анали-
тическому решению. В итоге удается получить функциональную связь
между отдельными параметрами и выяснить влияние каждого из них
на распределение температуры в конструкции. Но усложнение геомет-
рии конструкции, изменение условий теплообмена во времени, учет
контактного термического сопротивления в соединении обшивки с
подкреплением — все это сильно затрудняет аналитическое решение
задачи.
Тогда бывает целесообразно обратиться к более гибким способам
расчета, основанным на приближенной модели процесса теплопровод-
ности (см. § 25). Ниже для достижения определенности рассматривает-
ся применение этих способов к расчетной схеме, изображенной на рис.
26.4, а [36]. Схема охватывает достаточно большое число различных
конфигураций тонкостенных подкрепленных элементов, примеры кото-
рых (/—6) показаны на рис. 26.4,6. Излагаемые ниже способы расчета
нетрудно распространить на задачи с более сложной конфигурацией
тонкостенных подкреплений.
В общем случае принимается во внимание изменение во времени
условий теплообмена с воздушным потоком, в полости конструкции и
в соединении обшивки с полкой подкрепления. При необходимости мож-
но также учесть теплообмен излучением в конструкции и изменение
теплофизических характеристик ее материала с температурой. Но в
большинстве реальных случаев последние два фактора не играют реша-
ющей роли, и их обычно не принимают во внимание. Температура по
толщине обшивки и подкрепления считается одинаковой и не изменяе-
мой в направлении, нормальном к плоскости схемы на рис. 26.4, а.
Обшивка и подкрепление условно разбивают на участки конечной
ширины AXj. Участки объединяют в пять зон (/—V). Очевидно, что для
конфигураций, изображенных на рис. 26.4,6 (позиции 2 и 5), зона III
выпадает из рассмотрения. Используя допущения, рассмотренные в
251
§ 25, можно составить выражение для суммарного теплового потока,
поступающего в данный момент времени на /-тый участок:
Q, = aAxt (Тс — TL) + а'Ах, (Тс — 7\) 2Мг
Tj-i-Ti ! T^-Ti
+ \xt Дх£+1 + кх^ J "
(26.19}
Для участков зон / и /// значения коэффициента теплоотдачи а и
температуры среды Тс определяются условиями теплообмена обшивки
с воздушным потоком, а значения а' и Тс' — со средой в полости кон-
струкции. Толщина обшивки h считается постоянной, но ширина сосед-
них участков (ДХг-i и Дхг+1) может отличаться от ширины /-того уча-
стка. Опыт показывает, что при расчетах ширину участков обшивки
целесообразно выбирать переменной, уменьшая ее в направлении к ме-
сту соединения обшивки с подкреплением, где распределение темпера-
туры наиболее неравномерно.
Для i-того участка зоны // (рис. 26.4, в) величины а и Тс сохраня-
ют прежний смысл, а значения а' = ак и Tc' = Tj определяются условия-
ми контактного теплообмена с /-тым участком полки подкрепления
(зона IV). При разбивке на участки зон // и IV должно выполняться
условие Дхг=Дх.,-.
Для i-того участка зоны IV (рис. 26.4, г) значения а и Тс соответ-
ствуют условиям теплообмена полки подкрепления со средой в полости
конструкции. Значения а' = ак и Tc' = Tj определяются условиями кон-
тактного теплообмена i-того участка с /-тым участком обшивки (зо-
на II). Величины X и h теперь соответствуют коэффициенту теплопро-
водности и толщине полки подкрепления.
Наконец, для Z-того участка зоны V значения а и Гс, а' и Тс' опре-
деляются условиями теплообмена подкрепления со средой в полости
конструкции. Условия теплообмена могут быть различны с разных сто-
рон подкрепления. Поэтому в общем случае аУ=а' и ТС=^ТС'. Величина
h в уравнении (26.19) для конфигураций, изображенных на рис. 26.4,6,
позиции 2 и 5, равна половине толщины подкрепления, а в остальных
случаях — полной толщине.
В уравнении (26.19), помимо температур участков, от времени так-
же могут» зависеть величины а и Тс, а' и Гс/. Поступающий в /-тын
252
участок переменный во времени суммарный тепловой поток Qi вызы-
вает изменение температуры Tiy которое описывается уравнением
срйДх.-^-= Q., (26.20)
где с и р — удельная теплоемкость и плотность материала участка.
Подобные уравнения могут быть составлены для всех участков.
В итоге получается система из п обыкновенных дифференциальных
уравнений по числу участков в расчетной схеме. Начальным условием
для уравнений системы являются значения температур Tij0 участков в
момент времени t = 0. Эта система может быть решена с применением
моделирующих устройств или численным интегрированием на ЭЦВМ.
Производную в левой части уравнения (26.20) приближенно можно
заменить разностным соотношением (см. § 25)
dTi ~
dt
Тогда вместо системы дифференциальных уравнений получим систему
алгебраических уравнений, из которой по значениям температур Tith-\
в начале интервала времени Д/Л найдем температуры Tiik в конце
&-того интервала. При использовании неявной схемы алгебраические
уравнения имеют вид
срЛTi-k~Jk‘’k~' = Qi.k. (26.21)
Система таких уравнений наиболее эффективно решается на ЭЦВМ.
Для определения температурного состояния подкрепленной конст-
рукции удобно использовать моделирующие устройства и аналоги.
Принципы их построения разобраны в § 25. В качестве примера ниже
рассматривается составление электрических цепей для расчетной схемы
подкрепленной конструкции, содержащей 10 участков одинаковой ши-
рины Дх (рис. 26.5,а). Чтобы излишне не загромождать электрическую
схему, в задаче не учитывается теплообмен в полости конструкции.
На рис. 26.5,6 показана коммутация элементов аналоговой машины
(ЭАВМ) с усилителями постоянного тока. Между параметрами схемы
и решаемой задачи должны выполняться соотношения
R __ R' _ С = С'
Дх/ХЛ &x/k'h' 1/аДх 1/акДх ср^Дх c'p'h,'Ах
где штрихом помечены величины, относящиеся к подкреплению. На
вход верхнего ряда усилителей, соответствующих участкам обшивки,
через сопротивления Ra подаются напряжения ±ис, по абсолютной ве-
личине пропорциональные температуре внешней среды Тс. Если усло-
вия теплообмена в конструкции переменны по времени, то величины
«с, Ra и должны изменяться в процессе решения задачи. По изме-
няющимся по времени напряжениям uiy измеренным на выходе усили-
телей, из пропорции
= и‘~“° (26.23)
Тс Tq ис и0
определяются температуры участков. В пропорции TQ и uQ — начальная
температура конструкции и соответствующее ей напряжение, которое
задается в схему в момент начала решения задачи. Масштабом вре-
мени при переходе от процесса решения задачи на ЭАВМ к процессу
изменения температуры в конструкции служит отношение (Дх)2/а/?С,
где а = \1ср — коэффициент температуропроводности материала об-
шивки.
(26.22)
253
Модели процесса теплопроводности, которая описывается уравне-
ниями вида (26.20), соответствует аналог, состоящий из сопротивлений
и конденсаторов (рис. 26.5,в). Между параметрами электрической схе-
мы и рассматриваемой конструкции также выполняются соотношения
(26.22). Нестационарный процесс теплопроводности в конструкции ана-
логичен процессу зарядки конденсаторов электрической цепи, на вход
которой подается напряжение ис, пропорциональное температуре Гс.
Измеряя в процессе зарядки конденсаторов напряжения £/г- в узловых
Рис. 26.5
точках цепи и пользуясь пропорцией (26.23), можно определить тем-
пературное поле в обшивке и подкреплении в различные моменты вре-
мени. Масштаб времени остается таким же, как и для предыдущей
схемы.
Если термическим сопротивлением в соединении между обшивкой и
подкреплением можно пренебречь, то в электрической схеме сопротив-
ления /?к = 0 и узловые точки 3 и 7, 4 и 8 следует попарно соединить
накоротко. Тогда в процессе зарядки напряжения и3 = и7 и Ua = u8. Это
соответствует равенству температур Т3 = Т7 и Т4 = Т8. Учет теплообмена
в полости конструкции потребовал бы добавления еще одного ряда со-
противлений, присоединенных к узловым точкам 1, 2 и 5—10. Величина
этих сопротивлений должна быть пропорциональна термическому со-
противлению теплоотдачи в среду, находящуюся в полости конструк-
ции.
Модели процесса теплопроводности, которая описывается уравне-
ниями вида (26.21), соответствует аналог, состоящий только из сопро-
254
тивлений (рис. 26.5,г). Соотношение между сопротивлениями устанав-
ливается пропорцией
R' R° r'O
Дх/М ~~ kxj'k'h' ~ Mfrlcphkx ktklc'p'h' Дх
1/аДх 1/акДх
Задачи на этом аналоге решают по последовательным интервалам времени
A/fe. На каждом интервале в нижние точки схемы задают напряжения
пропорциональные температурам Tt^\- Напряжение устанавли-
вают пропорционально значению Tc.*- В верхних (узловых) точках схемы,
измеряют напряжения по которым из пропорции]
Tc,k 1\k Uc,k Ui,k
Tc,k Ti,k-\ [UQ,k~~ Ui,k-\
определяют температуры T\k. Расчет повторяют для всех последующих
интервалов времени. При этом величины сопротивлений /?'°, /?а и /?к
могут изменяться от интервала к интервалу в связи с изменением значе-
ний а и ак.
ОС
CL
О
CD
JD
О
<
□"
ГЛАВА V
РАСЧЕТНЫЕ СХЕМЫ. НАГРУЗКИ
§ 27. ОСОБЕННОСТИ КОНСТРУКЦИИ РАКЕТ
Большую часть стартового веса ракеты состав-
ляет топливо. Для ракет с жидкостным ракетным
двигателем (ЖРД) основной нагрузкой, определя-
ющей вес конструкции, является тяга двигателей, а
для ракет с ракетным двигателем на твердом топ-
ливе (РДТТ) основными нагрузками будут тяга и
давление в камере двигателя. Компоновка ракеты в
первую очередь определяется конструкцией элемен-
тов, воспринимающих эти нагрузки.
Кроме перечисленных основных нагрузок, на ра-
кету в полете действуют аэродинамические силы и
давление наддува в баках, нагрузки от управляю-
щих органов и т. д. Некоторые элементы конструк-
ции ракеты подвергаются в полете аэродинамиче-
скому нагреву. Нагрузки при транспортировке, при
установке на стартовое устройство и т. д. могут
также влиять на конструкцию ракеты.
Расчеты на прочность конструкции ракеты про-
изводятся по наиболее неблагоприятным комбина-
циям внешних нагрузок. Для различных элементов
ракеты эти комбинации нагрузок могут соответство-
вать разным случаям эксплуатации, которые назы-
ваются расчетными случаями.
Основные расчетные случаи для корпуса раке-
ты относятся к активному участку полета, для го-
ловной ее части — к участку входа в атмосферу.
Рассмотрим основные особенности конструкций
ракет, описание которых приведено в литературе
[32], [95], [119].
Одноступенчатые ракеты с ЖРД. На рис. 27.1,а
изображена типичная схема такой ракеты, где 1 —
головная часть, 2— переходной сухой отсек, 3, 5 —
баковые отсеки, 4 — межбаковый отсек, 6 — двига-
тельный отсек, 7 — ферма крепления двигателя, 8 —
двигатель, 9 — хвостовой отсек, 10 — стабилизатор.
При отделяемой головной части расчетные случаи
для элементов конструкции 2—8 соответствуют по-
лету на активном участке траектории. Баковые от-
секи 3 и 5 в основном нагружены осевыми силами и
внутренним давлением. Основной нагрузкой для су-
хих отсеков 2, 4, 6 является осевое сжатие.
256
Рис. 27.1
Переходной отсек 2, передняя коническая часть бака 3 и стабили-
заторы 10 на активном участке полета испытывают значительное тем-
пературное воздействие. Хвостовой отсек 9 подвергается максимальному
нагружению на стартовом устройстве. Стабилизаторы 10 нагружаются
аэродинамическими силами в полете, но могут также служить опорами
при стоянке ракеты на стартовом устройстве.
Одноступенчатые ракеты с РДТТ. Схема такой ракеты представлена
на рис. 27.1,6, где 1 — головная часть, 2 — переходной отсек, 3— при-
борный отсек, 4 — твердое топливо, 5 —
оболочка камеры сгорания, 6 — сопло
двигателя, 7 — хвостовой отсек, 8 — ста-
билизаторы.
Основная особенность конструкции
ракеты состоит в том, что топливный
отсек является одновременно камерой
сгорания. Вследствие этого оболочка 5
нагружается большим внутренним давле-
нием, которое определяет конструкцию и
вес этой оболочки. Само твердое топливо
нагружается давлением и инерционными
силами. Остальные отсеки одноступенча-
той ракеты с РДТТ загружаются анало-
гично соответствующим отсекам ракеты
с ЖРД.
Многоступенчатые ракеты. Схемы
таких ракет показаны на рис. 27.2:
а — ракета тандемной схемы, б — ракета
пакетной схемы и в — ракета смешанной
схемы.
Отсеки ракеты тандемной схемы ра-
ботают в тех же условиях, что и отсеки
обычной одноступенчатой ракеты. На ак-
тивном участке полета первой ступени
вторая ступень играет роль головной ча-
сти. Хвостовой отсек второй ступени нагружается значительными осевы-
ми нагрузками в конце работы двигателей первой ступени.
В пакетной схеме распределение осевых усилий между ускорите-
лями и ракетой зависит от последовательного включения основных дви-
гателей и двигателей ускорителей. Возможно два случая нагружения:
1) когда в начале работают только двигатели ускорителей и 2) когда
все двигатели работают одновременно.
При работе двигателей ускорителей отсеки ракеты могут работать
как на растяжение, так и на сжатие в зависимости от расположения
узлов крепления ускорителей. Так как вес конструкции ускорителей
меньше влияет на дальность полета, чем вес конструкции ракеты, то
положение узлов крепления ускорителей следует определять из условия
наиболее благоприятного нагружения корпуса ракеты. Например, для
уменьшения сжимающих усилий в корпусе ракеты целесообразно осе-
вые силы от ускорителей передавать через передние узлы крепления.
В конструкции смешанного типа нижняя часть центрального корпу-
са ракеты на активном участке полета нагружается реакциями второй
ступени и ускорителей.
На рис. 27.3 показаны схемы ракет «Европа» (а), «Титан II» (6),
«Минитмен» (в), а на рис. 27.4 — «Сатурн V». Все эти ракеты спроек-
тированы по тандемной схеме. Первые две ракеты с ЖРД (рис. 27.3, а
и 27.3, б) интересны тем, что в их конструкции нет оболочек двигатель-
ных отсеков и тяга двигателей первой ступени с помощью ферм пере-
17 Зак. 96
257
дается непосредственно на топливные баки. В конструкции ракеты
«Европа» нет межбаковых отсеков. Баки имеют общие днища. На
рис. 27.4 показана подробная схема мощной ракеты «Сатурн V». Здесь
4, 9 и 15 — двигательные отсеки третьей, второй и первой ступени соот-
ветственно. Они представляют собой обшивку, подкрепленную продоль-
ными и поперечными элементами. Такая конструкция предназначена
для восприятия больших осевых сил; /, 6, 11, 13 — сухие отсеки (пере-
ходные), 2, 3, 7, 8, 12, 14 — баковые отсеки, 5, 10, 18 — двигатели, 16 —
стабилизаторы, 17 — обтекатели двигателей, 19 — силовой привод пово-
Таблица 27.1
Тип ракеты Фау-2 Тор- -Аджена Блюстрик Атлас- - А джена Титан II Сатурн I Сатурн V
Стартовый вес, Т 13,0 52,0 93,0 125 136 544 2725
Диаметр максимальный, м 1,65 2,40 3,05 3,05 3,05 6,50 10,0
Периметр максимальный, м 5,18 7,54 9,58 9,58 9,58 20,4 31,4
Погонная нагрузка на периметр от ве- са, Т/м 2,51 6,90 9,70 13,0 14,2 26,6 86,6’
Стартовая тяга, Т 26,0 75,0 118 163,2 195 700 3400
Погонная нагрузка на периметр от тя- ги, Т/м : . . 5,02 9,95 12,3 17,0 20,3 34,3 108
258
ротного двигателя первой ступени. На том же рисунке показан узел Д
сечения I—I межбакового отсека 13 и двигательного отсека 9. Этот узел
интересен тем, что продольные элементы 20 отсека расположены на
внешней стороне обшивки 21, а поперечные элементы — шпангоуты 22—
на внутренней. При такой конструкции
шпангоуты не ослаблены вырезами от
продольных элементов.
В табл. 27.1 приведены данные по
весам, тягам и некоторым размерам
ряда ракет, а также величины нагру-
зок на единицу длины (погонных) пе-
Рис. 27.4
Рис. 27.3
риметра сечения корпуса от стартового веса и тяги. Из таблицы видно,
что величины погонных нагрузок растут с увеличением стартового веса
ракеты. Это позволяет создавать рациональные в весовом отношении
конструкции с высоким уровнем напряжений. Если в ранних ракетах
с относительно малой тягой критические напряжения составляли лишь
небольшую долю от величины предела текучести материала ат, то в тя-
желых ракетах типа «Сатурн» эти напряжения уже соизмеримы с от.
Другими словами, роль той части веса конструкции, которая определяет-
ся нагрузками, становится все более значительной.
§ 28. ВНЕШНИЕ НАГРУЗКИ
Действующие на ракету нагрузки можно разделить на поверхност-
ные и объемные. К поверхностным нагрузкам относятся аэродина-
мическое давление, давление газов в камере сгорания и сопле двига-
теля, реакции различных опорных устройств и т. д. Объемные на-
грузки являются следствием действия поля тяготения и сил инерции.
В каждый момент времени система всех сил, приложенных к ракете,
17
259-
находится в равновесии. Это означает, что вектор равнодействующей
объемных сил равен по величине и противоположен по знаку вектору
равнодействующей всех поверхностных сил. Это следствие принципа
Даламбера позволяет просто решать задачи, связанные с особенностя-
ми нагружения ракет. Силу тяги можно рассматривать как поверхност-
ную силу, направленную по оси двигателя. При полете вне атмосферы
эта сила является единственной поверхностной силой, приложенной к
ракете. Следовательно, в этом случае равнодействующая объемных сил
должна быть равна по величине и противоположна по знаку силе тяги.
Из этого следует, что ракету при полете без вращения можно рассмат-
ривать как тело, находящееся в некотором поле тяготения, направле-
ние и интенсивность которого определяется силой тяги двигателей.
Ускорение этого поля j=P!m, где Р — сила тяги, пг — масса ракеты.
Зеркало жидкости в топливных баках будет перпендикулярно к вектору
тяги двигателей.
То же явление будет и при полете без вращения в атмосфере, когда
отсутствуют поперечные силы. Только в этом случае ускорение услов-
Р__
ного поля тяготения будет равно j =-----, где X — сила аэродинами-
ки
ческого сопротивления.
Поверхностные нагрузки, действующие на ракету в различных усло-
виях эксплуатации, могут быть программными и случайными.
Основной программной нагрузкой на активном участке полета являет-
ся сила тяги двигателей, отклонение которой от номинального режима
весьма незначительно. Аэродинамические нагрузки зависят не только
от программных величин скорости и угла атаки, но и от случайных воз-
мущений в движении ракеты и случайных отклонений свойств атмо-
сферы от принятых в качестве стандартных. Характеристики так назы-
ваемой стандартной атмосферы приведены в ГОСТ 4401—64 и в кни-
ге [95].
В расчетах на прочность наиболее существенными случайными на-
грузками являются поперечные нагрузки от действия бокового ветра.
Некоторые статистические данные по распределению скоростей ветров
по высотам приведены в книгах [17], [24]. В качестве примера на
рис 28.1 представлено одно из распределений ветра, взятое из книги[17].
Кроме случайных ветров, приходится также учитывать струйные тече-
ния, существующие в атмосфере над некоторыми районами земного
шара. Для расчетов на прочность вместо вероятностных кривых рас-
пределения скоростей ветров удобно пользоваться их нормированными
значениями, обеспечивающими прочность ракеты при любых условиях
старта. Задание нормированных скоростей ветров делает нагрузки от
них детерминированными. В дальнейшем будем считать, что расчетные
скорости бокового ветра заданы для всех высот атмосферы.
Вопросы учета других случайных возмущений обычно решаются в
процессе проектирования конкретных конструкций. Некоторые из них
косвенно учитываются при назначении величин коэффициентов безопас-
ности (см. § 31).
Рассмотрим способы определения внешних нагрузок в различных
случаях эксплуатации баллистической ракеты.
Аэродинамические нагрузки на активном участке полета. Исходны-
ми данными для расчетов нагрузок служат результаты баллистических,
аэродинамических и динамических расчетов. В каждый момент време-
ни полета ракеты по траектории должны быть известны: высота полета
Н, плотность воздуха р, скорость ракеты и, число М=—, где а — ско-
а
рость звука на данной высоте, программный угол атаки апр, тяга дви-
гателей Р, аэродинамические коэффициенты сх, су, см, вес G и геомет-
260
рические параметры ракеты. К программному углу атаки добавляется
дополнительный угол атаки ав от действия бокового ветра. В первые
моменты действия бокового ветра, когда изменения параметров движе-
ния ракеты (угла тангажа, вектора скорости) еще очень малы, можно
дополнительный угол атаки от действия ветра определять по формуле
(рис. 28.2)
(28.1)
где и — скорость бокового ветра;
v— скорость полета.
Рис. 28.1
Рис. 28.2
Если в момент воздействия ветра программный угол атаки равен апр, то
суммарный угол атаки будет апр + ав. В последующие моменты времени,
когда изменение параметров движения ракеты существенно, суммарный
угол атаки
“ = “пр + ав + Да- (28-2)
где Да — изменение угла атаки при возмущенном движении ракеты.
Полные аэродинамические силы в скоростных осях х, у (см. § 17)
X=cxqSM, Y = cyqSMl (28.3)
ри2
где q = ----скоростной напор на данной высоте полета;
SM — площадь миделя ракеты. В осях хь уъ связанных с кор-
пусом ракеты,
Х\ = сХ1 qSM, = сУ1 qSM, (28.4)
где при малых углах атаки а
cXl = сх — асу, сУ1 = Су 4- асх.
Коэффициенты сх и су и соответственно cXi и сУх зависят от угла ата-
ки а и числа Л4 полета. Максимальные значения этих коэффициентов со-
ответствуют числам М = 1,0— 1,5. При малых углах атаки а можно счи-
тать, что сх не зависит от а, а су и сУ1 пропорциональны а.
261
Тогда
(28.5)
где Су и Cyt = Су + сх производные от су и сУ1 по а при а = 0. Для ра-
кеты Фау-2 зависимости коэффициентов сх и су от угла атаки а и числа М
приведены в книге [95].
Коэффициенты су, сх, определяют путем продувок моделей ракеты
в аэродинамических трубах и уточняют при полетных испытаниях.
Для расчетов на прочность ракеты силы Xi и У1 необходимо рас-
пределить по длине корпуса. Наиболее точно это можно сделать на
основе результатов продувок моделей на распределение давления. Од-
Рис. 28.3
нако в начальной стадии проектирования при отсутствии результатов
продувок моделей приходится пользоваться приближенными теоретиче-
скими методами.
Максимальное значение аэродинамических нагрузок соответствует
участку траектории полета со значением скоростного напора q = qmax-
При этом скорость полета сверхзвуковая (Л4>1). Для очень больших
чисел М справедлива теория Ньютона, согласно которой аэродинами-
ческое давление на поверхность тела определяется только величиной
нормальной составляющей скорости потока (50]. Этой теорией можно
воспользоваться для приближенного определения нагрузок при относи-
тельно небольших числах М полета. Ею, например, пользуются с попра-
вочными коэффициентами при определении нагрузок на носовую часть
сверхзвукового самолета [41]. Если аэродинамическое давление от дей-
ствия скоростного напора q представить в форме p = pq, то по теории
Ньютона
р = (28.6)
где vn—нормальная составляющая скорости потока v.
Если угол касательной к поверхности тела с осью вращения равен 0,
то при осесимметричном обтекании (рис. 28.3,а)
vn = v sin 0.
Соответственно
р = 2(?sln2 0.
(28.7)
262
Для конической поверхности угол [3 постоянный и распределение
давления по поверхности конуса равномерное. Для малых углов 0 мож-
но принять р = 2<?02.
При обтекании тела потоком под углом атаки составляющие ско-
рости vn будут переменными по окружности поперечного сечения (рис.
28.3, б):
ип = v sin (0 + a cos ср).
При малых углах 0 и а приближенно
vn = v (0 + а cos ф)
и давление определяется формулой
р = 2^(0 + асозф)2.
(28.8)
Интегрируя по поверхности тела, можно определить величины осевой
силы Xj и поперечной силы
s 2л
Xx = J j Р sinfi-rdqds,
о о
s 2Л
[ pcos0-cosq)-rdcpds,
б о
(28.9)
, dr
где as =--------элемент дуги меридиана,
sin 0
Для конуса при малом угле 0, когда sin 0=^=0 и cos0^= 1, получим
Х1 = 2 (₽ч+ Y1 = 2aqS^ <28Л0>
где SM = nJ?2 — площадь основания конуса.
Таким образом, по теории Ньютона
сХ1 = 2 (> + cVt=[2a. (28.11)
При уменьшении чисел М сверхзвукового потока коэффициент попе-
речной силы сУ1 возрастает. Поэтому при числах М порядка М = 2, соот-
ветствующих скоростным напорам, близким к q = ?max, вместо cyi = 2а в
расчетах можно принять [41]
^ = 3а. (28.12)
Тогда вместо соотношения (28.10) для получим
ri = 3a<7SM. (28.13)
Цилиндрические участки корпуса ракеты при сверхзвуковых скоростях
полета имеют, по сравнению с коническими участками, относительно мень-
ший коэффициент сУ1. В приближенных расчетах можно принять [41] сУ1 =
= 1,5а2Х, где X =— удлинение цилиндра. Соответственно поперечная си-
d
ла цилиндрической части корпуса
У\= l,5a2XgSM. (28.14)
Распределение этой силы по длине цилиндра можно принять равномер-
ным.
В приближенных расчетах аэродинамических нагрузок можно не учи-
тывать взаимное влияние различных отсеков. Тогда поперечная сила каж-
дого конического отсека определится фдрмулой У {° — 3a qSit где St- —
263
площадь проекции конической поверхности на плоскость, перпендикуляр-
ную к оси ракеты, и поперечная сила каждого цилиндрического отсека —
формулой У}0 = l,5a2?XzSz. Так как сумма площадей проекций кониче-
ских поверхностей на плоскость, перпендикулярную к оси ракеты, равна
5М — площади миделя ракеты, то полная поперечная аэродинамическая си-
ла для корпуса ракеты
Ух = 3a?SM + 1,5а2? Sz. (28.15)
Для двухступенчатой ракеты, показанной на рис. 28.4, получим
у<'> = JZLaqdt У(2) = — aq (d22 - d2}),
4 4
У(,3) ;= aq (dl-dl). (28.16)
4
Погонные нагрузки на цилиндрических участках корпуса ракеты
Силы У(1° конических отсеков можно прикладывать в точках, соот-
ветствующих центрам тяжести проекций поверхностей этих отсеков на
плоскость, проходящую через продольную ось корпуса.
При малых углах атаки, когда в первой формуле (28.11) можно пре-
небречь по сравнению с Р2, получим сХх = 2Р2. При этом значении cXi
получается заниженная величина лобового сопротивления. Более точная
формула [50] для конуса
1,56 +
М2)
(28.18)
лобовое сопротивление конуса от давления
X = (l,56 + -b^-)p'.^SM. (28.19)
Соответственно лобовое сопротивление каждого конического отсека корпу-
са можно определить по формуле
Х(0 = (1,56 + ) р!’7 qSit (28.20)
где Si, как и раньше, площадь проекции поверхности конического отсе-
ка на плоскость, перпендикулярную к оси ракеты.
Суммарное лобовое сопротивление конических поверхностей корпуса
ракеты от давления будет равно
х= fl,56 + -^Wp’’7S,.. (28.21)
264
Лобовое сопротивление корпуса Хтр, вызванное аэродинамическими
силами трения, можно приближенно оценить, приняв, что она состав-
ляет часть всего лобового сопротивления. Тогда полное лобовое сопро-
тивление корпуса ракеты определится приближенной формулой
Х + Хтр = ф,56+-^ (28.22)
\ м2 J
где k = 1,2 — 1,6.
Хотя полученные формулы для аэродинамических нагрузок и явля-
ются приближенными, однако это не вызывает значительных погрешно-
стей при определении напряжений в корпусе ракеты. Как уже отмеча-
лось в предыдущем параграфе, основной нагрузкой, определяющей
прочность ракеты, является сила тяги. Максимальные сжимающие уси-
лия в сечении корпуса в основном определяются осевыми силами инер-
ции масс, лежащих впереди этого сечения, и внутренним давлением
наддува (для баковых отсеков). Изгибающие моменты, вызванные по-
перечными аэродинамическими силами, относительно невелики. Макси-
мальные напряжения от этих моментов, как правило, меньше напряже-
ний от осевого сжатия. Поэтому вполне допустимо уточненные расчеты
аэродинамических нагрузок отнести к поверочным расчетам, когда уже
бывают известны результаты продувок моделей.
Уравновешивание ракеты на активном участке полета. Под уравно-
вешиванием ракеты понимают определение величин поперечных управ-
ляющих сил и сил инерции от поступательного и вращательного движе-
ний. Поперечная управляющая сила обычно создается или газовыми
рулями, или поворотными двигателями. Отклонение газовых рулей или
двигателей определяется работой автомата стабилизации. Величина
управляющей силы складывается из программной силы, заданной тра-
екторией полета, и дополнительной управляющей силы при стабилиза-
ции возмущенного движения. Для прочности ракеты наибольшее значе-
ние имеет величина управляющей силы при действии на корпус ракеты
бокового ветра. Программная управляющая сила обычно невелика и в
первом приближении в расчетах на прочность ее можно не учитывать.
Рассмотрим качественную сторону явлений, происходящих при воздей-
ствии бокового ветра на ракету. Для простоты будем считать, что на-
чальное невозмущенное движение ракеты соответствует вертикаль-
ному полету с нулевым углом атаки.
Составим приближенные линеаризованные уравнения возмущенного
движения ракеты как твердого тела при действии бокового ветра. Пусть
в момент времени t поперечная скорость центра масс ракеты равна vu
и угол поворота О. Если считать эти величины малыми, угол атаки по-
лучим в виде (рис. 28.5, а)
а = - ~ Vy---&. (28.23)
V
Аэродинамические силы в связанных осях хъ уг
X^c^qS^ Y^c^aqS,. (28.24)
Сила У1 приложена на расстоянии хд от передней точки ракеты.
Управляющая сила Ур приложена на расстоянии хр от той же точки
(рис. 28.5,6). Тяга двигателей направлена по оси ракеты. Проектируя
все силы на ось у и считая cos-0—1, sin-0 —-0, получаем (рис. 28.5, в)
= + —Ур. (28.25)
265
Составляя уравнение моментов относительно центра масс и пренебрегая
демпфирующим моментом, находим
1 = Y1 (%д ~%т) “ Гр (Х»~ (28.26)
В уравнениях (28.25) и (28.26) т — масса и / — массовый момент
инерции ракеты как твердого тела.
Рис. 28.5
К уравнениям движения (28.25) и (28.26) следует добавить уравне-
ние автомата стабилизации. Простейшее уравнение автомата может
иметь, например, следующий вид:
б + М = М, (28.27)
где б— угол отклонения газового руля или поворотного двигателя;
б — его производная по времени;
Ль k2 — характеристики автомата стабилизации; коэффициент k\ ха-
рактеризует запаздывание автомата.
Управляющее усилие Ур связано с углом 6 зависимостью
Ур = Лб, (28.28)
где А — коэффициент, учитывающий эффективность органа управления.
Система уравнений (28.25) — (28.28) позволяет с учетом формул
(28.23) и (28.24) определить все характеристики возмущенного движе-
ния, если задана скорость бокового ветра и. Для строгого определения
управляющего усилия Ур и расчетного угла атаки необходимо исследо-
вать весь переходной процесс, когда величины vy, Ф, б изменяются по
времени. Для статически устойчивой ракеты максимальная величина
силы У1 соответствует начальному моменту действия бокового ветра,
когда а = ав=—. При дальнейшем движении такой ракеты угол атаки
V
будет уменьшаться, так как ракета будет поворачиваться в направле-
нии уменьшения угла атаки. Это заключение, конечно, верно, если ско-
рость ветра не увеличивается в процессе движения ракеты. Для стати-
чески неустойчивой ракеты углы атаки в переходном процессе могут
оказаться большими ав. Поэтому при проектировании ракеты жела-
266
тельно избегать значительной статической неустойчивости, особенно на
режимах полета, когда скоростной напор близок к максимальному.
Достаточно точно значение управляющего усилия Ур можно опре-
делить только из решения уравнений возмущенного движения с учетом
работы автомата стабилизации. В начальной стадии проектирования
ракеты такие расчеты не всегда можно выполнить. В этих случаях
можно воспользоваться приближенным приемом, основанным на рас-
смотрении двух крайних случаев работы автомата стабилизации.
В первом случае принимают запаздывание автомата настолько боль-
шим, что угол отклонения управляющего органа 6 = 0 и соответственно
Ур = 0. Тогда из уравнения (28.26) определится угловое ускорение
= (28-29)
Во втором случае считают автомат стабилизации отрабатывающим
управляющую силу Ур, так что угловое ускорение ракеты = 0. Тог-
да из уравнения (28.26)
у = . (28.30)
хр — хт
В обоих случаях силу можно определять при угле атаки
Зная величины поперечной силы У1 и управляющей силы Ур, можно
определить поперечные перегрузки в каждом сечении корпуса.
В первом случае, когда Ур = 0 и аэродинамический момент уравно-
вешивается силами инерции, поперечная перегрузка в сечении
nUi=^-+ (х, -хт), (28.31)
mg gl
tn—масса ракеты;
I— массовый момент инерции ракеты;
g — ускорение силы тяжести у поверхности земли;
Х[ — координата рассматриваемого сечения.
Во втором случае, когда угловое ускорение равно нулю, перегрузка
во всех сечениях одинакова и равна
Пу = X1~YP = Г 1 _ *д~*т- 1 . (28.32)
mg mg [_ хр — хт J
Уравнениями (28.31) и (28.32) определяются перегрузки для ракеты
как для недеформируемого твердого тела. В динамических расчетах с
учетом упругости корпуса ракеты эти перегрузки соответствуют двум
первым формам собственных колебаний с нулевой частотой. Учет до-
полнительных динамических нагрузок от колебаний можно произвести
по методике, изложенной в гл. III.
Нагрузки, действующие на ракету при транспортировке. После по-
летных случаев случаи нагружения ракеты при транспортировке явля-
ются наиболее важными. Это объясняется тем, что в полетных случаях
основными являются осевые нагрузки, а роль изгибающих моментов и
перерезывающих сил относительно невелика.
При транспортировке корпус ракеты нагружается распределенными
поперечными нагрузками и относительно большими местными реакция-
ми опорных устройств. Нагрузки на элементы ракеты при транспорти-
ровке складываются из статических и динамических, определяемых ко-
лебаниями транспортных устройств. Статические нагрузки для различ-
267
них видов транспорта определить сравнительно легко. Динамические
нагрузки чаще всего бывают случайными (вероятностными). Их вели-
чины и повторяемость устанавливают на основании результатов обра-
ботки записей вибрационных и ударных перегрузок в реальных усло-
виях транспортировки. Таким образом, задаются расчетные значения
этих перегрузок и их повторяемость для различных видов транспорта.
В книге [24] приведены результаты большого числа экспериментов, их
анализ и рекомендации для расчета.
§ 29. АЭРОДИНАМИЧЕСКИЙ НАГРЕВ КОНСТРУКЦИИ
Нагрев конструкции, вызванный движением ракеты в плотных слоях
атмосферы, необходимо учитывать при проектировании. Этот фактор
влияет на выбор траектории полета, материалов конструкции, силовой
схемы и конструктивного выполнения отдельных узлов и агрегатов.
Влияние аэродинамического нагрева
тоспособности обшивки и силового
Рис. 29.1
прежде всего сказывается на рабо-
набора цилиндрических и кониче-
ских отсеков, оболочки баков и
ракетного двигателя твердого
топлива. При проектировании
это влияние в первую очередь
выясняют для активного участ-
ка полета по отношению к тон-
кой неподкрепленной обшивке,
которую для верхней оценки
возможных значений темпера-
туры принимают идеально те-
плоизолированной с внутренней
стороны.
Степень аэродинамическо-
J го нагрева обшивки зависит от
Тп многих параметров, среди кото-
рых наибольшую роль играют
скорость и плотность воздуш-
ного потока, обтекающего по-
верхность ракеты. В прилега-
ющем к поверхности слое поток, тормозится, часть его кинетической
энергии переходит в тепло, которое передается к поверхности ракеты,
в результате чего повышается температура конструкции. Часть тепла в
процессе нагрева излучается с поверхности в окружающее пространство.
Торможение частиц воздуха происходит неравномерно и зависит ог
расстояния до обтекаемой поверхности. Непосредственно на поверхности
обшивки благодаря силам трения относительная скорость частиц воз-
духа равна нулю. С удалением от поверхности относительная скорость
vx увеличивается, пока не достигнет предела который соответствует
обтеканию поверхности без трения (рис. 29.1,а). Прилегающий к по-
верхности слой потока, в пределах которого практически завершается
изменение скорости vx от 0 до называется пограничным.
Различная степень торможения частиц воздуха приводит к нерав-
номерному распределению температуры по толщине пограничного слоя.
Если обтекаемая потоком обшивка не -излучает в окружающее про-
странство и идеально теплоизолирована с внутренней стороны, то ча-
стицы воздуха на ее поверхности принимают температуру восстанов-
ления
Тг = Т6 (1 + ПЛ?) ,
(29.1)
где k — показатель адиабаты (для воздуха £=1,4). Ма—число Маха,
268
соответствующее скорости щ за пределами пограничного слоя. Вели-
чина г называется коэффициентом восстановления. Она показывает
долю кинетической энергии, которая переходит в тепло при торможе-
нии частиц воздуха на обтекаемой поверхности. Значение г зависит от
режима течения в пограничном слое и величины критерия Прандтля
Рг. Критерий Прандтля равен отношению кинетического коэффициента
вязкости к коэффициенту температуропроводности и характеризует по-
добие полей температуры и скорости в пограничном слое при обтекании
поверхности потоком. Для воздуха Рг = 0,7, что при ламинарном режи-
ме течения дает
г = ]ЛРг = 0,84, а при турбулентном — г=рлРг=0,89.
По мере удаления от поверхности обшивки температура воздуха
монотонно падает до значения соответствующего параметрам пото-
ка за пределами пограничного слоя (кривая 1 на рис. 29.1,6). Если
температура неизлучающей обшивки меньше температуры восстановле-
ния (ТП<ТГ), то обшивка нагревается, если же Тп>Тг, то она охлаж-
дается. Распределение температуры по толщине пограничного слоя для
этих случаев отмечено на графике кривыми 2 и 3. Величину и знак
удельного конвективного теплового потока, передаваемого к обшивке,
определяют по формуле
<7к = а(Тг-Тп), (29.2)
где а — коэффициент теплоотдачи.
При обтекании без угла атаки цилиндрической части корпуса раке-
ты можно считать, что T& = TH и = Ми, т. е. температура и число
Маха соответствуют параметрам невозмущенной атмосферы на высоте Н.
Тогда температура восстановления будет
Тг = Тн (1 + Т. (29.3)
Угол атаки при движении баллистической ракеты по траектории мал
и его влиянием на теплообмен при аэродинамическом нагреве цилинд-
рической части корпуса можно пренебречь.
При обтекании затупленной части конструкции, когда кинетическая
энергия потока полностью превращается в тепловую (г=1), темпера-
тура неизлучающей идеально теплоизолированной поверхности стано-
вится равной
г = т\(1 + -Ц^-М),
где Т*—температура торможения. Последний случай связан с обтека-
нием головной части ракеты и рассматривается в § 42. Там же разби-
раются вопросы, касающиеся теплообмена на поверхности конуса и за-
остренного тела вращения.
Для определения температуры восстановления и коэффициента теп-
лоотдачи необходимо знать скорость потока vH и параметры невозму-
щенной атмосферы на высоте Н. К этим параметрам относятся темпе-
ратура Тн, плотность рн (или давление рп) и скорость звука си. кото-
рая связана с температурой соотношением
где R— газовая постоянная воздуха.
Изменение этих параметров по высоте устанавливается таблицами
стандартной атмосферы. Эти таблицы составлены на основе осреднен-
ных данных экспериментальных измерений. Таким образом, параметры
269
стандартной атмосферы принимаются не зависящими от широты места,
времени года и суток и однозначно определяются высотой Н над уров-
нем моря. Распределение относительных температуры Th/Th—q и плот-
ности ря/рн=о воздуха по высоте показано на рис. 29.2. На уровне
моря (/7 = 0) принято Гн=о=
= 288° К и ря=о= 1,225 кг/м\
Действительные значе-
ния параметров атмосферы
могут отличаться от указан-
ных в таблицах стандартной
атмосферы [80]. В связи с
этим для определения верх-
него вероятного значения
температуры восстановления
в формуле (29.3) темпера-
туру часто берут с завы-
шением, а число Маха вы-
числяют по скорости звука
Си, соответствующей зани-
женному значению Тн. В
приведенных ниже числовых
примерах для расчета ис-
пользованы номинальные
табличные значения.
Для определения коэффициента теплоотдачи а от воздушного пото-
ка к поверхности ракеты можно использовать аналогию между тепло-
обменом и трением в потоке. Она следует из совпадения по форме диф-
ференциальных уравнений, описывающих переносы тепла и количества
движения в пограничном слое. Математическое выражение этой ана-
логии
St = scx (29.4)
связывает между собой критерий Стантона St и местный коэффициент
трения сх. Коэффициент пропорциональности s зависит от числа Пран-
дтля и при значении для воздуха Рг = 0,7 равен
s = у (Рг)-2/» = 0,64. (29.5)
При ламинарном режиме течения в пограничном слое местный коэффициент
трения
сх = 0,664//Re, (29.6)
а при турбулентном
сх = 0,0592 Re-0-2, (29.7)
где Re — критерий Рейнольдса. Смена ламинарного режима течения
турбулентным зависит от большого числа факторов и происходит в
диапазоне значений Re= (1,5ч-5) • 106. Критерий Рейнольдса
Re = vh(\x/t]v
где х — расстояние от точки образования пограничного слоя до рас-
сматриваемого участка поверхности обшивки, вычисляют по значениям
плотности р* и коэффициента вязкости т)* воздуха, взятых при опреде-
ляющей температуре
Л = Тн + 0,5 (Тп - Тн) 4" 0,22 (Тг - Тн).
270
Введение определяющей температуры позволяет учесть изменение фи-
зических свойств -воздуха по толщине пограничного слоя. Коэффициент
вязкости подсчитывают по формуле
т]е = 1,46• 10-6(7\)-(7\ + ПО) кг/м^сек,
а плотность воздуха определяют из соотношения
Р* = РнТн!Т\
в предположении, что давление в пограничном слое на цилиндрической
поверхности корпуса ракеты совпадает с давлением невозмущенной
атмосферы на данной высоте.
Критерий Стантона, определяемый по формуле (29.4), связывает
между собой интенсивность передачи тепла конвекцией и теплосодер-
жание потока. Он равен
St =--------, (29.8)
СР.Ы>Н
где —удельная теплоемкость воздуха, взятая при определяющей
температуре Т*. Зависимость удельной теплоемкости от температуры
показана на рис. 29.3 пунктиром.
Из соотношений (29.4) — (29.8) для ламинарного режима течения
получим
а = 0,425ср*рф vH/V Re, (29.9)
а для турбулентного
а = 0,038c^p^Re-°>2. (29.10)
В указанном выше диапазоне значений Re= (1,5-н5) • 106, который
характерен для смены режима течения в пограничном слое, практиче-
ски следует вести расчет одновременно по формулам (29.9) и (29.10) и
в дальнейшем использовать большее из полученных значений коэффи-
циента теплоотдачи.
271
Для расчета температуры восстановления и коэффициента тепло-
отдачи на поверхности конического отсека приведенные выше формулы
остаются справедливыми, но параметры невозмущенной атмосферы Тн,
vH, рд в них должны быть заменены параметрами Л4б, рб
потока, обтекающего коническую поверхность. Их можно определить
по методике, изложенной в работе [50].
При большой скорости полета (Мя^10) в пограничном слое воз-
никает весьма значительная разность температур Тт—Тп. В диапазоне
этих температур существенно изменяется удельная теплоемкость воз-
духа. Кроме того, в таких условиях заметное влияние на процесс тепло-
отдачи от воздушного потока к поверхности оказывают химические
реакции в пограничном слое, вызванные диссоциацией молекул возду-
ха. Из-за значительного изменения температуры по толщине погранич-
ного слоя концентрация диссоциированных газов у поверхности мень-
ше, чем на некотором расстоянии от нее. Проникая в результате диф-
фузии и перемешивания к поверхности, продукты диссоциации реком-
бинируют, выделяя тепло, что приводит к интенсификации теплообмена
в пограничном слое.
Влияние перечисленных факторов, которые играют важную роль
при теплообмене головной части ракеты на нисходящей ветви траекто-
рии полета в плотных слоях атмосферы, в значительной степени можно
учесть, если удельный конвективный тепловой поток к поверхности под-
считывать по формуле
qK = а' (Нг — Н„), (29.11)
где Нг и /7П — полные энтальпии воздуха при температурах Тг и Г1Г,
которые определяют по графику на рис. 29.3. Разность полных энталь-
пий Нт—Нп равна количеству энергии, которое необходимо затратить
на повышение температуры 1 кг воздуха от Ти до Тг. В эту энергию
входят тепловые эффекты химических реакций, которые происходят в
указанном диапазоне температур. При температурах Т<2000°К тепло-
емкость воздуха ср изменяется сравнительно мало, а влияние химиче-
ских реакций на теплообмен несущественно. Зависимость энтальпии от
температуры в этом диапазоне близка к линейной. При температурах
Г>2000°К начинает сказываться влияние химических реакций. Поэто-
му полная энтальпия воздуха, учитывающая тепловые эффекты этих
реакций, начинает быстро возрастать с увеличением температуры. На
ее величину также влияет давление р, от которого зависит степень дис-
социации молекул воздуха. Коэффициент теплоотдачи а', называемый
обычно энтальпийным, можно подсчитать по формулам (29.9) или
(29.10), опустив в них
Приведенными выше расчетными соотношениями можно пользовать-
ся не всегда. Дело в том, что при движении ракеты на большой высоте
благодаря разреженности атмосферы длина свободного пробега моле-
кул воздуха сравнима с толщиной пограничного слоя. Пограничный
слой в обычном понимании здесь отсутствует. Поэтому при расчете теп-
лообмена методы теории пограничного слоя становятся неприменимыми.
Их сменяют методы кинетической теории газов. В первом приближении
можно считать, что приведенные формулы справедливы, если
AfH/yRe<0,01. Конвективный теплообмен на высотах, где это условие
не выполняется, оказывает слабое влияние на температурное состояние
конструкции баллистической ракеты, и его можно не учитывать.
Помимо конвективного теплового потока, температурное состояние
обшивки зависит также от потока диэ ее собственного излучения в окру-
жающее пространство и величины лучистого теплового потока qa, который
поглощается обшивкой от внешних источников излучения, главным образом
от солнца. Тепловые потоки qK, q*3 и дл могут сильно отличаться по ве-
272
личине при различных условиях полета. На рис. 29.4 [36] показаны обла-
сти режимов полета (числа Мц и высоты Н), в которых можно учитывать
лишь определенные тепловые потоки: 1 — qK‘, 2 — qK и gH3; 3 — qK, ди3 и дл;
4 — и q^. Штриховкой отмечена примерная граница области Ми и /7, в
которой значение равновесной температуры Т обшивки, определяемой из
условия баланса всех действующих тепловых потоков, меньше 400 К.
Параметры Мп и Н для характерных траекторий баллистических ракет
укладываются, как правило, в областях 1 и 2. Поэтому равновесную
температуру Т идеально теплоизолированной
изнутри обшивки ракеты при текущих значе-
ниях Мп и Н можно найти из уравнения ба-
ланса
Як = Ям или а(Тг — Т) - есТцГ1,
где е и о() ^ 5,77-10“8 вш/м2( К)4—степень
черноты поверхности обшивки и коэффици-
ент излучения абсолютно черного тела. Это
уравнение можно привести к безразмерному
б = 1 , /V - = -^2- Т3Г, - —
а Тг
и решить его с помощью графика, показан -
ного на рис. 24.3.
Например, для значений vH — 1200 м/сек; Н = 20 км; х = 5 м
и
е- 0,8 последовательно определяем: из рис. 29.2 Ти/Тц=п = 0,78; р///рп=о=
= 0,07; затем подсчитываем: 7,/ = 0,78-288 = 225 К; Рн = 0,07-1,225 =
= 0,0856 кг/м1; сн = 20 Утп = 20]/225 = 300 м/сек; Ми=уц1Сц =
= 1200/300=4; при г= 0,84 (ламинарный режим) ТГ = Тц [1 -\ (k—1)гМ^/2} =
= 225 (1 0,168-4“) - 830°К; при г = 0,89 (турбулентный режим)
тг = Тн 11 4- (/г — 1) rMl/2] = 225 (1 + 0,178• 42) = 865 К.
Теперь следует задаться ожидаемым значением равновесной темпера-
туры. Пусть Т = Тп = 700°К. Тогда определяющие температуры примут
значения 1\=Тц 4 - 0,5 (Т„ — Тн) -|- 0,22 (Тг—Тц) = 225 -|- 0,5 (700—225)
+ 0,22 (830 — 225) = 596°К и 7\ = 225 -г 0,5 (700 — 225) 4- 0,22 (865-225) =
= 604 К. Так как разница между значениями Tt для ламинарного и тур-
булентного режимов течения в пограничном слое мала, то в последующих
расчетах принято одно значение 7\ =• 600°К. По нему определяют коэф-
фициент вязкости
П.= l,46-10-S(T4)'/2/(^ + 110) =
- 1,46- 10-с(600)7з/(600 -г 110) = 3,04- IO-5 кг/м-сек
и плотность воздуха
Р, - РпТц/T, = 0,0856-225/600 = 0,0322 кг/м1,
а по рис. 29.3 находят удельную теплоемкость сР ---^ 1,11 кдж/кг-град.
Критерий Рейнольдса
Re = Ц/zp.x/n. - 1200-0,0322-5/3,04-10-5 .= 6,35-106.
Так как Re>5-106, то режим течения турбулентный и коэффициент
теплоотдачи определяют по формуле (29.10)
18 Зак. 96
273
a-0,038cPep^HRe-°’2=0.038-1110-0,0322-1200(6,35- \G6)~Q^7lem/M2-град.
Затем вычисляют
W - (ecr0/a) (Тг)3 = (0,8-5,77-10~8/71) (865)3 - 0,422;
по рис. 24.3 находят $ = 0,814 и определяют
Т = ЪТГ = 0,814-865 = 705°К.
Полученное значение Т мало отличается от взятого в качестве пер-
вого приближения и поэтому может быть принято как окончательное.
В противном случае следовало бы повторить расчет при новом значе-
нии Т до тех пор, пока два последующих приближения не совпадут с
необходимой точностью.
Для различных чисел Мн полета результаты расчетов равновесной
температуры обшивки можно представить в виде зависимости Т1ТИ от
параметров Вл (рис. 29.5, а) и Вт (рис. 29.5,6). При ламинарном режи-
ме обтекания
Вл = 0,78-ЮЛ
_2kY’5Re4
тн=о'
при турбулентном
Вт = 0,876- 10-4е -^5- ( Tf1 Y 5Re0-2.
Р// \ ТН=0 '
Критерий Рейнольдса в обоих случаях вычисляют по параметрам невозму-
щенного воздушного потока
Re=-"^ .
Ли
Температура обшивки достигает равновесного значения при доста-
точно длительном установившемся полете с постоянной скоростью на
неизменной высоте. Но при движении баллистической ракеты по траек-
тории условия теплообмена существенно изменяются по времени: на
активном участке полета температура восстановления Тг непрерывно
возрастает, а коэффициент теплоотдачи а сначала увеличивается, а за-
тем по мере подъема ракеты на большую высоту начинает уменьшаться
несмотря на прогрессивный рост скорости полета.
Температура весьма тонкой обшивки с пренебрежимо малой полной
теплоемкостью будет принимать в полете так называемые мгновенные
равновесные значения T(t), которые соответствуют текущим значениям
а и Тг. Изменение температуры Т реальной обшивки из-за ее тепловой
инерции запаздывает по сравнению с изменением T(t). Запаздывание
274
тем значительнее, чем больше полная теплоемкость обшивки, причем
обшивка нагревается, когда T<T(t), и охлаждается, если
Для тонкой обшивки с постоянной по толщине температурой спра-
ведливо уравнение вида (26.1), которое в данном случае можно пред-
ставить так:
cph -~- = qK — qK3 = а(Тг-Т)- еа0Г, (29.12)
где Л, с и р — толщина обшивки, удельная теплоемкость и плотность
ее материала. Для решения этого уравнения можно использовать спо-
собы, изложенные в § 26. В качестве примера ниже рассматривается
расчет температуры обшивки на активном участке полета с помощью
графического способа, который в данном случае позволяет учесть изме-
нение во времени значений Тг и а, а также возможную зависимость
удельной теплоемкости материала обшивки и степени черноты ее по-
верхности от температуры [36].
Следует отметить, что интенсивность аэродинамического нагрева
обшивки при дозвуковой скорости полета довольно мала. Поэтому ин-
тегрирование уравнения (29.12) целесообразно начать с момента вре-
мени, соответствующего числу Мн= 1. Температуру обшивки в этот
момент времени, принимаемый за начальный (£ = 0), в приближенных
расчетах можно считать равной температуре восстановления при Ми = 1,
т. е.
7’0 = Л = 7’н(1 + -^-г).
Таблица 29.1
t мн и Ти Рн тг т а
k сек — км СК кг/м* °к °К вт/мР-град
0 0 1,00 1,6 278 1,039 328 328 —
1 5 1,55 4,0 267 0,802 382 338 305
2 10 2,20 6,6 253 0,596 470 364 277
3 15 2,95 10,0 229 0,395 585 406 209
4 20 4,00 14,0 225 0,217 865 462 129
5 25 5,10 19,0 225 0,100 1265 536 82
6 30 6,96 24,8 229 0,040 2210 606 35
В табл. 29.1 приведены значения Мн и Н с интервалом времени
А/ = 5 сек. Там же указаны температура Тн и плотность рн воздуха на
текущей высоте, вычисленные по графику на рис. 29.2. Подсчет значе-
ний критерия Рейнольдса показывает, что режим обтекания участка
обшивки, расположенного на расстоянии х = 5 м от передней точки ра-
кеты, на рассматриваемом участке полета будет турбулентным. Поэто-
му значения температуры восстановления Гг, приведенные в таблице,
подсчитаны по формуле
ТГ=ТИ 1 +
k-\
2
гМ*н - 7\(1+0,178Л^),
а начальная температура обшивки
TQ = TH 1 +
rl = 278 [1 + 0,178] = 328°К.
2 J
Приняты следующие параметры обшивки: с = 0,5 кдж]к.г- град; р =
= 7850 кг!м3; h= \ мм и е = 0,8. Для каждого момента времени с интер-
18* 275
валом Д/ = 5 сек, задаваясь рядом значений Т<ТГ и используя для
определения коэффициента теплоотдачи формулу (29.10), в координа-
тах Th, Т строим зависимость (рис. 29.6)
Л (Т) = [afe (7\ k - Т) - eaor}/cph,
где индекс k показывает номер интервала времени (&=1—6). При по-
строении на графике приняты следующие значения масштабов по осям
координат: mt =0,2 град! сек- мм и тт = 5 град 1мм.
По формуле (26.12) определяем угловой коэффициент ломаной
tgp = о,5-^- Д/ =0,5 = 5 - 0,1.
тт 5
Графическое построение для определения температур обшивки по
интервалам времени начинаем на графике из точки BQ, соответствую-
щей значению Г0 = 328°К. На пересечении первого луча с кривой зави-
симости 7\(Т) получаем точку ордината которой указывает темпе-
ратуру обшивки в конце первого интервала времени Л = 338°К. Далее
из точки Bi проводим отрезок ломаной BiO2, а затем — отраженный
луч, который с кривой зависимости Т2.(Т) дает точку пересечения В2
и т. д. Результаты графического определения температуры обшивки Т
приведены в предпоследнем столбце таблицы. По этим значениям с по-
мощью формулы (29.10) подсчитаны действительные величины коэф-
фициента теплоотдачи а, которые даны в последнем столбце таблицы.
Следует отметить, что при изменении толщины обшивки h кривые
зависимости Тк(Т) останутся прежними, но изменится масштаб
графика по оси абсцисс и пропорционально ему изменится угловой ко-
эффициент ломаной. Таким образом, при проектировании с помощью
графика на рис. 29.6 можно провести серию расчетов для обшивки из
заданного материала с различной толщиной и выбрать значение h, при
котором температура обшивки на активном участке полета ракеты
остается в допустимых пределах.
§ 30. ВНУТРЕННИЕ УСИЛИЯ В КОРПУСЕ РАКЕТЫ
Корпус ракеты представляет собой тонкостенную жесткую оболочку
вращения, усилия в каждом поперечном сечении которой могут быть
сведены к нормальной (осевой) силе N, перерезывающей силе Q и из-
276
гибающему моменту М (рис. 30.1). Построение эпюр нормальных, пере-
резывающих сил и изгибающих моментов по длине корпуса ракеты
необходимо для выбора расчетных случаев и проведения расчетов на
прочность.
Эпюра нормальных сил. Исходными данными для построения эпюры
нормальных сил являются: тяга двигательной установки Р, величина
аэродинамической осевой силы X и закон
#х(х), масса ракеты т и закон ее распре-
деления mv(x), давление наддува в баках
Pq. Все эти силовые факторы и масса ме-
няются вдоль траектории. В дальнейшем
при построении эпюр их считают неизмен-
ными и относят к определенному, фикси-
рованному моменту времени. Погонная
масса тх(х) и аэродинамическая нагруз-
ка qx(x) связаны с суммарными значе-
ниями т и X соотношениями
i i
т = тх (х) dx, X = qx (х) dx, (30.1)
о б
где I — длина ракеты. Аэродинамические
силы X и Y в настоящем параграфе соот-
ветствуют силам в связанной системе ко-
ординат. Индексы, принятые для этих сил
в § 28 и 17, здесь опущены.
При действии внешних сил Р и X
каждый элемент массы испытывает ста-
тическую перегрузку в осевом направле-
нии пх, которую определяют по формуле
(17.5). Нормальное усилие в сечениях
ее распределения по дл'ине
Рис. ЗОЛ
корпуса состоит из усилия Ai от внешних и инерционных нагрузок и ра-
стягивающего усилия Np от наддува на участках баков. В сечении с ко-
ординатой х усилие
^Vj. = Snx [ тх (х) [ Qx (х) dx’
б 6
(30.2)
Координата х может отсчитываться от условной точки пересечения тео-
ретического контура обвода головной части с осью х. Если тяга двига-
тельной установки Р приложена к корпусу в сечении х0, то при х>х0
нормальное усилие
N± = gnx тх (х) dx + J qx (х) dx — Р, (30.3)
б о
т. с. в сечении х = х0 осевое усилие имеет скачок на величину тяги Р,
при 0<х<х0 усилие определяемое формулой (30.2), — сжимающее,
при х>х0 (формула 30.3) N\ — растягивающее. Проведя интегрирова-
ние уравнения (30.3) по длине ракеты и воспользовавшись уравнения-
ми (30.1), получим зависимость для пх (17.5).
Уравнения (30.2) и (30.3) позволяют построить эпюры нормальных
сил для корпуса при статическом нагружении. В связи с тем, что реаль-
ный корпус является деформируемым телом, реагирующим на воздей-
ствие нагрузок, как правило, меняющихся по времени, кроме перегру-
зок статического характера, определяемых формулой (17.5), необходимо
учитывать динамические перегрузки пх . Определение осевых динами-
277
ческих перегрузок по длине корпуса, как для стержня, дано в гл. III.
Осевые усилия, возникающие от динамических перегрузок, самоуравно-
вешены и для любого сечения с координатой х определяются уравне-
нием
= % w т* юdx-
о
(30.4)
Итак, для построения эпюр нормальных сил нужно воспользоваться
уравнениями (30.2) — (30.4). Зависимости mx(x), qx(x), стоящие под
интегралами в этих уравнениях, обычно даются в виде графиков или
таблиц, поэтому получить аналитические выражения для N (х) неудает-
Рис. 30.2
ся. Приходится прибегать к численному интегри-
рованию. В начале расчета корпус разбивают по
длине на определенное количество равных участ-
ков /г = 204-50. Соответствующим сечениям при-
сваивают номера 0, 1, 2, ..., п. К этим сечениям
приводят аэродинамические и массовые усилия
так, чтобы сохранилось положение центра тяже-
сти и центра давления для всей ракеты. При
этом следует учитывать конкретный способ при-
ложения внешних и массовых усилий к корпусу
ракеты.
Тяга двигательной установки воспринимается
корпусом в сечении ее крепления к двигательно-
му отсеку. Аэродинамические усилия qx(x) пред-
ставляют собой распределенную по длине корпуса
нагрузку; управляющие силы приложены к оси
вращения руля. Инерционные силы пропорцио-
нальны массе оболочки корпуса, массам различ-
ных агрегатов и жидкого наполнения. Масса обо-
лочки считается распределенной по длине. Силы
инерции от массы агрегатов приложены в точках
крепления этих агрегатов к корпусу. Силы инер-
ции масс топлива воспринимаются днищами ба-
ков и переходят на корпус в местах крепления днищ.
Давление наддува р0 создает разгружающую осевую силу Np, дей-
ствующую на участке обечайки бака между передним и задним дни-
щами. Эта сила для цилиндрического бака равна Np = pQjtR2, для кони-
ческого несущего участка Np = pQnr2, где г — текущий радиус окружно-
сти сечения конуса.
Распределенные и сосредоточенные внешние и массовые усилия при-
водят к выбранным сечениям корпуса ракеты. Для этого сосредоточен-
ные нагрузки распределяют на два соседних сечения обратно пропор-
ционально плечам:
__р ai—1 рр ,__________р а1
д , .
(30.5)
Здесь Р — сосредоточенное усилие на /-том участке, А — длина участка,
и ai — расстояние от усилия Р до сечений j — 1 и / (рис. 30.2). Рас-
пределенную нагрузку q на /-том участке заменяют двумя сосредоточен -
ными силами
А А
Р/ = У qxdx, Р^_\ = у qdx — Р].
о о
(30.6)
278
На рис. 30.2 усилия Р и q представлены для наглядности как поперечные.
Соотношения (30.5) и (30.6) справедливы и для продольных и для по-
перечных сил.
Распределив для каждого /-того участка отдельно аэродинамичес-
кие, массовые усилия, тягу и управляющие силы, сложив /-тые силы со-
седних участков, приходящиеся на одно сечение, получают последователь-
ности: Pom; Plm\ Р2т\...\ Pjm;.. -\Рпт — сосредоточенных масс, PQX\ Р\х\
Рчх\ • • • ; Pjx\ • • • ; Рпх — аэродинамической осевой силы Pr; Pr±i —усилий
от тяги. При соблюдении уравнений (30.5), (30.6) массы Pjm должны в
сумме давать массу ракеты. Соответственно усилия Р]Х в сумме должны
быть равны аэродинамической осевой силе X.
Далее нужно просуммировать полученные силы для каждого i-того
сечения корпуса. Нормальные усилия определяются зависимостью
N. = gnx £ Pjm + £ PjX -£рг. (30.7)
/=о /=0 j=0
На участке бакового отсека из этих усилий следует вычесть величину
силы Np от давления наддува.
Вычисление усилий, необходимых при построении эпюр осевой силы
для корпуса ракеты, по зависимости (30.7) обычно сводят в таблицы.
В связи с тем, что в процессе проектирования эпюры усилий приходит-
ся строить несколько раз для различных расчетных случаев, рацио-
нально привести зависимость (30.7) к безразмерным параметрам и
разбить массу ракеты на составляющие, неизменные и меняющиеся в
процессе полета: массу сухого изделия тс и массу наполнения /пн. Со-
ответствующие массы в каждом /-том сечении обозначают
Р/m и Р”т, причем Pjm = Р^п + Р"т.
Выражение для нормального усилия тогда примет вид
= + + G = mg- <30-8)
/=0 /=0 /=0 /=0
Па участке баков, как и ранее, из полученных значений нужно вы-
честь Np = p0jtR2. В уравнении (30.8) коэффициенты, стоящие под зна-
ком суммы, меняются от 0 до 1 и могут быть представлены так:
— РС _ рн _ Р _ D
P/m=—Pjm = —^, PjX=^~, Pr = ~~ (30.9)
Осевые усилия, соответствующие динамической перегрузке пХд, равны
Л^д = (Р]т + Р*1ГП). (30.10)
/=0
Подсчет усилий по уравнению (30.8) для корпуса при статических на
грузках сведен в табл. 30.1. Столбцы 2, 3, 4 таблицы заполняют после
распределения масс и нагрузок по сечениям и приведения полученных
масс и усилий к безразмерным коэффициентам согласно уравнению
(30.9). В столбцах 6—9 производится суммирование коэффициентов
(интегрирование). Числовые значения коэффициентов, полученных в
столбцах 2—9, справедливы для любого расчетного случая полета раке-
ты. Для определенного случая при известных осевой перегрузке, весах
Gc и GH, суммарной аэродинамической нагрузке X и усилиях Р в столб-
цах 10—13 находят составляющие усилия а в столбце 14 —само
•осевое усилие Ni. Окончательное статическое усилие N по сечениям
корпуса указывают в столбце 16 после учета поправок, вносимых уси-
лием Хр от давления наддува на участках баковых отсеков.
279
Таким образом, для одной и той же ракеты, у которой в процессе
полета меняется только количество топлива, коэффициенты столбцов
2—9 таблицы остаются неизменными. Перегрузка пх в зависимости ог
веса ракеты и внешних сил определяется уравнением (17.5).
При проектировании часто приходится перемещать грузы сухой
части ракеты, добавлять или снимать некоторые агрегаты. В этом слу-
Таблица 30.1
№ 7е / J Р г V7S ] ж V/". —1 Л'
1 2 3 4 5 6 7 8
0
1
Продолжение табл. 30.1
№ с? н лх6с-(б) nxG"-(7) Х(8) Р(9) ^.=(10)+ Ч (И Ж12)- -(13) Л'р N-- -(14)-(15>
9 10 11 12 13 14 15 16
0
1
чае необходимо корректировать коэффициенты столбцов 2 и 6 и, есте-
ственно, вновь находить перегрузку по уравнению (17.5). Коэффициен-
ты остальных столбцов и последовательность операций остаются преж-
ними.
Эпюры перерезывающих сил и изгибающих моментов. Для построе-
ния этих эпюр, кроме закона распределения масс по длине ракеты
тх(х), необходимо знать величину поперечной силы У и ес распреде-
ление 7У(х), управляющее усилие Yp >и значение поперечной перегрузки
пу (см. § 28).
Перерезывающую силу в любом сечении х корпуса при n?y = const
можно найти по зависимости
Q = — gny J тх (х) dx + [ qy (х) dx. (30.11)
о 6
В тех случаях, когда следует учитывать вращательную перегрузку,
суммарное значение пу должно стоять под знаком интеграла.
Соотношение (30.11) справедливо от 0 до хь где приложено управ-
ляющее усилие. При х>%1 перерезывающая сила определяется уравне-
нием
Q = — g j‘ путх (х) dx + [^(x)dx —Ур. (30.12)
6 о
На торце корпуса при х=1 в полете Q = 0.
280
Изгибающий момент по длине корпуса для
ляется из соотношения
М = Qdx.
о
сечений х<х0 опреде-
(30.13)
Если в сечении с координатой
бающий момент, то для
х = Xq приложен сосредоточенный изги-
(30.14)
о
Если в последующих сечениях корпуса %i; х2, ••• приложены сосредото-
ченные моменты, то их следует добавить в правую часть уравнения
(30.14) для участков Х]<х<х2, х2<х, ... и т. д.
Величины усилий для построения эпюр перерезывающих сил при
динамической перегрузке пу можно получить из уравнения
д
<?д = g J «</д W tnx (х) dx.
6
(30.15)
Соответствующий изгибающий момент определяют по уравнению (30.13).
Эпюры изгибающих моментов и перерезывающих сил так же, как и
рассмотренные ранее эпюры N, строят по данным численных расчетов.
Численному интегрированию уравнений (30.11) и (30.13) должно пред-
шествовать распределение массовых и аэродинамических сил по участ-
кам интегрирования. При расчете поперечных массовых сил от жидко-
сти считается, что зеркало жидкости нормально к оси ракеты, так как
осевая перегрузка существенно больше поперечной на всем участке
активного полета. Массовые силы жидкости по длине от зеркала до
днища считаются распределенными равномерно. Массовые поперечные
усилия от агрегатов воспринимаются корпусом в узлах их крепления.
Для консольно закрепленных элементов, таких, например, как двига-
тель ЖРД, при действии поперечной перегрузки необходимо учитывать
в местах крепления нс только усилие, но и сосредоточенный момент.
При практических расчетах распределенные и сосредоточенные внеш-
ние и массовые усилия приводят к выбранным сечениям корпуса раке-
ты так же, как и ранее. Сосредоточенный момент Мо распределяется в
соседних /-том и j—1-м сечении согласно зависимостям (см. рис. 30.2)
, а;
М, = Л40 —, М/_1 = Л40 . (30.16}
Суммируя /-тые усилия соседних участков, получаем последователь-
ности: PQfn\ Pltn- Р2т\ ... ;РЛШ —сосредоточенных масс, PQy\ Р{у\ Р2у, ...
... ; Pjy, .. . ; Рпу — составляющих поперечной нагрузки, Ргу — усилий от
управляющих органов. Сумма всех элементарных масс Р-т должна рав-
няться массе ракеты, а центр тяжести Pjm должен совпадать с центром
тяжести хт изделия. Соответственно усилия Р?у в сумме должны быть
равны поперечной нагрузке У, а центр тяжести их совпадать с центром
давления ракеты. Для получения величин перерезывающей силы и изги-
бающего момента нужно теперь просуммировать полученные /-тые усилия.
Перерезывающая сила в i-том сечении
/=0 /-0 j=Q
281
изгибающий момент
М = Д £ Q. + £ Mjr. (30.18)
/=0 /=0
При построении безразмерных эпюр Q и М следует поступать так же,
как и при построении безразмерных эпюр нормальных сил. Массу ракеты
разделяют на составляющую сухого изделия и составляющую наполнения.
В каждом /-том сечении Р]т = Р^т + Р*т, где Р*т— элементарные массы
-от наполнения для эпюр М и Q. Уравнение для определения перерезы-
вающей силы в £:том сечении корпуса имеет вид
Q = - Gc £ «Л- - Gn £ л Д. + Y £ Pjy - Yp S Pry, (30.19)
/=0 /=0 j=0 j=0
где безразмерные коэффициенты . ,Ргу равны
Ч--—. = (30-2())
тс тп У У р
Для построения эпюры изгибающих моментов следует воспользо-
ваться уравнением (30.18).
Перерезывающую силу, соответствующую динамической перегрузке,
определяют так:
Q„ = G^nyR (Р-т + Р?т). (30.21)
/=0
Для определения динамического изгибающего момента значение QA
нужно просуммировать для каждого / от / = 0 до j = i и результаты в
каждом сечении умножить на А.
В табл. 30.2 определяются перерезывающие усилия и изгибающие
моменты по корпусу ракеты. Динамические нормальные и перерезыва-
ющие усилия и моменты пред-
ставлены в табл. 30.3. Можно
найти усилия и моменты для
любого тона колебаний, но для
этого нужно знать закон рас-
пределения осевой и попереч-
ной динамических перегрузок
по длине корпуса. Нахождение
величин и закона распределе-
ния динамических перегрузок
для корпуса как для стержня
дано в гл. III. Общие усилия и
моменты в корпусе ракеты рав-
ны сумме статической и дина-
мической компонент. Суммиро-
вание проводится после полу-
чения составляющих в табл.
30.1—30.3.
На рис. 30.3 построены ти-
пичные эпюры N(x), М(х) для
двухступенчатой ракеты.
Выше рассмотрены особенности определения внутренних усилий в
корпусе ракеты схемы «тандем». Построению эпюр N(x), Q(x), M(x)
для ракеты схемы «пакет» должны предшествовать расчеты по опреде-
лению реакций в связях ступеней. При статически определимом креп-
282
Таблица 30.2
№ Р1 Р? / Р1У РГУ SV7 ^РЗУ Ягу 6е (6) 6Л(7) у -(8) Ур(9) Q=-(10)~ —(11)4- 4-(12)-(13) Я Д(15) мг М
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
0
1
Таблица 30.3
№ 1 Рс ] Р» / pc-f-p” пх Д (4).Пл. Д £(6) Na=G-(7) Р? ] Р^+Р? пУ ул (10). гм *Д £(12) £(3) Qa=G-(13) =Д>(14)
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
0
1
лении ступеней реакции связей определить нетрудно, каждую ступень
при этом считают абсолютно жестким телом.
Например, система соединения ступеней ракеты «Титан Ш-С» ста-
тически определима. Осевая сила ускорителя первой 'ступени на кор-
пусе второй ступени воспринимается продольными лонжеронами.
Эксцентриситет тяги и лобовой силы дает радиальные составляющие на
корпус, воспринимаемые в двух сечениях.
Если по длине ракеты осевая сила воспринимается в двух или более
сечениях или радиальных связей больше двух, то такая система стати-
чески неопределима. Трудности определения реакций существенно воз-
растают. В этом случае корпус рассматривается как оболочка, под-
крепленная реальными усиливающими элементами (шпангоутами, лон-
жеронами). При нахождении коэффициентов уравнений метода сил не-
обходимо учитывать деформации как всего корпуса, так и отдельных
элементов, соединяющих ускорители с ракетой.
После определения реакций связей расчет внутренних усилий прово-
дят отдельно для каждого элемента пакета. Реакции связей при этом
считают внешними силами, и эпюры строят в той же последовательно-
сти, что и для схемы «тандем».
§ 31. КОЭФФИЦИЕНТ БЕЗОПАСНОСТИ. РАСЧЕТНЫЕ СЛУЧАИ
Задача расчета на прочность элементов конструкции ракеты — обес-
печить надежность работы конструкции при минимальном ее весе.
Формулировка условий достаточной надежности зависит от принимае-
мых критериев при оценке прочности и методов определения расчетных
предельных состояний конструкций.
В самолетостроении и ракетной технике в основном принят метод
расчета «по разрушающим нагрузкам». Особенность метода состоит в
том, что размеры элементов конструкции выбирают таким образом,
чтобы конструкция выдерживала без разрушения определенную норми-
рованную нагрузку. Эта нагрузка называется расчетной разрушающей
нагрузкой. Расчетная разрушающая нагрузка равна эксплуатационной
нагрузке, умноженной на коэффициент безопасности. Эксплуатацион-
ную нагрузку определяют по результатам баллистических и аэродина-
мических расчетов, продувок, полетных испытаний и пр. Таким образом,
все внешние усилия, действующие на ракету, перегрузки, внутренние
усилия, возникающие в корпусе в рабочих режимах полета, при транс-
портировке и старте, называются эксплуатационными. Эти нагрузки
связаны с расчетными нагрузками соотношениями
Хр-/Хэ, ур-/уэ, рр-/рэ, хр-ж Л4Р-/МЭ.
Здесь индексы «р» и «э» соответствуют расчетным и эксплуатационным
нагрузкам, f — коэффициент безопасности. Соответственно расчетная
перегрузка nP=fn?.
Степень надежности, с одной стороны, и весовая эффективность
конструкции, с другой, зависят от величины коэффициента безопасно-
сти f. Естественно, невыгодно создавать конструкции с большими зна-
чениями коэффициента безопасности — они будут иметь неоправданно
большой вес. При сильно заниженных значениях коэффициента без-
опасности возможно разрушение элементов конструкции в реальных
условиях эксплуатации. При назначении величины коэффициента без-
опасности должна учитываться степень точности определения эксплуа-
тационных нагрузок (т. е. погрешности в данных аэродинамических,
баллистических, тепловых и других расчетов, допуски на давление в
баках и пр.), а также известная условность в расчетах на прочность
(неполное соответствие силовой схемы реальной конструкции, отклонс-
284
пия от номинальных значений размеров, механических характеристик
материала и т. д.).
Для самолетов величина коэффициента безопасности лежит в пре-
делах /=1,5—2,0 [41]. В требованиях к расчету управляемых снарядов
в Англии указывается, что расчет конструкции на прочность в расчет-
ных случаях, соответствующих полету, должен проводиться с коэффи-
циентом безопасности /=1,33. Согласно требованиЯхМ к прочности бес-
пилотных летательных аппаратов, предъявляемым в США, для условии
загружения в полете коэффициент безопасности принят равным /=1,25;
в случаях обслуживания ракеты на земле коэффициент безопасности
повышается до /= 1,5 [118]. В большинстве случаев вводить одинако-
вый коэффициент безопасности для всех ракет и всех условий эксплуа-
тации нерационально. Учитывая недостаточную достоверность при опре-
делении отдельных составляющих нагрузки, иногда применяют разные
коэффициенты безопасности к этим составляющим. Например, величина
коэффициента безопасности на давление в баках при расчете на устой-
чивость может быть взята минимальной, в то время как соответствую-
щее значение коэффициента на внешние силы — несколько большей ве-
личины. Сравнительно небольшая величина коэффициента безопасности
для ракет обусловлена одноразовым их применением. Некоторые эле-
менты конструкции ракеты рассчитывают при повышенных коэффици-
ентах безопасности. Например, для баллонов высокого давления при
их заправке в присутствии людей коэффициент безопасности обычно
больше двух.
Для большинства элементов, работающих на растяжение, расчетной
разрушающей нагрузке должны соответствовать напряжения, равные
пределу прочности материала. Для отсеков, подверженных сжатию,
этой нагрузке должны соответствовать критические напряжения потери
устойчивости: для гладких отсеков — напряжения ахл (см. § 16), для
стрингерных и других подкрепленных отсеков — критические напряже-
ния потери общей устойчивости.
Приближенные методы определения разрушающих (предельных)
нагрузок для стержневых систем и оболочек освещены в § 15.
Для надежного определения разрушающих нагрузок реальных кон-
струкций ракет используют статические испытания. По результатам
испытаний определяют запас прочности элемента конструкции в расчет-
ных случаях загружения. Запас прочности
где Рф — фактическая разрушающая нагрузка по результатам испы-
таний;
Р»— расчетная разрушающая нагрузка.
Правильно спроектированная конструкция должна иметь запас проч-
ности, близкий к п = 1.
Необходимо отметить, что такие элементы конструкции ракеты как
двигатель ЖРД, находящийся в условиях интенсивного нагружения и
нагрева, рассчитывают не по разрушающим нагрузкам, а по допускае-
мым напряжениям или по допускаемым перемещениям [93]. Величину
запаса прочности при расчете по допускаемым напряжениям опреде-
ляют как отношение
где ав и ст’ — предел прочности материала и максимальное значение
эксплуатационного напряжения.
Подробнее особенности расчета двигателей по допускаемым напря-
жениям рассмотрены в § 48.
285
В связи с тем, что баллистическая ракета имеет программные траек-
тории полета, нагрузки в каждой точке трассы полета определяются на
основе баллистических и динамических расчетов. В некоторые моменты
времени полета напряжения в сечениях ракеты достигают наибольших
значений. Эти моменты соответствуют случаям наиболее опасных ком-
бинаций нагрузок и называются расчетными случаями.
Расчет элементов конструкции ракеты на прочность производится
в расчетных случаях по соответствующим им внешним нагрузкам.
Часто определить расчетные случаи бывает довольно сложно. Одна-
ко для ряда отсеков и агрегатов ракеты некоторые из таких случаев
можно указать заранее. Например, узлы крепления двигателя рассчи-
тываются на случай запуска при действии максимальной динамической
перегрузки, узлы крепления агрегатов внутри корпуса — на случай дей-
ствия максимальных перегрузок ri и п„ хвостовой отсек — на
г rj xmax i/max»
расчетные случаи при стоянке ракеты на стартовом столе при действии
максимальной ветровой нагрузки и т. д.
Понятно, что даже для этих элементов ракеты расчетные случаи
не исчерпываются теми, которые приведены. Детальные расчеты часто
выявляют новые и иногда более опасные расчетные случаи.
Для основных элементов ракеты, расположенных в средней части
(баков, переходных отсеков и т. д.), приходится определять расчетные
случаи на основе подробных расчетов на прочность.
В различные моменты времени полета и наземной эксплуатации каж-
дый отсек корпуса ракеты нагружается различными силами (сжимаю-
щими, изгибающими, сдвигающими, силами давления). Для упрощения
анализа расчетных случаев и комбинаций нагрузок удобно ввести по-
нятие определяющей нагрузки.
Усилие, от величины которого в первую очередь зависит силовая
схема и конструктивные особенности отсека, называется определяю-
щим. Так, для стабилизатора отделяющейся головной части ракеты
определяющей нагрузкой является внешнее аэродинамическое давле-
ние. Сухой отсек ракеты загружен осевым сжатием N, изгибающим мо-
ментом М и перерезывающей силой Q. Усилия сдвига обычно незначи-
тельны и являются второстепенным фактором. Сжатие и изгиб
определяют, в основном, конструкцию такого отсека. Для него опреде-
ляющей нагрузкой будет сжимающая эквивалентная силаЛ^^ = N + — .
/?
Для некоторых отсеков приходится рассматривать несколько опреде-
ляющих нагрузок. Например, для конического переходного отсека опре-
деляющая нагрузка — внешнее аэродинамическое давление и осевая
сила А^экв- Баки ракет в качестве определяющей нагрузки имеют ?УЭКВ
и давление наддува.
Эквивалентная сила
^экв = ^ + -^ (31.1)
А
характерна тем, что напряжения сжатия в сечениях корпуса от этой
силы равны суммарным напряжениям сжатия от действия осевой си-
лы N и изгибающего момента М.
Расчетные случаи для сухих отсеков средней части корпуса выби-
рают по максимальному значению величин Мэкв, вычисленных для раз-
личных точек траектории полета.
Зависимости NQKB от времени для различных сечений строят с по-
мощью уравнения (31.1), используя результаты предыдущего пара-
графа. Исходными данными для расчета являются внешние программ-
ные нагрузки и нагрузки от возмущенного движения ракеты по траек-
тории, а также распределение масс по длине корпуса ракеты и закон
их изменения по времени полета. По этим данным находят перегрузки
286
Рис. 31.1
пх и Пу в каждой точке траектории. Осевая перегрузка пх, определяе-
мая, в основном, программными нагрузками, увеличивается в полете.
Например, для ракеты «Титан 2» на старте пх»1,4, а в конце работы
двигательной установки первой ступени пх~9.
В сухом отсеке осевая сила N определяется уравнением (30.8). Она
складывается из сил инерции и сил аэродинамического сопротивления.
В сечениях передних и средних отсеков корпуса осевые силы обычно
возрастают по мере выгорания горючего вследствие увеличения осевой
перегрузки. Наиболее нагруженным сечением корпуса является, как
правило, сечение отсека, примыкающее к двигательной установке. На
рис. 31.1 построены харак-
терные кривые, отражаю-
щие изменение осевой си-
лы для различных сечений
в функции безразмерного
времени полета.
Поперечная перегруз-
ка nv, определяющая ве-
личину изгибающего мо-
мента в сечении корпуса,
складывается из двух час-
тей: программной попе-
речной перегрузки и пере-
грузки от возмущенного
движения. Вторая часть
перегрузки, зависящая, в
основном, от ветровой на-
грузки, обычно значитель-
но больше программной
перегрузки. Поперечная перегрузка при полете в атмосфере достигает
максимальных значений на участках траектории, где скоростной напор
q близок к <7тах- На участке траектории при полете в верхних слоях ат-
мосферы поперечная перегрузка весьма мала, величина ее определяется
силами от управляющих органов. Случаи наибольшей поперечной пере-
грузки соответствуют обычно максимальным изгибающим моментам в
сечениях корпуса ракеты.
Из уравнения (31.1) при известных силе N и моменте М легко найти
эквивалентную осевую силу Мжв в каждой точке траектории для раз-
личных сечений корпуса. На рис. 31.2 построена зависимость УУЭКВ от
времени для двух сечений корпуса бакового отсека ракеты Фау-2 [95].
Для сечения II—II расчетным является случай, когда /УЭКв2 = 15 500 кГ.
В сечении /—/ эквивалентная сила достигает максимальной величины
на 30-й секунде полета — Мжв1 = 12 800 кГ. Расчетные случаи для дру-
гих сечений корпуса можно найти построением подобных кривых.
Баки ракет нагружены нормальной силой N, изгибающим момен-
том М и внутренним давлением р. Определяющими нагрузками для них
являются эквивалентная сжимающая сила и внутреннее гидростатиче-
ское давление. Эквивалентная сжимающая сила для бака
N'3Ka = ЛГ + 2 -роп^, (31.2)
где ро — давление наддува, R — радиус обечайки бака. Гидростатиче-
ское давление складывается из давления наддува pQ и давления столба
жидкости пхуН
Р = Р0 + пхуН. (31.3)
Здесь у — удельный вес жидкости, пх — осевая перегрузка, Н — высота
столба жидкости от зеркала до рассматриваемого сечения.
287
Гидростатическое давление определяет окружные напряжения в обе-
чайке, окружные и меридиональные напряжения в оболочках днищ и
шпангоутах на стыке днищ с обечайкой.
Эквивалентная сила д^кв и гидростатическое давление р являются
определяющими нагрузками для расчета обечайки бака на устойчи-
вость от сжатия. Критические сжимающие напряжения в обечайке бака
зависят от величины внутреннего давления. Расчет обечайки произво-
дится на несколько расчетных случаев для различных комбинаций на-
грузок Л^экв И ’р.
Рис. 31.2
Участки обечайки бака, находящиеся над зеркалом жидкости, испы-
тывают интенсивный аэродинамический нагрев. В связи с тем, что на-
грев существенно снижает механические характеристики материала, не-
обходимо проводить расчет на прочность и устойчивость с учетом
влияния температуры. Особенности расчета баков различной конструк-
ции рассматриваются ниже, в § 33 и 34.
Как уже было указано, процесс нахождения расчетных случаев для
элементов корпуса ракеты весьма трудоемкий. Чтобы упростить расчет, на
стадии предварительного проектирования можно ориентироваться на мо-
менты времени полета, соответствующие наибольшим значениям скорост-
ного напора 9тах, тяги двигательной установки Ртах, температуры конст-
рукции Ттак, перегрузок /гХтах и а также величин (пхуН)тяк. Мо-
менты времени полета ракеты, соответствующие максимальным значениям
этих величин, в предварительных проектировочных расчетах могут рас-
сматриваться как расчетные случаи. Необходимо отметить, что последую-
щие расчеты позволяют точно определить расчетные случаи по ^эки)тах>
ртах и т. д.. Кроме полетных случаев, при расчетах рассматриваются слу-
чаи транспортировки ракеты и ее отсеков в горизонтальном положении,
случаи действия ветровых и сейсмических нагрузок.
Во всех этих расчетных случаях необходимо построить эпюры мо-
ментов Л1, нормальных и перерезывающих сил N и Q, эпюры гидро-
статического и аэродинамического давлений. Эти данные являются
исходными для проведения последующих расчетов на прочность.
ГЛАВА VI
РАСЧЕТ БАКОВ
§ 32. КОНСТРУКТИВНЫЕ СХЕМЫ И НАГРУЗКИ
Форма, конструкция и материал бака ракеты должны удовлетворять
различным, иногда противоречивым требованиям. Однако в основе
анализа силовой схемы, определения толщин элементов и веса бака
лежат прежде всего расчеты на прочность. Исходными данными для
расчетов на прочность баков являются нагрузки и температура.
Баки в различных расчетных случаях нагружены:
1) давлением наддува р0;
2) давлением столба жидкости пхуН, где пх— осевая перегрузка
с учетом динамичности (см. гл. Ill), Н и у— высота столба и удельный
вес жидкости;
3) силами реакции соседних отсеков. В поперечном сечении бака
действуют: М — изгибающий момент, N — осевая сжимающая сила и
Q — перерезывающая сила.
На прочность баков оказывает влияние температурное состояние
конструкции.
От внутреннего давления в сечении
Р = Ро + пхуН (32.1)
и усилий М, У, Q в обечайке бака возникают меридиональные Тъ окруж-
ные То и сдвигающие S погонные усилия. Наибольшие значения этих уси-
лий будут
1 — \ 2л/? + ~л№ 2 )
Л = (Ро + tlxyH) R,
(32.2)
(32.3)
(32.4)
Положительные значения сил 1\ и Т2 соответствуют растягивающим на-
пряжениям.
Усилие сдвига S в расчетах на прочность баков является второсте-
пенным фактором. Величины сил Тх и Т2 в первую очередь определяют
выбор того или иного конструктивного варианта бака и, как показы-
вают соотношения (32.2) и (32.3), зависят от давления наддува pQ.
При малых значениях давления наддува меридиональное усилие Ть
возникающее в обечайке корпуса бака, оказывается сжимающим. Сжа-
тая в осевом направлении обечайка может потерять устойчивость. На-
пряжения, соответствующие потере устойчивости обечайки гладкого
бака, весьма невелики. Для повышения устойчивости обечайки можно
применить панели стрингерной или вафельной конструкции. Существует
другой путь — увеличение давления наддува в баке pQ. Тогда осевые
сжимающие напряжения снижаются (32.2). Дальнейшее увеличение pQ
приводит к растяжению обечайки вдоль образующей. Соответствующие
19 Зак. 96
289
окружные усилия (32.3) при этом оказываются большими. При больших
окружных растягивающих усилиях баки целесообразно выполнять из
высокопрочных материалов. Отсутствие осевого сжатия позволяет де-
лать обечайки неподкрепленными. Баки этого типа называют глад-
кими из высокопрочного материала. Давление наддува в
них обычно выбирают так, чтобы в осевом направлении не возникали
сжимающие напряжения от силы N и момента М:
+ (32.5)
2 | 2лй nJ? I
Суммарные осевые напряжения при этом сравнительно невелики. Однако
внутреннее давление создает большие окружные напряжения
= (Ро + пхуН) ,
п
которые оказываются расчетными. Расчет обечаек баков при этом обыч-
но ведут на прочность от окружных растягивающих напряжений.
5)
Рис. 32.1
Примером баков гладкой конструкции могут служить баки ракеты
«Атлас» (рис. 32.1,а). Баки горючего (керосин) и окислителя (жидкий
кислород) представляют собой единый блок длиной около 18 м, диамет-
ром 3 м. В середине бака имеется полусферическая перегородка —
днище, разделяющая полости горючего и окислителя. Обечайка бака
изготовлена из 23 отдельных секций. Материал обечайки — нержавею-
щая холоднокатаная сталь с пределом прочности <ув= 140 кГ!мм2 (пре-
дел текучести от= 112кГ/юи2).Толщина стенок переменная: отЛ = 0,25ли£
в передней части до Л=1,1 мм у заднего днища. Весь период эксплуа-
тации, начиная с изготовления, в баках поддерживается избыточное
давление ро = О,7 кГ1см2 для предотвращения потери устойчивости тон-
костенной обечайки. Во время полета ракеты давление наддува в баке
горючего составляет 4,2 кГ1см2, а в баке окислителя— 1,8 кГ!см2. В ме-
стах сварки секций бака для компенсации потери прочности сварного
шва с внутренней стороны его накладывается усиливающая полоса,
привариваемая точечной сваркой.
Днища бака изготовлены из листов той же нержавеющей стали пу-
тем сварки отдельных секций. Нижнее и верхнее днища выполнены в
виде конуса с переходом в цилиндр.
На рис. 32.1,6 изображен блок баков ракеты «Центавр», изготов-
ленный также из тонколистовой нержавеющей стали. Бак горючего
(жидкий водород) — цилиндрический, с коническим передним днищем,
бак жидкого кислорода — чечевицеобразный.
290
Диаметр и толщины обечаек баков этого типа таковы, что конст-
рукция практически не может работать на сжатие. Секции бака
(й = 0,25 мм, /?=1500 мм) не способны воспринимать сжимающее на-
пряжение выше 2 кГ1мм\ что соответствует осевой силе 2Vi = 4800 кГ.
Давление же наддува р0=1,8 ат создает осевую силу Np= 130 000 кГ.
При отсутствии наддува достаточно небольшого сжимающего усилия,
чтобы обечайка потеряла устойчивость. Давление наддува позволяет
сохранить работоспособность конструкции.
При относительно небольших значениях внутреннего давления бак
может быть выполнен из листового алюминиевого сплава. По сравне-
нию с предыдущей схемой окружные напряжения здесь существенно
меньше. Обечайка в осевом направлении сжата. Расчет баков ведут,
в основном, на устойчивость как сжатых цилиндрических оболочек
с учетом внутреннего давления. Потеря устойчивости может происхо-
дить как в упругой, так и в пластической области работы материала.
На участке активного полета ракеты в атмосфере часть бака над зер-
калом жидкости испытывает интенсивный аэродинамический нагрев.
Механические характеристики материала обечайки при этом значитель-
но снижаются. Расчет на прочность должен проводиться с учетом влия-
ния температуры.
Гладкие баки из листового алюминиевого сплава применяются на
ракетах «Юпитер», «Редстоун» и пр. Цилиндрические участки баков
состоят из нескольких секций, свариваемых встык. Днища представ-
ляют собой сегменты сферы и соединены с цилиндрической обечайкой
через переходное кольцо.
Для повышения напряжений, соответствующих потере устойчивости
бака от осевого сжатия, обечайку подкрепляют продольными* и попе-
речными элементами. Такие баки называют стрингерными. Обе-
чайки стрингерных баков сжаты вдоль образующей. Давление наддува
здесь сравнительно невелико. Осевая сжимающая сила по длине бака
практически не меняется. При работе на сжатие все сечения равно-
опасны с точки зрения устойчивости. Поэтому такие баки часто выпол-
няют из панелей со слабо изменяющимся сечением.
В отличие от стрингерных, гладкие баки из высокопрочных материа-
лов рассчитывают только на внутреннее давление, величина которого
может существенно меняться по длине бака. Толщина обечайки в этих
баках у переднего днища отличается от толщины у заднего днища в не-
сколько раз.
Примером баков стрингерной конструкции являются баки ракеты
«Титан». На ракете «Титан I» отсек баков диаметром 3 м состоит из
двадцати отформованных панелей. Каждая панель с внутренней сто-
роны имеет Т-образные стрингеры. Изготовляют панели штамповкой
и вытяжкой на прессе, затем их подвергают механической обработке
и травлению. Предел прочности материала обечайки oR = 28 кГ]мм2.
Шпангоуты соединены с панелями при помощи сварки. Днища сделаны
из химически фрезерованных листов переменной толщины [119].
На рис. 32.2 изображен бак второй ступени ракеты «Титан Ш-С».
Вдоль образующей бака к обечайке прикреплены четыре лонжерона,
воспринимающих тягу боковых ускорителей. Лонжероны у заднего
торца соединены со шпангоутом, воспринимающим радиальные на-
грузки. Лонжероны в баке одновременно являются и подкрепляющими
элементами.
Для цилиндрических баков ракет больших диаметров, работающих
при небольшом давлении наддува, целесообразно применять так назы-
ваемую вафельную конструкцию. Обечайки бака могут изготовляться
из плит алюминиевого сплава. В процессе химического фрезерования
ячеек прямоугольной или ромбовидной формы часть материала уда-
19*
291
ляется. Остающиеся часто расположенные ребра делают оболочку
сильно анизотропной. Обечайку рассчитывают на устойчивость как ци-
линдрическую конструктивно-анизотропную оболочку, нагруженную осе-
вым сжимающим усилием и внутренним давлением. Величина критиче-
Рис. 32.2
ского напряжения в оболочке
зависит, в первую очередь, от
изгибной жесткости продоль-
ных ребер и жесткости на ра-
стяжение окружных ребер.
Баки вафельной конструк-
ции применены в ракетах «Са-
турн», «Тор» и др. На рис. 32.3,
32.4 и 32.5 представлены схемы
баков трехступенчатой ракеты
«Сатурн V». Из ракет «Сатурн»
самые большие баки — баки
ускорителя первой ступени
S—1С. Диаметр баков D= 10м.
Изготовлены они из сваривае-
мого, обладающего высокой
удельной прочностью при низ-
ких температурах и не имеющего склонности к хрупкому разрушению
алюминиевого сплава. Один из вариантов бака — стрингерной кон-
струкции.
Передний бак состоит из двух кольцевых секций, каждая секция —
из четырех листов. Обечайка другого варианта бака состоит из листов
вафельной конструкции с усиливающими ребрами в продольном и по-
перечном направлениях. Ребра высотой Л = 50 мм образуют прямоуголь-
42м
Рис. 32.3
ные клетки размером 25,4x25,4 мм при толщине оболочки бака
Ао = 4,6 мм. Днища баков полусферические высотой 3700 мм, изготов-
лены из того же материала.
Передний бак горючего третьей ступени ракеты «Сатурн V» — ва-
фельной конструкции, с ячейками ромбовидной формы. Бак окисли-
теля— чечевицеобразной формы, образован двумя полусферическими
днищами. Соединение днищ друг с другом и с обечайкой осуществляется
через прессованный шпангоут таврового сечения. Верхнее днище —
трехслойное, из двух тонколистовых полусфер, соединенных с промежу-
точным сотовым слоем из стеклопластика.
Рассмотренные баки выполнены по так называемой несущей
схеме. Их особенность — обечайка бака является одновременно и
корпусом ракеты, воспринимающим осевое сжатие и изгиб.
,292
Баки, расположенные внутри корпуса, самостоятельно воспринимаю-
щего внешние нагрузки, называют подвесными. На бак действуют
лишь внутреннее давление и местные силы, передаваемые узлами креп-
ления. При известном давлении наддува, осевой силе N и изгибающем
23 м
Рис. 32.4
моменте М в обечайке погонные усилия Т{ и Т2 определяют по зависи-
мостям (32.2), (32.3).
Среди имеющегося многообразия баков часто встречаются сфериче-
ские и торовые баки. Схема баков ракеты «Аджена А» изображена на
рис. 32.6,а. Передний бак окислителя— сферический, прикреплен кон-
сольно к коническому, участку
оболочки бака горючего .при
помощи сварки. Коническая
часть бака горючего переходит
в полусферический участок.
Блок баков прикреплен к пере-
ходному шпангоуту корпуса по
периметру наибольшего сече-
ния.
Расчет подобных баков на
прочность производится, в ос-
новном, на действие макси-
мального внутреннего давле-
ния. При расчете переходного
конического участка бака горючего необходимо учитывать осевые напря-
жения от сил реакции переднего бака. Возможны случаи, когда этот
участок сжат в осевом направлении, и тогда его нужно рассчитывать на
устойчивость.
Одна из схем торового бака изображена на рис. 32.6,6. Бак, обра-
зованный двумя концентрическими цилиндрическими оболочками, имеет
два торообразных днища с переходными кольцевыми элементами. На-
ружная оболочка бака нагружена осевой силой W, моментом М и дав-
лением р. Основным расчетным случаем для внутренней цилиндриче-
293
ской оболочки является случай наибольших окружных сжимающих
усилий от действия давления р (32.1). Наиболее рациональная конст-
рукция для внутреннего цилиндра — оболочка, подкрепленная попереч-
ным набором. Набор может быть выполнен в виде шпангоутов или
гофрированных элементов. Внутренняя часть торового бака соединена
с наружной диафрагмами или стержнями. Эти элементы передают на
корпус ракеты силы инерции массы топлива и тягу двигателя. Днища
бака рассчитывают на прочность как торообразныс оболочки, нагру-
женные давлением наддува и столба жидкости. Наружное кольцо креп-
ления днища сжато; его рассчитывают на устойчивость. Расчет внутрен-
него кольца ведут на прочность при растяжении.
Рассмотренные варианты конструкций баков не охватывают всего
многообразия имеющихся решений. Однако расчеты на прочность раз-
личных конструкций имеют много общего. Ниже рассмотрены расчеты
некоторых наиболее характерных элементов баков: обечаек гладких и
вафельных баков, днищ и соединительных колец.
§ 33. ГЛАДКИЕ БАКИ
Основные элементы баков гладкой конструкции — цилиндрические
и слабоконические обечайки — состоят из листов или панелей, имеющих
постоянную или переменную толщину вдоль образующей. Расчет обе-
чайки бака ведут: на прочность от действия внутреннего давления и на
устойчивость от осевых сжимающих усилий с учетом внутреннего
давления.
Расчет на прочность. Погонные усилия, возникающие в обечайке
бака, находят по формулам (32.2), (32.3), (32.4). При расчете бака
на прочность определяющим является окружное усилие Т2, зависящее
от давления р (32.3).
Расчету на прочность бака должно предшествовать определение
расчетных случаев для различных его сечений. В связи с тем, что по
времени полета ракеты величина осевой перегрузки возрастает, а вы-
сота столба жидкости Н падает, для различных сечений бака следует
найти зависимость величины давления по времени и определить макси-
мальное значение р. Так, при постоянном давлении наддува р0 макси-
мум р будет совпадать с наибольшим значением произведения пхН.
Этот момент времени и будет соответствовать расчетному случаю для
каждого сечения обечайки. По зависимостям (32.2) и (32.3) в расчет-
ных случаях определяются меридиональные и окружные усилия Т{ и Т2.
Возможны два вида напряженного состояния обечайки бака.
1. Окружное Т2 и меридиональное 7\ усилия — растягивающие. Этот
случай характерен для такого нагружения баков, когда первые два сла-
гаемых правой части формулы (32.2) меньше третьего слагаемого.
2. Окружное усилие Т2, растягивающее, а меридиональное -
сжимающее.
В том и в другом случае меридиональное усилие, как правило, по
абсолютной величине существенно меньше окружного.
Для баков при ?2>0 и Л>0 расчет на прочность ведут только от
окружных усилий. В проектировочном расчете из условия прочности
обечайки в окружном направлении определяют ее толщину, в повероч-
ном— при известной толщине определяют расчетные напряжения ор.
Эти напряжения должы быть меньше предела прочности материала:
ор (33.1)
h
Расчет баков, сжатых в осевом направлении (7\>0; прово-
дят следующим образом. Для каждой комбинации Т2 и 7\ в различных
сечениях определяют эквивалентные напряжения
291
(Тэ= r*~ri t (33.2)
величину которых приравнивают сгр = /сгэ. С учетом знака суммарные нап-
ряжения здесь будут больше, чем соответствующие окружные. Получен-
ные напряжения должны удовлетворять условию прочности сгр<ов.
Пример. Требуется определить толщину обечайки бака при диаметре D = 2500 мм,
давлении наддува р0=2,5 кГ/см2, удельном весе жидкости у=1430 кГ/м2. Материал
бака — алюминиевый сплав (Оа=25 кГ/мм2). Закон изменения осевой перегрузки пх (t)
по траектории принят таким же, как для ракеты «Фау-2» [95]. Рассмотрим два сечения
бака, отстоящие от уровня жидкости в начале полета на 2,5 и 5,0 м. Расход топлива
постоянный.
На рис. 33.1 изображены зависимости nx(t), (t) и H2(t), а также произведение
и nxH2(t). Кривые показывают, что при постоянном давлении наддува р0 расчет-
ными точками для обоих сечений будет 6-я секунда полета. При этом
Я1 = 2,1д, Н2 = 4,6м иил = 2,15.
Pl = Ро + пхУ^1 = 2,5 +’2,15 • 1430 -2,1- 10-4 = 3,15 кГ/см2.
р2 = р0 + пхуН2 = 2,5^2,15 • 1430-4,6- 1СГ4 = 3,91 кГ/см2.
Соответствующие погонные окружные усилия (T2)L = pY R ±= 3,15-1250-10-2 = 39,4 кГ/мм
и (Т2)2 = p2R = 3,91 • 1250- 10~- = 48,8 кГ/мм. Если меридиональное усилие 7\>>0 и
коэффициент безопасности f = 1,5, то толщины обечайки в сечениях 1 — 1 и 2 — 2 равны
/ц = (^2)1 //сгв = 39,4 • 1,5/25 = 2,36 мм
и
h2 = (T2)2 //ов = 48,8 • 1,5/25 = 2,93 мм.
Ниже рассматривается случай, когда меридиональное усилие 7\<0. Пусть 7\ =
= — 10 кГ/мм, а окружные напряжения в сечениях 1 — / и 2— 2 те же.В соответствии
с зависимостью (33.2) толщины обечайки в этих сечениях равны
= [(ТгК — Л1//ав = (39,4+ 10) • 1,5/25 = 2,96 мм
/i2 = [(T2)2 —Т1]//пв = (48,8 + 10) • 1,5/25 = 3,53 мм.
Расчет на прочность обечайки является основным для баков глад-
кой конструкции, когда в осевом направлении напряжения растягиваю-
щие. Если в осевом направлении в обечайке возникают напряжения
сжатия, необходимо дополнительно проводить расчет на устойчивость.
Расчет на устойчивость. Обечайку бака рассматривают как изотроп-
ную оболочку, нагруженную сжимающим усилием, изгибающим момен-
295
том и внутренним давлением. Напряжения, соответствующие потере
устойчивости такой оболочки,
<тхл = кыЕ — , (33.3)
АЛ АЛ 9 У /
где £ — модуль упругости материала оболочки, Л//? — отношение тол-
щины к радиусу, £хл— численный коэффициент. В практических расче-
тах коэффициент £хл можно представить в форме
kxn = kkpk^ (33.4)
Каждый из коэффициентов в этой формуле отражает влияние опре-
деленного фактора: k — зависимость напряжений потери устойчивости
от начальных несовершенств оболочки; kp — влияние внутреннего дав-
ления; kM-—неравномерность распределения сжимающих напряжений
по сечению, возникающих от осевого сжатия и изгиба; ki — влияние
пластических деформаций. Рассмотрим вкратце влияние каждого фак-
тора в отдельности на устойчивость оболочки.
Влияние начальных несовершенств. Напряжения, со-
ответствующие потере устойчивости оболочки, сильно зависят от на-
чальных несовершенств (начальных неправильностей формы) и с их
ростом заметно уменьшаются. Практически влияние начальных несо-
вершенств возрастает с уменьшением относительной толщины оболоч-
ки h/R. Поэтому коэффициент £, учитывающий влияние начальных
несовершенств, можно представить как функцию h/R. Для тщательно
изготовленных обечаек баков можно принять [25]
(33.5)
Так, например, для оболочки, имеющей параметр h/R = 1/500, £ = 0,2,
а при £/^ = 1/1800, £ = 0,1. На рис. 33.2 изображена зависимость (33.5),
а также представлены экспериментальные точки, полученные авторами
четырнадцати работ [25].
Влияние внутреннего давления. Теоретические и экспе-
риментальные исследования показывают, что внутреннее давление су-
щественно влияет на устойчивость цилиндрической оболочки, нагружен-
ной осевыми усилиями. Зависимость коэффициента устойчивости от
внутреннего давления может быть отражена соотношением [114]:
= 1 4-0,21а(Я/Я)0’6 _ Р%2
р 1 + За ’ а — E/i2 *
(33.6)
296
На рис. 33.3 представлены кривые kp = f(a) при разных значе-
ниях R/h. Существенное увеличение коэффициента устойчивости осо-
бенно характерно для очень тонких оболочек.
Влияние неравномерности распределения сжимаю-
щих напряжений. Сравнение коэффициентов устойчивости для ци-
линдрической оболочки, нагруженной осевой силой и нагруженной изги-
бающим моментом, показывает, что при одинаковых наибольших
сжимающих напряжениях устойчивость оболочки при изгибе примерно
на 25% выше, чем при осевом сжатии.
Совместное действие изгибающего момен-
та и освой силы можно учесть коэффици-
ентом [27]
„ 2М
1 + 1,25--
(33.7)
1+ NR
где W и М — осевое усилие с учетом раз-
грузки от давления и изгибающий момент
в сечении.
Влияние пластических де-
формаций. Потеря устойчивости боль-
Рис. 33.3
шинства сжатых и нагруженных внутрен-
ним давлением тонкостенных гладких оболочек происходит в упругой
области при сравнительно низком уровне сжимающих напряжений. Од-
нако в некоторых случаях, при определенном соотношении осевых и
окружных напряжений, в оболочке могут возникнуть пластические дефор-
мации. Величина напряжения потери устойчивости оболочки будет при
этом несколько меньшей. Потеря устойчивости оболочки будет происхо-
дить с образованием осесимметричных волн. Критические напряжения,
полученные по деформационной теории пластичности для цилиндриче-
ской оболочки, теряющей устойчивость за пределом упругости, будут [27],
<у1кр=4/Ёк£сА( (33.8)
о i\
где EK и Ес— касательный и секущий модули диаграммы растяжения
материала оболочки. Коэффициент 2/3 получен при условии образова-
ния осесимметричной волны и числе Пуассона ц = 0,5. Для упругой об-
ласти деформирования ЕК = ЕС = Е и уравнение (33.8) переходит в
<ткр = -2-Е—. (33.9)
кр 3 R
Коэффициент, показывающий, во сколько раз напряжения потери
устойчивости в пластической области меньше, чем в упругой при одной
и той же деформации е,
А?, = УУУУ.. (33.10)
Для оболочки, находящейся в двухосном напряженном состоянии,
величину коэффициента ki можно найти после определения интенсив-
ности напряжений
(Т • = + (зз др
При осевом сжатии и окружном растяжении зависимость (29.11) можно
представить в виде
°, = а2 /1 + Y + Y2, (33.12)
297
где
<Ji
а2
(33.13)
Предварительно рассмотрим, как определить коэффициент ki при
заданных сп и о2. По известной диаграмме растяжения о—е материала
оболочки можно построить зависимости Ек и Ес от е. Для известных
О1 и 02 по уравнениям (33.12) и (33.13) находим значение 0г-, по кото-
6,гЛ/мм'г
СИМОСТИ коэффициентов ki при этих Y от
рому определяем модули £к и
LIO *кг/мм' и из уравнения (33.10) вы-
числяем коэффициент Удоб-
но построить зависимость ко-
эффициента не от Of, а от
02 при различных значениях у.
Это можно сделать при помощи
уравнений (33.12) и (33.13).
На рис. 33.4 построена диа-
грамма растяжения 0—е алю-
миниевого сплава. Здесь же
приведены зависимости Ес и £к
от 8. Для значений у=0,1 —1,0
и 2,0 при разных 02 по уравне-
нию (33.12) найдены Of, затем
при помощи уравнения (33.10)
на рис. 33.5 представлены зави-
различных окружных напряже-
ний 02. Из этих кривых видно, что растяжение в окружном направлении
сжатой по оси цилиндрической оболочки вызывает уменьшение критиче-
ских напряжений в том случае, когда в оболочке интенсивность напря-
жений выше предела упругости.
Итак, учитывая основные факторы, влияющие на устойчивость ци-
(33.7), (33.10) можно получить величину коэффициента устойчиво-
сти kXJi. Однако критические напряжения по коэффициенту устойчиво-
сти сразу найти не удается, если в оболочке возникают пластические
деформации. Обратим внимание на то, что величина самого коэффи-
циента £хл зависит от уровня напряжений. Для определения напряже-
ний, соответствующих потере устойчивости оболочки, можно восполь-
зоваться методом последовательных приближений. В первом прибли-
298
жении коэффициент ki можно брать равным единице, т. е. считать, что
оболочка работает в упругой области. Затем по зависимостям (33.3)
и (33.4) можно определить критические напряжения охл = О1. Далее
при известном давлении находят G2 = pRlh и по уравнению (33.13) — у.
По рис. 33.5 определяют новый коэффициент ki. Его следует умножить
, на kkpkM — получают значение коэффициента &хл второго приближе-
ния. Далее находят критические напряжения второго приближения
и т. д. Иногда в качестве первого приближения для ki лучше взять
&; = 0,6—0,8. В ряде случаев это существенно ускоряет расчет. Отметим,
что теоретической верхней границей коэффициента устойчивости являет-
ся величина 0,605. Однако практически не удается получить коэффи-
циент £хл больше 0,45.
Изложенный метод расчета позволяет приближенно установить за-
висимости критических напряжений хлопка от различных факторов.
Для уточнения расчетов нужно пользоваться результатами эксперимен-
тов с баками или моделями баков, близкими к проектируемой конст-
рукции.
Пример. Обечайка бака гладкой конструкции толщиной /i = 3 мм и радиусом
£=1500 мм из алюминиевого сплава (£ = 7,2 • 103 кГ/мм2) нагружена осевым уси-
лием N и изгибающим моментом М, причем 2 M/NR = 0,2. Требуется определить напря-
жения, соответствующие потере устойчивости оболочки при р = 0.
Из соотношений (33.5), (33.6), (33.7) для R/h = 500 определяем [коэффициенты
k = 0,2; kp = 1,0; kM =1,04 и kL = 1,0. Коэффициент
А?хл = kkpkMki = 0,2 • 1,0 • 1,04 • 1,0 = 0,208.
Критическое напряжение хлопка согласно формуле (33.3)
h
ахл = k^E — = 0,208 • 7,2 • 103/500 = 3 кГ/мм2.
R
Далее нужно найти критические напряжения хлопка обечайки бака поц давлением р
и построить зависимость ахл = / (р). Диаграмма растяжения материала бака изображена
на рис. 33.4. Расчет сведен в табл. 33.1. По зависимостям (33.5), (33.6), (33.7) для
h 1
— =-------- и при р= 1; 2; 3; 4; 5 кГ/см2 определяем коэффициенты kp, kM\ kL. Про-
R 500
изведение этих коэффициентов для каждого давления заносим в первую строку. Затем
определяем о2 — pR/h. По зависимости (33.3)
находим ахл, полагая вначале ki = 1,0. Затем
проверяем, чему равен коэффициент ki. Для
этого вначале находим у = охл/о2 и по рис. 33.5
— величину коэффициента /?/. Из таблицы
видно, что для давлений р = 1; 2; 3 кГ/см2
оболочка теряет устойчивость в упругой области
= 1,0). Для давлений 4,0 и 5,0 кГ/см2 коэф-
фициенты k[ определяются методом последова-
тельных приближений. Полученная зависимость
охл = f (р) приведена на рис. 33.6. Из нее вид-
но, что внутреннее давление вначале сущест-
венно повышает критические напряжения хло-
пка. Наибольшие критические напряжения в обо-
лочке соответствуют давлению р = 3,0 кГ/см2.
При дальнейшем увеличении давления критиче-
ские напряжения хлопка падают.
Пользуясь полученным соотношением охл = /(р), можно получить
оптимальное, с точки зрения устойчивости, давление в баке. Для этого
по уравнению
N = рлТ?2 + охл (р) • ZnRh (33.14)
нужно построить зависимость осевой силы которую может выдер-
жать бак, в функции давления. Наибольшее значение силы соответ-
ствует оптимальному давлению в баке.
299
Таблица 33.1
р, кГ/см2 1 2 3 4 5
kkPkM 0,416 0,479 0,517 0,535 0,552
а2, кГ/mm* 5,0 10,0 15,0 20,0 25,0
ахл’ 6,0 6,9 7,45 7,7 7,95
у(1) 1,2 0,69 0,437 0,385 0,318
а<2> 1,0 1,0 1,0 0,75 0,425
а(2) яхл 0,4 0,235
а(х2л\ кГ/мм* 5,76 3,38
у(2) 0,288 0,135
А<3> 0,86 | 0,6 1
ь(3) лхл 0,46 0,331
сг(х3л\ кГ/мм2 6,62 4,77
у(3) 3,33 0,19
*<4> 0,8 0,56
а(4) ^хл 0,428 0,309
о^, кГ/мм2 6,17 4,45
y(4) 0,308 0,178
*’5) । 0,81 1 0,565
0,432 0,308
ахл, кГ/мм* 6,22 4,44
300
§ 34. БАКИ ВАФЕЛЬНОЙ КОНСТРУКЦИИ
Расчет обечайки бака вафельной конструкции (рис. 34.1,а) состоит
прежде всего в определении напряжений, соответствующих потере
устойчивости конструкции, подкрепленной частыми продольными и по-
перечными ребрами, при действии осевых сил и внутреннего давления.
Кроме того, необходимо выполнить расчет на прочность для определе-
ния окружных напряжений в различных сечениях обечайки.
tc--6R
Рис. 34.1
Для проведения расчета на устойчивость и определения напряжен-
ного состояния воспользуемся схемой конструктивно-анизотропной обо-
лочки.
Определение приведенных толщин конструктивно-анизотропной обо-
лочки. Считается, что оболочка при растяжении и изгибе в продольном
и поперечном направлениях имеет один и тот же модуль упругости, по
разную толщину. На рис. 34.1,6 изображены элементы сечений обо-
лочки. Площади сечений поперечных и продольных подкрепляющих
элементов обозначены через
/ш = Ьшаш и /с = ьсае- (34.1)
Здесь и далее индекс «ш» соответствует поперечным подкреплениям
(шпангоутам), а «с» — продольным (стрингерам). Приведенные тол-
щины оболочки при растяжении в кольцевом и меридиональном на-
правлениях будут
Лш = й0 + -^, hc=h0+-^, (34.2)
где й()—толщина обшивки, а /с и /ш —шаг подкреплений. Подсчитав мо-
мент инерции элементов сечений относительно центра тяжести, можно
найти приведенные толщины при изгибе
и
* ш
V (с
(34.3)
При 'подсчете момента инерции Jc обычно "пренебрегают кривизной
оболочки.
Эквивалентную толщину гладкой оболочки, равной по весу оболочке
вафельной конструкции, определяют из равенства
Л/Л-Ло^ш+/Л + /Х (34.4)
откуда
h’ — h0. (34.5)
Для гладкой оболочки площади подкреплений равны нулю (/ш = /с =0)
и толщины йш = hc = бш = Sc = h0. Для вафельной конструкции так же,
301
как и для гладкой, справедливы соотношения бш//1ш = бс/Лс = 1. Однако
величины 6Ш и бс, как правило, в несколько раз больше Лш и Лс, т. е.
--ш- j и Л_ » 1. (34.6)
Ащ Aq
Для расчета обечайки бака на устойчивость и прочность необходимо
воспользоваться уравнением, описывающим деформированное состояние
оболочки. Будем считать, что деформация и форма потери устойчивости
оболочки под действием внешних нагрузок осесимметричны. Все соот-
ношения получены для конструктивно-анизотропной оболочки. При рас-
смотрении оболочки постоянной толщины (/1ш = Лс = бш = 6с = Ло) резуль-
тирующие уравнения переходят в аналогичные для изотропной оболоч-
ки, которые получены ранее в гл. II.
Вывод уравнения осесимметричной деформации конструктивно-
анизотропной оболочки. К элементу, изображенному на рис. 34.2,а.
Рис. 34.2
приложены усилия, возникающие в продольных и поперечных сечениях
оболочки. Проектируя эти усилия на ось z, нормальную к поверхности,
получим
-------+ —2- = р, (34.7)
dx р R
где р — радиус кривизны образующей цилиндра после деформации,
R— радиус оболочки, Т2— окружное усилие. Сжимающее усилие вдоль
меридиана 7\ принято положительным. Перерезывающая сила Qi и из-
гибающий момент в продольном направлении Afi связаны соотношением
Выразим силовые факторы Afi; Qi; Т2 и кривизну 1/р через переме-
щения оболочки по нормали к поверхности w и в осевом направлении и.
Для цилиндрической оболочки соотношения между продольной еь попе-
речной деформациями е2 и перемещениями w и и имеют вид (см. гл. II)
e1=4L+2VT> (34.9)
ах ах2,
е2=^-. (34.10)
Кривизну меридиана через нормальное перемещение можно выразить так:
1 _ d2w
р dx2
(34.11)
302
Полагаем, что коэффициент Пуассона, как мало влияющий на напря-
женное состояние конструктивно-анизотропной оболочки, равен нулю
(ц = 0). Это позволяет представить соотношения Гука в виде
6!=-^-, е2 = ^. (34.12)
Е Е
Особенность принятой схемы конструктивно-анизотропной оболочки
состоит в том, что оболочка как бы имеет разную толщину по отноше-
нию к различным силовым факторам. Поэтому при определении погон-
ных усилий Гь Т2 и Mi напряжения ai и а2 должны суммироваться по
соответствующей толщине:
Лс/2 Лш/2 М2
1\ = — J' e1dz, Т2= у G^dz, Mv = j (^zdz. (34.13)
-4/2 -Аш/2 —6с/2
Учитывая соотношения (34.9), (34.10) и (34.12), можно определить
зависимости между усилиями и перемещениями:
Л = -Ehe4“- . Т2 = ЕАш , (34.14)
ах R
М1 = Е^-^- . (34.15)
12 dx2 v ’
В окончательном виде уравнение осесимметричной деформации обо-
лочки получаем, подставляя уравнения (34.8), (34.11) и (34.14), (34.15)
в соотношение (34.7):
+ T d^w +Ehn w (34.16)
12 dx4 dx2 R2
Таким образом, радиальное перемещение конструктивно-анизотроп-
ной оболочки определяется уравнением (34.16). Изгибающий момент и
окружное усилие можно найти из соотношений (34.15) и (34.14).
Обозначим
а2 = I / -----, р = 1. (34.17)
У R2f>l ЕЪ* У R2^ Е6®
Тогда уравнение (34.16) примет вид
^ + 2ф2-а2)-^-+(a2 + PW = 12-^з-. (34.18)
Общее решение уравнения (34.18) будет
до = (р#2/ЕНш) + Ci sh ах sin Рх + С2 sh ах cos Рх 4- С3 ch ах sin Рх +
+ C^ch ах cos Рх. (34.19)
Постоянные С2, С3, С4 определяем из граничных условий.
Решение (34.19) позволяет найти все силовые факторы в оболочке
при осесимметричной деформации.
Расчет обечайки бака на устойчивость. Величина радиального пе-
ремещения, соответствующего докритической форме равновесия доста-
точно длинной оболочки, определяется первым членом уравнения (34.19)
и равна WQ = pR2IEhul. Полное радиальное перемещение w можно пред-
ставить в виде двух слагаемых са = до0 + ^, где w — перемещение, отсчи-
тываемое от докритического состояния. Выразив через w соотношение
303
(34.16), получихм уравнение устойчивости конструктивно-анизотропной
оболочки
дЗ
Е — — + Т\ — + w = 0. (34.20)
12 dx* dx* Я2
Уравнение для изотропной оболочки имеет подобный вид (см. § 16),
но вместо коэффициентов Еб^/12 и EhjR2 стоят значения D и Eh/R2,
соответствующие жесткости на изгиб и растяжение изотропной оболочки.
При форме волнообразования w = sinXx, где X — параметр длины вол-
ны при потере устойчивости, из последнего уравнения можно получить
Т\ = -&с X2 4- -Eflui —
12 /?2 А2 ’
Определим критическое усилие при осесимметричной форме потери
устойчивости оболочки, приравняв нулю производную от 7\ по X2:
Р -1 /" др/гш
^р=41/ (34.21)
t\ J О
При этом Z = у/ 12/im/7?2d^ и длина полуволны оболочки I л/Х, т. е.
Величина соответствующей осевой силы при отсутствии внутреннего давле-
ния равна
N = 44 Е (34.22)
Для изотропной оболочки эквивалентной толщины h при тех же допуще-
ниях вывода критическое усилие равно
гир=1/44Л2- (34-23)
у о К
Эквивалентная по весу толщина изотропной оболочки через параметры
йо, йш и hc выражается соотношением (34.5). Критическое усилие этой
оболочки иначе можно представить в виде
лКР=1/ 4 4 <34-24>
у о
Эффективность подкрепленной конструкции может быть отражена
коэффициентом /гв, показывающим, во сколько раз критическое усилие этой
конструкции больше усилия гладкой:
Для вафельной оболочки безразмерные толщины йс и йш близки по
величине друг другу и равны hm hc (1,2 1,5) й0. Изгибная толщина
лежит в пределах бс = (2,0 -4- 5,0) hQ. При этом величина коэффициента
/г„-=2^3.
304
Расчетное критическое напряжение для вафельной обечайки бака
можно представить в форме
<тхл = £ле4 • (34.26)
А
Здесь h — эквивалентная толщина оболочки, определяемая соотношением
(34.5), А® л — коэффициент;
^хл = kkpkMk^ (34.27)
Коэффициенты k.kp,kM,ki отражают влияние начальных несовершенств
оболочки, внутреннего давления, изгибающего момента и пластических
деформаций. Значения этих коэффициентов и зависимость их от соот-
ветствующих факторов представлены в предыдущем параграфе. Коэф-
фициент kB устанавливает зависимость напряжения ахл от конструктив-
ных особенностей оболочки и определяется по формуле (34.25). Зна-
чение коэффициента &®л здесь может существенно превосходить вели-
чину 0,605.
При определении осевых напряжений в оболочке бака предполага-
лось, что на сжатие работает все сечение равномерно. Это возможно
лишь при отсутствии местных вмятин панелей в ячейках. В оконча-
тельных расчетах следует определять величину местных критических
напряжений панели. Напряжения, соответствующие местной потери
устойчивости панели между ребрами, определяют по уравнению [9]
<34-28>
А \ /
Коэффициент йхл определяется уравнением (33.4). Для вычисления
приближенного значения коэффициента £хл можно учитывать лишь k
и kp согласно формулам (33.5) и (33.6). Коэффициент kn для квадрат-
ной заделанной по краям панели /с = /ш равен 8,4. При величинах tmltQ,
отличных от единицы, можно использовать коэффициент kn для сжатой
в одном направлении плоской пластины, заделанной со всех сторон [9].
Сжатые продольные ребра проверяют на устойчивость. Для прямо-
угольных ребер критические напряжения потери местной устойчиво-
сти [27]
сткр~0,9-0,46Е(4)2- (34.29)
Определение окружных напряжений в оболочке. Окружные напря-
жения для безмоментной конструктивно-анизотропной оболочки опреде-
ляются соотношением G2 = pRlhm. Величину напряжений о2 для различ-
ных поперечных сечений оболочки можно уточнить, рассматривая
осесимметричную деформацию между двумя поперечными подкрепле-
ниями. Для этого нужно воспользоваться уравнениями (34.16) — (34.19),
куда вместо Аш подставить толщину оболочки h0. Начало координат
поместим посередине между подкреплениями (рис. 34.2,6). Граничные
условия для определения постоянных в уравнении (34.19) будут:
1) х = 0, wf 0; 2) х = 0, w'" = 0, так как Q = 0; 3) х = t/2, w' = 0;
4) х = t/2, w = (34.30)
так как w = д/?2/Е/ш и q = 2Q.
Здесь и далее в решении шаг t соответствует /ш. Первое и второе условия
показывают, что постоянные С2 = С3 = 0. Остальные условия приводят к
уравнениям
20 Зак. 96
305
1
(aCj — 0C4) ch a — sin 0 ——!- (0Сг + aC4) sh a — cos 0 —= 0;
2 2 2 2
Сг sh a — sin 0 ——C. ch a — cos 0 ——I-
2 2 4 2 1 2 ' Eh0
( ft
— J [a (a2 - 302) C, + 0 (02 - 3a2) C4] ch a sin 0 H-
ш I 2 2
(34.31)
+ [0 (3a2 — 02) C4 -j- a (a2 - 302) CJ sh a — cos 0 —)
2 2 J
)
Решив эти уравнения относительно Сг и С4, можно найти прогиб обо-
лочки w. Воспользовавшись далее вторым уравнением (34.14), в котором
нужно вместо Лш взять Ло, нетрудно определить окружное усилие Т2, а
затем, разделив его на ho,—напряжение <г2. При х == //2
шпангоута напряжения
о
U21 — ,
h0 [
Напряжения при х = 0
ch at — cos 0/
2 sh at + (a/0) sin 0/
сечении
(34.32)
a - pR
°20 — ~~
h0
1 —2
/ t n t n t
sh a — cos P — 4- (a/P) ch a — sin P —
(34.33)
sh at + (a/p) sin p/ -j- ya — (ch at — cos p/)
в
Параметр у равен
Rb2
у — 4
fut
(34.34)
Соотношения (34.32) и (34.33) показывают, что безразмерные окруж-
ные напряжения в оболочке e2Qho/pR и зависят от трех парамет-
ров у, Р//2 и a/р. Параметр у отражает влияние жесткости поперечного
подкрепления с площадью сечения /ш. При увеличении /ш окружные на-
пряжения о20 и о21 уменьшаются. Возрастание шага поперечных подкрепле-
ний р//2 приводит к некоторому увеличению напряжений. Отношение а/Р
меняется от 0 до 1. Уменьшение этого отношения несколько увеличивает
наибольшие напряжения. На рис. 34.3 изображены зависимости о20 и сг21
306
от длины шага при разных у для а = 0. Из графика видно, что для у> 1,0
и Р//2< 1,4 приближенно можно считать
#20 ~ <?21 ~ ^2 = ~~ • (34.35)
Лш
Меридиональные напряжения в обечайке бака равны
<h=~- (34.36)
Лс
Это выражение справедливо до момента образования вмятин в ячей-
ках— потери местной устойчивости.
Расчет на прочность обечайки бака состоит в определении напря-
жений о2 и си для ряда сечений. По известным окружным и меридио-
нальным напряжениям находятся эквивалентные напряжения. Для этого
можно воспользоваться условиями пластичности Треска-Сен-Венана
<тэ = <*2-(Д (34.37)
или Мизеса
<тэ = /о? — + <т|. (34.38)
При расчете на прочность баков обычно пользуются уравнением
(34.37), из которого находятся расчетные напряжения
/ (<т2 —(TJ, (34.39)
где / — коэффициент безопасности. Это уравнение и зависимости (34.35)
и (34.36) позволяют в проектировочных расчетах найти приведенную
толщину оболочки, если принять /lc~/lin-
Пример. Оболочка вафельной конструкции из алюминиевого сплава Е=7,2-103 кГ/мм2,
имеющая предел упругости сгу=25 кГ/мм2, нагружена осевым сжатием и внутренним
давлением р=3,0 кГ/см2. Параметры оболочки: радиус 7? = 1500 мм, шаг подкреплений
/ш = tc = t = 120мм, толщина обшивки hQ = 2,0 мм, высота ребер аш = ас = а = 10 мм,
ширина ребер Ьш = bc = b = 6 мм. Требуется определить расчетные напряжения хлопка
оболочки и величину окружных напряжений.
Приведенная толщина оболочки согласно формуле (34.2)
ab 10-6
Л = hc = ho +------= 2 4--------
ш с t 120
= 2,5 мм
и площадь подкреплений
= /с = ab = 10-6 = 60 мм2.
Для определения момента инерции нужно найти центр тяжести сечения. Относительно
наружной поверхности оболочки координата центра тяжести
hotho/2 + ab(hQ+a/2) 2,0-120-1,0 4- 10.6(2^5)
ит =---------------------=---------------------------- =2,2 мм.
' k 2,0-120 4- 10-6
hot + ab
Момент инерции сечения
М3 Ьа3
J = "1Т + ~12 + hot (Ут ~ Ло/2)2 + аЬ (Л°+ 0/2 “ ^т)2 =
190-2 О3 6-103
= ~ 1<?’ - -4 —— + 2,0-120(2,2 — 1,0)2 4- 10-6(2 4-5 — 2,2)2 = 2310 мм*.
Приведенные толщины на изгиб по формуле (34.3) равны
ЗЛ“ 3< 12-2310
120
= 6,12 мм.
20*
307
Эквивалентную по весу толщину оболочки находим из формулы (34.5)
Л = /*ш-£-Лс — Ло = 2,5-^ 2,5 — 2,0 = 3,0 мм.
Для оболочки h = 3tQ мм гладкой конструкции в предыдущем параграфе было
определено расчетное [напряжение о®л = 3,0 кГ/мм2 при нулевом давлении р = 0;
коэффициент &хл при этом равен 0,208. Для того чтобы определить коэффициент устой-
чивости для 'вафельной оболочки &°л нужно £хл = 0,208 умножить на kB, найденный по
формуле (34.25):
k _ V 6сдш________________у 6,123-2,5 _
В- (Лш + йс-Ло)2 “ (2,5 + 2,5 —2,0)2 ~2’63’
£®л = М» = 0,208-2,63 = 0,547.
Расчетные напряжения потери устойчивости вафельной обечайки бака
о“л = А®лЕ-^- = 0,547-7,2-103/500= 7,88 кГ/мм*,
R
т. е. в 2,63 раза больше напряжений гладкой оболочки того же веса. Для эквивалентной
по весу гладкой обечайки бака, находящейся под давлением р = 3,0 кГ/см2, коэффициент
^хл = 0,517 (см. § 33). Тогда расчетные напряжения потери устойчивости для вафельной
обечайки будут
а°л=£хлЛвЕ= 0,517-2,63-7,2-103/500 = 19,6 кГ/мм*.
R
Окружные напряжения в обечайке бака при р = 3,0 кГ/см2 вначале определим по
зависимости (34.35):
pR 3,0-1500
о о — —-
Йш 2,5
10“2 =18,0 кГ/мм2.
Из соотношений (34.32) и (34.33) найдем величину напряжений в поперечном под-
а
креплении а21 и посередине подкрепления а20. Положим, —- = 0, тогда параметр
Р
А,/зА_Л]/^-----------------
2 2 V R6C у дс 2 У 150-0,612 |/ 0,612
Из уравнения (34.34) определяем
„ _ _ *.-isoo.612- ,°Л„ _ ,0 4.
fui* Г Збс 0,6-12,0 |/ 3-0,612
р/
Напряжения сг20 и при найденных параметрах —— и у определяем из уравнений
(34.33) и (34.32). Величины напряжений равны о20 = 18,1 кГ/мм2 и o2i = 17,95 кГ/мм2.
Практическое совпадение напряжений о20, сг21 и о2 свидетельствует о правильном выборе
шага поперечных подкреплений и их жесткости. При более жестких поперечных подкрепля-
ющих элементах и большем расстоянии между ними величины напряжений сг20 и сг21 могут
значительно отличаться от о2.
§ 35. РАСЧЕТ ДНИЩ БАКОВ
При расчете на прочность днища рассматривают как безмоментные
оболочки вращения, нагруженные осесимметричной нагрузкой. Напря-
жения от изгиба в местах соединения днища с обечайкой бака и в зоне
крепления фланцев, как правило, в расчет не принимают. Изготовля-
ются днища обычно из пластических материалов, а для конструкций
такого типа местный изгиб не является причиной разрушения. В зоне
крепления фланцевых соединений люков и трубопроводов происходит
перераспределение мембранных напряжений. Расчеты показывают, что
фланцы влияют на напряженное состояние лишь локально (см. § 57),
и в предварительных расчетах это влияние не учитывают.
308
При расчете днищ прежде всего необходимо определить погонные
меридиональные Л и окружные Т2 усилия.
Определение усилий в днищах баков. Напряженное состояние без-
моментной оболочки вращения, нагруженной нормальным давлением,
описывается уравнениями (§ 9):
+ + <7е = °. (35.1)
.Il_ + 21 = q (35.2)
Ri R2 п
С помощью этих уравнений найдем усилия в днищах различной конфигу-
рации.
Рис. 35.1
1. Сферическое днище (рис. 35.1, а). Давление на поверхности днища
= Р Равно
р = Pq + пху [И + R (cos 6 — cos 0О)]. (35.3)
Воспользовавшись очевидными соотношениями для сферы
г = R sin 0, dr = R cos 0 d0, R± = R2 = Rt
после интегрирования уравнения (35.1), учитывая соотношения (35.2) и
(35.3), получим
Л = [Ро + Пху (И - tfcos е0)] 4 - + с-
2 3sin20
Постоянную С определяем из условия конечности усилия 7\ в по-
люсе оболочки при 0 = 0. Тогда выражение для меридионального усилия
в сферическом днище будет
г =Г1+—f— 1~cos39 -cose^l . (35.4)
2 лГ 2 L н \ 3 sin* 0 °7J
Окружное усилие Т2 находим из уравнения (35.2):
7. _ _PoR_ + н R_ Г1 + Л <2cos0 -cosео’— — 1~cos3e Y] . (35.5)
2 2 L Н \ 0 3 sin*0 J\ v '
Окружные и меридиональные усилия имеют максимальные значения
в полюсе при 0 = 0; при этом первый член в круглых скобках выражения
(35.4) стремится к единице:
Лтах = Лп,ах = у [ 1 + (1 ~ cos %)] • (35.6)
309
В месте сопряжения днища с кольцом при 0 = 0О меридиональное усилие
/Т’ P()R 1 г г R Г 1 । /? / 2 1 COS3 0р л \ ~| ,г\ г-
—----Ь ял#— Ч--------(-----------2---cos0o ) , (35.7)
° 2 хГ 2 [ Н\3 sin2 0о VJ
а радиальная составляющая сжимающая кольцо в его плоскости (рис. 35.1, в),
<? = 7\0cos00. (35.8)
В сферическом днище, изображенном на рис. 35.1, б, усилия 7\ и 7\
определяют в той же последовательности, что и в предыдущем случае. Ме-
ридиональное и окружное усилия равны
PoR и R Г1 /? / 2 I ' cos3 0 л \ /г, г-
1\ =---—-----пгуН— I--------(---------------cos0o) , (35.9)
2 хГ 2 [ Я \ 3 sin2 0 / _
Т2=—P°g——[1——?2cos6—cos60 —— 1~cos3e А]. (35.Ю)
2 2[ H\ 0 3 sin2 0 /J
В том случае, когда днище является общим для двух баков, в соот-
ношении (35.3) и последующих давление наддува р0 следует заменить пе-
репадом давлений Др.
2. Коническое днище (рис. 35.2). Давление на поверхности обо-
лочки распределено по закону
Р = Ро -пхуН (I +
R-r
Н
tgO
Из уравнений (35.1) и (35.2) определяют меридиональное
усилия
= i + tgo
2 sin 0 2 sin 0 L \ # 3 H J
(35.11)
окружное
(35.12)
(35.13)
И
Усилие на кольцо крепления днища определяется соотношениями
(35.8) и (35.12), куда вместо 0 нужно подставить 0О.
3. Торовое днище (рис. 35.3). Меридиональный и окружной радиусы
кривизны для тора Rx = 2? и = R 4--------—. Закон распределения давле-
sin 0
ния по 0 определяется соотношением (35.3). Интегрируя уравнение (35.1)
и используя условие ограниченности усилия при 0 = 0, получаем выраже-
ние для меридионального усилия
т = D r0+ (/?/2) sin 0 nxyHR2
1 ° г0-{г/? sin 0 ‘ г0 4-Я sin 0
— fl------— cos 0О) 4-
R \ Н °)
+ -А- Н------------1- sin 0 (1 — — cos 0(Л----— 1 ,cos39 I. (35.14)
2Н sin© 4Н cos Op 2 \ H J SH sin20 J
Окружные усилия находим из уравнения (35.2). Наибольшие усилия
в торовом днище — меридиональные на внутреннем контуре тора при
310
0 = —0О. Усилия во внутреннем и наружном кольцах определяются со-
отношениями (35.8) и (35.14), где для наружного кольца 0 = 0О, а для
внутреннего 0 = — 0о-
Как видим, для определения усилий в днищах баков любой конфи-
гурации исходными данными являются: закон распределения нагруз-
ки р, соотношения для главных радиусов кривизны и уравнения (35.1)
и (35.2).
Получив закон распределения погонных усилий по поверхности
днища и зная его толщину, можно найти напряжения ^ = Tjh в любой
точке, для оолыиинства днищ,
используемых в ракетной тех-
нике, расчетными являются
растягивающие напряжения. В
этом случае толщину днища
выбирают, исходя из условия
прочности, путем сравнения
расчетных напряжений с пре-
делом прочности материала
днища ов или пределом теку-
чести От- В связи с тем, что по-
гонные усилия по контуру дни-
ща непостоянны, иногда приме-
няют днища переменной толщины.
«Сатурн I» переменную толщину и
миниевого сплава.
Рис. 35.4
Так, на центральном баке ракеты
деет полусферическое днище из алю-
В ряде случаев днища могут быть нагружены внешним давлением.
Тогда толщину нужно выбирать из расчета на устойчивость. Значения
критических нагрузок для сферического сегмента, конической оболочки
и др., нагруженных внешним давлением, определяются соотношениями,
приведенными в книге [27].
Величины критических нагрузок для однослойных тонких днищ
весьма невелики. Поэтому в некоторых случаях для увеличения устой-
чивости оболочек используется трехслойная сотовая конструкция. На-
пример, наружный и внутренний слои днища ракеты «Сатурн II» со-
стоят из тонких металлических листов, а промежуточный слой — из сот.
Он выполнен из стеклопластика и выполняет также функции тепло-
изолирующей перегородки.
Расчет трехслойного днища. Рассмотрим особенности расчета сфе-
рического трехслойного днища (рис. 35.4). Будем считать, что нормаль-
ные напряжения воспринимаются лишь внутренним и наружным слоя-
ми, толщины которых h2 и h\. Промежуточный слой воспринимает
только усилия по нормали к поверхности. Температура внутреннего и
наружного слоев Т2 и 1\. Условия равновесия для каждого слоя
имеют вид
ех = ~.fl, <у = Рг~Рк . (35.15)
1 2/h 2 2/12 v !
Здесь рк— давление на промежуточный слой со стороны внутреннего
и наружного листов днища, R — радиус кривизны сферической оболочки.
Соотношения упругости наружного и внутреннего слоев
= 82=^(1-ц)+аТ2. (35.16)
Е2
Величины коэффициентов Пуассона ц и линейного расширения а для
внутреннего и наружного слоев считаем одинаковыми. Условие равен-
ства деформаций внутренней и наружной оболочек имеет вид
8Х = 82. (35.17)
зп
Решая уравнения (35.15)—(35.17) относительно рк, получаем
j
R . R \( ,
2E1hl ' 2Е,/г2 /
Для внутренней и наружной оболочек с одинаковыми
модулем упругости (h± = h2 = h, Е± = Е2 = Е) получим
Р1 + Рг +Е Jl_2_ (Т 7).
к 2 « 1-ц
Рк
соотношение
(35.18)
ТОЛЩИНОЙ и
(35.19)
Напряжения в наружном и внутреннем слоях находим по уравнениям (35.15):
*1 = (Р2 - Pi) + тг1- (П - Л), (35.20)
<т2 = (р2-Р1)-^--4т^-^-Т^- (35-21)
4/г 2 1 — р,
Соотношение (35.19) является исходным для определения шага и
жесткости сот. Величине рк>0 соответствует сжатие, а рк<0— отрыв
сот от наружных оболочек. Предельные значения усилий, при которых
происходит потеря устойчивости элементов при сжатии сот и отрыв
их от внешних слоев, определяют экспериментально.
Силовые и температурные напряжения по-разному влияют на проч-
ность наружных оболочек. Температурные напряжения в слоях само-
уравновешены и оказывают влияние лишь на местные критические на-
пряжения оболочки между сотами. Разрушения оболочки, изготовлен-
ной из пластического материала, от температурных напряжений обычно
не происходит. На прочность наружных слоев влияет только силовая
составляющая напряжений
<>! = <т2 = P2~P1 R. (35.22)
Ah
Расчет колец крепления днища к обечайке бака. Усилия в кольце-
вых элементах крепления днищ определяются соотношениями (35.7) и
(35.8). Более точные соотношения даны в гл. II. В большинстве баков
со сферическими, коническими и другими днищами в кольцах возни-
кают сжимающие напряжения. При определенной величине погонной
нагрузки, действующей на кольцо, = оно, изгибаясь в окружном
направлении, может потерять устойчивость. Величина критической на-
грузки для изолированного кольца определяется формулой
= (35-23)
где г—радиус, EJ— жесткость кольца.
По этой зависимости иногда ошибочно рассчитывают на устойчи-
вость кольца днищ баков при минимальном числе волн п = 2. Зависи-
мость (35.23) не учитывает поддерживающего влияния оболочек днища
и обечайки бака, которое оказывается существенным для реальных кон-
струкций. В работе [12] подробно исследована устойчивость кольцевых
элементов, соединяющих цилиндрическую обечайку с сегментом сфери-
ческой оболочки. Критическая нагрузка для системы кольцо—оболочка
определяется соотношением
— д2 — 1 EJ 1 £/lsin0« ______(1 + ft CQS Qp)2 x
^кр г3 1 -f- jll п [2л (п 4- cos 0O)— sin2 00
Г 1 a X sin 0O -f- 6n2
X----------X --------------—-------------
[ sin 0O (X sin 0O -ь 4n2 + 02)2 — (2n2 — P2)2
(35.24)
312
где
Р = — V 24(1 + И) ; I = ——----------"<^1>(-+И .
I R 1 + р 2п (п + cos Оо) — sin2 0О
I — длина цилиндрической обечайки, R — радиус сферического дни-
ща, h — толщина обечайки и днища (принята одинаковой). Расчеты
показывают, что для реальных размеров баков число волн, по которым
теряет устойчивость кольцо, п = 6—8.
В работе [12] получена также формула для определения критической
нагрузки для кольца сферического бака, загруженного радиальным уси-
лием q:
,__L-----------------------(35.251
'р г n[n-^(rh/F)(\ +ц)] \ г2 n2 J V
Здесь EF — жесткость кольца на растяжение. Соотношениями (35.24)
и (35.25) при расчетах пользуются так же, как и ранее (см. § 16) при
определении критического давления цилиндрической оболочки, т. е. за-
даются различным числом волн м = 2, 3, 4,..., до тех пор, пока не будут
получены минимальные значения ^Кр- Величины критических нагрузок,
получаемые по зависимостям (35.24) и (35.25) для реальных колец,
оказываются настолько большими, что соответствующие им напряже-
ния значительно превышают предел прочности <ув. Поэтому расчет колец
обычно приходится вести лишь на прочность при сжатии, используя
зависимости (35.24) и (35.25) только для контроля.
ГЛАВА VII
РАСЧЕТ СУХИХ ОТСЕКОВ
§ 36. КОНСТРУКТИВНЫЕ СХЕМЫ И НАГРУЗКИ
Сухими отсеками называют обычно все небаковые отсеки ракеты.
Сюда относят прежде всего двигательные отсеки ракет с ЖРД, меж-
баковые отсеки, обтекатели, переходные отсеки, корпус ракеты с под-
весными баками и т. д.
Конструкция и форма сухих отсеков зависят от назначения и общей
компоновки ракеты. Наибольшее распространение получили цилиндри-
ческие и конические отсеки, выполненные в виде оболочек вращения,
подкрепленных силовым набором. Некоторые конструкции переходных
отсеков изготовляются из элементов ферм.
Сухие отсеки слабо герметизированы, работают без наддува и на-
гружаются силами реакций соседних отсеков корпуса ракеты и мест-
ным аэродинамическим давлением. В сечениях отсеков действуют из-
гибающие моменты 7И, нормальные силы N и перерезывающие силы Q.
В расчетах отсеков на прочность необходимо учитывать температурное
состояние конструкции, определяемое, в первую очередь, аэродинами-
ческим нагревом. Сухие отсеки некоторых типов ракет, приспособлен-
ных к подводному старту, нагружаются большим внешним давлением.
Большим внешним давлением на активном участке полета нагружены
и конические элементы переходных отсеков.
Меридиональные усилия 1\ и усилия сдвига 3, возникающие в сече-
ниях сухого отсека, определяются формулами
f N I At X 1 zoz? 1 \
т1==—(-------1----- cos ф )--, (36.1)
S = ± —— tg Y^sincp, (36.2)
\ яг яг2 /
где ср— угловая координата в окружном направлении, у—угол конусно-
сти.
От внешнего давления р в отсеке возникают окружные усилия
Т.2 =----р—. (36.3)
cos у
Формулами (36.2) и (36.3) определяются усилия в коническом отсеке при
текущем радиусе г и угле конусности у. Для цилиндрического отсека
у 0, г = R = const и соотношения (36.1) — (36.3) упрощаются:
+—^4.^ (36.4)
S=-S-sin<p, (36.5)
я/?
Т2 = - pR, (36.6)
Усилия Г1, S и Т2 являются исходными для расчета отсеков.
314
Расчет цилиндрических сухих отсеков, находящихся в средней части
корпуса, ведут на случаи наибольшего значения эквивалентной сжи-
мающей силы Аэкв. Определяющими при выборе расчетных случаев для
конических участков переходных отсеков являются величины эквива-
лентной сжимающей силы Аэкв и внешнего давления р. Корпус двига-
тельного отсека рассчитывают на случай стоянки на стартовом столе,
когда отсек нагружен собственным весом ракеты и изгибающим мо-
ментом от ветровой поперечной нагрузки на корпус ракеты. Стыковые
соединения сухих отсеков рассчитывают, как правило, на случаи транс-
портировки.
Рассмотрим некоторые конструктивные варианты сухих отсеков, ос-
новным усилием для которых является меридиональное усилие 1\ (уси-
лия Т2 и S не равны нулю, но значительно меньше 7\).
Примером наиболее простого варианта сухого отсека являются
гладкие отсеки в виде неподкрепленной оболочки. Несущая способ-
ность конструкции, нагруженной осевой сжимающей силой, опреде-
ляется ее устойчивостью. Критические напряжения для цилиндрической
и слабо конической оболочки можно найти по зависимостям § 16. Для
неподкрепленной оболочки, например из магниевого сплава, с парамет-
ром — =300 (R — радиус, h — толщина оболочки) критическое напря-
h
жение окр = 2 кГ)мм2. Величина критического напряжения, как видно,
очень мала. Если критические напряжения сжатия сравнить с пределом
текучести материала от, то сгкР/о'т = 0,1—0,2. По этому отношению мож-
но судить об эффективности конструкции в весовом отношении. Для
гладких неподкрепленных отсеков, нагруженных осевой сжимающей на-
грузкой, характерны небольшие значения (уКр/пт. Они свидетельствуют
о невыгодности использования такой конструкции для сухих отсеков.
Однако эти конструкции все же применяют в виде коротких переход-
ных цилиндрических участков, соединяющих баки с сухими отсеками
вследствие их технологической простоты. Примером гладкого сухого
отсека может служить часть отсека ракеты «Аджена», примыкающая
к баку.
Ракета «Аджена» применяется как последняя ступень носителей
«Титан II и III» и «Атлас». Основной отсек корпуса представляет собой
цилиндрическую оболочку диаметром D= 1500 мм, состоящую из двух
частей. Передняя часть выполнена из листов магниевого сплава тол-
щиной h =1,8 мм и продольных подкрепляющих элементов — стринге-
ров. Задняя часть отсека изготовлена также из листов магниевого
сплава, но не имеет подкреплений. Толщина оболочки здесь 1г = 2,5мм.
На торцах неподкрепленного отсека имеются шпангоуты. К заднему
шпангоуту по периметру прикреплен блок баков. Через этот шпангоут
на корпус передается усилие от тяги ракетного двигателя. Расчетная
нагрузка для корпуса — сжимающая. Применение коротких гладких от-
секов может быть оправдано в тех случаях, когда они составляют не-
большую долю в весовом балансе конструкции.
Наиболее широко не только в баллистических ракетах, но и в дру-
гих летательных аппаратах применяются стрингерные и лонжеронные
отсеки. Конструкции этих отсеков обычно выполняют из обшивки, под-
крепленной продольными элементами — стрингерами и лонжеронами
(как правило, из прессованных профилей), а также поперечными коль-
цами — шпангоутами.
При конструировании отсека весьма трудно обеспечить устойчивость
обшивки между подкрепляющими элементами. Иногда приходится до-
пускать потерю устойчивости обшивки при сравнительно малой на-
грузке. Основными несущими элементами в этом случае являются про-
315
Рис. 36.1
дольные подкрепления. Конструкцию такого типа будем называть лон-
жеронной. Малый вес отсека этой конструкции достигается тем, что
удается допустить высокие напряжения в лонжеронах.
В тех случаях, когда в соответствии с требованиями эксплуатации
потеря устойчивости обшивки недопустима, приходится идти по дру-
гому пути. Применяется более толстая обшивка с частыми продоль-
ными подкреплениями. Это увеличивает критические напряжения об-
шивки. Одновременно оказывается возможным уменьшить сечение
продольных элементов. Для увеличения общей устойчивости отсек раз-
бивается на несколько участков шпангоутами. Конструкцию этого типа
назовем стрингерной.
Критические напряжения стрингерной и лонжеронной конструкции
значительно выше критических напряжений эквивалентной по весу
гладкой оболочки. В этих конструк-
циях удается достигнуть уровня на-
пряжений (Укр/<Тт = 0,4—0,5.
Стрингерные и лонжеронные
отсеки уже много лет применяются
в самолетостроении. В ракетной тех-
нике они использованы в конструк-
циях многих ракет. Хвостовой отсек
и корпус подвесных баков ракеты
«Фау-2» имеют продольные и попе-
речные подкрепления. В этой ракете
стальной корпус отсека подвесных
баков диаметром 1650 мм и длиной
6176 мм состоит из двух полуоболо-
чек, скрепленных по образующей
болтами. Обшивка корпуса толщи-
ной 0,6 мм имеет 24 продольных подкрепления (стрингера) и 8 лонже-
ронов, равномерно расположенных по периметру. Толщина стрингера
1,0 мм, лонжерона — 2 мм. По длине корпуса поставлены шпангоуты
корытообразного сечения. Отсек рассчитан на случай входа в плотные
слои атмосферы при действии значительных перегрузок, аэродинамиче-
ских нагрузок и нагрева. Этим, отчасти, объясняется применение сталь-
ного корпуса в ракете «Фау-2». Типичная схема корпуса сухого отсека
стрингерной конструкции, выполненного из алюминиевых сплавов, пред-
ставлена на рис. 36.1. Применение таких отсеков при невысоком уровне
нагрева эффективно в весовом отношении.
Одним из вариантов подкрепленной конструкции является панель-
ная конструкция. Для сухих отсеков применяют прессованные, меха-
нически и химически фрезерованные панели. Частые продольные под-
крепления в стрингерно-панельной конструкции и продольные и
поперечные в вафельной позволяют избежать потери устойчивости
обшивки. При расчете на общую устойчивость такую конструкцию мож-
но считать конструктивно-анизотропной оболочкой.
Выше мы отмечали, что при сжатии отсека, имеющего продольные
и поперечные подкрепления, трудно обеспечить устойчивость тонкой
обшивки между подкреплениями. При работе отсека на сжатие обшив-
ка, потерявшая устойчивость, является своего рода балластом. Для
повышения местных критических напряжений этой обшивки нужно су-
щественно уменьшить расстояние между подкреплениями, например
ширину клетки. Такая конструкция приближается к гофрированной.
Существует несколько вариантов сухих отсеков гофрированной
конструкции. Оболочка (двухслойная или трехслойная) состоит из од-
ного слоя гофра и одного или двух слоев гладкой обшивки. Листы
соединены при помощи сварки или склейки. Материал — алюминиевые
316
сплавы или нержавеющая сталь. Применяют гофры различного сече-
ния: трапециевидные, синусоидальные, омегообразные и др. Иногда ис-
пользуют конструкции в виде гофрированной обшивки, подкрепленной
мощными лонжеронами.
При расчете на общую устойчивость замкнутые цилиндрические и
конические гофрированные отсеки рассматривают как конструктивно-
ортотропные оболочки. Задача проектирования профиля гофра состоит
в том, чтобы обеспечить высокие
местные критические напряжения
плоских и скругленных элементов
гофра. Гофрированные панели, при-
меняемые в качестве обшивки и
имеющие по краям силовые элемен-
ты, рассчитывают как конструктив-
но-анизотропные пластины или по-
логие оболочки. При ориентировке
гофров вдоль действия сжимающей
нагрузки удается получить весьма
высокие критические напряжения.
Отношение оКр/пт можно повысить
до 0,7—0,8. Для отсеков, нагружен-
ных преимущественно осевым сжа-
тием, конструкция с продольным
направлением гофров является од-
ной из наиболее эффективных в ве-
совом отношении.
На ракетах «Сатурн», «Цен-
Рис. 36.2
тавр», «Атлас» широко применяются
отсеки, целиком состоящие из гоф-
ров, а также конструкции в виде гоф-
рированной обшивки, подкрепленной мощными лонжеронами. Переход-
ный отсек между второй и третьей ступенями ракеты-носителя «Сатурн»
(рис. 36.2) (120] состоит из двух секций цилиндрической оболочки дли-
ной 1140 мм и диаметром 6630 мм и конической оболочки длиной
1140 мм и диаметром верхней части 5560 мм. Передняя часть кониче-
ского отсека примыкает к баку окислителя третьей ступени, а цилинд-
рический отсек — к баку горючего предыдущей ступени. В конической
части переходного отсека имеется восемь лонжеронов, равномерно рас-
положенных по периметру. Между ними поставлено по семи лонжеро-
нов меньшего сечения. Всего в коническом отсеке 8 + 7x8 = 64 лонже-
рона швеллерообразного сечения. Цилиндрический отсек имеет вдвое
меньше продольных элементов. В торцовых сечениях конической и ци-
линдрической частей отсека, а также в месте перехода конуса в цилиндр
поставлены замкнутые круговые шпангоуты швеллерообразного сечения.
Примерно посередине длины каждого отсека установлены шпангоуты
меньшей жесткости. Шпангоуты в местах пересечения с лонжеронами
скреплены болтами через фитинги. Обшивка — трехслойная из сталь-
ных листов. Наружный и внутренний листы имеют толщину 0,2 мм, про-
межуточный гофрированный слой толщиной 0,05 мм пилообразного се-
чения приварен к этим листам в вершинах гофра. Каждый элемент
продольного гофра гофрирован еще в поперечном направлении
(рис. 36.3). Трехслойный лист суммарной толщиной 4 мм эквивалентен
по весу сплошному стальному листу толщиной 0,535 мм. Трехслойная
конструкция имеет жесткость на изгиб в продольном направлении в
140 раз больше жесткости сплошного эквивалентного по весу листа.
При испытаниях этого трехслойного материала на растяжение получе-
но разрушающее напряжение 100 кГ!мм?. При сжимающих нагрузках
317
вдоль гофров напряжения, соответствующие потере устойчивости, дости-
гали 56 кГ/мм2 при нормальной температуре [120].
Для отсеков, нагруженных осевыми силами и давлением, целесооб-
разно применять сотовые конструкции. Они сравнительно недавно
стали использоваться как в основных, так и во вспомогательных эле-
ментах корпуса носителей и космических аппаратов. Преимущество со-
товых панелей, состоящих из листов, прикрепленных при помощи сварки
Рис. 36.3
или склейки к двум сторонам заполнителя малого веса, заключается в
большой жесткости и хорошей местной устойчивости таких панелей при
малом весе.
Обычно при проектировании рассчитывают сплошную или каркас-
ную конструкцию, а затем преобразуют ее в эквивалентную конструк-
цию с сотовым заполнителем. В качестве заполнителя применяют ме-
таллы и пластмассы. Наиболее рациональная форма ячеек заполнителя
для изотропно нагруженных отсеков — шестигранные соты и вафли.
Обшивки и заполнитель в сотовых конструкциях, применяемых при вы-
соких температурах, целесообразно делать из одного материала во из-
бежание больших местных термических напряжений.
Сотовые панели применяют для обтекателей, перегородок и других
элементов, где требуется легкая, но жесткая конструкция. Корпус кос-
мического аппарата «Апполон» изготовлен, в основном, из сотовых па-
нелей. Кабина космонавтов состоит из панелей сотовой конструкции
толщиной 12,7 мм, толщина наружных листов по 2,28 мм. Материал
панели — нержавеющая сталь. Наружные листы соединены с сотами
при помощи сварки. Корпус двигательного отсека также состоит из
оболочки сотовой конструкции. Толщина панелей здесь 51 мм, толщина
наружного и внутреннего листов 1,27 мм. Материал сот и внешних ли-
стов— алюминиевый сплав.
В качестве переходных отсеков, расположенных у стыка ступеней
ракеты, иногда применяют стержневые конструкции, являющиеся эле-
ментами фермы. Подобные отсеки способны передать все компоненты
нагрузки с одной ступени на другую.
§ 37. СТРИНГЕРНЫЕ, ПАНЕЛЬНЫЕ И ЛОНЖЕРОННЫЕ ОТСЕКИ
Рациональной конструкцией сухого отсека, работающего в основном
на осевое сжатие, является оболочка, подкрепленная продольными н
поперечными элементами. Сжимающая сила воспринимается оболочкой
318
a;
Рис. 37.1
и продольными элементами. Назначение поперечных элементов — повы-
сить устойчивость обшивки и стрингеров. В зависимости от частоты
подкрепляющих элементов и их жесткости существуют различные фор-
мы потери устойчивости. Форма
потери устойчивости, при которой
обшивка теряет устойчивость
раньше подкрепляющих элемен-
тов, показана на рис. 37.1, а. На
рис. 37.1, б представлена форма
потери устойчивости, сопровож-
дающаяся изгибом стрингеров по
одной полуволне. При неправиль-
ной конструкции стрингера может
происходить потеря местной
устойчивости его элементов (рис.
37.1, в).
Расчетные формулы для эле-
ментов конструкции отсека. Обыч-
но длина панели обшивки (между
соседними шпангоутами) больше
ее ширины (между стрингерами!).
Поэтому для определения критических напряжений сжатия панели
можно пользоваться приближенной формулой для длинной пологой ци-
линдрической панели с радиусом кривизны /?, толщиной h и шириной
(расстоянием между стрингерами) tc:
°кр V + k
к
л.2
12(1 —ц2)
(37.1)
Первое слагаемое формулы (37.1) соответствует критическому на-
пряжению сжатой цилиндрической оболочки. Коэффициент &хл опре-
деляют по формуле (33.4). Второе слагаемое соответствует критиче-
скому напряжению длинной прямоугольной пластины. Коэффициент k
зависит от условий закрепления пластины. В предварительных проек-
тировочных расчетах можно принять &хл = 0,1. Минимальное значение
коэффициента й = 4,0 соответствует шарнирно опертой пластине. При
k = 4,0, йхл = 0,1 и ц = 0,3 формула (37.1) принимает вид
акр= +3,6£(Ау. (37.2)
Критическое напряжение потери устойчивости изолированного сжатого
стержня в упругой области определяют по формуле
°ко = с-------,
кр X2
(37.3)
где с — коэффициент, зависящий от характера закрепления концов стерж-
ня;
X = Z/p — гибкость стержня;
I—длина стержня; р = V J If — радиус инерции сечения.
Для шарнирно опертого стержня с=1,0, а для стержня с защем-
ленными концами с = 4,0. В реальных конструкциях закрепление стерж-
ния, как правило, упругое и значение коэффициента с лежит между
1,0 и 4,0. В предварительных проектировочных расчетах упругость за-
делки концов стержня учитывается коэффициентом с = 2,0.
Формула (37.3) справедлива только до значения гибкости X, соот-
ветствующей Окр^Оуп, где (ууп — предел упругости материала при сжа-
319
тии. Предельное значение гибкости, когда еще справедлива формула
(37.3), равно
(37.4)
При а>ауп происходит потеря устойчивости в пластической области и
вместо формулы (37.3) можно пользоваться уравнением
л2Ек
кр “ с
(37.5)
где Ек = dG/d&— касательный модуль диаграммы а — е материала. Урав-
нение (37.5) соответствует расчетам по касательному модулю [27] в теории
нсупругой устойчивости стержней. Расчеты по уравнению (37.5) произво-
дят графически. Строят график зависимости Х = л]/ сЕк1<зкр (рис. 37.2).
При отсутствии диаграммы а—г материала для приближенных расчетов
можно пользоваться эмпирической формулой
; / е
<\р = — (*в - От) Ч = Л1/ С~~ .
(37.6)
где ат — предел текучести материала;
ав — предел прочности.
Сжатые плоские элементы стержня в упругой области рассчитывают
на местную устойчивость по формуле для длинных пластин:
а л2 г? /' h \2
aKD = k ------------- £ -- ) >
кр 12(1 — p*) \ b ) '
(37.7)
где b — ширина элемента стержня; h — его толщина. Для плоского эле-
мента, ограниченного по краям двумя другими элементами (стенка
профиля, изображенного на рис. 37.3), можно принять коэффициент
& = 4,0, как для шарнирно опертой пластины. Для плоского элемента с
одним свободным краем (полки, рис. 37.3) & = 0,46, как для длинной
пластины, одна сторона которой свободна, другая шарнирно оперта.
320
Расчет местной устойчивости элементов стержня за пределом упру-
гости очень сложен и мало надежен. Надежные значения критических
напряжений обычно получают путем испытаний серии образцов на
сжатие.
Приближенно критическое напряже-
ние местной потери устойчивости можно
подсчитать по соотношению
О = в — (<j _ (Тт) b'h—, (37.8)
кр 1! v b т7 (&/ft)T v ’
где
Г F л2
(*/Л)т = 1/ —k-----------------.
Т V ат 12(1 —н2)
При этом для всех элементов стержня выполняется условие
л2
12(1 - р2)
(37.9)
при k = 4,0 и k •-= 0,46 соответственно получаем
(37.10)
Условия (37.10) соответствуют рациональной конфигурации сечения
любого тонкостенного стержня, когда можно не опасаться преждевре-
менной местной потери устойчивости. Формы поперечных сечений про-
дольных элементов показаны на рис. 37.4, а [103].
Рис. 37.4
Расчет стрингерного отсека. Стрингерным отсеком назовем вариант
конструкции, в котором толщина обшивки и расстояние между стрин-
герами выбраны так, что обшивка не теряет устойчивости до разруше-
ния отсека. Расчетное разрушающее напряжение сжатия для отсека
jiDh-\~fcn
где D — диаметр отсека;
Л —толщина обшивки;
(37.11)
21 Зак. 96
321
п — число и /с — площадь сечения стрингеров;
Л^экв — расчетная эквивалентная сжимающая сила.
Оптимальная в весовом отношении конструкция отсека из данного ма-
териала соответствует максимальному значению расчетного разрушающего
напряжения при заданной величине 7V3PKB. Величина расчетного разрушаю-
щего напряжения определяется значением погонной сжимающей нагрузки
гр _ ^ЭКВ
1 ” nD
Чем меньше величина тем труднее достичь высоких критических
напряжений сжатия, так как при уменьшении толщины обшивки увели-
чивается число стрингеров, соответственно уменьшается площадь их
сечения и критическое напряжение сжатия для стрингеров. Частое
подкрепление стрингеров шпангоутами приводит к увеличению веса
конструкции. Кроме того, при уменьшении толщины обшивки резко по-
вышается ее температура и соответственно снижаются механические
характеристики материала. Только в конструкции отсека с обшивкой,
подкрепленной частым гофром, удается использовать тонкую обшивку,
не теряющую устойчивость.
При выбранной толщине обшивки расстояние между стрингерами
определяют из условия, что сгкр обшивки равно расчетному разрушаю-
щему напряжению для всего отсека о. Из формулы (37.2) получим
/= 1,9/11/-------------
с у o — 0,\Eh/R
число стрингеров
(37.12)
(37.13)
(37.14)
(37.15)
неизвестной величиной
сжимающая сила, действующая на стрингер,
р = Л'экв-л£)/1а .
с п
площадь сечения стрингера
/с = Рс/О-
В формулах (37.12) — (37.15) единственной
является о. Величина этого напряжения должна определяться из усло-
вия минимального веса отсека. Для этого задаются несколькими значе-
ниями о, определяют площади стрингеров fc, подбирают форму сечения
стрингера и подкрепляющих его шпангоутов из условия, чтобы крити-
ческие напряжения потери общей и местной устойчивости были бы нс
меньше о.
Пример. Определим конструктивные размеры элементов стрингерного отсека диа-
метром D = 3000 мм, длиной I = 900 мм. Сжимающая ’сила Л^кв = 400-103 кГ мате-
риал — алюминиевый сплав, Е = 7,2-103 кГ/мм2, от = 28 кГ/мм2, ов = 40 кГ/мм2. При
толщине обшивки h = 2,5 мм и расчетном разрушающем напряжении о = 10 кГ/мм2 из
формулы (37.12) получим
Е
o — G,lEh/R
1,9-2,5
7,2-103
2,5
10—0,1*7,2-Ю3———
1500
= 135 мм.
Число стрингеров
tcD л-3000
п =-----=----------= 70.
tc 135
322
Усилие, приходящееся на один стрингер,
,V3KB~ nDh° 400 000 — лЗООО-2,5-10
Рс = —--------------=-------------------------= 2360 кг.
с п 70
Площадь стрингера
fc рс/а = 2360/10 = 236 мм2.
Из сортамента прессованных профилей выбираем стрингер в форме равнобокого
уголка 35x35x3,2, площадь сечения которого fc=236,2 мм2. Сечение стрингера вместе
с участком обшивки изображено на рис. 37.4, б. Критическое напряжение потери мест-
ной устойчивости для стрингера определяем по формуле (37.7) при £=0,46. Получаем
<уКр = 30 кГ1мм2, что значительно выше принятого значения а. Таким образом, потеря
местной устойчивости стрингера не лимитирует прочность отсека.
Для проверки стрингера на потерю общей устойчивости вычисляем момент инер-
ции стрингера с учетом площади обшивки между стрингерами относительно общего
центра тяжести стрингера и обшивки; кривизну обшивки не учитываем:
ypiyt
2,5-135 1,254-3,2-35-4,1 ->31» 8-3,2-21,6
Уч =-------=-------------------------------------------= 5,6 мм;
Vr. 2,5-1354-3,2-35 + 31,8-3,2
L
VI r V 3,2-31,83 135-2,53 35-3,23
Jx = \ (У1 - //т)2 =------“-----+------7^— +------77---+ 338-4,352 +
+ 112-1,52 > 102-162 = 41,6-103 .«.и4.
Площадь стрингера с присоединенной обшивкой
/ = /с 4- tch = 236 + 135- 2,5 = 574мм2.
Гибкость продольного элемента на длине всего отсека
_,06.
V Jx V 4,16- 104
Критические напряжения для стрингера с обшивкой как для стержня определяются
соотношением (37.3). При с = 2,0
л2Е л2-7,2-103
сг = с------= 2,0-------------= 12,7 кГ)мм2-
*р Ю62 '
Полученные напряжения выше тех, которыми мы задавались.
Если теперь повысить расчетное разрушающее напряжение а, то из условия устой-
чивости обшивки между стрингерами нужно увеличить число стрингеров и уменьшить
площадь их сечения. Это приводит к тому, что уменьшается момент инерции сечения
и гибкость продольных элементов на полной длине отсека. Условие общей устойчивости
(37.3) удается соблюсти, лишь разбив длину отсека на два или более участков шпан-
гоутами. Под длиной / в соотношении для гибкости К=1/р подразумевается длина каж-
дого участка.
Расчет панельного отсека. Сухие отсеки панельной конструкции из-
готовляют из панелей, получаемых прессованием или механической
обработкой толстых листовых заготовок. Панели только с продольными
ребрами (рис. 37.5, а, б) называются стрингерными, панели с продоль-
ными и поперечными ребрами — вафельными. В тех и других панелях
расстояние между ребрами выбирают из условия, чтобы обшивка (так
называемое полотно панели) не теряла устойчивости раньше общей по-
тери устойчивости отсека.
Расчет панельных отсеков, работающих при осевом сжатии, произ-
водится на общую устойчивость как конструктивно-анизотропной обо-
лочки, и на местную устойчивость, определяемую устойчивостью эле-
ментов панелей. При расчете баков вафельной конструкции была полу-
чена формула для критической величины погонной сжимающей силы
21* 323
при осесимметричной форме потери устойчивости (§ 34). Соответству-
ющее критическое напряжение сжатия можно определить по формуле
<37Д6)
где
Лш = h + hc = h + (37.17)
h —толщина обшивки;
/ш и fz —площади поперечного и продольного подкреплений;
и /с - шаг поперечного и продольного подкреплений;
— момент инерции поперечного сечения на длине tz.
Рис. 37.5
При расчете реальной конструкции нужно учитывать, что макси-
мальные критические напряжения зависят от формы потери устойчиво-
сти и начальных несовершенств. С учетом этих факторов формулу для
определения критических напряжений можно представить в виде
(Ткр = ^^ (37.18)
Ktlq, У tc
где коэффициент k отражает влияние формы потери устойчивости и
начальных несовершенств. Наиболее надежное значение коэффициента
k можно получить, исходя из результатов испытаний опытных отсеков
конструкций или их моделей. Если такие испытания не проводятся,
можно руководствоваться следующими соображениями. В панельных
конструкциях, изготовляемых из толстых листов, роль начальных несо-
вершенств существенно меньше, чем в гладкой обшивке из тонколисто-
вого материала. Если для гладких оболочек 6 = 0,2—0,3, то для панель-
ных— этот коэффициент порядка 6 = 0,3—0,5. Меньшее значение коэф-
фициента k соответствует стрингерно-панельному отсеку, большее —
вафельному, когда жесткость поперечных и продольных подкрепляю-
щих элементов одного порядка. Таким образом, для расчета отсеков
из стрингерных панелей можно пользоваться приближенной формулой
(37.18) с коэффициентом 6 = 0,3, для вафельных отсеков с коэффициен-
том 6 = 0,5. Расчет на местную устойчивость сводится к проверке устой-
чивости сжатой обшивки в клетке между соседними стрингерами и ре-
бер как пластинок по формулам (37.2) и (37.7).
Пример . Проведем расчет панельного отсека, нагруженного тем же усилием
и изготовленного из того же материала, что и стрингерный отсек. Пусть толщина
обшивки Zi = 2,0 мм, расчетное разрушающее напряжение с=12 кГ!мм2. Расстояние
324
между продольными подкреплениями из условия местной устойчивости обшивки долж-
но быть не более (37.12)
/ = 1 9ft 1/"----------------= 1,9-2,0 1//---------7’2'103--------= 97 шь
V a — 0,\Eh/R V 12 —0,1-7,2-103-2/1500
Выбираем /с = 60 мм. Тогда сила, приходящаяся на один продольный элемент,
Р = [N?— л Dh<3] = ------—----[400 000 — л-3000-2-12] = 1100 кГ.
nD экв л-3000
Площадь каждого элемента
Если теперь принять высоту подкрепления b = 20 мм, то толщина его будет h = 4,6 мм.
На рис. 37,5, а представлено выбранное сечение панели. Определим момент инерции се-
чения относительно центра тяжести
2s-
‘ 60-2,0-1,0 + 20-4,6-12
ут =-------- =-------------------------- =5,8 мм;
J y,Fi 60-2,0 + 20-4,6
i
V* \л 60-2,03
Jx = ), Ji + >, Fi (У ~ Ут? =----------- +
i
4.6-203
+-----------+ 120-4,82 + 92-6,22 = 9400 мм*.
Приведенная толщина обшивки отсека
f 92
ft =/t + -!—= 2,0+--------=3,53 мм.
c /с 60
Если в отсеке отсутствует поперечный набор, то =
Критические напряжения
при коэффициенте & = 0,3:
общей устойчивости отсека определим по уравнению
2Е -j / Jq hm
в = k —— I/ -----------=
р Rhe У tc
2-7,2-103 , Л 9400-2,0
Величина этих напряжений выше тех, которыми мы задавались, поэтому отсек удов-
летворяет условию общей устойчивости. Критические напряжения потери местной
устойчивости ребра при b)h=20/4,6 = 4,35 оказываются значительно выше предела теку-
чести материала.
Расчет лонжеронного отсека. Лонжеронным отсеком будем назы-
вать конструкцию, в которой допускается потеря устойчивости обшивки
раньше потери устойчивости продольных элементов — лонжеронов. Рас-
стояние между лонжеронами в такой конструкции отсека уже не лими-
тируется устойчивостью обшивки. Число лонжеронов выбирают из дру-
гих соображений. Так, в двигательных отсеках число лонжеронов
обычно бывает минимальным и определяется конструкцией двигатель-
ной установки. В переходных отсеках число лонжеронов может опреде-
литься требованиями более равномерной передачи усилий. Толщина
обшивки в лонжеронном отсеке может быть минимальной и опреде-
ляться температурными или технологическими условиями. При очень
тонкой обшивке следует опасаться сильного ее нагрева на активном
участке полета. Максимальная температура обшивки не должна быть
выше той, при которой происходит значительное снижение механиче-
325
ских характеристик материала. После потери устойчивости обшивка
почти не участвует в восприятии сжимающих усилий. Только узкая
полоса обшивки, прилегающая к лонжерону, работает совместно с ним
на сжатие. Эта часть обшивки называется присоединенной. Ширину
присоединенной обшивки 6Пр обычно определяют по приближенной фор-
муле Кармана:
4-=1'9Лк/\г'
(37.19)
где ол — напряжение в лонжероне;
h — толщина обшивки;
Е—модуль упругости материала.
Формула (37.19) получена из условия, что критическое напряжение
сжатия для длинной шарнирно-опертой пластины шириной 6Пр равно
напряжению ол- Площадь присоединенной обшивки при различных ва-
риантах крепления обшивки к лонжерону определяется следующим
образом. Если обшивка прикреплена
Рис. 37.6
к лонжерону так, как показано на
рис. 37.6,а, то половина ширины 6Пр,
определяемая формулой (37.19), долж-
на быть отложена от точки крепления
обшивки к лонжерону в обе стороны.
Общая ширина присоединенной обшив-
ки t при этом равна &Пр. Если обшивка
прикреплена к лонжерону так, как по-
казано на рис. 37,6,6 и ширина 6Пр
больше расстояния Д, то ширина при-
соединенной обшивки равна / = 2&Пр-
В том случае, когда Д меньше &Пр
(рис. 37.6,в), ширина присоединенной
обшивки равна / = Д + Ьпр. Таким обра-
зом, суммарная площадь лонжерона и
присоединенной обшивки равна fn + th.
Если п — число лонжеронов и /л —
площадь лонжерона, то
напряжение
сжимающее
*л
экв
(37.20)
п (f Л +
Это напряжение должно быть не больше критического напряжения
сжатия для лонжерона как стержня. Из условия Ол^^кр путем проб
можно определить площадь и момент инерции сечения лонжерона. Так
как обшивка не позволяет изгибаться лонжерону в плоскости, каса-
тельной к поверхности отсека, то при определении акр по формулам
(37.3) пли (37.6) момент инерции сечения нужно брать относительно
осп, параллельной этой плоскости. Если критические напряжения поте-
ри общей устойчивости лонжерона оказываются малыми, то отсек мож-
но подкрепить шпангоутами, разбив свободную длину лонжерона на
два или более участков. Форму сечения лонжерона выбирают с учетом
результатов расчетов его элементов на местную устойчивость.
Пример. Пусть лонжеронный отсек D = 3000 мм, 1 = 1000 мм нагружен сжима-
ющей силой А'ркв = 400-103 кГ. Материал отсека — алюминиевый сплав с механическими
характеристиками Е = 7,2-103 кГ/мм2’, ав = 40 кГ/мм2, от = 28 кГ/мм2. Определим
основные конструктивные размеры отсека.
При выборе толщины обшивки должны учитываться температурное воздействие и
технологические требования при изготовлении. Примем толщину обшивки h= 1,0 мм.
326
Для определения геометрии лонжерона нужно задаться числом лонжеронов п. Примем
л = 24. Тогда усилие, воспринимаемое однИхМ лонжероном,
№
' экв
п
400-1О3
24
= 16 700 кГ.
Чтобы продолжить расчет, нужно задаться величиной напряжений в лонжероне. При-
мем в первом приближении ал = сг = 25 кГ/мм2. Тогда площадь поперечного сечения
лонжерона с присоединенной обшивкой
Pq 16 700
f J- th = ----- =---------= 668 мм2.
1 a 25
Рис. 37.7
Выберем форму сечения лонжерона в виде трапециевидного отбортованного швел-
лера (рис. 37.7). У такого лонжерона две точки крепления к обшивке. При расстоянии
между точками большем 6Пр, площадь присоединенной обшивки равна Z/z = 2&np/i.
Из формулы (37.19) находим
/ Е / 7 2-103
/>пр = 1,9/t |/ — =1,9.1,о j/ —-------------= 32,2 мм.
Площадь присоединенной обшивки .равна
th = 2ЬпрЛ = 2-32,2-1,0 = 64,4 щщ2.
Площадь лонжерона Дч — 668 — 64,4 = 603,6 мм2. По сортаменту стандартных профи-
лей для подобного сечения выбираем профиль с геометрическими характеристиками
Дл = 608,8 мм2, Jx = 25,1 • 104 мм* (размеры сечения показаны на рис. 37.7). Местную
устойчивость полок лонжерона проверяем по формуле (37.7). Для наклонных полок bY =
= 47 мм, h = 3 мм\ принимая & = 4,0, получаем
окр = 0,9££ (h/bL)2 = 0,9-4- 7,2-10* X (3/47)2 > от;
для нижней горизонтальной полки
акр = 0,9/гЕ (/г/62)2 = 0,9X0,46*7,2.10* (3/19)2 >от.
Для определения общей устойчивости подсчитаем гибкость лонжерона с учетом присоеди-
ненной обшивки. Центр тяжести сечения (см. рис. 37.7)
I 608,8-25,11 —64,4-0,5
i — 22,7 мм. 673,2
Момент инерции
j = Jx + /л (Ул — Ух)2 + th (ух — i/0)2 =
= 25,1 • 10* + 608,8(25,1 — 22,7)2 Hz 64,4 (22,7 + 0,5)2 = 28,9-10* мм1.
327
Радиус инерции
/J _ / 28,9 Л О4
/л + /й V 608,8 + 64,4
гибкость
По формуле (37.3) находим критические напряжения общей устойчивости, считая с=2:
_ 2л2 Е _ 2-9,87-7,2-103
0кр= Д2 -- 23,32 >СТТ-
Полученные значения критических напряжений местной и общей устойчивости выше вели-
чины напряжений, принятых в качестве первого приближения. Лонжеронный отсек в
этом случае не теряет несущую способность.
Расчет сухих отсеков при действии перерезывающей силы. В рас-
четных случаях, соответствующих полету, перерезывающая сила Q со-
ставляет лишь незначительную часть сжимающей силы Мэкв. Сущест-
венной она может оказаться, например, при транспортировке. При этом
обшивка отсека может потерять устойчивость от действия сдвига или
сжатия со сдвигом. Если такая потеря устойчивости приводит к оста-
точным деформациям конструкции, то это может отразиться на проч-
ности отсека, что крайне нежелательно.
Рассмотрим устойчивость цилиндрической панели, образованной со-
седними стрингерами и шпангоутами. Для этого вначале определим
критические напряжения сдвига для цилиндрической панели длиной а,
шириной b по зависимости [9]
ткр = 0,1Е-^- +5,0рЕ-^-; Р= 1,0 + 0,8-^-. (37.21)
Критическое состояние при совместном действии сжатия и сдвига можно
оценить по приближенной зависимости [27], [91]
—(37.22)
^кр X ткр /
где О’ и т — расчетные, а сгкр и ткр — критические напряжения в панели.
§ 38. ГОФРИРОВАННЫЕ ОТСЕКИ
При малой величине сжимающей нагрузки на единицу длины пери-
метра поперечного сечения сухого отсека подкрепление тонкой обшивки
стрингерами становится нецелесообразным. Применение панельных от-
секов с очень тонкими продольными ребрами и тонкой обшивкой огра-
ничено технологическими возможностями. В этом случае целесообразно
применять гофрированные отсеки.
Гофрированные отсеки изготовляются из высокопрочного листового
материала. Они могут быть выполнены в виде тонкой обшивки, под-
крепленной продольным гофром, или в виде продольного гофра без
обшивки. Конструктивные варианты отсеков с продольным гофром по-
казаны на рис. 38.1: а, б — обшивка 1 подкреплена гофром 2 и шпан-
гоутами 3; в — гофрированный отсек без обшивки. Некоторые формы
гофра приведены на рис. 38.2: а — синусоидальная, б — прямоугольная,
в — омегообразная, г — трапециевидная.
Для определения величин разрушающих нагрузок и выбора конст-
руктивных размеров отсека проводят расчет на общую и местную устой-
чивость при осевом сжатии.
3 28
2
Рис. 38.1
°) 6) б) г)
Рис. 38.2
Расчет элементов гофрированного отсека на местную устойчивость.
Рассмотрим устойчивость гофра и отсека при сжатии.
Поперечное сечение гофра состоит из криволинейных и прямоли-
нейных участков (рис. 38.3,а). Расчет этих участков на устойчивость
можно свести к расчету цилиндрических оболочек и прямоугольных
пластинок. Для цилиндрических участков гофра критическое напряже-
ние сжатия в упругой области можно определить по формуле
cKp=--kE-^, (38.1)
329
где Лг — толщина гофра;
г — радиус сечения гофра;
Е — модуль упругости материала.
Для гофра с отношением радиуса к толщине г/Лг = 20—100 можно
приближенно принять & = 0,15. Если величина оКр, определенная по
формуле (38.1), окажется больше предела текучести материала от, то
следует принять о1ф = от.
Для плоских участков гофра критические напряжения сжатия мож-
но определить как для длинной пластинки:
акр=3,6Е^у, (38.2)
где b — условная ширина пластинки, равная 1,1 —1,2 ширины плоского
участка. Если окр, подсчитанная по формуле (38.2), больше от, то мож-
но ПРИНЯТЬ Окр = От-
Потеря устойчивости криволинейных участков гофра, как правило,
соответствует разрушению. Потеря же устойчивости плоских участков
не вызывает разрушения, так как плоская пластинка после потери
устойчивости продолжает нести нагрузку. Величина этой нагрузки за-
висит от значения критического напряжения. Если критические напря-
жения для криволинейных участков гофра, определенные по формуле
(38.1), выше критических напряжений в прямолинейных участках, то
приведенные разрушающие напряжения сжатия для гофра можно опре-
делить по формуле [116]
(Tpr = ^F£) (38.3)
Г Г
где 2пкр. — сумма усилий, воспринимаемых различными участками гофра;
Fr = Z Fi — суммарная площадь сечения гофра.
Площадь поперечного сечения гофра можно также подсчитать, умно-
жив шаг гофра t на его толщину hr и на коэффициент развертки т):
Ег=
где т] — отношение длины развертки гофра к его шагу.
Если критическое напряжение в каком-либо криволинейном участке
гофра меньше критических напряжений в плоских участках, то при-
ближенно можно принять
cfp.r = tfKp, (38.4)
где оКр — минимальное напряжение в криволинейном участке.
330
Если гофр соединен с тонкой обшивкой (рис. 38.3,6), то работа об-
шивки учитывается так же, как работа плоского участка гофра. Крити-
ческие напряжения для обшивки можно приближенно определять как
для длинной плоской пластинки
<ткР0 = 3,6^-М, (38.
\ о J
где /го — толщина обшивки, b = t — шаг гофра (рис. 38.3, б).
Обычно разрушающее напряжение для гофра выше, чем критиче-
ские напряжения для обшивки. В этих случаях приведенное разрушаю-
щее напряжение для гофра с обшивкой можно определить по формуле
gp
^кро о 4- tfp.r
(38.6)
где окр и Fo — критические напря кения и площадь сечения обшивки на
шаге b — t.
Величина разрушающей сжимающей силы для всего отсека, опреде-
ленная из условия местной устойчивости,
Л^кр = (Fo + Fr).
(38.7)
Расчет отсека на общую устойчивость. Гофрированный отсек пред-
ставляют как конструктивно-анизотропную оболочку. Расчет такой обо-
лочки на устойчивость можно произвести, пользуясь приближенным
методом, изложенным в предыдущем параграфе. Критическая сжимаю-
щая сила при общей потере устойчивости гофрированного отсека с об-
шивкой определяется формулой
Л'Кр = 4л*£|/А- (Ло+49 ’
(38.8)
где Jr — момент инерции сечения гофра с обшивкой на ширине шага /;
й0 — толщина обшивки;
/ш — площадь шпангоута;
/ — расстояние между шпангоутами.
Коэффициент k отражает форму потери устойчивости и влияние на-
чальных несовершенств. При малом числе подкрепляющих шпангоутов
можно принять, как и для стрингерно-панельного отсека (§ 37), & = 0,3.
Тогда
Л;р=1,2лЕ |/4(ло + 4)'
(38.9)
Общая устойчивость гофрированного отсека без обшивки может
определяться устойчивостью гофра на шаге t как сжатого стержня.
В зависимости от конфигурации гофра формы потери устойчивости
различны. Поэтому для гофрированных отсеков необходимо испытание
образцов конструкций.
В некоторых случаях предварительные расчеты выполняют, исходя
из условия устойчивости гофра как стержня при форме потери устой-
чивости, соответствующей изгибу в радиальной плоскости. При этом
можно воспользоваться формулой (37.3) из предыдущего параграфа
при с = 2. Таким же образом можно определить критические напряже-
331
ния для гофра с обшивкой. Критическая сила для всего отсека при та-
ком способе расчета определится по формуле
JVKP=2n^+ (38.10)
/ — расстояние между шпангоутами.
Для короткого отсека критическую силу можно определить по фор-
муле (38.10) без учета промежуточных шпангоутов. Если эта сила
окажется больше расчетной разрушающей силы, то для гофрирован-
ного отсека с обшивкой можно не производить контрольного расчета
по формуле (38.9).
Пример. Определим разрушающую нагрузку для гофрированного отсека, показан-
ного на рис. 38.1, а. Геометрия гофра ясна из рис. 38.3, б. Размеры отсека и гофра:
L = 3Z = 900 мм, R = 1000 мм, ho = 0,6 мм, t = 35,0 мм, Н = 16,0 мм, г = 4,00мм,
Фо = 1 рад, hr = 0,3 мм, Ь± = 4,0 мм, Ь2= 14,0 мм, Fo, = 28,0 мм2, т| = 1,49. Ме-
ханические характеристики материала отсека (алюминиевый сплав): сгт = 16,0 кГ/мм2,
Е = 7,0-103 кГ/мм2.
Расчет на местную устойчивость. По формуле (38.1), принимая k =
= 0,15, подсчитываем напряжения для криволинейных, а по формуле (38.2) — для
прямолинейных участков гофра. При подсчете критических напряжений для прямолиней-
ных участков условную ширину прямолинейных участков, как было сказано, возьмем
несколько больше, а именно = 4,5 мм, Ь2 = 16 мм. Для этих размеров поперечных
сечений гофра получим: для цилиндрического участка сгкр^>сгт; для плоских участков
гофра окР1>ат-
(4i \2 / 0 3 \2
—— \ = 3,6-7-103 X (—1— | - 8,84 кГ/мм2.
Ь' / \ 6,0 I
°2 / \ /
Для цилиндрического и первого плоского участков принимаем
°крц = +Р1 = от = 16 *Г/мм2.
При принятых размерах гофра и = гср0 = 4-1=4 мм
I
V= ~F~r '
16,0.0,3-4-4,0+ 16,0-0,3-2-4,0 + 8,84-0,3-14,0-2
=----------------!1!— -------------------------= 12,2 кГ мм2,
15,6
где
Fr = XFi = hv 2^ = 0,3(4-40 + 2-4,0 + 2-14,0)= 15,6 мм2.
Для обшивки
/ ho \2 / 0.6 V
о'ип =3,6Е( —=3,6-7,0-10* ---------) =7,41 кГ/мм2.
кро \ b J < 35 J
Приведенное разрушающее напряжение и разрушающую осевую силу для всего
отсека находим из условия местной устойчивости:
nKPoFo+ aprFr 7,41-28,0+12,2-15,6
СТр= r0 + Fr 28,0+15,6 -9,1 кГ/мм2-,
NkP = ^p^T~ (Го + О) = 9,1 2Я'100° (28,0 + 15,6) = 71,4-103 кГ.
Г О и
Приведенные разрушающие напряжения в гофре и обшивке получились сравнительно
невысокие ввиду относительно большой длины прямолинейных участков гофра. Для
повышения разрушающих напряжений высота и шаг гофра должны быть меньше.
Расчет на общую устойчивость. Для гофра и обшивки, изображен-
ных на рис. 38.3,6, погонный момент инерции в осевом направлении равен J г// = 31,2 льи3,
толщина обшивки Ло=0,6 мм, площадь поперечного сечения шпангоута /+=106 мм2,
расстояние /=300 мм. Критическая сжимающая сила
332
Л'кр=1,2 лЕ
\
-----) = 158-Ю3 кГ.
300 /
Определим критическую силу для отсека, считая, что он состоит как бы из
отдельных стержней. При / = 35 мм, Jr —1,09-103 мм\ с учетом промежуточных шпан-
гоутов (/=300 мм), получим
Хкр — 2/1-
л2Е7г 2л-1000
-----— = 2
/2---35
л2-7,0-103-1,09-103
3002
= 300-103 кГ.
Величина силы Л^р является наименьшей, и ее следует считать предельной для дан-
ного отсека.
Проектировочный расчет. В проектировочном расчете бывают зада-
ны размеры отсека (радиус R, длина L), известна величина расчетной
эквивалентной осевой сжимающей силы Л^Кв и температура отсека.
Требуется определить толщину обшивки, геометрические размеры гоф-
ра, подобрать материал отсека. Механические характеристики материа-
лов и зависимость этих характеристик от температуры считаем извест-
ными. Последовательность расчета рассмотрим на примере.
Пусть заданы: R = 1000 мм, L = 900 мм, температура 20°С, Л^кв =
- 100-103 кГ.
Прежде чем начать расчет, необходимо выбрать материал гофриро-
ванного отсека. Выбор материала определяется требованиями мини-
мального веса отсека, технологичностью и т. д. Пусть в результате все-
стороннего анализа выбран материал с механическими характеристи-
ками от=16,0 кГ/мм2, E = 1,Q*\№ кГ/mm2. Затем выбираем шаг гофра.
При выборе шага необходимо по возможности использовать стандарт-
ные промышленные гофры, имеющиеся экспериментальные данные по
гофрам, принять во внимание технологию изготовления отсеков [103].
Существенным обстоятельством при проектировании гофрированного
отсека является выбор отношения шага отдельного гофра к его высоте
t/H (см. рис. 38.3, а, б). Это отношение зависит от длины гофрирован-
ного отсека. Если в отсеке часто установлены шпангоуты, то эта вели-
чина может быть больше, т. е. гофр более пологий. Если же отсек имеет
мало шпангоутов или не имеет их совсем, то значение t/H уменьшается.
Пусть выбран шаг гофра /=35 мм, высота его //=16 мм. Теперь
нужно определить толщину и геометрию гофра, толщину обшивки. Для
этого подсчитаем минимальную и максимальную приведенную толщи-
ну, считая гофрированный отсек гладкой цилиндрической оболочкой.
Тогда минимальная приведенная толщина будет определяться условием
прочности, а максимальная приведенная толщина — условием устойчи-
вости гладкого отсека с тем же радиусом R и длиной L. Реальная при-
веденная толщина отсека будет находиться между этими крайними
величинами.
Расчетная величина напряжений в отсеке зависит от конструктив-
ной схемы отсека. Если в отсеке много вырезов, люков, то величину
расчетного разрушающего напряжения, принятого в качестве первого
приближения, следует взять меньше, например о = (0,6ч-0,7)от. Если же
отсек не имеет вырезов, то напряжение в первом приближении можно
принять выше — о= (0,8-г-0,9)от.
333
В рассматриваемом случае минимальная приведенная толщина
Пусть в первом приближении oi = 0,8oT. Тогда приведенная толщина
отсека будет равна АПР1 = 1,25 Лщщ = 1,25 • 1,2 = 1,5 мм. Приведенную
толщину нужно разбить на толщину обшивки и толщину гофра. Можно*
сделать тонкую обшивку и «толстый» гофр или, наоборот, толщину об-
шивки взять больше толщины гофра. Эти варианты для некоторой вы-
бранной формы сечения гофра следует оценить по зависимостям
(38.1) — (38.10). Обычно толщину обшивки можно брать больше тол-
щины гофра, так как приведенные разрушающие напряжения в гофре
из-за наличия криволинейных и более коротких прямолинейных участ-
ков всегда выше, чем критические напряжения в обшивке.
В результате такого анализа пусть выбран гофр с размерами:
/ = 35 мм, /7=16 мм, г = 4 мм, bi = 4 мм, Ьг=14 мм. Толщину обшивки
примем fto = 0,8 мм, оставшаяся толщина /z = ftnpi—h0= 1,5—0,8 = 0,7мм.
Для данной геометрии гофра коэффициент развертки т]= 1,49, т. е. дли-
на развертки гофра в 1,49 раза больше его шага. Поэтому
, h 0,7 п
hr — — = —-— = 0,47 мм.
П 1,49
Подсчитаем приведенные разрушающие напряжения в гофре и крити-
ческие напряжения в обшивке. Для цилиндрического участка
<гк_ = 0,15£ =0,15-7-103-^->ат;
крц г 4
для первого прямолинейного участка
<тКр = 3,6£( ) = 3,6-7.103(-^-) >ог;
\ ь\ / \ 4,5 J
для второго прямолинейного участка
/ h \2 / 0 47 \2
оКР2=3,6Е(-М = 3,6-7-103( ) > сгт.
\ / \ А О /
2 . U
В расчетах принята условная ^ширина плоских участков Ь\ = 4,5 мм,.
Ь2 = 16 мм вместо соответственно = 4 мм и Ь2 — 14 мм.
Для всего гофра приведенные разрушающие напряжения ор.г — от =
= 16 кГ/мм2. Критические напряжения в обшивке
сткРо 3,6Е (-у-)2 = 3.6 • 7 • 103 (уу-)2 13,1 кГ/мм2.
Приведенное разрушающее напряжение для гофра с обшивкой и раз-
рушающая сжимающая сила по условию местной устойчивости соответст-
венно равны
„ _ Wo + gP.rfr_ 13,1.0,8 - 35+ 16.0,47.35.1,49= 125 г.
р Го + ^г 0,8 • 35 4-0,47 • 35 • 1,49
jV“p = Op — (Fo + Fr) = 12,5 2я • 1000 (28 4- 24,5) = 118 • 103 кГ.
334
Критическую силу из условия общей устойчивости отсека определим по
формуле (38.9). Для гофра с обшивкой Jr//= 49,0 лш3, йо = 0,8 мм. При-
мем, что в отсеке шпангоутов нет, т. е. L = I = 900 мм, = 0. Тогда
ЛГкр = 1,2л£ /J/io+ -yj = 1,2л-7-103 /49-0,8 = 165-103 кГ.
Отсек при заданной величине осевой сжимающей силы несущую способ-
ность не теряет, так как NkP > Л^кв, УУкр>Л£кв.
Если значения разрушающей силы по условию местной устойчивости
или значение критической силы отличаются от заданной величины
например, то следует сделать расчет во втором приближении,
приняв значение приведенной толщины, например йпр2 = l,5Amin. Повторив
все вычисления, получим значения сил 7VKp второго приближения. Сделав
затем третье приближение, можно по трем значениям построить завиги-
мость 7VKp = / (Лпр) и, приравняв 7VKp = УУэкв, найти необходимое значе-
ние /гпр. Это значение Лпр уточняют в поверочном расчете.
При проектировании отсека с продольным гофром следует иметь в
виду, что данная конструкция целесообразна, если на отсек действуют
осевые сжимающие нагрузки. Если же отсек подвергается действию
внешнего давления, то конструкция оболочек, подкрепленных продоль-
ным гофром, становится неэффективной. В подобном случае нагруже-
ния при действии небольшего внешнего давления можно оценить в
первом приближении прочность отсека, считая гофр многоопорной бал-
кой, несущей поперечную нагрузку. Опорами являются шпангоуты.
Погонная нагрузка определяется при этом как произведение внешнего
давления на шаг гофра.
Предложенная методика расчета гофрированного отсека от действия
осевых сжимающих сил может служить лишь первым приближением.
Это связано с тем, что конструкции гофрированных отсеков могут изго-
товляться с различной точностью, с различными производственными
отклонениями. Кроме того, полученные выше теоретические зависимости
для гофра также являются приближенными. Поэтому после расчетов
необходимо провести серию экспериментов на моделях.
Гофрированные отсеки из тонкого листового материала могут под-
вергаться в полете значительному аэродинамическому нагреву. Так как
между обшивкой и гофром обычно существует хороший контактный
теплообмен, то температура гофра близка к температуре обшивки.
Это позволяет в приближенных расчетах не учитывать температурные
напряжения, вызванные перепадом температуры между обшивкой и
гофром. Нагрев конструкции следует прежде всего учитывать в измене-
нии механических характеристик материала. В случае значительного
перепада температуры между обшивкой и гофром, можно опасаться
преждевременной потери местной устойчивости обшивки вследствие
температурных напряжений. Расчет температурных полей в гофрирован-
ных конструкциях с обшивкой осложняется известной неопределен-
ностью величин контактных тепловых сопротивлений в местах соедине-
ния обшивки и гофра. Поэтому в тех случаях, когда можно ожидать
значительных перепадов и температур в конструкции гофрированных
отсеков, желательно производить их испытания с имитацией нестацио-
нарного нагрева.
Кроме сжатия, гофрированный отсек нагружается усилием сдвига.
Для цилиндрического отсека усилие сдвига
S = -5- sin ф, (38.11)
TiR
где Q — перерезывающая сила;
335
R — радиус отсека;
Ф — угловая координата в плоскости поперечного сечения, отсчи-
тываемая от линии действия перерезывающей силы Q.
Максимальные усилия сдвига соответствуют точкам с угловой ко-
ординатой ф = ± —.
В полетных случаях нагружения отсека при действии максимальной
сжимающей силы влияние усилий сдвига обычно несущественно, и в
приближенных расчетах их можно не учитывать. Однако в других
расчетных случаях, в частности при транспортировке ракеты, влияние
сдвигающего усилия может оказаться значительным. В этих случаях
необходимо проверять устойчивость конструкции гофрированного отсе-
ка от действия перерезывающей силы Q. Наиболее опасна потеря общей
устойчивости от сдвига. Критическое усилие сдвига приближенно мож-
но определить по формуле [41]
(38.12)
где Л =
L — длина отсека;
Z—расстояние между шпангоутами;
— момент инерции сечения шпангоута с присоединенной обшивкой
на длине I.
При нагружении отсека перерезывающей силой по формуле (38.12)
получаются несколько заниженные значения критических усилий сдвига.
§ 39. ПЕРЕХОДНЫЕ И ДВИГАТЕЛЬНЫЕ ФЕРМЫ
На рис. 39.1 изображена схема переходного отсека. Отсек состоит
из двух кольцевых шпангоутов, соединенных с обшивкой каждой сту-
пени ракеты и симметрично расположенных стержневых элементов
фермы. С каждой из ступеней ракеты на отсек действуют нагрузки, ве-
личины которых берут из эпюр моментов Л4, нормальных N и перере-
зывающих Q сил соответствующего расчетного случая.
Фермы неподвижно закрепленных двигателей выполняют по такой
же схеме, что и переходные отсеки. Нагрузки на ферму крепления дви-
гателя определяют следующим образом. Осевая сила
Л/ = (Р-6Л)Т]Д, (39.1)'
где Р — тяга двигательной установки, бд— вес камеры двигателя и
агрегатов, прикрепленных к ферме, пх — осевая перегрузка, т]д— коэф-
фициент динамичности. Величина коэффициента динамичности опреде-
ляется в гл. III. Наибольшие значения коэффициента динамичности
соответствуют старту, переходному режиму, отсечке двигателя. При-
ближенно коэффициент динамичности для старта можно определить,
зная отношение t\— времени выхода двигателя на режим к Т — перио-
ду собственных колебаний системы двигатель—ферма. Для
величину т]д определяют [108] по формуле
». = • + -£- (39.2)
Перерезывающая сила и изгибающий момент для фермы двигателя равны
Q = СдП,, (39.3)
М = GRnyl, (39.4)
336
где пу — поперечная перегрузка, Z — расстояние от центра тяжести ка-
меры и агрегатов до узлов крепления камеры к ферме. Зависимости
(39.1)— (39.4) показывают, что ферма должна рассчитываться в основ-
ном в двух расчетных случаях: в случае максимального осевого усилия
(обычно соответствует запуску) и в случае максимальной поперечной
перегрузки.
Остановимся на особенностях расчетной схемы переходных отсеков
и ферм крепления двигателя. Основную роль в напряженном состоянии
стержней фермы играют продольные усилия. Моменты и перерезываю-
щие силы, возникающие в стержнях, являются второстепенными фак-
торами. При расчете считают, что стержни фермы соединены идеаль-
ными шаровыми шарнирами. Торцовые сечения фермы при деформации
принимают плоскими, т. е. считают, что узлы фермы, соединяющие ее
со шпангоутом, прикреплены к твердому телу и лежат в одной плоско-
сти. Вследствие жесткости обшивки напряжения изгиба шпангоутов
«из плоскости», как правило, невелики. Основную роль в напряженном
состоянии шпангоута играет изгиб его ib своей плоскости. Таким обра-
зом, при расчете переходной отсек рассматривают как ферму, шарнир-
но прикрепленную к твердому телу в сечениях соединения со шпангоу-
тами. Шпангоуты рассчитывают как плоские рамы, нагруженные в
узлах крепления стержней. Расчет подобных ферм применительно к
узлам крепления двигателей самолетов изложен в книгах [9, 91]. Ниже
рассматривается упрощенный способ расчета фермы переходного
отсека.
Расчет усилий в элементах фермы. Для определения усилий, дей-
ствующих на узел элемента фермы (см. рис. 39.1), воспользуемся
соотношениями для погонных осевых 7\ и касательных S сил в цилинд-
рическом сечении корпуса радиуса г:
'Г N , М Л
7\ =---------1------cos 6,
2лг яг2
(39.5)
S = sin е + sin 0. (39.6)
ЛГ ЯГ2 /
Здесь 0 — угловая координата в сечении, отсчитываемая от вертикаль-
ной оси. При п узлах фермы на торце отсека расстояние между ними
у меньшего диаметра t = 2iirln. Обозначив номер узла через i (узел,
совпадающий с вертикальной осью, имеет номер Z = 0, остальные Z =
= 1, 2, ..., п—1), получим угол между узлом и вертикальной осью
л t • л 2яг
6, = — i или 0,- =------
г п
22 Зак. 96
337
Используя последние соотношения и уравнения (39.5) и (39.6), куда
вместо 6 подставим 0Z, находим осевую Р{ и касательную Т{ составляю-
щие усилия на каждый i-тый узел меньшего диаметра фермы:
Р = _L (n + — cos — \
(39.7)
2 _ М R — г \ . 2лг v
Л = —( Q +----------— sin —.
п \ г I J п
Максимальное осевое усилие приходится на узел, расположенный на вер-
тикальной оси:
Лпах = — (N+ — Y (39.8)
п \ Г J
Наибольшее касательное усилие — у узла на горизонтальной оси
Лпах = -(<? + — (39.9)
п \ г I /
Раскладывая усилие Pi на два направления: радиальное и в плоскос-
ти элемента фермы, а затем последнее вместе с 7\— на стержни, получим
усилие в каждом стержне
P = Pi^r + Ti---------—. (39.10)
2R sin —
п
Здесь плюс соответствует стержню, у которого суммируются усилия от
осевой и касательной составляющих, а минус — соседнему стержню, где
происходит вычитание сил. Длина стержня L связана с размерами отсека
и числом узлов соотношением
f Г"
L = 1/ R2 + г2 + Z2 — 2Rr cos
Усилие в любом стержне фермы таким образом равно
г 2л z
sin----
п 1 /хт 1 2М 2ш* \ L , /лч _ М R~r\ L п
Р = — [ N Н------cos---- — ± ( Q 4-------------}-----------
п \ г п J 21 \ г I J R л
sin —
L п J
(39.11)
Для стержней, узлы которых совпадают с вертикальной и горизон-
тальной осями, усилия равны
а п 21 к г )
(39.12)
От соотношения между величинами внешних нагрузок зависит, ка-
кое из этих усилий оказывается расчетным для элемента фермы —
стержня. Определяющей нагрузкой здесь является осевая сжимающая
сила N.
Расчет стержня фермы. Как мы уже знаем, расчетное усилие в
стержне фермы (см. рис. 39.1) можно определить по уравнениям (39.12).
Задача теперь состоит в том, чтобы по усилию Р и длине L подобрать
сечение стержня.
338
Сечение сжатых стержневых элементов фермы подбирают из расче-
та на устойчивость. Усилие, соответствующее потере устойчивости
стержня постоянного сечения, определяется формулой Эйлера. Соот-
ветствующие напряжения в стержне трубчатого сечения с моментом
инерции / = и площадью F = 2nRh равны
<гкр = С^-Е(^-)2, (39.13)
где R и L — радиус и длина трубы. Коэффициент с учитывает жест-
кость опор (с=1,0—1,5). Это соотношение справедливо при напряже-
ниях о, меньших предела текучести от. Для напряжений, превышаю-
щих от, критические напряжения определяют по экспериментальным
кривым [9] или по приближенной зависимости
(39.14)
где
х = лу777.
С точки зрения лучшего использования материала в конструкции
выгодно подбирать сечение так, чтобы напряжения были большими.
При заданных L и Е большие напряжения по соотношению (39.13) со-
ответствуют большим размерам сечения и малым толщинам. Стержень
трубчатого сечения малой толщины уже становится оболочкой. Оказы-
ваются возможными формы потери устойчивости, характерные для
оболочек (ромбовидные вмятины, гофры). Потерю устойчивости такого
вида для элементов фермы называют местной в отличие от потери об-
щей устойчивости стержня. Осевые сжимающие напряжения, соответ-
ствующие потере местной устойчивости цилиндрической оболочки,
определяют по формуле
<гкр=*еА (39.15)
К
р
где k — коэффициент, величина которого зависит от отношения —. Вдаль-
h
нейшем будем считать его постоянным и равным 0,15.
Исследуем влияние усилия Р и длины L на величину напряжений и
геометрию стержня. Из условия равнопрочное™ выгодно подобрать
сечение так, чтобы напряжения, соответствующие потере общей устой-
чивости (39.13), и местные критические напряжения (39.15) были рав-
ны напряжениям, возникающим в стержне от заданного усилия Р:
6=^-
2nRh
(39.16)
Исключив из соотношений (39.13), (39.15), (39.16) R и й, получим
а = 0- й)'/з Е2/з (39.17)
Показателем весовой эффективности всякого силового элемента
является отношение о/у, где у — удельный вес материала. Для сжатой
трубчатой стойки
а / л \7з £2/з / Р \7з
Пользуясь этой зависимостью, можно сравнивать весовую эффектив-
ность различных материалов при работе конструкции в упругой обла-
22*
339
сти. Введем коэффициент, показывающий, во сколько раз сравнивае-
мый материал эффективнее по весу, например, алюминиевого сплава
(AI):
n = • (39.18)
В табл. 39.1 на основании данных книги [121] представлены значе-
ния этого коэффициента для некоторых материалов. Наиболее выгодным
материалом для сжатых стержней при работе материала в упругой облас-
ти оказывается Be, затем идут Mg, Al и т. д. Эта последовательность
справедлива для температуры Т = 20 °C. При температуре 200 — 300 °C и
выше эффективными становятся Be, Ti и сталь. При напряжениях, превы-
шающих <гт, критические напряжения для стержня окр от и тогда пока-
затель весовой эффективности материала п — ----. Преимущества и
(СГт)а1/Yai
здесь остаются за Be, Ti и сталью.
Таблица 39.1
.Материал Е • 10“3, кГ/мм* у, кГ/м* п
А1 7,2 2850 1
Mg 4,2 1700 1,17
Ti 12,0 4500 0,885
Be 31,0 1800 4,17
Сталь 21,0 7800 0,75
Вернемся к силовому расчету отсека. В точках крепления стержней
фермы к шпангоутам возникают радиальные и касательные составляющие
усилий. Радиальные составляющие осевого усилия равны
2
i
Рг( = —(Ш
п \
2М
г
7? COS-----Г
п
а касательные составляющие в i-той точке
2 М я —г \ 2ш
Л =— Q Т-------------------) sin------.
п \ г I J п
Эти усилия на шпангоуте уравновешиваются касательными силами, пе-
редаваемыми с соседних отсеков. Особенности расчета шпангоутов,
загруженных системой сосредоточенных усилий, рассмотрены в § 45.
§ 40. ОТСЕКИ, РАБОТАЮЩИЕ НА ВНЕШНЕЕ ДАВЛЕНИЕ
Работоспособность нагруженного внешним давлением отсека, как
правило, определяется его устойчивостью, причем потеря устойчивости
отсеков тонкостенных конструкций современных летательных аппаратов
обычно происходит в упругой области.
Работающие на внешнее давление тонкостенные отсеки констук-
тивно выполняются в трех основных вариантах: оболочки, подкреплен-
ные силовым набором (обычно шпангоутами); оболочки, подкреплен-
ные поперечной гофрировкой, и анизотропные оболочки типа стекло-
пластиковых. Во всех этих случаях в основу расчета может быть поло-
340
жена формула для верхнего критического давления ортотропной обо-
лочки, полученная с помощью полубезмоментной теории (см. § 16):
р = (П2 _ 1) + а* ..(п*1!Гв . (40.1)
кр ' ' R» Rn*(n2—1) V ’
где l и R — длина и радиус оболочки;
D и В — жесткость оболочки на изгиб в окружном направлении и
на растяжение в осевом направлении;
п — число волн, образующихся в окружном направлении при
потере устойчивости и в каждом конкретном случае опре-
деляемое из условия минимума piKp.
Величина входящего в выражение (40.1) коэффициента а зависит
от способа закрепления краев оболочки. Так, если оба края оболочки
свободно оперты или соединены со шпангоутами, жесткими только в
своей плоскости, то а=1; если оба края оболочки жестко закреплены
относительно радиальных и осевых смещений, то а=1,5; для оболочки
с одним жестко заделанным краем, а другим свободным а = 0,6.
Для практических расчетов, особенно проектировочных, выражение
(40.1) неудобно тем, что число волн п каждый раз нужно находить под-
бором. Но, как уже отмечалось в § 16, для оболочек средней длины в
4 .----------------------------------------------------
данном случае при выполнении условия l/R<Z0,2ay BR2lD зависимость
(40.1) можно упростить и привести к формуле, аналогичной формуле
П. Ф. Папковича:
«°-2>
причем число окружных волн,
оценивается зависимостью
образующихся при потере устойчивости,
itR -.V 3BR2
а----- 1/ -----
I V D
Для достаточно длинных оболочек при l!R> 1,5а /BR2/D вторым слагае-
мым в выражении (40.1) можно пренебречь. Тогда при п = 2
__ 3D
^!кр &
«1кР
(40.2')
(40.3)
Ниже будут рассмотрены особенности расчета на устойчивость от-
секов, выполненных в различных конструктивных вариантах.
Расчет оболочки, подкрепленной шпангоутами. На рис. 40.1, а, по-
казана схема работающей на внешнее давление тонкостенной оболочки
с поперечным силовым набором (шпангоутами). Такая оболочка в за-
висимости от соотношения жесткостей шпангоутов и обшивки может
терять устойчивость по двум качественно различным формам. При отно-
сительно малой жесткости шпангоутов наименьшему значению верхнего
критического давления соответствует форма /; при большой жесткости
шпангоутов, наоборот, меньшее значение верхнего критического давле-
ния дает форма 2. Первую форму потери устойчивости иногда называ-
ют потерей общей устойчивости подкрепленной оболочки, а вторую —
потерей местной устойчивости, или потерей устойчивости обшивки меж-
ду подкреплениями.
Выражения «общая» и «местная» здесь довольно условны, посколь-
ку подкрепленная оболочка является единой упругой системой, и вся-
кая ее потеря устойчивости является, строго говоря, общей. Но эти
выражения удобны, так как они хорошо отражают качественную сто-
рону задачи: при потере местной устойчивости шпангоуты практически
сохраняют круговую форму, а деформируется, в основном, обшивка, а
при потере общей устойчивости шпангоуты деформируются вместе с
обшивкой.
341
На рис. 40.1,6 показан типичный график зависимости верхнего кри-
тического давления подкрепленной оболочки от жесткости на изгиб
шпангоутов EJ\ через Е7Э обозначено такое значение жесткости шпан-
гоутов, когда верхнее критическое давление, соответствующее потере
общей устойчивости, равно верхнему критическому давлению, соответ-
ствующему потере местной устойчивости обшивки между подкрепле-
ниями. При величине жесткости шпангоутов, меньшей EJ^, происходит
потеря общей устойчивости по форме /, и увеличение жесткости шпан-
гоутов приводит к росту значения критического давления. При величине
Жесткости шпангоутов, большей £7Э, происходит потеря местной устой-
чивости обшивки между подкреплениями по форме 2, и дальнейшее
увеличение изгибной жесткости шпангоутов никак не отражается на
величине критического давления. Если по условиям эксплуатации отсе-
ка нельзя допускать потерю местной устойчивости обшивки между под-
креплениями, то, очевидно, рациональной следует считать жесткость
шпангоута, примерно равную Е/э.
Поскольку реальные оболочки теряют устойчивость хлопком (см.
§ 16) при рХл<^Р1кр, то, строго говоря, рациональной была бы такая
жесткость шпангоутов, при которой совпадали бы давления хлопка при
потере общей и местной устойчивости. Но так как величина давления
хлопка зависит от трудно контролируемых начальных неправильностей,
то при проектировочных расчетах удобнее величину эффективной жест-
кости шпангоутов определять через верхнее критическое давление.
Для расчета на общую устойчивость подкрепленной шпангоутами
оболочки в формуле (40.1) следует принять
В = Eh, D = K
Eh?
12(1-Р) ’
В случае оболочки, подкрепленной равноотстоящими шпангоутами одина-
ковой жесткости,
= 1 + 12 -1 ~ |Г~ , (40.4)
I Eh* v
где h — толщина обшивки;
EJ — жесткость на изгиб шпангоута;
I — общая длина оболочки;
N—число промежуточных шпангоутов (не считая торцовых).
Если же жесткости шпангоутов и расстояния между ними хотя и
различны, но величины их одного порядка, то
К - 1 + 2 12(^J r2) У EJj sin2 (40.4')
j=i
312
Здесь Xj — расстояние от левого торца оболочки до /-того шпангоута,
имеющего изгибную жесткость EJj.
Значение нижнего критического давления потери общей устойчиво-
сти подкрепленной оболочки обычно незначительно отличается от зна-
чения верхнего критического давления. Поэтому в расчетах на общую
УСТОЙЧИВОСТЬ МОЖНО ПРИНЯТЬ Рхл~Р1кр-
Обшивку между подкреплениями можно рассчитывать на устойчи-
вость как гладкую шарнирно опертую оболочку длиной Z/(^+1) и тол-
щиной h (см. § 16).
Последовательность расчета подкрепленного шпангоутами отсека,
работающего на внешнее давление, покажем на конкретном примере.
Пусть задано /=1200 мм; /? = 600 мм; р = 6 кГ/см2; механические ха-
рактеристики материала: Е = 7,2-103 кГ/мм2, ц = 0,3; от = 26 кГ/мм2; по
торцам отсек оперт на жесткие в своей плоскости ребра. Требуется по-
добрать рациональную силовую схему подкрепленного отсека, т. е.
толщину обшивки, число и жесткость промежуточных шпангоутов.
Из условия прочности обшивка не может быть тоньше Лтт=р/?/ат~
1,39 мм. Последовательность расчета такова.
1. Задаемся толщиной обшивки /i^/imin, например, берем Л1 = 4 мм.
2. По формуле П. Ф. Папковича (16.23) определяем максимально
допустимое расстояние между шпангоутами
Ux = 0,92/?— (= 0,92.600--’---1 °- (Д-У/г = 238 мм
max Р \ R J 6 • 10-* \ 600 /
и, округляя в большую сторону, находим число шпангоутов и длину
пролета между ними:
Л' > (///max) - 1 = (1200/238) - 1 ^5;
= //(Д/ + 1) = 1200/(5 + 1) = 200 мм.
3. Обшивку между шпангоутами проверяем на возможность потери
устойчивости хлопком, причем, если экспериментальные данные отсутст-
вуют, берем рхл = р2кр = т2р1кр, где коэффициент v2 определяем по вели-
чине 0, из графика на рис. 16.2. Если окажется, что рхл<Р» то число
шпангоутов необходимо увеличить. В нашем случае 0 = 0,174 и v2 = 0,85,
рхл-г2.0,92£^+Д(А^ =
= 0,85 • 0,92 • 7,2 • 103 • 102 600(5+1) Р = 6,1 кГ/см*.
1200 \ 600 /
4. Жесткость шпангоутов определяем, приравнивая величины крити-
ческих давлений местной и общей потери устойчивости:
, л/? Г Е/i3/?-3 Т/д Г Eh ТЛ А лЯ [ „ Eh3 Я"3 "|3/* Г Eh Т *
/i L 312(1—И2) J L KJ /i(/V+l)L 3-12(1—h2)J L Я J
откуда Л = (N + I)4/» = (5 + I)4/’ - 11
и
j К— 1 h*1 = (И — 1) 43 - 1200
“ N+1 12(1 —р.2) “ (5+1) 12(1— 0,З2)
По найденной жесткости шпангоута следует подобрать его профиль.
Выполнив такой расчет для обшивок различных толщин, можно вы-
брать наиболее подходящий вариант в технологическом, конструктив-
343
ном и весовом отношениях. Следует отметить, что некоторый выигрыш
в весе можно получить, если использовать шпангоуты различной жест-
кости [5], чередуя более жесткие с менее жесткими (рис. 40.2).
Рис. 40.2
Рис. 40.3
Расчет оболочки, подкрепленной поперечным гофром. При неболь-
ших значениях внешнего давления минимальная толщина обшивки,
определяемая из условия прочности, оказывается малой, но зато из
условия устойчивости обшивку приходится подкреплять весьма боль-
шим числом шпангоутов. Тогда в некоторых случаях оказывается целе-
сообразно подкреплять оболочку не отдельными шпангоутами, а сплош-
ным гофром (рис. 40.3). Проиллюстрировать это можно следующим
оценочным расчетом. Пусть заданы габаритные размеры отсека I и /?,
величина внешнего расчетного давления р, значение коэффициента а,
определяемое из граничных условий, модуль упругости материала Е и
предел текучести от. Минимально допустимая из условия прочности
толщина обшивки, очевидно, равна hm-m = pR/вт- Тогда, используя фор-
мулу П. Ф. Папковича (16.23), при этом значении толщины обшивки
можно найти максимально допустимое из условий устойчивости рас-
стояние между шпангоутами
- тах . = 0,92а — (_^min_V/2 = 0,92 — (—\'2.
R Р \ R / (Тт\(гт7
Если окажется, что /тах^/> то, очевидно, оболочку вообще не надо
подкреплять шпангоутами. Если 1/20<:/тах//? .<;///?, то целесообразно
подкрепить оболочку соответствующим числом шпангоутов (как отме-
чалось выше, при этом следует просмотреть несколько вариантов с раз-
личными толщинами обшивки). Если, наконец, окажется, что
<1/20, т. е. если требуемое число шпангоутов превышает 20 на длине
оболочки, равной одному радиусу, то целесообразно подкреплять об-
шивку сплошным гофром [106]. Для металлических оболочек средней
длины с закрепленными торцами численные расчеты, грубо говоря, при-
водят к таким результатам: при р~ 100 кГ1см2 целесообразно приме-
нять гладкие неподкрепленные оболочки, при р~10 кГ1см2— подкреп-
лять оболочку шпангоутами, а при р~\ кГ/см2— сплошным (поперечным
гофром. Естественно, что эти рекомендации не являются абсолютными
и окончательный выбор силовой схемы работающего на внешнее дав-
ление отсека в каждом случае должен производиться с учетом конкрет-
ных конструктивных и технологических условий.
344
(40.5)
(40.6)
На общую устойчивость подкрепленный поперечным гофром отсек
тоже можно рассчитывать по формуле (40.1), приняв в ней
B = Ehn, D = E-r~,
° t
где h0 — толщина цилиндрической обшивки (см. рис. 40.3);
t — шаг гофра;
/г — момент инерции одного гофра с учетом обшивки относительно
оси I—I.
Величина внешнего критического давления оболочки с поперечным
гофром обычно незначительно отличается от величины верхнего крити-
ческого давления, определяемого формулой (40.1). Поэтому в расчетах:
МОЖНО ПРИНЯТЬ Рхл~Р1кр-
Кроме расчета гофрированного отсека на общую устойчивость, не-
обходимо производить расчет гофра и обшивки на местную устойчи-
вость аналогично тому, как это делалось для сжатой в осевом направ-
лении оболочки (см. § 38). Если гофр и обшивка имеют одинаковые
модули упругости (обычно их выполняют из одного и того же материа-
ла), то среднее окружное сжимающее напряжение в гофре и обшивке
можно подсчитать по формуле
pR ,
Ло + т]Лг
где г] — отношение длины развертки гофра к шагу гофра (величина q
обычно меняется в пределах 1,2—2,0). Подсчитанное по формуле (40.6)
значение сжимающего напряжения следует сравнить с критическими
значениями напряжений! гофра и обшивки из условия потери местной
устойчивости, найденными по формулам (38.1) — (38.6).
В качестве примера поверочного расчета определим критическое
давление из условий потери общей и местной устойчивости для отсека
с геометрией гофра, как на рис. 38.3,6. Механические характеристики
материала обшивки и гофра: Е = 7,0-103 кГ/мм2; от=16,0 кГ/мм2. Раз-
меры отсека R= 1000 мм; 1= 1000 мм.
Воспользуемся числовыми данными примеров, помещенных в § 38:
Jr/t =-31,2 мм3; h0 = 0,6 мм; hr = 0,3 мм; т] = 1,49.
Тогда формула (40.1) принимает вид (считаем а = 1)
р = (п2 — 1) -£- А. + а4 (nR/l^Eho . =
KlhP v ’ R? t 7?n4(n2—1)
_ , 2 _ 7,0 • 103 • 102 31 g j (л • 1000/1000)4 • 7,0 • 103 102 0,6 _
_ Л ' (1000)3 ’ + 1000л4 (n2 — 1) ~
= [(/I2 — 1)0,0218 H- 4,1 • 104/n4 (n2 — 1)] кГ/см2.
Таблица 40.1
7,0 • 103 • IO2
п 3 4 5 6 7 8
D 02-D — 0,174 0,326 0,524 0,762 1,04 1,38
/ л/? \4 В V / ) Rn*{n1-l) 63,2 10,7 2,76 0,908 0,362 0,160
Р1кр. кГ/см2 64,4 11,0 3,28 1,67 1,40 1,54
345
Задаваясь последовательно несколькими значениями числа волн п,
можно подсчитать соответствующие величины р1кр. Результаты такого
подсчета приведены в табл. 40.1 (на стр. 345). Наименьшее значение
критического давления получилось при п=7. Это значение р1кр=
= 1,40 кГ/см2 и будет верхним критическим давлением потери общей
устойчивости гофрированного отсека.
Поскольку в рассматриваемом случае
l/R = 1 < 0,2а V £/?*/£> =0,2-1 У(ЕЬа)^2/Е (Jr/t) =
= 0,2 Vh0R2/(Jr/t) = 0,2 уЛ),6 (1000)2/31,2 = 2,34,
то можно было для расчета воспользоваться и упрощенными зависимостя-
ми (40.2). Тогда
4 л/? ( Е Jr УЛ j Eha \'Л
Р1кр I \ 3R3 t ) \ R /
А л - 1000 / 7,0 - 103 • 10» 01 о\’/4/7,0- 103 • 102 • 0,6 УЛ ... г,
= 4-----------1 —--------------31,2 —---------------— =1,41 K.1ICM-.
1000 к 3(1000)3 у юоо /
1000
Как видно из приведенных результатов, разница в значениях /?1Кр
при расчете по формуле (40.1) и по упрощенным зависимостям (40.2)
в данном случае оказывается практически несущественной.
Для расчета гофра на местную устойчивость можно воспользовать-
ся результатами примера § 38. Поскольку для такого же профиля гоф-
ра там было найдено ор=9,1 кГ1мм2, то из формулы (40.6)
= 9д . юг 0,64- 1,49 - 0.3 = 0 955 кГ1смЪ'
Икр ₽ R 1000
За окончательное значение критического давления следует, есте-
ственно, взять наименьшее из двух полученных, т. е. Р1кр = Р11кР =
= 0,955 кГ/см2. При этом оказывается, что прочностные характеристики
материала используются далеко не полностью: окружные напряжения в
рассматриваемом гофрированном отсеке равны всего лишь примерно
половине предела текучести материала. Большое различие между най-
денными значениями критического давления из условий общей и местной
устойчивости показывает, что конструкция отсека нерациональна; ее
можно улучшить, взяв, например, более мелкий гофр. Тогда критические
напряжения из условия местной устойчивости увеличатся, а из условия
общей устойчивости снизятся. В результате отсек сможет выдержать
большее внешнее давление.
Проектировочный расчет гофрированного отсека состоит из серии
приведенных выше поверочных расчетов, причем с точки зрения веса
оптимальным будет тот вариант, при котором величина критического
окружного напряжения равна пределу текучести материала. Практиче-
ски удается достичь значения оКр= (0,8-=-0,9)от.
Расчет ортотропных стеклопластиковых оболочек. Одной из отличи-
тельных особенностей стеклопластиковых оболочек, изготовленных спо-
собом намотки ткани или нити, является весьма малая величина жест-
кости на сдвиг по сравнению с жесткостью на растяжение-сжатие в
окружном и осевом направлениях. Но выражение (40.1) было получено
на основе полубезмоментной теории оболочек, в которой угол сдвига
вообще считается равным нулю (см. § 16); другими словами, жесткость
на сдвиг принята равной бесконечности. Поэтому можно ожидать, что
для случая стеклопластиковых оболочек с малой жесткостью на сдвиг
из выражения (40.1) будут получаться завышенные результаты.
346
В одной из последних капитальных работ В. 3. Власова [26] был
предложен вариант полубезмоментной теории с учетом деформаций
сдвига. Им можно воспользоваться для определения верхнего крити-
ческого давления ортотропной стеклопластиковой оболочки. Не оста-
навливаясь подробно на самом решении, полностью аналогичном ре-
шению, изложенному в § 16, приведем окончательные результаты. Для
оболочки, опертой по обоим краям, вместо зависимости (16.33) полу-
чим
Р1кр —
-1) D
/?3
/ _______________а4#!________________
I I ) Г / ал/? \2 Bi
4 /?п4(п*-1) V-
| У til J ^12
(40.7)
где B\ = Exh, B[2=Gl2h (см. § 14). В формуле (36.7) коэффициент а= 1;
для других граничных условий значения коэффициента а можно при-
ближенно брать такими же, как и для случая полубезмоментной обо-
лочки без учета угла сдвига (см. § 16).
Как показывают расчеты, для длинных оболочек, теряющих устой-
чивость по малому числу волн, учет деформаций сдвига несуществен.
Но для коротких оболочек учет этих деформаций дает заметный эффект.
ГЛАВА VIII
РАСЧЕТ ГОЛОВНОЙ ЧАСТИ РАКЕТЫ
§ 41. НАГРУЗКИ И ВНЕШНИЕ ФОРМЫ
По своему характеру нагрузки, действующие на головную часть и
корпус ракеты в целом, аналогичны (см. § 28). Нагрузки, действующие
на головную часть, можно разделить на наземные и полетные.
Наземные нагрузки обусловлены наземной эксплуатацией ракеты.
Головная часть баллистической ракеты дальнего действия (БРДД)
транспортируется отдельно [95] и подвергается тем же нагрузкам, что
и корпус ракеты при транспортировке. После стыковки с носителем при
совместной транспортировке, подъеме и стоянке на головную часть ра-
кеты действуют поперечные и осевые нагрузки. Стыковые узлы между
головной частью ракеты и носителем при наземной эксплуатации на-
гружаются растягивающими усилиями от изгибающего момента и осе-
вой силы.
К полетным относятся нагрузки, действующие на активном уча-
стке траектории и на участке входа в плотные слои атмосферы. На
активном участке траектории стык головной части ракеты с носителем
нагружен изгибающим моментом и осевой сжимающей силой, равной
сумме лобового аэродинамического сопротивления и инерционной на-
грузки. Наиболее опасные случаи нагружения стыка соответствуют
максимальному скоростному напору и максимальным осевым перегруз-
кам. Величины нагрузок в этих случаях определяют из расчета ракеты
в целом (см. § 30). При действии максимальных осевых перегрузок
хвостовой отсек головной части нагружен максимальной осевой сжима-
ющей силой.
Определение максимальной перегрузки лХтах. Определяющими, с
точки зрения расчета на прочность конструкции головной части ракеты,
являются нагрузки, действующие на участке входа в плотные слои
атмосферы. В основе расчета нагрузок и температур на этом участке
лежит расчет траектории движения головной части. Параметры траек-
тории определяют путем численного интегрирования уравнений движе-
ния при известных величинах аэродинамических коэффициентов. Целе-
сообразно необходимые данные брать из аэродинамических и балли-
стических расчетов. Однако это не всегда возможно. Ниже излагается
метод определения осевых и поперечных нагрузок, величины которых
могут рассматриваться как первое приближение.
Основной внешней силой, действующей на головную часть ракеты,
является сила аэродинамического сопротивления. Без учета силы тяже-
сти, что дает небольшую погрешность [71], уравнение движения в на-
правлении вектора скорости для головной части ракеты с площадью
миделя S будет
>4=-^- (4L1>
Это уравнение точно проинтегрировать не удается, так как скорост-
ной напор q, коэффициент лобового сопротивления сх и масса головной
348
части ракеты меняются по времени. Проинтегрировать аналити-
g
чески это выражение можно лишь при следующих допущениях.
Для гиперзвуковых скоростей можно принять cx = const [50]. Вес
головной части ракеты меняется незначительно, и его также можно
считать постоянным. Наиболее серьезное допущение касается плотности
воздуха. Для определения нагрузок можно представить зависимость
для плотности в виде [71]
р=рое-^> (41.2)
где р0 — плотность воздуха на уровне моря;
Р — коэффициент;
Н —высота полета;
Н = HQ— s sin 60;
Но — высота, соответствующая началу интегрирования;
s — длина пути, отсчитываемая от начала интегрирования;
60 — начальный угол входа головной части в атмосферу.
При интегрировании принимаем 0o = const, т. е. считаем траекторию
участка входа в атмосферу прямолинейной. Подставим выражения для
плотности р и высоты Н в уравнение (41.1); получим
— = Г &е~»н, (41.3)
dt х 2Ры
где рм = Gr.q/S — нагрузка на мидель головной части. После интегриро-
вания получим
v = v0 ехр Г—сх--------е~(41.4)
0 L 20рм sin 0о J’
где v0— начальная скорость входа головной части в плотные слои
атмосферы при H = HOt когда 10.
Значение максимальной перегрузки в направлении вектора скорости
Получилось, что максимальная перегрузка не зависит от сх, рм (т. е. от
формы головной части) и //, а зависит только от Vo и sin 0О. Если в
левую часть уравнения (41.1) подставить значение перегрузки, а в пра-
вую— значение нагрузки на мидель головной части ракеты, то получим
выражение
пх = -~Я- (41.6)
Рм
В некоторый момент времени полета ’справедливо равенство пх =
= пХтж- Тогда из формулы (41.6) следует, что величины сх и рм опре-
деляют только величину максимального скоростного напора. Для го-
ловных частей с малым рм и большим сх при равных значениях v0 и
0о максимальное значение перегрузки будет при малых скоростных
напорах, и наоборот. Головные части с одинаковыми vQ и 0О испыты-
вают одну и ту же максимальную перегрузку, но на разных высотах.
Значение максимальной перегрузки можно получить как функцию
дальности полета L. Как известно [95], угол наклона вектора скорости
в конце активного участка полета (участок ОА) 0К примерно равен
углу наклона вектора скорости 0О при входе в плотные слои атмосферы
349
(участок ВС) (рис. 41.1). При оптимальном выборе параметров траек-
тории из условия максимальной эллиптической дальности
где R — радиус Земли.
Путем несложных преобразований можно получить зависимость скоро-
сти ик от дальности полета L:
— = 1/ 2 —in(L/2/?) , (41.8)
V 1 + sin (L/2/?) 7
где Vi — первая космическая скорость при /7 = 0.
Для значения 0 = 0,15-10~3 1/м в предположении, что Оо = Ок и
по формулам (41.5), (41.7), (41.8) можно получить зависимость
максимальной перегрузки от дальности полета.
Таким образом, при заданной дальности полета определяется вели-
чина максимальной лобо-
вой перегрузки, а по извест-
ному весу головной части
ракеты — максимальная ве-
личина силы лобового со-
противления X. Для голов-
ной части ракеты при нуле-
вом угле атаки выполняет-
ся равенство
Рис. 41.1
X --- X-t - С г, чП'Х -- cx,QS,
1 4 max
(41.9)
где Х\— сила лобового сопротивления в связанной системе координат
(§28).
Отсюда по известным значениям cXi и S определяется скоростной на-
пор 7, соответствующий моменту достижения nVmax:
Определение внешнего аэродинамического давления и внутренних
осевых усилий. Если известны коэффициенты cXl всей головной части
ракеты и отдельных ее элементов, то внешнее аэродинамиче-
ское давление определяется просто. По аналогии с распределе-
нием поперечных сил (см. § 28) силу аэродинамического сопротивления
X. раскладывают на отдельные составляющие, которые в дальнейшем
заменяют распределенными поверхностными силами.
Если коэффициенты cXi неизвестны, то внешнее аэродинамическое
давление можно приближенно определить по заданной геометрии голов-
ной части. Полная аэродинамическая сила лобового сопротивления,
действующая на головную часть при нулевом угле атаки,
Х1 = cXtqS =
где и St — коэффициенты лобового сопротивления и проекции площади
поверхности отдельных составляющих головной части на] плоскость,
перпендикулярную к оси ракеты xt (см. § 28). Отсюда следует, что
(41Л0)
350
а сила, приходящаяся на отдельный элемент головной части,
c^st
= (41.11)
S
Форма головной части ракеты изображена на рис. 41.2, а, где гСф —
радиус сферического носка, dH— диаметр сопряжения сферического
носка с конусом, у0 — угол сопряжения, рК1, рК1—углы образующей
соответственно переднего и заднего усеченного конусов с продольной
осью головной части, dj, d2— диа-
метры по задним торцам, /К1,
/К1 — длины усеченных конусов;
ZH — длина носка, /ц — длина ци-
линдрической части, I — длина го-
ловной части.
На рис. 41.2,6 показан вари-
ант неплавного сопряжения сфе-
рического носка с передним ко-
нусом.
При определении нагрузок на
головную часть ракеты можно не
учитывать сопротивление трения
и донное сопротивление. Для
формы головной части, изобра-
женной на рис. 41.2,6/, согласно
изложенному выше
Рис. 41.2
Ху = хГ + х?’ + Х(2),
• где Х|Н) — лобовое сопротивление носка;
Xi0, Х(2) — лобовое сопротивление соответственно переднего и заднего усе-
ченного конусов.
Лобовое сопротивление цилиндрической части незначительно, и при
определении нагрузок его можно не учитывать.
При больших числах А1, согласно работе [50], для носка в форме
сферического сегмента и конуса можно принять следующие зависимо-
сти для коэффициентов лобового сопротивления:
c(;)=2sln2y0fl-4-sin2y0\ Сх,=2р2, (41.12)
1 \ 2 /
где ₽к —угол в радианах.
В случае не плавного сопряжения носка с передней частью конуса
(см. рис. 41.2, 6)
С(Н) _ С(Н) _ [с(н) — С(н) ] г
Xl хпл хпл хсф
2^сф
где с(н) —коэффициент лобового сопротивления плоского носка, а —
то же сферического носка. В расчетах нагрузок можно принять =
лпл
= 1,83, = 1,0.
хсф
Внутренние осевые усилия по длине головной части ракеты
определяют так же, как и для всей ракеты без наполнения (см. § 30),
но длину каждого участка здесь берут равной 0,14-0,3 м. Характер рас-
пределения внутренних усилий зависит от распределения аэродинами-
ческих А^аэр и инерционных А/ин сил по длине.
351
Пример, Определим внешнее аэродинамическое давление на элементы поверхности
головной части, изображенной на рис. 41.2, а. Пусть площадь миделя сечения 3 =
= ~ ~ = 1,0 м2. Площади проекций поверхности носка SH, переднего и заднего усе-
ченного конусов Sj и 32 на плоскость, перпендикулярную к оси xlt будут равны:
nJ?
SH = 0,023 лг2; поскольку J2=0,6Ji, = ------ — Sn = 0,36-1,0 — 0,023 - 0,337 м2;
4
S2 = ~Y~ = -~- = 1,0 — 0,36 = 0,64 м2; уо = 65°; РК1 = 25° (0,436 рад);
РК1 = 34°20' (0,598 рад).
Носок сопрягается плавно, так как у0 + Рк =65-^ 25 = 90°. По формулам (41.12) нахо-
дим:
= sin2 Yo(1 — ~ sin2 у0^ = 2 sin2 65° Г1 — — sin2 65° = 0,966;
41} = 2рз = 2-0,4362 = 0,38; с<2) = 2р2 = 2-0,5982 = 0,715.
Полный коэффициент лобового сопротивления будет
с = У с^ --= 0,966 0,023 4-0,38 0,337 4-0,715 0,64 = 0,608.
xi X1 S
Величину полного аэродинамического сопротивления определим по формуле (41.9),
считая, что вес известен и дальность полета задана. Пусть для головной части ракеты
вес Gr ч = 1000 кГ, дальность полета £= 10 000 км. Тогда по формулам (41.7) и (41.8)
определяем 0к и ик.
По формуле (41.5), считая Р = 0,15-Ю-3 1/лг, найдем максимальную перегрузку
и = 55,6. Сила лобового сопротивления Х1 = 1000-55,6 = 55,6-103 кГ. Эту силу рас-
max
пределяем по элементам поверхности головной части пропорционально произведению коэф-
фициента лобового сопротивления на площадь Si по формуле (41.11). Для носка и
конусов
4">sh
Х<н) =
0,966-0,023
= 55 600------------= 2030 кГ,
0,608-1,0
... cx!si 0,38-0,337
X |) = Х1 - =55600 ’ о ’ = 11,7-Ю3 кГ,
1 cxS 0,608-1,0
,,, 42?s2 0,715-0,64
X 2) = %!---L-- = 55 600 - ’ = 41,9 -103 кГ.
1 crS 0,608 1,0
•*1
Сумма этих трех сил равна = 55,63-103 кГ, т. е. с точностью до третьего знака
величине силы Хх.
Полученные силы аэродинамического лобового сопротивления следует теперь рас-
пределить по поверхности элементов головной части. По образующей сферического
носка в меридиональной плоскости давление меняется по зависимости [50] рн = 2^ созу»
где у — Угол в плоскости меридиана. При у = 0 (в вершине носка) рн = 2д. Величину
скоростного напора можно определять по формуле
Xi
55 600
0,608-1,0
= 91,4-103 кГ!м2.
В этом случае рн = 2-91 400 = 182,8-103 кГ/м2, или 18,3 кГ)см2.
Если теперь принять [50], что давление по образующей конуса распределено по-
стоянно, то его величину можно определить, разделив полученные величины сил лобо-
вого сопротивления на соответствующие площади. Тогда
-Xi" 11 700
р = = —— = 34,7- Ю3 (3,47
и,оо/
Х(2) 41900
р =—!— = —— = 65,1-10’ кГ/ж3 (6,51 кГ1с^).
о2 и,04
352
На цилиндрической поверхности аэродинамическое давление в запас прочности можно
принять в первом приближении равным давлению на передний конус.
Таким образом все внешние силы, действующие на головную часть при нулевом угле
атаки, определены. Строим эпюру осевых сил по длине головной части. Считаем, что вес
головной части условно сосредоточен в двух точках в конце носового и начале хвостового
усеченного конусов и равен G1 = G2 = 500 кГ (рис. 41.3, а). Тогда на каждый груз будет
^г. ч^*тах
действовать инерционная сила --------- тах = 500-55,6 = 27,8-103 кГ. Все осевые аэро-
динамические силы уравновешены этими двумя
силами. На рис. 41.3, б построены эпюры осе-
вых СИЛ #ин, Л^аэр И Nx = Nw + ^аэр- Дл*
более точного построения эпюры осевых сил не-
обходимо вес головной части (считать распреде-
ленным по длине. Это относится к небольшим
грузам, весу теплозащитного покрытия, весу
конструкции.
Определение поперечных нагрузок.
Подъемная сила головной части возни-
кает при наличии угла атаки а вслед-
ствие перераспределения аэродинами-
ческих сил по окружности каждого
сечения. С наветренной стороны дав-
ление повышается, а с противополож-
ной— уменьшается. Поперечные аэро-
динамические силы уравновешиваются
инерционными силами поступательно-
го и вращательного движения. Дейст-
вие аэродинамических и инерционных
поперечных сил вызывает изгиб корпу-
са головной части.
Определим поперечные аэродина-
мические силы. В первом приближении
Рис. 41.3
для определения нагрузок учтем толь-
ко поперечные силы, возникающие на двух усеченных конусах. Для
всей головной части полная аэродинамическая поперечная сила равна
Yi — cyi4^t
(41.13)
где сУг — коэффициент поперечной аэродинамической силы;
q — скоростной напор;
S — площадь миделя головной части.
При малых углах атаки (см. § 28) можно представить коэффициент
сУ1 в виде линейной зависимости от угла атаки:
су. =
При гиперзвуковых скоростях полета (а эти скорости характерны для
головных частей) величина для конусов может быть принята [501 Рав‘
ной = 3. В этом случае поперечная сила на конусе равна
=3aqSlt
где — площадь проекции поверхности отдельных составляющих головной
части на плоскость, перпендикулярную к оси ракеты хг.
Для поверхности головной части, образованной системой усеченных
конусов, получим
у, = = 3aqS, (41.14)
где У*1’ — сила, создаваемая отдельным элементом поверхности;
S — площадь миделя.
23 Зак. 96
353
Для получения распределенной поперечной аэродинамической на-
грузки 7аЭр сосредоточенные аэродинамические силы У {° разносят про-
порционально текущему диаметру конусов. Тогда эпюра раэр для усе-
ченных конусов принимает форму
трапеции (рис. 41.4,6).
Для определения поперечных
сил, действующих на головную
часть ракеты, необходимо знать
величину угла атаки.
Угол атаки а складывается
из двух составляющих; ад обра-
зуется вследствие колебаний го-
ловной части ракеты при движе-
нии вдоль траектории, ав — от
действия порывов ветра.
Составляющую угла атаки ад
определяют из расчета траекто-
рий возмущенного движения го-
ловной части. Этот расчет доста-
точно сложен, так как параметры
траектории переменны. Сущест-
венными параметрами являются
начальный угол атаки и началь-
ная угловая скорость вращения
головной части. Величина их за-
висит от возмущений при отделе-
нии головной части от последней
ступени ракеты-носителя.
При наличии угла атаки зна-
чительно меняется величина аэ-
родинамического давления по
окружности поперечного сечения
головной части (рис. 41.5). Дав-
ление на коническую поверхность при малых углах атаки а можно опре-
делить для больших чисел М по зависимости
Рк = (₽К + а)г • (41.15)
Закон изменения давления по окружности поперечного сечения
можно принять в виде тригонометрического ряда
р = р0 + PiCOsq) + p2cos2cp, (41.16)
где угол ф отсчитывается от нижней точки окружности (см. рис. 41,5).
Коэффициенты ряда определяют приближенно, исходя из следующих
условий:
1. При ф=0 р = ртах» т- е- давлению, определяемому по формуле
(41.15) при а > 0.
2. При ф = р = ра=о, т. е. давлению, которое действует при нуле-
вом угле атаки.
3. При ф = л p==pmln, определяемому по формуле (41.15) при а<0,
причем pmIn >0.
Более точный метод определения давления по поперечному сечению
при обтекании конуса под ненулевым углом атаки можно найти в ра-
боте [50].
354
Для расчета поперечных нагрузок необходимо определить положе-
ние центра давления и центра масс по длине головной части. Коорди-
ната центра давления головной части
(41.17)
где — координаты точек приложения поперечных аэродинамических
сил. Положение центра масс головной части хт в общем случае опре-
деляют, как для всей ракеты
без наполнения.
Поступательная попереч-
ная перегрузка пу t для всей
головной части определяется,
как отношение внешней попе-
речной силы к ее весу: v
^, = 7—. (41.18)
Gr. ч
Поперечная перегрузка от вра-
щательного движения пВр ме-
няется линейно по длине голов-
ной части. Определим величи-
ну пВр. Вращающий момент от-
носительно центра масс голов-
ной части Рис. 41.5
Мг, =Л(ХТ —Хд).
(41.19)
Тогда угловое ускорение головной части с массовым моментом инерции
Л, будет
dP “ /21
, (Хт Хд) •
J zt
Величина поперечной перегрузки от вращательного движения для точ-
ки с координатой (см. § 28):
(i) = V1 (*т хд) (хт х1)
ВР Сг.ч
(41.20)
Полная поперечная перегрузка для этой точки равна сумме поступательной
и вращательной перегрузок
Массовый момент инерции /г, головной части ракеты определяется
как для всей ракеты.
Определение внутренних усилий при поперечном на-
гружении корпуса головной части начинается с распределения
инерционных сил по длине. Распределенные аэродинамические силы
считают известными (см. рис. 41.4). Определяют величины полных по-
перечных перегрузок по длине, находят величины инерционных попереч-
ных сил. Значение погонной нагрузки определяется по зависимости
9пог=?аэр—<7ин- Полученное значение погонной нагрузки дважды инте-
грируют. Первым интегрированием определяют перерезывающую силу,
23* 355
вторым — изгибающий момент по длине головной части. Перерезываю-
щая сила получается равной
а изгибающий момент
М = \Qdx =
где &Xi — размер каждого из i участков, на которые разбивают в рас-
чете головную часть ракеты по длине;
<7пог и Qi — средние значения погонной нагрузки и перерезывающий
силы на участке Дхг*.
В табл. 41.1 указан порядок определения величин для построения
эпюр Q и М.
Таблица 41.1
0 Л'1, м 0 0,1 0,2 0,3 2 Примечания
1 м
2 GL, кГ
3 (Х1 — Хт). М
4 Лвр
5 ПУ, 1
6 Qhh =
7 <7аэр»
8 ^пог;» Япог = ^аэр <7ин
9 Qi, кГ i Qi = 2 <?пог
10 &Mi=Qi&xi, кГм
11 М[, кГ-м Л1/ = V ДМ/ /=1
Пример. Определим внешние и внутренние силовые факторы при нагружении го-
ловной части поперечными аэродинамическими силами.
Пусть в результате аэродинамического и баллистического расчетов получен угол
атаки а = 4°, скоростной напор максимальный и равен q = 91,4-103 кГ/м2. Геометрия
головной части ясна из рис. 41.2, а. Условно, как и в предыдущем примере, примем, что
вес голозной части приложен поровну в двух точках с координатами = 0,333/, х(т2) =
Gr,4
= 0,8/ и равен в каждой точке Gr = G2 = —-— = 500 кГ. Считаем, что вся попереч-
ная сила образуется на двух усеченных конусах. Площади проекций поверхности каждого
конуса на плоскость, перпендикулярную к оси равны Si = 0,337 м2, S2 = 0,64 м2.
356
Для каждого конуса = 3aqSi = 3 -- 91400-0,337 = 6,44-103 кГ, аналогично
57,3
— 12,2-103 кГ. Полная поперечная сила равна их сумме + У(2) = 6440 +
+ 12 200 = 18 640+ 18,6-103 кГ. Координаты точек приложения этих сил х^ = 0,22/,
х^ = 0,9/, а координата центра давления
Хд~ S
0,337-0,22/+ 0,64-0,9/
0,337 + 0,64
= 0,664/.
Положение центра давления показано на рис. 41.4, а.
Затем находим положение центра масс головной части. На рис. 41.4 грузы прило-
жены в точках с координатами х^ = 0,333/, х(т2) = 0,8/, координата центра масс равна
0,4’ > + G.,42) 500•0,333/ + 500-0,8/
Gt + G2 ~ 500 + 500
Подсчитаем массовый момент инерции головной части для двух грузов на расстоянии
(х<2>-х<'>):
/2 = (х<т2) — х^)2 = 0,0545 .
1 4g g
Поперечная перегрузка по длине головной части
18 600
1000
Gr. qg
0,0545Gr „ l2g
(0,567/ — 0,664/) (0,567/ — %!)
= 18,6 p — 1,78^0,567 —+
Эпюра поперечной перегрузки п приведена на рис. 41.4, б.
Поперечная перегрузка в точке приложения первого груза с координатой х^^О^ЗЗ/
равна по этой зависимости = 10,8, для точки х(2) = 0,8/, п^2) == 26,4. Точка прило-
жения инерционных сил х^ равна
Gizi^’x'” 4- G2n*2)x^2) 500-10,8-0,333/ 4- 500-26,4-0,8/
хв =----------------------- =------------------!--------------- = 0,664/,
Л G.n^’ + G^2’ 500-10,8 + 500-26,4
XR хд» т- е- точка приложения равнодействующей инерционных сил совпадает с центром
давления. Следовательно, все вычисления сделаны правильно.
Теперь приложим по длине усеченных конусов головной части погонные усилия от
аэродинамических сил даэр и две сосредоточенные силы в точках приложения двух грузов
(см. рис. 41.4, а, б). В рассматриваемом примере инерционные погонные силы дин замене-
ны двумя сосредоточенными силами GinG) и G2n'2) (см. рис. 41.4, а). В случае если
учитывается непрерывное распределение масс по длине головной части, то прикладываем
Рин* Величина рин =- где — погонный вес головной части. Значения для рпог
дважды интегрируем и получаем величины Q и М. Эпюры Q и М показаны на рис. 41.6.
Определим величину аэродинамического давления по поперечному сечению усеченного
конуса головной части. Угол атаки a - 4°. Тогда для поперечного сечения переднего усе-
ченного конуса, для которого Рк =25°, получим по формуле (41.15) величины ртах,
Pa=0» Pmin*
2
= 46 800 кГ/м2 (4,68 кГ/см2)}
(25 J_ 4
' „ Q
о/ ,о
357
„ / 25 \2
ра=о = 2<?(₽к, ♦ 0)2 = 2-91 400 ( —— )
\ 0/,О /
= 34 700 кГ/м2 (3,47 кГ/см2);
Pmin = 2g (₽ - а)2 = 2-91 400 ( 23 4 ¥
\ О/,й /
= 24 600 кГ/м2 (2.46 кГ!см2).
Теперь, используя условия для определения коэффициентов ряда (41.16), получим
систему уравнений:
Ртах = Ро 4^ Р1 “Ь Рг»
Ра=о — Ро Рг»
Pmin — Ро Pi 41* Рг»
для которого рК2 = 34U2U'. При а = 4°
Рис. 41.6
откуда получаем р0 = 3,52 кГ/см2, р± = 1,11 кГ/см2, р2 = 0,05 кГ1см2. Величина дав-
ления по окружности как функция угла ф равна р = 3,52+ 1,11 cos ф + 0,05 cos 2ф.
В этом выражении последний член ряда/жределяет величину изгиба корпуса головной части
в окружном направлении. Аналогично можно определить коэффициенты ряда и получить
зависимость для величины давления как функции угла ф для заднего конуса. Подсчитаем
по формуле (41.15) только величину максимального давления на задний) усеченный конус,
имеем pmax = 2q ((3Кг + а)2 = 2-91 400 х
/ 34° 20' 4- 4° \
-------57 3^“J = 80,8’103 КГ/М2
(8,08 кГ)см2). Эта величина является
определяющей для расчета хвостового
отсека на устойчивость от внешнего
давления.
Таким образом в каждом
сечении по длине головной ча-
сти определены нормальная
осевая сила А', изгибающий мо-
мент М, перерезывающая сила
Q и аэродинамическое давле-
ние р. Это эксплуатационные
значения силовых факторов.
Для расчета на прочность и
устойчивость величину каждо-
го силового фактора необходи-
мо увеличить в f раз, где f —
коэффициент безопасности. Его
значения для разных силовых
факторов различны.
Внешние формы головных частей показаны на рис. 41.7 [123], [125].
Почти все головные части имеют притупленный носок. Носок через кони-
ческий переходник сопрягается с цилиндрической частью. Заканчивает-
ся головная часть стабилизирующей юбкой. На головных частях (/, 2)
устанавливается носовой медный конус, который поглощает тепло, а
головные части (5—9) имеют теплозащитное покрытие, которое пре-
пятствует проникновению внутрь больших тепловых потоков. Заострен-
ная головная часть ракеты «Фау-2» (10) не имела покрытия.
Расчет температуры конструктивных элементов выполняют для всех
сечений головной части. В большинстве случаев, как показывают рас-
четы, прогрев конструкции наступает позже момента действия макси-
мальных нагрузок (максимального скоростного напора). Следует особо
рассматривать случаи, где максимальные нагрузки совпадают по вре-
мени с наивысшей температурой. Для каждого сечения корпуса поэтому
вместе с нагрузками указывают и температуру (табл. 41.2). Такие таб-
лицы составляют для нескольких случаев по времени полета. Для каж-
дого сечения выбирают наихудшие сочетания нагрузок и температур.
358
Все проведенные расчеты нагрузок могут рассматриваться как пер-
вое приближение. Для точного определения нагрузок на головную часть
выполняют точные аэродинамические расчеты. Эти расчеты, в свою
очередь, уточняют путем продувок моделей головных частей в аэроди-
намических трубах при заданных числах М полета.
Рис. 41.7
Таблица 41.2
xlt м 0 0,1 0,2 1
Мэкв- кГ
Qp, кГ
рр, кГ/см2
Т, °C
§ 42. ТЕПЛОВАЯ ЗАЩИТА ГОЛОВНОЙ ЧАСТИ РАКЕТЫ
Головная часть баллистической ракеты при входе в плотные слои
атмосферы на нисходящей ветви траектории имеет скорость в несколь-
ко километров в секунду и обладает большим запасом кинетической
энергии. В плотных слоях атмосферы происходит торможение головной
части, так что ее кинетическая энергия у поверхности Земли в несколь-
ко раз меньше, чем в начале торможения. В процессе спуска разница
кинетических энергий переходит в тепло, значительная часть которого
идет на нагрев головной части и обтекающего ее поверхность воздуш-
ного потока. При проектировании головной части необходимо доби-
ваться того, чтобы на нагрев несущей части ее конструкции шла воз-
можно меньшая доля выделившегося тепла. Это достигается выбором
формы головной части и нанесением на ее поверхность термостойкого
покрытия.
Расчет конвективного теплообмена на поверхности конуса, обтекае-
мого воздушным потоком без угла атаки, можно провести по зависи-
359
мостям, приведенным в § 29. Отличие состоит лишь в том, что для
конуса необходимо учитывать местные значения параметров потока,
обтекающего его поверхность после присоединенной ударной волны
(косого скачка уплотнения). Равновесную температуру Т на поверхно-
сти конуса определяют по рис. 29.5, но теперь параметры Вл и Вт для
ламинарного и турбулентного режимов течения в пограничном слое
будут соответственно равны
Вл = 0,45-10-5^(1+0,4^) (42.1)
V 6 Рн К гн=о >
и
Вт = 0,76-10-4(1 + 1,8502) Р/^° (-Ти Y'5Re0 8, (42.2)
где е — степень черноты поверхности; g— коэффициент давления, опре-
деляемый по рис. 42.1 при заданных значениях полуугла конуса и
числа Мн полета. Отношения рн/рн=о и Th/Th=q характеризуют изме-
нение плотности и температуры воздуха по высоте Н; их находят по
таблицам стандартной атмосферы или по рис. 29.2. Критерий Рейнольдса
подсчитывают, исходя из параметров невозмущенного потока, по фор-
муле
Re = vh?hx _ ( (42
Пн
где ин — скорость полета, х — расстояние от передней точки конуса до
рассматриваемого участка поверхности, т]н— коэффициент вязкости
воздуха, вычисляемый по формуле
Пн = 1,46• 10-6 (Тн)3/2 (Тн + 110) кг!м• сек. (42.4)
В диапазоне значений Re= (1,54-5)* 106, в котором происходит смена
режимов течения в пограничном слое, при проведении практических
расчетов целесообразно принимать большее из двух значений Г, кото-
рые определяют по графикам на рис. 29.5,а, б. При вычислении темпе-
ратуры Т на поверхности заостренного тела вращения с криволиней-
ной образующей используют способ местных конусов. При этом в рас-
четные зависимости подставляют угол 0К, который составляет касатель-
ная к образующей поверхности в рассматриваемой точке с осью тела
вращения.
При сверхзвуковом обтекании головной части с закругленным нос-
ком возникает отсоединенная ударная волна с искривленным фронтом
(рис. 42.2). По своей интенсивности центральная часть ударной волны
близка к прямому скачку. За ней образуется так называемый ударный
слой сильно нагретого воздуха. Тепло от ударного слоя передается,
главным образом, конвекцией в пограничном слое, который возникает
на поверхности закругления. Благодаря высокой температуре воздуха
ударный слой обладает заметным по величине тепловым излучением,
но для типичных траекторий входа головных частей в плотные слои
атмосферы оно мало в сравнении с конвективным тепловым потоком,
и в расчетах его можно не учитывать.
В передней точке закругленного носка режим течения в погранич-
ном слое ламинарный, и для расчета удельного теплового потока мож-
но воспользоваться формулой
/-----/ \ 3,15
q0 = 1,1-108]/ - ?н — —-~Яп-------епЦм\ (42.5>
40 V рн=о \ / Я*-Я'
360
где vT = 7,9 км/сек, — первая космическая скорость у Земли, г0— радиус
закругления носка в м, Н* --= срТн + (и2н/2)— энтальпия заторможенного
воздушного потока, Нп и Н'— энтальпия воздуха при температурах поверх-
ности Тп и Т' = 300JK. Значения Нп и Н' определяют по рис. 29.3.
Формула (42.5) справедлива с точностью до 1О°/о в диапазоне значений
vH = (1,8-4- 7,9) км/сек и 1 > рн/ря=о > 8-10-5.
Распределение тепловых потоков q по образующей головной части
с закругленным носком зависит от режима течения в пограничном слое
и распределения давления. Если форму головной части приближенно
представить в виде полуэллипсоида вращения с полуосями а и b
(см. рис. 42.2), то отношение местного давления р к давлению ро в пе-
редней точке закругления будет
Х = 1 _ Az£H_cos2pK.
Ро Ро
Здесь рк — угол между каса-
тельной к образующей поверх- 3
ности в рассматриваемой точке
и осью головной части. Давле-
нием воздуха рн в невозмущен- 2
ном потоке обычно можно пре-
небречь в сравнении с давле-
нием ро. Поэтому j
~ sin2 рк. (42.6)
Ро
На рис. 42.3 построена за- о
висимость q/q0 от р/р0 для
различных отношений а/b при
ламинарном режиме течения в
пограничном слое. Следует от-
метить, что для полусферы и вытянутого вдоль оси головной части эл-
липсоида вращения (а/6^1) значение qQ является максимальным. При
а/&<1 максимум теплового потока q достигается на некотором удалении
от передней точки закругления.
При турбулентном режиме течения в пограничном слое тепловой
поток подсчитывают по формуле
/ Рм \°’8 / У» \ 3,18 (Т)
q = 25• 108 —!L— _Ф вт/мг, (42.7)
\ ?Н=0 / \ / х ’
361
где х— расстояние в м по образующей от передней точки закругления
до рассматриваемой точки поверхности, Ф — функция местного давле-
ния, которая изображена на рис. 42.3 пунктирной кривой. Эта функция
достигает максимума Фтах=0,261 при р/ро = О,58, что соответствует пе-
реходу от дозвукового обтекания поверхности головной части за удар-
ной волной к сверхзвуковому. При этом также достигает максимума
удельный тепловой поток q.
С помощью формул (42.5) — (42.7) и графика на рис. 42.3 из ба-
ланса конвективного и лучистого тепловых потоков на поверхности го-
ловной части с закругленным носком
q = ео0Т4
может быть найдена равновесная температура Т. Практически следует
вести расчет одновременно для ламинарного и турбулентного режимов
течения в пограничном слое и принимать большее из полученных зна-
чений q, что будет соответствовать большему значению равновесной
температуры. Этот способ расчета может быть уточнен по мере накоп-
ления данных об условиях перехода ламинарного пограничного слоя
в турбулентный при обтекании головной части с закругленным носком.
Теплозащитное . покрытие на поверхности головной части, которое
защищает несущую часть конструкции от непосредственного теплового
воздействия со стороны воздушного потока, подвергается также интен-
сивному механическому воздействию, создаваемому силами трения в
пограничном слое. Совместное влияние теплового и механического воз-
действий воздушного потока на теплозащитное (покрытие может при-
вести к разрушению его поверхности и уменьшению толщины слоя по-
крытия. Это разрушение происходит в сравнительно узком диапазоне
температур поверхности покрытия, который можно характеризовать
одним средним значением температуры Т*.
Если на всем участке входа головной части в плотные слои атмо-
сферы для выбранного вида теплозащитного покрытия выполняется
условие Т<Т*, то его поверхность не разрушается. В этом случае орга-
низация тепловой защиты головной части сводится к подбору такого
распределения толщины слоя покрытия по поверхности, который бы
обеспечивал сохранение температур контейнера и несущей части кон-
струкции в допустимых пределах. Для этого необходимо рассмотреть
процесс теплопроводности в оболочке головной части, которую в тепло-
вом отношении можно представить в виде двухслойной пластины, со-
стоящей из слоя термоизоляции и металлической стенки. Более под-
робно эта задача и способы ее решения разобраны в § 55.
Здесь же следует отметить, что слой термоизоляции с малым коэф-
фициентом теплопроводности Xi при интенсивном теплообмене с воз-
душным потоком отводит от поверхности сравнительно небольшую долю
теплового потока q, а остальная часть рассеивается с поверхности в виде
теплового излучения. Поэтому ее температура Ти практически следует
за текущим значением температуры Г. В приближенных расчетах целе-
сообразно принять Тп = Т и воспользоваться для определения зависи-
мости температуры Т(t) металлической стенки оболочки головной части
от времени t формулой, сходной с формулой (55.12):
оо Fo
Т (/) = То + Е Вп f [Т (|) - То] exp [(v;)2 а - Fo)] dl, (42.8)
п=1 6
где
Vn 4^ sin Vn cos Vn
362
Tq — начальная температура оболочки, v'n — корни характеристического
уравнения
ctg v = Kv9 К ,
с, р, h и pi, h\ — удельная теплоемкость, плотность и толщина метал-
лической стенки и слоя теплозащитного покрытия, Fo = ai///n —крите-
рий Фурье, в котором ai = Zi/ciPi— коэффициент температуропроводно-
сти покрытия. В формулу (42.8) входит зависимость равновесной
температуры от безразмерного времени — критерия Фурье — Т(£) =
= 7(Fo), что позволяет учесть изменение условий теплообмена голов-
ной части -с воздушным потоком в период ее входа в плотные слои
атмосферы.
Для головных частей ракет большой дальности равновесная тем-
пература поверхности Т на отдельных участках траектории входа в
плотные слои атмосферы превышает значение Г* для существующих
типов теплозащитных покрытий. В этот период поверхность покрытия
разрушается, причем фронт разрушения продвигается со скоростью
’ Р1[^ + ^1(^-То) + 0,5(Я;-Д)] ’
где е — степень черноты разрушающейся поверхности;
Я* —тепловой эффект процесса разрушения;
Н„ и Н'{— полные энтальпии газообразных продуктов разрушения при
температурах поверхности Т* и заторможенного воздушного
потока Г*.
Формула (42.9) получена на основе выражения (54.11), которое
описывает установившийся процесс разрушения теплозащитного по-
крытия при неизменных по времени условиях теплообмена с газовым
потоком (см. § 54). Здесь это выражение применено для определения
мгновенной скорости разрушения покрытия, соответствующей текущим
условиям теплообмена головной части при входе в плотные слои атмо-
сферы. В числитель формулы (42.9) дополнительно введен член, харак-
теризующий отвод тепла с поверхности покрытия излучением, а влияние
на теплообмен вдува в пограничный слой газообразных продуктов раз-
рушения учитывается в знаменателе этой формулы с помощью разности
энтальпий Н\— Н*.
По мере приближения головной части к поверхности Земли ско-
рость ее движения ии уменьшается, что приводит к уменьшению интен-
сивности теплообмена с воздушным потоком. В связи с этим равновесная
температура Т поверхности покрытия может стать ниже значения Г*
и процесс разрушения прекратится. Для расчета температуры металли-
ческой стенки оболочки головной части в последующий период ее дви-
жения к поверхности Земли снова можно воспользоваться формулой
(42.8) или применить численный способ, описанный в § 25.
Последовательность расчета разрушения теплозащитного покрытия
рассмотрим на примере.
Пусть требуется рассмотреть участок траектории головной части
при входе в плотные слои атмосферы, начиная с высоты /7 = 55 км.
Скорость движения на этой высоте vH = 7,2 км/сек. Изменение величин
Н и vH по времени t показано на рис. 42.4. Принято, что форма голов-
ной части представляет собой полусферу радиусом го = О,4 л/, состыко-
ванную с цилиндром, т. е. соотношение полуосей а/Ь = 1.
Расчет ведем для участка поверхности закругления, который соот-
ветствует максимуму конвективного теплового потока при турбулент-
363
ном режиме течения в пограничном слое. При этом согласно формуле
(42.6) p/po~sin2pK = 0,58 и рк = 50°. Расстояние до этого участка от пе-
редней точки закругления составит
х = [(л/2) — Рк] г0 = 0,283 м.
Например, для момента времени t = 10 сек параметры траектории
Н = 29 км и vh = 6,55 км/сек. По рис. 29.2 определяем ря/рн=0 = 0,017
и по формуле (42.7) вычисляем
_ / prr \0»8 /' \ 3,18 ф
,.25.10» /2- -2-
\ ?н=о j \ / х
= 25-108(0,017)0’8 х (Л^_у-18-------------°-261 = 17,4-106вт/ж2.
V \ 7,90 J (О,283)0,2
Этому значению соответствует равновесная температура поверхности со
степенью черноты е = 0,8
Т = q/E(J0 = р4/17,4• 106/0,8-5,77-10’8= 4400 К.
Н,нм, Vu-10'2
•10'7вгт1/м?
Результаты расчета тепло-
вых потоков по формуле (42.7)
для турбулентного режима те-
чения в пограничном слое при-
ведены на рис. 42.4. Там же
пунктирной кривой отмечено
изменение по времени тепловых
потоков, рассчитанных с по-
мощью формулы (42.5) в пред-
положении, что до рассматри-
ваемого участка сохраняется
ламинарный режим течения в
пограничном слое. При вычис-
лениях принято, что поверх-
ность теплозащитного покры-
тия разрушается при темпера-
туре Тп = Т* = 1200°С = 1473° К,
что по рис. 29.3 отвечает зна-
чению энтальпии воздуха Яп =
= 1560 кдэ/с/кг. Величина
полученная по формуле (42.5),
умножалась на отношение
?/<7о = О,68, взятое по рис. 42.3 при р/ро = О,58 и а/Ь=\.
Для того же момента времени ^=10 сек температура невозмущен-
ной атмосферы при // = 29 км ТН = 233°К (см. рис. 29.2), что при удель-
ной теплоемкости воздуха ср=1 кдж/кг- град дает значение энтальпии
заторможенного потока
//* = СрТн + (и^/2) = 1 • 233 + (6,552/2) • 103 = 2 1 630 кдж/кг.
Энтальпия воздуха при температуре Т" = 300°К равна
Я' = срГ = 1 -300 = 300 кдж/кг.
По формуле (42.5) с учетом значения q/q^ = 0,68 получаем
1,1-Ю8 g д
Рн=о
н*-нп
И* — Н'
LU2L о,68 ГоЖ (21 бзо -1.56L = 8.106 вт/м^
/ОЛ \ 7,90 J 21 630-300
364
В дальнейшем для расчета скорости разрушения теплозащитного
покрытия по формуле (42.9) до /=5 сек принимаем значения q, соот-
ветствующие ламинарному пограничному слою, а на остальной части
траектории — турбулентному пограничному слою. Для теплозащитного
покрытия Н* =6000 кдж/кг, pi=1600 кг/м\ Ci = l кдж]кг- град, TQ =
= 15°С = 288°К. Свойства газообразных продуктов разрушения покры-
тия для упрощения вычислений в данном примере приняты такими же,
как и для воздуха, т. е. Н\=Н* и = ЯП. Для момента времени
t= 10 сек по формуле (42.9) получаем
_________________я — __________________
Pi [#* + Q (П - То) + 0,5 (//* - Нп)]
__________17,4-10а —-0,8-5,77-10~8 (1473)4___________
1600 [6000 4- 1 (1473 — 288) + 0,5 (21 630 — 1560)]. 103
= 0,622-10"3 м/сек =
= 0,622 мм/сек.
Изменение скорости разрушения покрытия по времени показано на
графике. Площадь под кривой зависимости v от t, соответствующая
t
значению интеграла h* = j'vdt, равна толщине Л* разрушенного слоя
о
покрытия за время движения головной части на нисходящей ветви
траектории. В данном случае она составляет /г* =30 мм. Чтобы пре-
дотвратить повышение температуры несущей конструкции в последний
период движения головной части в плотных слоях атмосферы, началь-
ная толщина //о теплозащитного покрытия на рассматриваемом участке
поверхности должна превышать на несколько миллиметров значение Л*.
§ 43. УСТОЙЧИВОСТЬ СТАБИЛИЗИРУЮЩЕЙ ЮБКИ
В этом параграфе рассмотрена специфическая для расчета головной
части задача об устойчивости работающей на внешнее давление стаби-
лизирующей юбки (рис. 43.1,а). Расчет на прочность и устойчивость
остальных элементов конструкции головной части (силовые шпангоуты,
сжатая в осевом направлении оболочка, стыки и т. п.) может быть про-
изведен так же, как и для аналогичных элементов корпуса ракеты.
Устойчивость консольной цилиндрической оболочки с подкреплен-
ным краем. Сначала решим вспомогательную задачу об устойчивости
нагруженной внешним давлением ортотропной консольной цилиндриче-
ской оболочки, подкрепленной упругим шпангоутом (рис. 43.1,6). Эта
365
задача рассматривается в линейной постановке при следующих допу-
щениях: а) оболочка считается полубезмоментной; б) ось шпангоута
принимается нерастяжимой и лежащей в средней поверхности оболоч-
ки, а его жесткость при деформации из его плоскости пренебрежимо
малой.
Как было показано в § 16, для полубезмоментной оболочки систему
управлений (16.2) можно привести к одному разрешающему уравнению
(16.29) относительно нормального прогиба;
d4w . D д* f д*ш о д2иу . \ pR / dQw . д4^ \ т
д£* BR2 др* < др* др* J В \ дрв др* )
и, кроме того, получить четыре дополнительных соотношения, позво-
ляющих выразить через w перемещения и, и, а также осевое и сдвигаю-
щее усилия Л и S:
ц = — J wdfi, и =—Jб/р, (43.1)
= <43'2>
где В — жесткость оболочки на растяжение в осевом направлении,
D — жесткость оболочки на изгиб в окружном направлении.
Для замкнутой оболочки решение разрешающего уравнения можно
искать в виде
w = X sinnP,
(43.3)
где X — функция только осевой безразмерной координаты 5- Тогда это
уравнение приводится к обыкновенному дифференциальному урав-
нению
Xiv _ х*Х - 0, (43.4)
где
V = „4 (/12 _ 1) Г_^ _ (Л2_ 1) 1 (43 5)
В соответствии с порядком полученного уравнения для решения за-
дачи нужно сформулировать четыре граничных условия (по два для
каждого торца оболочки). Если считать, что левый торец оболочки при
g = 0 жестко закреплен относительно нормальных перемещений w и
упруго закреплен относительно осевых перемещений и, то двумя пер-
выми граничными условиями рассматриваемой задачи при 5 = 0 будут:
1) w = v = 0, следовательно, X=0,
2) си = Ть следовательно, X"=\cR/EH)X',
где с — жесткость упругого закрепления края оболочки в осевом на-
правлении. Заметим, что согласно гипотезе полубезмоментной теории
о нерастяжимости оболочки в окружном направлении условие w = Q
эквивалентно условию о = 0, как было показано в § 14.
Чтобы сформулировать третье и четвертое граничные условия, нуж-
но рассмотреть взаимодействие оболочки и шпангоута. Согласно допу-
щениям, полубезмоментной теории перерезывающее усилие Qi в обо-
лочке равно нулю, и поэтому полубезмоментная оболочка не может
передавать на шпангоут радиальных усилий. При потере устойчивости
торец оболочки может нагружать шпангоут только осевым и сдвигаю-
щим усилиями 7] и S. Но в настоящем решении жесткость шпангоута
при деформации на его плоскости принята пренебрежимо малой, по-
этому на торце оболочки осевое усилие должно обращаться в нуль,
и третьим граничным условием будет
3) 7\ = о, т. е. X" = 0 при £ = —1—.
R
366
Силовое взаимодействие оболочки и шпангоута сводится к тому, что
при потере устойчивости шпангоут загружается касательными усилия-
ми qx, равными сдвигающим усилиям S на торце оболочки. Изгиб
шпангоута под действием касательных распределенных усилий qx опи-
сывается уравнением [12]
EjJ-^- + 2-^- = (43.6)
т\ dpe dfP J 4 V 7
где EJT — изгибная жесткость торцового шпангоута, vT — касательные
перемещения точек оси шпангоута. Если считать край оболочки жестко
соединенным со шпангоутом и использовать соотношения (43.2) и (43.6),
то четвертым граничным условием будет
4) Ё7тХ = (4Ух"' при |= -1-.
\ К / А
Здесь £VT — приведенная изгибная жесткость шпангоута, зависящая от
числа волн п. Она определяется соотношением
EJT (-- Y п4 (п2 — I)2. (43.7)
т BR2 \ R J v 7 v 7
Решение уравнения (43.4), по форме совпадающего с уравнением
для свободно колеблющейся однородной балки (см. § 16), хорошо из-
вестно:
w = Ar sinXg + Л2 с os 4- H3shX^ + Л4сЬХ£. (43.8)
Использование сформулированных выше четырех граничных условий
приводит к системе однородных линейных уравнений относительно не-
известных Ль Л2, Л3 и Л4. Из условия равенства нулю определителя
этой системы получается характеристическое уравнение для определе-
ния собственных значений X.
Как показывают вычисления, если жесткость упругой заделки
ci>30-j-, то край оболочки можно считать жестко закрепленным от-
носительно осевого смещения и. В этом случае характеристическое
уравнение для X упрощается и принимает вид
£JT = а3----l-frchacosa--, (43.9)
cos a sh а — ch a sin а
. I
где а = X ——.
nR
Выражение для верхнего критического давления получают из выра-
жения (43.5):
рру0
(43.10)
где а; — наименьшее собственное значение, найденное из решения урав-
нения (43.9). Важно подчеркнуть, что входящая в выражение (43.10)
величина си сама зависит от числа волн п. Поэтому последовательность
определения минимального значения piKp должна быть такова: задав-
шись значением п, следует из уравнения (43.9) найти соответствующее
ему минимальное значение aj и только затем по формуле (43.10) под-
считать рщр. Повторив эти вычисления несколько раз, можно найти
минимальное значение piKp. При некоторых значениях EJT зависимость
Р1нр от п может иметь два минимума; в этом случае за критическое
значение следует, естественно, взять наименьшее из них.
367
Интересно отметить, что существует такое значение жесткости шпан-
гоута Е/э, при котором происходит качественная смена форм потери
устойчивости. Когда жесткость шпангоута меньше EJd, форма прогиба
оболочки при потере устойчивости такова, что максимальные нормаль-
ные перемещения имеет подкрепленный шпангоутом край оболочки
(рис. 43.2, форма 1).
Другими словами, форма потери устойчивости, подкрепленной шпан-
гоутом оболочки, аналогична форме потери устойчивости не подкреп-
ленной консольной оболочки.
При £/т>£/э максимум нор-
мальных перемещений сме-
щается к середине оболочки,
т. е. форма потери устойчиво-
сти становится аналогичной
форме потери устойчивости
оболочки с двумя закреплен-
ными краями (рис. 43.2, фор-
ма 2). Если при £/т<£/э уве-
личение жесткости шпангоута
ведет к существенному увели-
чению Р1кр, то при £/т>£/э
жесткость шпангоута практи-
чески перестает влиять на зна-
чение Р1кр (при £/т = £/э значе-
ние критического давления со-
ставляет примерно 0,90—0,98
от значения критического дав-
ления оболочки с обоими закрепленными краями). Отсюда очевидно,
что, с точки зрения общего веса оболочки, ставить шпангоут с жестко-
стью, значительно большей £/э, нецелесообразно. Как показывают чис-
ленные расчеты, для оболочек средней длины
£/э^ 0,450/. (43Л1)
Зависимость величины критического давления для оболочек средней
длины от жесткости торцового шпангоута может быть описана безраз-
мерным графиком, показанным на рис. 43.2, где по оси ординат отло-
жено отношение величины верхнего критического давления консольной
оболочки с торцовым шпангоутом к величине верхнего критического
давления опертой по двум краям оболочки, определяемого формулой
(16.37), а по оси абсцисс — безразмерная жесткость торцового шпан-
гоута.
Проверочный расчет стабилизирующей юбки. Цель проверочного
расчета — найти для заданной конструкции критические нагрузки при
потере общей и местной устойчивости. На рис. 43.1 показана стабили-
зирующая юбка, выполненная по схеме оболочки с поперечным сило-
вым набором (шпангоутами): металлическая обшивка толщиной h под-
креплена несколькими шпангоутами одинаковой жесткости на изгиб £/
и торцовым шпангоутом жесткости £/т. Обычно металлическая обо-
лочка стабилизирующей юбки снаружи покрывается слоем термоизоля-
ции, предохраняющим ее от аэродинамического нагрева. Слой термо-
изоляции увеличивает жесткость оболочки, что можно учесть в расчете,
например, путем введения эквивалентных толщин оболочки, как это
делалось в § 34 или в § 37. Но здесь в запас устойчивости просто будет
принято, что термоизоляция не увеличивает жесткости оболочки. Влия-
ние нагрева учитывается соответствующим понижением механических
характеристик материала обшивки и шпангоутов. Термические напря-
жения, вызываемые неравномерным иагревом, не учитываются.
368
Расчет обшивки на местную устойчивость между подкреплениями
можно выполнить по формуле (16.23):
где Rci—средний радиус i-того пролета между подкреплениями,
/z—длина i-того пролета по образующей конуса.
На местную устойчивость, естественно, следует просчитать все пролеты
между подкреплениями.
При расчете стабилизирующей юбки на общую устойчивость можно
(в запас устойчивости) заменить подкрепленную коническую оболочку
ортотропной полубезмоментной цилиндрической оболочкой, как пока-
зано пунктиром на рис. 43.1. Радиус этой ортотропной цилиндрической
оболочки равен максимальному радиусу конической оболочки, а жест-
кость на растяжение в осевом направлении и жесткость на изгиб в ок-
ружном направлении соответственно равны
Л = 1 12-!—н2,
/ ЕЛ»
где N — число промежуточных шпангоутов (без торцового);
/ — длина юбки по образующей.
Для определения критического давления эквивалентной ортотропной
цилиндрической оболочки можно воспользоваться результатами реше-
ния задачи, рассмотренной в начале этого параграфа. Расчет ведут
либо по зависимостям (43.9) и (43.10), либо по графику на рис. 43.2.
В последнем случае верхнее критическое давление
Р1кр =
(43.13)
где коэффициент т] берут по графику на рис. 43.2 в зависимости от ве-
личины относительной жесткости торцового шпангоута EJT/ID, а вели-
чину критического давления опертой по двум краям оболочки опре-
деляют по формуле (16.37):
Как следует из приведенного выше решения задачи об устойчивости
цилиндрической оболочки с подкрепленным краем, целесообразная ве-
личина жесткости торцового шпангоута примерно равна
EJ, 0,45 Г---------—-----I + (N + 1) EJ
9 | 12(1 -ц2)
(43.14)
Поскольку прием замены конической оболочки ортотропной цилиндри-
ческой весьма приближенный и заведомо идет в запас устойчивости,
то никакой дополнительной поправки на возможность хлопка оболочки
можно не делать, а просто принять р1Л~Р1кр-
§ 44. ОБТЕКАТЕЛИ. СИЛОВЫЕ ЭЛЕМЕНТЫ КОНСТРУКЦИИ
ГОЛОВНОЙ ЧАСТИ РАКЕТЫ
Расчет обтекателя. В настоящее время с помощью мощных ракет-
носителей производятся запуски космических аппаратов различного на-
значения: искусственные спутники Земли, автоматические межпланет-
24 Зак. 96 369
ные станции, пилотируемые космические аппараты. Космические аппа-
раты имеют, как правило, неблагоприятную, с точки зрения аэродина-
мики, форму. Поэтому они закрыты обтекателями, которые предохра-
няют аппараты от воздействия аэродинамических нагрузок и тепловых
потоков на участке выведения на заданную траекторию полета. На
Рис. 44.1
больших высотах, где аэродинамические нагрузки и тепловые потоки
малы, обтекатели сбрасываются.
Внешние формы обтекателей показаны на рис. 44.1, а некоторые-
геометрические данные приведены в табл. 44.1 [124]. Как видно из ри-
сунка, типичная конструкция, корпуса обтекателя состоит из носка в.
форме сферического сегмента и отсеков в форме усеченных конических
и цилиндрических оболочек.
Таблица 44.1
Номер по рис. 44.1 Длина, м Объем, м3 Назначение обтекателя
/ 1,96—3,66 1,98—4,53 Для спутников серии «Дискаверер»
2 2,92 2,88 Для ракеты «Аджена» по программе «Джемини»
3 4,06 3,71 «Рейнджер»
4 4,01 5,27 «Маринер III». «Маринер IV»,
5 5,66 7,68 Для спутника «Нимбус»
Для определения нагрузок, действующих на обтекатель в полете,
необходимо знать изменение по времени полета всех параметров дви-
жения, зависимость скорости ветра по высоте, величины аэродинамиче-
ских коэффициентов cXl, сУ1 для всего обтекателя и отдельных его-
элементов.
Вес обтекателя сравнительно невелик, поэтому величины инерцион-
ных сил малы по сравнению с внешними, в данном случае аэродина-
мическими, силами. Расчет нагрузок, действующих на обтекатель, сво-
дится в основном к определению в поперечных сечениях силовых фак-
торов от аэродинамических сил. Ниже излагается приближенная мето-
дика определения нагрузок, которая может рассматриваться как первое-
приближение.
370
Определим величины внешнего аэродинамического дав-
ления, действующего на каждый элемент поверхности обтекателя.
Рассмотрим нагружение носка в виде сферического сегмента с углом
в вертикальной плоскости у0, рис. 44.2,а. Величину аэродинамического
давления по поверхности носка рн приближенно принимаем согласно [50]
Ри Ра =PoCOs2Y>
р0 = 1,35----- arctg [1,96 (1 —М)].
(44.1)
Рис. 44.2
Для конической поверхности аэродинамическое давление при нулевом угле
атаки постоянно вдоль образующей и равно (§ 28)
рк =q( 1,56 + -Ь-—Лр'-7,
М2 ) к
(44.2)
где рк — угол в радианах.
При малых углах атаки а максимальную величину давления на ко-
ническую поверхность определим по формуле (см. § 28)
Ртах = Я ( 1,56 + (Рк 4- а)1’7.
\ М2 J
(44.3)
По окружности поперечного сечения обтекателя зависимость вели-
чины давления от угла ср можно подсчитать из выражения (41.16)
(см. §41).
При определении осевых сил, действующих на обтекатель, аэро-
динамическую силу сопротивления от трения не учитываем, так как ее
величина обычно составляет небольшую долю от волнового сопротив-
ления. Метод учета силы сопротивления от трения можно найти в ра-
боте [59].
При известных величинах давления в каждой точке по длине обте-
кателя определение осевых сил сводится к интегрированию (или сум-
мированию) проекций всех поверхностных сил на ось х{.
Для носка с углом у0 осевая сила, примерно равная силе лобового
сопротивления, будет (см. рис. 44,2,а).
24*
371
X(iH) — J р„ 2лг2сф sin у cos ydy = p0 • 2лг?ф j cos3 у sin ydy =
о о
= Роу г?ф<l — c°s4Yo) = РоЛГ^ф sin2Y0(1--------J- sin2Yo).
С учетом зависимости (44.1) получим
Х(!н) = р0длг2сф sin2Yo (1--sln2y0). (44.4)
Для конической поверхности осевая сила определяется как произ-
ведение величины давления на площадь проекции поверхности конуса
на плоскость, перпендикулярную к оси х{. Величина осевой силы, дей-
ствующей на цилиндрическую поверхность, невелика и ее учитывать
в расчете нагрузок не будем.
Полная осевая сила аэродинамического сопротивления равна сумме
осевых сил, действующих на элементы поверхности обтекателя
Хг = 2Х(1° = ХГ + Х(1°. (44.5)
Пример. Определим величины аэродинамического давления и осевые силы, дейст-
вующие на обтекатель, размеры которого показаны на рис. 44.2, а. На этом рисунке
у0 = 82°, рк = 8°, S = 1 ж2, гСф = 282 мм,
SH = лг2фsin2Yo = 0.98Л-2822 = 0,245 ж2, Sj = (S — SH) = (1,0]—J),245) = 0,755 + .
Другие данные: скоростной напор q = 6350 кГ/м2, число М= 1,5, угол атаки а = 4,7°.
Расчет начнем с определения величины давления на поверхности носка. Для М='1,5
р0 = 1,35------arctg [1,96(1 — М)] = 1,35 —— arctg [1,96 (1 — 1,5)] = 1,1;
Л л
рн = paq = pQq cos2y = 1,1- 6350 cos2 у = 6960 cos2 у; Рнтах = 0,69 кГ/см2.
Сила лобового сопротивления носка по формуле (44.4) для у0 — 82° равна
= РоЯЛГ^ф sin2 Yo (1 — у Sin2 Yo) = 1.1 • 6350 • 0,245 (1 — 0,49) = 870 кГ.
Для конуса аэродинамическое давление
/ 1,96 \ 7 / 1,96 \ f 8 \ U7
Рк = <?( 1,56 + —6350 1.56+= 543 /сГ/ле2;
\ М2 J \ 1,52 J \ 57,3 /
осевая сила
X)0 = pKSi = 543-0,755 = 410 кГ.
Полная осевая сила %! = Х<^ + Х)1' = 870 + 410 = 1280 кГ. Эпюра осевых сил по длине
обтекателя построена на рис. 44.2, б.
При наличии угла атаки а = 4,7° величина максимального давления для конуса при
Ф = 0 будет (см. § 41)
/ 1,96 \ ,7 / 1,96 \ / 8-М,7 \Ь7
Ртах = 41.56 + —— )(РК + а)1,7 = 6350 1,56 + -—- )( ) =
1VI у 1 । Э J \ □/ ,<5 j
= 1220 к,Г\м2 (0,122 кГ!см2).
Нагружение обтекателя в поперечном направлении про-
исходит при наличии угла атаки. Возникновение угла атаки а обуслов-
лено действием ветра и программным разворотом ракеты. Угол атаки
от действия ветра можно учесть по методике, изложенной в § 28, а про-
граммный угол известен.
Для определения величин поперечных аэродинамических сил нужны
значения коэффициентов подъемной силы сферического носка, усечен-
372
ного конуса и цилиндра. Для малых углов атаки поперечную силу, дей-
ствующую на полусферический носок, можно определить приближенно
по формуле
У'н) = х<н’ sin а = Х^а. (44.6)
Если радиус носка мал по сравнению с общей длиной обтекателя, то
при определении поперечных нагрузок можно считать, что сила прило-
жена в центре сферы.
Для конуса поперечная сила равна (см. § 28)
У(1° =•• Cy^q, где Cyt = 3.
Сила У1° приложена в геометрическом центре тяжести площади продоль-
ного сечения конуса.
Для цилиндра подъемную силу определяют по формуле (28.14):
У(!2) = l,5a2tyS2,
где X — удлинение цилиндрического отсека;
S2 — площадь поперечного сечения цилиндра.
Сила У(2) приложена в виде равномерной нагрузки (§ 28).
Силы У(1Н), У(1° и У(2) являются равнодействующими распределенных
поверхностных сил давления.
Пример, Для обтекателя, размеры которого приведены на рис. 44.2, а, определим
поперечные нагрузки, если известны: q = 6350 кГ/м2, a = 4,7°, SH= 0,245 л«2, Si =
= 0,755 д<2, S = S2= 1,0 jw2.
Поперечная сила, действующая на носок,
У|н) = X(!Н'а = 870 4,7 =71 кГ
57,3
и приложена в центре сферы.
Для усеченного конуса
4 7
У(,° = ЗаоЗ, = 3 —6350 0,755 = 1180 кГ.
1 57,3
Для цилиндрического отсека
Х = —
4гСф!
1000
4-282
= 0,89,
У(2) = l,5a2MS2= 1,5
4,7 \2
---— ) 0,89.6350-1,0 = 57 кГ,
57,3 )
Для построения эпюр Q и М примем, что сила на сферическом носке приложена
сосредоточенно, сила У^ распределена по трапеции, а сила приложена в виде равно-
мерной нагрузки. Полученные распределенные аэродинамические нагрузки дважды интег-
рируем. Для размеров, указанных на рис. 44.2, а и полученных выше значений сил, при
/1 = 3,0 м, /2= 1,89 /ц = 0,5 м на рис. 44.3 построены эпюры даЭп, Q и М. По
стыку с носителем действуют максимальные перерезывающая сила и изгибающий момент
(рис. 44.3)
Q = УW + у<0 + У <2> = 71 + 1180 + 57 » 1310 кГ,
/ о \
М = У]Н)/Н + У(1°4 + У(2)4 + 71-3,0+1189 (1,0 + — } + 57-0,5 « 2470 кГ-м.
Конструктивно-силовые схемы обтекателей опреде-
ляются характером разделения при сбросе и величинами нагрузок, ко-
торые действуют в осевом и окружном направлениях. Обтекатель, изо-
браженный на рис. 44.4, состоит из двух одинаковых частей 3 и 5,
373
Рис. 44.4
состыкованных продольными швами 4 на замках 11. С помощью тол-
кателей, которые создают момент относительно узлов /, половины об-
текателей откидываются. Узлы являются шарнирными опорами и пере-
дают растягивающие усилия. Перерезывающую силу воспринимают
шпильки S, установленные на шпангоуте носителя. Коническая часть
обтекателя не имеет продольных подкреплений, цилиндрическая обо-
лочка подкреплена стрингерным набором 7, так как по стыку 2 дей-
ствуют значительные нагрузки (сжатие, сдвиг). Эти сечения рассчиты-
вают на устойчивость как сечения стрингерного отсека. В окружном
(направлении обтекатель подкреплен шпангоутами 10, разрезанными
Р.ис. 44.5
продольными лонжеронами 9. Центр масс половины обтекателя обозна-
чен цифрой 6.
На стыке обтекателя с носителем действуют сосредоточенные растя-
гивающие усилия, приложенные к узлам крепления, погонные сжимаю-
щие нагрузки по контуру оболочки и сдвигающие усилия по бортам
•обтекателя. Характер погонных сжимающих сил и сдвигающих усилий
по стыку зависит от наличия вырезов, люфтов в концевом сечении об-
текателя и переднего отсека носителя. На распределение нагрузки
влияет предварительная затяжка стыковых болтов. Поперечная на-
грузка от порывов ветра может действовать в любом направлении. Если
программный угол атаки мал по сравнению с углом атаки из-за поры-
вов ветра, то нагрузку на стык можно считать независящей от направ-
ления действия силы. Тогда существенными будут два варианта нагру-
жения: 1) равнодействующая внешних сил действует в плоскости
стыковых узлов (рис. 44.5,а), 2) равнодействующая внешних сил дей-
ствует перпендикулярно к данному направлению (рис. 44.5,6).
В первом варианте момент М и осевая сила Nx воспринимаются
сосредоточенным усилием одного верхнего узла и распределенными по-
гонными усилиями, действующими по всему сечению стыка. Во втором
•варианте два узла растянуты, но погонные усилия распределены только
на полуокружности. Погонная сжимающая нагрузка в первом прибли-
жении (без учета ослаблений) может быть распределена по линейному
закону в обоих вариантах, причем /Vi— усилие на один стыковой узел,
.N2 — равнодействующая распределенных сил. Тогда для первого ва-
рианта из уравнений моментов относительно точек А и О
2МЛ = Л\-|- R - М + Nx± R = °,
^Mo = N2-^R-M-NxR = 0
получим
.. 2 М Nx
N, =------------,
3 R 3
м 2 М . 2
Л/, =--------------
2 3 R 3
375
Для второго варианта
%МА = 2Ni — R + Nx — R-M=0,
4 4
2М0 = n2 — r — m = o,
4
KT 2 M 1 .. 4 M
Nt =------------Nx, N2 =--------,
n R 2 л R
Здесь величина момента от сил учтена в М.
Пример, Определим усилия в стыковых узлах обтекателя при следующих данных:
₽ = 0,564 м, М = 2470 кГ-м, Nx = 1280 кГ. Значения и N2 будут: в первом ва-
рианте = 2500 кГ, N2 = 3780 кГ, во втором — Л\ = 2150 кГ, TV2 = 5580 кГ. Значе-
ние погонной сжимающей нагрузки во втором случае существенно больше, хотя растяги-
вающее усилие, действующее на узле, меньше. В первом варианте максимальная погонная
нагрузка равна
<7imax = Ms/31# = 2130 кГ/м, во втором — fomax = N2/2/? = 4950 кГ/м.
От этой сжимающей нагрузки рассчитывают на устойчивость соответствующую часть
цилиндрического отсека.
Шпангоуты в обтекателе подкрепляют тонкостенную обшивку при
нагружении внешним давлением. Их рассчитывают на устойчивость,
как кольца от максимального внешнего давления, и на прочность (из-
гиб и сжатие); при этом учитывают наличие двух шарниров по про-
дольному стыку в каждом шпангоуте.
Случай сброса обтекателя является расчетным для ряда кон-
структивных узлов обтекателя. Для определения нагрузок нужно рас-
смотреть уравнение вращательного движения половины обтекателя от-
носительно стыковых узлов и найти максимальное значение углового
ускорения. Затем определяют величины инерционных сил, строят эпюры
Л4, Q, N. Если Izx — массовый момент инерции половины обтекателя,
MZi — момент, создаваемый толкателем,^—вес половины обтекателя,
пХх —осевая перегрузка в момент сброса, то уравнение движения будет
/ — ]\Л 1 ^об и /
- ^.+ 2 «-/on-
Вариант I Вариант П
Рис. 44.6
причем /оп<0 на начальном
участке движения и /Оп>0
на среднем и конечном
участках движения (см.
рис. 44.4). В этом случае
М21 и /оп меняются по вре-
мени t. По мере увеличения
угловой скорости растет
центробежная сила, которая
вызывает движение полови-
ны обтекателя от ракеты-но-
сителя. При сбросе полови-
на обтекателя нагружается
массовыми силами. Величи-
на изгибающего момента и
нормальных сил зависит от
места расположения толкателей, от усилий в них и т. д. Расчет на проч-
ность и устойчивость проводится в каждом конкретном случае.
Силовые шпангоуты. В конструкции головной части ракеты в местах
крепления грузов действуют значительные сосредоточенные силы. Под.
узлами крепления грузов поэтому устанавливают силовые шпангоуты.
Усилия с центрально расположенного груза на обшивку могут пере-
даваться через тонкостенную коническую оболочку (рис. 44.6). Кони-
ческий переходной отсек крепится по всей окружности к шпангоуту
376
корпуса головной части. В этом случае на шпангоут не действуют со-
средоточенные силы и сечения шпангоута не подвергаются изгибу. Рас-
четная схема для шпангоута — кольцо под действием радиальной по-
гонной нагрузки. Если qr — радиальная нагрузка, Grp — вес груза,.
<р — угол наклона образующей передающего конуса с осью головной
части, R — средний радиус шпангоута, то
tg(p (44 7).
2л/?
Центр тяжести груза расположен на расстоянии 1Х от плоскости
шпангоута. От действия поперечных нагрузок возникает момент. Этот
момент дополнительно нагружает конус, шпангоут и корпус головной
части.
Варианты установки конуса показаны на рис. 44.6. В варианте / при
действии максимальной инерционной нагрузки шпангоут 1 растянут,
конус 2 сжат; при этом шпангоут рассчитывают на прочность, а ко-
нус— на устойчивость от осевого сжатия. В варианте // при той же
нагрузке шпангоут 1 сжат, конус 2 растянут; здесь, наоборот, шпангоут
рассчитывают на устойчивость от равномерно распределенной нагрузки,
а конус — на прочность.
При близком расположении узлов крепления груза к обшивке тонко-
стенные конусы превращаются в наклонные кольцевые шпангоуты
(рис. 44.7). В одном случае мощный шпангоут с наклонной стенкой
может уравновешивать внутренними растягивающими или сжимающими
усилиями (в зависимости от расположения) возникающие большие
осевые усилия (оба варианта). Погонная нагрузка на шпангоут опреде-
ляется выражением
^^~оГР?таХ <44-8>
2л/? cos ф
В точном расчете учитывают совместную работу шпангоута и об-
шивки корпуса головной части. Поперечная сила может.передаваться
на шпангоут либо касательными усилиями через шпангоут на обшивку,
либо нормальным давлением на внутренний пояс шпангоута. В первом
случае на шпангоут в его плоскости не действуют изгибающие момен-
ты, а во втором, наоборот, он загружен значительными по величине
изгибающими моментами.
В другом случае возможна передача осевого и поперечного усилий
от груза на продольные элементы-диафрагмы и мощный шпангоут.
Осевую нагрузку на одну диафрагму определяют при т диафрагмах
соотношением
гп
max’
(44.9)
377
При действии поперечной нагрузки ввиду того, что центр тяжести
груза расположен на расстоянии 1Х от плоскости шпангоута, продоль-
ные элементы испытывают дополнительную нагрузку. При диаметре
фланца крепления груза числе диафрагм т максимальная допол-
нительная нагрузка на диафрагму
(44.10)
Диафрагму рассчитывают на сдвиг от силы Рд + ДРд, обшивку кор-
пуса головной части ракеты в месте заделки диафрагмы— на устой-
чивость от усилий сдвига. Действующие касательные напряжения в об-
шивке определяются соотношением
-Г АРд
2М
тд
(44.11)
где I — длина диафрагмы;
/г0 — толщина обшивки корпуса.
Если груз расположен в корпусе
крепления располагаются на двух
несимметрично (рис. 44.8), то узлы
панелях между двумя силовыми
Рис. 44.8
шпангоутами. Осевая нагрузка уравновешивается потоком касательных
сил обшивки. Так как центр тяжести груза не совпадает с линией дей-
ствия потока касательных сил обшивки, то возникает момент. Этот мо-
мент через диафрагмы нагружает шпангоуты радиальными силами.
Если груз крепится на двух продольных диафрагмах длиной /, то по-
ток касательных сил по диафрагме
<7т =
_fi
2l xmax
Нагрузка на сварную точку с шагом t между диафрагмой и обшивкой
РТ = qt =
Grn t
—Гр —n
21 Лтах
Боковая поперечная нагрузка также создает момент, нагружающий
шпангоуты радиальными усилиями. Если расстояние между диафраг-
378
мами Ьп, то для шпангоутов, показанных на рис. 44.8, вертикальная
нагрузка приближенно равна
^гр / fl'll
R1 = —— -------------------Пх + -^ -I-----------------------пг,
2 \ I тах 2 Ьп
(44.12)
Ввиду симметрии поперечных нагрузок принимают пУ1 = n2l. После вы-
бора конструктивной схемы рассматривают различные сочетания на-
грузок, определяют наихудшие варианты загружения шпангоутов и
диафрагм. Эти случаи являют-
ся расчетными для элементов
конструкций шпангоутов и диа-
фрагм.
Днища. Головная часть
ракеты закрыта днищем. На
рис. 44.9 показано два возмож-
ных конструктивных варианта
днищ. В варианте I днище во-
гнуто внутрь головной части, в
варианте II — днище выпуклое.
Если конструкция герметичная
и давление внутри головной
части равно 1 ат, то в безвоз-
душном пространстве перепад давлении на оошивку также равен 1 ат.
Значение наружного давления определяют из расчета траектории
возмущенного движения головной части с учетом вращения вокруг по-
перечной оси. Если головная часть входит в атмосферу строго носовой
частью, то нагрузки на днище невелики. В простейшем случае нагрузку
на днище можно определить, если считать, что головная часть входит
в атмосферу днищем вперед. В этом случае а=180°. Тогда [см. § 41] для
дальности полета L= 10 000 км максимальная осевая перегрузка
n*max=55,6 и ПРИ нагРУзке на мидель рм = 1 000 кГ/м2 наружное давле-
ние на поверхность днища равно Р = /гхтах/9м = ^^6 кГ/см2.
В варианте / сферическое днище рассчитывают на устойчивость от
внутреннего давления и на прочность от внешнего, силовой шпангоут,
к которому крепится днище,— на прочность в первом случае и на устой-
чивость во втором. В варианте II днище рассчитывают на прочность
от внутреннего давления и на устойчивость — от внешнего, шпангоут
крепления в первом случае — на устойчивость, во втором — на проч-
ность.
ГЛАВА IX
РАСЧЕТ НА ПРОЧНОСТЬ ОТДЕЛЬНЫХ
ЭЛЕМЕНТОВ КОНСТРУКЦИИ
§ 45. СИЛОВЫЕ ШПАНГОУТЫ
Силовыми шпангоутами называют кольцевые элементы поперечного*
набора конструкции, на которые действуют сосредоточенные или рас-
пределенные на небольшой длине усилия. Таковыми являются шпан-
гоуты подвески грузов и агрегатов,
лизирующих элементов, шпангоуты,
Рис. 45.1
крепления управляющих и стаби-
на которые действуют усилия при
подъеме и транспортировке ра-
кет, и т. д.
На рис. 45.1,а изображен
шпангоут конического переходно-
го отсека ракеты. Осевое усилие,
воспринимаемое лонжеронами пе-
реходного отсека, создает ради-
альные составляющие в месте
стыковки конической части раке-
ты с цилиндрической. Торцевой
шпангоут конического отсека за-
гружен радиальными сосредото-
ченными усилиями, число которых
соответствует числу лонжеронов.
Величина каждого радиального*
усилия, действующего на шпан-
гоут,
г» f N . n М \,
pi = (-----Ь 2 —— COST )tgy.
\ п nR J
При изгибе корпуса моментом М сумма радиальных усилий Рг- равна
вертикальной составляющей, которая уравновешивается погонными уси-
лиями сдвига, передаваемыми на кольцо обшивкой.
На рис. 45.1,6 представлен случай нагружения шпангоута, на кото-
рый действуют усилия при подъеме ракеты. Закон распределения каса-
тельных сил по контуру кольца зависит от условий сопряжения отсека,
в котором заключен шпангоут, с соседними отсеками и от значений
параметра жесткости
(Eh)0R* ’
где R и I — радиус и длина отсека, (Е1)ш — изгибная жесткость шпан-
гоута, (Eh)о — жесткость обшивки. Ниже будет показано, как влияет
параметр жесткости на величину и закон распределения внутренних
усилий в кольце.
Для силовых шпангоутов, жесткость которых велика, можно счи-
тать, что усилия сдвига от радиальной силы Р
Яр = —sincp, (45.1)
nR
380
где ср— угловая координата, отсчитываемая от направления действия
силы Р. Усилие сдвига от момента SR в плоскости шпангоута
= (45. Г)
В жестком круговом шпангоуте по закону синуса уравновешивается
любая нагрузка, равнодействующая которой равна радиальному уси-
лию. Уравновешивание момента относительно центра жесткости осуще-
ствляется постоянными усилиями сдвига. Расчет шпангоута сводится,
таким образом, к расчету замкнутой кольцевой рамы, нагруженной
внешними силами и уравновешенной касательными усилиями.
Определение усилий в шпангоуте. На примере кругового штангоута,
нагруженного радиальной сосредоточенной нагрузкой Р, рассмотрим
порядок определения внутренних усилий в силовом шпангоуте. Будем
Рис. 45.2
считать, что высота сечения кольца мала по сравнению с радиусом и
контур шпангоута отождествляется с линией центров тяжести сече-
ний. Жесткость шпангоута здесь считаем постоянной. Существует не-
сколько методов определения внутренних усилий в кольце. Мы остано-
вимся на методе сил. Система, изображенная на рис. 45.2,а, двг!
раза статически неопределима. Разрежем кольцо по оси симметрии
при ср = О.
Из рис. 45.2,а видно, что
dMq = — qPR2 [ 1 — cos (ср — а) ] da, (45.2)
а с учетом уравнения (45.1), в котором ср заменяется на а, получим
Mq = — £ 1 — coscp---------ср sin ср J. (45.3)
Интегрирование уравнения (45.2) проведено от 0 до ср.
381
Значения нормальной и перерезывающей сил от касательных уси-
лий равны
Ng = ср siticp, (45.4)
2 л
р
Qq--= — (sinср—срcosq>). (45.5}
2 л
Соотношения для единичных моментов
= M2 = b/?(1—coscp). (45.6}
Коэффициенты канонических уравнений находим из уравнений
Л л
х R Г , л/? х /?2 р /1 \ j nR2
611 ТГ \ d(p = ТГ’ 612 = — О — cos<p)dtp = ——,
EJ J EJ EJ j EJ
о о
X R3 C/1 Х2Л Зл/?3 x P/?2 C/1
'’“-TT.V-1 2!;/' —^n(|-c°S4’-
о 0
Л
1 \ PR2 PR3 P /
— —cpslncp )dcp = — ——, d2(? = — —— (1 —coscp)( 1 — coscp —
x / ILJ Tt \
0
1 . \ , 7 PR3
-----Ф sin ф ) аф —---------.
2 J 8 EJ
Подставляя эти соотношения в канонические уравнения
Х1бц + ХД2 + = 0» ) /45 ух
^1^12 + X2S22 4" &2д — О I
и решая их, определяем неизвестные
Xj- ——, Х2 = —. (45.8}
4л 2 4л V 7
Изгибающий момент в любом сечении кольца равен
М = Мд + МД + М2Х2 (45.9)
или
М = —7^ (1--------“ C0S(P — Ф sin ф^. (45.10).
Воспользовавшись соотношениями, аналогичными (45.9), для нормальных
и перерезывающих усилий в кольце получим
р / 3 X
N = Г ф sin ср----— cos ф J, (45.11)
Q =-----ФС08Ф^- (45.12)
На рис. 45.2,6 построены кривые, представляющие закон изменения
внутренних силовых факторов по контуру шпангоута. Исходными за-
висимостями для построения кривых были уравнения (45.10) — (45.12).
Таким же путем можно определить внутренние усилия по контуру
шпангоута при любой внешней нагрузке. Некоторые случаи загружения
и результаты в виде графиков и формул приведены в книге [9]. Для
сложных случаев нагружения оказывается удобно строить эпюры вну-
382
тренних усилий по контуру шпангоута, пользуясь готовыми решениями
для простых случаев. Используя принцип независимости действия сил,
раскладываем внешнее усилие на ряд сил, для которых уже известны
зависимости М (ср), 7V(cp), Q (ср). В соответствии с коэффициентами, по-
лученными при разложении внешней нагрузки, суммируем эпюры от
этих сил. Получаем, таким образом, суммарные эпюры Л4, AZ, Q. На-
пример, закон изменения внутренних усилий для случая нагружения,
изображенного на рис. 45.1,а, можно получить, используя эпюры
рис. 45.2,6.
Вернемся к случаю загружения шпангоута одной радиальной силой..
Из эпюр рис. 45.2,6 видно, что наиболее нагруженным сечением шпан-
гоута является сечение при ср = л, где действует максимальный изгибаю-
щий момент. Для создания рациональной конструкции естественным, на
первый взгляд, кажется увеличение сечения шпангоута в этом месте,
даже если жесткость в остальных участках при этом снижается. Вы-
ясним, как влияет неравномерность жесткости шпангоута на распреде-
ление внутренних усилий.
Будем считать, *что жесткость шпангоута, нагруженного так же, как
и на рис. 45.2,а, не постоянна, а меняется по закону
7 =-----, (45.13)
1 -f- k COS ф
т. е. в сечении под силой жесткость максимальна, а при ср = 0 — мини-
мальна, причем коэффициент
__ J q J min J max
•^min J max
Решаем задачу, как и предыдущую, методом сил. Коэффициенты кано-
нических уравнений здесь равны
л/? Л л/?2
-----, о12 =--------
EJ0 EJQ
PR2 1
EJ0 2
б
EJ0 8 \ 21 J
Неизвестные Хг и X2 будут
d i-JL, 4
PR 3 6
4л
ЗР -142
1—— Л»
2
4л
Так же, как и для шпангоута постоянной жесткости, определяя изгибаю-
щий момент, нормальную и перерезывающую силу, получаем
1 — k — — k1 2 \
*32 I
---------cos ф — ср sin ср I,
1 — —k2 I
2 /
(45.14)
зва
2 3 \
1 — — k — — k* \
3 2 I
---------------sin cp 4- cp cos cp I •
1 ——ft2 /
2 /
Проследим за тем, как зависит величина изгибающего момента под си-
лой от соотношения Jq . Для этого в первом уравнении (45.14) положим
J max
<р = л. Отнесем затем эту величину к величине момента для шпангоута
постоянной жесткости. Тогда получим
М
м
(45.15)
На рис. 45.3 изображена зависимость g от /о/Лпах, из которой вид-
но, что существенное возрастание жесткости под силой увеличивает
момент в сечении. При /о//тах~^О момент увеличивается в 1,67 раза.
Напряжения же в сечении от изгибающего момента с увеличением
жесткости уменьшаются. Примем, что напряжения прямо пропорцио-
нальны моменту и обратно пропорциональны VJ (что справедливо для
двутавровых сечений). При той же площади поясов отношение напря-
жения в шпангоуте переменной жесткости о к напряжению в шпангоуте
постоянной жесткости о можно представить
График зависимости т] от JQ/Jmax изображен на рис. 45.3.
Выше рассмотрены случаи определения внутренних усилий в шпангоу-
тах большой жесткости. В работе [11] показано, что учет упругости обо-
лочки и шпангоута существенно влияет на перераспределение касательных
сил, а следовательно, и внутренних усилий по контуру кольца. На рис.
45.4 представлены эпюры изгибающих моментов для шпангоута конечной
жесткости, нагруженного радиальной силой Р. Шпангоут заключен в отсек
большой длины, имеющий ряд шпангоутов такой же жесткости, как и за-
381
груженный. Параметры жесткости шпангоута = 1 • 10“4 соответ-
(E/i)0/?4
ствуют на графике кривой М2, а - —^0,1 — кривой Mt. Здесь же
(Eh)0Rl
построена эпюра моментов М() для шпангоута бесконечно большой жест-
кости. Кривые Л40 и Mj отличаются друг от друга незначительно. Вели-
чину жесткости шпангоута, которая считается бесконечно большой, можно
оценить. Например, для отсека 7? = 1500 мм, h =3 мм со шпангоутами,
поставленными с шагом / 1500 мм, при параметре (Е})Ш1/(ЕН)О^ = 0,1
момент инерции шпангоута должен быть равен J 1010 мм4. Реальные
шпангоуты имеют жесткость существенно меньшую. Этот пример показы-
вает, что в ряде случаев следует учитывать упругость кольцевых элемен-
тов, снижающих внутренние усилия в шпангоутах. Однако расчет конст-
рукций в этом случае затруднен не только потому, что усложняется ре-
шение, но и в связи с тем, что не всегда верно можно определить усло-
вия сопряжения отсеков со шпангоутами и друг с другом (за счет люфтов,
заклепочных и других соединений). В работе [И] предлагается для слу-
чая загружения шпангоута радиальной силой проводить уравновешивание
не по всему контуру, а лишь на его части в секторе — < ср < при-
чем сила приложена при ср л. В этом случае касательные усилия на
участках, прилегающих к силе Р, распределены по закону
ЧР
q =----sin 2ср.
7 4R
На участке от ср = до ср = л величина изгибающего момента
лл Р/? Г 1 , 1 . 1 । 1 , 2
- ---------г------1----cos ср — sin ср 4---sin2 ср
2 [ л 8 Зл 2
а на участке от ср 0 до ср —
лл РР Г 1 3 । 1
Мо ------------------1----с OS
2 L л 8 Зл
Перерезывающая сила равна
Р Г 1 1 Р
Qi-—------------sin ср — cos ср 4-sin ср cos ср L Q2 ~---sin ср.
2 I Зл J 6л
Нормальное усилие в сечении
Р Г 1 1 Р
Ni = —--------cos ср — sin ср — cos2cp , N2=-------cos ср.
2 I Зл J 6л
Максимальный и изгибающий момент здесь равен
Мтах^0,169Р/?,
т. е. по сравнению со шпангоутом бесконечно большой жесткости в
1,41 раза меньше. Пользуясь методом наложения, таким же образом
можно построить эпюры внутренних усилий для случая изгиба шпан-
гоута сосредоточенным моментом.
Определение перемещений шпангоутов. Часто при расчетах возни-
кает задача определения перемещений контура шпангоута в радиаль-
ном w и касательном v направлениях под действием внешних сил. Ре-
шению ее должна предшествовать задача определения закона М = М (ср).
Не учитывая влияние нормальных и перерезывающих сил на псрсме-
25 Зак. 96
385
щения, обычно для определения w и v пользуются уравнением Бусси-
неска
+ —мм- (4516>
Интеграл этого уравнения равен
w = CiSin ф + C2cos(p + wM, (45.17}
где Wm — частное решение неоднородного уравнения, зависящее от вида
функции Л4(ф). Для случая нагружения шпангоута радиальной сосредо-
точенной силой Р уравнение (45.16) принимает вид
d2ay . PR3 f i 1 . \ /л к i qv
-----=-----------( 1---cos ср — cpsin® ). (45.18}
d(p2 2nFJ \ 2 у
Частное решение уравнения Wm можно найти методом подбора. Для урав-
нения (45.18) оно имеет вид
wm = PR— (1------— Ф sin ф + — ф2 cos ф\ (45.19)
2tiEJ \ 2 4 J
Общее решение описывается уравнением (45.17). Постоянные С± и С2 оп-
ределяют из граничных условий. Из условий симметрии системы постоян-
ная С± равна нулю. Константа С2 определяется из условия
л
ш cos фб(ф = О,
о
откуда получим
С2 = -^7(<3+Тя2} <45-20>
Тогда окончательное выражение для перемещения w будет
ш р-----8~ (з + ~|“ л2^созф---^-ф sin ф + ф2 cos ф^. (45.21)
На рис. 45.2, в построена эпюра радиальных перемещений w для кольца.
Касательное перемещение v в шпангоутах обычно находят, пользуясь
условием нерастяжимости средней линии кольца (е2 = 0), т. е. = w.
dtp
Интегрируя это соотношение и используя условие о нулевом касательном
перемещении при ф = 0, получим
PR3 Г 1 / ? \ 1 1
v =------ ф------( 11 + — л2 ' sin ф + ф cos ф i-ф2 sin ф .
2лЕ] |_ 8 \ 3 / 4 J
Расчет силового шпангоута обычно заканчивают подбором его сече-
ния. Существуют различные формы сечений шпангоутов: уголковые,
швеллерообразные, коробчатые, двутавровые и т. д. Иногда форму се-
чения шпангоута выбирают из конструктивных соображений, например
из условия стыковки. Одним из наиболее эффективных считается шпан-
гоут двутаврового сечения. Расчет шпангоута ведут в предположении,
что стенка тонкая и работает лишь на сдвиг, воспринимая всю перере-
зывающую силу. Нормальные напряжения воспринимаются только пол-
ками шпангоута. При определении напряжений в полках кривизну
шпангоута не учитывают. Основываясь на этом и зная закон распре
деления внутренних усилий по контуру Л4(ф), М(ф), (?(ф) и высоту
386
шпангоута И, приближенно определяют усилия в наружной и внутрен-
ней полках:
м
н ’
= Т ±
Площадь сечения полок выбирают на основании расчета на проч-
ность, приравнивая напряжения при расчетной нагрузке пределу проч-
ности, т. е. Рр//7 = ов- Отношение ширины полки к ее толщине подби-
рают из условий устойчивости, т. е. а=о'кр. Для упругой области
окр = kE(h/b)2 и для шпангоута, показанного на рис. 45.5,а, & = 0,46 [27]
как для пластины бесконечно большой длины, сжатой в осевом направ-
лении, опертой по трем сторонам и с од-
ной стороны свободной. Толщину стенки
шпангоута выбирают, приближенно пола-
гая, что касательные напряжения равно-
мерно распределяются по высоте, т. е.
T, = Q/Hhx. При расчетах определяется ве-
личина касательных напряжений, соот-
ветствующих потере устойчивости пласти-
ны от сдвига ткр. При работе стенки на
сдвиг иногда допускают потерю устойчи-
вости. Это обычно не вызывает разруше-
ния конструкции. В силовых шпангоутах,
в сечениях которых возникают большие
изгибающие моменты в радиальном на-
правлении, как правило, ставят шодкреп-
ляющие элементы (рис. 45.5,6). На каж-
дый элемент действует усилие
P = J±_L
Н R ’
Здесь l = Rq> — шаг подкрепляющих эле-
ментов.
В случае растянутого наружного пояса
мент нагружен сжимающей радиальной нагрузкой. Сечение его подби-
рают из условия устойчивости.
Определение температурных напряжений. Шпангоуты корпуса ра-
кеты, кроме силовых нагрузок, иногда в полете испытывают неравно-
мерный нагрев. В результате этого возникают температурные напряже-
ния. Ниже рассматривается задача определения температурных напря-
жений в круговом шпангоуте двутаврового сечения. Поле температур
принимается таким, что наружная полка нагрета до температуры Г,
а стенка и внутренняя полка — до То. Связь деформаций с напряже-
ниями наружного и внутреннего поясов
е1 = -^- + а(Т-Т0), е2 = -^-, (45.22)
Е Е
а радиальные перемещения
«1 = -^- + а/?(Т-'Т0)> и2= PAR~H)\ (45.23)
ef2
Рис. 45.5
и сжатого внутоеннего эле-
где pi и р2 — радиальная распределенная нагрузка у внутреннего и на-
ружного поясов в стенке.
Здесь R— радиус наружного контура шпангоута, Н — его высота^
а индексы (1) и (2) относятся соответственно к наружному и внутрен-
нему поясам. Стенка шпангоута по наружному и внутреннему конту-
рам загружена погонными усилиями /?1 и р2, равномерно распределен-
25=
387
ними по окружности. Отметим, что здесь не учитывается допущение
о том, что стенка не работает на нормальные напряжения.
Уравнение радиального перемещения стенки, которая здесь может
рассматриваться как диск, имеет вид [68]
Решение его будет
(45.24)
(45.25)
и = С±г + .
г
(45.26)
Напряжения на диске в радиальном направлении
_ Е f du и \
=----------{------1ц---- ,
1 — Ц2 \ dr г )
а с учетом зависимости (45.25) и того, что р = orht получим
1 — ц2 L г2 J
Условия сопряжения полки и стенки шпангоута при r = Ry р = р\ и = и}у
при r=R—Н, р = р2 и = и2 и соотношения (45.23) и (45.26) позволяют
определить напряжения в наружной и внутренней полках шпангоута.
Для случая, когда /?>//, F\=F2 = F и F<^Rh, напряжение в наружном
поясе будет
or1 = -JEa(7’-To)-^. (45.27)
Напряжения во внутреннем поясе имеют ту же величину, но обрат-
ный знак.
Зависимость (45.27) показывает, что напряжения в полках шпан-
гоута достигают весьма больших величин даже при небольших значе-
ниях температуры. Таким же путем можно определить напряжения
в полках при любом законе распределения температуры по высоте
шпангоута.
Температурные напряжения учитываются при расчете силовых эле-
ментов из материалов с относительно небольшим удлинением разрыва.
Конструкции из пластичных материалов, как правило, не разрушаются
от температурных напряжений. В расчетах учитывается лишь сниже-
ние прочностных характеристик материала, вызванное температурным
воздействием.
Выше рассматривались особенности так называемого упругого рас-
чета шпангоутов. Заслуживает внимания расчет кольцевых статически
неопределимых систем по несущей способности. Принципы расчета из-
ложены в книге [68].
§ 46. ПЕРЕДАЧА ПРОДОЛЬНЫХ СИЛ НА ТОНКОСТЕННЫЕ
ЭЛЕМЕНТЫ КОНСТРУКЦИИ
Тонкостенные цилиндрические и конические отсеки ракет часто на-
гружаются продольными сосредоточенными силами. Эти силы возникают,
например, в местах крепления двигательных и переходных ферм и стар-
товых устройств. Так как гладкие тонкостенные оболочки плохо воспри-
нимают сосредоточенные силы, то в районе приложения сосредоточенных
сил отсеки подкрепляются дополнительными элементами. Такими эле-
ментами являются лонжероны и шпангоуты. С помощью лонжеронов
сосредоточенные силы передаются на оболочку в виде усилий сдвига.
Шпангоуты позволяют передавать сосредоточенные силы, на оболочку в
388
виде распределенной нагрузки. Рациональная конструкция отсека, уси-
ленного лонжеронами и шпангоутами, должна передать сосредоточенные
силы на соседний отсек в виде нагрузки, близкой к равномерно распре-
деленной по периметру (рис. 46.1). Это особенно важно в том случае,
когда рассматриваемый отсек передает нагрузки ла топливный бак.
Выравнивание напряжений в сечениях отсека по мере удаления от
мест приложения сосредоточенных сил происходит в соответствии с об-
щим принципом Сен-Венана. Согласно принципу Сен-Венана две стати-
чески эквивалентные системы нагрузок создают в упругом теле напряже-
ния, существенно различные только в области, прилегающей к месту
приложения этих нагрузок. Следовательно, напряжения, вызванные са-
моуравновешенными нагрузками, будут затухать по мере удаления от
области их приложения. Если, например, к торцу цилиндрического отсека
(рис. 46.2) приложены четыре сосредоточенные силы Р и уравновеши-
2Р
вающая их распределенная нагрузка q =——, то напряжения по длине
як
оболочки будут затухать по мере удаления от торца. Длина зоны зату-
хания напряжений пропорциональна радиусу отсека R. Изменение макси-
мального напряжения по длине отсека можно представить в форме за-
тухающей экспоненциальной функции
2Р -ь 4-
в =----е я ,
TtR
где x/R— безразмерная осевая координата;
k — некоторый безразмерный коэффициент.
Исходя из уравнений § 13, можно показать, что для гладкой оболоч-
ки минимальная величина этого коэффициента порядка ^h/R, где h —
толщина оболочки. Таким образом, затухание напряжений в оболочке
зависит от малого параметра h/R. Чем тоньше оболочка тем медленнее
затухают напряжения, вызванные продольной самоуравновешенной на-
грузкой. Следовательно, для тонкой оболочки выравнивание напряжений,
389
вызванных продольными сосредоточенными силами, происходит на отно-
сительно большой длине. Это отличает тонкостенную оболочку от стерж-
ня сплошного сечения.
Подкрепление оболочки шпангоутами увеличивает приведенную тол-
щину и тем самым уменьшает длину зоны затухания нормальных напря-
жений. При большой жесткости шпангоутов на изгиб в своей плоскости
зону затухания приближенно можно определить без учета кривизны обо-
лочки (как для плоской пластины).
Строгое решение задачи о выравнивании напряжений в отсеке, за-
груженном сосредоточенными силами, связано с преодолением чрезвы-
чайно больших математических трудностей. Поэтому в практических
расчетах используют различные приближенные методы, основанные на
упрощенных схемах работы оболочки. В частности, можно использовать
расчетную схему, в которой тонкая обшивка рассматривается как эле-
мент конструкции, работающий только на сдвиг [98].
Ниже приведены решения некоторых задач о передаче сосредоточен-
ных сил на тонкостенные конструкции.
Нагружение плоской панели сосредоточенной силой. Рассмотрим
плоскую симметричную панель с обшивкой толщиной А, подкрепленную
тремя лонжеронами с площадями поперечных сечений и F2 (рис.
46.3, а). Будем считать, что панель подкреплена большим количеством
Рис. 46.3
поперечных элементов, достаточно жестких для того, чтобы можно было
положить удлинения в поперечном направлении равными нулю. На ле-
вом торце панели к среднему лонжерону приложена сила Р, на правом
торце все три лонжерона закреплены упруго. Определим, как по длине
панели изменяются усилия Л^ц и в лонжеронах и усилие сдвига S
в обшивке. При этом не будем учитывать продольные напряжения в
обшивке.
Из условия равновесия (рис. 46.3, б) следует, что в любом сечении
панели
N1 + 2N2=^P.
(46.1)
390
Рассмотрев равновесие элемента крайнего лонжерона (рис. 46,3,в), полу-
чим зависимость
N2 + dN2 — N2—Sdx = 0,
«откуда
S=N2, (46.2)
где штрихом обозначено дифференцирование по х.
Поскольку продольными напряжениями в обшивке мы пренебрегаем,
го из условия равновесия элемента обшивки в проекции на ось х следует,
что усилие сдвига S, а следовательно, и угол сдвига у постоянны по ши-
рине Ь. Величину угла сдвига у выразим через продольные перемещения
и и2 среднего и крайнего лонжеронов (рис. 46,3,г, где А и В—поло-
жения точек до деформации, Л j и Вх— после деформации):
(46.3)
Относительные удлинения 8Х и 82 среднего и крайних лонжеронов будут
81 — U\9 82 — И2,
(46.4)
•Удлинения лонжеро Тука с усилиями N нов ех, е2 и угол сдвига обшивки у связаны законом Ь N2 и S:
1 = -^-, е2=-^-, Y = (46.5) EF± EF2 Gh
где Е и G — модуль упругости материала лонжеронов и модуль сдвига
материала обшивки.
Продифференцировав зависимость (46.2) и использовав выражения
(46.1), (46.3), (46.4) и (46.5), получим дифференциальное уравнение
^относительно одной неизвестной функции М>(х):
N2— k2N2 = P Gh EFJ) ’ (46.6)
где 'Gb (-2- + -L Y (46.6')
b Решение уравнения (46.6) будет N. = \ EFr EF2 J 4- Cx sh kx 4- C2 ch kx. (46.7)
Для определения констант Сх и С2 используем граничные условия. Пос-
кольку левый торец крайнего лонжерона не нагружен, то, очевидно,
N2 = 0 при х =-- 0. (46.8)
Второе граничное условие при х = 1 получим, выразив угол сдвига через
деформации упругих закреплений лонжеронов на правом торце:
•V2 _ JV1
у - =------------— = —, (46.9)
b b Gh ’
где с жесткость упругих закреплений (см. рис. 46.3, а). Или, если ис-
пользовать соотношения (46.1) и (46.2), второе граничное условие можно
представить в виде
N2 — р ,
—— = ?------- при X = /.
Gh be r
(46.10)
391
В частности, при или с—>0 второе граничное условие соответст-
венно будет
N2 = 0 или N2 = Р/3 при х = I. (46.10')
Рассмотрим подробнее
граничного условия (46.8)
случай с —> оо (жесткая заделка). Из первого-
EFi
2 +------
EF,
(46.11)
Тогда из второго граничного условия (N2 = 0 при х = /) находим
Сх = — с2 th kl =--------------th kl (46.12)
„ . EFX
и, следовательно,
jV2 =------------(1 + th kl sh kx — ch kx). (46.13)
_ . EFr
Определив усилие N2, можно с помощью зависимостей (46.1) и
(46.2) найти усилие в среднем лонжероне М и усилие сдвига в обшивке
S. Интересно выяснить, на какой длине произойдет выравнивание напря-
жений по ширине панели. Для этого сначала условно рассмотрим бес-
конечно длинную панель тогда th&Z=l и зависимость (46.13) примет вид
?V2 =-----(1 — е~кх). (46.14)
„ . ЕЛ
И тогда, использовав зависимости (46.1) и (46.2), получим
Nj. = Р — 2N2 = Р------------, (46.15)
S = N'2 =-----—-------е~кх. (46.16)
. . ЕЕ,
С увеличением х усилие Л"2 монотонно возрастает и асимптотически при-
р
ближается к величине -------------. Соответственно напряженья в трех
2 + EF1lEF2
Р
лонжеронах выравниваются и стремятся к значению а =-----------.
F
Определим расстояние хъ при котором усилие Лг2 составит 90 % от
предельного значения. Тогда из зависимости (46.14) получим е_*х*~0,1,
2 3
откуда . Следовательно, с практически достаточной степенью;
k
2 3
точности зависимостью (46.14) можно пользоваться уже при —
и считать, что напряжения в лонжеронах выравниваются на длине х±
392
2 3
= —:. Величина хг обычно имеет порядок ширины обшивки между лон-
k
жеронами. Например, взяв Fr = F2 = 0,5 получим
при Е = 2,6С.
Нагружение цилиндрического от-
сека продольными силами. В каче-
стве второго примера определим изме-
нение усилий в лонжеронах и стрин-
герах по длине цилиндрического отсе-
ка, изображенного на рис. 46.4. Отсек
имеет четыре лонжерона с площадями
поперечных сечений /л и восемь стрин-
геров с площадями поперечных сечений
/с; радиус отсека R\ длина /, толщина
обшивки h\ материал обшивки и под-
креплений одинаковый. На левом тор-
це лонжероны нагружены силами Р\
правый торец отсека жестко заделан.
Считаем, что отсек подкреплен жестки-
ми в своей плоскости шпангоутами и
поэтому можно принять, что окружные
удлинения в обшивке равны нулю и от-
сек сохраняет круговую форму.
Чтобы учесть в решении жесткость обшивки в
Рис. 46.4
продольном направле-
нии, воспользуемся следующим приемом. Всю площадь поперечного сече-
ния обшивки 2л/?й «разнесем» равномерно на стрингеры и лонжероны,
прибавив условно к площади каждого из них А/ = —— и дальше в ре-
шении будем использовать площади лонжеронов и стрингеров F:1 и Fc
с учетом добавленной площади обшивки:
Рл /л + Fc = fc + . (46.17)
О о
Ввиду симметрии сдвигающие усилия в участках обшивки между
стрингерами будут равны нулю; работать на сдвиг будут только участки
обшивки, прилегающие к лонжеронам.
В такой постановке рассматриваемая задача о нагружении цилин-
дрического отсека продольными силами полностью эквивалентна рас-
смотренной выше задаче о нагружении плоской панели. Поэтому для
определения внутренних усилий в цилиндрическом отсеке можно вос-
пользоваться результатами, полученными для плоской панели, заменив
Fj на Лл, F2 на Fc, ширину обшивки в панели b на ширину работающей
к 2nR nR n
на сдвиг обшивки-----= —— .В частности, выравнивание напряжении
2 3
в сечении отсека произойдет на длине хг = —-—, где
k
k2 =
6Gft / 2 . 1 \
nR EFC Ерд )'
(46.18)
2 3
При />—-— усилия в лонжеронах #л в стрингерах Nc и усилие сдвига
k
S в обшивке определяются зависимостями:
393.
(46.19)
где продольная координата х отсчитывается от левого торца. В этой
задаче в площадь продольных подкреплений была включена площадь
поперечного сечения обшивки. Так, учитываемая в решении площадь
стрингера была равна Fc = fc + Af, где fc — площадь собственно стрин-
Л с 2nRh itRh, „
гера, а == ——— — —----------площадь обшивки, приходящаяся на один
стрингер. Таким приемом учета продольной жесткости обшивки можно
пользоваться при любом соотношении величин fc и Af. В частности, этот
прием решения применим и при fc = 0, т. е. тогда, когда стрингеров нет.
При этом для уточнения расчета число вводимых таким образом сосре-
доточенных площадей можно увеличивать.
Изгиб цилиндрического отсека двумя сосредоточенными силами.
Цилиндрический отсек радиуса /?, длины I имеет два лонжерона, кото-
рые нагружены на левом торце двумя равными, по противоположно
Рис. 46.5
направленными силами Р; правый торец отсека жестко заделан (рис.
-46.5, а). Площади поперечного сечения лонжеронов одинаковы и равны
F. Толщина обшивки h. Как и в предыдущей задаче, считаем, что об-
шивка отсека подкреплена большим числом жестких в своей плоскости
шпангоутов и можно нс учитывать деформации поперечных сечений
отсека в их плоскости.
Определим распределение усилий в лонжеронах и обшивке рассмат-
риваемого отсека.
Задачу будем решать с помощью приближенного энергетического
метода [98], причем, в отличие от рассмотренных выше примеров, учтем
в решении осевые нормальные напряжения в обшивке. Рассмотрим рав-
394
повссие части отсека длиной х, где координата х отсчитывается от левого
торца отсека.
В любом сечении отсека момент от осевых напряжений в обшивке
o.v и усилий в лонжеронах N должен быть равен изгибающему моменту
от заданных внешних сил:
2 f <JjiRcos <p R d <p + 2NR = 2PR. (46.20)
0
Так как перерезывающая сила в любом сечении отсека равна нулю
(изгибающий момент постоянен по длине отсека), то
2 xft/?sin cpdcp = 0. (46.21)
о
Распределение напряжений ох в обшивке отсека можно задать в
виде ряда Фурье с коэффициентами, зависящими от координаты х:
°х= £/„(*) COS Пф.
1,3,5
Вследствие симметрии конструкции и косой симметрии внешней нагрузки
суммирование производится только по нечетным значениям п. Функции
/п(х) можно определить из условия минимума потенциальной энергии
внутренних напряжений отсека (принцип Кастилиано). Для приближен-
ного решения задачи ряд Фурье обычно заменяют суммой конечного
числа слагаемых. Для иллюстрации энергетического метода решения
задачи ограничимся первым членом ряда. Тогда
о'х = Д (х) cos ср. (46.22)
Из уравнения (46.20) получим
(46.23)
nRh
Следовательно, выражение (46.22) можно представить в виде
<г. = — -(Р — JV) cos ф, (46.24)
nRh
где N'— переменное по длине отсека усилие в лонжероне.
Касательное напряжение в обшивке можно определить из уравне-
ния равновесия элемента обшивки в проекции на ось х (рис. 46.5, б):
= 0. (46.25)
дх R д<р v ’
Отсюда, учитывая зависимость (46.24) получим
т = г0 (х) — Rfi (х) sin ср = т0 (х) 4-— N' sin ср, (46.26)
лЛ
где то(х) — касательные напряжения при <р = 0.
Неизвестную функцию то(х) выразим через усилие W, используя
условие равновесия элемента лонжерона (рис. 46.5, в):
N' -|-2йт0(х) - 0. (46.27)
Теперь для т с учетом уравнений (46.26) и (46.27) получим выражение:
г =- -Y- ЛГ 1 + — sincpY (46.28)
395
Проверим выполнение условия (46.21), которое должно удовлетво-
ряться тождественно, поскольку выражение для т удовлетворяет урав-
нениями равновесия (46.25) и (46.27), а выражение для ох обеспечи-
вает постоянство изгибающего момента по длине отсека. Действительно,
подставив выражение для т в форме (46.28) в условие (45.21), получим
2 т hR sin ср dtp = 2N'R sin ср Н- — sin2 qQdcp = 0. (46.29)
b b 4
Таким образом, все силовые факторы в отсеке оказываются выра-
женными через одну неизвестную функцию М(х) —усилие в лонжероне.
Эту функцию найдем из условия минимума потенциальной энергии
отсека:
Ф = 2\~2EFdX+ 2 f ^~ZEhRdXd(f + 2 j f (46.30)
b bo о b
Здесь первое слагаемое соответствует потенциальной энергии растяги-
вающих напряжений в лонжероне, второе слагаемое—потенциальной
энергии нормальных напряжений в обшивке и последнее слагаемое —
потенциальной энергии касательных напряжений в обшивке.
Подставив выражения для ох и т из уравнений (46.24) и (46.28) в
формулу (46.30) и произведя интегрирование по угловой координате <р,
получим
i
Ф = JU (N,N')dx, (46.31)
о
где
U (N, N") = — + — (Р ~?V)2 -г (Л2 ~ 8) Р (N')2. (46.32)
EF л ERh 4nGh
Искомую функцию N (x), при которой потенциальная энергия минимальна,
определяют из уравнения Эйлера
dU_____d- / д£7 \ _ 0
dN dx \ dN' J
Для выражения U в форме (46.32) получим
N" — k2N =----------—------Р,
(л2 — 8) ER2
(46.33)
(46.34)
где
& =__________4G f 2 -i-
(л2 — 8) ER2 \
Общее решение уравнения (46.34)
xRh
F
W = С, sh kx 4- С» ch kx +
1 xRh + 2F
(46.35)
(46.36)
Для определения констант С\ и С2 надо составить граничные усло-
вия на левом (х = 0) и правом (х = /) торцах оболочки. На левом торце
имеем очевидное граничное условие: при х = 0 N]=P. Для составления
граничного условия на правом торце воспользуемся тем, что сечение
отсека х = 1 можо рассматривать как сечение в плоскости симметрии
отсека длиной 2Z, полученного зеркальным отражением рассматриваемого
отсека относительно плоскости заделки.
396
Для симметрично загруженного отсека длиной 2Z в плоскости сим-
метрии имеем N'=0. Таким образом, искомые граничные условия будут:
N = Р при х = 0,
N' =0 при х = I.
Из формулы (46.36) имеем
N' = Crk ch kx + C2k sh kx.
Из граничных условий получаем
Ci = —C2thkl = ~Р
2F \
nRh + 2F ’ ’
_______2F
nRh + 2F
Следовательно, усилие в лонжероне
N = P-----—-----r_^L(ch^x — thAsZshAx) + 1 .
nRh + ZF [ 2F
Касательное напряжение при ср = 0
т0 =-----— N' = — Р---------------(sh kx — th kl ch kx).
0 2h 2(JtRh + 2F}
При значительной длине отсека, когда можно принять th Л/ = 1, уси-
лие в лонжероне и величины нормальных и касательных
обшивке с учетом выражений (46.24) и (46.28) будут
N = Р------—----(1 +
nRh + 2F \ 2F J
о,. = Р----------(1 — е~кх) cos <р,
х nRh±2F
n knR e~liX f < 4 . \
х = Р-----------------( 1------sin ср V
2 TtRh, + 2F \ л J
Как и в двух предыдущих задачах, можно считать, что усилия в лонже-
ронах и напряжения в обшивке практически перестают меняться по дли-
2 3
не отсека при x = %i, где =—-—. При х>х{ напряжения в лонжероне
k
и обшивке будут приближенно равны
N 2Р 2Р п
О —-----= ------------, О' = ----------COS ф, X — 0.
л F nRh + 2F х jtRh + 2F т
Такое распределение напряжений соответствует решению, которое можно
получить, рассматривая отсек как балку, загруженную моментом 2PR.
Действительно, момент инерции поперечного сечения отсека равен
J xR3h + 2FR2,
а напряжения от изгибающего момента М = 2PR
MR 2Р
(Г =-----COS ф -------------COS ф.
х J nRh + 2F
Рассмотренные задачи иллюстрируют перераспределение внутренних
усилий в тонкостенных конструкциях, загруженных продольными сосре-
доточенными силами. При достаточном удалении от загруженного торца
напряжения в поперечных сечениях отсека определяются только вели-
чинами равнодействующих внешних сил и моментов.
(46.37)
(46.38)
напряжений в
(46.39)
(46.40)
e~kx
(46.41)
397
Полученные формулы для определения длины зоны хь где происхо-
дит перераспределение напряжений, соответствовали предположению о
недеформируемости поперечных сечений в их плоскости. В действитель-
ных конструкциях, когда шпангоуты имеют конечную жесткость на изгиб
и растяжение, длина зоны перераспределения напряжений может быть
большей.
Для коротких отсеков ракеты, когда длина отсека меньше его диа-
метра, передача продольных сосредоточенных сил с помощью лонжеро-
нов может оказаться неэффективной. На малой длине отсека только
небольшая часть продольных сил может быть передана на обшивку с
помощью усилий сдвига.
В этом случае на прилегающий отсек могут передаться большие со-
средоточенные силы реакций лонжеронов. Если эти силы опасны для
конструкции прилегающего отсека, то для их уменьшения можно отсек,
к которому приложены внешние сосредоточенные нагрузки, усилить
шпангоутом с относительно большой жесткостью на изгиб из его плос-
кости. В такой конструкции шпангоут, нагруженный силами, перпендику-
лярными к его плоскости, работает подобно криволинейному брусу, ле-
жащему на сплошном упругом основании.
Коэффициент жесткости упругого основания определяется величи-
ной жесткости на растяжение-сжатие в осевом направлении прилегаю-
щей к шпангоуту конструкции корпуса ракеты.
§ 47. БАЛЛОНЫ ВЫСОКОГО ДАВЛЕНИЯ, ТРУБОПРОВОДЫ,
СИЛЬФОНЫ
Расчет баллонов. В качестве балломов высокого давления в ракетах
применяются емкости разнообразной формы. Наиболее широко исполь-
зуются сферические так называемые шар-баллоны; получили также рас-
пространение баллоны в виде замкнутого кругового тора, цилиндриче-
ское с полусферическими днищами (рис. 47.1) и т. п. Эти емкости имеют
Рис. 47.1
некоторые преимущества по сравнению с шар-баллонами по условиям
компоновки, но зато уступают им по весу.
Давление является основной нагрузкой, определяющей толщину
стенки емкости и ее вес. Баллоны в ракете, как правило, крепят при
помощи лент с тендерами на специальных ложементах, так что нагру-
жение инерционными усилиями оказывается незначительным и в расчет
обычно не принимается. Местные усиления и малые размеры отверстий
в местах соединения заправочной и расходной трубок позволяют не учи-
тывать отверстий при расчете баллона.
Изготовляется большинство баллонов из штампованных элементов
путем сварки, так что при расчете обычно учитывается ослабляющее
влияние сварного шва. Материалы, применяемые для емкостей, должны
398
иметь высокие характеристики удельной прочности на растяжение. Этим
требованиям удовлетворяют высокопрочные стали и сплавы титана. Не-
давно баллоны высокого давления стали изготовлять из стекловолокни-
стых материалов.
Из условий эксплуатации и надежности конструкции коэффициент
безопасности при расчете баллонов высокого давления принимают боль-
шим (/>2). Расчет баллонов высокого давления на прочность сводится
к определению наибольшего усилия в оболочке, нагруженной равномер-
ным внутренним давлением, и выбору толщины оболочки таким образом,
чтобы расчетные напряжения в баллоне были равны пределу прочности
материала оп.
В сферической оболочке радиуса /?, нагруженной внутренним давле-
нием, напряженное состояние однородно, а
°i = <*2 = —,
2 2/i
и толщину стенки шар-баллона можно подобрать из соотношения
2ав&
Здесь — эксплуатационное давление, k — коэффициент прочности
сварного шва (/е = 0,85—0,95).
Напряжения в торовой оболочке кругового сечения, нагруженной
внутренним давлением, определяются зависимостями
. R .
Г + - Sin ф
а - 2 =
1 h г + R sin ф 2 2h
(47.1>
Здесь R — радиус сечения тора, г — радиус кольца, ф— угол между нор-
малью к поверхности оболочки и осью вращения. Наибольшие напряже-
л
ния возникают на внутреннем экваторе тора, где ф =— —,
R
а = _Р*_ L_______2
lmax h r — R
Толщину стенки торового баллона выбирают из соотношения
R
2
(47.2)
koa г ~ R
Цилиндрический баллон с полусферическими днищами, нагружен-
ный внутренним давлением, имеет некоторые особенности в распределе-
нии внутренних усилий. На участке сопряжения цилиндра с полусферой,
кроме мембранных напряжений, возникают изгибные напряжения от
краевого эффекта. Учет изгибных напряжений в баллонах высокого дав-
ления необходим в связи с тем, что конструкции, изготовленные из высо-
копрочных материалов, имеющих сравнительно небольшое относительное-
удлинение разрыва, часто разрушаются при испытаниях на участках
сопряжения с характерным изломом. Мембранные напряжения в цилинд-
ре ain = p/?/2/i, О2ц = Р^/Л, в сфере 0\c = (52c = pRl^h. Закон изгибающего
момента по осевой координате $, отсчитываемой от точки сопряжения
цилиндра с полусферой, описывается уравнением
м pRh_ sings
8 /3(1 —ц2)
399-
а дополнительные окружные напряжения, соответствующие краевому эф-
фекту,
(47.4)
o',. =---— e~as cos as.
2Д 4/i
Коэффициент а определяют из выражения
У RW
Для оболочек цилиндра и полусферы одинаковой толщины максимальные
напряжения в цилиндрической оболочке равны
Швах = (0,5 + 0,146), (<т2ц)тах = (1 + 0,0312). (47.3)
Вторые слагаемые отражают влияние краевого эффекта. Соотношения
(47.3) показывают, что наибольшие напряжения в баллоне — окружные.
Они практически не отличаются от мембранных, поэтому при расчете
такого баллона достаточно воспользоваться известным безмоментным
решением для окружных напряжений G2 = pR/h и толщину стенки бал-
лона определять из уравнения
Итак, для расчета баллонов высокого давления пользуются обыч-
но соотношениями (47.1), (47.2), (47.4). Эти зависимости показывают,
что толщина стенки баллона, а следовательно, и вес его тем меньше, чем
выше прочностные характеристики материала. Для увеличения предела
прочности материала, из которого изготовлен баллон, иногда идут на
некоторые конструктивные усовершенствования. Например, сферические
баллоны сжатого гелия на ракете «Атлас» помещают в емкости, содержа-
щие жидкий азот, температура которого Т = —195° С. При такой темпе-
ратуре значительно повышаются прочностные характеристики материала
баллона—титанового сплава (при Т = 20°С оп= 109 кГ1мм2, от = 96 кГ1мм2,
а при Т = — 195°С сгв= 164 кГ{мм2, <ут= 160 кГ1мм2). Это позволяет балло-
ны, находящиеся под давлением наддува р = 350 ат, при диаметре 407 мм
сделать сравнительно легкими. Вес одного баллона из титанового спла-
ва составляет всего G = 22,2 кГ.
Расчет трубопроводов. В ракетах с двигателем ЖРД встречаются
трубопроводы подачи горючего и окислителя к двигателю и так назы-
ваемые тоннельные трубы.
Трубопроводы подачи работают обычно при внутреннем давлении
Р Ро + пхун. (47.5)
Здесь Н — высота столба от зеркала жидкости в баке до расчетного се-
чения, пх — величина осевой перегрузки с учетом динамических особен-
ностей гидравлического тракта. Тоннельные трубы проходят внутри ба-
ков и загружаются внешним для них давлением наддува и столба
жидкости.
При транспортировке возникают поперечные перегрузки пу, создаю-
щие осевые напряжения в трубе. Трубопроводы подачи рассчитывают
прежде всего на прочность от внутреннего давления р:
fl
Напряжение при выбранной толщине трубы не должно превышать
предела прочности материала <тв- Это условие, как правило, не является
лимитирующим, и толщину труб выбирают из конструктивных или тех-
400
(47.6)
нологических соображений. В случае транспортировки незаправленных
баков при действии поперечной перегрузки напряжения в трубопроводе
определяют, как в балке длиной I (расстояние между точками крепления
труб), загруженной равномерно распределенной нагрузкой q = 2nRhyTny
(ут — удельный вес материала трубопровода). Трубу, закрепленную в
днищах бака, можно считать двухопорной балкой, максимальные осе-
вые напряжения в которой
" = Т Г' (47'7)
Эти напряжения должны удовлетворять условию прочности, т. е. о<ов,
а также условию устойчивости трубопровода как оболочки, т. е.
о<<уКр, где
о = kE —.
кр R
Для оболочки коэффициент k = 0,22.
При больших поперечных перегрузках к трубопроводам в баках кре-
пят растяжки, увеличивая тем самым количество опор балки. При этом
напряжения в трубопроводе следует определять известными способами,
как в многоопорной балке. Следует еще отметить, что при транспорти-
ровке ракеты возможно возникновение циклических поперечных перегру-
зок. При выборе шага растяжек на трубопроводах это учитывают и
стремятся к тому, чтобы частота колебаний трубы возможно больше
отличалась от частоты вынужденных колебаний системы.
Для обеспечения топливом поворотных двигателей, а также в уста-
новках с высоким уровнем вибраций применяют гибкие трубопроводы.
Они представляют собой эластичные трубы, обеспечивающие гибкость и
герметичность шланга, с несущей проволочной оплеткой из нержавеющей
стали. Наибольшее распространение получили шланги с внутренними
трубками из каучука и тефлона. Применяемые шланги могут работать
при давлениях до 300 ат и имеют сравнительно большие размеры. На-
пример, для двигателя Ф = 1 используются гибкие шланги до 350 мм
[122]. Расчет оплетки гибких шлангов можно вести так же, как и опле-
тенного корпуса РДТТ.
Тоннельные трубы рассчитывают на устойчивость от давления
p? = pzff рэ — суммарное эксплуатационное давление наддува и столба
жидкости. Простейший расчет показывает, что гладкие трубы теряют
устойчивость при очень малом внешнем давлении. Например, труба при
h= \ мм и R = 100 мм из алюминиевого сплава теряет устойчивость при
р = 0,2 кГ/см2. Для увеличения критического давления в тоннельных
трубах делают поперечные зиги (обычно омегообразного сечения). Эти
зиги являются своего рода шпангоутами, уменьшающими длину оболоч-
ки и повышающими ее устойчивость. Расчет тоннельных труб ведут в
следующей последовательности. Выбирают толщину трубы так, чтобы
окружные напряжения в ней удовлетворяли условиям прочности. Опре-
деляют шаг зигов I по уравнению
= (47.8)
Принимают коэффициент £ = 0,64. Находят радиус зига г или его момент
инерции из условия равноустойчивости участка трубы между зигами как
оболочки и зига как кольца:
(47.9)
26 Зак. 96
401
При больших радиусах г возможна местная потеря устойчивости — обра-
зование вмятины на внешнем контуре зига. Местные критические напря-
жения определяют приближенно по отношению
°кР = ^т-- (47.10)
Коэффициент k можно принять равным 0,15.
Расчет сильфонов. Сильфоны представляют собой оболочки враще-
ния, состоящие из торовых участков положительной и отрицательной
кривизны и соединенные плоскими круговыми пластинами; они приме-
няются для компенсации температурных и технологических деформаций
в трубопроводах.
Расчет сильфона сводится к определению его жесткости при осевом
и угловых перемещениях и
Рис. 47.2
расчету на прочность. Вопросы работы силь-
фонов и их расчет подробно освещены в ли-
тературе [68, 92]. Существует ряд методов
уточненного расчета сильфонов как оболо-
чек вращения. Применение этих методов,
однако, бывает затруднено из-за их гро-
моздкости. Удовлетворительные результаты
при определении жесткости сильфона дает
схематизация его как системы кольцевых
пластин. Пластины считают попеременно
заделанными по внутреннему и наружному
контурам (рис. 47.2). В такой схеме не учи-
тываются участки скругления, и поэтому
жесткость сильфона, полученная расчетным
путем, оказывается несколько выше дейст-
вительной.
Для определения жесткости сильфона
при осевом перемещении достаточно рас-
смотреть один элемент схемы — плоскую круговую кольцевую пластину,
нагруженную осевой силой Р. Наибольший прогиб для пластины, у кото-
рой отсутствуют угловые перемещения по внутреннему и наружному
контурам, определяется соотношением
w = — 3-—— (r2 — 1 — _4j?2 In2 7?Y (47.11)
Eh3 4л \ __ j /
_____ _ r
где R— отношение наружного радиуса пластины к внутреннему/? — —;
h — толщина пластины. При количестве волн гофрировки п число пла-
стин 2п и жесткость сильфона ,kp = PI2nw определяется зависимостью
Хр = ——-----— (r2 — 1 — _4/?2 In2 R
3(1 — и2) г2п \ Я2—1
(47.12)
При угловых перемещениях сильфон также представляют как систе-
му кольцевых пластин, но нагруженных изгибающим моментом. Угол
поворота а центрального кольца при неподвижном внешнем контуре
пластины
а _ 3 1-И2 М (/?2 + 1)1п/?-/?2+ ]
л Eh3 /?2 + 1
и отсюда нетрудно найти жесткость угловых перемещений сильфона
Хм = . Деформация сильфонов при поперечных перемещениях тру-
бопроводов и сохранении параллельности оси, как показано в книге
402
[68], сводится к угловым перемещениям. Связь между параллельным пе-
ремещениехМ А//, длиной сильфона L, количеством гофров п и углом а
определяется зависимостью
(47.14)
Толщину сильфонов определяют из расчета на прочность. Изгибные
напряжения ввиду небольшого ресурса работы и пластичности материа-
ла в расчет не принимают. Эксперименты показывают, что разрушению
сильфонов от внутреннего давления предшествует распрямление наруж-
ных участков гофров и, в конце концов, разрушение оболочки вдоль
образующей. Толщина стенки сильфона поэтому может быть определе-
на из соотношения
P3fR
h =
(47.15)
ГЛАВА X
РАСЧЕТ КОНСТРУКЦИИ
ЖИДКОСТНОГО РАКЕТНОГО ДВИГАТЕЛЯ
§ 48. ТИПИЧНЫЕ СИЛОВЫЕ СХЕМЫ. ОСОБЕННОСТИ
РАСЧЕТА НА ПРОЧНОСТЬ ОБОЛОЧКИ ЖРД
Известно, что ЖРД является наиболее теплонапряженным из совре-
менных тепловых двигателей. По количеству энергии, выделяющейся в
единицу времени в единице объема камеры сгорания, ЖРД в тысячи раз
превосходит стационарные тепловые установки. Такая теплонапряжен-
ность ЖРД связана с высокими давлением и температурой газов в ка-
мере сгорания, причем развитие и совершенствование двигателей ведет
к дальнейшему возрастанию этих параметров.
Специфика работы двигателя ставит перед его создателями довольно
трудные задачи. В общем комплексе подлежащих разрешению вопросов
важную роль играют вопросы, связанные с созданием надежно работаю-
щей, легкой и технологичной оболочки камеры ЖРД.
Схема конструкции и особенности нагружения камеры ЖРД. В кон-
струкции камеры ЖРД выделяют три основных элемента (рис. 48.1, а):
форсуночную головку /, оболочку камеры сгорания 2 и сопло 3; кро-
Рис. 48.1
ме того, в нее входят еще узлы крепления 4, входной коллектор 5 и ряд
других вспомогательных деталей. Наиболее характерным является тепло-
прочностной расчет оболочки камеры сгорания и поэтому на особенно-
стях ее нагружения мы остановимся подробнее.
Оболочка представляет собой двухстеночную осесимметричную кон-
струкцию. Внутренняя и наружная ее стенки скреплены между собой.
404
Различные виды скрепления стенок по геометрическому признаку можно
подразделить на три типа: продольные, винтовые и точечные связи.
Между стенками имеется пространство, называемое охлаждающим
трактом. По нему протекает один из компонентов топлива, используемый
для охлаждения оболочки. Вход охлаждающего компонента обычно
выполнен в виде коллектора в зоне сопла, а выход непосредственно свя-
зан с форсуночной головкой. В некоторых случаях часть оболочки сопла
может быть выполнена одностеночной в виде неохлаждаемого насадка.
Компоненты топлива через форсуночную головку поступают в каме-
ру сгорания, где происходит преобразование химической энергии топлива
в тепловую энергию продуктов сгорания, которые истекают через сопло,
создавая реактивную силу тяги двигателя. Характер изменения давления
газов рт и их температуры Тг по длине камеры показан на рис. 48.1,6.
Давление газов является одним из основных силовых факторов, на-
гружающих оболочку камеры. Вместе с тем интенсивный теплообмен
•с продуктами сгорания вызьНвает нагрев внутренней <и, в некоторой сте-
пени, наружной стенок. Изменение механических свойств материала сте-
нок с изменением температуры и значительные температурные дефор-
мации следует считать вторым основным фактором, влияющим на усло-
вия работы оболочки в целом, т. е. на ее общую прочность и жесткость.
Кроме этого, можно говорить о местной прочности <и жесткости
между связями каждой из стенок в отдельности, а также о прочности
элементов связи и их соединений со стенками. В этом случае необходимо
рассмотреть давление охлаждающей жидкости, которое на рис. 48.1,6
обозначено
Таким образом, исследование и расчет оболочки камеры как сило-
вого элемента двигателя распадаются на два основных направления:
1) общая прочность и жесткость оболочки как единого целого под дей-
ствием внутреннего давления и теплового воздействия; 2) местная проч-
ность и жесткость, в первую очередь, внутренней стенки между элемен-
тами связи под действием нагрева и перепада давлений \р = рж—рг.
При рассмотрении этих направлений особое внимание должно быть
уделено взаимной связи прочности оболочки и ее температурного состоя-
ния, связи условий работы оболочки как силового элемента двигателя с
особенностями его рабочего процесса. Важность учета взаимной зави-
симости этих факторов можно показать на простом примере. Под дей-
ствием перепада давлений Др внутренняя стенка прогибается в пролете
между элементами связи. В результате увеличивается площадь проход-
ного сечения охлаждающего тракта, падает скорость жидкости, ухудша-
ются условия охлаждения внутренней стенки, растет ее температура,
вызывающая снижение механических характеристик материала. Это
может привести к дальнейшему увеличению прогиба внутренней стенки,
к ее прогару или разрушению.
Материал оболочки, как правило, работает за пределом упругости.
Поэтому работоспособность оболочки камеры зависит не только
от силового воздействия на рабочем режиме, но и от последова-
тельности нагружения оболочки в процессе изготовления и испытания
двигателя. Остаточные деформации и напряжения, возникающие после
очередного нагружения, влияют на поведение оболочки при следующем
нагружении. Исследование истории нагружения оболочки камеры пред-
ставляет собой довольно сложную задачу. Для ее решения, помимо зна-
ния технологических, испытательных и рабочих режимов, включая режи-
мы пуска и остановки двигателя, необходимо располагать сведениями о
поведении материалов оболочки с учетом фактора времени при одновре-
менном изменении напряженно-деформированного состояния и темпе-
ратуры.
Специфическим режимом нагружения оболочки ЖРД является оп-
405
рессовка, когда подается давление в охлаждающий тракт при отсут-
ствии давления Дг в полости камеры. Такие условия обычно создаются
в процессе пуска двигателя, когда давление в камере сгорания еще не
поднялось, а охлаждающий компонент в тракте уже находится под дав-
лением. Кроме того, указанные условия возникают при опрессовке
охлаждающего тракта повышенным давлением в процессе технологиче-
ского контроля оболочки двигателя.
Реактивная сила тяги, создаваемая двигателем, с оболочки камеры
через узлы крепления и ферму передается на корпус ракеты. Узлы креп-
ления располагаются, как правило, в одной плоскости, нормальной к оси
двигателя. Они обычно устанавливаются в зоне форсуночной головки, а
для поворотных двигателей возможно также крепление камеры в зоне
критического сечения сопла или за цилиндрическую часть камеры сго-
рания. При проектировании и расчете узлов крепления необходимо учи
тывать ряд особенностей, связанных с передачей на оболочку камеры
сосредоточенных усилий.
Расположение узлов крепления двигателя на камере определяет вид
эпюры осевых сил в ее оболочке. Осевые силы оказывают некоторое
влияние на общую прочность и жесткость оболочки камеры. Характер
изменения осевой силы Nx по длине камеры при разных вариантах рас-
положения узлов крепления (/ — у головки, II— в конце цилиндрической
части камеры сгорания и III — в зоне критического сечения сопла) по-
казан на рис. 48.1,в.
Помимо статического нагружения оболочки на ее работоспособность
могут повлиять динамические режимы нагружения, так как ЖРД являет-
ся мощным источником колебаний в широком диапазоне частот. Ампли-
туды колебания давлений рг и которые определяют динамическое
нагружение оболочки, в особо неблагоприятных случаях могут быть со-
измеримы с номинальными значениями давлений. Возникновение коле-
баний давления связано с работой системы подачи компонентов и меха-
низмом горения топлива в камере сгорания.
Оболочка камеры подвергается прямому воздействию возмущающих
сил давления газов. При совпадении частоты собственных колебаний
конструкции с частотой колебаний давления наступает состояние резо-
нанса. Появляются большие амплитуды колебаний оболочки, что непо-
средственно сказывается на ее работоспособности. Резонансные колеба-
ния могут иметь и более сложную природу, когда переменное давление
газов вызывает изгибные (неосесимметричные) колебания оболочки
ЖРД. Это явление называется параметрическим резонансом.
Известно, что оптимальным режимом работы сопла ракетного двига-
теля является расчетный режим истечения, когда давление газов в
выходном сечении совпадает с атмосферным на данной высоте. Однако
при работе двигателя на различных высотах возникают нерасчетные ре-
жимы истечения газов. Типичным нерасчетным режимом работы сопла
с большим расширением газов является стендовое испытание двигателя
при нормальном атмосферном давлении р0. Оболочка сопла в этом слу-
чае оказывается нагруженной переменным по длине перепадом давлений
Ро—Рг, который может вызвать потерю устойчивости оболочки.
Таким образом, для двигателей с большим расширением сопла на-
гружение части его оболочки внешним давлением является одним из
расчетных случаев, подлежащих рассмотрению при проектировании обо-
лочки.
О критериях прочности и работоспособности ракетных двигателей.
В машиностроении используются три основных вида расчетов конструк-
ций на прочность: расчет по разрушающим (предельным) нагрузкам,
расчет по допускаемым напряжениям и расчет по допускаемым переме-
щениям или деформациям.
406
При расчете по разрушающим нагрузкам в основу кладут то зна-
чение нагрузки, при котором конструкция теряет насущую способность,
разрушается. Элементы тонкостенных конструкций^ работающие на сжа-
тие, обычно разрушаются в результате потери устойчивости, а элементы,
работающие на растяжение, — вследствие достижения напряжениями
предела прочности материала.
При расчете вводятся два основных коэффициента: коэффи-
циент безопасности и коэффициент запаса проч-
ности:
рр рразр
/ =------ и п =-----------
' рэ РР
(48.1)
где Рэ — значение эксплуатационной нагрузки; Р? — расчетное значение
разрушающей нагрузки; Рразр— фактическое значение разрушающей
нагрузки, определяемое экспериментально. Этот подход к прочностному
расчету использовался во второй части настоящего пособия. Но при ра-
счете ракетных двигателей наряду с расчетом по разрушающим нагруз-
кам используются также и расчеты по допускаемым напряжениям и
допускаемым перемещениям. Поэтому вместо коэффициента безопасно-
сти f и запаса прочности /г, определяемых зависимостями (48.1), при
расчете двигателей чаще пользуются просто понятием коэффициента
запаса, определяя его либо как отношение разрушающей и эксплуа-
тационной нагрузок, либо как отношение соответствующих напряжений.
Так, например, коэффициент запаса по пределу прочности равен
ив=,Ов/аэ, где оэ—максимальное значение эксплуатационного напряже-
ния, Оп — предел прочности материала.
Ниже указаны целесообразные подходы к расчету на прочность эле-
ментов жидкостного двигателя.
Камеру сгорания ЖРД на общую несущую способность целесооб-
разно рассчитывать по предельным нагрузкам, не считаясь с местными
концентрациями напряжений, поскольку обычно камера сгорания выпол-
няется из достаточно пластичных материалов. Расчет охлаждающего
тракта на местные прогибы ведут по допускаемым перемещениям [93].
Критерием работоспособности плоской форсуночной головки является
герметичность соединения форсунок с пластинами. Поэтому прочностной
расчет плоской головки следует вести по допускаемым деформациям.
Величины относительных удлинений, вызываемых изгибом и нагревом
плоской головки, следует сравнивать с теми их значениями (определяе-
мыми экспериментально), при которых нарушается герметичность соеди-
нения форсунок с пластинами [93]. Кроме того, если в камере имеются
сварные или паяные соединения и если материал в зоне пайки обладает
повышенной хрупкостью, то расчет этих соединений в некоторых случаях
возможен и по допускаемым напряжениям.
§ 49. ОСОБЕННОСТИ ТЕПЛООБМЕНА В ЖРД
Выше отмечалось (см. § 48), что тепловое воздействие является
одним из основных факторов, влияющих на работоспособность оболочки
двигателя. Оно определяется интенсивной передачей тепла от сильно
нагретых продуктов сгорания к оболочке путем конвекции и лучеиспус-
кания. От оболочки тепло отводится благодаря конвекции к жидкости,
движущейся по охлаждающему тракту (см. рис. 48.1,а). Для учета влия-
ния теплового воздействия на работоспособность двигателя необходимо
располагать сведениями, позволяющими количественно охарактеризовать
процессы теплообмена, происходящие в ЖРД. Поэтому на расчете усло-
вий теплообмена оболочки двигателя с газовым потоком и охлаждающей
жидкостью следует остановиться подробнее.
407
Расчет теплоотдачи газового потока к оболочке ЖРД представляет
собой одну из наиболее сложных задач конвективного теплообмена. По
длине камеры происходит переход от дозвукового течения продуктов
сгорания к сверхзвуковому, изменение давления рг и температуры Тг
движущегося газа (см. рис. 48.1,6), его химического состава и тепло-
физических свойств.
Интенсивность теплоотдачи, характеризуемая коэффициентом аг, в
первом приближении пропорциональна удельному массовому расходу
газа, равному произведению его плотности р на скорость w. Величина
pw также переменна по длине камеры. Эта величина в соответствии с
формулой
тп
где tn и Sr — массовый расход газов и площадь поперечного сечения
сопла, достигает максимума в наименьшем, критическом сечении сопла.
В соответствии с этим в критическом сечении от газов к оболочке обычно
передается максимальный удельный тепловой поток, а коэффициент
теплоотдачи достигает наибольшего значения. Распределение аг по длине
камеры довольно близко по характеру к изменению величины ро>.
Процесс передачи тепла конвекцией сосредоточен в пределах погра-
ничного слоя, в котором происходит торможение газа. У поверхности обо-
лочки газ тормозится полностью. Если тепло от поверхности, омываемой
продуктами сгорания, не отводится (идеально теплоизолированная стенка),
то ее температура ТГЛ1 принимает значение, близкое к Тг — температуре
адиабатического торможения газового потока. Если же тепло отводится в
охлаждающую жидкость, то Тг.п<^Тг, а от газов к оболочке передается
удельный тепловой поток
<7к^аг(Т;-Тг.п). (49.1)
Температура Тг определяется условиями горения компонентов топ-
лива в пристеночном слое. Если соотношения компонентов в этом слое
и в объеме камеры сгорания одинаковы, то значение Тг совпадает с тем-
пературой газов в камере сгорания. В некоторых случаях в пристеночный
слой подают избыточное количество одного из компонентов, чаще всего—
горючего. Это приводит к неполному сгоранию топлива в пристеночном
слое и снижению температуры Тг, что позволяет при прочих равных
условиях уменьшить конвективный тепловой поток, передаваемый от га-
зов к оболочке.
Для подсчета коэффициента теплоотдачи аг можно воспользоваться
зависимостью [21]
/ др* х 0,066
Nu =,0,0162 Ре0 82 .
где Nu и Ре — критерии подобия Нуссельта и Пекле. Критерий Нуссель-
та характеризует связь между интенсивностью теплоотдачи и темпера-
турным полем в пограничном слое при обтекании поверхности потоком.
Критерий Пекле устанавливает связь между передачей тепла в газовом
потоке конвекцией и теплопроводностью. Приведенная зависимость полу-
чена и экспериментально проверена для дозвуковых течений газа. Рас-
пространение ее на сверхзвуковой поток оправдано лишь при прибли-
женном расчете теплоотдачи. Разрешим эту зависимость относительно
коэффициента аг, который входит в критерий Нуссельта, и усредним
некоторые мало изменяющиеся с температурой величины; получим
аг = 4cp/n°’82£)_I’82 emlM2-град. (49.2)
408
Входящие в эту формулу параметры должны быть подставлены в строго
определенных единицах измерения: удельная теплоемкость газов ср в
кдж!кг-град, т в кг/сек, диаметр сечения сопла D в м.
Следует отметить, что в формулах (49.1) и (49.2) не учитывается
влияние на конвективный теплообмен дополнительного механизма пере-
дачи тепла, который связан с процессами диссоциации и рекомбинации
молекул газа в пограничном слое подобно тому, как это происходит при
обтекании ракеты воздушным потоком с большой сверхзвуковой ско-
ростью (см. § 29). Влияние этого фактора на теплообмен в двигателе
проявляется тем сильнее, чем выше температура ТГ.
Наряду с конвекцией передача тепла от продуктов сгорания к обо-
лочке в некоторой степени определяется и лучеиспусканием. Излучение
газов, в отличие от твердых тел, имеющих непрерывный спектр, проис-
ходит лишь при определенных длинах волн (в так называемых полосах
спектра). Поглощение и испускание лучистой энергии происходит во
всем объеме, занимаемом газом, в то время как для твердых тел эти
процессы протекают на их поверхности. Кроме того, излучение газов
зависит от переменных по длине двигателя состава, температуры и дав-
ления продуктов сгорания, от формы и размеров камеры. Эти особен-
ности в излучении газов вносят большие сложности в расчет лучистого
теплового потока, передаваемого к оболочке двигателя.
Для упрощения расчета камеру ЖРД обычно представляют в виде
замкнутой оболочки с поверхностью, соответствующей свойствам серого
тела, в полости которой находится однородный газ с постоянными по
объему параметрами. В такой схеме результативный лучистый поток qr
от газа, приходящийся на единицу поверхности оболочки, можно вычис-
лить, пользуясь сведениями из § 24.
Очевидно, что эффективное излучение газа совпадает с падающим
на поверхность оболочки (#г —<7пад) и состоит из собственного излуче-
ния газа с термодинамической температурой Тг и доли эффективного
излучения оболочки, которая пропускается газом без поглощения,
т. е.
Яг — ег9г + (1 -^г) Я »
где ег и 4Г — степень черноты и поглощательная способность газа по от-
ношению к излучению оболочки, сг0 = 5,77-10-8 вт/л2(°К)4— коэффи-
циент излучения абсолютно черного тела.
При </пад — д* и равенстве степени черноты е и поглощательной спо-
собности А оболочки-*для ее эффективного излучения из соотношений
(24.3) и (24.4) следует
Я* = eq° + (1 — Л) q„aA = Aq° + (1 — Л) q*, q° = <т0Т?.п
и
• о 1—А -
я ^я°-------— я,
А
где Тг.п — температура поверхности оболочки и q — результативный лучис-
тый поток от оболочки к газу, причем
Q = ~ Не-
последовательным исключением неизвестных величин q, q* и q*r четы-
ре представленных выше соотношения можно привести к уравнению
qr = е; (8Г q°T - Лг<7») = 8Г’<ТО (8ГТ? - ЛГТ£.П), (49.3)
409
где е*—эффективная степень черноты системы газ — оболочка,
1
д
< = t 1------------ (49.4)
При Лг = 0 (абсолютно прозрачный газ) е* = 1. Если газ поглощает все
падающее излучение (Лг == 1), то е* = А. Таким образом,
Для оболочек с большой поглощательной способностью (0,8<Л< 1) мож-
но пользоваться приближенной формулой
< = -^-(1 + Я). (49.5)
Для охлаждаемой оболочки ЖРД Тг.п С Тг. Поэтому в соотношении
(49.3) вторым членом в скобках можно пренебрегать по сравнению с пер-
вым и вести расчет по формуле
qr = 8*8га07^, (49.6)
в которой предварительно необходимо определить степень черноты газа
8Г. При температурах сгорания топлива в ЖРД наиболее существенным
излучением обладают водяной пар Н2О и углекислый газ СО2, которые
составляют значительную долю в продуктах сгорания современных дви-
гателей. Поэтому можно принять, что
ег == ен2о + еСо2 — Дег, (49.7)
где Дег ен2о£со2 — поправка, которая учитывает, что полосы спектра для
Н2О и СО2 частично перекрываются, так что излучение водяного пара в
некоторой степени поглощается углекислым газом, и наоборот. Степени чер-
ноты Н2О и СО2 можно подсчитать по эмпирическим формулам [2]
р0,2 ___
ен2о = 71 (рн2о00-64~ и есо2 = 7,1 /Рсо21 (49.8)
тг у тг
в которых парциальные давления рн2о и Рсо2 и суммарное давление газов
рг принимают в кГ!см\ а эффективную длину пути луча в газовом объе-
ме I — в м. Ее величину определяют по формуле
/=3,6^, (49.9)
Sr
где Ег и Sr — объем газа и поверхность оболочки, охватывающая этот
объем.
В действительности в камере ЖРД не удается выделить газовый
объем с постоянными параметрами, охваченный замкнутой оболочкой,
как это принято в рассмотренной выше расчетной схеме. Поэтому по
формулам (49.5) — (49.9) принято рассчитывать передачу тепла излуче-
нием в камере сгорания двигателя, а в сечениях сопла брать следующие
доли от рассчитанного лучистого потока: при О/Окр=1 (критическое се-
чение) — 0,5; D/DKY)= 1,5—0,15; О/ОКр = 2,5—0,04. В выходной части сопла
с большим расширением газов лучистым потоком можно пренебречь в
сравнении с конвективным.
Суммарный удельный тепловой поток
передаваемый от газа к оболочке на установившемся режиме работы
двигателя, воспринимается охлаждающей жидкостью. Для вычисления
410
коэффициента теплоотдачи аж к охлаждающей жидкости можно восполь-
зоваться зависимостью [14]
Миж = 0,027 Re0»8 i/P?; (чЛ.п)0'14.
Параметры, входящие в критерии Нуссельта (Nu), Рейнольдса (Re)
и Прандтля (Рг), берут при температуре Тж жидкости в рассматривае-
мом сечении охлаждающего тракта. Критерий Рейнольдса характеризует
гидродинамический режим течения жидкости. Его числовая величина
показывает соотношение между силами инерции и трения в потоке. Кри-
терий Прандтля характеризует подобие полей скорости и температуры
в пограничном слое при обтекании поверхности потоком. Последний со-
множитель в формуле учитывает направление передачи тепла и зависит
от отношения коэффициентов вязкости жидкости при температуре
Лк(Пж) и температуре Тхп охлаждаемой поверхности оболочки (т]х,п).
Этот сомножитель мало отличается от единицы, и в приближенных ра-
счетах его можно не учитывать.
Если разрешить приведенную выше зависимость относительно коэф-
фициента теплоотдачи, входящего в критерий Нуссельта, то получим
аж = 27сж 0^)°’2 (Рж^ж)0,8 Ргж2/з вт/м^-град, (49.10)
В эту формулу удельную теплоемкость сж охлаждающей жидкости
подставляют в кдж!кг-град, коэффициент вязкости т]ж— в кг!сек -м,
плотность рж — в кг/м\ скорость движения жидкости в охлаждающем
тракте шж— в м!сек. Эквивалентный диаметр £>0, м вычисляют по фор-
муле
D =
э П ’
где Зж и П — площадь и периметр поперечного сечения канала охлаж-
дающего тракта.
Температура жидкости вследствие ее подогрева возрастает по мере
движения от входного коллектора к форсуночной головке. На устано-
вившемся режиме работы двигателя величина Тж в фиксированном сече-
нии охлаждающего тракта остается постоянной; ее определяют по
формуле
где Гвх и т?к— температура жидкости на входе в охлаждающий тракт
и ее массовый расход. Так как суммарный удельный тепловой поток q
зависит от температуры Тг.п, которая неизвестна, то при определении
подогрева следует задаваться ожидаемым распределением температуры
Гг.п по длине камеры. Интегрирование ведут по длине s образующей
оболочки камеры в направлении движения жидкости, начиная от вход-
ного коллектора (см. рис. 48.1,а). В практических расчетах интегриро-
вание заменяют последовательным суммированием приращений темпе-
ратуры жидкости ДГЖ по участкам, в пределах каждого из которых все
параметры считаются постоянными.
После определения температуры жидкости в охлаждающем тракте
можно приступить к расчету распределения температуры в оболочке
двигателя. Здесь целесообразно рассмотреть наиболее простой случай,
когда элементы связи между внутренней и наружной стенками оболочки
отсутствуют или, по крайней мере, не участвуют существенным образом
в передаче тепла от внутренней стенки к охлаждающей жидкости. Усло-
вия теплообмена по поверхности стенки изменяются сравнительно мед-
411
ленно, поэтому передачей тепла вдоль нее посредством теплопроводности
можно пренебречь. Тогда внутреннюю стенку толщиной h' с коэффициен-
том теплопроводности материала V в тепловом отношении можно рас-
сматривать как плоскую, а распределение температуры в ней считать
одномерным (рис. 49.1, а). На поверхности при х' = 0 теплообмен с про-
дуктами сгорания определяется значениями аг, Тг и а на поверх-
ности, омываемой жидкостью, (x' = h')—значениями аж и Тж.
Для суммарного удельного теплового потока, передаваемого от газа
через стенку в жидкость, можно составить следующие соотношения:
Я — аг (TV Т’г.п) + <7Г = аг(Тг Тг.п),
<7=4? (Т’г.п-Тх.п),
h
Я =аж(Тх.п —Гж).
В первом из них Тг = Т* 4- (?г/аг) является приведенной температу-
рой газов, которая в форме уравнения Ньютона для конвективного тепло-
обмена позволяет учесть передачу тепла излучением. Из этих соотноше-
ний после исключения температур поверхностей стенки Тг.п и 7\.п получим
тг- тж---- (4911)
1----------------------------------------------------------------h' 1
+ а ; +
аг л аж
Распределение температуры по толщине стенки линейное
Т = Тг.п-(Л.п-Тх.п)4»
h
причем
Тх.п = тж + (<7/аж) и Тг.п = тх.п + (qh’/K'). (49.12)
Средняя температура по толщине внутренней стенки
г - 4- + Гг п) - тж + • (49-13}
2 аж 2Х
Температуру наружной стенки оболочки из-за малой интенсивности
ее теплообмена с внешней средой можно принять равной температуре
жидкости в рассматриваемом сечении охлаждающего тракта: Т" = Тп{.
Анализ влияния условий теплообмена и термического сопротивления
412
h'/K' внутренней стенки на ее температурное состояние удобно провести
графическим путем. Для построения диаграммы (рис. 49.1, б) по гори-
зонтали следует отложить отрезки, пропорциональные термическим со-
противлениям 1/аг, Л'/Л' и 1/аж, aja крайних вертикалях — температурам
Тг и Тж. Тогда отрезок прямой Тг—Гж в заштрихованной полосе будет
характеризовать распределение температуры по толщине внутренней
стенки, а ординаты точек его пересечения с соответствующими вертика-
лями будут соответствовать значениям характерных температур Тг.п, Tz,
Тх.п-
Изменение одного из параметров приводит к смещению отрезка в
заштрихованной области и позволяет судить об изменении температур-
ного состояния стенки. Например, увеличение интенсивности теплоотда-
чи в охлаждающую жидкость (рост коэффициента аж) приводит к пони-
жению температур всех точек стенки, причем степень понижения тем
больше, чем ближе находится рассматриваемая точка к охлаждаемой
поверхности. При падении величины аж наблюдается обратная картина.
Подобным образом можно показать, что температуры всех точек стенки
возрастают, если увеличиваются значения Гг, аг и Гж, и наоборот, темпе-
ратуры падают, если эти величины уменьшаются. Следует отметить, что
на температурном состоянии стенки благоприятно сказывается нанесение
на нагреваемую поверхность покрытия с высоким термическим сопротив-
лением.
Одним из параметров, который поддается изменению при проектиро-
вании оболочки двигателя, является термическое сопротивление h'/h'
внутренней стенки. Влияние изменения величины h'/k' на среднюю темпе-
ратуру Т* можно проанализировать с помощью диаграммы на рис.
49.1, в. Для этого фиксируют положение вертикали, соответствующей
срединной поверхности внутренней стенки, а остальные вертикали сме-
щают на расстояния, пропорциональные половине величины уменьшения
h'lK'. Так как для существующих двигателей аг<аж, то уменьшение
/г'/Х' приведет к падению средней температуры внутренней стенки. Для
выяснения влияния этого фактора на температуры Тг.п и Гхп следует
провести подобные построения, поочередно фиксируя положение верти-
калей, соответствующих нагреваемой и охлаждаемой поверхностям стен-
ки. В результате получим, что уменьшение ft'/V приводит к падению
Тг.п и росту Тх.п.
Этим объясняется стремление при проектировании оболочки двига-
теля уменьшать толщину внутренней стенки h' и применять для стенки
более теплопроводные материалы.
Пример, Пусть заданы следующие значения параметров, определяющих передачу
тепла от продуктов сгорания: Тг = Тг = 3500 °К = 3227 °C, ср = 4 кдж1кг-град\ пг =
= 40 кг/сек; длина и диаметр камеры сгорания Л=£) = 0,3 ж; рг = 40 кГ(см2\
рно= 15 кГ/см^', Рсог = Ю кГ[смг, Д = е = 0,8. Охлаждение оболочки ведется керо-
сином, расход тж = 12 кг)сек, зазор между стенками оболочки 6 = 1 мм, температура
керосина в рассматриваемом сечении охлаждающего тракта Тж = 100 °C. При этой тем-
пературе керосин имеет следующие теплофизические характеристики, необходимые для
расчета коэффициента теплоотдачи аж : сж = 2,22 кдж!кг-град', т|ж = 4,7-10~4 кг!м-сек\
коэффициент теплопроводности Хж = 0,133 вт/м-град-, рж = 750 кг/м3, что дает значе-
ние критерия Прандтля Ргж = сжт]ж/Хж = 7,85.
Рассмотрим два варианта выполнения внутренней стенки толщиной h' = 1 мм: сталь-
ная (X' = 14,5 вт!м-град) и медная (X' = 290 вгп1м-град).
Прежде всего по формуле (49.2) вычислим коэффициент теплоотдачи
ar = 4с*т°’82О-'‘82 = 4-4(40)°-82 (0,3)“1182 = 2960 вт/м?-град.
Затем по формулам (49.5)—(49.9) последовательно определим
Vr nD4J4
I = 3,6 —- = 3,6----------—
Sr лО£ + л£>2/2
= 0,6D= 0,18 м;
413
8н2о = 71 (Рн,оО°’6Р?’2/7’г = 71 (15 • 0,18)°>б(40)°-2/3500 = 0,077;
8co2 = 7,l^W / /7\ = 7,1 10 • 0,18 /]/350б = 0,146;
ег = 8н2о + 8со2 - 8н2о8со2 = 0,077 + 0,146 - 0,077 • 0,146 = 0,212;
е* = (1 + Я)/2 = (1 + 0,8)/2 = 0,9;
+ = 8*er<J0T* = 0,9 • 0,212 • 5,77 • 10"»(3500)< = 1,65 • 10» вт/м2.
Приведенная температура продуктов сгорания
Тг = Т* + (7г/аг) = 3500 + (1,65- 10е/2960) = 4058 °К = 3785 °C.
Скорость движения керосина в охлаждающем тракте
12
л (D -I- 2/г' + д) 6рж 3,14(300 + 2+ 1) 10-3.10-3-750 16,8 м/сек’
а эквивалентный диаметр щелевого охлаждающего тракта
п 4S* 4л (О+ 2/1'+6) 6
3 П л (D + 2/1') + л (D + 2/г' + 2d) 2' М'
Из формулы (49.10) получим
«ж = 27сж (-^-)0,2 (Рж^ж)°'8РГж А =
(4 7 • Ю-4 о 2
—-----r-Т- ) (750 • 16,8)0,8(7,85)—2/з = 17300 вт;.м--град.
2 • Ю“3 /
Для стальной стенки из формул (49.11) — (49.13) следует
3785 — 100
-----------— = 7,85 • 106em/,w2,
1 Ю-3 1-'
2960 + 14,5 + 17 300
________Тг-Тк
q 1_____/г' 1
--+ +-------
аГ л аж
7’x.n = 7'ж + (<?/«ж) = 100+ (7,85- 10»/17300) = 554 °C,
7’г.п = Т’х.п + (р/г'/^') = 554 + (7,85 • 10» - 10-3/14,5)= 1094 °C,
Т' = 0,5(Тх п + Тг п) = 0,5(554 -|- 1094) = 824 °C.
Для медной стенки соответственно получим
q = 9,21 • 106 em/M2. ТХ П = 632 ОС; Тг п = 664 °C; Г = 648 °C.
В первом варианте (стальная стенка) возникает опасность перегрева поверхности про-
дуктами сгорания. Во втором варианте (медная стенка) значение Тг п резко снижается
но возрастает температура Тх п, что может привести к разложению керосина на охлаж-
даемой поверхности, отложению на ней слоя кокса и последующему прогару стенки из-за
ухудшения условий ее охлаждения.
Интересно проследить за тем, как меняется температурное состояние
внутренней стенки с изменением давления рг в камере сгорания двига-
теля. Если при этом соотношение компонентов в пристеночном слое
остается неизменным, то температуру Тг и удельную теплоемкость газов
ср можно считать постоянными. Так как массовый расход пропорцио-
нален давлению рг, то коэффициент теплоотдачи в_ соответствии с фор-
мулой (49.2) аг~ (Рг)0’82. Зависимость величины qr от давления более
сложная. Расход охлаждающей жидкости также пропорционален давле-
нию рг. Если приближенно принять, что температура остается по-
стоянной в рассматриваемом сечении, то согласно формуле (49.10)
«ж~(Рг)0>8. Влияние давления рг на изменение условий теплообмена и
414
характерных те’мператур медной стенки для принятых выше данных
видно из табл. 49.1.
Изменение давления сильно влияет на величину суммарного удель-
ного теплового потока q, но мало сказывается на значениях характер-
ных температур медной стенки. В случае стальной стенки эти темпера-
туры изменяются значительно сильнее.
Таблица 49.1
рг, кГ/см2 20 40 60 80
аг, etn/м2- град 1680 2960 4120 5220
дг-10-6, вт!м2 1,21 1,65 1,99 2,28
о о — 3947 3785 3710 3665
аж, вт/м2-град 9900 17 300 23 900 30 200
д*Ю“6, вт/м2 5,49 9,21 12,43 15,50
тх.„, °C 655 632 620 614
Тг.п, °C 674 664 663 668
Г, °C 665 648 642 641
§ 50. ТЕМПЕРАТУРНОЕ СОСТОЯНИЕ ОБОЛОЧКИ ДВИГАТЕЛЯ
Уменьшение термического сопротивления внутренней стенки благо-
приятно сказывается на ее температурном состоянии. Но, как правило,
это одновременно приводит к снижению прочности и жесткости внутрен-
ней стенки либо из-за уменьшения ее толщины, либо в связи с тем, что
сплавы с высокой теплопроводностью имеют худшие механические ха-
рактеристики. Этого можно избежать, если внутреннюю и наружную
стенки скрепить между собой достаточно часто расположенными связями.
В качестве связей используют элементы различной конфигурации
(рис. 50.1, а—в) [14], которые обычно соединяют со стенками посред-
ством высокотемпературной пайки.
Помимо выполнения задачи скрепления стенок элементы связи в той
или иной мере участвуют в передаче тепла охлаждающей жидкости. При
часто расположенных связях их участие в передаче тепла становится
значительным и должно учитываться в расчете температурного состояния
оболочки двигателя. В связи с этим расчетную схему плоской стенки с
гладким щелевым охлаждающим трактом, рассмотренную в предыду-
щем параграфе, следует уточнить. Это уточнение можно сделать в доста-
точно общем виде для различных типов связей, в том числе для связей
в виде проволочных проставок и фрезерованных ребер (рис. 50.1,а, б).
Оболочку, выполненную в виде набора спаянных между собой профили-
рованных трубок, усиленных наружной стенкой, целесообразно рассмот-
реть отдельно.
Расчет распределения температуры в оболочке с частыми связями.
Если тепловой контакт между элементами связи с внутренней стенкой
415
считать идеальным и пренебречь участием наружной стенки в передаче
тепла охлаждающей жидкости, расчет оболочки сведется к расчету
плоской стенки с ребрами (рис. 50.1,г). Степень участия ребер в передаче
тепла жидкости зависит от соотношения между геометрическими разме-
рами ребер, коэффициентом теплопроводности Л их материала и коэффи-
циентом теплоотдачи к жидкости аж, который в дальнейшем принимается
одинаковым на всей охлаждаемой поверхности. Эффективность ребер
характеризуется коэффициентом kp, равным отношению тепловых пото-
Рис. 50.1
ков, проходящих через поверхность с ребрами и гладкую (без ребер)
поверхность стенки (36].
Если ребра выполнены из материала с высоким значением X, а вели-
чина а» мала, то температура Гх.п по всей охлаждаемой поверхности
примерно одинакова и коэффициент kp в этом случае равен отношению
площадей поверхности с ребрами 5Р и гладкой поверхности Sr, т. е.
<ил>
где b, h и I — пролет между ребрами, их толщина и высота. Тогда удель-
ный тепловой поток q, отнесенный к гладкой поверхности нагрева Sr,
будет
Я = аж^3 (Тх.п — Тж),
где Тж — температура охлаждающей жидкости. Для расчета температур-
ного поля в оболочке двигателя применимы формулы (49.11) — (49.13),
если в них вместо аш везде подставить произведение aMks. Коэффициент
ks здесь характеризует улучшение условий охлаждения оболочки бла-
годаря увеличению охлаждаемой поверхности.
С уменьшением теплопроводности материала ребер и возрастанием
коэффициента теплоотдачи аж распределение температуры по охлаждае-
мой поверхности становится неравномерным, температура Тх.п пони-
жается с удалением от основания ребер. Поэтому не все участки поверх-
ности стенки с ребрами одинаково эффективно участвуют в передаче
тепла жидкости и действительный коэффициент эффективности ребер
kp оказывается меньше, чем k8. Для определения коэффициента kp сле-
дует рассмотреть процесс теплопроводности в отдельно взятом ребре.
Если предположить, что температура Тх.п в основании ребра (х=0)
равна температуре охлаждаемой поверхности стенки в пролете между
ребрами, а распределение температуры в ребре является одномерным,
изменяющимся только по его высоте, то тепловой поток через его осно-
вание согласно формуле (25.7) будет равен
Q. = 2a./(r;.n-TJ-^-. г = (50.2)
416
С поверхности стенки в пролете между ребрами снимается тепловой
поток
Qb = ажЬ (Тх,„—Тж). (50.3)
Если же ребра отсутствуют, то тепловой поток через гладкую поверхность
стенки с прежней температурой 7\.п равен
<2г = аж(6+Л)(Л.п-Тж). (50.4)
Из соотношений (50.2) — (50.4) следует
Q0 + Qb b , 21 thg
Qr ’ b + h b + h £
(50.5)
Вновь для расчета температурного состояния оболочки двигателя
можно пользоваться формулами (49.11) — (49.13), заменив в них величи-
ну аж на произведение анЛр. Например, для подсчитанных в предыдущем
параграфе параметров, характеризующих условия теплообмена оболочки
с продуктами сгорания и охлаждающей жидкостью, ТГ=3285°С;
аг = 2960 вт!м2-град\ аж=17 300 вт1м2-град и при заданных Тж=100°С.
коэффициенте теплопроводности X=V = 290 вт/м-град и геометрических
размерах внутренней стенки с фрезерованными ребрами h'=b = h= \ мм,
1 = 6 = 2 мм получим
£ = /2ажДй I = /2-17300/290 • 10~3 • 2 • 10~3 = 0,69;
ГЬ 21 thg; _ 1 2-2 th 0,69 2 23
b + h + b + h £ ~ 1 + 1 + 1 +1 0,69 ~ ’
ТГ—ТЖ _________________________3285— 100_____________
1 /1' 1 “ (1/2960) + (1-10-з/290)-^(1/17300.2,23)
аг X
8,65 • 106 бпг/м2,
7\.п = ТЖ + (?/аж£р) - 100 + (8,65-106/17300-2,23) = 325 °C,
Л.п - Л.п + (qh'/V) = 355 °C и Г =-- 0,5 (7\.п + Тг.п) - 340 °C.
Сравнение полученных результатов со значениями температур, рассчи-
танными в примере предыдущего параграфа, показывает, что ребра
существенно улучшают условия охлаждения внутренней стенки.
В частном случае три £->0 (th£)/£—И и из соотношения (50.5) сле-
дует, что £р->(6 + 2/)/(& + й) =&s. Объясняется это тем, что термическое
сопротивление ребра становится малым в сравнении с термическим со-
противлением теплоотдачи к охлаждающей жидкости. Поэтому темпера-
тура боковых поверхностей ребра становится равной температуре осно-
вания, а коэффициент &р оказывается пропорциональным увеличению
охлаждаемой поверхности.
При неудачно выбранных параметрах вместо улучшения условий
охлаждения стенки с ребрами можно прийти к обратному результату.
Действительно, из соотношения (50.5) при 2/(th£)/£</z следует,что&р< 1,
т. е. тепловой поток, проходящий через стенку с ребрами, меньше, чем
через гладкую. Такое положение объясняется тем, что при этом условии
термическое сопротивление ребра становится больше, чем термическое
сопротивление теплоотдачи непосредственно к охлаждающей жидкости
с поверхности основания ребра. Граница рационального применения ре-
бер (&р=1) устанавливается соотношением
2/ = й.
27 Зак. 96
417
С другой стороны, при Л = 0, когда ребра вообще отсутствуют, снова
получается &р=1. Следовательно, при фиксированной ширине пролета &,
которая зависит от технологических возможностей изготовления оболоч-
ки и допустимого гидравлического сопротивления охлаждающего тракта,
существует оптимальная толщина ребра, которая обеспечивает макси-
мальное значение коэффициента т. е. наилучшие условия охлаждения
внутренней стенки.
Выше мы пренебрегали передачей тепла через торец ребра, темпе-
ратура которого может быть рассчитана по формуле вида (25.6) при
х = 1:
Т'—Тж
Т,= Тж н---
1 Ж Chg
Среднюю температуру Т" наружной стенки в этом случае можно принять
равной Тц что для данных рассмотренного выше примера составит
Г' = Тг = 280°С.
В действительности часть тепла через торцы ребер передается на-
ружной стенке, а от нее — охлаждающей жидкости. Верхняя оценка доли
от суммарного теплового потока, передаваемой через наружную стенку,
определяется выражением
^ax = pchS + (^r-; (50.6)
Оно получено в предположении, что температуры торца ребра и наруж-
ной стенки совпадают. Это выражение позволяет оценить максимальную
ошибку, которая может возникнуть при использовании приведенных
выше формул. Если участие наружной стенки в передаче тепла сущест-
венно (&тах>0,1), то расчет по этим формулам может дать слишком
завышенные в сравнении с действительными значения температур.
В таком случае для уточнения распределения температуры в оболочке
двигателя следует воспользоваться численным способом расчета или же
применить для решения задачи аналоги (см. § 25).
Уточненный расчет оболочки с ребрами. В качестве примера для
проведения уточненного расчета ниже рассматривается повторяющийся
элемент оболочки с фрезерованными ребрами (рис. 50.2,а), причем сталь-
ная наружная стенка имеет толщину Л"=1 мм и коэффициент теплопро-
водности V'=14,5 вт!м-град. Через плоскости симметрии, которые выде-
ляют этот элемент из оболочки (см. рис. 50.1,6), тепловой поток не про-
ходит. Поэтому они соответствуют идеально теплоизолированным
поверхностям. Теплообменом наружной стенки с внешней средой прене-
брегаем, так что соответствующая поверхность этой стенки также счи-
тается идеально теплоизолированной. Все необходимые для расчета ве-
личины приняты такими же, как и в предыдущем примере. При вычис-
ленном ранее значении £ = 0,69 и заданных 1 = 2 мм, Ь = \ мм по формуле
(50.6) получаем ^тах = 0,144, что свидетельствует о целесообразности про-
ведения уточненного расчета температурного состояния оболочки.
На рис. 50.2,6 показана область численного решения задачи. Вза-
имно перпендикулярными плоскостями (отмечены пунктиром) эта об-
ласть разбита на ячейки со сторонами Ах = Дг/ = 0,5 мм. Узловые точки
соединены между собой системой теплопроводящих стержней.
Перед численным решением задачи необходимо составить алгебраи-
ческие уравнения, которые связывают между собой температуры узло-
вых точек. Уравнение вида (25.8), полученное для внутренней узловой
точки области, в данной задаче справедливо для точек 5 и 20. Например,
для точки 5 оно имеет вид
4T\=T2 + T4 + Tq + T8.
418
Уравнение такого вида распространяется и на точки 4, 6, 9, 11, 13, 15,
19, 21—24. Все эти точки расположены на идеально теплоизолированной
поверхности, и их можно условно считать внутренними. Недостающие
для их окружения соседние узловые точки подбирают из соображений
симметрии. Например,
для точки 4
4Т4 = Т\-± 27\ + Т7,
для точки 23
4Т2з = 2Т20 -J- Т22 + T2V
цля точки 24
4Ти = 2Т21 + 2Т23.
Рис. 50.2
Уравнения для точек 1—3 составляют с учетом условий теплообмена
оболочки с газовым потоком. Например,
для точки 1
X' (Т2 - 7\) + К (Л - Л) + аг (Тг - Л)>- 0.
Дх Д V 2
для точки 2
к, Ьу/2 ,т _ т ) + X' (Т3 — Т.)
Дх Дх
+ V 4^- (Л - + «г (Тг- Т2у= 0.
При значениях %'=290 вт!м-град, аг=2960 вт/м^-град и 7’Г = 3285°С
соответственно получаем 2,005 = 7'2 + 7'4+17 град и 4,01 7’2 = 7’i + 7’3 +
+ 27’з + 34 град.
27* 419
Подобным образом составляются уравнения и для узловых точек,
расположенных на охлаждаемой поверхности оболочки. Например, для
точки 8
К (Л - т8) + X' (Т. - Ts) + X' 4- (т9- TJ +
\у \х Дх
) / Ьх_ _Ьу_Х т _ = 0
Дг/ 4 8/ ж \ 2 2 / °
При значениях аж = 17 300 вт;м2-град и Тж = 100 °C получаем
6,0678 = 27\ + Т7 4- Т9 + 27\о -! 6 град.
Наиболее сложными в данной задаче являются уравнения для точек
17 и 18, так как они лежат на границе двух участков оболочки, выпол-
ненных из разных материалов. При составлении уравнений необходимо
учитывать, что проводимость стержня между точками 17 и 18 опреде-
ляется свойствами обоих материалов. В частности, для точки 17
X' (Tlt - Т17) + X" (Т1в - Т17) 4- (X' + X") -^(Лз - Тп) 4-
Л// Дх Дх
+4-х- - т„)+«ж (+ 44) (г>к - =о.
Д// \ 2 2 /
После подстановки числовых значений параметров получаем
2,267\7 = Ти + 0,05 Т16 + 1,05Т\8 + 0,1 Т20 + 6 град.
Таким образом, для каждой узловой точки рассматриваемой области
можно составить алгебраическое уравнение. Систему из 24 уравнений
можно решить последовательными приближениями (итерациями). Для
этого нужно задаться ожидаемым распределением температур в узловых
точках и последовательно его уточнять с помощью составленных урав-
нений до тех пор, пока следующие друг за другом приближения не сов-
падут с необходимой точностью. Этот процесс можно запрограммировать
на ЭЦВМ. Кроме того, на ЭЦВМ подобная система алгебраических
уравнений решается точно с помощью определителей.
Для расчета температурного состояния оболочки двигателя целесо-
образно также использовать аналог в виде сетки электрических сопро-
тивлений (рис. 50.2, в), моделирующий процесс теплопроводности в си-
стеме теплопроводящих стержней, показанной на рис. 50.2,6. Этот аналог
можно также рассматривать как вычислительное устройство, решающее
систему составленных выше алгебраических уравнений.
Сопротивления аналога должны подчиняться соотношениям
-R- = = 20; = 1/(Хг = 196; = 1/а>к = 33,5.
R' R' Дх/Х' R' Wk'
Процесс решения задачи с помощью аналога сводится к измерению
потенциалов и в узловых точках сетки сопротивлений при задании на ее
вход разности потенциалов иг—ип<. Из пропорции
Т — Тж и — мж
Тг Т'ж wr мж
определяют температуры соответствующих узловых точек рассматривае-
мой области. На рис. 50.2,г указаны полученные значения температур
в °C, а на рис. 50.2,6 по этим значениям построены изотермы.
Разница между результатами расчета и данными приведенного выше
примера для температуры Тг.п составляет около 20°. Можно считать, что
420
такое уточнение температурного состояния внутренней стенки несущест-
венно для суждения о ее работоспособности. Это объясняется, в первую
очередь, тем, что наружная стенка в рассматриваемом случае выполнена
из плохо_ проводящего тепло материала. Средняя температура наружной
стенки 7v/ = 240°C, что на 40° меньше, чем по данным приведенного выше
примера. Эта разница также невелика с точки зрения влияния темпера-
туры на механические характеристики материала наружной стенки.
Рассмотренный пример показывает, что уточненный расчет дает
большую информацию о температурном состоянии оболочки двигателя
с частыми связями. В то же время данные расчета по приближенным
формулам являются достаточно надежными для целей проектирования
и расчета на прочность оболочки ЖРД.
Определение температурного поля в трубчатой оболочке. Один пз
возможных конструктивных вариантов выполнения охлаждаемой обо'
лочки двигателя представляет собой набор спаянных профилированных
трубок (см. рис. 50.1,в). Тонкостенные трубки набирают вдоль образую-
щей оболочки или укладывают по винтовой линии. Оболочка может
быть усилена наружной стенкой из металла или стеклопластика. Для
усиления применяется также оплетка из высокопрочной проволоки или
стекловолокна [107].
Рис. 50.3
В случае применения для наружной стенки низкотеплопроводного
материала типа стеклопластика можно считать, что она практически
не участвует в передаче тепла охлаждающей жидкости, которая проте-
кает по трубкам. При изготовлении наружной стенки из металла, когда
она спаивается вместе с трубками, ее роль в передаче тепла охлаждаю-
щей жидкости несколько возрастает, а условия охлаждения усиленной
оболочки в некоторой степени улучшаются в сравнении с оболочкой, со-
стоящей только из трубок. Введение в рассмотрение теплопроводности
в наружной стенке существенно усложняет решение задачи. Пренебре-
жение этим фактором приводит к некоторому завышению температуры
трубок, но позволяет получить достаточно простые расчетные формулы.
Точность этих формул тем выше, чем больше отношение коэффициентов
теплопроводности материала трубки и наружной стенки.
Расчетная схема для трубчатой оболочки в отличие от рассмотрен-
ных выше вариантов оболочек должна учитывать передачу тепла по-
средством теплопроводности вдоль поверхности трубки, омываемой га-
зовым потоком. В связи с этим повторяющийся элемент трубчатой обо-
лочки, выделенный на рис. 50.1,в штрихлунктирными линиями, пред-
ставляется в виде тонкой пластины толщиной ft, равной толщине трубки,
и шириной /1 + /2, равной половине периметра трубки (рис. 50.3,а) [36].
Одна сторона пластины омывается охлаждающей жидкостью темпера-
421
турой Тж, коэффициент теплоотдачи аж. К части противоположной по-
верхности пластины подводится удельный тепловой поток q от продуктов
сгорания. Остальная часть поверхности и торцы пластины идеально
теплоизолированы, что следует из принятого выше допущения и из усло-
вий симметрии рассматриваемого элемента оболочки.
Для применяемых в конструкции двигателя тонкостенных трубок из
материалов с высоким значением коэффициента теплопроводности X
критерий Bi = ажЛ/Х<0,1 (см. § 24). Поэтому перепадом температуры по
толщине трубки можно пренебречь и считать распределение температуры
одномерным, изменяющимся лишь по ее периметру. В такой постановке
задача сводится к рассмотрению установившегося процесса теплопровод-
ности в двух тонких стержнях конечной длины, состыкованных своими
основаниями. Подобная задача о температурном поле оболочки бака в
зоне уровня жидкости разобрана в § 26.
Для стержней, составляющих изображенную на рис. 50.3,а пластину,
распределение температуры удовлетворяет уравнениям
м^--аж(7\ - тж) + <? - о,
dx\
аж(Т2 —Тж) =0
dx2
с граничными условиями:
. dT 1 р, * dT 2 гч
при х± = /j —- = 0, при х2 = Z2 —- — 0;
dxx dx2
при Х1 = х2 = 0 7\ = Т2 = То и — + 0.
Решая эти уравнения, получаем следующие соотношения для расчета рас-
пределения температуры в трубке:
Л = тж + -^- [i + -Lz^2_chg(i-xj].
«Ж L ch g J
где
В большинстве практических задач нет необходимости рассчиты-
вать и анализировать непрерывное распределение температуры, а доста-
точно ограничиться значениями температур в некоторых характерных
точках и средними температурами отдельных участков трубки. Поэтому
целесообразно дать сводку формул для расчета этих характерных тем-
ператур:
Х1 = хч = 0
То = Тж 4- (?/аж) Ло,
Tl = + (?/аж)
Ti =ТЖ + (?/аж) Ki,
То = Тж + (<7/аж) Ло,
422
где
Shg I chd/l) ch Ц/I)
средние температуры участка 1 (см. рис. 50.3, а)
Т'=ТЖ + (9/аж) Л', Л' = 1 - (К№ th &Т),
участков в месте спая с соседней трубкой
7^* =Т 1 Q ~f(* = К о sh (I/O sh I
«ж 1-/’’ ~Т ch(l/7)
и в месте спая с наружной стенкой
— q — — К(\ sh £
Т" = тж + — К", к." 1.
Ж “Ж 6ch(g//)
средняя температура всей трубки
Т = Тж + (9/ажУГ/(1 + Г).
Температуру наружной стенки, которая усиливает трубчатую оболочку,
следует принимать равной температуре Т" соответствующего участка
трубки. _ __ _
Значения коэффициентов Л', К" и Л* численно равны долям сум-
марного теплового потока, которые снимаются охлаждающей жидкостью
с поверхности соответствующих участков трубки. Эти коэффициенты
характеризуют степень участия отдельных участков в передаче тепла
охлаждающей жидкости. Очевидно, что
К' +7С + Г= 1.
Пример. Пусть заданы:
h = 0,5 мм\ li = 1,25 мм\ 12 = 3,25 мм\ X = 290 вт!м-град\ Тж = 100 °C;
аж = 17 300 вт/м2-град-, ТГ = 3285 °C; аг = 2960 вт/мР-град.
Тогда
7=71/72= 1,25/3,25 = 0,385;
5 li = /17 300/290-0,5-10-3 -1,25- 10-з = 0,432;
До = 0,336; Д^ = 0,392; Kt = 0,198; ^ = 0,216;
Д'= 0,374; Д"=0,203 и Д* ]= 1 — Д'— Д" = 0,423.
Так как суммарный удельный тепловой поток q неизвестен, то его необходимо
предварительно определить из уравнения
q —каг (Тг Т ) — аг (Тг Тж) q К •
аж
Отсюда
Я = аг (Тг - Тж) I [ 1 + (аг /аж) К'] = 2960 (3285 - 100)/ [ 1
2960
17 300
0,374
= 8,85-Ю6 вт1м2.
По приведенным выше формулам определяют характерные температуры, значения ко-
торых (в °C) показаны на рис. 50.3, б.
На рис. 50.3, в приведены результаты решения на электрическом аналоге задачи
с теми же исходными данными, но с учетом теплопроводности в наружной стенке.
Толщина стальной наружной стенки Л"=1 мм, коэффициент теплопроводности
Z" = 14,5 вт/м • град. Хорошее совпадение результатов на рис. 50.3,6, в говорит об удов-
летворительной точности расчета по полученным выше формулам.
423
Расчет температуры неохлаждаемого насадка сопла. Выходная часть
сопла двигателя, которое имеет большую степень расширения газов,
может быть выполнена в виде неохлаждаемого тонкостенного насадка
(см. рис. 48.1,а). Стойкость материала насадка в газовом потоке зависит
от температурного состояния оболочки, которое_можно характеризовать
средним значением равновесной температуры Т. Это значение находят
из баланса действующих конвективных и лучистых тепловых пото-
ков [36]
аг (?; - Т) + qr -- ас (Т - Тс) + б'о0 Г4, (50.7)
где аг и ас — коэффициенты теплоотдачи газового потока и внешней среды»
Тс и Тг — температуры внешней среды и заторможенного газового по-
тока в пристеночном слое;
е'—степень черноты наружной поверхности насадка.
Наименее ясным в этом уравнении представляется определение ре-
зультативного лучистого потока qr от газов к оболочке. То обстоятель-
ство, что газ излучает и поглощает лишь в отдельных полосах спектра,
вызывает большие трудности при нахождении его поглощательной спо-
собности Аг по отношению к излучению насадка. В данном случае расчет
дополнительно осложняется тем, что оболочка насадка полностью не
охватывает всего объема излучающего газа, т. е. система газ — оболочка
не является замкнутой.
Излучение, падающее на внутреннюю поверхность насадка,
<7пад = <7* Фн (1 — 4) + ег ,
где и фн— эффективное излучение и коэффициент самооблученности
насадка;
ег и Тг — степень черноты и термодинамическая температура газа.
Коэффициент фн показывает, какая доля эффективного излучения
насадка вновь попадает на его поверхность, если газ в полости насадка
отсутствует.
В свою очередь, если считать оболочку серым телом (е=Л),
то
q* •=- ecr0 Т4 + (1 — А) дпад.
Из двух последних соотношений получаем
(50.8)
где ф= 1—фп. Поглощательную способность газов по отношению к эффек-
тивному излучению насадка приближенно можно считать равной их
степени черноты при температуре Г, т. е. /4г = ег(Л •
Коэффициент ф зависит только от геометрии насадка. Если насадок
выполнен в виде прямого кругового усеченного конуса, то этот коэффи-
циент равен [20]
1 4- О2 —0,5 [/(1+Р)2 + 4№ — >/ (Я — Р)2 Ч-4 7/2 Г , (509)
(1 + D) /(1 —О)2 + 4Й2
D—D^D^, H = H/D2,
где Н — высота насадка;
D± и D2 —диаметры его оснований (см. рис. 48.1, а).
424
Если насадок представляет собой поверхность вращения с криво-
линейной образующей, то Ф = фк(5к/5), где 5 и SK — площади внутренней
поверхности насадка и боковой поверхности вписанного в насадок усе-
ченного конуса. Следует отметить, что для замкнутой оболочки ср = О
и формула (50.8) переходит в полученное в § 49 соотношение (49.3) для
расчета лучистого теплообмена между объемом газа и охватывающей
его оболочкой.
Уравнение (50.7) с учетом соотношения (50.8) приводится к виду
N + 1, (50.10)
где
v Гн.г Mr — (1 — ^г) Ф1 + е % -a т
N =---------------------------о0 Т3, О' = —,
аг + ас т
- _ «Г 7^г + ас тс+%.г ег<?о^г
аг + ас
-г- -hi - лг) г 1 + (а - Лф].
fcH.r A L X А / J
Решение этого уравнения находим по рис. 24.3.
Пример. Пусть насадок выполнен в виде конической оболочки, размеры которой
/7 = 0,6 м\ DY= 1,2 м и D2 = 1,5 м. Для среднего сечения насадка диаметром £>ср =
= 1,35 м известно: Тг = 1300 °К; Г* = 3000°К; давление газов рг = 0,04 кГ]см2\ пар-
циальные давления Рн2о= 0,015 кГ1см2 и рсо*~ 0,01 кГ)см2. Как и в предыдущих
примерах этой главы, принято: удельная теплоемкость газов ср = 4 кдж1кг-град\ массо-
вый расход газов m = 40 кг/сек:, е = 4 = е' = 0,8; ас = 0.
Коэффициент теплоотдачи, рассчитанный по формуле (49.2),
аг = 4с’m0,82D~1,82 = 4-4 (40)°’82(1,35)-1’82 = 191 вт/м^-град.
Приведенная длина пути луча, вычисленная по формуле (49.9), равна /~0,6 м. Для
определения величины АГ следует вначале задаться ожидаемым значением равновес-
ной температуры, например Т'=1000°К. В результате вычислений по формулам (49.7)
и (49.8) получаем Лг = 0,043 и ег =0,0375. Далее при D = Dl/D2 = 0,8 и Я=Я/£>2 = 0,4 из
формулы (50.9) находим <р = срк=0,663, расчетом по приведенным выше формулам
получаем ен,г =0,885; 7' = 3028°К; JV=11,7. По рис. 24.3 при W=ll,7 находим 0 = 0,462
и вычисляем Т = 7'0 = 3028 • 0,462= 1400°К.
Расчет показывает, что для вновь полученного значения равновесной температуры
Аг =0,036. Но это уточнение в данном случае —Практически не влияет на определение
равновесной температуры. Поэтому значение Т'=1400°К можно принять за оконча-
тельное.
Если при определении равновесной температуры считать, что газовый объем пол-
ностью охватывается оболочкой (ср = О), то значение Т оказывается равным 1550°К.
В выходной части сопла с большим расширением газов лучистым
теплообменом продуктов сгорания с оболочкой можно пренебречь в срав-
нении с конвективным. Формально это отвечает условию ег=Лг = 0. При
этом условии полученные выше расчетные формулы заметно упроща-
ются. Равновесную температуру по-прежнему определяем из уравнения
(50.10), но теперь
N =----------2<Р + Я(1-ф) fl = JL
аг+«с ф + ^(1 —ф) Г ’
агТр + О>сТс
аг + ас
Для рассматриваемого примера при Тг = 3000°К; аг = 191 вт/:л2-град; = 0;
А = 0,8; ф = фк = 0,663 получаем Т= Т* = 3000°К; N = 11,2; fl= 0,466 и Т=1398°К.
425
Практически полное совпадение рассчитанных значений равновес-
ных температур с учетом и без учета излучения газа говорит о возмож-
ности использования для расчета упрощенных формул, в которых не
учитывается лучистый теплообмен между г_азом и оболочкой насадка.
Для сравнительно длинных насадков (//>0,5) характеризовать тем-
пературное состояние оболочки лишь одним значением средней темпе-
ратуры недостаточно. В таком случае следует провести расчет распре-
деления температуры по образующей насадка, разбивая его на несколько
кольцевых участков и рассматривая лучистый теплообмен между этими
участками.
§ 51. ОБЩАЯ НЕСУЩАЯ СПОСОБНОСТЬ КАМЕРЫ ДВИГАТЕЛЯ
При расчете камеры на общую несущую способность должны быть
известны: геометрия камеры, распределение давления газов по ее длине,
температурные поля в стенках, диаграммы растяжения и пределы проч-
ности материалов стенок в требуемом диапазоне температур. Расчет
носит поверочный характер.
В этом параграфе формулируется система допущений, с помощью
которой удается сравнительно просто произвести расчет камеры двига-
теля на прочность; потом на примере одномерной модели отмечаются
некоторые особенности работы двухслойной оболочки двигателя.
Система упрощающих допущений, используемых в дальнейших ре-
шениях, такова:
1. Тепловой расчет двигателя проводится для недеформированного
состояния и в дальнейшем считается, что ни местные прогибы охлаж-
дающего тракта, ни общая деформация камеры не влияют на темпе-
ратуру стенок.
2. Остаточные напряжения, возникающие в конструкции двигателя
в процессе его изготовления, не учитываются.
3. Считается, что температура и нагрузка меняются во время пуска
двигателя таким образом, что деформация материала стенок камеры
всюду является активной, и участки разгрузки отсутствуют.
4. Связи между стенками камеры принимаются абсолютно жесткими
и настолько частыми, что их действие на оболочки можно «размазать»,
т. е. заменить приведенным контактным давлением.
Вообще говоря, можно провести специальные уточненные исследо-
вания, свободные от того или другого из этих допущений, однако в боль-
шинстве случаев перечисленные упрощающие допущения не приводят к
большим погрешностям, но зато резко сокращают объем расчета.
Оценочный расчет «по кольцу». Материал стенок двигателя рабо-
тает обычно за пределом упругости и находится в сложном напряжен-
ном состоянии. Поэтому для полного расчета двигателя необходимо при-
влечь аппарат теории пластичности. Но прежде чем перейти к такому
расчету, целесообразно на простой модели установить основные законо-
мерности, свойственные двухстеночной конструкции камеры двигателя,
подвергнутой одновременному действию больших давлений и высоких
температур. Для этого можно произвести расчет двигателя «по кольцу»,
т. е. из цилиндрического участка камеры сгорания вырезать кольцо еди-
ничной ширины и считать напряженное состояние в стенках этого кольца
одноосным. Другими словами, в таком расчете «по кольцу» не учиты-
ваются осевые температурные удлинения и осевая сила. Кроме того,
будет предполагаться, что свойства материала наружной и внутренней
стенок определяются их средними температурами Т' и Т".
На такой простой модели, конечно, нельзя установить даже качест-
венно все закономерности, свойственные самой конструкции камеры, но
некоторые основные особенности удается легко проследить.
426
Из условия равновесия половины кольца (рис. 51.1,а) следует
Jr 6'h," = prR + ржб,
(51.1)
где Л' и h"— толщины внутренней и наружной стенок;
а' и б"— окружные напряжения во внутренней и наружной стенках;
R — средний радиус двухслойного кольца;
S — зазор между стенками.
Поскольку обычно б</?, а величина межрубашечного давления
имеет тот же порядок, что и величина давления газов рг, то вторым
слагаемым в уравнении (51.1) можно пренебречь; тогда получим
сг'Л' + v"h” = prR.
(51.2)
Рис. 51.1
Задача по нахождению о' и б'' является статически неопределимой, и по-
этому к уравнению (51.2) следует добавить уравнение в перемещениях.
Полные окружные удлинения внутренней и наружной стенок еп и явля-
ются суммами силовых и температурных удлинений:
еп е' + ет’ £п = е" + <51-3)
где е' и в"—температурные удлинения, определяемые соответствующими
средними температурами стенок. Силовые удлинения е' и е7 связаны с
напряжениями б' и б" диаграммами растяжения.
Поскольку связи между стенками считаются жесткими, то, очевидно,
е' + в; = е7 + е;. (51.4)
Если диаграммы растяжения б' = б' (б') и а"=сг"(е") при соответствую-
щих температурах Т и Т” заданы, то уравнений (51.2) и (51.4) достаточ-
но, чтобы найти б', б" и увеличение диаметра кольца в рабочем режиме
2А/? — 2/?е* при эксплуатационном давлении газов р*.
Для выяснения качественной стороны взаимодействия внутренней
и наружной стенок рассмотрим вначале случай упругой работы их мате-
риала; в этом случае легко получить аналитические выражения для ве-
личин напряжений и деформаций в оболочке камеры. Обозначив через
Е' и Е" модули упругости материалов внутренней и наружной стенок
427
при соответствующих температурах и учитывая, что при упругих дефор-
мациях в' = Е'&' и в" = Е''&'\ из уравнений (51.2) и (51.4) получим
Поскольку для оболочки камеры е^^е", то из полученных формул
следует, что наружная стенка всегда растянута, а внутренняя стенка мо-
жет быть как растянута, так и сжата в зависимости от соотношения меж-
ду давлением рг, величиной разности температурных удлинений (е^. — е")
и жесткостям и стенок E'h', E”h”.
Но, как уже отмечалось, материал стенок камеры чаще всего рабо-
тает за пределом упругости, что необходимо учитывать в расчете.
Так как диаграммы растяжения обычно заданы в виде графиков,
то решение приходится вести либо численным подбором, либо, что в дан-
ном случае удобнее, графически. При графическом решении следует пе-
рестроить диаграммы растяжения о, = о,(е/) и cfz, = cf"(е") в кривые
= и o"h" — f"(en). Для этого достаточно изменить масштаб диа-
грамм растяжения материала внутренней и наружной стенок в соответ-
ствии с их толщинами h' и h" и сместить начало отсчета по оси абсцисс
соответственно на величины ет и ет, , как показано на рис. 51.1,6 (диа-
грамма сжатия считается совпадающей с диаграммой растяжения).
Сложив графически эти две кривые, можно построить зависимость сум-
мы o,/z, + o,'/i'/ от полного удлинения еп; точка пересечения этой послед-
ней зависимости с прямой р3 R и даст рабочую точку А. Таким образом
можно определить величины напряжений во внутренней и наружной
стенках в рабочем режиме о,э и о"э. Следует подчеркнуть, что внутрен-
няя стенка в результате ее больших температурных удлинений обычно
оказывается сжатой.
После того как напряжения во внутренней и наружной стенках
будут определены, нетрудно подсчитать усилия в связях между оболоч-
ками. В современных двигателях используются настолько частые связи,
что их действие на стенки вполне можно заменить осредненным контакт-
ным давлением (положительное давление соответствует растягиваю-
щим усилиям в связях). Тогда, рассмотрев равновесие элемента внут-
ренней стенки, можно получить
Рк = (Рж-Рг) + -^. (51-5)
Как следует из формулы (51.5), в рабочем режиме связи могут работать
как на растяжение, так и на сжатие.
Если величины пределов прочности в'в и а" материалов стенок при
соответствующих температурах известны, то величину предельного давле-
ния легко можно определить по формуле
Сравнивая величину рабочего давления газов с величиной предельного
давления, судят о запасе прочности камеры.
В заключение следует подчеркнуть, что все полученные в расчете
«по кольцу» формулы не являются окончательными расчетными зависи-
428
мостями; они могут быть использованы только для ориентировочного
расчета. Основное значение приведенного решения «по кольцу» состоит
в его простоте и наглядности, в том, что с его помощью можно легко
проследить за влиянием того или иного параметра (толщин стенок, их
температур, величин давлений, материалов стенок) на величины напря-
жений в стенках и на величины усилий в связях. Кроме того, простая
модель двухслойного кольца, материал которого считается работающим
в одноосном напряженном состоянии, позволяет (по крайней мере, каче-
ственно) проследить за влиянием таких факторов, как повторные пуски
двигателя, остаточные технологические напряжения, и учесть реальную
последовательность нагружения при пуске двигателя [37, 93].
Уточненный расчет оболочки двигателя. Прежде всего следует опре-
делить запас прочности камеры по предельным нагрузкам. Для этого
подсчитанные в нескольких характер-
ных сечениях величины эксплуатаци-
онных суммарных внутренних усилий s'
7\ и Т2 сравнивают с подсчитанными в Л Р* ц\ /
тех же сечениях предельными значе-
ниями Т\ и Tf2-
При определении усилий Тх и Т2
камеру можно рассматривать как без-
моментную тонкостенную оболочку,
нагруженную внутренним давлением.
Площадь сечения охлаждающего трак-
та существенно меньше площади се-
чения самой камеры, и поэтому при
составлении уравнений равновесия
влиянием межрубашечного давления можно пренебречь. Важно под-
черкнуть, что задача нахождения 7\ и Т2 в безмоментной оболочке яв-
ляется статически определимой, и эти усилия не зависят ни от темпера-
туры, ни от свойств материала и толщин стенок камеры, ни от способа
их скрепления, а определяются исключительно геометрией самой камеры
и законом распределения давления газов.
Величину осевого усилия Т{ в любом сечении камеры легко опреде-
лить из условия равновесия в проекции на ось камеры, если известно
место крепления двигателя. Так, например, для сечений I—I и II—II
(рис. 51.2) соответственно
= Tl — -^L-R-----
2 2 2лЯ
где Р— тяга двигателя.
Величина окружного усилия Р2 определяется из уравнения Лапласа
—+ —=Рг. (51.7)
Rt R2 г V 7
где и /?2 — главные радиусы кривизны оболочки в рассматриваемом се-
чении камеры.
В упрощенном варианте расчета предельные значения усилий Т? и Т?
могут быть подсчитаны по формулам
тр = ?р •_= тр, тр = + crzr, (51.8)
где и cf— пределы прочности материалов стенок, определяемые по
средним температурам.
Проведя расчет камеры в нескольких сечениях, за окончательный за-
пас прочности следует взять наименьшее из полученных отношений
ТР
(51.9)
429
Если подсчитанный запас прочности не удовлетворяет конструктора,
то следует изменить какие-либо параметры в двигателе. Важно подчерк-
нуть, что все параметры двигателя тесно связаны между собой, и изме-
нение одного из них влечет за собой целую серию других изменений.
Так, изменение толщины стенок камеры вызывает изменение их темпе-
ратурного состояния, и прежде чем производить новый расчет на проч-
ность необходимо заново сделать тепловой расчет двигателя. Но измене-
ние толщины только одной наружной стенки обычно слабо сказывается
на изменении ее температуры и температурного состояния внутренней
стенки. Поэтому для данной толщины внутренней стенки, проделав один
раз тепловой расчет двигателя, можно из формул (51.9) и (51.8) подби-
рать толщину наружной стенки при заданном запасе прочности:
Для более полной оценки работоспособности камеры, кроме запаса
прочности по предельным нагрузкам, целесообразно еще определить
напряженно-деформированное состояние стенок камеры в рабочем ре-
жиме. Знание напряженно-деформированного состояния стенок необ-
ходимо также и для дальнейшего расчета местных деформаций в охлаж-
дающем тракте.
В рассматриваемом сечении предполагаются известными 7\ и Т2>
причем
h' /2 h' /2
= J <fxdz + <fxh", Т\= J ^dz + ^h". (51.11)
-h'A -Л72
Силовые удлинения в стенке камеры будут
еф — е<₽п 8т’ 8х “ 8хп ет ’
(51.12)
еф = ефП —е;, = —е;,
где £фп и 8хп — полные геометрические удлинения, вследствие допущения
о жесткости связей одинаковые для внутренней и наружной стенок в
каждом из сечений камеры, а ет — температурные удлинения, изменяю-
щиеся по толщине вместе с изменением температуры. Интенсивности де-
формаций в каждой точке определяются формулами § 4:
е;=-Аг V % + v;+<,
/3
е" = У у + е;е; + у.
/ 3
(51.13)
По диаграммам растяжения, соответствующим температурам в каждой
рассматриваемой точке, определяют интенсивности напряжений ы и
а/, а затем по соотношениям теории малых упруго-пластических дефор-
маций (см. '§' 5) подсчитывают величины осевых и окружных напряже-
ний по сечению стенок камеры:
430
Задача, следовательно, сводится к определению таких значений 8ХП и
ефп, при которых удовлетворяются уравнения (51.11). Поскольку в ре-
шение входят графически заданные зависимости сгг- от 8г, то определять
ехп И 8фП удобнее всего численным подбором. Преобразовав уравнения
(51.11) с использованием выражений (51.12) и (51.14), получим
Тг-4- т2 + FT тг_-Ь тх + fT
--------- ефп=-------, (51.15)
где
Л'/2 , * h'/2 , *
Л= ( — dz + ^-h", FT= + (51.16)
.) <• ei J t'i e'i
—h'l2 —h'l2
При определении величин Fx и FT по выражениям (51.16) или при
подсчете 1\ и Т2 по выражениям (51.11) толщину внутренней стенки
разбивают на несколько слоев. Число слоев следует выбирать в зависи-
мости от величины перепада температур по толщине внутренней стенки.
Так, для стальной стенки, когда перепад температур достигает несколь-
ких сот градусов, можно взять от трех до пяти слоев. Для медной внут-
ренней стенки при перепаде температур в несколько десятков градусов
вполне достаточно ограничиться одним-двумя слоями.
Последовательность подбора 8ХП и 8фп такова.
1. Задаются нулевые приближения для 8ХП и 8фп.
За нулевые приближения удобно брать величины полных окружных
и осевых удлинений, подсчитанных без учета влияния внутренней стенки,
т. е. принять, что
<•=—. °"=—• (51.17)
х Л" ’ Ф Д" >
Тогда, подсчитав величину интенсивности напряжений наружной стенки
=/Т2_ 7^4.72 _J_ (51Л8)
из диаграммы растяжения cf = cf (ер можно найти величину интенсивно-
сти деформаций наружной стенки е'^ и, воспользовавшись соотношениями
теории малых упруго-пластических деформаций (см. § 5), вычислить ну-
левые приближения:
(51.19)
2. По зависимостям (51.12) и (51.13) подсчитываются удлинения и
интенсивности деформаций в стенках камеры.
3. По диаграммам растяжения определяются интенсивности напря-
жений в стенках.
4. По формулахм (51.15) подсчитываются новые приближения для
полных окружных и осевых удлинений (величины усилий Т\ и Т2 счита-
ются известными). Подбор величин полных окружных и осевых дефор-
маций можно считать законченным, если последующие приближения
отличаются от предыдущих меньше, чем на заданную величину Ае (в
практических расчетах целесообразно ограничиться точностью
Ае^Ю-2 3 4).
431
Проделав то же для нескольких сечений камеры и определив для
них величины полных окружных и осевых удлинений ефП и 8ХП, судят о
том, как деформируется вся камера в рабочем режиме. При этом осевые
и радиальные перемещения камеры подсчитывают по величинам осевых
и окружных удлинений как для безмоментной оболочки (см. § 9). Если
эти величины перемещений удовлетворяют требованиям, предъявляе-
мым конструктором к камере двигателя, то прочностной расчет по общей
несущей способности можно считать законченным. В противном случае
нужно внести изменения в конструкцию камеры, заново определить
температурное состояние ее стенок и по полученным новым данным по-
вторить весь прочностной расчет.
Пример. Рассмотрим цилиндрическую камеру ЖРД с параметрами: средний радиус
камеры R = 150 мм, давление газов Рг=40 кГ1см2. Внутренняя стенка камеры медная
с продольными ребрами, наружная стенка из нержавеющей стали (рис. 51.3, а). В ре-
зультате теплового расчета (см. § 50) в рассматриваемом сечении имеем: средняя тем-
пература медной стенки Т' = 320°С, средняя температура ребер 7'реб = 280°С; средняя
температура наружной стенки Т" = 240°С. Диаграммы растяжения материалов стенок
при этих температурах приведены на рис. 51.3,6. Пределы прочности соответственно
равны: для наружной стенки сгв = 56 кГ!мм2, для внутренней стенки ов = 15 кГ^мы.1.
Величины температурных удлинений берем из книги [93], стр. 42: для внутренней стенки
гт =0,0058, для наружной стенки ет =0,0041.
Определим сначала запас прочности камеры по несущей способности.
Пренебрегая влиянием ребер, из зависимости (51.8) получаем
TP = aB/i" = 15-1 + 56-3,2 = 194 кГ/мм.
Для рассматриваемой цилиндрической камеры наибольшим будет окружное усилие
Тэ2 = рг£ = 40 • 10-2 • 150 = 60 кГ'мм,
и согласно формуле (51.9) запас прочности по несущей способности будет равен
Далее определим напряженно-деформированное состояние стенок камеры в рабо-
чем режиме. Сначала произведем расчет камеры «по кольцу». На рис. 51.4, а приведены
результаты такого графического расчета. Как видим, внутренняя стенка в рабочем
режиме оказалась сжатой, .причем усилие в ней (o,/i,)3=5 кГ1мм, следовательно,
окружное напряжение сг'~5 кГ1мм2\ усилие и напряжение в наружной стенке соответ-
ственно равны (o'7i")3 =62 кГ1мм и (/'=19 кГ/мм2; полное окружное удлинение
еп =0,0055. На рис. 51.4,6 показаны результаты аналогичного расчета «по кольцу» той
же самой камеры, но при толщине наружной стенки Л" = 2 мм.
Теперь проведем уточненный расчет, учитывающий двухосность напряженного со-
стояния в стенках камеры; при этом рассмотрим сечение, соответствующее сечению /
на рис. 51.2. Тогда
7\ = prR/2 = 30 &Г1мм\ Т2 = prR = 60 кГ/мм.
В нулевом приближении согласно формулам (51.17), (51.18) получаем
(ох)о = 9,4 кГ/мм2\ (с^)о = 18,8 кГ/мм2; (о-)0= 16,2 кГ1мм2.
Из диаграммы oz—ez находим (е£)0 = 0,0008, и далее из (51.19) получаем (еЛП)у=
= 0,0041; (Evn\) = 0,0049. В первом приближении согласно формулам (51.12) и (51.13)
находим
(е')! = 0,0025; (еД =0,0010; (е^ = —0,0008;
(<)е=-0,0017; Х)г> 0,0008; (8^ = 0.
При подсчете Fv и FT внутреннюю стенку на слои не разбиваем, а просто ведем
расчет по средним значениям температур и напряжений в стенке. Тогда по формулам
(51.16) находим Fi = 5400 кГ/мм\ FT = 225 кГ I мм. И в первом приближении по (51.15)
окончательно получаем (exn)i =0,0042; (e^n)i =0,0050.
432
Во втором приближении после повторения всех вычислений находим (exn)ll =
= 0,0042; (е^п)ц = 0,0050. Эти значения полных удлинений и принимаем за окончатель-
ные. Зная величины полных удлинений ехп и е^, используя зависимости (51.12) — (51.14)
и диаграммы растяжения, можно подсчитать величины напряжений в стенках камеры:
о'г = —4,3 кГ/мм2; оу = — 3,4 кГ/мм2; cr*=Jll,2 кГ/мм2; оу = 19,5кГ/мм2.
Если весь расчет повторить для толщины наружной стенки h" = 2 мм, то получим
8ЛП = 0,0041; = 0,0062.
И, наконец, если при той же
толщине h" = 2 мм произвести рас-
чет для сечения, соответствующего
сечению // на рис. 51.2, и учесть, что
в этом случае (при тяге Р = 87)
О)
Рис. 51.4
т PrR-
Т'= 2
= 21,5 кГ;ММ ,
то получим
ЕЛП = 0,0036; = 0,0083.
Рис. 51.3
Из сопоставления полученных результатов для ву, сгу, еуп^с результатами расчета
«по кольцу» видно, что качественно расчет «по кольцу» правильно Отражает реальную
картину, но в количественном отношении он дает довольно грубые результаты.
В изложенной схеме расчета не учитывалась ползучесть материала.
А между тем за несколько минут работы двигателя может заметно про-
являться кратковременная ползучесть материала стенок камеры. Учесть
в расчете эту кратковременную ползучесть проще всего с помощью тео-
рии старения [73]. Для этого весь расчет по определению напряженно-
деформированного состояния стенок камеры следует повторить для не-
скольких моментов времени работы двигателя, используя каждый раз
вместо статических диаграмм растяжения материала зависимости ог- от
8г, полученные перестройкой кривых простого последействия для тех же
моментов времени. В результате такого расчета находим зависимости
изменения полных окружных и осевых удлинений, а следовательно,
радиальных и осевых перемещений камеры по времени.
28 Зак. 96
433
§ 52. РАСЧЕТ ОТДЕЛЬНЫХ ЭЛЕМЕНТОВ КОНСТРУКЦИИ ЖРД
Усилия в связях и местные деформации охлаждающего тракта в
рабочем режиме. Местные прогибы -стенок камеры между связями воз-
никают как результат действия контактных усилий в связях. Если связи
между стенками растянуты,
показано на рис. 52.1,а; если связи сжаты, то местные деформации сте-
то -стенки камеры деформируются, как
нок имеют характер, показан-
ный на рис. 52.1,6; наконец, ес-
ли связи
вообще не нагружены, то рав-
ны нулю и местные деформа-
ции стенок.
Цель расчета — опреде-
лить усилия в связях, возника-
ющие в рабочем режиме ЖРД>
и местные прогибы, вызывае-
мые этими усилиями. Такой
расчет должен быть проведен для нескольких характерных сечений в ка-
мере сгорания, в зоне критического сечения и в сопловой части. Основное
внимание следует обращать на местные прогибы внутренней стенки, и
поэтому в дальнейшем изложение методики расчета ведется именно для
нее, хотя сама методика полностью применима и к расчету прогибов на-
ружной стенки.
Расчету на местные прогибы должен предшествовать расчет на общую
несущую способность камеры. Поэтому предполагаются известными осе-
вые и окружные напряжения в стенках cf, и о", а также полные
осевые и окружные удлинения вхп и 8фп. Кроме данных, необходимых для
расчета на общую несущую способность (см. §51), должны быть заданы
величина межрубашечного давления рж по длине камеры и геометрия свя-
зей между оболочками.
При определении усилий в частых связях реакции этих связей мож-
но осреднить, «размазать» по поверхности стенки, заменив их действие
на стенки камеры приведенным контактным давлением рк. Тогда из
условия равновесия элемента внутренней стенки можно получить
h' /2 /i'/2
Рк = ?Рж+-Б- f G'xdz+-^- ( Рг,
Al J A2 J
—ft'/2 —ft'/2
о)
Рис. 52.1
Р^о
5)
между оболочками
(52.1)
где R\ и /?2 — главные радиусы кривизны оболочки камеры в рассмат-
риваемом сечении, а коэффициент g равен отношению площади поверх-
ности стенки, на которую действует давление охлаждающей жидкости, к
площади поверхности стенки, на которую действует давление газа.
В частности, для изображенных на рис. 52.1 продольных связей
В рабочем режиме контактное давление может быть как положи-
тельным, так и отрицательным в зависимости от соотношения между
жесткостями и температурными внутренней и наружной стенок и от ве-
личины перепада давления на внутренней стенке. С точки зрения проч-
ности сварного или паяного соединения опасным является случай поло-
жительного контактного давления^ когда связи работают на растяжение.
Для оценки запаса прочности связей следует подсчитать величину рас-
тягивающего усилия, действующего на одну сварную точку или на еди-
ницу длины сварного или паяного шва, и сравнить его с соответствую-
434
щим значением разрушающего усилия. При этом величина разрушаю-
щего усилия должна определяться экспериментально для той
температуры, при которой работает соединение в рабочем режиме.
Усилие, приходящееся на единицу длины шва, очевидно, равно
(см. рис. 52.1)
<7шв = Рк(а+ *)• (52.2)
Если стенки камеры соединены между собой с помощью сварных точек,
то усилие, действующее на одну сварную точку, определится формулой
Ро = Рк$о,
где So — площадь поверхности оболочки, приходящаяся на одну свар-
ную точку.
В качестве примера определим контактное давление и усилие в
паяном шве для камеры, рассмотренной в предыдущем параграфе при
/i" = 3,2 мм\ межрубашечное давление считаем равным = 50 кГ1см2.
Из формулы (52.1) при 7?! = оо и 1/2 получим
рк = —50------— 3,4- 1 • Ю2 — 40 =— 17,3 кГ/см2.
к 2 150
Контактное давление оказалось отрицательным, и, следовательно, усилие
в паяном шве в рабочем режиме сжимающее:
= Рк (<* + Ь) = - 17,3 • 10-2 . (1 + 1) = _ 0,35 кГ/мм.
Определение местных прогибов стенки между связями — чрезвычай-
но сложная задача теории оболочек, так как материал стенки работает
за пределохМ упругости, свойства его в результате неравномерного нагре-
ва существенно изменяются по толщине, и в общем случае следует еще
учитывать геометрическую нелинейность задачи. Эти трудности удается
преодолеть с помощью численных методов решения. Кратко наметим
здесь общую схему решения, основанного на энергетическом методе
Ритца.
Если пренебречь изменением объема упруго-пластического тела, то
его полная энергия выразится зависимостью
г1
F = [ dV j — р \wdS, (52.3)
V0 s
где ai и ez — интенсивность напряжений и интенсивность деформаций;
dV — элементарный объем тела;
— р ^wdS — потенциал внешних сил;
s
dS — элемент поверхности оболочки.
Учитывая граничные условия, задаются функциями перемещений и,
v, w так, чтобы они зависели от п свободных параметров а^. При этом
функцией нормального прогиба wf как имеющей более наглядный физи-
ческий смысл, можно задаться непосредственно, а затем функции и и v
выразить (точно или приближенно) через w, например, с помощью соот-
ношений теории упругих оболочек. Выразив через выбранные функции
полную энергию, можно найти значения п произвольных параметров aj
из условия экстремума полной энергии, сводящегося к п уравнениям
вида
ог dV — р f wdS = 0, / = 1, 2, (52.4)
V 1 1 S
Если температура и соответствующие ей диаграммы растяжения
материала по толщине стенки известны, то решение по указанной схеме
28* 435
связано с преодолением только технических трудностей. Но при несколь-
ких свободных параметрах эти технические трудности настолько велики,
что решение полученной системы уравнений (52.4) возможно лишь на
быстродействующей вычислительной машине; «вручную» такую задачу
целесообразно решать, если ограничиться только одним свободным пара-
метром.
Изложенная общая схема расчета применима к любому типу связей,
в частности, к расчету камер с очень частыми связями. В этом случае
при определении местных прогибов кривизной стенки можно пренебречь
и заменить участок стенки между связями удлиненной пластинкой, за-
щемленной по краям и нагруженной равномерным давлением рк, уравно-
вешивающим реакции в связях (рис. 52.1). Прогибы такой пластинки
можно определить, считая ее геометрию неизменной при изгибе, но учи-
тывая составляющие прогиба, связанные с деформациями сдвига. Расчет
ведется для полоски единичной ширины, вырезанной из пластинки.
Подробное исследование вопроса о местных прогибах в оболочках
ЖРД с не очень частыми связями, когда стенку камеры нельзя заменять
плоской пластинкой, можно найти в книге [93].
Если требуется учесть ползучесть материала стенки, то весь расчет
(в том числе, конечно, и расчет на общую несущую способность) сле-
дует повторить для нескольких моментов времени, используя каждый раз
свои кривые растяжения, полученные перестройкой кривых простого
последействия по методу Ю. Н. Работнова (см. § 7).
Расчет оболочки сопла. Рассмотрим две задачи расчета сопла:
1) определение напряженно-деформированного состояния, усилий в свя-
зях и местных прогибов на охлаждаемом участке сопла и 2) расчет на
устойчивость неохлаждаемого насадка при работе двигателя на нера-
счетном режиме.
В основной части сопла давление газов мало, и его влиянием на нап-
ряжено-деформированное состояние стенок можно пренебречь. Тогда пол-
ные средние удлинения бфп и 8ХП и напряжения в стенках оф, , сг', cf ,
будут определяться только температурным состоянием сопла. В общем
случае расчет можно вести по схеме, изложенной в §51, но если жест-
кости стенок на растяжении в окружном и осевом направлениях пример-
но одинаковы, т. е. если сопло можно рассматривать как изотропное, то
расчет упрощается. Действительно, в этом случае независимо от геомет-
рии всей оболочки полные окружные удлинения будут равны полным осе-
вым удлинениям, силовые окружные удлинения равны силовым осевым
удлинениям и окружные напряжения в каждом слое по толщине стенок
равны осевым напряжениям в этом же слое. Другими словами, в каждом
слое по толщине стенок
= = < = е;=Еп-е; = е",
< = -^=- + еЛр + %>’ = 2е'-
V °
«• = 8” ’ + е'е' + е’1= 2е",
I 1^3 У X 1 X ф * ф ’
Ъ =а'
°; = /°? - =%=«п •
(52.5)
Из уравнений равновесия элемента оболочки получается соотношение
Л'/2
tf'dz = — tf'h".
(52.6)
436
Дальнейший расчет удобно вести графически подобно тому, как это
делалось в § 51 при упрощенном расчете камеры «по кольцу». Соответ-
ствующие графические построения приведены на рис. 52.2. Зависимость
усилия To = Gf,,iff в наружной стенке от величины полного удлинения
еп получена простой перестройкой диаграммы растяжения материала
наружной стенки при ее температуре Г", которую можно считать посто-
янной по толщине. При построении аналогичной зависимости для внут-
ренней стенки ее разбивают по толщине на несколько слоев AftK, для
каждого из них строят свою кривую, а затем их суммированием полу-
чают зависимость усилия во внутренней стенке
h'12
то= J G'dZ=^'bh'K
-h'/2
от величины полной' удлинения еп. Из условия равновесия (51.6) нахо-
дят рабочую точку Я, определяют величину полного окружного и осе-
вого удлинения еп = €фП = Гхп и величины осевых и окружных усилий в
стенках сопла. Когда будут
найдены полные удлинения и
усилия в наружной и внутрен-
ней стенках сопла, усилия на
связях и местные прогибы
охлаждающего тракта опреде-
ляют точно так же, как для ка-
меры сгорания.
Следует отметить, что пос-
ле выключения двигателя раз-
меры сопла могут уменьшаться
по сравнению с его начальны-
ми размерами. Физика этого
явления заключается в следу-
ющем. В работающем двигате-
ле нагретая внутренняя стенка
«распирает» более холодную
наружную стенку, что приводит к увеличению размеров сопла. Причем
внутренняя стенка (сжатая) обычно оказывается работающей далеко за
пределами упругости, и величина -полного удлинения в рабочем режиме
еп, естественно, бывает значительно меньше температурного удлинения
внутренней стенки (см. рис. 52.2). При остановке двигателя происходит
резкое охлаждение внутренней стенки и она стремиться уменьшиться в
размерах. А поскольку в рабочем режиме она была сжата за пределом
упругости и в ней остались пластические деформации сжатия, то темпера-
турное сокращение размеров внутренней стенки приведет к сжатию на-
ружной, т. е. размеры сопла уменьшатся по сравнению с начальными. Про-
иллюстрировать это можно таким примером (рис. 52.3). Для простоты рас-
суждений предполагается, что наружная стенка вообще не нагревается,
а материал внутренней стенки работает по диаграмме жестко-пластиче-
ского тела с упрочнением, причем его пределы текучести в холодном и
нагретом состоянии различны. Предполагается, также, что перед первым
пуском двигателя в стенках сопла нет никаких остаточных напряжений.
Описанным выше графическим решением по кольцу (см. § 51) опреде-
ляем рабочую точку А при первом пуске двигателя. Если при охлажде-
нии двигателя мысленно отделить внутреннюю стенку от наружной, то
она сокращается на величину 8Т от рабочей точки А до точки В (см.
рис. 52.3). Для определения действительного сокращения можно из точ-
ки В как из начала координат построить диаграмму растяжения холод-
ной внутренней стенки и графическим построением найти точку С
437
и, следовательно, величину остаточных напряжений и остаточных дефор-
маций в стенках сопла после первого пуска двигателя. Аналогичные
построения можно продолжить и для последующих пусков двигателя;
причем при повторных пусках сопло монотонно уменьшается в размерах.
В реальных двигателях описанная картина обычно усложняется ползу-
честью материала внутренней стенки, но характер явления остается
тем же.
При расчете на устойчивость неохлаждаемого насадка, нагружен-
ного на нерасчетном режиме работы внешним перепадом давления, мож-
но заменить его консольно закрепленной цилиндрической оболочкой,
как показано на рис. 52.4. Если материал и толщина оболочки неохлаж-
даемого насадка выбраны и температурное состояние его определено, то
дальнейший расчет на устойчивость можно проделать так же, как это
делалось при расчете на устойчивость стабилизирующей юбки (см. § 43).
Узлы крепления двигателя. Сила тяги ракетного двигателя является
равнодействующей всех поверхностных сил давления. На корпус ракеты
сила тяги передается с помощью узлов крепления двигателя. Выбор того
или иного вида конструкции узлов крепления обусловлен их расположе-
нием на камере двигателя и компоновкой всего двигательного отсека
ракеты. Некоторые возможные конструктивные схемы крепления двига-
теля приведены на рис. 52.5. Схемы а и в относятся к поворотным двига-
телям; здесь вопросы прочности играют подчиненную роль: основное —
конструктивное решение узла крепления, обеспечивающее требуемые
углы поворота всего двигателя. Для схемы б следует произвести расчет
на устойчивость (см. главу VII) сжатой в осевом направлении кониче-
ской оболочки, с помощью которой сила тяги передается на корпус раке-
ты. Для схемы г, где тяга передается с помощью кронштейнов высотой
//, силовое взаимодействие между кронштейном и оболочкой камеры
можно упрощенно представить, как показано на рис. 52.5,г, внизу. Пото-
ки касательных сил qx уравновешивают осевую силу; нормальные уси-
лия qn уравновешивают момент от сил Р/4 на плече И. Если qx принять
постоянным на длине L, a qn — изменяющимся линейно, то
Р 3 PH
Qx -•=-J Qn =--------х-
4 8L Чп 2 L3
Располагая экспериментальными данными по прочности сварного
шва, можно подобрать его длину L.
Расчет фермы в схеме д производится, как это было изложено в § 39.
Поскольку при возникают дополнительные нагружающие оболочку
р
радиальные силы Рг -----tgip, то места крепления двигателя в этом
4
варианте либо размещают непосредственно в зоне головки камеры, там,
438
двигатель обладает наибольшей радиальной жесткостью, либо ставят
дополнительный бандаж. (Это замечание относится и к схеме г, где тоже
возникают нежелательные радиальные силы дп.)
Рис. 52.5
Несколько камер могут образовывать связку; схема такой связки
показана на рис. 52.5,е. Каждая камера в ней имеет два силовых крон-
штейна крепления.
§ 53. ДИНАМИЧЕСКИЕ ЗАДАЧИ
Динамические явления в ЖРД очень сложны. Это обусловлено
прежде всего сложностью химических, тепловых и газодинамических
процессов, происходящих в камере и в сопле двигателя. г
Тонкостенные оболочки, из которых выполнен ЖРД, подверженные
действию переменных температур и давлений, находятся в состоянии
высокочастотных вибраций и, в свою очередь, сами являются мощным
источником вибраций, передаваемых на корпус ракеты и его элементы.
С другой стороны, вибрации оболочек и форсуночной головки приводят
к колебаниям давления жидкости перед форсунками и, как следствие, к
изменению величины впрыска топлива в камеру и поэтому оказывают
влияние на внутрикамерные процессы. Сложные формы оболочек за-
трудняют изучение динамических явлений в ЖРД.
Здесь мы поясним физические причины возникновения коле-
баний, которые полезно знать инженерам, занимающимся расче-
тами на прочность.
В зависимости от поставленных задач соотношения параметров и
интервала изучаемых частот в динамической схеме двигателя можно
выделить ряд частных динамических систем, по которым можно анализи-
ровать автоколебания, параметрические и вынужденные колебания
ЖРД. Существует несколько автоколебательных режимов, не связанных
с упругими колебаниями конструкции двигателя.
439
Например, одна из схем возникновения автоколебаний [51] основана
на том, что скорость впрыска топлива в камеру по отношению к пере-
паду давления на форсунках имеет запаздывание порядка времени ре-
лаксации топливоподающей магистрали, а горение топлива в камере
происходит после впрыска, спустя некоторое время, необходимое для
превращения топлива в продукты сгорания. Это время называется вре-
менем превращения (запаздывания горения). Период колебаний давле-
ния, которое в любой точке объема камеры считается одинаковым, при-
близительно равен удвоенному значению времени превращения и вре-
мени релаксации системы.
Другой механизм возникновения автоколебаний, не зависящий от
процесса впрыска топлива в камеру и названный поэтому внутрикамер-
ным [51], основан {на, том, что время запаздывания горения в колеба-
тельном режиме также является колеблющейся величиной. Скорость
горения достигает максимума при наибольшей скорости уменьшения
времени запаздывания и минимума — при наибольшей скорости возра-
стания времени запаздывания. Если эти колебания совпадают по фазе
с колебаниями давления в камере, то создаются благоприятные условия
для возбуждения автоколебаний.
В автоколебательную систему могут быть также включены продоль-
ные колебания газов в камере и колебания сжимаемой жидкости в тру-
бопроводе. Наилучшие условия для самовозбуждения автоколебаний
создаются в том случае, когда частота колебаний жидкости в трубе близ-
ка к одной из собственных частот колебаний газов в камере [51, 58].
В автоколебаниях могут участвовать и упругие стенки двигателя.
Колебания стенок (в том числе, и форсуночной головки) вызывают коле-
бания давления в межрубашечном пространстве и перед форсунками и
изменение величины впрыска топлива в камеру. В камере начинает пе-
риодически меняться давление и, если фазовые соотношения будут
неблагоприятны, оно будет вызывать упругие колебания стенок. Частота
автоколебаний в данном случае будет близка к частоте упругих колеба-
ний стенок; это, как правило, высокочастотные колебания. Рассмотрен-
ную схему можно усложнить, включив в нее колебания газов в камере.
Механизм возникновения низкочастотных автоколебаний (в том чис-
ле колебаний давления в камере), связанных с упругими колебаниями
корпуса и колебаниями жидкости в трубопроводах, рассмотрен в § 17.
Кроме автоколебаний, в ЖРД могут возникать и параметрические
колебания. Возможность возникновения параметрического резонанса для
цилиндрической оболочки ЖРД можно установить, руководствуясь сле-
дующими соображениями. Предположим, что в результате каких-либо
процессов, например автоколебаний, давление в камере сгорания изме-
няется по закону pr = po + Apsinp/, а в оболочке по какой-либо причине
вызваны колебания с изгибом поперечного сечения по форме, показан-
ной на рис. 53.1. Если давление будет достигать своего максимума в
каждый момент наибольшего искривления поперечного сечения оболочки,
то передача энергии в оболочку при этом будет наибольшая, возникнет
интенсивная ее раскачка. Изгибающий момент от сил давления обра-
зуется лишь, если оболочка получает искривление. Как и в примере с
маятником (см. рис. 17.5), параметрический резонанс может наступить,
когда <о=р/2, <о = р, (о= 1,5р, <о = 2р,...; при со = р/2 передача энергии и
амплитуды будут наибольшими.
Вывод уравнения параметрических колебаний цилиндрической обо-
лочки без учета изгиба образующих дан в работе [93]. Уравнение имеет
вид
qn + ю* (1 + е„ sta pt) qn = 0, (53.1)
где qn — обобщенная координата изгибных колебаний оболочки;
— частота изгибных колебаний n-го тона (п = 2, 3, ...)
440
= Т Га> + l«a— U 4г]> (53‘2)
m(n2+l) L Я J
е„ =-----------------, (53.3)
P, + (n’-l)EW
т— масса оболочки на единицу поверхности;
R — радиус оболочки.
Частота изгибных колебаний оболочки зависит от среднего давле-
ния в камере, с повышением которого частота возрастает. С увеличением
номера тона п частота изгибных колебаний возрастает, а параметр г?г
уменьшается, поэтому зона резонанса сужается. Диаграмма зон резо-
нанса, заимствованная из работы [23], показана на рис. 53.2. Наиболее
опасной является зона, соответствующая р/2со=1. Поэтому если для
камеры двигателя по формулам (53.2) и (53.3) вычислены еп и
<оп(«1=2), то, зная частоту р колебания давления можно по диаграмме
определить, возможно ли возникновение параметрического резонанса.
В сопле двигателя [6], как и в камере сгорания, также могут воз-
никнуть параметрические колебания. Для конического сопла изгиб
оболочки будет происходить, в основном, в окружном направлении при
прямых образующих конуса.
Под действием периодического изменения давления оболочка ЖРД
будет совершать вынужденные колебания. Форма колебаний при этом
будет осесимметричной, колебания оболочки сопровождаются растяже-
нием и сжатием ее в средней поверхности. Однако собственная частота
осесимметричных колебаний оболочки значительно выше частоты изгиб-
ных колебаний и поэтому для наступления резонансного состояния нуж-
на высокая частота изменения давления в камере.
Существует, кроме того, ряд важных инженерных задач по вибро-
прочности арматуры, различных трубопроводов и других устройств дви-
гателя. В таких задачах прежде всего необходимо определять частоты
собственных колебаний этих устройств и конструктивными мерами доби-
ваться того, чтобы они не совпадали с основными частотами ракеты —
частотами продольных и поперечных колебаний корпуса, частотами под-
вески двигателя в продольном и поперечном (угловом) направлениях.
При совпадении частот могут возникать значительные динамические на-
грузки на эти элементы.
В связи с тем, что во время работы двигатель находится в состоянии
вибраций, необходимо применять виброустойчивые соединения и там, где
это целесообразно, — виброгасители. Необходимо исключить возмож-
ность каких бы то ни было зазоров в соединениях различных конструк-
тивных элементов двигателя.
441
ГЛАВА XI
РАСЧЕТ КОНСТРУКЦИИ РДТТ
§ 54. ОСОБЕННОСТИ ТЕПЛООБМЕНА В РДТТ. РАСЧЕТ ТЕПЛОВОЙ
ЗАЩИТЫ ОБОЛОЧКИ ДВИГАТЕЛЯ ПРИ ФИЗИКО-ХИМИЧЕСКИХ
ПРЕВРАЩЕНИЯХ В ТЕРМОИЗОЛЯЦИИ
Для ракетного двигателя на твердом топливе (РДТТ) так же, как
для ЖРД, тепловое воздействие продуктов сгорания является одним из
основных факторов, определяющих работоспособность конструкции.
Влияние теплового воздействия проявляется в том, что от сильно нагре-
тых газов передаются значительные по величине тепловые потоки, кото-
рые аккумулируются неохлаждаемыми элементами конструкции двига-
теля, что вызывает непрерывное повышение их температуры. Поэтому в
отличие от ЖРД, где температурное состояние охлаждаемой конструк-
ции в течение почти всего времени работы (за исключением периодов
пуска и остановки двигателя) определяется процессами стационарной
теплопроводности, для большинства основных элементов конструкции
РДТТ температурное состояние является нестационарным, т. е. темпера-
тура существенно изменяется во времени. Это обстоятельство определяет
специфику тех задач, которые возникают при исследовании и расчете
температурных полей в конструкции РДТТ.
Необходимым условием для расчета температурных полей в РДТТ
является знание условий теплообмена продуктов сгорания с элементами
конструкции двигателя. Процессы теплообмена в ЖРД и РДТТ имеют
много общего, но для последнего они обладают некоторыми особенно-
стями, на которых следует остановиться.
Особенности теплообмена в РДТТ. Несущая часть оболочки камеры
сгорания РДТТ с достаточно большим временем работы защищена от
непосредственного воздействия сильно нагретых продуктов сгорания
слоем термостойкого покрытия. Форма заряда твердого топлива и после-
довательность его горения обычно таковы, что газовый поток омывает
с большой скоростью лишь поверхность соплового днища камеры сгора-
ния и оболочку сопла (см. рис. 57.1, стр. 468). У поверхностей переднего
днища и цилиндирической части камеры сгорания скорость движения
газов сравнительно невелика и определяется, в основном, механизмом
свободной конвекции. В связи с этим теплообмен на этих поверхностях
менее интенсивен, чем в сопловой части двигателя, что упрощает реше-
ние задачи тепловой защиты конструкции камеры сгорания.
Если заряд твердого топлива скреплен со стенками, то они могут
подвергнуться тепловому воздействию продуктов сгорания лишь после
выхода фронта горения топлива на поверхность скрепления. Для некото-
рых форм зарядов это происходит только в последние моменты работы
двигателя, так что температурное состояние цилиндрической оболочки
камеры сгорания, которая одновременно является частью корпуса ра-
кеты, определяется лишь условиями аэродинамического нагрева.
Если же между зарядом и цилиндрической оболочкой имеется зазор,
то он в начале работы двигателя заполняется горячими газами, которые
постепенно остывают, отдавая часть своего тепла оболочке. В этом слу-
чае ее температурное состояние, помимо аэродинамического нагрева,
442
определяется также условиями теплообмена с продуктами сгорания,
которые находятся в зазоре между оболочкой и зарядом.
У поверхности переднего днища образуется застойная зона, движе-
ние газов в которой происходит в соответствии с механизмом свободной
конвекции. Конвективный теплообмен на этой поверхности можно рас-
считать по зависимости, справедливой для условий свободной конвек-
ции {65],
Nu = / Gr ,
где Nu и Сг — критерии Нуссельта и Грасгофа. Критерий Нуссельта, как
уже отмечалось в § 49, характеризует связь между интенсивностью теп-
лоотдачи и температурным полем в газовом потоке у поверхности тела.
Критерий Грасгофа указывает на соотношение между подъемными си-
лами, обусловленными различием плотностей в отдельных точках газо-
вого объема, и силами трения. Разрешая приведенную зависимость отно-
сительно коэффициента теплоотдачи ак, который входит в критерий
Нуссельта, получим
где Хг, vr и Р = 1/273 — коэффициенты теплопроводности, вязкости и
объемного расширения газов;
Тк.с и Тп — температуры продуктов сгорания и поверхности
теплообмена;
D—диаметр днища;
j — ускорение полета (при испытаниях двигателя в
стендовых условиях j = g = 9,81 jn/cezc2).
Например, для топлива с температурой продуктов сгорания Тк.с = 2400 °К и давле-
нием рг = 30 кГ/см2 (vr=l,8-10~5 м21сек,, Хг = 0,12 вт!м-град) при j = 40 м!сек2,
D = 1 м, Тп = 1000 °К получаем ак = 107 впг/м2-град.
Помимо конвекции, передача тепла от продуктов сгорания к обо-
лочке двигателя происходит также излучением. Для однородных газо-
образных продуктов сгорания, которые не содержат твердых или жидких
частиц, расчет лучистых потоков можно провести по формулам
(49.5) — (49.9), приведенным при рассмотрении лучистого теплообмена
в ЖРД. Однако большинство современных твердых топлив при сгора-
нии выделяет газообразные продукты, содержащие твердую или жидкую
фазу в виде частиц углерода и тугоплавких окислов металлов. Излуче-
ние таких продуктов сгорания, в основном, определяется размерами,
количеством и температурой этих частиц. Но указанные параметры ча-
стиц плохо поддаются количественному учету, что затрудняет расчет
лучистого теплообмена в двигателе.
В приближенных расчетах для определения результативного лучи-
стого потока от продуктов сгорания к оболочке можно пользоваться
формулой
?г = ал(Тк.с-Тп), (54.1)
где ал — условный коэффициент теплоотдачи излучением, для которого
в первом приближении рекомендуется значение 600 вт^-град [65].
Суммарный тепловой поток, передаваемый от газов к оболочке ка-
меры сгорания, подсчитывается так:
= ^аг(Гк.с — Т„),
где аг=ак + ал — суммарный коэффициент теплоотдачи от газов к обо-
лочке, учитывающий передачу тепла конвекцией и излучением. Если
443
использовать данные приведенного выше примера для переднего днища
камеры сгорания двигателя, то получим аг = 707 вт!м2-град и
9 = аг(Гк.с—Гп)=707 (2400—1000) =0,99-106 вт/м2.
Передача тепла от газов к поверхности соплового днища и оболочке
сопла двигателя определяется, главным образом, механизмом вынуж-
денной конвекции, связанным с большой скоростью обтекания поверхно-
сти газовым потоком. Конвективный теплообмен здесь можно рассчи-
тать, как и в ЖРД, по формулам (49.1) и (49.2), которые следует пред-
ставить в виде
qK = ак (К ~ Т’п). (54.2)
ак = 4ср/и0,82 Z)-1»82 вт/м2- град. (54.3)
В формулу (54.2) для удельного конвективного теплового потока qK
входит температура заторможенного газового потока, которая принимается
постоянной по длине двигателя и равной температуре продуктов сгорания
в камере сгорания, т. е. Т* =ТКХ. В формулу (54.3) следует подставлять:
удельную теплоемкость с* газов при температуре 7^ — в кдж/кг-град,
расход газов через сопло m — в кг/сек и диаметр сечения сопла D — в м.
Для расчета лучистого теплообмена в зоне соплового днища можно
принять указанное выше приближенное значение коэффициента тепло-
отдачи излучением ал = 600 вт!м2-град. Это значение остается справед-
ливым и в дозвуковой части сопла до сечения с относительным диамет-
ром £>/jDkp = 1,2. В остальной части сопла по мере падения термодина-
мической температуры газов интенсивность лучистого теплообмена будет
быстро уменьшаться. Для расчета можно взять те же доли от принятого
значения ал, которые рекомендуется брать в ЖРД от лучистого потока
в камере сгорания (см. § 49): при £>/7)кр=1 (критическое сечение соп-
ла) —0,5; D/D^= 1,5—0,15; D/DKp = 2,5—0,04.
В качестве примера на рис. 54.1 показано изменение величин ак, ал и аг = ак + ал
по сечениям сопла РДТТ при следующих исходных данных: с? = 3 кдж[кг-град\ m =
= 17 кг!сек\ J)Kp = 0,1 м. В критическом сечении сопла
ак = 4с* zn0,82 D-1'82 = 4-3(17)°’82 (0,1)-1,82 = 8070 вт/м*-град,
ал = 0,5-600 = 300 вт^-град,
аг = ак ал = 8070 + 300 = 8370 вт[м2-град.
444
В камере сгорания при D/DK[) = 2
ак = (ак)кр(D/DKP)"’’82 = 8070 (2)-1’82 = 2280 вт!мг-град
И
ак = ак + ал = 2280 600 = 2880 etn/м2-град.
Из графика видно, что наиболее напряженным в тепловом отношении является
критическое сечение сопла двигателя. Здесь возникают наибольшие трудности в орга-
низации защиты конструкции от теплового воздействия газового потока. Вопросы рас-
чета температурного состояния конструкции в зоне критического сечения рассмотрены
в § 56. Там же изложен способ определения предельного температурного состояния
оболочки сверхзвуковой части сопла.
Конструкция соплового днища двигателя, которое включает в себя
дозвуковую часть сопла, обычно выполняется в виде двухслойной обо-
лочки, состоящей из металлической стенки и слоя теплозащитного по-
крытия. Способы расчета температурного поля в такой оболочке рас-
смотрены в § 55. В качестве теплозащитных покрытий в РДТТ
применяются материалы, которые претерпевают физико-химические
превращения и разрушаются при обтекании их поверхности высокотем-
пературным газовым потоком. Влияние этих процессов на теплообмен
с газовым потоком и работоспособность теплозащитного покрытия рас-
сматривается ниже.
Помимо рабочего режима, процессы теплообмена применительно к
РДТТ необходимо рассматривать и в период хранения двигателя. Дело
в том, что температурное поле в заряде твердого топлива влияет на его
напряженно-деформированное состояние в процессе хранения и работы
двигателя, а от температуры заряда перед пуском зависят баллистиче-
ские характеристики РДТТ [14]. Для литых зарядов, скрепленных со
стенками камеры сгорания, следует также принимать во внимание усло-
вия теплообмена оболочки с окружающей средой в период заливки топ-
лива, его полимеризации и последующего охлаждения до температуры
окружающей среды.
Для свободно вложенного заряда, когда между ним и оболочкой
имеется зазор, напряженно-деформированное состояние заряда в про-
цессе хранения связано с неравномерностью распределения температуры
но его объему. Температура заряда твердого топлива, которое обычно
плохо проводит тепло, изменяется медленнее, чем температура окру-
жающей среды. Значительные градиенты температуры в топливе могут
вызвать опасные термические напряжения, которые приводят к наруше-
нию целостности заряда при хранении, образованию трещин и увеличе-
нию поверхности горения, что может стать причиной взрыва двигателя
при пуске.
Степень неравномерности температурного поля в заряде зависит от
интенсивности его теплообмена с окружающей средой. Чем интенсивность
теплообмена меньше, тем равномернее температурное поле и менее
опасны термические напряжения. Помимо воздушного зазора, который
снижает интенсивность теплообмена между зарядом и оболочкой, тепло-
вое воздействие окружающей среды можно уменьшить с помощью на-
ружной теплоизоляции корпуса двигателя.
Наиболее совершенным способом поддержания заданного темпера-
турного режима заряда в процессе хранения является создание системы
термостатирования, которая автоматически подстраивается под изме-
нение условий теплообмена оболочки с окружающей средой. Расчет,
проектирование и настройка такой системы неразрывно связаны с ис-
следованием теплообмена в полости камеры сгорания и корпуса двига-
теля с окружающей средой.
Для заряда твердого топлива, скрепленного с оболочкой, поддержа-
ние заданного температурного режима с помощью системы термостати-
445
рования имеет еще более важное значение. Здесь опасны не только не-
равномерность температурного поля в заряде, но и большая разница
между температурой скрепления заряда с оболочкой и температурой
хранения. Дело в том, что коэффициент линейного расширения топлива
обычно выше, чем материала оболочки, из-за чего возникают напряже-
ния даже при одинаковой по объему заряда температуре. Однако вопро-
сы расчета и проектирования системы термостатирования носят специ-
фический характер и поэтому более подробно здесь не рассматриваются.
Расчет тепловой защиты оболочки двигателя при физико-химических
превращениях в термоизоляции. В РДТТ применяются теплозащитные
покрытия, поверхность которых разрушается при интенсивном нагреве
и механическом воздействии газового потока, а толщина покрытия
уменьшается по мере работы двигателя. Разрушение покрытия пред-
ставляет собой сложный физико-химический процесс, протекающий в
поверхностном слое при высокой температуре. Он сопровождается тер-
мическим разложением вещества, плавлением и испарением отдельных
составляющих покрытия, разрушением и уносом материала газовым по-
током.
Подобным образом разрушается обтекаемая продуктами сгорания
поверхность стеклопластика, который находит применение в РДТТ в ка-
честве конструкционного материала [14, 65]. Сначала в поверхностном
слое при сравнительно низкой температуре газифицируется связующее —
смола, а затем, по мере нагрева, оплавляется и уносится газовым пото-
ком наполнитель — стекловолокно. При проектировании оболочки РДТТ
из стеклопластика необходимо оценить, какая часть стенки подвергается
тепловому разрушению и какая сохраняет способность воспринимать на-
грузку.
Основная цель применения в РДТТ разрушающихся покрытий и
материалов состоит в том, чтобы защитить несущую часть конструкции
от теплового воздействия со стороны продуктов сгорания. При этом зна-
чительная доля подводимого от газового потока тепла расходуется па
физико-химические процессы, происходящие в поверхностном слое ма-
териала, а количество тепла, передаваемое посредством теплопроводно-
сти в глубь материала, сравнительно невелико.
Если предположить, что все физико-химические процессы происходят
на поверхности покрытия, омываемой продуктами сгорания, то уравне-
ние баланса тепла для этой поверхности примет вид
я' = — -ф- I + fpi (54.4)
дх |п
где q' — удельный тепловой поток, подводимый к поверхности от про-
дуктов сгорания;
Xi и рг — коэффициент теплопроводности и плотность покрытия;
v и Н* — скорость и удельный тепловой эффект процесса разрушения
покрытия.
Координатная ось х направлена в глубь покрытия по нормали к его
поверхности (рис. 54.2). При достаточной толщине покрытия условия
его теплообмена с внешней средой или с несущей частью конструкции
не влияют на процессы, происходящие в зоне движущейся поверхности.
На ней устанавливается постоянная температура Г* теплового разруше-
ния материала.
Если процесс разрушения покрытия является установившимся,
(и = const,q' = const), то из уравнения (54.4) следует, что градиент тем-
пературы dT\ldx|п также остается постоянным. Это значит, что профиль
(распределение) температуры в подвижной системе координат £ = х—vt,
начало которой связано с движущейся поверхностью покрытия, не изме-
446
няется по времени t. Преобразуя для данного случая одномерное диф-
ференциальное уравнение теплопроводности
д7\ _ „ d2Ti
-----—
dt 1
в подвижной системе координат, получаем обыкновенное дифференциаль-
ное уравнение
Л2Л , у dl\ _Q
a, d~
(54.5)
с граничными условиями: при £ = 0 Т = 7’* и при |->оо Т=Т0 — началь-
ной температуре покрытия. Решая это уравнение, получаем следующую
формулу для распределения температуры покрытия в зоне движущейся
поверхности [65]:
7*1 — То И (Те То) ехр
- —1
(54.6)
От разрушающейся поверхности в глубь покрытия отводится удель-
ный тепловой поток
-^44 =Х1 — (T,-T0)^c1P1v(T,-T0). (54.7)
дх |п d% |£=0 aL
Для определения скорости v в уравнении (54.4) осталось найти лишь
величину Она зависит от скорости и, так как на перенос тепла от
продуктов сгорания в пограничном слое будет оказывать влияние встреч-
ный поток газообразных продуктов разру-
шения со стороны поверхности покрытия. Т
Если встречное движение отсутствует
(покрытие не разрушается), то к поверхно-
сти с температурой Г* подводится удельный
конвективный тепловой поток ql{, который,
согласно формуле (54.2), равен
<7к = «к(^г-Т.), (54.8)
причем коэффициент теплоотдачи ак рассчи-
тывается по зависимости (54.3). Соотноше-
ние (54.8) условно можно рассматривать
с позиций стационарной теплопроводности в
плоской стенке (см. рис. 54.2) толщиной
h' = к'/ак, где V — коэффициент теплопро-
водности газов, которые движутся вдоль
поверхности параллельными слоями. Если
же эти слои в поперечном направлении про-
низываются со скоростью v' потоком про-
дуктов разрушения материала покрытия, то распределение температуры
Т' в условно принятой стенке, толщина которой предполагается прежней,
отличается от линейного и описывается дифференциальным уравнением
d?T' v' dr _ 0
d^ a' d% ’
где a'^Xlc'v' — коэффициент температуропроводности газообразных
продуктов разрушения материала покрытия. Это уравнение аналогично
соотношению (54.5), но описывает процесс теплопроводности в газе. Оно
447
имеет следующие граничные условия: при £ = 0 Т = Т* и при £ = —h'
Т = ТГ. Решая уравнение, получаем
[v
— -г И —1
1 , -г v г — , ; ----2—
Г v'
ехр --h
I а'
— 1
Отсюда конвективный тепловой поток, подводимый к поверхности по-
крытия,
Количественные оценки показывают, что vh'/a' = с'р'и'/ак<^ 1- Поэтому
в этой формуле целесообразно разложить экспоненциальную функцию в
ряд и в нем ограничиться лишь первыми тремя членами. Тогда
Поскольку на поверхности разрушения рV = р^, окончательно получим:
-1Г)-
(54.9)
Величину 1 — (c'piu^Qk) можно рассматривать как коэффициент,
характеризующий уменьшение конвективного теплового потока вслед-
ствие вдува газообразных продуктов разрушения покрытия в погранич-
ный слой. Вдув более холодных газов в пограничный слой можно орга-
низовать и без разрушения поверхности, например, пропусканием их
через пористую стенку. Однако этот способ требует усложнения кон-
струкции двигателя. __
Величину результативного лучистого потока qr от продуктов сгора-
ния можно считать такой же, как и для неразрушающейся поверхности,
так что суммарный удельный тепловой поток к разрушающейся поверх-
ности покрытия
< =<7к+<7г- (54.10)
Теперь из уравнения (54.4) с учетом соотношении (54.7) — (54.10)
определим скорость разрушения покрытия:
ак (Т — qr
V = -----------•
Pi [я* + С! (Т* -То) + -у- (?; - Т,)]
ий)
Заменив величину qr по формуле (54.1), окончательно получим:
аг(Тг*-7\)
v ~-----------------------------------
Pi [я, -Ь С1 (Т, -То) + -у-(Тг* - Т,)]
где аг = ак + ал и ал— условный коэффициент теплоотдачи излучением
(см. выше).
Если время работы двигателя tK, то толщина разрушенного слоя
покрытия составит ft* =vtK. Полученная формула остается приближен-
448
но верной и для переменных по времени условий теплообмена с газовым
потоком. В этом случае по формуле (54.11) вычисляют мгновенную ско-
рость разрушения покрытия, определяемую текущими значениями
ак, Тг и qr. Тогда толщину разрушенного слоя подсчитывают по соот-
ношению
h,= \vdt. (54.12)
б
Подобный прием использован в § 42 при решении задачи о разрушении
теплозащитного покрытия головной части ракеты при входе в плотные
слои атмосферы.
Толщина слоя покрытия до сих пор предполагалась настолько боль-
шой, что процесс теплопроводности в зоне движущейся поверхности по
зависел от условий теплообмена на противоположной поверхности.
Теперь необходимо дать количественную оценку начальной толщине Ло
слоя покрытия, при которой это допущение остается справедливым.
С практически достаточной точностью влиянием теплообмена на противо-
положной поверхности можно пренебречь, если ее температура Тк в кон-
це работы двигателя отличается от начальной температуры То менее чем
па 5% от разности Т*—То, т. е.
Гк~Г° <0,05. (54.13)
Т* ^0
Это условие выполняется в том случае, когда
vtK + -^-<h0. (54.14)
V
Если считать, что температура Тк несущей части конструкции в кон-
це работы двигателя должна удовлетворять условию (54.13), то формулу
(54.14) в виде
hQ=vtK-\-^- (54.15)
V
можно использовать для выбора начальной толщины теплозащитного
покрытия. При проектировании оболочки двигателя из стеклопластика к
найденной величине ho следует добавить слой толщиной Д/г0, который
будет воспринимать нагрузку.
Пусть заданы параметры, соответствующие дозвуковой части сопла в сечении с
относительным диаметром DIDkp = % (см. выше) : Т'Г = 2127°С; ак=2,28 квт)м? • град\
аг =2,88 квт!м2-град\ То = 2О°С; ai = 5-10~7 м21сек\ ci = l кдж)кг-град\ pi = 1600 кг/jn3;
//* = 6000 кдж/кг\ Т* = 1200°С; / = 2,5 кдж!кг-град\ /к=25 сек. Тогда, вычисляя по фор-
мулам (54.11) и (54.15), получаем скорость разрушения поверхности покрытия
у = 0,20 мм/сек, необходимую начальную толщину покрытия Ао = 12,5 мм. Толщина раз-
рушенного слоя Л* = у/и = 5 мм. Вдув газообразных продуктов разрушения в погранич-
ный слой уменьшает конвективный тепловой поток, передаваемый от газов, на 17,5%
(с/р 1 v/2«к =2,5-1600 -0,2-10“3/2 - 2,28=0,175).
§ 55. ТЕМПЕРАТУРНОЕ ПОЛЕ В МЕТАЛЛИЧЕСКОЙ СТЕНКЕ
С ТЕРМОИЗОЛЯЦИЕЙ
Наиболее часто для защиты поверхности несущей конструкции
РДТТ от теплового воздействия продуктов сгорания на нее наносят тер-
мостойкое покрытие. Для тонкостенных оболочек с теплозащитным
покрытием, которые являются типичным элементом конструкции двига-
теля, характерно малое отношение суммарной толщины металлической
29 Зак. 96
449
стенки и слоя покрытия к радиусу кривизны. Если это отношение не пре-
вышает 0,1, то с достаточной точностью подобную оболочку при реше-
нии задачи нестационарной теплопроводности можно рассматривать как
двухслойную пластину (рис. 55.1,а).
При сравнимых по величине толщинах слоев металла h и покрытия
hx первый имеет незначительное в сравнении со вторым термическое
сопротивление распространению тепла. Поэтому металлическую стенку
рассматривают лишь как слой, аккумулирующий тепло, а ее темпера-
туру Т считают одинаковой по толщине. В общем случае принимают, что
Рис. 55.1
с обеих сторон пластины происходит теплообмен, который описывается
уравнением Ньютона для конвекции. Условия теплообмена различны с
каждой стороны пластины, но не изменяются вдоль ее поверхности. Сле-
довательно, температура пластины меняется лишь в направлении одной
пространственной координаты z (одномерное температурное поле), на-
чало отсчета которой находится в плоскости контакта металла и слоя
покрытия. Характер распределения температуры l\(z, t) по толщине
пластины в произвольный момент времени показан на рисунке, причем
для температуры металлической стенки Т (t) = 7"i (0, t).
Если принять коэффициенты теплопроводности Xi и температуропро-
водности а\ материала теплозащитного покрытия постоянными, то рас-
пределение температуры по толщине покрытия будет описываться
линейным уравнением теплопроводности
”<..<) , А (55Л>
dt dz2 Q Р1
с граничными условиями
атхс/хх, п = аг _Т1 оь (55 2>
dz
%! dT1(dz “c lT1 (0’ Z) “ ?cl + СрЛ ’ (55’3)
где сир — удельная теплоемкость и плотность;
а — коэффициент теплоотдачи.
За начальное условие принимаем
Л (z, 0) = Т9. (55.4)
450
Параметры без индекса в соотношениях (55.1) — (55.4) относятся к
металлу, с индексами «1», «г» и «с» — соответственно к теплозащитному
покрытию, продуктам сгорания и внешней среде со стороны металли-
ческой стенки.
Сформулированная выше задача наиболее эффективно решается
операционным способом [56]. После преобразований получаем реше-
ние [35]
Т (z t) Bir Тг + Bic Тс + Bir Bic [Тс— (Тг— Тс) z]
Bip Bic -f- Bir Bic
00
2-‘У" exp [— Fo] I Bir (Тг— To) Г cos p„z +
n=\
+ (Bic - 1 + Bic (Tc - To) [cos И„ (1 - z) +
l гЛ J L
+ Bir sinHn(i~z) 11 ( (55
Цп J '
где
Fo = -^-, Bir=-^, Bic = K = z = —,
h\ M ciPi^i h
Zn = Bir + Bic - Яр* + (Bir + Bic + c os pn +
— множество корней трансцендентного уравнения
ctg ц 1 О К Bir) р2 BirBiс
и Bir + Bic- Кр2
(55.6)
которое называется характеристическим.
Критерий Фурье (Fo) является безразмерным временем процесса
нестационарной теплопроводности, критерии Био Bir и Bic характеризуют
интенсивность теплообмена на поверхность пластины, а параметр К
является отношением полных теплоемкостей металлической стенки и
теплозащитного покрытия. Из формулы (55.5) нетрудно получить выра-
жение для температуры металлической стенки, приняв z = 0.
При стендовых испытаниях двигателя температура внешней среды
обычно равна начальной, т. е. TC = TQ. Тогда вместо формулы (55.5)
получим
Л & 0 - То = 1 + Bicz~_____
Bir (Т* — То) Bir + Bic + Bir Bic
- Vexp [-14Fo] (Bic - Xp=>
цп 4 L i-м J
1
Температуру металлической стенки в этом случае определяют из формулы
Т (Л — То 1 ул 2 sin ii„ . 2 п 1
----—----2— ----------------------У ,------— exp f — р„ Fo].
Bir(T*-Te) Bir + Bic + BirBic
r n=l
Условия теплообмена пластины с продуктами сгорания и внешней
средой сильно отличаются по интенсивности, причем обычно Bir^> Bic
29* 451
и Bic< 1. В этом случае расчетные формулы можно упростить приняв
в них Bic = 0, т. е. считать, что пластина со стороны металла идеально
теплоизолирована. При расчете днищ и оболочки сопла это допущение
приводит к некоторому завышению температуры конструкции. После
упрощения для определения температуры покрытия получим соот-
ношение
-----; = У ,--ехр (— уп Fo] (cos vnz—Kvn sin vnz), (55.7)
Tr~7’o-----------------"
где
1 К 2 , / 1 . 2\ sin vn
yn = 1-----—Vn + 1 + —— Vn ------------2- COSVn
Bir \ Bir J vn
и vn — корни характеристического уравнения
tg v = Bir~Kv2J . (55.8)
v(l + KBir)
В практических расчетах в первую очередь определяют температуру
металлической стенки как элемента конструкции двигателя, несущего
нагрузку. Температуру Т(t) находят из соотношения (55.7) при z = 0:
6 =-----;-----У Вп ехр [— vn Fo],
т'~т‘ ±1
в„= —7-"- <55-9>
Угг Г п
Характеристическое уравнение (55.8) можно представить в графиче-
ской форме. Его правая часть обращается в нуль при значении (v)0 =
= / Bir//( и имеет асимптоту
3 l + KBir
Абсциссы точек пересечения кривых, соответствующих левой r/i, и
правой у<2. частям уравнения (55.8), равны vn (рис. 55.1,6). Из графика
видно, что при Bir>0 и любой величине (v)0 корни уравнения (55.8)
лежат в диапазонах
О < Vi < л/2 < v2 < Зл/2 Оз < 5л/2 ... (2п — 3) л/2 <
О„< (2n— 1) л/2.
Величина стоящая в показателе экспоненты в формуле (55.9),
сильно возрастает с повышением номера п. Поэтому бесконечный ряд
в этой формуле быстро сходится, являясь к тому же знакопеременным.
Для такого ряда отбрасывание членов, начиная с n-го, приведет к по-
грешности в вычислении, которая не будет превышать величину этого
члена. Анализ показывает, что наибольшие по абсолютной величине зна-
чения коэффициентов ряда равны
(ВЛах = 4(-1)"+>/(2п-1)л, т. е. (5^ = 1,273, (В2)тах =
= —0,424, (В3)тах = 0,255 и т. д. Если в ряду удержать всего один
первый член, то относительная погрешность менее 1°/0 будет при условии
0,01 > | (В2)тах
или Fo > 1,52.
452
Если удержать два члена, то максимально возможная относительная
погрешность не превосходит 1°/0 при условии
0,01 > (B3)max exp I" — Fo j или Fo > 0,15.
В большинстве случаев погрешность менее 1 % в результате отбра-
сывания третьего члена ряда обеспечивается, начиная с меньших значе-
ний Fo. При значениях Fo<0,15 величина T(t) лишь незначительно
отличается от То, так как изменение условий теплообмена на поверхно-
сти покрытия еще не успевает вызвать существенного изменения темпе-
ратуры металлической стенки. Поэтому в практических расчетах доста-
точно удерживать в ряду в формуле (55.9) не более двух членов.
Как было указано выше, параметр K=cphlcxpxh^ входящий в при-
веденные выше формулы, является отношением полных теплоемкостей
металлической стенки и слоя покрытия. С ростом этого отношения доля
тепла, аккумулированная покрытием, уменьшается и, начиная со значе-
ния /<^10, ее можно не учитывать. Тогда слой покрытия играет роль
лишь термического сопротивления, и расчет ведут по формуле
Г* — T(t)
г.- (- = ехр[-т], (55.10)
1 г 1 о
где т = atlcph\
а— приведенный коэффициент теплоотдачи;
а а
При относительная ошибка расчета по формуле (55.10) не
превышает 3,5%, причем с ростом величины Bir погрешность умень-
шается. Эта оценка может служить, в частности, ориентиром при опре-
делении времени установления равновесной температуры оболочки сопла
(см. § 56).
Если вместе с параметром К увеличивается и критерий Био
(Bir^10), то перепад температур Тг —Гп между продуктами сгорания
и поверхностью покрытия становится малым в сравнении с разностью
Тг—Т и им можно пренебречь, приняв t) =Ти=Тг. Тогда в фор-
муле (55.10) следует принять аг->оо и T=Ti = Xi^/cp/ift1.
При достаточно интенсивном теплообмене с газовым потоком
(Вг^10) условие Ti (/i!, t)=T r целесообразно использовать и в более
общем случае, когда полные теплоемкости металлической стенки и слоя
теплозащитного покрытия сравнимы между собой. Этот случай часто
встречается в расчетной практике. Термическое сопротивление теплоот-
дачи 1/ctr при этом оказывается, по крайней мере, на порядок меньше
термического сопротивления слоя покрытия /ii/Xi, и им можно прене-
бречь. В формулах (55.7) — (55.9) это соответствует переходу к Bir->oo.
Расчет температуры металлической стенки ведется, как и прежде, по
формуле (55.9), но коэффициенты ряда теперь равны
, 2sinv;
“п — ", ; ; у ,
+ sin cos vn
а значения v’n находят из решения характеристического уравнения
ctg v = Ку. (55.11)
Согласно формуле (55.9) относительная температура 0 металличе-
ской стенки определяется в этом случае лишь значениями К и Fo. Для
453
ее расчета удобно пользоваться номограммой (рис. 55.2), построенной
в полулогарифмических координатах. В таких координатах зависимость
0 от Fo при фиксированной величине К становится практически прямо-
линейной, начиная примерно со значений Fo=0,2—0,3. Излом прямых
при Fo = 0,5 вызван изменением масштаба номограммы по оси абсцисс.
Пример. Пусть требуется определить температуру Тк металлической стенки
соплового днища двигателя в конце его работы, если заданы: Тг = ТК с = 2400°К =
= 2127°С; То = 20°С; аг = 2880 вт/мР-град, ^ = 5 мм; = 0,8 вт/м-град; =
= 1 кдж/кг-град; рх = 1600 кг/м3; h — 3 мм; с — 0.5 кдж/кг-град; р = 8000 кг/м3;
время работы двигателя 25 сек. Расчетным путем получаем:
Bir = ap/ix/Xx = 2880-5-10~3/0,8 = 18,0;
К = cth/c^ht = 0,5-8000-3-10"3/1 • 1600-5-10~3 = 1,5;
ar = Xi/cxPi = 0,8/1-103-1600 = 5-10-7 м^/сек;
FoK = artjh} = 5-10-’ • 25/(5-10~3)2 = 0,5.
Так как Bir> 10, то можно пользоваться номограммой. По номограмме при Fo=0,5
и К = 1,5 интерполяцией между кривыми для К =1,4 и 1,6 находим, что 0 = 0,831.
Тогда ТК = Т (/к) = Т* - 0 (Т^ - То) = 2127 - 0,831 (2127 - 20) = 375°С.
При условии =Т* нетрудно учесть возможное изменение тем-
пературы газового потока по времени, т. е. Т* = Т* (/) = ТГ (Fo). Решая
подобную задачу для двухслойной пластины, идеально теплоизолированной
со стороны металлической стенки, получаем следующую расчетную
формулу для температуры металла:
сю Fo
Т (/) = то + £ Вп J [Т; (£) - То] exp [(v;)® а - Fo)] dt (55.12)
n=l 0
Это решение использовано, в частности, в § 42 для определения темпе-
ратурного состояния оболочки головной части ракеты с неразрушаю-
щимся теплозащитным покрытием.
Помимо строгого аналитического решения задачи нестационарной
теплопроводности для двухслойной пластины можно использовать при-
454
ближенный аналитический способ. Ниже этот способ рассматривается
для случая отсутствия теплообмена со стороны металлической стенки.
Процесс теплопроводности в пластине условно делится по времени
па две стадии (рис. 55.3). Первая стадия соответствует распространению
в глубь покрытия возмущения, вызванного на-
чалом теплообмена с газовым потоком, а вто-
рая— изменению температуры по всей толщи-
не пластины одновременно. Величина А*—
глубина проникновения температурного воз-
мущения, изменяется на первой стадии от О
до Аь
Сущность приближенного способа реше-
ния заключается в том, что дифференциальное
уравнение (55.1), описывающее процесс тепло-
проводности в слое покрытия, удовлетворяется
по координате z в среднем. Для этого его ин-
тегрируют по z в области, где протекает про-
цесс теплопроводности. Далее задача сводится
к решению обыкновенного дифференциального
уравнения, независимой переменной в котором
является время t.
Для рассматриваемой пластины распреде-
Рис. 55.3
ление температуры на первой стадии процесса
можно приближенно представить в виде квадратной параболы:
Л = П + (Тп-т0) (1-
\2
В это соотношение входят неизвестные А* и температура Тп поверх-
ности теплообмена с газовым потоком. Последнюю можно исключить с
помощью граничного условия (55.2), которое примет вид
адт;-?;) =24^-1 =2-^-(7’п-Т0).
OZ |п Л*
hj — z \2
h* J
(55.13)
Из двух последних формул получаем
Т*-То
т, = т,+ г '
«Л
Подставляя это выражение в уравнение (55.1) и интегрируя его по z
в пределах от hY—Аф до Аь можно получить дифференциальное уравнение
Ог^---_dh^_ = б
A,! dt
а+*
h
причем Аф = 0 при t = 0. Отсюда определяем связь глубины проникнове-
ния температурного возмущения с временем процесса:
=. _Л f 2 (\2 in (1 + a?h*
h? 12 3arh* 3 \ ar/i* J \ /
Температурное возмущение достигнет металлической стенки (А+ = Ах) за
время /х, что соответствует значению критерия Фурье
Fn______ 1 । 1
1 — ~ 12 3Bir
— 1п(1 + 44. (55.14)
455
В этот момент температура поверхности при z = hx равна
т*__________________________________________т
ТП = ТО + Bir —.
п 0 г 2-J-Bir
Если интенсивность теплообмена с газовым потоком велика (Bir->oo), то
Fox -> 1/12. При Fo'CFoj температура металлической стенки остается
равной начальной, т. е. Т =--Т0.
Распределение температуры в слое теплозащитного покрытия на вто-
рой стадии процесса теплопроводности также принимают параболическим:
т1 = т + ь1(^-Л + ь2(^-'\2.
\ /11 J \ /11 J
В это выражение входят три переменные по времени величины:
Ьи Ь2 и температура металлической стенки Т. После его подстановки в
уравнение (55.1) и интегрирования последнего от 0 до hr получаем
— + — + = «1-^-1 —=2аА- (55.15)
1 dt < 2 3 J 1 dz |г=л, dz |2=о Г
Из граничных условий при z = О
1 д7\ 1 dT гр гр
dz dt
находим дополнительное соотношение
= cph — . (55.16)
hi dt
Наконец, из граничного условия (55.2) при z =- h± имеем
ar(77 _T-Z>1_Z,2)=2j_(6i+262). (55.17)
hi
Из соотношений (55.15) — (55.17) исключаем Ьг и 62. В итоге полу-
чаем обыкновенное дифференциальное уравнение второго порядка:
. d2T. - + 2ЛХ------ -F Ао (Т - Гг) = °,
<ht у , I Ы \
\ h* ) I J
где
А _2 3 + Bir-b ЗК(1 +Bir) д 12Bir
1 K(4-FBir) ’ 0 К(4 + Bir) ‘
В момент времени t = tr (начало второй стадии процесса теплопровод-
ности) Т = Т0, Ь± ’= 0 и, согласно соотношению (55.16), dT/dt = Q.
Общим решением полученного уравнения будет
Т = Тг + exp [/7zxFo] + D2 exp [m2Fo],
где и /и2— корни характеристического уравнения
ш2 + 2А1ш 4- Ао = О,
т. е.
/«1.2 = — Д ± Y Al — Ао.
Постоянные DY и D2 определятся из начальных условий при t — tt:
T0 = T* + Dt exp 1/^FoJ + Z)2 exp [mJA],
0 = exp [rn^oj + D2m2 exp [/n2Foj].
456
В итоге получаем следующую зависимость для температуры метал-
лической стенки на второй стадии процесса теплопроводности:
Д—— = ——-— ехр (Fo— Foi)] 4-------------------—— exp [т2 (Fo — For) ]. (55.18)
Тг — То m2 — mi «1 — т2
Коэффициенты Ь± и Ь2, входящие в формулу распределения темпера-
туры по толщине теплозащитного покрытия, определяют из соотношений
bi = К (Т*г - То) {ехр [т, (Fo - F01)] - exp [m2 (Fo - Fo,)!},
— m2
2 r 2-|-Bir 2 + Bir
Например, для параметров, соответствующих переднему днищу двигателя (см. § 54)г
Т*Г = ТК с = 2400°К = 2127еС, аг = 707 вт / м2 - град, а также То = 20°С; h± = 4 мм\
= 0,47 вт/м-град} сх= 1,2 кдж/кг-град; рх= 1800 кг/м?\ h = 3 мм; с= 0,5 кдж/кг-град;
р — 8000 кг/м2; /к=25 сек, находим: Bir = 6; /(=1,4; а1=2,18*10-7 мР/сек и FoK= 0,34.
Далее из формулы (55.14) получаем Foi=0,113. Так как FoK> Fox, то конец работы двигателя
соответствует второй стадии теплопроводности в оболочке днища. Расчетным путем нахо-
дим: Л=5,49; Ао=5,14; —0,49; т2=—10,49; Тк = 160°С; 6Х=1215 гради62=410 град.
Распределение температуры по толщине покрытия при t = tK определяется зависимостью
z / г \2
Ti = тк 4- bl (z/hi) + b2 (z/hiP = 160J4- 1215 — 4- 410 ( — ) .
hi \ h-i J
В частности, температура поверхности теплообмена с газовым потоком
Tj = Тк + + Ь2 = 160 + 1215;+ 410 = 1785°С.
Если для сравнения при тех же исходных данных провести расчет по формулам (55.7) —
(55.9), то получим: = 0,689; = 2,927; Bi = 1,098; В2 = — 0,120;
Тк = Т* — (Г* — То) {В1 ехр [ — VjFoK] 4- В2 exp [ — v2FoK]} =
= 2127 — (2127 — 20) {1,098 ехр [— (0,689)2-0,34^— 0,120 ехр [— (2,927)2-0,34]} =
= 168°С и Тп = 1837°С. Совпадение результатов расчетов по точным и приближенным-
формулам можно считать удовлетворительным.
Для решения задачи нестационарной теплопроводности для двух-
слойной пластины можно также использовать приближенную математи-
ческую модель процесса теплопроводности (см. § 25). На рис. 55.4,а слой
покрытия разбит на участки шириной Дг, в середине которых помеща-
ются узловые точки, имеющие температуры 7\(/= 1,2,...,п). Узловая точка
с индексом О лежит в плоскости контакта металлической стенки и слоя
покрытия. Ей соответствует температура Т металла и полная теплоем-
кость cph + 0,5cipiДг. Считаем, что на обеих поверхностях пластины про-
исходит конвективный теплообмен (см. рис. 55.1).
Изменение температур узловых точек по времени описывается систе-
мой обыкновенных дифференциальных уравнений:
(cph. 4- 0,5 с1Р1Дг) + = + (Л - Г) 4- ас (Тс -Т),
at ixz
C]P1Az = + (Т - Л) + + (Т2 - Л),
dt Дг Дг
CiPi\z-^- = + (7,-1 -Tt) 4- + (Ti+I-T),
dt \z kz
457
Рис.
Температура Тп поверхности покрытия равна
Т = Т
1 п п
тг-тп
1 + -^-
arAz
(55.20)
Для интегрирования системы уравнений необходимо знать начальное
распределение температуры в узловых точках в момент времени 1 = 0.
Эту систему можно решить на аналоговой машине (ЭАВМ) с усилите-
лями постоянного тока или с помощью электрического аналога, состав-
ленного из /?С-ячеек (рис. 55.4, б, в). Параметры изображенных схем
должны подчиняться пропорциям
Ri Rr Rc Ci С
Az/Xi l/ar l/ac ’ CipiAz cph
На вход каждой схемы подаются напряжения и* и ис, пропорциональ-
ные температурам Т* и Тс. По измеренным напряжениям щ узловых то-
чек из пропорции —ТС)/(Т* — Тс) = (ui—uc)/(u*— ис) определяют тем-
пературы 7\-. Масштабом времени, который связывает электрический про-
цесс в схеме с процессом теплопроводности в пластине, является отно-
шение (^z^la^RC.
Если производные в левой части уравнений системы (55.19) заменить ко-
нечными разностями (см. §25), то для каждого интервала времени Д^
получим систему алгебраических уравнений:
[пК + у И + *)] Pk (П - Л-0 = TI>ft-7\ +
Pk k — Тi, i) — Tk — 2TL k 7*2, k,
(55.21)
Pk (Ti, k— Ti, k—1) = Ti— I, k — ^Ti, k + T'i+l, k,
А (Л k - Tn, *-i) = T„_,. k-Tn.h + T-r'k -~±-k— ,
— + (li/ar, k\z)
где
Pk =
Ti,k-\ и 7\ k — температуры i-той узловой точки в начале и в
конце /?-того интервала времени;
ac,k И Л,л, «г,k И Тг,Аг — коэффициенты теплоотдачи и температуры внеш-
ней среды и продуктов сгорания в конце интер-
вала.
Системе уравнений (55.21) соответствует электрический аналог (рис.
55.4, г), который позволяет провести решение задачи по последовательным
интервалам времени Д^. Сопротивления схемы подчиняются соотношению
Ri =.____________= Ro , Rr = Rc
AzMi ‘ A/fe/CiPiAz (Mk/cph \l/arJfe l/ac,/
На каждом интервале времени в нижние точки схемы задаются на-
пряжения пропорциональные температурам 7\ а>-ь а напряжения
459
и* k и uCtk устанавливаются пропорционально значениям 7* k и TCtk. В
верхних (узловых) точках схемы измеряются напряжения uitk, по которым
из пропорции (Tit k — TCt k)/(Tl k — Tc, k) = (u,i, k — uc, *)/(u*r, k — uc, k) опреде-
ляют температуры Tit k- Далее процесс решения повторяют для следую-
щего интервала времени. При этом сопротивления схемы могут изменять-
ся от интервала к интервалу, поскольку могут меняться значения Д/Л>
ас, аг, а также, в связи с изменением температуры, теплофизические ха-
рактеристики материалов.
Помимо электрического аналога, для решения системы уравнений
(55.21) можно воспользоваться методом прогонки (см. § 25). Рассмот-
рим применение этого метода на примере.
Пусть ас = 0 (теплообмен со стороны металлической стенки отсут-
ствует), и = 7, Д/ = 5 сек. Тогда для исходных данных приведенного выше
примера (см. стр. 454), получаем:
Дг - ^/(п + 0,5) = 5/(7 + 0,5) = 0,667 мм\
pk=--p = = (0,667-10—3)2/5 • 10“7 - 5 = 0,178;
[пК + 0,5 (Д + 1)] pk = [7-1,5 + 0,5 (1,5 + 1)] -0,178 - 2,09;
Хх/агДг - 0,8/2,88-10~3-0,667-10-3 = 0,416;
1/[0,5 + (М/«гМ 1 1/10,5 + 0,416] - 1,091.
Расчет по методу прогонки целесообразно вести с помощью таблицы,,
номера колонок которой соответствуют номерам узловых точек. В первых
трех строках табл. 55.1 приведены значения коэффициентов алгебраиче-
ских уравнений (55.21), представленных в форме трехчленных
— k + Д7\ k — C^Ti—\9k — Dit k.
Таблица 55.1
i 0 1 2 3 4 5 6 7
Ai 1 1 1 1 1 1 1 0
Bi 3,09 2,178 2,178 2,178 2,178 2,178 2,178 2,269
Ci 0 1 1 1 1 1 1 1
Di,i 41,8 3,56 3,56 3,56 3,56 3,56 3,56 2326
Ei 0,324 0,540 0,611 0,639 0,650 0,655 0,657 0
Fi,i 13,5 9,23 7,81 7,26 7,04 6,94 6,90 1448
4i 47,3 104 176 275 419 634 957 1448
98,8 18,5 31,3 49 74,6 113 170 2580
32 27,3 35,8 54,1 83,5 128,7 196,5 1725
104 222 361 533 733 999 1330 1725
Di з 217 39,5 64,3 94,8 130,5 178 237 2629
Лз 70,4 59,3 75,5 108,9 150,4 215 297 1818
178 331 504 700 925 1191 1491 1818
D[A 372 59 89,6 124,5 165 212 266 2645
Pi 4 120 97 114 152 206 274 355 1863
Ti\ 260 431 619 826 1055 1308 1580 1863
Di 5 544 76,7 110 147 188 232 281 2654
Fi\ 176 136 150 246 313 380 440 1892
345 521 713 921 1145 1383 1633 1892
460
В четвертой строке даны величины £\-,i для первого интервала времени
при условии, что начальные температуры узловых точек 7\,о = 2О°С.
Далее указаны значения коэффициентов £г- и F^ вычисленные после-
довательно по формулам
р Г k 1, k
Е: = ----------- и F; k ~ ----------- .
1 Bi-CtE^
И, наконец, приведены температуры Л,1 в °C узловых точек в конце пер-
вого интервала времени, которые определяются в обратном порядке
(от i+ 1 к I) по формуле (25.12)
Тi, k — Тi-\-\, kEi + Ft, k.
При этом для n-й узловой точки (п = 7) ТпА = FnA = 1448° С. Температу-
ра поверхности покрытия в конце первого интервала времени
Тп, 1 — Т П' 1 4-
К-Тп^
1 4“ 2 (Xi/ctrAz)
1448 + 2127-J448 = 1818оС
1 +2-0,41'6
Коэффициенты £г- остаются неизменными для всех интервалов.
В таблице для последующих четырех интервалов времени приведе-
ны значения Ditk, Fith и Tiik в °C. Таким образом, в последней строке
таблицы дано распределение температуры по узловым точкам в момент
времени £к = 25 сек, соответствующий концу работы двигателя. Темпера-
тура металлической стенки ТК = 345°С удовлетворительно согласуется со
значением, полученным выше с помощью номограммы. Температура
поверхности покрытия в конце работы двигателя будет
Тп, 5 == Тп, 5 4-
К-тпЛ
1 4-2(М/агЛ?)
= 1892 + --—— = 2020°С.
1+2-0,416
Отличие температуры поверхности покрытия от значения Т*=2127°С
и объясняет получение в расчете по номограмме, в котором принято Тп =
=T*t несколько завышенной величины Тк = 375°С, оценивающей «сверху»
нагрев металлической стенки при интенсивном теплообмене оболочки с
газовым потоком.
§ 56. ТЕМПЕРАТУРНОЕ ПОЛЕ В КОНСТРУКЦИИ СОПЛА
В конструкции сопла РДТТ можно выделить два характерных участ-
ка (см. рис. 57.1, стр. 468): один — в зоне критического сечения — выпол-
няется обычно в виде специального вкладыша, а другой — сверхзвуковая
часть сопла, называемая раструбом.
Расчет раструба. Раструб представляет собой, как правило, много-
слойную оболочку, состоящую из слоев металла и теплозащитного по-
крытия (14, 65]. Выходная часть оболочки сопла с большой степенью
расширения газов может не иметь теплозащитного покрытия. Суммар-
ная толщина всех слоев оболочки мала по сравнению с ее радиусом.
Поэтому в тепловом отношении оболочку раструба можно рассматри-
вать как плоскую многослойную пластину. Так как условия теплооб-
мена вдоль раструба изменяются сравнительно медленно, то распреде-
ление температуры в оболочке считается одномерным, изменяющимся
.лишь по ее толщине. Таким образом, для расчета нестационарного
температурного поля в раструбе можно воспользоваться способами,
изложенными в § 55.
Здесь целесообразно остановиться лишь на одном расчетном случае,
который может встретиться при проектировании раструба для РДТТ с
461
продолжительным временем работы. После начала работы двигателя*
температура каждого из участков_ раструба будет возрастать, пока не
достигнет равновесного значения Т, при котором подводимое от газов
количество тепла будет равно отводимому посредством излучения с
внешней поверхности раструба. Это значение будет наибольшим воз-
можным для данного участка оболочки, и его следует сравнивать с до-
пустимой температурой [Т], при которой применяемый в конструкции»
раструба материал сохраняет работоспособность в газовом потоке.
В направлении от среза сопла к критическому сечению интенсив-
ность теплообмена оболочки с газовым потоком увеличивается, в резуль-
тате чего возрастает величина Т. При проектировании раструба важно»
определить сечение сопла, в котором устанавливается равновесная тем-
пература, значение которой допустимо для применяемого материала
оболочки, т. е. выполняется условие Т=[Т]. Для части оболочки между
срезом сопла и этим сечением Т<[Т], и она может выполняться без теп-
лозащитного покрытия. Остальная часть оболочки нуждается в защите
от перегрева слоем покрытия, стойкого в газовом потоке.
Ниже последовательность расчета иллюстрируется на числовом при-
мере, в котором в качестве исходного принято распределение коэффици-
ента теплоотдачи аг от газового потока по сечениям сопла, рассчитанное
в § 54 (см. рис. 54.1). Это распределение повторено на рис. 56.1,п. Тем-
пература заторможенного газового потока 7г = 2400°К, допустимая тем-
пература материала раструба [Т]= 1700° К, степень черноты его внешней
поверхности е = 0,8, относительный диаметр среза_сопла £>/£)Кр = 5.
Если принять, что равновесная температура Т металлической обо-
лочки раструба постоянна по толщине, то уравнение баланса тепла для
произвольного сечения сопла будет иметь вид
аг(Т* — Т) = e6qT4; (56.1)
где По = 5,77-10-8 вт/>и2(оК)4— коэффициент излучения абсолютно чер-
ного тела. Отсюда при значении Т = 1700° К находим величину
г еа0Т< 0,8-5,77.10-8(1700)4 . 2 л
[аг1 =^=--5---= —----------------— = 550 вт м2-град,
7* —Г 2400— 1700
соответствующую сечению сопла, в котором выполняется условие Т = [Г].
Из рисунка следует, что это значение коэффициент теплоотдачи имеет
в сечении с относительным диаметром £>/£)Кр = 4,4.
462
Для определения равновесной температуры оболочки раструба бе»
теплозащитного покрытия (4,4<О/ОКр^5) уравнение (56.1) целесооб-
разно привести к безразмерному виду
где
W =_^о_(7”)3) fl = JL,
аг г Т*г
и для его решения воспользоваться рис. 24.3.
Например, для выходного сечения сопла по рис. 56.1, а находим аг = 430 вт/мР-град..
Затем вычисляем
N = (еа0/аг) (Т*)3 = (0,8-5,77-10~8/430) (2400)3 = 1,49
и с помощью рис. 24.3 определяем О = 0,68 и Т = ОТ* = 1630°К. Результаты расчета'
распределения температуры Т по сечениям этой части оболочки показаны на рис. 56.1 а.
Для того чтобы на остальной части металлической оболочки раст-
руба сохранилась температура Т=[Т], необходимо на его внутреннюю*
поверхность нанести теплозащитное покрытие. Уравнение баланса тепла,
для участка оболочки с покрытием имеет вид:
“г (Л* - тп) = А- (Тп - Т) г0оТ*.
где Тп, hr и Xi — температура поверхности покрытия, его толщина и коэф-
фициент теплопроводности. Отсюда находим
тп = Т* — Т4 и Й! = Тп~7 = Тг~т —
“г еа0Т4 ео0Т4 °г
Например, при Т — [Г] = 1700°К и значении = \вт1м-град для сечения сопла с
относительным диаметром £>/£)кр= 1,5 (аг = 3950 вт/мР-град) по этим формулам полу-
чим Тп = 2300°Ц и = 1,56 мм. Изменение величин Тп и hv по сечениям сопла пока-
зано на рис. 56.1, а.
Время /, за которое практически (например, с точностью 2%) уста-
навливается равновесное температурное состояние сопла, можно оценить-
следующим образом. Для металлической оболочки сопла без покрытия
изменение температуры Т по времени t описывается дифференциальным
уравнением вида (26.1):
Cpft^L = ar(Tr’-T)-ea0T\
где h, с и р — толщина, удельная теплоемкость и плотность материала
оболочки. С учетом равенства (56.1) это уравнение приводится к форме:
cph = аг (Т-Т)+ ео0 (Т4 - Т4). (56.2}
at
Процесс нагрева оболочки сопла начинается с температуры TQ.
На рис. 56.1,6 сплошной кривой показан характер изменения вели-
чины ?л = еа0(Г4—Г4) с изменением температуры Т. В первый период
нагрева, когда ^температура сопла мала в сравнении с ее равновесным
значением (Т<Т), что соответствует горизонтальной пунктир-
463.
ной линии на рисунке. Тогда вместо выражения (56.2) получим уравне-
ние
(56.3)
Ср/г^ = аг(Т;-Т)
без учета излучения оболочки, решением которого будет соотношение
т=:т;-(т;-т0)ехрГ--^'
В последующий период нагрева, когда температура Т близка к значению
Т, выражение для qn можно приближенно представить в виде
дл 4ео0Т3 (7 — Г),
что соответствует наклонной пунктирной линии на рисунке.
Точка пересечения пунктирных линий имеет абсциссу 7 = 0,75 Т. До
этого значения можно считать справедливой зависимость (56.3). Время
/1, отсчитываемое от начала нагрева, которое соответствует этому значе-
нию, определяют из формулы
cPh . 7Г 7*0
ti =----In--------
аг 7* —0,757
После момента времени t = изменение температуры оболочки сопла
приближенно описывается дифференциальным уравнением
cph = ах (Т — 7), ах = аг + 4еа073,
dt
интегрируя которое, получаем
Т = Т —
Z — G I
—а1—X •
c?h J
Из этой формулы можно найти значение /, при котором разница между
текущей и равновесной температурами составляет 2%, т. е. Т ^0,987,
1 = ti — in 4 Т~°.,9,8Т = ti + 2,52-^-.
aj Т «1
Например, для выходного сечения сопла (D/£)Kp = 5) при аг — 430 впг/м2. град;
Т = 1630°К; с = 0,25 кдж!кг-град; р = 8700 кг/л3; h = 1 мм и То — 20°С — 293°К по-
лучаем
430
О1 = 430 + 4-0,8-5,77-10“» (1630)3 = 1230 впг/м^град;
0,25-103.8700.10-3 2400 — 293
G —------------------1п —— — —- = 3 сек и t = 3 -Т 2,52 X
430 2400 — 0,75-1630
0,25.103.8700.10-3
X -----------------= 7,5 сек.
1230
Если полная теплоемкость слоя покрытия Cipj/zi мала в сравнении
с полной теплоемкостью металлической стенки ср/г, то для участка обо-
лочки с покрытием можно воспользоваться теми же формулами, заменив
в пих аг на приведенный коэффициент теплоотдачи
1
аг =------------.
—+ т"
а г М
В § 55 показано, что подобная замена приводит к ошибке не более 3,5%
при K = cph!c\p\h^ 10. Однако для оценки величины t «снизу» прене-
464
брсчь полной теплоемкостью покрытия можно и при меньших значениях
параметра К.
Например, для сечения сопла с относительным диаметром Z)/Z)Kp=l,5 при h —
= 3 мм и условии, что Т = [Т] = 1700°К, получим
сс,, =------------=-------------------------== 550 вт1м2-град,
(1,4) + (ММ) (1/3950)+ (1,56-Ю-з/1,
а1 = аг + 4£О'0Т3 = 550 Ц-4-0,8-5,77-10-8 (1700)3 = 1350 вт^-град]
0,25 • Юз. Q700 • 3 • 10-3 2400 — 2 93
tY =--------------------In -----------------= 7 сек
1 550 2400-0,75-1700
Z = 7 4- 2,52
0,25-103.8700-3-10-3
1350
= 19,3 сек.
Расчет вкладыша. В зоне критического сечения -сопла вкладыш
является наиболее тепло-напряженным элементом конструкции двигате-
ля. В этом сечении интенсивность теплообмена с газовым потоком мак-
симальна. В связи с этим во время работы двигателя возникает опас-
ность теплового разрушения и эрозии поверхности вкладыша, нарушения
теометрических размеров и формы газодинамического тракта двигателя,
что может привести к недопустимым отклонениям параметров РДТТ от
заданных значений. Поэтому основным требованием, которому должна
удовлетворять конструкция вкладыша, является стойкость его материала
в газовом потоке при условии сохранения геометрии обтекаемой поверх-
ности.
Это требование можно удовлетворить либо применением жаростой-
ких материалов, имеющих высокую температуру плавления, либо соз-
данием вкладыша в виде аккумулятора тепла, применив хорошо тепло-
проводный материал с низкой температурой плавления. Возможно
создание комбинированного вкладыша, имеющего на поверхности,
обтекаемой газовым потоком, слой жаростойкого материала и объем,
занятый материалом — аккумулятором тепла. Поглощение тепла этим
материалом существенно увеличивается, если использовать тепловые
эффекты, сопровождающие его плавление и последующее испарение.
Проектирование вкладыша и суждение о стойкости его материала в
газовом потоке неразрывно связано с определением температурного
состояния вкладыша. Можно выделить два основных расчетных случая.
Выбор первого связан с возникновением в период пуска двигателя боль-
ших градиентов температуры у поверхности вкладыша, обтекаемой газо-
вым потоком. При этом появляются значительные термические напря-
жения, которые особенно опасны для жаростойких материалов, обла-
дающих повышенной хрупкостью. Выбор второго расчетного случая
определяется прогревом вкладыша по всему объему в процессе работы
двигателя. Рассмотрение этого случая позволяет судить о силовом взаи-
модействии отдельных элементов конструкции вкладыша и допустимом
времени работы двигателя, в течение которого вкладыш сохраняет рабо-
тоспособность.
Температурное состояние вкладыша в первые моменты времени
после пуска двигателя решающим образом зависит от условий тепло-
обмена на его огневой поверхности, обтекаемой газовым потоком. Усло-
вия теплообмена на остальных поверхностях в этом случае играют не-
значительную роль, и их можно не учитывать. Тогда задачу нестацио-
нарной теплопроводности можно будет свести к задаче для тела весьма
больших размеров с внутренней полостью, ограниченной огневой поверх-
ностью вкладыша.
30 Зак. 96
465
Для малых интервалов времени t, прошедших с момента начала на-
грева вкладыша, допустимо считать, что тепловой поток, передаваемый
от газов с температурой торможения Тг к огневой поверхности с темпе-
ратурой Гп,
9 = аг(Т;-Тп)
далее распространяется по нормали к этой поверхности. Таким образом,
если выделить на ней элементарную площадку dS0 со сторонами dxQ и
dyQ (рис. 56.2,а), то тепловой поток, прошедший через эту площадку,
затем остается в пределах четырехгранной пирамиды. Ее грани явля-
ются плоскостями, перпендикулярными к огневой поверхности вкладыша.
Площадь сечения пирамиды dS на расстоянии г, отсчитываемом по нор-
мали от огневой поверхности вкладыша, будет
dS = dxdy = dx0(\^-^-')dy0( 1 + = dS</l + -4-V1 + -M,
\ А1 / \ К2 X А1 / \ К2 /
где и /?2 — радиусы кривизны рассматриваемого участка поверхности.
Распространение тепла в пирамиде описывается дифференциаль-
ным уравнением
ср
— dS = — dS
dt dz \ dz
Из двух последних соотношений при условии постоянства теплофизиче-
ских свойств (X, сир) материала вкладыша получаем
dT ,с d2T . dT ( 1
-----dS = a dS + a ---------
dt---dz2------------dz \ Ri
J_____। 2г
Rz RiR2
о*
(56.4)
Цель решения задачи — определить температурное поле в поверх-
ностных слоях вкладыша, для которых расстояния z малы в сравнении
с радиусами кривизны. Поэтому в уравнении (56.4) величинами порядка
и z//?2 можно пренебречь по сравнению с 1. Тогда получим линейное
дифференциальное уравнение с постоянными коэффициентами
dT
dt
d2T . о dT
= а---------\-2an-----,
dz2 dz
1
х = —
2
(56.5)
466
граничными условиями: при z = О
-Х-^- = аг(Тг-Т),
dz
при z—>ооТ ~*TQ и начальным условием —при t — О Т = TQ.
Решая уравнение (56.5), приходим к расчетной формуле
T — TQ = ехр [- xz] ?
т*__тп хХ
'г 'о 1+----------
«г
где
z - —Д=-, £ = f х 4- /ЕГ,
2 at ’ * \ X ) 1
f(z, £) = erfcz — ехр [£(2? + £)] erfc(z 4- £),
причем
оо
erf с и — f ехр [— В2] .
)/ л J
и
В частности, при u = 0 erfc u=l. Зависимость /(г, £) представлена на
рис. 56.2,6. Расчетом по приведенной формуле устанавливаем распреде-
ление температуры в поверхностных слоях вкладыша. Оно позволяет
определить напряженно-деформированное состояние этих слоев и оценить
опасность термических напряжений, возникающих при пуске двигателя.
При рассмотрении второго расчетного случая представление темпе-
ратурного поля вкладыша как одномерного обычно неприменимо. Лишь
в некоторых случаях для получения сугубо ориентировочных данных о
температурном состоянии вкладыша можно использовать расчетную
схему однородной или многослойной цилиндрической трубы или плоской
пластины с одномерным распределением температуры. Решение задачи
для однослойной пластины с независящими от температуры теплофизи-
ческими характеристиками легко получить из формулы (55.7) при Х = 0.
Если использовать расчетную схему цилиндрической трубы, то распре-
деление температуры по ее радиусу описывается более сложными зави-
симостями, чем для пластины. Расчетные формулы для однородной и
многослойной трубы можно найти в специальной литературе по неста-
ционарной теплопроводности.
Условия теплообмена с газовым потоком довольно сильно изменя-
ются вдоль оси вкладыша, а сам вкладыш может иметь весьма произ-
вольную форму и состоять из нескольких слоев с различными теплофи-
зическими характеристиками. Все это приводит к изменению темпера-
туры вкладыша в осевом направлении, т. е. температурное поле,
сохраняя в цилиндрических координатах осевую симметрию, оказывается
двухмерным. Расчет двухмерного нестационарного температурного поля
в неоднородном теле произвольной формы — задача довольно сложная.
В инженерной практике такую задачу рационально решать на основе
приближенной математической модели процесса нестационарной тепло-
проводности (см. § 25) с использованием ЭЦВМ или аналоговых
устройств.
§ 57. ПРОЧНОСТЬ КОРПУСА РДТТ
Типичные силовые схемы и особенности расчета на прочность РДТТ.
Двигатель па твердом топливе (РДТТ) является вторым, кроме ЖРД>
основным вариантом современного ракетного двигателя.
РДТТ используется как в качестве стартового ускорителя для кры-
латых ракет, так и в качестве маршевого двигателя для баллистических
30* 467
или крылатых ракет. Вопросы создания и расчета конструкции старто-
вых двигателей упрощаются вследствие сравнительно малого времени
их работы; кроме того, весовые характеристики стартовых двигателей не
столь важны для всей ракеты, как весовые характеристики маршевых
двигателей. Поэтому в дальнейшем изложении основное внимание будет
уделено расчету на прочность маршевых РДТТ с временем работы
порядка нескольких десятков секунд.
На рис. 57.1,а приведена типичная схема РДТТ. Двигатель имеет
корпус 1 с передним 5 и задним 3
Рис. 57.1
днищами и сопловый блок 4. Заряд
твердого топлива 2 может быть сво-
бодно вложен в корпус двигателя
(рис. 57.1,6) или прочно скреплен
с ним (рис. 57.1,в).
Работающий двигатель можно
рассматривать как сосуд, нагружен-
ный давлением горячих газов, обра-
зующихся в результате горения за-
ряда твердого топлива. Основное
назначение корпуса — выдержать в
течение заданного времени совмест-
ное воздействие внутреннего давле-
ния и высоких температур и пере-
дать на остальную часть ракеты си-
лу тяги. Кроме того, РДТТ обычно
является ч'астыо силового корпуса
всей ракеты и поэтому он восприни-
мает продольные и поперечные на-
грузки, а также испытывает внеш-
ний аэродинамический нагрев. С точ-
ки зрения прочности, величины на-
пряжений, вызываемых этими внеш-
ними продольными и поперечными
нагрузками, не опасны, поскольку обычно они малы по сравнению с ве-
личинами напряжений, вызываемых рабочим давлением газов. Но они
могут привести к потере устойчивости корпуса двигателя в том случае,
когда внешние нагрузки действуют на неработающий двигатель. Напри-
мер, это может произойти с двигателями второй и третьей ступени при
работающем двигателе первой ступени или с двигателем первой ступени
стоящей на старте ракеты.
Металлический корпус и металлические днища РДТТ целесообразно
рассчитывать по разрушающим (предельным) нагрузкам, дополняя в
некоторых случаях этот расчет проверкой по допускаемым перемеще-
ниям и допускаемым напряжениям. Так, для днищ с несимметрично рас-
положенными соплами дополнительной проверкой по перемещениям
будет определение угла поворота оси сопла, вызванное деформацией
всего днища. Этот угол не должен превышать допускаемого значения,
задаваемого при проектировании. Стеклопластиковый корпус двигателя
рассчитывают по разрушающим нагрузкам с дополнительной проверкой
по допускаемым напряжениям, так как стеклопластик — материал хруп-
кий, и поэтому необходимо проверять, не превышают ли допускаемых
значений величины местных напряжений, вызванных концентрацией
напряжений в местах стыков и в местах соединения стеклопластика с
металлом.
Особо следует отметить действие температур на конструкцию РДТТ.
Во-первых, корпус двигателя должен быть предохранен тем или иным
способом от непосредственного воздействия высоких температур горячих
газов. Во-вторых, должны быть приняты меры, чтобы изменения темпе-
468
ратуры на несколько десятков градусов в процессе изготовления и хра-
нения не приводили к значительным температурным напряжениям и
деформациям. Напряжения и деформации могут возникать вследствие
резкого (обычно почти в десять раз) различия между коэффициентами
линейного расширения топлива и материала корпуса двигателя или
вследствие неравномерного поля температур в крупногабаритных заря-
дах (при резком изменении температуры окружающей среды).
Сначала рассмотрим .расчет собственно корпуса двигателя, а затем
расчет днищ.
Расчет собственно корпуса двигателя. При расчете собственно кор-
пуса двигателя предполагается, что толщина изоляции выбрана и тем-
пература стенок корпуса двигателя известна; вопрос о выборе оптималь-
ной толщины изоляции корпуса будет рассмотрен отдельно.
Расчет цельнометаллического цилиндрического
корпуса. Расчет такого корпуса ведут по так называемой котельной
формуле и запас прочности п определяют из условия прочности в окруж-
ном напряжении:
л=_£в\ (57 Д)
P3R 7
где рэ — максимальное эксплуатационное давление в двигателе;
ав — предел прочности материала;
h и 7? — толщина стенки и радиус корпуса.
При этом предполагается, что либо сварные швы вообще отсут-
ствуют (корпус, изготовленный методом раскатки), либо технологически
обеспечена равнопрочность сварного шва и основного материала (кор-
пус, свернутый из листа с последующей сваркой).
Расчет стеклопластикового корпуса. В этом случае
необходимо принимать во внимание резкую анизотропию прочностных
свойств стеклопластика и запас прочности корпуса проверять как в
окружном, так и в меридиональном направлениях:
где (о’в)ф и (<Ув)х — соответственно пределы прочности стеклопластика
в окружном и меридиональном направлениях. За окончательный запас
прочности следует взять наименьший из двух полученных.
Стеклопластик, вопреки своему названию, — материал далеко не
пластичный. Диаграмма его растяжения вдоль стеклонитей остается
практически линейной вплоть до разрушения. В результате этого сило-
вые стсклопластиковые элементы конструкции чрезвычайно чувстви-
тельны ко всякого рода концентрациям напряжений. Именно поэтому
в стеклопластиковых корпусах РДТТ особого внимания заслуживают
все стыки. Конструктивно они должны быть выполнены таким образом,
чтобы концентрация напряжений в них была сведена к минимуму [14].
Расчет комбинированного корпуса. При расчете ком-
бинированного корпуса, состоящего из высокопрочной металлической
оболочки, усиленной обмоткой из стекловолокна с полимерным связую-
щим, можно выделить две задачи: 1) определение напряжений в метал-
лической оболочке и обмотке в рабочем режиме; 2) определение пре-
дельной величины внутреннего давления.
Стеклопластик при нагружении его вдоль волокон ведет себя упруго.
Если предположить, что в рабочем режиме и материал металлической
стенки работает в упругой области, то напряжения в комбинированном
корпусе определить легко. При этом можно считать, что начальные на-
пряжения, возникающие в металлической оболочке, пренебрежимо малы
по сравнению с рабочими напряжениями. Учет этих начальных напря-
469
жений тоже не составляет труда, но они не могут быть значительными,
поскольку тогда тонкостенная металлическая оболочка потеряла бы
устойчивость до нагружения внутренним давлением. Нагрев стенки счи-
тается незначительным и температурные удлинения тоже не учиты-
ваются.
Поскольку в РДТТ площадь критических сечений сопел значительно
меньше площади поперечного сечения корпуса, то можно считать, что
осевое усилие Ti = prR/2. Если металлическая оболочка укреплена про-
стой поперечной обмоткой, которая может воспринимать только окруж-
ные напряжения, то условиями равновесия, очевидно, будут
<4 /г' -г Gyh" = PrR, exh' --= prR/2, (57.3)
где Оф и вх—окружное и меридиональное напряжения в металлической
оболочке;
Оф — окружное напряжение в обмотке;
h' и h" — толщины металлической стенки и обмотки.
Условие равенства окружных удлинений металлической оболочки и
обмотки
= <57-4>
Е Е
где Е' и Е"— модули упругости металла и обмотки;
р/ —коэффициент Пуассона для металла.
Из условий (57.3) и (57.4) получим
' _ PrR ' _ Pr# l+p'(E"h”/2E'h
2/i' Ф h' l+(E"h"/E'h')
" _ prR E"_________1 — p72
Ф ~ h' Ef I(E''h"/E'h')
(57.5)
В более общем случае, когда корпус укреплен и продольно распо-
ложенной обмоткой, а материал металлической стенки работает за пре-
делом упругости, расчет может быть произведен по общей схеме расчета
двухслойной оболочки, изложенной в § 51 применительно к несущей
способности камеры ЖРД; при этом нетрудно учесть и температурные
деформации в комбинированном корпусе.
При определении предельного значения давления, т. е. при расчете
корпуса по несущей способности, можно ввести упрощающее допущение:
считать, что материал металлической стенки работает по диаграмме иде-
альной пластичности, причем предел текучести совпадает с пределом проч-
ности материала ав- Кроме того, поскольку удлинение разрыва стекло-
пластика обычно около 2 %, то можно считать, что ofl/£" > GqIE'. Тогда
величины предельного окружного (Т2)пр и осевого усилий в цилиндри-
ческом корпусе определятся так:
(7\)Пр = h' + а'в h”, (Т^ (57.6)
Оптимальным следует считать такое соотношение толщины металли-
ческой стенки и обмотки, при котором корпус равнопрочен в окружном
и осевом направлениях [126]. Поскольку в нагруженной внутренним дав-
лением цилиндрической оболочке 7^! = 7"2/2, то оптимальным будет
/г;;1т = А-, fJQ (57-7)
2 \ hQ /ОПТ 2
где hQ = p^R/бв — толщина металлического корпуса без обмотки при том
же расчетном давлении рг=^прэ.
470
Интересно оценить, какой выигрыш в весе можно получить, приме-
нив комбинированный корпус. Если ввести относительную массу единицы
поверхности силового корпуса (без учета массы термоизоляции)
— + 9"h"
т = ---
P'^o
(57.8)
где p' и p" —удельные веса металла и обмотки, то, используя соотноше-
ния (57.6), найдем
<57-9’
где Л = ———. При оптимальной величине h'/h0 = 1/2 получится
< р'
™ = + <57Л0>
2 \ Л J
При Л'/Ло <С 1/2 цилиндрическую металлическую оболочку следует
укреплять не только поперечной обмоткой, но и продольной. Тогда
PrR - Овй' 4- (Увйф, -у pfR = в'вЬ' + oahxt (57.11)
где и hx — соответственно толщина обмотки в окружном и осевом
направлениях. Из формул (57.11) следует
= hx = h'0-^-(— --4-Y (57-12)
ств Ло J ав 4 2 Ао 7
Относительный вес единицы поверхности корпуса двигателя будет
2 Л' < к) fto 2
(57.13)
Если при /г7/*о <!/2 укреплять
металлическую оболочку не про-
дольно-поперечной обмоткой, а на-
клонной к оси оболочки под некото-
рым углом а, то можно показать, что
при оптимальном а = а0Пт относи-
тельная масса комбинированного
корпуса будет определяться той же
зависимостью (57.13). На рис. 57.2
приведены зависимости т от отно-
шения h’lhfr построенные по выра-
жению (57.9) при и по вы-
ражению (57.13) при h'Ihb<xl2. Ин-
тересно отметить, что при /<<2 про-
стая поперечная обмотка в весовом
отношении оказывается выгоднее
продольно-поперечной и наклонной.
Нужно также подчеркнуть, что вы-
игрыш в весе по корпусу в целом при
продольночпоперечной и наклонной
обмотках практически еще меньше,
Рис. 57.2
471
чем на рис. 57.2, так как требуется заделка продольной и наклонной об-
моток на торцах оболочки.
Расчет днищ. Одна из основных трудностей расчета днищ состоит
в необходимости учета ослабляющего влияния имеющихся в них сопло-
вых отверстий (см. рис. 57.1,а). Различают два варианта нагружения
сопел: 1) во время работы двигателя на переднем днище сопла заглу-
шены, на заднем — открыты; 2) в процессе опрессовки двигателя при
заглушенных соплах на переднем днище могут быть заглушены и сопло-
вые отверстия на заднем днище. В связи с этим возникают две задачи:
1) расчет нагруженного внутренним давлением днища с заглушенным
соплом и 2) расчет днища с открытым соплом.
В настоящее время используют несколько подходов к решению задач
такого типа. Например, можно из линейного решения задачи об изгибе
упругой оболочки найти величины максимальных напряжений, возникаю-
щих в зоне отверстия днища; сравнивая эти величины напряжений с ве-
личинами напряжений в аналогичном днище без отверстия, можно полу-
чить так называемый к о эф ф и ц и е н т концентрации напряже-
ний. Величина этого коэффициента табулируется и в дальнейшем
используется в известной схеме расчета по допускаемым напря-
жениям. Но при изгибе тонких оболочек зона повышенных напря-
жений носит ярко выраженный локальный характер, связанный с подроб-
но рассмотренным в § 17 краевым эффектом. Поэтому расчет по допу-
скаемым -напряжениям с использованием коэффициента концентрации
напряжений оправдан только для очень хрупких материалов, а для
достаточно пластичных материалов, чаще всего используемых в реаль-
ных конструкциях, такой подход нецелесообразен, как это уже отмеча-
лось в § 11.
В некоторых случаях, помимо этого, определяют величину коэф-
фициента концентрации напряжений с учетом пластических деформаций
в зоне краевого эффекта. Такое решение дает более полное представ-
ление о распределении напряжений в реальном днище по сравнению с
решением в упругой области, но оно все же не устраняет основного недо-
статка самого подхода к расчету днищ по допускаемым напряжениям:
для пластичных материалов такой подход не дает возможности правиль-
но оценить работоспособность днища.
Как отмечалось выше, для ракетных двигателей логичнее вести ра-
счет на прочность не по допускаемым напряжениям, а по допускаемым
перемещениям. Для этого можно, использовав диаграмму растяжения
реального материала днища, с помощью машинного метода решения
типа шагового [97] выяснить картину поведения данного днища при дан-
ном варианте нагружения. Затем, имея полную информацию о пове-
дении днища под нагрузкой, можно обоснованно найти то значение
нагрузки, при котором днище еще сохраняет работоспособность в данном
конкретном варианте работы двигателя. Это, вероятно, наиболее совре-
менный и общий путь решения, но, насколько нам известно, задача о
прочности днищ с отверстиями машинными методами типа шаговых до
сих пор не исследовалась. (Шаговый метод с успехом был применен
В. И. Феодосьевым и С. М. Черняковым [97] к решению аналогичной
задачи о поведении сферической упруго-пластической оболочки с жест-
ким фланцем под действием сосредоточенных нагрузок.)
Наконец, возможен и расчет днища по предельной нагрузке, когда
материал реального днища заменяется идеальным жестко-пластическим
телом и определяется то значение нагрузки, при котором в результате
развития пластических деформаций конструкция из жестко-пластическо-
го тела перестает быть жесткой, превращается в механизм (см. § 15).
Расчет по предельным нагрузкам в такой трактовке тесно примыкает к
расчету по допускаемым перемещениям. Действительно, достижение
472
предельной нагрузки характеризуется прежде всего резким ростом пере-
мещений. Поэтому используемое ниже решение о предельной нагрузке
днища с отверстиями можно рассматривать как упрощенный первый этап
полного расчета днища по допускаемым перемещениям.
Рассмотрим две вспомогательные задачи о предельной нагрузке
сферической оболочки с закрытым и открытым патрубками под действием
внутреннего давления [82]; результаты решения этих задач легко пере-
нести на расчет сферических и эллиптических днищ РДТТ с заглушен-
ным и открытым соплами. При этом величину предела текучести жестко-
пластического тела следует определять, исходя из диаграммы растяже-
ния реального днища при данной температуре, как это схематично было
показано в § 15.
Предельное внутреннее давление сферической
оболочки с открытым патрубком. Если рассмотреть безмо-
ментное напряженное состояние сферической оболочки с отверстием без
патрубка, то легко найти (см. § 9)
р pRc /1 sin2 0О \ р pRc /1 । sin2 0р\
1 2 \ sin20/’ 2 2 \ sin20 /
где /?с — радиус сферы. Эпюры усилий 7\ и Т2 показаны на рис. 57.3, а;
поскольку для сферы без отверстия Т\ = Т2 = TQ = р/?с/2, то независимо
от диаметра отверстия максимальное значение (T2)max = pRc (при 6 = 60)
в два раза превышает значение усилия То в сфере без отверстия. Для
в)
г)
Рис. 57.3
сферы без отверстия предельное значение давления (рпр)0 = ^cs^hJR^ где
—предел текучести, hc — толщина сферы. Поэтому, если край отвер-
стия ничем не подкреплен, то независимо от диаметра отверстия величина
предельного давления будет равна
Pnp = -^--v^-p)o- (57.15)
*'С
Это значит, что величина предельного давления сферы с неподкреплеп-
ным открытым отверстием составляет всего половину величины предель-
ного давления сферы без отверстия. Подкрепление края отверстия будет
473
увеличивать значение предельного давления. В частности, практически
интересно выяснить, как влияют на величину предельного давления раз-
меры цилиндрического патрубка, соединенного со сферической оболочкой,
как показано на рис. 57,3,6. Не останавливаясь подробно на самом реше-
нии, изложим кратко только основные результаты, полученные А. Н. Се-
мененко [82] с помощью методов предельного анализа конструкций. Ре-
шение велось статическим и ки-_
нематическим методами (см. § 15), Ьопт
причем были рассмотрены пласти-
ческие механизмы разрушения обо-
лочки типа изображенных на рис.
57.3, в, г. Нижние границы предель-
ных нагрузок, найденные статиче-
ским методом, совпали с верхними
границами предельных нагрузок,
найденными кинематическим мето-
дом. Поэтому полученное решение
можно считать точным. °
2
Рис. 57.4 Рис. 57.5
Основные выводы из решения таковы:
1. Для каждого заданного угла 0О существует оптимальное отно-
шение толщины цилиндрического патрубка Ац к толщине сферической
оболочки Ас, т. е. существует оптимальное значение величины h = hnlhc,
при котором предельное давление достигает максимума (рис. 57.4, кри-
вая 7). Эта оптимальная безразмерная толщина цилиндрического па-
трубка (А) опт зависит от безразмерного радиуса сферической оболочки
Rc = Rdhc и угла 0о (рис. 57.5).
2. Предельное значение давления сферической оболочки с открытым
патрубком всегда меньше предельного значения давления сферической
оболочки без отверстия, причем при оптимальной относительной толщине
цилиндрического патрубка А=(А)0Пт относительное предельное давле-
ние Рпр = Рпр/(Рпр)о изменяется в зависимости от угла 0О (рис. 57.6).
3. Длина цилиндрического патрубка, влияющая на несущую способ-
ность сферической оболочки, равна 1^ )//?цЛц , где и Ац—радиус и
толщина цилиндрического патрубка.
Предельное внутреннее давление сферической
оболочки с заглушенным цилиндрическим патруб-
к о м. Аналогичными методами исследовалась задача о предельном внут-
реннем давлении сферической оболочки, соединенной с заглушенным ци-
линдрическим патрубком (рис. 57.7, а). Типичный пластический меха-
низм разрушения такой оболочки схематично показан на рис. 57.7,6.
474
Рис. 57.7
Рис. 57.8
В этом случае удалось получить значения верхних границ inpe-
дельных нагрузок, почти совпадающие со значениями нижних границ
предельных нагрузок (соответственно при решении кинематическим и
статическим методами).
Основные выводы из полученного решения следующие:
1. Для каждого значения угла 0О так же, как и для случая открытого
патрубка, существует оптимальная величина безразмерной толщины
цилиндрического патрубка h= (h) опт, при которой значение предельного
внутреннего давления достигает максимума (рис. 57.4, кривая 2). Зави-
симости оптимальной безразмерной толщины цилиндрического патрубка
от угла 0о для различных отношений Rdhc = Rc приведены на рис. 57.8.
2. Величина максимального предельного давления при h=(Ji)QnT
равна значению предельного давления сферической оболочки без от-
верстия. Другими словами, выбирая оптимальное значение для относи-
тельной толщины цилиндрического патрубка, можно выполнить сфери-
ческую оболочку с заглушенным патрубком равнопрочной сферической
оболочке, не ослабленной отверстием.
3. Длина зоны цилиндрического патрубка, влияющей на значения
предельного давления, равна 0,95 VR^ при оптимальной толщине
цилиндрического патрубка.
Выбор соотношения толщин несущей стенки и слоя термоизоляции.
Выше был рассмотрен расчет оболочки двигателя при заданной темпе-
ратуре несущей части конструкции. В действительности при проведении
проектировочного расчета металлической стенки изменение ее толщины
должно быть увязано с соответствующим изменением температуры, так
как будет меняться тепловая аккумулирующая способность стенки. Учи-
тывая .взаимное влияние параметров, характеризующих температурное
состояние и прочность оболочки, можно провести выбор оптимально-
го соотношения толщин металлической стенки h и слоя термоизоляции
йь который защищает стенку от непосредственного воздействия про-
дуктов сгорания. Под оптимальным понимается соотношение толщин,
которое обеспечивает минимальную массу оболочки при сохранении ею
работоспособности в течение всего времени работы двигателя.
Предполагается, что слой термоизоляции не несет нагрузку. Вся
нагрузка, вызванная давлением продуктов сгорания и внешними силами,
воспринимается металлической стенкой. Когда давление в камере сгора-
ния неизменно, расчетный случай обычно соответствует моменту времени
окончания работы двигателя, так как несущая стенка к этому моменту
прогревается наиболее сильно.
Условие сохранения оболочкой работоспособности может формули-
роваться по-разному в зависимости от особенностей конструкции и ма-
териалов двигателя. Здесь его можно принять в виде
(57.16)
т. е. максимальное погонное усилие в оболочке Тщах с учетом коэффици-
ента запаса п сопоставляется с разрушающим усилием для материала
при температуре Тк в конце работы двигателя. Масса единицы поверх-
ности оболочки
т ph + р^. (57.17)
где р и pi — плотности металла и термоизоляции, должна быть при этом
минимальна.
Возможность получить соотношение толщин h и h}, приводящих к
минимуму массы оболочки, следует показать сначала па основе общих
соображений.
476
На первый взгляд наиболее выгодным кажется сохранение в течение
всего времени работы двигателя возможно более низкой температуры
несущей стенки. Это позволило бы обеспечить достаточно высокое значе-
ние временного сопротивления о'в(71к) и при заданных величинах п и
Лпах (см. формулу 57.16) получить небольшую толщину металлической
стенки 1Л. Но оказывается, что для этого необходим слишком толстый
слой термоизоляции, так что масса оболочки в целом получается доста-
точно большой.
С увеличением толщины h возрастает количество тепла Q, которое
может воспринять металлическая стенка за время работы двигателя:
<3=ср/г(^к-7,о).
где с — удельная теплоемкость металла и 70— начальная температура
оболочки. Количество тепла Q возрастает не только с увеличением тол-
щины /г, но и с повышением температуры Гк, так как при большей тол-
щине h, как это видно из формулы (57.16), можно пойти на некоторое
снижение величины о'в(71к), которая для конструкционных материалов
падает с температурой.
Все это позволяет значительно снизить толщину слоя термоизоля-
ции, причем снижение массы термоизоляции оказывается большим неже-
ли увеличение массы металлической стенки при некотором увеличении
ее толщины h. Однако чрезмерное увеличение h в итоге приведет к зна-
чительному росту массы стенки, который уже не будет компенсироваться
снижением массы термоизоляции.
Таким образом, задача отыскания оптимального соотношения тол-
щин оболочки распадается на две, связанные между собой: 1) определе-
ние температуры Гк металлической стенки в конце работы двигателя
при различных соотношениях толщин h и б) подбор соотношения тол-
щин h и Ль обеспечивающих работоспособность оболочки при ее мини-
мальной массе.
Порядок решения этой задачи целесообразно проследить на примере.
Пусть заданы: п= 1,5; Лпах=80 кГ1мм\ зависимость ов от Т для
материала стенки такая:
Т °C 20 200 300 400 500 600
ав, кГ/мм2 60 58 56 52 40 20
Остальные параметры приняты такими же, как в примере расчета тем-
пературы стенки соплового днища двигателя (см. § 55): температура га-
зов Г* = 2400°К = 2127°С; Го = 2О°С; коэффициент теплопроводности тер-
моизоляции = 0,8 вт!м-град\ ее удельная теплоемкость с=4 кдж!кгХ
Хград и плотность pi = 1600 кг)м3\ с = 0,5 кдж!кг-град\ р = 8000 кг/м2-,
= 25 сек.
Теплообмен с продуктами сгорания считаем настолько интенсивным,
что температура поверхности термоизоляции Тп = Т*. В этом случае для
определения температуры Тк можно воспользоваться номограммой, приве-
денной на рис. 55.2. Номограмма связывает относительную температуру
6 = (Т* — Тк)/(Тг — То) с безразмерными параметрами Fo = и К =
= cJilCtPihb где аг = — коэффициент температуропроводности тер-
моизоляции, который в данном примере равен а1 = 5-10~7 м2!сек.
Предварительно вычисляем
- аА 5-10-’.25 12,5 ,
Fo = —— =-----------------= ——, где /гх в мм,
10"6/lf h\
Л1
477
и
д.__ cph ____ 0,5- 8000 h _ 2 5
QPi/zi 1 • 1600 hi ’ hi
Далее, задаваясь парами значений h и hlf находим значения Fo и Д’ и
по номограмме определяем величину 9, а по ней — температуру стенки
тк = т;-(т;-т0)о.
Результаты расчета представлены в виде семейства кривых па
рис. 57.9,а. Здесь же по формуле (57. Гб) пунктирной линией построена
зависимость необходимой по условию прочности толщины металлической
Рис. 57.9
стенки от ее температуры. Точки пересечения пунктирной кривой с семей-
ством кривых Тк(/г) при различных hx дают пары значений толщин тер-
моизоляции Л1 и металлической стенки /г, которые при заданных времени
работы tK и условиях нагрева обеспечивают работоспособность двига-
теля. Теперь из всех пар значений h и hx следует выбрать такую, при
которой масса оболочки минимальна. Для этого на рис. 57.9,6 по полу-
ченным выше точкам пересечения кривых построена зависимость h\ от /г,
а затем по формуле (57.17)—зависимость массы оболочки т от h.
Последняя кривая имеет минимум при значении /i* = 2,35 мм, которому
соответствует оптимальная толщина термоизоляции Л* = 5,0 мм. При
этом температура 7,к = 440°С (см. рис. 57.9,а), а рабочее напряжение в
металлической стенке о=Tmax/A* = 80/2,35 = 34 кГ/мм2.
В приведенном выше примере найдено оптимальное соотношение
толщин при условии, что свойства металла и термоизоляции заданы. Но
подобным же образом, если имеется выбор различных материалов стен-
ки и термоизоляции, можно провести сравнительные расчеты и подо-
брать наиболее выгодную их комбинацию.
§ 58. НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ЗАРЯДЕ ТВЕРДОГО ТОПЛИВА
Теоретическое определение условий нормального горения топлива и
истечения продуктов его сгорания, обеспечивающих заданный закон из-
менения тяги РДТТ по времени, является довольно сложной комплекс-
ной проблемой термодинамики и газодинамики. Задача изучения чисто
механического поведения заряда твердого топлива входит одной из со-
ставных частей в эту проблему.
478
Заряд твердого топлива можно рассматривать как конструкцию,
воспринимающую во время изготовления, транспортировки, хранения и
работы двигателя определенные нагрузки: инерционные, температурные
и перепады давлений.
В полете основными нагрузками, действующими на заряд твердого
топлива, являются инерционные силы и давление газов. Для случая сво-
бодно вложенного заряда продольные инерционные силы воспринима-
ются специальным опорным устройством (см. рис. 57.1,6), а для заряда,
скрепленного с корпусом, инерционные силы передаются непосредствен-
но на корпус двигателя. В свободно вложенном заряде давление газов
создает почти равномерное сжатие, обычно не приводящее ни к каким
неприятным последствиям. Заряд, скрепленный с корпусом двигателя,
можно рассматривать как нагруженный .внутренним давлением толсто-
стенный сосуд. Давление газов вызывает в нем сложное неоднородное
напряженное состояние, которое может привести к разрушению заряда
твердого топлива.
Кроме полетных инерционных нагрузок, для крупногабаритных
зарядов твердого топлива существенным оказывается действие собствен-
ного веса. Под действием этой силы в процессе длительного хранения и
транспортировки заряда из-за ползучести твердого топлива может неже-
лательно измениться геометрия заряда.
На процессе работы двигателя могут отразиться три основные вы-
зываемые этими нагрузками механические причины:
1) деформации заряда твердого топлива, происходящие в нем как
во время хранения, так и в рабочем режиме и изменяющие номинальную
геометрию заряда (например, проходное сечение внутреннего канала);
2) увеличение поверхности горения в результате разрушения, рас-
трескивания заряда твердого топлива, вызываемого действующими в нем
напряжениями;
3) разрушение заряда в конце работы двигателя вследствие потери
устойчивости под действием инерционных сил и перепадов давлений
(в основном, для свободно вложенного заряда).
Полное изложение этих вопросов выходит за рамки настоящего
учебного пособия; здесь будут только намечены пути решения и приведе-
ны некоторые наиболее простые результаты.
Основной задачей изучения механического поведения заряда твер-
дого топлива является определение его напряженно-деформированного
состояния. Для заряда не осесимметричной формы — это сложная трех-
мерная задача деформирования твердого тела, имеющего типичные для
полимера свойства (см. § 7).
Связь напряжений и деформаций в твердом топливе может быть
выражена зависимостями, рассмотренными в ’§ 7. Задача существенно
усложняется из-за того, что в зависимость напряжение — деформация
входит время. Поэтому для решения должны быть заданы начальные и
граничные условия.
В общем случае решение такого типа задач с учетом реальных
свойств твердого топлива, по-видимому, возможно только на ЭЦВМ с
использованием методов решения типа шаговых. Лишь в некоторых част-
ных случаях могут быть получены сравнительно простые аналитические
решения.
В качестве примера наиболее простого аналитического решения при-
ведем решение задачи о напряжениях и деформациях в заряде твердого
топлива, скрепленном с корпусом двигателя и имеющем форму круго-
вого цилиндра. Топливо будем считать работающим упруго; такое
упрощение свойств реального топлива возможно при определении на-
пряжений, вызываемых быстро нарастающим давлением при пуске дви-
479
гателя и при низких температурах [14], когда вязко-упругими свойства-
ми топлива можно пренебречь.
Напряжения и деформации в толстостенной трубе (задача Ляме
[73]). Сначала решим вспомогательную задачу по определению напря-
женно-деформированного состояния бесконечно длинной упругой толсто-
стенной трубы, нагруженной
постоянным по ее длине
dr)d(f внутренним и внешним дав-
лением (рис. 58.1,а). Все по-
перечные сечения в такой
трубе, естественно, остаются
плоскими и касательные на-
пряжения в них равны нулю.
Рассмотрим равновесие
элемента трубы (рис. 58.1,6).
В силу симметрии задачи ка-
сательные напряжения на
его боковых гранях равны
нулю; условие равновесия
действующих на гранях эле-
мента нормальных напряже-
ний в проекции на ось г
будет
(гаг)' — оф = О,
(58.1)
где штрихом обозначено дифференцирование по г.
Окружные и радиальные относительные удлинения еф и ег выража-
ются через радиальное перемещение ш:
еф = ег = w'. (58.2)
Удлинения Еф и ег связаны между собой условием совместности
деформаций, которое можно получить, исключив радиальное перемеще-
ние w и его производную w' из выражений (58.2):
(ГЕф)' — Ег = 0.
(58.3)
Поскольку материал трубы считается работающим упруго, то спра-
ведливы формулы закона Гука:
= 4'^~Н(ал + <Тф)]>
£
еФ = 4г[<7ф —P^r + orJ],
£
(58.4)
8Х = “[«х- Н(*Ф+ <*г)Ь
£
Исключив из этих формул напряжение ох, получим:
1 — ц2 г ц 1
Е_ =-----------------— вг-------Ого — LIE- ,
Е L ч
1 — и2 Г u, 3
Еф - —Оф — —(Уг -
Е | 1 — р, J
Теперь введем функцию напряжений F, связанную с напряжениями
ог и Оф зависимостями
аг = -М, оф = Г'. (58.6)
480
При таком выборе функции напряжений уравнение равновесия
(58.1) удовлетворяется тождественно, а из условия совместности дефор-
маций (58.3), использовав формулы (58.5) и зависимости (58.6), полу-
чим
---------J-/7 = o. (58.7)
Г г2
Решение дифференциального уравнения (58.7) ищем в виде
р = Сгп\ подставив это выражение в уравнение (58.7), приходим к ха-
рактеристическому уравнению для определения п:
п(п— l)+n— 1 -0, (58.7')
откуда получим п — ± 1, следовательно,
F -Схг + С,/-1. (58.8)
Для определения констант Cj и С2 должны быть заданы два гра-
ничных условия: на внутренней поверхности трубы (при r = ri) и на
внешней поверхности (при г = Г2). Формулы для определения напряже-
ний получаем из зависимостей (59.6):
аг = С. + -% сгф = С. - -%. (58.9)
Г2 г2
Радиальные и окружные удлинения находим по формулам (58.5):
[с, (1 - ад - а.] - Иех.
(58.10)
Интересно отметить, что если поперечные сечения трубы остаются
при деформации плоскими, то величины напряжений огг и оф не зависят
от осевого удлинения ех, а определяются только условиями на внутрен-
ней и наружной поверхностях трубы. Но в формулы (58.10) для ради-
альных и окружных удлинений входит величина ех; для ее определения
(а следовательно, и для определения осевого напряжения огх) должно
быть задано еще одно дополнительное условие.
Величину осевого напряжения ох можно найти, использовав третью
формулу закона Гука (59.4) и выражения (58.9) для радиальных и
окружных напряжений:
— Еех 4- р (<УГ -г Оф) = Еех + (58.11)
Изложенное решение справедливо и для трубы конечной длины,
если при нагружении все ее поперечные сечения остаются плоскими.
Кроме того, этим решением можно пользоваться для определения напря-
жений и деформаций в средней части достаточно длинной трубы.
Расчет упруго работающего цилиндрического скрепленного заряда.
Заряд, прочно скрепленный с камерой двигателя, обычно выполняется
из смесевого эластичного топлива, допускающего значительные дефор-
мации. Типичные для такого топлива механические свойства [14] при-
ведены ниже.
Модуль упругости:
при Т = 40°С.......................Е = 50 100 кГ/см2
» Т = 15°С.........................Е = 100 ч- 200 кГ!см2
» Т=— 40°С.........................Е = 1000 ч- 2000 кГ/см2
Коэффициент Пуассона...................р. = 0,35 4- 0,50
Коэффициент линейного расширения............а = 0,5- Ю-4 -?-1,5 - 10“41 /К°
31 Зак. 96 481
На основе приведенного выше решения задачи Ляме определим1
напряжения и деформации в скрепленном заряде, вызываемые давлением
газов в рабочем режиме, и температурные напряжения и деформации,
возникающие при
Рис. 58.2
изменении температуры всего двигателя (во время
хранения). Особенности крепления торцов заряда
учитывать не будем и заменим реальный двигатель,
упрощенной схемой (рис. 58.2). Обычно величина
модуля упругости материала корпуса двигателя на
несколько порядков превышает величину модуля
упругости топлива, поэтому при определении на-
пряженно-деформированного состояния заряда де-
формациями корпуса можно пренебрегать и рас-
сматривать его как абсолютно жесткий [14, 40].
Напряжения и деформации в заря-
де, вызванные давлением газов. По-
скольку деформациями камеры мы пренебрегаем^
то в рассматриваемом случае ех = 0. Граничные ус-
ловия для определения констант С\ и С2 составим,,
учитывая, что на внутренней поверхности заряда
при r = ri ог = —Рг, а на внешней его поверхности
при г = г2 равно нулю радиальное перемещение и, а следовательно, удли-
нение еф = ц/г; использовав формулы (58.9) и (58.10), получим два урав-
нения:
С1(1-2И)--^0,
г2
откуда
Ргт2 Q =
т2-(-1—2ц’ 2
где tn = rxlr2. Из формул (58.9) и (58.11) найдем
Рг"*2
т2 + 1 — 2ц
Г Г9
1 - ~ (1 - 2|х)
L г2
(58.14>
m2 + 1 — 2ц
Для заряда обычно наиболее опасно окружное напряжение оф на вну-
тренней поверхности (при г = г,):
(ТФ |г=г, = Рг
1 — т2 — 2ц
1 + т2 — 2ц
(58.15)'
При малых значениях отношения tn окружное напряжение оф|г=--лг
оказывается растягивающим и может вызвать разрушение заряда.
Очевидно, что увеличение радиуса канала заряда A/'i выражается
через окружное удлинение еф:
Е т2 4- 1 - 2ц 7
482
Определим нагрузки, передаваемые зарядом на корпус двигателя.
Величина нагружающего корпус двигателя давления рк равна радиаль-
ному напряжению в заряде при г = г2:
рк = — б г |г=г2
2т2(1—ц)
г т2 + 1 — 2ц
(58.17)
Величина осевой силы, нагружающей корпус двигателя, складывается из
двух составляющих: 1) равнодействующей сил давления рг на площади
поперечного сечения канала заряда лг? и 2) равнодействующей осевых
напряжений в заряде сгЛ на площади сечения заряда л(г2—г?). Использо-
вав третью формулу (58.14), получим
Nx = ргпг2 — <тлл (ri — г2) = рг лг22 т2- (58-18)
Температурные напряжения и деформации в
скрепленном заряде. Будем считать, что при температуре То на-
пряжения в заряде равны нулю; определим, какие напряжения и дефор-
мации возникнут в заряде, если температура заряда и корпуса двигателя
изменится и станет равной Т. Опять воспользуемся решением задачи
Ляме. Корпус двигателя, как и в предыдущем случае, считаем абсолютно
жестким; поэтому осевое удлинение заряда, обусловленное разностью
температурных удлинений топлива и материала корпуса двигателя,
будет
8х = (ак-а)(Т-Г0), (58.19)
где а и ак — коэффициенты линейного расширения топлива и материала
корпуса двигателя. Для определения констант Ci и С2 составим гранич-
ные условия на внутренней и наружной поверхностях заряда. Внутрен-
няя поверхность заряда (при г = г}) не нагружена и, следовательно, на
ней ог = 0. На наружной поверхности заряда (при г = г2) окружные удли-
нения обусловлены разностью температурных удлинений топлива и мате-
риала двигателя, т. е. аналогично осевым удлинениям имеем
еф = (ак—а) (Го—Т). Используя формулы (58.9) и (58.19), получим два
уравнения для определения констант С{ и С2:
ГС1(1—2И)—%] — р.(ак —<х) (То — Т) = 1 (58,20)
£ L г22 J
= (ак-а) (П-Т),
откуда
£ (Г — Т,) (ак — а) . Q
zna 4* 1 — 2р. ’ 2
Е(Т-Т0) (ак —а) г2
m2 Д 1 — 2ц 1
(58.21^
По формулам (58.9) и (58.11) находим напряжения в заряде:
= Е(Г-Т0) (ак — а) / j _ Д
т2 + 1 — 2ц \ г2
= Е(Т — Т0) (ак —а) А . Д
т24-1— 2р \ г2
_ Е (Т То) (ак — а) ,2 .
2ц V
(58.22)
31
483
По формулам (58.10) можно определить удлинения ег и еф в заря-
де. Коэффициент линейного расширения топлива значительно превы-
шает коэффициенты линейного расширения тех материалов (металлы,
стеклопластики), из которых изготовляют корпуса двигателей. Поэтому
наиболее опасные растягивающие напряжения будут возникать в заряде
при охлаждении двигателя, когда Т<Т0. При этом наибольшими будут
окружные напряжения у внутренней поверхности заряда (при г=гх):
(Гф |г=г, 2 £(г-^о)(ак-а)’ (58 23)
ф| 1 т2+1— 2ц
Представляют практический интерес и величины радиальных напря-
жений на наружной поверхности заряда (при г=г2), которые могут при-
вести к отслоению заряда от корпуса при охлаждении двигателя:
а. |г=г, = 'Е(т.~т°}(а*~а) (1 - /п2). (58.24)
m2 + 1 — 2ц
Изменение размера канала заряда Дгх определится так:
^Г1/Г1 = а (Т - То) + еф |Л=г,. (58.25)
Если считать ак а, то, используя приведенное выше решение, получим:
ДГ1/Г1 _ а (Т- Т0) <m2+1>(l+H (58.26)
1 v 0/ т2+1- 2ц
Так как /п = г1/г2<1, то при нагревании размер канала уменьшается, а
при охлаждении увеличивается.
Оценка работоспособности заряда твердого топлива производится
как по допускаемым перемещениям, так и по допускаемым напряжениям.
Типичный пример расчета по допускаемым перемещениям — определение
изменения геометрии заряда, вызванное ползучестью топлива под дейст-
вием собственного веса во время хранения или перепадами давлений и
инерционными нагрузками в момент пуска ракеты (14]. При пониженных
температурах топливо становится хрупким (пластические деформации
отсутствуют); разрушение, растрескивание заряда может в результате
резкого увеличения поверхности горения привести к взрыву всего двига-
теля. Поэтому при пониженных температурах (ниже так называемой тем-
пературы стеклования) расчет заряда твердого топлива следует произ-
водить по допускаемым напряжениям, учитывая концентрацию напря-
жений [14].
Вопрос о величине допускаемых напряжений для каждого типа
топлива должен определяться экспериментально.
§ 59. О ДИНАМИЧЕСКИХ ЯВЛЕНИЯХ В РДТТ
Высокочастотные колебания в ракетном двигателе твердого топлива
являются результатом возбуждения автоколебаний в сложной системе,
состоящей из твердого топлива, стенок двигателя, газовой среды и зоны
горения.
Одной из моделей, с помощью которой можно пояснить возбужде-
ние автоколебаний при горении, является модель возбуждения продоль-
ных автоколебаний газа в трубе. Если один конец трубы закрыт, а дру-
гой открыт, то формы собственных колебаний давления р и скорости
газа v будут такими, как показано на рис. 59.1,а.
484
Пусть в окрестности Дх какого-либо сечения х0 существует небольшая
зона теплоподвода Q (зона горения). Вариации давления и скорости
перед зоной теплоподвода в сечении х0 обозначим р\, щ в сечении
Хо + Дх —соответственно рг, ^2- Если расстояние между плоскостями,
ограничивающими зону Дх, считать малым по сравнению с длинами волн
собственных колебаний, так что волны колебаний не могут заметным
образом изменить своих амплитуд и фаз на расстоянии Дх, то все изме-
нения величин р и v в зоне горения будут связаны только с процессом
теплоподвода. Ввиду малости Дх будем считать, что р\ = р2 = р, но вслед-
ствие подвода тепла гмт^гм.
Пусть величины р и v изменяются по времени по гармоническому
закону, причем период колебаний равен Т. Тогда акустическая энергия,
излучаемая областью Дх за период колебаний, будет равна работе рас-
ширения газа [75]:
т
А = [ (у2 — гм) р dt, (59,1)
о
или
где ф— фазовый угол между {v2—гм) и р (рис. 59.1,6). Работа А будет
положительной, если ф по абслоютной величине меньше л/2.
В рассматриваемом примере колебательной системой является га-
зовая среда, источником энергии — зона теплоподвода, а обратной
связью — зависимость от давления и скорости колебаний энергии, излу-
чаемой зоной теплоподвода, или зависимость фазового угла ср от дав-
ления и приращения скорости (v2—гм). Если эти зависимости таковы,
что фазовый угол находится в пределах 0<|ф|<~~, то Л>0, область
теплоподвода излучает энергию в колебательную систему, колебания
будут нарастать.
Если л/2< | ф | <л, то Л<0, область Дх поглощает энергию из коле-
бательной системы, колебания будут затухать, система устойчива. При
| Ф | =л/2 система находится на границе устойчивости.
485
Предположим теперь, что труба с одним закрытым концом заполне-
на однородным горючим газом, газ у открытого конца подожжен и зона
горения распространяется по трубе к закрытому концу. Если сделать
допущение, что формы колебаний холодного и горячего газа в трубе
будут соответствовать рис. 59.1,а, то на основании выражения (59.1)
можно сделать вывод, что энергия, излучаемая зоной горения, будет
положительной и в системе могут возбуждаться нарастающие колеба-
ния, если зона горения будет располагаться на тех участках А/ трубы,
где графики функций р и v имеют
одинаковые знаки. При движении
зоны горения различные формы
колебаний будут возбуждаться,
затем затухать и вновь возбуж-
даться.
Кроме продольных колеба-
ний, могут возбуждаться радиаль-
ные и тангенциальные колебания
газов в трубе, причем механизм
их возникновения совпадает с ме-
Рис. 59.2 ханизмом возбуждения продоль-
ных автоколебаний.
Формы поперечных колебаний схематически представлены на
рис. 59.2. Концентрические окружности изображают узловые линии для
радиальных колебаний (рис. 59.2,а), узловые линии для тангенциальных
колебаний показаны на рис. 59.2,6.
В зависимости от схематизации и выбора модели исследования
можно говорить об автоколебаниях, если модель представляет собой
замкнутую систему с источником энергии, или о вынужденных колеба-
ниях, если в качестве модели выбрана незамкнутая колебательная си-
стема, а действие источника энергии и обратной связи заменено дейст-
вием внешней силы.
Например, если силу трения в маятниковой системе (см. рис. 17.3)
считать заданной: fTp = fosinpZ, то, подставив ее значение в правую часть
уравнения (17.9), получим уравнение вынужденных колебаний маятника.
Автоколебательные процессы в твердотопливных двигателях значи-
тельно сложнее только что рассмотренной упрощенной модели колеба-
ний столба газа. Это обусловлено тем, что здесь неоднородная и более
сложная колебательная система и очень сложные процессы, происходя-
щие в зоне горения.
Автоколебания совершаются на частотах, близких к частотам соб-
ственных колебаний системы [85, 102], и, по-видимому, на основании
этого в технической литературе по твердотопливным двигателям при
изучении автоколебаний часто применяются термины «резонансное горе-
ние», «резонансные колебания». Хотя термин «резонансное горение»
характеризует, в основном, процесс в зоне горения и относится к кате-
гории вынужденных колебаний, мы также будем его применять и в более
широком смысле слова, понимая его условность.
Проблема резонансного горения продолжает оставаться одной из
самых сложных при проектировании твердотопливных ракет. Этому во-
просу посвящено большое количество теоретических и эксперименталь-
ных исследований [14, 40].
Явления резонансного горения обладают специфическими свойства-
ми [40, 75]. Колебания в газовой полости происходят по формам соб-
ственных колебаний с амплитудами до нескольких десятков атмосфер.
Частотный спектр колебаний двигателя очень чувствителен к ряду
факторов, таких как физический и химический состав топлива, способ
486
•полимеризации, температура топливного заряда, способы крепления за-
ряда в камере и т. д. Поэтому, чтобы получить количественное воспро-
изведение изучаемых явлений в экспериментах, условия испытаний
должны повторяться со скрупулезной точностью.
При горении, сопровождающемся колебательными процессами, в
юиливе возникают весьма значительные механические деформации, ме-
няется характер его микроструктуры, что может оказывать влияние на
изменение средней скорости горения и соответствующее изменение сред-
него давления. Если твердое топливо чувствительно к деформациям, то
в условиях мощного акустического резонанса оно может разрушаться,
что в свою очередь, приведет к изменениям среднего давления.
Для расчета форм и частот собственных колебаний твердотопливный
двигатель может быть схематизирован в виде модели, показанной на
Рис. 59.3
рис. 59.3, где 1 — донная полость; 2— оболочка; 3 — сопловая полость;
4 — твердое топливо; 5 — зона горения. Наружные стенки обычно пред-
ставляют собой тонкостенную металлическую, стеклопластиковую или
комбинированную цилиндрическую оболочку. На одном конце оболочки
расположено сопло, другой конец заканчивается днищем. Внутри обо-
лочки находятся два вещества: заряд — твердое тело и газ сложного
•состава. Заряд может быть скреплен с оболочкой или свободно вложен
в нес. При определении форм и частот собственных колебаний в первом
приближении газ можно рассматривать как однородный и неподвижный.
Для упрощения расчет поперечных (радиальных и тангенциальных)
форм и частот колебаний обычно проводится без учета влияния донной
и сопловой частей оболочки.
Заманчиво также представить систему в виде двух парциальных:
отдельно газовая система с неподвижной наружной границей и отдельно
твердая система со свободной внутренней границей. Твердая система
может быть рассчитана по схеме толстостенного цилиндра [33]. Частоты
се радиальных колебаний будут повышаться с уменьшением толщины
свода топливной шашки. Частоты собственных колебаний твердой си-
стемы в значительной мере зависят от того, находится ли топливо в
контакте с оболочкой. Зазор в несколько сотых миллиметра «приводит к
полному изменению граничных условий. Размеры газовой зоны в про-
цессе горения увеличиваются. Поэтому частоты собственных колебаний
газовой среды будут уменьшаться [75].
Такое разделение системы будет справедливым лишь тогда, когда
скорость звука и плотность в твердой системе велики по сравнению с
этими же параметрами в газе. Однако для большого числа твердых
топлив скорость звука в твердой системе сравнима со скоростью звука
в газе. Кроме того, толщина твердой системы в общем случае одного по-
рядка с толщиной газовой системы. Эти два фактора делают разделение
системы во многих случаях неоправданным. В результате действительные
формы и частоты колебаний системы совершенно отличны от парцио-
нальных. В таких случаях надо решать задачу для твердой и газовой
систем совместно, обеспечив выполнение условий на границе их сопри-
487
косновения [40]. В общем случае акустическое движение газа вызывает
в твердой системе появление как волн расширения — сжатия, так и волн
сдвига. Анализ системы становится достаточно сложным, но может быть
выполнен с помощью современных вычислительных машин.
Передача энергии в колеблющуюся систему происходит в основном
в тонкой пограничной зоне (толщина порядка ста микрон) и поэтому
вполне понятно, что колебания будут возбуждаться только тогда, когда
узел волны давления удален от поверхности раздела двух сред. Этим и
объясняется, что колебания по данной тангенциальной или радиальной
форме не будут существовать непрерывно в течение всего процесса
горения, а должны, по крайней мере, прерываться несколькими периода-
ми устойчивости.
Самой сложной и менее изученной частью автоколебательной систе-
мы является тонкая пограничная зона, разделяющая твердую и газовую
части системы. Она характеризуется наличием крайне больших гради-
ентов температур, высокими скоростями энерго- и массообмена, разно-
образными сложными химическими реакциями и геометрически может
быть самой неопределенной.
В зависимости от учета различных явлений, происходящих в погра-
ничной зоне, предложено несколько моделей, объясняющих возможность
возникновения вибрационного горения. Среди них можно отметить сле-
дующие [40].
Модель Смита. Тепло от горящих газов подводится к твердой
поверхности. Поверхностный слой топлива выгорает со скоростью, при
которой температура поверхности сохраняет фиксированное значение.
Изменение величины теплового потока вызывает изменение скорости го-
рения. Волна повышенного давления, достигнув поверхности горения,
немедленно повысит скорость горения в этом месте. Это приведет к тому,
что такая волна, отразится, имея большую амплитуду, и продолжение
такого процесса может привести к нарастанию колебаний. В данной
модели не используется понятие запаздывания по времени.
Модель Грина. Эта модель связана с теплопередачей. Сущность ее
состоит в том, что на поверхности разложения твердого топлива колеба-
ния температуры усиливаются при запаздывании по времени между
колеблющимися скоростью реакции и температурой на поверхности.
Шиннар и Дишон усовершенствовали эту модель, показав, что можно
получить неустойчивые решения уравнений теплопередачи вблизи поверх-
ности без предположений о временном запаздывании.
Модель Чжень Синь-и. Указанная модель основана на влиянии
реактивных добавок в основое топливо. Окисление добавок рассматри-
вается как действие распределенных источников тепла, подводимого в
газовую систему. Дополнительный тепловой поток искажает акустиче-
ское поле, изменяя скорость звука в объеме камеры. Он может коле-
баться, но отстает по фазе от местных колебаний газа. Колебательный
подвод тепла, как и колебательный подвод массы, может вызвать не-
устойчивые колебания газовой смеси. В зависимости от ряда других
факторов дополнительные реактивные добавки могут как возбуждать
колебания, так и улучшать устойчивость работы двигателя.
Имеются работы, в которых указывается на то, что эрозионная ско-
рость (составляющая скорости газового потока, параллельная поверх-
ности горения) может также оказывать влияние на акустическую не-
устойчивость.
В книге [40] приведено значительное количество экспериментальных
данных по исследованию резонансного горения. Результаты эксперимен-
тов, в частности, подтверждают, что возбуждение колебаний происходит
па частотах собственных колебаний системы.
ЛИТЕРАТУРА
1. Авдуевский В. С. и др. Основы теплопередачи в авиационной и ракет-
ной технике. М., Оборонгиз, 1960.
2. Алем а со в В. Е. Теория ракетных двигателей. М., Оборонгиз, 1962.
3. А л футов Н. А. Определение нижнего критического давления упругой ци-
линдрической оболочки и поведение оболочки после потери устойчивости, «Расчеты на
прочность в машиностроении». Труды МВТУ им. Баумана, Сборник 89. М., Машгиз,
1958.
4. А л ф у т о в Н. А. О зависимости значения верхнего критического давления
цилиндрической оболочки от граничных условий относительно касательных составляю-
щих перемещений. Труды IV Всесоюзной конференции по теории пластин и оболочек.
Ереван, изд. АН Армянской ССР, 1964.
5. А л ф у т о в Н. А. Устойчивость цилиндрической оболочки, подкрепленной по-
перечным силовым набором и нагруженной внешним равномерным давлением. Инже-
нерный сборник, т. 23, 1956.
6. Ал фу то в Н. А. и РазумеевВ. Ф. Динамическая устойчивость опертой
по одному краю конической оболочки. Изв. АН СССР, ОТН, 1955, № 10.
7. Ананьев И. В. Тимофеев П. Г. Колебания упругих систем в авиацион-
ных конструкциях и их демпфирование. М., Машиностроение, 1965.
8. Андронов А. А., Витт А. А., Хайкин С. Э. Теория колебаний. М,,.
Физматгиз, 1959.
9. А с т а х о в М. Ф. и др. Справочная книга по расчету самолета на прочность.
М., Оборонгиз, 1954.
10. Бабаков И. М. Теория колебаний. М., Гостехиздат, 1958.
11. Б а л а б у х Л. И., Г а л к и н С. И. Приближенная теория основного напря-
женного состояния цилиндрической оболочки, подкрепленной упругими шпангоутами.
Труды VI Всесоюзной конференции по теории оболочек и пластин. М., Наука, 1966.
12. Бал абу х Л. И., Шаповалов Л. А. Контактные задачи сопряжения
безмоментных оболочек вращения с упругими кольцами. Изв. АН СССР, Механика и
машиностроение, 1962, № 4.
13. Баренблатт Г. И. Математическая теория равновесных трещин, обра-
зующихся при хрупком разрушении. Журнал прикладной механики и технической
физики, 1961, № 4.
14. Барре р и др. Ракетные двигатели. М., Оборонгиз, 1962.
15. Безухов Н. И. Основы теории упругости, пластичности и ползучести. М.,
«Высшая школа», 1961.
16. Б е р е з и н И. С. и Ж и д к о в Н. П. Методы вычислений. М., Физматгиз,
1962.
17. Бессе ре р К. У. Инженерный справочник по управляемым снарядам. М.,
Воениздат, 1962.
18. Биргер И. А. Остаточные напряжения. М., Машгиз, 1963.
19. Биргер И. А. Теория пластического течения при неизотермическом нагру-
жении. Изв. АН СССР, Механика и машиностроение, 1964, № 1.
20. Блох А. Г. Основы теплообмена излучением. М.—Л., Госэнергоиздат, 1962.
21. Болгарский А. В. и Щукин В. К. Рабочие процессы в жидкостно-
реактивных двигателях. М., Оборонгиз, 1953.
22. Боли Б. и Уэйнер Дж. Теория температурных напряжений. М., «Мир»,.
1964.
23. Б о л о т и н В. В. Динамическая устойчивость упругих систем. М., Гостехиз-
дат, 1956.
24. Б о н и и Э. А., 3 у к р о у М. Д ж., Б е с с е р е р К. У. Основы проектиро-
вания управляемых снарядов. М., Физматгиз, 1960.
25. В а н г а р т е н В., М о р т а н Е., С е й д П. Устойчивость упругих тонкостен-
ных цилиндрических и конических оболочек при осевом сжатии. «Ракетная техника и
космонавтика», 1965, № 3.
489-
26. Власов В. 3. Избранные труды. М., изд. АН СССР, 1962.
27. В о л ь м и р А. С. Устойчивость деформируемых систем. М., Наука, 1967.
28. В о л ь м и р А. С. и К и л ь д и б е к о в И. Г. О линейной теории устойчивости
цилиндрических оболочек. Инженерный журнал, т. 4, 1964, вып. 2.
29. Г о н т к с в и ч В. С. Собственные колебания пластин и оболочек (справоч-
ник). Киев, Наукова думка, 1964.
30. Гольденвейзер А. Л. Теория упругих тонких оболочек. М., Гостсхтеор-
издат, 1953.
31. Гухман А. А., Введение в теорию подобия. М., «Высшая школа», 1963.
32. Гэтленд К., Космонавтика ближайших лет. М., Воениздат, 1964.
33. Д и н и и к А. Н. Колебания цилиндра. Избранные труды, т. 2. ЛТ, изд.
АН СССР, 1955.
34. Жуковский Н. Е. О гидравлическом ударе в водопроводных трубах. Пол-
ное собрание сочинений, i. VII. М., ОНТИ НКТП, 1937.
35. Зарубин В. С. Расчет нагрева двухслойной металлической пластины.
Сб. статей «Некоторые вопросы механики» под ред. В. И. Фсодосьева. М., Оборонгиз,
1962.
36. Зарубин В. С. Температурные поля в конструкции летательных аппаратов.
М., Машиностроение, 1966.
37. Зарубин В. С. Исследование истории нагружения неравномерно нагретой
цилиндрической оболочки. Доклады научного совещания «Тепловые напряжения в
элементах конструкций», вып. IV. Киев, Наукова думка, 1964.
38. Ильюшин А. А. Пластичность. М., Госте.хиздат, 1948.
39. И с а н б а е в а Ф. С. Определение нижней критической нагрузки цилиндриче-
ской оболочки при всестороннем сжатии. Изв. Казанского филиала АН СССР, серия
физико-математических и технических наук, № 7. Казань, 1955.
40. Исследование ракетных двигателей на твердом топливе. Сб. переводов. М,
ПЛ, 1963.
41. Каи С. Н. и Свердлов И. А. Расчет самолета на прочность. М., Маши-
ностроение, 1966.
42. Качанов Л. М. Теория ползучести. М., Физматгиз, 1960.
43. Кениг. Влияние реактивной силы на изгибные механические характеристики
пакеты. «Вопросы ракетной техники», 1965, № 5.
44. Клинге н. Динамические нагрузки, обусловленные изменением скорости
зетра по высоте. «Ракетная техника и космонавтика», 1964, № 1.
45. К о ж е в н и к о в В. И. О величине критической силы при осевом сжатии ци-
линдрической оболочки (в линейной постановке). Изв. АН СССР, Механика и машино-
строение, № 3, 1964.
46. Коздоба Л. А. Электромоделирование температурных полей. Л., «Судо-
строение», 1964.
47. Колесников К. С. Низкочастотная неустойчивость номинального режима
жидкостного ракетного двигателя. Журнал прикладной механики и технической физи-
ки, 1965, № 2.
48. Колесников К. С. Колебания жидкости в цилиндрическом сосуде. М.,
изд. МВТУ, 1964.
49. К о ч и н Н. Е. Векторное исчисление и начала тензорного исчисления. М., изд.
АН СССР, 1951.
50. Краснов Н. Ф. Аэродинамика тел вращения. М., Машиностроение, 1964.
51. К рокко Л., Чжен С и н ь-и. Теория неустойчивости горения в жидкостных
ракетных двигателях. М., ИЛ, 1958.
52. Л е б е д е в А. А., С т р а ж е в а И. В., С а х а р о в Г. И. Аэромеханика
самолета. М., Оборонгиз, 1955.
53. Лебедев А. А., Чернобровкин А. С. Динамика полета. М., Оборон-
гиз, 1962.
54. Л ей бен зон Л. С. Собрание трудов, т. 1. М., изд. АН СССР, 1951.
55. Л о й ц я и с к и й Л. Г. и Л у р ь е А. И. Курс теоретической механики, ч. II.
М., Гостехиздат, 1954.
56. Лыков А. В. Теория теплопроводности. М., «Высшая школа», 1967.
57. Михеев М. А. Основы теплопередачи. М.—Л., Госэнергоиздат, 1956.
58. Мошкин Е. К. Динамические процессы в ЖРД. М., Машиностроение, 1964.
59. Н и л ь с е н Дж. Аэродинамика, управляемых снарядов. М., Оборонгиз, 1962.
60. Н о в о ж и л о в В. В. Теория упругости. Л., Судпромгиз, 1958.
61. Новожилов В. В. Теория тонких оболочек. Л., Судпромгиз, 1962.
62. О г и б а л о в Н. М., Суворова Ю. В. Механика армированных пласти-
ков. М, изд. МГУ, 1965.
63. О л ь ш а к В., М р у з 3., П е ж и н а П. Современное состояние теории пла-
стичности. М., «Мир», 1964.
64. О н и а ш в и л и О. Д. Некоторые динамические задачи теории оболочек. М.,
изд. АН СССР, 1957.
65. О р л о в Б. В. и М а з и н г Г. Ю. Термодинамические и баллистические ос-
новы проектирования ракетных двигателей на твердом топливе. М., Машиностроение,
1964.
-490
66. П а п к о в и ч П. Ф. Теория упругости. М., Оборонгиз, 1939.
67. П о ж а л о ст и н А. А. К расчету частот собственных колебаний пологой
сферической оболочки. Изв. вузов, Машиностроение, 1965, № 10.
68. Пономарев С. Д. и др. Расчеты на прочность в машиностроении, т. II
и III. М., Машгиз, 1958 .и 1959.
69. Прагер В. Проблемы теории пластичности. М., Физматгиз, 1958.
70. Проблемы высоких температур в авиационных конструкциях, Сб. статей. М.,
ИЛ, 1961.
71. Проблемы движения головной части ракет дальнего действия. Сб. статей. М.,
ИЛ, 1959.
72. Работ но в Ю. Н. Ползучесть элементов конструкций. М., Наука, 1966.
73. Р а б о т н о в Ю. Н. Сопротивление материалов. М., Физматгиз, 1962.
74. Р а б и н о в и ч Б. И. Об уравнениях поперечных колебаний оболочек с жид-
ким заполнением. Изв. АН СССР. Механика и машиностроение, 1964, № 1.
75. Рауше и бах Б. В. Вибрационное горение. М., Физматгиз, 1961.
76. Рейнер М. Деформация и течение. М., изд. нефтяной и горно-топливной
литературы, 1963.
77. Ржаницын А. Р. Устойчивость равновесия упругих систем. М., Гостехиз-
дат, 1955.
78. Ржаницын А. Р. Расчет сооружений с учетом пластических свойств мате-
риалов, изд. 2-е. М., Государственное издательство по строительству и архитектуре,
1954.
79. Рэлей. Теория звука, т. 1 и 2. М., Гостехиздат, 1955.
80. С а х а.р о в Г. И. и др. Нагрев тел при движении с большими сверхзвуковы-
ми скоростями. М., Оборонгиз, 1961.
81. Сейлем, Л а й б е р т. Осесимметричные колебания баков, частично запол-
ненных жидкостью под давлением. «Ракетная техника и космонавтика», 1965, № 1.
82. Семененко А. Н. Несуцая способность нагруженной внутренним давле-
нием осесимметричной сферической оболочки, сопряженной с открытым и заглушенным
цилиндрическим патрубком. Изв. вузов, Машиностроение, 1966, № 4 и 5.
83. Синярев Г. Б. и Добровольский М. В. Жидкостные ракетные дви-
гатели. М., Оборонгиз, 1957.
84. Стокер Дж. Нелинейные колебания в механических и электрических си-
стемах. М., ИЛ, 1953.
85. Стрелков С. П. Введение в теорию колебаний. М., Наука, 1964.
86. Тимошенко С. П. Теория упругости. М.—Л., ОНТИ, 1937.
87. Тимошенко С. П. Устойчивость упругих систем. М., Гостехиздат, 1955.
88. Тимошенко С. П. Колебания в инженерном деле. Физматгиз, 1959.
89. Тимошенко С. П., В о й н о в с к и й-К р и г е р С. Пластинки и оболочки.
М., Физматгиз, 1963.
90. Труды научно-технического совещания по изучению рассеяния энергии при
колебаниях упругих тел. Киев, изд. АН УССР, 1958.
91. Уманский А. А. Строительная механика самолета. М., Оборонгиз, 1961.
92. Ф е о д о с ь е в В. И. Упругие элементы точного приборостроения, М., Обо-
ронгиз, 1949.
93. Феодосьев В. И. Прочность теплонапряженных узлов жидкостных ракет-
ных двигателей. М., Оборонгиз, 1963.
94. Феодосьев В. И. Сопротивление материалов. М., Физматгиз, 1963.
95. Ф е о д о с ь е в В. И. и С и н я р е в Г. Б. Введение в ракетную технику. М.,
Оборонгиз, 1960.
96. Ф е о д о с ь е в В. И. Об одной задаче устойчивости, «Прикладная математика
и механика», т. 29, 1965, вып. 2.
97. Феодосьев В. И., Черняков С. М. О передаче сосредоточенных сил
на тонкостенную оболочку. Инженерный журнал «Механика твердого тела», 1966, № 6.
98. Ф е о ф а н о в А. Ф. Строительная механика авиационных конструкций. М.,
Машиностроение, 1964.
99. Ф люгге В. Статика и динамика оболочек. М., Госстройиздат, 1961.
100. Фрейн, Вонг. Метод предварительного анализа устойчивости с учетом
аэроупругости конструкций ракеты. «Вопросы ракетной техники», 1963, № 8.
101. Фрид, Миллер. Увеличение устойчивости автопилота методом демпфи-
рования изгибных колебаний корпуса ракеты. «Вопросы ракетной техники», 1962, № 5.
102. Харкевич А. А. Автоколебания. М., Гостехиздат, 1953.
103. Хертель Г. Тонкостенные конструкции. М., Машиностроение, 1965.
104. Ходж Ф. Г. Расчет конструкций с учетом пластических деформаций. М.,
Машгиз, 1963.
105. Черных К. Ф. Линейная теория оболочек, ч. I и II. Л., изд. ЛГУ 1962
и 1964.
106. Чижов В. Ф. Устойчивость гофрированной цилиндрической оболочки, на-
груженной внешним давлением. Изв. вузов, Машиностроение, 1964, № 3.
107. Шевелюк М. И. Теоретические основы проектирования жидкостных ра-
кетных двигателей. М., Оборонгиз, 1960.
491
108. Шиманский Ю. А. Динамический расчет судовых конструкций. Л., Суд-
промгиз, 1963.
109. Шмаков В. П. Об уравнениях осесимметричных колебаний цилиндрической-
оболочки с жидким заполнителем. Изв. АН СССР, Механика и машиностроение, 1964,
№ 1.
НО. Элли, Лебеттер. Расчет и измерение собственных колебаний многосту-
пенчатых ракет-носителей. «Ракетная техника и космонавтика», 1963, № 2.
111. Якоб М., Вопросы теплообмена. М., ИЛ, 1960.
112. Fop pl L. Eine neue elastische Materialkonstante. Ingenieur—Archiv, VII Bd.,
4 Heft, 1936.
113. G г a d о w c z у k M. H. Some remarks on the theory of shallow spherical'
shells, Ingenieur—Archiv, XXXII Bd., 5 Heft, 1963.
114. Koella H. H. Handbook of astronautical engineering, New York, Toronto,.
London, 1961.
115. Ma ken n a, Walker, W i n j e. A model for studying coupled engine—air-
frame longitudinal instability of liquid rocket system, AIAA, Preprint, № 81, 1964.
116. Sechl er E. E. and Newell J. S. Progress Report on Methods of Analy-
sis Applicable to Monocoque Aircraft Structures, Air Corps Technical Report, 1942, Jan.,.
15, № 4313.
117. Tse F. S., Morse I. E., Hinkle R. T. Mechanical vibrations, Boston,
1963 (перевод: Цзе, Морс, Хинкл. Механические колебания. М., Машиностроение,.
1966).
118. Journal of the RAS, VII, 1961, p. 39.
119. Burgess E. Long range ballistic missiles, London (перевод: Бургесс Э.
Баллистические ракеты дальнего действия. М., Воениздат, 1963).
120. Design News, v. 16, № 20, 1961, р. 16—17.
121. A discussion on new materials. London, 1964. (перевод: Механические свойст-
ва новых материалов. М., Мир, 1966).
122. Aircraft and Missiles Manufacturing, VII, 1959, p. 6—10.
123. Aviation Week, v. 72, № 15, 1960, p. 91.
124. Flight, v. 87, № 2918, 1965, p. 225—226.
125. Missiles and Rockets, v. 6, № 13, 1960, p. 32—33.
126. Джерард и Лакшмикантам. Оптимальные тонкостенные сосуды дав-
ления из анизотропного материала. Труды американского общества инженеров-механи-
ков, серия Е: «Прикладная механика», 1966, № 3, стр. 166 (русский перевод, изд. «Мир»).
ОГЛАВЛЕНИЕ
Стр.
Предисловие................................................................. 3
Вступительная статья ................................................... 8
Часть первая
.Глава I. Механика деформируемых тел.......................................11
§ 1. Основные понятия и уравнения....................................И
§ 2. Упругие тела. Вариационные уравнения. Температурные напряжения 20
§ 3. Изотропные, ортотропные и составные упругие тела................26
§ 4. Основные понятия теории пластичности............................34
§ 5. Деформационная теория пластичности .................39
§ 6. Теория течения. Особенности разрушения высокопрочных материалов 45
§ 7. Особенности деформирования сложных сред ........................49
.Глава II. Основы теории оболочек вращения постоянной толщины .... 60
§ 8. Геометрия оболочек ............................................ 60
§ 9. Безмоментная теория оболочек............................. ... 67
§ 10. Моментная теория оболочек. Классификация напряженных состояний 78
§ 11. Краевой эффект в моментной теории оболочек......................85
§ 12. Расчет пологой сферической оболочки и цилиндрического бака со
сферическими днищами ................................................94
§ 13. Моментная теория цилиндрических оболочек.......................106
§ 14. Приближенные теории расчета цилиндрических оболочек 115
§ 15. Расчет оболочек по предельным нагрузкам........................128
§ 16. Устойчивость оболочек..........................................136
Глава III. Основы динамических расчетов конструкций........................147
§ 17. Особенности динамического нагружения конструкций . 147
§ 18. Колебания упруго подвешенных масс..............................158
§ 19. Продольные колебания неоднородных стержней....................174
§ 20. Поперечные колебания неоднородных прямых стержней .... 185
§ 21. Колебания пластин и оболочек...................................202
§ 22. Продольные колебания корпуса ракеты ......................... 208
§ 23. Поперечные колебания корпуса ракеты 223
Глава IV. Задачи теплопроводности в тонкостенных конструкциях .... 229
§ 24. Условия теплообмена конструкции с окружающей средой. Основные
уравнения теплопроводности и краевые условия ...................... 229
§ 25. Способы решения задач теплопроводности.........................236
§ 26. Особенности расчета температуры в тонкостенных конструкциях . . 243
493
Часть вторая
Стр.
Глава V. Расчетные схемы. Нагрузки..........................................256
§ 27. Особенности конструкции ракет ....................256
§ 28. Внешние нагрузки ..... ....................... 259»
§ 29. Аэродинамический нагрев конструкции . .................268
§ 30. Внутренние усилия в корпусе ракеты..............................276
§ 31. Коэффициент безопасности. Расчетные случаи......................284
Глава VI. Расчет баков.................................................... 289'
§ 32. Конструктивные схемы и нагрузки ....................289
§ 33. Гладкие баки....................................................294
§ 34. Баки вафельной конструкции......................................301
§ 35. Расчет днищ баков...............................................308
Глава VII. Расчет сухих отсеков.............................................314
§ 36. Конструктивные схемы и нагрузки.................................314
§ 37. Стрингерные, панельные и лонжеронные отсеки 318
§ 38. Гофрированные отсеки............................................328
§ 39. Переходные и двигательные фермы.................................336
§ 40. Отсеки, работающие на внешнее давление..........................340
Глава VIII. Расчет головной части ракеты....................................348
§ 41. Нагрузки и внешние формы........................................348
§ 42. Тепловая защита головной части ракеты...........................359
§ 43. Устойчивость стабилизирующей юбки..............................365
§ 44. Обтекатели. Силовые элементы конструкции головной части ракеты 369
Глава IX. Расчет на прочность отдельных элементов конструкции .... 386
§ 45. Силовые шпангоуты...............................................386
§ 46. Передача продольных сил на тонкостенные элементы конструкции 388
§ 47. Баллоны высокого давления, трубопроводы, сильфоны .... 398
Часть третья
Глава X. Расчет конструкции жидкостного ракетного двигателя.................404
§ 48. Типичные силовые схемы. Особенности расчета на прочность обо-
лочки ЖРД.............................................................404
§ 49. Особенности теплообмена в ЖРД...................................407
§ 50. Температурное состояние оболочки двигателя......................415
§ 51. Общая несущая способность камеры двигателя......................426
§ 52. Расчет отдельных элементов конструкции ЖРД......................434
§ 53. Динамические задачи.............................................439
Г лава XI. Расчет конструкции РДТТ..........................................442
§ 54. Особенности теплообмена в РДТТ. Расчет тепловой защиты обо-
лочки двигателя при физико-химических превращениях в термоизо-
ляции ................................................................442
§ 55. Температурное поле в металлической стенке с термоизоляцией . . 449
§ 56. Температурное поле в конструкции сопла....................461
§ 57. Прочность корпуса РДТТ....................................467
§ 58. Напряжения и деформации в заряде твердого топлива .... 478
§ 59. О динамических явлениях в РДТТ .................................484
Литература
494
489
Лев Иванович Балабух,
Константин Сергеевич Колесников,
Владимир Степанович Зарубин,
Николай Анатольевич Алфутов,
Валерий Иванович Усюкин,
Вениамин Федорович Чижов.
ОСНОВЫ СТРОИТЕЛЬНОЙ МЕХАНИКИ РАКЕТ
Художественный редактор И. К. Гуторов
Редактор Т. М. Минаева
Художник Л. М. Чернышов
Технический редактор А. С. Кочетова
Корректор С. К. Марченко
Т-00642 Сдано в набор 17/V 1968 г.
Подписано к печати 27/1 1969 г. Формат 70X108l/i6
Объем 31 печ. л. 43,40 усл. печ. л. Уч.-изд. л. 33,87
Изд. № от 44/66 Тираж 6000 экз. Цена 1 р. 37 к.
Тематический план издательства «Высшая школа»
(вузы и техникумы) на 1969 г. Позиция № 69
Москва, К-51, Неглинная ул., д. 29/14,
Издательство «Высшая школа»
Типография Изд-ва МГУ. Москва, Ленинские горы. Зак. 96