Author: Смирнов В.И.
Tags: фундаментальные и общие проблемы математики математика высшая математика
Year: 1974
Text
В. И. СМИРНОВ
КУРС
ВЫСШЕЙ МАТЕМАТИКИ
ТОМ ПЕРВЫЙ
ИЗДАНИЕ ДВАДЦАТЬ ТРЕТЬЕ,
СТЕРЕОТИПНОЕ
Допущено Министерством
высшего и среднего специального образования СССР
в качестве учебника
для студентов механико-математических
и физико-математических факультетов университетов
издательство «наука»
главная редакция
физико-математической литературы
МОСКВА 1974
Б17
С 50
УДК 510 @22)
20203-016
053@1)-74
ОГЛАВЛЕНИЕ
Предисловие к восьмому изданию 7
Предисловие к двадцать первому изданию 8
ГЛАВА I
ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ
§ 1. Переменные величины 9
1. Величина и ее измерение (9). 2. Число A0). 3. Величины посто-
постоянные и переменные A2). 4. Промежуток A3). 5. Понятие о функ-
функции A3). 6. Аналитический способ задания функциональной зависи-
зависимости A6). 7. Неявные функции A7). 8. Табличный способ A8).
9. Графический способ изображения чисел A9). 10. Координа-
Координаты B1). 11. График и уравнение кривой B2). 12. Линейная
функция B4). 13. Приращение. Основное свойство линейной функ-
функции B5). 14. График равномерного движения B7). 15. Эмпирические
формулы B8). 16. Парабола второй степени B9). 17. Парабола тре-
третьей степени C2). 18. Закон обратной пропорциональности C3).
19. Степенная функция C5). 20. Обратные функции C7). 21. Много-
Многозначность функции C8). 22. Показательная и логарифмическая
функции D1). 23. Тригонометрические функции D3). 24. Обратные
тригонометрические, или круговые, функции D7).
§ 2. Теория пределов. Непрерывные функции 49
25. Упорядоченное переменное D9). 26. Величины бесконечно
малые E1). 27. Предел переменной величины E7). 28. Основные
теоремы F1). 29. Величины бесконечно большие F3). 30. Моно-
Монотонные переменные F5). 31. Признак Коши существования пре-
предела F6). 32. Одновременное изменение двух переменных величин,
связанных функциональной зависимостью G0). 33. Примеры G4).
34. Непрерывность функции G5). 35. Свойства непрерывных функ-
функций G7). 36. Сравнение бесконечно малых и бесконечно больших
величин (81). 37. Примеры (83). 38. Число е (84). 39. Недоказанные
предложения (88). 40. Вещественные числа (89). 41. Действия над
вещественными числами (92). 42. Точные границы числовых мно-
множеств. Признаки существования предела (94). 43. Свойства не-
непрерывных функций (96). 44. Непрерывность элементарных функ-
функций (99).
ГЛАВА II
ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ
§ 3. Производная и дифференциал первого порядка 103
45. Понятие о производной A03). 46. Геометрическое значение
производной A05). 47. Производные простейших функций A08).
1*
4 ОГЛАВЛЕНИЕ
48. Производные сложных и обратных функций A11). 49. Таблица
производных и примеры A15). 50. Понятие о дифференциале A17).
51. Некоторые дифференциальные уравнения A20). 52. Оценка
погрешностей A22).
§ 4. Производные и дифференциалы высших порядков 124
53. Производные высших порядков A24). 54. Механическое значение
второй производной A26). 55. Дифференциалы высших порядков A27).
56. Разности функций A28).
§ 5. Приложение понятия о производной к изучению функций... 131
57. Признаки возрастания и убывания функций A31). 58. Максимумы
и минимумы функций A34). 59. Построение графиков A39). 60. Наи-
Наибольшее и наименьшее значения функций A42). 61. Теорема Ферма
A48). 62. Теорема Ролля A49). 63. Формула Лагранжа A51). 64. Фор-
Формула Коши A54). 65. Раскрытие неопределенностей A55). 66. Раз-
Различные виды неопределенностей A57).
§ 6. Функции двух переменных 160
67. Основные понятия A60). 68. Частные производные и полный
дифференциал функции двух независимых переменных A62).
69. Производные сложных и неявных функций A64).
§ 7. Некоторые геометрические приложения понятия о производ-
производных 166
70. Дифференциал дуги A66). 71. Выпуклость, вогнутость и кривиз-
кривизна A68). 72. Асимптоты A71). 73. Построение графиков A73). 74. Па-
Параметрическое задание кривой A75). 75. Уравнение Ван-дер-Ваальса
A79). 76. Особые точки кривых A80). 77. Элементы кривой A84).
78. Цепная линия A86). 79. Циклоида A87). 80. Эпициклоиды и ги-
гипоциклоиды A89). 81. Развертка круга A92). 82. Кривые в полярных
координатах A92). 83. Спирали A94). 84. Улитки и кардиоида A95).
85. Овалы Кассини и лемниската A97).
ГЛАВА III
ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ
§ 8. Основные задачи интегрального исчисления и неопределен-
неопределенный интеграл 199
86. Понятие о неопределенном интеграле A99). 87. Определенный
интеграл как предел суммы B02). 88. Связь определенного и неоп-
неопределенного интегралов B08). 89. Свойства неопределенного инте-
интеграла B13). 90. Таблица простейших интегралов B14). 91. Правило
интегрирования по частям B15). 92. Правило замены переменных.
Примеры B16). 93. Примеры дифференциальных уравнений первого
порядка B20).
§ 9. Свойства определенного интеграла 223
94. Основные свойства определенного интеграла B23). 95. Теорема
о среднем B26). 96. Существование первообразной функции B30).
97. Разрыв подынтегральной функции B31). 98. Бесконечные пре-
пределы B35). 99. Замена переменной под знаком определенного ин-
интеграла B36). 100. Интегрирование по частям B39).
ОГЛАВЛЕНИЕ 5
§ 10. Приложения понятия об определенном интеграле ........ 241
101. Вычисление площадей B41). 102. Площадь сектора B44).
103. Длина дуги B46). 104. Вычисление объемов тел по их попереч-
поперечным сечениям B53). 105. Объем тела вращения B55). 106. Поверхность
тела вращения B56). 107. Определение центров тяжести. Теоремы
Гульдина B60). 108. Приближенное вычисление определенных ин-
интегралов; формулы прямоугольников и трапеций B64). 109. Форму-
Формула касательных и формула Понселе B65). ПО. Формула Симпсо-
на B66). 111. Вычисление определенного интеграла с пере-
переменным верхним пределом B71). 112. Графические способы B73).
113. Площади быстро колеблющихся кривых B74).
§ 11. Дополнительные сведения об определенном интеграле 275
114. Предварительные понятия B75). 115. Разбиение промежутка на
части и образование различных сумм B78). 116. Интегрируемые
функции B80). 117. Свойства интегрируемых функций B84).
ГЛАВА IV
РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ
ВЫЧИСЛЕНИЯМ
§ 12. Основные понятия из теории бесконечных рядов 289
118. Понятие о бесконечном ряде B89). 119. Основные свойства
бесконечных рядов B91). 120. Ряды с положительными членами.
Признаки сходимости B93). 121. Признаки Коши и Даламбера B95).
122. Интегральный признак сходимости Коши B98). 123. Знакопе-
Знакопеременные ряды C01). 124. Абсолютно сходящиеся ряды C02). 125.
Общий признак сходимости C05).
§ 13. Формула Тейлора и ее приложения 306
126. Формула Тейлора C06). 127. Различные виды формулы Тейло-
Тейлора C10). 128. Ряды Тейлора и Маклорена C11). 129. Разложение е*
C12). 130. Разложение sin x и cos л: C14). 131. Бином Ньютона C15).
132. Разложение logO+лг) C21). 133. Разложение arctgx C25).
134. Приближенные формулы C27). 135. Максимумы, минимумы и
точки перегиба C28). 136. Раскрытие неопределенностей C30).
§ 14. Дополнительные сведения из теории рядов 332
137. Свойства абсолютно сходящихся рядов C32). 138. Умножение
абсолютно сходящихся рядов C33). 139. Признак Куммера C35).
140. Признак Гаусса C36). 141. Гипергеометрический ряд C39). 142.
Двойные ряды C41). 143. Ряды с переменными членами. Равномер-
Равномерно сходящиеся ряды C45). 144. Равномерно сходящиеся последова-
последовательности функций C48). 145. Свойства равномерно' сходящихся
последовательностей C51). 146. Свойства равномерно сходящихся
рядов C54). 147. Признаки равномерной сходимости C55). 148. Сте-
Степенные ряды. Радиус сходимости C57). 149. Вторая теорема
Абеля C58). 150. Дифференцирование и интегрирование степен-
степенного ряда C60).
глава v
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
§ 15. Производные и дифференциалы функции 363
151. Основные понятия C63). 152. О предельном переходе C65).
153. Частные производные и полный дифференциал первого
в ОГЛАВЛЕНИЕ
порядка C67). 154. Однородные функции C69). 155. Частные произ-
производные высших порядков C71). 156. Дифференциалы высших
порядков C73). 157. Неявные функции C75). 158. Пример C77).
159. Существование неявных функций C79). 160. Кривые в про-
пространстве и поверхности C81).
§ 16. Формула Тейлора. Максимумы и минимумы функции от не-
нескольких переменных 385
161. Распространение формулы Тейлора на случай функции от
нескольких независимых переменных C85). 162. Необходимые усло-
условия максимума и минимума функции C86). 163. Исследование мак-
максимума и минимума функции двух независимых переменных C88).
164. Примеры C91). 165. Дополнительные замечания о нахождении
максимумов и минимумов функции C93). 166. Наибольшее и наи-
наименьшее значения функции C94). 167. Относительные максимумы
и минимумы C95). 168. Дополнительные замечания C98). 169. При-
Примеры D01).
ГЛАВА VI
КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ
И ИНТЕГРИРОВАНИЕ ФУНКЦИИ
§ 17. Комплексные числа 404
170. Комплексные числа D04). 171. Сложение и вычитание комп-
комплексных чисел D07). 172. Умножение комплексных чисел D08).
ПЗ. Деление комплексных чисел D11). 174. Возвышение в сте-
степень D12). 175. Извлечение корня D14). 176. Показательная функ-
функция D16). 177. Тригонометрические и гиперболические функции D18).
178. Цепная линия D22). 179. Логарифмирование D27). 180. Сину-
Синусоидальные величины и векторные диаграммы D28). 181. При-
Примеры D31). 182. Кривые в комплексной форме D34),, 183. Представ-
Представление гармонического колебания в комплексной форме D37).
§ 18. Основные свойства целых многочленов и вычисление их
корней 437
184. Алгебраическое уравнение D37). 185. Разложение многочлена
на множители D39). 186. Кратные корни D40). 187. Правило Горне-
ра D42). 188. Общий наибольший делитель D45). 189. Вещественные
многочлены D46). 190. Зависимость между корнями уравнения и
его коэффициентами D47). 191. Уравнение третьей степени D47).
192. Решение кубического уравнения в тригонометрической фор-
форме D51). 193. Способ итерации D54). 194. Способ Ньютона D58).
195. Способ простого интерполирования D59).
§ 19. Интегрирование функций 461
196. Разложение рациональной дроби на простейшие D61). 197. Ин-
Интегрирование рациональной дроби D63). 198. Интеграл от
выражений, содержащих радикалы D66). 199. Интегралы
вида ^R(x, Уах2 + Ьх + с)Aх D67). 200. Интегралы вида
$ R (sin ху cos л:) dx D70). 201. Интегралы вида \ еах [Р (х) cos Ъх +
+ Q(x)sinbx] dx D72).
Алфавитный указатель 475
ПРЕДИСЛОВИЕ К ВОСЬМОМУ ИЗДАНИЮ
Настоящее издание весьма существенно отличается от предыду-
предыдущего. Из книги исключен материал, относящийся к аналитической
геометрии. В связи с этим пришлось сделать перегруппировку остав-
оставшегося материала. В частности, все имеющиеся в настоящем томе
приложения дифференциального исчисления к геометрии собраны в
§ 7 (глава II). Далее, в первый том отнесена глава, посвященная
комплексным числам, основным свойствам целых многочленов и си-
систематическому интегрированию функций. Прежде она была главой I
второго тома.
Не останавливаясь на мелких добавлениях и изменениях в изло-
изложении, мы укажем на существенные добавления. Принимая во внима-
внимание, что в следующих томах приходится встречаться с довольно тон-
тонкими и сложными вопросами современного анализа, мы сочли полез-
полезным в конце § 2 (глава I) после изложения теории пределов поместить
изложение теории иррациональных чисел и ее применений к доказа-
доказательству признаков существования предела и свойств непрерывных
функций. Там же мы приводим строгое определение и исследование
свойств элементарных функций. В главе V, посвященной функциям
нескольких переменных, мы приводим доказательство существования
неявных функций.
Изложение ведется таким образом, что крупный шрифт может
читаться самостоятельно. В мелкий шрифт отнесены примеры, неко-
некоторые отдельные дополнительные вопросы, а также весь тот теоре-
теоретический материал, о котором мы упоминали выше, и лоследние па-
параграфы главы IV, также содержащие дополнительный теоретический
материал более сложного характера.
Профессор Г. М. Фихтенгольц сделал мне ряд ценных указаний
в отношении изложения, которыми я воспользовался при окончатель-
окончательной редакции этой книги. Считаю своим приятным долгом выразить
ему мою глубокую благодарность.
В. Смирнов
ПРЕДИСЛОВИЕ К ДВАДЦАТЬ ПЕРВОМУ ИЗДАНИЮ
В настоящем издании основной текст и весь план книги остались
без перемен, но в ряде мест были сделаны изменения в изложении
материала. Особенно это коснулось теории пределов и дополнитель-
дополнительных сведений об определенном интеграле.
В. Смирнов
ГЛАВА Г
ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ
И ТЕОРИЯ ПРЕДЕЛОВ
§ 1. ПЕРЕМЕННЫЕ ВЕЛИЧИНЫ
1. Величина и ее измерение. Математический анализ имеет ос-
основное значение в ряде наук и, в частности, в естественных науках
и технике. В отличие от остальных-наук, из которых каждая инте-
интересуется лишь некоторой определенной стороной окружающего нас
мира, математика имеет дело с самыми общими свойствами, прису-
присущими всем доступным для научного исследования явлениям.
Одним из основных понятий является понятие о величине и ее
измерении. Характерное свойство величины заключается в том, что
она может быть измерена, т. е. тем или иным путем сравнена с не-
некоторой определенной величиной того же рода, которая принимается
за единицу меры. Самый процесс сравнения зависит от свойства ис-
исследуемой величины и называется измерением. В результате же из-
измерения получается число, выражающее отношение рассматриваемой
величины к величине, принятой за единицу меры.
Всякий закон природы дает нам соотношение между величинами
или, вернее, между числами, выражающими эти величины. Предметом
исследования математики и являются как раз числа и различные соот-
соотношения между ними, независимо от конкретного характера тех ве*
личин или законов, которые привели нас к этим числам и соотно-
соотношениям.
Итак, каждой величине соответствует измеряющее ее число.
Но число это существенно зависит от принятой при измерении еди-
единицы или масштаба. При увеличении этой единицы будет умень-
уменьшаться число, измеряющее данную величину, и, обратно, число это
будет увеличиваться при уменьшении единицы.
Выбор масштаба обусловливается характером исследуемой вели-
величины и обстоятельствами, при которых производится измерение. Ве-
Величина масштаба при измерении одной и той же величины может
меняться в самых широких пределах, — например, при измерении длины
10 ГЛ. I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ \ 2
в точных оптических исследованиях принимают за единицу длины
один ангстрем (одну десятимиллионную долю миллиметра, 10~7мм);
в астрономии же употребляют единицу длины, называемую световым
годом, т. е. расстояние, проходимое светом в течение одного года
(за одну секунду свет проходит примерно 300 000 км).
2. Число. Число, которое получается в результате измерения, мо-
может быть целым (если единица содержится целое число раз в из-
измеряемой величине), дробным, или рациональным (если существует
другая единица, которая содержится целое число раз как в измеря-
измеряемой величине, так и в выбранной раньше единице, — короче, когда
измеряемая величина соизмерима с единицей меры), и, наконец, ир-
иррациональным (когда такой общей меры не существует, т. е. данная
величина оказывается несоизмеримой с единицей меры).
Так, например, в элементарной геометрии доказывается, что диа-
диагональ квадрата несоизмерима с его стороной, так что, если мы бу-
будем измерять диагональ квадрата, приняв за единицу длины его сто-
сторону, то полученное при измерении число j/2 будет иррациональным.
Иррациональным же оказывается и число тс, измеряющее длину ок-
окружности, диаметр которой принят за единицу.
Для уяснения понятия об иррациональном числе полезно обра-
обратиться к десятичным дробям» Всякое рациональное число, как извест-
известно из арифметики, может быть представлено или в виде конечной
десятичной дроби или в виде бесконечной десятичной дроби, при-
причем в последнем случае бесконечная дробь будет периодической (чис-
(чистой периодической или смешанной периодической). Так, например,
производя деление числителя на знаменатель по правилу деления де-
десятичных дробей, мы получим
^- = 0,151515. .. = 0,A5), ~ = 0,2777... = 0,2 G).
Наоборот, как известно из арифметики, всякая периодическая деся-
десятичная дробь выражает рациональное число.
При измерении величины, несоизмеримой с принятой единицей,
мы можем сначала подсчитать, сколько раз полная единица заклю-
заключается в измеряемой величине, затем сколько раз десятая доля еди-
единицы заключается в полученном остатке величины, затем сколько
раз сотая доля единицы заключается в новом остатке и т. д. Таким
путем при измерении величины, несоизмеримой с единицей, будет
образовываться некоторая бесконечная непериодическая десятичная
дробь* Всякому иррациональному числу соответствует такая беско-
бесконечная дробь и, наоборот, всякой бесконечной непериодической де-
десятичной дроби соответствует некоторое иррациональное число. Если
в этой бесконечной десятичной дроби оставить лишь несколько пер-
первых десятичных знаков, то получится приближенное значение по
2 J § i. ПЕРЕМЕННЫЕ ВЕЛИЧИНЫ
И
недостатку иррационального числа, представляемого этой дробью.
Так, например, извлекая квадратный корень по обычному правилу до
третьего десятичного знака, получим
Числа 1,414 и 1,415 будут приближенными значениями ]/^2 с точ-
точностью до одной тысячной по недостатку и по избытку.
Пользуясь десятичными знаками, можно иррациональные числа
сравнивать по величине друг с другом и с рациональными числами.
Во многих случаях приходится рассматривать величины разных
знаков: положительные и отрицательные (температура выше и ниже 0°
и т. п.). Такие величины выражаются соответственно положительны-
положительными и отрицательными числами. Если а и Ь — положительные числа
и а>Ь, то — а < — Ь, и любое положительное число, включая нуль,
больше любого отрицательного числа.
Все рациональные и иррациональные числа располагаются в не-
некотором определенном порядке по своей величине. Все эти числа
образуют совокупность вещественных чисел.
Отметим одно обстоятельство, связанное с представлением веще-
вещественных чисел десятичными дробями. Вместо любой конечной деся-
десятичной дроби мы можем написать бесконечную десятичную дробь
с девяткой в периоде. Так, например: 3,16 = 3,1599... Если не
пользоваться конечными десятичными дробями, то получится точное
биоднозначное соответствие между вещественными числами и бес-
бесконечными десятичными дробями, т. е. всякому вещественному числу
соответствует бесконечная десятичная дробь и всякой бесконечной деся-
десятичной дроби соответствует вещественное число. Отрицательным числам
соответствуют бесконечные десятичные дроби с предшествующим им
знаком минус.
В области вещественных чисел выполнимы первые четыре дей-
действия, кроме деления на нуль. Корень нечетной степени из любого
вещественного числа имеет всегда одно определенное значение. Корень
четной степени из положительного числа имеет два значения, которые
различаются только знаком. Корень четной степени из отрицатель-
отрицательного вещественного числа не имеет смысла в области вещественных чисел
«/-0=0).
Строгая теория вещественных чисел и действий над ними будет
нами изложена в [40].
Арифметическим, или абсолютным, значением числа а на-
называется само число а, если а — положительное число или нуль,
и число —а, если а — отрицательное число. Абсолютное значение
числа а обозначается символом \а\, так что |а| = а, если а^О,
и j а | = — а, если а < 0. Так, например, | 5 | = 5 и | — 5 | = 5 и
вообще | а \ = | — а |. Нетрудно видеть, что абсолютное значение
суммы j a -\-b\ будет равно сумме абсолютных значений слагаемых,
12 ГЛ. 1. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ | 3
т. е. равно | а | -(-1Ь | только в том случае, если слагаемые имеют
одинаковый знак, а при разных знаках слагаемых |{?|С11Н^1
так что во всех случаях
Так, например, при а = — Зи Ь = — 7 мы имеем знак равенства,
а при а = Ъ и Ь = —7 имеем |3-|-( — 7) [ ===== 4 и |3| + | — 7|==10,
т. е. знак неравенства.
Точно так же легко видеть, что
\а-Ь\^\а\-\Ь\,
причем считается, что |а |^ | Ъ |. При \а\ <^\Ь\ неравенство также
справедливо, ибо слева стоит положительная величина, а справа —
отрицательная.
Абсолютное значение произведения равно произведению абсо-
абсолютных значений сомножителей, и абсолютное значение частного
(делитель отличен от нуля) равно частному абсолютных вначений
делимого и делителя, т. е.
а
Т
3. Величины постоянные и переменные. Величины, исследуемые
в математике, разделяются на два класса: постоянные и переменные.
Постоянной величиной называется величина, которая при дан-
данном исследовании сохраняет одно и то же, неизменное, значение.
Ей соответствует, таким образом, при фиксированной единице меры
определенное число.
Переменной величиной называется такая величина, которая по
тем или иным причинам может принимать различные значения при
данном исследовании.
Из этих определений ясно, что понятие о постоянной и перемен-
переменной величине в значительной мере условно и зависит от обстоятельств,
при которых изучается данное явление. Одна и та же величина, ко-
которая при одних условиях могла рассматриваться как постоянная,
при других условиях может стать переменной, и наоборот.
Так, например, при измерении веса тел важно знать, производится
ли взвешивание в одном и том же месте земной поверхности или
в разных: если измерение производится в одном и том же месте, то
ускорение силы тяжести, от которой и зависит вес, будет оставаться
величиной постоянной, и различие в весе между разными телами бу-
будет зависеть только от их массы; если же измерения производятся
в разных местах земной поверхности, то ускорение силы тяжести не
может считаться постоянным, так как оно зависит от центробежной
4 J § 1. ПЕРЕМЕННЫЕ ВЕЛИЧИНЫ 13
силы вращения Земли; благодаря этому одно и то же тело на эква-
экваторе весит меньше, чем на полюсе, что и можно обнаружить, если
производить взвешивание не на рычажных, а на пружинных весах.
Равным образом при грубых технических расчетах можно считать,
что длина входящих в конструкцию стержней есть величина неизмен-
неизменная; при более же точных, когда приходится принимать во внимание
действие изменения температуры, длина стержней оказывается пере-
переменной, что, конечно, значительно усложняет все расчеты.
4. Промежуток. Характер изменения переменной величины может
быть самым разнообразным. Переменная величина может принимать
либо всевозможные вещественные значения, без всяких ограничений
(например время t, отсчитываемое от некоторого определенного на-
начального момента, может принимать всевозможные, как положитель-
положительные, так и отрицательные, значения), либо значения ее ограничиваются
некоторыми неравенствами (например абсолютная температура 7ю, ко-
которая должна быть больше—273° С); наконец, переменная величи-
величина может принимать лишь некоторые, а не всевозможные значе-
значения (только целые — число жителей данного города, число моле-
молекул в данном объеме газа — или только соизмеримые с данной
единицей и т. п.).
Укажем некоторые, наиболее распространенные в теоретических
исследованиях и на практике способы изменения переменных величин.
Если переменная величина х может принимать все вещественные
значения, удовлетворяющие условию а ^ х ^ Ь, где а и b — задан-
заданные вещественные числа, то говорят, что х изменяется в проме-
промежутке (а, Ь). Такой промежуток, со включенными концами, назы-
называют иногда замкнутым промежутком. Если переменная х может
принимать все значения из промежутка (а, 6), кроме его концов, т. е.
а<^х<^Ь, то говорят, что х изменяется внутри промежутка
(а, Ь)% Такой промежуток с исключенными концами называется откры-
открытым промежутком. Кроме того, областью изменения х может быть
и промежуток, замкнутый с одной стороны и открытый с другой:
а^х<^Ь или а<^х^.Ь.
Если область изменения х определяется неравенством д^.х, то
говорят, что х изменяется в промежутке (a, -f- сю), который замкнут
слева и открыт справа. Точно так же при неравенстве х^Ь
мы имеем промежуток (—со, Ь), открытый слева и замкнутый
справа. Если х может принимать любые вещественные значения,
то говорят, что х изменяется в промежутке (— оо, -}- оо), открытом
с обеих сторон.
В дальнейшем через (а, Ь) мы всегда будем обозначать замкнутый
промежуток. Часто для замкнутого промежутка пользуются обозна-
обозначением [а> Ь]. Исключение одного или обоих концов из промежутка
мы будем оговаривать особо.
14 ГЛ. 1. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ ( 5
б. Понятие о функции. Чаще всего в приложениях приходится
иметь дело не с одной переменной величиной, а с несколькими сразу.
Рассмотрим, например, 1 кг воздуха. Переменные величины, определя-
определяющие его состояние, будут: давление р(кг/м2)у под которым он на-
находится; объем v(m3), который он занимает; температура его t(°C).
Предположим пока, что температура воздуха поддерживается равной
0°С. Число t есть в данном случае постоянная, равная нулю. Оста-
Остаются переменные р и v. Если менять /?, то будет меняться и v; на-
например, если воздух сжимать, то объем уменьшается. Давление р
мы можем менять произвольно (по крайней мере в пределах, доступ-
доступных технике), а потому мы можем называть р независимой переменной;
при каждой фиксированной величине давления газ, очевидно, должен
занимать вполне определенный объем; стало быть, должен существо-
существовать такой закон, который позволяет при каждом значении р найти
соответствующее ему значение и Этот закон хорошо известен — это
закон Бойля — Мариотта, который гласит, что объем, занимаемый
газом при постоянной температуре, обратно пропорционален давлению.
Применяя этот закон к нашему килограмму воздуха, можно найти
зависимость между v и р в виде уравнения
__ 273 - 29,27
Переменная величина v называется в данном случае функцией
независимой переменной р.
Отвлекаясь от этого частного примера мы можем сказать, что,
теоретически говоря, для независимой переменной характерным
является множество ее возможных значений, и мы можем по
произволу выбирать для нее любое значение из этого множества
ее возможных значений. Так, например, множеством значений неза-
независимой переменной х может служить какой-либо промежуток (а, Ь)
или внутренность этого промежутка, т. е. независимая переменная х
может, например, принимать любые значения, удовлетворяющие нера-
неравенству а^х^Ь или неравенству a<ix<Zb. Может случиться, что
х принимает любые целочисленные значения и т. д. В указанном
выше примере роль независимой переменной играло р, и объем v был
функцией р. Дадим теперь определение функции.
Определение. Величина у называется функцией независи-
независимой переменной х, если любому определенному значению х (из
множества ее возможных значений) соответствует определен-
определенное значение у.
. Если, например, у есть функция от х, определенная в промежутке
(а, Ь), то это значит, что любому значению х из этого промежутка
соответствует определенное значение у.
Вопрос о том, какую из двух величин, х или у, считать незави-
независимой переменной, есть часто вопрос только удобства. В нашем при-
5 i § 1. ПЕРЕМЕННЫЕ ВЕЛИЧИНЫ 15
мере мы могли бы, меняя произвольно объем v и определяя каждый
раз давление р> считать независимой переменной vf а давление р рас-
рассматривать как функцию от v. Решая написанное выше уравнение
относительно р, получим формулу, выражающую функцию р через
независимую переменную:
273.29,27
Р v
Сказанное о двух переменных без труда распространяется и на
случай какого угодно числа переменных; и здесь мы можем отли-
отличить переменные независимые от зависимых, или функций.
Возвращаясь к нашему примеру, положим, что температура t не
будет уже 0° С, а может меняться. Закон Бойля — Мариотта должен
быть при этом заменен более сложной зависимостью Клапейрона:
ро = 29,27 B73 + *),
которая показывает, что при изучении состояния газа можно менять
произвольно лишь две из величин р, v и *, а третья будет полностью
определена, если даны значения этих двух. Мы можем принять за неза-
независимые переменные, например, р и *, тогда v будет функцией от них:
v_ 29,27B73 + 0
Р '
либо же независимыми переменными можно считать v и *, а р будет
функцией от них.
Приведем другой пример. Площадь 5 треугольника выражается
через длины сторон а, Ь, с по формуле
где р— полупериметр треугольника:
Р~ 2 '
Стороны a, Ь, с можно менять произвольно, лишь бы только каждая
сторона была больше разности и меньше суммы двух других. Таким
образом, переменные я, Ь, с будут независимыми переменными,
ограниченными неравенствами, S—функцией от них.
Мы можем также задать произвольно две стороны, например а, Ь,
и площадь 5 треугольника; пользуясь формулой
S = -^ab sin С,
где С — угол между сторонами а> Ь, мы можем тогда вычислить С.
Здесь уже величины a, b, S будут независимыми переменными, С —
функцией. При этом переменные я, b, S должны быть ограничены
неравенством
16 ГЛ. 1, ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ 1 6
Следует заметить, что в этом примере мы получаем для С два
значения, смотря по тому, возьмем ли мы для С острый или тупой
из двух углов, имеющих один и тот же синус
Мы приходим здесь к понятию о многозначной функции, о котором
подробнее будем говорить ниже.
6. Аналитический способ задания функциональной зави-
зависимости. Всякий закон природы, дающий связь одних явлений с дру-
другими, устанавливает функциональную зависимость между величинами.
Существует много способов для изображения функциональных
зависимостей, но самое важное значение имеют три способа: 1) ана-
аналитический, 2) способ таблиц и 3) графический, или геометри-
геометрический.
Мы говорим, что функциональная зависимость между величинами
или, проще, функция изображена аналитически, если величины
эти связаны между собой уравнениями, в которые они входят, под-
подвергаясь различным математическим операциям: сложению, вычитанию,
делению, логарифмированию и т. д. К аналитическому изображению
функций мы приходим, когда исследуем вопрос теоретически, т. е.,
установив основные предпосылки, мы применяем математический
анализ и получаем результат в виде некоторой математической формулы.
Если мы имеем непосредственное выражение функции (т. е. зави-
зависимой переменной) при помощи математических действий над дру-
другими, независимыми переменными, то говорят, что функция аналити-
аналитически задана явно. Примером явного задания функции может слу-
служить выражение объема газа v при постоянной температуре через
давление (явная функция одной независимой переменной):
_ 273-29,27
~~ Р
или выражение площади 5 треугольника через стороны:
(явная функция от трех независимых переменных). Выпишем еще
пример явного задания функции от одной независимой переменной х:
у=*2х2-Зх + 7. A)
Часто бывает неудобно или невозможно выписывать формулу, ко-
которая выражает функцию через независимые переменные. При этом
пишут коротко так:
7 ] § 1. ПЕРЕМЕННЫЕ ВЕЛИЧИНЫ
17
Эта запись обозначает, что у есть функция независимой переменной
х и / есть символический знак зависимости у от х. Вместо /можно,
конечно, употреблять и другие буквы. Если мы рассматриваем разные
функции от ху то должны употреблять и разные буквы для симво-
символической записи зависимости от х:
f(x), F(x), ф(дг) и т. д.
Такой символической записью пользуются не только в том слу-
случае, когда функция задана аналитически, но и в самом общем случае
функциональной зависимости, которой мы определили в [5].
Аналогичной короткой записью пользуются и для функций от
нескольких независимых переменных:
v = F(x, у, г).
Здесь v есть функция переменных х, у, z.
Частное значение функции получим, придав независимым перемен-
переменным частные же значения и выполнив действия, указанные знаками
/, F,... Так, например, частное значение функции A) при л:»*-^ будет
Вообще частное значение некоторой функции f(x) при х = х0
обозначается f(x0). Аналогично — для функций от нескольких пере-
переменных.
Не надо смешивать общего понятия функции, которое было нами
дано в [5J, с понятием аналитического выражения у через х. В общем
определении функции говорится лишь о некотором законе, согласно
которому любому значению переменной х из множества ее возмож-
возможных значений соответствует определенное значение у. При этом не
предполагается никакое аналитическое выражение (формула)у через х.
Отметим еще, что можно определить функцию различными анали-
аналитическими выражениями на разных участках изменения независимой
переменной х. Так, например, мы можем определить функцию
у на промежутке @, 3) следующим образом: у = х-\-6 при
0<х<2 и j/=ll—-2х при 2<;х^3. При таком задании
любому значению х из промежутка @, 3) соответствует определен-
определенное значение у, что и соответствует определению функции.
7. Неявные функции. Функция называется неявной, если мы
имеем не непосредственное аналитическое выражение ее через пере-
переменные независимые, а только уравнение, которое связывает ее
значение со значениями переменных независимых. Так, например,
если переменная величина^ связана с переменной величиной х уравнением
18 ГЛ. Т. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ 1 8
то у есть неявная функция независимой переменной х; с другой
стороны, можно и х считать неявной функцией независимой пере-
переменной у.
Неявная функция v от нескольких независимых переменных х} у, z,...
определяется вообще из уравнения
F(x,ytz,...t v) = 0.
Вычислять значения этой функции мы можем тогда, когда раз-
разрешим уравнение относительно v и тем самым представим v в виде
явной функции от х, у у z,...:
В приведенном выше примере у выражается через х в виде
Однако для получения различных свойств функции v совсем нет
необходимости решать уравнение, и очень часто бывает, что удается
достаточно хорошо изучить неявную функцию по самому уравнению,
которым она определяется, не решая его.
Например, объем газа v есть неявная функция давления р и тем-
температуры t, определяемая уравнением
Угол С между сторонами а и Ь треугольника площади 5 есть
неявная функция а, Ь и S, определяемая уравнением
аЬ sin C=2S.
8. Табличный способ. Аналитический способ представления функ-
функций применяется главным образом при теоретических исследованиях.
На практике же, когда приходится на самом деле вычислять много
частных значений различных функций, аналитический способ пред-
представления часто оказывается неудобным, так как он требует в каж-
каждом случае производства всех необходимых вычислений.
Чтобы избежать этого, вычисляются частные значения наиболее
употребительных функций, при большом числе частных значений
независимых переменных, и составляются таблицы. Таковы, напри-
например, таблицы значений функций
У = х2, —, /л7, тих, ^-тих2, log10 лг, log10sinx, и т. д.,
с которыми постоянно приходится иметь дело на практике. Суще-
Существуют и другие таблицы, более сложных функций, которые тоже
приносят большую пользу: таблицы бесселевых функций, эллиптичес-
© I § 1, ПЕРЕМЕННЫЕ ВЕЛИЧИНЫ 19
ких и т. д. Существуют таблицы и для функций от нескольких
переменных, простейший пример которых представляет обыкновенная
таблица умножения, т. е. таблица значений функций z=*xy при
различных целых значениях х к у.
Иногда приходится вычислять значения функций при таких част-
частных значениях независимых переменных, которых в таблицах нет,
а есть только соседние к ним значения; для того, чтобы можно
было пользоваться таблицами и в этом случае, существуют различ-
различные правила интерполяции; одно из таких правил было дано еще
в курсе средней школы при пользовании таблицами логарифмов
(partes proportionates).
Важное значение имеют таблицы тогда, когда при их помощи
изображаются функции, аналитическое выражение которых нам неиз-
неизвестно; с этим приходится иметь дело, когда производится экспе-
эксперимент. Всякое опытное исследование имеет целью обнаружить
скрытые для нас функциональные зависимости, и результат всякого
опыта представляется в виде таблицы, связывающей между собой
соответствующие значения исследуемых при этом опыте величин.
Л). Графический способ изображения чисел. Переходя к гра-
графическому способу изображения функциональной зависимости, мы
начнем со случая графического изображения одной переменной.
Всякое число х может быть изображено некоторым отрезком.
Для этого достаточно, условившись раз навсегда в выборе единицы
длины, построить отрезок, длина которого равна как раз данному
числу х. Таким образом, всякая ве-
величина не только может быть вы- g _ д д + ^
ражена числом, но также и геомет- **< ° ° ¦ >°—*¦
рически изображена отрезком.
Для того чтобы можно было та- Рис. 1.
ким путем изобразить и отрица-
отрицательные числа, условимся откладывать отрезки на одной и той же
прямой линии, приписав ей притом определенное направление (рис. 1).
Условимся, далее, обозначать всякий отрезок знаком АВ, причем точ-
точку А будем называть началом, В — концом отрезка.
Если направление от А к В совпадает с направлением прямой,
отрезок изображает число положительное; если же направление
от А к В противоположно направлению прямой, то отрезок изобра-
изобразит число отрицательное (А1В1 на рис. 1). Абсолютное же значе-
значение рассматриваемого числа выражается длиной изображающего его
отрезка независимо от направления.
Длину отрезка АВ будем обозначать через \АВ\; если отрезок
АВ изображает число х, то будем писать просто
20 ГЛ. I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ [ 9
Для большей определенности можно раз навсегда условиться
помещать начало всех отрезков в заранее выбранную точку О пря-
прямой. Тогда всякий отрезок О А, а потому и изображаемое им число х,
будет вполне определяться точкой А, концом отрезка (рис. 2).
Обратно, задав число х, можем и
х> о Vх* ш- у п0 величине и по направлению
определить отрезок ОА, а по-
Рис 2. тому и конец его А. Точке О
(начало) соответствует х = 0.
Итак, если провести направленную прямую XX (ось) и отме-
отметить на ней неподвижную точку О (начало), то каждому
вещественному числу х будет соответствовать определенная
точка А этой прямой, такая, что отрезок О А измеряется чис-
числом х. Обратно, всякой точке А оси соответствует вполне
определенное вещественное число х, измеряющее отрезок ОА.
Это число х называется абсциссой точки А; если нужно ука-
указать, что точка А имеет абсциссу х, то пишут А {х).
Если число х меняется, то изображающая его точка А передви-
передвигается по оси. Установленное выше понятие о промежутке при таком
графическом изобраэюении числа х становится совершенно нагляд-
наглядным, а именно: если х меняется в промежутке а^х^Ь, то соот-
соответствующая точка на оси XX будет находиться в отрезке, концы
которого имеют абсциссы а и Ь.
Если бы мы ограничились одними рациональными числами, то
точке А не соответствовало бы никакой абсциссы, если отрезок ОА
несоизмерим с принятой единицей, т. е., иначе говоря, одни рацио-
рациональные числа не заполняют всех точек прямой. Это заполнение
достигается введением иррациональных чисел. Основным положением
при графическом изображении одной переменной величины является
указанное выше положение: всякой точке оси XX соответствует
определенное вещественное число и, наоборот, всякому веществен-
вещественному числу соответствует определенная точка оси XX.
Возьмем на оси XX две точки: точку А\ с абсциссою Х\ и
точку Л2 с абсциссою x2. При этом отрезку ОА\ будет соответ-
соответствовать число хь а отрезку ОЛ2— число дг2. Нетрудно показать,
рассматривая всевозможные взаимные расположения точек At и Л2,
что отрезку AiA2 будет соответствовать число (х%— хх), так что длина
этого отрезка будет равна абсолютному значению разности (лг2 — Xi):
Если, например, дг1 = —3 и х% = 7, то точка А\ лежит слева
от О на расстоянии, равном 3, а точка Л2 лежит справа от О на
расстоянии, равном 7. Отрезок А\А% будет иметь длину 10 и будет
to)
§ l. ПЕРЕМЕННЫЕ ВЕЛИЧИНЫ
21
направлен так же, как ось XX, т. е. ему будет соответствовать
число 10 = 7 — (— 3) = Хо — хх. Предоставляем читателю разобрать
другие возможности расположения точек Ах и Л2.
10. Координаты. Выше мы видели, что положение точки на пря-
прямой Х'Х может быть определено вещественным числом х. Пока-
Покажем теперь аналогичный способ определения положения точки на
плоскости.
Проведем на плоскости две
взаимно перпендикулярные оси
XX и Y'Y и возьмем за начало
на каждой из них их точку пере- /
сечения О (рис. 3). Положитель-
Положительные направления на осях указаны
стрелками. Точкам оси XX со-
соответствуют вещественные числа,
которые мы обозначим буквой х.
Л
и
9я
i
•
?
I
i
i
i
-•
¦ -
81
[
°\
г
г
1
-
—
1
1
1
м
i
i
•
I
ш
Рис. 3.
Точкам оси Y Y также соответ-
соответствуют вещественные числа, кото-
которые мы будем обозначать буквой у. Если нам заданы определенные
значения х и у, то мы имеем определенные точки А и В на осях
Х'Х и Y'Y] зная точки А и В, можем построить точку М пересече-
пересечения прямых, параллельных осям и проведенных через точки А и В.
Каждой паре значений величин х, у соответствует одно
вполне определенное положение точки М на плоскости чертежа.
Обратно, каждой точке М плоскости соответствует вполне
определенная пара значений величин х, у, отвечающих точкам пере-
пересечения Л, В прямых, проведенных через точку М параллельно осям,
с осями XX и ГГ.
При указанных на рис. 3 направлениях осей Х'Х> Y'Y надо х
считать положительным, если точка А лежит направо, и отрицатель-
отрицательным, если она лежит налево от точки О; у будет положительным,
если точка В лежит сверху, отрицательным, — если снизу, от О.
Величины х} у, определяющие положение точки М на плос-
плоскости и в свою очередь определяемые положением точки М, на-
называются координатами точки ¦ М. Оси Х'ХУ Y'Y называются
координатными осями, плоскость чертежа — координатной плос-
плоскостью XOY, точка О — началом координат.
Величина х называется абсциссой, у — ординатой точки М.
Задавая точку М ее координатами, пишут М(ху у).
Самый способ изображения называется способом прямоуголь-
прямоугольных координат.
Знаки координат точки М при различных ее положениях в раз-
различных координатных углах (I—IV) (рис. 3) можно представить та-
такой таблицей:
22
ГЛ. I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ [ 11
м
X
У
I
+
+
и
—
11)
—
-
IV
+
—
Совершенно ясно, что коорди-
координаты х и у точки М равны рас-
расстояниям точки М до осей коор-
координат, взятым с соответствующи-
соответствующими знаками. Отметим, что точки
оси XX имеют координаты (х> 0),
а точки оси У У—координаты
@, у). Начало координат О имеет
координаты @,0).
11. График и уравнение кривой. Возвратимся к величинам х и у,
которые изображает точка М. Пусть х и у связаны функциональной
зависимостью; это значит, что, меняя по произволу х (или v), мы
будем получать каждый раз соответствующее значение у (или х).
Каждой такой паре значений х и у соответствует определенное по-
положение точки М на плоскости XOY; если же значения эти будут
меняться, то точка М будет передвигаться по плоскости и при дви-
движении своем опишет некоторую линию (рис. 4), которая называется
графическим изображением (или, проще, графиком или диаграммой)
рассматриваемой функциональной за-
зависимости.
Если зависимость задана аналити-
аналитически в виде уравнения в явной форме
У=П*)
или в неявной форме
У
1
(
и
1
cJm
V
X.
V
то уравнение это называетя уравне- Рис 4
нием кривой, а кривая — графиком
уравнения или графиком функции. Кривая и ее уравнение суть
лишь различные способы выражения одной и той же функциональной
зависимости, т. е. все точки, координаты которых удовлетворяют
уравнению кривой, лежат на этой кривой и, обратно, коорди-
координаты всех точек, лежащих на кривой, удовлетворяют ее уравнению.
Если дано уравнение кривой, можно, пользуясь листом графленой
бумаги, построить, более или менее точно, самую кривую (вернее,
можно построить какое угодно число точек, лежащих на этой кри-
кривой); чем больше таких точек построим, тем яснее будет для нас фор-
форма кривой; такой способ называется построением кривой по точкам.
Выбор масштаба имеет существенное значение при построении
кривых; при этом можно выбирать разные масштабы при построе-
построении х и у. При одинаковых масштабах для х и у плоскость упо-
уподобляется листу бумаги, разграфленному на квадраты, при разных
же масштабах —на прямоугольники. В дальнейшем будет подразу-
подразумеваться, что масштабы для х и у одинаковы.
ц ] § 1. ПЕРЕМЕННЫЕ ВЕЛИЧИНЫ 23
Читателям рекомендуется здесь же построить по точкам несколько
графиков простейших функций, меняя притом масштабы для х и у.
Введенные выше понятия о координатах точки М, об уравнении
кривой и графике уравнения устанавливают тесную связь между
алгеброй и геометрией. С одной стороны, мы получаем возможность
наглядным геометрическим путем изображать и исследовать аналити-
аналитические зависимости, с другой стороны, оказывается возможным
сводить решение геометрических вопросов к чисто алгебраическим
действиям, в чем и заключается основная задача аналитической
геометрии, разработанной впервые Декартом.
Ввиду чрезвычайной важности формулируем еще раз факты,
лежащие в основе аналитической геометрии. Если на плоскости от-
отметить две координатные оси, то всякой точке плоскости будет
соответствовать пара вещественных чисел — абсцисса и ордината
этой точки, и, наоборот, всякой паре чисел будет соответство-
соответствовать определенная точка плоскости, имеющая первое число своей
абсциссой и второе число своей ординатой. Кривой на плоскости
соответствует функциональная зависимость между х и у, или,
что то же, уравнение, содержащее переменные х и у, которое
удовлетворяется в том и лишь в том случае, если вместо х и у
подставить координаты какой-либо из точек кривой. Наоборот,
уравнению, содержащему две переменные х и у, соответствует
кривая, состоящая из тех точек плоскости, координаты которых,
будучи подставлены вместо х и у в уравнение, удовлетворяют ему.
В дальнейшем мы рассмотрим основные примеры графиков функ-
функций, а теперь приведем некоторые общие соображения. Пусть мы
имеем уравнение в явной форме: y=f(x), где f(x) — однозначная
функция, определенная, например, в промежутке (а,Ь), т.е. такая
функция, что любому х из {а, Ь) соответствует одно определенное
значение f(x)\ график указанной функциональной зависимости состоит
из точек (х,у), полученных указанным только что способом. Перпен-
Перпендикуляр к оси ОХ, проведенный через любую точку этой оси, абс-
абсцисса которой принадлежит (а, Ь), встретит график в одной точке
(однозначность f(x)). В случае уравнения F(x,y) = 0 в неявной
форме дело обстоит сложнее. Может случиться, что уравнению не
соответствует ни одной точки. Это имеет место, например, для
уравнения х^-^-у* -\-3==0, ибо при любых вещественных х и у
левая часть положительна. Уравнению (х — ЗJ -(- (у — 5J = 0 соот-
соответствует, очевидно, только одна точка C, 5).
Построение графика совершается автоматически в самопишущих при-
приборах; переменной х является обычно время; у — величина, изменение кото-
которой с течением времени нас интересует, например барометрическое давле-
давление (барограф), температура (термограф). Важное значение имеет индика-
индикатор, который записывает зависимость между объемом и давлением газа,
заключенного в цилиндре парового или газового двигателя.
24
ГЛ. Т. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ
112
12. Линейная функция. Простейшая функция, которая вместе
с тем имеет важные приложения, — двучлен первой степени:
у = ах+Ь, B)
где а и Ь—данные числа. Эта функция называется линейной функ-
функцией. Мы покажем, что ее график — прямая линия. Рассмотрим сна-
сначала тот случай, когда число Ь равно нулю. При этом функция B)
имеет вид:
у = ах. C)
Она выражает тот факт, что переменная у прямо пропорциональна
переменной х, и число а называется коэффициентом пропорциональ-
пропорциональности.
Значения
0 0
удовлетворяют уравнению C), т.е. соответствующий этому уравнению
график проходит через начало координат О-
у л
N
Рис. 5.
Рис. 6.
Обращаясь к чертежу (рис. 5), мы видим, что уравнение C) выра-
выражает следующее геометрическое свойство исследуемого графика:
какую бы точку М на нем мы ни взяли, отношение ординаты y=NM
этой точки к ее абсциссе x=ON есть постоянная величина а. Так
как, с другой стороны, это отношение равно тангенсу угла а, обра-
образуемого отрезком ОМ с осью ОХУ то отсюда видно, что геометри-
геометрическое место точек М есть прямая, проходящая через начало коор-
координат О под углом а (или тс-|-а) к оси ОХ. Мы считаем а от
оси ОХ до прямой против часовой стрелки.
Одновременно с этим обнаруживается и важное геометрическое
значение коэффициента а в уравнении C): а есть тангенс угла а,
который образует прямая, соответствующая этому уравнению,
с осью ОХ, вследствие чего а называется угловым коэффициентом
прямой. Заметим, что если а — число отрицательное, то угол а будет
тупой и соответствующая прямая будет расположена так, как указано
на рис. 6.
13 1
§ 1. ПЕРЕМЕННЫЕ ВЕЛИЧИНЫ
25
Обратимся теперь к общему случаю линейной функции, а именно
к уравнению B). Ординаты у графика этого уравнения отличаются
от соответствующих ординат графика уравнения C) постоянным сла-
слагаемым Ь. Таким образом, мы получим непосредственно график урав-
уравнения B), если график уравнения C), изображенный на рис. 5 (при
а>>0), передвинем параллельно оси О У на отрезок Ь\ наверх, если
Ь положительно, и вниз, если оно отрицательно. Таким образом,
мы получим прямую, параллельную исходной прямой и отсекающую
на оси OY отрезок ОМ0 = Ь (рис. 7).
Итак, график функции B) есть
прямая линия, причем коэффициент
а равен тангенсу угла, образованного
этой прямой с осью ОХ, а свободный
член Ь равен отрезку, отсекаемому
этой прямой на оси OY, считая от
начала О.
Коэффициент а иногда называют
просто уклоном прямой, a b — началь-
начальной ординатой этой прямой. Наоборот,
если нам дана какая-нибудь прямая L, не параллельная оси О У, то
нетрудно написать уравнение вида B), соответствующее этой прямой.
Согласно предыдущему, достаточно взять коэффициент а равным
тангенсу угла наклона этой прямой к оси ОХ и Ь равным отрезку,
отсекаемому этой прямой на оси OY.
Отметим один частный случай, который представляет известную
особенность. Пусть а = 0. Уравнение B) дает нам при всяком х:
т. е. получается такая „функция" от х, которая при всех значениях х
сохраняет одно и то же значение Ь. Нетрудно видеть, что графиком
уравнения BХ) будет прямая, параллельная оси ОХ и отстоящая от
этой оси на расстоянии \Ь\ (сверху, если &Х), и снизу, если &<0).
Чтобы не делать специальных оговорок, мы будем говорить, что
уравнение BХ) также определяет функцию от х.
13. Приращение. Основное свойство линейной функции. Уста-
Установим одно новое важное понятие, с которым часто приходится
иметь дело при исследовании функциональной зависимости.
Приращением независимой переменной величины х при переходе
от начального значения хг к конечному х2 называется разность
между конечным и начальным значениями: хх — х^ Соответ-
Соответствующим приращением функции y=f(x) называется разность
между конечным и начальным значениями функции:
26
ГЛ. Т. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ
113
Эти приращения часто обозначают так:
Ах = хг — хь Ау =у% — у1т
Заметим при этом, что приращение может быть как положитель-
положительной, так и отрицательной величиной, так что величина, получив
„приращение", не обязательно должна увеличиться.
Обратим внимание на то, что запись Алг надо рассматривать как
единое целое для обозначения приращения х.
Обратимся к случаю линейной функции:
Ь и у! = а*!-]-&.
или
Вычитая почленно, получим
Уъ—У\ = <*(** —*д
Д_у = а Ал:.
D)
Равенство это показывает, что линейная функция у-=-ах-\-Ь
обладает тем свойством, что приращение функции (у2—У\) про-
пропорционально приращению неза-
независимой переменной {х^ — jct),
причем коэффициент пропор-
пропорциональности равен а, т. е.
угловому коэффициенту, или
уклону графика функции.
Если мы обратимся к самому
~/^ щ ~щ~ ^ ~" графику (рис. 8), то приращению
г независимой переменной соответ-
Рис. 8. ствует отрезок МХР = kx =
= лг2 — хг-и приращению функ-
функ—уь и формула D) непосредственно
вытекает из рассмотрения треугольника М^РМ*
Положим теперь, что некоторая функция обладает указанным вы-
выше свойством пропорциональности приращений независимой перемен-
переменной и функции, выражаемым формулой D). Из этой формулы следует
или
Будем считать исходные значения переменных хг и ух вполне
определенными и обозначим разность (у{ — ахх) одной буквой Ъ\
ции— отрезок PMi = hy=
У* = ах% + Oi — ахг).
Так как окончательные значения переменных х% и у.2 мы можем
брать любыми, то вместо букв х% и у2 можно просто писать
§ 1. ПЕРЕМЕННЫЕ ВЕЛИЧИНЫ
27
буквы х и у, и предыдущее равенство перепишется в виде
у = ах + Ь,
т. е. всякая функция, обладающая указанным выше свойством
пропорциональности приращений, есть линейная функция у = ах-\-
J- Ь, причем а есть коэффициент пропорциональности.
Итак, линейная функция и график ее, прямая линия, могут слу-
служить для изображения всякого закона природы, в котором имеет
место пропорциональность между приращениями исследуемых вели-
величин, что случается весьма часто.
14. График равномерного движения. Наиболее важное приложение,
которое дает механическое истолкование уравнения прямой и его коэффи-
коэффициентов, — это график равномерного движения.
Если точка Р движется по некоторому пути
(траектории), положение ее вполне определяется
расстоянием, отсчитываемым по траектории в ту
или иную сторону от некоторой данной ее точки У* S=f(t)
А до точки Р. Это расстояние, т. е. дуга АР, Mo<f
называется пройденным путем и обозначается
буквой s, причем s может быть и положитель-
ным и отрицательным: значения s в одну сто-
сторону от начальной точки А считаются поло- Рис. 9.
житсльными, а в другую — отрицательными.
Пройденный путь s есть некоторая функция от времени t, приняв кото-
которое за независимую переменную, можем построить график движения, т. е.
график функциональной зависимости (рис. 9)
его не следует смешивать с самой траекторией движения.
Движение называется равномерным, если путь, проходимый точкой за
любой промежуток времени, пропорционален этому промежутку, другими
словами, если отношение
?lzjSl As
пройденного за промежуток времени от tx до t2t к величине этого
промежутка есть постоянная величина, которая
называется скоростью движения и обозначается
через v.
В силу сказанного выше, уравнение графика
равномерного движения имеет вид
Рис.
s = vt + s0;
самый график есть прямая, угловой коэффи-
коэффициент которой равен скорости движения, на-
начальная же ордината s0 есть значение s при t = 0.
На рис. 10 изображен график движения
точки Р, которая двигалась с постоянной ско-
ско, р д
ростью vt в положительном направлении от момента 0 до момента tt (угол
с осью t острый), затем с постоянной же, но большей скоростью v2, в том
же направлении (угол острый, но больший) до момента t2, а затем с посто-
постоянной, но отрицательной скоростью v8 (в обратном направлении, угол тупой)
28
ГЛ. I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ
[15
до начального своего положения. В случае, когда приходится иметь дело
с многими точками, движущимися по одной и той же траектории (напри-
(например при составлении расписания движения поездов или трамваев), такой
графический способ является единственно удобным на практике средством
для определения встреч движу-
7 8 9 10 11 12 щихся точек и вообще для обо-
обозрения всего движения (рис. 11).
130
120
110
100
90
80
70
ВО
50
kO
30
20
10
О
(А
VI
/
\
/
л
f
\
\
\ )
f
V
/
V
ч
1
L
г
->
'
1
1
1
1
\
/
/ 1
Уу
А
/\
\
\
7
г
\
\
/(
j
1
у
\
\
V
\
15. Эмпирические формулы.
Простота построения прямой и
выражаемого ею закона пропор-
пропорциональности приращения функ-
функции и независимой переменной
делает график прямой весьма
удобным средством при нахожде-
нахождении эмпирических формул, т. е.
таких, которые выводятся непо-
непосредственно из данных опыта, без
особого теоретического исследо-
исследования.
Изобразив графически полу»
ченную из опыта таблицу на ли-
листе миллиметровой бумаги, мы
найдем ряд точек, и если мы же-
желаем получить приближенную
эмпирическую формулу для изу-
изучаемой функциональной зависи-
зависимости в виде линейной функции,
нам остается провести прямую,
которая если и не проходит сразу через все построенные точки (что, конечно,
почти никогда невозможно), то, по крайней мере, проходит между этими
8 9
Рис. 11.
10 11
12
4,0
3,9
3,8
3,7
3,6
3,5
г*
О
|
о
0,5
1,0
Рис. 12.
точками и при этом так, чтобы по возможности одинаковое число точек ока-
оказалось как по одну, так и по другую сторону от прямой, и все они лежали до-
достаточно к ней близко. В теории ошибок и обработки наблюдений изучаются
более точные способы как для построения указанной прямой, так и для су-
суждения о совершаемой при таком приближенном представлении погрешности.
16]
1. ПЕРЕМЕННЫЕ ВЕЛИЧИНЫ
29
Но при менее точных исследованиях, с которыми приходится иметь дело
в технике, построение эмпирической прямой проще всего производить по
способу „натянутого шнурка", сущность которого ясна из самого названия.
Построив прямую, с помощью непосредственного измерения определяем ее
уравнение
JF y = a
которое и дает искомую эмпирическую формулу. При выводе этой формулы
надлежит иметь в виду, что очень часто масштабы для величин хну бы-
бывают различны, т. е. одна а та же длина, отложенная на осях ОХ и OY,
изображает разные числа. В этом случае угловой коэффициент а не будет
равен тангенсу угла, образуемого прямой с осью ОХ, но будет отличаться
от него множителем, равным численной величине отношения между едини-
единицами длины, принятыми при изображении величин л: и у.
Пример (рис. 12).
X
V
0,212
3,721
0,451
3,779
0,530
3,870
0,708
3,910
0,901
4,009
1,120
4,089
1,341
4,150
1,520
4,201
1,738
4,269
1,871
4,350
Отв.
у «а 0,375л:+ 3,65.
(Знаком я» мы обозначаем здесь и в дальнейшем приближенное равенство.)
16. Парабола второй степени. Линейная функция
есть частный случай целой функции п~й степени, или многочлена
(полинома) п-й степени:
у = аохп + аххп-х + ... +ап^х + ап9
простейший случай которого после линейной функции есть трехчлен
второй степени (п = 2):
у = ах2 -\-bx-\-c\
график этой функции называется параболой второй степени или
просто параболой.
Пока мы будем исследовать лишь простейший случай параболы:
у = ах\ E)
Кривая эта без труда может быть построена по точкам. На рис. 13
изображены кривые у = х2 (а—1) и у = — х* (а = —1). Кривая,
соответствующая уравнению E), расположена целиком над осью ОХ
при а^>0 и под осью ОХ при я<^0. Ордината этой кривой воз-
возрастает по абсолютному значению, когда х возрастает по абсолют-
абсолютному значению, и тем быстрее, чем больше абсолютная величина а.
30
ГЛ. I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ [ 16
На рис. 14 изображен ряд графиков функции E) при различных
значениях а, которые проставлены на чертеже при соответствующих
этим значениям параболах.
Уравнение E) содержит только х2, а потому не меняется при за-
замене х на (—х), т.е. если некоторая точка (х,у) лежит на пара-
параболе E), то и точка (— х, у) лежит на той же параболе. Две точки
у-ах2
1
\
-г
V
/
/
/
/
V
\
/
i
\
\
/
/
3
г
-1
-2
-з
J
/
\
\
1
7
/
f
h
/
I
\
\
\
\
\
Z *~
Рис. 13.
(х,у) и (— х,у), очевидно, симметричны относительно оси О К, т. е.
одна из них является зеркальным изображением другой относительно
этой оси. Таким образом, если повернуть правую часть плоскости на
180° вокруг оси О У и совместить ее с левой частью, то часть па-
параболы, лежащая справа от оси О К, совпадает с частью параболы,
лежащей слева от этой оси. Иначе говоря, ось О У есть ось сим-
симметрии параболы E).
Начало координат оказывается самой низкой точкой кривой при
с>0 и самой высокой при а<0 и называется вершиной параболы.
Коэффициент а вполне определяется, если задать одну точку М0(х0, у0)
параболы, отличную от вершины, так как тогда имеем
j6 I § I. ПЕРЕМЕННЫЕ ВЕЛИЧИНЫ
после его уравнение параболы E) примет вид
31
F)
Существует весьма простой графический способ построения какого
угодно числа п точек параболы при заданных вершине, оси симметрии и любой
ее точке Мо> отличной от вершины.
Абсциссу и ординату данной точ- ifj
ки Мо (*о. Уо) Делим на п Равных ча-
частей (рис. 15) и через начало коорди-
0 1 Z 3 4 5 6 7 8
Рис. 15.
\
\
-2
\
\
V-
\
X
-1
3
2
si
0
/ /
/
i
o'fi
/
У
Г i
1
V
'"л
1
I
к
17
г
Рис. 16.
нат проводим лучи к точкам деления ординаты. Пересечение этих лучей с
прямыми, проведенными через точки деления абсциссы параллельно оси OY,
и дает точки параболы. Действительно, по построению мы имеем (рис. 15):
п—1 , п-—\
т. е. на основании (б) точка Мх (хъ ух) также лежит на параболе. Доказа-
Доказательство для других точек аналогично.
Если имеются две функции:
и соответствующие им графики, то координаты точек пересечения
этих графиков удовлетворяют обоим написанным уравнениям, т. е.
абсциссы этих точек пересечения суть решения уравнения
/iW=/2D
Указанное обстоятельство легко использовать для приближенного
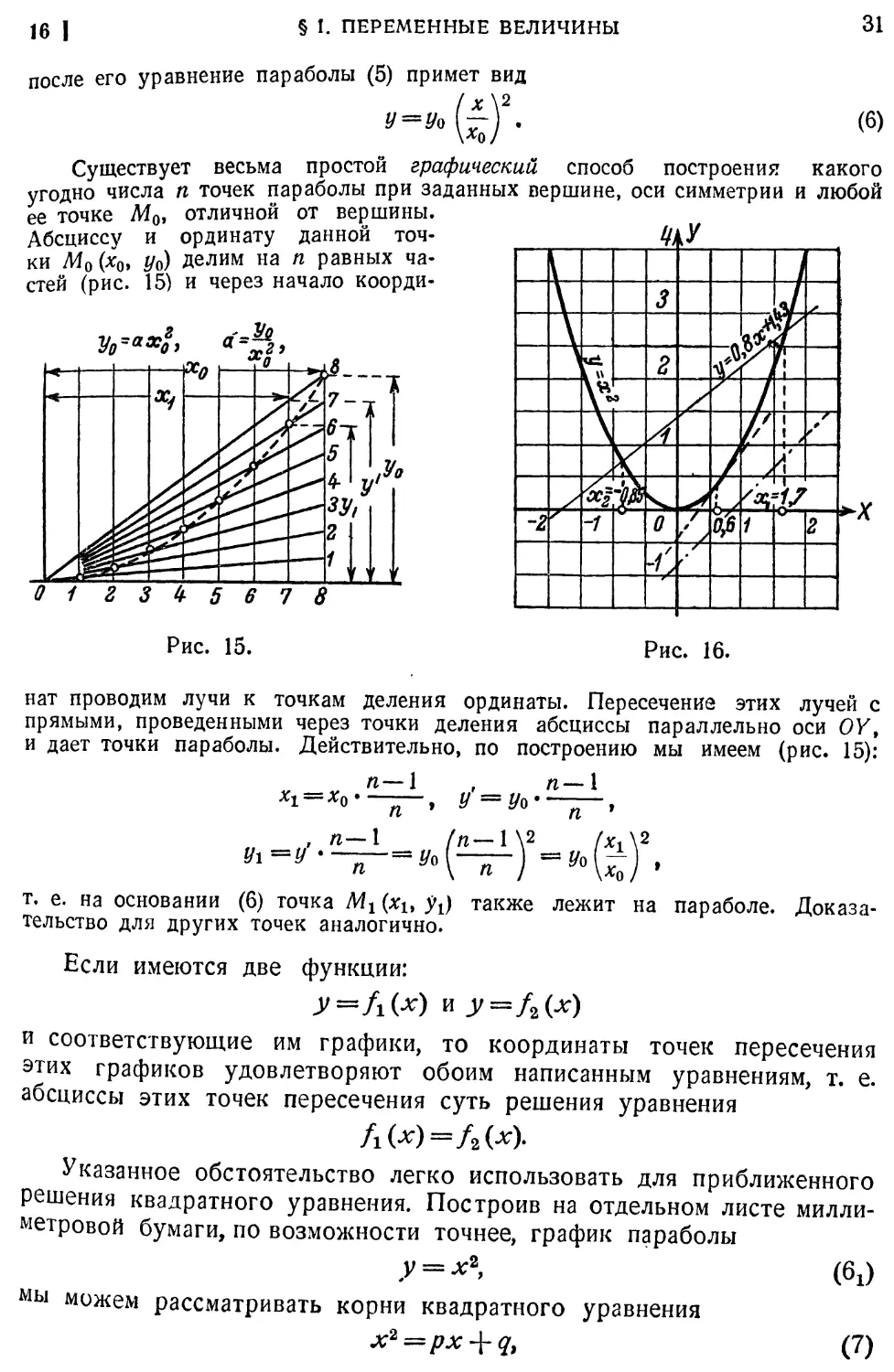
решения квадратного уравнения. Построив на отдельном листе милли-
миллиметровой бумаги, по возможности точнее, график параболы
мы можем рассматривать корни квадратного уравнения
G)
32
ГЛ. I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ 1 17
как абсциссы точек пересечения параболы FХ) и прямой y=px-\-q»
так что решение уравнения G) сводится к нахождению на чертеже
упомянутых точек пересечения. На рис. 16 изображены три случая,
когда таких точек будет две, одна (касание прямой с параболой) и
ни одной.
17. Парабола третьей степени. Многочлен 3-й степени
имеет своим графиком кривую, называемую параболой третьей сте-
степени. Мы рассмотрим эту кривую в простейшем случае
у = ах3, (8)
При положительном а знаки х и у одинаковы, а при отрицатель-
отрицательном а — различны. В первом случае кривая расположена в первом
и третьем координатных углах, а во
втором случае —во втором и чет-
четвертом углах. На рис. 17 изображен
вид этой кривой при различных
значениях а.
Если х п у одновременно заме-
заменить на (— х) и (— у), то. обе части
уравнения (8) изменят знак, и урав-
уравнение по существу не изменится,
т. е. если точка (х,у) лежит на кри-
кривой (8), то и точка (—х, — у)
также лежит на этой кривой. Точки
(ху у) и (—дг, — у) лежат, очевидно,
симметрично относительно начала О,
т. е. отрезок, их соединяющий, де-
делится началом О пополам. Из пре-
предыдущего следует, что всякая хорда
кривой (8), проходящая через на-
начало координат О, делится этим на-
началом пополам. Иначе это выражают
так: начало координат О есть центр кривой (8).
Отметим еще один частный случай параболы третьей степени:
у = ах3 + сх. (9)
Правая часть этого уравнения есть сумма двух слагаемых, и, следо-
следовательно, для построения этой кривой достаточно провести прямую
у = сх A0)
и взять сумму соответствующих ординат линий (8) и A0) непосред-
непосредственно из чертежа. Различные виды, которые может при этом при-
принять кривая (9) (при а=1 и различных с), изображены на рис. 18.
Рис. 17.
§ 1. ПЕРЕМЕННЫЕ ВЕЛИЧИНЫ
33
Построив кривую
получим удобный (при небольшой точности вычислений) графический способ
для решения уравнения 3-й степени
так как корни этого уравнения суть не что иное, как абсциссы точек пере-
пересечения кривой
у = л;5
с прямой
y
Чертеж нам покажет (рис. 19), что таких точек пересечения может быть
одна, две или три, но одна — наверно, т. е. уравнение 3-й степени имеет,
по крайней мере, один вещественный корень. Строго доказано это будет
впоследствии.
1л
+М01-2-3
f
2 I И
///
III
III!
3
г
I
//
(Ж
L
V
I
У
y^otf+cx
I
Рис. 18.
Рис. 19.
18. Закон обратной пропорциональности. Функциональная зави-
зависимость
^ X
(И)
выражает закон обратной пропорциональности между переменными
х и у. При увеличении х в несколько раз у уменьшается во столь-
столько же раз. При т^>0 переменные х и у одного и того же знака,
т. е. график расположен в первом и третьем координатных углах, а
при т <^ 0 — во втором и четвертом. При лг, близких к нулю, дробь
j- велика по абсолютной величине. Наоборот, при больших по абсо-
абсолютной величине значениях х дробь — мала по абсолютной величине.
34
ГЛ. I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ
Непосредственное построение этой кривой по точкам приведет
нас к рис. 20, на котором изображены кривые (И) при различных
значениях ту причем сплошной линией начерчены кривые, соответ-
соответствующие случаю т^>0, пунктирной — случаю /и<^0, и у каждой
кривой проставлено соответствующее ей значение т. Мы видим, что
каждая из построенных кривых, которые называются равнобочными
гиперболами, имеет бесконечные ветви, приближающиеся к осям
координат ОХ и OY при беспредельном увеличении абсциссы х или
ординаты у точки на рассматриваемой ветви. Эти прямые называются
асимптотами гиперболы.
У,
Рис. 20.
Рис. 21.
Коэффициент т в уравнении (И) определяется вполне, если задать любую
точку MQ (xOi у0) изучаемой кривой, так как тогда
хоуо=1п;
уравнение же A1) перепишется в виде
ху=х0у09 A2)
или
х0 х '
Отсюда вытекает графический способ построения какого угодно числа
точек равнобочной гиперболы, если заданы ее асимптоты и какая-нибудь
ее точка Мо (xOi y0). Приняв асимптоты за оси координат, проведем из
начала координат произвольные лучи ОРи ОР2,... и отметим точки пере-
пересечения этих лучей с прямыми у=у0 и х = х0.
Проводя через каждые две такие точки, лежащие на одном луче, пря-
прямые, параллельные осям координат, получим в пересечении этих прямых точки
гиперболы (рис. 21). Это вытекает из подобия треугольников ORQt и OSPt:
=
:ЩИЛИ-о
т. е. точка Мх (xl} yt) лежит на кривой A2).
.
§ 1. ПЕРЕМЕННЫЕ ВЕЛИЧИНЫ
35
19. Степенная функция. Функции у = ах, у = ах2, у = ахъ и
v==~ которые мы выше исследовали, суть частные случаи функ-
функции вида
у = ахп, A3)
где а и п — какие угодно постоянные. Функция A3) вообще назы-
называется степенной функцией. При построении кривой мы ограничимся
лишь положительными значениями х и случаем а=1. На рис. 22 и
23 изображены графики, соответствующие различным значениям п.
Ук
Рис. 22.
Рис. 23.
Для всех значений п уравнение у = хп дает j/=l при лг=1, т. е.
псе кривые проходят через точку A, 1). При положительных значе-
значениях п кривые при х> 1 подымаются вверх тем круче, чем больше
величина п (рис. 22). При отрицательных п (рис. 23) функция у~хп
равносильна дроби. Например, вместо у = х~2 можно написать j/ = — .
В этих случаях при возрастании х ординаты у, наоборот, убывают.
Заметим при этом, что при дробном п с четным знаменателем мм
2_
считаем значение радикала положительным; например, х2 = У~~х счи-
считаем положительным (при лг>0).
Две постоянные аил, входящие в уравнение A3), определятся, если
задать две точки кривой M&t, уг) и М2(х2, у2), после чего окажется
У1=ах*1> У2=*ахп1 A4)
одно уравнение на другое, исключаем а:
У2 " W/ •
36 ГЛ. 1. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ
затем, логарифмируя, находим п по формуле
log xt — log x2 *
найдя n, из любого из уравнений A4) получим д.
Графический способ построения какого угодно числа точек кривой A3)
по двум заданным ее точкам Mt (х1У у^) и М2 (x2t у2) изображен на рис. 24.
Проводим через точку О два произвольных луча под углом а к оси ОХ
и р к оси О У; из данных точек Mt и М2 опускаем перпендикуляры на коор-
координатные оси до пересечения их с лучами в точках Sit S2> Tv Га и с осями
Рис. 24.
в точках Qu Q2; Rv R2. Через точку R2 проводим R2Tb параллельно RiT%
и через точку S2 проводим S2Q9 параллельно SjQ2. Проводя, наконец, через Г3
и Q8 прямые, параллельные соответственно осям ОХ и ОУ, получим в их
пересечении точку Mz (xz% уг) кривой. Действительно, из подобия треуголь-
треугольников находим
OQZ = OS2 OS2 = OQt
т. е.
откуда
0Q2 0Q,
или
xs __ л:2
и точно так* же можно показать, что
-*¦
Принимая во внимание A4), находим
1
т. е. точка (xzt уг) лежит действительно на кривой A3), что и требовалось
доказать.
20 i § 1. ПЕРЕМЕННЫЕ ВЕЛИЧИНЫ 37
20. Обратные функции. Для исследования дальнейших элемен-
аоных функций введем новое понятие, а именно, понятие об обрат-
обратной функции. Как мы уже упоминали в [5], при исследовании функ-
функциональной зависимости между переменными х и у> вопрос о выборе
независимой переменной находится в нашем распоряжении и решается
исключительно соображениями удобства. Пусть имеется некоторая
функция y=f{x)> причем х играет роль независимой переменной.
функция, которая определяется из той же функциональной
зависимости y=f(x), если в ней рассматривать у как независим
мую переменную, а х как функцию
называется обратной по отношению к данной функции f(x), a
эта последняя функция часто называется прямой.
Обозначения для переменных не играют существенной роли и,
обозначая в обоих случаях независимую переменную буквою х, мы
можем сказать, что <р (лг) будет обратной функцией для функции f(x).
Так, например, если прямые функции суть
у = ах-\-Ь, у = хп,
то обратные будут
X — Ь
Нахождение обратной функции по уравнению прямой функции назы-
называется ее обращением.
Пусть мы имеем график прямой функции у=/(х). Нетрудно
видеть, что этот же график может служить и графиком обратной
функции jt = <p(y). Действительно, оба уравнения y = f(x) и лг = <р(у)
дают одну и ту же функциональную зависимость между х и у.
В прямой функции произвольно задается х. Откладывая по оси ОХ
от начала О отрезок, соответствующий числу лг, и восставляя из
конца этого отрезка перпендикуляр к оси ОХ до пересечения с гра-
графиком, мы получаем, взяв длину этого перпендикуляра с соответ-
соответствующим знаком, значение у, отвечающее взятому значению лг. Для-
обратной функции ;е = ср(у) мы должны только откладывать заданное
значение у по оси О К от начала О и восставлять из конца этого
отрезка перпендикуляр к оси OY до пересечения с графиком. Длина
этого перпендикуляра с соответствующим знаком дает нам значение х,
отвечающее взятому значению у.
При этом возникает неудобство, что в первом случае независимая
переменная х откладывается по одной оси, а именно оси ОХ, а во
втором случае независимая переменная у откладывается по другой оси,
а именно по оси ОУ. Иначе говоря, при переходе от прямой функ-
функции >=/(лг) к обратной x==(f(y) мы можем оставить тот же график,
ГЛ. I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ
I 21
s
ч
/
\
\
\
•
У
i
0
X
\
i
1 )
/
\
/
J
--
/
i
f
i/
-At
\\
но должны помнить, что при этом переходе ось для изображения
значений независимой переменной становится осью значений функции,
и наоборот.
Чтобы избежать этого неудобства, мы должны при упомянутом
переходе повернуть плоскость как целое таким образом, чтобы оси
ОХ и О У поменялись местами. Для этого, очевидно, достаточно
повернуть плоскость чертежа вме-
вместе с графиком на 180° вокруг
биссектрисы первого координат-
координатного угла. При этом повороте оси
поменяются местами, и обратную
функцию лг = ср (у) надо уже писать в
обычном виде: у = ср (х). Итак, если
прямая функция у=/(х) задана
графически, то для получения гра-
графика обратной функции ^ = ср(лг)
достаточно повернуть плоскость
графика на 180° вокруг биссек-
биссектрисы первого координатного угла.
На рис. 25 график прямой функ-
Рис. 25. ции изображен сплошной линией, а
график обратной функции — пунк-
пунктиром. Пунктиром же изображена биссектриса первого координатного
угла, вокруг которой надо повернуть всю плоскость чертежа для
получения пунктирной кривой из сплошной кривой.
21. Многозначность функции. Во всех графиках элементарных
функций, которые мы рассмотрели выше, характерным был тот факт,
что прямые, перпендикулярные оси ОХ, пересекали график не больше,
чем в одной точке, и большею частью именно в одной точке. Это
значит, что у функции, определяемой этим графиком, заданному зна-
значению х соответствует одно определенное значение д/. Иначе про
такую функцию говорят, что она однозначна.
Если же прямые, перпендикулярные оси ОХ, пересекают график
в нескольких точках, то это значит, что заданному х соответствует
несколько ординат графика, т. е. несколько значений у. Такие функ-
функции называются многозначными. Мы уже упоминали о многознач-
многозначных функциях раньше [5].
Если прямая функция у=/(х) однозначна, то обратная функция
у = ср(лг) может оказаться и многозначной. Это видно, например,
из рис. 25.
Разберем подробнее один элементарный случай. На рис. 13
изображен сплошной линией график функции у = х*. Если повер-
повернуть чертеж вокруг биссектрисы первого координатного угла на 180°,
то получится график обратной функции у= у/х (рис. 26).
21 1
§ 1. ПЕРЕМЕННЫЕ ВЕЛИЧИНЫ
Рассмотрим его подробнее. При отрицательных х (левее оси OY)
прямые, перпендикулярные оси ОХ, вовсе не пересекают графика,
т е. функция у = Vх не определена при х < 0. Это соответствует
тому факту, что корень квадратный из отрицательного числа не
имеет вещественных значений. Наоборот, при любом положительном
х прямая, перпендикулярная оси ОХ, пересекает график в двух точ-
точках т. е. при заданном положительном х мы имеем две ординаты
графика: MN и MNX. Первая ордината дает для у некоторое поло-
положительное значение, а вторая дает такое же по абсолютной величине
отрицательное значение. Это со-
соответствует тому факту, что корень
Рис. 26.
Рис. 27.
квадратный из положительного числа имеет два значения, равные
по абсолютной величине и обратные по знаку. Из чертежа видно
также, что при х = 0 мы имеем одно только значение у = 0. Итак,
функция у=|/лг определена при лгг^О, имеет два значения при
х^>0 и одно при х — 0.
Заметим, что мы можем сделать нашу функцию у=\/х одно-
однозначной, взяв лишь часть графика на рис. 26. Возьмем, например,
только ту часть графика, которая находится в первом координатном
угле (рис. 27). Это соответствует тому, что мы рассматриваем лишь
положительные значения квадратного корня. Отметим также, что
часть графика функции у=-/х, изображенная на рис. 27, полу-
получается из той части графика прямой функции >/ = л;2(рис. 13), кото*
рая лежит правее оси ОК. Часть графика функции
у = ]Гх ИЛИ у = X2 ,
лежащая в первом координатном угле, уже была изображена нами
на рис. 22.
Займемся теперь тем случаем, когда обращение однозначной
прямой функции приводит к однозначной же обратной функции.
Для этого нам придется ввести новое понятие.
40 ГЛ. I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ ( 21
Функция у=/(х) называется возрастающей, если при увели-
увеличении независимой переменной х соответствующие значения
у возрастают, т. е, если из неравенства хг> хг следует
/()C)
2
При том расположении осей ОХ и О У, которым мы пользуемся,
возрастанию х соответствует перемещение по оси ОХ вправо, а воз-
возрастанию у — движение по оси OY вверх. Характерной особенностью
графика возрастающей функции является тот факт, что при движении
вдоль кривой в сторону возра-
возрастающих х (вправо) мы движем-
движемся и в сторону возрастающих у
(вверх).
Рассмотрим график какой-ни-
какой-нибудь однозначной возрастающей
функции, определенной в проме-
промежутке а <- х <: Ъ (рис. 28). Пусть
/(а) = с и /(ft) = d, причем,
очевидно, в силу возрастания
функции c<id. Если мы возьмем
Рис. 28. какое-нибудь значение у из про-
промежутка c^y^d и в соответ-'
ствующей точке восставим перпендикуляр к оси О Y, то этот перпен-
перпендикуляр встретит наш график в одной точке, т. е. всякому у из
промежутка o^y^d отвечает одно определенное значение х.
Иначе говоря, функция, обратная возрастающей функции, будет
однозначной.
Нетрудно видеть из чертежа, что и эта обратная функция будет
возрастающей.
Аналогичным образом, функция y=f(x) называется убывающей,
если при увеличении независимой переменной х соответствующие
значения у, наоборот, убывают, т. е. если из неравенства х2<х^
следует f(x1)>f(x2). Как и выше, можно утверждать, что функция,
обратная убывающей функции, будет однозначной убывающей функ-
функцией. Отметим еще одно важное обстоятельство. Во всех рассуждениях
мы предполагаем всегда, что график функции представляет собою
сплошную кривую без разрывов. Этот факт равносилен особому
аналитическому свойству функции f(x), а именно, непрерывности этой
функции. Строгое математическое определение непрерывности функ-
функции и исследование непрерывных функций будет нами дано в § 2.
Целью настоящей главы являются лишь предварительное ознакомление
с основными понятиями, систематическое изучение которых будет
дано в следующих главах.
В отношении терминологии заметим, что когда мы говорим о
функции без упоминания о ее многозначности, то мы подразумеваем
всегда однозначную функцию.
221
§ I. ПЕРЕМЕННЫЕ ВЕЛИЧИНЫ
41
22. Показательная и логарифмическая функции. Возвращаемся
еперь к исследованию элементарных функций. Показательная функ-
функция определяется уравнением
У = а\ A5)
причем мы считаем, что основание а есть заданное положительное
число (отличное от единицы). При целом положительном х значение
ах очевидно. При дробном положительном х выражение а* опреде-
р
ляется как радикал а4 =Уар, причем, в случае четного q, мы ус-
условливаемся брать положительное значение радикала. Не входя сей-
сейчас в подробное рассмотрение значений ах при иррациональном хУ
заметим только, что мы получим приближенные значения а* при ир*
рациональном х все с большей степенью точности, если заменим ир-
иррациональное х его приближенными значениями так, как это было
указано выше [2]. Например, приближенными значениями аУ2, где, как
известно, У~2= 1,414213..., будут
Вычисление ах при отрицательном х сводится к вычислению а* прл
положительном х в силу формулы: a~x=z—t являющейся определе-
определением степени при отрицательном показателе. Из упомянутого выше
соглашения считать радикалы в выраже-
L
нии а = у ар всегда положительными
вытекает, что функция ах при любых
вещественных х всегда положительна.
Кроме того, можно показать, на чем
мы не останавливаемся, что при а^>1
функция ах — возрастающая функция,
а при 0 <^ а <^ 1 — убывающая функ-
функция. Более подробное исследование этой
функции будет нами дано дальше [44].
На рис. 29 изображены графики
функции A5) при различных значени-
значениях а. Отметим некоторые особенности
графиков на рис. 29.
Прежде всего при любом а Ф О мы имеем по определению а°= 1,
и, следовательно, при любом а график функции A5) проходит через
точку 3/= 1 на оси OY, т. е. через точку с координатами @,1). Если
Q^>1, то кривая идет слева направо (в сторону возрастающих х),
поднимаясь беспредельно вверх, а при движении влево кривая
Рис 29.
42
ГЛ. 1. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ
|22
беспредельно приближается к оси ОХ, нигде ее не достигая. При
а<^\ расположение кривой относительно осей будет иным. При дви-
движении направо кривая беспредельно приближается к оси ОХ, а при
движении влево беспредельно уходит вверх. Так как а* всегда поло-
положительно, то график, конечно, всегда расположен над осью ОХ. За-
Заметим еще, что график функции у=\-Лх можно получить из графика
функции у = а?, поворачивая чертеж вокруг оси О К на 180°. Это
вытекает непосредственно из того, что при упомянутом повороте х
переходит в (—х), а #-* = (—Y*.
Заметим еще, что если а = 1, то у = Xх, и при всяком значении х
мы имеем у=1 [12].
Логарифмическая функция определяется уравнением
A6)
По определению логарифма функция A6) будет обратной для функ-
функции A5). Мы можем, таким образом, получить график логарифми-
логарифмической функции (рис. 30) из графика показательной, повернув кривые
рис. 29 на 180° вокруг биссектрисы первого координатного угла.
Рис. 30.
Рис. 31.
Ввиду возрастания функции A5) при а^>\ обратная функция A6)
будет также однозначной возрастающей функцией от х, причем, как
это видно из рис. 29, функция A6) определена лишь при х^>0
(отрицательные числа не имеют логарифмов). Все графики рис. 30,
соответствующие различным значениям а, пересекают ось ОХ в точ-
точке х=\. Это соответствует тому факту, что логарифм единицы при
любом основании равен нулю. На рис. 31 изображен для ясности один
график функции A6) .при а^>1.
С понятием о логарифмической функции тесно связаны понятия о лога-
логарифмической шкале и теория логарифмической линейки.
Логарифмической шкалой называется такая шкала, нанесенная на данной
прямой, длина делений которой соответствует не самому числу, обозначаю-
§ 1. ПЕРЕМЕННЫЕ ВЕЛИЧИНЫ 43
23 ]
ление а ег0 логарифму, обыкновенно по основанию 10 (рис. 32).
ЩС м образом, если при некотором делении шкалы стоит число х, то длина
«Г*ка U равна не х, a log10*. Длина отрезка между двумя точками шкалы,
обозначенными через х и у, будет равняться (рис. 32)
5Г— Lv = \ogioy — log10A: = log10-?- ;
ля получения же логарифма произведения ху достаточно к отрезку ~Ъс при-
прибавить отрезок 1у> так как полученный таким путем отрезок будет равен
= log10 (xy).
Таким образом, имея логарифмическую шкалу, можно приводить умно-
умножение и деление чисел просто к сложению и вычитанию отрезков на шкале,
И "fit
xxy
Рис. 32.
что проще всего осуществляется на практике с помощью двух тождествен-
тождественных шкал, из коих одна может скользить вдоль.другой (рис. 32 и 33). В этом
и заключается основная идея устройства логарифмической линейки.
X
4 5 6 7 в 3 1 I
у:х у
Рис. 33.
Для вычислений часто употребляется логарифмическая бумага, которая
представляет собой разграфленный лист, причем, однако, точки деления на
осях ОХ и OY соответствуют не обыкновенной, а логарифмической шкале.
23. Тригонометрические функции. Мы остановимся лишь на
четырех основных тригонометрических функциях:
у = sin х, у = cos х,
y = tgx, y =
причем независимую переменную х будем выражать в радианной мере,
т. е. за единицу угла примем центральный угол, которому соответ-
соответствует дуга окружности, по длине равная радиусу.
График функции y = sinx изображен на рис. 34. Из формулы
44
ГЛ. I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ
123
ясно, что график функции ys=cosx (рис. 35) может быгь получен
из графика функции y = sin.xr простым передвижением его вдоль
оси ОХ налево на отрезок у.
Рис. 34.
Рис. 35.
На рис. 36 представлен график функции д/ = tg jc. Кривая состоит
из ряда одинаковых отдельных бесконечных ветвей. Каждая ветвь
помещается в вертикальной полосе ширины тс и представляет собою
возрастающую функцию от х. Наконец, на рис. 37 представлен график
функции y = ctgx, также состоящий из отдельных бесконечных ветвей.
При передвижении графиков функций j/ = sin.*r и y = cosx вдоль
оси ОХ направо или налево на отрезок 2тс эти графики совмещаются
сами с собой, что соответствует тому факту, что функции sin лг и
cos* имеют период 2тс, т. е.
sin(jc±2ir) = sin.xr и cos (x dr 2тс) = cos x
при любом х. Совершенно так же графики функций y = tgx и
y = ctgx совмещаются сами с собой при передвижении их вдоль
оси ОХ на отрезок тс.
Графики функций
y=Asinax, y = Aco$ax (А>0, а>0) A7)
весьма схожи с графиками функций y=sinx и y = cosx. Чтобы
получить, например, график первой из функций A7) из графика
y = $inx, надо длины всех ординат этого последнего графика
23|
§ 1. ПЕРЕМЕННЫЕ ВЕЛИЧИНЫ
45
Рис. 36.
Рис. 37.
46
ГЛ. I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ I 23
умножить на Л и изменить масштаб по оси ОХ так, чтобы точка с абс-
абсциссой х попала бы в точку с абсциссой ~. Функции A7) также
2я
периодические, но имеют период —.
Графики более сложных функций
у = A sin (ах + Ь), у = A cos (ax + 6),
A8)
которые называются простыми гармоническими кривыми, получают-
получаются из графиков функций A7) передвижением вдоль оси ОХ на от-
отрезок — влево (мы считаем &>0). Функции A8) имеют также пе-
2я
риод —.
Графики функций вида
у = Аг sin агх + Вг cos агх + А2 sin а2х + В2 cos a2x,
представляющих собою сумму нескольких слагаемых типа A7), мож-
можно строить, например, складывая ординаты графиков отдельных
\
Si
N
\1
W
1
•Л
Л
1
/
Л'
f
)
0
1
J
0,
/ ^
\
л
1
% i
ж-
•
«
i
/
Ч
\
ТС
\
\
\
\
/
j
f
/\ 1
V
/
1
1
i
I
»
А
f
f
\
j
Ч
\
J
V
*
я
\
Рис. 38.
слагаемых. Полученные таким образом кривые называются обычно
сложными гармоническими кривыми. На рис. 38 указано построе-
построение графика функции
Заметим при этом, что функция
у = Ах sin fljjt: + Вх cos ахд: A9)
может быть представлена в виде A8) и изображает простое гармо-
гармоническое колебание.
лл , § 1. ПЕРЕМЕННЫЕ ВЕЛИЧИНЫ 47
24 I
Действительно, положим
Мы имеем, очевидно,
и, кроме того, 2 %2
а потому, как известно из тригонометрии, всегда можно найти такой
угол ЬХУ чтобы было
cos bx = m, sinbx = n. B1)
Подставив в A9) вместо Ах и Вх их выражения B0) и пользуясь
равенствами B1), получим
у = A (cos bx - sin axx -j- sin &t • cos axx),
т. e.
у = A sin (а^лт -f- Jj).
24. Обратные тригонометрические, или круговые, функции.
Эти функции получаются при обращении тригонометрических функций:
y = sinx, cosat, tgx, ctg.*:
и обозначаются, соответственно, символами
у = arc sin x, arc cos дг, arctgA;, arcctgAr,
что представляет собою не что иное, как сокращенное обозначение
названий: угол (или дуга), синус, косинус, тангенс или котангенс ко-
которого соответственно равен х.
Остановимся на функции
B2)
График этой функции (рис. 39) получается из графика функции
y=sinx по правилу, указанному в [20]. Весь этот график располо-
расположен в вертикальной полосе, ширины два, опирающейся на отрезок
— 1^х^-|-1 оси ОХ, т. е. функция B2) определена лишь в про-
промежутке — 1^лг<:-|-1. Далее, уравнение B2) равносильно уравне-
уравнению sin у = Ху и, как известно из тригонометрии, при заданном х мы
получаем бесчисленное множество значений для угла у. Из графика
мы видим, действительно, что прямые, перпендикулярные к оси ОХ
в точках промежутка —l^JC^+b имеют с графиком бесчис-
бесчисленное множество общих точек, т. е. функция B2) есть многозначная
Функция.
Непосредственно из рис. 39 мы видим, что функция B2) станет
однозначной, если мы вместо всего графика ограничимся лишь его
48
ГЛ. I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ
[24
частью, начерченной более жирно сплошной линией, что соответству-
соответствует условию — рассматривать только те значения угла у, имеющего
данный siny = xf которые лежат в промежутке (—5-,^>V
На рис. 40 и 41 указаны графики функций д; = arc cos лт и
у = arc tg x и отмечены жирно сплошной линией те части графика,
которые надо оставить, чтобы сделать функцию однозначной (чертеж
у ^
J7D
-/
Ф*
Рис. 39.
Рис. 41.
для arc ctg x предоставляется сделать читателям). Заметим при этом,
что функции д/ = агс tgx и ^/ = 3^ ctg лг определены при всех вещест-
вещественных значениях х.
Отмечая из чертежа интервал изменения у на отмеченной жирно
части кривой, мы получаем таблицу ограничений, при которых функ-
функции становятся однозначными:
У
Неравен-
Неравенства для у
arc sin x
71 ТС
-т<>'<т
arc cos x
0<>><7С
arc tg x
тс тс
arc ctg x
0<y<n
Нетрудно показать, что определенные таким образом функции,
которые называются главными значениями круговых функций, удовле-
удовлетворяют соотношениям
arc sin x -f- arc cos лг= —t arc tg x 4- arc ctg x — ^ . B3)
• § 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ 49
^5 ]
§ 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ
25. Упорядоченное переменное. Когда мы говорили о независимой
переменной х, для нас было важно лишь множество тех значений,
которые может принимать х. Например, это могло быть множество
значений, удовлетворяющих неравенству О^дг^1. Сейчас мы будем
рассматривать переменную величину х, принимающую последователь-
последовательно бесчисленное множество значений, т. е. сейчас для нас является
важным не только множество значений ху но и тот порядок, в кото-
котором она принимает эти значения. Точнее говоря, предполагается
следующее: 1) если xf и х" два значения переменной величины х, то
имеется возможность отличить среди них предыдущее и последующее,
причем если х' предшествует х", а х" предшествует х"\ то х' пред-
предшествует х'"\ 2) никакое значение х не является последним, т. е.
какое бы значение переменной величины х мы ни взяли, существу-
существует бесчисленное множество значений, следующих за ним. Такую пере-
переменную величину называют упорядоченной переменной. В дальней-
дальнейшем мы для краткости просто будем говорить переменная величина.
Отвлекаясь, как всегда, от конкретного характера величины (длина,
вес и т. д.) термином „упорядоченная переменная величина" или просто
„переменная величина* обозначают всю бесконечную последователь-
последовательность ее значений, т. е. бесконечную последовательность чисел.
Важным частным случаем упорядоченной переменной величины
является тот случай, когда имеется возможность пронумеровать всю
ее последовательность значений (первое, второе, третье и т. д.):
так что из двух значений хр и xq то является последующим, кото-
которое имеет больший значок. В качестве примера положим, что общий член
последовательности хп определяется формулой хп = ~% (п = 1,2, 3,...),
так что последовательность имеет вид
1111 m
п
Пусть, далее, лгп = О,11 ... 1, т. е. хп есть десятичная дробь, у ко-
которой целая часть равна нулю, а после запятой стоит п единиц; полу-
получим последовательность
п
0,1; 0,11; 0,111, ... , 0,11 ... 1, ... B)
Вставляя между двумя числами последовательности A) число нуль,
получим новую последовательность
у» 0, -у, 0, у, 0, jg, .M? C)
50 ГЛ. I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ I 25
для которой х1 = ~2,Хъ — 0, лг3 = -|-, Хь = 0, х5 = уй т- Д- Среди
значений этой переменной величины встречаются и одинаковые,
а именно хр=0 при четном р. Отметим, что переменная A) убыва-
убывающая, т. е. всякое ее значение меньше всех предшествующих значе-
значений, а переменная B) возрастающая, т. е. всякое ее значение больше
всех предшествующих. Переменная C) не является ни убывающей,
ни возрастающей.
Укажем теперь примеры упорядоченной переменной, значения
которой нельзя пронумеровать. Положим, что переменная величина
х принимает все различные значения, удовлетворяющие неравенству
а — k^x<^a, где а и k — некоторые числа и ?^>0. При этом
считается, что из двух значений х' и лг" последующим является боль-
большее. Иначе говоря, переменная величина х возрастает, принимая все
значения из промежутка а — k^x<^ay замкнутого слева и откры-
открытого справа. Она принимает любые значения из этого промежутка
меньшие а, но не принимает значения а. Первым значением перемен-
переменной является значение х = а — ky а дальнейшая нумерация значений
переменной невозможна. Если мы положим, что возрастающая пере-
переменная удовлетворяет не неравенству а — k^x<^a, а неравенст-
неравенству а — k<^x<^a, то при этом нет и первого значения перемен-
переменной х. Совершенно аналогично можно рассматривать и убывающую
переменную х на промежутке a<^x^a-\-k или на промежутке
а <^ х <^ а -\- k.
Укажем теперь пример, аналогичный предыдущим, но в котором
переменная не является ни возрастающей, ни убывающей. Перемен-
Переменная величина х принимает все различные значения, удовлетворяющие
неравенству а — k^x^a-\-kt кроме значения х = а. Если х' и У —
различные значения х> у которых абсолютные величины разностей
\х—а\ и |У— а\ различны, то последующим считается то, у кото-
которого эта абсолютная величина меньше (то, которое ближе на оси
ОХ к а), а если х' — а и х" — а отличаются лишь знаком (У и х"
одинаково удалены от а, но находятся на оси ОХ с разных сторон
от а)у то последующим считается то, у которого указанная разность
отрицательна (то, которое на оси ОХ лежит слева от а). В
этом примере переменная х приближается к а на промежутке
а — k^x^a-\-k с разных сторон, принимая все значения, кроме
х = а; первое значение переменной x — a-^-k, второе х = а — /г,
а дальнейшая нумерация невозможна. Если вместо промежутка
а — k^x^a-\-k взять промежуток а — k<^x<^a-\-k при преж-
прежнем определении порядка изменения х, то нет возможности указать
и первое значение х.
В дальнейшем мы часто будем иметь дело с переменными величи-
величинами, связанными функциональной зависимостью. Пусть переменная х
есть функция переменной L В соответствии с этим введем обозна-
. § 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ 51
x(t). Пусть ? —некоторое упорядоченное переменное. Этим
Сдается и упорядоченность значений х (t), а именно, если f и f при-
С°ялежат последовательности значений t и f предшествует tf\ то
"читаем, что среди значений х (t) значение х (f) предшествует х (О-
В дальнейшем мы будем иметь в основном те случаи, когда среди
начений упорядоченной переменной t нет одинаковых. Но x(t)
может принимать и одинаковые значения при различных t
Естественно сказать, что упорядоченное переменное t упорядочивает
переменную x(t) или является упорядочивающей переменной для x(f).
Отметим, что для пронумерованной переменной хь x2f х3, ... роль
t играет значок 1, 2, 3, ..., т. е. в этом случае t принимает после-
последовательные значения 1, 2, 3, ... и таким образом нумерует значения
переменной х.
Возникает вопрос о действиях над упорядоченными переменными.
Если, например, х и у — упорядоченные переменные, то без предва-
предварительных соглашений неясно, что обозначает сумма х-\-у или про-
произведение ху, ибо как х, так и у принимают бесчисленное множество зна-
значений, и остается неясным, какие значения х и у надо складывать или
перемножать, чтобы получить новую переменную х-\-у или ху. Если
хну — пронумерованные переменные, а хь х2, ... и уь у2) ... —
последовательные значения х и у, то сумма х-\-у определяется как
пронумерованное переменное, имеющее последовательность значений
В общем случае для определения действия над упорядоченными пере-
переменными необходимо, чтобы они имели одну и ту же упорядочивающую
переменную. Пусть переменные х и у — функции х (t) и у (t) одной и
той же упорядоченной переменной t, которая упорядочивает x(t)
и y(t). Сумма х и у определяется как упорядоченная переменная
•*@+.УОО> которая упорядочивается той же переменной t.
Для явлений, происходящих во времени, последовательность значе-
значений переменной величины может естественно устанавливаться их
последовательностью во времени, и часто пользуются схемою времени
и применяют термины „доа и „послеа вместо „предыдущее" и „после-
„последующее" значения.
Настоящий параграф посвящен в основном теории пределов, являю-
являющейся основою современного математического анализа. В этой теории
рассматриваются некоторые основные случаи изменения величин.
26. Величины бесконечно малые. Каждому значению переменной
величины х соответствует точка К на числовой оси ОХ, имеющая
абсциссу Ху и изменение х изобразится перемещением точки К по
оси ОХ, Положим, что все различные положения точки К при из-
изменении х остаются внутри некоторого конечного отрезка оси ОХ
^ равносильно тому, что длина отрезка ОК, где О— начало
52 ГЛ. 1. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ [ 26
координат на оси ОХУ остается меньше определенного положительного
числа М. В этом случае переменная величина х называется ограни-
ограниченной. Принимая во внимание, что длина ОК есть | х |, мы приходим
к следующему определению.
Определение. Переменная величина х называется ограни-
ограниченной, если существует такое положительное число М, что
\х\<^М для всех значений х.
Примером ограниченной величины может служить sin t, где t —
любая упорядоченная переменная. В этом примере М есть любое число,
большее единицы.
Рассмотрим теперь тот случай, когда точка /С, последовательно
перемещаясь, беспредельно приближается к началу координат. Точ-
Точнее говоря, положим, что точка К при своем последовательном пе-
перемещении попадает внутрь любого наперед заданного малого от-
отрезка «S\S оси ОХ с серединой О и при дальнейшем движении
остается внутри этого отрезка. В этом случае говорят, что величина
х стремится к нулю, или есть величина бесконечно малая.
Обозначим длину, отрезка «Sr5 через 2s. Буквой е мы обозначили
тем самым любое заданное положительное число. Если точка К на-
находится внутри S'S, то длина (Ж<^е и, наоборот, если длина
О/С<е, то точка К находится внутри «^«S. Мы можем, таким обра-
образом, высказать следующее определение:
Определение. Переменная величина х стремится к нулю
или есть бесконечно малая, если при любом заданном положи-
положительном числе е существует такое значение величины х, что
для всех последующих значений выполнено неравенство |j*r|<^e.
Ввиду важности понятия бесконечно малой величины дадим дру-
другую формулировку того же определения:
Определение. Величина х называется стремящейся к нулю
или бесконечно малой, если \ х | при последовательном изменении х
делается и при дальнейшем изменении остается меньше любого
наперед заданного малого положительного числа е.
Термином „бесконечно малая величина* мы обозначаем вышеопи-
вышеописанный характер изменения переменной величины, и не надо смеши-
смешивать понятия бесконечно малой величины с часто употребляющимся
в практике понятием очень малой величины*
Положим, что при измерении длины некоторого участка мы по-
получили 1000 м с каким-то остатком, который считаем очень малым
по сравнению со всей длиной и им пренебрегаем. Длина этого остатка
выражается определенным положительным числом, и термин „беско-
„бесконечно малый" в данном случае, очевидно, неприменим. Если бы в дру-
другом, более точном измерении мы встретились с такою же длиной, то
перестали бы уже считать ее очень малой и приняли бы ее во вни-
внимание. Мы видим, таким образом, что понятие малой величины
л/, * 2 ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ 53
26 |
понятие относительное, связанное с практическим характером
измерения.
Положим, что переменная величина х принимает последовательно
значения
пусть в есть любое заданное положительное число. Чтобы
убедиться в том, что х есть величина бесконечно малая, нам надо
показать, что | хп |, начиная с некоторого значения п> меньше е, т. е.
нам надо установить существование такого целого чисда N, чтобы
было
\хп\<^г при условии
Это число N зависит от е.
Рассмотрим в качестве примера бесконечно малой величины вели-
величину, принимающую последовательно значения
. D)
Нам надо удовлетворить неравенству
?"<е или fllog10<?<Jog108
Принимая во внимание, что Iog10 q отрицателен, можем переписать
предыдущее неравенство в виде
ибо при делении на отрицательное число смысл неравенства меняется,
и, следовательно, за N мы можем принять наибольшее целое число,
заключающееся в частном log10 e : log10 q. Таким образом, рассматривае-
рассматриваемая величина, или, как обычно говорят, последовательность D),
стремится к нулю.
Если мы в последовательности D) заменим q на (—q), то разница
будет лишь в том, что у нечетных степеней появится знак минус,
абсолютные же величины членов этой последовательности останутся
прежними, а потому и в этом случае мы будем иметь величину бес-
бесконечно малую.
Если величина х бесконечно малая (х стремится к нулю), то это
обычно обозначают следующим образом: Нтлг = 0, или для прону-
пронумерованной переменной: Нтдгл = 0, где Нт — начальные буквы латин-
латинского слова limes, что по-русски значит предел. В дальнейших дока-
доказательствах мы, кроме первой теоремы, будем проводить доказатель-
доказательство для пронумерованных переменных. В первой теореме мы прове-
проведем доказательство как для пронумерованных переменных, так и в
общем случае.
54 ГЛ. 1. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ { 26
Докажем два свойства бесконечно малых величин.
1. Сумма нескольких (определенного числа) бесконечно малых
есть также бесконечно малая величина.
Рассмотрим, например, сумму w = x-]-y-{-z трех бесконечно
малых величин. Пусть эти переменные пронумерованы и
Х\, х%, дг3, ...; у\7 уъ у& ...; zi9 z^ z3t ...
— их последовательные значения. Для w получаем последовательные
значения
Пусть е — любое заданное положительное число. Принимая во вни-
внимание, что х, у и z — бесконечно малые, можем утверждать: суще-
существует такое Nb что |агл|<^~ при n^>Nt; такое Nb что Ij^K-g-
при n^>N<? такое N& что |гл|<С4- при n^>N^ Обозначая через N
наибольшее из чисел Nit N& NB, можем утверждать, что
и, следовательно,
^ + Т'^^ при
т. е. |?2>л|<О ПРИ n^>N, откуда и следует, что w — величина бес-
бесконечно малая.
Рассмотрим теперь общий случай, когда дг, у, z суть функции
х (t), у (t), z (t) одной и той же упорядочивающей переменной t и
w (t) = х (t) -f-у (t) -f- z (t). Принимая во внимание, что х7 у> z — бес-
бесконечно малые, можем утверждать: существует такое значение t = f*
что \x(t)\ <С4~ ^ля всех последующих значений t; существует такое
значение t = t", что |^@|<С4" ^ля всех последующих значений t;
существует такое значение if", что \z(t)\ <[4- для всех последующих
значений t Обозначая через t0 такое из трех значений f, t", f пе-
переменной ty что два других или предшествуют ему или совпадают с
ним, можем утверждать, что
для всех ty следующих за tQ, и потому
01<1^@Ц-Ьп@1 + !^
Для всех '» следующих за *0, т. е. w — бесконечно малая.
fi . § 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ 55
2 Произведение величины* ограниченной на величину бесконечно
малую есть величина бесконечно малая.
Рассмотрим произведение ху пронумерованных переменных, где
еличина х — ограниченная и у — бесконечно малая. Из этого усло-
условия следует: существует такое положительное число Ж, что | хп К М
при любом п; существует такое N, что Ьл|<~ при л>М При
\\ \*\\\<М при
т е. |хпУп I<Се ПРИ n^>N, откуда и следует, что произведение ху —
бесконечно малая.
Заметим, что последнее свойство остается подавно справедливым,
если х = С—постоянная величина. При этом роль числа М может
играть любое число, большее, чем С, т. е. произведение постоянной
величины на бесконечно малую есть величина бесконечно малая. В
частности, если х — бесконечно малая, то и (— х) — бесконечно малая.
Ввиду основного значения понятия бесконечно малой величины
для дальнейшего мы остановимся еще на этом понятии и приведем
некоторые дополнительные замечания.
Считая 0<^#<^1, вставим между двумя членами последователь-
последовательности D) число нуль. Получим последовательность
q, О, q\ О, q\ О, ...
Нетрудно видеть, что и эта переменная стремится к нулю, но при
этом она бесчисленное множество раз принимает значение нуль. Это
не противоречит определению величины, стремящейся к нулю. Пред-
Предположим, что все последовательные значения „переменной* равны
нулю. Для пронумерованной переменной это значит, что хп = 0 при
всяком л, а в случае х (t), где t — упорядоченная переменная, это зна-
значит, что x(t) = 0 при всех значениях t. Такая „переменная", по су-
существу, есть постоянная величина, но она формально подходит под
определение бесконечно малой величины. Например, для пронумеро-
пронумерованной переменной (^ = 0 при любом п) \хп\<^г для любого задан-
заданного положительного в при всех п. Если хп = С при всех п и С —
число, отличное от нуля, то такая последовательность не есть, оче-
очевидно, бесконечно малая величина.
Возьмем те три примера упорядоченной переменной из [25], в
которых нельзя пронумеровать переменную, и положим в этих
примерах а = 0. Первый из них — возрастающая переменная, прини-
принимающая все значения из промежутка —k^.x<^0. При заданном
е^>0 для всех значений этой переменной, следующих после значения
х === — ?> если е ^k, имеем |х \<^е. Если же s^>k, то | х |<^е для
всех значений х. Таким образом, х стремится к нулю (от меньших
значений). Совершенно аналогично х стремится к нулю и в остальных
56 ГЛ. I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ [ 26
двух случаях: когда х— убывающая переменная, принимающая
все значения из промежутка 0<^x^.k> и когда х принимает все
значения (различные) из промежутка —k^.x^:-\-k, кроме лг = О,
с определением последовательности значений, указанной в [25]. Для
переменной х с указанными выше способами стремления к нулю
введем специальные обозначения: в первом случае будем писать
х—+ — 0 (х стремится к нулю от меньших значений); во втором
х -—>-}- 0 (х стремится к нулю от больших значений); в третьем слу-
случае лг-— ±0 (лг стремится к нулю с двух сторон).
Имеется, конечно, бесчисленное множество способов, какими про-
пронумерованная или не пронумерованная переменная х может стремить-
стремиться к нулю. Во всех этих случаях мы будем писать х—> (). В указан-
указанных выше трех случаях мы у нуля пишем знаки. Характерная осо-
особенность первого из этих трех случаев состоит в том, что х, воз-
возрастая, принимает все значения, меньшие нуля и достаточно близкие
к нулю. Во втором случае тот же характер изменения х связан с
убыванием х. В третьем случае х принимает все значения, доста-
достаточно близкие к нулю, как меньшие, так и большие, кроме значения
нуль. Из двух значений х' и х'\ не одинаково удаленных от нуля
(т. е. | х' | Ф | х" |), последующим считается то, которое ближе к нулю,
а из двух значений, одинаково удаленных от нуля (У = — х'\ по-
последующим считается отрицательное значение.
Сделаем еще одно замечание. Из определения бесконечно малой
величины следует, что при доказательстве того, что перемен-
переменная х — бесконечно малая, достаточно ограничиться рассмот-
рассмотрением лишь тех значений х, которые следуют после какого-
либо определенного значения x = xQ, причем это последнее зна-
значение можно выбирать произвольно.
В связи с этим полезно в теории пределов сделать добавление
к определению ограниченной величины, а именно, не надо требовать,
чтобы для всех значений величины у выполнялось неравенство
|^ а достаточно дать такое более общее
Определение. Величина у называется ограниченной, если
существует такое положительное число М и такое значение у0>
что для всех последующих значений выполняется неравенст-
неравенство \у\<М.
При таком определении ограниченной величины доказательство
второго свойства бесконечно малых остается без изменения. Для про-
пронумерованного переменного из второго определения ограниченной
величины следует первое, так что второе определение не является
более общим. Действительно, если \хп\<^М при n^>N, то, обозна-
обозначая через М наибольшее из чисел:
...» \xN\ и М,
мы можем утверждать, что |^|<^+1 при всяком п.
$ 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ 57
27 Предел переменной величины. Переменную величину мы на-
и' бесконечно малой, если соответствующая ей движущаяся по
ОХ точка Я обладает тем свойством, что длина отрезка ОК
°С\ последовательном изменении Я становилась и при дальнейшем
П*менении Я оставалась меньше любого заданного положительного
И ела е. Положим теперь, что это свойство выполняется не для
отрезка (Ж> а для отрезка АК, где А есть определенная точка на
оси ОХ с абсциссой а (рис. 42). В этом случае промежуток S'S
длины 2е будет иметь середину
не в начале координат, а в точке
Л с абсциссой х = а, и точка Я
при своем последовательном пе-
перемещении должна попасть внутрь
этого промежутка и там при даль-
дальнейшем перемещении оставаться. В этом случае говорят, что постоян-
постоянное число а есть предел переменной величины х, или что переменная
величина х стремится к а.
Учитывая, что длина отрезка АК есть \х — а\ [9], мы можем
сформулировать следующее определение.
Определение. Пределом переменной величины х называется
такое число а, что разность х — а есть величина бесконечно
малая.
Отметим, что при этом и величина а — х есть величина бесконечно
малая. Принимая во внимание определение бесконечно малой величины,
можно сформулировать определение предела а следующим образом.
Определение. Пределом переменной величины х называется
такое число а, что имеет место следующее 'свойство: при любом
заданном положительном числе е существует такое значение
переменной х, что для всех последующих значений выполняется
неравенство \ х — а | < е (или, что то же, \ а — х \ <С е).
В случае пронумерованного множества хь х2, х3, ... при любом
заданном положительном числе е надо установить существование
такого целого положительного числа N, что \хп — а\<С.г (или
Iа — *п | < е) при п > N.
Если а есть предел х (х стремится к а), то пишут:
lim лг = а, или х->а.
В случае пронумерованной переменной: хь х2, х3, ... говорят
также, что а есть предел указанной последовательности (последова-
(последовательность стремится к а) и пишут:
lim л;л = а, или
Обратим внимание на некоторые непосредственно ясные следствия
определения предела, на доказательстве которых мы не останавливаемся.
58 ГЛ. I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ [ 27
1. Переменная величина не может стремиться к различным
пределам, т. е. или вовсе не имеет предела или имеет один опре-
определенный предел.
2. Переменная величина, имеющая предел, равный нулю, есть
бесконечно малая величина, и, наоборот, всякая бесконечно малая
величина имеет предел, равный нулю.
3. Если две переменные хп и уп (п—\, 2, 3, ...) или x(t) uy(t)
имеют пределы а и b и удовлетворяют при своем последователь-
последовательном изменении неравенствам хп^уп (п — \, 2, 3, ...) или x(t)^
y то и а^Ь.
Заметим, что если переменные удовлетворяют неравенству хп <^уп>
то для их пределов может получиться и знак равенства, т. е.
Ь
4. Если три переменные хп, уп и zn удовлетворяют неравен-
неравенству xn^yn^.zn, a xn и zn стремятся к одному и тому же
пределу а, то и переменная уп стремится к пределу а.
Существование предела а у переменной х равносильно тому, что
разность х — а = а есть бесконечно малая, причем упорядоченность а
определяется упорядоченностью л:. Для пронумерованной переменной:
Отсюда следует, что
5. Существование предела а у переменной х равносильно тому,
что х можно представить в виде суммы числа а и бесконечно
малой величины, т. е. х = а-\-<х или хп = а-{-ап, где а или ал —
бесконечно малые.
6. При определении предела а переменной х достаточно ограни-
ограничиться рассмотрением лишь тех значений х, которые следуют
после какого-либо определенного значения х = х0, причем это по-
последнее значение можно выбирать произвольно, т. е. можно не
обращать внимания на значения, предшествующие х0.
7. Если последовательность хь хъ хъ, ... стремится к а, то
всякая бесконечная частичная подпоследовательность хП1, хП2,
Хпв> ...» выделенная из вышеуказанной, также стремится к а.
В частичной подпоследовательности значки пь пъ пг, ... образуют
какую-либо возрастающую последовательность целых положительных
чисел.
Для непронумерованной переменной х, стремящейся к а, анало-
аналогичное свойство имеет место при некоторой оговорке. Положим, что
из последовательности значений х мы исключили некоторые значения
(возможно, бесчисленное множество значений), но сделали это так,
что для любого фиксированного значения х = х0 оставшаяся после-
последовательность значений х содержит значения, для которых х = х0
есть предшествующее значение. При этом оставшаяся последователь-
последовательность значений при прежнем упорядочивании значений есть упорядо-
упорядоченная переменная, стремящаяся к а.
27 ] §2- ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ 59
В качестве примера рассмотрим пронумерованную переменную
п
^ = 0,1, х* = 0,11, ,.., д:л = 0,11 ... 1, ...
и докажем, что ее предел равен -^-. Составим разность
1 _]_ ]_ _J_ 1 1
"9" Xl~W 9 *а~900' •" • T~X
Неравенство сГ~шг<Сг равносильно неравенству
9.юл>1 или /i>logie-™
и за N можно принять наибольшее целое число, содержащееся в раз-
разности log10 Iog109 (считаем s<-q-).
Рассмотрим теперь сумму первых п членов бесконечно убывающей
геометрической прогрессии
Как известно,
о _Ь-Ъдп
*»— \ — q '
и, придавая п значения 1, 2, 3, .... получим последовательность
Si, »>2> оз, . ..
Из выражения Sn имеем
Правая часть является произведением постоянного множителя -.
и бесконечно малого множителя qn [26]. В силу второго свойства
бесконечно малых [26] разность =— Sn есть величина бесконечно
Ь
малая и, следовательно, число -л есть предел последовательности
1 — q
*^1> *S*2> • • •
Вернемся к непронумерованной переменной величине х из [25],
определяемой неравенствами: a — k^x<^ay или a<^x^a-\-k, или
а — k^.x^a-\-k кроме x=a, с указанной в [25] последователь-
последовательностью значений. Эта переменная х имеет, очевидно, во всех трех
случаях предел а, и мы будем обозначать эти три случая изменения х
следующим образом: х-->а — 0, х—+а-\-0, х-*а±0 [ср. 26]. Отме-
Отметим, что это обозначение не связано с величиною положительного
числа k, ибо, как указано выше, при определении предела можно не
обращать внимания на значения, предшествующие какому-либо значе-
значению дг.
60 ГЛ. I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ [ ft
Сделаем еще несколько замечаний и приведем примеры.
Упорядоченная „переменная* величина х, все значения которой
равны числу а, подходит под определение величины, стремящейся к а,
Например, для пронумерованной переменной (лгд = а при любом п)
\хп — а | = 0 меньше любого заданного положительного е при всех п
[ср. 26]. Такое рассмотрение постоянной величины как частного слу-
случая переменной будет нам удобно впоследствии.
Отметим еще, что если переменная х имеет предел, например а*
то \х — а |<^& при заданном е^>0, начиная с некоторого значения хг
и, следовательно, при этом |х\<^|а|-f-в, т. е. х величина ограни*
ценная (см. замечание в [26]).
Переменная величина, как мы уже упоминали, не всегда имеет
предел. Возьмем, например, пронумерованную переменную jc*! = 0,1#
лг2 == 0,11, .#з = 0,111, ..., имеющую предел -д-, и переменную ух=з
— -j> Уъ == 2г» ^з= 23» ...» имеющую предел нуль. Пронумерованная
переменная ^ = 0,1, z2 = у, ^3 = 0»11» *к = -ср> ** = 0>т> 2в=*
= 28, ... не имеет предела. Последовательность ее значений zlt Z&,
z& ... имеет предел -q-, а последовательность значений z^ zit гб, ,.^
имеет предел нуль.
Возьмем указанную выше последовательность yl = -^-i Уъ=1ъ*
уъ = —, ,.. , имеющую предел нуль, и вставим между двумя ее чле-
членами числа 1, у, -22 ..., которые вдвое больше предыдущего числа*
Эта последняя последовательность также стремится к нулю. Полу*
чится последовательность, стремящаяся к нулю:
JL 1 !_ _L JL JL
2 ' 22' 2 ' 23 J 22' " *"
Члены этой последовательности, приближаясь беспредельно к нулк*
от положительных значений, не всегда убывают: второй больше пер-
первого, четвертый больше третьего и т. д.
Рассмотрим непронумерованную переменную, которая, убывая HI
промежутке A<^лг^5), стремится к единице, т. е. лг—> 1-^-0. Есл$
мы исключим значения лг, удовлетворяющие условию 3<^лг^4, то
оставшееся множество значений х при прежнем упорядочивании (убы**
вание) также будет стремиться к единице. Если мы исключим значе-
значения ху удовлетворяющие условию 1 <^х*^ 2, то при прежнем порядке
(убывание) оставшееся множество будет упорядоченным, но буде*
стремиться не к единице, а к двум. Если же мы исключим значе-
значения х, удовлетворяющие условию 1<*'<2| то оставшееся
, §2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ 61
тво значений х при прежнем порядке (убывание) не будет упорядо-
С иным, ибо будет иметь последнее значение х==2. Этот пример свя-
4 с тем замечанием, которое мы сделали выше об исключении зна-
3еНйй из непронумерованной упорядоченной переменной.
28. Основные теоремы. Дальнейшие теоремы мы будем проводить
для пронумерованных переменных. В общем случае доказательство
совершенно аналогично [ср. 26].
1. Если слагаемые алгебраической суммы нескольких {опреде-
{определенного числа) переменных имеют пределы, то и их сумма имеет
предел, и этот предел равен сумме пределов слагаемых.
Рассмотрим алгебраическую сумму х—y-\-z и положим, что про-
пронумерованные переменные хп> уп и zn (п— 1, 2, 3, ...) имеют пре-
пределы а, Ь и с. В силу этого имеем
где ап, р„ и 7/1 — величины бесконечно малые. Для последовательных
значений суммы х—y-\-z имеем
Первая скобка в правой части есть постоянная, а вторая — беско-
бесконечно малая величина [26]. Следовательно [27],
то есть
lim (х — у -f- z) = о- — Ь -}- с = lim х — limj/ + Hm z.
2. Если сомножители произведения нескольких переменных
имеют пределы, то и произведение имеет предел и этот предел
равен произведению пределов сомножителей.
Рассмотрим произведение двух сомножителей ху и положим, что
пронумерованные переменные хп, уп (л=1, 2, 3, ...) имеют пределы
а и Ъ. В силу этого имеем
где ал и рл — величины бесконечно малые. Для последовательных зна-
значений произведения хпуп имеем
Сумма, стоящая в правой части р скобках, есть сумма бесконечно
малых. Действительно, первые два слагаемые ее суть произведения
постоянных а и b на бесконечно малые, а в третьем слагаемом
62 ГЛ. I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ I 28
первый множитель ал->0 и потому есть ограниченная величина, а
второй множитель рл — бесконечно малая величина. Таким образом,
в правой части первое слагаемое аЬ есть «постоянная, а второе (скоб-
(скобка) — бесконечно малая [26]. Следовательно, xnyn-*ab, то есть
lim (ху) ~аЬ = lim x • lim у.
3. Если делимое и делитель •— переменные величины, имеющие
пределы, и предел делителя отличен от нуля, то и частное
имеет предел и этот предел равен частному пределов делимого
и делителя.
Рассмотрим частное xfy и положим, что пронумерованные пере-
переменные хПУ уп (я=1, 2, 3, ...) имеют пределы а и bt причем # ^ 0.
Докажем, что —-^тг* Для этого достаточно показать, что разность
Уп О
— — -г- есть бесконечно малая. По условию
Уп Ь J
где <хп и ря — бесконечно малые. Имеем
Хп_ _ а _ а + ап _ ^
Уп ~Ь- 6 + рл b
Знаменатель дроби, стоящей в правой части, состоит из двух множи-
множителей и, в силу предыдущих двух теорем, стремится к Ь\ Следова-
Следовательно, начиная с некоторого значения п, знаменатель будет больше
— ф ф 0), и дробь u{uxq ч будет, начиная с указанного значения п,
2
заключаться между нулем и -р-, т. е. будет величиной ограниченной.
Величина {Ьап — а$п) есть бесконечно малая. Итак, разность — — -г
есть бесконечно малая. Следовательно, — -> тг» то есть
Уп *
,. х a lim х /Л. . Лч
lim — = -7- = -р (lim V 9^ 0).
^/ 6 lim г/ v -^ ^ у
Отметим некоторые следствия доказанных теорем. Если х стремится
к пределу а, то переменная bxk, где b — постоянная и k — целое поло-
положительное число, будет стремиться, согласно теореме 2, к пределу Ьак.'
Рассмотрим многочлен
f{x) = аохт + а^™-1 + ... + akxm-k + ...
где коэффициенты ak — постоянные. Применяя теорему 1 и пользуясь
только что сделанным* замечанием, можно утверждать, что при стремле-
стремлении х к а этот многочлен будет стремиться к пределу
lim f(x) =/(a) = аоат + агат^ +... +
akam-k +... + ат^а + ат.
I 52. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ S3
Точно так же мы можем утверждать, что при указанном измене-
изменении х рациональная дробь
будет стремиться к пределу
^ 0.
Все эти утверждения имеют место при любом способе стремле-
стремления х к пределу а.
Вместо многочленов, расположенных по степеням одной перемен-
переменной, мы могли бы, конечно, рассматривать многочлены, расположенные
по степеням нескольких переменных, стремящихся к пределам.
Так, например, для пронумерованных переменных, если \imxn = a и
\imyn = b, то
lim (х% + хпуп +у%) = а* + аЬ + Ь\
29. Величины бесконечно большие. Если переменная величина х
стремится к пределу, то она, как мы упоминали, очевидно, ограни-
ограничена.
Теперь мы рассмотрим некоторые случаи изменения неограничен-
неограниченных величин.
Как и раньше, вместе с величиной х мы будем рассматривать
соответствующую ей точку К, перемещающуюся по оси ОХ. Пусть
эта точка К перемещается так, что какой бы большой отрезок ТТ
с серединой в начале координат мы ни взяли, точка К при своем
последовательном перемещении окажется вне этого отрезка и при
дальнейшем перемещении будет оставаться вке его. В этом случае
говорят, что х есть величина бесконечно большая, или стремится
к бесконечности. Пусть 2М—длина отрезка ТТ. Принимая во вни-
внимание, что длина отрезка 0К=\х\, можем высказать следующее
определение:
Величина х называется бесконечно большой, или стремящейся
к бесконечности, если |лг|, при последовательном изменении х,
делается и при дальнейшем изменении остается больше любого
заданного положительного числа Jtf. Иначе говоря: величина х
называется бесконечно большой при соблюдении следующего условия:
пРи любом заданном положительном числе М существует такое
значение переменной х, что для всех последующих значений
соблюдается неравенство |*|>М.
В частности, если бесконечно большая величина х при своем
оследовательном изменении, начиная с некоторого своего значения,
64 ГЛ. I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ [ 2$
остается постоянно положительной (точка К справа от точки О%
то говорят, что х стремится к плюс бесконечности (-f-oo). Если жй
величина х остается отрицательной (точка К слева от точки О), щ
говорят, что х стремится к минус бесконечности (—со).
Для обозначения бесконечно большой величины употребляют сим*
волы: Um.r==oo, lim x = -f- со, Птл; = — оо. Вместо lim# = oq
можно, очевидно, писать lim | лг | = -|~оо.
Термин „бесконечно большой* служит лишь для краткого обо*
значения вышеуказанного характера изменения переменной величина!
х> и здесь, как и в. понятии бесконечно малой величины, надо отли*
чать понятие бесконечно большой величины от понятия очень боль*
той величины.
Если, например, величина х принимает последовательно значений
1, 2, 3, ..., то, очевидно, \шх = -\-оо. Если ее последовательный
значения будут: —1, —2, —3, ..., то lim at ===== — оо, и, наконец^
если эти значения будут: —1, 2, —3, 4, ..., то мы можем напи*
сать: Нтлг = оо.
Рассмотрим еще в качестве примера величину, принимающую
последовательно значения
и пусть М^>1—любое заданное число. Неравенство
cf>M
равносильно следующему:
и, следовательно, если N есть наибольшее целое число, заключаю*
щееся в частном log10 М: log10 q, то будем иметь
qn^>M при условии n^>N,
т. е. рассматриваемая переменная стремится к -f-°a
Если в последовательности E) заменим q на (— q), то изменятср
лишь знаки при нечетных степенях q, абсолютные же значения членов
последовательности останутся прежними и, следовательно, при отрй*
дательных значениях qt по абсолютному значению больших единицы*
последовательность E) стремится к бесконечности.
В дальнейшем, когда мы будем говорить, что переменная величий?
стремится к пределу, то будем подразумевать, что этот предел ко*
нечен. Иногда говорят, что »переменная величина стремится к бескб?
нечному пределу % обозначая этими словами бесконечно большуФ
величину.
Из предыдущих определений непосредственно вытекает так09
т
следствие: если переменная х стремится к нулю, то переменная ^
j $ % ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ 65
т __ заданная постоянная, отличная от нуля, стремится к бесконеч-
ости, а если X стремится к бесконечности, то — стремится к нулю.
30. Монотонные переменные. При рассмотрении переменной вели-
величины мы часто не в состоянии найти ее предел, но нам важно знать,
что этот предел существует, т. е. что переменная стремится к пре-
пределу. Укажем один важный признак существования предела.
Положим, что переменная величина х постоянно возрастает
(точнее говоря, никогда не убывает) или постоянно убывает (точнее
говоря, никогда не возрастает). В первом случае всякое значение
величины не меньше всех предыдущих и не больше всех последующих.
Во втором случае оно не больше всех предыдущих и не меньше
всех последующих. В этих случаях говорят, что величина меняется
монотонно.
Соответствующая ей точка К на оси ОХ будет тогда переме-
перемещаться в одном направлении — в положительном, если переменная
возрастает, и в отрицательном, если она убывает. Непосредственно
ясно, что могут представиться лишь
дне возможности: или точка К бес- • -/Ч>—о-о-о—о *^А
предельно удаляется по прямой ** кгкзК(*- А
(х—>-[-оо или—оо), или точка К Рис. 43.
беспредельно приближается к не-
некоторой определенной точке А (рис. 43), т. е. переменная х стре-
стремится к пределу. Если, кроме монотонности изменения, известно еще,
что величина х ограничена, то первая возможность отпадает, и можно
утверждать, что величина стремится к пределу.
Рассуждение это, основанное на интуиции, очевидно, не имеет
доказательной силы. Строгое доказательство мы приведем позже.
Указанный признак существования предела обычно формулируют
так: если переменная величина ограничена и меняется монотонно,
то она стремится к пределу.
Рассмотрим в качестве примера последовательность
где х есть данное положительное число. Мы имеем
и =и « — G)
*фи значении п^>х дробь — будет меньше единицы и ип<^ип.ь
временная unt начиная с некоторого своего значения, при
1) Символ п\ есть сокращенное обозначение произведения 1-2-3 ... а
называется „факториал пи
3 П ТЛ г> _ *
68 ГЛ. I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ \ 31
увеличении п будет постоянно убывать, оставаясь больше нуля. Со-
Согласно признаку существования предела, эта переменная будет стре-
стремиться к некоторому пределу и. Будем в равенстве G) беспредельно
увеличивать целое число п. В пределе мы получим
и = w О или и = 0,
то есть
lim J = 0. (8)
Если мы в последовательности F) заменим х на (—х), то изме-
изменится лишь знак у членов с нечетным значком п, и эта последова-
последовательность по-прежнему будет стремиться к нулю, т. е. равенство (8)
справедливо при любом заданном значении х как положительном,
так и отрицательном.
В этом примере мы вычислили предел к, предварительно убедив-
убедившись, что он существует. Если бы этого последнего мы не сделали,
то примененный нами метод мог бы привести и к ошибочному ре-
результату. Рассмотрим, например, последовательность
Имеем, очевидно,
un = un_xq.
Не заботясь о существовании предела ип, обозначим его буквою и.
Переходя в написанном равенстве к пределу, получим
u = uq9 т. е. w(l—q) = 0
и, следовательно,
и = 0.
Но это неверно, ибо при <7^>1, как известно, lim qn==-]-oo [29].
31. Признак Коши существования предела. Указанный в [30]
признак существования предела является лишь достаточным, но не
необходимым условием существования предела, ибо, как мы знаем
[27], переменная величина может стремиться к пределу, меняясь и не
монотонно.
Французский математик Коши дал необходимое и достаточное
условие существования предела, которое мы сейчас и сформулируем.
Если предел известен, то характерным для него является тот факт,
что, начиная с некоторого значения переменной, абсолютное значение
разности между пределом и переменной меньше любого заданного
положительного е. Согласно признаку Коши, для существования пре-
предела необходимо и достаточно, чтобы, начиная с некоторого значе*
ния переменной, разность между любыми двумя последующими зна-
, § 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ 67
ниями переменной была меньше любого заданного положительного е.
Дадим точную формулировку признака Коши.
Признак Коши. Для того чтобы переменная х имела пре-
предел необходимо и достаточно выполнение следующего условия:
при любом заданном положительном числе е существует такое
значение х, что для любых последующих значений /«/ вы*
полняется неравенство: \х? — *"|<>
Положим, что мы имеем пронумерованную переменную
Согласно признаку Коши, необходимое и достаточное условие суще-
существования предела у этой последовательности состоит в следующем:
при любом заданном положительном е существует такое N (завися-
(зависящее от г), что
\хт — ^/il<?> если т и n>iV. (9)
Необходимость этого условия доказывается очень просто. Если
наша последовательность имеет предел а, то напишем хт — хп =
= (хт — а)-{-(а — хп), откуда следует
Но, в силу определения предела, существует такое N, что
\хт — ^1^4" и \а — xn\<^Y> если т и n^>N, и, тем самым,
\хт—xn\<Ce> если т и n^>N. Короче говоря, если значения х
становятся сколь угодно близкими к а, то они становятся сколь
угодно близкими и друг к другу.
Не приводя пока строгого доказательства достаточности условия
Коши, дадим ему наглядное пояснение (рис. 44).
Рис. 44.
Пусть Ms — точка координатной оси, соответствующая числу Xg.
Положим, что условие (9) выполнено. Согласно этому условию су-
существует такое значение N=Nlf что
при
т* е. все точки Ms при s^>Nx находятся внутри отрезка A[Ah длина
которого равна двум и середина которого есть точка с абсциссой xN .
Точно так же существует значение N=N% такое, что
1
68 ГЛ. I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ [ 3|
причем можно считать, что N%^NV Из сказанного следует, что все
точки xs при 5^>А/2 находятся внутри отрезка /, длина которого-
равна единице и середина которого есть точка с абсциссой xNr (|
другой стороны, все эти точки должны находиться внутри отрезка
А[АЬ откуда следует, что отрезки / и АхАу должны иметь общук?
часть. Пусть. А»А% — эта общая часть. В силу сказанного выше точки
Ms при 5^>Л^ должны находиться внутри отрезка А'2А^
Точно так же существует N= Л/з^Л^ такое, что | xs— xN
при s^> A/3. Аналогично предыдущему, построим отрезок Л3Л3, длин$
которого не превосходит -^ и который принадлежит отрезку Л2А^:
причем все точки Ms при s^>Nz будут находиться внутри него. По*
111 .
лагая e=-j, -^, ... , —, ... , получим, таким образом, ряд от-
отрезков АпАп, из которых каждый последующий заключается в пре*
дыдущем и длины которых стремятся к нулю. Концы этих отрезков
будут, очевидно, стремиться к одной и той же точке Л, и число щ
соответствующее этой точке, и будет пределом переменной величину
х, так как из описанного выше построения следует, что при достав
точно большом значении 5 все точки Ms будут сколь угодно близки
к точке Л.
В качестве приложения признака Коши рассмотрим уравнение Кеплер%
которое служит для определения положения планеты на своей орбите. Урав*
нение это имеет вид
х = q sin x -\- a,
где а и q — данные числа, из которых второе заключено между нулем й;
единицей, а х—неизвестное. Возьмем любое число х0 и построим последов
вательность чисел
хх = q sin x0 -j- a, x2 — q sin xt -f- a, ... ,
xn = q sin хп^ + а, хплл = q sin xn + a, ...
Вычитая из второго из этих равенств почленно первое, получим
х2 — xv = q ( sin xt — sin xQ) = 2q sin -^—^cos -1—-—-.
Принимая во внимание, что |sina|^|a| и | cos a | ^ 1, получим
\x x \^j2q "** == a \x x I (Щ
Совершенно так же можем получить следую!дее неравенство:
или, пользуясь неравенством A0), можем написать
I х* — *21 ^ f I *x — ^о I-
I § 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ 69
Продолжая подобные вычисления, получим при всяком п неравенство
*п\<ЯЛ\Х1 — Хо\- (И)
Рассмотрим теперь разность хт— хт считая для определенности
Хт — Хп = Хт — Хт-\ "Г хт-\ хт~2 i хт-2 хт~г "Г • • • "F ¦*" гс+1 — -*"п-
Пользуясь неравенством A1) и формулой для суммы членов геометри-
геометрической Прогрессии, будем иметь
| Хт — хп \ ^\хт — xm~i I + I хт-\ — хт-2 | +
+ I хт-2 — xm-z 1 + • • • "Г" I хпл-\ — хп I ^
— JT0 f.
При беспредельном увеличении п множитель qn стремится к нулю [25|,
множитель 1л*! — хо\ постоянный: дробь—^ZZ всегда заключается между
нулем и -j • , т. е. ограничена, ибо, при т > п, qm~n заключается между
нулем и единицей. Таким образом, при беспредельном увеличении п и лю-
любом т > п разность хт — хп стремится к нулю, и условие (9) выполнено.
Мы можем, согласно условию Коши, утверждать, что существует предел
В равенстве
Хп+i == Я sin хп *т~ а
будем беспредельно увеличивать п. Пользуясь тем, что lim sin xn = sin ? пря
lim .*¦„ = ?, как это мы покажем в [34], в пределе получим
? = # sin ?-f- а, A2)
т. е. предел ? переменной хп есть корень уравнения Кеплера.
При построении последовательности хп мы исходили из произвольного
числа л-0. Однако покажем, что уравнение Кеплера не может иметь двух
различных корней, откуда следует, что lim xn не зависит от выбора х{) и
равняется единственному корню уравнения Кеплера.
Положим, что кроме ? оно имеет еще корень ?t, и покажем, что ^=5.
По условию, кроме A2) имеем
?х = q sin ?j -f- a.
Вычитая из этого равенства почленно равенство A2), получим
&! — ? = q ( sin ?t — sin ?) = 2q sin —Цт— cos l "Т**
откуда
sin —
2
"° I sin a | ^: | a f при любом угле a, и последнее неравенство приводит к
следующему:
lei-eKfiei — ei.
силу о <с q <c 1 последнее неравенство может иметь место только при
1*1 —?1 = 0, т. е. ?1=?, откуда и следует, что уравнение Кеплера имеет
только один корень.
70 ГЛ. I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ ( 32
32. Одновременное изменение двух переменных величин, свя-
связанных функциональной зависимостью. Пусть имеется функция
y = /(je), определяемая на некотором множестве значений ху напри-
например в некотором промежутке. Используя значения х из указанного
множества, мы можем строить различные упорядоченные множества
значений переменной х и при этом будем получать соответствующие
упорядоченные множества значений переменной y = f(x) [25]. Упо-
Упорядоченная переменная х является упорядочивающей для f(x). Мы
рассмотрим в этом параграфе один важный случай такого про-
процесса.
Пусть функция f{x) определена на некотором промежутке, со-
содержащем точку х —с внутри. Выбирая достаточно малое положи-
положительное ky можем считать, что тем самым f(x) определена на проме-
промежутке с — k*^x*^c-\-k.% Рассмотрим три случая упорядочивания
значений х: х —> с — 0, х —> с -|- 0; х —> с±0 — и соответствующую
этим случаям упорядоченную переменную /(х). Пусть в первом слу-
случае эта переменная имеет предел. Обозначим его буквою А\. В этом
случае пишут:
Hm f(x)=A%. A3)
х-+с -0
Совершенно аналогично во втором случае, при наличии предела
(обозначим его буквою Ля), пишут:
lim /(х)=А2. (И)
Часто пределы A3) и A4) обозначают символами f(c — 0) и f(c-\-0)9
так что
Hm f(x) = f(c — 0), Hm./(*)=/(*
х-*с — 0 x-*c+Q
Отметим, что это — пределы f(x) при стремлении х к с слева я
справа. В третьем случае х стремится к с с двух сторон и сущест-
существование предела
Hm f(x) = B A5)
х-+ с ±0
равносильно, очевидно, следующему: существуют пределы A3) и A4),
и они равны (А\ = Аъ). При этом В= Аг = А%.
Не следует смешивать символы f(c — 0) и f(c-\-0) с f(c), т. е.
со значением f(x) при х = с. Выше мы совершенно не пользовались
этим значением, и при предыдущих рассуждениях f(x) может быть
v не определена при х = с. Если функция определена при х = с и
Дс —0)=/(*+0)=/(О,-т. е.
Hm
х-+с +0
f § 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ 71
говорят, что функция непрерывна при х = с (в точке с). Поль-
Туясь определением предела для х и f(x), легко указать условия,
равносильные существованиям пределов A3), A4) и A5). Существо-
ание предела A3) равносильно, очевидно, тому, что f(x) становится
сколь угодно близким к Аь когда х достаточно приближается к
числу су оставаясь меньше с. Точнее говоря, A3) равносильно сле-
следующему: при любом заданном положительном числе е существует
такое положительное число т], что
|/(^) —Л1|<е, если
При этом т] зависит от выбора s. Совершенно аналогично, A4) рав-
равносильно следующему: при любом заданном положительном числе s
существует такое положительное число ?], что
|/С*) —Ла|<е, если 0<> —*<т), A40
и A5)' равносильно следующему: при любом заданном положительном
числе е существует такое положительное число т], что
если \х —
Отметим еще следующий очевидный факт: если существует пре-
предел A5), то f(x) при любом законе стремления упорядоченной
переменной х к с имеет предел В, Аналогичное замечание имеет
место и для пределов A3) и A4) при стремлении х к с слева и
справа.
В дальнейшем мы подробно рассмотрим понятие непрерывности
и свойства непрерывных функций. Сейчас мы обратимся к тем слу-
случаям, когда х или f(x) стремятся к бесконечности [29]. Предыдущие
определения легко обобщаются и на эти случаи. Нетрудно, например,
видеть, что
lim = — оо, lim == —т— оо -
Х-+С— 0 л с х-+с-\-0 Л L
lim tgx = -\-oo, lim igx = — со.
Положим, что f(x) определена при всех достаточно больших х
и что упорядоченная переменная х любым образом стремится к -\~ оо
[29]. При этом f{x) есть также упорядоченная переменная, и может
существовать для нее конечный предел
lim f(x) = A. A6)
X -»• -f-OO
^то равносильно следующему: при любом заданном положительном
числе е существует такое число Ж, что
\f{x) — Л|<е, если х>М. Aбх)
72 ГЛ. I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ [ 32
В частности, упорядоченность х может состоять в том, что х бес-
беспредельно возрастает, принимая все достаточно большие веществен-
вещественные значения. Совершенно аналогично можно рассмотреть случай
х-> — сю.
Если f(x) определена при всех х, достаточно больших по аб-
абсолютной величине, и упорядоченное переменное х стремится к со
[29], то может аналогично предыдущему существовать конечный
предел
lim/(x)= АУ
что равносильно следующему: при любом заданном положительном
числе е существует такое положительное число М, что
\/(х) — Л|<е, если
В частности, х может стремиться к со, принимая все различные
значения, достаточно большие по абсолютной величине. Их можно
упорядочить так же, как это мы делали в [25] для ненумерованной
переменной х, удовлетворяющей условию а — k^x<^a-{-k (кроме
х = а). Отметим, что для пронумерованной переменной хь х%, х2,... ,
имеющей предел я, вместо \\тхп — а часто пишут lim хп==а.
п-*со
В этом случае #-->оо обозначает, что п возрастает, принимая все
целые положительные значения.
Можно говорить и о бесконечных пределах f(x). В частности,
lim f(x) = — оо
обозначает, что при любом заданном отрицательном числе Mi су-
существует такое число М, что f(x)<^Mh если х^>М. Аналогично
можно определить и другие случаи бесконечного предела.
Нетрудно проверить справедливость следующих равенств:
lim x's = -{-oo, lim х3 = — со,
X -* -f- оо х-* — со
lim — = 0, Iimx2 = -|~oo>
X -> ОО •*" X -+ CO
-. 2х2— 1 ,. 2~*3F. 2
А4-А
Ilm У2 1 1 = lim г—=0.
л:-»оо л "Г l jf-j-co J J |__
~ X2
Рассмотрим еще один физический пример. Положим, что мы на-
нагреваем некоторое твердое тело, и пусть t0 его начальная темпера-
32
§ 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ
73
Tvpa. При нагревании температура тела будет повышаться, пока не до-
достигнет точки плавления. При дальнейшем нагревании температура
буцет оставаться неизменной до тех пор, пока тело не перейдет це-
целиком в жидкое состояние, а затем опять начнется повышение темпе-
температуры образовавшейся жидкости. Аналогичная картина произойдет и
при превращении жидкости в газообразное состояние. Будем рассмат-
рассматривать количество сообщенного телу тепла Q как функцию темпе-
температуры. На рис. 45 изображен график этой функции, причем на го-
горизонтальной оси откладывается температура, а на вертикальной —
01 to
с
-4
л
Рис. 45.
-1
Рис. 46.
количество поглощенного тепла. Пусть t\ — температура, при кото-
которой тело начинает переходить в жидкое состояние, и t% — темпера-
температура, при которой жидкость начинает переходить в газообразное
состояние. Очевидно:
lim
¦* ti — о
= орд. АВ
lim <3 = орд. Л С.
Величина отрезка ВС дает скрытую теплоту плавления, а вели-
величина отрезка EF—скрытую теплоту парообразования.
Вели пределы /(с — 0) и /(с + 0) существуют и различны, то
разность /(с-|-0)—f(c — 0) называется разрывом, или скачком,
функции f(x) при х = с (в точке х = с).
Функция j/ = arctg имеет при х = с скачок тс. Только что
X ~~~ С
рассмотренная функция Q(t) имеет в точке плавления t = t± скачок,
равный скрытой теплоте плавления.
При определении предела/(х) при стремлении х к с мы считали,
что х стремится к с, никогда с мим не совпадая. Эта оговорка суще-
существенна, потому что значение f(x) при х = с иногда или не суще-
существует, или не имеет ничего общего со значениями /(х) при х> близких
к с* Так, например, функция Q(t) не определена при i — t^
74 ГЛ. I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ | 33
Рассмотрим еще пример для пояснения сказанного. Положим, что
на промежутке (— 1, —|— 1) функция определена следующим образом;
у=х-\-\ при—
у = х—1 при
у = 0 при х = 0.
На рис. 46 воспроизведен график этой функции, состоящий из двух
отрезков прямых, из которых исключены конечные точки (при jc = O), и
одной отдельной точки — начала координат. В этом случае
lim f(x) = l, lim /(*)=—1, /@) = 0.
* —-0 *-*-{-0
33. Примеры. 1. Известно, что при любом х имеет место нера-
неравенство | sin л; |=^:| л; | и знак равенства имеет место лишь при лг = О.
Напомним, что величина х при этом выражается в радианах. Из ска-
сказанного следует, что для любого заданного положительного числа е
мы имеем |sin.xr|<^e, если |лг|<^е, т. е.
lim sinx = 0.
2. Далее, имеем:
т. е. 0^1 — cos х <; 4р, откуда следует, что [27]
lim cosjc=1.
3. Рассмотрим частное
Эта функция определена при всех х кроме х = 0, ибо при ^ = 0 й
числитель и знаменатель обращаются в нуль и дробь теряет смысл.
С Исследуем изменение у при х —* ± 0. При из-
изменении знака х величина у не меняется, так
что достаточно предполагать, что х —¦ -f- 0. По-
Покажем, что у—*\ при х—»-{-0. Тот же предел
получится и при дг—> — 0. Отметим, что тео-
теорему о пределе частного применить нельзя, ибо
и числитель и знаменатель стремятся к нулю
при лт—>-|-0.
Будем рассматривать х как центральный
Рис. 47. угол в круге радиуса единица (рис. 47). При-
Принимая во внимание, что пл. Д А0В<^ш. сек-
сектора АОВ<^ил. Л АОС, получим
sinx<A;<
34 1
§ 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ 75
откуда, деля на ^ sin ¦*> получим
^ sin х
или
sin х ^ ,. -ч
> cos х. A7)
^ X
Но cos х-->1 при лг—> + 0, откуда
v sin х 1
hm —^- = 1
и, в силу сказанного выше,
,. sin л: .
hm = 1.
Определим для данного случая число т], которое входит в усло-
условие (I5j). Вычитая из единицы три части неравенства A7), получим
откуда следует, что
sin х .
х
если 1 — cos лг<^е. Но, как мы видели выше, 1 — cos дг<^-к-, и
достаточно выбрать — <^е, т. е. |лг|<^у2е. Итак, в данном случае
j/2e может играть роль числа т\.
34. Непрерывность функции. Приведем еще раз определе-
определение непрерывности функции f{x) в точке х = с> если эта функция
определена в этой точке и вблизи нее слева и справа.
Определение. Функция f {x), определенная при х = с и всех
значениях х, достаточно близких к с, называется непрерывной
при х = с (в точке с), если существует предел f(x) при х-->с±0
и этот предел равен f (с):
lim f(x)=f(c). A8)
x-+c±0
Напомним, что это равносильно тому, что существуют пределы
/(с — 0) и /(с_}-0) слева и справа и Что эти пределы равны
между собою и равны f(c), т. е. f(c — 0)=f(c-\-0)=f(c).
Из сказанного в [32] следует, что это равносильно также сле-
следующему: при любом заданном положительном числе е существует
такое положительное число % что
I/M-/WK" при |Jf-c|<Tj. A9)
76 ГЛ. I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ [ 34
Не нужно оговаривать, что х Ф с, ибо f (х)—f(c) — 0 при х = с.
Иначе зто можно формулировать так:/(х) —f(c)—>0 при х — с—»±0.
Разность х — с есть приращение независимой переменной, а
разность f(x)—f(c)— соответствующее приращение функции. По-
Поэтому указанное выше определение непрерывности часто форму-
формулируют так:
Функция называется непрерывной в точке х = с, если беско*
нечно малому приращению независилсои переменной (от начального
значения х = с) соответствует бесконечно малое приращение
функции.
Заметим, что свойство непрерывности, выражаемое равенством A8),
сводится к возможности находить предел функции простой подста-
подстановкой вместо независимой переменной ее предела.
Из формул, приведенных в конце [28], мы видим, что целый много-
многочлен от х и частное таких многочленов, т. е. рациональная функция
от 'х, суть функции, непрерывные при любом значении х, кроме тех
значений, при которых знаменатель рациональной функции обращается
в нуль.
Непрерывной, очевидно, будет и функция у = Ъ> сохраняющая при
всяком х одно и то же значение [12].
Все элементарные функции, рассмотренные нами в первой главе
(степенная, показательная, логарифмическая, тригонометрические и
обратные круговые), непрерывны при всех значениях х, при которых
они существуют, кроме тех значений, при которых они обращаются
в бесконечность.
Так, например, logl0x есть непрерывная функция от х при всех
положительных значениях х\ tg лг есть непрерывная функция от х
при всех значениях х, кроме значений
где k есть любое целое число.
Отметим еще функцию uv, где и и v суть непрерывные функции
от xf причем предполагается, что и не принимает отрицательных
значений. Такая функция называется степенно-показательной. Она
точно так же обладает свойством непрерывности, исключая те
значения х} при которых и и v одновременно равны нулю или
и = 0 и и<0.
Высказанное нами утверждение о непрерывности элементарных
функций нуждается, конечно, в доказательстве, но мы примем это без
доказательства. В дальнейшем мы рассмотрим этот вопрос подроб-
подробнее. Докажем только непрерывность функции sin x при любом x = ct
пользуясь определением A9). Мы имеем [ср. 31]
о . х — с х 4- с
sin х — sin с = 2 sin —к— cos ——-,
35 j § 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ 77
откуда следует
in х — sin с ] = 2
sin
sin
х— с
cos
sin
X — С
Wo 1 sin ct | ^ | а | при любом угле а, и, следовательно,
| sin х — sin с \ ^ | х — с |.
Чтобы иметь | sin х — sin с | <^ е, где s — заданное положительное
число, достаточно считать, что \х — с\<^г, т. е. роль -ц в опреде-
определении A9) может играть число е.
-Нетрудно показать, что сумма или произведение произвольного
конечного числа непрерывных функций есть также непрерывная
ерункция; то же относится и к частному двух непрерывных
функций за исключением тех значений независимой переменной,
при которых, знаменатель обращается в нуль.
Рассмотрим лишь случай частного. Положим, что функции у(х)
и О(лг) непрерывны при х = а и что ф(а)^0. Составим функцию
Пользуясь теоремой о пределе частного, получим
lim cp (х)
что и доказывает непрерывность частного f(x) при х = а.
Отметим один простой пример. Раз у = sin x есть непрерывная
функция от х, то y = b sin х, где Ь — постоянная, также будет непре-
непрерывной функцией, так как она является произведением непрерывных
функций у — Ь (см. выше) и y = sinx.
Вернемся теперь еще к функции у = . При х = 0 эта функ-
х
ция неопределенна, но мы знаем, что lim y=\. Поэтому, если мы
х-+±0
положим у-= 1 при х = 0} то у будет непрерывной функцией в точке
Подобнее нахождение предела функции при стремлении л; к ее
точке неопределенности называется раскрытием неопределенности,
а самый предел, если он существует, называют иногда истинным зна-
значением функции в ее упомянутой точке неопределенности. В дальней-
шем мы будем иметь много примеров раскрытия неопределенностей.
35. Свойства непрерывных функций. Выше мы определили
свойство непрерывности функции при заданном значении х. Положим
Теперь, что функция определена в конечном промежутке а
78 ГЛ. I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ [ 35
Если она непрерывна при любом значении х из этого промежутка,
то говорят, кто она непрерывна в промежутке (я, Ь). Заметим
при этом, что непрерывность функции на концах промежутка х = а
и хх=Ь состоит в следующем:
lim /(*)=/(a), lim f(x)=f(b).
x->a + Q x-*b — 0
Все непрерывные функции обладают следующими свойствами:
1. Если функция f(x) непрерывна в промежутке (а, ?), то
существует в этом промежутке, по крайней мере, одно такое
значение х, при котором f(x) принимает свое наибольшее значе-
значение и, по крайней мере, одно такое значение х, при котором
функция принимает свое наименьшее значение.
2. Если функция f(x) непрерывна в промежутке (а, Ь), при-
причем f(a) = m и f{b) = n, и если k — любое число, заключающееся
между т и п, то существует в промежутке (а, Ь), по крайней
мере, одно такое значение х, при котором значение f(x) равно k;
в частности, если /(а) и f(b) разных знаков, то существует
внутри промежутка (а, Ь\ по крайней мере, одно такое значе-
значение х, при котором f(x) обращается в нуль.
Эти два свойства становятся непосредственно ясными, если при-
принять во внимание, что в случае непрерывности функции соответствую-
соответствующий ей график будет представлять собою непрерывную кривую. Это
замечание не может, конечно, служить доказательством. Самое понятие
о непрерывной кривой, наглядное с первого взгляда, оказывается чрез-
чрезвычайно сложным при ближайшем его рассмотрении. Строгое доказа-
доказательство указанных двух свойств, так же как и следующего, третьего,
основано на теории иррациональных чисел. Мы примем эти свойства
без доказательства.
В последних номерах настоящего параграфа мы выясним основы
теории иррациональных чисел и связь этой теории с теорией пре-
пределов и свойствами непрерывных функций. Заметим, что второе
свойство непрерывных функций можно еще формулировать так: при
непрерывном изменении х от а до b непрерывная функция f(x)
проходит, по крайней мере, один раз через все числа, лежащие меж-
между /(а) и f{b).
Ha рис. 48 и 49 изображен график непрерывной в промежутке
(а, Ь) функции, у которой f(a)<^0 и /(#)^>0. На рис. 48 график
один раз пересекает ось OXt и при соответствующем значении X
функция f (х) обращается в нуль. В случае рис. 49 таких значений
будет не одно, а три.
Мы переходим теперь к третьему свойству непрерывных функций,
которое является менее наглядным, чем два предшествующих.
3. Если f(x) непрерывна в промежутке (а, Ь) и. если x = xQ есть
некоторое значение х из этого промежутка, то в силу условия A9)
35
§ 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ
79
[34] (заменяя с на х0) для любого заданного положительного г суще-
существует такое т], зависящее, очевидно, от е, что
\f(x)— /(дто)|<е, если \х —
причем мы считаем, конечно, х также принадлежащим промежутку
tuj Ь). (Если, например, дго = д, то х обязательно больше а, а если
j?ft = &, то х<^Ь.) Но число т\ может зависеть не только от г, но
и от того, какое именно значение х = х0 из промежутка (а, Ь) мы
рассматриваем. Третье свойство непрерывных функций заключается
в том, что на самом деле для у
любого заданного е суще-
ъ
Рис. 48.
Рис. 49.
ствует одно и то же tj для всех значений х0 из промежутка (а> V).
Иными словами, если f(x) непрерывна в промежутке (а, Ь), то
для любого заданного положительного е существует такое по-
положительное т], что
для любых двух значений х? и х" из промежутка (a, b)t удовлет-
удовлетворяющих неравенству
1*"-*Ч<ч- С21)
Это свойство называется равномерной непрерывностью. Таким
образом, если функция непрерывна в промежутке (а, Ь), то она
будет равномерно непрерывна в этом промежутке.
Отметим еще раз, что мы предполагаем функцию f(x) непрерыв-
непрерывной не только для всех лг, лежащих внутри промежутка (а, Ь), но и
Для значений' х = а и х = Ь.
Мы поясним свойства равномерной непрерывности еще на одном
простом примере. Предварительно перепишем предыдущие неравенства
в другом виде, заменяя букву х' на х и У на (х-)-/*)- При этом
x' = h представляет собою приращение независимой переменной
80 ГЛ. Т. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ [ 35
и f(x-{-h)—f(x)— соответствующее приращение функции. Свойство
равномерной непрерывности запишется так:
|/(*+А)_/(*)|<е, если |й|<1),
где х и (х -\- h) — любые две точки из промежутка (а, Ь).
Для примера рассмотрим функцию
В данном случае мы имеем
h) —f(x) = (a: + hf — x2 =
При любом заданном значении х выражение Bxh -f- /г2), дающее приращение
нашей функции, стремится, очевидно, к нулю, если приращение независимой
переменной стремится к нулю. Этим еще раз подтверждается [34], что взятая
функция непрерывна при всяком значении х. Тем самым она будет непре-
непрерывна, например, в промежутке —\^.х^2. Покажем, что она будет равно-
равномерно непрерывна в этом промежутке. Нам надо удовлетворить неравенству
12xh + h21 < s B2)
соответствующим подбором числа yj в неравенстве |А|<т), причем х и
(лг + Л) должны принадлежать промежутку (—1, 2). iMbi имеем
12xh + h21 ^ | 2xh | + h2 = 2 | * 11 h | + /г2.
Но наибольшее значение |лт| в промежутке (—1, 2) равно двум, и потому
мы можем заменить предыдущее неравенство более сильным:
12xh + h21 ^ 4 | h |
Будем считать во всяком случае | Л | < 1. При этом Л2<|Л|, и мы можем
переписать предыдущее неравенство в виде:
12xh + h21 < 4 | h | + | h \ или | 2xh + Л21 < 5 | h |.
Неравенство B2) будет, наверное, удовлетворено, если мы подчиним | h |
условию 5 | h | < е. Таким образом, Л должно удовлетворять двум неравенствам
|Л|<1 и |Л|<~.
Следовательно, за число к] мы можем взять наименьшее из двух чисел 1 и
-?-. При малых s (а именно при s<5) мы должны взять т] = -^-, и во вся-
ком случае очевидно, что найденное yj будет, при заданном е, одним и тем же
для всех х из промежутка (— 1, 2).
Указанные свойства могут уже не иметь места в случае разрывных
функций или функций, непрерывных только внутри промежутка. Рассмот-
Рассмотрим функцию, график которой изображен на рис. 46. Она определена на
промежутке (— 1, + 1) и имеет разрыв при л: = 0. Среди ее значений имеются
сколь угодно близкие к единице, но она не принимает значения, равного
единице, и значений, больших единицы. Таким образом, среди значений этой
функции нет наибольшего. Точно так же среди этих значений нет и наимень-
наименьшего. Элементарная функция у = х не принимает внутри промежутка @, 1)
ни наибольшего, ни наименьшего значения. Если рассматривать эту же функ-
функцию в замкнутом промежутке @, 1), то она будет достигать своего наимень-
наименьшего значения при л: = 0 и наибольшего при д?=1. Рассмотрим еще функ-
gg j § 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ 81
i ию /(.*•) = sin—, непрерывную в промежутке 0<х<с:1, открытом слева.
При стремлении х к нулю аргумент — беспредельно растет, и sin — колеб-
колеблется между (—1) и (+1) и не имеет предела при x---f-0. Покажем, что
указанная функция не обладает равномерной непрерывностью в промежутке
к <- г -^ 1. Рассмотрим два значения: х' = — и х" =-т-л—-.—р—, где я— целое
"~~~ tin DЛ -f- 1) тс
положительное число. Оба они принадлежат упомянутому промежутку при
любом выборе п. Далее, мы имеем
/ (л;') = sin пп = 0, / (х") = sin ( 2пк -f- ~\ = 1.
Таким образом,
^Х ' Dл + 1) те пк9
При беспредельном возрастании целого положительного числа п разность
х" — х' стремится к нулю, а разность f(x")—f(x') остается равной единице.
Отсюда видно, что не существует положительного т\ для промежутка 0 < х ^ 1
такого, что из B1) следует \f(x") —f{x') | < 1; это соответствует выбору
е = 1 в формуле B0).
Возьмем функцию /(;c)==A:sin—. При х—»-\-0 первый множитель х
стремится к нулю, а второй sin — не превышает единицы по абсолютной
величине, а потому [32] f(x)-+0 при x—*-f-0. При х = 0 второй множитель
не имеет смысла, но если мы дополним определение нашей функции, положив
/@) = 0, т. е. будем считать f(x) = xsin— при 0<х<^\ и/@) = 0, то
получим функцию, непрерывную в замкнутом промежутке @, 1). Функции
sin-— и xsin — обладают, очевидно, непрерывностью при любом х, отличном
х х
от нуля.
36, Сравнение бесконечно малых и бесконечно больших ве-
величин. В дальнейшем буквами а и р мы будем обозначать упорядо-
упорядоченные переменные, которые имеют одну и ту же упорядочивающую
переменную (значок п или переменную t), так что мы можем произ-
производить элементарные действия над этими переменными.
Q
Если переменные аир стремятся к нулю, то к их частному —
теорема о пределе частного неприменима и мы без дополнительных
исследований ничего не можем сказать о существовании предела у
этого частного.
Положим, что а и В стремятся к нулю, но не принимают в про-
Цессе изменения значения нуль и что отношение — стремится к пре-
АелУ а, конечному и отличному от нуля. При этом и отношение ~
82 ГЛ. Т. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ | 36
стремится к пределу —, конечному и отличному от нуля. В этом
случае говорят, что аир — бесконечно малые одного и того же
порядка.
Q
Если предел отношения - равен нулю, то говорят, что р — бес-
бесконечно малая высшего порядка по сравнению с а или что а —
бесконечно малая низшего порядка по сравнению с р. Если отноше-
отношение — стремится к бесконечности, то ~ стремится к нулю, т. е. р бу-
будет низшего порядка по сравнению с а и а высшего порядка по
сравнению с р. Легко показать, что если а и р бесконечно малые
одного и того же порядка и f бесконечно малая высшего по-
порядка по отношению к а, то она бесконечно малая высшего по-
порядка и по отношению к р. По условию —-—0, и отношение^ имеет
предел, конечный и отличный от нуля. Из очевидного равенства
? = -•-, в силу теоремы о пределе произведения, непосредственно
следует, что ? —* О, что И доказывает наше утверждение.
Отметим важный частный случай бесконечно малых одного и
того же порядка. Если - —* 1 (при этом и -—*1], то бесконечно
малые а и р называются эквивалентными. Из равенства = -—1
непосредственно следует, что эквивалентность а и р равносильна
тому, что разность р — а есть бесконечно малая высшего порядка
по отношению к а. Из равенства ^—^—= 1 —g точно так же следует,
что эквивалентность равносильна тому, что р—а есть бесконечно
малая высшего порядка по отношению к р.
Если отношение \, где k — постоянное положительное число,
стремится к пределу, конечному и отличному от нуля, то говорят,
что р бесконечно малая порядка k no сравнению с а. Если -^—+с,
где с — число, отличное от нуля, то -^->1, т. е. р и со? — экви-
эквивалентные бесконечно малые, и следовательно, разность 7 = р—са*
есть бесконечно малая высшего порядка по сравнению с р (или по
сравнению с а*). Если принять а за основную бесконечно малую,
то равенство p = cafe-f-f> г#е Т — бесконечно малая высшего по-
порядка по сравнению с aft, представляет собой выделение из беско-
бесконечно малой р бесконечно малого слагаемого со!* (простейше-
(простейшего вида по отношению к а), так что остаток -у есть Уже ^ес-
конечно малая высшего порядка по сравнению с р (или по сравне-
сравнению с а*).
37 ] § 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ 83
Аналогичным образом производится сравнение бесконечно боль-
больших величин и и v. Если - стремится к пределу, конечному и
отличному от нуля, то говорят, что и и v бесконечно большие вели-
величины одного и того же порядка. Если > О, то > оо. В этом
случае говорят, что v бесконечно большая низшего порядка по
сравнению с и или что и бесконечно большая высшего порядка по
сравнению с v. Если »1, то бесконечно большие называются
эквивалентными. Если -?, где k — постоянное положительное число,
имеет предел, конечный и отличный от нуля, то говорят, что v
бесконечно большая &-го порядка по сравнению с и. Все сказанное
выше о бесконечно малых имеет место и для бесконечно больших»
Отметим еще, что если отношение - или - вовсе не имеет пре-
а U
дела, то соответствующие бесконечно малые или бесконечно боль-
большие называются несравнимыми.
37. Примеры.
1. Выше мы видели, что
-. sin х л
lim = 1,
о х
т. е. sin х и х суть эквивалентные бесконечно малые, и, следовательно, раз-
разность sin х — х есть бесконечно малая высшего порядка по отношению к х.
Дальше мы увидим, что эта разность эквивалентна —7Гх3> Тв е* является
бесконечно малой третьего порядка по сравнению с х.
2. Покажем, что разность 1 — cos л: есть бесконечно малая второго по-
порядка по отношению к х. Действительно, применяя известную тригономет-
тригонометрическую формулу и элементарные преобразования, получим
1 — cos x
Если л:—»0, то а = ?г также стремится к нулю, и, как мы показали,
. х
у 2 sin а , 1-1 — cos х 1
lim = hm = 1, и, следовательно, lim ^ — "о"»
х~+0 X (х-+0 ^ X—+QX ?
2
т- е. действительно, 1 — cos x бесконечно малая второго порядка по сравне-
сравнению с х.
3. Из формулы
84 ГЛ. 1. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ I 38
следует
|/Т+Т—1_ 1
х ~~~ у \ _|_ х _j_ \'
откуда
lim ! = тг.
т. е. }^\ -\- х — 1 и х суть бесконечно малые одного порядка, причем
У~\-\-х—1 эквивалентна ~^-х.
4. Докажем, что многочлен степени т есть бесконечно большая по-
порядка т по сравнению с Л'. Действительно,
аохт + а,хт~1 + ... + ат_хх + ат =
л:-»оо •*
Нетрудно видеть, что два многочлена одной и той же степени, при а* —*оо,
суть бесконечно большие одного и того же порядка. Их отношение имеет
пределом отношение их старших коэффициентов. Например,
4 ""ЛШсо 7 , 1 , i. 7 '
"*" X ^ X2
Если степени двух многочленов различны, то при х—*со тот из них будет
бесконечно большой высшего порядка но сравнению с другим, степень ко-
которого больше.
38. Числе е. Рассмотрим один важный для дальнейшего пример
переменной величины, а именно, рассмотрим переменную, прини-
принимающую значения
где пу возрастая, принимает целые положительные значения и стре-
стремится, таким образом, к -\-оо. Применяя формулу бинома Ньютона,
получим
. Мя_1 I * ] 1 п(п—\) 1 . п(п-\)(п—2) 1 ,
л]-1!" 1 „Т 2! п** 3! п3 •"
38
§ 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ ?5
Написанная сумма содержит (я-f-l) положительных слагаемых,
р увеличении целого числа п, во-первых, увеличится число сла-
слагаемых и, во-вторых, каждое из прежних слагаемых также увели-
увеличится, так как в выражении общего члена*)
4,(i_±\(i_2\. .Ji-k—
4,
/г! остается без изменения, а разности, стоящие в круглых скобках,
увеличатся при увеличении п. Таким образом, мы видим, что рас-
рассматриваемая переменная при увеличении п увеличивается, и для
того, чтобы убедиться в существовании предела этой переменной,
достаточно доказать, что она ограничена.
Заменим в выражении общего члена каждую из упомянутых раз-
разностей единицей, а все множители, входящие в k\, начиная с '3,
заменим на 2. От такой замены общий член увеличится, и мы будем
иметь, применяя формулу для суммы членов геометрической про-
прогрессии
1-4
^
f 1 \п
т. е. переменная A-| J ограничена. Обозначим предел этой пере-
переменной буквой е:
lim ( 1-] ) =е (п — целое положительное). B3)
+ Л п I
п
Этот предел не может быть, очевидно, больше 3. В формуле B3)
целое п может, очевидно, стремиться к -\- со любым образом.
Докажем теперь, что выражение A -j ) стремится к тому же
пределу <?, если х—+ -j-oo, принимая любые значения.
Пусть п — наибольшее целое число, заключающееся в х, т. е.
1) Произведение fl j f 1 ] . . . f 1 ^-j получается из дроби
nk
если каждый из k coMHO^KHTev^eH, стоящих в числителе, разделить на /?,
финимая во внимание, что число сомножителей п в знаменателе также
равно /г.
86 ГЛ. I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ [ 38
Число п стремится, очевидно, вместе с х к -{- оо. Принимая во
внимание, что при увеличении положительного основания, большего
единицы, и показателя степени увеличивается и сама степень, можем
написать
Но, в силу равенства B3),
lim 1-4 р-р = hm
+ 1+_
Hm A + Й"+1= Вт r(±)"(
Таким образом, крайние члены неравенства B4) стремятся к пре-
пределу е, а потому к тому же пределу должен стремиться и средний
член, т. е.
lim (l+lVW B5)
Рассмотрим теперь тот случай, когда х стремится к —оо. Введем
вместо х новую переменную у, полагая
х = — 1 —у, откуда у = — 1 — х.
Из последнего равенства видно, что, при стремлении х к —оо
у стремится к -(-оо.
1 -| ) замену переменных и принимая
во внимание равенство B5), получим
„m (l+l)'= lim (_=2-Г^= lim
Если х стремится к оо, имея любые знаки, т. е. | jvt [ —> —|— оо,
то из предыдущего следует, что и в этом случае
lim (l+±VW B6)
Впоследствии мы покажем удобный путь для вычисления числа е
с любой степенью точности. Число это, как оказывается, есть число
иррациональное [и с точностью до седьмого десятичного знака оно
выражается так: е = 2,7182818,..
оо 1 § 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ 87
оо I
/ ? \ X
Нетрудно теперь найти предел выражения A-J— , где k — дан-
данное число. Пользуясь непрерывностью степенной функции, получим
где буквою у обозначено частное ^-, стремящееся к бесконечности
одновременно с х.
( k\n
Выражения вида A-| ) встречаются в теории так называемых
сложных процентов. Предположим, что приращение капитала проис-
происходит ежегодно. Если капитал а отдан из р процентов годовых, то
по истечении года наращенный капитал будет a(l-\-k), где k = ^^\
по прошествии второго года он будет a(l-f-&J, и, вообще, по про-
прошествии т лет он будет a(l-\-k)m.
Положим теперь, что приращение капитала происходит через —
часть года. При этом число k уменьшится в п раз, так как про-
процентная такса р рассчитана на год, а число промежутков времени
увеличится в п раз, и наращенный капитал через т. лет будет
Пусть, наконец, п увеличивается беспредельно, т. е. приращение
капитала происходит через все меньшие промежутки времени и в пре-
пределе— непрерывно. По прошествии т лет наращенный капитал будет
Ъ \ тп Г ( Ъ \я Щ
П1 п-+оо W n> i
ekm
Примем число е за основание логарифмов. Такие логарифмы на-
называются натуральными логарифмами и их обычно обозначают
просто знаком log (или In) без указания основания.
При стремлении переменной х к нулю в выражении ** ~гл;
числитель и знаменатель стремятся к нулю.^Раскроем эту неопре-
неопределенность. Введем новую переменную уу полагая
* = 1,т. е. у = ±,
откуда видно, что, при х—*0, у стремится к бесконечности. Введя
эту новую переменную и пользуясь непрерывностью функции logx
при х^>0 и формулой B6), получим
88 ГЛ. I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ [ ЗЭ
Из этого ясна целесообразность сделанного выбора основания ло-
логарифмов. Точно так же, как при радианном измерении углов, истин-
sin х п
ное значение выражения при х = 0 равно единице, в случае
х
натуральных логарифмов истинное значение выражения °g '~^XJ
при х = 0 тоже равно единице.
Из определения логарифмов вытекает следующее соотношение:
Логарифмируя это соотношение по основанию е> получим
log Лг = loga N • log а или \oga N=logN- j~.
Соотношение это выражает логарифм числа N при любом осно-
основании а через его натуральный логарифм. Множитель М = - на-
называется модулем системы логарифмов с основанием а; при а =10
он выражается с точностью до седьмого десятичного знака так:
М = 0,4342945...
39. Недоказанные предложения. При изложении теории пре-
пределов мы оставили недоказанными несколько предложений, кото-
которые сейчас перечислим: существование предела у монотонной
ограниченной переменной [30|, необходимое и достаточное условие
существования предела (признак Коши) [31] и три свойства непре-
непрерывных в замкнутом промежутке функций [35]. Доказательство этих
предложений основывается на теории вещественных чисел и действий
над ними. Изложению этой теории и доказательству упомянутых выше
предложений будут посвящены следующие номера.
Введем еще одно новое понятие и формулируем еще одно пред-
предложение, которое также будет доказано ниже. Если мы имеем мно-
множество, состоящее из конечного числа вещественных чисел (например,
мы имеем тысячу вещественных чисел), то среди них будет как наи-
наибольшее, так и наименьшее. Если же мы имеем бесконечное множе-
множество вещественных чисел и даже таких, что все эти числа принад-
принадлежат определенному промежутку, то, все же не всегда среди этих
чисел будет наибольшее и наименьшее. Например, если мы рассмот-
рассмотрим множество всех вещественных чисел, заключающихся между 0
и 1, но не будем причислять к этому множеству самих чисел 0 и 1,
то среди этого множества чисел нет ни наибольшего, ни наимень-
наименьшего. Какое бы число, близкое к единице, но меньше ее, мы ни взяли,
найдется другое число, лежащее между взятым числом и единицей.
В данном случае числа 0 и 1, не принадлежащие к взятому множе-
множеству чисел, обладают по отношению к нему следующим свойством;
л , § 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ 89
чисел нашего множества нет чисел, больших единицы, но при
заданном положительном числе в есть числа, большие A—е).
Точно так же среди чисел нашего множества нет чисел, меньших
у1Я но при любом заданном положительном числе* е есть числа, мень-
меньшие:'@ Ч"?)- ^ти числа 0 и * называются точной нижней и точной
верхней границами указанного выше множества вещественных чисел.
Перейдем от этого примера к общему случаю.
Пусть имеется некоторое множество Е вещественных чисел. Го-
Говорят, что оно ограничено сверху, если существует такое число М,
что все числа, принадлежащие множеству Е, не превосходят М.
Точно так же говорят, что множество ограничено снизу, если суще-
существует такое число т, что все числа, принадлежащие множеству
ЕУ не менее, чем т. Если множество ограничено сверху и снизу,
то его просто называют ограниченным.
Определение. Точной верхней границей множества Е на-
называют такое число C {если оно существует), что среди чисел,
принадлежащих Е, нет чисел, больших р, но при любом задан-
заданном положительном е есть числа, большие ф — г). Точной ниж-
нижней границей множества Е называется такое число а (если оно
существует), что среди чисел, принадлежащих Е, нет чисел, мень-
меньших а, но при любом заданном положительном е есть числа,
меньшие (а -\-г).
Если множество Е не ограничено сверху, т. е. существуют числа
из Е, большие любого заданного числа, то множество не может
иметь точной верхней границы. Точно так же, если множество Е не
ограничено снизу, то оно не может иметь точной" нижней границы.
Если среди чисел множества есть наибольшее, то оно, очевидно, и
является точной верхней границей множества. Точно так же, если
среди чисел множества есть наименьшее, то оно и является точной
нижней границей множества Е. Но, как мы видели, не всегда среди
чисел бесконечного множества есть наибольшее или наименьшее.
Однако можно показать, что у множества, ограниченного сверху,
всегда имеется точная верхняя граница, а у множества, ограни-
ограниченного снизу, — точная нижняя граница. Отметим еще, что из оп-
определения точных границ непосредственно следует, что точная верх-
верхняя и точная нижняя граница может быть только одна.
Указанными в настоящем номере предложениями мы будем часто
пользоваться в дальнейшем.
Следующие номера, напечатанные мелким шрифтом, могут быть
пропущены при первом чтении.
40. Вещественные числа. Начнем с изложения теории вещественных
чисел. Мы исходим из множества всех рациональных чисел, целых и дроб-
^1Х> как положительных, так и отрицательных. Все эти рациональные числа
°ЖНо себе представить расположенными в порядке их возрастания. При
Том» если а и b два любых различных'рациональных числа, то между
90 ГЛ. I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ | 40
ними можно вставить сколько угодно рациональных чисел. Действительно
пусть а<Ь, и введем положительное рациональное число г = , где
п — какое-нибудь целое положительное число. Рациональные числа a -f- г,
0 + 2г, ... , а-\-(п—\)г лежат между а и Ь, и, ввиду произвольности
в выборе целого положительного числа я, наше утверждение доказано.
Назовем сечением в области рациональных чисел всякое разделение
всех рациональных чисел на такие два класса, что любое число одного
(первого) класса меньше любого числа другого (второго) класса. При этом,
очевидно, если некоторое число находится в первом классе, то и всякое
меньшее его число также находится в первом классе, и если некоторое
число находится во втором классе, то и всякое большее число также нахо-
находится во втором классе.
Положим, что среди чисел первого класса есть наибольшее число. При
этом, в силу упомянутого свойства совокупности рациональных чисел, можно
утверждать, что среди чисел второго класса нет наименьшего числа. Точно
так же, если среди чисел второго класса есть наименьшее, то среди чисел
первого класса нет наибольшего. Назовем сечение — сечением первого родаг
если среди чисел первого класса есть наибольшее или среди чисел второго
класса есть наименьшее. Легко построить такие сечения. Возьмем какое-*
нибудь рациональное число Ь и отнесем к первому классу все рациональные
числа, меньшие Ь, ко второму классу — все рациональные числа, большие ^
а само число Ь отнесем или к первому классу (оно будет там наибольшим)
или ко второму классу (оно будет там наименьшим). Беря за Ь всевозмож-
всевозможные рациональные числа, мы получим таким образом всевозможные сечения
первого рода. Мы будем говорить, что такое сечение первого рода опре*
деляет то рациональное число Ь> которое является наибольшим в первом
или наименьшим во втором классе.
Но существуют и сечения второго рода, у которых в первом классе
нет наибольшего числа, а во втором классе нет наименьшего числа. Построим
пример такого сечения. Отнесем к первому классу все отрицательные
-рациональные числа, нуль и те положительные рациональные числа, квадрат
которых меньше двух, а ко второму классу отнесем все те рациональные
положительные числа, квадрат которых больше двух. Так как не существует,
рационального числа, квадрат которого равен двум, то все рациональные числа
окажутся распределенными, и мы будем иметь некоторое сечение. Покажем, что
в первом классе нет наибольшего числа. Для этого достаточно показать, что
если число а принадлежит первому классу, то есть числа, большие а, также,
принадлежащие первому классу. Если а отрицательно или нуль, то это
очевидно; положим, что а > 0. По условию составления первого класса
а2 <с 2. Введем положительное рациональное число г = 2 — а2 и покажем»
что можно определить настолько малое положительное рациональное число х$
чтобы (а-\-х) также принадлежало первому классу, т. е. чтобы имелось
неравенство
2 —(д + л:J>0 или г — 2ах — л:2>0,
т. е. дело сводится к нахождению такого положительного рационального
числа, которое удовлетворяет неравенству х2 -\- 2ах < г. Считая х < 1, иыееш
х2 < х, и, следовательно, х2 + 2ах < х + 2tf* = Bа + 1) л:, т. е. нам доста-
достаточно удовлетворить неравенству Bа -(- 1) х <С г, таким образом, х опреде*
ляется из двух неравенств
Очевидно, можно найти сколько угодно таких положительных рациональ-
рациональных х, которые удовлетворяют обоим этим неравенствам. Совершенно так же
яЛ i § 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ 91
н0 показать, что во втором классе построенного сечения нет наимень-
ь о числа. Итак, мы построили пример сечения второго рода. Основным
шСмеНТ0М теории является следующее соглашение: мы считаем, что всякое
Ь\чение второго рода определяет некоторый новый объект — иррацио-
альное число. Разные сечения второго рода определяют разные иррацио-
^атьные числа. Нетрудно догадаться, что построенный выше пример сече-
сечения второго рода определяет то иррациональное число, которое мы обычно
обозначаем /2.
Можно расставить теперь все введенные таким образом иррациональные
числа вместе с прежними рациональными в порядке возрастания, который
интуитивно изображается для нас точками направленной оси ОХ. Если а есть
некоторое иррациональное число, то мы обозначим через I (а) и II (а) первый
и второй классы того сечения, которое определяет иррациональное число а.
Мы считаем число а большим, чем любое число из I (а), и меньшим, чем
любое число из II (а). Таким образом, любое иррациональное число сравни-
сравнивается с любым рациональным. Остается определить понятия больше и
меньше для любых двух различных иррациональных чисел аир. Поскольку
а и р различны, классы I (а) и 1 (Р) не совпадают, и один из классов заклю-
заключается в другом. Положим, что I (а) заключается в I (р), т. е. всякое число
из I (а) принадлежит 1 (р), но есть числа из I (р), принадлежащие II (а). При
этом мы по определению считаем а < р. Таким образом, совокупность всех
рациональных и иррациональных чисел, т. е., иначе говоря, совокупность всех
вещественных чисел расположена в порядке. При этом, пользуясь данными
выше определениями, нетрудно показать, что если а, Ь и с — вещественные
числа а< b и Ь < с, то а < с.
Отметим прежде всего одно элементарное следствие из указанных опре-
определений. Пусть а—некоторое иррациональное число. Поскольку в классе I (а)
нет наибольшего, а в классе II (а) нет наименьшего числа, то непосредст-
непосредственно очевидно, что между а и любым рациональным числом а можно вста-
вставить сколько угодно рациональных чисел. Пусть теперь а<р — два различ-
различных иррациональных числа. Часть рациональных чисел из I (P) входит в II (а), и
отсюда непосредственно следует, что между аир также можно вставить
сколько угодно рациональных чисел, т. е. вообще, между двумя различ-
различными вещественными числами можно вставить сколько угодно рацио-
рациональных чисел.
Мы переходим теперь к доказательству основной теоремы теории ирра-
иррациональных чисел. Рассмотрим совокупность всех вещественных чисел и
произведем в ней какое-нибудь сечение, т. е. распределим все вещественные
числа (не только рациональные, но и иррациональные) на два класса I и II
так, чтобы любое число из I было меньше любого числа из II. Докажем, что
при этом обязательно или в классе I будет наибольшее число или в классе II
будет наименьшее число (одно исключает другое, как и выше для сечения
в области рациональных чисел). Для этого обозначим через Г совокупность
всех рациональных чисел из I и через IP — совокупность всех рациональ-
рациональных чисел из II. Классы (Р, IP) определяют некоторое сечение в области рацио-
рациональных чисел, и это сечение определит вещественное число а (рациональное
Или иррациональное). Положим для определенности, что это число а принад-
принадлежит классу I при упомянутом выше распределении всех вещественных
чисел на два класса. Покажем, что а должно быть наибольшим числом из
класса I. Действительно, если бы это было не так, то существовало бы
в классе I вещественное число р, большее а. Возьмем некоторое рациональ-
рациональное число г, лежащее между а и р, т. е. а < г < р. Оно должно принадле-
принадлежать классу I и, следовательно, классу Р.
Таким образом, в первом классе сечения (Р, IP), определяющего числа а,
уходится число г, большее, чем а. Этого быть не может, и, следовательно,
аше предположение, что а не наибольшее число класса! — неправильно.
92 ГЛ. I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ | $|,
Совершенно так же можно показать, что если а попадает в класс II, то ощ
должно быть там наименьшим числом.
Итак, мы доказали следующую основную теорему:
Основная теорема. # любом сечении, произведенном & обласщ
вещественных чисел, обязательно: или первый класс содержит наибол^
шее число или второй класс содержит наименьшее число.
Всем рассуждениям настоящего номера легко придать простой геометру
ческий смысл. Сначала мы рассматриваем на оси ОХ только точки с рацио-
рациональными абсциссами. Сечению в области рациональных чисел соответствует
разрез прямой ОХ на две полупрямые. Если разрез происходит в точ^
с рациональной абсциссой, то полу.чается сечение первого рода, причеи
абсцисса той точки, в которой происходит разрез, причисляется сама иди
к первому или ко второму классу. Если же разрез производится в точк?,
которой не соответствует рациональная абсцисса, то получается сечение
второго рода, определяющее иррациональное число, которое и принимается
за абсциссу той точки, в которой произведен разрез. После заполнения ц±
ких пустых точек иррациональными абсциссами всякое рассечение прямой
происходит уже в точке с некоторой вещественной абсциссой. Все щ
является лишь геометрической иллюстрацией и не имеет доказательной силы,
Нетрудно, пользуясь данным onp-еделением иррационального числа а, обра*
зовать бесконечную десятичную дробь, соответствующую этому числу [ф
Всякий конечный отрезок 9Tqft дроби должен принадлежать I (а), но если м|*
увеличим на единицу последнюю цифру этого отрезка, то соответствующей
рациональное число должно находиться в II (а).
41. Действия над вещественными числами. Теория иррациональных
чисел, кроме данных выше определений и основной теоремы, содержит еще
определение действий над иррациональными числами и исследование свойс1?!
зтих действий. При определении действий мы будем руководствоваться*
сечениями в области рациональных чисел, и, поскольку эти сечения опреде-
определяют не только иррациональные, но и рациональные числа (сечения первогр
рода), определение действий будет годиться вообще для всех вещественны^
чисел, причем для рациональных чисел они будут совпадать с извест-
известными. При изложении настоящего номера мы ограничимся только общими
указаниями. ?
Сделаем предварительно одно замечание. Пусть а — некоторое вещ(р
ственное число. Возьмем какое-нибудь (малое) рациональное положительно!"
число г, затем рациональное а из I (я) и составим арифметическую про-
прогрессию
я, а-{-г, а-\-2г, ... , а-\-пг, ...
При больших п числа (а -+- пг) попадут в И (а), и, следовательно, буЩ
существовать такое целое положительное k, что [а-\-(k—1)г] принадлЙ*
жит I (а) и (а-\- kr) принадлежит II (а), т. е.: ^
Заме ч а н и е: В любом сечении рациональных чисел существуют
в разных классах числа, отличающиеся на любое заданное положителъ*
ное рациональное число г, как бы мало оно ни было.
Перейдем теперь к определению сложения. Пусть а и р — два вещ$?
ственных числа. Пусть а — любое число из I (а), а' — из II (ос), Ь — из \Щ
и Ь'—из II ф). Составим всевозможные суммы (а-\-Ь) и (a' -j- b'). Во всякоИ
случае имеем: а + Ь < а' + Ь'. Составим новое сечение рациональных чисел,
относя ко второму классу все рациональные числа, большие всех (а-\-Ь)$
и относя к первому классу все остальные рациональные числа. При этоМ
любое число первого класса меньше любого числа второго класса, в0
числа (а + Ь) отходят в первый класс и все числа (а' + Ь') — во второй класб
Составленное новое сечение определит некоторое вещественное числО|
I § 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ 93
ос мы и назовем суммой (а + Р). Это число, очевидно, больше или равно
К?1Ч, (я 4" ^) и мсньше или равно всем (а' -\- Ь'). Принимая во внимание, что
HCC|nv сделанного выше замечания, числа а и а', а также Ь и Ь' могут от-
В ДрУг от ДР)'га на любое малое положительное рациональное число,
показать, что может существовать только одно число, удовлетво-
цшисе указанным выше неравенствам. Непосредственно проверяется, что
^ <у-кение удовлетворяет обычным законам, известным для рациональных
Ч11ССЛ а + Р = Р + а
Например, чтобы получить (Р + а), пам наД° будет составлять вместо
сумм (а-\-Ь) и (о' + ?') суммы (? + я) и (Ь' -\-а'), но эти суммы совпадают
с'прежними, так как переместительный закон сложения для рациональных
чисел известен.
Пусть а — некоторое вещественное число. Определим число (—а) сле-
следующим сечением: в первый класс относим все рациональные числа из класса
if (а) с измененным знаком, а во второй класс — все числа из I (а) с изме-
измененным знаком. Таким образом, получится действительно сечение в области
рациональных чисел, и для числа (— а), как нетрудно проверить, имеем
-(-«) = «, « + (-«) = <).
Нетрудно видеть, что если а > 0, то (— а) < 0, и наоборот. Назовем абсолют-
абсолютным значением числа а, отличного от нуля, то из двух чисел а и (—а),
которое больше нуля. Обозначим, как и раньше, абсолютное значение числа а
СИМВОЛОМ | а |.
Переходим теперь к умножению. Пусть а и р— два положительных
вещественных числа, т. е. а > 0 и р > 0. Пусть а — любое положительное
число из I (а), Ь—любое положительное наело из I (р), а' и Ь' — любые
числа из II (а) и II (Р) (они уже обязательно положительны). Составляем
новое сечение, относя ко второму классу все рациональные числа, большие
всех произведений ab> и к первому классу — остальные рациональные числа.
Все аЬ попадут в первый класс и все а'Ь' — во второй класс. Новое сечение
определит некоторое вещественное число, которое мы и назовем про-
произведением ар. Это число больше или равно всем аЬ и не превосходит
всех а'Ь', и только одно это вещественное число удовлетворяет этим не-
неравенствам.
Если одно из чисел а, р или оба — отрицательны, то мы приводим умно-
умножение к предыдущему случаю, вводя в определение умножения обычное
правило знаков, т. е. мы полагаем а$ = ±.\а\ | р |, причем берем знак (-(-),
если числа аир оба меньше нуля, и берем знак (—), если одно из чисел
больше нуля, а другое меньше нуля.
При умножении на н^ль принимаем определение, что а -0 = 0 •<х = 0.
Непосредственно проверяются основные законы умножения:
а? + аТ, "
и произведение нескольких сомножителей может равняться нулю в том и
только в том случае, если хоть один из сомножителей равен нулю.
Вычитание определяется как действие, обратное сложению, т. е. а—р = д;
равносильно х-\-$ = а. Добавляя к обеим частям этого равенства (—р),
получим, в силу упомянутых выше свойств сложения: х = а-\-(—Р), т. е.
разность должна обязательно определяться по этой формуле, и действие
вЬ1читания сводится к сложению. Остается проверить, что полученное выра-
выражение для х действительно удовлетворяет условию л' + р = а, но это непо-
непосредственно вытекает из свойств сложения. Отметим справедливость обыч-
Ого свойства: неравенство а >> 8 равносильно а — р > 0. Прежде чем пере-
*°дить к делению, определим чиело, обратное данному. Если а есть рацио-
94 ГЛ. I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ ( 42
нальное число, отличное от нуля, то обратным называют число —. Пусть
а — вещественное число, отличшое от нуля. Пусть сначала а>0, и пусть а'—
любое число из II (а) (оно — рационально и положительно). Определим число,
обратное а, следующим сечени<ем: к первому классу отнесем все отрицатель-
отрицательные числа, нуль и числа —7, а ко второму классу — остальные числа. Пусть
некоторое положительное число сг принадлежит первому классу нового
сечения. Это значит, что сг =—„ где а\—из II (а). Возьмем любое поло-
жительное рациональное число с2 < С{. Его можно представить в виде
с2 = —г, где а'2 — рационально и а!2 > а[, т. е. а'2 также принадлежит II (а).
а2
Иначе говоря, если некоторое положительное число принадлежит первому
классу нового сечения, то всякое меньшее рациональное положительное
число также принадлежит этому первому классу. Туда же входят по усло-
условию все отрицательные числа и нуль. Отсюда видно, что сечение, опреде-
определяющее число, обратное а, произведено нами с соблюдением того основного
условия, что любое число второго класса больше любого числа первого
класса. Это число, обратное а- обозначим символом —.
а 1 1
Если а < 0, то мы определим обратное число формулой — = — -j—г.
Пользуясь определением умножения, получим а—= 1.
Переходим теперь к делению. Это есть действие, обратное умножению,
т. е. а:$ = х равносильно дф=г=а, и, как при вычитании, нетрудно показать,
что если C:у?0, то получается единственное частное: лг=а»-о->и» таким об-
образом, деление сводится к умножению. Деление на нуль невозможно.
Возведение в целую положительную степень сводится к умножению.
Извлечение корня определяется как действие, обратное возведению в сте-
степень. Пусть а — вещественное положительное число и п—некоторое целое,
большее единицы. Произведем следующее сечение рациональных чисел:
к первому классу отнесем все отрицательные числа, нуль и все положитель-
положительные числа, п-е степени которых меньше а, а ко второму классу — остальные
числа. Пользуясь определением умножения, нетрудно показать, что положи-
положительное число р, определяемое этим сечением, удовлетворяет условию:
п,—
рл = а, т. е. р является арифметическим значением корня у а. Если/г —чет-
—четное, то вторым значением будет (—р). Аналогично определяется корень не-
нечетной степени из вещественного отрицательного числа (один ответ). Более
подробно о показательной функции будет сказано потом. Отметим еще сле-
следующий важный результат: раз справедливы основные законы действий, то
тем самым будут справедливы и все правила и тождества алгебры, если
под буквами разуметь вещественные числа.
42. Точные границы числовых множеств. Признаки существования
предела. Докажем теперь теорему о точных границах множества вещест-
вещественных чисел, которую мы формулировали в [39].
Теорема. Если множество Е вещественных чисел ограничено сверху,
то оно имеет точную верхнюю границу, и если Е ограничено снизу, то
оно имеет точную нижнюю границу.
Ограничимся доказательством первой части теоремы. По условию все
числа из Е меньше некоторого числа М. Произведем сечение вещественных
42 I § 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ 95
чисел следующим образом: ко второму классу отнесем все числа, большие
всех чисел из Е, а к первому — остальные вещественные числа. Во второй
класс попадут, например, все числа (М+р), где р^О, а в первый класс
попадут, например, все числа из Е. Пусть р— вещественное число, опреде-
определенное произведенным сечением. По основной теореме [40] оно будет наи-
наибольшим в первом классе или наименьшим во втором. Покажем, что р и
есть точная верхняя граница Е, Во-первых, среди Е нет чисел, больших р,
ибо все числа Е попали в первый класс. Далее, наверно существуют числа Еу
большие (р — е) при любом е > 0, ибо, если бы таких чисел не было, то
число (р 2") было бы больше всех чисел Е и должно было бы попасть
во второй класс, а в действительности оно меньше р и находится в первом
классе. Теорема, таким образом, доказана. Очевидно, что если р принадле-
принадлежит Еу то оно будет наибольшим из чисел Е.
Докажем теперь существование предела у монотонной ограниченной
переменной [30]. Итак, пусть переменная х все время возрастает или, по
крайней мере, не убывает, т. е. всякое ее значение не меньше любого пре-
предыдущего. Пусть, кроме того, х ограничено, т. е. существует такое число М,
что все значения х меньше М. Рассмотрим совокупность всех значений х.
По доказанной теореме существует точная верхняя граница р для этой со-
совокупности. Покажем, что р и есть предел х. Пусть е — произвольное поло-
положительное число. По определению точной верхней границы найдется значе-
значение л:, большее (р=—е). Тогда, в силу монотонности, и все последующие зна-
значения х будут больше (р — е), но, с другой стороны, они не могут быть
больше р, и, в силу произвольности е, мы видим, что р = Нтдг. Точно так
же можно разобрать и случай убывающей переменной.
Прежде чем переходить к доказательству признака Коши [31], докажем
одну теорему, которой мы будем пользоваться.
Теорема. Пусть имеется последовательность конечных проме-
промежутков
(*иА)» («2, ь*),.-, («я. ьп),...
причем каждый следующий промежуток заключается в предыдущем, т. е.
an+i ^ ап и Ьп+1 ^ Ьт и пусть длины этих промежутков стремятся к
нулю, т. е. (Ьп — ап)~*0. При этом концы промежутков ап и Ьп стре-
стремятся к общему пределу при возрастании п.
По условию теоремы мы имеем al^a2^i... и, кроме того, an<ibi
при любом п. Таким образом, последовательность аи а2У ... будет монотон-
монотонной и ограниченной, а потому будету иметь предел: ап —> а. Из условия
{Ьп — ап)-+0 вытекает Ъп=-ап-\-гп, где ел—*0, и, следовательно, Ьп имеет
предел, также равный а.
Перейдем теперь к доказательству признака Коши. Ограничимся случа-
случаем переменной, значения которой можно пронумеровать:
•**1> Х2> . .., ХПу ... (^')
"адо доказать, что необходимое и достаточное условие существования пре-
предела последовательности B7) заключается в следующем: для любого задан-
заданного положительного е существует такой значок ./V, что
\хт — хп I < е ПРИ т и n>N. B8)
окажем, что это условие достаточно, т. е. что при выполнении этого
ВИя B7) И
у д, р
Н1г послеДовательность B7) имеет предел. Из наших прежних рассужде-
и [31] вытекает, что если условие выполнено, то можно построить после-
вательность промежутков
96 ГЛ. Т. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ [ 43
со следующими свойствами: каждый следующий заключается в предыдущем,
длины (bk — ak) стремятся к нулю и всякому интервалу (ак, bk) соответст-
соответствует такое целое положительное число А/д,, что все xs при s :> Л^ принад-
принадлежат (ak, bk). Эти интервалы (ak> bk) суть отрезки A'kAk из [31]. По дока-
доказанной выше теореме имеется общий предел:
lim ak= lim bk = a. B9)
k-*CQ k—»-OO
Покажем, что а и есть предел последовательности B7). Пусть задано
положительное число s. В силу B9) существует такое целое положитель-
положительное /, что промежуток (ah bL) и все следующие промежутки лежат внутри
промежутка (а — е, а + е).
Отсюда следует, что и- все числа xs при s > TV; принадлежат этому же
промежутку, т.е. \а — xs | < е при s > TV/. Ввиду произвольности е мы
видим, что а есть предел последовательности B7), и достаточность усло-
условия B8) доказана. Необходимость этого условия была доказана нами
раньше [31]. Доказательство остается в силе и для не пронумерованной
переменной.
43. Свойства непрерывных функций. Переходя к доказательству фор-
формулированных раньше [35] свойств непрерывных функций, начнем с доказа-
доказательства вспомогательной теоремы.
Теорема I. Если f(х) непрерывна в промежутке (а, Ь) и задано
какое-нибудь положительное число г, то этот промежуток можно
таким образом разбить на конечное число новых промежутков, что
\f(x2)—f(xj)\<.z} если только xt и х2 принадлежат одному и тому
же новому промежутку.
Будем доказывать от обратного. Предположим, что теорема несправед-
несправедлива, и придем к нелепости. Итак, пусть невозможно разбить (at b) на части
указанным образом. Делим наш промежуток средней точкой на два проме-
промежутка: (я, -—п—) и (—pj—, b\. Если бы теорема была справедлива для
каждого из этих двух промежутков, то она, очевидно, была бы справедлива
и для всего промежутка (af b). Итак, мы должны считать, что, по крайней
мере, один из двух полученных промежутков нельзя разбить на части ука-
указанным в теореме образом. Берем ту половину промежутка, для которой
теорема не выполняется, и делим его опять на две равные части. Как и вы-
выше, по крайней мере для одной из новых половинок теорема не выпол-
выполняется. Берем эту половинку, делим ее опять помолам и т. д. Таким обра-
образом, мы получаем последовательность промежутков
(a, b), (aly bjy (tfo, b2), ..., (ап, bn)y ...,
из которых каждый следующий есть половина предыдущего, так что длина
(Ьп — ап), равная „п , стремится к нулю при возрастании п. Кроме того,
для всякого промежутка (аПУ Ьп) теорема не выполняется, т. е. нельзя ника-
никакой (апу Ьп) разбить на новые промежутки так, чтобы \f(x2)—/(.*i)|<e,
если только xt и х2 принадлежат одному и тому же новому промежутку.
' Покажем, что это нелепо.
По теореме из [42] ап и Ьп имеют общий предел:
1ипял = Нт&я = а, C0)
причем этот предел, как и все числа ап и Ьт принадлежит промежутку (а, Ь)<
Положим сначала, что а — внутри (а, Ь). По условию, f (х) непрерывна при
х = а, и, следовательно [34], при заданном в теореме е существует такое rit
43 J § 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ 97
что для всех х из промежутка (а — tj, а + т)) выполняется неравенство
<f C1)
Если Xt и х2 — два любых значения из промежутка (а — tj, <* + *]), то мы
имеем
/ (хм) -/ (xt) =/ (х2) -/(«)+/ («) -/ (xj,
откуда
\f(x2)
и, в силу C1),
\f(x2)-f(x1)\<* C2)
для любых xi и х2 из промежутка (а — yj, а + Y]). Но, в силу C0), будет су-
существовать промежуток (#/, #/), принадлежащий промежутку (а—yj, a + Yj).
Поэтому неравенство C2) и подавно будет выполняться для любых ху и х2
из этого промежутка (#/, bt), т. е. для промежутка (ah bj) теорема выпол-
выполняется даже без всякого его подразделения на части. Это противоречит тому,
что, как мы видели выше, для всякого промежутка (аПУ Ьп) теорема не вы-
выполняется. Таким образом, теорема доказана, если а—внутри промежутка
(af b). Если а совпадает, -например, с левым концом промежутка, т. е. а = а%
то доказательство будет таким же, но вместо промежутка (а—yj, а-f-*]) надо
будет взять промежуток (а, а + *]).
Перейдем теперь к доказательству третьего свойства из [35].
Теорема II. Если f(х) непрерывна в промежутке (а, Ь), то
она равномерно непрерывна в этом промежутке, т. е. при любом
заданном положительном е существует такое положительное у\, что
\f(x")—f(x') |<s для любых значений х' и х" из (а, Ь), удовлетворяю*
щих неравенству \х" — х' \<л\.
В силу теоремы I мы можем подразделить (л, Ь) на конечное число
новых промежутков так, чтобы \f(x2)—/ (*i) | <-у, если только xt и ха
принадлежат одному и тому же новому промежутку. Пусть yj—длина са-
самого короткого из новых промежутков. Покажем, что именно при этом
числе т] наша теорема выполняется. Действительно, если х' и х" — два зна-
значения из (а, Ь), удовлетворяющих/неравенству \х" — х' \ < yj, то или х' и х"
принадлежат одому и тому же новому промежутку, или они находятся
в двух прилегающих друг к другу новых промежутках. В первом случае, по
построению новых промежутков, имеем: \f(x")—/(х')\<С-к-, а потому и
подавно \f(x") —f(x') | < s. Переходя ко второму случаю, обозначим через y
точку, в которой соприкасаются те два прилегающих друг к другу проме-
промежутка, к которым принадлежат х' и х'\ В данном случае мы можем напи-
написать
/ (*О-/(*')=/(**)-/G)+/(?)"-/(*')>
т. е.
\f{x*) -/(*') I <\/(х') —/G) I + |/G) -/СО |. C3)
Но
I/(*')-/(!) К \и 1/G)-/(ОКу, C4)
..»ч..л«. я. Г
98 ГЛ. I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ [ 43
так как точки х' и |, а также f и х'. находятся в одном и том же новом
промежутке. Неравенства C3) и C4) дают нам \f{x")—/(лг')|<е, и тео-
теорема доказана.
Теорема I приводит нас также к такому следствию:
Следствие. Функция, непрерывная в промежутке (а, Ь), ограничена
сверху и снизу, т. е. просто ограничена в этом промежутке. Иными сло-
словами, существует такое число М, что для всех значений х из (а, Ь) выпол-
выполняется неравенство \f(x)\<zM. Действительно, возьмем некоторое опреде-
определенное ео>О, и пусть п0 — число тех новых промежутков, на которые надо
разбить (а, Ь), чтобы удовлетворить теореме I при взятом значении е = ?0.
Для любых двух точек, принадлежащих одному и тому же новому проме-
промежутку, мы имеем \f(x2)—f(xt) | < е0. Отсюда непосредственно следует, что
для любого х из промежутка (а, Ь) мы имеем \f(x)—f(a)\<:noto, т. е.
все значения /(х) заключаются между / (а) — noto и /(я) + яо?о«
Поскольку совокупность всех значений f(x) в промежутке (а, Ь) огра-
ограничена сверху и снизу, она имеет точную верхнюю границу и точную ниж-
нижнюю границу [42]. Обозначим первую через р, а вторую через а. Докажем
теперь первое свойство из [35].
Теорема III. Непрерывная в промежутке (а, Ь) функция достигает
в этом промежутке своего наибольшего и наименьшего значения.
Нам надо доказать, что в промежутке (а> Ь) существует такое значение
х, при котором f (х) равно р, и такое значение х,при котором f (х) равно а.
Ограничимся доказательством первого утверждения и будем доказывать от
обратного. Положим, что f (х) ни при каком х из (а, Ь) не равно р (следо-
(следовательно, всегда меньше р). Составим новую функцию
Поскольку знаменатель не обращается в нуль, новая функция также
будет непрерывной в промежутке (а, Ь) [34]. С другой стороны, из опреде-
определения точной верхней границы следует, что при произвольном б > О суще-
существуют для а^х^Ь значения/(*), лежащие между (р — е) и р. При этом:
0<Р—/(х)<г и ср (х) >—. Поскольку е можно брать произвольно ма-
малым, мы видим, что непрерывная в промежутке (#, Ь) функция у(х) не огра-
ограничена сверху, что противоречит указанному выше следствию теоремы I.
Докажем, наконец, второе свойство из [35]. Пусть f (х) непрерывна
в (а, Ь) и k — некоторое число, лежащее между f (а) и f (Ь). Для определен-
определенности положим, что /(а) < k </ (b). Составим новую функцию
непрерывную в промежутке (а, Ь). Ее значения на концах промежутка будут
F(a)=f (а) -¦*<<>, F (b)=f (b)-k> О,
т. е. значения F (х) на концах промежутка — разных знаков. Если мы дока-
докажем, что внутри (а, Ь) есть такое значение х0, при котором F(xo) = O, то
при этом f(x0) — /г = 0, т. е. f (xo) = k, и второе свойство будет доказано.
Итак, достаточно доказать следующую теорему:
Теорема IV. Если f (х) непрерывна в промежутке (a, b)y a f(a) и
f(b) разных знаков, то внутри промежутка существует по крайней
мере одно такое значение х0, при котором f(x'0) = 0.
Доказываем от обратного, как и теорему III. Пусть f (х) нигде в про-
промежутке (а, Ь) не обращается в нуль. При этом новая функция
*м=тЬ) C5)
44 ] § 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ 99
будет также непрерывной в промежутке (я, Ь) [34]. Пусть задано какое-ни-
какое-нибудь е > 0. В силу теоремы I мы можем расставить внутри промежутка
(а, Ь) конечное число точек так, что, причисляя к этим точкам еще концы
промежутка, мы будем иметь разность значений f (х) в любых двух сосед-
соседних расставленных точках, по абсолютной величине меньшую, чем е. Прини-
Принимая во внимание, что f(a) и f (b) разных знаков, мы ,можем утверждать,
что найдутся такие две соседние из вышеупомянутых точек ?t и ?2, в кото-
которых/(х) разных знаков. Итак, с одной стороны, /(?0 и /(?2) разных зна-
знаков и, с другой стороны, |/(?2)—/Ei)|<e. Но если у двух вещественных
чисел разных знаков абсолютное значение разности меньше е, то каждое из
этих чисел по абсолютному значению меньше е, т. е. например, |/(Si) | < е.
Но тогда, в силу C5), | <р (^) | > —, и ввиду того, что s можно брать про-
произвольно малым, мы видим, что непрерывная в промежутке (я, Ь) функ-
функция <р (х)—не ограничена в этом промежутке, что нелепо. Теорема, таким
образом, доказана.
44. Непрерывность элементарных функций. Мы показали раньше не-
непрерывность многочлена и рациональной функции [34]. Рассмотрим теперь
показательную функцию
у = а* (д>0), C6)
причем для определенности будем считать а^>\. Эта функция вполне опре-
определена при всех рациональных положительных значениях х. Для отрица-
отрицательных х она определяется формулой:
«* = JF*. C7)
и, кроме того, fl° = l. Таким образом, она определена при всех рациональ-
рациональных х. Из алгебры известны также правила сложения и вычитания показа-
показателей при умножении и делении.
Если х есть положительное рациональное число —, то
ах = "
где радикал считается арифметическим. Очевидно, что яР>1, и из опреде-
определения корня вытекает, что 0*>1 при лг>0 (применить определения из
[41]). Из C7) вытекает, что /0 <с ах <^\ при д:<;0. Покажем теперь, что
ax'2>>aXi1 если х2 "> х1У т. е. что ах — возрастающая функция. Действи-
Действительно,
причем х2 — л:1>0, и, следовательно, оба сомножителя справа положи-
положительны. Покажем еще, что ах—+\, если х—*0, принимая рациональные зна-
значения. Положим сначала, что х—*0 через все рациональные значения,
убывая (справа). При этом ах убывает, но остается больше единицы, и, сле-
следовательно, имеет предел, который мы обозначим через /. При упомянутом
выше изменении х переменная 2х также стремится справа к нулю по всем
рациональным значениям. Мы имеем, очевидно,
и, переходя к пределу, получим
/ = /2 или /(/—1)=^
4*
100 ГЛ. Т. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ | 44
т. е. /=1 или / = 0. Но вторая возможность отпадает ввиду я*>1. Итак,
ах —* 1, если х—> 0 справа. Из C7) вытекает, что тот же предел будет и
тогда, когда х —*0 слева. Итак, вообще: ах —*1, если лг—*О, принимая ра-
рациональные значения. Отсюда вытекает непосредственно, что если х, при-
принимая рациональные значения, стремится к рациональному пределу Ьу то
аХ—^аР, Действительно,
а* — аь = аь (ах~ь — 1).
Разность (х — Ь) стремится к нулю и (ах~ь—1), по доказанному, также
стремится к нулю.
Определим теперь функцию C6) при иррациональных х. Пусть а — не-
некоторое иррациональное число, а I (а) и II (а) — первый и второй классы
сечения в области рациональных чисел, определяющих а. Положим, что х~+а,
возрастая и проходя через все рациональные числа из I (а). Переменная ах
возрастает, но остается ограниченной, а именно она меньше, чем ах'\ где х"—
любое число из II (а). Таким образом, при упомянутом изменении х пере-
переменная ах имеет предел, который мы пока обозначим через L. Точно так
же, если х—*а, убывая и пробегая рациональные числа из II (а), то ах также
имеет предел. Покажем, что этот предел также равен L Пусть х' — из I (а)
и х* — из II (а). Мы имеем
ах" — ах' = ах' (ах"~х' — 1) < L (ах"~х' — 1),
т. е.
0 < ах" — ах' < L (а*""* — 1).
Для х' и хй', близких к а, разность (хт — х') сколько угодно близка к
нулю и, в силу написанного неравенства, то же можно сказать и о разности
(а*" —а*), откуда и вытекает наше утверждение о совпадении пределов. Мы
принимаем по определению аа равным упомянутому пределу L, т. е. а% есть
предел, к которому стремится ах, когда х—>а через рациональные зна-
значения. Теперь .функция C6) определена при всех вещественных х. На осно-
основании сказанного выше легко доказать, что это будет возрастающая функ-
функция, т. е. aX2>aXl, если хх и х2 — любые вещественные числа, удовлетво-
удовлетворяющие неравенству х2 > xv При доказательстве надо рассмотреть отдельно
случаи, когда хх и х2 — оба иррациональны или одно из пих рационально.
Остается еще доказать, что эта функция будет непрерывна при всяком ве-
вещественном х. Сначала надо показать, что ах-+\ при х—>б, причем счи-
считаются допустимыми все вещественные значения х. Это можно показать
совершенно так же, как выше это было сделано для рациональных х. Далее,
как и выше, пользуясь формулой
а* — а* = а* (ах-а—\)9
мы можем показать, что ах —* а'а при х—><*, что и дает непрерывность ах
при любом вещественном х.
Нетрудно проверить, что все основные свойства показательной функции
справедливы при любых вещественных показателях. Пусть, например, а и р—
два иррациональных числа и пусть х —> а и _у—- р, причем переменные х
и _у, меняясь, одновременно принимают рациональные значения. Для рацио-
рациональных показателей мы имеем
ахаУ = ах+У.
Переходя к пределу и пользуясь доказанной непрерывностью показа-
показательной функции, получим то же свойство для иррациональных показателей:
44 1 § 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ 101
Докажем еще правило перемножения показателей при возвышении сте-
степени в степень:
Если р = я есть целое положительное, то написанная формула непосред-
непосредственно вытекает из правила сложения показателей при умножении. Если
р = Б- есть рациональное положительное число, то
Для рациональных отрицательных чисел указанное правило непосредст-
непосредственно вытекает из формулы C7). Положим теперь, что р иррационально,
и пусть рациональные числа г стремятся к р. Мы имеем, по доказанному
выше,
(ау = а«
Переходя к пределу и пользуясь непрерывностью показательной функ-
функции, причем слева принимаем аа за основание, мы и получим (да)Р = я°Ф.
Прежде чем переходить к логарифмической функции, сделаем некото-
некоторые замечания об обратных функциях, о чем мы уже говорили коротко во
введении [20]. Еслиз>=/(*) — возрастающая непрерывная функция в про-
промежутке (а, Ь)у причем /(а) = А и /(?) = #, то, в силу второго свойства
непрерывных функций, при возрастании х от а до Ь через все веществен-
вещественные значения f (х) будет возрастать от А до В, проходя через все проме-
промежуточные значения. Таким образом, всякому значению у из промежутка
(Л, В) будет соответствовать определенное л: из (я, Ь)} и обратная функ-
функция х = <р (у) будет однозначной и возрастающей. Если х = х0 находится
внутри (а, Ь), уо=/(хо) и х пробегает малый промежуток (дг0 — е, л + е),
то у будет пробегать некоторый промежуток (у0 — i^, .УоЧ""^)* Обозначал
через 5 наименьшее из двух положительных чисел Yjt и yj2, мы можем утвер-
утверждать, что если у принадлежит промежутку (^0 — &, .Уо + 8)> составляющему
лишь часть промежутка (у0 — v\i, у0 + 1Гъ)» то соответствующие значения х
тем более принадлежат прежнему промежутку (лг0—-s, *0 + e), т. е.
I 9 (У) — 9 (Уо) I < е» если только \у—у01 < t. Ввиду произвольности s
это дает нам непрерывность функции х = у(у) в точке у~у0- Если х0
совпадает, например, с концом я, то в предыдущих рассуждениях вместо
(х0 — е, дго + е) надо взять промежуток (х0, л4-е)- Аналогично можно
разобрать случай убывающей непрерывной функции/(х).
Вернемся к функции C6). Раз а> 1, то а= 1 +6, где #>0, и формула
бинома Ньютона дает при целом положительном п > 1:
откуда видно, что ах беспредельно возрастает при беспредельном возраста-
возрастании х. Далее, из C7) следует, что ах —*0 при х—*• — оо. Принимая во вни-
внимание сказанное выше об обратных функциях, можем утверждать, что
функция
x = logay9 C8)
обратная C6), будет однозначной, возрастающей непрерывной функцией при
v>0. Такие же результаты получаются и для случая 0<я<1, но только
Функции C6) и C8) будут убывающими.
Введем теперь новое понятие о сложной функции. Пусть дг = /(лг) есть
Функция, непрерывная в промежутке а ^х ^Ьу причем ее значения при-
принадлежат промежутку (с, d). Пусть, далее, z=.F(y) есть функция, нсире-
102 ГЛ. 1. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ f 44
рывная в промежутке c^y^d. Понимая под у указанную выше функцию
от х, мы получим сложную функцию от х:
Говорят, что эта функция зависит от х через посредство у. Она опре-
определена в промежутке a^ix^b. Нетрудно видеть, что она будет и непре-
непрерывной в этом промежутке. Действительно, бесконечно малому приращению х
соответствует бесконечно малое приращение у в силу непрерывности f (х),
а бесконечно малому приращению у соответствует бесконечно малое прира-
приращение z в силу непрерывности F (у).
Рассмотрим теперь степенную функцию
z = хь C9)
с любым вещественным показателем Ь, причем переменную х мы считаем
положительной. Из рассуждений с показательной функцией непосредственно
следует, что функция C9) имеет определенное значение при всяком х > 0.
Пользуясь определением логарифма и применяя, например, натуральные ло-
логарифмы, мы можем написать вместо C9):
Полагая y = b\ogx и г = еУу мы можем рассматривать эту функцию как
сложную функцию от ху и непрерывность показательной и логарифмической
функций докажет нам непрерывность функции C9) при всяком л:>0.
Мы доказали выше [34] непрерывность функции sin x при всех значе-
значениях х. Так же доказывается непрерывность функции cos x при всех х. Из
формул
sin х . cos л:
tg х = , ctg х = ——
ь cos х' ь sin x
непосредственно следует [34] непрерывность tgx и ctgx при всех л*, кроме
тех, при которых знаменатель обращается в нуль.
Функция у = sin х есть непрерывная возрастающая функция в проме-
промежутке f ^-, yJ- Пользуясь сказанным выше об обратных функциях, мо-
можем утверждать, что главное значение функции х = arc sin у будет непре-
непрерывной возрастающей функцией в промежутке —1 ^д? ^ 1- Аналогично до-
доказывается непрерывность и остальных обратных круговых функций.
ГЛАВА IT
ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ
§ 3. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
ПЕРВОГО ПОРЯДКА
45. Понятие о производной. Рассмотрим движущуюся по напра-
направленной прямой линии точку. Пройденный ею путь s, отсчитываемый
от определенной точки прямой, есть, очевидно, функция времени U
s=f(t),
так что всякому определенному моменту времени t соответствует
определенное значение 5. Придадим t приращение Ь?\ и тогда но-
новому моменту времени t-\-bl будет соответствовать путь s-j-As.
В случае равномерного движения, приращение пути пропорционально
As
приращению времени, и в этом случае отношение -г- выражает по-
постоянную скорость движения. В общем случае это отношение зависит
как от выбранного момента времени t, так и от приращения М и
выражает среднюю скорость движения за промежуток времени от t
до t -\- ?d. Эта средняя скорость есть скорость воображаемой точки,
которая, двигаясь равномерно, за промежуток времени Д^ проходит
путь As. Например, в случае равномерно ускоренного движения мы
будем иметь
1Г =дГ
Чем меньше промежуток времени Д?, тем с большим правом мы
можем считать движение рассматриваемой точки за этот промежуток
времени равномерным, и предел отношения — , при стремлении Д?
104 ГЛ. И. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ I 45
к нулю, определяет скорость v в данный момент t
As
А/-*0 А* *
Так, в случае разномерно ускоренного движения
x; = lim -гг= Hm igt-j~vo~\--^-gAt\=:gt-^~vu.
Скорость v есть так же, как и путь ,9, функция от t\ функция
эта называется производной функции f(t) no t; таким образом,
скорость есть производная от пути по времени.
Положим, что некоторое вещество вступает в химическую реак-
реакцию. Количество этого вещества х, вступившее уже в реакцию
к моменту времени t, есть функция от t. Приращению времени At
будет соответствовать приращение Ах величины х> и отношение -j-
выражает среднюю скорость химической реакции за промежуток
времени At, а предел этого отношения, при стремлении At к нулю,
выражает скорость химической реакции в данный момент времени L
Отвлечемся теперь от примеров и дадим общее определение про-
производной. Положим, что функция y=f(x) определена при некотором
фиксированном значении х и при всех значениях к нему достаточно
близких, т. е. при всех значениях вида x-\-h, где h — любое поло-
положительное или отрицательное число, достаточно малое по абсолют-
абсолютному значению. Величину h называют обычно приращением незави-
независимой переменной х. Вместо h пишут часто Ах. Соответствующее
приращение функции будет: Ay=f(x-\-h)—f(x). Составим отно-
отношение этих приращений:
m
Ах~~~ h V>
Это отношение определено при всех значениях /г, достаточно малых
по абсолютной величине, т. е. в некотором промежутке — k ^ /г ^ -|- k
кроме /г = 0. Поскольку х фиксировано, отношение A) является
функцией только от h.
Определение. Если отношение A) имеет предел (конечный)
при стремлении h к нулю (/г->±0), то этот предел называется
производной функции f(x) при заданном х.
Иначе говоря, производной данной функции f(x) при заданном
значении х называется предел отношения -j~- приращения Ду функции
к соответствующему приращению Lx независимого переменного, когда
это последнее стремится к нулю (Дх->±0), если упомянутый пре-
предел существует. Для обозначения производной пишут у\ или f(x):
46 1 § 3. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ПЕРВОГО ПОРЯДКА 105
Операция нахождения производной называется дифференцированием
функции.
Дробь A) при h->±0 может и не иметь предела, и тогда
производная при заданном значении х не существует. Существование
предела /'(х) равносильно следующему [32]: при любом заданном
числе е^>0 существует такое число ?]^>0, что
е, если\к\<т[ п
Предполагая, что производная существует, можем написать
где р -> 0 при h->±0. Далее, имеем
откуда следует, что f(x~\-h)—/(•*)-> 0 при h->±0, т. е. если
при некотором значении х производная f (х) существует, то
при этом значении х функция f(x) непрерывна. Обратное утверж-
утверждение неправильно, т. е. при непрерывности функции при заданном х еще
нельзя утверждать, что при этом значении х существует производная.
Обратим внимание на то, что при отыскании производной у не-
непрерывной функции мы имеем дробь A), у которой и числитель и
знаменатель стремятся к нулю, причем знаменатель h в нуль не обра-
обращается. Отметим один частный случай. Если у = сх, то числитель
дроби есть c{x-\-h) — cx = ch, а вся дробь равна с, т. е. не зависит
от h. Ее предел при h -> ± 0 также равен с.
При фиксированном х значения f(x) и f(x) суть числа. Если
функция и производная существуют при всех х внутри некоторого
промежутка, то f'(x) является функцией от х внутри этого проме-
промежутка. В рассмотренном выше случае f(x) = cx производная f(x)
равна числу с при всех х.
46. Геометрическое значение производной. Для выяснения
геометрического значения производной обратимся к графику функ-
функции yz=zf(x). Возьмем на нем точку М с координатами (х, у) и
близкую к ней, тоже лежащую на кривой, точку N с координатами
(х-\-Ах, у-\-Ау). Проведем ординаты М{-М^\л NXN этих точек и из
точки М проведем прямую, параллельную оси ОХ. Мы будем иметь
(рис. 50):
=A> B)
Отношение -г- равно, очевидно, тангенсу угла аи образованно-
образованного секущей MN с положительным направлением оси ОХ. При
106
ГЛ. И. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ
[48
стремлении Ах к нулю точка TV будет, оставаясь на кривой, стремиться
к точке М\ предельным положением секущей MN будет касатель-
касательная МТ к кривой в точке Ж, и, следовательно, производная /г(х)
равна тангенсу угла а, образованного касательной к кривой
в точке М (х, у) с полоэюительным
направлением оси ОХ, т. е. равна
угловому коэффициенту этой ка-
касательной.
При вычислении отрезков по фор-
формулам B) надо принимать во внима-
внимание правило знаков и помнить, что
приращения Ах и Ау могут быть как
положительными, так и отрицатель-
отрицательными.
Точка N, лежащая на кривой,
может стремиться к Ж с любой
стороны. На рис. 50 мы придали касательной определенное направ-
направление. Если бы мы придали ей прямо противоположное направление,
то это привело бы к изменению угла а на величину и и не повлияло
на величину тангенса этого угла. В дальнейшем мы вернемся еще
к вопросу о направлении касательной. Сейчас для нас это несущест-
несущественно.
Мы видим таким образом, что существование производной связано
с существованием касательной к кривой, соответствующей уравнению
у=/(х), причем угловой коэффициент касательной tga=/'(jc) дол-
должен быть конечным. Иными словами, касательная не должна быть
параллельна оси ОУ. В этом последнем случае
% Зп
а= -к- или а = —.г-, и тангенс такого угла
равен бесконечности.
Непрерывная кривая может в отдельных
точках вовсе не иметь касательной или иметь
касательную, параллельную оси OY (рис. 51),
и при соответствующих значениях х функция
f(x) не имеет производной. Таких исключитель-
исключительных точек может быть сколь угодно много на кривой. Доказывается
также, что существуют такие непрерывные функции, которые не
имеют производной ни при одном значении х. Кривая, соответствую-
соответствующая такой функции, недоступна нашим геометрическим представлениям.
Остановимся несколько подробнее на тех случаях, которые пред-
представлены на рис. 51.
Предварительно введем понятия о производной справа и произ-
производной слева. Положим, что h стремится к нулю не произвольным
образом, а со стороны отрицательных значений или со стороны
положительных значений, т. е. /г-> — 0 или /г-^-j-O. Если при этом
46 1
§ 3. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ПЕРВОГО ПОРЯДКА
107
отношение A) имеет предел (конечный), то он обозначается обычно
символом fix — 0) или, соответственно, fix-\-Q) и называется
производной слева или, соответственно, производной справа. Суще-
Существование производной fix) равносильно тому, что существуют про-
производные fix — 0) и fix-\-0) и что они равны. При этом /'(.*;) =
/() + )
Если существуют различные производные f {х — 0) и f(x-\-0),
то это соответствует тому случаю, когда в соответствующей точке х
существуют слева и справа касательные, не параллельные оси ОУ
(предельные положения секущей), но эти касательные различны, т. е.
они не лежат на одной прямой, проходящей через точку с абсциссой
х. Этот случай представлен точкой My на рис. 51. В точках М% и
УИ3 отношение A) при /г-> — 0 и /z->-|-0 стремится к бесконечно-
бесконечности. Обратим внимание на знак этой бесконечности.
Для точек N, лежащих на кривой слева от Ж2, величина /г<^0 и
f{x-\-h)—f(x)<^0 при /г, достаточно близких к нулю, так как
ордината слева меньше ординаты в точке Ж2. Таким образом, в этом
случае отношение A) положительно, и при /г-> — 0 оно стремится
к (-J- со) (касательная слева параллельна оси OY). Справа от М2
величина h ^> 0 и по-прежнему f(x -\~ h) —f(x) <^ 0, т. е. отношение A)
отрицательно и оно стремится к (— со) при /г —^—]— 0. Переходим
к точке Ж3. Здесь слева /*<^0 и fix-\-h)—/(х)<^0, а справа
/г^>0 и f(x-\-h)—f(x)^>0, т. е. слева и справа отношение
A) положительно и оно стремится к
(-j-oo) как при /г~> — 0, так и при
/г —^—[—- 0, т. е. в этом случае отно-
отношение A) стремится к (-(-оо) при
/г -> ± 0.
Отметим, что при определении про-
производной мы требовали, чтобы отно-
отношение A) стремилось к конечному
пределу при h -> db 0. Если этот пре-
предел при /г -* ± 0 равен (-|- оо)- или
(— со), то мы все же не говорим, что
при соответствующем значении х су-
существует производная, равная (-)- оо)
или (— со).
Возможны, конечно, и такие точки на кривой y=f(x), в кото
рых нет и производных fix — 0) и /'(лг-j-O). Такая кривая изобра-
изображена на рис. 52. Она не имеет указанных производных при х—с.
Если непрерывная функция задана только на промежутке (я, Ь\
то при х = а мы имеем возможность образовать только правую произ-
производную /' (а + 0), а при х — Ь — только левую производную /' ф — 0).
Когда говорят, что fix) имеет в промежутке (a, b) i3auKHy-
том) производную fix), то во внутренних точках промежутка эту
У ,
и
f(c)
Рис. 52.
108 гл. и. понятие о производной и его приложения I 47
производную надо понимать в обычном смысле, а на концах проме-
промежутка в только что указанном смысле.
Если f(x) определена в промежутке (А, В), более широком, чем
(а, Ь), т. е. А <^Д и В^>Ь, и имеет внутри (Л, В) обычную про-
производную f (х), то тем более она будет производной в указанном
смысле и на промежутке (а, Ь).
47. Производные простейших функций. Из понятия производ-
производной следует, что для определения производной надо составить
приращение функции, разделить его на соответствующее прира-
приращение независимой переменной и найти предел этого отношения
при стремлении приращения независимой переменной к нулю. При-
Применим это правило к некоторым простейшим функциям.
I. у = Ь (постоянная) [12].
y = limllzA=iim 0 = 0,
h
т. е. производная постоянной равна нулю.
II. у = хп (п — целое положительное число).
i xn + nhxn~l + v 4h2xn~2 +... + hn—xn
= \\m fl_ :
= lim Г/иг* + n(n~l) hxn~* +... + Нп~Л = nxn~x.
В частности, если у = х, то j/=l. В дальнейшем мы обобщим
это правило дифференцирования степенной функции на любые значе-
значения показателя п.
/0_sinx 2 cos [x + T sm-g-
-r =hm
h-+0 n Л —О
= hm cos(x + ~l —7.— ==cos.
h smY
2
так как при стремлении ~ к нулю —^ > 1 [33].
Т
2 sin (х + т>-) sin у
= 1,т ^ = 11т
. h
.. . / , h\ Sin 2
= — lim sin [ x 4" ^y —i— = — sin x.
2
47 ] § 3. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ПЕРВОГО ПОРЯДКА 109
V. y=logx
у = lim '"к кл •*""; ~ '"а л = lim
¦_„..Ч+4)_,
так как при /г->0 переменная а = —также стремится к нулю и
a
VI. _у = си (х), где с — постоянная и и (х) есть функция от х.
, ,. си(х + Л) — си (х) ,. м(х + Л) — а (*) ,, v
у = hm —v ~ ,; — = с lim v ~ I *-?= си (х)}
h-+Q п Л-*0 п
т. е. производная от произведения постоянной величины на пере-
переменную равна произведению этой постоянной на производную от
переменного сомножителя, или, другими словами, постоянный мно-
множитель можно выносить за знак производной.
VII. j/ = loge*.
Как мы знаем, \ogax = \ogx* -. [38]. Применяя правило VI,
получим
!!
у х log а'
VIII. Рассмотрим производную от суммы нескольких функций;
для определенности ограничимся тремя слагаемыми:
у = и (х
y=Hm
h
_и Ги
A-.0 L
— w(x)
J
т. е. производная суммы нескольких функций равна сумме произ*
водных этих функций.
IX. Рассмотрим теперь производную от произведения
функций:
г _ ]im ц (x + h)v (х + h) — и (х) v (х)
л-о
НО ГЛ. II. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ [ 47
Прибавляя к числителю величину и (х -f- h) v (х) и вычитая из него
ту же величину, получим
h
1 • / I у \ v (х 4- h) — v (х) , «. , ч и (х + Л) — и (х)
= hm м(х + л) —-—!—^ — 4- hm г; (х) ——!—{¦ ^-^ =
Л-^0 П h-+Q П
т. е. для случая двух сомножителей мы показали, что производная
произведения равна сумме произведений производных каждого из
сомножителей на остальные.
Докажем справедливость этого правила для трех сомножителей,
соединяя два сомножителя в одну группу и применяя правило
к случаю двух сомножителей:
у — и (х) v (х) w (х),
У = {[и (х) v (х)] w (X)}' = [и (х) v (х)] w' (х) + w (х) [и (х) v (*)]' =
= и (х) v (х) w' (х) + и (х) 1/ (х) w (х) + и' (х) v (х) w (х).
Применяя известный метод математической индукции, нетрудно рас-
распространить это правило на случай любого конечного числа сомно-
сомножителей.
X. Пусть теперь у есть частное:
и(х)
u(x-\-h) и (х)
-/_i:^, V(X + fl)~~V(x) _
h
Вычитая и прибавляя к числителю второй из дробей произведе-
произведение u(x)v(x), получим, принимая во внимание непрерывность v(x):
*v(x)
v! (x) v (x) — v' {x) и (х)
т. е. производная дроби (частного) равна производной числителя,
умноженной на знаменатель, минус производная знаменателя,
умноженная на числитель, все разделенное на квадрат знаме-
знаменателя*
48 ] § 3. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ПЕРВОГО ПОРЯДКА Ш
XL y = tgx.
г sin х\' ( sin х)' cos л: — (cos x)' sin x cos3 x + sin2 л: 1
У \~cos~x) cos2 х cos2 х cos2 x •
XII. y = ctgx.
f cos x\' (cos x)' sin л: — ( sin x)' cos x — sin2 л: — cos2 x 1
У == \sin x). sin2x sin2 л: sin2 лг*
При выводе правил VI, VIII, IX и X мы предполагали, что функ-
функции и(х), v(x), w{x) имеют производные, и доказали существование
производной у функции у.
48. Производные сложных и обратных функций. Напомним
понятие о сложной функции [44]. Пустьy=f(x) — функция, непре-
непрерывная в некотором промежутке a^x^bf причем ее значения
принадлежат промежутку c^y^d. Пусть далее, z = F(y)— функ-
функция, непрерывная в промежутке c^y^d. Понимая под у выше-
вышеуказанную функцию от х, мы получим сложную функцию от х:
Говорят, что эта функция зависит от х через посредство у.
Нетрудно видеть, что эта функция будет непрерывна в промежутке
а^х^Ь. Действительно, бесконечно малому приращению х соот-
соответствует бесконечно малое приращение у в силу непрерывности функ-
функции f(x), а бесконечно малому приращению у соответствует беско-
бесконечно малое приращение z в силу непрерывности F(y).
Прежде чем переходить к выводу правила дифференцирования
сложной функции сделаем одно замечание. Если z = F(y) имеет
производную при у=у0, то, согласно сказанному в [45], мы можем
написать
C)
где переменная а есть функция Ау, определенная при всех Ау, до-
достаточно близких к нулю и отличных от нуля, причем а->0, если
Д_у -> 0, оставаясь отличным от нуля. Равенство C) остается спра-
справедливым для Ajy = O при любом выборе а, ибо при Aj/ = O и
А^ = 0. В силу сказанного выше естественно положить а = 0 при
Ау = 0. При таком соглашении мы можем считать, что в формуле C)
а -> 0, если Ау -> 0 любым образом, даже и принимая значение,
равное нулю. Формулируем теперь теорему о производной сложной
Функции.
Теорема. Если y = f(x) имеет в точке x = xQ производную
Р (Хц) и z = F(y) имеет в точке Уо = / (х^) производную F* (у^,
то сложная функция F (J (х)) имеет в точке х = х0 производную,
равную произведению F (у^) f (Хц).
112 гл. и. понятие о производной и его приложения [ 48
Пусть Длг — приращение (отличное от нуля), которое мы придаем
значению х0 независимой переменной х, и Ay=/(;co-f- Ад:)—/(х$)—•
соответствующее приращение переменной у (оно может оказаться и
равным нулю). Пусть, далее, Аг = F (у0 -f- Ад/) — F(y0). Производная
от сложной функции z — F(f(x)) по х при х = х0 равна, очевидно,
пределу отношения-г- при Д#-^0, если этот предел существует.
Разделим обе части C) на Длг:
При стремлении Ах к нулю и Ly -> 0, в силу непрерывности функ-
функции j/=/(.#) в точке х = хф а потому, как мы указали выше,
а->0. Отношение —• стремится при этом к производной /'(х0), и,
переходя в написанном выше равенстве к пределу, получим
что и доказывает теорему. Отметим, что непрерывность f{x) при x = xQ
вытекает из предположенного существования производной /'(лг0) [45].
Доказанная теорема может быть формулирована в виде следую-
следующего правила дифференцирования сложных функций: производная
сложной функции равна произведению производной по промежу-
промежуточной переменной на производную от промежуточной перемен-
переменной по независимой переменной:
z'x = F'(y)f(x).
Переходим к правилу дифференцирования обратных функций.
Если y=f(x) непрерывна и возрастает в промежутке (а, Ъ) (т. е.
большим значениям х соответствуют и большие у), причем A=f(a)
и B=f{b)y то, как мы знаем [21 и 44], в промежутке (Л, В) су-
существует однозначная и непрерывная обратная, также возрастающая
функция д; = ср(у). В силу возрастания, если Ал: ф 0, то и Ду ф О,
и наоборот, и в силу непрерывности из Алг~>0 следует Ау->0, и
наоборот. (Совершенно аналогично рассматривается случай убываю-
убывающих функций).
Теорема. Если f(x) имеет в точке лг0 производную f (х^),
отличную от нуля, то обратная функция <р (у) имеет в точке
_уо=/(лго) производную
h
Обозначая через Ал: и &у соответствующие приращения хну, т. е.
Д* = 9 (Уо + А.У) — ? СУо),
48
§ 3. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ПЕРВОГО ПОРЯДКА
ИЗ
и принимая во внимание, что оба они отличны от нуля, можем
написать:
Ах
Как мы видели выше, кх и Ау одновременно стремятся к нулю,
и последнее равенство в пределе и приводит к D). Доказанная тео-
теорема может быть формулирована в виде сле-
следующего правила дифференцирования обратных
функций: производная обратной функции рав-
равна единице, деленной на производную перво-
первоначальной функции в соответствующей
точке.
Правило дифференцирования обратных функ-
функций имеет простое геометрическое истолкова-
истолкование [21]. Функции х = у(у) и y=f(x) имеют Рис. 53.
один и тот же график на плоскости XOY с той
лишь разницей, что для функции х = у(у) ось независимой пере-
переменной есть ось О К, а не ОХ (рис. 53). Проводя касательную МТ
и вспоминая геометрическое значение производной, получим
причем на рис. 53 угол C, как и а, считается положительным. Но,
очевидно, Р = у— а, и, следовательно,
Если лг = ср(у) есть функция, обратная y=f(x)t то, очевидно,
и наоборот — функцию y=f(x) можно считать обратной функции
?у
Применим правило дифференцирования обратных функций к пока-
показательной функции.
XIII. ^ = 0* (а>0).
Обратная функция в данном случае будет
и, в силу VII,
т XJfJ у log a »
откуда по правилу дифференцирования обратных функций
У = , = у log а или (ax)f = о>х log a.
114 гл. и. понятие о производной и его приложения I 48
В частном случае при а = е имеем
Полученная формула, вместе с правилом дифференцирования слож-
сложных функций, даст нам возможность вычислить производную от
степенной функции.
XIV. у = хп (лг^>0; п — любое вещественное число).
Эта функция при всех х^>0 определена и имеет положительные
значения [19].
Пользуясь определением логарифма, мы можем представить нашу
функцию в виде сложной функции
Дифференцируя по правилу дифференцирования сложных функций,
получим
v = еп l°s х — = хп — = пхп~х.
•* хх
Этот результат нетрудно обобщить и на случай отрицательных зна-
значений х, если только сама функция при этом существует, например,
Применим правило дифференцирования обратных функций к на-
нахождению производных обратных круговых функций.
XV. j/ = arcsin х.
Мы рассматриваем главное значение [24] этой функции, т. е. ту
дугу, которая находится в промежутке (—у, +т)' ФУН1Ш«ИЮ ЭТУ
можно рассматривать как обратную функцию по отношению к функции
x==s'my и, согласно правилу дифференцирования обратных функций,
имеем
' _ _L — * _ 1 _ 1
причем у радикала надо брать знак (-}-)> так как cosy имеет знак
(-]-) в промежутке (—у, у). Точно так же можно получить
(arc cos x)' = — .,
У 1 — х1
причем рассматривается главное значение arc cos x, т. е. та дуга, ко-
которая заключается в промежутке @, тс).
XVI. у = arc tg x.
Главное значение arctgx заключается в промежутке ( ^-, у),
и функцию эту можно рассматривать как обратную по отношению
49 ] § 3. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ПЕРВОГО ПОРЯДКА 115
к функции x = tgy\ следовательно,
1 1 2
=y=-jl=== У==
Точно так же получим
(arc ctg x)r = — rqr~2 •
XVII. Рассмотрим еще дифференцирование функций вида:
где и и v — функции от х (степенно-показательная функция).
Мы можем написать
у = ev l°2 u,
и, применяя правило дифференцирования сложных функций, получим
Применяя правило дифференцирования произведения и дифференци-
дифференцируя log it, как сложную функцию от х, будем иметь окончательно
у = ev l°s * (v log u -f- ~ vt\
или
49. Таблица производных и примеры. Приведем таблицу всех
выведенных нами правил дифференцирования.
1. (*)' = 0.
2. (cu)' = cu'.
3. («1 + М2 + ... + ^У=«; + Г/2 + .-. + ^.
4. (щщ...uj = щщщ...un + щщщ...ия-|-.м + ЩЩЩ...it'n.
- / uY u'v — v'u
5- \т) =-^r--
6. (xny = nxn~1 и (дг)'=1.
7. i^
8. (ex)f = ex и (ax)r = ax log a.
9. (sin Ar)'=cosjtr.
10. (cos x)' = — sin #.
11. (tg at)'= —i—,
4 & ' cos2 ^ •
16 ГЛ. II. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ
12. (ctg*)'= 4—.
v & J sm2 л:
13. (arc sin л:)'= 1
V /1 — х2
14. l
15. (arctgx)f
16.
17. (w7 = то* и + г/* log и v.
18. >/i=j/i-Hi (у зависит от х через посредство и).
Применим выведенные правила к нескольким примерам.
1. у = х*—3х2 + 7х— 10.
Применяя правила 3, 6 и 2, получим
у' = 3л:я — 6л:+ 7.
о * 'з"
Применяя правило 6, получим
3. у = 5
Полагая u = sinx, применим правила 18, б и 9:
у' = 2а • и' = 2 sin л* cos л: = sin 2x.
4. у = sin (л:2).
Полагая и = х2, применим те же правила:
у1 = cos и • и' = 2х cos (^с2).
Полагая сначала и = х -\- Ухг + 1 и затем v = x2-\-\, применим два
раза правило 18, а также правила 7, 3 и 6:
У =¦
+ yV + i ' {/лг2 +1 ~Yx* 4-1'
50 ] § 3. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ПЕРВОГО ПОРЯДКА 117
п
Положим ц = 2-1-1 и пРименим правила 18, б и 5:
У1'1 (
х
7. ^ = л:*
Применяя правило 17, црлучим
у = л:-*, х -\- xx\ogx = Xх A -f-
8. Функция у задана уравнением
E)
как неявная функция от х. Требуется найти производную у.
Если бы мьт решили данное уравнение относительно у, то получили бы
yz=f(x), левая часть уравнения после подстановки у =/(лг), очевидно, обра-
обращается тождественно в нуль. Но производная от нуля как производная от
постоянной, равна нулю, а потому, если мы продифференцируем левую часть
данного уравнения но ху считая, что у есть заданная этим уравнением функ-
функция от х, то должны получить нуль:
2х . ?У , л г Ь2х
- + -^/ = 0, откуда У = -^.
В этом случае, как мы видим, у' выражается не только через х, но и
через у, но зато нам не пришлось для отыскания производной решать урав-
уравнение E) относительно у, т. е. находить явное выражение функции.
Как известно из аналитической геометрии, уравнению E) соответствует
эллипс, и найденное выражение у' дает угловой коэффициент касательной
к этому эллипсу в точке с координатами {х, у).
50. Понятие о дифференциале. Пусть Ад: — произвольное прира-
приращение независимой переменной, которое мы считаем уже не завися-
зависящим от х. Мы будем называть его дифференциалом независимой
переменной и обозначать знаком Ах либо dx. Знак этот ни в коем
случае не является произведением d на х, а служит лишь символом
для обозначения произвольной, не зависящей от х величины.
Дифференциалом функции называется произведение ее произ-
производной на дифференциал независимой переменной.
Дифференциал функции у=/(х) обозначают символом dy или
():
dy = df(x)=f(x)dx. F)
Из этой формулы естественно получается выражение производной
в виде частного двух дифференциалов:
118 гл. и. понятие о производной и его приложения \ 50
Подчеркнем, что дифференциал dx независимого переменного,
входящий в определение дифференциала функции и в формулу F),
может принимать совершенно произвольные значения. Фиксируя какое-
либо значение dxf мы по формуле F) получаем соответствующее
значение dy при заданном х. Если мы счи-
считаем dx приращением независимого перемен-
переменного xt то надо, чтобы не только х, но и
x-\-dx принадлежали промежутку, на кото-
котором определена функция. Но и при этом диф-
дифференциал функции dy не совпадает, кроме
исключительных случаев, с приращением
функции, соответствующим приращению dx
независимого переменного.
Чтобы выяснить разницу между этими
понятиями, обратимся к графику функции.
Возьмем на нем некоторую точку М(ху у)
и другую точку N. Проведем касательную МТ, ординаты, соответ-
соответствующие точкам М и N, и прямую МР параллельно ОХ (рис. 54).
Мы будем иметь
МР = ММ = Ах (или dx),
Р!\!=ку (приращение у),
отсюда
dy =f (x) dx = МР tg Z. PMQ = PQ.
Дифференциал функции изображается отрезком PQ, не совпадаю-
совпадающим с отрезком PN, который изображает приращение функции. От-
Отрезок PQ изображает то приращение, которое получилось бы, если бы
в промежутке (х} х -}- dx) мы заменили отрезок MN кривой отрезком
MQ касательной, т. е. если бы мы считали, что в этом промежутке
приращение функции пропорционально приращению независимой пере-
переменной, и коэффициент пропорциональности взяли бы равным угло-
угловому коэффициенту касательной МТ, или, что то же, равным про-
производной Г (х).
Разность между дифференциалом и приращением изображается
отрезком NQ. Покажем, что если Ах стремится к нулю, то разность
эта есть величина бесконечно малая высшего порядка по сравнению
с Их [36].
Отношение ^- в пределе дает производную, а потому [27]
50 j § д. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ПЕРВОГО ПОРЯДКА 119
где е есть величина бесконечно малая одновременно с Ах. Из этого
равенства получим
F byf{
или
Ду = dy -J-, s Дат,
откуда видно, что разность между dy и Ду равна (—еДлг). Но
отношение (—гкх) к Д.г, равное (—г), стремится к нулю вместе
с Ах, т. е. разность между dy и Ду есть величина бесконечно малая
высшего порядка по сравнению с Дх. Заметим, что знак этой раз-
разности может быть любым. На нашем чертеже и Ал: и эта разность
имеют знак (-[-)•
Формула F) дает правило нахождения дифференциала функции.
Применим его к некоторым частным случаям.
I. Если с есть постоянная, то
т. е. дифференциал постоянной равен нулю,
I1. d [си (х)] == [си (x)]r dx = си' (х) dx = c du (x),
т. е. постоянный множитель можно выносить за знак дифферен-
дифференциала.
III. d + + r
= du (x) -f- do (x) -f- dw (x)>
т. е. дифференциал суммы равен сумме дифференциалов слагаемых.
IV. d [и (х) v (х) w (х)] = [и (х) v (х) w (x)]' dx =
= v(x)w (х) и (х) dx + и (х) w (x) vr (x) dx -j- и (х) v (x) wr (x) dx =
= v(x)w (x) du (x) -\-u(x)w (x) dv (x) + и (х) v (x) dw (x)>
т. е. дифференциал произведения равен сумме произведений диффе-
дифференциалов каждого из сомножителей на все остальные сомно-
сомножители.
Мы ограничились случаем трех сомножителей. Тот же вывод
годится и для любого конечного числа сомножителей.
*. v (*) и' № dx~~u (*)v' (х) dx_
v (x) da (x) — и (х) dv (x)
— Щх)? »
т. е. дифференциал частного (дроби) равен произведению диффе-
дифференциала числителя на знаменатель минус произведение дифферен-
дифференциала знаменателя на числитель, все деленное на квадрат зна-
знаменателя.
120 ГЛ. II. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ [ 51
VI. Рассмотрим сложную функцию у=/(и), где и есть функция
от х. Определим dy, предполагая у зависящим от х:
dy =у'х dx = f (it) • и'х dx = f (u) du,
т. е. дифференциал сложной функции имеет тот же вид, какой
он имел бы в том случае, если бы вспомогательная функция и
была независимой переменной.
Рассмотрим численный пример для сравнения величины приращения
функции с се дифференциалом. Возьмем функцию
у =/(*) = хг + 2х2 + 4х + 10
и рассмотрим ее приращение
/B,01) —/B) = 2,013 + 2 • 2,012 + 4 • 2,01 + 10 — B3 + 2 . 22 + 4 .2 + Ю).
Производя все действия, получим для приращения величину
Ау =/B,01) —/B) = 0,240801.
Несравненно проще вычислить дифференциал функции. В данном случае
dx = 2>Q\—2 = 0,01 и дифференциалом функции будет
dy = (Зд:2 + 4х + 4) dx = C . 2* + 4 • 2 + 4). 0,01 = 0,24,
Сравнивая dy и Ау, видим, что они совпадают до третьего десятич-
десятичного знака.
51. Некоторые дифференциальные уравнения. Мы показали, что, заме-
заменяя в промежутке (.v, x-\-dx) приращение функции ее дифференциалом, мы
применяем закон прямой пропорциональности между приращениями функции
и независимой переменной с соответствующим коэффициентом пропорциональ-
пропорциональности, и что такая замена приводит к ошибке, которая является бесконечно
малой высшего порядка по сравнению с dx. На этом основано применение
анализа бесконечно малых к исследованию явлений природы.
Наблюдая некоторый процесс, стараются разбить его на малые элементы,
к каждому из которых, пользуясь его малостью, применяют закон прямой
пропорциональности. В пределе получают таким образом уравнение, пред-
представляющее собою соотношение между независимой переменной, функцией
и их дифференциалами (или производной). Уравнение это называется диффе-
дифференциальным уравнением, соответствующим рассматриваемому процессу.
Задача нахождения самой функции по дифференциальному уравнению есть
задача интегрирования дифференциального уравнения.
Итак, при применении анализа бесконечно малых к изучению какого-
либо закона природы, необходимо составить дифференциальное уравнение
рассматриваемого закона природы и -' проинтегрировать его. Эта последняя
задача обычно бывает гораздо труднее первой, и о ней мы будем говорить
впоследствии. В дальнейших примерах выведем дифференциальные уравнения,
соответствующие некоторым простейшим явлениям природы.
1. Барометрическая формула. Давление атмосферы р, рассчитываемое
на единицу площади, есть, очевидно, функция высоты h над поверхностью
земли. Рассмотрим вертикальный цилиндрический столб воздуха с площадью
поперечного сечения, равной единице. Проведем два поперечных сечения
А и Av на высотах h и h-\-dh. При переходе от сечения А к сечению А±
давление р уменьшится (если dh > 0) на величину, равную весу воздуха,
который заключается в части цилиндра между А и AL. Если dh мала, можем
51 1 § 3. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ПЕРВОГО ПОРЯДКА 121
приближенно считать плотность р воздуха в этой части цилиндра постоян-
постоянной. Площадь основания столбика ААХ равна единице, его высота dh и, сле-
следовательно, объем dh, а искомый вес р dh. Итак, уменьшение р (при dh > 0)
равно р dh:
dp — — р dh.
Согласно закону Бойля — Мариотта, плотность р пропорциональна давле-
давлению р:
р = ср (с — постоянная),
и мы окончательно получаем дифференциальное уравнение
dp = — ср dh или -~ = — ср.
2. Химические реакции первого порядка. Пусть некоторое вещество,
масса которого есть а} вступает в химическую реакцию. Обозначим буквою
л* ту часть этой массы, которая ужа вступила в реакцию к моменту вре-
времени t, отсчитываемому от начала реакции. Очевидно, х есть функция от t.
Для некоторых реакций можно приближенно считать, что количество веще-
вещества dx} вступившее в реакцию за промежуток времени от момента t до
момента t + dt, при малом dt пропорционально dt и количеству вещества,
которое к моменту t оставалось не вступившим в реакцию:
dx = c (а — х) dt или — = с (а — л:).
Преобразуем это дифференциальное уравнение, вводя вместо х новую
функцию у = а— л:, где у обозначает массу, которая остается не вступив-
вступившей в реакцию к моменту времени t. Принимая во внимание, что а есть
постоянная, получим
dy dx
dt dt'
и дифференциальное уравнение химических реакций первого порядка может
быть переписано в виде
d
3. Закон охлаждения. Положим, что некоторое тело, нагретое до высо-
высокой температуры, помещается в среду, имеющую постоянную температуру 0°.
При охлаждении тела его температура 0 будет функцией времени t, которое
мы будем отсчитывать от момента помещения тела в среду. Количество
тепла dQ, отданного телом за промежуток времени dt, будем приближенно
считать пропорциональным длительности dt этого промежутка и разности
температур тела и среды к моменту времени t (закон охлаждения Ньютона).
Мы можем тогда написать
dQ = c1ti dt (ct — постоянная).
Обозначив буквою k теплоемкости тела, имеем
где мы пишем знак (—), так как db в рассматриваемом случае отрицательно
(температура понижается). Сравнивая эти два выражения dQ, получим
db=*—cbdt (c^j) или ^=--^0;
122 гл. п. понятие о производной и его приложения [ 52
с есть величина постоянная, если мы будем считать теплоемкость k посто-
постоянной. Выведенные нами дифференциальные уравнения имеют одинаковую
форму. Все они выражают то свойство, что производная пропорциональна
самой функции с отрицательным коэффициентом пропорциональности (— с).
В [38] мы показали, что при непрерывных процентах с основного капи-
капитала а через t лет образуется наращенный капитал aekt, где k — процент-
процентная такса, выраженная в сотых долях:
у = aekt. G)
Вычисляя производную, получим
t ky, (8)
т. е. в этом случае мы получаем то же свойство пропорциональности произ-
производной и самой функции, благодаря чему свойство это называют законом
сложных процентов. Впоследствии мы покажем, что функция G) дает все
решения дифференциального уравнения (8) при произвольном значении
постоянной а, вместо которой будем писать С.
Таким образом, решения наших уравнений могут быть представлены
в виде (заменяя k на —с):
b(t)=Ce~cty (9)
где С—постоянная. Определим теперь физическое значение постоянной С
в каждой из предыдущих формул. Подставляя в первую из формул /г = 0,
получим
С = р@)=ро,
где р0 есть, таким образом, давление атмосферы при Л = 0, т. е. на поверх-
поверхности земли. Вторая из формул при ? = 0 даст нам
С=у(Р),
т. е. С есть масса, не вступившая в реакцию в начальный момент времени,
и ее мы раньше обозначали буквою а. Наконец, подставляя t = 0 в третью
из формул (9), убедимся также, что С есть начальная температура 60 тела
в момент его помещения в среду. Итак, окончательно имеем
p(h)==Poe-chj y(t) = aer<*t b(t) = %e~ct. A0)
52. Оценка погрешностей. При практическом определении или неточ-,
ном вычислении какой-либо величины х получается ошибка Ах, которая на-*
зывается абсолютной ошибкой или абсолютной погрешностью наблюдения
или вычисления. Она не характеризует точности наблюдения. Например,
ошибка около 1 см при определении длины комнаты практически допустима,
а такая же ошибка при определении расстояния двух близких предметов
(например, свечи от экрана фотометра) указывает на большую неточность
измерения. Поэтому вводят еще понятие об относительной погрешности,
Ал:
которая равна абсолютной величине отношения
абсолютной погреш-
погрешности к значению самой измеряемой величины.
Положим теперь, что некоторая величина у определяется из уравнения
= f(x). Ошибка Ах при определении величины х повлечет за собой ошиб-
ошибку Ау. При малых значениях Ах можно заменить приближенно Ду дифферен-
дифференциалом dy, так что относительная погрешность при определении величины^
выражается формулой
\dy
52!
§ 3. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ПЕРВОГО ПОРЯДКА
123
Примеры. 1. Сила тока i определяется, как известно, по тангенс-галь-
тангенс-гальванометру из формулы:
i = С tg ср.
Пусть tfcp — ошибка при отсчете угла ср:
с , di с , 2
/
at =
COS^cp
COS" ср • С tg ср
di
" sin 2cp "Y'
при определении i будет тем
откуда видно, что относительная ошибка
меньше, чем ближе ср к 45°.
2. Рассмотрим произведение uv:
и, следовательно,
т. е. относительная ошибка произведения не больше суммы относитель-
относительных ошибок сомножителей.
То oice правило получаем и для частного, так как
и v du — и dv
v v2 '
d 4-
d(uv)
uv
-—
d
du
и
(uv)
uv
dv
V
du
и
9
и
V
du_
и
dv^
v :
V
и
V
du
и
dv
V
3. Рассмотрим формулу для площади круга:
2nr dr
~^r =
Q
Q =
dQ = 2Tzr dr, ~^r =
Q
o dr
т. е. относительная ошибка при определении площади круга по написанной
выше формуле равна удвоенной относительной ошибке при определении
радиуса.
4. Положим, что определяется угол ср по логарифму его синуса и тан-
тангенса. Согласно правилам дифференцирования имеем
d (logl. sin Ч) = l
откуда
d (log,, tg T) =
CQS
d (log10 sincp), rf<p = l
sin cp cos cp flf (logi0 tg
A1)
Предположим, что при определении log10 sin ср и log10 tg ср мы сделали
одну и ту же ошибку (эта ошибка зависит от числа десятичных знаков
в той таблице логарифмов, которой мы пользуемся). Первая из формул A1)
Даст для rfcp величину по абсолютному значению большую, чем вторая из
формул A1), так как в первой формуле произведение log 10 - sincp делится,
а во второй формуле умножается на cos ср, а | cos ср | <с 1. Таким образом,
ири вычислении углов выгоднее пользоваться таблицей для logi0tgcp.
124 ГЛ. II. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ [ 53
§ 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
ВЫСШИХ ПОРЯДКОВ
53. Производные высших порядков. Производная f (х) функ-
функции y—f(x) есть, как мы знаем, также функция от х. Дифферен-
Дифференцируя ее, мы получаем новую функцию, которая называется второй
производной, или производной второго порядка, первоначальной
функции f(x) и обозначается так:
/', или f"(x). .
Дифференцируя вторую производную, получаем производную
третьего порядка, или третью производную:
/", или /'"(*).
Применяя таким образом операцию дифференцирования, получим
производную любого п-ro порядка у{п\ или /(л) (х).
Рассмотрим несколько примеров.
1. jf== еа'\ У = аеах, у" = а*еах,..., /п) = апеах.
2. у = (ах + Ь)\ У = ak (ах + bf'\
y" = a*k(k-\)(ax+b)k-\...,
3. Мы знаем, что
(sin х)' = cos х = sin (•# + у)» (cos лг) = — sin x = cos L*r -{- у J,
т. е. дифференцирование sin x и cos x приводится к прибавлению
числа ^у к аргументу, а потому
(sin х)" = [sin (x + !) J = sin [x + 2 у) • (*.+ l)'=sin (jp + 2-J),
и, вообще,
){n) i{ + ~^ и
A+лг)«'
б. Рассмотрим сумму функций
Применяя правилб дифференцирования суммы и считая, что соот-
соответствующие производные функций и, v и w существуют, получим
53 ] § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 125
т. е. производная любого порядка от суммы равна сумме произ-
производных того же порядка. Например,
у = ;сз_4дг2-|-7лг+10; / = 3*» — 8х + 7, /' = 6* — 8; /" = 6,
уD) = 0 и, вообще, j/(/l) = 0 при л^>3.
Таким же путем можно показать, вообще, что производная п-го
порядка от многочлена т-й степени равна О, если п^>т.
Рассмотрим теперь произведение двух функций y = uv. Применяя
правила дифференцирования произведения и суммы, получим
у = u'v -\- uv,
у" = u"v + uv + и V + uv" = u"v -f 2w V + вгЛ,
У' = «"'* + «V + 2tfV + 2и V + «V + игГ =
Мы подмечаем следующий закон составления производных: чтобы
составить производную п-го порядка от произведения uv, надо
(и -+- v)n разложить по формуле бинома Ньютона и в полученном
разложении заменить показатели степеней у и nv указателями
порядка производных, причем нулевые степени (u° = v°=l), вхо-
входящие в крайние члены разлоэюения, заменить самими функциями.
Правило это называется правилом Лейбница и символически его
записывают в следующем виде:
Докажем справедливость этого правила, пользуясь способом
доказательства по индукции. Положим, что для л-й производной
это правило справеддиво, т. е.
У> = (ii + v)W = u<n)v-f у ц^1 V + п {П~Х) u(W + ... +
+ n(n-\)...(n-k+\) u(*-*)v(k)+^% + mW. A)
Чтобы получить yin+l\ надо написанную сумму продифференцировать
по х. При этом произведение u^n~k)v{k) в общем члене суммы, со-
согласно правилу дифференцирования произведения, заменится суммой
u(n~k+\)v(k) _i_u{n-k)v(k+i)a j^0 B символических обозначениях эту сумму
можно написать в виде
un-kvk(u-\-v).
Действительно, раскрывая скобки и заменяя показатели степеней
указателями порядка производных, мы и получим сумму и<л-*+1Мл*-|-
4- ?/(«-*V*+iL jy^bI ВИДИМ) таким образом, что для получения д/(л+1)
надо каждое слагаемое в сумме A), а потому и всю эту сумму,
126 гл. и. понятие о производной и его приложения [ 54
помножить символически на (u-\-v), и, следовательно,
= (и + ()
Мы показали, что если правило Лейбница справедливо для неко-
некоторого п, то оно справедливо и для (я-f-l). Но непосредственно мы
убедились, что оно справедливо для п=1, 2 и 3, а следовательно,
оно справедливо и для всех значений п.
Рассмотрим в качестве примера
и найдем уП00):
1^
(За:8 — l)"f + - - - + ^ (Зл:2—
+ ; (g
1 • Z ¦ о
Все производные многочлена второй степени, начиная с третьей, равны
тождественно нулю и (ех){п) =ех, вследствие чего мы получим
у юо) = ех (Зх2 — 1) + 10О?* • 6л: + 4950^ -6 = ех (Зх2 + 6Q0x + 29 699).
54. Механическое значение второй производной. Рассмотрим
прямолинейное движение точки:
где, как всегда, t есть время и 5 — путь, отсчитываемый от опреде-
определенной точки прямой. Дифференцируя один раз по t> получим ско-
скорость движения:
Составим вторую производную, которая представляет собою
предел отношения -^ при стремлении А^ к нулю. Отношение ~
характеризует быстроту изменения скорости за промежуток времени
Д? и дает среднее ускорение за этот промежуток времени, а предел
этого отношения при стремлении td к нулю дает ускорение w рас-
рассматриваемого движения в момент времени t:
w=f"(t).
Положим, что f(i) есть многочлен второй степени:
s = at*-{-bt 4-с, v = (lat-{-by w = 2a,
т. е. ускорение w постоянно и коэффициент а = у w. Подставляя
? = 0, получим b = v0, т. е. коэффициент & равен начальной скорости,
и c = sQ, т. е. с равно расстоянию точки в момент времени ? = 0
от начала координат на прямой. Подставляя найденные значения а,
b и с в выражение для 5, получим формулу для пути в равномерно
55 ] § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 127
ускоренном (w^>0) или равномерно замедленном (w<^0) движении:
Вообще, зная закон изменения пути, мы можем, два раза диффе-
дифференцируя по t, определить ускорение w, а следовательно, и силу /,
производящую движение, так как, согласно второму закону Ньютона,
f=niw> где т — масса движущейся точки.
Все сказанное годится лишь для прямолинейного движения.
В случае криволинейного движения, как доказывается в механике,
f (t) дает лишь проекцию вектора ускорения на касательную к тра-
траектории.
Рассмотрим для примера случай гармонического колебательного
движения точки М, когда расстояние 5 этой точки от некоторой
определенной точки О на прямой, по которой движется трчка М,
определяется по формуле:
2
= a sin ( —
где а — амплитуда, т — период колебания и со — фаза суть величины
постоянные. Определим, дифференцируя, скорость v и силу /:
2па /2л , , \ г 4л2т . /2л . , \ 4ъ2т
v — — cos — t -4- со , / = mw = 2— a sin — t -4- to = — 5,
т. е. сила по величине пропорциональна длине отрезка ОМ и на-
направлена в противоположную сторону. Иными словами, сила направ-
направлена всегда от точки М к точке О и пропорциональна удалению
точки М от точки О.
55. Дифференциалы высших порядков. Введем теперь понятие
о дифференциалах высших порядков функции y=f(x). Ее диффе-
дифференциал
dy=f(x)dx
является, очевидно, функцией от лг, но не надо забывать при этом,
что дифференциал независимой переменной dx считается уже неза-
независящим от х [50] и при дальнейшем дифференцировании выносится
за знак производной как постоянный множитель. Рассматривая dy
как функцию от х, можно составить дифференциал этой функции;
он называется дифференциалом второго порядка первоначальной
функции f(x) и обозначается символами d*y, или d2f(x):
dly = d {dy) = [/' {x) dx]' dx =/" (x) dx\
Составляя опять дифференциал полученной функции от х, придем
к дифференциалу третьего порядка:
d'y = d (d2y) = [/" (х) dx*$ dx =/'" (x) dx*
128 гл. и. понятие о производной и его приложения [ 56
и, вообще, составляя последовательно дифференциалы, придем к поня-
понятию о дифференциале п-го порядка функции f{x) и получим для
него выражение:
dnf\x\ или dny=f^n)(x)dxn. B)
Эта формула позволяет представить производную п-го порядка
в виде частного:
/°°(*)=g. C)
Рассмотрим теперь случай сложной функции у=/(и), где
и — функция некоторой независимой переменной. Мы знаем [50],
что первый дифференциал этой функции имеет тот же вид, как
и в том случае, когда и — независимая переменная:
dy=f(u)du.
При определении дифференциалов высших порядков мы получим
формулы, отличные по виду от формулы B), ибо мы не имеем уже
права считать du величиной постоянной, так как и не является
независимой переменной. Так, например, для дифференциала второго
порядка будем иметь, применяя правило для нахождения дифферен-
дифференциала произведения, выражение
d*y = d [f (и) du] = du d [f(u)} +/' (и) d (du) =/" (a) du% +/'(«) d\
которое содержит, по сравнению с формулой B), добавочное
слагаемое f(u)dhu
Если и есть независимая переменная, то du надо считать величи-
величиной постоянной и d2u = 0. Положим теперь, что и есть линейная
функция независимой переменной t> т. е.
u = at-\-b.
При этом du = a dty т. е. du есть опять величина постоянная, а по-
потому дифференциалы высших порядков сложной функции будут
выражены по формуле B):
dnf(u)=fin)(u)diin9
т. е. выражение B) для дифференциалов высших порядков годится
в том случае, если х есть независимая переменная или линейная
функция независимой переменной,
56. Разности функций. Обозначим буквою h приращение независи-
независимой переменной. Соответственное приращение функции y=f(x) будет
D)
Его называют иначе разноетью первого порядка функции f(x).
Эта разность есть, в свою очередь, функция от х} и мы можем найти
56 ] § <*. производные и дифференциалы высших порядков 129
разность этой функции, вычисляя значение этой функции при
x-\-h и х и вычитая из первого результата второй. Эта разность
называется разностью второго порядка первоначальной функции f (х)
и обозначается символом At2y. Нетрудно выразить А'2у через значения
самой функции f(x)\
tfy = A (Ay) = \f(x-\- 2А) -f(x + h)\ — [f(x + h) - f(x)} =
E)
Эта разность второго порядка также есть функция от лг, и, опре-
определяя разность этой функции, получим разность третьего порядка
t^y первоначальной функции f(x). Заменяя в правой части равен-
равенства E) х на jc —j— Л и вычитая из полученного результата правую
часть равенства E), будем иметь выражение для Д3у:
А3у = \/(х + ЗА) - 2/(лг + 2/г) + f(k + h)\ -
-[/(*+2ft) —2/(* +A)+ /(*)] =
А^ + А) —
Таким образом, можно последовательно определить разность
любого порядка, и разность п-го порядка Алу будет иметь следую-
следующее выражение через значения функции f(x):
+ ... + (-l)V(x). F)
Выше мы убедились в справедливости этой формулы при п— 1, 2
и 3. Для ее полного доказательства надо применить обычный способ
доказательства от п к (лг -|— 1). Заметим, что для вычисления Апу
надо знать {п-\-\) значения функции f(x) при значениях аргумента:
х, лг-f-A, x-f-2/z,..., x-\-nh. Эти значения аргумента образуют
арифметическую прогрессию с разностью /г, или, как говорят, являются
равноотстоящими значениями.
При малых значениях h = dx разность Ау мало отличается от диф-
дифференциала dy. Точно так же разности высших порядков будут давать
приближенные значения дифференциалов соответствующих порядков,
и наоборот. Если, например, функция задана таблично при равно-
равноотстоящих значениях аргумента, то мы, не имея аналитического
выражения функции, не в состоянии точно вычислить значения
ее производных различных порядков, но вместо точной форму-
лы C) можем получить приближенное значение производных, вы-
вычисляя отношение -т-^. Составим для примера таблицу разностей и
130
ГЛ. II. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ
[56
дифференциалов функции у = х3 в промежутке B, 3), принимая:
Дат = А = 0,1.
Для составления этой таблицы были вычислены последователь-
последовательные значения функции у = хъ> из них при помощи вычитания,
согласно формуле D), были получены значения Aj/, из них также
при помощи вычитания получились значения А2у и т. д. Такой спо-
способ последовательного вычисления разностей, конечно, проще, чем
вычисление по формуле F). Дифференциалы вычисляются по извест-
известным формулам, указанным наверху таблицы, причем надо положить
с/* = А = 0,1.
X
2
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3
У
8,000
9,261
10,648
12,167
13,824
15,625
17,576
19,683
21,952
24,389
27,000
1,261
1,387
1,519
1,657
1,801
1,951
2,107
2,269
2,437
2,611
— ¦
№у
0,126
0,132
0,1 за
0,144
0,150
0,156
0,162
0,168
0,174
—
—
0,006
0,006
0,006
0,006
0,006
0,006
0,006
0,006
—
—
My
0
0
0
¦fi
0
0
0
—
—
—
dy=3x^dx
:
1,200
1,323
1,452
1,587
1,728
1,875
2,028
2,187
2,352
2,523
—
rf2y =
= 6xdx2
0,120
0,126
0,132
0,138
0,144
0,150
0,156
0,162
0,168
—
—
d3y=6dx3
0,006
0,006
0,006
0,006
0,006
0,006
0,006
0,006
—
—
—
d*y = 0
0
0
0
0
0
0
0
—
—
—
—
Сравним точное и приближенное значения второй производной у9
при х=2. В рассматриваемом случае у" = 6х и /'=12 прилг=2.
Приближенно эта производная выражается отношением -р-, и при
х = 2 мы получим
0,126
;=12Д
Если f(x) есть многочлен от х:
= f(x) = а
то, вычисляя Ду по формуле D), получим для Ау выражение в виде
целого многочлена (т—1)-й степени со старшим членом maQhxm~l>
что нетрудно проверить. Таким образом, в случае у = х'6> Ау будет
многочленом второй степени от х, Ь?у — многочленом первой сте-
степени, А3у — постоянной и А4у — нулем (см. таблицу). Предлагаем
читателю в качестве упражнения показать, что значения d?y должны
в рассматриваемом примере на одну ступень запаздывать но сравне-
сравнению с А2;/, что видно из таблицы.
57 J § 5. приложение к изучению функций 131
§ 5. ПРИЛОЖЕНИЕ ПОНЯТИЯ О ПРОИЗВОДНОЙ
К ИЗУЧЕНИЮ ФУНКЦИЙ
57. Признаки возрастания и убывания функций. Знание про-
и?водной дает возможность изучать различные свойства функций. Мы
начнем с наиболее простого и основного вопроса, а именно с во-
вопроса о возрастании и убывании функции.
функция f{x) называется возрастающей в некотором проме-
промежутке, если в этом промежутке большим значениям независи-
независимой переменной соответствуют и большие значения функции,
т. е. если
при й>0.
Наоборот, если мы имеем:
при й>0,
то функция называется убывающей.
Если мы обратимся к графику функции, то промежутки воз-
возрастания будут соответствовать тем частям графика, на которых
большим абсциссам соответствуют и большие ординаты. Если мы,
как это сделано на рис. 55, направим ось ОХ вправо и ось OY
наверх, то промежутку возрастания у
функции будут соответствовать та-
такие части графика, что при движе-
движении вдоль кривой вправо в направ-
направлении возрастающих абсцисс мы
подымаемся вверх. Наоборот, проме-
промежуткам убывания соответствуют ча-
части кривой, опускающиеся вниз при
движении вдоль кривой вправо. На
рис. 55 часть графика АВ соответ-
соответствует промежутку возрастания, а
часть ВС— промежутку убывания.
Из чертежа непосредственно ясно,
что на первом участке касательная
образует с направлением оси ОХ угол а, отсчитываемый от оси ОХ
до касательной, тангенс которого положителен. Но тангенс этого
угла есть как раз первая производная f (х). Наоборот, на участке ВС
направление касательной образует с направлением ОХ угол а (в
четвертой четверти), тангенс которого отрицателен, т. е, для этого
случая Г(х) будет величиной отрицательной. Сопоставляя получен-
полученные результаты, мы приходим к следующему правилу: те проме-
промежутки, в которых Г(х)^>0, суть промежутки возрастания
Функции, а те промеоюутки, в которых f'(x)<^Q, суть проме-
промежутки убывания функции.
Рис. 55.
132 ГЛ. II. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ [ 57
Мы пришли к этому правилу, пользуясь чертежом. В дальней-
дальнейшем дадим для него строгое аналитическое доказательство. Сейчас же
мы применим полученное правило к некоторым примерам.
1. Докажем неравенство
Xs
sin х >jc —^- при х > 0.
Для этого составим разность
/(x)= sin x—ix —-g-j.
Определим производную /' (х):
Принимая во внимание, что по абсолютной величине сама дуга больше
своего синуса, можем утверждать, что f'(x)>0 в промежутке @, +оо),
т. е. в этом промежутке / (х) возрастает, но /@) = 0, и потому
= sin л: — (* —^)>° ПРИ
т. е.
л:8
sin х > х ~- при х > 0.
2. Точно так же можно доказать неравенство
x>log A+*) при л->0.
Составим разность
f(x) = x — log
откуда
Из этого выражения видно, что при х >¦ 0 и /' (х) "> О, т. е. f (х) возра-
возрастает в промежутке @, +оо), но/@) = 0, и, следовательно,
f(x) = x — log(l+jc)>0 при *>0,
т. е.
х > log A + х) при х > 0.
3. Рассмотрим уравнение Кеплера, о котором мы говорили в [31]:
х = q sin x + а @ <; q <. 1).
Мы можем переписать его в виде
f(x) = x — q sin л: — а = 0.
Составляя производную /' (л:), получим
/' (х) = 1 — <7 cos х.
Принимая во внимание, что произведение q cos x по абсолютному значе-
значению меньше единицы, так как по условию q заключается между нулем
57
§ 5. ПРИЛОЖЕНИЕ К ИЗУЧЕНИЮ ФУНКЦИЙ
133
и единицей, можем утверждать, что /'(л*) > 0 при любом значении х,
а потому f (х) возрастает в промежутке (—оо, + оо) и, следовательно, не
может обратиться более одного раза в нуль, т. е. уравнение Кеплера не
может иметь более одного вещественного корпя.
Если постоянная а кратна тс, т. е. a = kTi, где k — целое число, то, непо-
непосредственно подставляя л- = /гтс, получим f(kn)=0J и x = kn будет един-
единственным корнем уравнения Кеплера. Если а не кратно тс, то можно найти
такое целое число k, что
kn < fl< (k+ 1)тс.
Подставляя x = kn и (& + 1)тс, получим
/ (kn) = kn — а < О,
/ (k+Тк) = (к + 1) тс — а > 0.
Но если /(/№) и /(&+ 1тс) разных знаков, то /(х) должно обращаться в нуль
внутри промежутка (kn, k + 1тс) [35], т. е. внутри этого промежутка будет
находиться единственный корень уравнения Кеплера.
4. Рассмотрим уравнение
/ (х) = Зл'5 — 25л:8 + 60лг+ 15 = 0.
Составим производную /' (л*) и приравняем ее нулю:
f (х) = 15л:4 — 75л:2 + 60= 15 (х* — 5х2 + 4) = 0.
Решая это биквадратное уравнение, получим, что /' (л*) обращается
в нуль при
* = —2, —1, +.1 и +2.
Таким образом, весь промежуток (—оо, +оо) мы можем разбить на
пять промежутков:
(-оо, -2), (-2, -1), (-1, 1), A, 2), B, +оо),
внутри которых/'(л:) сохраняет уже неизменный знак, а потому /(лг) ме-
меняется монотонно, т. е. или возрастает или убывает, и не может поэтому
внутри' каждого из этих промежутков иметь более одного корня. Если на
концах какого-либо из этих промежутков f (х) имеет разные знаки, то
уравнение f (х) = 0 имеет внутри такого промежутка один корень, а если
эти знаки одинаковые, то внутри соответствующего промежутка корней нет.
Таким образом, для определения числа корней уравнения остается опре-
определить знаки f (х) на концах каждого из пяти указанных промежутков.
Для определения знака f (х) при л: = ±;оо представим f (х) в виде
При стремлении х к (— оо), f(x) стремится к (—оо), ибо л:5 при этом
стремится к (— оо), а выражение, стоящее в круглых скобках, — к 3. Точно
так же убедимся в том, что при стремлении х к (+оо) и f (х) стремится
к (+оо). Подставляя значения л: = — 2, — 1, 1 и 2, получим следующую
таблицу:
Л*
f(x)
— оо
—
— 2
—
— 1
—
1
+
2
_)_
+
134
ГЛ. П. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ
58
Оказывается, что / (х) имеет разные знаки только на концах промежутка
(— 1, -|- 1), и, следовательно, рассматриваемое уравнение имеет только один
вещественный корень, заключающийся внутри этого промежутка.
Выше мы определили возрастание и убывание функции в проме-
промежутке. Иногда говорят, что функция возрастает или убывает в точке
x = Xq. Это значит следующее: функция возрастает при x = xQy
если f(x)<^f(Xo) при х<^х0 и f(x)^>f(x0) при х^>х0, причем х
считается достаточно близким к х0. Аналогично определяется убыва-
убывание функции в точке. Из понятия производной непосредственно
вытекает достаточное условие возрастания и убывания в точке лго>
а именно, если /' (хо)^>О, то функция возрастает в точке xQ,
и если f'(xQ)<^0y то функция убывает в точке xQ. Действительно,
если, например, Г(Хо)^>0, то отношение
имеющее предел Г(Хц\ будет также положительным при
всех /г, достаточно малых по абсолютной величине, т. е. числитель
и знаменатель будут одинаковых знаков. Иначе говоря, будет:
/ —/С*о)>О при /г>0 и /(лто + А)— /(*о)<° ПРИ
что и дает возрастание в точке лт0.
68. Максимумы и минимумы функций. Обратимся вновь к рас-
рассмотрению графика некоторой функции f{x) (рис. 56). На этом
графике мы имеем последовательное чередование промежутков воз-
возрастания и убывания функции. Дуга АМХ
соответствует промежутку возрастания.
Следующая за ней дуга МхМг — проме-
промежутку убывания, следующая 7И.2Ж3 — опять
промежутку возрастания и т. д. Те точки
кривой, которые отделяют промежутки
возрастания от промежутков убывания,
являются вершинами кривой. Рассмотрим,
. х например, вершину Mv Ордината в этой
вершине больше всех ординат кривой,
достаточно близких к рассматриваемой и
лежащих как слева, так и справа от нее.
Говорят, что такой вершине соответствует максимум функции f(x).
Это приводит к следующему общему аналитическому определению:
функция f(x) достигает максимума в точке х = хъ если ее зна-
значение /(хг) в этой точке больше всех ее значений в ближайших
точках, т. е. если приращение функции
А]
Рис. 56.
при всяких h как положительных, так и отрицательных, доста-
достаточно малых по абсолютному значению.
58 ] § 5. приложение к изучению функций 135
Обратимся к рассмотрению вершины УИ2. В этой вершине, наоборот,
ордината меньше всех соседних с ней ординат, лежащих как слева,
так и справа, и говорят, что этой вершине соответствует минимум
функции; аналитическое определение будет: функция f {х) достигает
минимума в точке х = хъ если
при всяких h, как положительных, так и отрицательных, доста-
достаточно малых по абсолютному значению.
Из чертежа мы видим, что как в вершинах, соответствующих
максимуму функции, так и в вершинах, соответствующих минимуму,
касательная параллельна оси ОХ, т. е. ее угловой коэффициент /' (х)
равен нулю. При этом предполагается, конечно,
что касательная и тем самым производная су-
существуют. Но параллельность касательной
оси ОХ может иметь место и не только в вер-
Ук Г(х)>0
м
f'(x)>0
шинах кривой. Так, например, на рис. 57 мы
имеем точку кривой Ж, которая не является
вершиной и в которой все же касательная парал-
параллельна оси ОХ. Рис. 57.
Положим, что Г(х) обращается в нуль при
некотором значении х = х0, т. е. в соответствующем месте графика
касательная параллельна оси ОХ. Исследуем знак f'(x) при зна-
значениях х, близких к х0. Рассмотрим следующие три случая.
I. При значениях х, меньших х0 и достаточно близких к дг0, f'(x)
положительна, а при значениях х, больших х0 и достаточно близких
к -^о» f (х) отрицательна, т. е., иными словами, /'(х) при переходе х
через х0 переходит через нуль от положительных значений к отри-
отрицательным.
В этом случае мы имеем слева от х = х0 промежуток возрастания
и справа—промежуток убывания, т. е. значению х = х0 соответ-
соответствует вершина кривой, дающая максимум функции f(x) (рис. 56).
II. При значениях лг, меньших хОу Г (х) отрицательна, а при
значениях х, больших дг0, положительна, т. е. /'(х) при переходе
через нуль идет от отрицательных значений к положительным.
В этом случае слева от точки х = х0 мы имеем промежуток убы-
убывания, а справа — промежуток возрастания, т. е. значению х = х9
соответствует вершина кривой, дающая минимум функции (рис. 56).
III. При значениях х как меньших, так и больших х& /' (х) имеет
один и тот же знак. Положим, например, что это есть знак (-]-)•
В этом случае соответствующая точка графика лежит внутри
промежутка возрастания и вовсе не является вершиной (рис. 57).
Сказанное приводит нас к следующему правилу нахождения тех
значений х, при которых f(x) достигает максимума или минимума;
1) нужно составить Г(х)\
136
ГЛ. II. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ
J58
2) найти те значения х, при которых f (x) обращается в нуль,
т. е. решить уравнение f'(x) = 0;
3) исследовать изменения знака Г(х) при переходе через эти
значения по следующей схеме:
X
f'(x)
x0— h
i
x0
0
*. + *
i
максимум
минимум
возрастает
убывает
Обозначения х0 — h и xQ-{-h в приведенной таблице показывают,
что нужно определить знаки функции f(x) при значениях х> мень-
меньших и больших дг0, но достаточно близких, так что h считается
достаточно малым положительным числом.
При этом исследовании предполагается, что /'(дго) = О, но при
всех х, достаточно близких к лг0 и отличных от xQi fix) отлична
от нуля.
Обратим еще внимание, что в случае рис. 57 касательная
в точке М с абсциссою дг0 находится по разные стороны от кривой
в окрестности этой точки. В данном случае f'(xo) = Q и f'(x)^>0
при всех х, близких к х0 и отличных от xQ, и весь участок кривой
с точкой х0 внутри дает промежуток возрастания, несмотря на то,
что/'(*о) = 0.
Иногда вместо указанного выше определения максимума дают
несколько другое, а именно: функция f(x) достигает максимума
в точке х = Х\у если ее значение f(xx) в этой точке не меньше ее
значений в ближайших точках, т. е. если приращение функции
f(xx-{-h) — f(xi)^0 при всяких h, как положительныхУ так и
отрицательных, достаточно малых по абсолютной величине.
Аналогично минимум в точке х% можно определить неравенством
f(x%-\-h)—/(х2)^0. Если при этом определении функция имеет
в точке максимума или минимума производную, то эта производная
должна, как и выше, обращаться в нуль.
Рассмотрим пример. Пусть требуется найти максимумы и минимумы
функции
f(x) = (x-l)*(x-2)\
Составим первую производную
— 7) = 5 (*-!)(* —
58
§ 5. ПРИЛОЖЕНИЕ К ИЗУЧЕНИЮ ФУНКЦИЙ
137
Из последнего выражения видно, что /' (х) обращается в нуль при сле-
следующих значениях независимой переменной: xL = \, х2 = -^- и х3 = 2.
Переходим к их исследованию. Прил;=1 множитель (х — 2J имеет знак
плюс, множитель 1х ^-) —знак минус. При всех значениях х как меньших,
так и больших единицы, но достаточно близких к единице, знаки этих множи-
множителей будут те же самые и, следовательно, произведение этих двух множите-
множителей имеет безусловный знак,минус при всех значениях х, достаточно близ-
близких к единице. Обратимся, наконец, к рассмотрению последнего множителя
(х—1), который как раз обращается в нуль при лг=1. В случае х < 1
он имеет знак минус, а при х > 1—знак плюс. Таким образом, все произ-
произведение, т. е. /' (х), имеет при х < 1 знак плюс и при х > 1 знак минус.
Откуда следует, что значению х=\ соответствует максимум функции/(л:).
Подставляя значение jc = 1 в выражение самой функции f (х), мы получим
величину найденного максимума, т. е. ординату соответствующей вершины
графика функции
Повторяя аналогичные рассуждения и для остальных значений лг2 = -^
и л*3 = 2, мы получим следующую табличку:
X
f(x)
fix)
\—h
+
возр.
1
0
0
макс.
1+Л
—
i-
—
убывает
7
5
0
108
3125
миним.
+
2 —Л
+
2
0
2 + Л
+
возрастает
В указанном нами способе исследования максимумов и миниму-
минимумов функции представляется несколько затруднительным, особенно
в более сложных примерах, определение знака /''(х) при значениях.*;
как меньших, так и больших испытуемого. Во многих случаях этого
можно избегнуть, если ввести в рассмотрение вторую производную
f" {х). Положим, что нам надо испытать значение x = xQt при кото-
котором /'(jco) = O. Подставим это значение х = х0 в выражение второй
производной и положим, что мы получили положительную величину,
т. е. /"(Хо)^>О. Если принять f{x) за основную функцию, то f"(x)
будет ее производной и положительность этой производной в точке
x = Xq показывает, что сама основная функция Г (х) возрастает
в соответствующей точке, т. е. Г(х) при переходе через нуль
в точке х = Хъ должна идти от отрицательных значений к положи-
положительным. Таким образом, в случае f" (х0)^>0 в точке х = х^ функ-
Ция f(x) будет достигать минимума. Точно так же можно
показать, что в случае Г(х0)<^0 в точке х = хо функция f(x)
достигает максимума. Если, наконец, при подстановке х=х0
138
ГЛ. ТТ. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ
58
в выражение /" (х) мы получим нуль, т. е. /" (хо) = О, то пользование
второй производной не дает возможности исследовать значение
x = xQ> и приходится обращаться к непосредственному исследованию
знака Г {х). Мы получаем, таким образом, изображенную в таблице
схему:
X
f W
0
Г (х)
+
0
максимум
минимум
сомнительный случай
Из приведенных рассуждений непосредственно следует, что при
наличии производной второго порядка необходимым условием мак-
максимума является неравенство f"(x)^0, а необходимым условием
минимума — неравенство /"(je)^O. При этом мы можем определять
максимум условием f(xx -\- h) —f(x^) ^ О и минимум — условием
f(x<i-\-h)—/(х2)^0, как мы об этом говорили выше.
Пример. Требуется найти максимумы и минимумы функции
/ (х) = sin х + cos x.
Эта функция имеет период 2тг, т. е. не меняется при замене х на х-\-2%.
Достаточно исследовать промежуток изменения х от 0 до 2гс. Составим
производные первого и второго порядка
/' (л:) == cos a: — sin x, f" (х) = — sin х — cos x.
Приравнивая первую производную нулю, получим уравнение
cos х — sin x = 0 или tg х = 1.
Корни этого уравнения из промежутка @, 2л) будут
Исследуем эти значения х по знаку /" (х):
=— sin ~ — cos -?• = — V~2 < 0; максимум /(-?-) = V%
f"[-r) = —sin ~— cos-^ = уг2">0; минимум /f-^j = — Y%
В заключение обратим внимание на одно обстоятельство, которое
иногда имеет место при нахождении максимумов и минимумов. Может
случиться, что на графике функции имеются такие точки, в которых
касательной или вовсе нет или она параллельна оси ОY (рис. 58).
В точках первого рода производная Г (х) вовсе не будет суще-
59 I § 5. приложение к изучению функций 139
ствовать, а в точках второго рода она будет равна бесконечности,
так как угловой коэффициент прямой, параллельной оси О К, равен
бесконечности. Но, как непосредственно видно из чертежа, в таких
точках может встретиться максимум или минимум функции. Таким
образом, мы должны, строго говоря, до-
полнить предыдущее правило нахождения
максимумов и минимумов следующим ука-
указанием: максимум и минимум функции
f(x) может встретиться не только
в тех точках, где f (х) обращается в
нуль, но и в тех точках, где она не
существует или обращается в беско- у)
нечность. Исследование таких точек надо рис>
производить по первой из схем, указан-
указанных выше, а именно—г путем определения знака f (х) при значе-
значениях, меньших и больших исследуемого.
Во всем предыдущем мы занимались простейшим случаем непре-
непрерывной функции f(x) с непрерывной производной, имеющей конеч-
конечное число нулей в исследуемом промежутке. При последнем заме-
замечании отсутствие производной допускается также в конечном числе
точек. Вообще настоящий и следующие два параграфа имеют целью
быть наглядным введением в исследование свойств функций. Далее
мы вернемся к строгому аналитическому изложению.
Пример. Требуется найти максимумы и минимумы функции
f(x) = (x-\)^x~2.
Составим первую производную
2
Она обращается в нуль при х = -^- и в бесконечность при х = 0.
Исследуем последнее значение: числитель написанной выше дроби имеет при
х = 0 знак минус и при всех значениях ху как больших, так и меньших
нуля, но близких к нему, он будет иметь хот же знак. Знаменатель дроби
при х <с 0 имеет знак минус, а при х>>0 знак плюс. Следовательно, вся
Дробь имеет при х < 0 и близких к нулю знак плюс, а при х > 0 — знак
2
минус, т, е. при л: = 0 мы имеем максимум /@) = 0. В точке х = -g- будем
иметь минимум
T 3 у-90
20
B\ 3 V/T 3
59. Построение графиков. Разыскание максимумов и минимумов
Функции f(x) существенным образом облегчает построение графика
140
ГЛ. II. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ
! 59
этой функции. Выясним на некоторых примерах простейшую схему
построения графиков функций.
1. Пусть требуется построить график функции
У __. /д- 1 J (л: 2K
исследованной нами в предыдущем номере. Мы получили там две вершины
этой кривой, а именно, максимум A, 0) и минимум f-^-, —41W) • 0™стим
эти точки на чертеже. Кроме того, полезно отметить и следы искомой кривой
у на осях. При jc = O мы имеем у = — 8, т. е. след
' на оси ОУ будет у = — 8.
Приравнивая у нулю, т. е.
(х — IJ (х — 2K = 0,
мы получим следы на оси ОХ. Один из них, лг=1,
как мы уже выяснили, является вершиной, а дру-
другой, х = 2, как это было выяснено в предыдущем
номере, вершиной не является, но в соответствую-
*-Х щей точке графика касательная параллельна оси
ОХ. Искомая кривая изображена на рис. 59.
2. Вычертим кривую
Составим первую производную
У = — 2хё~~ х .
Приравнивая у' нулю, получим значение лг = О, ко-
которому, как нетрудно видеть, соответствует верши-
вершина (максимум) кривой с ординатой у=\. Эта же
Рис. 59. точка дает и след кривой на оси ОК. Приравнивая
у нулю, получим уравнение ё~х =0, которое не
имеет решений, т. е. следов на оси ОХ кривая не имеет. Заметим, кроме
того, что при стремлении х к (+оо) или (—оо) показатель степени у е~~*
стремится к (—ос), и все выражение стремится к нулю, т. е. при беспре-
-2fi -1? -
10
дельном удалении направо и налево кривая беспредельно приближается к
оси ОХ. Соответствующая всем полученным данным кривая изображена на
рис. 60.
3. Построим кривую
59 I § 5. ПРИЛОЖЕНИЕ К ИЗУЧЕНИЮ ФУНКЦИЙ HI
которая дает график так называемого затухающего колебания. Множитель
sin bx по абсолютному значению не превышает единицы, и вся кривая будет
расположена между двумя кривыми
у = егах и у = — е~ах.
При стремлении х к (+оо) множитель е~ах, а следовательно, и все про-
произведение е~ах sin bx будет стремиться к нулю, т. е. при беспредельном уда-
удалении направо кривая будет безгранично приближаться к оси ОХ. Следы
кривой на оси ОХ определятся из уравнения
sin bx = 0,
т. е. будут
х = -г (k — целое число).
Определим первую производную
у = — ае~ах sin bx + be~ax cos bx = e~ax (b cos bx — a sin bx).
Но выражение, стоящее в круглых скобках, может быть, как известно, пред-
представлено в виде
b cos bx — a sin bx = К sin (bx -f- <p0),
где К и ср0 — постоянные. Приравнивая первую производную нулю, получим
уравнение
sin (bx + ср0) = О,
которое дает
= knt т. е. лг= ^°- (k — целое число). A)
Когда х переходит через эти значения, sm (bx -\-у0) будет всякий раз
менять свой знак. То же можно, очевидно, сказать и относительно произ-
производной у', так как
у = Ке~ах sin (bx + ср0),
а множитель е~ах знака не меняет. Следовательно, этим корням соответствуют
поочередно максимумы и минимумы функции. В случае отсутствия показа-
показательного множителя е~ах мы имели бы синусоиду
у = sin bx,
и абсциссы ее вершин получились бы из уравнения
cos bx = 0,
т. е.
(k—целое число).
Мы видим, таким образом, что показательный множитель не только
уменьшает амплитуды колебаний, но и смещает абсциссы вершин кривой.
Сравнивая уравнения A) и Aл), нетрудно видеть, что это смещение равно
постоянной величине! — ~ — ~-). На рис. 61 изображен график затухаю-
затухающего колебания при я = 1 и Ь = 2п. Вершины кривой не находятся на пунк-
пунктирных линиях, соответствующих уравнениям у = + е~ах. Это происходит
вследствие указанного выше смещения вершин.
142 гл. тт. понятие о производной и его приложения I 60
4. Построим кривую
__ х* — 3х
У g .
Составляем производные первого и второго порядка
, *2 —1 „
Приравнивая первую производную нулю, получим значения ^ = 1 и
#2 =—1. Подставляя эти значения во вторую производную, убедимся, что
первому значению будет соот-
соответствовать минимум, а вто-
второму — максимум. Подставляя
эти значения в выражение для
у, определим соответствующие
вершины кривой:
(-• т). ('¦ -4)-
Полагая д: = 0, получим # = 0,
т. е. начало координат @, 0)
лежит на кривой. Наконец,
иУ > X
Рис. 61.
Рис. 62.
приравнивая у нулю, получим, кроме # = 0, еще два значения #= ± J^3,
т. е. окончательно точки пересечения кривой с осями координат будут @, 0),
(У^ 0) и (—Кз7 0). Отметим еще, что при одновременной замене х и у
на (—х) и (—у) обе части уравнения кривой меняют лишь знак, т. е.
начало координат есть центр симметрии кривой (рис. 62).
60. Наибольшее и наименьшее значения функций. Пусть рас-
рассматриваются значения функции f(x) при значениях независимой пере-
переменной х из промежутка (а, Ъ\ т. е. при а-^х^Ъ, и пусть тре-
требуется найти наибольшее и наименьшее из этих значений. При ука-
указанном условии функция f(x) будет достигать наибольшего и наи-
60
§ 5. ПРИЛОЖЕНИЕ К ИЗУЧЕНИЮ ФУНКЦИЙ
143
меньшего значения [35], т. е. соответствующий этой функции график
будет иметь в упомянутом промежутке наибольшую и наименьшую
ординаты. Согласно приведенным выше правилам, мы сможем найти
все максимумы и минимумы функции, заключающиеся внутри про-
промежутка (а, Ь). Если функция f(x) имеет свою наибольшую орди-
ординату внутри этого промежутка, то эта наибольшая ордината будет,
очевидно, совпадать с наибольшим максимумом функции внутри
промежутка (я, Ь). Но может оказаться, что наибольшая ордината
находится не внутри промежутка, а на одном из его концов х = а
или х = Ь. Поэтому для нахождения, например, наибольшего зна-
значения функции недостаточно сравнить все ее максимумы внутри
промежутка и взять наибольший, но необходимо также принять во
внимание и значение функции на концах промежутка. Точно так же
для определения наименьшего значения функции надо взять все ее
минимумы, лежащие внутри промежутка, и граничные значения функ-
функции при х = а и х = Ь. Заметим при этом, что максимумы и ми-
минимумы могут вовсе отсутствовать, а наибольшее и наименьшее
значения у непрерывной функции в ограниченном промежутке (а, Ь)
обязательно будут существовать.
Отметим некоторые частные случаи, когда нахождение наимень-
наименьших и наибольших значений производится наиболее просто. Если,
например, функция f(x) возрастает в промежутке (я, Ь)у то, оче-
очевидно, при х = а она будет принимать
наименьшее, а при х = Ь наибольшее
значение. Для убывающей функции
картина будет противоположной.
Если функция имеет внутри проме-
промежутка один максимум и не имеет ми-
минимумов, то этот единственный макси-
мум и дает наибольшее значение функ-
функции (рис. 63), так что в этом случае
для определения наибольшего значения
Функции вовсе не надо определять значений функций на концах про-
промежутка. Точно так же, если функция имеет внутри промежутка один
минимум и не имеет вовсе максимумов, то упомянутый единственный
минимум и дает наименьшее значение функции. Указанные только
что обстоятельства будут иметь место в первых из четырех изло-
изложенных ниже задач.
1. Дан отрезок длины U Требуется разделить его на две наста так,
чтобы площадь прямоугольника, построенного на них, была наибольшей.
Пусть х —длина одной из частей отрезка, (/ — *) — длина другой его
части. Принимая во внимание, что площадь прямоугольника равна произве-
произведению его соседних сторон, видим, что задача сводится к нахождению тех
значений х% при которых функция
*(/ — X)
наиб, значь
Рис. 63.
144 гл. тт. понятие о производной и его приложения f 69
достигает наибольшего значения в промежутке @, /) изменения х. Составим
производные первого и второго порядка
/'(*) = (/ — х) — * = / — 2лг, /"(*) = —2 <0.
Приравнивая первую производную нулю, получим единственное значение
л; = -—, которому и соответствует максимум, так как f" (x) постоянно
отрицательна. Таким образом, наибольшая пло-
площадь будет у квадрата со стороною -~-.
2. Из круга радиуса JR вырезается сектор
и из оставшейся части круга склеивается ко-
конус. Требуется определить угол вырезанного
сектора так, чтобы объем конуса был наи-
большим.
Рис- 64« Примем за независимую переменную х не
угол вырезанного сектора, а его дополнение до
2тс, т. е. угол оставшегося сектора. При значениях х, близких к 0 и 2тс,
объем конуса будет близок к нулю, и, очевидно, внутри промежутка @, 2тс)
будет существовать такое значение х> при котором этот объем будет наи-
наибольшим.
При склеивании оставшейся части круга в конус (рис. 64) получится
такой конус, у которого образующая равна /?, длина окружности основания
равна Rx, радиус основания г — -?-- и высота
Объем этого конуса будет
При отыскании наибольшего значения этой функции мы можем не об-
пз
ращать внимания на постоянный множитель —Ц-. Оставшееся произведение
х2У~4п2 — х2 положительно и, следовательно, будет достигать наибольшего
значения при тех же значениях х, при которых достигает наибольшего зна-
значения его квадрат. Таким образом, мы можем рассматривать функцию
внутри промежутка @, 2к). Составляем первую производную
f (х)= \6п2хг— 6хъ.
Она существует, при всех значениях х. Приравнивая ее нулю, получим
три значения:
Первые два значения не лежат внутри промежутка @, 2л). Остается един-
единственное значение хг = 2п у —, лежащее внутри этого промежутка;
но выше мы видели, что наибольшее значение внутри этого промежутка
50 I § 5. приложение к изучению функций 145
должно встретиться, а следовательно, и не исследуя значения л*3, можем
утверждать, что ему будет соответствовать наибольший объем конуса.
3. Прямою L плоскость разделена на две части (среды) I и II. Точка
двигается в среде I со скоростью vlt в среде II — со скоростью v2. По
какому пути должна двигаться точка, чтобы возможно скорее попасть
из точки А среды I в точку В среды II?
Пусть AAt и BBt— перпендикуляры из
точек Aw В на прямую L. Введем следующие
обозначения: AAt = a, BBt = by AlBl = c, и
на прямой L будем отсчитывать абсциссы в на-
направлении A^Bt (рис. 65). —? = Л??\Г~Т^Ь
Ясно, что как в среде /, так и в среде // 1 уг fv4 х
путь точки должен быть прямолинейным, но ir \1
путь по прямой АВ не будет, вообще говоря, В
„скорейшим путем". Итак, „скорейший путь" р ^
будет состоять_из двух прямолинейных от- *
резков AM и MB, причем точка М должна
лежать на прямой L. За независимую переменную х выберем абсциссу точки
М: х = АХМ. Время ty наименьшее значение которого ищется, определится
по формуле
V у
в промежутке (—oo, + oo). Составим производные первого и второго
порядков:
f(x)= X С~Х
a2 + x2 v2yb2 + (c—xJ
м2 , b2
Обе производные существуют при всех значениях х, и /" (л:) всегда имеет
знак (-)-). Следовательно, /' (х) возрастает в промежутке (—со, -\- оо) и не
может обратиться в нуль более одного раза. Но
/' @) = / < 0
Vb2 + 2
f(c)= 4_^>0,
viy a2 + с2
а потому уравнение
/'W = o
имеет единственный корень х0 между 0 и с, которому соответствует един-
единственный минимум функции /(а:), так как /* (х) > 0. Абсциссы 0 и с соот-
соответствуют точкам Ах и Вlt а потому искомая точка М будет находиться
между точками At и Bv что можно было бы показать и из элементарных
геометрических соображений.
Поясним геометрический смысл полученного решения. Обозначим через
а и C углы, составленные отрезками/AM и ВМ с перпендикуляром, восста-
вленным из точки М к L. Абсцисса х искомой точки М должна обращать
нуль /' (х), т. е. должна удовлетворять уравнению
v2 У Ь2 + (с — л-J *
146 гл. тт, понятие о производной и его приложения 160
которое можно переписать так:
vtAM v2BM
или
sin a sin p sin a __ vt
„скорейший путь" будет тот, при котором отношение синусов углов а и Р
будет равно отношению скоростей в средах / и //. Результат этот дает нам
известный закон преломления света, и, следовательно, преломление света
совершается так, как будто луч света выбирает ;'„скорейший путь" из точек
одной среды в точки другой.
4* Положим, что экспериментально определяется величина дг, и п одина-
одинаково тщательно произведенных наблюдений дают для нее п значений
«1, «2» ". » аП>
неодинаковых ввиду неточности инструментов. „Наиболее вероятным" значе-
значением величины х будем считать то, при котором сумма квадратов ошибок
будет наименьшей. Таким образом, нахождение этого значения приводится
к нахождению х из условия наименьшего значения функции
у уЛ) \Л, UiJ -J- \Л U2) -р ... -р \Л, lift)
в промежутке ( — со, +оо). Составляем производные первого и второго
порядков
с — а2)+ ... +2(х — ап),
Приравнивая первую производную нулю, получим единственное значение
которому будет соответствовать минимум ввиду положительности второй
производной. Таким образом „наиболее вероятным" значением х является
среднее арифметическое значений, полученных из наблюдений.
5. Найти кратчайшее расстояние точки М до окружности.
Примем за начало координат центр окружности О, за ось ОХ—пря-
ОХ—прямую ОМ. Пусть ОМ — аи пусть R есть радиус окружности. Уравнение
окружности будет
а расстояние точки М с координатами (а, 0) до любой точки окружности
Будем искать наибольшее значение квадрата этого расстояния. Подставив
вместо у2 его выражение R? — х2 из уравнения окружности, мы получим
функцию
f(x) = (х—аJ + (Я2 — х2) = — 2ах + а2 + #2,
где независимая переменная х может изменяться в промежутке (— /?^ х ^ /?).
Так как первая производная
/'(*)=-2а
60 1
§ 5. ПРИЛОЖЕНИЕ К ИЗУЧЕНИЮ ФУНКЦИЙ
147
отрицательна при всех значениях х, то функция f(x) убывает и достигает,
следовательно, наименьшего значения при x = R на правом конце проме-
промежутка. Кратчайшим расстоянием будет длина отрезка РЖ (рис. 66).
6. В прямой круговой конус вписать прямой круговой цилиндр (с основа-
основанием, лежащим в основании конуса) так, чтобы его полная поверхность была
наибольшей.
М
Рис. 66.
Рис. 67.
Обозначим радиус основания и высоту конуса буквами R и Я, а радиус
основания и высоту цилиндра — буквами г и h. Функция, наибольшее значе-
значение которой ищется, будет в данном случае
Переменные величины г и h связаны между собой тем условием, что цилиндр
вписан в данный конус. Из подобия треугольников ABD и AMN имеем
(рис. 67):
MN BD h H
_ —^ ^____ tl TTTI _____^ —— ___
AN ~~ AD1 R-r ~~ R »
откуда
R
-я.
Подставляя это значение h в выражение для S, получим
Таким образом, S оказывается функцией одной независимой перемен-
переменной г, которая может изменяться в промежутке 0 ^ г ^ R. Составим произ-
производные первых двух порядков:
Приравнивая нулю -т—, получим для г одно значение
HR
Для того чтобы это значение находилось внутри промежутка @, R), необхо-
необходимо выполнение неравенств
0< o
2 (Я-/?)
2 (Я-/?)
148 гл. п. понятие о производной и его приложения f 61
Первое из этих неравенств равносильно тому, что И должно быть
больше R. Умножая обе части второго неравенства" на положительную вели-
величину 2 (Я—R), получим
d2S
При выполнении этого условия -~-2 имеет знак (—); значению B) соответ-
соответствуют единственный максимум функции 5 и наибольшая величина поверх-
поверхности цилиндра. Эту величину можно легко определить, подставляя значе-
значение г из B) в\выражение для 5.
Предположим теперь, что значение B) не лежит внутри промежутка
(О, R), т. е. что не выполнено одно из неравенств C). При этом могут пред-
представиться две возможности: или Н <^. R или Н > R, но R^>-^. Обе они
могут быть охарактеризованы одним неравенством
И ^ 2R D)
«с
Преобразуем выражение для —:
dl = 2* Br + H-?t H}=2^[BR-H)r+ H (R-r)}.
Из этого выражения видно, что при выполнении условия D) -т->0 при
0<г</?, т. е. функция S возрастает в промежутке (О, R), а потому дости-
достигает наибольшего значения при г = R. При этом значении г, очевидно,
/г = 0, и полученное решение можно рассматривать как сплющенный цилиндр,
основание которого совпадает с основанием конуса и вся поверхность кото-
которого приводится к 2tzR2.
61. Теорема Ферма. Выше мы изложили, пользуясь элементарными
геометрическими соображениями, способы исследования возрастания
и убывания функций, нахождения их максимумов и минимумов, а также
наибольших и наименьших значений. Сейчас мы переходим к строгому
аналитическому изложению некоторых теорем и формул, которые
дадут нам аналитическое доказательство справедливости приведенных
выше правил, а также позволят продвинуть исследование функций
еще несколько дальше. В дальнейшем изложении мы будем уже вполне
отчетливо и подробно перечислять все условия, при которых соответ-
соответствующие теоремы и формулы имеют место.
Теорема Ферма. Если функция f(x) непрерывна в проме-
промежутке (а, Ь), в каждой точке внутри этого промежутка имеет
производную и в некоторой точке х = с внутри промежутка
достигает наибольшего (или наименьшего) значения, то в этой
точке х = с первая производная равна нулю, т. е. f (с) = 0.
Итак, положим для определенности, что значение f(c) является
наибольшим значением функции. Для того случая, когда это есть
наименьшее значение, доказательство может быть проведено совер-
совершенно аналогичным образом. Итак, согласно условию, точка х — с
62
§ 5. ПРИЛОЖЕНИЕ К ИЗУЧЕНИЮ ФУНКЦИЙ 149
лежит внутри промежутка и разность f(c-\-ti)—f(c) будет отри-
отрицательной или, во всяком случае, не положительной, при любом h
как положительном, так и .отрицательном:
/(с + й)-/(с)<0.
Составим отношение
f(c + h)-f(c)
Числитель написанной дроби, как сказано, меньше или равен нулю,
а потому
/<« + *)-/(«) <0 прий>0,
/(« + *)/W ^ 0 при/г<о.
h
Точка х = с лежит внутри промежутка, и в ней по условию
существует производная, т. е. написанная выше дробь стремится
к определенному пределу f(c), если h стремится к нулю любым
образом. Положим сначала, что h стремится к нулю со стороны поло-
положительных значений. При этом, переходя к пределу в первом .из
неравенств E), получим
»^0.
Точно так же переход к пределу при h -> 0 во втором неравен-
неравенстве E) дает
Сопоставляя эти неравенства, мы получим требуемый результат:
/'@ = 0.
62. Теорема Ролля. Если функция f(x) непрерывна в проме-
жутке (а, Ь), имеет производную в каждой точке внутри этого
промежутка и значения функции на концах этого промежутка
равны, т. е. f(a)=f(b), то внутри промеэюутка существует, по
крайней мере, одно такое значение х —с, при котором производ-
производная обращается в нуль, т. е. f(c) = 0.
Непрерывная функция f(x) должна достигать в рассматриваемом
промежутке наименьшего значения т и наибольшего значения М.
Если бы оказалось, что эти наименьшее и наибольшее значения оди-
одинаковы, т. е. т = М, то отсюда следовало бы, очевидно, что функция во
всем промежутке сохраняет постоянное значение, равное т (или Ж). Но,
как известно, производная от постоянной равна нулю, и, следова-
следовательно, в этом простом случае во всякой точке внутри промежутка
производная была бы равна нулю. Обращаясь к рассмотрению общего
случая, мы можем, следовательно, считать, что т<^М, Так как
150
ГЛ. II. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ
[ 62
значения функции на концах по условию одинаковы, т.е. f(a) =f(b),
то, по крайней мере, одно из чисел т или М отлично от этого обще-
общего значения на концах. Положим, например, что это будет М, т. е. что
наибольшее значение функции достигается не на концах, а внутри
промежутка. Пусть х=с будет та точка, где это значение достигается.
Согласно теореме Ферма, мы будем иметь в этой точке /' (с) = 0, что
и доказывает теорему Ролля.
Й частном случае, если f(a)=f(b) = O, можно теорему Ролля
формулировать кратко так: между двумя корнями функции заклю-
заключается, по крайней мере, один корень
первой производной.
Теорема Ролля имеет простое геометри-
геометрическое значение. По условию, f(a)=f(b)t
т. е. ординаты кривой y=f(x)} соответ-
—*-Х ствующие концам промежутка, равны, и
внутри этого промежутка существует про-
производная, т. е. кривая имеет определенную
касательную. Теорема Ролля утверждает, что при этом внутри про-
промежутка будет существовать, по крайней мере, одна такая точка,
в которой производная будет равна нулю, т. е. в которой касатель-
касательная будет параллельна оси ОХ (рис. 68).
Замечание. Если не выполнено условие теоремы Ролля о су-
существовании производной /' (х) во всех точках внутри промежутка,
то теорема может оказаться и неверной.
Так, например, функция
1) и /(— 1)=/A) = 0, но произ-
произРис#
непрерывна в промежутке (— 1,
водная
Зу х
внутри промежутка в нуль не обращается. Происходит это оттого,
что f (х) не существует (обращается в бесконечность) при х = 0
у (рис. 69). Другой пример дает
кривая, изображенная на рис. 70.
У
а ос Ъ
Рис. 70.
В этом случае мы имеем кривую y=f(x)y у которой /(а) =/(#) = 0.
Однако из чертежа видно, что касательная внутри, промежутка (а, Ъ)
63 ] § 5. ПРИЛОЖЕНИЕ К ИЗУЧЕНИЮ ФУНКЦИЙ 15)
не может быть параллельна оси ОХ, т. е./'(х) не обращается в нуль.
Происходит это оттого, что кривая в точке x = ol имеет две различ-
различные касательные, справа и слева от этой точки, и, следовательно,
в этой точке не существует определенной производной, и условие
теоремы Ролля о существовании производной во всех точках внутри
промежутка не выполнено.
63. Формула Лагранжа. Положим, что функция f(x) непрерывна
в промежутке (а, Ь) и имеет внутри этого промежутка производную,
но условие f(a)=f(b) теоремы Ролля может быть не выполнено.
Составим функцию
где X — постоянная, которую мы определим так, чтобы новая функ-
функция F (х) удовлетворяла упомянутому условию теоремы Ролля, т. е.
потребуем, чтобы
F(a)=F(b)
ИЛИ
откуда
Х_" f(b)-f(a) ^
Применяя теперь к F(х) теорему Ролля, можем утверждать, что
меж&у а и b будет находиться такое значение х—-с, при котором
откуда, подставляя найденное выше значение X,
Последнее равенство можно переписать так:
№-f(a) = (b-a)f'(c).
Равенство это называется формулой Лагранжа. Значение с заклю-
заключается между а и by г потому отношение с,~~ = 0 заключается между
нулем и единицей, и мы можем написать
с = а + в(Ь-а) (
и формула Лагранжа перепишется в виде:
Полагая b = a-\-h, получим еще следующий вид формулы:
152 гл. н. понятие о производной и его приложения [ 63
Формула Лагранжа дает точное выражение для приращения
f{b)—f{a) функции f(x)y а потому называется также формулой
конечных приращений.
Мы знаем, что производная постоянной равна нулю. Из формулы
Лагранжа мы можем вывести обратное предложение: если производ-
производная f[(x) во всех точках промежутка (а, Ь) равна нулю, то
функция f(x) постоянна в этом промеэюутке.
В самом деле, возьмем произвольное значение х из промежутка
(а, Ь) и, применяя формулу Лагранжа к промежутку (ау х), получим:
но по условию /'(<•) = О и, следовательно,
f(x)—f(a)=09 т. e. f(x) = f(a) = постоянной.
Относительно величины с, входящей в формулу Лагранжа, мы
знаем только то, что она заключается между а и Ъ, и поэтому фор-
формула Лагранжа не дает возможности точного вычисления приращения
функции через производную, но с ее помощью можно произвести
оценку той ошибки, которую мы делаем, заменяя приращение функ-
функции ее дифференциалом.
Пример. Пусть
Производная
и формула Лагранжа даст
М
logio (a + h) - log10 a ^h-^-^ @ < 0 < 1)
или
М
log10 (a + h) = log10 a + h
Заменяя приращение дифференциалом, получим приближенную формулу
М М
log10 (а + К) — log10 я = Л —, log10 (a + h) = log10a + Л — .
Сравнивая это приближенное равенство с точным, полученным по формуле
Лагранжа, увидим, что ошибка
иМ . М WM
h h
а
Полагая а = 100 и Л = 1, получим приближенное равенство
log,, 101 = log,, 100 + ^ = 2,00434...
с ошибкой
63
§ 5. ПРИЛОЖЕНИЕ К ИЗУЧЕНИЮ ФУНКЦИЙ 153
Заменяя в числителе этой дроби 0 единицей, а в знаменателе нулем,
¦-IM дробь и можем поэтому сказать, что ошибка вычисленного значе-
значения log10 101 меньше
JjL = 0,00004...
Перепишем формулу Лагранжа в виде:
/(»)-/(«) =f(c) (a<c<b).
Обращаясь к графику функции у = f(x) (рис. 71), заметим, что
отношение
f (Р) — f (я) СВ
b — а ас
лает угловой коэффициент хорды АВ, a f(c) дает угловой коэф-
коэффициент касательной в некоторой точке М дуги АВ кривой. Таким
образом, формула Лагранжа равносильна
следующему утверждению: на дуге кри-
еой имеется такая точка, в которой
касательная параллельна хорде. Частным
случаем этого утверждения, когда хорда
параллельна оси ОХ, т. е. /(а)—/(Ь),
является теорема Ролля.
Замечание. Из формулы Лагранжа 01
непосредственно вытекают те признаки Рис. 71,
возрастания и убывания, которые были
установлены нами выше из чертежа. Действительно, положим, что
внутри некоторого промежутка первая производная /' (х) положи-
положительна и пусть х и х -\-h — две точки из этого промежутка. Из фор-
формулы Лагранжа:
видно, что при положительных h разность, стоящая слева, будет вели-
величиной положительной, так как оба множителя в произведении, стоя-
стоящем справа, в этом случае положительны. Таким образом, предполагая
положительность производной в некотором промежутке, мы получили
/(*+*)-/(*)> 0,
т. е. функция возрастает в этом промежутке. Точно так же из напи-
написанной выше формулы непосредственно вытекает и признак убывания.
Заметим здесь же, что рассуждения, приведенные нами при дока-
доказательстве теоремы Ферма, остаются вполне применимыми и для того
случая, когда в рассматриваемой точке функция достигает не обяза-
обязательно наибольшего или наименьшего значения, а только лишь макси-
максимума или минимума. Эти рассуждения докажут, что в таких точках
первая производная должна быть равна нулю, если она существует.
154 гл. п. понятие о производной и его приложения [ 64
64. Формула Коши. Положим, что функции f(x) и ср(дг) непре-
непрерывны в промежутке (а, Ь) и в каждой точке внутри этого проме-
промежутка имеют производную, причем производная ср' (х) ни в одной из
точек внутри промежутка не обращается в нуль. Применяя к функ-
функции <р(х) формулу Лагранжа, получим
— ?(«) = (* — «)?'fa) (
но по условию <р' fa) ^ О И> следовательно,
Составим функцию
где X — постоянная, которую мы определим так, чтобы было
то есть
откуда
i_ f(b)-f{a)
— (b)()
При таком выборе X к функции F(x) приложима теорема Ролля,
и, следовательно, будет существовать такое значение х = с, при
котором
Г (с) =/' (с) + Х?' (с) = 0 (а < с
Это уравнение дает
откуда, подставляя найденное для X значение, получим
f(b)-f(a) _/'(с) (а<Г
или
/Jb)-f(a) __Г[а
ИЛИ
h)-~f(a)_f'
Это и есть формула Коши, Полагая в этой формуле у(х) = ху
будем иметь <p'(x)=l, и формула примет вид:
т. е. мы получили формулу Лагранжа как частный случай формулы
Коши.
55 ] § 5. приложение к изучению функций 155
65. Раскрытие неопределенностей. Положим, что функции
и ty(x) непрерывны при а<^х^а-\-k, где k — некоторое положи-
положительное число, имеют непрерывные производные и ф'' (х) не обра-
обращается в нуль при указанных значениях х. Положим, кроме того, что
lJfflcp(jc) = O и Нтф(х) = 0 при л:->а-|-0 [26]. Полагая ср(а) =
— б(а) = 0, мы получим функции, непрерывные вплоть до х = а,
т. е. при a^x^a-\-k. При лг-^a-j-O к частному тт>> которое
при jc = a представляет собою неопределенность вида -^-, не приме-
применима теорема о пределе частного. Укажем способ раскрытия такой
неопределенности, т. е. способ нахождения предела у4-4 при х-> а -\~ 0.
Докажем предварительно следующую теорему: если при сделан-
сделанных выше предположениях отношение ^ стремится к пре-
пределу Ь при х-+а-\-0, то к тому же пределу стремится и отно-
отношение функций ^Щ.
Принимая во внимание, что
и применяя формулу Коши [64], получим
<Р (х) 9 (х) — ср (а) срг (?)
Заметим, что при сделанных относительно <р (лг) и ф (jc) предположе-
предположениях применима формула Коши.
Если дг—>а-[~0, то ?, заключающееся между а и х ш зависящее
от х, стремится к а. При этом, по условию, правая часть равенства G)
стремится к пределу Ь, а потому я левая часть имеет тот же предел.
Отметим, что этот предел может быть и бесконечным. Таким образом
приходим к правилу:
При разыскании предела частного |-рт в случае неопределенно-
0 ,
emu g- можно заменить отношение функции отношением их
производных и отыскивать предел этого нового отношения.
Правило это дано французским математиком Лопиталем и назы-
называется обычно его именем.
Если отношение производных ^,г( также приводит к неопределен-
0
ности Q- и функции ср' (х) и <]/ (х) удовлетворяют тем условиям, кото-
которые мы выше формулировали для ср(х) и ф(х), то и к отноше-
нию йу / у\ можно применить правило Лопиталя, и т. д.
156
ГЛ. И. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ
65
Мы рассмотрели случай а<^х ^а-\- k. Совершенно аналогично
рассматривается случай а — k^x<^ay т. е. х—>а — 0. В дальней-
дальнейших примерах предел не зависит от того, стремится ли х справа или
слева, и мы пишем х —> а.
Мы рассмотрели тот случай, когда х стремится к конечному пре-
пределу а. Правило справедливо и для того случая, когда х стремится
к бесконечности. На доказательстве этого мы не останавливаемся.
Приложим правило Лопиталя к нескольким примерам.
1.
2. lim
x-*o x
x — sin л:
= lim
A->0 1
1 — cos л:
т. е. разность л: —sin л: есть бесконечно малая третьего порядка по сравне-
сравнению с л*.
о 1itY, х — xcosx ,. 1 — cos x + ^sin х
о, nm = urn ¦ =
x-*o x— sin x x-+o 1— cos л*
__ jj sin x-{- sin x + x cos x ___ ^m 2 cos* + cos x — x sin дг
x-+o sinx a:-*u cos л:
-==3.
Результат этого примера приводит к практически удобному способу
спрямления дуги окружности.
Рассмотрим окружность, радиус которой примем за единицу. За ось ОХ
выберем один из диаметров этой окружности, а за ось OY—касательную
в конце этого диаметра (рис. 72). Возьмем некоторую дугу ОМ и пусть на
оси OY имеется отрезок ON, равный дуге ОМ,
и проведем прямую NM. Пусть Р — точка ее
пересечения с осью ОХ. Обозначим через и
длину дуги ОМ (радиус принят за единицу).
Уравнение прямой NM в отрезках имеет вид:
¦**• Для вычисления длины отрезка ОР заметим,
что на прямой NM лежит точка М с коорди-
Рис. 72. натами
л: = OQ = 1 — cos и, у = QM = sin и.
Эти координаты должны удовлетворять написанному уравнению:
1 — cos и . sin и , Лп м — и cos и
7TF1 = !» откуда ОР= : .
ОР и J и— sinw
Результат примера 3 показывает, что, при ОР-+3 и—*0, т. е. точка Р
на оси ОХ будет стремиться к точке D, расстояние которой от начала
координат равно утроенному радиусу окружности. Отсюда получается про-
простой способ приближенного спрямления дуги окружности. Для* спрямления
дуги ОМ надо отложить от точки О отрезок OD, равный трем радиусам
окружности, и провести прямую DM. Отрезок ONV отсекаемый этой прямой
на оси О У, и даст приближенно длину дуги ОМ. Способ этот приводит
к очень хорошим результатам, особенно для небольших дуг; но даже для
дуги те/2 относительная ошибка составляет приблизительно 5%.
66 ] § 5. ПРИЛОЖЕНИЕ К ИЗУЧЕНИЮ ФУНКЦИЙ 157
66. Различные виды неопределенностей. Доказанное в [65]
правило применимо и к случаю неопределенностей вида —. В
дальнейшем мы не будем отличать стремление х к а слева или
справа и будем писать для краткости х—> а. Предположим, что при
этом непрерывные функции о (х) и ф (х) стремятся к (-J- со) или
/ . со). Для определенности пусть
lim ср (х) = lim ф (х) = -f- сю (8)
х-+а х-*а
Покажем, что отношение -|у^ стремится к тому же пределу Ь> при-
причем предполагается, что ф'' (х) не обращается в нуль при значениях х,
близких к а.
Рассмотрим два значения независимой переменной х и х0, близ-
близкие к а и такие, что х заключаются между х0 и а. По формуле
Коши будем иметь
но, с другой стороны,
у W
i
«К*)
Отметим, что из (8) непосредственно следует, что ср (х) и ф (х)
отличны от нуля при значениях х, близких к а. Сравнивая эти два
выражения, получим
(х)
или
1 —.
1 у
гДе 5 заключается между х и лг0 и, следовательно, между а и д:0.
Возьмем х0 достаточно близким к а; тогда, в силу условия (9), мы
можем считать, что первый множитель в правой части .равенства A0)
будет сколь угодно мало отличаться от b при любом выборе х между
хо и а. Закрепив, таким образом, значение xQy будем приближать
158 гл. и. понятие о производной и его приложения [ 66
х к а. Тогда в силу условия (8) второй множитель в правой части
равенства A0) будет стремиться к единице, а потому мы можем
утверждать, что отношение Vt-{, стоящее в левой части равенства A0),
при значениях х, близких к а, будет сколь угодно мало отличаться
от Ь, т. е.
Из доказанной теоремы следует, что правило Лопиталя применимо
и для раскрытия неопределенностей вида --.
Отметим еще некоторые виды неопределенностей. Рассмотрим
произведение <?(x)ty(x), и пусть
lim <р (х) = 0
х-+а
И
lim ф (х) = со.
х-+ а
Это будет неопределенность вида 0 • со. Нетрудно привести ее
0 оо
к виду -д- или -:
Рассмотрим, наконец, выражение <р (#)*(¦*) и пусть
lim ср (х) = 1 и lim ф (х) = оо.
Это будет случай неопределенности вида I00. Рассмотрим лога-
логарифм данного выражения
log [ср {xf И] = ф (х) log ср (х),
который приводится к неопределенности вида 0 • оо. Раскрывая эту
неопределенность, т. е. находя предел логарифма данного выражения,
мы тем самым будем знать и предел самого выражения. Совершенно
так же раскрываются неопределенности вида со0 и 0°.
Рассмотрим теперь примеры.
рХ рХ
1. lim — = lim %r==J^ODf
lim Ё^-з lim — == lim ~ = + oo
Х-+ + ОЭХ2 АГ-».-|-00 2л: at-^-j-oO 2
ex
Совершенно так же можно убедиться в том, что отношение — при
любом положительном значении п стремится к бесконечности, когда
х —» + оо, т. е. показательная функция ех возрастает быстрее любой
66 I § 5. ПРИЛОЖЕНИЕ К ИЗУЧЕНИЮ ФУНКЦИЙ 159
положительной степени х при беспредельном возрастании х.
J_
2. Hm ^?= Hm —4^= Hm -^ = 0 (я >0),
т. е. log x возрастает медленнее любой положительной степени х.
1
= Hm —^—=
3. lim л:л1с^л;= Hm —^—= lim
=-_ lim — = 0 (л>0).
4. Найдем предел хх при стремлении лс к (+0). Логарифмируя это выра-
выражение, получим неопределенность вида 0 • со. Эта неопределенность в силу
примера 3 даст в пределе нуль, а следовательно
lim xx =\,
х->-\-0
5. Найдем предел отношения
lim x + sinx.
#-юо X
Числитель и знаменатель написанного отношения стремятся к бесконеч-
бесконечности. Заменяя по правилу Лопиталя отношение функций отношением про-
производных, получим
lim 1 + cos-y.
X -*00 1
Но 1 + c°sa: при беспредельном возрастании л: ни к какому пределу не
стремится, ибо cos .г будет все время колебаться между (+1) и (—1);
однако нетрудно видеть, что само данное отношение стремится к пределу
lim * "Г ьш л -s lim
Итак, в этом случае неопределенность раскрывается, но правило Лопи-
таля ничего не дает. Этот результат не противоречит доказанной теореме;
ибо в теореме утверждалось лишь то, что если отношение производных
стремится к пределу, то к тому же пределу стремится и отношение функ-
функций, но не наоборот.
6. Отметим еще неопределенность вида (оо±оо). Она приводится обычно
к неопределенности вида -^г» Например,
* Ulim
\2)
*-«? х
\\т(-± Ulim ? .
-*о\ sin л: х-\-х2) х-+ъ (x-\-x2)smx
ыражение представляет собою не
Раскрывая ее указанным выше способом, получим
Последнее выражение представляет собою неопределенность вида ~^ч
160 гл. и. понятие о производной и его приложения [ 67
§ 6. ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
67. Основные понятия. До сих пор мы рассматривали функцию
одной независимой переменной. Рассмотрим теперь функцию двух
независимых переменных u=f(xy у).
Для определения частных значений такой функции должны быть
заданы значения независимых переменных: х = х0, у = у0. Каждой
такой паре значений х и у соответствует определенная точка Мо
на координатной плоскости с координатами (jc0, y0), и вместо того,
чтобы говорить о значении функции при х = х0, у=у0, можно
говорить о значении функции в точке М0(х0, у0) плоскости. Функция
может быть определена на всей плоскости или только в некоторой
ее части, в некоторой области. Если f(x, у) есть целый много-
многочлен от ху у, например,
и=/(х, у) = *
то можно считать, что эта формула определяет функцию на всей
плоскости. Формула
определяет функцию внутри окружности х2-{-у<2=\ с центром
в начале координат и радиусом единица и на самой окружности,
где и = 0. Аналогом промежутка на плоскости является область,
определяемая неравенствами й^х =^#i, а%^:у ^.Ь%. Это — прямо-
прямоугольник со сторонами, параллельными осям, причем граница этого
прямоугольника также включается в область. Неравенства ai<^.xr<^j,
а.2<^у <^Ы определяют только внутренние точки прямоугольника.
Если граница области причисляется к ней, то область называется
замкнутой. Если граница не причисляется, к области, то область
называется открытой [ср. 4]. Определим понятие предела для функ-
функции f(x, у) двух переменных [ср. 32]. Положим, что функция опре-
определена во всех точках М(х, у\ достаточно близких к точке М0(а, Ь).
Определение. Говорят, что число А есть предел f(x,y)
при стремлении М (х, у) к MQ (a, b)y и пишут
\\mf{xy у) = Ау или Ит/(дг, у) = Ау
х-* а М-+Мо
если для любого заданного положительного числа е существует
такое положительное число г\, что
\А—/(хуу)\<г} если \х — а|<7] и \у — Ъ\<т\-
При этом предполагается, что исключена пара значений х — а,
у — Ь(М не совпадает с Жо). Если точка Мо лежит на границе той
области, в которой определена f(x, у), то М, стремящаяся к УИ0,
должна принадлежать области, в которой определена функция /(х, у).
67 ] § 6. ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ 161
Пусть имеется какая-либо пронумерованная последовательность
точек Мп(хпУ уп)} стремящаяся к М0(а, Ь), т. е. такая, что последо-
последовательность хп имеет предел а, а последовательность уп— предел Ь.
Можно доказать, что если последовательность чисел un=f(xnt уп)
для любой такой последовательности точек Мп(хт уп) имеет один
и тот же предел Д то А есть предел f(x> у) при стремлении
М (ху у) к Мо (пу Ь) в смысле сформулированного выше определения.
Положим, что f(Xy у) определена в точках М0(а, Ь) и во всех
точках, достаточно близких к М0(а, Ь) [ср. 32].
Определение. Функция f(x, у) называется непрерывной
в точке М0(а, Ь), если
, y)=f(a, b)y или lim/(#, y)=f(ay b).
MM
Функция называется непрерывной в некоторой области, если она
непрерывна в каждой точке этой области.
Так, например, функция и=}/1—х1 — у2 непрерывна внутри
круга, в котором она определена. Про нее можно также сказать,
что она остается непрерывной, если мы к кругу присоединим и его
границу, т. е. окружность, на которой и = 0.
Пусть В — ограниченная замкнутая область на плоскости и
f(x, у) — непрерывная в В функция (непрерывная внутри В и вплоть
до границы В). Такая функция обладает свойствами, аналогичными
свойствам функции одной независимой переменной, непрерывной
в конечном замкнутом промежутке [35]. Доказательства этих свойств,
по существу, те же, что и доказательства из [43]. Сформулируем
лишь результаты.
1. Функция f(x, у) равномерно непрерывна в В, т. е. при любом
заданном положительном числе е существует такое положи-
положиесли (хи уО и (дг2, у2) принадлежат В и
2. Функция /(х, у) ограничена в В, т. е. существует такое
положительное число Ж, что \/(х, у)\<^М для всех (х, у),
принадлежащих В.
3. Функция f(x, у) достигает в В наибольшего и наимень-
наименьшего значений.
Обратим внимание на одно следствие, которое вытекает из опре-
определений непрерывности функций. Если /(лг, у) непрерывна в точке
(а, Ь) и если мы положим y = bt то функция f(x, b) одной пере-
переменной х непрерывна при х = а. Аналогично, /(а, у) непрерывна
при у = ь.
162
ГЛ. П. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ
г
68. Частные производные и полный дифференциал функ-
функции двух независимых переменных. Допустим, что у функции
и=/(лг, у) переменная у сохраняет постоянное значение и меняется
только дг, то есть и становится функцией одного х и можно вычис-
вычислить ее приращение и производную. Обозначим через Д^и прираще-
приращение и, которое эта функция получает, когда у остается постоянным,
а х получает приращение Адг:
Axti =f(x + Адг, у) — /(дг, у).
Производную получим, найдя предел
Нт
Ал:
= lim
Ах
Производная эта, вычисленная в предположении, что у остается
постоянным, называется частной производной функции и по х и
обозначается так: - f' , или fx(x, у), или ~.
Заметим, что ~ нельзя толковать как дробь, но лишь как сим-
символ для обозначения частной производной. Если /(лг, у) имеет част-
частную производную по х, то она является непрерывной функцией х
при фиксированном у.
Точно так же определяется приращение Дуг и частная произ-
производная от и по у, вычисленная в предложении, что х не меняется:
Ау
Если, например, и = х*-\-у*, то ^ =
Рассмотрим уравнение Клапейрона
С помощью этого уравнения одна из величин /?, v и Т может быть опре-
определена в зависимости от двух других, причем эти последние должны уже
считаться'независимыми переменными. Мы получим следующую таблицу:
Независимые
переменные
Функции
Частные
производные
dv
dT
V
R
Р
Т,р
dv
'dp
RT
P*
dp
dT
P
R
V
T,v
V
dp
'dv
RT
t/2
dT
dp
P
V
R
, v
pv
~R
dT'
'dv
P
R
68 ] § 6. ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ 163
Отсюда получается следующее соотношение
дТ dp dv
Если бы в левой части равенства мы произвели сокращение, то полу-
получили бы не (— 1), а (+ 1). Но в этом равенстве частные производные вычи-
dv
слены при различных предположениях: -^=, — в предложении, что р постоян-
дТ др
но; -ч при. v постоянном; ~- — при Т постоянном, а потому упомянутое
сокращение недопустимо.
Обозначим через Аи полное приращение функции, получаемое
при одновременном изменении как х, так и у:
ku=f(x+kxf y-\-ky) — f(x, у).
Прибавляя и вычитая f(xy y-\-ky\ можем написать
?Ш = [/(Х + Ьх, y + Ly)—f(x, y + &y)] + \f(x, y + by) — f(Xt у)].
В первой квадратной скобке мы имеем приращение функции и
при неизменном значении {у -\- Aj/) переменной у> во второй квадратной
скобке — приращение той же функции при неизменном значении х.
Положим, что f(xy у) определена внутри некоторой области В,
что точка (лг, у) находится внутри В и что Ajc и Aj/ взяты настолько
малыми по абсолютной величине, что прямоугольник с центром (х> у) и
длиной сторон 2 | Длг | и 2 | Ад/1 также находится внутри В, Предпо-
Предположим, кроме того, что f(xf у) имеет внутри В частные производ-
производные. Применяя к каждому из приращений, входящих в выражение Aw,
формулу Лагранжа, что мы можем сделать, так как в каждом слу-
случае меняется только одна независимая переменная, получим
Аи —fx (х -f B^xf у + Ау)Алг + f'y (х, у -f BxAy) Ay,
где б и 0х заключаются между нулем и единицей. Предполагая не-
ди dtt
прерывность частных производных ^- и ^-, мы можем утверждать,
что при стремлении Дат и Ау к нулю, коэффициент при Алг будет
стремиться к /^ (лг, у), а коэффициент при ky — к fy (x, у), а потому
имеем
Аи = [?(*, y) + *]bx+\fy(x, y) + Si]by
или
Аи = f'x (х, у) Ах + /; (х, у) Ау + еДлт 4- 8, Ау, A)
где вив! — величины бесконечно малые одновременно с Ад; и Hay.
Формула эта аналогична формуле
Дд/ = у Их 4* е Алг,
164 гл. п. понятие о производной и его приложения I 69
доказанной нами в случае функции одной независимой переменной
[50]. Произведения гАх и е^у будут бесконечно малыми высших
порядков по сравнению соответственно с Ах и Ду.
Напомним, что в предыдущих рассуждениях мы исходили из
предположения не только существования, но и непрерывности част-
частных производных -~ и ~ в некоторой области, содержащей точку
(х, у) внутри себя.
В сумме первых двух слагаемых в правой части формулы A)
заменим Ах и Ау произвольными величинами dx и dy (дифферен-
(дифференциалами независимых переменных). Мы получим таким путем выра-
выражение
du =fx (*, у) dx -f- f'y (x, у) dy,
или
которое называется полным дифференциалом функции и [ср. 60].
Ввиду вышеуказанных свойств еДх и etAy можно сказать, что
при малых значениях \dx\ и \dy\ полный дифференциал du дает
приближенное значение полного приращения Аи, соответствующее
приращениям dx и dy независимых переменных [50].
С другой стороны, очевидно, что произведения j- dx и ч- dy дают
приближенную величину приращений kxu и Avw, и, таким образом,
при малых приращениях независимых переменных полное прираще-
приращение функции приближенно равно сумме ее частных приращений
Aw r^dur^ kx
Равенство B) выражает весьма важное свойство функций от не-
нескольких независимых переменных, которое можно назвать „свойством
наложимости малых действий". Сущность его заключается в том, что
соединенный эффект от нескольких малых действий Ах и Ау с доста-
достаточной точностью может быть заменен суммой эффектов от каждого
малого действия в отдельности.
69. Производные сложных и неявных функций. Положим теперь
что функция н=/(х, у) зависит через посредство х и у от одной
независимой переменной ty т. е. допустим, что х и у суть не незави-
независимые переменные, но функции независимой переменной ty и опре-
da ,
делим производную - от и по t
Если независимая переменная t получит приращение Д?, то функ-
функции х и у получат соответственно приращения Ах и Aj/, а и получит
приращение Aw:
Аи = f(x -f- Ах, у -j- Aj>) —/ (х, у).
69 ] § 6. функции двух переменных 165
В \6$] мы видели, что приращение можно написать в виде:
Д//=/;С* + вД*, у-\- Ау) Дл?+ /;(*, j/ + etAy) Ду.
Разделим обе части этого равенства на Д?
Мы предполагали, что хну допускают производную по t, а сле-
следовательно, и подавно будут непрерывными функциями от t Поэтому
при стремлении М к нулю Ах и Ду также будут стремиться к нулю,
и, в силу предполагаемой непрерывности ^ и -^, написанное равен-
ство в пределе даст нам
ъ =fx (x, y)Tt~^fy ^ y) df C)
Равенство это выражает 'правило дифференцирования сложной
функции в случае функции нескольких переменных.
Предположим, в частности, что роль независимой переменной t
играет переменная х, т. е. что функция u=f(x, у) зависит от неза-
независимой переменной х как непосредственно, так и через посредство
переменной у> которая является функцией от х. Принимая во внима-
внимание, что — =1, получим на основании равенства C)
CLX,
а?=их.у) + Гу(х,у)&. D)
Производная — называется полной производной от и по х в отли-
отличие от частной производной f'x (x, у).
Доказанное правило дифференцирования сложных функций при-
применяется для нахождения производной неявной функции. Положим,
что уравнение
F(x,y) = 0 E)
определяет у как неявную функцию от х, имеющую производную
/ = ?'(*)¦
Подставляя у = у(х) в уравнение E), мы должны были бы получить
тождество 0 = 0, так как у = у(х) есть решение уравнения E). Мы
видим, таким образом, что постоянную нуль можно рассматривать
как сложную функцию от х, которая зависит от х как непосредственно,
так и через посредство у = <р (х).
Производная по х от этой постоянной должна равняться нулю;
применяя правило D), получим
166 ГЛ. И. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ I 70
откуда
, К(х, у)
Fy(x,y)'
В полученное таким образом выражение для у' может войти как х,
так и у, и если' нужно получить выражение у' только через незави-
независимую переменную х, то придется решить уравнение E) относи-
относительно у.
§ 7. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ
ПОНЯТИЯ О ПРОИЗВОДНЫХ
70. Дифференциал дуги. В интегральном исчислении будет пока-
показано, каким образом находится длина дуги кривой, будет выведено
выражение для дифференциала длины дуги и будет доказано, что
отношение длины хорды к длине стягиваемой ею дуги стремится
к единице, когда дуга беспредельно сжи-
сжимается к точке.
Пусть дана некоторая кривая y=f(x)9
и будем отсчитывать на ней длину дуги от
некоторой фиксированной точки А в опре-
определенном направлении (рис. 73). Пусть 5 —
у длина дуги AM от точки А до переменной
точки Ж. Величина s, как и ордината у,
Рис. 73. является функцией абсциссы х точки М.
Если направление AM совпадает с принятым
направлением кривой, то 5^>0, а в противном случае 5<^0. Пусть
М(х, у) и N(x-\-Ax, y-\-ky) — две точки кривой и As— разность
длин дуг AN и АМУ т. е. приращение длины дуги при переходе из
М в N. Абсолютное значение As есть длина дуги MN, взятая со
знаком плюс. Из прямоугольного треугольника имеем
откуда
Ах2 =
или
/As\2
Ш\2 (As \2 л х(Ау\*
ST) \Ах) — 1 + \Ах! •
Касательная МТ, если она существует, является предельным поло-
положением секущей MN при стремлении N к М вдоль кривой, т. е. при
Дх->±0.
Переходя к пределу в предыдущем равенстве (предполагается суще-
существование касательной), получим, принимая во внимание, что, в силу
70 ] § 7. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ 167
сказанного выше (-jfj —¦ 1:
ИЛИ
— = ±]/"i + /*• A)
Мы должны брать знак (-J-), если при возрастании дг и s возрастает,
и знак (—), если 5 убывает при возрастании х. Будем для опреде-
определенности считать, что имеет место первый случай (изображенный на
рис. 73). Из формулы A) при этом следует
ds = УI-\-yr* dx или, в силу у' = ¦/-,
ds = Ydx*-\-dy\ т. е. ds* = dx* -f dy\ B)
Если радикал считается положительным, то получается арифметическое
значение ds. Формула B) является, по существу, иной записью преды-
предыдущей формулы или формулы A). Она, как мы увидим в дальнейшем,
удобна для приложений. Более подробное рассмотрение длины дуги
будет дано в [103].
Естественным параметром при определении положения точки М на
кривой является длина 5 дуги AM. Эту величину 5 можно принять
за независимую переменную, и при этом координаты (х, у) точки М
будут функциями s:
Более подробно мы будем говорить о «параметрическом задании кри-
кривой» в [74]. Теперь мы выясним геометрический смысл производных
от х и у по s.
Положим, что точка N расположена так, что направление дуги MN
совпадает с принятым направлением кривой, т. е. As^>0. При стрем-
стремлении N к М направление секущей MN в пределе дает определенное
направление касательной к кривой в точке М. Это направление каса-
касательной мы назовем положительным направлением касательной. Оно
связано с принятым направлением самой кривой.
Пусть ах — угол, образованный направлением MN с положительным
направлением оси ОХ. Приращение Ах абсциссы х есть проекция
отрезка MN на ось ОХ, и, следовательно,
дх=Ш. cos <*! (Ш =
причем в этом равенстве MN считается положительным. Деля обе
части этого равенства на длину дуги MN9 равную Д-s, получим
Ах VAx2 + ДУ*
g= to У *****
168
ГЛ. 11. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ
171
По условию As^>0, а потому при стремлении N к М отношение
Дх2 4- Ду2
д-1—— стремится к (-f- 1), а угол <хх стремится к углу а, обра-
образованному положительным направлением касательной М Т с положи-
положительным направлением оси ОХ. Написанное выше равенство даст нам
в пределе
dx ,оч
Точно так же, проектируя MN на ось OYt получим
sina=4v.
ds
D)
71. Выпуклость, вогнутость и кривизна. Случаи выпуклости и
вогнутости кривой в сторону положительных ординат представлены
на рис. 74 и 75.
Одна и та же кривая у=/(х) может, конечно, состоять и из
выпуклых и из вогнутых частей (рис. 76). Точки, отделяющие
У
Рис. 74.
Рис. 75.
выпуклые части кривой от ее вогнутых частей, называются
точками перегиба.
Если будем, двигаясь по кривой в сторону возрастания х, следить
за изменением угла ос, образуемого касательной с положительным
направлением оси ОХ, то увидим (рис. 76),
что на участках выпуклости этот угол
убывает, а на участках вогнутости
возрастает. Такое же изменение, следо-
следовательно, будет претерпевать и tg a, т. е.
производная f (х), так как с увеличением
(уменьшением) угла а и tg a увеличивается
(уменьшается). Но промежутки убывания
f (х) суть те промежутки, где производ-
производная этой функции отрицательна, т. е.
f'
Выпунп
Вогнут.
Перегиб -
Рис. 76.
фу р
()dO> и точно так же промежутки возрастания f'(x) суть те
промежутки, где f"(x)^>0. Мы получим, таким образом, теорему:
Кривая обращена выпуклостью в сторону положительных орди-
ординат на тех участках, где Г(х)<^0> и вогнутостью на тех, где
71 I
§ 7. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ
169
f()^ Точки перегиба суть те ее точки, при переходе через
которые f"(x) меняет знак.
Из этой теоремы мы путем рассуждений, аналогичных приведенным
раньше рассуждениям [58], получаем правило нахождения точек пере-
перегиба кривой: чтобы найти точки перегиба кривой, надо определить
те значения х, при которых f" (x) обращается в нуль или не
существует, и исследовать изменение знака f"{x) при переходе
через эти значения х, пользуясь следующей таблицей:
/" (х)
точка перегиба
ч—
вогн. вып.
1
вып. вогн.
нет точки перегиба
выпукл.
++
вогн.
1
Наиболее естественное представление об искривлении кривой мы
получим, если будем следить за изменением угла а, составляемого
касательной с осью ОХ при движении по кривой. Из двух дуг оди-
одинаковой длины As та дуга будет более искривлена,
для которой касательная повернется на больший
угол, т. е. для которой приращение Аа будет
больше. Эти соображения приводят нас к понятию
о средней кривизне As и о кривизне в данной
точке: средней кривизной дуги As называется
абсолютная величина отношения угла Аа между
касательными в концах этой дуги к длине As дуги. Предел этого
отношения при стремлении As к нулю называется кривизной кри-
кривой в данной точке (рис. 77).
Таким образом, для кривизны С мы получаем выражение:
Рис. 77.
с=
ds
Но tga есть первая производная у', т. е.
a = arctgy\
откуда, дифференцируя по х сложную функцию arctg/:
Как мы только что показали
ds — ± /l-\-y'*dx.
Деля do. на Us, получим окончательно выражение для кривизны
С—±:
у"
+/¦>
¦>¦'••
E)
170 ГЛ. II. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ [ 71
На участках выпуклости надо брать знак (—), а на участках
вогнутости знак (-f-) для того, чтобы С получило положительное
значение.
В тех точках кривой, где не существует производных у' или у'\
не существует и кривизны. Вблизи тех точек, где у" обращается
в нуль, и, следовательно, кривизна обращается в нуль, кривая походит
на прямую. Это будет, например, вблизи точек перегиба.
Положим, что координаты х, у точек кривой выражены через
длину дуги s. В этом случае, как мы видели
dx . dy
cosa = dl' sma = Ts-
Угол а будет также функцией s, и, дифференцируя написанные
равенства по s, получим
da d2x da d2y
-Sina^ = ^?> C0SVs = ^-
Возводя обе части этих равенств в квадрат и складывая, будем иметь
откуда
Величина у?, обратная кривизне, называется радиусом кривизны.
Для радиуса кривизны R мы будем иметь, в силу E), следующее
выражение
— ^О+У1
У"
F)
или
причем значение корня берется положительным.
В случае прямой линии у есть многочлен первой степени от х,
а потому у" тождественно равна нулю, т. е. вдоль всей прямой кри-
кривизна равна нулю, а радиус кривизны — бесконечности.
В случае окружности радиуса г будем иметь, очевидно (рис. 78):
As = rAa и Я = Шп — =г,
аа
т. е. радиус кривизны вдоль всей окружности постоянен. Впослед-
Впоследствии мы увидим, что таким свойством обладает только окружность.
72 ]
§ 7. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ
171
.--. О
Рис. 78.
Рис. 79.
Заметим, что изменение радиуса кривизны совсем не так наглядно, как
изменение касательной. Рассмотрим линию, состоящую из отрезка АВ пря-
прямой и дуги ВС окружности, касательной к отрезку в конце В (рис. 79).
На участке АВ радиус кривизны равен бесконечности, на участке же ВС
он равен радиусу окружности г и,
таким образом, в точке В он терпит
разрыв непрерывности, хотя при
этом направление касательной ме-
меняется непрерывно. Этим обстоятель-
обстоятельством объясняются толчки вагонов
на поворотах. Допустим, что вели-
величина скорости движения вагона v
остается неизменной. В этом случае,
как известно из механики, сила будет
направлена по нормали к траектории
и равна т -^, где т есть масса движущегося тела и R — радиус кривизны
траектории. Отсюда видно, что в точках разрыва непрерывности радиуса
кривизны и сила будет претерпевать разрыв непрерывности, что и обуслов-
обусловливает толчок.
72. Асимптоты. Перейдем теперь к изучению бесконечных вет-
ветвей кривой, на которых одна из координат х или у или обе вместе
беспредельно возрастают. Гипербола и па-
парабола дают нам примеры кривых с беско-
бесконечными ветвями.
Асимптотой кривой с бесконечною
ветвью называется такая прямая, что
расстояние точек кривой до этой пря-
прямой при беспредельном удалении по беско-
бесконечной ветви стремится к нулю.
Покажем сначала, как находить асимпто-
асимптоты кривой, параллельные оси OY. Уравне-
Уравнение такой асимптоты должно иметь вид:
Рис. 80.
где с — постоянная, и в этом случае при движении по соответствую-
соответствующей бесконечной ветви х должно стремиться к с, а у — к бесконеч-
бесконечности (рис. 80). Мы получаем, таким образом, следующее правило.
Все асимптоты кривой
параллельные оси OY, можно получить, найдя те значения х== с,
при приближении к которым f(x) стремится к бесконечности,
Для исследования того, как расположена кривая относительно асимп-
асимптоты, надо определить знак f{x) при стремлении х к с слева и справа.
Перейдем теперь к нахождению асимптот, непараллельных оси ОК.
В этом случае уравнение асимптоты должно иметь вид
172 ГЛ. 11. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ I 72
где 5э т] — текущие координаты асимптоты, в отличие от х, у —теку-
—текущих координат кривой.
Пусть с» есть угол, образованный асимптотой с положительным
направлением оси ОХ, Ш — расстояние точки кривой до асимптоты
и ~Щг __ разность ординат кривой и асимптоты при одинаковой
абсциссе х (рис. 81). Из прямоугольного треугольника будем иметь
и, следовательно, условие
UmMK = 0
мы можем заменить условием
ИшЖ1 = 0. G)
В случае асимптоты, непараллельной оси OY, при движении по
соответствующей бесконечной ветви х стремится к бесконечности.
Принимая во внимание, что МКХ есть разность ординат кривой и
асимптоты при одинаковых абсциссах, можем
у4 переписать условие G) так:
м ^^ Hm \f(x) — ax — b] = 09 (8)
откуда мы и должны получить значения а я Ь.
Условие (8) можно переписать в виде:
Рис.81.
Но первый множитель х стремится к бесконечности, а потому выра-
выражение, стоящее в квадратных скобках, должно стремиться к нулю
то есть
Найдя а, мы определим Ъ из основного условия (8), которое можно
переписать в виде:
й= lim [/(х) — a*].
ЛГ-+ОО
ЛГ-+ОО
Итак, для существования асимптоты, непараллельной оси 0Y,
рт°'й
необходимо и достаточно, чтобы при движении по бесконечной
ветви х беспредельно возрастало и чтобы существовали пределы
a=Mmf-&9 Ь=\\т[1\х)-ах\,
73 ] § 7. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ 173
и тогда уравнение асимптоты будет
Для исследования расположения кривой относительно асимптоты, надо
отдельно разобрать случаи стремления х к (-(- оо) и (— оо) и в каждом
из этих случаев определить знак разности
Если он будет (-)-), то кривая располо-
расположена над асимптотой, а если (—), то под
асимптотой. Если же эта разность при бес-
беспредельном возрастании х не будет сохра- ^
нять неизменного знака, то кривая будет коле-
колебаться около асимптоты (рис. 82). Рис. 82.
73. Построение графиков. Укажем теперь схему действий, кото-
которые надо проделать при построении кривой
более полную, чем это сделано в [59].
Для этого нужно:
а) определить промежуток изменения независимой переменной х\
б) определить точки пересечения кривой с осями координат;
в) определить вершины кривой;
г) определить выпуклость, вогнутость и точки перегиба кривой;
д) определить асимптоты кривой;
е) выяснить симметричность кривой относительно осей координат,
если таковая существует.
Для более точного вычерчивания кривой полезно также наметить
еще ряд точек кривой. Координаты этих точек можно вычислить,
пользуясь уравнением кривой.
1. Вычертим кривую
*~~ 4(лг —I)'
а) х может изменяться в промежутке (—оо, +оо).
б) Полагая * = 0, получим у=.—j-; полагая у = О, получим лг = 3, т. е.
/ 9 \
кривая пересекается с осями координат в точках @, ——) и C, 0).
в) Составляем первую и вторую производные
2
' W— 4(лг_-1J '
Применяя обычное правило, получим вершины C, 0) — минимум, (— 1, — 2) —
максимум.
174 ГЛ. ТТ. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ [ 73
г) Из выражения второй производной видно, что она положительна при
jc>1 и отрицательна при лг<1,.т. е. промежуток A, оо) есть промежуток
вогнутости кривой, а промежуток (—оо, 1) есть промежуток выпуклости.
Точек перегиба нет, так как f"(x) меняет знак лишь при х = 1, а этому
значению х соответствует, как мы сейчас увидим, асимптота, параллельная
оси OY.
д) При х=\ у обращается в бесконечность, и кривая имеет асимптоту
лг = 1.
Будем теперь искать асимптоты, непараллельные оси OY:
(х—3)а
_9_
х
т. е. асимптота будет
___1_ 5_
4 4
Предлагаем читателю исследовать расположение кривой относительно
асимптоты.
е) Симметрии не имеется.
Нанося все полученные данные на чертеж, получим кривую (рис. 83).
2. Исследуем кривые:
которые дают форму тяжелой балки, изгибающейся под влиянием собствен-
собственного веса, причем первая кривая относится к тому случаю, когда концы
балки могут свободно поворачиваться, а вторая — когда они заделаны наглухо.
Общая длина балки 2я, начало координат в середине балки и ось ОУ на-
направлена вертикально вверх.
а) Очевидно, нас интересует изменение х лишь в промежутке (—а, -\-а).
б) Полагая х = 0, получим у — Ьса* и y1 = cai, т. е. в первом случае
прогиб середины балки в пять раз больше, чем во втором. При х = ± а,
y=yi = 0, что соответствует концам балки.
в) Определим производные
У = — 4сл: (За2 — л:2), у" = — 12с (а2 — л;2),
у[ = — 4сх (а2 — л:2), у1; = — 4с (а2 -^ Зл:2).
В обоих случаях в промежутке (— а> Ц- а) будет существовать минимум
при х = 0, что соответствует прогибу середины балки, о котором мы гово-
говорили выше.
г) В первом случае у" > 0 в промежутке (— а, + а), т, е. в первом слу-
случае вся балка обращена вогнутостью вверх. Во втором случае у'{ обращается
а
в нуль при х = ±: г—- и меняет притом знак, т. е. соответствующие точки
У 3
будут точками перегиба балки.
74
§ 7. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ
175
д) Бесконечных ветвей нет.
е) В обоих случаях уравнение не меняется при замене х на (—х)9 т. е.
в обоих случаях кривая симметрична относительно оси ОК.
На рис. 84 изображены обе кривые. Для простоты нами взят случай
я=1, с = —1; на практике длина балки значительно больше ее прогиба,
У
г
1
и г
х 2 J^~if"
Рис. 83.
Рис. 84
т. е. а значительно больше с, так что внешний вид кривой прогиба будет
несколько иной (какой?).
Предлагаем читателю найти точки перегиба кривой
у = е~*2
и сравнить с рис. 60, на котором изображен соответствующий график.
74. Параметрическое задание кривой. При отыскании уравне-
уравнения геометрического места по данному его свойству не всегда бывает
удобно или возможно выразить это свойство непосредственно в виде
уравнения, связывающего текущие координаты лг, у. В таком случае
бывает полезно ввести третью, вспомогательную переменную вели-
величину, через которую можно выразить отдельно абсциссу х и орди-
ординату у любой точки геометрического места.
Совокупность двух полученных таким путем уравнений
О»
также может служить для построения и исследования кривой, так
как при каждом значении t она определяет положение соответствую-
соответствующей точки кривой.
Такой способ задания кривой называется параметрическим,
вспомогательная же переменная t — параметром. Для получения
уравнения кривой в обычном (явном или неявном) виде как зависи-
зависимости, связывающей х и у, нужно из двух уравнений (9) исклю-
исключить параметр t, что можно сделать, хотя бы решив одно из этих
Уравнений относительно t и подставив полученный результат в другое,
176 гл. п. понятие о производной и его приложения [ 74
С параметрическим заданием кривых особенно часто приходится
иметь дело в механике, при исследовании траектории движущейся
точки, положение которой зависит от времени t> а потому и коор-
координаты суть функции от t. Определив эти функции, мы и получим
параметрическое задание траектории.
Так, например, параметрическое уравнение окружности с центром
в точке (xQ, у0) и радиусом г будет
x = xo-\-r cos t, y — yo-\-r sin t. A0)
Перепишем эти уравнения:
х — х0 = г cos t, у — у0 = г sin t.
Возводя обе части в квадрат и складывая, исключим параметр t
и получим обычное уравнение окружности
Точно так же непосредственно ясно, что
x = acos?, y = bsint A1)
есть параметрическое уравнение эллипса
— 4- — = 1
а2 ' Ь2 *
Положим, что у, как функция от х, определена параметрически
формулами (9).
Приращение параметра Д? вызовет соответствующие приращения
Ах и Ау, и мы получим, деля числитель и знаменатель дроби -г—
на Д?, следующее выражение для производной от у до х:
1. by ,. Ы ф' (t)
yx = hm -г-= lim -г—= r, ;.;¦
ИЛИ
Составим вторую производную от у по х:
Применяя правило нахождения дифференциала частного, получим [501
._<Pydx-tPxdy
у щ?—
74 1 § 7. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ 177
Но, в силу (9),
dx = <р' @ dt, <Рх = <р"
d у = f @ dt, d*y = ф* (t) dt\
Подставляя это в A3) и сокращая на dt*, получим окончательно
%йш Ф" @?'(')-?" (РФ'(О
у = ww •
Заметим, что выражение у" по формуле A3) отличается от выра-
выражения той же производной по формуле C) из [55J (при п = 2)
потому что это последняя формула выведена лишь в том предполо-
предположении, что х есть независимая переменная, а при параметрическом
представлении (9) независимой переменной является t. Если х есть
независимая переменная, то dx считается уже постоянным [50],
т. е. не зависящим от лг, и d*x — d(dx) = 0 как дифференциал по-
постоянной. При этом формула A3) переходит в A5).
Имея возможность определить у и у", мы тем самым можем
решить вопрос о направлении касательной к кривой, о выпуклости
и вогнутости кривой и т. д.
В качестве примера рассмотрим кривую, заданную уравнением
0 (fl>0) A6)
и называемую „листом Декарта".
Введем переменный параметр ty полагая
y = tx, A7)
и рассмотрим точки пересечения прямой A7) с переменным угловым коэф-
коэффициентом t и кривой A6). Подставляя в уравнение A6) выражение у из
уравнения A7) и сокращая на х2, получим
а уравнение A7) даст нам тогда
Sat2
Эти уравнения дают параметрическую форму представления листа Декарта.
Определим производные от х и у по t\
-** _баD--'3)
2t(\ -Н3)-ЗгУ _ iat B -<
—аа ~
178
ГЛ. ТТ. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ
[74
Для исследования изменениями^ разобьем весь промежуток (—оо,-J-oo)
изменения t на такие отдельные части, внутри которых производные х\ и y't
сохраняют неизменный знак и не обращаются
в бесконечность. Для этого нам придется от-
отметить значения:
*==~1> 0> уги
о
Рис. 85.
при которых эти производные обращаются в
нуль или бесконечность. Знаки x't и y't внутри
этих промежутков определятся без труда по
формулам A8); вычислив значения х и у на
концах промежутков, мы получим, таким об-
образом, приведенную ниже таблицу.
В соответствии с этой схемой мы полу-
получим кривую, изображенную на рис. 85.
Промежуток
t
(-со, -1)
(- 1, 0)
(У\ +оо)
+
+
+
—
—
y't
+
+
—
X
возрастает от 0 до +°°
возрастает от —со до 0
возрастает от 0 до у/~4а
убывает от у^4а
до у/~2а
убывает от у^2а до 0
V
убывает от 0 до —оо
убывает от + со до 0
возрастает от 0 до у^2л
возрастает от ^2а
до у/~4а
убывает от ^f\a до 0
Для вычисления углового коэффициента касательной имеем формулу
Обратим внимание на то, что хну обращаются в нуль при ^ = 0 и
г = со, и кривая, как это видно из чертежа, пересекает сама себя в начале
координат
координат.
Формула A9) дает нам
= 0 при
/ /О /3\
y^=r lim -iif—LL= lim
г 0,
L
оо при
75 ] § 7. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ 179
т. е. две ветви кривой, взаимно пересекающиеся в начале координат, ка-
касаются— одна оси ОХ и другая оси OY.
При стремлении t к (— 1) х и у стремятся к бесконечности, и кривая
имеет бесконечную ветвь. Определим асимптоту:
угловой коэффициент асимптоты равен lim J^- = lim ' ~* * ) =— 1,
J х-+оэ х t->-\ 3at(\-\-t8)
т. е. уравнение асимптоты будет
у = — х — а или х
75. Уравнение Ван-дер-Ваальса. Если считать, что газ точно следует
законам Бойля — Мариотта и Гей-Люссака, то получается, как известно,
следующая зависимость между упругостью газа /?, его объемом у и абсо-
абсолютной температурой Г:
py = RT,
где R— постоянная, одна и та же для всех газов, если рассматривать одну
„грамм-молекулу" газа, т. е. число граммов газа, равное его молекулярному
весу.
Существующие газы не подчиняются строго указанной зависимости, и
Ван-дер-Ваальсом была дана другая формула, гораздо более точно выражакь
щая явление. Формула эта имеет вид:
где а и Ъ — положительные постоянные, различные для различных газов.
Решая уравнение относительно р, получим
Исследуем зависимость р от у, считая Т постоянным, т. е. рассматривая
случай изотермического изменения состояния газа. Найдем первую производ-
производную от р по у:
~2a(y — bf
dp ___ RT 2а 1 Г
dv ~ (v — bJ^ v'[~ (v — ЬJ[
B1)
Мы будем рассматривать только значения v>b. По поводу физического
смысла этого условия, а также кривых, которые будут получены, отсылаем
читателя к курсам физики. Приравнивая производную нулю, получим урав-
уравнение
Щ?Я.-*Т-Ь B2)
Исследуем изменение левой части этого уравнения при изменении v от Ь
до (-}- с») и для этого определим ее производную по v, помня, что произве-
произведение RT по условию постоянно:
V
J ~~
п
2(v — b)v* — Sv2(v — bf_ 2а (у — Ъ) {у — Щ
откуда видно, что эта производная положительна при Ь<:у <ЗЬ и отрица-
отрицательна при у >> ЗЬ, т. е. левая часть уравнения B2) возрастает в промежутке
(Ь, ЗЬ) и убывает при дальнейшем увеличении у, а потому при у = ЗЬ она
180
ГЛ. И. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ
[76
— RT.
RT>
RT<
достигает максимума, равного
8а
21Ь
Непосредственной подстановкой нетрудно также убедиться, что левая
часть уравнения B2) при v=b и v = -\~co обращается в (—RT) и, следова-
следовательно, имеет знак (—). Если найденный
максимум ее также отрицателен, т. е. если
8а
21Ь >
то левая часть уравнения B2) постоян-
постоянно отрицательна, а в этом случае из
выражения B1) видно, что производная
dp
~~ постоянно отрицательна, т. е. р убы-
убывает с возрастанием v.
Наоборот, если
8а
27Ь '
то левая часть уравнения B2) дости-
достигает положительного максимума при
г/ = 3&, и уравнение B2) имеет один
корень vx в промежутке (Ь, Щ и дру-
другой корень v2 в промежутке C#, +со).
При переходе v через значение vx ле-
левая часть уравнения B2) и, следователь-
следовательно
но, -~- переходит от знака (—) к знаку
(-J-), т. е. этому значению v соответ-
соответствует минимум р. Точно так же убе-
убедимся, что значению v = v2 соответству-
соответствует максимум р.
Если, наконец,
8а
RT=z B3\
— 21Ь '
то максимум левой части уравнения B2) равен нулю, значения v = v1 н
v = v2 сливаются в одно значение v — ЗЬ, при переходе через это значение
левая часть уравнения B2) и -—- сохраняют знак (—), т. е. р постоянно убы-
убывает с возрастанием v, и значению v = 3b соответствует точка перегиба К
кривой. Соответствующие этой точке перегиба значения v — Vfa p=ipk и
значение температуры Г= 7^, определяемое из условия B3), называются
критическими объемом, упругостью и температурой газа. На рис. 86 указан
вид кривых, соответствующих трем рассмотренным случаям.
76. Особые точки кривых. Рассмотрим уравнение кривой в неявной форме
F(x,y) = 0. B4)
Угловой коэффициент касательной к такой кривой определяется по фор-
где (х, у) — координаты точки касания.
76 J § 7. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ 181
Рассмотрим тот частный случай, когда F(x,y) есть целый многочлен от
х и у. В этом случае кривая B4) называется алгебраической. Частные про-
производные Fx(x/y) и F'v(x,y) будут иметь вполне определенные значения,
если вместо х и у подставить координаты любой точки М кривой B4), и
уравнение B5) даст нам определенный угловой коэффициент касательной, во
всех случаях, кроме тех, когда координаты точки (х, у) обращают в нуль
частные производные F'x (х,у) и F' (х,у). Такая точка М называется особой
точкой кривой B4).
Особой точкой алгебраической кривой B4) называется точка, коорди-
координаты которой удовлетворяют уравнению B4) и уравнениям
Fx(x,y) = Q, F'y(x,y)=:0. B6)
Для эллипса
х2 v2
_ 4--^--— 1
а* ^ Ь2 "~ 1
условие B6) даст нам х=у — 0, но точка @, 0) належит на эллипсе, а по-
потому эллипс особых точек не имеет. То же можно утверждать и относи-
относительно гиперболы и параболы.
В случае листа Декарта
условия B6) будут иметь вид:
Зх2 — Зау~0 и 3/ — Зах = 0,
и непосредственно видно, что начало координат @,0) является особой точ-
точкой кривой. При исследовании листа Декарта мы показали, что в начале
координат кривая пересекает сама себя, и две ветви кривой, пересекающиеся
в этой точке, имеют в ней различные касательные: для одной из ветвей
касательной является ось ОХУ для другой — ось OY.
Особая точка, в которой пересекаются различные ветви кривой так,
что каждая ветвь имеет свою особую касательную, называется узловой
точкой кривой.
Таким образом, начало координат является узловой точкой листа Декарта.
Укажем еще на примерах некоторые типы особых точек алгебраических
кривых.
1. Рассмотрим кривую
у2 — ах* = 0 (а> 0),
называемую полукубической параболой. Нетрудно проверить, что коорди-
координаты @,0) обращают в нуль левую часть этого уравнения и ее частные
производные по х и у> и, следовательно, начало координат является особой
точкой кривой. Для исследования вида кривой вблизи этой особой точки
построим эту кривую. Ее уравнение в явной форме будет
Для построения кривой достаточно исследовать ту ее часть, которая
соответствует знаку (+), ибо часть кривой, соответствующая знаку (—),.
будет симметрична с первой частью относительно оси ОХ. Из уравнения
видно, что х не может быть меньше нуля и что при возрастании
л от 0 до (-[- оо) и у возрастает от 0 до (+ оо).
Определим производные первых двух порядков:
3 г— З/а"
182
ГЛ. II. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ
I 76
При д: = 0 и/ = 0, и заметив, что х может стремиться к нулю, принимая
лишь положительные значения, можем утверждать, что ось ОХ будет каса-
касательной к кривой справа в начале координат. Кроме того видно, что для
исследуемой части кривой у" сохраняет неизменный знак (+) в промежуток
(О, +оо), т. е. эта часть обращена вогнутостью в сторону положительных
ординат.
На рис. 87 изображена исследуемая кривая (при а=\). В начале коор-
координат встречаются, не продолжаясь дальше, две ветви кривой, причем обе
Рис. 87.
Рис. 88.
ветви в точке встречи имеют одну и ту же касательную и расположены
по разные стороны от этой касательной вблизи особой точки (в дан-
данном случае — везде). Такая особая точка называется точкой возврата
первого рода.
' 2. Рассмотрим кривую
(у — **)» —*» = <).
Нетрудно проверить, что начало координат является особой точкой кривой.
Уравнение кривой в явной форме будет
у = х2±. У***
Из этого уравнения видно, что х может изменяться от 0 до (+ со). Опре-
Определим производные двух первых порядков:
У= 2* ±-|-/Р, у" = 2±^-У"х
и исследуем отдельно обе ветви кривой, соответствующие знакам (+) и (—).
Заметим, прежде всего, что в обоих случаях, при х = 0 и у = 0 и так
же, как в предыдущем примере, ось ОХ будет для обеих ветвей касатель-
касательной справа.
Исследуя обе ветви обычным способом, получим следующие результаты:
для первой ветви при возрастании х от 0 до (-J- со) и у возрастает от 0 до
(+со), и кривая вогнута; на второй ветви имеется вершина (максимум) при
л: = —, точка перегиба при х = т&? и точка пересечения с осью ОХ
при *= 1.
7G1
§ 7. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ
183
Принимая во внимание все указанное, получим кривую, изображенную
на рис. 88.
В начале координат встречаются, не продолжаясь дальше, две ветви
кривой, причем обе ветви в точке встречи имеют одну и ту же
касательную и расположены по одну сторону от этой касательной
вблизи особой точки. Такая особая точка называется точкой возврата
второго рода.
3. Исследуем кривую
у — х* + хв = 0.
Начало координат есть особая точка кривой. Уравнение кривой в явной
форме будет
у = ±:х2 |Л—х2.
Уравнение кривой в неявной форме содержит только четные степени х и у,
а потому оси координат суть оси симметрии кривой, и достаточно иссле-
исследовать часть кривой, соответствующую положительным значениям х и у.
Из уравнения кривой в явной форме видно, что х может изменяться от (—1)
до 1. Ограничимся вычислением первой
производной У
, л: B — Зх2)
V^-x*
При х = 0 и _у=У = 0, т. е. в начале
координат, касательная совпадает с осью
ОХу а при х =з 1, у = 0 и у' = оо, т. е.
в точке A,0), касательная параллельна
оси ОУ. По обычным правилам найдем,
что кривая будет иметь вершину при
/4-
ринимая во внимание
Рис. 89.
все сказанное и, в частности, симметричность кривой, получим кривую,
изображенную на рис. 89. В начале координат две ветви кривой, соот-
соответствующие знакам (+) и (—) перед корнем, взаимно касаются. Такая
особая точка называется точкой соприкосновения.
4. Исследуем кривую
у* — х2(х— 1)=0.
Начало координат есть особая точка кривой. Явное уравнение кривой будет
у = ± у х2(х— 1>
Принимая во внимание", что подкоренное выражение не может быть отрица-
отрицательным, можем утверждать, что либо * = 0, либо х^\. При л: = 0 и
У=0. Исследуем теперь ветвь кривой, соответствующую знаку (-J-). При
увеличении х от 1 до (+оо) у увеличивается от 0 до (+оо). Из выражения
первой производной
32
видно, что, при д" = 1,у обращается в бесконечность, т. е. в точке A, 0)
касательная параллельна оси ОУ. Вторая ветвь кривой, соответствующая
знаку (—), будет симметрична с исследованной относительно оси ОХ.
184
ГЛ. И. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ
[77
5
k
3
г
1
0
-1
-2
-з
I /
У
/
t ( * ?
I
. \
\
\
5
3
2
1
0
-i
-2
-3
У
/
*-"*7 6 3 4
Принимая все это во внимание, получим кривую, изображенную на рис. 90.
В рассматриваемом случае координаты точки О @, 0) удовлетворяют урав-
уравнению кривой, но вблизи нее нет других точек кривой. В этом случае
особая точка называется изолированной точкой.
Указанными выше типами особых точек исчерпываются всевозможные
случаи особых точек алгебраических кривых, но может случиться, что в не-
некоторой точке алгебраической кри-
кривой произойдет совпадение несколь-
нескольких особых точек, одинаковых или
разных типов.
Кривые не алгебраические назы-
называются трансцендентными.
Предлагаем читателю показать,
что уравнению
у =з х log х
соответствует кривая, изображенная
на рис. 91. Начало координат являет-
является точкой прекращения кривой.
77. Элементы кривой. При-
Приведем основные формулы, связан-
Рис. 91. ные с понятием касательной к
кривой и ее кривизны, и введем
еще некоторые новые понятия, связанные с понятием касательной.
Если уравнение кривой имеет вид:
У =/(*), B7)
то угловой коэффициент касательной есть производная f(x) от у
по х, и уравнение касательной может быть написано в виде:
где (х, у) — координаты точки касания и (Х> У) — текущие коор-
координаты касательной. Нормалью к кривой в точке (х, у) кривой
называют прямую, проведенную через эту точку перпендикулярно
к касательной в этой точке. Как известно из аналитической гео-
геометрии, угловые коэффициенты перпендикулярных прямых обратны
по величине и по знаку, т. е. угловой коэффициент нормали будет
( г), и уравнение нормали можно написать так:
Рис. 90.
или
(Х — х)-\-у(У — у) = 0. B9)
Пусть М есть некоторая точка кривой, Т и N — точки пересе-
пересечения касательной и нормали кривой в точке М с осью OX, Q —
основание перпендикуляра, опущенного из точки М на ось ОХ
(рис. 92). Отрезки QT и QN, лежащие на оси ОХ, называются
77]
§ 7. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ
185
подкасательной и поднормалью кривой в точке М, и отрезкам
этим соответствуют определенные числа, положительные или отри-
отрицательные, смотря по направлению этих отрезков на оси ОХ. Длины
отрезков МТ и MN называются длиною касательной и длиною
нормали кривой в точке М, причем дли-
длины эти мы будем считать всегда положи-
положительными. Абсцисса точки Q на оси ОХ
равна, очевидно, абсциссе х точки М.
Точки Т и N суть точки пересечения
касательной и нормали с осью ОХ, а по-
потому для определения абсцисс этих точек
надо положить в уравнении касательной
и нормали К=0 и полученные уравне-
уравнения разрешить относительно X. Мы по-
получим, таким образом, для абсциссы точки
Т выражение (х — ~], а для абсциссы точки N — выражение
(х-\-уу). Нетрудно теперь определить величину подкасательной и
поднормали:
_ JL
У ~ V ' I C0)
Из прямоугольных треугольников MQT и MQN можно опреде-
определить теперь длины касательной и нормали:
\Ш\=
C1)
причем знак (±) надо выбирать так, чтобы выражения в правой
части оказались положительными.
Напомним еще формулу для радиуса кривизны кривой [71]:
/? = ±A+-Г) *. C2)
у" V J
Обозначая длину нормали буквою п> получим из второй из фор-
формул C1):
У '
и, подставляя это значение у\ -\-у* в формулу C2), будем иметь
еще следующее выражение для радиуса кривизны:
C2,)
186 гл. и. понятие о производной и его приложения [ 78
Если кривая задана параметрически
то первая и вторая производные у' и у" от у по х выражаются по
формулам [74]
v>_dy _V(t)
у ~ dx ~ ср' (;) '
„ _ rfV rfx - d'x dy _ ф" (t) y' (Q - y" (Q <]/ (Q
В частности, подставляя эти выражения в формулу C2), получим вы-
выражения радиуса кривизны в рассматриваемом случае:
к ~ — d*y dx — d*x dy ~ — ф" (t) <?' (t) — у" (
где a есть угол, образуемый касательной с осью ОХ
Если кривая задана неявно
F(x9y) = 0,
то в силу формулы B5) получим следующее уравнение касательной
F'x (х, у) {Х-х) + Fy (х, у) (Y -у) = 0. C5)
78. Цепная линия. Цепной линией называется кривая, которая при соот-
соответствующем выборе координатных осей имеет уравнение:
Кривая эта дает форму равновесия тяжелой вити, подвешенной за два
конца. Ее нетрудно построить по правилам, указанным в [73], и вид ее ука-
указан на рис. 93. Определим первую и вторую производные от у:
откуда
2?
е а)
Подставляя это выражение A+^'2) во вторую из формул C1), получим
для длины нормали кривой
79 1
§ 7. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ
187
и подставляя выражение для п и у" в формулу C2J, получим
" — а*у*у а *'
т. е. радиус кривизны цепной линии равен длине нормали MN. При х = 0
ордината^ цепной линии принимает наименьшее значение у = а, и соответ-
соответствующая точка Л кривой называется ее вер-
вершиною.
На рис. 93 указаны еще некоторые вспо-
вспомогательные линии, которые нам понадобятся
впоследствии. При замене х на (— х) уравне-
уравнение цепной линии не меняется, т. е. ось OY
есть ось симметрии цепной линии.
79. Циклоида. Вообразим круг радиуса
а, который катится без скольжения по непо-
неподвижной прямой. Геометрическое место, опи-
описанное при таком движении некоторой точкой
М окружности круга, называется циклоидой.
Примем прямую, по которой катится круг,
за ось ОХ', за начало координат примем на- Рис« 93.
чальное положение точки М, когда окруж-
окружность касается в ней оси ОХ, и через t обозначим угол поворота окружно-
окружности. Обозначим далее: через С — центр окружности, через TV—точку каса-
касания окружности в ее некотором положении с осью ОХ} через Q"—основание
Рис. 94.
перпендикуляра, опущенного из точки М на ось ОХ, и через R—основание
перпендикуляра, опущенного из точки М на диаметр NNt окружности (рис. 94).
Принимая во внимание, что ввиду отсутствия скольжения
ON = луге
= at,
можем выразить координаты точки М, описывающей циклоиду, через пара-
параметр t = Z. NCM:
х = OQ = ON — QN = at — a sin t = a (t — sin t\
у = ~QM = ~NC — ~RC = a — a cos t = a A — cos t).
Это и дает нам параметрическое представление циклоиды.
Заметим прежде всего, что достаточно рассмотреть изменение t в про-
промежутке @, 2тг), который соответствует полному обороту окружности. После
этого полного оборота точка М опять совпадает с точкой касания О' окруж-
окружности и оси ОХ, но только передвинется на отрезок 00' = 2тш. Часть кри-
188 гл. п. понятие о производной и его приложения | 79
вой, которая получится при дальнейшем движении, будет тождественна
с дугой 00' и получится, если мы перенесем эту дугу на отрезок 2па вправо,
и т. д. Вычислим теперь первые и вторые производные от х и у по t:
-^ = ?'(/) = a (I-cos/), -g-= <!/(*) = я sin*,
d2x d2v
— = <p" (t) = a sin tt -^ .= ф" @ = a cos t.
C6)
Угловой коэффициент касательной в силу первой из формул C3) будет:
. . 2 sin тг cos тг j.
, я sin * 2 2 t
Формула эта приводит к простому способу построения касательной к
циклоиде. Соединим точку Nt с точкой М кривой. Угол MNtN есть впи-
вписанный угол, опирающийся на дугу NM = t, и, следовательно, он равен
-к-. Из прямоугольного треугольника RMNt получим (рис. 94):
Сравнивая это выражение с выражением для у', видим, что прямая MNt
и есть касательная к циклоиде, то есть:
Чтобы построить касательную к циклоиде в ее точке М, достаточно
соединить эту точку с концом Nt того диаметра катящегося круга, дру-
другой конец которого находится в точке касания окружности и оси ОХ.
Прямая MNy соединяющая точку М с другим концом только что упомя-
упомянутого диаметра, перпендикулярна к прямой MNU так как угол NXMN
опирается на диаметр, и мы можем поэтому утверждать, что прямая MN
есть нормаль к циклоиде. Длина нормали л = MN определится непосред-
непосредственно из прямоугольного треугольника NtMN:
п = 2а sin -~-.
Радиус кривизны циклоиды получим, пользуясь формулой C4) и выра-
выражениями'C6):
[а2 A —cos tJ + a2 sin21]3/* __ _^_ а B — 2cos Q3/a _
~~ a cost • а A — cos t) — a sin t • a sin t ~" ~~ cos t — 1 """
= a •
A - cos 0l/2= 4a sin
В последнем выражении мы оставляем лишь знак (+), так как для
первой ветви циклоиды t заключается в промежутке @, 2л), и sin -^ не может
быть величиной отрицательной.
Сравнивая это выражение с выражением для длины нормали п, будем
иметь # = 2п> т. е. радиус кривизны циклоиды равен удвоенной длине нор-
нормали (МС^ на рис. 94).
80 1
§ 7. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ
189
Если бы точка М, которая описывала циклоиду, лежала не на окруж-
окружности круга, а внутри или вне ее, то при качении круга она описала бы
кривую, которая соответственно называется укороченной или удлиненной
циклоидой (иногда обе эти кри-
кривые называют трохоидой). УД
Назовем через h расстоя-
расстояние СМ точки М от центра
катящегося круга. Остальные
обозначения оставим те же.
Разберем сначала случай h < «,
т. е. тот случай, когда точка М
находится внутри круга (рис.
95). Непосредственно из черте-
чертежа имеем:
= at — h sin t, y — QM =
= NC — RC = a — h cos t-
В случае h > а уравнения
будут те же, но кривая примет
вид, указанный на рис. 96.
Рис. 95.
Рис. 96.
80. Эпициклоиды и гипоциклоиды. Если круг, с окружностью которого
связана точка М, катится не по прямой ОХУ а по некоторой неподвижной
у окружности, то получатся два обширных клас-
са кривых: эпициклоиды, если катящийся
круг расположен вне неподвижного; гипоцик-
гипоциклоиды, если катящийся круг расположен вну-
внутри неподвижного.
Выведем уравнение эпициклоид. Поме-
-$ стим начало координат в центр неподвиж-
неподвижного круга; ось ОХ направим по прямой, со-
соединяющей этот центр О с точкой К> которая
является начальным положением точки М,
когда обе окружности касались друг друга в
этой точке. Обозначим буквою а радиус катя-
катящейся окружности, через Ъ — радиус неподвиж-
неподвижной окружности и примем за параметр t угол,
образуемый с осью ОХ радиусом ON непод-
неподвижной окружности, проведенным в точку каса-
касания окружностей, когда подвижная окружность
повернулась на угол ср = /_NCM (рис. 97).
Ввиду того, что качение окружности происходит без скольжения, можем
написать дуга KN = луге NM,
Т" е' bt = a- = —
Из чертежа непосредственно находим
Г= ОС cos /. КОС — СУЙ cos t
Рис. 97.
= (а + b) cos t — a cos {t + <р) = (а + Ь) cos t — a cos *" t,
=ОЛ1 = 1С—RC = OCsin ? KOC — CMsin ? SMC =
= (a + b) sin t — a sin {t + <f) = (a + b) sin t — a sin ~*~ ¦ t.
C7)
190
ГЛ. И. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ
[80
Кривая состоит из ряда одинаковых дуг, каждая из которых соответ-
соответствует полному обороту подвижного круга, т. е. увеличению угла ср на 2те,
а угла t на —. Таким образом, концы этих дуг соответствуют значениям
4ак
2рак
Для того чтобы когда-нибудь мы пришли в начальную точку кривой А',
необходимо и достаточно, чтобы один из этих концов совпал с /f, т. е. чтобы
существовали целые числа р и q, удовлетворяющие условию
ибо точке К соответствует некоторое число полных оборотов около точки О.
Предыдущее условие может быть написано так:
Такие числа р и q будут существовать тогда и только тогда, когда а и Ъ —
отрезки, соизмеримые между собою; в противном же случае отношение -г
есть число иррациональное и не может сде-
сделаться равным отношению двух целых чисел.
Отсюда следует, что эпициклоида пред-
представляет замкнутую кривую тогда и только
тогда, когда радиусы подвижного и непо-
неподвижного кругов соизмеримы; в противном
же случае кривая эта незамкнутая и, вый-
дя из точки Ку в нее никогда больше не
возвратится.
Рис. 98. Это замечание относится и к гипоцик-
гипоциклоидам (рис. 98), уравнение которых может
быть получено из уравнения эпициклоид простою заменой а на (— а):
= (Ь — a) cos t -f- a cos t,
= (b — a) sin t — a sin
•t
C8)
Отметим некоторые частные случаи. Положим, что в случае эпициклоиды
Ь = а, т. е. радиусы неподвижного и подвижного кругов равны. Мы получим
в этом случае кривую, состоящую из одной ветви (рис. 99), и, подставив
в уравнения C7) Ь = а, получим уравнения этой кривой:
х = 2а cos t — a cos 2t,
у = 2а sin t — a sin 2t.
Кривая эта называется кардиоидой.
Определим расстояние г точек М (х, у) этой кривой до точки AT, имею-
имеющей координаты (а} 0), и для этого приведем к более удобному виду выра-
выражения для (х — а) и у:
х — а = 2а cos t — а (cos21 — sin21) — a = 2a cos t ~~ 2a cos-1—2a cos t (I — cos t)%
у = 2a sin t — 2a sin t cos t = 2a sin t A — cos t)t
§ 7. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ
191
откуда
4tf2cos2*(l— cos tJ + 4а2 sin21 (\ — costJ =2a(l—cost).
Разность (л:—а) и у суть проекции отрезка КМ на оси ОХ и О У, но
из написанных выше выражений видно, что (х— а) и у равны произведению
длины отрезка КМ соответственно на cos t и sin t, и мы можем поэтому
утверждать, что отрезок КМ образует угол t с положительным направлением
оси ОХу т. е. параллелен радиусу ON,
Результат этот будет для нас важен
в дальнейшем при выводе правила
построения касательной к кардиоиде.
ч
Рис. 99.
Рис. 100.
Введем угол 6 == тс — t, образованный отрезком КМ с отрицательным
направлением оси ОХ. Для г мы получим тогда
r = 2a(l+cos0).
Уравнение это является уравнением кардиоиды в полярных координатах,
и мы более подробно исследуем эту кривую, когда будем говорить о поляр-
полярных координатах.
Отметим теперь некоторые частные случаи гипоциклоид. Полагая в урав-
уравнениях C8) Ь = 2а, получим
х = 2а cos t = Ъ cos t, у = 0,
т. е. если радиус неподвижного круга вдвое больше радиуса подвижного
круга, то точка М двигается по диаметру неподвижного круга.
Положим теперь, что Ь = 4а. В этом случае гипоциклоида будет состоять
из четырех ветвей (рис. 100), и в этом частном случае она называется астро-
астроидой. Уравнения C8) при Ь = Аа дадут нам
х = Ъа cos t + a cos 3? = За cos t + а D cos31 — 3 cos t) = 4a cos31 = b cos31,
у = За sin t — a sin 3t = 3a sin t — a C sin t — 4 sin31) = 4a sin31 = b sin81.
Возведя ' обе части уравнений в степень 2/з и складывая почленно полу-
полученные уравнения, исключим па'раметр t и получим уравнение астроиды
в неявной форме
а
192
ГЛ. IT. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ
[81
81. Развертка круга. Разверткой круга называется кривая, которую
описывает конец М гибкой нити, постепенно сматывающейся с неподвижной
окружности радиуса а, и притом так, что в точке /С, где нить отделяется от
окружности, она остается касательной к окружности (рис. 101).
Приняв за параметр угол t, образуемый с положительным направлением
оси ОХ радиусом, проведенным в точку АГ, и принимая во внимание, что
/<7И = дуге AI(=at, получим уравнение
развертки круга в параметрической
у "\ форме:
х = прохОМ = прохО/С+ прохКМ =
= a cos t + at sin tt
у = npOYOM = npOYOK + nip0YKM =
= a sin t — at cos t.
Определим, пользуясь первой из
формул C3), угловой коэффициент ка-
касательной:
**х
л cos ^
Рис. 101.
a cos t -j- at sin t
— a sin t -f- я sin ? + atf cos *
Угловой коэффициент нормали к развертке круга будет, следовательно,
равен
откуда видно, что прямая МК и будет нормалью к развертке круга. Свой-
Свойство это, как мы увидим впоследствии, имеет место и для разверток любых
кривых.
82. Кривые в полярных координатах. Положение точки М на
плоскости (рис. 102) определяется в полярных координатах: 1) ее
расстоянием г от некоторой данной точки О (полюс) и 2) углом 6,
который образует направление у
отрезка ОМ с данным направле-
направлением (L) (полярная ось). Часто
X
15
Рис. 102.
Рис. 103.
называют г—радиусом-вектором и б — полярным углом. Если
принять полярную ось за ОХ, а полюс — за начало координат, то
имеем, очевидно (рис. 103):
x = rcos6, jy = rsin8. C9)
Данному положению точки М соответствует одно определенное
положительное значение г и бесчисленное множество значений б,
821
§ 7. НЕКОТОРЫЙ ГЕОМЕТРИЧЕСКИЙ ПРИЛОЖЕНИЯ
которые отличаются слагаемым, кратным 2тс. Если М совпадает с О,
то г = 0 и б — совершенно неопределенно.
Всякая функциональная зависимость вида г = /(9) (явная) или
р (г, 0) = О (неявная) имеет в полярной системе координат свой
график. Чаще приходится иметь дело с явным уравнением
г=/(9). D0)
В дальнейшем мы будем рассматривать не только положительные,
но и отрицательные значения г, причем если некоторому значению 1
соответствует отрицательное значение г, то условимся откладывать
это значение г в направлении, прямо про-
противоположном тому направлению, которое
определяется значением б.
Считая, что на некоторой заданной
кривой г есть функция б, мы видим, что
уравнения C9) представляют собой пара-
параметрическую форму уравнения этой кри-
кривой, причем хну зависят от парамет-
параметра б как непосредственно, так и через по-
средство г. Мы можем поэтому прилагать Рис. 104.
в данном случае формулы C3) и C4)
[77]. Обозначая через а угол, составленный касательной с осью ОД
будем иметь, применяя первую из формул C3),
rr
— г sin
где через г' мы обозначаем производную от г по б.
Введем еще в рассмотрение угол jx между положительными на-
направлениями радиуса-вектора и касательной к кривой (рис. 104). Мы
имеем:
и, следовательно,
cos {л = cos a cos б -f- sin a sin 6,
sin p. = sin a cos б — cos a sin 6.
Дифференцируя равенства C9) по 5 и принимая во внимание, что
dx dy
j? и ф соответственно равны cos a и sin a, получим
cos a = cos б % — r sin Ъ~,
ds ds'
sina —
ds
ds
Подставляя эти выражения cos а и sin а в написанные выше выра-
выражения для cos \ъ и sin [а, будем иметь
dr . rdft
" ds' ds
7 П \Л Гииппла * I
194 гл. и. понятие о производной и его приложения ( 83
и, следовательно,
, ГС1Ь Г 7
db
Из C9) следует
dx = cos 6 dr — г sin 6 dO,
dy = sin 8 dr + r cos б d0,
а потому
ds = У (rf*J + (dyJ = У (rfrJ + r2 (rf8J, D2)
й равенство a = [x + 6 дает нам, если мы разделим числитель и зна-
знаменатель на dd:
Из формулы же D1Х) имеем
где г' и г" — производные первого и второго порядка от г по б.
Подставляя полученные выражения производных в предыдущую фор-
формулу, будем иметь для радиуса кривизны:
83. Спирали. Разберем три вида спиралей:
спираль Архимеда: r = a6,
» гиперболическую: r0=a, (fl>0;
п логарифмическую: r = bea®.
Спираль Архимеда имеет вид, изображенный на рис. 105, причем
пунктир соответствует части кривой при 8<0. Отрицательным значениям б
соответствуют и отрицательные значения г, и их надо откладывать в направ-
направлении, противоположном тому направлению, которое определяется значе-
значением 6.
Всякий радиус-вектор встречает кривую бесчисленное множество раз>:
причем расстояние между каждыми двумя последовательными точками пере-
пересечения есть величина постоянная, равная 2ап. Это видно из того, что на-
направление ради ус а-вектор а, соответствующее некоторому данному значе-
значению б, не меняется, если к б прибавить 2я, 4я... ; длина же г, определяемая
из уравнения г = аб, будет получать приращения 2ап, 4ал, ...
Гиперболическая спираль изображена на рис. 106. Предполагая б > 0%
исследуем, что будет происходить с кривой1 когда б стремится к нулю.
Уравнение
841
§ 7. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ
195
показывает, что г будет стремиться при этом к бесконечности. Возьмем
некоторую точку М на кривой при достаточно малом значении 0 и опустим
перпендикуляр MQ на полярную ось X. Из прямоугольного треугольника MOQ
получим (рис. 106):
¦?гп • п л sin 8
QM = г sin 0 = —g—,
а при стремлении б к нулю
1- 'гл л ж л- SJn в
lim QM = lim a —н— = а.
Итак, расстояние между точкой М кривой и полярной осью, при стрем-
стремлении 0 к нулю, стремится к а, и кривая будет иметь асимптоту LK* парал-
параллельную полярной оси и проведенную на расстоянии а от нее.
I _ -К
Рис. 105.
Рис. 106.
Далее, видим, что г не обращается в нуль ни при каких конечных зна-
значениях 0, а только стремится к нулю, когда 0 стремится к бесконечности.
Кривая будет поэтому беспредельно приближаться к полюсу О, закручиваясь
около него, но никогда не пройдет через О в противоположность спирали
Архимеда. Такая точка называется, вообще,
асимптотической точкой кривой.
Логарифмическая спираль изображена на
рис. 107.
При 0=0, r — b и при стремлении 0 к (+ оо)
и г стремится к ( + оо), а при стремлении 0 к
(—оо) г стремится к нулю, никогда не обра-
обращаясь в нуль. В рассматриваемом случае
г' = abeaB и tg у. = -С- = — .
т. е. радиус-вектор образует с касательной к
логарифмической спирали постоянный угол ja.
Рис. 107.
84. Улитки и кардиоида. Построим круг на диаметре ОА = 2а (рис. 108);
из точки О, лежащей на окружности, будем проводить радиусы-векторы и
на каждом из них будем откладывать постоянную длину h = DM от точки
пересечения D этой прямой с окружностью. Геометрическое место точек М
называется вообще улиткою.
Замечая, что
OD = 2acos0 и ШТ=г,
находим уравнение улитки
г = 2а cos 0 + Л.
196
ГЛ. И. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ
I 84
Если h > 2д, то уравнение это дает для г только положительные зна-
значения, и соответствующая кривая изображена на рис. 109. Если h<.2a, тог
будет принимать и отрицательные значе-
значения, кривая имеет вид, изображенный
на рис. 110. В точке О кривая пересекает
Рис. 108.
Рис. 109.
самое себя. Наконец, при Л = 2в уравнение улитки будет
г = 2а A+ cos 6),
т. е. в этом случае улитка представляет собою кардиоиду [80], которая только
иначе расположена, чем в [80]
(рис. 111). Значению 6 = я будет
соответствовать г = 0, т. е. кривая
пройдет через точку О.
Рис. ПО.
Рис. 111.
Определим первую и вторую производные от г по 8:
г' = — 2а sin 0, г" = — 2а cos в.
Вычислим
г 2a(l
8
то есть
^ = у + у. D4)
Как было показано раньше [80], кардиоиду можно себе представить как
кривую, описанную точкой круга, катящегося по упомянутому выше кругу
85 I § 7. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ 197
с диаметром ОЛ = 2а, причем диаметр катящегося круга равен диаметру
неподвижного круга. Пусть С — центр неподвижного круга, М — некоторая
точка кардиоиды, N — точка касания катящегося круга в его положении,
соответствующем этой точке, с неподвижным кругом, и NNi—диаметр по-
подвижного круга (рис. 111). Выше [80] мы видели, что прямые ОМ и CNt —
параллельны *), т. е. угол ACN=b и, следовательно,
дуга NM = дуге ON = п — 0.
Угол MNiN, как вписанный, опирающийся на дугу NM, равен -~ ^-,
и, наконец, угол, образованный направлениями ОМ и NtM, равен
откуда видно, что NtM и есть касательная к кардиоиде в точке М. Мы полу-
получаем, таким образом, следующее правило:
Чтобы построить касательную к кардиоиде в ее точке М, доста-
достаточно соединить эту точку с концом Nt того диаметра катящегося
круга, другой конец которого находится в точке касания катящегося
круга с неподвижным; нормаль пройдет по прямой MN.
Выведенное выше правило построения касательной к кардиоиде полу-
получается просто из кинематических соображений. Известно, что вообще движе-
движение неизменяемой системы на плоскости в каждый данный момент сводится
к вращению вокруг неподвижной точки (мгновенного центра), причем, вообще
говоря, положение этой точки меняется с течением времени. В случае каче-
качения, указанного на рис. 111, мгновенный центр есть точка соприкосновения N
катящегося круга с неподвижным, и, следовательно, скорость движущейся
точки М, направленная по касательной к кардиоиде, перпендикулярна
к лучу NM, т. е. этот луч есть нормаль к кардиоиде, а перпендикулярная
к нему прямая NtM — касательная к кардиоиде. Из этих соображений сле-
следует, что приведенное правило построения касательной годится, вообще, для
кривых, описанных некоторой точкой окружности, катящейся без скольжения
по неподвижной кривой.
85. Овалы Кассини и лемниската. Овалы Кассини получаются как гео-
геометрическое место точек М, для которых произведение расстояний от двух
данных точек Ft и Fa есть величина постоянная:
Обозначим длину F%F2 через 2а, направим полярную ось по линии FtF%
и полюс О поместим в середине отрезка FtF9. Из треугольников OMFt и
OMFa (рис. 112) находим
FtM2 = г2 + а2 + 2ar cos 9, F2M* = г2 + а* — 2аг cos 9
Подставляя эти выражения в уравнение овалов и возводя его обе части
в квадрат, получим после элементарных преобразований
г4 — 2a2r2 cos 28 + я* — Ь* = 0,
откуда
г2 = а2 cos 26 ± ]Лa4 cos2 26 — (а4 — Ь*).
1) В [80] эти две прямые были КМ и ONL (рис. 99).
198
ГЛ. 11. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ
[ S5
Случаи, соответствующие а2<Ь2 и а2 > Ь2, изображены на рис. 112,
причем второму случаю соответствует кривая, состоящая из двух отдельных
замкнутых кривых. Мы рассмотрим более подробно лишь тот важный слу-
случай, когда а2 = Ь2. Соответствующая кривая называется лемнискатой, и ее
уравнение будет
г2 = 2л2 cos 20.
Уравнение это дает вещественные значения для г, только когда cos 20 ^>0,
т. е. когда 0 лежит в одном из промежутков
И), (т*. ?)• (?¦
причем г обращается в нуль при
тс
Зтс 5я 7п
~4> TJ T'
Нетрудно на основании этих соображений построить кривую (рис. 113).
Рис. 112.
Рис. ИЗ.
В точке О кривая будет пересекать самое себя, и пунктирные прямые
представляют собою касательные к двум ветвям кривой, пересекающимся
в точке О. Дифференцируя обе части уравнения лемнискаты по 0, получим
2а2 sin 20
2rrr = — 4а2 sin 20 или г' = —
откуда
Г
•к
2а2 sin 20
Переходя от полярных координат к прямоугольным, из формулы C9) имеем
r2 = jc2+y, cos0 = —, sin0=^-.
Уравнение лемнискаты можно написать в виде
r2 = 2a2(cos20— sin20);
подставляя предыдущие выражения, получим уравнение лемнискаты в прямо-
прямоугольных координатах
х2 + у* = 2а2 Х*~У\, или (л:2 + УJ = 2а2 (л:2 —.у2),
х —|— _V
откуда видно, что лемниската есть алгебраическая кривая четвертого порядка.
ГЛАВА III
ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ
§ 8. ОСНОВНЫЕ ЗАДАЧИ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
И НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
86. Понятие о неопределенном интеграле. Одной из основных
задач дифференциального исчисления является задача нахождения про-
производной или дифференциала данной функции.
Первой основной задачей интегрального исчисления является
обратная задача — отыскание функции по заданной ее производной
или дифференциалу.
Пусть дана производная
или дифференциал
dy=f(x)dx
неизвестной функции у.
Функция F{x), имеющая данную функцию f(x) своей производ-
производной или/(х)с1х своим дифференциалом, называется первообразной
данной функции f(x).
Если, например,
f{x) = x\
то первообразной функцией будет, например, F(x) = -^x^ Дейст-
Действительно,
Допустим, что мы нашли какую-нибудь первообразную F(x)
функцию данной функции /(лг), которая имеет f(x) своей производ-
производной, т. е. удовлетворяет соотношению
F(x)=f(x).
Так как производная от произвольной постоянной С равна нулю,
мы имеем также
200 ГЛ. Ш. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ I 86
т. е. наряду с F (х) и функция F (х) -f- С есть также первообразная
функция для f(x).
Отсюда следует, что если задача нахождения первообразной
функции имеет хоть одно решение, то она имеет и бесчисленное
множество других решений, отличающихся от упомянутого на про-
произвольное постоянное слагаемое. Можно, однако, показать, что этим
и исчерпываются все решения задачи, а именно:
Если F(x) есть какая-либо из первообразных функций для
данной функции f(x), то любая другая первообразная функция
имеет вид
где С есть произвольная постоянная.
В самом деле, пусть F\ (x) есть любая функция, имеющая f(x)
своей производной. Мы имеем
F\(x)=f(x).
С другой стороны, и рассматриваемая функция F (х) имеет f{x) своей
производной, т. е.
F'{x)=f{x).
Вычитая это равенство из предыдущего, получаем
F[ (х) - F (х) = [Ft (x) - F (x)]' = 0,
откуда, в силу известной теоремы [63],
где С есть постоянная, что и требовалось доказать.
Полученный нами результат можно еще формулировать так: если
производные (или дифференциалы) двух функций тождественно
равны, то сами функции отличаются лишь постоянным слагаемым.
Самое общее выражение для первообразной функции называется
также неопределенным интегралом от данной функции f{x) или
от данного дифференциала f(x)dx и обозначается символом
\f{x)dx}
причем функция /(х) называется подынтегральной функцией, а
f(x) dx — подынтегральным выражением.
Найдя какую-нибудь первообразную функцию F (х), в силу дока-
доказанного выше можем написать
где С есть произвольная постоянная.
Приведем механическое и геометрическое истолкование неопре-
неопределенного интеграла. Пусть у нас имеется закон аналитической зави-
зависимости скорости от времени:
86
S 8. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
201
я требуется найти выражение пути 5 от времени. Так как скорость
движения точки по заданной траектории есть производная ^т от пути
по времени, то задача сводится к нахождению первообразной данной
функции /(/), т. е.
s = \ f(t) dt.
Мы получаем бесчисленное множество решений, отличающихся на
постоянное слагаемое. Эта неопределенность ответа имеет место
вследствие того, что мы не фиксировали того места, от которого
отсчитываем пройденный путь s. Если, например, v = gt-\-v0 (равно-
(равномерно ускоренное движение), то для 5 мы получим выражение
ибо, как нетрудно проверить, производная выражения A) по t сов-
совпадает с заданным выражением v = gt-\-v0. Если мы согласимся
отсчитывать 5 от той точки, которая соответствует значению t = 0,
т. е. если согласимся считать 5 = 0 при * = 0, то мы должны будем
в формуле A) положить постоянную С=0. В предыдущих рассуж-
рассуждениях мы обозначили независимую переменную не буквой х, а бук-
буквой t, что, конечно, не имеет существенного значения.
Перейдем теперь к геометрическому истолкованию задачи на-
нахождения первообразной функции. Соотношение / = /(дг) показывает,
что график искомой первообразной функцим,
или, как говорят, интегральная кривая
есть кривая, касательная к которой при лю-
любом значении х имеет заданное направление,
определяемое угловым коэффициентом
B)
Иными словами, при любом значении неза-
независимой переменной х соотношением B) за- рис, Ц4.
дано направление касательной к кривой и
требуется найти эту кривую. Если построена одна такая интегральная
кривая, то все кривые, которые мы получим, передвигая ее на любой
отрезок параллельно оси О У, будут иметь при одном и том же зна-
значении х параллельные касательные с тем же угловым коэффициентом
У=/(х) (рис. 114), что и исходная кривая. Упомянутый параллель-
параллельный перенос равносилен прибавлению к ординатам кривой постоян-
постоянного слагаемого С, и общее уравнение кривых, отвечающих задаче,
будет
y = t{x)-\-C C)
202
ГЛ, III, ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ
I 87
Для того чтобы вполне определить положение искомой инте-
интегральной кривой, т. е. выражение искомой первообразной функции,
нужно задать еще какую-нибудь точку, через которую интегральная
кривая должна пройти, хотя бы точку пересечения ее с некоторой
прямой
параллельной оси О У. Такое задание равносильно заданию началь-
начального значения^ искомой функции y = F(x), которое она должна
иметь при заданном значении х — х0. Подставляя эти начальные
значения в уравнение C), мы получим уравнение для определения
произвольной постоянной С:
и окончательно первообразная функция, удовлетворяющая поставлен-
поставленному начальному условию, будет иметь вид:
Прежде чем выяснить свойства неопределенного интеграла и спо-
способы нахождения первообразной функции, мы изложим вторую основ-
основную задачу интегрального исчисления, и выясним ее связь с форму-
формулированной уже нами первой задачей — задачей нахождения перво-
первообразной функции. Существенным для дальнейшего является новое
понятие, а именно понятие определенного интеграла. Для того чтобы
естественно прийти к этому новому понятию, мы будем исходить из
интуитивного представления площади. Оно же будет служить нам и
для выяснения связи между понятием определенного интеграла и по-
понятием первообразной функции. Таким образом, рассуждения следую-
следующих двух номеров, основанные на интуитивном представлении пло-
площади, не являются строгими доказательствами новых фактов. Логи-
Логически строгая схема по-
построения основ интеграль-
интегрального исчисления указана в
конце [88]. Она приведена
полностью в конце настоя-
настоящей главы.
87. Определенный ин-
интеграл как предел суммы.
Отметим на плоскости ХО Y
график функции f(x), при-
причем мы считаем, что этот график представляет собою непрерывную
кривую, лежащую целиком над осью ОХ, т. е. считаем, что все орди-
ординаты этого графика положительны. Рассмотрим площадь Sa&, ограни-
ограниченную осью ОХ, этим графиком и двумя ординатам^ х~а и х=Ь
(рис. 115), и постараемся найти величину этой площади. Разобьем
Рис. 115.
87 I § 8. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
для этого промежуток (а, Ь) на п частей в точках
203
Рассматриваемая площадь Sab разобьется на п вертикальных по-
полос, причем k-я полоса имеет основание длины (xk — xk_i). Обозначим
через mk и Mk соответственно наименьшее и наибольшее значения
функции f(x) в промежутке (xk_h xk)y т. е. наименьшую и наиболь-
наибольшую ординаты нашего графика в этом промежутке. Площадь полоски
лежит между площадями двух прямоугольников с общим основанием
(*к-ь *k) (Рис- 116) и с высотами mk и Mk. Эти прямоугольники
являются входящим и выходящим прямоугольниками для k-ft полоски.
0
г
га
it
— -
г
5«
1
Рис. И 6.
Рис. 117.
Таким образом, величина площади k-ft полоски заключается между
площадями упомянутых двух прямоугольников, т. е. между двумя
числами
а потому вся рассматриваемая площадь Sab будет лежать между сум-
суммами площадей упомянутых входящих и выходящих прямоугольников,
т. е. вся площадь Sab будет лежать между суммами
(хп — хп^
D)
Таким образом, мы имеем неравенство
E)
Построим теперь вместо входящего и выходящего прямоугольни-
прямоугольников для каждой полоски какой-либо средний прямоугольник, прини-
принимая, как всегда, за основание (xk — xk_i) и взяв за высоту какую-
либо ординату f(lk) нашего графика, соответствующую любой точке %k
из промежутка (xk_i9 xk) (рис. 117). Рассмотрим сумму площадей
204 ГЛ. И1. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ I 87
этих средних прямоугольников:
Она, так же как и площадь Sab, будет заключаться между суммами
площадей входящих и выходящих прямоугольников, т. е. мы будем
иметь неравенство
G)
Будем теперь беспредельно увеличивать число п делений промежутка
(а, Ь) и притом так, чтобы наибольшая из разностей (хк — хк_х)9
стремилась к нулю. Так как функция f(x) по условию непрерывна,
то разность (Мк — mk) между наибольшим и наименьшим ее значе-
значениями в промежутке (хк_ь хк) будет стремиться к нулю при беспре-
беспредельном уменьшении длины этого промежутка, независимо от его по-
положения в основном промежутке (а, Ь) (свойство непрерывной функ-
функции [35]). Таким образом, если мы обозначим через е„ наибольшую
из разностей
(Ж, — тиО, (Ж2 — т& ...,(Mk — mk\ ..., {Мп_х — mn_v\ (Mn — тп\
то, в силу сказанного, при упомянутом выше предельном переходе
число ел будет стремиться к нулю. Определим теперь разность между
суммой площадей выходящих прямоугольников и суммой площадей
входящих прямоугольников:
r?i\)(xx— * о) -Ь (М* — /и*) (аг« — ДгО + ...+ •
+ (Мк — тк) (хк — xk_x) -f-... + (Мп — тп) (хп — хп_х\
откуда, заменяя все разности (Мк — тк) наибольшей гп и помня, что
все разности (хк — хк_х) — положительны:
то есть
(хп — хп_х)\ = гп (хп — х0) = гп {р — а).
Мы можем, таким образом, написать
то есть
\im(Sn — sn) = 0. (8)
С другой стороны, при всяком п мы имели
^ Sn (9)
87 1 «8. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 205
и величина площади Sab есть определенное число. Из формул (8) и
(9) непосредственно следует, что величина площади Sab является
общим пределом sn и Sn> т. е. площадей выходящих и входящих
прямоугольников:
Hm sn — lim Sn = Sab.
Так как, с другой стороны, сумма средних прямоугольников 5я,
как мы видели, лежит между $п и Sn, то и она должна стремиться
к площади Sab, т. е.
lim Sn = Sab*
Эта сумма S'n является более общей по сравнению с суммами sn и
Sny так как в ней мы можем произвольно выбирать 5Л из проме-
промежутка (дгл_1, xk) и, в частности, можем брать f(ik) равной наимень-
наименьшей ординате тк или наибольшей Mk. При таком выборе сумма S'n
превращается в суммы sn и Sn.
Предыдущие рассуждения приводят нас к следующему:
Если функция f(x) непрерывна в промежутке (а, Ь) и если
мы, разбив этот промежуток на п частей в точках
и обозначив через x = bk любое значение из промежутка (xk-h *Д
вычислим соответствующее значение функции f(ik) и составим
суммуJ)
то при беспредельном возрастании числа делений п промежутка
и беспредельном уменьшении наибольшей из разностей (xk — xk^t)
эта сумма стремится к определенному пределу. Предел этот
равен площади, ограниченной осью ОХ, графиком функции f(x) и
двумя ординатами: х — а,х = Ь.
Упомянутый предел называется определенным интегралом от
функции f(x), взятым по переменной х между нижним пределом
х==а и верхним х = Ь, и обозначается следующим символом
\f(x)dx.
а
Заметим, что существование предела / суммы A0) при беспре-
беспредельном уменьшении наибольшей из разностей (xk—xk_x)y сводится
п
1) Знак 2 / (?fc) (xu — xk_t) есть сокращенное обозначение суммы F).
206
ГЛ, III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ
(
о
к следующему утверждению: при любом заданном положительном
числе 8 существует такое положительное число т), что
<е
при любом разбиении и выборе точек \к из промежутка (xk-b xk),
если наибольшая из (положительных) разностей xk — ^-1<Л- Этот
предел / и является определенным интегралом.
Отметим, что множество значений сумм A0) при всевозможных
разбиениях промежутка (а, Ь) на части и всевозможном выборе ?Л
нельзя упорядочить так, чтобы об-
образовалась упорядоченная пере-
переменная. Предел суммы надо пони-
понимать лишь так, как это указано
выше (с помощью 8 и ч\).
Выше мы предполагали, что
график функции / (х) находится
Рис. 118. целиком над осью ОХ, т. е. что все
ординаты этого графика положи-
положительны. Рассмотрим теперь общий случай, при котором некоторые части
этого графика находятся над осью, а другие под осью ОХ (рис. 118).
Если мы и в этом случае составим сумму F), то слагаемые
/(?&) (xk — xk~i)> соответствующие частям графика, лежащим под осью
ОХ, будут отрицательными, так как разность (хк — хк^г) положи-
положительна и ордината f (fck) отрицательна.
После перехода к пределу получится определенный интеграл,
который будет учитывать площади, находящиеся над осью ОХ со
знаком (+) и под осью ОХ со знаком (—), т. е. в этом общем
случае определенный интеграл
f(x) dx
будет давать алгебраическую сумму площадей, заключенных между
осью ОХ, графиком функции f(x) и ординатами х=*а и х = Ь.
При этом площади над осью ОХ будут получаться с положи-
положительным знаком, а под осью ОХ —с отрицательным.
Как мы увидим в дальнейшем, мы приходим к нахождению пре-
предела суммы вида F) не только в вопросе вычисления площади, но
и во многих, весьма разнообразных, других задачах естествознания.
Приведем только один пример. Пусть некоторая точка М передви-
передвигается по оси ОХ от абсциссы х = а к абсциссе х = Ь, и на нее
действует некоторая сила Г, направленная также по оси ОХ. Если
сила Т постоянная, то работа, которую она совершает при передви-
передвижении точки из положения лг = а в положение х~Ь, определяется
87 I § 8. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 207
произведением R=T {Ъ — а), т. е. произведением величины силы на
пройденный точкой путь. Если сила Т—переменная, то написанная
формула больше неприменима. Положим, что величина силы зависит
от положения точки на оси ОХ, т. е. является функцией абсциссы
точки Т=/(х).
Чтобы вычислить работу в этом случае, разобьем весь путь,
пройденный точкой, на определенные части
и рассмотрим одну из этих частей (xk_i, xk). С ошибкой тем мень-
меньшей, чем меньше длина (xk — xk_i)} мы можем считать, что сила,
действовавшая на точку при передвижении ее от xk_x к xk, посто-
постоянна и совпадает со значением этой силы f($,k) в некоторой точке %k
из промежутка (xk_ly xk). Поэтому для работы на участке (xk_lt xk)
мы получим приближенное выражение
и для всей работы будем иметь приближенное пока выражение вида:
При беспредельном увеличении числа делений п и беспредельном
уменьшении наибольшей из разностей (xk — хк_г) мы получим в пре-
пределе определенный интеграл, дающий точную величину искомой работы:
Отвлекаясь от каких бы то ни было геометрических или механи-
механических истолкований, мы можем теперь установить понятие об опре-
определенном интеграле от функции f(x) по промежутку а^х^Ь как
о пределе суммы вида F). Второй основной задачей интегрального
исчисления и является изучение свойств определенного интеграла и,
прежде всего, его вычисление. Если f(x) — заданная функция, ах = а
и х = Ь — заданные числа, то определенный интеграл
\f(x)dx
а
есть некоторое определенное число. Знак ^ представляет собою
измененную букву 5 и должен напоминать о той сумме, которая
при предельном переходе дала величину определенного интеграла.
Подынтегральное выражение f(x)dx должно напоминать о виде сла-
слагаемых этой суммы, а именно о f$k) (xk—лгл_1). Буква х, стоящая
под знаком определенного интеграла, называется обычно переменной
208
ГЛ. III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ
(88
интегрирования. Отметим по поводу этой буквы одно важное об-
обстоятельство. Величина интеграла, как мы уже упомянули, есть опре-
определенное число, не зависящее, конечно, от обозначения переменной
интегрирования х, и мы можем в определенном интеграле обозна-
обозначать переменную интегрирования любой буквой. Это не будет иметь,
очевидно, никакого влияния на величину интеграла, которая зависит
лишь от того, каковы ординаты графика f(x) и пределы интегриро-
интегрирования а и Ь. Итак, обозначение независимой переменной никакой
роли не играет, т. е., например,
\f{x)dx = \f(t)dt
Вторая задача, интегрального исчисления — вычисление опреде-
определенного интеграла — представляет собою на первый взгляд довольно
сложную задачу составления суммы вида F) и затем перехода к пре-
пределу. Заметим, что при этом предельном переходе число слагаемых
в упомянутой сумме будет беспредельно расти, а каждое из них
будет стремиться к нулю. Кроме того, на первый взгляд эта вторая
задача интегрального исчисления не имеет никакой связи с первой
задачей о нахождении первообразной функции для заданной функ-
функции/(лг). В следующем номере мы покажем, что обе задачи тесно связаны
ь
одна с другой и что вычисление определенного интеграла \f{x)dx
а
совершается весьма просто, если известна первообразная функция
для f(x).
88. Связь определенного и неопределенного интегралов. Рас-
Рассмотрим опять площадь Sab, ограниченную осью ОХ, графиком
функции f(x) и ординатами х = а и х = Ь. Вместе с этой площадью
рассмотрим и часть ее, ограниченную левой ординатой х = а и не-
некоторой подвижной ординатой, отвечающей переменному значению х
{рис. 119). Величина этой площади Sax будет, очевидно, зависеть от
того, в каком месте мы поставим правую ординату, т. е. будет
функцией от х. Эта величина будет изображаться определенным
интегралом от функции /(jc), взятым от нижнего предела а до верх-
88 I § 8. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 209
него предела х. Так как буква х занята для обозначения верхнего
предела, то мы для избежания путаницы будем обозначать перемен-
переменную интегрирования другой буквой, а именно, буквой L Таким обра-
образом, мы можем написать:
Sax=\f(t)dL (И)
а
Здесь мы имеем определенный интеграл с переменным верхним
пределом лг, и его величина есть, очевидно, функция этого предела.
Покажем, что эта функция является одной из первообразных функ-
функций для f(x). Для вычисления про-
производной от этой функции рассмот-
рассмотрим сперва ее приращение A5ajc,
соответствующее приращению Длг
независимой переменной х. Очевид-
Очевидно, имеем (рис. 120):
Обозначим через т и М, соот- х
ветственно, наименьшую и иаиболь- Рис. 120.
шую ординаты графика f{x) в про-
промежутке (х, х -f- Длг). Криволинейная фигура P\PQQi> начерченная
в большом масштабе на рис. 120, будет целиком лежать внутри пря-
прямоугольника с высотой М и основанием кх и будет заключать внутри
себя прямоугольник с высотой т и тем же основанием, а потому
т Длг < A Sax ^ M Дат,
или, разделив на Адг:
Когда Ах -> 0, обе величины т и М в силу непрерывности функ-
функции f(x) стремятся к общему пределу — ординате P1P = f(x) кри-
кривой в точке х, а потому
что мы и хотели доказать. Полученный результат мы можем фор-
формулировать следующим образом: определенный интеграл с перемен-
переменным верхним пределом
\
есть функция этого верхнего предела, производная от которой
равна подынтегральной функции f(x) при верхнем пределе. Иначе
говоря, определенный интеграл с переменным верхним пределом
есть первообразная функция для подынтегральной функции.
210 ГЛ. III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ [ 88
Установив связь между понятиями определенного и неопределен-
неопределенного интегралов, покажем теперь, каким образом можно вычислять
величину определенного интеграла
ь
\f{x)dx,
а
если известна какая-либо первообразная функция F(x) для f(x).
Как мы показали, определенный интеграл с переменным верхним
пределом есть тоже первообразная функция для f(x), и в силу [86]
можем написать
\ A2)
где С есть некоторая постоянная. Для определения этой постоянной
заметим, что если у площади Sax правая ордината совпадает с левой,
т. е. х = а, то величина площади обращается, очевидно, в нуль,
т. е. левая часть в формуле A2) обращается в нуль при х = а.
Следовательно, тождество это при х = а дает
, т. e. C= — F(a).
Подставляя найденное значение С в A2), получим
Наконец, полагая здесь х = Ь, будем игегь
ь ь
\f(t)dt = F(b) — F(a) или \f (x) dx = Fib) — F(a). A3)
а а
Разность вида \F(b) — F(a)] будем в дальнейшем обозначать
ь
символом F(x) .
а
Мы приходим, таким образом, к следующему основному правилу,
выражающему величину определенного интеграла через значение
первообразной функции: величина определенного интеграла равна
разности значений первообразной функции для подынтегральной
функции при верхнем и нижнем пределах интегрирования.
Формулированное правило показывает, что нахождение первооб-
первообразной функции, т. е. решение первой задачи интегрального исчи-
исчисления, решает и вторую задачу, т. е. вычисление определенного
интеграла, и освобождает, таким образом, нас при вычислении опре-
определенного интеграла от сложных операций образования суммы F) и
перехода к пределу.
88 1 § 8. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 211
В качестве примера найдем определенный интеграл
Первообразной функцией для х2 является функция -^-л? [86].
о
Пользуясь выведенным нами правилом, будем иметь
—
Если бы мы, не пользуясь первообразной функцией, стали вычислять
предложенный определенный интеграл непосредственно из его определения
как предела суммы, то пришли бы к гораздо более сложному вычислению,
которое вкратце воспроизведем. Разобьем промежуток @, 1) на п равных
частей точками
В данном случае мы имеем п следующих промежутков:
длина каждого из которых равна —. При составлении суммы F) примем
за Iff левый конец промежутка, т. е.
ei—U> 52 — ~, S3 = —, ••• , Ъп=—-—•
Все разности *?—#?_1 = —, и, замечая, что значения подынтегральной
функции f(x)=x2 на левых концах промежутков будут:
можем написать
1 , 1 1
Для вычисления суммы, стоящей в числителе, напишем ряд очевидных
равенств:
1+3.12+13
2 + 3.22 + 2*
212 ГЛ. lit. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ | 88
Складывая почленно, получим
2» + За + ...Ч-л8=:(л-1) + 3[1+2 + ... + («-1)] +
+ 3[Н + 22 + ... + <«-1)81+1'+ 2*+ ... + (*-1)'.
Производя сокращения и применяя формулу суммы арифметической про-
прогрессии, можем написать
откуда
Подставив полученное выражение в A4), имеем
1
Г 2^ г п(п— 1)Bл — 1) 1 ,. Л 1WO 1\ 2 1
J n—oo 6/r on^oo\ w/\ nj 6 3
Уяснив основные задачи интегрального исчисления и связь между
ними, мы посвятим следующий номер дальнейшему рассмотрению
первой задачи интегрального исчисления, а именно задаче выяснения
свойств неопределенного интеграла и его разыскания.
Наши предыдущие рассуждения об определенном интеграле осно-
основывались на чисто геометрических соображениях, а именно на рас-
рассмотрении площадей Sab и Sax. В частности, доказательство основ-
основного факта, что сумма F) имеет предел, исходило из допущения,
что для всякой непрерывной кривой имеется определенная площадь
$аь- ^Ри Bce^ наглядности такого допущения оно не является строго
обоснованным, и единственно математически строгий путь был бы
обратный: не опираясь на геометрическую интерпретацию, доказать
непосредственно аналитическим путем существование предела 5
суммы
Л= 1
каковой потом уже принять за определение площади Sab. Это
доказательство мы приведем в конце настоящей главы и притом
при более общих предположениях относительно функции f(x)y чем
ее непрерывность.
Заметим еще, что геометрическая интерпретация являлась суще-
существенным моментом и при доказательстве того основного предло-
предложения, что при непрерывности подынтегральной функции производ-
производная от определенного интеграла по верхнему пределу равна подын-
подынтегральной функции при верхнем пределе. В следующем параграфе
настоящей главы мы приведем и строгое аналитическое доказатель-
доказательство этого предложения. Оно, совместно с доказательством существо-
существования определенного интеграла от непрерывной функции, позволяет
89 I § * НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 213
утверждать, что для всякой непрерывной функции имеется первооб-
первообразная, т. е. неопределенный интеграл. Дальше мы выясним основ-
основные свойства неопределенного интеграла, и будем считать, что имеем
дело лишь с непрерывными функциями.
При изложении свойств определенного интеграла мы строго до-
докажем основную формулу A3). Таким образом, единственным недока-
недоказанным фактом останется факт существования предела суммы A0)
для непрерывной функции f(x). Это доказательство, как мы уже
сказали, приводится в конце главы.
89. Свойства неопределенного интеграла. В [86] мы видели, что
две первообразные функции для одной и той же функции отличаются
лишь постоянным слагаемым. Это приводит нас к первому свойству
неопределенного интеграла.
I. Если две функции или дяа дифференциала тождественны,
то неопределенные интегралы от них могут отличаться лишь
на постоянное слагаемое.
Наоборот, чтобы проверить, что две функции отличаются
постоянным слагаемым, достаточно показать, что их производ-
производные (или дифференциалы) тождественны.
Следующие свойства II и III непосредственно вытекают из поня-
понятия о неопределенном интеграле как первообразной функции, т. е.
из того, что неопределенный интеграл
\f{x)dx
есть такая функция, производная которой по х равна подынте-
подынтегральной функции f(x), или дифференциал которой равен подын-
подынтегральному выражению f(x)dx.
И. Производная от неопределенного интеграла равна подынте-
подынтегральной функции, а дифференциал — подынтегральному выраже-
выражению:
d\f{x)dx=f(x)dx. A5)
Ш. Одновременно с A5) мы имеем
и эту формулу можно еще переписать так [50]:
A6)
что в соединении со свойством И дает: рядом стоящие знаки du\,
в каком бы порядке они ни следовали, взаимно уничтожаются,
если условиться отбрасывать произвольную постоянную в равенстве
между неопределенными интегралами.
214 ГЛ. III. ПОНЯТИЕ, ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ [ 90
IV. Постоянный множитель можно выносить из-под знака
интеграла:
\ \1). A7)
V. Интеграл от алгебраической суммы равен алгебраической
сумме интегралов от каж&ого слагаемого:
\(u-\-v — w)dx = \udx-\- \vdx— \wdx-\-C. A8)
Правильность формул A7) и A8) нетрудно обнаружить, диффе-
дифференцируя обе части и убеждаясь в тождественности полученных про-
производных. Например, для равенства A7):
(\Af(x)dxy=Af(x),
(A \f(x) dx + С/ = A (\f(x)dxY = Af(x).
90. Таблица простейших интегралов. Для получения этой таб-
таблицы достаточно прочесть в обратном порядке таблицу простейших
производных [49], после чего мы получим
J dx =
xmdx— , 1 + С, если тф — 1,
1 sin x dx = — cos x-\-C, \ cos x dx= sin x -f- C,
Для проверки этой таблицы достаточно установить, что производ-
производная правой части равенства тождественна с подынтегральной функцией
левой части. Вообще, зная ту функцию, от которой данная функция
f(x) есть производная, мы тем самым получаем ее неопределенный
интеграл. Но обыкновенно, даже в самых простых случаях, заданные
J) Иногда не пишут произвольного постоянного слагаемого после неоп-
неопределенного интеграла, подразумевая, что неопределенный интеграл уже
содержит такое слагаемое. Равенство A7) при этом будет
= A \f(x)dx.
01 I § 8. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 215
функций не находятся в таблице интегралов, что и делает задачу
интегрального исчисления гораздо более трудной, чем задачу диф-
дифференциального исчисления. Все дело приводится к преобразованию
данного интеграла к таким, которые заключаются в таблице про-
простейших.
Преобразование это требует навыка и практики и облегчается
применением нижеследующих основных правил интегрального исчи-
исчисления, а также свойств IV, V из [89].
91. Правило интегрирования по частям. Мы знаем, что если
иу г> — две какие угодно функции от х с непрерывными производ-
производными, то [50]
или
В силу свойств I, V и III мы заключаем отсюда
—J nda + C
что и дает формулу интегрирования по частям:
\ [ A9)
Она сводит вычисление интеграла ^udv к вычислению интеграла
\vdii, причем этот последний может оказаться более простым.
Примеры.
1. J \ogxdx.
Полагая здесь
u = \ogx, dx = dvf
имеем прежде всего
dx
откуда, в силу A9),
V log*d* = A:log*— \ хи— = #!og#—x+ С.
На практике отдельные преобразования выписывать не нужно; все дей-
действия производятся по возможности в уме.
2. ^ $ j J
216 ГЛ. 1П. ПОНЯТИЕ OB ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ | 92
что дает окончательно
$ e*x*dx = е* \х* — 2х + 2} + С.
3. ^ sin х • xsdx = \ хь • sin x dx = jj *8rf (— cos л*) =
= — х9 cos л: — ^ (— cos л-) dx* = — a:8 cos x + 3 ^ a:2 • cos x /tx =
= — л*8 cos л* + 3 ^ л:2*/ sin л: = — л:8 cos jc + Зл:2 sin x — 3 ^ sin x d\ =
= — л:8 cos л: + Зл:2 sin лг — 6 ^ л: sin л: tfx =
= — xs cos л: + Зл*2 sin л: — б ^ л-rf (— cos л*) =
= — л:8 cos x + Зл:2 sin x + бл* cos x — 6 ^ cos л* dx =
= — л:8 cos x -f- Зл:2 sin x -j- бл: cos x — б sin x + С
Способ, показанный в этих примерах, применяется, вообще, при
вычислении интегралов типа:
^ eaxxmdx, \ sin Ьх • xmdx, \ cos ?x • xmdx,
где /я есть любое целое положительное число; нужно заботиться
лишь о том, чтобы при последовательных преобразованиях степенью
все время понижалась, пока не дойдет до нулевой.
92. Правило замены переменных. Примеры. Интеграл
часто можно упростить, введя вместо х новую переменную tt положив
B0)
Для преобразования неопределенного интеграла к новой пере-
переменной t no формуле B0) достаточно преобразовать к новой
переменной его подынтегральное выражение:
B1)
Для доказательства в силу свойства I [89] нам достаточно уста-
установить совпадение между дифференциалами от левой и правой частей
формулы B1). Произведя дифференцирование, имеем
d(\f (x)dx) = f(x)dx = f {<?(()]<?'(t)dt,
d(\fW (')] ?' @ dt) = f\9 @] ?' @ dt
Часто вместо подстановки B0) употребляют обратную
92 ] § 8. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 217
Примеры.
1. § (ах + Ь)т dx (при т ф— 1).
Для упрощения интеграла полагаем
ах -f b = t, adx = dt> dx = —.
Подставив это в данный интеграл, находим
Для вычисления этого интеграла употребляется подстановка Эйлера,
о которой более подробно сказано ниже. Новая переменная t вводится здесь
по формуле
|/д:2+ a = t — х, t = x + Ух2 + а.
Для определения х и dx возвышаем в квадрат:
=
Подставив все это в данный интеграл, имеем
JT+~a J i* + a ' 2 t*
вычисляется при помощи особого приема, с которым мы познакомимся
подробнее позже, а именно при помощи разложения подынтегральной
Функции на простейшие дроби.
218 ГЛ. Ш. ПОНЯТИЕ ОВ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ [ 92
Разложив знаменатель подынтегральной функции на множители:
л:2 — а2 = (х — а) (х + а)у
представим ее в виде суммы более простых дробей:
1 А , В
¦ -г -
х2 — а2 х — а ' х + в '
Для определения постоянных А и В освобождаемся от знаменателя, что
дает тождество
1 = А (х + а) + В (х — а) = (А + В) х + а (А — В),
которое должно иметь место при всех значениях х. Оно будет выполнено,
если определим А и В из условий
Итак, имеем:
х2 — а2 2а\х — а
J дг2-в2 2a|.J x-a J
: I [log (x - а) - log (x + в)] + С = 1 log ?-p5 + С.
7. Интегралы более общего вида:
tnx-j-n
приводятся к разобранным уже раньше, если в знаменателе подынтеграль-
подынтегральной функции выделить полный квадрат. Имеем
Полагаем далее
что дает
mx + n = m(t — ?
где мы положили А = т и 5 = л ^-. Положив, наконец,
где знак (-{-) или (—) нужно взять в зависимости от знака левой части
этого равенства и а считается положительным, мы можем переписать дан-
данный интеграл в виде:
tdt
92 | § 8- НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 219
Первый из этих интегралов вычисляется сразу, если положить
t2 ± а2 = г, 2t dt = dz,
что дает
z 1. L ..
Второй же интеграл имеет вид, разобранный в примерах 3 (+) и б (—).
8. Интегралы вида:
приводятся к разобранным выше тем же приемом выделения полного ква-
квадрата. Применяя обозначения примера 7, можем переписать данный интеграл
в виде: '
Г
Vx2+px+q
tdt . D С dt U 2 p2\
Первый из этих интегралов вычисляется при помощи подстановки
которая дает
t dt С zdz С
= 1 = I
Vt2 + b J « J
Второй интеграл уже разобран в примере 5 и равен log(t-\-]ft2 +#).
9." Аналогичным приемом выделения полного квадрата интеграл
Jmx 4- п ,
— dx
yq-\-px — х2
можно привести к виду:
и имеем
при помощи подстановки а2 — t2 = z2. Второй интеграл разобран в примере 4.
in f • 2 ^ Г* 1—cos 2л: , 1 / 1 . о \ . п
10. 1 sin2 х dx = 1 ^ dx = -у (х — -тг sin 2х \ + С «
= -^ (х — sin х cos л*) + С.
'• ~т (х + sin х cos х) + ^
220 ГЛ. III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ I
11. Интеграл
приводится к разобранному уже при помощи интегрирования по частям:
Прибавив и вычтя а в числителе подынтегральной функции последнего
интеграла, перепишем предыдущее равенство в виде:
у х 2+а
или
dx
yx2
откуда окончательно
С
у jrqrj tf jc = -i- [л: Vx2+a + л log (л: + /л:2 + л)] + С.
93. Примеры дифференциальных уравнений первого порядка. В [51]
мы рассматривали простейшие дифференциальные уравнения. Самое общее
дифференциальное уравнение первого порядка имеет вид:
F(x, у, у') = 0.
Это есть соотношение, связывающее независимую переменную х, неиз-
неизвестную функцию у и ее первую производную у'. Обыкновенно можно
решить это уравнение относительно/ и переписать его в виде:
где f(x, у) есть известная функция от д: ну.
Не рассматривая этого уравнения в .общем случае, что будет сделано
во втором томе, остановимся лишь на некоторых простейших примерах.
Уравнение с разделяющимися переменными, — когда функция f(x> у)
представляется в виде отношения двух функций, из которых одна зависит
только от х, а другая только от у:
Помня, что у = ~, можем переписать это уравнение в виде:
Ф (У) *>=»?(*)«**.
так что в одну часть уравнения входит только буква х, в другую — только
буква у; это преобразование и называется разделением переменных. Так как
в силу свойства I [89] получаем
$Ф(У)Ф = $?(*)** + С, B3)
откуда и можно, взяв интегралы, определить искомую функцию у.
93 I § 8- НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 221
Примеры. 1. Химические реакции первого порядка. Обозначив через
а количество вещества, имевшегося к началу реакции, через х — количество
вещества, вступившего в реакцию к моменту t, мы имеем [51] уравнение
~=с(а —л:), B4)
где с — постоянная реакции. Сверх того мы имеем условие
х = 0. B5)
Разделяя переменные, находим
dx
а — х
или, интегрируя
где Сх — произвольная постоянная. Отсюда выводим
а-*=**-*-*-Се"*,
где С = е * есть также произвольная постоянная. Ее можно определить
из условия B5), в силу которого предыдущее равенство при * = 0 дает
а= С, и окончательно
1
2. Химические реакции второго порядка. Пусть в растворе содержатся
два вещества, количества которых к началу реакции, выраженные в грамм-
молекулах, суть а и Ь. Допустим, что к моменту t в реакцию вступают
равные количества обоих веществ, которые мы обозначим через дг, так что
количества оставшихся веществ будут а — х и Ь — х.
По основному закону химических реакций второго порядка скорость
течения реакции пропорциональна произведению этих оставшихся количеств,
т. е.
d-± = k(a-x)(b-x).
Нужно интегрировать это уравнение, присоединив к нему еще начальное
условие
х
0.
Разделяя переменные, имеем
(a-x)(b-x)-*att
или, интегрируя,
„-~, B6>
где С, — произвольная постоянная.
Для вычисления интеграла в левой части мы применим способ разложе-
разложения на простейшие дроби (пример 6) [92]:
1 = А . В
(а — х) (Ь — л') а — х b — х *
1 == A (b — х) + В (а — х) = — (А + В) х + (АЬ + Ва),
222 ГЛ. III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ
что дает
откуда
1
так что
[ 93
— (Л + В) = 0;
Подставляя в B6), имеем:
° я— л: N
Ь — х
а — х '
где С = е(& Cl. Искомая функция х определяется отсюда без всякого труда.
Предлагаем читателям разобрать особый случай a = bt когда предыду-
предыдущие формулы теряют смысл.
3. Найти все кривые, пересекающие под данным постоянным углом
радиусы-векторы, проведенные из начала коор-
координат *) (рис. 121).
Пусть М (Ху у) есть точка искомой кривой.
Из чертежа мы имеем
ш = а— 0,
Рис. 121.
¦«•-^¦-«-тЧпйт-:
Обозначив для удобства вычислений
__ 1
gw —
и освобождаясь от знаменателей, перепишем полученное дифференциальное
уравнение в виде
или, умножив обе части на dx,
х dx+ydy = a(xdy—ydx). B7)
Это уравнение интегрируется весьма просто, если перейти от прямо-
прямоугольных координат х, у к полярным г, 0, приняв ось ОХ за полярную ось
и начало координат О за полюс. Мы имеем [82]
что дает
') Вообще углом между двумя кривыми называется угол между касатель-
касательными к ним, проведенными в точке пересечения кривых.
94 J § 9. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА 223
Уравнение B7) перепишется после этого в виде:
dr
Интегрируя, имеем
Полученные кривые называются логарифмическими спиралями.
§ 9. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
94. Основные свойства определенного интеграла. Мы уже
говорили, что определенный интеграл
ъ
I=\f{x)dx, a<b, A)
а
где (я, Ь) — конечный промежуток и /(лг) — непрерывная в нем
функция, есть предел сумм вида [87]
ь п
$ /(*) dx = Urn 2 /E*) С** - **-i). B)
a k=\
Этот предел надо понимать следующим образом: при любом задан-
заданном положительном 8 существует такое положительное число rj, что
<е
при любом разбиении и выборе точек Ел из промежутков (xk_b xk),
если наибольшая из (положительных) разностей xk — xk.x < tj.
Кратко говоря, интеграл A) есть предел сумм B) при любом
выборе !-? и стремлении наибольшей из разностей х^ — х^\ к нулю.
Отметим, что при этом число слагаемых суммы B) беспредельно
возрастает. Строго говоря, определение упомянутого предела B) надо
понимать так, как это указано выше (с помощью 8 и г\).
В конце главы мы докажем существование упомянутого предела
сумм B) для непрерывных функций и некоторых классов разрывных
функций. В дальнейшем, если не оговорено особо, мы будем считать^
подынтегральную функцию непрерывной на промежутке интегрирования.
Мы предполагали, что нижний предел а интеграла меньше верхнего
предела Ь. Если # = ?, то из толкования интеграла как площади
следует, что естественно считать
а
C)
Это равенство является определением интеграла для того случая,
когда верхний предел равен нижнему.
224 ГЛ. Ш. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ ( 9t
При а]>? принимается следующее определение:
ь а
— \f(x)dx. D)
Ь
В интеграле, стоящем в правой части, нижний предел b меньше
верхнего а и интеграл понимается обычным образом, как указано
выше. Если бы мы для интеграла, стоящего слева, построили сумму B),
то для нее (а^>Ь) мы получим
и все разности (xk — xk_x) отрицательны. Если мы перейдем к инте-
интегралу, стоящему в правой части равенства D), т. е. будем считать а
верхним пределом и Ь нижним, то промежуточные точки xk надо
будет считать в обратном порядке, и в сумме B) все разности пере-
переменят знак. Эти соображения делают естественным определение D)
в том случае, когда а^>Ь.
Отметим еще очевидное равенство
ь ъ
$ dx= \ \dx = b — a. E)
а а
Действительно, раз подынтегральная функция при всех х равна еди-
единице, то
— а) + (дг2 — хх) + {хг — лг
Но сумма, стоящая в квадратных скобках, равна постоянной {Ь — а).
Переходим к перечислению и доказательству свойств определен-
определенного интеграла. Первые два из них суть определения, выраженные
равенствами C) и D).
I. Определенный интеграл с одинаковыми верхним и нижним
пределами считается равным нулю.
II. При перестановке между собой верхнего и нижнего преде-
пределов определенный интеграл, сохраняя абсолютное значение, ме-
меняет лишь знак:
а Ь
\f(x)dx=-[f(x)dx.
Ь а
III. Величина определенного интеграла не зависит от обозна-
обозначения переменной интегрирования:
а
Это уже было выяснено в [87].
94 I $ 9. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА 225
IV. Если дан ряд чисел
a, ft, i, • • •, A, /,
расположенных в каком угодно порядке, то
i ь с i
\ \ F)
Эту формулу достаточно установить для случая трех чисел а, Ь, с9
после чего нетрудно распространить доказательство на какое угодно
число слагаемых.
Допустим сперва, что a <ib <Cc. Из определения вытекает, что
Нш 2
причем предел этот будет один и тот же, каким бы мы способом
ни разбивали на части промежуток (а, с), лишь бы только наиболь-
наибольшая из разностей (Х{ — Xi_x) стремилась к нулю. Мы можем усло-
условиться разбивать промежуток (а, с) так, чтобы точка Ъ, лежащая
между о и с, каждый раз оказывалась одной из точек деления.
Но тогда сумма
разобьется на две такого же типа, с той лишь разницею, что при
составлении одной мы будем разбивать на части промежуток (а, Ъ\
при составлении же другой — промежуток (Ь, с\ и притом так, что
в обоих случаях наибольшая из разностей (Х( — -#7-i) стремится
к нулю. Каждая из этих сумм будет стремиться соответственно к
\f{x)dxy
а Ь
и мы получим, фиксируя последовательность разбиений и числа
\f(x)dx \ l
что и требовалось доказать.
Пусть теперь Ь лежит вне промежутка (а, с\ например а
По доказанному сейчас мы можем написать
) dx = J /(*) dx + J f{x) dx,
Q о ы
226 ГЛ. Ш. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ [ 95
откуда
ebb
\ f(x)dx= \ f(x)dx — \ f(x)dx.
а а с
Но в силу свойства II имеем
Ь С
— \f(x)dx=\ f{x)dx,
с b
т. е. опять
с b с
\f{x)dx = \ f(x)dx + \f(x)dx.
a a b
Аналогичным путем можно рассмотреть и все остальные возмож-
возможные случаи взаимного расположения точек.
V. Постоянный множитель можно выносить из-под знака
определенного интеграла, т. е.
ь ь
\
а
ибо
п Ъ
= A Jim 2 /(У (хг - x.t_x) = A\ f(x) dx.
VI. Определенный интеграл от алгебраической суммы равен
алгебраической сумме определенных интегралов от каждого сла-
слагаемого, ибо, например,
\ 2
= lim 2 /(W (xt -х(.г) - lim 2
95. Теорема о среднем. VII. Если в промежутке (а, Ь) функции
f(x) и <f(x) удовлетворяют условию
О, G)
95 I
то и
§9. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
<?(x)dx
227
(8)
короче говоря, неравенства можно интегрировать.
Составим разность
ь ь ь
\ <t{x)dx—\f{x)dx = \ [<?(x)—f(x)]dx =
a a a
= Urn ? [<P (У-/&)](*,-*,_,).
В силу неравенства G) слагаемые, стоящие под знаком суммы, по-
положительны или, по крайней мере, неотрицательны. Следовательно,
то же можно сказать о всей сумме и ее пределе, что и приводит
к неравенству (8).
Приведем еще геометрическое по-
пояснение сказанного. Допустим сперва,,
что обе кривые
y=f(x\ y = <
лежат над осью ОХ (рис. 122). Тогда о
фигура, ограниченная кривой y=f(x),
осью ОХ и ординатами4 х== а и х = Ь,
лежит целиком внутри аналогичной фигуры, ограниченной кривой
у = (р (х), а потому площадь первой фигуры не превосходит площади
второй, т. е.
ь ъ
Общий случай какого угодно расположения данных кривых отно-
относительно оси ОХ при сохранении условия G) приводится к преды-
предыдущему, если передвинуть чертеж настолько кверху, чтобы обе кри-
кривые оказались над осью ОХ; это передвижение прибавит к каждой
функции f{x) и <р(х) одно и то же слагаемое с.
Легко показать, что если в G) имеет место знак <^, то и в (8)
имеет место знак <\ Напомним, что функции f{x) и <р (х) считаются
непрерывными.
Следствие. Если в промежутке {а, Ь)
|/М|<?М<Д (9)
то
— a),
A0)
228 ГЛ, Ш. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ
В самом делеу условия (9) равносильны следующим:
— Л* < —? ДО </(*)*??(*)< +А*.
Интегрируя эти неравенства в пределах от а до Ъ (свойство VII)
и пользуясь E), получаем
ь ь ь
— М(Ь — а)^ — $ <р (х)dx< $ /(*)rf*< 5 ТС*)dx^м(ь —' а)>
а а а
что равносильно неравенствам A0).
Полагая у(х) = \/(х)\, получаем из A0) важное неравенство:
x, A00
которое является обобщением на случай интеграла известного свой-
свойства суммы: абсолютная величина суммы меньше или равна сумме
абсолютных величин слагаемых. В написанной формуле знак равен-
равенства имеет место, как нетрудно понять, лишь в том случае, когда
f(x) не меняет знака в промежутке (а, Ь).
Из того же свойства VII вытекает весьма важная теорема.
Теорема о среднем. Если функция <р(х) сохраняет знак
в промежутке (а, Ь), то
\ f(x) г (х) dx=*№ \<?(x)dx, A1)
а а
где I есть некоторое значение, принадлежащее промежутку (а, Ь).
Будем для определенности считать <р(лг)^О в промежутке (а, Ь)
и обозначим через т и М соответственно наименьшее и наибольшее
значения f(x) в промежутке (а, Ь). Так как, очевидно,
(причем оба знака равенства имеют место одновременно, только когда
f{x) постоянна) и ср(^)^О, то
/тр (х) ^ / (х) <р (х) ^ Мер (лг),
и в силу свойства VII, считая Ь^>а,
ь ь ь
Отсюда ясно, что существует такое число Р, удовлетворяющее
неравенству т^Р^М, что
ь ь
\ \ A2)
95 | § 9. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА 229
Так как функция f(x) непрерывна, она принимает в промежутке
(а, Ь) все значения, лежащие между наименьшим т и наибольшим М,
в том числе и значение Р [35]. Поэтому найдется такое значение ?
внутри промежутка (а, Ь), для которого
что и доказывает формулу A1).
Если ср(х)^0 в промежутке (а, Ь)> то ~(р(д;)^О в промежутке
(а, Ь). Применяя к ней доказанную теорему, получим
ь ь
\ f{x)[^ft(x)\dx = fQb\[—ftix)\dxi
а а
вынося знак (—) за знак интеграла и умножая обе части на (—1),
придем к формуле (И).
Точно так же, если Ъ <^ #, то из предыдущего следует формула:
Переставляя в обеих частях пределы интегралов и умножая на
(—1), придем к формуле A1), которая доказана, таким образом,
во всей общности.
В частности, полагая <р(лг)=1, получим важный частный слу-
случай теоремы о среднем:
ь ь
\ f(x)dx = f$)\dx = f$)(b — a). A3)
a a
Значение определенного интеграла равно произведению длины
промежутка интегрирования на значение подынтегральной функ*
ции при некотором промежуточ-
промежуточном значении независимой пере-
менной.
Если а^>Ьу эту длину нужно
взять со знаком (—). Геометрически
предложение это равносильно, тому,
что, рассматривая площадь, ограни-
ограниченную любой кривой, осью ОХ и Рис. 123.
двумя ординатами х = а, х = Ь,
всегда можно найти равновеликий ей прямоугольник с тем же осно-
основанием (Ь — а) и с высотой, равной одной из ординат кривой в
промежутке (а, Ь) (рис. 123).
Нетрудно показать, что число 5, входящее в формулу (М) или
A3), всегда можно считать лежащим внутри промежутка (а, Ь).
230 ГЛ. III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ | 96
96. Существование первообразной функции. VIII. Если верх*
ний предел определенного интеграла есть величина переменная,
то производная интеграла по верхнему пределу равна значению
подынтегральной функции при этом верхнем пределе.
Заметим, что величина интеграла
ь
\f(x)dx
а
при данной подынтегральной функции f(x) зависит от пределов ин-
интегрирования а и Ь. Рассмотрим интеграл
\f{t)dt
а
с постоянным нижним пределом а и переменным верхним пределом х9
причем переменную интегрирования мы обозначаем буквою t в от-
отличие от верхнего предела х. Величина этого интеграла будет функ-
функцией верхнего предела х:
X
F{x) = \f(t)dt A4)
а
и, надо доказать, что
Для доказательства вычислим производную функцию F(x)> исходя
из определения производной [45]:
dx
Мы имеем
х + Н х x-\-h
F(x + h)= \f{t)dt= \f{f)dt-\- \f(t)dt
a ax
(в силу свойства IV), откуда
F(x-\-h) = F(x)+ \ f(t)dt,
x
причем
Применяя A3), имеем
x-\-h
— F{pc)= \ f(t)dt=f?)ht
X
97 1 § 9. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА 231
где h может быть как положительным, так и отрицательным, если
a<^x<^b; h^>0 при х = а и h<^Q при х = Ь. Число ? принадле-
принадлежит промежутку, концы которого суть х и x-\-h, так что если h
стремится к нулю, то 5 стремится к х и /(?) — к f{x) в силу не-
непрерывности этой функции. Из последней формулы непосредственно
следует, что F(x) — непрерывная функция при a^ix^b, т.е. опре-
определенный интеграл, рассматриваемый как функция верхнего пре-
предела, есть непрерывная функция в промежутке (а, Ь). Деля обе
части последней формулы на h:
h)-F(x) _
—
и устремляя h к нулю (/г-y-f-O при х = а и /г-> — 0 при х = Ь),
получим
Об определении производной на концах замкнутого промежутка мы
уже говорили в [46].
Из предыдущего следует также, что:
IX. Всякая непрерывная функция f(x) имеет первообразную
функцию или неопределенный интеграл.
Функция A4) есть та первообразная функция для /(лг), которая
обращается в нуль при х = а.
Если Fi(x) есть одно из выражений первообразной функции,
то, как мы видели в [88],
\ F1(b)^Fl(a). A5)
97. Разрыв подынтегральной функции. Во всех предыдущих
рассуждениях предполагалось, что подынтегральная функция f(x)
непрерывна во всем промежутке интегрирования (а, Ь).
Введем теперь понятие интеграла и для некоторых разрывных
функций.
Если в промежутке (а, Ь) имеется точка с, в которой
подынтегральная функция f(x) терпит разрыв, но при этом
интегралы
с—V b
\ f(x)dx, J f(x)dx (a<ft)
а с -\- е"
стремятся к определенным пределам, когда положительные
числа е' и е" стремятся к нулю, то эти пределы называют-
называются определенными интегралами от функции f(x), взятыми
232 ГЛ. Ш. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ
соответственно между пределами (а, с) и (с, Ь), т, е.
( С —S'
\f(x)dx — \\m \ f(x)dx,
ь ь
\f(x)dx = \\m \ f(x)dx,
если эти пределы существуют.
Мы положим в этом случае
\f(x)dx=\f(x)dx+\f(x)dx.
Функция F(x), определенная формулой A4), обладает, как нетрудно
видеть, следующими свойствами:
р (x) — f(x) во всех точках (а, Ь), кроме x = ct и Р(х) непре-
непрерывна во всем промежутке (а, Ь)у включая х = с.
Если точка с совпадает с одним из концов промежутка (а, Ь)>
надо рассматривать вместо двух только один из пределов:
b Ь — г
lim \ f(x)dx или lim \ f(x)dx.
Наконец, если точек разрыва с в промежутке (а, Ь) не одна, а
несколько, то нужно разбить промежуток на части, в каждой из
которых будет уже только по одной точке разрыва.
При сделанном выше соглашении о смысле символа
ь
\f(x)dx
а
свойство IX и формула A5)
будут наверно иметь место, если F'1(x)==f(x) во всех точках
(ау Ь), кроме х — с, и F^(x) непрерывна во всем промежутке (а, Ь)>
включая х = с.
Утверждение это достаточно доказать для случая одной точки
разрыва с внутри промежутка (а, Ь\ так как случай нескольких
точек разрыва и случай, когда с = а или Ъ> исследуются совершенно
аналогичным образом.
Так как в промежутках (а, с — е'), (с-\-г\ Ь) функция /(х)
также непрерывна, то к этим промежуткам применима формула A5),
97 I § 9- СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
и мы имеем
233
b
\
В силу непрерывности Fx (x) мы можем написать
с
\f(x)dx=Wm [Ft(с — е')-F,(а)| = F,(с) — F,(а),
4-0
\f{x)dx = Hr
Vim
т. e.
= Ft (b) - Ft (a),
\f{x)dx=\ f{x)dx + \f{x)dx =
а а с
= [Pi (c) — Л (a)l -f [fi (*) — i
что и требовалось доказать.
С точки зрения геометрической, рассмотренный случай встречается
тогда, когда кривая y=if(x) имеет разрыв
в точке с, но так, что плошадь кривой
все же существует. Рассмотрим, например,
график функции, определенной следующим
образом:
/(х) = ^ + ^ при
f(x) = x при
(рис. 124). Площадь, ограниченная этой
кривой, осью ОХу ординатой х = 0 и пе-
переменной ординатой х — хи есть непре-
непрерывная функция от ху несмотря на то, что
функция f(x) терпит разрыв при лг = 2.
С другой стороны, нетрудно найти перво-
первообразную функцию для f(x), которая была
бы непрерывна во всем промежутке @, 3).
Это будет, например, функция Fx (x), определяемая следующим образом:
ftW = T + T при
= Y при
/ г
Рис. 124.
Действительно, дифференцируя, убеждаемся, что
234
ГЛ. III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ
|97
в промежутке @, 2) и F[(x) = x в промежутке B, 3). Кроме того, оба на-
написанных выражения Ft (x) при дг = 2 дают одну и ту же величину 2, что и
обеспечивает непрерывность Ft (x). Площадь, ограниченная нашей кривой,
осью ОХ и ординатами л: = 0, лг = 3, выразится формулой
Я О 3
в чем нетрудно убедиться и непосредственным рассмотрением чертежа.
У
Рассмотрим еще функцию у = х" 2/з (рис. 125). Она обращается в бес-
бесконечность при х = 0, но ее первообразная функция Здг1/з остается непре-
непрерывной при этом значении х, а потому можем написать
другими словами, хотя рассматриваемая кривая при приближении л: к нулю
уходит в бесконечность, тем не менее она имеет совершенно определенную
площадь между ординатами х = —1 и х = 1.
Для функции ^з первообразная функция ( ) обращается сама в бес-
бесконечность при х = 0, формула A5) неприменима к этой функции в том
случае, когда точка 0 лежит внутри промежутка (я, Ь); кривая -^ в таком
промежутке конечной площади не имеет.
Заметим, что интегралы от разрывных функций в конечном про-
промежутке (а, Ь) в. некоторых случаях имеют смысл и непосредственно,
как пределы сумм, указанных в начале [94]. Это будет иметь, на-
например, место в том случае, когда f(x) имеет конечное число точек
разрыва в промежутке (а, Ь) и ограничена в нем, т. е. существует
такое положительное число М, что \f(x)\<^M при всех х из(а,Ь).
Значения в точках разрыва не влияют при этом на величину инте-
интеграла. Мы будем говорить об этом в [116]. Если же функция не
98 I § 9- СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА 235
ограничена, т. е. \/(х)\ принимает сколь угодно большие значения,
то непосредственное определение интеграла как предела суммы не-
невозможно. Это имеет место для примера, соответствующего рис. 125.
Здесь необходимо определять интеграл как интеграл по укорочен-
укороченному промежутку с дальнейшим переходом к пределу
^ х 3 dx = lim ^ x 3 dx-f- lim \ x~^dx.
Такие интегралы называются обычно несобственными.
Для функции —g- не существует конечного предела
1
lim \ —2dx= -j-co-
е —¦ -|- О «J х"
е
Такие интегралы называются расходящимися. Указанный выше инте-
интеграл от jr~2/3 называется сходящимся, поскольку указанные выше
пределы при s'-> — 0 и е" -> -[- О существуют.
В следующем параграфе мы рассмотрим несобственные интегралы
по бесконечному промежутку. В этом последнем случае непосред-
непосредственное определение интеграла как предела суммы невозможно и
интеграл по существу несобственный.
98. Бесконечные пределы. Предыдущие рассуждения можно рас-
распространить и на случай бесконечного промежутка и положить
4-00 b
$ f(x)dx= lim \f(x)dx, A6)
b b
\ f(x)dx= lim \f(x)dx; A7)
-oo a-+-coa
если эти пределы существуют.
Условие это наверно выполнено, если первообразная функция
Fi(x) стремится к определенным пределам, когда х стремится
к (-J- со) или к (— со). Обозначив эти пределы просто через Ft (-]- со)
и Fx (— со), будем иметь
00
\ f{x) dx = lim [F, (*) - F, (a)] = F, (+ oo) - F, (a), A8)
a b-+-\-co
b
\ f(x) dx=hm [F, (b) - F, (a)] = F, (b) - Fi (- сю), A9)
— oo a-* — oo
+ oo a oo
[ f(x)dx— \ f(x)dx-\-\f(x)dx = Fl(-}-oo)—Fl(—oo)i B0)
236
ГЛ. HI. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ
что и является обобщением формулы A5) на случай бесконечного
промежутка.
Часто соотношение A6) пишут в виде
оо b
\f(x)dx = lira \/(x)dx.
С точки зрения геометрической, при выполнении предыдущего
условия можно сказать, что бесконечная ветвь кривой у=/(х), ко-
которая соответствует лг->±оо, имеет площадь.
Если пределы A6) или A7) существуют, то говорят,- что соответ-
соответствующие интегралы сходятся или что это — сходящиеся инте-
интегралы. В противном случае говорят, что интегралы расходятся.
Пример. Кривая у = г—ц—^, уходящая в бесконечность при х = ±. оо,
все же ограничивает с осью ОХ конечную площадь (рис. 126), так как
-{-оо
dx
\+х'-
= arc Xgx
TT" I = TC«
При вычислении этого интеграла следует помнить, что для функции
arc tg х нужно брать ке любое значение этой многозначной функции, а именно
-1,5
-0,5 0 0,5
Рис. 126.
1,5
то, которое было определено в [24], для того чтобы она сделалась однознач-
однозначной, т. е. между (— — J и ( + -9-J I в противном случае предыдущая формула
теряет смысл.
99. Замена переменной под знаком определенного интеграла.
Пусть f(x) — непрерывна в промежутке (а, Ь) или даже в более
широком промежутке (Л, В), о котором будет сказано ниже. Пусть
далее функция <р(г) однозначна, непрерывна и имеет непрерывную
производную <g (t) в промежутке (а, Р), причем
7(а) = а и ?(?) = *. B1)
99 | «9. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА 237
Положим далее, что значения ср (t) при изменении t в проме-
промежутке (а, Р) не выходят из промежутка (а, Ь) или из того более
широкого промежутка (Л, В)> в котором f{x)— непрерывна. При
этом сложная функция /[<р@] есть непрерывная функция t в про-
промежутке (а, р).
При высказанных предположениях, если ввести вместо х новую
переменную интегрирования к
x = <?(t), B2)
то определенный интеграл преобразуется по формуле
ь р
\ f(x) dx = $/1<р @1 i @ dt. B3)
а а
В самом деле, введем вместо рассматриваемых интегралов — ин-
интегралы с переменными пределами
X t
F(x) =\f(y)dy, 1Г@ = \f\y(z)\ <f'(z)dz.
a a
В силу B2) F(x) есть сложная функция t:
/?(х) = /7[ср(О|= \fiy)dy.
а
Вычисляя ее производную по правилу дифференцирования сложных
функций, имеем
dF(x) dF (x) dx
dt ~ dx It'
но, в силу свойства VIII [96),
из формулы же B2) следует
dx ,
откуда
d-L^L = f (х) ср' @ = /[ср @] ср' @.
Вычислим теперь производную от функции ЧГ (t). В силу свой-
свойства VIII и сделанных нами предположений имеем
Функции ч7@ и /^(л:), рассматриваемые как функции от U
имеют, таким образом, одинаковые производные в промежутке (а, Р),
238 ГЛ. III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ | 99
а потому [89] могут отличаться лишь на постоянное слагаемое, но
при t = cn мы имеем
т. е. эти две функции равны при ? = а, а потому и при всех зна-
значениях t в промежутке (а, fi). В частности, при t = $ имеем
что и требовалось доказать.
Весьма часто вместо подстановки B2):
употребляют обратную
* ]() B4)
Тогда пределы аир определяются сразу по формулам
но нужно здесь иметь в виду, что выражение B2) для х, которое
получим, если решим уравнение B4) относительно х, должно
удовлетворять всем указанным выше условиям, в частности, функ-
функция <р@ должна быть однозначной функцией от t. Если это свой-
свойство ср(О не соблюдено, то формула B3) может оказаться неверной^
Введя в интеграле
A dx=2
вместо х новую независимую переменную t по формула
t = x\
в правой части формулы B3) получим интеграл с одинаковыми пределами
+1, +1, равный, следовательно, нулю, что невозможно. Ошибка происходит
вследствие того, что выражение х через t:
*=+ уг
есть функция многозначная.
Пример. Функция /(л:) называется четной функцией х, если / (— х) =
в=/(л"), и нечетной функцией, если /(—х) =—/(*). Например, cos* есть
четная функция и sin x — нечетная.
Покажем, что
если f(x) — четная, и
\ f(x)dx = 0,
если / (х) — нечетная.
ДОС 1 § 9. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА 239
Разобьем интеграл на два [94, IV]:
$ f{x)dx=* \ f(x)dx+]f(x)dx.
— а —а 0
В первом интеграле совершим замену переменной дг = — t и восполь-
воспользуемся свойствами II и III [94]:
\ \
\ f (х) dx = - jj / (-1) dt = \f (- *) Л = J / (_
a a 0 0
откуда, подставляя в предыдущую формулу,
( /W dx Jifl-x) dx + \f(x) dx=A\f(-x) +f(x)\ dx.
-a 0 0 0
Если /(x) — четная функция, то сумма [/(— л:) +/ (х)] равна 2/ (х), а если
/(д:) — нечетная, то эта сумма равна нулю, что и доказывает наше утвер-
утверждение.
100. Интегрирование по частям. Формула интегрирования по
частям [91] для определенных интегралов может быть написана
в виде:
ь ь ь
\u{x)dv(x) = u(x)v{x)\ —\v(x)du(x). B5)
a a a
Действительно, интегрируя почленно тождество [91]
и (х) dv (х) = d [и (х) v (х)] — v (x) du (x),
получим
но в силу свойства IX [96],
что и дает формулу B5). Считается, конечно, что и (х) и v (x) имеют
непрерывные производные в промежутке (а, Ь).
Пример. Вычислить интегралы
гс/2 л/2
[ sinn х dx, [ cos" x dx.
Положим
к/2
/л = jj sinnxdx*
о
240 ГЛ. Ш. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ | 100
Интегрируя по частям, имеем
я/2
я= ( sin* jtein
я/2 я/2
/я= ( sin* jtein xdx = — ^ sin'1'1 xd cos лг
:— sin" л: cos л:
о б
— 1) sin* x cos x • cos л* д?лг =
= (я — 1) \ sinrt~2A- cos2 лг tf* = (я — 1) ( sin"'2* A — sin2.v)<fjr =
х = (я — 1) /л_8 — (я —
т. е.
откуда, решая относительно" /я:
/•«^/.-г B6)
Формула эта называется формулой приведения* так как приводит вычи-
вычисление интеграла /п к такому же интегралу, но с меньшим значком (п—2),
Различим теперь два случая в зависимости от того, есть ли п число
четное или нечетное.
1. n = 2k (четное). Имеем, в силу B6),
2k — 1 , _Bk- I) B/g — 3) _ _{2k — 1) Bfe — 3) ...3> 1
2k /2*-*— 2Л.B/г — 2) 2k~* 2ЛB/г —2)...4.2
и так как
то окончательно
Bk — l)Bfe— 3)...
'2*"~ 2ЛBЛ —2)... 4-2 2 *
2. я = 2k + 1 (нечетное). Аналогично предыдущему находим
— 2)... 4-2 Т
те/2
О
а потому
2k Bk 2) 4 » 2
J*k+l = Bk + \)Bk— 1)... 5-3#
Интеграл
я/2
lxdx
\ cosn.
ем, но i
cos'* х их = ^ sin-*1 (~ — х \ dx%
можно вычислить таким же путем, но проще привести его к предыдущему,
заметив, что
101 I § 10. ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ 241
откуда, положив
~к X — Г, X — -о * >
на основании формулы B3) и свойства II [94] имеем
те/2 0 те/2
\ cosnxdx*=— J smntdt~ \ sinntdt.
Ь те/9 О
Объединяя полученные результаты, можем написать
| | = »?jjg^ » Z ,' ¦' f B7,
§ 10. ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ
ИНТЕГРАЛЕ
101, Вычисление площадей. Мы переходим к приложениям по-
понятия определенного интеграла к вычислению площадей, объемов и длин
дуг. При этом мы будем руководствоваться во многом наглядными
соображениями. Точное определение площади и объема с разных то-
точек зрения будет нами дано в последующих томах.
В [87] мы видели, что площадь, ограниченная кривой y=f{x\
осью ОХ и двумя ординатами х = а и х = Ь, выражается опреде-
определенным интегралом у
\f(x)dx
Этот интеграл, как мы видели, дает рис 127,
алгебраическую сумму площадей, в
которой каждая площадь, расположенная под осью ОХ, входит со
знаком (—). Для того чтобы получить сумму площадей в обычном
смысле, нужно вычислить
\\Пх)\Aх.
а
Так, сумма заштрихованных на рис. 127 площадей равна
г g ft k b
\f(x)dx-\/{x)dx + \f(x)dx — \f(x)dx-\- \f(x)dx.
а с g h к
Площадь, заключенная между двумя кривыми
A)
242 ГЛ. III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ I Ю1
и двумя ординатами
лг = а, х = Ь,
в том случае, когда одна кривая лежит над другой, т. е.
в промежутке (а, Ь), выражается определенным интегралом
\{f(x)-9(x)]dx. B)
а
Допустим сперва, что обе кривые лежат над осью ОХ. Непосред-
Непосредственно из рис. 128 видно, что искомая площадь 5 равна разности
площадей, ограниченных данными кривыми с осью ОХ
что и требовалось доказать. Общий случай какого угодно располо-
расположения кривых относительно оси ОХ приводится к разобранному,
если передвинуть ось ОХ настолько кни-
книзу, чтобы обе кривые оказались над осью
ОХ; это передвижение равносильно при-
прибавлению к обеим функциям f(x) и <р(х)
одного и того же постоянного слагаемо-
слагаемого, причем разность f(x) — у(х) остается
без изменения.
Рис. 128. Предлагаем в виде упражнения дока-
доказать, что если данные две кривые пере-
секаются так, что одна кривая лежит частью ниже, а частью
выше другой, то сумма площадей, лежащих между ними и орди-
ординатами х = а, х = Ь, равна
ь
C)
Часто вычисление определенного интеграла называют квадрату-
квадратурой. Это связано с тем, что определение площади, как указано выше,
сводится к вычислению определенного интеграла.
Примеры. 1. Площадь, ограниченная параболой второй степени.
у = ах2 -f~ Ьх + с,
осью ОХ и двумя ординатами, расстояние между которыми есть h, равна
и
D)
101 ]
§ 10. ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
243
где Ух и у2 означают крайние ординаты кривой, у0 — ординату, равноотстоя-
равноотстоящую от крайних.
При этом предполагается, что кривая лежит над осью ОХ.
При доказательстве формулы D) мы можем, не ограничивая общности,
считать, что крайняя ордината слева направлена по оси QY (рис. 129), так
как передвижение всего чертежа параллельно оси ОХ не изменяет ни вели-
чины рассматриваемой площади, ни
взаимного расположения крайних и
средней ординат, ни величин этих
ординат. Но при этом предположении,
Рис. 129.
Рис. 130.
допустив, что уравнение параболы имеет вид у = ах2 + Ъх -f- с, мы выра-
выразим искомую площадь 5 в виде определенного интеграла
h
^а^+ Ь ~-+ ch =~ Bah*
При наших обозначениях мы имеем
= с, у2 = ах2 + Ьх + с\ = ah2 + bh4-c,
v=0 \x—h
yl = ax2 + bx + с
откуда следует
Ух +У* + 4Уо = 2ah2 + 3bh + 6с,
что и доказывает наше утверждение.
2. Площадь эллипса. Эллипс, уравнение которого
симметричен относительно координатных осей, а потому искомая площадь S
равна учетверенной площади той части эллипса, которая лежит в первом
координатном углу, т. е.
а
6 = 4 f ydx
244
ГЛ. III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ
101
(рис. 130). Вместо того, чтобы определить у из уравнения эллипса и под-
подставить полученное выражение в подынтегральную функцию, мы восполь-
воспользуемся параметрическим представлением эллипса:
х = a cos t, y = b sin t> E)
и введем вместо х новую переменную t\ у выразится тогда сразу вторым
из уравнений E). Когда х меняется от 0 до я, t меняется от у до 0, и
так как все условия правила замены переменных [99] в данном случае вы-
выполнены, то
U 0 x/s
5 = 4 1 b sin t d (a cos t) = — Aab 1 sin21 dt = 4ab i sin21 dt.
По формуле B7) [100] при Ы1 мы имеем
F)
откуда находим окончательно
5 = nab.
При а = Ь, когда эллипс обращается в
круг радиуса а, получим известное выра-
выражение па2 для площади круга.
3 В
3. Вычислить площадь,
между двумя кривыми
заключенную
Данные кривые (рис. 131) пересекают-
Рис. 131. ся в двух точках @, 0), A, 1), коорди-
координаты которых мы получим, решая совмест-
совместно уравнения этих кривых. Так как в промежутке @, 1) имеем ]/
то искомая площадь S в силу B) выражается формулой
102. Площадь сектора. Площадь сектора, ограниченная кривой,
уравнение которой в полярных координатах есть
r=fD G)
и двумя радиусами-векторами
е=о, е=р, (8)
проведенными из полюса под углами а и р к полярной оси, выра-
выражается формулой
Р . Р
(9)
102 1 § Ю. ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ 245
Для вывода формулы (9) разобьем рассматриваемую площадь
(рис. 132) на малые элементы, разделив угол между радиусами-век-
радиусами-векторами (8) на п частей. Рассмотрим площадь одного из таких малых
секторов, ограниченного лучами 6 и
G-j-Дб. Обозначив через AS его пло-
площадь, через т\л М — наименьшее и наи-
наибольшее значения функции г=/(б) в
промежутке (б, б-|-Дб), мы видим, что /M'^\\^Q
AS заключается между площадями двух
круговых секторов того же растворе-
растворения Аб, но радиусов т и М, т. е. /?&~*CiT ^
т^ рис. ,32.
а потому, обозначив через Р некоторое число, лежащее между т
и Ж, можем написать
AS = ~P2A6.
Так как непрерывная функция /F) в промежутке F, G-f-Аб)
принимает все значения между т и Ж, то в этом промежутке навер-
наверное найдется такое значение 6', при котором
а тогда
Если теперь будем увеличивать число элементарных секторов
AS так, что наибольшее из значений А6 стремится к нулю, и если
вспомним сказанное в [87], то в пределе получим
I J гЗД),
а
что и требовалось доказать.
Заметим, что основная идея приведенного доказательства фор-
формулы (9) заключается в замене площади сектора AS площадью кру-
кругового сектора того же растворения Аб и радиуса /(б'). Приняв
вместо точного выражения A0) приближенное:
AS = i-
где г==/@") и 6" — любое значение из промежутка (б, б-f-AO), для
площади этого сектора мы получим в пределе тот же результат:
A1)
246
ГЛ. III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ
[ 103
При таком выводе подынтегральное выражение в формуле A1)
получает простой геометрический смысл: -^- r2d0 есть приближенное
выражение площади элементарного сектора растворения dO и потому
называется просто элементом площади в полярных координатах.
Пример. Найти площадь, ограни-
ограниченную замкнутой кривой
г = a cos 30 (а > 0).
Кривая эта, построение которой
по точкам не представляет никакого
труда, изображена на рис. 133 и на-
называется трилистником. Полная пло-
площадь, ею ограниченная, равна ше-
шестикратной площади заштрихованной
у части, соответствующей изменению 6 от
0 до -д-, так что по формуле (9) имеем
—a2cos2 36 ^/0 =
Рис. 133.
=«2 Г cos2 30 d C0)=я2 i i
103. Длина дуги. Пусть имеется дуга А В некоторой кривой.
Впишем в нее ломаную линию (рис. 134) и будем увеличивать
число сторон этой ломаной так, чтобы наибольшая из длин сторон
стремилась к нулю. Если при этом периметр ломаной будет стре-
стремиться к определенному пределу, не
зависящему от того, какие именно ло-
ломаные мы вписываем, то дуга назы-
называется спрямляемой, а упомянутый
предел называется длиной этой дуги.
Это же определение длины годится и
для замкнутой кривой.
Пусть кривая задана явным урав-
уравнением y=f(x), причем точкам А и В
соответствуют значения х = а и х = Ь
^), и пусть f(x) имеет непрерывную производную в промежутке
которому и соответствует дуга АВ. Мы покажем, что
при этих условиях дуга АВ спрямляема и что ее длина выражается
определенным интегралом.
Пусть АМгМ<2... Мп_хВ — вписанная ломаная, причем ее верши-
вершинам соответствуют значения
Рис. 134.
103 1 § Ю. ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ 247
и обозначим yi=f(xi). Принимая во внимание формулу для длины
отрезка из аналитической геометрии, для периметра ломаной полу-
получим следующую формулу
Р= 2V(*i -*м)" + (Уг ~Уг-lf =
) -f (^-i
Пользуясь формулой конечных приращений
П*д -/(*м) =f (W (*t - x^) (x
получим для длины отдельной стороны ломаной выражение
из которого мы видим, что требование того, чтобы наибольшая из
сторон стремилась к нулю, равносильно требованию, чтобы наиболь-
наибольшая из разностей (хг—Xi_t) стремилась к нулю. Для периметра
ломаной получаем выражение
а оно действительно имеет предел, равный интегралу
ь
Таким образом, длина / дуги АВ выражается формулой
1= J /l-ff(jc)& A2)
Пусть xF<^xrr — какие-либо два значения из промежутка (а, Ь\
а Ж' и Мп — соответствующие точки на дуге А В, Применяя тео-
теорему о среднем, получаем следующую формулу для длины /'
дуги ММ':
/'= J l/l +P(x)dx= /1 +/'2(У (хГ-tf) &<Ь<*Г).
Для длины хорды М'М", пользуясь формулой конечных приращений,
получаем формулу
ММ" = V(x" - x?f + [f(x") -f{x')f =
248 ГЛ. III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ | ЮЗ
Отсюда следует
Если точки М и М" стремятся к точке М с абсциссой х, то х'
и х"-+х, а тем самым Ъх и 52->дг, и из последней формулы мы
получаем
ATM" f
Этим мы пользовались в [70].
Положим теперь, что кривая задана параметрически
причем точкам Л и 5 соответствуют значения /==а и ? = [3^р
Мы предполагаем, что значениям t из промежутка a^f^p соот-
соответствуют точки кривой А В так, что различным t соответствуют
различные точки этой кривой, которая сама себя не пересекает и
не замкнута (рис. 134). Далее мы предполагаем, что в промежутке
a^t^$ существуют непрерывные производные ср'(/) и ф'(?).
Пусть, как и выше, ЛЖД ... Мп_хВ — вписанная ломаная и
tQ = a<^tl<^h<^ ... <^tn_1<^tn = $ — соответствующие значения
параметра t Для периметра ломаной получим выражение
р = 2 /[? ft) - у ft-i)]2+IWi) -
i = l
или, применяя формулу конечных приращений,
р = 2 /?'2 <**)+Г W) ft - ^-i) ft-i < ^ и ъ < til A з)
Можно показать, что требование того, чтобы наибольшая из сторон
ломаной стремилась к нулю, равносильно требованию того, чтобы
наибольшая из разностей (tt — t^) стремилась к нулю. Это может
быть доказано и без предположения существования производных
?'(<) и f @-
Выражение A3) отличается от суммы, дающей в пределе интеграл
0Л, (И)
ввиду того, что аргументы xi и т}, вообще говоря, различны.
Введем сумму
q = gVv* Ы + Г
|03 I $ 10- ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ 249
которая в пределе дает интеграл A4). Для того чтобы доказать,
что и сумма A3) стремится к пределу A4), надо показать, что
разность
п
стремится к нулю.
Умножая и деля на сумму радикалов, получим
уы+уы
Так как
W С
то
I* - ? I < S If (*<> - f ('l) I («I - 'i-i>
Числа т; и т) принадлежат промежутку (tt_v tt), и, в силу равно-
равномерной непрерывности ф'(?) в промежутке а^^^З, можно утвер-
утверждать, что наибольшая из величин | ф' (ij) — ф' (т/) |, которую мы
обозначим через 8, стремится к нулю, если наибольшая из разностей
ifi — *j_i) стремится к нулю. Но из предыдущей формулы следует:
откуда очевидно, что р — <7->0. Таким образом, сумма A3), выра-
выражающая периметр вписанной ломаной, стремится к интегралу A4),
т е
т. е.
Эта формула для длины / остается справедливой и в случае зам-
замкнутой кривой. Чтобы убедиться в этом, достаточно, например,
разбить замкнутую^ кривую на две незамкнутые, к каждой применить
формулу A6) и "сложить полученные значения /. Точно так же,
если некоторая кривая L состоит из конечного числа кривых Lk,
каждая из которых имеет параметрическое представление, удовле-
удовлетворяющее указанным выше условиям, то, вычисляя по формуле A5)
Длину каждой кривой Lk и складывая эти длины, получим длину
кривой L
250 ГЛ. III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ [ 103
Рассмотрим переменное значение t из промежутка (а, C), кото-
которому соответствует переменная точка М дуги А В. Длина дуги AM
будет функцией от t и будет выражаться формулой
8 @ = J уУЧО+ФЧОЛ- A6)
а
Принимая во внимание правило дифференцирования интеграла по
верхнему пределу, получим
то есть
ds =
откуда, принимая во внимание, что
получаем формулу для дифференциала дуги [70]
а формула A5) может быть, без указания переменной интегрирова-
интегрирования, переписана в виде
f f
l=\ds=\
(A) (A)
\
(A)
Пределы (А) и (В) указывают на начальную и конечную точки
линии.
Если ?'2@ + f2@>° при всех t из (а, Р), то, согласно A7),
мы получим производную от параметра t no s:
ds
Наличие непрерывных производных y'{t) и ф'@ при условии
?'2 @ ~Ь Ф'2 @ ^> 0 гарантирует нам непрерывно изменяющуюся каса-
касательную вдоль Л Б.
Если кривая задана в полярных координатах уравнением
то, введя прямоугольные координаты х и у, связанные с полярными
гиб соотношениями
* = rcos9, y = rsinO A8)
[82], мы можем рассматривать эти уравнения, как параметрическое
задание кривой с параметром 0.
103 I § I0- ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ 251
Мы имеем тогда
dx=cosQdr — rsinQdO,
dy = sin 0 dr -f- r cos 6 dd,
dx1 + dy* = (dr? + r2 (db?,
откуда,
ds = /(dx? + (dy? = /(dr?-\-r2(dd?, A9)
и если точкам А и В соответствуют значения аир полярного
угла 0 (рис. 135), то формула A5) даст нам
*- -.,
5 =
Выражение для ds A9), которое назы-
называется дифференциалом дуги в полярных
координатах, можно получить и непо-
непосредственно из чертежа, заменив беско- Рис
нечно малую дугу ММ ее хордой и вычи-
вычислив последнюю, как гипотенузу прямоугольного треугольника MNM,
катеты которого MN и NM приближенно равны, соответственно,
rdb и dr.
Примеры. 1. Длина дуги s параболы jy = x2, отсчитываемой от вер-
вершины @, 0) до переменной точки с абсциссой х, по формуле A2) выра-
выражается интегралом
1х
B1)
= f YY+y^dx= [ V\ + 4x*dx = Y [ }t
(мы положили г = 2лг).
В силу примера 11 [92] имеем
Подставив это в B1), получим без труда
s = ~ [2х У\+4х2 + log Bx +
2. Длина эллипса
в 5илУ симметричности его относительно осей координат, равна учетверен-
н°й длине той его части, которая лежит в первом координатном углу. Пред-
Представив эллипс параметрически уравнениями
х = a cos t% у = Ь sin t
252 ГЛ. Ш. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ I Ш
и заметив, что точкам А и В соответствуют значения параметра 0 и у, мы
получим для искомой длины / следующее выражение по формуле A5):
os4dt. B2)
Интеграл этот не может быть вычислен в конечном виде; для него
можно указать только способ приближенного вычисления, который будет
приведен ниже.
3. Длина дуги логарифмической спирали
г =
[83], отсекаемой радиусами-векторами G = а, 6 = % в силу B0) выражается
интегралом
4. В [78] мы рассматривали цепную линию, пусть М (х, у) есть какая-
либо ее точка. Вычислим длину дуги AM (рис. 93). Принимая во внимание
выражение для A +/2) из [78], получим
Ь
откуда
а2 + (дуга AMJ = а2 + а2?2 = а2 A + у12) = у2,
т. е. длина дуги AM равна катету прямоугольного треугольника, гипотенуза
которого равна ординате точки М, и другой катет которого равен а. Мы
получаем, таким образом, следующее правило построения длины дуги AM:
Из вершины А цепной линии, как центра, надо описать окружность
радиусом, равным ординате точки М; отрезок OQ оси ОХ от начала
координат О до точки пересечения Q оси ОХ с упомянутой окруж-
окружностью и будет представлять собою спрямленную dvzy AM (рис. 93).
В предыдущих формулах при выборе знаков мы руководились тем
обстоятельством, что для точек, лежащих на правой части цепной линии,
у' имеет знак (+).
5. Для циклоиды, рассмотренной в [79|, определим длину дуги / ветви
00х (рис. 94) и площадь S, ограниченную этой ветвью и осью ОХ:
2% 2тс
/ = \ VW(t)\2 + W @1* dt = \ Уаг{\ — cos О2 + я8 sin2* dt =
2тс 2те
2к 2тс 2tc
а [ V2 — 2costdt = а [ у 4sin2 $ dt^2a [ sin у
—
sin у dt e
j = 8a,
104|
§ 10. ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
253
т е длина дуги одной ветви циклоиды равна учетверенному диаметру
катящегося круга;
2* 2*
2а 2* 2*
S = \ У dx = \ ф (t) ср' (О Л = а2 V A —cos tJ
о о о
dt
2тг
2 С
_ 2 cos * + cos21) dt = 2iza2 — 2л2 [ sin >]2* +
~ sin 2tf* =
т. е. площадь, ограниченная одной ветвью циклоиды и той неподвижной
прямой, по которой катится круг, равна утроенной площади катяще-
катящегося круга.
Вычисляя /, при извлечении корня
-, мы должны выбрать
арифметическое значение корня, что и сделали, ибо при изменении t от 0
до 2л функция sin -^—положительна.
6. Кардиоида, рассмотренная в [84], симметрична относительно полярной
оси (рис. 111), а потому для вычисления ее длины / достаточно вычислить
длину дуги при изменении в в промежутке @, п) и полученный результат
удвоить:
тс it
/ = 2^ /г2 + г'2 db = 2 ^
о о
4а2 A + cos ОJ + 4а2 sin26 db =
cos ~ dO = 8<z [ 2 sin -]*•= 16а,
т. е. длина дуги кардиоиды в восемь раз больше диаметра катящегося
(или неподвижного) круга.
104. Вычисление объемов тел по их поперечным сечениям.
Вычисление объема данного тела сводится также к вычислению опре-
Рис. 136.
Деленного интеграла, если мы умеем определять площадь поперечных
сечений тела, перпендикулярных данному направлению.
Обозначим через V объем данного тела (рис. 136) и допустим,
что нам известны площади всех поперечных сечений тела плоско-
плоскостями, перпендикулярными данному направлению, которое мы примем
254
ГЛ. HI. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ
[ 104
за ось ОХ Всякое поперечное сечение определится абсциссой х точ-
точки пересечения его с осью ОХ> а потому площадь этого поперечного
сечения будет функцией от х, которую мы обозначим через S(x) и
будем считать известной.
Пусть, далее, а и Ъ означают абсциссы крайних сечений тела.
Для вычисления объема V разобьем его на элементы рядом попе-
поперечных сечений, начиная от х = а
и кончая х = Ь\ рассмотрим один
из таких элементов A Vy образо-
образованный сечениями с абсциссами
х и х -f- Ах Заменяем объем. А V
объемом прямого цилиндра, вы-
высота которого равна Ддг, а осно-
основание совпадает с поперечным
сечением нашего тела, соответ-
соответствующим абсциссе х (рис. 137). Объем такого цилиндра выразится
произведением S(x)kx> и, таким образом, мы получим следующее
приближенное выражение для нашего объема V:
где суммирование распространено на все те элементы, на которые
разбито наше тело поперечными сечениями. В пределе, когда число
элементов беспредельно возрастает и наибольшее из Ад; стремится
к нулю, написанная сумма превращается в определенный интеграл,
который и дает точное значение объема V, $
что приводит к следующему предложению. -—¦°^
Если для данного тела известны все
его поперечные сечения плоскостями, перпен-
перпендикулярными некоторому данному направ-
направлению, принятому за ось ОХ, то объем -'
тела V выражается формулой
ь
V=\S(x)dx, B3)
а РИС. 138.
где S(x) означает площадь поперечного сечения с абсциссой х,
а и Ь — абсциссы крайних сечений тела.
Пример. Объем „цилиндрического отрезка"\ отсекаемый от прямого
кругового полуцилиндра плоскостью^проведенной через диаметр его осно-
основания (рис. 138). Примем диаметр АВ за ось ОХ, точку А — за начало коор-
координат; обозначим радиус основания цилиндра через г, угол, образуемый
верхним сечением отрезка с его основанием, через а.
Поперечное сечение, перпендикулярное диаметру АВ, имеет вид прямо-
прямоугольного треугольника PQR, и его площадь выражается формулой
__ 1 _ — 1
2 2
105)
§ 10. ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
255
Далее, по известному свойству окружности, отрезок PQ есть среднее
геометрическое между отрезками АР, РВ диаметра АВ, а потому
PQ2 = АР. РВ = х Bг — х),
i\ окончательно
Применяя формулу B3), для искомого объема V получим
'2г
= J S (x)dx = ~ tg a f х Bг -
если ввести „высоту" отрезка /? = rtga.
105. Объем тела вращения. В случае, когда рассматриваемое
тело получается от вращения данной кривой у=/(х) вокруг оси ОХ,
Рис. 139. Рис. 140.
поперечные его сечения будут круги радиуса у (рис. 139), а потому
v с*)=$ *
т. е. объем тела, получаемого при вращении вокруг оси ОХ части
кривой
У =/(*)>
заключенной между ординатами х = а, х=Ь, выражается фор-
формулой
ь
W—\^dx. B4)
а
Пример. Объем эллипсоида вращения. При вращении эллипса
х2 v2
а2 ^ Ъ*
вокруг большой оси получается тело, называемое удлиненным эллипсоидом
РЩения (рис. 140). Крайние значения абсциссы х в рассматриваемом
256 ГЛ. III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ
случае будут (—а) и (+а), а потому формула B4) дает
[ Л 06
B5)
Точно так же мы сможем вычислить и объем сжатого эллипсоида
вращения, который получается при вращении нашего эллипса вокруг малой
оси. Нужно только переставить между собой буквы х, у, а и bt что дает
В случае а =
которого равен -~-
о
B6)
-ь -ь V ""'
оба эллипсоида обращаются в шар радиуса а, объем
106. Поверхность тела вращения. Площадью поверхности,
получаемой при вращении кривой в плоскости ХО Y вокруг оси ОХ,
называется предел, к которому стремится площадь поверхности,
получаемой при вращении вокруг той же оси ломаной, вписанной
в данную кривую, когда число сторон этой ломаной беспредельно
увеличивается, а наибольшая из длин сторон стремится к нулю
(рис. HI). Если вращается часть кривой, заключенная между
точками А и В, то поверхность F
тела вращения выражается формулой
(В)
F= J 2nyds, <27)
(А)
где ds есть дифференциал дуги дан-
данной кривой, т. е.
Рис, 141. В этой формуле кривая может быть
задана как угодно, в явной или в па-
параметрической форме; символы (А) и (В) показывают, что нужно
интегрировать между теми пределами для независимой переменной,
которые соответствуют данным точкам кривой А и В.
Будем считать, что уравнение кривой задано в параметрической
форме, причем роль параметра играет длина дуги 5 кривой, отсчи-
отсчитываемая от точки Л, и обозначим через / длину всей кривой АВ.
Эта кривая, конечно, считается спрямляемой. Мы имеем: х = ф (s),
j/ = if($). Разобьем, как всегда, промежуток @, /) изменения s на
частичные промежутки
О =
sn = /.
fO6 I § l0- ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ 257
Пусть значению $ = $,• соответствует точка Mt кривой, причем, оче-
очевидно, Жо совпадает с А и Мп — с Б. Обозначим через qt длину
отрезка M^iMi9 через Д$г—длину дуги M^Mi и положим yi = ty(si).
Используя формулу для поверхности усеченного конуса, находим
следующую формулу для поверхности, получаемой от вращения
ломаной AMiMi... Mn_tB:
ИЛИ
2 S
i = 1 i= t
Пусть 8 — наибольшее из абсолютных значений | yt — yt_x J. В силу
равномерной непрерывности функции ф(я) в промежутке O^s^l
величина 8 стремится к нулю, если наибольшая из разностей (st — s^)
стремится к нулю. Но мы имеем
откуда следует, что второе слагаемое в выражении Q стремится
к нулю. Исследуем первое слагаемое, для чего перепишем его в виде
Покажем, что вычитаемое в этом выражении стремится к нулю. Для
этого заметим, что непрерывная в промежутке @, /) функция y=-ty(s)
ограничена, и, следовательно, существует такое положительное
число т> что |jv_i|^/ra при всех и Поэтому
уw (А^, - ft) I < 21 ^(Д5, - Л) = т (/ - 2
Но если наибольшая из разностей (s( — $^х) стремится к нулю, то
и наибольшая из длин хорд q{ стремится к нулю, и периметр впи-
вписанной ломаной стремится к длине дуги
откуда
2
1 = 1
258 ГЛ. Ш. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ [ 106
Таким образом, в выражении Q остается исследовать лишь слагаемое
2 S
/== 1 i= 1
Но предел этой суммы и приводит нас к интегралу B7). Таким
образом, мы и получаем эту формулу. Если кривая задана параме-
параметрически через любой параметр tt то мы имеем [ср. 103]
i
F = J 2* <|> @ /9" @ + f2 @ Л, B8,)
и в случае явного уравнения у=/(х) линии АВ:
ь
F= faf(x) /l+f*{x)dx. B80
Пример. Поверхность эллипсоида вращения, удлиненного и сжатого.
Рассмотрим сперва поверхность удлиненного эллипсоида вращения. При-
Применяя обозначения примера [105], по формуле B8) имеем
Из уравнения эллипса мы имеем:
откуда
— а —а
Вводя сюда выражение для эксцентриситета эллипса
имеем (см. пример [99])
О
106 ] § Ю. ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ 259
Интегрируя по частям, имеем (ср. пример 11 [92])
откуда
и окончательно
С УТ=? dt = ^
Г=1*~+ arc sin t]t
B9)
Эта формула годится в пределе и для е = 0, т. е. когда # = я, и эллип-
эллипсоид превращается в шар радиуса а. В скобках при этом оказывается не-
неопределенное выражение, раскрывая которое [65], имеем
arc sin г
?=0
= 1.
Перейдем теперь к сжатому эллипсоиду вращения. Переставив между
собой буквы х и у, а и Ь, мы находим:
= 2*
I
где х считается функцией от у. Но из уравнения эллипса имеем
откуда
J
2«b* \аг -, /V
e \b У Ь2
и окончательно
C0)
260
ГЛ. 111. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ
tO7
107. Определение центров тяжести. Теоремы Гульдина. Если
дана система п материальных точек
Мх (хь у{), Ж2 (хь у& ..., Мп (хп, уп),
массы которых равны, соответственно,
/я„ tnb ..., тп,
то центром тяжести системы Q называется точка, координаты
которой xQy yG удовлетворяют условиям
п п
MXG = SmiX» МУо = S т*У» C])
i=l i=l
где М означает полную массу системы
п
м — 2 щ*
1=1
При определении центра тяжести можно каким угодно образом
группировать точки системы, разбивая их на частные системы с тем,
чтобы при вычислении координат центра тяжести Q всей системы
заменять всю группу точек, вошедших в какую угодно частную
систему, одной точкой, а именно ее центром тяжести, приписав ей
массу, равную сумме масс вошедших в нее точек.
Мы не будем останавливаться на доказательстве этого общего
принципа, которое не представляет труда и легко может быть про-
проверено на простейших частных случаях
системы с тремя, четырьмя и т. д. точ-
точками.
В дальнейшем мы будем иметь дело
не с системами точек, а с тем случаем,
когда масса заполняет сплошь некоторую
плоскую фигуру (область) или линию.
Для простоты ограничимся рассмотре-
нием лишь однородных тел, плотность ко-
которых примем за единицу, так что масса
такой фигуры будет равняться ее длине, если она имеет вид линии,
и площади, если она имеет вид плоской области.
Пусть сперва нужно определить центр тяжести дуги кривой АВ
(рис. 142), длина которой 5. Следуя предыдущему общему принципу,
разобьем дугу АВ на п малых элементов As. Центр тяжести всей
системы можно вычислить, заменив каждый из этих элементов одной
точкой, центром тяжести рассматриваемого элемента, сосредоточив
в ней всю массу элемента Am = As1).
Рис. 142.
J) Центр тяжести каждого такого элемента, вообще говоря, не лежит на
кривой, хотя и будет тем ближе к ней, чем меньше элемент, что и указано
схематически на рис. 142.
107 1 § Ю. ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
26!
Рассмотрим один из таких элементов As и обозначим координаты
его концов через (х, у\ (х-\-Ах, у-\-Ау)\ координаты же его цент-
центра тяжести обозначим через (х, JJ). При достаточном уменьшении
элемента As, можем считать, что точка (х, у) сколь угодно мало
отстоит от точки (х, у).
По формулам C1) имеем, как и в [104],
(В)
= ^]x Am ==?зс As = \im?x As == $ xds> C2>
(А)
(В)
]?yAm==2iyAs = \imYlyAs= $ yds, C3)
(А)
откуда, вычислив $ по формуле
(В) {В) ^
* = J rfs= \
(А (А
J
(А)
(А)
и определим координаты центра тяжести О.
Из формул C2) и C3) вытекает важная теорема:
Теорема I Г у л ь д и н а. Площадь поверхности, полученной при
вращении дуги данной плоской кривой вокруг некоторой оси, лежа-
щей в ее плоскости и не пересекающей ее, равняется произведе-
произведению длины вращающейся дуги на длину пути, описанного при
этом вращении центром тяжести дуги.
В самом деле, приняв ось вращения за
ось ОХ, для поверхности F тела, описанно-
описанного при вращении дуги A3, имеем B7) [106]
(В)
F = 2я J у ds =
(А)
а х х+йх Ь X
[в силу C3)], что и требовалось доказать.
Рассмотрим теперь некоторую плоскую Рис. 143.
область S (площадь которой обозначим
также через S). Допустим для простоты, что эта область (рис. 143)
ограничена двумя кривыми, ординаты которых обозначим через
Следуя общему принципу, указанному в начале этого номера,
разобьем фигуру на п вертикальных полосок AS прямыми, параллель-
параллельными оси OY. При вычислении координат центра тяжести О фигуры мы
можем заменить каждую такую полоску ее центром тяжести, сосре-
сосредоточив в нем .массу полосок Am = AS. Рассмотрим одну из таких
полосок; обозначим через х и х-\-Ах абсциссы ограничивающих ее
прямых МхМг и
через Х> ^ — координаты центра тяжести.
264
ГЛ. III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ
1 108
108. Приближенное вычисление определенных интегралов; формулы
прямоугольников и трапеций. Вычисление определенных интегралов на
основании формулы A5) [96] с помощью первообразной функции не всегда
возможно, так как, хотя первообразная функция и существует, если подын-
подынтегральная функция непрерывна, однако она далеко не всегда может быть
найдена фактически, и даже тогда, когда ее можно найти, она имеет часто
весьма сложный и неудобный для вычислений вид. Поэтому важное значение
имеют способы приближенного вычисления определенных интегралов.
Большая часть их основывается на истолковании определенного инте-
интеграла как площади и как предела суммы
ъ п
^ / (х) dx = lim ^ / №/) (хi — *м). C8>
a i=l
Во всем дальнейшем мы условимся раз навсегда делить промежуток
(а> Ь) на п равных частей; длину каждой части обозначим через Л, так что
Ь —а . ., / ,ч
Обозначим далее через у-г значение подынтегральной функции y—f(x)
При Х = Х( (< = 0, 1, ..., П)\
yi=f(xd=f{a+lh). C9)
Эти величины мы считаем известными; их можно получить непосред-
непосредственным вычислением, если функция/(х) задана аналитически, или снять
прямо с чертежа, если она изображена графически.
Полагая в сумме, стоящей в правой части C8), ?i = x/_1 или х^ мы
получим две приближенные формулы прямоугольников'.
D1)
где знак (я») обозначает приближенное равенство.
Чем больше число я, т. е. чем меньше /г, тем эти формулы будут точнее
и в пределе, при п —> со и h —* 0,
дадут точную величину определен-
определенного интеграла.
Таким образом, погрешности
формул D0) и D1) стремятся к
нулю при возрастании числа орди-
ординат. При данном же значении числа
ординат верхний предел погрешно-
погрешности особенно просто определяется
для того случая, когда данная функ-
»Х ция f(x) монотонна в промежутке
Х5Х& Х2 ^'Х8 (я> Ь) (рис. 146). В этом случае ясно
непосредственно из чертежа, что по-
Рис. 146. грешность каждой из формул D0) и
D1) не превышает суммы площадей
заштрихованных прямоугольников, т. е. не превышает площади прямоуголь-
Ь — а
j-ика с тем же основанием = Л и высотой, равной сумме высоту—Уо
109
10. ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
263
заштрихованных прямоугольников, т. е. величины
Ъ — а,
D2)
Формулы прямоугольников вводят вместо точного выражения площади
кривой y=f{x) приближенное ее выражение — площадь ступенчатой лома-
ломаной линии, составленной из горизонтальных и вертикальных отрезков, ограни-
ограничивающих прямоугольники.
Иные приближенные выраже-
выражения мы получим, если вместо сту-
ступенчатой ломаной линии будем
брать другие линии, которые доста-
достаточно мало отличаются от данной
кривой; чем ближе такая вспо-
вспомогательная линия подходит к
кривой у =/(лг), тем меньше бу-
будет погрешность, которую мы со-
совершаем, приняв за величину пло-
площади— площадь, ограниченную
вспомогательной линией.
Так, например, если мы заменим данную
маной линией, ординаты которой при х =
Рис.
кривую вписанной в нее ло-
ло, р р совпадают с ординатами дан-
данной кривой (рис. 147), другими словами, заменим рассматриваемую площадь
суммою площадей вписанных в нее заштрихованных трапеций, то получим
приближенную формулу трапеций:
Ь— а
\Уо
-х + уп].
D3)
109. Формула касательных и формула Понселе. Увеличим теперь
число делений вдвое, подразделив каждое из делений пополам. Мы получим
таким путем 2л делений (рис. 148):
У4 .^-Ji^^^^K __ h
которым будут соответствовать ор-
ординаты:
Рис- 148- Уо> У1/2у У и —t У и У1 + 1/4 —» Уп
(ординаты у0У yv ...9уп будем называть четными, ординаты у1/а, уа/а, ...,
Уп — i/a — нечетными).
В конце каждой нечетной ординаты проведем касательную до пересече-
пересечения ее с двумя соседними четными ординатами и заменим данную площадь
суммою площадей построенных таким путем трапеций. Полученная таким
262 ГЛ. III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ | 107
При достаточном сужении полоски, т. е., при уменьшении ее
ширины Алг, точка (ху у) сколь угодно мало будет отстоять от сере-
середины Р отрезка прямой М^МЬ вследствие чего можем писать при-
приближенные равенства
Далее, масса Д/тг полоски, равная ее площади AS, может быть
приравнена площади прямоугольника с основанием Ajc и высотой,
сколь угодно мало отличающейся от длины отрезка MiM^=y^— у\>
т. е.
Lin ~ (у% —ух) кх.
Применяя формулу C1), можем написать
MxQ = SxG = %xbm = lim2 [*{у г —Уд] А* =
ъ
= \x{y2—yi)dx, C4)
ъ
=lim 2 [т(J;^ - ^}]А^ = J т (-у1. - J'D ^- <35>
а
Из формулы C5) вытекает
Теорема II Гульдина. Объем тела, получаемого при вра-
вращении плоской фигуры вокруг некоторой оси, лежащей в ее пло-
плоскости и не пересекающей ее, равен произведению площади вра-
вращающейся фигуры на длину пути, описанного ее центром тяже-
тяжести при вращении,
В самом деле, приняв ось вращения за ось ОХ, нетрудно заме-
заметить, что объем рассматриваемого тела вращения V равен разности
объемов тел, получаемых при вращении кривой у% и кривой yi9
а потому, согласно B4) [105],
в силу C5), что и требовалось доказать.
Полученные две теоремы Гульдина весьма полезны как при опре-
определении поверхности или объема фигур вращения, когда известно
положение центра тяжести вращающейся фигуры, так и обратно —
при определении центра тяжести фигуры, когда известны объем
или поверхность производимой ею фигуры вращения.
107 J
§ 10. ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
263
Примеры. 1. Найти объем V кольца (тора), получаемого при вращении
круга радиуса г (рис. 144) вокруг оси, лежащей в его плоскости на расстоя-
расстоянии а от центра (причем г < а, т. е. ось вращения не пересекает окружность).
Рис. 144.
Центр тяжести вращающегося круга находится, очевидно, в его центре,
а потому длина пути, описываемого центром тяжести при вращении, равна
2па. Площадь вращающейся фигуры равна %г2, а потому по теореме II Гуль-
дина имеем
V=izr2'2na = 2n2ar2. C6)
2. Найти поверхность F кольца, рассмотренного в примере 1.
Длина вращающейся окружности равна 2тсг; центр тяжести по-прежнему
совпадает с центром окружности, а потому в силу теоремы I Гульдина
имеем
F = 2пг • 2па = 4п2аг. C7)
3. Найти центр тяжести G полукруга ра-
радиуса а. Примем основание полукруга за ось
ОХ и направим ось ОУ по перпендикуляру
к ОХ, восставленному в центре (рис. 145); в
силу симметричности фигуры относительно
оси OY ясно, что центр тяжести G лежит на
оси OY. Остается найти только yG. Для этой
цели применим теорему II Гульдина. Тело,
получаемое при вращении полукруга вокруг оси ОХ, есть шар радиуса ау
и его объем равен -j- nas. Площадь S вращающейся фигуры равна -^ я2, a
потому
4. Найти центр тяжести G' полуокружности радиуса а.
Выбирая координатные оси, как и в предыдущем примере, видим опять,
что искомый центр G' лежит на оси OY, так что остается найти yQt, При-
Применяя теорему I Гульдина и заметив, что поверхность тела вращения F в
данном случае равна 4тсд2, длина s = rctf, получим
4%а2 ==
• 2%yG,y yG,=z2^L.
Как и следовало ожидать, центр тяжести полуокружности лежит ближе
к ней, чем центр тяжести ограничиваемого ею полукруга.
266 ГЛ. III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ ( НО
образом приближенная формула называется формулой касательных:
ь
b^ 1/] = *i. D4)
Одновременно с предыдущими описанными трапециями рассмотрим
вписанные трапеции, которые получим, соединив хордами концы соседних
нечетных ординат; присовокупим к ним еще две крайние трапеции, обра-
образованные хордами, соединяющими концы ординат у0 и _yi/2» Уп _ i/2 и jyn.
Сумму площадей полученных трапеций обозначим через
2 Г^1/2П-^з/2-Г-".-Г-4У/г_1/2
кривая у =/(лг) в промежутке (а, Ъ) не имеет точек перегиба,
т. е. только выпукла или только вогнута, то площадь S кривой заклю-
заключается между площадями ах и с2, и естественно поэтому принять за прибли-
приближенное выражение для 5 среднее арифметическое 1 ~~Г 2, что дает формулу
Понселе:
ь
Нетрудно видеть, что погрешность этой формулы при сделанном пред-
предположении о виде кривой не превосходит абсолютного значения
/а+УЛ-1/, Уо+Уп\Ь-а
2 2~/^-» DЬ)
причем выражение, стоящее в скобках, равно, как это нетрудно показать из
свойства средней линии трапеции, отрезку средней ординаты, отсекаемому
хордами, соединяющими между собой концы край-них четных и крайних не-
нечетных ординат.
110. Формула Симпсона. Оставив в силе предыдущее подразделение на
четное число частей, заменим данную кривую рядом дуг парабол второй
степени, проведя их через концы каждых трех ординат:
у о, Л/.« у» л> Л/.» у* -'• Уп-v Уп-ч* уп-
Вычисляя площадь каждой из полученных таким путем криволинейных
фигур по формуле D) [101], мы получим приближенную "формулу Симпсона:
я1 „/1д D7)
На выводе погрешности этой формулы, а равно и погрешности формулы
трапеций, мы здесь останавливаться не будем. Заметим, вообще, что выра-
ПО ]
10. ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
267
жсние погрешности в виде определенной формулы имеет скорее теоретиче-
теоретическое, чем практическое значение, так как обыкновенно дает слишком гру-
грубый предел.
По поводу предыдущего построения заметим, что соответствующим под-
подбором я, Ь и с в параболе у = ах2 + Ьх + с можно всегда заставить ее
пройти через заданные три точки плоскости с различными абсциссами.
На практике для точности результата существенное значение имеет плав-
плавный ход кривой, и в соседстве с точками, где кривая более или менее резко
меняет вид, нужно вести вычисления с большей точностью, для чего необ-
необходимо вводить более мелкие подразделения промежутка. Во всяком случае
полезно перед вычислением составить себе хотя бы только приблизительное
представление о ходе кривой.
Весьма существенное значение при приближенных вычислениях имеет
схема расположения действий. Для того чтобы дать представление о ней,
а также чтобы сравнить точность, даваемую различными выведенными выше
приближенными формулами, мы приводим следующие примеры:
*/«
1, S= \ sin х dx= I,
о
п = 10,
= 0,
= 0,078 539 81,
= 0,026 179 94
у2
Уг
Уь
Уъ
Уь
У7
У*
У*
II
sin 9°
sin 18°
sin 27°
sin 36°
sin 45°
sin 54°
sin 63°
sin 72°
sin 81°
0,156 4345
0,309 0170
0,453 9905
0,587 7853
0,707 1C68
0,809 0170
0,8910065
. 0,951 0565
0,987 6883
5,853 1024
У*/2
УЧ2
УУш
У°/2
Уп/2
У1В/2
У"/ш
У"/2
У"/ш
sin 4°,5
sin 13°,5
sin 22°,5
sin 31°,5
sin 40°,5
sin 49°,5
sin 58°,5
sin 67°,5
sin 76°,5
sin 85°,5
0,078 4591
0,233 4454
0,382 6834
0,522 4986
0,649 4480
0,760 4060
0,852 6402
0,923 8795
0,972 3699
0,996 9173
6,372 7474
Уо
Ую
sin 0°
sin 90°
0,000 0000
1,000 0000
268
ГЛ. 111. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ
Формула прямоугольников по недостатку
Е,
Уо
5,853 1024
0,000 0000
t b — a
0,767 3861
1,196 1198
Е 5,853 1024 \gS
S = 0,919 4080
1,963 5059
ПО
Формула прямоугольников по избытку
Е,
У«
5,853 1024
1,000 0000
Ь — а
0,835 8873
Г, 196 1198
E 6,8531024
0,032 0071
S я» 1,076 5828
Формула
касательных
]а
Ь — а
0,804 3267
1,1961198
\g S 0,000 4465
S ««1,001 0290
Формула трапеций
2 Ei
Уо+Ую
11,706 2048
1,000 0000
b — a
g 2n
1,104 0158
2,895 0899
E 12,706 2048 lgS 1,999 1057
5 ^ 0,997 9430
Формула Понселе
1
2
(У1
E2
+ J>io)
/, +У">/2)
12,745 4948
0,250 0000
—0,268 8441
12,726 6507
5^0,999 5487
1,999 8039
110 J § 10. ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
Формула Симпсона
269
2 Ei
4Е2
Уо+Ую
11,706 2048
25,490 9896
1,000 0000
IgS
b — a
g Qa
1,582 0314
2,417 9685
38,197 1944 lg S
S^ 1,000 0000
1,999 9999
2. S=
±?±- dx = -j- log 2 = 0,272 198 2613...,'
„=10, Lzz?=bl b-a= 1
У*
Уз
Уа
Уъ
Уь
Ъ
Уъ
Уэ
Ei
0,094 3665
0,1753092
0,240 7012
0,290 0623
0,324 3721
0,345 5909
0,356 1263
0,358 4065
0,354 6154
2,539 5503
Л/,
Л/,
Л/,
Л/,
Л/,
yJ5/a
у»/.
У»/,
0,048 6685
0,136 6865
0,210 0175
0,267 3538
0,308 9926
0,336 4722
0,352 0389
0,358 1540
0,357 1470
0,351 0273
2,726 5583
Уо
У ю
0,000 0000
0,3465736
\) Эта формула будет выведена во втором томе.
ГЛ. III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ
Формула Понселе
I НО
1
1
5,453 1166
0,086 6434
—0,099 9239
a s =
Формула
2 ?i
4L2
Уо+Уп
Симпсона
5,079 1006
10,906 2332
0,346 5736
5,439 8361
16,331 9074
= ^2 *« 0,271 9918
п = 20,
log 2 = 0,693 147 18'...
— а 1 Ъ — а
1
2п
40'
6л 120е
У1
Уз
Уз
ЗУ
>>5
У*
Уч
У*
У*
Ую
У и
Уи
Уи
Уи
Ухъ
Ум
У17
Уи
Уи
Ei
0,952 3810
0,909 0909
0,869 5653
0,833 3333
0,800 0000
0,769 2307
0,740 7407
0,714 2857
0,689 6552
0,666 6667
0,645 1613
0,6250000
0,606 0606
0,588 2353
0,571 4287
0,555 5556
0,540 5405
0,526 3146
0,512 8205
13,116 6666
УЧ%
У*/а
Уэ/а
Ухз/2
У15/а
у19/2
У"/ш
У23/а
*¦/.
У27/а
У"/»
Узз/а
У35/]
^37/2
Узе/,
Е2
0,975 6097
0,930 2326
0,888 8889
0,851 0638
0,8163266
0,784 3135
0,754 7169
0,727 2727
0,701 7543
0,677 9661
0,655 7377
0,634 9207
0,615 3846
0,597 0149
0,597 7101
0,563 3804
0,547 9451
0,533 3333
0,519 4806
0,506 3291
13,861 3816
Ill 1 § 10. ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
Формула трапеций
1,000 0000
0,500 0000
2 Si
У0 + У20
26,232 1332
1,500 0000
27,732 1332
271
Формула Понселе
27,722 7632
0,375 0000
—0,370 4847
27,727 2785
Формула Симпсона
2 Si
4S3
У0+У20
26,232 1332
55,445 5264
0,500 0000
83,177 6596
1^0,69314716
111. Вычисление определенного интеграла с переменным верхним
пределом. Во многих вопросах приходится вычислять значения определен-
определенного интеграла
F{x)J\f{x)ix
при переменном верхнем пределе.
Основываясь на формуле трапеций D3), можно указать следующий спо-
способ получения приближенных значений этого интеграла, конечно, не при всех
значениях х} а только при тех, которыми подразделен на части промежуток
(я, Ь), т. е.
F(a), F(*i), F(xJ9 ..., F(xh)% ..., /*(*«-!)• F(b).
D3)
По формуле D3) мы имеем
a + kh
D9)
Эта формула дает возможность, вычислив значение F(Xk), перейти, к
следующему значению F(xk+l) = F(xk + h).
Вычисление это можно располагать по схеме, приведенной, на стр. 272.
272
ГЛ. III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ
Г in
ш
с»
•si
и
II
5»
СО
в
+
ч*
О
О
о
•si
«—¦ |сч
со*
*
со*
со
со*
•si
-!*
со"
+
IT
со*
со'
со
¦si
со*
+ +
СО чр
со со
«3
СО
со
со
со
со
•si
со"
со
со
со
со
+
к»
со
со
со
во
со
со
со
*г
со"
со
СО
со
+
со*
II
со
S
ю
со
со
со
ее
со
со*
-1С
со
со
со
00°
в*
со
со
•si
со
о
«
112
§ 10. ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
273
112. Графические способы. Эти вычисления можно произвести графи-
графически, если дан график кривой y=f(x); мы получим таким путем по-
построение графика интегральной
кривой
E0)
по графику кривой
Прежде всего, если имеем
достаточно делений, то мы мо-
можем принять приближенно
*~Х
т. е. если график кривой E0)
начерчен, то величины-^ полу-
получаются непосредственно из чертежа, как ординаты кривой при (рис. 149)
— . 2k~ 1 и
xk-4* - а + —2~ П'
Наметим на оси ОУ точки:
На оси ОХ влево от точки О построим отрезок ОР, равный единице.
Проведем лучи
РАЬ РА2, РА3, ...,
и через точки MOf Mly М2}... — им параллельные, так что
M0Mt (| PAit M,M21| РА2} М2МВ || РЛ3, ...
Точки Мо, Mlt M2i ... и будут точками искомой приближенной инте-
интегральной кривой, так как нетрудно из чертежа убедиться, что
/2 = h (yl/2 +y*/t), *гМ8 = h (у1/з + у3/а /2
а это, в силу приближенного равенства E1), показывает
в силу формулы D8).
Указанное построение проделано для того случая, когда масштаб для
функции F(x) совпадает с масштабом для f(x). Если масштаб для площади
другой, то построение остается тем же с тою только разницей, что отре-
отрезок ОР имеет длину не единицу, а /, причем / равно отношению масштаба
Для F(x) к масштабу для f(x).
Графическое приближенное построение повторного интеграла
®(x)=\dx(]f(x)dx)
а а
основано на формуле прямоугольников D0) [108|.
274 ГЛ. ITT. ПОНЯТИЕ OS ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ
Положим, как и раньше, что
Рассматривая только значения лг0, xiy х2,..., хт... независимой пере-
переменной ху мы по формуле D0) имеем приближенное равенство
Применяя ту же формулу и к функции Ф (x)f имеем
Ф (хк) = h[F(лго) + F (х,) + ... + F(хк_,)]
Отсюда вытекает следующее построение ординаты Ф (xk) (рис. 150): по-
построив точку Р, как и раньше, мы на
A<L оси OY откладываем отрезки
Проведя лучи
PBU Р?2, РЯ3,..., PBk,...>
строим точки
Мо, Ми М2,..., Mkf...,
проводя
Р 0
х0 х< хг xs
Рис. 150.
{||Р53,...
| РВ2,
Эти точки и будут точками иско-
искомой приближенной кривой, начерченной,
однако, в неизменном масштабе A: Л), ибо из построения ясно, что
XiMt = Лу0, х2М2 = hy0 + h (Уо
в силу E2). Если длина ОР есть не единица, а /, то построенная кривая
дает ординату кривой Ф (х)} измененную в отношении 1 : /Л. Следует огово-
оговорить, что при всем удобстве указанных построений точность их невелика,
и их можно употреблять лишь при сравнительно грубых расчетах.
113. Площади быстро колеблющихся кривых. Выше [ПО] было указано,
что для успешного применения различных приближенных формул, для вычис-
вычисления определенных интегралов надлежит разбивать кривую, площадь кото-
которой определяется на участки, в каждом из которых она имеет плавную
форму. Это требование весьма затруднительно для кривых, ведущих себя не-
неправильно, имеющих много колебаний вверх и вниз. Для определения пло-
площадей таких кривых по предыдущим правилам приходится вводить слишком
много подразделений, что значительно усложняет вычисления.
В таких случаях полезно применять другой способ, а именно разбивать
площадь на полоски, параллельные не оси О У, а оси ОХ: для приближен-
114 1 § 11. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ 275
ного определения площади кривой, изображенной на рис. 151, откладываем
на оси ОУ наименьшую и наибольшую ординаты аир кривой и разделяем
промежуток (а, р) на п частей в точках
У о = а» У и • • •» JVi-i» Уь • • •» 3>я-и Уп = Р.
Проведя через точки деления прямые, параллельные оси ОХ, мы
разобьем всю площадь на полоски, состоящие из отдельных частей; за
Рис. 151.
приближенное выражение площади UPt полоски мы можем принять произ-
произведение ее основания iyi—yi_t) на сумму длин // отрезков любой прямой
заключенных внутри рассматриваемой площади; сумма эта непосредственно
может быть определена на чертеже. Обозначив эту сумму через /,-, мы полу-
получаем для искомой площади S приближенное выражение вида
3>о (Ь — в) + (Ух —Уо) h + (У2 —.Vi) h + • • • + (Уп — Jto-i) In*
которое будет тем точнее, чем больше число делений и чем круче колеба-
колебания кривой.
Надлежащее развитие основной идеи этого способа привело к понятию
об интеграле Лебега, значительно более общему, чем изложенное выше
понятие об интеграле Римана [94, 116].
§ И. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ОПРЕДЕЛЕННОМ
ИНТЕГРАЛЕ
114. Предварительные понятия. Последние номера настоящей
главы будут посвящены строгому аналитическому рассмотрению поня-
понятия интеграла, и в дальнейшем мы докажем существование опреде-
определенного предела у суммы вида:
276 ГЛ. III. ПОНЯТИЕ Об ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ [ Н4
не только для случая непрерывных функций. Для этого нам необхо-
необходимо ввести некоторые новые понятия, связанные с рассмотрением
разрывных функций.
Пусть функция f(x) определена в некотором конечном проме-
промежутке (а, Ь). Мы будем рассматривать только ограниченные функ-
функции, т. е. такие функции, все значения которых в упомянутом про-
промежутке остаются по абсолютной величине меньшими некоторого
определенного положительного числа, т.е. функция f(x) называется
ограниченной в промежутке (а, Ь), если существует такое поло-
положительное число В, что при всяком х из упомянутого проме-
промежутка мы имеем:
Если функция f(x) непрерывна, то, как мы уже упоминали [35],
она достигает в этом промежутке наибольшего и наименьшего значе-
значений, а потому, очевидно, будет и огра-
ограниченной. Наоборот, разрывные функ-
функции могут быть как ограниченными, так
и неограниченными. В дальнейшем мы
будем рассматривать только ограничен-
ограниченные разрывные функции. Положим, на-
например, что функция / (х) имеет график,
изображенный на рис. 152. В точке
х = с мы имеем разрыв непрерывно-
непрерывности функции, и значение функции в
самой точке лг = с, т. е./(с), должно
быть определено каким-нибудь образом путем дополнительного усло-
условия. В остальных точках промежутка, включая концы а и Ь, функция
непрерывна. Кроме того, при стремлении переменной х к значению
х = с от меньших значений, т. е. слева, ордината f(x) стремится
к определенному пределу, геометрически изображаемому отрезком NMX.
Точно так же при стремлении х к с от больших значений, т. е.
справа, f(x) стремится тоже к определенному пределу, изображаемому
отрезком NM%, но этот последний предел отличен от упомянутого
выше предела слева. Упомянутый предел слева обозначают обычно
символом /(с — 0), а предел справа — символом f(c-\-0) [32]. Этот
наиболее простой разрыв непрерывности функции, при котором
существуют конечные определенные пределы как слева, так и
справа, называется обычно разрывом первого рода. Значение функ-
функции в самой точке х = с, т. е. /(с), будет, вообще говоря, отличным
как от f(c — 0), так и от f(c -)-0) и должно быть определено до-
дополнительно. Если функция непрерывна в промежутке (а, Ь), включая
концы, за исключением конечного числа точек, в которых она имеет
разрывы первого рода, то график такой функции состоит из конеч-
114 ] § И. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ 277
ного числа кривых, непрерывных вплоть до своих концов, и из от-
отдельных точек в местах разрыва непрерывности (рис. 153). Такая
функция, несмотря на свою разрывность, будет, очевидно, ограни-
ограниченной во всем промежутке. Но, конечно, функции и с более
сложными разрывами могут быть огра-
ограниченными.
В дальнейшем мы часто будем рас-
рассматривать множества всех значений,
которые некоторая функция f(x) при-
принимает на каком-либо заданном про-
промежутке изменения независимой пере-
переменной. Если взятая функция ограни-
чена в рассматриваемом промежутке,
то множество ее значений в этом проме- рис- 153*
жутке ограничено сверху и снизу, а
потому это множество имеет точную верхнюю и точную нижнюю
границы [39]. Если, например, f(x) непрерывна в рассматриваемом
промежутке (замкнутом), то, как известно [35], она достигает в этом
промежутке наибольшего и наименьшего значений. В данном случае
эти наибольшее и наименьшее значения функции и будут точными
верхней и нижней границами значений f{x) в рассматриваемом про-
промежутке.
Рассмотрим 'другой пример. Если функция f(x) есть возра-
возрастающая функция, то она принимает наибольшее значение на правом
конце промежутка и наименьшее — на левом. Эти значения, так же
как и в предыдущем случае, будут точными верхней и нижней гра-
границами значений f(x). В обоих рассмотренных примерах точные
границы значений функции сами являлись частными значениями
функции, т. е. сами принадлежали к рассматриваемой совокупности
значений функции. В более сложных случаях разрывной функции
точные границы значений функции могут сами и не являться значе-
значениями функции, т. е. могут и не принадлежать к множеству значе-
значений функции.
Пусть т — точная нижняя граница множества значений ограничен-
ограниченной функции f(x) на некотором конечном промежутке (а, Ь) и М —
точная верхняя граница. Возьмем новый промежуток (а\ Ь'), который
является частью (я, Ь).
Пусть т и М — точные нижняя и верхняя границы множества
значений f(x) на (а\ Ь'). Так как множество значений f\х) на (а\ Ь')
содержится в множестве значений f(x) на более широком промежутке
(я> Ь)} то можно утверждать, что т'^т и М'^М, т. е. имеет
Лемма 1. Если некоторый промежуток заменить его частью,
то точная верхняя граница значений fix) не может увеличиться,
а точная нижняя граница не может уменьшиться*
278 ГЛ. III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ [ П5
115. Разбиение промежутка на части и образование различ-
различных сумм. Пусть конечный промежуток (я, Ь) разбит на конечное
число частей промежуточными значениями х:
a = xo<xi<x*<'..<xk-i<xk<--<xn-i<xn = f>- 0)
Такое разбиение будем обозначать одной буквой 8; значения хк
называются точками деления 8. У различных разбиений число частич-
частичных промежутков и точки деления xk, вообще говоря, различны.
Длины частичных промежутков для разбиения A) обозначим: 8^ =
= xk — xk_x (k=\, 2,..., п). Пусть f(x) — ограниченная функция,
заданная на промежутке (я, Ь). Напишем сумму, соответствующую
разбиению 8 A), предел которой, если он существует, дает опреде-
определенный интеграл от f{x) по промежутку (я, Ь)\
"(8. У=2/0*)8*. B)
Она зависит от 8 и выбора точек \к. Рассмотрим множество значе-
значений f(x) в промежутке (xk_b xk). В силу ограниченности функции f(x)9
это — ограниченное множество. Обозначим через mk точную нижнюю
и через Mk — точную верхнюю границы значений f(x) в промежутке
(хк-ь xk) {k=\, 2,..., п) и в слагаемых суммы B) заменим /(?*) на
mk, а также на Mk. Мы получим две суммы, зависящие только от
разбиения 8 промежутка {а, Ь)\
s(B)=|>A; 5(8)= 2 ma- C)
Из определения тк и Mk непосредственно следует
откуда ввиду положительности 8^ будем иметь
D)
Пусть, как и выше, т и М — точные нижняя и верхняя границы зна-
значений f(x) на всем промежутке (а, Ь). Используя лемму 1, нетрудно
видеть, что имеют место неравенства
и, кроме того, очевидно,
п и
115 1 § П. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ 279
Умножая неравенства E) на положительные числа 8А и суммируя по k
от k = 1 до k = n, получим
тф — а) < 5(8) < М(Ь — а),
т. е. множество значений s(8) и 5E) при всевозможных разбиениях 8
ограничено сверху и снизу. Обозначим буквою i точную верхнюю
границу множества значений s(8) и буквою / — точную нижнюю гра-
границу значений 5(8) при всевозможных разбиениях 8:
«*<*, S^l. F)
Отметим, что неотрицательная разность М — т называется обычно
колебанием функции f(x) на промежутке (а, Ь). Разность Mk — mk
есть колебания функции f(x) на промежутке {xk_b xk).
Введем теперь некоторые новые понятия. Разбиение 8' промежутка
(а, Ь) назовем продолжением разбиения 8, если всякая точка деления 8
есть и точка деления 8', т. е. 8' получается из 8 добавлением новых
точек деления (если 8' не совпадает с 8). Если Ьх и 82 — два разбие-
разбиения, то произведением их назовем такое разбиение (а, Ь), точки деле-
деления которого получаются объединением точек деления как Ьь так и
82. Произведение разбиений обозначим символом 8Д. Это понятие
применимо и для нескольких сомножителей. Разбиение 8Д является,
очевидно, продолжением как разбиения Ьъ так и разбиения 82.
Лемма 2. Если разбиение 8' есть продолжение разбиения 8,
то 5(8)<5(8') и 5(8)^5(8').
При переходе от 8 к 8' каждый из промежутков (xk_b xk) под-
подразделения 8 может разбиться на части. Положим, например, что этот
промежуток разбился на три части (xk_b ak), (ak, $k), (pft, xk), длины
которых Vj} = aLk—xk_l9 Vg) = ^k — ak9 bf = xk — %, и пусть Mkv,
Mf, MT—точные верхние границы множества значений/(jc) в ука-
указанных промежутках. В силу леммы 1: М&\ М™ и MT ^Mk> и сумма
ЪТ -\-ЪТ -\-lf = bk = xk — xk_v Слагаемое Mkbk суммы 5(8) при пе-
переходе к 8' заменяется суммой трех слагаемых:
МШ* + Mfbf + Mfbf
и, в силу сказанного выше,
M4W + МТЪТ + Mfbf < Mk {If + bf + 8^) = ЖА,
т. е. при переходе от 8 к 8' каждое слагаемое Mkbk суммы или за-
заменяется конечной суммой, которая меньше или равна Mkbk, или
остается без изменения. Отсюда и следует, что 5(8)^5(8'). Совер-
Совершенно аналогично доказывается, что s (8) ^ s (8'), и лемма доказана.
Принимая во внимание, что mk ^ Mk и 8^ положительны, легко
видеть, что при одном и том же 8 мы имеем 5(8)^5(8). Покажем,
2&0 ГЛ. III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ I 116
что такое же неравенство имеет место и для любых различных раз-
разбиений.
Лемма 3. Если Ъх и 82—любые два разбиения, то s (Ь{) ^ S (Ь2).
Рассмотрим произведение 8j82 разбиений 8j и 82. Поскольку 8,8.2
есть продолжение Ьх и 82, из леммы 2 следует, что 5EjB2)^: ^ (Bj) и
и пользуясь неравенством 5(8182)^5(8182), получаем
Лемма доказана.
Из этой леммы непосредственно следует, что верхняя грань i
множества значений 5(8) при всевозможных разбиениях 8 и нижняя
грань I для 5(8) удовлетворяют неравенствам
Займемся теперь суммами о (8, lk), которые удовлетворяют нера-
неравенствам D). При фиксированном разбиении 8, в силу определения
mk и Mk> можно при любом k выбрать %k так, чтобы f(tk) было
сколько угодно близко к Mk или даже (в некоторых случаях) совпа-
совпадало с Mky т. е. можно выбрать ik так, чтобы сумма о (8, tk) была
сколь угодно близкой к S(b) или даже в некоторых случаях, чтобы
о(8, lk) совпадало с 5(8). С другой стороны, в силу D), о (8, tk)^
г^?(8). Отсюда следует, что S(b) есть точная верхняя граница зна-
значений а (8, lk) при всевозможных выборах \k. Аналогично доказы-
доказывается, что 5(8) есть точная нижняя граница значений о (8, lk), т. е.
имеет место
Лемма 4. При фиксированном разбиении 8 величина s(8) есть
точная нижняя граница значений о (8, tk) при всевозможных
выборах %ky a S(b) есть точная верхняя граница множества зна-
значений о (8, $k) при тех же условиях.
116. Интегрируемые функции. Укажем теперь необходимое и
достаточное условие существования интеграла у ограниченной функ-
функции f(x) или, как говорят, необходимое и достаточное условие
интегрируемости f(x). Через [х(8) в дальнейшем будем обозначать
наибольшую иа длин частичных промежутков, входящих в подраз-
подразделение 8.
Теорема. Необходимое и достаточное условие интегрируе-
интегрируемости ограниченной функции f (х) на конечном промежутке (а, Ь)
состоит в том, чтобы разность
стремилась к нулю, если |х(8) стремится к нулю.
Иначе говоря, это условие, назовем его условием А, состоит в сле-
следующем: при любом заданном положительном числе е существует
116 1 § П. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ 281
такое положительное число т], что неотрицательна разность:
S(b)— 5(8)<e, если [х(8)<т].
Достаточность. Положим, что условие А теоремы выполнено,
т. е. S(b) — s(8)->0 при |х(8)->0. При этом из G) следует, что
i = I и что s(8) и S(b) стремятся к / при ц.(8)->0. Отсюда следует,
в силу D), что и сумма о (8, lk) стремится к / при |х (8) -> О и любом
выборе lk. Точнее говоря: )/—с (8, ^)|<С^? при ц(&)<Сз причем
т]^>0 определяется заданием е^>0. Таким образом, доказано, что/(х)
интегрируема и число / есть величина интеграла. Достаточность усло-
условия А доказана.
Необходимость. Положим, что f(x) интегрируема. Докажем,
что выполнено условие А. Обозначим /0 величину интеграла от f(x).
Из его определения следует: для любого е^>0 существует такое
^ ЧТО
т> если
при любом выборе bk. В силу леммы 4, при любом фиксированном
возможен такой выбор \k = i'k и %k = Ц, что
|o(8,-6i)-5(8)|<-j и |а(8, «)-
Мы можем написать
-f- [/0 — в(S, 6i
откуда, в силу (9) и A0), получаем при
т. е. }S(b) — 5(8)|<^е при р-(8)<^7], а это и есть условие А. Необ-
Необходимость условия доказана.
Замечание 1. Из доказательства достаточности следует, что
i = I при выполнении условия А, и при этом величина интеграла
равна /. Поэтому из необходимости условия А следует, что равен-
равенство i = l является необходимым условием интегрируемости.
Замечание 2. Можно показать, что для любой ограниченной
функции f(x) будет: $(&)->? и S(b)->I при [х(8)~>0. Отсюда сле-
следует, что если i = /, то (?(§) — 5 (8)) -> 0 при [х (8) -* 0, и потому равен-
равенство i = 1 не только необходимо, но и достаточно для интегрируемо-
интегрируемости f{x).
282 ГЛ. III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ I 116
I. Если f(x) непрерывна на замкнутом промежутке (я, Ь), то она
равномерно непрерывна на нем. Кроме того, на каждом из промежут-
промежутков (xk_v xk) она достигает своего наименьшего значений mk и наи-
наибольшего Mk. В силу равномерной непрерывности f(x) при любом
заданном е ^> О существует такое т] ^> 0, что 0 ^ Mk — mk <^, J_ -,
если |^(8)<^7]. При этом
т.е. S(b) — s(8)<^e, если jx(S)<^^. Таким образом, условие А
выполнено, и, следовательно, всякая непрерывная функция инте-
интегрируема.
II. Положим теперь, что ограниченная функция f{x) имеет конечное
число точек разрыва. Для определенности будем считать, что f{x)
имеет одну точку разрыва х = с, лежащую внутри (я, Ь). Отметим
прежде всего, что разности Mk — mk на любом частичном промежутке
не превосходят колебания М — т функции на всем промежутке
(а, Ь):
Mk — mk^M — m, A=l, 2,..., п. A1)
Пусть задано положительное число е. Выделим точку с из проме-
промежутка (а, Ь) малым фиксированным промежутком {аь bt) (рис. 154),
таким, что а<^а1<^с<^Ь1<^Ь и Ьх — ах<^ъ. На замкнутых проме-
промежутках (а, а{) и (&!, Ь) функция f(x)
о 000 о непрерывна, а тем самым и равномерно
а а1 с \ * непрерывна. Поэтому для каждого из
рис> 154. этих ДВУХ промежутков существует такое
число т], что \f(x")—/(J^)|<![e, если У
и х" принадлежат (а, ах) или (Ьь Ь) и \х!' — /|<^ni. Числа г\ могут
оказаться разными для (a, at) и (bif b), но если мы возьмем наимень-
наименьшее из этих двух чисел % то оно будет годиться для обоих проме-
промежутков. Пусть 8 — любое такое разбиение (а, Ь), что соответствую-
соответствующее ему (а (8) меньше чисел т) и е:
ц(8)<7] и |л(8)<е, A2)
т. е. меньше наименьшего из двух чисел ч\ и е.
Оценим соответствующую такому 8 сумму (8), состоящую из не-
неотрицательных слагаемых. Промежутки (xk_if xk)f принадлежащие 8,
разобьем на два класса. К первому отнесем те, которые целиком
укладываются в (а, аг) или (bit b\ a ко второму классу остальные час-
частичные промежутки разбиения 8. Это будут те промежутки (xk_b xk),
которые или принадлежат (ai9 bx) или частью налегают на этот про-
116 1 § И. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ 283
межуток. Сумма длин Ьк промежутков первого класса, очевидно, меньше
(Р — а), а эта сумма для промежутков второго класса меньше Зе. Это
вытекает из неравенства bx — #i<O> второго из неравенств A2) и
того факта, что число частью налегающих на (av bx) промежутков
разбиения Ь не больше двух. Далее, для промежутков первого класса,
в силу непрерывности f(x) на (а, ах) и (Ьь Ь\ первого из нера-
неравенств A2) и определения числа % имеем Мк — тк<^г. Для проме-
промежутков второго класса используем неравенство A1). Таким образом,
имеем для суммы по промежуткам первого класса
и для промежутков второго класса
и
Окончательно
A3)
если р. (8) удовлетворяет неравенствам A2). Квадратная скобка в пра-
правой части A3) есть определенное число, и принимая во внимание
возможность произвольного выбора малого положительного числа е,
мы можем утверждать, что выполнено условие А, т. е. всякая ограни-
ограниченная функция f{x)y имеющая конечное число точек разрыва
непрерывности, интегрируема.
III. Рассмотрим тот случай, когда/(дг) — монотонная ограниченная
на конечном промежутке (а, V) функция. Для определенности будем
считать, что f(x) не убывает, т. е. f(ci)^f(c2)f если сг<^с2. При
этом на каждом промежутке (xk-i, *k) мы имеем mk=f(xk_1) и
-М* =/(**)• Отсюда следует
S(b) - * (8)= J] (Mk - mk) h = 2 [f(xk) -f(xk.x)} bk.
Но &?=^(л(8) и разности f(xk) — f{xk_x) неотрицательны, и, следова-
следовательно,
2
Принимая во внимание, что
2
284 ГЛ. III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ
получаем
откуда следует, что
SF)-sF)<e, если H(fi)</(fr)l/(fl) ПР" /Ф)>/(а).
Если f(b) = f(a), то /(лг) — постоянная.
Таким образом, всякая монотонная ограниченная функция ин-
интегрируема.
Заметим, что монотонная функция может иметь и бесчисленное
множество точек разрыва, так что случай (III) не исчерпывается слу-
случаем (II). В качестве примера можем привести функцию, равную
нулю при 0^лг<С-2"» равную у при -к-^х <С-^} равнуюv.-^- при
о Q
-^-^лг<С-т-> и т- д* и> наконец, равную 1 при лг=1. У этой неубы-
неубывающей функции точками разрыва будут на промежутке @, 1) значения
*.-! А А 1
Упомянем о том, что монотонная ограниченная функция должна
иметь во всякой точке разрыва х = с пределы /(с —0) и /(?-}-0). Это
непосредственно следует из существования предела у монотонной и
ограниченной последовательности чисел [30].
При выводе условий интегрируемости мы всегда предполагали f(x)
ограниченной. Можно доказать, что это условие является необходимым
условием интегрируемости, т. е. существования определенного предела
у суммы B). Если это условие ограниченности не выполнено, то все же
в некоторых случаях можно определить интеграл от f(x) по проме-
промежутку (а, Ь), но уже не как предел суммы B). В этом случае инте-
интеграл называется несобственным. Основы учения о несобственном инте-
интеграле выяснены нами в [97]. Более подробно это будет изложено
во втором томе.
Если промежуток интегрирования (а, Ь) бесконечен в одну или в обе
стороны, то понятие об определенном интеграле по такому промежутку
также не приводится непосредственно к пределу суммы вида B).
В этом случае мы имеем тоже несобственный интеграл (см. [98] и вто-
второй
117. Свойства интегрируемых функций. Пользуясь найденным
выше необходимым и достаточным условием интегрируемости, нетрудно
выяснить основные свойства интегрируемых функций.
I. Если f(x) интегрируема в промежутке (a, b), и мы изме-
изменим произвольно значения f(x) в конечном числе точек из (а, Ь),
117 ) § П. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ 285
tno новая функция будет также интегрируема в (а, Ь) и вели-
величина интеграла от этого не изменится.
Ограничимся рассмотрением того случая, когда мы изменили зна-
значение f(x) в одной точке, например в точке х = а. Новая функ-
функция ср(х) везде совпадает с f(x), кроме х = а, а ср(#) берем произг
вольно. Пусть т и М — точные нижняя и верхняя границы f(x)
в (а, Ь). Точная нижняя граница у(х) будет, очевидно, больше или
равна т, если у(а)^т, и будет <р(а)> если ТС^Х^- Точно так же
точная верхняя граница <р(х) будет меньше или равна М, если
ср(а)^Ж, и будет ср(я), если <p(a)^>M. Сравнивая сумму A2) для
f(x). и ср(лг), замечаем, что разница может быть только в первом
слагаемом (при ? = 1). Но это первое слагаемое, очевидно, для f(x)
и ср (х) стремится к нулю, так как Sj —> 0 и {Мх — т^) ограничено.
Сумма остальных слагаемых, кроме первого, также, очевидно, стре-
стремится к нулю, так как f(x) интегрируема, и вся сумма (8) для f(x)
должна стремиться к нулю. Интегрируемость <р(-*0 доказана. Совпа-
Совпадение значений интеграла для f{x) и ср (лг) очевидно, ибо при соста-
составлении сумм B) мы всегда можем считать $t отличным от а, а зна-
значения f(x) и у(х) во всех точках, кроме х = а, совпадают.
II. Если f(x) интегрируема в промежутке (а, Ь), то она
интегрируема в любом промежутке (с, а1), составляющем часть
(а, Ъ).
Это легко следует из того, что сумма (8), состоящая из неотри-
неотрицательных слагаемых, для промежутка {с, d) не больше, чем эта сумма
для (а, Ь)у при условии, что в этой последней сумме х = с и лг = й
суть точки деления. В силу интегрируемости f(x) на (а, Ь) сумма (8)
для (а, Ь) стремится к нулю при jx (S) -—> 0 при любых точках деления.
Тем более и сумма для (с, d) стремится к нулю, если [а(В)—*0 для
частичных промежутков из (с} d), т. е. f(x) интегрируема на (с, d).
Заметим, что с может совпадать с a, a d может совпадать с Ь. Совер-
Совершенно так же, как и в [94], доказывается равенство
l\ (а<с<Ь).
III. Если f(x) интегрируема в (а, Ъ), то и cf{x), при любом
постоянном с, также интегрируема в (а, Ь).
Считая, например, с^>0, можно утверждать, что для функции с/(х)
надо заменить прежние mk и Mk на cmk и cMk. Сумма (8) приобретет
лишь множитель с и будет по-прежнему стремиться к нулю. Свойство V
из [94], очевидно, сохраняется и доказывается по-прежнему.
IV. Если f\{x) и fi(x) — функции, интегрируемые в (а, Ь), то
их сумма
также интегрируема в (af b).
286 ГЛ. HI. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ I П7
Пусть m'k, M'k, tn'k, Ml — точные нижние и верхние границы ft (х)
и fz(x) в промежутке (хк-ь xk). Таким образом, все значения /, (х)
в промежутке (xk_h xk) больше или равны т'ъ, а все значения f^(x)
там же больше или равны т%. Отсюда ср (х) ^ m'k -f- т% в проме-
промежутке (xk_h xk).
Точно так же доказывается, что y(x)^Mk-\-Ml в проме-
промежутке (хк_ъ xk). Обозначая через mk и Mk точную нижнюю и точную
верхнюю границы у(х) в промежутке (xk_b xk), имеем, таким
образом,
откуда следует неравенство
Mk — mk < {M'k + Ml) — (m'k + ml),
то есть
Mk — mk^ (М'к — m'k) + (Ml — ml).
Составляя сумму (8) для ср (х), получим
О
Обе суммы, стоящие справа, стремятся к нулю при jj, (Ь) —> 0, так
как функции fi (x) и /2 (х) по условию интегрируемы. Следовательно,
сумма (8) для <р(лг), т. е. сумма
j](Mk-mk)bky
и подавно стремится к нулю, т. е. <р(лг) также интегрируема. Дока-
Доказательство распространяется легко на случай алгебраической суммы
любого конечного числа слагаемых. Свойство VI из [94] доказывается,
как и раньше.
Аналогично предыдущему доказываются следующие свойства:
V. Произведение fx (x) /2 (х) двух функций, интегрируемых
в (а, Ь), будет функция, также интегрируемая в (а, Ь).
VI. Если f(x) интегрируема в (а, Ь) и точные нижняя и верхняя
границы т и М функции f(x) в (а, Ь) одного и того же знака,
то и fj-ir есть функция, интегрируемая в (а, Ь).
VII. Если f(x) интегрируема в (а, Ь), то и ее абсолютное зна-
значение \f(x)\ также есть функция, интегрируемая в (а, Ь).
Неравенство A0) из [95] может быть доказано, как и выше.
Совершенно так же остается справедливым и свойство VII из [95],
117 ] § 11. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ 287
если f(x) и <рС*О — интегрируемые функции. Теорема о среднем
читается так:
Если f(x) и ср (лг) интегрируемы в промежутке (а, Ь) и ср(х)
сохраняет знак в этом промежутке, то
где (х — некоторое число, удовлетворяющее неравенству т^
а т и М — точные нижняя и верхняя границы f(x) в (а, Ь).
Б частности,
ь
Доказательство будет таким же, что и раньше [95]. Пользуясь
этой формулой, нетрудно установить, что
F{x) = \f(t)dt
а
есть непрерывная функция от лг, и Ff(x)=f(x) при всех значениях х,
где f(x) непрерывна. Наконец, установим основную формулу инте-
интегрального исчисления для интегрируемых функций. Пусть Fl(x) —
непрерывная в промежутке (а, Ь) функция, и при любом значении х
внутри промежутка (а, Ь) имеется производная F'1(x)=f(x)) где
f(x) — интегрируемая в (а, Ь) функция.
При этом имеет место основная формула
Разбивая промежуток на части и применяя к каждой части (xk_h xk)
формулу конечных приращений [63], можем написать
Далее, суммируя по k и принимая во внимание, что (III из [116])
п
2 [^i (xk) — Ft (xk_i)] = Fx (b) — Fx (a),
мы получим
288 гл. itt. понятие об интеграле и его приложения \ 117
Равенство это справедливо при любом разбиении промежутка (а, Ь)
на части ввиду специального выбора точек ik, определяемого фор-
формулой конечных приращений A4). Переходя к пределу, получим вместо
суммы интеграл
что и требовалось доказать. Заметим, что при определении интеграла
значения f(x) на концах промежутка (а} Ь) не играют роли, в силу
свойства I настоящего номера.
Г Л А В А IV
РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ
ВЫЧИСЛЕНИЯМ
§ 12. ОСНОВНЫЕ ПОНЯТИЯ ИЗ ТЕОРИИ БЕСКОНЕЧНЫХ РЯДОВ
118. Понятие о бесконечном ряде. Пусть дана бесконечная после-
последовательность чисел
«1, Щ> «з» ...» ил, ... A)
Составив сумму п первых членов последовательности
*л = И1 + «а+ ... +wm B)
мы получим, таким образом, другую бесконечную последовательность
чисел
Sit &2, . ., , $п, ...
Если эта последовательность стремится к пределу [конеч-
[конечному):
$ — lim sn>
говорят, что бесконечный ряд
и\ + Щ+ ... +"*+ ... C)
сходится и имеет сумму s, и пишут:
.. +нл+ ... D)
Если же sn не стремится к пределу, то говор ят, что бес-
бесконечный ряд C) расходится.
Иначе говоря, бесконечный ряд C) называется сходящимся, если
сумма его первых п слагаемых при беспредельном возрастании п
по всем целым положительным значениям стремится к пределу,
и этот предел называется суммою ряда.
10 В, И. Смирнов, т. I
290 ГЛ. IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ [ 118
О сумме бесконечного ряда можно говорить только тогда, когда
он сходится, и тогда сумма первых членов ряда sn является прибли-
приближенным выражением для суммы ряда 5. Погрешность гп этого прибли-
приближенного выражения, т. е. разность
называется остатком ряда.
Очевидно, что остаток гп есть в свою очередь сумма бесконеч-
бесконечного ряда, который получается из данного ряда A), если в нем
отбросить пер'вые п членов с начала:
Точная величина этого остатка в большинстве случаев остается
неизвестной, и потому особенно важной является приближенная оценка
этого остатка.
Простейший пример бесконечного ряда представляет геометриче-
геометрическая прогрессия
Рассмотрим отдельно случаи
Мы знаем ?27], что при |<?|<^1 геометрическая прогрессия имеет
конечную сумму s= < , и потому оказывается сходящимся рядом;
действительно, при этом
а а — aqn aqn
S~Sn~V^q \ — q —T^q'
— sn—+ 0 при я—*оо, так как qn —*0 при |у|<^1 [26]. При
||^ из выражения sn видно, что sn—>оо при я-^оо, так как
qn—+oo при | q \^> 1 [29]. При q = 1 мы имеем sn = an, и, очевидно,
также sn —* оо, так что при | q \ ^> 1 и q = 1 геометрическая про-
прогрессия оказывается расходящимся рядом. При # = —1 мы полу-
получаем ряд
а — а-\-а — а-\- ...
Сумма sn первых п его членов равна нулю, если п четное, и
равна а, если п нечетное, т. е. sn не стремится к пределу, и ряд
расходится; однако при всех значениях п эта сумма в отличие от
предыдущего случая остается ограниченной, так как принимает только
значения 0 и а.
Если абсолютная величина sn — суммы п первых членов ряда
C) —- стремится к бесконечности при беспредельном возрастании п,
119 ] § 12. ОСНОВНЫЕ ПОНЯТИЯ ИЗ ТЕОРИИ БЕСКОНЕЧНЫХ РЯДОВ 291
то ряд C) называется собственно расходящимся. В дальнейшем,
говоря о собственно расходящемся ряде, мы для краткости будем
говорить просто расходящийся ряд.
119. Основные свойства бесконечных рядов. Сходящиеся беско-
бесконечные ряды обладают некоторыми свойствами, которые позволяют
действовать с ними, как с конечными суммами.
I. Если ряд
имеет сумму s, то ряд
.. +яня+ ..., F)
получаемый из предыдущего умножением всех членов на одно
и то же число а, имеет сумму as, ибо сумма ап первых п членов
ряда F) есть
а потому
lim on = lim asn = a lim sn = as.
II. Сходящиеся ряды можно почленно складывать и вычитать,
т. е. если
+ + .. +г>я+ ... =о,
то ряд
(u1±vl) + (u,±v2)+ ... +(un±vn)+ ... G)
также сходится и сумма его равна 5±а, ибо сумма первых
членов ряда
Другие свойства суммы, например независимость суммы от порядка
слагаемых, правило перемножения двух сумм и т. п., в применении
к бесконечным рядам будут рассмотрены ниже в § 14. Заметим пока,
что они справедливы не для всякого ряда. Сочетательный закон спра-
справедлив, очевидно, для любого сходящегося ряда, т. е. можно объеди-
объединять в группы любые рядом стоящие слагаемые. Это сводится к тому,
что вместо всех sn(n= 1, 2, 3,...) мы берем подпоследовательность snk,
что не меняет предела 5 [27].
III. Свойство сходимости или расходимости ряда не нару-
нарушится, если в ряде отбросить или приписать к нему любое конеч-
конечное число членов с начала.
10*
292 ГЛ. IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ [ 119
Действительно, рассмотрим два ряда
Второй получается из первого отбрасыванием первых двух слагаемых.
Если обозначить через sn сумму первых п членов первого ряда,
а через ап — то же для второго ряда, то, очевидно
причем если п —> оо, то и значок (л — 2) —¦* оо. Отсюда видно, что
если sn имеет предел, то и ол_2 имеет предел, и наоборот. Эти пре-
пределы 5 и о, т. е. суммы взятых двух рядов, будут, конечно, различны,
а именно
IV. Общий член ип сходящегося ряда стремится к нулю при
беспредельном возрастании п:
limwrt = 0, (8)
ибо очевидно, что
и если ряд сходится и имеет сумму s, то
lim sn_t = lim sn = s9
откуда
lim un = lim sn — lim $„_! = 5 — 5 = 0.
Таким образом, условие (8) необходимо для сходимости ряда,
но оно не достаточно: общий член ряда может стремиться к нулю,
и ряд все же может быть расходящимся.
Пример. Гармонический ряд
Здесь мы имеем
ип = > 0 при п —*¦ оо.
Нетрудно, однако, показать, что сумма п первых членов ряда (9) беспре-
беспредельно возрастает. Для этого сгруппируем слагаемые, начиная со второго,
в группы из 1, 2, 4, 8, ... членов:
120 1 § 12. ОСНОВНЫЕ ПОНЯТИЯ ИЗ ТЕОРИИ БЕСКОНЕЧНЫХ РЯДОВ 293
так что в &-й группе будет 2k~x членов. Если в каждой группе заменим все
члены последним, наименьшим членом группы, то получится ряд
1 1 9 , 1 1 1 1
сумма первых п членов которого, равная 1+-^-(л—1) , стремится, оче-
очевидно, к (+оо). Взяв достаточно большое число членов ряда (9), мы можем
получить какое угодно число п групп, и сумма этих членов будет еще больше,
чем
м_}„(я—1I и отсюда видно, что для ряда (9) sn-+
120. Ряды с положительными членами. Признаки сходимости.
Особенное значение имеют ряды с положительными (не отрицатель-
отрицательными) членами, для которых все числа
иь и2, и3, -••»'««, ...3*0.
Для них мы установим ряд признаков сходимости и расходимости.
1. Ряд с положительными членами может быть только либо
сходящимся, либо же собственно расходящимся; для такого ряда
$n-+s или 5п-> + оо.
Для того чтобы ряд с положительными членами был сходя-
сходящимся, необходимо и достаточно, чтобы сумма sn его первых
членов при всяком п оставалась меньше некоторой постоянной Аг
не зависящей от п.
Действительно, для такого ряда сумма sn не убывает при возра-
возрастании п, так как при этом добавляются новые положительные (неот-
(неотрицательные) слагаемые, и все наши утверждения вытекают из разоб-
разобранных раньше свойств возрастающих переменных [30].
Для суждения о сходимости или расходимости рядов с положи-
положительными членами часто полезно бывает сравнить их с другими, более
простыми рядами, чаще всего с геометрической прогрессией.
Для этого мы установим признак:
2. Если каждый член ряда с положительными членами
начиная с некоторого члена, не превосходит соответствующего
члена сходящегося ряда
v1 + v2 + v3 + ... + vn + ..., A2)
то и ряд A1) также сходится.
Если же, наоборот, каждый член ряда A1), начиная с неко-
некоторого п, не меньше соответствующего члена расходящегося
ряда A2) с положительными членами, то и ряд A1) также
расходится.
294 ГЛ. TV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ [ 120
Допустим сперва, что мы имеем
причем ряд A2) сходится. Не ограничивая общности, мы можем счи-
считать, что это неравенство выполняется при всех значениях пу отбросив,
в случае надобности, те первые члены, для коих оно не выполняется
(свойство III [119]). Обозначив через sn сумму п первых членов
ряда A1), через ап — аналогичную сумму для ряда A2), мы имеем,
в силу A3),
Но ряд A2) по условию сходится, и, обозначив через о сумму
ряда A2), имеем
а потому и
откуда, в силу 1, вытекает сходимость ряда A1).
Пусть теперь выполняется неравенство
un^vn. A4)
Мы имеем, очевидно,
но ряд A2) теперь расходится, и сумма ап первых его п членов
может быть сделана больше сколь угодно большого данного наперед
числа; тем же свойством, в силу A5), обладает и sn, т. е. ряд A1)
будет также расходящимся.
Замечание. Из сходимости (или расходимости) ряда A2) выте-
вытекает и сходимость (или расходимость) ряда
где k — какое угодно постоянное положительное число.
Действительно, из сходимости ряда ?vn вытекает и сходимость
ряда %kvn в силу I [119]. Наоборот, если ^рп расходится, то и
ряд Yfcvn должен быть расходящимся, ибо, если бы он сходился,
то, умножая его члены на у, мы, в силу I [119], имели бы и схо-
сходимость ряда 2рп. Из сказанного вытекает:
Ряд A1) сходится, если
un^kvn> A6)
причем ряд ]?vn — сходящийся и k — какое-нибудь положительное
число; ряд A1) расходится, если
un^kvn9 A7)
причем ряд ?vn—расходящийся.
121 ] § 12. ОСНОВНЫЕ ПОНЯТИЯ ИЗ ТЕОРИИ БЕСКОНЕЧНЫХ РЯДОВ 295
Сравнивая данный ряд с геометрической прогрессией, мы полу-
получим два основных признака сходимости рядов с положительными
членами.
121. Признаки Коши и Даламбера. 3. Признак Кош и. Если
общий член ряда с положительными членами A1)
начиная с некоторого значения п, удовлетворяет неравенству
где q не зависит от п, то ряд сходится.
Если же, наоборот, начиная с некоторого значения, имеем
1, A9)
то ряд A1) расходится.
Не ограничивая общности, можем допустить, что неравенства A8)
или A9) выполняются при всех значениях п (свойство III [119]). Если
выполнено A8), то
т. е. общий член данного ряда не превосходит соответствующего
члена бесконечной убывающей геометрической прогрессии, а потому,
в силу 2, ряд будет сходящимся. В случае же A9) имеем
и ряд A1), общий член которого не стремится к нулю (больше еди-
единицы), не может быть сходящимся (свойство IV [119]).
4. Признак Даламбера. Если отношение последующего
члена ряда к предыдущему ——, начиная с некоторого значения п,
ип~1
удовлетворяет неравенству
^-^q<l, B0)
где q не зависит от п, то ряд A1) сходится.
Если же, наоборот, начиная с некоторого значения п, имеем
«Я-1
B1)
то данный ряд расходится.
Допустив, как и раньше, что неравенства B0) или B1) выпол-
выполняются при всех значениях п в случае B0), мы имеем
296 ГЛ. IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ. [ 121
откуда, перемножая почленно и сокращая общие множители,
т. е. члены ряда меньше членов убывающей геометрической про-
прогрессии
и, в силу 2, ряд (И) сходится. В случае же B1)
т. е. члены ряда не убывают по мере удаления от начала, следо-
следовательно, ип не стремится к нулю при п—*оо, и ряд сходиться не
может (свойство IV [119]).
Следствие. Если при беспредельном возрастании п
Упп или -^- B2)
ип~1
стремится к конечному пределу г, то ряд
сходится при условии г<М и расходится при условии г^>1.
Пусть сперва г<О« Выберем число е настолько малым, чтобы
было также и
При больших значениях п величина ^ип или -^- будет отличаться
от своего предела г не больше, чем на е, т. е. мы, начиная с неко-
некоторого достаточно большого значения п, будем иметь
<1 B30
или
г-е<^<г + е<1. B3,)
Применяя признаки Коши или Даламбера при # = r-f-e<^U
в силу B30 или B3а), сразу заключаем о сходимости данного ряда.
Аналогичным образом доказывается и расходимость его при усло-
условии г^> 1 или если хоть одно из выражений B2) стремится к (-f-oo).
Примеры. 1. Ряд
1+ + Й
<24>
121 | § 12. ОСНОВНЫЕ ПОНЯТИЯ ИЗ ТЕОРИИ БЕСКОНЕЧНЫХ РЯДОВ 297
Применяя признак Даламбера
а потому данный ряд сходится при всех конечных значениях х (положи-
(положительных).
2. Ряд
!*• т
Здесь мы имеем
хп хп~1 ип п — 1
п п * п~1 п — 1' мл_х п '
а потому, по признаку Даламбера, данный ряд сходится при 0<л:<1 и
расходится при х > 1.
3. Ряд
со
2 rn sin2 па (г > 0). B6)
Применяя признак Коши, имеем
ип = г11 sin2 ла, лГщь '==-r i/^sin2 па ^ г,
а потому данный ряд сходится, если г < 1.
Признак Даламбера в данном случае не дает никакого результата, ибо
отношение
ип _ г Г sin /га |2
И/1-1 bsin (л— 1)а J
не стремится ни к какому пределу и даже не остается все время < 1
или ^ 1.
Вообще можно показать, что признак Коши сильнее признака Далам-
Даламбера, т. е. он может применяться во всех случаях, когда применяется при-
признак Даламбера, но сверх того и в некоторых других, когда последний не
может применяться. Но зато пользование им сложнее, чем признаком Далам-
Даламбера, в чем нетрудно убедиться хотя бы на первых двух из разобранных
выше примерах.
Заметим, далее, что бывают случаи, когда и признак Коши и признак
Даламбера применяться не могут; это случается, например, всякий раз, когда
т, е. когда г = 1. Мы имеем тогда дело с сомнительным случаем, когда
вопрос о сходимости или расходимости должен быть разрешен каким-либо
иным путем.
Так, например, для гармонического ряда
298 ГЛ. IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ I 122
который, как мы видели в [119], есть ряд, расходящийся, мы имеем
и, таким образом, вопрос о сходимости или расходимости гармонического
ряда не мог быть решен с помощью признаков Коши или Даламбера.
С другой стороны, дальше мы докажем, что ряд
есть ряд сходящийся.
Но для него мы имеем опять
т. е. опять-таки сомнительный случай, если применять признаки Коши или
Даламбера.
122. Интегральный признак сходимости Коши. Предположим,
что члены данного ряда
Щ + Щ-\-Щ+ ...+ия+... B7)
положительны и не возрастают, т. е.
И1^и^...^ия^ия+1^...>0. B8)
Изобразим члены ряда графически, откладывая по оси абсцисс
независимую переменную п, принимающую пока только целые значения,
а по оси ординат — соответствующие значения ип (рис. 155). Всегда
можно найти такую непрерывную функ-
функцию y=f(x), которая при целых значе-
значениях х = п принимает как раз значе-
значения ип; для этого достаточно провести
непрерывную кривую через все по-
построенные точки; будем при этом счи-
считать, что и функция y=f(x) не воз-
возрастающая.
1 8 3 ? 2 6 7 8 9* Л При таком графическом изображении
сумма п первых членов данного ряда
Рис. 155. , , , ,
представится как сумма площадей „выходящих" прямоугольников,
1) В предыдущих вычислениях существенно обратить внимание на то,
что если положить х = — , то х—*0 и —log — = xlogx-+0 [66]. Отсюда,
VT
логарифмируя выражение 1/ —, убеждаемся, что оно стремится к единице.
122 ] § 12. ОСНОВНЫЕ ПОНЯТИЯ ИЗ ТЕОРИИ БЕСКОНЕЧНЫХ РЯДОВ 29Э
которая заключает внутри себя площадь фигуры, ограниченной кри-
кривой y=f(x), осью ОХ и ординатами х=1, х = #-[-1, а потому
sn^ j f(x)dx. B9)
i
С другой стороны, та же фигура заключает внутри себя все
„входящие" прямоугольники, сумма площадей которых равна
Щ + иъ + Ч + • • • + ил+1 = sn+i — Wi, C0)
а потому
п Н-1
i /W^. C1)
Эти неравенства приводят нас к следующему признаку.
5. Интегральный признак Кош и. Ряд B7)
члены которого положительны и не возрастают при возраста-
возрастании п, сходится или собственно расходится, смотря по тому,
имеет ли интеграл
1= ^f(x)dx C2)
конечное значение или равен бесконечности.
Напомним при этом, что f(x) должна убывать при возрастании х.
Пусть сперва интеграл / имеет конечное значение, т. е. кривая
y=f(x) имеет конечную площадь [98]. Из положительности f(x)
вытекает
п -f- 1
а потому, в силу C1),
т. е. сумма sn остается ограниченной при всех значениях п, и на осно-
основании признака I [120] ряд B7) будет сходящимся.
Пусть теперь /=оо, т. е. интеграл
f(x)dx
при увеличении п может быть сделан больше любого заданного
наперед числа N. Тогда в силу B9) и сумма sn может быть сделана
больше Л/, т. е. ряд B7) будет собственно расходящимся.
300 ГЛ. IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ [122
Аналогичным путем можно показать, что остаток ряда B7) не
превосходит интеграла
00
]f{x)dx.
П
Замечание. При применении признака Коши в интегралеC2)
нижний предел, равный единице, можно заменить любым числом а,
большим единицы, так как интегралы с нижним пределом еди-
единица и а одновременно или сходятся или расходятся [98].
Примеры. 1. Гармонический ряд
Здесь мы имеем
а потому можно положить
тогда
|/ х W
и интеграл расходится, ибо \ogx-+-\-co при х-*-f оо; данный ряд, как мы
уже знаем, расходящийся.
2. Более общий ряд
00
? 9-
где р — любое число, большее нуля (при р ^ 0 ряд, очевидно, расходящийся).
Здесь мы имеем
1 . „ оо
logx
, если р = 1.
Отсюда ясно, что интеграл расходится, если р^\, и сходится и равен
г, если р > 1. Действительно, в последнем случае показатель 1 —р < О,
xl~P = р_1 —> 0 при х -* + оо, и, следовательно,
1-Я'
\-p~p-r
Следовательно, в силу признака Коши, ряд C3) будет сходящимся, если
р> 1, и расходящимся, если р^ 1.
123 ] § 12. ОСНОВНЫЕ ПОНЯТИЯ ИЗ ТЕОРИИ БЕСКОНЕЧНЫХ РЯДОВ 301
123. Знакопеременные ряды. Переходя к рядам с какими угодно
членами, мы рассмотрим прежде всего ряды знакопеременные, у кото-
которых члены попеременно положительны и отрицательны. Такие ряды
удобнее писать не так, как раньше, а в виде
причем числа
Щ, щ, и3> •-. > пп> ...,
считаются положительными *).
Относительно знакопеременных рядов можно доказать следующее
предложение:
Для того чтобы знакопеременный ряд сходился, достаточно,
чтобы абсолютные значения его членов убывали и стремились
к нулю при возрастании п. Остаток такого ряда по абсолют*
ному значению не превосходит абсолютного значения первого из
отброшенных членов.
Рассмотрим сперва суммы четного числа членов ряда
Так как по условию абсолютные значения членов ряда убывают
(лучше сказать, не возрастают) при возрастании л, то, вообще,
и и2л+1 —
а потому
т. е. переменная 52л — не убывающая. С другой стороны, мы имеем
Чп = «1 — («2 — %) — («4 — Ив) — • • • — (И2л-2 — ll'lnU) — Щ
так как все разности в скобках неотрицательны, т. е. переменная sin
остается ограниченной при всех значениях п. Отсюда следует, что,
при беспредельном возрастании п, 52л стремится к конечному пре-
пределу [30], который мы обозначим через s:
Далее, мы имеем
52л+1 = 52л-f"H2rt+i —¦ 5 при п —¦со,
так как по условию н2л+1 — 0.
1) Здесь мы считаем, что первый член ряда положительный; если он
отрицательный, то ряд запишется в виде — и1 + и2 — и8 + и4 — ...
302 ГЛ. IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ [ 124
Мы видим, таким образом, что как сумма четного,, так и сумма
нечетного числа членов ряда C4) стремится к одному и тому же
пределу s, т. е. ряд C4) сходящийся и имеет сумму 5.
Остается еще оценить остаток тп ряда. Мы имеем
причем одновременно надо брать верхние или нижние знаки. Иначе
откуда, рассуждая как и раньше, имеем
что и требовалось доказать.
Из формулы
Гя = ± К»я+1 — "
в квадратных скобках которой стоят неотрицательные количества,
следует, что знак гп совпадает с тем знаком, который надо брать
перед квадратной скобкой, т. е. совпадает со знаком ±ип+1. Итак,
при указанных в теореме условиях знак остатка знакоперемен-
знакопеременного ряда совпадает со знаком первого из отброшенных членов*
Пример. Ряд
1±±
есть знакопеременный ряд, абсолютные значения членов которого беспре-
беспредельно убывают при п—*оо, а потому он будет сходящимся. Мы увидим
в дальнейшем, что его сумма равна log 2. Однако для действительного вы-
вычисления log 2 этот ряд не годится, так как для того чтобы остаток его
был меньше 0,0001, нужно взять 10 000 его членов:
|гя|<—1-^^0,0001; п^ 10000.
Итак, ряд этот хотя и сходится, но сходится очень медленно; для того
чтобы иметь с такими рядами дело на практике, нужно предварительно пре-
преобразовать их из медленно сходящихся в быстро сходящиеся, или, как гово-
говорят, улучшить сходимость.
124. Абсолютно сходящиеся ряды. Из прочих рядов с какими
угодно членами мы остановимся лишь на рядах абсолютно сходящихся.
Ряд
»!+»! + »•+... + »!!+••• C5)
сходится, если сходится ряд, составленный из абсолютных значе*
ний членов данного ряда, т. е. ряд
|и1|+|я«Жив|+...+ |ия| + ... C6)
Такие ряды называются абсолютно сходящимися рядами.
124 ] § 12. ОСНОВНЫЕ ПОНЯТИЯ ИЗ ТЕОРИИ БЕСКОНЕЧНЫХ РЯДОВ 303
Итак, допустим, что ряд C6) сходится, и положим
*« = у(| tin I + ап), дал = у(| ия| — wj.
Оба числа т>я и wnf наверно, неотрицательны, так как очевидно
(ип, если ип^*0, ГО, если ип^0,
CO
V V
oo
V
С другой стороны, как г>я, так и г»я не превосходят \ип\, т. е.
общего члена сходящегося ряда C6), а потому, в силу признака 2
сходимости рядов с положительными членами [120], оба ряда
будут сходящимися.
Так как мы имеем
то будет сходиться и ряд
который получается вычитанием ряда 2 wn из РяДа 2
Сходящиеся ряды с положительными членами представляют ча-
частный случай абсолютно сходящихся рядов, признаки сходимости
которых получаются непосредственно из признаков сходимости рядов
с положительными членами.
Признаки сходимости 1—5, выведенные в [120, 121, 122] для
рядов с положительными членами, применяются и к рядам с ка-
какими угодно членами, если только условиться заменить везде ип
на | ип |. При этом условии останутся в силе и признака расхо-
расходимости 3 и 4 и следствие из них [121].
В частности, в формулировках признаков Коши и Даламбера
нужно заменить
}/~ип я —— на }/"| ип | I
Так, например, если -^- ^tf'O» т- е- прт^К^ т0
я-i I л-11
согласно признаку Даламбера [121], ряд с положительными членами
304 ГЛ. IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ [ 124
C6) сходится, а следовательно, ряд C5) сходится абсолютно. Если
же —— ^51, т. е. | ия | ^ | ия_11, то, при возрастании п, члены ип
не убывают по абсолютному значению, а потому не могут стремиться
к нулю, и ряд C5) расходится. Отсюда, как и в следствии [121],
—*г<М, то ряд C5) абсолютно сходится;
следует,
если же
что
«я
Л—1
если
\, то ряд C5) расходится.
Замечание. Заметим еще, что если члены некоторого ряда
C5) по абсолютному значению не больше некоторых положитель-
положительных чисел | ип | <; ап и ряд ах -f- a2 + • • • ~Ь ап Н~ • • • из &тих чисел
сходится, то ряд C6) и подавно сходится [120], т. е. ряд C5)
абсолютно сходится.
Примеры. 1. Ряд (пример [121])
00
2_
п=\
абсолютно сходится npji всех конечных значениях х как положительных, так
и отрицательных, ибо
===!iiJ._0
п
при всех конечных значениях х.
2. Ряд
у и
— п
абсолютно сходится при | х \ < 1 и расходится при I х \ > 1, так как
п—\ ,
х .
3. Ряд
1 sin па
я = 1
абсолютно сходится при |г|<1, ибо для него:
Необходимо заметить, что далеко не всякий сходящийся ряд есть вместе
с тем и абсолютно сходящийся, т. е. остается сходящимся, если каждый
член ряда заменить его абсолютным значением. Так, например, знакоперемен-
знакопеременный ряд
125 ] § 12. ОСНОВНЫЕ ПОНЯТИЯ ИЗ ТЕОРИИ БЕСКОНЕЧНЫХ РЯДОВ 303
как мы видели, — сходящийся; если же заменить каждый член его абсолют-
абсолютным значением, получим расходящийся гармонический ряд:
,,1,1,1,
1+ + + +
Абсолютно сходящиеся ряды обладают многими замечательными
свойствами, которые изложены в § 14. Так, например, только они
обладают свойством конечных сумм — независимостью суммы от по-
порядка слагаемых.
125. Общий признак сходимости. В заключение настоящего
параграфа упомянем о необходимом и достаточном условии сходимости
ряда
Сходимость эта по определению равносильна существованию предела
у последовательности
Sb % S3, ..., ?„...,
где sn — сумма п первых членов ряда. Но для существования этого
предела мы имеем следующее необходимое и достаточное условие
Коши [31]:
для любого заданного положительного е суще cm вует т акоеЫ, что
\*т — SJ<S
при всяких т и n^>N. Положим для определенности, что т^>п и
пусть т = п-{-р, где р — любое целое положительное число. Заметив,
что тогда
*т ~ sn = Sn+p — *п = («1 + Щ + ... + Un + И/i+l + • • • + 'W —
— (wi -f w2 + ... + un) — un+l -f- нЛ+2-}-... -f un+p,
мы можем высказать следующий общий признак сходимости ряда.
Для сходимости бесконечного ряда
«1 + «2 + Щ + • • • + Un + • • •
необходимо' и достаточно, чтобы для любого заданного положи-
положительного е существовало такое число N, что при всяком n^>N
и при всяком положительном р выполняется неравенство
I «/141 + Пп+Ъ + • • • + Ил+р К S>
т. е. сумма какого угодно числа последовательных членов ряда,
начиная с ип+ь остается по абсолютному значению меньше е,
коль скоро /z^>M
Необходимо заметить, что при зсей теоретической важности этого
общего признака сходимости ряда, применение его на практике обычно
затруднительно.
306 ГЛ. IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ [ 126
§ 13. ФОРМУЛА ТЕЙЛОРА И ЕЕ ПРИЛОЖЕНИЯ
126. Формула Тейлора. Рассмотрим многочлен п-й степени:
f(x) = а0 + ахх -f- а2лг2 +... + апхп;
придадим х приращение h и вычислим соответствующее значение
функции f(x-\-h). Это значение, очевидно, можно разложить по сте-
пеняхМ /г, раскрывая различные степени (х-\-Н) по формуле бинома
Ньютона и располагая окончательный результат по степеням /г. Коэф-
Коэффициенты при различных степенях h будут многочленами, зависящими
от х:
A)
Для этого мы изменим обозначения, написав в тождестве A) а
вместо х и вместо x-\-h просто х. Тогда окажется
h = x—а,
и, вместо A), мы получим
и нужно только определить многочлены:
iD ..., Ап(х).
-аГАп(а). B)
Для определения AQ(a) положим в этом тождестве х = а, что
даст
Для определения Ах(а) продифференцируем тождество B) по х
и затем положим х = а\
Дифференцируя еще один раз по х и полагая затем х = а, полу-
получим Л2(я)
126
§ 13. ФОРМУЛА ТЕЙЛОРА И ЕЕ ПРИЛОЖЕНИЯ
307
Продолжая эти операции, дифференцируя к раз и полагая затем
= а, мы получим
Итак, мы имеем
Л0(а)=/(а),
после чего формула B) примет вид
k\
fitl) (n\
•—sr (*-*?' C)
Эта формула верна только в том случае, когда f(x) есть много-
многочлен степени не выше п, и она дает разложение такого многочлена
по степеням разности (х — а).
Положим теперь, что f(x) — не многочлен, а какая-либо функция,
определенная внутри некоторого промежутка / и имеющая непрерыв-
непрерывные производные до порядка (п-\-1). Пусть значение х = а нахо-
находится внутри /. В дальнейшем считаем, что х принадлежит /.
Обозначим через Rn(x) разность между f(x) и правой частью
формулы C), т. е. положим
Дифференцируем последовательно это тождество:
/»(*)=/» (а)+
-а)+ ...+
D.)
Полагая в D) и последних тождествах х = а, получаем
E)
308 ГЛ. IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ | 126
Дифференцируя последнее из равенств Dt) еще один раз, найдем
Р? + Ъ(х)=/& + 1)(х). F)
Из соотношений E) и F) мы без труда получим выражение для
Rn (х), ибо по основной формуле интегрального исчисления
X
а
откуда, принимая во внимание E) и интегрируя по частям, выводим
последовательно
X X
Rn{x)= J Ra(t)dt = — J Rn(t)d{x-t) =
a a
x
= -#.@ C* - 01* +1 Rn(<)(* - t)dt=
= J
Для уяснения сделанных преобразований заметим следующее.
Переменная интегрирования обозначена буквой t, так что х под
знаком интеграла надо считать постоянным и дифференциал х рав-
равным нулю, и потому, например,
Лх-tf ^(x-tr *, л (х-if ,,
и, вообще,
Точно так же выражение
126 ] § 13. ФОРМУЛА ТЕЙЛОРА И ЕЕ ПРИЛОЖЕНИЯ 309
обращается в нуль, так как при подстановке ? = х обращается в нуль
множитель (х— t)nt а при подстановке t = a множитель /^)(а) = 0
в силу E).
Мы получаем таким путем следующее важное предложение:
Формула Тейлора. Всякая функция f(x), имеющая внутри
некоторого промежутка, содержащего точку х = а внутри себя,
непрерывные производные до (я-(-1)-го порядка включительно, при
всех значениях х внутри этого промежутка может быть раз-
разложена по степеням разности (х — а) в виде
G)
где Rn(x), остаточный член формулы, имеет вид
-t)n dt
Весьма часто в приложениях встречается другая форма остаточ-
остаточного члена, которая непосредственно получается из (8) при приме-
применении теоремы о среднем [95]. Под знаком интеграла в правой части
формулы (8) функция (х — t)n сохраняет знак, а потому по теореме
о среднем мы имеем
Подставляя верхний и нижний пределы, получим
п+\
Л + 1
так как при t = x написанное выражение обращается в нуль. Под-
Подставляя это в предыдущую формулу, будем иметь
Rn(x) = (x-ay»*fa$, (9)
где 6 есть некоторое среднее значение, лежащее между а и лг. Эта
форма остаточного члена называется остаточным членом в форме
Лагранжа, и формула Тейлора с остаточным членом Лагранжа
будет
между a и 4
x _
310 ГЛ. IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ [ 127
127. Различные виды формулы Тейлора. При п = 0 мы полу-
получаем кз G^ выведенную раньше [63] формулу конечных прираще-
приращений Лагранжа;
формула Тейлора является, таким образом, непосредственным обоб-
обобщением формулы конечных приращений.
Переходя к прежним обозначениям и написав х вместо а и
x-\-h вместо х, перепишем формулу Тейлора G) в виде
так как при новых обозначениях (х — а) надо заменить на /г. Зна-
Значение Е, лежащее при прежних обозначениях между а и х, будет
лежать между х и (x-\-h)t и его можно обозначить через (х-{-Щу
где 0<^6<^1. В силу (9) остаточный член формулы A0) можно,
таким образом, написать в виде:
Левая часть формулы A0) есть приращение А^ функции y=f(x)>
соответствующее приращению или, что то же, дифференциалу /г
независимой переменной. Вспомнив выражения для дифференциалов
высших порядков [56], мы имеем
dy =y'dx =f (х) h, d*y = у" (dxf =/" (х) h\ ...,
dny=y{n) (dx)n=f{n)(x)hn,
откуда
dn+1y
причем символ -, , •:>.
обозначает результат подстановки в вы-
выражение ¦ , i ТчГ вместо х суммы лг—{— 0Л.
В этом виде формула Тейлора особенно интересна тогда, когда
приращение h независимой переменной есть величина бесконечно
малая. Формула A2) дает тогда возможность выделить из прираще-
приращения функции Ду бесконечно малые слагаемые различных порядков
относительно h.
В частном случае, когда исходное значение а независимой пере-
переменной есть нуль, формула Тейлора G) принимает вид
^f^ ^ x), A3)
128 J § 13. ФОРМУЛА ТЕЙЛОРА И ЕЕ ПРИЛОЖЕНИЯ 311
где
и % лежащее между 0 и лг, можно обозначить Qx, где 0, зависящее
от ху удовлетворяет неравенству О<^0<^Ь Формула A3) называется
формулой Маклорена,
128. Ряды Тейлора и Маклорена. Если f(x) имеет при х = а
и х близких к а производные всех порядков, то мы можем написать
формулу Тейлора при любом значении п. Перепишем формулу Тей-
Тейлора в виде:
где
т. е. Sn+\(x) есть сумма первых (п-\-\) членов бесконечного ряда
Если при некотором значении х и беспредельном возрастании я
lim #„(*) = 0, A5)
Й-+ОО
то, в силу сказанного в [118], указанный выше бесконечный ряд
сходится при указанном значении х и его сумма равна f{x). Таким
образом, получается разложение функции f(x) в бесконечный сте-
степенной ряд Тейлора:
-a)?$+ ... +(*-в)"?^Ц-... A6)
по степеням разности (х — а).
В дальнейшем мы всегда будем иметь дело с тем случаем, когда
условие A5) имеет место не для отдельного значения дг, а для всех х
из некоторого промежутка.
Таким же образом формула Маклорена дает нам при соблюдении
условия A5) разложение f(x) в ряд Маклорена
A7)
Оценка Rn(x) имеет важное значение для приближенного вычисления
значений функции f(x) при помощи разложения ее в степенной ряд.
Применим предыдущие соображения к разложению и приближен-
приближенному вычислению простейших функций.
312 ГЛ. IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ | 129
129. Разложение ех. Прежде всего мы имеем
f(x) = e\ f'(x) = e\ ...,W
а потому
и формула Маклорена с остаточным членом A4) дает
Мы видели (пример [121]), что ряд
оо
я=0
есть абсолютно сходящийся при всех конечных значениях х, а по-
потому при всяком х имеем
Д-Я+1.
____() При n-OQ,
так как это выражение есть общий член сходящегося ряда1).
С другой стороны, множитель е^х в выражении остаточного члена,
наверно, не превосходит ех при х^>0 и единицы при дг<^0, а по-
потому остаточный член стремится к нулю при всех значениях х, и
мы получим разложение
которое имеет место при всех значениях х.
В частности, при х=\ получаем выражение для е, весьма удоб-
удобное для вычисления е с любой степенью точности
Пользуясь этой формулой, вычислим число е с шестью десятичными
знаками. Если мы приближенно положим
См. также пример в [34].
129 1
§ 13. ФОРМУЛА ТЕЙЛОРА И ЕЕ ПРИЛОЖЕНИЯ
313
причем знак (<) поставлен потому, что в знаменателе дробей множители
(П _(_ 2), (п + 3), (п + 4), ...заменены меньшим числом (л+1), отчего все
дроби увеличились.
Можно поэтому указать следующие пределы, между которыми заклю-
заключается число е:
Если желаем получить для е приближенное значение, отличающееся от
истинного не более, чем на 0,000 001, положим я =10; тогда
+
'" + 101'
и ошибка не превзойдет ТлТТл<3« Ю~8. В этой формуле первые два ела-
гаемых вычисляются точно; остальные восемь слагаемых нужно вычислить
с семью знаками, так как при этом ошибка каждого слагаемого не больше
0,5 единицы седьмого знака, т. е. 0,5-10~7, а вся ошибка не больше
10~7.0,5-8 = 4.10,
т. е. четырех единиц седьмого знака, а потому общая ошибка по абсолют-
абсолютному значению не будет превышать 4,3 • 10~7. Мы имеем
1
2!s
1
31"
1
4!""
1
51 ~
1
6!""
1
71""
1
81~
1
9!~
1 _
2 = 2,000000
= у = 0,500 000
ГЗ '
= J- = 0,041 666
314
* =0,008 333
415
S^L = 0,001 388
:-i= = 0,000 198
6!7
= 4о = 0,000 024
s-gjg = 0,000 002
1
= ——=0,000 000
0
0
7
7
3
9
4
8
8
3
(точно)
(по избытку)
(по недостатку)
(по избытку)
(по недостатку)
(по избытку)
<?*« 2,7182818.
Значение е с 12 знаками есть 2,718 281828 459.
314 ГЛ. IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ [ 130
130. Разложение sin# и cos*. Мы имеем [53]:
/(*)=sin*, /'(*)= sin (* + -j), ..., /<*>(*) = sin
откуда
= 0, f@)=l, Г@) = 0,/w@) = -l, ...,
после чего формула A3) дает
smx—U 3!~Г*5!~ ••* "
— \)пх2п+1
\)пх
В остаточном члене множитель
как мы видели выше,
то—г~отг,
стремится к нулю при п —> оо, а абсолютное значение синуса не
превышает единицы, и, следовательно, остаточный член стремится
к нулю при всех конечных значениях х, т. е. разложение
имеет место при всех значениях х.
Аналогичным образом мы можем доказать, что разложение
?
B0)
имеет место при всех значениях х.
Ряды A9) и B0) весьма удобны для вычисления значений функций
sin х и cos # при малых значениях угла х. При всех значениях х,
как положительных, так и отри-
отрицательных, они знакопеременные,
так что если мы взяли такое число
членов, что дальнейшие идут убы-
убывая, то ошибка по абсолютному
значению не превосходит первого
0,5 1>0 1,5 2,0 ^2,5 3,0щ 3,5 * из отброшенных членов [123].
При больших значениях х
Рис. 156. ряды A9) и B0) также сходятся,
но медленно, и для вычисления
неудобны. На рис. 156 показано взаимное расположение точной кри-
кривой sin х и первых трех приближений:
хъ
_
Х
131 ] I 13. ФОРМУЛА ТЕЙЛОРА И ЕЕ ПРИЛОЖЕНИЙ 315
Чем больше членов взято в приближенной формуле, тем в боль-
большем промежутке приближенная кривая близка к точной. Заметим,
что во всех написанных формулах угол х выражается в дуговой
мере, т. е. в радианах [33].
Пример. Вычислить sin 10° с точностью до 10~8. Прежде всего пере-
переводим градусную меру в дуговую
Остановившись на приближенной формуле
. тс тс 1 / тс
мы делаем ошибку, не превосходящую
^ < 4. 10- (^
В правой части предыдущей формулы sin y^ надлежит вычислять каж-
каждое слагаемое с шестью знаками, так как тогда полная ошибка будет не
больше
2 • 0,5 - 10~6 + 4 . Ю-6 = 5 • 10~в.
С указанной точностью мы имеем
~ = 0,174 533, ~( -V = 0,000 886, sin ~ = 0,173 647,
1 о О \ 1 о / 1 о
причем за первые четыре знака можно ручаться.
131. Бином Ньютона. Здесь мы имеем, считая х^>—1, т. е.
Л-х)т~\
)...(m—
где т — любое вещественное число, так что формула A3) дает нам:
где остаточный член может быть определен по формуле (8) при
0
Принимая во внимание, что в данном случае
> = т(т — 1)... (т — п) A + ff-n~\
316 ГЛ. IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ I 131
можем написать
m(OT1i(W") { B2)
Применяя к интегралу теорему о среднем A3) из [95] и обозначая
через 6х, где 0<в<1> значение t, лежащее между 0 и х и вхо-
входящее в упомянутую теорему о среднем, получим
Rn{х) = т(т-\)„.(т-п) {х_
B3)
Если /?л->0, то ряд
< , m . m(m—1) о , . m(m —1) ...(/м — л
1+урН -i~-*2+ + — ^—|^
ур2i|^ Х-2ДГЯ+... B4)
должен быть сходящимся [118]. Мы имеем
\и
п+1
X
\х\ при л->оо,
а потому ряд сходится (абсолютно) при | х \ < 1 и расходится при
|х|>1 [124]. Хотя ряд B4) и сходится при |х|<1, однако еще
неясно, что при этом его сумма равна (l+-^)m> и приходится еще
доказывать, что Rn(x)->~0 при |дг|<1. Множитель
х
п\
в выражении B3) для Rn(x) будет общим членом сходящегося
ряда B4), в котором т заменено на (/гг — 1), а потому [118] стре-
стремится к нулю при я->оо.
Множитель L ~ ¦] не превосходит единицы при всех значе-
значениях п. В самом деле, в рассматриваемом случае — 1<лг<+1»
а потому как при положительных, так и при отрицательных значе-
значениях х будет 0 < 1 < б < 1 +Ьх, откуда
Последний множитель тх(\ +0х)т~1 также остается ограничен-
ограниченным, так как число A -\-tix) лежит между 1 и 1 -\-ху и тх{\ -\-Ьх)т~х
лежит между пределами тх и tnxj\ -\-x)m~\ не зависящими от п.
|31 ] § 13. ФОРМУЛА ТЕЙЛОРА И ЕЕ ПРИЛОЖЕНИЯ 317
Из сказанного ясно, что Rn(x) по формуле B3) представляется
в виде произведения трех множителей, из которых один стремится
к нулю, а два других остаются ограниченными при беспредельном
возрастании п, а потому и
Rn(x)—>0 при П—+ОО.
Итак, разложение
имеет место при всех значениях х, удовлетворяющих условию
Когда показатель т есть число целое и положительное, то ряд B5)
заканчивается на члене п = т и превращается в элементарную фор-
формулу бинома Ньютона. В общем же случае разложение B5) дает
обобщение бинома Ньютона для какого угодно показателя т.
Полезно отметить особо некоторые частные случаи бинома:
TJ_==l+x + ^+.x3+...+*"+..., B6)
X 1 -\-х = 1 -\--^х — YT4X ' 2.4.6х ~~ 2.4-6.8Х г--"
|/'Г+Т~ 2Х» 2.4^ 2.4.6Х "т" 2-4-б-8Х ~ •••
Заметим, что функция A-\-х)т при всяких л:]>—1 имеет поло-
положительные значения [19,44], т. е. сумма ряда B4) при —1<^х<^-\- 1
положительна. В частности, например, ряд B7) дает в этом проме-
промежутке положительное значение
Примеры. 1. Извлечение корней. Формула B5) особенно удобна для
извлечения корней с любой степенью точности. Пусть нужно извлтечь корень
тя-й степени из целого числа А. Всегда можно подобрать целое число а
так, чтобы m-я степень а была, по возможности, ближе к Д так что, поло-
положив Л = ат4-Ь, причем \Ъ\<. ат, мы имели бы
Так как здесь
ат
< 1, то обозначив отношение — через дг, мы можем
ат
вычислить 1/ 1 -f- — по формуле бинома Ньютона, причем ряд будет схо-
сходиться тем лучше, чем меньше абсолютное значение рассматриваемого
отношения.
318 ГЛ. IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ [ 131
Вычислим, например, |/1000 с точностью до 10~5, Мы имеем
L 5 128 5 10 V128J 5 10 15^128] "Т
Остановимся на написанных членах и оценим ошибку, подставляя в фор-
формулу B3)
1 о 3
Множитель h | , как было указано, заключается между нулем и
единицей. Множитель A + §х)т~1 будет
3 \-«/e /125\Ve /6\Ve
ибо
1б/1Г 6^ ?
V 5 < 5 < 3'
Окончательно из формулы B3) получим
Вычисление оставшихся членов нужно вести с шестью знаками, так как
тогда полная ошибка не превзойдет
4 • 3 • 0,5 • 10~в + 5 • 10 == 6,5 • 10 < Ю-6.
Вычисление можно расположить следующим образом:
1
5
1
5
4
"То"
1 = 0,2
А = 0,08
^ = 0,048
X
X
X
А = 0,023 4375 X
ь|§J= 0,000 549 X
а!)= 0,000 013 X
0,2 = 0,004 687
0,08 = 0,000 044
0,048 = 0,000 001
0,004 732
_ 0,004 732 = 0,995 268
4
3,981 072
2. Приближенное вычисление длины эллипса. В [103] было полученс
следующее выражение для длины / эллипса с полуосями а и Ь\
те/, те/2
/ = 4 С Ya2sin2t + b4o^Tdt = 4а f I/ sin2t + ~ cos21 dt
0 и
|31 ] § 13. ФОРМУЛА ТЕЙЛОРА И ЕЕ ПРИЛОЖЕНИЯ 319
[формула B2)]. Вводя в рассмотрение эксцентриситет е эллипса
получаем:
«/я
/ = 4а \ / 1 — г2 cos2 tdt? B9)
К
Интеграл этот точно вычислить нельзя, но его можно вычислить с какой
угодно степенью точности, разложив 1) подынтегральную функцию в ряд по
степеням е:
1 2 \ 2
2cos2HY
~ecosH— Y 2
1 .2-3 .,...—
= 1 о- e2 cos21 д е4 cos4 ? —у^ ee cos61 -f- /?3,
причем ошибка /?3, если ее оценить по формуле B3) при п = 3, удовлетворяет
неравенству
L I А А
2' ..___. Л 1-е V»A_A.___.J4-5-l
b2.3 ^y
'' C0)
так как
Подставив это выражение в B9) для /, интегрируя и вспомнив фор-
формулы B7) [100], находим
те/а те/2 те/2 я/а
f \ t — jQt«[ cosU dt + ^
«/2 те/а те/2 те/2
= 4йГ V ^ — — е2 f cos2 tdt — -g&i \ cos* tdt — jQt«[
x) Разложение это, наверно, возможно, так как для эллипса е<1, и по-
потому слагаемое —e2cos2*, которое играет здесь роль х в формуле бинома
«ьютона, по абсолютному значению меньше единицы.
320 ГЛ. IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ [ 131
где, в силу формулы A0х) [95] и неравенства C0),
KU „..,„, 175 ** ^ 0,05е*
Формула C1) сама по себе удобна для вычисления длины эллипса, осо-
особенно для малых эксцентриситетов. Основываясь на ней, можно указать
простое геометрическое построение приближенного выражения для длины
эллипса, при котором нужно иметь дело только с окружностями.
Обозначим через lt и /2, соответственно, среднее арифметическое и сред-
среднее геометрическое полуосей эллипса:
и сравним длину / эллипса с длинами 2nlu 2nl2 двух окружностей радиу-
радиусов /t и /2.
Замечая, что
и разлагая в ряды по формуле бинома Ньютона, получим без труда следую-
следующие выражения:
2ic/, = 2ш [1 -1 е2 -1 «* -1 е« + Pl], C2)
причем ошибки рх и р2> если их оценить по формуле B3), удовлетворяют
неравенствам:
5 е8 77 б8
lpil<32 утТг' lp8l<5l2(i_s2)'/4-
Отсюда ясно, что при малом эксцентриситете, когда можно пренебречь
высшими степенями е по сравнению с е2# можно принять за длину эллипса
длину любой из двух окружностей, радиусы которых равны среднему
арифметическому или среднему геометрическому полуосей. Если желательна
большая точность, составим выражение
а . 2nlt + p • 2тс/8, C4)
подобрав множители аир так, чтобы по возможности большее число членов
в выражениях C1) и C4) совпадали между собой. Так как первые два члена
каждого из выражений C1), C2) и C3) совпадают, то, прежде всего, должно
быть
« + Р —1.
Приравнивая, далее, между собой коэффициенты при е4 в выражениях C1)
и C4), получаем
та+1-н или
Решая полученные два уравнения относительно аир, находим
3 1
132 1 § 13. ФОРМУЛА ТЕЙЛОРА И ЕЕ ПРИЛОЖЕНИЯ 321
Подставив это в C4), имеем
а-2*/, +р-2*/, = 2* (|-/,—i-/,)^
1^ C5>
т. е. оказывается, что совпадают члены не только с е4, но и с е°, и расхо-
расхождение формул C1) и C5) начинается только с членов с е8. Приняв во вни-
внимание найденные выше оценки для р, pt и р2 и заметив, что
11 1175, 5 3 77 1
и < + +
ножем окончательно сказать: с ошибкой, не превосходящей -. g-, за дли."
ну эллипса с полуосями а,Ь и эксцентриситетом г можно принять длину
окружности радиуса г, причем
3 а + Ь 1 лГ-т
132. Разложение log A +л:)«1) Это разложение можно получить
из общей теории, но мы применим другой способ, который с успе-
успехом употребляется и во многих других случаях.
Выразим log(l-f-jc) в виде определенного интеграла. Мы имеем,
очевидно, при х^>—1:
х
- = log A -4-1)\ = log A -4- x) — log 1 = log A
то есть
Но имеет место тождество
которое непосредственно получается, если делить единицу на 1 —|— ^
и остановиться на остатке (—l)ntn. Таким образом,
1О?(
J) Функция log л: не может быть разложена в ряд по степеням х, так
как при лг = О она сама и ее производные терпят разрыв непрерывности
и обращаются в бесконечность.
322 ГЛ. IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ I 132
где
х
Rn (х) — (— 1)я \ fqrj • C6)
Ряд
X ""т"з" *'• • п г»*»»
для которого
\п I И — lit ||
наверно расходящийся при |.г |> 1 (следствие [121]), а потому нужно
рассматривать только случай |дг|<^1, х = ±\. При этом случай
х = —1 также должен быть отброшен, ибо при х = — 1 функция
log(l-j-Ar) обращается в бесконечность.
Итак, остаются случаи: 1) |jc|<^1 и 2) х=\. В случае 1), при-
применяя к выражению C6) для Rn(x) теорему о среднем [96] и при-
принимая во внимание, что Vх не меняет знака при изменении t от О
до х, имеем
откуда, в силу условия |#|<^1, следует
1 1
\Rn(*)\<
п+\ 1+блг*
Множитель ¦ t , fl— в правой части предыдущего неравенства
остается ограниченным при всех значениях п, так как заключается
между пределами 1 и у-г-—, не зависящими от я, а потому при рас-
1 -|- X
| X
сматриваемых значениях х
-»0 при я—>оо.
Тот же результат мы получим и в случае 2), когда х=1. Та же
формула C7) при х=1 показывает
\Rfl (*I =я д. 1 lXfl^nJ-1»
т. е. опять
/?ЛA) —*0 при я—»оо.
132 I § 13. ФОРМУЛА ТЕЙЛОРА И ЕЕ ПРИЛОЖЕНИЯ 323
Итак, разложение
? ? fcd?? ... C8)
имеет место при всех значениях х, удовлетворяющих неравенствам
—1<*<+1. C9)
В частности, при х=\ имеем равенство
о котором уже было упомянуто выше [123]. Формула C8) непосред-
непосредственно для вычисления логарифмов не годится, так как в ней пред-
предполагается, что х удовлетворяет неравенствам C9) и, кроме того,
ряд в правой части ее сходится недостаточно быстро. Ее можно пре-
преобразовать в более удобный для вычислений вид. Для этого подста-
подставим в равенство
(—х) вместо х, что дает
log(l-x) = -x-
и вычтем почленно. Мы получим
Положив здесь
мы имеем
1ов-г-*_2Г г | * . z8 . 1 г* . 1
или
Эта формула годится уже при всех положительных значениях а
и z, так как при этом лг = 2 ^_ заключается между нулем и еди-
единицей. Она тем более удобна для вычисления, чем меньше дробь
г
2^ , -, или, что то же, чем меньше z по сравнению с а.
324 гл. w. ряды и их приложения к приближенным вычислениям [ 132
Формула D1) весьма полезна для вычисления логарифмов. Хотя факти-
фактически таблица логарифмов была вычислена не с помощью рядов, которые
во время Непера и Бригга были еще неизвестны, все же формула D1)
может с успехом применяться для проверки и для быстрого вычисления
таблицы логарифмов. Положим в D1J = 1 и возьмем последовательно
а = 15, 24, 80, мы получим
где ряды, обозначенные через Р, Qf /?, сходятся весьма быстро. Эти равен-
равенства дают нам уравнения
41og2— Iog3 — log5 = 2P,
— 31og2 —
_41og2 + 41og3 —
для определения чисел log 2, log 3, log 5, решая которые, найдем без труда
log2=14P+10Q + 6R,
log3 = 22P+16Q+10/?,
log 5 = 32P -f 24Q + UR.
Полученные таким путем логарифмы будут натуральными; с их помощью
мы находим модуль М десятичной системы логарифмов:
М== кГТО = °>4342944819 •••»
зная который, можем от натуральных логарифмов переходить к десятичным
по формуле
log10 х = М log х.
Аналогичным путем, пользуясь разложениями на множители
а = 2 400= 100-23-3, a + z— 2 401 = 74,
а= 9 800= 100.2- 72, a + z= 9 801 =34. И2,
а = 123 200 = 100 .24. 7.11, а + г == 123 201 == 3е. 132,
с= 2 600= 100-2 -13, а + ^= 2 601 =32.172,
с= 28 899 = 32.132-19, й + ^= 28 900= 100 • 172,
мы вычислим log 7, log 11, log 13, ...
Определив логарифмы простых чисел, мы уже без помощи рядов,
а только одними сложениями и умножениями на целые множители опреде-
определим и логарифмы составных чисел, которые, как известно, всегда можно
разложить на простые множители.
133 ] § 13. ФОРМУЛА ТЕЙЛОРА И ЕЕ ПРИЛОЖЕНИЯ 325
133. Разложение arc tgje. Здесь мы будем поступать так же,
как и при разложении log(l-)-jc). Мы имеем
Получаем, интегрируя,
X
Yjrj* = arc tg t = arc tg # — arc tg 0 = arc tg лг,
где arctg.r, как и в примере из [98], имеет главное значение. Мы
имеем, следовательно,
X X
гхсщх =
V3 v-5 / \\П-1у2П~1
у ^ L I \ l ) л 1 Г) (\г}
3 ' 5 2л — I ' п \ *
где
X
Rn(x) = (—l)n f щ^-. D2)
о
Ряд
Х^\Х*_ | (— \)п~1Х*п~1 |
для которого отношение
lift Z/Z "~~" О а о
й^г =аггт^-^ при л-*°°
наверно, расходится при л:2]>1; нам поэтому достаточно ограни-
ограничиться случаем лг2^ 1, т. е.
-Ю< + 1, D3)
Считая сначала 0<[лг^1, из формулы D2), в силу VII [95], по-
получим:
так как, очевидно,
Если х<^0, то, вводя вместо t новую переменную, t = — т,
получим
— X
'"" dx.
326 ГЛ. IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ [ 133
Здесь верхний предел (—х) уже положителен, а потому опять
имеет место указанная выше оценка для \Rn{x)\t т. е. разложение
+'- D4>
имеет место #/ш ясгл; значениях х, не превосходящих единицу по
абсолютному значению,
В частности, при х = \ получаем
arctgl =_ = 1__ + ^ —...
Ряд этот, ввиду весьма медленной сходимости, непригоден для вычис-
вычисления числа я. Ряд D4) сходится тем быстрее, чем меньше л*. Положим,
например,
XS=T И ^=агс18"*
Мы имеем
1 А
5 5 ¦ а 6 120
tg4 =
l~~25 X 144
Так как tg 4cp мало отличается от единицы, то угол 4<р мало отличается
от—. Введем эту малую разность
Отсюда выводим
120
l
что дает
Оба ряда в скобках — знакопеременные [123], а потому, ограничившись
в каждом из них лишь написанными членами, мы сделаем ошибку, не пре-
превосходящую
Желая получить п с точностью до 10~6, мы будем вычислять отдельные
члены с семью знаками, так как тогда ошибка при определении -j- не пре-
превзойдет
4 . 4 • 0,5 . Ю-7 + 0,5 • 10~7 + 0,5.10~e < 2 . 10%
а ошибка при определении я не превзойдет 8»10~%
134 J § 13. ФОРМУЛА ТЕЙЛОРА И ЕЕ ПРИЛОЖЕНИЯ
Вычисление будем производить по следующей схеме:
327
4-= 0,200 000 О
= 0,000 064 0
+ 0,200 064 0
1
3-58
= 0,002 666 7
_i—- = 0,000 001 8
/ • о
— 0,002 668 5
0,197 395 5
X 4
1 0,789 582 О
-239 = —0ДО4 184 1
0,785 397 9
X 4
Значение числа п с восьмью знаками есть 3,141 591 65.
Можно получить при | х | ^ 1 разложение
х
1 л:8 . 1 • 3 х
1 -3-5 ... B/г — 1) х2п+1
'2.4-6... 2/г ЪГТЛ
D5)
134. Приближенные формулы. Ряд Маклорена, в случае его
сходимости, дает возможность приближенно вычислять функцию /(лг),
заменяя ее конечным числом членов разложения:
Чем меньше лг, тем меньше членов можно брать в этом разло-
разложении для вычисления /(лг) с желаемой точностью. Если х весьма
мало, то достаточно ограничиться только первыми двумя членами,
отбросив все остальные. Таким образом получается весьма простая
приближенная формула для f(x), которая при малых х вполне
может заменить часто весьма сложное точное выражение для f{x).
Приведем такие приближенные формулы для наиболее важных
функций:
COS ЛГ ^^ 1 — -
ах ?*& 1 -\-x\oga,
log (\-\-х) *& х.
Пользуясь этими приближенными формулами при лг, близких
к нулю (положительных или отрицательных), можно значительно
упрощать сложные выражения.
328 ГЛ. IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ [ 135
Примеры.
1.
п — т
п п
1 1
3. Определить увеличение объема тела при нагревании (объемное рас-
расширение), когда известен коэффициент линейного расширения а. Если один
из линейных размеров тела при 0е есть /0, то при нагревании до t° он будет
а, коэффициент расширения, для большинства тел — весьма малая величина
(< 10~5). Так как объемы относятся, как кубы линейных размеров, можем
писать
* 0+«')'. v = V0(\+at
Vo 1
т. е. число За дает нам коэффициент объемного расширения. Для плотно-
плотности р, которая обратно пропорциональна объему, найдем аналогичную зави-
зависимость:
? A+
Понятно, что все эти приближенные формулы годятся только при доста-
достаточно малых х, в противном же случае они оказываются уже неточными, и
необходимо привлекать к рассмотрению дальнейшие члены разложения.
135. Максимумы, минимумы и точки перегиба. Формула Тей-
Тейлора позволяет сделать существенное дополнение к правилу нахо-
нахождения максимума и минимума функций, изложенному в [58]. В даль-
дальнейшем мы считаем, что f(x) имеет непрерывные производные до
порядка п в точке х=х0 и ее окрестности.
Если при х = х0 обращаются в нуль (п—1) первых производ-
производных функции f(x):
причем п-я производная /(/I)(-^o) отлична от нуля, значение х9
соответствует вершине кривой, если п, т. е, порядок первой не
обращающейся в нуль производной, есть число четное, и притом:
максимум, если /(л) (лг0) < 0,
минимум, если
если же п есть число нечетное, то значение х$ соответствует
не вершине, а точке перегиба*
135 ) § 13. ФОРМУЛА ТЕЙЛОРА И ЕЕ ПРИЛОЖЕНИЯ 329
Для доказательства нужно рассмотреть разности
где h — достаточно малое положительное число. По самому опреде-
определению максимума и минимума [58] в точке х0 будет максимум, если
обе эти разности меньше нуля, минимум, если обе они больше
нуля. Если же эти разности при сколь угодно малых положитель-
положительных h будут разных знаков, то при лг0 не будет ни максимума, ни
минимума. Разности же эти могут быть вычислены по формуле Тей-
Тейлора, если подставить туда лг0 вместо а и it h вместо *) h:
f(x.-h) =
По условию:
Г(Хъ)=Г (jco) = ...=/('i-1)(^o) = O, /(л) (*о) Ф 0;
значит,
%W 0 + Щ
При достаточно малом положительном h множители /(л) (х0 -f- Щ
и f{n) (х0 — byh), в силу предполагаемой непрерывности /{п) (х)} имеют
одинаковый знак, а именно знак числа /(л) (лг0), отличного от нуля.
Мы видели, что точка дг0 может быть вершиной тогда и только
тогда, когда обе разности f(xo±h)—/(х0) одинакового знака, и в
силу сказанного сейчас это может случиться только, если п число
четное, ибо только тогда выражения f(x,±h)—/(х0) будут иметь
одинаковые знаки; в противном же случае, когда п нечетное, множи-
множители hn и (—\)nhn будут разных знаков, и исследуемые разности
также будут разных знаков.
') Остаточный член мы берем в форме Лагранжа; число 0, лежащее
между нулем и единицей, при \-\-h) и (—h) не одно и то же, почему мы
написали 0Х во второй формуле.
830 ГЛ. IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ I 136
Допустим теперь, что п четное; тогда общий знак разностей
( rt h) —/(лг0) совпадает со знаком /(л) (х0). Если /(п) (хо)<^ 0,
то f(xo±h)—f(x0)<^0, и мы имеем максимум; если же /(w) (xQ)^>0,
то f(xQ±h)—/(хо)^>О, и получаем минимум.
Если же п — число нечетное, то, во всяком случае, я^З, для
второй производной f"(x) мы получаем из формулы Тейлора выра-
выражение:
г {х,-к>=
откуда, рассуждая таким же образом, как и раньше, убеждаемся, что
ввиду нечетности (п — 2) функция /* (jc), обращаясь в нуль при
х = х0, меняет знак, т. е. значение х^ соответствует точке пере-
перегиба [71], что и требовалось доказать.
136. Раскрытие неопределенностей. Пусть имеем отношение
функций
которые при х = а обращаются в нуль. Для раскрытия неопреде-
неопределенного выражения
9(х)\
при ср(а) = ф(а) = О разлагаем числитель и знаменатель по формуле
Тейлора:
2i -!-••• "Г
+¦
(«+1I
и, по сокращении рассматриваемого отношения на некоторую сте-
степень (лг — а), полагаем х = а.
136 ] § 13. ФОРМУЛА ТЕЙЛОРА И ЕВ ПРИЛОЖЕНИЯ 331
Примеры.
1-cos 2л: .. V 2 + 24 + '") _
1. hm
...)-1-3*
97 — "о" •
^1
Тот же прием приносит пользу и при раскрытии неопределенностей
других видов. Рассмотрим один пример.
2. Hm О^л:8— 5л:2+ 1 — х).
.v-»oo
Здесь мы имеем неопределенность вида (оо—со). Мы имеем
При достаточно больших, по абсолютному значению, х разность /- 5 j
близка к нулю, и мы можем применить формулу бинома Ньютона B5) при
*и = -о-, заменяя х на —(-- — — ]
МТ/3 1 Ч5 М , зз у/5 и»
Подставляя это в фигурную скобку и сокращая единицы, полечим
где все невыписанные члены содержат только отрицательные степени лг, т. е.
в пределе при лг->оо обращаются в нуль, и, следовательно,
lim
Возможность предельных переходов в бесконечных рядах, которые мы
применяем в настоящем номере, легко может быть оправдана, на чем мы не
останавливаемся.
332 ГЛ. IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ [ 137
§ 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
ИЗ ТЕОРИИ РЯДОВ
137. Свойства абсолютно сходящихся рядов. Понятие об абсолютно
сходящемся ряде было дано в [124]. Теперь мы установим важнейшие его
свойства.
Сумма абсолютно сходящегося ряда не зависит от порядка сла-
слагаемых.
Докажем это предложение сперва для рядов с неотрицательными чле-
членами, которые, как мы знаем [120], могут быть только или сходящимися
(а потому и абсолютно сходящимися), или собственно расходящимися.
Итак, пусть дан сходящийся ряд с положительными (неотрицательными)
членами
. A)
Обозначим через sn сумму его п первых членов, через s—его сумму.
Мы имеем, очевидно,
Переставив члены ряда A) каким угодно образом, мы получим другое рас-
распределение членов, которому будет соответствовать ряд
Vl + vt + v9+ ... +vn+ ..., B)
состоящий из тех же членов, что и A), но в другом порядке, так что каж-
каждый член из ряда A) имеет определенный номер в ряде B), и наоборот.
Обозначим через ап сумму п первых членов ряда B). При любом значении п
можно найти настолько большое число т, чтобы все члены, входящие в сумму
сл, вошли в smi а потому
°п ^ *т < з.
Таким образом, показано существование, постоянного числа s, не зави-
зависящего от я, такого, что при всех значениях п имеем
откуда [120] вытекает сходимость ряда B). Обозначим через а его сумму.
Очевидно, что
о rss lim Qn ^ s-
/I-»-00
Переставив в предыдущих рассуждениях ряды A) и B), мы таким же путем
покажем, что
и из неравенств а ^ s, s ^ а вытекает
sea.
Обратимся теперь к рядам с какими угодно членами. Так как по усло-
условию ряд A) абсолютно сходящийся, то ряд с положительными членами
00
l«il + l«i|+ .» +l»nl+ -.- S 1«»1 C)
сходится и по доказанному сумма его s* не зависит от порядка слагаемых.
С другой стороны, оба ряда
оо оо
2
/1=1
(ср. [124]) также имеют положительные члены и также сходятся, так как
138 1 § 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ 333
общий член каждого из них не превосходит | ип |, т. е. общего члена сходя-
сходящегося ряда C).
В силу доказанного каждый из них не зависит от порядка членов; не
будет зависеть от порядка членов и разность их, которая совпадает с сум-
суммой ряда A), что и требовалось доказать.
Следствие. В абсолютно сходящемся ряде можно каким угодно
образом группировать слагаемые и складывать их затем уже по группам,
ибо такая группировка приводит к перемене порядка слагаемых, отчего
сумма ряда не изменится.
Замечание. Если из абсолютно сходящегося ряда выделить любую
последовательность его членов, то полученный таким путем ряд также будет
абсолютно сходящимся, так как такому выделению соответствует выделение
последовательности членов в ряде C) с положительными членами, что-, оче-
очевидно, не нарушает сходимости этого ряда. В частности, будут сходящимися
ряды, составленные в отдельности из положительных и отрицательных чле-
членов сходящегося ряда. Обозначим через sf сумму ряда, составленного из
положительных членов, и через (—s")— сумму ряда, составленного из отри-
отрицательных членов. При беспредельном возрастании п сумма sn первых п
членов всего ряда может содержать сколь угодно много членов из обоих
упомянутых рядов, и в пределе, очевидно, получим
s = lim sn = s* —s".
Нетрудно показать, что когда ряд сходится не абсолютно, то ряды,
составленные из его положительных и отрицательных членов, являются соб-
собственно расходящимися. Так, например, для неабсолютно сходящегося
ряда [124]
1~2" + " —T+i"
ряды
,,1.1,1, 1 1 1 1
1 + +++ и
расходятся. Сумма п первых членов первого ряда стремится к (+ оо), а вто-
второго ряда—к (— оо) при беспредельном возрастании п. Пользуясь указанным
выше обстоятельством, Риман показал, что, меняя надлежащим образом
порядок членов неабсолютно сходящегося ряда, можно сделать его сумму
равной какому угодно числу. Таким образом, оказывается, что понятие об
абсолютно сходящемся ряде тождественно с понятием о ряде, сумма кото-
которого не зависит от порядка слагаемых.
Заметим еще, что если мы в каком-нибудь сходящемся (не обязательно
абсолютно сходящемся) ряде переставим местами конечное число слагаемых,
то суммы первых п членов sn останутся при всех достаточно больших п
теми же, т. е. сходимость ряда не нарушится, и сумма ряда останется преж-
прежней. Предыдущее же рассуждение и результаты относятся и к тому случаю,
когда переставляют бесконечное число слагаемых.
138. Умножение абсолютно сходящихся рядов. При перемножении
двух абсолютно сходящихся бесконечных рядов можно применять пра-
правило умножения конечных сумм: произведение равно сумме ряда, который
получим, если каждый член одного ряда умножим на каждый член дру-
другого и полученные произведения сложим. Порядок слагаемых здесь без-
безразличен, так как построенный таким путем ряд будет также абсо-
абсолютно сходящимся.
Данные абсолютно сходящиеся ряды пусть будут
534 ГЛ. IV, РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ [ 138
Рассмотрим сперва частный случай, когда оба они с положительными
членами1 и притом когда само умножение совершается следующим порядком:
E)
Покажем, прежде всего, что ряд E), все члены которого также положи-
положительны, сходится, а затем уже, что его сумма S равна so.
Обозначим через Sn сумму п первых членов ряда E). Можно всегда
выбрать настолько большое число т, чтобы все члены, входящие в состав Sn,
вошли и в произведение сумм:
т. е. чтобы оказалось Sn ^ smomi т. е.
Sn < so, F)
так как sm^s, om^o$ откуда и следует сходимость ряда E) [120].
Обозначив сумму ряда E) через 5, из неравенства F), очевидно, имеем
Рассмотрим теперь произведение snan. При данном л, очевидно, можно,
найти настолько большое т, чтобы все члены, входящие в состав произве-
произведения сумм sn и оп, вошли в сумму Sm; мы получим тогда
^ 5,
а потому и в пределе, я-юэ,
snan -+so^S. G)
Неравенство это в соединении с F) дает S = so, что и требовалось
доказать.
Пусть теперь ряды D) — абсолютно сходящиеся, но с какими угодно
членами. Следовательно, сходятся ряды с положительными членами
I 1 + 1 «2 [ + - + I «Л| + "• И \Vx\ + \Vt\+...+ \Va\+...b
а потому, в силу только что доказанного, сходится и ряд
Отсюда видно, что составленный по предыдущему правилу ряд E) будет
в этом случае абсолютно сходящимся. Обозначим теперь через
соответственно положительные члены рядов D) и абсолютные значения от-
отрицательных членов. Мы знаем (замечание [137]), что ряды, составленные из
этих членов, сходятся; положим
в'- 2 а;, а'= 2 Ь'п, •'- 2 а"п> а"= 21 Ьп> («
139 J § 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ 335
Как известно [137], мы имеем
S = Sf—S", а = а'—а".
Как показано, ряды (8) с положительными членами можно почленно
перемножать между собой; сумма произведений рядов
sV, s"a", —s'o", —s'V
содержит как раз те и только те члены, которые входят в ряд E), а потому
имеем
S = sV + s"c" — S'a" — s'V = (sr — S") (a' — o") = S<J,
что и требовалось доказать.
Пример. Ряд
сходится абсолютно при | q \ < 1, а потому
139. Признак Куммера. Признаки Коши и Даламбера сходимости и рас-
расходимости рядов [121], при всей их практической важности, все же являются
весьма частными и неприменимы во многих даже сравнительно простых
случаях. Проводимый ниже признак обладает гораздо большей общностью.
Признак Куммера. Ряд с положительными членами
Й1 + И.+ -. +ия+... (9)
сходится, если существует такая последовательность положительных
чисел ctj, a2, ,.., ал, ... , что, начиная с некоторого значения п,
было всегда
^ (Ю)
где а — некоторое положительное число, не зависящее от п; ряд (9)
расходится, если при тех же значениях п:
^ (И)
00
и, кроме того, ряд \ расходящийся.
Не ограничивая общности, мы можем считать, что условия теоремы вы-
выполняются, уже начиная с я==1. Пусть сперва выполнено условие A0). Мы
выводим из него, положив я=1, 2, 3, ... ,
откуда, складывая почленно и приводя подобные члены, находим
а («а + • • • + Чп) ^ «А — «*«* < aA-
Мы видим отсюда, что ряд (9) с положительными членами, сумма п первых
a.Ui
членов которого без ut остается меньше постоянного числа -1—-, не зави-
зависящего от п, сходится [120].
ГЛ. TV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ [ 140
Пусть теперь выполнено условие A1). Оно дает нам
1
т. е. отношение ^5±1 не меньше соответствующего отношения членов рас-
и
ходящегося ряда
и
п
Расходимость ряда (9) будет следовать тогда из следующей леммы о ря-
рядах с положительными членами:
Дополнение к признаку Даламбера. Если, начиная с неко-
некоторого значения п, отношение ?"±1 не превосходит соответствующего
ип
отношения ^^ членов сходящегося ряда
v
то и ряд
сходится. Если же отношение ^±1 остается не меньшим соответств\>ю-
ип
щего отношения членов расходящегося ряда A2), то и ряд A3)—расхо-
A3)—расходящийся.
Действительно, пусть сперва имеем
причем ряд A2) сходится. Мы имеем последовательно
откуда, перемножая, находим
й?<:^ или и <:Й1«
— ^ — , ИЛИ Un ^ -~ Vn,
Из последнего неравенства и замечания в [120] [при fc = —) следует
\ vi!
сходимость ряда A3). Аналогичным образом можно доказать и расходи-
расходимость его, в случае, если -2±!^-?±! и ряд A2) расходится.
140. Признак Гаусса. Весьма важные применения имеет следующий
Признак Гаусса1). Если в ряде с положительными членами (9)
1) В сущности, обобщение признака, действительно установленною
Гауссом.
140 ] § 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ 337
отношение —— можно представить в виде
—— =l+~ + -Tif где р> 1 и !«„[<Л, A4)
причем А не зависит от п, т. е. величина <лп остается ограниченной, то
ряд (9) сходится, если ^>1, и расходится, если р-^1.
Заметим, что во всех случаях, исчерпываемых этим признаком, признак
Даламбера неприменим [121]. Сама же формула A4) получается при разло-
разложении отношения —2- по степеням —, т. е. при выделении членов различ-
ных порядков малости относительно —, конечно, если это возможно.
Переходя к доказательству, мы исследуем отдельно случаи: 1) ^1 и
2) fi. = 1. В случае 1) мы положим в признаке Куммера ал = л, причем заме-
заметим, что ал>0 и ряд У,— расходится [119]. Мы имеем, очевидно, в дан-
данном случае
un+i J п-*оо
Если fA > 1, то, начиная с некоторого значения п, будем иметь
и
где a—любое положительное число, меньшее ja — 1, и ряд (9) будет схо-
сходящимся. Если же /х < 1, то, начиная с некоторого значения п, мы будем
иметь
ип
т. е. ряд (9) будет расходящимся [139]. В случае 2) мы имеем
Положим в признаке Куммера ап = п log n и составим ряд
где суммирование можно начинать с любого целого положительного я, так
как первые слагаемые не влияют на сходимость [118]. Докажем расходимость
написанного ряда, пользуясь интегральным признаком Коши [122]. Нам надо
доказать расходимость интеграла
00
dx
л: log л:
a
Но мы имеем
оо
= С *.iog(log*)
log a
338 ГЛ. IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ [ ИО
и функция log (log x) беспредельно возрастает при возрастании х, т. е. на-
написанный выше интеграл действительно расходится, а потому и ряд A5) рас-
расходится. Составим теперь разность ап—- ал+1, пользуясь A4):
un+i
+-j- + ^)log/i-(«+I)log(я+1)=-
(п + 1) log n + "^рД П - (п + 1) log (п + 1)
log п
Множитель и>п остается по условию ограниченным, отношение же ?_х-
стремится к нулю при п -> оо, так как по условию р— 1 >0, и log n возра-
возрастает слабее любой положительной степени п (пример 2 из [66]). Если поло-
положить := —Ху то х—>-0, и второе слагаемое справа будет
т. е. оно стремится к (—1) [38]. Мы видим, таким образом, что в данном
случае ряд \ — расходится и (ап— ад+1)->—1 при я->со, а по-
потому, при достаточно больших л, будет: ап — ап+1 < 0, т. е. ряд (9) бу-
u
un+i
дет расходящимся [139], что и требовалось доказать.
Приведенные выше признаки сходимости могут применяться и к рядам
с какими угодно членами, если заменить в них ип на | ип |. Но в этом слу-
случае они дают только возможность сказать, будет ли данный ряд абсолютно
сходящимся или не будет таковым. Из них можно будет извлечь, вообще
говоря, условие абсолютной сходимости, но не условие расходимости, так
как мы знаем, что ряд может быть не абсолютно сходящимся, но и не рас-
расходящимся [124]. Таким путем мы получаем:
Дополнение к признаку Гаусса. Ряд
с какими угодно членами, для которого
где р > 1 и \ <*п | < Л, будет абсолютно сходящимся при р. > 1.
Нетрудно показать, что он будет расходящимся при ц<0. В самом
деле, в этом случае мы имеем, принимая во внимание ограниченность сод,
>> 1 при л —> со,
а потому, начиная с некоторого значения л, в силу условия fx<Of
т. е., начиная с этого значения л, члены ряда возрастают по абсолютному
значению, и общий член ряда ип не может стремиться к нулю при л->оо,
т. е. ряд A7) будет расходящимся.
141 1 § 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ 339
141. Гипергеометрический ряд. Применим предыдущие общие сообра-
соображения к так называемому гипергеометрическому ряду, или ряду Гаусса:
+ n!Y(V+D —
Некоторые функции, встречающиеся в приложениях, приводятся к таким
рядам. Непосредственной подстановкой чисел а, Р и у легко проверить, на-
например, следующие равенства
F(l, р, р; х)=1++*++«+
F(-m, р, Р; х)-
f(a pp;,)l| B0)
Для исследования сходимости ряда A9) составим отношение последую-
последующего члена к предыдущему
т. е. по следствию из A21) ряд A9) сходится при |*|<1 и расходится при
|*| >1« Остаются только случаи: 1)*=1 и 2) *=•— 1. Заметим еще, что
при всех достаточно больших п множители (а+n), (Р + л) и (у+п) будут
положительными, так что при *=1 все члены ряда при достаточно боль-
большом п имеют один и тот же знак, а при *= — 1 получится при больших п
знакопеременный ряд.
В первом случае имеем, разлагая по формуле прогрессии (считая п до-
достаточно большим) и перемножая полученные абсолютно сходящиеся ряды
почленно [138]:
W
"" "*"
где величина ©я остается ограниченной. Далее, в рассматриваемом случае,
отбросив достаточно большое число начальных членов в ряде
-1)
мы получим ряд с членами одного знака, применяя к которому признак
Гаусса, получаем абсолютную сходимость при
p + l, т.е. Y-a-
и расходимость при
Y—а —р + 1^1, т.е. Y—а —
340 ГЛ. IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ [ 141
Во втором случае, при х = — 1, мы получаем знакопеременный, начи-
начиная с некоторого члена, ряд
Мы имеем здесь, как и раньше
п _. , т—«—8+1 | "я
а потому, применяя дополнение к признаку Гаусса, получаем сходимость
при
7—а—p+l>lf т. е. 7~ а—
и расходимость при
7 — а—р+1<0, т, е. т—«—Р< — Ь
В случае
¦7_в_Р=_1
можно показать, что общий член ряда стремится к пределу, отличному от
нуля, т. е. ряд будет расходящимся [119]. Наконец, в случае
—1<7 — а —р<0
можно доказать, что абсолютные значения членов ряда, убывая, стремятся
к нулю при п-+со, т. е. [123] ряд будет сходящимся, но не абсолют-
абсолютно. На доказательстве этих двух последних утверждений мы останавли-
останавливаться не будем.
Применяя это к разложению бинома
_л:+_Л_
i т(т — \)...(т — п+\)
которое получается из A9) (|3 = 7 — произвольно) заменой а на (— т) и х
i;a (— х) и которое, как мы знаем, сходится при |х|<1 и расходится при
) х | > 1, получим, что написанный ряд будет:
абсолютно сходиться при т>0, если х= —1,
расходиться при /п*^0, если л* = —1,
абсолютно сходиться при т>0, если л: = 1,
не абсолютно сходиться при — 1 < т ^0, если х = 1,
расходиться при т^—1, если лг = 1,
обращаться в полином при /п = целому числу ^0.
Мы покажем дальше [149], что если ряд бинома сходится при x = ±\f
то сумма его равна A ± 1)т, т. е., соответственно, 2т или 0.
Заметим, что в предыдущем мы считали а, р и ] отличными от нуля и
целого отрицательного числа. Для 7 это важно, так как в противном случае
члены ряда теряют смысл (знаменатель обращается в нуль), а если а или р
есть нуль или целое отрицательное число, то ряд обрывается и превра-
превращается в конечную сумму.
142 1
§ 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ
341
142. Двойные ряды. Рассмотрим прямоугольную таблицу чисел, ограни-
ограниченную сверху и слева, но уходящую в бесконечность направо и вниз:
1
3
«11
«21
«81
«mi
«12
«22
«32
«m2
«13
«23
«83
«тз
... «,„ ...
... Щп ...
... «зл •••
... итп ...
B2)
Она содержит бесчисленное множество строк, номера которых указы-
указываются первым значком, и столбцов, номера которых даются вторым знач-
значком при букве и. Таким образом, и^ означает число, стоящее в пересечении
1-й строки с k-м столбцом таблицы.
Допустим сперва, что все числа uik положительны.
Для того чтобы определить понятие о сумме всех чисел таблицы B2),
наметим в плоскости чертежа точки с целыми положительными координа-
координатами М (/, k) и проведем ряд кривых
пересекающих координатные оси в первом
координатном углу и подчиненных лишь
тому условию, чтобы каждая точка М при
достаточно большом п попала внутрь пло-
площади (Сл), ограниченной кривой Сп и
координатными осями ~(рис. 157), и чтобы
площадь (Сп) заключалась внутри (Сл+1).
Составим сумму Sn всех чисел uik, соот-
соответствующих точкам, попавшим внутрь пло-
площади (Сп). При возрастании п эта сумма,
очевидно, будет возрастать, и поэтому мо-
могут представиться лишь два случая: или 1) сумма Sn остается ограниченной
при всех значениях л, и тогда существует конечный предел
lim Sn = 5,
Л-fOO
или 2) сумма Sn при возрастании п беспредельно возрастает.
В случае 1) говорят, что двойной ряд
Рис. 157.
00
1
B3)
сходится и имеет сумму S. В случае 2) двойной ряд B3) называется
расходящимся.
Сумма сходящегося ряда B3) с положительными членами не зави-
зависит от способа суммирования, т. е. от выбора кривых Сш и может
342 ГЛ. IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ [ 142
быть получена также путем суммирования ряда по строкам или
столбцам
s(f;b (?) <24>
т. е. вычислением сперва суммы всех членов каждой строки (или каждого
столбца) таблицы, а затем сложением полученных сумм.
В самом деле, построим какую-нибудь другую систему кривых С[, С^...,
С'пУ ... , обладающих тем же свойством, что С» С2, ... , Сп ... Обозначим
через 5^ сумму всех чисел таблицы, соот-
соответствующих точкам, попавшим внутрь пло-
площади (С„). При заданном п можно всегда вы-
выбрать настолько большое т, чтобы площадь
(Сд) оказалась внутри (Ст), и тогда
\° \° \° nn°
Рис. 158.
т. е. в силу предыдущего существует конеч-
ный предел
Переменив роли кривых Сп и Сп, мы точно так же докажем, что
что возможно лишь при условии
Сумму двойного ряда B3) можно получить, хотя бы взяв за Сп лома-
ломаные, составленные из отрезков прямых (рис. 158):
i = const, k = const.
Мы получим таким путем суммирование „по квадратам*!
S = «П + («12 + «22 + «2i) + ... +
B5)
Суммируя же „по диагоналям", получим
S = «И + («12 + «2l) + («18 + «22 + «8l) +
+ («1Л + «2,*-1 +-.-+ tint) + • • •
Для доказательства формул B4) заметим прежде всего, что сумма какого
угодно числа членов таблицы B2) меньше 5, а потому и сумма членов,
стоящих в любой строке или в любом столбце, также всегда меньше 5, от-
откуда вытекает сходимость каждого из рядов
|42 ] § 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ 343
Мы имеем сверх того для любых конечных значений чисел тип:
т со
sm= J] ( У\
B6)
В самом деле, будем рассматривать только первые т строк таблицы B2).
Взяв из них элементы первых р столбцов, мы имеем, очевидно
р т
БЛ2, «,.)«*•
По правилу сложения рядов [119] имеем
оо т р т
S't+S'a+ ... +S' = У1 (У! И;Л== Ига У! (
так как выражение, стоящее под знаком предела, не больше S.
Аналогичным образом доказывается и второе из неравенств B6). Нера-
Неравенства B6) показывают, что оба ряда
00 СО ОО
il fel il
сходятся и имеют суммы, не превосходящие 5, т. е.
и
С другой стороны, ясно, что при любом выборе системы кривых Сп все
члены, входящие в состав суммы Sn войдут в состав обеих сумм
при достаточно большом /w, т. е.
а потому и в пределе
S= lim
Ввиду j'^Sh aff^S, это возможно лишь при условии
а' = а" = S,
что и требовалось доказать.
Из двойных рядов с какими угодно членами мы остановимся только на
абсолютно сходящихся рядах, т. е. таких, для которых двойной ряд,
составленный из абсолютных значений
сходится.
344 ГЛ. IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ [ 142
Применяя рассуждения, аналогичные рассуждениям [124], можем показать,
что и для таких рядов существует сумма
со со оо со
'!*)• B7)
которая также не зависит от способа суммирования и, в частности, может
быть получена суммированием по строкам и по столбцам.
Замечание. Многие свойства абсолютно сходящихся простых рядов
распространяются и на двойные абсолютно сходящиеся ряды; в частности,
замечание из [124]: если каждый член двойного ряда по абсолютному
значению не превосходит члена сходящегося двойного ряда с положитель-
положительными членами, то данный ряд абсолютно сходящийся.
Точно так же распространяется свойство 2) из [120].
Примеры. 1. Ряд
со
B8)
2 ш
сходится при а>1, р>1, ибо, суммируя по квадратам, мы имеем
где А и В обозначают сумму рядов
со оо
сходящихся при а> 1, Р> 1 [122].
2. Ряд
У * B9)
i, k = I
сходится при ct>2 и расходится при о =^2, так как, суммируя по диагона-
диагоналям, мы имеем
откуда, подставляя вместо fl j сначала у, т. е. меньшее число, а за-
затем 1, т. е. большее число, находим
1A, , 1 I ^ 9 . 1 , , 1
143 | § 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ 345
сю
Сходимость ряда Л -^ при а > 2 и расходимость его при а ^ 2
доказывают наше утверждение.
3. Если а и с положительны и Ь2 —' ас < 0, то ряд
C0)
сходится при р>1 и расходится при р^
Пусть сперва #:>0. Так как, очевидно
то, обозначив через Аг меньшее из чисел а и с, через А2 — большее из
чисел а, Ь, с, имеем
2A1ik ^ ai* + 2bik + ck* < А2 (i + k)\
откуда, ограничиваясь единственно интересным случаем р > 0, выводим
что в силу примеров 1 и 2 и сделанного выше замечания дает сходимость
при р>1 и расходимость при p^.\t причем существенно отметить, что
множители — и /о . чр от / и /г не зависят.
Пусть теперь ^<0. Обозначив через Ао большее из чисел а, с, \b\f
в силу очевидного неравенства (]/"а^J +(")/"cifeJ ^2 Ylk
2(b + VTc) ik ^ а/2 + 2bik + ck2 < Ао
причем b + ]^ас > 0, так как по условию \b\<z У ас. Дальше доказательство
проводится так же, как и в случае ?>0.
143. Ряды с переменными членами. Равномерно сходящиеся ряды.
Формулы Тейлора и Маклорена представляют примеры рядов, члены которых
зависят от переменной х. Во второй части курса мы познакомимся с весьма
важными тригонометрическими рядами, которые имеют вид:
оо
2 (<*п cos пх + bn sin nx),
я = 1
^лены которых зависят также не только от я, но и от переменной х.
Мы займемся теперь, вообще, рядами с переменными членами, завися-
зависящими от некоторой независимой переменной х.
Пусть имеется бесконечная последовательность функций
и, (х), и2 (*), иь (л:), ... , ип (х), ..., C1)
определенных в промежутке (а, Ь). Составим из них ряд
щ (х) + и2(х) + и9 (х)+ ... +ип(х)+ ... C2)
Он может сходиться для каких-либо значений х из (я, Ь) и расходиться для
других х. Сумма первых п членов ряда C2) srt(^)_ecTb, очевидно, функция
346 ГЛ. IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ [ 143
от х. Для значений х} при которых ряд C2) сходится, мы можем говорить
о его сумме $ (х) и остатке rn(x) = s (х)— sn(x). При этом
s(x)= lim sn(x). C3)
П -»- 00
Если ряд C2) сходится при всех х из (а} Ь), т. е. при а^х^Ь, то
говорят, что он сходится в промежутке (а, Ь).
Если ряд C2) сходится в промежутке (а, Ь) и имеет сумму s(x), то это
значит, что при каждом данном значении х из (д, Ь), задав произвольно
положительное число е, можно найти такое число N, чтобы при всех значе-
значениях п > N мы имели | гп (х) \ < е при п > N, причем, очевидно, это число N
будет зависеть от выбора е. Необходимо, однако, отметить, что N будет,
вообще говоря, зависеть еще от выбранного значения х, т. е. может иметь
различные значения при заданном е и различном выборе х из промежутка
(а, Ь)у и его мы будем обозначать через N (х). Если при любом данном по-
положительном г можно найти такое число N, не зависящее от х, чтобы
при любом значении х из промежутка (а, Ь) выполнялось неравенство
|гл(*)|<е C4)
при всех и > N, то ряд C2) называют равномерно сходящимся в проме-
промежутке (а, Ь).
Рассмотрим, например, ряд
111
C5)
1
-\)(х
причем х меняется в промежутке @, a)t где а — любое данное положитель-
положительное число.
Нетрудно видеть, что ряд можно переписать так:
_f_JL__ L_\
\х + п — \ х + п) • • • »
так что в данном случае
S*(*)=7"XT' SW= limsrt(A:) = O, гл(л:) =
х "Тп п-»оо
и если мы хотим сделать
|г„(^I==^<е, C6)
то достаточно взять
я>-^- — x*=N(x). C7)
Если теперь мы хотим, чтобы неравенство C6) выполнялось при всех
значениях х в промежутке @, а), при условии n>Nt независимо от взятого
значения л*, то достаточно положить Лг= — ^zN(x), так как тогда нера-
неравенство C7), а потому и C6), при условии п>ЛГ, будет выполнено наверное
143 ] § 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ 347
при всех значениях х в промежутке @, а). Итак, ряд C5) будет равномерно
сходящимся в промежутке @, а).
Не всякий ряд обладает свойством равномерной сходимости, так как не
для всякого ряда можно указать не зависящее от х число N, которое
было бы не меньше всех TV (л:) в промежутке (а, Ь).
Рассмотрим, например, в промежутке Q^x^l ряд
* + *<д---1)+х«(*-1)+ ... +х»-Чх-\)+ ..¦ C8)
Сумма первых п членов будет
sn(x) = x + (x*-x) + (x*-x*)+ ... +(дс«—л»),
то есть
sn (х) = х\
и, следовательно [26]
s (х) = lim sn (x) = 0 при 0 ^ х < I
П-+СО
И
гп (х) = s (х) — sn (x) = — хп при 0 ^ х < 1.
При А" = 1 мы имеем, подставляя в C8) х=\, ряд
1+0 + 0+...,
то есть
sn (х) = 1, 5 (х) = lim sn (*) = 1, rn (x) = s (x) — вя (jt) = 0
при jc=1 и при любом п. Ряд C8) сходится во всем промежутке О^сх^ 1,
но в этом промежутке сходимость неравномерна. Действительно, в силу
гп(х) = — хп при 0^дг<14 если мы хотим, чтобы выполнялось неравен-
неравенство C4) | гп (х) | < е, то должно быть хп < е, т. е. п log x < log e, или, деля
на отрицательное число log дг, получим
log e
log**
Итак, в данном случае N(x) = r-^— и не может быть заменено меньшим.
При приближении х к единице, log х —¦ 0, функция N (х) возрастает бес-
беспредельно, и нельзя указать такое значение N, чтобы неравенство C4) вы-
выполнялось при n^>N во всем промежутке @, 1). Вследствие этого обстоя-
обстоятельства, хотя ряд C8) и сходится во всем промежутке @, 1), в том числе
и при х=\, однако сходимость его будет все медленнее при приближении х
к единице; для достаточного приближения к сумме ряда нужно будет брать
все больше членов, чем ближе х будет к единице. Заметим, однако, что при
самом значении лг=1 ряд просто обрывается на втором члене.
Укажем теперь другое определение равномерной сходимости, равносиль-
равносильное прежнему определению. Выше мы формулировали [125] необходимое и
достаточное условие сходимости ряда. В рассматриваемом случае оно форму-
формулируется так: для сходимости ряда C2) в промежутке (я, Ь) необходимо и
достаточно, чтобы при любом заданном положительном е и любом х из (а, Ь)
существовало такое N, что
I ия+1 (х) + ип+2 (*)+...+ и Л+р (х) |< в C9)
при п > N и любом целом положительном р. Это Af при заданном е может
зависеть еще от выбора х. Если же при любом заданном положитель-
положительном е существует число N одно и то же для всех х из (а, Ь) такое, что
348 ГЛ. IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ I 144
при и > N и любом целом положительном р выполняется C9), то говорят,
что ряд C2) сходится равномерно в промежутке (а, Ь).
Надо показать, что это новое определение равномерной сходимости
равносильно прежнему определению, т. е. если ряд равномерно сходится
в прежнем смысле, то он равномерно сходится и в новом смысле, и наобо-
наоборот. Итак, пусть сначала ряд равномерно сходится в прежнем смысле, т. е.
\гп(х)\<.г при n>N, где х — любое значение из (а, Ь) и N не зависит
от х. Мы имеем, очевидно
«я+1 (*) + И/и-2 (*)+••.+ «я+р (*) = гп (х) — гл+р (х) D0)
и, следовательно,
I «л+1 (х) + ап+2 (х) + ... + ип+р (*) К | гл (л:) | + | гя+р (х) |,
что при n>N и, следовательно, n-\-p>N дает
D1)
Ввиду произвольного выбора е мы видим, что ряд равномерно сходится
в новом смысле. Положим теперь, что ряд равномерно сходится в новом
смысле, т. е. что выполнено неравенство C9) при я > N, не зависящем от х$
любом целом положительном р и любом х из (а, Ь). Из этого следует, что
ряд сходится, и мы можем образовать
гп (х) = ял+1 (х) + ип+2 (х) + ... = lim [ия+1 (д:) + ия.г8 (*) + ...+ «я+р (-v)l,
р-^оо
причем из неравенства C9) при /?—*оо получаем в пределе |гЛ(х)|^е при
п> N, т. е. из нового определения равномерной сходимости, в силу произ-
произвольности е, вытекает прежнее, и равносильность обоих определений до-
доказана.
Отметим, что при первом определении равномерной сходимости C4) мы
используем гп (х) и тем самым уже дополнительно предполагаем, что ряд
сходится. Второе определение равномерной сходимости C9) включает и са-
самый факт сходимости ряда.
144. Равномерно сходящиеся последовательности функций. Последо-
Последовательность функций
«,(*),«,(*),-.«„(¦*) <42>
которую мы рассматривали выше, была определена с помощью ряда C2);
sn (x) означало сумму п первых членов ряда. Но можно рассматривать по-
последовательность D2) саму по себе, считая ее данной, и уже по ней по-
построить ряд, суммой п первых членов которого является n-Pi член последо-
последовательности sn(x). Члены этого ряда определяются, очевидно, по формулам:
«1 (х) = st (х), и2 (х) = s2 (х) — st (х), ..., ип (х) = sn (x) —s^i (х), ... D3)
Очень часто последовательность D2) бывает проще D3), как это имело
место и в рассмотренных примерах.
Таким путем мы приходим к понятиям о сходящейся и равномерно
сходящейся последовательности функций:
Если дана последовательность функций D2):
Si(x), 8Ш(Х), ... , 5Я(*), ... ,
определенных в промежутке (a, b)t и если при каждом значении х в этом
промежутке существует предел
s {х) = lim sn (x), D4)
rt-* 00
144 1
§ 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ
349
то последовательность D2) называется сходящейся в промежутке (я, Ь),
функция же s (х) называется предельной функцией последовательности D2).
Если, сверх того, при любом данном наперед положительном е суще-
существует такое число N, не зависящее от х, что неравенство:
\ s (x) —^sn (x) | <; е D5)
имеет место при всех значениях п>N во всем промежутке (а, Ъ), то
последовательность D2) называется равномерно сходящейся в промежут-
промежутке (а, Ь). Условие D5) можно заменить равносильным ему
\sm(x)-sn(x)\<* D6)
при т и л > N.
Условие равномерной сходимости последовательности D2) равносильно
условию равномерной сходимости ряда
«i (х) + н2 (*) + ... + ип (х) + ..., D7)
где D3):
и, (х) = st (х), tt2 (х) = s2 (х) — Si (л:), ..., ип (х) = sn (х) — sn_t (х), ...
Равносильность условий D5) и D6) при исследовании равномерной схо-
сходимости последовательностей может быть доказана совершенно так же, как
выше была установлена равносильность условий C5) и C6) для бесконечных
рядов. Отметим еще, что из равномерной
сходимости sn (x) в промежутке («, Ь)
непосредственно следует и равномерная >«t sffl-f
сходимость в любой части (а, Ь). » ' ' J
Понятие о равномерной сходимо-
сходимости последовательностей может быть
Рис. 159.
Рис. 160.
истолковано и геометрически. Если мы изобразим графически функции s(x)
и sn (x) при различных значениях /г, то для равномерно сходящейся последо-
последовательности наибольший отрезок ординаты, заключенной между кривыми
sn (х) и s(x), должен стремиться к нулю, при n-^оо для всех х из (а, Ь);
для неравномерно сходящейся последовательности это условие не будет вы-
выполнено.
Обстоятельство это наглядно проверяется на рис. 159 и 160, сделанных1)
Для разобранных выше примеров:
*) Для большей наглядности рис. 159 и 160 выполнены в разных мас-
масштабах для хну.
350 ГЛ. TV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ I 144
В случае рис. 160 предельная функция s (x) графически изображается
отрезком @, 1) оси ОХ, исключая точку 1, и отдельной точкой с координа-
координатами A, 1).
Правда, в последнем примере предельная функция s(x) не непрерывна.
Но нетрудно привести пример сходящейся последовательности, предельная
функция которой непрерывна, но которая тем не менее сходится неравно-
неравномерно. Таким свойством обладает хотя бы последовательность (рис. 161)
ПХ (О^х^а). D8)
Мы имеем, очевидно, при д:=^0:
ft* 1_ х
\
и, при я—*со, первый множитель справа »0, а второй стремится к —,
ft X
т. е. $п(х)-+0 при хфО. При д: = 0, очевидно, sw@) = 0 при всяком ft, и,
следовательно, при всех х из @, а),
У где а —некоторое положительное
10
0,5
ЧИСЛО,
s (х) = lim srt (x) = 0.
Однако максимальная величина
отрезка ординаты между кривыми
п z1 sn(x) и s(x), которая в рассматри-
п-2 ваемом случае приводится просто к
,п'*» ординате кривой sn(x), так как
°>5 1>° Ь5 W s(x) = 0, будет ^ (и бУдет соответ-
Рис. 161. V 1 v
ствовать значению х = —), Так как
п}
она не стремится к нулю при п—»>оо, то последовательность D8) не будет
равномерно сходящейся в промежутке @, а); и, действительно, если мы хотим,
чтобы было
I s (х) — sn (х) |
то, решая относительно п неравенство 2-й степени
и считая е достаточно малым, получим
Функция эта возрастает беспредельно при дг—*0, что и обуславливает
неравномерную сходимость последовательности.
Заметим, наконец, что те же рис. 160 и 161 показывают, что последо-
последовательность хп равномерно сходится в промежутке @, q), где q — любое
положительное число, меньшее единицы, а последовательность . 2 2 равно-
равномерно сходится в промежутке (q, а), где 0 < q < а, в чем нетрудно убедиться
и непосредственным вычислением.
145 ] § 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ 351
145. Свойства равномерно сходящихся последовательностей. 1. Пре-
Предельная функция равномерно сходящейся в промежутке (а, Ь) последова-
последовательности непрерывных функций также непрерывна.
Пусть
— данная последовательность функций, причем все они непрерывны в проме-
промежутке (а} Ь)} и пусть
s (л:) = \\т sn (x)
П-+СО
ее предельная функция. Нам нужно доказать, что, задав наперед сколь
угодно малое положительное число е, можно найти такое число 5, чтобы
было [35]:
— s(x)\<t, если |Л|<&, D9)
при условии, что оба числа х и х -f- h лежат в промежутке (а> Ь). Мы можем
писать при любом п:
^l8(X + h) — Sn(X + h)\ +
В силу определения равномерной сходимости, мы можем выбрать п на-
настолько большим, чтобы во всем промежутке (а, Ь), в том числе и при зна-
значениях х и х + Л, было
\s(x + h)-Sn(X + h)\<~9 \8(Х)-8П(Х)\<±.
Выбрав так п и фиксировав его, в силу непрерывности функции sn (x)
[351, мы можем найти такое число &, чтобы было
\sn{x + b) — sn(x)\<4f9 если |Л|<&.
Сопоставив все эти неравенства, мы и получим неравенство D9).
Если последовательность функций сходится неравномерно, то предельная
функция может и не быть непрерывной, примером чего может служить
хотя бы последовательность хп в промежутке @, 1).
Обратное утверждение, однако, неверно, — и для неравномерно сходя-
сходящейся последовательности предельная функция может быть непрерывной,
например, для последовательности:
пх
\+п2х2'
2. Если
8Х(Х), 8Ш(Х), ..., ЯЛ (ЛГ), ...
есть равномерно сходящаяся последовательность непрерывных в проме-
промежутке (а, Ь) функций а (а, р) — любой промежуток, лежащий в (а, Ь), то
\ sn (x) rf* — $ s (x) dx, n -> оо E0)
а а
или, иначе,
lim \sn(x)dx = \ lim sn(x)dx. E1)
352 ГЛ. IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ [ 145
Если пределы интегрирования переменные, например, р = лг, то после-
последовательность функций
]sn(t)dt
= 1, 2, 3, ...)
E2)
также сходится равномерно в промежутке (а, Ь). Процесс этот назы-
называется переходом к пределу под знаком интеграла.
Заметим прежде всего, что в силу свойства 1) предельная функция s (x)
также непрерывна. Рассмотрим теперь разность
s (х) dx — J sn (x) dx = ^ [s (x) — sn (x)] dx.
Задав число е, мы можем, в силу равномерной сходимости, найти такое
число N, чтобы при всех значениях п > N, во всем промежутке (а, Ь) мы
имели
|s(*) — sn(x)\<z,
а потому [95], A0t)
Р P. P
а а а
Итак, для любого промежутка (а, C), заключающегося в (а, Ь), имеем
Р Р
Р.
(b — a)
при п > N: Правая часть неравен-
неравенства не зависит от а и р и стре-
стремится к нулю, если е — 0. Ввиду про-
произвольности г мы можем формули-
формулировать результат так: при любом
заданном положительном ех суще-
существует N, не зависящее от а и р,
такое, что
Р
I} s (х) dx — ^ sn (x) dx\<et
а а
при л > N. Отсюда непосредственно
вытекает формула E0). Полагая
р = х и принимая во внимание не-
независимость N от р, видим, что
Рис. 162. последовательность E2) сходится рав-
равномерно для всех х из (а, Ь).
Для неравномерно сходящихся последовательностей эта теорема может
оказаться и неверной. Пусть, например,
sn (х) = пхе
@ ^ х ^
(рис. 162). Нетрудно показать, разбирая отдельно случаи х>0 и лг = О, что
при всяком х в промежутке @, 1)
sn (•*) ~* 0 при п —»оо,
145 1
§ 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ
353
так что здесь s (л:) = 0. Последовательность эта, однако, не может быть
равномерно сходящейся, так как наибольшая ордината кривой у = sn (х),
или, что то же самое, наибольшая величина разности sn (х) — s (x), которая
получается при лг=——, возрастает беспредельно при я-*со.
у 2л
С другой стороны, мы имеем
1 1
г»
sn(x)dx-=.n 1 хё~
в то время как
3. Ясли функции последовательности
имеют непрерывные производные
1
б промежутке (а> Ь), причем последовательность s'n (x) равномерно схо-
сходится к предельной функции с (х), а последовательность sn (x) сходится
к предельной функции s (x), то sn (x) также сходится равномерно и
или иначе
г_*оо dx
lim sn (x)
dx
E3)
E4)
Процесс этот называется переходом к пределу под знаком производной.
Пусть а — любое постоянное, х — переменное значение на промежутке
(а, Ь)> В силу свойства 2) мы имеем
X X
lim J s'a (x) dx = f a (x) dx.
Но
j s; (х) й?л: = sn (х) — 5Я (а) -^sW-5 (а),
а
а потому предыдущая формула дает
s(x) — 5 (а) = Jа
а
354 ГЛ. IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ [ 146
Дифференцируя это равенство и пользуясь известными свойствами опре-
определенного интеграла (свойство VII) [95}, мы имеем
что и требовалось доказать. Остается доказать равномерную сходимость по-
последовательности sn (х). Имеем
X
sn С*) = sn (а) + $ s'n (х) dx.
а
Последовательность sn (а) сходится и вовсе не содержит х. Последова-
Последовала
тельность ^ s'n (x) dx сходится равномерно в силу свойства 2). Отсюда и вы-
а
текает равномерная сходимость sn (х), так как из определения равномерной
сходимости непосредственно вытекает, что сумма двух равномерно сходящихся
последовательностей есть также равномерно сходящаяся последовательность.
Кроме того, всякая сходящаяся последовательность, члены которой не содер-
содержат х, как, например, sn (а), подходит под определение равномерно сходя-
сходящейся последовательности.
Заметим еще, что мы доказали равномерную сходимость sn (x) во всем
промежутке (а, Ь), используя лишь равномерную сходимость s'n (x) и сходи-
сходимость sn (а), и, следовательно, при формулировке последнего свойства доста-
достаточно потребовать сходимости sn (х) в одной точке х = а. Отсюда, как мы
уже сказали, будет вытекать равномерная сходимость sn (x) во всем проме-
промежутке (я, Ь).
146. Свойства равномерно сходящихся рядов. Если в предыдущих
предложениях мы будем считать sn (x) суммой п первых членов данного
ряда
«1 (*) + «¦(*)+ - +««(*)+ •••>
a s (х) — суммой всего ряда, то непосредственно получим аналогичные пред-
предложения для рядов с переменными членами.
1. Если члены ряда
и, (х) + и2 (х) + .... + ип (х) + ... E5)
непрерывные в промежутке (а, Ь) функции и ряд сходится равномерно,
то и сумма его s (х) есть непрерывная функция в промежутке (а, Ь).
2. Если члены ряда E5) непрерывные в промежутке (а, Ь) функции
и ряд сходится равномерно, то его можно почленно интегрировать между
какими угодно пределами а, р, лежащими в промежутке (а, Ь), т. е.
$ 2 %(*)dx = § J ип (x)dx. E6)
а п = \ л = 1 а
Если пределы интегрирования переменные, например, р = х, то ряд,
который получается почленным интегрированием
XX X
$ и, (х) dx + J и2 (х) dx + ... + 5 М-*) dx + ..., E7)
а а а
также равномерно сходится & промежутке {а, Ь).
147 ] § 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ 355
3. Если ряд E5) сходится в промежутке (я, Ь) а его члены имеют
непрерывные в промежутке (а, Ъ) производные и'^ (х),..., и'п (x)t ..., причем
ряд, составленный из производных
сходится равномерно в промежутке (а, Ь), то и данный ряд сходится
равномерно и его можно дифференцировать почленно, т. е.
п = 1 п= 1
При выводе этих предложений из теорем [145] надо только иметь в виду,
что указанные в предложениях свойства имеют, как мы уже знаем, место
в случае конечного числа слагаемых. Так, например, если члены ряда ип {х)
суть непрерывные функции, то и функции
sn (х) = fli (х) + и2 (х) + ... + ип (х)
непрерывны при любом п [34].
147. Признаки равномерной сходимости. Укажем некоторые достаточ-
достаточные условия равномерной сходимости.
Ряд функций, определенных в промежутке (а, Ь)\
сходится равномерно в промежутке (о, Ь), если выполнено одно из следую-
следующих условий:
(А) Можно найти последовательность положительных постоянных
Mlt М2, ,.., МЯ| ...
таких, что
I «л (х) | ^ Мп в промежутке (а, Ь) E9)
и ряд
М1 + Мш+...+Мя+... F0)
сходящийся (признак Вейерштрасса).
(Б) Функции ип (х) могут быть представлены в виде
ИяИ = здD F1)
где aL, a2y .^, f am .... суть постоянные, такие, что ряд
*! + «•+...+*я+... F2)
сходится; функции же vx (x)} ..., vn (дг),... вс^ неотрицательны, остаются
меньше постоянного положительного числа М и при каждом значении х
в промежутке (а, Ь)\
Vi (x) ^v2 W^m,^^W5...i0^ vn (x) < М F3)
(признак Абеля).
Доказательство (А). Так как ряд F0) сходится, то при данном
е можно найти такое число N, чтобы при всех п > N и при всех р мы
имели [125]:
356 ГЛ. IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ [ 147
в силу же неравенств E9) и
откуда [143] и вытекает равномерная сходимость ряда E5).
Доказательство (Б). Положим
°P = fln+i + fl^+ - +ап+р >=Ь 2, ...),
откуда непосредственно следует
<W = ai и an+k = °'k-°Li
Оценим выражение
W/m (*) + ап+2 (х) + ... + ип+р (х) =
= «л+i^n+i (х) + an+2vn+2 (х) + ... + an+pvn+p (x).
Подставляя вместо an+k их выражения через a'k и собирая члены с оди-
одинаковыми о^, получим
р»я+р (а:) =
+ Vi If л+p-i W - ^n+p Wl + VW
Принимая во внимание, что vn+p (x) и все разности vn+k^(x) —
по условию неотрицательны, можем написать
или, обозначая через о' наибольшее из абсолютных значений |aj|, |о^|,..., |о'|
• + [Vn+p-1 (X) — Vn+p (X)] + Vn+p {X) }
получаем, производя сокращения,
I Un+i (х)+ ...+ ип+р (х) | ^:a'vn+1 (х). F4)
Из определения <s'k и сходимости ряда F2) вытекает, что для любого
заданного положительного е существует такое N, что при п > N и всяком к
мы имеем
1°а1<яэ апотомУи °г<ж-
Принимая во внимание еще, что по условию 0 ^ vn+p (х) ^ М, получаем
в силу F4),
I ВЛ+1 (Х)+ .- + «ц+р W | < •
при п>N и любом р. Так как N не зависит от л:, то отсюда и вытекает
равномерная сходимость ряда E5) в промежутке (a, b).
148 1 § 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ 357
Примеры.
1. Ряды
<б5>
2
/1=1 /1=1
сходятся равномерно во всяком промежутке, так как при всяком х имеем:
иряд2^
cos пх
1 I sin пх
1
пР
при р>1 сходящийся [122] (признак Вейерштрасса).
оо
2. Если ряд ^ ап сходится, то и ряд
/1 = 1
2 Э <вв>
1
2
л-1
равномерно сходится в промежутке (O^x^l) при любом /, так как, поло-
положив здесь
удовлетворим всем условиям признака Абеля.
148. Степенные ряды. Радиус сходимости. Весьма важный пример при-
приложения изложенной выше теории рядов с переменными членами предста-
представляют степенные ряды, т. е. ряды вида:
а0 + atx + а2х* + ... + апх" + ... , F7)
с которыми мы уже встретились при исследовании формулы Маклорена.
Подробное изучение свойств этих рядов относится к теории функций ком-
комплексной переменной, а потому здесь мы укажем только самые основные
свойства.
Первая теорема Абеля. Если степенной ряд F7) сходится при
некотором значении * = ?, то он сходится абсолютно при всех значе-
значениях х, для которых
1*1<|6|. F8)
Наоборот, если он расходится при *==?, то расходится и при всех
значениях х, для которых
1*1>|6|=г. F9)
Пусть сперва ряд
сходится, тогда общий член сходящегося ряда должен стремиться к нулю,
т. е.
агАп—+® ПРИ п-+со,
а иотому можно найти такую постоянную М, чтобы при все* значениях п
мы имели
358 ГЛ. IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ \ 149
Придадим теперь х любое значение, удовлетворяющее условию F8), и
положим
х
4=1 т
Мы имеем, очевидно
\*Л*п\=\*пФ^\ = \*пФ\\%
т. е. общий член ряда F7) при рассматриваемом значении х по абсолютной
величине не превосходит общего члена бесконечно убывающей геометри-
геометрической прогрессии, а потому ряд F7) сходится абсолютно [124].
Вторая часть теоремы очевидна, так как если бы ряд F7) сходился при
некотором значении х, удовлетворяющем условию F9), то по доказанному
сейчас он должен был бы сходиться при всяком ?, для которого | ? | < | х |,
что противоречит условию.
Следствие. Существует вполне определенное число R, которое
называется радиусом сходимости ряда F7) и которое обладает следую-
щими свойствами:
ряд F7) сходится абсолютно при \x\<.R,
ряд F7) расходится при \ х | > R.
В частности, может оказаться, что R = 0, и тогда ряд F7) расходится
при всех значениях х, отличных от нуля, или же R = oot и тогда ряд F7)
сходится при всех значениях х.
Отбросив первый случай, рассмотрим такое положительное значение
x — k, при котором ряд F7) сходится. Такое значение наверное существует,
если, вообще, существуют значения лг^О, при которых ряд F7) сходится.
Если мы будем увеличивать число ?, то могут встретиться лишь два случая:
или все время ряд F7) будет оставаться сходящимся при х = ?, даже когда
? увеличивается беспредельно; тогда мы имеем, очевидно, R = со; или же будет
существовать такое постоянное число Л, которое обладает тем свойством,
что при всех ?<Л ряд F7) сходится, но при ?>Л ряд делается расхо-
расходящимся.
Существование такого числа Л интуитивно-геометрически вполне оче-
очевидно, так как на основании первой теоремы Абеля, если ряд при каком-
нибудь значении & сделается расходящимся, то он будет расходиться и при
всех больших значениях. Строгое доказательство .существования числа А
может быть проведено на основании теории иррациональных чисел. Очевидно,
что это число Л и будет радиусом сходимости R ряда F7).
Проведем доказательство существования R. Разобьем все вещественные
числа на два класса следующим образом: к первому классу отнесем все
отрицательные числа, нуль и такие положительные числа $, что ряд F7)
сходится при | х | = ?, а ко второму классу отнесем все остальные веществен-
вещественные числа. В силу доказанной теоремы любое число первого класса меньше
любого числа второго класса, т. е. мы произвели сечение в области веще-
вещественных чисел, а потому или в первом классе есть наибольшее число или
во втором есть наименьшее число [40]. Нетрудно видеть, что это число и
будет радиусом сходимости R ряда. Если все числа попадут в первый класс,
то надо считать R = cq,
149. Вторая теорема Абеля. Если R есть радиус сходимости ряда
F7), то ряд сходится не только абсолютно, но и равномерно в любом
промежутке (а, Ь), лежащем целиком внутри промежутка (~-Rt -f- R),
т. е* для которого
149 1 § 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ 359
Если же ряд сходится и при х = R или х = — R} то он будет равно-
равномерно сходящимся и в промежутке (я, R) или (— R, Ь).
Заметим, прежде всего, что, не нарушая общности, мы можем считать
/?=1, введя вместо х новую независимую переменную t по формуле
после чего ряд F7) превратится в степенной ряд относительно переменной t,
а промежуток (—R, -\- R) перейдет в (—1, 1).
Если /?= 1, то, по определению радиуса сходимости, ряд F7) будет схо-
сходиться абсолютно при всяком значении лг = ?, для которого |?|<cl. Рассмо-
Рассмотрим теперь любой промежуток (а, #), лежащий внутри (— R, R), так что
— 1 <а<Ь<\.
Выберем за ? любое число, лежащее внутри (— 1, 1), но по абсолютному
значению большее | а | и \Ь\. При всяком х в промежутке (а, Ь) имеем
и так как ряд
сходится абсолютно и члены его не зависят от х, то по признаку Вейер-
штрасса ряд F7) сходится равномерно в промежутке (а, Ь).
Допустим теперь, что ряд F7) сходится и при лг=1, т. е. что ряд
ао + ai + а2 + • • • + ап + • ••
сходится. Полагая
vn(x)=xn,
мы можем применить к ряду F7) признак Абеля, который покажет, что ряд
F7) будет равномерно сходиться во всем промежутке (а, 1), где а — любое
число, большее — 1.
Случай, когда ряд F7) сходится при х = —1, приводится к предыду-
предыдущему, если заменить х на (—х).
Обозначим через f (х) сумму ряда F7). Она существует, конечно, лишь
при тех значениях х, при которых ряд сходится. Пусть R — радиус сходи-
сходимости ряда. Принимая во внимание равномерную сходимость ряда во всяком
промежутке (а, Ь), для которого
— R<a<b<R, G0)
и свойство 1) из [146], можем утверждать, что сумма ряда f(x) есть
непрерывная функция во всяком из указанных промежутков (а, Ь). Иначе
говорят, что f(x) непрерывна внутри промежутка (— /?, -{-R). Дальше
мы увидим, что эта функция имеет сколько угодно производных внутри
промежутка (— R, + Я)- Если ряд F7) сходится и при х = R, то в силу
доказанной равномерной сходимости во всяком промежутке (a, R)} где
а> — Rtf(x) будет непрерывной функцией в этом промежутке, и, в част-
частности, f(R) будет пределом f(x) при стремлении х к R слева [35]:
/¦(/?)= lim /(*). G1)
X-+R-0
Аналогично при сходимости ряда для х = — R.
Выше мы видели, что разложение бинома Ньютона [131]
/1 i ч»« 1 I тп , ш (т — I) о I
о+*>"•«= i+-jt ¦* i—Tj—-х + -
360 ГЛ. IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ [ 150
^имеет радиус сходимости /?=1 ив некоторых случаях сходится при х = ± 1^
В силу только что доказанного можно утверждать, что если, например, ряд*
сходится при jc = 1, то его сумма при этом равна
lim
150. Дифференцирование и интегрирование степенного ряда. Пусть
— радиус сходимости ряда
* +. + апх* + ... G2)
а0
а2х*
Интегрируя его почленно от 0 до л: и дифференцируя его, мы получим два
других степенных ряда
^х*+...+^1х"+> + ... G3)
2 + ... + папхп~х +... G4)
Покажем, что они имеют тот же радиус сходимости R. Для этого надо
показать, что они сходятся, если | х | < R, и расходятся, если | х | > /?.
По доказанному, ряд G2) сходится равномерно во всяком промежутке
(—#i> +#i)i r^e 0<7?!<^, ив силу свойства 2) из [146] его можно в этом
промежутке интегрировать почленно от 0 до х, т. е. можно утверждать, что
ряд G3) сходится при любом х, для которого | х | < Rt и что при этом сумма
ряда G3) равна
$
где f(x) — сумма ряда G2). Покажем теперь, что и ряд G4) сходится, если
| л: < R. Возьмем такое х> выберем какое-нибудь число ?, лежащее между
I* и R> т. е.
|*|<6</?, G5)
и положим
Для членов ряда G4) получаем оценку
и, в силу предыдущего,
*»-» 1
Применяя к ряду
он сходится при 0
п~х признак Даламбера, нетрудно показать, что
и, следовательно [119],
щп-i __ о при п -+ со, G6)
а. потому, при всех достаточно больших п:
Но в силу G5), ряд 2 ufff1 сходится абсолютно, а потому и ряд G4) схо-
сходится абсолютно при взятом значении х. Итак, оба ряда G3) и G4) сходятся,
если | х | < R} т. е. при почленном интегрировании и дифференцировании
150 1 § 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ 361
степенного ряда его радиус сходимости не может уменьшиться. Но отсюда
непосредственно следует, что он не может и увеличиться. Действительно,
если бы, например, радиус сходимости ряда G3) был R\ причем Rr > R, то
при дифференцировании ряда G3) мы получили бы ряд G2), и его радиус
сходимости должен быть не меньше R', а по условию он равен Ry причем
R < R'. Итак, ряды G3) и G4) имеют тот же радиус сходимости, что и ряд
G2). Дифференцируя ряд G4) еще раз, получим, в силу доказанного выше,
степенной ряд
2а2 + 3. 2asx + 4 . Sa4x2 +... + п (п — 1) апхп~2 +...
с тем же радиусом сходимости R и т. д. То же будем иметь и при повтор-
повторном почленном интегрировании ряда G3) от 0 до х. Все полученные от
почленного дифференцирования и от почленного интегрирования от 0 до х
ряды равномерно сходятся во всяком промежутке (я, b), удовлетворяющем
условию G0). Вспоминая свойства 1), 2) и 3) из [146], можем сформулиро-
сформулировать следующий результат.
Сумма степенного ряда
ао + а1х + а2х* + ... + апхп + ... , G7)
радиус сходимости которого есть R, есть непрерывная внутри промежутка
(— R, + R), т. е. при — R < х < + R, функция, имеющая внутри этого
промежутка производные всех порядков. Эти производные могут быть
получены почленным дифференцированием ряда G7). Последовательное
почленное интегрирование от 0 до х при — R < х < -J- R также может
производиться почленным интегрированием ряда G7). Почленное диффе-
дифференцирование и интегрирование степенного ряда не меняют его радиуса
сходимости.
Отметим, что промежуток (—R, -J- R) может быть и открытым промежут-
промежутком (—оо, +°°)> т- е. все сказанное справедливо и для того случая, когда
радиус сходимости ряда G7) равен бесконечности.
Полагая
мы получаем, таким образом,
/' (х) = ах + 2а,
/<*>(*) =/г! я„ЧЧ"+ 1)л...3-2ял+1 * + ...,
откуда следует при х = 0,
Подставив эти выражения для я0, av a2> ..., ап в G8), получим
т. е. степенной ряд совпадает с разложением своей суммы по формуле
Маклорена.
Изложенная теория степенных рядов распространяется без труда на
степенные ряды вида
<*о + ai (х - а) + о2 {х- а)* + ... + ап (х-а)" +... G9)
362 ГЛ. IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЁННЫМ ВЫЧИСЛЕНИЯМ \ 150
Везде роль х будет играть разность (х— а). Радиус сходимости Д ряда
G9) определяется из того условия, что ряд сходится при \х — а \ <. R и рас-
расходится при | х — а | > R. Если обозначить через/(л:) сумму ряда G9) в про-
промежутке
(80)
то для коэффициентов ап получаем выражение
т. е. ряд G9) в промежутке (80) совпадает с разложением своей суммы
в ряд Тейлора.
Мы вернемся еще к теории степенных рядов в третьем томе при изло-
изложении теории функций комплексной переменной.
В качестве примера предлагается вывести из теории степенных рядов
разложения функций log (l-f-лг), arctgx, arc sin л:, заметив, что
X
dx
X
С dx
arc sin x = l
— Г2
и исследовать область применимости полученных разложений.
ГЛАВА V
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
§ 15. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ
151. Основные понятия. В § б главы II, посвященном функциям
двух переменных, мы начали с изложения основных понятий, касаю-
касающихся таких функций. Сейчас мы будем говорить о функциях многих
переменных и, кроме того, более подробно остановимся на понятии
предела.
Функцию f(x, у) мы считаем определенной или на всей плоско-
плоскости или в некоторой области. Таким образом, всякой точке (х, у)
из этой области соответствует определенное значение f(x, у). Если
рассматриваются только внутренние точки области, то такая область
называется открытой. Если к области причисляется ее контур, то
область называется замкнутой.
Аналогичным образом, если ввести прямолинейную, прямоуголь-
прямоугольную систему координат OX, OY, OZ в пространстве, то, вместо
тройки чисел (х, у, z) мы можем говорить о точке М пространства
с координатами (х, у, z). Будем считать, что функция f(x> у, z)
определена во всем пространстве или в некоторой области простран-
пространства, которая может быть открытой или замкнутой. В наиболее про-
простых случаях границами области (их может быть и несколько) бу-
будут некоторые поверхности. Так, например, неравенства
определяют замкнутый прямоугольный параллелепипед, ребра кото-
которого параллельны координатным осям. Неравенства
определяют открытый параллелепипед. Неравенство
определяет замкнутую сферу с центром (а, Ь, с) и радиусом г. Если
исключить знак равенства и оставить только знак <^, то получится
364 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ I 151
открытая сфера. Понятие предела и непрерывности для функции
трех переменных определяют совершенно так же, как и [67] для
двух переменных.
Для функций f(xb х2> ..., хп) многих переменных при я>3
уже теряется геометрическая наглядность пространства, однако и
в этом случае часто сохраняют геометрическую терминологию. По-
Последовательность п вещественных чисел (хь хь ..., хп) называют
точкой. Множество всех точек образует я-мерное пространство.
Области такого пространства определяются неравенствами. Так, на-
например, неравенства
сг ^ хх ^ db c2^x2^d2i . •., сп ^ хп ^ dm
определяют я-мерный параллелепипед или, как иногда говорят, «-мер-
«-мерный промежуток. Неравенство
определяет я-мерный шар. Окрестностью точки (аь аь ..., ап)
называется множество точек, определенных последним неравен-
неравенством при некотором выборе г или неравенствами \xk — ak\^p
(k=l, 2, ..., п\ где р —некоторое положительное число.
Если функция f(xLt x2, .... хп) определена в окрестности точ-
точки (аь а2, ..., ап), то говорят, что f{xb x2> ..., хп) стремится
к пределу А при стремлении точки М(хь х2, •.., хп) к точке
М0(аь а2) ..., ап\ и пишут
lim f(xb x2i ..., хп) = А или lim f(xb x2> ..., хп) — А,
если для любого заданного положительного числа 8 существует та-
такое положительное т), что |Л—f(xlt x2t ..., ^я)|<;в, если толь-
только \о>ъ — Хь\<ч\ при k = 1, 2, ..., п, причем считается, что
точка М(хь х2У ..., хп) не совпадает с М0(аь а2, ..., ап). Если
f(xv х2У ..., хп) определена и в точке М0(аь а2, ..•, ап\ то не-
непрерывность в этой точке определяется равенством [ср. 67]:
lim f(xv x2> ..., xn)=f(ai9 a2, ..., ал).
Справедливы указанные в [67] свойства функции, непрерывной
в замкнутой области.
Как в случае функции одного переменного [34], справедливы
утверждения о непрерывности суммы, произведения и частного не-
непрерывных функций. Последнее —в том случае, когда знаменатель
отличен от нуля в точке (аь а2, ..., ап).
152 ] § 15. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ 365
152. О предельном переходе. Остановимся более подробно на понятии
предела, ограничиваясь случаем функции двух переменных. Если существует
предел
lim/(x, у) = Л, A)
х-* а
у-+Ь
то будем говорить, что существует предел по обеим переменным. Как мы
знаем [67], это значит, что /(х, у) стремится к пределу А при любом законе
стремления точки М (х, у) к Мо (at b). В частности
lim f(xyb) = A и lim / (а, у) = Л. B)
х -+а у->Ь
В первом случае М (х, у) стремится к Мо (а, Ь) по прямой, параллельной
оси ОХ, а во втором случае — по прямой, параллельной оси OY. Отметим,
что из существования пределов B) и их равенства еще не вытекает суще-
существование предела A). В качестве примера рассмотрим функцию
и положим 0 = 0 и Ь = 0. Мы имеем
lim/(x, 0)= lira х<0 == lim 0 = 0 и lim
*-><) лг-0 Х2+02 аг-0 V-0
у
а предел A) в этом случае не существует. Действительно, полагая — = tg в,
можем переписать нашу функцию в виде
/ (л:, у) = , = *»а = sin a COS а. C)
\ «^ л:2+у2 1 +tg2a v '
Если точка М (х, зО стремится к М @, 0) по прямой, проходящей через
начало и образующей угол а0 с осью ОХ, то /(х, >>), выражаемая формулой
C), остается постоянной, и ее величина зависит от выбора а0, откуда и сле-
следует, что предел A) не существует в рассматриваемом примере. Отметим,
что формула C) не определяет функцию в самой точке М @, 0).
Кроме предельного перехода A), можно рассматривать еще повторные
пределы, соответствующие предельному переходу сначала по х при постоян-
постоянном у% отличном от Ь, а затем по у, или наоборот:
lim [lim/(x, у)] или lim [lim f(xt у)]. D)
х-*ay-*b у-* b x -*a
Может оказаться, что оба повторных предела существуют, но различны. Так,
например, для функции
мы имеем, как нетрудно проверить,
lim [lim f(x, y)] = l, lim [lim /(x, у)] ==— 1.
Но имеет место
Теорема. Если существует предел по обеим переменным A), и при
всяком х, достаточно близком к а и отличном от а, существует предел
lim
366 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ I 152
то существует первый повторный предел D) и он равен А, т. е.
Km ?(x)=A F)
х-*а
Из существования предела A) следует [67], что для любого заданного
положительного е существует такое положительное yj, что
И—/(*.301<* ПРИ I* — *1<Ч и \у — b\<tl, G)
причем (л:, у) не совпадает с (а, Ь). Фиксируем л:, отличное от а, так, чтобы
иметь \х—я|<7). Принимая во внимание E) и переходя в неравенстве G)
к пределу по у, получим
\А — ср (х) | ^ е при \х — д|<т] и хфа,
откуда, ввиду произвольности е, следует равенство (б).
Замечание. Совершенно так же, если мы предположим, что суще-
существует предел A) и что при всяком у, достаточно близком к Ъ и отличном
от Ь, существует предел
Ит/(лг,.у) —«Ь60>
х-*а
то существует второй повторный предел D) и он равен А, т. е.
Нтф(у) = А
Если предел A) существует и равен f(a, b), т. е. A—f(a, b), то функ-
функция f(x, у) непрерывна в точке (я, Ь) или, как говорят, непрерывна по обеим
переменным в точке (а, Ь). При этом, в силу B),
lim f(x, b)=f(a, b), lim f(a, y)=f(a, b),
x-+a у -+ b
т. е. функция непрерывна по каждой переменной в отдельности в точке
(а, Ъ), о чем мы говорили и раньше [67]. Наоборот, из непрерывности по
каждой переменной еще не вытекает непрерывности по обеим переменным.
Действительно, определим функцию формулой C) вне начала координат и по-
положим /@, 0) = 0. Как мы упоминали выше, мы имеем при этом
/(x, 0)=0 и lim
лг-ч.0 у-*0
т. е. функция непрерывна по каждой1 переменной в точке @, 0). Но она не
является непрерывной по обеим переменным, ибо, как мы видели, не суще-
существует определенного предела f(x, у) при стремлении М (х, у) к Мо @, 0).
Если /(л:, у) имеет в некоторой области, содержащей точку (л:,у) внутри
себя, частные производные, то, как мы показали [68], имеет место формула
/(* + Д*, У + АУ) —/(*, У) =f'x (х + Uxy у + Ay) Ал: +/у (дг, у + ОхД.у) Д^
(о.<е и е1<1).
Положим, что частные производные ограничены в упомянутой области, т. е.
по абсолютной величине не превышают некоторого числа М. При этом на-
написанная формула дает
|/(* + Алг, у + Ау) —/(а:, у
и правая часть этого неравенства стремится к нулю при Дл:-»0 и Ду-^О,
откуда следует
lim f(x + Ax,y + Ay) =/ (*, у),
Lx ~* 0
Ay -¦ 0
153 1 $ 15. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ 367
т. е. если f(x, у) имеет внутри некоторой области ограниченные частные
производные, то она непрерывна внутри этой области.
Функция C) при дополнительном соотношении /@, 0)=»0 равна нулю
на всей оси ОХ и на всей оси OY и в точке Мо (О, 0) она имеет, очевидно,
частные производные, равные нулю. В остальных точках она также имеег
частные производные:
, , у* — х2у , . хъ — ху%
т. е. указанная выше функция имеет частные производные на всей плоскости.
Все же она, как мы видели, не обладает непрерывностью в точке @, 0). Это
объясняется тем, что частные производные могут принимать сколь угодно
большие по абсолютной величине значения при приближении точки (лг, у)
к началу координат.
153. Частные производные и полный дифференциал первого
порядка. В [68] мы ввели понятие о частных производных и полном
дифференциале функции двух переменных. Эти понятия могут быть
распространены и на случай функции любого числа переменных*
Для примера рассмотрим функцию четырех переменных
w=f(x, у, zy t).
Частной производной от этой функции по х называется предел
1. f(x + h,y, г, t)—f(x, у, *, t)
А-±0 h
если он существует, и для обозначения этой частной производной
употребляют символы
Г,(х. у, z, 0, или д'1* * *' *>, или g.
Аналогично определяются частные производные и по другим пере-
переменным.
Полным дифференциалом функции называется сумма ее частных
дифференциалов:
где dx, dy, dzy dt — дифференциалы независимых переменных (про-
(произвольные величины, не зависящие от х, у, z, t).
Дифференциал есть главная часть приращения функции:
&w=f(x-\-dx> y-\-dyr z-\-dz> t-\-dt) — f(x, у, z, t%
а именно (ср. [68]):
где е1э е2, ез, е4 стремятся к нулю, если dx, dy, dz, dt стремятся
к нулю, причем предполагается, что функция w имеет непрерывные
368 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ \ 153
частные производные внутри некоторой области, содержащей точку
(лг, у, z> t) внутри себя.
Точно так же может быть обобщено и правило дифференци-
дифференцирования сложных функций. Предположим, например, что лг, у и z
суть не независимые переменные, но функции независимой перемен-
переменной L Функция w будет в этом случае зависеть от t как непосред-
непосредственно, так и через посредство х, у, г, и полная производная
от w no t будет иметь выражение
dw dw , dw dx , dw dy , dw dz
Мы не останавливаемся на доказательстве этого правила, так
как оно состоит в буквальном повторении того, что мы говорили
в [69]. Если переменные х, у, z зависят, кроме t, и от других
независимых переменных, то в правой части формулы (8) мы должны
dx dy dz дх ду dz
вместо -гг. -?, -7т писать частные производные -^г, ^г, т-.
at at at Ot at dt
В этом случае и функция w будет, кроме t, зависеть и от других
независимых переменных, и в левой части равенства (8) мы также
dw dw , т
должны -тт заменить на ^-. Но эта последняя частная производ-
dw
ная отлична от частной производной -^-, стоящей в правой части
равенства (8) и вычисленной лишь поскольку w непосредственно
зависит от (; для отличия эту частную производную, вычисленную
непосредственно по t, заключают иногда в скобки, так что равен-
равенство (8) принимает в рассматриваемом случае вид
dw fdw\ , dw dx . dw dy , dw dz Q
В случае функции от одной переменной, мы видели, что выра-
выражение ее первого дифференциала не зависит от выбора независи-
независимой переменной [50]. Покажем, что это свойство остается спра-
справедливым и в случае функции от нескольких переменных.
Рассмотрим для определенности случай функции от двух пере-
переменных
2 = ср(л:, у).
Положим, что х и у суть функции независимых переменных и и v.
Согласно правилу дифференцирования сложных функций, имеем
cte dz^dx \dz_dy. ^Jl дг дх . dzdy
du дх да * ду ди' dv дх dv ' ду dv*
Полный дифференциал функции по определению равен
. dz , , dz ,
dzdu+dv
154 ] § 15. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ 369
Подставляя выражения частных производных, получим
, dz (дх , , дх , \ , дг (ду » , ду , \
дх \ди • dv 1 1 ду\ди • dv j
Но выражения, стоящие в круглых скобках, суть полные диффе-
дифференциалы х и уу и мы можем написать
, dz . , dz ,
dzdx + dy
т. е. дифференциал сложной функции имеет то же выражение, ко-
торое он имел бы, если бы х, у были независимыми переменными.
Свойство это позволяет распространить правило нахождения
дифференциала суммы, произведения и частного на случай функции
от нескольких переменных:
где и и v — функции нескольких независимых переменных. Действи-
Действительно, пользуясь доказанным свойством, мы можем, например,
написать
d (uv) = v^ du -j—j-L dv = vdu-\-u dv.
154. Однородные функции. Дадим определение однородной функ-
функции нескольких переменных: функция нескольких переменных назы-
называется однородной функцией этих переменных степени т, если
при умножении этих переменных на произвольную величину t
функция умножается на tm, т. е. имеет место тождество
f(tx, ty) = tmf(x, у) или f(tx, tyt tz) = tmf(x, уу z) A0)
при любых допустимых значениях переменных х, у, z, t. Число т
может быть любым фиксированным вещественным числом. Если, на-
например, m = -j> T0 tm= \ft и t должны быть положительными. По-
Положим, что функция f(x, у) выражает некоторый объем, что х и у
суть длины некоторых линий и что в выражении f(x, y\ кроме этих
линий, входят отвлеченные числа. Умножение х и у на t (положи-
(положительное число) равносильно уменьшению линейного масштаба в t раз
(при t^>\ или увеличению при ?<М), и, очевидно, что при этом
функция f(x, y)t выражающая объем, должна умножаться на t\ т. е.
в рассматриваемом случае функция f(x, у) будет однородной функ-
функцией третьей степени. Так, например, объем конуса выражается через
радиус его основания х и высоту у по формуле v — -rr ъх*у. Эта
370 гл. v. функции нескольких переменных [ 154
функция будет однородной третьей степени при всех вещественных
х, у и t. Такой же функцией будет и любой однородный многочлен
от х и у третьей степени, т. е. такой многочлен, в каждом члене
которого сумма показателей х и у равна трем:
/(*, j/) = ах* -f bx*y -f сху* + dy\
Дроби
г \г ху
+ у21 х2+у2> х2+у2
суть однородные функции степеней соответственно 1, 0 и (— 1).
Отметим, что /(х, у)= j/rx*-{-y\ где радикал считается арифметиче-
арифметическим, будет однородной функцией первой степени при всех веще-
вещественных х и у и при всех t^>0. Действительно,
причем оба радикала считаются положительными.
Дифференцируя тождество A0) по t и применяя правило диффе-
дифференцирования сложной функции, получим, полагая u = tx и v — ty:
xfa(u, v)+yfv(tt, v) = mtm-lf(x, у).
Полагая t = 1, находим
xfx (х} у) +у/у (х, у) = mf (х, у), A1)
что выражает следующую теорему Эйлера, об однородных
функциях:
Сумма произведений частных производных однородной функции
на соответствующие переменные равна произведению самой этой
функции на степень ее однородности.
При доказательстве мы считаем естественно, что функция f(x> у)
имеет непрерывные частные производные при соответствующих зна-
значениях переменных, которыми мы пользовались при доказательстве.
Если т = 0, то, положив в тождестве A0) t = —, мы получим
X
/(*, j/)=/(l, ?) или f(x, у, *)=/(l, ?, |),
т. е. однородная функция нулевой степени есть функция отноше-
отношения всех переменных, кроме одной, к этой последней переменной.
Часто однородную функцию нулевого измерения называют просто
однородной*
155 ] § 15. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ 371
155. Частные производные высших порядков. Частные произ-
производные функции от нескольких переменных суть в свою очередь
функции тех же переменных, и мы можем определить их частные
производные. Таким образом мы получим частные производные вто-
второго порядка первоначальной функции, которые также будут функ-
функциями тех же переменных, и их дифференцирование приведет к част-
частным производным третьего порядка первоначальной функции, и т. д.
Так, например, в случае функции u=f(x, у) от двух переменных,
«1 ди ди
дифференцируя каждую из частных производных ^- и j~ еще раз по
х и уу получим четыре производные второго порядка, которые обо-
обозначаются так:
fxs(X> У)> fxy(X, у), fyX(X, у), />(Х, у),
ИЛИ
d2f(x, у) d*f(x,y) d2f(x, у) d2f(x, у)
дх2 ' дхду > дудх ' ду2 '
или, наконец,
д2и д2и д2а д2а
дх27 дхду ' дудх * Ъу2*
Производные /хУ(х, у) и /уХ(х, у) отличаются лишь порядком
дифференцирования. В первом случае дифференцирование произво-
производится сначала по х и потом по у, а во втором случае — в обрат-
обратном порядке. Покажем, что эти две производные тождественны
между собою, т. е. что результат дифференцирования не зависит
от порядка дифференцирования.
Составим выражение
со =/(* + *, y + k)— f(x + h, у)—fix, y + k)-\-f(x,y).
Полагая
> У) =f(x + К У) —/to У\
можем написать выражение о) в виде
со = [/(х + Л, yJrk)-f(x, y + k)]-[f(x + h, y)-f(x, у)} =
==<pto у + ь) — ?to у)-
Применяя два раза формулу Лагранжа [63], получим
Буквы 0 с различными значками означают числа, лежащие между О
и 1. Знаком fy (x-\-h, y-\-$ik) мы обозначаем частную производную
функции f(x, у) по ее второму аргументу у} когда туда вместо х
и у подставлены, соответственно, x--\-h и y-\-Qik. Аналогичные
обозначения применяются и для других частных производных.
372 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ'ПЕРЕМЕННЫХ [ 155
Точно так же, полагая
/ -/(*, У),
можем написать
й, у) —
= А [Л (* + 8.А, у + k) — fx(x + евй, .у)] = ААД, (JC + 88А,
Сравнивая оба выражения, полученных для со, будем иметь
или
Предполагая непрерывность написанных производных второго порядка
и устремляя h и к к нулю, получим
/?*(*> У)=/ху(х> У).
Это рассуждение приводит к следующей теореме.
Теорема. Если f(x, у) имеет внутри некоторой области
непрерывные производные f"yx(x, у) и f"xv(x, у), то во всех точ-
точках внутри упомянутой области указанные производные равны.
Рассмотрим теперь две производные третьего порядка
fxiy(X, У) И fyx»(X9 у),
отличающиеся лишь порядком дифференцирования. Принимая во
внимание, что по доказанному результат двукратного дифференци-
дифференцирования не зависит от порядка дифференцирования, можем написать
Гх*у(х, У) — -^Г^—— дудх —Тхух{х, у) =
= fyxx(X, у)=/'ух2(х, у),
т. е. и в этом случае результат дифференцирования не зависит от
порядка дифференцирования. Это свойство без труда обобщается на
производные любого порядка и на случай функции любого числа
переменных, и мы можем высказать общую теорему: результат
дифференцирования не зависит от порядка, в котором произво-
производится дифференцирование.
Заметим, что при доказательстве мы пользовались не только
существованием производных, но и их непрерывностью внутри
некоторой области.
В дальнейшем мы будем всегда предполагать непрерывность про-
производных, о которых мы будем говорить, и в силу доказанной теоремы
для производных высших порядков надо лишь указывать порядок
производной п, те переменные, по которым производится дифферен-
дифференцирование, и число дифференцирований по каждой переменной.
156 | § 15. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ 373
Так, например, в случае функции w—f(x, у, z, f), пользуются
следующим обозначением:
dnf (xt у, г, Л
которое показывает, что взята производная п-то порядка, причем
дифференцирование произведено а раз по х, Р раз по у, у раз по
^ и 8 раз по L
156. Дифференциалы высших порядков. Полный дифференциал
du функции от нескольких переменных есть в свою очередь функ-
функция тех же переменных, и мы можем определить полный дифферен-
дифференциал этой последней функции. Таким образом мы получим дифферен-
дифференциал второго порядка d2u первоначальной функции и, который также
будет функцией тех же переменных, а его' полный дифференциал
приведет нас к дифференциалу третьего порядка d3u первоначальной
функции и т. д.
Рассмотрим подробнее случай функции u = f(x, у) двух пере-
переменных х и у и будем предполагать, что переменные х и у суть
независимые переменные. По определению
ЩЛ Я^Иу, A2)
При вычислении d2u будем принимать во внимание, что диффе-
дифференциалы dx и dy независимых переменных надо рассматривать как
величины постоянные, а потому их можно выносить за знак диффе-
дифференциала
Вычисляя точно так же dsu, мы получим
Эти выражения d2u и d3u приводят нас к следующей символи-
символической формуле для дифференциала любого порядка:
)/. A3)
374 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ 156
причем формулу эту надо понимать так: сумму, стоящую в круглых
скобках, надо возвысить в степень п, применяя формулу бинома
Ньютона; после чего показатели степеней у у- иг надо считать
J ох ду
указателями порядка производных по х и у от функции /.
Мы убедились в справедливости формулы A3) при #, равном
1, 2 и 3. Для полного ее доказательства необходимо применить
обычный способ доказательства от п к (п + 1). Положим, что фор-
формула A3) справедлива при некотором п. Определим дифференциал
(п-{- 1)-го порядка:
где символом
мы обозначаем, вообще:
Принимая во внимание, что для dnu формула A3) считается до-
доказанной, можем написать
т. е. формула доказана и для dnJrX w.
Формула A3) обобщается без труда и на случай функции лю-
любого числа независимых переменных. Формула A3) справедлива, как
мы знаем [153], не только в том случае, когда х и у суть незави-
независимые переменные. Но при выводе выражения dhi существенным
было считать dx и dy величинами постоянными, и формула A3)
справедлива лишь в тех случаях, когда dx и dy могут считаться
постоянными.
Это будет справедливо, если хну суть независимые переменные.
Положим теперь, что х и у суть линейные функции независимых пе-
переменных z и t:
x = az-{- bt-\-c, у = axz -f- bxt -\- cb
me коэффициенты и свободные члены — постоянные. Для dx и dy
получим выражения
dx = a dz -f- b dty dy = aldz-\- bx dt.
Ho dz и dt, как дифференциалы независимых переменных, должны
считаться постоянными; то же можно сказать, следовательно, в этом
случае и относительно dx и dy; мы можем поэтому утверждать,
157 | § 15. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ 375
что символическая формула A3) справедлива как в случае, когда
х и у суть независимые переменные, так и в том случае, когда
они суть линейные функции (целые многочлены первой степени)
независимых переменных.
Если dx и dy нельзя считать постоянными, то формула A3) уже
не будет справедливой. Разберем выражение dru в этом общем слу-
случае. При вычислении
мы уже не имеем права выносить dx и dy за знак дифференциала,
как это делали выше, но должны применять формулу для диффе-
дифференциала произведения [153].
Мы получим, таким образом,
Сумма первых двух слагаемых в правой части этого равенства
даст нам выражение, которое мы имели выше для d'hi, и оконча-
окончательно получим
+ Ш?.*х + &<%Я-*у. A4)
т. е. в рассматриваемом общем случае выражение для d-и будет
содержать добавочные слагаемые, зависящие от d*x и d2y.
157, Неявные функции. Укажем сейчас правила дифференциро-
дифференцирования функций, заданных неявно. При этом мы будем предполагать,
что написанные уравнения действительно определяют некоторую функ-
функцию, имеющую соответствующие производные. В [159] при некото-
некоторых условиях мы докажем это. Если у есть неявная функция от х:
F(x, у) = 0, A5)
то первая производная / этой функции определяется, как мы знаем,
из уравнения [69]:
Fx{x, y) + Fy(x, у)у' = Ъ. A6)
Уравнение A6) мы получали, предполагая в равенстве A5) у
функцией от х и дифференцируя обе части этого тождества по х.
Поступая так же с A6), получим уравнение для определения второй
производной у"\
F** (*i У) + 2/^j, {х9 у) у + /> (*, у)у'* + Fy (х, у) у" = 0. A7)
376 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ ] 157
Дифференцируя еще раз по лг, получим уравнение для определе-
определения третьей производной у'" и т. д.
Обратим внимание на то, что в получаемых таким образом
уравнениях коэффициент при искомых производных неявной функции
будет один и тот же, а именно F'y(x, у), и потому, если при неко-
некоторых значениях х и у, удовлетворяющих уравнению A5), этот
коэффициент отличен от нуля, то при этих значениях указанный
выше прием даст вполне определенные значения для производных
любого порядка неявной функции. При этом, конечно, предпола-
предполагается существование частных производных от левой части уравне-
уравнения A5).
Рассмотрим уравнение с тремя переменными
Ф(*, У> z) = 0.
Такое уравнение определяет z как неявную функцию от независи-
независимых переменных х и у, и если заменить в левой части этого урав-
уравнения z именно этой функцией от х и у, то левая часть уравнения
станет равна тождественно нулю. Таким образом, дифференцируя
левую часть этого уравнения по независимым переменным х и у
в предположении, что z есть функция от них, мы должны получить
нуль:
Ф'х(х> У> г) + ФИх, у, z)zx = 0,
Ф'у(х, у, г)-\-Фг{х, у, z)zy = 0.
Из этих уравнений определятся частные производные первого
порядка z'x и Zy. Дифференцируя первое из написанных соотноше-
соотношений еще раз по хг получим уравнение для определения частной про-
производной Zx2 и т. д. Во всех получаемых уравнениях коэффициент
при искомой производной будет Ф'г(х, у, z). Рассмотрим теперь си-
систему уравнений
<р(лг, у, 2) = 0, ф(х, у, г) = 0. A7J
Будем считать, что эта система определяет у и z как неявные функ-
функции от х. Дифференцируя оба уравнения системы по х в предполо-
предположении, что у и z суть функции от ху получим систему уравнений
первой степени для определения производных у' и г от у и z по х:
<?'х(х, у, *) + ъ(х, у, *)•/ + ?*(*> У> z)-/ = 0,
<!>*(•*> У» <г) + <|>И*> У> 2)-у' + фИ*> у, г)./ = 0.
Дифференцируя эти соотношения еще раз по х, получим систему
уравнений для определения вторых производных у" и z". Диффе-
Дифференцируя еще раз по х, получим систему уравнений для определения
у'" и аГ и т. д.
158 j § 15. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ 377
Производные п-го порядка у(л) и 2(л) будут при этом опреде-
определяться из системы вида:
У> *)-/я) + ?;С*. У> z).z(n) + A = 0,
у, г)-у(л) + фИ*> у, z)*z{n)+B = 0,
где А и В — выражения, содержащие производные порядка ниже п.
Такая система, как это известно из элементарной алгебры, будет
давать одно определенное решение, если выполнено условие:
<?'у(х, У> г)-$'г(х, у> z) — <?'g(x, у, г)-$'у(х9 у, г)фО.
При всех тех значениях х, у и z, удовлетворяющих системе A7Д
при которых это условие выполнено, описанный выше прием при-
приведет к вполне определенным значениям производных.
Если имеется система т уравнений с (т-\-п) переменными, то
такая система определяет, вообще говоря, т переменных как неяв-
неявные функции остальных п переменных, и производные этих неявных
функций могут быть получены указанным выше приемом последова-
последовательного дифференцирования уравнений по независимым переменным.
158. Пример. Рассмотрим- в качестве примера уравнение
ax2 + by2 + cz2 = \, A8)
которое определяет г как функцию от х ъ у. Дифференцируя по х, получим
ах + сг-г'х*=0, A9)
и точно так же, дифференцируя по у, получим
откуда
*> _ ах „' _ ЬУ
х cz У cz
Дифференцируя соотношение A9) по х и по у, а соотношение A9г) по^у,
получим
а + cz'J + С2 2J2 = 0, cz'xz'y + С2 2^ = 0, b + ^^2 + С? ^2 = 0,
откуда
a A- cz'J* • />2«.2 л/1?2 д. л2 v2
cz cz
gjggv q^a:^
z
z* *
ь +
CZ
Покажем теперь другой способ вычисления частных производных, осно-
основанный на применении выражения полного дифференциала функции. Дока-
Докажем предварительно вспомогательную теорему. Пусть нам удалось каким-
нибудь образом получить выражение полного дифференциала dz функции
378 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ I 158
двух независимых переменных х и у в виде
dz = р dx -(- q dy.
С другой стороны, мы знаем, что
dz = z'xdx + z'v dy.
Сравнивая эти два выражения, получим
'y dy.
Но dx и dy, как дифференциалы независимых переменных, суть вели-
величины произвольные. Полагая dx = l и dy=0 или dx = 0 и dy = \, полу-
получим
/> = *; и q = Zy
Итак, если полный дифференциал функции z двух независимых пере-
переменных х и у может быть представлен в виде
dz=p dx + q dy,
то р = z'x и q = z'y.
Теорема эта справедлива и для функции любого числа независимых
переменных. Совершенно так же можно показать, что если дифференциал
второго порядка может быть представлен в виде
d2z = rdx2 + 2s dxdy + t dy2,
mo r = zx2} s = zxy и t = z"y%.
Вернемся теперь к рассмотренному примеру. Вместо того, чтобы опре-
определять производные левой части соотношения A8) по х и у, определим ее
дифференциал, помня, что выражение первого дифференциала не зависит от
выбора независимых переменных [153]:
ах dx -\-bydy-\- cz dz = 0, B0)
откуда
_, ах . Ьу ,
dz = dx dy.
cz cz J
и, следовательно, в силу доказанной теоремы,
, ах , by
* cz У cz
Определим теперь дифференциал левой части соотношения B0), прини-
принимая во внимание, что dx и dy должны считаться при этом постоянными:
adx2 + b dy2 + с dz2 + cz d2z = 0
или
_г9 а j 2 ^^а 1^2 а л а Ъ , ~ 1 tax . . by \2
d2z = dx2 dy2 dz2 = dx2 dy2 — dx4--^-dy) —
cz cz J z cz cz J z \cz " cz y)
и, следовательно
„ acz2 + a2x2 9 ___abxy „ _ bcz2 + b2y*
Таким образом, определив дифференциал некоторого порядка, мы полу-
получим все частные производные соответствующего порядка.
159 ] § 15. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ 379
159. Существование неявных функций. Наши рассуждения носили
формальный характер. Мы предполагали во всех случаях, что соответствую-
соответствующее уравнение или система уравнений определяют неявным образом неко-
некоторую функцию, имеющую производную. Сейчас докажем основную теорему
существования неявных функций.
Рассмотрим уравнение
F(xty) = 0 B1)
и укажем те условия, при которых оно определяет единственным образом у
как функцию от х> непрерывную и имеющую производную.
Теорема. Пусть х = xQ и у =у0 —решение уравнения B1), т. е.
пусть F (х, у) и ее частные производные первого порядка по х и у — не-
непрерывные функции при всех х и у, достаточно близких к х0 и у0, и
пусть, наконец, частная производная Fy (дг, у) отлична от нуля при
х = хо,у=уо. При этом существует при всех х, достаточно близких
к х0, одна определенная функция у (х), удовлетворяющая уравнению B1),
непрерывная, имеющая производную и удовлетворяющая условию:
У (•*¦<>) =.Уо-
Положим для определенности, что Fy (х, у) > 0 при х = х01 у—у0. Так
как по условию эта производная непрерывна, то она будет положительной
и при всех значениях х и у, достаточно близких к х0 и у0, т. е. существует
такое положительное число /, что F (х} у) и ее частные производные не-
непрерывны и
Fy(xt y)>0 B3)
при всех х и у, удовлетворяющих условию
Далее, функция F (x0J у) одной переменной у обращается в нуль при
yz=zy0, в силу B2), и есть возрастающая функция от у в промежутке
СУо — U Уо + 0» в СИЛУ B3) и B4). Таким образом, числа F(xQ} у0 — /)
и F(xQ, уо-\-1) будут разных знаков: первое — отрицательное, а второе —
положительное. Принимая во внимание непрерывность функции F (х, у),
мы можем утверждать [67], что F (х, у0 — /) будет отрицательным, а
F (х, уо-\-1) — положительным при всех х, достаточно близких к х0, т. е.
существует такое положительное число /lf что
F (*i У о — 0 < ° и F (х> У о + 0 > 0 B5)
при \х — xu\^lv Обозначим через т наименьшее из двух чисел: / и lt.
Принимая во внимание B4) и B5), мы можем утверждать, что выполнены
неравенства B3) и B5), если х и у удовлетворяют неравенствам
Если возьмем какое-нибудь определенное х, лежащее в промежутке
,— w, л*о + /и)| т. е. удовлетворяющее первому из неравенств B6), то
х, у), как функция от у, будет в силу B3) возрастающей функцией в
промежутке (у0 — /, уо + 1)} и, в силу B5), будет разных знаков на концах
этого промежутка. Следовательно, она будет обращаться в нуль при одном
определенном значении у из этого промежутка. В частности, если х = х0,
то, в силу B2), это значение у будет у=у0. Мы доказали, таким образом,
существование в промежутке (х0 — т} xQ-\-m) определенной функции у(х),
являющейся решением уравнения B1) и удовлетворяющей условию у (лг0) =
=>V Иначе говоря, из предыдущих рассуждений следует, что, при всяком
380 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ \ 159
фиксированном х из промежутка (лг0 — т, хо-\-т), уравнение B1) имеет
единственный корень, лежащий внутри промежутка (у0— А.Уо + 0-
Покажем теперь, что найденная функция у (х) будет непрерывной при
xs=zxo. Действительно, при любом заданном малом положительном е числа
F (*о> JVo —е) и F (xo> Уо +е) будут, в силу B5), разных знаков, а следова-
следовательно, будет существовать такое положительное t\y что F (х, у0—е) и
F (х* УоЛ~г) — разных знаков, если только \х — л:01 < ц, т. е., иначе говоря,
при \х — х01 < г\ корень уравнения B1), т. е. значение найденной функции
у (х), удовлетворяет условию \у—у01 < е, что и доказывает непрерывность
у (х) при х = х0.
Покажем теперь существование производной у'(х) при х = х0. Пусть
Ах = х— xQ и пусть Ау=у—у0 есть соответствующее приращение у. Сле-
Следовательно, х = хо-\- Ах и у—уо-\- Ау удовлетворяют уравнению B1), т. е.
F(xo + Axt уо + Ау) = 0, и в силу B2) можем написать
F (х0 + Аху у, + Ау) - F (х01 у0) = 0.
Принимая во внимание непрерывность частных производных, можем
переписать это равенство так [68]:
[F'Xu (х0, у0) + tj Д* + [Fyo (xot у0) + .,] Ау = 0, B7)
где et и s2-^0» если Ах и Ду — 0, и где мы обозначили через F'Xu (x0J у0) и
Fyo (х0У у0) значения частных производных при х = х0, у =у0. Из доказан-
доказанной выше непрерывности следует, что Ау —> 0, если Дл: —* 0.
Уравнение B7) дает нам
Ду _ F'Xo (^о> Уо) + gi
Ах" F'yo(xQ} уо) + гй>
переходя к пределу при Ах — 0, получим
,(x) По (*.. у»)
( )
Мы доказали непрерывность и существование производной функции
у (х) только при х = х0. Если мы возьмем какое-либо другое значение х
из промежутка (х0 — т, х0 + т) и соответствующее значение у из про-
промежутка (у0 — /, уо + /), являющееся корнем уравнения B1), то для этой
пары значений х, у опять выполнены все условия нашей теоремы, и в силу
доказанного у (х) будет непрерывной и будет иметь производную при взя-
взятом значении х из упомянутого промежутка.
Совершенно так же, как и выше, формулируется и доказывается теорема
о существовании неявной функции z (x, у), определяемой уравнением
Ф(х, у, z) = 0.
Рассмотрим теперь систему
, у, z) = 0, ф {х, у, z) = 0, B8)
определяющую у и г как функции от х.
Для этого случая имеет место
Теорема. Пусть х = х0, у =уо> z = zo —решение системы B8), пусть
<р (х, у, z)% ф (Xj у, z) и их частные производные первого порядка — непре-
непрерывные функции (х, у, z) при всех значениях этих переменных, доста-
достаточно близких к (xot y0, z0), и пусть выражение
160 I § 15, ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ 381
отлично от нуля при х — хо> v=^o» 2 = г0. При этом существует при
всех значениях х, достаточно близких к лг0, одна определенная система
двух функций у (x)t z (x), удовлетворяющая уравнениям B8) непрерывных,
имеющих производные первого порядка и удовлетворяющих условию
() ()
Уо> (o) o
а доказательстве этой теоремы мы останавливаться не будем. В третьем
томе мы рассмотрим общий случай любого числа функций с любым числом
переменных.
160. Кривые в пространстве и поверхности. Начнем с указа-
указания некоторых фактов, известных из аналитической геометрии. Пусть
трехмерное пространство отнесено к прямолинейным прямоугольным
осям OX, OY, OZ, так что всякая точка определяется координатами
х, у, z. Пусть а, Ь9 с — какая-либо тройка чисел, причем по крайней
мере одно из чисел отлично от нуля. Такой тройке чисел соответ-
соответствует два прямо противоположных направления в пространстве,
у которых направляющие косинусы (косинусы углов, образованных
этими направлениями с осями ОХ, О У, OZ) пропорциональны чис-
числам (а, Ь, с).
Упомянутые косинусы выражаются формулами:
а л Ь
cosa = =, cosB=
cos т =
Выбор знака у радикала (верхнего или нижнего) определяет одно
из прямо противоположных направлений.
Пусть имеются две тройки чисел (a, bt с) и (aly bXi сх). Ра-
Равенство
аах -\- bbi -(- ссх = 0
выражает условие перпендикулярности соответствующих этим трой-
тройкам чисел направлений.
Как известно из аналитической геометрии, всякому уравнению с
тремя переменными
F{x; у, г) = 0, B9)
или в явной форме
*=/(*, У), C0)
соответствует, вообще говоря, некоторая поверхность в пространстве,
отнесенном к прямоугольным осям ОХ, О К, OZ.
Линия в пространстве может быть рассматриваема, как пересе-
пересечение некоторых двух поверхностей, и может быть, следовательно,
определена совокупностью двух уравнений
Fx{x,y, 2) = 0, F%(x9 у, г) = 0. C1)
382 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ 160
Иначе кривую можно определить в параметрической форме уравне-
уравнениями:
* = ?(')> У = Ф(О. * = (*(*). C2)
Длина дуги кривой, как и в случае плоской кривой, определяется
как предел периметров ломаных линий, вписанных в эту дугу, при
беспредельном уменьшении каждой из сторон этой ломаной. Рассу-
Рассуждения, которые мы не будем приводить, так как они совершенно
аналогичны рассуждениям [103] в случае плоской кривой, показы-
показывают, что длина дуги выражается определенным интегралом
(Afg) h
5= \ /(dx? + (dyf-\-(dz? = $ V <?'*(*)+ V*(t) + *'4t)dt9 C3)
(Ali) h
где tx и t% суть значения параметра t, соответствующие концам Mi
и Ж2 дуги, и дифференциал дуги имеет выражение
ds = V(dx)* + (dy)* + (dz)*. C4)
Если роль параметра t играет длина дуги 5 кривой, отсчиты-
отсчитываемая от некоторой определенной точки ее, то совершенно так же,
как это мы делали в случае плоской кривой [70], можно показать,
dx dy dz
что производные -г-, ~-, -г- равны направляющим косинусам каса-
касательной к кривой, т. е. равны косинусам углов, образованных поло-
положительным направлением этой касательной с осями координат.
Принимая во внимание C2) и C3), мы получаем для этих коси-
косинусов формулы:
cosa = -
cos р==-
COS Y =
C5)
при соответствующем выборе знака у радикала, зависящем от вы-
выбора направления касательной.
Выше мы считали, что функции C2) имеют непрерывные произ-
производные и по крайней мере одна из них отлична от нуля. Таким об-
образом, направляющие косинусы касательной к кривой в точке (х, у, z)
пропорциональны у {t)t ф'@> ^'(О илй dx, dy} dz и уравнение каса-
касательной может быть написано в виде
X — x_Y—y_Z—z
160 ] § 15. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ 383
ИЛИ
X х ' У Z z c\f\\
Введем теперь новое понятие, а именно понятие касательной пло-
плоскости к поверхности
F( у, г) = 0. C7)
Пусть Мъ(хо> уо> *о)— некоторая точка этой поверхности и L — ли-
линия C2), лежащая на поверхности и проходящая через точку Жо,
так что при некотором t = tQ имеем лг0 = ср (?0), уо = ф(?о), <гв = а)(^0).
Предполагаем, что у функции C7) в точке Жо и ее окрестности имеются
непрерывные частные производные по х, у и z, причем по крайней
мере одна из этих производных отлична от нуля. Пусть аналогичное
свойство имеют и функции C2) при t = t0 и в окрестности этого
значения.
Если подставим C2) в левую часть уравнения C7), то получим
тождество по t> поскольку L лежит на поверхности C7). Дифферен-
Дифференцируя это тождество по ty получим
м{*> У> *)«>'(*) = О,
где вместо х, у, z надо подставить функции C2), и в точке Мо
Fx (xQ) у0, ^о) ?' (^о) + Fy (х*> Уо> ^о) ф' (^о) + Fz (xQ} у0, г0) <of (*e) = 0. C8)
Как мь! видели, ср'(^0)> ф'(^о)> W4^o) пропорциональны направляющим
косинусам касательной к линии L в точке Жо, и равенство C8) по-
показывает, что касательная в точке УИ0 к любой линии L, лежащей
на поверхности C7) и проходящей через точку Жо, перпендикулярна
к некоторому определенному, не зависящему от выбора L направле-
направлению, у которого направляющие косинусы пропорциональны числам
Fx(xo> Уо> zo)> Fy(xQy yo> ^o)» Fz(xQ, y0, zQ). Мы видим, таким образом,
что касательные в точке Жо ко вс^м линиям, лежащим на поверх-
поверхности и проходящим через точку Мо, лежат в одной и той же пло-
плоскости. Эта плоскость называется касательной плоскостью к по-
поверхности C7) в точке УИ0. Она проходит, очевидно, через точку Жо.
Пусть
+z0) = 0 C9)
— уравнение этой плоскости. Как известно из аналитической геомет-
геометрии, коэффициенты Л, В, С должны быть пропорциональны направ-
направляющим косинусам нормали к этой плоскости, т. е. в данном случае
пропорциональны Fx(xQ) yOr z0), Fy(xQ> у0, <га), Fz(xQi у0, ,г0). В даль-
дальнейшем вместо точки Ж0(лт0, у0, z^) мы применим общее обозначение
точки М (х} у, <г). Таким образом, А, В и С должны быть пропор-
пропорциональны F*(x» У* z)> Fy{x} у, z), Fg(x} у, <г), и, следовательно,
384 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ ( 160
уравнение касательной плоскости окончательно может быть написано
в виде:
+ F*(x, y,z)(Z-z) = 0, D0)
где X, К, Z — текущие координаты касательной плоскости, а х, у,
z — координаты точки касания М.
Нормаль к касательной плоскости, проходящая через точку каса-
касания М, называется нормалью к поверхности. Ее направляющие
косинусы пропорциональны, как мы сейчас видели, частным произ-
производным F'x(xy у, z\ Fy(x} у у г), F'z{x> у, z), и уравнение ее, следо-
следовательно, будет
F^(x, у, z) — F'y(x, у, z) — F'g(x, у, z) •
Если поверхность задана уравнением в явной форме: z=f(x, y)}
то уравнение C7) будет иметь вид
F(x, y> z) = f(x, y) — z = 0,
и, следовательно,
F'x(x,.yt z)=fx(x, у), F'y(x9 у, z)=fy(x, у), F'2(x, у, z) ——1.
Обозначая, как это обыкновенно делается, частные производные
fx(x, у) и fy(x, у) буквами р и q, получим уравнение касательной
плоскости
y) — (Z — z) = 0 D2)
и нормали к поверхности
Х—х _Y—y_Z-z (
Для эллипсоида
а* ^ Ь* ^ с2 "" 1
уравнение касательной плоскости в некоторой его точке (дг, у, г) будет
ИЛИ
Правая часть этого уравнения равна единице, так как координаты
(xt yf z) точки касания должны удовлетворять уравнению эллипсоида, и
окончательно уравнение касательной плоскости будет
161 I § 16, ФОРМУЛА ТЕЙЛОРА 385
§ 16. ФОРМУЛА ТЕЙЛОРА. МАКСИМУМЫ И МИНИМУМЫ
ФУНКЦИИ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
161. Распространение формулы Тейлора на случай функции
от нескольких независимых переменных. Для простоты письма
ограничимся случаем функции /(лг, у) от двух независимых перемен-
переменных. Формула Тейлора дает разложение f(a + hf b + k) по сте-
степеням h и k приращений независимых переменных [127]. Введем
новую независимую переменную t, полагая
Мы получим, таким образом, функцию одной независимой пере-
переменной t:
A)
езависимой пе
, b + kt),
причем
ф@)=/(а, Ь) и ФA)=/(а + А, b + k). B)
Пользуясь формулой Маклорена с остаточным членом Лагранжа,
можем написать [127]:
?^?Qi). C)
Выразим теперь производные <р(р) @) и <р(л+1) (б) через функцию
f(x, у). Из формулы A) мы видим, что х и у суть линейные функ-
функции независимой переменной t и
dx — hdt, dy = kdt
Мы можем поэтому пользоваться символической формулой при
определении дифференциала любого порядка функции ф(?) [156]:
откуда
При ^ = 0 имеем х = а и у~Ь, при ^ = 6 имеем x —
й8^ а потому
Подставляя эти выражения в формулу C) и пользуясь еще формулами
386 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ I 162
B), получим окончательно формулу Тейлора
Заменяя в этой формуле а на х, Ь на у и обозначая прираще-
приращения h и k независимых переменных через dx и dy, а приращение
функции, т. е. f(x-\-dx, y-\-dy)—f(x,y)> через Af(x, у), можем
написать формулу в следующем виде:
Правая часть этой формулы содержит дифференциалы различных
порядков функции f(x, у), а в последнем члене указаны те значения
независимых переменных, которые надо подставить в производные
(п-\-\)-то порядка, входящие в этот член. Аналогично случаю функ-
функции от одной независимой переменной формула Маклорена, дающая
разложение функции f(x, у) по степеням х, у} выводится из фор-
формулы Тейлора D), если положить там
e = 0, b = 0; h = x, k=y.
При выводе формулы D) мы предполагали, что функция f(x,y)
имеет непрерывные частные производные до порядка (я-|-1) в неко-
некоторой открытой области, содержащей отрезок прямой, соединяющий
точки (а, Ь) и (a-\-h, b-\-k). При изменении t от нуля до единицы,
переменная точка x = a-\-ht, y = b-\-kt описывает упомянутый
отрезок. При п = 0 получаем формулу конечных приращений
Отсюда, как и в [63], непосредственно следует, что если внутри
некоторой области частные производные первого порядка равны
везде нулю, то функция сохраняет внутри упомянутой области
постоянное значение.
162. Необходимые условия максимума и минимума функции.
Пусть функция /(лг, у) непрерывна в точке (а, Ь) и некоторой ее
окрестности. Аналогично случаю одной независимой переменной мы
будем говорить, что функция f(x, у) двух независимых переменных
достигает максимума в точке (а> Ь\ если значение f(a, b) не
меньше всех смежных значений функции, т. е. если
А/=/(а + К Ъ + k) —f(a, b) < 0, E)
при всех h и k достаточно малых по абсолютной величине.
162 ] § 16. ФОРМУЛА ТЕЙЛОРА 387
Точно так же мы будем говорить, что функция f(x, у) дости-
достигает минимума при х = а и y = bt если
А/=/(а + /г, b + k)—f(a9 *K*0 E0
при всех значениях h и k достаточно малых по абсолютной
величине.
Итак, пусть х = а> у = Ь — значения независимых переменных,
при которых функция f(xf у) достигает максимума или минимума.
Рассмотрим функцию f(x, b) одной независимой переменной х.. По
условию она должна достигать максимума или минимума при х = а,
а потому ее производная по х при х = а должна или обращаться
в нуль или же не существовать [58]. Таким же рассуждением убе-
убедимся, что и производная функция /(а, у) по у должна или обра-
обращаться в нуль или не существовать при у = Ь. Мы приходим, таким
образом, к следующему необходимому условию существования макси-
максимума или минимума: функция f(x, у) двух независимых перемен-
переменных может достигать максимума или минимума лишь при тех
значениях х и у, при которых частные производные первого по-
порядка - Ч' и * д обращаются в нуль или не существуют.
Совершенно так же, меняя только х или только уу мы можем,
пользуясь сказанным в [58], утверждать, что при наличии произ-
производных второго порядка необходимым условием максимума являются
неравенства *^х[ ^ ^ 0 и *^х* У* ^ 0, а необходимым условием
минимума — неравенства д^*1"^0 и д^^'2 ^ ^0.
Предыдущие рассуждения остаются в силе и в случае функции
любого числа независимых переменных. Мы можем высказать, таким
образом, следующее общее правило:
Функция нескольких независимых переменных может дости-
достигать максимума или минимума лишь при тех значениях неза-
независимых переменных, при которых частные производные первого
порядка обращаются в нуль или не существуют. В дальнейшем
мы ограничимся рассмотрением того случая, когда указанные частные
производные существуют.
Дифференциал первого порядка равен сумме произведений частных
производных по независимым переменным на дифференциалы соответ-
соответствующих независимых переменных [153], и мы можем поэтому утвер-
утверждать, что при значениях независимых переменных, при которых
функция имеет максимум или минимум, ее дифференциал первого
порядка должен обращаться в нуль. Эта форма необходимого усло-
условия удобна, потому что выражения первого дифференциала не зависят
от выбора переменных [153]. Приравнивая нулю частные производ-
производные первого порядка, мы получаем систему уравнений, откуда опре-
определяются те значения независимых переменных, при которых функция
388 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ 163
может достигать максимума или минимума. Для полного решения
вопроса необходимо еще произвести исследование полученных зна-
значений для того, чтобы решить, достигает ли функция, действительно,
при этих значениях независимых переменных максимума или минимума,
а если достигает, то чего именно — максимума или минимума. В сле-
следующем номере мы покажем, как производится это исследование
в случаях функции двух независимых переменных.
163. Исследование максимума и минимума функции двух
независимых переменных. Пусть система уравнений
^)=0) -^-=0, (б)
выражающая необходимое условие максимума или минимума, дала
нам значения х = а и у = Ь, которые надо исследовать. Предполо-
Предположим, что f(x, у) имеет непрерывные частные производные до вто-
второго порядка в точке (а, Ь) и некоторой ее окрестности.
Согласно формуле Тейлора D), при п = 2 можем написать
Принимая во внимание, что х = а и у = Ь являются решением
системы F), можем переписать это равенство так:
b + k)-f(ay Ь) =
h = r cos a, k = r sin а.
При малых по абсолютному значению h и k, и г будет мало, и
наоборот, и условия А и &->0, с одной стороны, и г->0, с дру-
другой — между собой равносильны.
Формула G) примет вид:
(8>
Принимая во внимание непрерывность производных второго
порядка и считая h и k или, что то же, г бесконечно малыми,
можем утверждать, что производные в правой части формулы (8),
163 I § 16. ФОРМУЛА ТЕЙЛОРА 389
вычисленные при значениях а -[- Щ Ь -\- Qk, бесконечно мало отли-
отличающихся от a, by сами бесконечно мало отличаются от чисел
а2/(а, Ъ) _ д*/(а, Ь) _R d*f(af Ь) _г
да2 ~Лз dadb ~ D> db2 ~и'
а потому коэффициенты при cos2 а, cos а sin а, sin2 а в квадратной
скобке формулы (8) можно заменить соответственно на А -(- st, 2B -f- e2,
C-f- е3, где е1э е2» ез СУТЬ величины, бесконечно малые одновременно
с h и k (или с г).
Формулу (8) можно после этого переписать так:
А/= ~ [A cos2 a + 2? sin а cos а + С sin2 а + е], (9)
где
е = sx cos2 а -{- 2e2cos а sin а -}- е3 sin2 а
есть величина, бесконечно малая одновременно с h и k (или с г).
Из определения максимума и минимума следует, что если правая
часть равенства (9) при всех достаточно малых значениях г сохраня-
сохраняет знак (—), то значениям х = а и у = Ь соответствует максимум
функции f(x, у); если она сохраняет знак (-)-), то указанным значе-
значениям будет соответствовать минимум функции; если же, наконец, при
сколь угодно малых значениях г правая часть равенства (9) может
иметь как знак (-{-), так и знак (—), то значениям х — а и у = Ь
не соответствуют ни максимум, ни минимум функции.
При исследовании знака правой части равенства (9) могут пред-
представиться следующие четыре случая:
I. Если трехчлен
Л cos2 а + 2В sin а cos а -f С sin2 а A0)
не обращается в нуль ни при одном значении а, то как непрерывная
функция от а он сохраняет неизменный знак [56]. Пусть это будет
знак (-]-). В промежутке @, 2тс) эта непрерывная функция достигает
своего наименьшего (положительного) значения т, В силу периодич-
периодичности cos аи sin а это же наименьшее значение т будет иметь мес-
место и для любых значений а. Величина | е | при всех достаточно малых
значениях г меньше т, и при этом знак правой части равенства (9)
определяется знаком трехчлена A0), т. е. будет (-(-); в этом случае
мы будем иметь минимум.
II. Положим теперь, что трехчлен A0), не обращаясь ни при ка-
каких значениях а в нуль, сохраняет знак (—). Пусть — т наименьшее
(отрицательное) значение этого трехчлена в промежутке @, 2тс) из-
изменения а. Величина |е| при достаточно малых значениях г меньше
ту и при этом знак правой части равенства (9) будет постоянно (—),
т. е, в этом случае мы будем иметь максимум.
III. Положим теперь, что трехчлен A0) меняет знак. Пусть при
<х = а1 он равен положительному числу -\-тъ а при а = а2 —
390 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ I 163
отрицательному числу — /гс2. При всех достаточно малых значениях г
|е| будет меньше тх и т* При таких значениях г и при a = at и
а2 знак правой части равенства (9) будет определяться знаком трех-
трехчлена A0), т. е. будет (-)-) при a = aj и (—) при а = а~2- Таким обра-
образом, в рассматриваемом случае знак правой части равенства (9) может
быть и (-)-) и (—) при сколь угодно малых значениях г, т. е. в этом
случае мы не будем иметь ни максимума, ни минимума.
IV. Положим, наконец, что трехчлен A0), сохраняя неизменный
знак, может обращаться в нуль при некоторых значениях а. В этом
случае без дальнейшего исследования знака е мы не можем сделать
никаких заключений о знаке правой части равенства (9), и этот слу-
случай остается сомнительным в нашем исследовании.
Итак, все свелось к исследованию знака трехчлена A0) при из-
изменении а, и мы укажем простые признаки, позволяющие судить, с
каким из указанных четырех случаев мы имеем дело.
1. Положим сначала, что А Ф 0. Трехчлен A0) мы можем пред-
представить в виде:
(A cosa + B sin aJ + (ЛС —В2) sin2 a nn
{ }
Если AC — Z?2^>0, то числитель написанной дроби представляет
собою сумму двух положительных слагаемых, которые не могут об-
обратиться в нуль одновременно. Действительно, второе слагаемое об-
обращается в нуль, только если sina = 0, но при этом cosa = ±l,
и первое слагаемое обращается в Л2 ф 0. Таким образом, в рассма-
рассматриваемом случае знак выражения A1) совпадает со знаком Л, и,
следовательно, при Л^>0 будем иметь случай (I), т. е. минимум, а
при Л <^ 0 — случай (II), т. е. максимум.
2. Предполагая по-прежнему АфО, положим, что АС—?2<[0.
Числитель дроби A1) будет иметь знак (-)-) при sina = 0 и знак
(—) при ctga = — -г а потому при указанных условиях мы будем
иметь случай (III), т. е. не будет ни максимума, ни минимума.
3. Если при АфО мы положим, что АС—?2 = 0, то числитель
дроби A1) приводится к первому слагаемому и, сохраняя неизменный
знак (-)-), обращается в нуль при ctga = — -v, т. е. при этих усло-
условиях мы имеем дело с сомнительным случаем (IV).
4. Положим, что Л = 0, но ВфО. Трехчлен A0) имеет тогда
вид: sin a BB cos a -f- С sin a). При значениях a, близких к нулю, вы-
выражение, стоящее в круглых скобках, сохраняет неизменный знак,
совпадающий со знаком Д а первый множитель sin a имеет разные
знаки, смотря по тому, будет ли а больше или меньше нуля, т. е.
имеет место случай (III) — ни максимума, ни минимума.
5. Предположим, наконец, что А = В=0. Тогда трехчлен A0)
дриведется к одному слагаемому С sin2 a и, следовательно, не меняя
164 I
§ 16. ФОРМУЛА ТЕЙЛОРА
391
знака, может обращаться в нуль, т. е. мы имеем дело с сомнитель-
сомнительным случаем.
Принимая во внимание, что в случае 4 будет АС — Б2<^0, в
случае 5 имеем ЛС —Б2 = 0, можем высказать следующее правило:
для нахождения максимумов и минимумов внутри области при
предположении, что функция f(x, у) непрерывна там и имеет
непрерывные производные до второго порядка, надо составить
частные производные fx(x\ у) и f'y{x, у) и решить систему урав-
уравнений
Пусть х = а, у = Ь — какое-нибудь решение этой системы. По*
ложив
д*/(а, Ь) _ А д*/(а, Ь) _ d2f(a, b) _ п
Э55 ~А' dadb —Uy Ж* ~U
производим исследование решения по следующей схеме:
АС —В2
А
+
+
МИН.
макс.
—
ни мин.
ни макс.
0
сомнит.
случай
164. Примеры. 1. Рассмотрим поверхность z=f(x, у). Уравнение каса*
тельной плоскости к ней будет [160]:
и f'y (x, у).
где р и q обозначают частные производные fx (л:, у)
Если при некоторых значениях х = а и у = Ъ
функция z достигает максимума или минимума,
то соответствующая точка называется вершиною
поверхности: в такой точке касательная плоскость
должна быть параллельна плоскости ХУ> т. е. част-
частные производные р и q должны обращаться в
нуль, и поверхность должна быть расположена
по одну сторону от касательной плоскости, вблизи
точки касания (рис. 163). Но может случиться,
что р и q в некоторой точке обращаются в нуль,
т. е. касательная плоскость параллельна плоско-
плоскости XYy но поверхность вблизи этой точки рас-
расположена по обе стороны от касательной плоско-
плоскости, ив этом случае при соответствующих зна-
значениях х и у функция z не будет достигать ни Рис. 163.
максимума, ни минимума.
Укажем еще на одну возможность, которая может осуществиться в слу-
случае, названном нами в предыдущем сомнительным. Положим, что при х = а,
у = Ь касательная плоскость параллельна плоскости ХУ, и поверхность
392
ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
I 164
расположена по одну сторону от касательной плоскости, но имеет с нею
общую линию, проходящую через точку касания. В этом случае разность
f(a + ht b + k)-f(a, b)t
не меняя знака при достаточно малых по абсолютному значению h и ky будет
обращаться в нуль при h или k, отличных от нуля. Нетрудно осуществить
этот случай, представив себе, например, круговой цилиндр, ось которого парал-
параллельна плоскости XY. В этом случае также говорят, что функция f(x, у)
имеет максимум или минимум при х = а иуг=Ь [162].
Поверхность
есть гиперболический параболоид. Приравнивая нулю частные производные
от г по х и уу получим лс=_у = О, и касательная плоскость к поверхности
в начале координат будет сов-
совпадать с плоскостью XY. Со-
Составим частные производные
второго порядка:
д2г
дхду'
1
и, следовательно,
АС~В' ^F
Т. е. При JCsaajy = 0 фуНКЦИЯ
г не достигает ни максимума,
ни минимума, и вблизи начала
координат поверхность распо-
расположена по обе стороны от ка-
касательной плоскости (рис. 164).
2. На плоскости даны п точек Mi(ah ^)(/==l, 2, ..., п). Требуется
найти точку М такую, чтобы сумма произведений данных положительных
чисел /я; на квадраты расстояний ее до точек М/ достигала минимума. Пусть
(лг, у) — координаты искомой точки М. Упомянутая выше сумма будет:
Рис. 164.
W = 2j mi l(x — aiJ + (У — biYV
Приравнивая нулю частные производные w'x и w'y, получаем
h ••- +тпап mxbt + m2b2 + ... + ™rfin
тп
A2)
Нетрудно проверить, что в рассматриваемом случае А и АС — В2 будут
больше нуля, и, следовательно, найденным значениям х и у действительно
будет соответствовать минимум т. Этот минимум является наименьшим
значением w на плоскости (х, у), ибо w —» + оо при беспредельном удалении
точки (х>у).
Если М(—материальные точки и mi — их массы, то формула A2) опре-
определяет координаты центра тяжести системы точек М^
165 1 § 16. формула тейлора 393
165. Дополнительные замечания о нахождении максимумов и мини-
минимумов функции. Предыдущие рассуждения распространяются и на случай
большего числа независимых переменных. Пусть, например, дана функция
трех независимых переменных f(x, у, z). Для нахождения тех значений неза-
независимых переменных, при которых эта функция достигает максимума или
минимума, надо решить систему трех уравнений с тремя неизвестными [162]
fx(x, у, г) = 0, fy(xt у, *)= 0, /;(*, у, 2) = 0. A3)
Пусть лг = а, у = Ь, 2 = с — одно из решений этой системы. Наметим кратко
путь для исследования этих значений. Формула Тейлора дает нам приращение
функции в виде суммы однородных полиномов, расположенных по степеням
приращений независимых переменных:
~П да +Л дГ~^1 Тс
Значения х = а, у = Ь, г = с удовлетворяют уравнениям A3). Поэтому
df(a, b, с) д/(а, Ь, с) д/(а, Ь, с) _.
й Si r« дь +1 ^ -У-
Если совокупность членов второй степени относительно h, ft, t
обращается в нуль только при Л=? = /=гО, то знак правой части A4) при
Л, k, /, достаточно малых по абсолютному значению, совпадает со знаком
выражения A5), и если этот знак (+), то f(a, b, с) является минимумом
функции f(xt у, z), если же (—), то мы имеем дело с максимумом. Если
выражение A5) может иметь разные знаки, то /(в, Ь, с) не является ни
максимумом, ни минимумом функции. Если же, наконец, выражение A5), не
меняя знака, обращается в нуль при некоторых значениях Л, ?, /, отличных
от Л = &==/ = 0, то этот случай остается сомнительным и требуется иссле-
исследование тех членов правой части A4), которые содержат h, k и / в степени
выше второй.
Приведем полное исследование этого сомнительного случая в частном
примере функции двух независимых переменных
и=х2 — 2ху + у2 + Xs + у8.
о ди да
.значения лг=^ = О обращают в нуль частные производные ^— и -д—.
Кроме того, имеем
т. е. мы имеем дело с сомнительным случаем. Характерная особенность
этого случая состоит в том, что совокупность членов второго измерения
в выражении функции а представляет собою полный квадрат, и мы можем
в рассматриваемом примере написать
394 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ 166
При х—у = 0 и и обращается в нуль. Для исследования знака а при х
и у, близких к нулю, введем полярные координаты
л; = Г cos а, у == г sin а.
Подставляя эти значения х и у, получим
U = г2 [(cos а — sin аJ + Г (cos3 а + sin3 а)].
При любом значении а в промежутке @, 2тс), отличном от -т- и -j-,
cos a — sin
и, следовательно, для всякого такого значения а можно выбрать такое поло-
положительное число г0, что при r<ir0 знак выражения, стоящего в квадратных
скобках, будет (+). При « = -д- этот знак'также
будет (+), но при а = —- мы получим знак (—),
и, следовательно, при х=у = 0 функция и не
будет иметь ни максимума, ни минимума.
Рассмотрим еще функцию
и = (у — л:2J — хК
** * Нетрудно проверить, что при х=у = 0 част-
Рис. 165. ные производные -с— и -^- обращаются в нуль,
и что мы имеем дело с сомнительным случаем.
Выбирая для х сколь угодно малое значение и полагая у = х2, мы видим,
что функция и приведется к (—хъ) и ее знак будет зависеть от знака х>
т.е. при х=у~0 функция и не будет достигать ни максимума, ни мини-
минимума. Вводя полярные координаты, мы получили бы
U =Г2 (sin2 а — 2r COS2a sin a + f2 COS4 a — Г3 COS5 a),
и из этого выражения видно, что при всяком значении а, не исключая и зна-
значений а = 0 и тс, можно найти такое положительное число г0, чтобы было
и>0 при г<:г0У т. е. на всякой полупрямой, выходящей из начала коорди-
координат, функция и имеет знак (+) вблизи начала координат. Однако, |сак мы
видим, это не влечет за собой минимума в начале координат, где « = 0, ибо
нельзя найти упомянутое число г0 так, чтобы оно было одно и то же для
всех значений а.
В [76] мы построили кривую (у — л:2J — л:5=0 и видели, что она в начале
координат имеет точку возврата второго рода, а левая часть этого уравнения
имеет знак (—) вблизи начала координат, если рассматривать ее значения
в точках, заключающихся в заштрихованной области между двумя ветвями
кривой (рис. 165).
166. Наибольшее и наименьшее значения функции. Положим, что тре-
требуется найти наибольшее значение некоторой функции /(л:, у), -заданной
в определенной области. Указанный в [163] прием позволяет нам найти все
максимумы функции внутри этой области, т. е. те точки внутри области,
в которых значения функции не меньше, чем в соседних с ними точках. Для
нахождения наибольшего значения функции надо принять во внимание зна-
значения функции на границе (контуре) данной области и сравнить ее макси-
максимумы внутри области со значениями на контуре. Наибольшее из всех этих
значений и будет наибольшим значением функции в данной области. Ана-
Аналогично находится и наименьшее значение функции в данной области. Для
разъяснения сказанного рассмотрим пример.
167
§ 16. ФОРМУЛА ТЕЙЛОРА
395
На плоскости дан треугольник ОАВ (рис. 166), образованный осями
ОХ и 0Y и прямой
-^ +3^ —1=0. A6)
Требуется найти такую точку этого треугольника, для которой сумма
квадратов ее расстояний до вершин треугольника была бы наименьшей.
Принимая во внимание, что вершины А и Б имеют координаты A, 0) и
@, 1), мы можем написать выражение для вышеупомянутой суммы квадратов
расстояний переменной точки (л:, у) до вершин
треугольника:
Приравнивая нулю частные производные пер-
первого порядка, получим х =y = 1/s, и нетрудно
показать, что этим значениям соответствует ми-
минимум z = i/8. Исследуем теперь значения z на
контуре треугольника. Для исследования z на
стороне ОА надо в выражении для z поло-
положить у = 0:
z = 2x2 + (x— 1J+1> рис< 16б<
причем х может меняться в промежутке @, 1),
Поступая согласно [60], убедимся, что z на сто-
стороне ОА принимает наименьшее значение 2 = 5/3 в точке С, для которой
x = 1/i. Точно так же и на стороне ОБ наименьшее значение г будет равно
5/8 и будет достигаться в точке D, для которой у = 1/3. Для исследования
значений z на стороне АВ надо, согласно уравнению A6), в выражении z
положить у = 1 — х:
причем х может меняться в. промежутке @, 1). В данном случае наименьшее
значение z будет г = 8/2 и будет достигаться в точке Е, для которой х =у = 1/2.
Мы получаем, таким образом, следующую таблицу возможных наименьших
значений функции:
г
1 1
3 ' 3
4
3
5
3
5
3
1 1
2 ' 2
3
2
Из этой таблицы мы видим, что наименьшее значение г = 4/3 будет
достигаться в точке (Va» Va)- Рассматриваемая задача может быть также
решена и для любого треугольника, и искомая точка является центром тяжести
треугольника.
167. Относительные максимумы и минимумы. До сих пор мы
рассматривали максимумы и минимумы функции, предполагая, что те
переменные, от которых функция зависит, суть независимые пере-
переменные. В подобных случаях максимумы и минимумы называются
абсолютными. Перейдем теперь к рассмотрению того случая, когда
переменные, от которых зависит функция, связаны некоторыми
396 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ I 167
соотношениями. В подобных случаях максимумы и минимумы назы-
называются относительными.
Пусть требуется найти максимумы и минимумы функции
/ (Xi, Х%у ..., ХтУ Xm+if ¦,. , Хт+п)
от (т~\-п) переменных хь которые связаны п соотношениями
A=1, 2, ..., п).
В дальнейшем для сокращения письма мы не будем писать аргу-
аргументов у функций. Разрешая п соотношений A7) относительно п
переменных, например,
мы выразим их через остальные т независимых переменных
Х\у Хч, «• • у Хт\
подставляя эти выражения в функцию /, получим функцию от т
независимых переменных, т. е. придем к задаче отыскания абсолют-
абсолютных максимумов и минимумов. Но такое разрешение системы A7)
часто бывает практически затруднительным и даже невыполнимым,
и мы укажем другой способ решения задачи, способ множителей
Лагранжа.
Пусть в некоторой точке М(хь хъ ,.., Хт+п) функция / до-
достигает относительного максимума или минимума. Предполагая су-
существование производных в точке М, можем утверждать, что пол-
полный дифференциал функции / должен -обращаться в нуль в точке
М [162]:
т + я
2& A8)
С другой стороны, дифференцируя соотношения A7), получим в той
же точке М следующие п равенств:
т-\-п
2
2 Ш
Умножим эти последние уравнения на неопределенные пока мно-
множители
^1> ^2> • • • 9 ^Я
и сложим их все почленно друг с другом и с соотношением A8):
167 | § 16. ФОРМУЛА ТЕЙЛОРА 397
Определим эти п множителей так, чтобы коэффициенты при п диф-
дифференциалах
• • • 9 dxm+n
зависимых переменных были равны нулю, т. е. определим Хь Х2, ..,,
из п равенств
&=° B0>
i ..., т-\-п).
Тогда в левой части соотношения A9) останутся лишь члены,
содержащие дифференциалы независимых переменных
йхъ dxb ..., dxm>
то есть
Но дифференциалы dxb dxb ...t dxm независимых переменных
суть величины произвольные. Приравнивая один из них единице,
а остальные нулю, мы видим, что из равенства B1) вытекает, что
все коэффициенты этого равенства должны быть равны нулю [158],
то есть
lfrfe 1Й=0 (s=1' 2 т)- B2)
Надо считать, что во всех предыдущих формулах, начиная с A8),
переменные xs заменены координатами той точки М, в которой /
достигает, по предположению, относительного максимума или мини-
минимума. В частности, этр относится и к уравнениям B0), из которых
должны быть определены \ь Х2, ..., Хл.
Таким образом, уравнения B2), B0) и A7) выражают необходимое
условие того, что в точке (хъ хъ ..., хт+п) достигается относи-
относительный* максимум или минимум.
Уравнения B2), B0) и A7) дадут нам (т-\-2п) уравнений для
определения {т-\-п) переменных xs и п множителей Х?.
Из системы B2) и B0) видно, что для определения тех значений
переменных xs, при которых функция f достигает относитель-
ного максимума или минимума, надо приравнять нулю частные
производные по всем xs от функции Ф, определяемой равенством
считая Хь Х2, .. t, Хл постоянными, и присоединить п уравнений
связи A7).
В следующем параграфе мы кратко изложим вопрос о достаточных
условиях.
398 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ 168
Отметим, что при выводе указанного правила мы предположили
не только существование производных у функций / и ср^, но и воз-
возможность определения множителей Хх, Х2, ##f, Хд из уравнения B0).
В связи с этим указанное правило может не дать нам некоторых зна-
значений (хъ хь ..,, хт+п), для которых достигается относительный
максимум или минимум. Мы выясним сейчас более подробно это
обстоятельство в простейших случаях и уточним теорию.
168. Дополнительные замечания. Пусть ищутся относительные макси-
максимумы и минимумы функции / (л:, у) при одном дополнительном условии
Ч(х,у) = 0, B3)
и предположим, что, например, относительный максимум достигается в точке
(х0, Уо), так что <р (xQJ у0) = 0. Пусть у (х, у) имеет непрерывные частные
производные первого порядка в точке (л:0, у0) и ее некоторой окрестности,
и предположим, кроме того, что
<^0 (•**<)» Уо)^<>. B4)
При этом уравнение B3) определит единственным образом в окрестности
х = х0 функцию у = (о (х), непрерывную, с непрерывной производной и такую,
что у0 = о) (х0) [157]. Подставляя у = <о(лг) в функцию f (х, у), мы можем
утверждать, что функция f[x, <о (л:)] одного переменного х должна достигать
максимума при х = х0 и, следовательно, ее полная производная по х должна
обращаться в нуль при х = лг0, то есть
f'x0 (лГо> У о) +/у0 (*о» Уо) »' (-^o) == 0.
Подставляя ^ = 0)(-^) в B3) и дифференцируя по л:, получим в точке
(А-о, у0) [69]:
^0 (хоу У о) + <?'Уо (^о» У о) w' М = 0.
Умножая второе уравнение на X и складывая почленно с первым, получим
Определяя X из условия f'yo + tyy0 = 0» что возможно, в силу B4), будем
иметь f'XQ + WxQ == ^» т# е* придем к двум уравнениям
/;„ + ^0 = 0; /;о + Хср;о = 0, B5)
к которым надо присоединить еще уравнение <р (лг0, д>0) = 0, чем и оправды-
оправдывается способ множителей. Если условие B4) не выполнено, т. е.
<?Уо С*о» У о) =°> но ?io (^o» .Vo) ФЪ, то можно повторить все предыдущие рас-
рассуждения, меняя х и у ролями. Если в точке (лг0, у0) мы имеем
<Pi0 (*о. У о) = 0 и yQ (лг0, у0) = 0, B6)
то мы не можем доказать, что точка (лг0, у0) получается при помощи пра-
правила множителей.
Равенства B6) показывают, что точка (х0, у0) является особой точкой
кривой B3) [76]. Дадим сейчас пример такой задачи, для которой имеют
место условия B6) в точке относительного минимума.
Пусть требуется найти кратчайшее расстояние от точки (— 1, 0) до точек,
лежащих на полукубической параболе^2 — х3 = 0, изображенной на рис.87
[76]. Таким образом, ищется минимум функции /== (х -\-1J+^2 при условии
168 I § 16. формула тейлора 399
ср=3;2 — л:3 = 0. Геометрически очевидно, что минимум достигается в точке
(О, 0), лежащей на полукубической параболе, причем эта точка является
особой точкой параболы. Способ множителей приведет нас к следующим
двум уравнениям:
При подстановке л: = 0, y=zO первое уравнение приводит к нелепому
равенству 2 = 0, а второе — удовлетворено при любом X. В данном случае
способ множителей не приведет нас к точке @, 0), в которой достигается
относительный минимум.
Совершенно аналогично можно показать, что если в точке (лг0, у0У г0)
функция достигает максимума или минимума, при одном дополнительном
условии у (х, уу z) = 0, и притом, по крайней мере, одна из частных про-
производных первого порядка функции ср отлична от нуля в точке (х01 у0У zo)> то
эта точка может быть получена по способу множителей.
Аналогичны рассуждения и в более общих случаях, но при этом при-
приходится ссылаться на теорему существования неявных функций для систем
уравнений, о чем мы упоминали в [157]. Пусть, например, функция f(xy у, z)
достигает относительного максимума в точке (xQy yQy г0) при двух дополни-
дополнительных условиях
<?(х,уу *) = 0, ф(дг, уу г)=0 B7)
и при обычных предположениях существования и непрерывности производ-
производных, и пусть мы имеем
Ьо (*о» Уоу *о) V2o С*о> У» *о) — Ьо (•**<)> Уоу *о) ?yQ (*o> Уоу *о) Ф °- B8>
При этом уравнения B7) определяют единственным образом функции:
У = со1(л-); z = <as(x) такие, что _у0 = Ш1 (-^о)» zo = Ш2 (хо)- Подставляя эти
функции в функцию /, получим функцию одного х, которая имеет максимум
при x=zxOi откуда следует
f'x0 (хо, Уо> *0) +fy0 ^oi Уоу «о) wi (*o) +/;о (^о. Уо> *о) \(хо) = 0.
Подставляя указанные функции в B7) и дифференцируя по х в точке
(•*"<)> Уоу 2о)» получим
Умножаем эти равенства на \it X2 и складываем с предыдущим
(/'Хо+wXt+»,g+<ryt+la1,,+wyj+w.+*«?;,+x^;0)=°- <29>
Принимая во внимание B8), можем утверждать, что из двух уравнений
мы сможем определить At и Х2, и уравнение B9) после этого приведет нас
к равенству
чем и оправдывается способ множителей для данного случая. К уравнениям
C0) и C1) надо добавить еще
? С*о» 3>о> zo) = ° й Ф (-^о» Уоу zo) = 0.
Вместо условия B8) мы могли бы поставить аналогичное условие, диф-
дифференцируя не по у0 и г01 а по xQ и у0 или по дг0 и 20. Но если не только
400 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ | 168
выражение, стоящее в левой части B8), но и два других аналогичных выра-
выражения, которые получаются при дифференцировании по х0 и у0 или по х0
и 20, равны нулю, то мы не сможем оправдать способ множителей для точки
(•*о» Уоу zo)- Можно показать, что во всех рассмотренных в следующем номере
примерах мы не можем иметь такого случая. Так, например, в примере 1
мы имеем одно дополнительное условие C2). и в левой части этого условия,
по крайней мере, одно из чисел Д В и С отлично от нуля. Если, например,
СфЪ, то производная левой части C2) по z равна числу Си, следовательно,
отлична от нуля во всякой точке (х, у, z). Это и указывает на то, что
в рассматриваемом случае всякий ответ должен Получаться по способу
множителей.
Приведем теперь короткие указания о достаточных условиях относи-
относительного максимума или минимума, ограничиваясь тем случаем, когда мы
имеем две независимые переменные. Пусть ищутся относительные макси-
максимумы и минимумы функции / (лг, у, z) при наличии одной связи у(х,у, 2) = 0.
Составляем функцию Ф ==/-{-Х<р. Положим, что, приравнивая нулю ее про-
производные первого порядка по х, у, z и учитывая уравнение связи, мы полу-
получали значения х = лг0, у =у0, z = zoy Х = Х0. Мы должны испытать получен-
полученные значения переменных, т. е. определить знак разности f(xf у, z)—
—/(*о» Уо> 2о) ПРИ всех (*» У> *)» достаточно близких к (л:0, у0, z0) и удо-
удовлетворяющих уравнению связи ср (х, у, z) = 0. Введем функцию ф (дг, у, z) =я
t=sf(^t У* г) + ло<р (лг, у, z). Из уравнения связи непосредственно следует,
что вместо разности f(x, у, z)—f(xQ1 y0, z0) можно взять разность
ф (х, yt z) — ф (лг0, yot z0) и исследовать ее знак. Частные производные пер-
первого порядка функции ф (х, у, z) в точке (лг0, jy0, z0) обращаются по условию
в нуль. Разлагая последнюю разность по формуле Тейлора и ограничиваясь
членами со вторыми производными, получим выражение вида [ср. 165]:
ф (х, у, z) — ф (х0, yOf z0) =
2alsdx dz + 2
где через aik мы обозначим значения соответствующих частных производ-
производных второго порядка функции ф (л:, у, z) в точке (лг0, yot z0) и через dxf
dyy dz — приращения переменных. Положим, что <р^о (лг0> у0, го)^Ь-О, так что
уравнение связи определяет я = со(л:, у), причем z0 == <•> (л:0, yQ). Из уравне-
уравнения связи получаем
<?'х (^ У* z)dx + 9у (х* У* *) аУ + 9г (** У* z)dz = °-
Подставляя значения ^ = ^0,^=^0» ^ = ^о> выражаем dz через dx и dy:
Z"" bo (X<» У Of «о) Х ?i0 (^oi Уо> *e) ^
Подставляя это выражение dz в предыдущую формулу и собирая подобные
члены, получим
ф (л:, yt z) — ф (лг0, ^0, г0) = A dx* + 2В dx dy + Cdy*+ ...
Теперь можно использовать признак максимума и минимума из [163]. Так,
например, если АС — Ва>0 и Л>0, то в точке (лг0, у0, zo) функция
f (x> V, z) имеет относительный минимум. Из рассуждений, приведенных
в [163], непосредственно следует, что для обоснования указанного правила
достаточно предположить, что функции /(лг, у, г) и ср (лг, у, z) имеют в точке
(*о> Уо> 2о) и ее окрестности непрерывные производные до второго порядка.
Мы не останавливаемся более подробно на вопросе о достаточных
условиях относительного максимума и минимума. Существенными в преды-
предыдущих рассуждениях являлись замена разности f(x% у, z)—f(x01y01 zQ)
169 J § 16. ФОРМУЛА ТЕЙЛОРА 401
разностью <|/ (х, у, z) — ф (х0, у0, г0), у которой производные первого порядка
в точке (лг0, у01 z0) равны нулю, а также факт, что дифференциал dz зави-
зависимого переменного определялся через дифференциалы dx, dy независимых
переменных из уравнения первой степени. Аналогичным образом надо посту-
поступать для выяснения достаточных условий и при другом числе переменных
и связей.
169. Примеры. 1. Требуется найти кратчайшее расстояние от точки
(а, Ь, с) до плоскости
Ax + By + Cz + D = 0. C2)
Квадрат расстояния от данной точки (а, Ъ, с) до переменной точки (х, у, z)
выражается формулой
г2 = (а: — оJ + (у - by + (г - сJ. C3)
В данном случае координаты (а:, у, z) должны удовлетворять уравнению C2)
(точка должна находиться на плоскости). Найдем минимум выражения C3)
при условии C2). Составляем функцию
Приравнивая нулю ее частные производные по х, у, z, получим
л- = я—1-ХЛ у=*Ь— уХ^, * = <? — --Х^. C4)
Подставляя эти значения в условие C2), можем определить X?t
2(Aa
( '
Мы получили единственный ответ, и так как наименьшее значение
должно существовать, то ему и должны соответствовать найденные значе-
значения переменных. Подставляя значения C4) в выражение C3), получаем выра-
выражение для квадрата расстояния от точки до плоскости:
где Хх определяется по формуле C5).
2. Разложить данное положительное число а на три положительных
слагаемых х, у, z так, чтобы выражение
C6)
было наибольшим (m, n, p — данные положительные числа).
Найдем максимум выражения C6) при условии
= a. C7)
Вместо максимума выражения C6) можно искать максимум его логарифма
т log х -J- n log у + р log z.
Составляем функцию
Ф ==m log AT + nlog^+ptog z + ^i {x-\-y-\-z — а).
402 ГЛ. V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ I 169
Приравнивая нулю ее частные производные, получим
Л
и соотношение C7) дает
х Л у- 2- * —-?.
Л1 Л1 Л1
. т+п+р
*i = ,
__ та па ра ,««»
т+п + р9 У—т + п + р' Z~~ m + n + p> ( '
то есть
причем найденные значения переменных суть положительные числа. Можно
показать, что при поставленных условиях выражение C6) должно иметь
наибольшее значение, и единственность ответа показывает, как и в примере 1,
что найденным значениям переменных и со-
соответствует, именно, наибольшее значение
выражения C6).
Формулы C8) показывают, что для реше-
решения задачи число а надо разбить на части,
пропорциональные показателям т, п и р.
Предлагаем читателю в последних двух
примерах провести исследование достаточных
условий по методу, указанному в предыдущем
параграфе.
3. Проводник длины 10 разветвляется на
р lfi7 одном из своих концов на k отдельных про*
водников длин /s(s = l, 2, ..., k), причем
сила тока в соответствующих частях про-
проводника есть ?0, iit ..., ik. Спрашивается, как надо выбрать площади
поперечных сечений qOf qu ..., qk отдельных частей проводника для того,
чтобы при данной разности потенциалов Е для цепей (/0, l^ (/0> h\ •••
• ••»('о> h) пошло наименьшее количество материала V (рис. 167).
Обозначим буквою с сопротивление проволоки из данного вещества,
длина которой и площадь поперечного сечения равны единице.
Функция V переменных q0, qt, ..., qki наименьшее значение которой
ищется, будет
Принимая во внимание данную разность потенциалов Е, можем напи-
написать k соотношений
T V qQ qs 1
Составим функцию
*m I \ Яо Qs I \
Приравнивая нулю частные производные от Ф по qot qlt ..., qk, получим
Г D°)
/,-^-0E=1,2,...,^.
169 ] § 16. ФОРМУЛА ТЕЙЛОРА 403
Из условий C9) получим
Ч\ ^ Чъ "* Чк ~~~ с Чо
обозначив буквою сг общую величину этих отношений, можем написать
а * С q§
Из уравнений D0) имеем
Подставив эти выражения \s в первое из уравнений D0), получим
или
0о = -
1TZW
откуда окончательно
я, = -J- [ V. + >Ч (%+'!<*+ ... +%)]•
Подставляя это выражение q0 в соотношения D1), получим для qv
Я 2 Як-
с1ф! у, \
Таким образом, необходимые условия максимума и минимума V дают
нам единственную систему положительных значений для q^ qv ... , qk; но из
физических соображений ясно, что при некотором выборе площадей попе-
поперечных сечений должно получаться наименьшее количество материала, и
можно поэтому утверждать, что полученные значения qQ} qv ..., q^ и дадут
решения задачи.
ГЛАВА VI
КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ
И ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
§ 17. КОМПЛЕКСНЫЕ ЧИСЛА
170. Комплексные числа. Если ограничиваться только веще-
вещественными числами, то, как известно, действие извлечения корня не
всегда выполнимо; корень четной степени из отрицательного числа
не имеет ответа в области вещественных чисел. В связи с этим уже
квадратное уравнение с вещественными коэффициентами не всегда
имеет вещественные корни. Это обстоятельство приводит, естественно,
к расширению понятия о числе, к введению новых чисел более общей
природы, частным случаем которых являются вещественные числа.
При этом существенно определить эти числа и действия над ними
таким образом, чтобы для новых чисел остались в силе все основные
законы действий, известные для вещественных чисел. Это, как мы
покажем дальше, оказывается возможным.
Не только указанная выше невыполнимость, в некоторых случаях,
действия извлечения корня, но и простые геометрические соображения
приводят к естественному расширению понятия о числе. Мы и будем
руководиться этими геометрическими соображениями при расширении
понятия о числе.
Мы знаем, что всякое вещественное число графически можно
изобразить или как отрезок, отложенный на данной оси ОХ, или же
как точку на этой оси, если условимся начала всех отрезков поме-
помещать в начало координат; обратно — всякому отрезку или точке на
оси ОХ соответствует определенное вещественное число.
Если теперь вместо одной оси ОХ рассматривать всю плоскость,
отнесенную к координатным осям ОХ, О У, то, обобщив надлежащим
образом понятие о числе, мы получим возможность каждому вектору,
лежащему в этой плоскости, или каждой ее точке сопоставить неко-
некоторое число, которое мы назовем комплексным.
Если условимся не различать между собой векторы, равные по
длине и одинаково направленные, то можно сопоставить веществен-
вещественное число не только всякому вектору на оси ОХ} но, вообще, вся-
170 1 § П. КОМПЛЕКСНЫЕ ЧИСЛА 405
кому вектору, параллельному оси ОХ. В частности, вектору длины
единица, направление которого совпадает с положительным напра-
направлением оси ОХ, соответствует вещественное число единица.
Вектору длины единица, направление которого совпадает с поло-
положительным направлением оси OY, сопоставим символ /, называемый
мнимой единицей. Всякий вектор MN плоскости может быть пред-
представлен как сумма двух векторов МР и PN, параллельных осям коор-
координат (рис. 168). Вектору МР, параллельному оси ОХ, соответствует
некоторое вещественное число а. Вектору PN, параллельному оси О К,
пусть соответствует символ Ы, где Ь — вещественное число, абсолют-
абсолютное значение которого равно длине вектора PN и которое будет
положительным, если направление PN совпадает с положительным
направлением оси О У, и отрицательным, если направление PN проти-
противоположно положительному направлению О К
Таким образом, естественно, вектору MN со-
поставить комплексное число, имеющее вид
Отметим тот факт, что знак (-f-) в написанном
выражении а-\-Ы не есть знак действия. Это
выражение надо рассматривать как единый
символ для обозначения комплексного числа.
После определения сложения комплексных чисел Рис. 168.
мы вернемся к рассмотрению этого знака.
Вещественные числа а и Ъ представляют собой, очевидно, вели-
величины проекций вектора MN на координатные оси.
Отложим от начала координат вектор О А (рис. 168), совпадаю-
совпадающий по длине и направлению с вектором MN. Конец этого вектора А
будет иметь координаты (а, Ь), и этой точке А мы можем сопоста-
сопоставить то же комплексное число а~\-Ы, что и векторам ММ и О А*
Итак, всякому вектору плоскости (всякой точке плоскости)
соответствует определенное комплексное число a -f- Ы. Веществен-
Вещественные числа а и b равны проекциям рассматриваемого вектора на
координатные оси (координатам рассматриваемой точки).
Придавая в выражении а -\- Ы буквам а и Ь всевозможные веще-
вещественные значения, получим совокупность комплексных чисел; а назы-
называется вещественной и Ы — мнимой частью комплексного числа.
В частном случае вектора, параллельного оси ОХ, комплексное
число совпадает со своей вещественной частью:
а-\-Ы = а. A)
Таким образом, вещественное число а мы считаем частным слу-
случаем комплексного числа.
406 ГЛ. VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ | 170
Понятие о равенстве двух комплексных чисел вытекает из их
геометрической интерпретации. Два вектора считаются равными, если
они имеют одинаковую длину и совпадающее направление, т. е.
если они имеют одинаковые проекции на координатные оси, а потому
два комплексных числа считаются равными между собой тогда
и только тогда, когда в отдельности равны их вещественные
и мнимые части, т. е> условие равенства комплексных чисел будет
ах-{- bxi = a%-\- b%i равносильно ах = аь ЪХ = Ъ^ B)
В частности,
а-\-Ы = 0 равносильно а = 0; Ь = 0*
Вместо того, чтобы определить вектор MN его проекциями а и
Ь на координатные оси, мы можем определить его двумя другими
величинами, а именно: его длиною г и углом ср, который направле-
направление MN образует с положительным направлением оси ОХ (рис. 168).
Если же мы считаем, что комплексное число а -\- Ы соответствует
точке с координатами (я, Ь\ то Т и ср будут, очевидно, полярными
координатами этой точки. Как известно, имеют место соотношения:
а = г cos ср, ^ = г sin ср, г = ]/а2 -f- b\
а Ь . Ь
— sin y= 9 = arctg—
— y2 b2 Y Y2 + b2 r a
C)
Положительное число г называется модулем, ср ~ аргументом
комплексного числа а -[- bi. Аргумент определяется лишь с точностью
до слагаемого, кратного 2тг, так как всякий вектор MN совместится
сам с собой, если его повернуть на любое число полных оборотов
в ту или иную сторону вокруг точки М. В случае г = 0 комплекс-
комплексное число равно нулю, и его аргумент совершенно неопределенен.
Условие равенства двух комплексных чисел состоит, очевидно, в том,
что модули их должны быть равны, а аргументы могут отли-
отличаться лишь слагаемым, кратным 2тс.
Вещественное число имеет аргумент 2?тс, если оно положитель-
положительное, и B&-[-1)тс, если оно отрицательное, где k — любое целое
число. Если вещественная часть комплексного числа равна нулю,
то комплексное число имеет вид Ы и называется чисто мнимым.
Соответствующий такому числу вектор параллелен оси О К, и
аргумент чисто мнимого числа Ы равен (-^--j-2&тс), если
если
Модуль вещественного числа совпадает с его абсолютным значе-
значением. Для обозначения модуля числа a -j- bi пишут это число между
двумя вертикальными чертами:
\а-\-Ы\= /а* + Ь\
171 ] § 17. КОМПЛЕКСНЫЕ ЧИСЛА 407
В дальнейшем мы будем часто обозначать комплексное число
одной буквой. Если а есть комплексное число, то его модуль будет
обозначаться символом | а |. Пользуясь выражением C) для а и Ь,
можем выразить комплексное число через его модуль и аргумент
в виде
г (cos 9"W sin ?)•
В этом случае говорят, что комплексное число написано в тригоно-
тригонометрической форме.
171. Сложение и вычитание комплексных чисел. Сумма век-
векторов представляет собою замыкающую многоугольника, составлен-
составленного из слагаемых векторов. Принимая во внимание, что проекция
замыкающей равна сумме проекций составляющих, мы приходим
к следующему определению сложения комплексных чисел:
xf) + (а2 + М +... + (ая + bnt) =
D)
Нетрудно видеть, что сумма комплексных чисел не зависит от по-
порядка слагаемых (переместительный закон) и что слагаемые можно
объединять в группы (сочетательный закон), ибо такими свойствами
обладают сумма вещественных чисел ak и сумма вещественных
чисел bk.
Как мы упоминали выше, комплексное число а-\-Ы отожде-
отождествляется с вещественным числом #. Точно так же число 0 -\- bt
записывают просто в виде Ы (чисто мнимое число). Пользуясь опреде-
определением сложения, мы можем утверждать, что комплексное число
a-\-bi есть сумма вещественного числа а и чисто мнимого числам/,
то есть а + 6 = (а + °0 + @ + *0-
Вычитание определяется как действие, обратное сложению, т. е.
разность
¦* + У1 = (ai + ь i0 — (fh
определяется из условия
i) = ах + ЬХ1,
или, в силу D) и B): x-\-a$ = a1; y-\-b% = bl, т. е. х = ах — аъ
y = bt — ?2, и окончательно получаем
(в1 + bYi) - (в, + Ь4) = (at — а%) + (*, - bJL E)
Вычитание комплексного числа (fli-\-b4)> как мы видим, равно-
равносильно сложению уменьшаемого (at -j- b±i) и комплексного числа
(— а2 — Ь4\ Это соответствует следующему: вычитание векторов
сводится к сложению вектора уменьшаемого с вектором, по ве-
величине равным вычитаемому, а по направлению ему противопо-
противоположным.
408
ГЛ. VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ
172
Рассмотрим вектор А^А
ствует комплексное число
Этот вектор представляет собой, очевидно, разность векторов ОАХ и
начальной точке Л2 которого соответ-
соответи концу А\— число ^
ОАч (рис. 169) и, следовательно,
ветствует комплексное число
ему соот-
соотравное разности комплексных чисел, соответ-
соответствующих его концу и его началу.
Установим теперь свойства модуля суммы
и разности двух комплексных чисел. Прини-
Принимая во внимание, что модуль комплексного
числа равен длине соответствующего этому числу вектора и что одна
сторона треугольника короче суммы двух других, получим (рис. 170)
Рис. 169.
причем знак равенства будет иметь место лишь в том случае, когда
векторы, соответствующие комплексным числам ъх и о^, имеют одина-
одинаковое направление, т. е. когда аргументы этих чисел или равны, или
отличаются на кратное 2тс. Доказанное свойство имеет, очевидно,
место и в случае любого числа слагаемых:
... П
т. е. модуль суммы меньше или равен сумме
модулей слагаемых, причем знак равенства
имеет место лишь в том случае, когда аргу-
аргументы слагаемых равны или отличаются крат-
кратным 2тс.
Принимая во внимание, чтр сторона треуголь-
треугольника больше разности двух других сторон, можем, 0
кроме того, написать
Рис. 170.
т. е. модуль суммы двух слагаемых больше или равен разности
модулей этих слагаемых. Равенство будет иметь место лишь в том
случае, когда направления соответствующих векторов противоположны.
Вычитание векторов и комплексных чисел приводится, как это мы
видели выше, к сложению, и для модуля разности двух комплексных
чисел будем, как и для модуля суммы, иметь (рис. 170)
Ы — I ч\ <|<ч — **\ <КИ-1а21-
172. Умножение комплексных чисел. Произведение двух ком-
комплексных чисел мы определяем аналогично произведению веществен-
вещественных чисел, а именно: произведение рассматривается как число,
172 } § 17. КОМПЛЕКСНЫЕ ЧИСЛА 409
составленное из множимого, как множитель составлен из единицы.
Вектор, соответствующий комплексному числу с модулем г и аргу-
аргументом <р, может быть получен из единичного вектора, длина кото-
которого равна единице и направление которого совпадает с положи-
положительным направлением оси ОХ, путем его удлинения в г раз и пово-
поворота в положительном направлении на угол ф.
Произведением некоторого вектора а4 на вектор а2 назовем век-
вектор, который получится, если к вектору blx применить [вышеуказан-
[вышеуказанные удлинение и поворот, при помощи которых вектор а2 полу-
получается из единичного вектора, причем последнему соответствует,
очевидно, вещественная единица.
Если (rx> <pi)> (г* ъ) СУТЬ модули и аргументы комплексных
чисел, соответствующих векторам ai и а2, то произведению этих
векторов будет, очевидно, соответствовать комплексное число с мо-
модулем гхг% и аргументом (ф1-|-ф2)« Мы приходим, таким образом,
к следующему определению произведения комплексных чисел:
Произведением двух комплексных чисел называется такое
комплексное число, модуль которого равен произведению модулей
сомножителей и аргумент — сумме аргументов сомножителей.
Таким образом, в том случае, когда комплексные числа напи-
написаны в тригонометрической форме, будем иметь
Т\ (cos f t -f-1 sin cpx) ¦ r2(cos cp2 -{- / sin ср2) =
[ cos (<pt -f- <ря) -И sin (<
Выведем теперь правило составления произведения для того слу-
случая, когда комплексные числа даны не в тригонометрической форме:
Пользуясь указанным выше обозначением модулей и аргументов
сомножителей, можем написать
ах = rx cos <pt, bx == гi sin ср1? а2 = r2 cos cp2, b% = ra sin <p2;
согласно определению умножения F):
x = rfa cos ((pt + (р2), у = rfa sin (?! + срз),
откуда
х = гхгг (cos cp! cos <р2 — sin ffx sin <p2) =
= rx cos ф! • r2 cos фа — rx sin <pt • r2 sin cp2 = axa% — ЬхЪгу
у =r rxr% (sin (px cos cp2 + cos ?t sin ?a)= ri sin Ti' r« cos ?«+
-f- rx cos ф! • r2 sin ф2 = bxa% + a^
и окончательно получим
G)
410 ГЛ. VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ [ 172
В случае Ь1 = Ь% = 0 сомножители являются вещественными
числами ах и а2 и произведение приводится к произведению ахаг
этих чисел. В случае а1 = а% = 0 и ^1 = &2=1 равенство G) дает
т. е. квадрат мнимой единицы равен (-—1).
Вычисляя последовательно целые положительные степени /, по-
получим
и вообще, при всяком целом положительном ?:
Правило умножения, выражаемое равенством G), можно форму-
формулировать так: комплексные числа надо перемножать, как буквен-
буквенные многочлены, считая Р = —1.
Если а есть комплексное число а-\-Ы> то комплексное число
а — Ы называется сопряженным с а, и его обозначают через а. Со-
Согласно формулам C) имеем |a|2 = a2-f- b*.
Но из равенства G) вытекает
(а + Ы) (а — Ы) = а2 + Ъ\
а следовательно,
| a |2 = (а + Ы)(а — Ы) = aa,
т. е. произведение сопряженных комплексных чисел равно квад-
квадрату модуля каждого из них.
Отметим еще очевидные формулы
<х + а = 2я, а__а = 2^. (8)
Из формул D) и G) непосредственно следует, что сложение и
умножение комплексных чисел подчиняются переместительному за-
закону, т. е. сумма не зависит от порядка слагаемых, а произведение —
от порядка сомножителей. Нетрудно проверить и справедливость
сочетательного и распределительного законов, выражающихся сле-
следующими тождествами:
(а2 -{- а2) -j- а3 = аА -f- (a3 -f- a3),
Предоставляем сделать это читателю.
Заметим, наконец, что произведение нескольких сомножителей
будет иметь модуль, равный произведению модулей сомножителей,
и аргумент, равный сумме аргументов сомножителей. Таким
образом, произведение комплексных чисел будет равно нулю тогда
и только тогда, когда, по крайней мере, один из сомножителей
равен нулю.
173 ] § 17. КОМПЛЕКСНЫЕ ЧИСЛА 411
173. Деление комплексных чисел. Деление комплексных чисел
определяется как действие, обратное умножению. Таким образом,
если (г1э срх) — модуль и аргумент делимого, а (г2, <р2)— модуль и
аргумент делителя, то нетрудно видеть, что деление имеет один
определенный результат, если делитель отличен от нуля, и что мо-
модуль частного будет —, а аргумент его (cpj — ср^)- Обозначая частное
в виде дроби, можем написать
г, (cosy,-Иsin 9l) = rj_ _ } + s.n _
r2 (cos ср2 4-1 sm cp2) r2 L VT1 JlJ ' VT1 TZ7J v '
Итак, модуль частного равен частному модулей делимого и
делителя, и аргумент частного равен разности аргументов де~
лимого и делителя. Если г2 = 0, то формула (9) теряет смысл.
Если делимое и делитель даны не в тригонометрической форме, а
в виде ax-\-bxi и a2-j-#2j, то, выражая в формуле (9) модули и
аргументы через а1у аь Ъь Ъъ получим следующее выражение для ча-
частного:
fli + bj a1a2-{-b1b2 , b1a2— atb2 .
"r h
которое можно получить и непосредственно, рассматривая i как
иррациональность и умножая числитель и знаменатель на комплекс-
комплексное число, сопряженное со знаменателем, для того чтобы освобо-
освободиться от иррациональности в знаменателе
i) (a2 — b2i) _ (gAg2 + Ma) + (bxa% — a
и окончательно,
bxb2 , bxa2 — ajJ
Раньше [172] мы указали на то, что переместительный, сочета-
сочетательный и распределительный законы сохраняют свою силу и при
сложении и умножении комплексных чисел, а потому для выражений,
содержащих комплексные числа, оказываются справедливыми все те
преобразования, которые являются следствиями этих законов и ко-
которые хорошо известны в применении к вещественным числам. Сюда
относятся, например: правило вынесения за скобку, раскрытие ско-
скобок, простейшие формулы, формула бинома Ньютона в случае целого
положительного показателя, формулы, относящиеся к прогрессиям,
и т. д.
Отметим еще одно важное свойство выражений, содержащих
комплексные числа, связанные знаками первых четырех действий.
Из формул D), E), G) и A0) непосредственно вытекает следующее
412 ГЛ. VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ I 174
предложение: если в сумме, разности, произведении и частном за-
женим все числа сопряженными, то и результаты действий за-
заменятся сопряженными.
Так, например, заменяя в формуле G) Ьх и Ъ% на (— bt) и (— Ь^)у
получим
{а1 — bxi) (а2 — Ь4) = {ахаг — bxb^) — (bta% -f-
Указанное свойство будет, очевидно, справедливым и для лю-
любого выражения, содержащего комплексные числа, связанные зна-
знаками первых четырех действий.
174. Возвышение в степень. Применяя формулу F) в случае п
равных сомножителей, получаем правило возвышения комплексного
числа в целую положительную степень
[г (cos cp -j- i sin ср)]л = rn (cos яср -f- / sin n<f), A1)
т. е. для возвышения комплексного числа в целую положительную
степень нужно его модуль возвысить в эту степень и аргумент
умножить на показатель степени.
Полагая в формуле A1) г=1, получаем формулу Моавра
(cos cp + i sin <р)л = cos щ -\- i sin щ. A2)
Примеры. 1. Разлагая левую часть равенства A2) по формуле би-
бинома Ньютона и приравнивая вещественные и мнимые части согласно усло-
условию B), получим выражения для cos щ и sin щ через степени coscpH sin1)
cos n<p = cos* <p — (") cos/l~2 <P sin2
+ (?) cos»cp sin4 9 + ... + (— \f («л) cos71-* 9 sin2* <
n
A—IJ sin«9 (/г—четное)
+ ... + < Ц1
(—1) * n cos <p sin'19 (n — нечетное);
sin л<р = (") cos'1 <p sin^ — C) cosn~8 9 sin8 9 + E) cos71'5 <p sin5 9 —... +
+ (- 1)* 0*+1) cos"*-* 9 sin2^9 +... +
2
(—1) 2 sinn9 (n — нечетное).
^(— 1) 2 n cos 9 sin"9 (/г — четное)
A) 2
*) Символом (Jj) мы обозначаем число сочетаний из п элементов
по т, то есть
/п \ __ /г (п— 1) ...(/г — W+1) /г!
174 ] § 17. КОМПЛЕКСНЫЕ ЧИСЛА 413
В частности, при « = 3 формула A2) после раскрытия скобок будет
иметь вид
cos8 9 + 3/ cos3 9 sin 9 — 3 cos 9 sin2 9 — i sin8 9 = cos З9 + / sin З9,
откуда
cos З9 = cos8 9 — 3 cos 9 sin2 9, sin З9 = 3 cos2 9 sin 9 — sin3 9.
2. Просуммируем выражения
An = 1 + r cos 9 + r2 cos 29 +... + rn~x cos (n —1)9,
Положим
г = г (cos 9 + / sin 9) ]
и составим комплексное число
An + Bnl=\ +r(cos9 + * sin 9) + г2 (cos 2<? + t sin 29) + ...+
[cos(л —1)9 + * sin (л — 1)<p].
Пользуемся равенством A1) и формулой для суммы геометрической про-
прогрессии
A — rn cos /19) — 1гп sin Щ
1=3 A —г cos 9) — ir sin 9 *
Умножая числитель и знаменатель последней дроби на величину
A—rcos9) + ir sin 9» сопряженную со знаменателем, получим
А 4-/? fl— К1 -~ r" cos п^ "" *r" sin wcp^ ^! -" r cos y) + fr sin ^ —
л ^ л3 A— r cos9J + r2sin29 "
A — r/> CoS ^y) (i — r cos 9) -f- rw+1 sin 9 sin ^9
~ ra —2r C0S9+I
) /t sjn щ
rn+1 cos (n — 1)9 — rn cos Д9 — r cos 9 4"
r2 — 2r cos9+1
. rff+1 sin (n — 1)9 — rn sin 719 -}- г sin 9
*i r2 — 2r cos 9 -f-1
Приравнивая вещественные и мнимые части согласно условию B), будем
иметь
Ап = 1 + г cos 9 + г2 cos 29 + ••• + rn~x cos (л — 1) 9 =
rn+l cos (/г — 1)9 — rn cosny — г cos 9 + 1
г2 — 2r cos 9 + 1 *
_ гЛ+1 sin (n — 1)9 — rn sin /19 + г sin 9
r8 — 2r C0S9+I "•
414 ГЛ. VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ I 175
Считая, что абсолютное значение вещественного числа г меньше еди-
единицы, и беспредельно увеличивая п, получим в пределе суммы бесконеч-
бесконечных рядов
A4)
sin 29¦+... = -7Г^
В выражениях Ап и Вп положим г=1, тогда получим
cos (п — 1)9 — cos щ — cos 9 4* \ _
.4- COS (Я— 1) т — о/1 ч
1 v ' /т 2A — cos9)
2 sin-1 sin (я — -1\<р + 2 sin2 ^ &1[п — ±)ч+ sin-t
4sin2-|- 2 sin i
sin ~ cos
'. A50
sinY
Аналогичным образом получим
sin 9+ sin 29 + ".+ sin (/1 — 1)9 = . A52)
175. Извлечение корня. Корнем п-й степени из комплексного
числа называется такое комплексное число, п-я степень которого
равна подкоренному числу.
Таким образом, равенство
Y* (cos cp -f-1 sin cp) = р (cos <|> + / sin ф)
равносильно равенству
рп (cos лгф -}- / sin Щ) = г (cos cp -}- / sin cp).
Но у равных комплексных чисел модули должны быть равны и
аргументы могут отличаться лишь кратным 2тс, т. е.
рп = г, Щ = с
откуда
где |/"г есть арифметическое значение корня и & — любое целое
число. Таким образом, мы получаем
>/r(cos<p-f-isincp)=i/ r ^cos-^-^ \-tsm -s-^—j, A6)
175 | § 17. КОМПЛЕКСНЫЕ ЧИСЛА 415
т. е. для извлечения корня из комплексного числа надо извлечь
корень из его модуля, а аргумент разделить на показатель корня»
В формуле A6) число k может принимать всевозможные целые
значения; однако можно показать, что различных значений корня
будет только п} и они буд^Гг соответствовать значениям
А = 0, 1, 2,..., (п — 1). A7)
Чтобы доказать это, заметим, что правые части в формуле A6) бу-
будут различными при двух различных значениях k = kx и k = k% тогда,
+ 2k + 2k
когда аргументы — и —¦ — отличаются не кратным 2т:, и бу-
будут одинаковыми, если указанные аргументы отличаются кратным 2 тс.
Но разность (&! — k%) двух чисел из ряда A7) по абсолютному
значению меньше п, а потому разность
_ kx — k
2 2
п
не может быть кратна 2ти, т. е. п значениям k из ряда A7) соответ-
соответствуют п различных значений корня.
Пусть теперь &2 — целое число (положительное или отрицатель-
отрицательное), не заключающееся в ряде A7). Мы можем представить его
в виде
где q — целое число и kt — одно из чисел ряда A7), а потому
9 + 2 V _ т + ЗМ | 2
т. е. значению k% соответствует то же значение корня, что и значе-
значению kb заключающемуся в ряде A7). Итак, корень п-й степени из
комплексного числа имеет п различных значений.
Исключение из этого правила представляет лишь частный случай,
когда подкоренное число равно нулю, т. е. г = 0. В этом случае
все указанные выше значения корня равны нулю.
Примеры. 1. Определим все значения у i. Модуль i равен единице
и аргумент -^-, а потому
cos|- + / 8inTe cos-i—§ +i sin —з № = 0, 1, 2).
Мы получаем следующие три значения для /7:
п_ . ]l___Vj_y _L . 5я , . . 5тс__ / 1
Зтс . Зтс
cos -~- + 1ш sm 15- = — *•
416 ГЛ. VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ [ 176
2. Рассмотрим все значения j/T, т. в. все решения двучленного урав-
уравнения
Модуль единицы равен единице и аргумент —нулю, а потому
П, П/ ; 2klt 2&Jt
п п »»»•••*
Обозначим буквой 8 то значение этого корня, которое получается при & = 1;
е = cos (-/ sin —.
п ' п
Согласно формуле Моавра:
ft_ ?^5Lj.- • 2kK
"" п п f
т. в. все корни уравнения zn = \ имеют вид
е* (? = 0, 1, 2, .... п-1),
причем надо считать е° = 1.
Рассмотрим теперь двучленное уравнение вида
гп = а.
Вместо г введем новое неизвестное и, полагая
Я/—
г — иуа,
где j/аГесть одно из значений корня /i-й степени из а. Подставляя выра-
выражение для z в данное уравнение, получим для и уравнение
Отсюда видно, что все корни уравнения гп =а могут быть представ-
представлены в виде
где у/~а — одно из п значений этого корня и ък принимает все значения
корня П'й степени из единицы.
176. Показательная функция. Мы рассматривали раньше показа-
показательную функцию ех в случае вещественного показателя х. Обобщим
теперь понятие о показательной функции на случай любого ком-
комплексного показателя. При вещественном показателе функция ех
может быть представлена в виде ряда [129]
Определим аналогичным рядом показательную функцию и
в случае чисто мнимого показателя, т. е. положим
Отделяя вещественные и мнимые члены, имеем отсюда
еУ1
==[1 ~!г+1г~1г + -"
176 I § 17. КОМПЛЕКСНЫЕ ЧИСЛА 417
откуда, вспомнив разложения cosy и sin у в ряд [130], получаем
?^ = cos y-\-i sin у. A8)
Эта формула и определяет показательную функцию при чисто
мнимом показателе. Заменяя у на (—у):
e'yi = cosy — lsiny A9)
и решая уравнения A8) и A9) относительно cosy и sin у, получим
формулы Эйлера, выражающие тригонометрические функции через
показательные с чисто мнимым показателем:
?2i, sinJ/==??i-2l. B0)
Формула A8) дает новую показательную форму комплексного
числа, имеющего модуль г и аргумент <р:
г (cos <р 4" I sin ?)= re9i-
Показательную функцию при любом комплексном показателе
x-{-yi определяем формулой
ex+yi _ ех, eyi _ ех (C0S y _|_ f sin ^ ^21)
т. е. модуль числа exJpyt будем считать равным ех, а аргумент
равным у.
Нетрудно обобщить на случай комплексных показателей прави-
правило сложения показателей при умножении. Пусть z = x-\-yl a
ег • ег* = ех (cos у -f- i sin у) • e*i (cos j^ -j- ^ sin y^,
или, применяя правило умножения комплексных чисел [172],
ег • e*i = e***i [cos (у + У1) +1 sin
Но выражение, стоящее в правой части этого равенства, согласно
определению B1), представляет собою
9 т0 есть ez+zi.
Правило вычитания показателей при делении
может быть непосредственно проверено путем умножения частного
на делитель.
В случае целого положительного п будем иметь
а раз
Л A. R И. Пмипнпа. г. I
418 ГЛ. VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ [ 177
Пользуясь формулами Эйлера, мы сможем выразить любую целую поло-
положительную степень sin ф и соэф, а также и произведение таковых степеней,
в виде суммы членов, содержащих лишь первые степени синуса или косинуса
кратных дуг:
B2)
Разложив правые части этих равенств по формуле бинома Ньютона,
перемножив их и приведя в полученных разложениях показательные функции
к тригонометрическим, согласно формулам A8) и A9), мы получаем искомое
выражение.
Примеры. 1.
16 " 16 "Г 16 ~*~ 16 "^ 16 "*" 16
* 3 3.1
2.
128
8=5 128 в
3 3 1 1
¦= 64 C0S ф *~ 64 C0S Зф "" 64 C0S 5ф "" 64 C0S 7ф *
Заметим при этом, что любая целая степень cos ф и четная степень sin ф
представляют собою четные функции ф, т. е. не меняют своей величины при
замене ф на (—ф), и выражение таких четных функций ф будет содержать
лишь косинусы кратных дуг. Если же функция есть нечетная функция ф,
т. е. если эта функция меняет знак при замене ф на ( — ф), как это будет
иметь, например, место в случае нечетной степени sin ф, то разложение такой
функции будет содержать лишь синусы кратных дуг, и свободный член в этом
разложении будет наверное отсутствовать. Все эти обстоятельства будут
нами выяснены более подробно при изложении тригонометрических рядов.
177. Тригонометрические и гиперболические функции. До сих
пор мы рассматривали тригонометрические функции лишь в случае
вещественного аргумента. Определим тригонометрические функции
при любом комплексном аргументе z по формулам Эйлера:
ezi _j_ e-zi . ^ ezi _ e-zi
g Sin Z^
_^ e j e . ^
COS Z g , Sin Z—
9
причем выражения, стоящие справа, при любом комплексном z имеют
смысл, указанный в [176].
Пользуясь этими формулами и основными свойствами показатель-
показательной функции, нетрудно проверить справедливасть формул тригоно*
177 1 § 17. КОМПЛЕКСНЫЕ ЧИСЛА 419
метрии в случае комплексного аргумента. Предлагаем читателю в ка-
качестве упражнения доказать, например, соотношения
sin2* + cos2* =1,
sin (* + zx) = sin * cos zx + cos * sin zb
COS (* + *x) = COS * COS *! — Sin * Sin Zx.
Функции tg* и ctg* определяются по формулам
. sin;
tg* =
ь cos z
Введем теперь гиперболические функции. Гиперболические синус
и косинус определяются по формулам
ег е-в
, СП * = COS /* г~
th _5!l? &—e~z _e*z—l
Z~~chz = ez+e-z "~^+l*
sh2 ^г—^ ^ е2г—1
Пользуясь этими формулами, нетрудно проверить, например, сле-
следующие соотношения:
B3)
Таким образом возникает гиперболическая тригонометрия с фор-
формулами, аналогичными формулам обычной тригонометрии круга.
Заменяя в формуле обычной тригонометрии sin* на / sh* и cos* на
ch *, получим аналогичную формулу гиперболической тригонометрии.
Это обстоятельство вытекает непосредственно из формул, определяю-
определяющих гиперболические функции,
sh (^i ± z2) = sh ^ ch ,г2 ± ch гг sh г^
ch (zx ± z2) = ch zi ch ,г2 dt sh zx sh ^2,
sh 2z = 2 sh г ch z, ch 2г
420
ГЛ. VT. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ
I 177
Пользуясь этим указанием, нетрудно получить следующие формулы
приведения суммы гиперболических функций к логарифмическому
виду:
•ch-
2
sh zx — sh z% = 2 sh
0, — Zs 1
1 n 2 ch ¦
¦ch-
B4)
Рассмотрим теперь гиперболические функции при вещественных
значениях аргумента:
У т gx—q-x gx _j_ 0-х
~ 2 • chx= 2 f
е2х— 1
График функции д; = сЬдг предста-
представляет собой цепную линию [78], к бо-
более подробному изучению которой мы
перейдем в [178]. Графики функций
chAr, shx, th -хг, cthA: изображены на
рис. 171.
Непосредственно дифференцируя,
получаем следующие выражения произ-
производных:
Рис. 171.
dx
ch2*
tf ch*
tf cth*
dx ~
Отсюда получаем таблицу интегралов:
l shAT^Ar = ch^r + C,
Г dx
Г dx _
J sh2 *
Самое название „гиперболические функции* произошло вследствие
177 1
§ 17. КОМПЛЕКСНЫЕ ЧИСЛА
421
того, что функции cht и sht играют ту же роль для параметриче-
параметрического представления равнобочной гиперболы
какую функции cost и smt — для окружности
Параметрическое представление окружности есть
x = acost, y = aslnt,
равнобочной же гиперболы
х = a ch t, у = a sh t,
как в этом нетрудно убедиться при помощи соотношения
ch2 * — sh2*=l.
Геометрическое значение параметра t в обоих случаях, окруж-
окружности и гиперболы, также одинаково. Если мы обозначим через 5
у \
Рис. 172.
Рис. 173.
площадь сектора А ОМ (рис.172), а через ?0 площадь всего круга
(?0 = тш2), то, очевидно,
Пусть теперь 5 обозначает площадь аналогичного сектора равнобоч-
равнобочной гиперболы (рис. 173). Мы имеем
X
5=пл. OMN—ш. AMN=~xy— fydx =
a
x
— ~2ГХ /^2 — a2 — l /x2*—a2 dx*
422 ГЛ. VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ [ 178
Вычисляя интеграл по формуле из [92], находим:
_а* — а* log (х + Ух* ~ я2)]* =
Если теперь, обозначая опять через 50 площадь круга, положим
то найдем без труда
х Г х2 a
—+ 1/ Т" — 1
откуда, складывая почленно и умножая на -y:
а2 = ash*,
т. е. мы и получаем параметрическое представление равнобочной ги-
гиперболы.
178. Цепная линия. Исследуем кривую провисания гибкой однородной
тяжелой нити, подвешенной на концах At и А2 (рис. 174).
В плоскости этой кривой направим ось ОХ горизонтально, ось ОУ вер-
вертикально вверх. Выделим элементы MM1=-ds нити. На каждый из них дей-
действуют натяжения Т и 7\ от оставшихся частей нити и вес элемента. Натя-
Натяжения приложены в концах М и Mt элемента и направлены по касательным
(причем Т—по отрицательному, 1\ — по положительному направлению ка-
касательной). Вес мы можем принять пропорциональным длине элемента
dp = р ds,
где р — линейная плотность нити (вес погонной единицы длины).
Для равновесия необходимо и достаточно, чтобы равнялась нулю сумма
проекций действующих на элемент сил как на горизонтальное, так и на вер-
вертикальное направление. Так как проекция веса элемента ds на горизонталь-
горизонтальное направление равна нулю, то горизонтальные составляющие сил Т и Тх
должны быть равны по величине и противоположны по знаку. Обозначим
через То общую величину их горизонтальной составляющей.
Далее, из чертежа мы получаем для вертикальных составляющих натя-
экений соответственно выражения
-rotg« = -ro/ и Г§ tg (а+ |/а) = Гв (у+ */).
178]
§ 17. КОМПЛЕКСНЫЕ ЧИСЛА
423
Здесь da — прирост угла а, образованного касательной с осью ОХ, при
перемещении из точки М в точку Mif и d/ — соответствующее прираще-
приращение углового коэффициента касательной, т. е. величины tga.
Рис. 174.
Приравнивая нулю сумму проекций Г, 7\ и силы веса р ds на ось О К,
получим
то есть
что можно написать так:
Todyf = р ds,
^р/
Переменные здесь разделяются [93]:
dx.
B5)
заметим, что k есть постоянная, прямо пропорциональная горизонтальной
составляющей натяжения и обратно пропорциональная линейной платности
нити. Интегрируем полученное уравнение
откуда
е =у -j- у
чтобы определить у, введем обратную величину
е = / в/
У + /1+У2
Вычитая почленно это равенство из предыдущего, находим
у ~~ 2
424 ГЛ. VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ | 178
Интегрируя еще раз, получим уравнение искомой кривой нити
<2б>
Произвольные постоянные Ct и С2 определяются из условия, что кривая
проходит через точки At (av bt) и А2 (а21 Ь2). Однако в приложениях наиболь-
наибольший интерес представляет не само уравнение кривой провисания, т. е. по-
постоянные Cj и С2, а соотношение между горизонтальным и вертикальным
расстояниями точек подвеса и длиной дуги АгА2.
При исследовании зависимости между этими тремя величинами мы мо-
можем, конечно, совершить параллельный перенос координатных осей.
Поместив начало в точку (— С1У —С2), мы можем считать, что в уравнении
B6) CjssCjssO, и это уравнение заменится более простым
?л ¦ К
откуда ясно, что кривая провисания есть цепная линия.
Пусть при указанном выборе координатных осей точка подвеса Ах имеет
координаты (а1} bj) и А2 — координаты (а2, Ь2). Обозначив через /, Л, s гори~
зонтальное и вертикальное расстояния точек подвеса и длину нити, будем
иметь
«2
«1 «1 «1
По формулам B4) находим
откуда на основании первого из соотношений B3)
s2 — h2 = 4k2sh24-
что и дает искомую зависимость между /, h и s. Ее можно переписать в сле-
следующей форме:
Sri fTr
^. B7)
2k
Если точки подвеса и длина нити заданы, то величины /, h и s известны
и мы получаем уравнение для определения параметра k, или если линей-
линейная плотность р нити также известна, то уравнение B7) может служить для
определения горизонтальной составляющей натяжения Го. Положим для
сокращения письма:
178 ] § 17. КОМПЛЕКСНЫЕ ЧИСЛА 425
Уравнение B7) превратится в
she _
Вспомнив разложение показательной функции в степенной ряд [1291, найдем
she __ е^—е-1 —1 . е2 ?* ?6
е 2; 3! 51 7! *"''
откуда видно, что при возрастании е от 0 до +оо отношение также посто-
постоянно возрастает от 1 до +оо. Стало быть, при всяком заданном значении
с ^> 1 уравнение B7j) имеет один положительный корень, который можно
вычислить, пользуясь таблицами гиперболических функций J). Данные вели-
величины /, h и s должны при этом удовлетворять
условию
U2
или
которое очевидно и из геометрических сообра-
соображений, так как Yh2-\-l2 есть хорда А±А21 as— '
дуга цепной линии между теми же точками.
Пусть, например,
$ = 100 м% / = 50 м% Л = 20 м, р =20 кг/м,
мы получим
с = 0,02 V Ю 000 — 400 = 0,8 • /б" = 1,96
и по таблицам гиперболических функций найдем корень уравнения B74);
откуда
) = *Р = ^Р = -о-5?тЕ-'20 = 232 кг.
Пусть точки подвеса находятся на одинаковой высоте. Исследуем стрелу
провисания нити / (рис. 175):
Разлагая показательную функцию в ряд, получим
i
2!
B8)
Точно так же будем иметь для s=flyre AtA2 [формула B7) при Л = 0]:
±=k[e™-e~™) = l + ±~i+±^lF+... B9)
1) Например, таблицы Янке и Эмде,
426 ГЛ. VT. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ [ 178
Ограничиваясь в ряде B8) одним слагаемым, определим приближенно k:
В разложении B9) удержим первые два слагаемых и подставим найден-
найденное для к выражение
Дифференцируя это соотношение, получим зависимость между удлине-
удлинением нити и увеличением стрелы провисания:
или df^^T-^-As,
Уравнение B5) было нами получено в предположении, что на всякий
элемент нити действует сила тяжести, пропорциональная длине элемента.
В некоторых случаях, например при рассмотрении цепей висячих мостов,
эту силу тяжести надо считать пропор-
пропорциональной длине не самого элемента,
но его проекции на горизонтальную ось.
Это случится тогда, когда нагрузка от
> настила моста настолько велика по
сравнению с собственным весом цепи,
что последней можно пренебречь. В этом
случае вместо уравнения B5) будем
иметь
Tody' = р dxf
откуда
У = слТ х2 -f- Ctx -f- С2,
т. е. кривая провисания будет параболой.
Положим, что концы нити At и А2 находятся на одинаковой высоте,
и поместим начало координат в вершину параболы (рис, 176), так что
уравнение ее будет
у е= ах*
Как и выше, определим длину пролета lz=zAtA% и стрелу прогиба /=0Л.
Из уравнения параболы получим
/=а—, откуда а = -^-ч
Вычислим длину дуги АХА2) равную удвоенной дуге ОЛа1
i
s = l
. + 4а2 х2 <
179 ] § 17. КОМПЛЕКСНЫЕ ЧИСЛА 427
По формуле бинома Ньютона имеем
/1+4а2д:2 = A + 4а2 X2I!2 = 1 + 2а2X2 — 2а4*4 + ...
и, интегрируя, находим разложение для s:
Подставим вместо а найденное выше его выражение:
где е = у-. Ограничиваясь в написанном разложении двумя первыми сла-
слагаемыми, получим приближенную формулу
8 /2
совпадающую с аналогичной формулой для цепной линии.
17&. Логарифмирование. Натуральным логарифмом комплек-
комплексного числа г (cos ср —|— ^ sin ср) называется показатель степени,
в которую надо возвысить е, чтобы получить логарифмируемое
число. Обозначив натуральный логарифм символом Log, можем ска-
сказать, что равенство
Log [r (cos ср -|-1 sin ср)] = х +
равносильно следующему:
ex+yi _ r ?co
Последнее равенство можно написать так:
ех (cos у -\- i sin у) = г (cos ср —|— / sin ср),
откуда, сравнивая модули и аргументы, получим
e* = r, y = <? + 2kiz (* = 0, ±1, ±2,...)>
то есть
л: = log r и x-\-yi = logr-]-(y-{-2kiz)l
и окончательно:
Log [r (cos ср -f / sin ср)] = log г + (ср + 2k%) tt C0)
т. е. натуральный логарифм комплексного числа равен комплек-
комплексному числу, вещественная часть которого есть обычный ло-
логарифм модуля, а мнимая часть представляет собою произведе-
произведение i на одно из значений аргумента.
Мы видим, таким образом, что натуральный логарифм любого
числа имеет бесчисленное множество значений. Исключение состав-
составляет лишь нуль, логарифм которого не существует. Если мы под-
подчиним значение аргумента неравенству
428 ГЛ. VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ [ 180
то получим так называемое главное значение логарифма. Для отли-
отличия главного значения логарифма от общего его значения, даваемого
формулой C0), пользуются для главного значения обозначением log
вместо Log, так что
где — тс < р
С помощью логарифма определим комплексную степень любого
комплексного числа. Если и и v — два комплексных числа, причем
и ф 0, то положим
Заметим, что Log и, а потому и ii° имеют, вообще говоря, бес-
бесчисленное множество значений.
Примеры. 1. Модуль i равен единице и аргумент ~2~~, а потому
Logt = (-J- + 2**)* (Л = 0, ± 1, ± 2,...).
2. Определим ih
180. Синусоидальные величины и векторные диаграммы. Укажем
на применение комплексных величин при изучении гармонических колеба-
колебаний. Рассмотрим переменный ток, сила которого J в каждый момент вре-
времени имеет во всей цепи одно и то же значение, определяемое по формуле
у =/т sin (** + *), C2)
где t — время, a jmt а и «р — постоянные.
Постоянная jm которую мы будем считать положительной, называется
амплитудой) постоянная о> называется частотой и связана с периодом Т
соотношением
постоянная ср называется фазой переменного тока.
Ток, сила которого определяется по формуле C2), называется синусои-
синусоидальным. Сказанное применяется и для напряжения
v = trmsinH + (p1), C3)
и в дальнейшем мы будем рассматривать силы тока и напряжения, изме-
изменяющиеся по синусоидальному закону, определяемому формулами C2) и C3).
Существует простое геометрическое изображение синусоидальных вели-
величин одной и той же частоты. Через некоторую точку О плоскости прово-
проводим луч, который мы будем вращать с угловой скоростью со по часовой
стрелке; этот луч назовем осью времени.
Пусть начальное положение оси времени при* = 0 совпадает с осью ОХ
Построим вектор бл (рис. 177) длины jm который образует угол <$, с на-
начальным положением оси времени (напомним, что положительным направле-
направлением отсчета углов мы считаем направление против часовой стрелки).
180 I
§ 17. КОМПЛЕКСНЫЕ ЧИСЛА
429
В момент t вектор О А будет образовывать угол (<р + «0 с осью вре-
времени, повернувшейся на угол со?; проекция вектора ОА на направление, пер-
я
пендикулярное оси времени и получающееся поворотом ее на угол
про-
против часовой стрелки, или, короче говоря, взятая с надлежащим знаком
длина перпендикуляра, опущенного из конца вектора ОА на ось времени,
и дает нам, очевидно, величину J =i/msin((u* + cp).
Рис. 177.
Для изображения другой синусоидальной величины того же периода
надо будет отложить вектор длины у^» образующий с первым вектором угол
Таким образом, при помощи неподвижных векторов на плоскости мы
можем изображать синусоидальные величины одной и той же частоты. Дли-
Длина всякого вектора дает амплитуду соответствующей величины, а угол
между двумя векторами представляет собой разность фаз соответствующих
этим векторам величин. Построенные указанным образом векторы дают так
называемую векторную диаграмму системы синусоидальных величин одно-
одного и того же периода.
Геометрическая сумма нескольких векторов векторной диаграммы, со-
согласно теореме о проекции замыкающей, будет соответствовать синусоидаль-
синусоидальной величине того же периода, равной сумме синусоидальных величин,
соответствующих слагаемым векторам.
Пользуясь определением умножения, приведенным в [172], можно при-
придать операциям с векторными диаграммами удобный аналитический вид.
В дальнейшем мы будем обозначать векторы теми же буквами, но жир-
жирным шрифтом.
Произведение вектора j на комплексное число re*?1 будем считать
равным вектору, который получается из вектора j, если его длину умно-
умножить на г и повернуть его на угол ср, т. е. будем считать, что произведе-
произведение гё*1 j получается согласно приведенному в [172] правилу умножения
комплексного числа, изображающего вектор j, на комплексное число re*?1.
Если комплексное число ге& написать в виде (а + fa')» T0 произведение
можно представить в виде суммы двух векторов
430 ГЛ. VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ [ 180
причем первое слагаемое есть вектор, параллельный вектору j, а второе
слагаемое есть вектор, перпендикулярный вектору j.
Разлагая какой - либо вектор ji на два взаимно перпендикулярных напра-
направления, можем представить его в виде
При этом \а + Ы\ равно, очевидно, отношению длин векторов j и j$, а аргу*
мент числа (а + Ы) представляет собой угол, образованный вектором j^ с век-
вектором j. Этот угол дает разность фаз величин, соответствующих векторам jx и j,
Введем понятие о среднем квадратичной значении синусоидальной ве-
величины C2), которое мы обозначим символом М (j2). Оно определяется ра-
равенством
Интегрируя выражение
y»-/S,sta« (arf+ф) —g- /«,--j- /*, cos 2(со/+ <р)
в пределах от 0 до Т =—, получим
1 г 1 1—1
Корень квадратный из среднего квадратичного значения называется эф-
эффективным, или действующим, значением величины:
На практике при построении векторных диаграмм обычно принимают
длину вектора равной не амплитуде, а эффективному значению величины,
т. е. по сравнению с описанным выше построением длины векторов умень-
уменьшают в отношении 1: 1^2.
Дифференцируя формулу C2), получим
^¦«ю/да cos И + ф) = co/m sin (tot + ф +yj,
т. е, производная -J отличается от j лишь тем^ что амплитуда умножается
на © и к фазе прибавляется -^-.
Выведенное соотношение в векторных обозначениях напишется так;
§-т. C4)
Интегрируя формулу C2) я отбрасывая произвольную постоянную, что
необходимо делать, если мы желаем получить также Синусоидальную
181 1 § 17. КОМПЛЕКСНЫЕ ЧИСЛА 431
величину того же периода, имеем
dt = — - ]т cos (со* + <р) = -Jm sin(<о* + у — Jj^ t
откуда следует *)
181. Примеры. 1. Рассмотрим цепь переменного тока, в которую вве-
введены последовательно: сопротивление R, самоиндукция L и емкость С,
Обозначив через v напряжение и через j силу тока, будем иметь известное
из физики соотношение:
Ограничимся пока только явлениями установившимися и притом тем
случаем, когда и напряжение и сила тока оказываются синусоидальными
величинами одного и того же периода. Предыдущее уравнение можно пере-
переписать в векторной форме, введя вместо v и j векторы напряжения и тока
v и j:
v = Rj + Ld +
вспомнив формулы C4) и C5), находим отсюда
v = ^j + (oz:/j + ^j = (^ + w/)j=:Cj, C6)
где
u = (uL L, С = Я + и/. C7)
too
Полученная зависимость между векторами напряжения и тока имеет вид
обычного закона Ома с тою только разницей, что вместо омического сопро-
сопротивления здесь входит комплексный множитель С, который называется ка-
кажущимся сопротивлением цепи и состоит из суммы трех „сопротивлений":
омического (R), сопротивления от самоиндукции (ыЫ) и сопротивления
от емкости (--^г ].
\соЫ /
Формула C6) дает вместе с тем разложение вектора v на две составляю-
составляющие: R\ — по направлению у и ui\ — по направлению, перпендикулярному к j.
Первая называется ваттной, вторая — безваттной составляющими напряже-
напряжения. Эти термины станут ясными, если мы вычислим среднюю мощность W
тока нашей цепи, которая определяется как среднее арифметическое по всему
периоду от мгновенной мощности vj:
т т
W = j С vjdt = ^?? f sin (<o* + ?х) sin (со* + Ъ) dt;
<Pj означает здесь фазу напряжения, <р3 — фазу тока, так что
^= vm sin (со* + ?1), у =jm sin (со*
J) Символ -J обозначает вектор, соответствующий синусоидальной вели-
величине -?, а символ \jd* — вектор, соответствующий \ j dt.
432 ГЛ. VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ I 181
Без труда находим
W = ^ J [cos (Tl - Ъ) - cos Bш^ + Ъ)] dt
= ^ J [cos (Tl - Ъ) -
= Щ^ COS (?l — <р2) == veffjeff COS fo - Ъ). C8)
Таким образом, наибольшая по абсолютному значению средняя мощность
получается, когда фазы напряжения и тока совпадают или отличаются на п;
наименьшая, равная нулю, мощность получается, когда эти фазы отличаются
на л/2.
При составлении этого выражения W безваттная составляющая ui\
вектора v дает среднюю мощность, равную нулю, ибо вектор ui\ перпенди-
перпендикулярен вектору j, т. е. для него cos (срх— <р2)=0, и вся средняя мощность,
которая переходит в джоулево тепло, получается лишь от ваттной („рабочей")
составляющей.
Соотношение C6) можно переписать в виде
j = ^v = Y]V, где ч =
или
Комплексный множитель т) называется кажущейся проводимостью цепи,
он равен обратной величине кажущегося сопротивления. Предыдущая же
формула дает разложение вектора тока на ваттную и безваттную составляю-
составляющие (по направлению v и перпендикулярно к нему).
2. Основные правила для вычисления сопротивления сложной цепи постоян-
постоянного тока, в которую включены сопротивления последовательно или парал-
параллельно, правила, которые выводятся из законов Ома и Кирхгофа, остаются
в силе и для цепей с переменным установившимся синусоидальным током,
если только условимся мгновенные значения напряжения и тока заменить
соответствующими векторами, а омические сопротивления — кажущимися.
Так, если в цепь включены последовательно кажущиеся сопротивления
то векторы напряжения и тока будут связаны соотношениями:
v = C'j, где C'eCi + C + ..м C9)
т. е. при последовательном включении кажущиеся сопротивления склады»
ваются.
Наоборот, если те же сопротивления включены параллельно^ то мы по-
л^им соотношение
v = C"j, где i7=xl + L+... , D0)
т. е. при параллельном включении складываются кажущиеся проводимости.
Графически построение полного кажущегося сопротивления при последо-
последовательном включении кажущихся сопротивлений Ct, С2,... сводится просто
к построению геометрической суммы векторов, изображающих эти комплекс-
комплексные числа.
181 ]
§ 17. КОМПЛЕКСНЫЕ ЧИСЛА
433
Укажем построение в случае параллельного включения двух кажущихся
сопротивлений Сх и С2. Мы имеем по предыдущему правилу
Положив
мы будем иметь
С" =
Ро
Это приводит нас к следующему геометрическому построению (рис. 178I).
Находим прежде всего сумму Ci + С3 = ОС; затем строим Д AOD, подоб-
подобный Д СОВу для чего поворачиваем Д СОВ в положение С'0?' и проводим
прямую AD || С'В'-
Из подобия треугольников выводим:
то есть Р=
Ро
что и требовалось доказать.
3. Рассмотрим связанные колебания двух цепей, находящихся в магнит-
магнитном соединении (рис. 179). Пусть vl9j\ означают внешнюю электродвижущую
В
Рис. 178.
Рис. 179,
силу и силу тока в цепи I, j\ — силу тока в цепи II (без внешней электро-
электродвижущей силы); Rv R2> Ll} L21 Clt C2 — соответственно: сопротивления,
коэффициенты самоиндукции и емкости этих цепей, М — коэффициенты
взаимной индукции цепей I и II.
Имеем соотношения
dj.
dt
И
hdt,
hdt.
x) На чертеже мы для упрощения направили ось ОХ по вектору Clf что
приводится к предположению 0Х =0. В общем случае достаточно повернуть
ось ОХ на угол 0Х по часовой стрелке.
434 ГЛ. VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ [ 182
Если рассматривать установившийся процесс, в котором напряжение и
ток меняются по синусоидальному закону одинаковой частоты, то эти уравне-
уравнения можно переписать в векторной форме:
-) j2 =
где Ex и ?2— кажущиеся сопротивления цепей I и II, если они взяты сами
по себе. Решая относительно jj и j2, получим без труда
i -
Переписав первое уравнение в виде:
мы можем сказать, что наличие цепи II изменяет кажущееся сопротивление С
цепи I на слагаемое—=—.
182. Кривые в комплексной форме. Если вещественные числа условимся
изображать точками на данной оси ОХУ то изменение вещественной перемен-
переменной приводится к передвижению соответствующей точки по оси ОХ Совер-
Совершенно аналогично изменению комплексной переменной С = лг+у/ приводится
к передвижению изображающей точки по плоскости X0Y.
Особенно интересен тот случай, когда переменная С при своем измене-
изменении описывает некоторую кривую; это случится тогда, когда вещественная
и мнимая части, т. е. координаты х и у, суть функции некоторого параметра щ
который мы будем считать вещественным
* = <Pi(«)» У = ?«(«)• D1)
Мы будем тогда писать просто
С =/(«), где /(a) = <Pi («)
и будем называть это уравнение—уравнением рассматриваемой кривой D1)
в комплексной форме.
Уравнения D1) дают параметрическое представление кривой в прямо*
угольных координатах. К представлению ее в полярных координатах мы при-
придем, если напишем переменную С в показательной форме:
С = реЧ р = <Ы")> 0 = <Ы«).
В этом выражении множитель р есть не что иное, как ) С |, множитель
же е®*, который в случае вещественных С F = 0 или к) совпадает со „знаком"
(±. 1), есть вектор длины единицы и обозначается символом
(сокращенное латинское слово „Signum" — знак).
К необходимости рассмотрения уравнений кривых в комплексной форме
приводят векторные диаграммы. Если мы в соотношении
182 I § 17. КОМПЛЕКСНЫЕ ЧИСЛА 435
будем считать вектор тока j постоянным, но будем менять какую-нибудь из
различных постоянных цепи, то будет меняться кажущееся сопротивление ?
и вектор v; конец этого вектора v опишет кривую, которая называется диа-
диаграммой напряжения, построив которую, мы получим ясную картину
изменения вектора v. Точка ? также опишет кривую (диаграмма сопроти-
сопротивления), которая только выбором масштаба будет отличаться от диаграммы
напряжения (за единицу будет принят вектор j).
Рассмотрим теперь уравнения некоторых простейших кривых.
1. Уравнение прямой, проходящей через данную точку So^^o+W* и
образующий угол а с осью ОХ:
параметр и означает здесь расстояние, отсчитываемое от точки ?0 до
2. Уравнение окружности с центром в точке ?0 и радиусом г:
3. Эллипс с центром в начале координат и полуосями а и Ьу причем
большая ось направлена по оси ОХ, имеет в комплексной форме уравне-
уравнение [177]:
Если большая ось образует угол <p0 с осью ОХ, то уравнение эллипса примет
вид
В общем случае, когда центр эллипса находится в точке ?0 и большая ось
образует угол ф0 с осью ОХ, эллипс будет иметь уравнение
Если b=а, уравнение это обращается в уравнение окружности радиуса а:
где (фо + «)| так же как и и,— вещественный параметр. Если 6 = 0, получим
отрезок прямой:
pui JLp-lti
Ф*1 —Y—-
образующий угол ф0 с осью ОХ, длины 2а, середина которого в точке ?0,
ибо параметр v = a cos м — вещественный, подобно м, но может принимать
значения только между (—а) и (+а).
Рассматривая случаи окружности и отрезка прямой как предельные
случаи эллипса, получающиеся, когда малая полуось становится равной боль-
большой или обращается в нуль, мы можем теперь сказать вообще, что уровне-
нив
'* D2)
где So» Mi» y^—какие угодно комплексные числаь всегда представляет
уравнение эллипса.
В самом целе, положив
436
ГЛ. VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ
\ 182
можем переписать уравнение D2) в виде
откуда ясно, что рассматриваемая кривая есть действительно эллипс с центром
в точке Со, полуосями (Afx ± М2), и большая ось которого образует угол <р0
с осью ОХ, т. е. имеет направление биссектрисы угла между векторами /х1
и fx2. При М2=:0 эллипс обращается в окружность, при M2~ML — в отрезок
прямой.
4. При исследовании явле-
явлений переменного тока в цепях с
Рис. 180.
Рис. 181.
непрерывно распределенными сопротивлениями, емкостями и самоиндукцией
большое значение имеют кривые, уравнение которых в комплексной форме
имеет вид
С = ^и, D3)
где v и 7 — какие угодно комплексные постоянные.
Положив v = N^01, [7 = а + Ы и переходя к полярным координатам,
имеем отсюда
С == 9ен = Л^0*
то есть
откуда
или окончательно
т. е. рассматриваемая кривая есть логарифмическая спираль [рис. 180, соот-
соответствующий случаю-^- > 0 ).
Более сложные кривые типа
184 ] § 18. ОСНОВНЫЕ СВОЙСТВА ЦЕЛЫХ МНОГОЧЛЕНОВ 437
можно получить, построив „составляющие спирали*
и вычисляя геометрически при каждом значении и сумму соответствующих
значений tlf С2, ... , С* (рис. 181).
183. Представление гармонического колебания в комплексной форме.
Гармоническое затухающее колебание выражается формулой
х = Ae~et sin (со* + <р0), D4)
где А и е — положительные постоянные. Введем в рассмотрение комплексную
величину
Вещественная часть этой комплексной величины совпадает с выражением D4).
Таким образом, мы можем представить любое гармоническое затухающее
колебание как вещественную часть комплексного выражения вида:
С = «!"',
где аир — комплексные числа. В случае формулы D5):
(f)
а = Ае и р = <о + е/.
ичес
Выр
В случае чисто гармонического колебания без затухания е = 0 и (J будет
числом вещественным. Выражение D5) для С совпадает с выражением D3) при
и н =
Отсюда видно, что при изменении t точка С описывает логарифмическую
спираль, причем полярный угол 6 есть линейная функция времени t:
т. е. радиус-вектор из начала координат в точку С вращается вокруг начала
с постоянной угловой скоростью со. Проекция точки С на ось ОХ совершает
затухающие колебания D4). Если е = 0, то точка С движется по окруж-
окружности р=Д и ее проекция на ось ОХ движется по закону гармонического
колебания без затухания:
х = A sin (at + <Po)*
§ 18. ОСНОВНЫЕ СВОЙСТВА ЦЕЛЫХ МНОГОЧЛЕНОВ
И ВЫЧИСЛЕНИЕ ИХ КОРНЕЙ
184. Алгебраическое уравнение. В настоящем параграфе мы
будем заниматься исследованием целого многочлена (полинома):
где Oq, d, ... , ak> ... , ап — данные комплексные числа и z — ком-
комплексная переменная, причем старший коэффициент a§ мы можем
считать отличным от нуля. Основные действия с многочленами
438 ГЛ. VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ [ 184
хорошо известны из элементарной алгебры. Мы напомним только
основной результат, касающийся действия деления. Если/(г) и <р(<г) —
два многочлена и степень ср(г) не выше степени /(г), то f(z)
мЪжно представить в виде:
где Q(z)n R(z) — также многочлены, причем степень R(z) ниже
степени ср(г). Многочлены Q(z) и R(z) называются, соответственно,
частным и остатком при делении f(z) на ср(,г). Частное и остаток
суть вполне определенные многочлены, так что представление f(z)
в указанном выше виде через ср (z) единственно.
Значения z, при подстановке которых многочлен обращается
в нуль, называются корнями этого многочлена. Таким образом,
корни /(г) суть решения уравнения
.. +akz"-*+ ...+ ал_1г + ап = 0. A)
Написанное уравнение называется алгебраическим уравнением
п-й степени.
При делении f(z) на двучлен (z — а) частное Q(z) будет много-
многочленом^— 1)-й степени со старшим коэффициентом а0, остаток же R
не будет содержать z. По основному свойству деления имеет место
тождество
Подставляя в это тождество z = ay получим
т. е. остаток, получаемый при делении многочлена f(z)na{z — а),
равен /(а) (теорема Безу).
В частности, для того чтобы многочлен /(г)делился на B — а)
без остатка, необходимо и достаточно условие
т. е. для того чтобы многочлен делился на двучлен (z — а) без
остатка, необходимо и достаточно, чтобы z = a было корнем
этого многочлена.
Таким образом, зная корень z = a многочлена /(-г), мы можем
выделить из этого многочлена множитель (г — а):
f(z) = (z-a)fx(z)9
где
Д (г) = b, z*-1 + bx zn-* + ... + »л_, z
нахождение остальных корней приводит к решению уравнения
*,*»-» + $!*'-*+ ... + V
(п — 1}-й- степени.
185 ] :§ 18. ОСНОВНЫЕ СВОЙСТВА ЦЕЛЫХ МНОГОЧЛЕНОВ 439
Для дальнейшего нам необходимо иметь ответ на следующий
вопрос: имеет ли всякое алгебраическое уравнение корни? В случае
неалгебраического уравнения ответ может быть отрицательным. Так,
например, уравнение
е* = 0 (z = x-\-yi)
вовсе корней не имеет, так как модуль ех левой части ни при
одном значении х в нуль не обращается. Но в случае алгебраиче-
алгебраического уравнения на поставленный выше вопрос имеется утвердитель-
утвердительный ответ, который и заключается в следующей основной тео-
теореме алгебры: всякое алгебраическое уравнение имеет по
крайней мере один корень.
Мы примем здесь эту теорему без доказательства. В третьем томе
при изложении теории функций комплексной переменной мы дадим
ее доказательство.
185. Разложение многочлена на множители. Всякий многочлен
f(z) = а0 zn + a, **-i + ... + ая.! г + ая, B)
согласно основной теореме, имеет корень z = zly а потому делится
на (z — zx)y и мы можем написать [184]
Второй множитель произведения, стоящего в правой части этого
равенства, имеет, согласно упомянутой основной теореме, корень z =
= z%, а потому делится на (z — ?2)> и мы можем написать
/ (z) = (г- zj (z - *0 (a0z*-2 + ...).
Продолжая таким образом выделять множители первой степени,
мы получим окончательно следующее разложение f(z) на множители:
/(*) = ao(z-zj(z-*,).;.(z-zn), C)
т. е. всякий мйогочлен п-й степени разлагается на (#-f-l) мно-
множителей, один из которых равен старшему коэффициенту, а
остальные суть двучлены первой степени вида (z — а).
При подстановке z = zs(s= 1, 2,..., п) по крайней мере один
из множителей в разложении C) обратится в нуль, т. е. значе-
значения z = zs суть корни f{z).
Любое значение z, отличное от всех zs, не может быть кор-
корнем f(z)f так как при таком значении z ни один из сомножителей
в разложении C) в нуль не обратится.
Если все числа zs различны между собой, то f(z) имеет ровно п
различных корней. Если среди чисел zs есть одинаковые, то число
различных корней/(г) будет меньше п.
Таким образом, мы можем высказать теорему: многочлен п-й сте-
степени {или алгебраияеское уравнение п-й степени) не может иметь
более п различных корней.
440 ГЛ. VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ [ 186
Непосредственным следствием этой теоремы является следующее
предложение: если известно, что некоторый многочлен степени
не выше п имеет более п различных корней, то все коэффици-
коэффициенты этого многочлена и свободный член равны нулю, т. е. этот
многочлен равен нулю тождественно.
Положим, что значения двух многочленов fx (z) и /2 (z) степени
не выше п совпадают более чем при п различных значениях z. Их
разность f\(z)—A(z) есть многочлен степени не выше п, имею-
имеющий более п различных корней, а потому эта разность обращается тож-
тождественно в нуль и f\{z) и /2(г) имеют одинаковые коэффициенты.
Если значения двух многочленов степени не выше п совпадают
более чем при п различных значениях z, то все коэффициенты
этих многочленов и свободные члены одинаковы, т. е. эти мно-
многочлены тождественно равны между собой.
Это свойство многочленов лежит в основе так называемого ме-
метода неопределенных коэффициентов, которым мы в дальнейшем бу-
будем пользоваться. Практически сущность этого метода сводится к то-
тому, что из тождественного равенства двух многочленов вытекают
равенства коэффициентов этих многочленов при одинаковых степенях z.
Разложение C) было нами получено путем выделения множите-
множителей первой степени из многочлена f(z) в определенном порядке.
Покажем теперь, что окончательный вид разложения не зависит от
того, каким образом мы выделяли указанные множители, т. е. что
многочлен имеет единственное разложение на множители вида C).
Положим, что, кроме разложения C), имеет место разложение
f(z) = bQ(z — z[)(z- &\.. (z — zn). C,)
Сравнивая эти два разложения, можем написать тождество
— z*)...(z — zn) = bo(z — z\)(z — z'2)...{z — z'n).
Левая часть этого тождества обращается в нуль при z = zl; сле-
следовательно, то же должно иметь место и по отношению к правой
части, т. е. по крайней мере одно из чисел z'k должно быть равным zv
Можно, например, считать, что z\ =Z\. Сокращая обе части написан-
написанного тождества на {z — zt), получим равенство
а0 (г — z2)... {г — zn) — b0 (z — zr2)... (z — z'h),
справедливое при всех значениях z, кроме, может быть, z = zit Но
при этом, в силу доказанного выше предложения, это равенство также
должно быть тождеством. Рассуждая так же, как и выше, докажем,
что Z2 =<z2 и т. д. и, наконец, что Ь0 = а0, т. е. разложение (Зх) должно
совпадать с разложением C).
186. Кратные корни. Среди чисел zs, входящих в разложение
C), могут быть, как мы уже упоминали, и одинаковые. Соединяя в
186 ] § 18. ОСНОВНЫЕ СВОЙСТВА ЦЕЛЫХ МНОГОЧЛЕНОВ 441
разложении C) одинаковые сомножители в одну группу, можем напи-
написать его в виде:
/(z) = во(* — *0*1 (z — z,)k2 ...{г — zmfm, D)
где числа zv га,..., zm различны и
Если в написанном таким образом разложении имеется множи-
множитель (z — zs)ks , то корень z = zs называют корнем кратности ks
и вообще корень z = a многочлена f (z) называется корнем крат-
кратности k, если f(z) делится на (z — a)k и не делится на (z — a)k+1.
Укажем теперь другой признак кратности корня. Для этого
введем в рассмотрение формулу Тейлора. Заметим прежде всего,
что можем определить производные от многочлена f{z) по тем же
формулам, какие имели место при вещественной переменной:
f (z) = naozn-t + (n-\) atzn-* +... + (п - k) ak
f" (z) = n(n—\) aQzn~2 -f (n — 1) (п — 2) axzn~* +
Формула Тейлора
F)
представляет собою элементарное алгебраическое тождество, содержа-
содержащее буквы а и z, справедливое не только при вещественных, но и
при комплексных значениях этих букв.
Выведем теперь условие того, чтобы z = a было корнем f(z)
кратности k. Перепишем F) в виде:
= (,- a)"[I
Многочлен, стоящий во второй квадратной скобке, имеет степень ниже
степени (z — a)k, и отсюда видно [184], что первая квадратная скоб-
скобка есть частное, а вторая — остаток при делении f(z) на (z—a)k.
442 ГЛ. VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ [ 187
Для того чтобы/(г) делилось на (z — a)k, необходимо и достаточно,
чтобы этот остаток был равен тождественно нулю. Рассматривая его как
многочлен относительно переменной (z — а), получаем следующее
условие:
/(а) =/*(а) = ...«=/<*-» (а) = 0. G)
К этому условию мы должны еще добавить условие
f{k)(a) ф 0, (8)
ибо если бы и /{k\a) = 0, то/(г) делился бы не только на (z — a)k,
но и на (z — а)ш. Итак, условия G) и (8) являются необходимы-
необходимыми и достаточными условиями того, чтобы z = a было корнем
кратности k многочлена f(z).
Положим ty(z)=f (z), следовательно,
f(z)=/"D f (z)=f"(z), ..., ф<*-»(г) =/*>(*).
Если z = a есть корень кратности k многочлена f(z)y то, в силу
G) и (8):
ф() ф'(а) = ... = ф(*-2)(а) = 0 и ^к'1\а)ф0,
т.е. z = a будет корнем кратности (k—1) для ty(z) или, что то же,
для f(z), т. е. корень кратности k некоторого многочлена явля-
является корнем кратности (k—I) для производной этого многочлена.
Применяя последовательно это свойство, убедимся, что он будет
корнем кратности (k — 2) для второй производной, корнем крат-
ности (k — 3) для третьей производной и т. д. и, наконец, кор-
корнем первой кратности, или, как говорят, простым корнем для
производной (k — 1)-го порядка.
Таким образом, если для f(z) имеет место разложение
f(z) = a,(z- zxp (z — ztf* ...{г — zjm, (9)
то для f (z) будем иметь
f (z) = (z - ztfi-1 (z — *2)Vi ...(*_ Zmfm-y о D (io)
где о) (z) — многочлен, не имеющий уже корней, общих с f(z).
187. Правило Горнера. Укажем теперь практически удобное правило
для вычисления значений/(г) и производных при заданном значении z = a.
Пусть при делении/(г) на (z — а) получается частное fl (z) и остаток
rv при делении fx (z) на (z — а) — частное /2 (z) и остаток г2 и т, д.;
/(*) = (*-а)Л () + ^,
/,(«) = (г — а)/8(*) + г2, г, =Л (а),
Л (*) = (*-*)/•<*) +г., г, =/,•(*),
187 ] § 18. ОСНОВНЫЕ СВОЙСТВА ЦЕЛЫХ МНОГОЧЛЕНОВ 443
Перепишем формулу F) в виде:
Сравнивая эту формулу с первым из написанных выше равенств, по-
получим
Z() /ip q?L
/lB) = Z_?.+ ip.B
Поступая точно так же с fx (z\ найдем:
f (9\ /"(<*) , f"(a) ,„• -v, , fln)(a) ,„ а,п-2 r _ f (a)
и, вообще,
Положим теперь
f{z) = aozn
/i (*) = bQz*-
и покажем, каким образом можно вычислять коэффициенты частного bs и
остаток Ьп. Раскрывая скобки и собирая члены с одинаковыми степенями z,
получим тождество
aozn + а^'1 Н 1- ап_& + ап =
= (* - в) (V11 + ^
и сравнивая коэффициенты при одинаковых степенях г:
«о = Л» a1 = b1 — bQa, a2 = b2 — bxa, . . . , дл_! = bn_t — ?л_20,
«я = bn — ^д.^,
откуда
^o = до» ^i = ^оа + aiy b2 = bta + а2, . . • , ^л_х = Ьп_2а + «я-1,
*я = ^л-1« + «я = гх.
Эти равенства и дают возможность последовательно определить величины bs.
Точно так же, обозначив частное и остаток при делении/t (г) на (z — я),
Л (*) = Vrt~2 + Мл~3 + . . . + ся-32 + ^я-2; сл_! = г2,
будем иметь
т. е. коэффициенты с5 вычисляют последовательно при помощи bst так же
как bs при помощи as.
Указанный прием вычисления называется правилом, или алгорифмом,
flk) (a)
Горнера 1). Применяя это правило, мы получим величины J ь. «
J) Вообще алгорифмом называют определенное правило, согласно кото*
рому надо производить математические операции, чтобы получить Tpedye*
мый ответ.
444 ГЛ. VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ [ 187
Приведем схему вычислений, которая понятна без пояснений:
а01 а1У а2, я3, ...,
+ boa, btat b2at ...,
b21 b8,
сга, с2а,
., bn_2t bn_ly
., cn_sa, cn_2a
с»,
с -г -
= ao> h
mQ=aQ
(я-1)!
m0 =
_ /m> (fl)
n!
Пример. Найти значения функции
f(z) = 25 + 224 — 2z2 —
и ее производных при z = —5.
ЮО
:— 5
1, 2, 0, —2, —25, 100
—5, 15, —75, 385, —1800
1, —3, 15, —77, 360
—5, 40, —275, 1760
—1700 =/(—5)
1 —8, 55. —352
—5,
65, -600
1, —13, 120
~5,
90
1, —18
— 5
1
/'(—5)
-1 1!
f (—5)
2!
3!
4!
/(V) (__5)
1 5!
188 1 § 18. ОСНОВНЫЕ СВОЙСТВА ЦЕЛЫХ МНОГОЧЛЕНОВ 445
188. Общий наибольший делитель. Рассмотрим два много-
многочлена fx (z) и /а (г). Каждый из них имеет определенное разложение
на множители вида C). Общим наибольшим делителем D (г) этих двух
многочленов называется произведение всех двучленных множителей
вида (z—а)у входящих как в разложение fx (г), так и в разложение /2 (г),
причем эти общие множители берутся с показателем степени, равным
наименьшему из показателей, с которым они входят в разложения ft (z)
и А («г). Постоянные множители при составлении общего наибольше-
наибольшего делителя никакой роли не играют. Таким образом, общий наиболь-
наибольший делитель двух многочленов есть многочлен, корни которого суть
общие двум упомянутым многочленам корни с кратностью, равной на-
наименьшей из тех двух кратностей, с которыми они входят в упомя-
упомянутые многочлены. Если данные многочлены не имеют общих корней,
то говорят, что они взаимно простые. Совершенно аналогично пре-
предыдущему можно определить и общий наибольший делитель несколь-
нескольких многочленов.
Для составления общего наибольшего делителя указанным выше спо-
способом необходимо иметь разложение данных многочленов на множители
первой степени. Но нахождение разложения C) сводится к решению
уравнения f(z) = 0, что и составляет одну из основных задач алгебры.
Можно, однако, подобно тому, как это делается в арифметике
для общего наибольшего делителя целых чисел, указать другой спо-
способ отыскания общего наибольшего делителя, не требующий разложе-
разложения на множители, — способ последовательного деления. Способ этот
состоит в следующем. Положим, что степень Д (z) не ниже степени /2 (z).
Первый* многочлен делим на второй, затем второй многочлен /2 (z)
делим на остаток, получаемый при первом делении, этот первый ос-
остаток делим на остаток, получаемый при втором делении, и т. д.,
пока не получится деление с остатком, равным нулю. Последний ос-
остаток, отличный от нуля, и является общим наибольшим дели-
делителем двух данных многочленов. Если этот остаток не содержит z,
то данные многочлены будут взаимно простыми. Таким образом, на-
нахождение общего наибольшего делителя сводится к делению мно-
многочленов, расположенных по убывающим степеням переменной. Раз-
Разделив Л (г) и /2 (-г) на D(z), мы получим взаимно простые многочле-
многочлены. Один из них или оба могут не содержать г.
Сравнивая разложения (9) и A0), мы видим, что общий наиболь-
наибольший делитель D(z) многочлена f(z) и его производной f'(z) будет
причем мы опускаем постоянный множитель, что является несущест
венным.
Разделив f(z) на D(z), получим
— zm),
446 ГЛ. VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ f 189
т. е. при делении многочлена f(z) на общий наибольший дели-
делитель f{z) и /' (г) получается многочлен, имеющий все корни прос*
тые и совпадающие с различными корнями f{z).
Получение такого многочлена называется операцией освобождения
многочлена f(z) от кратных корней. Мы видим, что для этого нет
необходимости решать уравнение Дг) = 0.
Если f(z) и /' (z) взаимно простые, то f(z) имеет все корни прос-
простые и наоборот.
189. Вещественные многочлены. Рассмотрим теперь многочлен
с вещественными коэффициентами:
f(z) = aoz» + axzn-i +... + an_xz + am
и пусть этот многочлен имеет комплексный корень z = a-{-bl
(b ф 0) кратности k, т. е.
f(a + W) =/' (а + Ы) = ... =/<*-*> (а + Ы) - 0,
Заменим теперь в выражении f(a-\-bi) и в производных все ве-
величины сопряженными. При этой замене коэффициенты aSf как числа
вещественные, останутся прежними и лишь (а + W) перейдет в
(а — Ы)> т. е. многочлен f{z) останется прежним, но вместо
z*=*a-\-bl в него будет подставлено z*=a — bL После замены
комплексных чисел сопряженными, как известно [173], и общий
результат, т. е. значение многочлена, переходит в сопряженное. Таким
образом получим
f(a - Ы) = /' (а -&)=....= /<*-!) (а - Ы) = 0,
fk(a-bt) = A-Bl^0,
т. е. если многочлен с вещественными коэффициентами имеет
комплексный корень z = a-{-bi(b фО) кратности k, то он должен
иметь и сопряженный корень z = a — bl той же кратности.
Итак, комплексные корни многочлена f{z) с вещественными ко-
коэффициентами распределяются по парам сопряженных корней. По-
Положим, что переменная z принимает лишь вещественные значения,
и обозначим ее буквою х. Согласно формуле C)
f{x) = а0 (х - zx) (х - z2)... (х - zn).
Если среди корней z будут комплексные, то соответствующие им
множители также будут комплексными. Перемножив попарно мно-
множители, соответствующие паре сопряженных корней, получим
-(а-И)] = [(* - а)-Ы][(х - а)
где
/7= -2а, у==а2
191 ] § 18. ОСНОВНЫЕ СВОЙСТВА ЦЕЛЫХ МНОГОЧЛЕНОВ 447
Таким образом, пара комплексных сопряженных корней дает вещест-
вещественный множитель второй степени, и мы можем высказать следующее
положение: многочлен с вещественными коэффициентами разла-
разлагается на вещественные множители первой и второй степени.
Разложение это имеет следующий вид:
f(x) = а0 (х - *!)** (х - *а)*.... (х - xrfr (х* +Plx + qtfi X
X(x*+p2X + q2y*...(x*+ptX + qtyt. A1)
где хь х2, f,., хг — вещественные корни f(x) кратности kb k2,. ¦., kr
и множители второй степени происходят от пар комплексных соп-
сопряженных корней кратности 1Ь /2> •••> h*
190. Зависимость между корнями уравнения и его коэффи-
коэффициентами. Пусть, как и раньше, zb z2> ..., zn СУТЬ корни уравнения
aozn + ахгп-г + ... + an_xz + ап = 0.
Согласно формуле C), будем иметь тождество:
aozn + axzn~x +... + an_xz + an = a0(z- zL) (z - z2) \..(z — zn).
Применяя в правой части известную из элементарной алгебры фор-
формулу для перемножения биномов, отличающихся вторыми членами,
можем привести написанное тождество к виду
где Sk обозначает сумму всевозможных произведений из чисел zs
E=1, 2, ,,., п) по k множителей в каждом. Сравнивая коэффициен-
коэффициенты при одинаковых степенях z, получим
1 а0J 2"~яр"' ''•' k — \~- ;—,¦.«, п — к — ; Оо»
или в раскрытом виде
Zl i Z2 \ • ' • 1 %п — ~ у
«о
A2)
Формулы эти являются обобщением известных свойств корней
квадратного уравнения на случай уравнения любой степени. Они да-
дают, между прочим, возможность составить уравнение, когда известны
его корни.
191. Уравнение третьей степени. Мы не будем подробно заниматься
вопросом о фактическом вычислении корней алгебраических уравнений.
Вопрос этот излагается в учебниках по приближенным вычислениям. Мы
448 ГЛ. VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ [ 191
остановимся лишь на случае уравнения третьей степени и укажем также
некоторые методы вычисления, которые будут полезны и в дальнейшем.
Начнем с исследования уравнения третьей степени
yS + a1y2 + a2y + as=Q. A3)
Вместо у введем новую неизвестную х, полагая
у = х + а.
Подставив это в левую часть уравнения A3), получим уравнение
+ at) х2 + (За2 + 2at а + а2) х + (<х* + а^2+ а2а + а3) = 0.
Если положим os= — ^-, то член с х2 пропадает, и, следовательно, подста-
подстановка
преобразует уравнение A3) к виду
/ (х) = л:3 + рх + Я = 0, A4)
не содержащему члена с х2.
Если р и q — вещественны, то уравнение A4) может иметь или все три
вещественных корня, или один вещественный и два мнимых сопряженных
корня [189]. Чтобы решить, какой из этих случаев имеет место, составим
первую производную левой части уравнения
Если/?>0, то/'(л:)> 0, и f(x) все время возрастает и будет иметь
лишь один вещественный корень, ибо при переходе от х = — оо к лг = + °°
функция / (х) меняет знак (—) на (+). Положим теперь, что р < 0. Функция
/(л:), как нетрудно видеть, будет иметь максимум при дг = —1/ —^ и
минимум при х = 1/ —тг • Подставляя эти значения х в выражение функ-
функции/^), получим для максимального и минимального, значений этой функ-
функции, соответственно, выражения
2 Г р
з
Если оба эти значения одного знака, т. е.
ИЛИ
т+ё>0>
то уравнение имеет только один вещественный корень, который заключается
в промежутке (—оо, — 1/ —f-) или в промежутке ( +l/ — ~, + оо).
Если же упомянутое выше максимальное значение f(x) имеет знак (+),
а минимальное (—), т. е.
~Л "Г" 97 ^ » (***i)
191
§ 18. ОСНОВНЫЕ СВОЙСТВА ЦЕЛЫХ МНОГОЧЛЕНОВ
449
ТО /(—-(
иметь соответ-
ственно знаки (—), (+), (—), (+), и уравнение A4) будет иметь три ве-
вещественных корня. Заметим, кроме того, что при р > О, наверно, выполнено
условие A5!). Предоставляем читателю показать, что в случае
27
A58)
уравнение A4) имеет кратный корень + 1/ —~ и
0, и из A53) следует /?<0. При р = 0 и
—
корень —, причем
O
мы считаем /?^0, и из A53) следует /?<0. При р = 0 и q^zO мы имеем
неравенство A5±), и уравнение A4) принимает вид Xs + <7 = 0> т. е. х = j/ — #,
откуда следует, что уравнение A4) имеет один вещественный корень [175].
При p = q = 0 уравнение A4) будет: л;3 = 0 и имеет корень л: = 0 третьей
кратности.
Полученные результаты собраны в еле- У.
дующей таблице: ' «•
л:8 + рх + q = 0
4 + 27 <U
Один вещественный и два
мнимых сопряженных корня
Три вещественных различ-
различных корня
Три вещественных корня,
среди которых есть кратный
На рис. 182 изображен график функ-
ции
при различных
/ 2 ъ
относи-
/ р
тельно ( V + ^y
предположениях
4 ' 27/' В случае A5з)
ному корню соответствует точка касания *
кривой с осью ОХ.
Выведем теперь формулу, выражающую корни уравнения A4) через его
коэффициенты. Формула эта для практических вычислений не годится, и
в следующем номере мы, пользуясь тригонометрическими функциями, извле-
извлечем из нее практически удобный способ вычисления корней.
Вместо неизвестных х введем две новые неизвестные и и v, полагая
A6)
х = и
Подставим в уравнение A4)
(a + v) (Sav+p) + q=zQ.
A7)
450 ГЛ. VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ [ 191
Неизвестные и и v подчиним условию
и тогда уравнение A7) дает нам
и8 + Vs = — q.
Таким образом, вопрос приведен к решению двух уравнений:
w = -f, u*+v* = -q. A8)
Возводя обе части первого из уравнений в куб, имеем
и, следовательно, и3 и и8 суть корни квадратного уравнения
т. е.
4 +27 ' V"y 2 К 4 +27' A9)
Окончательно, согласно формуле A6), найдем
2 ~ V 4+-Т- B0)
Эта формула для решения кубического уравнения A4) носит название
формулы Кардана — итальянского математика XVI столетия.
Обозначим для краткости через jRt и R2 выражения, стоящие под знаком
кубических корней в формуле B0):
Каждый из кубических корней имеет три различных значения [175], так
что написанная формула даст, вообще говоря, девять различных значений х,
и только три из них будут корнями уравнения A4). Посторонние значения х
получились вследствие того, что мы возводили первое из уравнений A8) в
третью степень. Для нас могут подойти лишь те значения, для коих и и v
связаны первым из соотношений A8), т. е. в формуле B0) мы должны брать
только те значения корней кубических, произведение которых равно (—тг).
Обозначим буквою е одно из значений кубического корня из единицы:
2я" . 2я 1 . /3\
е = cos у + i sin — = — -^ + ly~ i>
• 4щ . . . 4tz 1 УЗ .
и пусть y/~Rl и y/~R2—какие-либо значения корней, удовлетворяющие ука-
указанному выше условию. Умножая их на е и е2, получим все три значения
корня [175].
192 | § 18. ОСНОВНЫЕ СВОЙСТВА ЦЕЛЫХ МНОГОЧЛЕНОВ 451
Принимая во внимание, что е3=1, получим следующее выражение для
корней уравнения A4), считая р и q— любыми комплексными:
e№ B1)
192. Решение кубического уравнения в тригонометрической форме.
Положим, что коэффициенты р и q уравнения A4) — числа вещественные.
Формула Кардана, как мы уже упоминали, неудобна для вычисления корней,
и мы выведем более практичные формулы. Рассмотрим отдельно четыре
случая.
Из написанного следует, что р < 0. Подкоренные выражения Rx и R2 в фор-
формуле B0) будут комплексными, но, несмотря на это, все три корня уравнения
будут, как известно, вещественными [191]. Положим
откуда [171]
— h B2)
Согласно формуле Кардана, имеем
Ф + 2kn
XJL^—
+
+ f r (^cos^-Cg 'sm з—) (u==0> '• 2)-
Принимая в обоих слагаемых равные значения для kt получим для произ-
произведения эти
будем иметь
ведения этих слагаемых положительное число: У~г* =—-§-. Окончательно
о
(k=0r 1, 2), B3)
где г и ф определяются по формуле B2), причем нетрудно показать, что
если мы возьмем различные ф, удовлетворяющие второму из уравнений B2),
то получим одинаковый набор корней по формуле B3).
Н. ? + §>0ир<0.
Уравнение A4) имеет один вещественный корень и два комплексных со-
р3 а2
пряженных [191], причем из написанного следует, что — ^ < ~-т Введем
вспомогательный угол со, полагая
B4,)
452 ГЛ. VI. КОМПЛЕКСНЫЕ ЧИСЛА. НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ [ 192
Это даст нам
i+i- V-1+1 -•—/-* v* г •
ибо, в силу B41),
Вводя, наконец, угол <р по формуле
tg?=]/'tgy, B4.)
получим следующее выражение для вещественного корня:
L.
B5l)
Предлагаем читателю, пользуясь формулой B1), показать, что мнимые
корни будут иметь выражения:
B5.)
от &у
III. ?+f*
В этом случае, как и в предыдущем, уравнение A4) буцет иметь один
вещественный корень и два мнимых сопряженных. При этом 1/ ^- может
быть и меньше и больше, чем
, и мы вместо формулы B4t) введем
угол to следующим образом:
]/§=! tgco. B6J
Это дает
созш
192 | § 18. ОСНОВНЫЕ СВОЙСТВА ЦЕЛЫХ МНОГОЧЛЕНОВ 453
Вводя новый угол <р по формуле
tg?=]/tg|-) B62)
окончательно будем иметь
Xi= у T(tg<f~ctg?)==~2l/'/fctg2?<
Мнимые корни будут
IV ? + 11-0
iv. 4 -т- 2? —и.
Уравнение A4) имеет кратный корень, и в этом случае, как и в случае /? = 0,
решение уравнения не представляет никаких затруднений.
Пользуясь выведенными тригонометрическими формулами, можно при по-
помощи таблицы логарифмов вычислить корни кубического уравнения с боль-
большой степенью точности.
Пример 1.
Полагая х=у— 3, приведем уравнение к виду
^з — 4у — 1=0,
и это уравнение имеет три вещественных корня [191]. Формулы B2) дают
cos <p, и, находя самый угол <р, определяем корни по формулам B3):
1/27 —
cos ср = jljq— у lg cos «p = 1,51156
- = 23°40'59", у +О36°° =143°40'59';
о
lgTT=0>3635°
= 0,32529, lg (—у2) = 0,26970, lg (—y3) = 1,40501
ух = 2,1149, у2 = —1,8608, у3 == —0,2541
:! = —0,8851, х2 = —4,8608, хв = — 3,2541
454 ГЛ. VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ | 193
П р и м е р 2.
8
Определяем угол to по формуле B4t) и угол <р—по формуле B42) и затем
вычисляем корни по формулам B5Х) и B52):
lg sin со = 1,60206, <о=23°34'11*, -^ = 11°47'20'
Igtg <р= 1,77318, ср = 30°40'31', 2<р = 61°21'02'
lg -^Дг- = 0,05672, ~т-1- = 1,11395
V—P ctg 2<p = 1,97602, Y—P ctg 2cp = 0,94628
xi = —2,2790, x2y xs = 1,1395 ± 0,94628/
193. Способ итерации. Во многих случаях, имея приближенное значе-
значение л*0 искомого корня Е с небольшим числом десятичных знаков, удобно
улучшать это приближенное значение корня. Одним из способов такого
исправления приближенного значения корня является способ итерации, или
способ последовательных приближений* Этот способ, как выяснится из
дальнейшего, годится не только цля алгебраического, но и для трансцендент-
трансцендентных уравнений.
Положим, что уравнение
/(*) = 0 B8)
мы переписали в виде
/iW=/iD B9)
причем /i (jc) таково, что уравнение
при любом вещественном т имеет один вещественный корень, который
легко вычислить с большой степенью точности. Вычисление корня уравне-
уравнения B9) при помощи метода итерации состоит в следующем: подставляя
приближенное значение х0 искомого корня в правую часть уравнения B9),
определяем второе приближение хх к искомому корню из уравнения
/iW=/.W
Подставляя xt в правую часть B9) для следующего приближения лга,
решаем уравнение Д (х) =/2 (хх) и т. д. Таким образом определится после-
последовательность значений
•^0» *^1» ^2» • • • » ^/1» * • • I C0)
причем
/iW | C1)
193
§ 18. ОСНОВНЫЕ СВОЙСТВА ЦЕЛЫХ МНОГОЧЛЕНОВ
455
Нетрудно указать геометрический смысл полученных приближений. Иско-
Искомый корень есть абсцисса точки пересечения кривых
У=ЛМ C2,)
и
У =/*(*)• C2.)
На рис. 183 и 184 изображены обе эти кривые, причем в случае рис. 183
производные f[ (x) и f'u (x) имеют в точке пересечения одинаковые знаки,
а в случае рис. 184 — разные знаки, и в обоих случаях
Равенствам C1) соответствует следующее построение: проводим пря-
прямую х = х0, параллельную оси О К, до пересечения ее в точке (х0, у0) с кри-
кривой C22); через эту точку пересечения проводим прямую у =.Уо> параллельную
\
Рис. 183.
Рис. 184.
-+.*
оси ОХ, до пересечения ее в точке (xv у0) с кривой C2j); через точку (х1} у0)
проводим опять прямую x = xlt параллельную оси О У, до пересечения ее
с кривой C22) в точке (xit ух)\ через эту последнюю точку проводим пря-
прямую у~Ух до пересечения ее с кривой C2Х) в точке (х2, ух) и т. д. Абсциссы
точек пересечения и дают нам последовательность C0).
Если первое приближение взято достаточно близко к 6, то эта последо-
последовательность, как видно из чертежа, стремится к 5, как к пределу, причем
в случае, когда /[ (?) и /2' (?) одинаковых знаков, получается ступенчатая
ломаная линия, стремящаяся к ? (черт. 183), а если f'x (?) и f2 (У разных
знаков, то эта ломаная линия стремится к 5, имея форму спирали (черт. 184).
Мы не будем приводить условий и строгого доказательства того, что после-
последовательность C0) стремится к $ как к пределу. Во многих случаях это
можно непосредственно обнаружить из чертежа.
Особенно удобен для приложения указанный способ в том случае, когда
уравнение B9) имеет вид
Пусть ? есть корень этого уравнения, приближенное значение которого
456
ГЛ. VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ
I 193
нам известно. Ряд последовательных приближений будет
Можно показать, что действительно лгЛ —^ ^ при п —* оо, если функция
/2(х) имеет производную /;D которая
У удовлетворяет условию
*+№ в промежутке
6-
Пример 1. Рассмотрим уравнение
л:5 — х — 0,2 == 0. C3)
Его вещественные корни суть абсциссы
точек пересечения линий (рис. 185)
Рис. 185.
у = х + 0,2, C42)
и, как видно из рис. 185, уравнение C3)
имеет один положительный и два отрица-
отрицательных корня.
В точках пересечения А и В> соот-
соответствующих положительному корню и
большему по абсолютному значению отрицательному корню, угловой
коэффициент прямой C42) меньше по абсолютному значению, чем угловой
коэффициент касательной к кривой C4t), т. е. при вычислении этих корней
методом итерации уравнение C3) надо представить в виде
Принимая за первое приближение при вычислении положительного корня
xQ = 1, получим таблицу A).
|/*Л + 0,2
хх = 1,037
х& = 1,0434
а:8 == 1,0445
хк = 1,04472
*Л + 0,2
1,2
1,237
1,2434
1,2445
(I)
Значение хА дает искомый корень с точностью до четвертого знака. При
вычислении отрицательного корня, большего по абсолютному значению,
примем за первое приближение х0 = —1 и получаем таблицу (II).
В точке С, которой соответствует отрицательный корень, меньший по
абсолютному значению, угловой коэффициент касательной к кривой C4j) по
абсолютному значению меньше единицы, и потому при применении метода
итерации уравнение C3) надо представить в виде
193 | § 18. ОСНОВНЫЕ СВОЙСТВА ЦЕЛЫХ МНОГОЧЛЕНОВ
Принимая за первое приближение х0 = 0, получим таблицу (III).
457
У*»+ 0,2
Xl = —0,956
л:2 = — 0,9456
л:3 = — 0,9430
лг4 = -0,9423
л:5 = — 0,94214
*в = -0,94210
*„ + 0,2
-0,8
-0,756
—0,7456
—0,7430
—0,7423
—0,74214
(И)
Во всех трех случаях приближение к корню происходило по ступенчатой
линии, как это изображено на рис. 183, в чем нетрудно убедиться из рис. 185,
и во всех трех случаях приближения хп стремятся при увеличении п к ис-
искомому корню, изменяясь монотонно.
4~0,2
*1==-0,2
дг2 = —0,20032
хъ
—0
—0,00032
Пример 2.
x = \gx. C5)
Корни этого уравнения суть абс-
абсциссы точек пересечения линий
(рис. 186)
и, как видно из рис. 186, уравнение
имеет по одному корню в каждом из
промежутков
я = 0, ±1, ±2,...
Для положительных корней будет
иметь место приближенное равенство
Рис. 186.
где буквою ап мы обозначаем я-й положительный корень уравнения C5).
Вычислим корень а1? близкий к -у. Для применения метода итерации пе-
перепишем уравнение C5) в виде
х = arc tg x
* Зл
и примем за первое приближение л*0= ^.
458 ГЛ. VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ [ 194
При вычислении последовательности приближений
хп = arc tg хп^
надо всегда брать значение арктангенса, содержащееся в третьей четверти.
Пользуясь таблицами логарифмов и выражая дуги в радианном измерении,
получим:
хо = 4,7124, ^==4,5033,
х2 = 4,4938, х3 = 4,4935.
194. Способ Ньютона. Процесс итерации, указанный на рис. 183 и 184,
состоит в приближении к искомому корню по прямым, параллельным коор-
координатным осям. Мы укажем теперь другие процессы итерации, для которых
применяются и прямые, наклонные к координатным осям. Одним из таких
способов является способ Ньютона.
Рис. 188.
Пусть л:о и х0 — приближенные значения корня ? уравнения
C6)
и положим, что в промежутке (л*о, х0) это уравнение имеет один только ко-
корень ?. На рис. 187 и 188 изображен график кривой
У =/(*).
Абсциссы точек N и Р суть приближенные значения х'о и х0 корня ?,
который является абсциссой точки А В точке р проведена касательная PQX
к кривой, и из точки пересечения Qt этой касательной с осью абсцисс про-
проведена ордината QtQ кривой; в точке Q проведена касательная QRX к кри-
кривой и из точки RL проведена ордината RXR кривой и т. д.
Точки Pv Qi} /?!,..., как видно из чертежа, стремятся к точке А, так
что их абсциссы л*0, xv x2 ,... являются последовательными приближениями
для корня ?. Выведем формулу, выражающую хп через хпл.
Уравнение касательной PQX будет
195
§ 18. ОСНОВНЫЕ СВОЙСТВА ЦЕЛЫХ МНОГОЧЛЕНОВ
459
Подставляя К = 0, найдем абсциссу точки Qt:\
и, вообще,
у. f\Xfi-l) „ 1 9
C7)
C8)
То обстоятельство, что хп действительно являются приближениями к
корню ?, мы усмотрели просто из чертежа, который сделан для того случая,
когда f(x) монотонна и остается выпуклой (или вогнутой) в промежутке
(х'о, х0), другими словами, когда /' (х) и /" (х) сохраняют знак в этом про-
промежутке [57, 71]. На строгом аналитическом доказательстве этого мы оста-
останавливаться не будем.
Заметим, что если бы мы применили способ Ньютона не к концу х0У а
к концу х'о, то не получили бы приближения к корню, как это показывает
проведенная пунктиром касательная. В случае рис. 188 кривая обращена
вогнутостью в сторону положительных ординат, т. е. /" (х) > 0, и способ
Ньютона, как мы видим, надо применять к тому концу, где/(л:)>0. Из
рис. 187 вытекает, что при /" (х) <0 способ Ньютона нацо применять к тому
концу, где ордината /(х)<0. Мы приходим, таким образом, к следующему
правилу: если f (x) и f" (x) в промежутке {Xq, xq) не обращаются в нуль,
а ординаты /(Xq) и f(x0) разных знаков, то, применяя способ Ньютона
к тому концу промежутка, где знаки f(x) и f"(x) совпадают, получим
последовательные приближения для единственного корня уравнения C6),
заключающегося в промежутке (х'о, х0).
195. Способ простого интерполирования. Укажем еще один способ
приближенного вычисления корня. Через концы N и Р дуги кривой прове-
проведем прямую. Абсцисса следа В этой прямой на оси абсцисс и даст приближен-
приближенное значение корня (рис. 189). Пусть, как и раньше, х'о и х0 — абсциссы кон-
концов промежутка. Уравнение прямой NP будет
¦У
Полагая К=0,
точки В:
или
или
найдем выражение абсциссы
C9)
(Хо — X'o
f(xo)-f(x'o) ¦
(xo — xo)f(xo)
Рис. 189.
Замена участка кривой отрезком прямой, проходящей через конечные
точки кривой, равносильна замене функции f (х) в исследуемом промежутке
многочленом первой степени, имеющим те же конечные значения, что и f (x)t
или, что то же, равносильно предположению, что в указанном промежутке
изменения f(x) пропорциональны изменениям х. Этот прием, называемый
обычно простым интерполированием, применяется, например, при пользова-
пользовании таблицами логарифмов (partes proportionales). Указанный нами прием
вычисления корня называется также иногда правилом ложного положения
(regula falsi).
460
ГЛ. VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ
195
Если применять одновременно как способ простого интерполирования,
так и способ Ньютона, получается возможность оба предела х'{) и х0 прибли-
приблизить к корню ?.
Положим, например, что на конце х0 знаки fix) и /" (л:) совпадают, так
что способ Ньютона надо применять
именно к этому концу.
Применяя оба способа, получим
два новых приближенных значения
(рис. 190):
х=х f}**\
К приближенным значениям х[ и
хх можно опять применить те же
формулы и получим новые значения
Рис. 190.
х -х -
Таким образом получим два ряда значений
X , X , X у . . . ,
О' 1* 2* '
qj X1,
приближающихся к корню ? слева и справа.
Если у значений х'п и хп совпадают несколько первых десятичных зна-
знаков, то у корня ?, который заключается между хп и хю должны быть те же
самые десятичные знаки.
Пример. Уравнение
/(л:) = х5-л--0,2 = 0,
которое мы рассматривали в примере 1 [193], имеет один положительный
корень в промежутке 1<сх<с1,1, и в этом промежутке
/' (д:) = 5jc4 — 1 и /" (л:) = 20л'3
знака не меняют. Таким образом, мы можем положить
Вычисляем значения функции f (х):
= _0,2, /A,1) =0,31051,
откуда видно, что на правом конце (хо=\,\I f (х) и /" (х) имеют один и
тот же знак (-{-), и, следовательно, способ Ньютона надо применять именно
к правому концу. Предварительно вычисляем значение/ (х) на правом конце:
/'A,1) = 6,3205.
Согласно формулам C7) и C9), будем иметь
0,51051
=1.039,
6,3205
196 ] § 19. ИНТЕГРИРОВАНИЕ ФУНКЦИЙ 461
Для следующего приближения вычисляем:
/A,039) = — 0,0282, /A,051) =0,0313, /' A,051) = 5,1005,
откуда
что дает значение корня с точностью до двух единиц в четвертом знаке [193J:
1,04469 <5< 1,04487.
§ 19. ИНТЕГРИРОВАНИЕ ФУНКЦИИ
196. Разложение рациональной дроби на простейшие. Выше
мы указали ряд приемов для вычисления неопределенных интегралов.
В настоящем параграфе мы дополним эти указания и придадим им
более систематический характер. Первым вопросом будет вопрос
об интегрировании рациональной дроби, т. е. частного двух многочле-
многочленов. Прежде чем переходить к решению этого вопроса, мы устано-
установим формулу, которая дает представление рациональной дроби в виде
суммы некоторых дробей простейшего вида. Это представление назы-
называется разложением рациональной дроби на простейшие
Пусть имеется рациональная дробь
F(x)
Если это — дробь неправильная, т. е. степень числителя не ниже
степени знаменателя, то, производя деление, можем выделить целую
часть — многочлен Q (х) и представить дробь в виде
где jj-' есть уже правильная дробь, у которой степень числителя
ниже степени знаменателя. Кроме того, мы будем считать эту дробь
несократимой, т. е. будем считать, что числитель и знаменатель
взаимно простые [188].
Пусть х = а есть корень знаменателя кратности k:
f(x) = (x-a)kfl(x) и Д(а)^0.
Докажем, что дробь можно представить в виде следующей суммы:
\Х —п) J~i \Х) {X —Cl) (Л* — О.) ь jTj \Х)
где А — некоторая постоянная и второе слагаемое правой части —
правильная дробь. Составим разность
у (л) А <?(х) — А/1(х)
(A--fl)*/i(*) {x-af — (х-а)Ь/\(х)
462 ГЛ. VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ f 196
и определим постоянную А так, чтобы числитель дроби, стоящей
в правой части написанного равенства, делился на (х — a) [184J:
откуда
При таком выборе А только что упомянутую дробь можно со-
сократить на (х— а), и мы придем таким образом к тождеству B).
А
Оно показывает, что, выделяя слагаемое вида , __ к, которое и на-
называется простейшей дробью, мы можем понизить показатель степени
множителя (х— а), входящего в знаменатель, по крайней мере, на
единицу.
Положим, что знаменатель разлагается на множители:
/ (х) = (х- aOki (х - a,t... С* - am)k™.
Постоянный множитель мы не пишем, так как он может быть
отнесен к числителю. Применяя последовательно указанное выше
правило выделения простейшей дроби, получим разложение правиль-
правильной рациональной дроби на простейшие:
4S ¦ <'-> i ,jf
- a2)*2 ~ (л: — a2)ft2-' ~ * ' * ~ jc-«2
A(m)
m
x-a
Укажем теперь способы определения коэффициентов, входящих
в правую часть написанного тождества. Освобождая его от знамена-
знаменателя, придем к тождественному равенству двух многочленов и, при-
приравнивая их соответствующие коэффициенты, получим систему урав-
уравнений первой степени для определения искомых коэффициентов. Из-
Изложенный способ, как мы уже упоминали выше [186], называется
способом неопределенных коэффициентов.
Можно поступать и иначе, а именно, придавать в упомянутом
выше тождественном равенстве многочленов различные частные зна-
значения переменной х. Этим способом подстановки можно еще поль-
пользоваться и предварительно продифференцировав любое число раз
упомянутое 'тождество.
Можно доказать, на чем мы останавливаться не будем, что раз-
разложение C) единственно, т. е. что его коэффициенты имеют вполне
197 1 § 19. ИНТЕГРИРОВАНИЕ ФУНКЦИЙ 463
определенное значение, не зависящее от способа разложения. В даль-
дальнейшем мы дадим примеры применения указанных выше способов
определения неизвестных коэффициентов разложения.
В случае вещественности многочленов ср(лг) и f(x) правая часть
тождества C) может все-таки содержать мнимые члены, происходя-
происходящие от мнимых корней знаменателя. Мы приведем другое разложе-
разложение рациональной дроби, свободное от этого недостатка, но огра-
ограничимся при этом лишь тем случаем, когда знаменатель дроби имеет
только простые корни, так как в приложениях имеет наибольшее
значение именно этот случай.
Паре комплексных сопряженных корней знаменателя х=а±Ы
будет соответствовать сумма простейших дробей
A + Bl . A — Bi
x — a — bi*x — a+bi '
Приводя эти дроби к одному знаменателю, получим простейшую
дробь вида
Таким образом, в рассматриваемом случае вещественная рацио-
рациональная дробь разложится на вещественные простейшие:
У W — А1 | А2 I \ Аг 1
f(x) х — at ¦ л:— а2 ~г '"•.*: — яг '
причем в первой строке стоят дроби, соответствующие вещественным
корням знаменателя, ха во второй — дроби, соответствующие парам
комплексных сопряженных корней.
197. Интегрирование рациональной дроби. Интегрирование
рациональной дроби в силу формулы A) приводится к интегриро-
интегрированию многочлена, что даст также многочлен, и к интегрированию
правильной рациональной дроби, что мы и будем сейчас рассматри-
рассматривать.
Если знаменатель дроби имеет только простые корни, то, в силу
формулы D), все приведется к интегралам двух видов:
П.
464 ГЛ. VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ ( 197
Вспоминая сказанное [92], получим ответ вида
Таким образом, в рассматриваемом случае интеграл выразится
через логарифмы и арктангенсы.
Рассмотрим теперь тот случай, когда знаменатель правильной
рациональной дроби содержит кратные корни. Обратимся к разложе-
разложению C). Мнимые числа, которые могут в нем встретиться, будут
играть лишь промежуточную роль в дальнейших вычислениях и
в окончательном результате исчезнут.
При интегрировании простейших дробей, знаменатель которых
выше первой степени, мы получим также рациональную дробь:
\ k-S ^Х =
Сумма полученных после интегрирования дробей даст алгебраи-
алгебраическую часть интеграла, которая по приведении к общему знамена-
знаменателю будет, очевидно, правильной дробью вида
Числитель со (х) есть многочлен степени, по крайней мере, на
единицу ниже степени знаменателя, а знаменатель представляет со-
собою общий наибольший делитель D(x) знаменателя интегрируемой
дроби f(x) и ее первой производной f (х) [188].
Сумма остальных непроинтегрированных дробей
х — а1 * х — я2 '*•*'* — ат
при приведении к общему знаменателю окажется правильной дробью
вида
(х — ах)(х-а2).„(х-ату
где 1&\(х) есть многочлен степени, по крайней мере, на единицу ниже
степени знаменателя, а знаменатель представляет собою частное
Di(x) от деления /(х) на D(x). Таким образом, мы получим следу-
следующую формулу Остроградского:
<5>
Многочлены D(x) и Dj(x) мы можем определять и не зная кор-
корней f(x) [188]. Укажем теперь, как определить коэффициенты мно-
197 ] § 19. ИНТЕГРИРОВАНИЕ ФУНКЦИЙ 465
гочленов (»(х) и щ(х)у степени которых мы можем считать на еди-
единицу ниже степеней соответствующих знаменателей. Дифференцируя
равенство E), освобождаемся от знаков интеграла. Освобождаясь
в полученном таким образом тождестве от знаменателя, будем иметь
тождественное равенство двух многочленов и, применяя к нему метод
неопределенных коэффициентов или подстановки, сможем определить
коэффициенты со (л:) и и>х(х).
Формула Остроградского дает, таким образом, алгебраическую
часть интеграла правильной рациональной дроби и тогда, когда корни
знаменателя неизвестны. Знаменатель дроби, стоящей под знаком ин-
интеграла в правой части равенства E), содержит только простые корни,
и, разлагая эту дробь на простейшие, мы сумеем вычислить этот
интеграл, причем, как это мы только что видели, он выразится че-
через логарифмы и арктангенсы. Для проведения последней операции
нам надо знать корни Ог(х).
Пример. Согласно формуле Остроградского
С dx g*» + P* + T
Дифференцируем по х
1 Bа
и, освобождаясь от знаменателя, имеем
1 = Bал: + р) (х3 + 1) - Зл:2 (ал:2 + $х + -т) + (Ъх* + вх + ч) (х3 + 1).
Сравнивая коэффициенты при л:5, получаем 5 = 0, и сравнивая затем коэф-
коэффициенты при л:2, получим у = 0. Подставляя в написанное тождество
^ = Ь = 0 и сравнивая коэффициенты при остальных степенях, будем иметь:
е — а = 0, т] — 2р = 0, 2а + е = 0, 0 + tj = 1,
откуда окончательно:
1 2
а = т = 5 = е = 0, Р = -з~, 7] = Т
и, следовательно,
dx
Sdx _ х 2 С
(*t + l/- 3(^+1) 3 J
Последний интеграл вычисляется разложением дроби на простейшие:
1 A
Освобождаемся от знаменателя:
1 = А (х2 - х + 1) + (Мх + ЛО (х + 1).
Полагая * = — 1, получим Д=— а затем, сравнивая коэффициенты
при х2 и свободные члены
466 ГЛ. VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ I
и, следовательно,
1 1 х — 2
Окончательно получим
dx
откуда
+ -4= arctg 2x~Z} + С
3/3 /3 ¦
198. Интеграл от выражений, содержащих радикалы. Рассмо-
Рассмотрим некоторые другие типы интегралов, которые приводятся к инте-
интегралам от рациональной дроби.
1. Интеграл
cx + d) > \cx + d) ' •••
где /? — рациональная функция своих аргументов, т. е, частное мно-
многочленов от этих аргументов, а X, [i, ... —рациональные числа.
Пусть /я — общий знаменатель этих дробей. Введем новую перемен-
переменную к
ах
гт dx
При этом, очевидно, х} -зт-*и выражения
будут рациональными функциями t, и интеграл F) приведется к ин-
интегралу от рациональной дроби.
2. Биномный дифференциал. К интегралу F) приводятся в не-
некоторых случаях интегралы от биномных дифференциалов:
а + bxn)pdxt G)
где т, п и р — рациональные числа.
Положим x = tn:
1 л
_
109 | § 19. интегрирование функций 467
Если р или —^1— есть целое число, то п
есть интеграл вида F). Из очевидного равенства
Если р или —^1— есть целое число, то полученный интеграл
[ 1
следует, что и в том случае, когда —— \-р — целое число, инте-
интеграл G) приводится к виду F).
Существует теорема Чебышева, согласно которой указанные
три случая исчерпывают все случаи, в которых интеграл от бином-
ного дифференциала выражается через элементарные функции.
199. Интегралы вида i R(X, i/ax* ~\-bx-\-c) dx. Интегралы
вида
R(x, yax%-\-bx-\-c)dx) (8)
где R — рациональная функция своих аргументов, приводятся к ин-
интегралам от рациональной дроби при помощи подстановок Эйлера,
В случае а ^> О можно пользоваться первой подстановкой Эйлера:
l/ял;2 -f- bx -\- с = t — \/ах.
Возвышая обе части этого равенства в квадрат и решая относительно х,
получим
2tya-
откуда видно, что дг, -? и j/ад:2 -\-bx-\-c будут рациональными
функциями от t и, следовательно, интеграл (8) приведется к инте-
интегралу от рациональной дроби.
В случае с^>0 можно пользоваться второй подстановкой Эйлера:
\/ ах* -f- bx-\-c
Предлагаем читателю убедиться в этом.
В случае а<^0 трехчлен (ах2-j-bx-{-с) должен иметь вещест-
вещественные корни jcj и хь ибо в противном случае он имел бы при всех
вещественных значениях х знак (—), а -/ах2 -f- bx -f- с был бы вели-
величиной мнимой. В случае вещественности корней упомянутого трех-
трехчлена интеграл (8) приводится к интегралу от рациональной дроби
при помощи третьей подстановки Эйлера:
/а(х — xt) (х — Хъ) = t(x — *2),
в чем и предлагаем убедиться читателю.
468 ГЛ. VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ [ 199
Подстановки Эйлера приводят большей частью к сложным выклад-
выкладкам, а потому мы укажем другой прием вычисления интеграла (8).
Обозначим для краткости письма:
у = j/aA;2-f- bx -f- с.
Всякая положительная четная степень у представляет собою мно-
многочлен от х, а потому подынтегральную функцию нетрудно привести
к виду
v)— Ш1 (*) + "»(*) .У
где оM(дг) — многочлен от х. Освобождаясь от иррациональности
в знаменателе и совершая элементарные преобразования, можно пре-
преобразовать написанное выражение к виду
Первое слагаемое есть рациональная дробь, интегрировать кото-
которую мы уже умеем. Выделяя из дроби (°7 ( , целую часть и разлагая
оставшуюся правильную дробь на простейшие, мы придем к интегра-
интегралам вида
f -^40 :dX (9)
S ix-arvZr + bx + , ' A0)
где ср(лг) — многочлен от х.
При этом мы предполагаем, что многочлен со8 (х) имеет лишь
вещественные корни.
Прежде чем переходить к рассмотрению интегралов (9) и A0),
отметим два простейших частных случая интеграла (9):
С dx
2
Формулу A1) нетрудно получить при помощи первой подстановки
Эйлера. Интеграл A2) уже был нами разобран раньше [92].
199 ] § 19. ИНТЕГРИРОВАНИЕ ФУНКЦИЙ 469
Для вычисления интеграла (9) удобно пользоваться формулой:
dx
=с> A3)
где ty(x) — многочлен степени на единицу ниже, чем ср(х), и X —
постоянная. На доказательстве формулы A3) мы останавливаться не
будем. Дифференцируя соотношение A3) и освобождаясь от знаме-
знаменателя, получим тождественное равенство двух многочленов, откуда
и можно определить коэффициенты многочленов ф (х) и постоянную X.
Интеграл A0) приводится к интегралу (9) при помощи подстановки
х— я = у.
Пример.
с
х—\
)x-\ J(jc —1) Ka:» —
~dx-
Но
х — \
а потому
J/a:2-a"+1 J (л;— 1) Ух2 —
, rfjc=a ^+
(л: — 1) у л:» — л: + 1 J/a:2-a"+1 J (л;— 1) Ух2 — * + Г
Согласно формуле A3)
С—-^ ^==./,2-^ + i+xC—gf
J/a:2-a:+1 ^/л:2-д:+1 •
Дифференцируя это соотношение и освобождаясь от знаменателя, получим
тождество
2х = а Bх - 1) + 2Х,
откуда
l х
и, следовательно, в силу формулы A1),
х
Подставляя
470 ГЛ. VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ [ 200
получим
окончательно
Интеграл (8) является частным случаем абелева интеграла, который
имеет вид:
^ )dx, A4)
где R — рациональная функция своих аргументов и у— алгебраическая
функция от х, т. е. функция от х, которая определяется из уравнения
левая часть которого есть целый многочлен относительно хну. Если
где Р (х)— многочлен третьей или четвертой степени от х, то абелев инте-
интеграл A4) называется эллиптическим интегралом. Мы займемся этими инте-
интегралами в третьем томе. Даже и этот последний, а тем более и общий абелев
интеграл, вообще говоря, не выражается через элементарные функции.. Если
степень многочлена Р (х) выше четвертой, то интеграл A4) называется ги-
гиперэллиптическим.
Если соотношение A5), которое выражает у как алгебраическую функ-
функцию от ху обладает тем свойством, что хну могут быть выражены в виде
рациональных функций вспомогательного параметра t, то, очевидно, абелев
интеграл A4) приводится к интегралу от рациональной дроби. В указанном
случае алгебраическая кривая, соответствующая соотношению A5), назы-
называется уникурсальной. В частности, подстановки Эйлера служат доказатель-
доказательством уникурсальности кривой
уз = ах2 + Ьх + с.
200. Интегралы вида \^(sinAr, cosx)dx. Интеграл вида:
С ^(sinAr, cosx)dx, A6)
где R — рациональная функция своих аргументов, приводится к инте-
интегралу от рациональной дроби, если ввести новую переменную
200 ] § 19. ИНТЕГРИРОВАНИЕ ФУНКЦИЙ 471
Действительно, согласно известным формулам тригонометрии, по-
получим
2t I — t*
8Ш*=Г+1Г» C0SX = T+-p>
и, кроме того,
2dt
\ dx = -
откуда и вытекает непосредственно наше утверждение.
Укажем теперь некоторые частные случаи, когда выкладки могут
быть упрощены.
I. Положим, что /?(sinAr, cos at) не меняется при замене sinjc и
cos х, соответственно, на (— sin х) и (— cos at), т. е. предположим,
что i? (sin4 at, cos at) имеет период тт. Так как
sillJC== COS AT tg AT,
то /?(sinлг, cos*) оказывается рациональной функцией от cosat и
tg at, не меняющейся при замене cos х на (— cos х), т. е. содержа-
содержащей только четные степени cos x:
R(sinx, cos x) = Rt (cos2 at, tgAr).
В рассматриваемом случае для приведения интеграла A6) к инте-
интегралу от рациональной дроби достаточно положить
t = tgx.
Действительно, при этом
. dt n 1
dx cos2at
Итак, если R (sin дг, cos х) не меняется при замене sin х и cos лг,
соответственно, на (—sin лг) и (—cos л:), то интеграл A6) при-
приводится к интегралу от рациональной дроби при помощи под-
подстановки t = igx.
2. Предположим теперь, что /?(sinAr, cosat) меняет лишь знак
при замене sin а: на (—sin at). Функция
7? (sin л;, cos л:)
sin л:
не будет вовсе меняться при указанной замене, т. е. будет содер-
содержать только четные степени sinAr, а следовательно:
, cos x) = /?i (sin2 x, cos a:)-sin a:.
Подставляя t = cos at, получим
R(sinx, cQsx)dx = — [ Ri(l—t\ t)dt,
f
472 ГЛ. VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ \ 201
т. е. если R(sinx, cos .г) при замене sin л; на (—sin.*;) меняет
лишь знак, то интеграл A6) приводится к интегралу от рацио-
рациональной дроби при помощи подстановки ?=cos.r.
3. Точно так же нетрудно показать, что если /?(sin.r, cos х) при
замене cos х на (—cos x) меняет лишь знак, то интеграл A6)
приводится к интегралу от рациональной дроби при помощи под-
становки t =
201. Интегралы вида С eax \P (х) cos bx + Q (л:) sin bx\ dx. Ин-
Интеграл вида:
[ A7)
где ср (х) — многочлен п-й степени от х, интегрированием по частям
можно упростить:
еах9(х) dx = 1 е^ (х) -1 J e^' (x) dx.
Таким образом, выделяя из интеграла слагаемое, имеющее вид
произведения еах на многочлен п~й степени, мы можем понизить сте-
степень многочлена под знаком интеграла на единицу. Продолжая та-
таким образом интегрировать по частям и принимая во внимание, что
получим
^ , A8)
где ф (х) — многочлен той же n~ft степени, что и ср (х), т. е. инте-
интеграл от произведения показательной функции еах на многочлен
п-й степени имеет вид такого же произведения.
Дифференцируя соотношение A8) ¦ и сокращая обе части полу-
полученного тождества на еаху можем определить коэффициенты поли-
полинома ф(дг) по способу неопределенных коэффициентов.
Рассмотрим теперь интеграл более общего вида:
f еах [Р (х) cos bx + Q (x) sin bx] dx, A9)
где Р(х) и Q(x) — многочлены от х. Пусть п — наибольшая из
степеней этих двух многочленов. Вводя в качестве вспомогательного
средства комплексные величины, можем привести интеграл A9) к
201 ] § 19. ИНТЕГРИРОВАНИЕ ФУНКЦИЙ 473
интегралу A7), а именно, подставив вместо cos ^лг и sin bx их выра-
выражения по формулам Эйлера [176]:
pbxi _L p-bxi pbxi e~bxi
cos bx = ^ , sin bx = к-. ,
получим
С eax [P(x) cos bx -j- Q (x) sin bx ] dx =
где ср (л;) и срх (х) — многочлены степени не выше п. Применяя фор-
формулу A8):
f еах [Р (х) cos bx -f Q (л;) sin ^лг] rfjc =
<**w) -^ ф (лг) + ^ («-") * ф! (лг) + С,
где ф(лг) и ty\(x) — многочлены степени не выше п} и подставляя
е± bxi _ cos ^х Ч- / sjn frXi
окончательно имеем
(* лх
у е [Р(х) cos bx -(- Q (jc) sin ^лг] rfx =
= ^ [/? (x) cos for -f 5(x) sin for] +C, B0)
где R(x) и ^(лг) — многочлены степени не выше п. Таким образом,
мы видим, что интеграл A9) имеет выражение того же вида,
что и его подынтегральная функция, причем степень многочленов
в выражении интеграла надо брать равной наибольшей из сте-
степеней многочленову стоящих в подынтегральной функции.
Дифференцируя соотношение B0), сокращая полученное тождество
на еах и приравнивая коэффициенты одинаковых членов вида
л:5 cos bx и Xssin bx{s= 0, 1, 2, ... , п), стоящих в правой и левой
частях, получим систему уравнений первой степени для определения
коэффициентов многочленов R(x) и S(x). Заметим при этом, что,
если cos bx или sinbx под знак интеграла и не входят, в правой ча-
части формулы надо обязательно писать обе тригонометрические
функции, помня высказанное выше правило определения степеней
многочленов R(x) и S(x).
К интегралам вида A9) приводятся непосредственно интегралы
вида:
sin(a^xr-f-^i) sin (a*xr-f-?2)... cos{cxx-\-d^cos(c^x-\-d,2)...dx.
Действительно, пользуясь известными тригонометрическими фор-
формулами, выражающими сумму и разность синусов и косинусов в виде
474 ГЛ. VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ [ 201
произведения, можно, наоборот, произведение каких-либо двух из вы-
вышеупомянутых тригонометрических функций выразить в виде суммы
или разности синусов и косинусов. Применяя несколько раз это пре-
преобразование, можем довести число тригонометрических множителей
под знаком интеграла до одного и таким образом получим интеграл
вида A9).
Пример. Согласно формуле B0):
1 еах sin bx dx = еах (A cos bx + B sin bx) + С.
Дифференцируем и сокращаем на еах:
sin bx = (aA + ЬВ) cos bx + ( — bA + aB) sin bx,
откуда
аА -f- ЬВ = 0, — М-f-а^:== Ь то есть А~ —
и окончательно
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Абеля интеграл 470
— признак 355
— теоремы 357, 358
Абсолютная величина 11
— погрешность 122
Абсолютный максимум и минимум
395
Абсцисса 20, 21
Алгебраическая кривая 181
— функция 470
Алгебраическое уравнение 438
Аналитическая геометрия 23
Аналитический способ задания функ-
функции 16 •
Аргумент комплексного числа 406
Архимедова спираль 194
Асимптота 34, 171
Асимптотическая точка 195
Астроида 191
Безу теорема 438
Бесконечно большая величина 63
— малая величина 52
, порядок 81, 82
, свойства 54, 55
, сравнение 81
, эквивалентность 82
Бесконечный ряд 289
Биномиальный ряд 315
Биномный дифференциал, интегриро-
интегрирование 466
Вейерштрасса признак 355
Векторная диаграмма 429
Вещественная часть 405
Вещественные числа 11, 89
, действия 92
Вогнутость и выпуклость 168
Возврата точка 182, 183
Возрастающая функция 40, 131, 134
Гармонические кривые 46
Гармонический ряд 292, 300
Гармоническое колебание 46
в комплексной форме 437
Гаусса признак 336, 338
— ряд 339
Геометрическая прогрессия 290
Гипербола 34
Гиперболическая спираль 194
Гиперболические функции 419—421
Гипергеометрический ряд 339
Гиперэллиптический интеграл 470
Гипоциклоиды 189
Горнера правило 442
Границы числового множества (верх-
(верхняя, нижняя) 89, 94
График функции 22, 173—175
Графический способ задания функ-
функции 19
решения уравнений 33
Графическое изображение 22
Гульдина теоремы 261, 262
Даламбера признак 295, 336
Двойные ряды 341
Действительные числа см. Вещест-
Вещественные числа
Декартов лист 177, 181
Дифференциал 117
— высшего порядка 127, 128
—, геометрическое истолкование
118
— дуги 166, 251, 382
— полный 164, 367, 373
—, применение к приближенным вы-
вычислениям 122
Дифференциальное уравнение 120,
220
Дифференцирование 105
—, интеграл по верхнему пределу
230
476
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Дифференцирование, правила 115,
164, 176, 375—377
— ряда, равномерно сходящегося 355
степенного 361
Длина дуги 246—251, 382
— касательной 185
— нормали 185
Дробное число 10
е (число) 85
—, приближенное вычисление 313
Замена переменных 216, 236
Замкнутая область 160, 363
Замкнутый промежуток 13
Затухающие колебания 141
Знакопеременный ряд 301
Изолированная точка кривой 184
Интеграл неопределенный 199, 213,
214
— определенный 205, 210, 223—241
Интегральная кривая 201
Интегральный признак Коши 299
Интегрирование биномных дифферен-
дифференциалов 466
— иррациональных выражений 219,
220, 466, 467
— по частям 215, 239
—, правила 213—216
— рациональных дробей 217, 218,
463—466
— ряда, равномерно сходящегося 354
—.—, степенного 360
— тригонометрических и показатель-
показательных выражений 470—474
Интегрируемая функция 280—288
Интерполирования способ 459
Интерполяция 19, 459
Иррациональное число 10, 91
Истинное значение функции 77
Итерации способ 454
Кардана формула 450
Кардиоида 190, 196, 253
Касательная плоскость 383
— прямая 106, 166, 186
Касательных способ 458
— формула 266
Кассини овал 197
Квадратура 242
Кеплера уравнение 68, 69, 132, 133
Колебание функции 279
Комплексное число 404
, действия 407—416
-, показательная форма 417
—: — сопряженное 410
, тригонометрическая форма 407
Конечных приращений формула 152
Координатная плоскость 21
Координаты 21
— полярные 192
Корень многочлена 438
Косинус 44, 108, 314
Котангенс 44, 111
Коши признак существования пре-
дела 67
— признаки сходимости ряда 295,
299, 305
— формула 154
Кратные корни многочлена 441
Кривизна 169
Кубическое уравнение 448, 451
Куммера признак сходимости ряда 335
Лагранжа способ множителей 396
— форма остаточного члена ряда Тей-
Тейлора 309
— формула 151
Лейбница правило 125
Лемниската 198
Линейная функция 24—26
Логарифм натуральный 87, 427
Логарифмическая бумага 43
— линейка 42
— спираль 195, 252, 436
— функция 42, 101, 109, 158, 321
— шкала 42
Ложного положения правило 459
Лопиталя правило 155—159
Маклорена ряд 311
— формула 311
Максимум и минимум функции 134—
139, 328
, правила отыскания 135,
136
нескольких переменных
386, 388—394
абсолютный 395
относительный 396,
398—401
Мнимая единица 405
— часть 405
Многозначная функция 16, 38
Многочлен 29, 437—447
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
477
Множество числовое, ограниченное
сверху, снизу 89
Множителей неопределенных метод
Лагранжа 396
Моавра формула 412
Модуль комплексного числа 406
— перехода для логарифмов 88
Монотонная переменная 65
Наибольшее и наименьшее значения
функции 142, 143, 148, 161, 394,
395
Начало 20
— координат 21
Начальная ордината 25
Независимая переменная 14
Неопределенные выражения 155—159,
330
Неопределенный интеграл 200, 213,
214
Неопределенных коэффициентов спо-
способ 462
Непрерывная функция 40, 71, 75—81,
96-102, 161
Несобственный интеграл 235
Нечетная функция 238
Неявная функция 17, 165, 375,
379
Нормаль к кривой 184
— к поверхности 384
Ньютона способ 458
Область определения функции зам-
замкнутая 160, 363
открытая 160, 363
Обратная функция 37, 101, 111, 112
Обратные круговые функции 47, 48,
114, 325
, главное значение 48
Общий наибольший делитель много-
многочленов 445
Объем тела 253—256
Ограниченная функция 161, 276
Однозначная функция 23, 38
Однородная функция 369
Окрестность 364
Определенный интеграл 205, 210,
223—241
, вычисление с помощью пер-
первообразной 210
— —, приближенное вычисление
263-274
, свойства 223
Определенный интеграл, связь с не-
неопределенным 208
, теорема о среднем 228, 229
Ордината 21
Основная теорема алгебры 439
Особые точки кривой 181
Остаток ряда 290, 302
Остаточный член в формуле Тейлора
309
Остроградского формула 464
Ось 20
Открытая область 160, 363
Открытый промежуток 13
Относительная погрешность 122, 123
Парабола 29, 242, 251
— третьей степени 32
Параболоид гиперболический 392
Параметр 175
Параметрическое задание кривой
175
Первообразная функция 199, 210
Перегиба точка 168, 328
Переменная величина 12
— интегрировании 207
— монотонная 65
— независимая 14
— ограниченная 52, 56
упорядоченная 49
Площадь 241—246
— поверхности вращения 256
Погрешность абсолютная 122
— относительная 122, 123
Подкасательная 185
Поднормаль 185
Подстановка, замена переменной
216
— дробно-линейная 466
— тригонометрические 470
— Эйлера 467
Подстановки способ 462
Подынтегральная функция 200
, разрыв 231
Подынтегральное выражение 200
Показательная функция 41, 99, ИЗ,
158, 312, 416-418
Полином 29
Политропические кривые 35
Полная производная 165, 368
Полное приращение 163
Полный дифференциал 164, 367, 373
сложной функции 368
Полукубическая парабола 181
Полюс 192
Полярная ось 192
478
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Полярное уравнение кривой 192
Полярные координаты 192
Полярный угол 192
Понселе формула 266
Последовательность 53
— функций 348—354
Последовательных приближений спо-
способ 454
Постоянная величина 12
Правильная дробь, разложение на
простейшие 461
Предел переменной 57—63
— функции 70
многих переменных 160
повторный 365
Прекращения точка 184
Приближенное вычисление опреде-
определенного интеграла 263—274
— равенство 29
— решение уравнений 454—461
Приближенные формулы 327
Приведения формула 240
Признаки сходимости ряда 293—305,
335—383, 355
Приращение переменной 25, 104
— функции 25
нескольких переменных 162, 163
Производная 104, 108—111, 115, 116
— высшего порядка 124, 371
— неявной функции 165, 375
—, правила вычисления 108—115,
177
— слева 107
— справа 107
— частная 162, 367, 371
Промежуток 13
Прямоугольников формула 264
Равномерная сходимость последова-
последовательности 348
ряда 345
Равномерная непрерывность функций
79, 161
Радиус кривизны 170, 185, 186, 194
— сходимости 358
Радиус-вектор 192
Развертка круга 192
Разности функций 128, 129
Разрыв подынтегральной функции 231
— функции 73, 276
Раскрытие неопределенностей 77,
155—159, 330
Рациональная дробь, разложение на
простейшие 461 J
Рациональное число 10
Рол ля теорема 149
Ряды абсолютно сходящиеся 302, 332,
333
— двойные 341
— знакопеременные 301
— Маклорена 311
— равномерно сходящиеся 345
— расходящиеся 289
— степенные 357, 360—362
— сходящиеся 289
— Тейлора 311
— тригонометрические 345
Сечение в числовой области 90
Симпсона формула 266
Синус 43, 108, 314
Синусоидальные величины 428
Скачок функции 73
Сложная функция 101, 111 120, 128,
165
Соприкосновения точка 183
Спирали 194
Спрямляемая дуга 246
Сравнения признак 293, 294
Среднего значения интеграла форму-
формула 228, 229
Степенная функция 35, 36, 108
Степенно-показательная функция 76,
Степенные ряды 357, 360—362
Сумма ряда 289
Табличный способ задания функции
18
Тангенс 44, 111
Тейлора ряд 311
— формула 309, 385, 441
Тор 263
Трансцендентные кривые 184
Трехчлен второй степени 29
Тригонометрические ряды 345
— функции 43—47, 418
, разложение в степенной ряд
314
Трилистник 246
Трохоида 189
Убывающая функция 40, 131, 134
Угловой коэффициент прямой 24
Узловая точка кривой 181
Уклон прямой 25
Улитка 195
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
479
Уникурсальная кривая 470
Упорядоченная переменная
Уравнение кривой 22
— поверхности 381
49
Ферма теорема 148
Функциональная зависимость
Функция 14
Целая функция 29
Целое число 10
Центр кривой 32
— тяжести дуги 260
плоской фигуры 261
системы точек 392
16
Цепная линия 186, 252, 422
Циклоида 187, 252, 253
Частная производная 162, 367, 371
Четная функция 238
Эйлера подстановки 467
— теорема 370
— формулы 417
Эквивалентные бесконечно малые и
бесконечно большие величины 82
Эллипс 243, 251, 318, 435
Эллипсоид 255, 256, 258, 384
Эллиптические интегралы 470
Эмпирические формулы 28
Эпициклоида 189