Многообразия Эйнштейна. Том 1 - Бессе А.

Author: Бессе А.
Tags: топология геометрия математика
ISBN: 5-03-002065-9
Year: 1990
Similar
Гладкие многообразия
Лекции по геометрии. Семестр III. Гладкие многообразия
Современная геометрия: Методы и приложения. Том II. Геометрия и топология многообразий
Гладкие многообразия и наблюдаемые
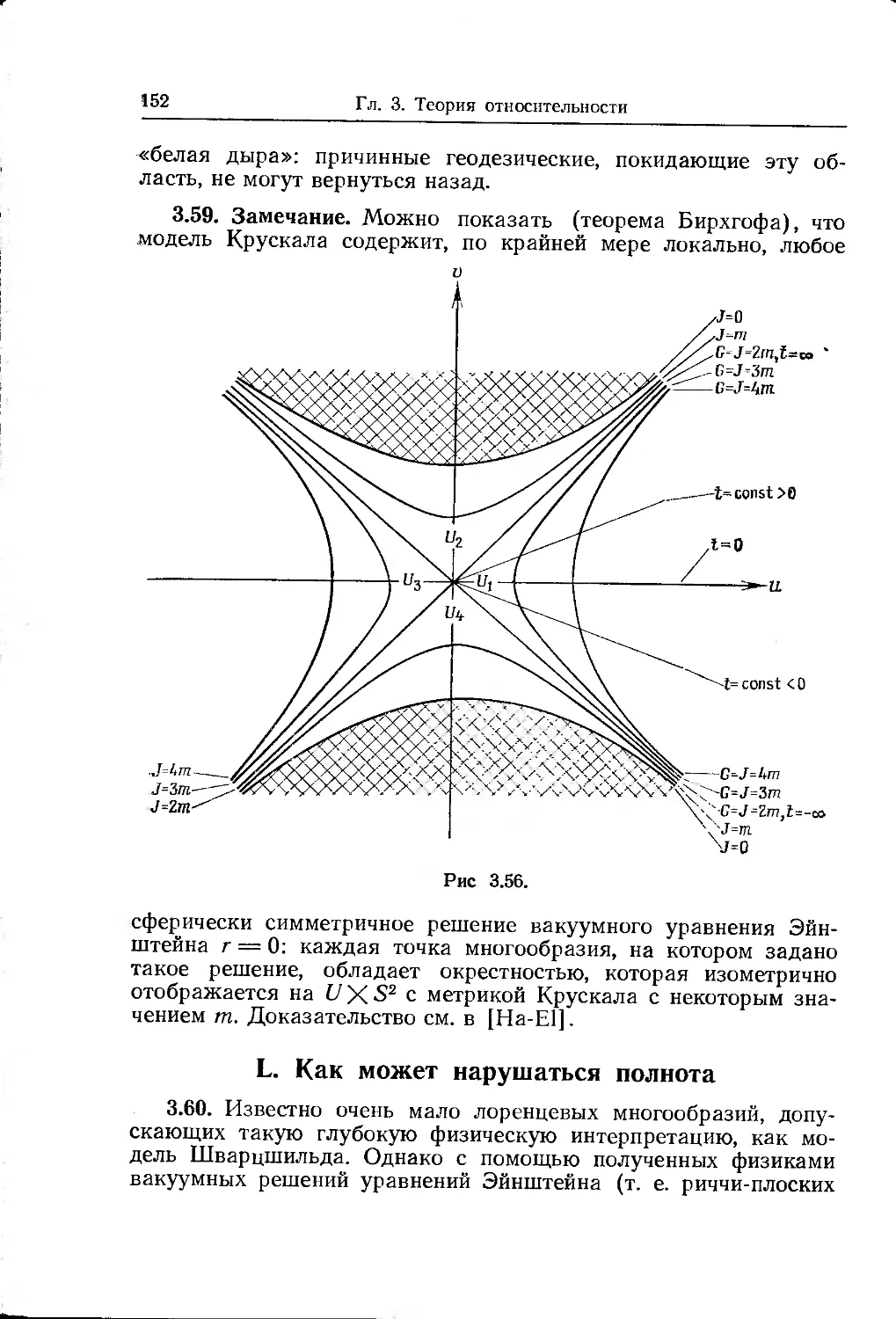
Text
                    Arthur L. Besse
Einstein Manifolds
With 22 Figures
Springer-Verlag
Berlin Heidelberg New York
London Paris Tokyo
А.Бессе
Многообразия
Эйнштейна
В двух томах
Том I
Перевод с английского
Д. В. Алексеевского
Москва «Мир» 1990
Цдппстгк'^-’П
ББК 22.152
Б53
УДК 515.1
Бессе А.
Б53 Многообразия Эйнштейна: В 2-х т. Т. I. Пер. с англ,—
М.: Мир, 1990. —318 с.
ISBN 5-03-002065-9
Книга известного французского математика, посвященная одному
из современных и активно развивающихся направлений геометрии. Мно-
гообразия Эйнштейна — это многомерный аналог поверхностей постоян-
ной кривизны, которые возникли в общей теории относительности и
связаны с кэлеровой и кватернионной геометрией, алгебраическими по-
верхностями и полями Янга — Миллса. Автор начинает с основных
понятий и дает обзор применяемых методов в различных приложениях.
Русское издание выходит в двух томах.
Для математиков (геометров, специалистов по группам Ли, ал-
гебраической геометрии, функциональному анализу), для физиков-тео-
ретиков, аспирантов и студентов университетов.
г~°
ББК 22.152
Г» Г1 R Л И О 'Г Е V А.
Ад:,!	- Д . Г-ОГО
педагогического мне.и гу»а
Редакция литературы по математическим наукам
ISBN 5-03-002065-9 (русск.)
ISBN 5-03-001423-3
ISBN 3-540-15279-2 (аигл.)
© Springer-Verlag Berlin Heidelberg 1987
All rights reserved
Authorized translation from English language
edition published by Springer-Verlag Berlin
Heidelberg New York Tokyo
© перевод на русский язык, Д. В. Алексеев-
ский, 1990
От переводчика
Книги Артура Ланселота Бессе пользуются заслуженной из-
вестностью в нашей стране. Его новая книга посвящена много-
образиям Эйнштейна — римановым многообразиям постоянной
кривизны Риччи или, иначе говоря, римановым многообразиям,
тензор Риччи rg которых пропорционален метрике g, т. е. ге =
= kg. Это соотношение можно рассматривать как квазилиней-
ное дифференциальное уравнение в частных производных отно-
сительно римановой метрики g. Оно называется вакуумным урав-
нением Эйнштейна с космологической постоянной к.
Книга содержит энциклопедически полное изложение полу-
ченных к настоящему времени результатов относительно много-
образий Эйнштейна и обзор различных методов исследования и
решения уравнения Эйнштейна. На первый взгляд может пока-
заться, что тема книги является довольно специальной и состав-
ляет один из разделов римановой геометрии. Ошибочность такого
взгляда становится очевидной после прочтения вдохновенно
написанного введения. Глубокая эрудиция и педагогическое
мастерство автора позволили ему убедительно показать, что
уравнение Эйнштейна является одним из фундаментальных не-
линейных уравнений геометрии и математической физики и тесно
связано с целым рядом разнообразных вопросов. В книге содер-
жится не только практически полный курс римановой и кэлеро-
вой геометрий (гл. 1 и 2), но также продуманное изложение ряда
глубоких теорий и результатов, связанных тем или иным образом
с многообразиями Эйнштейна. Значительная их часть не была
отражена в монографиях. В качестве примеров можно указать
теорию римановых субмерсий, теорию однородных римановых
и кэлеровых многообразий, теорию твисторов и описание кон-
формно полуплоских метрик Эйнштейна, краткий курс общей
теории относительности, классификацию групп голономии, полу-
ченную ближайшим другом и идейным вдохновителем автора —
Марселем Берже, теорию значений скалярной кривизны и об-
суждение проблемы Ямабе, теоремы гиперболизации Тёрстона
и др.
В книге приводятся наброски доказательств и обсуждения
таких важных и глубоких результатов, как теорема Чигера —
Громола о структуре многообразий неотрицательной кривизны
Риччи, теорема Гамильтона о существовании метрики постоян-
ной кривизны на компактном 3-многообразии положительной
кривизны, теоремы Коисо о структуре пространства модулей мет-
рик Эйнштейна, теорема Яу, решающая знаменитую проблему
Калаби и играющая важную роль в дифференциальной геомет-
рии, алгебраической геометрии и теоретической физике.
6
От переводчика
По существу задача изучения и построения многообразий
Эйнштейна служит автору полигоном для отработки и развития
мощных методов решения нелинейных проблем, использующих,
помимо геометрических соображений, различные идеи из алгеб-
ры, анализа, топологии, теории дифференциальных операторов.
При этом кратко излагаются и сами эти методы, как правило
без технических подробностей, но четко, с упором на идейную
сторону дела. Отметим также использование лаконичных, тща-
тельно продуманных обозначений, позволяющих упростить гро-
моздкие выкладки, п наличие большого числа формул и таблиц,
которые содержат обширную информацию, полезную для широ-
кого круга читателей.
Чем же замечательно уравнение Эйнштейна и каков его гео-
метрический смысл? Напомним, что основным инвариантом ри-
манова многообразия (М, g) является его тензор кривизны R =
= №iki), который определяет 2-секционную кривизну /С(о) по
направлению любой касательной 2-плоскости о с ТХМ (т. е. гаус-
сову кривизну поверхности, образованной геодезическими, выхо-
дящими из точки х в направлении 2-плоскости о). Тензор Риччи
определяется как свертка	тензора кривизны, а его
значение rg(X, Х)= RtjkiXiXk на единичном векторе Х^ТМ (кри-
визна Риччи) с точностью до множителя п—1, n = dimAf, рав-
но среднему значению секционных кривизн по направлению 2-
плоскостей, содержащих вектор X. Таким образом, многообразие
Эйнштейна характеризуется тем, что для него усредненное зна-
чение секционных кривизн постоянно.
Более глубокую геометрическую и физическую интерпрета-
цию уравнения Эйнштейна предложил Э. Картан. Он определил
понятие p-секционной кривизны в направлении произвольной р-
плоскости, 2 р п—1, и показал, что (п—1)-секционная
кривизна определяется тензором Риччи (точнее, его бездивер-
гентной частью — тензором Эйнштейна). Поэтому уравнения Эйн-
штейна можно рассматривать как условие постоянства (п— 1)-
секционной кривизны или, более физично, как условие того, что
введенный Картаном вектор момента сил кривизны, действую-
щий на гиперплоскость в касательном пространстве, ортогонален
этой гиперплоскости и имеет постоянную величину. Это позво-
ляет рассматривать уравнение Эйнштейна как аналог закона
Паскаля для идеальной жидкости.
С математической точки зрения выделенность уравнения Эйн-
штейна проявляется в том, что оно является фактически един-
ственной системой квазилинейных уравнений второго порядка
для метрики, в которой число уравнений равно числу неизвест-
ных. Кроме того, уравнение Эйнштейна является уравнением
От переводчика
7
Эйлера—Лагранжа для простейшего лагранжиана в простран-
стве метрик — полной скалярной кривизны. По существу это
единственный лагранжиан, линейно зависящий от кривизны.
Впервые уравнение re = Kg было предложено А. Эйнштейном
как уравнение гравитационного поля в вакууме. В настоящее
время уравнение Эйнштейна играет важную роль в различных
моделях теории поля. Таким образом, рассматриваемые в книге
вопросы имеют глубокую связь с современной теоретической
физикой.
Содержание книги подробно отражено во введении. Отметим
только, что в ней можно выделить четыре основные темы.
I.	Изучение общих свойств локальных и глобальных решений
уравнения Эйнштейна и структуры пространства модулей метрик
Эйнштейна (гл. 4, 5, 12).
II.	Изучение и построение метрик Эйнштейна, допускающих
достаточно большую группу изометрий, например транзитивную
группу (в этом случае уравнение Эйнштейна сводится к системе
алгебраических уравнений) или группу с орбитами коразмерно-
сти 1 (в этом случае уравнение Эйнштейна сводится к системе
обыкновенных дифференциальных уравнений), а также метрик
Эйнштейна, согласованных с расслоением (гл. 7, 8, 9).
III.	Изучение различных специализаций уравнений Эйнштей-
на и метрик Эйнштейна, определяемых условиями согласования
с той или иной дополнительной геометрической структурой
(гл. 10—14). При этом важную роль играет классификация
групп голономии, из которой следует, что локально неприводи-
мое риманово многообразие с группой голономии Hol =# SO (я),
О(п) либо имеет группу голономии О(п/2) и является кэлеро-
вым, либо является многообразием Эйнштейна. В кэлеровом
случае уравнение Эйнштейна упрощается и сводится к одному
уравнению типа уравнения Монжа—Ампера на одну скалярную
функцию — кэлеров потенциал.
IV.	Изучение различных обобщений уравнения Эйнштейна, в
том числе уравнения Янга—Миллса для римановой связности
(гл. 16).
Без сомнения, новая книга А. Бессе, посвященная бурно раз-
вивающейся области математики — многообразиям Эйнштейна,
будет полезна широкому кругу математиков и физиков, интере-
сующихся современной дифференциальной геометрией и ее при-
менением.
Д. В. Алексеевский
От автора
Для того чтобы собрать в этой книге столь разные резуль-
таты, мне пришлось обратиться к друзьям, к счастью, более уче-
ным, чем я. Это Женевьева Аверу, Лионель Берар-Бержери,
Марсель Берже, Жан-Пьер Бургиньон, Анджей Дердзиньский,
Дени М. Де Тюрк, Поль Годушон, Найджел Дж. Хитчин, Жо-
зет Уйо, Герман Кархер, Джерри Л. Каждан, Норихито Коисо,
Жак Лафонтен, Пьер Панею, Альбер Поломбо, Джон А. Торп,
Лиан Валер и другие.
Я благодарен за финансовую поддержку, которую оказали
мне Университет Париж-VII, Математический центр Политех-
нической школы, Национальный совет научных исследований,
Университет Шамбери и Генеральный совет Савойи.
Наконец, позволю себе поприветствовать здесь моего пред-
шественника и однофамильца Жана Бессе из Цюриха, который
прославился в теории функций комплексной переменной (см.,
например, [Bse]).
Ваш Л
г____]_э
Артур Бессе
Le Faux, 15.09.1986
Глава О
Введение
А. Определения и краткие пояснения
0.1. «Риманово многообразие фактически составлено из бес-
конечного числа маленьких кусочков евклидовых пространств»
(Э. Картан). Говоря современным языком, риманово многооб-
разие (Л1, g) состоит из следующих объектов: компактного
С“-многообразия М и метрического тензорного поля g, представ-
ляющего собой положительно определенную билинейную сим-
метрическую дифференциальную форму на М. Другими словами,
с каждой точкой р многообразия М ассоциирована евклидова
структура gp в касательном пространстве ТГМ многообразия Л4
в точке р, причем отображение p<-^gP имеет класс С°°. Гово-
рят, что g есть риманово, метрика на М.
0.2. Римановой структурой называется класс изометричных
римановых многообразий (подробности см. в гл. 4, 12). Два ри-
мановых многообразия (Л4, g) и (М', g') называются изомет-
ричными, если существует диффеоморфизм f: М-^М', перево-
дящий g' в g, т. е. f*g' = g. Другими словами, если обозначить
через Л (или, точнее, через Л(М)} множество римановых мет-
рик на М, то множество римановых структур на М есть про-
странство орбит Л /Ч£> множества Л относительно группы © =
= ®(.Л4) диффеоморфизмов многообразия М.
0.3. Как мы уже сказали, римановы многообразия представ-
ляют собой обобщение евклидовых пространств. Они также
естественным образом появляются в механике, см. [Ab-Ма] и
[CB-DW-DB]. Дальнейшим обобщением являются финслсровы
многообразия, которые получаются, если ассоциировать (беско-
нечно гладким образом) с каждой точкой р структуру банахо-
вой нормы в касательном пространстве ТРМ. Но несмотря на
то, что финслеровы многообразия естественным образом возни-
кают в механике и физике, они оказались менее важными, чем
римановы многообразия, и хорошие публикации о них появ-
ляются редко (см. тем не менее работы Э. Картана [Саг 10],
X. Буземана [Bus 1], X. Рунда [Run], М. Громова [Gro 3]).
10
Гл. 0. Введение
0.4. Теперь рассмотрим компактное С°°-дифференцируемое
многообразие М размерности п и поставим вопрос:
СУЩЕСТВУЮТ ЛИ НА М НАИЛУЧШИЕ (ИЛИ НАИБОЛЕЕ.
УДОБНЫЕ, ИЛИ ВЫДЕЛЕННЫЕ) РИМАНОВЫ
СТРУКТУРЫ?
Об этом меня спросил мой хороший друг Рене Том в Страс-
бургской математической библиотеке в 1958 г. Для простоты
ограничимся случаем компактного многообразия. Если рассмат-
ривать метрики Эйнштейна как критические точки функционала
U (см. 0.12 и гл. 4), то в компактном случае можно надеяться
доказать существование таких структур (несмотря на то, что
в конце концов этот подход разочаровывает, см. 4.1). Неком-
пактный случай также представляет интерес (см. гл. 15).
0.5. Для поверхностей (п = 2) ответ на поставленный вопрос
известен: наилучшими римановыми структурами на компактной
поверхности М являются структуры постоянной кривизны.
В двумерном случае существует лишь одно понятие кривизны,
а именно гауссова кривизна, которая представляет собой функ-
цию К'. M->R. Если М вложено в R3 с естественной индуци-
рованной римановой метрикой, то гауссова кривизна есть про-
изведение главных кривизн, или обратная величина к произ-
ведению главных радиусов кривизны. На любой компактной
поверхности существует хотя бы одна риманова метрика посто-
янной кривизны, а с помощью масштабного преобразования зна-
чение кривизны можно сделать равным 1, 0 или —1. Более того,
на поверхности М римановы структуры фиксированной постоян-
ной кривизны 1, 0 или —1 образуют прекрасное конечномерное
подмногообразие (с особенностями) пространства ,</£>, так на-
зываемое Пространство Модулей. Например, на двумерной сфере
S2 и на вещественной проективной плоскости RP2 существует
ровно одна риманова структура постоянной кривизны 1. На ком-
пактной поверхности М (ориентируемой или не ориентируемой)
с эйлеровой характеристикой %(М)<; 0 римановы структуры по-
стоянной кривизны —1 зависят от —3%(Л4) вещественных пара-
метров. Например, для ориентированной поверхности рода у
имеем бу — 6 параметров. Подробности см. в § В гл. 12.
0.6. А как будет выглядеть естественное обобщение поверхно-
сти постоянной кривизны для римановых многообразий размер-
ности больше двух? Мы утверждаем, что хорошим обобщением
оказывается многообразие постоянной кривизны Риччи.
А. Определения и краткие пояснения
И
0.7. О кривизне Риччи можно прочесть в гл. 1. Здесь мы
лишь напомним определение. Кривизна Риччи риманова много-
образия (Л4, g)— это квадратичная дифференциальная форма
(или симметрическая билинейная форма), которая обозначается
буквой г (или rg, если нужно указать соответствующую метри-
ку). Ограничение билинейной формы г на диагональ определяет
функцию на расслоении UM единичных касательных векторов
(которая тоже обозначается через г). Эта функция представляет
собой след эндоморфизма кривизны и выражается через 4-тен-
зор кривизны R по формуле r(x) = trace(zt—*/?(x, z)x). Можно
дать и эквивалентное определение: для хе UM значение r(x)
есть сумма Х"=2^(х> х«) секционных кривизн К(х, х,) для про-
извольного дополнения х до ортонормированного базиса
(х1, Х2, .... Хп).
0.8. Существуют три основных понятия кривизны риманова
многообразия, (i) Риманов тензор кривизны R (эквивалентный
функции секционной кривизны К, определенной на касательных
плоскостях), который представляет собой биквадратичную фор-
му, содержащую полную информацию о метрике g на уровне
кривизны, (ii) Определенная выше кривизна Риччи г — след R
относительно g. (iii) Наконец, скалярная кривизна s — скаляр-
ная функция на М, представляющая собой след s = tracegr
квадратичной формы г относительно g. Заметим, что при ц=2
все три кривизны эквивалентны. При п = 3 кривизна Риччи со-
держит всю ту же информацию, что и риманов тензор кривизны.
Главным образом по этой причине наша книга посвящена мно-
гообразиям размерности п 4.
0.9. Простые рассуждения показывают, что квадратичная
форма Риччи г: UM^>- R равна константе X тогда и только
тогда, когда r = Kg. Такие римановы многообразия называются
многообразиями Эйнштейна. После нормировки метрики всегда
можно считать, что имеет место один из трех случаев:
r = g
г = 0
r = ~g
(когда Z > 0),
(когда Л = 0),
(когда Л < 0).
Соответствующее значение константы 1,0 или —1 мы будем на-
зывать знаком многообразия Эйнштейна.
0.10. Назовем первую причину, по которой метрику Эйн-
штейна можно считать хорошим кандидатом на роль привиле-
гированной метрики на данном многообразии.
12
Гл. 0. Введение
Может показаться, что в качестве «наилучших» метрик есте-
ственно выбрать метрики постоянной кривизны (однородность
на уровне кривизны). Постоянство секционной кривизны (как
функции на грассмановом многообразии касательных 2-плоско-
стей многообразия Л4) приводит к тому, что после нормировки
метрики риманово многообразие становится локально изомет-
ричным единственному модельному пространству той же постоян-
ной кривизны, т. е. стандартной сфере (Sn, сап) с канонической
структурой сап (индуцированной, например, стандартным вло-
жением S"cR'1+1), если кривизна положительна, или евкли-
дову пространству (R", сап) (рассматриваемому как риманово
многообразие), если кривизна равна нулю, или, наконец, гипер-
болическому пространству (Нп, сап), если кривизна отрица-
тельна. В частности, существует ровно одна односвязная полная
нормированная структура постоянной секционной кривизны 1,0
или —1. Соответствующие многообразия диффеоморфны Р" или
S". Следовательно, большинство многообразий размерности п 4
не допускают таких метрик. Для п = 3 ситуация пока остается
неясной (см. § С гл. 6).
Что же касается римановых метрик постоянной скалярной
кривизны, то они существуют на любом компактном многообра-
зии произвольной размерности, а при п 3 образуют бесконеч-
номерное семейство (см. § F гл. 4). Таким образом, этих мет-
рик оказывается слишком много для того, чтобы считать их
привилегированными. Короче говоря, постоянство секционной
кривизны — это слишком сильное условие, а постоянство ска-
лярной кривизны — слишком слабое. Остается только постоян-
ство кривизны Риччи.
С наивно аналитической точки зрения постоянство кривиз-
ны Риччи привлекательно еще и потому, что метрика и кри-
визна Риччи зависят от одинакового числа параметров, а имен-
но от п(и-(- 1)/2 параметров. Мы увидим, что метрики постоян-
ной кривизны Риччи образуют конечномерное семейство.
Правда, встает вопрос о существовании таких метрик. Но нам
по крайней мере встретится множество примеров.
0.11. Для любителей линейных представлений (скажем, для
алгебраически мыслящих читателей) отметим, что действие
ортогональной группы на тензор кривизны 7? риманова много-
образия определяет разложение этого тензора на части, соот-
ветствующие неприводимым компонентам этого действия: R =
= U + Z + VF. Часть W— это знаменитый тензор конформной
кривизны Г. Вейля, часть U эквивалентна скалярной кривизне
s, a Z есть бесследовая часть кривизны Риччи. Таким образом,
условие Z = 0 эквивалентно условию Эйнштейна. Более по-
А. Определения и краткие пояснения
13
дробно об этом подходе и об условиях U = 0 и W = 0 см § G.
Н гл. 1.
0.12. Назовем теперь вторую причину (на самом деле это
сразу две причины). Грубо говоря, условие Эйнштейна для ри-
манова многообразия (Л4, g0) эквивалентно тому, что метрика
go является критической точкой функционала полной скалярной
кривизны
S. g । > sgPg
м
на пространстве	метрик объема единица. Это означает,
что для любой вариации go + th, где h принадлежит т. е.
пространству билинейных симметрических дифференциальных
форм на М, производная
Ь=о
равна нулю. Простота функционала и естественность понятия
критической точки говорят в пользу метрик Эйнштейна.
0.13. Еще одна причина связана с историей физики. А. Эйн-
штейн, работая над теорией относительности и рассматривая не
римановы, а лоренцевы многообразия (которым соответствует
тензорное поле g сигнатуры (—, —, ..., —, -|-) в отличие от
положительной определенности (+, •••, +) римановой метри-
ки, см. гл. 3), в 1913 г. предположил, что полевые уравнения
взаимодействия гравитационного и других полей имеют вид
г — ^-sg = T, где Т — тензор энергии-импульса. В частности,
«отсутствие массы» приводит к риччи-плоским многообразиям,
для которых г = 0. А. Эйнштейн получил это условие как урав-
нение Эйлера — Лагранжа для вариационной задачи. Действи-
тельно, вычисления показывают (см. 4.17), что градиент функ-
ционала S равен г — уsg. Рассматривая только метрики
объема единица, мы приходим к условию постоянства кривизны
Риччи, которое определяет метрики Эйнштейна. Это необходи-
мый шаг, поскольку для большинства многообразий требование
«быть риччи-плоским» оказывается слишком сильным. Напри-
мер, компактное многообразие М с первым числом Бетти
(Л1) > dim Л1 по теореме Бохнера 6.56 не допускает риччи-
плоской метрики.
0.14. Уточним нашу цель. Мы пользуемся термином «много-
образия Эйнштейна» для римановых многообразий постоянной
14
Гл. 0. Введение
кривизны Риччи, потому что так давно уже принято среди ма-
тематиков, и не претендуем на получение результатов по мате-
матической физике. По своему отношению к нашей работе
физики-теоретики делятся на две группы. Одни считают, что
все, что мы делаем, — просто ерунда. Другие думают, что гео-
метрия римановых многообразий (например римановых много-
образий Эйнштейна) может им пригодиться хотя бы как источ-
ник идей. Она может даже принести реальную пользу, по-
скольку комплексификация позволяет перейти к более общей
модели, в рамках которой разница в знаке сигнатуры исчезает.
То же самое можно сказать и о теории Янга — Миллса.
0.15. Третья причина связана с тем, что в двумерном случае
постоянство кривизны Риччи эквивалентно постоянству кри-
визны, и здесь все обстоит замечательно (см. 0.5 и § В гл. 12):
на любой компактной поверхности существуют метрики постоян-
ной кривизны, которые образуют прекрасное конечномерное
множество. По поводу трехмерного случая см. § С гл. 6.
0.16. Эта книга посвящена многообразиям Эйнштейна раз-
мерности п > 4. В § D, Е мы обсудим книгу в целом, а в § F, G
дадим подробный обзор содержания по главам. Для простоты
мы разбили весь материал на три части: существование, при-
меры и единственность. Надеемся, что это окажется полезным
при первом знакомстве с предметом (см. обзоры [Вег 6] и
[Вой 5, 10]).
В. Зачем нужна книга о многообразиях Эйнштейна?
0.17. В сентябре 1979 г. в Эспальоне, во Франции, состоялся
симпозиум по многообразиям Эйнштейна. Именно там я понял,
что о них стоит написать книгу. Тема, кажется, уже вполне
созрела: хотя многие фундаментальные вопросы все еще
остаются открытыми, сделаны и большие успехи — в частности,
благодаря доказательству гипотезы Калаби (которое дали
Т. Обин в случае отрицательной скалярной кривизны и С. Т. Яу
в случае неположительной кривизны), а также результатам, по-
лученным Н. Коисо для пространств модулей. Сейчас исследо-
вания в этой области быстро развиваются. Кроме того, известно
уже довольно много примеров многообразий Эйнштейна разных
типов.
0.18. Многообразия Эйнштейна не только интересны сами по
себе, но и связаны с многими важными областями римановой
геометрии: с римановыми субмерсиями, однородными римано-
выми пространствами, римановыми функциями и их критиче-
С. Существование
15
скими точками, теорией Янга — Миллса, четырехмерными авто-
дуальными многообразиями, группами голономии, кватернион-
ными многообразиями и, наконец, через теорию КЗ-поверх-
ностей с алгебраической геометрией. Все эти области сейчас
процветают. В то же время связей между многообразиями Эйн-
штейна и геодезическими, а также спектром лапласиана, ка-
жется, пока не установлено1).
0.19. Я стремился включить в эту книгу все, что известно
о многообразиях Эйнштейна, и даже упомянутые выше смежные
разделы. Признаюсь, что кое-где воспользовался многообра-
зиями Эйнштейна как предлогом для того, чтобы обратиться к
особенно близким мне вопросам геометрии. Некоторые очень
сложные доказательства (см., например, § С гл. 11) в книге
лишь намечены, чтобы не увеличивать слишком сильно ее
объем, — однако только в тех случаях, когда в литературе легко
найти исчерпывающие доказательства.
0.20. Во всех главах изложение носит замкнутый характер.
Поэтому многие вещи повторяются несколько раз. Но в конце
концов, повторение даже полезно. Когда мне не хватало компе-
тентности в некоторых вопросах, я обращался к друзьям, кото-
рые также внесли вклад в эту книгу. Мы провели множество
встреч, чтобы добиться максимальной согласованности различ-
ных частей. Особенно трудно было согласовать обозначения
(см. 0.39). Всем авторам воздается должное в соответствующих
главах, поэтому здесь мы не будем на этом останавливаться.
Если у кого-то возникнут жалобы, их можно подать в суд по
месту жительства автора: департамент Сены, Франция.
С. Существование
0.21. Сегодня все выглядит совершенно по-разному при
п = 4 и при п 5. Как это ни смешно, при п 5 мы не знаем
ответа даже на простейший вопрос: любое ли компактное мно-
гообразие обладает хотя бы одной метрикой Эйнштейна? Можно
сказать, что мы не знаем, является ли условие эйнштейновости
при н > 5 сильным условием или нет. Конечно, при этом мы
не требуем, чтобы константа Эйнштейна имела определенный
знак: априори он может быть произвольным. Существование
’) В статье [Алексеевский Д. В. О длине минимальных геодезических в
кватернионных многообразиях.— Тезисы конференции «Вопросы геометрии
«в целом», Новосибирск, 1987, с. 4] показано, что для чстырехмерпых мно-
гообразий (а также для произвольных кватерннонно-кэлеровых многообра-
зий) условие эйнштейновости позволяет получить некоторые оценки длины
минимальных геодезических. — Прим, перев.
16
Гл. 0. Введение
на многообразии М метрики Эйнштейна положительного знака,
как известно, влечет за собой компактность многообразия и ко-
нечность его фундаментальной группы (см. 6.52). Отметим так-
же, что для многообразий Кэлера — Эйнштейна мы располагаем
топологическими условиями во всех комплексных размерностях
(см. § А гл. 11).
0.22. Случай четырехмерных многообразий изучен лучше.
Здесь условие эйнштейновости означает, что оператор кривизны
коммутирует с оператором Ходжа, действующим на 2-формах.
Это коммутационное соотношение накладывает сильные огра-
ничения на подынтегральные выражения в формулах Чженя
для класса Эйлера и класса Понтрягина. (Отметим, что в че-
тырехмерном случае существует лишь один класс Понтрягина
и одно число Понтрягина.) Если %(А1) — эйлерова характери-
стика многообразия М, a pi(Af) — его число Понтрягина, то из
указанного коммутационного соотношения следует неравенство
(М) |,
поэтому не каждое компактное четырехмерное многообразие
обладает метрикой Эйнштейна. Например, его эйлерова харак-
теристика должна быть неотрицательной. Более сложными при-
мерами нарушения этого неравенства могут служить связные
суммы пяти или более комплексных проективных плоскостей, а
также двух или более торов. Однако вопрос о том, будет ли это
неравенство достаточным условием, остается открытым. Пре-
дупредим читателя, что при п 5 условие эйнштейновости не
накладывает никаких ограничений на подынтегральные выра-
жения в формулах Чженя для чисел Эйлера и Понтрягина
(см. 6.41).
D. Примеры
0.23. Несмотря на простоту условия г = 7.g, не следует ду-
мать, что можно легко найти примеры многообразий Эйнштейна.
Если я вас не убедил, попробуйте сами построить пример, кото-
рого нет в книге, и если вам это удастся, пожалуйста, сразу же
напишите мне. Еще труднее найти риччи-плоское компактное
многообразие. Автор будет счастлив угостить вас обедом в са-
мом лучшем ресторане в обмен на такое многообразие!
1.	Алгебраические примеры
0.24. Как проще всего строить римановы многообразия по-
стоянной кривизны Риччи? Пусть М — однородное риманово
многообразие, т. е. группа изометрий G = Isom(Af) действует
D. Примеры
17
на М транзитивно. В этом случае многообразие М можно пред-
ставить в виде фактор-пространства M—G/H, где G — группа
Ли, а Н — ее замкнутая компактная подгруппа. Группа G со-
храняет любой инвариант римановой метрики. В частности,
скалярная кривизна s остается постоянной. Если мы хотим,
чтобы кривизна Риччи была постоянной функцией на расслое-
нии UM единичных касательных векторов, достаточно потребо-
вать, чтобы группа G действовала на UM транзитивно (в этом
случае говорят, что многообразие G/H изотропно). Ясно, что
можно ограничиться транзитивностью в одной точке, т. е. по-
требовать, чтобы линейное представление изотропии Ad Н дейст-
вовало транзитивно на единичной сфере касательного простран-
ства ТРоМ некоторой точки. Но это чрезвычайно сильное условие.
Оно означает, что метрическое пространство двухточечно одно-
родно. Все такие пространства исчерпываются симметрическими
пространствами ранга единица, т. е. евклидовыми пространст-
вами, сферами, различными проективными пространствами и
двойственными ко всем этим пространствам некомпактными
пространствами.
0.25. Эли Картан сделал очень важное замечание (см.
[Саг 12] или [Wol 3], с. 137): однородное риманово многообра-
зие M = G/H автоматически оказывается эйнштейновым, если
его представление изотропии Ad Н в ТР,М неприводимо. Дейст-
вительно, представление Ad Н сохраняет две квадратичные фор-
мы в ТРМ: метрику g и кривизну Риччи г. Поскольку одна из
них положительно определена, из теории приведения и нз не-
приводимости Ad Н следует, что эти формы пропорциональны.
Отметим, что по той же причине однородное многообразие М =
= G/Н с неприводимым линейным представлением изотропии
обладает единственной (с точностью до пропорциональности)
инвариантной римановой метрикой, которая автоматически ока-
зывается эйнштейновой.
0.26. Простейшим способом, описанным в 0.24, можно по-
строить только симметрические пространства ранга единица.
Замечание Эли Картана позволяет получить более широкий
класс примеров. Прежде всего, все неприводимые римановы
симметрические пространства изотропно неприводимы. Этот
класс включает в себя пространства постоянной кривизны, раз-
личные проективные пространства, а также грассмановы много-
образия. В 7.51 мы покажем, что изотропно неприводимых
римановых пространств G/Н, грубо говоря, в два раза больше,
чем неприводимых симметрических пространств. Некоторые из
них чрезвычайно интересны тем, что размерность стабилизатора
2 А. Бессе, т. 1
18
Гл. 0. Введение
очень мала по сравнению с размерностью группы изометрий
(см. табл. 7.106, 7.107).
0.27. Поиск всех однородных римановых компактных много-
образий Эйнштейна — задача алгебраическая, но вовсе не про-
стая. Теоретически ее можно решить, анализируя пары (д, 1))
алгебр Ли, соответствующих группам G, Н. Чем больше непри-
водимых компонент имеет представление изотропии Ad И, тем
сложнее становится задача, поскольку растет число различных
инвариантных метрик на G/H. Совсем недавно в этой классифи-
кации были сделаны большие успехи (см. гл. 7, а также
[DA-Zi] и [Wa-Zi]). Для того чтобы дать некоторое представ-
ление о том, насколько неканоническим может быть однородное
многообразие Эйнштейна, приведем несколько примеров. На
S4n+3 и Сргп+i существуют неканонические однородные метрики
Эйнштейна, на S15 существует не менее двух таких метрик, а
на группе SO(ri)—не менее п различных метрик Эйнштейна
(при 12). На S2XS3, S3XS3, S6XS7 и S7X$7 существуют
метрики Эйнштейна, не являющиеся метриками прямого произ-
ведения.
2.	Примеры из анализа
0.28. До 1980 г. не было известно никаких классов компакт-
ных многообразий Эйнштейна, кроме класса однородных много-
образий. Но еще в 1954 г. Э. Калаби высказал гипотезу — как
мы теперь знаем, верную, — которая позволяет описать широкий
класс компактных многообразий нулевой кривизны Риччи, т. е.
риччи-плоских римановых многообразий, или многообразий Эйн-
штейна знака нуль.
Рассмотрим компактные кэлеровы многообразия. В этом
случае результаты Чженя позволяют очень красиво интерпрети-
ровать кривизну Риччи. Прежде всего, с помощью комплексной
структуры кривизна Риччи преобразуется в замкнутую диффе-
ренциальную 2-форму р (по поводу кэлерова случая см. гл. 2).
Согласно теореме де Рама, эта 2-форма определяет некоторый
вещественный класс когомологий, который (с точностью до мно-
жителя 2л) представляет собой не что иное, как первый класс
Чженя Ci (М) нашего комплексного многообразия. Э. Калаби
предположил, что если первый класс Чженя компактного кэле-
рова многообразия равен нулю, то оно допускает риччи-плоскую
кэлерову метрику.
0.29. В 1955 г. Э. Калаби доказал единственность такой мет-
рики (в любом кэлеровом классе). Доказательства существо-
вания пришлось ждать до 1976 г., когда С. Т. Я у получил тео-
D. Примеры
19
рему существования, в основе которой лежит существование
решения нелинейного уравнения в частных производных типа
Монжа — Ампера, — результат, тоже не дававшийся аналитикам
долгое время. В устных сообщениях Калаби распространил
свою гипотезу на тот случай, когда класс ci (М) отрицательно
определен, а метрика Эйнштейна имеет знак —1. В 1976 г. эта
гипотеза была независимо доказана Т. Обином и С. Т. Яу.
0.30. Сейчас известно множество примеров компактных кэле-
ровых многообразий с нулевым или отрицательным первым
классом Чженя (см. § А гл. 11). Отметим только, что алгебраи-
ческая гиперповерхность степени d в комплексном проективном
пространстве С/Эт+1 имеет нулевой первый класс Чженя, если
d = т + 2, и отрицательный, если d > т + 2. Но для того чтобы
можно было оценить сложность гипотезы Калаби и задачи по-
строения многообразий Эйнштейна, предупредим читателя, что
эти гиперповерхности не будут эйнштейновыми в индуцирован-
ной кэлеровой метрике в СРт+1. Таким образом, методы ана-
лиза позволяют получить метрики Эйнштейна лишь в неявном
виде. Отметим также, что неплоские однородные римановы мно-
гообразия не могут быть и риччи-плоскими. Пока что мы не
знаем других примеров компактных риччи-плоских многообра-
зий, кроме тех, что приведены выше.
3.	Спорадические примеры
0.31. Помимо уже указанных примеров мы знаем только две
конструкции многообразий Эйнштейна, причем они позволяют
получить лишь несколько новых многообразий. В основе первой
лежит результат Ш. Кобаяси. Рассмотрим компактное много-
образие Кэлера — Эйнштейна знака -(-1 и главное S'-расслоение
над ним, отвечающее классу когомологий, кратному кэлерову
классу базового многообразия. На тотальном пространстве
этого расслоения существует метрика Эйнштейна. К сожалению,
таким способом удается получить только однородные метрики.
0.31а. В 1979 г. Д. Пейдж нашел совершенно новый пример
метрики Эйнштейна на связной сумме двух комплексных проек-
тивных плоскостей (это многообразие можно также получить
раздутием точки комплексной проективной плоскости или как
нетривиальное 52-расслоение над S2). Л. Берар-Бержери по-
строил на основе конструкции Д. Пейджа общий метод. Однако
пока с помощью этого метода удалось получить лишь неболь-
шое число новых компактных многообразий Эйнштейна. Не-
компактный случай намного проще.
2*
20
Гл. 0. Введение
Е. Единственность и модули
0.32. Рассмотрим задачу классификации всех структур Эйн-
штейна на данном компактном многообразии М. В двумерном
и трехмерном случаях вопрос достаточно ясен (см. § В, G
гл. 12), однако для мало что известно. Отметим, что ни
для одного многообразия не доказана единственность структуры
Эйнштейна, даже для S4 и СР2.
0.33. Сформулируем основные результаты, касающиеся един-
ственности.
1.	На сфере Sn каноническая метрика является изолирован-
ной точкой в пространстве структур Эйнштейна, а также един-
ственной метрикой Эйнштейна среди метрик секционной кри-
визны Ке[3п/(7п— 4), 1]. Вероятно, эта оценка неточна. При
п = 4 мы располагаем точной оценкой: К е [1/4, 1].
2.	Компактное комплексное однородное многообразие допу-
скает ровно одну (с точностью до голоморфных преобразований)
метрику Кэлера — Эйнштейна (И. Мацусима, см. гл. 8)'). Однако
на нем могут существовать другие метрики Эйнштейна, некэле-
ровы или кэлеровы относительно других комплексных структур.
Например, так обстоит дело с многообразием, которое полу-
чается раздутием одной точки проективной плоскости СР2 (см.
0.31).
3.	Единственности явно нет на сферах 54"+3, для которых
Г. Йенсен построил примеры неканонических метрик Эйнштейна
при любом п. Они являются однородными. Аналогичные при-
меры построены и для других классических многообразий (см.
82 и 9.8).
0.34. Есть ли такие многообразия, для которых все структуры
Эйнштейна известны? В четырехмерном случае ответ будет по-
ложительным. Такими многообразиями являются тор (а также
его фактор-многообразия), на котором все метрики Эйнштейна
являются плоскими (по теореме об обращении кривизны в
нуль), и КЗ-поверхность (и ее факторы по группе Z2), на кото-
рой все метрики Эйнштейна являются кэлеровыми относительно
одной из комплексных структур. Множество структур Эйнштейна
образует конечномерное подмногообразие в пространстве .#/©
римановых структур (т. е. классов диффеоморфных римановых
метрик), которое имеет размерность 6 для Тл и размерность 57
для КЗ-поверхности (см. § В гл. 12).
0.35. Пусть М — компактное многообразие, а <о (М)—под-
множество структур Эйнштейна из пространства Л'/© римано-
*) При дополнительном предположении, что оно односвязно и допускает
кэлерову метрику. — Прим, перев.
F. Краткий обзор содержания по главам
21
вых структур. Напомним, что множество ё (Л4) называется
Пространством Модулей многообразия М. Что можно сказать
о пространстве <^(Л4)? Прежде всего бросим неискушенный
взгляд на его касательное пространство. Рассмотрим кривую
g(t) в ё(М), для которой rs(t} = Z (t)g (/), \ft, и g(0) = g. Про-
дифференцировав эту кривую по t при t = 0 и положив
h = |f ’ мы Д°кажем> что функция Х(0 не меняет знака.
Поэтому можно считать, что Х(£)= 1, 0 или —1. В этом случае
можно показать, что тензор h удовлетворяет эллиптическому
уравнению в частных производных. Отсюда следует, что про-
странство ё (М) в каждой точке инфинитезимально конечно-
мерно. Поэтому можно предположить, что пространство ё(М),
грубо говоря, состоит из связных компонент конечной размер-
ности.
0.36. Мы наметили огромную программу. Ее трудность носит
не аналитический характер. Скорее она определяется алгебраи-
ческой сложностью глобальной системы уравнений в частных
производных rg = Xg.
Недавно Н. Коисо осуществил часть этой программы. Преж-
де всего он обнаружил, что формальное касательное простран-
ство, о котором шла речь в 0.35, в общем случае не является
касательным пространством к ё (М) в точке g. Он построил
примеры, в которых решение h указанного эллиптического урав-
нения не является касательным вектором никакой кривой g(t)
из ё(М). Однако он доказал, что ё (М) всегда является ана-
литическим подмножеством некоторого гладкого подмногообра-
зия из •</©. Таким образом, пространство ё(М) в некотором
смысле конечномерно. Более того, оно хаусдорфово.
0.37. Сейчас многими умами владеет задача описания мно-
жества констант Эйнштейна на данном компактном многообра-
зии. Речь идет о множестве таких вещественных чисел X, для
которых существует метрика g полного объема единица с rg =
— "kg. Мы знаем только, что это множество счетно. Неизвестно,
является ли оно дискретным подмножеством прямой и ограни-
чено ли оно снизу. Легко показать, что оно ограничено сверху
(см. § G гл. 12).
F. Краткий обзор содержания по главам
Главы 1 и 2. Основные сведения
0.38. Годами меня уговаривали написать трактат по рпмано-
вой геометрии. Я устоял против этого соблазна и включил в
первые две главы лишь те сведения, которые используются в
22
Гл. 0. Введение
книге. Некоторые не совсем стандартные понятия и результаты
можно найти в § Н гл. 0, § G, I, К гл. 1 и § Н, I гл. 2.
0.39. Особое внимание уделяется проблеме обозначений, ко-
торая вызвала оживленную дискуссию. Самые большие труд-
ности возникли с кривизной и со скалярной кривизной. В конце
концов мы пришли к такому (не единодушному) соглашению:
К — секционная кривизна;
R — тензор кривизны;
г—кривизна Риччи;
s — скалярная кривизна.
Мы решили отказаться от развернутых обозначений типа ric,
ricci или seal, поскольку при этом некоторые уравнения оказы-
вается невозможно прочесть: например, Al (ricci) = seal -h —
— ricci (6ft).
Глава 3. Теория относительности
0.40. Подчеркнем, что эта книга посвящена собственно ри-
мановым многообразиям, т. е. многообразиям с положительно
определенной метрикой. Однако объект нашего изучения тесно
связан с теорией относительности Эйнштейна (и не только на-
званием), а также с лоренцевыми
многообразиями. Поэтому мы реши-
ли, что в книгу стоит включить не-
которые основные понятия и ре-
зультаты теории относительности
(тензор энергии-импульса и т. д.).
Поскольку лоренцева геометрия са-
ма стала обширной математической
дисциплиной, пришлось делать от-
бор материала. Надеемся, что он
устроит читателей-неспециалистов.
0.41. На первый взгляд риманова
и лоренцева геометрии имеют много
общего: канонические связности,
геодезические, тензоры кривизны
и т. д. Но на самом деле эта общая часть — всего лишь общая
исходная точка для движения в разных направлениях. Например,
взглянув на уравнения Эйнштейна, специалист по римановой
геометрии поступит в соответствии с этой книгой: займется
вопросами существования, единственности, проблемой модулей
и т. д. Физик же начнет с пространственноподобной гиперповерх-
ности и постарается с помощью уравнений Эйнштейна про-
F. Краткий обзор содержания по главам
23
должить индуцированную на ней риманову метрику, чтобы полу-
чить лоренцеву метрику в пространстве-времени. Риманова гео-
метрия занимается эллиптическими уравнениями в частных про-
изводных, а лоренцева геометрия — гиперболическими уравне-
ниями. Кроме того, в лоренцевой геометрии обычно рассматри-
ваются некомпактные многообразия и сингулярности. Взаимоот-
ношения этих двух областей лучше всего иллюстрирует рисунок,
который приводится в работе Ч. Н. Янга [Yan] (рис. 0.41).
По лоренцевой геометрии написаны замечательные книги:
[Be-Eh], [На-El], [Mi-Th-Wh], [ONe3], [Sa-WuJ.
Глава 4. Римановы функционалы
0.42. В этой главе развивается идея из 0.12: риманово мно-
гообразие (М, g) является многообразием Эйнштейна тогда и
только тогда, когда g есть критическая точка функционала
S(g)=\ Sggg на пространстве Mi(M). У математика сразу
J м
возникает множество естественных вопросов. Существует ли
хорошая теория Морса для вычисления второй вариации этого
функционала (индексной формы)? Существуют ли другие по-
добные функционалы и что представляют собой их критические
метрики? В гл. 4 вошло все, что известно по этому поводу, но
здесь остается больше открытых вопросов, чем получено резуль-
татов. Отметим, что в этой главе мы встретимся с вариацией
метрики, с пространством М/S) римановых структур, а также с
недавно развитой теорией допустимых знаков скалярной кри-
визны.
Глава 5. Кривизна Риччи как уравнение
в частных производных
0.43. Если забыть о метрике g, то ее кривизна Риччи ге
оказывается просто бедной сироткой в пространстве ^2М би-
линейных симметрических дифференциальных форм на данном
компактном многообразии М. В связи с этим в голову приходит
множество вопросов. В частности, вопрос существования и един-
ственности метрики g с заданным тензором Риччи г. В гл. 5
рассматриваются вопросы именно такого типа. В последнее
время на многие вопросы были получены ответы. Трудность
состоит в том, что уравнение в частных производных rg = г от-
носительно неизвестной метрики g является сильно нелиней-
ным, неэллиптическим и имеет весьма своеобразный вид. Его
24
Гл 0 Введение
основная особенность заключается в переопределенности, обус-
ловленной тождествами Бьянки.
0.44. В этой главе читатель найдет много результатов. Ока-
зывается, встречаются и настоящие сиротки, т. е. формы г, не
индуцированные никакой метрикой, и дети, и даже единствен-
ные дети. Здесь же доказывается, что любая метрика Эйнштей-
на g вещественно аналитична (в соответствующих координатах)
в силу характера уравнения rg = ‘kg. Этот результат имеет важ-
ные следствия. И наконец, приводится результат Гамильтона
о существовании метрик Эйнштейна на некоторых 3-многообра-
зиях и набросок его доказательства.
Глава 6. Многообразия Эйнштейна и топология
0.45. В эту главу включен материал, о котором шла речь
в § С. Рассматриваемая в ней проблема положительной скаляр-
ной кривизны лежит в самом сердце сегодняшних исследований.
Глава 7. Однородные римановы многообразия
0.46. Как отмечалось в § D, среди однородных пространств
можно найти множество примеров многообразий Эйнштейна.
Об однородных римановых многообразиях написано огромное
количество статей и несколько монографий, но систематическое
изложение этой темы в книгах встречается не слишком часто
(исключение составляет книга Кобаяси и Номидзу [Ko-No2]).
Поэтому мы сочли целесообразным включить в гл. 7 систе-
матическое введение в эту теорию. Мы приводим также таб-
лицы, потому что они нам нравятся, а в существующей литера-
туре их не очень много.
Глава 9. Римановы субмерсии
0.47. Идея римановых субмерсий возникает при изучении
римановых метрик в расслоении Е-+-В. Метрики римановых
субмерсий в некотором смысле являются ближайшими к метри-
кам римановых произведений. Грубо говоря, для римановых
субмерсий (особенно для субмерсий с вполне геодезическими
слоями) кривизну тотального пространства Е можно выразить
через кривизны метрик базы В и слоя F. Самое удивительное
свойство заключается в том, что секционная кривизна по каса-
тельным к базе В направлениям всегда больше или равна кри-
визне ее горизонтальных лифтов. Метод субмерсий позволяет
F. Краткий обзор содержания по главам
25
построить множество примеров (см. § G—К гл. 9), поэтому нам
кажется, что систематическое изложение теории может ока-
заться полезным.
Глава 10. Группы голономии
0.48. Группа голономии риманова многообразия (М, g)
(строго говоря, в некоторой точке ре М, однако группы голо-
номии в различных точках изоморфны) представляет собой
подгруппу HczO(TpM) ортогональной группы касательного про-
странства ТРМ, которая состоит из всевозможных параллельных
переносов вдоль петель с началом в точке р. Может показаться,
что этот объект никак не связан с метриками Эйнштейна. Од-
нако тождества Бьянки и тот факт, что группа голономии по-
рождается операторами кривизны многообразия (М, g), остав-
ляют очень мало вариантов ортогонального представления
HczO(n). Многообразие (Л4, g) всегда можно считать неприво-
димым, так как в противном случае все сводится к рассмотре-
нию группы голономии неприводимых сомножителей. Для не-
приводимого риманова многообразия либо H — SO(n), либо
Н = U (п/2) (и тогда мы имеем дело с кэлеровым многообра-
зием), либо группа Н относится к очень короткому списку. При
этом в силу тождеств Бьянки все римановы многообразия с
группой голономии из этого списка автоматически оказываются
многообразиями Эйнштейна.
0.49. Сделаем несколько замечаний. Во-первых, исследования
по группам голономии практически не проводились с 1955 по
1975 г. Затем они возобновились, и большинство открытых
проблем было решено. В частности, доказательство гипотезы
Калаби (в риччи-плоском случае) позволило получить примеры
римановых многообразий с группами голономии SU(n/2) и
Sp(n/4). Во-вторых, после книги Лихнеровича [Lie 3] не появи-
лось ни одного учебника, где излагалась бы теория групп голо-
номии. В-третьих, в тот короткий список, который мы упомянули,
входит группа Н = Sp(l)Sp(n/4). Многообразия с такой груп-
пой голономии называются кватернионно-кэлеровыми и рассмат-
риваются в гл. 14.
Главы 8 и 11. Кэлеров случай
0.50. Это центральные главы книги. Изложение в них ведется
весьма подробно (исключение составляет доказательство тео-
ремы существования). Решение проблемы Калаби позволяет по-
строить широкий класс многообразий Эйнштейна, и в частности
26
Гл. 0. Введение
риччи-плоских многообразий. Сейчас нет другого способа полу-
чения таких многообразий, поскольку однородные римановы
многообразия не могут быть риччи-плоскими, не будучи пло-
скими.
0.51. Попутно мы излагаем теорию компактных однородных
комплексных пространств, которая лежит на пересечении ал-
гебры и анализа. В литературе существует не слишком много
описаний этих пространств, в точности совпадающих с орбитами
присоединенного представления компактных групп Ли (теория
Кириллова — Сурьо). Мы попытались дать современное изло-
жение.
Глава 12. Пространство Модулей эйнштейновых структур
0.52. Это ключевая глава: в ней рассматривается основная
проблема теории многообразий Эйнштейна. Мы приводим здесь
подробный обзор последних результатов Коисо, о которых го-
ворилось в § Е.
Глава 13. Автодуальность
0.53. Для ориентированных четырехмерных римановых мно-
гообразий тензор Вейля W распадается на две части, W+ и W~,
относительно действия группы 50(4). Условие W~ = 0 опреде-
ляет конформно полуплоские многообразия. Мы изучаем эти
многообразия, поскольку благодаря Р. Пенроузу есть надежда
построить классификацию конформно полуплоских многообра-
зий Эйнштейна или хотя бы получить новые примеры с по-
мощью трехмерных комплексных многообразий. Мы приводим
схему доказательства утверждения о том, что единственными
конформно полуплоскими многообразиями Эйнштейна с s ^0
являются многообразия S4 и СР2 с каноническими метриками
и риччи-плоские КЗ-поверхности. К сожалению, с помощью
комплексных многообразий удалось построить только неком-
пактные примеры. Изложение в этой главе ведется весьма под-
робно, так как эти результаты получены недавно и еще не
вошли в книги.
Глава 14. Кватернионно-кэлеровы многообразия
0.54. Существуют римановы многообразия размерности 4т
с группой голономии, содержащейся в Sp(l)Sp(m)<= О(4т).
Они образуют особый класс римановых многообразий. Мы
знаем не слишком много таких примеров. Во-первых, отметим,
F. Краткий обзор содержания по главам
27
что группа Sp(l)Sp(m) входит в тот короткий список, о кото-
ром шла речь в 0.51, поэтому соответствующие многообразия
автоматически оказываются эйнштейновыми. Во-вторых, для
кватернионно-кэлеровых многообразий можно воспользоваться
твисторной конструкцией, заменив в ней комплексные числа
кватернионами. В этой главе рассматриваются также римановы
многообразия с группой голономии, принадлежащей группе
Sp(m) cz О (4т). Они называются гиперкэлеровыми. Решение
проблемы Калаби позволяет описать широкий класс таких мно-
гообразий.
Глава 15. Немного о некомпактном случае
0.55. Мы уделяем основное внимание компактным многооб-
разиям, однако и в некомпактном случае существуют красивые
результаты, например глубокая теорема существования полных
многообразий Кэлера — Эйнштейна. В гл. 15 приводится крат-
кий обзор этой быстро развивающейся области и дается по-
дробная библиография.
Глава 16. Обобщения условий Эйнштейна
0.56. Произведение двух многообразий Эйнштейна обычно
не является многообразием Эйнштейна, но соответствующая
метрика все же оказывается достаточно «хорошей». Она имеет
параллельную кривизну Риччи; Dr — 0. Обратно, если Dr = 0,
то метрика (по крайней мере локально) является произведе-
нием метрик Эйнштейна.
0.57. Условие Dr = 0— это естественное обобщение условия
эйнштейновости. Можно убедиться, что из него следует гармо-
ничность тензора кривизны. Этому и аналогичным условиям
посвящено довольно много работ. Мы постарались дать полный
обзор полученных результатов.
Приложение. Пространства Соболева
и эллиптические операторы
0.58. Поскольку для изучения дифференциальных уравнений
в частных производных, которые рассматриваются в этой книге,
используется аппарат анализа, мы приводим в приложении все
необходимые сведения.
28
Гл. 0. Введение
G. Путеводитель
Если вас интересуют
группы Ли и алгебры Ли
алгебраическая геометрия
анализ
контрпримеры
существование
геометрия
кэлерова геометрия
лоренцевы многообразия
мотивировки
открытые проблемы
обзор
топология
единственность
другие вопросы
короткая прогулка
длинное путешествие
читайте главы
1, 2, 7, 8, 10
11, 12.К, 13, 14
4, 5, 9, 11, 15, прилож.
6, 11
5, 7, 9, 11, 15
0.Н, 3, 8, 9, 10, 11
2, 8, 11
1, 3, 6.D, 7.1, 10.J
0
0.1
0
6
9, И, 12
предметный указатель
0 и § А каждой главы
0, 3, 5, 6, 15, 10, 7, 9
Н. Как почувствовать кривизну Риччи
За свою долгую жизнь я понял, что кривизну Риччи очень
трудно ПОЧУВСТВОВАТЬ. Надеюсь, читателю поможет мой
опыт. Исторически Г. К. Риччи ввел свою кривизну по следую-
щим соображениям. Если М cz R"+1 — вложенная в евклидово
пространство гиперповерхность, то на ней определена вторая
фундаментальная форма, представляющая собой квадратичную
дифференциальную форму на М. Ее собственные значения (от-
носительно метрики g) называются главными кривизнами ги-
перповерхности М, а соответствующие главные направления
задают линии кривизны. Однако если (М, g)—абстрактное ри-
маново многообразие, то нет ни такой формы, ни выделенных
направлений, ни собственных значений. Для того чтобы испра-
вить дело, Риччи ввел след тензора кривизны (как в 0 7). Но,
кажется, он так и не использовал этот инвариант. Это не уди-
вительно: собственные направления тензора Риччи в абстракт-
ном римановом многообразии, видимо, не обладают интерес-
ными геометрическими свойствами (исключение составляют кон-
формная риманова геометрия (см. [Fer] и [Eis], с. 181) и не-
которые специальные многообразия, которые рассматриваются
в гл. 16).
0.60. Для того чтобы понять геометрический смысл кривизны
Риччи, нужно представить себе объем. Суть в том, что кри-
Н. Как почувствовать кривизну Риччи
29
визна Риччи — это след, след представляет собой производную
определителя, а определитель связан с объемом. Рассмотрим
геодезический шар В(р, t), т. е. множество точек из М, рас-
стояние от которых до фиксированной точки р меньше t. Мы
увидим, что кривизна Риччи появляется в формуле асимптоти-
ческого разложения объема vol(B(p, t)) по t. При этом даже
удается получить оценки, справедливые при всех t. Асимптоти-
ческое разложение имеет вид
vol(B(p, /)) = <о (n) tn (1
(6 (п + 2)) s ^ + ° (^)) 
где <о(и) — объем единичного шара в R", a s(p) — скалярная
кривизна в точке р. Кривизна Риччи играет важную роль в до-
казательстве этой формулы.
0.61. Имея дело с мерой в (М, g), удобно перейти к каса-
тельному пространству с помощью экспоненциального отобра-
жения. Рассмотрим функцию 6(х, t), которая определяется на
произведении t/pMX R+ уравнением
ехР₽ (Pg) = 6 (x> Z) dPx ® dt’
где d,,x — каноническая мера на единичной сфере UPM cz ТРМ,
a dt — мера Лебега на прямой R. Можно доказать (см.
[Не-Ка])— или хотя бы убедить себя, поиграв с полями Якоби
и определителями, — что
6 (х, /) = /"-’(!- узг (х) /2 + о (И).
Здесь г(х)—кривизна Риччи (рассматриваемая как квадратич-
ная форма) в точке х. Грубо говоря, кривизна Риччи характе-
ризует отклонение величины телесного угла в римановом много-
образии (М, g) (который измеряется площадью единичной
сферы дВ(р, I)) от величины соответствующего угла в евкли-
довом пространстве. Отсюда сразу следует формула для 0(х, t),
поскольку vol (В (р, /)) = \	6 (х, t) d„x.
Jx^UpM
0.62. Р. Бишоп ([Bis]) сделал чрезвычайно важное откры-
тие: что кривизна Риччи определяет некоторое глобальное не-
равенство. Дело обстоит так. Предположим, что г^(п—l)kg
для некоторого вещественного числа k. Наилучшее такое k —
это просто наименьшее собственное значение квадратичной фор-
мы г относительно метрики g. Теорема Бишопа утверждает, что
функция t F—>
6 (х, t)
является невозрастающей,
30
Гл. 0. Введение
где Sk — значение функции (0(х,	для модельного про-
странства постоянной секционной кривизны k (т. е. t при k = 0,
sinV^/V^ ПРИ &>0 и sinh V — W/V — k при£<0).
Эта функция рассматривается на отрезке [0, /], на котором
функция 0(х, s) не обращается в нуль (условие, равно-
сильное тому, что число t меньше первого сопряженного значе-
ния в направлении вектора х). В частности, для любых значе-
ний х и t, удовлетворяющих этим условиям, выполняется нера-
венство 6 (х, t) (t).
0.63. Теорема Бишопа — это фундаментальная теорема рима-
новой геометрии. Она означает, что важнейшим числовым инва-
риантом компактного многообразия (Л4, g) является k(g)—наи-
меньшее собственное значение кривизны Риччи. Предположим,
например, что k(g) — 0, т. е. кривизна Риччи неотрицательна:
г 0. Тогда для каждой точки р и каждого числа t > 0 вы-
полняется неравенство vol(B(p, /)) ^ со(н)Милнор доказал,
что в этом случае фундаментальная группа имеет полиномиаль-
ный рост (см. [Mil 1], а также 6.61).
0.64. Громов обнаружил, что неравенство Бишопа можно
проинтегрировать. Если обозначить через Sk модельное про-
странство постоянной секционной кривизны k, то
,	, vol (В (р, t))
функция 11—->—I ,является невозрастающеи
для любой точки реЛ1 и числа t, не превосходящего диаметра
diarn(g) многообразия (Л1, g). Таким образом, инвариант k,
наряду с диаметром, несет значительную информацию о рима-
новом многообразии. Основной результат Громова в этой об-
ласти заключается в том, что множество всех римановых мно-
гообразий можно снабдить метрической структурой хаусдор-
фова типа. Пусть дано натуральное число п, положительное
число D и вещественное число К. Подмножество множества
всех римановых многообразий размерности п, диаметр которых
ограничен сверху числом D, а кривизна Риччи ограничена
снизу числом К, является предкомпактным подмножеством ука-
занного выше огромного метрического пространства.
0.65. Это утверждение о предкомпактности порождает об-
ширную программу получения оценок всевозможных римановых
инвариантов, зависящих только от размерности, диаметра и
инварианта k(g). В последнее время многим математикам уда-
лось получить такие оценки различных инвариантов: нижнюю
Н. Как почувствовать кривизну Риччи
31
и верхнюю границы собственных значений лапласиана много-
образия (М, g); верхнюю границу наилучшей константы в нера-
венствах Соболева; нижние границы константы Чигера h(g) и
изопериметрической константы Ci(g), границы ядра уравнения
теплопроводности и собственных функций лапласиана. Громов
высказал гипотезу, что числа Бетти многообразия М также
можно оценить с помощью этих трех инвариантов. В то же
время известно, что число гомотопических типов многообразий
невозможно оценить лишь с помощью этих инвариантов (см.
[Wai]).
0.66. Для получения указанных границ недостаточно распо-
лагать объемами шаров и оценкой Бишопа. Нужно воспользо-
ваться приемом, предложенным Громовым и основанным на глу-
бокой теореме Альмгрена о существовании и регулярности
экстремальных гиперповерхностей в многообразии (М, g). Идеи
Галло позволяют свести все к следующей картине. Пусть И —
гиперповерхность в (М, g), снабженная полем единичных нор-
малей hi~>-x(h). Тогда можно определить экспоненциальное
отображение произведения Н X R в М вида F(h, t) =
= exph(t-x(h)) и вновь задать функцию 6, позволяющую вы-
числить меру и определяемую условием F*(pg) = B(h, t)p.H®dt.
Здесь ря — каноническая риманова мера в Н. Е. Хайнце,
Г. Кархер и (независимо) М. Маэда доказали неравенство,
двойственное к неравенству Бишопа:
e(h,
где v(/i)—средняя кривизна гиперповерхности Н в точке h, а
s' — производная по t функции sk пз 0.62. Это неравенство
выполняется для всех h е Н и всех t до первой фокальной точки
h. Через k = k(g) мы обозначили наименьшее собственное зна-
чение кривизны Риччи многообразия (М, g).
0.67. Кривизна Риччи тоже имеет ограниченные возможности.
Например, в 0.66 гиперповерхность Н нельзя заменить подмно-
гообразием произвольной размерности: чтобы получить верх-
нюю границу для 6, нужно знать нижнюю границу не только
кривизны Риччи, но и секционной кривизны (см. [Не-Ка]).
Кривизны Риччи достаточно только в том случае, если подмно-
гообразие представляет собой гиперповерхность или точку. При
этом неравенство Бишопа дает оценку лишь с одной стороны
(верхнюю границу объема при наличии нижней границы кри-
визны Риччи). Легко показать, что получить аналогичную
оценку с другой стороны невозможно: если бы выполнялись оба
неравенства, то для многообразий постоянной кривизны Риччи,
32
Гл. 0. Введение
т. е. для многообразий Эйнштейна, было бы справедливо равен-
ство vol(B(p, /)) = vol (В (Sfc, /)) для всех р <= М и /eR+. Но
из него следует постоянство секционной кривизны (см. [Gr-VaJ,
с. 183), а мы знаем, что существуют многообразия Эйнштейна
непостоянной секционной кривизны. Есть одно исключение: трех-
мерные многообразия, для которых Эшенбург и О’Салливан
доказали двухстороннее неравенство (см. [Es-OS]). В трехмер-
ном случае условие эйнштейновости, как известно, равносильно
постоянству секционной кривизны.
0.68. Между кривизной Риччи и объемом есть и другая связь.
Для кэлерова многообразия кривизна Риччи, преобразованная
с помощью комплексной структуры в 2-форму типа (1,1), пред-
ставляет собой не что иное, как вторую производную d'd"
функции объема. При этом связь с указанными выше неравен-
ствами остается во многом загадочной (см. 2.100).
0.69. Из неравенства Бишопа следует теорема Майерса о
диаметре и фундаментальной группе риманова многообразия
положительной кривизны Риччи. По-видимому, для многообра-
зий отрицательной кривизны Риччи неравенство Бишопа не
имеет никаких следствий. Для некомпактных многообразий не-
отрицательной кривизны Риччи Дж. Чигер и Д. Бромол полу-
чили красивый геометрический результат: если такое многооб-
разие обладает прямой (т. е. геодезической, которая является
кратчайшей кривой между любыми своими точками), то оно
представляет собой произведение M = MXR с метрикой пря-
мого произведения (см. 6.65).
I.	Основные открытые проблемы
Мы сконцентрируем внимание на тех проблемах, которые
непосредственно связаны с материалом этой книги (более ши-
рокий круг вопросов обсуждается, например, в [Yau 7]).
Пока, к сожалению, нет «общих» примеров глобально опре-
деленных метрик Эйнштейна. Мы располагаем только глобаль-
ными кэлеровыми и однородными примерами, а также знаем,
что локальная задача является корректной.
Найдено несколько симметрических решений, причем иног-
да — с помощью элементарных алгебраических рассуждений,
как в случае однородных пространств с неприводимым пред-
ставлением изотропии. С примерами кооднородности один дело
обстоит значительно хуже: большинство из них было получено
почти случайно, и лишь немногие оказались компактными.
Остается открытой проблема описания метрик Эйнштейна ко-
I. Основные открытые проблемы
33
однородности два на компактном многообразии. Локальное ис-
следование двумерной системы, которая возникает в этом слу-
чае, кажется вполне разумной задачей, но. несмотря на ряд
серьезных попыток, переопределенные граничные условия до
сих пор не удалось полностью учесть и согласовать. Вполне мо-
жет оказаться, что случай более высокой неоднородности будет
проще, поскольку коразмерность сингулярных компонент про-
странства орбит связана с тем, как орбиты общего положения
в пределе переходят в сингулярные орбиты.
К этой проблеме можно подойти и с другого конца: можно
попробовать показать, что многие многообразия не допускают
метрик Эйнштейна. Иными словами, можно поставить вопрос:
имеются ли топологические (или другие) препятствия к сущест-
вованию метрик Эйнштейна? Пока такие препятствия обнару-
жены только в четырехмерном случае. Таким образом, остается
полностью открытым фундаментальный вопрос: являются ли
многообразия, допускающие метрику Эйнштейна, редкими или,
наоборот, многочисленными?
Может оказаться, что случай положительных метрик Эйн-
штейна отличается от случая отрицательных метрик Эйнштейна
так же, как в кэлеровом случае: для каждой размерности из-
вестно лишь конечное число положительных, но бесконечно
много отрицательных многообразий Кэлсра — Эйнштейна. Кро-
ме того, положительный случай, по-видимому, связан с сущест-
вованием нетривиальных изометрий. До сих пор не известно ни
одного примера положительной метрики Эйнштейна без изо-
метрий. Было бы интересно найти хотя бы одну такую метрику!
Функциональный подход к евклидовым уравнениям Эйнштей-
на1), и в частности предложенная физиками интерпретация
этих уравнений с помощью классических приближений кванто-
вых явлений (см. [Jackiw] или [Perry]), позволяют предполо-
жить, что функционал S полной скалярной кривизны (см. гл. 4)
должен во многих случаях иметь критические точки. Таким
образом, он может быть связан с топологией классифицирую-
щего пространства В©(М) группы диффеоморфизмов ©(М) мно-
гообразия, которое можно отождествить с пространством
Jt(А4) /© (АД римановых структур на М—пространством, на
которое можно опустить функционал S.
Среди предварительных вопросов, которые полезно изучить
в связи с этими проблемами, отметим вариант условия Пале —
Смейла, который можно сформулировать следующим образом.
Дана последовательность метрик, отклонение которых от метрик
*) То есть уравнениям Эйнштейна для положительно определенной мет-
рики.— Прим, перев.
3 А. Бессе, т. 1
34
Гл. 0. Введение
Эйнштейна стремится к нулю (это отклонение можно охаракте-
ризовать, например, квадратом нормы бесследовой части тен-
зора Риччи относительно фиксированной фоновой метрики).
Верно ли, что эта последовательность содержит подпоследова-
тельность, сходящуюся к метрике Эйнштейна? Другой, более
сложный вопрос: существует ли такое число е > 0, зависящее
только от размерности, что любое многообразие, допускающее
метрику, отклонение которой от метрики Эйнштейна меньше е,
допускает и метрику Эйнштейна? Известные нам четырехмерные
препятствия не исключают такой возможности (см. [Pol 1]).
Можно поставить и более специальные вопросы.
Для риччи-плоских многообразий. Все известные примеры
риччи-плоских компактных многообразий имеют специальную
группу голономии (Hol #=SO(n), О(п)). Верно ли это в общем
случае ? Если верно, то можно надеяться получить классифика-
цию всех компактных риччи-плоских многообразий.
Для различных метрик Эйнштейна на фиксированном мно-
гообразии Эйнштейна. Что представляет собой множество кон-
стант Эйнштейна (для эйнштейновых метрик полного объема
единица)? В частности, могут ли на одном многообразии су-
ществовать метрики Эйнштейна с константами Эйнштейна про-
тивоположных знаков? Если это невозможно, замечание о том,
что положительные и отрицательные метрики Эйнштейна отно-
сятся к существенно разным семействам, приобретает дополни-
тельный вес.
Глава 1
Основные сведения
А. Введение
1.1.	В этой главе собраны наиболее важные сведения, кото-
рые используются в книге. В частности, мы напоминаем опреде-
ления основных понятий римановой (и псевдоримановой) гео-
метрии. Это нужно главным образом для того, чтобы ввести не-
обходимые обозначения. Поэтому большинство основных теорем
приводится без доказательств, тем более что доказательства
можно найти в таких классических учебниках по римановой
геометрии, как [Ch-Eb], [Hel 1], [Ко-No 1, 2], [Spi].
Мы также приводим результаты, которые нс входят в эти
учебники, хотя и являются стандартными. Такне результаты
сопровождаются полными доказательствами. Это относится,
в частности, к разложению тензора кривизны на неприводимые
компоненты (§ G, Н), к формуле Вейценбёка (§ I) и к первой
вариации поля тензора кривизны при вариации метрики (§ К).
Подчеркнем, что эта глава служит в основном для ссылок и не
является полным курсом римановой геометрии. Специалисты мо-
гут нс читать главу целиком, а пользоваться ею только по мере
надобности (неспециалистам можно посоветовать прочесть один
из названных учебников).
1.2.	Мы предполагаем, что читатель знаком с основными по-
нятиями дифференциальной топологии, дифференциальной гео-
метрии, алгебраической топологии и теории групп Ли, такими,
как многообразие, дифференцируемое отображение, расслоение
(особенно главное и векторное), касательное расслоение, тензор
и тензорное поле, дифференциальная форма, спинор и спинор-
ное поле, группа Ли (и ее дифференцируемое действие), алгебра
Ли и экспоненциальное отображение (для группы Ли), диффе-
ренциальный оператор и его символ, сингулярные гомологии в
когомологии, когомологии де Рама, гомотопические группы
и т. д.
1.3.	Если не оговорено противоположное,
все многообразия предполагаются гладкими (т. е. при-
надлежащими классу С°°), конечномерными, хаусдорфо-
выми, паракомпактными и (как правило) связными, а все
отображения (в частности, все действия групп Ли) — глад-
кими.
3*
36
Гл. 1. Основные сведения
При изучении дифференциальных операторов предположение
гладкости часто оказывается не самым удобным, поэтому мы
будем работать с пространствами Соболева. Теория этих про-
странств и некоторые дополнительные сведения из анализа при-
водятся в приложении.
1.4.	Обозначения. Обозначим через Т^-^М векторное рас-
слоение г раз ковариантных и s раз контравариантных тензоров
на «-мерном многообразии М. При этом сделаем два исключе-
ния: касательное расслоение П0- 1>Af будем обозначать через
ТМ, а кокасательное расслоение Т^’°>М — через Т*М. Заметим,
что T^r’s)M = rrM0^)STM.
Обозначим через Л sМвекторное расслоение s-форм на М. Та-
ким образом, /\s М= /\s (Т*М). Вообще, символ Л означает
операцию альтернирования, а символы S и ®— симметризацию.
Пространство сечений векторного расслоения удобно обозна-
чать соответствующей рукописной буквой')- Например, вектор-
ное пространство гладких (г, s) -тензорных полей на М (т.е сече-
ний расслоения	будем обозначать через	В част-
ности, fZ'TW означает пространство векторных полей на М.
Обозначим через пространство С-'-финкиий на М, а
через П''Л4— пространство дифференциальных р-форм на М.
В дифференциальной геометрии часто используются объекты,
которые сами не являются тензорными полями (например, связ-
ности и дифференциальные операторы), но с которыми можно
ассоциировать тензорные поля (например, поле тензоров кри-
визны Римана). Для характеризации тензорных полей мы часто
будем использовать следующий результат.
1.5.	Теорема (фундаментальная лемма дифференциальной
геометрии). Пусть р: Е-+М— векторное расслоение конечного
ранга над многообразием М, а Е — векторное пространство его
сечений. Пусть А:	— линейное отображение. Тогда для
существования (всегда единственного) сечения а дуального век-
торного расслоения Е*-+М, для которого
А(Х)(х) = а(Х(х))
при всех х^ М, Х^ё, необходимо и достаточно, чтобы отобра-
жение А было Я?? М-линейным, т. е. чтобы для любой функции
f е Я?М выполнялось равенство
	A(fX) = fA(X).
') В дальнейшем пространство сечений векторного расслоения Е часто
обозначается через Соо(£). — Прим, перев.
А. Введение
37
Мы будем применять эту теорему главным образом к ’ё’М-
полилннейным отображениям A: (И~ М)гМ)s. В этом слу-
чае будем говорить, что отображение А «определяет» (г, s) -тен-
зорное поле. В качестве иллюстрации приведем два хорошо
известных примера.
(а)	Внешний дифференциал da дифференциальной р-формы
а определяется своими значениями на (р +1) векторных полях
Хо, Xi	Хр по формуле
(l.5a) da(X0, Х„ Хр) = £ (-1)’ а (Хо, ..., Хь .... Хр) +
1=0
+	2	X,], Х„, Xt, .... Xh Хр),
где X, означает пропуск аргумента Л',.
Легко проверить, что правая часть этой формулы ’g’M-поли-
линейна.
(Ь)	Производная Ли Lx А от (г, s)-тензорного поля А вдоль
векторного поля X определяется своими значениями на вектор-
ных полях Хь ..., X, по формуле
(1.5b)	LxA(Xx, ..., Xr) =
= Х-Л(Х„ ..., Хг}-£ А(Х„ ..., [X, X,], ..., Хг),
если А является (г, 0)-тензором, и по формуле
(1.5с)	LxA(Xx, ..., Хг) =
= [Х, Л(ХЬ ..., хг)1-£ д(хь ..., [X, Х+ ..., хд
если А является (г, 1)-тензором. При этом выполняется
условие
(1.5d) оператор Lx линеен и является оператором дифферен-
цирования относительно тензорного произведения (£).
Отметим, что выражение LXA является ^М-линейным отно-
сительно Xi, ..., X,, но не является ^М-линсйным относи-
тельно X.
(с)	Наконец, напомним, что для дифференциальной р-формы
а эти производные связаны соотношением
(1.5е)	Lxct = ix da-\- d (ixa),
38
Гл. 1. Основные сведения
где ix: QpAl->Qp-'7W есть внутреннее произведение (на вектор-
ное поле X), задаваемое формулой
(1.5f) 1Л₽(Х2, .... Хр) = ₽(Х, Х2, .... Хр), если р > О,
г’х₽ = 0, если р == 0.
В. Линейные связности
1.6.	Понятие связности, играющее ведущую роль в диффе-
ренциальной геометрии, имеет много различных аспектов и до-
пускает различные эквивалентные определения (см. коммента-
рий М. Спивака [Spi], т. 5, с. 604). В гл. 9 нам понадобится
общее (геометрическое) понятие связности Эресмана. Мы дадим
ее определение и рассмотрим ее связь со стандартными поня-
тиями связности в главном и векторном расслоении. Во многих
учебниках (см., например, [Ко-No 1]) сначала определяются
связности в главном расслоении Здесь мы напомним только
понятие линейной связности в векторном расслоении как ко-
вариантной производной (этот подход принадлежит Ж. Л. Ко-
зюлю) .
1.7.	Определение. Пусть р: Е-*-М— векторное расслоение
над многообразием М. Линейной связностью пли ковариантной
производной в расслоении Е называется отображение
V:
{X, s) > \xs,
удовлетворяющее для любых векторных полей X, Y из 2ГМ, лю-
бых сечений s, t из <S и любых функций /, h из ’ё'М условиям
Vf X hYS = [Vxs + ^VyS,
(1.7)	Vx (s + /) = Vxs + Xxt,
Vx (M) = (f) s + fVxS.
1.8	. Замечания, (а) Для любого сечения s e <£' отображение
Vs: ЕГМ-+<£, заданное формулой (Vs) (X) = \\s, является ‘g’Al-
линейным. Таким образом, по теореме 1.5 отображение Vs яв-
ляется дифференциальной 1-формой на М со значениями в Е.
В частности, мы можем определить Vxs для любого касатель-
ного вектора X из ТМ В то же время отображение si—>Xxs не
является ^М-линейным (на самом деле V есть дифференциаль-
ный оператор первого порядка, см. § I).
(Ь)	Из теоремы 1.5 сразу следует, что для любых связно-
стей V и V' в векторном расслоении Е разность
А (X, s) — Vxs — Vxs
В. Линейные связности
39
^Al-линейна и, значит, определяет сечение расслоения
А1 М®Е'®Е.
Обратно, для любой связности V в Е и сечения .1 расслоения
А 1 М®Е*®Е отображение VAs = vAs + А (X, s) является связ-
ностью в Е.
(с)	Приведем пример связности. Пусть В ХЕ— тривиализо
ванное векторное расслоение над В. Тогду существует един
ственная связность, называемая тривиальной связностью, для
которой постоянные сечения (т. е. сечения $ вида s(6) = (6, g),
где | — постоянный элемент из Е) удовлетворяют условию
Va-s = 0 для всех X е ZTM.
Рассмотрим, например, произвольную связность V в вектор-
ном расслоении Е над М и локальную тривиализацию (U, q)
расслоения Е, где 17 —открытое подмножество в М, a q пред-
ставляет собой С^-изоморфизм расслоений
p~l(U)^UXF.
Тогда EXE снабжено тривиальной связностью Х и в (17)
можно определить связность Vrf, соответствующую связности V5
при изоморфизме <р. Разность Г между V и V<p представляет
собой сечение расслоения A U®E*®E. Оно называется тен-
зором Кристоффеля связности V относительно тривиализации <р.
Если при этом U есть область определения карты многообра-
зия М с координатами (х‘) и если мы отождествим слой Е с
Rp, то компоненты Г“₽ тензора Г относительно канонических
базисов (д/дх1) в TU и (ес:) в R₽ будут классическими симво-
лами Кристоффеля связности V.
1.9.	Рассмотрим гомоморфизм векторных расслоений
(где р и q — векторные расслоения, p°h = f°q и ограничение
отображения h на каждый слой расслоения q линейно).
Для любой линейной связности V в Е существует единствен-
ная такая линейная связность V' в Е, что для любого касатель-
ного вектора Х^ТК и любых сечений s и t расслоений р и q
соответственно, согласованных в том смысле, что $ ° f = h о t, вы-
полняется равенство

40
Г.ч. 1. Основные сведения
В частности, для любого отображения f: N-+M линейная
связность V в Е (векторном расслоении над М) индуцирует ли-
нейную связность W, которая называется индуцированной связ-
ностью в индуцированном векторном расслоении f*E над N.
1.10.	Пусть £], Е2— два векторных расслоения над М. Тогда
любая линейная связность V в прямой сумме Е = Е[&Е2 век-
торных расслоений естественным образом определяет линейные
связности V1 в £[ и V2 в Е2. Для любого векторного поля X е
и любого сечения	расслоения Е связность V1 за-
дается формулой
= РЦ ^xs\\
где в правой части sj рассматривается как сечение расслоения
Е, а рг[ есть проекция прямой суммы Е = Е{ ф Е2 на первое
слагаемое.
Из теоремы 1.5 непосредственно следует, что (в тех же обо-
значениях) отображение (X, Si)<—= pr2(\xs1) определяет
сечение расслоения Д 1 М ® Е\ ® Е2 (здесь рг2 означает проек-
цию на второе слагаемое). Позже нам встретятся ситуации,
в которых эта конструкция окажется полезной (см., например,
гл. 9).
1.11.	Определение. Кривизной Е'' линейной связности V в
векторном расслоении Е называется 2-форма на Л1 со значе-
ниями в Е*®Е, задаваемая формулой
(1-11)	Ex,ys = V[X, yjs — [Vx, Vy] S
для любых векторных полей X, Y<=ZTM и сечения s е <S.
Из теоремы 1.5 следует, что 7?v есть тензорное поле. По-
скольку кривизна является важнейшим инвариантом связности,
полезно отметить, что существует много других интерпретаций
Е (например, интерпретация Эресмана (9.53b)). Приведем одну
из них.
1.12.	Рассмотрим дифференциальные р-формы на М со зна-
чениями в Е, т. е. сечения расслоения /хРМ®Е. Определим
ассоциированный с V внешний дифференциал dX следующим
образом: для любого сечения а расслоения Л р М ® Е его
дифференциал dva есть сечение расслоения Л М®Е, зада-
ваемое формулой
сГа (Хо, ..., Хр) = X (-I)1 VXi (а (Хо, Х<, Хр)) +
i
+ X (-1)’+,а([й, XJXO, ..., Х{, •••> Xi, Хр),
В. Линейные связности
41
где Хо, ..., Хр — векторы из ТХМ, а Хо, ...» Хр — их продол-
жения до векторных полей в окрестности точки х. Тогда
(1.12)	R$, Ys = -d' (d's) (X, Y).
Отметим, что, вообще говоря, d'" ° dv =# 0 в отличие от случая
обыкновенного внешнего дифференциала.
1.13. Примеры, (а) Кривизна тривиальной связности три-
виального расслоения равна нулю.
(Ь) Если V = V + v4, где А—сечение расслоения Д1 Л4 ®
® Е* ® Е, то легко проверить, что
Rx. ys — Rx. ys = — (dvA)x, у s — Ax (Лу$) + Ay (/Vs).
где сечение А рассматривается как 1-форма со значениями в
Е*®Е. Это показывает, что кривизина /Д в общем случае не
равна нулю, поскольку любая 1-форма А определяет связность
V. Более того, эта формула позволяет вычислить кривизну связ-
ности \ относительно локальной тривиализации. Для этого надо
выразить V через тривиальную связность и символы Кристоф-
феля.
1.14.	Теорема (дифференциальное тождество Бьянки). Пусть
V — связность в векторном расслоении Е над М. Тогда
(1.14)	dV?v = 0.
Доказательство. Утверждение теоремы вытекает из опреде-
ления кривизны (1.12) и тождества (dv □ dv) ° dv=d? ° (dv ° dv). □
1.15.	Еще несколько определений. Сечение s векторного рас-
слоения Е со связностью V называется параллельным, если
Vs = 0. Заметим, что для любой точки х <= М существуют такая
окрестность U и такой конечный набор сечений (s«)te/ расслое-
ния Е над U, что (s£ (y))i образует базис слоя Еу для у е U
и Vsi(x) = 0. (Достаточно рассмотреть локальную тривиализа-
цию Е.)
Если векторное расслоение Е снабжено какой-либо дополни-
тельной структурой (послойной евклидовой метрикой h, комп-
лексной структурой I, епмплектической формой со или эрмитовой
тройкой (g, J, со)), то линейная связность V в Е называется
соответственно евклидовой (или метрической), комплексной,
симплектической или эрмитовой, если соответственно поле h, J, со
или (g, J, со) параллельно. В этом случае кривизна /Д связности
V обладает дополнительными свойствами, для любых Х, Уе
42
Гл 1. Основные сведения
f= ТХМ эндоморфизм Rx, у слоя Ех является соответственно ко-
сосимметрическим, комплексным, кососимплектическим или ко-
соэрмитовым.
В том случае, если Е есть касательное расслоение базового
многообразия М, возникают дополнительные объекты.
1.16.	Определение. Линейной связностью D на многообразии
А1 называется линейная связность в касательном расслое-
нии ТМ.
1.17.	Пусть V — линейная связность в векторном расслоении
Е над М. Если s е <S— сечение Е, то Vs — сечение расслоения
Т*М®& (см. замечание 1.8(a)). Пусть D — линейная связность
на М. Тогда D и V индуцируют линейную связность (которая
тоже будет обозначаться V) на Г’АЮЕ'. Поэтому можно опре-
делить вторую производную V(Vs), которук? мы обозначим V2s.
Она представляет собой сечение расслоения Г*2,0>Л1 ® Е, зада-
ваемое формулой
(V2s),y, у = Vx (VyS) — VpyyS.
Для (V2s) x, у мы будем также использовать обозначение
(VVs) (X, У), или Vy ys, или даже (V2s) (X, У).
По индукции можно определить итерированные ковариант-
ные производные Vr’s как сечения расслоения Т<р' 0)Л1 0 Е вида
.........................х-
Важно отметить, что порядок векторов А), ..., Хр играет су-
щественную роль, поскольку ковариантные производные (в от-
личие от обычных) в общем случае не коммутируют.
1.18.	Определение. Тензором кручения Т линейной связности
D на многообразии М называется (2,1)-тензорное поле
(1Л 8)	Та, у = DXY - DyX - [X, У].
То, что Т есть тензорное поле, следует из теоремы 1.5.
1.19.	Замечания, (а) Кручение по определению кососим-
метрично относительно ковариантных переменных.
(Ь) Для любого (2,1)-тензорного поля А на М формула
DXY = DXY + Ах, у задает новую связность В с тензором кру-
чения Т, который имеет вид
Тх.У = ^Х.У + ^Х.У — Лу, А-
В. Линейные связности
43
В частности, для любой связности D на М с тензором кручения
Т формула (X, Y)t-^-DxY—^ТХУ задает связность без кру-
чения (т. е. с нулевым тензором кручения).
(с) Если D — связность без кручения на М, скобка вектор-
ных полей выражается через D по формуле
[X, У] = DXY — DYX.
Обратно, внешний дифференциал дифференциальных форм
можно выразить через D. Для а е Й₽Л1 и векторов Хо, ..., Хр
имеем
rfa(X0, ..., Хр) = Е(-1)‘ (ДХ/<х) (*о.У, ..., Хр).
1.20. Вернемся к соотношениям между итерированными ко-
вариантными производными. Простейшее соотношение описы-
вается так называемой формулой Риччи
(1.21)	Vx, у$ Vy xs =	7?x ys Vr ,
где T — поле кручения связности D, a Rv— кривизна связно-
сти V.
Заметим, что если связность D не имеет кручения (или,
иначе говоря, симметрична), то правая часть не содержит Vs.
Пусть V*s = VxS + Bxs — другая связность. Тогда
Vx, yS = Vx, YS “Ь Ух^у 8 У	(УXs) “Ь ^Х (Уг8) “Ь Вх Уу8)'
Это позволяет получить формулу для Для третьих произ-
водных можно получить много формул, из которых мы приведем
только две.
1.22.	Следствие. Формулы Риччи для третьих производных
имеют вид
(1.22а) Vx, у, г8 Vy, х, z8 ~ ~~ ^х, у (Уг8) “Ь ^rx yzs ^тх, у. zS'
(1.22b) Vx, у, zs — Vx, z. y8 =
= — (Vx7?v)y z s ~ ^y, z (Vxs) — Tyf z8 ~ \dxt)y zs'
Доказательство, (а) Применим 1.21 к Vs. (b) Применим Vx
к 1. 21.	□
1.23.	Напомним, что линейная связность D на многообразии
М индуцирует связность в любом тензорном расслоении и к этой
связности также можно применять полученные формулы. В част-
44
Гл. 1. Основные сведения
ности, поскольку кручение Т и кривизна R связности D явля-
ются тензорными полями на М, можно рассматривать их кова-
риантные производные DpT, DPR любого порядка р, которые
тоже представляют собой тензорные поля на М. Эти поля удов-
летворяют ряду соотношений. Простейшие соотношения вклю-
чают Т, R и их первые ковариантные производные. Они назы-
ваются тождествами Бьянки. Нам уже встретилось одно из
них — дифференциальное тождество Бьянки для произвольных
расслоений со связностью над многообразием.
1.24.	Теорема. Пусть D — линейная связность на М. Тогда
ее тензоры кручения Т и кривизны R удовлетворяют соотно-
шению
^Х, Y, Z (Rx, + ^TXt у? + (ВхТ)у, = U.
Доказательство. Проведем вычисления в локальной карте <р.
Соответствующая тривиальная связность D® имеет нулевую
кривизну и нулевое кручение Тч>. Поэтому тензор кручения Т
связности D выражается через тензор Кристоффсля Г —О— D®
по формуле
Tx.Y = Y— Гу, X-
Для завершения доказательства достаточно выразить R через
R® и вычислить циклическую сумму.	□
1.25.	Предложение. Дифференциальное тождество Бьянки для
связности V в произвольном векторном расслоении Е (над много-
образием М, снабженным линейной связностью D с кручением Т)
имеем вид
(1.25а)	у z ((Vx/?v)r ? +	= o.
В частности, если D не имеет кручения, то
(1.25b)	^х, y, z (Vx^)y, z = 0.
Доказательство. Достаточно выразить (1.14) через интегри-
рованные ковариантные производные.	□
1.26.	Определение. Если D — линейная связность на много-
образии М, то ее геодезической называется гладкая кривая
с:	для которой
D£c = 0
(т. е. векторное поле d/dt на интервале 1 параллельно относи-
тельно индуцированной связности C*D в индуцированном рас-
слоении с*ТМ над /).
В. Линейные связности
45
Напомним, что из общей теоремы существования решений
обыкновенного дифференциального уравнения следует, что для
любого касательного вектора X е ТХМ существует единственная
геодезическая сх: I-+M, для которой сх (0) = х, сх(0) =
= 7'°с	)=Х, а I — максимальный интервал.
Для любого х е М обозначим через 3)х множество касатель-
ных векторов X е ТХМ, для которых 1 принадлежит области
определения / геодезической сх. Обозначим через 3) объедине-
ние 3)х по всем х е М. Тогда 3)х открыто в ТКМ, а 3) открыто
в ТМ.
1.27.	Определение. Отображение ехр: 3)^-М, задаваемое
формулой exp (X) = сх (1), называется экспоненциальным ото-
бражением.
Будем обозначать через ехрА ограничение отображения ехр
на 3)х = 3) А ТХМ.
1.28.	Теорема. Дифференциал отображения ехрх в нуле 0,е
е ТХМ есть тождественное отображение ТХМ (при отождествле-
нии 1\тхм с тхму
В частности, по теореме о неявной функции отображение
ехрх индуцирует диффеоморфизм ехрА	некоторой
окрестности Ux точки 0х в ТХМ на некоторую окрестность
точки х в М. Этот диффеоморфизм определяет локальную си-
стему координат в окрестности Vx точки х.
1.29.	Определение. Линейная связность D на многообразии
М называется полной, если область 3) определения экспонен-
циального отображения совпадает с многообразием М.
Дифференциал отображения ехрА в других точках области
3)х описывается инфинитезимальной деформацией, переводящей
геодезические в геодезические, которая порождает векторные
поля специального вида вдоль геодезических.
1.30.	Определение. Пусть даны связность D на многообразии
М и ее геодезическая с. Полем Якоби вдоль с называется век-
торное поле J вдоль с (т. е. образ сечения расслоения с*ТМ
при касательном отображении Тс), удовлетворяющее уравнению
(1.30)	DcDcJ + Rt, j с ^Тс, J = 0-
Заметим, что (1.30) представляет собой дифференциальное
уравнение второго порядка вдоль с. Поэтому поле J полностью
определено, если в некоторой точке c(t) известны значения
/с(О и (ПД)сщ.
46
Гл. 1. Основные сведения
1.31.	Предложение. Для любых векторов У^Т,М и Х<=Д)х
дифференциал (7\ехрд) (У) равен значению в точке с%(1) одно-
значно определенного поля Якоби J вдоль сх с начальными
условиями / (0) = О, (£)<;/) (0) = У.
Из предложения 1.31 следует, что дифференциал отображе-
ния ехрЛ вырожден тогда и только тогда, когда поле Якоби,
равное в начальной точке нулю, вновь обращается в нуль в не-
которой точке t > 0.
1.32.	Определение. Будем говорить, что точки с(0) и с(0
сопряжены вдоль геодезической с, если существует ненулевое
поле Якоби вдоль с, для которого J(0) —/(/) = 0.
Изучение сопряженных точек играет важную роль в диффе-
ренциальной геометрии (см., например, [Ch-Eb] относительно
риманова случая).
С. Римановы и псевдоримановы многообразия
1.33.	Определение, (а) Псевдоримановой метрикой сигна-
туры (р, q) на гладком многообразии Л1 размерности п = р + q
называется такая гладкая симметрическая дифференциальная
2-форма g на М, что для любой точки хе М форма gx на ТХМ
невырожденна и имеет сигнатуру (р, q). Пара (М, g) назы-
вается псевдоримановым многообразием.
(Ь) Если q = 0 (т е. форма gx положительно определена),
форма g называется римановой метрикой, а пара (М, g) — ри-
мановым многообразием.
(с) Если р = 1 и q > 0, форма g называется лоренцевой
метрикой, а пара (Л4, g)— лоренцевым многообразием.
1.34.	В качестве первого примера рассмотрим плоские мо-
дельные пространства Пусть g0—невырожденная симметриче-
ская билинейная 2-форма на Р" сигнатуры (р. q), где п = р + q.
Структура векторного пространства в R" индуцирует канониче-
скую тривиализацию 7’R" = R"X R" (с помощью параллельных
переносов). Каноническая псевдориманова метрика g (ассоции-
рованная с gG) на R" определяется требованием, чтобы при
отождествлении 7\R! с R" форма gx отождествлялась с go.
1.35.	Другие примеры можно получить с помощью следую-
щей общей конструкции.
Пусть I: N М — погружение, a g — псевдориманова мет-
рика на М. Предположим, что для любой точки А'еЛ' подпро-
странство (Txi) (TXN) пространства 7’,(Д)Л4 невырожденно (т. е.
С. Римановы и нсевдорпмаповы многообразия
47
индуцированная форма i*g в TN невырожденна). Тогда i*g есть
псевдориманова метрика на N.
1.36.	Другие модельные пространства. Рассмотрим, напри-
мер, каноническую 2-форму gp сигнатуры (р, п + 1—р) на
R"+1 (т. е. gp = dx2i-j- ... + dx2p — dxp+\ — ... — dx„+i). Как и
в 1.34, форма gp индуцирует псевдориманову метрику на Rn+1.
Рассмотрим вложенные подмногообразия
S" = {x = R"+1; gp+1(x, х) = +1},
77" = {x = R"+1; gp(x, х) = -1].
Соответствующие вложения i удовлетворяют предположениям
1.35. Следовательно, i*g — псевдориманова метрика, a (Sp,
i*gP) и (47Р, i*gp+i)—псевдоримановы многообразия сигнатуры
(р, п — р).
В частности, если п — р, риманово многообразие 5" и связ-
ная компонента точки (0, .... 0,1) многообразия 77" (состоя-
щего из двух связных компонент, задаваемых неравенствами
Лп+1 >0 и Xn+i < 0) называются канонической сферой Sn и ка-
ноническим гиперболическим пространством Нп.
Подробности см., например, в [Wol 4], с. 67.
1.37.	Пусть (714, g) и (A4',g') — два псевдоримановых много-
образия сигнатур (р, q) и (pz, q'). Произведение М%М' яв-
ляется многообразием, а его касательное расслоение допускает
каноническое расщепление Т (М X 714') = ТМ ф ТМ'. Для любой
точки (х, х')е7ИХ714' определим симметрическую 2-форму
g®g' на Их. x')(7W X ЛГ) = 7\Л1ф ТХ’М' как прямую сумму фор-
мы gx на Д714 и формы g', на ТХ,М'. Очевидно, g®g' пред-
ставляет собой псевдориманову метрику сигнатуры (р-R р',
q + q') на М X 714'. Она называется метрикой произведения.
1.38.	Пусть (714, g)—псевдориманово многообразие. Для лю-
бой точки хеЛ1 невырожденная квадратичная форма gx опре-
деляет канонический изоморфизм ТХМ >ТХМ, а также канони
ческий изоморфизм между любым тензорным пространством
Т{ф‘‘1}М и пространством 7'х₽+1’9-1)717 (последнее можно заме-
нить любым пространством Tx's}M с г + s = р + q).
Этот изоморфизм часто обозначают ь («бемоль»), а обрат-
ный к нему изоморфизм — # («диез»), поскольку в классиче-
ских тензорных обозначениях они соответствуют опусканию и
подниманию индексов (см. 1.42).
48
Гл. 1. Основные сведения
Композиция изоморфизма Т^'Q>М —> Т*’ Р^М с «отображением
вычисления значений» (спаривающего векторное пространство
с двойственным) представляет собой невырожденную квадратич-
ную форму (которая тоже обозначается gx) на любом простран-
стве	а значит, и на его подпространствах, таких, как
ЛхЛ1 или Sp (Т*хМу Заметим, что если форма gx положительно
определена на ТХМ, то она положительно определена и на лю-
бом пространстве Т'х₽’<7>Л1.
1.39.	Теорема (основная теорема (псевдо)римановой геомет-
рии). На любом псевдоримановом многообразии (Л4, g) сущест-
вует единственная линейная связность D (так называемая связ-
ность Леви-Чивита), которая
(а)	является метрической (т. е. Dg — 0),
(b)	не имеет кручения (т. е. Т = 0).
1.40.	Определение. Римановым тензором кривизны риманова
многообразия (Л4, g) называется поле тензоров кривизны его
связности Леви-Чивита D.
Заметим, что, поскольку D не имеет кручения, тождества
Бьянки 1.24, (1.25b) и формула Риччи (1.21) принимают более
простой вид.
1.41.	Найдем компоненты всех этих тензоров в локальных ко-
ординатах.
Пусть <р; U -+ V — карта М, т. е. <р есть диффеоморфизм от-
крытого подмножества U cr Rn на открытое подмножество
V cz М. Координатные функции х' на R" определяют координат-
ные функции х1 о Ф '1 на V, которые мы тоже будем обозначать
х‘. Дифференциальные 1-формы (dx!) определяют базис в T*V.
Обозначим через (д,) двойственный базис в TV. Тензорные поля
dx'®dx', i, j = 1, ..., п, определяют базис пространства ТХ'О>У
в каждой точке х е V. Поэтому ограничение метрики g на V
можно записать в виде
п
g= £ gijdx^dx',
i.i = l
где gij — функции на V, причем gij = gji-
Теперь мы можем охарактеризовать связность Леви-Чивита
D ее компонентами относительно базиса (<?,). Положим
С. Римановы и псевдоримановы многообразия	49
Тогда символы Кристоффеля (Гц) задаются формулой
г* = 4 £ Skl (diSji + д!Ёц -
где (gkl) — матрица, обратная к матрице (§,-,)- Символы Г?,
представляют собой компоненты тензора, являющегося разно-
стью связности D и тривиальной связности на V, индуцирован-
ной картой ф (ср. с замечанием 1.8(c)).
Наконец, компоненты Rifk кривизны /?, определяемые ра-
венством
выражаются через Гц- по формуле
Riik = d,Tlik - dtrlik + X (г^Г/т - rfftrL).
m = l
1.42. В классическом тензорном исчислении принято правило,
позволяющее избежать частого употребления знака суммы X-
Оно состоит в том, что по повторяющимся индексам всегда под-
разумевается суммирование (обычно от 1 до « = dimM). На-
пример, мы пишем
г* = 42gkl (didil + djgil - dl§ij),
R'nk = dfrllk - dtrlik + rrkr‘m - rTkrlim.
Еще одно правило позволяет избежать большого числа множи-
телей gij и gkl. Оно называется правилом поднимания и опуска-
ния индексов. Пусть дан тензор А е Тх’^М, имеющий в локаль-
ном базисе компоненты А1.....»/ Компоненты соответствую-
щих ему тензоров из	и Ух 11 s+I)Al обозначаются так:
4;-.Х
(в правых частях равенств подразумевается суммирование по
повторяющимся индексам). Существует еще несколько согла-
шений, более или менее широко используемых. Например, 6;
означает символ Кронекера
6'i = 1 для любого i, i>i — Q при i =£ !
4 а. Бессе, т. 1
50
Гл. 1. Основные сведения
Скобка [ ] обычно означает альтернирование индексов, скобка
{ }—циклическую сумму и т. и. Однако, используя эти обозна-
чения, мы все же будем напоминать читателям их смысл.
1.43. Пусть (Л4, g)— псевдориманово многообразие. Геодези-
ческие, экспоненциальное отображение и поля Якоби его связ-
ности Леви-Чивита D называются геодезическими, экспонен-
циальным отображением и полями Якоби многообразия (М, g).
Многообразие (М, g) называется полным, если его связность
Леви-Чивита D полна
Отметим, что в локальных координатах (х‘) геодезическая
c(0 = U/(0)/=i,„ удовлетворяет системе п дифференциальных
уравнений второго порядка
(1.43)	х* + У, r*.fex/xfc = 0,	1 = 1, ..., п,
I,	Л=1	1
где точка означает производную по /.
1.44.	С помощью экспоненциального отображения можно
следующим образом задать в окрестности любой точки хен М
локальные координаты специального вида. Зафиксируем орто-
нормированный базис (Хь ..., Хц) пространства ТХМ. Он опре-
деляет изоморфизм a:	>ТАМ. Пусть U — окрестность нуля
в ТХМ, а V—-окрестность точки х в М, такие, что ехрх осущест-
вляет диффеоморфизм U на V (см. 1.28). Тогда
ехрхоа: a-1(Z7)->l/
— локальная карта многообразия М в окрестности точки х. Со-
ответствующие координаты называются нормальными коорди-
натами (с центром х).
Отметим, что базис (гЛ) совпадает с (X,) в точке х, но,
вообще говоря, не является ортонормнрованным в других точ-
ках множества V.
Поскольку ехрл отображает радиальные лучи (/>—>tX) про-
странства ТХМ на геодезические сх, в нормальных координатах
геодезические, выходящие из точки х, описываются радиаль-
ными лучами (с центром х).
Нормальные координаты характеризуются следующим об-
разом.
1.45.	Теорема (фольклор, см. [Eps]). Локальные координа-
ты (л") в псевдоримановом многообразии (Л4, g), заданные в
открытом шаре с центром в начале координат, являются нор-
мальными координатами (с центром в точке х) тогда и только
С. Римановы и псевдоримановы многообразия
51
тогда, когда компоненты (gu) метрики g в этих координатах
удовлетворяют соотношениям
Хёц(х1, .... хп)х> = х‘.
Фактически это не что иное, как классическая лемма Гаусса,
которая обычно формулируется следующим образом.
1.46.	Теорема (лемма Гаусса, см., например, [Ch-Eb]). Пусть
(М, ё)— псевдориманово многообразие, х — точка из М и X
е Фх с: ТХМ. Тогда
(а)	^(1>(Гхехрх)(Х), (7'xexpJ(X)) = ^(X, X);
(Ь)	если gx(X, У) = 0 для некоторого вектора Y^.TXM, то
ёсх о» ((ГхехРх) W- (тх ех!\) (у)) = °-
1.47.Определение. Элементом объема pg псевдориманова мно-
гообразия (М, g) называется единственная плотность (т. е.,
в локальных координатах, абсолютная величина /г-формы),
удовлетворяющая условию
ygu>.....х„) = 1
для любого ортонормированного базиса (X,) пространства ТХМ.
Очевидно, в локальных координатах (д')
pg = Vl det (gu) 11 dxl A ... Д dxn |,
так что pg эквивалентна мере Лебега в любой локальной си-
стеме координат.
Существует формула, выражающая pg в нормальных коор-
динатах через поля Якоби.
1.48. Определение. Пусть (д")—нормальные координаты в
М. Рассмотрим функцию 6 = Vl det (gi,) |.
Заметим, что 0 не зависит от выбора базиса (Xi), опреде-
ляющего нормальные координаты (так как все они ортонорми-
рованные).
Для произвольного неизотропного вектора X е S)x cz ТХМ
зафиксируем ортонормированнып базис (X,) в ТХМ, для кото-
рого вектор Хп пропорционален X, и рассмотрим п — 1 полей
Якоби /ь ..., Jn-i вдоль сх с начальными условиями
Л(0) = 0, (Dd/f-)(0) = X,.
4*
52
Гл. 1. Основные сведения
1.49. Предложение. Если с%(1) лежит в области определения
нормальных координат, то
6 (ехрх X) = | det (Д,	7„_1)|(ехрЛЛ).
Это сразу следует из (1.31) и (1.46). Определитель рассмат-
ривается относительно ортонормированного базиса.
1.50. Если многообразие (Л1, g) ориентировано, обозначим
через cog форму объема многообразия (Л4, g)—каноническую
n-форму, для которой pg — |cog| и которая принадлежит классу
форм данной ориентации. Заметим, что g(ug, (og) = (—l)s, где
s — число —1 в сигнатуре g (т. е. g имеет сигнатуру (п — s, s).
Сформулируем более общее определение.
1.51.Определение. Для любого числа р, 0 р п, определим
оператор Ходжа * как единственный изоморфизм векторных
расслоений
*: Д Л4->Д М,
для которого
а Л (* p) = g(a, p)(og
для любых а, ре Л^ЛТ, хе.М.
Оператор обладает следующими свойствами.
1.52.	Предложение, (а) *1=о)й и -:<<ой = (—l)s;
(b)	для любых иеД/'Ми реЛ Р М выполняется равен-
ство
g(a, *₽) = (-l)p(re“p,g(*a, р);
(с)	на пространстве Д М
1.53.	Замечание. В четномерном случае (n=2tri) оператор
* индуцирует автоморфизм пространства Д М. В римановом
случае (s = 0) этот автоморфизм является
—	инволюцией, если т четно,
—	комплексной структурой, если т нечетно.
Эти факты влекут за собой важные геометрические след-
ствия. Например, для 4-мерного риманова многообразия М рас-
щепление Д2Л4 на два собственных подпространства оператора
« приводит к понятию автодуальности, которое изучается в
гл. 13.
В случае 4-мерного лоренцсва многообразия (s = l) опера-
тор * индуцирует комплексную структуру в Д2 М, которая при-
С. Римановы и псевдорнмановы многообразия
53
меняется для классификации тензоров кривизны пространства-
времени (см. 3.14).
1.54.	Еще несколько обозначений. Напомним, что псевдори-
манова метрика индуцирует канонические изоморфизмы (ь и #)
между тензорными пространствами. Однако для наиболее важ-
ных объектов мы не будем пользоваться этими изоморфизмами,
а введем специальные обозначения
Пусть f — гладкая функция на М
(а)	градиентом функции / называется векторное поле Df =
= #df (или df''), т. е. Df удовлетворяет соотношению g(Df, X) =
= Xf = df (X) для X <= ТМ-,
(Ь)	гессианом функции f называется ковариантная произ-
водная 1-формы df, т. е. Ddf (будем также пользоваться обо-
значением D2f); он удовлетворяет соотношению Ddf(X, У) =
= X(Yf)— (DxY)f и симметричен;
(с)	лапласианом функции f называется взятый со знаком
минус след ее гессиана относительно метрики g:
bf=-tre(Ddf) = -g(g, Ddf).
Отметим, что А есть эллиптический оператор тогда и только
тогда, когда метрика g риманова.
1.55.	Поскольку метрика g индуцирует псевдоевклидову
структуру в слоях любого тензорного расслоения, каждый диф-
ференциальный оператор А, действующий между пространства
ми тензорных полей, обладает каноническим формально сопря-
женным оператором А*. Например, для ковариантной произ-
водной
D-. д-(т’s) М П'ТИ ® Т^г-s» М
формально сопряженный оператор
£>*: Q'Af ®	s) М -► 9^- s> М
описывается следующим образом. Если aeQ[<U®5"lrs,4f
и Xi, ..., Хг—векторные поля, то (D*a) (Xt, ..., Хг) есть взя-
тый со знаком минус след (££) ТТИ-значной 2-формы
(X, Y)^(Dxd)(Y, Х1г Хг)
относительно метрики g Все это относится и к естественным
подрасслоениям расслоения ПГ-5,Л4 В римановом случае опе-
ратор D*a задается формулой
(Л) (%....... ХГ) = - £ (Пг.а) (Уй ..., Хг),
где (У,)/=1 п — произвольный ортоиормированный базис.
54
Гл. 1. Основные сведения
В наиболее важных частных случаях мы будем пользоваться
специальными обозначениями.
1.56.	Определение. Пусть d: Q;’A1 —Q',+1M — внешний диф-
ференциал на р-формах многообразия М. Формально сопряжен-
ный к нему оператор обозначается 6 и называется кодифферен-
циалом.
Оператор 6 можно задать разными способами:
(а)	выберем локальную ориентацию М и рассмотрим соот-
ветствующий оператор Ходжа «т; тогда
6 = — *g о d о *g;
(b)	рассмотрим /\'+ М как подпространство пространства
Л1 м® /\рм- тогда 6 представляет собой ограничение опе-
ратора D* на Л Л4;
(с)	в римановом случае, если (X(-)i=1	„— ортонормирован-
ный базис векторных полей, то
(6а)......Xp) = -Z(Dr.a)(yz, .... Хр).
1.57.	Оператор Д = df> + bd: Q'’A1 —QMl называется лапла-
сианом Ходжа — де Рама на р-формах.
1.58.	Дивергенцией divX (или 6Х) векторного поля X назы-
вается кодифференциал двойственной 1-формы, т. е. divX=
= 6(А>). в римановом случае
divX = - Xg(Dr.X, Yt),
i = l
где (У,) — ортонормированный базис.
1.59.	Вместо форм можно рассматривать симметрические
тензоры. Композиция ковариантной производной
D: ^PM^Q,M®^PM==?’,M®&’PM
с симметризацией
^1м®^рм- ^^р+,м
представляет собой дифференциальный оператор
6’: &,РМ-»?’Р+'М.
Формально сопряженный к нему оператор
6: ^Р+1Л1 ^Л1
D. Римановы многообразия как метрические пространства
55
называется дивергенцией. Отметим, что 6 есть просто ограниче-
р+1
ние оператора D*, действующего в ®	Т.Н, на подпростран-
ство
1.60.	Лемма. В пространстве \-форм оператор б*:
удовлетворяет условию
8a = —'/aLa#g,
где La# — производная Ли по направлению векторного поля а*
{двойственного к 1 -форме а).
В частности, 6*а = 0 тогда и только тогда, когда а* —
киллингово векторное поле.
Доказательство.
6а (X, У) = '/2 ((ОАа) (У) + (£>га) (X)) =
= >/2 {Ха (У) - а (ОАУ) + Уа (X) - а (DyX)} =
= '/2{X-g(a\ У)-£(а«, DxY) +
+ Y-g(a\ X)-g(a", DYX)} =
= '/2 U У) + g (DY^, X)} =
= -V2(W)(x, У)
(ср. с доказательством теоремы 1.81).
D. Римановы многообразия
как метрические пространства
Риманово многообразие имеет еще один важный инвариант —
расстояние.
На протяжении всего параграфа предполагается,
что (Al, g) — риманово многообразие.
1.61.	Определение. Пусть (М, g) — риманово многообразие.
(а)	Длиной кусочно гладкой кривой с: [а, 6]->7Й назы-
вается число
ь
L(c)= Vg(c, c)dt.
а
(Ь)	Для любой пары точек х, у е М обозначим через d(x, у)
точную нижнюю грань длин всех кусочно гладких кривых, соеди-
няющих х и у.
56
Гл. 1. Основные сведения
Отметим, что если кривая с является геодезической, то функ-
ция g(c, с) постоянна и Л(с) = (6 — а)д/й (О с); нижняя грань
d(x, у) достигается не всегда.
1.62.	Теорема. Для любого риманова многообразия (М, g)
функция d является расстоянием и топология метрического
пространства (Af, d) совпадает с топологией многообразия М.
Из леммы Гаусса 1.46 следует, что расстояние реализуется
(по крайней мере локально) геодезическими, т. е. справедлива
следующая теорема.
1.63.	Теорема. У любой точки х^М существует такая
окрестность Ux cz М, что для любой точки у Ux расстояние
d(x, у) равно длине единственной геодезической, соединяющей
х и у в Ux.
1.64.	Следствие. Каждая геодезическая реализует расстояние
между любой парой ее достаточно близких точек; обратно, каж-
дая кривая, обладающая этим свойством, является геодезиче-
ской (с точностью до параметризации).
В метрическом пространстве, как и в римановом многообра-
зии, существует понятие полноты. К счастью, эти понятия наи-
лучшим образом согласованы. Это составляет содержание сле-
дующей теоремы.
1.65.	Теорема (Е. Хопф — В. Ринов). Для риманова многооб-
разия (Л1, g) следующие условия эквивалентны:
(а)	(М, g) со связностью Леви-Чивита полно;
(Ь)	(Л4, d) полно как метрическое пространство;
(с)	ограниченные подмножества М относительно компактны.
Из каждого из этих условий следует, что
(d)	любые две точки х, у е М соединяет хотя бы одна гео-
дезическая.
Отметим, что может существовать много геодезических, сое-
диняющих две точки, и что из свойства (d) не следует полнота
(М ё)-
1.66.	Следствие. Компактное риманово многообразие полно.
(Это утверждение в общем случае несправедливо для псевдо-
римановых многообразий, но верно в предположении их одно-
родности, см. гл. 7.)
Отметим, что геодезическая, соединяющая две точки, не
всегда реализует расстояние между ними. Минимальные гео-
дезические играют очень важную роль в римановой геометрии.
D. Римановы многообразия как метрические пространства
57
При этом существенно, что предел минимальных геодезических
есть минимальная геодезическая.
1.67.	Лемма. Пусть (ck) — последовательность геодезических,
а (М— такая последовательность вещественных чисел, что для
любого k
d(ck(O), ck(tk)) = tk.
Предположим, что векторы (щ(0)) сходятся в ТМ к некоторому
вектору X, а числа (/*) сходятся к числу t при k^-co. Тогда
геодезическая с, для которой с (0) = X, удовлетворяет условию
d (с (0), с (/)) — t.
Укажем несколько элементарных следствий. Напомним, что
диаметром риманова многообразия (М, g) называется точная
верхняя грань расстояний между парами точек из М, а лучом
(соответственно прямой) называется такая бесконечная геоде-
зическая с: [0, оо [->М (соответственно с: ]—оо, -|-оо
что для любых двух точек х, у на с расстояние d(x, у) равно
длине участка геодезической с между х и у (т. е. с имеет мини-
мальную длину среди всех кривых, соединяющих любые две ее
точки).
1.68.	Теорема. Если многообразие (М, g) компактно, то его
диаметр конечен и существует такая пара точек х, у е М, что
расстояние d(x, у) равно диаметру.
Если многообразие (7И, g) полно и некомпактно, то оно
имеет бесконечный диаметр и для любой точки х е М сущест-
вует луч с, для которого с (0) = х.
Заметим, что некомпактное риманово многообразие (Л1, g)
может не иметь прямых. Однако если М имеет два «конца», то
в нем существует прямая, соединяющая эти концы.
Наконец отметим, что понятие сопряженных точек (см. опре-
деление 1.32) и понятие расстояния связаны следующим об-
разом.
1.69.	Теорема. Пусть с — геодезическая на римановом много-
образии (Al, g), a t0 — такое число, что точки с(0) и с (/о) сопря-
жены вдоль с. Тогда геодезическая с не реализует расстояние
между с(0) и c(t) при t > to-
Отметим, что первая точка раздела вдоль с (т. е. такая точка
c(t\), что геодезическая с реализует расстояние между с(0) и
c(t) при t < ti, но не реализует его при t > Л) может встре-
титься раньше, чем первая точка, сопряженная с с(0) вдоль с.
58
Гл. 1. Основные сведения
Е. Римановы погружения, изометрии
и киллинговы векторные поля
1.70.	Определение. Пусть (М, g) и (Л7, А) — два псевдорима-
новых многообразия. Гладкое отображение f; M-+-N называется
псевдоримановым погружением, если f*h = g или, что эквива-
лентно, если для любой точки х е Л1 касательное отображение
Txf удовлетворяет условию
h((Txf)X, (Txf)Y) = g(X, Y)
для любых /, }'g ТхМ.
Отметим, что такое отображение f, очевидно, является по-
гружением, а ограничение h на (Txf) (ТХМ) невырожденно.
Обратно, пусть f: M-f-N— гладкое погружение, a h — псевдо-
риманова метрика на М, для которой все подпространства
(Txf) (Т,:М) невырожденны. Тогда f—псевдориманово погруже-
ние риманова многообразия (М, f*h) в (N, /г). Отметим, что
f(M) будет подмногообразием в N только в том случае, если
f — вложение.
1.71.	Пусть f: (М, g)-»(N, h)—псевдориманово погружение.
Тогда касательное расслоение ТМ многообразия М можно рас-
сматривать как подрасслоение индуцированного векторного рас-
слоения f*(TN), наделенное псевдоевклидовой структурой, инду-
цированной метрикой h, и линейной связностью D, индуцирован-
ной связностью Леви-Чивита метрики h (см. 1.9). Обозначим
через NM ортогональное дополнение к ТМ в f*(TN). Расслоение
NM называется нормальным расслоением (погружения). Со-
гласно 1.10, связность D индуцирует связности в расслоениях
ТМ и NM и некоторый тензор. Ясно, что индуцированная в ТМ
связность совпадает со связностью Леви-Чивита метрики g. Обо-
значим через V индуцированную в NM связность и назовем вто-
рой фундаментальной формой погружения f тензор
И: ТМ ® ТМ -> NM,
значение которого на двух векторных полях U, V^!7~M за-
дается формулой
II (U, V) = JY(DU\/),
где U, V е ТГ М, a — ортогональная проекция на NM. Зада-
дим также тензор В\ TM®NM->TM формулой g{ByX, V) =
= — g(II(fA V), X), где U, V^TXM, X<=NxM.
Е. Римановы погружения, изометрии и киллинговы векторные поля 59
1.72.	Теорема. Пусть f; (М, g)-+(N, h)— псевдориманово
погружение. Пусть U, V, U7 — векторные поля на М, а X, У —
сечения расслоения NM. Тогда
(a)	DpV = DVX + II (17, V) (формула Гаусса),
(b)	DVX = BVX + \jjX (уравнение Вайнгартена),
(с)	(R(U, V)U, V) = (R(U, V)U, V) + |II(t/, V)F— (II(L/, U),
II (V, V)) (уравнение Гаусса),
(d)	(R(U, V)W, X) = ~((\ull)(Y, W), X) + ((VpII)(U, W), X)
(уравнение Кодацци — Майнарди),
(e)	(R(U, V)X, Y) = (R? (U, V)X, Y) - (BVX, BVY) + (BVX, ВиУ)
(уравнение Риччи),
где R, R, Rv — кривизны связностей D, D и V, fl ?И — ковари-
антная производная тензора II. Буква g для краткости опу-
щена.
1.73.	Определения. Пусть f: (М, g)-^-(N, h)—псевдорима-
ново погружение.
(а)	Вектором средней кривизны погружения f в точке х^М
называется вектор нормали
п
//x = trII = S II (Xz, Xt),
»=i
где Xi, ..., Xn — ортонормированный базис TXM.
(b)	Точка х е М называется омбилической, если сущест-
вует такой нормальный вектор v е NXM, что
II (U, V) = gx (U, V) v, VC/, V ее ТХМ.
(с)	Говорят, что f имеет постоянную среднюю кривизну, если
поле векторов средней кривизны И параллельно, т. е. ХН = 0.
(d)	Если все точки многообразия М омбилические, то по-
гружение f называется омбилическим.
(е)	Если Н = 0, погружение f называется минимальным.
(I) Если 11 = 0, погружение f называется вполне геодези-
ческим.
Отметим, что, вообще говоря, из (d) не следует (с).
Если размерности многообразий М и N равны, псевдорима-
ново погружение локально (но, вообще говоря, не глобально)
является диффеоморфизмом и сигнатуры многообразий (7И, g)
и (N, h) совпадают.
1.74.	Определение. Изометрией называется псевдориманово
погружение, являющееся диффеоморфизмом.
Изометрии римановых многообразий можно охарактеризо-
вать с помощью расстояния.
60
Гл. 1. Основные сведения
1.75.	Теорема. Сюръективное гладкое отображение f: (M,g)—>~
->(М, h) римановых многообразий является изометрией в том
и только в том случае, если оно сохраняет расстояния, т. е.
dh(f(x), f(y)) — dg(x, у) для х, у е М.
Очевидно, композиция двух изометрий и обратный диффео-
морфизм f~l изометрии f являются изометриями. Поэтому мно-
жество всех изометрий псевдориманова многообразия (Л4, g) на
себя образует группу, которая называется группой изометрий и
обозначается ЦМ, g). Группа изометрий как подгруппа группы
диффеоморфизмов многообразия М имеет естественную тополо-
гию («компактно открытую» топологию).
1.76.	Примеры, (а) Пусть даны псевдориманово многообра-
зие (М, g) и произвольный диффеоморфизм a;	Тогда а
есть изометрия (N, a*g) на (М, g).
(b)	Любой параллельный перенос в плоском модельном
пространстве (Rn, g0) из примера 1.34 является изометрией.
Вообще, группа /(R", go) представляет собой полупрямое про-
изведение RnX)O(gn) группы параллельных переносов Rn и
ортогональной группы О (go) метрики g0.
(с)	Группа O(gP) (соответственно O(gp+1)) преобразований
пространства R"+I (см. 1.36) сохраняет подмногообразие Sp
(соответственно Н”) и индуцирует на нем группу изометрий.
Можно показать, что эта группа есть полная группа изометрий
многообразия (Sp, fgp'l (соответственно (Нр, 1*ур+1У).
(d)	Вообще, если (А4, g)—псевдориманово подмногообразие
псевдориманова многообразия (М, h), как в 1.35, то любая
изометрия (N, h), сохраняющая М (т. е. такая, что f(M) = M),
индуцирует изометрию многообразия (А4, g).
Сформулируем основной результат для группы ЦМ, g).
1.77.	Теорема (С. Б. Майерс, Н. Стинрод [My-Sy]). Пусть
(А4, g) — псевдориманово многообразие.
(а)	Группа ЦМ, g) всех изометрий является группой Ли,
гладко действующей на М\
(Ь)	для любой точки хе М стационарная подгруппа
Ц (М, g) = {/ е 7 (М, g), f (х) = х}
является замкнутой подгруппой группы ЦМ, g). Более того,
представление изотропии
р: Ц (М, g) -> GL (ТХМ),	= Txf
задает изоморфизм группы 1ЦМ, g) на замкнутую подгруппу
ортогональной группы О(ТХМ, g.Y)e GL(TXM).
Е. Римановы погружения, изометрии и киллинговы векторные поля 61
1.78. Следствие. Если (М, g)— риманово многообразие, то
/ДМ, g) есть компактная подгруппа группы 1 (М, g). Более
того, если многообразие М компактно, то группа 1(М, g) ком-
пактна.
1.79. Замечания, (а) Вообще, на любом римановом многооб-
разии (М, g) группа 1 (М, g) действует совершенно (см.
[Yau 6]).
(b) ^Группа ЦМ, g) может быть компактной (например, три-
виальной) даже в том случае, если многообразие (М, g) не-
компактно или нериманово.
(с) Можно показать, что dim 1 (М, g) <2 --	, причем ра-
венство имеет место только в том случае, если (М, g) имеет
постоянную секционную кривизну.
Поскольку изометрия сохраняет метрику g, она сохраняет
связность Леви-Чивита, геодезические, элементы объема и раз-
личные типы кривизны (определенные в § F). Рассмотрим со-
ответствующие инфинитезимальные понятия.
1.80.	Определение. Пусть (ЛТ, g)—псевдориманово многооб-
разие. Векторное поле X на М называется киллинговым, если
порожденная им локальная однопараметрическая группа диф-
феоморфизмов состоит из локальных изометрий.
1.81.	Теорема. Для векторного поля X следующие условия
эквивалентны:
(а)	поле X киллингово:
(Ь)	производная Ли метрики g вдоль X равна нулю, т. е.
Lxg = 0;
(с)	ковариантная производная DX кососимметрична отно-
сительно g, т. е. g(DYX, Z) + g(DzX, Y) = 0.
Кроме того, любое киллингово поле X обладает следующими
свойствами:
(d)	производная Ли связности D вдоль X равна нулю, т. е.
LXD = 0;
(е)	ограничение X на любую геодезическую является полем
Якоби-,
(f)	вторая ковариантная производная D2X удовлетворяет
условию
D2u vX = R(X, U)V.
Доказательство. Напомним, что производная Ли любого тен-
зорного поля (или связности) А вдоль X задается формулой
62
Гл. 1. Основные сведения
где q)t — (локальная) однопараметрпческая группа диффеомор-
физмов, порожденная X. Отсюда сразу следуют свойство (d) и
эквивалентность условий (а) и (Ь). Далее,
(Lxg) (У, Z) = X - g (У, Z) - g ([X, У], z) - g (Y, [X, Z]) =
= g(DxY, Z) + g(Y, DxZ)-g(DxY, Z) +
+ g(DYX, Z)-g(Y, DxZ) + g(Y, DZX) =
= g(DYX, Z) + g(Y, DZX),	•
что доказывает эквивалентность условий (с) и (Ь). Свойство (е)
следует из определения полей Якоби, так как изометрии пере-
водят геодезические в геодезические. Наконец, свойство (f)
выводится из (е) с помощью поляризации и алгебраического
тождества Бьянки.	□
1.82.	Замечания, (а) Условия (d), (е), (f) не гарантируют,
что X — киллингово поле.
(Ь) Скобка двух киллинговых векторных полей является
киллинговым векторным полем. Таким образом, пространство
всех киллинговых векторных полей является подалгеброй Ли
алгебры Ли всех векторных полей.
1.83.	Теорема. На полном многообразии (М, g) любое кил-
лингово векторное поле полно, т. е. порождает однопараметри-
ческую группу изометрий. Следовательно, алгебра Ли киллин-
говых векторных полей является алгеброй Ли группы Ли изо-
метрий I (М, g).
В заключение сформулируем теорему несуществования, до-
казанную С. Бохнером ([Вос 1]), в которой используется кри-
визна Риччи, введенная в 1.90.
1.84.	Теорема. Пусть (М, g) — компактное риманово много-
образие кривизны Риччи г.
(а)	Если г отрицательно, т. е. r(U, U) < 0 для любого не-
нулевого касательного вектора U, то не существует ненулевых
киллинговых векторных полей и группа изометрий I (М, g)
конечна.
(Ь)	Если г неположительно, т. е. г (С, 77)^0 для любого
U е ТМ, то любое киллингово векторное поле параллельно и
связная компонента единицы группы I(M, g) есть тор.
(с)	Если г = 0, то размерность пространства киллинговых
векторных полей равна первому числу Бетти bi(M, R).
Укажем отправную точку доказательства, которое прово-
дится по той же схеме, что и 1.155. Соответствующая формула
Вейценбёка вытекает из 1.81(f) и имеет вид D*DX = Ric(A),
F. Многообразия Эйнштейна
63
где X — произвольное киллингово векторное поле. Скалярно
умножая это соотношение на X и интегрируя по М, получим
J|DX|2pg=Jr(X, X)pg,
м	м
откуда и следует утверждение теоремы.
F. Многообразия Эйнштейна
Прежде всего перечислим свойства риманова тензора кри-
визны R, с которыми мы уже познакомились.
1.85.	Предложение. Поле тензоров кривизны R псевдорима-
нова многообразия (М, g) обладает следующими свойствами-.
(1.85а) R есть (3,1) -тензор-,
(1.85b) тензор R кососимметричен по двум первым аргументам,
т е.
R(X, Y)=—R(Y, X);
(1.85с) оператор R (X, У) кососимметричен относительно g, т. е.
g(R(X, Y)Z, U)=—g(R(X, Y)U, Z);
(1.85d) (алгебраическое тождество Бьянки)
R(X, Y)Z + R(Y, Z)X+R(Z, Х)У = 0;
(1.85e) g(R(X, Y)Z, U) = g(R(Z, U)X, У);
(1.85f) (дифференциальное тождество Бьянки)
(DR)(X, Y, Z) + (DR)(Y, Z, X) + (DR)(Z, X, Y) = 0.
Тождество (1 85e) доказывается с помощью тождеств (b),
(c), (d) (упражнение).
1.86.	С помощью метрики g можно отождествить кривизну
с (4, 0)-тензором
(X, У, Z, U)^g(R(X, Y)Z, U).
Мы будем также использовать (2, 2)-тензор, определяемый кри-
визной R, который обозначим через 5?. Благодаря симметриям
его можно рассматривать как линейное отображение /\2 М ->
—> А2М, определяемое условием
g(<Z(X/\Y), ZXU) = g(R(X, У), Z, U)
для любых векторов X, У. Z, U.
64
Гл. 1. Основные сведения
Тождество (е) показывает, что есть симметрическое ото-
бражение относительно псевдоевклидовой структуры, индуци-
рованной метрикой g на А2 М (см также 1.106).
1.87.	Определение (п^2). Секционная кривизна неизотроп-
ной 2-плоскости ст в ТХМ задается формулой
H(a) = g(R(X, Y), X, Y)/(g(X, X) g (Y, Y) — g(X, У)2),
где {X, Y} — произвольный базис плоскости о.
1.88.	Предложение. Секционная кривизна многообразия
(М, g) равна константе k для любой касательной 2-плоскости
в точке х тогда и только тогда, когда тензор кривизны имеет вид
(1.88) R(X, Y)Z = k(g(Y, Z)X-g(X, Z)Y).
Отметим, что для модельного пространства R" кривизна
R и= 0, в то время как модельные пространства Sp и Нр (см.
1.36) имеют постоянную секционную кривизну k, равную +1
и —1 соответственно.
Дифференциальное тождество Бьянки препятствует слиш-
ком простому масштабному изменению кривизны.
1.89.	Теорема (Ф. Шур). Пусть п^З. Если для любого
х^М секционные кривизны 2-плоскостей aczTxM равны (чис-
лу, которое априори может зависеть от х), то многообразие
(М, g) имеет постоянную секционную кривизну.
Вследствие алгебраических симметрий тензора кривизны R
лишь одна его свертка приводит к нетривиальному тензору.
1.90.	Определение. Тензором кривизны Риччи (иначе кри-
визной Риччи или тензором Риччи} г псевдориманова многообра-
зия (М g) называется 2-тензор
r(X, y) = tr(Z^->R(X, Z)Y),
где tr означает след линейного отображения Z1—->R(X, Z)Y.
Отметим, что тензор Риччи симметричен. (Это следует из
того, что связность Леви-Чивита нс имеет кручения.)
1.91.	Замечание. Иногда мы будем рассматривать тензор
Риччи как (1,1)-тензор и обозначать его Ric: ТМ-+ТМ. По
определению
r(X, У) = g (RicX, У).
Отметим, что Ric есть ^-симметрическое отображение. В част-
ности, в римановом случае оператор Ric имеет вещественные
собственные значения (что не всегда справедливо в псевдорима-
F. Многообразия Эйнштейна
65
новом случае). Кроме того, в римановом случае тензор Риччи
связан с «локальной» функцией 0 (определенной в 1.48) сле-
дующим неравенством.
1.92.	Предложение. Пусть (М, g)— риманово многообразие,
с — геодезическая с с(0) = х, а 6 — функция, определенная
в 1.48 в нормальных координатах с центром х. Определим функ-
цию ф формулой ф(с(/)) = -|-(6(с(/)))1/<"''|). Тогда
(1.92)	(п—l)g(c, с)ф-}-г(с, с)ф^0.
Из предложения 1.82 можно вывести, что если многообразие
(М, g) полно и г(Х, Х)^(п—l)a2g(X, X) для некоторого
а > 0 и всех X е ТМ, то любая геодезическая с имеет сопря-
женные точки с(0) и с(/0), где 0	Отсюда и из 1.69
вытекает теорема Майерса 6.51. Вообще, нижняя грань значений
г является верхней гранью роста объема «метрического шара»
В(х, t)= {у е М, d(x, у)^ /} (см. 0.62). Для лоренцевых мно-
гообразий аналогичные формулы приводят к так называемым
«теоремам неполноты» (см. [На-Е1]).
Конечно, след г относительно g также является важным
инвариантом.
1.93.	Определение. Скалярная кривизна псевдориманова мно-
гообразия (Л1, g) определяется как функция s = trgr.
Более подробно скалярная кривизна изучается в гл. 4. От-
метим, что на любом многообразии М существуют метрики по-
стоянной скалярной кривизны (см. гл. 4). Производные г и s
связаны следующей формулой.
1.94.	Предложение. Справедливо соотношение бг =---
где б — дивергенция симметрического Ч-тензорного поля, опре-
деленная в 1.59.
Доказательство. Достаточно рассмотреть след дифферен-
циального тождества Бьянки	□
1.95.	Определение. Псевдориманово многообразие (М, g) на-
зывается эйнштейновым (или многообразием Эйнштейна), если
существует такое вещественное число 1, что
(1.95)	r(X, Y) = Tg(X, У)
для любых А', У е ТХМ, х es М.
1.96. Замечания, (а) Это понятие представляет интерес
только при п 4. Действительно, если /г = 1, то г = 0. Если
5 А. Бессе, т. 1
66
Гл. 1. Основные сведения
п — 2, то в любой точке хе М для X, )' е ТХМ имеем г(Х, У) =
— sg (X, Y). Поэтому двумерное псевдориманово многообра-
зие является эйнштейновым тогда и только тогда, когда оно
имеет постоянную (секционную или скалярную) кривизну. Если
п = 3, то многообразие (М, g) эйнштейново тогда и только
тогда, когда оно имеет постоянную (секционную) кривизну
(упражнение!).
(Ь) При замене g на t~g, где t — положительная константа,
тензор Риччи г не меняется, поэтому для многообразия Эйн-
штейна константа X из L95 меняется на V2.
1.97. Теорема. Если п 3, то п-мерное псевдориманово мно-
гообразие является эйнштейновым тогда и только тогда, когда
для любой точки х ед М существует такое число к:;. что
1.97)	rx = kxgx.
Доказательство. Утверждение «только тогда» тривиально.
Для доказательства достаточного условия применим оператор
дивергенции б к обеим частям равенства (1.97). Получим
бг =---^-ds = —JZ,
откуда Z----^-s = const. С другой стороны, след равенства
(1.97)	относительно g дает nk = s. Значит, X. = const. □
1.98.	Многообразия Эйнштейна (особенно римановы) состав-
ляют главный предмет изучения в этой книге. Поэтому в после-
дующих главах приводится множество примеров таких много-
образий (см., в частности, гл. 7). Сейчас мы приведем только
тривиальные примеры. Любое многообразие постоянной сек-
ционной кривизны является эйнштейновым. В частности, много-
образия Rra, Sp, Нр с метриками, описанными в 1.34 и 1.36,
эйнштейновы.
1.99.	Предложение. Произведение двух псевдоримановых
многообразий Эйнштейна с одной и той же константой X есть
многообразие Эйнштейна с Toil же константой.
Отметим, что произведение двух многообразий Эйнштейна
с различными константами не является многообразием Эйн-
штейна. Такие произведения можно рахо актеризовать следую-
щим образом.
1.100.	Теорема. Если тензор Риччи г риманова многообразия
{М, g) параллелен (т. е. Dr = Q), то (по кремней мере локаль-
G. Разложение алгебраических тензоров кривизны
67
но) многообразие (М, g) представляет собой произведение (как
в 1.37) конечного числа многообразий Эйнштейна.
Это утверждение следует из теоремы разложения де Рама
(см. 10.43).
В 7.117 приводится пример лоренцева многообразия с
£>г = 0, которое не разлагается в произведение многообразий
даже локально и не является многообразием Эйнштейна.
G. Разложение алгебраических тензоров кривизны
на неприводимые компоненты
1.101.	В этом параграфе мы покажем, что тензор кривизны
псевдориманова многообразия естественным образом распа-
дается на три части, соответствующие скалярной кривизне, бес-
следовой части тензора Риччи и тензору кривизны Вейля (при
/1^=4). Этот важный факт не приводится в большинстве учеб-
ников по римановой геометрии, хотя он давно известен и яв-
ляется классическим.
Основное наблюдение заключается в том, что расслоение, в
котором живут тензоры кривизны, в силу свойств симметрии
(см. 1.85) является приводимым относительно естественного
действия ортогональной группы и, следовательно, разлагается
в сумму неприводимых компонент. Так определяется канониче-
ское разложение тензора кривизны.
1.102.	Начнем с обзора псевдоевклидовой геометрии с точки
зрения представлений ортогональной группы в высших тензор-
ных пространствах. Мы также рассмотрим случай специальной
ортогональной группы в размерности 4, в котором имеется до-
полнительное разложение тензора Вейля ориентированных че-
тырехмерных римановых многообразий. Эти результаты проли-
вают дополнительный свет на роль скалярной кривизны и кри-
визны Риччи и позволяют получить очень простые доказатель-
ства некоторых классических результатов.
1.103.	Пусть Е представляет собой /г-мерное вещественное
векторное пространство (тг>1). Тогда каждое тензорное про-
странство T{h' l}E = &jk E'Qf&E есть пространство представле-
ния линейной группы GL(E). Действие элемента y^GL(E) в
этом пространстве задается формулой
У (|j ® . . . 0 U ® Xj ®	® Xt) =
= (\~*£1) ®	® (Ч-1^) ® (YM) ®	® (УХ[),
где	lk^E* и х,.....xt i= Е.
5*
68
Гл. 1. Основные сведения
Пусть q — невырожденная квадратичная форма на Е. Тогда
q определяет отождествление Е с Е*. Более того, если у при-
надлежит ортогональной группе O(q), задаваемой формой q,
то ^у-1 = у и, значит, О (q) -модули Е и Е* изоморфны. Поэтому
можно расматривать только тензорные степени пространства Е.
Напомним, что SkE означает k-ю симметрическую степень Е,
а Лг Е означает l-ю внешнюю степень Е. Символом о мы обо-
значаем симметрическое произведение тензоров, нормируемое
условием х ° х = х ® х.
1.104.	Конечно, О (q)-модуль Е неприводим. Хорошо извест-
но, что модуль Е приводим (даже как GL (Е)-модуль). Обо-
значим через SoE пространство бесследовых симметричных
2-тензоров. Напомним, что q индуцирует след, представляющий
собой линейное отображение tr9: S2f-»-R.
1.105.	Предложение. Разложение О(q)-модуля	Е на не-
приводимые компоненты имеет вид
&Е = A2£®S2£®R?.
Доказательство. Очевидно, что любая форма
k е (^)2 Е (=	Е*) допускает разложение
k = Д2 k + slk + (tr9 k/n) q,
где
/\2k(x, y) = ~(k(x, y) — k(y, x)),
S2k(x, y) = -^-(k(x, y)+k(y, л-)),
Sok (x, y) = S2k — (trQ k/n) q.
Нетривиальное утверждение заключается в том, что модули
SoE и /\2Е неприводимы. Оно следует из теории инвариантов:
достаточно проверить, что пространство О (q)-инвариантных ква-
дратичных форм на Е трехмерно (подробности см. в [Wey],
§ II.9, 11.17, [Bes 2], доклад IX, или [Be-Ga-Ma], с. 82—83). □
1.106.	Рассмотрим тензоры, удовлетворяющие тем же алге-
браическим тождествам, что и тензоры кривизны псевдорима-
нова многообразия в одной точке. Свойства 1.85(a), (Ь), (с),
(е) показывают, что при отождествлении касательного простран-
ства Е = ТХМ с сопряженным пространством Е* с помощью
метрики q=gx тензор кривизны в точке х принадлежит про-
странству S2A2£.
G. Разложение алгебраических тензоров кривизны
69
Более того, известно, что пространство &)k Е приводимо как
GL (Е) -модуль. Действительно, симметрическая группа ©fe (и ее
групповая алгебра R(©*)) определяет естественные GL(E) -мор-
физмы. При этом GL(E)-неприводимые компоненты GL(E)-мо-
дуля &)к(Е) оказываются ядрами некоторых идемпотентов из
'Е(©й), так называемых симметризаторов Юнга (см. [Wey],
гл. IV, или [Nai], § II. 3).
В частности, алгебраическое тождество Бьянки (1.85d) со-
ответствует следующему симметризатору Юнга.
1.107.	Определение. Назовем отображением Бьянки b идем-
потент в Е, который имеет вид
b (Е) (х, у, z, 0 = 4" (х> z< 0 + Я (У, z> 0 + Е (z> V У, 0)>
где	x,y,z,t^E\
Очевидно, что эндоморфизм b является GL(E) -эквивариант-
ным, что Ъ2 = Ъ и что Ъ отображает S2/ 2Е в себя. Поэтому
имеет место GL(E) -эквивариантное разложение
S2 Л2£ = Kerfc® Im 6.
Простые вычисления доказывают, что 1ш&=Л4£- Отсюда,
в частности, следует, что b = 0 на S2 /\2Е при п = 2, 3. Другими
словами, тождество Бьянки для этих размерностей вытекает из
других тождеств для кривизны.
1.108. Определение. Назовем пространство *&Е = Ker b
(в S2 /\2Е) пространством аглебраических тензоров кривизны.
Очевидно, тензор кривизны псевдориманова многообразия
в любой точке х е М лежит в 'ёТ^М. Ключевое утверждение
этого параграфа заключается в том, что пространство ё’Е
можно разложить как О (q)-модуль, где q = gx. Определим для
алгебраических тензоров кривизны понятия, соответствующие
тензору Риччи и скалярной кривизне.
1.109. Определение. Сверткой Риччи называется О (q) -экви-
вариантное отображение
с: S2 /\2E->S2E,
задаваемое формулой
с (Е) (х, у) = tr Е (х, - у, •)
для Е S2 Л2 Е, х, у е Е*.
70
Гл. 1. Основные сведения
1.110. Определение. Произведением Кулкарни — Номидзу
двух симметрических 2-тензоров h, k называется 4-тензор h A k,
задаваемый формулой
h ® k (х, у, z, t) = 1г (х, у) k (у, /) + h (у, t) k (х, z) —
— h (х, t) k (у, z) — h (у, z) k (x, z),
где x, у, z, E*.
С помощью простых вычислений можно доказать
1.111.	Предложение.
(a)	h ® k = k ® h;
(b)	h®k принадлежит <&E',
(c)	q ®q равно удвоенному тождественному отображению
пространства /\2 Е (при отождествлении End(A2£) =
= 02Л2£).
Отметим, что в римановом случае тензор кривизны многооб-
разия постоянной секционной кривизны k равен ^-gx®gx.
1.112.	Замечание. Произведение Кулкарни — Номидзу пред-
ставляет собой частный случай естественного произведения в-
градуированной алгебре ^p_0<S2(A₽£'), задаваемого формулой
(а о р) - (|т о v) = (а Л ц) о (р Л v).
Напомним, что форма q индуцирует квадратичные формы
(также обозначаемые через q) на пространстве Е и его под-
пространствах S2E и S2/\2E. Если отождествить пространства
S2E и S2 (Л2£) с подпространствами пространств EndE
и End(A2E) соответственно, то в обоих случаях q(h, k) =
= tr(/io/j) где означает композицию эндоморфизмов. Из
этого замечания и прямых вычислений вытекает
1.113.	Лемма. При п> 2 отображение
q®-:S~E->^E, k^q®k
инъективно, а сопряженное к нему отображение совпадает со
сверткой Риччи, ограниченной на ®(Е) с S2 А2 Е.
Теперь сформулируем основной результат.
1.114.	Теорема. Если п~^4, то О (у)-модуль ®Е разлагается
в ортогональную сумму однозначно определенных неприводимых
G. Разложение алгебраических тензоров кривизны
71
модулей:
<1.114)	<&Е = <иЕ®£,Е®ЖЕ,
где
<llE = Rq®q,
&E = Rq®(S20E),
1ЕЕ = Ker (c J- ^E) = Ker c f] Ker b.
Доказательство. Существование такого разложения вытекает
из леммы 1.113 (для S2E — P.q ®S2E). Ключевым моментом
вновь оказывается доказательство неприводимости слагаемого
7ЕЕ. Оно вытекает из теории инвариантов, поскольку простран-
ство О (q) -инвариантных квадратичных форм на пространстве
q?E трехмерно. Точнее, это пространство порождается формами
q(R, R), q(c(R), c(R)) и (tr c(R))2 (см. [Bes 2], доклад IX, и
[Be-Ga-Ma], с. 82—83).
1.115. Замечание. В рамках теории представлений можно
показать, что пространства SoE и WE (точнее, их комплекси-
фикации) являются неприводимыми О (q) -модулями, старшие
веса которых равны удвоенным старшим весам модулей Е и
А2к.
1.116. Определение, (а) Пространство 7ЕЕ называется про-
странством тензоров Вейля;
(Ь) для любого алгебраического тензора кривизны R обо-
значим через W (или 1П(/?)) его компонент}' из 7ЕЕ и назовем
се тензором Вейля тензора R.
Используя тензор Риччи и его след, нетрудно найти тензор
Вейля W в явном виде. Действительно, для любого h <= S2E
простые вычисления показывают, что
c(q®h) = (n-2)h+(trh) q.
Поэтому, вводя обозначения г — с (R), s = trr, получаем
(1.116)	+
S
где z = г — — q.
Тензор V/ можно рассматривать как остаток от деления
R на q.
72
Гл. 1. Основные сведения
Н. Применение к римановой геометрии
Пусть (Л4, £) —псевдориманово многообразие. Для любой,
точки ге /И тензор кривизны Rx (при отождествлении ТХМ =
— Т^М) принадлежит ‘ё’Т^М (с q = g‘x)- При этом г = с(^)
есть кривизна Риччи, a s = trr — скалярная кривизна. Соотно-
шение (1.116) позволяет дать следующее определение.
1.117.	Определение. Тензором Вейля W n-мерного псевдори-
манова многообразия (Л4, g) (с 4) называется тензор
Вейля его тензора кривизны, рассматриваемый как (3,1)-тензор.
Явное выражение для тензора W, рассматриваемого как
(4,0)-тензор, вытекает из (1.116). В § J мы покажем, что IF за-
висит только от задаваемой g конформной структуры, в част-
ности, W =0 тогда и только тогда, когда многообразие
(Л4, g) конформно плоско (при п ^4), см. 1.164.
1.118.	Из определения 1.95 следует, что многообразие (Л4, g)
является эйнштейновым тогда и только тогда, когда во всех
точках х^М компонента кривизны R, лежащая в SZ (Тх Л4),
равна нулю. Отметим, что многообразие имеет постоянную сек-
ционную кривизну тогда и только тогда, когда компоненты /?,
лежащие в ЗДТХМ) и Ж’(ГЛ7И), равны нулю.
Различные компоненты R не вполне независимы как поля,
поскольку их производные связаны определенными соотноше-
ниями. Первое фундаментальное соотношение имеет вид бг =
—----^-ds (см. 1.94). В 4.72 и 16.3 мы получим еще три анало-
гичных соотношения.
1.119.	Если п==2 или 3, ситуация упрощается.
(а)	Если п = 2, то
S2 /\2 E = Rq®q, R = -®-q®q, r — ^-q.
При этом s = 2k, где k — гауссова кривизна (т. е. секционная
кривизна 2-плоскости ТХМ).
(Ь)	Если п = 3, то
S2 Л2 Е = (R<7 ® q) Ф (So£ ® q), R = q ® q + (г-q} ® q.
В частности, кривизна Риччи определяет тензор кривизны и
справедливо следующее предложение.
1.20.	Предложение. Двумерное или трехмерное псевдорима-
ново многообразие является эйнштейновым тогда и только
тогда, когда оно имеет постоянную секционную кривизну.
Н. Применение к римановой геометрии
73
1.121.	Рассматривая подгруппы O(q), можно получить более
тонкие разложения. В геометрическом случае такая ситуация
возникает, если многообразие М снабжено дополнительной
•структурой (например, эрмитовой пли кватернионной). Теория
становится особенно интересно, когда группа голономии мно-
гообразия (Л4, g) меньше, чем О(п) (см. гл. 10).
Здесь мы рассмотрим только случай специальной ортого-
нальной группы SO(q), геометрически соответствующий ориен-
тированному многообразию М. Известно, что компоненты раз-
ложения (1.114) также неприводимы относительно группы
SO(q) при п=#4 (см. [Kir] или [Bes 2], доклад IX). Но при
п = 4 возникают новые явления. Они связаны с непростотой
группы SO(q) (или ее комплексификации, если сигнатура q
равна (1, 3)).
1.122.	В этом пункте Е означает ориентированное четырех-
мерное векторное пространство, a q — положительно определен-
ную квадратичную форму в Е. Мы ограничимся анализом этого
случая, поскольку для других сигнатур складывается иная си-
туация (см. 1.130).
Рассмотрим оператор Ходжа *, определенный в 1.51.
Прежде всего отметим, что он индуцирует изоморфизм
SO(4)-модулей Д4Е и Д°£ = ₽ (напомним, что как О(4)-мо-
дули они неизоморфны). Кроме того, оператор * индуцирует
автоморфизм пространства Д2Е, являющийся самосопряжен-
ным оператором. Поэтому оператор «• можно рассматривать как
элемент пространства S2 Д2Е. Важно, что оператор « как авто-
морфизм Д2Е является инволюцией. Положим
Д Е = {а с= Д Е, * а = а},
Д Е = {а е= Д Е, * а = — а}.
Очевидно, что /\2 Е =/\ Е® Д Е. Точнее, справедливо
1.123.	Предложение. Два SO(4)-модуля Д Е и Д Енепри-
водимы и трехмерны, но не изоморфны. При этом SO (4) -модуль
&)2 Е допускает следующее разложение в сумму однозначно
определенных неприводимых подмодулей:
02 Е= Д + Е® Д~ E®SoE®Rq.
Доказательство этого и следующего утверждения см в [Ast]
или [Bes 2], доклад IX.
Сформулируем еще одно важное свойство этих модулей.
74
Гл. 1. Основные сведения
1.124.	Лемма. Подпространство Д + Е<8> Д £с®4£ есте-
ственным образом отождествляется с ЗбЕ. Поэтому отображе-
ние q®- индуцирует канонический изоморфизм S2E на
Д + £® Д” Е.
1.125.	Замечание. Пространство Д2£ (как SO(4)-модуль)
изоморфно алгебре Ли so (4) группы £0.(4) (с присоединенным
действием SO (4)). Этот изоморфизм отображает подпростран-
ства Д £ и Д £ на два коммутирующих трехмерных идеала
алгебры Ли so(4), изоморфных so(3) (см. [Bes 2], приложе-
ние I).
' Перейдем к описанию разложения SO (4)-модуля S2 Д2£"
на неприводимые подмодули. Ясно, что элемент *е Д4£ по-
рождает все пространство Д4£?«₽. Легко проверить, что для
любого /?е£2Д2£ справедливо равенство b(R) = q(R, *). По-
этому из разложения Д2£ сразу следует
1.126.	Теорема. Пространство S2 /\2Е (как SO (4)-модуль)
допускает следующее ортогональное разложение на неприводи-
мые подмодули:
S2 .д2 £ = КМл+£ФКМл-£®(Д + £® Д~ £)ф
®S0( Д + £) ®50(Д ~е\
Легко видеть, что
wa+e + Id/-E = Id^EId^+E - IdfCE = *•
Поэтому RIdp+E®Rld^-E= Rq® </®R * и R* = Д4£.
1.127.	Положим
7£+£ = £0(Д + £),
Ж-£ = £о(Д- £).
Поскольку S6E— Д + £® Д £, имеем ЖЕ = Ж+Е®7Е~Е.
Поэтому разложение SO (4)-модуля ‘gE на неприводимые под-
модули имеет вид
ЪЕ = <UE ® S6E ® Ж+£ ф 7£-£.
Это разложение отличается от 1.114 лишь тем, что тензор
Вейля разлагается на две компоненты, W+ и W~.
Н. Применение к римановой геометрии
75
1.128.	Различные подпространства можно характеризовать
свойствами их элементов (рассматриваемых как самосопряжен-
ные операторы в /\2Е) в композиции с оператором *. При этом
S6E = {R^S2 /\2 Е‘, *R = — *r},
№+E={r<=So Л2Е; *R = R* = R},
7Г“£={/?е5оЛ2£; */? = /?* = -/?}.
Отсюда следует, что элемент R^S2/\2E, рассматриваемый
как линейный оператор в А Е= /\ £ Ф А Е, задается мат-
рицей
W+ + ^Id
Z*
z
w~ + ^ld
где R = s-Id + Z + IE+ + W~— разложение на неприводимые
компоненты (см. 1.127).
Многообразия Эйнштейна размерности 4 можно охарактери-
зовать следующим образом.
1.129.	Следствие. Для четырехмерного риманова многообра-
зия (М, g) с тензором кривизны R следующие условия эквива-
лентны:
(а)	многообразие (Л1, g) эйнштейново:
(Ь)	при любом выборе локальной ориентации <R — R*;
(с)	секционная кривизна любой 2-плоскости а<^ТхМ,
х е Л1, совпадает с секционной кривизной ортогональной 2-пло-
скости o'- cz ТХМ.
Все результаты пунктов 1.126—1.129 принадлежат И. М Зин-
геру и Дж. Торпу [Si-Th].
Отметим, что в окрестности любой точки х^М всегда мож-
но выбрать ориентацию.
1.130. Замечание, (а) Если квадратичная форма q имеет сиг-
натуру (2, 2), то такие же рассуждения приводят к аналогич-
ному результату, поскольку в этом случае «-2= 1.
(Ь) Если сигнатура q равна (1, 3), то разложение <&Е имеет
другой вид, поскольку -х-2 = —1 (т. е. в А2 Е имеется естествен-
ная комплексная структура ). Соответствующее разложение
(найденное А. Петровым) изучается в гл. 3.
Разница объясняется тем, что группа SO(3, 1) проста, в то
время как группы SO (4) и SO (2, 2) непросты (хотя все они
имеют одинаковые комплексификации).
76
Гл. 1. Основные сведения
Как было показано в 1.119, при п — 2 или 3 тензор кривизны
имеет специальные свойства и его разложение отличается от
«общего случая» п 4. В действительности при п = 4 тензор
кривизны также обладает специальными свойствами (помимо
уже сформулированных), которые понадобятся нам в гл. 4, 12.
Начнем с некоторых общих определений.
1.131.	Определения. Пусть R— алгебраический тензор кри-
визны.
(а)	Обозначим через R симметрический 2-тснзор
п
Я(Х, у) = £ EiEt-EkR(x, et, eh ek)R(y, eh eh ek),
i, i,k = l
где x, у <= £*, a (e£)— ортонормированный базис в £*, для ко-
торого
Q(eb e,) = 61/Ez, ez = ± 1.
О
(b)	Обозначим через R линейный оператор в £2£
о	П
(Rh) (х, у) = X е£Л (£ (х. et) у, et)
i=l
для /igS2£, где х, у, ei те же, что в (а), и £ рассматривается
как элемент из £ ® £*•
Простые вычисления доказывают
1.132.	Предложение.
(a)	tr £ = <?(£, £);
(b)	тензор R симметричен-,
(с)	тензор R эйнштейнов (т. е. г —тогда и только
тогда, когда R отображает пространство S2E в себя.
°
Тензор R подробно изучается в [Bo-Ка]. Этот тензор есте-
ственным образом возникает при инфинитезимальной вариации
кривизны Риччи, в частности, при изучении Пространства Моду-
лей многообразий Эйнштейна (см. 12.30).
1.133.	Замечание. Из предложения 1.132 следует, что если
v 1
при и = 4 тензор R эйнштейнов, то R = -4- q(R, R)q. Обратное
утверждение неверно. Например, тензор кривизны прямого про-
изведения S2 X Н2 двух пространств противоположной постоян-
ной кривизны удовлетворяет соотношению £ = -^-|£|2д, по-
скольку для него s = W = 0, но многообразие S2 X Н2 неэйн-
штейново.
1. Лапласианы и формулы Вейценбёка
11
I.	Лапласианы и формулы Вейценбёка
1.134.	На римановом многообразии (М, g) можно опреде-
лить ряд дифференциальных операторов, связанных с тензорным
полем g, которые дают информацию о геометрии многообра-
зия М. Мы уже видели, что среди дифференциальных операто-
ров первого порядка, действующих на тензорных полях, особую
роль играет связность Леви-Чивита. Она отображает тензор-
ные поля порядка k в тензорные поля порядка k + 1 (мет-
рика позволяет игнорировать вариантность). Ее главный сим-
вол uDt Т*М ® (ф6 ТМ) ->ф/гН ТМ представляет собой тож-
дественное преобразование (при отождествлении Т*М с ТМ
с помощью метрики).
1.135.	Нас будет интересовать специальное семейство диф-
ференциальных операторов второго порядка, играющее в гео-
метрии важную роль. Прежде всего опишем это семейство.
Главный символ стл дифференциального оператора А второго
порядка, действующего на сечения векторного расслоения Е,
отображает S2T*M<8>E в Е. Для удобства мы будем называть
оператор А оператором Лапласа, если для Ъ,^Т*М и е^Е
выполняется условие оА (g ® £ ® е) = — g (g, g)e (метрику на ко-
векторах мы также обозначаем через g). Можно дать и другие
определения.
Особенно важную роль играет грубый лапласиан (V*)V
связности V в векторном расслоении Е. Далее мы предполагаем,
что Е — эрмитово векторное расслоение. Символом V* обозна-
чается оператор, формально сопряженный к связности V. За-
метим, что оператор V*V можно записать в виде —tr V’V, где
V1 — ковариантная производная в расслоении Т*М ® Е, задавае-
мая формулой V1 = V® 1т*м + If ® D.
1.136.	Основное свойство операторов рассматриваемого се-
мейства состоит в следующем. Говорят, что оператор Лапласа
А допускает разложение Вейценбёка, если
Л = V’V+ #(/?*),
где оператор К (Rv) линейно зависит от кривизны 7?v е
ей2(УИ, End£) связности V в расслоении Е.
1.137.	Разложение Вейценбёка имеет большое значение по
следующей причине: существует метод (предложенный Бох-
нером, см. [Вос 1]) доказательства теорем об обращении в нуль
ядра оператора Лапласа, допускающего разложение Вейцен-
бёка, и оценки наименьшего собственного значения этого one-
78
Гл. 1. Основные сведения
ратора. Метод работает главным образом на компактных мно-
гообразиях. Если А —	+ К (Ev), то
Иф, ф) Ре = {(V*V<p, ф) + (К Ф, <р} gg =
м	м
= $ I Уф F Pg + (Л (Ev) ф, ф) hr
М	М
Если К (Ev) — неотрицательно определенный эндоморфизм в
каждой точке, то правая часть представляет собой сумму двух
неотрицательных слагаемых. Поэтому из Дер = 0 следует, что
У<р = 0 и К (Ev) Ф = 0.
Если эндоморфизм Д (Ev) строго положителен, то, очевидно,
Ф = 0. Такие рассуждения стали классическими в дифферен-
циальной геометрии и будут неоднократно использоваться в этой
книге для различных операторов А. Игра обычно начинается с
выбора подходящего оператора второго порядка. Формула
Вейценбёка проверяется непосредственно. При этом бывает
удобно работать во вспомогательном расслоении коэффициен-
тов, например в касательном расслоении, как в 12.69, 16.9 или
16.54.
1.138.	Дадим некоторые комментарии. Если векторное рас-
слоение Е снабжено ковариантной производной, то с каждым
дифференциальным оператором А порядка k, отображающим
сечения расслоения Е в сечения другого векторного расслоения
F, можно связать такую последовательность (а,), fl. G
е=С°° (SlT*M® Е, F), относительных символов, что Д = £/==оагу'.
При этом ak совпадает с главным символом оператора А. Таким
образом, с помощью ковариантной производной можно дать
более алгебраическое описание дифференциальных операторов.
В этом контексте можно сказать, что оператор Лапласа до-
пускает разложение Вейценбёка, если его относительный сим-
вол первого порядка равен нулю, а относительный символ
нулевого порядка линейно зависит от кривизны. Эти условия
автоматически выполняются для естественных римановых диф-
ференциальных операторов на подрасслоениях касательного рас-
слоения (полную теорию см. в [Eps], (Str] или [Тег]).
1.139.	Для любого линейного представления р группы О(п)
(а также SO(n) или Spin (и) для ориентированного или, соот-
ветственно, спинорного многообразия) в пространстве Е опре-
делено ассоциированное векторное расслоение Ер и канониче-
ская End Ер-значная 2-форма cpeQ2(7W, EndEp), которая со-
I Лапласианы и формулы Веппеибёка
79
ответствует О (/г) -эквивариантному отображению р о i: А 2 IR" —>
—► о (п) — > End Е. Здесь i — естественное отождествление внеш-
него квадрата стандартного представления группы О(и) с ее
алгеброй Ли е(п).
Если R е С00 (Д2 ГМ® Д2 ГМ) — риманов тензор кривиз-
ны, то можно построить сечение
ср ® ср (R) <= С°° (End Е 0 End Е)
и (перемножая эндоморфизмы) сечение с2р (R) е С°° (End Е),
линейно зависящее от R. Если соа, 1	--• —ортонор-
мированный баЗИС пространства /\~ТМ И /? = ^а+р^арюа®юр>
то
(1 .140)	Ср (R) Raf,cp (®а) ср (юр)-
а. р
Как мы знаем (см. 1.86), Raf,=^R^a. Поскольку эндоморфизмы
Ср(оа) кососимметричны, эндоморфизм cp(R) самосопряжен.
1.141.	Оператор вида
(1.142)	А = D*£> + pc2 (R)
(где р — константа) обладает важным свойством: если группа
голономии связности Леви-Чивпта редуцируется к подгруппе
GczO(n), то оператор А коммутирует с ортогональными проек-
циями на подрасслоения расслоения Ер, определяемыми разло-
жением представления p|G в сумму неприводимых компонент.
1.143. Примером такого оператора может служить так назы-
ваемый лапласиан Лихнеровича на р-тензорных полях. В [Lie 2]
А. Лихнерович ввел оператор Ат, определив его действие на
поле 7 е С“ (®р ГМ) формулой
д£Г = £*£)Е+ ГТ,
где
(Г?')/ ... = 5	••• • • *’р ~	' .....lP~
Непосредственно проверяется, что
(1.144)	Г/? = —2с2 (/?),
где р — естественное представление группы О(п) на р-тензорах.
80
Гл. 1. Основные сведения
1.145.	Дифференциальный оператор второго порядка, описы-
вающий деформацию первого порядка метрики Эйнштейна,
представляет собой лапласиан Лпхнеровича на симметрических
2-тензорных полях (см. [Ве-Eb] и гл. 12). Член, содержащий
кривизну, можно описать указанным выше инвариантным спо-
собом.
1.146.	Мы приведем разложения Вейценбёка для ряда опе-
раторов:
(i)	лапласиана Ходжа Ая = dd* + d*d, действующего на
внешние дифференциальные /?-формы;
(ii)	комплексного лапласиана дд' + д*д, действующего на
внешние дифференциальные формы типа (0, р) на кэлеровом
многообразии (см. гл 2);
(iii)	лапласиана Дирака S)2, действующего на комплексном
спинорном расслоении ЁЛ1 (см. 1.147);
(iv)	лапласиана Дирака (^5V)2, действующего на сечения
расслоения 'ЕМфЕ, где Е — расслоение коэффициентов со связ-
ностью V.
1.147.	Оператор Дирака C°°(SA1)-^- C°°(SM) на спинор-
ном многообразии задается формулой
ЕЕ) — <т ° D,
где <т: С°° (Т*М ® ХМ) —> С°° (SA4) — отображение клиффордова
умножения
о (а ® ср) = а - ср.
Таким образом,
Е)2ц> = сгТЛр,
где E)2q>	С°° ГМ&2М) и
(1.148)	ог2(а® 0®<р) = а • Р • <р.
Но для клиффордова умножения
а-р + р-а=—2g (a, Id,
поэтому
(1Л 49)	S)2qp = D'Dy + с2 (Е) <р.
В то же время элемент а= У, a^etEej алгебры Ли о(п) при
спинорном представлении б переходит (см. [Hit 2]) в
Q (а) = ~ V £ aijei  et.
Поэтому
У ст2 (е, ® е, ® а<р) = у • е, • ср = —46 (а) ср.
I. Лапласианы и формулы Вейценбёка
81
Сравнивая эту формулу с (1.149), получаем
^ = D,D-4c26(R).
Непосредственные вычисления с использованием симметрии тен-
зора кривизны показывают, что
S Rijkiei -erek-ei = -2sld <= С°° (End (2*4)),
и мы получаем формулу Лихнеровича ([Lie 4])
(1.150)	£>2 = D*D + -^s.
1.151.	Часто бывает удобно работать с расслоением коэффи-
циентов.
Оператор Дирака С°° ('EM ® Е) —» С°° (ЕМ ® Е) для рас-
слоения коэффициентов Е со связностью V задается формулой
^>v = (a® 1)(D® 1 + 1 ®v).
Таким образом,
(1.151)	(S)v)2 = v'V + cl (R ® 1 + 1 ® Rv). ’
Поэтому, согласно 1.147,
(1.152)	(^v)2 = vi*vi + ^.s + c2(1 + /?V)i
где
cl (1 ® Rv) (<p ® e) = У et  e} - <p ® Rz/ (e).
В частном случае (который рассматривается в гл. 13), когда
(Е, V) есть векторное расслоение, ассоциированное с главным
расслоением реперов со связностью Леви-Чивита и представ-
лением р, получаем
cl (1 ® Rv) = -4с6 ® р (R) е= С°° (End (SM ® £)),
где
(1 -153)	Сб ® р (R) = Е R«,	(<оа) ® р (fi>p).
а, р р	1
Рассмотрим в качестве расслоения коэффициентов спинор-
нос расслоение 2*4. Тогда (см. [At-Bo-Sh], [Hit 2]) при чет-
ном п
2*4 ®2М с-® Д₽ Т'М,
р=0
а при нечетном п
й	14]
2*4® 2*4 ~ ® Л2"Г7*4~ 0 Л2₽+17с*4.
р=0	р=о
6 А. Бессе, т. 1
82
Гл. 1. Основные сведения
Клиффордову умножению в левой части отвечает в правой части
умножение, которое задается оператором е(а)—i(a) при чет-
ном п и оператором ±e(a)± -»i(a) при нечетном п, где е(а) —
внешнее умножение на 1-форму a, a i(a) — сопряженное к нему
внутреннее умножение.
Следовательно,
n ( d + d* при четном п,
1 ± * d ± d * при нечетном п
и в обоих случаях
(Z>D)2 = dd* + d‘d = &,
где Д — лапласиан Ходжа.
Поэтому в силу 1.151
Д = dd" = d'd = D*D — 4 (е£ ® 1 + ce ® ce) (R).
Для тензорного квадрата р представления 6 соответствующее се-
чение ср еС°°(Нот (A2Т'М, SA40XA4)) имеет вид
ср = св® 1 + 1 ®с0
и, следовательно,
с2 (/?) = (^ ® 1 + 2св ® с6 + 1ВД) (/?).
Но с2р (/?) = ---jg-s есть скаляр. Значит,
(4® 1 + <?6®св) (т?)=±4(/?),
и мы получаем
(1.154)	D~ 2ср (Я)-
Это не что иное, как лапласиан Лихнеровича (см. 1.143).
1.155. Еще более специальный случай — представление на
1-формах, т е. стандартное л-мерное представление группы
О (л).
В этом случае
dd* + d'd = £>*£> — 2 £-j- R^ (8> ег =
= D*D + г,
что приводит к теореме Бохнера об обращении в нуль (см.
[Вос 1J, а также гл. 6): если г > 0, то первое число Бетти
компактного многообразия равно нулю.
1.156. Кэлерово многообразие можно охарактеризовать как
риманово многообразие, группа голономии которого содержится
J. Конформная деформация рямановых метрик
83
в U(m)^S0(2m). Согласно [At-Bo-Sh] и [Hit 2], в этом слу-
чае спинорное расслоение YA4 имеет вид
т л
SA4~ф Л 7сМ®А,/2,
р=0
где Д'/2— линейное расслоение, ассоциированное с 2-значным
представлением
det~1/2: t/(m)->t/(l).
(Отметим, что в формулах Вейценбёка глобальные вопросы
существования ориентации и спинорной структуры не играют
роли.)
Таким образом, из (1.157) следует изоморфизм
ф Л °’Р ТсМ ~	® №1/2,
который приводит к следующей формуле для оператора Ди-
рака:
0D = л/2 (д + д*)
(см. [Hit 2]). Поэтому
дд* + д*д = -^(0г>')2.
В силу (1.152)
дд* + д*д = D'D + -j-« - 4 (сб ® ср) (/?).
В этом случае кривизна расслоения коэффициентов равна поло-
вине формы Риччи, а собственные значения оператора
—4 (с6 ® Ср) (R) равны 4	(± гДе 1	1 т> — яв-
ственные значения формы Риччи. Поскольку
1=1
принцип Бохнера (об обращении в нуль, см. 1.37) с учетом изо-
морфизма Дольбо позволяет доказать теорему Бохнера и Яно
[Bo-YaJ: если на кэлеровом многообразии г > 0, то Нр(М, О) =
= 0 для р > 0, где С — пучок голоморфных функций на М.
Другие теоремы об обращении в нуль, которые доказы-
ваются с помощью спинорного подхода, см. в [Mic] и [Hsi].
J. Конформная деформация римановых метрик
Мы рассмотрим здесь простейшие негомотетичные деформа-
ции (псевдо) римановой метрики: конформные деформации. Они
заключаются в умножении длин всех векторов в каждой точке
6*
84
Гл. 1. Основные сведения
на масштабный множитель (зависящий от точки) без изменения
углов.
1.158.	Определение. Две псевдоримановы метрики g и g} на
многообразии М называются
(а)	(поточечно) конформными, если существует такая
С°°-функция f, что gl = e2fg;
(b)	конформно эквивалентными, если существует такой диф-
феоморфизм а многообразия М, что метрики a*gr и g пото-
чечно конформны.
Отметим, что если метрики g’ и g конформно эквивалентны,
то а есть изометрия метрики e2fg на g1. Поэтому мы ограни-
чимся изучением случая, когда g' =e2fg.
Выразим различные инварианты метрики g' через инва-
рианты метрики g и производные функции f (относительно
связности Леви-Чивита D метрики). Как и прежде, буквы R, г,
s, W означают различные тензоры кривизны метрики g. Напом-
ним, что Df означает градиент, Af— лапласиан, a Ddf — гессиан
функции f относительно метрики g (см. 1.54).
1.159.	Теорема. Пусть (М, g) — псевдориманово многообра-
зие, a f — функция на М. Тогда инварианты псевдоримановой
метрики g} = e2fg имеют следующий вид:
(а)	связность Леви-Чивита:
D\Y = DXY + df (X) Y + df(Y)X-g(X, Y) Df;
(b)	(4, 0) -тензор кривизны:
7?1 = e2f (> - g ® (Ddf -df°df + ±\df |2g)) ;
(с)	(3, \)-тензор Вейля:
Wl = W;
(d)	тензор Риччи:
P = r-(n- 2)(Ddf - df °df) + (Af - (n - 2)| df \2)g;
(e)	бесследовая часть тензора Риччи:
Zl = Z-(n-2)(Ddf-df°df)---^(&f + \df\2)g;
(f)	скалярная кривизна:
s* = e-2f (s	2 („ _ 1) Af - (n - 2) (n - 1) | df |2);
(g)	элемент объема:
pg, =
J. Конформная деформация римановых метрик	85
(h)	оператор Ходжа на р-формах (для ориентируемого Л1):
(п—2р) f
(i)	кодифференциал на р-формах:
б*|3 =e-2f (60 — (n — 2p)iDfP);
(j)	(псевдо)лапласиан на р-формах:
Д*а = e-2f (Да — (п — 2р) d (iDfd) — (п — 2р — 2) iDf da +
+ 2(n — 2p)df/\iDfa— 2df Л 6а),	□
1.160.	Замечания, (а) Канонические изоморфизмы # и b
между ТМ и Т*М различны для g и g1. В частности, (4,0)-тен-
зоры Вейля связаны соотношением W1 = e2fW, и наоборот, если
понимать как (3,1) -тензор, то исчезает множитель e2f.
(b) Если нас интересует только один инвариант, то для
упрощения формул часто бывает удобно выбрать масштабный
множитель иначе, В частности, справедливо
1.161. Следствие, (а) Если gx = ф4Лл-2)§-, п 3, ф > 0, то
(1.161а)	ф(п+2)/(П-2)я1 = 4 2^11 Дф + 5ф.
(b) Если g1 — <p~zg (<p > 0), то
(1.161b) Zl = Z + ^-(Ddq> + -^g).
(с) Если g1 = x~ig, т > 0, то
(1.161с)	А1а = тАа4- п~2^—— iDxda-(-
4- ~~ g2P & (4ота) + Л ба.
Формула (1.161а) связана с гипотезой Ямабе (см. гл. 4 и ука-
занную там литературу). Формула (1.161b) изучается, в част-
ности, в [ОЬа].
Отметим, что некоторые инварианты не меняются при кон-
формных деформациях. Например, на четномерном ориентиро-
ванном многообразии *g' = *g на у-формах. Этим результатом
можно воспользоваться, в частности, для 4-многообразий.
1.162. Следствие. Пусть М — компактное четномерное много-
образие. Тогда для любой функции f гармонические ~ -формы
для метрик g и gl = e?fg совпадают.
«6
Гл. 1. Основные сведения
1.163. Приведем другой пример. Пусть с — изотропная геоде-
зическая на псевдоримановом многообразии (М, g), т. е. с удов-
летворяет условию g(c(t), c(t)) — O (и, значит, метрика g нери-
манова). Тогда с точностью до параметризации кривая с будет
изотропной геодезической и для псевдоримановой метрики e2fg
на М, где f — произвольная функция. Действительно,
D\c = 2df (с) с.
Полагая с1 = с о <р, где вещественная функция <р (t) находится из
уравнения <р" + 2<p'df(c) (c(t)) — 0, получаем ZJ’c, = 0.
Наконец, отметим, что вторая фундаментальная форма по-
гружения при (поточечной) конформной деформации объемлю-
щей метрики меняется не слишком сильно. Пусть II — вторая
квадратичная форма риманова погружения t: (М, g)-+(N, h).
Тогда вторая квадратичная форма II1 риманова погружения
i:	(М, e2<foi'lg)->(N, e^h)
имеет вид
II1 (U,	— V) — g(U, V)Jf(Df),
где Jf(Df) означает нормальную компоненту градиента функ-
ции f.
Основным конформным инвариантом является тензор Вейля.
В частности, поскольку для плоской метрики W = 0, тензор
Вейля оказывается препятствием к тому, чтобы псевдориманова
метрика была локально конформна плоской метрике.
1.164.	Определение. Псевдориманово многообразие (Л4, g)
называется конформно плоским, если у любой точки xg М су-
ществует такая окрестность V и такая функция f на V, что мно-
гообразие (V, e2fg) является плоским.
Отметим, что функция f не обязательно должна быть опре-
делена на всем М. Оказывается, при п 4 тензор Вейля яв-
ляется единственным препятствием к тому, чтобы многообразие
было конформно плоским.
1.165.	Теорема. При п^4 псевдориманово п-мерное много-
образие (М, g) является конформно плоским тогда и только
тогда, когда его тензор Вейля равен нулю.
Подробное доказательство см. в [Eis], с. 85, или в [Grr],
с. 188. В соответствии с теоремой 1.159, это условие равносильно
локальной разрешимости переопределенной системы уравнений
второго порядка
Ddf-dfodf + {\df\2-^)g = r.
J. Конформная деформация римановых метрик
87
Основная идея заключается в том, что при п >4 и W — 0 усло-
вия интегрируемости высших порядков отсутствуют.	□
1.166.	Замечание. Необходимое, но не достаточное условие
того, чтобы многообразие было конформно плоским, состоит в
существовании базиса из разложимых 2-форм, являющихся соб-
ственными векторами тензора кривизны Л. Это понятно, по-
скольку при W — О
1.167.	Примеры. 1) Любое многообразие постоянной секцион-
ной кривизны конформно плоско.
2)	Произведение многообразия постоянной секционной кри-
визны на S1 или на R конформно плоско.
3)	Произведение двух римановых многообразий, одно из ко-
торых имеет секционную кривизну 1, а другое (—1), конформно
плоско.
Вот краткое доказательство утверждения 3). Не совсем
строго можно написать, что g = gM + gu на Т (М X W) =
= TMy^TN. Тогда RM = gM®gM и RN = — gN®gN- Отсюда
R — Rm + Rn — ём ®ём — ён® ёк — (ём~\~ ён) ®
® (ём ёи) — ё® (ём ён)
и, значит, W = 0.
Можно проверить, что примерами 2) и 3) исчерпываются все
римановы произведения, являющиеся конформно плоскими.
1.168.	Этот же формализм позволяет получить простое до-
казательство следующего результата Э. Картана ([Саг 4]):
гиперповерхность в конформно плоском римановом многообра-
зии (с п 5) является конформно плоской тогда и только
тогда, когда ее вторая фундаментальная форма имеет либо
одно собственное значение, либо два, из которых одно имеет
кратность единица. (Часть «тогда» связана со свойствами тен-
зоров Кодацци, которые изучаются в гл. 16.)
Отметим, что теорема 1.165 неприменима при п — 2 и 3, так
как в этом случае тензор Вейля исчезает из разложения R и
результаты оказываются совсем другими.
1.169.	Теорема. Любое двумерное псевдориманово многооб-
разие конформно плоско.
Эта теорема чаще встречается в другой формулировке,
утверждающей существование «изотермических координат» (т. е.
локальных координат (х, у), в которых g = e2f (dx2 + dy2)).
«8
Гл. 1. Основные сведения
Впервые она была доказана К. Ф. Гауссом ([Gau]) в аналити-
ческом случае, а затем А. Корном ([Ког]) и Л. Лихтенштейном
([Lit]) в случае С°° (см. также оригинальное доказательство
Ж. Ж. Чженя в [Chr 1] или его изложение в [Spi], т. 4, с. 455).
В силу теоремы 1.159 это равносильно локальной разрешимости
уравнения 2Af + s = 0. Поскольку в римановом случае оператор
А является эллиптическим, локальная разрешимость уравне-
ния немедленно следует из теоремы 45 приложения.	□
1.170.	В трехмерном случае существует другое препятствие
к тому, чтобы многообразие было конформно плоским: одна из
неприводимых компонент тензора DR, так называемое тензор-
ное поле Вейля-Схоутена. Оно обращается в нуль тогда и только
тогда, когда многообразие (М, g) конформно плоско. Поскольку
кривизна R определяется тензором Риччи г (при п — 3), тензор
Вейля — Схоутена определяется компонентой разложения тен-
зора Dr. В 16.4 (v)d) мы увидим, что многообразие (Л1, g) кон-
формно плоско тогда и только тогда, когда тензор Dr симме-
тричен.
Отметим наконец, что полной классификации конформно
плоских многообразий пока нет, однако доказана
1.171.	Теорема (Н. Кюйпер, [Кдп]). Конформно плоское ком-
пактное односвязное риманово многообразие конформно экви-
валентно канонической сфере (той же размерности).
К- Первая вариация поля тензоров кривизны
1.172.	Для любого компактного многообразия М множество
«Л? всех римановых метрик на М открыто в пространстве 9^М
с компактно открытой топологией, а также с Л*-топологией. На-
помним, что определение L^-нормы (см. приложение, 3) осно-
вано на выборе метрики на М. Однако для компактного много-
образия М топология, задаваемая такой нормой, не зависит от
выбора метрики. (В геометрических задачах мы фактически
имеем дело с римановыми структурами, т. е. с римановыми мет-
риками, рассматриваемыми с точностью до диффеоморфизмов.
Этот подход развивается в гл. 4, 12.)
1.173.	Формулы для различных тензоров кривизны в локаль-
ных координатах выглядят не очень приятно (см. 1.42). Однако
они показывают, что отображения g i—> Rg (соответственно	rg,
g'f—>sg) из Ж в С°° (/\2 Af<8> Д2Л1) (соответственно 9^М, ff’M)
являются квазилинейными дифференциальными операторами вто-
рого порядка. В частности, они дифференцируемы, если Ж снаб-
К. Первая вариация поля тензоров кривизны
89
жено некоторой £л-нормой (Л 2), а пространство значений — со-
ответствующей £^_г-нормой. При этом для g^.Jt дифференциалы
этих отображений в точке g являются линейными дифферен-
циальными операторами второго порядка, которые обозначаются
через /?', r'g и s'. Они были вычислены в локальных координа-
тах специалистами по теории относительности (см. [Bln],
[Lie 2]). Опишем обобщенный подход, близкий к подходу, ко-
торый развивается в [В1е].
1.174.	Теорема. Пусть (Л4, g) —псевдориманово многообра-
зие и	Тогда дифференциалы в точке g по направлению
h связности Леви-Чивита и различных тензоров кривизны опи-
сываются следующими формулами:
(а)	для связности Леви-Чивита:
g (D'gh (X, У), Z) = 4 {Dxh (У, Z) + DYh (X, Z) - Dzh (X, У)};
(b)	для (3, \)-тензора кривизны:
R'gh (X, У) Z = (£>у0;/г) (X, Z) - (DxD'gh) (У, Z);
(с)	для '(4, 0) -тензора кривизны:
R'gh (X, X, Z, U) zh (X, U) + £>2 vh (У, Z) -
- D2X zh (У, U) - D* vh (X, Z) + h (R (X, У) Z, U) -
— h(R(X, Y)U, Z)J;
(d)	для тензора Риччи:
(e)	для скалярной кривизны:
s'eh = \ (trs Л) + 6е ( «/) - g (rg, А).
Доказательство. Поскольку разность двух связностей есть
тензорное поле, дифференциал связности Леви-Чивита является
симметрическим (2,1)-тензорным полем. Из определения 1.39
следует, что
(1.175)	g(DxY, Z) =4-{Хг(У, Z) + Yg(Z, X)-Zg(X, У)-
-g(X, [У, Z]) + g(y, [Z, X]) + g(Z, [X, У])}
для любых векторных полей X, У, Z. Отсюда легко выводится
(1.174а).
90
Гл. 1. Основные сведения
1.176.	Обозначение. Иногда бывает удобно вместо DJ* рас-
сматривать (3,0)-тензорное поле
Cgh(X, Y, Z) = g(D'gh(X, У), Z).
1.177.	Для того чтобы вычислить дифференциал кривизны R,
продифференцируем (1.11):
R'gh (X, Y)Z = D'gh (У, £>XZ) + Dy (D’Ji (X/Z)) -
- D'gh (X, DyZ) - Dx (D'gh (У, Z) + D'gh ([X, У], Z).
Отсюда немедленно следует (1.174b).
1.178.	Замечание. Мы не будем доказывать формулу (1.174с),
поскольку в книге она не используется: мы привели ее только
для полноты. Заметим, что производная не коммутирует с опе-
рациями изменения типа тензорного поля и вычисления следа
(2,0)-тензора, поскольку эти операции используют метрику. Од-
нако отметим, что	/
(а)	с помощью тождества Риччи/ (1.21) можно убедиться,
что тензорное пойе R'gh симметрично относительно пар (X, Z)
и (У, U);
(Ь)	симметрии тензора R'g(h) можно сжато отразить на
уровне символов (см. приложение, 15):
otR'g(h) = -^(tot)®h.
1.179.	Для того чтобы вычислить r'g, отметим, что операция
вычисления следа линейного отображения коммутирует с диф-
ференцированием. Поэтому, обозначая через (X) ортонорми-
рованный репер, получаем
r'gh(X, Y)=t^DKi{Cgh)(X, У, X^-D^C^X,, У, ХД
Легко видеть, что второй член равен ~ Dgd (trg/z), а первый член
можно представить в виде
Т Ё (°1,. х* (Г, X,) + rh (X, X,) - Kh {X. Г)).
£=1
Теперь из тождества Риччи (1.21) следует
С*х,. х* (У. X,) = ci. х л (Г. X,-) + л (К (X,, X) У,х,) +
+ Л(Я(Х,. Х)Х„ Г).
К. Первая вариация поля тензоров кривизны
91
Собирая все члены и замечая, что D*Dh = — ^=}Т)2Хx h (где
D* — формально сопряженный к D оператор, определенный в
1.55), получаем
(1.180а) r'h = -^(D^Dh + roh + hor-
- 2Rgh - 26*6 h - D d (tr_A)).
Здесь 5g обозначает дивергенцию, б* — формально сопряжен-
ный к ней оператор (см. 1.59), a h о k есть (2,0)-тензор, по-
строенный с помощью метрики из композиции операторов h и kr
рассматриваемых как (1,1)-тензоры, т. е. как линейные отобра-
жения ТМ на себя; наконец, символ Rg обозначает действие
кривизны на симметрические 2-тензоры, определенное в 1.131.
Остается заметить, что оператор
(1.180b)	Д£А = D‘Dh + rg°h + h°rg — 2Rgh
есть не что иное, как лапласиан Лихнеровича, определенный
в 1.143 (и ограниченный на симметрические (2,0)-тензоры). От-
сюда следует (1.174d).
1.181.	Для того чтобы вычислить s', проще всего продиффе-
ренцировать формулу se = trg rg:
s'eh=~g{h, rg) + ^g{r'gh).
Заметим, что
\ (M=Ч (M). ‘4 К (V))=- ‘V (M).
4,f = -trs(D1,df).
Отсюда немедленно следует (1.174e).	□
1.182.	Замечание. Символ оператора s' задается формулой
(1.182)	c^s'(А) = — | / |2 trgA — А (/*, /*).
Он, очевидно, сюръективен, если ковектор t не равен нулю.
Поэтому формально сопряженным к оператору s' является пе-
реопределенный эллиптический оператор, отображающий ¥?М в
S^M по формуле
(1.183)	(s;)* f = Dg df + (Agf) g - frg,
где f — произвольная функция на M. Впоследствии (в 4.33) нам
понадобится
92
Гл. 1. Основные сведения
1.184.	Предложение. Дифференциал \'g лапласиана, дейст-
вующего на функции, задается формулой
<1.184) (D = g (Dg df, h)-g (df, 6gh + ±d (tr/)).
Доказательство. Прежде всего вычислим дифференциал 6g
оператора 6g, действующего на дифференциальные 1-формы.
Поскольку б а = D*a — — tr (D а], имеем
б'Л (а) = g (h, Dga) — trg (Dji (а)).
Согласно (1.174a),
<1.185) &'gh (а) = g (h, Da) — g (a, bgh + у d (trgfc)) .
Подставляя a — df в (1.185), получаем (1.184). /	□
Дифференциалы объема и элемента объема находятся с по-
мощью простых вычислений.
1.186.	Предложение. Пусть (М, g) — псевдориманово много-
образие.
(а)	Дифференциал y'g элемента объема задается формулой
(b)	Предположим дополнительно, что многообразие М ком-
пактно, и положим vol(Af)g= pg. Тогда
м
voi (Myg h=\v'Ji=-±\ (tr/) pg.
м	м
Отметим, что для заданного элемента объема рб любой дру-
гой элемент объема pg] записывается в виде PgI=fPg, где f —
положительная функция на М.
1.187.	В качестве примеров применения этих формул приве-
дем простое следствие (1.174е) и (1.186b) для компактных мно-
гообразий Эйнштейна.
Если многообразие (М, g) эйнштейново, то rg = -^-sgg, где
sg — const. Значит, g (rg, h)=^J sgg (g, h) = ^-sg trg h. Если, кро-
ме того, многообразие М компактно, то интеграл дивергенции
(а также лапласиана) по М всегда равен нулю. Поэтому из
1.
К. Первая вариация поля тензоров кривизны	93
формулы (1.174е) для компактного эйнштейнова многообразия
(М, g) следует
Sir	2 Г
(s?) = - т ss \ (trg h) Hg = - - Sg \ tty-
MM	M
Таким образом, мы доказали
1.188.	Предложение (М. Виль, [Vil]). Пусть (М, g)— ком-
пактное эйнштейново многообразие и	Тогда
Г .	9
J(s?) Mg = --sgvol(M)'g/i.
м
В частности, если sg = 0 или vol (44)g h = 0, то функция s'g не может
иметь постоянный знак, если не равна тождественно нулю.
Отметим, что интеграл (s'ft) pg не равен производной по h
м
от полной скалярной кривизны j (sg) pg, которая более подробно
м
изучается в гл. 4.
Глава 2
Основные сведения (продолжение):
кэлеровы многообразия
2.1.	Эта вводная глава содержит замкнутое в себе изложе-
ние элементов кэлеровой геометрии как части римановой гео-
метрии. Приведенные здесь сведения понадобятся нам в даль-
нейшем, особенно в гл. 8, 11, 12, 14.
Мы попытались по возможности преодолеть распространен-
ное среди математиков, занимающихся римановой геометрией,
нежелание иметь дело с комплексной геометрией. Для этого мы
решили работать только с вещественными объектами, почти не
используя комплексных координат. Это заставило нас перепи-
сать некоторые доказательства, особенно в § Н.
Мы отдаем предпочтение тем вопросам, в которых важную
роль играет тензор Риччи. Другие аспекты теории освещаются
в обширной литературе, написанной на эту тему: в [Chr 2],
[Gr-Ha], [Hir], [Ко-No 2], [Ко-No 2], [Ko-Mo], [Wei], [Wei] и
многих других работах.
А. Почти комплексные и комплексные многообразия
2.2.	Определение. Почти комплексной структурой на связ-
ном многообразии называется гладкое поле автоморфизмов ка-
сательного расслоения ТМ, удовлетворяющее условию
Рх = - Idx, xgeM,
где Id — тождественное преобразование.
Другими словами, почти комплексная структура на многооб-
разии М задается действием поля С комплексных чисел на ТМ,
превращающим ТМ в комплексное векторное расслоение над М.
2.3.	Размерность п почти комплексного многообразия (М, I)
всегда четна. Положим
п — 2m,
где m — комплексная размерность М. Комплексный оператор J
определяет в М выделенную ориентацию, относительно которой
адаптированный ортонормированный репер {еь Je\, ..., em, Jem}
ориентирован положительно.
А. Почти комплексные и комплексные многообразия
95
2.4.	Почти комплексная структура J задает расщепление
комплексифицированного касательного расслоения ТсМ =
ssTAf®RC на два дополнительных взаимно сопряженных комп-
лексных подрасслоения:
{2.4)	ТсМ ~ Т'М © Т"М,
где в каждой точке х е М слоем Т'ХМ (соответственно Т"М)
является собственное подпространство оператора Jx с собствен-
ным значением -j-i (соответственно —I). Обратно, любое комп-
лексное подрасслоение Т'М расслоения ТсМ, дополнительное к
сопряженному, определяет почти комплексную структуру J
на М.
2.5.	Элементы из Т'М (соответственно из Т"М) называются
комплексными векторами типа (1,0) (соответственно типа
(0,1)). Любой вещественный касательный вектор X можно пред-
ставить— и притом единственным образом — в виде суммы
х = и + и,
где U (соответственно £7) есть его компонента типа (0,1) (соответ-
ственно типа (0,1)). В свою очередь комплексные компоненты
U и £7 выражаются через Х\
U = ^{X — ИХ), U = (X + iJX).
Это определяет С-линейный изоморфизм ТМ на Т'М и С-анти-
линейный изоморфизм ТУИ на Т"М.
Расщепление (2.4) комплексифицированного касательного
расслоения ТсМ индуцирует расщепление всех комплексных
тензорных расслоений на различные типы. В частности,
{2.6)	Д> = £ ЛР(Г2И)*® Л’(Т"МГ,
р+?=г
где /\СМ= /\ ®С есть расслоение С-значных r-форм, а
/\Р(Т'МУ (соответственно Д?(Т"Л£)*) обозначает расслоение
С-линейных внешних р-форм (соответственно </-форм) на Т'М
соответственно на Т"М).
2.7.	Обозначим расслоение f\P (Т'М)* ®/\Q (Т"М)* через
Дс 9 М. Его элементы называются комплексными формами
типа (р, q).
При p — q обозначим расслоение вещественных форм типа
(р, р) через /\р’РМ.
96 Гл. 2. Основные сведения (продолжение): кэлеровы многообразия
Комплексный оператор J индуцирует на кокасательном рас-
слоении Т*М ~ Д1М комплексный оператор, который также обо-
значается через J и задается формулой
(2.8)	Jt,(X) = -t,(JX), УЪ>е=ГхМ, VXeETxM, Ухе=М,
2.9. Замечание. Выбор знака объясняется тем, что действие
J должно быть согласовано с отождествлением касательного
и кокасательного расслоений, определяемым эрмитовой метри-
кой (см. 2.19).
Оператор ] можно продолжить на все /\*СМ: для любой
формы <р типа (р, q)
(2.10)	/<р = г<«'-Р>(р.
2.11.	Интегрируемость. Почти комплексная структура У назы-
вается интегрируемой, если выполняется одно из следующих
эквивалентных условий:
(i)	внешний дифференциал dQ любой 1-формы 6 типа (1,0)
принадлежит идеалу, порожденному 1-формами типа (1,0) (или,
что эквивалентно, dQ не имеет компонент типа (0,2));
(ii)	комплексный тензор кручения, или тензор Нийенхейса,
N, задаваемый формулой
(2.11)	4N (X, Y) = [X, У] + J [JZ, У] + J [X, /У] - [JZ, ГУ],
VX, У е= ТХМ, Ух е= М,
равен нулю (в правой части X, У обозначают произвольные про-
должения векторов X, У до локальных векторных полей);
(iii)	Скобка любых двух векторных полей типа (1,0) явля-
ется векторным полем типа (1,0).
2.12.	Эквивалентность этих трех условий установить нетруд-
но. Выполнение любого из них приводит к тому, что почти комп-
лексная структура J индуцируется единственной комплексной
структурой (по теореме Ньюлендера — Ниренберга, см. [Ne-Ni],
а также [Koh], [Ног 1], [Mai 1]).
2.13.	Напомним, что комплексное многообразие комплексной
размерности m представляет собой паракомпактное хаусдорфово
топологическое пространство, допускающее покрытие откры-
тыми множествами, которые гомеоморфны открытым подмноже-
ствам Ст с голоморфными функциями перехода (см., например
[Chr 2], с. 1). Отсюда следует, что комплексное многообразие
есть гладкое многообразие, касательное расслоение которого
снабжено почти комплексной структурой J, интегрируемой в
смысле 2.11.
А. Почти комплексные и комплексные многообразия
97
С другой стороны, почти комплексная структура J на много-
образии не может индуцироваться двумя неэквивалентными
комплексными структурами (см. [Ko-No 2], с. 123). Заметим,
что касательное расслоение комплексного многообразия, рас-
сматриваемое как комплексное векторное расслоение, является
голоморфным, т. е. допускает голоморфные функции перехода.
2.14.	Если почти комплексная структура J интегрируема, то
внешний дифференциал dtp любой формы <р типа (р, q) является
суммой форм типа (р + 1, q) и типа (р, q+1 )> которые обозна-
чаются через сГф и d"q> соответственно. Таким образом, мы по-
лучаем два дифференциальных оператора d' и d", сумма кото-
рых равна внешнему дифференциалу:
(2.15)	d = d' + d".
При этом
d'd" + d"d' = 0, d'2 = 0, d"2 = 0.
Определим новый вещественный дифференциальный оператор
dc, действующий на формы по формуле
(2.16)	dc<p = — Г1 </7ф = (— 1 )г 7 dJ<p,
где ф есть r-форма. Тогда
dc = i(d"-d')
или, что эквивалентно,
d" = ±(d-idc), d'= ~(d-\-idc).
Квадрат оператора dc равен нулю, а операторы d и dc анти-
коммутируют:
ddc + dcd — 0, (dc)2 = 0.
С другой стороны,
(2.17)	ddc = 2id'd".
2.18.	Пусть Е — комплексное векторное расслоение над М.
Комплексная Е-значная r-форма определяется как сечение рас-
слоения Д r М ®СЕ.
Если расслоение Е снабжено iC-линейной связностью V, то,
как и в вещественном случае, можно определить внешний диф-
ференциал dv в пространстве Е-значных форм. Если М снаб-
жено почти комплексной структурой 7, расслоение /\сМ®сЕ
очевидным образом расщепляется на типы, а если структура 7
7 А. Бессе, т. 1
98 Гл. 2. Основные сведения (продолжение): кэлеровы многообразия
интегрируема, то расщепляется в сумму
dv = dv'+dv",
как и в скалярном случае. Оператор dvc определяется так же,
как в 2.16. Однако квадраты всех этих операторов уже не равны
нулю, а зависят от кривизны V.
Далее буква М обозначает комплексное многообразие или,
что эквивалентно, многообразие размерности п = 2т, снаб-
женное интегрируемой почти комплексной структурой /.
В. Эрмитовы и кэлеровы метрики
2.19.	Определение. Эрмитовой метрикой на многообразии М
называется такая риманова метрика g, что
g (JX, JY) = g (X, У), VX, Y е ТХМ, Vx е М.
Это означает, что метрический тензор имеет тип (1,1), т. е.
/-инвариантен.
2.20.	Мы сохраним одни и те же обозначения для объектов
римановой геометрии и их полилинейных продолжений на комп-
лексифицированные расслоения.
В частности, скалярное произведение (•, •) комплексных
тензоров или форм С-билинейно. Оно индуцирует С-линейные
изоморфизмы Т’СМ ТСМ и Ь: ТСМТ'СМ, переставляю-
щие типы. Отметим, что подрасслоения Т'М и Т"М вполне изо-
тропны относительно скалярного произведения.
2.21.	Оператор Ходжа «- (см. 1.51) отображает формы типа
(р, q) в формы типа (т— q, т — р). Операторы « и J, дейст-
вующие на формы, коммутируют.
2.22.	Определим с помощью оператора Ходжа «• операторы
кодифференцирования, соответствующие дифференциальным
операторам d, d', d" и dc:
б =—i>' =—*d"*, 6" = —*d'*, 6C =—*dc*
(ср. c 1.56). Пары (d, 6), (d', 6"), (d", 6'), (dc, 6е) состоят из
операторов, формально сопряженных друг другу относительно
глобального скалярного произведения
(q>, ф)=	(ф, ф)це.
м
В. Эрмитовы и кэлеровы метрики
99
2.23.	Оператор Ходжа * и операторы кодифференцирования
можно определить и на комплексных £-значных формах, где
Е — произвольное комплексное векторное расслоение с С-ли-
нейной связностью V.
2.24.	Определим эрмитово скалярное произведение h в ZcAf:
(2.24)	h(U, V) = g(U, V), VU, V <еДТсМ)х, VxeeM.
Ограничение h на подрасслоение Т'М при отождествлении 2.5
подрасслоения Т'М с ТМ индуцирует эрмитово скалярное про-
изведение Н в ТМ:
(2.25)	И (X, Y) = 1- [g (X, У) - ig (JX, К)],
уХ, УееТхМ, VxeeM.
2.26.	Установим линейное взаимно однозначное соответствие
между векторным расслоением SX’XM вещественных симметриче-
ских J-инвариантных билинейных форм и расслоением Л ’’1 М,
сопоставив сечению Ь расслоения 2-форму 0:
(2.26)	0(Х, Y) = b(JX, У), ЧХ,У^ТхМ, УхееМ.
Говорят, что /-инвариантные билинейные формы Ь и 0 ассоции-
рованы друг с другом. При этом 2-форма 0 называется положи-
тельной (соответственно отрицательной), если форма b положи-
тельно (соответственно отрицательно) определена.
2.27.	Определение. Кэлеровой формой <о эрмитовой метрики
называется 2-форма, ассоциированная с метрическим тензором.
Кэлерова форма <о равна (с точностью до множителя —1/2)
мнимой части эрмитова скалярного произведения Н.
2.28.	Определение. Эрмитова метрика называется кэлеровой,
если комплексный оператор J параллелен относительно связ-
ности Леви-Чивита:
(2.28)	DJ = 0oDxJY = JDXY, VX, У <^ТХМ, VxeAl.
2.29.	Предложение. Эрмитова метрика является кэлеровой
тогда и только тогда, когда форма со замкнута.
Доказательство. Если метрика кэлерова, то тензоры g и J
параллельны. Но тогда форма со параллельна и, значит, зам-
кнута. Обратное утверждение является более тонким (см.
[Ko-No], с. 148).	□
2.30.	Предложение. Эрмитова метрика является кэлеровой
тогда и только тогда, когда в окрестности любой точки хеМ
7*
100 Гл. 2. Основные сведения (продолжение): кэлеровы многообразия
существует геодезическая комплексная система координат, т. е.
комплексная система координат, относительно которой данная
метрика совпадает с плоской метрикой с точностью до малых
второго порядка:
<2.30)	g{d/dz, d/dz^ = 6afi, D(d/dza) = 0
в точке х для а, р — 1, ..., т.
Доказательство. См. (Wei], с. 196, [Gr-Ha], с. 108, (D-G-M-
S], с. 265.
Отметим, что экспоненциальное отображение (см. 1.27) яв-
ляется голоморфным и, значит, задает комплексные геодезиче-
ские координаты только в плоском кэлеровом многообразии.
2.31.	Построим с помощью кэлеровой формы два линейных
оператора L и А, действующих на формы. Оператор L внешнего
умножения произвольной формы <р на о задается формулой
(2.31)	£ф = (оА<р,
а оператор А внутреннего умножения на <в определяется как
(формально) сопряженный к L, т. е. как свертка с <в.
Форма <р называется примитивной, если Аф = 0. Если <р есть
2-форма, то скаляр Аф равен просто скалярному произведению
(ф, (в) кэлеровой формы <в и ф, т. е. следу tr ф формы ф относи-
тельно (В.
2.32.	Предложение. Если эрмитова метрика кэлерова, то
(2.32)	[A, d] = - 6е,	[A, dc] = 6.
Доказательство. Одно из этих равенств легко следует из дру-
гого. В силу предложения 2.30 достаточно проверить их для ка-
нонической плоской метрики в С"‘. Для этого нужно провести
довольно хлопотные, но несложные вычисления (см. [Gr-Ha],
с. 111—114).	□
2.33.	Применив (2.32) к замкнутой 2-форме ф типа (1,1),
получим
(2.33)	бф = —йс(1гф).
В частности, форма ф гармонична тогда и только тогда, когда
она имеет постоянный след. С другой стороны, формулы (2.32)
остаются справедливыми и для Е-форм, где Е— векторное рас-
слоение с линейной связностью V. Для любой 2-формы Ф типа
(1,1) со значениями в Е соотношение (2.33) принимает вид
(2.34)	б^ф = — /V (tr Ф),
В. Эрмитовы и кэлеровы метрики
101
где tr Ф есть след формы Ф по базовым индексам, т. е. свертка
Ф с со. Применяя это соотношение к кривизне R кэлеровой мет-
рики, рассматриваемой как замкнутая 2-форма со значениями
в A^Af, мы немедленно получаем, что кривизна кэлеровой мет-
рики гармонична тогда и только тогда, когда ее тензор Риччи
параллелен (см. [Mat 3]; более сильный результат приводится
в гл. 16).
2.35.	Замечание. Легко проверить, что коммутатор В =
= [A, L] действует на r-форму ф по формуле
Вср = (т — г) ф.
С другой стороны,
[В, L] = - 2L,	[В, А] = 2А.
Таким образом, мы получили линейное действие комплексной
алгебры Ли ©1(2, С) специальной линейной группы второго
порядка в пространстве комплексных форм в любой точке М.
Применяя хорошо известную теорию представлений алгебры
Ли ©1(2, С), легко получаем теорему Лефшеца о разложении:
Ф =	2 ЕРФР, (г ~ тУ — тах (0> г ~ т)>
Р52(г-т)+
где ф — произвольная r-форма, а фр — примитивные (г—2р)-
формы. Если кэлерова форма замкнута, то это действие инду-
цирует действие ©1(2, С) в пространстве комплексных когомо-
логий, и мы получаем аналогичное разложение пространства
когомологий через примитивные когомологии. (Подробности, а
также другие результаты, в том числе трудную теорему Леф-
шеца, см. в [Wei], гл. V, или [Gr-Ha], гл. 7.)
2.36.	Любую вещественную билинейную форму ф можно рас-
сматривать как гомоморфизм ТМ-*-Т*М, если положить
ф (X) = 1хф,
а также (если воспользоваться метрикой g = (-, •)) как эндо-
морфизм ТМ, задаваемый формулой
(ф(Х), Г) = ф(Х, У).
В зависимости от контекста ф(Х) означает либо вектор, либо
двойственную ему 1-форму. Если р— вещественная 2-форма
типа (1,1), а b — ассоциированная с ней симметрическая форма
(см. 2.6), то соответствующие эндоморфизмы ТМ связаны со-
отношением
P(X) = 6(JX).
Эндоморфизм р (соответственно Ь) симметричен (соответствен-
но кососимметричен) и коммутирует с J, т. е. является косоэрми-
102 Гл. 2. Основные сведения (продолжение): кэлеровы многообразия
товым (соответственно эрмитовым) в вещественном смысле.
Продолжив эндоморфизм р (соответственно b) С-линейно на
ТсМ и затем ограничив его на Т'М, мы получим косоэрмитов
(соответственно эрмитов) в комплексном смысле эндоморфизм
эрмитова голоморфного касательного расслоения (Т'М, h).
2.37.	Одновременное использование вещественного и комп-
лексного подходов может привести к недоразумениям. Напри-
мер, след формы р, рассматриваемой как (вещественный) эндо-
морфизм ТМ, равен нулю, в то время как след этой же формы,
рассматриваемой как С-линейный эндоморфизм Т'М, есть чисто
мнимое комплексное число, вообще говоря отличное от нуля.
Оно называется комплексным следом формы р, обозначается
trcP и связано с определенным в 2.31 вещественным следом tr р
формулой
(2.37)	trc Ф = i • tr ф.
2.38.	Для 2-формы ф типа (1,1) разложение Лефшеца при-
нимает вид
(2-38)	ф = 2£±.й) + ф0(
где примитивная часть <р0 формы ф совпадает с ее бесследовой
частью.
2.39.	Отметим, что эндоморфизм, ассоциированный с кэле-
ровой формой «о, совпадает с J, a tr<o = m.
(2.40). Слой Д1’1 расслоения /\1’1М можно отождествить
с алгеброй Ли и(щ) унитарной группы U (т) с помощью любой
из предложенных интерпретаций. Расслоение Л *’1М можно
отождествить с векторным расслоением, ассоциированным с
присоединенным представлением Adt7(m) группы U(т) на
u(m) и естественным главным U(m) -расслоением, определенным
эрмитовой метрикой.
Отметим, что последнее расслоение можно описать как рас-
слоение адаптированных ортонормированных реперов на ТМ
(см. 2.3) или как расслоение ортонормированных реперов на
Т'М относительно эрмитова скалярного произведения h.
С. Тензор Риччи и форма Риччи
2.41. Помимо обычных свойств симметрии тензора кривизны
кривизна R связности Леви-Чивита кэлеровой метрики удовле-
творяет соотношению
(2.42)	R (X, У) (JZ) = J (R (X, У) z), VX, У, Z е ТХМ, Vx 6= М.
С. Тензор Риччи и форма Риччи	103
Таким образом, кэлерова кривизна R является вещественной
2-формой типа (1.1) со значениями в векторном расслоении
косоэрмитовых эндоморфизмов ТМ как в вещественном, так и
в комплексном смысле (см. 2.36), т. е. в Д1'1^.
Кроме того, кэлерову кривизну можно рассматривать как
симметрическое сечение векторного расслоения Д *’1М <8> Д *’1М
или как поле симметрических эндоморфизмов векторного рас-
слоения Д *’1М. Все эти интерпретации кэлеровой кривизны
оказываются полезными.
2.43.	Кэлерова кривизна, рассматриваемая как поле эндо-
морфизмов, называется оператором кэлеровой кривизны. Он
совпадает с оператором, индуцированным на расслоении
/\,,1Мс /\2СМ римановым оператором кривизны, действую-
щим на Д2 М.
2.44.	Определение. Формой Риччи р называется образ Р(ы)
кэлеровой формы и при действии оператора кэлеровой кри-
визны.
2.45.	Предложение. Тензор Риччи г кэлеровой метрики пред-
ставляет собой вещественную симметрическую билинейную
форму типа (1,1), а ассоииированная с ним 2-форма есть форма
Риччи р.
Доказательство. Пусть {ei, Je\, .... em, Jem}—ортонорми-
рованный базис касательного пространства ТХМ в любой точке
х е М, а X, У — векторы из ТХМ. Тогда
tn	m
г(Х, У)= Е (R(ea, Х)еа, У)+ Е (R(Jea, X)Jea, У) =
а=1	а=1
tn	тп
= Е (R(ea, X)Jea, JY) - Е (Ж, Х)еа, JY) =
а=1	а=1
m
= Е (R(ea, Jea)X, JY).
а=1
Второе равенство получается с помощью (2.42), а последнее
равенство эквивалентно алгебраическому тождеству Бьянки 1.24.
Таким образом, в произвольном адаптированном ортонормиро-
ванием базисе {еа, Jea}, а = 1, .... пг, кэлерова форма при-
нимает вид
tn
(2.46)	ы = Е еа A Jea.	□
а=1
2.47. Предложение. Форма Риччи р замкнута.
104 Гл. 2. Основные сведения (продолжение): кэлеровы многообразия
Доказательство. В силу свойств симметрии кэлеровой кри-
визны R форма р равна свертке кривизны R, рассматриваемой
как Д ’’1М- значная 2-форма, и кэлеровой формы со, рассматри-
ваемой как Д *’1 М-значная 0-форма
р = R Л и.
Вообще, если ф и ф представляют собой Д *’1 ЛТ-значные р-фор-
му и //-форму соответственно, то через ф Л ф обозначается ска-
лярная (р + q) -форма, которая получается, если взять скаляр-
ное произведение их послойных частей и внешнее произведение
базовых частей. Легко убедиться, что
(2.48)	d (<р Л ф) = dD<p Л ф + (— 1)р<7ф Л сРф.
Применяя это соотношение к R Л © и учитывая, что Д *’1 Al-
значная форма R замкнута в силу дифференциального тож-
дества Бьянки (см. 1.14), а форма со замкнута как параллельная
форма, мы немедленно получаем требуемый результат. □
2.49.	Замечание. Из этого доказательства следует более об-
щее утверждение о том, что образ 7?(<р) любой параллельной
2-формы ср типа (1,1) при действии оператора кэлеровской
кривизны замкнут.
2.50.	Тензор Риччи г в римановой геометрии входит в виде
слагаемого нулевого порядка в известную формулу Бохнера
(см. 1.155)
(2.51)	A£ = 6Z)£ + r(X),
где g— произвольная 1-форма, а X — двойственное к ней век-
торное поле (обозначения см. в 2.36). Аналогичная ситуация
складывается в кэлеровой геометрии, где г входит в еще одну
формулу Вейценбёка, содержащую операторы D+ и D~, которые
определены на 1-формах (а тем самым ввиду метрической двой-
ственности и на векторных полях) следующим образом. Для
любой 1-формы g билинейная форма DZ, представляется в виде
(2.51)	Dl = D+l + D~l,
где Z)+g (соответственно Z)_g) есть /-инвариантная (соответ-
ственно J-косоинвариантная) форма. Другими словами, Z)+g и
Z)-g есть части типа (1,1) и типа (2,0) + (0,2) формы Dc.
2.53.	Предложение. Пусть g—произвольная 1-форма, а X —
двойственное к ней векторное поле. Тогда
b(D4-D-$ = r(X).
С. Тензор Риччи и форма Риччи
105
Доказательство. Если X — векторное поле, то /?(•, -)Х есть
77И-значная 2-форма
/?(•, • )X — — dDDX
(см. 1.12). С помощью 2.36, 2.32 и замечания 2.34 получаем
г (X) = - р (JX) = AdD DJX = - (&D)C DJX = t>D(J • DJX),
где J-DJX означает действие (2.8) оператора J на ГМ-значную
1-форму DJX. Остается заметить, что J-DJX отождествляется
с разностью D+g— ZJ-g.	□
2.54.	Замечание. Ограничение оператора б на пространство
вещественных билинейных форм типа (1,1) (соответственно
типа (2,0)+ (0,2)) есть формально сопряженный к D+ (соответ-
ственно к Z)-) оператор.
2.55.	Замечание. Сравнивая (2.53) с формулой Бохнера, по-
лучаем
(2.55)	=
для любой 1-формы g.
Отсюда следует, что 1-форма g гармонична на компактном
многообразии тогда и только тогда, когда она принадлежит
ядру оператора D+.
Отметим, что Z>+| не зависит от выбора кэлеровой метрики.
На самом деле гармоничность g равносильна голоморфности ее
(1,0)-составляющей (см. 2.102).
2.56.	Замечание. Сравнивая (2.52) с разложением
(2.56)	DZ = ^dl + ^(Lxg)0-^&Z-g
билинейной формы £)g относительно действия ортогональной
группы О (2m), где X, как обычно, означает двойственное к g
векторное поле, а (-)о означает бесследовую часть формы отно-
сительно g, мы немедленно получаем соотношение
(2.56а)	6£>-g = 46(Lxg)0-4^-d6g
или, что то же самое (см. (1.60)),
(2.56b)	6£)^ = 6d’g-у dfig
для любой 1-формы.
106 Гл. 2. Основные сведения (продолжение): кэлеровы многообразия
D. Голоморфная секционная кривизна
2.57.	Определение. Голоморфной секционной кривизной на-
зывается функция Н, задаваемая на расслоении единичных ка-
сательных векторов UM формулой
(2.57)	Н (X) = (R(X, JX)X, JX), VX<=UxM,
Другими словами, Н (X) есть секционная кривизна комплексной
прямой, задаваемой вектором X, т. е. 2-плоскости, натянутой на
X и JX.
2.58.	Голоморфная секционная кривизна определяет весь
тензор кэлеровой кривизны, подобно тому как секционная кри-
визна определяет весь риманов тензор кривизны (первое
утверждение легко выводится из второго). Как и в римановом
случае, если функция Н постоянна на каждом слое 1)ХМ, то она
постоянна всюду (при т>1). Оператор кэлеровой кривизны,
соответствующий постоянной голоморфной секционной кривизне,
равной с, имеет вид
(2.58)	R = | ((m + 1) Id (	+ Id Г л, ,	,
где т — комплексная размерность М\ Rio— тривиальное ве-
щественное линейное подрасслоение расслоения /\1’1М, порож-
денное кэлеровой формой со; AJ’1 Л1— векторное расслоение
вещественных примитивных 2-форм типа (1,1); Id — тождест-
венный оператор. Отметим, что тождественный оператор на
/\'-1М не является оператором кэлеровой кривизны никакой
кэлеровой метрики, так как он не удовлетворяет первому тож-
деству Бьянки.
2.59.	Пример. Комплексным проективным пространством
СРт называется многообразие комплексных прямых в Ст+1,
проходящих через начало координат, или, что эквивалентно,
СРт есть фактор-пространство многообразия Cm+1—{0} по
естественному действию группы С *. Пусть Ui — образ открытого
множества в C,'m+I — {0}, заданного в декартовых координатах
(z1, ..., zm+l) условием z1’=/= 0 при проектировании С"4-1 —
— {0}—►СР"1. На каждом множестве Lit определены комплекс-
ные координаты {<%“}, а = 1, ..., т, где
za	za+i
iXa = —r, а < z; txa - —j- , a i.
z	zl
Таким образом, в CiP"’ задана структура комплексного много-
образия. Рассмотрим теперь 2-форму <вс типа (1,1), которая в
D. Голоморфная секционная кривизна
107
каждой окрестности Ut задается формулой
т
(2.59)
<йс =4-мс ios (1 + у, । I2).
\	а=1 J
где с — положительное число. Эта 2-форма является кэлеровой
формой кэлеровой метрики, которая называется метрикой Фу-
бини— Штуди (с параметром с). Голоморфная секционная кри-
визна этой метрики постоянна и равна с.
Стандартная метрика Фубини — Штуди соответствует с — 4.
2.60.	Пример. Комплексным тором (комплексной) размер-
ности m называется фактор-пространство пространства С"1 по
некоторой решетке Г. Плоская метрика в Ст индуцирует пло-
скую кэлерову метрику в Ю.^/Г, где Г — произвольная решетка.
Обратно, любое плоское компактное кэлерово многообразие го-
ломорфно накрывается комплексным тором (см. [Bie]).
2.61.	Пример. Пусть Dm — единичный шар в С"1. Тогда
2-форма
z	m
(2.61)	<йс = 4 ddc log ( 1 - УI z“ |2
\	а=1
является кэлеровой формой полной кэлеровой метрики в Dm,
параметризованной положительным числом с, которая назы-
вается метрикой Бергмана. Голоморфная секционная кривизна
этой метрики постоянна и равна —с.
Стандартная метрика Бергмана соответствует с — 4.
2.62.	Обратно, любое компактное кэлерово многообразие по-
стоянной голоморфной секционной кривизны с изометрично
СРт с метрикой Фубини — Штуди при с > 0 или компактному
фактору Dm с метрикой Бергмана по дискретной группе изо-
метрий при с < 0 (см. [Ko-No], с. 170).
2.63.	Разложение тензора кэлеровой кривизны. Разложение
Лефшеца 2.35 для Д1,1 М индуцирует разложение тензора кэ-
леровой кривизны, рассматриваемого как сечение расслоения
До 1 М® Д ’’1М. Получаем?
(2.63)	р =	<й®<й + 4-(й®р04-4-р0®<й4-в,
III	III
где ро — примитивная часть формы Риччи, а В — сечение под-
расслоения До 1 М® До ' М.
108 Гл. 2. Основные сведения (продолжение): кэлеровы многообразия
Тензор В, рассматриваемый как эндоморфизм Др’Л1, допу-
скает разложение
(2.64)	+
где след Во равен нулю, a tr В означает след В.
Поскольку след оператора кэлеровой кривизны равен s/2,
где s — скалярная кривизна, мы заключаем, что
(2.6S)	(гВ = 4(1-Л).
2.66.	Из определения 2.57 следует, что голоморфная секцион-
ная кривизна постоянна тогда и только тогда, когда р0 и Во
равны нулю. В этом случае скалярная кривизна тоже постоянна
и равна
(2.66)	s — m (in — 1) с,
где с — значение голоморфной секционной кривизны.
2.67.	Сравнивая разложения 1.114 и (2.63) римановой кри-
визны, получаем следующие соотношения между нормами:
(2.67)
| ро |2 = (m — 1)| Z |2,
s2 = 4m(2m- 1)| U |2.
Отсюда следует
2.68.	Предложение. Нормы компонент U и W кривизны кэ-
лерова многообразия (комплексной) размерности m > 1 свя-
заны неравенством
(2.68)	l^l2>^rlt/|2.
При m > 2 равенство имеет место тогда и только тогда, когда
голоморфная секционная кривизна постоянна. В частности, при
т>2 любая конформно плоская кэлерова метрика является
плоской.
2.69.	Замечание. При т = 2 неравенство (2.68) сводится к
очевидному неравенству
\W+ |2<| Н7|2,
а равенство имеет место тогда и только тогда, когда кэлерова
метрика является автодуальной или конформно полуплоской
(U7- = 0).
Е. Классы Чженя
109
Если, кроме того, метрика является конформно плоской, то
кривизна редуцируется к своей компоненте Z. В частности, кри-
визна гармонична (см. § Е гл. 16), а тензор Риччи, согласно
2.34, параллелен. Легко показать, что любое компактное кон-
формно плоское кэлерово многообразие комплексной размер-
ности 2 локально накрывается произведением римановых по-
верхностей с метриками постоянной кривизны, различающейся
только знаком.
Е. Классы Чженя
2.70.	Характеристические классы комплексного многообразия
М выражаются через кэлерову кривизну R произвольной кэле-
ровой метрики следующим образом. Пусть Р — вещественная
Ас1{/(т)-инвариантная симметрическая р-полилинейная форма на
алгебре Ли и(т). Благодаря Аб^тгинвариантности она инду-
цирует симметрическую р-полилинейную форму на векторном
расслоении Л1М, которая тоже обозначается Р. Эта форма
определяет на М вещественную дифференциальную 2р-форму
типа (р, р)
(2.70)	ср (R) = -^Р (R,..., R),
где R, конечно, рассматривается как Д *’1 41-значная 2-форма.
Можно доказать, что форма cp(R) замкнута и ее класс кого-
мологий не зависит от выбора кэлеровой метрики (см. [Chr 3],
с. 113—115). Таким образом, мы получаем гомоморфизм из про-
странства I(m) Аб{/(т)-инвариантных симметрических г-полили-
нейных форм на u(m) в пространство когомологий Н*(М, R),
который называется гомоморфизмом Чженя — Вейля. Его образ
называется пространством характеристических классов многооб-
разия М.
2.71.	Замечание. Мы получим этот же гомоморфизм, если в
качестве R возьмем кривизну любой комплексной связности, т. е.
линейной связности, относительно которой комплексная струк-
тура J параллельна (см. 1.15).
Заметим, что любой элемент Ре/(М) полностью опреде-
ляется ассоциированной с ним полиномиальной функцией Р на
u(m). При этом Р является полной поляризацией Р. Поэтому
I (т) отождествляется с кольцом Ас1(Дт)-инвариантных полино-
мов, а гомоморфизм Чженя—Вейля является кольцевым гомо-
морфизмом. Кольцо 1(т) порождается единицей и т элемен-
тарными симметрическими полиномами
(2.72)	др (А) = др (diag (iXI( ..., iZ.J) == (Л,, ...» Лт),
р — 1, ..., т,
НО Гл. 2. Основные сведения (продолжение): кэлеровы многообразия
где diag(i'Ai, .tXm) — диагональная каноническая форма про-
извольной косоэрмитовой матрицы А
о 1
diag(^i.....i^m) =
I О

a <jp есть p-я элементарная симметрическая функция
Xm)= £ Z,-J . . . Л;.
t[< ... <lp
2.73.	Определение. Вещественным р-м классом Чженя ср(М)
называется образ полиномиальной функции ор при гомомор-
физме Чженя — Вейля. Соответствующая 2р-форма аД/?) назы-
вается каноническим представителем класса ср(М), ассоцииро-
ванным с кэлеровой метрикой.
2.74.	Лемма. Пусть Sp— полная поляризация полинома др,
рассматриваемого как функция на Л^М. Тогда
(2.74)	Sp(<pb <Рр)=-^2 Лр(<Р! л ... л <рр).
При р = 1 имеем Лф = 2|(ф). Из свойств симметрии опера-
тора кривизны вытекает
2.75.	Предложение. Первый класс Чженя С|(Л4) представ-
ляется 2-формой -2~р.
2.76.	Следствие. Вещественный класс когомологии формы
Риччи р зависит только от комплексной структуры в М.
Позже мы докажем это непосредственно (см. 2.101).
При р = 2 с использованием квадрата Л2 оператора Л из
2.32 доказывается
2.77.	Лемма.
(2.77)	22(ф, Ф) = 7-Л2(фл Ф) = у(1г<р • trap —(ф, ар)) =
=	trф tr 'ф — (Фо, Фо)],
где фо, ар0— примитивные части ф и ар соответственно (см. 2.32).
Доказательство (упражнение).	□
Е. Классы Чженя
111
Рассмотрим симметрическую билинейную форму q на
(2.78) q (<р, ф) = 4г (ЯР А ф) = tr <р • tr ф — (<р0, Фо)] -
Vqp, »|:(= Ах ' (М), Xfx е М.
Она невырожденна и имеет сигнатуру (1, т2— 1). Форма q
индуцирует на Д1,1 Л4 ® Д1’1Л1 невырожденную симметриче-
скую билинейную форму сигнатуры (т4— 2т2 + 2, 2т2— 2),
которая тоже обозначается q. Обозначим через q(R, R) квадрат
нормы кэлеровой кривизны R относительно q.
Пусть с2(^)= 4^2-S2(A R) есть канонический представи-
тель второго класса Чженя. Из (2.27) легко выводится, что
(2.79)	Jf(c2(R)) = -^q(R, RY
Получим с помощью разложения 2.63 для R формулу Апта
([Apt]). Имеем
(2.80)	4 А>(с, (Л)) =	(т^+Т) - 2-^1 Р» F +1 В. Р) =
=	((2m—3)(m—l)|t/|2—(2m—3)|Z|2+| W |2),
в то время как
(2.81)
Значит,
(2.82)	4 Л2 (2(-ш+~ с2(7?) ~ ci(/?)) =
Интегрируя по М, получаем
(2.80а) (m2 g)f (с2 U [®Г-2) (М) =
1 С /	— 1	2	2 (т 1) I |2 г । р г2А __
= &?Ц4^+П S---------------— |P°I +lBol)Pg —
м
= -glj- J ((2m - 3)(m - 1)1 и |2 - (2m - 3)| Z |2 + | W |2) pg,
м
<2-8|а>	дМ	Р«’
м
112 Гл. 2. Основные сведения (продолжение): кэлеровы многообразия
<2'82а» (^2jr((^iyJL^-c5)UM"'!)<AO =
S (- (1 - 7?)IР»f + ^1 В° 0 !*«•
м	__
2.83. Замечание. Левые части (2.80а), (2.81а), (2.82а) зави-
сят только от классов Чженя Cj и с2 и от кэлерова класса [со]
(см. 2.114).
Более того, при т — 2 числа Чженя c2t и с2 зависят только
от выделенной ориентации многообразия. Они связаны с сигна-
турой о и характеристикой Эйлера — Пуанкаре % соотноше-
ниями
(2.84)	с2 = Зт + 2х, с2 = х-
В частности, при пг — 2 формула (2.82а) принимает вид
(2.85) Зс,-= z-Зт =	(--11р„|* + |В.|>) ц,.
м
F. Форма Риччи как форма кривизны
линейного расслоения
2.86. Пусть L — голоморфное линейное расслоение над М,
т. е. комплексное векторное расслоение (комплексного) ранга 1
с голоморфными функциями перехода. Будем считать, что L
снабжено эрмитовым скалярным произведением h в слоях и
связностью V, согласованной с h. Зафиксируем локальный голо-
морфный репер I в L, т. е. локальное голоморфное сечение без
нулей. Тогда связность V задается локальной 1-формой т]:
(2.87)	vx/ = n(X)/, УХевТхМ. Vx(=M.
Согласованность V и /г означает, что
X-h(l, l) = h(yxl, + Vx/) = (n + n)W-ft(/, 0
или, короче, что
(2.88)	т) 4- т) = d log | /12,
где |/| означает квадрат й(/, /) нормы I.
С другой стороны, кривизну /?' можно определить обычным
способом:
(2.89)	Rx (X, Y)1 = Vy (yxl) -	(V/) - V[y. X]l = - dn (X, Y) I.
Таким образом, кривизну /?v можно рассматривать как гло-
бально определенную скалярную 2-форму, локально равную
F. Форма Риччи как форма кривизны линейного расслоения
113
—dr\. В частности, форма /?v замкнута и в силу 2.88 является
чисто мнимой скалярной формой.
2.90.	Предложение. Кривизна равна нулю тогда и только
тогда, когда в окрестности любой точки из М существует парал-
лельное сечение расслоения L.
Доказательство. Это предложение является частным случаем
более общего утверждения из теории линейных связностей, но
оно легко проверяется непосредственно. Действительно, если
2?v = 0, то локальная форма связности относительно локального
голоморфного сечения I по лемме Пуанкаре равна (возможно,
в меньшей окрестности фиксированной точки х е М) точной
форме d(logf). Сечение f-l является параллельным.	□
Среди эрмитовых связностей мы выделили класс предпочти-
тельных связностей, которые удовлетворяют дополнительному
условию
2.91.	Сечение Vtjl равно нулю для любого голоморфного се-
чения I и вектора О типа (1,0).
Легко убедиться, что для такой связности
(2.92)	т] == d'log | /12
и, значит,
(2.93)	= — d"d' log 1112,
где I — произвольное локальное голоморфное сечение без нулей.
Отметим, что из (2.92) следуют существование и единствен-
ность предпочтительной связности, которая называется эрмито-
вой связностью или связностью Чженя пары (L, h) (см. [Chr 2],
§ 6).
2.94.	Для этой связности любое локальное параллельное се-
чение голоморфно, так как если сечение f-l параллельно, а I
голоморфно, то df имеет тип (1,0), т. е. функция f голоморфна.
2.95.	На комплексном многообразии существуют два выде-
ленных голоморфных линейных расслоения (не считая тривиаль-
ного): каноническое линейное расслоение К и двойственное к
нему расслоение К*.
Каноническое линейное расслоение К есть расслоение
Дт (7’,Л1)*-форм типа (т, 0), а антиканоническое линейное рас-
слоение К* есть расслоение Л Т'М кососимметрических
контравариантных тензоров типа (т, 0).
Оба этих расслоения наследуют послойную эрмитову метрику
от послойной эрмитовой метрики h расслоения Т'М и связности,
8 А. Бессе, т. 1
114 Гл. 2. Основные сведения (продолжение): кэлеровы многообразия
индуцированные в К и К* связностью Леви-Чивита, являются
эрмитовыми.
Тензор кривизны связности Чженя в К. (соответственно в
Л*) есть след (соответственно минус след) — в комплексном
смысле — вертикальной части кэлеровой кривизны Р.
Учитывая симметрию оператора кэлеровой кривизны, сразу
получаем
2.96.	Предложение. «Форма Риччи р с точностью до множи-
теля i (соответственно —i) равна тензору кривизны канониче-
ского линейного расслоения К. (соответственно антиканониче-
ского расслоения К*).
2.97.	Следствие. Форма Риччи равна нулю тогда и только
тогда, когда в окрестности любой точки из М существует па-
раллельная (следовательно, голоморфная) форма типа (т, 0).
Доказательство. Это утверждение непосредственно следует
из предложений 2.90 и 2.96.	□
2.98.	Следствие. Пусть {еа}, а=1, ..., т, — локальный го-
ломорфный репер расслоения Т'М. Пусть (ga^) — эрмитова мат-
рица, составленная из скалярных произведений (®а> е₽)’ а
det(£a₽)“ ее определитель. Тогда форму Риччи р можно ло-
кально представить в виде
(2.98)	Р = — id'd" log det (gn₽)	.
Доказательство. Согласно 2.93 и 2.96,
(2.99)	р = — id'd" log Ш2,
где I — локальное голоморфное сечение без нулей расслоения
К*. В частности, для / = ei Л ... Л ет получим 1112 — det (gap).
□
2.100.	Следствие. Форма Риччи р зависит только от комп-
лексной структуры и формы объема pg кэлеровой метрики g.
Доказательство. Это утверждение тривиально следует из
2.98.	□
2.101.	Замечание. Пусть go — фиксированная кэлерова мет-
рика на комплексном многообразии М с формой объема pg(i и
формой Риччи ро. При замене метрики g0 кэлеровой метрикой g
форма объема меняется на pg — fpg, где f—положительная
функция, а форма'Риччи — на pg = pgo— id'd" log f. Это утверж-
дение следует из 2.98.
G. Теория Ходжа
115
Таким образом, форма Риччи любой кэлеровой метрики на
комплексном многообразии М определяет один и тот же класс
когомологий.
Можно поставить вопрос: любая ли 2-форма pg„ — id'd" log f,
где f — положительная функция, является формой Риччи кзле-
ровой метрики?
Другими словами: любая ли форма объема р, т. е. 2т-форма
без нулей, индуцирующая ориентацию М, является формой
объема кэлеровой метрики?
Это знаменитая проблема Калаби. Ответ таков: да, если М
компактно (см. гл. 11).
G. Теория Ходжа
Рассмотрим операторы Лапласа
Д = df> + 6d, Д' = d'6' + d'd', Д" = d"t>" + f>"d",
Дс = dc6c + 6е Дс.
Сформулируем одну из главных особенностей кэлеровой мет-
рики.
2.102.	Предложение. Операторы Лапласа кэлеровой метрики
удовлетворяют соотношениям
(2.102)	Д = Дс = 2ДС = 2Д".
В частности, риманов лапласиан Д коммутирует с J и сохра-
няет тип формы.
Доказательство. Это очевидное следствие предложения 2.33.
□
Далее мы предполагаем, что многообразие М компактно.
2.103.	Хорошо известно, что р-е пространство когомологии с
комплексными коэффициентами Нр(М, С.) изоморфно простран-
ству гармонических комплексных р-форм. Точнее, пространство
Н*(М, С) изоморфно пространству когомологии, ассоциирован-
ному с внешним дифференциалом d, действующим в простран-
стве комплексных внешних форм (теорема де Рама), и в каж-
дом классе d-когомологий существует ровно одна гармоническая
форма (теория Ходжа).
Рассмотрим теперь d''-когомологии, ассоциированные с опе-
ратором d", действующим на комплексных внешних формах.
В этом случае также можно доказать (теория Дольбо, см. [Hir],
§ 15), что каждый класс d''-когомологий содержит ровно одну
8*
116 Гл. 2. Основные сведения (продолжение): кэлеровы многообразия
Ангармоническую форму. Таким образом, для каждой пары
(р, q) пространство когомологий Hp<q(M, С) изоморфно про-
странству форм типа (р, q), аннулируемых оператором А".
В кэлеровой случае Д" = уА и пространство Нр-ЦМ, С)
представляет собой подпространство пространства Нр+ч(М, С).
Получаем разложение
(2.104)	Hr(M, С) = S Hp'q(M,C).
p+q=r
Обозначим через Нр<ч комплексную размерность простран-
ства НР’ЦМ, С), а через br (r-е число Бетти)—комплексную
размерность пространства НЦМ, .С).
Поскольку оператор А" вещественный, комплексное сопря-
жение индуцирует кососимметрический изоморфизм Нр- ЦМ, С)->
-> Нч-р(7W, С), который называется двойственностью Серра.
В частности,
(2.105)	hp' 4 = h4’ р, \/р, 9 = 0, 1, ..т.
Отсюда сразу следует, что числа Бетти нечетного порядка четны
(возможно, равны нулю).
2.106.	С другой стороны, кэлерова форма и ее степени гар-
моничны. Значит, hP’p=/= 0 для р = 0, 1, ..., т. Следовательно,
числа Бетти четного порядка больше нуля.
Таким образом, мы выявили топологическое препятствие
к существованию кэлеровой метрики на компактном комплекс-
ном многообразии.
2.107.	Например, так называемые многообразия Калаби —
Экмана, т. е. произведения S2^IXS2,+I, р2 + 92>1, снабжен-
ные естественной комплексной структурой, не допускают кэлеро-
вой метрики (см. [Chr], с. 4—6).
2.108.	Замечание. Изоморфизм между Нр'ЦМ, С) и ядром
оператора А" на формах типа (р, q) имеет место для произволь-
ной эрмитовой метрики. В этом случае пространства Нр>ЦМ, С)
связаны с обычными когомологиями спектральной последова-
тельностью Фролихера, которая в кэлеровом случае вырож-
дается и с помощью которой выводится неравенство
(2.108)	£ hp,q.
p+q~r
G. Теория Ходжа
117
В общем случае справедливо равенство
т
(2.108а)	х= S (~\)p+qhp’q,
р, <7=0
где % — характеристика Эйлера — Пуанкаре (см. [Gr-Ha] с. 444).
Сформулируем еще одно важное следствие предложения
2.102.
2.109.	Предложение (<Мс-лемма). Для любой вещественной
(1<1с-замкнутой р-формы <р разложение Ходжа можно записать
в виде
(2.109)	<р = d ба + dc dp + <рн,
где а, р — вещественные р-формы, а ц>ц — гармоническая часть
формы ф.
Доказательство. См. [D-G-M-S], 5.11.	□
2.110.	Следствие. Любая вещественная d-точная 2-форма
Ф = <2£ типа (1,1) является ddc-точной.
Доказательство. Применить 2.109 к 1-форме g, которая яв-
ляется г/с1е-замкнутой, поскольку ф = /ф.	□
2.111.	Определение. Формой Леви вещественной функции f
называется вещественная (1,1)-форма у ddcq>. Локальная функ-
ция с нулевой формой Леви называется плюригармонической.
Комплексный лапласиан (т. е. взятый со знаком минус след
формы Леви) на кэлеровом многообразии связан с римановым
лапласианом А формулой
(2.112)	Af = — (ddcf, со).
2.113.	Следствие. Для компактного кэлерова многообразия
справедлива теорема 2.115. В то же время легко доказать (см.,
например, [Wei 1]), что для любого комплексного многообразия
произвольная замкнутая (1,1) -форма является (локально) фор-
мой Леви вещественной функции.
В частности, кэлерова форма кэлерова многообразия являет-
ся формой Леви некоторой вещественной функции, которая
определена с точностью до плюригармонического слагаемого и
называется кэлеровым потенциалом.
2.114.	Определение. Кэлеровым классом кэлеровой формы со
называется множество кэлеровых форм из класса когомологий
[<о] формы (О.
118 Гл. 2. Основные сведения (продолжение): кэлеровы многообразия
Согласно 2.110, любой элемент кэлерова класса формы и
имеет вид
(2.114)	<o' = (o + dd7,
где f — вещественная функция, определенная с точностью до
константы.
2.115.	Пусть (Е, h) — голоморфное эрмитово расслоение, т. е.
голоморфное векторное расслоение Е с послойной эрмитовой
метрикой h. С помощью связности Чженя V, ассоциированной
с h, построим, как и выше, операторы d, d", 6", А" и т. д. (ин-
декс V в их обозначениях мы опускаем). Легко проверить, что
оператор d" не зависит от h и является когомологическим опе-
ратором в пространстве Е-значных форм (т. е. (d")2 = 0). По-
этому можно рассмотреть соответствующее пространство кого-
мологий Hp-q(M, Е), изоморфное пространству Е-значных
(р, д)-форм, аннулируемых оператором X" (зависящим от h).
При р = 0 пространство //0><7(Л4, Е) изоморфно пространству
когомологий многообразия М с коэффициентами в пучке ё рост-
ков голоморфных сечений Е, которое определяется, например,
по Чеху (см. [Hir], § 15).
Пусть hP’q(E) обозначает комплексную размерность про-
странства	Е). Определим число Эйлера х(Л4, ё) мно-
гообразия М относительно ё формулой
tn
(2.116)	x(Af, #)=£ (-\)q h{Q’q} (Е).
<;=0
Знаменитая теорема Римана — Роха — Хирцебруха утверждает,
что число %(М, ё} можно представить в виде интеграла по М
от универсального полинома (зависящего только от размерности
М и ранга Е) от классов Чженя М и Е (см. [Hir], § 21).
2.117.	В частности, число Эйлера х(Л4, О} относительно струк-
турного пучка О (пучка голоморфных сечений тривиального ли-
нейного расслоения), равное
tn
(2.117)	%(М, С)= £ (-—l)qh°’q,
<7=0
можно представить в виде интеграла по М от универсального
полинома (зависящего только от т) от классов Чженя много-
образия М, следовательно (см. 2.70), от кэлеровой кривизны.
2.118.	Примерами эрмитовых голоморфных векторных рас-
слоений служат расслоение /\Р(Т'М) и двойственное к нему
расслоение ДР’°M Д₽ (Г'Л!)*, р=1, гп.
Н. Голоморфные векторные поля и инфинитезимальные изометрии 119
Голоморфные сечения расслоения Д ’ М называются голо-
морфными р-формами.
Пространство голоморфных р-форм отождествляется с
Нр’°(М, С). В частности, на компактном многообразии все го-
ломорфные р-формы замкнуты.
По двойственности Серра размерность пространства голо-
морфных р-форм равна /г°-₽, р = 1, т.
В частности, если компактное кэлерово многообразие М не
допускает ненулевых голоморфных р-форм для р > 0, то
%(Я 0=1.
Н. Голоморфные векторные поля
и инфинитезимальные изометрии
Пусть М — компактное почти комплексное многообразие.
2.119.	Определение. Инфинитезимальным автоморфизмом
почти комплексной структуры 1 называется вещественное век-
торное поле X, сохраняющее J:
(2.119)	LxJ = 0<^[X, JY]~J[X, У],
Пространство всех таких полей образует конечномерную ал-
гебру Ли относительно скобки векторных полей. Точнее, спра-
ведлив следующий хорошо известный результат (см [КоЬ 4],
с. 1—4).
2.120.	Группа автоморфизмов компактного почти комплекс-
ного многообразия есть группа Ли преобразований 21(44). Ал-
гебра Ли правоинвариантных векторных полей на 21(44) есте-
ственным образом отождествляется с алгеброй Ли инфинитези-
мальных автоморфизмов почти комплексной структуры.
Далее мы предполагаем, что 44 — компактное комп-
лексное многообразие с кэлеровой метрикой g.
2.121.	Предложение. Вещественное векторное поле X яв-
ляется инфинитезимальным автоморфизмом комплексной струк-
туры тогда и только тогда, когда ее часть типа (1,0) голо-
морфна.
Доказательство. Достаточно доказать, что для любой голо-
морфной 1-формы 0 типа (1,0) функция 0(A) голоморфна. Для
120 Гл. 2. Основные сведения (продолжение): кэлеровы многообразия
любого векторного поля Y имеем
do(X, У) = х-е(У)-у-е(Х)-е([х, у]),
de(x, /У) = х-е(/У)-/у-е(Х) —б([х, /У]) =
= IX • 6(У) — /У • 6(Х) - г0([Х, У]).
С другой стороны, dQ имеет тип (2,0), поскольку форма 0 голо-
морфна. Поэтому d6(X, JY) = idQ(X, У). Отсюда
/У • 0 (X) =/У • 0 (X),
что доказывает голоморфность локальной функции 0(Х).	□
2.122.	Следствие. Алгебра Ли %(М) инфинитезимальных
автоморфизмов комплексной структуры имеет естественную
структуру комплексной алгебры Ли голоморфных векторных
полей. Группа 51 (7И) автоморфизмов комплексной структуры
имеет естественную структуру комплексной группы Ли.
Доказательство. Компонента типа (1,0) поля /X равна iX1-0
и голоморфна одновременно с полем X10. Утверждение, что X и
JX одновременно являются или не являются инфинитезималь-
ными автоморфизмами комплексной структуры, непосредственно
следует также из обращения в нуль тензора комплексного кру-
чения N.	О
2.123.	Для краткости будем называть инфинитезимальный
автоморфизм комплексной структуры вещественным голоморф-
ным векторным полем. Используя оператор D~, введенный в
2.52, получаем
2.124.	Предложение. Вещественное векторное поле X голо-
морфно тогда и только тогда, когда
(2.124)	£)~Х = 0.
Другими словами. Di, имеет тип (1,1), где g — двойственная к X
1-форма.
Доказательство. Достаточно воспользоваться (2.119) и обра-
щением в нуль кручения связности D.	□
2.125.	Следствие (А. Лихнерович [Lie 1]). Пусть М — ком-
пактное кэлерово многообразие размерности п = 2т. Тогда
(i)	если т = 1, то алгебра Ли конформных векторных полей
совпадает с алгеброй Ли вещественных голоморфных векторных
полей-,
(ii)	если m~> 1, то любое конформное векторное поле яв-
ляется киллинговым (см. 1.80);
Н. Голоморфные векторные поля и инфинитезимальные изометрии 121
(iii)	любое киллингово векторное поле является (веществен-
ным) голоморфным векторным полем;
(iv)	точнее, вещественное векторное поле является киллин-
говым тогда и только тогда, когда оно голоморфно и сохраняет
форму объема.
Доказательство. Достаточно воспользоваться замечанием
2.54, формулой (2.65b) и предложением 2.124.	□
2.126.	Следствие. Разложение Ходжа 1 -формы g, двойствен-
ной вещественному голоморфному векторному полю X, можно
представить в виде
(2.126)	g = df + dc/z + g0,
где f, h—корректно определенные вещественные функции с нуле-
вым интегралом по М, a g0— гармоническая часть g.
Доказательство. Достаточно применить ddc-лемму 1.109 к
1-форме g, которая является сйс-замкнутой, поскольку dg имеет
тип (1,1), так же как Z)g.	□
2.127.	Определение. Вещественная функция f, входящая в
разложение Ходжа (2.126), называется голоморфным потен-
циалом (относительно кэлеровой метрики g) вещественного го-
ломорфного векторного поля X.
2.128.	В силу предложения 2.125(iv) голоморфный потенциал
обращается в нуль тогда и только тогда, когдй поле X кил-
лингово.
2.129.	Отметим, что вещественная функция h из (2.126) яв-
ляется голоморфным потенциалом вещественного голоморфного
векторного поля —JX.
2.130.	Замечание. Если X — киллингово векторное поле, то
1-форма Zg замкнута в силу 2.126 и 2.128. С другой стороны,
производная Ли кэлеровой формы по направлению X равна
(2.131)	Lxa> = d (ixa) = dZg.
Поэтому киллингово поле является гамильтоновым векторным
полем относительно симплектической структуры, заданной кэ-
леровой формой.
Этот результат следует из более общего утверждения о том,
что на компактном римановом многообразии киллингово поле
сохраняет все гармонические поля, в частности кэлерову форму
(см. [Lie 1], с. 130).
122 Гл. 2. Основные сведения (продолжение): кэлеровы многообразия
2.132.	Отметим, что поля X и JX могут одновременно быть
киллинговыми только в том случае, если поле X параллельно.
Это следует из (2.56), так как при этом £)g = -g-dg в силу 2.56
и 1-форма g замкнута.
2.133.	Замечание. Из 2.100 и 1.125(iv) следует, что два объ-
екта, ассоциированных с кэлеровой метрикой, а именно форма
Риччи р и алгебра Ли инфинитезимальных автоморфизмов кэ-
леровой метрики (т. е. киллинговых полей), по существу зависят
не от всей метрики, а только от комплексной структуры и формы
объема.
Структура на многообразии, заданная комплексной структу-
рой и формой объема, называется унимодулярной комплексной
структурой. Она представляет собой GL(m, C)(~|SA(2m, С)-
структуру, для которой соответствующая GL(m, С)-структура
интегрируема. Сама эта структура является интегрируемой
тогда и только тогда, когда соответствующая форма Риччи равна
нулю. По теореме Калаби — Яу (см. 11.15) любая унимодуляр-
ная комплексная структура на кэлеровом многообразии инду-
цируется кэлеровой метрикой, которая определена неоднозначно.
2.134.	Предложение (Ж- Л. Козюль [Kos], с. 567). Пусть
М — компактное кэлерово многообразие с формой Риччи р. Если
X, Y — два инфинитезимальных автоморфизма кэлеровой мет-
рики, то
(2.134)	р(Х, У) =-4-6(7[X, J]).
Доказательство. Напомним сначала (см. 1.58), что диверген-
ция 6Z векторного поля Z по определению равна 6g, где g—
двойственная 1-форма. Дивергенция 6Z зависит только от формы
объема pg и задается формулой
(2.135)	=	(6Z) pg.
(Она отличается знаком от обычной дивергенции.)
Дивергенция скобки любых двух векторных полей U, V
равна
(2.136)	6([(7, V]) = t/-6V — V-6U.
Эта формула легко проверяется непосредственно или выводится
из тождества
(2.137)	[Д, К]Ь = -6(СД Д КЬ) + б£/. уЬ-бу.дь,
Приступим к доказательству предложения. Пусть g—1-форма,
двойственная к полю X. Из приведенного ниже предложения
Н. Голоморфные векторные поля и инфинитезимальные изометрии 123
2.140 следует, что
р(Ю==г(/Ю = 4д^-
Поскольку поле ]Х голоморфно, из (2.33) и 2.126 вытекает
б dll = [Л, dc] dll = - dcX dll = dcbcJt,
где 6cJ£ = 6g равно нулю по условию. Таким образом,
Р(ё)=4^
и, значит,
р(Х, У) = 1у-б(/Х),
что в силу 2.136 равно
Р(Х, У) = 1/Х.бУ + 4-б([У, JX]).
Поскольку 6У = 0 и поле У голоморфно, предложение дока-
зано.	□
2.138.	Предложение. Если тензор Риччи компактного кэле-
рова многообразия отрицательно определен, то группа 21 авто-
морфизмов комплексной структуры конечна.
Доказательство. Из (2.53) следует, что
(2.138)	<г(Х), Х) = <£>+Х, £)+Х>-<£>“Х, D~x}
для любого векторного поля X, где < •, • > — глобальное скаляр-
ное произведение. Теперь из 2.124 следует, что алгебра Ли
21 (Л4) группы 21 (Л4) равна нулю. Далее, поскольку форма Риччи
р с точностью до множителя i равна кривизне канонического
расслоения К, расслоение К является обильным. Это, в част-
ности, означает существование голоморфного вложения М а
с= СР'\ которое отождествляет 21 (ЛТ) с алгебраической комп-
лексной подгруппой Ли группы PGL(jV-|- 1, С) проективных
преобразований. Отсюда следует, что число связных компонент
группы 21 (А4) конечно. Значит, и сама дискретная группа 21 (М)
конечна (подробнее см. [КоЬ 4], с. 82—86).	□
2.139.	Замечание. Из 2.138 сразу следует, что если тензор
Риччи г равен нулю, то любое голоморфное векторное поле па-
раллельно.
С другой стороны, если г > 0, ненулевые голоморфные поля
не могут быть параллельными.
124 Гл. 2. Основные сведения (продолжение): кэлеровы многообразия
Объединяя (2.53) и (2.55) с предложением 2.124, получаем
2.140.	Предложение (А. Лихнерович). На компактном рима-
новом многообразии вещественное векторное поле X голоморфно
тогда и только тогда, когда
(2.140)	|д&-г(Х) = 0,
где £ — двойственная к X 1 -форма.
Более того, вещественное поле X голоморфно тогда и
только тогда, когда глобальное скалярное произведение
Д£ — г (X), тождественно равно нулю.
2.141.	Для доказательства теоремы Калаби — Футаки (см.
2.160) полезно расписать соотношение (2.140) более подробно,
используя разложение Ходжа формы Риччи
(2.141)	р = у + ddcF,
где у — гармоническая часть р, a F — корректно определенная
вещественная функция с нулевым интегралом по М.
2.142.	Определение. Функция F называется потенциалом
Риччи кэлеровой метрики.
2.143.	Если X — вещественное голоморфное векторное поле,
то 1-форма г(Х) имеет разложение Ходжа такого же типа (см.
(2.126)), что и двойственная к X 1-форма £. Это утверждение
вытекает непосредственно из 2.140, но его можно получить и
другим способом. Заметим, что внешний дифференциал dr(X),
равный с точностью до знака производной Ли от формы Риччи
по направлению JX, является, как и р, (1,1)-формой, так как
поле JX голоморфно. Теперь утверждение следует из сИс-леммы
(2.109). Точнее, справедливо
2.144.	Предложение. Для любого вещественного голоморф-
ного векторного поля X I-форма г(Х) равна
(2.144)	г (X) = d (f + X • F) + dc (h - JX • F),
где f,h — вещественные функции с нулевыми интегралами по
М, определяемые уравнениями
(2.145)	bf + (dd°f, у) = 0, bh + (ddch, у) = 0
или равносильными им уравнениями
(2.146)	66е (f • со — f • у) = 0, &6c(h • со — h • у) = 0,
где f и h — голоморфные потенциалы X и —JX.
Н. Голоморфные векторные поля и инфинитезимальные изометрии 125
Доказательство. С помощью разложения 2.142 получаем
г (X) = - р (JX) = - ddcF (JX) - у (JX).
Поскольку поле JX голоморфно, как и X, первый член в правой
части равен
(2.147)	—ddcF(JX) = -LJXdcF + d(iIxdcF) = d(X • F) - dc(JX • F).
Проводя рассуждения 2.143 для у, получим разложение Ходжа
второго члена в виде
— y(JX) = df + dch,
где f и h определяются (с точностью до постоянного слагае-
мого) из уравнений
Af = -6(у(/Х)), Д/г = -6с(у(7Х)).
Используя козамкнутость у, легко получить (2.145).	□
2.148. Следствие. Голоморфный потенциал f вещественного
голоморфного векторного поля X удовлетворяет уравнению
(2.148)	Af — f — X  F = — ^ (X  F) pg,
м
где f определяется из (2.145).
2.149.	Замечание. Потенциал Риччи F связан со скалярной
кривизной s уравнением
(2.149)	ls = tr р = у s0-AF,
где у s0 — const есть след гармонической 2-формы у.
В частности, постоянство скалярной кривизны равносильно
обращению в нуль потенциала Риччи.
В этом случае уравнение (2.148) принимает вид
(2.150)	|AF-f = 0.
Обратно, используя вторую часть предложения 2.140, легко
проверить, что если s = const, то векторные поля (df)* и (dcf)*
голоморфны (причем последнее является инфинитезимальной
изометрией) для любого решения f уравнения 2.150.
Другими словами, каждое слагаемое разложения Ходжа для
£ является 1-формой, двойственной вещественному голоморф-
ному векторному полю.
В частности, гармоническая составляющая g параллельна.
Отсюда немедленно следует
126 Гл. 2. Основные сведения (продолжение): кэлеровы многообразия
2.151.	Предложение (А. Лихнерович [Lie 1]). На компакт-
ном кэлеровом многообразии постоянной скалярной кривизны
комплексная алгебра Ли §1 (Af) расщепляется в сумму абелевой
алгебры Ли параллельных векторных полей и комплексной ал-
гебры Ли голоморфных векторных полей, ортогональных про-
странству гармонических 1-форм. Последняя алгебра Ли яв-
ляется комплексификацией вещественной подалгебры Ли инфи-
нитезимальных изометрий вида (dcf)#, где f — произвольное ре-
шение уравнения
(2.151)	\2f + (ddcf, р) = 0.
2.152. Из 2.151 сразу следует, что связная группа изометрий
является максимальной компактной связной подгруппой группы
Sl(Af) (см. [Lie 1]).
I. Теорема Калаби — Футаки
2.153. Определение. Функционалом Футаки называется ве-
щественная линейная форма на пространстве 51 (А1) вещест-
венных голоморфных векторных полей, заданная формулой
(2.153)	SF(X) = \(X- F) pg, X е= а (М).
м
Функционал 3~ можно также представить в виде
(2.154)	(i) ff~(X)=(df, dF),
(И) <Г(Х)=$т)Ив,
м
(iii) FT (X) = - | J (fs) pg,
M
где f — голоморфный потенциал X, a F — потенциал Риччи.
2.155. В частности, <F(X) = 0, если поле X киллингово.
Действительно, в этом случае X-F = 0, поскольку X сохраняет
р и у в (2.141).
2.156. Для получения важного следствия 2.160 вычислим
первую производную функционала FT как функцию на про-
странстве ЛИ кэлеровых метрик на М со значениями в сопря-
женном пространстве 31 (М)*. Ввиду неоднородности функцио-
нала ограничим его на пространство J(\ кэлеровых метрик
полного объема 1. При этом точки из отождествляются с
кэлеровыми формами, а направление первой вариации в
I. Теорема Калаби—Футаки
127
точке о задается (1,1)-формой И, удовлетворяющей соотно-
шению
(2.157)	J(tr/7)pg = O.
м
Первые вариации формы объема, формы Риччи скалярной кри-
визны и оператора Лапласа в направлении Н описываются сле-
дующей леммой.
2.158.	Лемма.
(i)	=	• pg,
(ii)	p'(H) = -±-ddc(trH),
(iii)	=	p),
(iv)	Д' (Я) ф = (H, ddcty),
где ф — вещественная функция.
Доказательство, (i) pg == am; (ii) paj5 = — у dd<: log det(£ag)
(cm. 2.98); (iii) yS = (P, co); (iv) Аф = — (ddcty, co).	□
2.159.	Предложение. Первая вариация ST в точке
в направлении Н имеет вид
(2.159)	У' (Н)(Х) = {Н, fy-fei),
где f — голоморфный потенциал X, a f определяется уравне-
нием (2.145).
Доказательство. &~'(Н)(Х) = ( (Х-F'(Я)) •!*.,+ (XF)n'JH)=
м	м
= {f, А (Г (//)))+ ^(Х  F)tr И  pg,
где в силу 2.149 и 2.158
A (F' (Я)) = (AF)' (Я) - А' (И) (F) =
= (Н, у) — yAtr Н +	sco—-р,	□
Используя (2.148), получаем нужный результат.
2.160.	Следствие (Калаби — Футаки). Функционал ST постоя-
нен на каждом кэлеровом классе.
128 Гл. 2. Основные сведения (продолжение): келеровы многообразия
Доказательство. Достаточно воспользоваться (2.159), учи-
тывая, что 2-форма fy— fa в силу 2.146 является (Мс-козамк-
нутой.
2.161.	Замечание. Следствие 2.160 является обобщением ре-
зультата А. Футаки ([Fut]), принадлежащим Е. Калаби
([Cal 7]). В теореме Футаки предполагается, что кэлеров класс
кратен первому классу Чженя (с положительным множителем).
В этом случае гармоническая составляющая у формы Риччи
кратна со и 2-форма fy — fa тождественно равна нулю. Другими
словами, соответствующая метрика является критической точ-
кой для ST.
Обратно, используя то, что гармоническая ненулевая форма
не может равняться нулю на непустом открытом множестве
(см. [Аго]), из (2.159) легко получить, что критическими метри-
ками функционала ST являются либо кэлеровы метрики, кэле-
ров класс которых пропорционален классу Чженя, либо кэле-
ровы метрики, относительно которых все вещественные голо-
морфные векторные поля являются инфинитезимальными изо-
метриями и, значит, параллельны в силу 2.132.
2.162.	Замечание. Согласно 2.149, если кэлеров класс [со]
содержит кэлерову метрику постоянной скалярной кривизны, то
функционал Футаки равен нулю для любой метрики из [со].
Глава 3
Теория относительности
А. Введение
3.1.	Интерес к многообразиям Эйнштейна был вызван интер-
претацией условия Эйнштейна г = 0 как уравнения для грави-
тационного поля в отсутствие материи. Эйнштейн получил это
уравнение в 1915 г. Краткая история открытия полевых урав-
нений Эйнштейна, начиная с ранних работ, изложена в
[Mi-Th-Wh], с. 431—434.
3.2.	Эту главу мы начнем с обсуждения физической интер-
претации различных понятий четырехмерной лоренцевой гео-
метрии. Затем кратко обсудим физический и геометрический
смысл уравнения Эйнштейна. Далее рассмотрим классифика-
цию Петрова тензоров кривизны 4-многообразия Эйнштейна —
Лоренца и достаточно подробно изучим модель Шварцшильда,
описывающую гравитационное поле вне сферически симметрич-
ной звезды. В заключение кратко обсудим метрику Тауба —
НУТ1) и теоремы сингулярности, утверждающие, что при неко-
торых «физически разумных» предположениях пространство-
время не может быть геодезически полным.
В. Физическая интерпретация
3.3.	Пространство-время специальной теории относительности
представляет собой пространство Минковского R4, т. е. вектор-
ное пространство R4, снабженное лоренцевым скалярным про-
изведением g сигнатуры (-j-------). Выбор g-ортонормиро-
ванного базиса {ео, щ, ег, ез} в R4 определяет в R4 систему
координат (хо, Xi, х2, х3), которую можно рассматривать как
выделенную сопутствующую систему координат некоторого
наблюдателя, считающего себя неподвижным. Координата хо
описывает время, измеренное этим наблюдателем, а 3-плоскость
х3 = const — пространство одновременных с точки зрения этого
наблюдателя событий. История наблюдателя описывается кри-
*) То есть метрику Тауба — Ньюмена—Унтп — Тамбурпно. — Прим,
перев.
9 А. Бессе, т. 1
130
Гл. 3. Теория относительности
вой	а, Ь, с): в момент времени t по часам наблюда-
теля он находится в точке пространства (а, Ь, с).
Частица с ненулевой массой покоя, движущаяся относи-
тельно «покоящегося» наблюдателя, описывается в сопутствую-
щей ему системе координат параметризованной кривой ₽(/) =
= (f,	x2(t), x3(t)). Измеренная наблюдателем скорость
этой частицы равна
1Ш+Ш+ШГ-
Принцип, согласно которому скорость любой частицы относи-
тельно наблюдателя должна быть меньше скорости света, озна-
чает, что
или, поскольку xo(t) = t, что
Это условие, согласно которому частица движется относи-
тельно наблюдателя со скоростью, меньшей скорости света, не
зависит от параметризации кривой р. При желании можно вы-
брать в качестве параметра t длину дуги т, а не координату х0.
Параметр г характеризует собственное время частицы, т. е.
время, измеренное в системе координат, связанной с частицей.
Условие, что скорость частицы, движение которой описывается
кривой р, относительно наблюдателя меньше скорости света, не
зависит от наблюдателя и инвариантно выражается неравен-
ством g (р, Р) > 0.
3.4.	Пространство-время общей теории относительности
представляет собой гладкое четырехмерное многообразие М,
снабженное метрикой сигнатуры Лоренца (-|----------). Каса-
тельный вектор v в точке многообразия М называется времени-
подобным, если g(v, и) > 0, пространственноподобным, если
g(v, v)<Z 0, и изотропным, если g(v, и) = 0. Движение частицы
с ненулевой массой покоя в М описывается времениподобной
кривой р, т. е. кривой, для которой g(p, р) > 0. Обычно кривую
р параметризуют параметром t, задаваемым условием g(р (/),
p(/))==z/7i2, где m — масса покоя частицы. Если m~ 1, то гово-
рят, что р описывает движение пробной частицы. Безмассовая
частица, например фотон, движется по изотропной кривой, т. е.
по кривой р с изотропным вектором скорости P(f) (при всех t).
С. Полевое уравнение Эйнштейна
131
3.5.	Пробные частицы можно рассматривать как наблюда-
телей в пространстве-времени. Единичный времениподобный
вектор v в точке р е М можно рассматривать как вектор 4-ско-
рости пробной частицы, пролетающей через точку р. Он назы-
вается инфинитезимальным наблюдателем в точке р. С каждым
инфинитезимальным наблюдателем v ассоциируется простран-
ство покоя — подпространство касательного пространства
ТРМ, состоящее из векторов, ортогональных к v. Если кривая р
описывает движение частицы с массой покоя пг (т. е. g(0, 0) =
= mz), a v есть инфинитезимальный наблюдатель в точке 0(f),
то 0 (/) = av + а', где а е w е и-1. Вектор w называется
3-моментом частицы относительно наблюдателя v, а вектор
w/a— 3-скоростью частицы относительно v.
Эти понятия обсуждаются более подробно в [Sa-Wu], гл. 1,2.
С. Полевое уравнение Эйнштейна
3.6.	В общей теории относительности лоренцева метрика g
интерпретируется как гравитационный потенциал. Поэтому она
должна быть связана уравнением поля с распределением
массы-энергии, которое порождает гравитационное поле. Пред-
ложенное Эйнштейном уравнение поля имеет вид
1 -г
r-Tsg = T,
где Т — тензор энергии-импульса.
Тензор энергии-импульса Т представляет собой симметриче-
ское дважды ковариантное тензорное поле на М. Величина
Т(у, v) описывает плотность энергии в точке р, измеренную
наблюдателем v. Ковектор Т (р, •) описывает плотность мо-
мента, а симметрическая билинейная форматах — тензор на-
пряженности массы-энергии в точке р, измеренные наблюдате-
лем в. Отметим, что, поскольку форма g [ отрицательно опре-
делена, тензор напряженности можно привести к диагональному
виду в g (ох'°РтоноРмиРованном базисе. Диагональные эле-
менты называются главными давлениями в точке р распреде-
ления массы-энергии с точки зрения наблюдателя v.
Подробнее о физическом смысле тензора энергии-импульса
Т см. [Sa-Wu], гл. 3, и [Mi-Th-Wh], гл. 5.
3.7.	Уравнение Эйнштейна допускает различные обоснова-
ния. Упомянем три из них.
(i)	Тензор энергии-импульса является дважды ковариант-
ным тензорным полем. Поэтому нужно искать дважды кова-
риантное тензорное уравнение. Тензор r — —sg, стоящий в ле-
9*
132
Гл. 3. Теория относительности
вой части уравнения Эйнштейна, является простейшим дважды
ковариантным тензором, который можно построить из метриче-
ских коэффициентов gt, и их первых двух производных таким
образом, чтобы он был линейным по вторым производным и без-
дивергентным. Условие бездивергентности интерпретируется как
закон сохранения.
(ii)	Уравнение г— ysg = 0, описывающее гравитационное
поле в вакууме, можно получить как уравнение Эйлера вариа-
ционной задачи для функционала j sgpg (см. гл. 4).
(iii)	В «классическом пределе» уравнение Эйнштейна сво-
дится к уравнению Пуассона, описывающему ньютоновскую
гравитацию.
Подробности см. в [Fra], [Mi-Th-Wh] и [Web].
3.8.	Замечание. Решением уравнения Эйнштейна мы назы-
ваем метрику g и тензор энергии-импульса Т, описывающий тот
или иной вид материи. При этом тензоры g и Т должны быть
связаны уравнением Эйнштейна.
Если Т = 0 (вакуум), требуется просто найти метрику g,
удовлетворяющую уравнению г—^sg = Q. В других случаях
требуется найти g и Т. Один из развивающихся подходов со-
стоит в постановке задачи Коши для g и Т на пространственно-
подобной гиперповерхности и в трактовке уравнения Эйнштейна
вместе с дополнительным уравнением div7’ = 0 как эволюцион-
ного уравнения (см., например, [На-El], гл. 7).
3.9.	Замечание. Взяв след обеих частей уравнения Эйнштей-
на, получим
$ = — trace Т,
где оператор Т задается равенством g(T(v), w) = T(v, w) для
всех v, w^TpM, р<=М. Поэтому при 7’ = 0 уравнение Эйн-
штейна
r-±sg = T
принимает вид r — Q. Таким образом, любое вакуумное решение
уравнения Эйнштейна описывается риччи-плоским простран-
ством-временем. Иногда рассматривают модифицированное
уравнение Эйнштейна
r--^sg + Kg = T,
где 1 — константа (так называемая космологическая постоян-
ная). В этом случае вакуумное пространство-время задается
решением уравнения г = eg, где с — const. Это модифицирован-
D. Приливные напряжения
133
ное уравнение было весьма популярно на заре создания общей
теории относительности, но теперь считается, что оно не согла-
суется с наблюдениями.
D. Приливные напряжения
3.10.	Величина ускорения, с которым близкие свободно па-
дающие пробные частицы сближаются или удаляются друг от
друга, измеряется секционной кривизной. Пусть дана свободно
падающая пробная частица, описываемая времениподобной гео-
дезической у. Бесконечно близкая свободно падающая частица,
расположенная в начальный момент времени в направлении
вектора w от геодезической -у(ау_1_у(0), g(w, w) =—1) и дви-
жущаяся в начальный момент времени параллельно -у, описы-
вается полем Якоби 157 вдоль -у с начальными условиями U7(0) =
= w, IF'(0) = 0. Пространственное удаление этих двух частиц
измеряется функцией / = [—^(IF, W) ]1/2. Вычислив первые две
производные функции f и воспользовавшись уравнением Якоби,
получим f/(0) = 0, f"(0) = —К(у(0)Ло>). Таким образом, в слу-
чае положительной секционной кривизны близкие свободно па-
дающие частицы стремятся сблизиться, а в случае отрицатель-
ной секционной кривизны — разлететься.
Предупреждение. Связь между знаком кривизны и поведе-
нием времениподобных геодезических в литературе трактуется
по-разному, в зависимости от сигнатуры используемой метрики.
Многие авторы используют метрику сигнатуры (•-----1- + +),
т. е. рассматривают метрический тензор другого знака. Это при-
водит к изменению знака секционной кривизны, но, конечно, не
меняет геометрии геодезических, поскольку собственные значе-
ния оператора W->-R(W, у)у остаются прежними.
3.11.	Пусть задан инфинитезимальный наблюдатель v. Сим-
метрическая билинейная форма g(R(v, -)v, •) в его простран-
стве покоя vz интерпретируется как приливный тензор напря-
жений, измеренный этим наблюдателем. Поскольку форма g f ох
отрицательно определена, указанная выше билинейная форма
приводится к диагональному виду в g-ортонормированном ба-
зисе. Диагональные члены являются главными приливными
напряжениями, измеренными наблюдателем v. Отметим, что
главные напряжения есть критические значения функции wt—*
+—> — R (v Л te>) на единичной сфере в пространстве и-1-. Число
—^-r(v, v), равное одной трети суммы главных приливных на-
пряжений, измеренных наблюдателем v, называется средним
приливным напряжением относительно наблюдателя v.
134
Гл. 3. Теория относительности
Подробное обсуждение этого круга вопросов см. в [Tho 2].
3.12.	Одно из следствий уравнения Эйнштейна состоит в том,
что гравитационные силы вынуждают средние приливные на-
пряжения становиться отрицательными (или по крайней мере
неположительными). Действительно, поскольку traceТ = —s,.
уравнение Эйнштейна можно представить в виде
Г = т — у (trace Т) g.
Поэтому среднее приливное напряжение относительно инфини-
тезимального наблюдателя v будет неположительным, если
г (v, v) = T(v, v)—trace Т i>0.
Условие Г (о, и)—trace Т 0, которое выполняется для лю-
бого инфинитезимального наблюдателя v, называется сильным
энергетическим условием. Оно выполняется почти для всех
разумных физических моделей и означает, что сумма плотности
энергии и трех главных давлений должна быть неотрицатель-
ной для любого инфинитезимального наблюдателя v.
В пространстве-времени, удовлетворяющем сильному энерге-
тическому условию, среднее приливное напряжение всюду не-
положительно, и, таким образом, близкие свободно падающие
частицы в среднем стремятся сблизиться.
Е. Нормальные формы кривизны
3.13.	По причине индефинитности метрики теория нормаль-
ных форм тензора кривизны для лоренцевых многообразий ока-
зывается более тонкой, чем в римановом случае. Например, в
римановом случае всегда существует ортонормированный базис
пространства /\2ТрМ, состоящий из собственных векторов опе-
ратора кривизны 7?: А2 ТрМ~> /\2ТрМ. В лоренцевой случае,
это, вообще говоря, не так.
3.14.	Геометрически наиболее интересны нормальные формы
тензора кривизны, обусловленные выбором базиса пространства
ТРМ, а не пространства /\2ТрМ. Чтобы получить такие нормаль-
ные формы для четырехмерных лоренцевых многообразий, удоб-
но превратить /\2ТрМ в комплексное векторное пространство
с помощью оператора Ходжа ».
3.15.	Напомним, что выбор ориентации <в в пространстве ТРМ
(т. е. элемента сое f\4TpM с g(a>, ®) = —1) определяет опера-
Е. Нормальные формы кривизны
135
тор *: /\2ТрМ-г /\2ТрМ, где аЛр = §(*а, Р)со. Для заданного
ортонормированного базиса {е0, еь е2, е3} пространства ТрМ
с g(e0, е0) >0, goAg1Ag2Ag3 = (o легко вычислить матрицу [*]
оператора Ходжа относительно базиса {е0 Л gb g0Ag2, е0 Л е3,
е.2 л ез» е3 Л gb ei л ег} пространства /\2ТрМ. Она имеет вид
/0 —IX
=	0 )’
где 1 — единичная матрица 3X3. Таким образом, оператор
Ходжа действует на /\2ТрМ как комплексный оператор. По-
этому, полагая ia = «а для /\2ТрМ, мы превращаем
f\2TpM в комплексное трехмерное векторное пространство.
3.16.	Симметрическая билинейная форма h на /\2ТрМ
h(a, ₽) = g(a, ₽) — »g(* a, ₽)
представляет собой невырожденное эрмитово скалярное произ-
ведение в комплексном векторном пространстве /\2ТРМ. Можно
проверить, что каждый ортонормированный базис {во, е\, е2, ез}
пространства ТРМ определяет /i-ортонормированный базис
{е2 Л g3, g3Agb e]Ag2} пространства /\2ТрМ.
3.17.	Обратно, для любого /i-ортонормированного базиса
{«1, а2, а3} пространства f\2TpM найдется такой g-ортонорми-
рованный базис {ео, ei, еъ, ез} пространства ТРМ, что е1 Ле2 = ад,
g3 A gj = а2, е2 л е3 = ± аь Действительно, поскольку
а£ А а£ = g (* аг, аг) со = Im (Л(аг, аг))«> = 0,
каждый бивектор а, разложим и, значит, определяет 2-плоскость
Pi ст ТРМ. Поскольку
g (ab a,-) = Re (h (аь a,)) = 1,
все эти плоскости пространственно подобны (g(v, е)<0 для
О I' G Pi). Поскольку
а. Ла7 = £(*а£, 0/)®= — (1т/г(аг, aj))a = О,
эти 2-плоскости попарно пересекаются. Выберем единичные век-
торы
в] *= r2 п Рз,
е2 е Р3, для которого g(eit е2) = 0 и е1Ле2 = а;й
€3 е Р2, для которого g (еь е3) = 0 и е3 Л gj = а2,
-е0 ст ТРМ, для которого g (е0, ег) = 0, г = 1, 2, 3, и e0Agj Ag2Ag3=a).
136
Гл. 3. Теория относительности
Тогда из условия ft-ортогональности бивектора ои и бивекторов
сс2, аз следует, что ои = ±е2 Л е3.
3.18.	Для четырехмерных лоренцевых многообразий с по-
мощью оператора Ходжа можно описать О (g) -инвариантные
подпространства пространства алгебраических тензоров кри-
визны (ср. с 1.128). Напомним, что Я&^^^Я имеет постоян-
ную кривизну; R е^<=^Я определяется своим тензором Риччи,
имеющим нулевой след; ЯеУоЯ имеет нулевой тензор
Риччи. Эти условия можно следующим образом интерпретиро-
вать с помощью матриц.
3.19.	Относительно ортонормированного базиса пространства
/\2ТрМ, описанного в 3.15, матрица [Q] квадратичной формы
Q(a, 0) = £(Яа, р) и матрица [Я] эндоморфизма Я: Л2ГрЛГ->-
-> /\ТрМ имеют вид
[/?] =
-А —
В С )'
где А, В, С — матрицы 3X3, причем матрицы А и С симметри-
ческие. Ядро свертки Риччи состоит из таких тензоров R, для
которых trace А = О, С = —А и В = В1, Таким образом, Я е
е Ж *Я = Я* и trace Я = 0. Отображение г -> g ® г задает-
изоморфизм пространства симметрических ковариантных 2-тен-
зоров на пространство Ж-1-: если R — g®r, то С = А и В —
= —В1. Поэтому Я G 5" -<=> «Я = —Я* и /? e -<=>• Я есть ска-
лярный оператор.
3.20.	В частности, условие эйнштейновости многообразия М
(т. е. условие Я+ Ж) эквивалентно условию Я* = *Я.
Если воспользоваться комплексной структурой пространства
ТРМ (см. 3.15), можно сказать, что многообразие М является
эйнштейновым тогда и только тогда, когда эндоморфизм
R: /\2ТрМ-> /\2ТрМ, Vр <= М, является комплексно линейным.
Мы используем этот факт для получения нормальных форм тен-
зора кривизны лоренцевых многообразий Эйнштейна.
3.21.	Итак, если М — многообразие Эйнштейна, то Я — комп-
лексно линейный эндоморфизм пространства f\2TpM. Пусть
{₽ь ₽2, ₽з} — базис пространства f\2TpM, в котором матрица
[Я] эндоморфизма Я принимает нормальный жорданов вид.
Возможны три случая.
Е. Нормальные формы кривизны
137
(Z[ 0 0 \
О z2 О I
О О 2Г3/
для некоторых Zi, Z2, z3 &С. В этом случае стандартные рас-
суждения (вычисление обеих частей равенства й(7?р,-, Р/) =
= A(Pi, /?Р/)) показывают, что =	р;) = 0, если zt=/=z/.
Другими словами, собственные векторы эндоморфизма R по-
парно й-ортогональны, если собственные значения попарно раз-
личны. Если существуют одинаковые собственные значения, то
собственные подпространства попарно й-ортогональны и базис
{Pi. Рг, Рз} можно ортогонализовать с помощью процедуры Гра-
ма— Шмидта. Поэтому в любом случае можно считать базис
{Рь Рг, Рз} й-ортонормированным. Другими словами, матрица
[й] эрмитовой формы й имеет вид
(1 0 0\
0 10.
0 0 1/
/.г, 01 0 X
3.23. Случай II: [7?]=| 0 z2 1 I для некоторых zu г2еС.
х0 0 z2/
В этом случае стандартные рассуждения показывают, что
й12 = й^ = 0, а если z{ Ф z2, то и й[3 = 0. Если zx = z2 и й13 =/= 0,
то, заменив Р[ на Р[ + ар2 и выбрав подходящее значение аеС,
можно добиться того, что й13 = 0. Наконец, с помощью замены
базиса {рь р2, р3} базисом вида {арь йр2, йр3 + ср2} можно
добиться того, -что йц = й23=1, й33 = 0. Матрица [й] в этом
базисе, который мы по-прежнему будем обозначать {рь р2, р3},
принимает вид
(1 0 0\
0 0 1.
0 1 0/
(z 1 0\
0 z 1 I для некоторого
0 0 z)
Z 6= С.
В’ этом случае стандартные рассуждения показывают, что
Лц = й[2 = 0 и й13 = й22. Заменив базис {рь р2, р3} подходящим
базисом вида {ар1; аР2 + Рь «Рз + йРг + cpj, можно добиться
того, что й13= 1, й23 = й33 = 0. Матрица [й] относительно этого
138
Гл. 3. Теория относительности
нового базиса (рь р2, Рз) принимает вид
(0 0 1 \
0 10.
1 0 07
3.25. Для того чтобы превратить полученные нормальные
формы тензора кривизны R в нормальные формы R относи-
тельно g-ортонормированного базиса в ТРМ, нужно перейти
к Л-ортонормированному базису {аь а2, а3}’пространства /\2ТрМ,
а затем воспользоваться 3.17. Для типа I базис {рь р2, р3) уже
является ортонормированным, т. е. можно положить «/ = Ру,
/= 1, 2, 3. Для типа II можно положить «ц = рь , а2 = У2Р2 4-
+ Рз, a3 = i(—У2Р2 + Рз). Для типа III можно положить а,=
= V2P1 Ч~ Рз» «2—Р2, a3 = i(—V2P1 + Рз)- Матрица эндоморфиз-
ма относительно базиса {ab 02, 03} принимает вид
(zt 0 OX /zt 0 (OX	/z 1 ОХ
0 z2 0 I, (II) 0 z2 +1	0 I, (III) I 1 z i I.
0 0 z3J X 0 i z2 — 1 /	\ 0 i z)
3.26. Теперь рассмотрим g-ортонормированный базис {eo, eu
62, e3} пространства TPM, соответствующий базису {он, a2, a3}
(см. 3.17), и вычислим матрицу [7?] эндоморфизма R относи-
тельно^базиса {е0 А е0 Л е2, е0 А е3, е2 Л е3, е3 А еь et А е2} про-
А2 ТрМ. Учитывая, что * R = R * и ie} A ek = * et A ekt
странства
получим
U?] =
A -B\
В A
где A -j- iB есть матрица эндоморфизма R относительно базиса
{«i, «2, аз}- (Для типа III при этом, возможно, придется заме-
нить е2 на —е2.) Для каждого из трех типов матрицы А и В
имеют следующий вид (где z, = X,- + ip,):
(X] 0 0 X	/ Ц1 0 0 X
0 Х2 0 I, В = | 0 р2 0 I,
о о х3/	\ 0 0 р,3/
AXj	0	0\	/р.] 0 0\
(II)	Л = 1 0 Л2+1 О , В= о р2 1 I,
\ О	О	Х2 — 1 /	V 0 1 р2/
(X 1 о\	/о о ох
1 X 0 I, В = [ 0 0 11.
0 0 х/	XQ 1 о/
F. Метрика Шварцшильда
139
3.27.	Эти нормальные формы были получены Петровым в
1954 г. и описаны в его книге [Pet]. Они интенсивно использо-
вались при изучении гравитационного излучения (см., напри-
мер, [Pir]). В наших рассуждениях мы следовали [Tho 1]. От-
метим, что из алгебраического тождества Бьянки 1.24 вытекает,
что pi + ц2 + Из = 0 для типа I, pi -f- 2ц2 =0 для типа II и ц = 0
для типа III.
F. Метрика Шварцшильда
3.28.	Наиболее полезное решение вакуумного уравнения
Эйнштейна г —0 было найдено Шварцшильдом в 1916 г., вскоре
после того, как Эйнштейн сформулировал общую теорию отно-
сительности. Это решение моделирует гравитационное поле вне
изолированной статической сферически симметричной звезды.
3.29.	Пространство-время М называется статическим, если
на М существует такое нигде не обращающееся в нуль времени-
подобное киллингово векторное поле X (см. 1.80), что распре-
деление ортогональных 3-плоскостей интегрируемо. Интеграль-
ными многообразиями этого распределения будут простран-
ственноподобные гиперповерхности, локально изометричные
друг другу. Локально эти гиперповерхности задаются уравне-
нием t = const для некоторой временной функции t.
3.30.	Пространство-время М называется сферически симмет-
ричным, если на нем действует изометриями специальная орто-
гональная группа SO(3), причем все орбиты этой группы
являются либо пространственноподобными гиперповерхностями,
либо точками. При этом двумерные орбиты всегда имеют по-
стоянную положительную кривизну.
3.31.	Условия статичности и сферической симметричности
выполняются для произведения М = R X /XS2 (где / —откры-
тый интервал), снабженного произвольной метрикой скрещен-
ного произведения
g = F2 (Р) dt2 - dp2 - G2 (р) da2,
где t и р — стандартные координаты в iR и /, a dc2 — стандарт-
ная метрика (постоянной кривизны 1) на сфере S2. Координат-
ная функция t является глобальной временной функцией. Груп-
па SO(3) действует на М изометриями, причем ее орбитами
служат 2-сферы (t, р) = const. Сфера t = t0, р = ро с индуциро-
ванной метрикой G2(po)do2 изометрична евклидовой 2-сфере
радиуса G(p0).
140
Гл. 3. Теория относительности
Мы найдем (почти не проводя вычислений) тензор Риччи
такой метрики, а затем укажем условия, которым должны удов-
летворять функции F и G, чтобы метрика имела нулевую кри-
визну Риччи*
3.32.	Прежде всего отметим, что при каждом feR гипер-
поверхность {/} X / X «S2 вполне геодезична, поскольку она
представляет собой множество неподвижных точек изометрич-
ного отражения (обращения времени). Поскольку любое век-
торное поле постоянной длины, ортогональное вполне геодези-
ческой гиперповерхности, является параллельным вдоль этой
гиперповерхности, для любого касательного к R вектора х и
ортогональных ему векторов у, z .выполняется равенство
R(y, z)x = 0. Отсюда следует, что d/dt есть собственный вектор
тензора Риччи г.
3.33.	Аналогично, гиперповерхность RX/X51 является
вполне геодезическим подмногообразием для любой большой
окружности 51 в S2 (так как она является множеством непо-
движных точек отражения в S2). Значит, R(y, z)x = 0, если х —
касательный к S2 вектор, а векторы у, z перпендикулярны х. По-
этому любой касательный к S2 вектор является собственным
значением тензора г.
3.34.	Таким образом, пространства, касательные к сомножи-
телям R и S2, а следовательно (в силу ортогональности), и к /,
являются собственными пространствами тензора г. Это озна-
чает, что тензор Риччи диагоналей относительно разложения
Af = RX/XS2. Остается лишь вычислить его диагональные
члены, являющиеся суммами секционных кривизн.
3.35.	Эти секционные кривизны находятся следующим об-
разом.
Прежде всего отметим, что кривая р)(р) = (Л р, р) яв-
ляется геодезической многообразия М для любых <eR и
р е S2, поскольку она параметризована длиной дуги, а ее траек-
тория представляет собой множество неподвижных точек группы
изометрий, порожденной отражением прямой IIR относительно
точки t и отражением сферы S2 относительно большой окруж-
ности, проходящей через точку р. Векторное поле d/dt является
полем Якоби вдоль геодезической у(/. р>, следовательно,
(3.35а) К (d/dt Л д/др) = {batdod/dt, d/dt}/\\ d/dt Л д/dp ||2 = F"/F.
Аналогично, для любого единичного касательного к S2 вектора
х поле d/dQ, где 0 — угловая координата большой окружности
S1 в S2, соответствующей х, является полем Якоби вдоль у.
F. Метрика Шварцшильда
141
Поэтому
(3.35b) К (д/др Л х) = {D2g/gpd/dQ, д/дв)/\\ д/дд Л д/др if = G"/G.
Таким образом, мы вычислили кривизны двумерных вполне гео-
дезических подмногообразий в гауссовых координатах.
Для того чтобы найти остальные секционные кривизны, за-
метим, что на каждой гиперповерхности R X {р} X S2, заданной
уравнением р = const, индуцируется метрика риманова произ-
ведения
gp = F2(p)dt2-G2(p)d<y2.
Вторая фундаментальная форма этой гиперповерхности относи-
тельно единичного нормального векторного поля д/др задается
формулой (Од/д(£р) (х, у) = — 2gp (S • х, у), следовательно,
/ — FF' 0	\
S к 0 —GG'h ) ’
где h = da2. Из уравнения Гаусса следует, что
(3.35с)	^(_^_лх)=-^--^,
где х — касательный к S2 вектор, и
(3.35d)	К (х Л у) = - А- + (-^)2,
где х, у — касательные к S2 векторы.
3.36.	Таким образом, тензор Риччи имеет собственные зна-
чения
F"	F' G'
(3.36а)	=	+
F"	G"
(3.36b) гр = ^ + 2-^-,
/О ОС ч	G" . F' G' 1 I <G'\2
(3.36.с) гх = — + — . — — — + j (кратности два).
3.37.	Теперь мы можем решить уравнение Эйнштейна г = 0
для метрики скрещенного произведения на R X IX S2. Условие
0 = r/ = -^-(F'G2)' (см. (3.36а))
показывает, что F'G2 = const. Положим
(3.37а)	т = F'G2.
Условие
OX rp - rt = 2	(см. (3.36а) и (3.36b))
142
Гл. 3. Теория относительности
показывает, что G'/F = const. Изменив масштаб t, будем счи-
тать, что G'/F = 1. Тогда
(3.37b)	G' = F,
(3.37с)	G" = F' — m]G2 (см. (3.37а)).
Используя эти соотношения, получаем из (3.36с)
(3.37d)	rx = -^^~l+F2).
Условие гх = 0 выполняется тогда и только тогда, когда
Таким образом, метрика
(3.37е)	g = F2(p)dt2-dp2-G2(p)do2
на R X / X S2 удовлетворяет вакуумному уравнению Эйнштейна
г = 0 при условии, что
(3.371)
где т — некоторая константа.
3.38.	Эту метрику можно привести к более привычному виду,
если ввести вместо р новую координату p = G(p). В результате
замены метрика принимает вид
g = (1 - -^-) dt2 - (1 - dp2 - p2 da2,
полученный Шварцшильдом. Если рассматривать максимальную
область изменения координаты р, то эта метрика представляет
собой статическую сферически симметричную метрику в R X
X(2m, oo)XS2. Функция p = G(p) обычно интерпретируется
как расстояние до центра звезды (хотя ни измерениями времени
прохождения отраженного светового сигнала, ни тригонометри-
ческими измерениями расстояния нельзя воспользоваться для
подтверждения того, что приращение р измеряет радиальное
расстояние).
3.39.	Замечание. С помощью связывающих F и G уравнений
из 3.37, формул для кривизны из 3.35 и полученных в 3.32 и 3.33
результатов, касающихся обращения в нуль многих компонент
G. Планетные орбиты
143
кривизны, можно описать собственный базис и собственные зна-
чения оператора кривизны R.
(3.39а) R имеет двумерное собственное подпространство
{d/dt Л d/dp, х Л у} с собственным значением —2т X
XG(p)-<
(3.39b) R имеет четырехмерное собственное подпространство
{d/dt Л х, d/dp Л у}, где х, у — касательные векторы
сферы S2, с собственным значением т  G (р)~3.
Такой разложимый собственный базис удобен для вычисле-
ний. Отметим также, что тензор R в каждой точке пропорцио-
нален тензору Вейля многообразия S2 X S2.
G. Планетные орбиты
3.40.	Решение Шварцшильда моделирует гравитационное
поле вне звезды, а константа т при изучении периодов планет-
ных орбит интерпретируется как масса звезды.
3.41.	Рассмотрим некоторую планету, вращающуюся вокруг
звезды. Ее движение описывается времениподобной геодезиче-
ской у пространства-времени М. Эта геодезическая лежит во
вполне геодезическом подмногообразии iR XIX S1, где S1 —
большая окружность сферы S2, являющаяся проекцией у на S2.
Поэтому у записывается в виде
Y(S) = (/(S)> p(s), e(s)),
где 6 — угловая координата на S1.
3.42.	Орбита называется круговой, если р = а для некоторой
константы а. В этом случае
(3.42а)	Y = ^ + e-A.,
(3.42b)	= t^ + (t2FF' - 02GG') |p_0	+ 0	.
Поэтому уравнение геодезических Z)yy = O означает, что
(3.42с)	t = ё = 0, ё2 =	(a) i2.
Таким образом, функции i и 6 постоянны и, поскольку F'=
= m/GzH G' — F (см. (3.37с) и (3.37b)),
(3.42d)	<*2=ттат'г-
144
Гл. 3. Теория относительности
Выберем в качестве параметра s собственное время вдоль гео-
дезической у (другими словами, длину дуги). Тогда
F2(a)i2-G2(a)G2 = 1.
Поскольку F = (1 — 2т/G)1/2,
(3.42е)	F=(l-^-)”.
Таким образом, планета движется по круговой орбите тогда и
только тогда, когда
(3.42f)	t (s) = ± (1 -	s + ci,
0 (s) = ± [ G2 (a) (G (a) _ 3m) ] S + C2
для некоторых констант ci, c2eR. Обычно в первой формуле
выбирают знак -ф, т. е. I > 0.
3.43.	Этими результатами можно воспользоваться для вы-
числения периода орбиты. Относительно собственного времени
период орбиты равен ТР =|2л/й |. Относительно космического
времени период равен Гс = | /1ТР = | 2л//0 |. Поскольку G интер-
претируется как расстояние от центра звезды и i =
(. 3m X ~1/2 .	.	-
= \-----G (а) J ‘ при G(a)—^oo, для больших круговых
орбит
T2P^T2c = 4n2i2/G2 = ^-G\a).
Это не что иное, как третий закон Кеплера для периода обра-
щения планеты, вращающейся вокруг звезды массы т.
3.44.	Замечание. Такое использование ньютоновских понятий
(расстояние от звезды, круговые орбиты) в релятивистской мо-
дели оказалось возможным только благодаря специфике рас-
сматриваемой модели. В частности, существенную роль играет
наличие выделенного космического времени t и стандартного
пространственного сечения IX S2. Отметим, что при очень боль-
ших значениях G космическое время и стандартное простран-
ственное сечение можно определить (в хорошем приближении)
с помощью ньютоновских измерений, поскольку кривизна умень-
шается как m/G\ т. е. при больших G рассматриваемая модель
мало отличается от ньютоновской. Таким образом, модель
Шварцшильда описывает плавный переход (при уменьшении G)
от почти ньютоновской модели к модели, которая так сильно
отличается от ньютоновской, что плохо поддается воображению
G. Планетные орбиты
145
(см. 3.45). Наш реальный мир находится где-то посредине:
эксперименты по измерению времени на земле и в нашей пла-
нетной системе показывают малые отклонения от ньютоновской
модели.
3.45.	Замечание. Отметим, что круговые планетные орбиты
могут существовать только при 1 (Ца)- ~ ^~2 > т- е- когда
G(a)>3m. При стремлении G(a) к Зт период обращения
относительно собственного времени стремится к нулю. Если
G(a) = 3m, круговая орбита y(s) = (t(s), G~l(3m), 6($)) будет
Наблюдатель вне
фотонной сферы
неподвижный^
в космической
системе отсчета
Фотонная сфера
Фотоны"
Наблюдатель
на фотонной сфере!
неподвижный
в космической
системе отсчета
Рис. 3,46.
геодезической при f = 6 = 0 и i2 = 27m262. Такие орбиты яв-
ляются изотропными геодезическими. Они интерпретируются как
траектории фотонов. «Сфера» G_1 (3m) X S2 с: IX S2 называется
фотонной сферой, поскольку фотон, испускаемый в касательном
к этой сфере направлении, всегда остается на ней.
3.46.	Интегральные кривые киллингова векторного поля d/dt
интерпретируются как мировые линии «космически неподвиж-
ного» (но не свободно падающего!) наблюдателя. Космически
Ю А. Бессе, т. I
146
Гл. 3. Теория относительности
неподвижные наблюдатели на фотонной сфере могут увидеть
свое собственное прошлое. Действительно, все направленные в
прошлое изотропные геодезические, выходящие из точки р в ка-
сательном направлении к фотонной сфере, фокусируются в точке
р', которая расположена в прошлом на траектории космического
наблюдателя, проходящей через р (см. рис. 3.46). Космически
неподвижные наблюдатели вне фотонной сферы в принципе
тоже могут заглянуть в свое прошлое, если наведут телескопы
на точки, близкие к фотонной сфере (см. рис. 3.46). Однако для
звезд радиуса > 3m, таких, как наше Солнце (а также Земля),
это не так, поскольку решение, описывающее вакуум, не распро-
страняется на сферу г = 3т.
Н. Прецессия перигелия
3.47.	Анализ круговых планетных орбит допускает обобще-
ние на случай почти круговых орбит и позволяет изучить пре-
цессию перигелия.
Пусть геодезическая у (s) ==(/(§), p(s), 6(s)) описывает кру-
говую планетную орбиту в М, как в 3.42. Можно считать, что
p(s) = a, t(s) = bs и 0(s) = cs, где константа aeR такова, что
G(a)>3m, fe = (l—3m/G(a))-V2 и c=[m/G2(a) (G(a) — 3m)p/2.
Тогда период орбиты относительно собственного времени равен
2л/с. Рассмотрим почти круговую орбиту, которая лежит на
вполне геодезической гиперповерхности RX/XS1, содержащей
-у. Инфинитезимально такая орбита описывается полем Якоби.
Для краткости мы будем обозначать оператор X>->R(X, у) у
через fy • X. Найдем с помощью 3.39 его собственные век-
торы и собственные значения в у3-. Имеем
fy-W = mG~3 -W—.Kw-W,
rv7	l F d . G d
где W	b  G + c • F dt .
Очевидно, эти собственные векторы не параллельны, но
со ;= (рр (—), г) = (1 - 3m/G) be = (1 - 3m/G)1/2 с =
Отметим, что ньютоновская теория требует, чтобы выполнялось
со = с. Поскольку параллельное векторное поле вдоль мировой
линии физически реализуется как угловой момент вращающе-
гося тела, из условия со = с/b можно сделать следующий вывод:
если ось вращения планеты (имеющей круговую орбиту) лежит
в орбитальной плоскости, то эта ось медленно вращается вперед
I. Геодезические вселенной Шварцшильда
147
-относительно своего положения, соответствующего ньютоновской
теории (прецессия Фокера). Запишем уравнения Якоби в виде
(’•«’’ + •* £)" +	+1* <) = 0
«ли в эквивалентном виде
(ji -f- 2сор.) • W = 0,	—2<оЛ -р ji	(/Ср — <о2) р> 0.
Положив 1 + 2юр = const, получим
Р + (/Ср + 3/СШ) ц = fl + (1 — 6m/G) с2ц = const.
Решение р, = const соответствует почти круговым орбитам. Пе-
риодические решения имеют период (1—6m/G)~I/22n/c. Таким
образом, в случае слегка удлиненной орбиты перигелий дости-
гается вновь через отрезок времени, слегка превосходящий пе-
риод (в (1—6m/G)1/2 раз). Эта формула описывает знамени-
тый релятивистский эффект: смещение перигелия Меркурия на
43 угловые секунды в столетие.
I. Геодезические вселенной Шварцшильда
3.48.	Обобщение результатов предыдущего параграфа позво-
ляет получить качественную информацию о поведении любых
геодезических вселенной Шварцшильда М. Например, если
у (s) = (t (s), р (s), 6 (s)) — произвольная геодезическая, лежащая
на вполне геодезической гиперповерхности RX/X^’cAf, то
р = Gz6 и е = F2t постоянны вдоль у. Действительно, G26 =
= — ^у, и F2i = (у,	, но эти скалярные произведения
д д	т.
ПОСТОЯННЫ ВДОЛЬ у, поскольку ПОЛЯ -gg- и киллинговы. Если
у — причинная геодезическая (т. е. времениподобная или изо-
тропная), то ц и е можно интерпретировать как угловой момент
и полную энергию пробной частицы, движение которой описы-
вается геодезической у.
3.49.	Рассмотрим подробнее случай, когда у
геодезическая. Тогда
есть изотропная
Отсюда
0 = (у, у) = F2!2 - р2 - G262.
p2=/?2/2_G202
р*	еа
G1 — 2m
1 G
U1
G2 •
10*
148
Гл. 3. Теория относительности
Поскольку р 2 О, вдоль каждой изотропной геодезической вы-
полняется неравенство

Функция (J----q-J/G2 достигает максимального значения
1/27т2 при G = 3m. Поэтому возможны три случая.
3.50.	Случай /: р2 > 27т2е2. В этом случае геодезическая
остается вне гиперповерхности G = Зт. Функция G достигает
минимума вдоль каждой максимально продолженной изотропной
геодезической такого типа, лежащей в области G > 3m. Эти
геодезические описывают мировые линии фотонов, которые до-
стигают точки максимального приближения к фотонной сфере
и затем удаляются на бесконечность.
3.51.	Случай II: р2 = 27т2е2. Этот случай соответствует изо-
тропным геодезическим, которые накручиваются на фотонную
сферу (см. 3.45), а также изотропным геодезическим, которые
асимптотически приближаются по спирали к фотонной сфере
с внешней или внутренней стороны.
3.52.	Случай III: р2 < 27т2е2. В этом случае функция ^-(G°p
отделена от нуля вдоль геодезической -у, поскольку
Значит, функция G монотонна вдоль у. Вдоль максимальной
изотропной геодезической этого типа функция G стремится
к значению 2m, когда аффинный параметр s стремится к неко-
торому конечному значению. Такие геодезические неполны. Они
описывают фотоны, испускаемые или поглощаемые звездой.
J. Отклонение луча света
3.53.	Изотропные геодезические с р2 > 27т2е2 (типа I) опи-
сывают мировые линии фотонов, пролетающих мимо звезды.
С точки зрения наблюдателя луч света, проходящий вблизи
звезды и описываемый такой геодезической, отклоняется грави-
J. Отклонение луча света
14»
тационным полем звезды (см. рис. 3.53). Угол отклонения можно
оценить следующим образом.
3.54.	Предположим, что как наблюдатель, так и источник
света расположены очень далеко от звезды, т. е. там, где гео-
метрия Шварцшильда близка к геометрии Минковского. Угол
Рис. 3.53.
отклонения <р определяется как угол между направлениями на
звезду, вычисленными в геометрии Шварцшильда и в асимпто-
тическом пространстве Минковского. Он приближенно равен
,	г00
6с — л, где6с=\ 6 ds—центральный угол, образованный двумя
лучами мировой линии. Для того чтобы оценить 0С, заметим,
что функция 6 (s) —	6 ds монотонна, поскольку функция
0 = |i/G2 знакопостоянна. Поэтому вдоль у функцию 6 можно
рассматривать как параметр. Как и в 3.52, имеем
= {'2 - [((1 _	/ ° °р)2]}<° ° рГЛЛ
Если положить v — m/G ° р, это уравнение принимает вид
(£)2“(=7-”’+2Л
Обозначим через 6о значение 6, при котором функция G ° р до-
стигает минимума (а функция v — максимума), и положим
150
Гл. 3. Теория относительности
v0 — v (в0)  Тогда
Следовательно, функцию можно представить в виде
Таким образом,
СО	t)0
1	(	^-o3V1/2
J („2	2X1/2 ( 1	2 р , J dv >
o’	—v	)	V	^о — о/
?°	1	(
> 2 J Л,2 _ 2X1/2 I 1 + д2_ 2 Jdv — n-j- 4v0.
о vo V ) V °0 — ° /
Значит, угол отклонения ф не меньше, чем 4п0 = 4т/Go, где
Go — минимальное значение G на -у. Для луча света, проходя-
щего вблизи Солнца, полученное таким способом значение хо-
рошо согласуется с наблюдениями. Отметим также, что время
движения луча, проходящего вблизи звезды (измеренное наблю-
дателем, расположенным далеко от звезды), оказывается боль-
ше, чем предсказывает ньютоновская теория (эффект Шапиро).
В более крутых световых конусах вблизи звезды световой луч
затрачивает больше координатного времени, чем может ожидать
наблюдатель, находящийся вдали от звезды (конечно, если он
не владеет теорией относительности).
К. Расширение Крускала
3.55.	Модель Шварцшильда можно расширить таким обра-
зом, чтобы причинные геодезические, достигающие границы
G — 2т за конечное время, продолжались дальше. Наиболее из-
вестный способ такого расширения состоит во вложении модели
Шварцшильда в U X S2, где U — подходящее открытое множе-
ство в R2 с метрикой вида
g = Н2 (и, и) (dv2 — du?) — J2 (и, и) da2.
Здесь da2 обозначает стандартную метрику на сфере S2.
3.56.	Определим / (неявно) с помощью уравнения
(i- l)e"2m = u2-v2,
К. Расширение Крускала
15Г
где те ₽, и положим
Я = (32т3//)>-//2т.
Тогда метрика g является риччи-плоской метрикой в L'X.S2,
где
U — {(u, v) R2; v2 — и2 < 1}.
Это пространство-время известно как модель Крускала. Отобра-
жение fy..Id: R X 7 X 52-> t/X S2, где f:	—отобра-
жение, задаваемое уравнениями
ы==	----iy/2e~G<p>/4mcosh(//4/n),
v = ( °2т----1 У'2e~G (p)/4m sinh (t^rri),
является изометричным вложением модели Шварцшильда в мо-
дель Крускала (в [Stp] объясняется, как найти такое расшире-
ние). Отметим, что при этом вложении функция / на t/X«S2 со-
ответствует функции G на R XIX S2.
Описанное вложение отображает модель Шварцшильда на
t/iXS2, где Ну = {(«, о)е U, и > 10]}. Типичные кривые уров-
ня координатных функций t и G модели Шварцшильда показаны
на рис. 3.56.
3.57.	Область t/2XS2, где Uz — {{и, о)е U, v > |ц|}, назы-
вается черной дырой Шварцшильда. Если звезда сжимается в
точку и ее «радиус» Jo становится меньше 2т, то метрика Кру-
скала в области Jo < J < 2т описывает гравитационное поле
между звездой и горизонтом J — 2т. Отметим, что, поскольку
все световые конусы на рис. 3.56 имеют наклон ±1, все причин-
ные кривые, вдоль которых время модели Крускала v возрас-
тает и которые входят в черную дыру, должны остаться в ней
навсегда, т. е. окончиться в точке J — 0. В частности, любая
звезда, сколлапсировавшая внутрь своего радиуса Шварцшильда
J = 2т, обречена на непрерывный коллапс вплоть до J = 0.
Собственное время, необходимое геодезической для достижения
границы / = 0, конечно, поэтому модель Крускала также гео-
дезически неполна. Однако эту модель уже нельзя расширить,
поскольку, например, величина || 7? ||2 = tr R ° R не ограничена
вблизи J — 0.
3.58.	Область /7зХ«52, изображенная на рис. 3.56, изомет-
рична модели Шварцшильда t/iXS2 при изометрии (u, v, р)*-^
ь—>(—u,v,p) многообразия t/XS2. Область t/4XS2 изометрична
Uz'X.S2 при изометрии обращения времени (и, v, р)>—>(и,—v,p)
многообразия t/X«S2. Область (74X«S2 интерпретируется как
152
Гл. 3. Теория относительности
«белая дыра»: причинные геодезические, покидающие эту об-
ласть, не могут вернуться назад.
3.59. Замечание. Можно показать (теорема Бирхгофа), что
модель Крускала содержит, по крайней мере локально, любое
Рис 3.56.
сферически симметричное решение вакуумного уравнения Эйн-
штейна г — 0: каждая точка многообразия, на котором задано
такое решение, обладает окрестностью, которая изометрично
отображается на U X 52 с метрикой Крускала с некоторым зна-
чением т. Доказательство см. в [На-El].
L. Как может нарушаться полнота
3.60. Известно очень мало лоренцевых многообразий, допу-
скающих такую глубокую физическую интерпретацию, как мо-
дель Шварцшильда. Однако с помощью полученных физиками
вакуумных решений уравнений Эйнштейна (т. е. риччи-плоских
L. Как может нарушаться полнота
153
лоренцевых многообразий) можно показать, как сильно разли-
чаются геометрические свойства римановых и лоренцевых мно-
гообразий. Хорошим примером может служить метрика Тауба —
НУТ, открытая в 1951 г. Таубом и расширенная в 1963 г. Нью-
меном, Унти и Тамбурине. Это риччи-плоская метрика в RXS3.
Ее группа изометрий U(2) имеет пространственноподобные
орбиты S3. На этих орбитах индуцируются метрики Берже, т. е.
они с точностью до масштабного множителя изометричны гео-
дезическим сферам в 'СР2 или в двойственном ему пространстве.
Риччи-плоская метрика получается каноническим варьирова-
нием стандартной метрики на расслоении RXS3-*S2 (где
S3-*S2 — расслоение Хопфа), как показано в 9.67. Странное по-
ведение геодезических в пространстве Тауба — НУТ проявляется
главным образом на двумерных вполне геодезических слоях.
Подробности можно найти в [На-El], с. 174—178. Здесь мы рас-
смотрим (также следуя [На-El]) более простой плоский дву-
мерный пример подобного поведения геодезических, открытый
в 1967 г. Мизнером (метрика, индуцированная в слоях про-
странства Тауба — НУТ, не является плоской).
Рассмотрим дискретную группу изометрий G лоренцевой пло-
скости, порожденную преобразованием
(х\ /cosh я sinh л \ /х\
7 ) -> I . .	,	) • I т ), ds2 — dx2 — dt2.
tj \ sinh л cosh л/ /
Она действует вполне разрывно на полупространствах x-pt > О
и —x-\-t>G (однородных, но не полных, см. 7.113), но не на
всей лоренцевой плоскости. Фактор-пространством в обоих слу-
чаях является произведение S’XR- После преобразования
/:= 1/4(72 — х2), : = 2arctanh(х/i) (определенного только в
пересечении подпространств) метрика в S*X!R+ принимает вид.
ds2 — —y dt2-p tdty2.
В результате замен ф±=ф=р1о§/ метрика принимает вид
ds2+ = 2с?ф+ dt +t • (с?ф+)2 на S1 X R,
dsP_ = —2dty_ dt -pt  (chj>_)2 на S' X R-
Первый цилиндр изометричен фактор-пространству первой полу-
плоскости x-pt > 0, а второй — фактор-пространству второй по-
луплоскости. Таким образом, мы получили два аналитических
продолжения лоренцева многообразия (S1 X R+, ds2) до лорен-
цевых многообразий (S’ X R, ds2+~) и (S1 X R, ds2_~), причем не
существует хаусдорфова лоренцева многообразия, содержащего
154
Гл. 3. Теория относительности
оба расширения. Эти расширения изотропно геодезически не-
полны, хотя на рис. 3.60 это можно заметить не сразу. Одно
•семейство изотропных геодезических состоит из образующих
цилиндра = const с аффинным параметром t. Они полны.
Окружность t = 0 выглядит как замкнутая изотропная геодези-
ческая. Другие изотропные геодезические спирально накручи-
ваются на цилиндр и полны при |^]->-оо. В противоположном
Рис. 3.60. Плоские неполные лореи-
цевы многообразия (Мизнер, 1967).
направлении они бесконечно ча-
сто накручиваются на цилиндр
и, как можно предположить,
глядя на рис. 3.60, асимптотиче-
ски подходят к предельной
геодезической / = 0. Однако
анализ параметризации пока-
зывает, что все обстоит совсем
не так, как может показаться
привычному к римановой гео-
метрии глазу. Например,
(s)	— —2 logs,	t — 0
есть аффинная параметриза-
ция «замкнутой» геодезической
t = 0, которая, таким образом,
неполна при s —0. При каж-
дом новом обороте значение
аффинного параметра умень-
шается на меньшую величину,
поэтому конечному изменению
аффинного параметра изотроп-
ной геодезической соответст-
вует бесконечное число обо-
ротов. Эту неполноту легко
можно было обнаружить и в
описании многообразия как факторизованной полуплоскости, но
читатель, вероятно, согласится, что человек, привыкший к ри-
мановой геометрии, не мог ожидать ничего подобного, глядя на
простую плоскую метрику без особенностей
2йф+ dt -j- Цс1ф+)2 на S’X Ik-
М. Теоремы о сингулярности
3.61.	Расширение Крускала модели Шварцшильда было от-
крыто в 1960 г. Это открытие положило начало периоду интен-
сивных исследований по общей теории относительности, когда
М. Теоремы о сингулярности
155
физики начали использовать глобальные дифференциально-гео-
метрические методы для изучения сингулярностей простран-
ства-времени. Было обнаружено, что при некоторых разумных
физических предположениях следует ожидать появления сингу-
лярностей в гравитационных моделях. В заключение мы сфор-
мулируем одну из наиболее знаменитых теорем о сингулярности,
доказанную Пенроузом в 1965 г.
Теорема. Пусть пространство-время М обладает следующими
свойствами-.
(i)	тензор Риччи г всюду неотрицательно определен-,
(ii)	любая максимально продолженная причинная геодези-
ческая из М имеет в некоторой точке ненулевое приливное
напряжение-,
(iii)	М не содержит замкнутых времениподобных кривых-,
(iv)	М содержит ловушечную поверхность, т. е. компактную
пространственноподобную 2-поверхность, для которой оба семей-
ства изотропных геодезических нормалей к S являются сходя-
щимися х).
Тогда пространство-время М геодезически неполно.
Условие (i) означает, что плотность энергии всюду неотрица-
тельна. Условие (iv) означает, что в пространстве-времени
имеется гравитационный коллапс. В модели Крускала 2-сфера
1	(«) П 1 (&) является замкнутой ловушечной поверхностью
при всех а < 2m и b е IR.
Доказательство этой теоремы и подробное обсуждение этой
и аналогичных теорем читатель найдет в [На-Е1].
3.62.	Замечание. В этой главе мы рассматривали главным
образом вакуумные модели пространства-времени. Это вызвано
тем, что (i) вакуумные метрики являются эйнштейновыми, а кни-
га посвящена именно пространствам Эйнштейна, и (ii) лучше
обсудить подробно один важный пример, чем поверхностно рас-
смотреть несколько. Однако существует обширная литература
по общей теории относительности, в которой многое может оча-
ровать математика, занимающегося римановой геометрией. Осо-
бенно рекомендуем книги [Be-Eh], [На-El], [Mi-Th-Wh],,
[ONe3], [Pen 2], [Sa-Wu], [Stp] и [Web].
*) Это означает, что соответствующие этим нормалям вторые квадра-
тичные формы имеют отрицательный след (относительно метрики), т. е. сред-
ние кривизны поверхности по этим направлениям отрицательны, см. [Be-Ehf
и [На-Е1]. — Прим, перев.
Глава 4
Римановы функционалы
А. Введение
4.1. Со времен Лагранжа хорошо известно, что уравнения
классической механики можно получить как решение вариацион-
ной задачи для некоторого функционала в конфигурационном
пространстве, который называется действием (см. [Ab-Ма],
[Аги]). Гильберт показал (см. [Hil]), что уравнения общей тео-
рии относительности можно получить исходя из действия
§1—» 5бцб (которое является полной скалярной кривизной).
В статье Гильберта высказываются пророческие идеи о роли
группы диффеоморфизмов, которую он уже рассматривает как
«калибровочную группу».
Напрашивается естественный способ доказательства суще-
ствования метрик Эйнштейна: достаточно показать, что полная
скалярная кривизна, соответствующим образом нормированная
(см. 4.16), имеет критические точки. Увы, эти ожидания слиш-
ком наивны.
Применение прямых вариационных методов, часто весьма
успешно работающих в нелинейном анализе (см., например,
[Nir 4]), в данном случае вызывает серьезные затруднения.
Действительно, поскольку существуют компактные многообра-
зия, не допускающие метрик Эйнштейна (такие, как S1 X 52
или S1 X S3, см. гл. 6), в трех- и четырехмерном случаях нельзя
получить нужных результатов средствами одного лишь анализа.
Хотя аналогичные примеры в размерностях больше четырех не-
известны, естественно предположить, что доказательство суще-
ствования метрик Эйнштейна прямым вариационным методом
потребует некоторых геометрических предположений относи-
тельно многообразия. Теорема Гамильтона (см. [Ham 2] и гл. 5)
устанавливает такой результат, но только в трехмерном случае.
Если ограничить функционал полной скалярной кривизны
на класс поточечно конформных метрик, то множество критиче-
ских точек расширяется. Критическими точками при этом оказы-
ваются метрики рассматриваемого класса с постоянной скаляр-
ной кривизной (см. 4.25). Вопрос о существовании таких крити-
ческих точек составляет содержание знаменитой проблемы Яма-
В. Основные свойства римановых функционалов
157
бе. Для случая общего положения она решена (но не пол-
ностью1)) в размерности п 6. Основные трудности связаны
с нарушением условия Пале — Смейла (см. [Nir 4], II. 1).
В § В приводятся основные свойства римановых функциона-
лов, которые будут использоваться в дальнейшем. Большинство
этих свойств следует из инвариантности функционала относи-
тельно группы диффеоморфизмов. В § С доказывается теорема
Гильберта (точнее, ее риманов вариант, что не меняет дела),
а в § D обсуждается проблема Ямабе.
Объединяя результаты Ямабе и Т. Обина с результатами
Каждана — Варнера для скалярной кривизны и с описанными
в гл. 6 топологическими препятствиями, можно получить полное
описание функций (включая константы!), которые являются
скалярными кривизнами метрик на данном компактном много-
образии (§ D, Е). Эти результаты мы излагаем более подробно:
они представляют собой прекрасные примеры применения ана-
лиза в геометрии и не столь сложны для читателя-геометра, как
гипотезы Ямабе и Калаби.
Параграф F посвящен изучению множества © метрик фик-
сированного объема и постоянной скалярной кривизны. В общем
случае это пространство является бесконечномерным многооб-
разием, а все критические точки функционала полной скалярной
кривизны, ограниченного на это многообразие, являются мет-
риками Эйнштейна. С помощью множества © можно дать гео-
метрическую интерпретацию вторых производных полной ска-
лярной кривизны. Это сделано в § G.
В § Н дается обзор результатов по квадратичным функцио-
налам. Подробности можно найти в [Вег 4], [Mut 1, 2], [Pat].
Результаты разочаровывают, однако эти вопросы представляют-
ся нам интересными, и не только потому, что они далеки от пол-
ного решения.
В. Основные свойства римановых функционалов
4.2. Пусть Лм, или просто Л, — множество римановых мет-
рик на компактном многообразии М. В компактной открытой
С°°-топологии Л есть ожрытый выпуклый конус. Пусть © —
группа диффеоморфизмов М на многообразии Л. Тогда суще-
ствует естественное правое действие группы R* X © на Л:
(Л <Р) • g = t2tfg.
Ясно, что две метрики из одной орбиты имеют одинаковые гео-
метрические свойства. Правда, можно возразить, что такие гео-
’) Полное решение было анонсировано Р. Шоэном.
158
Гл. 4. Римановы функционалы
метрические характеристики, как объем и длина кривой, у этих
метрик различны. Однако все различие сводится к масштабному
множителю, являющемуся степенью t. Классы изометричных
метрик описываются точками пространства Л/% орбит группы
2), которое часто называют пространством римановых структур.
Классы глобально гомотетичных метрик описываются точками
пространства ^£1/2), где
(4.3)
•^i — J g g= Л, j Pg — 1
I м
Теорема Д. Эбина о срезе ([Ebi 2]) устанавливает основное
свойство действия группы 2). Мы приведем только инфинитези-
мальный вариант этой теоремы. Грубо говоря, она утверждает,
что инфинитезимально пространства Л/% и Л\/% устроены как
многообразия. Касательное пространство к 21-орбите данной
метрики g есть образ дифференциального оператора первого по-
рядка
(4.4)	б*:
задаваемого формулой
б £	2 L^g
(см. 1.59). Поскольку символ <т<(б*)(х)—t°x оператора б*
инъективен, из приложения 32 следует, что пространство Т&Л —
= разлагается в ортогональную (относительно глобального-
скалярного произведения) прямую сумму
(4.5а)
^2M = Im б’Ф Ker6g.
Здесь дивергенция 6g выступает как оператор, формально сопря-
женный к оператору б’, определенному в 1.59. Ясно, что каса-
тельное пространство ТеЛ\ = {/ie^2Af, g'>g = 0) содержит
Im б*, поэтому разложение (4.5а) можно уточнить:
(4.5b)
ТвЛх = Im 6g Ф (Ker 6g П ТЪЛ^.
Здесь мы нормируем полный объем ЛА считая его равным еди-
нице. Возможна и дальнейшая нормщжвка: Дж. Мозер доказал,
что любые две С°°-плотности на компактном многообразии М
с одинаковыми интегралами по М сопряжены диффеоморфизмом.
Поэтому, если ц — положительная плотность с полным объемом
единица, то любая метрика из Л\ оказывается ©-эквивалентной
некоторой метрике из множества
(4.6)	Л’ц = {g ge Л, pg = |ij <= Лх
(см. [Msr] или [Ham 1], с. 203).
В. Основные свойства римановых функционалов
159
4.7.	Определение. Вещественная функция F на Л называется
римановым функционалом, если Г(ф*§) = F(g) для любого диф-
феоморфизма <р и метрики g е Л.
4.8.	Комментарии, (i) Поскольку <р есть изометрия многооб-
разия (М, g) на многообразие (М, q>*g), образ F(g) зависит
только от римановой структуры, задаваемой метрикой g, и
функцию F можно рассматривать как функцию на фактор-про-
странстве .</£>.
(ii)	Для сравнения приведем тривиальный пример нерима-
нова функционала. Зафиксируем точку р е М и рассмотрим
функционал g'—>sg(p), сопоставляющий каждой метрике ее ска-
лярную кривизну в точке р. Очевидно, он нериманов.
(iii)	В [Pal 3] Р. С. Пале исследует естественные лагран-
жианы для римановых метрик. Они определяются как ©-инва-
риантные отображения Лм-^&М, зависящие только от Л-струи
некоторого порядка k метрики g. Все функционалы, которые мы
будем рассматривать, имеют вид	L(g)p.e, где L-—есте-
ственный лагранжиан.
4.9.	Определение. Риманов функционал называется диффе-
ренцируемым (соответственно дифференцируемым до порядка
г), если для некоторого целого k функция F дифференцируема
(соответственно дифференцируема до порядка k) на Л относи-
тельно 1,2-нормы (напомним, что все такие нормы эквива-
лентны).
В этой главе мы дважды (4.36, 4.44) воспользуемся теоре-
мой о неявной функции (в банаховой и ILH-категории), поэтому
понятия производной по направлению нам недостаточно. Однако
во всех рассматриваемых случаях дифференцируемость легко
проверяется: функционал вида£>—> P(Rg) где Р — поли-
ном, очевидно, дифференцируем. При этом, интегрируя по ча-
стям, легко проверить, что-^- F(g + th) | = F' • h — (fl, h) , где
симметрический 2-тензор а является полиномом от кривизны и
ее первых двух ковариантных производных (конкретные при-
меры см. ниже). Это приводит к следующему понятию.
4.10.	Определение. Говорят, что дифференцируемый риманов
функционал F обладает градиентом в точке g, если существует
такое а е что для любого h е
F'p-h = {a,h\.
160
Гл. 4. Римановы функционалы
Градиент а обозначается grad Г. Если F обладает градиентом
в каждой точке, то отображение £•—>grad Eg задает векторное
поле на Л. Это векторное поле удовлетворяет следующему ус-
ловию интегрируемости (см. [В1е]), которое восходит к Гиль-
берту (см. [НИ], с. 403).
4.11.	Предложение. Если риманов функционал F обладает
градиентом grad Fg в точке g, то
6g (grad Fs) = 0.
Доказательство. Поверхность уровня функционала F, прохо-
дящая через g, содержит орбиту точки g относительно группы
диффеоморфизмов. Поэтому градиент этого функционала ^-ор-
тогонален касательному пространству Im 6^ этой орбиты. □
4.12.	Замечание. Подобная формула справедлива и для L2-
скалярного произведения, если рассматриваются соответствую-
щие градиент и дивергенция. Однако она не несет дополнитель-
ной информации.
Инвариантность функционала относительно группы диффео-
морфизмов влечет за собой некоторые следствия для метрик,
допускающих достаточно много изометрий. Следующее предло-
жение позволяет получить концептуальное доказательство изве-
стных ранее результатов о специальных функционалах (см.
[Mut2], [Pat]).
4.13.	Предложение (Д. Бликер, [В1е]). Пусть (TH,g)— изо-
тропно неприводимое однородное пространство с канонической
римановой метрикой (см. 7.39). Тогда для любого риманова
функционала F, обладающего градиентом, существует такая кон-
станта К, что grad Fg = Kg.
Доказательство. Для любой изометрии <р метрики g имеем
<р* (grad Fg) = grad Fg. Рассматривая изометрии, сохраняющие
точку р, и учитывая неприводимость группы изотропии, мы по-
лучаем, что gradFg(p) = K(p)g(p). Из однородности простран-
ства следует, что К(р) = const.	□
4.14.	Следствие. Изотропно неприводимые однородные мет-
рики являются критическими точками любого риманова функ-
ционала, ограниченного на М\.
4.15.	Замечание. Предложение 4.13 и следствие (4.14) спра-
ведливы, в частности, для неприводимых симметрических про-
странств (см. гл. 7).
С. Полная скалярная кривизна: свойства первого порядка
161
С. Полная скалярная кривизна:
свойства первого порядка
4.16.	Определение. Полной скалярной кривизной компактного
риманова многообразия (М, g) называется число S (g) = \ sgpg.
Функционал g'—^Skg) есть однородный функционал степени
п/2. Поэтому мы можем либо ограничить его на Л\, либо нор-
мировать, рассмотрев однородный функционал S/(vol)<n_2)/".
Далее мы опускаем символ g в тексте доказательств в тех слу-
чаях, когда это не приводит к недоразумениям.
4.17.	Предложение. Для любого компактного риманова мно-
гообразия (М, g) функционал S дифференцируем и
s?A=<(V2)^-rg> h)8-
Следовательно, grad Sg = (sg/2)g— rg.
Доказательство. Напомним, что s' • h = A (tr A) + 6 (6Л) —
— (^> rg)’ см- (l-174e). {Значит, по формуле Стокса S'-A =
Л>- °
4.18.	Замечание. При п = 2 из 4.17 следует, что S'=0. Зна-
чит, число S(g) не зависит от метрики и является инвариантом
многообразия. Это неудивительно, так как -^sgpg есть просто
интегрант Гаусса — Бонне в размерности 2.
4.19.	Следствие, (i) Для любого риманова многообразия
(М, g)
Vg + Tdsg = 0-
(ii)	Если dimAl > 2 и для некоторой функции f выполняется
равенство rg = fg, то f = const и многообразие (М, g) эйн-
штейново.
Доказательство. Напомним, что 6(fg) = —df (см. 1.59).
В компактном случае утверждение (i) следует из предложе-
ния 4.11, примененного к 4.17. В общем случае, взяв диверген-
цию от обеих частей рд^енства r = fg, получим l/2ds — df.
С другой стороны, s = trr = nf. Отсюда ds = df = 0.	□
4.20.	Замечание, (i) Формула 4.19 обычно доказывается
с помощью дифференциального тождества Бьянки (см. 1.94).
И А. Бессе, т. 1
162
Гл. 4. Римановы функционалы
На самом деле оба тождества Бьянки следуют из инвариантно-
сти S относительно группы диффеоморфизмов. Этот подход, не-
явно содержащийся в статье Гильберта [Hil], был развит
Дж. Кажданом ([Kaz 2]).
(ii)	Равенство дивергенции нулю трактуется физиками как
закон сохранения. Это объясняет ту роль, которую играет тензор
rg — (sg/2)g в эйнштейновых уравнениях поля (см. 3.7 и
[На-Е1]).
Сформулируем результат Гильберта.
Далее мы предполагаем, что dimAf>2.
4.21.	Теорема. Для компактного риманова многообразия
(Л4, g) объема 1 следующие условия эквивалентны:
(i)	(Л4, g) эйнштейново;
п-2
(ii)	g есть критическая точка функционала S/vol 2 ;
(Ш) g есть критическая точка функционала S на JK.\\
(iv) g есть критическая точка функционала S на множестве
Л’у. метрик g с фиксированной формой объема = у.
Доказательство. Ясно, что условия (ii) и (iii) эквивалентны,
так как S — однородный функционал степени п/2—1. Напом-
ним, что
Tg-{йе 9>2М, (h, g) = 0),
= {h (= 9ю M, trgft = O).
Метрика g является критической точкой функционала S ( Jtj
(соответственно S [“ УРр, тогда и только тогда, когда ортогональ-
ная проекция вектора grad Sg — (s/2)g— г на ТвМ\ (соответ-
ственно на TgNц) равна нулю. В обоих случаях это означает,
что г — fg для некоторой функции f. Результат следует теперь
из 4.18.	□
4.22.	Замечание. Заметим, что grad Sg f Л3^ = — g — r — z.
Теорема 4.21 допускает следующую конечномерную версию.
Пусть G — компактная группа Ли, транзитивно действующая
на М. Обозначим через множество G-инвариантных рима-
новых метрик полного объема 1. Тогда Ж°\ — конечномерное
многообразие. Скалярная кривизна sg любой метрики g е
постоянна и равна Sg.
D. Существование метрик постоянной скалярной кривизны 163
4.23.	Теорема (Пале, [Pal 3], [Ра! 12]). Метрика g^Jt°
является эйнштейновой тогда и только тогда, когда g есть кри-
тическая точка функционала S [ Лл .
Доказательство. Утверждение теоремы следует непосред-
ственно из принципа симметричной критичности (см. [Ра! 12]
и [Ра! 4]). Пусть компактная группа Ли G действует на много-
образии V (в нашем случае Л\), a F (у нас S) есть G-инва-
риантная функция на V. Положим Vе = {v eV', y-v — v,
VyeG}. Принцип гласит, что критические точки функционала
F [ Vе являются критическими точками F [ V. Подробное обсу-
ждение этого принципа в общем случае см. в [Ра! 2] и
[Ра! 4].	□
4.24.	Замечание. Г. Йенсен ([Jen2]) доказал утверждение4.23
для М = G с помощью прямых вычислений и рассмотрел вопрос
существования нетривиальных критических точек. Дальнейшие
результаты см. в гл. 9 и в работе Д’Атри и Циллера [DA-Zi].
Возникает вопрос, возможна ли вариационная интерпрета-
ция других геометрических свойств. Следующее предложение
является исходным пунктом для атаки на знаменитую проблему
Ямабе: существует ли метрика постоянной скалярной кривизны,
поточечно конформная данной метрике g на компактном много-
образии?
4.25.	Предложение. Для компактного риманова многообразия
(М, g) следующие условия эквивалентны:
(i)	скалярная кривизна постоянна-,
(ii)	g есть критическая точка функционала S на множестве
Confog метрик, поточечно конформных g и имеющих тот же
полный объем.
Доказательство. Утверждение (ii) справедливо тогда и только
тогда, когда S'- fg— 0 для любой функции f с нулевым интегра-
лом. Но это означает (см. 4.17), что функция s ортогональна лю-
бой такой функции f. Поскольку функция f = sg —	Sg^e
ортогональна sg и константам, отсюда следует, что sg—const. □
D. Существование метрик
постоянной скалярной кривизны
4.26.	С учетом предложения 4.25 напрашивается естественный
способ получения таких метрик: минимизация скалярной кри-
визны в конформном классе. При этом удобно рассматривать S
как функционал на пространстве функций. Принимая во внима-
11*
164
Гл. 4. Римановы функционалы
ние нормировку, положим для любой положительной С°°-функ-
ции f
(4.27)	Ye (f) = S (fa)/vol (M, fg)in~2>,n.
Напомним, что если f = f4,(n~2\ то
(см. 1.161a). Имеется и другое представление Yg.
YS(V =
£и (4 п — 2 ।	+
(п-2)/п
(Un,(n_%
4.28. Определение. Инвариантом Ямабе p,(g) метрики g на-
зывается точная нижняя грань полных скалярных кривизн мет-
рик из конформного класса метрики g того же полного объема,
что метрика g.
Приведенная выше формула показывает, что
(4.29)
inf CL4n-2 ‘^g+v2)^
feMf>0	|2n/(n-2) gg)(n~2)/n
Соответствующее уравнение Эйлера — Лагранжа имеет вид
4 &еГ + sef = Н (g) fn+»“n~2>.
Его нетривиальные решения дают метрики постоянной скаляр-
ной кривизны (а именно gi — f4/in~2)g). Этот факт нам уже из-
вестен из 4.25. Благодаря работам Ямабе [Yam 2], Н. С. Тру-
дингера [Tru 1] и Т. Обина [Aub 2], [Aub 3] (см. также книгу
[Aub 6]) известно, что нижняя грань p(g) достигается при до-
вольно общих предположениях.
4.30. Теорема ([Aub 2]). (i) Для любого компактного ри-
манова многообразия (М, g) выполняется неравенство p(g)
fx(S", сап). Если p.(g) < p,(S", сап), то в конформном классеg
существует метрика полного объема 1 постоянной скалярной
кривизны.
(11) Условие p(g) < fi(S", сап) выполняется, если n^G и
многообразие (М, g) не является конформно плоским.
Доказательство см. в [Aub 2]. Основным моментом является
доказательство утверждения (i). Согласно лемме Соболева
D. Существование метрик постоянной скалярной кривизны
165
•о вложении (см. приложение, 8), существует вложение
Li <=*• L4 (2 q ) > компактное при q <	2  Идея до-
казательства состоит в том, чтобы, используя компактность, ре-
шить сначала вспомогательную вариационную задачу, в которой
2/х
число----77 из 4.29 заменяется меньшим числом q, а затем ис-
п. — 2	4
2ft
следовать сходимость при q —► _ 2 . Для этого нужно найти
наилучшую константу в неравенстве Соболева ([Aub 3]).
Эта теорема не дает полного решения проблемы Ямабе1),
однако позволяет доказать существование «большого числа»
метрик постоянной скалярной кривизны на данном компактном
многообразии. Для этого нам понадобится следующее свойство.
4.31. Предложение (Л. Берар-Бержери, [Вё Вег 4]). Если
пространство метрик снабжено С2-топологией, то отображение
непрерывно.
Набросок доказательства. Ясно, что отображение ц полуне-
прерывно сверху. Для доказательства непрерывности снизу ис-
пользуется следующий прием: с помощью леммы Мозера (точ-
нее, ее модификации с параметрами из [Ebi 1], с. 38) отображе-
ние р ограничивается на пространство метрик с одной и той же
формой объема. Подробное доказательство (использующее не-
равенство Гёльдера) мы предоставляем читателю.	□
4.32. Теорема, (i) На любом компактном связном многооб-
разии существует метрика постоянной отрицательной скалярной
кривизны.
(ii) Если на М существует метрика g, для которой sg О
и sg 0, то на М существуют метрика постоянной положитель-
ной скалярной кривизны и метрика нулевой скалярной кривизны.
Доказательство. Утверждение (i) следует из теоремы 4.30,
если показать, что существует метрика строго отрицательной
полной скалярной кривизны. Соответствующая теорема суще-
ствования доказана А. Аве и Т. Обином ([Avz 1], [Aub 1],
[Aub 2]), однако Л. Берар-Бержери [Вё Вег 4] предложил бо-
лее простое доказательство.
Выберем открытый шар Dn в М. Пусть Sp X Ен лежит внутри
Dn, причем р q — п, п 1, q 2. Зафиксируем положитель-
ную функцию f на DQ, зависящую только от расстояния до на-
') Р. Шоэн анонсировал полное утвердительное решение проблемы Ямабе
(см. [See]). В то же время проблема Ямабе не имеет решения на многих
полных некомпактных многообразиях (см. [Jin]).
166
Гл. 4. Римановы функционалы
чала и тождественно равную 1 вблизи границы D4. Если g2 и §з
обозначают канонические метрики на Sp и Dq, то формула
_ 2р
g\^f +
определяет на Sp X Dq метрику, которая продолжается до не-
которой метрики g на М. Имеем
~ Sg^g ”1” S
М	M—SpXDq St’xD'1
Первое слагаемое не зависит от f, а второе можно преобразо-
вать следующим образом:
$ ^-voKs”, fe)	'’X-X И О*-
SPX£>9	D9
Поскольку р<п—2, коэффициент при |cZf|2 отрицателен. Те-
перь мы можем выбрать функцию f так, чтобы она была огра-
ничена (скажем, числами 1 и 2), а интеграл | df |2pg, оказался
настолько большим, чтобы число S (g) — sgpg было отрица-
тельным.
(ii) Пусть g — метрика csg^0. Тогда эллиптический само-
сопряженный оператор 4 ” ~ 2' ^gf + $gf положителен. Он строго
положителен, если sg Ф 0. Его первое собственное значение X(g)
строго положительно (см. приложение, 37). Поэтому для любой
функции
5 (4 Нт । ‘‘f t + »Z)	> > (е) II f £
м
Неравенство [i(g)> 0 вытекает теперь из неравенства Гёльдера.
Теперь, используя утверждение (i) и непрерывность отобра-
жения р, можно найти такую метрику gi, что p(gi) = 0. Приме-
нив теорему Обина 4.30 к gi, получим метрику нулевой скаляр-
ной кривизны. Если p.(g) < p(S", сап), то те же рассуждения
дают метрику положительной скалярной кривизны. Даже в слу-
чае, если p(g) = p(Sn, сап), можно уменьшить [1(g), вновь ис-
пользуя свойство непрерывности.	□
4.33.	Замечание. В своих статьях о функциях, которые реа-
лизуются как скалярные кривизны метрик из данного конформ-
ного класса, Дж. Каждан и Ф. Варнер использовали функцио-
нал gi—>h(g) так же, как мы использовали р в доказательстве
Е. Образ отображения
167
теоремы 4.32 (см. [Ka-Wa 4], § 3). Поскольку первое собствен-
ное значение положительного эллиптического оператора поло-
жительно, стандартная теория возмущения (см. [Kat]) показы-
вает, что функционал g*~*X(g) дифференцируем по g. Каждан
и Варнер доказали, что критические точки функционала X,
ограниченного на Jlt\, являются метриками Эйнштейна. Чита-
тель может проверить это с помощью формулы (1.184).
Е. Образ отображения скалярной кривизны
4.34.	Теперь мы готовы ответить на следующий вопрос: ка-
кие функции на данном компактном многообразии являются ска-
лярными кривизнами римановых метрик? Заметим, что
(i)	существуют многообразия, на которых нет метрик поло-
жительной скалярной кривизны, например КЗ-поверхности
(см. [Lie 4]) и торы (см. [Gr-La 1] или [Sc-Ya]). Кроме того,
существуют многообразия, на которых нет метрик неотрицатель-
ной скалярной кривизны (см. [Ka-Wa 4]); простейшим приме-
ром может служить связная сумма торов (см. [Gr-La 1],
[Sc-Ya]).
(ii)	Мы сформулируем несколько теорем существования мет-
рик постоянной скалярной кривизны.
Согласно результатам Дж. Каждана и Ф. Варнера, если мы
знаем постоянные функции, являющиеся скалярными кривиз-
нами, то фактически мы знаем и все функции, являющиеся ска-
лярными кривизнами. Используя (i) и (ii), Каждан и Варнер
доказали следующую классификационную теорему ([Ka-Wa 3]),
уточненную Л. Бераром-Бержери.
4.35.	Теорема. Компактные многообразия М размерности
п^З делятся на три класса:
(А)	любая С°°-функция на М является скалярной кривизной
некоторой С°°-метрики-,
(В)	функция на М является скалярной кривизной некоторой
метрики тогда и только тогда, когда она тождественно равна
нулю или отрицательна в некоторой точке (при этом любая
метрика нулевой скалярной кривизны является риччи-плоской);
(С)	функция на М является скалярной кривизной тогда и
только тогда, когда она отрицательна в некоторой точке.
Доказательство. Прежде всего нужно проверить локальную
сюръективность отображения £•—(4.36), а затем воспользо-
ваться тем тривиальным фактом, что если f принадлежит образу
отображения то это верно и для f °<р, где <р—любой диф-
феоморфизм.
168
Гл. 4. Римановы функционалы
Из координатного представления sg видно, что отображение
скалярной кривизны g^—^Sg определяет квазилинейный диф-
ференциальный оператор второго порядка. Теорема вложения
Соболева (см. приложение, 8) показывает, что при р> п этот
оператор продолжается до отображения пространства метрик
класса Lp в Lp (М). В этом контексте можно воспользоваться
теоремой о неявной функции для банаховых пространств.
4.36.	Предложение. Если линеаризованное отображение s'o
отображения скалярной кривизны сюръективно в точке go и
р>п, то Lp- продолжение отображения gt—>sg локально сюръ-
ективно, т. е. существует такое е > 0, что для f ^Lp (М) с || f —
— sg0||<8 существует Ьр-метрика g, для которой f=sg. Если
при этом f е С°°, то g С°°.
Доказательство. Определим отображение F окрестности нуля
в ЕР(М) в Lp (М), положив F (f) = sgo + s'g\f, где Sg* — формаль-
но сопряженный к s' оператор (см. приложение, 16). К функ-
ции F, имеющей в нуле дифференциал s'o ° s'*, можно применить
теорему о неявной функции. Теперь остается только воспользо-
ваться нелинейной теоремой регулярности (см. приложение, 41).
Из приложения 32а следует, что сюръективность s'* эквива-
лентна сюръективности s'. Следующее предложение показы-
вает, что в случае общего положения эти условия выполняются.
4.37.	Предложение (Ж.-П. Бургиньон, [Bou 1], VIII.8). Если
Kers'*#= 0, то либо многообразие (М, g) риччи-плоско и
Ker s'* = R - 1, либо его скалярная кривизна равна положитель-
ной константе и sg/(n—1) есть собственное значение лапла-
сиана.
Доказательство. Возьмем дивергенцию от s'* • f (см. 1.21).
В силу тождества Риччи (1.187) имеем 6(Ddf)~ dkf — r(Af, -).
Поэтому, используя 4.19, получаем d (s'* •/) = l/2f ds = 0. Из
теории эллиптических операторов (см. [Аго] и [Ног 3]) следует,,
что если функция f равна нулю на открытом множестве, то она
тождественно равна нулю. Следовательно, s = const. Тогда
tr (s'* • == (n — 1) Af — sf = 0. Если s = 0, to f = const, и, воз-
вращаясь к s'* • f, мы видим, что это возможно только при
условии rg — 0.	□
Дальнейшее исследование уравнения s'*f — 0 см. в [Коо]
и [Laf 3]. Нетрудно убедиться, что предложение 4.37 не яв-
Е. Образ отображения скалярной кривизны
169
ляется оптимальным результатом. Действительно, для стандарт-
ной метрики на S2'X.S2 лапласиан имеет собственное значение
s/4, но Kers'* = 0. Как бы то ни было, условие, что sg/(n—1)
не принадлежит спектру, снова появится в следующем пара-
графе.
4.38.	Лемма (доказательство см. в [Ka-Wa 2]). Если
dim М = п> 2 и f^C° (М), то Ь^-функция fi принадлежит за-
мыканию множества {[ ° ф, (р ей} тогда и только тогда, когда
inf f fi (х) sup f почти всюду.
4.39.	Лемма. Пусть fo *&№ — скалярная кривизна некоторой
метрики. Если функция	такова, что X(Im(f0))cz Im(fi)
для некоторого числа Z > 0, то fi является скалярной кривизной
некоторой метрики.
Доказательство леммы. Заменив метрику гомотетичной,
можно считать, что Х= 1. Если fn = s„ и Kers'* = 0, то к go
можно применить теорему 4.36 о неявной функции, причем вы-
брать (ре® так, чтобы ||f — Л°ф11р<е. Если Кег6'*=/=0 (и в
силу 4.37 sgo = const), то можно выбрать метрику g2 с
sg2=/= const, для которой по-прежнему Im(sg2) cz Im (Л) (если
взять метрику g2 достаточно близкой к go). Остается восполь-
зоваться этими соображениями для g2.	□
4.40.	Завершение доказательства теоремы 4.35. Если много-
образие М обладает метрикой неотрицательной скалярной кри-
визны, не равной тождественно нулю, то из 4.32 (ii) следует
существование на М метрик постоянной положительной, отрица-
тельной и нулевой скалярной кривизны. Применяя в каждом
случае лемму 4.39 с функцией f0, равной постоянной скалярной
кривизне, получаем, что любая функция является функцией ска-
лярной кривизны. Другие случаи рассматриваются аналогично.
То, что из условия sg — 0 следует rg — 0 (в случае В), будет
доказано в 4.49.	□
4.41.	Замечания, (i) Если dim.M = 2, то с помощью анало-
гичных рассуждений (заменив теорему 4.32 теоремой о кон-
формном представлении) можно получить следующее обращение
теоремы Гаусса — Бонне ([Ka-Wa 1]). Пусть %(Л1)>0 (соот-
ветственно %(Л1) = 0; х(Л4)<0). Тогда функция f на М яв-
ляется гауссовой кривизной некоторой метрики тогда и только
тогда, когда f положительна в некоторой точке (соответственно
f = 0 или принимает значения обоих знаков; f отрицательна в
некоторой точке).
170
Гл. 4. Римановы функционалы
(ii)	Использование Соболевских пространств Lpk (а не Lk,
как в большинстве работ по линейной эллиптической теории)
является существенным; ZA-норма нужна для леммы 4.38 об
аппроксимации, которая, очевидно, не справедлива для равно-
мерной нормы. Кроме того, для применения теоремы о неявной
функции в 4.36 необходимо, чтобы выполнялось условие р >
> dim М.
F. Многообразие метрик
постоянной скалярной кривизны 1)
4.42.	Поскольку многообразие Л римановых метрик и его.
подмногообразия являются многообразиями Фреше, моделиро-
ванными пространством обычная теорема о неявной функ-
ции к ним неприменима. Эта трудность преодолевается с по-
мощью аппарата ILH-многообразий, развитого X. Омори
[Ото]. Напомним, что в силу леммы Соболева (см. приложе-
ние, 8) пространства сечений С°°(Е) любого векторного расслое-
ния Е над М есть обратный предел limT->TC 1% (Е). Переход от
гильбертовых многообразий, моделированных пространствами
L2S (к которым применима теорема о неявной функции), к
ILH-многообразиям, моделированным пространством С°°(Е),
аналогичен переходу от L2S к Сх в эллиптической теории. Для
того чтобы избежать технических сложностей, мы не приводим
полных доказательств, которые можно найти в работах Н. Коисо
[Koi 1] и [Koi 2].
Поскольку мы уже знаем, что любое компактное многообра-
зие несет «много» метрик постоянной скалярной кривизны, вве-
дем множество
(4.43а) S =	volg = l, sg = const).
Нам понадобятся два описания этого множества. С одной сто-
роны, ясно, что geS тогда и только тогда, когда sg =
С другой стороны, постоянство sg эквивалентно тому, что
AgSg = 0. Поэтому инфинитезимальные деформации, сохраняю-
щие это условие с точностью до первого порядка, суть те дефор-
мации, которые лежат в ядре дифференциального оператора чет-
вертого порядка
(4.43b)	%-/i = Ag(s;-A),
поскольку А^ (Л) • f = 0, если f = const.
*) Этот параграф при первом чтении можно опустить.
F. Многообразие метрик постоянной скалярной кривизны
171
Следующая теорема Н. Коисо ([Koi 1 ]) показывает, что в
точках общего положения множество ® является бесконечно-
мерным многообразием, и позволяет получить локальный ва-
риант теоремы Ямабе.
4.44. Теорема. Пусть g0^<5, причем sgJ(n—l) не является
положительным собственным значением лапласиана Дв0. Тогда
в некоторой окрестности точки go множество ® есть ILH-nod-
многообразие в Л \ и
Tg0& = Кег % П {h е 9^М, (h, go)go = 0).
Отображение	из ^Л1Х® в Л есть локальный
ILH-диффеоморфизм окрестности точки (l,go) на окрестность
точки go-
Набросок доказательства. Сначала покажем, что отображе-
ние g i-> S (g) = sg — $ м sg\igo из Лх в <&gJA = {f е <&М, (f, l)go =
= 0} есть ILH-субмерсия. Действительно, его Lp~ продолжение
является субмерсией в гильбертовой категории для достаточно
большого р (т. е. для р > (п/2) + 2, см. приложение 8). Сюръ-
ективность вытекает из предположения о спектре (достаточно
положить h = fg). Из эллиптической теории следует, что
Ker S' (go) = Ker ago Q {h, (h, go)go = 0}
есть прямое слагаемое. Действительно, поскольку символ а*
сюръективен, имеет место ортогональное разложение
(4.45) Т*ЛХ = {h, (h, g0) = 0} = (Ker П VO 0 Im V
Второе утверждение теоремы следует из ILH-теоремы о неяв-
ной функции после того, как установлено разложение
&’2M = Tg<5®‘&M- go
в предположении, что sgJ(n — l)^Sp (Ag0). Это разложение, ко-
торое уже не является ортогональным, также выводится с по-
мощью эллиптической теории.	□
4.46.	Замечания, (i) Условие SgJ(n — 1) ф Sp (Да), возмож-
но, несущественно для первого утверждения теоремы, но оно су-
щественно для второго утверждения. Если многообразие (М, g)
имеет постоянную скалярную кривизну и допускает конформ-
ное некиллингово векторное поле X, то sg/(n — 1) ф Sp (Дй).
Действуя на g потоком поля X, получаем однопараметрическое
•семейство метрик, конформных g, одинаковой скалярной кри-
визны.
172
Гл. 4. Римановы функционалы
(ii)	Покажем, что теорема 4.44 применима к любому много-
образию Эйнштейна, кроме стандартной сферы. Напомним не-
равенство Лихнеровича для первого собственного значения М
лапласиана: на любом компактном многообразии	- rmin>
(см. [Lie 1], с. 135, [Be-Ga-Ma], с. 179—181, или [Gal 3]).
Если теперь g—метрика Эйнштейна и sg/(n—1) принадлежит
спектру, то имеет место равенство и по теореме Обаты (см. [Be-
Ga-Ma] или [ОЬа]) многообразие (М, g) изометрично стан-
дартной сфере.
Появятся ли у функционала полной скалярной кривизны но-
вые критические точки (помимо метрик Эйнштейна), если огра-
ничить его на ®? Вот частичный ответ на этот вопрос.
4.47.	Предложение. Пусть g — метрика постоянной скалярной
кривизны Se на многообразии М и пусть sg/(n — 1) ф Sp+Ag.
Если g — критическая точка полной скалярной кривизны, огра-
ниченной на ®, то (М, gj— многообразие Эйнштейна.
Доказательство. Для h^T имеем S' • h = h, г — g) —
~{h, z).Согласно 4.45, если Sg [	— 0, то существует та-
кая функция f, что z = a*f — s'* Ef. Вычислив след, получим
О = (п — 1) Дй/ — s ДД откуда z = 0.	□
4.48.	Замечание. Даже при условии sg/(n — 1) Sp (Дб) про-
странство Ker <Zg Г)	можно рассматривать как формальное
касательное пространство к ®. Поэтому S [ © имеет крити-
ческую точку тогда и только тогда, когда существует такая
функция f с нулевым средним значением, что
z& = DEdf + (Egf) g — frg.
Случай f = 0 соответствует метрике Эйнштейна. Но существо-
вание ненулевого решения этого уравнения является очень силь-
ным условием: единственный случай соответствует стандартной
сфере (согласно 4.46, это уравнение эквивалентно уравнению
Обаты Ddf — — fS’ если метрика g эйнштейнова). Можно
предположить, что этим случаем все и исчерпывается.
Из предложения 4.47 вытекает важное следствие для много-
образий типа (В) из 4.35. Оно получено Ж.-П. Бургиньоном
(см. [Bou 1]), но мы приводим новое доказательство.
4.49.	Следствие. Пусть компактное многообразие М не несет
метрик неотрицательной ненулевой скалярной кривизны sg 0.
G. Снова о полной скалярной кривизне: свойства второго порядка 173
Тогда любая метрика ненулевой скалярной кривизны является
риччи-плоской.
Доказательство. Нуль есть максимум функционала S [ ® и,
следовательно, его критическое значение.	□
4.50.	Примеры (ср. с § D гл. 6). (i) На КЗ-поверхности лю-
бая метрика нулевой скалярной кривизны является риччи-
плоской.
(ii)	На торе любая метрика нулевой скалярной кривизны
является плоской.
4.51.	Замечание. Дж. Каждан обобщил эти результаты на
некомпактный случай (см. [Kaz3]).
G. Снова о полной скалярной кривизне:
свойства второго порядка
Напомним, что для функционалов, определенных на откры-
том подмножестве U векторного пространства Е, можно ввести
понятие второй производной: для этого нужно взять первую
производную от первой производной, рассматриваемой как функ-
ция на {/><£ (см. [Die] или [Ham 1]). Однако это понятие не
обобщается на случай многообразия, если на нем не задана
связность, специально придуманная для этой цели (см. [Die],
XVIII. 18, или [Pal 1]). Тем не менее понятие второй производ-
ной в критической точке всегда имеет смысл. Это можно прове-
рить непосредственно или с использованием расслоения струй.
Следующей леммой мы воспользуемся в 4.10 и 4.64.
4.52.	Лемма. Пусть F — риманов функционал, имеющий вто-
рые производные. Тогда для любой метрики g^jft и вектор-
ного поля Х^ТГМ
F"(g)(b*X, -) = 0.
Это утверждение справедливо и для функционала F \ Jt\, при
условии что g — его критическая точка.
Доказательство. Сформулированное свойство эквивалентно
©-инвариантности F с точностью до третьего порядка. □
4.53.	Для того чтобы вычислить S", рассмотрим однопара-
метрическую деформацию g(t)— g-\- th-\-(t2/2) k метрики g, ко-
торая принадлежит М\ с точностью до третьего порядка. Мы
уже знаем, что в первом порядке это условие означает, что
174
Гл. 4. Римановы функционалы
(trg h) pig = 0. Поскольку
dt2 ^g (О lt=0 ~ ~2 ~dt trg (0 "I"	^g (O If—0 =
=4[m+t(w-i4K.
условие второго порядка имеет вид \ (tr„ft) р. = \ ( | h\2 —
— 2~tr2ft) pig. Следовательно,
(4.54)	4T?Sg(0|^o = -^-^—rg(f)+ ySg(Ogr(Z), h + tk^ =
= (— r' • h + у (s' • h) g + sh, h} + {—r + ±-sg, kj +
+ у (— r + Ts’ <trg + 2<r>	— {sh, h}.
4.55.	Предложение (см. [Вег 4], с. 290, и [Mut 1]). Если g—
метрика Эйнштейна полного объема 1, то вторая производная
функционала S \ jK\ в точке g равна
S''	= {h - у И’ Dh + 6* 6ft + б (6ft) g + 4- (A trgft) g -
~^(trgh)g+ Rgh).
Доказательство. Поскольку метрика g эйнштейнова, сумма
последних четырех слагаемых из (4.54) равна (1/л—l/2)s||ft||2
и, согласно (1.180а),
r'-h = 1/2D*Dh— Ъ*Ыг- l/2Dgd(trgft) + (s/n)ft — Rh
и
s' • ft = A (trg ft) + 6 (6ft) — (s/n) trg ft.	□
Следующее замечание показывает, как можно интерпрети-
ровать этот оператор, который выглядит достаточно сложно.
4.56.	Замечание. Если ограничить S на конформный класс
метрик, то в силу 4.25 его вторая производная в точке g, яв-
ляющейся метрикой постоянной скалярной кривизны, имеет
смысл. В самом деле, согласно 4.53, получаем S" (fg, fg) = (п —
— 2)/2 • {(п—1) Agf — sgf, f}g. Из этой формулы вытекают три
следствия.
(i)	Индекс критической точки всегда конечен. В частности,
полагая М = Sl X S"-1 с канонической метрикой, где S1 — до-
G. Снова о полной скалярной кривизне: свойства второго порядка 175
статочно длинная окружность, можно получить сколь угодно
большой индекс.
(ii)	Как можно предположить исходя из теоремы 4.44, мет-
рика g является вырожденной критической точкой тогда и
только тогда, когда sgl(n — 1) ф. S^txg. В этом случае нуль-про-
странство совпадает с собственным подпространством оператора
Ag, соответствующим собственному значению sg/(n—1).
(iii)	Если g есть метрика Эйнштейна, отличная от стандарт-
ной метрики сферы, то из 4.46 следует, что g является невы-
рожденной критической точкой и ее индекс равен нулю. Это
свойство можно рассматривать как инфинитезимальный вариант
результата Обаты ([ОЬа]), утверждающего, что метрика Эйн-
штейна (отличная от стандартной метрики сферы) является
единственной метрикой постоянной скалярной кривизны в своем
конформном классе метрик с нормированным объемом.
Вернемся к изучению S\dtb Мы уже знаем (см. 4.52), что
ядро S" содержит Im б*, поэтому необходимо исключить три-
виальные деформации. В силу замечания 4.56 форму S" (fg, fg)
можно считать уже известной. Остается рассмотреть ортого-
нальное дополнение к пространству {6gg 4- fg}, т. е. к 67’(О)П
ntrg’(O). Следующая лемма показывает, что это пространство
допускает интересное геометрическое описание.
4.57.	Лемма, (i) Для любого компактного риманова много-
образия (М, g) алгебраическая сумма Im б* +	• g замкнута
в 9^М и имеет место ортогональное разложение
= (Im 6g + <&М • g) © (6g1 (0) fl trg1 (0)).
причем оба слагаемых бесконечномерны.
(ii)	Если многообразие (М, g) отлично от стандартной сферы
и эйнштейново, то разложение можно уточнить:
=	Im б;х © (6g1 (0) fl trg1 (0)),
причем третье слагаемое является касательным пространством
к многообразию © метрик постоянной скалярной кривизны
объема 1.
Доказательство. Воспользуемся приемом Хёрмандера (см.
(Ног 2], с. 135): применим эллиптическую теорию к оператору
(X, f) 1—>6pf + fg, отображающему	в ^2Af. Как опе-
ратор бистепени (1,0) он является переопределенным эллипти-
ческим оператором, поэтому разложение (i) следует из прило-
жения 34.
176
Гл. 4. Римановы функционалы
Если многообразие (Л4, g) отлично от стандартной сферы
и эйнштейново, то на нем не существует некиллинговых кон-
формных векторных полей (см. 4.46). Поскольку подпростран-
ства Im 6* и 'S’M-g замкнуты, отсюда следует более тонкое раз-
ложение.
Напомним (см. 4.44), что Те<& = Ker ag П TgM\. Поскольку
Imd’caj1^)) (постоянство скалярной кривизны метрики сохра-
няется при диффеоморфизмах), ограничивая разложение=
= Im 6* ф Ker dg на Те<£>, получаем
Те<5 = Im d^© (di1 (0) (] ai1 (0) (] ТеЯ^.
Учитывая, что метрика g эйнштейнова, имеем
= Ag (Ag (tr g/i) + 6g (dgft) -	trgft) .
Если dg/i = 0 и agh = 0, то функция Ag(trJi'j—ecTb
константа. Эта константа равна нулю, если h е Т gJ(x. Исполь-
зуя полученную Лихнеровичем нижнюю оценку первого соб-
ственного значения лапласиана (см. 4.46), заключаем, что
trg /i = 0.	□
4.58.	Замечания, (i) Побочным результатом этого доказа-
тельства в эйнштейновом случае является разложение для
Э^М, которым мы воспользовались в доказательстве локальной
теоремы Ямабе 4.42.
(ii) Для стандартной сферы также получаем
V (0) fl ai1 (0) fl Т8ЯХ = ai1 (0) f) tri1 (0).
Однако геометрическая интерпретация при этом не сохраняется.
Полученные результаты обобщает следующая теорема
М.. Берже и Н. Коисо (см. [Вег 4] и [Koi 3]). Положим
(4.59)	<&gM = {fe= <&М, {f, l>g = 0}.
4.60.	Теорема. Пусть (М, g) — компактное многообразие Эйн-
штейна, отличное от стандартной сферы. Тогда имеет место ор-
тогональное относительно S" разложение
Т&ЯХ = Im б* ф <&g (М) • g® di1 (0) f] tri1 (0).
При этом
(i)	первое слагаемое принадлежит ядру Sg;
G. Снова о полной скалярной кривизне: свойства второго порядка 177
(ii)	для f е ^еМ и Л е 6g1 (0) (1 trg 1 (0) выполняется равенство
S" (fg + h,fg + h)=^ [(n - 2) <(n - 1) Agf - sef, f)g -
— {D*Dh — 2Rh, h)g].
В частности, ограничение S" на второе слагаемое положительно
определено, а ядро и коиндекс ограничения S" на третье сла-
гаемое конечны, поэтому S" I4 7^© имеет конечный коиндекс.
Доказательство. Нам осталось доказать лишь отдельные де-
тали. То, что S"(fg, h) = 0, если dgh = 0 и trff/г = 0, выводится
из (4.54) с помощью повторного интегрирования по частям,
a S" (h, h) вычисляется непосредственно. Оператор D*D яв-
ляется самосопряженным и положительным и имеет инвариант-
ное подпространство 6g1 (0)П trg1 (0), поскольку для любой
метрики Эйнштейна
6ДЛ = D* D6 + (s/n) б
(см. [Lie 2]). Утверждение о конечности следует из приложе-
ния 32.	□
4.61.	Замечания, (i) Эти результаты остаются справедливыми
и для стандартной сферы, если во втором слагаемом заменить
ортогональным дополнением к сферическим гармоникам
первого порядка.
(ii)	Из результатов Бургиньона — Эбина — Марсдена [Во-
Eb-Ма] следует, что пространство 6g1 (0) П trg1 (0) всегда бес-
конечномерно.
Из определения второй производной вытекает следующий
результат (в гл. 12 для него приводится более прямое доказа-
тельство, которое фактически сводится к тем же рассуждениям).
4.62.	Следствие. Инфинитезимальные эйнштейновы деформа-
ции, сохраняющие полный объем и ортогональные к орбите
группы диффеоморфизмов, являются решениями системы урав-
нений
6g/f = 0, trg/i = O, D* Dh — 2Rh = 0.
Поскольку вся геометрическая информация содержится в Tg<&,
в соответствии с обычной терминологией вариационного исчис-
ления можно дать следующее определение.
4.63.	Определение. Метрика Эйнштейна g на М называется
устойчивой, если квадратичная форма S" [ б~1 (0) П tr“1 (0) строго
12 А- Бессе, т. 1
178
Гл. 4. Римановы функционалы
отрицательна, т. е. существует такое X > О, что (£)* Dh — 2Rh,
ft) X || Л ||2 для всех h <= 6g1 (0) f] trj1 (0) = Tg@>.
В частности, устойчивые метрики Эйнштейна инфинитези-
мально устойчивы. Поэтому, согласно важной теореме Н. Коисо
(см. 12.49), они недеформируемы. В связи с этим мы отложим
обсуждение устойчивости до § Н гл. 12, а здесь лишь приведем
несколько примеров устойчивых метрик Эйнштейна:
(а)	стандартная сфера;
(Ь)	компактное многообразие Эйнштейна строго отрицатель-
ной секционной кривизны;
(с)	стандартное комплексное проективное пространство.
С другой стороны, рис. 9.72 показывает, что сферы Йенсена
неустойчивы.
4.64.	Замечание. В работе Лафонтена [Laf 2] изучается пол-
ная масса кривизны Риччи, т. е. функционал g н-> Vr (g) = \ [хг.
JAf
Ясно, что это однородный функционал степени нуль. Эйнштей-
новы не риччи-плоские метрики являются критическими точ-
ками для Vr. Сопоставим формулы для S и Vr. Полагая г = Eg
и используя лапласиан Лихнеровича Дд, получаем для
и h е 6g1 (0) Пtrg* (0)
s; (fg + h, fg + ft) = у [(n _ 2) <(n - 1) Dgf - mf, f) -
— {DLh — 2eh, ft)],
(V;)g(/g + ft, fg + ft) = ||e|(n-4)/2[(n-2)<(n-l)D2f-neD/ /)-
— (£)2 ft _ 2EDLh, ft)].
Отсюда видно, что свойства S" из теоремы 4.60 справедливы
и для V".
Н. Квадратичные функционалы
Перейдем к рассмотрению функционалов, которые представ-
ляют собой интегралы полиномов второй степени от кривизны.
Поскольку нас интересуют римановы функционалы, эти поли-
номы должны быть инвариантны относительно естественного
действия групп в пространстве тензоров кривизны (см. [Gil],
[Pal]). Базис такого пространства состоит из полиномов s2,
|г|2, |R|2. Имеется и другой важный базис: |S|2, |Z|2, |Ц7|2
Н. Квадратичные функционалы
179
(см. 1.114). Положим
(4.65)	Sr(S>=Llr«|!,‘«’
SR(g)= JlR.I’Ug, SZ(g)=	srte)= Jnr,fH,.
МММ
Это однородные функционалы степени — 2.
4.66.	Предложение. Функционалы Ss и Sr дифференцируемы
и имеют градиенты
(grad Ss)g = 2Dg ds+ 2 (AgSg) g + ± s2gg - 2sgrg,
(grad Sr)g = D*gDgrg + Dg dsg + ± (Agsg) g +
Доказательство. Имеем
Ss' • h = y $ s2 (tr Л) + 2 ss' (A) Hg =
м	м
= у <s2g, h) + 2 (s, s' (Л)> = (y s2g + 2s'* (s), h).
Аналогично,
Srg-A = y J | r |2tr (Л) |ig + 2(r, r'(h)) — 2(ror, h)
M
(как и в 4.53, необходимо учесть вариацию скалярного произве-
дения). Напомним, что г' (Л) = у Д£/г — 6*6Л — у Dd tr (Л), где
Д£/г = D*Dh + hor~\-roh — 2Rh (см. (1.180b)), откуда г'*(Л) =
= уД£Л —6*6Л —y(6(6A))g. Имеем grad Srg = у | г |2 g—2г ° г+
+ 2/* (г)-
Для завершения доказательства достаточно воспользоваться
4.19.	О
4.67.	Следствия, (i) Метрики Эйнштейна являются критиче-
скими точками функционалов Ss Jft\ и Sr\Jt\.
(ii)	Если dimAl = 4, то метрика является критической точ-
кой для Ss тогда и только тогда, когда она эйнштейнова или
имеет нулевую скалярную кривизну.
(iii)	Если dimAl = 4 и g — критическая точка для Sr\Jt,\,
то скалярная кривизна метрики g постоянна.
12*
180
Гл. 4. Римановы функционалы
Доказательство. Первое утверждение доказывается элемен-
тарно. Если п = 4, то tr (grad Srg) — 2As и tr (grad Ssg) = 6As.
□
4.68.	Замечание. Для любого полинома Р от п переменных
определим функционал J Р($ь ••> sn)Pg> где st— фундамен-
тальные симметрические полиномы от собственных значений
re. С помощью аналогичных вычислений можно показать (см.
[Laf2]), что любая метрика Эйнштейна является критической
точкой для FP I4 Однако могут существовать и другие кри-
тические точки (см. 4.74).
Формулу для grad SR можно упростить, если воспользовать-
ся соответствующими дифференциальными операторами. Вве-
дем оператор dD: 9^2М.->С°° (Л2 М®Т*М), положив
(4.69)	dgh(x, у, z) = Dxh(y, z) — Dyh(x, z)
(ср. с 1.12). Таким образом, dgh. есть внешний дифференциал
формы h, рассматриваемой как 1-форма со значениями в каса-
тельном расслоении. Этот подход развивается в [Вой 9]. Фор-
мально сопряженный к dD оператор будем обозначать через 6D.
4.70.	Предложение. Функционал SR дифференцируем и имеет
градиент
grad SRg = 2&°d°re - 2Rg + ± I Rg Г g.
(Ср. c [Ber4], c. 202. Напомним, что Rab — RajkiPibb, cm. 1.131.)
Доказательство. Для того чтобы избежать недоразумений,
мы будем рассматривать только ковариантные тензоры. Тогда
SR'-h = 2 ( (/?, R'(h)) gy g + | h R I2 tr (Л) pg - 4 ((& h)glig.
M	MM
Напомним, что R' (h)(x, y, z, t)—DyC(h)(x, z,t)—DXC (h) (y'z, /)-[-
-[-_/?(%, y, z, где C (h) — ковариантный 3-тензор, ассоции-
рованный с вариацией связности (см. 1.177). Отсюда
$ (R, R' (h)) pg = — 2 (R, DC (h)) + (Я, К) =
м
= — 2{D*R, C(h)) + {R, К).
Поскольку 2С (h) (у, z, t) == Dyh (z, t) + Dzh (y, t) — Dth (y, z) (cm.
1.177), достаточно рассмотреть кососимметрическую no z,t часть.
Поэтому
2{D*R, C(h)) = {D*R(y, z, /), dDh(z, t, y)\
Н. Квадратичные функционалы
181
В силу дифференциального тождества Бьянки D*R (у, z, t) =
— —dDr(z, t, у), следовательно,
— 2 {D*R, С (h)) = <6DdDr, h).	□
4.71.	Замечание. Убедившись, что f>DdDr = 2D* Dr + 2r ° r —
О
— 2RrD ds, мы придем к формуле 6.1 из [Вег 4].
4.72.	Следствие, (i) Метрика Эйнштейна (и, шире, метрика
с параллельным тензором Риччи} является критической точкой
для SR t М\ тогда и только тогда, когда R — ~17? |2 g.
(ii) Если dim М = 4, то метрики Эйнштейна, а также кон-
формно плоские метрики нулевой скалярной кривизны являются
критическими точками для SR. При этом любая критическая
для SR метрика имеет постоянную скалярную кривизну.
Доказательство. Утверждение (i) следует из формулы 4.66.
Для доказательства (ii) заметим, что при п = 4 справедливо-
тождество
(4.72)	R_^R\2g=^z + 2Wz,
где z = г—— g (ср. с 1.118). Поскольку W = s = 0, из 16.3
следует, что dDr = 0. Значит, grad ST? = 0 и в этом случае. По-
следнее утверждение вытекает из наблюдения, что в четырех-
мерном случае tr(gradS/?) = 2As.	□
4.73.	Пример. Напомним, что, согласно 4.13, изотропно не-
приводимые симметрические пространства являются критиче-
скими точками для -S7?.
4.74.	Контрпример. Существуют неэйнштейновы метрики, яв-
ляющиеся критическими точками для Sr и SR-. достаточно взять
произведение двух компактных пространств постоянной кри-
визны, у которых кривизны отличаются только знаком. Это не-
удивительно, поскольку при возведении в квадрат теряется ин-
формация о знаках собственных значений г.
4.75.	Контрпримеры. В размерности п > 4 известно множе-
ство примеров метрик Эйнштейна, не являющихся критическими
точками для S7? Г Jft\, например сферы Йенсена (см. 9.82) или
произведение плоского многообразия на риччи-плоское, но не
плоское многообразие (о существовании таких многообразий
см. гл. 11).
Перейдем к изучению функционалов SZ и SIF.
182
Гл. 4. Римановы функционалы
4.76.	Легко проверить, что функционал SZ обладает теми же
свойствами, что и Sr. Функционал SI1? давно изучается специа-
листами по теории относительности. С помощью тех же рассуж-
дений, что и выше, можно доказать, что он дифференцируем
и имеет градиент. В четырехмерном случае его градиент назы-
вается тензором Баха и обозначается через В. С помощью пред-
ложений 4.66, 4.70 и формулы (4.72) можно показать, что
<4.77)	В = - 26DD'W - 2 IFг
(см. [Вас]). Очевидно, что конформно евклидовы метрики яв-
ляются критическими точками для SIF, но существует и много
других критических точек.
4.78.	Предложение. Пусть М — компактное четырехмерное
многообразие. Метрики из следующих двух классов являются
критическими точками для SIF:
(i)	метрики, локально конформные метрикам Эйнштейна-,
(ii)	конформно полуплоские метрики, т. е. метрики, для ко-
торых W+ или W~ есть нуль (в предположении, что М ориенти-
руемо).
Доказательство, (i) Если g— метрика Эйнштейна, то в силу
дифференциального тождества Бьянки D*W = 0 (см. § А гл. 16).
Отсюда следует (i), так как обращение в нуль тензора Баха
есть локальное свойство, инвариантное относительно конформ-
ных деформаций метрики.
Утверждение (ii) можно проверить непосредственно, однако
в 4.82 мы приведем для него прямое глобальное доказательство.
Дальнейшие результаты см. в работе А. Дердзиньского
[Der 3].
4.79.	Замечание. Нам неизвестны примеры конформно полу-
плоских компактных многообразий, не являющихся конформно
эйнштейновыми.
4.80.	Векторное пространство SO (4)-инвариантных квадра-
тичных форм на пространстве четырехмерных тензоров кри-
визны имеет базис |S|2, |Z|2, 1IF+|2, |IF-|2 (см. 1.126).
Соответствующие функционалы на пространстве римановых
метрик на данном компактном ориентированном 4-многообра-
зии М связаны двумя линейными соотношениями. Формула
Гаусса — Бонне показывает, что%(М) — (1/8п2) ^ (| R |2—4| г |2 +
+ s2)jxg (или 1/8п2^м(|5|2 — |Z|2+|IF|2)pg), а формула для си-
Н. Квадратичные функционалы
183.
гнатуры — чтоо-(Л4) = (1/12л2)	— I |2) (см. 6.31
и 6.34). С помощью 4.66,4.70 и алгебраического тождества
7? —|2g = -|-z + 2W7z легко проверить, что в четырехмер-
ном случае производная функционала SR — 48r + 8s равна
нулю.
Этот факт впервые был установлен Ланцошем ([Lan2]) еще
до того, как Чжень открыл обобщенную формулу Гаусса — Бон-
не. Однако Ланцош пришел к заключению, что этот лагражиан
«не вносит вклад в образование поля и может быть опущен».
Взгляды математиков и физиков поистине различны!
Обратно, исходя из формулы Гаусса — Бонне и формулы
для сигнатуры, мы получаем прямое доказательство следствий
4.72 (ii) и 4.78 (ii), а также следующую дополнительную инфор-
мацию (ср. с [Bo-La]).
4.81.	Предложение, (i) Метрики Эйнштейна реализуют абсо-
лютный максимум функционала SR, равный 8л2%(Л1);
(ii) конформно плоские метрики нулевой скалярной кри-
визны реализуют абсолютный минимум функционала SR, рав-
ный —8л2/(Л4);
(iii) конформно полуплоские метрики реализуют абсолют-
ный минимум функционала SW, равный 12л21 о(М) |.
Эти результаты обусловливают топологические препятствия
к существованию таких метрик на четырехмерных компактных
многообразиях (ср. с 6.35).
Между функционалом SR (а также SW) и функционалом
Янга — Миллса существует некоторая аналогия (ср. с [At-Hi-
Si], [Bo-La] и гл. 13). В обоих случаях рассматривается квад-
рат нормы кривизны в данном расслоении. Однако есть и важ-
ные различия. Функционал Янга—Миллса определен на любом
векторном расслоении с фиксированной метрикой, причем варьи-
руется метрическая связность. Функционалы 87? и 81Г опреде-
лены на расслоении /\2ТМ, причем при варьировании метрики
изменяются также связность и норма в этом расслоении. Воз-
вращаясь к формуле
grad SRs = 26D8dD8r8 -2R8 + ^\Rs ||
(cm. 4.70), мы видим, что первое слагаемое полностью анало-
гично градиенту функционала Янга — Миллса. Два дополни-
тельных слагаемых соответствуют вариации метрики вдоль
слоев.
184	Гл. 4. Римановы функционалы
В высших размерностях ситуация совершенно меняется.
Пусть М — произвольное компактное многообразие размерности
«^5. Тогда, как показал М. Громов (см. [Gro4]), на М суще-
ствуют римановы метрики объема 1 со сколь угодно малым
значением функционала S7?.
Квадратичные функционалы представляют большой интерес
в кэлеровом случае. Если ограничиться метриками из данного
класса когомологий, то здесь возникают дополнительные соот-
ношения между функционалами: все они выражаются через
один функционал. При этом градиент ограниченного функцио-
нала допускает приятную геометрическую интерпретацию (см.
§ Е гл. 11).
Глава 5
Кривизна Риччи как уравнение
в частных производных
В этой главе мы исследуем свойства отображения, сопостав-
ляющего метрике ее тензор Риччи, как дифференциального опе-
ратора. Напомним, что кривизна Риччи заданной метрики g
(5.1)	Ric(g) = r
локально выражается через первые и вторые частные производ-
ные этой метрики. Мы будем считать тензор г заданным и изу-
чать свойства соответствующей метрики g.
Возникает ряд естественных вопросов.
(i)	Задано тензорное поле г; существует ли метрика, удов-
летворяющая (5.1)?
(ii)	Какие ограничения на г (скажем, на компактном мно-
гообразии) гарантируют единственность такой метрики (с точ-
ностью до постоянного множителя)?
(iii)	Как гладкость г влияет на гладкость g?
Мы также исследуем аналог формулы (5.1) для метрик
Эйнштейна
(5.2)	Ric (g) == kg
(для некоторой константы к) в контексте теории дифферен-
циальных уравнений и рассмотрим для |(5.2) те же вопросы.
А. Точечная (инфинитезимальная) разрешимость
Мы ничего не добьемся, пока не решим уравнение (5.1)
хотя бы в одной точке. Пусть этой точкой является начало ко-
ординат в 1Н"(п^З), и пусть задана симметрическая п X п
матрица г,-/. Мы хотим найти такую метрику g в окрестности
начала координат в R”, что
Ric (g) |х_0 = Гц.
Для этого вычислим Ric(g) в локальных координатах:
(5.3)	Wete),, = l^{-^+-^-
z z—'	I дх1 дх1 дх дх
s, t
д3ёц d2gst ) ,
dxs dxf дх' dx’ J ®
186 Гл. 5. Кривизна Риччи как уравнение в частных производных
где (gst) — матрица, обратная к (gst), a Q — функция от мет-
рики g и ее первых производных, однородная степени 2 по пер-
вым производным. Будем искать g в простом виде gq =
где ф (х) = однородный квадратный полином.
С помощью (5.3) легко получаем, что если
п п
1 Ё
/	S = 1 t = l
— rst I xsx* Г dxl ® dxl,
TO
Ric(g)L=0 = r-
Задача решения уравнения (5.2) в одной точке тривиальна:
примерами таких решений могут служить метрики постоянной
кривизны.
В. От точечной разрешимости
к локальной: препятствия
Пытаясь продолжить решение в точке хотя бы до уровня
1-струи, мы немедленно сталкиваемся с трудностями. Основная
причина связана с инвариантностью (5.1) относительно группы
диффеоморфизмов. Действительно, если ф<, t е R, — семейство
диффеоморфизмов с фДр) = р и ф0 = Id, a Riem(gj—риманов
тензор кривизны метрики g, то из инвариантности	,
'(5.4)	ф; (Riem (g)) = Riem (ф^ (g))
следует (в качестве условия интегрируемости) стандартное тож-
дество Бьянки. Оно получается, если продифференцировать
(5.4.) по t в точке t — 0 и заметить, ,что возникающее тожде-
d<p, I
ство справедливо при любых значениях —1 (по поводу та-
кого подхода к тождеству Бьянки см. [Kaz 2]). Для кривизны
Риччи условия интегрируемости принимают вид бг -j- -у ds = О
или, в локальных координатах,
(5.5) 0 = Bian (g, r)k = £ gli (rik.f - ± rtj. , k = 1,2, ..., n,
i, i
где точка с запятой означает ковариантную производную. Тож-
дество (5.5) можно записать более подробно:
45.6) o = Biante,r). = ^«[Q-l^-)-
_yrz
к \ дх' 2 дх1 ) j ’
В. От точечной разрешимости к локальной препятствия
187
где k = 1, п. Мы будем называть (5.5) условием интегри-
руемости, несмотря на то, что оно содержит не только г, но и
неизвестную метрику g. (Другими словами, поскольку в (5.1)
входит столько же уравнений, сколько неизвестных (а именно
I 2 II, и поскольку тождество Бьянки добавляет п уравне-
ний для g, система (5.1) — (5.5) переопределена.) Следуя
Де Тюрку ([DeT 1]), покажем, что уравнение (5.1) не всегда
имеет решение, поскольку для некоторых тензоров г может не
существовать метрик g, удовлетворяющих тождеству Бьянки
(5.6).
5.7. Пример. В локальных координатах (х1, ..., хп) для про-
извольной функции qtj(х2, хп) не существует римановой
метрики с тензором Риччи
п
г = х1 dx1 ®dx1 + У Яа(х2, xn)dxt^dxl
t, i=2
в любой окрестности точки из гиперплоскости х1 — 0. Действи-
тельно, если г есть тензор Риччи метрики g, то должно выпол-
няться тождество Бьянки (5.5). В частности, положив k — 1
в (5.6), получим	/
4-£п=о
на гиперплоскости х1 = 0, что невозможно для положительно
определенной метрики g.
Если в этом примере заменить х1 на (х1)р, то p-я производ-
ная тождества Бьянки не выполняется в начале координат, хотя
при соответствующем (зависящем от gij) выборе метрики все
тождества, полученные дифференцированием тождества Бьянки
меньше чем р раз, выполняются. Следующий пример Де Тюрка
показывает, что возможна ситуация, когда решение отсутствует
в изолированной точке.
5.8. Пример. В любой окрестности начала координат не су-
ществует римановой метрики с кривизной Риччи
(5.9)	г — У, xlx’ dx10 dx’.
i. i
Однако г есть тензор Риччи некоторой римановой метрики
в Rn\{0}.
Сначала докажем первое утверждение. Обозначим через
Bian(g, г), выражение (5.6) при k = 1. Тогда для г из (5.9)
188 Гл. 5. Кривизна Риччи как уравнение в частных производных
в силу (5.6)
д Bian (g, г)]
— дх1
L=2>"
i
что, очевидно, противоречит положительной определенности g.
Существование метрики с тензором Риччи (5.9) вне начала
координат проще всего проверить в сферических координатах,
где р2=(-к1)2+	+ (х”)2. В этих координатах (5.9) прини-
мает вид
(5.10)	r = p2(dp)2.
Непосредственные вычисления показывают, что если метрика g
в локальных координатах (у1, -.., уп) имеет вид
2
(5.11)	g = (h (у1)) <"~2> [h' {iff (dy^ + (dy2)2 + ... + (dz/")2],
где	h — произвольная	гладкая положительная
я Л' =
dh
dy' ’
то кривизна Риччи этой метрики равна
Ric (g) = a2 hh (dy1)2,
функция,
n I
тде а2 = _ 2'' Сравнение с (5.10) показывает, что (5.11) за-
дает искомую метрику, если положить р = //’, считая у;, j 2,
угловыми координатами, и определить функцию Л(р) из урав-
нения аА'(р) = рЛ(р), т. е. положить
fc(p) = exp-g-.
•Отметим, что эта метрика вырождается в начале координат,
так как коэффициент при (dp)2 обращается в нуль.
5.12. Пример. Вблизи начала координат не существует мет-
рики произвольной сигнатуры с тензором Риччи
г = Е (1/2х' + ЧгХ1 + Е х*) dx1 ® dx1.
i, i \	k )
В этом случае тождество Бьянки (5.6) принимает вид
Emg'mft—0. k=\, 2, ..., п, что противоречит невырожден-
ности g.
Мораль этих примеров такова: тождество Бьянки является
препятствием для разрешимости уравнения Риччи (5.1) и даже
для локальной разрешимости — по крайней мере для полино-
миального г. Отметим, что во всех примерах тензор г в рас-
С. Локальная разрешимость уравнения Ric(g) = г
189
сматриваемой точке вырождается (как квадратичная форма).
Интуитивно это вызывает некоторые подозрения. Действительно,
если Ric(g) = г, то
<5.13)	Ric (<p* (g)) = ф* (Ric (g)) = ф’ (г)
для любого диффеоморфизма ф. Поскольку метрика g всегда не-
вырожденна, орбита вырожденного тензора г относительно
группы диффеоморфизмов «меньше» орбиты g. Естественно
предположить, что это вызовет трудности. Обратимся теперь
к невырожденному случаю.
С. Локальная разрешимость уравнения Ric(g) = r
для невырожденного тензора г
5.14. Теорема (Де Тюрк, [DeT 2]). Пусть r^Cm<a
0<а< 1) есть поле симметрических (2,0)-тензоров в окре-
стности точки р многообразия размерности п^З. Если тензор г
в точке р обратим, то существует такая Cm< а-риманова метрика
g, что Ric (g) = г в некоторой окрестности точки р. Если при
этом поле г вещественно аналитично, то существует вещественно
аналитическая метрика g любой сигнатуры с Ric (g) = г.
Вероятно, вторая часть этой теоремы справедлива и без
предположения аналитичности. В лоренцевой случае Де Тюрк
([DeT 3]) получил для класса Ст< “ даже более сильный резуль-
тат. Он доказал разрешимость задачи Коши для уравнения
Риччи на малом промежутке времени (т. е. существование мет-
рики лоренцевой сигнатуры с заданными начальными усло-
виями, удовлетворяющими некоторым необходимым условиям
связи) в предположении невырожденности г.
В первом доказательстве теоремы 5.14, данном в [DeT 2], ис-
пользовалась локальная теория эллиптических систем уравне-
ний в частных производных, а также специальная итерацион-
ная процедура. Впоследствии Де Тюрк [DeT 5] нашел более пря-
мое доказательство, которое мы и воспроизведем здесь.
Идея доказательства состоит в применении теоремы о ло-
кальной разрешимости эллиптических уравнений (теорема 45 из
приложения), однако, поскольку уравнение Ric(g)= г не эллип-
тично, потребуются некоторые дополнительные рассуждения.
Существует несколько способов установления неэллиптичности.
Сначала рассмотрим линеаризацию Ric'(g) квазилинейного
оператора Ric в точке g (см. приложение, уравнение 24) и вос-
пользуемся координатами, в которых g,-, = бц в точке р. Из яв-
ного представления (5.3) получим (в соответствии с § F прило-
жения), что главный символ o^(Ric'(g)) в точке | —	...
190
Гл. 5. Кривизна Риччи как уравнение в частных производных
..., |„) е= Т*рМ равен
(5.15)	[а£ (Ric' (g)J й],7 = - |	| g |2 +
“Ь ^2
S
При фиксированном g=/=0 отображение o5(Ric'(g)) является
эндоморфизмом пространства симметрических матриц. Легко
проверить (положив, например, g =(1,0, ..., 0)), что ядро
этого отображения состоит из матриц вида Л,7 = vfa + vfa или
Л = £®и + v где v = (vt) —произвольный ковектор. По-
скольку символьное отображение не является изоморфизмом, си-
стема Риччи неэллиптична.
Второй способ установления неэллиптичности основан на
рассмотрении потока <р/ на многообразии. Дифференцируя (5.13)
в точке t = 0, получаем
Ric (g) = Ric' (g) (Lxg),
где X —поле скоростей потока <р<. Правая часть содержит
третьи производные X, а левая — только первые. Значит, справа
некоторые члены должны сокращаться. Поскольку символ ото-
бражения Ric' содержит только старшие производные, эти рас-
суждения показывают, что тензоры из образа L,xg лежат в ядре
символа aE(Ric'(g)). Более подробно, Lxg — Ь*Х, откуда
(Ric' (g)) ° (6*) = 0.
Но образ о^(6*) состоит в точности из тензоров вида Л = £®
®о + 17®£.Суть формулы (5.15) заключается в том, что именно
эти тензоры, возникающие при действии группы диффеоморфиз-
мов, являются единственным препятствием к эллиптичности опе-
ратора g->- Ric(g). Это обстоятельство оказывается решающим
при изучении Ric(g) как дифференциального оператора.
Существует еще один способ доказательства неэллиптич-
ности системы Риччи, основанный на локальной теореме разре-
шимости из § К приложения. Мы знаем, что система Риччи
всегда разрешима в точке g. Поэтому из ее эллиптичности сле-
довала бы локальная разрешимость. Но это противоречит при-
мерам из § В.
Напомним, что приведенные в § В примеры неразрешимости
существенно обусловлены тождеством Бьянки (5.5), которое
следует из инвариантности оператора Риччи относительно груп-
пы диффеоморфизмов. Идея Де Тюрка состоит в таком исполь-
зовании группы диффеоморфизмов, чтобы она не мешала, а по-
С. Локальная разрешимость уравнения Ric(g) = г	191
могала доказательству разрешимости. Для этого уравнение
Риччи (5.1) заменяется уравнением
Ric (g) = q>* (г),
решениями которого одновременно являются метрика g и диф-
феоморфизм ф. Это уравнение содержит вторые производные
метрики g, но лишь первые производные ф. Поэтому оно не
удовлетворяет определению эллиптичности, данному в приложе-
нии. Однако это уравнение оказывается переопределенным эл-
липтическим уравнением в смысле более общего определения
эллиптичности по Дугласу — Ниренбергу, если тензор г обратим
(см. [DeT 5]). Альтернативный подход состоит в том, чтобы рас-
сматривать лишь диффеоморфизмы ф специального вида, напри-
мер зависящие от первых производных g, и т. п. Приведем, по-
видимому, простейшую схему, в которой диффеоморфизм ф за-
висит от искомой (неизвестной) метрики.
В конечном счете мы пытаемся решить уравнение Ric(g) = r.
Поэтому выберем в качестве начального приближения метрику
go, для которой Ric (go) = г в точке р. Будем искать такое (ма-
лое) h, что
(5.16)	Ric (g0 + h) = (exp (о (ft)))* г,
где exp (и(ft)) — диффеоморфизм, отображающий хеЛ4 в
expz(o(ft)(х)), a v — векторное поле
W = £ (Г-1)^ (g0 + ft)St (ftS₽; t ~ | hst._ ₽) .
(?, s, t
Здесь гичка с запятой означает ковариантную производную от-
носительно метрики go. Важное следствие такого выбора со-
стоит в том, что главный символ правой части (5.6) оказывается
равным
‘A Е + hlsUs - Щ).
I	s
Сравнение с (5.15) показывает, что главный символ (5.15) ра-
вен —i-ftf/|g|2 и система эллиптична в обычном смысле. При-
меняя к ней локальную теорему разрешимости (приложение,
теорема 45), получаем первое утверждение теоремы 5.14. (За-
метим, что exp (v (h)) является диффеоморфизмом некоторой ок-
рестности точки р, поскольку можно считать, что ft == Vft = О
в точке р.) Отсюда следует и аналитическая часть теоремы, по-
скольку для невырожденной метрики g0 произвольной сигнатуры
система (5.16) всегда имеет нехарактеристические направления
и к ней можно применить теорему Коши — Ковалевской.
192 Гл. 5. Кривизна Риччи как уравнение в частных производных
Можно также поставить задачу нахождения связности (не
обязательно метрической) заданной кривизны Риччи. Она менее
трудна, поскольку неизвестных здесь намного больше, чем урав-
нений, т. е. задача недоопределена. Гаски ([Gas 1,2]) получил
доказательство локального существования в аналитическом и
Ст>“ случаях. Это доказательство упростил Де Тюрк ([DeT 1]),
который заметил, что задача фактически является эллиптической
и недоопределенной. Вопреки ожиданиям симметрии тензора
Риччи оказываются не связанными с симметриями связности.
D. Локальное построение метрик Эйнштейна
Рассмотрим вопрос локального существования решений урав-
нения (5.2) для метрик Эйнштейна. Гаски ([Gas3]) показал,
что если 2-струя метрики g удовлетворяет условию Ric(g) = kg
в одной точке, то она продолжается до метрики Эйнштейна g
в окрестности этой точки. Точнее, Гаски доказал следующую
теорему.
5.17.	Теорема (Гаски, [Gas3]). Пусть задан алгебраический
тензор кривизны Ro (см. § G гл. 1), т. е. тензор /?о = R'iki в R”,
и 3, удовлетворяющий первому тождеству Бьянки. Пусть go —
невырожденная метрика, удовлетворяющая в начале координат
условиям Riem (g0) = Ro, Ric (go) = kg0 с некоторой константой
к. Тогда в некоторой окрестности начала координат существует
такая вещественно аналитическая метрика g, что
(i)	g = go, Riem(g) = Ro в начале координат;
(ii)	Ric(g)=Z,g в некоторой окрестности начала координат.
Если при это метрика go риманова, то метрика g также ри-
манова.
Этот результат доказывается с помощью теории Картана —
Кэлера. Поскольку тождество Бьянки для метрик Эйнштейна
тривиально, многие технические трудности, встречающиеся при
доказательстве соответствующего утверждения теоремы 5.14,
исчезают.
Отметим также, что Де Тюрк ([DeT 3]) доказал и обсудил
локальную теорему существования решения задачи Коши для
(5.1) в лоренцевом случае.
Е. Регулярность метрик с гладким тензором Риччи
Верно ли, что если Ric(g) = г и тензор г гладкий, то и рима-
нова метрика g гладкая? Это тоже чисто локальный вопрос. От-
вет основан на теории регулярности решений эллиптических
Е. Регулярность метрик с гладким тензором Риччи
193
уравнений (см. приложение). В нашем изложении мы будем
следовать работе Де Тюрка и Каждана ([De-Ka]). Следующий
пример показывает, что при решении этого вопроса необходима
некоторая осторожность.
5.18.	Пример. Пусть g— стандартная плоская метрика, а <р —
диффеоморфизм класса С3. Тогда тензор Ric (ф* (g)) = 0 веще-
ственно аналитический, в то время как метрика <p*(g) имеет
лишь класс гладкости С2. Рассматривая произведения вида
М" = Т2 X Nn~2, где Т2 — плоский тор, а диффеоморфизм <р яв-
ляется гладким на N, можно получить более сложные примеры.
Для того чтобы решить вопрос о регулярности, введем есте-
ственные локальные координаты, в которых метрика оказывает-
ся максимально гладкой. Как было показано в [Sa-iSh] и [De-
Ka] , такими координатами являются гармонические координаты,
в которых каждая координатная функция гармонична. Отметим,
что, вопреки наивному предположению, геодезические нормаль-
ные координаты не обладают нужным свойством, так как в них
гладкость может понизиться на две производные (см., напри-
мер, [De-Ka], 2.3.) Гармонические координаты впервые исполь-
зовал Эйнштейн ([Ein]) в специальном случае, а затем — Лан-
цош ([Lan 1]), который заметил, что формула для кривизны
Риччи в этих координатах упрощается. В случае двумерных мно-
гообразий классические изотермические координаты являются
гармоническими.
Для доказательства существования гармонических координат
в окрестности данной точки р рассмотрим некоторую коорди-
натную карту (х1, ..., хп) и будем искать гармонические функ-
ции и1(х), ип(х) с и’ (р) = 0 и взаимно ортогональными век-
торами gradn'(p). Из локальной теоремы разрешимости (при-
ложение, теорема 45) следует, что такие функции существуют.
Далее, из теории регулярности эллиптических уравнений (при-
ложение, теорема 41) следует, что если в исходных координатах
метрика имеет класс Гёльдера Ск’а (или С“), то гармонические
координаты и< имеют класс Склл- “ (или С“). Располагая этими
фактами, мы легко докажем следующее предложение, утвер-
ждающее, что в гармонических координатах метрика имеет мак-
симальную гладкость.
5.19.	Предложение. Если метрика g^Ck’a, 1 k оо
(или g се С“) в некоторой карте, то любой тензор Т, имеющий
класс Ск’ “ (или О) в этой карте, имеет тот же класс гладкости
в гармонических координатах. В частности, g се Ck’ “ (или
g се С“) в гармонических координатах.
Доказательство. Согласно сказанному выше, отображение,
переводящее данные координаты в гармонические, имеет класс
13 А. Бессе- т. 1
194 Гл. 5. Кривизна Риччи как уравнение в частных производных
гладкости Ck+l-a. Преобразование тензора T^Ck-a к этим
гармоническим координатам использует только первые производ-
ные этого отображения. Значит, в гармонических координатах
Т €= Ck’“.	□
Теперь мы можем ответить на локальный вопрос, будет ли
метрика g с гладким тензором Риччи Ric(g) гладкой. Чтобы
избежать трудностей примера 5.18, мы будем либо использо-
вать гармонические координаты, либо предполагать, что тензор
Ric(g) невырожден в рассматриваемой точке. После формули-
ровки теоремы мы приведем несколько поясняющих примеров.
5.20.	Теорема (Де Тюрк—Каждая, [De-Ka]). Пусть g <= С2
есть риманова метрика в окрестности точки р.
(а)	Если тензор Ric(g) невырожден в точке р и в некото-
рых локальных координатах Ric(g)e Ck- “ (или Са) вблизи р,то
в этих же координатах g<^ Ck>a (или Са).
(Ъ)	Если в гармонических координатах Ric(g) е Ck- “, Л > 0
(или С“), вблизи р, то в этих же координатах g^Ck+2’a
(или О).
5.21.	Замечания, (i) Как мы видели в 5.18, утверждение (а)
неверно без предположения о невырожденности Ric(g). Возни-
кает желание попытаться доказать, что в случае (а) на самом
деле g е Ck+2’ “, однако это не всегда так. Действительно, если
g — метрика Эйнштейна, например стандартная метрика на Sn,
а <р: Sn-^-Sn— диффеоморфизм класса Cft+r «, то gt = ф*(g)е
е= Ck’ “ и, значит, Ric(g]) = cgi е Ck> а, где с = const 0. Итак,
в этом случае метрика не будет более гладкой, чем ее тензор
Риччи (ср. с теоремой 5.26).
(ii) В замечании 4.10 из работы [De-Ka] приводится при-
мер, показывающий, что при замене гармонических координат
нормальными геодезическими координатами утверждение (Ь)
оказывается неверным (исключение составляют случаи глад-
кости (С00) и вещественной аналитичности (С“)).
(iii) Отметим, что гладкость тензора Риччи не меньше глад-
кости полного тензора кривизны. Поэтому теорема 5.20 также
показывает, как регулярность Riem(g) влияет на регулярность
метрики g.
Доказательство теоремы 5.20. (а) Поскольку тензор Ric(g)
обратим в точке р, метрика g должна удовлетворять следую-
щему основному уравнению, введенному Де Тюрком ([DeT 2]):
Ric (g) + 6* (г-1 Bian (g, г)) = г.
Это равенство, очевидно, справедливо, поскольку Bian(g, г) = 0
(см. (5.5)). Важно, что данное уравнение, как заметил Де Тюрк,
Е. Регулярность метрик с гладким тензором Риччи
195
эллиптично. Отметим также, что, поскольку Bian(g, г) содержит
первые производные от г, уравнение содержит вторые производ-
ные от г. Отсюда следует, что если r=Ric(g') имеет класс
Ck’ “, то коэффициенты уравнения имеют класс Cft~2- “. Для за-
вершения доказательства воспользуемся теоремой об эллипти-
ческой регулярности (приложение, теорема 41).
Ь) Пусть Г‘/г есть символы Кристоффеля метрики g в коор-
динатной карте (х1, ..., х") и Г* X», /’g‘f^if- Вычисления по-
казывают, что Ах^ = Г* и
Ric (g)n = — у gr-s +
r, s
, 1 V ( dV . dYr\ .
+ ~ / Дёп —r + gr/ —r) । • • • >
2	\ dx1	dx1 )
r
где многоточие обозначает члены низших порядков, содержащие
только первые производные метрики. В частности, в гармони-
ческих координатах 0 = Ахй = Г*, т. е.
(5.22)	Ric{g)^ = — ^^grs~dxrj^- + низшие члены.
г, s
Таким образом, в гармонических координатах дифференциаль-
ное уравнение Ric(g) = r эллиптично (приложение, § G), т. е.
можно применить теорему об эллиптической регулярности. □
Объединяя теорему 5.20 и предложение 5.19, получаем
5.23. Следствие, (а) Если в некоторых координатах риманова
метрика g е Ck> a(k 2) и Ric(g’)e &• a(l k), то в гармони-
ческих координатах g е Cft+2’ “.
(b) Если, кроме того, тензор Ric(g') обратим, то в гармони-
ческих координатах g е С‘+2- “.
5.24. Замечание. Возникает естественный вопрос о регуляр-
ности отображения, сопоставляющего метрике связность, т. е.
о том, как регулярность метрики связана с регулярностью коэф-
фициентов связности. Де Тюрк и Каждан ([De-Ka]) показали,
что если связность Леви-Чивита Г метрики g имеет класс Ck- а,
то метрика g имеет класс С*+*> “. Это верно для невырожденной
метрики любой сигнатуры, не обязательно римановой. Для до-
казательства достаточно заметить, что дифференциальный опе-
ратор первого порядка S’-»-Г является переопределенным и эл-
липтическим. Поэтому к нему можно применить теорему о ре-
гулярности решений эллиптических уравнений.
13*
'196 Гл. 5. Кривизна Риччи как уравнение в частных производных
F. Аналитичность метрик Эйнштейна
и ее применение
.Любая метрика Эйнштейна g удовлетворяет условию
<(5.25)	Ric (g) = eg,
где с — константа (если dim At ^3). Согласно замечанию' 5.21,
при изометрии гладкость метрики может измениться. Предложе-
ние 5.19 показывает, что оптимальная гладкость достигается
в гармонических координатах. Результаты этого параграфа не
вызывают удивления, но оказываются важными.
5.26.	Теорема (Де Тюрк—Каждан, [De-Ka]). Пусть (М, g) —
^связное риманово многообразие Эйнштейна класса С1 с dim At
3.	Тогда метрика g вещественно аналитична в гармонических
.и в геодезических нормальных координатах. В частности, для М
существует атлас карт, в которых метрика аналитична, с веще-
ственно аналитическими функциями перехода.
Доказательство. В силу (5.22) уравнение (5.25) в гармони-
ческих координатах является квазилинейным и эллиптическим.
Кроме того, это уравнение вещественно аналитично по всем
своим переменным. Поэтому все его решения вещественно ана-
литичны в этих координатах (приложение, теорема 41). Но
тогда метрика g аналитична и в геодезических нормальных
координатах (поскольку, если метрика аналитична в некоторых
координатах, то она аналитична и в геодезических нормаль-
ных координатах). Аналитичность функций перехода следует
из того, что они гармоничны (если рассматривать переход от
одной гармонической карты к другой, а метрика аналитична.
□
Отсюда немедленно вытекает существование локального изо-
метрического вложения.
5.27.	Следствие. Любое риманово многообразие Эйнштейна
(At, g) класса С2 с dim At = п 3 локально и изометрично
вкладывается в .Rn(n+1)/2.
Доказательство. По теореме 5.26 можно выбрать локальные
координаты, в которых метрика g вещественно аналитична.
Утверждение следует теперь из теоремы Картана — Жане (см.
[Jan], [Саг 7], а также [Spi], ;т. 5) о том, что любая веще-
ственно аналитическая метрика локально и изометрично вкла-
дывается в R«(«+i)/2.	□
„	п (п + 1)
Пока неизвестно, можно ли снизить размерность —---------
для многообразий Эйнштейна при п > 3. В трехмерном случае
G. Метрики Эйнштейна на трехмерных многообразиях
197
метрики Эйнштейна имеют постоянную секционную кривизну,
т. е. локально изометричны стандартным метрикам на S3, 'R3
или Н3 (гиперболическое пространство). Имеются очевидные
локальные изометричные вложения S3->-R4, №->R5 (см. [Spi],
с. 241). Отметим, что Н3 не вкладывается локально и изомет-
рично в R4 (см. [Spi], с. 195).
Второе приложение теоремы 5.26 связано с единственностью
продолжения метрики Эйнштейна.
5.28.	Следствие. Пусть g\, g2— две полные метрики Эйн-
штейна на связном односвязном многообразии М. Если g\ = g2
(как тензорные поля) на некотором открытом множестве, то
с точностью до диффеоморфизма gx = g2 всюду на М. Другими
словами, существует такой диффеоморфизм f: М-+М, что g\ =
= f4g2).
Доказательство. Поскольку, согласно теореме 5.26, метрики
аналитичны, это утверждение следует из теоремы Майерса (см.
[Муе], теорема 3, а также [Ко-No 1], следствие 6.4, с. 256). От-
метим существенность требования полноты (достаточно рассмот-
реть диффеоморфные образы двух открытых подмножеств в R"
с разными объемами) и односвязности (достаточно рассмотреть
два плоских тора с разными объемами).	□
5.29.	Замечание. Может вызвать недоумение тот факт, что
уравнение Риччи (5.1) и уравнение Эйнштейна (5.25) оказы-
ваются эллиптическими в одних координатах и неэллиптиче-
скими в других (в то время как определение эллиптичности не
зависит от выбора координат). Объяснение состоит в том, что
при замене координат в этих уравнениях меняются не только
независимые переменные, но и зависимые, поскольку сама иско-
мая метрика преобразуется как тензор. Между тем утвержде-
ние о «независимости понятия эллиптичности» относится только
к изменению независимых переменных.
G. Метрики Эйнштейна на трехмерных многообразиях
Займемся теперь глобальными вопросами. Сначала рассмот-
рим вопрос существования глобального решения уравнения
(5.2).
5.30.	Теорема (Гамильтон, [Наш 2]). Пусть М — связное
компактное гладкое 3-многообразие (без границы), допускаю-
щее метрику g со всюду положительно определенным тензором
Риччи Ric(g). Тогда М допускает метрику постоянной положи-
тельной секционной кривизны.
198
Гл. 5. Кривизна Риччи как уравнение в частных производных
5.31.	Замечание. Из теоремы (5.30) вытекает, что М есть
сфера S3 или ее фактор по дискретной группе. В некотором
смысле эта теорема представляет собой вариант гипотезы Пуан-
каре в контексте римановой геометрии. Отметим также, что по
теореме Обина ([Aub 1]) достаточно потребовать, чтобы выпол-
нялось Ric(g)^sO со строгим неравенством в одной точке (од-
нако многообразие S2 X S1 с бесконечной фундаментальной
группой не допускает метрики положительной кривизны Риччи,
т. е. одного условия Ric(g)^0 недостаточно).
Возникает естественный вопрос: справедлив ли аналог тео-
ремы 5.30 для отрицательной кривизны Риччи? Многообразие
S2 X 51 может служить контрпримером, поскольку, как пока-
зали Гао и Яу, оно обладает метрикой строго отрицательной
кривизны Риччи. С другой стороны, на нем не существует мет-
рик отрицательной секционной кривизны, так как в этом случае
его универсальной накрывающей было бы пространство R3, а не
S2 X R, как на самом деле.
5.32.	Основная идея доказательства состоит в построении
семейства метрик gt, fe[0, оо), где go — заданная метрика
с Ric(go)>0, a limgf— искомая метрика постоянной кри-
/->ОО
визны. Семейство gt описывается как интегральная кривая не-
которого векторного поля в пространстве Фреше бХ-римановых
метрик. Проще всего попытаться определить векторное поле как
градиент некоторого функционала энергии. Следуя Гильберту
(см. гл. 4), можно было бы взять в качестве такого функцио-
нала полную скалярную кривизну S(g) = ( sgpg. В этом случае
поток задается уравнением
д 2 о
-gt-g~sEg~2rg.
К сожалению, в общем случае это уравнение не имеет решений
(даже на малом интервале времени). Действительно, оно при-
водит к обращенному вспять по времени уравнению теплопро-
водности для скалярной кривизны. Но для последнего уравне-
ния известны примеры начальных условий, не определяющих
локальных решений. Для того чтобы исправить положение, Га-
мильтон рассмотрел уравнение
(5.33)	^g^g-^,
где р — среднее значение скалярной кривизны:
Р = \S£^s!
м / м
G. Метрики Эйнштейна на трехмерных многообразиях
199
Уравнение (5.33) имеет решение, по крайней мере на малом
интервале времени, для любого компактного многообразия с лю-
бой начальной метрикой. Гамильтон показал, что в случае ком-
пактного 3-многообразия с начальной метрикой, имеющей по-
ложительную кривизну Риччи, уравнение (5.33) имеет решение
gt, определенное при всех t. При этом кривизна Риччи метрики
gt положительна для любого t, а при /->оо метрика gt стре-
мится к метрике постоянной положительной кривизны.
Полное доказательство этих утверждений технически слиш-
ком сложно для того, чтобы приводить его здесь: получение
оценок, необходимых для доказательства сходимости gt, тре-
бует большого числа локальных выкладок. Тем не менее мы по-
пробуем передать дух этого доказательства, приведя небольшое
число характерных вычислений.
Первая сложность возникает при попытке доказательства
существования решения на малом интервале времени. В отли-
чие от многих вариационных задач (например, задачи о гармо-
нических отображениях), для которых градиентное поле приво-
дит к параболическим уравнениям, в данном случае уравнение
(5.33) не параболично. Причина та же, по которой уравнение
(5.1) не эллиптично: из инвариантности уравнения (5.33) отно-
сительно группы диффеоморфизмов вытекает его вырожден-
ность. Гамильтон ([Наш2]) преодолел эту трудность с по-
мощью мощной техники анализа — теоремы о неявной функции
Нэша — Мозера. Фактически он доказал общую теорему о
«слабо параболических» системах, которая применима в дан-
ном случае. Недавно Де Тюрк ([DeT 4]) наметил доказатель-
ство этой части теоремы Гамильтона в духе теоремы 5.14. Ос-
новным аналитическим средством доказательства является клас-
сическая теорема существования и единственности для парабо-
лических уравнений ([La-So-Ur], теорема 5.2, с. 320, теорема
9.1, с. 341—342, [Наш], с. 120—121).
Обратимся к вопросам существования решения на большом
интервале времени и сходимости решения. Чтобы упростить
вычисления, заметим вслед за Гамильтоном, что с помощью за-
мены переменных уравнение (5.33) можно преобразовать к виду
(5.34)	^-g = -2Ricte).
Для этого, исходя из (5.34), выберем ф(/) так, чтобы при всех t
метрика g = ф£ имела объем p.g= 1, и положим / = ф (/) dt,
В результате элементарных вычислений получим
д	2
-^£ = -pg-2Ric(g).
at	п
200 Гл. 5. Кривизна Риччи как уравнение в частных производных
Следовательно, можно получить оценки кривизны решения с по-
мощью технически более простого уравнения (5.34), а затем
пересчитать их для (5.33). Отметим, что решение уравнения
(5.34) через конечное время Т «взрывается», т. е. становится
сингулярным. Важный момент доказательства существования
решения (5.33) при всех t е [0, оо] заключается в проверке того,
гг
что \ ty(f)dt = oo.
Jo
Покажем теперь, что если g0 имеет положительную кривизну
Риччи, то же самое верно для gt при всех t > 0. Поскольку это
свойство масштабно-инвариантно, без потери общности можно
работать с (5.34). Первый шаг состоит в выводе уравнения, опи-
сывающего эволюцию тензора Риччи (см. также гл. 1). Далее
мы рассматриваем только трехмерный случай (г = 3).
5.35.	Лемма. Если метрика g удовлетворяет (5.34) и г =
= Ric(g), то
~д7 гч = Е ^РЧга-. рч) “ 6s</ + 3sr>/ ~ ~ 2v}
P.Q
и
-^ = -Д« + 2|г|2,
где
VИ = S gpqriprqj,
s=£ Sp4rpq,
v=Tlgp4Vpq = trV = \rr.
PQ
Лемма непосредственно вытекает из формулы для первой
вариации тензора Риччи (см. (1.183)) с учетом того, что пер-
вая вариация метрики равна —2гц (приведенное выражение
представляет собой лапласиан Лихнеровича от —г,,,ср.с 1.143).
Используется также тот факт, что при п — 3 секционная кри-
визна выражается через тензор Риччи.
Доказательство того, что положительность кривизны Риччи
сохраняется, как и доказательство других важных оценок, ос-
новано на следующем принципе максимума для тензоров (см.
[Нагл 2], теорема 9.1, а также [Нагл 4]).
5.36.	Лемма. Пусть при 0 С t С Т симметрический тензор
Mij удовлетворяет уравнению
Л M{i = - ДМ17 + £ k + Nth
k
G. Метрики Эйнштейна на трехмерных многообразиях
201
где тензорное поле Ыц (М, g) гладко зависит от М и g, причем
X/, / N>0, если только МцУ' = 0; zk — произвольное
векторное поле; лапласиан берется относительно метрики g (как
г, так и g могут зависеть от t). Тогда если М 0 при t = 0,
то это верно и при 0 t Т.
Леммы 5.35 и 5.36 позволяют доказать следующую лемму
(ход доказательства типичен для многих оценочных результа-
тов этой книги).
5.37.	Лемма. Пусть gt удовлетворяет условию (5.34) при
0 < t <Т. Если скалярная кривизна sgo > 0, то sgf > 0 при
0 t < 7'; если Ric(g0) > 0, то Ric (gt) > 0 при 0 t <Z Т.
Доказательство. Из леммы 5.35 следует, что скалярная кри-
визна s(x, t) = Sgt удовлетворяет неравенству
ds
~dt
— As.
Поэтому, согласно принципу максимума, s(x, t) > s(x, 0) > 0
при t > 0. Аналогичное доказательство утверждения, что из
Sgo< 0 следует sgf < 0, не проходит: метод уравнения тепло-
проводности, по-видимому, «предпочитает» положительную кри-
визну.
Утверждение для Ric(gt) доказывается аналогично, только
вместо элементарного принципа максимума используется лемма
5.36 с г‘ =0. Пусть
Nti = — 6sz/ + 3srz/ — (s2 — 2v) gn.
Заметим, что, если собственные значения г равны X, р, v, соб-
ственные значения N равны (р— v)2— 2Х2 + Х(ц. + v) и двум
другим выражениям, получающимся в результате перестановок
Л, р, v. Например, если Х=0, то соответствующее собственное
значение А равно (р— v)2^0.	□
С помощью следующей важной оценки можно показать, что
отношение собственных значений тензора Риччи решения урав-
нения (5.34) остается ограниченным при всех t. Эта оценка до-
казывается применением принципа максимума к эволюцион-
ному уравнению для тензора гц/в.
5.38.	Лемма. Если s > 0 и гц> esgij для некоторого е > 0
и t = 0, то оба неравенства справедливы для всех t, для кото-
рых существует решение.
Для того чтобы оценить отношения собственных значений
г,/, достаточно объединить лемму 5.38 с тривиальной оценкой
202 Гл. 5. Кривизна Риччи как уравнение в частных производных
r s£- Таким образом, кривизна Риччи (а значит, и секцион-
ная кривизна) оценивается с помощью скалярной кривизны.
Исследуем условия, при которых решение уравнения (5.34)
«взрывается» в момент Т. Взрыв может произойти только в том
случае, если скалярная кривизна gt стремится к бесконечности.
Действительно, если функция и ограничена, то компоненты тен-
зора кривизны также ограничены. Но вычисления показывают,
что норма каждой ковариантной производной кривизны
удовлетворяет эволюционному уравнению вида
А|^7?|2==__д|^|2-2|^+1/?|2+ £ (d‘R\diR\dkR).
i + j=k
Здесь (•[•[•) есть некоторая линейная комбинация сверток
соответствующих сомножителей. Согласно интерполяционному
неравенству (т. е. неравенству Гёльдера, проинтегрированному
по частям),
~	J|d'7?|2
и	и
для всех k, где С зависит от k и от max|s|. Поэтому из ограни-
ченности max|s| выводится ограниченность | dkR |2 и | dkR |р
(с помощью интерполяции), а также ограниченность max|5z/?|
(с помощью неравенства Соболева). Следовательно, решение gt
эволюционного уравнения (5.34) при t-*-T ведет себя хорошо.
Поэтому должно выполняться условие lim maxs= оо.
t-+T
На следующем шаге мы убедимся, что mins—>-оо при 1-+Т.
Следовательно, объем gt при t^»-T стремится к бесконечности
ST
расходится (ф по опре-
о
делению есть множитель, связывающий решение (5.33) с реше-
нием (5.34)). Отсюда вытекает существование решения уравне-
ния (5.34) при всех t.
Для того чтобы доказать, что mins-»-oo, оценим модуль гра-
диента | Ds | функции s:
(5.39)	| Ds К -J- т^3'2 + С (n), Vr] > 0.
Оценка (5.39) получается из эволюционногоо уравнения для ве-
личины
с помощью принципа максимума (эти вычисления представляют
собой наиболее сложную и тонкую часть доказательства). По-
G. Метрики Эйнштейна на трехмерных многообразиях
203
скольку maxs-^oo при t-+T, из (5.39) следует существование
такого 7’i = 7’i(f)), что C(i]) < ц2 (max s)3/2 при 7\<t<T.
Значит, |du| r]2(maxs)3/2 при t>T\. Из этой опенки сразу
вытекает, что х(х)^(1—i])maxs в любой точке х, расстояние
от которой до точки максимума функции меньше чем
~(maxs)~l/2 Но по теореме Майерса (об ограниченности диа-
метра сверху) любая точка удовлетворяет этому условию при
достаточно малом 1]. Следовательно, min (1 — tj) maxs и
Для завершения доказательства теоремы 5.30 достаточно
убедиться, что решение уравнения (5.33) на самом деле схо-
дится к предельной метрике и что эта метрика имеет постоян-
ную секционную кривизну. Ключевой шаг заключается в про-
верке того, что при t-^- оо разброс собственных значений кри-
визны Риччи решения уравнения (5.33) стремится к нулю. Для
решения уравнения (5.34) это равносильно стремлению вели-
чины
(X — ц)2 + (Л — у)2 + (н — у2)
(Л + в + v)2
к нулю при t Т, где X, ц, v — собственные значения г. Равно-
сильность доказывается с помощью принципа максимума, по-
скольку последнее выражение в обозначениях леммы 5.35 мож-
но переписать в виде
3» — s2
Стремление этой величины к нулю выводится из принципа мак-
симума, примененного к эволюционному уравнению для вели-
чины
где константа 6 >0 выбрана специальным образом. Из прин-
ципа максимума следует ограниченность последней величины
при t -+ Т (в то время какх—>-оо).
Получив эти опенки и вернувшись с помощью масштабного
преобразования к исходной метрике (5.33), мы убеждаемся, что
собственные значения ее тензора Риччи при t-^-oo стремятся
к одной и той же константе. Следовательно, предельная мет-
рика имеет постоянную секционную кривизну, что и завершает
набросок доказательства теоремы 5.30.	□
5.40.	Замечание. Сразу возникает вопрос, можно ли обоб-
щить этот результат на высшие размерности. Видимо, эволю-
204 Гл. 5. Кривизна Риччи как уравнение в частных производных
ционный процесс «предпочитает» положительную кривизну: он
всегда увеличивает скалярную кривизну. Обобщению мешает то,
что при п 4 тензор Риччи не определяет тензор кривизны. Это
меняет характер многих вспомогательных эволюционных урав-
нений, использованных в доказательстве, и становится непонят-
ным, как сохранить полученные оценки. В то же время в дока-
зательстве не применяются никакие аналитические соображе-
ния, использующие трехмерность (например, тонкие Соболевские
оценки или условия Пале — Смейла). Поэтому некоторые обоб-
щения действительно удается получить (см. [Mag], |Ham 4],
а также [Вой 12]).
Н. Теорема единственности для кривизны Риччи
Перейдем ко второму вопросу, поставленному в начале
главы: когда тензор Риччи однозначно определяет метрику. По-
скольку Ric(cg) = Ric(g) для с — const > 0, единственность
может иметь место только с точностью до масштабного множи-
теля (или, для метрики произведения, с точностью до независи-
мых масштабных множителей на каждом сомножителе). Для
краткости мы по-прежнему будем говорить о единственности
(с учетом сделанного замечания). Теорема Гамильтона, обоб-
щенная Де Тюрком и Коисо ([De-Ko]), утверждает, что стан-
дартные метрики на некоторых симметрических пространствах
однозначно определяются своими тензорами Риччи.
5.41.	Теорема. Пусть М — неприводимое риманово симмет-
рическое пространство компактного типа, a go — стандартная
(симметрическая) метрика на М, нормированная так, что
Ric (go) = go- Тогда любая риманова метрика g\ на М с тензо-
ром Риччи Ric(gi)=g0 пропорциональна g0, т. е. gi = cg0,
с = const > 0. При этом априори метрика g\ не должна удов-
летворять никаким условиям однородности.
Для сферы S" эту теорему доказал Гамильтон ([Нагл 3]),
а в остальных случаях — Де Тюрк и Коисо. Она является след-
ствием более общего результата 5.42 и наблюдения, что из ра-
венства связностей Леви-Чивита метрик g и g следует равен-
ство их тензоров Риччи. Самое сильное утверждение, которое
можно получить с учетом теоремы о разложении де Рама 10.43
(если не делать дополнительных предположений типа предпо-
ложений теоремы 5.41), заключается в том, что кривизна Риччи
однозначно определяет связность Леви-Чивита.
5.42.	Теорема ([De-Ko]). Пусть (М, g)—компактное много-
образие Эйнштейна с Ric (g) = g и неотрицательной секционной
I. Несуществование глобальных решений
205
кривизной. Тогда любая риманова метрика g на М с Ric(g) = g
имеет такую же связность Леви-Чивита, как метрика g.
Ключевым моментом доказательства является вывод фор-
мулы для &g(gikgik) в предположении, что тождественное ото-
бражение Id: (М, g)->(M, g) является гармоническим. В этом
случае gikgik есть плотность энергии гармонического отображе-
ния. В рассматриваемом случае, когда 0<Ric(g) = g, имеем
gikgtk = seal (g) = s, и формула для Ag(gikgik) приводит к не-
равенству
(5.43)	- As > 2gikgil (g^i - Rijkt),
причем равенство достигается только в том случае, если мет-
рики g и g имеют одинаковые связности Леви-Чивита. Здесь че-
рез Rijki обозначен тензор кривизны метрики g, а гармоничность
отображения Id: (М, g)-^-(M, g) равносильна дифференциаль-
ному тождеству Бьянки для кривизны Риччи 1.94. Для завер-
шения доказательства теоремы 5.42 остается заметить, что из
предположений теоремы следует неотрицательность правой
части (5.43). Значит, —As^O. Но тогда s = const и в (5.43)
имеет место равенство. Следовательно, связности Леви-Чивита
метрик g и g совпадают.	□
Мы рассмотрели случаи, когда метрика, или по крайней
мере связность, однозначно определяется своим тензором Риччи.
Однако во многих случаях имеет место существенная неодно-
значность. Примером может служить 19-мерное семейство не-
когомологичных риччи-плоских метрик на КЗ-поверхности, по-
лученное с использованием решения проблемы Калаби (см.
гл. 12, § J, К). Калаби ([Cal 5]) построил и явные примеры не-
когомологичных кэлеровых метрик с одним и тем же тензором
Риччи. Во всех этих примерах семейство метрик с данным тен-
зором Риччи конечномерно. Возникает вопрос: всегда ли не-
единственность конечномерна?
I. Несуществование глобальных решений
В этой главе мы привели ряд результатов, касающихся
локального существования и несуществования решений урав-
нения
Ric (g) = г.
Следуя Де Тюрку и Коисо, опишем ситуацию, в которой реше-
ния существуют локально, но не глобально.
5.44 Теорема ([De-Ko]). Пусть (М, g) — компактное рима-
ново многообразие. Тогда существует такая константа c0(g), что
206 Гл. 5. Кривизна Риччи как уравнение в частных производных
при c>c0(g) не существует римановых метрик g на М с
Ric(g)=cg. В частности, если секционная кривизна
< 1/(п—1) или g есть метрика Эйнштейна с Ric(g)=g, то с0 =
= (g) = 1.
Для доказательства заметим, что в предположениях теоремы
правая часть неравенства (5.43) строго положительна. Значит,
—Д$ > 0, что невозможно, поскольку в точке максимума функ-
ции s выполняется неравенство —Д$ 0.	□
Сравним эту теорему с результатом Бохнера: если Ric (g) =
= г > 0, то первое число Бетти многообразия М равно нулю.
Таким образом, для большинства многообразий М решения
не существует. Мы рассматривали более тонкую ситуацию, когда
уравнение Ric (g)=cr имеет решение при малых с > 0, но не
имеет решений при больших с.
Глава 6
Многообразия Эйнштейна и топология
А. Введение
Какие компактные многообразия допускают метрики Эйн-
штейна? Полный ответ на этот вопрос, по-видимому, пока не
получен (исключение составляет двумерный случай, см. § В).
По крайней мере для размерностей 3 и 4 можно указать неко-
торые многообразия, не допускающие метрик Эйнштейна.
6.1.	Многообразие Эйнштейна размерности 3 всегда имеет
постоянную кривизну. Поэтому его универсальная накрываю-
щая диффеоморфна R3 или S3. В частности, многообразие
S2XS‘ не имеет метрик Эйнштейна. В последнее время глубо-
кие исследования В. Тёрстона существенно уменьшили разрыв
между необходимыми и достаточными условиями существова-
ния метрик Эйнштейна для 3-многообразий. Оказалось, что
лишь для небольшого числа исключений ответ неизвестен.
Большинство многообразий допускают метрики Эйнштейна от-
рицательной скалярной кривизны. В § С мы перечислим топо-
логические ограничения на 3-многообразия Эйнштейна и сфор-
мулируем без доказательств некоторые теоремы гиперболиза-
ции В. Тёрстона.
6.2.	В четырехмерном случае топологические препятствия
к существованию метрики Эйнштейна на многообразии свя-
заны с тем, что интегральные формулы для сигнатуры и эйле-
ровой характеристики принимают особый вид. Из работ
М. Берже, Дж. Торпа и Н. Хитчина известно, что эйлерова ха-
рактеристика х(Л4) и сигнатура т(7И) компактного 4-многообра-
зия Эйнштейна М удовлетворяют неравенству
I т (М) |<2/зХ(М).
Те же свойства лежат в основе неравенства М. Громова
для компактного 4-многоообразия Эйнштейна М. Здесь ||А1||
означает симплициальный объем Громова (см. § D).
208
Гл. 6. Многообразия Эйнштейна и топология
6.3.	В размерности п> 4 не известно никаких топологиче-
ских препятствий к существованию метрик Эйнштейна. Было
бы замечательно, если бы любое многообразие размерности
п> 4 (или по крайней мере большинство таких многообразий)
допускало метрику Эйнштейна отрицательного знака. Для мет-
рик Эйнштейна положительного знака (X > 0) существуют два
типа результатов.
6.4.	Результаты первого типа возникают благодаря взаимо-
действию тензора Риччи и фундаментальной группы. Если тен-
зор Риччи г полного риманова многообразия удовлетворяет не-
равенству
г kg, k = const > 0,
то по теореме С. Б. Майерса многообразие М и его универсаль-
ная накрывающая компактны и, значит, фундаментальная груп-
па (Л4) конечна. Если компактное риманово многообразие
имеет неотрицательную кривизну Риччи, то, согласно Дж. Ни-
геру и Д. Громолу, его универсальная накрывающая изомет-
рична произведениюМ X R’, где М — компактное многообразие.
Поэтому для некоторой конечной группы ЕсзлДМ) в фактор-
группе Jii (Л1) /F существует подгруппа iZ4 конечного индекса.
Эти и более давние результаты приводятся в § Е.
6.5.	Результаты второго типа связаны со скалярной кривиз-
ной. А. Лихнерович в 1963 г. доказал с использованием опера-
тора Дирака, что для компактного четырехмерного спинорного
многообразия A-род является препятствием к существованию
метрики с положительной скалярной кривизной. Этот резуль-
тат, обобщенный последовательно Н. Хитчином, М. Громовым
и X. Б. Лоусоном, исключительно важен для решения проблемы
существования метрик положительной скалярной кривизны.
С его помощью можно строить примеры односвязных многооб-
разий, не допускающих метрик Эйнштейна положительного
знака, которые нельзя получить на основе результатов 6.2—6.4.
Эта теорема приводится в § F.
Наконец, в § G приводится схема доказательства теоремы
Нигера — Громола, которая упоминалась в 6.4.
В. Существование метрик Эйнштейна
в двумерном случае
6.6.	Согласно предложению 1.120, метрика двумерного мно-
гообразия является эйнштейновой тогда и только тогда, когда
она локально изометрична одному из модельных пространств
В. Существование метрик Эйнштейна в двумерном случае
209
S2, R2 или Н2, снабженных канонической метрикой. Это позво-
ляет строить многообразия Эйнштейна, склеивая многообразия
с границами, что приводит к элементарному доказательству
следующей теоремы.
6.7.	Теорема. Любое 2-многообразие допускает полную мет-
рику постоянной кривизны.
6.8.	Опишем сначала процесс склеивания многообразий по-
стоянной кривизны —1 с геодезическими границами.
Для в > 0 обозначим е-окрестность геодезической L гипербо-
лической плоскости № через 7\. Пусть Tt,i (соответственно Tt, i)
есть фактор-пространство окрестности Те по единственному со-
храняющему (соответственно меняющему) ориентацию движе-
нию плоскости И2, ограничение которого на L является сдвигом
на величину I. Пусть Mi, М2 есть 2-многообразия, внутренности
которых имеют постоянную кривизну, a L\, Li — компоненты их
границ, являющиеся геодезическими длины I. Тогда при доста-
точно малом е любую изометрию <р геодезической Lt на замкну-
тую геодезическую L+ из Tt, i можно продолжить до изометрии
e-окрестности Lt в М,- на каждую из двух половин многообразия
Tt, i. Это определяет гомеоморфизм окрестности геодезической
Li — L2 в склеенном многообразии М^фМг на Tt, t, ограни-
чение которого на М, является изометрией. Таким образом, мы
получаем метрику Эйнштейна на М\ U<p М2. Аналогично, любое
изометричное двулистное накрытие L\—*-L~ продолжается до
изометрии е-окрестности L\ в М\ на Тё.пг- Это определяет мет-
рику Эйнштейна на многообразии Mi mod ср, где ср — сдвиг гео-
дезической L\ на 1/2.
Следующий шаг заключается в разрезании 2-многообразия
на простые части. Это делается с помощью чисто топологиче-
ских соображений.
6.9.	Пусть М есть 2-многообразие (возможно, открытое).
Рассмотрим пару (с, U), где с — гладкая простая замкнутая
кривая в М, a U — ее регулярная окрестность. Выберем макси-
мальное множество таких пар (с, U), что
(i)	с не ограничивает диск в М,
(ii)	если (с, U) #= (с', U'), то замыкания U, U' не пересе-
каются, а кривые с, с' не гомотопны в М.
Разрежем многообразие М вдоль кривых с на части, являю-
щиеся (возможно, открытыми) многообразиями с границей
(точнее, эта операция заключается в удалении регулярных окре-
стностей U). Возможно, получится всего одна часть, например
если указанные кривые с отсутствуют или имеется только одна
14 А- Бессе, т. 1
210
Гл. 6. Многообразия Эйнштейна и топология
односторонняя кривая. Пусть Р — некоторая часть. Мы полу-
чим новое многообразие Р без границы, приклеив ко всем ком-
понентам границы многообразия Р диски. Сразу видно, что
(а) многообразие Р имеет род нуль, т. е. любая односвязная
замкнутая гладкая кривая в Р ограничивает диск; (Ь) много-
образие Р имеет не более одного конца, т. е. дополнение
Р — Л’ любого компакта имеет не более одной неограниченной
связной компоненты. Отсюда следует, что Р диффеоморфно S2
или R2. Поэтому многообразие Р диффеоморфно либо дополне-
нию конечного числа непересекающихся дисков в S2, либо до-
полнению локально конечного числа дисков в R2. Легко видеть,
что число дисков в первом случае не превосходит 3-х, а во вто-
ром случае не превосходит единицы.
6.10.	За исключением тех случаев, когда Р = М = S2 или
R2, каждая часть относится к одному из следующих типов:
диск = S2— диск;
кольцо — S2 — 2 диска;
«штаны» = S2— 3 диска;
проколотый диск = R2— диск.
Диск появляется только в том случае, если его граница дву-
кратно накрывает одностороннюю кривую в М. При этом по-
лучается только одна часть и М = RP2.
Кольцо появляется только в том случае, если две компоненты
его границы накрывают одну и ту же кривую в М. При этом
также получается только одна часть и М представляет собой
тор или бутылку Клейна.
Для проколотого диска существуют три возможности: он мо-
жет появиться один (при этом его граница двукратно накры-
вает одностороннюю кривую в М, а М представляет собой ленту
Мёбиуса), либо склеенным с другим проколотым диском (тогда
М есть открытый цилиндр), либо, наконец, склеенным со «шта-
нами».
6.11.	Многообразия, которые получаются в результате склеи-
вания одного, двух или трех проколотых дисков со «штанами»,
называются бесконечными, дважды бесконечными или трижды
бесконечными «штанами».
Предложение. Каждый из четырех типов «штанов» допускает
полную метрику постоянной кривизны —1 с геодезическими
компонентами границы любой заданной длины.
Доказательство. Такие метрики получаются в результате
склеивания двух одинаковых гиперболических шестиугольников
по трем сторонам. Длины оставшихся трех сторон можно вы-
С. Трехмерный случай
211
брать произвольным образом, в том числе нулевыми, для того
чтобы включить случай кратно бесконечных «штанов». □
6.12.	Завершение доказательства теоремы. Многообразия S2
и iRP2, очевидно, допускают метрики постоянной положительной
кривизны. Многообразия R2, тор, бутылка Клейна, лента Мё-
биуса и цилиндр допускают полные метрики нулевой кривизны.
Если многообразие М не диффеоморфно ни одному из исключи-
тельных многообразий этих трех типов, то все части его разло-
жения представляют собой «штаны». Снабдим каждую часть
метрикой кривизны —1 таким образом, чтобы все компоненты
границы имели длину е^2. Тогда любой выбор изометрий соот-
ветствующих компонент границы, являющихся окружностями,
определяет (в соответствии с 6.8) метрику Эйнштейна на ис-
ходной поверхности М.		□
6.13.	Этот метод принадлежит В. Тёрстону (см. [Thu 1],
[Fa-La-Po], [Bsr]). Он позволяет получить наилучшее описа-
ние пространства Тейхмюллера поверхности, а также , приме-
няется, например, для классификации диффеоморфизмов по-
верхностей. Приведенные рассуждения показывают, что если
риманова структура постоянной кривизны —1 на поверхности
существует, то она неединственна (исключение составляют
трижды бесконечные «штаны»). Подробности см. в § В гл. 12.
6.14.	Замечание. Знак постоянной кривизны (1, 0 или —1)
определяется знаком эйлеровой характеристики (если'считать,
что —оо имеет отрицательный знак). Как правило, имеет место
знак —1. Лишь небольшое число исключительных поверхностей
имеют знаки +1 и 0.
С. Трехмерный случай
6.15.	Риманова метрика на 3-многообразии является эйн-
штейновой тогда и только тогда, когда она имеет постоянную
секционную кривизну (предложение 1.120). Однако в отличие
от двумерного случая каждое 3-многообразие допускает метрику
постоянной кривизны. Сформулируем некоторые необходимые
условия.
6.16.	Если 3-многообразие М допускает метрику постоянной
кривизны, то его универсальная накрывающая диффеоморфна
3-сфере S3 или пространству R3. В частности, зт2 (Д4) = 0. Точ-
нее, любая вложенная 2-сфера S2 в М ограничивает вложенный
3-шар В3 в М. В этом случае будем говорить, что многообразие
М примерно (см. [Roh]). Ясно, что на S2 X S1 не существует
14*
212
Гл. 6. Многообразия Эйнштейна и топология
метрики постоянной секционной кривизны. Это верно для лю-
бого многообразия М, которое разлагается в нетривиальную
связную сумму М = N =#= Р (где N и Р не диффеоморфны S3).
6.17.	Поскольку имеется только десять существенно различ-
ных компактных многообразий, допускающих плоскую метрику,
а многообразия, допускающие метрику постоянной кривизны 1,
хорошо изучены (см. [Wol 1]), мы ограничимся случаем отри-
цательной кривизны. Пусть многообразие М компактно и до-
пускает метрику постоянной секционной кривизны —1. Тогда
его фундаментальная группа то (7И) изоморфна дискретной ком-
пактной подгруппе Г группы движений гиперболического 3-про-
странства Н3 (см. 1.37). Любой элемент из Г гиперболичен, т. е.
сохраняет некоторую геодезическую в И3. Любые два коммути-
рующих элемента сохраняют общую геодезическую, следова-
тельно, соответствуют некоторым итерациям одной и той же
замкнутой геодезической в М, т. е. являются степенями некото-
рого элемента из Г. В частности, Г не содержит подгрупп, изо-
морфных Z Ф Z. В этом случае мы будем говорить, что М гомо-
топически атороидально.
6.18.	Вообще, фундаментальная группа компактного много-
образия секционной кривизны —1 не может содержать нецик-
лических разрешимых подгрупп (это свойство находит отраже-
ние в понятии аменабельной группы, см. [Grf]). Действительно,
любая нециклическая аменабельная дискретная группа движе-
ний пространства Н3 содержит негиперболический элемент.
6.19.	С помощью этих простых свойств уже можно строить
примеры неэйнштейновых многообразий. Рассмотрим два про-
стых способа построения 3-многообразий: S'-расслоения над
поверхностью и расслоения над окружностью. Тип S'-расслое-
ния над S2 зависит от целого числа feeZ = ni(Diff (S1)). При
k >0 слой имеет порядок k в лДЛД) и расслоение Mk-+S2 на-
крывается расслоением Хоифа M\ = S3->S2. Эти многообразия
допускают метрику постоянной кривизны 1. Если k 0, то
Л] (ЛД) — Z и Мк не допускает метрики постоянной кривизны.
Если S — поверхность с х(Х)^0, то S'-расслоение М над X
не будет гомотопически атороидальным. Действительно, слой
определяет нетривиальный центральный элемент подгруппы
конечного индекса в лДТИ), поэтому М не допускает метрики
кривизны 1 или —1. Однако среди десяти плоских 3-многооб-
разий два (произведение S'XK и еще одно многообразие F)
расслаиваются над бутылкой Клейна К и два (Т3 и S' X К)
расслаиваются над Т2.
С. Трехмерный случай
213
6.20.	Любое 3-многообразие М, которое расслаивается над
окружностью со слоем, являющимся поверхностью 2, можно
получить из LX [0.1] путем отождествления граничных ком-
понент с помощью диффеоморфизма <р поверхности 2. Конструк-
ция многообразия М зависит только от класса изотопии эле-
мента (р. Тем не менее таким способом можно получить мно-
жество различных примеров.
(а)	Сферические или ₽Р2-расслоения над S’ накрываются
произведением S2XS' и, значит, не допускают метрик постоян-
ной кривизны.
(Ь)	Если S есть поверхность с х (2)	0, то изотопические
классы диффеоморфизмов 2 взаимно однозначно соответствуют
внешним автоморфизмам группы jti(S). Например, если S = Т2
есть 2-тор, то ^-расслоение Aftp задается матрицей <р е GL(2, Z).
Фундаментальная группа лДЛ!,,,) является расширением Z2
с помощью ф и, значит, разрешима. Поэтому Л1ч, не допускает
метрики кривизны —1. Однако многообразие Л4.„ может быть
плоским. Для этого необходимо и достаточно периодичности
элемента <р. Отметим, что Л41(, гомотопически атороидально тогда
и только тогда, когда <р имеет два различных вещественных соб-
ственных значения.
(с)	Для всех компактных плоских 3-многообразий, кроме
одного (многообразия F из 6.19), число Бетти bx (М, R) =И= 0.
Эти многообразия расслаиваются над окружностью. В семи
случаях слоем является тор, а в двух других — бутылка Клейна
К. Другие К-расслоения над окружностью не допускают метрики
постоянной кривизны.
(d)	Предположим, что %(2)<0. Если диффеоморфизм <р
периодичен, то 7H<r накрывается произведением 2XS1 и, зна-
чит, не является гомотопически атороидальным. На самом деле
многообразие 7ИЧ, гомотопически атороидально тогда и только
тогда, когда никакая итерация <р не сохраняет изотопический
класс кривых. В этом случае диффеоморфизм <р называется не-
приводимым или псевдоаносовским (см. [Fa-La-Po]). Изве-
стно (см. 6.24), что в этом случае Мч допускает метрику кри-
визны — 1.
Приведенные нами примеры не очень представительны.
В действительности, как показывают недавно полученные
В. Тёрстоном результаты, большинство примарных 3-многообра-
зий допускают метрику кривизны —1. Начнем с приятного до-
статочного условия, которое, впрочем, весьма далеко от необ-
ходимого.
6.21.	Определение. Двусторонняя поверхность N, вложенная
в 3-многообразие М, называется несжимаемой, если любая про-
214
Гл. 6. Многообразия Эйнштейна и топология
стая замкнутая кривая в N, ограничивающая в М диск, внут-
ренность которого не пересекается с N, ограничивает также не-
который диск в N. Компактное 3-многообразие называется
хакеновым, если оно примарно и содержит двустороннюю не-
сжимаемую поверхность, отличную от сферы.
6.22.	Среди многообразий из примеров 6.19 и 6.20 хакено-
выми являются все те, которые строятся без помощи сфер и
проективных плоскостей.
6.23.	Теорема (В. Тёрстон, [Thu 3]). Компактное ориенти-
руемое хакеново многообразие допускает метрику постоянной
кривизны —1 тогда и только тогда, когда оно гомотопически
тороидально.
6.24.	Теорема 6.23 применима к многообразиям M(f, расслоен-
ным над окружностью, если <р есть неприводимый диффеомор-
физм ориентируемого слоя. Это позволяет получить довольно
неожиданные примеры гиперболических многообразий. Действи-
сальным накрытием базовой окружности, имеет бесконечный
объем, в то время как объем его шаров растет линейным обра-
зом. Такое явление невозможно в двумерном случае. Первые
примеры такого рода были получены Т. Йоргенсеном [Jor]. Из-
ложение доказательства теоремы 6.23 для многообразий, рас-
слоенных над окружностью, см. в [Sul].
В [Thu 2] В. Тёрстон отметил, что формулировка теоремы
6.23 не вполне удовлетворительна. По-видимому, предположение
о хакеновости играет в доказательстве чисто техническую роль
и не имеет глубокой связи с постоянством кривизны. Опишем
еще один метод В. Тёрстона, который позволяет построить еще
больше компактных 3-многообразий постоянной кривизны.
6.25.	Зацеплением в компактном 3-многообразии называется
объединение конечного числа попарно непересекающихся про-
стых замкнутых кривых. Процесс хирургии Дена вдоль зацеп-
ления L состоит в удалении регулярной окрестности L и вклеи-
вании ее обратно некоторым другим способом. Многообразия,
получаемые таким образом, зависят от дискретного параметра,
поскольку элемент Diff (T2)/Diff {D2 X S2) определяется парой
взаимно простых целых чисел.
6.26.	Теорема (В. Тёрстон, [Thu 1]). Пусть L — зацепление
в компактном многообразии М. Предположим, что М — L до-
пускает полную метрику постоянной кривизны —1 конечного
объема. Тогда все {кроме конечного числа) многообразия, кото-
С. Трехмерный случай
215
рые получаются из М с помощью хирургии Дена вдоль L, до-
пускают метрики кривизны —1.
6.27.	Любое компактное 3-многообразие можно получить из
3-сферы S3 с помощью хирургии Дена вдоль некоторого зацеп-
ления L (см. [Roh]). Более того, можно выбрать зацепление L
таким образом, чтобы его дополнение допускало полную мет-
рику постоянной кривизны —1. Еще одна важная теорема
В. Тёрстона характеризует узлы, дополнения к которым обла-
дают этим свойством (см. [Thu 2]). Таким образом, в опреде-
ленном смысле почти любое компактное 3-многообразие допу-
скает метрику постоянной кривизны —1.
6.28.	Тем не менее вопрос о том, какие компактные много-
образия допускают метрику постоянной кривизны, до конца не
решен. Например, любое компактное риманово многообразие
строго отрицательной секционной кривизны обладает свой-
ствами 6.17 и 6.18 (см., например, [Gro 6]). Однако неизвестно,
допускает ли такое многообразие метрику постоянной отрица-
тельной секционной кривизны. На аналогичный вопрос для мно-
гообразий отрицательной кривизны Риччи недавно получен от-
рицательный ответ. Он следует из замкнутости класса таких
многообразий относительно взятия связных сумм, а также связ-
ных сумм с линзовыми пространствами и произведениями вида
SXS1 (см. [Gao]). Для контраста напомним, что компактное
3-многообразие положительной кривизны Риччи допускает мет-
рику постоянной кривизны по теореме Гамильтона 5.30.
6.29.	В 0.4 мы упомянули, что одной из причин изучения
метрик Эйнштейна является поиск наилучших римановых мет-
рик на данном компактном многообразии. В [Thu 2] В. Тёр-
стон предложил альтернативную формулировку этой задачи для
случая 3-многообразий:
— Наилучшей метрикой на 3-многообразии (если она суще-
ствует) является локально однородная метрика. В трехмерном
случае существует ровно восемь односвязных однородных ри-
мановых пространств G/Н, где G — максимальная группа изо-
метрий риманова многообразия G/Н, допускающих фактор-про-
странства конечного объема. Эти пространства подробно опи-
саны в [Sco]. Очевидно, что к ним относятся стандартная cqbe-
ра, евклидово и гиперболическое пространство.
— Не всякое 3-многообразие М локально однородно, по-
этому необходимо допустить возможность разрезания многооб-
разия на части. Первый шаг состоит в разложении в связную
сумму «наименьших» многообразий. Это можно сделать кано-
ническим образом. Полученные части называются примерными
216
Гл. 6. Многообразия Эйнштейна и топология
слагаемыми многообразия Л4. Как мы уже видели, не все при-
марные многообразия локально однородны, поэтому необходимо
дальнейшее разбиение. Разрезая М вдоль нетривиально вло-
женного 2-тора, мы получаем семейство открытых многообразий.
Если каждая часть обладает полной локально однородной мет-
рикой, можно считать, что поставленная задача выполнена.
— В настоящее время эта задача решена (за исключением
случая компактных гомотопически атороидальных многообра-
зий). Если многообразие М не является гомотопически аторои-
дальным, то в нем существуют нетривиально вложенные под-
многообразия, являющиеся 5*-расслоениями или, в более общем
случае, расслоениями Зейферта. Максимальное среди этих под-
многообразий, которое всегда существует и единственно с точ-
ностью до изотопии, называется характеристическим подмного-
образием многообразия М (см. [JohJ). По одной из теорем
В. Тёрстона ([Thu 2], теорема 2.3) дополнение к характеристи-
ческому подмногообразию допускает полную метрику кривизны
— 1 (за исключением случаев, когда существует полная плоская
метрика). Теперь остается только каноническим образом раз-
бить расслоение Зейферта на локально однородные части. Боль-
шинство частей вновь снабжается гиперболической метрикой.
Остальные семь типов геометрии встречаются лишь в неболь-
шом (хотя и бесконечном) числе особых случаев.
D. Четырехмерный случай
6.30.	Важным топологическим инвариантом n-мерного диф-
ференцируемого многообразия М является его эйлерова харак-
теристика х(М), которая определяется следующим образом.
Обозначим через bi = dim Н‘ (М, R) числа Бетти многообра-
зия Л4. Тогда
х(М)=1](-1)'^.
г = 0
Например, %(S2ra) = 2, x(S2,n+1) = 0, x(CPm) = m.
Если M есть компактное ориентированное риманово много-
образие размерности 2m, то обобщенная теорема Гаусса — Бон-
не [Ko-No 2] позволяет представить %(Л4) в виде интеграла
некоторого полинома степени m от кривизны.
6.31.	В четырехмерном случае это выражение принимает
очень простой вид (см. [Bes 2], доклад X):
Z(M) = i J (II и II2 - IIZ II2 + II WII2) pg,
D. Четырехмерный случай
217
где U, Z, W—неприводимые компоненты тензора кривизны
R многообразия М (см. 1.114).
6.32.	Если (М, g)—многообразие Эйнштейна, то Z = 0. По-
этому у_(Л1)^0 и х(Л1)=0 только в плоском случае (/? — ()).
Эта теорема принадлежит М. Берже ([Вег 2[). В частности,
S'XS3 и Т4Ф Т4 не допускают метрик Эйнштейна.
6.33.	Предположим теперь, что М есть компактное ориен-
тированное 4/г-многообразие. Тогда ^-произведение определяет
симметрическую билинейную форму В на H2k(M,Z)
В (a, ₽)=<aU0,
где a, fi е Н2к (М, Z ), а [М] обозначает фундаментальный класс
гомологий многообразия М.
6.34.	Сигнатура билинейной формы В (т. е. разность между
числом положительных и числом отрицательных квадратов ее
канонического вида) называется сигнатурой многообразия М и
обозначается т(Л4). Это число является топологическим инва-
риантом и в четырехмерном случае может быть найдено но
формуле (см. [Bes 2])
т W W V11 W + i|2 ~11 W~ ||2)
м
где W± — неприводимые компоненты тензора Вейля относитель-
но действия специальной ортогональной группы (см. 1.126).
Сравнивая формулы для х(Л4) и т(М) с заданной ориента-
цией и с противоположной ориентацией (когда т заменяется на
—т), получаем следующую теорему.
6.35.	Теорема (Дж. Торп, [Tho], [Hit 1]). Пусть М — ком-
пактное ориентированное ^-многообразие Эйнштейна. Тогда его
эйлерова характеристика %(М) и сигнатура т(М) связаны не-
равенством
х(М)>3/21ЛЛ1) |.
6.36.	Случай, когда имеет место равенство = т(М) |,
был исследован Н. Хитчином ([Hit 1]). Предположим для опре-
2
деленности, что у %(Л4) =— т (М) (мы увидим, что если дости-
гается равенство, то многообразие М можно считать комплекс-
ным и, значит, естественным образом ориентированным). Срав-
нивая подынтегральные выражения для % и т, получаем
II и II2 + IIW+II2 + II w~ II2 = II w~ 1Г - IIw+ II2,
откуда U — IF+ = 0 и R = IF-.
218
Гл. 6. Многообразия Эйнштейна и топология
Предположим, что Z? =А 0. Расслоение 2-форм над М, слои
которого отождествляются с алгеброй Ли 50(4), разлагается от-
носительно действия оператора Ходжа * в прямую сумму соб-
ственных подрасслоений
Л2М=Л+гИ® V.M.
Слои расслоений Л + М и Л М отождествляются с su(2).
Рассмотрим кривизну SI естественной связности расслоения
2/И. Она представляет собой 2-форму со значениями в эндо-
морфизмах расслоения 2/И. Для любых векторных полей
X, Y <= С'Х(ТМ) и 2-формы о) е П2(Л4)
$(Х, У)ш = [/?(Х, У), <о].
Обозначим через $+ и кривизны связностей, индуцирован-
ных в расслоениях Д + Л1 и Л М. Тогда	+ 5?-, и если
форма <D е; О2(Л4) является сечением расслоения Л+Л1, то
$(Х, У)ш = 5?+(Х, У)Ю = [Я(Х, У), ш].
Поскольку кривизна R = W~ отображает Л М в себя,
имеем £5?+ = 0. Следовательно, эйлерова характеристика много-
образия М положительна (так как R 0). Отсюда вытекает
равенство bi(M) = 0. Действительно, если Ь\ (Л4) > 0, то в М
существует гармоническая 1-форма. Поскольку кривизна Риччи
многообразия равна нулю, из теоремы Бохнера следует, что эта
1-форма параллельна. Но тогда двойственное к ней векторное
поле не равно тождественно нулю, что противоречит положи-
тельности эйлеровой характеристики.
Предположим теперь, что многообразие М односвязно. Тогда
расслоение Д М тривиально и группа голономии редуцируется
к SU (2). Значит, многообразие М кэлерово и имеет нулевую
кривизну Риччи, а тем самым и нулевой первый класс Чженя.
Такое многообразие по определению является КЗ-поверхностью
(см. 12.104).
Если М не является КЗ-поверхностью, то из теоремы 6.65
следует (см. [Ch-Gr 1]), что группа Л| (М) конечна (поскольку
у(Л1)>0). Значит, универсальное накрытие М конечнократно.
Поэтому универсальная накрывающая М является компактным
многообразием М с нулевыми первым числом Бетти и первым
классом Чженя. Таким образом, М есть КЗ-поверхность. □
6.37.	Теорема (Н. Хитчин, [Hit 1]). Пусть М — компактное
ориентированное ^-многообразие Эйнштейна. Если его эйлерова
D. Четырехмерный случай
219
характеристика х(Л1) и сигнатура т(Л'/) связаны соотношением
|т(М)1 = 4%(М),
О
то кривизна Риччи многообразия М равна нулю и либо много-
образие М плоско, либо его универсальная накрывающая яв-
ляется КЗ-поверхностью. В последнем случае М есть либо КЗ-
поверхность (Л1 (Л4) — 1), либо поверхность Энриквеса (л1(7И) =
== Z2), либо фактор-пространство поверхности Энриквеса по
свободно действующей антиголоморфной инволюции (ni (Л1) =
— £ 2 X г) •
6.38.	Теорема 6.35 позволяет строить примеры односвязных
многообразий, не допускающих метрик Эйнштейна. Например,
если М. = (СР2)^Г, т. е. 7И есть связная сумма р экземпляров
СР2 с естественной ориентацией, то
Х(Л1) = р + 2, т(М) = р.
Поэтому при р 4 многообразие (СР2)^р не допускает метрик
Эйнштейна. Предыдущая теорема показывает важность КЗ-по-
верхностей и мотивирует изложение следующего результата.
6.39.	Определение. Риманово 4^-многообразие (М, g) назы-
вается гиперкэлеровым, если оно допускает три параллельные
комплексные структуры /, /, К, для которых // = —Л — К,
и метрика g эрмитова относительно каждой из них. Можно по-
казать, что это равносильно включению Hol (g) cz Sp(k) (см.
10.33, 14.3).
6.40.	Теорема. Пусть g — риманова метрика на дифферен-
цируемом многообразии М, которое гомотопически эквивалентно
КЗ-поверхности. Тогда следующие условия эквивалентны-.
(i)	скалярная кривизна метрики g неотрицательна-,
(ii)	многообразие (М, g) гиперкэлерово;
(iii)	кривизна Риччи метрики g равна нулю.
Доказательство. Любая КЗ-поверхность М является спинор-
ным многообразием, поскольку w2(M) s щ (M)mod 2 и, значит,
w2(M)~ 0. При этом А (М) =	——К и по теореме Лих-
неровича (см. § F) многообразие М не допускает метрики по-
ложительной скалярной кривизны. Таким образом, многообра-
зие М принадлежит классу В из теоремы 4.35. В частности, лю-
бая метрика на М неотрицательной скалярной кривизны будет
риччи-плоской, т. е. из (i) следует (iii).
220
Гл. 6. Многообразия Эйнштейна и топология
Мы знаем (см. 6.36), что расслоение автодуальных 2-форм
Л + М на М тривиально. Значит, существуют три параллельных
сечения /, /, К расслоения Д М, для которых I2 — J2 =
= №==—Id и IJ — —Л = К. Таким образом, многообразие
(/И, g) гиперкэлерово. Наконец, (ii) влечет за собой (iii)
(см. 10.67), поскольку риманово многообразие с группой голо-
номии SU автоматически имеет нулевую кривизну Риччи
и Sp(l) = St/(2).	□
6.41.	Замечание. Можно показать (см. [Pol 1]), что неравен-
ство из теоремы 6.35 не характеризует многообразия Эйнштей-
на. Это неравенство остается справедливым при различных пред-
положениях, ограничивающих колебание значений кривизны.
Метод, использованный для доказательства теоремы 6.35,
по существу является чисто алгебраическим. Мы находим инте-
гральные представления двух характеристических чисел и затем
сравниваем подынтегральные выражения в каждой точке. Мож-
но показать, что, начиная с размерности п = 6, существуют ал-
гебраические контрпримеры (см. [Ger], [Во-Ро]) к любым
естественным обобщениям неравенства для подынтегральных
выражений характеристических чисел, справедливого при п = 4.
Если в условия теоремы 6.35 включить требование постоян-
ства знака секционной кривизны, то будет справедливо более
сильное неравенство
|-г(М)|<(-|-)3/2х(М)
(см. [Hit 1]).
6.42.	Приведем еще одно следствие формулы (6.31). Пусть
(М, §)—четырехмерное многообразие Эйнштейна отрицательно-
го знака, нормированное так, что г = —(п—l)g\ Тогда
| U Р =	— = 6 и, значит, % (М) vol (М, g). Однако
существуют многообразия, на которых метрика с г —(п—l)g
не может иметь сколь угодно малый объем: препятствием ока-
зывается так называемый симплициальный объем Громова.
6.43.	Симплициальный объем представляет собой топологи-
ческий инвариант компактного ориентированного многообразия.
Пусть многообразие М имеет размерность п. Фундаментальный
класс [Л1] есть класс сингулярных гомологий из Нп(М, R), т. е.
класс эквивалентности сингулярных циклов, представляющих
собой линейные комбинации симплексов:
с — 22 ^iOi, Kt G R, dc = 0.
D. Четырехмерный случай
221
Симплициальный объем ||Л4|| многообразия М по определению
равен точной нижней грани сумм вида
SKI,
соответствующих циклам с=2^Хгсг, представляющим класс
[М].
6.44.	Очевидно, что если существует отображение степени d
многообразия М на многообразие N, то
iiMn>idi-imi.
Поскольку сфера Sn допускает отображения на себя любой сте-
пени, ||S"II =0 при всех 1. Более того, М. Громов показал,
что Ц7ИЦ =0 для всех односвязных многообразий М.
Вообще, обращение в нуль симплициального объема зависит
только от фундаментальной группы (см. [Gro 2]).
6.45.	В то же время существуют многообразия М с ||А1|| #= 0,
например многообразия, допускающие метрику отрицательной
секционной кривизны (см. теорему Тёрстона, [Gro 2], с. 10,
20). Для поверхности Л4сх(Л1)<;0 существует элементарное
доказательство того, что ||Л1||=—2%(М).
Другие примеры можно получить с помощью связных сумм,
поскольку
\\M#N || = || М11 + 11ЛГЦ,
если dim М = dim N 3, а также с помощью произведений,
поскольку
||Л1Х/И1>С||Л1||-||ЛП|,
где константа С зависит только от dim(A!XAr)- В четырехмер-
ном случае можно взять С = 8.
6.46.	Центральным результатом, полученным для симпли-
циального объема, является основное неравенство М. Громова:
если (М, g) — компактное многообразие с г —(п—1)^, то
vol (М, g) С'||М||, где константа С зависит только от размер-
ности. В четырехмерном случае можно взять С' = -у^- (см.
[Gro 2], с. 12). С помощью 6.42 получаем следующую теорему.
6.47.	Теорема (М. Громов, [Gro 2], с. 87). Пусть М — ком-
пактное ^-многообразие. Если М допускает метрику Эйнштейна,
то
|| М || < 2592л2х (М).
6.48.	Пример. Пусть S — замкнутая поверхность рода у.
Удалим р открытых шаров из произведения S X 2 и обозначим
222
Гл. 6. Многообразия Эйнштейна и топология
через Л1 многообразие, склеенное из двух таких многообразий
с границей. Тогда %(Л1)=8(у—I)2 — 2р и т(Л1) = 0. С другой
стороны,
||Л1||>2||ЕХ2||>32(у-1)2,
поскольку М допускает отображение степени 2 на S X При
соответствующем выборе у и р получаем 0 < 2592л2/(Л1) <
< i|Al||. Значит, многообразие М не допускает метрики Эйн-
штейна. Это заключение нельзя получить из теоремы 6.35.
6.49.	Замечание. С помощью соотношения 6.34 в теорему 6.47
можно внести следующее уточнение. Для 0е[0,3/2] положим
0'= 2-33~9л~2 (с/4—О2). Если М — компактное 4-многообразие
Эйнштейна, то для любого 0 е [0, 3/2]
6|т(М)| + 6'||ЛЦКх(Л1).
Е. Кривизна Риччи и фундаментальная группа
6.50.	Из условия положительности кривизны Риччи вытекают
различные ограничения на фундаментальную группу. В то же
время неизвестно никаких топологических препятствий к суще-
ствованию метрик отрицательной кривизны Риччи г, даже если
допускать только компактные и полные метрики. Если кривизна
Риччи отрицательна, то метод Бохнера дает только дифферен-
циально-геометрическую информацию (но не дает топологи-
ческой).
Следующие теоремы формулируются для римановых много-
образий неотрицательной кривизны Рцччи. Из теоремы Т. Обина
([Aub]) следует, что любое компактное риманово многообразие
неотрицательной кривизны Риччи, которая положительна в не-
которой точке, допускает метрику положительной кривизны
Риччи. Таким образом, случаи г >0 и г^О весьма близки. Это
иллюстрация явления устойчивости, описанного в [Ch-Eb].
Первый результат для многообразий с г > 0 был получен
С. Б. ЛАайерсом в 1935 г. Он основан на формуле для второй
вариации (см. [Ch-Eb]).
6.51.	Теорема ([Муе]). Пусть (Al, g)— полное риманово мно-
гообразие, кривизна Риччи которого удовлетворяет условию
г^(п—l)k2g, где k = const > 0. Тогда М —компактное мно-
гообразие с диаметром d (Л1)	
6.52.	Следствие. Компактное риманово многообразие (Ai, g)
положительной кривизны Риччи имеет конечную фундаменталь-
ную группу.
Е. Кривизна Риччи и фундаментальная группа
223
Это следует из того, что универсальная накрывающая Л1
многообразия М имеет такую же кривизну, как Л1, и по тео-
реме 6.51 является компактной.	□
6.53.	Пример. Тор Тт — Rm/Zm есть компактное многообра-
зие с фундаментальной группой Zm. Следовательно, на нем не
существует метрики положительной кривизны Риччи, но, ко-
нечно, существуют плоские метрики.
6.54.	Следствие 6.52 не обобщается на полные некомпактные
многообразия. Л. Берар-Бержери и П. Набоннан привели при-
меры многообразий положительной кривизны Риччи размерно-
сти п 4, которые имеют фундаментальную группу 7, (см.
[Nab]). Расмотрим на многообразии ] 0, оо [ X S"-1 X R метрику
dS2 = dr2 _|_ h2 go _|_ f2 dt2t
где go — стандартная метрика на сфере Sn-1, f — ограничение
на R+ четной положительной О-функции, a h — ограничение
на R+ положительной нечетной функции с /г'(0)= 1. Можно
показать, что g — dr2 + h2(r)g0 есть полная метрика в R". Та-
ким образом, мы получаем полную метрику в R"+1 как скре-
щенное произведение (М, g) — (Rn, g)X,f R (см. 7.11). Связная
компонента единицы группы изометрий многообразия (Л1, g)
содержит подгруппу, изоморфную Z. Поэтому Rn+1/Z есть диф-
ференцируемое многообразие с положительной кривизной Риччи
и фундаментальной группой Z.
В трехмерном случае складывается другая ситуация.
Р. Шоэн и С. Т. Яу доказали следующий сильный результат.
6.55.	Теорема ([Sc-Ya 4]). Полное некомпактное риманово
3-многообразие положительной кривизны Риччи диффеоморф-
но R3.
С. Бохнер в 1946 г. доказал для первой группы когомологий
R) компактного многообразия (М, g) следующий ре-
зультат.
6.56.	Теорема ([Вос 1]). Пусть (М, g)—компактное рима-
нсвэ многообразие неотрицательной кривизны Риччи. Тогда
dim И1 (М, R) = bi dim М и универсальная накрывающая М
многообразия М разлагается в прямое произведение Rbi X М.
Если кривизна Риччи положительна, то Н1(М, R)=0.
Доказательство основано на анализе гармонических 1-форм
с использованием формулы Вейценбёка (см. гл. 1, § I)
(t/6 + f>d)a — D*Da + г (а*),
224
Гл. 6. Многообразия Эйнштейна и топология
которая позволяет выразить лапласиан 1-формы а через грубый
лапласиан и кривизну Риччи. Здесь D означает связность Леви-
Чивита, а а'* — векторное поле, двойственное к 1-форме а отно-
сительно метрики g. Поскольку оператор D*D неотрицателен,
из условия г > 0 следует отсутствие гармонических форм. Если
г 0, то все гармонические формы параллельны. Но по тео-
реме Ходжа — де Рама число Бетти Ъ\ равно размерности про-
странства гармонических 1-форм.	□
6.57.	Для многообразий положительной кривизны Риччи этот
результат оказывается более слабым, чем теорема Майерса,
поскольку из конечности Л1 (А1) автоматически следует, что
П*(М, R) = 0. С. Галло ([Gal 4]) и М. Громов ([Gro 1]) полу-
чили следующее обобщение этого результата.
6.58.	Теорема. Пусть М — компактное связное п-мерное ри-
маново многообразие. Обозначим через k нижнюю грань значе-
ний кривизны Риччи, а через d — диаметр М. Тогда существует
такое положительное число е, зависящее только от п и d, что
b\ (М) п при k —е- vol (М)2/п.
6.59.	Пример. Для тора 7’m = Rm/Zm имеем bl = m.
6.60.	Следующая теорема, доказанная Дж. Милнором *),
уточняет теорему Бохнера и дает информацию об алгебраиче-
ской структуре фундаментальной группы.
Пусть М — некоторое многообразие, a G — подгруппа его
фундаментальной группы, порожденная конечным числом обра-
зующих 36= {hi, ..., ftp). Каждому натуральному числу s
можно поставить в соответствие число y(s) приведенных слов
длины не больше $, построенных из образующих ftj и обратных
к ним элементов. Отображение уж:	называется функ-
цией роста группы G, ассоциированной с системой образую-
щих 36.
6.61.	Теорема ([Mill]). Пусть (М, g) — полное риманово
многообразие неотрицательной кривизны Риччи. Тогда функция
роста (s) любой конечно порожденной подгруппы фундамен-
тальной группы Л1 (Л1) удовлетворяет неравенству
yx(s)^ksn,
где k — некоторая константа и п = dim М.
') Эта теорема впервые была доказана в работе [Шварц А. С. Объемный
инвариант накрывающих.— Докл. АН СССР, 1955, т. 105, № 1, с. 32—34].—
Прим, перев
Е. Кривизна Риччи и фундаментальная группа
225
Доказательство основано на следующей теореме сравнения,
принадлежащей Р. Л. Бишопу ([Bis], см. также 0.64) *).
Пусть х0— точка универсальной накрывающей многооб-
разия М, a v(r)— объем шара радиуса г с центром в х0. Тогда
из неотрицательности кривизны Риччи следует, что v (г)	<£>пгп,
где со„ — объем единичного шара в
Образующие hi, hp можно интерпретировать как преоб-
разования скольжения в М. Если W = maxi=].....pd(x0, ht(x0)),
то объем шара с центром в точке хо радиуса lEs содержит по
крайней мере y(s) различных точек вида А(х0), /гелДМ).
При достаточно малом е шары В(х0, в) и /zB(x0, в), /ie
е Л1 (М), /г #= Id не пересекаются. Поэтому шар В (х0, W's + в)
содержит по крайней мере y(s) попарно непересекающихся ша-
ров вида h (В (х0, в)). Значит,
(s) v (в)< v (Ws + в).
Отсюда в силу неравенства Бишопа следует теорема 6.61. □
6.62.	Замечание. Для некомпактного многообразия М пока
неизвестно, следует ли из существования полной метрики неот-
рицательной кривизны Риччи конечная порожденность его фун-
даментальной группы.
6.63.	Пример ([Mill]). Пусть G— нильпотентная группа
матриц вида
1 а Ь\
0 1с],
0 0 17
а К — подгруппа целочисленных матриц. Тогда G/К есть ^-рас-
слоение над S1. Можно проверить, что группа щ(С/К) имеет
полиномиальный рост четвертой степени. Значит, G/К не допу-
скает метрики неотрицательной кривизны Риччи.
Структура многообразий неположительной кривизны Риччи
была исследована Дж. Чигером и Д. Бромолом (см. [Ch-Gr 1]).
Новые доказательства их результатов приводятся в [Es-He],
Напомним некоторые определения из 1.68.
6.64.	Определение. Прямой (соответственно лучом) в пол-
ном римановом многообразии называется геодезическая, реа-
лизующая расстояние между любой парой своих точек и опре-
’) Этот результат доказан ранее П. Гюнтером в работе [Finige Satze
fiber das Volumenelement aines Riemanschen Raumes. — Publ. Math. Debrecen,
1960, 7, № 1—4, 78—93].— Прим, nepee.
15 А. Бессе, т. 1
226
Гл. 6. Многообразия Эйнштейна и топология
деленная при всех значениях параметра t (соответственно при
/е[0, + со[).
6.65.	Теорема (Дж. Чигер, Д. Громол, [Ch-Gr 1 ]). Пусть
(М, g) — связное полное риманово многообразие неотрицатель-
ной кривизны Риччи. Тогда оно разлагается в прямое произве-
дение (М X R9, g X go), где go — каноническая плоская метрика
в R’, а (М, g) — полное риманово многообразие неположитель-
ной кривизны Риччи, не содержащее прямых.
6.66.	Замечание, (а) Топологическое следствие последнего
утверждения заключается в том, что М имеет не более одного
конца.
(Ь)	Доказательство этой фундаментальной теоремы будет
намечено в конце § G этой главы. Из доказательства будет
видно, в частности, что функция Буземана (см. 6.79) любого
луча в М является субгармонической.
(с)	В предположении неположительности секционной кри-
визны эта теорема была доказана В. А. Топоноговым ([Тор]).
Классификация полных некомпактных двумерных многообразий
неотрицательной гауссовой кривизны принадлежит С. Кон-Фос-
сену ([Coh]).	_
(d)	Отметим, что если размерность М равна нулю (соот-
ветственно единице), то М есть точка (соответственно окруж-
ность S1) и многообразие (М, g) плоско.
(е)	В частном случае^ когда многообразие (М, g) риччи-
плоско, многообразие (М, g), очевидно, тоже риччи-плоско.
Если при этом dimM^3, то многообразие (М, g) плоско.
(f)	В частном случае, когда многообразие (М, g) однородно,
многообразие (М, g) также однородно. Кроме того, оно ком-
пактно, так как любое некомпактное однородное риманово мно-
гообразие имеет по крайней мере одну прямую (упражнение!).
Наконец, если многообразие М компактно, теорема 6.65 дает
большую информацию о фундаментальной группе и о накры-
вающих многообразия М. Доказательства следующих результа-
тов см. в [Ch-Gr 2].
6.67.	Следствие (Дж. Чигер, Д. Громол, [Ch-Gr 1,2]).
Пусть (М, g) — компактное связное риманово многообразие не-
отрицательной кривизны Риччи. Тогда
(а)	существует такая конечная нормальная подгруппа F
группы щ(М), что группа nt(M)/F является расширением
группы Z.q с помощью конечной группы-,
(Ь)	риманова универсальная накрывающая (М, g) многооб-
разия (М, g) изометрична прямому произведению (М X R9,
g X go), где g0 — каноническая плоская метрика в R4, а(М, g) —
F. Скалярная кривизна и спинорное препятствие	227
комапактное односвязное риманово многообразие неотрицатель-
ной кривизны Риччи',
(с)	многообразие (М, g) является конечнократным накры-
тием над таким многообразием (М, g), что многообразие (M,g)
диффеоморфно Al X Тч, локально изометрично (М X Tq, g X gi)
и 'расслаивается над некоторым плоским тором (74gi);
(d)	если группа изометрий описанного многообразия (М, g)
конечна (что имеет место, когда (М, g) риччи-плоско), то опи-
санное в (с) конечнократное накрытие многообразия (М, g) гло-
бально изометрично многообразию (М У^Т4, g X g\).
Для того чтобы проиллюстрировать утверждение (с), рас-
смотрим пример из [Ch-Gr2]. Прямое произведение S2 X R
(с канонической метрикой) допускает свободное действие груп-
пы Z: образующая Z действует на S2 как поворот на угол а
с иррациональным отношением и действует на R как сдвиг.
Многообразие М = (S2X'R)/Z диффеоморфно произведению
52XS', расслаивается над S1 и локально изометрично римано-
вому прямому произведению S2XS1. Однако никакое накрытие
многообразия М не изометрично риманову прямому произведе-
нию S2 X S1.
Следствие 6.67 выводится из теоремы 6.65 с помощью сле-
дующих рассуждений. Пусть (М, g)—компактное риманово мно-
гообразие, универсальная накрывающая (Л4, g) которого не-
компактна. Тогда (М, g) содержит по крайней мере одну пря-
мую (упражнение!).
F. Скалярная кривизна и спинорное препятствие
Результаты предыдущего параграфа позволяют получить
примеры неодносвязных многообразий размерностей п 5, не
допускающих метрик Эйнштейна положительного знака. Суще-
ствуют и односвязные примеры, которые возникают при изуче-
нии более слабого условия: существования метрик положитель-
ной скалярной кривизны.
Основная идея заключается в использовании формулы Вей-
ценбёка для оператора Дирака.
6.68.	Пусть (M,g) — спинорное многообразие, т. е. многооб-
разие с нулевым вторым классом Штифеля—Уитни. Обозначим
через С1(7\2И) алгебру Клиффорда пространства (ТХМ, g(x))
и положим Cl (n)= C1(R"). Пусть dimAf=n. Тогда С1 (п)-рас-
слоение Е над М определяется как векторное расслоение, слои
которого являются С!(п)-модулями. Такое расслоение естествен-
15*
228
Гл. 6. Многообразия Эйнштейна и топология
ным образом снабжается послойной метрикой и связностью,
ассоциированной со связностью Леви-Чивита D в М. Эту связ-
ность мы также будем обозначать буквой D. Определим опера-
тор Дирака следующим образом. Пусть <р — сечение расслоения
Е, а (/,)— локальный ортонормированный базис векторных по-
лей на М. Положим
W = X • De ф,
/ = 1	1
где точка означает умножение Клиффорда.
Главный символ оператора SD в точке а е Т*М задается
клиффордовым умножением на а. Поэтому главный символ опе-
ратора S)2 равен —||<z||27d (см. приложение, 15).
Операторы 3) и S)2, очевидно, являются эллиптическими и
самосопряженными.
6.69.	Примеры. Если Е есть расслоение алгебр Клиффорда
над М, то оператор SD равен оператору d + б. Если Е =
есть спинорное расслоение над М, то, согласно 1.150,
<6.70)	.®2 = £>’£> +4-s,
где s — скалярная кривизна метрики g.
Для компактного многообразия М без границы простран-
ство Ж = Ker(.2)) = Ker(2>2) называется пространством гармо-
нических спиноров.
В четномерном случае расслоение разлагается в прямую
сумму двух подрасслоений S+M и S~7W, которые называются
расслоениями положительных и соответственно отрицательных
спиноров. Оператор Дирака отображает сечения каждого из
этих подрасслоений в сечения другого подрасслоения. Положим
2>+— 25|S+M. Напомним, что индекс оператора @)+ по опреде-
лению равен dim Ker .25+ — dim Coker S)+. Применение метода
Бохнера к формуле Вейценбёка (6.70) приводит к следующему
результату.
6.71.	Теорема (А. Лихнерович, [Lie4]). Пусть (M,g)—ком-
пактное спинорное многообразие. Если скалярная кривизна s
метрики g неотрицательна и не равна тождественно нулю, то
в М отсутствуют ненулевые гармонические спиноры. В частно-
сти, если М — четномерное многообразие, то индекс S)+ равен
нулю.
Если s = 0, то все гармонические спиноры параллельны.
6.72.	С помощью теоремы Атьи — Зингера об индексе ([At =
= Si3]), которая устанавливает связь индекса оператора
F. Скалярная кривизна и спинорное препятствие
229
С A-родом А(М), т. е. специальным характеристическим числом
многообразия М, А. Лихнерович показал, что компактное связ-
ное спинорное многообразие размерности п = 4m, допускающее
метрику положительной скалярной кривизны, имеет нулевой
А-род.
Например, в четырехмерном случае А (М) = т (М). По-
скольку КЗ-поверхность является спинорным многообразием и
имеет сигнатуру —16 (см. 12.108), она не допускает метрики
положительной скалярной кривизны (и, в частности, метрики
Эйнштейна положительного знака). С другой стороны, комп-
лексная проективная плоскость СР2 имеет сигнатуру 1 и не яв-
ляется спинорным многообразием. Она допускает метрику поло-
жительной скалярной кривизны. Таким образом, предположе-
ние о том, что многообразие М является спинорным, в тео-
реме 6.71 является существенным.
6.73.	Н. Хитчин улучшил результат Лихнеровича, используя
уточненный вариант теоремы об индексе ([At-Si 3]).
Теорема об индексе естественным образом формулируется
на языке К-теории. При этом индекс эллиптического оператора
интерпретируется с помощью групп К-теории. Понятие А-рода
можно обобщить таким образом, чтобы оно также формулиро-
валось на языке К-теории. Это было сделано Дж. Милнором
([Mil 2]). Существует сюръективный гомоморфизм а кольца
•спинорных кобордизмов Й®р1П на кольцо КО* (точка), для ко-
торого а(М) = А(М), если п = 8т.
Из теоремы об индексе следует, что
dim Ker S)+ — dim Ker = A (M), если n = 4m,
dimKer^ = a(A4)mod2, если n2 = 8m + 1,
dim Ker 2£>+ = a (M) mod 2, если n = 8m + 2.
6.74.	Следствие (H. Хитчин, [Hitl]). Пусть M — компактное
спинорное многообразие. Если оно допускает метрику положи-
тельной скалярной кривизны, то а (М) = 0.
6.75.	Пример ([Hit 1]). Некоторые экзотические сферы раз-
мерности п = 8m + 1 и 8m + 2 являются спинорными многооб-
разиями с а(А4)=#0. Следовательно, они не допускают метрики
положительной скалярной кривизны (и, в частности, метрики
Эйнштейна положительного знака).
6.76.	Красота результата Н. Хитчина заключается в том, что
в односвязном случае необходимое условие a (А4) = 0 существо-
230
Гл. 6. Многообразия Эйнштейна и топология
вания метрики положительной скалярной кривизны, по-види-
мому, является и достаточным.
Пусть $ — класс компактных многообразий, допускающих
метрики положительной скалярной кривизны. Следует отметить,
что условие а — 0 инвариантно относительно кобордизмов. В не-
котором смысле условие принадлежности к классу $ также ин-
вариантно относительно кобордизмов. Точная формулировка
утверждения, доказанного М. Громовым и X. Б. Лоусоном, та-
кова. Пусть многообразие М размерности п > 5 односвязно и
является (соответственно не является) спинорным. Если М
спин-кобордантно (соответственно ориентированно-кобордантно)
многообразию из $, то оно принадлежит ф. С учетом результа-
тов С. Смейла достаточно проверить устойчивость класса $ от-
носительно хирургии в коразмерности 3. Доказательство
устойчивости с помощью явной конструкции было получено
Р. Шоэном и С. Т. Я у ([Sc-Ya3]).
Образующие кольца ориентированных кобордизмов имеют
явные реализации, которые, как нетрудно проверить, принадле-
жат 5р. Поэтому любое односвязное компактное многообразие
размерности п > 5, не являющееся спинорным, допускает мет-
рику положительной скалярной кривизны. Случай кольца спин-
кобордизмов является более тонким, однако кольцо односвяз-
ных спин-кобордизмов отличается от кольца ориентированных
кобордизмов только кручением. Кроме того, существуют спинор-
ные образующие кольца	(кватернионные проективные
пространства), которые принадлежат $. Отсюда М. Громов и
X. Б. Лоусон сделали вывод, что идеал, порожденный классом
5р в кольце Qs>5, имеет конечный индекс в Кег а. Другими сло-
вами, если М есть односвязное компактное спинорное много-
образие размерности п>5с а(Л1) —0, то некоторая связная
сумма МФ ... ФМ допускает метрику положительной скаляр-
ной кривизны.
6.77.	Для неодносвязных многообразий возникают и другие
препятствия к существованию метрики положительной скаляр-
ной кривизны. Здесь мы не будем их обсуждать, поскольку они
не приводят к построению новых примеров многообразий, не
допускающих метрик Эйнштейна положительного знака. Эти
препятствия возникают для достаточно больших фундаменталь-
ных групп (см. [,Sc-Ya3, 4], [Gr-Lal,3]), причем некоторые из
них не очень сильно зависят от самой группы (см. [Сгг]). От-
метим, что случай конечной фундаментальной группы не сво-
дится к односвязному случаю. Существуют многообразия
G. Доказательство теоремы Чигера—Громола
231
с а(М)#=0, универсальная накрывающая которых компактна и
обладает метрикой положительной скалярной кривизны (см.
[ВёВег4] и [Rbg 1,2]).
G. Доказательство теоремы Чигера—Громола
о полных многообразиях неотрицательной
кривизны Риччи
6.78.	Как мы уже видели в § Е, существуют три основные
теоремы о топологии многообразий неотрицательной кривизны
Риччи:
(а)	теорема Майерса 6.51, набросок доказательства кото-
рой приведен в 1.92;
(Ь)	теорема Бохнера 6.56, доказательство которой основано
на формуле Вейценбёка 1.155;
(с)	теорема Чигера — Громола 6.65.
До последнего времени доказательство теоремы Чигера —
Громола не приводилось ни в одной книге. Недавно
Дж. X. Эшенбург и Е. Хайнце ([Es-He]) нашли вполне эле-
ментарное доказательство этой теоремы, в котором, в частности,
не используется теория регулярности решений эллиптических
уравнений (в отличие от первоначального доказательства). Мы
приведем набросок оригинального доказательства Чигера —
Громола с упрощениями, предложенными в [Es-He], Для удоб-
ства читателя сформулируем доказываемый результат в экви-
валентной форме, несколько отличающейся от исходной.
6.79.	Теорема (Дж. Чигер, Д. Громол, [Ch-Gr 1], Дж. Эшен-
бург, Е. Хайнце [Es-He]). Пусть (М, g)— полное связное рима-
ново многообразие неотрицательной кривизны Риччи. Предпо-
ложим, что многообразие (M,g) допускает прямую. Тогда оно
является римановым произведением (A4XR, gY,dt2), где
(М, g) — полное связное риманово многообразие неотрицатель-
ной кривизны Риччи, a dt2 — каноническая метрика на пря-
мой 'R.
Доказательство. Ключевой момент доказательства заклю-
чается в рассмотрении функции Буземана луча. Пусть
У [0, + оо[—>-Л4—произвольный луч. Функции
ft(x) = t — d(x, у(0)
образуют равностепенно непрерывное семейство неубывающих
по t функций на М, ограниченных функцией d(x, у(0)), причем
граница достигается на у. Поэтому предел
6= lim ft
+оо
232
Гл. 6. Многообразия Эйнштейна и топология
существует и является непрерывной функцией на М, ограничен-
ной функцией d (х, у (0)), причем граница достигается на у.
Назовем b функцией Буземана луча у. Отметим, что функция
b может не принадлежать классу С1. Для того чтобы устранить
возможную негладкость функции Ь, введем понятие опорной
С°°-функции (которое интенсивно используется в [Wu 4]).
6.80.	Определение. Функция h называется опорной Сх-функ-
цией для непрерывной функции f в точке х0 М если
(а)	функция h определена и принадлежит классу С°° в не-
которой окрестности точки хо',
(b)	h(x0) = f(x0)-
(с)	h(x) f(x) для всех х <= W.
Приведем схему, по которой можно найти опорную функцию
для функции Буземана Ь луча у при условии, что многообразие
(М, g) имеет неотрицательную кривизну Риччи. Для любой
точки хо е М и числа t 0 обозначим через Xt начальный еди-
ничный касательный вектор минимальной геодезической, соеди-
няющей хо и у(£). Пусть X есть предельная точка семейства
Xt^.TXtrM при Лемма 1.67 показывает, что геодезическая
сх, заданная вектором X, является лучом. Положим
bx, t(x) = b (х0) +1 — d (х, сх (0).
6.81.	Лемма. Функции bx,t являются опорными (^-функ-
циями для функции Буземана b луча в точке х0. Если мно-
гообразие (М, g) имеет неотрицательную кривизну Риччи, то
где п — размерность М.
Доказательство. Поскольку сх есть луч, точки cx(t) не при-
надлежат множеству раздела точки х0 и, обратно, точка хо не
принадлежит множеству раздела точек cx(t). Поскольку функ-
ция расстояния принадлежит классу С°° вне множества раздела,
отсюда следует, что функция bx, t принадлежит классу С°° в не-
которой окрестности W точки хо- Далее, bx, t (х0) — b (хо) » по-
скольку d(xo, cx(t)) = t в силу минимальности сх. Имеем
bXt t(x)~b (*) = b (х0) + t — d (х, сх (0) — b (х) =
= lim (и — d (х0, у (и)) +1 — d (х, сх (/)) — и + d (х, у (и))).
и-»о°
Пусть у« есть минимальная геодезическая, соединяющая точку
хо с у (и), а Хи — ее начальный касательный вектор (см.
G. Доказательство теоремы Чигера—Громола	233
рис. 6.81). Тогда при и > t получаем
d(x0, У (и)) = t + d (у„ (0, у (и)).
Следовательно,
bx, t(x)~b (х) = Нт (d (х, у (и)) — d (у„ (0, У (и)) — d (х, сх (0)) <
U->oo
<	Нт (d (у (и), сх (0) — d (у„ (0, у (и))) <
U->oo
<	Нт d (сх (0, Уи (0)-
Существует такая последовательность ип, что Нт ип — оо и
гг->оо
Нт Хи = X. Отсюда следует, что bx t (х) — b (х)	0. Последнее
П->ео П	’
утверждение леммы вытекает из равенства
i (х) = — Arf (х, сх(0)
и следующей леммы.
6.82. Лемма, (а) Пусть СХо есть множество раздела точки хо
риманова многообразия (M,g). Тогда функция f (х) — d (хо, х)
принадлежит классу С°° на множестве W — М\ ({х0}UСХо) и,
удовлетворяет условиям ||£>f|| = 1 и Д/(х0) = — оо.
234
Гл. 6. Многообразия Эйнштейна и топология
(Ь) Если, кроме того, кривизна Риччи многообразия (M,g)
неотрицательна, то на IF
П — 1
Af >------— •
Доказательство. Утверждение (а) является стандартным и
вытекает, например, из леммы Гаусса 1.46. Докажем утвержде-
ние (Ь). Его можно проверить с помощью элементарных вы-
числений, но мы приведем другое доказательство. Оно основано
на наблюдении, что в силу условия ||£>f||= 1 функция f опреде-
ляет риманову субмерсию W R (где R снабжено стандартной
метрикой dt2). Поэтому можно воспользоваться формулами
О’Нейла для субмерсии, приведенными в гл. 9. При этом из од-
номерности базы R следует, что тензор А равен нулю, а тензор-
Т удовлетворяет условиям
TvV = - Ddf (U, V)Df,
где U, V — вертикальные векторы (т. е. Uf = Vf = 0) и
N — (Af)Df.
Поскольку И ||2 =	IINII2 + 11 Т° ||2 <^^7 ll^ll2, имеем
(отметим, что Hf(Df,U) = 0 для любого U). Из (9.36с) легко
выводится, что
0 < г (Df, Df) = Df (Af) - || Ddf ||2 < Df (Af) -	(Af2).
Пусть с есть интегральная кривая поля Df (т. е. горизонтальная
геодезическая римановой субмерсии f). Рассмотрим функцию
одной переменной
Ф(0==Д/(с(0).
Она удовлетворяет условиям
0 + <рЛ---—г Ф2, lim ф = — со.
п 1	/->0
Положим ф = Тогда ф' =	и ф(0) = 0. Следо-
1	, t	_
вательно, — — = ф } .	□
Докажем теперь ключевой результат, касающийся функций
Буземана.
G. Доказательство теоремы Чигера—Громола
235
6.83.	Предложение. Пусть (М, g)— полное риманово много-
образие неотрицательной кривизны Риччи. Тогда функция Бузе-
мана любого луча субгармонична, т. е. для любого геодезиче-
ского замкнутого шара В в М гармоническая функция h, опре-
деленная в В и совпадающая с b на границе дВ, удовлетворяет
в В неравенству h Ь.
Доказательство. Поскольку функция h гармонична, она при-
надлежит классу С°° (см. приложение, 31). Пусть bx,t есть по-
строенная выше опорная функция для b в точке х0. Тогда
bx, t — h есть опорная функция для b — h, удовлетворяющая не-
равенству
Поскольку b — h = 0 на дВ, неравенство h b немедленно вы-
текает из следующего обобщения принципа максимума Э. Хоп-
фа, доказанного Э. Калаби.	□
6.84.	Предложение (Э. Калаби, [Cal 8], Э. Хопф, [Нор]).
Пусть f — непрерывная функция на связном римановом много-
образии (М, g). Предположим, что для всех хеМ и е>0 су-
ществует такая опорная С°°-функция fx, е для функции f в точке
х, что &fx, е(х) е. Тогда функция f может достигать максимума
только в том случае, если она является константой.
Доказательство. Предположим, что существует точка х мак-
симума функции Д причем f не постоянна ни в какой окрестно-
сти U7 точки х. Выберем такой замкнутый геодезический шар В
с центром х, что функция f на его границе дВ не равна тожде-
ственно f(x). Положим д'В ={у дВ, f(x) — f(y)}=/=dB. Выбе-
рем O’-функцию <р на М. так, чтобы она равнялась нулю в точке
х, была отрицательна на д'В, положительна в некоторой точке
из дВ\д'В, а ее градиент Dip не обращался в нуль на В (см.
рис. 6.84). Для любого а>0 положим ha =	—1- Тогда ha
есть С^-функция на М, причем йа(х) = 0, функция ha отрица-
тельна на д'В и Д/га = (—а2||£)ф||2 + аАф) е“(р. Из компактности
В следует существование такого а, что ДЛа < 0 на В. Зафикси-
руем такое а. Далее, существует такое т] > 0, что (f + т]йа) (у) <
< f(x) для всех у^дВ. Но тогда функция f + т]йа достигает
максимума (^f(x)) в некоторой точке z, не принадлежащей
внутренности Ва шара В. Для любого е > 0 функция fz, е + r]/irx
является опорной О-функцией для f + т]/га в точке z и дости-
гает максимума в точке z. Следовательно, Д (^ t +(г)	0.
С другой стороны, Дйя(г)<0 и Afz,e(z)^e для любого е > 0.
Получаем противоречие.	□
236
Гл. 6. Многообразия Эйнштейна и топология
6.85.	Завершение доказательства теоремы 6.79. Пусть у —
прямая в М. Она определяет два луча у+(/) = y(t) и у_(/) =
= у(—t). Обозначим через Ь+ и Ь- соответствующие функции
Буземана, являющиеся субгармоническими непрерывными функ-
циями на М. Очевидно, что (b+ + b_) (х) = lim (2/ — d (х, у (/)) —
1->оо
— d(x, у (—t)))	0 и Ь+ + й_ = 0 на у. Применяя предложе-
ние 6.84 (с определенными выше опорными функциями), заклю-
чаем, что Ь+ = —Ь_ на М. Значит, функция Ь+ одновременно
субгармонична и супергармонична, т. е. гармонична и, следова-
тельно, принадлежит классу С°°. Опорные функции bx, t и by. t
для функций Ь+ и Ь- в точке х также являются функциями
класса С°°, имеют единичный градиент в точке х и удовлетво-
ряют неравенству bx,t <1 Ь+ — — Ь- — by, t, причем можно
считать, что bx, t(x) =— by,t(x). Отсюда следует, что норма
градиента функции 6+ равна 1. Теорема вытекает теперь из сле-
дующей леммы.
6.86.	Лемма. Пусть (М, g)— связное полное риманово мно-
гообразие неотрицательной кривизны Риччи, a f — С°°-функция
на М с ||Z)f||— 1. Тогда М есть риманово произведение (Л?ХК,
g'X.dt2), a f — проекция на второй сомножитель.
Доказательство. Как и в доказательстве леммы 6.82, можно
рассматривать f как риманову субмерсию на многообразие
(R,d/2). Сохраняя обозначения леммы 6.82, рассмотрим функ-
G. Доказательство теоремы Чигера—Громола
287
цию ф = Af о с. Пусть £ есть первообразная функции w j. • По-
ложив g — е~\ немедленно получим, что
• 5" = (-7^т+т^т)£<0-
Поскольку функция £ положительна на R, она постоянна. Но
тогда ф =0, Af = 0, ||£>df||= 0 и Т = 0. Это означает, что рима-
нова субмерсия f является римановым произведением, по-
скольку многообразие R односвязно.	□
Глава 7
Однородные римановы многообразия
А. Введение
7.1.	В этой главе мы изложим общую теорию однородных
римановых многообразий и построим с ее помощью примеры
однородных многообразий Эйнштейна. Пока что полная клас-
сификация однородных многообразий Эйнштейна не получена
даже в компактном случае. В частности, остается открытым
следующий вопрос.
7.2.	Проблема. Классифицировать компактные односвязные
однородные многообразия M=G/K (с компактными G и К),
которые допускают G-инвариантную метрику Эйнштейна.
Эта проблема подробно обсуждается в 7.54. Отметим, что
М. Ванг и В. Циллер привели примеры компактных односвяз-
ных многообразий G/К, не допускающих G-инвариантной мет-
рики Эйнштейна (см. 9.95).
7.3.	Тем не менее известно много примеров однородных мно-
гообразий Эйнштейна. После общих определений, связанных
с однородными римановыми многообразиями (§ В), и вычисле-
ния их кривизн (§ С) мы приведем простейшие примеры одно-
родных многообразий Эйнштейна: пространства постоянной кри-
визны и проективные пространства (§ D). Затем мы получим
(без всяких вычислений) еще целый ряд примеров многообра-
зий Эйнштейна, рассмотрев изотропно неприводимые простран-
ства, и приведем (без доказательства) классификацию строго
изотропно неприводимых пространств, полученную Дж. А. Воль-
фом.
Мы также приведем несколько общих результатов, касаю-
щихся однородных многообразий Эйнштейна (§ Е), которые
вытекают из более общих результатов для кривизны Риччи, и
дадим обоснование (§ Е) следующей грубой классификации.
7.4.	Теорема. Пусть (Л4, g) — однородное многообразие Эйн-
штейна постоянной скалярной кривизны s.
(а)	Если s > 0, то многообразие М компактно и имеет ко-
нечную фундаментальную группу.
(Ь)	Если s = 0, то М плоско.
В. Однородные римановы многообразия
239
(с)	Если s < 0, то М некомпактно.
В связи с 7.4 (с) встает следующий вопрос.
7.5.	Вопрос (Д. В. Алексеевский). Пусть M=G/K — неком-
пактное однородное многообразие Эйнштейна. Верно ли, что К
есть максимально компактная подгруппа в G?
7.6.	Позже мы приведем другие примеры многообразий
Эйнштейна. В § F мы изложим развитую Э. Картаном теорию
римановых симметрических пространств и набросаем схему их
классификации, а в § G приведем (без доказательства) класси-
фикацию М. Ванга и В. Циллера метрик Эйнштейна, являю-
щихся стандартными однородными метриками. Все эти примеры
сведены в табл. 7.102—7.109 в § Н. В гл. 9, 15 приводятся дру-
гие примеры однородных метрик Эйнштейна.
7.7.	В § I мы рассмотрим случай лоренцевых однородных
многообразий. При этом мы не будем строить общую теорию,
а лишь отметим основные отличия от риманова случая и про-
иллюстрируем их примерами (некоторые примеры являются
эйнштейновыми).
В. Однородные римановы многообразия
7.8.	Определение. Риманово многообразие (Af, g) называется
однородным, если группа I(M,g) его изометрий транзитивна на
А1 (т. е. для любых точек х, у е М существует изометрия, пере-
водящая х в у).
Следуя духу эрлангенской программы Ф. Клейна ([К1е]),
мы будем пользоваться более тонким определением. Напомним,
что на заданном многообразии может транзитивно действовать
несколько групп. Поэтому такое многообразие можно рассмат-
ривать как фактор-пространство различных групп (примеры
см. в 7.13).
7.9.	Определение. Риманово многообразие (Al, g) называется
G-однородным (или однородным относительно группы Ли G),
если G есть замкнутая подгруппа группы I(M,g), действующая
на М транзитивно.
7.10.	Замечания, (i) Отметим, что группа G не обязана со-
впадать с I(M,g). Например, группа изометрий евклидова про-
странства состоит из всех движений, а ее собственная подгруппа
параллельных переносов действует транзитивно.
(ii)	Мы предполагаем замкнутость G только для простоты
изложения. Действительно, если G есть транзитивная и эффек-
240
Гл. 7. Однородные римановы многообразия
тивная ') группа преобразований многообразия М, сохраняющая
некоторую риманову метрику g, то замыкание G группы G
в группе диффеоморфизмов Diff (М) является замкнутой под-
группой группы I(М, g), транзитивно действующей на М.
7.11.	Стационарная подгруппа. Поскольку G есть замкнутая
подгруппа группы I(M, g), стационарная подгруппа (или ста-
билизатор') K = {f^G, f(x) = x} произвольной точки х^М
является компактной подгруппой группы IX(M, g).
Отметим, что компактность М равносильна компактности G.
Поскольку изометрия f однозначно определяется образом
f(x) одной точки х и соответствующим касательным отображе-
нием Txf, линейное представление изотропии %(f) = Txf стацио-
нарной группы К в GL(TXM) является точным (т. е. инъек-
тивным) .
7.12.	Замечание об эффективности. В соответствии с опреде-
лением 7.9 мы должны предположить, что группа G действует
на G/К эффективно, т. е. /С не содержит нетривиальных нор-
мальных подгрупп группы G.
В общем случае, если даны группа Ли G и ее компактная
подгруппа К., то группа G не всегда действует эффективно на
G/К (а соответствующее представление изотропии не всегда
является точным). Пусть С — максимальная нормальная под-
группа группы G, принадлежащая /С. Тогда G' = G/С действует
на G/К со стационарной подгруппой К' = К/С и это действие
группы G' на G/K — &/К' эффективно.
Как правило, в конкретных примерах мы не будем явно опи-
сывать эффективно действующую группу G', поскольку это
всегда можно сделать с помощью простых вычислений. Напри-
мер, комплексное проективное пространство СРп обычно за-
дается как однородное пространство SU(п + 1)/S (17(1) G(n)).
Однако группа G — SU(п + 1) действует на СРп не эффек-
тивно. Здесь С = Z„+i (центр SI7(n + l)) и G'=SU(n-]-
+ \)/Zn+l = PSU(n+ 1).
Однако во всех примерах в этой и следующей главах дей-
ствие G на G/К является почти эффективным, т. е. К не содер-
жит недискретных нормальных подгрупп группы G. В этом слу-
чае группы G и G' (а также К и К') имеют одну и ту же ал-
гебру Ли. В таблицах из § Н указаны алгебры Ли групп G и К
(см. 7.101).
7.13.	Примеры. Транзитивные действия на сферах. Стандарт-
ную сферу Sn можно рассматривать как однородное многообра-
*) Эффективность означает, что только единица группы действует на М
как тождественное преобразование. — Прим, перев.
В. Однородные римановы многообразия
241
зие SO(n + l)/SO(n), однако существуют и другие компакт-
ные связные группы Ли, транзитивно и эффективно действую-
щие на сферах. Д. Монтгомери и X. Самелсон ([Mo-Sal]) и
А. Борель ([Вог 1,2]) классифицировали все такие группы и
получили следующий список.
G	SO in)	U (n) SU (n)	Sp’(n) Sp (1)	Spin) U (1)	Sp (n)
Сфера	S„-i	S2n-1		S4rt-1	
К	SOJn-l)	U in—1) S<7(n-l)	Sp(n-l)Sp(l)	Sp(n-l)U(l)	Sp(n— 1)
tn	0	1 1	1	2	6
g2	Spin (7)	Spin (9)
S6	S7	S15
S£J(3)	g2	Spin (7)
0	0	1
Здесь действие группы G на соответствующей сфере Sp опреде-
ляется таким специальным линейным представлением р группы
G в пространстве ₽₽+*, для которого G транзитивно действует
на единичной сфере в Rp+l. Например, мы имеем естественные
представления SO(n) в R", U (п) в lC"(=R2") и Sp(n)Sp(l)
в Н"(= R4") (по поводу последней группы см. [Hel 1], а также
гл. 10, 14). Далее, К обозначает стационарную подгруппу, ат —
размерность пространства G-инвариантных римановых метрик,
рассматриваемых с точностью до гомотетии (т. е. с точностью
до изометрии и масштабного преобразования метрики). В сле-
дующем параграфе (см. 9.86) мы рассмотрим G-инвариантные
метрики, которые являются эйнштейновыми.
7.14.	Замечание. Отметим наличие большого числа вклю-
чений между указанными группами: SU (и) cz U (и) cz SO (2n),
Sp(n)czSO(2n), Sp(n)G(l)cG(2n), Sp(n) cz Sp(n) G(l) c
cz Sp (n) Sp (1) cz SU (in), G2 cz SO (7), SU (4) cz Spin (7) cz SO (8),
Spin (9) cz SO (16).
Включение вида G cz G' позволяет отождествить одну и ту
же сферу с однородными пространствами группы G и группы
G', однако на сфере обычно существуют G-инвариантные мет-
рики, которые не являются G'-инвариантными. Имеются только
три исключения: G2 cz SO(7), Spin(7)cz SO(8) и SU(n)cz U(n)
16 А. Бессе, т. I
242
Гл. 7. Однородные римановы многообразия
(п>2). В частности, группы Gz, )Spin(7) и SU(n) не являются
полными группами изометрий никакой римановой метрики на
соответствующей сфере.
Напомним, что любая SO (п) -инвариантная метрика на сфере
S"-1 пропорциональна стандартной и имеет полную группу изо-
метрий О(п). Таким образом, даже SO(ri) не является полной
группой изометрий никакой римановой метрики на S"-1.
7.15.	Примеры. Проективные пространства. Напомним, что
проективные пространства являются однородными многообра-
зиями:
RP" = SO (п + 1)/О (п),
СР" = SU (п + 1 )/S (Я-(1)17 (п)),
HP" = Sp (п + 1)/Sp (и) Sp (1),
CaP2 = P4/Spin (9).
Все группы из 7.13 транзитивно действуют на RPn. Кроме
того, Sp(n) транзитивно действует на 'СР2”-1 (при отождествле-
нии Ц" с С2") со стационарной подгруппой Spin—1)0(1).
Этим исчерпывается весь список компактных связных групп
Ли, действующих на проективных пространствах транзитивно и
эффективно (А. Л. Онищик, [Oni]). О соответствующих метри-
ках Эйнштейна см. 9.86.
7.16.	Примеры. Торы. Единственной компактной связной
группой Ли, действующей на торе Тп эффективно и транзитивно,
является сам тор Тп (Д. Монтгомери, X. Самелсон, [Mo-Sa 2]).
7.17.	Некоторые некомпактные примеры. Гиперболическое
пространство является однородным многообразием Нп =
— SO0(n, 1)/SO(n), где SOo(n, 1) — связная компонента еди-
ницы ортогональной группы 0(п, 1), заданной квадратичной
формой сигнатуры (n, 1) в R"+* (ср. с 1.36). Существуют также
комплексный, кватернионный и октавный аналоги гиперболиче-
ского пространства:
CHn = SU(n, l)/S(U(n)U(l)),
HHn = Sp(n, l)/Sp(n)Sp(l),
Ca№ = №7Spin (9)
(для особых простых групп Ли мы используем те же обозначе-
ния, что в [Hel 1]). Отметим, что существует много различных
замкнутых подгрупп группы SO0(n, 1) (соответственно
St7(n+ 1), Sp-(n, 1)> №°)> транзитивно действующих в Нп (со-
ответственно в СНп, НЯ", СаЯ2). В частности, существует раз-
решимая подгруппа группы SOQ(n, 1) (соответственно SU(n, 1),
С. Кривизна
243
Sp(n, 1), Ft2), действующая просто транзитивно в Нп (соот-
ветственно в СНп, ННп, СаН2). Это следует, например, из раз-
ложения Ивасавы G = KAN (см. [Hel 1]).
7.18.	Зафиксируем G-инвариантное риманово многообразие
(XI, g) и точку хеМ. Тогда К = Gf|/X(A1, g) есть компактная
подгруппа группы G и М диффеоморфно фактор-пространству
Рис. 7.19. фу— геодезическая, у е К; (2)у (0 — касательный вектор к у
в точке </ = у(0; ® строго выпуклый шар В (х, г) с центром в точке х;
@ изометрия f с f(y) — x; ® Tyf(y(t)) определяет геодезическую б длины г,
выходящую из точки х; (6) геодезическая (-1°б удлиняет у на г.
G/F (см., например, [Cha], с. 109—111, или [Hel 1], с. 113).
В частности, компактность М равносильна компактности G. От-
метим, что группа G действует на М эффективно, т. е. К. не со-
держит нормальных подгрупп группы G. С помощью изометрий
можно продолжить любую геодезическую сколь угодно далеко
(см. рис. 7.19). Это позволяет получить следующий хорошо из-
вестный результат.
7.19.	Теорема. Однородное риманово многообразие полно.
Подробное доказательство см. в [Ко-No 1], с. 176. См. так-
же пояснение к рис. 7.19.
С. Кривизна
7.20.	Обозначим через g алгебру Ли группы G. Для любого
/ед будем обозначать через Exp (/X) однопараметрическую
подгруппу группы G, порожденную X. Действие группы Ехр(/Х)
16*
244
Гл. 7. Однородные римановы многообразия
на М позволяет рассматривать ее как однопараметрическую
группу (pt диффеоморфизмов многообразия Л4, где
Ф/ (у) = Ехр (tX) у.
Отождествим X е g с векторным полем на М, порожденным
группой (pt. При этом g отождествляется с множеством киллин-
говых векторных полей на (М, g), которые порождают однопа-
раметрические группы, лежащие в G. (Напомним, что G не обя-
зательно должна быть полной группой изометрий.) Здесь есть
одна тонкость.
7.21.	Предостережение. Пусть [•, •]— скобка Ли векторных
нолей на М, а [ • , • ]0 — скобка Ли в алгебре Ли g (мы будем
иользоваться этими обозначениями на протяжении всей главы).
Тогда при описанном выше отождествлении для любых элемен-
тов X, У е g выполняется равенство
[X, У]0 = - [X, У].
Комментарии, а также более подробное изложение других ре-
зультатов этого параграфа см. в [Wai] или в [KO-No 2], с. 469.
7.22.	Подалгебра Ли с leg, соответствующая стационарной
подгруппе К, отождествляется с подалгеброй киллинговых полей
из д, которые обращаются в нуль в точке х. Пусть Adc есть
присоединенное представление группы G в д. Из компактности
К следует, что Ado (К) есть компактная линейная группа пре-
образований пространства g. С помощью известной процедуры
усреднения можно построить Ado (К)-инвариантную евклидову
метрику в g и Adc (К)-инвариантное дополнение р к I в g (как
ортогональное дополнение к I относительно этой метрики). За-
фиксируем раз и навсегда такое инвариантное дополнение р
(вообще говоря, не единственное) и отождествим его с ТХМ,
сопоставив элементу Хер значение соответствующего киллин-
гова поля в точке х. При этом представлении изотропии у груп-
пы К в ТХМ отождествится с ограничением присоединенного
представления Adc подгруппы К на р.
7.23.	Обозначим через (-, •) скалярное произведение в р, со-
ответствующее евклидовой метрике gx в ТХМ при отождествле-
нии ТХМ — р. Отметим, что это скалярное произведение
Adc (К)-инвариантно, поскольку К действует изометриями и со-
храняет точку х. Таким образом, с каждой G-инвариантной ри-
мановой метрикой на М мы связали Ado (К)-инвариантное ска-
лярное произведение в р. Обратно, справедлива
7.24.	Теорема. Пусть G — группа Ли, К — ее компактная
подгруппа, не содержащая нормальных подгрупп группы G,
С. Кривизна
245
а р— Ado (/С)-инвариантное дополнение к I в g. Тогда каждое
Ado (К) -инвариантное скалярное произведение (•, •) в р одно-
значно определяет риманову метрику g в G/К = М таким об-
разом, что группа G действует (слева) на (М, g) изометриями,
а скалярное произведение, индуцированное метрикой g в р (как
описано в 7.23), совпадает со скалярным произведением (-, •).
Подробное доказательство см. в [Ko-No 2], с. 200. Идея до-
казательства состоит в том, что метрика gy в ТУМ определяется
как f*gx, где f— преобразование из G, переводящее у в х. □
7.25.	Примеры. Пусть G есть произвольная связная группа
Ли. Тогда G транзитивно действует на себе левыми сдвигами.
Поэтому любое скалярное произведение в алгебре Ли g группы
G разносится левыми сдвигами до G-инвариантной римановой
метрики на G. Такая метрика обычно называется левоинва-
риантной римановой метрикой. В этом случае К={е}, 1 = 0
и V = g.
7.26.	Пункты 7.23 и 7.24 показывают, что G-однородное ри-
маново многообразие (М, g) в определенном смысле полностью
определяется Ade (К)-инвариантным скалярным произведением
в р. Вследствие этого кривизну многообразия (М, g) можно
выразить через скалярное произведение ври скобки Ли в g.
Отметим, что ввиду инвариантности кривизны относительно изо-
метрий достаточно вычислить ее только в точке х.
Далее, тензор кривизны в точке х отождествляется с
Ado (А)-инвариантным тензором пространства р. Сначала опи-
шем связность Леви-Чивита.
7.27.	Лемма. Пусть X, Y, Z — киллинговы векторные поля на
римановом многообразии (M,g). Тогда
(7.27)	2g(DxY, Z) = g([X, У], Z) + g ([X, Z], Y) + g(X, [У, Z]).
Доказательство. Если X, Z — киллинговы поля, то
g([X, Z], Х) = g (DXZ, X)-g(DzX, X) = g(DxX, Z).
Поляризуя это равенство, получаем
g(DxY, Z) + g(DYX, Z) = g([X, Z], Y) + g(X, [У, ZJ).
Теперь (7.27) следует из равенства DxY—DyX — [X, У].	□
7.28.	Предложение. Пусть (М, g) есть G-однородное рима-
ново многообразие и р определено как в 7.22. Пусть X, У—
киллинговы векторные поля из р. Тогда
(7.28а)	(DXY)X = - | [X, У]„ + U (X, У),
246
Гл. 7. Однородные римановы многообразия
где отображение U: VXV~определяется условием
(7.28b)	2(U(X, У), Z) = ([Z, Х]¥, У) + (X, [Z, У]₽)
для всех Z е р.
Доказательство следует непосредственно из (7.27) и (7.21).
(Здесь и далее [ - ,  ]р и [ • , • ]f обозначают компоненты
скобки [  , - ]0, лежащие ври?.)
7.29.	Замечание. Отметим, что если X и У — киллинговы век-
торные поля, то поле DXY не всегда киллингово. Поэтому фор-
мула (7.28а) справедлива только в точке х. Конечно, значение
поля DXY в другой точке у е М можно вычислить, применяя
изометрию f с f (х) = у, но нам это не понадобится.
7.30.	Теорема. Пусть X, У — произвольные векторы в точке х
однородного риманова многообразия М. Тогда, с учетом отож-
дествлений 7.22, 7.23 и (7.28b), справедлива следующая фор-
мула для кривизны:
(7.30)	gx(R(X, Y)X, У) = -||[Х, У]Д2-4([Х, [X, У]3Ь, У)—
-|([У, [У, ХШ Х) + | [/(X, У)|2 —(t/(X, X), U(Y, У)).
В частности, если ] X | — | У| = 1 и (X, У) — 0, то формула (7.30)
задает секционную кривизну 2-плоскости, натянутой на X и Y.
Доказательство.
gx{R(X, У)Х, У) = (Ал.г]Х, У)-(ДхДгХ, У) + (ДуДхХ, У) =
= -(дух, [Х,у])-Х(ад У) + (Дух, ДХУ) +
+ У (DxX, У) - (DxX, DyY) = I DyX |2 -
~(DxX, £>уУ) + У ([X, У], X) =
= 11 [X, У]г I2 + ([X, У]„, U (X, У)) +1 и (X, У) I2-
-(t/(X, X), U(Y, У)) + ([У, [X, У]], X) +
+ ([Х, У], [У, Х])= |Д(Х, У)|2-
- (U (X, X), и (У, У)) + 11 [X, УЬ I2 +
+ 4-(1Н> Х]ь У) + 4(Х, [[X, У]ь У]р) +
+ ([К, [X, У](]ь X) + ([У, [X, УЬ]„, X) -
— |[Х, У]р I2.
С. Кривизна
247
Учитывая Ado (/С)-инвариантность скалярного произведения,
получаем ([У, [X, К]е]Р, Х) = (У, [[X, У]{, Х]р). Отсюда следует
(7.30).	□
7.31.	В дальнейшем мы будем отождествлять тензоры кри-
визны в точке х с тензорами пространства р с помощью отожде-
ствления ТХМ = р. Например, будем писать
gx(R(X, Y)X, Y) — (R(X, Y)X, У).
Обозначим через (Xt) ортонормированный базис простран-
ства (у, (•, •)). Для того чтобы упростить формулу для кри-
визны Риччи, положим Z = '£iU(Xi, Х{).
7.32.	Лемма. Вектор Z = ^{U (Х{, Х£) однозначно характе-
ризуется как вектор из р, удовлетворяющий условию
(7.32)	(Z, X) = tr(adX), VX е р
(где tr(adX) означает след линейного отображения ad Хе
GEE End (g)).
Доказательство. Поскольку [X, t] е р, имеем
tr (ad X) =	([X, Xb, X) = (Z, X).	□
Отметим, что Z = 0 тогда и только тогда, когда группа G
унимодулярна.
С помощью непосредственных вычислений в базисе (X,) по-
лучаем
7.33.	Следствие;. Кривизна Риччи г в точке х задается фор-
мулой
(7.33)	Г (X, х) = -1 £ I [X, хь I2 - 4 Е (И. и. ы -
/	i
-	е ах и, хм»,Xt)+4 Е и*" ху -
i	i, I
-	([Z, Х]р, X).
Эту формулу можно немного упростить, если ввести форму
Картана — Киллинга.
7.34.	Определение. Формой Картана — Киллинга В алгебры
Ли g называется симметрическая Ad G-инвариантная билиней-
ная форма на g, задаваемая равенством В(Х, У) = tr(adX«<
[□ad У), X, У eg.
248
Гл. 7. Однородные римановы многообразия
7.35.	Скалярное произведение (•, ) на р можно продолжить
до Adc (Л-)-инвариантного скалярного произведения на g (кото-
рое также обозначается (•, •)), полагая (I, р) = 0 и выбирая на
f произвольное Ad(А)-инвариантное скалярное произведение
(существующее в силу компактности А).
Дополнив ортонормированный базис (X,) пространства р
ортонормированным базисом (У;) пространства I, получим
ортонормированный базис пространства g = t -|- р. Для любого
А' е g имеем
(7.35)	В (X, Х)=Х(И. [х, Х,],]„ X,) + L([X, [X. V,],],. Г,).
Отсюда следует
7.36.	Лемма. Ограничение формы В на I отрицательно опре-
делено.
(В частности, —В f f есть Ado (К)-инвариантное скалярное
произведение в I.)
Доказательство. Применяя (7.35) к X е f и учитывая ad I-
инвариантность, получаем
(7.36)	В (X, X) = - X | [X, Хг]„ |2 - £ | [X, V/]l |2.
Таким образом, В(Х, Х)^0. Кроме того, В(Х, X) = 0 тогда и
только тогда, когда X принадлежит центру алгебры Ли g. Но
тогда из эффективности G следует, что Х = 0 (см. 7.12).	□
Отметим, что подпространство р не обязательно В-ортого-
нально к f и форма В не обязательно знакоопределена и невы-
рожденна на р.
7.37.	Если теперь Хер, то простые вычисления, использую-
щие ad {-инвариантность, показывают, что
<7.37а) £ ([X, [X, И,],],, V,)= Z ([X, [X, Х,],|,„ X,),
откуда следует, что
(7.37b) В(Х, X) = 2 S ([X. -|Х, X,],],. X,) +
+ Е ([X, [х, X,],],, X,).
Отсюда вытекает
D. Примеры однородных многообразий Эйнштейна
249
7.38.	Следствие. Кривизну Риччи г в точке х можно предста-
вить в виде
(7.38)	г(Х, Х) = —Хг],|2~4В<Х’ *> +
i
+ zZ(^>	*).
«. 1
Наконец, мы получаем следующую формулу для скалярной
кривизны.
7.39.	Следствие. Скалярная кривизна s в точке х (а значит,
и всюду) задается формулой
(7.39)	s = - | £ |[Хг, ХД I2 - | £ В (Xlt Xt) -1Z I2.
i, I	I
D. Примеры однородных многообразий Эйнштейна
7.40.	Поскольку риманово многообразие постоянной секцион-
ной кривизны, очевидно, является многообразием Эйнштейна,
мы получим примеры однородных многообразий Эйнштейна,
рассмотрев однородные римановы многообразия постоянной сек-
ционной кривизны, такие, как
S" = SO(n + l)/SO(nb
Rn = D(n)/SO (и)
► co стандартными метриками.
Hn = SO0(n, 1)/$О(я),
Некоторые фактор-пространства этих многообразий также од-
нородны, например !RP" = SO(n-f- 1)/О(п), Тп (или, шире,
T₽XlR"_₽), а также некоторые фактор-пространства сферы Sn
(см. полный список в [Wol4], с. 89). Отметим, что нетривиаль-
ные фактор-пространства многообразия Нп не являются одно-
родными.
7.41.	Другие примеры однородных метрик Эйнштейна, об-
общающие уже приведенные, можно получить, если рассмотреть
симметрические пространства, например проективные простран-
ства
СРп — SU(n-[- 1)/S (U (1) U (n)),
HP” = Sp (n + 1)/Sp (n) Sp (1),
CaP3 = F4/Spin(9).
Напомним, что компактные симметрические пространства
ранга один *) являются двухточечно однородными (см., напри-
') Определение симметрического пространства см. ниже в § F. Ранг
симметрического пространства определяется как размерность максимального
плоского вполне геодезического подмногообразия. Проективные пространства
имеют ранг 1. — Прим, перев.
250	Гл. 7. Однородные римановы многообразия
мер, [Hel 1]), т. е. группа изометрий G транзитивна на расслое-
нии единичных, векторов. Отсюда легко следует их эйнштейно-
вость.
В четырехмерном случае приведенный список примеров по
существу оказывается исчерпывающим. Полный перебор, осно-
ванный на классификации С. Исихары четырехмерных одно-
родных пространств ([Ish 1]), приводит к следующему ре-
зультату .
7.42.	Теорема (Г. Р. Йенсен, [Jen 1]). Любое четырехмер-
ное однородное многообразие Эйнштейна симметрично.
А. Дердзиньский получил доказательство этой теоремы без
помощи перебора (устное сообщение).
Отметим, что даже в пятимерном случае проблема полной
классификации однородных многообразий Эйнштейна все еще
остается открытой.
Следующее простое замечание позволяет получить много
примеров многообразий Эйнштейна без вычисления их кри-
визны.
7.43.	Определение. G-оцнородное многообразие М — G/K.
(с компактной подгруппой К) называется изотропно неприво-
димым, если представление изотропии группы К неприводимо.
Заметим, что в обозначениях 7.22 это условие означает, что
представление Ado (К) группы К в пространстве р неприводимо.
7.44.	Теоремам (Дж. А. Вольф, [Wo! 3]). Пусть G-однородное
многообразие М = G/К изотропно неприводимо. Тогда суще-
ствует единственная (с точностью до гомотетии) G-инвариант-
ная риманова метрика на М. Эта метрика является эйнштей-
новой.
Доказательство. Любая G-инвариантная риманова метрика
на М задается некоторым Ado (К) -инвариантным скалярным
произведением (•, •) в р. Из неприводимости группы Adc(A)
следует, что все Ado (К)-инвариантные скалярные произведения
в р, а тем самым и все G-инвариантные римановы метрики в М
пропорциональны.
Кроме того, любая Ado (К)-инвариантная симметрическая
билинейная форма на V пропорциональна форме (•,•). В част-
ности, тензор Риччи г пропорционален метрике в точке х,
а тем самым (ввиду однородности) и всюду. Поэтому G-инва-
риантная риманова метрика в М является эйнштейновой. □
7.45.	Примеры. Основные примеры изотропно неприводимых
пространств — это неприводимые симметрические пространства,
которые мы рассмотрим подробнее в § F. В некомпактном слу-
чае других примеров не существует, т. е. справедливо
D. Примеры однородных многообразий Эйнштейна
251
7.46.	Предложение. Любое некомпактное изотропно непри-
водимое пространство является симметрическим.
Доказательство. Пусть М = G/K — изотропно неприводи-
мое пространство связной группы Ли G. Выберем р и (•, •)
как в 7.22. Имеем g — I + V- Обозначим через Н максимальную
компактную подгруппу группы G, содержащую К. Ее алгебра
Ли 1) содержит t, и, очевидно, Adc К-инварнантна. Из AdG(A)-
неприводимости пространства р следует, что его AdG (К)-инва-
риантное подпространство ф Г) Р либо совпадает с р, либо равно
нулю. В первом случае G — Н и многообразие M—G/K ком-
пактно. Во втором случае Н = ft (поскольку максимальная
компактная подгруппа Н связной группы Ли G связна) и М —
— G/К есть симметрическое пространство (см. 7.79).	□
7.47.	Другие примеры. В работе [Wol 3] Дж. А. Вольф клас-
сифицировал G-однородные римановы многообразия G/К, для
которых связная компонента единицы стационарной подгруппы
К имеет неприводимое представление изотропии. Мы будем на-
зывать их строго изотропно неприводимыми пространствами,
поскольку это условие немного сильнее, чем условие из 7.43.
Отметим, что эти условия совпадают, если группа ft связна,
например, если группа G связна, а многообразие G/К одно-
связно.
Доказательство результата Вольфа весьма длинно, поэтому
мы его не приводим (см. [Wol 3], а также [Wa-Zi 1], где пред-
ложено новое концептуальное доказательство и исправлены не-
точности классификации). Полный список изотропно неприво-
димых пространств приводится в табл. 7.102—7.107 как состав-
ная часть более общей классификации стандартных однородных
многообразий. Здесь мы укажем только некоторые компактные
примеры с простой классической группой G (если группа G не
проста, то строго изотропно неприводимое пространство G/K
является симметрическим).
7.48.	Конструкция изотропно неприводимых пространств, од-
нородных относительно простой классической компактной
группы Ли. Пусть р — неприводимое точное представление ком-
пактной группы Ли К в пространстве !RW. Если представление р
допускает инвариантную комплексную или симплектическую
структуру или не допускает таких структур, то оно определяет
вложение p(ft) группы К в группу G = SU{J—^, или
или SO (ft) соответственно. Очевидно, p(ft) есть компактная
подгруппа группы G и фактор-пространство G/p(ft) является
G-однородным пространством (если p(K)=?=G, то G действует
252
Гл. 7. Однородные римановы многообразия
на 6/р(А) почти эффективно). Первый класс примеров описы-
вается следующим предложением.
7.49.	Предложение (Дж. А. Вольф, [Wol 3]). Пусть К —
простая компактная группа Ли без центра, ар — ее присоеди-
ненное представление. Тогда однородное многообразие
SO (dim А) /р (А) изотропно неприводимо.
На самом деле присоединенное представление Ado группы
<z = SO (dim А), ограниченное на А, имеет вид Д2р и разла-
гается в сумму самого представления р (присоединенного пред-
ставления группы р(А) на ее алгебре Ли) и другого представ-
ления %, которое есть в точности представление изотропии
группы р(А) в SO (dim А)/р(А). Представление % неприводимо
(хотя это не очевидно). Концептуальное доказательство этого
факта приводится в [Wa-Zi 1].
7.50.	Можно получить и другие примеры, рассмотрев неко-
торые хорошо известные представления. Обозначим через р
естественное представление группы SO(n) в 'R", группы SU(ri)
в С" и группы Sp(n) в Нп — R4”- Символами S и А мы бу-
дем обозначать симметрическое и соответственно внешнее про-
изведение представлений. Напомним, что тензорное произведе-
ние двух симплектических представлений вещественно, в то
время как тензорное произведение вещественного и симплекти-
ческого представлений симплектично. С помощью конструк-
ции 7.48 получаем следующие примеры изотропно неприводи-
мых пространств:
к	p	G
SU(p) SU(q)	Pi ® Pi	SU (pq)
Sp (1) Sp (ft)	Pi ® Pi	SO (4n)
Sp (1) SO (n)	Pi ® Pi	Sp (n)
SU(n)	A2 Pi	
SU (n)	S2P1	su ("Ч+ ~)
SO (n)	S2Pi - 1 «)	SO ( n (”2+1} - 1)
Sp (ft)	S2Pi - 1 2)	SO (2n* — n — 1)
I) Это представление группы SO(n) в пространстве бесследовых
симметрических 2-тензоров.
2) Это представление группы Sp(n) в пространстве бесследовых
эрмнтово-кватернионных матриц.
Е. Общие результаты для однородных многообразий Эйнштейна 253
7.51.	Замечание. Существует более общая конструкция, при-
надлежащая Уоллу (см. конец [Wol 3]), которая обобщает 7.49
и 7.50 и позволяет получить ряд новых примеров. Пусть G/K—
компактное неприводимое симметрическое пространство. Тогда,
за небольшим числом исключений (сводящихся по существу
к вещественным и кватернионным грассманианам), применение
конструкции 7.48 к представлению изотропии группы К приво-
дит к несимметрическим строго изотропно неприводимым про-
странствам (при этом в комлексном и кватернионном случаях
надо брать только один сомножитель группы К).
Конструкция Уолла позволяет получить практически все
несимметрические строго изотропно неприводимые пространства,
за небольшим числом исключений (таких, как SO(7)/G2 и од-
нородные пространства особых групп Ли). Концептуальное до-
казательство этого результата приводится в [Wa-Zi 1]. Окон-
чательный точный результат состоит в следующем.
7.52.	Теорема (Дж. А. Вольф, [Wol 3]). Компактное одно-
связное строго изотропно неприводимое пространство либо яв-
ляется неприводимым симметрическим пространством (содер-
жащимся в табл. 7.102—1.105), либо принадлежит к одному из
семейств из табл. 7.106 или к конечному списку из табл. 7.107.
Замечание. Недавно А. Грей сообщил автору, что эта клас-
сификация впервые была получена О. В. Мантуровым [Man 1,
2, 3] (с некоторыми неточностями).
Е. Общие результаты для однородных многообразий
Эйнштейна
Применим общие результаты, полученные для кривизны Риччи,
к однородным многообразиям Эйнштейна. Начнем с многооб-
разий Эйнштейна положительной скалярной кривизны.
7.53.	Теорема. Пусть (М, g)—однородное многообразие Эйн-
штейна положительной скалярной кривизны. Тогда многообра-
зие М компактно и имеет конечную фундаментальную группу.
Кроме того, группа всех изометрий G компактна, а ее макси-
мальная полупростая подгруппа действует на М транзитивно.
Доказательство. Первое утверждение является частным слу-
чаем теоремы Майерса 6.51, поскольку метрика g полна, а кри-
визна Риччи положительна и постоянна. Второе утверждение —
это простое упражнение по топологии.	□
Вопрос о полной классификации компактных однородных
многообразий Эйнштейна положительной скалярной кривизны
254
Гл. 7. Однородные римановы многообразия
остается открытым. В частности, еще не решена следующая
проблема.
7.54.	Проблема. Классифицировать компактные односвязные
однородные многообразия M = G/K (с компактными G и К),
допускающие G-инвариантную риманову метрику Эйнштейна.
Мы уже видели в 7.44, что изотропно неприводимые G-од-
нородные пространства допускают ровно одну G-инвариантную
метрику Эйнштейна (с точностью до пропорциональности).
С другой стороны, в 9.95 мы приведем (следуя М. Вангу и
В. Циллеру) примеры компактных односвязных однородных
пространств G/К, не допускающих G-инвариантных метрик
Эйнштейна. Некоторые из них не допускают никаких однород-
ных метрик Эйнштейна (инвариантных относительно произволь-
ной транзитивной группы G).
В гл. 9 мы построим много примеров однородных про-
странств G/К, допускающих две или более непропорциональные
G-инвариантные метрики Эйнштейна. В число этих примеров
входят сферы S2<?+3 = Sp(^+ \)/Sp(q) (см. 9.82).
Следующий вопрос тем не менее остается открытым.
7.55.	Проблема. Пусть М = G/K — компактное односвязное
однородное пространство (с компактными G и К). Является ли
множество G-инвариантных метрик Эйнштейна на М. (рассмат-
риваемых с точностью до пропорциональности) конечным? Дру-
гими словами, может ли существовать нетривиальное семейство
непропорциональных G-инвариантных метрик Эйнштейна?
Отметим, что в некомпактном случае можно привести при-
меры нетривиальных семейств однородных метрик Эйнштейна
(отрицательной скалярной кривизны). Такими примерами яв-
ляются некоторые семейства ограниченных однородных обла-
стей в С", п > 7, с метрикой Бергмана, построенные в [PiSh]
(автору сообщил об этом Ж. Э. Д’Атри).
Сформулируем теперь общие результаты, полученные для
однородных многообразий Эйнштейна отрицательной скалярной
кривизны.
7.56.	Теорема. Пусть (М, g) — однородное многообразие Эйн-
штейна отрицательной скалярной кривизны. Тогда многообра-
зие М и группа G некомпактны.
Доказательство непосредственно следует из теоремы Бох-
нера 1.84.	□
Сформулируем следующую гипотезу.
Е. Общие результаты для однородных многообразий Эйнштейна 255
7.57.	Гипотеза (Д. В. Алексеевский, [Ale 4]). Пусть М =
= G/K—некомпактное однородное многообразие Эйнштейна.
Тогда К есть максимальная компактная подгруппа группы G.
7.58.	Эта гипотеза представляется чересчур оптимистической,
поскольку при более слабом предположении отрицательности
кривизны Риччи соответствующее утверждение неверно. М. Лей-
те и И. Доти-Миателло [Le-DM] показали недавно, что группа
SL(n, R), п 3, допускает левоинвариантную метрику отрица-
тельной кривизны Риччи.
Если гипотеза верна, существует разрешимая группа Ли
G изометрий, действующая на М просто транзитивно. Тогда
задача сводится к классификации левоинвариантных метрик
Эйнштейна на разрешимых группах Ли. Известно много приме-
ров таких метрик, как симметрических (см., например, 7.17),
так и несимметрических (см., например, тезисы Э. Д. Делоффа
[Del]). Напомним также, что существуют построенные в явном
виде семейства непропорциональных левоинвариантных метрик
Эйнштейна. Однако полная классификация получена только в
у нимодулярном случае, где справедлива
7.59.	Теорема (И. Доти-Миателло, [DoM]). Пусть G—уни-
модулярная разрешимая группа Ли. Тогда любая левоинва-
риантная метрика Эйнштейна на G является плоской.
Доказательство. Воспользуемся формулой (7.38). Из усло-
вий теоремы следует, что Z = В = 0. Поскольку производная
алгебра Ли и = [g, g] разрешимой алгебры Ли g нильпотентна,
она имеет нетривиальный центр с. Пусть (X,) (соответственно
(Y,) и (Zk)) есть ортонормированный базис с (соответственно
ортогонального дополнения с в п и ортогонального дополнения п
в g). Тогда [Х;, У/] = 0 и [X/, Zk] е с. Отсюда следует, что
(7.59) г (Xz, Xt) = -1 £ (По Zk], Хг)2 +
k. i'
+ 4 £ ([xr, zk], xt.)2 +1 £ ([У,., zk], x£)2 +
i', k	j, k
+ 4£([y„ yr], xf)2 + |£ ([zk, zd, x{)2.
i,	Г	k, k'
Следовательно, Хгг(Хг, Xt-)^0. Поскольку группа G неком-
пактна, метрика может быть эйнштейновой только в том слу-
чае, если г = 0, и утверждение теоремы вытекает из приведен-
ной ниже теоремы 7.61.	□
256
Гл. 7. Однородные римановы многообразия
7.60.	Замечания, (i) Более общий результат относительно
кривизны Риччи получен в [DoM].
(ii)	В нильпотентном случае этот результат получен Е. Хайн-
це ([Hei]).
В более простом риччи-плоском случае мы располагаем пол-
ной классификацией.
7.61.	Теорема (Д. В. Алексеевский, Б. Н. Кимельфельд, [А1-
Ki 1]). Однородное риччи-плоское многообразие является пло-
ским и, значит, изометрично произведению плоского тора на
евклидово пространство.
Доказательство (по [Be Вег 1]). По теореме 6.65 Чигера —
Громола универсальная накрывающая (fit, g) риччи-плоского
однородного многообразия является римановым произведением
евклидова пространства и компактного односвязного однород-
ного риччи-плоского многообразия N. По теореме Бохнера 1.84
многообразие N сводится к точке.	□
Поскольку существует много групп, транзитивно действую-
щих на евклидовом пространстве, классификация плоских
G-однородных многообразий является более сложной1). Отме-
тим только следующий результат (см., например, [Be Вег 1]).
7.62.	Теорема. Риманово G-однородное многообразие (М, g)
является плоским тогда и только тогда, когда оно удовлетворяет
следующим условиям:
(i)	максимальная связная нильпотентная нормальная под-
группа Gi группы G абелева-,
(ii)	стационарная подгруппа К содержит максимальную
связную полупростую подгруппу группы G;
(iii)	если gi—алгебра Ли группы Ли Gi и дополнительное
к стационарной подалгебре подпространство р выбрано так, что
оно содержит gb то ограничение скалярного произведения (•, •)
на gi является Ad (G)-инвариантным.
F. Симметрические пространства
7.63.	Определение. Риманово многообразие (М, g) называет-
ся симметрическим (или римановым симметрическим простран-
ством), если для любой точки х^.М существует такая изомет-
рия fx многообразия (М, g), что fx(x) — х, Тх (fx) = — 1<Дхм.
*) Описание плоских G-однородных многообразий, см., например, в ра-
боте [Алексеевский Д. В., Солодовников А. С., Винберг Э. Б. Геометрия
пространств постоянной кривизны.— ВИНИТИ. Итоги науки и техники. Фун-
дам. напр., 1988, т. 29, с. 5—146].— Прим, перев.
F. Симметрические пространства
257
Изометрия fx (определенная однозначно, если многообразие
М связно) называется (центральной) симметрией с центром
в точке х.
7.64.	Изучение римановых симметрических пространств на-
чато в знаменитой работе Э. Картана [Саг 6]. Картан получил
их полную классификацию. В настоящее время существует об-
ширная литература по симметрическим пространствам (см., на-
пример, [Hel 1], [Ko-No 2], гл. 9, или [Los]). Мы не будем
подробно излагать эту теорию, а лишь напомним некоторые
свойства симметрических пространств и воспользуемся ими для
вычисления кривизны Риччи.
7.65.	Предложение. Риманово симметрическое пространство
(Л4, g) однородно.
Набросок доказательства. Прежде всего многообразие М
полно, так как любой отрезок геодезической можно продолжить
с помощью симметрий с центрами в его концах (см. рис. 7.65а).
Далее, для любых точек у, z е М симметрия относительно сере-
дины любого геодезического отрезка, соединяющего у и z (и су-
ществующего в силу полноты), переставляет точки у и z
(см. рис. 7.65b). Таким образом, группа изометрий действует
транзитивно.	□
7.66.	Обозначим через G связную компоненту единицы груп-
пы изометрий I(M,g), а через К — стационарную подгруппу
фиксированной точки хе М Тогда симметрия fx с центром в х
принадлежит К и порождает инволютивный автоморфизм о
группы G
a(f) = fx
Положим G° = {f^G, a (f) = f} и обозначим через Go связную
компоненту единицы группы G°. Тогда справедлива
7.67.	Теорема (Э. Картан). (i) Пусть М — связное симметри-
ческое пространство, а о — инволютивный автоморфизм группы
G, соответствующий произвольной точке х^М. Тогда Ga zd/Czd
с Go.
(ii)	Обратно, если а — инволютивный автоморфизм группы
Ли G, а К — компактная подгруппа группы G, удовлетворяющая
условию G° zd К гэ Go, то любая G-инвариантная риманова мет-
рика на G/К симметрична.
Доказательство. Мы докажем только (i). Доказательство (ii)
см. в книге [Hell]. Пусть f е К. Тогда f(x) = x и о (/)(*) =
17 А. Бессе, т. 1
258
Гл. 7. Однородные римановы многообразия
=	(х) = X. Более того, Tx(o(f)) = Tx(fx □ f ° fx l) = Tx(fx) о
°Txf °Tx(fx') — Txf, откуда f = o(f).
Пусть ft — однопараметрическая подгруппа в Go. Тогда
о (ft) — ft и, значит, fx°ft = ft°fx. В частности, fx (ft (x)) = ft (x),
t. e. ft(x) есть неподвижная точка для fx. Но fo(x) — x и х есть
Рис. 7.65а. ф геодезическая; (2) точка х „возле конца"; @ действие fx;
@ геодезическая fx (у), продолжающая у.
Рис. 7.65b. ф точки у и z на М; (2) произвольная геодезическая у, соеди-
няющая у и z; @ центральная точка х на у, @ fx отображает у в z.
изолированная неподвижная точка для fx. Значит, ft(x) = x для
всех t и ft е К.	□
7.68.	Пусть й — алгебра Ли группы G, а I — ее подалгебра,
соответствующая К. Пусть cr = AdG(fx)—автоморфизм алгебры
Ли £, индуцированный автоморфизмом о группы G. Положим
V =	сг(х) = —X}. Тогда р есть AdG(К)-инвариантное под-
пространство. С другой стороны, сг(Х) — X для X е f и I есть
общая алгебра Ли групп Ли Ga, К и Go. Справедлива
F. Симметрические пространства
259
7.69.	Фундаментальная лемма. Пусть о — инволютивный ав-
томорфизм алгебры Ли g, а I, р— его собственные подпростран-
ства с собственными значениями 1 и —1. Тогда
[f, f]cf, [f, р]ср, [p.pjczf.
Доказательство. Докажем, например, последнее включение.
Пусть X,	Тогда ФХ = —X, csY = —У и
[X, У]0 = [оХ, сгУ]д = а([Х, У])д. Значит, [X, У]де=1. □
7.70.	Риманово однородное пространство, для которого
[р, р] cz I, не всегда является симметрическим, однако всегда яв-
ляется локально симметрическим (см. определение 10.76), а его
универсальное накрывающее пространство является симметри-
ческим. Примерами служат линзовые пространства S2"+1/Zp,
р>3.
7.71.	Описанный выше выбор дополнения р позволяет легко
вычислить кривизну симметрического пространства, поскольку
в этом случае U — 0 (т. е. симметрические пространства яв-
ляются естественно редуктивными, см. 7.84). Используя ad(f)-
инвариантность скалярного произведения и тот факт, что опе-
ратор adX при Хер переставляет I и р, легко доказать
7.72.	Предложение. Тензор кривизны и тензор Риччи сим-
метрического риманова пространства определяются формулами
(7.72а)	(/? (X, У) X, У) = — ((ad X о ad X) У, У),
(7.72b)	г (X, У) = - tr ((ad X о ad У) f р, X, У е р.
С помощью инволюции о легко выводится, что В (I, р) = 0,
и доказывается
7.73.	Теорема. Кривизна Риччи риманова симметрического
пространства имеет вид
Доказательство. Поскольку оператор adX для Хер пере-
ставляет подпространства I и р,
tr ((adX<= ad У) [ р) = tr ((adXo ad У) ) f) = yS(X, У).
(Отметим, что тензоры R и г зависят только от g и р.)	□
7.74.	Следствие. Пусть (М, g)— риманово симметрическое
пространство. Тогда метрика g эйнштейнова в том и только
том случае, если ограничение формы В на р либо тождественно
17*
260
Гл. 7. Однородные римановы многообразия
равно нулю, либо знакоопределено и пропорционально скаляр-
ному произведению (•, -) в р.
Очевидно, скалярная кривизна будет положительной, нуле-
вой или отрицательной, если форма В соответственно отрица-
тельно определена, равна нулю или положительно определена.
7.75,	Предположения следствия 7.74 очевидным образом
выполняются, если симметрическое пространство изотропно не-
приводимо, т. е. если присоединенное представление Ado (/С)
группы К в пространстве р неприводимо. В этом случае будем
говорить, что симметрическое пространство неприводимо. Сле-
дующий результат представляет собой важный шаг на пути
классификации симметрических пространств.
7.76.	Теорема. Односвязное риманово симметрическое про-
странство разлагается в риманово произведение евклидова про-
странства и неприводимых римановых симметрических про-
странств.
Набросок доказательства. Мы приведем только основные
идеи доказательства. Читатель может попробовать сам восста-
новить все технические детали или обратиться к книге [Hel 1]
за полным доказательством.
Пусть р = ф*=ор(-— единственное разложение простран-
ства v в прямую сумму подпространств fi, для которого
(i)	В [- рг = Лг(-, •) t Ри
(ii)	В (рг, £,) = (&-, р;-) = 0, i^=j;
(iii)	рг есть Ad0 (^-инвариантное подпространство;
(iv)	при / #= 0 представление Adc (А) (* рг неприводимо;
(v)	Ло = 0 (возможно, что ро — 0 или r = 0).
Напомним, что форма В f f отрицательно определена. Ис-
пользуя Ad (б)-инвариантность формы В, легко доказать, что
[р0, Ро] = 0 и [рг, р/] = 0 при i^=j. Для каждого t АО поло-
жим ft- = [pt, pt]czf. Заметим, что B(fz, f7) = 0 при i j и tf
есть идеал алгебры Ли f. Обозначим через f0 такой идеал, что
f = ®I.=of/. Тогда gz = fi ® рг есть идеал алгебры Ли g и
[0/, 0/1 —0 при i=^=j. Таким образом, алгебра Ли g разла-
гается в прямую сумму идеалов д = ф/=о0о
Обозначим через Gt подгруппу группы G, порожденную под-
алгеброй Qi, и положим Ki — Gif) К. Ограничение (, •) Г pi опре-
деляет Gi-инвариантную риманову метрику gt в однородном
пространстве М,- — Gi/Ki. При этом (Mi,gt), очевидно, является
симметрическим пространством, и нетрудно проверить, что ри-
F. Симметрические пространства
261
маново многообразие (М, g) разлагается в риманово произведе-
ние многообразий (Mi, gi). Кроме того, (Л10, g0)—евклидово
пространство, а (Mi, gi), t > О, — неприводимые симметрические
пространства.	□
7.77.	Из доказательства следует, что если симметрическое
пространство (Л4, g) неприводимо, то ро = 0 и форма В на g не-
вырожденна. Последнее утверждение означает, что алгебра
Ли g полупроста. Рассмотрим отдельно компактный и неком-
пактный случаи.
7.78.	Теорема. Если неприводимое симметрическое простран-
ство (М, g) некомпактно, то алгебра Ли I стационарной под-
группы К является максимальной компактной подалгеброй ал-
гебры Ли g группы G.
Доказательство. Поскольку группа G некомпактна, форма В
не может быть отрицательно определена на g. С другой сто-
роны, форма В отрицательно определена на I. Так как пред-
ставление Абс(К)Гу неприводимо, отсюда следует, что форма В
положительно определена на р. Пусть Г — максимальная ком-
пактная подалгебра в g, содержащая I. Тогда форма В отрица-
тельно определена на V и, значит, I' = 1.	□
7.79.	Следствие; Некомпактное неприводимое симметрическое
пространство имеет вид G/К, где G — вещественная простая не-
компактная группа Ли без центра, а К — максимальная ком-
пактная подгруппа группы G.	□
7.80.	Замечание. Такие симметрические пространства назы-
ваются пространствами типа III, если группа G абсолютно про-
ста (т. е. комплексификация дс = д ® С алгебры Ли g является
простой комплексной алгеброй Ли), и пространствами типа IV
в противном случае, т. е. если G является комплексной простой
группой Ли. Список всех таких симметрических пространств
приводится в табл. 3, 4 в § Н.
7.81.	Теорема. Пусть (М, g) — компактное односвязное не-
приводимое симметрическое пространство. Тогда либо G — про-
стая группа, либо существует такая вещественная простая ком-
пактная односвязная группа Ли Н с центром Z, что G = (Я X
X Н)/Z и К = Н/Z, где Z и Н вложены в Н\Н с помощью
диагонального вложения ht-^-(h, h).
Замечание. В последнем случае симметрические простран-
ства Ну(Н/Н называются пространствами типа II. Список та-
ких пространств приводится в табл. 2 в § Н.
262
Гл. 7. Однородные римановы многообразия
Доказательство. Будучи полупростой, алгебра Ли g разла-
гается в прямую сумму простых идеалов д,-. Автоморфизм о
из 7.68 переставляет эти идеалы. Если о (g;) = g„ то рг — {х е g„
о(х)==—х} является ненулевым Adc (К)-инвариантным подпро-
странством пространства р и в силу неприводимости совпадает
с р. В этом случае алгебра Ли g = g, проста.
Пусть теперь о (дг) = д7, где i #= /. Тогда = {(х, — о (х)) е
е Я/ Ф 9/} есть AdG (Aj-инвариантное подпространство простран-
ства р и, значит, р = pz, 9 = 9/® д,. Положим i) = дг- и отожде-
ствим д, с t) с помощью в. Тогда д = I) ф I) и f = {(x, о (х)) е
9i Ф 9/} = {(*, х)е!>фЯ-	□
7.82.	Нам осталось рассмотреть случай компактных неприво-
димых симметрических пространств с простой группой G. Такие
пространства называются пространствами типа I. Следующий
прием позволяет свести классификацию этих пространств
к классификации вещественных простых групп Ли. Пусть
gC = 9 £> С — комплексификация алгебры Ли д, a Gc— одно-
связная комплексная группа Ли с алгеброй Ли д . Очевидно,
что gi = t Ф ip есть вещественная подалгебра алгебры Ли дс.
Обозначим через G] соответствующую ей подгруппу группы Gc.
Поскольку fczgi, группа Gi содержит Д, и легко проверить, что
G\/K есть некомпактное неприводимое симметрическое про-
странство типа III. Теперь классификация пространств типа I
следует из классификации вещественных простых групп Ли и их
максимальных компактных подгрупп. Все пространства типа I
перечисляются в табл. 1 в § Н.
7.83.	Замечания. (1) Этой конструкцией можно пользоваться
для всех неприводимых симметрических пространств. Простран-
ство Afi = G\/K называется двойственным к исходному про-
странству М. Пространства типов I и III, а также пространства
типов II и IV двойственны друг другу.
(2)	Отметим, что неприводимые симметрические простран-
ства типов I и II являются компактными эйнштейновыми мно-
гообразиями неотрицательной секционной кривизны, а непри-
водимые симметрические пространства типов III и IV неком-
пактными эйнштейновыми многообразиями неположительной
секционной кривизны. (Можно показать, что при переходе
к двойственному пространству меняется только знак кривизны,
см. [Hel 1].)
G. Стандартные однородные многообразия	263
G. Стандартные однородные многообразия
В ряде специальных случаев сложные формулы (7.30),
(7.33), (7.38), (7.39) упрощаются.
7.84.	Определение. Пусть (М, g)— однородное риманово мно-
гообразие, а подпространство р определено как в 7.22. Мет-
рика g называется естественно редуктивной (относительно р),
если V = 0.
Отметим, что понятие естественной редуктивности опреде-
ляется выбором группы G и подпространства р. Следующая
теорема характеризует естественно редуктивные пространства.
7.85.	Теорема (Б. Костан, [Kos]). Ado (К) -инвариантное ска-
лярное произведение (•, •) в р определяет естественно редук-
тивную G-инвариантную риманову метрику в М = G/К тогда
и только тогда, когда на идеале g' = Р + [р, §] алгебры Ли g су-
ществует невырожденная симметрическая билинейная форма q,
для которой
(i)	<7(8'01, V) = 0;
(ii)	ограничение q на у совпадает с (-, •);
(iii)	форма q является Ad G'-инвариантной (где G' — под-
группа Ли G, соответствующая подалгебре g').
Доказательство см. в работе [Kos], а также в более поздней
работе [DA-Zi], с. 4.
Отметим, что форма q не обязательно должна быть положи-
тельно определена на g'. Группа G' действует на М транзитивно,
и метрика g естественно редуктивна относительно G' и р. Об-
ратно, если q — невырожденная симметрическая Ad(G)-инва-
риантная билинейная форма на g, причем ее ограничение на f
невырожденно, а ограничение на ^-ортогональное дополнение Iх
к f положительно определено, то форма </1 определяет есте-
ственно редуктивную метрику в однородном пространстве
G/К с G' = G. Поэтому при решении большинства вопросов
можно считать, что G' = G.
Следующий специальный случай является объектом особого
изучения для компактных многообразий.
7.86.	Определение. G-однородное риманово многообразие
(М, g) называется нормальным, если в алгебре Ли g существует
такое Ad(G)-инвариантное скалярное произведение q, что р
есть ^-ортогональное дополнение к f в g и метрика g опреде-
ляется ограничением q на р.
264
Гл. 7. Однородные римановы многообразия
7.87.	Предложение. Секционная кривизна естественно редук-
тивного G-однородного риманова многообразия задается фор-
мулой
(7.87а)	{R(X, Y)X, У) = ( [ [X, У]£, X],, У) J-( [X, У]„ |2
или эквивалентной формулой
(7.87b) (R{X, Y)X,Y)=q( [X, У]{, [X, У]{) + {| [X, У],|2.
Отметим, что секционная кривизна нормального G-однород-
ного риманова многообразия всегда неотрицательна (и тожде-
ственно равна нулю, только если G = Тп и К = {1}). Это, во-
обще говоря, не верно для естественно редуктивных пространств
(поскольку форма q не обязательно должна быть положительно
определена на f).
Введем оператор Казимира представления изотропии.
7.88.	Определение. Пусть q— невырожденная симметрическая
ad f-инвариантная билинейная форма на алгебре Ли f. Операто-
ром Казимира TV-мерного представления р алгебры Ли f назы-
вается элемент
ср,9 = -Ер(п,-)оР(к/)
алгебры Ли glfiR"), где (U/) и (V/)—дуальные базисы про-
странства t (т. е. q(Ui, V/) — 6ij).
Отметим, что Ср,9 коммутирует с любым элементом
из p(f).
7.89.	Предложение. Кривизна Риччи естественно редуктив-
ного G-однородного риманова многообразия задается фор-
мулой
(7.89а) г (X, X) = -1В (X, X) + ± £ Ч ( И, X,-]f, [X, Х,-]{)
или, если д' — д {ср. с. 7.85), формулой
(7.89b) г (X, X) = - | В (X, X) + | (Сх, ,Х, X),
где %; /<—>-д!(р)— представление изотропии.
G. Стандартные однородные многообразия
265
Доказательство. Формула (7.89а) следует из формул (7.87b),
(7.37b) и Ad (G') -инвариантности формы q. Формула (7.89b) по-
лучается теперь в результате преобразований
(Сх,9х, Г) = - £ (Р/, [V/, г) =
= -£<?( [г, и, кд],, ц-) =
= -£([к, [х, xjj,, хг) =
= £<7 ([К XJt, И, XJt).	□
Конкретизируем эти формулы для частного случая.
7.90.	Определение. G-однородное риманово многообразие на-
зывается стандартным, если оно нормально и q = —В.
Заметим, что группа G в этом случае компактна и полупро-
ста, поскольку форма В отрицательно определена. Если G есть
простая компактная группа Ли, то любое естественно редук-
тивное G-однородное риманово многообразие является стан-
дартным (с точностью до масштабного множителя). Это сразу
следует из доказательства 7.44.
7.91.	Предложение. Пусть М = G / К — компактное изотропно
неприводимое пространство. Тогда его (единственная с точ-
ностью до пропорциональности) G-инвариантная риманова
метрика является стандартной (при соответствующей норми-
ровке) .
Отметим, что в отличие от однородных метрик изотропно не-
приводимых пространств стандартные однородные метрики не
всегда эйнштейновы. Например, стандартная метрика на
SU(n) -однородном пространстве S2"-1 = SUW/SUfn—1) не
эйнштейнова. Это сразу следует из формулы (7.89b).
7.92.	Предложение. Стандартное однородное риманово мно-
гообразие эйнштейново тогда и только тогда, когда оператор
Казимира Съ-в, где % — представление изотропии алгебры Ли1
в р, скалярен.
Отметим, что ограничения оператора Сх,-в на %(I)-инва-
риантные подпространства представляют собой скалярные опе-
раторы Kid, но, вообще говоря, с различными А. Поэтому
условия предложения 7.92 накладывают сильные ограничения
266
Гл. 7. Однородные римановы многообразия
на представление если оно приводимо. В частности,
представление % не может иметь инвариантных век-
торов.
7.93.	Предложение. Если стандартное риманово однородное
многообразие G/К эйнштейново, т. е. г = kg, то */4 X V2 и
(i)	X =И= 'Л тогда и только тогда, когда многообразие G/K
локально симметрично-,
(ii)	X — */4 тогда и только тогда, когда К = {!}•
Доказательство. Поскольку (Сх, -вХ, X) 0, причем равен-
ство имеет место тогда и только тогда, когда % = id, имеем
Х^:1^, причем X = */4 тогда и только тогда, когда К={1}.
Учитывая (7.35) и Ad(G)-инвариантность формы В,
имеем
Чг^чХ, Х) = -1ДВ(Х, X)- X (И, A<]v, [X, Х£-]р).
Отсюда следует, что X sg: 1/2, причем X = ’/2 тогда и только
тогда, когда [V, Й с t.	□
7.94.	Замечания, (i) Можно получить и более явную фор-
мулу для константы Эйнштейна X стандартной однородной мет-
рики Эйнштейна. Разложим алгебру Ли I в прямую сумму
центра Го и простых идеалов ..., Ir с Si — dim Г, и обозначим
через Bt. форму Картана — Киллинга алгебры Ли Г,, пропор-
циональную В:
Ви=С1В\1(.
Тогда
Г
(7.94)	x=4. + ^.£s,(l_C1).
i=l
(ii)	Формула (7.89b) и предложения 7.92 и 7.93 впервые
были получены в работе [Wa-Zi 2]. В этой работе М. Ванг
и В. Циллер полностью классифицировали односвязные стан-
дартные однородные римановы многообразия с простой алгеб-
рой G, которые являются эйнштейновыми. Они также построили
ряд нетривиальных примеров стандартных G-однородных эйн-
штейновых многообразий с непростой группой G. В случае не-
простой группы G возникает много естественно редуктивных
G-однородных эйнштейновых многообразий (см. гл. 9), боль-
шинство которых не являются стандартными. Мы не будем
доказывать классификационную теорему для случая простой
G. Стандартные однородные многообразия
267
группы G, а лишь сформулируем ее (теорема 7.99). Начнем
с некоторых примеров.
7.95.	Примеры. Конструкция, описанная в 7.49, позволяет
получить следующий класс примеров. Пусть К—компактная
полупростая группа Ли с тривиальным центром. Присоединен-
ное представление определяет вложение группы К в SO (dim К).
Стандартная риманова метрика в SO (dim К)/К эйнштейнова.
7.96.	Будем использовать обозначения из 7.48 и 7.50. Стан-
дартная однородная метрика на однородном пространстве
G/p(K) (не являющемся строго изотропно неприводимым) бу-
дет эйнштейновой в следующих случаях.
к	p	0
SO (п) ... SO (и) -К 1 k раз S (U («) ... и (n)) L >3 Sp (ti) ... Sp (n) j " SO (ti) SO (ti) Sp (ti) Sp(ti) Sp (n)U(2n — 1) SO (n) U (n + 1) S (U (I) U (mi) U (m2)) *)	z	pi 0 id 0 ... 0 id	-j < + id 0 p, 0 ... 0 id + ... > t + id 0 id 0 ... 0 pi ' Pi® Pi Pi® Pi Pi ® id + id 0 p! Pi 0 id + id 0 Pj Pi ® id ® id + id 0 p! 0 pi	SO (kti) SU (kti) Sp (kti) SO (n2) SO (4n2) Sp (3n — 1) SO (3м + 2) SU (I + mitrii)
)Если т% + mil + l=lm т (т >т > 2).
1 Z	1 X \	1	£	}
7.97.	Следующая конструкция обобщает предыдущие при-
меры (см. также замечание 7.51). Пусть Gi/Kt, i=l, —
последовательность компактных неприводимых симметрических
пространств размерности dim (G,-//C) = п,- с представлением изо-
тропии щ. Тогда стандартная однородная метрика пространства
SO(tii)/ni(Kt) эйнштейнова в том и только том случае, если
группа К, проста или же Gi/Ki = SO(2n)/SO(n)SO(n) или
Sp(2n)/Sp(n)Sp(n). (Это следует из изотропной неприводимо-
сти пространств, если группа К проста или указана в четвертой
или пятой строке таблицы из 7.96.) Предположим, что это усло-
вие выполняется для всех I, и рассмотрим однородное простран-
ство SO(N)/p(K), где N = Xint, K = Ki- ... • Кг и
р = 0 id 0 ... 0 id -J- id 0 Л2 0 ... 0 id	id 0 id 0 ... & лг.
268
Гл. 7. Однородные римановы многообразия
Стандартная однородная метрика пространства SO(N)/p(K)
эйнштейнова тогда и только тогда, когда отношение nt/dim/G
не зависит от i.
Примеры 7.95 получаются в тех случаях, когда пространства
Gi/Kt являются изотропно неприводимыми симметрическими
пространствами типа II. Условие независимости отношения
Mi/dim Ki от i выполняется, если рассматриваются одинаковые
симметрические пространства (а также в ряде других слу-
чаев). Простейшим является случай, когда Gt/Ki —
= SO(n+ \)/SO(n).
7.98.	Изолированным примером является многообразие М —
= Spin(8)/G2, где G2 с: Spin (7) с Spin (8). Первое включение
с фактор-пространством Spin (7)/G2 — S7 описано в 7.13, а вто-
рое является стандартным включением, также с фактор-про-
странством S7.
Многообразие М топологически диффеоморфно произведе-
нию S7 X S7 (хотя и не изоморфно ему как однородное про-
странство). Стандартная Spin (8)-инвариантная метрика на М
является эйнштейновой, но не изометрична метрике произведе-
ния. (Представление изотропии % группы G2 есть сумма двух
7-мерных неприводимых представлений, задаваемых включе-
нием G2 cz Spin (7).)
7.99.	Теорема (М. Ванг—В. Циллер, [Wa-Zi 2]). Компакт-
ное односвязное стандартное G-однородное риманово многооб-
разие простой группы G является эйнштейновым тогда и только
тогда, когда оно содержится в табл. 1, 2 (с G — H), 5, 6, 7
или 8 из § Н.
Н. Таблицы
7.100.	Введение. В следующих таблицах перечисляются не-
которые G-однородные римановы многообразия:
(а)	в табл. 1, 2, 3, 4 неприводимые симметрические простран-
ства (типов I, II, III, IV соответственно);
(Ь)	в табл. 5, 6 — другие строго изотропно неприводимые
пространства;
(с)	в табл. 7, 8 — другие пространства (с простой группой
G), для которых стандартная риманова метрика является эйн-
штейновой.
Мы не перечисляем все эти пространства в явном виде, по-
скольку явно указать соответствующие группы G и К не так
просто.
Н. Таблицы
269
7.101.	Мы указываем только алгебру Ли g группы G и под-
алгебру Ли f стационарной подгруппы К.
Это позволяет определить многообразие М с точностью до
конечных накрытий. Подробности см. в [Hel 1], [Wol 3] и
[Wa-Zi 2].
Отметим, что в общем случае описания f как алгебры Ли
недостаточно, поскольку могут существовать различные ее вло-
жения в g (исключение составляет ряд специальных случаев,
таких, как симметрические пространства). Поэтому в таблицах
мы по мере надобности описываем также вложение подалгебры
f в д, часто путем отсылки к соответствующему месту данной
главы.
Ввиду наличия изоморфизмов между классическими груп-
пами малых размерностей одни и те же пространства могут
встречаться в таблицах несколько раз. Для того чтобы избе-
жать этого, мы накладываем ограничения на размерности. Пе-
речислим изоморфизмы между классическими алгебрами Ли:
(1)	ёо(2, С) = С; ёо(2) = ёо(1, 1) = ёо(1, H) = R;
(2)	ё1 (2, С) = ёо (3, 1) = ёо (3, С) = ёр (1, С); ёи (2) = ё! (1, Н) =
= (3) = ёр(1); ёи(1, 1) = ё1(2, ₽) = ёо(2, 1) = ёр(1, R);
(3)	ёо(4, С) = ё1(2, С)фё1(2, С); - ёо (4) = ёи (2) ф ёи (2);
ёо(2, 2) = ё1(2, ₽)®ё!(2, R); ёо (2, (Н) = ёи (2) ф ё1 (2, R);
(4)	ёо(5, С) = ёр(2, С); ёо (5) = ёр (2); ёо(4, 1) = ёр(1, 1);
ёо (3, 2) = ёр (2, R);
(5)	ё((4, R) = eo(6, С); ёи(4) = ёо(6); ёи(3, 1) = ёо(3, И);
ёи(2, 2) = ёо(4, 2); ё( (4, R) —ёо(3, 3); ё! (2, 1Н) = ёо(5, 1);
(6)	ёо(4, Ц) = ёо(6, 2).
Отметим, наконец, что существуют различные обозначения
для одних и тех же алгебр Ли. Например, для алгебры Ли
51 (п, Ц) часто используется обозначение 5U*(2n), а для алгебры
Ли 5о(и, Н)—обозначение 5о*(2п). Что касается особых алгебр
Ли, то символом £6 обозначается компактная особая алгебра
Ли, а символом £б — некомпактная алгебра Ли с характером б,
комплексификацией которой является алгебра Ли Е8. Анало-
гичные обозначения используются для особых алгебр Ли типов
Е7, Е8, F4, G2 (подробности см. в [Hel 1]).
270
Гл. 7. Однородные римановы многообразия
7.102.	Таблица 1. Компактые неприводимые симметрические
пространства типа I
9	t	dim М	Условия |	•	е	dim М.
ёп (р + q)	ёи (p) ® ®ёи(<7)®Р	2р<7	><Р<<7	£6	ёи(6)фёи (2)	40
ёи (га)	ёо (га)	(га-1)(га+2) 2	3 га	£6	ёо(1О)фК	32
ёи (2га)	ёр (га)	(«-1)Х X (2га + 1)			ёр(4)	42
ёо (2га)	ёи(га)®8?	га (га — 1)	5 ’С га	Ев	Ft	26
ёо (р + <?)	ёо (р) ф ёо (<?)	PQ	1 <Р<<7 7<р + q	£т	ёи(8)	70
ёр(га)	ёи(га)фР	п (п + 1)	2<га	Е,	ёо(12)фёи(2)	64
ёр (р + q)	(Р)Ф §»(<?)	4рр	1<Р<Р	Ет	W	54
g2	ёи(2)фёи (2)	8		Ев	ёо (16)	128
Ft	ёо (9)	16		Ев	£тфёи(2)	112
Ft	ёр(3)фёи(2)	28				
7.103.	Таблица 2. Компактные неприводимые симметриче-
ские пространства типа II
t	dim 2И	Условия		I	dim M
ёи (га)	га2 — 1	2=5		F\	52
ёо (га)	га (га — 1) 2	7s		Ев	78
ёр (га)	га (2га + 1)	2s	Zn	E,	133
g2	14			Ев	248
Примечания.
(i)	Здесь g = I © I и I диагонально вложено в g.
(ii) М есть связная простая компактная группа Ли.
Н. Таблицы
271
7.104.	Таблица 3. Некомпактные неприводимые симметриче-
ские пространства типа III
0	1	dim М	Условия	0	1	dim М
ёи (р, q)	ёи (р)е фёи (p)©R	2рЧ	1 <Р<?	Е2	ёи(6)фёи(2)	40
ё! (n, R)	ёо (п)	(п— 1)(п+2) 2	3 с и	р —14	ёо(10)фР	32
ё! (п, И)	ёр (п)	(п-1)Х X (2«+1)	2 < п	П6	ёр (4)	42
ёО (п, И)	ёи (п) ф R	п (п — 1)	5 rS' п	р-26	F<	26
ёо (р. q)	ёо (р) ф ёо (р)	РЧ	1 <Р<<7 7<Р + <7	£7 п7	ёи (8)	70
ёр (п, R)	ёи (п)фР	П (п + 1)	2 < п	£ —Э	ёо(12)фёи(2)	64
ёр (Р, q)	ёр(р)фёр(р)	4рр	1 <Р<<7	р-25 |£7	Ее Ф R	54
G2	ёи(2)фёи (2)	8		р8 ,:8	ёо (16)	128
р—20	ёо (9)	16		р—24	Вуфёи (2)	112
F4 Г 4	ёр(3)фёи (2)	28				
Примечания.
(i)	Здесь M — G/K, где G— некомпактная абсолютно простая
вещественная группа Ли, а К — ее максимально компактная
подгруппа.
(ii)	Двойственность (см. 7.83) связывает пространства типов I
и III, указанные в соответствующих строках таблиц 1, 3.
7.105.	Таблица 4. Некомпактные неприводимые симметриче-
ские пространства типа IV
0	£	dim М	Условия	в	1	dim М
ё!(п, С)	ёи (п)	п2 — 1	2<п			52
ёо (ft, С)	ёо (п)	п(п — 1) 2	7<«	Ef>		78
272
Гл. 7. Однородные римановы многообразия
Продолжение табл. 4
8	f	dim М	Условия	•	1	dim М
йр (и, С)	йр («).	га(2га+ 1)	2<га	£-С С7	Е7	133
I Осч о		14		Ооо	Е8	248
Примечания.
(i)	Здесь M — G/K, тле G — простая комплексная группа Ли,
а К — ее максимально компактная подгруппа.
(ii)	Двойственность (см. 7.83) связывает пространства типов
II и IV, указанные в соответствующих строках таблиц 2, 4.
7.106.	Таблица 5. Компактные несимметрические строго изо-
тропно неприводимые пространства
(а) Бесконечные семейства
8	t	Условия	•	Г	Условия
	йи (га)	5 "С га	а,	йо (га)	5 <; га
	Йи (га)	3 'С га	йо ((га - 1) х X (2га 4-1))	йр(га)	3 'С га
йи (рр)	Йи (р) $ ® йи (Р)	2<Р<<7 р + q Ф 4	йо (га (2га + 1))	йр(га)	2 5^п(*)
йо (га2 — 1)	sit (га)	3 'С га (*)	Йо (4га)	«Р(1)Ф ®йр(«)	2<га
	Йо (га)	7<га(*)	йр(п)	йр(1)© @ ЙО (га)	3 "С га
Примечание. Эти пространства описаны в 7.50 и 7.49 (послед-
ние отмечены знаком (*)).
7.107. Таблица 6. Компактные несимметрические строго изо-
тропно неприводимые пространства
(Ь) Особые пространства
0	f	Прим,	8	t	Прим.	9	t	Прим.
йи (16)	йо (10)	1	йо(133)	£7	3	£в	йи(3)	4
Н. Таблицы
273
Продолжение табл. 6
0 		t	Прим.	0	t	Прим.|	.1	’ 1	Прим..!
ЙИ (27)	Е6		ЙО(248)	Et	3	E6	3 йи (3)	4, 5
ЙО (7)	g2	2	W)	Йи (2)	1	Е6	g2	4
Йо (14)	g2	3	3₽(7)	ЙИ (6)	1	|е.	62©йи (3)	4
ЙО (16)	Йо (9)		йр(10)	ЙО (12)	1	|Ет	йи (3)	4
Йо (26)	Ft	1	й₽(16)	S»(3)		е7	йи(6)фйи(3)	4
ЙО (42)	йр (4)	1	йр (28)	e7	1	Iе’	G2 © йр (3)	4
ЙО (52)	Ft	3	G2	SU (3)	4	Iе-	Г 4 © йи (2)	4
Йо (70)	ЙЦ (8)	1	g2	ЙО (3)	4	Iе-	йи (9)	4
Йо (78)	Е6	3	Fi	йи(3)фйи(3)	4	е8	Ft ф G2	4
Йо (128)	ЙО (16)		F‘	О2фйи (2)	4	|в.	£6©йи (3)	4
Примечания.
(1)	Определено в 7.51.
(2)	Определено в 7.13.
(3)	Определено в 7.49.
(4)	Здесь I— максимальная подалгебра в g.
(В рассматривае-
мых случаях это однозначно характеризует вложение leg,
см. [Dyn 2].)
5) pt означает сумму f ф f ф ... ф f (р раз).
7.108.	Таблица 7. Компактные нестрого изотропно неприво-
димые G-однородные многообразия с простой группой G, для
которых стандартная метрика эйнштейнова
(а)	Бесконечные семейства
0	t	Условия	0	t	Условия
йи (kn)	/гйи (п) ф ©(fe-l)R	3</г 1<« (О	ЙО (п2)	йо (п) ф йо (п)	3<п
йи (Z + pq)	йи(/)фйи(р)ф © (?) Ф 2R	2 С Р < q, Ipq = р2 + + ?2+ 1	йо (4п2)	ёр (п) ф йр (п)	2 п
18 А. Бессе, т. 1
274
Гл. 7. Однородные римановы многообразия
Продолжение табл. 7
8	с	Условия	0	с	Условия
ёо (У)	р(1)	см. прим. (2)	ёр (kn)	6ЙР («)	3^fe 1^«(1)
ёо {Зп -|- 2)	ёи (п+1)ф ©ёо (/г)ф₽	3 п	ёр (Зп — 1)	ён (2п - 1)ф фёр(«)фК	1 п
Примечания.
(1)	k • I) означает § ® ... ® I) (k раз).
(2)	Здесь £ = Ji ф ... ф fr, г > 1. В этом случае существуют
такие компактные неприводимые симметрические простран-
ства Gi/Ki, что соответствующие пары (g,, Ъ) удовлетво-
ряют одному из трех условий:
либо подалгебра Ли ft- проста,
либо (дг, fz) = (ёо (2п), аа (п) ф §о («)),
либо (gz, fz) = (ёр (2п), ёр(п) ф ёр(п)), и отношения dimGz/dim/Cz
не зависят от i. Буква р означает представление nz ® rd ® ...
... ® rd ф rd ®л2® ... ®rd + ... -j-rd®rd® ... ® пг ал-
гебры Ли £ в пространстве Кл’, где N = £z (dim Gz— dimKz),
а л, — представление изотропии алгебры Ли fz для однород-
ного пространства Gi/Ki (см. 7.97).
7.109.	Таблица 8. Компактные нестрого изотропно неприво-
димые G-однородные многообразия простой группы G, для ко-
торых стандартная метрика эйнштейнова
(Ь) Особые многообразия
S	t	р (см. прим. 1) или t) (см. прим. 2)	9	Г	
ёо (8)	g2	Pi® id (1)	Es	R8	Картановская подалгебра
ёо (26)	йр(1)фйр(5) Фёо (6)	(Pi ® Pi ®'Л® ® (id® id® р,) (1)	Ее	8ёи (2)	ёо (16) (5)
Ft	ёо (8)	ёо (9)	Ее	4ёи (2)	£вфёи (3)
Ее	R6	Картановская подалгебра	Ее	4ёи (3)	Явфёи (3)
Ее	Зёи (2)	Зёи (3) (3)	Ее	2ёи (3)	ёи(9) (6)
Н. Таблицы
275
Продолжение табл. 8
e	t	p (см. прим. 1) или $ (см. прим. 2)	•	t	5
Ea	SO (8)©R2	So(lO)@R	E8	2Su (5)	t максимальна
Ee	&>(6)©Su (2)	Su(6)©Su (2)	Ea	So (9)	Su (9)
e7	R7	Картановская подалгебра	E.	SO (9)	SO (16) (7)
e7	7Su (2)	So (12) © Su (2)	Ea	2So (8)	So (16)
e7	So (8)	Su (8)	&	S»(2)	t максимальна
e7	SO (8)© ©3SU (2)	So(12)©Su(2) (4)		2Й)) (2)	SO (16) (8)
Примечания.
(1)	Здесь р — представление алгебры Ли t в Rw, задающее вло-
жение f в so (N);
pi — стандартное представление или же единственное семи-
мерное неприводимое представление алгебры Ли б2.
(2)	За исключением первых трех случаев, мы задаем вложение
t в g либо с помощью явного описания, либо указанием мак-
симальной картановской подалгебры b алгебры Ли g, со-
держащей t. Согласно [Dyn 2], тип алгебры Ли 1) полностью
характеризует ее вложение в g. Вложение t cz I; всегда счи-
тается стандартным (за исключением случая (7)). Напом-
ним, что однородное пространство G/К определяется как
пространство, соответствующее паре (g, t).
(3)	3Su (2) = 3S0 (3) Зёи (3), где последнее включение опреде-
ляется включением ёо (3) cz Su (3).
(4)	30 (8) © 2Su (2) = So (8) © ёо (4) <zz SO (12).
(5)	83u (2) = 480 (4) czz so (16).
(6)	Включение 2Su(3) cz Sit (9) задается представлением
Pi® Pi-
(7)	Включение So (9) cz во (16) задается полуспинорным пред-
ставлением.
(8)	Включение Sp(2) ©Sp(2) czSo(16) задается представле-
нием pi ® p|.
18*
276
Гл. 7. Однородные римановы многообразия
I. Немного об однородных лоренцевых
многообразиях
7.110.	Существует теория однородных лоренцевых многооб-
разий (или, шире, однородных псевдоримановых многообразий).
Она аналогична теории однородных римановых многообразий,
но является более сложной. Это связано с тем, что в лоренце-
вом, или псевдоримановом, случае стационарная подгруппа мо-
жет быть некомпактной. Поэтому Adc(К)-инвариантное допол-
нение V к подалгебра f в алгебре Ли g может не существовать.
Вместо £ приходится работать с фактор-пространством g/f, на
котором естественным образом индуцируется действие стацио-
нарной группы К. Мы не будем развивать общую теорию для
этого случая (см., например, гл. 10 из [Ко-No 2]), а лишь рас-
смотрим несколько примеров, иллюстрирующих разницу между
римановым и лоренцевым случаями, особенно для многообразий
Эйнштейна.
7.111.	Определение. Лоренцево многообразие (М, h) назы-
вается G-однородным, если G есть замкнутая подгруппа группы
изометрий	действующая на М транзитивно.
7.112.	Примеры, (i) Пространство Минковского, т. е. много-
образие (R", /гсап), где hcan = dx\ — dx% — ... — dx2n. Оно будет
G-однородным для любой замкнутой подгруппы G группы
КяХО(1,п—1), которая содержит все параллельные переносы.
Это пространство является модельным для лоренцевой геомет-
рии. Оно плоско (т. е. R = 0) и, конечно, односвязно и полно.
(ii)	Полные лоренцевы многообразия постоянной ненулевой
кривизны, представляющие собой дискретные факторы про-
странства
S? = SOo(l, n)/SO0(l, п- 1)
и универсальной накрывающей Н” пространства
Hi = SO (2, п- l)/SOo(l, n- 1).
Они часто реализуются как подмногообразия
=	... — х2 = 1} о: Rn+I
с метрикой, индуцированной метрикой Минковского dxl—
— dx2 — ... — d.Xn в Rn+I, и, следовательно, подмногообразия
ггП (2,2	2	2___ _рп+1
Н\ = \Хо Ч- -- «^2 - • • • -	- 1 J
I. Немного об однородных лоренцевых многообразиях 277
с метрикой, индуцированной метрикой
dxo -f- dxi — dxl — ... — dxh в Rn+1
(см. [Wol 4]).
7.113.	Пример неполного многообразия. Рассмотрим двумер-
ное пространство Минковского (R2, dx2 — dy2) и его открытое
подмногообразие Л4 = {(х, р)е •R2, х + у > 0}.
Ясно, что (Af, dx2 — dy2} есть плоское неполное односвязное
лоренцево многообразие. При этом оно оказывается однород-
ным. Действительно, рассмотрим неабелеву группу Ли G —
— ‘R X R с умножением
(a, t) (a', t') = (а + а'е*, t +1').
Группа G просто транзитивно действует на М как группа изо-
метрий по формуле
(a, t) (х, у) = (х ch t + у sh t + а, х sh t + у ch t — a).
Таким образом, многообразие М однородно и, значит, теорема
7.19 несправедлива для лоренцевых многообразий даже в пред-
положении их локальной симметричности. (В рассматриваемом
примере кривизна Д равна нулю и, следовательно, параллель-
на, что означает локальную симметричность.)
7.114.	Определение. Лоренцево (или, в более общем случае,
псевдориманово) многообразие (Af, h) называется симметриче-
ским, если для каждой точки х s М существует такая изомет-
рия Д многообразия М, что fx (х) — х и Txfx = — IdTxM.
7.115.	Замечания, (i) Так же, как в римановом случае, до-
казывается, что симметрическое лоренцево многообразие одно-
родно и полно.
(ii)	Пример 7.113 показывает, что односвязное однородное
локально симметрическое лоренцево многообразие может не
быть симметрическим.
(iii)	С другой стороны, полное односвязное локально сим-
метрическое лоренцево многообразие является симметрическим
(см. [Ko-Wo2], гл. 11).
(iv)	Отметим, что полнота означает только, что любая гео-
дезическая допускает неограниченное продолжение. Теорема
Хопфа — Ринова несправедлива для псевдоримановых многооб-
разий. Например, многообразие Hi полно (и симметрично), но
не любые две его точки можно соединить геодезической.
7.116.	Теория симметрических лоренцевых многообразий су-
щественно отличается от риманова случая. Здесь мы лишь ука-
278
Гл. 7. Однородные римановы многообразия
жем (см., например, [Ca-Wa]), что любое односвязное симмет-
рическое лоренцево многообразие является произведением сим-
метрического риманова многообразия (с метрикой —g при на-
шей нормировке) и одного из трех многообразий:
(i)	(R, d/2);
(ii)	полного односвязного лоренцева многообразия постоян-
ной кривизны;
(iii)	одного из многообразий, описанных в 7.117.
7.117.	Специальный класс симметрических примеров. Пусть
'(R", (-, - ))—каноническое евклидово пространство, a f: R"->
—>R"— произвольный симметрический эндоморфизм. Рассмот-
рим разрешимую алгебру Ли g = R2”-2 = R« X Rn X R X R co
скобкой
[(x, y, t, u), (xr, y', t', u')] — (uf (y') — u'f (у), их' — u'x,
(x, f (/))-« f(z/)), 0).
Тогда 1 = {(x, 0,0,0)} есть абелева подалгебра и у={0, y,t, и)}
•есть ad l-инвариантное дополнение к I в g.
Определим на )) симметрическую билинейную форму
q ((0, у, t, и), (0, у', Г, и')) = tu' — uf — {у, у').
Она имеет сигнатуру (l,n+ 1) и ad 1-инвариантна.
Пусть G — односвязная разрешимая группа Ли с алгеброй
Ли g, а К—подгруппа, соответствующая подалгебре I. Тогда
подгруппа К замкнута в G и форма q определяет G-инвариант-
ную лоренцеву метрику в многообразии M—G/K с помощью
той же конструкции, что и в римановом случае (см. 7.24).
7.118.	Теорема [Ca-Wa]. Построенное в 7.117 однородное ло-
ренцево многообразие (М, h) симметрично. Его кривизна Риччи
равна нулю тогда и только тогда, когда tr f — 0, а секционная
кривизна равна нулю тогда и только тогда, когда f = 0.
Доказательство см. в работе [Ca-Wa], Вычисления, анало-
гичные вычислениям § С, можно проводить и в данном случае.
7.119.	Следствие. Существуют риччи-плоские, но не плоские
симметрические лоренцевы многообразия размерности п~^ 4.
(Ср. с. 7.61.)
7.120.	Замечания, (i) В четырехмерном случае, т. е. при
п = 2, из условий I/ #= 0 и trf =0 следует, что (с точностью до
гомотетии) в соответствующем базисе эндоморфизм f имеет вид
/ = diag(l,—1). Соответствующее риччи-плоское четырехмер-
I. Немного об однородных лоренцевых многообразиях 279
ное лоренцево многообразие имеет кривизну типа II по класси-
фикации Петрова (см. 3.23).
(ii)	Отметим, что при соответствующем выборе f многооб-
разие М имеет компактные фактор-пространства по дискретной
группе изометрий (см. [Ca-Wa]).
(iii)	Отметим, наконец, что если tr f о, то соответствую-
щее многообразие (Л1, ft) является неприводимым симметриче-
ским пространством, но не является эйнштейновым многооб-
разием.
Глава 8
Компактные однородные кэлеровы
многообразия
0. Введение
8.1.	Единственными известными примерами комплексных
многообразий, допускающих метрики Кэлера— Эйнштейна по-
ложительной скалярной кривизны, являются компактные одно-
родные кэлеровы многообразия.
Эти многообразия интенсивно изучались в различных аспек-
тах в 50-е годы. При дополнительном предположении односвяз-
ности они являются орбитами присоединенного представления
компактной группы Ли и каноническим образом снабжаются
метрикой Кэлера — Эйнштейна.
Мы приведем схему доказательства первого утверждения
(теорема 8.89) и полностью докажем второе (теорема 8.2).
Затем опишем все инвариантные кэлеровы структуры и вы-
делим среди них каноническую симплектическую структуру Ки-
риллова — Костана — Сурьо.
Наконец, мы дадим грубую классификацию орбит классиче-
ских компактных простых групп Ли.
8.2.	Теорема. Пусть G — связная компактная группа Ли,
действующая с помощью присоединенного представления на
своей алгебре Ли д.
Каждая орбита М группы G в g допускает каноническую
G-инвариантную комплексную структуру g и единственную
(с точностью до гомотетии) G-инвариантную метрику Кэлера —
Эйнштейна h, согласованную с I (и имеющую положительную
скалярную кривизну).
Любая метрика Кэлера — Эйнштейна на комплексном мно-
гообразии (М, I) однородна относительно своей группы изомет-
рий и получается из h с помощью некоторого автоморфизма
комплексной структуры I.
Существование на орбитах компактных групп Ли комплекс-
ной структуры доказано в работе [Вог 2], § 29 (см. также
[Вог 4], [Seri] и [Bo-Hi], § 12).
Существование инвариантной метрики Кэлера — Эйнштейна
фактически установлено Ж- Л. Козюлем (см. [Koz 1], (5.1) и
теорема 3).
Эквивалентность всех метрик Кэлера — Эйнштейна относи-
тельно комплексных автоморфизмов доказана И. Мацусимой
(см. [Mat 1]).
А. Орбиты присоединенного представления компактной группы Ли 28£
А. Орбиты присоединенного представления
компактной группы Ли
8.3.	Прежде чем доказывать теорему, рассмотрим некоторые-
вопросы геометрии орбит группы G как вложенных подмного-
образий евклидова пространства. Для этого раз и навсегда за-
фиксируем G-инвариантное скалярное произведение (•, •) в ал-
гебре Ли д. Конкретный выбор этого произведения несуществен;
можно, например, считать, что оно с точностью до знака совпа-
дает с формой Киллинга.
Мы построим в явном виде каноническую G-инвариантную-
почти комплексную структуру на каждой орбите М и докажем
ее интегрируемость. Затем с помощью формулы Ж. Л. Козюля
из гл. 2 вычислим G-инвариантную форму Риччи р, ассоцииро-
ванную с комплексной структурой, и покажем, что она поло-
жительно определена. Отсюда сразу следует первая часть тео-
ремы. Второе утверждение теоремы вытекает из некоторого спе-
циального свойства связной группы изометрии компактного-
многообразия Кэлера — Эйнштейна положительной скалярной
кривизны и из важного результата С. Монтгомери.
8.4.	Поскольку центр группы G тривиально действует на д,
его можно считать тривиальным. Тогда алгебра Ли окажется
полупростой, а группа G будет ее присоединенной группой.
8.5.	Пусть g = SfL1g(-— разложение алгебры Ли g в пря-
мую сумму простых идеалов, a G —Hf=1G(-— соответствующее
разложение группы G, где Gz— присоединенная группа алгебры
Ли д. Тогда каждая орбита группы G в пространстве g разла-
гается в прямое произведение орбит М, групп Gt- в дг-, которые
мы будем называть простыми сомножителями орбиты.
Орбита М называется полной, если ни один из ее сомножи-
телей Aft- не сводится к точке. В этом случае каждая группа Gi
действует на соответствующем многообразии М, эффективно.
В этой главе предполагается, что g есть полупростая
алгебра Ли, G — ее присоединенная группа, а М — полная
орбита группы G в д. Общие элементы алгебры д обоз-
начаются через U, V, W, ..., а общий элемент орбиты М
обозначается через w, если он рассматривается как точка
из М, и через W, если он рассматривается как элемент
алгебры Ли. Присоединенный оператор ad (UP) также обоз-
начается через adOT для w е М.
282
Гл. 8. Компактные однородные кэлеровы многообразия
8.6.	Фундаментальные векторные поля. Каждый элемент U
алгебры Ли g индуцирует однопараметрическую группу преоб-
разований <рД6/) орбиты М
<pt(t7)(r) = Ad(exp(Z -	Xfw^M, Vfe=R.
Соответствующее векторное поле Хи на М имеет вид
(8.6)	Хи^) = [и, Г] = - ad (Г) (t/), Vwe=M,
и называется фундаментальным векторным полем, порожден-
ным элементом U.
8.7.	Лемма. Скобка двух, фундаментальных векторных полей
Хи и Xv, порожденных элементами U и V, является фундамен-
тальным векторным полем — Хщ п, порожденным элементом
V].
Доказательство. Формула (8.6) позволяет рассматривать
поля Хц, Xv как векторные поля на всем пространстве д. Их
скобка имеет вид
[Хщ Xv] (w) = [V,	- [U, Xv] =
= [V, [67, Г]] - [G, [К, Г]] =
= [[К, G], Г].
Ограничивая ее на М, получаем поле Хщ, v]. □
8.8.	Замечание. Зафиксируем точку w0 е М. При этом орбита
М отождествляется с фактор-пространством G/Gw*, где GWa —
стабилизатор точки w0- Легко видеть, что правоинвариантное
векторное поле на G, индуцированное элементом U Q, проек-
тируется в фундаментальное векторное поле Хи.
Таким образом, мы получаем гомоморфизм алгебры Ли пра-
воинвариантных векторных полей на G в алгебру Ли гладких
векторных полей на М. Поскольку группа G действует на М
эффективно, этот гомоморфизм инъективен. Согласно 8.6, он не
зависит от выбора точки w0 е М.
8.9.	Касательное расслоение орбиты М. Поскольку группа G
действует на М транзитивно, значения фундаментальных век-
торных полей Хи в любой точке w е М порождают все каса-
тельное пространство TWM.
Пространство TWM является аффинным подпространством
пространства д, проходящим через точку w, а его направляющим
подпространством является векторное подпространство Im ad®—
образ эндоморфизма adw пространства д. Для простоты мы бу-
дем писать Mw вместо Imadw и отождествлять TWM с Mw:
(8.10)	TWM ~ М„.
А. Орбиты присоединенного представления компактной группы Ли 283-
8.11.	В частности, гладкое векторное поле на орбите М можно
рассматривать как гладкую g-значную функцию на М, значе-
ние которой в точке w принадлежит подпространству Mw.
8.12.	Предостережение. В данном контексте важно различать
скобку элементов алгебры Ли g и скобку векторных полей на
орбите М.
8.13.	Определение. Нормальной метрикой на орбите М назы-
вается G-инвариантная риманова метрика, индуцированная.
AdG-инвариантным скалярным произведением в д.
Свойство G-инвариантности скалярного произведения (•, •),
инфинитезимально выражается соотношением
(8.14)	([Г, G], V) + (G, [W, V]) = 0, XfU, V, Г e g.
Эндоморфизм adw кососимметричен относительно скалярного
произведения и определяет разложение пространства g в орто-
гональную сумму
(8.15)	g = Kerada,®Imadai,
где Ker adw — ядро оператора adw.
8.16.	В частности, ограничение adw на Im adw не имеет ядра.
Таким образом, мы получаем кососимметрический автоморфизм.
касательного расслоения ТМ, равный adw в точке w.
8.17.	Подпространство Keradw является алгеброй Ли ста-
ционарной группы Gw точки w.
Ассоциированное с ним аффинное подпространство, проходя-
щее через точку w, является слоем в точке w нормального рас-
слоения орбиты М. Этот слой мы также будем отождествлять
с векторным подпространством Ker adw, которое для краткости
обозначим через Lw.
8.18.	Отметим, что w <= Lw. Таким образом, существует вы-
деленное (гладкое) сечение — так называемое тавтологическое
сечение — нормального к М расслоения. Это сечение не обра-
щается в нуль нигде на М.
8.19.	Сформулируем два свойства компактных групп Ли (до-
казательства см. в [Lie], вып. 23).
Пусть G — связная компактная группа Ли. Тогда
(i)	все максимальные торы группы G сопряжены (их раз-
мерность называется рангом группы G);
(ii)	централизатор C(S) любого тора S группы G представ-
ляет собой объединение всех максимальных торов, содержащих
S (в частности, он связен).
•284
Гл. 8. Компактные однородные кэлеровы многообразия
8.20.	Предложение. Стабилизатор Gw любой точки w М свя-
зен и совпадает с централизатором своего связного центра Sw
Доказательство. Стабилизатор Gw равен централизатору за-
мыкания однопараметрической подгруппы exp(Cw), а значит,
юн связен в силу 8.19 (ii).
Алгебра Ли связного центра Sw группы Gw является цент-
ром алгебры Ли Lw. Поскольку оператор adm не имеет ядра в Mw,
алгебра Ли Lw совпадает с централизатором подалгебры в д.
Поэтому централизатор тора Sw в G есть связная компонента
единицы группы Gw, т. е. сама группа Gw.	□
8.21.	Предложение. Объединение всех подалгебр sw, w е М,
есть тотальное пространство тривиального векторного подрас-
слоения нормального расслоения орбиты М в д.
Доказательство. Зафиксируем точку w0 е М. Тогда отобра-
жение, сопоставляющее элементу Z е Точку Ad (g)  2 е
е ®ad(g)-ta>0> является изоморфизмом и не зависит от выбора эле-
мента g класса смежности g • Gw„.	□
8.22.	Определение. Элемент w алгебры Ли g называется ре-
гулярным, если его стационарная подалгебра Lw абелева или,
что эквивалентно, если совпадает с Lw
Орбита регулярного элемента называется многообразием
(полных) флагов группы G.
8.23.	Мы покажем, что регулярные элементы образуют от-
крытое всюду плотное множество в д. Поэтому орбиты общего
положения являются многообразиями флагов.
Согласно 8.17, нормальное расслоение многообразия флагов
тривиально. В частности, классы Штифеля — Уитни и классы
Понтрягина многообразия флагов равны нулю.
Согласно 8.19, многообразия флагов отождествляются с фак-
тор-пространствами G/Т группы G по максимальным торам Т.
В. Каноническая комплексная структура
8.24.	Представление изотропии. Касательное пространство
TWM ~ Mw к орбите М в точке w, очевидно, инвариантно от-
носительно операторов adLca и AdGw. Действие AdGi2j f Mw отож-
дествляется с представлением изотропии группы Gw
Представление изотропии группы Gw и его ограничение на
связный центр Sw группы Gw вполне приводимо. Поэтому
Sw-модуль Мш разлагается в ортогональную прямую сумму
<8.25)	Mw = £ Ew, t, dimM = n = 2m,
В. Каноническая комплексная структура
285
двумерных неприводимых 5го-модулей Ew, ,, действие группы Sw
на которых в соответствующем базисе задается матрицей
(8.26) Га.(з) =
(cos2 ла, (s) — sin 2 ла,-(s)
sin2na,(s) cos2na,(s)
Vs G
Здесь а, —вес представления Га., который можно рассматри-
вать либо как линейную форму на ба,, принимающую целочис-
ленные значения на решетке ехр-‘(е), либо как линейную функ-
цию на Sw со значениями в R/Z.
8.27.	Отметим, что все формы а, отличны от нуля. Действи-
тельно, оператор adw |'Afa) не имеет ядра и, значит, ai(w)^=0
для i=l, ..., т.
8.28.	Положительные корни. Действие группы Sw в Ew,,- от-
носительно любого ортонормированного базиса пространства
Ew, i, задается матрицей Гс. (S) или Г-о, (s) в зависимости от
ориентации. Из двух противоположных форм ±а, выберем ту,
значение которой на векторе w положительно, и обозначим ее
через а,-.
8.29.	Определение. Формы а,- называются положительными
корнями Группы Sw В fi.
С помощью скалярного произведения корни можно отожде-
ствить с элементами пространства 6W.
Каждое подпространство Ew,, имеет выделенную ориента-
цию. Положительными (ортонормированными) базисами для
этой ориентации считаются базисы, относительно которых дей-
ствие. группы Sw задается матрицей raf-
8.30.	Почти комплексная структура в многообразии Af.
Ориентацию двумерного евклидова пространства EW1,- можно
рассматривать как комплексную структуру. Объединяя эти комп-
лексные структуры, получаем комплексную структуру Jw на
всем пространстве Мш TWM.
Из 8.26 следует, что естественное действие алгебры Ли gw
на Mw в ограничении на подпространство Ею, имеет вид
(8.31)	[Z, Хг] = 2а,- (Z) JWX,-, VZ <= VX, е EWi t, Vi=l, ..., m.
Описанное разложение З^-модуля Mw, вообще говоря, не яв-
ляется однозначным, поскольку некоторые корни а,- и а,- могут
совпадать. Объединяя подпространства Ew,i, соответствующие
одинаковым корням а,- = а, мы получаем однозначно опреде-
ленное разложение
(8.32)	Mw = £ Ew,a
286
Гл. 8. Компактные однородные кэлеровы многообразия
Sw-модуля Mw в сумму собственных подпространств
Е = У Е
Каждое подпространство Ew, а определяется подгруппой Sw,
а его размерность равна удвоенной кратности та корня а. Оче-
видно, разложение G-инвариантно, когда w пробегает орбиту М.
Из 8.31 немедленно следует, что комплексная структура Jw
на подпространстве Ew, а имеет вид
(8.33)	*]-
Отсюда видно, что комплексная структура Jw не зависит от раз-
ложения Sw-модуля Mw на неприводимые компоненты.
8.34.	Таким образом, мы определили почти комплексную
структуру J на отрбите М. Из 8.33 следует, что она G-инва-
риантна.
8.35.	Замечание. Для любой точки w е М автоморфизмы Jw
и adw касательного пространства ТШМ=^ Mw коммутируют:
adm о = JW°	% = —2ла (оу) X, VX е EWj а, Va <= Ф.
В дальнейшем мы будем рассматривать Jw как эндоморфизм
пространства д, считая его равным нулю на Lw. Этот эндомор-
физм также коммутирует с adw. В силу произвольности w мы
получаем (гладкое) поле эндоморфизмов аффинного простран-
ства д.
Обозначим через Па оператор ортогонального проектирова-
ния пространства g на Mw. Тогда
(8-36)	П = — J2.
х z	W	W
8.37. Комплексифицированное касательное расслоение ор-
биты М. Обозначим через Afw = Afw®C комплексификацию
пространства Mw и продолжим по С-линейности действие
группы Sw и оператора Jw на М^,.
Каждая компонента Ew. i = Ew, t ® С разложения Sm-MO-
дуля Mw разлагается в прямую сумму двух взаимно сопря-
женных одномерных собственных подпространств Tw, г и Tw,i,
соответствующих собственным значениям 2niai, и —2juat-.
Пусть Tw (соответственно Tw) обозначает прямую сумму
всех подпространств Tw,t (соответственно Tw, /). Тогда
(8.38)	Л12 = Tw е Tw, Vw е= М.
В. Каноническая комплексная структура
287
Это разложение, очевидно, G-инвариантно. Ограничение опера-
тора Jw на Tw (соответственно Tw) имеет вид ild (соответ-
ственно —ild). Поэтому пространства Tw (соответственно Tw),
w е М, являются слоями комплексного векторного расслоения
векторов тина (1,0) (соответственно (0, I)) над орбитой М.
8.39.	Предложение. G-инвариантная почти комплексная
структура J на М интегрируема.
Доказательство. Нужно показать, что тензор кручения А
структуры 1 равен нулю (см. 2.11). Для этого достаточно про-
верить, что 4ЛГ {Ху, Xv) = 0, где Хи, Xv — фундаментальные
векторные поля (см. 8.6).	□
8.40.	Лемма. Для любых фундаментальных векторных полей
Хи, Xv векторное поле 4N(Xy, Xv) имеет вид
4NW {Ху, Xv) = [ [(/, V] + [JWU, V] + Jw [U, Jw, V] -
- [jwu, jwv], in Vw e m.
Доказательство. Поскольку поле J инвариантно относительно
фундаментальных векторных полей, формула (2.11) принимает
вид
4N {Ху, Xv) = [Ху, Xv] - [/Ху, /Ху].
По лемме 8.7 первая скобка равна —Xju, yj.
Для того чтобы вычислить вторую скобку, продолжим (как
при доказательстве леммы 8.7) векторные поля на все простран-
ство д. Нам понадобится следующая лемма.
8.41.	Лемма. Производная dxJw поля J в точке w по направ-
лению вектора X е Twq задается формулой
{dxJw) V = [G, /ШУ] - Jw [U, V], VV «= Twq = g, Vw е g,
где U — произвольный элемент из д, для которого adw[/=—X.
Доказательство. Вектор X является касательным вектором
к кривой
w (0 — Ad (exp tU) w
в точке w. Из G-инвариантности оператора J следует, что
/.(tjV = Ad (exp tU) ° Jw ° Ad (exp (— tU)) W
для W e g. Дифференцируя это равенство no t, получаем
утверждение леммы.	□
Доказательство леммы 8.40 (продолжение). Имеем
[/Ха, /Ху]. = d(1xu}w {JXV) - d(JXv}w {JXv),
288
Гл. 8. Компактные однородные кэлеровы многообразия
где
d(TXu}w = RV, /XJ + [(d(W£/) J) (JV), W].
Аналогичная формула справедлива и для второго слагаемого.
По лемме 8.41
[/Ху, /Хг]и = [ [JU, JV]-J[JU, V]-J[U, /V], W],
что и завершает доказательство леммы 8.40.	□
Лемма 8.40 позволяет свести вопрос об интегрируемости
почти комплексной структуры на орбите М к некоторому чисто
алгебраическому вопросу относительно алгебры Ли g и поля
эндоморфизмов /. Точнее говоря, лемму 8.40 можно перефор-
мулировать следующим образом.
8.42.	Почти комплексная структура f на М интегрируема
тогда и только тогда, когда для любых элементов U, V е g и
w е М элемент
4SW (U, V) = [CZ, V] + Jw [JWU, V] + Jw [CZ, JWV] - [JWU, JWV]
принадлежит нормальному подпространству Lw.
Для любой фиксированной точки w е М можно считать, что
элементы U, V принадлежат Mw. Удобнее, однако, иметь дело
с комплексными векторами. Поэтому мы будем предполагать,
что элементы U, V принадлежат A1S и имеют тип (1,0) или
(0, 1), см. 8.37.
Если U и V имеют разный тип, то, очевидно, SW(U, Е) = 0.
Если элементы U, V имеют тип (1,0), то
2SW (С/, V) = [CZ, V] + iJw [CZ, V], VCZ, V e= Tw.
Пусть теперь элементы U, V принадлежат собственным под-
пространствам Tw i и Tw, j соответственно. Тогда их скобка
[С/, V] либо равна нулю, либо является собственным вектором
для adze, с собственным значением 2ni(at + a,) (w). Поскольку
(а,- + a,) (w) > 0, коммутатор [CZ, V] принадлежит простран-
ству Tw и, значит, SW(U, Е) = 0. Это завершает доказательство
предложения 8.39.	□
С. G-инвариантная форма Риччи
8.43.	Как мы установили в 2.100, форма Риччи кэлеровой
метрики зависит только от комплексной структуры и формы
объема.
На каждой орбите М существует единственная (с точностью
до гомотетии) G-инвариантная форма объема: форма объема й
С. G-иивариантиая форма Риччи
289
нормальной метрики. Поэтому форма Риччи любой G-инва-
риантной кэлеровой метрики, согласованной с канонической
G-инвариантной комплексной структурой /, является корректно
определенной 2-формой, которая полностью определяется комп-
лексной структурой J.
8.44.	Фундаментальные векторные поля Хи на орбите М со-
храняют (по определению) любые G-инвариантные геометриче-
ские объекты. В частности, они сохраняют Q и J и, значит, яв-
ляются инфинитезимальными автоморфизмами любой G-инва-
риантной кэлеровой структуры (в силу предложения 2.125 (iv)).
Поскольку любой вектор касательного пространства TWM
является значением фундаментального векторного поля (опреде-
ленного с точностью до элемента из Lw), форма Риччи р пол-
ностью определяется своими значениями на фундаментальных
векторных полях. Применяя формулу Ж. Л. Козюля (2.134),
получаем
(8.45)	рю (X, У) = - 4 б (7 [X, У]) (w),
где X, У — фундаментальные векторные поля, соответствующие
элементам U, Veg. Согласно 8.7 и 8.35, векторное поле
/И, У] в точке w е М равно
7[Х, У](щ)-7„,[Г, [G, V] ] = [W, JW[U, V]].
Остается вычислить дивергенцию этого векторного поля (кото-
рое, очевидно, не является фундаментальным).
8.46. Определение. Адаптированным базисом пространства
Mw называется базис {Xt, JXi}, i = 1, ..., m, составленный из
положительно ориентированных ортонормированных базисов
{Xi, JXi} неприводимых подмодулей Ew, i из разложения Sw-mo-
дуля Mw (см. 8.25).
8.47. Предложение. G-инвариантная форма Риччи р в точке
w е М имеет вид
QAT) Рга (X, У) = ( Е Иь ОД [£Л V]),
где {Xi, JXt}, i = 1, — произвольный адаптированный базис про-
странства Mw, а X, У — фундаментальные векторные поля, соот-
ветствующие элементам U, V.
Доказательство. Продолжим каждый вектор адаптирован-
ного базиса {X;,JXi}, i = l, ..., m, до локального векторного
поля на М с помощью параллельного переноса вдоль геодези-
ческих нормальной метрики, выходящих из точки w. Мы полу-
19 А. Бессе, т. 1
290
Гл. 8. Компактные однородные кэлеровы многообразия
чим поле ортонормированных реперов {ek}, k = 1, ...» 2т, в ок-
рестности точки w е М, причем ковариантная производная каж-
дого векторного поля ek в точке w будет равна нулю. Поскольку
нормальная метрика на орбите М индуцирована евклидовой
метрикой пространства д, ковариантная производная любого
векторного поля g в точке w по направлению ek равна проек-
ции на TWM si Mw производной по направлению ek произволь-
ного продолжения поля g на д. Поэтому
2m	2m
(8.48) 6gOT = — Е ([efe, ё] (w). ek) = — £ (defeU. ek)
fe=i	fe-i	B
для любого векторного поля g на М.
Применяя лемму 8.41 и формулу (8.48) к векторному полю
w gw = [U7, Jw [ V] ], получаем
2m
Pw {X, Y) = ->/2 бёа. = */2 E (W, Jw [U, V] ], ek) +
2m
+ 7?E ([Г, ^([CZ, V]),ek) =
*=1	*
= 72E ([efe, JW[CZ, VJ], ek)-
k=l
2m
- 7г E ( №. [acC1 (ek), Jw [U, V] ] ], efe) +
2m
+ 72 E ([W, 7w[adw‘(eft), [C7, V]]], ek).
k^i
Первая сумма, очевидно, равна нулю. Это же верно и для вто-
рой суммы, поскольку векторы ad^'e^ и adE.Cfe пропорцио-
нальны, так как каждый вектор ek принадлежит (по построе-
нию) одному из подпространств EWti. Третт я сумма равна
2m	2m
- 72 Е ([<Л И, [ad;1 (еь), Jw о adw (eft)]) = 7г E (fa, fa}, [tZ, V])
fe-1	Ы
m
= E ([cz. И. [xz, /x.-]),
*:=i
что и завершает доказательство предложе шя 8.47.	□
8.49.	Следствие. Сумма у (да) =	>	[X,, JXJ не зависит
Заяи/ю. Ома я/шяддлРЖШ' центру
С. G-инварнантная форма Риччи
291
алгебры Ли Lw и равна сумме ^ае_ц- та- а положительных
корней группы Sw в пространстве g с учетом их кратности.
Доказательство. Поскольку алгебра g полупроста, она со-
впадает со своим коммутатором [д, д]. Отсюда и из 8.47 сле-
дует первое утверждение.
Если U е Lw, то соответствующее фундаментальное поле X
в точке ю обращается в нуль. Поэтому из (8.47) следует, что
([у (w), t/], V) = 0, Lw, VV е g.
Это показывает, что [у (w), И] = 0 для Vt/ е Lw, т. е. у(ау) при-
надлежит центру алгебры Lw.
Наконец, рассмотрим произвольный элемент Z ед 5W. Для
i=l, ..., m имеем
(Z, [Xh JXi]) = (JXi[Z, Xl]) = 2nai(Z).
Отсюда
(Х z') = 2n X ai (Z) = 2n X ma-a(Z),
\i=l	Z	i=l	a e Ф
что и завершает доказательство.	□
8.50.	Для того чтобы доказать положительность формы
Риччи, нам придется немного углубиться в теорию корней по-
лупростых алгебр Ли.
Как мы уже отметили в 8.19, стабилизатор Gw любой точки
w е М представляет собой объединение всех максимальных то-
ров, содержащих тор Sw. Пусть Т — один из этих максимальных
торов. Поскольку ограничение присоединенного представления
группы G на Т вполне приводимо, получаем корневое разло-
жение
(8.51)	д = яф X (Хуэ
± (Д.У' P.Q
где Н—алгебра Ли группы Т, а Е+ат двумерные неприво-
димые Г-мо дул и, на которых представление группы Т задается
матрицами Г± ат (см. (8.26)), а соответствующие веса ±ar£ Н*
отождествляются с помощью скалярного произведения с эле-
ментами алгебры Н. Множество 7?с всех весов ±аг образует
систему корней в абстрактном смысле (см., например, [Ser 2],
гл. V). В частности, все пары ±а? отличны друг от друга.
Подпространства Lw и Mw инвариантны относительно дей-
ствия тора Т. Поэтому множество распадается на два под-
множества и D, состоящих из весов представления Adr на
подпространствах Lw и Mw соответственно. Пока не выбрана
19*
292
Гл. 8. Компактные однородные кэлеровы многообразия
ориентация двумерных неприводимых компонент £± а?,, веса
определены только с точностью до знака.
Разложение
(8.52)
Т’-модуля Mw на неприводимые подмодули является одновре-
менно разложением модуля Mw на неприводимые подмо-
дули. Поэтому веса ±аг- тора Sw представляют собой ограниче-
ния весов ±ат тора Т на подпространство пространства Н*
(или, при отождествлении Н* — Н, ортогональные проекции ве-
сов на подпространство = ^в).
8.53.	Определение. (Положительными) дополнительными
корнями тора Т (относительно да) называются веса представле-
ния Ad?, ограничения которых на являются (положитель-
ными) корнями тора Sw.
Отметим, что множество D+ положительных дополнительных
корней тора Т совпадает с множеством тех элементов из
которые принимают положительное значение на векторе w.
8.54.	Для дополнительного корня ат е D+ обозначим через
Хат, JXaT} ортонормированный базис пространства Е+ ог (кото-
рое мы будем также обозначать через Еат). Очевидно, что
скобка [Х„г, /Ли?-] коммутирует с подалгеброй Н и, значит, при-
надлежит Н. Эта скобка равна 2пат. В силу следствия 8.49
сумма положительных дополнительных корней (относительно да)
любого максимального тора, содержащего Sw, принадлежит про-
странству и равна у (да).
8.55.	Лемма. Скалярное произведение суммы элементов D+
и любого элемента D+ положительно и не меньше скалярного
квадрата этого элемента.
Доказательство ([Koz 1], с. 574, лемма 2, или [Bo-Hi], 14-8).
Зафиксируем элемент ат е D+ и выберем элемент р? е D+, ска-
лярное произведение которого на корень ат отрицательно. На-
помним два факта из общей теории систем корней полупростой
алгебры Ли:
(а„, рт)
(i) число k — —2 У1—Ц- является целым и положи-
тельным;
(8.56) (ii) для I = 0, 1, ..., k векторы Р? + 1ат являются
весами представления Ad? и принадлежат D+ (по-
скольку (Рг + 1ат} (да) > 0 при I > 0).
С. G-иивариаитная форма Риччн
293
Сумма 2Lz=o (₽r + far) равна (fe + 0 Рт + k~- + — аг, а ее
скалярное произведение на элемент ат равно нулю.
Множество D представляет собой объединение непересекаю-
щихся цепочек {Pr + far}, Z = 0, k, которые задаются па-
рами (рг, ат) с отрицательным скалярным произведением, и эле-
ментов, скалярное произведение которых на а? неотрицательно
(например, ат).	□
8.57. Предложение. G-инвариантная форма Риччи р положи-
тельно определена.
Доказательство. Согласно 8.47 и 8.48,
рш (X, У) = 2л (у (да), [U, V]), VX, У е= Mw ~ TWM,
где U, V — элементы из д, которые переводятся оператором ad®
в X, У, и у(да)е$ш. Отсюда видно, что рш(Х, У) = 0, если век-
торы X, У принадлежат различным неприводимым компонентам
Ей,, i и Еш, j разложения Gw-модуля Mw. С другой стороны, для
любого вектора Xi е EWj i
(8.58)	р. (X, «,) -	| х, F, ; = 1....т.
Пусть Т — максимальный тор, содержащий Sw. Тогда at
есть ортогональная проекция положительного дополнительного
корня ат е D+, а у (да), согласно 8.54, есть сумма всех элемен-
тов из D+. Скалярное произведение (у(да), а,) равно (у (да), аг)
и положительно по лемме 8.55.
8.59.	Следствие. Каждая орбита М допускает единственную
(с точностью до гомотетии) G-инвариантную метрику Кэлера —
Эйнштейна, согласованную с канонической комплексной струк-
турой. Эта метрика имеет положительную скалярную кривизну.
Доказательство. Форма р является формой Риччи любой
G-инвариантной кэлеровой метрики на М, согласованной с ка-
нонической комплексной структурой. Поскольку форма р поло-
жительно определена, ее можно рассматривать как кэлерову
форму кэлеровой метрики g0 = р(-, J, •), которая, очевидно, яв-
ляется метрикой Кэлера — Эйнштейна скалярной кривизны
n = diniRM. Любая G-инвариантная метрика Кэлера — Эйн-
штейна пропорциональна g0, поскольку ее кэлерова форма про-
порциональна р.	□
8.60.	Предложение. Любую метрику Кэлера — Эйнштейна на
орбите М, согласованную с канонической комплексной структу-
рой, можно получить из G-инвариантной метрики Кэлера—
Эйнштейна с помощью автоморфизма комплексной структуры.
294
Гл. 8. Компактные однородные кэлеровы многообразия
Доказательство (см. [Mat3], теорема 3). Пусть gt— мет-
рика Кэлера — Эйнштейна на М, согласованная с канонической
комплексной структурой /. Согласно следствию 8.59, существует
единственная G-инвариантная метрика Кэлера — Эйнштейна g0
с таким же, как у gi, полным объемом. Пусть Go и Gi— связ-
ные группы изометрий метрик g0 и gi. Группа G может ока-
заться собственной подгруппой группы Go, но в любом случае
последняя является компактной группой Ли без центра (см.
8.88 (i)). Поэтому по теореме 11.52 группы Go и Gi являются
компактными вещественными формами связной группы комп-
лексных автоморфизмов St (А1) комплексного многообразия
(AT, J), которая, таким образом, является комплексной полупро-
стой группой Ли. Отсюда следует, что группы Go и G] сопря-
жены элементом <р eSl(Af):
(8.60)	G! = (Ad<p)G0.
Напомним теперь следующий результат Д. Монгомери.
8.61.	Любая максимально компактная подгруппа транзитив-
ной группы Ли преобразований компактного односвязного мно-
гообразия М действует на М транзитивно ([Моп]).
Будучи компактной вещественной формой полупростой комп-
лексной группы Ли, группа G является максимальной компакт-
ной подгруппой группы St (АГ). Кроме того, многообразие М од-
носвязно по теореме 11.26. Значит, группа G\ действует на АГ
транзитивно. Форма объема метрики g\ равна <р*£20, по-
скольку обе формы инвариантны относительно транзитивной
группы Gj и имеют одинаковый полный объем. Преобразова-
ние ср сохраняет (по определению) каноническую комплексную
структуру. Отсюда следует, что форма Риччи pi метрики g\ яв-
ляется образом <р*р0 формы Риччи р0 метрики g0, что и завер-
шает доказательство. В процессе доказательства этого утверж-
дения мы доказали также
8.62.	Следствие. Любая метрика Кэлера — Эйнштейна на ор-
бите М, согласованная с канонической комплексной структурой,
однородна, т. е. имеет транзитивную связную группу изометрий.
8.63.	Теорема 8.2 полностью доказана.	□
D. Симплектическая структура
Кириллова — Костана — Сурьо
8.64.	Мы построили на каждой орбите АГ компактной полу-
простой группы Ли G каноническую G-инвариантную комплекс-
ную структуру и G-инвариантную метрику Кэлера — Эйнштейна,
D. Симплектическая структура Кириллова—Костана—Сурьо	295
которая определяется своей кэлеровой формой р вида (8.58),
где y(w) можно рассматривать как «константу», точнее, как
G-инвариантное сечение тривиального расслоения 5 над М. Оп-
 ределим теперь 2-форму F на М, положив
(8.65) FW(X, Y) = (w, [G, У]), VX, Yc=TwM~Mw,
где, как и прежде, G = adwX, V = adwy, a w рассматривается
как тавтологическое сечение расслоения s (см. 8.18).
1	8.66. Предложение. 2-форма F является кэлеровой формой
G-инвариантной кэлеровой структуры, согласованной с канони-
I ческой комплексной структурой.
Доказательство. Форма F, очевидно, G-инвариантна. По-
этому предложение непосредственно вытекает из следующих
трех лемм.
|	8.67. Лемма. Внешний дифференциал G-инвариантной
2-формы В имеет вид
(8.67) dB{X, Y, Z) = B([X, Y], Z) + B([Y, ZJ, X) + В([Z, XJ, У),
где X, Y, Z — произвольные фундаментальные векторные поля
на М.
,	Доказательство. Учитывая G-инвариантность формы В, имеем
X-B(Y, Z) = B([X, У], Z) + B(y, [X, Z]).
С другой стороны, для любых векторных полей X, У, Z
dB(X, У, Z) — X-B(Y, Z) + Y B(Z, X) + Z-B(X, У)
-B([X, У], Z) —В([У, Z], X)-B([Z, X], У).
Из этих равенств немедленно следует утверждение леммы. □
8.68.	Лемма. Форма F замкнута.
Доказательство. Пусть X, У, Z — фундаментальные вектор-
ные поля, соответствующие элементам U, V, Т е g. С помощью
леммы 8.67 получаем, что в любой точке w е М
dFw(X, У, Z) = FW([X, У], Z) + FW([Y, Z], X) + FW([Z, X], У)
= (ш, f[G, V], ГЦ-[[К Г], G] + [[Г, G], У]).
Правая часть равна нулю в силу тождества Якоби.	□
8.69.	Лемма. Форма F имеет тип (1, 1) и положительно опре-
делена.
296
Гл. 8. Компактные однородные кэлеровьт многообразия
Доказательство. Рассмотрим снова разложение Ads -мо-
дуля Mw на неприводимые подмодули £ш,Представив Fw (X, Y)
из (8.65) в виде ([IF, t/],V), мы убедимся (как в 8.57), что
FW(X, У) = 0, если элементы X, У принадлежат различным под-
модулям и что Fw(Xi,JXi) = (2nai(w))~i- |Х,|2, если Х; е
Е Поскольку at(w)>0 для 1 = 1, ..., т, доказательство
завершается так же, как доказательство предложения 8.57. □
8.70.	Форма F представляет собой симплектическую струк-
туру на М, которая есть не что иное, как симплектическая
структура Кириллова — Костана— Сурьо (см., например, [Kir],
§ 15). Мы будем называть ее канонической симплектической
структурой орбиты М.
Отметим, что в общем случае F не совпадает с кэлеровой
формой G-инвариантной метрики Кэлера — Эйнштейна (ср.
с. 8.58 и 8.65).
8.71.	Замечание. Каноническая симплектическая 2-форма F
является формой, ассоциированной с автоморфизмом ad^1 ка-
сательного расслоения ТМ с помощью нормальной метрики
(8.71) F(X, y) = (ad"*X, У), VX, У «= Mw с- TWM, Vw<=M.
Аналогичные 2-формы, ассоциированные с adw и Jw, являются
невырожденными и даже положительно определенными фор-
мами типа (1, 1), но, вообще говоря, не являются замкнутыми.
В частности, нормальная метрика эрмитова, но, вообще говоря,
не кэлерова (см. предложение 8.86).
Е. Инвариантные кэлеровы метрики на орбитах
Определенные выше кэлеровы G-инвариантные формы р и F
имеют вид
(8.72) Bw (X, К) = (о (ш), [17, V]), VX, У е TWM Mw, Vty g= М,
где X = adwt/, y = adraV, а сг есть некоторое G-инвариантное
сечение расслоения s над М (см. 8.58, 8.65).
8.73. Лемма. Пусть о есть G-инвариантное сечение расслое-
ния 5. Тогда формула (8.72) задает ненулевую G-инвариантную
замкнутую 2-форму типа (1, 1). Эта форма положительно опре-
делена тогда и только тогда, когда для любого положительного
корня а представления MSw и любой точки w е М скалярное
произведение (a, cr(w)) положительно.
Доказательство. Форма В, очевидно, G-инвариантна. Ее
замкнутость доказывается так же, как в лемме 8.68. Рассмат-
297
Е. Инвариантные кэлеровы метрики на орбитах
ривая разложение Аб5а)-модуля Mw на неприводимые подмо-
дули £ю,мы убеждаемся, что (как в доказательстве леммы
8.69)
В(Х, У) = 0, если
(о (ги), а.)
<8.74) В(XJXJ =	| X, |2, G= Ew< tl Vi = 1«..., m.
Отсюда сразу следует утверждение леммы.
8.75.	Определение. Будем говорить, что 2-форма В вида
(8.72) является образом G-инвариантного сечения ст при транс-
грессии.
8.76.	Предложение. Любая замкнутая G-инвариантная
2-форма В является образом (единственного) G-инвариантного
сечения расслоения 5 при трансгрессии.
Доказательство. Условие Gw-инвариантности формы В запи-
сывается в виде
Bw (Ad (b)  X, Ad (b) Y) = BW (X, Y), VX, Y e= Mw, Vw 6= M,
Vb<=Gai
или, на инфинитезимальном уровне, в виде
(8.77)	Bw ([Z, X], У) + Bw (X, [Z, У]) = О,
VX, Y^MW, Vwg=M, VZ<=LW.
Будем рассматривать В как С-билинейную форму на комплек-
сифицированном касательном расслоении.
Пусть Т — максимальный тор, содержащий Sw (и, значит,
содержащийся в Gw), a t — его алгебра Ли. Рассмотрим разло-
жение Adr-модуля Mw в сумму одномерных собственных под-
пространств:
(8.78)	< = £ Ч+S 9-аГ,
“reD+ ar<=D+
где — собственное подпространство веса +2niar, причем
подпространства да^ и сопряжены. С помощью (8.77) легко
доказать, что
(i)	Bw (X, У) = 0, если X, У — собственные векторы типа
(1,0), соответствующие различным корням ат,
(8.79)	BW(X, Х) = гф(аг) |X |2, если X — собственный вектор,
соответствующий корню йге9+, где ф(аг) зависит
только от аг.
298
Гл. 8. Компактные однородные кэлеровы многообразия
Поскольку В есть замкнутая G-инвариантная 2-форма, из
леммы 8.67 следует, что в точке w
(8.80)	O^B^ad^G, V], adw Z) + Bw (adw [V, Z], ad^G)
+ Ba,(ad!i,[Z, G], adw V), Vw <= M, VG,» V, Z <= gc.
Пусть ar, pr — такие корни из D+, что ат + е £)+. Пусть
G, V, Z — единичные собственные векторы типа_(1,_0) из Mw,
соответствующие корням ат, рг, ат + pr, a G, V, Z — сопря-
женные к ним векторы типа (0, 1), соответствующие корням
—ат, —рг, —аг — рг. В силу С-одномерности собственных под-
пространств имеем
[G, V] = Л • Z, [V, Z] = р  G, [Z, G] = V V,
где X, р, v — ненулевые комплексные числа. Из равенств
([G, V], Z) + (V, [G, Z]) = 0 = ([V, Z], G) + (Z, [V, G]),
где (•, •) означает С-билинейное продолжение скалярного про-
изведения, сразу следует, что числа X, р, v равны. Применив
соотношение (8.80) к тройке (G, V, Z), получим
0 = ((ar + Pr)(w))2 • В (Z, Z) + (аг (да))2 • В (D, U) + pr (w))2 - В (V, V)
для любых единичных векторов G, V, Z из даз„ др/. и да7.+рг
соответственно (предполагается, что пара корней аг, рг е D+
замкнута, т. е. ат + рг е D+). Следовательно,
((аг + Рг) М)2 Ф (аг + Рг) = (“г М)2 Ф («г) + (Рг М)2 Ф (Рд)
для любой замкнутой пары корней аг, Рг-
Поскольку положительные корни порождают все простран-
ство t, существует единственный элемент о(ш)е1, для которого
,	.	(а.т, a (w))
(8.81)	=	VoreDt.
Любые два максимальных тора, содержащие Sw, сопряжены
элементом b е Gw, переставляющим собственные подпростран-
ств3 9аг> не меняя ограничений корней ат на iw. С другой сто-
роны, элемент о(щ) принадлежит пересечению различных под-
алгебр t, т. е. лежит в
Описанная конструкция, очевидно, G-инвариантна. Мы по-
лучили G-инвариантное сечение о расслоения 5, образом кото-
рого при трансгрессии является форма В.	□
Е. Инвариантные кэлеровы метрики на орбитах
299
8.82.	Следствие. Замкнутые G-инвариантные 2-формы на М
имеют тип (1, 1) относительно канонической комплексной струк-
туры.
Из предложения 8.76 и леммы 8.73 немедленно следует
8.83.	Предложение. Гомоморфизм трансгрессии задает
взаимно однозначное соответствие между множеством G-инва-
риантных. кэлеровых метрик на орбите М, согласованных с ка-
нонической комплексной структурой, и множеством G-инва-
риантных сечений расслоения 5 над М, для которых скалярные
произведения на все положительные корни положительны.
8.84.	Замечание. Зафиксируем точку w0 g /И и обозначим
через р естественную проекцию G -+GlGw<^ М. Тогда G-инва-
риантные сечения о расслоения 5 взаимно однозначно соответ-
ствуют элементам Оо s®0- Каждый элемент оо е sW1J опреде-
ляет биинвариантную 1-форму на слое GWo расслоения р. Хо-
рошо известно (и легко проверяется), что пространство биин-
вариантных 1-форм на GWq отождествляется с пространством
первых когомологий де Рама H'fjr<(Gw; R). С другой стороны,
гармонические формы на М (относительно любой G-инвариант-
ной римановой метрики) G-инвариантны. Поэтому трансгрессия
индуцирует изоморфизм пространства H'dr(Gw', R) на H2DR(M; R).
Из предложения 8.83 сразу следует
8.85.	Предложение. Если расслоение 5 над М имеет ранг 1,
то М допускает единственную (с точностью до пропорциональ-
ности) G-инвариантную кэлерову метрику. Она является мет-
рикой Кэлера — Эйнштейна. При этом каноническая симплек-
тическая структура совпадает с кэлеровой формой G-инвариант-
ной метрики Кэлера — Эйнштейна (нормированной соответ-
ствующим образом).
8.86.	Замечание. Рассмотрим орбиты, для которых ранг рас-
слоения s равен 1, или, что эквивалентно, орбиты таких элемен-
тов w е д, централизатор которых в g имеет одномерный центр,
порожденный элементом w.
Такие орбиты существуют только в том случае, если ал-
гебра Ли g проста. Среди них содержатся все неприводимые
кэлеровы симметрические пространства, для которых представ-
ление изотропии неприводимо (см. 7.45, 7.75 и табл. 2 в гл. 10).
В этом случае все G-инвариантные метрики пропорцио-
нальны. В частности, нормальная метрика является метрикой
Кэлера — Эйнштейна.
Обратно, из доказательства предложения 8.76 (см. 8.79,
8.81) сразу следует, что нормальная метрика является кэлеро-
300
Гл. 8. Компактные однородные кэлеровы многообразия
вой в том и только в том случае, если для любой точки w е М
все положительные корни а, группы Sw совпадают или, что экви-
валентно, если все положительные корни а, имеют на w оди-
наковые значения щ(да). Отсюда очевидным образом вытекает
симметричность нормальной метрики. Действительно, нормаль-
ная метрика на орбите М симметрична тогда и только тогда,
когда для любой точки w е М скобка [Mw, Mw] принадлежит Lw.
F. Компактные однородные кэлеровые многообразия
8.87.	Определение. Компактным однородным кэлеровым мно-
гообразием называется компактное кэлерово многообразие М,
на котором связная группа изометрий G действует транзитивно.
8.88.	Сформулируем без доказательства два основных ре-
зультата, касающихся односвязных компактных однородных
кэлеровых многообразий:
(i)	связная группа изометрий не имеет центра, см. [Mail],
[Bo-Re];
(ii)	стационарная группа В произвольной точки совпадает
с централизатором C(S) некоторой торической подгруппы S
группы G, причем в качестве S можно взять связный центр
группы В (в частности, группа В связна), см. [Mat 1 ], [Вог4],
[Ser 1], [Lie 5].
8.89.	Теорема. Любое компактное односвязное однородное
кэлерово многообразие изоморфно (как однородное комплекс-
ное многообразие) орбите присоединенного представления его
связной группы изометрий, снабженной канонической комплекс-
ной структурой.
Доказательство. Пусть М — односвязное компактное одно-
родное кэлерово многообразие, G — его связная группа изомет-
рий, Во — стабилизатор фиксированной точки хо е М, a So —
связный центр группы Во. Согласно 8.88 (ii), группа Во пред-
ставляет собой централизатор группы So в G.
Пусть Т — максимальный тор группы G, содержащий So
(и, значит, лежащий в Во), a g, b, 50, t—алгебры Ли групп G,
Во, So, Т соответственно.
Снабдим g произвольным G-инвариантным скалярным про-
изведением и обозначим через ш0 ортогональное дополнение к b
в д. Подпространство т0, очевидно, Абв0-инвариантно и ото-
ждествляется с касательным пространством ТХ„М.
Любая G-инвариантная комплексная структура на М опре-
деляет Абв„-инвариантную комплексную структуру J на ш0.
F. Компактные однородные кэлеровы многообразия
301
Рассмотрим разложение
(8.90) g = t© £ Е+а = 1ф £	ф £ £
+ SG	± ₽т <=	± ат е= D 1
Adp-модуля g в сумму неприводимых подмодулей.
Корень из Rc называется простым, если он не разлагается
в сумму двух положительных корней (относительно некоторого
упорядочения).
8.91. Простые корни образуют базис пространства t, причем
каждый положительный корень является суммой простых кор-
ней (см. [Ser 2]).
Среди простых корней системы RG содержатся все простые
корни системы Rb„, которые остаются простыми и для системы
Rg, поскольку множество D+ замкнуто (т. е. (D+ ф D+) П Ro cz
с. D+). Таким образом, мы имеем базис
{'рг, ..., r~s₽j-, 'аг.’а,}, r = rank(G),
s = dim (So)
пространства t, состоящий из простых корней {^г, ..., r~spr}
системы Ro и простых корней {‘аг, .... sar}, лежащих в D.
Обозначим через
W,.... r’W, W,.... W}
дуальный базис относительно нормальной метрики и рассмот-
рим линейную комбинацию
(8.92)	w = У, wt • 'а*
1 = 1
векторов *'а* с положительными коэффициентами w,-. Отметим,
что разложения Adr-модулей Ь и Шо на неприводимые подмодули
имеют вид
b0=t(b X	m0= X А±„
1	+ aT<=D
(обозначения см. в 8.50—8.57).
Эндоморфизм J пространства т0 продолжается до Ads, инва-
риантного эндоморфизма, равного нулю на Ьо, который также
обозначается через /. Этот эндоморфизм сохраняет подпростран-
ства Е+ аг, ± ar е D, и определяет на них выделенную ориен-
тацию. Обозначим через аг корень, соответствующий этой
ориентации. Он называется положительным корнем комплекс-
ной структуры J.
302
Гл. 8. Компактные однородные кэлеровы многообразия
Доказательство следующих двух результатов можно найти
в [Bo-Hi],
8.93.	Интегрируемость комплексной структуры J эквивалентна
замкнутости множества D+ положительных корней комплексной
структуры J. (Замкнутость D+ означает, что сумма двух корней
из D+, являющаяся корнем, принадлежит D+, см. [Bo-Hi],
лемма 12-4.)
8.94.	Множество весов Нс относительно Adr можно упоря-
дочить таким образом, что корни из D+ останутся положитель-
ными ([Bo-Hi], предложение 13-7).
Ясно, что Ьо есть централизатор элемента w в алгебре Ли g.
Следовательно, стабилизатор точки w в группе Adc (связный
в силу 8.19) совпадает с Во. Кроме того, скалярное произведе-
ние w и любого положительного корня комплексной структуры
J положительно. Таким образом, М изоморфно орбите точки
w, снабженной канонической комплексной структурой.
С учетом теоремы 8.89 теорему 8.2 можно переформулиро-
вать следующим образом.
8.95.	Теорема (И. Мацусима, [Mat3]). Любое компактное
односвязное однородное кэлерово многообразие допускает един-
ственную (с точностью до пропорциональности) метрику Кэ-
лера— Эйнштейна, инвариантную относительно связной группы
изометрий исходной метрики. Эта метрика Кэлера — Эйнштейна
получается из исходной метрики с помощью автоморфизма
комплексной структуры.
8.96.	Замечание. Предложение 8.60 позволяет построить на
каждом компактном односвязном кэлеровой многообразии М
семейство различных (но изометричных) метрик Кэлера —
Эйнштейна, согласованных с комплексной структурой, которое
параметризовано открытым подмножеством связной группы
?[(М) автоморфизмов комплексной структуры (ср. с. 11.46).
В неодносвязном случае справедлива
8.97.	Теорема ([Mat3], [Bo-Re]). Любое компактное одно-
родное кэлерово многообразие является кэлеровым произведе-
нием плоского комплексного тора и односвязного компактного
однородного кэлерова многообразия.
8.98.	Следствие. Компактное однородное кэлерово многооб-
разие допускает метрику Кэлера — Эйнштейна тогда и только
тогда, когда оно односвязно или является комплексным тором.
G. Пространство орбит
303
8.99.	Замечание. Борель и Реммер ([Bo-Re]) доказали бо-
лее общее утверждение о том, что любое компактное однород-
ное комплексное многообразие кэлерова типа (т. е. допус-
кающее кэлерову метрику) представляет собой произведение
комплексного тора и компактного односвязного однородного
комплексного многообразия кэлерова типа (как однородных
комплексных многообразий). При этом последнее является ра-
циональным алгебраическим многообразием (см. [Got]).
В [Bo-Re] доказано, что любое компактное однородное комп-
лексное многообразие кэлерова типа допускает кэлерову мет-
рику, которая превращает его в однородное кэлерово многооб-
разие.
Если односвязное многообразие М допускает метрику Ка-
лера — Эйнштейна положительной скалярной кривизны, то оно
является проективно алгебраическим (см. 11.11).
G. Пространство орбит
Пусть G, как обычно, есть компактная связная группа Ли
с тривиальным центром, Т—максимальный тор G, a g и t —
алгебры Ли групп G и Т. (Алгебра Ли максимального тора на-
зывается картановской подалгеброй алгебры Ли g.)
8.100.	Предложение (Р. Ботт). Пересечение любой орбиты
М присоединенного представления группы G в g с картановской
подалгеброй t есть конечное непустое множество точек.
Доказательство ([Bot 2]). Пусть Z—регулярный элемент
из t, т. е. t совпадает с централизатором Z в g, и пусть fz —
функция, заданная формулой
f7 (да) = (Z, Г), Vw е М.
Если а.'о — критическая точка функции fz на М, то для любого
вектора X е TWtM
0 = dfz (щ0) (А) = (Z, X), УХ е Т^М ~ М^.
Отсюда
0 = (Z, [Го, t/]) = ([Z, Го], H),Vt7eg,
и, значит, [Z, Го] = 0, т. е. Го е t. Подалгебра t содержится
в LWo (см. обозначение в 8.17). Поэтому ортогонально пере-
секается с t в точке щ0- Таким образом, пересечение Мf] t
дискретно и, значит, конечно.	□
8.101.	Замечание. Если w0 есть точка пересечения орбиты М
с t, то люба друга? точка пересечения получается из w0 дей-
ствием такого элемента g Е G, который сохраняет максималь-
304
Гл. 8. Компактные однородные кэлеровы многообразия
ный тор Т, т. е. элемента из нормализатора NT тора Т в G.
Группа W(G) автоморфизмов тора Т, индуцированных элемен-
тами из NT, т. е. фактор-группа Nr/T, называется группой Вейля
группы G относительно тора Т. Группа W(G) конечна (см.
[Ada], с. 29). Мы показали, что пересечение Мf] t является
орбитой группы Вейля W(G).
Рассмотрим снова систему корней RG группы G, которые
отождествляются с элементами картановской подалгебры t
с помощью G-инвариантного скалярного произведения. Регу-
лярный элемент Ze t определяет такое упорядочение системы
Rc, при котором положительными корнями считаются такие i
корни, что их скалярные произведения на Z положительны. При
этом картановская подалгебра как вещественное векторное про-
странство порождается простыми корнями {'ат, .... гат}, см.
доказательство теоремы 8.95.
8.102.	Определение. Замкнутой (соответственно открытой)
положительной камерой Вейля С (соответственно С) называется
множество векторов из t, скалярные произведения которых на
положительные (или, что эквивалентно, простые) корни неот-
рицательны (соответственно положительны).
Стенками замкнутой камеры Вейля С называются гиперпло-
скости ‘И, ортогональные простым корням ‘ат, i = 1, ..., г.	(
Напомним следующий известный результат ([Ada], с. ПО).
8.103.	Пересечение орбиты любого элемента из t относи-
тельно группы Вейля W(G) с положительной камерой Вейля С
состоит ровно из одного элемента.
Отсюда немедленно следует
8.104.	Предложение. Любая орбита М группы G в g есть ор-
бита однозначно определенного элемента w0 из замкнутой ка-
меры Вейля С.
8.105.	Замечание. Орбита М является многообразием фла-
гов тогда и только тогда, когда ее представитель из С лежит
в С. Многообразия флагов представляют собой орбиты общего
положения. Другие орбиты являются орбитами элементов w0,
принадлежащих одной или нескольким стенкам камеры Вейля.
Из доказательства предложения 8.100 следует, что размерность
тора SWe в точности равна рангу г группы G минус число сте-
нок 'Н, содержащих w0-
Многообразия флагов в некотором смысле порождают все
орбиты.
4
G. Пространство орбит
305
8.106.	Предложение. Каждое многообразие флагов группы G
допускает голоморфное расслоение над любой орбитой со слоем,
являющимся многообразием флагов.
Доказательство. Рассмотрим камеру Вейля С и орбиты 7Й
и М двух элементов z0 и w0, принадлежащих С и С соответ-
ственно.
Поскольку элемент z0 регулярен, касательное пространство
ТгоМ отождествляется с ортогональным дополнением t-1- карта-
новской подалгебры t в д. Касательное пространство TWaM
отождествляется с подпространством пространства t-1-, ортого-
нальным к ядру оператора admo. В обозначениях 8.51 имеем
£ Еат TWeM~ £ Еат,
°-t^rg	атг-о+
где R^ — множество положительных корней (для заданного
упорядочения корней), a D+ — множество положительных до-
полнительных корней относительно w0 (см. 8.53). Определим
G-эквивариантное отображение Ф: 7Й->7И, положив
(8.107)	Ф ((Ad g) z0) = (Ad g) w0, Vg^G.
Отображение Ф определено корректно, поскольку стабилизатор
точки z0 — максимальный тор Т — содержится в стабилизаторе
GWo точки wo- Очевидно, что отображение Ф является сюръек-
тивным и гладким.
Касательное отображение йФ в точке z0 имеет вид
(8.108)	дФго (X) = абШо • ad’1 (X), VX <= TZaM ~ MZo,
и на каждой неприводимой компоненте Еат сводится к умно-
жению на aT(w0) /a.T{z0). Отсюда видно, что отображение Ф
имеет максимальный ранг и перестановочно с операторами ком-
плексной структуры многообразий М и М. Учитывая G-эквива-
риантность, заключаем, что Ф есть локально тривиальное голо-
морфное расслоение.
Слой над w0 является компактным однородным кэлеровым
многообразием, изоморфным GW.JT, т. е. многообразием флагов
группы Gw„ (см. 8.89). Это завершает доказательство. □
8.109.	Следствие. Многообразия флагов компактной группы
Ли G изоморфны как комплексные однородные многообразия.
20 А Бессе, т. I
4
306
Гл. 8. Компактные однородные кэлеровы многообразия
8.110.	С помощью тех же рассуждений можно доказать бо-
лее общее утверждение о том, что орбиты двух элементов Wi
и W2, имеющие один и тот же стабилизатор в группе G, изо-
морфны как комплексные однородные многообразия.
Н. Примеры
8.111.	Пример. Орбиты группы SU(N). Алгебра Ли &i(N)
состоит из всех бесследовых косоэрмитовых матриц порядка N.
Картановской подалгеброй t служит абелева алгебра Ли диа-
гональных матриц из su(7V). Положим
где X; можно рассматривать как линейные формы, сопоставляю-
щие набору (Ль ..., Zjv) его i-ю компоненту.
Веса представления АсК, где Т — максимальный тор диаго-
нальных матриц из SU(N), соответствующий подалгебре 1,
имеют вид (Л,- — Лу), i=/=j. Положительными корнями относи-
тельно естественного упорядочения являются формы (Л, — Лу),
i < /, а простыми корнями — формы (Л/ — Л<+1), t= 1, ..., N—1
(см. [Ada]).
Замкнутая положительная камера Вейля С задается нера-
венствами
^1	... Лдь
Согласно 8.104, любая орбита группы Adsnw является орбитой
некоторого элемента из С. Каждый элемент из С можно пред-
ставить в виде
i£» = (p.b ..., Pi, р2, ..., р2, • ••. Р9, •••, рД
q
где р, > р2 ... > р9, 1 < pi < N, Е pt = N, V/ = 1, .... 9.
Н. Примеры
307
Легко видеть, что централизатор элемента w зависит не от
значений щ, а лишь от их кратностей (рь ..., pq) и является
подгруппой S(t/(pi)X ••• X U(pq)) группы SU(N).
Таким образом, любая орбита группы SU(N) изоморфна
(как SU(N) -однородное многообразие) одному из фактор-про-
странств
St/(TV)	~ U(N) __ Msum
S (U (P1) X ... X U (pq)) ~ U (Pi) X  • • X V (P(l)	.M'
где (pi, pq)—произвольное (упорядоченное) разбиение
числа N в сумму положительных чисел.
Согласно 8.110, многообразие М^^.р ) наделяется струк-
турой комплексного однородного многообразия.
8.112.	Вопреки ожиданию, орбиты, соответствующие двум
ризбиениям числа N, которые отличаются только порядком сла-
гаемых, могут иметь совершенно различные комплексные струк-
туры (см., например, [Bo-Hi]).
С геометрической точки зрения многообразие ^(pJ^-.Pq)
представляет собой многообразие флагов типа (рь ..., pq)
в C'v, т. е. наборов (Plt ..., Pq) взаимно ортогональных (отно-
сительно естественной эрмитовой метрики) подпространств Р{
пространства Cw, для которых dim Pi = pi, i — 1, ..., q.
Легко видеть, что определенное таким образом многообразие
флагов группы изоморфно многообразию обобщенных флагов
пространства CN (в обычном смысле).
Размерность центра группы S((7(pi)X ••• ХЩр<?)) равна
(q—1). Поэтому орбиты, для которых эта размерность равна
единице (см. 8.86), имеют вид
St/ (W)	U (N)	.	_
S (I/ (р) х V(q))~ U(p)X U(q) ’ Р^Я
и представляют собой грассмановы многообразия комплексных
р-подпространств пространства Cw. Одним из них является
комплексное проективное пространство QPN-X, снабженное при
р — 1 канонической комплексной структурой, а при р =
— N — 1 — сопряженной комплексной структурой. (Эти две ком-
плексные структуры эквивалентны.)
Хорошо известно (и легко проверяется), что нормальные
метрики этих многообразий являются кэлеровымн (относительно
канонической комплексной структуры) и симметрическими
(см. 8.86).
8.113.	Пример. Орбиты группы SO(2N). Алгебра Ли 50(2/V)
состоит из всех кососимметрических вещественных матриц по-
рядка 2N. Картановской подалгеброй t служит абелева алгебра
20*
308
Гл. 8. Компактные однородные кэлеровы многообразия
Ли матриц вида
_________________________
T°-^i0
| х2 о ; 0
о
; о - х„ 1
{ Ад, 0 ।
О
Весами представления Adr, где Т — максимальный тор, соот-
ветствующий подалгебре t, являются 1-формы (X,-— X/),
±(Х;4-Х;), i =# /. Положительными корнями относительно стан-
дартного упорядочения являются 1-формы (Х£-— Х;), (Л£ + Х/),
i < /, а простыми корнями — формы (Х£— X£+i), i= 1, ..., N—1,
и (Xjv-i + Хл), см. [Ada], пример 4.19, с. 8.
Замкнутая положительная камера Вейля С задается нера-
венствами
X] ... X^v-i I Хд, |.
Любой элемент из С можно представить в виде
(Mi, • • -, Рь Р2, • • • > Иг, • • • >	.М<р 0, 0, ..., 0),
V ✓	—V	/	X——>V —	>— —v	z
₽1	Р2	Pg	I
где
Ц, > Ц2 . . . > Цд > 0,
ч
^Pi + l = N,
i = l
или в виде
(Ml, ..., р.ь р.2, ..., р.2, ..., Ц9, ..., р.,, — р,9),
Р]	Р2	Рд
где
<7
> р.2 > ... > р,9 > 0, 1 «с Pi «С N, Е Pi = N.
i=l
Н. Примеры
309
Стабилизатор элемента любого типа вновь зависит только от
упорядоченного набора (рь .pq, I) или (рь pq). В пер-
вом случае стабилизатор имеет вид
U(Pl)X ... XU(pa)XSO(2l),
а во втором — вид
U(Pl)X ... XU(Pq_l)XU(Pq).
Здесь U (pi) — унитарная группа порядка р, каноническим об-
разом вложенная в группу S0(2pt), которая в свою очередь
диагональным образом вложена в SO(2N). Далее, О (pq) — уни-
тарная подгруппа группы SO(2pq), заданная комплексной струк-
турой J пространства R2f\ для которой
Je\=e-2, Je2Pq-3 = espq-2, Je2pq-\ =— e2Pq,
где	e2Pi?-i, e2Pq)— стандартный базис пространства R2₽«.
8.114.	Геометрически различаются три типа многообразий:
(1)	многообразия	р/j (где (рь ..., pq) — упорядочен-
ное разбиение числа (N—-/), 0</^Az), представляющие со-
бой многообразия комплексных флагов типа (рь ..., pq) в R27V,
т. е. упорядоченных наборов (Рь ..., Pq) взаимно ортогональ-
ных подпространств Р,- размерностей dim Р, = р,-, снабженных
комплексными структурами, которые согласованы со стандарт-
ной евклидовой метрикой;
(2)	многообразия	(где (/?,, ..., pq) — упорядочен-
ное разбиение числа N), представляющие собой многообразия
положительных комплексных флагов типа (рь .... pq), т. е. опи-
санных выше флагов, удовлетворяющих одному дополнитель-
ному условию: комплексная структура R27V, которая является
суммой комплексных структур флагов, индуцирует канониче-
скую ориентацию пространства R2W;
(3)	многообразия M^p^2N\Pq) отрицательных комплексных
флагов типа (рь ..., pq) (где (рь ..., pq) — упорядоченное раз-
биение числа N), определяемые так же, как в (2), с одним отли-
чием: комплексная структура пространства R2W индуцирует
ориентацию, противоположную канонической.
Многообразиями Л1рЯ-(2д), Мцу)<2Л,), A/^(2/V) исчерпываются
все орбиты, стабилизаторы которых имеют одномерный центр.
Два последних многообразия сопряжены элементом из O(2N),
который не лежит в SO(2N) и переставляет соответствующие
канонические комплексные структуры. Они представляют собой
многообразия комплексных структур в R27V, согласованных со
стандартной евклидовой метрикой и индуцирующих стандартную*
310
Гл. 8. Компактные однородные кэлеровы многообразия
(соответственно противоположную стандартной) ориентацию.
Многообразие М(°_2Ы)— это многообразие собственных под-
пространств пространства 'К2Л' размерности 2(N—•/), снабжен-
ных комплексной структурой, которая согласована с индуци-
рованной евклидовой метрикой.
Нетрудно проверить, что нормальная метрика будет кэлеро-
вой и симметрической для многообразий Ajfvj(2W), 7И^)(2Л)
^днффеоморфных —{/(jy/J > но не будет ни кэлеровой,
ни симметрической для многообразия	за исключением
случая l = N—1. Исключительное симметрическое многооб-
разие	изоморфно многообразию
SO (27V)	________SO (27V)	,	„
U (I) X SO (27V — 2) ~ SO (2) X SO (27V -2)	'	’ Л
Его можно интерпретировать как многообразие ориентирован-
ных 2-плоскостей пространства IR2'V.
8.115.	Пример. Орбиты группы SO(2Af+l). Ранг группы
SO(2Af4-l) равен N, как и для группы SO(2N). Алгебра Ли
so(2A'r-f- 1) состоит из кососимметрических вещественных мат-
риц порядка 2Л' + 1. Картановская подалгебра t состоит из
матриц вида
! о -<
; ?ч__о i____
У о — Z2 I
; а2 о । 0
| 0	|
! о ।
Весами представления Adz, где Т—максимальный тор, со-
ответствующий подалгебре t, являются 1-формы (Х>— Х;),
t #= j, ± (Л; + Л,/), i #= /, ±V Положительными корнями отно-
сительно стандартного упорядочения служат 1-формы (Z,,- — X/),
.i < /, (Z; + А,/), i j, и At-, а простыми корнями—1-формы
Н. Примеры
311
(X, — A;+i), i — 1,	N—1, и Луу (см. {Adaj, пример 4.20).
Замкнутая положительная камера Вейля С задается нера-
венствами
Л ।	Ло 14 ... 14 Л у ^4 0.
Как и в предыдущем примере, стабилизаторы элементов из С
имеют вид
щР{)хщР2)х ... xu(Pq)xso(2i+1),
где
Q
N, Y'Pi^N-l.
i=\
Соответствующие орбиты М^р^.^р}) представляют собой мно-
гообразия комплексных флагов типа (рь ..., pq}, определяемые
так же, как в примере 8.113.
Стабилизаторы с одномерным центром имеют вид
U(N -l)XSO('2l+ 1).
Соответствующие орбиты являются многообразиями (2/V—
— 2Z)-мерных подпространств пространства R2W+1, снабженных
комплексной структурой, согласованной с индуцированной ев-
клидовой метрикой. Как и в 8.86, легко проверить, что нор-
мальная метрика орбиты M(SvL<zf+l> не будет ни кэлеровой, ни
симметрической, за исключением случая I — N—1. В этом слу-
чае орбита изоморфна многообразию
SO (21V+ 1)	SO (21V 4- 1)
и (1) x so (21V - 1) — SO (2) X so (21V — 1) ’
Это тоже многообразие ориентированных 2-плоскостей в R2A,’+1.
8.116.	Пример. Орбиты группы Sp(N). Алгебра Ли
состоит из косоэрмитовых кватернионных матриц порядка.
N. Картановская подалгебра t является абелевой алгеброй Ли.
матриц вида
i^i
(Л] , . . . , Луу) —
где Л,- — вещественные числа.
(Луу
-312 Гл. 8. Компактные однородные кэлеровы многообразия
Весами представления Adr, где Т — максимальный тор, со-
ответствующий подалгебре И, служат 1-формы (X,-— X/), i^j,
±(Х, + Х7), i=/=j, и ±2Хй Положительными корнями относи-
тельно стандартного упорядочения являются корни (X,-— Х;),
i<j, (X; -1- X,), i^=j, и 2Xt, а простыми корнями—-корни
(X,- — Х/+1), i=l, ..., N— 1, и 2XW (см. [Ada], пример 4.18,
с. 85).
Замкнутая положительная камера Вейля С задается нера-
венствами
4>о.
Xi 'S5 Х2
Стабилизаторы элементов из С имеют вид
t/(Pi)X ... XU(pq)XSp(l),
где (pi, ..., pq)-—произвольное упорядоченное разбиение числа
(N — /),()</< А.
Для того чтобы дать геометрическую интерпретацию соот-
ветствующих орбит AfpPW p^t рассмотрим Sp(N) как группу
комплексных автоморфизмов пространства ,С2ЛГ, сохраняющих
каноническую комплексную симплектическую структуру и ка-
ноническую эрмитову метрику пространства С2Л' (см. [Chv], I,
§ VI—VIII).
Легко убедиться, что	Pq) изоморфно (как Sp(N)-
однородное пространство) многообразию изотропных флагов
типа (pi, ..., pQ), т. е. наборов (Plt ..., Pq) взаимно ортого-
нальных (относительно эрмитовой метрики) комплексных под-
пространств Pt комплексных размерностей dim Р£ = pi, вполне
изотропных относительно симплектической структуры.
Поскольку любое комплексное одномерное подпространство
пространства С2Л/ изотропно, среди орбит группы Sp(N) суще-
ствует комплексное проективное пространство СР2*’-’, изо-
морфное
SP (АГ)
L (1)XSP (IV-1)
(см. 7.15).
Вообще, стабилизаторы с одномерным центром имеют вид
U(N ~ l)XSp(l).
Соответствующие им орбиты	являются многообразиями
вполне изотропных комплексных (N—Z)-мерных подпро-
Н. Примеры	313'
странств пространства С2Л'. Среди них есть только два много-
образия, для которых нормальная метрика кэлерова (и, значит,
симметрическая): многообразие(Л,) = СР2Л"-1 и многообразие
изоморфное
Sp (ТУ)
С/ (АГ)
и отождествляемое с многообразием вполне изотропных ком-
плексных TV-мерных подпространств в С2ЛГ (см. 8.86).
Содержание т. II
Глава 9. Римановы субмерсии
§ А. Введение. § В. Римановы субмерсии. § С. Инварианты А и Т.
§ D. Формула О’Нейла для кривизны. § Е. Полнота и связности. § F. Ри-
мановы субмерсии с вполне геодезическими слоями. § G. Каноническая
вариация. § Н. Применение к однородным многообразиям Эйнштейна.
§ I. Другие примеры однородных многообразий Эйнштейна. § J. Скрещен-
ные произведения. § К. Примеры неоднородных компактных многообразий
Эйнштейна положительной скалярной кривизны.
Глава 10. Группы голономии
§ А. Введение. § В. Определения. § С. Обращение в нуль ковариантных
производных инвариантов голоиомии. Примеры. § D. Римановы произведения
и голоиомия. § Е. Структура I. § F. Голономия и кривизна. § G. Симмет-
рические пространства и их голономия. § Н. Структура II. § I. Неодносвяз-
ный случай. § J. Лоренцевы многообразия. § К. Таблицы.
Глава 11. Метрики Кэлера — Эйнштейна и гипотеза Калаби
§ А. Метрики Кэлера—Эйнштейна. § В. Доказательство гипотезы Калаби
н ее следствия. § С. Набросок доказательства теорем Обила- Калаби—Яу.
§ D. Компактные комплексные многообразия с положительным первым
классом Чженя. § Е. Экстремальные метрики.
Глава 12. Пространство Модулей эйнштейновых структур
§ А. Введение. § В. Типичные примеры: поверхности и плоские многообра-
зия. § С. Основной аппарат. § D. Инфинитезимальные эйнштейновы дефор-
мации. § Е. Формальная интегрируемость. § F. Структура пространства
предмодулей. § G. Множество констант Эйнштейна. § II. Устойчивость
эйнштейновых структур. § I. Размерность Пространства Модулей. § J. Де-
формация метрик Кэлера—Эйнштейна. § К. Пространство Модулей на
КЗ-поверхности.
Глава 13. Автодуальность
§ А. Введение. § В. Автодуальность. § С. Конформно полуплоские много-
образия. § D. Конструкция Пенроуза. § Е. Обращение конструкции Пен-
роуза. § F. Построение конформно полуплоских многообразий Эйнштейна.
Содержание т. II
315
Глава 14. Кватернионно-кэлеровы многообразий
§ А. Введение. § В. Гиперкэлеровы многообразия. § С. Примеры гппср-
кэлеровых многообразий. § D. Кватернионно-кэлеровы многообразия.
§ Е. Симметрические кватернионно-кэлеровы многообразия. § F. Кватер-
нионные многообразия. § G. Пространство твисторов кватернионных много-
образий. § Н. Применение теории пространств твисторов. § I. Примеры не-
симметрических кватернионно-кэлеровых многообразий.
Глава 15. Немного о некомпактном случае
§ А. Введение. § В. Конструкция неоднородных метрик Эйнштейна.
§ С. Конструкции, использующие расслоения. § D. Ограниченные области
голоморфности.
Глава 16. Обобщения условий Эйнштейна
§ А. Введение. § В. Естественные линейные условия на Dr. § С. Тензоры
Кодацци. § D. Случай DreC“(Q®S): римановы многообразия с гармо-
ническим тензором Вейля. § Е. Случай DreC”(S): римановы многооб-
разия с гармонической кривизной. § F. Случай CreC“(Q). § G. Случай
ВгеС“(Я): римановы многообразия, удовлетворяющие условию (Dr) (А',
X) = 0 для всех касательных векторов X. § Н. Ориентированные римано-
вы 4-многообразия с 6И7+ = 0.
Приложение. Пространства Соболева и эллиптические опера-
торы
§ А. Пространства Гёльдера. § В. Пространства Соболева. § С. Теоремы
вложения. § D. Дифференциальные операторы. § Е. Сопряженные опера-
торы. § F. Главный символ. § G. Эллиптические операторы. § Н. Оценки
Шаудера и /."-оценки линейных эллиптических операторов. § I. Сущест-
вование решений линейных эллиптических уравнений. § J. Регулярность ре-
шений эллиптических уравнений. § К- Существование решений нелинейных
эллиптических уравнений.
Дополнение
§ А. Бесконечное множество констант Эйнштейна на S2XS2m+1. § В. Явные
метрики с группой голономии б2 и Spin (7). § С. Неоднородные метрики
Кэлера—Эйнштейна положительной скалярной кривизны. § D. Единствен-
ность метрик Кэлера—Эйнштейна положительной скалярной кривизны.
§ Е. Гиперкэлеровы фактор-многообразия.
Оглавление
От переводчика...................................................5
От автора	............................... g
Глава 0. Введение .......	........... . 9
А.	Определения и краткие пояснения ...	................. 9
В.	Зачем нужна книга о многообразиях Эйнштейна?.............14
С.	Существование ............................... .	.... 15
D.	Примеры............................ .	... 16
Е.	Единственность и модули	. ... 20
F.	Краткий обзор содержания по главам ...	. ... 21
G.	Путеводитель........................................... .28
Н.	Как почувствовать кривизну Риччи............ .	28
I.	Основные открытые проблемы . .	...........32
Глава I. Основные сведения •	.	 •	- 35
А.	Введение .	.	35
В.	Линейные связности........................................ 38
С.	Римановы и псевдоримаповы многообразия ...	46
D.	Римановы многообразия как метрические пространства.........55
Е.	Римановы погружения, изометрии и кнллннговы векторные поля 58
F.	Многообразия Эйнштейна.....................................63
G.	Разложение алгебраических тензоров кривизны на неприводимые
компоненты........................................... .	.	67
Н.	Применение	к римановой	геометрии	72
I.	Лапласианы	и формулы	Вейценбёка	...	77
J.	Конформная	деформация	римановых	метрик	83
К.	Первая вариация поля тензоров кривизны .	88
Глава 2. Основные сведения (продолжение): кэлеровы мно-
гообразия ...........................................   •	•  . 94
А.	Почти комплексные и комплексные многообразия	.94
В.	Эрмитовы и кэлеровы метрики	....	.98
С.	Тензор Риччи и форма Риччи	. .	102
D.	Голоморфная секционная кривизна .	.106
Е.	Классы Чженя . ...........................................109
F.	Форма Риччи как форма кривизны линейного расслоения	.112
G.	Теория Ходжа ...	.................... .	...........115
Н.	Голоморфные векторные поля и инфинитезимальные изометрии 119
I.	Теорема Калаби — Футаки...................................126
Оглавление
317
Глава 3. Теория относительности.................................129
А.	Введение..................................... .	. .	. . 129
В.	Физическая интерпретация ....	.	. 129
С.	Полевое уравнение Эйнштейна	131
D.	Приливные напряжения ...	.133
Е.	Нормальные формы кривизны ............................... 134
F.	Метрика Шварцшильда .	.	. 139
G.	Планетные орбиты .................. . 143
Н.	Прецессия перигелия ...	.	146
I.	Геодезические вселенной Шварцшильда	. 147
J.	Отклонение луча света................................... 148
К.	Расширение Крускала ....	150
L.	Как может нарушаться полнота	.	152
М.	Теоремы сингулярности ....	154
Глава 4. Римановы функционалы..................................156
А.	Введение................................................ 156
В.	Основные свойства римановых функционалов	...	157
С.	Полная скалярная кривизна: свойства первого порядка .	.	161
D.	Существование метрик постоянной скалярной кривизны .	163
Е.	Образ отображения скалярной кривизны . .	167
F.	Многообразие метрик постоянной скалярной кривизны .	170
G.	Снова о полной скалярной кривизне: свойства второго порядка . 173
Н.	Квадратичные функционалы .	.	.178
Глава 5. Кривизна Риччи как уравнение в частных произ-
водных .......	.183
А.	Точечная (инфинитезимальная) разрешимость . .	.	183
В.	От точечной разрешимости к локальной: препятствия	. 186
С.	Локальная разрешимость уравнения Ric(g) — г для невырожден-
ного тензора г....................................  .	.	189
D.	Локальное построение метрик Эйнштейна . .	.	192
Е.	Регулярность метрик с гладким тензором Рнччи .	192
F.	Аналитичность метрик Эйнштейна и ее применение .	196
G.	Метрики Эйнштейна на трехмерных многообразиях	197
Н.	Теорема единственности для кривизны Риччи ...	. 204
I.	Несуществование глобальных решений .	205
Глава 6. Многообразия Эйнштейна и	топология	207
А.	Введение................................ . 207
В.	Существование метрик Эйнштейна в двумерном случае .	. 208
С.	Трехмерный случай ...	.211
D.	Четырехмерный случай.................. . 216
Е.	Кривизна Риччи и фундаментальная группа	. 222
F.	Скалярная кривизна и спинорное препятствие .............. 227
G.	Доказательство теоремы Нигера — Громола о полных многообра-
зиях неотрицательной кривизны Риччи ........................ 231
318
Оглавление
Глава 7. Однородные римановы многообразия . .	238
А.	Введение .	. .	...	... 238
В.	Однородные римановы многообразия................  239
С.	Кривизна........................ ...............  243
D.	Примеры однородных многообразий Эйнштейна.................. 249	Г
Е.	Общие результаты для однородных многообразий Эйнштейна .	253
F.	Симметрические пространства................................256
G.	Стандартные однородные многообразия .	. . 263
Н.	Таблицы........................................ • 268
I.	Немного об однородных лоренцевых многообразиях ...	276
Глава 8. Компактные однородные кэлеровы многообразия 280
0. Введение .	.	.................................280
А.	Орбиты присоединенного представления компактной группы Ли 281
В.	Каноническая комплексная структура	..... 284
С.	G-инвариантная форма Риччи............................... .	288
D.	Симплектическая структура Кириллова — Костана — Сурьо .	. 294
Е.	Инвариантные кэлеровы метрики на орбитах	. .	. . 296
F.	Компактные однородные кэлеровы многообразия	... 300
G.	Пространство орбит ....	......... 303
Н.	Примеры..................................................  306
Содержание т. II................................................ 314
г
УВАЖАЕМЫЙ ЧИТАТЕЛЬ!
Ваши замечания о содержании книги, ее
оформлении, качестве перевода и другие про-
сим присылать по адресу: 129820, Москва,
И-НО, ГСП, 1-й Рижский пер., д. 2, издатель-
ство «Мир».
НАУЧНОЕ ИЗДАНИЕ
Артур Бессе
МНОГООБРАЗИЯ ЭЙНШТЕЙНА
В 2-х томах
Т. I
Зав. редакцией чл.-корр. АН СССР В. И. Арнольд
Зам. зав. редакцией А. С. Попов
Научный редактор О. Р. Чуян
Мл. науч. ред. Т. А. Денисова, Н. С. Полякова
Художник О. С. Василькова
Художественный редактор В. И. Шаповалов
Технический редактор М. А. Страшнова
Корректор В. И. Киселева
ИБ № 7195
Сдано в набор 04.09.89, Подписано- к печати 23.03.90,
Формат 60X90716. Бумага типографская № 1. Печать
высокая. Гарнитура литературная. Объем 10,0 бум. л.
Усл. печ. л. 20,00. Усл. кр.-отт. 20,00. Уч .-изд. л. 17,96-
Изд. № 1/6724. Тираж 4250 экз. Зак. 287. Цена 2 р. 50 к.
Издательство «Мир» В/О «Совэкспорткннга» Госу-
дарственного комитета СССР по печати
129820, ГСП, Москва, И-ПО, 1-й Рижский пер., 2.
Набрано в Ленинградской типографии № 2 голов-
ного предприятия ордена Трудового Красного Зна-
мени Ленинградского объединения «Техническая
книга» им. Евгении Соколовой Государственного
комитета СССР по печати. 198052, г. Ленинград,
Л-52, Измайловский проспект, 29. Отпечатано в Ле-
нинградской типографии № 4 ордена Трудового
Красного Знамени Ленинградского объединения
«Техническая книга» им. Евгении Соколовой Госу-
дарственного комитета СССР по печати. 190000>-
Ленинград, Прачечный пер., 6.