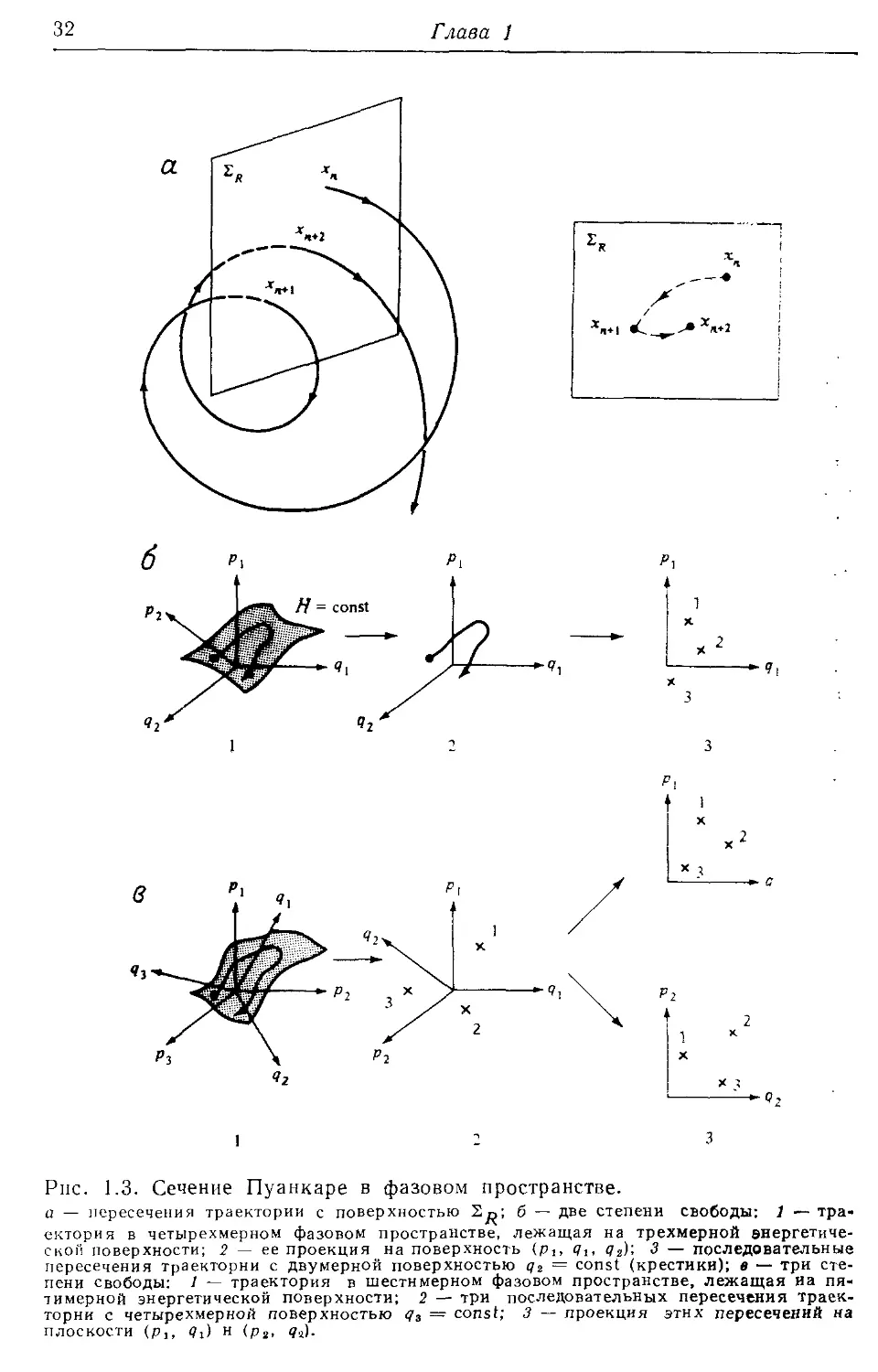
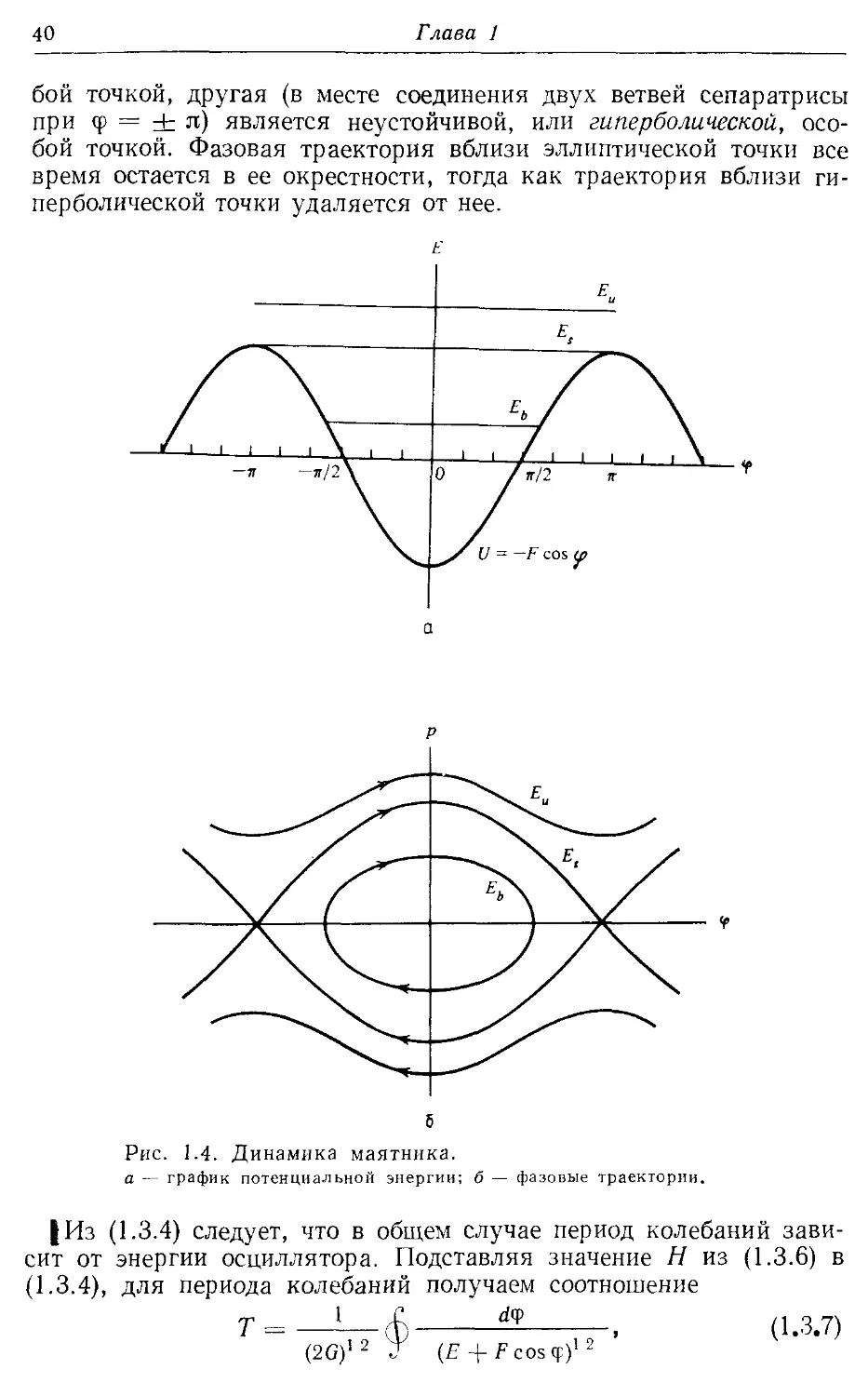
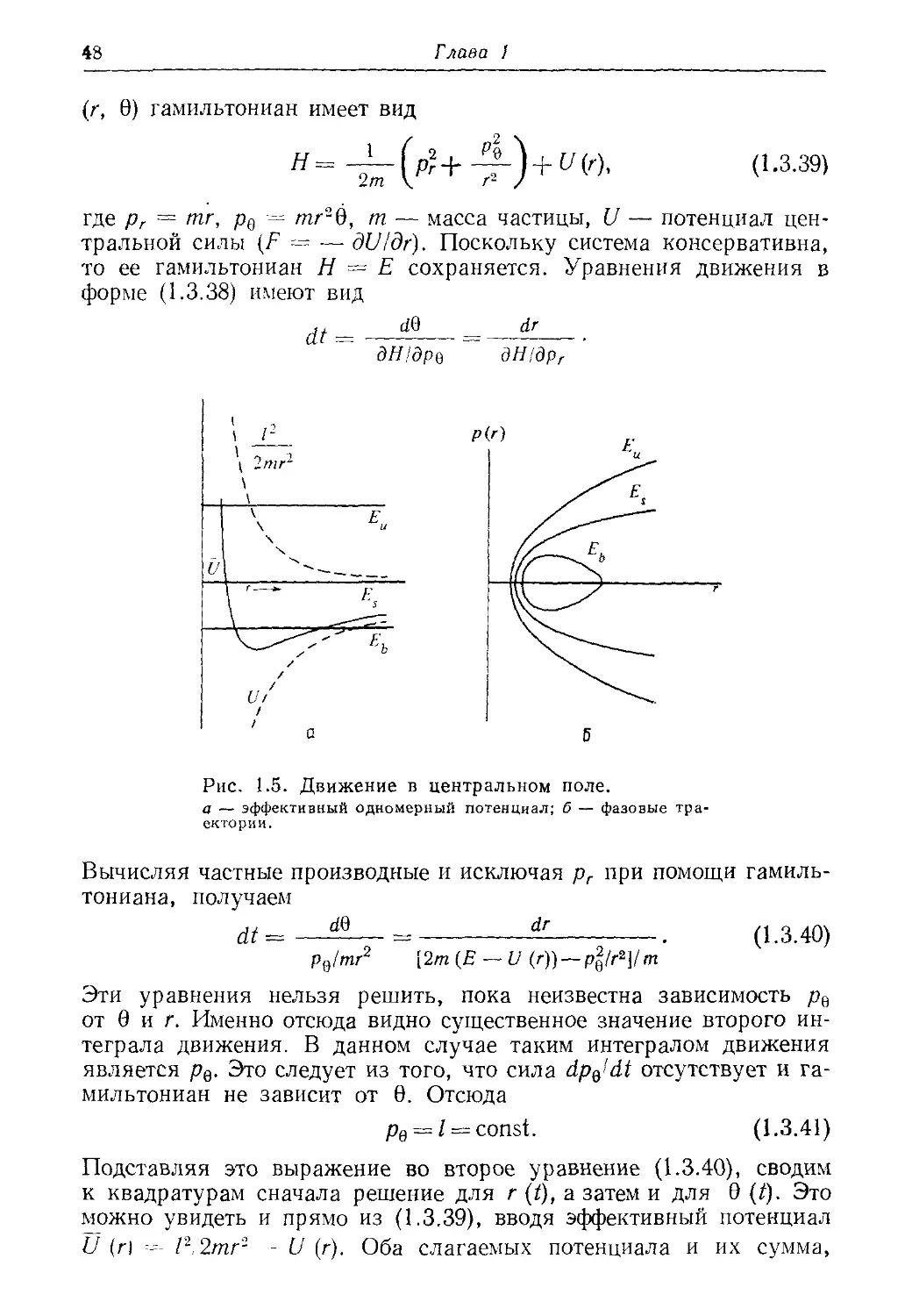
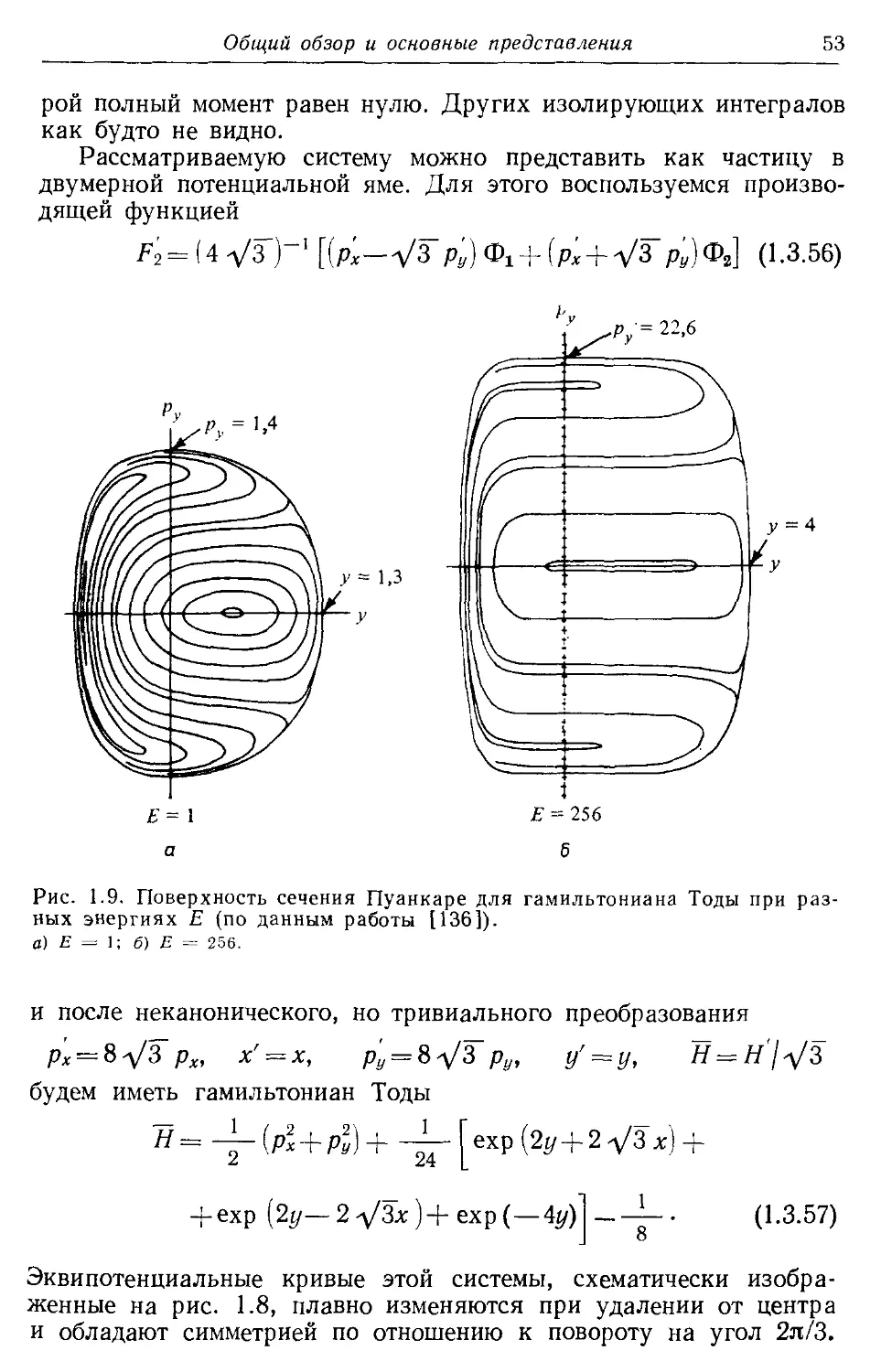
Author: Лихтенберг А. Либерман М.
Tags: физика монография нелинейная механика статическая физика
Year: 1984
Text
А.Лихтенберг, М.Либерман
РЕГУЛЯРНАЯ И СТОХАСТИЧЕСКАЯ ДИНАМИКА
Монография известных американских физиков, профессоров
Калифорнийского университета (Беркли) А.Лихтенберга и М.Либерман а
посвящена новой быстро развивающейся и малоизвестной области, пограничной
между нелинейной механикой и статистической физикой. Основное внимание
уделено выяснению физической сущности и механизма, а также условиям
возникновения динамического хаоса, т. е. случайного движения полностью
детерминированных систем классической механики. Подробно рассмотрены
характерные примеры таких явлений и некоторые приложения. Значительное
место отведено описанию и иллюстрации различных методов теоретического
анализа и практического расчета хаотических процессов.
Предназначена для широкого круга научных работников и инженеров в
области механики, физики и в определенной степени химии и биологии, а также
для преподавателей, аспирантов и студентов старших курсов соответствующих
специальностей.
ОГЛАВЛЕНИЕ 1)
*) Звездочкой отмечены параграфы и пункты, содержащие основной
материал.
Предисловие редактора перевода 5
Предисловие 11
Глава 1. Общий обзор и основные представления 13
§1.1. Вводные замечания 13
* § 1.2. Теория преобразований в механике 20
* 1.2а. Канонические преобразования 21
* 1.26. Движение в фазовом пространстве 25
* 1.2в. Переменные действие — угол 34
§ 1.3. Интегрируемые системы 38
* 1.3 а. Одна степень свободы 38
1.36. Линейные дифференциальные уравнения 43
1.3в. Несколько степеней свободы 47
* § 1.4. Системы, близкие к интегрируемым 59
* 1.4а. Две степени свободы 59
* 1.46. Более чем две степени свободы 71
§ 1.5. Диссипативные системы 73
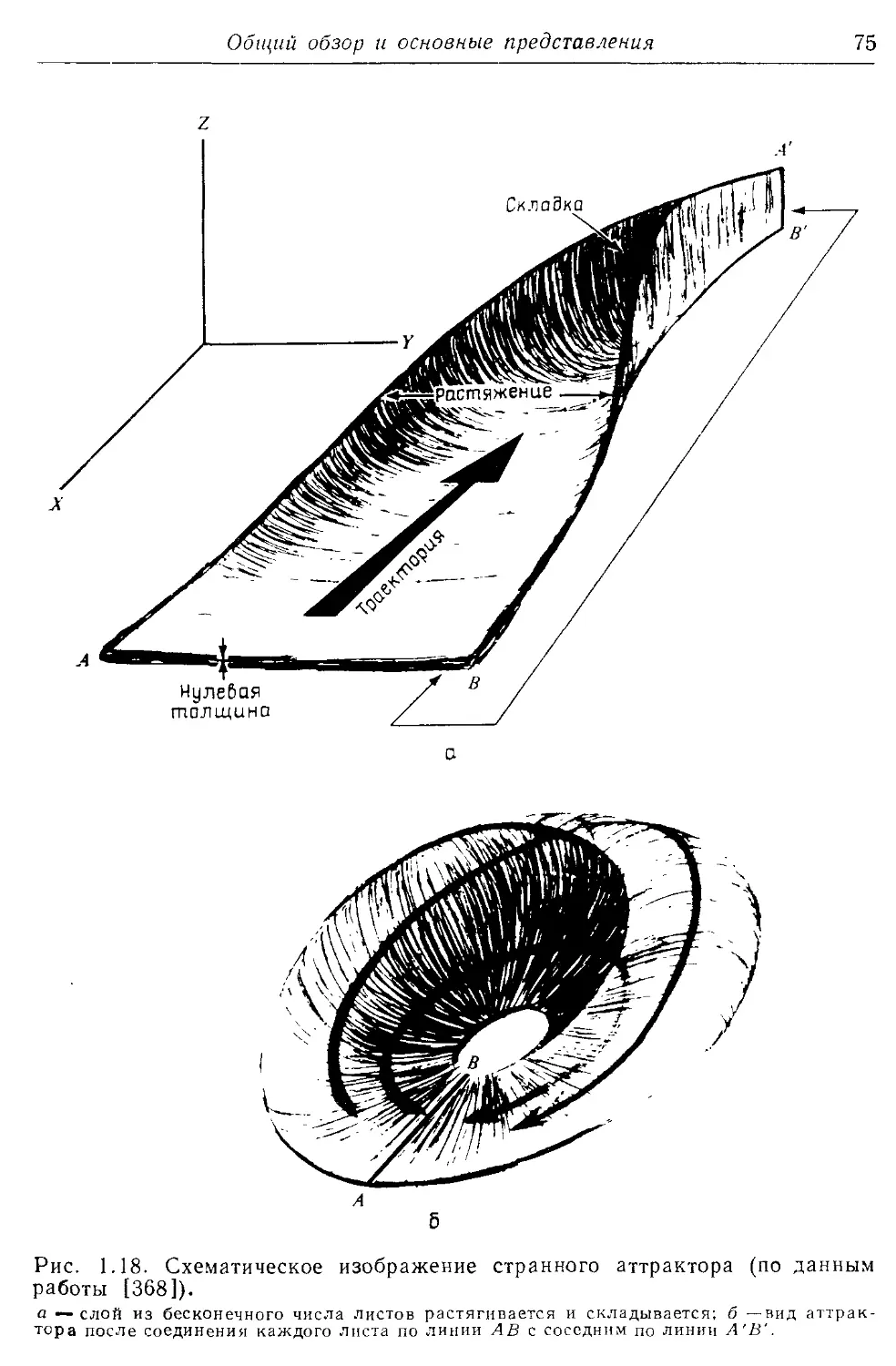
1.5а. Странные аттракторы 74
1.56. Модель Лоренца 76
Глава 2. Каноническая теория возмущений 81
§ 2.1. Введение 81
2.1а. Степенные ряды 84
2.16. Асимптотические ряды и малые знаменатели 87
2.1 в. Влияние резонансов 89
* § 2.2. Классическая теория возмущений 89
* 2.2а. Одна степень свободы 90
* 2.26. Несколько степеней свободы 95
§ 2.3. Адиабатическая инвариантность 104
* 2.3а. Введение и основные понятия 104
* 2.36. Каноническая адиабатическая теория 107
* 2.3в. Медленно изменяющийся гармонический осциллятор 111
2.3г. Неканонические методы 114
§ 2.4. Резонансная теория возмущений 121
* 2.4а. Устранение резонансных знаменателей 123
* 2.46. Вторичные резонансы 130
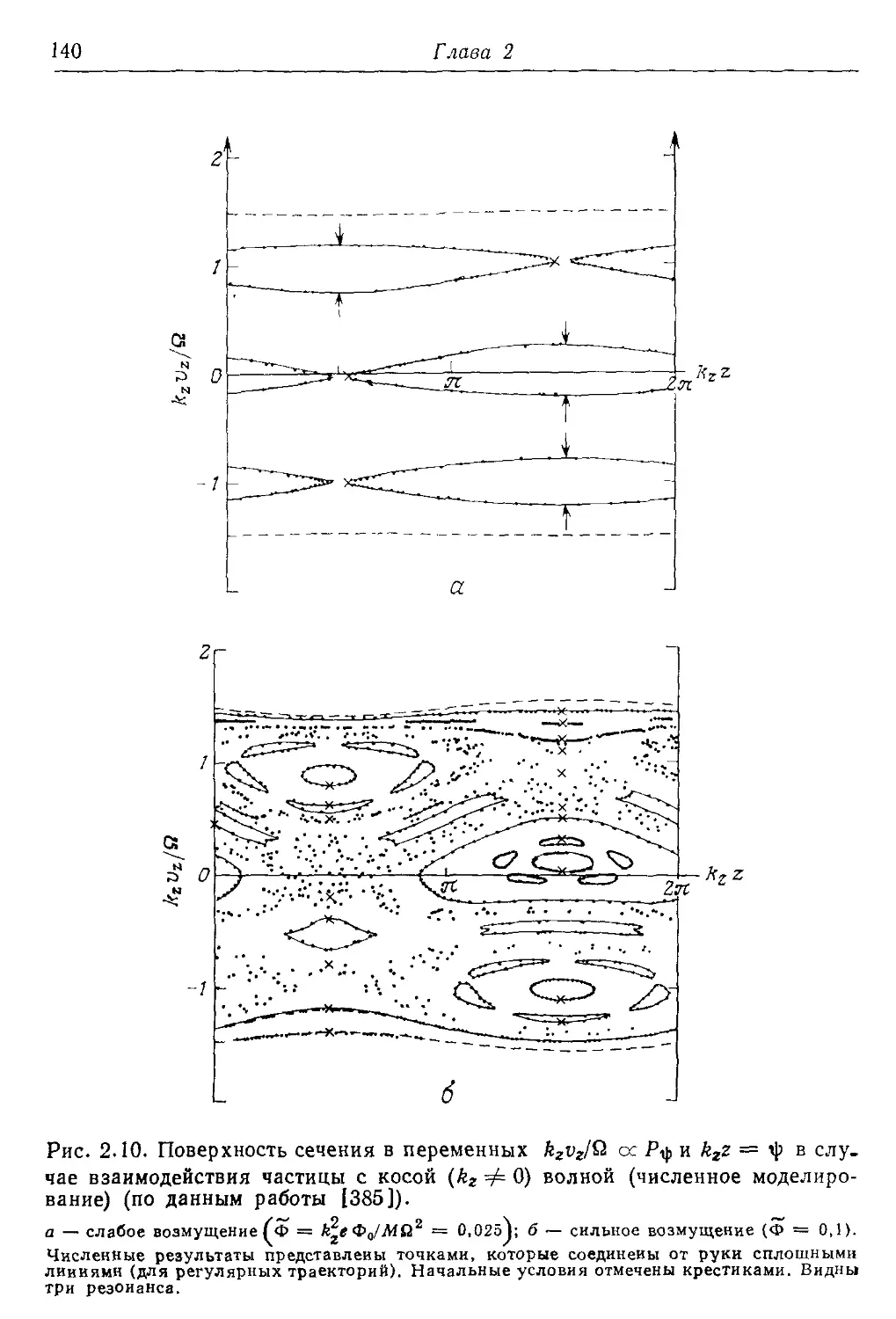
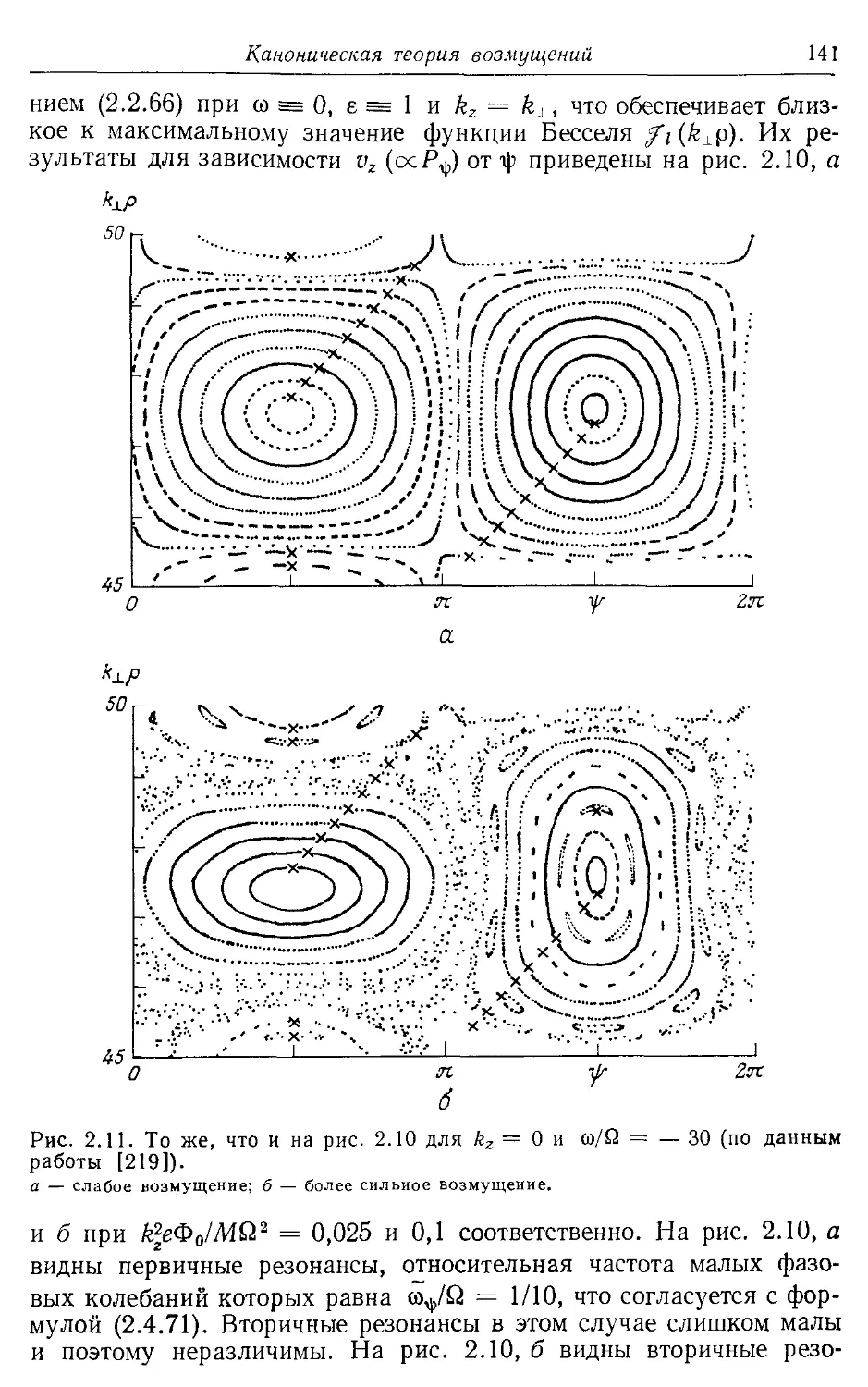
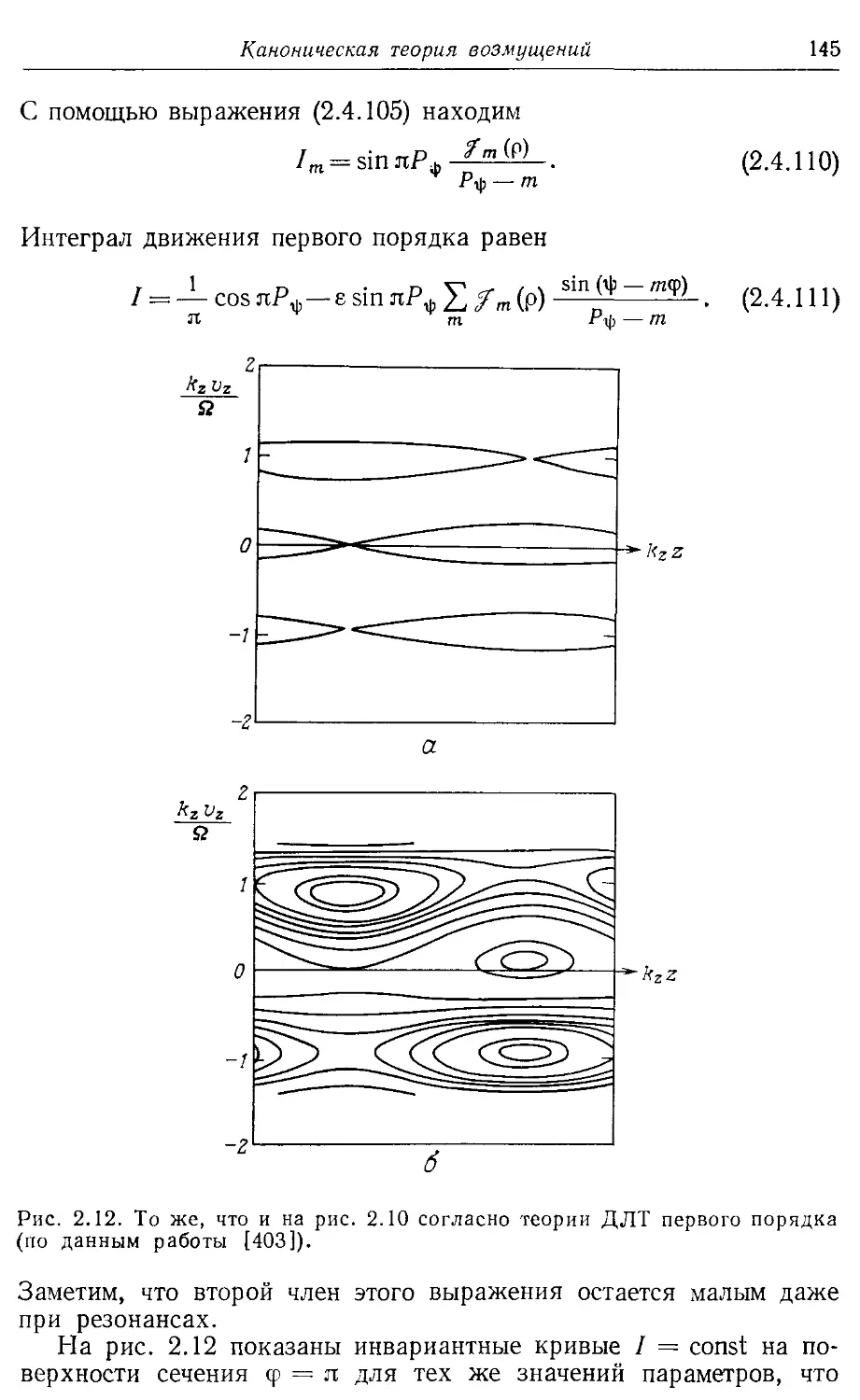
* 2.4в. Резонансное взаимодействие волны и частицы 135
2.4г. Глобальное устранение резонансных знаменателей 142
§ 2.5. Метод преобразований Ли 146
2.5а. Общая теория 148
2.56. Ряды Депри 149
2.5в. Адиабатические инварианты 154
§ 2.6. Сверхсходимость 162
2. 6а. Метод Колмогорова 165
2.66. Периодические траектории 167
Глава 3. Отображения и линейная устойчивость 175
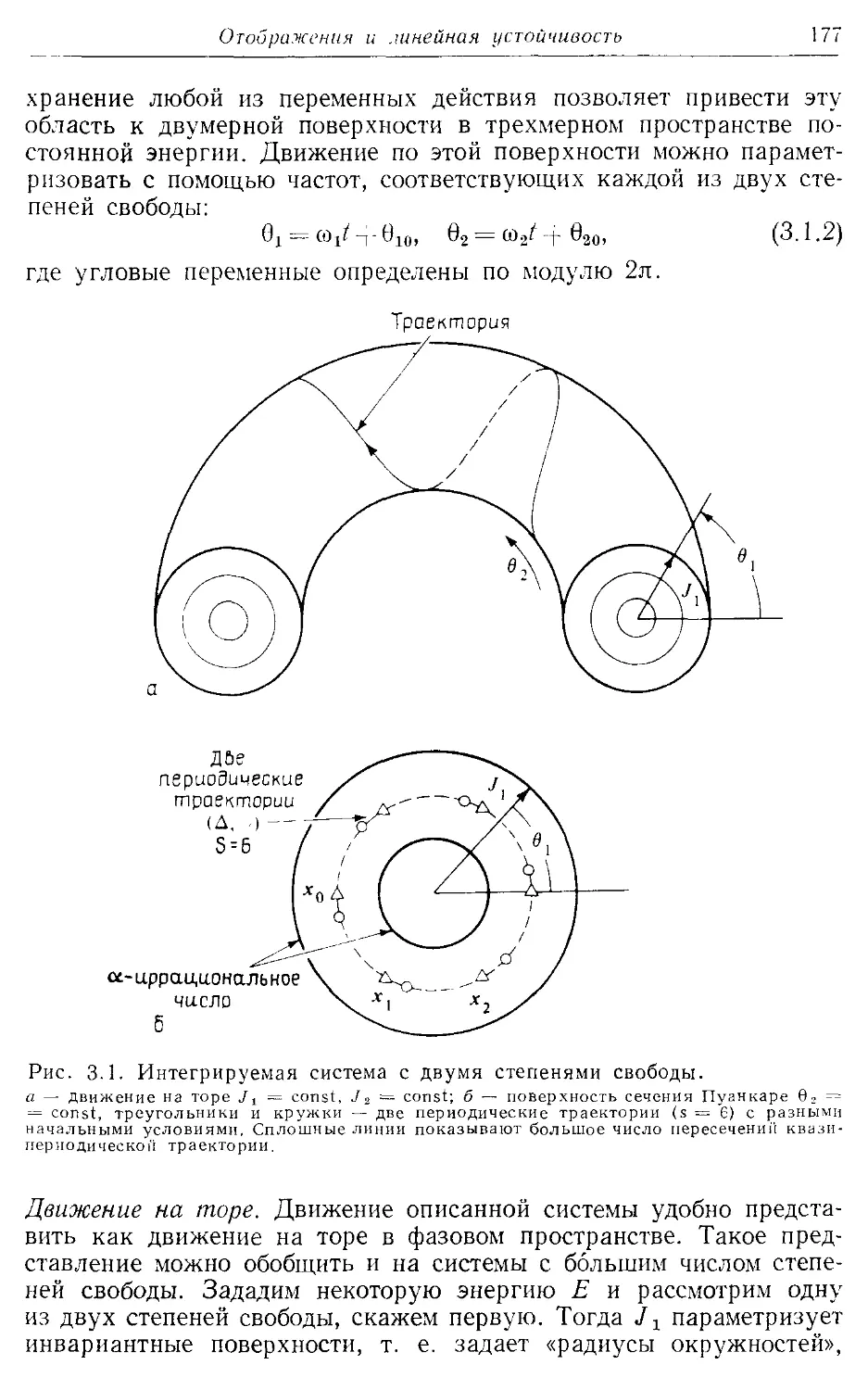
* § 3.1. Гамильтоновы системы как канонические отображения 176
* 3.1 а. Интегрируемые системы 176
* 3.16. Системы, близкие к интегрируемым 180
* 3.1 в. Уравнения Гамильтона и отображения 182
* § 3.2. Типичное поведение канонических отображений 184
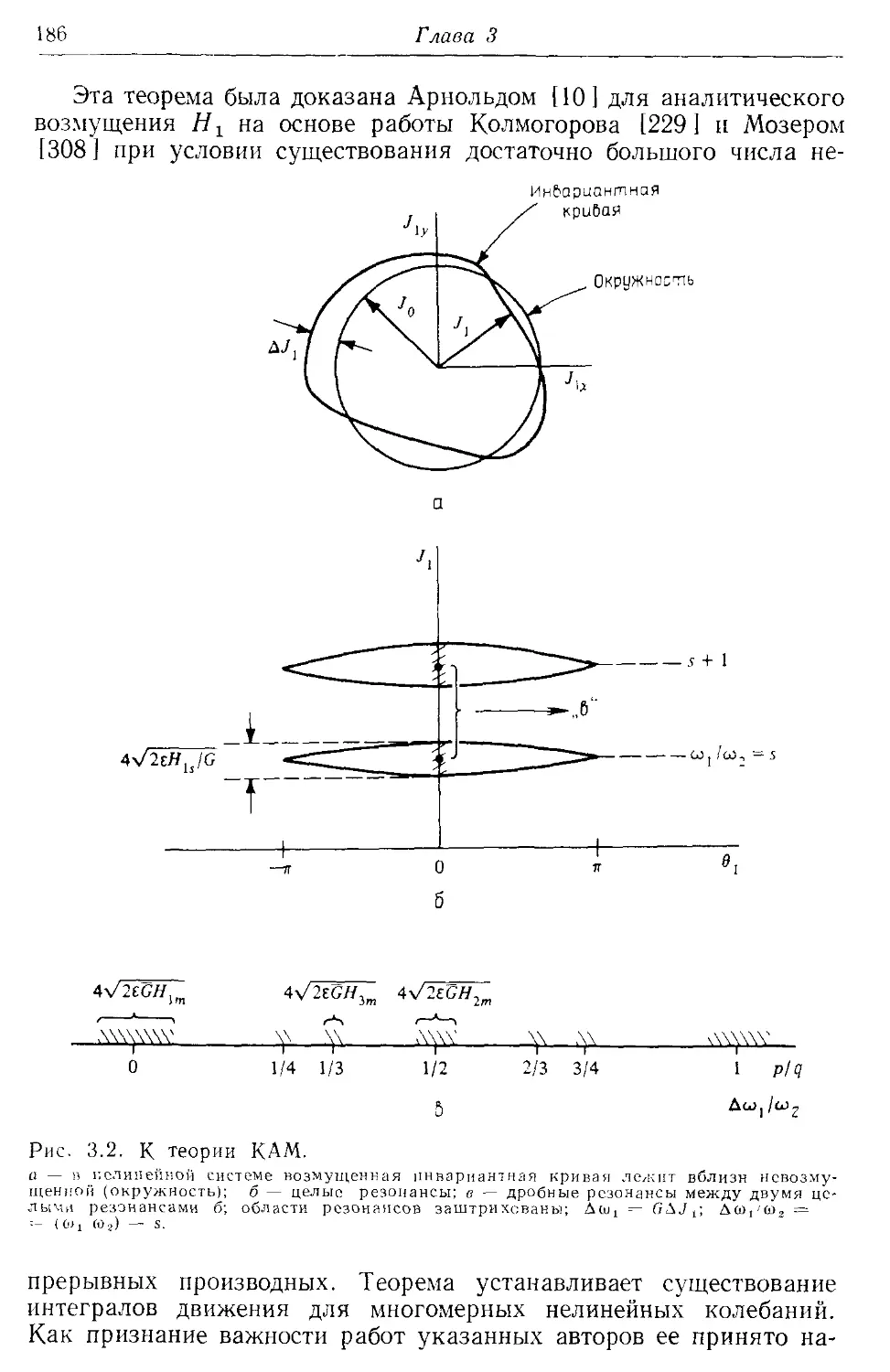
* 3.2а. Иррациональные числа вращения и теория КАМ 185
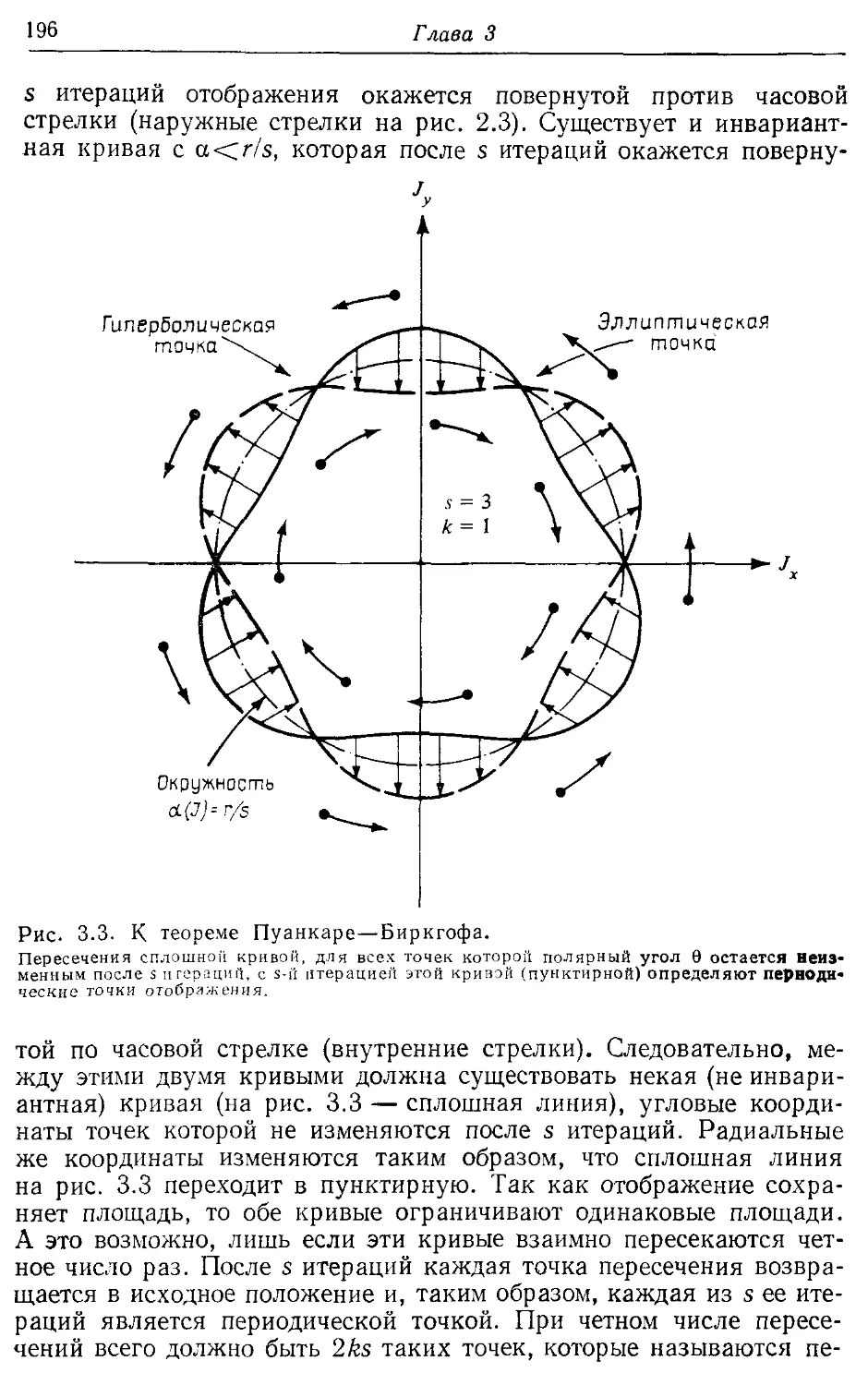
* 3.26. Рациональные числа вращения и структура резонансов 195
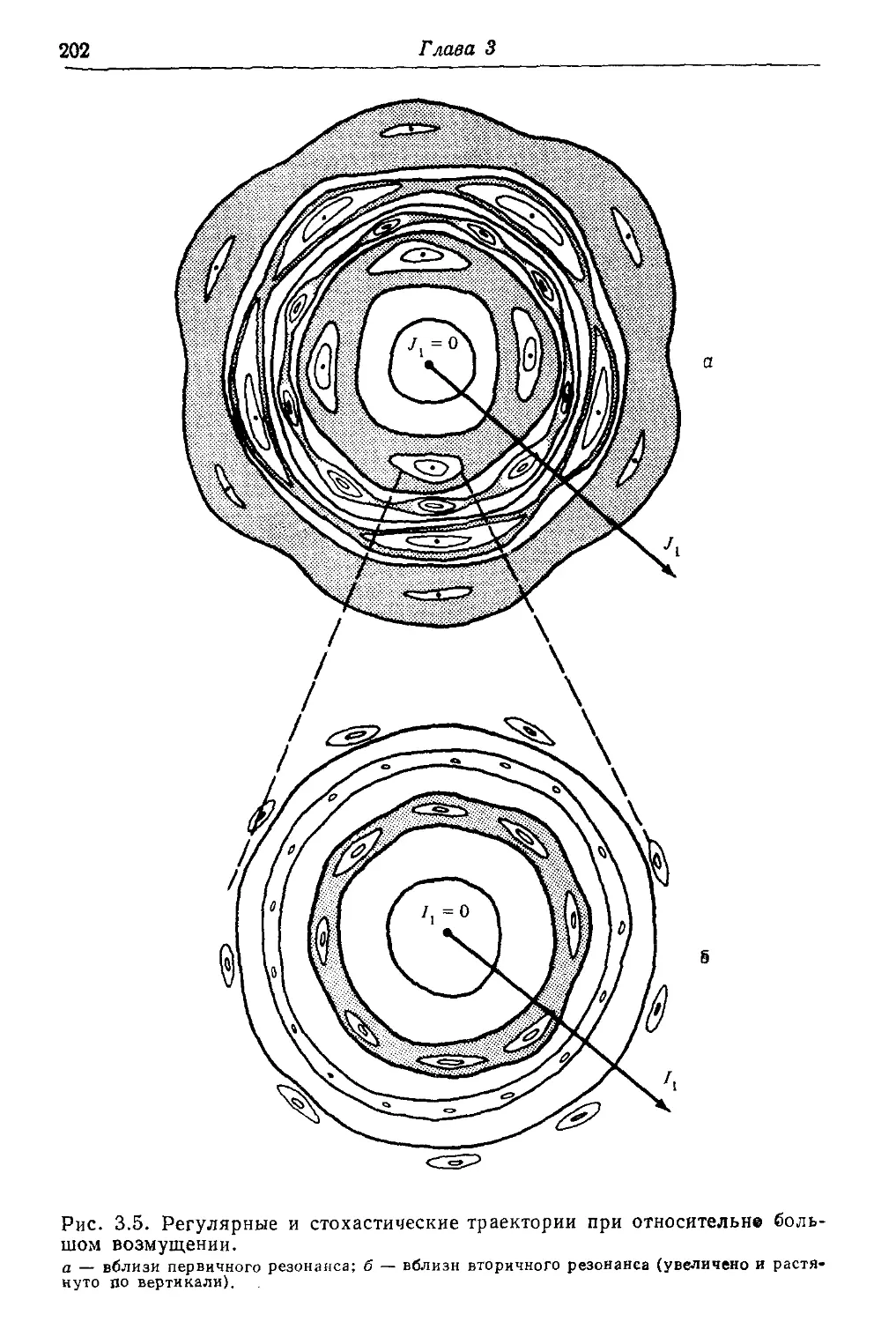
* 3.2в. Полное описание нелинейного отображения 200
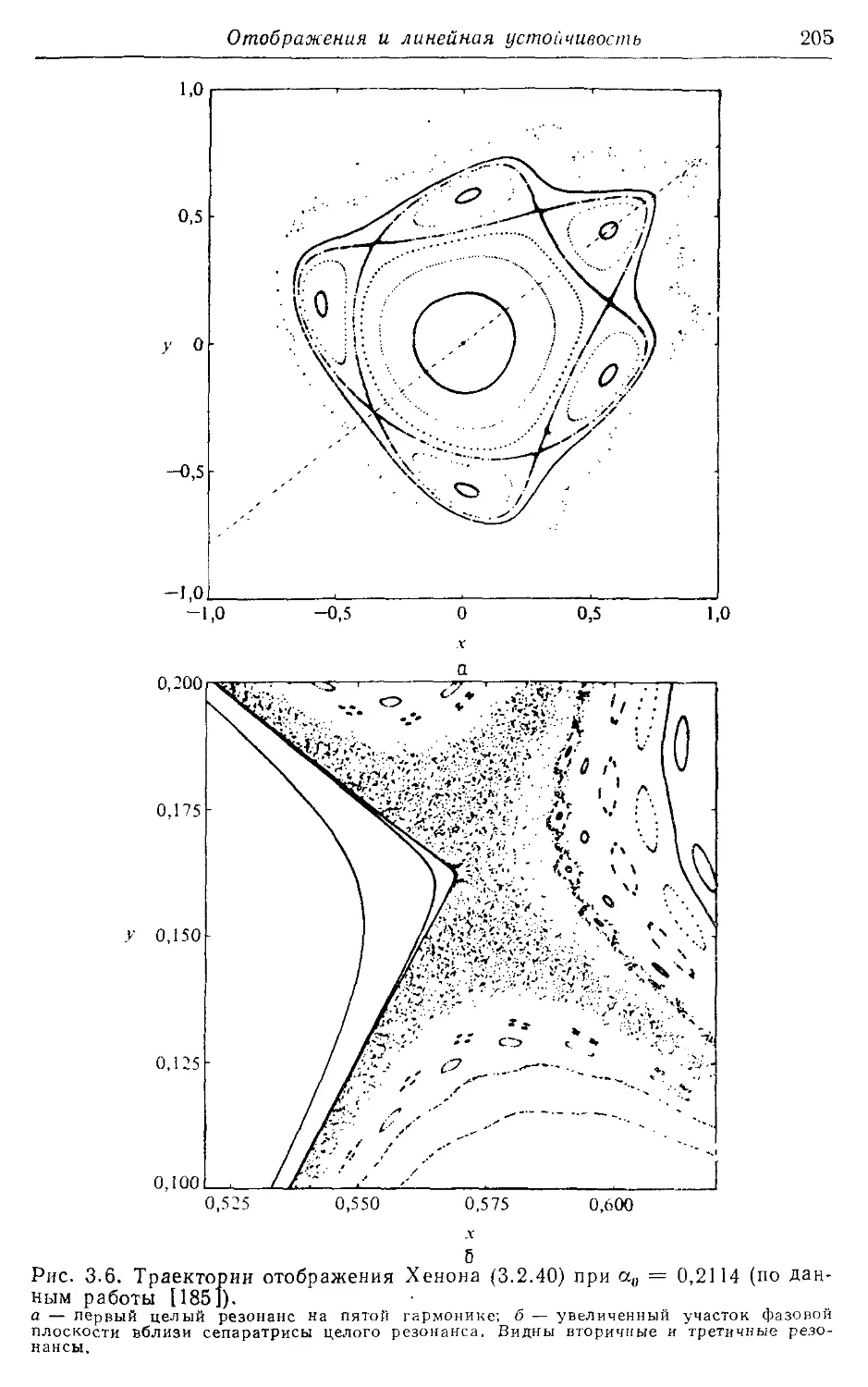
* 3.2г. Численный пример 204
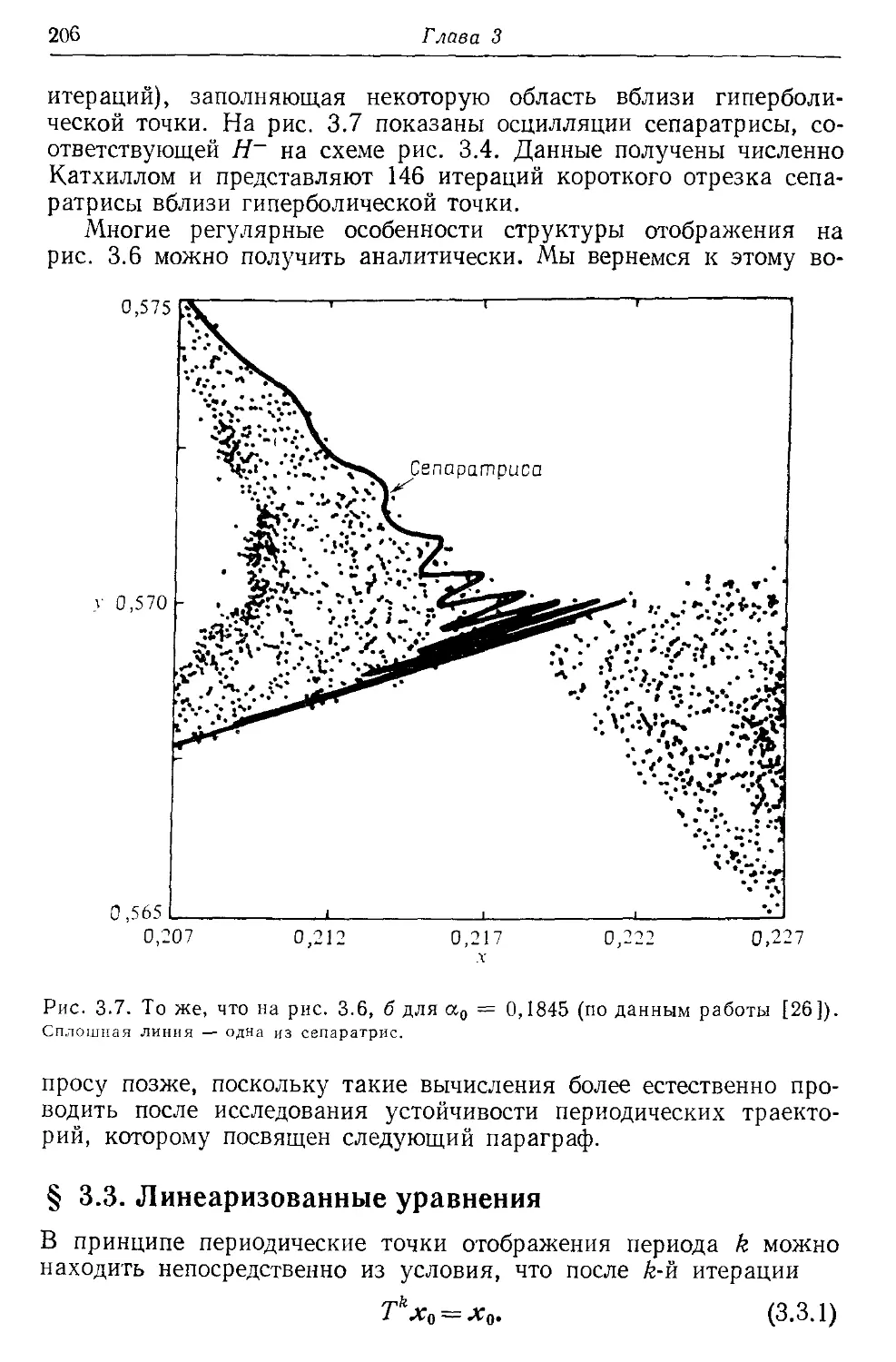
§ 3.3. Линеаризованные уравнения 206
3.3а. Собственные значения и собственные векторы 207
* 3.36. Двумерные отображения 212
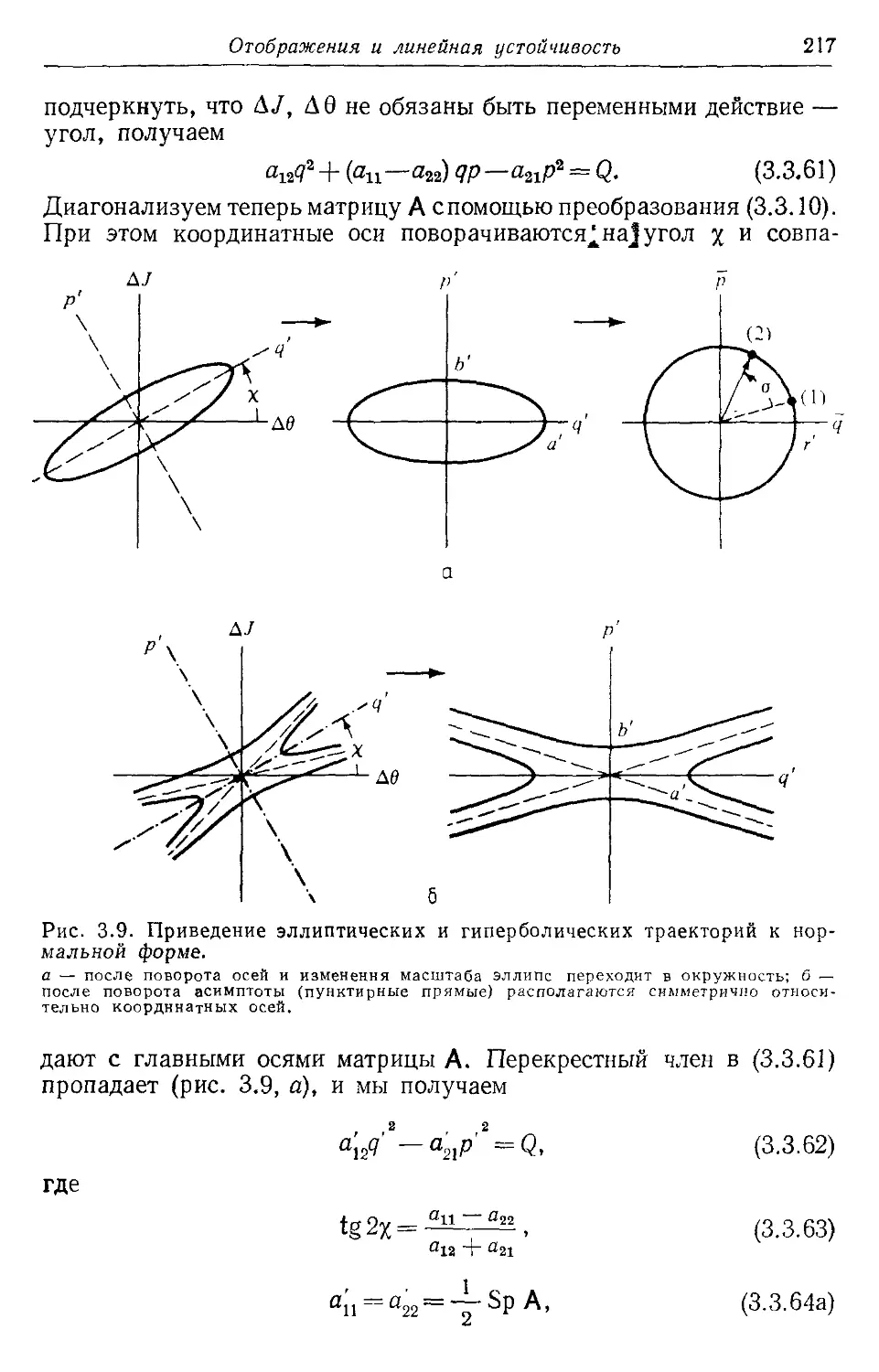
* З.Зв. Линейная устойчивость и инвариантные кривые 215
* § 3.4. Ускорение Ферми 220
* 3.4а. Физические задачи и их модели 221
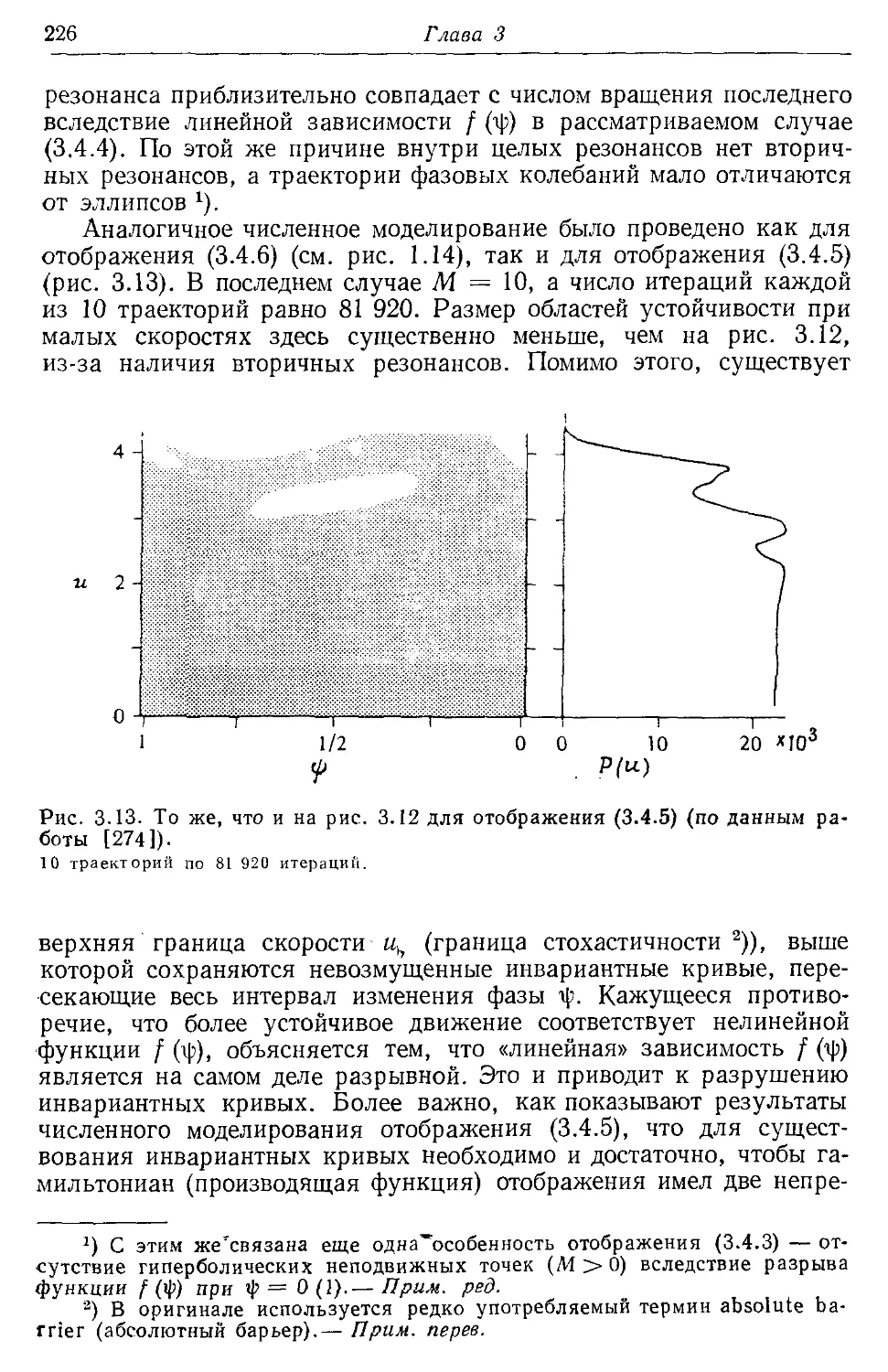
* 3.46. Численное моделирование 224
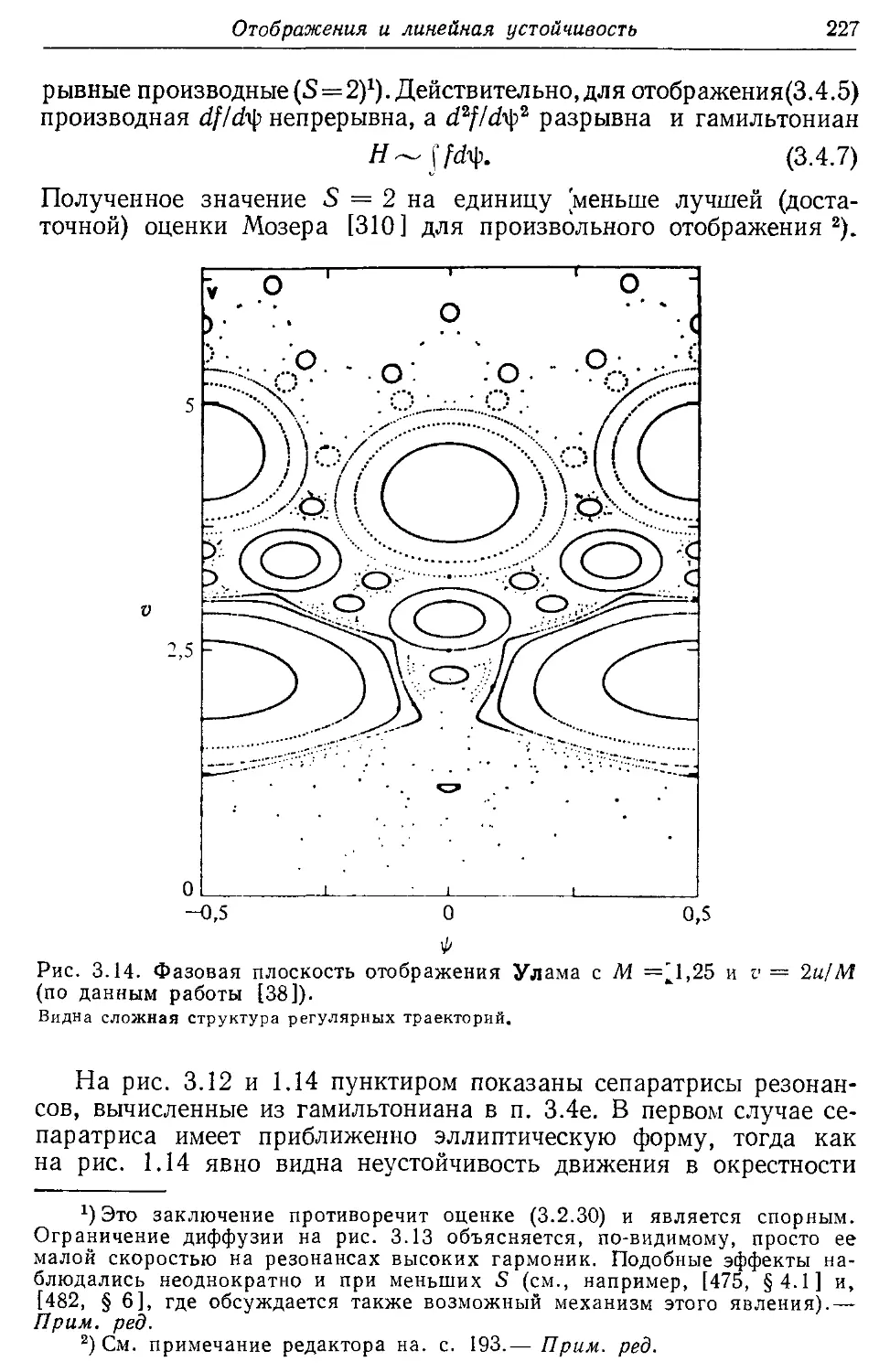
* 3.4в. Периодические точки и их линейная устойчивость 228
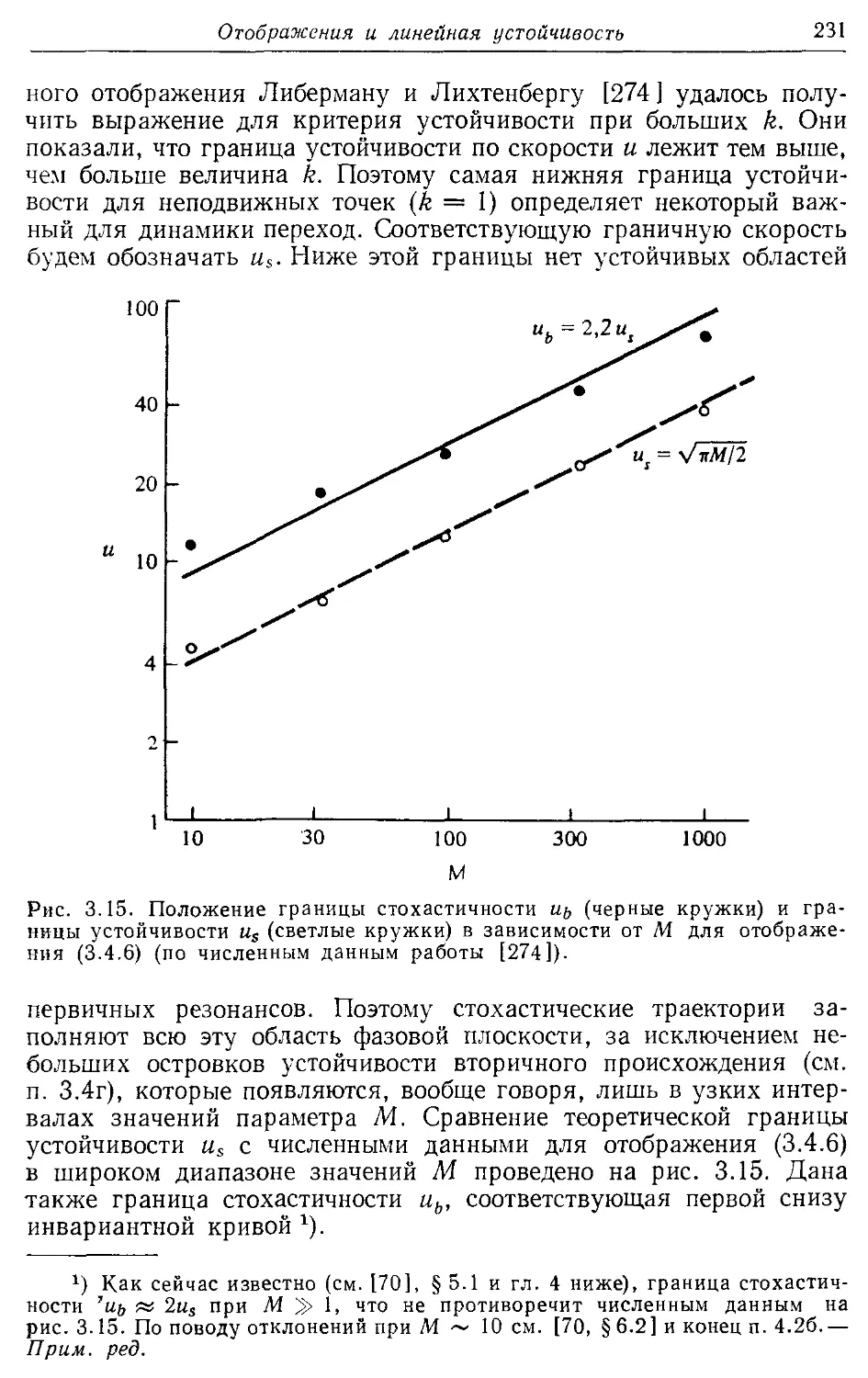
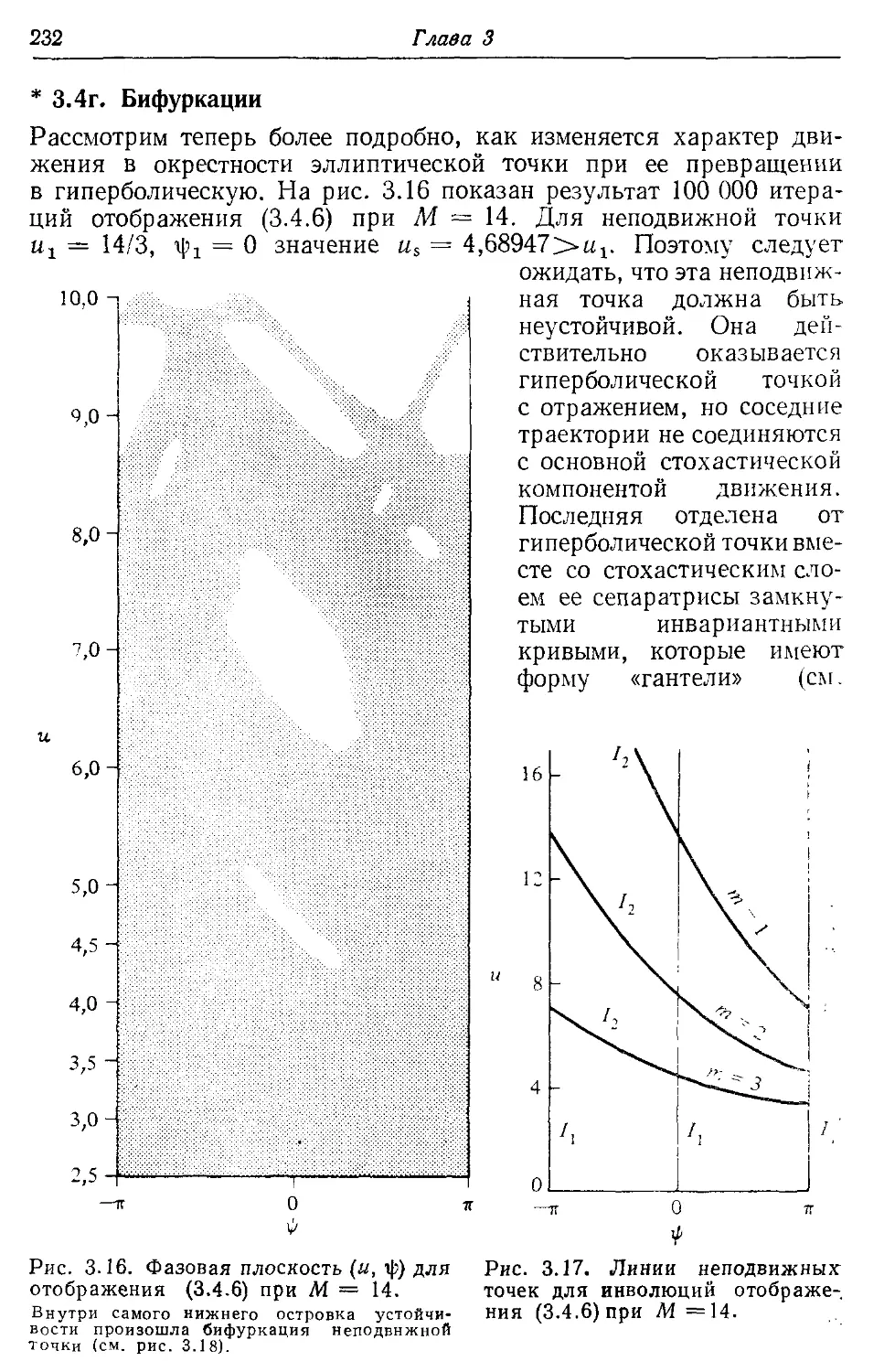
* 3.4г. Бифуркации 232
* 3.4д. Уравнения Гамильтона 235
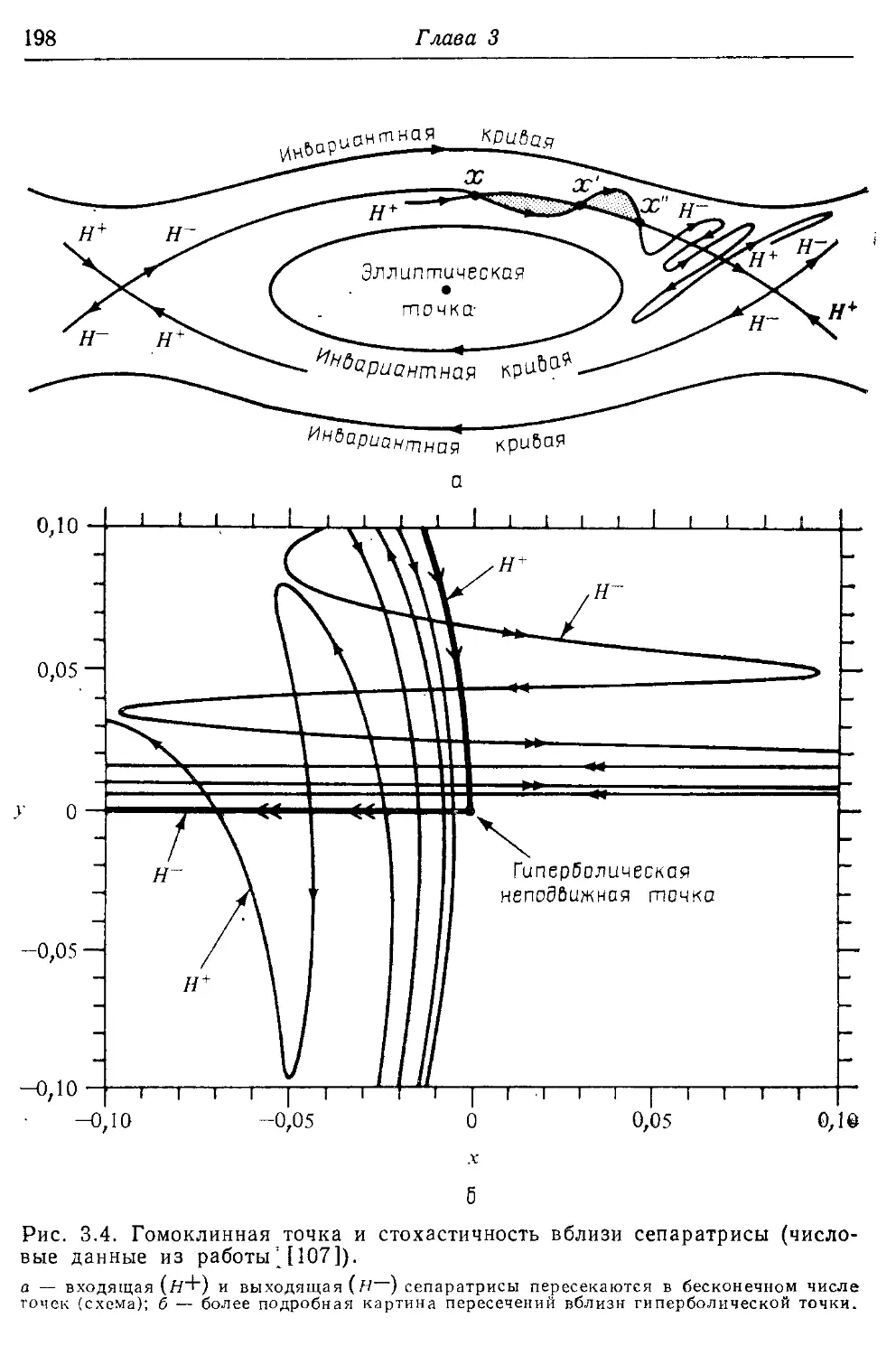
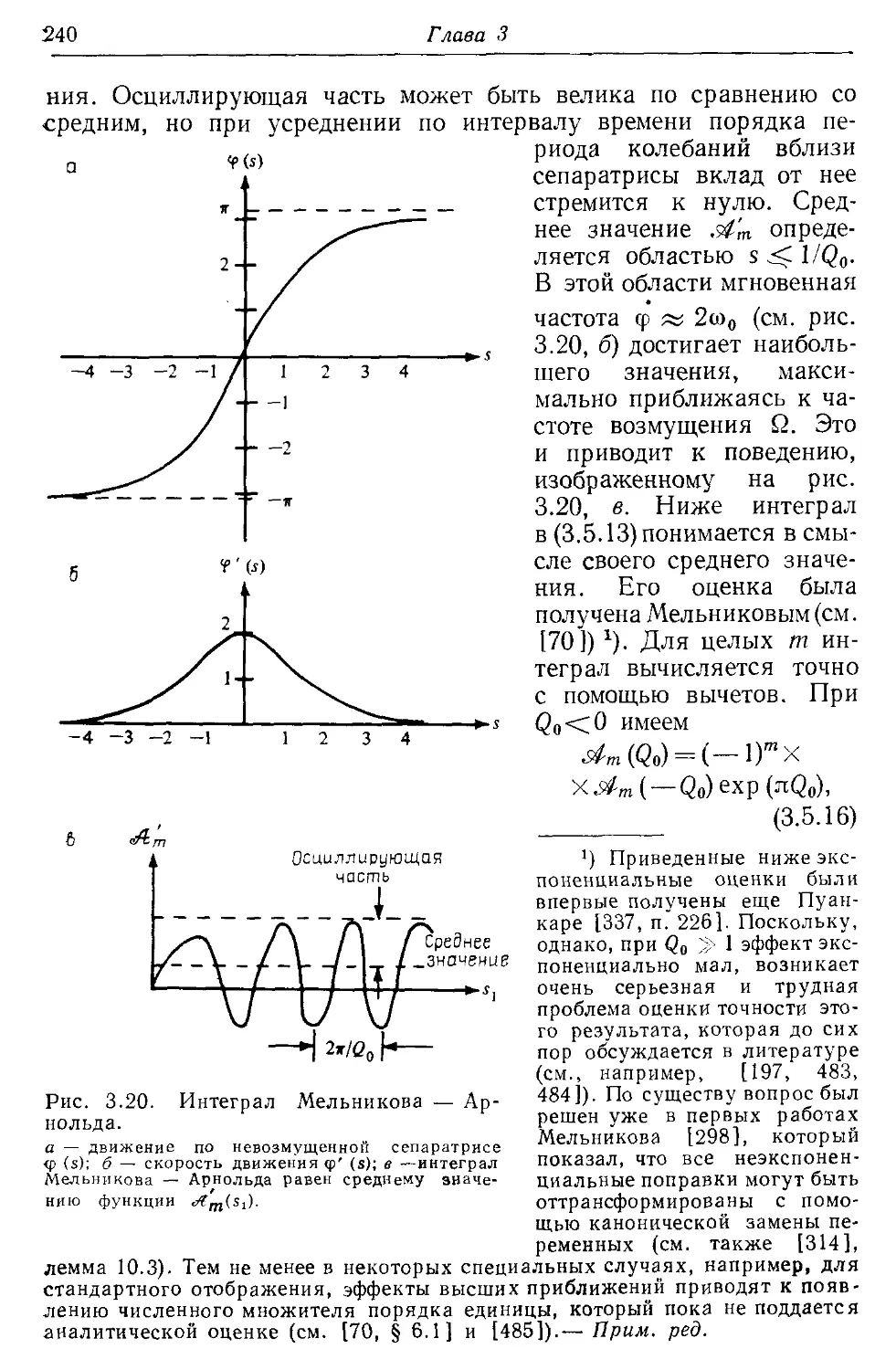
* § 3.5. Движение в окрестности сепаратрисы 236
* 3.5а. Вынужденные колебания маятника 238
* 3.56. Сепаратрисное отображение 241
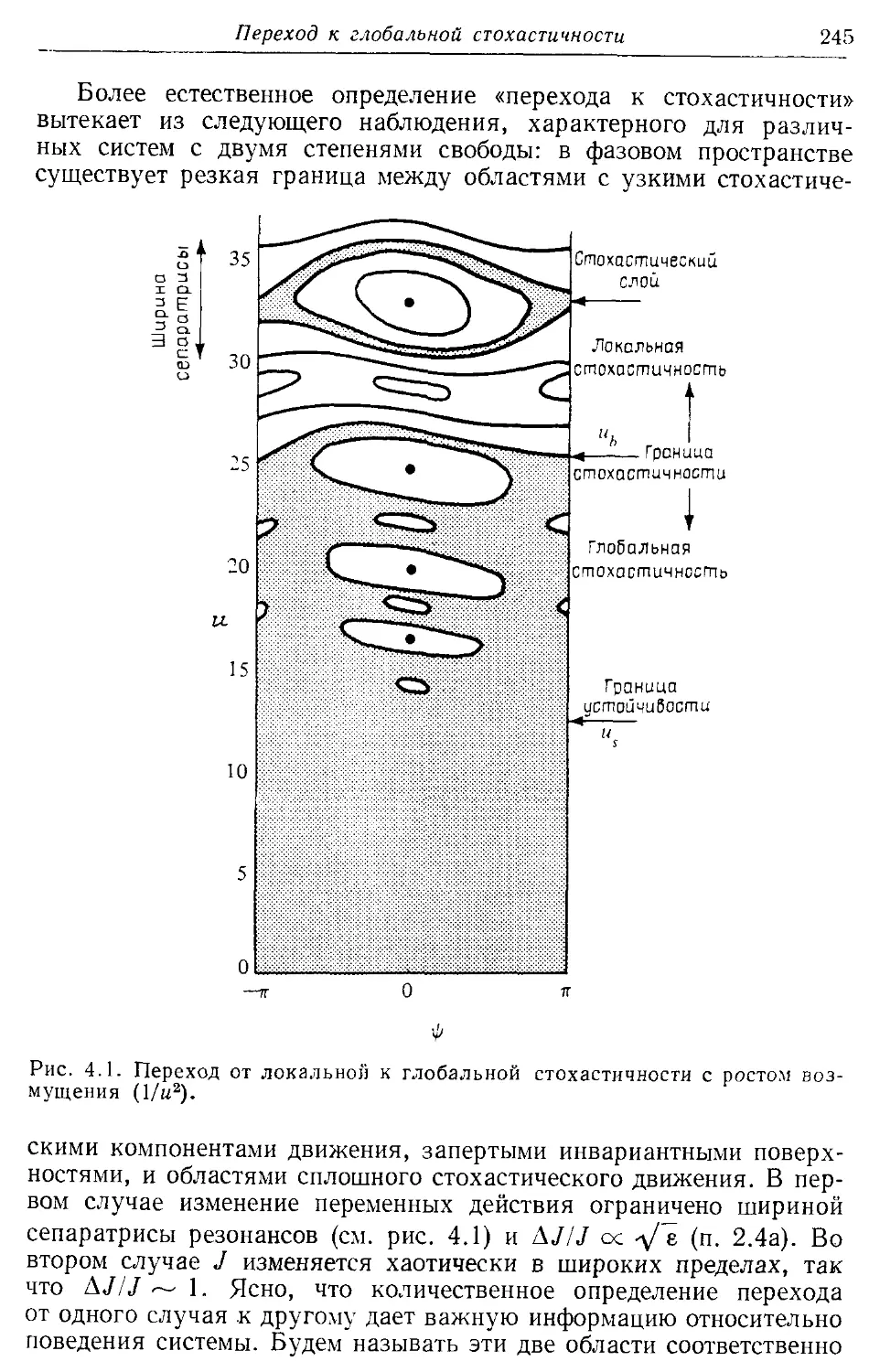
Глава 4. Переход к глобальной стохастичности 244
* §4.1. Введение 244
*4.1а. Качественное описание критериев перехода 246
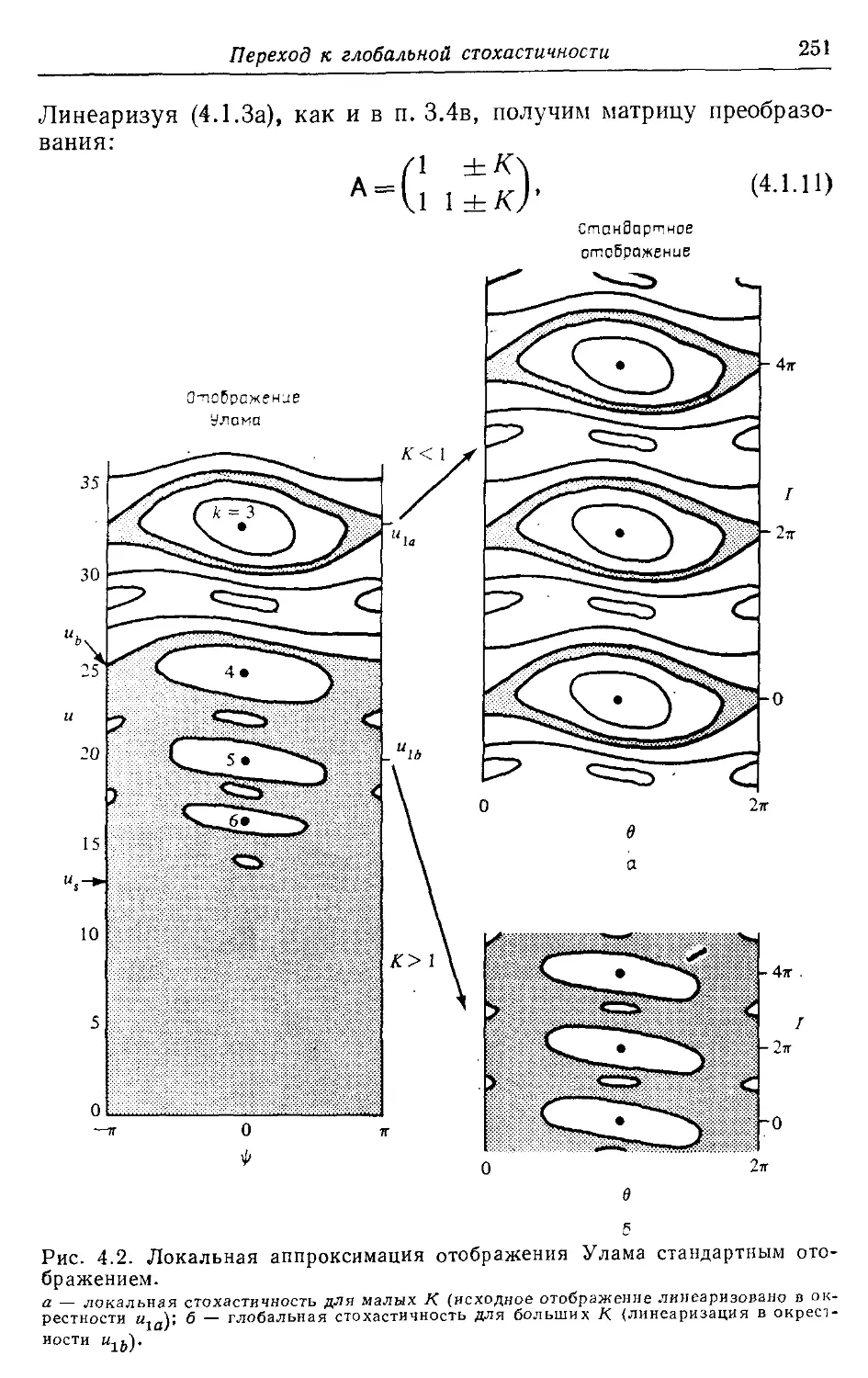
* 4.16. Стандартное отображение 249
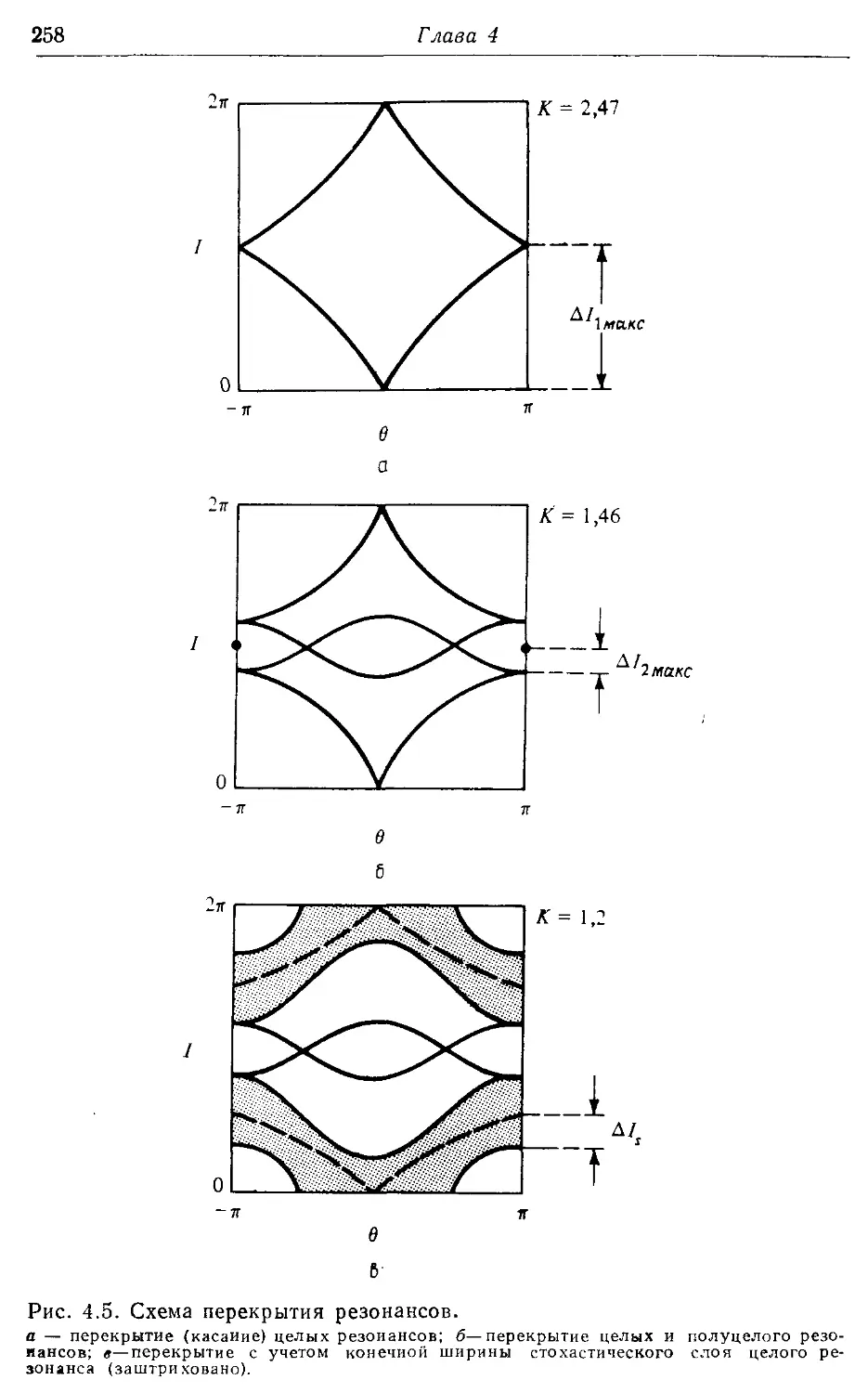
* § 4.2. Перекрытие резонансов 257
* 4.2а. Схема получения критериев 257
* 4.26. Вычисление критериев перекрытия 257
§ 4.3. Вторичные резонансы 263
4.3а. Центр резонанса 263
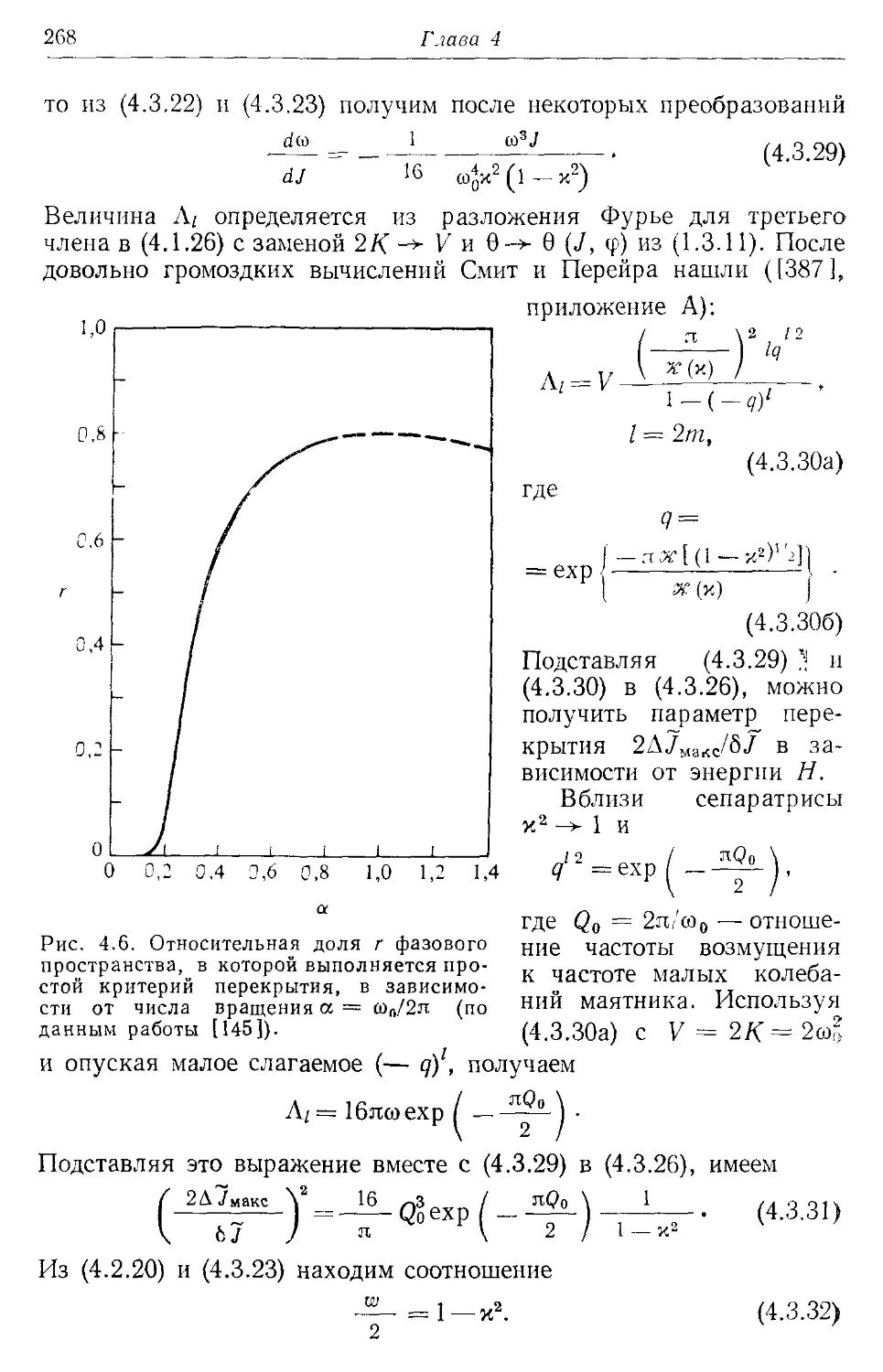
4.36. Сепаратриса 267
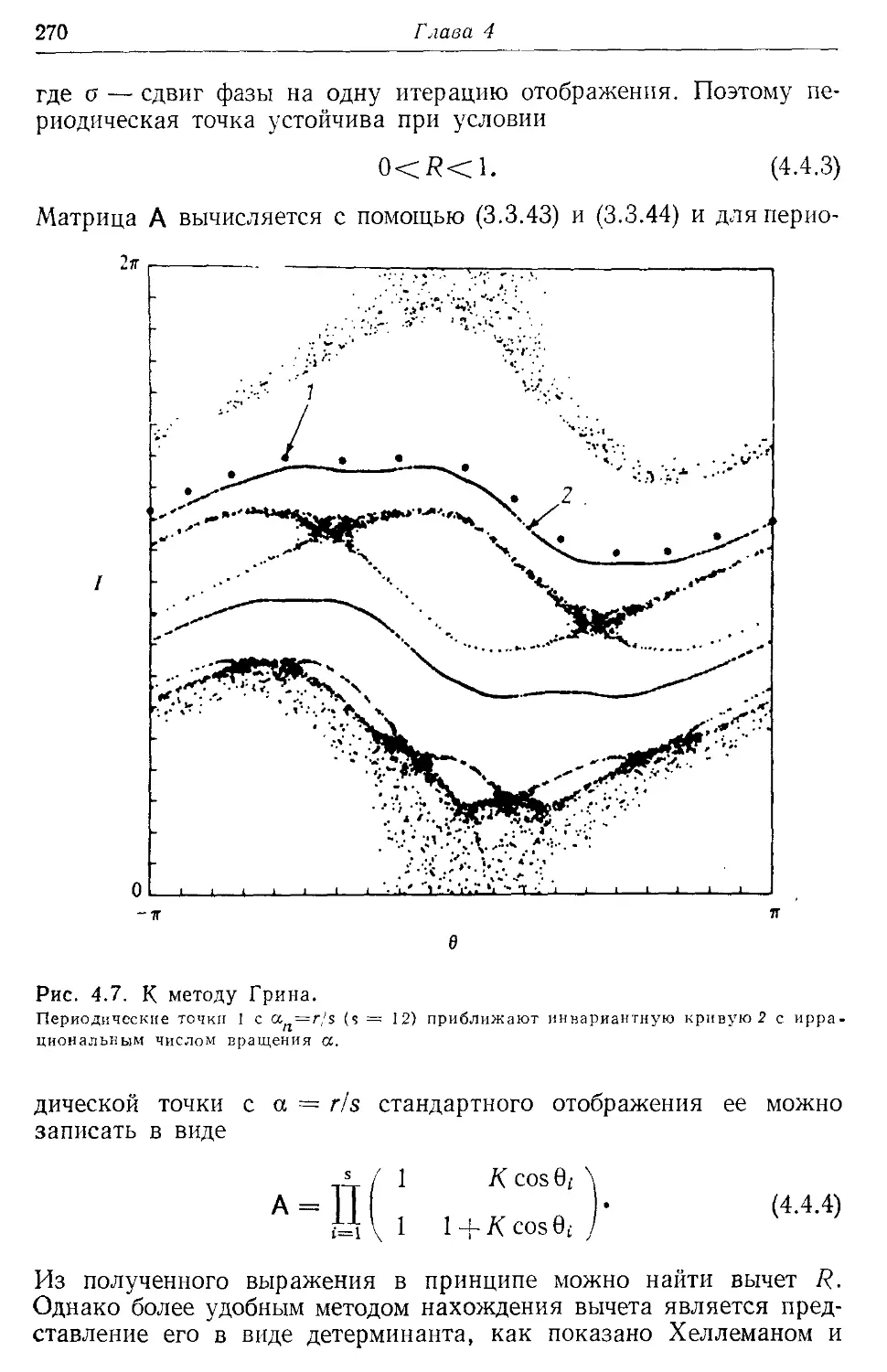
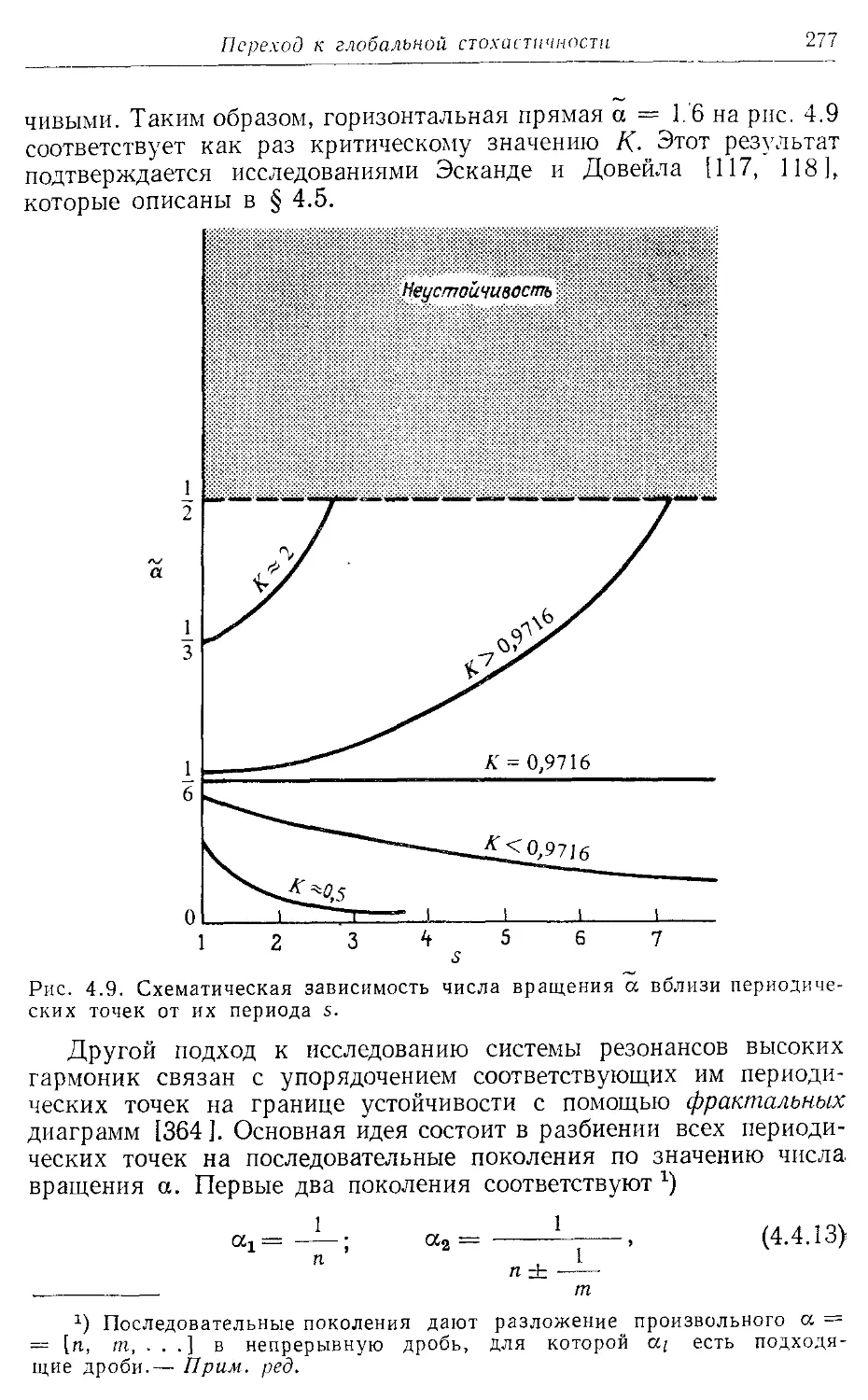
* § 4.4. Резонансы высоких гармоник 269
* 4.4а. Основы метода Грина 269
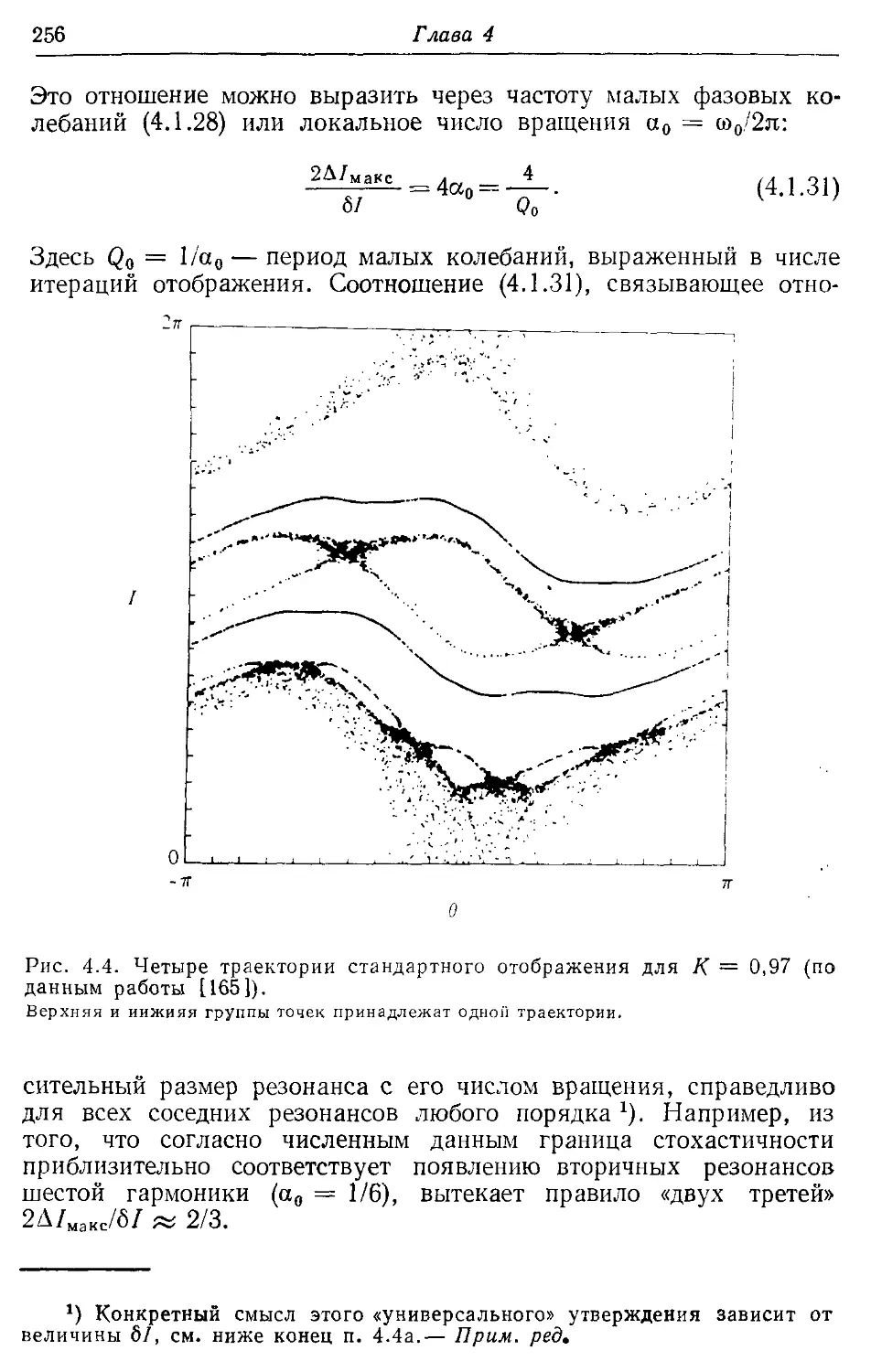
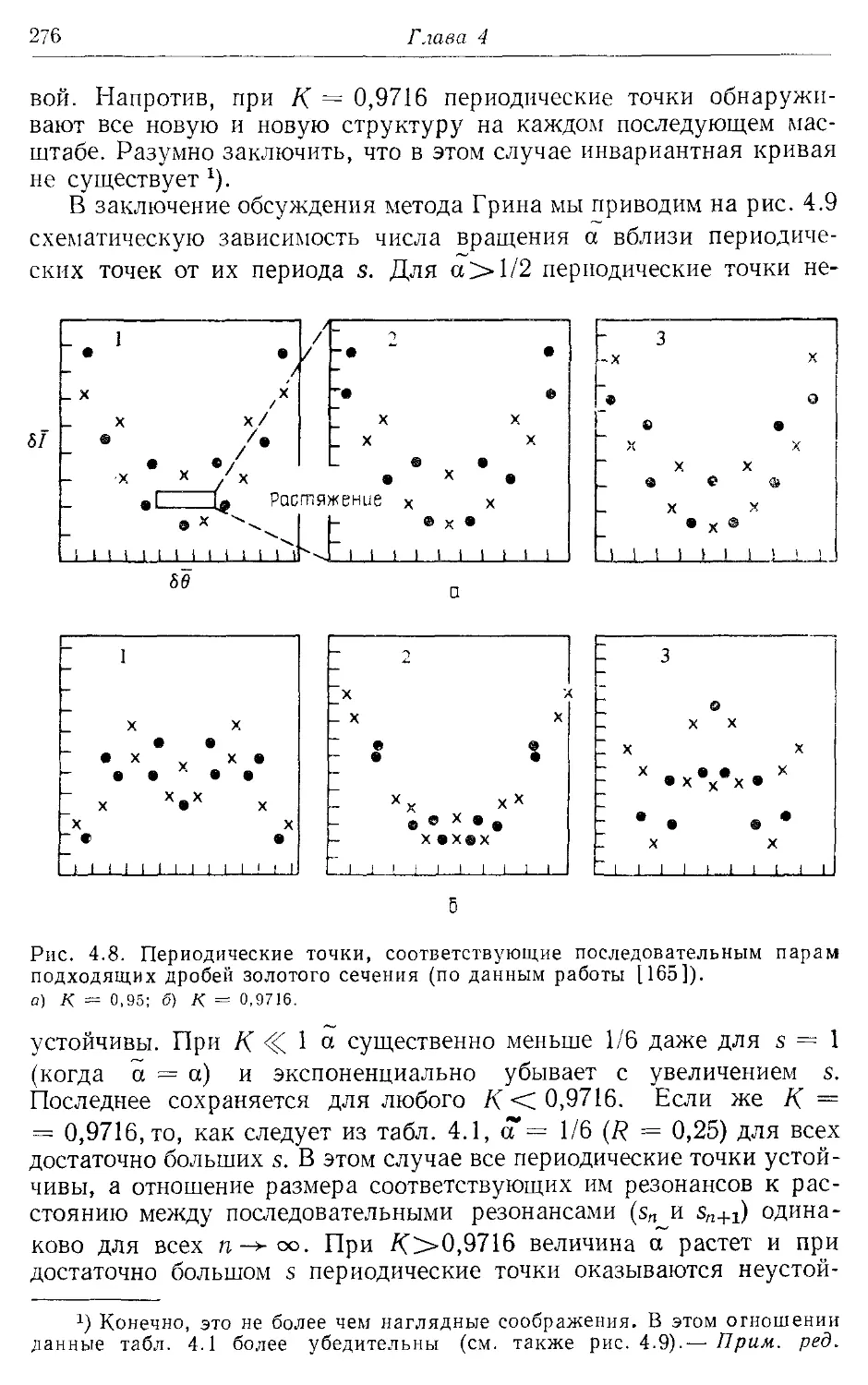
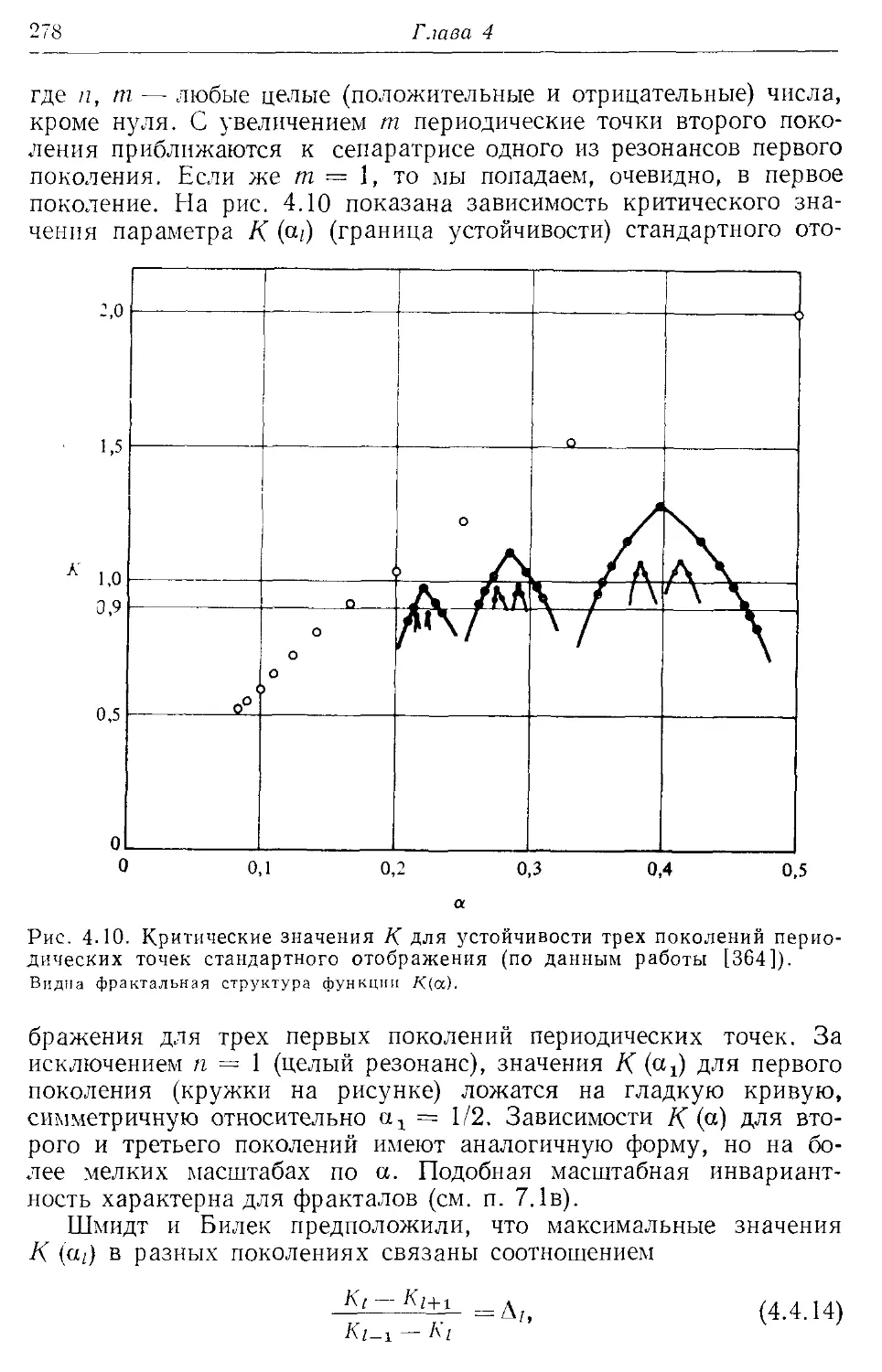
* 4.46. Численные эксперименты 274
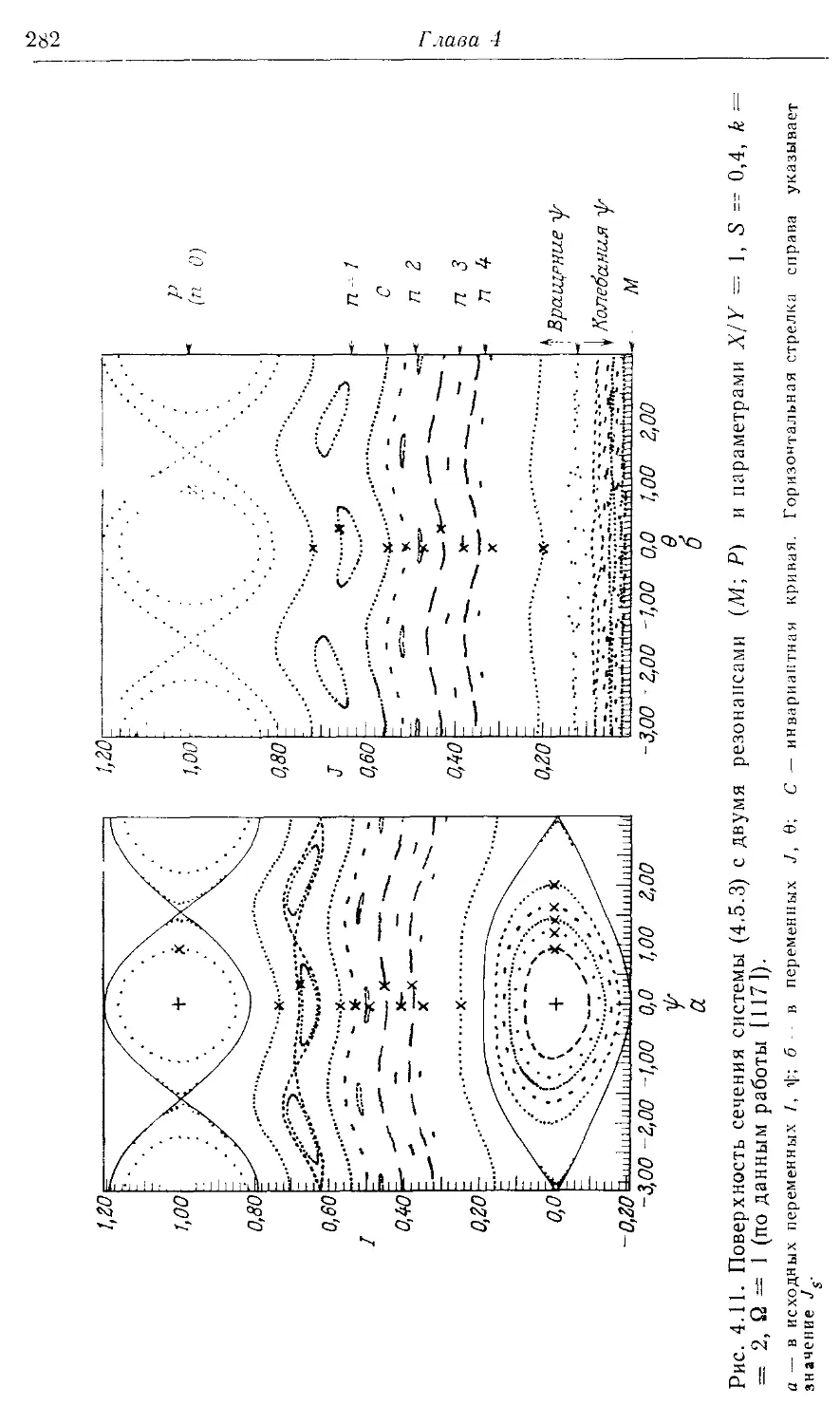
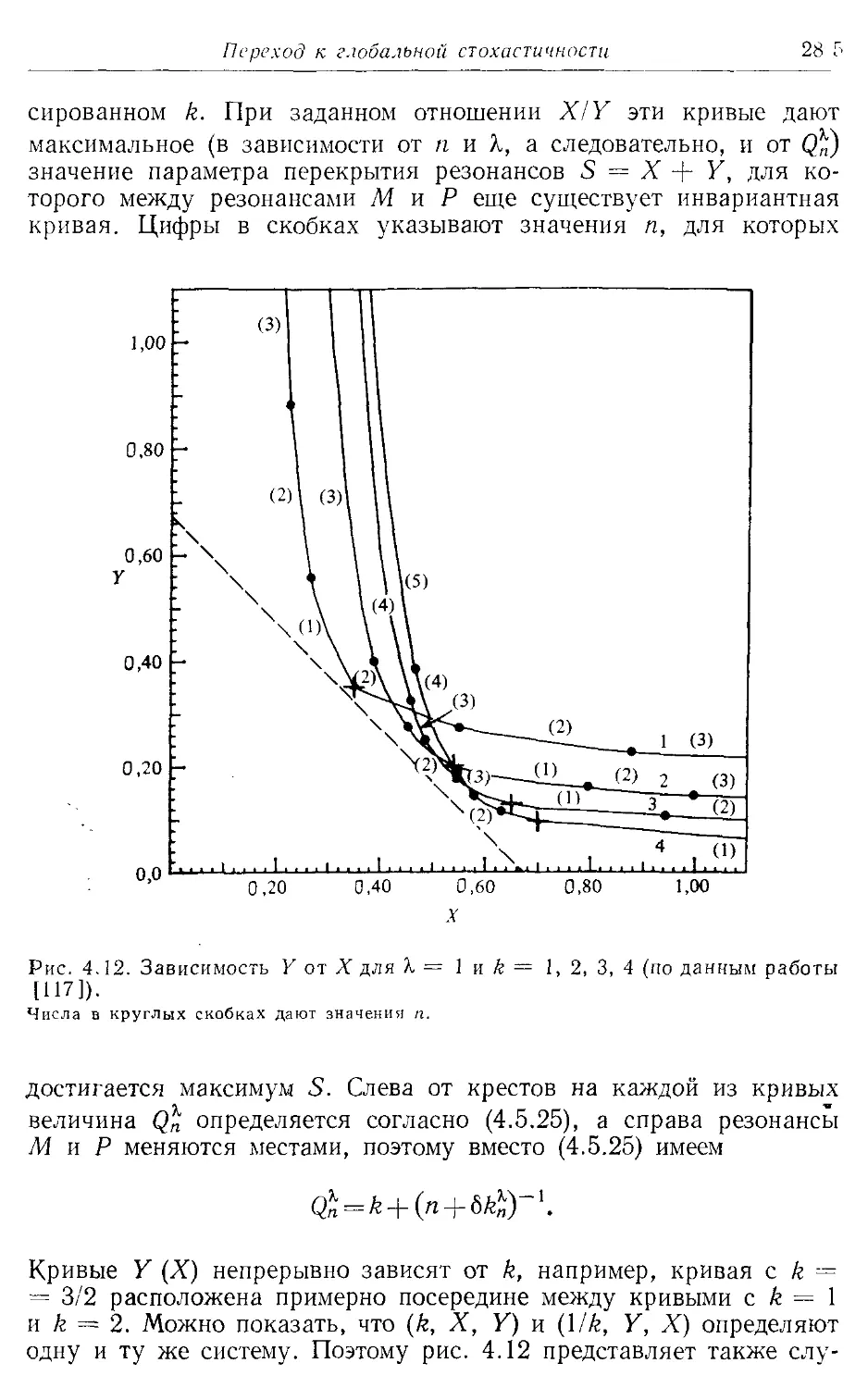
§ 4.5. Метод ренормализации для двух резонансов 279
§ 4.6. Вариационные методы 287
* § 4.7. Заключение 288
Глава 5. Стохастическое движение и диффузия 290
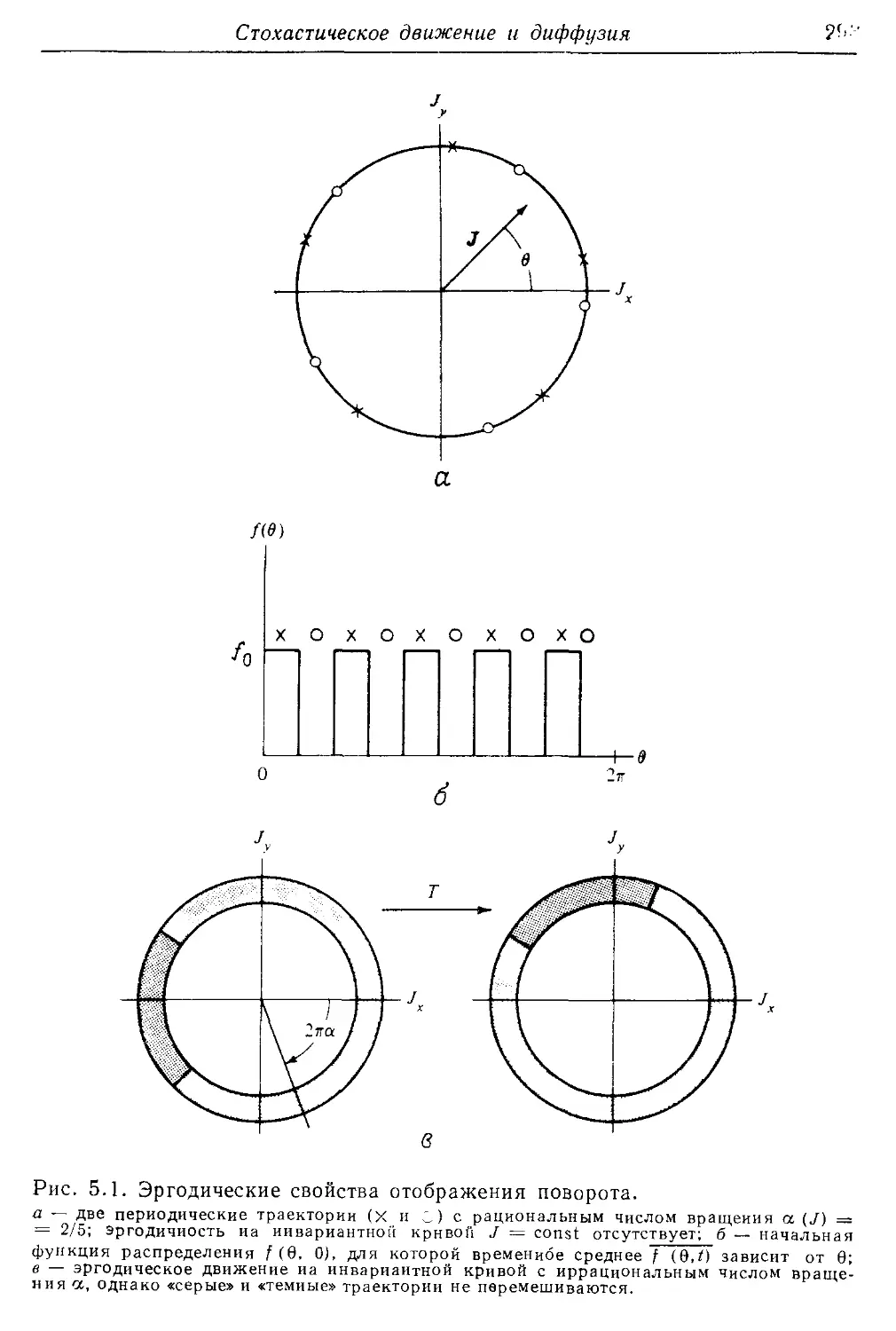
§5.1. Введение 290
§ 5.2. Основные понятия 291
* 5.2а. Эргодичность 291
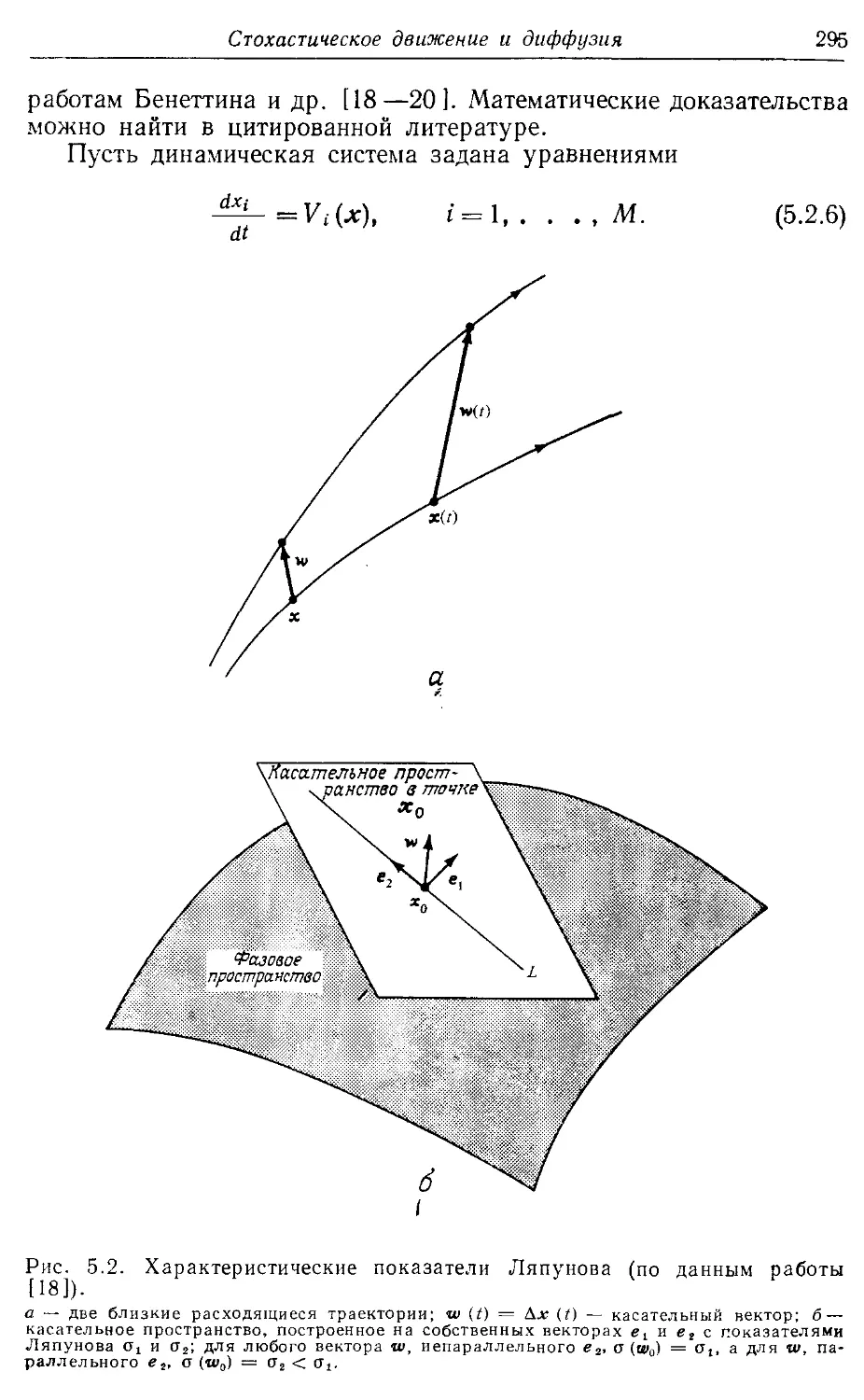
* 5.26. Характеристические показатели Ляпунова 294
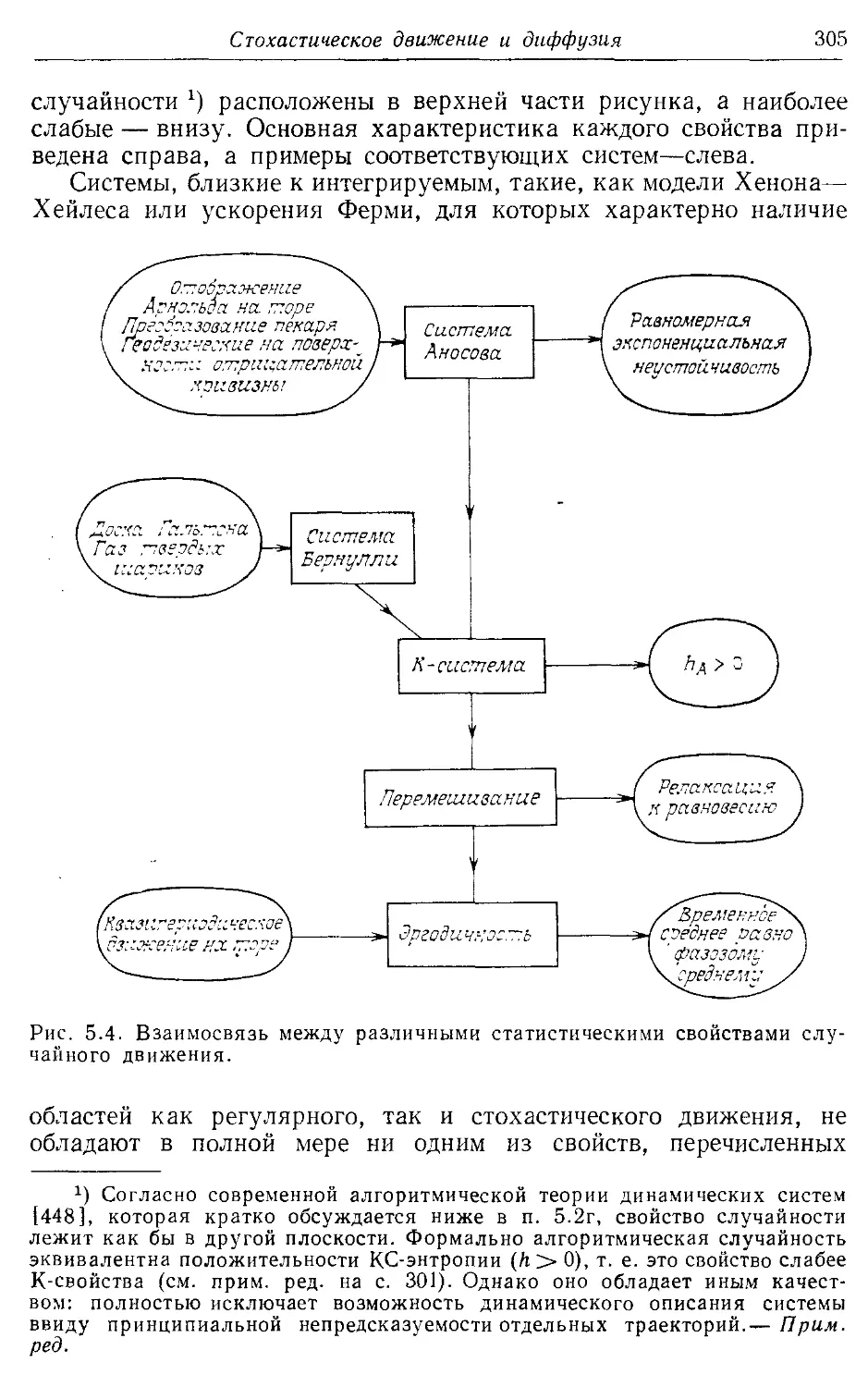
5.2в. Основные свойства стохастичности 298
5.2г. Случайность и ее численное моделирование 306
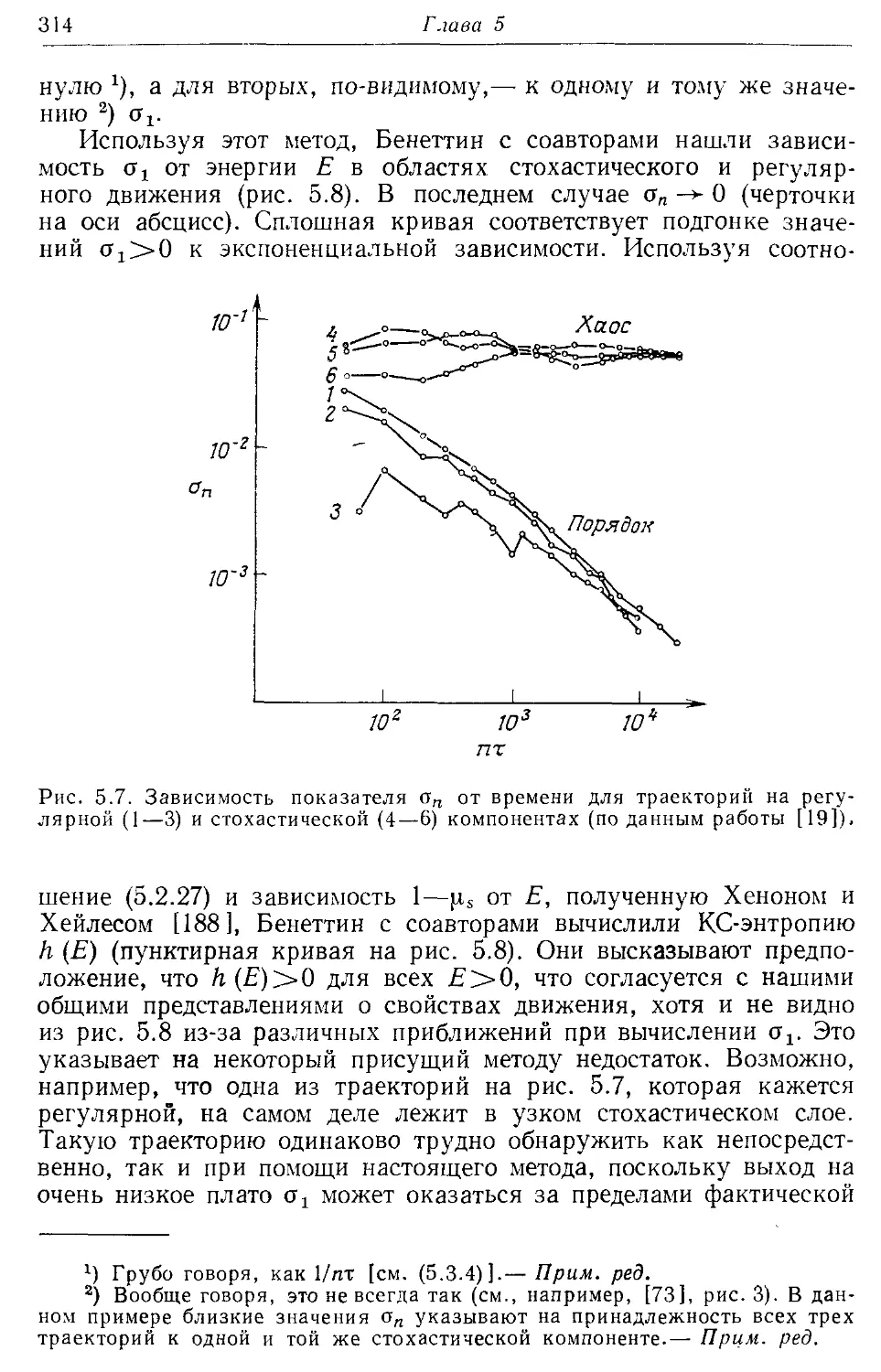
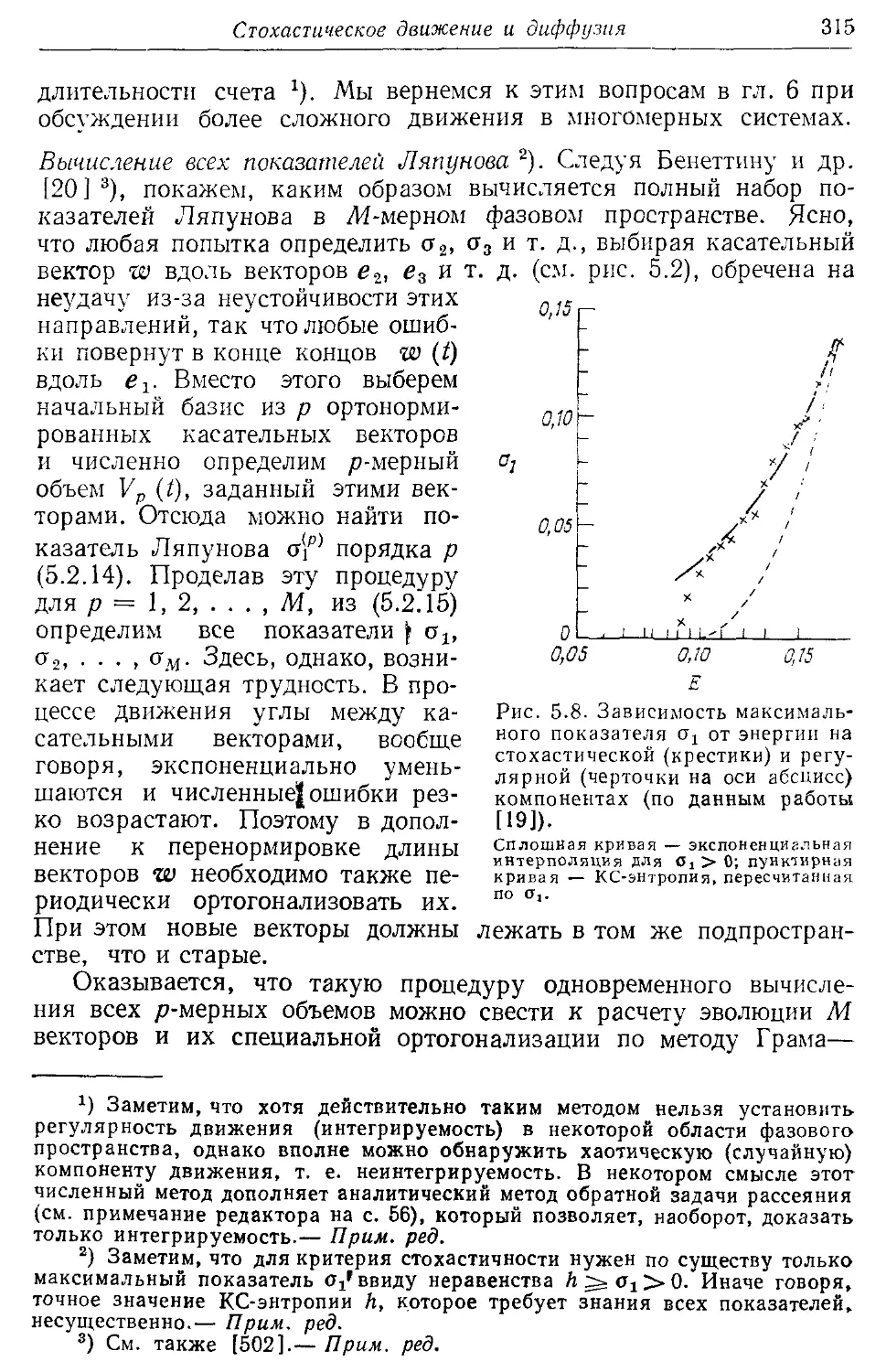
§ 5.3. Определение показателей Ляпунова и КС-энтропии 310
5.3а. Аналитические оценки 311
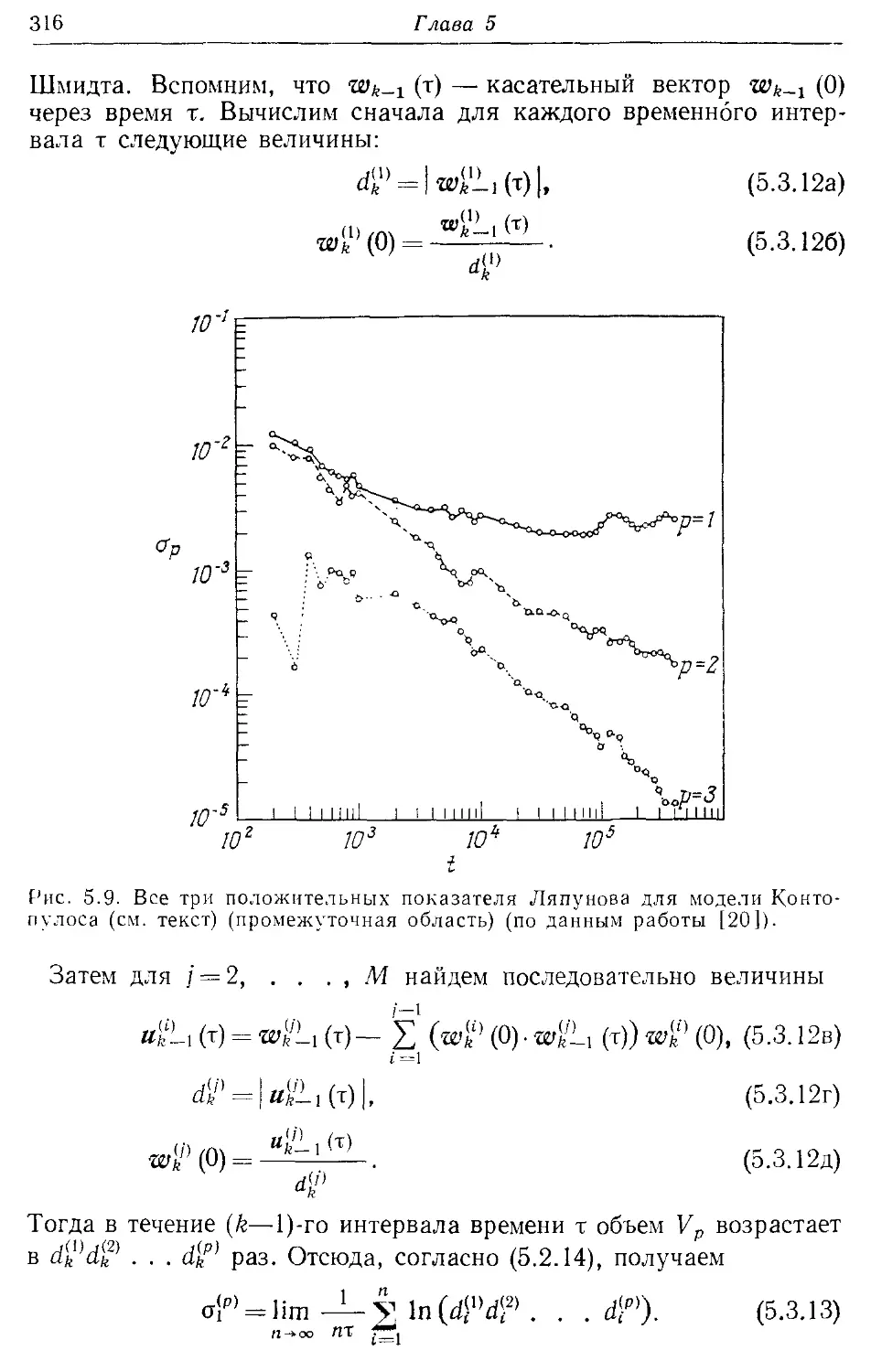
5.36. Численные методы 312
§ 5.4. Диффузия в пространстве действий 317
* 5.4а. Уравнение Фоккера—Планка 318
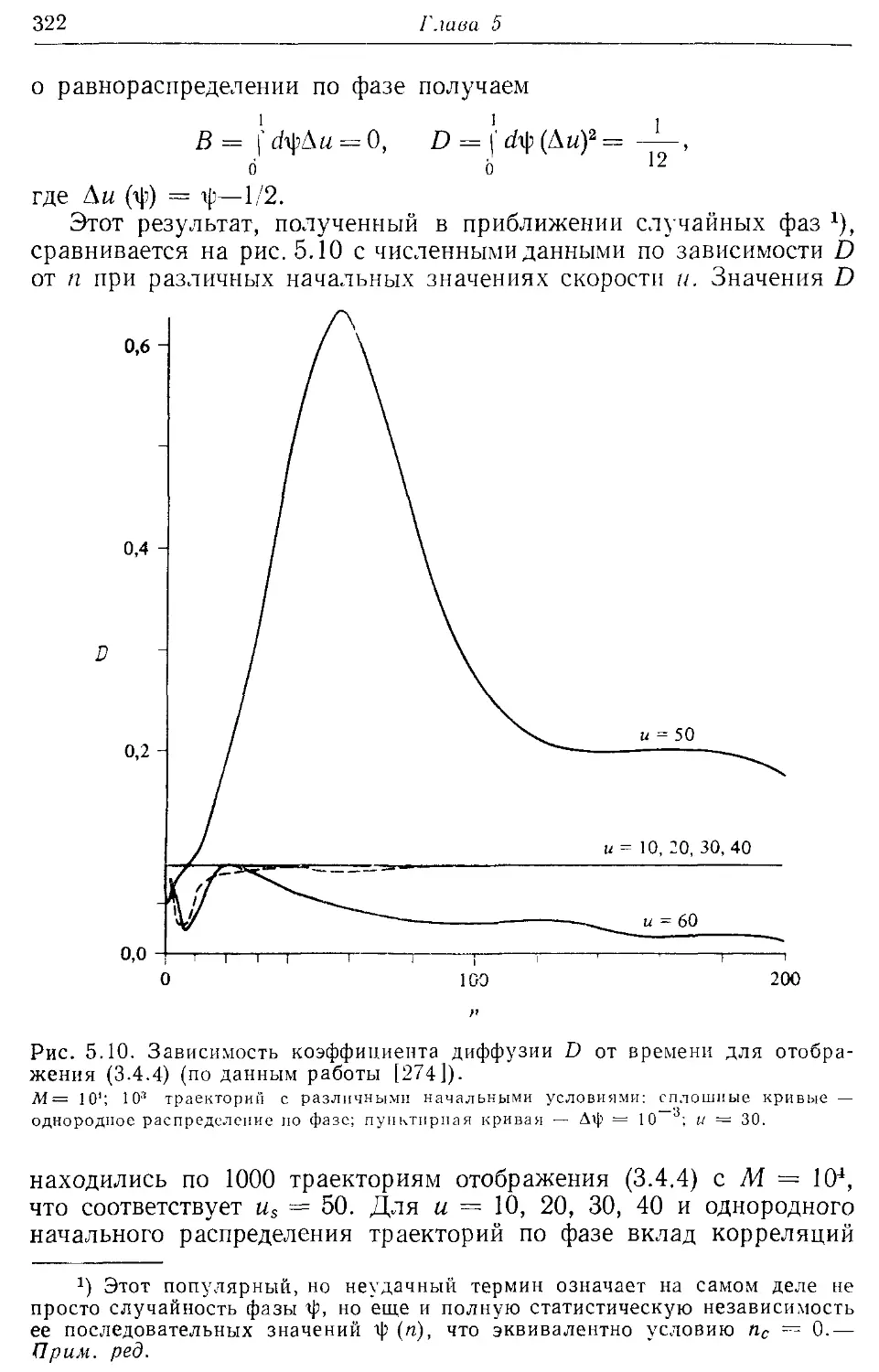
* 5.46. Коэффициенты переноса 321
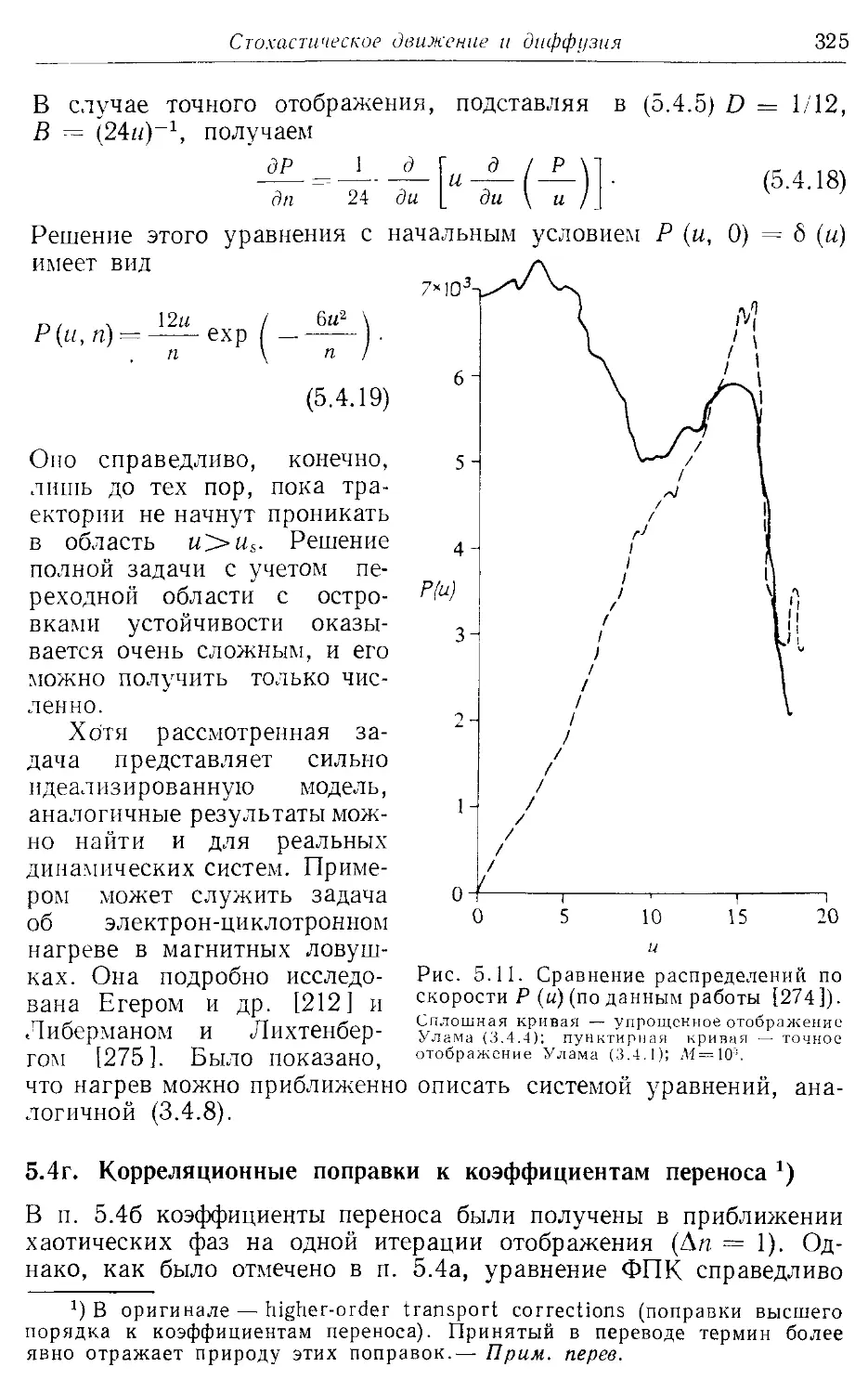
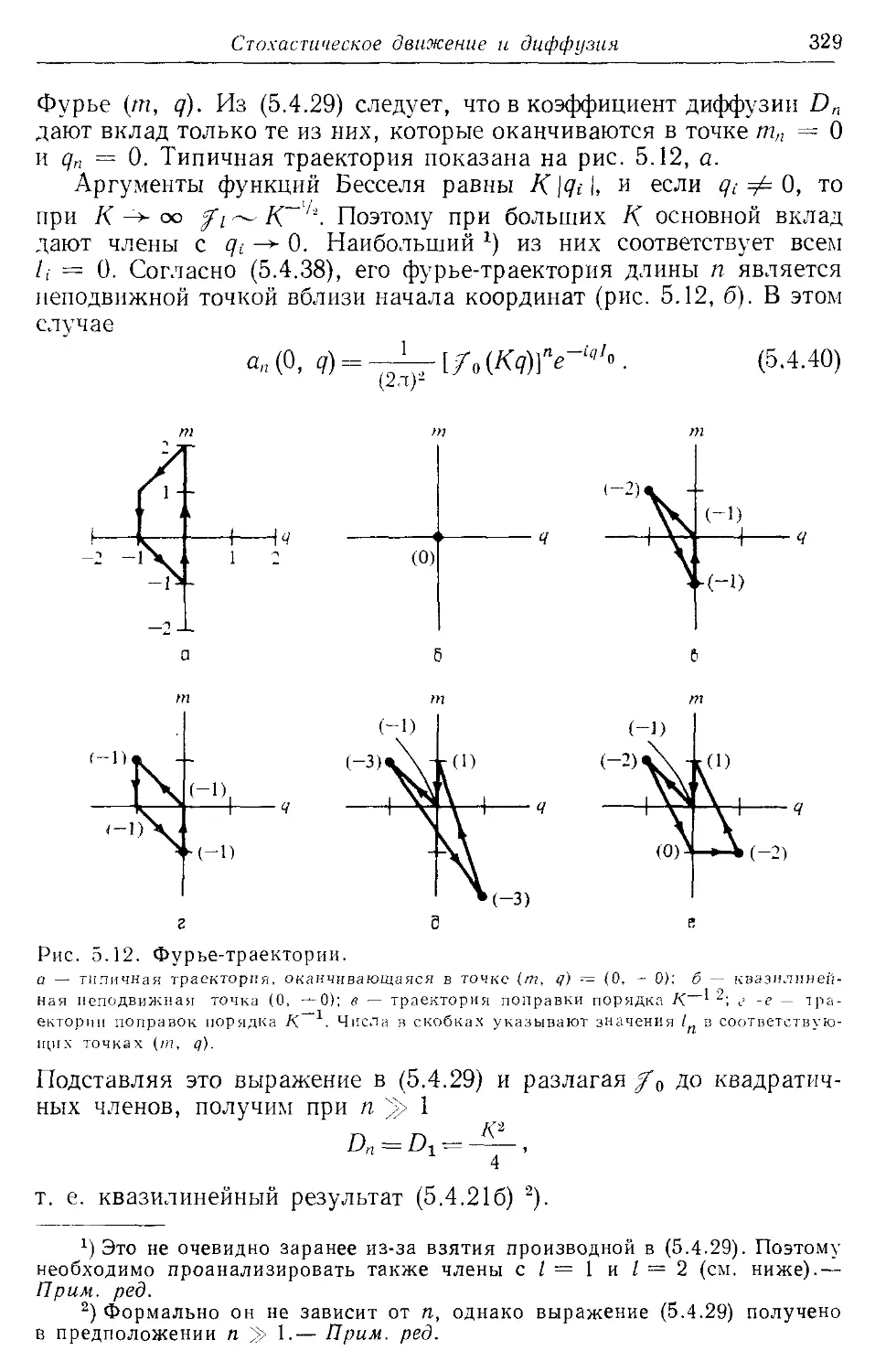
* 5.4в. Стационарные и нестационарные решения 324
5.4г. Корреляционные поправки к коэффициентам переноса 325
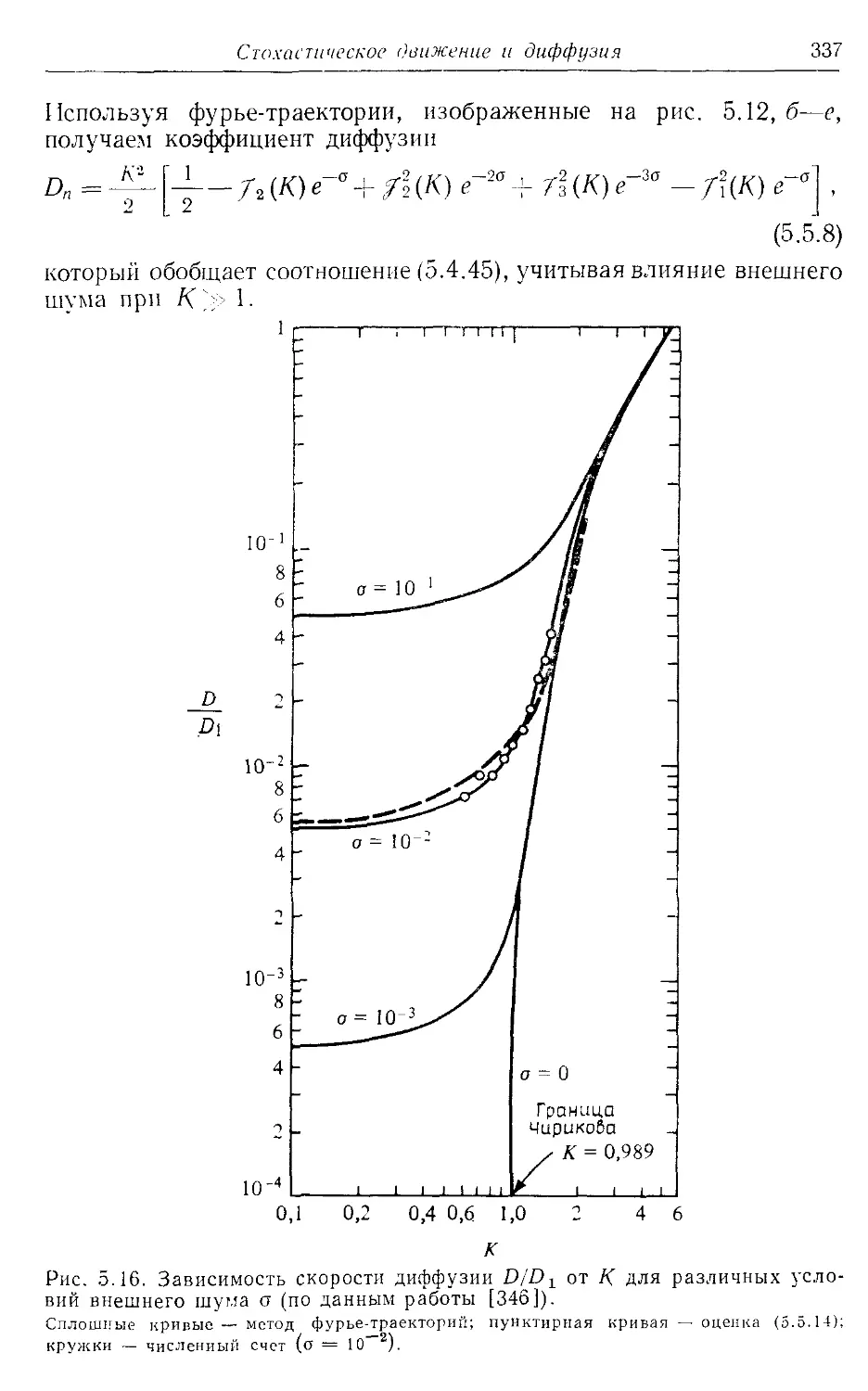
§ 5.5. Влияние внешнего шума 332
5.5а. Введение 332
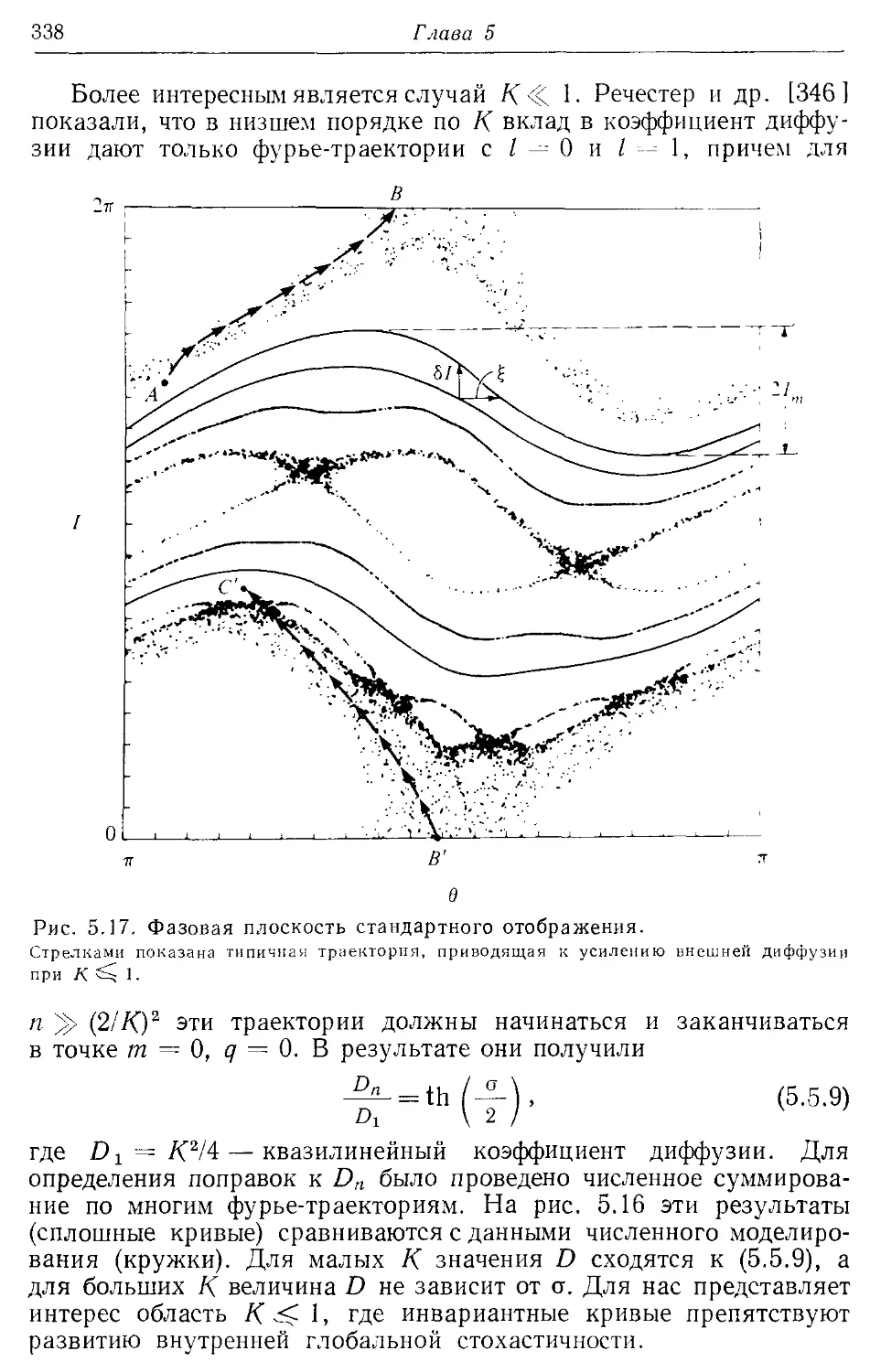
5.56. Диффузия в присутствии резонансов 335
Глава 6. Многомерные колебания 341
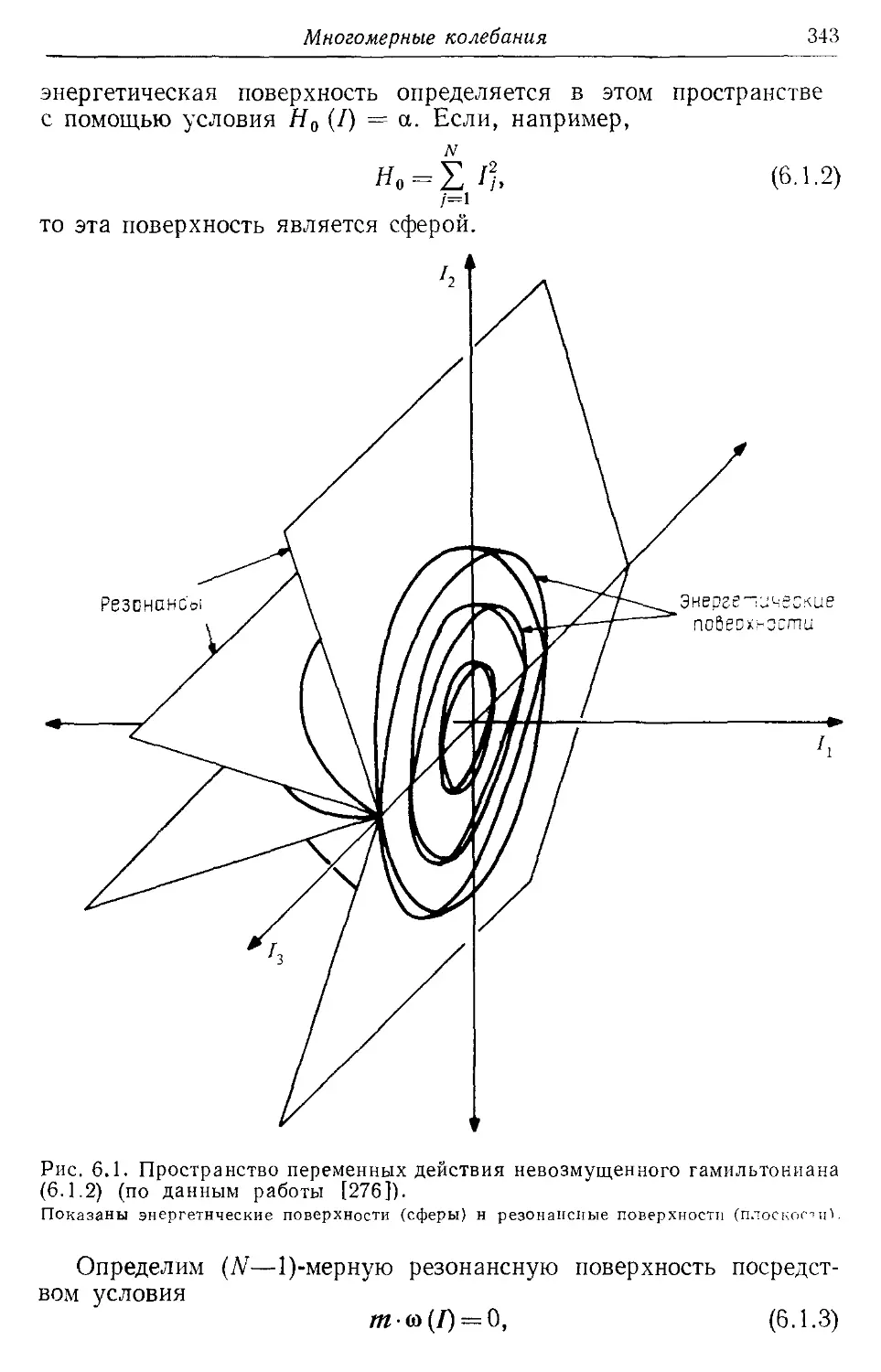
* § 6.1. Резонанс многомерных колебаний 341
* 6.1а. Геометрия резонансов 342
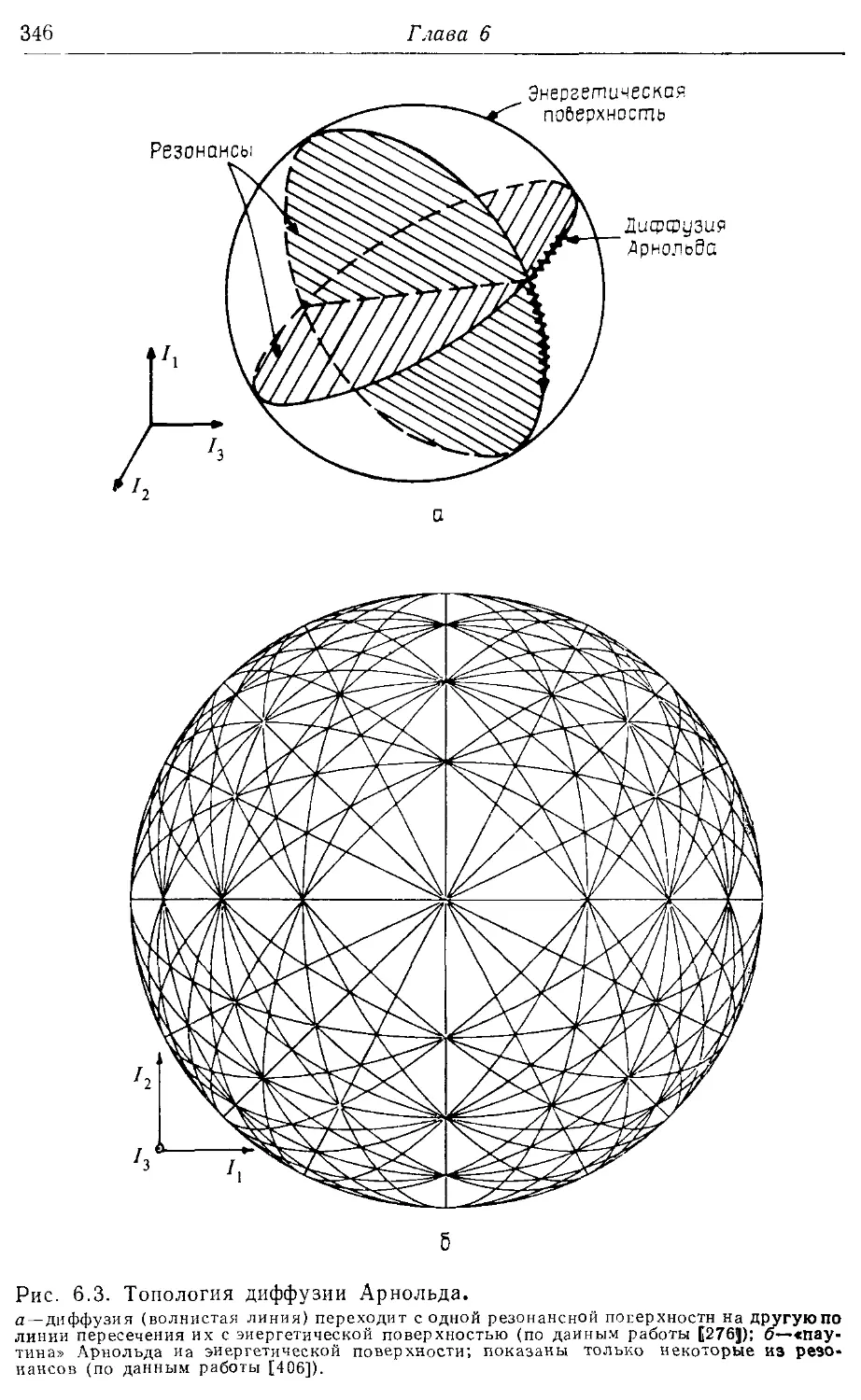
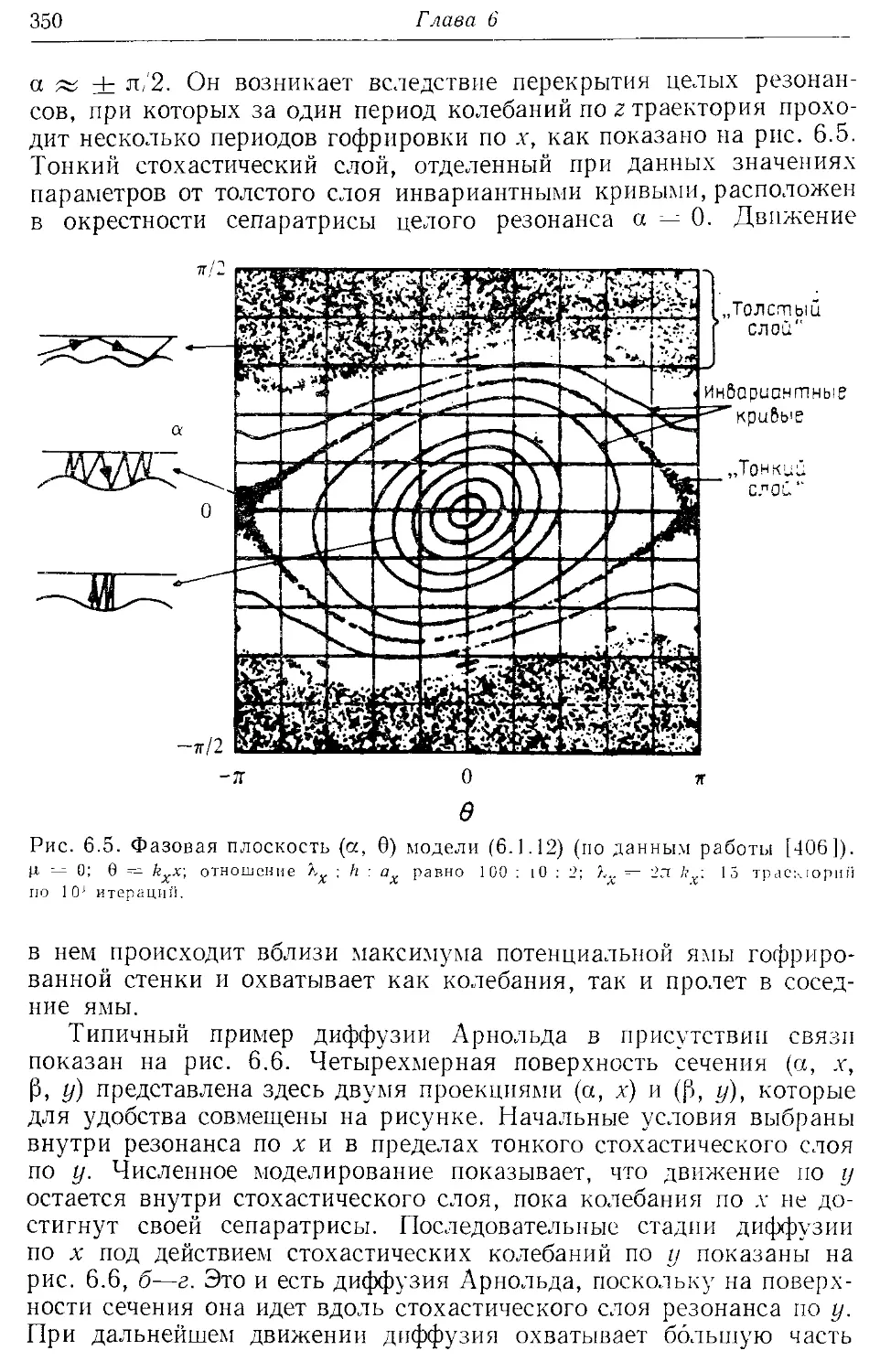
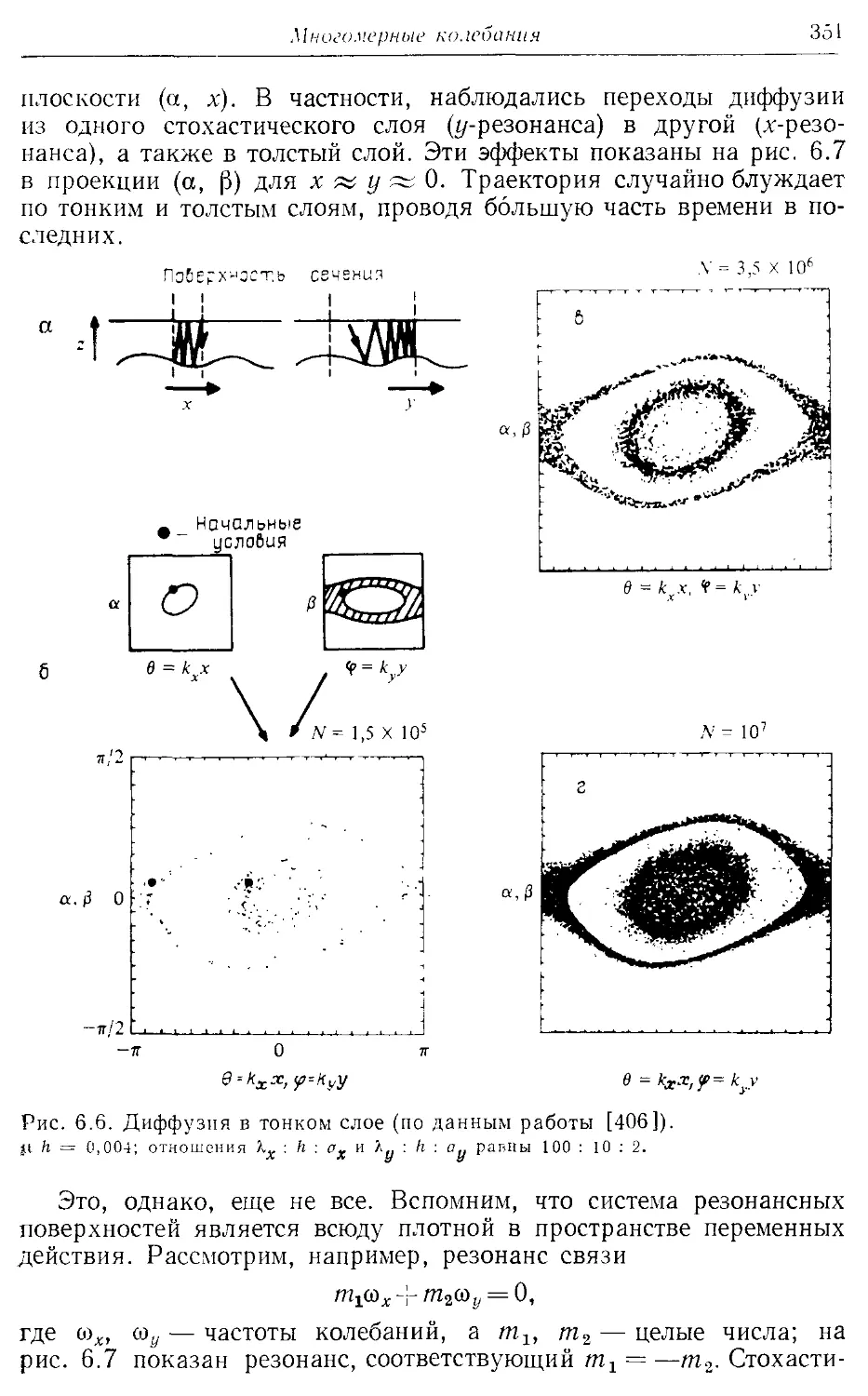
* 6.16. Примеры диффузии Арнольда 347
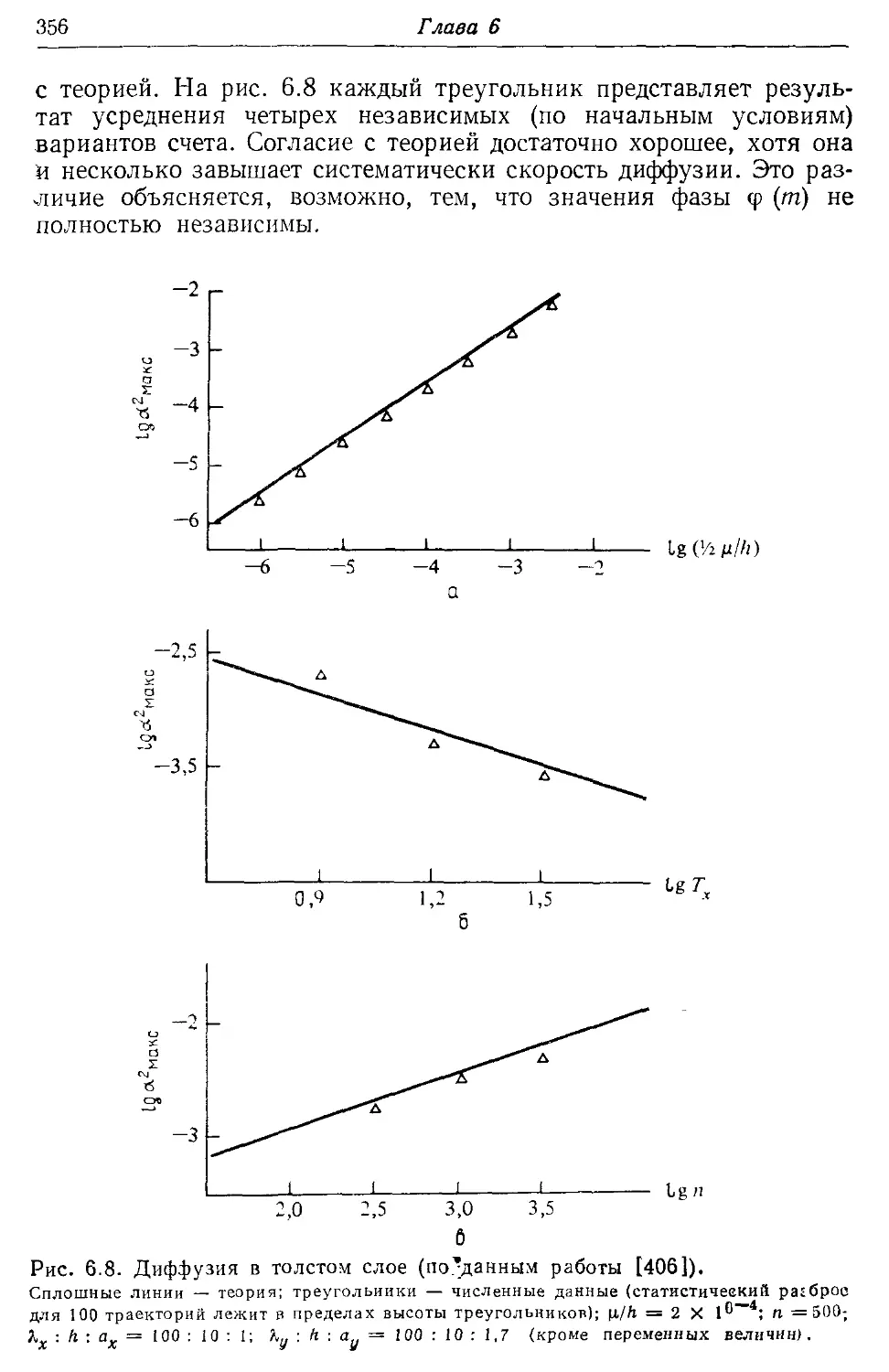
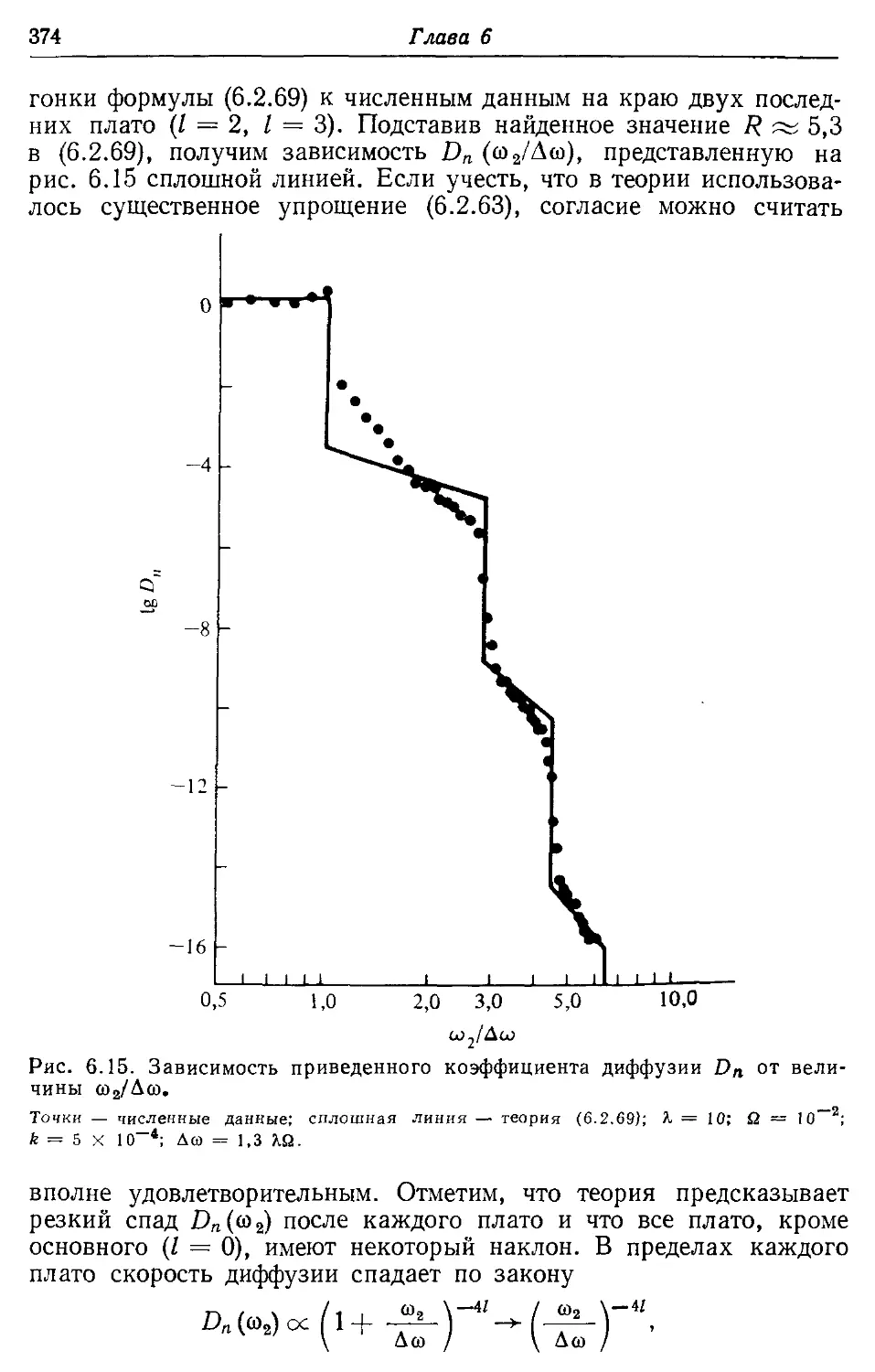
§ 6.2. Скорость диффузии вдоль резонансов 353
* 6.2а. Расчет диффузии в модели стохастической накачки 353
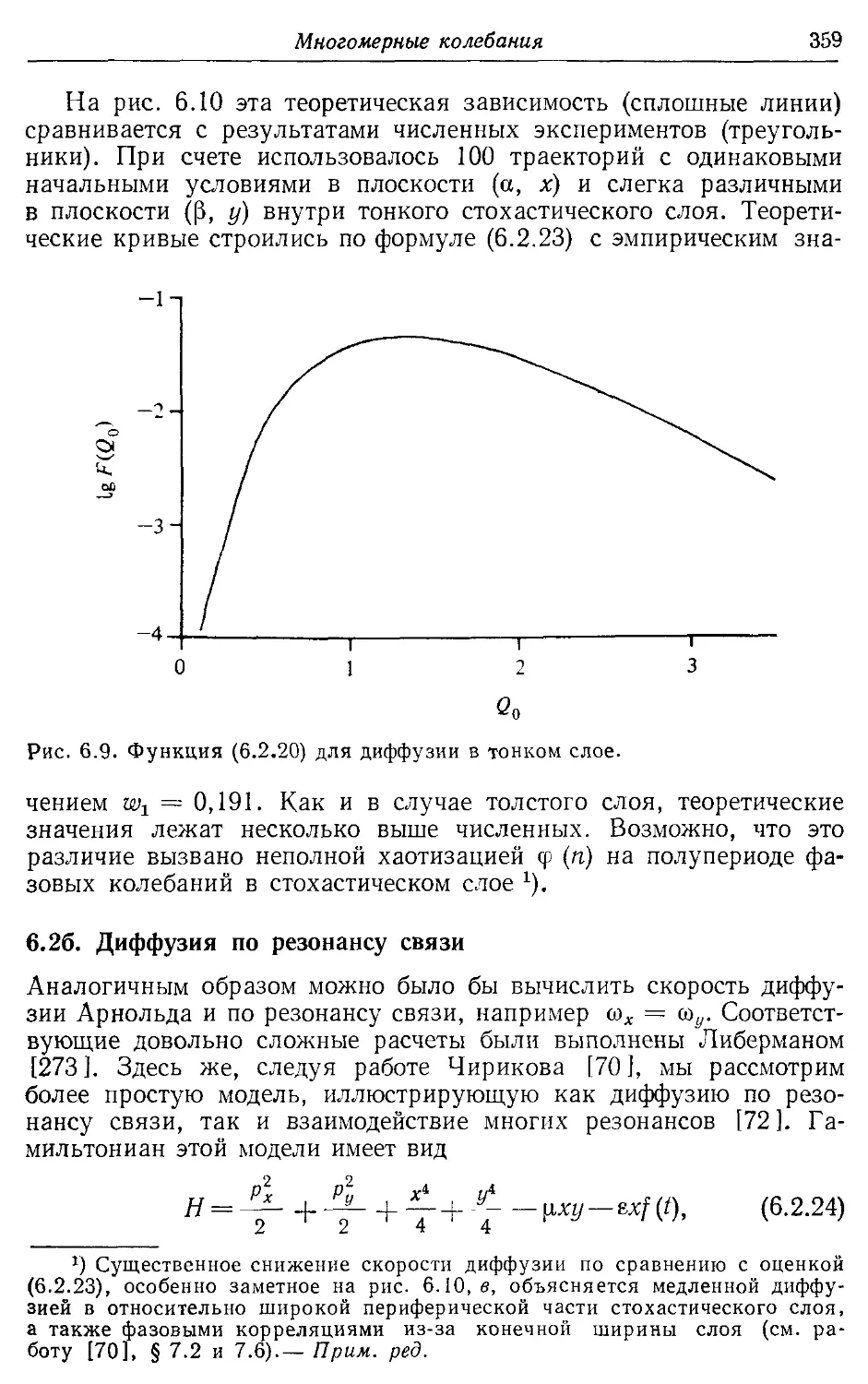
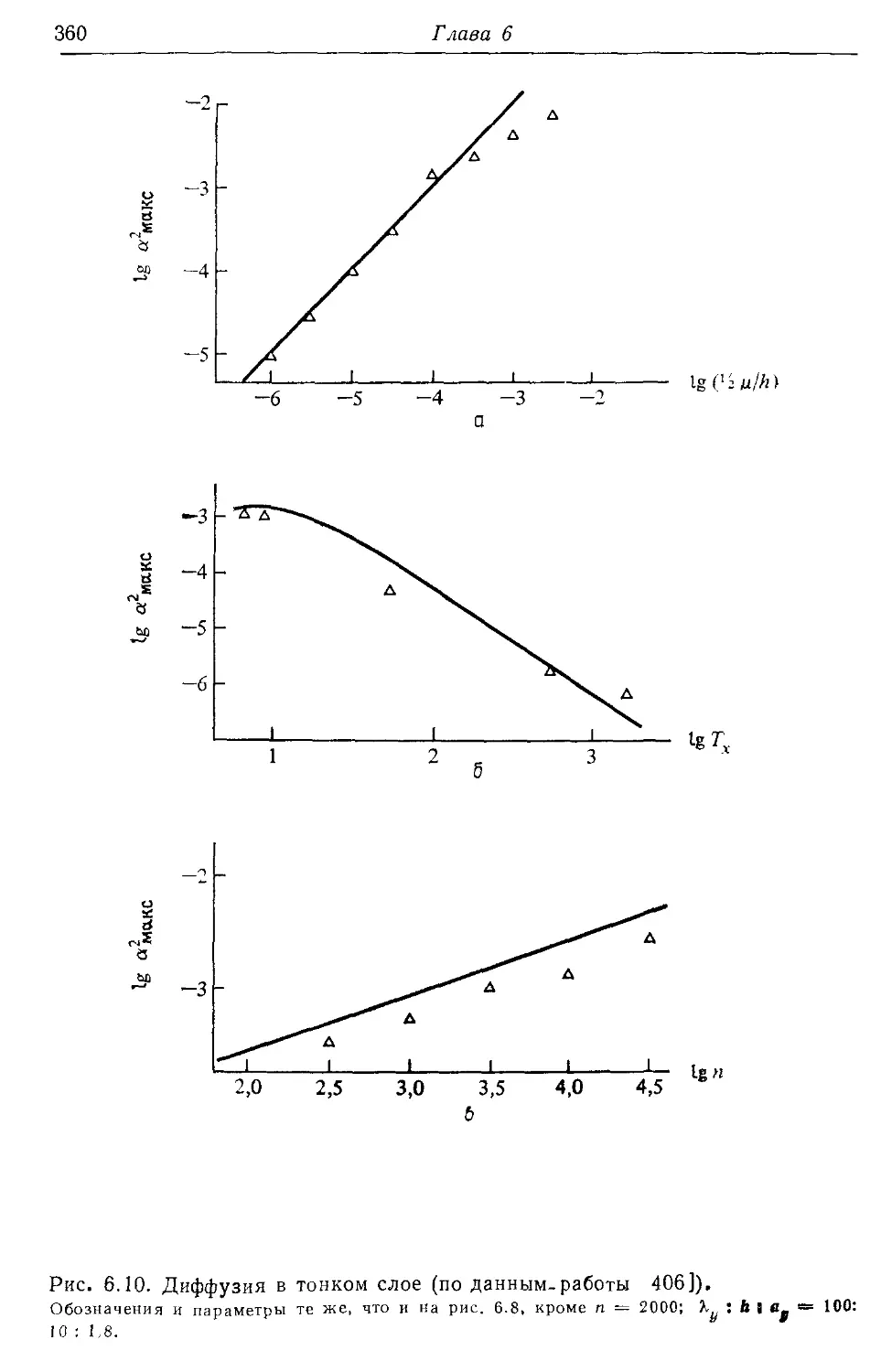
6.26. Диффузия по резонансу связи 359
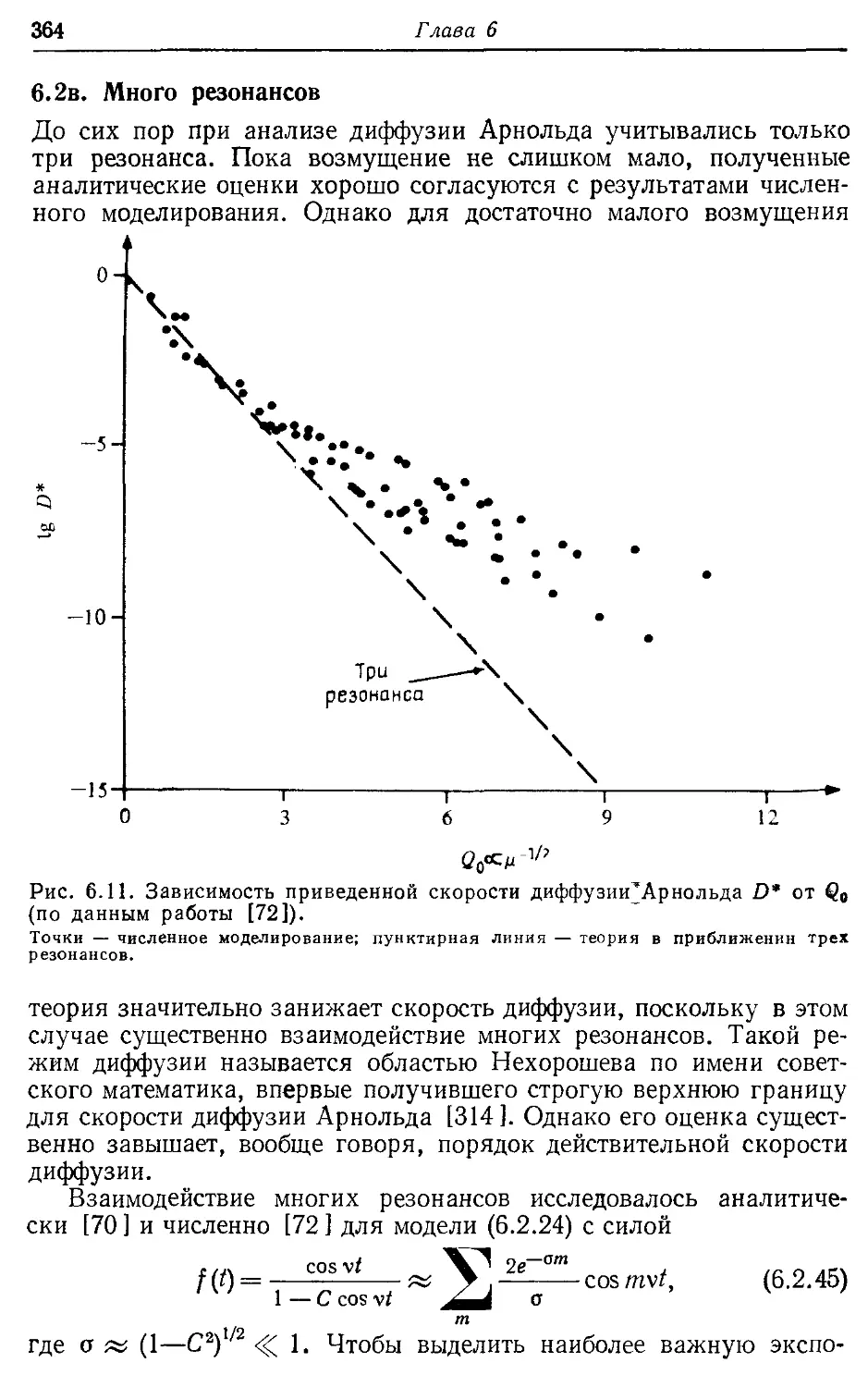
6.2в. Много резонансов 364
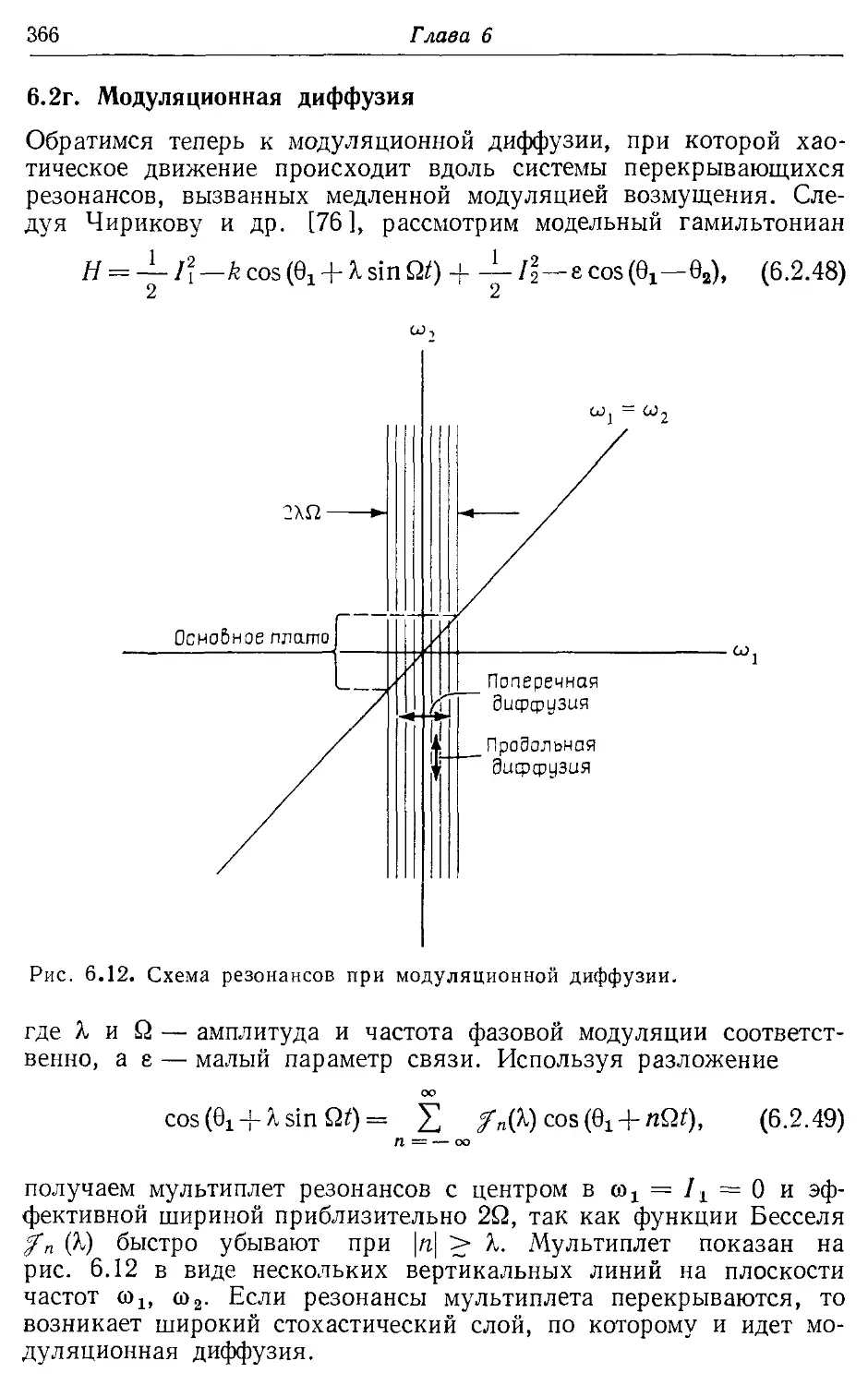
6.2г. Модуляционная диффузия 366
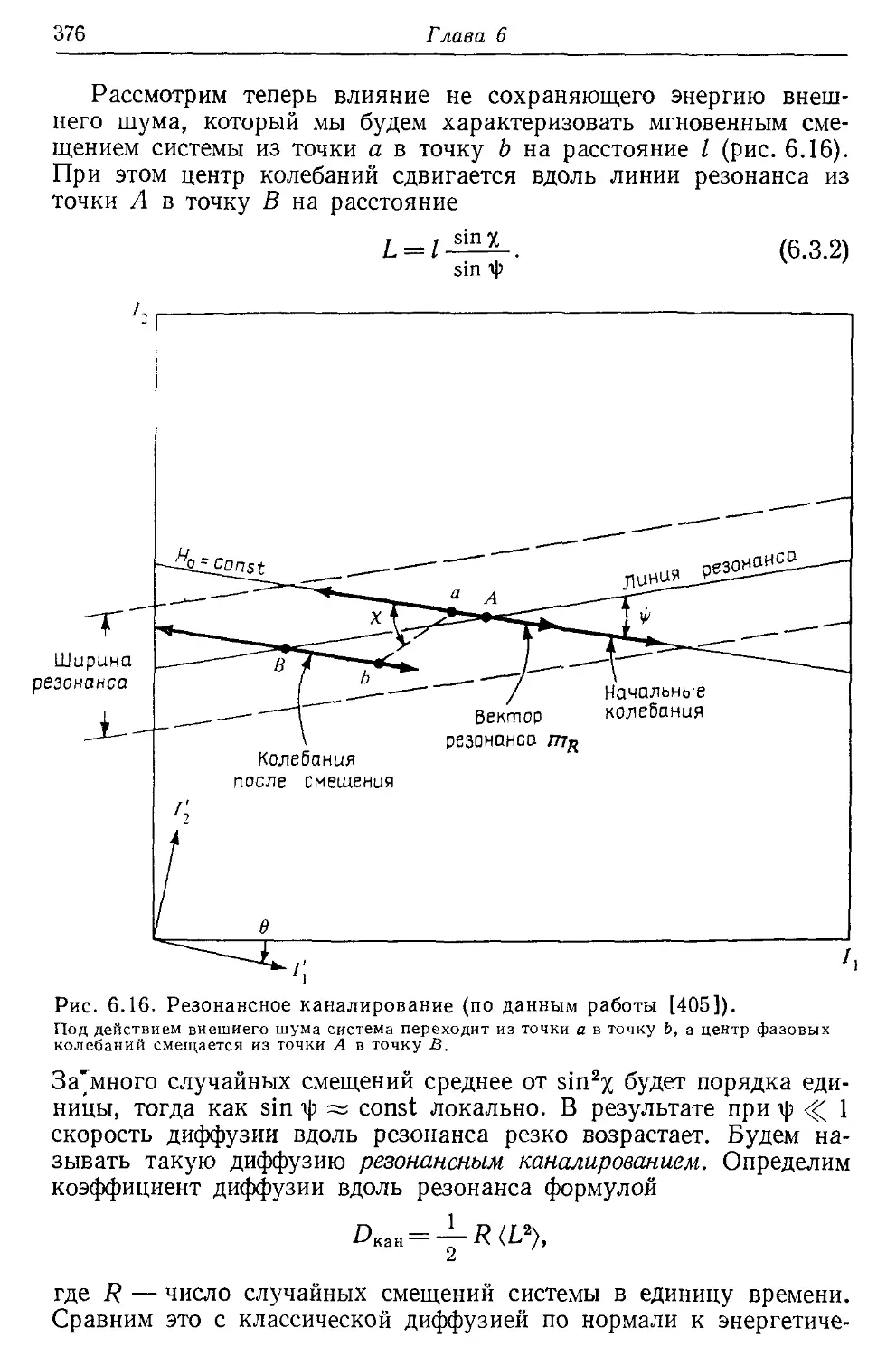
§ 6.3. Внешняя диффузия 375
6.3а. Резонансное каналирование диффузии 375
6.36. Диффузия резонанса 382
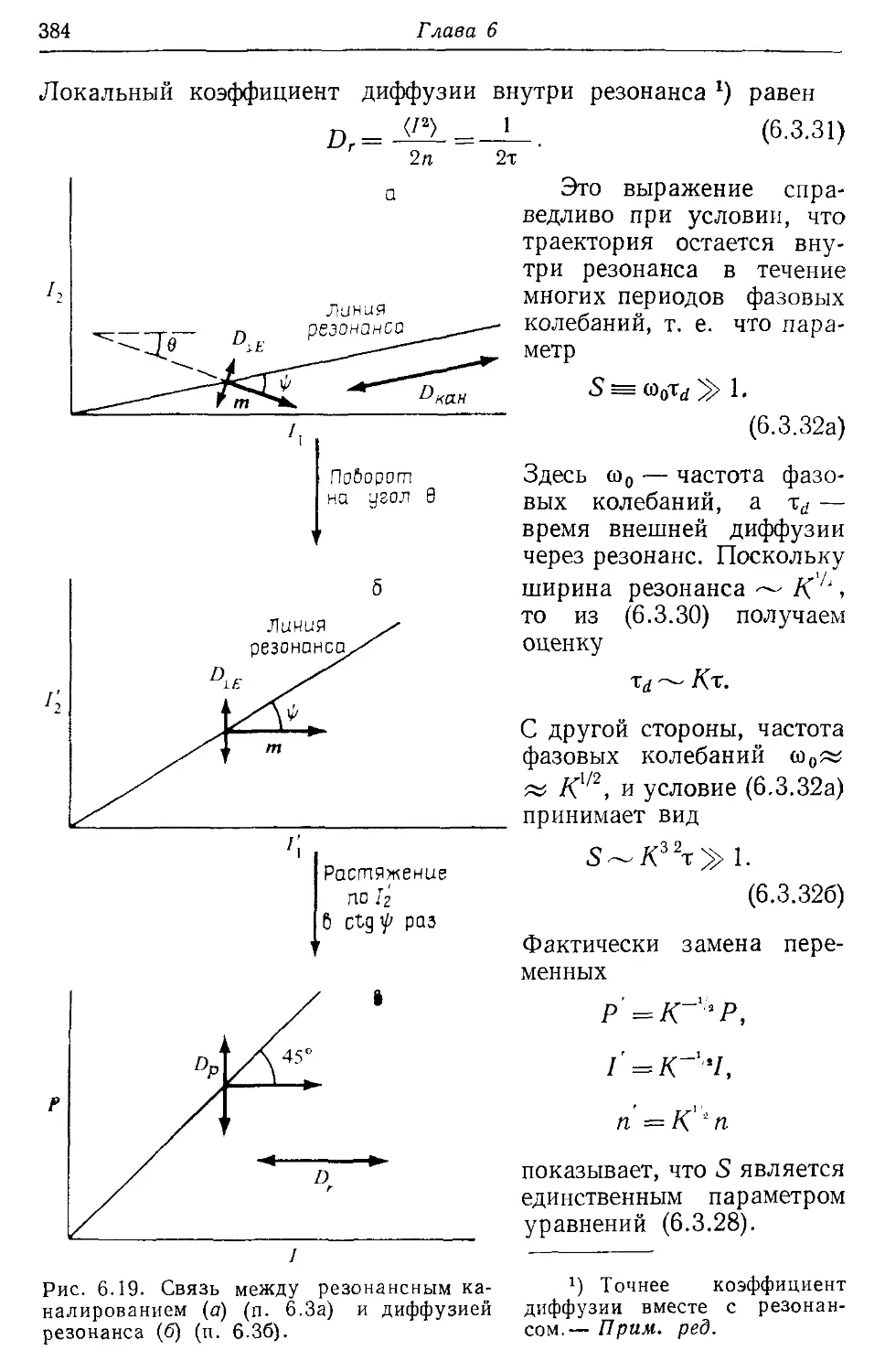
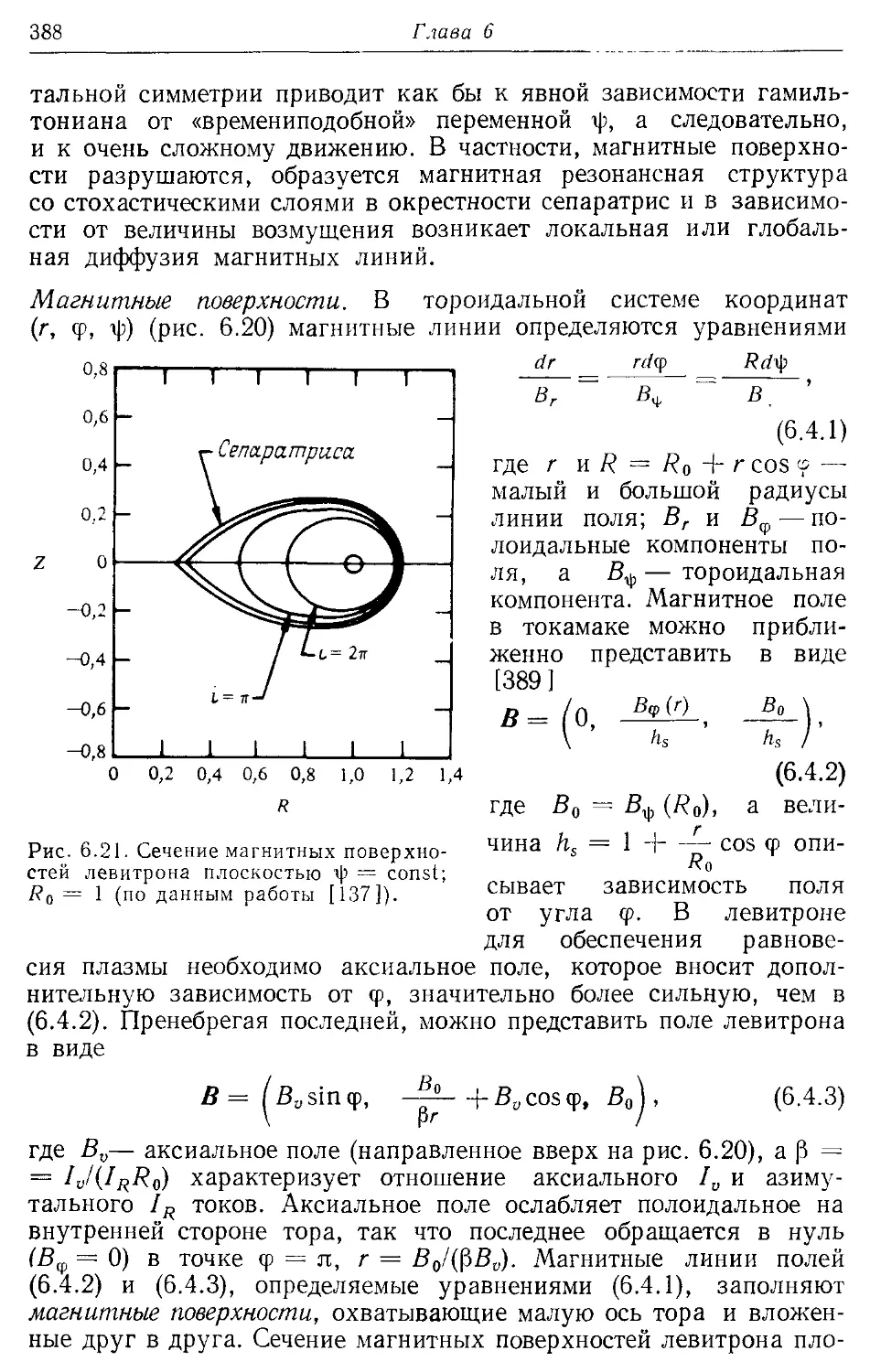
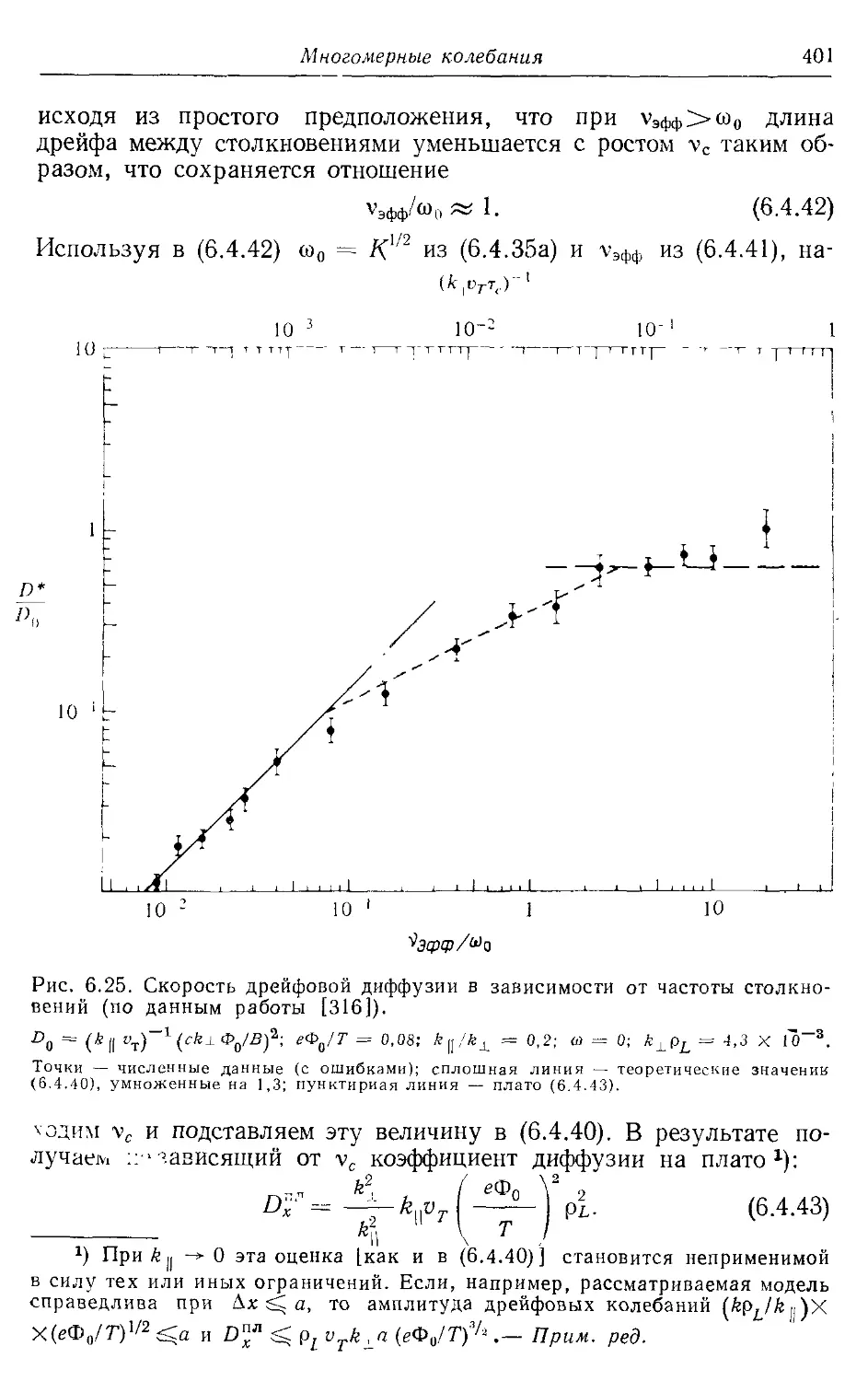
§ 6.4. Диффузия в тороидальных магнитных ловушках 386
6.4а. Динамика магнитных линий 386
6.46. Дрейфовые поверхности и диффузия в статических полях 392
6.4в. Диффузия в нестационарных полях 395
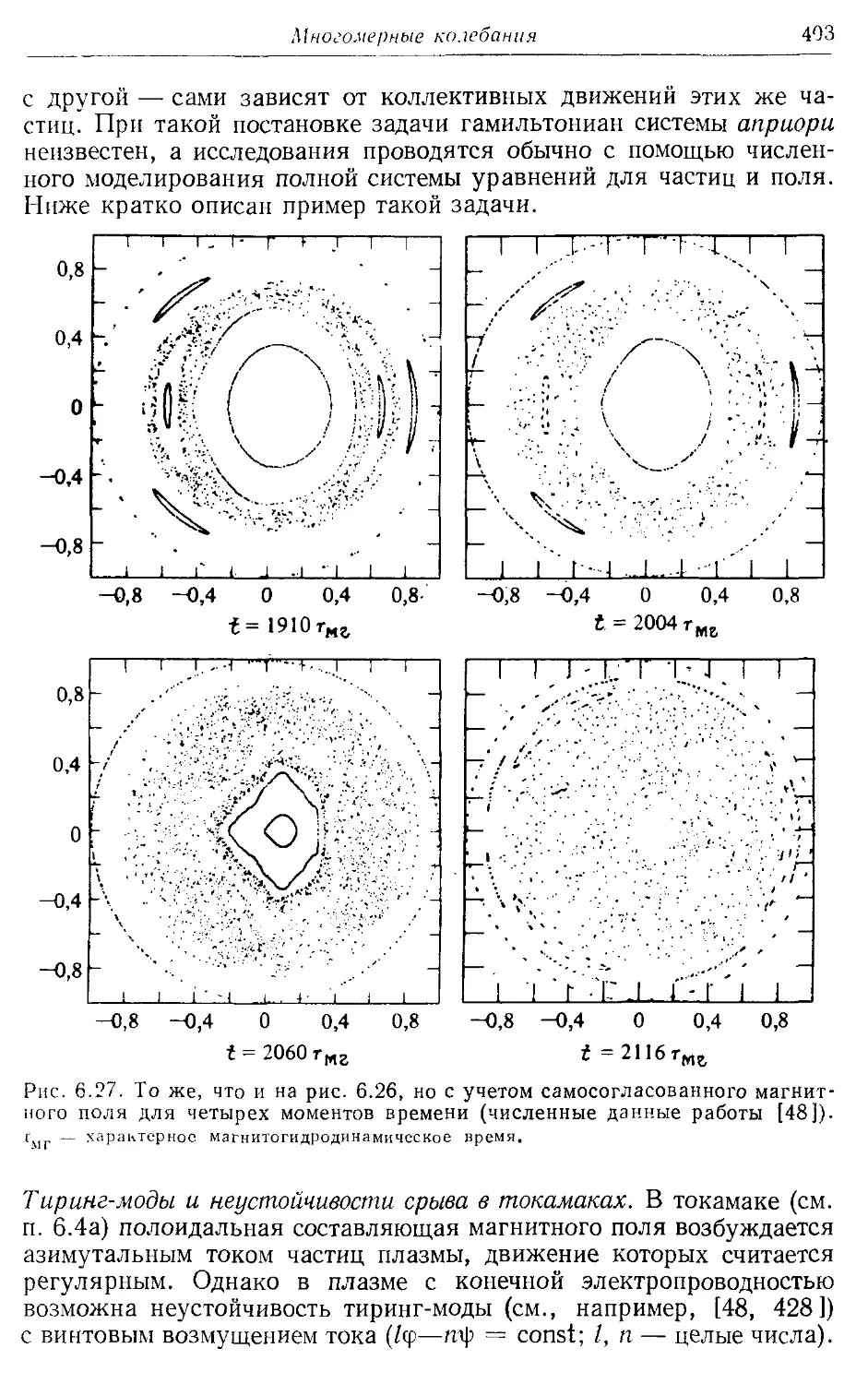
6.4г. Самосогласованная задача 402
§ 6.5. Системы со многими степенями свободы 404
Глава 7. Диссипативные системы 410
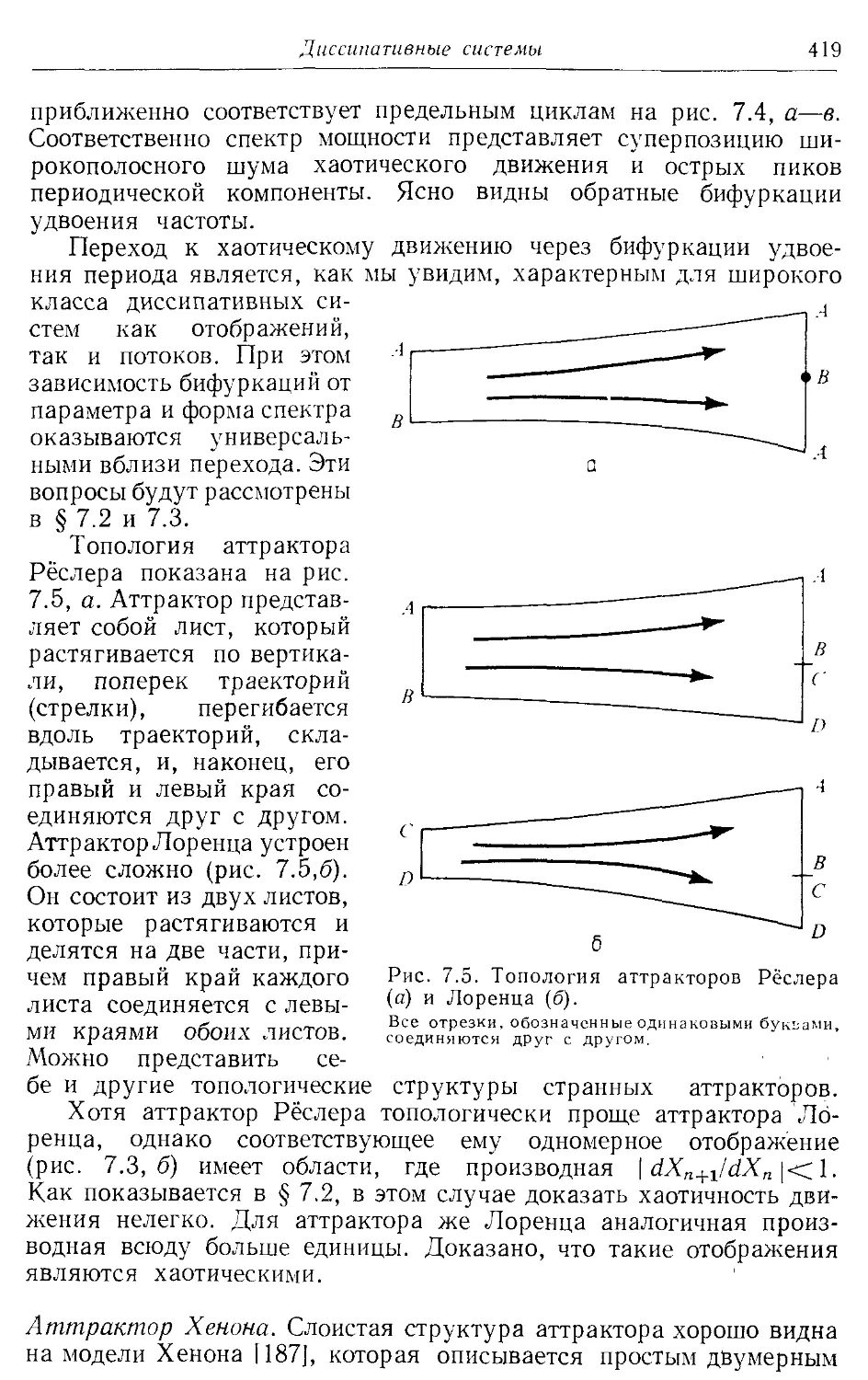
§ 7.1. Простые и странные аттракторы 410
7.1 а. Основные свойства 411
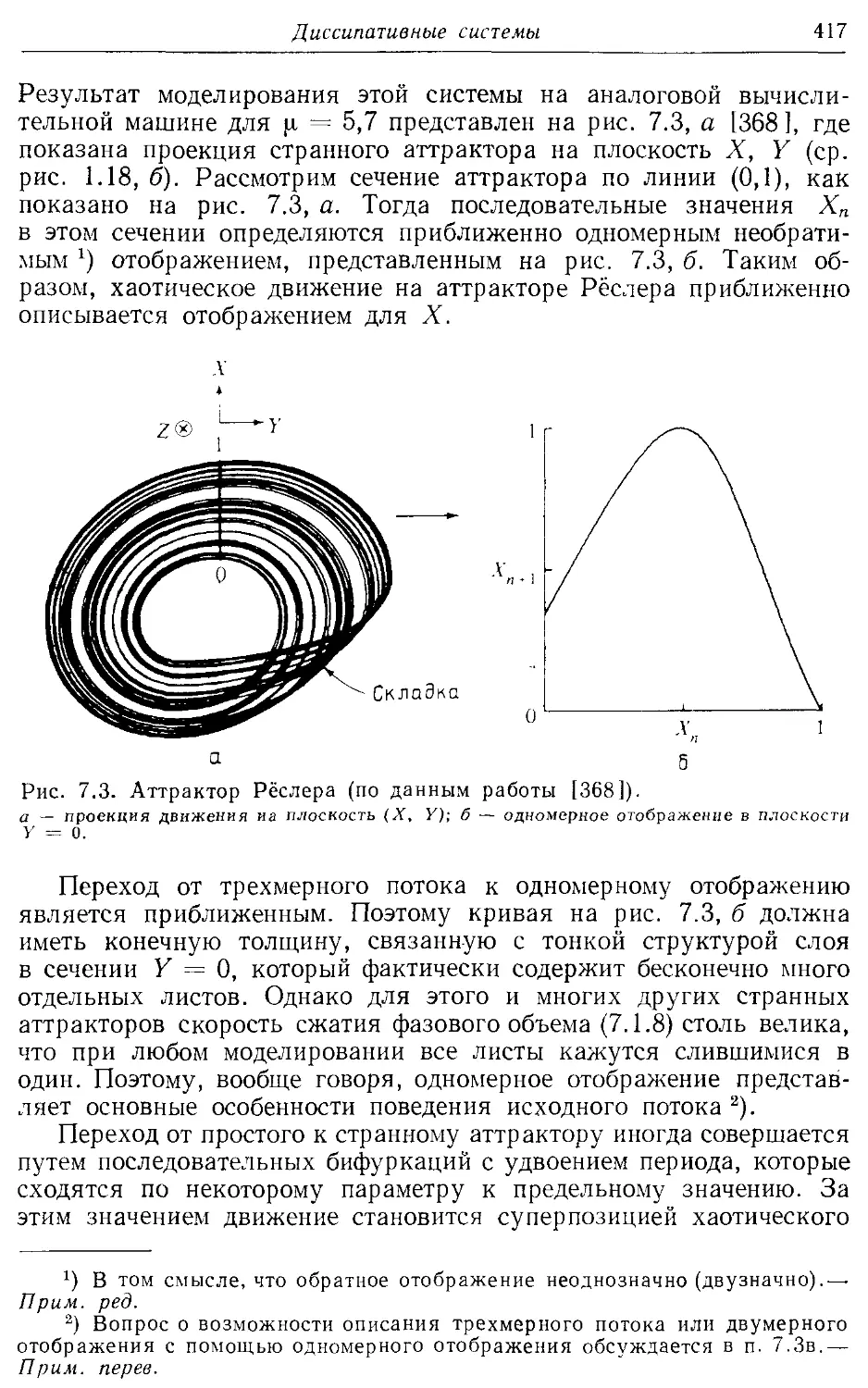
7.16. Примеры странных аттракторов 416
7.1 в. Геометрия странных аттракторов 422
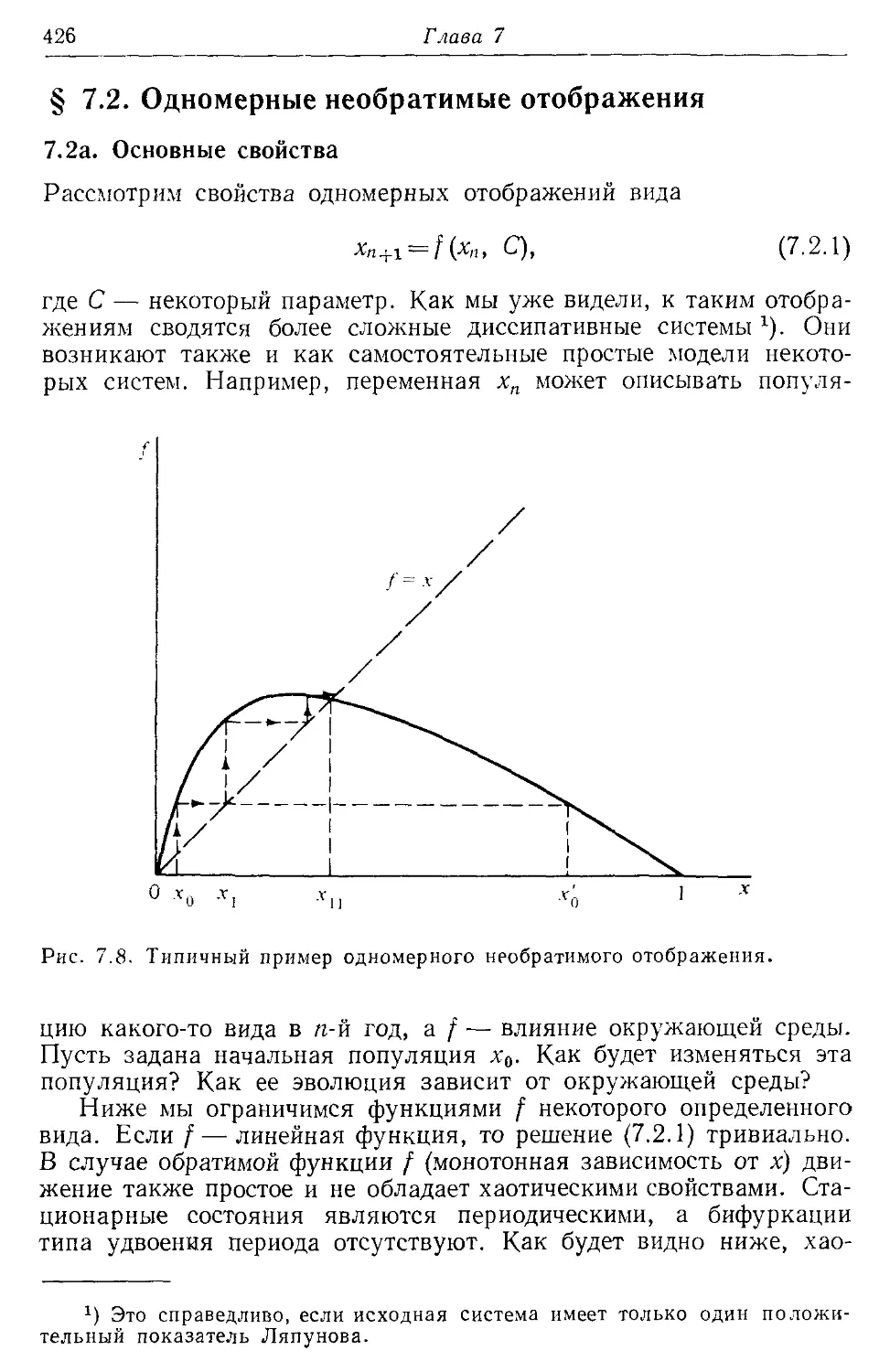
§ 7.2. Одномерные необратимые отображения 426
7.2а. Основные свойства 426
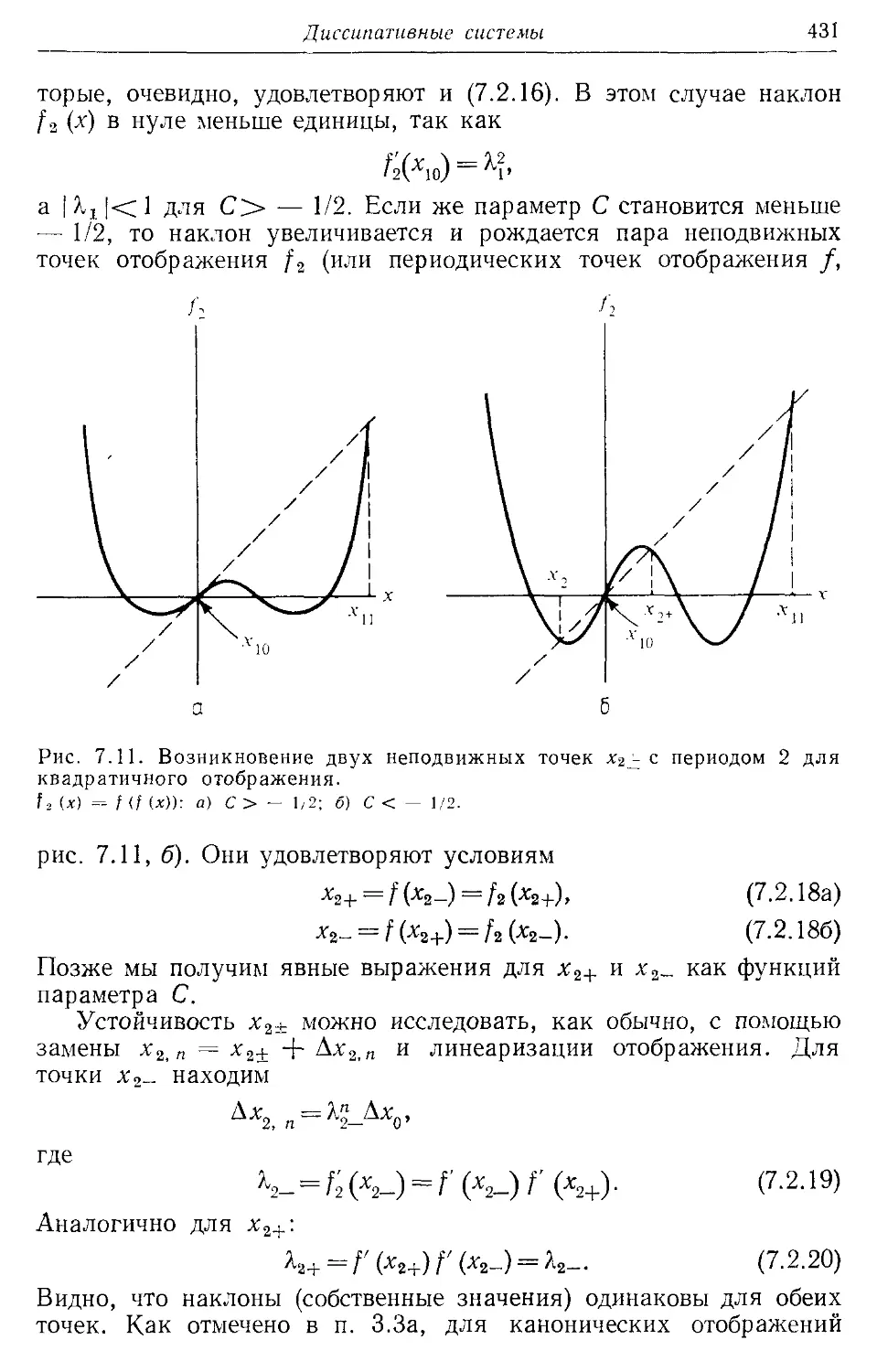
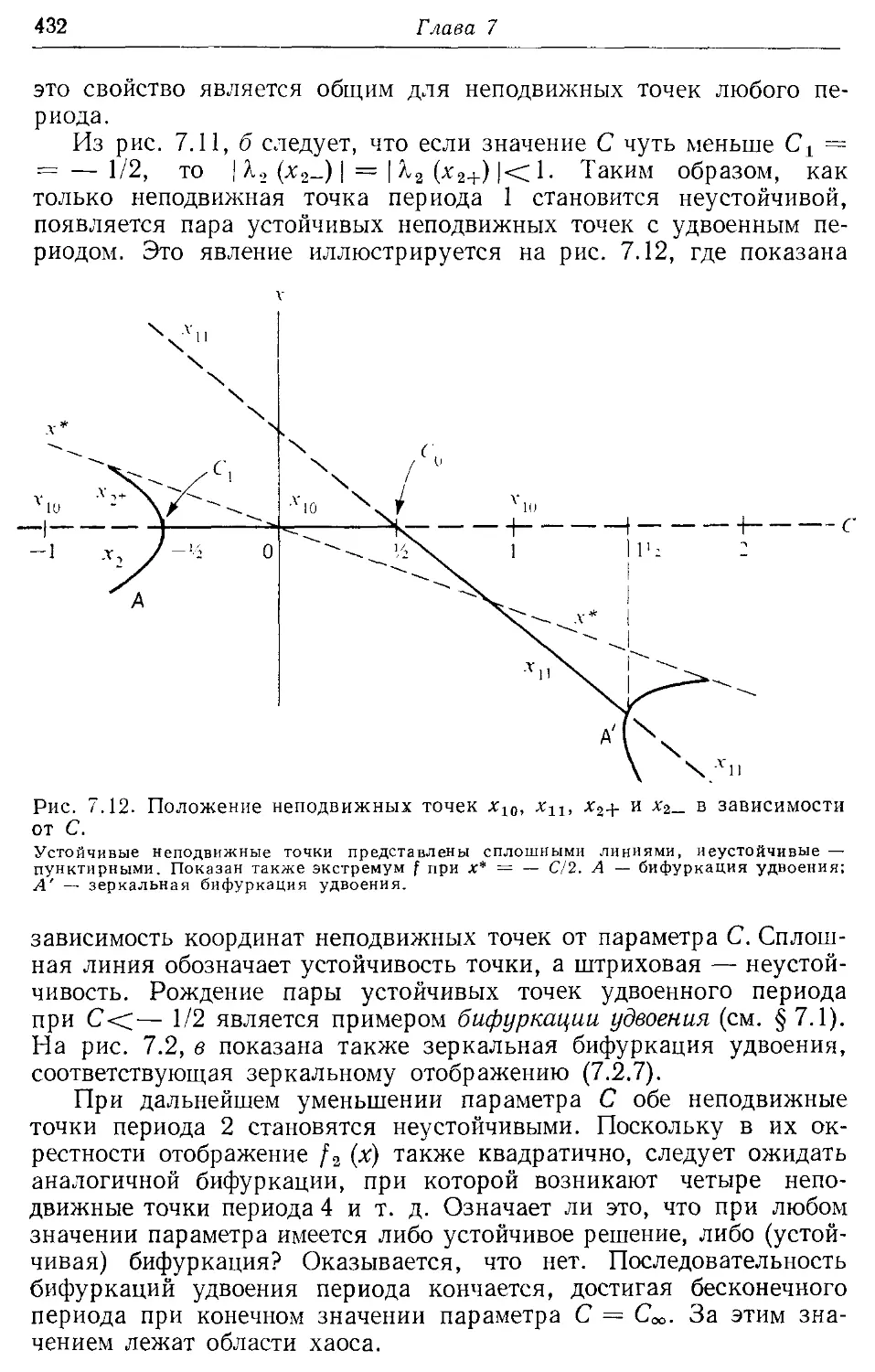
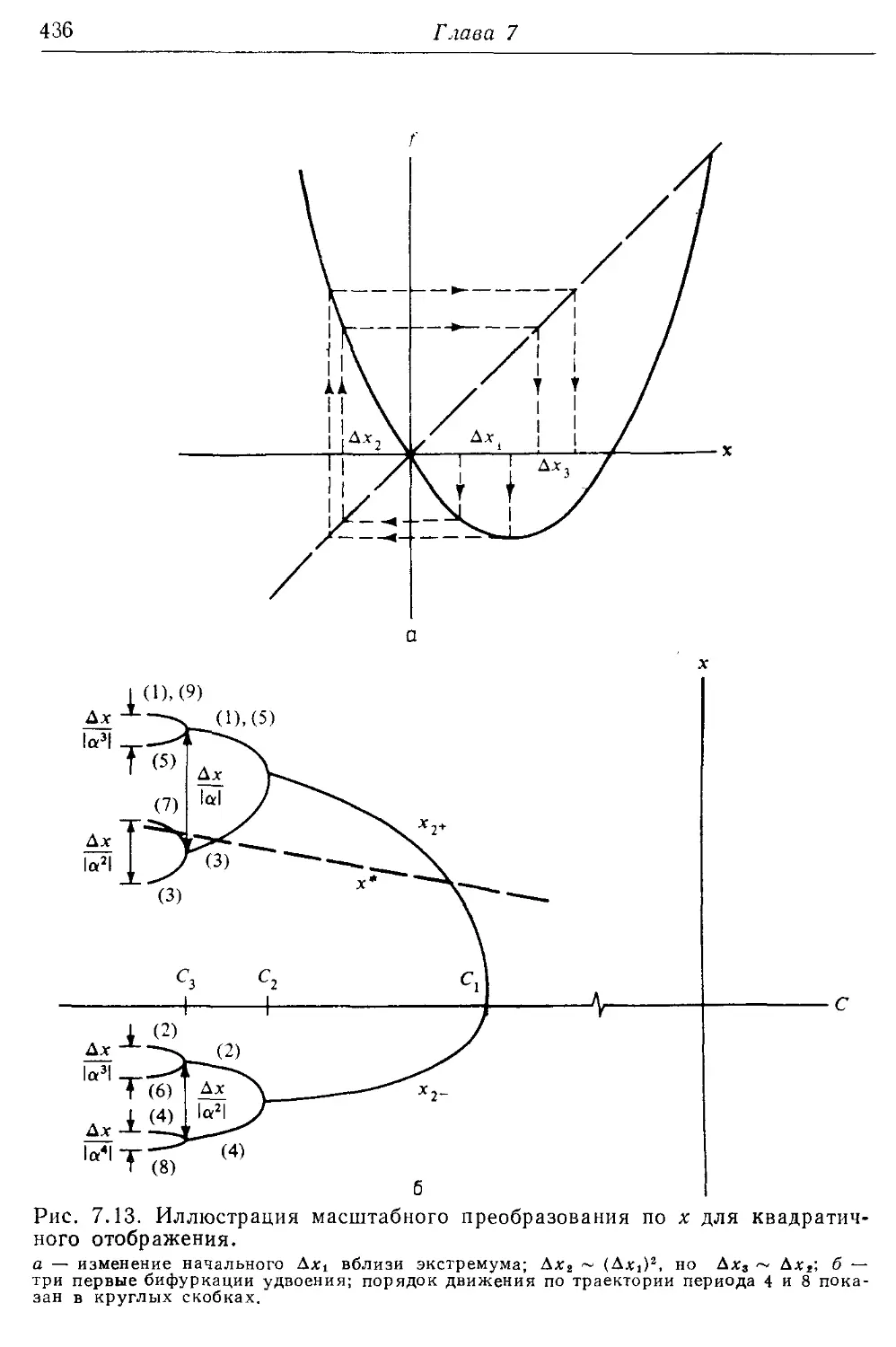
7.26. Периодическое движение 430
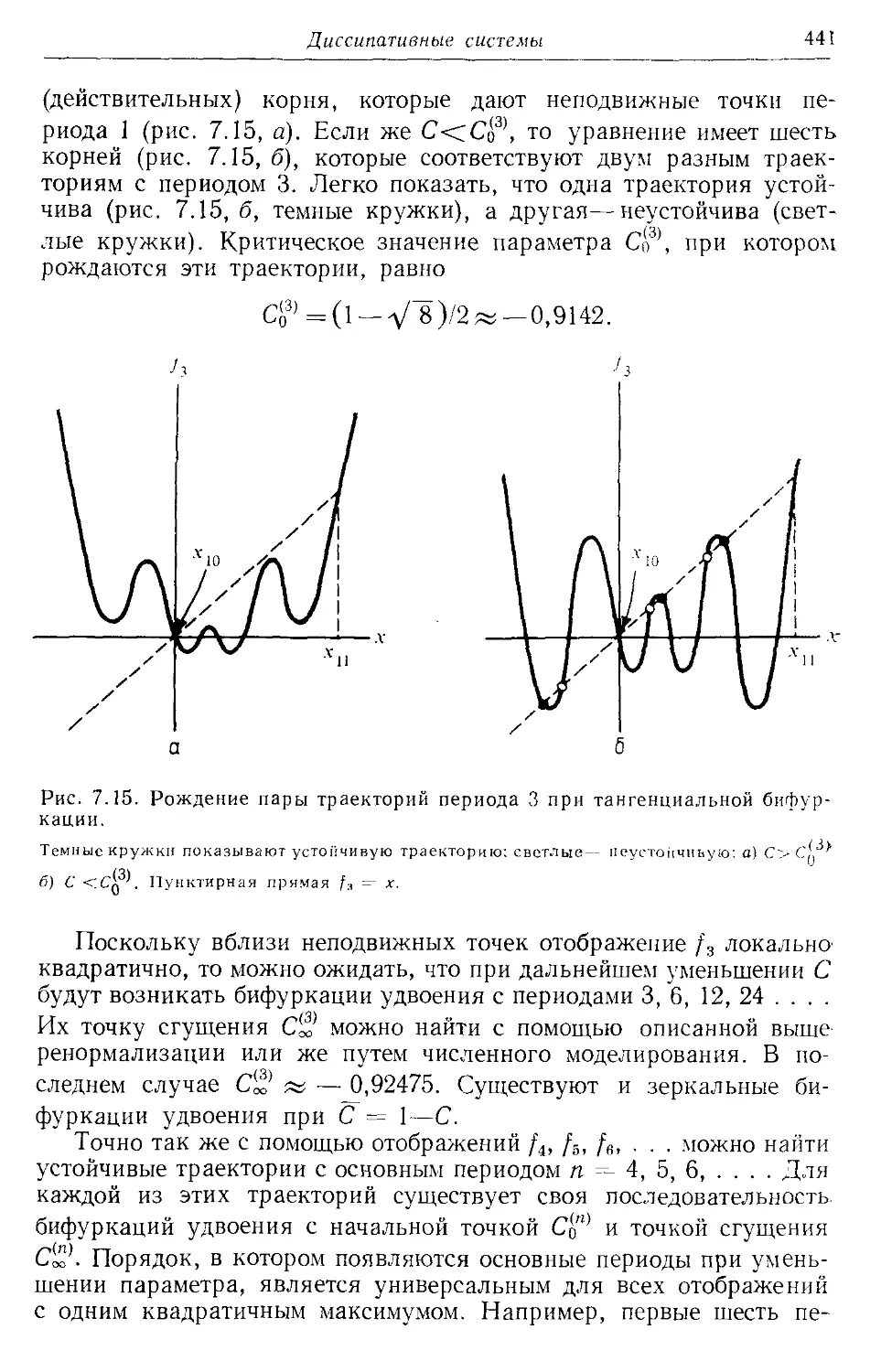
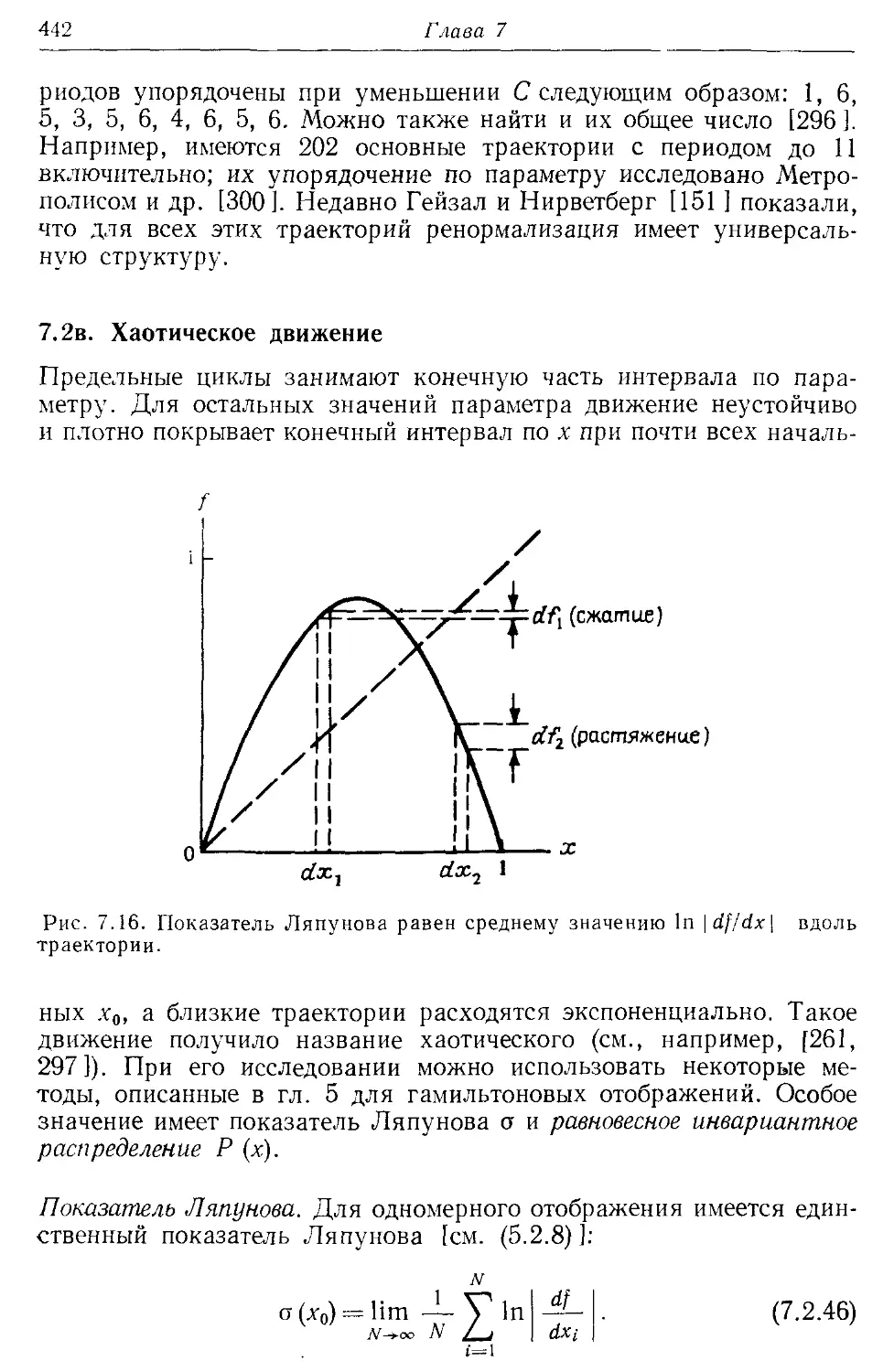
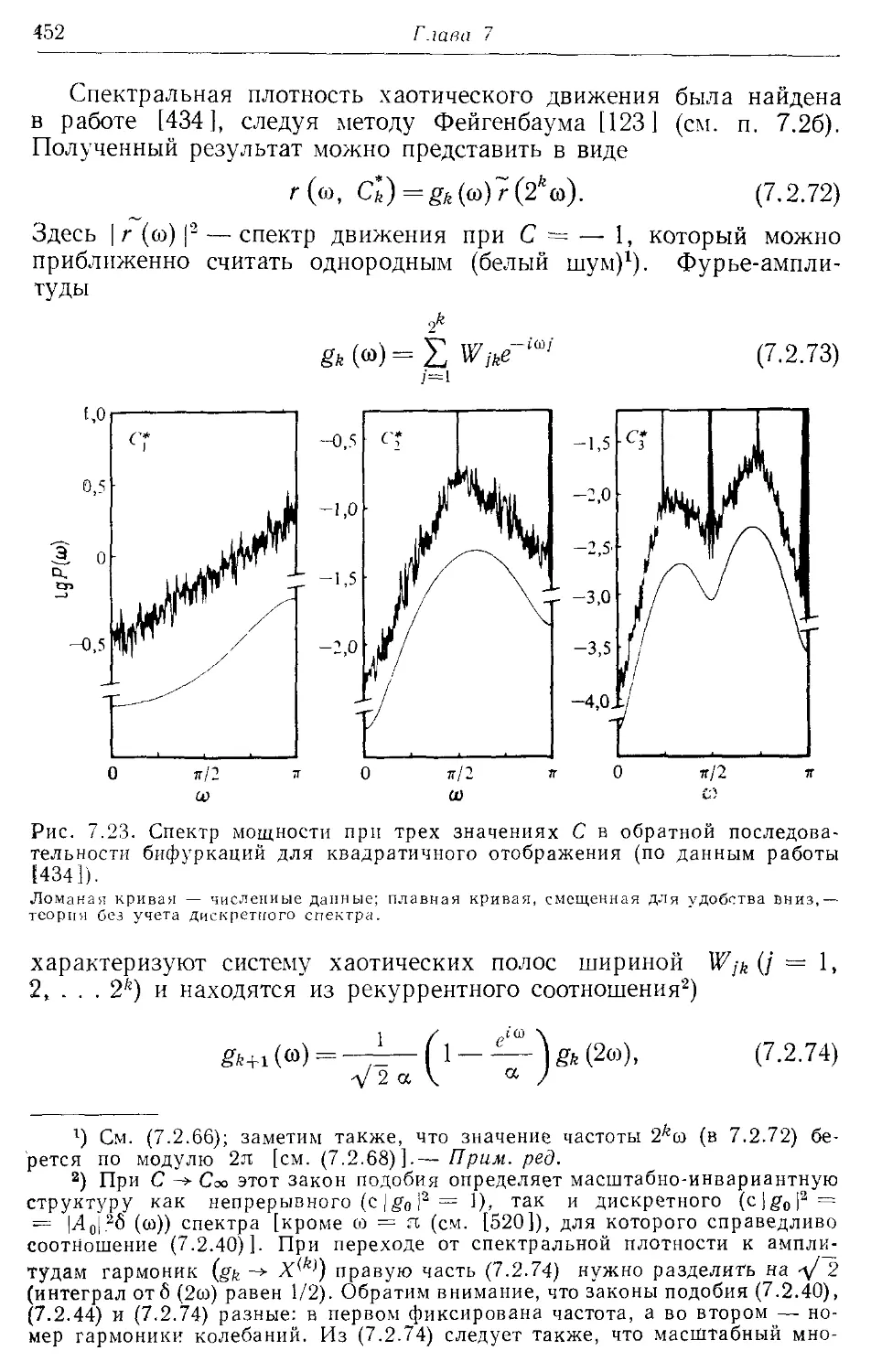
7.2в. Хаотическое движение 442
§ 7.3. Двумерные отображения и связанные с ними потоки 453
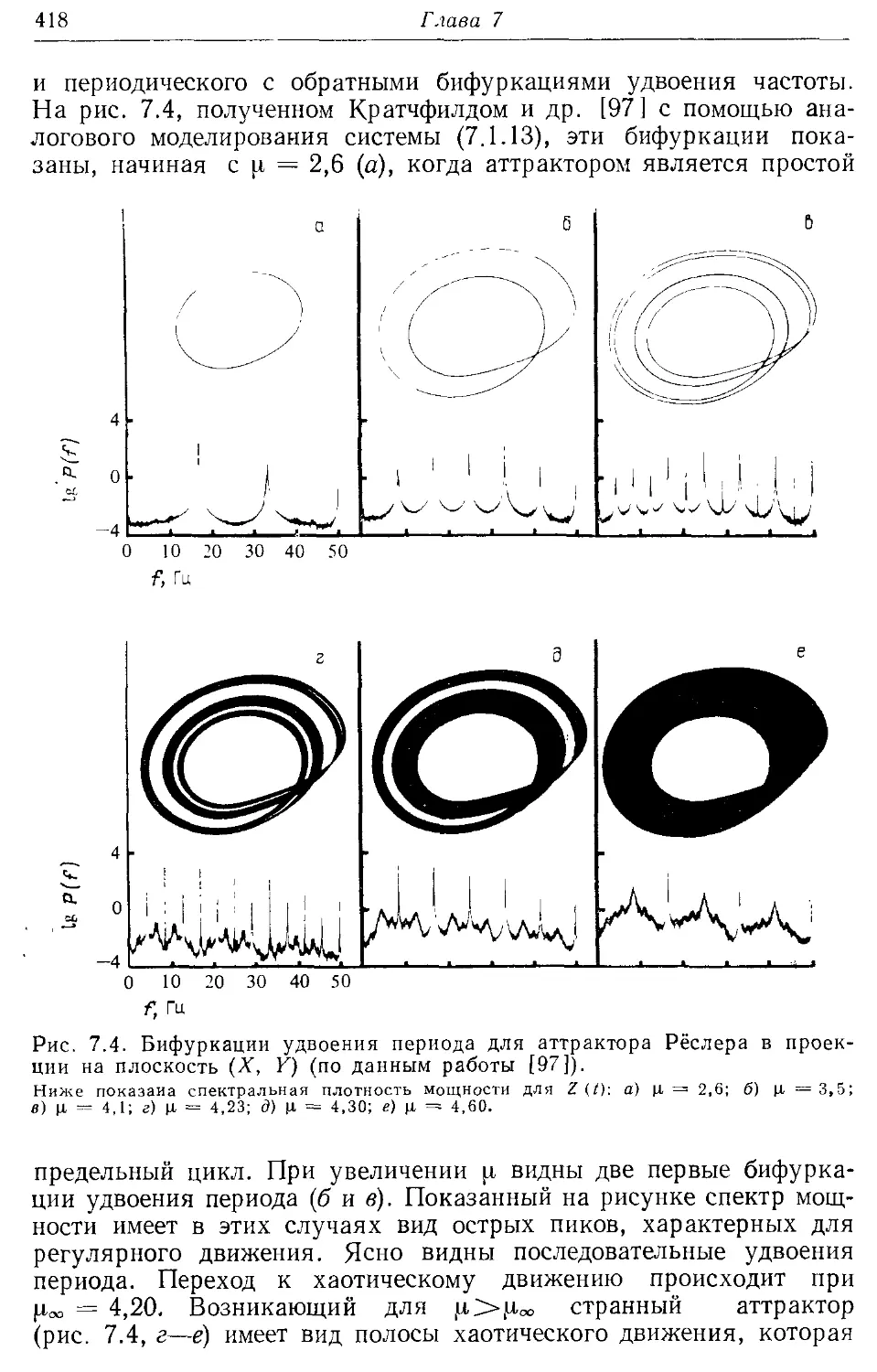
7.3а. Бифуркации удвоения периода 453
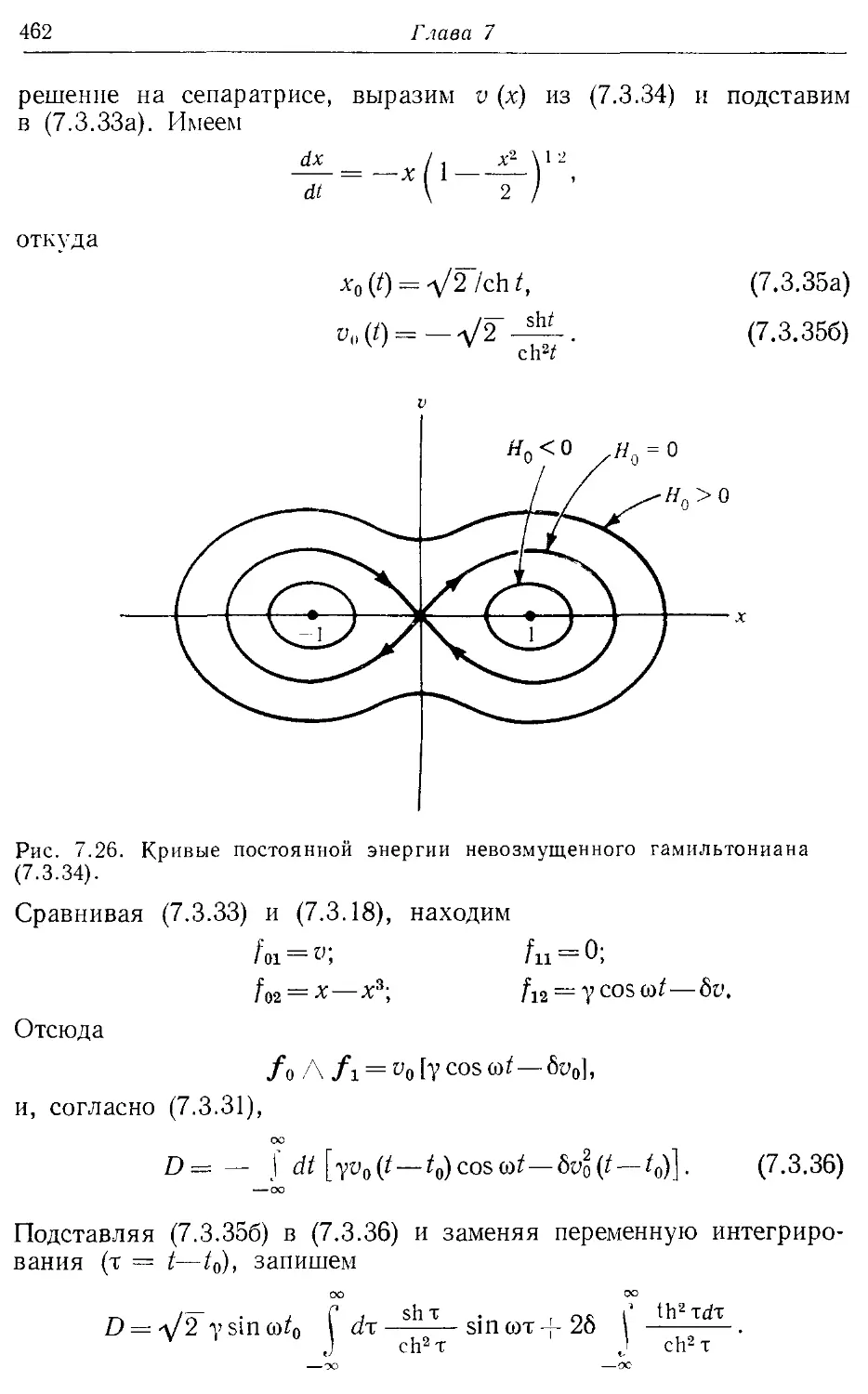
7.36. Движение вблизи сепаратрисы 457
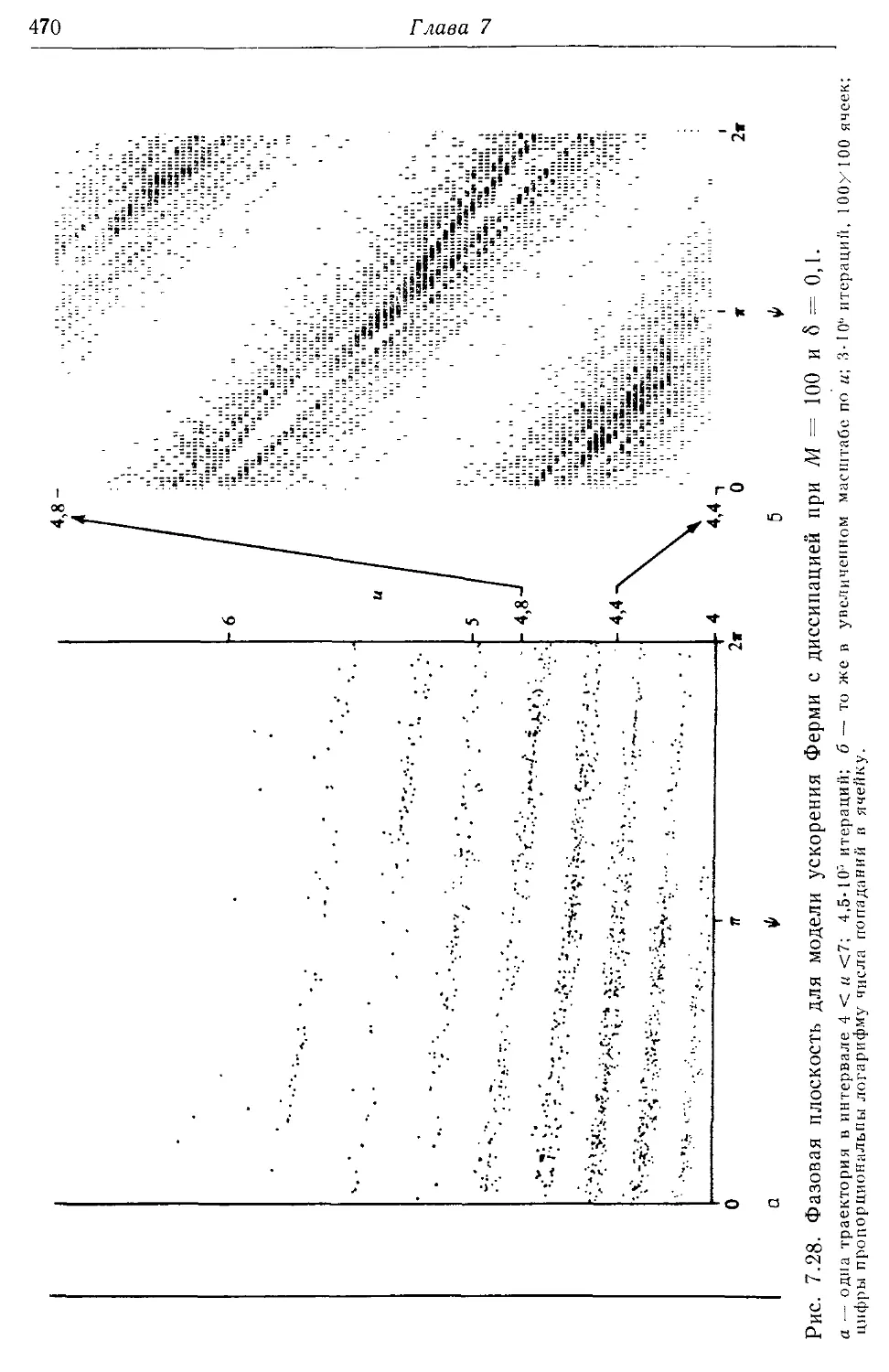
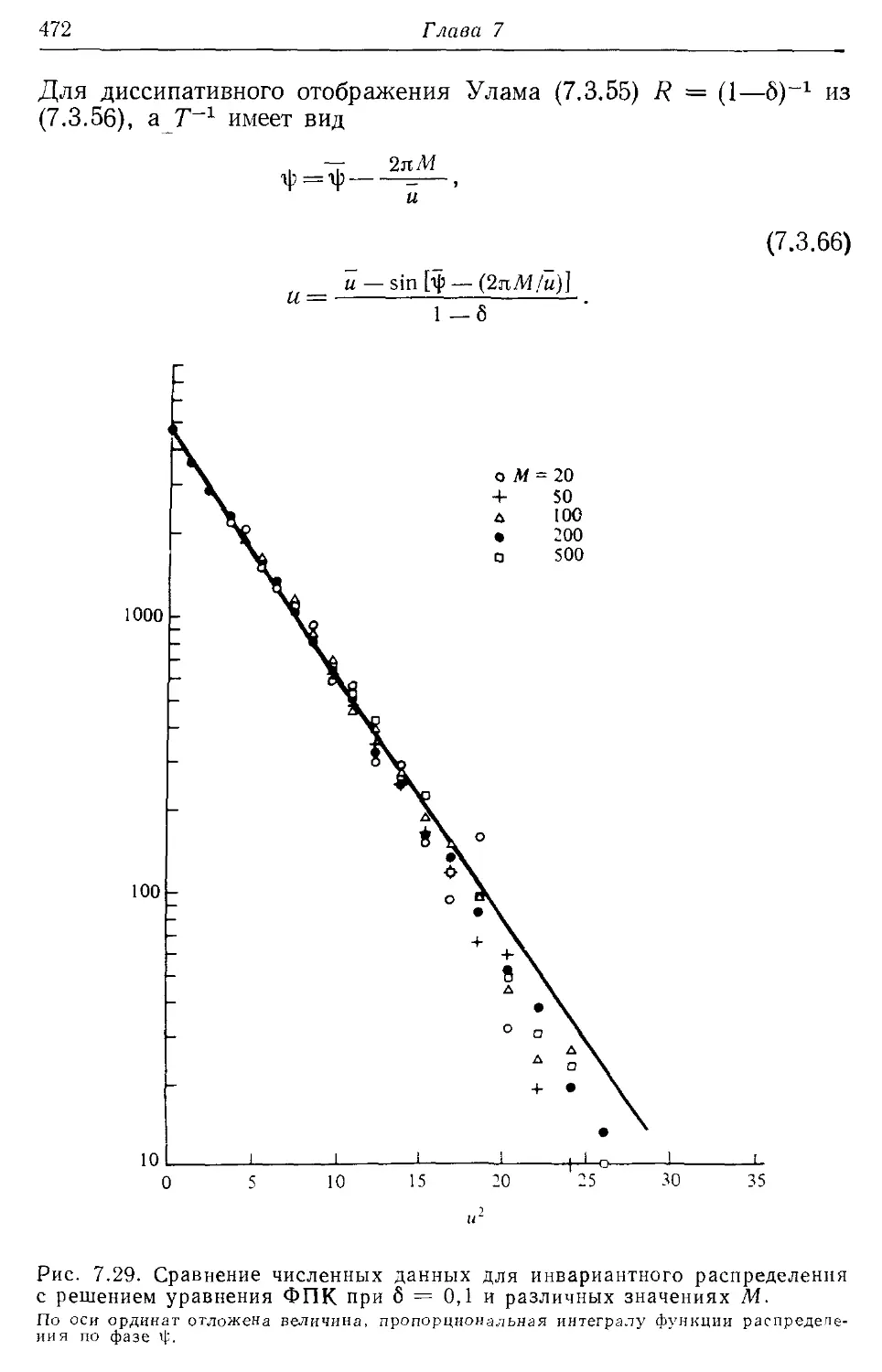
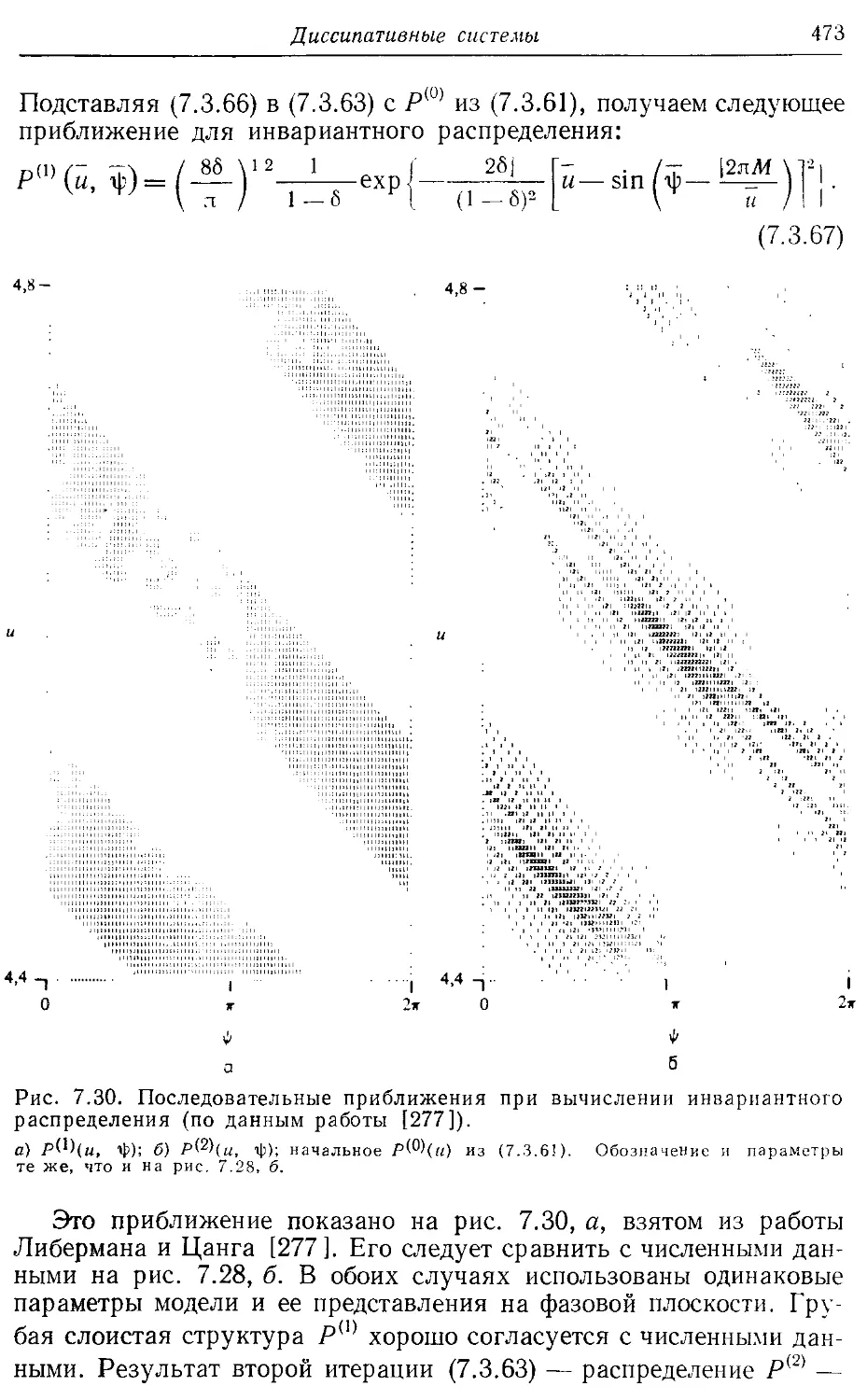
7.3в. Вычисление инвариантных распределений 466
§ 7.4. Проблема турбулентности 474
7.4а. Представление Фурье 474
7.46. Переход к турбулентности 478
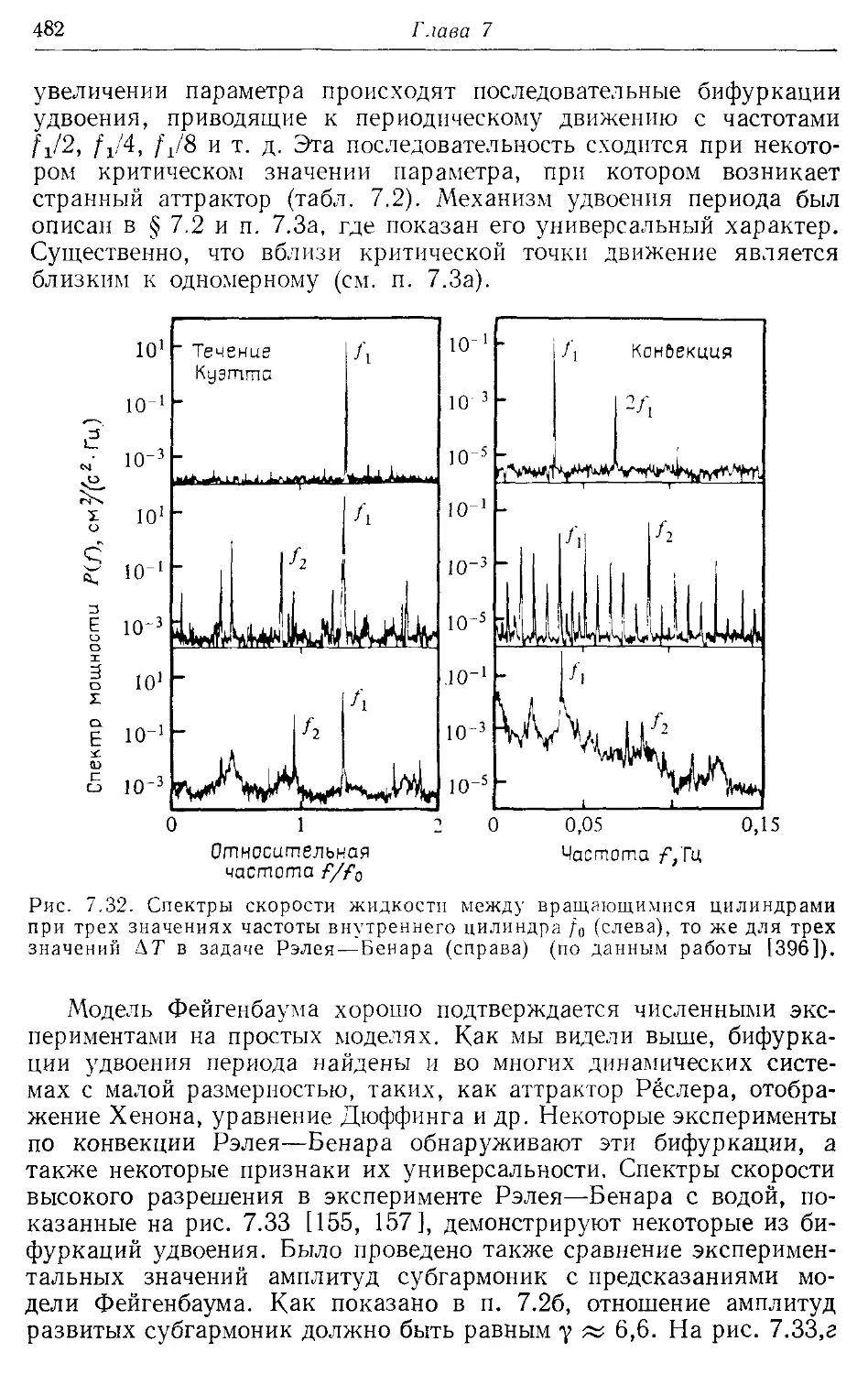
Дополнение А. Некоторые приложения 486
А. 1. Небесная механика 486
А.2. Ускорители и встречные пучки 488
А.З. Магнитные ловушки 490
А.4. Нагрев плазмы 492
А. 5. Химическая динамика 494
А. 6. Квантовые системы 495
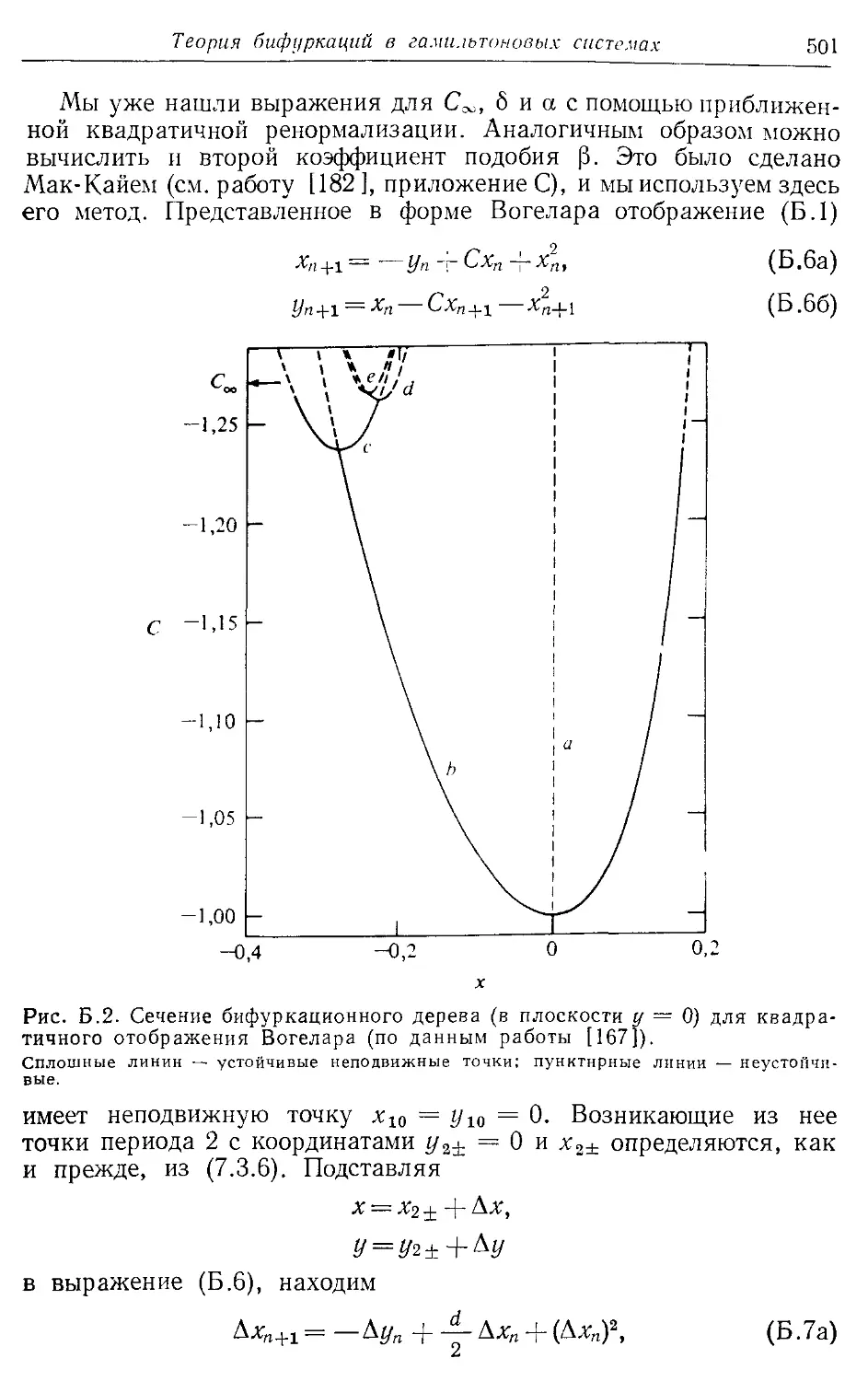
Дополнение Б. Теория бифуркаций в гамильтоновых системах 497
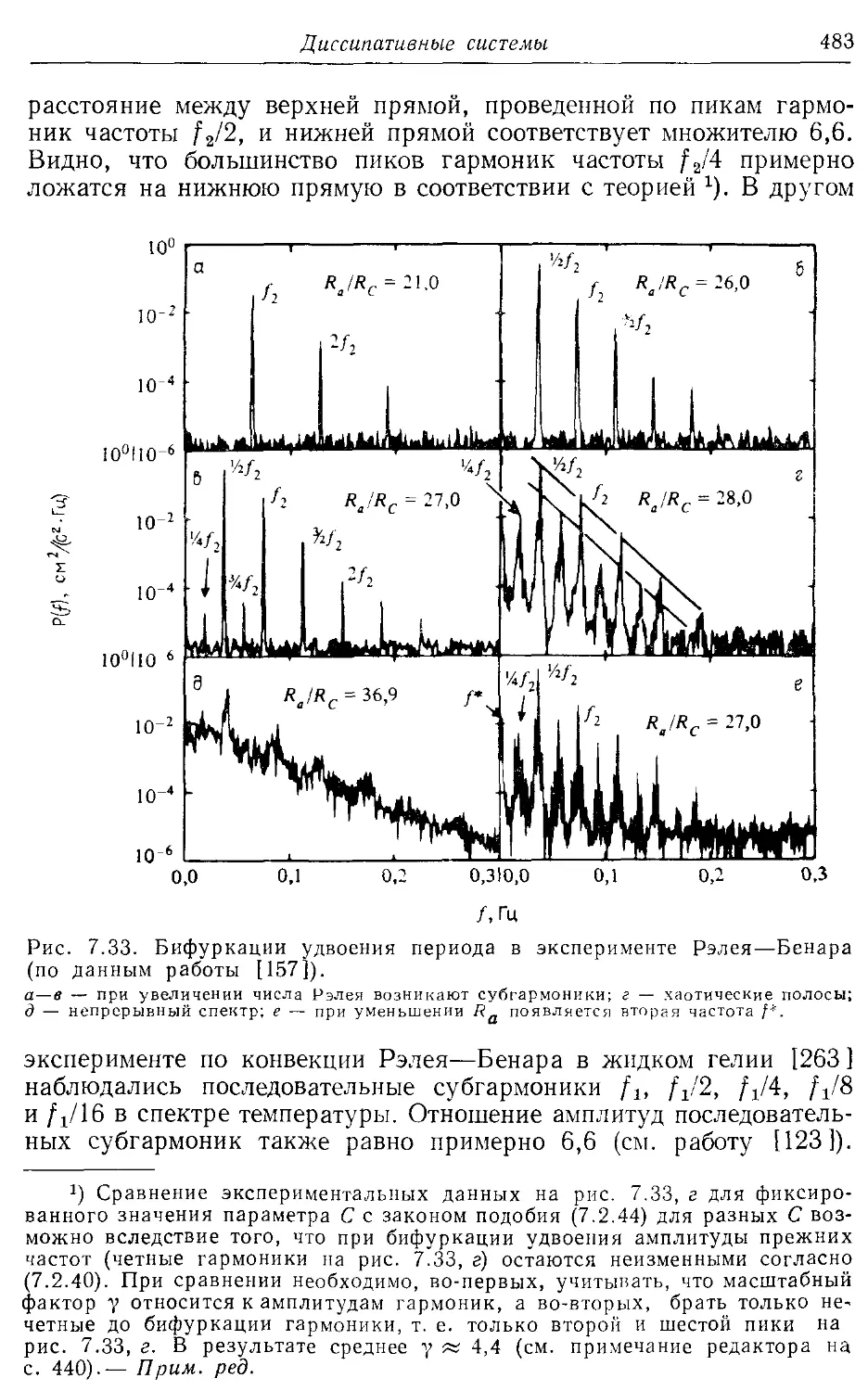
Список основных обозначений 504
Литература 506
Именной указатель 522
Предметный указатель 523
ИМЕННОЙ
Абловиц (Ablowitz) 57
Авез (Avez) 199, 200, 290
Алексеев В. М. 307, 487
Альфвен (Alfven) 490
Аносов Д. В. 19, 302
Арнольд В. И. 15, 18, 186, 190, 199,
200,290,341,364,465,491
Бардет (Bardet) 493
Баунтис (Bountis) 58, 171, 172. 174,
271
Белоусов Б. П. 494
Бенеттин (Benettin) 294, 295, 297,
308,313,315,317
Берк (Berk) 494
Берман Г. П. 497
Бернштейн (Bernestein) 492
Берри (Berry) 162. 290, 299, 496
Берс (Bers) 98, 139
Бивинс (Bivins) 407
Билек (Biaiek) 253, 273
Биркгоф (Birkhoff) 14, 15, 104, 199,
487
Боголюбов Н. Н. 13, 104. 114, 115.
317,319,444,490
Борн (Born) 92
Брамбилла (Brambilla) 394
Брахнч (ВгаЫс) 220, 221, 228
Бриджес (Bridges) 467
Брудно А. А. 307
Брунс (Bums) 487
Будкер Г. И. 336, 395, 489
Бэкстер (Baxter) 492
Вайдал (Vidal) 495
Ватанабе (Watanabe) 494
ГалеевА.А. 336, 381,395
Гальгани (Galgani) 408
Гаррен (Garren) 491
Гарридо (Garrido) 147, 487
Гейзал (Geisal) 442
Гелл (Gell) 395)
Голдстейн (Goldstein) 20
УКАЗАТЕЛЬ
Голуб (Gollub) 481
Грин (Green G.) 181, 247, 489
Грин (Greene J.) 194, 214, 220, 247,
252, 269, 273, 274, 279, 308, 500
Гроссман (Grossmann) 449
Густавсон (Gustavson) 65, 487
Депри (Deprit) 147. 487
Джакалья (Giacaglia) 92, 104, 147, 154
Довейл (Doveil) 248, 277, 503
Драгт (Dragt) 199, 200, 490, 491
Дуннет (Dunnett) 122, 142
Дьюар (Dewar) 147, 149
Erep (Jaeger) 247, 325, 492
Жаботинский А. М. 494
Жданова Т. А. 324
Жебехели (Szebchely) 488
Забуский (Zabusky) 407
Зальцман (Saltzman) 476
Заславский Г. М. 220, 221, 294, 425,
496, 497
Зигель (Siegel) 488
Зисок (Zlsook) 450, 451
Зубарев Д. Н. 114
Израйлев ф. М. 324, 467, 469
Казати (Casati) 497
Кари (Сагу) 147, 164. 165, 332
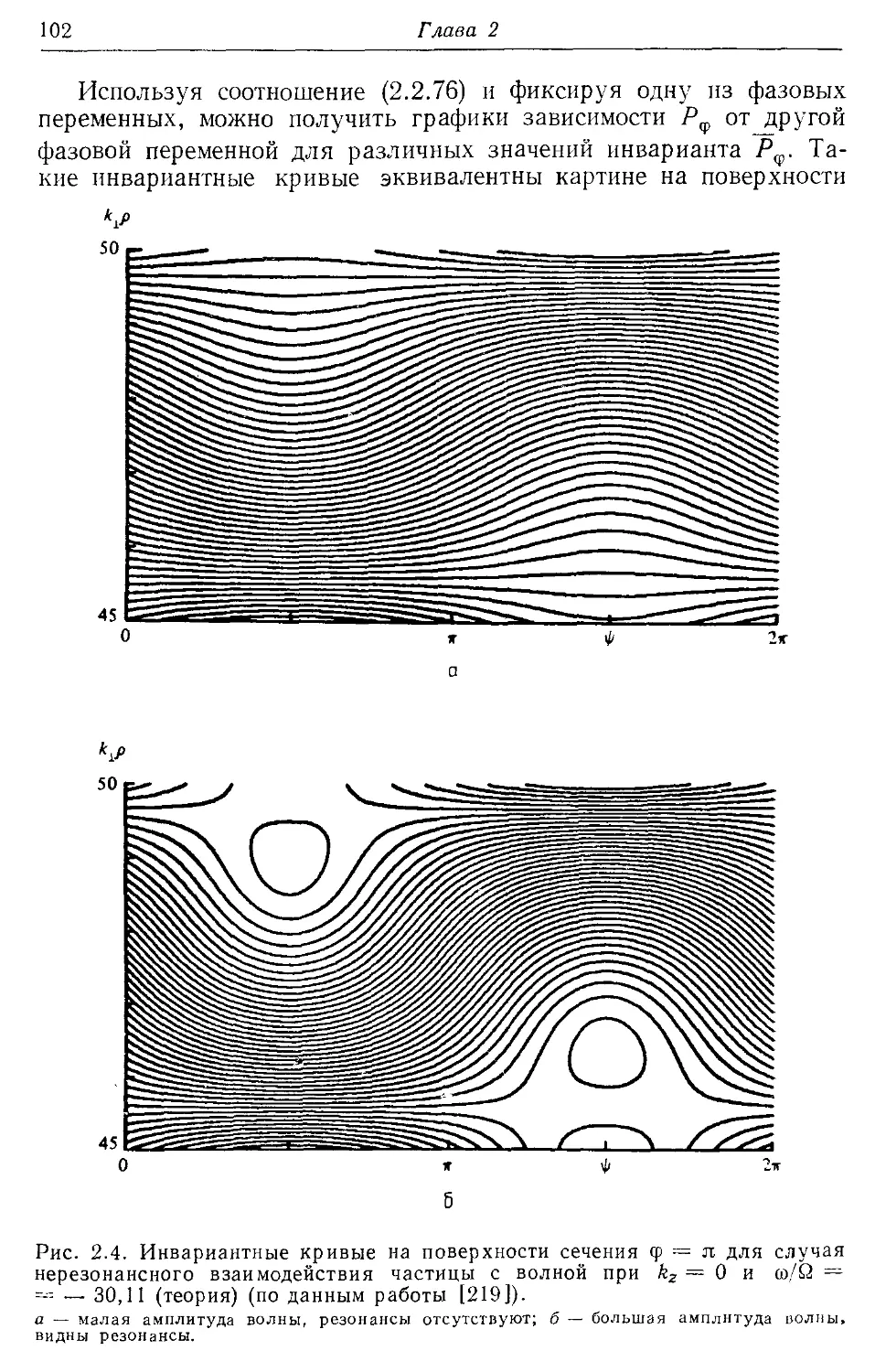
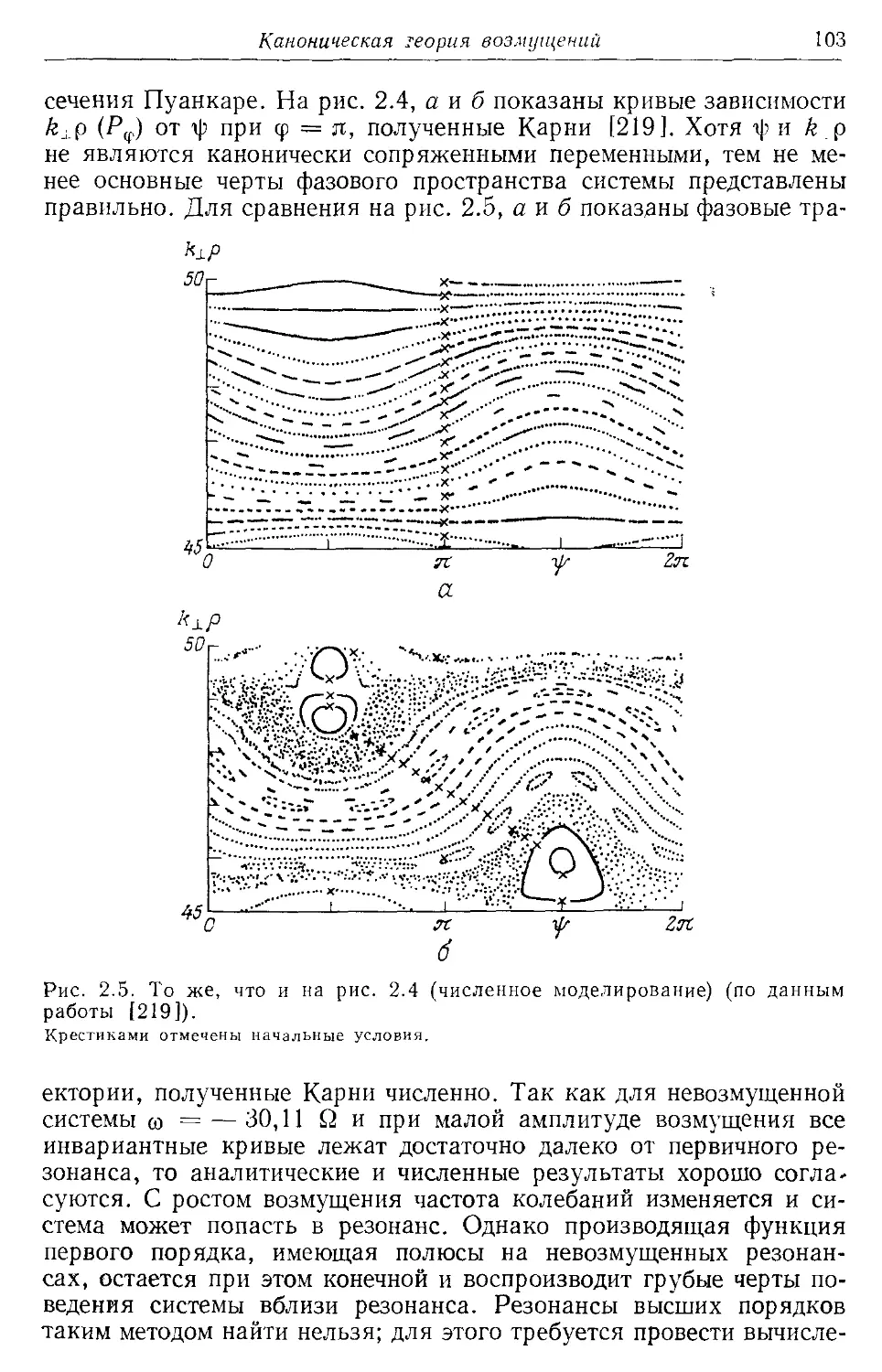
Карни (Кагпеу) 98, 103, 139, 142, 332
Кауфман (Kaufman) 98, 139, 147
Клейн (Klein) 248
Колле (Collet) 448
Колмогоров А. Н. 15, 82, 162. 168
186,300,318,406,487
Коломенский А. А. 489
Контопулос (Contopoulos) 190, 317,
487, 488
Копель (Kopell) 495
Коэн (Cohen) 375, 381, 382, 386, 491
Кратчфилд (Crutchfield) 418, 484
Крилин (Krilin) 490
Крускал (Kruskal) 13, 88, 104, 114,
490
Крылов Н. М. 13, 114. 319, 444
Крылов Н. С. 294, 300
Кулсруд (Kulsrud) 88
Куммер (Kummer) 488
Курант (Courant) 46, 489
Лакина (Lacina) 490
Ландау Л. Д. 20, 319, 478, 479
Лансфорд (Lunsford) 142, 190, 273,
279
Ласлет (Laslett) 489
Лебедев А. Н. 489
Левис (Lewis) 46
Лейнг (Laing) 142
Ли (Li) 248
Либерман (Lieberman) 111, 220, 221,
231, 291, 324, 325, 335, 353, 359,
473, 492
Линдштедт (Lindstedt) 82, 85
Литлджон (Littlejohn) 115, 147
Лифшиц Е. М. 478
Лихтенберг (Lichtenberg) 111, 126,
220, 221, 222, 231, 235, 247, 252,
291, 324, 325, 335, 394, 489, 492,
494, 503
Лич (Leach) 46
Лози (Lozi) 422
Лоренц (Lorenz) 19, 20, 76, 77, 79,
448, 476, 480
Лэнфорд (Lanford) 414
Ляпунов А. М. 294
Мак-Кай (МасКау) 501
Мак-Лафлин (McLaughlin) 457
Мак-Намара (McNamara) 65, 104, 142,
147, 148, 154, 160, 164. 487
Манневиль (Manneville) 484
Маркус (Marcus) 497
Марсден (Marsden) 348
Мартнн-Лёф (Martin-Lot) 306
Мейс (Meiss) 332
Мельников В. К. 199, 240, 348, 457,
459
Метрополис (Metropolis) 442
Мисюревич (Misiurewicz) 422
Митропольский Ю. А. 13, 114
Мозер (Moser) 15, 162, 186, 190, 193,
199, 227, 488
Морозов А. Д. 457
Найфе (Neyfeh) 147
Невинс (Nevins) 395, 399
Некрасов А. К. 492
Нехорошее Н. Н. 73, 364, 365
Нирветберг (Nierwetberg) 442
Нойес (Noyes) 495
Нортроп (Northrop) 121, 154, 490
Оселедец В. И. 294, 297
Отт (Ott) 422, 478, 497
Паста (Pasta) 14, 56, 348, 406
Перейра (Pereira) 267, 268
Персиваль (Percival) 248, 287, 288
Песин Я. Б. 294, 301
Петухов В. А. 489
Погуце О. П. 395
Помо (Pomeau) 484
Пуанкаре (Poincare) 13, 15, 16, 28, 82,
87, 90, 104, 197, 200, 240, 294,
348, 487
Пустыльников Л. Д. 221
Рабинович М. С. 489
Рассел (Russel) 424
Раулэндс (Rowlands) 375, 381, 382,
385, 467
Ренно (Rannou) 308
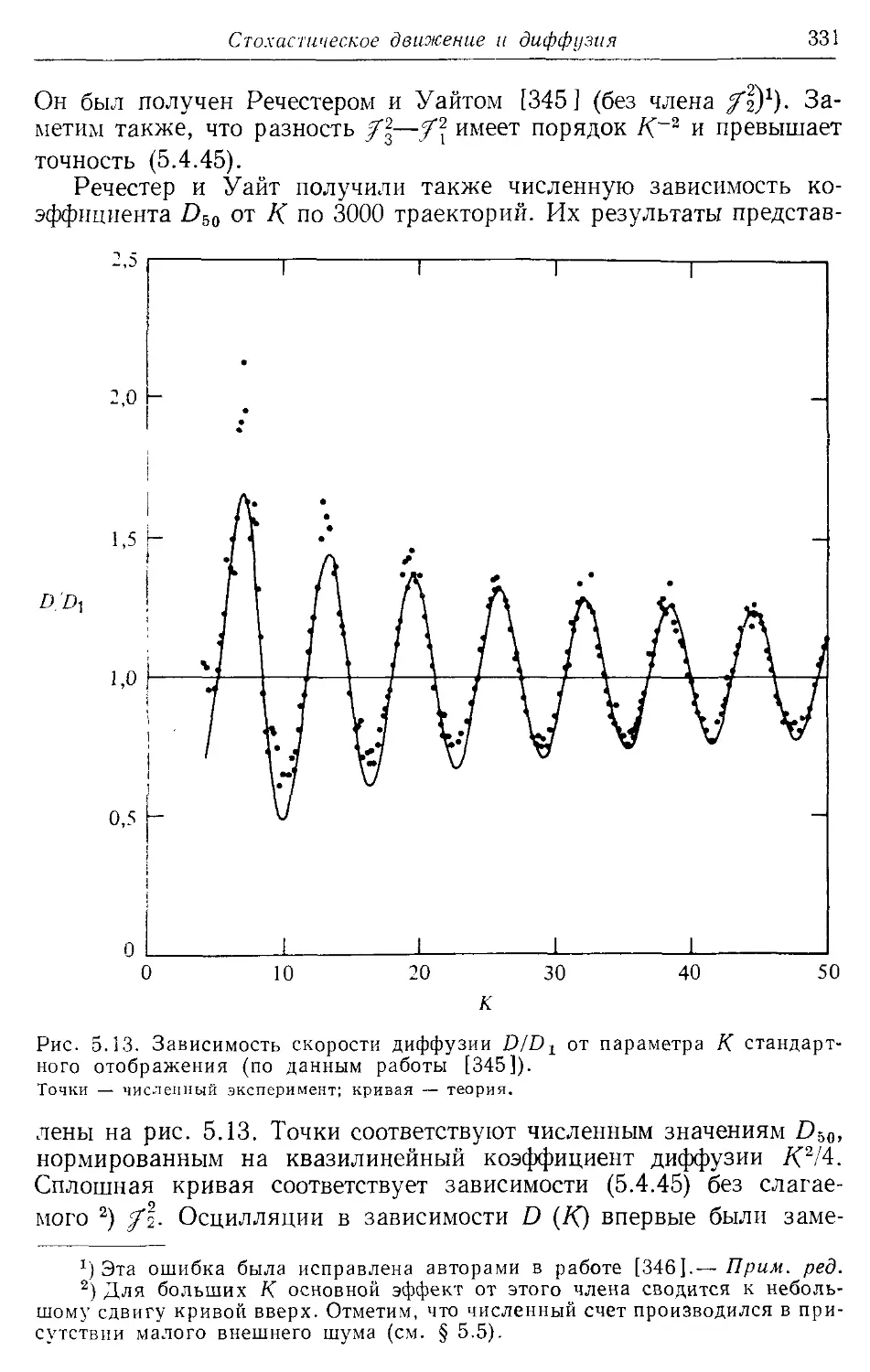
Речестер (Rochester) 326, 331, 336,
338, 392
Рёслер (Rossler) 416
Родионов С. Н. 491
Розенблют (Rosenbluth) 247, 392, 491
Ронлии (Rognlien) 493
Рудник (Rudnick) 443
Рютов Д. Д. 385
Рюэль (Ruelle) 19, 478, 480, 495
СагдеевР. 3.336, 381,395
Саймон (Syrnon) 46
Самек (Samec) 493
Сегур (Segur) 57
Сейдл (Seidi) 492
Сиамбис (Siambis) 491
Синай Я. Г. 17,71,300,496
Ситников К. Н. 487
Смейл (Smale) 199, 487
Смит (Smith) 98, 139, 267, 268, 493
Снайдер (Snyder) 46
Спротт (Sprott) 492
Стикс (Stix) 392
Стоддард (Stoddard) 408
Ступаков Г. В. 385
Суинни (Swinney) 481
Табор (Tabor) 249
Тейлор (Taylor) 142
Теллер (Teller) 490
Теннисон (Tennyson) 73, 341, 342,
353, 368, 375, 379, 381
Tofla(TodaM1
Томае (Thomae) 449
Треве (Treve) 422, 478
Тэкенс (Takens) 19, 193, 478. 480
Уайес (Wyeth) 493
Уайт (White) 326, 331,336
Уайтмен (Whiteman) 65, 104, 154, 487
Уинтнер (Wintrier) 488
Уиттекер (Whittaker) 20, 55, 154, 486,
487
Улам (Ulam) 14, 56, 68, 220, 348, 406
Уотерс (Waters) 407
Фармер (Farmer) 424, 425
Фейгенбаум (Feigenbaum) 20, 434,
438 452, 481
Ферми (Fermi) 14, 56, 68, 204, 220,
348, 406
Филд (Field) 495
Филоненко Н. Н. 392
Финн (Finn) 147, 199, 200, 392
Форд (Ford) 54, 190, 247, 273, 279,
294, 299, 407, 408
Фрёлинг (Froehling) 425
Фрёшле (Froeschle) 294, 348, 407
Фукуяма (Fukuyama) 98, 139, 269
Фурсов В. С. 489
Хагихара (Hagihara) 488
Хастье (Hastie) 491
Хатори (Hatori) 494
Хаулэнд (Howland) 147, 164
Хедлунд (Hedlund) 294
Хейлес (Heiles) 54, 64, 290, 294, 314
Хеллеман (Helleman) 165, 171, 270,
290, 433, 448, 453, 478, 486
Хенон (Непоп) 16, 54, 64, 204, 290,
294,314,416,419,421
Хереворд (Hereward) 489
Хертвек (Hertweck) 490
Ховард (Howard) 405, 491, 493
Холл (Hall) 56, 58
Холмс (Holmes) 348, 437, 461, 463
Хольт (Holt) 57
Хопф (Hopf) 294, 478
Хори (Hori) 147, 487
Хьтоберман (Huberman) 443, 450,
451,484
Цанг (Tsang) 473
Цейпель (Von Zeipel) 13, 87, 90
Чандрасекар (Chandrasekhar) 490
Чарчилл (Churchill) 488
Чириков Б. В. 17, 43, 68, 73, 111, 121,
122, 127, 164, 181, 193—195,
220. 221, 246, 247, 249, 252. 257,
262, 294, 311,332, 342, 353, 360,
365, 366, 375, 381, 382, 386, 469,
486,488,490,491,492,497
Шарковский А. И. 440
Шейдекер (Scheidecker) 294, 407
Шепелянский Д. Л. 497
Шлютер (SchlQter) 490
Шмидт (Schmidt) 252, 253, 273
Штерн (Stern) 104, 154
Эдмондс (Edmonds) 492
Экман (Eckmann) 448, 478, 484
Эминицер (Eminhizer) 165
Эсканде (Escande) 248, 277, 503
ПРЕДМЕТНЫЙ
Адиабатический инвариант 13, 17,
31,37,88,104,124,134,154
— процесс 87, 111, 1 12,349
Адиабатическое возмущение 106,
107, 154, 367
Аносова системы 302—305, 308
Аттрактор, геометрия 74, 75, 78,
417^22
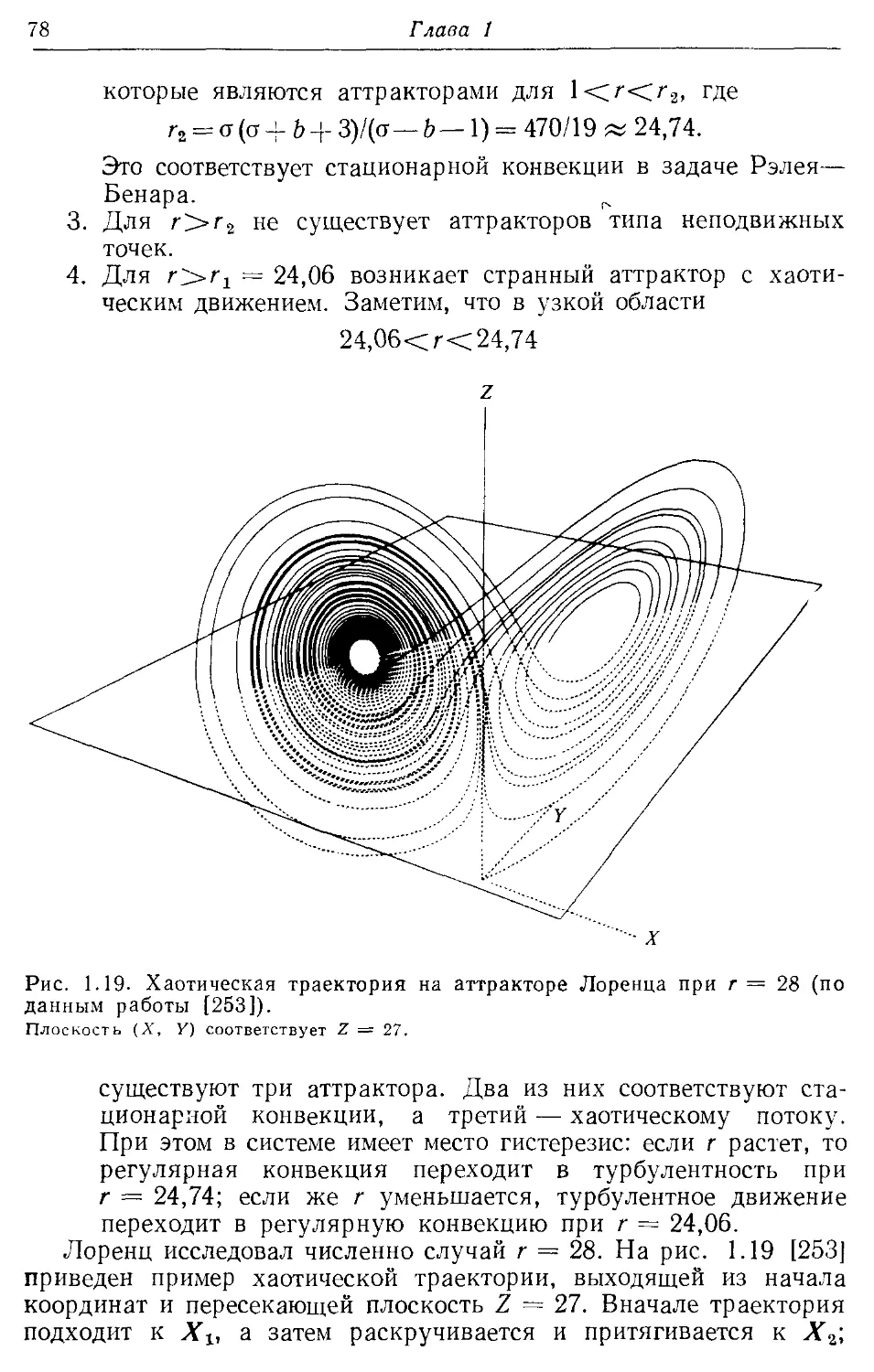
— Лоренца 78—80, t77
— область притяжения 414
— простой 19, 73, 74. 76—80, 413,
414, 440-^42, 464
— странный (хаотический) 19, 20,
74—76, 78, 80, 416-^25, 463,
464, 469
размерность 19, 74, 422—425
—Хенона 419^22
Бернулли свойство 304
— сдвиг 303, 304
— система 303—305
Бильярдная модель 348 353
Бифуркации 77, 78, 232, 415, 416,
430—432,440,442,453
— обратные 416, 448. 449
— теория 415, 416, 433^38, 45-i—
457. 497
Вырождение 126, 129, 130, 137, 138,
189—191
Вычет 269
— средний 271
Газ твердых шариков 70, 305
Гальтона доска 305
Гамильтониан автономный 23, 24, 59,
100, 148, 292, 298
— канонические преобразования
90—98, 132—134, 147, 180, 189,
259—261
— неавтономный 97, 98, 110, 111,
154, 184, 235, 236, 255, 259, 354
— переход к отображению 182, 183
УКАЗАТЕЛЬ
— стандартный 43, 127, 236
— фурье-разложение 92, 95, 97, 98,
123, 124, 132, 144 189, 235, 236,
281,474-^76
Гармонический осциллятор 36, 89,
129
— — медленно изменяющийся 87,
111,119,121,156,157
Гетероклинные точки 199—201
Гиперболические точки (траектории)
40, 196—201, 204, 206, 218, 219,
230, 232, 254, 458^60, 462
Гомоклинные точки 198—201, 306,
307. 458
Грина критическое значение 275—
277
Грубость см. Устойчивость
структурная
Депри ряды 149, 259
Диссипативные системы 73, 410
Диффузия Арнольда 18, 19, 59, 71—
73, 249, 292, 317, 341, 346, 347,
350—352, 357—365, 367
— внешняя 332, 337, 338, 375
— в пространстве действий 317
— модуляционная 18, 19, 342, 366
— неоклассическая 336, 395
— по резонансам 335, 353
— резонанса 382
— резонансное каналирование 375,
385. 386
—скорость 331, 337, 340, 353, 372,
373, 377, 378, 399^02
квазилинейная 326, 383
— тензор 377—379
— уравнение 291, 319—321
— частиц в ловушке 386
Золотое сечение см. Число вращения
Иерархия инвариантов 110, 111
— резонансов 62, 203, 204
Инвариант см. Интеграл движения
Инвариантная кривая (поверхность)
17, 18, 33, 60—69, 72, 102, 103,
178, 185—200, 215, 231, 232, 247,
248, 272, 273, 279—281, 350
Инвариантное распределение (мера)
291,444-^48,466
на аттракторе 444—448, 466
Интеграл действия 13, 20, 31
Интегралы движения 33, 34, 48, 55,
60, 98, 176, 203
адиабатические см.
Адиабатический инвариант
глобальные 38, 47, 52, 60, 98.
143—146
изолирующие 348, 487
инволюция 38
локальные 124, 200
К-системы 300, 301, 303, 305
Канторово множество 76, 422—424
Касательный вектор 295, 296
Квазипериодические колебания 35,
49, 74, 178, 294, 305
Компонента движения 232, 292, 294,
301,311,312,314
Корреляции 332
— связь с коэффициентами переноса
321, 325, 326
— убывание 244, 332
Коэффициенты переноса 291, 319,
321,325
Крупноструктурное разбиение
("огрубление") 97, 299, 300
Ляпунова показатели 244, 294, 301,
442—444,448
вычисление 310
обобщенные 297
Магнитные ловушки ПО, 111, 386,
490
Малые знаменатели см. Резонансные
знаменатели
Марковский процесс 318
Матрицы 207—209, 214—220. 296
— симплектические 209—212
Маятник 39, 42, 93, 95, 152—154 237
238, 263—269
— как модель резонанса 42, 127, 236,
255
— точное решение 39—42, 267
Мельникова—Арнольда интеграл
239—241,465
Метод Венцеля —Крамерса—
Бриллюэна (ВКБ) 13
— Грина 247, 248, 269
—Дуннета—Лейнга— Тейлора
(ДЛТ) 142—146
— касательных Ньютона 163, 181,
213
— Уиттекера конструирования
интегрируемых систем 55, 58
— усреднения см. Теория
возмущений асимптотическая
— Фурье-траекторий 326—332
Методы вариационные 287
в теории возмущений 168—374
Модель Контопулоса 316, 317
— Леннарда-Джонса 408
— Лоренца 20, 57, 76, 77, 475^77.
484
— Ферми—Паста,— Улама 14,
405^07
—Хенона—Хейлеса 16, 54, 58, 59,
63—67,171-174,313
Нелинейность колебаний 86,187—
191
параметр 127, 189
умеренная 194, 195
Неподвижные (периодические) точки
125, 127, 130, 195, 214, 215, 228,
229, 232— 234, 242, 250—253,
276, 277, 430
Непрерывная дробь 271—273, 277
Округления ошибки 290, 308, 309,
335
Отображение Арнольда 302, 305
— Вогелара 500, 501
— в сечении Пуанкаре 79, 179, 180,
238,241,242,411
— гамильтониан 183, 184, 235.
236,255,256
— диссипативное 464, 465, 468
— Заславского 425
— инволюции 181, 213, 214, 233, 242
— каноническое 179—182, 184. 228
— Катана— Йорке 425
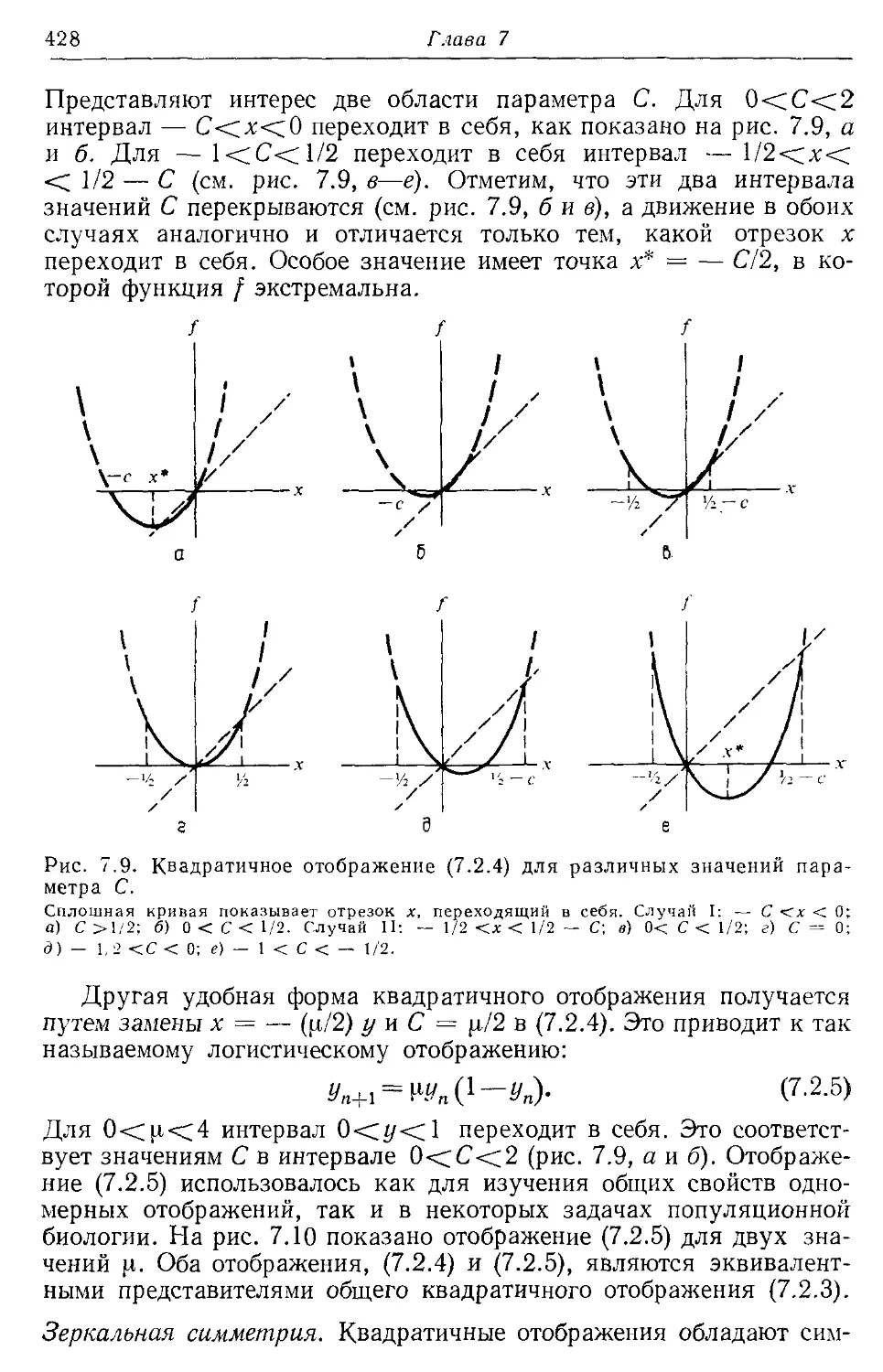
— квадратичное 204, 427—429
—линеаризованное 207, 214—220,
229, 296, 298. 321
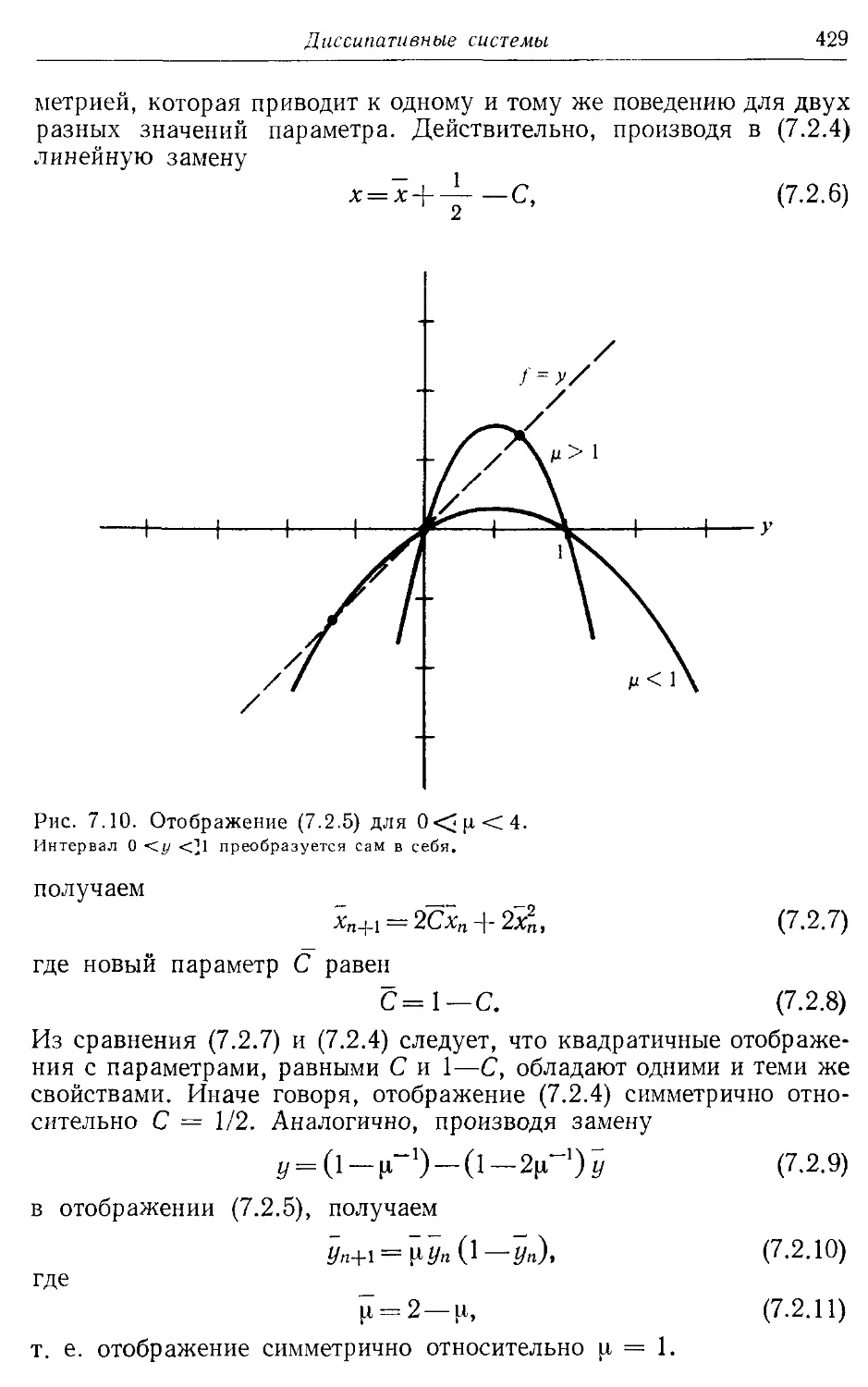
— логистическое 428, 429, 447, 448
— необратимое 76, 426
— обратимое 411
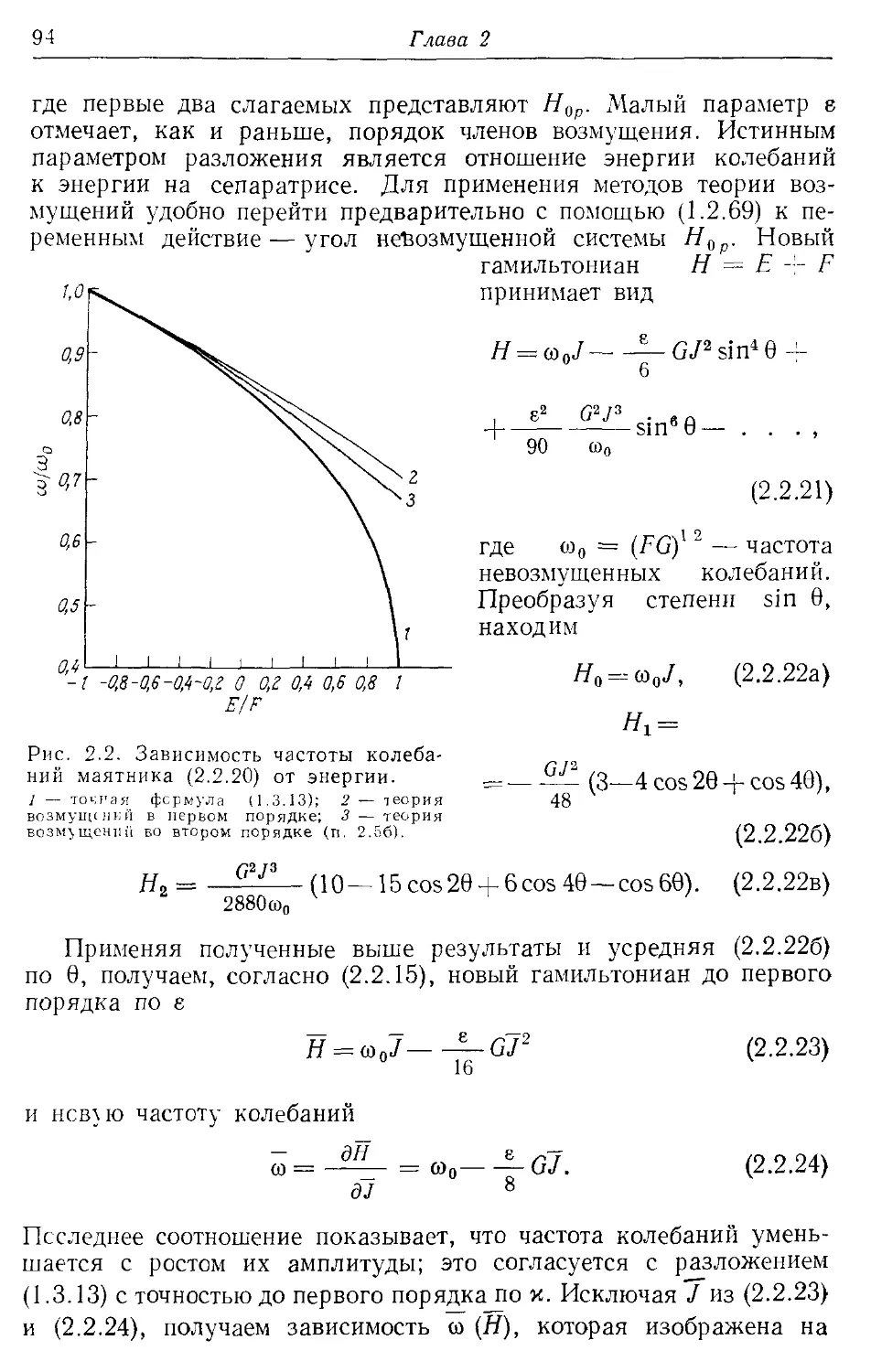
—одномерное 76, 79, 80, 233, 234,
426,
— поворота 179—182. 195, 204, 293,
333,382
— Пуанкаре 79, 179. 235, 238, 298,
348,411,453
— сепаратрнсное 241, 250
— стандартное 181, 331,338, 382
— Улама 222—224, 227, 242, 249,
250,321,325,334,468
Параметры подобия 433—438, 451,
456, 457, 497—503
Пенлеве свойство 47—59
Перекрытие резонансов 71, 257,
367—369, 405
критерии 17, 68, 246, 247, 289,
367
простое 257
улучшенное 258—262
Перемежаемость 484, 485
Переменные действие — угол (фаза)
31, 34, 36, 37, 41, 90, 95, 107, 342,
361,389
— дрейфовые 99, 100
— канонические 107, 178, 222, 223,
300. 323, 324
— обобщенные 22, 148. 154
— разделение 38. 115
— смешанные 147
Перемешивание 17, 70, 298—300,
305, 448
Переход к стохастичностн 245
турбулентности 478
Периодическая 8-функция 184, 235
Периодические траектории 60, 74,
125, 167, 178, 179, 207
Правило двух третей 256, 288
Предельный цикл 74, 416, 464, 480—
482
Преобразование каноническое 95,
107, 123, 148, 149, 162, 354, 362,
378, 389
—пекаря (отображение) 71, 299, 305
Производящая функция 90, 182, 362,
378
Ли 25, 148. 180,259
смешанных переменных 9о, 123
Фурье-разложение 92, 95—98,
101, 109, 259, 369
Пространство действий 344—347
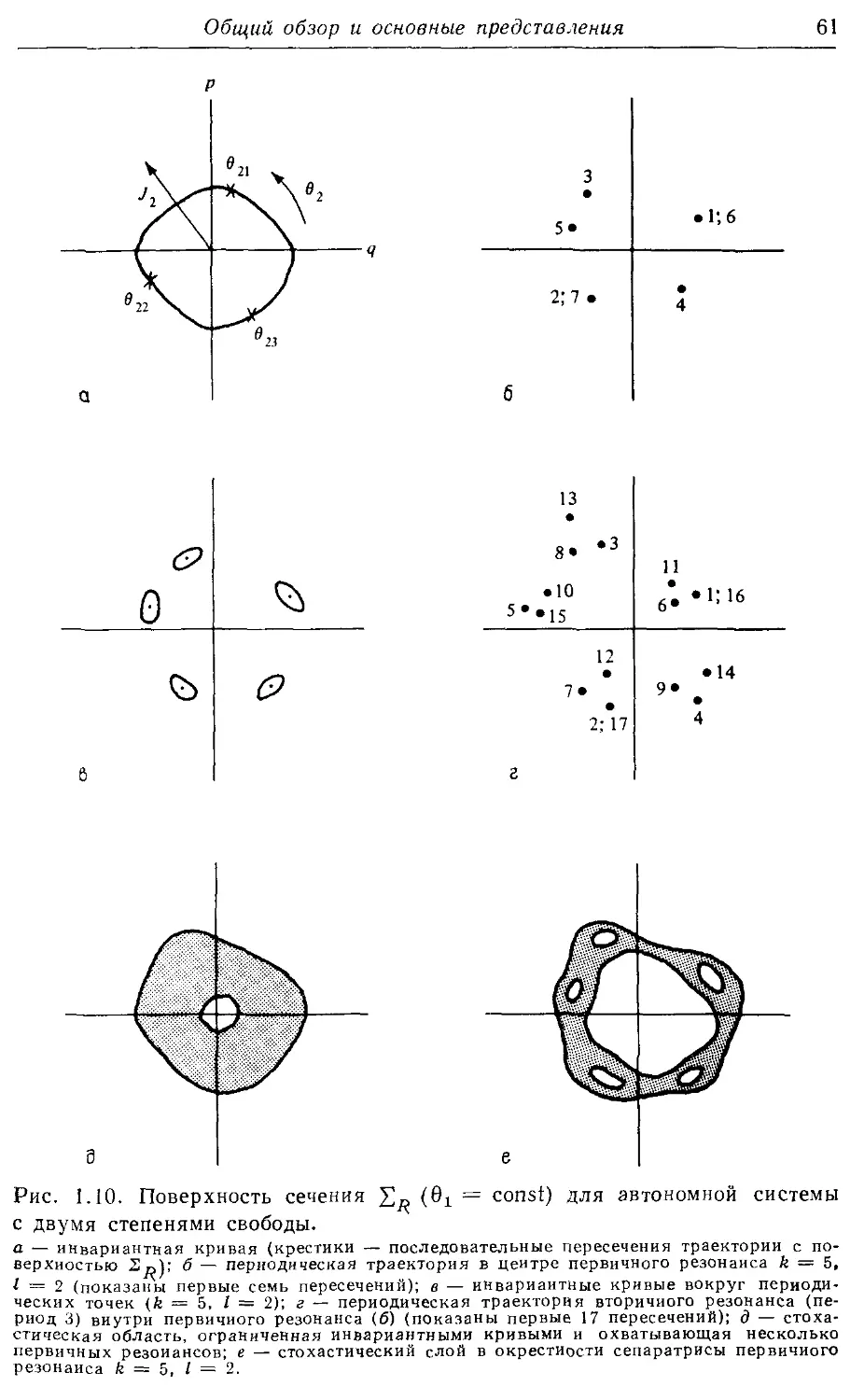
Пуанкаре сечение 15, 31—34. 53, 60,
61, 65—67, 69, 102, 103, 140, 141,
177,411
Резонанс волна—частица 98—104,
135, 144—146, 161, 162, 280
— вторичный 61, 62, 130, 138, 139,
192, 202, 203, 205, 237, 263, 281
— высших гармоник 125, 269—274,
365
порядков 109
— дрейфовый 394—397
— многомерный 341
— первичный 61, 62, 126—130, 146,
186, 195, 200—205, 225, 228, 236,
237, 257— 260
— прохождение 112, 113, 367
— связи 359,375,379, 390
—центр 127—129, 132, 134, 263, 397
Резонанса два 279—281
Резонансные знаменатели 83, 87, 89,
96,98,109,187
устранение 123, 160
глобальное 142
— поверхности 343—346, 379
Резонансов взаимодействие 360, 364
— уровни 139, 168
Ренормализация 135, 248, 277—279,
433—438, 455^57, 501—503
— в стохастическом слое 257, 269
— Грина 269—211
— для двух резонансов 248, 279—287
— точная теория 433—435, 440, 453,
497
Рэлея— Бенара конвекция 20, 67,
475, 476
Сверхадиабатичность 491
Секулярные члены 82, 85
Сепаратриса 39, 41, 42, 49, 61—64,
67, 73, 128, 191, 197—200, 206,
234, 237, 267
Символическая траектория 304
Системы, близкие к интегрируемым
24, 36, 42, 59, 62, 89, 90, 180, 305,
310
— интегрируемые 38, 51, 54, 55, 70,
125,176—180,310,315
конструирование 55
примеры 39, 51, 177
— квантовые 307, 309, 495
Сложность алгоритмическая 306, 307
Случайность 290, 294. 299, 305, 307
— связь со сложностью 306, 307
Случайные последовательности 306,
307
— фазы (приближение) 70, 71, 291,
322
Собственные векторы 207, 215—220,
296, 297, 303
— значения 207, 215—220, 230, 297,
303
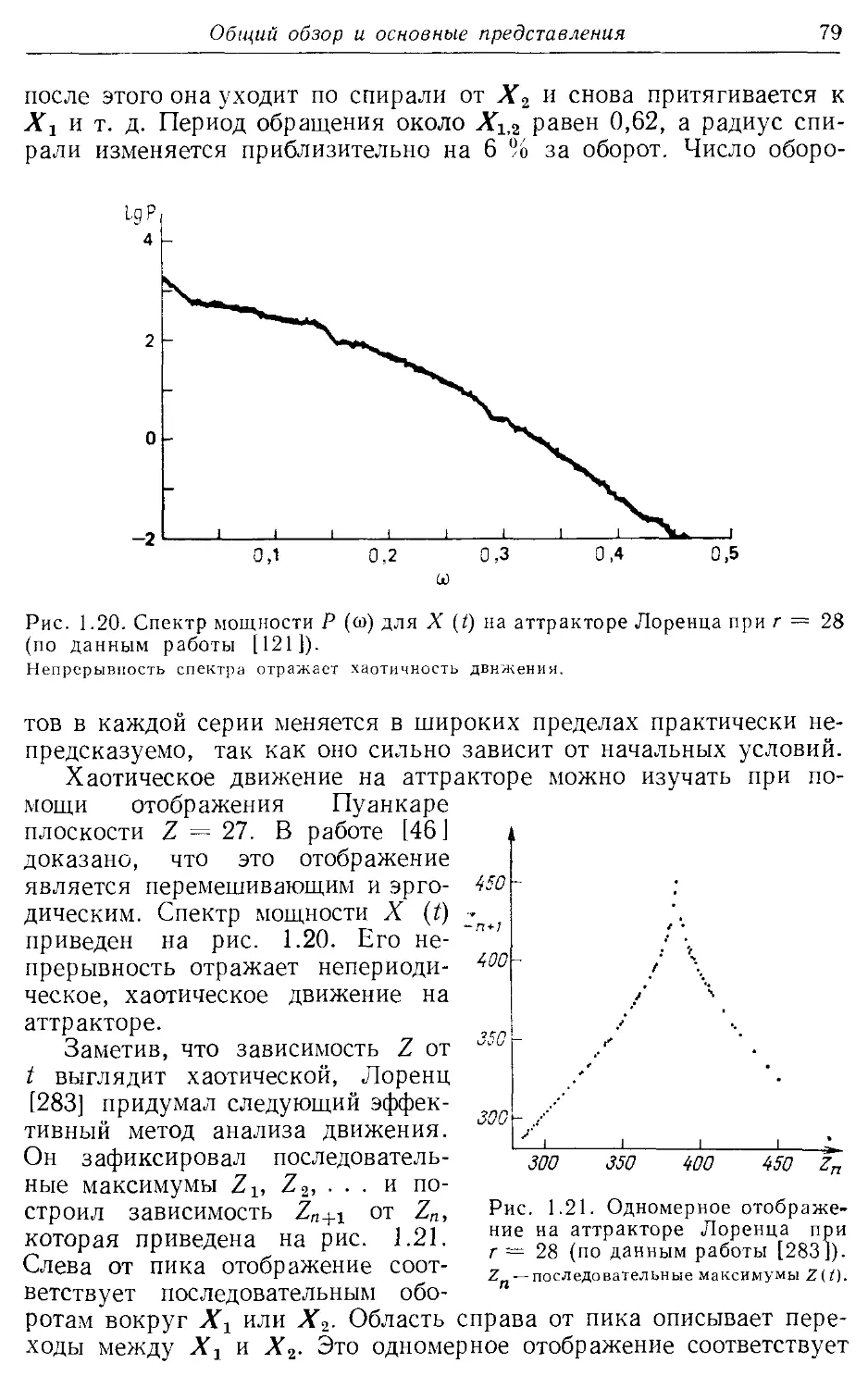
Спектр мощности 79, 438—440,
449^53
Стохастическая накачка 353
Стохастический слой 61—63, 65,
71—73 237, 238, 242, 243, 261—
263, 347
модуляционный 366—371
толстый 349—352, 354
тонкий 350—352, 357
Стохастичность глобальная 70 71
194 245, 246, 248, 249, 254, 290
— граница 226, 231, 242, 246, 253—
256
— критерии 200, 241, 246, 257, 291
310,312,315
— локальная 69, 245, 246, 254
—области 74, 201—206,245
— параметр 181, 249
— свойства 291, 298, 442, 449
Теорема Алексеева—Брудно 307
— Лиувилля 27,412
— Пуанкаре— Бендиксона 413,416
— Пуанкаре—Биркеофа 195
Теория возмущений асимптотическая
13, 87, 104, 105, 114—118, 203,
235,236
вариационная см.
Вариационные методы
каноническая 81, 107, 369
классическая 89
Ли 145
неканоническая 1 !4
резонансная 17, 43, 121, 203
235 262, 263, 390
сверхсходящаяся 82, 162
— Колмогорова— Арнольда—
Мозера (КАМ) 38, 60, 68, 165,
184,185,203,224
Тоды цепочка 47, 51—54, 57
Тор см. Инвариантная поверхность
Турбулентность гидродинамическая
474
— химическая 494
Удвоение периода 76, 430—432,
453^57, 498
Уравнение Дюффинга 461—465
— Фоккера—Планка—Колмогорова
(ФПК) 318, 468^72
У-системы см. Аносова системы
Ускорение Ферми 59, 68, 69, 220, 262,
263, 468
Устойчивость движения, граница
231,245
линейная 127—130, 207, 215,
228, 242, 247, 252, 253
островки 224, 225, 232, 245,
251—254,469
— структурная 302, 308,
Фазовая траектория 128, 129, 131,
178, 254, 414, 462
Фазовое пространство 18, 19, 25—
27, 32, 58, 254, 255, 299, 307, 458
разбиение 245, 246, 951, 300
расширенное 28—30, 95, 223
сокращенное 29, 33
Фазовые колебания 130, 134, 226, 236
частота 136, 130, 236, 384
Фокус 74, 414—416, 463, 464, 468
Фрактальная размерность см.
Аттракторы
Фрактальные диаграммы 277—279
Хаос см. Стохастичность,
Случайность
Число вращения 179, 180, 241, 256,
281
золотое сечение 194, 272, 275—
277
иррациональное 185
рациональное 195, 272, 279
Эллиптические точки (траектории)
39, 42, 197, 201, 204, 216—218,
224 232, 254
Энергетическая поверхность 292,
297, 343—346, 375, 376, 379, 385
Энтропия (КС-энтропия) 244, 300,
301, 303—305, 307, 513
— вычисление 301, 311, 315
— связь с показателями Ляпунова
301
Эргодичность 14, 17, 70, 291, 299,
305 487
ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
Книга, перевод которой предлагается читателю, написана из-
известными американскими физиками, профессорами Калифорний-
Калифорнийского университета (Беркли) А. Лихтенбергом и М. Либерманом.
Она посвящена весьма необычной области классической механики,
которая получила название стохастической, или хаотической, ди-
динамики.
Фундаментальное значение исследований в этой области, бурно
развивающихся особенно в последнее десятилетие, состоит в том,
что они вскрывают динамическую природу случайности и стати-
статистических законов, преобразуя частную гипотезу «молекулярного
хаоса», выдвинутую Больцманом более ста лет тому назад, в общую
теорию динамического хаоса.
Многочисленные приложения хаотической динамики в самых
разных областях физики и техники, а также других наук обязаны
тому существенно новому и принципиально важному обстоятель-
обстоятельству, что статистические законы, а вместе с ними простое статисти-
статистическое описание более не ограничены (нашим незнанием!) только
очень сложными системами с большим числом степеней свободы.
Напротив, при определенных условиях, которые сводятся в основ-
основном к сильной (экспоненциальной) локальной неустойчивости дви-
движения в некоторой области фазового пространства, динамический
хаос возможен, например, всего при двух степенях свободы кон-
консервативной гамильтоновои системы. Источник чрезвычайной слож-
сложности, характерной для индивидуальной реализации случайного
процесса, оказался совсем не там, где его искали со времен Больц-
мана! Дело вовсе не в сложном устройстве конкретной динамиче-
динамической системы (и } ж тем более не в числе ее степеней свободы) и даже
не во внешнем «шуме» (что есть только иное выражение сложности
другой системы — окружающей среды), а в точно заданных началь-
начальных условиях движения. В силу непрерывности фазового простран-
пространства в классической механике эти начальные условия содержат
бесконечное количество информации, которое при наличии силь-
сильной неустойчивости и определяет предельно сложную, непредска-
непредсказуемую и невоспроизводимую картину хаотического движения.
Такая система не «забывает» свои начальные условия, а наоборот,
следует им во всех мельчайших деталях и именно это и приводит
к хаосу, который с самого начала заложен в этих деталях. Конечно,
с точки зрения физики все это — весьма существенная идеализа-
Предисловие редактора перевода
ция, но в то же время это как раз тот самый предельный случай,
который открывает новую перспективу реальной динамики и не
только классической, но и квантовой.
Предлагаемая читателю книга является почти единственной 1)
физической (несмотря на обилие формул) монографией в рассмат-
рассматриваемой области; она представляет собой одну из первых попыток
дать цельную картину по существу нового раздела физики. Ее ав-
авторы в течение многих лет успешно работают в этой области, им
принадлежит здесь ряд интересных и важных результатов, они
хорошо известны среди специалистов как за рубежом, так и в на-
нашей стране. Один из авторов, проф.А. Лихтенберг, знаком также и бо-
более широкому кругу советских читателей по переводу его книги [3 1.
Новая книга рассчитана на широкий круг специалистов. Од-
Однако она не является популярной и при активном чтении треб\ет
значительной работы, переосмысления многих привычных понятий.
Авторы ставят своей задачей не только рассказать о новой области
или дать обзор новых результатов, но и научить читателя (желаю-
(желающего!) работать в этой области и помочь ему овладеть методами тео-
теоретического анализа и практических расчетов. Основной направ-
направляющей нитью изложения является детальное и всестороннее об-
обсуждение перехода от простых и хорошо известных регулярных
нелинейных колебаний к разл ичным режимам хаотического движе-
движения (гл. 3—5), включая такие тонкие эффекты, как диффузия Ар-
Арнольда (гл. 6). Авторы подобрали небольшое число достаточно про-
простых и характерных примеров, к которым они многократно
возвращаются при описании различных эффектов или методов ана-
анализа. Это существенно облегчает, на наш взгляд, понимание и ос-
освоение основного материала. Книга хорошо иллюстрирована; она
включает разнообразные результаты численного моделирования,
что значительно способствует наглядности изложения.
В книге рассматривается в основном гамильтонова динамика.
Диссипативным системам посвящена только гл. 7. Изложение здесь
более конспективно, особенно это касается наиболее интересного
§ 7.4 «Проблема турбулентности». Тем не менее материал этой главы
служит хорошим введением в современную теорию диссипативных
динамических систем.
В основу анализа гамильтоновой динамики положена резонанс-
резонансная теория возмущений (§ 2.4), опирающаяся на ясные физические
представления и позволяющая количественно исследовать такие
сложные задачи, как, например, стохастический слой вокруг
сепаратрисы нелинейного резонанса. Основная идея здесь заклю-
заключается в том, что переход с ростом возмущения от регулярного дви-
движения к хаосу происходит через изменение топологии инвариант-
г) Совсем недавно из печати вышла монография Заелавского [1], посвя-
посвященная той же проблеме с одним, однако, существенным добавлением: в
нее включены вопросы квантовой теории динамического хаоса. Математиче-
Математические монографии также немногочисленны (см., например, [2]).
Предисловие редактора перевода
ных кривых в окрестности нелинейных резонансов. Система резо-
нансов является, вообще говоря, всюду плотной в фазовом про-
пространстве и имеет иерархическую структуру, которая характери-
характеризуется бесконечной последовательностью уровней: первичные
резонансы между невозмущенными колебаниями, вторичные резо-
нансы с колебаниями на первичных резонансах и т. д.
Наряду с этим описаны и другие новые методы в теории нели-
нелинейных колебаний, в том числе и малоизвестные нашему читателю.
Это относится прежде всего к использованию преобразований Ли
(§ 2.5), методу Дуннета—Лейнга—Тейлора (п. 2.4г) и ренормали-
зации (§ 4.4 и„4.5).
Наряду с чисто динамическими задачами рассмотрено также
совместное влияние резонансов и внешнего шума (§ 6.3). Прин-
Принципиально важно, что динамический хаос возможен в отсутствие
какого-либо внешнего случайного возмущения. Однако не менее
существенно и то, что в условиях глобального хаоса всегда при-
присутствующий реально слабый шум не изменяет статистические свой-
свойства системы. С другой стороны, при некоторых условиях, напри-
например вблизи границы перехода к динамическому хаосу, совместное
действие шума и резонансов может быть совсем иным, нежели каж-
каждого из этих факторов в отдельности.
Один из недостатков книги — некоторая перегруженность раз-
различными, иногда очень специальными методами и задачами. От-
Отчасти это сделано авторами сознательно в расчете на то, что книга
может служить своего рода справочником для тех, кто уже освоил
основы хаотической динамики. Чтобы помочь начинающим, основ-
основные разделы книги отмечены звездочкой.
Другой недостаток связан с неустановившейся терминологией
и как следствие значительной долей специального «жаргона». В ка-
качестве примера можно указать на не разграниченные четко поня-
понятия «хаотический» и «стохастический» (см. примечание авторов на
с. 74). Представляется, что первый термин является вообще более
предпочтительным, поскольку второй имеет и совсем иной смысл.
Так, существует обширная область исследований «стохастических
процессов» под действием внешних случайных возмущений. При
переводе мы старались внести в терминологию единообразие, в не-
некоторых случаях это отмечено в примечаниях редактора или пере-
переводчиков.
В книге имеются повторения, часть которых с разрешения ав-
авторов была сокращена при переводе. Были исправлены также оче-
очевидные опечатки и неточности. Спорные положения, а также не-
некоторые свежие или почему-либо не отраженные в книге интерес-
интересные результаты отмечены в примечаниях редактора. Там же даны
пояснения к основному тексту.
Рассматриваемые в книге приложения носят в основном иллю-
иллюстративный, педагогический характер. Краткая сводка некоторых
других приложений дана в дополнении А. Как отмечают авторы,
Предисловие редактора перевода
нет никакой возможности сколько-нибудь полно осветить все разно-
разнообразные приложения теории динамического хаоса. Все же хо-
хочется добавить к их списку два более фундаментальных приложе-
приложения в нелинейной теории поля. Одно из них связано с открытыми
в работе [4] (см. также [5, 6]) хаотическими колебаниями гравита-
гравитационного поля в однородных анизотропных космологических мо-
моделях общей теории относительности вблизи особенности. Инте-
Интересно отметить, что сложную исходную систему уравнений Эйн-
Эйнштейна удается свести в конечном счете к простому одномерному
отображению х = 1 х (mod 1), которое и определяет хаотическую
динамику космологической модели. Это отображение дает также
пример простейшей динамической системы с хаотическим движе-
движением. Еще один аналогичный пример — отображение х — kx
(mod 1), где целое &>1 (см. п. 5.2г).
Другое приложение относится к калибровочным полям Янга—
Миллса, ответственным за взаимодействие элементарных частиц.
Классические однородные модели такого поля описывают в отли-
отличие от предыдущего примера локальную (внутреннюю) динамику
поля, которая также оказывается, вообще говоря, хаотической
[7—9]. В простейшем случае такая однородная модель сводится
к обычной гамильтоновой системе с двумя степенями свободы и по-
потенциальной энергией U = (хуJ.
Отметим также красивое явление генерации магнитного поля
за счет развития локальной неустойчивости движения замагничек-
ной плазмы [10].
Естественно, что в такой обширной и быстро развивающейся
области, как динамический хаос, даже самая «свежая» монография
не успевает отразить некоторые новые результаты, с одной стороны,
и не в состоянии вместить все аспекты этой многогранной про-
проблемы, с другой стороны. Ниже мы коснемся трех таких вопросов,
которые указывают также на границы применимости существующей
теории динамического хаоса.
Первый вопрос относится к «аномальным» (аномально сложным)
статистическим свойствам динамического хаоса. В отличие от ста-
статистических гипотез, в качестве которых естественно выбирать
простейшие предположения, статистические свойства определяются
здесь динамикой системы и могут оказаться весьма сложными. Та-
Такова, например, гидродинамическая турбулентность. Исследова-
Исследования последних лет показали, что статистические «аномалии» дина-
динамического хаоса — весьма распространенное явление, связанное,
в частности, со сложной иерархической (масштабно-инвариантной)
структурой границы хаоса в фазовом пространстве [11—14] (см.
также конец § 5.4). Несмотря на экспоненциальную локальную
неустойчивость движения, это приводит к степенному затуханию
корреляций: С (х) к т"р; /><1- Диффузионное описание может
оказаться в таких условиях совершенно неприменимым.
Предисловие редактора перевода
Другой интересный вопрос: к чему ведет динамический хаос?
Как мы теперь знаем или, лучше сказать, наконец, поняли, конеч-
конечным продуктом хаоса совсем не обязательно является унылое ста-
статистическое равновесие, которое может оказаться просто неустой-
неустойчивым. Классический пример этого — джинсовская неустойчивость
гравитирующего газа, которой в конечном счете все мы обязаны
как своим существованием, так и неисчерпаемым разнообразием
окружающего нас мира. Аналогичные коллективные (когерентные)
процессы давно и широко изучаются в плазме. Сюда же относится
и так называемая «химическая динамика» (см. дополнение А.5).
Недавно все это получило привлекательное название «синерге-
«синергетика». С точки зрения физики такие процессы естественно называть
вторичной динамикой. К ней относится по существу вся класси-
классическая механика макроскопических тел, в частности, и вся небес-
небесная механика (первичной является в этом случае молекулярная
динамика). Одна из характерных особенностей вторичной дина-
динамики — ничтожное число ее степеней свободы по сравнению с пер-
первичной системой. Однако именно эти коллективные степени сво-
свободы и определяют наиболее существенную глобальную структуру
системы и ее эволюцию, тогда как все остальное есть лишь не-
некоторый общий термодинамический «фон». В этом же состоит, по-
видимому, и ответ на вопрос о предельном поведении динамиче-
динамической системы с очень большим числом степеней свободы, который
кратко обсуждается в конце § 6.5. Дело здесь не столько в размере
сохраняющихся областей регулярного движения, сколько в воз-
возможности возникновения вторичной динамики.
Наконец, еще один очень важный вопрос: в какой мере такой
своеобразный феномен, как динамический хаос, сохраняется в (бо-
(более фундаментальной) квантовой механике? В отличие от класси-
классического хаоса, природа и механизм которого в основном выяснены,
исследование квантовой динамики соответствующих систем только
начинается (см. дополнение А.6). Тем не менее уже сейчас ясно,
что квантовые эффекты кардинально изменяют характер этого яв-
явления и притом весьма неожиданным образом. Поскольку это ка-
касается временной эволюции системы, в квантовой механике воз-
возможна (и, по принципу соответствия, необходима) лишь временная
имитация тех или иных свойств классического хаоса [15] (см. также
[1, 16, 17]). В действительности же квантовое движение является
почти периодическим из-за дискретности спектра любой ограни-
ограниченной в фазовом пространстве системы, а также дискретности са-
самого фазового пространства в квантовой механике. Временной
классический хаос уступает место пространственному хаосу кван-
квантовых стационарных состояний [18, 19].
Перевод книги выполнен канд. физ.-мат. наук В. В. Вечеславо-
вым (предисловие, гл. 2, дополнения), В. Г. Давидовским (гл. 3, 6),
канд. физ.-мат. наук Ф. М. Израйлевым (гл. 4, 7) и канд. физ.-мат.
наук Д. Л. Шепелянским (гл. 1, 5).
'10 Предисловие редактора перевода
Мы весьма признательны авторам книги, профессорам А. Лих-
тенбергу и М. Либерману, за помощь при подготовке русского из-
издания.
Б. В. Чириков
ЛИТЕРАТУРА
1. Заславский Г. М. Стохастичность динамических систем.— М.: На\ка,
1983.
2. Корнфельд И. П., Синай Я- Г., Фомин С. В. Эргодическая теория —
М.: Наука, 1980.
3. Лихтенберг А. Динамика частиц в фазовом пространстве.— М.: Атом-
издат, 1972.
4. Лифшиц Е. М., Лифшиц И. М., Халатников И. М.— ЖЭТФ, 1970,
т. 59, с. 322.
5. Ландау Л. Д., Лифшиц Е. М. Теория поля.— М.: Наука, 1973, с. 498.
6. Лифшиц Е. М., Халатников И. М., Синай Я- F., Ханин К. М.,
Щур Л. Н.— Письма в ЖЭТФ, 1983, т. 38, с. 79.
7. Матинян С. Г., Саввиди Г. К., Тер-Арутюнян Н. Г.—Письма в ЖЭТФ,
1981, т. 34, с. 613.
8. Чириков Б. В., Шепелянский Д. Л.— Ядерная физика, 1982, т. 36, с. 1563.
9. Николаевский Е. С, Щур Л. Н.~ ЖЭТФ, 1983, т. 85, с. 3.
10. Арнольд В. И., Зельдович Я- Б., Рузмайкин А. А., Соколов Д. Д.—
ЖЭТФ, 1981, т. 81, с. 2052.
П. Channon S. R., Lebowitz J. L.— Ann. X. V. Acad. Sci., 1980, v. 357,
p. 108.
12. Чириков Б. В., Шепелянский Д. Л.— В кн.: IX Международная конфе-
конференция по нелинейным колебаниям. Киев: Наукова думка, 1983.
т. II.
13. Чириков Б. В.— Lecture Notes in Physics, 1983, v. 179, p. 29.
14. Karney С F. F.— Physica, 1983, v. 8D, p. 360.
15. Израйлев Ф. М., Чириков Б. В., Шепелянский Д. Л.— Soviet Scientific
Reviews, 1981, v. 2C, p. 209.
16. Чириков Б. В.— УФН, 1983, т. 139, с. 360.
17. Шепелянский Д. Л.— Physica, 1983, v. 8D, p. 208.
18. Шнирельман А. И.— УМН, 1974, т. 29, № 6, с. 181.
19. Berry M. V.— J. Phys., 1977, v. ЮА, p. 2083.
Элизабет и Марлен
ПРЕДИСЛОВИЕ
В настоящей монографии рассматривается стохастическое, или хаоти-
хаотическое, движение нелинейных колебательных систем. Это — быстроразви-
вающаяся область нелинейной механики с приложениями во многих обла-
областях науки и техники, включая астрономию, физику плазмы, статистиче-
статистическую механику и гидродинамику. Основное внимание уделяется динамиче-
динамической стохастичности в гамильтоновых системах, когда хаотическое движение
обусловлено самой динамикой, а не внешним шумом. Вместе с тем рассмат-
рассматривается также и влияние шума на движение динамической системы. В по-
последней главе подробно обсуждаются основные особенности хаотического
движения диссипативных систем.
Исследования в этой области начались еще в прошлом веке, когда Пу-
Пуанкаре и другие пытались построить теорию нелинейных возмущений пла -
нетных движений. Однако только новые математические результаты, полу
ченные в 60-х гг., вместе с результатами численного моделирования на бы-
быстродействующих ЭВМ послужили основой современного подхода к этой
проблеме. Так как новые методы частично обязаны математическим достиже-
достижениям, появились уже две или три математические монографии, отражающие
эти результаты. Однако их язык и изложение труднодоступны специалистам
других наук и инженерам, не говоря уже о том, что в них не содержатся
конкретные методы для проведения практических расчетов.
В нашей книге главное внимание уделяется выяснению физической сущ-
сущности явлений, а не математической строгости. Мы приводим практические
методы описания движения, определения перехода от регулярного к стоха-
с тическому поведению, а также нахождения основных характеристик стоха-
стохастичности. При этом мы существенно опираемся на численное моделирова-
моделирование для иллюстрации и подтверждения этих методов.
Монография задумана как пособие для тех физиков и инженеров, ко-
которые захотят познакомиться с этой областью механики, и как справочник
для исследователей, уже знакомых с такими методами. Книгу можно ис-
использовать также как учебное пособие по механике для аспирантов. Мы
предполагаем, что читатель имеет обычную вузовскую подготовку по мате -
матике и физике, включая основы гамильтоновой механики. Знакомств о
с аналитической механикой желательно, но не обязательно. Подробный об -
зор необходимого материала дается в § 1.2 и 1.3.
Основные идеи динамической стохастичности в гамильтоновых системах
вводятся в § 1.4. В гл. 2—6 мы последовательно переходим от регулярного
к стохастическому движению. Чтобы помочь читателю, мы отмечаем звез -
12 Предисловие
дочкой (*) те параграфы и пункты (п.), в которых содержится основной ма-
материал. Они и составляют ядро нашего изложения. Особенно важным яв-
является п. 2.4а о резонансной теории возмущений. Материал книги был ус-
успешно использован в 30-часовом курсе лекций для аспирантов в Беркли.
В дополнение к основному материалу рассмотрены также и другие важ-
важные вопросы. Влияние внешнего шума на динамику системы с двумя степе-
степенями свободы представлено в § 5.5 (с использованием результатов п. 5.4г),
для большего числа степеней свободы — в § 6.3, а некоторые приложения
рассмотрены в § 6.4. Описание диссипативных систем в гл. 7 является более
или менее независимым от обсуждения гамильтоновых систем. При изучении
материала гл. 7 следует обращаться к введению в § 1.5, а также к описа-
описаниям метода сечения Пуанкаре в п. 1.26 и показателей Ляпунова в п. 5.26
и § 5.3. Бифуркации удвоения периода рассмотрены в п. 7.26, 7.3а и в до-
дополнении Б (см. также п. 3.4г). Другие специальные вопросы, такие, как
теория возмущений Ли (§ 2.5), методы ускоренной сходимости (§ 2.6), неко-
некоторые аспекты теории ренормализации (§ 4.3 и 4.5), неканонические методы
(п. 2.3г), глобальное устранение резонансных знаменателей (п. 2.4г и, ча-
частично, 2.5в), вариационные методы (п. 2.66 и § 4.6) и модуляционная диф-
диффузия (п. 6.2г), можно отложить до ознакомления с основным материалом.
Данная монография подготавливалась в течение трех с половиной лет.
Многие друзья и коллеги поддерживали нас в этом. Мы хотим выразить здесь
признательность всем тем, кто просмотрел основные разделы рукописи и чьи
замечания существенно улучшили окончательный вариант текста. Мы бла-
благодарны X. Абарбанелю, Дж. Кари, Б. В. Чирикову, Р. Коэну, Д. Эсканде,
Дж. Форду, Дж. Грину, Р. Хеллеману, П. Холмсу, Дж. Ховарду, О. Лэн-
форду, Д. Лихтенбергу, Р. Литлджону, Б. Мак-Намаре, Г. Мотцу, К- Спар-
роу, Дж. Л. Теннисону и А. Вайнстейну. Полезные замечания были сделаны
также Дж. Казати, А. Кауфманом, Я. Персивалем и Г. Смитом. Нам также
приятно отметить значительное влияние многих опубликованных работ
Б. В. Чирикова в этой области. Некоторые изложенные в книге идеи были
развиты авторами во время работы по контрактам с Национальным научным
фондом, министерством энергетики и научно-исследовательским управле-
управлением военно-морских сил. Один из авторов (А. Л.) благодарит за гостепри-
гостеприимство колледж св. Екатерины в Оксфорде, а другой (М. Л.) столь же призна-
признателен Имперскому колледжу в Лондоне, где была подготовлена значитель-
значительная часть рукописи.
А. Лихтенберг,
М. Либерман
Глава 1
ОБЩИЙ ОБЗОР И ОСНОВНЫЕ
ПРЕДСТАВЛЕНИЯ
§ 1.1. Вводные замечания
Эта книга появилась в результате исследований по нелинейной
динамике. Целью исследований было выяснение поведения отдель-
отдельного осциллятора при медленном изменении его параметров, с од-
одной стороны, и поведения нескольких слабо взаимодействующих
осцилляторов — с другой. Эти две проблемы, которые первона-
первоначально рассматривались независимо, оказались тесно связанными
между собой в случае многомерных систем.
Существенный прогресс в понимании эффекта медленного из-
изменения параметров был достигнут на Сольвеевской конференции
1911 г. благодаря Эйнштейну, который указал на значение интег-
интеграла действия в физике. Он отметил, что «адиабатическое» посто-
постоянство действия, продемонстрированное впервые Лиувиллем
и Грином за три четверти века до этого, прямо связано с физиче-
физическим представлением о том, что число квантов в медленно меняю-
меняющейся системе должно оставаться постоянным. Появившийся в ре-
результате метод Венцеля—Крамерса—Бриллюэна (метод ВКБ 1427,
235, 41 ] ) стал основой волновой механики, а также теории распро-
распространения волн в неоднородных средах. Соответствующую мате-
математическую теорию развили Боголюбов и Митропольский [33]
и Крускал [239]. Сейчас она широко известна как метод усред-
усреднения х).
Другое направление исследований, касающееся связанных не-
нелинейных осцилляторов, началось с попыток решить задачу трех
тел в небесной механике, которая служит упрощенной моделью
Солнечной системы. Ранние работы по этой проблеме восходят к
трудам Гамильтона и Лиувилля середины XIX в., которые стиму-
стимулировали развитие гамильтоновой механики, лежащей в основе
большинства современных исследований. К концу XIX в. многие
идеи, касающиеся устойчивости нелинейных систем, были рассмот-
рассмотрены Пуанкаре [337] и применены им к проблемам небесной ме-
механики. Именно в этот период Пуанкаре, Цейпель [419] и другие
разработали методы теории возмущений, которые оказались столь
плодотворными при описании поведения нелинейных систем на
х) Асимптотические методы использовались уже Пуанкаре ([337],гл. 8)
и были развиты для решения широкого круга задач нелинейной механики
Н. М. Крыловым, Н. Н. Боголюбовым и их школой (см., например, [242)
и [447, т. 1]).— Прим. ред.
]4 Глава 1
коротком интервале времени. Появление квантовой теории зна-
значительно стимулировало эти исследования. Так, резонансная тео-
теория возмущений, позволяющая учесть локальное резонансное
взаимодействие между двумя степенями свободы, была сформули-
сформулирована уже на заре квантовой механики [34]. Классическая тео-
теория возмущений, а также более современный формализм Ли (см.,
например, [102]) будут рассмотрены в гл. 2.
Важный вопрос, на который не смогла ответить ранняя теория
возмущений, был вопрос о длительной устойчивости Солнечной
системы. Преобладало мнение, что движение планет является «ре-
«регулярным» (квазипериодическим) и в конечном счете может быть
вычислено при помощи новых математических методов. Это мнение
подкреплялось известными решениями задачи двух тел и других
простых механических задач, а также интерпретацией палеонтоло-
палеонтологических данных, которые наводили на мысль о регулярности дви-
движения Земли вокруг Солнца в течение сотен миллионов лет.
Противоположный вгляд на механические системы со многими
степенями свободы был выдвинут Больцманом при попытке понять
поведение разреженных газов. Он считал, что движение молекул
следует рассматривать как случайное, причем каждой молекуле
доступна вся энергетически разрешенная область фазового про-
пространства. Эта точка зрения известна как эргодическая гипотеза,
ставшая основой классической статистической механики. Она была
с успехом использована при объяснении многих наблюдаемых
свойств вещества.
Первую попытку численной проверки эргодической гипотезы
Больцмана для системы с умеренным числом степеней свободы
предприняли Ферми, Паста и Улам [127], которые использовали
модель в виде цепочки нелинейно взаимодействующих сосредото-
сосредоточенных масс. К их удивлению, численные эксперименты не подтвер-
подтвердили ожидаемое стохастическое движение модели.
Это глубокое противоречие между существованием интегрируе-
интегрируемых систем, с одной стороны, и эргодических, с другой, было симп-
симптомом некоторой фундаментальной нерешенной проблемы класси-
классической механики. Определенный вклад в разрешение этого противо-
противоречия внес Пуанкаре: он продемонстрировал, что в окрестности не-
неустойчивых неподвижных точек движение имеет чрезвычайно слож-
сложный характер. Это был первый намек на то, что регулярные силы
могут порождать стохастическое движение в нелинейных колеба-
колебательных системах. Впоследствии Биркгоф [29] показал, что при
рациональном отношении частот для двух степеней свободы (ре-
(резонанс) всегда существуют как устойчивые, так и неустойчивые
неподвижные точки. Резонансы все более высокого порядка и бо-
более мелкого масштаба последовательно изменяют топологию фазо-
фазовых траекторий и приводят к образованию «цепочки островов».
Было установлено, что ряды теории возмущений не описывают та-
такие резонансы.
Общий обзор и основные представления 15
Хотя работы Пуанкаре и Биркгофа продемонстрировали чрез-
чрезвычайную сложность топологии фазового пространства, вопрос
об эргодичности движения, т. е. о том, покрывает ли траектория
всю энергетически доступную область фазового пространства или
же она ограничена какими-то интегралами движения, оставался
до недавнего времени без ответа. Теорема Колмогорова [229],
доказанная при различных ограничениях Арнольдом [10]
и Мозером [308] (теорема КАМ), утверждает, что при воз-
возмущении интегрируемых систем инвариантные поверхности
сохраняются для большинства начальных условий. Хотя
движение вблизи сепаратрисы каждого резонанса и является
стохастическим, оно ограничено соседними инвариантными по-
поверхностями и не является эргодическим. В гл. 3 мы рас-
рассмотрим теорию КАМ и связанные с ней топологические ре-
результаты, которые служат обоснованием многих методов, описан-
описанных в этой книге.
Наряду с достижениями теории возмущений и другими мате-
математическими результатами, одной из основных побудительных при-
причин возрождения интереса к нелинейной механике было изобрете-
изобретение цифровой ЭВМ. Уже с самого начала использование ЭВМ для
интегрирования уравнений движения было соединено с методом
сечения Пуанкаре, при котором такое интегрирование Л'-мерных
уравнений заменяется итерацией соответствующего (N—1)-мерного
отображения. В результате оказалось возможным наблюдать за
движением системы в фазовом пространстве в течение сотен тысяч
колебаний. Обнаруженные уже в первых экспериментах удиви-
удивительно тонкие пространственные структуры движения быстро при-
привлекли внимание как теоретиков, так и экспериментаторов. Отсюда
две основные особенности нашего изложения материала: мы сущест-
существенно опираемся на результаты численного моделирования, с од-
одной стороны, и на соответствие между непрерывным движением
(JV-мерным потоком) и его дискретным (N—1)-мерным отображе-
отображением Пуанкаре — с другой (см. гл. 3). Центральным моментом
нашего описания динамики является численный эксперимент, ко-
который считается, как правило, окончательной проверкой теорети-
теоретического анализа. Примеры численного моделирования приводятся
в каждой главе также для иллюстрации и пояснения физической
сущности явлений.
Из детальных численных экспериментов и соответствующих
теоретических исследований возникла весьма необычная картина
фазового пространства слабо возмущенных систем. Вблизи резо-
нансов топология невозмущенных инвариантных поверхностей
изменяется и образуется характерная резонансная структура, по-
похожая на «цепочку островов». Внутри островов топология также
изменяется, приводя к еще более мелкой резонансной структуре
и т. д. Однако вся эта структура — только часть полной картины
движения, которая включает также плотную систему тонких слоев
1G Глава 1
со стохастическим движением. Анализу этой структуры посвящена
большая часть гл. 3.
Для слабо возмущенных систем с двумя степенями свободы тон-
тонкие стохастические слои отделены друг от друга инвариантными
поверхностями, а стохастические колебания переменных действия
внутри слоя оказываются экспоненциально малыми (по возмуще-
возмущению). С увеличением возмущения возможен переход, при котором
изолирующие инвариантные поверхности разрушаются и стоха-
стохастические слои сливаются, приводя к глобальному стохастиче-
стохастическому движению. Фазовое пространство можно разделить при этом
на три области. Одна из них содержит в основном стохастические
траектории. Она связана 1) со второй областью, значительную часть
которой составляет по-прежнему стохастическая компонента дви-
движения, но внутри ее уже имеются большие острова регулярного
движения. Третья область содержит главным образом регулярные
траектории и отделена от первых двух инвариантными поверхно-
поверхностями. Классический пример, иллюстрирующий переход от почти
регулярного к существенно стохастическому движению, был пред-
предложен Хеноном и Хейлесом [188] для моделирования динамики
в задаче трех тел2). Численные эксперименты и связанные с ними
эвристические теории, развитые за последние двадцать лет, про-
прояснили основные процессы и позволили определить величину воз-
возмущения, при которой происходит такой переход. Эти результаты
иллюстрируются в гл. 3 на примере ускорения Ферми, первона-
первоначально предложенного для объяснения происхождения космиче-
космических лучей. Рассматривается модель, в которой упругий шарик
колеблется между неподвижной и вибрирующей стенками. Далее,
в гл. 4, определяются условия перехода от локализованной стоха-
стичности к глобальной. При этом используются различные под-
подходы к задаче (см., например, [70, 165J).
Все упомянутые методы применялись при исследовании широ-
широкого круга задач как на начальном этапе развития теории, так
и в последующих приложениях. Приложение к задаче трех тел
и ее многочисленным вариантам ознаменовало по существу начало
широких исследований в данной области3). Возникают и новые за-
захватывающие приложения в астрономии, например структура
колец Сатурна или пояса астероидов. Качественно это удается по-
понять на основе представления о резонансах с большими возмущаю-
возмущающими телами. Однако количественные данные о ширине колец
Сатурна и люков в распределении астероидов, а также недавно
наблюдавшуюся с космических кораблей сложную структуру ко-
колец Сатурна еще предстоит объяснить.
2) Траекториями движения.— Прим. ред.
2) Этот пример возник из задачи о движении звезды в поле галактики.—
Прим. ред.
3) Это, пожалуй, преувеличение, вспомним хотя бы классические труды
Пуанкаре по небесной механике.— Прим. ред.
Общий обзор и основные представления
Другим важным приложением является движение заряженной
частицы в магнитном и электрическом полях. Прежде всего было
установлено, что магнитный момент является адиабатическим инва-
инвариантом, связанным с ларморовским вращением заряженной ча-
частицы [7]. В дальнейшем были рассмотрены адиабатические ин-
инварианты и для других степеней свободы частицы. Эта задача сти-
стимулировала развитие асимптотических разложений и техники ус-
усреднения, а также исследования Чирикова 167], в которых он изу-
изучал переход между регулярным и стохастическим движением и
установил первый критерий такого перехода (критерий перекры-
перекрытия резонансов). В дальнейшем был проведен учет влияния высоко-
высокочастотного поля вследствие его резонанса с ларморовским враще-
вращением. В результате был найден предел для высокочастотного на-
нагрева, связанный с существованием инвариантных кривых. Род-
Родственная задача о движении частицы в намагниченной плазме под
действием волны, иллюстрирующая многие из вышеупомянутых
особенностей движения, используется в качестве примера для ре-
резонансной теории возмущений (гл. 2) и для определения перехода
от адиабатического поведения к стохастическому (гл. 4). Другим
интересным приложением теории является движение частиц в уско-
ускорителях. Именно в этой области были проведены некоторые ранние
исследования поведения многомерных нелинейных систем. Урав-
Уравнения Гамильтона могут быть использованы также и для описания
других типов траекторий, таких, как магнитные линии или лучи
в геометрической оптике. В случае аксиально симметричной то-
тороидальной геометрии гамильтониан, описывающий магнитные
линии, оказывается интегрируемым. К настоящему времени уже
проведен ряд исследований по разрушению тороидальных магнит-
магнитных поверхностей возмущениями, возникающими как от внешних
токов, так и от самосогласованных токов удерживаемой плазмы.
Подобные приложения используются ниже в качестве примеров, а
также кратко обсуждаются в дополнении А.
Существование движений, которые проявляются при численном
моделировании как случайные, надежно установлено. Однако ма-
математические попытки охарактеризовать стохастичность с помощью
таких понятий, как эргодичность, перемешивание и тому подобное,
далеко не всегда оказывались успешными 1). Синай [377] доказал
эти свойства для газа твердых шариков. Было показано также,
что некоторые модельные гамильтоновы системы обладают даже
более сильными стохастическими свойствами. Эти результаты, опи-
описанные в гл. 5, дают основание считать, что случайность движения
имеет место и для типичной гамильтоновой системы в том случае,
когда она обладает поведением, характерным для идеализирован-
идеализированных моделей.
х) Здесь, по-видимому, имеются в виду трудности аналитического выяв-
выявления указанных свойств в конкретных динамических системах. — Прим.
ред.
Ig Глава 1
Кажущаяся стохастичность 2) движения в подобных сложных
системах дает основание говорить о принципиально новом подходе
к статистической .механике и поэтому привлекает, к себе все более
широкий круг исследователей в этой области. Сложность движе-
движения вблизи неустойчивых периодических решений и тот факт, что
эти неустойчивые траектории образуют в фазовом пространстве
всюду плотное множество, служат серьезным доводом в пользу
такой точки зрения. В последнее время значительные усилия были
направлены на выяснение связи стохастического движения с по-
показателями Ляпунова, которые определяют скорость экспоненци-
экспоненциальной расходимости близких траекторий. Это важно также и с
практической точки зрения для вычисления усредненной по
фазам скорости диффузии по переменным действия. В прошлом
такие вычисления проводились в предположении о случайности
фаз. Ясно, что это предположение несправедливо при наличии ин-
инвариантных кривых, ограничивающих область изменения фаз.
Даже в случае полной эргодичности, когда движение охватывает
всю энергетическую поверхность, необходимо еще определить мас-
масштаб времени, на котором фазы становятся случайными. Прове-
Проведенные численные и аналитические исследования позволили глубже
понять проблему убывания фазовых корреляций вблизи инвариант-
инвариантных поверхностей. Эти вопросы будут рассмотрены в гл. 5.
Существует значительное различие между стохастичностью в си-
системах с двумя и большим числом степеней свободы. Используя
топологические соображения, Арнольд [12] показал2), что для си-
систем с более чем двумя степенями свободы стохастические слои свя-
связаны между собой и образуют в фазовом пространстве плотную
«паутину». Для начальных условий на этой паутине стохастиче-
стохастическое движение идет вдоль слоев, приводя к глобальной диффузии,
не ограниченной инвариантными поверхностями. Этот механизм
принято называть диффузией Арнольда. Она может быть быстрой
или медленной в зависимости от толщины стохастических слоев.
Такая диффузия существует (в принципе) для сколь угодно малых
возмущений интегрируемых систем. Еще один интересный эффект
в многомерных системах связан с медленной модуляцией одного
из периодических движений3). В этом случае стохастическое движе-
движение вдоль паутины может значительно усиливаться за счет так
называемой модуляционной диффузии. Этот механизм противоре-
противоречит интуитивному представлению о том, что медленная модуляция
должна приводить к адиабатическому поведению*). В многомерных
системах резонансы могут значительно влиять на диффузию также
х) Этот осторожный термин сейчас уже не оправдан (см., например,
[448] и популярные статьи [61, 449—452]).— Прим. ред.
2) См. также [462].— Прим. ред.
3) Имеются в виду невозмущенные колебания по одной из независимых
степеней свободы.— Прим. ред.
4) См. примечание редактора на с. 367.— Прим. ред.
Общий обзор и основные представления 19
и благодаря внешней стохастичности (шуму). Для систем с двумя
степенями свободы действие шума эквивалентно, вообще говоря,
наличию третьей степени свободы и приводит к диффузии вдоль
резонансов. При этом резонансы могут значительно увеличивать
скорость диффузии. Считается, что эти процессы могут ограничи-
ограничивать время жизни частиц и интенсивность пучков в накопительных
кольцах. В гл. 6 мы рассмотрим диффузионные процессы в много-
многомерных системах, включая диффузию Арнольда и модуляционную
диффузию, а также совместное действие внешнего шума и резонан-
резонансов.
Новая область явлений возникает в диссипативных системах,
фазовый объем которых не остается постоянным, а сокращается
со временем. Конечное состояние в этом случае представляет со-
собой движение на некотором подпространстве, называемом аттрак-
аттрактором, размерность которого меньше размерности исходного фа-
фазового пространства. Изучение регулярного движения в таких
системах восходит к Ньютону и в дальнейшем было связано с раз-
развитием теории обыкновенных дифференциальных уравнений. На
этой ранней стадии было выяснено, что траектория может притя-
притягиваться к таким простым аттракторам, как неподвижные точки,
замкнутые траектории и торы, на которых устанавливается, со-
соответственно состояние равновесия, периодическое и квазипериоди-
квазипериодическое движение. И только сравнительно недавно, в пионерской
работе Лоренца [2831, было показано, что и в диссипативных си-
системах встречается хаотическое движение. Лоренц обнаружил та-
такой аттрактор в модели, описываемой системой обыкновенных не-
нелинейных дифференциальных уравнений. Рюэль и Тэкенс [355 ]
использовали для аттрактора с хаотическим движением термин
«странный аттрактор»1). Топология странных аттракторов весьма
примечательна. Она характеризуется масштабной инвариант-
инвариантностью2), при которой структура аттрактора повторяется на все
более мелких пространственных масштабах. Такие структуры, на-
называемые фракталами, обладают любопытным свойством дробной
размерности, промежуточной между размерностью точки и линии,
линии и плоскости и т. д.
Когда геометрическая структура странных аттракторов была
выяснена, возникла качественная картина движения, важной осо-
особенностью которой является близкое соответствие между движе-
х) В литературе уже отмечалась странность этого термина [74]. Для сов-
современной эргодической теории подобный аттрактор является, напротив,
естественным. Его существование вытекает, в частности, из теоремы Аносова
[8] о структурной устойчивости хаоса для динамических систем определен-
определенного класса, которые получили позднее название систем Аносова. С другой
стороны, упоминаемая ниже фрактальная структура хаотического аттрак-
аттрактора не является универсальной, это может быть, например, и просто тор.—
Прим. ред.
2) В оригинале — geometric invariance (геометрическая инвариант-
инвариантность).— Прим. перге.
20 Глава 1
ннем на странном аттракторе и движением, описываемым некото-
некоторым одномерным необратимым отображением. Такие отображения
не возникают непосредственно из диссипативных потоков1), но яв-
являются важными примерами простых систем с хаотическим пове-
поведением и находят приложение в таких разных областях, как эко-
экономика и экология. При изменении параметра эти отображения
испытывают последовательные бифуркации, такие, что период пре-
предельного цикла каждый раз удваивается. Бифуркации накапли-
накапливаются при некотором критическом значении параметра, выше ко-
которого движение становится хаотическим. Фейгенбаум [122 J пока-
показал, что этот процесс является в некотором смысле универсальным.
Однако фактически странные аттракторы появились впервые
в трехмерных потоках и связанных с ними двумерных отображе-
отображениях. В этом случае также имеет место последовательность бифур-
бифуркаций с удвоением периода. Для понимания поведения таких си-
систем важно знать движение вблизи сепаратрисных слоев и инва-
инвариантные распределения2). Несмотря на соответствие между одно-
одномерными и двумерными отображениями, наше знание последних
недостаточно. Например, в настоящее время нет никакого метода
для отыскания перехода к странному аттрактору в многомерных
системах.
Появление странных аттракторов в трехмерных потоках, та-
таких, как модель Лоренца, указывает на один из возможных меха-
механизмов возникновения гидродинамической турбулентности. Это
стимулировало исключительно точные экспериментальные изме-
измерения вблизи перехода от ламинарного к турбулентному течению
в реальных жидкостях. Модель Лоренца была получена фактически
из задачи о конвекции Рэлея—Бенара в подогреваемом снизу слое
жидкости с учетом только трех мод движения. Хаотическое движе-
движение в трехмерной модели Лоренца представляет возможную кар-
картину турбулентности и в некоторых реальных гидродинамических
системах, которая оказывается проще, чем первоначальные пред-
представления Ландау [251 ]. Динамика диссипативных систем рассмат-
рассматривается в гл. 7, включая одномерные и двумерные отображения,
а также гидродинамические приложения.
*§1.2. Теория преобразований в механике
В этом параграфе дается краткий обзор основных понятий гамиль-
тоновой механики, необходимых для анализа динамики в фазовом
пространстве. Изложение материала близко к книге Голдстейна
[156] (гл. 8 и 9) и существенно опирается на курс Уиттекера [430].
Большинство длинных доказательств опущено.
:) Это не совсем так, первый пример такого отображения был построен
еще Лоренцем [283] (см. также [210] и п. 1.56).— Прим. ред.
2) То есть инвариантную меру на аттракторе.— Прим. ред.
Общий обзор и основные представления 2I
* 1.2а. Канонические преобразования
Различные эквивалентные формы уравнений движения можно по-
получить друг из друга путем преобразования переменных. Одна из
таких форм получается в результате введения функции Лагранжа
L[q,q, t) = T[q )-U(q, t), A.2.1)
где q и q — векторы координат и скоростей по всем степеням сво-
свободы, Т — кинетическая энергия, U — потенциальная энергия и все
связи предполагаются независящими от времени. Уравнения дви-
движения Лагранжа для каждой из координат qt имеют вид
d dL ^ 6L __ q A2 2)
dt д-( dqi
Эти уравнения можно получить либо из вариационного принципа
(б ) Ldt — 0), либо путем прямого сравнения с законами движе-
движения Ньютона. Определим гамильтониан посредством соотношения
Н(Р, Я, 0 = 2 qiPi-L (q, q, t), A.2.3)
i
где q рассматривается как функция q и новой переменной р. Вы-
Вычисляя дифференциал Н, получаем
дН . V^ дН . , дН ,,
d^+ >——dpi + -—dt =
V (ft--~-) dg, + V
где мы подставили A.2.2) в третью сумму справа. Уравнение A.2.4)
может быть удовлетворено только, если определить р,- как
Pi = ^~- A.2.5)
qi
При этом первая сумма справа в A.2.4) тождественно обращается
в нуль. Приравнивая коэффициенты при дифференциалах, полу-
получаем уравнения движения, содержащие только первые производ-
производные,
Pi= —, A.2.6а)
dqc
?< = Нг- A-2-6б>
dp
22 Глава 1
-i^-=_-^-. A.2.7)
dt dt v '
Переменные p, q называются обобщенными импульсами и коор-
координатами, а соотношения A.2.6) и A.2.7) есть уравнения
Гамильтона. Исследование характера решений этих уравнений
составляет основное содержание настоящей монографии. Любой
набор переменных р, q, временная эволюция которых дается урав-
уравнениями вида A.2.6), называется каноническим, а сами р,- и qt —
сопряженными переменными.
Производящие функции от смешанных переменных. Пусть мы хо-
хотим перейти от канонических переменных q, p к новым перемен-
переменным q, p. Их можно связать при помощи некоторой функции от
одной старой и одной новой переменных следующим образом. Так
как лагранжиан получается из вариационного принципа, то, ис-
используя A.2.3), находим
S y{ (bptqi-Hip, q, О)л]=0. A.2.8)
Это уравнение справедливо как для старых, так и для новых ка-
канонических переменных. Поэтому интеграл в A.2.8) для разных
переменных может отличаться только на полный дифференциал:
q, t) = '2ptqi — H[p, q, t) + -±-Fl(q, q, t\,
1 l at
A.2.9)
где мы выбрали функцию F — F\, зависящей от q и q. Раскрывая
полную производную от Flt получаем
y^^yi ( )
dt АЛ dqi Ч ¦ ~L dqi Ч dt V
1 i
Считая переменные в A.2.10) независимыми, из A.2.9) (сравнивая
соответствующие члены и требуя, чтобы члены с qi и qc по отдель-
отдельности равнялись нулю) находим
/Jf=-^-. A.2.11а)
dqi
-рс=-ф-, A.2.116)
dqi
q, t) = H(j>, q, t)^-^-F1{q, q, i). A.2.11b)
Общий обзор и основные представления 23
Можно определить производящие функции и от других пар смешан-
смешанных (старой и новой) канонических переменных:
F2\q,~p, t), Fs(p,~qt t), F,ip, p, /I.
Если, например, ввести F2 при помощи преобразования Лежандра
F2(q, p, t) = F1lq, q, d+2», A.2.12)
i
где q— функция q и р, то получим каноническое преобразование
в виде
Pi = -^-, A.2.13а)
qt = -^-, A.2.136)
OP
Н\р, q, t) = H(p, q, t)-~F2{q, P, t). A.2.13b)
Производящие функции F3 и F4 определяются соотношениями, ана-
аналогичными A.2.12), и приводят к соответствующим каноническим
преобразованиям.
Канонические преобразования позволяют, по крайней мере
формально, решить уравнения движения динамической системы
следующим образом. Рассмотрим отдельно случай гамильтониана,
зависящего явно от времени, и случай автономного гамильтониана,
не зависящего от времени. В первом случае положим Н = 0. Тогда
производные по времени от новых переменных равны нулю в силу
уравнений Гамильтона. Поэтому новые переменные не зависят от
времени и их можно интерпретировать как начальные значения
исходных (непреобразованных) переменных. Таким образом, ка-
каноническое преобразование фактически оказывается решением,
определяющим значения координат и импульсов в произвольный
момент времени в зависимости от их начальных значений. Подста-
Подставив A.2.13а) в A.2.13в) с Н = 0, получим уравнение в частных
производных для производящей функции Fг:
которое называется уравнением Гамильтона—Якоби. Во втором
случае, когда Н не зависит от времени явно, достаточно положить
Н равным константе. Тогда преобразование A.2.13в) приводит к
уравнению Гамильтона—Якоби в виде
Е. A.2.15)
Если переменные в уравнениях A.2.14) и A.2.15) не разделяются,
24 Глава 1
то решить их столь же трудно, как и исходные канонические урав-
уравнения. Однако метод Гамильтона—Якоби очень удобен для полу-
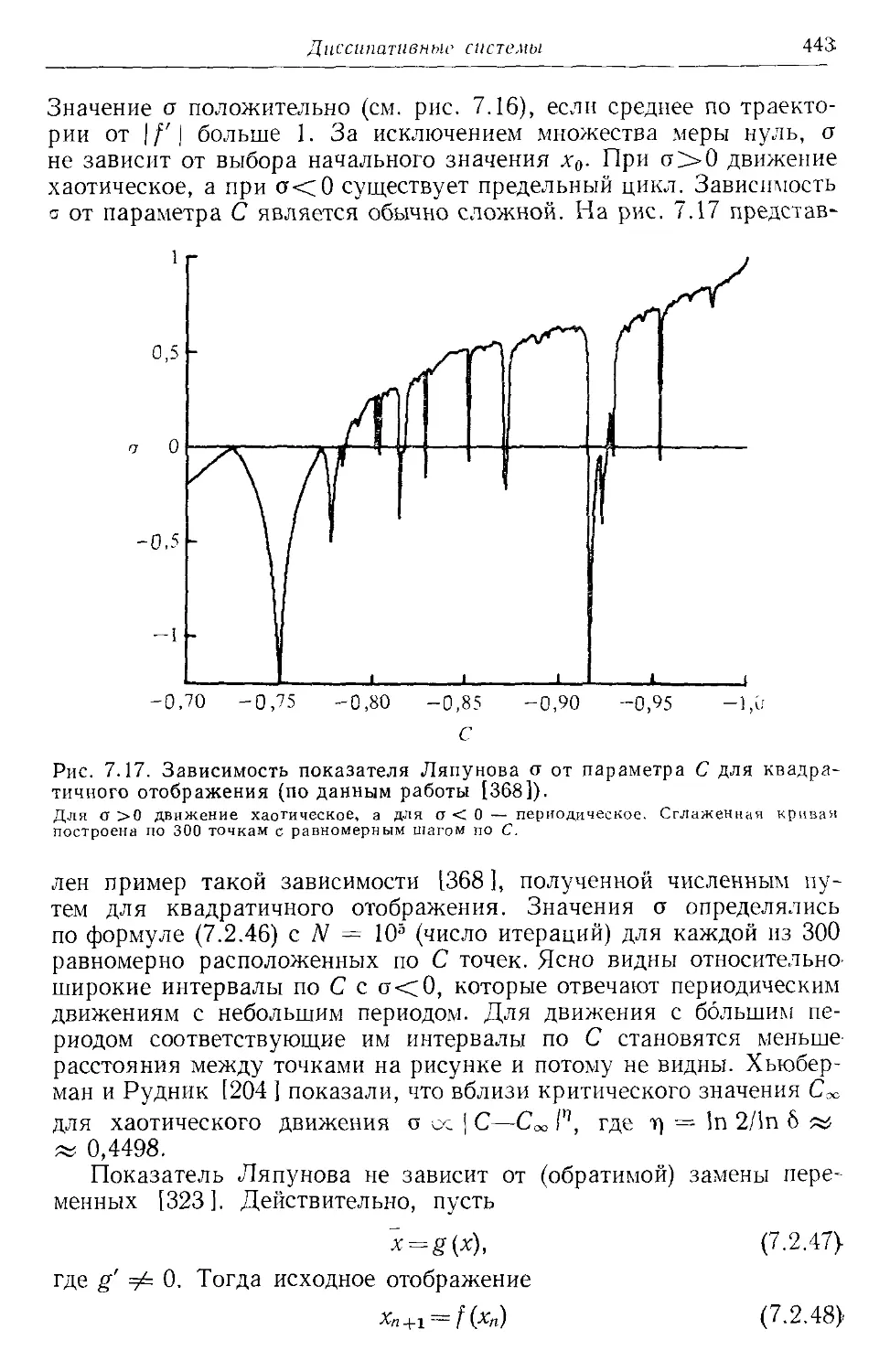
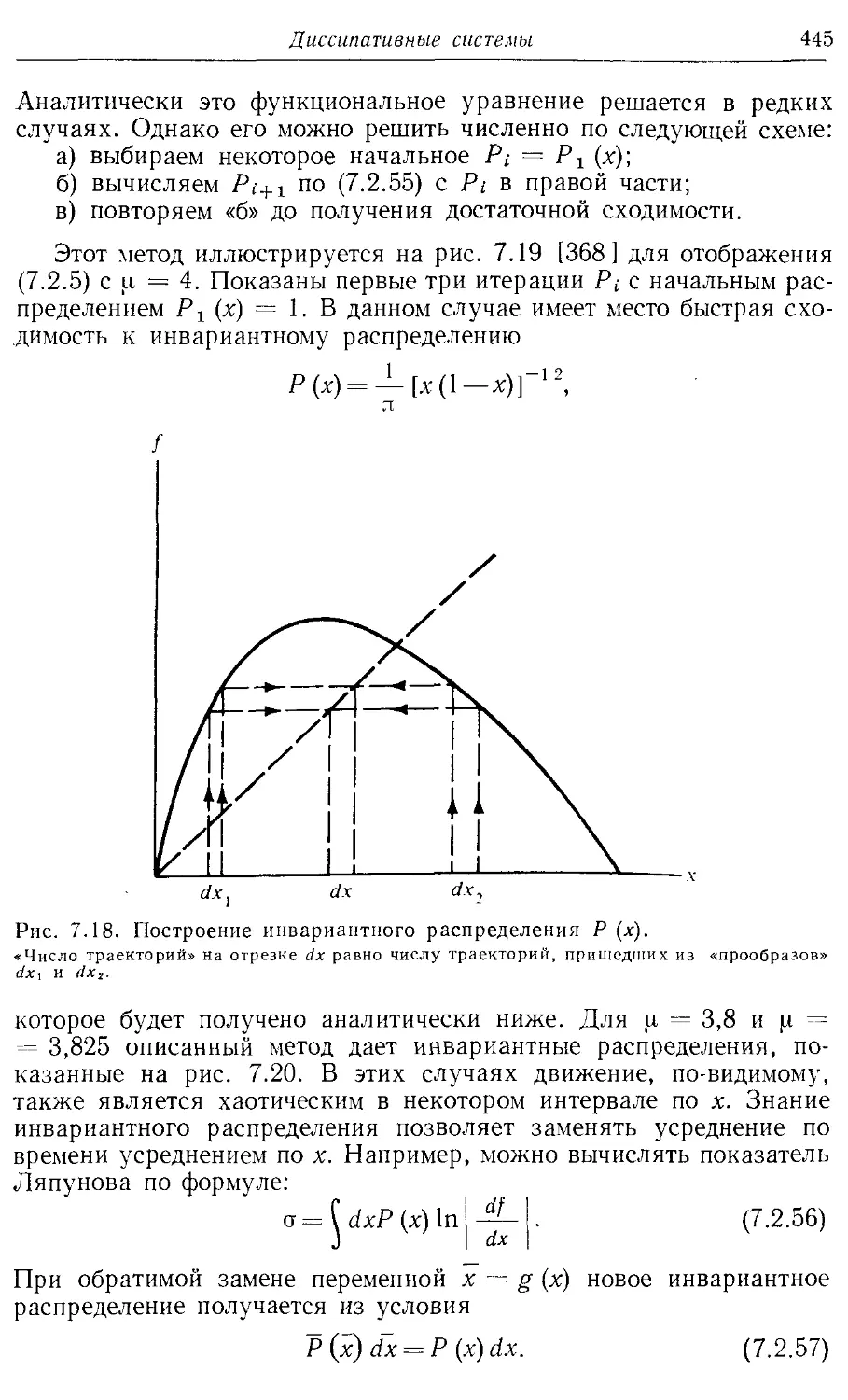
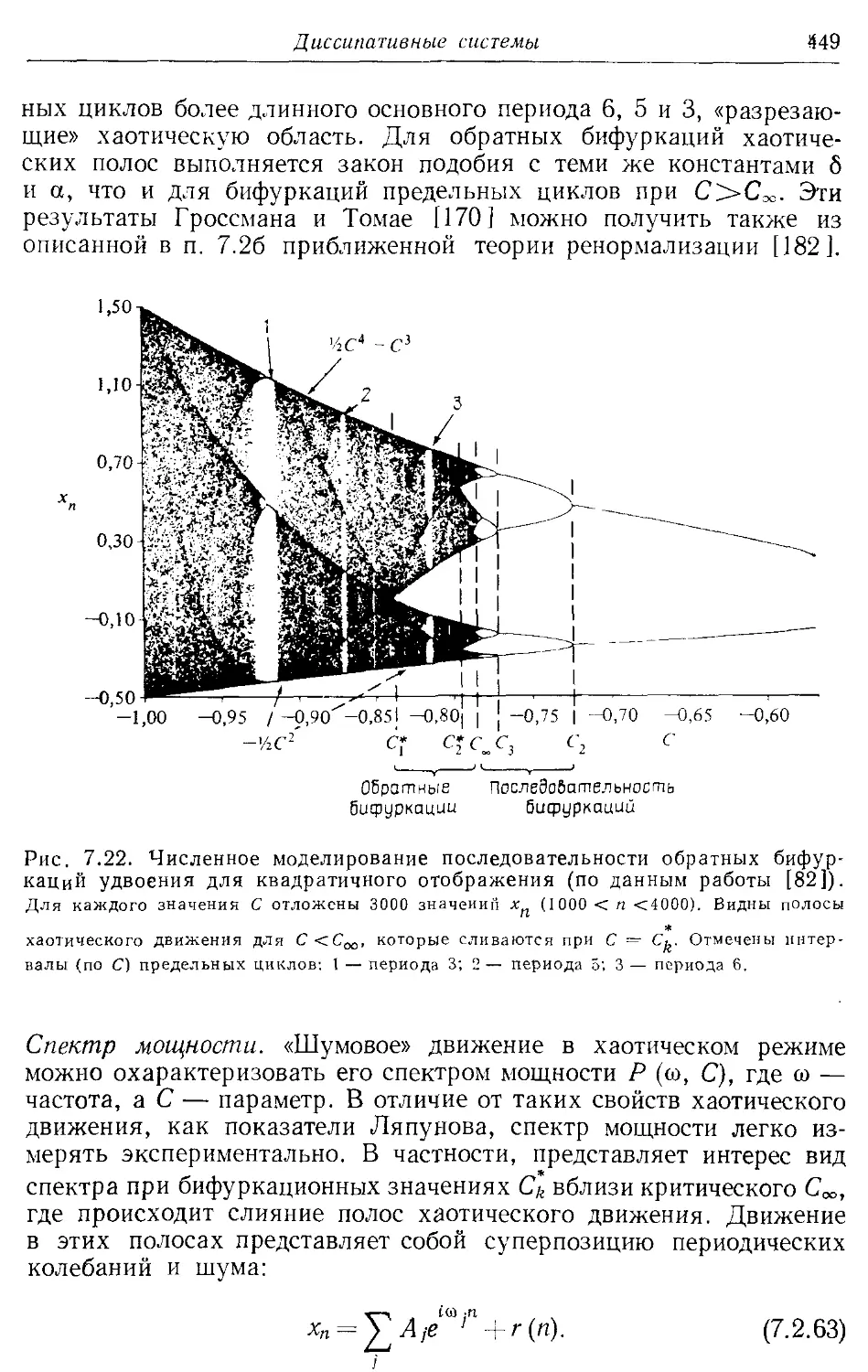
получения приближенных решений в виде рядов для систем, близких
к системам с разделяющимися переменными, или, как их чаще на-
называют, для систем, близких к интегрируемым.
Скобки Пуассона. Важной динамической величиной являются
скобки Пуассона:
[и, у] = у/-^_ J?L_J5L-*L-), A.2.16)
^,J \ dqk dpk dqk dpk j
k
где и и v — произвольные функции канонических переменных.
Уравнения движения можно записать с помощью скобок Пуассона
следующим образом. Выбрав в качестве и координату, а в качестве v
гамильтониан системы, получим
[qt Н] = V / dqi дН дН dqi ) дИ
dPk дрк I dpi
k
Сравнивая с уравнениями Гамильтона, имеем
qi = [qi, H] A.2.17)
и аналогично
pi = lpc, Щ. A.2.18)
Скобки Пуассона удовлетворяют правилу антикоммутации
[и, v] = —[v, и] A.2.19)
и тождеству Якоби
[[и, v], w)-r[[w, и], v]~[[v, w], u] = 0. A.2.20)
Используя уравнения Гамильтона, можно записать полную про-
производную по времени от произвольной функции % = -/ (q, р, t)
в виде
A.2.21)
dt ^J \ dqt dpi dpi dqi j ' dt " dt
с
При отсутствии явной зависимости от времени д% dt = 0. Если
к тому же и скобки Пуассона равны нулю, то говорят, что функ-
функция х коммутирует с гамильтонианом и является интегралом дви-
движения. Ясно, что если гамильтониан не зависит от времени явно,
то и он является интегралом. Такие гамильтонианы называются
автономными. Выберем в качестве функции % один из импульсов р{
и пусть он не является явной функцией времени t. Если при этом
гамильтониан не зависит от сопряженной координаты (т. е.
Общий обзор и основные представления 25
qi = 0), то из A.2.21) вытекает, что dpc'dt = 0 и, следова-
следовательно, pi является интегралом движения
Pi = а,- = const, A.2.22)
a
'qi = -^H-=(oi = const. A.2.23)
d
Интегрируя A.2.23), получаем решение в виде
q{ = <*it + fr. A.2.24)
Если можно найти такое каноническое преобразование, что все
новые импульсы оказываются постоянными, то решение в новых
канонических переменных описывается соотношениями A.2.22)
и A.2.24). Обратное преобразование в этом случае дает полное ре-
решение в исходных переменных. Производящей функцией такого
преобразования служит решение уравнения Гамильтона—Якоби
A.2.15).
Другой метод интегрирования уравнений движения связан с ис-
использованием производящей функции w (р, q, s), задающей кано-
каноническое преобразование (от старых переменных р, q к новым пе-
переменным р, q) в виде уравнений Гамильтона:
dpi _ _ dw dgt _ дш A2 25)
ds dqi ds dpi
где s— произвольный параметр. При этом связь новых и старых
переменных дается соотношениями
P = p(s), ~q = q{s). A.2.26)
Функция w называется производящей функцией Ли и зависит только
от старых переменных. Использование такой функции упрощает
вычисление высших порядков теории возмущений. Мы обсудим
этот метод в § 2.5.
В заключение заметим, что успех метода канонических преобра-
преобразований определяется разумным выбором преобразования. Сами
по себе эти преобразования не приводят к новой физике, но могут
помочь при анализе или физической интерпретации того или иного
движения, свойства которого остаются, однако, неизменными как
в старых, так и в новых переменных.
* 1.26. Движение в фазовом пространстве
Рассмотрим уравнения Гамильтона A.2.6) в общем случае N сте-
степеней свободы, когда индекс i пробегает значения от 1 до N.
Решение уравнений A.2.6) содержит 2N постоянных, соответст-
соответствующих начальным значениям координат и импульсов. Они одно-
однозначно определяют эволюцию системы, которую можно представ-
26
Глава 1
лять себе как движение точки в 2/V-MepHOM пространстве. Предпо-
Предположим, что мы решили уравнения A.2.6) и нашли зависимость р
и q от времени. Тогда мы можем проследить траекторию движения
в 2 JV-мерном пространстве с координатами р и q от некоторого мо-
момента времени tlt соответствующего начальным значениям рх и qlt
до более позднего момента t2. Такое объединенное пространство
(р, q) называется фазовым пространством системы. Примеры трех
фазовых траекторий показаны на рис. 1.1, где фазовое пространство
представлено в двух измерениях, так что абсцисса характеризует
N координат q, а ордината — N импульсов р. Рассмотрим три важ-
важных свойства фазового пространства.
Рис. 1.1. Траектории в фазовом пространстве.
1. В любой заданный момент времени траектории в фазовом
пространстве не пересекаются. Это очевидно из того факта,
что начальные условия однозначно определяют последующее
движение. Поэтому если бы две траектории совпали, т. е.
в какой-то момент времени их значения р и q оказались бы
одинаковыми, то и последующее их движение было бы оди-
одинаковым. Если гамильтониан не зависит от времени, то тра-
траектории в фазовом пространстве также не зависят от времени
и, следовательно, вообще не могут пересекаться. Очевидно,
что в расширенном фазовом пространстве с добавочной вре-
временной координатой траектории не будут пересекаться, даже
если гамильтониан периодически зависит от времени1).
2. Любая граница С\ в фазовом пространстве, охватывающая
некоторое множество начальных условий в момент времени tlt
трансформируется к моменту времени t2 в границу С2, охва-
охватывающую траектории того же множества. Это свойство вы-
г) Периодическая зависимость здесь несущественна и упомянута, оче-
очевидно, только для того, чтобы расширенное фазовое пространство было ком-
компактным (ограниченным).— Прим. ред.
Общий обзор и основные представления 27
текает непосредственно из предыдущего, поскольку любая
траектория в момент пересечения границы совпадает с од-
одной из граничных траекторий, а значит, и движется вместе
с ней. Отсюда можно получить ограничения на движение
большой группы траекторий, определяя движение гораздо
более узкого класса траекторий, принадлежащих границе.
3. Рассмотрим некоторый ансамбль начальных условий, каж-
каждое из которых представляет возможное состояние системы.
Представим вероятность ансамбля, или его плотность рас-
распределения в фазовом пространстве, в виде
т = т(р, q, t).
Если нормировать т. так, чтобы выполнялось условие
ndPidqt=\, A.2.27)
где интегрирование распространяется на все фазовое про-
пространство1), то из уравнения непрерывности
находим
дх ,
( • дх , dpi , • дх д qi \ Л
\ dpi dpi dqc dqi J
dt JmU\ dpi dpi dqc dqi J A.2.29;
i
Согласно уравнениям Гамильтона A.2.6), второй и четвер-
четвертый члены суммы сокращаются, и мы получаем уравнение
>, A.2.30)
_^_ . dpi dqi I dt
выражающее несжимаемость потока в фазовом пространстве.
Этот результат известен как теорема Лиувилля, которая ока-
оказывается мощным инструментом анализа гамильтоновой ди-
динамики (подробное обсуждение и примеры см. в работе [265 ]).
Интегральные инварианты. Благодаря вышеперечисленным свой-
свойствам анализ движения в^фазовом пространстве приводит к значи-
значительным упрощениям при исследовании динамических задач. В ча-
частности, из A.2.30) немедленно следует, что гУУ-мерный интеграл
\Udpidq{, A.2.31)
вычисленный в определенный момент времени t, является инва-
инвариантом движения. Иерархия таких инвариантов разной размер-
г) Такая нормировка обычно невыполнима из-за неограниченности фа-
фазового пространства и несущественна для дальнейшего.— Прим. ред.
28 Глава 1
ности впервые изучалась Пуанкаре [337). Они были названы им
интегральными инвариантами. Общий вывод таких инвариантов
дается в работе [43011). Интегральные инварианты имеют фунда-
фундаментальное значение для теории гамильтоновых систем и могут
быть приняты в качестве ее основы [13]. Мы рассмотрим первый
член этой иерархии [для которой A.2.31) является N-м и послед-
последним членом]:
Г C^dpdqi = const, A.2.32)
J J *
где интеграл берется в определенный момент времени по некоторой
двумерной поверхности в фазовом пространстве.
Применив теорему Стокса к A.2.32), получим инвариант
2 Ptdqt = const, A.2.33)
где интегрирование производится теперь по замкнутой в фазовом
пространстве кривой при фиксированном значении t. Величина
A.2.33) называется относительным интегральным инвариантом
системы. В общем случае применение теоремы Стокса понижает
размерность области интегрирования на единицу и преобразует
интегральный инвариант, взятый по произвольному гиперобъему,
в относительный инвариант, взятый по замкнутой гиперповерх-
гиперповерхности. Относительные интегральные инварианты особенно важны
для колебательных систем (см. ниже).
Расширенное фазовое пространство. Рассмотрим теперь гамиль-
гамильтониан Н, явно зависящий от времени. Вариационный принцип
A.2.8), из которого получаются уравнения Гамильтона, справед-
справедлив при интегрировании по любому параметру, не зависящему от
вариации. Обозначим такой параметр через ? и перепишем A.2.8)
в виде
<*<Н ..н «¦ \^._п A.2.34)
Положив
-t, A.2.35)
получим новую форму вариационного уравнения
б
где —Hut можно рассматривать как дополнительные импульс
См. также [13].— Прим. перев.
Общий обзор и основные представления 29
и координату в некотором новом расширенном фазовом простран-
пространстве размерности BN + 2). Поток параметризуется теперь новым
«временем» ?,.
Новый гамильтониан Я для расширенного набора канониче-
канонических переменных (р, —Я, q, t) можно получить с помощью про-
производящей функции
Л'
F2 = H~PiQi + ~pN+1t. A.2.36)
Используя A.2.13в), находим Я (р, q, t) = Я (р, q, t) — Я, и ка-
канонические уравнения принимают вид
dpi _ дН dgi дН ,. g дуч
dt, dqi d^ dpi
Новый гамильтониан, определяющий поток в расширенном фазо-
фазовом пространстве, не зависит явно от «времени» ?. Кроме того урав-
уравнения A.2.37) с i = N -г \ дают: t (?) = ? и Я = const. Таким
образом, движение системы с гамильтонианом, зависящим от вре-
времени, эквивалентно движению с дополнительной степенью свободы
и гамильтонианом, не зависящим от времени1).
Справедливо и обратное. Рассмотрим независящий от времени
гамильтониан Я для системы с N степенями свободы в 2ЛЛмерном
фазовом пространстве. Выберем любую из обобщенных координат
в качестве нового «времени» ?. Тогда канонически сопряженный
ей импульс представляет новый гамильтониан Я, зависящий от
«времени» и описывающий движение системы с (N—1) степенями
свободы в сокращенном фазовом пространстве размерности BN—2).
Пусть, например,
Н(р, д) = Н0. A.2.38)
Положим
Pi = pi, qt = qi, i=l, Л/— 1 A.2.39)
и разрешим A.2.38) относительно pN — pN (p, q, qN). Выбирая
Я - — рЛ, и l, — qN, мы получаем уравнения Гамильтона A.2.37)
в сокращенном фазовом пространстве (р, q), где новый гамильто-
гамильтониан оказывается явной функцией «времени» ? (подробности см.
в работе [430], § 141).
Таким образом, теория, развитая для независящего от времени
гамильтониана с N степенями свободы, применима также и к га-
гамильтониану, зависящему от времени, но cN—1 степенями свободы.
В частности, независящий от времени гамильтониан с двумя сте-
1) Эти рассуждения несколько формальны. Более существенно то, что
движение по дополнительной координате задано, например, t (t) = ?.
В этом состоит также отличие от рассматриваемого далее движения в сокра-
сокращенном фазовом пространстве.— Прим. ред. ¦ :
30
Глава 1
пенями свободы динамически эквивалентен гамильтониану с од-
одной степенью свободы, зависящему от времени.
Интеграл действия. Рассмотрим связь между относительным ин-
интегральным инвариантом A.2.33), для которого интегрирование
проводится в некоторый определенный момент времени t, и интег-
интегралом действия для одномерной колебательной системы с незави-
независящим от времени гамильтонианом. Интеграл действия опреде-
определяется как
^dq, A.2.40)
2л
\y
Рис. 1.2. Контур интегрирования для вычисле-
вычисления переменной действия.
где интегрирование производится по одному периоду колебаний.
В терминах расширенного фазового пространства выражение
A.2.33) для одномерного осциллятора можно переписать в виде
V (pdq— Я dt) = const,
причем интегрирование производится при ? = const. Поскольку
выбор Z, произволен, то новый путь интегрирования, который вклю-
включает и изменение времени, может быть выбран так, что часть его
будет проходить вдоль действительной траектории системы в фа-
фазовом пространстве. Для специального случая Я = const второе
слагаемое обращается в нуль при интегрировании по любому зам-
замкнутому контуру, и мы получаем
j)pdq = const. A.2.41)
Если теперь выбрать пучок траекторий, вокруг которого про-
производится интегрирование, как это показано на рис. 1.2, то полный
путь интегрирования будет состоять из двух частей
&pdq=[pdq+ \pdq, A.2.42)
У с\ с2
где путь Сх охватывает один период колебаний. При этом конечные
Общий обзор и основные представления 31
точки кривой Сг имеют одинаковые значения q, и поэтому путь С.:
можно выбрать так, что q = const. Вследствие этого из A.2.40)
и A.2.42) получаем
[р dq = const = 2л/. A.2.43)
Отсюда вытекает эквивалентность интеграла действия и относи-
относительного интегрального инварианта в рассматриваемом случае1).
Значение интеграла действия определяется прежде всего тем, что
он является каноническим импульсом в переменных действие —
угол (см. § 1.2в). Помимо этого, он оказывается адиабатическим
инвариантом движения, т. е. остается приблизительно постоянным
в случае медленного, по сравнению с периодом колебаний, изме-
изменения гамильтониана со временем. Адиабатическое постоянство
действия подробно рассматривается в § 2.3 и имеет фундаменталь-
фундаментальное значение для понимания регулярного движения в системах
с гамильтонианом, зависящим от времени, и в системах с несколь-
несколькими степенями свободы.
Сечение Пуанкаре. Метод сечения Пуанкаре является одним из ос-
основных методов анализа гамильтоновой динамики. Для автоном-
автономных систем с двумя степенями свободы фазовое пространство че-
четырехмерно. Выберем в фазовом пространстве некоторую двумер-
двумерную поверхность j^R (см. рис. 1.3, а) и рассмотрим последователь-
последовательные пересечения ее траекторией. Пересечение происходит каждый
раз, когда траектория проходит сквозь поверхность в некотором
определенном направлении (например, слева направо).
В частности, удобно выбрать поверхность сечения J^R следую-
следующим образом. Заметим прежде всего, что траектория лежит на
трехмерной энергетической поверхности Я (р1( р2. <7i» <b) = Но
в четырехмерном фазовом пространстве [см. рис. 1.3, б (/)]. Это
уравнение определяет любую из четырех переменных, скажем р2,
как функцию трех остальных
Р2 = Ръ(Ръ <7ъ Ь)- A.2.44)
Рассмотрим проекцию траектории на трехмерный объем (ръ qx, q.2)
на рис. 1.3, б B). Если движение ограничено, то траектория бу-
будет все время пересекать определенную плоскость q2 = const вну-
внутри этого объема. Эту плоскость, заданную координатой qx и со-
сопряженным импульсом plf удобно выбрать в качестве поверхности
сечения ?л. В общем случае последовательные пересечения траек-
траектории с поверхностью J^R будут произвольно распределены в не-
г) Этот результат можно получить и проще, заметив, что при Н = const
смещение вдоль фазовой траектории эквивалентно изменению начальных
условий.— Прим. ред.
32
Глава 1
Рис. 1.3. Сечение Пуанкаре в фазовом пространстве.
а — пересечения траектории с поверхностью 2р; б — две степени свободы: 1 — тра-
траектория в четырехмерном фазовом пространстве, лежащая на трехмерной энергетиче-
энергетической поверхности; 2 — ее проекция на поверхность {Pi, Qi, q2)', 3 — последовательные
пересечения траектории с двумерной поверхностью q2 = const (крестики); в — три сте-
степени свободы: / — траектория в шестнмерном фазовом пространстве, лежащая иа пя-
пятимерной энергетической поверхности; 2 — три последовательных пересечения траек-
траектории с четырехмерной поверхностью q3 = const; 3 — проекция этих пересечений на
плоскости (/?], qx) н {р3, д^).
Общий обзор и основные представления 33
которой ограниченной области ?Л. В случае существования до-
дополнительного (помимо Яо) интеграла движения
Цръ Рг. Яъ %) = const A.2.45)
из A.2.44) и A.2.45) следует
Pi = Pi(Gi> <7г)- A.2.46)
Поэтому последовательные пересечения должны лежать на неко-
некоторой инвариантной кривой, определяемой уравнением A.2.46)
с дг = const. Таким образом, существование интегралов движе-
движения можно определить из анализа пересечений траекторий с по-
поверхностью Y,r- После того как существование интеграла установ-
установлено, можно исследовать локальную устойчивость и другие инте-
интересные свойства инвариантных кривых.
Отметим, что рассматриваемая поверхность сечения (ри <7i)
как раз и является сокращенным фазовым пространством исходной
гамильтоновой системы, э последовательные пересечения полу-
получаются друг из друга путем канонического преобразования, опреде-
определяемого уравнениями Гамильтона. Поэтому площадь, ограничен-
ограниченная замкнутой кривой, на поверхности сечения сохраняется. Это
важное свойство можно получить и непосредственно следующим
образом. Запишем общие дифференциальные соотношения
wi_ дХ 4- дХ d
dq д]х
A.2.47)
где X и \i можно рассматривать как начальные координату и им-
импульс на поверхности сечения. Выразив частные производные че-
через производящую функцию F2 (X, р) и разрешив A.2.47) относи-
относительно dp и dq, получим
A.2.48)
dp= -J^.dk+-±-dii,
где введены обозначения dF.2/dX = Fx и т. д. Детерминант коэффи-
коэффициентов A.2.48), эквивалентный якобиану преобразования от пе-
переменных (X, ц) к (q, p), равен единице, что и доказывает сохранение
площади при преобразовании1). Это свойство двумерной поверхно-
поверхности сечения в четырехмерном фазовом пространстве в дальнейшем
х) В общем случае исходные переменные p,q не являются каноническими
на поверхности сечения и сохраняется некоторая их функция Ж (р, q) —
«наведенная» мера.
34 Глава 1
будет играть важную роль как при численном поиске интегралов
движения (§ 1.4), так и при выяснении устойчивости линеаризо-
линеаризованного движения вблизи периодического решения (§ 3.3).
Метод сечения Пуанкаре можно обобщить и на системы с чис-
числом степеней свободы Лг>2. Для независящего от времени гамиль-
гамильтониана системы с N степенями свободы размерность энергетиче-
энергетической поверхности в фазовом пространстве равна 2N—1 [рис. 1.3, в
(/) 1. Исключим, как и раньше, одну из переменных, например pN,
и рассмотрим последовательные пересечения траектории с BN—2)-
мерной поверхностью qN = const с координатами plt . . . , /?лт-ц
qlt . . . , qN-_i [рис. 1.3,6 B)\. При этом поверхность сечения по-
прежнему представляет собой сокращенное фазовое пространство
с сохраняющимся объемом. В случае существования одного или
более интегралов движения все пересечения будут лежать на од-
одной поверхности, размерность которой меньше 2N—2. В против-
противном случае они будут заполнять некоторый BN—2)-мерный объем.
Если движение по разным степеням свободы многомерной си-
системы почти независимо, то удобным способом наглядного пред-
представления движения служат проекции поверхности сечения на
плоскости (pi, cji), как показано на рис. 1.3, в (<?). Для регулярного
движения с точно разделяющимися переменными {pit qt) площадь
сохраняется в каждой плоскости (pit q{). При этом для каждой
степени свободы существует свой интеграл движения и все проекции
лежат на некоторой кривой в каждой из плоскостей (pi, qi). Однако
в общем случае при A^>2 даже для регулярной траектории пере-
пересечения, спроектированные на произвольную плоскость (/?,-, </,),
не лежат на кривой, а заполняют некоторый конечный слой, размер
которого зависит от выбора переменных (pit qt). В рассматривае-
рассматриваемом случае пересечения лежат фактически на (N—1)-мерной по-
поверхности, проекция которой на любую из плоскостей (pi, qt) за-
занимает область конечной площади. Примеры многомерного движе-
движения описаны кратко в п. 1.4в и подробно — в гл. 6.
* 1.2в. Переменные действие — угол
Для системы с одной степенью свободы и гамильтонианом, не за-
зависящим от времени, всегда существует интеграл движения. В мно-
многомерном случае, если переменные в уравнении Гамильтона—Якоби
полностью разделяются, можно найти N интегралов движения,
которые «развязывают» все N степеней свободы. Обозначим произ-
производящую функцию F2 через 5 и примем, что в случае полного раз-
разделения переменных решение имеет вид
S = SS<(<7<, «1 • ¦ • «n), A-2.49)
i
где а; — новые импульсы, связанные с N интегралами движения.
Общий обзор и основные представления 35
Если, кроме того, гамильтониан можно записать в виде суммы г)
I
то из-за независимости переменных qi уравнение Гамильтона—
Якоби A.2.15) распадается на N уравнений
a. A.2.50)
Решив их, найдем зависимость S; от qi. Новые импульсы а? ока-
оказываются при этом постоянными разделения для уравнения Гамиль-
Гамильтона—Якоби и удовлетворяют соотношению
2>; = Я0. A.2.51)
i
Связь между старыми и новыми каноническими переменными
дается соотношением A.2.13). Новый гамильтониан Н зависит
только от импульсов а;, и уравнения Гамильтона решаются три-
тривиально.
Выбор постоянных а; в качестве новых импульсов является
произвольным. Вместо этого можно выбрать любые N величин
Jit являющихся независимыми функциями а;:
Ji = /((«). A.2.52)
Если эти N уравнений обратить,
at = ai(J), A.2.53)
и подставить в A.2.49), то получим производящую функцию для
преобразования к новым импульсам J,-:
S(g, J) = S(q, а (У)) A.2.54)
и новый гамильтониан
#(•/) = !>,(./). A.2.55)
i
Решение уравнений Гамильтона и в этом случае тривиально.
Для периодических систем с полностью разделяющимися пе-
переменными очень удобно выбрать функции J (а) специальным об-
образом. При этом под периодическими мы подразумеваем такие
системы, в которых по каждой степени свободы либо р? и д? яв-
являются периодическими функциями времени одного периода, либо
pi периодически зависит от qt. В первом случае говорят о колеба-
колебаниях, а во втором — о вращении. Периоды движения по каждой
степени свободы не обязательно одинаковы. Если они не находятся
в рациональном отношении, то движение называется квазиперио-
квазипериодическим2). Для определения переменных действия </, как функций се
г) Это условие, вообще говоря, излишне и приведено, видимо, только
для упрощения изложения (см., например, [453]).— Прим. перев.
2) В оригинале —conditionally periodic (условно периодическое) — ме-
менее распространенный синоним квазипериодического.— Прим. перев.
36 Глава 1
запишем интеграл A.2.40), используя для р{ выражение A.2.13а),
где /1( . . . , Jи — новые сохраняющиеся импульсы. Обращение
этого выражения дает новую производящую функцию 5 (q, J).
Согласно A.2.24), сопряженные координаты имеют вид
8/ = @f*-j-p/, A.2.57)
где сог и pt- — постоянные. Интегрируя Э( по полному периоду
колебаний Т, получаем
t+T
Qt = f d8, = (O(T. A.2.58)
i
Но, с другой стороны, из A.2.136) следует
dQt=^--^-dqt. A.2.59)
J
Подставляя это выражение в A.2.58), меняя порядок дифферен-
дифференцирования и интегрируя по периоду, находим
Сравнение A.2.58) с A.2.60) дает
ш,Т = 2п, A.2.61)
т. е. постоянные сог есть просто частоты колебаний. Таким обра-
образом, использование переменных действие — угол представляет
собой удобный способ получения частот колебаний, не требующий
выяснения деталей движения. При исследовании движения систем,
близких к интегрируемым, удобно предварительно перейти к пе-
переменным действие — угол в интегрируемой части системы, а уже
затем использовать теорию возмущений или другие методы.
Гармонический осциллятор. Проиллюстрируем достоинства пере-
переменных действие — угол на примере гармонического (линейного)
осциллятора, гамильтониан которого имеет вид
H = G-?—-F^- = a, A.2.62)
2 2 V '
где G, F я а — постоянные. Определив р (q, а) и вычислив интеграл
^ A-2'63)
1) Выражение A.2.60) сразу получается из определения A.2.56) для
при р = J, q = 8.— Прим. ред.
Общий обзор и основные представления 37
где 4„акс = Bа/FI2, получим
/ = a(FG)-I/2. A.2.64)
Отсюда и из A.2.55) гамильтониан равен
tf = (FGI/2J A.2.65)
и не зависит от угловой переменной. Частота колебаний равна
соо =дНШ = (FG)i2. Подставляя а из A.2.64) в A.2.62), полу-
получаем одно из уравнений канонического преобразования
p = p(q, J) = [2RJ-R2q2)V2, A.2.66)
где R = (F/GV2. Из A.2.13а)
о
и из A.2.136) находим второе уравнение
A.2.67)
о
которое после интегрирования дает
A.2.68а)
С учетом A.2.66) имеем
/? = B/#I2cose. A.2.686)
Уравнения A.2.68) определяют преобразование от переменных
действие — угол к исходным переменным р, q. Это преобразование
обычно получается при помощи производящей функции типа
Fx (q, q), которая имеет вид
Fx= ±-Rq* ctgB. A.2.69)
Отметим также, что эллипс, определяемый уравнением A.2.62),
можно канонически преобразовать в круг, изменяя масштаб: р =
= л/Rp'; q = q'Уд/R. Отсюда, ясно, что в переменных действие —
угол (J, Э) движение представляет собой вращение некоторого век-
вектора постоянной длины J. Это немедленно приводит к уравнениям
преобразования A.2.68), из которых видно также, что величина R
равна отношению полуосей исходного эллипса.
Ниже мы увидим, что переход к переменным действие — угол
особенно эффективен в случае медленного изменения величин F
и G со временем или в зависимости от координаты по другой сте-
степени свободы. В этом случае J является адиабатическим инвариан-
инвариантом движения, т. е. мало изменяется даже при значительном из-
изменении соо и Я (см. также [265], гл. 2). Для нелинейных колеба-
38 Глава 1
ний преобразование A.2.68) не приводит к переменным действие—
угол. Тем не менее, как мы увидим в гл. 2, его можно использовать
при построении рядов теории возмущений. Общий же метод вве-
введения переменных действие — угол, развитый в этом параграфе,
применим, как будет видно ниже, и к нелинейному осциллятору.
§ 1.3. Интегрируемые системы
Рассмотрим гамильтонову систему с N степенями свободы. Если
уравнение Гамильтона—Якоби разделяется на N независимых урав-
уравнений, по одному на каждую степень свободы, то гамильтониан
и движение системы называются интегрируемыми (иногда исполь-
используются термины полностью интегрируемый или полностью разде-
разделяющийся). Постоянные разделения а; называются изолирующими
или глобальными интегралами движения1), поскольку каждый та-
такой интеграл «отделяет» одну степень свободы. Система с N степе-
степенями свободы интегрируема тогда и только тогда, когда сущест-
существует N независимых изолирующих интегралов.
Эти интегралы должны быть в инволюции, т. е. их скобки Пуас-
Пуассона друг с другом должны обращаться в нуль: [a,-, ct/J = 0. Это
гарантирует, что переменные а,- образуют полный набор новых им-
импульсов. Любая полная система N функций от а, например пере-
переменные действия Jс, также определяет набор изолирующих интег-
интегралов, скобки Пуассона которых автоматически обращаются в
нуль (подробности см. в работе [430], § 147).
*
1.3а. Одна степень свободы
Согласно соотношению A.2.21), для системы с одной степенью сво-
свободы и независящим от времени гамильтонианом Н величина
Н(р, q) = E A.3.1)
является интегралом движения. Поэтому все такие системы интег-
интегрируемы. При этом импульс р зависит только от координаты q
(но не от времени). Разрешив A.3.1), получим
Р = Р(Я, Е). A.3.2)
*) В отечественной литературе используется также не совсем удачный
термин — однозначный (конечнозначный) интеграл. Заметим, что понятия
изолирующий и глобальный характеризуют, вообще говоря, разные свой-
свойства интеграла движения, поскольку «изоляция» может быть и локальной
как, например, в теории КАМ (см. п. 3.2а ниже). Исключение с помощью
каждого интеграла одной степени свободы, т. е. двух динамических перемен-
переменных, возможно только при условии обсуждаемой ниже инволюции, или ком-
коммутирования, интегралов, что означает совместимость соответствующих им
циклических координат. В противном случае интеграл позволяет исключить
лишь одну динамическую переменную (см., например, [337], п. 14).— Прим.
ред.
Общий обзор и основные представления 39
Зависимость переменных р и q от времени можно определить из
второго уравнения Гамильтона A.2.66), которое дает
дН'др
или, после интегрирования,
A.3.3)
3
** A.3.4)
дН/др
Так как дН/др зависит только от переменных р и q, которые свя-
связаны соотношением A.3.2), то интегрирование уравнений движе-
движения сводится к квадратуре. Однако интеграл можно найти, вообще
говоря, только численно.
Модель маятника. Проиллюстрируем описанную выше процедуру
на простом примере маятника. Подобный гамильтониан возникает
по существу во всех задачах с нелинейными резонансами, и эта
модель лежит в основе нашего подхода к нелинейной динамике,
рассматриваемой в последующих главах. Уравнения движения
маятника имеют вид
р=—fsinq), (f = Gp, A.3.5)
где F = mgh; G — \!{mh2); mg— сила тяжести, действующая на
массу т; h — длина маятника. Угол отклонения от вертикали <р
и момент импульса р, сопряженный ф, удовлетворяют уравнениям
Гамильтона. Гамильтониан есть сумма кинетической энергии
— Gp2 и потенциальной энергии U = — F cos <p:
Н= -i-Gp2 —/гсозф=?. A.3.6)
Соотношение A.3.4) сводит задачу к квадратуре и позволяет вы-
выразить решение через эллиптические интегралы. Однако многое
можно узнать и прямо из анализа соотношения A.3.6) при различ-
различных значениях энергии Е, как это показано на рис. 1.4. Значение
гамильтониана Е соответствует полной энергии системы. Если Е
больше максимального значения потенциальной энергии F, то им-
импульс р всегда отличен от нуля. Это приводит к неограниченному
изменению ф, т. е. к вращению. При этом для р;>0 движение про-
происходит слева направо с энергией Еи. Для E<c.F движение огра-
ограничено (внутри потенциальной ямы) и соответствует колебаниям
маятника. Если же Е = F = Es, то движение происходит по се-
сепаратрисе, а период колебаний становится бесконечным. Движение
имеет две особые точки при р = 0: одна находится в начале коор-
координат при ф = 0 и является устойчивой, или эллиптической, осо-
40
Глава 1
бой точкой, другая (в месте соединения двух ветвей сепаратрисы
при ф = ± я) является неустойчивой, или гиперболической, осо-
особой точкой. Фазовая траектория вблизи эллиптической точки все
время остается в ее окрестности, тогда как траектория вблизи ги-
гиперболической точки удаляется от нее.
Рис. 1.4. Динамика маятника.
а — график потенциальной энергии; б — фазовые траектории.
^Из A.3.4) следует, что в общем случае период колебаний зави-
зависит от энергии осциллятора. Подставляя значение Н из A.3.6) в
A.3.4), для периода колебаний получаем соотношение
Т
(Щ
1 2
(? + Fcos(F)
1 2
0.3.7)
Общий обзор и основные представления 41
которое можно выразить через эллиптические интегралы. В част-
частности, из A.3.5) видно, что на сепаратрисе как возвращающая сила,
так и скорость обращаются в нуль при ф = я, и поэтому период Т
становится бесконечным.
Чтобы записать гамильтониан маятника в переменных действие—
угол (У, 8), вычислим действие аналогично A.2.63). В результате
получим
Тмаке
J(E) = ~ ]" [-^-(?-^со5ф1)]12<%, A.3.8)
в(Ф, Е)= (G-^-W ** _, A.3.9)
\ dE I J [B/G) (E + F cos qh)]1 2
где Фмакс = л/2 для вращения (E^>F) и cos фмакс = — HIF для
колебаний (E<.F). Новый гамильтониан получается путем подста-
подстановки Я == Е в A.3.8) и обращения функции /(Я). Выражения
A.3.8) и A.3.9) приводятся к эллиптическим интегралам и их можно
представить в виде [383, 344]:
(*) — A — х2)Х(х), х<1,
, A.3.10)
(J)
[Ж (х)]-1 Т (tj, х), х<1,
A.3.11)
Здесь R = (F/GI2, а /С (х) и ?Г (х) — полные эллиптические ин-
интегралы первого и второго рода:
0 * Ш A.3.12)
Я2
Г 19
о'
где х sin I") = sin — ф, 2х2 = 1 + EIF, а 9~ — эллиптический ин-
интеграл первого рода. Величина к характеризует относительную
энергию маятника, так что на сепаратрисе х = 1; для колебаний
х<1, а для вращения х>-1.
Соотношения dJIdE = 1/со и A.3.10) определяют частоту
ю(х) я [ \Ж(х)]-\
шв 2
42 Глава 1
где юо=(Я/I2 A.3.14)
— частота малых колебаний вблизи эллиптической точки. Асимп-
Асимптотическое выражение для Ж при х -*¦ 1 дает частоту вблизи се-
сепаратрисы
A-х2)
12
«о I _м„ Г 4
я/1п
' ' (х2-!I2
A.3.15)
При х -*¦ 1 частота логарифмически обращается в нуль. Уравнение
сепаратрисы можно получить из A.3.6) и условия Е = F:
''" ^(l+cos9sI2, A.3.16)
G
где индекс s отвечает значениям переменных на сепаратрисе. Отсюда
п i 2@р ГГ1с _JPs_ /I q 171
//S — ^П CUb ^ , {I .О. I 1 J
где плюс и минус соответствуют верхней и нижней ветвям сепарат-
сепаратрисы. Уравнение Гамильтона
q>s = Gps A.3.18)
с учетом A.3.17) дает
I ^UJ (Л HJo ' 1Д.О.1^7/
at 2
Разрешая это уравнение относительно dt и интегрируя с начальным
условием ф = 0 при t = 0, получаем
A.3.20)
cos(q>/2)
0
или, после обращения,
<ps = 4arctg[exp(a>oQ] — п. A.3.21)
Траектории вблизи сепаратрисы очень похожи на саму сепаратрису,
за исключением того, что период движения стремится к бесконеч-
бесконечности при приближении к сепаратрисе A.3.13).
Гамильтониан A.3.6) был получен для модели маятника. Од-
Однако оказывается, что такого вида гамильтониан получается почти
во всех близких к интегрируемым системах, в которых имеет место
резонанс между степенями свободы. В окрестности значений пере-
переменных действия, соответствующих точному резонансу, разложе-
разложение неинтегрируемой части гамильтониана в ряд Фурье дает члены,
Общий обзор и основные представления 43
которые вызывают медленные изменения, описываемые гамильто-
гамильтонианом вида A.3.6). Предположим, что угловые переменные ф
и а|)> соответствующие разным степеням свободы, находятся в ре-
резонансе, так что отношение их частот <мф/с0ф для каких-то значений
переменных действия близко к рациональному числу г/1. Тогда
можно произвести каноническое преобразование к новой медлен-
медленной переменной
9 = /ф—п|; A.3.22)
и исключить одну из быстрых угловых переменных, например ф.
Канонически сопряженный 8 импульс связан с отклонением дейст-
действия, например J4, от точного резонансного значения Уо. Если те-
теперь произвести усреднение по быстрой угловой переменной г|),
то получится гамильтониан с одной степенью свободы, совпадающий
по форме с гамильтонианом маятника A.3.6). Поскольку такой га-
гамильтониан всегда возникает при фурье-преобразовании возмуще-
возмущения с последующим применением резонансной теории возмущений
и усреднения, он был назван Чириковым [70 ] «универсальное опи-
описание нелинейного резонанса». Мы будем называть его стандарт-
стандартным гамильтонианом. Он играет фундаментальную роль во всем
нашем изложении материала. Соответствующая теория возмущений
рассматривается в § 2.4 и широко используется в последующих
главах.
1.36. Линейные дифференциальные уравнения
Прежде чем перейти к анализу нелинейной системы с двумя степе-
степенями свободы, рассмотрим хорошо изученное математически ли-
линейное дифференциальное уравнение второго порядка с перемен-
переменными коэффициентами. Как известно, решение такого уравнения
существует и соответствует регулярному движению1). Рассмотрим
дифференциальное уравнение
x + f(t)'x + g(t)x=0, A.3.23)
где / (t) и g (t) считаются пока произвольными функциями времени.
Так как это уравнение является линейным уравнением второго
порядка, его общее решение можно построить при помощи двух
линейно независимых решений х1 и хг. Важное свойство этого урав-
уравнения получается из анализа вронскиана
W =
Х\
х
A.3.24)
*) Это зависит от вида функций f (t) и g (f) в A.3.23).— Прим. ред.
44
Глава 1
Дифференцируя обе части равенства по t, находим
dW
it
Хг
A.3.25)
где второй определитель обращается в нуль, так как он имеет оди-
одинаковые строки. Подставляя выражение для хх и х2 из A.3.23)
и раскрывая определитель, находим
fxt + gxx).
После сокращения членов gxxx2 имеем
W = —fW.
Интегрирование этого выражения дает
A.3.26)
Если / (t) = 0, то диссипация в системе отсутствует х) и полу-
получающееся уравнение
x + g(t)x = 0 A.3.27)
соответствует гамильтониану
± A.3.28)
cq = xnp = x. В этом случае A.3.26) сводится к
W = const. A.3.29)
Это соотношение справедливо независимо от того, является ли
g (t) периодической функцией или нет.
Решение любого дифференциального уравнения второго порядка
однозначно определяется начальными значениями функции и ее
производной. Поэтому для каждого из независимых решений можно
написать преобразование от начального момента времени t = О
к любому другому моменту времени в виде
Хг @ =
@)
! @),
хх @=т21х1 @) + т22 хг @),
где коэффициенты /и« зависят от времени, но не от начальных ус-
условий. Из A.3.29) вытекает, что детерминант матрицы
т21
detM =
= 1.
A.3.30)
1) Функция / @ может характеризовать также изменение параметров
системы, например массы.— Прим. ред.
Общий обзор и основные представления 45
Этот результат получается, если записать матрицу преобразования
двух решений в виде
/ x1(t) x2{t) \ ( mn m12\fx1@) х2@) \
x2{t) J \ m21 гпп/ХЫО) x2@)
Вычисляя детерминант в обеих частях равенства и используя тот
факт, что детерминант произведения матриц равен произведению
их детерминантов, получим преобразование для вронскиана
Поскольку W (t) = W @), то det М = 1, что эквивалентно усло-
условию сохранения площади. В дальнейшем мы будем рассматривать
только такие консервативные *) системы.
Периодические коэффициенты. Если g (t) имеет период т, то A.3.27)
имеет два независимых решения вида
x(t) = w(t) explicit)], A.3.31)
где w (t) — периодическая функция времени
w(t) = w(t + i).
При этом
exp {i [Мр (/ + т) —гр @]} =ехр {id),
где а не зависит от времени. Поэтому г|) тоже периодическая функ-
функция времени. Уравнение A.3.31) представляет собой общее реше-
решение Флоке для линейного уравнения с периодическими коэффици-
коэффициентами. Дифференцируя A.3.31) два раза, подставляя результат
в A.3.27) и сокращая ?'*, получаем для действительной и мнимой
частей:
ш—wty2 + g(t)w = 0, A.3.32а)
2гя)-$~\-Щ = 0. A.3.326)
Перепишем второе уравнение в виде
2w + JL = о,
г) Имеется в виду сохранение не энергии, а площади на фазовой пло-
плоскости системы (х, х). Заметим, что последнее сразу следует из того, что при
f = 0 рассматриваемая система является гамильтоновой A.3.28) в перемен-
переменных х, х.— Прим. ред.
46
Глава !
или, после интегрирования,
A.3.33) ч
Подставляя это соотношение в A.3.31) и переходя к действитель-
действительным функциям, находим
х(/) = w @ cos if @, A.3,34)
где "ф = 1 df ш2. Используя соотношение
А,
cos2oH-sin2i{5=l A.3.35)
и выражая sin i|; и cos г|з с помощью A.3.34), получаем инвариант 2)
/(*, х, t) = [w~2x2^{wx—wxf]. A.3.36)
Хотя явный вид функции w (/) в общем случае неизвестен, но из
существования решения следует, что для гамильтониана A.3.28)
всегда существует инвариант /. Подставляя A.3.33) в A.3.32а),
получаем уравнение для до:
=0.
A.3.37)
Решение этого уравнения не проще, чем исходного A.3.27). Однако
Левис [259] заметил, что любое решение A.3.37) определяет через
соотношение A.3.36) решение A.3.27) для всех начальных условий.
Инвариант A.3.36) полезен при изучении движения частиц в уско-
ускорителях с жесткой фокусировкой [94], когда функция g (t) кусочно
постоянна и можно явно найти w (t). Точное решение известно
также и в случае g (t) = a + 6 cos t, который приводит к уравне-
уравнению Матье. Левис [259 ] показал, что для произвольной функции
инвариант A.3.36) можно построить при помощи теории возмуще-
возмущений.
Отметим, что проведенный выше анализ применим к линейным
неавтономным системам с одной степенью свободы, которые соот-
соответствуют некоторому специальному классу гамильтонианов с двумя
степенями свободы. Так как неавтономные линейные системы вто-
второго порядка интегрируемы, то неудивительно, что всегда можно
найти соответствующий инвариант. Попытки Саймона [397 ] и Ле-
виса и Лича [260] обобщить эти методы на нелинейные системы
не привели пока к новым полезным результатам.
х) В общем случае A.3.33) содержит произвольную постоянную: ф =
= C/w2; соответственно изменяются и A.3.36), A.3.37).— Прим. ред.
г) Этот инвариант, полученный впервые Курантом и Снайдером [94],
имеет простой физический смысл сохранения «энергии» в переменных:
х -->¦ x/:j; t -> г|; (подробности см., например, в работе [232]).— Прим. ред.
Общий обзор и основные представления 47
1.3в. Несколько степеней свободы
Для систем с несколькими степенями свободы соотношение A.3.3)
принимает вид
Jl*«* A.3.38)
d.
дН/дрг дН/др2 dH/dpN
Только в том случае, когда производная дН1дрг — / (qj зависит
лишь от qlt первое уравнение решается в квадратурах. Аналогич-
Аналогичное утверждение имеет место и для последующих уравнений. В об-
общем случае необходимо решать всю систему дифференциальных
уравнений совместно. Однако, если в дополнение к гамильтониану
имеются другие интегралы движения, тогда число совместно ре-
решаемых уравнений может быть уменьшено на единицу для каждого
дополнительного изолирующего интеграла движения. Изолирую-
Изолирующим является такой интеграл, который в некоторых канонических
переменных приводится к уравнению: dH/dpi = / (qi). Преобразо-
Преобразование к переменным действие — угол удовлетворяет даже более
жесткому условию dHidpi = const. Однако само преобразование
зависит от существования изолирующего интеграла. Последний же
может быть достаточно глубоко скрыт в динамике системы, так что
обнаружить его не так-то легко. Изолирующие интегралы связаны
с симметриями динамической системы. Эти симметрии могут ока-
оказаться очевидными, и тогда необходимое преобразование перемен-
переменных, обеспечивающее решение в квадратурах, определяется не-
непосредственно. Это справедливо, например, для частицы в поле
центральных сил (см. ниже). Когда присутствие симметрии в си-
системе не очевидно, как, например, в случае рассматриваемой ниже
цепочки Тоды, найти изолирующий интеграл не просто. В настоя-
настоящее время не существует какого-либо метода, позволяющего опре-
определить все изолирующие интегралы произвольной гамильтоновой
системы или хотя бы установить их полное число. Поэтому не су-
существует и никакого общего способа проверки на интегрируемость
(N изолирующих интегралов) для системы с N степенями свободы.
Если в системе нет очевидной симметрии, то догадаться о существо-
существовании скрытого изолирующего интеграла и обнаружить его часто
удается лишь при помощи численных экспериментов.
Центральные силы. Проиллюстрируем нахождение изолирующего
интеграла (помимо полной энергии) и сведение решения к квадра-
квадратурам на простом примере движения частицы в поле центральных
сил. Хорошо известно, что эта задача интегрируема. Без потери
общности задача сводится к двумерному движению в плоскости,
определяемой начальной скоростью частицы и положением сило-
силового центра. Третья степень свободы тривиально отделяется при
помощи изолирующего интеграла pz = 0. В полярных координатах
48
Глава 1
(г, 9) гамильтониан имеет вид
A.3.39)
где pr — mr, Pq — mr-Q, m — масса частицы, U — потенциал цен-
центральной силы {F ~ — dUldr). Поскольку система консервативна,
то ее гамильтониан Н = Е сохраняется. Уравнения движения в
форме A.3.38) имеют вид
dt = М = dr
дН1дрг
I
1
и\
\
\
\
\
\
/
/
и/
1
/
а
Еи
Рис. 1.5. Движение в центральном поле.
а — эффективный одномерный потенциал; б — фазовые тра-
траектории.
Вычисляя частные производные и исключая рг при помощи гамиль-
гамильтониана, получаем
dt^—*— = d± . A.3.40)
pQ/mr2 [2m(E — U(r)) — p$/r*]lm
Эти уравнения нельзя решить, пока неизвестна зависимость ре
от 9 и г. Именно отсюда видно существенное значение второго ин-
интеграла движения. В данном случае таким интегралом движения
является рв. Это следует из того, что сила dp^dt отсутствует и га-
гамильтониан не зависит от 6. Отсюда
= / = const.
A.3.41)
Подставляя это выражение во второе уравнение A.3.40), сводим
к квадратурам сначала решение для г (t), а затем и для 0 (/). Это
можно увидеть и прямо из A.3.39), вводя эффективный потенциал
U (г) ---- Р,2тг'- - U (г). Оба слагаемых потенциала и их сумма,
Общий обзор и основные представления
49
или эффективный потенциал, показаны на рис. 1.5, a U (г) =
= — klft при 2<Р<;0; задача Кеплера соответствует |J = 1.
Указаны также три значения полной энергии системы Eb, Es и Еи,
соответствующие финитному, сепаратрисному и инфинитному дви-
движениям. Фазовые кривые представлены на рис. 1.5, б. Движение
здесь аналогично случаю одной степени свободы (рис. 1.4), за исклю-
исключением того, что сепаратриса теперь замыкается на бесконечности.
Рис. 1.6. Пример ограниченной траектории для
Р Ф 1 (некулоновское взаимодействие).
Финитное движение на плоскости (г, 6), ограниченное окружно-
окружностями радиуса гх и г2, показано на рис. 1.6 для Р Ф 1. Пространст-
Пространственная траектория не замкнута, так как отношение периодов по г
и 8 не равно целому числу1). Это — пример квазипериодического
движения. Тем не менее пересечения траекторий с плоскостью
6 = const образуют в этом случае замкнутую кривую в координатах
г, рг вследствие существования двух изолирующих интегралов рв -=
= / и Н = Е. Для Р =1 (задача Кеплера) частоты движения по г
и 8 одинаковы и траектория образует замкнутую кривую (эллипс)
в плоскости (г, 8).
1) Точнее, рациональному числу.— Прим. ред.
50 Глава 1
Рассмотрим теперь преобразование к переменным действие —
угол. Подставляя производящую функцию в A.3.39), получаем урав-
уравнение Гамильтона—Якоби A.2.15) в виде
dSr
2т \\ дг
где мы использовали преобразование pi = dSldqt и учли, что пе-
переменные разделяются. После умножения на 2тг2 гамильтониан
принимает вид A.2.50):
[^M^Jl =P, A.3.43)
дв I I 2т
и мы снова приходим к сохранению момента импульса. Это, конечно,
прямо следует из того, что 6 является циклической переменной,
т. е. гамильтониан от нее не зависит. Второе уравнение в A.3.43)
дает
dSr V = 2т(Е — U(г)) —. A.3.44)
дг
Запишем переменные действия в виде
—— d6, A.3.45)
Щ^-dr. A.3.46)
Подставляя A.3.43) и A.3.44) в A.3.45) и A.3.46), соответственно
получаем
JB = ^-~]ldQ = l, A.3.47)
2я о
Пусть, например, U (г) = — klr. Простое интегрирование ([156],
§ 9.7) дает
(^) A.3.49)
Отсюда новый гамильтониан
A.3.50)
2 {Jг + ^еJ
где мы заменили / на /е. Заметим, что переменные действия входят
только в виде суммы. Следовательно, в системе имеется вырожде-
Общий обзор и основные представления
51
ние1). Это значит, что движения как по г, так и по Э имеют одну и ту
же частоту 2)
дН дН mk*
со =
dJr
(Jr -г
A.3.51)
что приводит к замкнутой траектории. Если центральная сила за-
зависит от г по-другому, то траектория уже не будет замкнутой, как
показано на рис. 1.6.
Цепочка Тоды. В качестве второго примера интегрируемого гамиль-
гамильтониана рассмотрим трехчастичную цепочку Тоды [408] 3), гамиль-
Рис. 1.7. Трехчастичная цепочка Тоды.
тониан которой имеет вид
Н = [р\-тР2 + Рз) + ехр[— (фх — ф3)] -гехр [ — (ф2—фх)] -г
-гехр[ —(фа —фа)] —3. A.3.52)
Система состоит из трех частиц, движущихся по кольцу (рис. 1.7);
между ними действуют отталкивающие силы, уменьшающиеся по
1) В оригинале — intrinsic degeneracy (внутреннее вырождение).—
Прим. перев.
2) В других канонических переменных (например, рх = Jr + /е, Рг)
вырождение означает, что одна из основных частот системы (со2 = дН!дрг)
равна нулю.— Прим. ред.
3) См. также [454].— Прим. ред.
52
Глава 1
экспоненциальному закону. Помимо энергии, имеется, очевидно,
другой изолирующий интеграл — полный момент
Рг = Рх + Рг + Рз = const. A.3.53)
Это следует из инвариантности гамильтониана при вращении си-
системы как целого (<р,- —>- q>f + ф0), а также непосредственно из урав-
уравнений Гамильтона. Чтобы учесть это явно, перейдем к новым мо-
Рис. 1.8. Эквипотенциальные кривые для гамильтониана
Тоды.
Стрелка показывает направление роста потенциала.
ментам Рх = ръ Р2 = /?2 и Р3, определяемому формулой A.3.53).
Используя производящую функцию
F, = Лф1 + Р&2 + (рз — Pt — Рдщ, A.3.54)
получим
+ ехр [ — (Ф2
ехр (Ф,) —3,
A.3.55)
где координаты Ф; канонически сопряжены с Pi. Так как гамиль-
гамильтониан не зависит от Ф3, то, как непосредственно видно, Р3 =
= const. Без потери общности можно положить Р3 = 0, что со-
соответствует выбору такой вращающейся системы отсчета, в кото-
Общий обзор и основные представления
53
рой полный момент равен нулю. Других изолирующих интегралов
как будто не видно.
Рассматриваемую систему можно представить как частицу в
двумерной потенциальной яме. Для этого воспользуемся произво-
производящей функцией
у)Ф2\ A.3.56)
У = 1,3
Рис. 1.9. Поверхность сечения Пуанкаре для гамильтониана Тоды при раз-
разных энергиях Е (по данным работы [136]).
а) Е = 1; б) Е = 256.
и после неканонического, но тривиального преобразования
будем иметь гамильтониан Тоды
-4г/)]-^-. A.3.57)
+ ехр Bг/-
Эквипотенциальные кривые этой системы, схематически изобра-
изображенные на рис. 1.8, плавно изменяются при удалении от центра
и обладают симметрией по отношению к повороту на угол 2л/3.
54 Глава 1
Если разложить гамильтониан Н по х и у до кубических членов,
получим гамильтониан Хенона—Хейлеса
Я =~{р:-^Р1 + х2 + у2)^х2у--!Гу*. A.3.58)
Движение, описываемое этим гамильтонианом, рассматривается
в следующем параграфе. Известно, что эта система неинтегрируема:
Хенон и Хейлес [188] обнаружили в численных экспериментах,
что при увеличении энергии Н' = Е происходит переход от регу-
регулярного движения к стохастическому. При этом оказалось, что
стохастичность присутствует в какой-то мере при любой энергии.
Все это указывает на отсутствие в системе изолирующего интеграла.
Форд и др. [136] исследовали численно гамильтониан Тоды Н,
ожидая получить такой же результат. Каково же было их удивле-
удивление, когда они обнаружили, что траектории остаются регуляр-
регулярными для произвольной энергии Н = Е, т. е. все пересечения тра-
траектории с поверхностью х = 0 ложатся на гладкие инвариантные
кривые. На рис. 1.9 кривые показаны для значений Е = 1 и Е =
= 256. Эти результаты резко расходятся с данными следующего
параграфа, согласно которым в модели Хенона—Хейлеса траекто-
траектории, заполняющие значительную часть площади, явно видны вплоть
до такой низкой энергии, как Е = 1/8. Это различие связано, ко-
конечно, с тем, что у цепочки Тоды есть скрытая симметрия и соот-
соответствующий ей изолирующий интеграл. Воодушевленный числен-
численными результатами Форда, Хенон [186] нашел явное аналитиче-
аналитическое выражение для этого интеграла
1 = 8рх (р2х-Зр1) + (рх -'г л/3~ ру) ехр [B«/-2 УЗх)] —
— 2рхехр(—4у)-\- (рх— л/W ру) ехр [{2y + 2^/3x)] = const.
A.3.59)
Инвариантные кривые на рис. 1.9 можно непосредственно вычис-
вычислить, если положить х = 0 и исключить рх из A.3.57) с помощью
A.3.59). Существование трех изолирующих интегралов Н, Р3 и /
обеспечивает интегрируемость гамильтониана Тоды х) A.3.52). Од-
Однако даже в исходных переменных интеграл / не соответствует
какому-либо очевидному закону сохранения или симметрии.
Нахождение интегрируемых гамильтонианов. Существуют ли ка-
какие-либо общие методы проверки на интегрируемость конкретного
гамильтониана? На сегодняшний день ответ на этот вопрос отрица-
отрицательный. Можно, однако, поставить вопрос по-другому: существуют
1) Вообще говоря, необходимо еще проверить коммутируемость интегра-
интегралов, что было сделано для произвольного числа степеней свободы в работе
[455].— Прим. ред.
Общий обзор и основные представления 55
ли методы конструирования потенциалов, приводящих к интегри-
интегрируемым гамильтонианам? Такой метод действительно существует
по крайней мере для ограниченного круга задач. Впервые этот ме-
метод был применен Уиттекером ([430], § 152) к исследованию дви-
движения частицы, которое описывается гамильтонианом
H=-j~p\+~^-pl+V(ql,qt). A.3.60)
Уиттекер поставил вопрос: существуют ли такие функции V, для
которых система имеет интеграл не выше второй степени по р:
I(p, q) = ap2l + bp22^cp1p2 + ep1 + fp2^rg, A.3.61)
где коэффициенты зависят от д? Чтобы такая функция была интег-
интегралом движения, необходимо выполнение условия
[/, #] = 0. A.3.62)
Подставляя A.3.60) и A.3.61) в A.3.62) и приравнивая коэффи-
коэффициенты при рТр", получаем систему уравнений в частных произ-
производных для этих коэффициентов, выраженных через потенциал V
и его первые производные. Линейные по р члены приводят к неза-
независимым уравнениям
-*L-=o, -2L=o, -dL + -^-=o, A.3.63)
dq d? d7 dq
e^L+/_^L=0. A.3.64)
Для остальных членов:
да ,, db _ ,, db , дс
д<7г dq\ dq*
дс { да п A-3.65)
qx q2
A.3.66)
дУ с dV -0
b
dqz dq2
Так как уравнения A.3.63) и A.3.64) независимы от A.3.65) и
A.3.66), то первые можно решить отдельно, что приводит к линей-
линейному по р инварианту:
который существует для аксиально симметричного потенциала
{i l). A.3.67)
56 Глава 1
Это не что иное, как сохраняющийся момент импульса, с которым
мы познакомились в задаче о центральных силах. Поищем решения,
не связанные с этой симметрией. Положив е = / = 0, получим
из A.3.65) и A.3.66):
dq\ dqj ) dqxda2
, /_дс__ 2 да \ дУ B дЬ _ дс \ дУ =Q
\ &?i dq2 I dq-t \ d<?i dq2 / dqz
A.3.68)
где a, b и с определяются из дифференциальных уравнений A.3.65).
Уиттекер показал, что уравнение A.3.68) имеет характеристики
вида
аа а* — т
где х и у связаны с ^ и ^ простым преобразованием координат,
а а и у — постоянные интегрирования. Если выбрать за новые пе-
переменные параметры этих конфокальных эллипсов и гипербол
х = ~ • у = -j- К«2-т2) (y2- P2)]1 \
то дифференциальное уравнение для V, A.3.68), будет иметь ре-
решение
V= ^W-^P) , A.3.69)
где г|) и ф — произвольные функции.
Этот интересный результат, однако, не привел пока к новым ре-
решениям физических задач. Тем не менее в последнее время проис-
происходит возрождение интереса к конструированию интегрируемых
гамильтонианов1). Холл [174] применил такой метод к движению
частицы в статических электрическом и магнитном полях, явно
введя в задачу векторный потенциал. При этом он обнаружил, что
решение Уиттекера не является полным, так как в нем не учиты-
учитываются ограничения, связанные с сохранением энергии 2). Им были
рассмотрены также и другие классы инвариантов, не квадратичных
х) Наибольшее влияние на это оказала работа [456] (стимулированная
в свою очередь знаменитой проблемой Ферми—Паста—Улама [127]), в ко-
которой был предложен мощный метод обратной задачи рассеяния, позволяю-
позволяющий конструировать целые семейства интегрируемых гамильтонианов. Сов-
Современное состояние вопроса см., например, в книге [457].— Прим. ред.
2) Речь идет о том, что из-за сохранения энергии изменения р1 и р2 в
A.3.61) не являются независимыми. Поэтому условия интегрируемости
Уиттекера A.3.63) — A.3.66) достаточны, но не необходимы (см. также
1458]).— Прим. ред.
Общий обзор и основные представления 57
по импульсам. Целью этих исследований было найти самосогласо-
самосогласованное решение для токов в плазме, обеспечивающих ее удержа-
удержание. Однако вследствие чувствительности интегрируемости к не-
небольшим изменениям потенциала, о чем свидетельствует сравнение
потенциала Тоды с его приближением в форме потенциала Хенона
и Хейлеса, кажется маловероятным, что для реальных потенциа-
потенциалов таким путем удастся достичь полной интегрируемости движе-
движения. В связи с этим представляет интерес вопрос: насколько силь-
сильным может быть возмущение интегрируемой системы, чтобы
большая часть траекторий осталась регулярной? Этот вопрос под-
подробно рассмотрен в гл. 2 и 4.
Другой подход развивается Хольтом [198]. Он рассмотрел га-
гамильтониан
H = H0 + eV A.3.70)
и потребовал, чтобы потенциал V был выбран так, чтобы все члены
ряда теории возмущений со степенью е, выше заданной, были бы
тождественно равны нулю. При помощи такой процедуры ему уда-
удалось построить инвариант A.3.59) для гамильтониана Тоды. Он
показал также, что этот инвариант можно получить и методом
Уиттекера, если включить кубические по р члены. Процедура
остается при этом прежней, как описывалось для квадратичных
по р инвариантов, но становится гораздо более сложной. В общем
случае такой метод не способен определить, существует ли инва-
инвариант для гамильтониана вида A.3.70), поскольку невозможно
рассмотреть все типы инвариантов. С другой стороны, если сущест-
существует инвариант невысокой степени по р (как, например, р3 для це-
цепочки Тоды), то его можно найти и, таким образом, доказать ин-
интегрируемость исходного гамильтониана. Однако для систем с бо-
более чем двумя степенями свободы подобная техника не проходит
даже для ограниченного класса инвариантов.
Недавно был предложен еще один метод проверки динамиче-
динамической системы на интегрируемость, использующий так называемое
свойство Пенлеве. Последнее означает, что все подвижные особен-
особенности решения в плоскости комплексного времени являются только
простыми полюсами. Подвижными называются особенности, за-
зависящие от начальных условий. Абловиц и др. [4] показали, что
существует тесная связь между уравнениями в частных производ-
производных, имеющими солитонные (интегрируемые г) решения, и соот-
соответствующими им обыкновенными дифференциальными уравне-
уравнениями, обладающими свойством Пенлеве. Сегур [366] продолжил
эти исследования и показал, что модель Лоренца для диссипативной
системы (см. § 1.5), обладающая в общем случае хаотическим по-
*) Существования солитонов, вообще говоря, недостаточно для интегри-
интегрируемости (см., например, [459]).— Прим. ред.
58 Глава 1
ведением, оказывается интегрируемой1) как раз для тех значений
параметров, при которых уравнения обладают свойством Пенлеве.
Ряд хорошо известных примеров гамильтоновых систем был рас-
рассмотрен Баунтисом и др. [37]. Полученные результаты опять-таки
подтверждают точное соответствие между интегрируемостью и
свойством Пенлеве. Хотя это и не доказано строго, однако, по край-
крайней мере для систем рассмотренного класса (две степени свободы
и квадратичный по импульсам гамильтониан), накопилось уже до-
достаточно много данных в пользу такого соответствия 2). В принципе
этот метод применим и к системам более высокой размерности, хотя
для них это соответствие еще не проверено.
Один из методов нахождения специальных интегрируемых га-
гамильтонианов состоит в выборе гамильтониана определенного
вида, зависящего от некоторых произвольных параметров, и под-
подборе таких значений этих параметров, при которых имеет место
свойство Пенлеве. Например, для обобщенного гамильтониана
Хенона—Хейлеса A.3.58)
Н (
из этого условия удается определить параметры \х, А и В [37 J.
Такая же задача была решена Холлом [174] с помощью метода
Уиттекера (с инвариантами до 4-го порядка) в применении к обоб-
обобщенному гамильтониану Хенона—Хейлеса. Оба подхода дают сле-
следующие условия интегрируемости:
а) ц=1, А = В,
б) [i = 6, А и В любые,
в) ц, = 16, В = Ш,
которые были проверены прямым вычислением. Неизвестно, од-
однако, существует ли какая-либо фундаментальная связь между
методами Пенлеве и Уиттекера.
Как известно, системы с одной степенью свободы всегда интег-
интегрируемы, а системы с двумя степенями свободы — как исключе-
исключение. Что же произойдет при дальнейшем увеличении числа степе-
степеней свободы? Как уже отмечалось выше, даже нахождение отдель-
отдельных интегрируемых потенциалов становится в этом случае очень
трудным, чтобы не сказать невозможным. Однако, как показано
в § 6.5, область фазового пространства, занятого регулярными тра-
х) Под интегрируемостью диссипативной системы здесь понимается, по-
видимому, существование простого аттрактора — устойчивого фокуса или
предельного цикла.— Прим. ред.
2) См., однако, работу [460], где показано, что для сохранения соответст-
соответствия с интегрируемостью свойство Пенлеве необходимо модифицировать.
Дальнейшие исследования этого вопроса см. также в работе [461].— Прим.
ред.
Общий обзор и основные представления 59
екториями, может как возрастать1), так и уменьшаться при увели-
увеличении числа степеней свободы. Примечательно, что при переходе
к системам, описываемым дифференциальными уравнениями в ча-
частных производных, которые имеют в некотором смысле бесконеч-
бесконечное число степеней свободы, снова обнаруживаются большие
классы интегрируемых систем. При этом, как обсуждалось выше,
уравнения в частных производных, имеющие солитонные (интег-
(интегрируемые) решения, можно свести к обыкновенным дифференци-
дифференциальным уравнениям, обладающим свойством Пенлеве. Для даль-
дальнейшего обсуждения методов решения и соотношения между диф-
дифференциальными уравнениями в частных и обыкновенных произ-
производных мы отсылаем читателя к специальной литературе [249, 366].
*§ 1.4. Системы, близкие к интегрируемым
Обратимся теперь к качественному описанию типичного случая
таких гамильтоновых систем, которые можно рассматривать как
возмущения интегрируемых систем. Мы будем называть такие си-
системы близкими к интегрируемым. Рассмотрим сначала простой
случай автономного гамильтониана с двумя степенями свободы,
или, что эквивалентно, неавтономного (зависящего от времени)
гамильтониана с одной степенью свободы. Как мы видели в п. 1.26,
неавтономные системы можно свести к автономным путем увеличе-
увеличения числа степеней свободы на единицу. Отличительной чертой
систем, близких к интегрируемым, является присутствие причуд-
причудливо перемешанных друг с другом областей как регулярного, так
и стохастического движения. При этом стохастические области от-
отделены друг от друга областями с регулярными траекториями.
Стохастические траектории естественно возникают в результате
движения, задаваемого детерминированными уравнениями Гамиль-
Гамильтона, которые не содержат никаких специальных «стохастических»
сил. Мы проиллюстрируем это на двух примерах, широко обсуж-
обсуждавшихся в литературе: модель Хенона—Хейлеса и ускорение
Ферми. Для автономных систем с более чем двумя степенями сво-
свободы области стохастичности уже не разделяются регулярными
траекториями, а образуют стохастическую «паутину», что приво-
приводит к так называемой диффузии Арнольда, которая качественно
описана в конце этого параграфа.
*1.4а. Две степени свободы
Рассмотрим автономную систему с двумя степенями свободы, близ-
близкую к интегрируемой, т. е. систему с гамильтонианом вида
H(ju уа, еь е2) = я0(А, /2) + еЯ1(/1, у2> е1( а,), A.4.1)
где У, 9 — переменные действие — угол невозмущенного движе-
Это утверждение спорно, см. примечание на с. 409.— Прим. ред.
60 Глава 1
ния, а е — малый параметр возмущения. Функция Но зависит
только от переменных действия, а зависимость Нх от углов в яв-
является периодической.
Типичный характер движения в таких системах сейчас вполне
понятен. Траектории лежат на трехмерной поверхности Я = const
в четырехмерном фазовом пространстве. При этом, согласно теории
КАМ. (гл. 3), регулярные траектории заполняют конечную долю
фазового пространства. Остальные траектории характеризуются
стохастическим, или хаотическим, поведением. Стохастические
и регулярные траектории очень сложно переплетены друг с другом,
причем стохастическая траектория подходит сколь угодно близко
к каждой точке фазового пространствах), подобно тому как любое
иррациональное число может быть сколь угодно точно аппроксими-
аппроксимировано рациональными числами.
Регулярные траектории. Из-за того что зависимость регулярных
траекторий от начальных условий оказывается разрывной, их
присутствие еще не означает наличия в системе изолирующего (гло-
(глобального) интеграла или определенной симметрии. Однако там,
где такие траектории существуют, им соответствуют точные интег-
интегралы движения. Для регулярных траекторий угловые переменные
зависят от времени либо квазипериодически (типичный случай),
либо периодически. В первом случае частоты движения несоизме-
несоизмеримы, и траектория плотно покрывает поверхность инвариантного
тора, заданного сохраняющимися значениями переменных дейст-
действия. В последнем случае траектория замыкается через целое число
оборотов вокруг тора (более полное представление об инвариантных
торах дано в гл. 3). Наиболее удобными методами исследования
регулярных траекторий являются теория возмущений и метод се-
сечения Пуанкаре, рассмотренный в § 1.2.
Различные типы регулярных траекторий и их пересечения с по-
поверхностью ?я @х = const) для системы с двумя степенями свободы
представлены на рис. 1.10. Случай а соответствует типичной тра-
траектории, покрывающей поверхность тора. Движение вокруг глав-
главной оси тора периодично по 6Х с периодом 2я. При этом последо-
последовательные пересечения поверхности ?я при 82= 021, 022, 9гз ¦ • ¦
ложатся на замкнутую инвариантную кривую и плотно покрывают
ее за большой промежуток времени. Случай б соответствует резо-
резонансу
k«>1(J) + lu2{J) = 0, A.4.2)
где а>г = 01? со2 = 02, k и / — целые числа. Резонансная траекто-
траектория замкнута. При k = 5, 1 = 2 она пересекает поверхность ?я
в пяти точках, которые называются неподвижными, или периоди-
*) В общем случае это справедливо лишь в пределах одной хаотической
компоненты движения, которая для системы вида A.4.1) может охватывать
максимум всю энергетическую поверхность.— Прим. ред.
Общий обзор и основные представления
61
2; 7 .
,Г,6
о
5»
г
13
•
8»
• 10
•15
7«
• 3
12
•
2; 17
11
•
6»
9»
.1
•
•
4
:i6
14
Рис. 1.10. Поверхность сечения ?„ (в1 = const) для автономной системы
с двумя степенями свободы.
а — инвариантная кривая (крестики — последовательные пересечения траектории с по-
поверхностью 2„); б — периодическая траектория в центре первичного резонанса k = 5,
1 = 2 (показаны первые семь пересечений); в — инвариантные кривые вокруг периоди-
периодических точек (fe = 5, I = 2); г — периодическая траектория вторичного резонанса (пе-
(период 3) внутри первичного резонанса (б) (показаны первые 17 пересечений); д — стоха-
стохастическая область, ограниченная инвариантными кривыми и охватывающая несколько
первичных резоиансов; е — стохастический слой в окрестности сепаратрисы первичного
резонанса к = 5, / = 2.
62 Глава 1
ческими, точками движения. Поскольку при таком движении тра-
траектория невозмущенного гамильтониана замкнута и периодична,
то мы называем такой резонанс первичным. Резонанс б — специ-
специальный случай инвариантной кривой, когда число вращения klt
рационально. Резонансы и их взаимодействие играют важную роль
в возникновении стохастического движения в системах, близких
к интегрируемым.
Случай в соответствует типичной траектории в окрестности пер-
первичного резонанса (рис. 1.10,6). Пересечения траектории с поверх-
поверхностью Хд образуют пять гладких замкнутых кривых {первичных
островов), окружающих неподвижные точки (случай б). Наконец,
случай г иллюстрирует еще более сложное движение: замкнутую
периодическую траекторию, которая за 15 оборотов по вг три раза
обходит первичный резонанс k — 5; / = 2; Этот случай представ-
представляет пример вторичного резонанса между колебаниями на первич-
первичном резонансе и невозмущенным движением. Вторичные резонансы
возникают под действием возмущения Я3 и в свою очередь окру-
окружены резонансами еще более высокого порядка.
Теперь ясно, насколько сложна структура регулярных траекто-
траекторий. Первичные резонансы приводят к возникновению вторичных
резонансов и так до бесконечности. Расчет регулярных траекторий
(инвариантных кривых и резонансов) рассматривается в гл. 2 и 3.
Области стохастичности. Известно, что стохастические траекто-
траектории занимают конечную область энергетической поверхности в фа-
фазовом пространстве, а их последовательные пересечения заполняют
конечную площадь поверхности сечения. Пример двух стохасти-
стохастических траекторий приведен на рис. 1.10. В случае д траектория
заполняет кольцеобразный стохастический слой, заключенный ме-
между двумя инвариантными кривыми, подобными тем, что изобра-
изображены в случае а. В этой области существуют также и регулярные
траектории, но соответствующие им островки устойчивости, окру-
окружающие неподвижные точки (см. § 3.3), либо обходятся стохасти-
стохастической траекторией, либо их размер слишком мал и их просто не
удается разглядеть. В случае е показан стохастический слой вблизи
островков случая в, заполненный одной стохастической траекторией.
Стохастическое движение всегда возникает возле сепаратрис,
которые разделяют инвариантные кривые различной топологии.
Действительно, вблизи сепаратрисы частота колебаний со стремится
к. нулю, см. A.3.15). Поэтому условие резонанса с частотой невоз-
невозмущенных колебаний юп:
ka> — co0 = 0 A.4.3)
приводит к тому, что при приближении к сепаратрисе расстояние
по переменной действия между соседними резонансами (k и k + 1)
также стремится к нулю. Область стохастичности вблизи сепарат-
Общий обзор и основные представления 63
рисы будем называть стохастическим слоем х). В системах с двумя
степенями свободы при малом возмущении е эти слои оказываются
очень тонкими и отделены друг от друга инвариантными кривыми,
ввиду чего переход траектории из одного слоя в другой невозмо-
невозможен. С увеличением е инвариантные кривые, разделяющие сосед-
соседние резонансы и их стохастические слои, сильно искажаются и
в конце концов разрушаются. В результате происходит слияние
стохастических слоев и возникает глобальная, или сильная, стоха-
стичность. Условие такого перехода рассмотрено в гл. 4, а харак-
характер хаотического движения — в гл. 5.
Некоторое указание на причину возникновения стохастичности
вблизи сепаратрисы можно получить из картины перекрытия ре-
зонансов, которое приводит к чрезвычайно запутанному движению,
в особенности с учетом резонансов высоких порядков. К такому
же заключению можно прийти и с другой точки зрения, рассмотрев
траекторию самой сепаратрисы. Как из теоретического анализа,
так и из численных экспериментов следует, что с учетом возмуще-
возмущения сепаратриса не является уже такой гладкой кривой, как в ин-
интегрируемой системе (рис. 1.4), а напротив, также оказывается
чрезвычайно сложной. Движение вблизи сепаратрисы подробно
обсуждается в п. 3.26. При достаточно малом возмущении инва-
инвариантные поверхности ограничивают область стохастического дви-
движения (см. 3.2а), однако с увеличением возмущения резонансы бо-
более высоких порядков отодвигают инвариантные поверхности от
сепаратрисы и тем самым расширяют область сложного движения.
Мы видели, что вблизи резонанса фазовые траектории сильно
возмущены. Тем не менее внутри резонанса существуют замкну-
замкнутые периодические траектории (неподвижные точки на рис. 1.10, б
и г). Устойчивость линеаризованного вблизи них движения также
связана со стохастичностью. Линейная устойчивость решений
в окрестности периодической траектории приводит к регулярному
движению, которое может быть разрушено слабым нелинейным воз-
возмущением только за большой промежуток времени. Неустойчивые
решения приводят к экспоненциальной расходимости траекторий,
скорость которой можно принять за меру стохастичности (см.
гл. 5). Можно ожидать, что в той области фазового пространства,
где все или почти все периодические решения линейно неустойчивы,
движение будет хаотическим.
Модель Хенона—Хейлеса. Рассмотрим в качестве иллюстрации хо-
хорошо известный пример движения в двумерном потенциале
U(х, y)=-j
х) В оригинале — resonance layer (резонансный слой). В переводе ис-
используется более распространенный в отечественной и зарубежной литера-
литературе термин стохастический слой.— Прим. перев.
64
Глава 1
показанном на рис. 1.11. Впервые эта модель исследовалась чис-
численно Хеноном и Хейлесом [188] в качестве простого примера не-
нелинейной системы с несколькими (двумя) степенями свободы.
В дальнейшем эта система детально изучалась многими авторами.
К сожалению, в этом примере встречаются некоторые трудности,
Рис. 1.11. Замкнутые эквипотенциальные кривые (U =
= const < 1/6) для модели Хенона—Хейлеса A.4.4) (по
данным работы [291]).
которые не являются типичными для нелинейных систем и требуют
особого подхода. Тем не менее этот численный пример хорошо иллю-
иллюстрирует интересующие нас вопросы. Ход потенциала в декарто-
декартовых координатах х, у показан на рис. 1.11. Гамильтониан частицы
в таком потенциале можно записать в виде Н = Но -(-еЯ1= Е,
где
A.4.5а)
-у3.
A.4.56)
Для удобства масса частицы принята равной единице, а малый
Общий обзор и основные представления 65
параметр е определяется выбором энергии: е — Е12. Если Е
меньше граничной потенциальной энергии U = 1/6, то частица
будет удерживаться внутри потенциальной ямы. Существование
инвариантных кривых в этом случае можно определить по картине
на поверхности сечения (у, ру). В пределе малых колебаний гамиль-
гамильтониан можно записать в переменных действие — угол в виде
(см. п. 1.2в):
A.4.6)
В данном случае частоты колебаний аг и ю2 равны единице. Если
учесть теперь слабое возмущение A.4.56), то полный гамильтониан
примет вид
Я = оIУ1 + со2/2 + еЯ1(/1) /2, еъ 02). A.4.7)
При достаточно малой энергии траектории на поверхности сечения
оказываются замкнутыми кривыми почти для всех начальных ус-
условий, за исключением очень близких к резонансным. Эти кривые
можно найти либо численно, решая уравнения движения, либо
путем вычисления интеграла движения по теории возмущений с уче-
учетом членов достаточно высокого порядка по е (см. гл. 2). Если в раз-
разложении взять мало членов, то замкнутые кривые еще будут по-
получены, но они не будут похожи на численные. С другой стороны,
если в разложении взять слишком много членов, то ответ будет
отличаться от правильного решения, так как ряд асимптотический.
Мак-Намара и Уайтмен [291] вычислили У2 с точностью до второго
и третьего порядков по е для начальной энергии Е = 0,01 и различ-
различных начальных условий. Их результаты показаны на рис. 1.12, а
и б. Видно, что в данном примере члены высокого порядка оказы-
оказываются очень существенными и даже изменяют характер движения.
Так, наблюдаемые в численном эксперименте (рис. 1.12, в) траек-
траектории, замкнутые вокруг точек А и В, появляются лишь в четвер-
четвертом порядке теории возмущений. Необходимость использовать
высокие порядки теории возмущений возникает далеко не во всех
системах, близких к интегрируемым. В данном случае это является
следствием двух особенностей модели Хенона—Хейлеса: 1) невоз-
невозмущенные колебания линейны и 2) частоты этих колебаний совпа-
совпадают. Сравним численные результаты Хенона и Хейлеса с теорией
возмущений Густавсона [171] восьмого порядка (рис. 1.13). Для
энергий Е = 0,042 A/24) и Е = 0,083 A/12) возникает впечатле-
впечатление, что инвариантные кривые существуют везде, а ряд теории
возмущений сходится к правильному пределу. Однако ни то ни
другое, строго говоря, не является верным, поскольку наряду
с инвариантными кривыми имеются очень тонкие стохастические
слои, распределенные по всей поверхности сечения и связанные
с резонансами между двумя степенями свободы. Толщина этих
слоев экспоненциально мала по параметру Е~1. Поэтому для ма-
66
Глава 1
-0,1?
+0,15
лых значений Е слои занимают ничтожную часть полной площади
поверхности сечения и неразличимы на картинках, получаемых
в численных экспериментах.
Для более высокой на-
начальной энергии Е = 0,125
наблюдается три типа траек-
траекторий: простая инвариантная
кривая как и при низкой
энергии; многопетлевая тра-
траектория, например представ-
представляющая цепочку из пяти
маленьких островов, подобная
изображенной на рис. 1.10, в,
для которой пересечения
«перескакивают» от одной
петли к другой, и, по-види-
по-видимому, эргодическая траекто-
траектория (аналогичная изображен-
изображенной на рис. 1.10, е) с пере-
пересечениями в случайных точ-
точках. Для последней траек-
траектории переменные действия
не только не являются инте-
интегралами движения, но и не
могут быть получены из раз-
разложений теории возмущения.
С другой стороны, даже для
граничной энергии (Е = 1/6)
интегралы сохраняются в ма-
малых изолированных областях
фазовой плоскости. Присут-
Присутствие таких островов устой-
устойчивости означает существо-
существование интеграла движения
вблизи первичного резонанса,
связанного с частотами не-
невозмущенных колебаний по х
и у. Методы вычисления таких
интегралов, а также разме-
Рис. 1.12. Инвариантные кривые
на поверхности сечения модели
Хенона—Хейлеса; Е = 0,01 (по
данным работы [291 ]).
а — во втором порядке (по е); б —
в третьем порядке; в — численное мо-
моделирование.
Общий обзор и основные представления
67
¦¦'•'/:.•
>~т
Е = Г8
, . у
{ ¦ ; i'i ¦ у
.--'' E= 1/24
0
¦'ч. „\4>-s*'¦' '• • • --V"''-¦'? =1/12
-¦?¦'¦ ..¦'•¦•
? = I '
. ¦¦¦' л
4^,
1
У
1,6
Рис. 1.13. Сравнение аналитической (слева) и найденной численно (справа)
структуры поверхности сечения модели Хенона—Хейлеса (по данным ра-
работы [17Ц).
68 Глава 1
ров островков устойчивости приведены в § 2.4 вместе с подроб-
подробными примерами.
Хотя существует несомненное соответствие между расчетами
устойчивых областей по теории возмущений и результатами числен-
численного моделирования, это еще не означает, что устойчивость сохра-
сохраняется в любой момент времени, как это предсказывает теория воз-
возмущений, поскольку слабые резонансы высокого порядка могут
разрушить эту устойчивость. Однако на помощь приходит теория
КАЛ1, которая гарантирует, что, во всяком случае, для достаточно
малого возмущения инвариантные кривые существуют и близки
к невозмущенным. Это дает основание предположить, что те кри-
кривые, которые выглядят гладкими и устойчивыми, наверное, близки
к хорошим инвариантным кривым, хотя, возможно, и имеют ка-
какую-то невидимую структуру. Опираясь на это предположение,
мы развиваем эвристический критерий разрушения интегралов
движения, связанный с критерием перекрытия соседних резонансов,
который был предложен Чириковым [67]. Сравнивая эти критерии
с численными экспериментами, можно получить достаточно надеж-
надежные количественные оценки разрушения интегралов движения. Эти
вычисления — основная тема гл. 4.
Ускорение Ферми. Как уже было отмечено в § 1.2, существует тес-
тесная связь между гамильтоновыми системами с двумя степенями
свободы и сохраняющими площадь отображениями двумерной по-
поверхности на себя. Преобразование, задающее последовательные
пересечения траектории с некоторой поверхностью, является именно
таким отображением. И обратно, динамическую систему, заданную
отображением, можно описать и гамильтонианом, который полу-
получается разложением отображения в ряд Фурье х).
Рассмотрим пример динамической системы, которую можно
описать сохраняющим площадь отображением; он иллюстрирует
характер стохастических траекторий в системах с двумя степенями
свободы. Отображение описывает движение шарика между непод-
неподвижной и колеблющейся стенками. Этот пример Улама [415] моде-
моделирует механизм ускорения космических лучей, предложенный
Ферми [126].Обозначим через ип скорость шарика (в единицах удвоен-
удвоенной амплитуды скорости стенки), перед его п-и столкновением с ко-
колеблющейся стенкой, а через г|)„ — фазу колебаний стенки в мо-
момент столкновения. Тогда отображение имеет вид
, A.4.8а)
v) Имеется ввиду фурье-разложение по времени, см. п. 3.1в.— Прим.
ред.
Общий обзор и основные представления
69
где М — некоторое приведенное расстояние между стенками, а
скорость шарика ип берется по абсолютной величине.
Динамика такого отображения может быть прослежена на мно-
многие тысячи итераций, что позволяет получить детальное представ-
Локолизобанная
стохасгпичносгпь
25-
20-
15-
U
10-
5-
0 -
¦-i::=v ;::: '-:".:;: ¦ ¦¦:::'::::1:l'i?::;=Yil:^::==^^
::j:i:::::::i=::; ;:;i:;-"= :!-:::::=:!!:гШ;!!:Ш! SSIir ::::::::':::::=
Глобальная
стохасгпичносгпь
с . остробками
устойчивости
-
Сплошная
стохастичнасть
-
+1Г
Рис. 1.14. Поверхность сечения для задачи Ферми (по данным работы [274]).
Показано заполнение фазовой плоскости одной траекторией за 623 000 итераций Пунк-
Пунктирные кривые рассчитаны по резонансно!! теории возмущений.
ление о поведении системы и, в частности, исследовать ее статисти-
статистические свойства. На рис. 1.14 изображена плоскость (и, гр) после
623 000 итераций для М = 100 и начальной скорости и0 яг; 1.
Плоскость разделена на 200 у 100 ячеек х), причем в неотмечен-
неотмеченные ячейки траектория не попадала. Видно, что на фазовой пло-
плоскости имеются три области: 1) область больших значений и, в ко-
которой преобладают инвариантные кривые, а узкие и ограниченные
стохастические слои расположены только вблизи резонансных се-
1) Для и ^25, см. п. 3.46.— Прим. ред.
70
Глава 1
паратрис; 2) единая стохастическая область при промежуточных
значениях и, в которой еще остаются островки устойчивости во-
вокруг периодических траекторий, и 3) область стохастичности для
малых и, в которой все первичные периодические траектории, по-
видимому, неустойчивы. В областях 2 и 3 имеет место сильная, или
глобальная, стохастичность движения. В последней из них, не-
несмотря на существование некото-
некоторых корреляций между последо-
последовательными значениями фазы т}\
можно использовать приближение
хаотических фаз и диффузионное
уравнение для скорости и. Более
подробно этот вопрос будет рас-
рассмотрен в гл. 5.
Эргодические системы. Подобно
полностью интегрируемым систе-
системам, эргодические системы, в ко-
которых отсутствуют регулярные
траектории, оказываются в неко-
некоторых отношениях более простыми,
5
Рис. 1.15. Два примера систем, обладающих эргодичностью и перемешива-
перемешиванием (по данным работы [14]).
а — разверчка тора, по которому движутся твердые диски, V. = ?>\ б — преобразование
пекаря; перемешивание происходит в результате раскатыьання, разрезания и склады-
складывания.
чем системы, близкие к интегрируемым. Хотя в эргодических си-
системах и нельзя пользоваться понятием отдельных траекторий,
но зато можно установить ряд общих статистических свойств. При-
Примером такой системы может служить движение бильярдного шара,
сталкивающегося с неподвижным диском (рис. 1.15, а). Траекто-
Траектория шара изображена сплошной линией со стрелками, указываю-
указывающими направление движения. Отражения от диска происходят по
обычному закону: угол падения а равен углу отражения C. Движе-
Движение считается пространственно периодическим по обоим направле-
направлениям. При этом можно считать, что траектория, проходящая че-
через одну сторону ячейки периодичности, возвращается с противо-
Общий обзор и основные представления 71
положной стороны под тем же углом. Синай [377] показал, что эта
система обладает и эргодичностью и перемешиванием. Она пред-
представляет интерес и для статистической механики [133].
Другим хрошо известным примером эргодической системы яв-
является «преобразование пекаря», которое отображает единичный
квадрат на себя:
У о' 2
О-4-9)
Для наглядности используя знаменитого арнольдовского кота [14]-
находим, что это преобразование похоже, см. рис. 1.15, б, на дейст,
вне пекаря, раскатывающего, разрезающего и складывающего свое
тесто. Движение этой системы является неустойчивым и обладает
свойством перемешивания.
Таким образом, имеются явные свидетельства в пользу стати-
статистических свойств отображений в областях неустойчивого движе-
движения. Что же касается более сильного предположения о возможно-
возможности использовать приближение хаотических фаз, когда движение
системы напоминает случайное блуждание в импульсном прост-
пространстве, то это зависит также от наличия существенно различных
временных масштабов для перемешивания по фазе и по импульсу.
Для многих динамических систем перемешивание по фазе происхо-
происходит гораздо быстрее, чем по импульсу, что и позволяет ввести раз-
разные масштабы времени.
* 1.46. Более чем две степени свободы
Все вышеописанные эффекты для автономных систем с двумя сте-
степенями свободы имеют место и для систем с более чем двумя степенями
свободы. В типичном случае стохастические и регулярные траекто-
траектории тесно сосуществуют в 2Л^-мерном фазовом пространстве и на
BN—2)-мерной поверхности сечения, а стохастические слои рас-
расположены вблизи резонансов. Толщина слоев растет с увеличением
возмущения, что приводит в конце концов к перекрытию первич-
первичных резонансов, движению поперек слоев и сильной стохаспшчно-
сти. Однако при достаточно малом возмущении первичные резо-
нансы не перекрываются. В этом случае возникает новое физиче-
физическое явление — движение вдоль слоев, или так называемая диф-
диффузия Арнольда.
Диффузия Арнольда. Для двух степеней свободы двумерные инва-
инвариантные поверхности (торы) разделяют трехмерный энергетиче-
энергетический «объем» в фазовом пространстве на изолированные слои, по-
подобно тому как линии на плоскости выделяют изолированные об-
72
Глава I
ласти (рис. 1.16, а). Но уже для трех степеней свободы трехмерные
торы не разделяют пятимерный энергетический «объем», как линии
не могут изолировать трехмерную область (рис. 1.16,6). Таким
образом, при iV>2 инвариантные Af-мерные торы не разделяют
BjV—1)-мерную энергетическую поверхность на отдельные обла-
области. Поэтому при iV>2 в типичном случае все стохастические слои
на энергетической поверхности связаны в единую сложную сеть —
паутину Арнольда. Эта паутина пронизывает все фазовое простран-
пространство, подходя сколь угодно близко к любой его точке. Для началь-
ИиВариантные
A
кри&ые
V
Рис. 1.16. Топология энергетической поверхности (поданным работы [273])-
а — двумерная энергетическая поверхность (плоскость) разделяется инвариантными кри-
кривыми на изолированные области; б — трехмерная энергетическая «поверхность» (объем)
не разделяется одномерными кривыми.
ных условий на паутине стохастическая траектория пересекает
в конце концов любую область энергетической поверхности, даже
когда возмущение е -»- 0. Это и есть диффузия Арнольда.
Слияние стохастических траекторий в единую сеть было дока-
доказано [12] для специальной нелинейной системы. В общем случае
такого доказательства до сих пор нет, но известно несколько чис-
численных примеров диффузии Арнольда. С практической точки зре-
зрения возникают два основных вопроса: 1) какова относительная
мера стохастической компоненты в интересующей нас области фа-
фазового пространства и 2) какова скорость диффузии Арнольда для
тех или иных начальных условий. Оценку размеров стохастиче-
стохастической компоненты можно получить из критерия перекрытия резо-
нансов (см. гл. 6).
Так же как и в системах с двумя степенями свободы, перекры-
перекрытие резонансов приводит к образованию стохастического слоя ко-
конечной ширины и вызывает движение поперек слоя. Новой особен-
особенностью диффузии Арнольда является движение вдоль стохастиче-
стохастического слоя, которое возникает при взаимодействии по крайней
Общий обзор и основные представления 73
мере трех резонансов. Схема такого движения изображена на
рис. 1.17. В плоскости (Jv 9Х) показана проекция резонанса и его
стохастического слоя. Ось переменной действия J2 перпендику-
перпендикулярна этой плоскости. Для консервативной системы с двумя сте-
степенями свободы сохранение энергии и изменение J х только в пре-
пределах стохастического слоя ограничивают изменение J 2. Однако
при наличии еще одной степени свободы или в случае зависимости
гамильтониана от времени последнее ограничение отпадает, и ста-
становится возможным движение вдоль стохастического слоя по /,.
Стохастический
слой
Быстрая
Эиффуэия
Рис. 1.17. Быстрая диффузия идет поперек стохастического слоя, а медлен"
ная диффузия Арнольда—вдоль слоя.
При взаимодействии трех резонансов скорость диффузии Ар-
Арнольда была найдена Чириковым [70] и Теннисоном и др. [40611 ).
Это рассматривается в гл. 6. В общем случае взаимодействия мно-
многих резонансов строгая оценка сверху была получена Нехороше-
вым [314]. Однако, вообще говоря, она значительно завышает ско-
скорость диффузии. Обзор численных экспериментов по диффузии Ар-
Арнольда в области взаимодействия многих резонансов [72 ] дан
в гл. 6.
§ 1.5. Диссипативные системы
В отличие от гамильтоновых систем с их фундаментальным законом
сохранения фазового объема для диссипативных систем харак-
характерно его постоянное уменьшение со временем. Это приводит к
тому, что все траектории движения притягиваются к некоторой
поверхности (аттрактору), размерность которой меньше, чем у ис-
исходного фазового пространства. При этом уравнения движения
уже не являются каноническими, но их можно записать, вообще
х) Первые оценки для скорости диффузии Арнольда приведены в [146].-
Прим. ред.
74 Глава 1
говоря, в виде системы дифференциальных уравнений первого по-
порядка:
J^=V(x), A.5.1)
где для iV-мерного фазового пространства векторы х и V имеют
N компонент. Траектория х (/) называется в этом случае yV-мерным
потоком. В случае регулярного потока движение на аттракторе
является простым. Это может быть, например, неподвижная точка
(фокус) или периодическая траектория (предельный цикл). Для
двумерных потоков существуют фактически только эти две возмож-
возможности.
Для трехмерных потоков, помимо фокусов и предельных цик-
циклов, возможны и квазипериодические траектории с двумя основ-
основными частотами. По аналогии можно было бы ожидать, что это и есть
единственно возможные аттракторы. Однако это не так. Было по-
показано, что в трехмерных (и большей размерности) диссипативных
системах существуют аттракторы с очень сложной геометрической
структурой. В частности, они имеют дробную размерность (см.
п. 7.1в) и называются обычно странными аттракторами. Движе-
Движение на странных аттракторах является хаотическим г).
1.5а. Странные аттракторы
Грубо говоря, странный аттрактор—это такой аттрактор, на кото-
котором близкие траектории расходятся экспоненциально. В качестве
примера представим себе трехмерный поток в виде слоя из беско-
бесконечного числа двумерных листов. Слой растягивается вдоль одного
из направлений и складывается, как показано на рис. 1.18, а. При
этом края слоя (АВ и А'В') гладко соединены между собой. Так как
на краю А'В' имеются два отдельных листа, а на краю А В только
один, то для гладкости их соединения необходимо бесконечное
число листов. В противном случае возникли бы разрывы, ведущие
к необратимости потока. Эскиз окончательной структуры такого
аттрактора представлен на рис. 1.18, б.
Из схемы аттрактора видно, что, несмотря на экспоненциальную
расходимость, траектории ограничены 2). Далее, оказывается, что
1) Термин «хаотический» обычно используется для описания случайного
движения в диссипативных системах, тогда как термин «стохастический»
чаще относится к гамильтоновым системам. Хотя мы и пытались придержи-
придерживаться такого соглашения, не следует думать, что эти два термина соответст-
соответствуют различной «степени случайности»; по существу мы рассматриваем их
как синонимы.
2) Проблема согласования расходимости близких траекторий на аттрак-
аттракторе с его ограниченностью возникает только при минимальной размерности
аттрактора, равной двум (имеется в виду обычная, целая размерность, ср.
п. 7.1в). При большей размерности расходимость в линейном приближении
сменяется перемешиванием траекторий; хаотический аттрактор может иметь
при этом простую форму, например, тора.— Прим. ред.
Общий обзор и основные представления
75
НулеВая
толщина
Рис. 1.18. Схематическое изображение странного аттрактора (по данным
работы [368]).
о —слой из бесконечного числа листов растягивается и складывается; б —вид аттрак-
аттрактора после соединения каждого листа по линии АВ с соседним по линии А'В'.
76 Глава I
структура аттрактора повторяется на все более и более мелких
пространственных масштабах. Такая масштабная инвариантность,
характерная также и для структуры резонансов в гамильтоновых
системах, служит основой анализа динамики как гамильтоновых,
так и диссипативных систем. Подобная многослойная структура,
которую можно описать математически как некоторое канторово
множество, рассматривается в § 7.1.
Уравнения A.5.1), приводящие к возникновению странного
аттрактора, зависят обычно от некоторого параметра (аналогичного
величине возмущения в гамильтоновых системах), изменение кото-
которого меняет характер движения. На примерах модели Хенона—
Хейлеса и ускорения Ферми мы видели, что в гамильтоновых си-
системах при увеличении возмущения траектории из регулярных ста-
становятся стохастическими. Подобно этому, и в диссипативных си-
системах при изменении параметра возможен переход от периодиче-
периодического движения к хаотическому на странном аттракторе. Во мно-
многих случаях такой переход происходит путем последовательного
удвоения периода движения вплоть до некоторого критического
значения параметра, за которым структура аттрактора изменяется
и движение становится хаотическим. Дальнейшее увеличение па-
параметра может привести к обратному процессу или к появлению
простого аттрактора другой симметрии. Еще одна интересная осо-
особенность таких систем заключается в том, что обычно можно найти
поверхность сечения, на которой движение сводится приближенно
к необратимому одномерному отображению. Необратимость озна-
означает здесь многозначность обратного отображения. Такие отобра-
отображения возникают во многих физических задачах и будут подробно
рассмотрены в § 7.2.
Не все из перечисленных свойств легко увидеть из одного при-
примера. Сейчас мы рассмотрим первый пример странного аттрактора—
модель Лоренца [283]. В § 7.4 мы снова вернемся к этому примеру
для того, чтобы изучить физическую систему, из которой он воз-
возникает. В § 7.1 рассмотрены другие примеры, позволяющие шире
взглянуть на различные явления, связанные с хаотическим движе-
движением в диссипативных системах.
1.56. Модель Лоренца
Этот поучительный пример хаотического потока возник из гидро-
гидродинамических уравнений, описывающих конвекцию Рэлея—Бе-
нара. Слой жидкости конечной толщины подогревается снизу та-
таким образом, что между верхней холодной и нижней горячей по-
поверхностями поддерживается постоянная разность температур. Дви-
Движение жидкости описывается уравнением Навье—Стокса. Предпо-
Предполагая поток двумерным, его можно охарактеризовать двумя пере-
переменными: функцией тока г|> и отклонением В распределения темпе-
температуры от стационарного (линейного по вертикали).
Общий обзор и основные представления 77
Уравнения в частных производных для возмущенного потока
можно преобразовать к системе обыкновенных дифференциальных
уравнений. Для этого следует разложить функции г|) и G в двойной
ряд Фурье по х и г с амплитудами, зависящими только от времени t.
Оставив ограниченное число членов, получим движение в конечно-
конечномерном фазовом пространстве. Вывод этих уравнений движения
из уравнения Навье—Стокса приведен в § 7.4.
Лоренц [283 ] исследовал упрощенную модель, в которой было
оставлено только три «наиболее важных» фурье-амплитуды. В этом
приближении уравнения принимают вид
Х=— oX--oY,
Y=~XZ-rX — Y, A.5.2)
где X — амплитуда конвективного движения; Y — разность тем-
температур для течений вверх и вниз; Z — отклонение вертикального
температурного профиля от линейного, а о, г, Ъ — безразмерные
параметры, физический смысл которых обсуждается в § 7.4.
Модель Лоренца интенсивно исследовалась во многих работах
(см. литературу в работе [180]). Значения параметров а и Ъ обычно
фиксированы (ст =10, b = 8/3), и поведение системы исследуется
в зависимости от г. Перечислим некоторые элементарные свойства
модели Лоренца [252, 283, 411].
1. Уравнения инвариантны относительно преобразования:
Х-^ — X, Y-+—Y, Z-+Z.
2. Фазовый объем сокращается с постоянной скоростью (см.
п. 7.1а)
Л = М- 4- -**- + JL- = __ (а + b + 1),
дХ ' dY * dZ K '
которая весьма велика для обычно используемых значений
параметров: о = 10, Ь = 8/3, Л та — 13,7. За единицу вре-
времени объем сокращается в ё~А та 106 раз.
3. При г = 0 и />0 решение ограничено и X, Y, Z -v 0 для
t —*- оо.
С ростом г характер решений меняется следующим образом.
1. Для ()<;/¦<; 1 единственным аттрактором является непод-
неподвижная точка в начале координат. Это соответствует стацио-
стационарной теплопроводности в задаче Рэлея—Бенара.
2. Для г>>1 аттрактор теряет устойчивость и возникают две
новые неподвижные точки
*i.2 = (±[*(r-l)]12, ±[b(r~l)]12, r-1),
78
Глава I
где
которые являются аттракторами для 1
гг = о(о-\-Ь + 3)/(ст—6— 1) = 470/19 да 24,74.
Это соответствует стационарной конвекции в задаче Рэлея—
Бенара. ^
3. Для г>г2 не существует аттракторов типа неподвижных
точек.
4. Для г^>г± — 24,06 возникает странный аттрактор с хаоти-
хаотическим движением. Заметим, что в узкой области
24,06<г< 24,74
"¦'¦- х
Рис. 1.19. Хаотическая траектория на аттракторе Лоренца при г = 28 (по
данным работы [253]).
Плоскость {X, У) соответствует Z = 27.
существуют три аттрактора. Два из них соответствуют ста-
стационарной конвекции, а третий — хаотическому потоку.
При этом в системе имеет место гистерезис: если г растет, то
регулярная конвекция переходит в турбулентность при
г = 24,74; если же г уменьшается, турбулентное движение
переходит в регулярную конвекцию при г = 24,06.
Лоренц исследовал численно случай г = 28. На рис. 1.19 [253]
приведен пример хаотической траектории, выходящей из начала
координат и пересекающей плоскость Z = 27. Вначале траектория
подходит к Хг, а затем раскручивается и притягивается к Хг;
Общий обзор и основные представления
79
после этого она уходит по спирали от Х2 и снова притягивается к
Хг и т. д. Период обращения около Xbi равен 0,62, а радиус спи-
спирали изменяется приблизительно на 6 % за оборот. Число оборо-
LgP
4
-2
0,1
0,2
0,3
0,4
0.5
Рис. 1.20. Спектр мощности Р (со) для X (t) на аттракторе Лоренца при г = 28
(по данным работы [121]).
Непрерывность спектра отражает хаотичность движении.
тов в каждой серии меняется в широких пределах практически не-
непредсказуемо, так как оно сильно зависит от начальных условий.
Хаотическое движение на аттракторе можно изучать при по-
помощи отображения Пуанкаре
плоскости Z = 27. В работе [46 J
доказано, что это отображение
является перемешивающим и эрго- 450
дическим. Спектр мощности X (t) _* ^
приведен на рис. 1.20. Его не-
непрерывность отражает непериоди-
непериодическое, хаотическое движение на
аттракторе.
Заметив, что зависимость Z от
t выглядит хаотической, Лоренц
[283] придумал следующий эффек-
эффективный метод анализа движения.
Он зафиксировал последователь-
последовательные максимумы Zi, Z2, . . . и по-
построил зависимость Zn+X от Zn,
которая приведена на рис. 1.21.
Слева от пика отображение соот-
соответствует последовательным обо-
оборотам вокруг Хг или Х2. Область справа от пика описывает пере-
переходы между Хг и Х2. Это одномерное отображение соответствует
400-
350
300
300
350
400
450 Zn
Рис. 1.21. Одномерное отображе-
отображение на аттракторе Лоренца при
г = 28 (по данным работы [283]).
SO Глава I
приближению, при котором бесконечно много листов аттрактора
соединяются в один. Оно оказывается весьма хорошим из-за боль-
большой скорости сокращения фазового объема.
Это одномерное отображение позволяет непосредственно понять
хаотический характер движения на аттракторе Лоренца. Дейст-
Действительно, производная зависимости Zn+1(Zn) везде больше еди-
единицы, а это, как легко показать (см. п. 7.2в), сразу приводит к экс-
экспоненциальной расходимости близких траекторий. Соответствие
между странными аттракторами и одномерными отображениями
будет использовано в гл. 7.
Глава 2
КАНОНИЧЕСКАЯ ТЕОРИЯ
ВОЗМУЩЕНИЙ
§ 2.1. Введение
При анализе нелинейных задач широко используются методы тео-
теории возмущений: вместо исходной динамической системы изучается
близкая к ней интегрируемая система, на которую действует «воз-
«возмущение». Характеризуя различие между этими системами малым
параметром е и располагая невозмущенным решением, мы ищем воз-
возмущенное решение в виде разложения по степеням е. Например,
в случае слабой нелинейности линейная система интегрируется
непосредственно, а возмущенное решение можно получить в виде
ряда.
В этой схеме неявно предполагается, что исследуемая система
является интегрируемой. Как мы видели в гл. 1, обычно это не так,
и большинство многомерных динамических систем не интегрируемы.
В таких системах хаотические траектории, связанные с резонан-
сами между различными степенями свободы, занимают конечный
фазовый объем, а их распределение среди регулярных траекторий
оказывается всюду плотным. Теория возмущений не в состоянии
описать всю сложность такого хаотического движения, что фор-
формально выражается в расходимости соответствующих рядов.
Даже в случае начальных условий, при которых траектории
являются регулярными, имеются трудности при применении тео-
теории возмущений. Под действием возмущения регулярные траекто-
траектории в некоторой окрестности резонансов изменяют свою тополо-
топологию. Возникает характерная резонансная структура, напоминаю-
напоминающая «острова», описанные в § 1.4, причем их фазовый объем также
конечен. Эти острова являются «микромирами» исходной возму-
возмущенной системы, содержащими собственные хаотические и регуляр-
регулярные траектории. Обычная теория возмущений не отражает измене-
изменения топологии фазового пространства и для описания регулярного
движения вблизи определенного резонанса или ограниченной си-
системы резонансов была разработана специальная резонансная тео-
теория возмущений. В настоящее время не существует методов, кото-
которые позволяли бы находить регулярные траектории с учетом всей
иерархии резонансов 1).
J) Это не совсем так. Во-первых, существует техника построения сходя-
сходящихся рядов, например, в теории КАМ [11, 310, 463]. Кроме того, в послед-
последнее время развиваются методы масштабно-инвариантного описания резо-
резонансной структуры (см., например, [117, 165. 369] и §4.4, 4.5).— Прим.
ред.
82 Глава 2
Изменение топологии фазового пространства вблизи резонан-
сов, хаотические области и характер движения в них составляют
основное содержание последующих глав этой книги. В данной
главе мы рассмотрим методы теории возмущений, которые исполь-
используются для получения решений, «аппроксимирующих» в некотором
смысле реальное движение в многомерных нелинейных системах.
Решение в форме ряда может приближенно правильно отражать
грубые черты истинного движения даже тогда, когда реальная тра-
траектория является хаотической или изменяет существенно свою
топологию, но при этом целиком содержится в узком слое вблизи
сепаратрисы и окружена регулярными траекториями. С другой
стороны, теория возмущений не в состоянии дать хотя бы качест-
качественное описание хаотического движения в тех областях фазового
пространства, где перекрываются основные резонансы.
Если действительная траектория регулярна, то, казалось бы,
можно надеяться получить решение в виде равномерно сходяще-
сходящегося ряда. Однако описываемые в этой главе классические ряды,
будучи весьма полезными при некоторых теоретических вычис-
вычислениях, оказываются расходящимися. В классических методах ам-
амплитуда и частота колебаний представляются рядами по степе-
степеням е при фиксированных начальных условиях. Поскольку резо-
резонансы распределены в пространстве частот всюду плотно, то по
мере изменения частоты в высших порядках теории возмущений
в дело вступают все новые и новые резонансы. Это обстоятельство
приводит к расходимости рядов, которые в лучшем случае оказы-
оказываются асимптотическими.
Поиск сходящихся решений привел Колмогорова к разработке
методов сверхсходящихся разложений [229]. Им же была предло-
предложена техника, при которой частота удерживается постоянной, а
начальные условия в процессе выполнения разложения изменяются.
Это позволило построить сходящиеся ряды для «достаточно малых»
возмущений и «достаточно далеко» от резонансов (теория КАМ).
Рассмотрение теории возмущений мы начнем с краткого описа-
описания некоторых ее методов, используя простые примеры динамиче-
динамических систем и исследуя движение непосредственно по определяю-
определяющим его дифференциальным уравнениям. Даже для нелинейного
осциллятора с одной степенью свободы (интегрируемая система)
разложение только амплитуды колебаний в степенной ряд приво-
приводит к появлению неограниченно растущих во времени секулярных
членов и расходимости. Решая совместные уравнения для ампли-
амплитуды и частоты колебаний, Линдштедт [278 J и Пуанкаре [337 ] прео-
преодолели секулярность и получили сходящиеся ряды. Их техника
описана в п. 2.1а и представлена в общей канонической форме
в п. 2.2а. Этот материал составляет основу дальнейшего изложения
теории возмущений.
В случае двух и более степеней свободы резонансы между ос-
основными частотами и их гармониками вызывают дополнительные
Каноническая теория возмущений 83
сингулярности, связанные с так называемыми малыми знаменате-
знаменателями, что приводит к расходимости классических рядов даже для
регулярных решений. Для формального подавления этой расходи-
расходимости х) были предложены некоторые методы, в частности метод
усреднения. Этот метод дает возможность непосредственно вычис-
вычислять адиабатические инварианты, которые являются приближен-
приближенными интегралами движения и получаются путем усреднения по
быстрой угловой переменной системы. Адиабатические инварианты
определяются формально с помощью асимптотических рядов по
параметру возмущения е. Относящиеся сюда приемы описаны в
п. 2.16, а их представление в канонической форме дано в § 2.3.
Следует, однако, иметь в виду, что метод усреднения приводит
к неверному выводу о том, что возмущенная система всюду интег-
интегрируема. Истинное движение, которому отвечает структура фазо-
фазового пространства с перемежающимися областями хаотичности и
островами устойчивости, подменяется всюду интегрируемым дви-
движением, вытекающим из существования адиабатических инвари-
инвариантов 2). Будет такое описание «справедливо» или нет, определяется
величиной возмущения и той степенью детальности, с которой срав-
сравниваются между собой реальное движение и предсказания адиаба-
адиабатической теории. Это обстоятельство подчеркивалось в п. 1.4а,
где для задачи Хенона и Хейлеса (см. рис. 1.13 и последующее об-
обсуждение) сопоставлены истинные траектории и результаты вычис-
вычислений с помощью адиабатических инвариантов. Формальная рас-
расходимость 3) (для любого конечного е) асимптотического ряда, пред-
представляющего адиабатический инвариант, является еще одним сви-
свидетельством того, что метод усреднения искажает действительную
структуру фазового пространства. Тем не менее этот метод весьма
полезен при изучении движения в нелинейных системах.
Вблизи резонансов регулярные решения сильно возмущены
и претерпевают топологические изменения. В такой ситуации клас-
классическая теория возмущений приводит к появлению малых знаме-
знаменателей и расходимости рядов, как это показано в п. 2.1в. Неко-
Некоторой специальной заменой переменных эта резонансная сингу-
сингулярность устраняется, что делает возможным использование обыч-
обычного метода усреднения. Именно такая резонансная теория возму-
возмущений, описанная в § 2.4, составляет основу нашего метода изу-
*) Правильнее было бы сказать — для построения формальных рядов,
которые, вообще говоря, расходятся.— Прим. ред.
2) В общем случае более естественно было бы говорить о переменных
действия, которые являются приближенными интегралами движения не
только для адиабатического (медленного) возмущения, но и просто для ма-
малого возмущения. Используемые в тексте термины «адиабатическая теория».
«адиабатическое приближение» и т. п. следует понимать именно в таком рас-
расширенном смысле.— Прим. ред.
3) Имеется в виду, что асимптотические ряды могут с успехом приме-
применяться для анализа движения, хотя они и являются расходящимися. —
Прим. ред.
84 Глава 2
чения хаотического движения. Ее детальному рассмотрению по-
посвящены п. 2.4а и б. В качестве примера подробно исследуется дви-
движение в магнитном поле заряженной частицы, взаимодействующей
с электростатической волной (см. п. 2.4в). Предложенное в работе
[111] обобщение этого метода, позволяющее одновременно избав-
избавляться от малых знаменателей целой группы резонансов, описано
в п. 2.4г.
Для простоты изложения все методы рассматриваются лишь
в первом порядке по е, а канонические преобразования выполняются
с помощью зависящей от смешанного набора переменных произво-
производящей функции. Эти методы можно перенести и на более высокие
порядки [34], но последовательное распутывание старых и новых
переменных становится алгебраически сложным, а соответствую-
соответствующие ряды оказываются громоздкими. Однако высшие приближе-
приближения часто необходимы, как, например, в задаче Хенона и Хейлеса,
где первый порядок теории возмущений дает неверный результат
даже в предельном случае очень низкой энергии. В § 2.5 мы знако-
знакомим читателя с теорией преобразований Ли, которая пришла на
смену старым способам получения классических рядов в высоких
порядках по е. Методы Ли иллюстрируются на примерах задач
с одной степенью свободы и вычисления адиабатических инвариан-
инвариантов высших порядков.
В § 2.6 рассматриваются сверхсходящиеся ряды и проводится
сопоставление их с классическими рядами (п. 2.6а). Специальное
применение этих методов к вычислению периодических траекторий
в нелинейных системах описано в п. 2.66.
2.1а. Степенные ряды
Проиллюстрируем использование степенных рядов на примере ин-
интегрируемого слабо нелинейного осциллятора с одной степенью
свободы. Это может быть показанный на рис. 2.1, а маятник, ко-
колеблющийся с небольшой амплитудой и описываемый гамильто-
гамильтонианом A.3.6). Разлагая первое из уравнений A.3.5) до третьего
порядка по ф, запишем дифференциальное уравнение движения в виде
есох B.1.1)
6
где х = ф — угол отклонения от вертикали, со0 = (FGI2 — ча-
частота малых колебаний, е — малый безразмерный параметр, вве-
введенный в кубический член, чтобы явно выделить его как возмуще-
возмущение; в конце вычислений мы положим к = 1 х).
Если представить х в виде ряда
х = хо + e-Ki + e^-r . . , B.1.2)
1) Это справедливо, конечно, только при условии, что в системе остается
другой (неявный) малый параметр, например амплитуда колебаний в рас-
рассматриваемом случае.— Прим. ред.
Каноническая теория возмущений
85
и приравнять коэффициенты при одинаковых степенях е, то в ну-
нулевом порядке получим уравнение гармонического осциллятора
x0 = Acosa0t. B.1.3)
Уравнение движения в первом порядке по е имеет вид
х\ + «Ota =
cos3
B.1.4)
Представляя cos3co0/ в этом уравнении в виде суммы двух членов
cos 3 со01 = (cos Зю0/ + 3 cos (о0/),
^лл\\\\\\\\\\\\\\\\Ч
\\\\\\\\\\\ЖУ х\\\\\\\\\\\\\\\\\Ж\
• Быстро
I
I
I
I
а 5
Рис. 2.1. Нелинейные колебания.
а — маятник; 6 — адиабатическое возмущение; в — пример резонанса.
С U
находим, что первый из них дает «хорошее» частное решение
А3
192
COS3(D(/,
B.1.5)
в то время как второй оказывается резонансным и ему отвечает
частное решение
xlb =
16
sin со,/ -)- 2 cos co00.
B.1.6)
Видно, что первое слагаемое растет линейно со временем — это
и есть секулярный член. В рассматриваемом случае секулярность
возникает вследствие выбора неподходящего разложения, при ко-
котором не принимается во внимание зависимость частоты колебаний
от их амплитуды.
Корректный подход, разработанный Линдштедтом [278], со-
состоит в одновременном разложении по степеням е как амплитуды,
так и частоты колебаний. Предположим, что х = х (со/) является
86 Глава 2
периодической функцией со/ с периодом 2я, и разложим х и со по
степеням е, так что наряду с B.1.2) имеем
со = соо — ею! + е2оJ + .... B.1.7)
Подстановка этих разложений в уравнение B.1.1) дает
(too-г280H0)!+ . . . ) 1лго + елг1 + . . . ) +
+ со5(^0+ех1-1- . . .) — ей)о(дг0 + ел:]1+ . . .K=0,
B.1.8)
где штрихи означают производные по аргументу со/. В нулевом
порядке имеем
хо^х0 = 0, B.1.9)
и решение х0 — A cos со/. Уравнение первого порядка
xl + 2-^Xo + Xi -Хо = 0 B.1.10)
«о 6
после подстановки в него выражения для х0 приобретает вид
х\ + хх = 2 -^- A cos со/ + — A3 cos©/ + —!— A3 cos 3©/.
«0 8 24
B.1.11)
Условие периодичности х (со/) требует, чтобы коэффициент при
cos со/ равнялся нулю, так как в противном случае возникают
секулярные члены. Следовательно, мы выбираем величину сох так,
чтобы исключить секулярность
со1=~^-А2соо, B.1.12)
и получаем характерное для маятника уменьшение частоты коле-
колебаний с возрастанием амплитуды. При таком выборе сох решение
уравнения B.1.11) есть
дз
х, = Л, cos со/ + В, sin со/ cos3co/. B.1.13)
1 1 г 1 ig2 v /
В частности, для начальных условий
получаем выражение
*!= -^— (coscu/^cos3co/), B.1.15)
которое описывает изменение х (со/), вызванное нелинейностью.
Рассмотренную процедуру можно выполнить и в более высоких
порядках по е. Основу метода составляет предположение о перио-
периодичности х с частотой со, отличной от частоты малых колебаний сй0-
Каноническая теория возмущений 87
Дополнительная свобода, возникающая вследствие разложения со,
позволяет исключать секулярность в каждом порядке по е, чем
и достигается равномерная сходимость решения. Каноническая
форма метода Линдштедта, представленная в п. 2.2а, была разра-
разработана Пуанкаре [337] и Цейпелем [419].
2.16. Асимптотические ряды и малые знаменатели
Рассмотрим колебания гармонического осциллятора с медленно
изменяющейся возвращающей силой (или частотой). Эта задача
существенно отличается от предыдущей наличием явной зависимо-
зависимости от времени, так что фактически мы имеем дело с двумя степе-
степенями свободы. Запишем уравнение движения такого осциллятора
(рис. 2.1, б) в виде ; L,
x-w2(e0x = 0, B.1.16)
где малый безразмерный параметр е введен опять-таки для явного
выделения возмущения и по окончании вычислений полагается
равным единице. Истинным малым параметром разложения в рас-
рассматриваемом случае является отношение периода колебаний к ха-
характерному временному масштабу изменения возвращающей силы
1 со
со со
B.1.17)
Ниже используется разложение не непосредственно для .v, a
для некоторой вспомогательной переменной у, скорость изменения
членов разложения которой тем меньше, чем выше их порядок.
Прежде всего, переходя к новой независимой переменной т = et,
запишем уравнение B.1.16) в виде
со2(т)х = 0. B.1.18)
е
Введем теперь новую переменную у посредством равенства
х = ехр [\yd%\. B.1.19)
Обозначая dx!dx как х', находим
х' = ух, х" = у*х^г у'х.
Подстановка последних соотношений в уравнение B.1.18) приво-
приводит к уравнению Риккати
e2(/-f/)-f со2 = 0. B.1.20)
Представим у в виде степенного ряда
. . . B.1.21)
88 Глава 2
и подставим это разложение в B.1.20). В низшем порядке по е
находим
а в следующем порядке
2i/oi/i-yo = O. B.1.22)
Использование B.1.21) и B.1.22) совместно с B.1.19) дает
Интегрируя второе слагаемое и учитывая равенство у0 = + гсо,
получаем
х = -^—exp [±i\<adt]. B.1.23)
со1 2
Рассмотрим медленное изменение частоты от значения ы1 при
до значения со2 при ^>^2 и вычислим интеграл действия
ldx B.1.24)
J
2л
в каждой из этих двух областей (t<it1 и t^>t2), где со по предпо-
предположению не изменяется.
Полагая р — /пх и переходя в B.1.23) к действительному ре-
решению
х = Лео2cos (со^f 6),
находим, что / = A/2) тА'1 в обеих областях, несмотря на то что
как частота со, так и энергия Е = A/2) тх„акс = <°^ могли изме-
измениться сколь угодно сильно. Действие / является, таким образом,
адиабатическим инвариантом движения, т. е. сохраняется в пре-
пределах точности используемых разложений, полученных в предпо-
предположении медленности изменения параметров. Существование ин-
инварианта позволяет легко получить решение, хотя гамильтониан
и не сохраняется.
Вычисление действия в области t1<.t<,t2, где происходит
медленное изменение параметров, приводит к тому же результату.
Более того, описанное разложение можно выполнить во всех по-
порядках по малому параметру. Это было сделано Кулсрудом [244]
для линейного осциллятора и затем обобщено Крускалом [239 ]
и другими (см. [265] и § 2.3) на более сложные системы. Подчерк-
Подчеркнем еще раз существенное отличие этого разложения от разложе-
разложения, описанного в п. 2.1а. Наличие явной зависимости от времени
эквивалентно движению с двумя степенями свободы. При этом ре-
решения в виде рядов, как правило, не сходятся к точным решениям,
а оказываются асимптотическими. Это понятие будет подробно рас-
рассмотрено в начале § 2.3.
Каноническая теория возмущений 89
2.1 в. Влияние резонансов
Если рассмотренный в п. 2.1а осциллятор подвергается периоди-
периодическому во времени внешнему возмущению или если медленные
изменения параметров осциллятора, описанные в п. 2.16, являются
периодическими, то резонансы между колебаниями осциллятора
и внешним возмущением разрушают сходимость разложений и из-
изменяют или разрушают интегралы движения. Проиллюстрируем
возникающие при этом трудности на простом примере.
Рассмотрим вынужденные колебания линейного осциллятора
B-1.25)
где внешняя сила g (t) является периодической функцией времени
с периодом 2n/Q. Решение однородного уравнения B.1.25) есть
xh = A cosco,/ + ?siniO(/. B.1.26)
Представим внешнюю силу g (t) в виде ряда Фурье
оо
g (/) = -^- + ? [ап cos пШ + bn sin n Qt) B.1.27)
2 п=\
и подставим это выражение в уравнение B.1.25). Разлагая частное
решение хр (t) в ряд Фурье, для n-го члена получаем
_ ancosnQt + bns,mnQt ^ ,^ . „а)
Видно, что при cog « n2Q2 имеет место резонанс, приводящий к рас-
раскачке колебаний. Наш пример иллюстрируется на рис. 2.1, в, на
котором показан ребенок, раскачивающий качели.
Если осциллятор нелинейный, как, например, рассмотренный
в п. 2.1а, то в однородном решении присутствуют все гармоники
с частотами, кратными основной частоте со0. В этом случае резо-
резонансы возникают всякий раз, когда отношение частот co0'Q яв-
является рациональным числом, т. е. имеет место всюду плотная си-
система резонансов. Но, как мы уже знаем, частота колебаний яв-
является функцией их амплитуды. Резонансы же изменяют ампли-
амплитуду, а значит, и частоту колебаний, нарушая тем самым точное
выполнение резонансных условий. Таким образом, малые знаме-
знаменатели, препятствующие сходимости классических рядов в окрест-
окрестности резонансов, отражают определенное физическое явление,
которое приводит к локальному изменению характера фазовых тра-
траекторий.
*§ 2.2. Классическая теория возмущений
Большинство многомерных или подверженных внешним воздейст-
воздействиям динамических систем являются неинтегрируемыми (см. § 1.3).
Однако для тех систем, которые близки к интегрируемым, можно
90 Глава 2
попытаться получить решение с желаемой точностью, если предста-
представить производящую функцию в виде ряда по степеням малого па-
параметра и затем решать уравнение Гамильтона—Якоби последо-
последовательно в каждом порядке. Как уже отмечалось, малые знамена-
знаменатели препятствуют сходимости этих рядов. Тем не менее получен-
полученные таким путем результаты можно использовать для вполне удов-
удовлетворительного описания поведения системы в некоторых обла-
областях фазового пространства. Более того, этот метод оказывается
весьма полезным при построении приближенных решений и для
систем с одной степенью свободы, когда явное интегрирование урав-
уравнений движения затруднительно, а также для предварительного
перехода к переменным действие — угол в невозмущенных систе-
системах с несколькими степенями свободы.
* 2.2а. Одна степень свободы
Рассмотрим гамильтониан следующего вида:
Я = Я0(/)-ЬеЯ1(/, е)+Е2Я2(/, 9)+ . . .. B.2.1)
Здесь использованы переменные действие — угол для первого сла-
слагаемого Но, поэтому ему отвечает решение
J = J0, B.2.2а)
e = <o*-fp, B.2.26)
со == дН0Ш, B.2.2b)
где Jo. ю> Р — постоянные, не зависящие от t. Следуя Пуанкаре
[337] и Цейпелю [419], мы ищем преобразование к таким новым
переменным 7, 8, для которых новый гамильтониан Н есть функция
только переменной действия J. Используя производящую функцию
S G, 9), представим S и Н в виде степенных рядов по е
S = 76 + eS1-i- • • • , B.2.3)
Н^Н.+ гН^ . . . , B.2.4)
причем член низшего порядка в S выбран так, чтобы порождать
тождественное преобразование J = / и 6 = 6. Старая переменная
действия и новая угловая переменная определяются из выражений
A.2.13а) и A.2.136) соответственно
J = 7^e dSl(? 9) -г • • . , B.2.5а)
ах)
е^е-е-^^-^- -f . . . . B.2.56)
dJ
Для получения нового гамильтониана необходимо выразить ста-
старые переменные через новые с помощью соотношений B.2.5) и за
Каноническая теория возмущений
тем использовать формулу A.2.13в). В первом порядке по е это
сделать нетрудно
J = 7 + s dSl^J> 6) f
дв
B.2.6а)
9 = 6 — е dSl^ §) -1- . . . . B.2.66)
Тогда из A.2.13в) имеем
Я G, 0) = Я(/G, в), 9G, 6I. B.2.7)
Разлагая правую часть последнего равенства в степенной ряд
по е и используя B.2.6), получаем
Я0(/G,ё)) = Я0G) + е-^--%- + . . . , B.2.8а)
dJ dQ
eH^Ji'J, [6)" еG'[ei^f^ji/, e)+ . . .. B.2.86)
Подстановка этих выражений в B.2.7) позволяет найти члены но-
нового гамильтониана нулевого (Яо) и первого (Ну) порядков
Я0 = Я0G), B.2.9)
H^^mjMLJL +я1G, Ъ). B.2.Ю)
Так как мы ищем новый гамильтониан, который зависит только
от переменной действия J, то необходимо путем выбора функции Si
в B.2.10) компенсировать зависящую от 6 часть Н1. Определим
среднюю (Ну) и переменную [Ну] части Нг посредством выраже-
выражений
(Hi)^-~ | нги, e)S, B.2.П)
{Я1} = Я1-<Я1>. B.2.12)
Из равенства B.2.10) находим два соотношения
Я1 = <Я1>, B.2.13)
@_^_=_{Я1}. B.2.14)
<эе
Объединяя B.2.9) и B.2.13), получаем преобразованный гамиль-
гамильтониан с точностью до членов первого порядка
Я = Я0G] + е<Я1(у, Щ B.2.15)
92 Глава 2
с новой частотой со ¦— дН dJ. При этом предполагается, что урав-
уравнение B.2.14) можно разрешить относительно функции Sv с по-
помощью которой исключается \Нг\. Видно, что новый гамильто-
гамильтониан в первом порядке получается путем усреднения старого га-
гамильтониана по фазе.
Чтобы найти функцию Sx, представим [Н^, и Sx в виде рядов
Фурье
//,; = ^ tfwl7le'4 B.2.16а)
п =0
Sx= 1.Sln\l'e^. B.2.166)
Из B.2.14) немедленно следует, что S10 = const x), a
Sln=—-^_, n т^О. B.2.17)
Если со (J) ф 0, то ряд Фурье для 5Х сходится и позволяет выпол-
выполнить преобразование переменных B.2.6).
Разложения высших порядков. Иногда необходимо провести разло-
разложения до более высокого порядка по е либо из-за того, что поправки
первого порядка равны нулю, либо из-за желания повысить точ-
точность вычислений. Процедуру Пуанкаре—Цейпеля можно выпол-
выполнить в любом порядке по е, но распутывание старых и новых п е
ременных, ведущее от B.2.5) к B.2.8), требует утомительных алге-
алгебраических выкладок. Если полного обращения переменных не
требуется, то вычисление нового гамильтониана, а следовательно,
и возмущенной частоты колебаний становится относительно про-
простым.
Подробное рассмотрение вычислений в высших порядках со-
содержится в § 2.5, где представлены современные методы с исполь-
использованием преобразований Ли. Здесь мы ограничимся тем, что вы-
выпишем в явном виде соотношения, необходимые для определения
нового гамильтониана с точностью до второго порядка по е. Более
детальное обсуждение рядов Пуанкаре—Цейпеля можно найти
в работах Борна [34] и Джакалья [153].
Предположим, что в соотношении B.2.1) только Яо и Нг от-
отличны от нуля. Пусть 5 и Я представлены степенными рядами по е
вида B.2.3) и B.2.4), тогда выражения B.2.8а) и B.2.86) можно
выписать явно
1) Функцию S10 нельзя найти из B.2.14), но можно просто положить
= 0, не нарушая этого условия.— Прим. ред.
Каноническая теория возмущений 93
яду (у, е))=я„(УН
Jmd m] dJ'" \ со /
т, п
B.2.18а)
f, е), е)= яду, е
B.2.186)
Полагая Я функцией только переменной действия У и приравнивая
Я = Я с помощью выражения B.2.18), получаем в нулевом и пер-
первом порядке по е соотношения B.2.9) и B.2.10) соответственно.
Во втором порядке по е находим (без обращения 8):
/7 — дН<> dSl j ' д'н° I dSl У j_ dHl dSl
B.2.19а)
Поскольку Я, является функцией только У, то имеем
+ ^я^^^\ , B-2Л9б)
772
а периодическая по 8 функция 52 определяется из условия
д#0 552 _ | 1 д-Н0
dl dQ | 2 d~f \ дв I d~j дв
'B.2.19b)
скобки ( ) и f j, как и раньше, соответствуют усредненной и ос-
осциллирующей частям выражения. Частота колебаний вычисляется
обычным образом как со = дН/dJ.
Маятник. Для иллюстрации описанного выше метода разложения
рассмотрим нелинейные колебания маятника, гамильтониан ко-
которого имеет вид [см. A.3.6)]:
Я„ = — Gp2 — F cos ф = Е. B.2.20)
В качестве невозмущенной системы Яо р выберем квадратичную
часть гамильтониана, которая соответствует линейным колебаниям,
а оставшиеся члены будем считать возмущением. Раскладывая Яр
в ряд Тейлора и опуская постоянную, получаем
Нр = -L Gp2 +- — /V —/V+ — ^Ф6— • • ¦ ,
2 2 4! 6!
94
Глава 2
где первые два слагаемых представляют ЯОр. Малый параметр е
отмечает, как и раньше, порядок членов возмущения. Истинным
параметром разложения является отношение энергии колебаний
к энергии на сепаратрисе. Для применения методов теории воз-
возмущений удобно перейти предварительно с помощью A.2.69) к пе-
переменным действие — угол неЪозмущенной системы Яо Новый
Я = Е -I- F
гамильтониан
принимает вид
-G/2sin46
+ ¦
90
ш0
-sine8— . . . ,
B.2.21)
-о,б-ОА-о,г о о,г оа а,е о,8 :
E/F
Рис. 2.2. Зависимость частоты колеба-
колебаний маятника B.2.20) от энергии.
/ — точг'эя формула A.3.13); 2 — теория
возмущений в первом порядке; 3 — теория
возмещении во втором порядке (п. 2.56).
GV3
2880ш0
¦A0— 15cos2e
где oj0 = (FG){ 2 — частота
невозмущенных колебаний.
Преобразуя степени sin 8,
находим
B.2.22а)
= — — C—4 cos 26 + cos 48),
B.2.226)
Э —cos 69). B.2.22b)
Применяя полученные выше результаты и усредняя B.2.226)
по 8, получаем, согласно B.2.15), новый гамильтониан до первого
порядка по е
= соо7
GT
T
B.2.23)
и нсв\ ю частоту колебаний
дН
со =
dJ
= соо —GJ.
B.2.24)
Последнее соотношение показывает, что частота колебаний умень-
уменьшается с ростом их амплитуды; это согласуется с разложением
A.3.13) с точностью до первого порядка по х. Исключая / из B.2.23)
и B.2.24), получаем зависимость ю (Я), которая изображена на
Каноническая теория возмущений 95
рис. 2.2 кривой 2; ее можно сопоставить с точным результатом
A.3.13), представленным на рис. 2.2 кривой /.
Производящую функцию i?! можно найти путем интегрирования
уравнения B.2.14):
Г, /2
Sj_= ——(8sin26— sin 46). B.2.25)
192ш0
Используя это выражение, нетрудно получить преобразование
B.2.6) от старых переменных к новым.
* 2.26. Несколько степеней свободы
Если возмущенный гамильтониан описывает автономную систему
с несколькими степенями свободы или явно зависит от времени даже
для одной степени свободы, то рассмотренные выше разложения
оказываются расходящимися. Чтобы убедиться в этом, обобщим
метод Пуанкаре—Цейпеля на случай автономного гамильтониана
с N степенями свободы. Явную зависимость от времени можно
учесть с помощью дополнительной степени свободы в расширенном
фазовом пространстве. Запишем
Я (У, 0) = Я0(У) + еЯ1(У, в), B.2.26)
где У и 0 — iV-мерные векторы переменных действия и углов не-
невозмущенной системы Яо, а Н1 — периодическая функция всех
угловых переменных
#i = 2 Я1« We»»'в. B.2.27)
m
В последнем выражении использовано обозначение
B.2.28)
где те — целые числа, по которым производится iV-кратное сумми-
суммирование в B.2.27). Будем снова искать преобразование к таким
переменным J, 8, для которых новый гамильтониан Я зависит только
от J. Введем производящую функцию
с 7 flj_p VS. (~~f\ pim-Q to 9 9Q\
m
которая в нулевом порядке по е отвечает тождественному преобра-
преобразованию, а в первом содержит iV-кратную сумму, периодическую
по 8. Как и в одномерном случае, выразим старые переменные че-
через новые с помощью этой производящей функции и подставим их
в A.2.13в). Приравнивая коэффициенты при одинаковых степенях е,
находим в нулевом порядке
ЯО(У) = ЯОG), B.2.30)
96 Глава 2
и в первом порядке
SiU в) Л-H^J, 81. B.2.31)
1 (j
Здесь вектор частот й> невозмущенного движения определяется
формулой
й)(У)= аЯ°Р . B.2.32)
Усредняя по <?сеж угловым переменным, имеем
Я = Но G) -Ь е <//х G, в)) B.2.33)
щ.-^-=— {tfij. B.2.34)
Решение 52 последнего уравнения можно получить путем интегри-
интегрирования вдоль траекторий возмущенного движения. Действительно,
так как в выражении
dSj = dS1 dSj. dl , dS^ dJ
dt dt ^ dQ dt ^ gj dt
B 2 35)
в нулевом порядке первый и третий члены правой части равны
нулю, то производная dSJdt равна левой части B.2.34) и можно
написать
Si=— |{Я1G, 6@.)} Л. B.2.36)
Интегрируя ряд Фурье для Нъ окончательно получаем
Я""A) е'от'9+ B.2.37)
тфО ч '
Мы сразу же сталкиваемся с проблемой малых знаменателей, так
как для любого J всегда найдется такое т, что mm {J) окажется
сколь угодно близко к нулю, и сходимость рядов явно нарушается.
Подчеркнем еще раз, что это обстоятельство отражает в равной
мере трудности как математического, так и физического характера.
Оно возникает из-за фактического действия резонансов, которое,
как будет показано в § 2.4, изменяет топологию фазовых траекто-
траекторий. Несмотря на это, значительные усилия были потрачены на
попытки по крайней мере «отодвинуть» секулярность в более высо-
высокие порядки разложения. В защиту этих, казалось бы бесперспек-
бесперспективных, методов заметим, что они дают решения, сходящиеся к ис-
истинным решениям в определенных областях фазового пространства
для конечных, но больших интервалов времени. Более того, в не-
некоторых случаях такие решения хорошо аппроксимируют движе-
Каноническая теория возмущений 97
ние в течение любого времени, если используется крупноструктур-
крупноструктурное разбиение фазового пространства 1). Последний результат свя-
связан с фактической сходимостью (согласно теории КАМ) определен-
определенных решений для некоторых значений J. Как мы увидим ниже, в
случае двух степеней свободы эти решения жестко ограничивают
резонансные траектории, которые вынуждены, таким образом,
оставаться вблизи нерезонансных траекторий.
Явная зависимость от времени. Для системы с одной степенью сво-
свободы и явной зависимостью гамильтониана от времени мы получим
в первом порядке по е некоторые соотношения, которые понадо-
понадобятся нам в дальнейшем. Начнем с гамильтониана
Я = Яо(^) + еЯ1(^, 6, t), B.2.38)
в котором возмущение периодично по 8 с периодом 2я и по времени
с периодом 2n/Q, a
Я1=2Я1№(/)е'('е+тй0. B.2.39)
/, т
Как и в п. 2.2а, выбираем производящую функцию 5 в виде
5 = 76 + 653.G, 6, t). B.2.40)
При этом переход от старых переменных к новым выполняется с по-
помощью B.2.6). Из-за явной зависимости Нг от времени соотноше-
соотношение B.2.7) изменяется:
77G, 8, t) = H{J, 9, n + e-^AJ^L. B.2.41)
dt
Разложение по е дает
77о = #0G), B.2.42)
Н1 = JEl. + со _Ф_ + Нг. B,2.43)
Подбирая, как и прежде, Sx таким образом, чтобы уничтожить
переменную часть Яь находим в первом порядке по е
Н = Н0 + г(Н1), B.2.44)
где усреднение производится как по 8, так и по /, а
-^i-+co^L = —{Ях}. B.2.45)
dt да
Для нахождения Sx произведем фурье-разложение
at)_ {2.2.Щ
^J /со (j) + mQ
1, m - 0
To есть при конечной точности описания.— Прим. ред.
98 Глава 2
Мы вновь сталкиваемся с малыми знаменателями, препятствующими
сходимости рядов.
Классическая каноническая теория возмущений может быть
весьма полезна при определении интегралов движения, если си-
система находится достаточно далеко от первичных (т. е. проявляю-
проявляющихся в низшем порядке теории возмущений) резонансов. Для
иллюстрации выберем функцию Нъ содержащую только одну гар-
гармонику по 0:
Ях =?/(./, t) + V(J, OcosO. B.2.47)
Чтобы найти Sj явно, представим Н± и Sx рядами Фурье
Нг G, ё, /J = ? Ь1т(Т) cos (IQ— m°t\, B.2.48)
S^J, 0, /)=2a/m(/)sin(/0 — mQt], B.2.49)
где суммирование производится по всем пг для / = 0 и / = 1. Под-
Подставляя B.2.49) в B.2.45), определяем коэффициенты aim при /,
m ф 0:
alm= ^—. B.2.50)
tnQ — la \J)
В области таких значений /, при которых знаменатели не малы,
функции aim не имеют особенностей. В первом порядке по е новый
гамильтониан, как и в одномерном случае, имеет, согласно B.2.44),
вид __
Я = Я0G) + е&00G). B.2.51)
Новая переменная действия равна
7с т я л г о dSj(J, 8, t) .» g _„.
v ' ' ' 58 v '
Любая функция вида / (/), так же как и J, является интегралом
движения. Ниже (п. 2.4г) мы используем этот факт для построения
глобальных интегралов движения.
Взаимодействие частицы с волной. Проиллюстрируем методы и ог-
ограничения канонической теории возмущений в случае нескольких
степеней свободы на практически интересном примере взаимодейст-
взаимодействия заряженной частицы с электростатической волной в одно-
однородном магнитном поле (рис. 2.3). Такая задача была рассмотрена
Смитом и Кауфманом [385, 386 ] для случая волны, распространяю-
распространяющейся наклонно к магнитному полю, а для случая перпендикуляр-
перпендикулярного распространения это сделали Карни и Берс [222], а также
Фукуяма и др. [145].
Введем прежде всего переменные действие — угол для невоз-
невозмущенной системы, гамильтониан которой имеет вид
B.2.53)
Каноническая теория возмущений
99
Здесь М — масса частицы, е — ее заряд, с — скорость света. Обо-
Обозначая через х, у, "г орты координатных осей, запишем векторный
потенциал однородного магнитного поля Во в виде
А(х)=— Воух.
Импульс
— A
B.2.54)
B.2.55)
канонически сопряжен радиусу-вектору частицы х -^ хх — yy—zz.
С помощью производящей функции
1
1 —
¦{y-Yfdgy-xY
B.2.56)
и соотношений A.2.11) переходим к новым дрейфовым переменным:
tgcp= —, B.2.57а)
\
Me I Mvl
ц = —
^ B.2.576)
= y-f psintp, B.2.57b)
, B.2.57г)
k*\
где
Q =
Me
B.2.58) Рис. 2.3. Траектория частицы
в однородном магнитном поле
В
— ЛЭРМОРОВСКаЯ ЧаСТОТа, Ц — МаГ- * — волновой вектор электростати-
„ ' .) о . о ческой волны.
нитныи момент, v-± = vLx -f- v2,
р = vJQ. — ларморовский радиус, X и Y — дрейфовые коорди-
координаты ларморовского центра, Рф и ф — момент импульса и угловая
координата. Новыми импульсами являются величины />ф, МпХ
и Рг\ им отвечают координаты ср, Y и z соответственно. Преобразо-
Преобразованный гамильтониан имеет вид
Р2
B.2.59)
Предположим, что возмущением является электростатическая
волна с электрическим полем Е = — 7Ф, где
ф=
B.2.60)
100 Глава 2
В дрейфовых переменных имеем
//j = eCDosin (kzz-{-k±Y—й^рэтф— cot), B.2.61)
где
р(Р_)= /ifsL_V'2. B.2.62)
Так как возмущенный гамильтониан
Я' = Я0 + еЯ1 B.2.63)
не зависит от импульса MQX, то Y = const и, сдвинув z или t
на постоянную величину, можно исключить постоянную фазу k , F
из B.2.61). Нелинейность колебаний возникает благодаря зависи-
зависимости фазы kzz—/гхр sin ср—со^ от sin ф и р. Поскольку гамильто-
гамильтониан зависит только от линейной комбинации kzz—со^, то можно
исключить зависимость от времени, перейдя в систему отсчета
волны. Это осуществляется с помощью производящей функции
F2 = (kzz—со/)Рф + Рфф. B.2.64)
Используя соотношения A.2.13), получим новые переменные Рф,
гр и новый гамильтониан Я:
Рг= -^- =kzP^, B.2.65а)
= kzz—at, B.2.656)
k2p2
Я= —^^^^ РфШ + РфО + ееФ0 sin (г|з—^хр sin ф) = ? = const.
B.2.66)
Здесь, как и прежде, е — малое возмущение (в конце вычислений
полагают, что е = 1). Резонансные гармоники возмущения можно
выявить с помощью разложения в ряд по функциям Бесселя
2^ ?
B.2.67)
Мы уже видели, что необходимо оставаться достаточно далеко
от первичных резонансов для того, чтобы амплитуды Фурье убы-
убывали быстрее резонансных знаменателей. В нашем случае убывание
амплитуд Фурье определяется функциями Бесселя fm (k_L p). Не-
Невозмущенные частоты колебаний находятся из B.2.67):
=а, B.2.68а)
Каноническая теория возмущений 101
Возмущение возбуждает только резонансы между основной часто-
частотой сйф и гармониками частоты юф, поэтому условие резонанса
имеет вид
со„,—/nQ = 0. B.2.69)
Для kz = 0 из B.2.686) получаем
w + /nQ = 0. B.2.70)
Для kz Ф 0, разрешая B.2.69), находим резонансные значения Р^\
^ B.2.71)
Мы исследуем эти резонансы с помощью резонансной теории воз-
возмущений в п. 2.4в.
Поскольку Яф является переменной действия, то для косой
волны резонансы B.2.71) неизбежны. Рассмотрим поэтому перпен-
перпендикулярную волну (kz = 0) в предположении, что условие резо-
резонанса B.2.70) не выполнено. В этом случае, как будет показано
ниже, при достаточно малом возмущении первичные резонансы
отсутствуют. Из B.2.34) и B.2.67) находим
Q JEL. = _ еФо? fm (кГр) sin (ip-тф),
о, + о?
dip аф m
B.2.72)
где р = р {Р<р)- Решение этого уравнения имеет вид
С помощью последнего выражения можно связать старые перемен-
переменные действия Рф, Ру с новыми:
"°Д~аФ) ¦ B-2.74)
Обращая, в первом порядке получаем
!п^"Ф) = const. B.2.75)
<„(^р) ^
m
Подобным же~образом находим
Р^Р,+ геФ0 V [mfm(Ахр) "°С»-"Ф) = COnst,
m
B.2.76)
причем р (Pw) определяется выражением B.2.62).
102
Глава 2
Используя соотношение B.2.76) и фиксируя одну из фазовых
переменных, можно получить графики зависимости Яф от другой
фазовой переменной для различных значений инварианта Р9. Та-
Такие инвариантные
50 г- —
кривые эквивалентны картине на поверхности
Рис. 2.4. Инвариантные кривые на поверхности сечения ф = п. для случая
нерезонансного взаимодействия частицы с волной при кг = 0 и ш/Я =
— — 30,П (теория) (по данным работы [219]).
а — малая амплитуда волны, резонансы отсутствуют; 6 — большая амплитуда волны,
видны резонансы.
Каноническая теория возмущений
103
сечения Пуанкаре. На рис. 2.4, а и б показаны кривые зависимости
&j-P (Pif) от \р при ф = я, полученные Карни [219]. Хотя t[i и & р
не являются канонически сопряженными переменными, тем не ме-
менее основные черты фазового пространства системы представлены
правильно. Для сравнения на рис. 2.5, а я б показдны фазовые тра-
50г
Рис. 2.5. То же, что и на рис. 2.4 (численное моделирование) (по данным
работы [219]).
Крестиками отмечены начальные условия.
ектории, полученные Карни численно. Так как для невозмущенной
системы со = — 30,11 Q и при малой амплитуде возмущения все
инвариантные кривые лежат достаточно далеко от первичного ре-
резонанса, то аналитические и численные результаты хорошо согла-
согласуются. С ростом возмущения частота колебаний изменяется и си-
система может попасть в резонанс. Однако производящая функция
первого порядка, имеющая полюсы на невозмущенных резонан-
сах, остается при этом конечной и воспроизводит грубые черты по-
поведения системы вблизи резонанса. Резонансы высших порядков
таким методом найти нельзя; для этого требуется провести вычисле-
104 Глава 2
ния во втором порядке резонансной теории возмущений (§ 2.4).
Области хаотического движения вообще не описываются рассмат-
рассматриваемой теорией возмущений, однако их размер можно оценить,
как это будет показано в гл. 4.
§ 2.3. Адиабатическая инвариантность
* 2.3а. Введение и основные понятия
В п. 2.16 мы видели, что для осциллятора с медленно и аперио-
апериодически изменяющимся параметром можно построить разложение,
которое дает адиабатический инвариант движения. Параметром
разложения являлось отношение периода быстрых колебаний ос-
осциллятора к характерному времени медленного изменения пара-
параметра. Такую же процедуру можно использовать и в многомерных
системах для построения рядов, не содержащих явно малых знаме-
знаменателей. Этот метод, впервые предложенный Пуанкаре [337], был
затем более строго обоснован Биркгофом [29].
Систематическая техника таких разложений, разработанная
Боголюбовым и сотр. [242, 33, 32], получила название метода
усреднения 1). Несколько иная форма этого метода, более подходя-
подходящая для канонического представления, была предложена Круска-
лом [239] (см. п. 2.3г). Крускал показал, что адиабатические ин-
инварианты можно построить в любом порядке по параметру разло-
разложения и что получающиеся при этом ряды оказываются асимпто-
асимптотическими. В работах Боголюбова и Крускала рассматривается
широкий класс систем дифференциальных уравнений, не обяза-
обязательно гамильтоновых. Полезные канонические формы методов вы-
вычислений были введены Мак-Намарой и Уайтменом [292 ] и Штер-
Штерном [391, 392]. Однако в более высоких порядках разложения на
смену им пришла техника преобразований Ли [290] (см. § 2.5).
Связь между различными методами рассматривается в обзорах
Мак-Намары и Уайтмена [292] и Джакальи [153].
Асимптотические ряды. Биркгоф [29] впервые показал, что ос-
осциллятор с медленно,изменяющейся частотой
2) В оригинале — multiple scale method of averaging [метод усреднения
с несколькими масштабами (времени)] —термин, который в отечественной
литературе не употребляется. Заметим, что понятие усреднения (как при-
приближенного метода) уже подразумевает наличие в задаче по крайней мере
двух различных масштабов времени. По поводу специальных методов теории
возмущений, в которых эти масштабы вводятся явно, см., например, работу
[313].— Прим. ред.
Каноническая теория возмущений
105
допускает решение в виде асимптотического ряда. Это значит, что
последовательные приближения
xn{t,
точного решения х (t, г)
можно построить таким об-
образом, что для любых фик-
фиксированных п и t
, e) —
k=Q
B.3.1)
Так как
lime~"exp
0,1
-Xn{t,t)]=0. B.3.2)
Напомним некоторые важ-
важные свойства асимптоти-
асимптотических рядов. Во-первых,
две различные функции
могут соответствовать од-
одному и тому же асимпто-
асимптотическому ряду. Поэтому
построение асимптотиче-
асимптотического ряда еще не опреде-
определяет однозначно представ-
представляемую им функцию.
Предположим, что две
функции хх и х2 отлича-
отличаются на экспоненциально
малую величину при е-И):
0,01
0,001
0,0001
0,1
10
10в
\Х~х\
B.3.3)
B.3.4)
1МО.КС
10
б
то асимптотическое разло-
разложение функции Лх есть
Хп = 0 для всех п (см.
рис. 2.6, а). Следователь-
Следовательно, функции хх и х2 пред-
представляются одним и тем же
асимптотическим рядом.
Фактически прямые вы-
вычисления обнаружили такие экспоненциально малые изменения
адиабатических инвариантов в колебательных системах с медленно
Рис. 2.6. Свойства асимптотического ряда-
а — функция Ах = ехр (— 1/е), для которой
асимптотическое разложение есть тождественный
нуль; б — расходимость асимптотического ряда
при фиксированном е. Последовательные аппро-
аппроксимации Хп вначале приближаются к истинному
значению х, а затем удаляются от него. «Наи-
«Наилучшая» аппроксимация отвечает номеру п =
= "макс-
106 Глава 2
изменяющимися параметрами1) (см., например, [81, 191, 200]).
Для многомерных систем 2) эти экспоненциально малые изменения
инвариантов являются следствием резонансов, вызывающих то-
топологическую перестройку фазового пространства, а при доста-
достаточно сильном возмущении и разрушение инвариантов. Таким об-
образом, «адиабатический» инвариант, представляемый асимптоти-
асимптотическим рядом, является в пределе е ->¦ 0 приближением порядка
ехр (— b/в) точного решения, траектория которого может лежать:
а) на гладкой инвариантной поверхности, б) на инвариантной по-
поверхности резонанса, в) в тонком стохастическом слое.
Второе свойство асимптотических рядов заключается в их фор-
формальной расходимости: для любых фиксированных ей/ имеем 3)
x(t, e) — Xn(t, e)|->-oo, я-^оо. B.3.5)
Общее поведение Хп с ростом я при фиксированном е иллюстри-
иллюстрируется на рис. 2.6, б. Вначале увеличение я улучшает аппроксима-
аппроксимацию, но для /;, больших некоторого ямаКс (в), последующие при-
приближения становятся все хуже и хуже и расходятся при п-^>-оо.
Поэтому следует вычислять лишь ямакс первых членов разложе-
разложения, сумма которых будет отличаться от точного решения, грубо
говоря, на величину последнего (с номером ямакс) члена.
Наконец, отметим, что асимптотическое разложение для адиа-
адиабатических инвариантов несправедливо на интервалах времени,
значительно превышающих время «медленных» изменений в системе;
иными словами, адиабатический инвариант не может даже при-
приближенно сохраняться при ?->оо. Такое несохранение адиаба-
адиабатических инвариантов, известное как диффузия Арнольда, возни-
возникает в системах с тремя и более степенями свободы и является
основным содержанием гл. 6.
Медленное возмущение. Рассмотрим отличие в порядках членов
разложения для случая, когда возмущение мало и когда оно мед-
медленное, или «адиабатическое». Для малого возмущения гамильто-
гамильтониан имеет вид
H=H0(J, О + еЯ^/, 9, 0+ • •
где Яо описывает полностью интегрируемое движение, а е — ма-
малый параметр, характеризующий величину неинтегрируемой части
Н. Для малого возмущения производные от Яо и Нг полагаются
величинами того же порядка, что и сами Яо и Нlt т. е.
#i!
дНй
dt
—
0
3J
х) Для экспоненциальной малости существенна аналитическая зависи-
зависимость параметров от времени (см., например, [11, 244, 464]).— Прим. ред.
2) А также в случае явной периодической зависимости параметров от
времени.—• Прим. ред.
3) Это не всегда так, как показывает только что рассмотренный пример
функции Лх (<), определяемой формулой B.3.3) (см. также [465], § 1.3).—
Прим. ред.
Каноническая теория возмущений 107
Для медленного возмущения производные по времени прини-
принимаются по порядку величины в е раз меньше тех членов, из которых
они получены, т. е.
-е Но\
dt
Чтобы явно выделить эти порядки величин, запишем
#о=#о И,
так что
dt
где штрих означает дифференцирование по аргументу т = гг.
В этом параграфе нас будут интересовать такие системы, для
которых изменения во времени и движение по всем степеням сво-
свободы, кроме одной, являются медленными. С учетом этого запишем
гамильтониан в виде
H = H0(J, гу, eQ + eH^J, 9, гу, et)+ . . . , B.3.6)
где /, 9 — переменные действие — угол для невозмущенного
(е = 0) движения по единственной «быстрой» степени свободы, а
у = (р, q) — «медленные» канонические переменные (не обяза-
обязательно действие—угол) по остальным степеням свободы. Так как
при в = 0 система имеет фактически одну степень свободы, она
всегда является интегрируемой и можно ввести переменные /, 9.
При этом малый параметр е в B.3.6) будет «автоматически» давать
правильные порядки величин при дифференцировании Я в рядах
теории возмущений.
* 2.36. Каноническая адиабатическая теория
Построим классический адиабатический инвариант с точностью
до первого порядка для гамильтониана B.3.6). В нулевом порядке
таким инвариантом является действие /, связанное с быстрой сте-
степенью свободы. Чтобы учесть эффект возмущения ъНх, произведем,
как и в п. 2.26, преобразование от J, в, у к J, 9, _у, такое, что но-
новый гамильтониан
Я = //0+87?! + . . . B.3.7)
не будет зависеть от «быстрой» фазы 9. Вводя производящую функ-
функцию
S = 7Q+p-g-[-eS1[7, 9, р, <?,/)+. . . , B.3.8)
108 Глава 2
получаем в первом порядке по е:
ае
B.3.9а)
е=ё—е-^-, B.3.96)
dJ
B.3.9b)
dq
h B.3.9r)
qq
dp
Подставляя эти выражения в Яо и удерживая члены порядка"г,
находим '
Яо (J, гу, et) = Яо G, ejy, в*) + ею -^-, B.3.10)
где со = dHJdJ— быстрая частота. Заметим, что члены
_ дН0 dS1 дН0 ^ dS, B 3 11)
dq dp dp dq
имеют второй порядок малости по е и потому опущены. С помощью
выражения A.2.13в) получаем
и/7 п ~ ^ и 1 т n a I dS (j, В, ер, ее, et)
H(J, 8, гу, г() — Н(J, 8, гу, е^ + е ь^— f ч'—L,
d (et)
B.3.12)
Разлагая Н, Н и S, используя B.3.9) и приравнивая коэффи-
коэффициенты при одинаковых степенях е, находим в нулевом порядке
Яо G, гу, et) = Яо G, гу, et) B.3.13)
и в первом порядке
77,G, Э, гу, е*) = ш-^г- +//1G,8,еу, е/), B.3.14)
где S1==S1(,/, 9, е_у, е^), а член dSJdt в B.3.12) имеет второй
порядок малости и поэтому не вошел в B.3.14).
Выберем теперь S1 таким образом, чтобы исключить перемен-
переменную по 0 часть Hv Считая медленные фазы постоянными,^введем
среднее только по 9
2я
и переменную часть
{//1)е = Я1-(Я1M. B.3.16)
Каноническая теория возмущений 109
Разделение B.3.14) на среднюю и переменную части дает для Я
в первом порядке
ЯG, гу, et) = #„+ е(Hx)e, B.3.17)
причем Si легко находится из уравнения
<о-^- =— {Ях}й. B.3.18)
39
Адиабатическим инвариантом нулевого порядка является невоз-
невозмущенное действие /. В первом порядке новым инвариантом бу-
будет J, для которого в старых переменных из B.3.9а) имеем х)
7(/, 9, еу, ef) = J—e-^i-, B.3.19)
или с учетом B.3.18)
Фактически любую функцию от J можно взять в качестве адиаба-
адиабатического инварианта.
Малые знаменатели. Где же сингулярности, с которыми мы столк-
столкнулись в п. 2.26 и которые препятствовали сходимости рядов?
Их проще всего обнаружить, если принять, что в первом порядке
по е величины у являются переменными действие — угол: _у =
= (Jy, 6„). В этом случае, не опуская членов B.3.11) и dS^dt,
вместо выражения B.3.18) получаем
(o^L, +есв„- dSi +8_ggi_ =_{я1к. B.3.21)
сЮ д(еву) д(е0
Так как функции 5Х и {Я^д периодичны по всем угловым пере-
переменным и по Q/, их можно разложить в ряд Фурье
S — / Т ^Ш (^' ^) i (kS+m-Wy+lQet) /9 о 99\
(
ki 0
Отсюда видно, что малые знаменатели возникают вследствие ре-
зонансов высокого порядка (ш, I — большие числа) между медлен-
медленными и быстрыми колебаниями. Вблизи этих резонансов нельзя
пренебрегать членами порядка е в B.3.21). Поэтому нет ничего
2) Нижеследующие соотношения справедливы, вообще говоря, только
в том (редком) случае, когда невозмущенная система Яо (е) интегри-
интегрируема как при 8=0, так и при е Ф 0, несмотря на явную зависимость от
времени и многомерность. Иначе поправки к адиабатическому инварианту
будут зависеть и от функции На (е).— Прим. ред.
110 Глава 2
удивительного в том, что адиабатические ряды, в которых резо-
резонансные эффекты не учитываются, оказываются асимптотическими,
т. е. формально расходящимися и справедливыми лишь для интер-
интервалов времени, меньших или порядка характерного времени мед-
медленных изменений 1).
Описанное выше адиабатическое разложение можно выполнить
и в более высоких порядках. В каждом порядке необходимо решать
уравнение для 5„, подобное уравнению B.3.18) для S1. При этом
резонансные знаменатели никогда не появляются, а их действие
все время отодвигается во все более высокие порядки. Выражения
для адиабатических инвариантов высших порядков приведены
в § 2.5.
Иерархия инвариантов. Построение адиабатического инварианта,
если он действительно существует, фактически снижает число сте-
степеней свободы с N до N—1 (в пределах точности адиабатического
приближения). Это происходит потому, что задаваемый асимптоти-
асимптотическим рядом по степеням е преобразованный гамильтониан
Я = Н 11, еу, et, e)
не зависит от 0, а / — константа. Если среди оставшихся степеней
свободы найдется еще одна, колебания по которой являются бы-
быстрыми по сравнению с другими, то можно ввести второй малый
параметр е2, перейти к переменным действие — угол по этому бы-
быстрому движению для невозмущенной (е3 = 0) системы и найти
второй адиабатический инвариант. Этот процесс можно продол-
продолжить, что приведет к возникновению иерархии инвариантов и эф-
эффективному снижению числа степеней свободы вплоть до единицы.
Такая ситуация хорошо известна в физике плазмы для движения
заряженной частицы в магнитной ловушке. Вначале определяется
инвариант, связанный с быстрым ларморовским вращением, — маг-
магнитный момент ц, затем — продольный инвариант Уц, отвечающий
более медленным колебаниям между магнитными пробками, и,
наконец,— потоковый инвариант Ф, связанный с дрейфовым дви-
движением. Эти три степени свободы показаны на рис. 2.7 (более под-
подробное обсуждение данной задачи можно найти в работе [175]).
В рассматриваемом случае тремя малыми параметрами являются:
1) е — отношение частоты продольных колебаний к ларморовской
частоте; 2) е2 — отношение частоты дрейфового движения к ча-
частоте продольных колебаний и 3) е3 — отношение частоты измене-
изменения во времени магнитного поля к дрейфовой частоте.
Вся иерархия инвариантов ограничена условиями справедли-
справедливости адиабатической теории, и резонансы могут привести к изме-
1) Поскольку резонансные эффекты, вообще говоря, экспоненциально
малы, их влияние, например в виде диффузии Арнольда, проявляется на
значительно большем масштабе времени (см. § 6.2).—¦ Прим. ред.
Каноническая теория возмущений
111
нению пли разрушению этих инвариантов. Для частицы, движу-
движущейся в статической магнитной ловушке, такие процессы были
исследованы Чириковым 167, 70]. Аналогичные исследования для
частицы, находящейся в ловушке и взаимодействующей с перемен-
переменным электрическим полем, были проведены Егером и др. [212],
а также Либерманом и Лихтенбергом 1274]. В случае более чем
двух степеней свободы частицы подвержены диффузии Арнольда
даже при отсутствии перекрытия первичных резонансов. Однако,
как показано в гл. 6, при е -»~ 0 как скорость диффузии Арнольда,
Рис. 2.7. Иерархия адиабатических инвариантов для заряженной частицы
в магнитной ловушке: магнитный момент \i, продольный инвариант J ц, по-
потоковый инвариант Ф.
так и общий фазовый объем стохастических слоев, по которым
идет диффузия, стремятся к нулю. Поэтому в практических прило-
приложениях иерархия адиабатических инвариантов соответствует ис-
истинному движению с очень хорошей точностью. Адиабатическая
теория является и останется впредь одним из плодотворных под-
подходов к пониманию движения в динамических системах.
* 2.3в. Медленно изменяющийся гармонический осциллятор
С целью иллюстрации общего метода и резонансных эффектов вы-
вычислим адиабатический инвариант первого порядка для медленно
изменяющегося линейного осциллятора
F(r)q\
B.3.23)
где малый параметр введен посредством переменной т = et. Вна-
Вначале перейдем к переменным действие ¦— угол J, 9 для невозму-
невозмущенного гамильтониана Я/о = Я/ (е = 0) с помощью производя-
производящей функции
FAQ, в, x)=^-/?G2ctg0, B.3.24)
112 Глава 2
где R (г) = (FIGI2. Из A.2.11) получаем уравнения преобразова-
преобразований A.2.68) и новый гамильтониан
J sin 29. B.3.25)
2 R
Здесь соо (т) = (FGf 2, а штрих означает дифференцирование по т.
Наша система приведена теперь к виду B.3.6) и допускает приме-
применение метода Пуанкаре—Цейпеля.В нулевом порядке адиабати-
адиабатическим инвариантом является
/ = -^- = const, B.3.26)
т. е. число квантов йсоо сохраняется при медленном изменении ча-
частоты осциллятора [114]. Для определения инварианта первого
порядка применим выражение B.3.20) к гамильтониану B.3.25),
что сразу даст
7= .7A + еР sin 20) = const, B.3.27)
где Р (et) — R'/2a0R. Видно, что в первом порядке величина J
испытывает небольшие колебания с частотой, в 2 раза превышаю-
превышающей частоту осциллятора. Постоянство / можно проверить, взяв
производную по времени (обозначена точкой) от B.3.27),
Т= / + ePJ sin 29 + 2е<оо/Р cos 29 -f б (еа). B.3.28)
В силу канонических уравнений для гамильтониана B.3.25) пер-
первый и третий члены сокращаются и в первом порядке по е остается
T=eP/sin20. B.3.29)
Если медленное возмущение имеет обычный порядок малости, т. е.
Р ~ гР, то / ~ е3 и, следовательно, / является инвариантом пер-
первого порядка.
Прохождение через резонанс. Рассмотрим теперь изменение адиаба-
адиабатического инварианта, обусловленное резонансами между колеба-
колебаниями осциллятора и медленными периодическими изменениями
его параметров. Разложим Р в ряд Фурье
Р = е2 ajnaiet, B.3.30)
пфй
здесь ecox — частота медленных изменений, причем отношение
Каноническая теория возмущений 113
©!/©„ порядка единицы. Подставляя выражение для Р в формулу
2.3.29), получаем
где мы заменили J па J с точностью до величин первого порядка
по е. Интегрирование B.3.31) по периоду медленных колебаний
дает AJ/J —- е2, если частоты га>1 и <и0 несоизмеримы. В противном
случае, т. е. при
Ю0 __ _?_ (О Q ОО\
80)! 2
где s — целое число порядка е, члены суммы с п — ± s не за-
зависят от времени и интеграл по периоду медленных колебаний дает
-AL — е21 «s [ - 2яе~1 ~ е. B.3.33)
Таким образом, если резонанс поддерживается в течение времени
tp ~ 2яе~1/ц»1, то инвариант первого порядка разрушается, что
свидетельствует о сильном нарушении адиабатичности2). Это не
означает, однако, что интеграл движения вообще не существует,
просто он имеет другой вид. Действительно, в п. 1.36 мы видели,
что линейный осциллятор B.3.23) с периодически изменяющимися
во времени коэффициентами является интегрируемой системой,
откуда и следует существование некоторого интеграла движения.
С другой стороны, для нелинейного осциллятора возможно как
сохранение невозмущенного интеграла движения, так и его топо-
топологическое изменение или полное разрушение. Хотя нелинейный
1) Соотношение B.3.31) справедливо только по порядку величины, так
как уравнение B.3.29) содержит еще одно слагаемое eP J sin 29 =
= s2P*J озо sin 40 [см. B.3.27I. Для нижеследующих оценок это, однако,
несущественно.— Прим. ред.
2) Связь рассмотренной задачи с прохождением резонанса требует по-
частотно-
яснения. Пусть, например, Р (т) = P0cos ( Qot ~\ — sin (тсоЛ ) —
V wx J
модулированное возмущение с частотой Q (т) = Qo + Я cos (тсох). Резонанс
проходится, если при некотором % — тр частота Q (%р) = со0. В этом случае
амплитуда |<zs| ~ в" 2 и А/// ~ л/г, что уточняет оценку B.3.33). Вряд
ли можно говорить о сильном нарушении адиабатичности [на ин-
интервале времени ~ (ecoj)}, так как А/ < J. Однако даже первая поправка
к / B.3.27) уже теряет смысл. Если же резонанс не проходится, т. е.
Q (т) Ф ш0 для любого т, то амплитуда а5 экспоненциально мала и адиаба-
тичность имеет место в полной мере. Различные режимы прохождения ре-
резонанса, в том числе и для нелинейного осциллятора, исследованы, напри-
например, в работах [466, 68, 467].— Прим. ред.
114 Глава 2
осциллятор представляет больший интерес, мы ограничились здесь
линейной системой в целях иллюстрации методов построения раз-
разложений.
2.3г. Неканонические методы
Для некоторых типов задач изложенные выше классические ме-
методы неприменимы. В первую очередь речь идет об уже упоминав-
упоминавшейся задаче о дрейфовом движении заряженной частицы в маг-
магнитном поле (см. рис. 2.7). Гамильтониан в этом случае имеет вид
где
= mv+ —A(q, t) B.3.35)
с
— канонический импульс, а векторный потенциал А связан с маг-
магнитным полем соотношением В = V X А. Движение заряженной
частицы в однородном магнитном поле Во хорошо известно и сво-
сводится к ларморовскому вращению и равномерному перемещению
вдоль поля. Небольшие неоднородности поля могут заметно изме-
изменить характер движения, приводя как к колебаниям вдоль поля,
так и к поперечному дрейфу (см. рис. 2.7). Очевидно, что при ма-
малой неоднородности поля частота ларморовского вращения велика
по сравнению с частотами колебаний и дрейфа. В качестве малого
параметра в уравнениях движения можно принять отношение х)
т/е ~ е, что гарантирует большое значение частоты вращения
О, = еВ/тс ~ е~х. Однако в гамильтоновой формулировке B.3.34)
главные члены как по р, так и по Л имеют порядок Bel me ~ ?~х
и почти сокращаются, что затрудняет оценку порядков величин
по е. Эта трудность связана не с самим дрейфовым приближением,
а лишь с его гамильтоновым описанием 2). Подобные задачи побу-
побудили Крылова и Боголюбова [242], Боголюбова и Зубарева [32],
Боголюбова и Митропольского [33 ] и Крускала [239] сформули-
сформулировать адиабатическую теорию возмущений для системы диффе-
дифференциальных уравнений общего вида, необязательно гамильтоно-
*) Этот параметр является формальным, поскольку он никак не связан
с реальным возмущением в задаче — с неоднородностью поля.— Прим. ред.
2) Это утверждение спорно, см., например, [468]. Отмеченные трудности
связаны отчасти с тем, что обычно невозмущенным считается движение ча-
частицы в однородном магнитном поле, которое является инфинитным, т. е.
качественно отличается от финитного возмущенного движения частицы в маг-
магнитной ловушке. По поводу другого выбора невозмущенной системы в этой
задаче см. [464].— Прим. ред.
Каноническая теория возмущений 115
вых или необязательно в канонических переменных J). Как и в ка-
каноническом случае, эти методы предполагают наличие быстрой пе-
переменной по одной степени свободы и медленных по остальным сте-
степеням свободы и содержат усреднение на коротком масштабе
времени. Будучи эффективными и очень общими, эти методы не-
неизбежно оказываются и очень громоздкими, особенно в высших
порядках. В канонической формулировке дифференциальные урав-
уравнения получаются из скалярной функции Н; это же касается и пре-
преобразования переменных, которое определяется скалярной произ-
производящей функцией. В случае общего метода усреднения а) эти упро-
упрощающие обстоятельства отсутствуют.
Рассмотрим вначале метод Крускала и проиллюстрируем его
на примере вычисления адиабатического инварианта первого по-
порядка для медленно изменяющегося гармонического осциллятора.
Мы выбрали работу Крускала, а не Крылова и Боголюбова, по-
поскольку Крускал показывает, как неканонические возмущенные
решения связаны с переменными действия в тех случаях, когда
дифференциальные уравнения можно получить из гамильтониана.
Обращаем внимание читателя на недавно разработанный Литл-
джоном [281 ] метод, в котором используются неканонические пе-
переменные, но дифференциальные уравнения и преобразования пе-
переменных определяются, как и в методе Пуанкаре—Цейпеля, ска-
скалярными функциями. Подход Литлджона есть нечто среднее между
классической канонической теорией и общими методами усредне-
усреднения Крылова и Крускала (подробнее см. в [281 ]) 3).
Метод усреднения Крускала. Следуя Крускалу, рассмотрим авто-
автономную систему дифференциальных уравнений
x = f(x, e), B.3.36)
обладающую тем свойством, что при е =0 (/ = /0 (х)) траектория
х (t) является замкнутой («петля»). Прежде всего преобразуем пе-
переменные, чтобы разделить движение на быструю и медленную
части. Если х — jV-компонентный вектор, то должно быть N—1
«медленных» переменных _у = _у (х), описывающих движение са-
самой петли и удовлетворяющих условию
=/o-V^ = 0. B.3.37)
о
1) Поскольку это касается работ Боголюбова и его школы, следует заме-
заметить, что их основной мотивировкой были приложения к широкому кругу
задач, в которых нельзя пренебречь диссипацией и гамильтонов формализм
неприменим. — Прим. ред.
2) См. примечание редактора на с. 104. Используемый здесь и ниже тер-
термин «общий метод усреднения» подчеркивает, что такой метод не ограничен
гамильтоновыми системами.— Прим. ред.
3) Обобщение метода Литлджона на релятивистский случай содержится
в работе [472].— Прим. ред.
116 Глава 2
При этом оставшаяся «быстрая» переменная 0 = 0 (л:), периоди-
периодическая в нулевом порядке (е = 0), определяет движение вдоль
петли. В новых переменных уравнения B.3.36) принимают вид
y = egrC», 9),
• . а, B.3.38)
0 = соC>, 9),
где быстрая фаза 0 связана с одной из медленных переменных tji
которая в каноническом случае была бы переменной действия для
быстрой степени свободы. Преобразования переменных можно пред-
представить, как и в каноническом случае, в виде разложения по малому
параметру е.
Общий метод усреднения заключается в том, чтобы найти та-
такие «хорошие» переменные z и "ф, эволюция которых не зависит
от г|з:
Z = ей (z),
• г,/ ч B.3.39)
причем z, ty, h и Q можно определить независимо в каждом по-
порядке по е. Необходимо, таким образом, найти четыре уравнения,
устанавливающие связь величин n-го порядка с теми же величинами
(п—1)-го порядка. Поскольку величины нулевого порядка можно
определить непосредственно, то полное решение находится по ин-
индукции. Для получения этих соотношений выразим полные произ-
производные B.3.39) через переменные у и 0 с помощью выражений
B.3.38) и уравнений преобразования г = г (у, 0), г|> = "ф (у, 0):
г = у Z ¦ eg + —it- со = еЛ (z),
у дв B.3.40)
Дополнительно потребуем периодичности z и
г {у, Q + 2n) = z(y, 6),
B Я 4П
2я. l -°- ;
Из последнего выражения видно, что if играет роль угловой пере-
переменной. Для определения z и -ф как функций _у и 0, введем произ-
произвольно следующие начальные условия:
*{У0) = У B 3-42)
B-342)
Возможен и другой выбор начальных условий, однако выбор B.3.42)
упрощает преобразование переменных. Получим теперь выражения,
позволяющие определять z, t|\ h, Q в любом порядке по е. Предпо-
Каноническая теория возмущений 117
ложим пока, что мы сумели каким-то образом найти величины у,
0, g и со точно, хотя в действительности их можно представить и
в виде разложений. Разделив B.3.40) на со, интегрируя и определяя
постоянные из начальных условий, получаем
е
У„г-г) —. B.3.43а)
¦* ' (?>
¦ф= \(Q(z) — ey$-g) — - B.3.436)
J со
о
Условия периодичности дают
2л
-VJt-8)— = °> B.3.44а)
2я
-ev^-g-) —=2я. B.3.446)
Уравнения B.3.43) и B.3.44) являются теми четырьмя уравнениями,
которые позволяют находить неизвестные величины г, t|), A, Q в лю-
любом порядке по е. В канонической теории они соответствуют разде-
разделению уравнения B.3.14) для производящей функции Sx на среднюю
и переменную части *).
Следующим шагом является разложение z и -ф в ряд по степе-
степеням е, например:
г=Е^, B.3.45)
я
после чего А и Q также можно представить рядами, например:
B.3.46)
В нулевом порядке по е имеем z0 = у. В первом порядке эти
переменные определяются из выражений B.3.43) и B.3.44) при
z = у и h = hi следующим образом. Из B.3.43а) находим
M*)-V-ff)-J-. B.3.47)
См. уравнения B.3.49) — B.3.52).— Прим. ред.
118 Глава 2
я из условия периодичности B.3.44а)
2)-Vyy-*)-f- = 0- B.3.48)
2л
о
Используя Vs,yg = g" и определяя среднюю часть соотношением
2Я 2л
—> B.3.49)
/
о о
а интеграл от переменной части g посредством
е
, B-3.50)
получаем из B.3.48) и B.3.47)
h1(z) = (g), B.3.51)
zx=-g. B.3.52)
Аналогичные вычисления с использованием уравнений B.3.436)
и B.3.446) определяют -ф в первом порядке по е. Заметим, что фи-
физический смысл этих преобразований заключается в том, что в каж-
каждом порядке переменные определяются таким образом, чтобы их
средняя часть была равна нулю и интегрирование по углу не при-
приводило бы к появлению секулярных членов. Сами переменные мо-
могут иметь при этом различную природу. Для осциллятора с од-
одной степенью свободы и медленно изменяющейся частотой вели-
величина у может быть гамильтонианом. В случае нескольких степеней
свободы с не зависящим от времени гамильтонианом величина у
может представлять вектор переменных действия. В любом случае,
согласно формальной схеме Крускала, инвариант должен опреде-
определяться обычным образом:
2л N
2^
0 k=l
где pk, Ци могут быть либо компонентами z, либо в более общем
случае функциями от г. Крускал демонстрирует каноническую при-
природу / и 4", вычисляя для них скобки Пуассона
№, /] = 1. B.3.54)
Фактическое вычисление является довольно сложным, но уже сам
вид выражения B.3.53) для J показывает, что это действительно
переменная действия.
Каноническая теория возмущений 119
Медленно изменяющийся осциллятор. Проиллюстрируем метод Кру-
скала на примере изменяющегося во времени гармонического ос-
осциллятора. Хотя этот метод был разработан для применения в
многомерных системах, его основные черты можно показать и на
одномерной модели. Имеем
dt
B.3,55)
Gp,
dt F<
причем для упрощения принято G = const. Чтобы привести B.3.55)
к стандартному виду автономной системы уравнений первого по-
порядка, введем новую независимую переменную т = et. Обозначая
точкой производную по времени, получаем
p=-F(T)q, B.3.56)
т= е.
В нулевом порядке по е имеем т = const и, следовательно, F =
= const. Пусть векторная переменная _у равна
У = (Н, т), B.3.57)
т. е. имеет компоненты Них. Здесь Н — гамильтониан системы
H=-L-q*+-^-p*, B.3.58)
который в нулевом порядке сохраняется. Величины Н и т являются
(с точностью до знака) каноническими переменными расширенного
фазового пространства. Решение нулевого порядка есть просто
гармонические колебания
= <70sin(GV + P)
), l ¦" '
где, как и прежде, R = {FIGI2 и ю0 = (FGI2. Определяя угло-
угловую переменную посредством 6 = соо t -;- |3, находим из B.3.59)
B.3.60)
Мы хотим перейти к новым «хорошим» переменным, не зависящим
от быстрой фазы. Для этого надо использовать преобразования
B.3.43) и B.3.44) последовательно в каждом порядке по е. Чтобы
найти необходимые производные Я и 8, продифференцируем B.3.58),
подставляем в него B.3.56) и получаем
H=—F'q*, B.3.61)
120 Глава 2
где F' — производная по т. Из B.3.58) и B.3.60) можно выразить
q и р через Нив:
q2 = _2H_ sin2Q)
F B.3.62)
Подставляя q- в выражение для Я и учитывая равенство R'/R —
= F'I2F, имеем
'^)) B.3.63)
«ли
3> = (Я, T) = eg(H, т, 6). B.3.64)
Аналогичным путем, дифференцируя B.3.60) и используя B.3.56),
определяем производную для угловой переменной:
• 1 ( ?>' Рп Г. / J?n \21
Н =
B.3.65)
Выражая Rqlp из B.3.60) и преобразуя, получаем
6 = со0 + е -^— sin 20 = со (Я, т, 9). B.3.66)
Уравнения B.3.63) и B.3.66) можно теперь использовать для по-
получения «хороших» переменных гиф Применяя B.3.63), B.3.64)
и B.3.66) при вычислении выражения B.3.49), в первом порядке
•находим
(^ ) B-3.67)
и, согласно B.3.51), А2 = (g). Полагая z = (Я, т), вычисляя ин-
интеграл B.3.50) и используя B.3.51), получаем
Аналогичные вычисления приводят к тривиальному результату
% = т, что^вместе с B.3.68) позволяет определить в первом порядке
«хорошие» переменные z = (Я, т), так что z не зависит от if. Подоб-
Подобным же образом строятся и преобразования для угловой перемен-
переменной я|з.
Каноническая теория возмущений 121
Получив хорошие переменные, можно выразить через них ин-
интеграл движения
2л
7—J-^-JL-Jp-ft-,*. B.3.69)
где р и q — функции Н и я|з. В первом порядке по е достаточно'
выполнить интегрирование по 6 вместо if: это упрощение исполь-
использовано в работе Нортропа и др. [321 ]. Используя выражения
B.3.62) и вычисляя производную от q, получаем
2я
7= —!—f -^-cos26d9.
2я J со„
о
С помощью B.3.68) в первом порядке по е находим
7 =
2я J w0 \ 2ю0 R
о
Производя интегрирование, получаем выражение для адиабатиче-
адиабатического инварианта
Н /, + >bR' sin2e\. B.3.70)
ш0 w
Это выражение совпадает с выражением B.3.27), полученным'в^ка-
нонической теории возмущений. Если Н вычисляется в области,
где параметры не изменяются, то R' = 0 и мы приходим к обыч-
обычному выражению
-^- = const, B.3.71)
с
которое, как это видно из B.3.70), справедливо только в нулевом
порядке.
§ 2.4. Резонансная теория возмущений °
Вблизи резонанса невозмущенной системы малые знаменатели
появляются уже при вычислении адиабатических инвариантов
первого порядка (см. § 2.3). Эти знаменатели можно устранить
J) В оригинале — secular perturbation theory (секулярная теория воз-
возмущений). Принятый в переводе термин более непосредственно отражает
назначение теории, тогда как секулярнои в прямом смысле является класси-
классическая нерезонансная теория возмущений (см. § 2.2).— Прим. ред.
122 Глава 2
путем канонического преобразования к специальным (резонанс-
(резонансным) переменным. Такое преобразование можно наглядно пред-
представить себе как переход во «вращающуюся» в фазовом простран-
пространстве систему отсчета. При этом новые переменные описывают мед-
медленные фазовые колебания на резонансе, центр которого соответству-
соответствует неподвижной эллиптической точке на новой фазовой плоскости х).
Такая техника применялась ранее в нелинейной теории движения
частиц в ускорителях (см. [255 I, где приведена также дополни-
дополнительная литература) и при изучении электронного циклотронного
резонанса в магнитной ловушке [367]. Этот метод близок к исполь-
использованному Чириковым в работе [67] 2). После устранения резо-
резонансных знаменателей применяются описанные выше (§ 2.3) методы
усреднения по быстрой фазе. В дальнейшем рассматривается авто-
автономная гамнльтонова система с двумя степенями свободы. Обобще-
Обобщение на неавтономные системы не представляет труда путем введе-
введения расширенного фазового пространства (см. § 1.2).
Если возмущение достаточно велико, то появляются вторичные
резонансы, которые могут в свою очередь изменить или разрушить
интегралы первичных резонансов, вычисленные в п. 2.4а. Малые
знаменатели вторичных резонансов можно устранить аналогично
тому, как это делается для первичных резонансов (п. 2.46). Меха-
Механизм, с помощью которого вторичные резонансы разрушают интег-
интегралы первичных резонансов, повторяет механизм разрушения не-
невозмущенных интегралов первичными резонансами; он составляет
основу методов анализа перехода от регулярного движения к хао-
хаотическому в гамильтоновых системах (гл. 4).
В качестве иллюстрации в п. 2.4в рассмотрен резонанс между
волной и частицей, который описан ранее в п. 2.26. Отыскивается
резонансный интеграл движения и демонстрируется влияние вто-
вторичных резонансов. Все это поясняется с помощью некоторых ре-
результатов численного моделирования.
Преобразование к резонансным переменным — не единствен-
единственный способ описания топологических изменений адиабатического
инварианта вблизи резонанса. Имеется определенная свобода вы-
выбора инварианта, так как если / — инвариант невозмущенной си-
системы, то и любая функция / (/) тоже инвариант. Выбирая dlldJ =0
вблизи резонансных значений /, можно учесть изменения в топо-
топологии возмущенной системы. Этот метод, разработанный Дуннетом
и др. [111 ] (метод ДЛТ), описан в п. 2.4г и иллюстрируется на том
же примере резонанса волна—частица.
х) Возможность устранения резонансных знаменателей связана с учетом
нелинейности, точнее, неизохронности колебаний (зависимости их частоты
от амплитуды); см. ниже в этом параграфе и п. 3.2а.— Прим. ред.
2) Подобные методы использовались во многих работах (см., например,
[33, 232, 469]).— Прим. ред.
Каноническая теория возмущений 123-
* 2.4а. Устранение резонансных знаменателей
Рассмотрим гамильтониан
H = H0(J) + eH1(J, в), B.4.1)
где Яо описывает интегрируемую систему, а Нг является периоди-
периодической функцией Э:
#i= 2 HLm{j)einB. B.4.2)
I, m
Здесь п = (/, гп) — целочисленный вектор. Если между невозму-
невозмущенными частотами имеется резонансное соотношение
J^-^J-, B.4.3)
где г, s — целые числа и
со1(/)= 5-, a.2(J) =-^—~, B.4.4)
то попытка найти решение с помощью теории возмущений, описан-
описанной в § 2.2 и 2.3, приводит к малым резонансным знаменателям.
Будем считать, что условие B.4.3) относится либо к первичному
резонансу в системе, либо ко вторичному резонансу с фазовыми
колебаниями на первичном резонансе. В обоих случаях резонансные
знаменатели можно устранить с помощью преобразования, которое
исключает одну из переменных действия Jx или J 2. Выберем про-
производящую функцию
F2 = (rQ1—sQ2)J1 + QiJ2, B.4.5)
которая задает каноническое преобразование от J, 6 к J, Ъ:
/1=^?-=ri1, B.4.6а)
J2= — =^2 — S^b B.4.66)
91= -^- =г61—s8a, B.4.6b).
ея= -^~ =ея. B.4.бг>
dJ2
Скорость изменения новой резонансной переменной
ё1== reu
B.4.7)
характеризует медленные отклонения от резонанса.
При использовании производящей функции вида B.4.5) имеется
произвол в том, какую из исходных фазовых переменных оставить-
124 Глава 2
неизменной. Предположим, что 02 — наименьшая из двух частот,
и примем в 2 = 62, тогда усреднение гамильтониана по быстрой
фазовой переменной после преобразования будет проводиться по
более медленной из исходных фазовых переменных. Такой выбор
особенно удобен, если предстоит устранять знаменатели резонан-
сов высших порядков, так как в последних остается при этом более
низкая гармоника *).
Применяя преобразование B.4.6) к гамильтониану B.4.1) и ис-
используя A.2.13в), находим
H = H0[j) + bH1[J, в), B.4.8)
B.4.9)
I, m
Для получения преобразованного гамильтониана первого порядка
можно, как и в § 2.3, усреднить по переменной Э2 [ср. B.3.17)],
что дает
Я = Я0(у) + еЯ1(У, 9,), B.4.10)
Яо = ЯоG), B.4.11)
! (У, e)V;= ? H_pr,ps[j)e-tp»> . B.4.12)
Это усреднение справедливо вблизи резонанса, где 62^> 6V Так
как Я не зависит от 82, то
72 = 720 = const. B.4.13)
Это — первый^член ряда, представляющего адиабатический ин-
инвариант для гамильтониана B.4.8). Из B.4.66) видно, что 7% яв-
является комбинацией инвариантов невозмущенной системы:
J* = h +—^i = const. B.4.14)
г
Таким образом, введение резонансных переменных позволило в яв-
явном виде найти новый инвариант системы вблизи резонанса. Од-
Однако для резонанса высокого порядка, когда s ^> г, новый инва-
инвариант /2 просто пропорционален исходному инварианту J v Сле-
1) Это замечание непонятно и несущественно для дальнейшего. Конеч-
Конечный результат не должен зависеть от выбора переменной 82, в качестве ко-
которой, кстати, можно взять и любую комбинацию 6Х, 62, линейно независи-
независимую от 9j.— Прим. ред.
Каноническая теория возмущений 125
довательно, существенны только резонансы низких гармоник 1).
Поскольку J г = const, то движение, определяемое гамильто-
гамильтонианом B.4.10) в переменных J ъ Ъъ имеет фактически одну сте-
степень свободы и, следовательно, интегрируемо. Неподвижные точки
710, 910 на фазовой плоскости /1( 91; соответствующие периоди-
периодическим решениям для возмущенного гамильтониана, находятся
из условия
-^-=0, дЯ =а B415)
Для невозмущенного гамильтониана периодические решения при
резонансном значении J B.4.3) вырождены по Э, т. е. существуют
для всех Э. Возмущение снимает вырождение и оставляет только
периодические решения, удовлетворяющие B.4.15) (см. также об-
обсуждение теоремы Пуанкаре — Биркгофа в п. 3.26).
Обычно амплитуды Фурье Я_рл ps быстро убывают с ростом р.
Поэтому интегрируемое движение в переменных 7Ъ 6~х можно
описать с хорошей точностью, удерживая лишь члены с р = 0, ± 1:
77 = Но (J)+eHM(j) +2еЯг._5 G) cos9b B.4.16)
где принято Я_г, s = Яг, _s, что всегда можно обеспечить триви-
тривиальной заменой вх—>- 8Х -f- const.
Применяя B.4.15) к гамильтониану B.4.16), получаем
= 0, B.4.17)
0. B.4.18)
Из B.4.18) следует существование двух неподвижных точек 910 = 0
и 910 = я. При точном резонансе2)
0 B.4.19)
и уравнение B.4.17), определяющее J10, принимает вид
дН dHr_s =0> B.4.20)
где положительный знак соответствует 810 = 0, а отрицательный —
610 = я.
г) Это замечание справедливо, но по другой причине: обычно, хотя и не
всегда, резонансы высших гармоник очень слабые и соответственно область
резонанса с измененной топологией инвариантных поверхностей оказывается
узкой по переменным действия [см. B.4.31)).— Прим. ред.
2) Отметим, что условие точного резонанса по невозмущенным частотам
B.4.19) совместимо с B.4.15), вообще говоря, лишь в нулевом порядке по е
(см. B.4.17)].— Прим. ред.
126 Глава 2
Рассмотрим два случая.
1. Резонанс в невозмущенной системе имеет место только при
некоторых значениях Jt и У2- Такая система (и ее гамильтониан
Но) называется невырожденной х). Это наиболее типичный случай,
при котором невозмущенный гамильтониан после преобразования
зависит от обеих переменных действия
И —НпA 7.Л B 4 91 \
2. Условие резонанса B.4.3) выполняется для любых Jг, J2.
Такая система называется вырожденной 2). Очевидно, что в этом
случае
и после преобразования B.4.6а), B.4.66)
Ho=H0(j2), B.4.23)
т. е. Яо не зависит от J х. Вырождение по отношению к одному из
первичных резонансов довольно часто встречается в физических
системах 3), представляющих интерес. Однако этого почти никогда
не происходит по отношению ко вторичным резонансам в силу
очень сложной зависимости их частот от переменных действия.
Особенности вырожденных систем рассматривались Егером и Лих-
тенбергом [212] и Израйлевым [207 ]4).
Невырожденный случай. Из гамильтониана B.4.16) с учетом B.4.21)
получаем оценки
. Г'~" B.4.24)
откуда следует, что B.4.16) можно разложить в окрестности не-
неподвижной точки по переменной J1 (но не по 8-J. Обозначая
А/1=71— 710, B.4.25)
имеем
11 о \ *» / ^- -• * 0 ' ** 0 '
dJ l 2 дЦ
B.4.26)
1) В оригинале — accidentally degenerate (случайно вырожденная).
Этот термин используется в отечественной литературе в совершенно ином
смысле, соответствующем случаю 2, рассмотренному ниже.— Прим. перев.
2) В оригинале — intrinsically degenerate (внутренне вырожденная).—
Прим. перев.
3) Например, в случае линейных невозмущенных колебаний. Классиче-
Классическим примером вырождения для нелинейной системы является задача Кеп-
Кеплера (см. п. 1 .Зв).— Прим. ред.
4) Любопытные эффекты вырождения рассмотрены также в работах
[134, 470].— Прим. ред.
Каноническая теория возмущений 127
Вторым членом в правой части B.4.26) можно пренебречь в силу
B.4.19). Подставляя B.4.26) в B.4.16), опуская постоянную и удер-
удерживая лишь члены низшего порядка по е и Л/1( находим гамиль-
гамильтониан, описывающий движение вблизи резонанса
J—Fcos9~, B.4.27)
здесь G — параметр нелинейности
GG0)=-^^, B.4.28)
дА
а
F [Jo\ = — 2еЯ,, _s (Vo). B.4.29)
Этот примечательный результат показывает, что движение вблизи
любого резонанса *) подобно движению маятника с его колебаниями
вращением и сепаратрисой. Приближение B.4.27) использовалось
Чириковым [70 ] и другими авторами для описания типичного по-
поведения гамильтоновых систем вблизи резонанса; оно же является
основой нашего подхода при изучении хаотического движения
в окрестности сепаратрисы резонанса. Гамильтониан B.4.27) дает
в некотором смысле универсальное описание движения вблизи ре-
резонанса, поэтому мы будем иногда называть АН стандартным
гамильтонианом.
Перестройка движения под действием возмущения вблизи ре-
резонанса иллюстрируется на рис. 2.8, а. При GF>0 устойчивая
и неустойчивая неподвижные точки расположены при Q1 = 0 и
0j— л соответственно. Частота колебаний вблизи устойчивой не-
неподвижной точки (центр резонанса) мала:
'/ _S)V». B.4.30)
Эта частота уменьшается вплоть до нуля при приближении к сепа-
сепаратрисе, оставаясь все время много меньше частоты 62, которая
по порядку величины равна единице. Максимальное отклонение
ДА макс мало, происходит на сепаратрисе (при Qx= 0) и равно
половине ее ширины
Д71макс = 2 (-^)'/2 ~(e^,J'/>. B.4.31)
]) Правильнее было бы сказать—типичного резонанса, поскольку «при-
«приближение маятника» B.4.27) справедливо все же лишь при определенных
условиях — так называемой умеренной нелинейности, во-первых [см.
C.2.36)], и малости кратных гармоник, во-вторых (противоположный при-
пример см. в работе [471], § 4.2).— Прим. ред.
128
Глава 2
AJ
Центр резонанса
I
ия щазы
Сепсоатриса
Вращение фазы
Рис. 2.8. Фазовые траектории вблизи резонанса.
а — невырожденный случай; полуширина резонанса Д^1макс и частота фазовых коле-
колебаний со, малы (~ е'2); б — вырожденный случай; ширина резонанса порядка единицы.
а частота порядка е.
Каноническая теория возмущений 129
Вблизи центра резонанса фазовые траектории являются эллипсами
с отношением полуосей
h , _?)'/2. B.4.32)
Для полного решения задачи следовало бы выполнить преобразо-
преобразование к переменным действие — угол медленных колебаний (или
вращения). Однако такое преобразование необходимо по существу
лишь при учете вторичных резонансов и мы отложим его до п. 2.46.
Вырождение. Действуя, как и в предыдущем случае, но учитывая
независимость гамильтониана Яо от 7х [см. B.4.23)], вместо B.4.24)
получаем оценки
71~еЯ|.,_5, е1~еЯ0,0~еЯг,_5, B.4.33)
из которых следует, что отклонение по 7г и 0Х одного порядка,
поэтому нельзя разлагать гамильтониан B.4.16) только по Jъ
как это было сделано выше. В общем случае для анализа движения
системы B.4.16) можно перейти к новым переменным действие—
угол (см. п. 1.3а). Выясним сначала общий характер движения,
разлагая гамильтониан B.4.16) в окрестности центра резонанса
вх = 0 по степеням AJX и Авг = вг до квадратичных членов.
Имеем
1 даЯ0,0 | .") \2 I
dJl
i — И Г ) i ш'ол
— no.o\Jo)-i — s--±, ,
B.4.34)
B.4.35)
cos §i = l -(A9iJ+. . .. B.4.36)
Линейные по А]г члены выпадают в силу B.4.20); опуская постоян-
постоянные, мы приходим к гамильтониану гармонического осциллятора
\ B.4.37)
где
G= -Д-+В д2Нал +е д*Нг-*-, B.4.38)
ayf ^f ayf
F=—2eHr,_s. B.4.39)
130 Глава 2
Но при вырождении первый член в B.4.38) равен нулю, поэтому
как G, так и F оказываются величинами порядка г. Частота малых
колебаний вблизи центра резонанса равна
51 = (G/?I2—е, B.4.40)
а отношение полуосей эллипса —
.= fJlY2~l. B.4.41)
Вблизи центра резонанса вырождение определяется соотношением
B.4.38) и происходит при уменьшении первого слагаемого до нуля.
Аналогичным образом вблизи неустойчивой неподвижной точки
9Х = + я получаются гиперболические фазовые траектории с
асимптотами, наклоненными к оси 8а под углами ± %> где
- B.4.42)
Поведение вырожденной системы иллюстрируется на рис. 2.8, б.
Грубо говоря, оно похоже на невырожденное, если только G Ф 0.
Различия между ними, существенные для отображений и теории
КАМ, обсуждаются в п. 3.2а; там же кратко рассмотрен особый слу-
случай G = 0. Вообще говоря, характерная для вырождения слабая
нелинейность приводит к сложному поведению системы, тогда как
невырожденный случай оказывается обычно более простым для
анализа.
* 2.46. Вторичные резонансы
Если возмущение е не очень мало, то существенную роль играют
вторичные резонансы [см. B.4.9) ], которые изменяют или разру-
разрушают адиабатический инвариант J 3. Это резонансы между гармо"
никами фазовых колебаний на первичном резонансе (п. 2.4а) и не-
невозмущенными колебаниями основной частоты со2. В адиабатиче-
адиабатическом пределе их структура показана на рис. 2.9, а. Устранение
малых знаменателей вторичных резонансов можно провести по об-
общей схеме п. 2.4а, хотя здесь имеются, как будет видно ниже, не-
некоторые дополнительные особенности. Начнем с усредненного га-
гамильтониана B.4.10), в который необходимо ввести новые перемен-
переменные действие — угол (Iu ср^ для фазовых колебаний. Вместо ре-
решения уравнения Гамильтона—Якоби A.2.5.0) исследуем, как и
в п. 2.2а, движение в окрестности центра резонанса с помощью
теории возмущений. Обозначим через /Со преобразованный гамиль
тониан и, следуя логике принятых обозначений, будем писать /2
Каноническая теория возмущений
131
вместо Jo. В приближении B.4.16) из B.2.23) сразу же получаем
() &( 5-^-G/f+ . . ., B.4.43)
Id
Рис. 2.9. Фазовые траектории вблизи вторичного резонанса.
а — вторичный резонанс ntfli = со2 в переменных У,, 6iJ б — преобразование к перемен-
переменным действие — угол I it фх невозмущенных фазовых колебаний на первичном резонансе;
в — преобразование к резонансным переменным вторичного резонанса.
132 Глава 2
где G и tOj — функции /2, определяемые выражениями B.4.38)
и B.4.40). Если усреднение по 62 справедливо, то разложение
B.4.43) является формальным решением задачи. Оно не зависит
от угловых переменных, и, следовательно, существуют два интег-
интеграла движения: /2 = 72 и It. Преобразование к переменным Ilt
Фх показано на рис. 2.9, б.
Чтобы учесть эффект вторичного резонанса, восстановим член
Н\, отброшенный при усреднении по 82:
Н\ G,0) = Я, [Щ - Нх G,6). B.4.44)
Представим его в виде ряда Фурье
Я, = У 'Я, „G) exp [ i — 6, + i (I — + т) 6,1, B.4.45)
J-J \_ г \ г ) J
где штрих означает, что член с h + mr = 0 из суммы исключен.
В окрестности центра резонанса (810 = 0)
Н\ = \} Hi т(/ш+ Л/1,/2) exp u — A9i-f-
l.m
B.4.46)
Преобразуя это возмущение к переменным действие — угол
низшего порядка, т. е. для линейных колебаний переменных Д/^
КЬХ [см. A.2.68)], и обозначая Ъ% через ср2, находим
Я/,тG10,/2) ехр п'(I — +т ) ф2 exp i —
Urn
B.4.47)
где R = (F/GI2. Мы рассматриваем невырожденный случай и по-
потому пренебрегаем отклонениями А/х, считая их малыми в силу-
B.4.32). Разлагая вторую экспоненту, получаем
/Ci = V Тгт„ G10,/j exp Un^+ill— + m\<p2j, B.4.48)
I,m,n
где
rten = ^,mG10,/2)/J-(^-)"*|. B.4.49)
а /„ — функция Бесселя. Из B.4.48) [видно, что возможны ре-
Каноническая теория возмущений 133
зонансы между ф2 и ф1( поэтому усреднение по ф2 может привести
к отличному от нуля результату. Чтобы получить новый инвариант,
запишем полный гамильтониан, используя B.4.43) и B.4.48) в виде
аналогичном гамильтониану B.4.1) с некоторым новым параметром
возмущения е2. Эта аналогия позволяет для устранения сингуляр-
сингулярности вторичных резонансов снова использовать метод, описанный
в п. 2.4а. Рассмотрим резонанс
_ЩН-=-?_. B.4.51)
@1 Я
где
ю2=-^- = ю2^1, B.4.52)
Щ = ^~г12 B.4.53)
согласно B.4.4) и B.4.30). Аналогично B.4.6) перейдем к новым
переменным Iъ /2, ф1( ф2 с медленной фазой
ф1 = Рф1—q фг B.4.54)
Соответствующая производящая функция имеет вид
F2 = (р ф!—q фа) ~1г + ф2^2- B.4.55)
Усреднение B.4.48) по быстрой фазе ф2 с учетом B.4.51) приводит
к соотношению
nq+^l-j
где Is/r — целое число. Это соотношение удовлетворяется, если
в B.4.48) оставить только слагаемые с
n=—jp, l = kr, tn = jq—ks, B.4.56)
где /, k — любые целые числа. При / == ± 1, например, р-я гармо-
гармоника фазовых колебаний по фх находится в резонансе с <7-й гармо-
гармоникой колебаний по ф2 = 02; резонансам более высоких гармоник
отвечают значения |/|>1. Выполняя усреднение для гамильто-
гамильтониана К, получаем
Л./йФ.). B.4.57)
G) =/Се (/i G)ЛG)), B.4.58)
.-I/C,,.,/-1'*'- B-4.59)
134 Глава 2
В последнем выражении амплитуда Фурье /-й гармоники колебаний
по фх равна
Поскольку К не зависит от ц>2, мы сразу же получаем адиабатиче-
адиабатический инвариант фазовых колебаний
72 = /в + -!L /х = const B.4.61)
р
(таким образом, фазовые колебания оказываются интегрируемыми).
Сравнивая выражения B.4.57) и B.4.59) с B.4.10) и B.4.12), ви-
видим, что все результаты п. 2.4а применимы и в отношении вторич-
вторичного резонанса (см. также рис. 2.9, в).
Амплитуда фазовых колебаний. Для оценки величины вторичного
резонанса возьмем наибольший член в B.4.60) с | /1 = 1 и \k\ = \,
а также положим q = 1, что отвечает резонансу с основной часто-
частотой невозмущенных колебаний по 62 = ср2. Из B.4.49) следует,
что он пропорционален функции Бесселя
причем индекс р — целое число и в силу B.4.51) имеет порядок е ' .
Так как /1маКс порядка R, то максимальное значение аргумента
B1 XIR)X 2 порядка единицы. Отсюда при большом р (малом е) функ-
функцию Бесселя можно оценить как
l
Из этого выражения следует, что амплитуда Фурье резонанс-
резонансного члена пропорциональна If 2, так что размеры резонанса быстро
падают с убыванием Iг. Заменяя в формулах B.4.30), B.4.31) H_riS
на К-р.я и учитывая оценку B.4.62), приходим к заключению,
что амплитуда и частота колебаний Т1 меньше, чем для J1 по край-
крайней мере в |(е~1;'2)!]1/2 раз. Явное выражение для гамильтониана
вторичного резонанса будет получено в п. 2.4в.
Хотя анализ вторичных резонансов проводится аналогично ана-
анализу первичных резонансов, полученные результаты обладают
некоторыми особенностями. Так, размер вторичного резонанса за-
зависит от г значительно сильнее, чем первичного (~ е'/2), поэтому
при достаточно малом е вторичные резонансы несущественны х).
С другой стороны, при относительно больших е для определения
границы справедливости адиабатической инвариантности вторичные
J) Напомним, что этот вывод, как и вышеприведенные оценки для вто-
вторичных резонансов, справедлив лишь для малых фазовых колебаний на пер-
первичном резонансе. Вблизи сепаратрисы резонанса положение существенно
изменяется (см. п. 4.36).— Прим. ред.
Каноническая теория возмущений 135
резонансы могут быть столь же важны, как и первичные резо-
нансы.
Быстрое уменьшение размера вторичных резонансов с возмуще-
возмущением приводит к устойчивости движения внутри резонансов (в «ост-
«островах») при умеренной величине возмущения. Более того, даже при
весьма больших возмущениях, как, например, в случае на
рис. 1.13, в, интегралы движения сохраняются не только внутри
первичных, но и внутри вторичных резонансов. Следствия этой
устойчивости будут более подробно рассмотрены ниже.
Описанная процедура устранения малых знаменателей вторич-
вторичных резонансов в окрестности центра первичного резонанса [213]
является одним из вариантов метода ренормализации, в котором
преобразование от резонанса я-го порядка к резонансу (п ~ 1)-го
порядка строится таким образом, чтобы сохранить форму гамиль-
гамильтониана, изменяя лишь его параметры. Эта идея является основой
некоторых методов анализа перехода от регулярного движения
к хаотическому; эти методы анализа будут рассмотрены в гл. 4.
2.4в. Резонансное взаимодействие волны и частицы
Вернемся к примеру [в п. 2.26 — влиянию электростатической
волны на движение заряженной частицы в магнитном поле. Рас-
Рассмотрим случай резонанса между невозмущенным ларморовским
вращением частицы и колебаниями волны. Как мы видели выше,
в этом случае нельзя найти интегралы движения с помощью класси-
классической теории возмущений из-за появления резонансных знамена-
знаменателей. Однако резонансная теория возмущений дает возможность
устранить эти знаменатели локально. Следуя работе [267], рас-
рассмотрим две задачи: 1) волна распространяется под углом к маг-
магнитному полю (kz Ф 0), что соответствует невырожденному случаю;
2) волна распространяется перпендикулярно магнитному полю
(кг = 0), что соответствует вырождению.
Невырожденный случай. При kz Ф 0 условие резонанса B.2.71)
выполняется для различных значений т и импульса частицы Рг.
Выберем определенный резонанс т — I и перейдем к резонансным
переменным с помощью производящей функции B.4.5), которая
для гамильтониана B.2.67) принимает вид
ф)^ фф B.4.63)
Имеем
H=JLp\^u (Рф—/Рф)— /V» + ееФ0 2 fm(k_p) X
2М т
X sin[ij5—(m—Оф], B.4.64)
где р — функция переменных действия. Достаточно близко от ре-
136 Глава 2
зонанса переменная т|з изменяется медленно и можно провести ус-
усреднение по быстрой фазе ц>. В результате остается единственный
член с т = / и усредненный гамильтониан равен
Н = -^-Р1 + & (РФ— /Лц) — ?м>» + ееФо/i (fe±p) sintj>. B.4.65)
2М
Если произвести замену 1|з -> 1|э + л/2, так что sin ip -> cos ij;, то
Я примет вид B.4.16). Так как Н не зависит от ф, имеем
Рфо. B.4.66)
Согласно B.4.18) и B.4.20), неподвижные точки соответствуют
гро = О; я B.4.67а)
и
А. Рф— /Й— о = ± ееФ0^_ /; (А±р), B.4.676)
ЛГ ' дР
где
Уравнение B.4.676) неявно определяет величину Р^о. Линеаризуя
по Ру (но не по if), получаем гамильтониан маятника B.4.27) с па-
параметрами [см. B.4.28) и B.4.29)]
G = -|' B-4.69)
F = —ееФ0// (*j.po). B.4.70)
Согласно B.4.30), частота малых^колебаний равна
' k2 1/2
±± ¦ B.4.71)
М
Максимальная амплитуда (на сепаратрисе) получается из B.4.31)
^ B.4.72)
Как Ыф, так и ДРфМакс пропорциональны е1/2. Определим с по-
помощью B.2.71) расстояние между соседними резонансами
^ B.4.73)
Отношение удвоенной амплитуды колебаний импульса к рассто-
расстоянию между резонансами равно
2ДРф макс = 4м1|) # /2 4 74>
Q
Каноническая теория возмущений
137
Вырождение. Сравним полученные результаты с вырожденным слу-
случаем, когда в гамильтониане B.4.65) kz = 0. Проводя разложение
в окрестности центра резонанса как по АРФ, так и по А-ц?, прихо-
приходим к гамильтониану гармонического осциллятора с
B.4.75)
'/Oxpo). B.4.76)
Частота малых колебаний и максимальное отклонение импульса
равны
dPi
1/2
АР,[
B.4.77)
B.4.78)
Здесь со,), имеет порядок е, а АР^макс порядка единицы. Сравнивая
B.4.77) с B.4.71) и B.4.78) с B.4.72), мы видим, что при вырождении
частота малых колебаний в е~1/2 раз меньше, а максимальное от-
отклонение импульса во столько же раз больше, чем при отсутствии
вырождения.
В отличие от случая волны, распространяющейся под углом
к магнитному полю, частота возмущения теперь фиксирована и
равна со, поэтому резонанс возможен с одной из гармоник частоты
Q, хотя и при разных значениях импульса Р^. Действительно,
подставив kz = 0 в B.4.676), получаем уравнение
B.4.79)
определяющее значение Р^ для неподвижных точек. Корни этого
уравнения лежат в некотором интервале значений k±p.
Для со + ZQ = 0, например, их можно найти из условия
—~ fiik.pj^O. B.4.80)
Если же со + IQ = бсо, то, согласно B.4.79), резонанс имеет место
при условии
бсо
B.4.81)
В рассматриваемой задаче вырождение возникает, когда направ-
направление распространения волны становится нормальным к магнит-
138 Глава 2
ному полю. Чтобы увидеть, как происходит переход, учтем члены
порядка е в выражении B.4.38) для параметра G:
А-^г /ДМ- B-4.82)
М
Вырождение наступает при
— <ееФ0 -^- f, (/г,р) . B.4.83)
/И
Вторичные резонансы. Для получения гамильтониана вторичного
резонанса, как и в п. 2.46, перейдем к переменным /, 8 для малых
фазовых колебаний. При kz Ф 0 находим
B.4.85)
где G и Ыф определяются выражениями B.4.69), B.4.71), a R =
= (FiGf12. Низший порядок возмущения выражается в перемен-
переменных /, 8 аналогично B.4.47)
?т (k_p) sin [*o+(-^-)I/2sine —(m -
B.4.86)
Оставляя главный член суммы с т = / + 1, для резонанса гармо-
гармоники п получаем
/C1 = /Cnsin(^o + ne—ф), B.4.87)
где
2/ \11.2
Перейдем к новым медленным переменным
'=п6— ф-И'о —. B.4.88а)
/ = «7. B.4.886)
Каноническая теория возмущений 139
Усредняя B.4.86) по быстрой фазе ф, находим гамильтониан вто-
вторичного резонанса
А~К = — Gs(Alf— Fscos§, B.4.89)
где для Gs и Fs с помощью формул B.4.84) и B.4.87) при е зы 1
имеем
Gs= ^-n\ B.4.90а)
8
Ft = -Kn. B.4.906)
Частота малых колебаний и максимальное отклонение импульса
аналогично предыдущему равны
»S = (^GSI2, B.4.91)
Л7 — _%®s_. (9 4 Q91
'-"макс— \id.~x.vi,)
Gs
Расстояние б7 между соседними вторичными резонансами (гар-
(гармоники п и п + 1) можно найти, используя B.4.886) и соотношения
ф^^Й = 0, B.4.93)
откуда (при п > 1)
б7=-^4-- B.4.94)
С помощью выражения B.4.92) для hTM3KC получаем для вторич-
вторичного резонанса
_2AW =Jgi_, B.4.95)
б/ Шф
что совпадает по форме с аналогичным соотношением B.4.74) для
первичного резонанса. По индукции заключаем, что это отношение
сохраняет свой вид и для резонансов более высоких уровней (тре-
(третичных и так далее), т. е. оно является универсальным. Заметим,
что вторичным и более высокого уровня резонансам отвечают не-
невырожденные гамильтонианы.
Численные эксперименты. Детальные численные исследования были
выполнены Смитом и Кауфманом [385, 386] для невырожденного
случая (косая волна) и Карни, Берсом, Фукуямой и др. [222, 220,
145] для вырожденного случая (перпендикулярная волна).
Для косой волны Смит и Кауфман исследовали движение вблизи
резонансов с / = kzvJQ — — 1; 0; 1 в системе отсчета волны
(со = 0). Они выбрали k± BE!M)U2!Q —1,48, где Е дается выраже-
140
Глава 2
2L
<C^> .. - *7^==7ГГГа-.
Рис. 2.10. Поверхность сечения в переменных kzVz/Q ее Р$ и 62z = ф в слу.
чае взаимодействия частицы с косой (kz Ф 0) волной (численное моделиро-
моделирование) (по данным работы [385]).
а — слабое возмущение (ф
Численные результаты представлены точками, которые соединеиы от руки сплошными
лиииямн (для регулярных траекторий). Начальные условия отмечены крестиками. Видны
три резонанса.
z« Ф0/ЛШ2 = 0,025); б — сильное возмущение (Ф = 0,1)-
Каноническая теория возмущений
141
нием B.2.66) при со == 0, е = 1 и kz = k±, что обеспечивает близ-
близкое к максимальному значение функции Бесселя ft(k±p). Их ре-
результаты для зависимости vz (осРф) ото)) приведены на рис. 2.10, а
.,, J
» '. • I I : /
111!
t
Zti
a
50
....•¦ ¦. ..:.:•:"¦.::;.;• ...,-¦¦.. л*-"
.il* ¦'{.¦ "'?' '^"^•"'¦"^."¦¦^x'v^^- :-
¦¦•.-••¦.¦¦•¦•;•¦ -..,'¦¦'¦¦ ~ ¦¦•/;•;¦•.¦.¦• •¦;•• 'k.4* ~- :."—-' *••;.'i
31
6
Zut
Рис. 2.11. To же, что и на рис. 2.10 для kz = 0 и co/Q = — 30 (по данным
работы [219]).
а — слабое возмущение; б — более сильное возмущение.
и б при &2еФ0/Л1&2 = 0,025 и 0,1 соответственно. На рис. 2.10, а
видны первичные резонансы, относительная частота малых фазо-
фазовых колебаний которых равна (оф/й = 1/10, что согласуется с фор-
формулой B.4.71). Вторичные резонансы в этом случае слишком малы
и поэтому неразличимы. На рис. 2.10, б видны вторичные резо-
142 Глава 2
нансы пятой гармоники, т. е. с частотой co^/Q — 1 5, что опять
согласуется с B.4.71). Размеры вторичных резонансов можно при-
приблизительно вычислить из соотношения B.4.92). Разбросанные
в окрестности сепаратрис резонансов / = — 1 и I = 0 точки пред-
представляют стохастические траектории (см. § 1.4). Решения, полу-
полученные в данной главе с помощью метода усреднения, совершенно
не отражают стохастическое поведение. Обратим также внимание
на резонансы второй гармоники, расположенные между областями
главных резонансов; это явление обсуждается в последующих
главах.
Сопоставим эти результаты с тем, что получается в случае пер-
перпендикулярной волны, который численно исследован Карни [219 J.
На рис. 2.11, а и б приведены его результаты для поверхности се-
сечения ф = л при / = — 30. Относительная частота малых фазовых
колебаний первичного резонанса а = со^/й та 1/9 для меньшего
возмущения и а ж 1/5 для большего. В первом случае инвариант-
инвариантные кривые почти совпадают с полученными из усредненного га-
гамильтониана B.4.65) 1) при kz = 0. При большем возмущении воз-
возникает, как и ожидалось, цепочка из пяти островов и другие уже
привычные нам детали. Размер первичных резонансов примерно
одинаковый в обоих случаях, поскольку, как было показано выше,
этот размер не зависит от возмущения. Как и для косой волны, ис-
исследование проводилось при значениях kxp, близких к максимуму
tfi (k±p). Аналогичные результаты для другой задачи были полу-
получены Фордом и Лансфордом [134].
2.4г. Глобальное устранение резонансных знаменателей
Теперь мы опишем метод ДЛТ (Дуннета—Лейнга—Тейлора) [111],
позволяющий в некоторых случаях устранять знаменатели сразу
всех первичных резонансов. Этот метод был вначале использован
при изучении движения заряженной частицы в пространственно
периодическом магнитном поле [111], а позже применен для ана-
анализа резонансного взаимодействия волны и частицы (п. 2.4в); по-
последний случай рассмотрен ниже. Обобщение этого метода на бо-
более высокие порядки по параметру разложения выполнено Мак-
Намарой [290] и будет описано в конце следующего параграфа.
Метод ДЛТ был разработан для изучения автономных систем
с двумя степенями свободы и невозмущенным гамильтонианом Но
специального вида
Яо(/) = а(У1) + со2Уг, B.4.96)
где со 2 — постоянная частота, так что обе частоты а1 и со2 не за-
!) Только для одной (по-видимому, правой) Гполовины поверхности се-
сечения на рис. 2.И. Для другой половины фазовые колебания связаны с чле-
членом пг ф I в гамильтониане B.4.64) ( | m—11 = 1). То же касается и частоты
малых колебаний, например, значение а = 1/5 относится только к правому
резонансу на рис. 2.11, б.— Прим. ред.
Каноническая теория возмущений 143
висят от одной из переменных действия (в нашем случае от У2).
Такая форма гамильтониана не является исключительной и даже
типична для неавтономных систем с одной степенью свободы, ко-
которые можно изучать в расширенном фазовом пространстве (см.
п. 1.26) 1).
Метод ДЛТ использует определенную свободу в выборе интег-
интегралов движения. На поверхности сечения Э2 = const инвариантные
линии являются прямыми Jг = const. Но и любая функция /0 (Jx)
также приводит к этим же прямым
I0(JJ = const. B.4.97)
Поэтому /0 тоже можно рассматривать как интеграл невозмущен-
невозмущенного движения и выбирать его конкретную форму по своему усмот-
усмотрению.
Непригодность классической теории возмущений для описания
движения вблизи резонанса обсуждалась в п. 2.26; там же и в
п. 2.4в были рассмотрены конкретные примеры резонансных знаме-
знаменателей. Неудача классического подхода имеет простое физическое
объяснение: топология истинных инвариантных кривых / = const
отличается вблизи резонанса от топологии невозмущенных инва-
инвариантных кривых /0 — const. Вообще говоря, при малом е линии
/0 -г е/ j = const могут топологически отличаться от линий /0 =
= const, только если 1г велико. Поэтому появление больших зна-
яений /х есть просто отражение топологических изменений в теории
возмущений. Это наводит на мысль о том, что можно улучшить
теорию возмущений, если выбрать такие невозмущенные интегралы
движения, чтобы отличие в топологии обеспечивалось при малых
Iг. Так будет в том случае, когда dlJdJ-y обращается в нуль, т. е.
инвариантные кривые /0 = const соответствуют максимуму или
минимуму по невозмущенному действию J г.
Теория возмущений. Для построения разложения нового инвари-
инварианта / заметим, что, согласно A.2.21), любой интеграл движения
удовлетворяет условию
[/, Я] = 0. B.4.98)
Разлагая Н и /, получаем
H(J, в) = Я0G) + еЯ1(У, в)+ • • ., B.4.99)
/ (У, в) = /0 (Л) + e/j (J, в) + . . . , B.4.100)
где /0 выбрано так, что является функцией только Jх. Приравни-
Приравнивая коэффициенты при одинаковых степенях е, находим, что в ну-
нулевом порядке условие
[/„, Яо] = 0 B.4.101)
х) Метод ДЛТ применим и непосредственно к неавтономным системам
с одной степенью свободы, причем без ограничений на вид невозмущенного
гамильтониана Яо (J).— Прим. ред.
144 Глава 2
всегда удовлетворяется, ибо по построению /0 и Ио не зависят от
угловых переменных. В первом порядке имеем
Ни Яо] + [/о, Н1} = 0, B.4.102)
или
щЛ±+щЛ1. = Л±Лк.. B.4.103)
Разлагая Нг\\ 1г в ряд Фурье
nld+diB.4.104a)
B.4.1046)
l,m
получаем из B.4.103)
,m = lJ^-Hlm. B.4.105)
Чтобы найти инвариант, положим
_di°_ = Д cr m,(co1/' + co2m')) B.4.106)
dJx f'.m'
где Ci',m' — некоторые коэффициенты, а произведение берется по
всем тем значениям индексов /', т', для которых амплитуды Фурье
Hi'.m' отличны от нуля. По построению dIQ/dJ1 обращается в нуль
на каждом резонансе, и величины Iim, согласно B.4.105), оказы-
оказываются конечными. Новый инвариант имеет вид
/ = /0 + е/г = const, B.4.107)
где /0 находится интегрированием B.4.106), а 1г определяется ра-
равенствами B.4.105) и B.4.1046).
Резонанс волна — частица. Для иллюстрации метода рассмотрим
гамильтониан B.2.67) для волны, распространяющейся под углом
45° к магнитному полю [403]. Перейдем в систему отсчета волны
(со == 0) и введем безразмерные переменные: k± = kz = 1, Q — 1(
М = 1, еФ0 = 1, р = BРфI/2. Имеем
Я = — Pi+Pcp-fe, V fm(p)sin(ty—mq>). B.4.108)
В соответствии с B.4.106) полагаем
%) ф B.4.109)
т
Каноническая теория возмущений
145
С помощью выражения B.4.105) находим
/m = Sin яРф /т(Р) .
— т
Интеграл движения первого порядка равен
B.4.110)
-. B.4.111)
kzz
Рис. 2.12. То же, что и на рис. 2.10 согласно теории ДЛТ первого порядка
(по данным работы [403]).
Заметим, что второй член этого выражения остается малым даже
при резонансах.
На рис. 2.12 показаны инвариантные кривые / = const на по-
поверхности сечения ф = л для тех же значений параметров, что
146 Глава 2
и результаты численного моделирования на рис. 2.10. Согласие
между этими рисунками хорошее, хотя, конечно, области хаотиче-
хаотического движения, которые наблюдаются при сильном возмущении
на рис. 2.10, б, нельзя получить из инвариантных кривых.
Отдельный резонанс. Сравним интеграл движения / в методе ДЛТ
с интегралом резонансной теории возмущений в случае одного ре-
резонанса. Для гамильтониана
Н = а (А) + со2У2 + г A sin (Ш±~tn%) B.4.112)
преобразование B.4.6) к резонансным переменным дает
Н = а (/ /,) + со2 ( J2—mJi) + гА sin 9,. B.4.113)
Так как Н не зависит от 9а, то /2 = const. Поскольку Я = const,
то
Ч-бЛэте, B.4.114)
также является интегралом движения. Применяя метод ДЛТ, по-
получаем из B.4.106) уравнение
dlo _ da m
%. B.4.115)
dj1 dJi I
В результате приходим к интегралу -движения /, который точно
совпадает с Т.
Распространение метода ДЛТ на более общие, чем B.4.96), га-
гамильтонианы до сих пор не сделано. Неясно также, как выбирать
/0 в тех случаях, когда амплитуды Н[т всех гармоник отличны от
нуля, так как при этом производная dlJdJ^ должна обращаться
в нуль для всех рациональных значений отношения частот. Тем
не менее в пределах этих ограничений метод ДЛТ весьма полезен
для глобального устранения резонансных знаменателей 1).
§ 2.5. Метод преобразований Ли
При использовании теории возмущений часто необходимо иметь
разложение выше первого- порядка. Так было в задаче Хенона и
Хейлеса (см. п. 1.4а), где1в силу вырождения потребовалось про-
провести вычисления по крайней мере во втором порядке, чтобы по-
получить хоть какое-то представление об истинных фазовых траекто-
траекториях даже при низкой энергии. Имеются и другие случаи (см.,
например, п. 2'.5в), когда в первом порядке получается нулевой
результат, а отличные от нуля члены возникают только во втором
или более высоких порядках. '
*) Отметим, что преимущество метода ДЛТ реально проявляется только
в том (по-видимому, редком) случае, когда подбором коэффициентов С/т про-
произведение B.4.106) можно представить как достаточно простую функцию
Jx.— Прим. ред.
Каноническая теория возмущений 147
Применение классических методов Пуанкаре—Цейпеля для
разложения выше первого порядка становится все более и более
утомительным. При классическом подходе для преобразований от
старых переменных У, 8 к новым У, 9 используется производящая
функция смешанного набора переменных, например 5 (8, J, t).
В результате и само преобразование также получается в смешанных
переменных
9(8,7, 0=-aSF'7'f)-. B.5.1)
dJ
в то время как желательно было бы определить новые переменные
как функции старых 9 (8, J, t), или наоборот. То же самое спра-
справедливо и для соотношения между новым и старым гамильтониа-
гамильтонианами
Н (в, J,t) = H (в, J, t) + I^AJL. B.5.2)
Если Н, Н и S можно представить в виде рядов по степеням е, то
относительно нетрудно получить разложение в любом порядке [34 ].
Однако уже во втором порядке по е появляются громоздкие выра-
выражения [см., например, B.2.19) ] без какой-либо явной системы в
них. В более высоких порядках количество алгебраических выкла-
выкладок становится удручающе велико, а физические закономерности
оказываются глубоко скрытыми.
Значительным шагом в развитии гамильтоновой теории возму-
возмущений явилось введение преобразований Ли в работах Хори [199]
и Гарридо [150]. При использовании этих преобразований не воз-
возникают функции смешанного набора переменных, а все члены ря-
рядов получаются в результате последовательного применения ско-
скобок Пуассона, что делает теорию канонически инвариантной.
Депри [102] усовершенствовал этот метод и получил соотношение
для определения я-го члена разложения преобразования в степен-
степенной ряд по е. Дьюар [105] разработал вариант метода, пригодный
для изучения систем, не допускающих- представления преобразо-
преобразования в виде степенного ряда. Драгт и| Финн [107] использовали
метод Ли при изучении сохранения магнитного момента в диполь-
ном поле. Хаулэнд [203] применил этот метод в сверхсходящейся
теории возмущений Колмогорова. Существенный вклад в разра-
разработку метода внесли Кауфман и сотр. [214, 51, 52, 22*4, 225], а также
Мак-Намара [290]. Новая техника построения разложений, осо-
особенно эффективная в высоких порядках, описана Кари [50], ко-
который следовал работе Драгта и Финна [108]. Изложение метода
Ли содержится в монографиях Найфе [313] и Джакалья [153],
а также в методических статьях Кари [49, 50] и Литлджона [280].
Наше изложение основано главным образом на последних статьях.
148 Глава 2
В п. 2.5а описаны основы метода Ли, который затем исполь-
используется для получения степенных разложений Депри (п. 2.56). В ка-
качестве иллюстрации получены поправки второго порядка к гамиль-
гамильтониану маятника. С помощью модификации метода Ли в п. 2.5в
рассмотрены ряды для адиабатических инвариантов и их приложе-
приложение к вычислению инварианта второго порядка изменяющегося во
времени гармонического осциллятора, а также средней силы, дей-
действующей на заряженную частицу в поле электростатической
волны. В заключение кратко описана методика Мак-Намары [290 ]
получения адиабатических инвариантов высших порядков. В ка-
качестве примера рассмотрен резонанс волна—частица.
2.5а. Общая теория
Начнем с рассмотрения автономных систем; случай явной зависи-
зависимости гамильтониана от времени исследуем позже. Пусть х={р, q) —
вектор обобщенных импульсов и координат, представляющий
положение системы в фазовом пространстве. Введем производящую
функцию Ли w (х, е) с помощью уравнения
-^=[х, w(x, г)], B.5.3)
de
которое можно рассматривать как уравнение Гамильтона с «га-
«гамильтонианом» w и «временем» 8, записанное посредством скобок
Пуассона. Его решение при любом е и начальном условии х:
х = х(х, е) B.5.4)
представляет собой каноническое преобразование от х к х, для ко-
которого выполняются соотношения
[<ji, чЦ = [Ph Pi] = 0; [qt, Pi] = 6if. B.5.5)
Введем отвечающий преобразованию B.5.4) эволюционный оператор
Т, который переводит любую функцию g в преобразованной точке
х (х, е) в соответствующую функцию / в начальной точке, т. е. ра-
равенство
f = tg B.5.6)
означает
f(x)=g[* (*,*)]• B-5.7)
В частности, если g (x) — х, то
х=Тх. B.5.8)
Для явного определения преобразования Т введем оператор Ли L'-
L = [w, ]. B.5.9)
Каноническая теория возмущений 149
Из B.5.3) и B.5.8) получаем операторное уравнение
— =— ft, B.5.10)
de
которое допускает формальное решение
f = exp[—jL(e)de]. B.5.11)
Для любого канонического преобразования, в том числе и для
порождаемого функцией w, новый гамильтониан Н связан со ста-
старым гамильтонианом Н соотношением
Н(х{х,г)) = Н{х), B.5.12)
т. е. новый гамильтониан в новой точке равен старому гамильто-
гамильтониану в старой точке. В силу B.5.6) и B.5.7) получаем
Ц=Т~ХИ. B.5.13)
Для неавтономных систем w, L, Т являются явными функциями
времени t, которое считается фиксированным при выводе преобра-
преобразования Т. По этой причине все полученные выше соотношения
до B.5.11) включительно остаются справедливыми. Однако старый
и новый гамильтонианы не совпадают, и равенство B.5.13) не вы-
выполняется. Правильное соотношение [49]
^51' B.5.14)
J dt
о
[ср. с A.2.Ив) или A.2.13в)] было впервые получено Дьюаром
[105]. Вместе с выражениями B.5.9) и B.5.11) для операторов L
и Т оно дает полное описание канонических преобразований с по-
помощью производящих функций Ли.
2.56. Ряды Депри
Разложим w, L, Т, Н и Н по степеням е [102, 49]:
а> = 2 е"а;„+1, B.5.15)
/1=0
L=SeBLB+lf B.5.16)
/1=0
t=^enfn, B.5.17)
/1=0
Я=2еп#я, B.5.18)
/1=0
!50 Глава 2
Я=2ое"Я„, B.5.19)
тде [см. B.5.9I
Ln = [wn]. B.5.20)
Подставляя B.5.16) и B.5.17) в B.5.10) и приравнивая коэффици-
коэффициенты при одинаковых степенях е, получаем рекуррентное соотно-
соотношение для Т„ (п>0):
Тп = 1-"у tntn-m, B-5.21)
л ^о
которое вместе с условием Го = 1 позволяет определить Тп через
Ln во всех порядках. Заметим, что в общем случае эти операторы
не коммутируют, т. е. Lib/ Ф LjLi и т. д.
Нам потребуются обратные операторы Т\,х, для определения
которых продифференцируем равенство ТТ~Х = 1 по переменной е,
откуда
dT~l =LT~\ B.5.22)
de
Последнее уравнение позволяет написать рекуррентное соотноше-
соотношение для Г-1 («>0, Г-1 = 1):
77'=-"-У Ln-mfn\ B.5.23)
В первых трех порядках находим
ti = —Lu B.5.24а)
Т2= -L2-f— L\, B.5.246)
Т3= LL3-j--LL2L1+^-LIL2--i-^. B.5.24в)
3 0 о b
ТГ1 = ?-ь B.5.25а)
7Т' = —L2-f—??, B.5.256)
2 2 '
7У = 4-?з+— L,L2 + -i-^i+4^- B.5.25b)
об о b
•Основное правило отыскания 7Y1 по заданному Г„ таково: вместо
Ln подставляем — Ln и изменяем на обратный порядок записи всех
произведений некоммутирующих L-операторов.
Каноническая теория возмущений 151
Чтобы получить уравнения для wn, умножим B.5.14) на t слева
и продифференцируем по е
dT -fj + f J*L J*L + t B.5.26)
de de dг dt
Исключая df/de с помощью B.5.10) и умножая слева на Т1, на-
находим
dw dH t-jj j,—l dH ,„ r (-,„,
Используя степенные разложения, в я-м порядке (п ф 0) имеем
dWn =пН„ У Lr, m#m V mf~lmHm C>5 28>
о m=0 от =1
Переписывая первый член первой суммы в виде LnH0 = LnH0 =
= [wn, Ho f, приходим к окончательному результату
п—\
Down = п \Нп—Нп) - ? (Ln^mHm + mfn-mHj, B.5.29)
где учтено, что в нулевом порядке Но = Но, и введено обозначение
полной производной по времени вдоль невозмущенных траекторий
?>oS3-J-+[ , HQ]. B.5.30)
Уравнения B.5.29) до третьего порядка таковы
'Hx — H1, B.5.31а)
2)~Ll{Hi + H1), B.5.316)
B.5.31b)
Уравнение B.5.31а) следует сравнить с эквивалентным ему урав-
уравнением первого порядка B.2.10), полученным по методу Пуанкаре—
Цейпеля. В обоих случаях по заданному Нг мы выбираем некото-
некоторое Н\ обычно так, чтобы устранить секулярности в производящей
функции wx или Slt а затем определяем саму производящую функ-
функцию. Полученное wx используется в правой части уравнения
B.5.316), где #2 выбирается таким образом, чтобы устранить се-
кулярность в w2 и т. д. вплоть до любого желаемого порядка.
Хотя система уравнений вида B.5.31) формально справедлива
при любом числе степеней свободы, но если их больше одной, то
возникают резонансные знаменатели, так же как и при использо-
использовании производящих функций от смешанного набора переменных.
152 Глава 2
Формальный способ их устранения до любого порядка описан
в п. 2.5в.
Маятник. Для иллюстрации применения рядов Депри продолжим
рассмотрение примера в п. 2.2а и получим описание нелинейных
колебаний маятника во втором порядке. Старый гамильтониан
B.2.22) был записан в переменных действие — угол невозмущенной
(линейной) системы J, 8. В нулевом порядке из B.2.22а) имеем
Я0(/) = со0/. B.5.32)
В первом порядке B.5.31а) дает
СОо_^1. = Я1_Я1, B.5.33)
где Нх определяется выражением B.2.226)
Я1= ^— C — 4 cos 28 + cos 48).
48 v
Выбирая Ях так, чтобы исключить порождающее секулярность
среднее от Нъ имеем
Hl(J) = (H1)= — G/2, B.5.34)
16
где скобки ( ) означают среднее по 8. Уравнение B.5.33) при-
принимает вид
I-* г iff I со с, оел
где скобками {) обозначена переменная часть. Интегрируя B.5.35),
"находим выражение для wx:
цу1 = —L_J^L (Sin 48- 8 sin 28). B.5.36)
192 w0
Заметим, что в первом порядке Н1 в B.5.34) я w1 в B.5.36) совпа-
совпадают с полученными ранее выражениями B.2.23) и B.2.25), где
вместо J фигурирует J. Переходя ко второму порядку, переписы-
переписываем уравнение B.5.316)
со0 = 1\п<1—П2)—L\ \п\ + п\) (Z.o.oi)
C6
через средние и переменные части в виде
8W2
оь
= 2(H2-(H2)-{H2})-2[w1, (Н$-1щ, №}]. B.5.38)
Снова выберем Я2 так, чтобы обратить в нуль среднее от правой
части этого уравнения. Среднее от первых скобок Пуассона уже
Каноническая теория возмущений 153-
равно нулю, так как w1 содержит только переменную часть. Вторые
скобки Пуассона есть произведение двух функций и их среднее от-
отлично от нуля. Положим
H2 = (Ht) + -L([wlt {H,}]). B.5.39)
Выражая второй член с помощью B.2.226) и B.5.36), находим
[шъ \Н1\] = ' — A7 — 9cos29 +cos69). B.5.40).
1152 со0
Используя это соотношение и B.2.22в), получаем
н ' °2р
/72 = •
256 ш0
Заметим, что Я2 не есть просто среднее от Я2, а содержит допол-
дополнительное слагаемое, квадратичное по величинам первого порядка.
Для получения Я2 достаточно знать w1 и вообще для определения
Нп необходимо иметь w вплоть до порядка (п—1). Чтобы найти w2r
надо проинтегрировать уравнение B.5.38), которое с учетом B.5.39)*
принимает вид
Щ= -2 \Нъ)-2[щ, <Я1>]-{[а;1> (Я,)]]. B.5.41)
(Го
Решение этого уравнения не представляет большого интереса и здесь,
не приводится. Суммируя Яо, Нх и Я2, получаем во втором по-
порядке (е = 1)
Я = (й0/ —GP 1- ^-. B.5.42)
16 256 ш0
На первый взгляд кажется странным, что новый гамильтониан яв-
является функцией только старого действия /. Последнее становится,,
однако, понятным, если учесть, что в методе Ли определяющими
являются операции над функциями, а не над их аргументами. Это
видно уже из вывода преобразования B.5.8) с помощью преобразова-
преобразования функций B.5.6). Аргументы же функций [например, J в
B.5.42) ] являются формальными переменными и должны быть
заменены в конце вычислений на преобразованные переменные
Т
Так как Я зависит только от /, то новая частота с точностью
до второго порядка равна
B.5.43а)
dJ [ 8 ш0 256
') Отмеченное выше недоразумение связано просто с неудачным обозна-
обозначением; гамильтониан B.5.42) зависит не от старой, а от формальной пере-
переменной, которую следовало бы обозначить другой буквой.— Прим. ред.
154 Глава 2
Это выражение следует сравнить с результатом B.2.24) первого
порядка. Исключая действие J из B.5.43а), с помощью соотноше-
соотношения Н (J) = Е + F, где Н (J) дается формулой B.5.42) с заменой
J на J, а «о = FG, получаем зависимость частоты колебаний от
энергии
Эта зависимость показана на рис. 2.2 в виде кривой 3.
2.5в. Адиабатические инварианты
Несмотря на влияние резонансов, которое даже в первом порядке
по е приводит к локальному изменению или разрушению адиаба-
адиабатических инвариантов, часто возникает необходимость в получении
асимптотических разложений более высоких порядков. Такие вы-
вычисления оказываются очень громоздкими, если используется
процедура усреднения Крускала или Боголюбова, потому что вы-
выполнение совместных обратных преобразований переменных бы-
быстро усложняется. Явные выражения для преобразований до вто-
второго порядка были получены в работе Мак-Намары и Уайтмена
[292]; конкретный пример, использующий некоторые упрощения,
рассмотрен Нортропом и др. [321 ].
Другой, более простой метод, использующий скобки Пуассона,
был предложен еще Уиттекером [430 ] и развит в работах Мак-
Намары и Уайтмена [292] и Джакалья [153]. Оба метода по су-
существу эквивалентны до второго порядка, как было показано Мак-
Намарой и Уайтменом [292 ], а для некоторого класса задач и во
всех порядках, согласно Штерну [391 ]. Позднее Мак-Намара уста-
установил [290], что использование скобок Пуассона является частным
случаем метода преобразований Ли. Последний метод сменил ста-
старую технику, в том числе и с использованием скобок Пуассона;
он положен в основу нашего описания адиабатических инвариан-
инвариантов высших порядков. Подробности старых методов можно найти
в цитированных выше работах.
Порядки величин при адиабатическом возмущении. При медленном
возмущении гамильтониан имеет вид (см. п. 2.3а)
H = H0(J, 9, 83'. eO+etfiO/, 9, гу, et)+ . . . . B.5.44)
Здесь J, в переменные действие — угол для единственной быстрой
-степени свободы и у = (р, q) — обобщенные переменные остальных
медленных степеней свободы. Порядок производных по у и по
времени t на единицу выше порядка тех членов, из которых они
получены. Построенные в п. 2.56 ряды не отражают этого измене-
Каноническая теория возмущений 155
ния порядков и потому должны применяться с осторожностью.
Для медленных возмущений оператор Ли имеет вид
L = Lf + eLs, B.5.45)
где быстрая часть
дв dJ dJ дв
а медленная
^^
d(eqi) д(ер.) д (apt) d(zqt)
i
и w ~ w (J, 6, ey, et). Из выражения B.5.23) видно, что 7V1 опре-
определяется через коэффициенты степенных разложений Lf и Ls как
полином я-го порядка по е. Наконец, член dwjdt в уравнении
B.5.29) имеет порядок е: dwjdt—*- edwjd (et). Для решения этого
уравнения можно разложить wn и Нп по степеням е, например:
со
ш„= ^ eVw, B.5.47)
и приравнять в B.5.29) коэффициенты при одинаковых степенях е.
В результате получается цепочка уравнений, из которой можно,
последовательно найти wnQ, wnl . . . . На каждом шаге #„* выби-
выбирается так, чтобы устранить секулярность по быстрой переменной 0.
Фактически в п-м порядке теории возмущений необходимо найти
члены wmk только для тп + k ^ п. Эта процедура эквивалентна
в любом порядке описанному в § 2.3 методу усреднения. Она яв-
является более удобной, поскольку в порядках величин быстрых и
медленных переменных автоматически устанавливается разница
на единицу; это позволяет проводить усреднение по быстрой пере-
переменной в любом порядке теории возмущений и исключать возник-
возникновение секулярных членов. Однако все присущие методу усред-
усреднения ограничения (см. § 2.3) проявляются и здесь.
Первое уравнение цепочки (k = 0) есть
юв-^5- = «(^«о—tin)— У, (Lf, n-mHmo + mtf~\_mHm), B.5.48)
56 m=l
причем выражения для Tfl получаются из выражений B.5.25)
заменой L на Lf. Каждое уравнение цепочки имеет вид
со9^ = п77„, + Ф, B.5.49)
где Ф — известная функция медленных переменных и времени.
В процессе решения этой цепочки уравнений резонансные знаме-
знаменатели никогда не возникают, ибо левая часть B.5.49) является
156 Глава 2
производной только от быстрой фазовой переменной. Однако, как
мы уже знаем, резонансы между быстрыми и медленными колеба-
колебаниями приводят к тому, что ряд, представляющий wn, оказывается
ас имптотическим.
Процедуру получения инварианта выше первого порядка лучше
всего продемонстрировать на конкретном примере. Вначале мы
продолжим вычисления п. 2. Зв и получим адиабатический инва-
инвариант второго порядка для медленно изменяющегося гармониче-
гармонического осциллятора. В качестве второго приложения теории найдем
среднюю силу, действующую на заряженную частицу в поле вы-
высокочастотной электростатической волны.
Медленно изменяющийся гармонический осциллятор. Из выраже-
выражения B.3.25), обозначая штрихом дифференцирование по аргументу
&t и записывая для простоты со вместо со0, получаем гамильтониан
H = a>J + e — — Jsin'2Q, u.5.50)
2 со
где
со = со(еО. B.5.51)
Примемте выражении B.3.23) G — 1, F = со2 (et). В нулевом по-
порядке Яо= Яо; в первом порядке уравнение B.5.31а) имеет вид
aJw^+eJw1_ = j} H ( 552)
зе а(ео
Чтобы решить это уравнение с точностью до е, полагаем
Щ^Щя + ewa, Я, = Яю + еЯп, B.5.53)
что приводит к системе •„
(OJ^ = 7710_-L-^L./sin2e) B.5.54а)
30 2 со
(a_dw1L_ = 7} | дщо_^ B.5.546)
дд J 3(80
Чтобы избежать секулярности в w10 и wllt следует выбрать Я10=0
и Яп = 0, поэтому
= 0. B.5.55)
Интегрируя B.5.54а) и подставляя полученное выражение для w10
в B.5.546), находим
Щ = Щ» + «ihi = — — J cos 20 — /—V / sin 26. B.5.56)
4 со2 8со \ со2 /
Каноническая теория возмущений 157
Во втором порядке уравнение B.5.316) принимает вид
со
59 ' d(et)
Поскольку это уравнение следует решить в нулевом порядке по
е, опустим второй член в левой части, а во втором члене правой
части положим Lt= ?/г = lw10, J; с учетом #2 = 0, согласно
B.5.50), получим
со -^- = 2Я20— [w10; HJ. B.5.58)
Скобки Пуассона
[Що, Hj]= )r-^-J B.5.59)
4 со3
яе содержат переменной части. Чтобы избежать секулярности,
полагаем
7?20= x-S^JLjt B.5.60)
8 ш3
откуда w20 = 0.
Подставляя вместо формальной переменной / переменную /,
для нового гамильтониана второго порядка находим
B.5.61)
Я со77.
8 ш3
Дифференцируя это выражение по /, определяем новую частоту
Согласно B.5.8), можно выразить новое действие J через старые
переменные
7=77.' B.5.63)
Используя B.5.24а) и B.5.246), во втором порядке имеем
— е2
J = J — e[w1, J]-\ [w10, [w10, J]]. B.5.64)
2
В эту зависимость входит функция первого порядка wx. Используя
определяющее ее выражение B.5.56), получаем
/sn + )/+/
2 со2 8 \ ш2 / 4со \ ш2 /
B.5.65)
В силу B.5.61) J = const, и соотношение B.5.65) описывает инва-
инвариантные кривые на плоскости (/, 0). Этот результат совпадает
158 Глава 2
с полученным в работах [282, 391, 429], однако использование
преобразований Ли позволило существенно упростить вычисления.
Движение в быстро осциллирующем поле. В качестве второго при-
примера найдем среднюю силу, действующую на заряженную частицу
в поле электростатической волны с медленно изменяющейся ампли-
амплитудой х). Хорошо известно, что средняя сила пропорциональна
квадрату амплитуды волны, поэтому потребуется провести вычис-
вычисления во втором порядке. Примем гамильтониан в виде
Hw(p, х, Ц = —^~р*~ееФ{екх)со?,(кх — Ы), B.5.66)
1т
где параметр е соответствует адиабатическому возмущению. Вводя
расширенное фазовое пространство и считая Е = — Hw импуль-
импульсом, канонически сопряженным времени t, находим
Не(р, Е, х, /) = —p2 + ?4-eeO>(e/h:)cos(/ex— со/). B.5.67)
С помощью производящей функции
Ft = (—kx + <af)Je + kxJ4 B.5.68)
имеем
a>Je, ф kx,
at д/ф
B.5.69)
Новый гамильтониан Н зависит от быстрой 6 и медленной еф фаз:
Я = Я0 + ееФ(еф)соз9, B.5.70)
а гамильтониан невозмущенного движения
Яо = ^-(Лр-^еJ + со7е B.5.71)
1т
определяет частоты колебаний
«Ф=^(^-./е) = К, B.5.72)
*2 — JB) = ® — kv,. B.5.73)
m
г) Это неудачный пример для демонстрации преимущества метода преоб-
преобразования Ли, поскольку рассматриваемая задача гораздо проще и в более
общем виде решается с помощью классического метода усреднения (см.,
например, [453], § 30).— Прим. ред.
Каноническая теория возмущений 159
Условие адиабатичности (соф <С &>е; е = 1) требует, чтобы частица
была далеко от резонанса с волной
» vx. B.5.74)
Введем теперь преобразования Ли. В нулевом порядке по е
гамильтониан Яо = Я„, а в первом порядке
B.5.75)
Функцию о»! необходимо найти с точностью до е, поэтому полагаем
W1 = W10-\-EW11,
B.5.76)
и находим
*= Яю—еФсо5В, B.5.77а)
36
OV О (Ёф)
Так как среднее от еФ cos 8 равно нулю, то выбираем Я10 = О
и интегрируем B.5.77а)
wlo= sin В. B.5.78а)
Используя это выражение в B.5.776) и полагая Я1Х = 0, после
интегрирования находим
ши — cos 6. B.5./об)
@0 @0
Переходя ко второму порядку теории, мы должны найти w2
в нулевом порядке по е, поэтому опускаем в уравнении B.5.316)
члены высших порядков, учитываем, что Я2 = 0, Нг == 0, дНr!dJe-^
= 0, и получаем
2Я20 + ^--^-. B.5.79)
а ае ил а/е ^е
Выберем Я го так, чтобы исключить секулярность по 8:
B-5-80)
Вычисляя это выражение с помощью B.5.78а), приходим к квадра-
квадратичной зависимости гамильтониана от амплитуды волны
. B.5.81)
1m Am (со — kvxf 2т
Средняя сила равна
160 Глава 2
Возвращаясь в усредненном гамильтониане Н = Но -f- еЯх + е2Яг
к исходным переменным, получаем выражение в виде суммы кине-
кинетической и эффективной потенциальной энергии (е = 1):
= const. B.5.82)
р^_.ди9м =__?^__фф; . B58з)
ИХ 2/Л (СО — &/*J
Видно, что эта сила обращается в нуль вблизи максимума или ми-
минимума амплитуды волны, причем минимум отвечает устойчивым
колебаниям частицы.
При приближении к резонансу средняя сила, согласно B.5.83),
неограниченно возрастает, но при этом нарушается условие адиа-
батичности (соф ^ сое). Этот случай можно исследовать в рамках
резонансной теории возмущений, или в более высоком порядке,
с помощью комбинации метода ДЛТ и преобразований Ли, как это
будет описано ниже.
Устранение резонансных знаменателей. Адиабатические инвари-
инварианты, как это было показано в § 2.4, в окрестности резонансов пре-
претерпевают топологические изменения. Для отдельного резонанса
замена переменных вида B.4.6) (резонансные переменные) позво-
позволяет учесть изменения топологии и составляет основу резонанс-
резонансной теории возмущений, изложенной в п. 2.4а в первом порядке
по е. Поскольку для двух степеней свободы движение полностью
разделяется на быстрое и медленное, то методы этого параграфа
применимы и для нахождения интегралов движения более высоких
порядков вблизи резонансов.
В работе [290 ] Мак-Намара соединил технику преобразований
Ли с методом ДЛТ (п. 2.4г). Напомним, что с помощью этого ме-
метода для определенного класса задач удается построить интеграл
движения первого порядка с учетом влияния сразу всех первич-
первичных резонансов. Метод основан на том факте, что если J — интег-
интеграл невозмущенной системы, то и любая функция /0 (/) также
является интегралом. Выбирая /0 (/) так, чтобы производная
dIJdJ обращалась в нуль при резонансных значениях J, можно
учесть топологические изменения интеграла / возмущенной си-
системы. Техника преобразований Ли позволяет легко ввести функ-
функцию/о вместо / следующим образом. В соответствии с методом
этого параграфа эволюционный оператор Т вычисляется с точ-
точностью до желаемого порядка п. Затем, вместо записи интеграла
в форме B.5.63), т. е.
7= 77 = const, B.5.84)
положим
7 1 B.5.85)
Каноническая теория возмущений 161
и выберем /„ (У) так, чтобы устранить полюсы функции / (У). Мак-
Намара показал, что необходимость выбора /0 (У) возникает только
после того, как будет достигнут я-й порядок разложений, и дал
правила такого выбора.
Резонансное взаимодействие волны и частицы. Применим последний
метод к решению рассмотренной ранее в п. 2.26 задачи для волны,
распространяющейся под углом 45° к магнитному полю, с гамиль-
гамильтонианом B.4.108). В первом порядке уравнение B.5.31а) прини-
принимает вид
Р*^+^= -Z /m(p)sin(^-mcp). B.5.86)
Запишем решение этого уравнения:
т =0
С помощью B.5.25а) находим интеграл движения
7 = Io(P*) + t[wlt /0], B.5.88)
или
$? B-589)
Если выбрать dI0/dP^ согласно B.4.109), то все резонансные зна-
знаменатели в B.5.87) сокращаются и для / получается выражение
B.4.111). Первичные резонансы при Р^ = + 1, 0, — 1 хорошо
описываются полученным интегралом движения (см. п. 2.4г).
Переходя ко второму порядку, следует решить уравнение
B.5.316) и найти w2. С помощью B.5.25) получаем интеграл движе-
движения в виде
7 = I0 + e[wlt Io] + -^-[wt,Io] + -^-lwlt [wu /„]]. B.5.90)
Эта функция имеет полюсы второго порядка при целых Р^ и по-
полюсы первого порядка при полуцелых Р^. Чтобы устранить все
эти полюсы, выберем
^ B.5.91)
sinnP^si
dP ф
Инвариантные кривые (/ = const) показаны на рис. 2.13; их сле-
следует сравнить с инвариантными кривыми первого порядка
(рис. 2.12, б) и с численными результатами (рис. 2.10, б).Полуце-
б).Полуцелые резонансы, как и нерезонансные области, хорошо воспроиз-
162
Глава 2
Рис. 2.13. То же, что и на рис. 2.10, б во втором порядке по е = 0,1 (по дан-
данным работы [290]).
водятся на рис. 2.13. Однако целые резонансы сильно искажены,
хотя для меньшей величины возмущения согласие гораздо лучше
1290]. Здесь остается еще много неясных вопросов1).
§ 2.6. Сверхсходимость
Рассмотрим теперь некоторый класс методов теории возмущений,
предложенных Колмогоровым 1229] и играющих, как показано
в гл. 3, фундаментальную роль при доказательстве теоремы КАМ.
Их основной чертой является чрезвычайно быстрая сходимость
последовательных приближений. Во всех до сих пор рассмотрен-
рассмотренных в этой главе методах гамильтониан Н — Но ~г еН1 подвер-
подвергался таким последовательным каноническим преобразованиям,
при которых порядок возмущения по е изменялся на единицу на
каждом шаге:
') Это замечание относится, по-видимому, не столько к самой задаче,
сколько к возможностям и пределам применимости метода ДЛТ.— Прим.
ред.
Каноническая теория возмущений 163
Это ясно видно, например, из системы уравнений B.5.31). Выбирая
производящую функцию Ли w±, мы исключаем \иН1\, но остается
е2//2; выбирая w», исключаем \г~Н2\, но остается е3Н3 и т. д. Кол-
Колмогоров показал, что последовательность канонических замен пе-
переменных можно организовать таким образом, чтобы оставшееся
на каждом шаге возмущение было порядка квадрата предыдущего:
Выполнив п преобразований, можно получить таким путем реше-
B") т
ние задачи с точностью порядка е . 1акая процедура носит
название сверхсходимости или иногда квадратичной сходимости х).
Продемонстрируем оба обсуждаемых подхода на имеющей само-
самостоятельный практический интерес задаче отыскания корня урав-
уравнения
/(х) = 0. B.6.1)
Следуя Мозеру 1310] и Берри [26], предположим, что нам известно
некоторое значение х0 (обычно это решение невозмущенной задачи),
которое можно принять в качестве начального приближения для
корня. Следующее приближение хг найдем из первых двух членов
разложения Тейлора вокруг х0:
/(*о)-/'(*о)(*1 —*о) = 0. B.6.2)
Для получения приближения хп на п-м шаге необходимо опреде-
определить корень полинома п-й степени
B.6.3)
т =0
Выберем малый параметр е = х—х0 и представим функцию / (х)
рядом по степеням е. Вычитая из этого ряда выражение B.6.3),
получаем, что ошибка еп =-- х—хп после п-то приближения является
величиной порядка е":
1 f{n+l) ix \
еп ! 1 ^^ еге+1 . B.6.4)
(п -f 1)! /' (х0) К '
Такая линейная сходимость характерна для обычных методов тео-
теории возмущений.
Чтобы продемонстрировать квадратичную сходимость, вос-
воспользуемся методом касательных Ньютона. Первый шаг этого ме-
метода представлен уравнением B.6.2). Ошибка ех первого шага
J) В отечественной литературе употребляется также термин «ускорен-
«ускоренная сходимость» [463].— Прим. перев.
164 Глава 2
оценивается с помощью разложения / (х) относительно точки х0
до е2:
е1~а(хо)(л:-хоJ = а82, B.6.5)
где
а(*о)=—^-П*оУП*о). B-6.6)
Таким образом, ошибка е1 имеет порядок е2. На следующем шаге
повторим процедуру разложения / (х) вокруг точки хх (а не х0)
и найдем
*-* = —гыГ- B-6J)
Ошибка этого шага с учетом B.6.5) равна
е2 ~ ее {хх) (х—ххJ ~ а (хх) а2 (х0) е4 B.6.8)
и является величиной порядка е4. Быстрая сходимость обеспечи-
обеспечивается за счет того, что значение переменной, вокруг которого вы-
выполняется разложение, с каждой итерацией приближается к точ-
точному значению. По индукции для ошибки после п итераций имеем
П
k—i
B.6.9)
Вообще говоря, /"//' -~ 1, так что ошибка уменьшается квадра-
квадратично на каждом шаге. Однако, если
/"//' — е-1, B.6.10)
[это соответствует резонансу вблизи разыскиваемого значения
корня, / (х) -— (х—хг)~и, лгг-~лг0], то и тогда квадратичная сходи-
сходимость оказывается сильнее х). Аналогично сверхсходящееся раз-
разложение в теории К.АМ также подавляет действие малых резонанс-
резонансных знаменателей.
Сверхсходящиеся разложения не нашли пока широкого приме-
применения в практических расчетах. Как мы увидим ниже, соответст-
соответствующие вычисления оказываются при этом слишком громоздки:™.
Чириков [70 ] демонстрирует сверхсходимость на примере маят-
маятника, используя производящую функцию от смешанного набора
переменных. Однако более естественно применить сверхсходимость
в сочетании с преобразованиями Ли. Для автономных систем это
впервые было сделано Хаулэндом [203 ]. Мы рассмотрим эту тех-
технику в п. 2.6а, следуя Кари [49 ], метод которого применим также
и для неавтономных систем. В работе Мак-Намары [290] кратко
обсуждается возможность использования сверхсходящихся преоб-
!) Фактически для сходимости требуется, чтобы f"/f'~ 8 т;т<1(е->0);
похожее условие возникает и при доказательстве теоремы К.АМ (см. п. 3.2а).
Каноническая теория возмущений 165
разований Ли для вычисления интегралов движения вблизи резо-
нансов.
Получение приближенных решений для систем, близких к ин-
интегрируемым, тесно связано с отысканием периодических решений
в таких системах. Последние важны, поскольку они образуют
плотное множество и позволяют анализировать близкие решения
с помощью линейной теории (см. § 3.3). Хеллеман, Эминицер и др.
[116] разработали в последнее время весьма эффективные сверх-
сверхсходящиеся методы нахождения периодических решений. Эти
методы описываются в п. 2.66 и иллюстрируются на примере за-
задачи Хенона—Хейлеса.
2.6а. Метод Колмогорова
Следуя Кари [49], рассмотрим гамильтониан
оо
Н= 2 е"Я„(лг, 0. B.6.11)
где Яо — интегрируемая часть, а вектор х — (J, 6) означает пе-
переменные действия — угол для Яо. Введем последовательные пре-
преобразования Ли, приводящие к последовательности новых гамиль-
гамильтонианов, занумерованных с помощью верхнего индекса. Исполь-
Используя метод Депри (п. 2.56), начнем с уравнений B.5.31) для первой
производящей функции Ли шA):
Я^ = Яо, B.6.12а)
Hlt B.6.126)
~H2)-[w{l\ {H^ + H,)]. B.6.12b)
Обычно эти уравнения интегрируются одно за другим. В каждом
порядке новый гамильтониан Н\1) выбирается так, чтобы исклю-
исключить секулярность в ш;1', после чего определяется сама функция да'1'"
Затем w\J подставляется в следующее уравнение и весь процесс
повторяется. Интегрирование каждого из уравнений есть единич-
единичный «шаг» процедуры, и после п таких шагов мы получаем новый
гамильтониан Я, зависящий с точностью порядка е" только от пе-
переменной действия J.
В методе Колмогорова гамильтонианы и производящие функции
выбирают иначе. Основное правило состоит в том, что одновре-
одновременно решаются все те уравнения, правые части которых не содер-
содержат Wi. При этом, как и прежде, Hi выбирается таким образом,
чтобы устранить секулярности в да,-. Во всех оставшихся уравне-
уравнениях Wj (/>i) полагаются равными нулю, после чего из них опре-
определяются Я,-. Выполнение всей этой процедуры является единич.
ным «шагом» разложения.
166 Глава 2
На первом шаге мы можем «одновременно» решить только одно
авнение, а
из уравнения
уравнение, а именно B.6.126). Полагая Н\1) = (Нг), находим w\[)
IH^. B.6.13)
Гамильтониан Н^ определяется из B.6.12в) при w^ = 0 и т. д.
Нельзя одновременно *) с w\l) найти, например, w$\ так как в
уравнение B.6.12в) входит неизвестная еще функция w\i].
Приступая ко второму шагу, вводим новый «старый гамиль-
гамильтониан»
ЯA) = 5 епН2\ B.6.14)
71=0
в котором
{l) {]eH\l\ B.6.15а)
0, B.6.156)
/>1. B.6.15b)
Таким образом, в новом невозмущенном гамильтониане полностью
учтено решение, полученное на предыдущем шаге. Поскольку воз-
возмущение не содержит теперь члена первого порядка, то Н\2) -- 0;
wf* =0 и //о2' -- Яо1'. Система уравнений Депри принимает вид
B.6.16a)
B.6.166)
* = 4 [Н?>-H\l)) - [wf\ W + M1}], B.6. 16b)
где
D^ = — -f [ , Яо"] B.6.17)
— полная производная по времени вдоль траекторий первого по-
порядка исходной системы. Теперь мы можем одновременно решить
два первых уравнения B.6.16а) и B.6.166), устраняя секулярности
в w{P и wf] выбором #22! и #з2> соответственно. В остальных урав-
') То есть на этом же шаге; если же мы сначала найдем Е){'* из B.6.13),
а затем подставим его в B.6.12в), то вернемся к обычной теории возмуще-
возмущений.— Прим. ред.
Каноническая теория возмущений 167
нениях полагаем ш}-2) = 0 и используем их для определения Я}2),
/>3. В результате находим новый гамильтониан
ljB) _ rjB) , „4r/B) ; р5н'2> ' CO К 1«Л
где
w<2) _ 77B) ^ -273B) ^ P 377B) ^9 r 1Q1
Hf} = Hf\ />3, B.6.20)
причем Яо2) является функцией только переменных действия, а
возмущение не содержит членов порядка е2 и е3.
На третьем шаге можно сразу устранить члены возмущения
порядка с четвертого по седьмой. Это следует по индукции из об-
общего уравнения Депри B.5.29). Пусть возмущение в Я</1) имеет по-
порядок е или выше. Используя преобразование с производящей
функцией w(n+l\ получим а/?-+1) = 0, Цп+1) = 0, G'-1)J-n+1) = 0
и Я/"+1) = 0 для /<2". Отсюда находим, что для m<2"+1 урав-
уравнение B.5.29) записывается в виде
-т\Пт Г1т I. \AXt.LV)
Следовательно, уравнения с номерами от т = 2п до т = 2"+! —1
можно решить одновременно.
Отметим, что каждый шаг в методе Колмогорова оказывается
намного сложнее, чем в обычной теории возмущений. Более того,
на каждом шаге требуется проводить интегрирование вдоль новых
траекторий системы. Возможно, что это есть выражение всеобщего
«закона сохранения»: на одну и ту же высоту можно взобраться
либо за много мелких шагов, либо за несколько крупных! Мы ду-
думаем, что метод Колмогорова не лучший способ выполнения прак-
практических вычислений 1). С другой стороны, он совершенно необхо-
необходим в теории КАМ для получения сходящихся рядов вне резонан-
сов.
2.66. Периодические траектории
Для замкнутых периодических траекторий в системах с несколь-
несколькими степенями свободы удается построить сходящиеся решения.
Это становится возможным потому, что условие точной периодич-
периодичности позволяет представить траекторию простым рядом Фурье
и избежать, таким образом, появления резонансных знаменателей
Y) Это заключение авторов представляется преждевременным, так как
еще не накоплен достаточный опыт практических расчетов с использованием
сверхсходящихся методов. Можно, например, отметить, что если требуется
умеренная точность, скажем, до ~ е3 включительно, то сверхсходимость
заведомо упрощает вычисления (см. [70], § 2.2; 5.1).— Прим. ред.
168 Глава 2
(п. 2.26). Однако, чтобы обеспечить периодичность в рамках теории
возмущений, необходимо изменять начальные условия в каждом
из последовательных приближений, поддерживая частоту неизмен-
неизменной х). Это отличается от обычной схемы теории возмущений, в ко-
которой для заданных начальных условий точность последовательных
приближений повышается за счет переопределения частоты.
Метод построения периодических решений с фиксированной ча-
частотой и фазой был разработан Хеллеманом, Эминицером и сотр.
Этот метод использовался во многих задачах, например вынужден-
вынужденные колебания ангармонического осциллятора [116], модель Хе-
нона и Хейлеса [183] (см. п. 1.4а) и отображение Хенона [178]
(см. п. 3.2г). Авторы называют свой метод «обратным» ввиду отме-
отмеченной выше необычной последовательности действий — от ча-
частоты к начальным условиям.
Хотя мера всех периодических траекторий равна нулю, они
являются всюду плотными в фазовом пространстве. Наглядно пе-
периодические траектории соответствуют рациональным числам на
отрезке, мера которых равна нулю, но которые тем не менее сколь
угодно хорошо приближают любое иррациональное число. Поэ-
Поэтому на первый взгляд может показаться, что отыскание периоди-
периодических траекторий эквивалентно получению вообще всех траекто-
траекторий. На самом деле это не так, поскольку периодические траекто-
траектории, вообще говоря, не ограничивают апериодические тр аектории.
Даже если в начальный момент они близки, то позже могут ока-
оказаться произвольно далеко друг от друга в фазовом пространстве.
В отличие от этого при двух степенях свободы инвариантные торы
ограничивают близкие траектории и поэтому являются значительно
более важными для описания динамики системы. Тем не менее и
в общем случае периодические траектории могут оказаться весьма
полезными по двум причинам. Во-первых, они могут выявлять не-
некоторые особенности общей структуры движения, например ре-
зонансы различного уровня с определенным числом вращения. Во-
вторых, можно исследовать их устойчивость, что будет использо-
использовано в § 4.4 при определении глобальной устойчивости движения.
Вариационный метод. Рассмотрим замкнутую траекторию в авто-
автономной системе с N степенями свободы. Движение при этом является
периодическим, т. е. существует N—1 резонансных условий вида
h- @ = 0, B.6.22)
где все ./V-мерные целочисленные векторы 4 линейно независимы -).
1) Этот прием, служащий фактически основой теории К.АМ, был предло-
предложен Колмогоровым [229] (см. также [И]).— Прим. ред.
2) Вектор основных частот со не имеет в данном случае определенного
смысла [ср. B.6.24) и C.1.5)], полная же система частот определяется со-
соотношением B.6.23).— Прим. ред.
Каноническая теория возмущений 169
Все частоты являются целыми кратными основной частоты обра-
обращения
(о,- = тгй)Л. B.6.23)
Это позволяет представить координаты qj и скорости q,- с помощью
рядов Фурье
<7/ = Z Q/*/™'', B.6.24а)
^ma'i. B.6.246)
m=—ю
Вариационное уравнение для замкнутой траектории удобнее
всего записать с помощью лагранжиана A.2.1). Из принципа Га-
Гамильтона получаем
bj>L{'qh qi)dt = 8{L)=0t B.6.25)
где (L) — интеграл по периоду обращения 2п/о)г. Считая q,- и q,-
функциями коэффициентов Фурье Q/m и варьируя эти коэффици-
коэффициенты, находим
^,m. B.6.26)
oQjm
Из вариационного исчисления известно, что
dQjm
если удовлетворяются уравнения Лагранжа
d d(L) d(L) n
dt g-.
B.6.27)
B.6.28)
Заметим, что (L) — чисто алгебраическая функция Q,-m (и со,.).
Если задано (L), то Q,-m находятся как корни системы уравнений
B.6.27), которые определяют стационарную точку функции (L).
Трудность вычисления этих корней связана с тем, что в общем слу-
случае стационарная точка Q не отвечает ни максимуму, ни минимуму
(L), а является седловой (см. рис. 2.14). Тип этого седла разрывно
зависит от изменения Qjm (а также, следовательно, и от начальных
значений qj и qj). Используем для вычисления корней простой ме-
метод касательных Ньютона. Введем векторную переменную Q, со-
составленную из коэффициентов Q/m, и положим / = d(L)!dQ, тогда
из B.6.27)
^fO, B.6.29)
dQa
где Qo — начальное приближение корней, a AQ — первая поправка.
170
Глава 2
Подставляя выражение для /, имеем
AQ- d4L} = -
d(L)
B.6.30)
Диагонализуя матрицу кривизны дг (L)'dQ20 (см. рис. 2.14),
приходим к следующим заменам:
B.6.31)
d{L)
dQ0
Рис. 2.14. Двумерное седло.
Q — стационарная точка усредненного лагранжиана <?>. Q,, Q2 — исходные переменные;
с,, с2 — новые переменные, в которых матрица кривизны диагональна.
Уравнение B.6.30) принимает вид
Хп(Со)Асп= —(L)n(c0),
B.6.32)
где п нумерует компоненты вектора с в диагонализованной системе.
Среди значений кривизны К (с) имеются как положительные, так
и отрицательные. Пронумеруем их в порядке возрастания от от-
отрицательных к положительным, при этом одно из значений кт (с) =
— 0 (см. [179]). Однако в процессе итераций эта упорядоченность,
вообще говоря, не сохраняется. Положение можно исправить, введя
в метод Ньютона корректирующую поправку
(А„—Л)Дс„=—<L)n, B.6.33)
где Я выбирается так, чтобы знак %п—% при итерациях не изме-
изменялся. Такой прием обеспечивает линейную сходимость к сп. Бо-
Каноническая теория возмущений 171
лее того, когда решение с подходит достаточно близко к с, можно
убрать л и восстановить квадратичную сходимость. В качестве Я
удобно выбрать %т (с), так как при п § т разность Хп (с) — %т(с) §0
и Хт -*¦ 0 при с —>¦ с, как и требуется для сходимости в B.6.33).
Таким образом, вместо обычных начальных условий
<7/@) = ?Q/m. B.6.34а)
т
qj@)=mrYmQim, B.6.346)
т
мы задаем теперь значение п = т, для которого кривизна равна
нулю, или
(L)m(c) = 0 B.6.35)
для любого вектора с, что гарантирует im= 0 в первом порядке
по Асш.
В практических расчетах используются исходные (Q), а не диа-
гонализованные (с) переменные и конечные ряды Фурье. Были при-
придуманы и различные другие приемы для сокращения вычислений
и ускорения сходимости; подробности можно найти в цитированных
выше оригинальных статьях.
Задача Хенона и Хейлеса. Продемонстрируем применение изложен-
изложенного общего метода к системам с двумя степенями свободы, следуя
работам Баунтиса [35] и Хеллемана и Баунтиса 1183]. Условие
резонанса имеет вид
scoi — га2 = 0, B.6.36)
где
B.6.37)
г
— некоторая постоянная, а г и s — взаимно простые целые числа.
Частоты (Oj и со 2 теперь уже не являются независимыми, а кратны
общей частоте обращения
B.6.38)
Г S
Период обращения равен тг — 2я,'сог. Обозначая соответствующие
частотам cot и со2 координаты через х и у, можно представить ре-
решение в виде рядов Фурье B.6.24а) по каждой степени свободы:
x(t)= У. Aneinar\ y(t)= I Bnf?™'-. B.6.39)
nnr""°J
В рассматриваемом методе можно было бы задать со,, и два из
четырех начальных условий х, у, х, у, а коэффициенты Фурье Ап,
172 Глава 2
Вп и оставшиеся два условия найти путем последовательных при-
приближений. Поскольку, однако, для обеспечения периодичности
траектории достаточно задать только г и s, то можно фиксировать
три начальных условия, а частоту со, и четвертое условие найти
с помощью рядов. Так как главными частотами в B.6.39) являются,
конечно, исходные частоты B.6.36), то можно ожидать, что глав-
главными в фурье-разложении B.6.39) будут члены с амплитудами А-_г
и B_s. Выделение этих членов помогает достижению быстрой схо-
сходимости решения.
Для иллюстрации метода рассмотрим, следуя Баунтису [35],
потенциал Хенона и Хейлеса, заданный выражением A.4.4) (см.
также рис. 1.11). Уравнения Лагранжа имеют вид
х=— х—2ху, B.6.40а)
у'=— у-\- У2— х\ B.6.406)
Чтобы явно ввести фигурирующие в B.6.36) частоты, перепишем
эти уравнения в форме
B.6.41а)
!]. B.6.416)
Правые части этих уравнений считаются в некотором смысле ма-
малыми, на что указывает введенный малый параметр е. Уравнения
B.6.41) эквивалентны B.6.33) [183]. Разложим теперь коэффици-
коэффициенты Фурье в B.6.39) по степеням е:
Оо оо
j=0 П=—оо
B.6.42)
со оо
/А ^^ / ^^ D itl(i) t
/=0 п=—оо
Подставляя эти выражения в B.6.41), получаем систему рекуррент-
рекуррентных соотношений
(r2-n2)a2An,i+1=(rWr-\)Ani-2 ? AkjBn^,jt B.6.43a)
k=— оо
оо оо
k=—оо k~—оо
B.6.436)
из которых можно найти все коэффициенты, кроме главных п = ± г
и п = ± s, так как для последних левая часть уравнений обра-
обращается в нуль. Эти коэффициенты проще всего получить, задав
Каноническая теория возмущений
173
в дополнение к г и s три начальных условия. Выберем, например,
х = х0 при t = 0 и будем считать коэффициенты Фурье действи-
действительными (Л„ = Л_„, 5„ = 5_„), откуда следует х @) = г/ @) = 0.
Тогда амплитуда Аг определяется непосредственно из B.6.42) с по-
помощью рекуррентного соотношения
B.6.44)
а= 1
1 1
А г, /+1 ~~гхо 7Г °l
2 2
Рис. 2.15. Начальные условия х0, у0 периодических решений системы Хе-
нона — Хейлеса при х0 = у0 = Одля различных значений a^Es/r, где s, r —
взаимно простые числа (по данным работы [183]).
а частота находится из уравнения B.6.43а) при нулевой левой
части:
¦[А г,-
B.6.45)
Вместо того чтобы находить Во и Bs из уравнения B.6.436) при
п = 0 и п = s соответственно, обратим процедуру для ускорения
сходимости. Если использовать уравнение B.6.436) с нулевой ле-
174 Глава 2
вой частью и единственными отличными от нуля коэффициентами
Во,о. б+s.o и А±г.о> то в первом приближении имеем
(sV-l)--2B0,0 = 0. B.6.46)
Это дает возможность найти Bs из рекуррентного соотношения,
которое получается с помощью B.6.436) при п = 0:
2В.?./+1 = ВП/- ? В*/+2М*Л B.6.47)
ft +s fe
Входящие сюда величины В01- определяются в любом порядке из
того же самого уравнения при п ~ s:
Во, /+!=-——Hi—s2g),)Bs/— i BkjBs^k,j~~ AkjAs_kiA.
¦itssj 1 к u, s к 1
B.6.48)
Соотношение B.6.47) эквивалентно условию B.6.35). Все осталь-
остальные коэффициенты Ап и Вп получаются рекуррентно из уравне-
уравнений B.6.43) с некоторым разумным максимальным значением п.
После этого начальное значение у определяется в любом порядке
прямо из B.6.39).
С помощью этой процедуры Баунтис [35 ] построил кривые за-
зависимости начальных координат х0, у0 при постоянном значении
отношения а --- s'r и непрерывно изменяющейся частоте аг. Ве-
Величины а выбраны так, чтобы наилучшим образом аппроксимиро-
аппроксимировать значение а = 1 (отношение частот малых колебаний). Полу-
Полученные результаты приведены на рис. 2.15. Каждая кривая посто-
постоянного а соответствует определенному диапазону непрерывного
изменения ыг. Однако зависимость решения от а разрывна, т. е.
малые изменения а приводят к совершенно другим значениям сог,
г и s.
Следуя подходу создателей метода, мы использовали уравнения
движения в форме Лагранжа. Однако все это можно было бы про-
проделать и в канонической форме с помощью подстановки х -- р. хотя
для периодических траекторий такая формулировка не дает каких-
либо очевидных преимуществ. Что на самом деле желательно, так
это иметь дело с лагранжианами, содержащими невысокие степени
координат. В противном случае метод становится слишком громозд-
громоздким из-за необходимости перемножать сразу много рядов Фурье,
что приводит к появлению многократных сумм в рекуррентных со-
соотношениях для коэффициентов х).
г) В работе [473] предложен другой метод нахождения периодических
траекторий, свободный от этих недостатков.— Прим. ред.
Глава 3
ОТОБРАЖЕНИЯ И ЛИНЕЙНАЯ
УСТОЙЧИВОСТЬ
Некоторые топологические соображения помогают наглядно пред-
представить, а затем и понять многомерное движение. Они естественно
приводят к разностным уравнениям, т. е. к отображению динами-
динамической траектории системы на некоторое подпространство ее
фазового пространства. В случае двух степеней свободы такие
отображения дают простую и наглядную картину движения. Бо-
Более того, использование отображений — обычно наиболее удобный
путь проведения как аналитических и численных расчетов стоха-
стохастического движения, так и математических доказательств сущест-
существования различных типов траекторий. Вместе с тем регулярное
движение, как мы видели в гл. 2, часто бывает удобно описывать
дифференциальными уравнениями. Переход от дифференциальных
уравнений (Гамильтона) к отображениям и обратно широко ис-
используется при анализе движения большинства нелинейных ди-
динамических систем.
Мы рассмотрим три случая возникновения отображений:
а) непосредственно из физической постановки задачи, напри-
например, для модели ускорения Ферми, которая обсуждалась
в гл. 1 и подробно рассмотрена в § 3.4;
б) как результат последовательных пересечений динамической
траектории с некоторой поверхностью 1), например, в задаче
Хенона — Хейлеса (гл. 1);
в) как результат аппроксимации движения, справедливой на
некотором ограниченном интервале времени или только в не-
некоторой области фазового пространства, например, в задаче
о движении в окрестности сепаратрисы маятника под дейст-
действием периодического возмущения (§ 3.5).
В этой главе мы рассмотрим канонические отображения для свя-
связанных нелинейных осцилляторов с произвольным числом N сте-
степеней свободы, но особенно подробно для N = 2.
В § 3.1 устанавливается связь между гамильтоновыми систе-
системами и каноническими отображениями путем использования ме-
метода сечения Пуанкаре в фазовом пространстве. На примере ото-
отображения поворота показывается, как построить отображение по
Так называемый метод сечения Пуанкаре (см. п. 1.26).— Прим. ред.
176 Глава 3
данному гамильтониану и как по отображению восстановить га-
гамильтониан. Эти результаты применимы, вообще говоря, к систе-
системам как с двумя, так и с большим числом степеней свободы.
В § 3.2 обсуждаются строгие математические результаты, ка-
касающиеся важных особенностей поведения системы, включая тео-
теорему КАМ, которая устанавливает устойчивость квазипериодиче-
квазипериодических колебаний под действием достаточно малого возмущения.
Проанализированы условия «умеренной» нелинейности, которая
необходима для теоретического анализа регулярного движения.
На основании теоремы Пуанкаре—Биркгофа о неподвижной точке
рассматривается структура фазового пространства вблизи устой-
устойчивых и неустойчивых периодических траекторий, в том числе
и стохастические слои. Излагая математические результаты, мы
не стремимся к строгости. Читателям, интересующимся математи-
математическими аспектами теории, следует обратиться к обзорам Арнольда
и Авеза [14] и Мозера [310 J, в которых приведены многие матема-
математические доказательства.
В § 3.3 мы рассмотрим линеаризованное движение и его устой-
устойчивость в окрестности неподвижных точек. Для иллюстрации при-
применения этих методов к системам с двумя степенями свободы в § 3.4
рассматривается модель ускорения Ферми, описываемая с помощью
отображения. Неподвижные точки (периодические решения) и их
устойчивость исследуются аналитически и сравниваются с числен-
численными результатами. Получена также гамильтонова форма отобра-
отображения. Наконец, в § 3.5 рассматривается задача о движении маят-
маятника под действием периодического возмущения в окрестности се-
сепаратрисы. Производится переход от уравнений Гамильтона к ото-
отображению и рассмотрен характер линеаризованного движения.
Такой подход был использован Чириковым [70 ] при анализе пе-
перехода от регулярного к стохастическому движению. Этот метод
будет изложен в гл. 4. Он применяется также при оценке скорости
диффузии Арнольда в гл. 6.
* § 3.1. Гамильтоновы системы как канонические
отображения
* 3.1а. Интегрируемые системы
Рассмотрим осциллятор с двумя степенями свободы, гамильтониан
которого Н не зависит от времени. Так как система предполагается
интегрируемой, то можно ввести переменные действие — угол (см.
п. 1.2в) и
H(Jlt /2) = ?, C.1.1)
где Е — сохраняющаяся энергия системы, a Jг, J2 — интегралы
движения. Сохранение энергии позволяет уменьшить размерность
области движения в фазовом пространстве с четырех до трех. Со-
Отображения и .линейная устойчивость
177
хранение любой из переменных действия позволяет привести эту
область к двумерной поверхности в трехмерном пространстве по-
постоянной энергии. Движение по этой поверхности можно парамет-
параметризовать с помощью частот, соответствующих каждой из двух сте-
степеней свободы:
61 = и1^-в10, ег = и^4-в2о. C.1.2)
где угловые переменные определены по модулю 2л.
Траектория
Лбе
периоЭические
траектории
(Д, ¦
ос- ирраидональ ное
число
б
Рис. 3.1. Интегрируемая система с двумя степенями свободы.
а — движение на торе J ± — const, J2 ~ const; б — поверхность сечения Пуанкаре 62 ~
= const, треугольники и кружки — две периодические траектории (s = 6) с разными
начальными условиями. Сплошные линии показывают большое число пересечении квази-
пернодическон траектории.
Движение на торе. Движение описанной системы удобно предста-
представить как движение на торе в фазовом пространстве. Такое пред-
представление можно обобщить и на системы с большим числом степе-
степеней свободы. Зададим некоторую энергию Е и рассмотрим одну
из двух степеней свободы, скажем первую. Тогда J\ параметризует
инвариантные поверхности, т. е. задает «радиусы окружностей»,
178 Глава 3
а угол 9Х характеризует положение системы на окружности. Для
полного описания необходимо учесть угол 82, так что инвариант-
инвариантная поверхность оказывается тором, как показано на рис. 3.1, а.
Задание J х и Е определяет также Js, а вместе с ним и отношение
^ C.1.3)
0J
поскольку coj = coj (J) и со., = со2 (,/). При а = r's, где г, s —
взаимно простые целые числа, частоты соизмеримы, и движение
на торе вырождается в периодическую траекторию, которая замы-
замыкается после г оборотов по 9Х и s оборотов по 92. В общем случае
а — иррациональное число, и траектория покрывает всю поверх-
поверхность тора. Поскольку г и s могут быть очень большими, периоди-
периодические траектории расположены в фазовом пространстве всюду
плотно.
Представление о движении на торе особенно полезно, потому
что его можно обобщить и на системы с более чем двумя степенями
свободы. Сохранение каждой из переменных действия уменьшает
размерность инвариантной поверхности на единицу. Так, если у
системы с N степенями свободы в 2 N-мерной фазовом пространстве
все N переменных действия сохраняются, движение происходит
по N-мерной поверхности, или многообразию, и описывается N
угловыми переменными. Топологически эта поверхность является
N-мерным тором, т. е. по аналогии с рис. 3.1,а N фазовых пере-
переменных взаимно ортогональны и определены по модулю 2л, а по-
положение поверхности задается переменными действия.
Важным следствием этих представлений является то, что в про-
произвольных канонических переменных
/>=/>(/, в), q = q(J, в) C.1.4)
движение интегрируемой системы можно записать в виде
), C.1.56)
где т — целочисленный, а р — постоянный N-мерные векторы.
Уравнения C.1.5) следуют из фурье-разложения по угловым пере-
переменным и в общем случае описывают квазипериодические колеба-
колебания р и q.
Для получения периодического решения положим х)
/я-(о = 0. C.1.6)
Так как вектор т имеет целочисленные компоненты, то отношение
частот со* является рациональным числом, т .е. со(- = я,-соо, где це-
1) Имеется в виду, что N = 2.— Прим. ред.
Отображения и линейная устойчивость 179
лые числа tii не имеют общего множителя. Траектория замыкается
через период
j ^5 C.1.7)
где iii — число оборотов по г-й степени свободы с частотой со,-.
Отображение поворота. При изучении фазовых траекторий, осо-
особенно в случае двух степеней свободы, удобно использовать метод
сечения Пуанкаре, подробно описанный в п. 1.26. Для гамильто-
гамильтониана C.1.1) в качестве поверхности сечения можно выбрать либо
плоскость (/ь 0^ F., = const), либо плоскость (J2, 92) (9Х= const).
В первом случае последовательные пересечения с плоскостью
(Jх, Qx) отделены друг от друга интервалом времени At = 2я/со2,
причем J\ = const (см. рис. 3.1, а). За это время Q1 увеличивается
на co1Af = 2яа (Jх), где а — число вращения. Так как /2 ¦=
= J2 {J\, Е), то при заданном Е величину а можно считать функ-
функцией только Jг. Опуская для упрощения записи индекс 1, полу-
получаем уравнения, описывающие переход от «-го к (п -1 1)-му пере-
пересечению:
Jn+x=Jn, C.1.8а)
ел+1 = ея-]-2яа(/л+1), C.1.86)
где для дальнейшего мы записали а как функцию Jn+i, а не /„. Ото-
Отображение C.1.8) называется отображением поворота1). При та-
таком отображении окружности переходят в себя, но число вращения
зависит, вообще говоря, от радиуса окружности. При иррацио-
иррациональном а любая траектория равномерно заполняет окружность
при п —>- оо. При рациональном а — rls, где г и s — взаимно про-
простые числа, получаются периодические траектории с периодом s
итераций. Две такие траектории с s = 6 показаны на рис. 3.1, б.
Отображение поворота не обязательно записывать в переменных
действие — угол. Например, уравнения
C.1.9a)
C.1.96)
где \р — параметр, определяют линейное отображение поворота.
Возмущение этого отображения будет описано в п. 3.2г.
Как отмечалось в п. 1.26, двумерное отображение поворота
должно сохранять площадь:
———— =[о„+1, Jn+i}= 1- C.1. Ш)
о (Jn.' °л)
Аналогичное соотношение выполняется и для C.1.9).
J) В оригинале —twist mapping (закручивающее отображение).— Прим.
перев.
180 Глава 3
Эти результаты обобщаются и на интегрируемые системы с TV
степенями свободы (Н = const). Выбирая, скажем, QN = const
в качестве поверхности сечения, получаем отображение поворота
для N—1 оставшихся пар переменных действие — угол:
Л+1 = Л, C.1.11а)
вя+1 = вп + 2ла(У„+1), C.1.116)
где <Xj = со^/содд — число вращения для г-й пары. Условия на
скобки Пуассона, эквивалентные сохранению площади двумерного
отображения, очевидно выполняются.
* 3.16. Системы, близкие к интегрируемым
Отображения, сохраняющие площадь. Рассмотрим малое возмуще-
возмущение интегрируемой системы с двумя степенями свободы. При этом
гамильтониан зависит от угловых переменных
H(J, в) = Я0(У) + еЯ1(У, в). C.1.12)
На поверхности сечения 82 = const (mod 2я) отображение пово-
поворота C.1.8) перейдет теперь в возмущенное отображение поворота
C.1.13а)
1, в„), C.1.136)
где fag — периодические функции 9. Так как это отображение
получается из гамильтоновых уравнений, оно должно сохранять
площадь. Мы выбрали функции / и g зависящими от Jn+1, а не
от Jn, так что сохранение площади принимает особенно простую
форму. В самом деле, соотношения C.1.13) можно получить из про-
производящей функции
1, в„), C.1.14)
причем
a — ds4-ldJn+x, C.1.15a)
/=— д$/дв„, C.1.156)
g = d&/dJn+i, C.1.15b)
откуда
-4- = 0, (o.l.lu)
dJn+i д6„
и площадь сохраняется. Метод преобразований Ли ([108], см.
также § 2.5) позволяет получить отображения, в которых Jn+1
и 6„+1 явно выражаются через /„ и 0„. Однако они неудобны для
наших целей.
Если / зависит от Jn+1, то Jn+l зависит от /„ неявно [см.
C.1.13а)]. Численно величину Jn+1 легко найти, используя метод
Отображения и линейная устойчивость 181
касательных Ньютона или метод последовательных приближений,
в котором новое приближение J(n\-\ находится путем подстановки
предыдущего Jl^+\ в функцию/. Оба метода обеспечивают быструю
сходимость (см. § 2.6) х).
Во многих интересных случаях / не зависит от J и g ~ 0. Тогда
C.1.13) принимают вид явного отображения поворота 2):
^+1 = /» + е/(еи), C.1.17а)
9п+1 = 9п + 2яа(Л+1). C.1.176
В дальнейшем мы подробно рассмотрим два таких отображения:
упрощенное отображение Улама (§ 3.4) и сепаратрисное отображе:
ние (§ 3.5).
Если линеаризовать C.1.176) в окрестности неподвижной точки
Jп+1 = Jn = Jo, Для которой a (Jo) — целое число, то
Ja = J0 + AJn. C.1.18)
Вводя новую переменную действия
In = 2na'AJn, C.1.19)
приходим к обобщенному стандартному отображению
In+1 = In + Kf*(Qn), C.1.20a)
%+! = % +1 „+i, mod2jt. C.1.206)
Здесь
К = 2ла'е/макс C.1.21)
— параметр стохастичности, а /* = ///макс — приведенное из-
изменение переменной действия, нормированное на единицу. Таким
образом, обобщенное стандартное отображение локально (по /)
и эквивалентно произвольному возмущенному отображению пово-
поворота. В случае /* = sin 6„ оно переходит в стандартное отобра-
отображение (известное также, как отображение Чирикова — Тейлора)
1„+1 = 1п +К sinQn, C.1.22а)
en+i=en + /n+1. C.1.226)
Отображение C.1.22) использовалось Чириковым [70] и Грином
[165] для оценки перехода от регулярного движения к хаотиче-
хаотическому. Эти вопросы рассмотрены в гл. 4.
Достаточно симметричные отображения можно представить в
виде произведения более простых отображений. Представление яв-
явного отображения поворота как произведения двух инволюций и ис-
х) Обсуждение важного вопроса о существовании и единственности ре-
решения для неявного отображения, а также условий сходимости последова-
последовательных приближений содержится в работе [474].— Прим. ред.
2) В оригинале—radial twist mapping (радиальное закручивающее ото-
отображение).— Прим. перев.
182 Глава 3
пользование такого представления для нахождения неподвижных
точек описано в п. 3.36 и 3.4г.
Обобщение возмущенного отображения поворота на случай
большего числа степеней свободы при Я = const получается с по-
помощью производящей функции
^2 = Уп+1-9п + 2я^(Уп+1) + &^(У„+1, 6„). C.1.23)
Отсюда находим (N—1) пару канонических (по построению из F2)
отображений
г„+1, Э„), C.1.24а)
1п+ъ е„). C.1.246)
Если ,? не зависит от Уп+1, получается BN—2)-мерное явное ото-
отображение поворота. Примером такого отображения могут служить
разностные уравнения в задаче о бильярде. Эта задача упомина-
упоминалась в п. 1.46 и подробно рассмотрена в гл. 6.
Вводя х -¦= (У, в), можно символически записать все такие ото-
отображения в виде
хп+1 = Тхп. C.1.25)
* 3.1 в. Уравнения Гамильтона и отображения
Как уже отмечалось, переход от уравнений Гамильтона к отобра-
отображению и обратно используется при анализе движения динамиче-
динамических систем. Как мы увидим в следующем параграфе, типичное
поведение гамильтоновых систем описывается обычно в терминах
отображений. Используя отображение, легко провести также чис-
численное моделирование нелинейных колебаний на времени порядка
миллионов периодов. Наконец, аналитический вывод диффузион-
диффузионных уравнений для хаотического движения получается, опять-таки
исходя из отображений. Вместе с тем регулярные свойства отобра-
отображений часто легче получить из уравнений Гамильтона. Как мы уви-
увидим ниже, отображения можно представить в виде некоторых спе-
специальных уравнений Гамильтона. Это позволяет связать анализ
отображений с общей теорией гамильтоновых систем. Покажем
сначала, как перейти от уравнений Гамильтона к отображению,
и наоборот.
Переход к отображению. Для двух степеней свободы функции f
и g возмущенного отображения поворота C.1.13) можно найти в пер-
первом порядке по е следующим образом. Интегрируя уравнение Га-
Гамильтона
-i^-=— e-^i- C.1.26)
dt dOj
Отображения и линейная устойчивость 183
на одном периоде движения по 82, получаем
t-^-(Jn+Xt J2, 8n + (o^, е20 + со20, C.1.27)
ob
где (напомним) J2> сох и <д2 — функции Jn+1, и использованы не-
невозмущенные переменные J, в, т. е. интегрирование производится
по невозмущенной траектории. Изменение переменной действия J
определяется соотношением
е/(/п+1, Qn) = bJ1(Jn+1, 0„). C.1.28I)
Соответствующее изменение фазы наиболее удобно определить
из условия сохранения площади C.1.16). Для возмущенного ото-
отображения поворота это дает
g(J,Q)=-[JL-dQ. C.1.29)
J dJ
В случае явного отображения поворота g = 0.
При вычислении изменения одной из переменных действия не
обязательно выражать невозмущенное движение по остальным сте-
степеням свободы в переменных действие—угол. Для гамильтониана
H = H0(Jlt p2, ft)-f еЯ^, 9Ъ рг, q2). C.1.30)
Уравнение C.1.26) остается прежним, откуда с точностью до е
имеем
, pa(t), q,(t)). C.1.31)
Мы вернемся к этому выражению при рассмотрении сепаратрис-
ного отображения в § 3.5.
Описанная процедура обобщается и на случай N степеней сво-
свободы, что приводит к изменению N—1 переменной действия
Т N
AJ= —8 \ dt (</n_i-l> ¦/«, 9/г ~Т~ &"> 9д/ -f Йи^) C.1.32)
J E6
о
и е/ = Л/. Как и в C.1.15), функция g" в C.1.23) находится путем
интегрирования / по 8„, откуда g = d$/dJn+1, и отображение
C.1.24) полностью определено.
Переход к уравнениям Гамильтона. Рассмотрим явное отображение
поворота C.1.17). Часто бывает желательно представить отображе-
1) В этом соотношении J2 выражено с точностью до е через Jx из гамиль-
гамильтониана #„ (Jг, J2) = const— Прим. ред.
184 Глава 3
ние в форме уравнений Гамильтона, причем роль «времени» играет
номер итерации п х). Это можно сделать, вводя в C.1.17а) периоди-
периодическую дельта-функцию:
оо сю
6i(«)= 2 б(п—т) = 1 +22 cos2ziqn, C.1.33)
где последнее выражение есть разложение Фурье. Тогда C.1.17)
принимает вид
-^- = 6/@N!^), C.1.34а)
dn
=2na(J), C.1.346)
dn
где J (n), 6 (я) — значения величин /„, 9„ как раз перед моментом
«времени» п. Уравнения C.1.34) имеют гамильтонову форму и со-
соответствуют гамильтониану
H(J, 9, п) = 2л fa(/)d/ —еб^л) \f(Q)dQ. C.1.35)
Отметим, что гамильтониан Н этой системы с одной степенью сво-
свободы явно зависит от времени 2). Описанный метод легко обоб-
обобщается и на случай явного отображения поворота с N степенями
свободы. Мы используем гамильтониан C.1.35) для отображения
Улама в § 3.4.
*§ 3.2. Типичное поведение канонических
отображений
Рассмотрим общее поведение системы связанных нелинейных ос-
осцилляторов и структуру их фазового пространства. Основным ре-
результатом здесь является теорема КАМ, гарантирующая существо-
существование инвариантных торов для систем как с двумя, так и с боль-
большим числом степеней свободы. Однако некоторые следствия тео-
теоремы КАМ существенно различаются для этих двух случаев. Так,
диффузия Арнольда возможна лишь в последнем случае. Мы от-
отложим обсуждение этого вопроса до гл. 6. Здесь же для иллюстра-
иллюстрации теоремы КАМ и характерной структуры фазового пространства
мы ограничимся рассмотрением двумерных (сохраняющих площадь)
отображений с некоторыми естественными обобщениями на случай
большего числа степеней свободы.
1) При этом считается, что п изменяется непрерывно. Напомним также,
что «время» п не совпадает с физическим временем t (dn/dt » (Одг/2я), при-
причем зависимость t (п) может быть очень сложной, так как содг = wjv(-/i)>
a Jt — может изменяться хаотически.— Прим. ред.
2) И конечно, совершенно не похож на исходный физический гамильто-
гамильтониан Н с двумя степенями свободы. Тем не менее траектории обеих систем
совпадают для целочисленных моментов «времени» п. Однако для привязки
к физическому времени t необходимо знать зависимость co2 (J\) да
со2 (ylt У2 (^о. ^i))i или исходный гамильтониан Яо (Уг, /2)-— Прим. ред.
Отображения и линейная устойчивость 185
* 3.2а. Иррациональные числа вращения и теория К AM
С учетом возмущения гамильтониан системы зависит от угловых
переменных C.1.12) и, как мы видели в гл. 2, резонансы между
степенями свободы могут нарушить сходимость рядов теории воз-
возмущений. Тем не менее можно доказать теорему (теорема КАМ),
согласно которой при выполнении определенных (перечисленных
ниже) условий существуют инвариантные торы
У = Л-Ы>A, е), C.2.1а)
в = 1+иA, е). C.2.16)
Здесь и и v периодичны по \ и равны нулю при е = 0, а вектор \
связан с невозмущенными частотами х) на торе соотношением
| = to. Условия применимости теоремы КАМ следующие:
1) частоты должны быть линейно независимы в некоторой об-
области J (условие нелинейности невозмущенных колебаний 2))
1><(о* (¦/)?= О, C.2.2)
i
где со; — компоненты вектора ю — dHJdJ, а пц — компо-
компоненты целочисленного вектора гп\
2) возмущение должно иметь достаточно большое число непре-
непрерывных производных (условие гладкости возмущения);
3) система должна находиться достаточно далеко от всех резо-
нансов, так что
т-&\ > у\т\~х C.2.3)
для всех т. Здесь т зависит от числа степеней свободы и глад-
гладкости возмущения Нъ а у зависит от величины возмущения
еН 1 и нелинейности G невозмущенного гамильтониана Но.
Поскольку неравенство C.2.3) не может выполняться при слишком
большом значении у, которое растет с | еЯх | и 1/G, инвариантные
торы существуют лишь при достаточно малой величине возмуще-
возмущения. Из условий 1 и 3 следует также и условие умеренной нелиней-
нелинейности 3). Если условия теоремы выполнены, то, например, окруж-
окружности отображения поворота слегка деформируются под действием
возмущения, не изменяя топологии, как это показано для сечения
инвариантного тора на рис. 3.2, а.
1) Лучше было бы сказать средними частотами, поскольку успех теории
КАМ связан прежде всего с фиксацией средних частот, а не начальных ус-
условий, как это обычно делается (см. примечание редактора на с. 168). Именно
для этих фиксированных частот и справедливы условия C.2.2) и C,2.3), при-
приведенные ниже.— Прим. ред.
2) Это последнее условие имеет вид: det (dcoi/dJi;) ф 0 [см. C.2.10)];
условие же C.2.2) следует из C.2.3).— Прим. ред.
3) См. C.2.36).— Прим. перев.
186
Глава 3
Эта теорема была доказана Арнольдом [10] для аналитического
возмущения Н^ на основе работы Колмогорова [229] и Мозером
[308 ] при условии существования достаточно большого числа не-
Иноариангпная
кривая
Окружность
А.
У
S + 1
Си>! /CO., = S
Рис. 3.2. К теории КАМ.
а — в нелинейной системе возмущенная инвариантная кривая лежит вблизи нсвозму-
щенной (окружность); б — целые резонансы; о — дробные резонансы между двумя це-
лычи резонансами б; области резонансов заштрихованы; кы1 — GSJt; Дсо, ¦ со2 =
=- @)! (О г) — S.
прерывных производных. Теорема устанавливает существование
интегралов движения для многомерных нелинейных колебаний.
Как признание важности работ указанных авторов ее принято на-
Отображения и линейная устойчивость 187
зывать теоремой КАМ. Ниже мы обсудим смысл теоремы, идею до-
доказательства и значение условий ее применимости.
Проиллюстрируем трудности доказательства теоремы на при-
примере двумерного отображения поворота C.1.13). Последовательные
пересечения возмущенной траектории с поверхностью 02 = const
(см. рис. 3.1, а) описываются разностными уравнениями, которые
определяют новые значения переменных J ъ Q1 на поверхности се-
сечения через их предыдущие значения. Предположим, что инвари-
инвариантная кривая вида C.2.1а) удовлетворяет уравнению
J1(Q1) + v(B1), C.2.4)
где v Fj) — некоторая известная периодическая функция. Попро-
Попробуем решить это уравнение путем разложения в ряд Фурье по 9Х:
h (ЭО = 2 akem'; v (8X) = 2 Ьье™1. C.2.5)
k k
Тогда
Jt (9j - 2л«) — Jj @X) = — V ak [1 —exp (ik2na)] exp {ikQJ,
k
C.2.6)
откуда
a* = ^ . C.2.7)
1 — exp (ik 2яа)
Коэффициенты а^ убывают медленнее, чем bk, а при рациональных
а некоторые из них не определены. В этом и состоит проблема ма-
малых знаменателей, препятствующих сходимости рядов теории воз-
возмущений. Если а зависит от Jlt то величину J x нужно выбирать
так, чтобы ни один знаменатель не оказался резонансным. Для
этого необходимо соответствующим образом изменить процедуру
разложения, а также потребовать достаточно быстрого убывания
коэффициентов bk- Доказательства теоремы КАМ чрезвычайно
сложны и мы не будем их здесь излагать. Основная идея доказа-
доказательства состоит в изменении начальных условий на каждом шаге
разложения таким образом, чтобы все время оставаться достаточно
далеко от всех резонансов и тем самым иметь возможность продол-
продолжать разложение.
Нелинейность 1), Мы уже знаем, что при наличии резонанса между
степенями свободы невозмущенной системы фазовые траектории
2) В оригинале — linear independence or sufficient nonlinearity (линей-
(линейная независимость, или достаточная нелинейность). Термин «линейная не-
независимость частот» обычно связывается только с условием вида C.2.2), ко-
которое может выполняться и для линейного осциллятора с постоянными ча-
частотами. Поэтому в переводе используется в этом случае термин «нелиней-
«нелинейность (колебаний)», понимаемый в смысле условия C.2.10), приведенного
ниже.— Прим. ред.
188 Глава 3
существенно искажаются под действием возмущения. Если невоз-
невозмущенные частоты зависят от переменных действия, то изменения
последних выводят систему из резонанса и тем самым ограничивают
эти изменения. Если максимальные колебания J много меньше не-
невозмущенного значения Jo, то возможно существование инвариант-
инвариантных кривых, расположенных «вблизи» невозмущенных J = Jo.
В этом и состоит смысл условия нелинейности невозмущенных ко-
колебаний. Это условие гарантирует, что в выражении C.2.1а)
v (|, е) ->- 0 при е ->- 0.
Чтобы полнее изучить этот вопрос, найдем условие линейной
зависимости частот. Для простоты рассмотрим систему с двумя
степенями свободы и предположим, что частоты coj (J u /2) и
со.2 (Jъ Jг) связаны соотношением
/((»!, С02) = 0.
Дифференцируя, получаем
df
для любых dJ х и dJ 2. Это уравнение удобно записать в матричном
виде
df
©,/ =| ]| | = 0. C.2.8)
dJ-i
Если det ©^ Ф 0, то единственное решение: /а = 0. Это означает,
что не существует справедливого для всех / соотношения вида
0. C.2.9)
Следовательно, необходимое условие нелинейности колебаний
можно записать в виде 1)
det @,^0. C.2.10)
Именно в такой форме его обычно и приводят.
Для некоторого заданного резонанса условие C.2.10) можно
ослабить, потребовав лишь, чтобы частота не оставалась постоян-
постоянной 2) вдоль направления фактического приращения J. Действи-
1) В теории КАМ это условие необходимо для компенсации сдвига ча-
частот из-за возмущения (Дш) путем изменения начальных условий (ДУ), т. е.
для разрешимости системы линейных уравнений Дш = otj-AJ относительно
AJ.— Прим. ред.
2) Точнее, чтобы не сохранялось условие резонанса т-ч> = 0.— Прим.
Отображения и линейная устойчивость 189
тельно, рассмотрим систему с двумя степенями свободы и гамиль-
гамильтонианом B.4.1):
I, m
Выбирая резонанс с I = r, m = s и а>г!&1 = r^s> подставляя в
C.2.8) с dflda1 = r, d//dw2 = — s и учитывая, что из уравнений
Гамильтона dJ1ldJ2 = — г Is, получаем условие на нелинейность
в виде
г2 2rs l-s2 — -ф 0; C.2.12)
? 2
оно используется также при доказательстве теоремы КАМ. В слу-
случае произвольного числа степеней свободы аналогичный результат
приведен в § 3.3 работы [70]:
пи д2Но т/фО. C.2.13)
Поучительно получить соотношение C.2.12) с помощью резо-
резонансной теории возмущений (§ 2.4). Используя производящую
функцию B.4.5),
F2 = (rQ1—sQ2)~J1 + %J2, C.2.14)
перейдем в гамильтониане C.2.11) к новым переменным B.4.6).
Разлагая гамильтониан в окрестности резонансного значения пе-
переменной действия и усредняя по быстрой фазе, находим в низшем
порядке по е:
3^ JavOI C.2.15)
^ +гъ
где для простоты амплитуда Hrs принята действительной. Если
d2H0ldjf, то нелинейность появляется лишь в более высоком по-
порядке, и ширина сепаратрисы не будет ограничена величиной по-
порядка s1/2. Таким образом, мы получили условие на нелинейность,
эквивалентное C.2.12):
^Яо_ C.2.16)
d~J2
Это условие разделяет системы на невырожденные (с?Н0Ш\ ф 0)
или сально нелинейные, и вырожденные (d2Ti0ld~j\ = 0), или слабо
нелинейные. Именно невырожденные системы удовлетворяют ус-
условиям теоремы КАМ. Покажем эквивалентность условий C.2.16)
и C.2.12). Представляя C.2.16) в виде
дН0 dJt дН0 dJ2
д~]\ dJl \ dJl a7[ dJ2 dlx
и учитывая, что dJ JdJ\ — г, a dJ\ldJx = — s, получаем C.2.12).
190 Глава 3
Величину необходимой нелинейности G при заданном е можно
оценить, потребовав, чтобы максимальное изменение переменной
действия A/j было много меньше невозмущенного значения J0.
Полная ширина сепаратрисы равна А/1 = rAJ1. Используя
C.2.15), находим
или
G> 32r4iHrs ¦ C.2.18)
Вырождение, при котором не выполняется условие C.2.10),
встречается во многих системах, представляющих физический ин-
интерес. Возникает естественный вопрос: существуют ли инвариант-
инвариантные кривые для таких систем? Представляется, что обычно, хотя
и не всегда, общая структура теории КАМ сохраняется и в этом
случае г). Мы уже рассматривали два таких примера: задачу Хе-
нона—Хейлеса (§ 1.4) и резонанс волна—частица (§ 2.4). Еще
один пример — «эффекты встречи» в накопительных кольцах
[404] 2). Во всех этих задачах не зависящая от фаз часть гамиль-
гамильтониана имеет вид
H0 = (*0-J + eH10(J), C.2.19)
а нелинейность возникает из члена возмущения с т = 0. Хотя
величина нелинейности G порядка е, условие на нелинейность
C.2.18) все еще может выполняться. Таким образом, инвариант-
инвариантные кривые могут существовать и для вырожденных систем. Если
теперь рассмотреть резонансы второго и более высоких порядков,
как это было сделано в § 2.4, то соответствующие им гамильтонианы
оказываются, как правило, невырожденными. Таким образом,
структура фазового пространства вырожденных и невырожденных
систем является, вообще говоря, сходной.
Отметим, что есть также особые случаи вырождения, когда
инвариантные кривые не существуют. Интересным примером слу-
служит система, рассмотренная Лансфордом и Фордом 1286], а также
Контопулосом [89]. Следуя Контопулосу, запишем гамильтониан
системы в виде
Н = Wj/! -гco2/2 -f- GK/3-ге [ct cos(m^Qi т2в2 -',- тз9з) +
-f P cos («A -r п2% -|- л893)], C.2.20)
где аир — некоторые нелинейные функции U, a miy П{ — целые
числа. Так как гамильтониан зависит только от двух линейных
х) Обобщение на вырожденные системы проведено Арнольдом и Мозе-
ром (см. [11], § 10 и [374], § 34).— Прим. ред.
2) См. также [207].— Прим. ред.
Отображения и линейная устойчивость 191
комбинаций фаз, то преобразование вида B.4.5) оставляет лишь
две новые фазы:
+ 8 [acos Bi + рcos92], C.2.21)
где Q1 = m1Q1 + m292 + m393, 9~2 = л191 + Я292 + ^з^з. И1 =
= m1w1-r m2co2 -f- m3co3 и т. д. Поскольку гамильтониан не за-
зависит от 63, то 73 — сохраняется, и задача приводится к двум сте-
степеням свободы. Однако если выбрать частоты так, что coj = <д2 = О,
как это сделали Лансфорд и Форд, то гамильтониан приведенной
системы принимает вид
Н = е [a cos ех + р cosej. C.2.22)
В отличие от задачи с волной (см. п. 2.4в) разделение на быстрые
и медленные переменные здесь невозможно. Следовательно, не-
неприменима и резонансная теория возмущения. Фактически рас-
рассматриваемая система вообще не имеет малого параметра 1), т. е.
не близка к интегрируемой. В таком случае нет основания ожидать
существования инвариантных кривых даже в пределе е —*- 0. Это
и было обнаружено Лансфордом и Фордом путем численного ин-
интегрирования уравнений движения 2).
Условие на гладкость возмущения. Необходимую гладкость воз-
возмущения (число его непрерывных производных) можно определить,
исходя из представления о том, что инвариантные кривые сущест-
существуют только вне всех резонансных областей. Если все фазовое про-
пространство между двумя резонансами низшего порядка заполнено
другими резонансами, разумно заключить, что инвариантные
кривые здесь не существуют. Рассмотрим снова простейший случай
двух степеней свободы с гамильтонианом C.2.11). Будем считать,
что невозмущенный гамильтониан Но зависит от J2 линейно, и по-
положим сй1/со2 = s. Тогда расстояние между целыми резонансами
по частоте Ьах — со2 — const и не зависит от J г и J2 (см. рис. 3.2,6).
Между этими целыми резонансами расположены дробные резо-
нансы с отношением частот co^'cog = s + plq, где р, q — целые
числа и p<zq. В C.2.11) при / = q это соответствует целым числам
т(р, q) = p + sq. C.2.23)
Используя выражение B.4.31) для ширины сепаратрисы отдель-
отдельного резонанса
1) Поскольку характер ее движения вообще не зависит от величины е,
которая определяет лишь масштаб времени.— Прим. ред.
2) Принятое выше условие шг = со2 = 0 означает наличие двух незави-
независимых резонансов в невозмущенной линейной системе C.2.20). Отсутствие
таких резонансов и есть дополнительное условие применимости теории КАМ
к вырожденным системам (см. примечание редактора на с. 190).— Прим.
ред.
192 Глава 3
а также соотношения AJ г = qAJ 1 и G = q2d2H0!dJ\ = q2G, по-
получаем
' °" "" Z ^'/2. C.2.24)
где суммирование производится по всем вторичным резонансам.
Поскольку
Аыг= ~ AJ1 = GAJ1, C.2.25)
то отношение суммарной ширины вторичных резонансов, заштри-
заштрихованных на рис. 3.2, в, к расстоянию между первичными резонан-
сами равно
— = 2-1 »,„• C.2.26)
Предположим теперь, что возмущение в гамильтониане имеет S
непрерывных производных. Так как величина т пропорциональна
д, то фурье-амплитуды убывают при больших q по закону 1)
Ао C.2.27)
где Ло — некоторая постоянная. Подставляя эту оценку в C.2.26
и замечая, что
^H^ — qH^, C.2.28)
получаем
4B80Л,)'/'
| ()
При 5>2 эта сумма сходится к некоторому положительному числу
о. Таким образом, независимо от коэффициента перед суммой мы
приходим к важному условию существования инвариантных торов:
5>2. C.2.30)
Можно сравнить этот результат с условием применимости тео-
теоремы КАМ, записав соотношение C.2.3) для случая двух степеней
свободы в виде
а>1 г
s
>YS~(T+1). C.2.31)
') В случае двух степеней свободы достаточно наложить условие на глад-
гладкость только по одной из фаз, так как зависимость от другой фазы можно
исключить переходом к отображению. Оценка для коэффициентов Фурье
C.2.27) справедлива при следующих дополнительных условиях (см., на-
например, [548]): 1) \Нцт\ убывают монотонно с q; 2) (S -f- 1)-я производная
ограничена и имеет конечное число разрывов.— Прим. ред.
Отображения и линейная устойчивость 193
Левую часть этого неравенства можно рассматривать как относи-
относительную ширину одного из дробных резонансов, которая исклю-
исключается неравенством C.2.31). Просуммируем теперь по всем дроб-
дробным резонансам, лежащим между двумя целыми резонансами, т. е.
на единичном интервале отношения частот со1/со2, учитывая, что
число возможных значений г на этом интервале не превышает s.
Суммарную величину исключаемого интервала Ж (по мере Лебега^
см., например, [374]) можно найти, умножая C.2.31) на s и затем
суммируя по s. Получаем
^s~\ C.2.32)
s=l
Сравнивая выражения C.2.32) и C.2.29), мы видим, что т соот-
соответствует величина 5/2, а^~ (eGAoI/Vco2. Как и в C.2.29), сумма
в C.2.32) сходится при т>1. Как показал Мозер (см. [374]), этого
хватает для существования инвариантных торов. Если учесть, что
гамильтониан C.2.11) является интегралом соответствующего ото-
отображения [см. C.1.27)], то отсюда можно прийти к заключению,
что для существования инвариантных кривых двумерных отобра-
отображений достаточно двух непрерывных производных для самого ото-
отображения или трех производных для соответствующего гамиль-
гамильтониана. Мозер утверждает [310], что для доказательства сущест-
существования инвариантных кривых достаточно потребовать1) 5>4,
и высказывает предположение, что это условие можно фактически
ослабить до 5>3. Приведенные в п. 3.46 численные данные указы-
указывают на существование инвариантных кривых 2) при 5 > 2, ана-
аналогичный результат был получен Чириковым [70]. Однако при
5 = 0 это уже не так (п. 3.46). С другой стороны, Тэкенс [402]
построил пример, в котором нет инвариантных кривых и при
5 = 2. Таким образом, как и Мозер [310], мы можем предполо-
предположить, что условия 5>3 всегда достаточно для существования ин-
инвариантных кривых 3). Можно также думать, что в некоторых слу-
1) Здесь и ниже приведены значения S для гамильтониана. Следует иметь
в виду, что в общем случае параметр гладкости S может быть и не целым
числом, как это видно из фурье-представления возмущения C.2.27).—
Прим. ред.
2) Этот вывод противоречит условию C.2.30) и является спорным, в ча-
частности, в работах [70, 475] интерпретация аналогичных численных дан-
данных совсем иная (см. примечание редактора на с. 227).— Прим. ред.
3) При сравнении условия C.2.30) с цитированными результатами ма-
математических работ следует иметь в виду, что в последних рассматриваются
любые возмущения определенного класса непрерывности (по Гёльдеру) С1,
не ограниченные неявно принимаемыми в основном тексте дополнительными
условиями (см. примечание редактора на с. 192). Если понимать S как па-
параметр убывания коэффициентов Фурье в C.2.27), то утверждение Мозера
соответствует S > 3 и подтверждается последними результатами Германа и
Рюссмана (см. [476]), а гипотеза Мозера S>2 опровергается контрприме-
контрпримерами Германа для любого S<3.— Прим. ред.
194 Глава 3
чаях инвариантные кривые могут существовать и при двух непре-
непрерывных производных возмущения в гамильтониане.
Расчеты, приводящие для двух степеней свободы к условию
C.2.30), были выполнены Чириковым [70] в общем виде для N
степеней свободы. Он получил следующее необходимое условие су-
существования инвариантных торов 1):
2. C.2.33)
Для этого же случая Мозер [309] получил строгое достаточное
условие
S>2N + 2 C.2.34)
в предположении, что величина у, стремящаяся к нулю вместе с е,
выбрана также достаточно малой. Отметим, что это более сильное
требование, чем гипотеза Мозера S>3 для двумерных отобра-
отображений 2).
Достаточная иррациональность и умеренная нелинейность. Пред-
Предполагая, что сумма в C.2.29) сходится к некоторому о, мы видим,
что инвариантные кривые не существуют, если а = co^coa лежит
внутри одного из заштрихованных на рис. 3.2, в интервалов 3).
Так как ширина этих интервалов пропорциональна (eG)'1- и убы-
убывает с ростом q, то необходимо, чтобы величина а лежала доста-
достаточно далеко от любого рационального значения plq. При малых
е это условие легко выполнимо, но с ростом е инвариантные кривые
существуют лишь для таких иррациональных а, которые наиболее
плохо аппроксимируются рациональными числами. С этой точки
зрения самым иррациональным числом является золотое сечение:
а = (д/5—l)'2 = ag. Грин [165] дал очень точный критерий
возникновения сильной стохастичности в предположении4), что ин-
инвариантная кривая с а = ag разрушается последней (с ростом е).
Мы опишем метод Грина и его результаты в гл. 4.
Положив левую часть C.2.29) равной единице, получим усло-
условие малости возмущения е:
^i-, C.2.35)
J) Обобщение этого результата на случай явной квазипериодической
зависимости от времени дано в работе [477].— Прим. ред.
2) Оценку Мозера C.2.34) можно, по-видимому, улучшить, если учесть,
что фактически гладкость по одной из N фаз несущественна (см. примечание
редактора на с. 192), т. е. N -*¦ N—1. Считая, как и выше, S параметром
в C.2.27) (см. примечание редактора на с. 193), получаем S > 2N—1. Оценка
C.2.33) при этом не изменится.— Прим. ред.
3) Правильнее сказать, что пока мы не уверены, существуют ли инвари-
инвариантные кривые внутри этих интервалов. На самом деле размер областей,
где они действительно разрушаются, много меньше (см. [70] и п. 4.26).—
Прим. ред.
4) Обсуждение этой гипотезы см. в работе [76].— Прим. ред.
Отображения и линейная устойчивость 195
а также (при заданном е) некоторое ограничение на нелинейность
сверху. Используя выражения C.2.18) и C.2.35), приходим к ус-
условию умеренной нелинейности
32еЛп _ со?
¦ г9- <G< —¦ C.2.36)
/2 32еЛ0а2 V '
При этом в C.2.18) мы положили (r2lq2) Hrs~-A0. Аналогичные
оценки были получены Чириковым [70].
При доказательстве теоремы КАМ [308] возмущение е прихо-
приходится, вообще говоря, полагать чрезвычайно слабым. Чириков
[67] нашел, что критическую величину возмущения можно оце-
оценить из условия перекрытия целых резонансов, изображенных на
рис. 3.2, б. Численные эксперименты показали, что этот критерий
дает разумную оценку для величины возмущения, при которой
разрушаются последние инвариантные кривые, проходящие между
этими резонансами. Используя аналитические и численные ре-
результаты с учетом дробных резонансов q = 2 и q = 3, Чириков
[70 ] усовершенствовал критерий перекрытия и получил весьма
точные предсказания для границы стохастичности. Критерий пе-
перекрытия резонансов и связанные с ним другие критерии перехода
к стохастичности для некоторого класса типичных возмущений
будут подробно рассмотрены в гл. 4.
* 3.26. Рациональные числа вращения и структура резонансов
Продолжим изучение возмущенного отображения поворота C.1.13).
Как мы уже знаем, согласно теореме КАМ, инвариантные кривые
с иррациональным значением а, достаточно удаленным от рацио-
рациональных значений rls, сохраняют свою топологию и лишь слегка
деформируются при малом возмущении. Однако при рациональных
значениях а = rls и вблизи них теорема КАМ неприменима. Для
исследования структуры отображений в этом случае воспользуемся
более ранней теоремой.
Теорема Пуанкаре—Биркгофа. В случае невозмущенного отображе-
отображения поворота C.1.8) любая точка на окружности a (J) = rls яв-
является периодической1) с периодом s (см. рис. 3.1,6). Теорема
Пуанкаре—Биркгофа утверждает, что возмущенное отображение
поворота будет иметь 2ks периодических точек (k = 1, 2, . . .).
Поясним это, используя рис. 3.3.
Предположим для определенности, что a (J) возрастает с /.
Тогда вне кривой, соответствующей рациональному значению
a (J) = rls, существует инвариантная кривая a>r/s, которая после
х) В оригинале — fixed point (неподвижная точка), термин, который
относится не к исходному отображению Т, а к его s-й степени Ts, т. е. к ото-
отображению после s итераций.— Прим. перев.
196
Глава 3
s итераций отображения окажется повернутой против часовой
стрелки (наружные стрелки на рис. 2.3). Существует и инвариант-
инвариантная кривая с a<zr/s, которая после s итераций окажется поверну-
J
Гиперболическая
точка"
Эллиптическая
точка
*- J
Рис. 3.3. К теореме Пуанкаре—Биркгофа.
Пересечения сплошной кривой, для всех точек которой полярный угол в остается Неиз-
Неизменным после s итераций, с s-й итерацией этой кривой (пунктирной) определяют периоди-
периодические точки отображения.
той по часовой стрелке (внутренние стрелки). Следовательно, ме-
между этими двумя кривыми должна существовать некая (не инвари-
инвариантная) кривая (на рис. 3.3 — сплошная линия), угловые коорди-
координаты точек которой не изменяются после s итераций. Радиальные
же координаты изменяются таким образом, что сплошная линия
на рис. 3.3 переходит в пунктирную. Так как отображение сохра-
сохраняет площадь, то обе кривые ограничивают одинаковые площади.
А это возможно, лишь если эти кривые взаимно пересекаются чет-
четное число раз. После s итераций каждая точка пересечения возвра-
возвращается в исходное положение и, таким образом, каждая из s ее ите-
итераций является периодической точкой. При четном числе пересе-
пересечений всего должно быть 2ks таких точек, которые называются пе-
Отображения и линейная устойчивость 197
риодическими точками Пуанкаре—Биркгофа. Теорема ничего не
говорит о величине k, хотя обычно k = 1.
Если мы более подробно рассмотрим отображение в окрестно-
окрестности периодических точек на рис. 3.3, то заметим, что существуют
два различных типа поведения. Вблизи эллиптической точки (см.
рис. 3.3) соседние точки как бы вращаются вокруг нее. В противо-
противоположность этому вблизи гиперболической точки соседние точки
уходят из ее окрестности. Мы уже встречались с поведением такого
типа при рассмотрении движения в фазовом пространстве простого
маятника в § 1.3. Там мы нашли цепочки чередующихся эллиптиче-
эллиптических и гиперболических точек, причем первые окружены регуляр-
регулярными траекториями, а вторые соединены между собой сепаратри-
сепаратрисами. Такая картина является типичной для нелинейных колеба-
колебаний при малом возмущении.
Эллиптические точки. В § 2.4 путем перехода к переменным, свя-
связанным с эллиптической точкой, нам удалось исследовать все бо-
более и более мелкие области регулярного движения на фазовой
плоскости. Мы видели, что вокруг эллиптической точки сущест-
существует своя система резонансов (периодических точек) более высокого
порядка, движение вокруг которых повторяет исходное на более
мелком масштабе. Было показано также [см. B.4.62) и последующее
обсуждение], что возмущение в высших порядках очень быстро умень-
уменьшается с s (пропорционально 1/s!). Если исходное возмущение мало,
то фазовая плоскость заполнена, в основном, инвариантными кри-
кривыми, топология которых такая же, как и у невозмущенной си-
системы. Остальная часть фазовой плоскости вокруг эллиптических
точек заполнена инвариантными кривыми другой топологии. Можно
ли сказать, что вся фазовая плоскость заполнена инвариантными
кривыми все возрастающей сложности и все более мелких масштабов,
пока с ростом возмущения вся эта структура внезапно не разру-
разрушается, переходя в стохастичность? Оказывается, что нет. В ти-
типичном случае области стохастичности существуют в окрестности
сепаратрис (связанных с гиперболическими точками) при любом
возмущении и растут вместе с ним.
Гиперболические точки. Рассмотрим поведение отображения в ок-
окрестности гиперболической точки. Мы уже знаем, что осциллятор
с одной степенью свободы, как, например, маятник, имеет сепа-
сепаратрису, которая соединяет гиперболические точки, приближаясь
к одной из них и удаляясь от другой. У маятника есть лишь одна
гиперболическая точка, но в общем случае имеется цепочка из ks
гиперболических точек. В интегрируемом случае они соединяются
между собой гладкой сепаратрисой. В случае же неинтегрируемой
системы с несколькими степенями свободы или соответствующего
отображения вида C.1.13) ситуация оказывается значительно бо-
более сложной. Следуя Берри [26 ], мы качественно опишем картину
У О
-0,05 —
-0,10'
Гиперболическая
непоЭйижная точка
-0,10
|
-0,05
0,05
0,16
Рис. 3.4. Гомоклинная точка и стохастичность вблизи сепаратрисы (число-
(числовые данные из работы^ [107]).
а — входящая (н+) и выходящая (н~) сепаратрисы пересекаются в бесконечном числе
точек (схема); б — более подробная картина пересечений вблизи гиперболической точки.
Отображения и линейная устойчивость 199
поведения сепаратрис, основанную на работах Пуанкаре [337],
Биркгофа [30] и Смейла [381 ] х). Близкое изложение содержится
в книгах Арнольда и Авеза [14] и Мозера [310].
Гиперболическая точка соединяет четыре траектории: две вхо-
входящие (//+) и две выходящие (Н~). Точка х принадлежит сепарат-
сепаратрисе #+, если в результате последовательных отображений Тпх
она приближается к гиперболической точке при п-> с». Если же
это происходит в результате обратных отображений Т~пх, то точка
х принадлежит сепаратрисе Н~. Поскольку на сепаратрисе период
колебаний бесконечен, движение точки х становится все более и
более медленным по мере приближения к гиперболической точке.
Рассмотрим теперь две соседние гиперболические точки одного
и того же резонанса. В отличие от интегрируемой системы сепарат-
сепаратриса Н~, выходящая из гиперболической точки, не соединяет ее
с соседней, а в типичном случае пересекает сепаратрису Н+, при-
приходящую в соседнюю (сдвинутую по фазе на 2n/ks) гиперболиче-
гиперболическую точку. Место пересечения называется гомоклинной точкой,
так как она соединяет выходящую и входящую сепаратрисы од-
одного и того же резонанса. Пересечения сепаратрис соседних резо-
нансов называются гетероклинными точками. Легко показать, что
если существует одно пересечение, то их существует и бесконечно
много.
Такое чрезвычайно сложное поведение можно представить себе
несколько более наглядно с помощью следующей схемы, как это
было сделано впервые Мельниковым [298]. Рассмотрим гипербо-
гиперболическую точку и ее отображение, как показано на рис. 3.4, а.
Из пересечения сепаратрис Н~ и Н+ в гомоклинной точке х сле-
следует, что они пересекаются и в точках х', х" и т. д. При этом точка
х" расположена к х' ближе, чем х' к х. Так как области, заклю-
заключенные между взаимно пересекающимися кривыми Н~ и #+ (они
заштрихованы на рисунке), являются отображениями одна другой,
то их площади равны. Следовательно, между точками х' и х" кри-
кривая Н~ отклоняется от Н+ сильнее, чем между хих'. Последующие
пересечения сепаратрис все более и более сближаются, а амплитуда
осцилляции Н~ возрастает. На рисунке не изображена сепаратриса
Н+, приближающаяся к левой гиперболической точке сверху. Она
осциллирует так же сильно, как и Н~ справа. Все сказанное от-
относится и к двум другим сепаратрисам в нижней части рисунка.
На рис. 3.4, б приведены численные результаты Драгта и Финна
[107], иллюстрирующие пересечение сепаратрис в окрестности
гиперболической точки. Сепаратриса Н~, выходящая из соседней
гиперболической точки слева, осциллирует при приближении к ги-
гиперболической точке справа, а сепаратриса Н+ (не показанная на
рис. 3.4, а) осциллирует, удаляясь от нее.
1) Важную роль в этих исследованиях сыграли также работы Мельни-
Мельникова [298, 299].— Прим. ред.
200 Глава 3
Для численного определения сепаратрис, например Н~, выби-
выбираем произвольную точку на кривой Н~ вблизи той гиперболиче-
гиперболической точки, из которой она выходит, и проводим прямую между
выбранной точкой и ее отображением. Последовательные итерации
этого отрезка и дают осциллирующую сепаратрису Н~, прибли-
приближающуюся к соседней гиперболической точке справа.
Сами по себе гомоклинные точки еще не дают полной картины
всей этой очень сложной области вблизи сепаратрисы. Так как пе-
период фазовых колебаний обращается в бесконечность на сепарат-
сепаратрисе, то в ее окрестности имеется бесконечно много вторичных
резонанов, соответствующих высоким гармоникам частоты фазо-
фазовых колебаний. Каждый из этих резонансов имеет свою собствен-
собственную систему чередующихся эллиптических и гиперболических то-
точек, со своим сложным движением в их окрестности и многократ-
многократными пересечениями как своих сепаратрис, так и сепаратрис пер-
первичного резонанса в гетероклинных точках. Все эти сепаратрисы,
по-видимому, всюду плотно заполняют доступное им фазовое про-
пространство. Пересечение сепаратрис фактически показывает, что
в этой области не могут существовать инвариантные торы вследст-
вследствие изменения топологии траекторий1). Подробное обсуждение
этих вопросов дано Драгтом и Финном [107]. Однако для малых
возмущений все это чрезвычайно сложное поведение происходит
лишь в ограниченной инвариантными кривыми области фазового
пространства (рис. 3.4, а).
* 3.2в. Полное описание нелинейного отображения
Теперь мы можем полностью описать структуру отображения, на-
например поверхность сечения нелинейного осциллятора с двумя
степенями свободы. Очень схематично топология такого отображе-
отображения дана Арнольдом и Авезом [14]. Рассмотрим случай умеренного
возмущения, когда многие невозмущенные инвариантные кривые
(J = const, см. рис. 3.1, б) сохраняются и при наличии возмущения.
Будем считать для определенности, что daJdJi<0, a a =
= со01/со02 = 1/л (иррациональное число) при Jх = 0. С ростом
J\ частота (а1 уменьшается, пока не достигнет значения, соответст-
соответствующего первому существенному резонансу сох = со2/4. При этом
на поверхности сечения образуется цепочка из четырех островков.
Другими словами, если начальные условия траектории совпадают
х) Связь гомоклинной структуры с неинтегрируемостью обсуждалась
еще Пуанкаре [337] и была строго доказана в работе [478] (см. такжеИ479,
480]). Следует, однако, иметь в виду, что это локальная неинтегрируемость,
имеющая место лишь на множестве начальных условий, вообще говоря, ма-
малой меры, дополнительном к большинству начальных условий, для которых
инвариантные торы сохраняются согласно теории КАМ (см. ниже и [477]).—
Прим. ред.
Отображения и линейная устойчивость 201
с периодической точкой отображения, то соответствующая траекто-
траектория, помеченная точками лг0, лг1( ... на рис. 3.1, б, сделает четыре
витка вокруг тора. Для близких соседних точек величина
dJJdt Ф 0, и их траектории на поверхности сечения охватывают
периодические точки. В § 2.4 было показано, как рассчитывать
такие замкнутые кривые, другие примеры будут приведены в § 3.4
и 3.5 и в последующих главах. Наши предыдущие качественные
рассуждения привели к выводу о чередовании эллиптических и ги-
гиперболических точек на поверхности J = const, что совпадает с ре-
результатами § 2.4 на основе теории возмущений. Наличие гомоклин-
ных и гетероклинных точек в окрестности гиперболической точки
обусловливает существование области хаотического движения,
ограниченной инвариантными кривыми.
Увеличивая J ъ мы придем к следующему существенному ре-
резонансу ©х = со2/5 с цепочкой из пяти островков. При дальнейшем
увеличении J ± будут последовательно встречаться резонансы с чис-
числом островков, равным шести, семи и т. д. При этом между каж-
каждыми двумя из этих главных резонансов существует еще и беско-
бесконечно много промежуточных резонансов, соответствующих всем
промежуточным рациональным отношениям частот. Однако вели-
величина последних резонансов, как было показано в § 2.4, быстро
убывает. Так, например, одним из промежуточных резонансов ме-
между двумя главными резонансами с а = 1/4 и а = 1/5 является
резонанс с а = 2/9, т. е. с г = 2 и s = 9. Его размер относится
к размеру резонанса с а = 1/5 как квадратный корень из отноше-
отношения соответствующих амплитуд фурье-разложения возмущения.
В самом деле, используя выражение B.4.31), получаем
еЯл — '/г, C.2.37)
д2Н01д1\
где #r,_s — амплитуда фурье-разложения соответствующей ре-
резонансной гармоники. Максимальная величина фурье-амплитуды
равна (см. п. 2.46):
где fs — функция Бесселя. В результате находим грубую оценку
отношения размера резонансов:
\1ЩЪ « 0,1. C.2.38)
AJ(s/r = 5)
Таким образом, относительный размер резонансов более высоких
гармоник весьма мал.
В итоге мы приходим к качественной картине структуры отоб-
отображения, представленной на рис. 3.5, а. Инвариантные кривые
изображены здесь сплошными линиями. Те из них, которые окру-
202
Глава 3
Рис. 3.5. Регулярные и стохастические траектории при относятельнв боль-
большом возмущении.
а — вблизи первичного резонанса; б — вблизи вторичного резонанса (увеличено и растя-
растянуто по вертикали).
Отображения и линейная устойчивость 203
жают начало координат {J х = 0), при наличии возмущения уже
не являются окружностями и соответствуют новым интегралам
движения Jx = const, a J x является периодической функцией
фазы. Приближенные значения этих инвариантов можно получить
методом усреднения (§ 2.3). Инвариантные кривые, окружающие
эллиптические точки, нельзя найти таким способом, но они полу-
получаются с помощью резонансной теории возмущений (§ 2.4). Для тра-
траекторий же вблизи сепаратрис интеграл движения не существует,
и они заполняют на поверхности сечения некоторую конечную об-
область. Несколько таких областей показаны на рис. 3.5, а штрихов-
штриховкой. Они ограничены инвариантными кривыми. Между резонансом
с а = 1/4 и а = 1/5 расположен более мелкий, но все еще различи-
различимый резонанс с а = 2/9. Есть, конечно, и все другие промежуточ-
промежуточные резонансы. Однако они не показаны на рисунке либо потому,
что имеют слишком малые размеры и неразличимы в принятом мас-
масштабе, либо потому, что они целиком погружены в хаотические
области других резонансов.
Что же мы увидим, если увеличить масштаб в окрестности ка-
какого-либо островка одного из резонансов? Для этого перейдем сна-
сначала к новым переменным^!, Qx (§ 2.4) и введем новую переменную
действия
/i=^Pi4 C-2.39)
соответствующую замкнутой траектории вокруг эллиптической
точки с заданным а. При этом траектории исходного резонанса
преобразуются в систему концентрических окружностей. Однако
резонансы между этими колебаниями и основными частотами си-
системы приводят к возникновению вторичных резонансов, которые
деформируют окружности. Мы уже рассматривали вторичные ре-
резонансы в п. 2.46 и нашли, что их размер и частота фазовых колеба-
колебаний экспоненциально малых) с показателем, пропорциональным
A/а)'1'. Для ширины вторичных t резонансов можно получить
оценку, аналогичную C.2.37). Мы отложим это до гл. 4, а сейчас
ограничимся качественной иллюстрацией результата с помощью
рис. 3.5, б. Отметим, что отношение размера вторичных резонансов
к расстоянию между ними значительно меньше, чем для первичных
резонансов. Эта качественная картина резонансов разных масшта-
масштабов подтверждает вывод теории КАМ (п. 3.2а): при достаточно
малом возмущении большая часть фазового пространства запол-
заполнена инвариантными торами.
Следующие соображения помогут лучше представить себе эту
иерархию резонансов. Возьмем произвольную точку поверхности
сечения и будем растягивать область вокруг этой точки, пока не
х) Точнее, см. оценку B.4.62).— Прим. ред.
204 Глава 3
увидим какую-то резонансную структуру. Для достаточно малого
возмущения выбранная точка будет с большой вероятностью ле-
лежать на инвариантной кривой, хотя вокруг нее и расположены сто-
стохастические области различных резонансов. Повторим теперь эту
процедуру, т. е. снова выберем произвольную точку в пределах
растянутой области и продолжим растяжение области, пока не уви-
увидим структуру следующего масштаба. В этом новом масштабе зна-
значительно меньшая часть площади будет стохастической, и вероят-
вероятность выбранной точки попасть на инвариантную кривую сущест-
существенно возрастает. На каждом следующем масштабе доля стохасти-
стохастической области будет экспоненциально уменьшаться, а вероятность
попадания произвольной точки на инвариантную кривую будет
быстро стремиться к единице. Тем не менее всегда существует ко-
конечная вероятность попадания и в стохастическую область. Если
это случилось, то все последующие растяжения будут обнаружи-
обнаруживать уже только стохастические траектории.
* 3.2г. Численный пример
Исследования нелинейной динамики (в том числе и методом сече-
сечения Пуанкаре) путем численного интегрирования уравнений Га-
Гамильтона очень трудоемки, поскольку шаг интегрирования должен
быть много меньше характерного периода движения. В отличие
от этого прямое итерирование заданного на том же периоде ото-
отображения может быть легко выполнено на сотни тысяч периодов
и дает в существенных чертах ту же картину движения, что и урав-
уравнения Гамильтона. Такие отображения интенсивно использова-
использовались в различных исследованиях нелинейных колебаний. В § 3.4
мы рассмотрим этим методом задачу об ускорении Ферми [126].
Здесь же проиллюстрируем некоторые обсуждавшиеся выше осо-
особенности на примере квадратичного отображения поворота, иссле-
исследованного Хеноном [185]:
\ У о ) \ лг0 sin г{з + (г/0—
где г|э = 2яа0, а а0 — число вращения соответствующего линей-
линейного отображения поворота C.1.9).
Вблизи начала координат, которое является эллиптической точ-
точкой отображения, нелинейный член xl мал. На рис. 3.6, а и б вос-
воспроизведены результаты Хенона для г|> = 76,11°. На рис. 3.6, а
виден первый главный резонанс с а = 1/5, что соответствует углу
поворота 72°. Следовательно, нелинейность в данном случае за-
замедляет вращение. Исследование отображения в окрестности ги-
гиперболической точки этого резонанса приводит к любопытной кар-
картине, представленной на рис. 3.6, б. Видны вторичные и третич-
третичные резонансы, а также хаотическая траектория (длиной в 50 000
Отображения и линейная устойчивость
205
1,0
0,5
у о
-0,5
-1,0
-1,0
-0,5
0,5
1,0
0,200
0,175
У 0,150
0,125
0,100
о . \;
'•::&?&<..¦ >й ••¦••л
0,525
0,550
0,575
0,600
Рис. 3.6. Траектории отображения Хенона C.2.40) при а„ = 0,2114 (по дан-
данным работы [185]).
а — первый целый резонанс на пятой гармонике; б — увеличенный участок фазовой
плоскости вблизи сепаратрисы целого резонанса. Видны вторичные и третичные резо-
нансы.
206
Глава 3
итераций), заполняющая некоторую область вблизи гиперболи-
гиперболической точки. На рис. 3.7 показаны осцилляции сепаратрисы, со-
соответствующей Н~ на схеме рис. 3.4. Данные получены численно
Катхиллом и представляют 146 итераций короткого отрезка сепа-
сепаратрисы вблизи гиперболической точки.
Многие регулярные особенности структуры отображения на
рис. 3.6 можно получить аналитически. Мы вернемся к этому во-
0,575
v 0,570
0,565
'.••¦•л\
- %^:'^
!1.'л • . ,
i—
%
>'j
1
^ Сепаратриса
i
1
i
:V.:".f:V'^.*":
,» .'... •./.Л:.ч.;
1 ,__
' л!
1
* "#\
0,207
0,212
0,217
x
0,222
0,227
Рис. 3.7. To же, что на рис. 3.6, б для а0 = 0,1845 (поданным работы [26]).
Сплошная линия — одна из сепаратрис.
просу позже, поскольку такие вычисления более естественно про-
проводить после исследования устойчивости периодических траекто-
траекторий, которому посвящен следующий параграф.
§ 3.3. Линеаризованные уравнения
В принципе периодические точки отображения периода k можно
находить непосредственно из условия, что после k-й итерации
Т Ха = Xq.
C.3.1)
Отображения и линейная устойчивость 207
Однако при больших k эти вычисления становятся слишком трудо-
трудоемкими. Вместо этого можно исходить и прямо из гамильтониана.
Уравнения, которые надо при этом решать, соответствуют перио-
периодическим траекториям и их можно записать на поверхности се-
сечения в виде
-^-=0, C.3.2)
где вектор х = (р, q). В общем случае решение этих уравнений
можно найти лишь в форме рядов [116].
После того как периодические точки отображения найдены,
можно исследовать их устойчивость в линейном приближении. Это
делается следующим образом. Полагая х — х0 + Ах и сохраняя
только линейные по Ах члены, получаем уравнение вида
Axn+k^A-Axn, C.3.3)
где А — матрица, не зависящая от Ах.
В предыдущием параграфе было показано, что малые возмуще-
возмущения интегрируемой системы приводят к возникновению последо-
последовательности чередующихся эллиптических (устойчивых) и гипер-
гиперболических (неустойчивых) точек. Об этом говорят, в частности,
численные данные, приведенные в п. 3.2г. Однако в случае больших
возмущений топологические соображения х) уже неприменимы и
в принципе все периодические точки могут быть неустойчивыми.
В случае неинтегрируемых гамильтоновых систем линейная устой-
устойчивость является, по-видимому, необходимым и достаточным ус-
условием для нелинейной устойчивости 2) в том смысле, что первая
гарантирует существование инвариантных торов достаточно близко
к периодической траектории 3).
3.3а. Собственные значения и собственные векторы
Обозначив для простоты х = (р, q) = Ахп и х = (р, q) == Axn+k,
перепишем линеаризованное уравнение уИ-мерного отображения
C.3.3) в виде
х = Ах, C.3.4)
где А — матрица М X М, не зависящая от х. Предположим, что
ранг матрицы равен М, следовательно, det А ф 0. Собственным
*) По-видимому, имеются в виду скорее наглядные представления на ос-
основе рис. 3.3.— Прим.. ред.
2) Это справедливо лишь при дополнительных условиях, в частности
указанных в примечании авторов ниже (см. примечание редактора на
с. 191).— Прим. ред.
3) Особыми случаями являются числа вращения а = 1/3; 1/4.
208 Глава 3
значением системы C.3.4) является постоянная, входящая в урав-
уравнение
Ах = 1х, C.3.5)
так что некоторый вектор х остается неизменным с точностью до
множителя. Из C.3.5) следует, что X удовлетворяет характеристи-
характеристическому уравнению
det(A — M) = 0; C.3.6)
где I — единичная матрица. Это — алгебраическое уравнение
М-го порядка, имеющее М корней. Каждое собственное значение
соответствует нормальной моде колебаний, или фундаментальному
решению. Из C.3.5) следует также, что для устойчивости
колебаний lim Xn должен быть ограничен *). Векторы Xk, соответст-
вующие значениям Xk, называются собственными векторами, или
нормальными колебаниями. Эти векторы можно найти, решая
однородную систему уравнений
В •¦**=?></*/* = 0, C.3.7)
;
где В (А/г) = А —М- Если все собственные значения А различны,
решение можно получить следующим образом. Перенесем члены
с / = / в правую часть уравнений C.3.7) и опустим уравнение с
i = I. Положим Xik = CkBu, где с& — произвольная постоянная,
а Вц Ф 0 — алгебраическое дополнение элемента Ъц матрицы В.
Получившуюся таким образом неоднородную систему М—1 урав-
уравнений решаем стандартным методом Крамера и получаем
x!k = ckBu; /=1 м- C-3.8)
Поскольку ранг матрицы В равен (М—1), то по крайней мере одно
Вц Ф 0. В случае совпадающих собственных значений метод
решения остается таким же, но некоторые из векторов Xk будут
зависеть от нескольких произвольных постоянных.
Рассмотрим матрицу X, столбцы которой составлены из компо-
компонент разных собственных векторов Xk- Если, кроме того, все собст-
собственные значения различны 2), то из C.3.5) находим
А-Х = Х-Л, C.3.9)
где А — диагональная матрица с элементами Ац = А<. Отсюда
Л = Х-1-А-Х, C.3.10)
1) Это справедливо, вообще говоря, лишь в том случае, когда матрица
А не зависит от х0 (см. ниже п. 3.36, З.Зв, 5.26 и работу [55)].— Прим. ред.
2) Случай совпадающих собственных значений см. в [13] или в любом
учебнике по линейной алгебре.
Отображения и линейная устойчивость 209
т. е. X диагонализует А. Введем новые векторы
я* = Х-1-**; лг* = Х-«*. (З.З.П)
Из C.3.5) получаем
A.ak = huk, C.3.12)
т. е. Uk являются собственными векторами матрицы Л и из них можно
образовать ортонормированный базис ен-
Симметрия собственных значений. Если преобразование, задавае-
задаваемое А, является каноническим, то М равно четному числу 2N и вы-
выполняются следующие соотношения для скобок Пуассона:
[йи ?/] = [Й, р/]=0, C.3.13)
Введем 2УУ-мерную антисимметричную матрицу
ГО — I \
0 j. C-3.14)
каждый элемент которой есть блок N X N; Гт — Г = — Г,
(Т означает транспонирование) и det Г = 1. Тогда соотношения
C.3.13) можно записать в виде
[xh */] = S aikTklan = r//t C.3.15)
где
aik = dxjdxk. C.3.16)
Из C.3.15) следует, что в рассматриваемом случае не все элементы
матрицы А независимы. В матричной форме имеем
А-Г-АТ = Г C.3.17а)
или
АТ-Г-А = Г. C.3.176)
Матрица, удовлетворяющая этому условию, называется симплек-
тической.
Покажем, что если X — собственное значение матрицы А, то
1А также является ее собственным значением. Поскольку собствен-
собственные значения произвольной матрицы не изменяются при транспо-
транспонировании, то из C.3.5) имеем
АТу = Ху, C.3.18)
или
(Ат)-1.у=-^->». C.3.19)
210
Глава 3
Из C.3.17а) получаем
C.3.20)
Значит, 1А тоже является собственным значением матрицы А с соб-
собственным вектором х = Т-у. Отсюда
C.3.21)
Re Л
Рис. 3.8. Собственные значения симплектической матрицы.
Так как матрица А вещественная, то комплексные собственные
значения появляются только в виде комплексно сопряженных пар.
Если же Я комплексная величина и | Я | Ф 1, то собственные значе-
значения образуют четверки:
Я, Я*, 1/Я, 1/Я*,
симметричные относительно вещественной оси и единичной окруж-
окружности (рис. 3.8). В случае Im Я = 0 собственные значения Я, 1/Я
лежат на вещественной оси. При \Х\Ф I движение всегда неустой-
неустойчиво. Если же | Я | = 1, то собственные значения Я и Я* = 1/Я ле-
лежат на единичной окружности и движение устойчиво.
Легко показать, что из симметрии собственных значений сле-
следует, что характеристическое уравнение C.3.6) можно записать
в виде
iN~l ' ' ~ 1 ' ' =0 C.3.22)
Отображения и линейная устойчивость 211
с симметричными коэффициентами:
«1 = Оалг-1, «2 = «2лг-2. .... C.3.23)
Итак, если все собственные значения различны, то для устой-
устойчивости движения необходимо, чтобы все они лежали на единич-
единичной окружности. В случае же кратных X вопрос об устойчивости
*более сложен (см. [13]). Вообще говоря, при этом имеет место так
называемая пограничная устойчивость *).
Теперь мы покажем, что если матрица А симплектическая,
то и матрицу X тоже можно представить в симплектической форме
путем умножения ее столбцов на определенные константы Си- Рас-
Рассмотрим антисимметричную матрицу.
S = X-r-XT, C.3.24)
элементы которой
St] = XfT-xj. C.3.25)
Из выражений C.3.9) и C.3.24) получаем
A-S-AT = S, C.3.26а)
или
XiXjSu^Sij. C.3.266)
Значит, Si/ФО, лишь если ЯД/= 1. Учитывая соотношение,
C.3.21), находим, что отличные от нуля элементы матрицы S удов-
удовлетворяют соотношениям
S,.{+N = —St+N.{, i = l,...,N. C.3.27)
Положив 5,-, {+N = — 1 и xi = Cix'i, получаем из C.3.25)
Ctcl+Nx'tT • Г • x't+N = — 1. C.3.28)
Это уравнение позволяет определять, например Ct+N по заданным с,-.
Таким образом, S= Г по построению. Сравнивая C.3.24) с C.3.17а),
видим, что матрица X симплектическая. Так как N постоянных ci
можно выбрать произвольно, то построенная матрица X не единст-
единственная.
Используя C.3.176), можно показать, что х\-Т-хг инвариантно
по отношению к симплектическому преобразованию х=Ах,
т. е.
^I-r-^ = ^T-r.^2. C.3.29)
1) Устойчивым является лишь глобальное (нелинейное) движение, в ли-
линейном же приближении по Ддс движение в этом случае неустойчиво, хотя
jA,| = 1 [см. C.3.71) и рис. 5.5]. Эта неустойчивость существенна при чис-
численном определении перехода от регулярного движения к хаотическому.—
Прим. ред.
212 Глава 3
Это соотношение часто используется как определение симплектиче-
ского преобразования. Положив хх = х, х2 = Ал:, найдем, что
квадратичная форма
Q = xT-T-A-x C.3.30)
является инвариантом отображения А.
Только в случае двух степеней свободы, когда для X получается
квадратное уравнение, собственные значения и собственные век-
векторы можно легко найти в явном виде. Однако именно этот случай
соответствует двумерным отображениям, которые занимают цен-
центральное место в нашем анализе нелинейных колебаний. Что ка-
касается большего числа степеней свободы, то аналитические реше-
решения здесь удается получить лишь в некоторых специальных случаях.
* 3.36. Двумерные отображения
Двумерное отображение задается системой двух разностных урав-
уравнений первого порядка. Выпишем здесь еще раз уравнения C.1.13)
для возмущенного отображения поворота, положив для упроще-
упрощения записи е г= 1:
в„), C.1.13а)
1, On), C.1.136)
где / и g — периодические по 8 функции с периодом 2я (или иногда
для удобства с периодом единица), а число вращения а = coj/coj
определяет изменение фазы 9Х (здесь мы опустили индекс 1) на пе-
периоде фазы 82. Поскольку величины а, / и g записаны как функции
переменной Jn+1 (а не /„), то симплектический характер отображе-
отображения выражается в форме простого условия сохранения площади
C.1.16). Отметим, что вовсе не обязательно записывать отображе-
отображение в переменных действие—угол, примером служит отображение
Хенона C.2.40).
Периодические точки. Отображение C 1 13) имеет периодическую
точку х0 = (/„, 80) периода k, если
xo=Tkxo, C.3.31)
причем х0 не является периодической точкой меньшего периода.
Иначе говоря, первый возврат в начальную точку происходит
ровно через k итераций отображения. Для любого k существует
счетное множество периодических точек. Они образуют группы,
или периодические траектории {дг01, х02 xok], где л:0,- =
= Тсх01, а длина каждой траектории равна ее периоду k. Система
периодических траекторий имеет иерархическую структуру [164].
Для получения всех периодических точек периода k нужно ре-
решить 2k + 2 алгебраических уравнения:
..,*, C.3.32а)
Отображения и линейная устойчивость 213
= б.' + 2ла (Л+1) + g (Ji+1, в,),
C.3.326)
+ m = 0, 1, . . .,
где m — целое число взаимно простое с к. За исключением случая
k = 1 и, возможно, k = 2, решать такую систему уравнений очень
трудно не только аналитически, но даже и численно. При боль-
больших k простые методы нахождения корней, вроде метода касатель-
касательных Ньютона, становятся непригодными ввиду близости соседних
решений в Bk + 2)-мерном пространстве. Специальные вариа-
вариационные методы, разработанные для решения этой задачи [116,
179, 183], описаны в § 2.6.
В случае явного отображения поворота, когда / не зависит от
/ и g = 0, последовательные подстановки выражений для Xt в вы-
выражения для Xi+X приводят к уравнениям с двумя неизвестными
вида
МЛ, 60 = 0, C.3.33)
ЫЛ, 00 = 0.
Но и эти уравнения очень трудно решить при большом k из-за чрез-
чрезвычайно сложного характера функций fx и /2.
Произведение инволюций. Существует важный класс отображений,
периодические точки которых можно найти из уравнения с одним
неизвестным. Если отображение (или соответствующий гамильто-
гамильтониан) обладает симметрией определенного типа, то его можно пред-
представить в виде произведения двух инволюций [104, 166]
T = ItIx. C.3.34)
По определению отображение инволюции возвращает систему в на-
начальное состояние после двух итераций, т. е.
/? = /; 11= I, C.3.35)
где / — тождественное отображение. Явное отображение поворота
можно представить в виде произведения двух инволюций при ус-
условии, что функция / антисимметрична относительно некоторого
угла (для простоты положим этот угол равным нулю). В этом слу-
случае отображение I\ задается уравнениями:
7=/л + /(9л), C.3.36а)
0= —0л, C.3.366)
а отображение /2 есть
Л+1 = 7, C.3.37а)
9„+1=— ё + 2лаG). C.3.376)
Использование инволюций чрезвычайно облегчает нахождение пе-
периодических точек. В самом деле, так как все точки отображения
214 Глава 3
инволюции имеют период 2, то особыми могут быть лишь непод-
неподвижные точки (с периодом 1). А такие точки легко можно найти.
Например, отображение I\ имеет следующие линии неподвижных
точек х^.
91 = 0, л, mod 2л C.3.38)
независимо от значения Jlt а /2 имеет линии неподвижных точек
х2 при
292 = 2яа(/2), тос12я. C.3.39)
Используя C.3.34) и C.3.35), можно показать, что если как х, так
и Тпх являются неподвижными точками отображения /х (или /2),
то л: является также и неподвижной точкой отображения Т2П.
В § 3.4 мы воспользуемся этим методом для определения периоди-
периодических точек отображения Улама. Грин использовал этот метод
для нахождения периодических точек большого периода в случае
стандартного отображения [165] и в задаче Хенона—Хейлеса
[166]. В обоих случаях отображение, а значит, и нечетная степень
отображения представимы в виде произведения инволюций. Поэ-
Поэтому периодические точки этих отображений можно найти рассмот-
рассмотренным методом. Так, например, отображение Т3 можно предста-
представить в виде произведения двух инволюций следующим образом:
T8 = (Vi/0(/iVj). C.3.40)
Линеаризованное отображение. Разложим отображение вокруг пе-
периодической траектории периода k:
х01 —>- лгО2 —>- • . • —>¦ xuk -> лгО1
и найдем линеаризованные уравнения движения в окрестности
точки х01:
&Хп+к = М {Хок) ¦ кХп+k-! = М (Хок) ¦ М (ЛГо.А-i) • hXn+k-2
C.3.41)
и т. д. или
bxn+k = AvAxn. C.3.42)
Здесь
А! = М(д:о*)-М(л;о, ft_J---M(Jfoi) C.3.43)
— упорядоченное произведение k матриц М; = М (хо1), взятых
в последовательных точках периодической траектории, каждая
из которых
djn+1
\
C.3.44)
Отображения и линейная устойчивость 215
есть матрица Якоби отображения. В окрестности точки лг0,- анало-
аналогичным образом приходим к выражению
At = M(_rM(-,---Mft C.3.45)
которое получается из Ах циклической перестановкой матриц.
Для возмущенного отображения поворота матрицу М можно
получить путем подстановки выражения C.1.13а) для Jn+1 в
C.1.136), откуда (е = 1)
Ми = Ми 2п-^.+-^г); C.3.46)
Здесь 6 = 9„, / = Jn+i, а якобиан отображения
определяет изменение фазовой площади. Полагая det М = 1, по-
получаем условие сохранения площади C.1.16).
Для неподвижной точки Ai = Mi и движение в ее окрестности
определяется матрицей Ма. В случае же периодической точки с пе-
периодом, большим 1, собственные значения и собственные векторы
находятся из уравнения
/К1х = кх C.3.48)
для движения вблизи точки х01 или из уравнения
А2 з» = Я»у C.3.49)
для движения вблизи точки х02 и т. д. Однако подстановка А2 =
= Mi-Ai-МГ1 в уравнение C.3.49) приводит его к уравнению
C.3.48) с у = Mi*. По индукции аналогичным образом связаны
также любые At- и A»_i. Отсюда следует, что собственные значения
и условия устойчивости одинаковы для всех точек одной периоди-
периодической траектории. Собственные же векторы для точки xoi выра-
выражаются посредством соотношения
Jfi = М <_i-М (_>••• Mi ¦•*! C.3.50)
через собственные векторы точки х01.
* З.Зв. Линейная устойчивость и инвариантные кривые
Собственные значения линеаризованного отображения являются
корнями уравнения C.3.6):
/аи—к а3
или
+ l=0, C.3.51)
216 Глава 3
где
Sp A=au + a2»
и det A = 1 ввиду сохранения площади. Корни уравнения C.3.51)
равны
^[(^Jр2. C-3.52)
Произведение корней к^кг = 1, а их сумма %х + ^2 есть веществен-
вещественное число. Возможны три случая.
1. Корни Klt Я2 являются комплексно сопряженными и лежат
на единичной окружности (а Ф 0):
Хи2 = е±*. C.3.53)
Это соответствует устойчивым решениям, причем
SpA = 2cosa, C.3.54)
|SpA|<2. C.3.55)
2. Корни действительны и взаимно обратны
C.3.56)
так что
\Kt\ = e±a C.3.57)
и
|SpA| = |2cha|>2. C.3.58)
Это соответствует экспоненциально растущему и убывающему
решениям. Первое (неустойчивое) решение может быть двух
видов:
[SPA>2(^>1) и SpA<—2(ЯХ< —1).
3. Корни равны
^ = ^ = ±1. C.3.59)
Существование этих трех случаев следует также и непосредственно
из симметрии собственных значений. Выясним теперь физический
смысл этих решений.
Эллиптические траектории. В случае 1 общее решение имеет вид
АУЛ = a cos па + b sin па,
А9„ = с cos па + d sin na
C.3.60)
и описывает движение по эллипсу вокруг периодической точки.
Уравнение эллипса можно получить из инвариантной квадратич-
квадратичной формы C.3.30). Введя обозначения р = А/ и q = А9, чтобы
Отображения и линейная устойчивость
217
подчеркнуть, что 4/, 40 не обязаны быть переменными действие —
угол, получаем
аиЯг + (а1х—a22)qp—a21p* = Q. C.3.61)
Диагонализуем теперь матрицу А спомощью преобразования C.3.10).
При этом координатные оси поворачиваются^на|угол % и совпа-
совпаду
-Ав
AJ
.'Я
¦Ав
Рис. 3.9. Приведение эллиптических и гиперболических траекторий к нор-
нормальной форме.
а — после поворота осей и изменения масштаба эллипс переходит в окружность; б —
после поворота асимптоты (пунктирные прямые) располагаются симметрично относи-
относительно координатных осей.
дают с главными осями матрицы А. Перекрестный член в C.3.61)
пропадает (рис. 3.9, а), и мы получаем
a'12q' —a2lp' =Q,
где
— «22
C.3.62)
C.3.63)
C.3.64а)
218 Глава 3
a'i2—a2i = ai2 — a2i> C.3.646)
а'.м' = — (Sp AJ— 1. C.3.64b)
Последние два уравнения можно разрешить относительно недиаго-
недиагональных элементов матрицы А. В случае 1 а'п и а^\ имеют проти-
противоположные знаки, и выражение C.3.62) переходит в уравнение
эллипса с отношением полуосей
1/2
C.3.65)
Наконец, преобразование р' = Rxl2p, q' = R~l2q переводит тра-
траекторию в окружность, а отображение сводится к простому линей-
линейному повороту на угол а. Если ввести нелинейные члены, пропор-
пропорциональные более высоким степеням Дл:, то получим возмущенное
отображение поворота со всей своей сложной иерархической струк-
структурой, показанной на рис. 3.5.
Гиперболические траектории. В случае 2 общее решение имеет вид
п C-3-66)
де„=ся"+<*А,гп
и описывает движение по одной или по обеим ветвям гиперболы,
Производя поворот к главным осям (см. рис. 3.9, б), снова при-
приходим к уравнению C.3.62). Однако теперь а'п и а'2\ имеют оди-
одинаковый знак, и мы получаем гиперболу с асимптотами
p' = ±Rq'. C.3.67)
Переписав C.3.66) в этой повернутой системе координат, видим,
что при положительной величине К1 движение происходит только
по одной ветви гиперболы. Если же Х± — отрицательная величина,
то при каждой итерации отображения р' и q' отражаются относи-
относительно начала координат и движение происходит по обеим ветвям
гиперболы, как показано на рис. 3.10.
В обычном случае, когда эллиптические и гиперболические пе-
периодические точки чередуются, гиперболические траектории
остаются на одной ветви гиперболы. Примером может служить ма-
маятник с гамильтонианом A.3.6), который для простоты мы пере-
перепишем в виде
#= — р2 —cos ф = const. C.3.68)
Соответствующие траектории в фазовом пространстве показаны
на рис. 1.4. Линеаризуя гамильтониан в окрестности неподвижных
точек р = 0 и ф = 2пп, получаем
= const. C.3.69)
Отображения и линейная устойчивость
219
Аналогично в окрестностях точек /) = 0и
р2 — (АфJ = const.
C.3.70)
Очевидно, что выражение C.3.69) описывает эллипсы, а C.3.70) —
гиперболы. Это соответствует неподвижным точкам ср = 0 и ср = я,
как показано на рис. 1.4.
Гиперболические точки второго вида (с отражением) также
важны для нашего анализа. Как будет видно из дальнейшего, та-
такие точки возникают при сильном возмущении, когда эллиптиче-
эллиптическая точка превращается в гиперболическую с отражением. В этом
/у
/4
а о
Рис. 3.10. Три последовательных отображения начальной точки Xi-
а — вблизи обыкновенной гиперболической точки^х >1; б — вблизи гиперболической
точки с отражением ^ < — 1.
случае все неподвижные точки отображения 7* становятся гипер-
гиперболическими, и движение в окрестности данного резонанса стано-
становится стохастическим. Это будет явно показано в § 3.4.
Случай равных собственных значений. Случай 3, когда 'К1 = Х^ =
= ± 1, особый в том смысле, что он является пограничным между
устойчивым и неустойчивым движениями. При А,! = к2 = 1, пе-
переходя к главным осям, отображение можно привести к виду
Ли-* \
C.3.71)
Это отображение описывает сдвиг вдоль прямой р' = const *).
Линия неподвижных точек соответствует р'о = 0. Аналогично этому
J) Возможен также случай, когда С21 = 0, а а\2 = Ш2- При этом сдвиг
происходит вдоль прямой q' = const.
220 Глава 3
при кг = Я2 = — 1 сдвиг происходит вдоль двух прямых р' =
= ± const. Начальному условию р'о = 0 соответствует луч. Пе-
Периодические точки с периодом 2 лежат на прямой р'о = 0, причем
если <7о>О, то 9* = — <7о и т. д. Согласно теореме Пуанкаре —
Биркгофа, при включении нелинейного возмущения, некоторые
из этих периодических точек сохраняются и ведут с ростом возму-
возмущения к бифуркациям, которые будут рассмотрены в п. 3.4г. В § 4.4
мы покажем также, что случай Хг = к2 = — 1 особенно важен
при определении перехода между ограниченным и неограниченным
стохастическим движением по методу Грина [165].
*§ 3.4. Ускорение Ферми
Предложенный Ферми [126] механизм ускорения космических
лучей за счет столкновения их с движущимися магнитными по-
полями моделируется колебаниями частицы между неподвиж-
неподвижной и осциллирующей стенками. Если фаза колебаний стенки
в момент удара является случайной, то частица в среднем уско-
ускоряется. Более интересен вопрос: может ли стохастическое ускоре-
ускорение возникать из нелинейной динамики без дополнительного ус-
условия о случайности фазы, например, при периодическом движе-
движении стенки. Численное моделирование последнего случая, прове-
проведенное Уламом и сотр. [415], показало, что движение частицы яв-
является, по-видимому, стохастическим, но ее средняя энергия не воз-
возрастает.
Эти результаты Улама были объяснены с помощью аналитиче-
аналитических и численных методов Заславским и Чириковым [443 ] и более
полно Брахичем [38 ] и Либерманом и Лихтенбергом [274 ]. Они
показали, что в случае гладкой зависимости скорости стенки от
времени фазовая плоскость движения разбивается на три различ-
различные области: 1) область малых скоростей, в которой все неподвиж-
неподвижные точки неустойчивы, что приводит к стохастическому движению
практически во всей этой области; 2) область промежуточных ско-
скоростей, где внутри стохастической компоненты имеются островки
устойчивости, окружающие эллиптические точки, и 3) область боль-
больших скоростей, в которой стохастические слои в окрестности се-
сепаратрис изолированы друг от друга инвариантными кривыми,
которые пересекают весь интервал изменения фазы. Именно по-
последняя область и ограничивает набор энергии частицей. Если же
зависимость скорости стенки от времени недостаточно гладкая, то
области 3 не существует в согласии с теорией КАМ.
Модель ускорения Ферми явилась одной из первых задач по
определению условий существования инвариантных кривых. В со-
сочетании с простотой численного моделирования на «большие вре-
времена» она стала как бы пробным камнем в понимании динамики
нелинейных гамильтоновых систем с двумя степенями свободы.
Отображения и линейная устойчивость 221
Важно поэтому выяснить, что в этой задаче типично для систем,
близких к интегрируемым, а что зависит от модели. Ниже мы под-
подробно исследуем ряд таких моделей.
*3.4а. Физические задачи и их модели
В литературе рассматривалось несколько моделей ускорения Ферми,
которые приводят к различным отображениям на поверхности се-
сечения Пуанкаре. Модель Улама показана на рис. 3.11, а. Точное
НепоЭ&цжнпя сгпенка
I-
Осциллирующая стенка
а б
Рис. 3.11. Модели ускорения Ферми.
а — модель Улама: частица совершает колебания между неподвижной и осциллирующей
стенками; б — модель Пустыльникова: частица отражается от осциллирующей стенки
в поле тяжести с ускорением g.
отображение для этой модели исследовано Заславским и Чирико-
вым [443 ] и Либерманом и Лихтенбергом [274 ] для пилообразной
зависимости скорости стенки от времени хш (t), Брахичем [38] для
пилообразной и параболической функции хш (/), а Лихтенбергом
и др. [272] в случае произвольной скорости xw(t). «Упрощенное»
отображение для модели Улама, в котором пренебрегается смеще-
смещением подвижной стенки, было введено Либерманом и Лихтенбер-
Лихтенбергом] [274 ] и исследовалось ими для произвольной скорости стенки х).
Пустыльников [339] исследовал другую модель (рис. 3.11,6),
в г которой частица сталкивается только с одной осциллирующей
стенкой и возвращается к ней в постоянном поле тяжести 2). Здесь
также можно ввести упрощенное отображение, которое приводится
к стандартному отображению (см. п. 4.16).
J) В случае пилообразной скорости такое отображение исследовано также
в работе [443].— Прим. ред.
2) Эта модель была введена и исследована Заславским [481, § 2Б].—
Прим. ред.
222 Глава 3
Точное отображение Улама. В случае когда скорость подвижной
стенки задается пилообразной функцией времени, Заславский
и Чириков получили следующую систему точных разностных урав-
уравнений движения частицы:
U^y C.4.1а)
(%) C.4.16)
<—г|>„), C.4.1 в)
4 /
, mod 1. C.4.1г)
Здесь а — амплитуда колебаний стенки, / — минимальное рас-
расстояние между стенками, ип — безразмерная скорость частицы
(амплитуда скорости стенки равна 1/4), п — число столкновений
с подвижной стенкой, 1|з„ — фаза подвижной стенки в момент столк-
столкновения. Фаза гр изменяется от 0 до 1/2 при движении стенки из
положения А в положение В и от 1/2 до 1 при обратном движении
(см. рис. 3.11, а). Знак плюс в выражении C.4.1а) соответствует
соотношению C.4.16) на предыдущем шаге, знак минус — соот-
соотношению C.4.1в).
Хотя уравнения C.4.1) и является точными, они не сохраняют
фазовую площадь, т. е. переменные и и гр оказываются неканониче-
неканоническими. Чтобы перейти к каноническим переменным, запишем, сле-
следуя Лихтенбергу и др. [272], разностные уравнения в переменных,
относящихся к столкновениям частицы с неподвижной стенкой.
Введем ип = vnl2u>a — новую нормированную скорость частицы
и 8„ — фазу подвижной стенки в момент га-го столкновения частицы
с неподвижной стенкой. Будем считать, что движение подвижной
стенки задается выражением xw = aF (ty), где F — четная перио-
периодическая функция фазы гр = со* с периодом 2л. Тогда получим сле-
следующую систему неявных уравнений, аналогичную C.4.1):
C.4.2а)
, C.4.26)
«п+1
L L- C.4.2в)
Un
Отображения и линейная устойчивость 223
Здесь % — фаза подвижной стенки в момент столкновения с ча-
частицей после ее га-го столкновения с неподвижной стенкой, М =
= U2na, a F' — импульс, получаемый частицей при столкновении.
Легко видеть, что скорость частицы v является канонически со-
сопряженной ее расстоянию х до неподвижной стенки, а фаза 0 иг-
играет роль переменной времени, сопряженной энергии частицы
Е = и2. Это означает, что если в расширенном фазовом простран-
пространстве (у, х, — Е, t) выбрать поверхность сечения х = 0, то для остав-
оставшейся пары переменных (— Е, 9) отображение C.4.2) сохраняет
площадь. В самом деле, найдя якобиан непосредственно из системы
C.4.2), получаем
[д (Еп+\, б/г+l)
д(Еп, в„)
= 1. C.4.3)
Упрощенное отображение У лама. Система уравнений C.4.1) су-
существенно упрощается, если пренебречь смещением колеблющейся
стенки. Такая упрощенная модель сохраняет наиболее характер-
характерные черты физически более реальной исходной модели и вместе
с тем легко обобщается на случай произвольного закона скорости
стенки. Мы проведем сравнение результатов численных экспери-
экспериментов для точного и упрощенного отображений. Каноническими
переменными упрощенного отображения являются скорость ча-
частицы перед /г-м столкновением с движущейся стенкой и фаза ко-
колебаний стенки. При пилообразном законе изменения скорости
стенки отображение имеет вид
. + фл - C.4.4а)
2
М modi. C.4.46)
«Л+1
Здесь и = vIV — безразмерная скорость частицы, VIA — ампли-
амплитуда скорости стенки, М = //16а, безразмерное время пролета
равно М/и = 21/vT, где Т = C2a/V)'/a — период колебаний
стенки. В выражении C.4.4а) стоит абсолютная величина, тем са-
самым учитывается изменение направления скорости при u<zl, ко-
которое имеет место в точном отображении C.4.1). В наиболее инте-
интересной области «>-1 это несущественно.
Упрощенное отображение можно получить и непосредственно
из точного C.4.1) при На > 1 иа»1. Упрощенные уравнения
легко обобщаются на случай нелинейной зависимости / (ф) =
= — F' (г|)) в C.4.2). Например, отображение
ия+1 = |ил + Bфя—1)[1 — B%,-im C.4.5а)
^ modi C.4.56)
un+i
224 Глава 3
соответствует кубической зависимости, а отображение
. C.4.6а)
C.4.66)
— синусоидальной (аналитической) зависимости. В последнем слу-
случае интервал изменения фазы гр принят равным 2зх, а не 1. Все эти
отображения сохраняют фазовую площадь. Нелинейные законы
изменения скорости стенки являются фактически более регуляр-
регулярными, чем «линейный», в том смысле, что для первых функция
/ (г|з) более гладкая в точке г|з = 0. Как отмечалось ранее, для су-
существования инвариантных кривых, согласно теореме КАМ, не-
необходимо, чтобы возмущение имело достаточное число непрерывных
производных. В случае пилообразного закона изменения скорости
стенки уже само возмущение (скорость) является разрывным, и
поэтому можно думать, что в этом случае не существует инвариант-
инвариантных кривых, пересекающих весь интервал изменения фазы ip. Мы
увидим, что это и в самом деле так. Более того, по крайней мере для
отображения Ферми мы сможем определить, сколько же непрерыв-
непрерывных производных требуется для применимости теоремы КАМ.
*3.4б. Численное моделирование
Современные быстродействующие ЭВМ позволяют получить сотни
тысяч итераций рассмотренных выше отображений. Для исследо-
исследования всей фазовой плоскости разобьем интервал фазы @,1) или
@,2я) на 100 ячеек, а интервал скорости @, «маКс) на 200 ячеек.
На рис. 3.12 приведены численные результаты для упрощенного
отображения C.4.4) с М — 10 после 163 840 итераций для каждой
из 10 траекторий, использованных в счете. На рисунке отмечены
ячейки, в которые попала хотя бы одна из этих траекторий. В пра-
правой части рисунка показано распределение плотности Р (и), про-
проинтегрированное по фазе и по всем итерациям. Начальные условия
движения выбраны случайно в области малых скоростей частицы.
При этом каждая траектория заполняет всю стохастическую ком-
компоненту движения, и конечное распределение на фазовой плоскости
не зависит от начальных условий. Незаполненные траекториями
островки устойчивости ограничены инвариантными кривыми, и по-
поэтому частицы не могут попасть в них извне. Центрами островков
являются эллиптические точки. Ниже мы покажем, что при
u<z.— Мч* линеаризованное движение в окрестности всех непод-
неподвижных точек неустойчиво. Это видно и непосредственно из кар-
картины фазовой плоскости на рис. 3.12. Эллиптическая точка при
и — М соответствует резонансу 1 : 1 между колебаниями частицы
и стенки. При меньших значениях скорости частицы (Mlи = 2,
Отображения и линейная устойчивость
225
3, 4, . . .) расположены целые резонансы 2:1, 3:1, 4:1,...,
при которых стенка совершает соответственно два, три, четыре
и т. д. колебания за время одного колебания частицы.
1/-
0 О
20
Р(и)
ЗОХ Ю3
Рис. 3.12. Фазовая плоскость (и, i|i) и функция распределения Р (и) для ото-
отображения C.4.4) (по данным работы [274]).
10 траекторий по 163 840 итераций; М = 10. Пунктирная кривая рассчитана по резо-
резонансной теории возмущений.
Между этими целыми резонансами (k = 1) находятся дробные
резонансы с k~>\. Так, например, между целыми резонансами
М/и = 1 (и = 10) и М/и = 2 (и — 5) расположен резонанс М/и =
= 3/2 (и т 6,67), соответствующий трем колебаниям стенки на
два колебания частицы (см. рис. 3.12). Этот резонанс отделен в
свою очередь от целого резонанса другими резонансами с еще боль-
большими k. Число вращения дробных резонансов вблизи края целого
226
Глава 3
резонанса приблизительно совпадает с числом вращения последнего
вследствие линейной зависимости / (г|з) в рассматриваемом случае
C.4.4). По этой же причине внутри целых резонансов нет вторич-
вторичных резонансов, а траектории фазовых колебаний мало отличаются
от эллипсов х).
Аналогичное численное моделирование было проведено как для
отображения C.4.6) (см. рис. 1.14), так и для отображения C.4.5)
(рис. 3.13). В последнем случае М = 10, а число итераций каждой
из 10 траекторий равно 81 920. Размер областей устойчивости при
малых скоростях здесь существенно меньше, чем на рис. 3.12,
из-за наличия вторичных резонансов. Помимо этого, существует
4 -
2 -
1/2
0 0 10
Р(и)
20
Рис. 3.13. То же, что и на рис. 3.12 для отображения C.4.5) (по данным ра-
работы [274]).
10 траекторий по 81 920 итераций.
верхняя граница скорости ц, (граница стохастичности 2)), выше
которой сохраняются невозмущенные инвариантные кривые, пере-
пересекающие весь интервал изменения фазы ty. Кажущееся противо-
противоречие, что более устойчивое движение соответствует нелинейной
функции / (\р), объясняется тем, что «линейная» зависимость / (гр)
является на самом деле разрывной. Это и приводит к разрушению
инвариантных кривых. Более важно, как показывают результаты
численного моделирования отображения C.4.5), что для сущест-
существования инвариантных кривых необходимо и достаточно, чтобы га-
гамильтониан (производящая функция) отображения имел две непре-
*) С этим же'связана еще одна'особенность отображения C.4.3) — от-
отсутствие гиперболических неподвижных точек (М > 0) вследствие разрыва
функции /(ф) при $ = 0 (I).—Прим. ред.
а) В оригинале используется редко употребляемый термин absolute ba-
barrier (абсолютный барьер).— Прим. перев.
Отображения и линейная устойчивость
227
рывные производные (S=2I). Действительно, для отображенияC.4.5)
производная dfldty непрерывна, a d2f/dty2 разрывна и гамильтониан
C.4.7)
Полученное значение 5 = 2 на единицу меньше лучшей (доста-
(достаточной) оценки Мозера [310] для произвольного отображения2).
-0,5
Рис. 3.14. Фазовая плоскость отображения Улама с М =^1,25 и v = 2и/М
(по данным работы [38]).
Видна сложная структура регулярных траекторий.
На рис. 3.12 и 1.14 пунктиром показаны сепаратрисы резонан-
сов, вычисленные из гамильтониана в п. 3.4е. В первом случае се-
сепаратриса имеет приближенно эллиптическую форму, тогда как
на рис. 1.14 явно видна неустойчивость движения в окрестности
х)Это заключение противоречит оценке C.2.30) и является спорным.
Ограничение диффузии на рис. 3.13 объясняется, по-видимому, просто ее
малой скоростью на резонансах высоких гармоник. Подобные эффекты на-
наблюдались неоднократно и при меньших S (см., например, [475, §4.1] и,
[482, § 6], где обсуждается также возможный механизм этого явления).—-
Прим. ред.
2) См. примечание редактора на. с. 193.— Прим. ред.
228 Глава 3
сепаратрисы из-за образования вторичных резонансов. Некоторый
перекос резонанса по сравнению с расчетным вызван пренебреже-
пренебрежением поворотом главных осей (см. рис. 3.9, а).
Хотя численные данные на рис. 3.12 и 3.13 хорошо представ-
представляют крупномасштабную структуру фазовой плоскости, они не
отражают более мелкие детали этой структуры. Последние можно
выявить, если проводить численное моделирование с большим ко-
количеством начальных условий. Именно такое исследование было
выполнено Брахичем [38] для отображений с различными / (гр),
а также для точного отображения C.4.1). В последнем случае1)
его результат для М = 1,25 показан на рис. 3.14. При сравнении
с рис. 3.12 следует учесть сдвиг фазы на 1/2. На рис. 3.14 хорошо
виден целый резонанс k = 1 при v = 2,2, а также дробные резо-
нансы с& = 3и& = 2, расположенные соответственно при боль-
больших скоростях v. Вблизи целого резонанса имеется еще и резонанс
с k = 6, который деформирует сепаратрису первого. Резонанс
k = 6 связан с небольшой нелинейностью из-за смещения стенки
и зависимости Ми для сдвига фазы. Наконец, в верхней части
рис. 3.14 виден вторичный резонанс пятой гармоники, относящийся
к целому первичному резонансу k = 1. Последний похож на вто-
вторичные резонансы для отображения Хенона (см. рис. 3.6).
*3.4в. Периодические точки и их линейная устойчивость
Периодические точки. Рассмотрим периодические точки различных
отображений для ускорения Ферми. Запишем упрощенное отобра-
отображение в виде
«/+1 = 1 "/ + /№/) I, C.4.8а)
% %4C.4.86)
Отметим несколько простых свойств этого отображения. Просумми-
Просуммировав уравнение C.4.8а) по k итерациям и принимая, что «/>/(%)
при всех /, получим фазовое соотношение для любой группы пе-
периодических точек, лежащих на одной периодической траектории
•отображения
Е/(%) = 0. C.4.9)
/=i
Взяв такую же сумму для уравнения C.4.86), получим «среднюю»
скорость Ukm периодической точки периода k:
uhm = ^L, C.4.10)
х) В работе [38] исследовалось несколько иное отображение, однако
качественно сложная структура фазовой плоскости на рис. 3.14 характерна
и для отображения C.4.1).— Прим. ред.
Отображения и линейная устойчивость
229
где m—взаимно простое с k целое число, а
_ к
иш = 1Тх^щ\ C.4.11)
/=i
Целое число m нумерует периодические траектории с данным k.
Разброс скорости каждой периодической точки (k, m) лежит в пре-
пределах Аымакс = (k— 1) |/|макс.
Как видно из рис. 3.12—3.14, периодические точки, окружен-
окруженные большими областями устойчивости, расположены при и "'}/ 1,
где величина е = | / \MaKClukm мала. Они соответствуют первич-
первичным резонансам и сохраняются даже в пределе е ->¦ б. При е = О
периодические точки (k, m) имеют координаты: гр/ = ip0 + 2njm/k;
Uj = kM'm; / = 1, . . . , k; г|H — любая величина. Значение я|-0
становится, однако, определенным при малом, но конечном е.
Расположение неподвижных точек (периода k = 1) для различных
отображений приведено в табл. 3.1.
Таблица 3.1. Расположение и устойчивость неподвижных точек (k=\)
Отображение
Точное C.4.1)
Упрощенное C.4.4)
/^¦ф—1/2
Упрощенное C-4.6)
/=sirn[\
Упрощенное C.4.5)
Положение
т=1,2,3. . . .
ui
1/2 М(+1/8)/т
1/2 М/т
0 М/т
я М/т
1/2 М/т
Устойчивость
Устойчивы при и±> —(Af+1/8I,2
—»— Mi > — М1/2
2
Неустойчивы
Устойчивы при Hi > (Л1/2I/2
Линейная устойчивость. Теперь мы проведем подробный анализ
устойчивости неподвижных точек, представленных в табл. 3.1.
Начнем с отображения C.4.4). Линеаризуя его в неподвижных точ-
точках ых = М/т; % = 1/2, получаем
C.4.12)
\%). C.4.13)
м
= Лг|>„ (Ды„
Откуда для матрицы преобразования вектора (Аи, Дгр) имеем
А= __^L i_ JL ¦ C.4.14)
230 Глава 3
При этом det А = 1, как и должно быть в силу сохранения фазовой
площади. Согласно C.3.55), условие устойчивости имеет вид
м
2—
<2, C.4.15)
ЛГ . C.4.16)
I Sp A I =
или
При Mj<C — Mlf2 величина SpA<; —2, что соответствует гипер-
гиперболической точке с отражением. Именно такая неподвижная точка
возникает, когда эллиптическая точка превращается в гиперболи-
гиперболическую на границе устойчивости. Физический смысл такого превра-
превращения можно пояснить, вычислив угол поворота а вокруг непод-
неподвижной точки, определяемый выражением C.3.54):
coscr = — SpA. (ЗАЛ7)
На границе устойчивости cos a = ¦— 1 и, следовательно, сдвиг
фазы о = п. Это явление хорошо известно и детально исследовано
в самых разных областях, как, например, распространение волн
в периодических структурах [42] или движение частиц в ускори-
ускорителях [94].
В качестве примера превращения эллиптических точек в гипер-
гиперболические с отражением рассмотрим отображение C.4.6). Все
неподвижные точки с % = л (и разными пг и Mj) являются гипер-
гиперболическими (без отражения), так как для них SpA = 2 -f-
+ 2лт2/М>2 при любом гпфО. Для неподвижных точек с % = О
величина SpA = 2—2nm2/M. Поэтому те из них, для которых
ш<BМ/яI/2, или
ll/2, C.4.18)
оказываются эллиптическими (устойчивыми), а остальные — ги-
гиперболическими с отражением. При меньших скоростях все непод-
неподвижные точки становятся гиперболическими (неустойчивыми), а
движение в их окрестности — стохастическимх). Как видно из.
табл. 3.1, условия устойчивости для разных отображений отли-
отличаются только численным множителем. Можно показать [274],
что для отображения C.4.6) условие устойчивости периодических
точек периода k = 2 имеет вид ы2> (лМУ/2, т. е. граница устой-
устойчивости по скорости лежит выше, чем для неподвижных точек
(k = 1).
Анализ устойчивости периодических точек с k = 3, 4, 5, . . .
становится все более и более трудным. Однако в случае упрощен-
Это не совсем точно, см. рис. 3.18.— Прим. ред.
Отображения и линейная устойчивость
231
ного отображения Либерману и Лихтенбергу [274 ] удалось полу-
получить выражение для критерия устойчивости при больших к. Они
показали, что граница устойчивости по скорости и лежит тем выше,
чем больше величина к. Поэтому самая нижняя граница устойчи-
устойчивости для неподвижных точек (к = 1) определяет некоторый важ-
важный для динамики переход. Соответствующую граничную скорость
будем обозначать us. Ниже этой границы нет устойчивых областей
100
40
20
10
10
30
100
м
300
1000
Рис. 3.15. Положение границы стохастичности щ (черные кружки) и гра-
границы устойчивости us (светлые кружки) в зависимости от М для отображе-
отображения C.4.6) (по численным данным работы [274]).
первичных резонансов. Поэтому стохастические траектории за-
заполняют всю эту область фазовой плоскости, за исключением не-
небольших островков устойчивости вторичного происхождения (см.
п. 3.4г), которые появляются, вообще говоря, лишь в узких интер-
интервалах значений параметра М. Сравнение теоретической границы
устойчивости us с численными данными для отображения C.4.6)
в широком диапазоне значений М проведено на рис. 3.15. Дана
также граница стохастичности иь, соответствующая первой снизу
инвариантной кривой х).
г) Как сейчас известно (см. [70], § 5.1 и гл. 4 ниже), граница стохастич-
стохастичности 'и;, да 2us при М > 1, что не противоречит численным данным на
рис. 3.15. По поводу отклонений при М ~ 10 см. [70, § 6.2] и конец п. 4.26.—
Прим. ред.
232
Глава 3
* 3.4г. Бифуркации
Рассмотрим теперь более подробно, как изменяется характер дви-
движения в окрестности эллиптической точки при ее превращении
в гиперболическую. На рис. 3.16 показан результат 100 000 итера-
итераций отображения C.4.6) при М ~ 14. Для неподвижной точки
«1 = 14/3, ip! = 0 значение us = 4,68947>ы1. Поэтому следует
ожидать, что эта неподвиж-
10,0
9,0-
8,0-
7,0-
6,0-
5,0-
4,5-
4,0 -
3,5-
3,0-
2,5
—it О
Рис. 3.16. Фазовая плоскость (и, ty) для
отображения C.4.6) при М — 14.
Внутри самого нижнего островка устойчи-
устойчивости произошла бифуркация неподвижной
точки (см. рис. 3.18).
ная точка должна быть
неустойчивой. Она дей-
действительно оказывается
гиперболической точкой
с отражением, но соседние
траектории не соединяются
с основной стохастической
компонентой движения.
Последняя отделена от
гиперболической точки вме-
вместе со стохастическим сло-
слоем ее сепаратрисы замкну-
замкнутыми инвариантными
кривыми, которые имеют
форму «гантели» (см.
16
8
4
0
-
-
ч
Л
\
V
—л- 0 тг
Рис. 3.17. Линии неподвижных
точек для инволюций отображе-
отображения C.4.6) при М =14.
Отображения и линейная устойчивость 233
рис. 3.18). При этом внутри сепаратрисы имеются две перио-
периодические точки периода 2, которых не было при «s<C«i.
Топология фазовой плоскости на этом малом масштабе в какой-то
степени похожа, хотя и не полностью, на глобальную топологию,
в которой инвариантные кривые окружают отдельные периодиче-
периодические точки или изолируют друг от друга сепаратрисы.
Чтобы найти положение только что описанных периодических
точек периода 2, запишем отображение C.4.6) в виде произведения
двух инволюций /х и /2, как это было сделано в п. 3.36. Линии не-
неподвижных точек инволюций 1г и /2 определяются выражениями
C.3.38) и C.3.39) и показаны на рис. 3.17. В частности, неподвиж-
неподвижные точки /, определяются выражением
и — . C.4.19)
(г|> \ пт)
Используем теперь результат п. 3.26, устанавливающий связь ме-
между неподвижными точками с периодом k = 2 и k = 1. Если обо-
обозначить
/ _Ш_ \ 3.4.20)
\ г|) + лт I
то
Тх = (п, $),
где
лМ .
и = + SIn '
(
2яМ о
—-— — 2лт.
C.4.21)
Чтобы и точка (и, "ф) была неподвижной точкой инволюции /2,
необходимо выполнение соотношения
^!sin\|;. C.4.22)
(лга)!-12 пМ
При М = 14, т = 3, полагая sin of « а|з—гр3/6, получим г|; =
= ±0,23351, а и определяется выражением C.4.19). Эти периоди-
периодические точки показаны на рис. 3.18 вместе с сепаратрисой, которая
имеет форму восьмерки и принадлежит неустойчивой неподвижной
точке.
Что же произойдет при дальнейшем уменьшении величины М,
а вместе с ней и и{? Для выяснения этого вопроса заметим, что
для и в уравнении C.4.6а) вблизи кривой /2 можно использовать
выражение C.4.19). В результате получаем одномерное отображе-
отображение
234
Глава 3
ип+1 « u,,-j-sin л / т ]
\ ип I
C.4.23)
Такие отображения естественно возникают при изучении диссипа-
тивных систем и подробно описаны в § 7.2. Мы покажем там, что
с уменьшением М происходит целый каскад последовательных би-
4,85
4,80
4,75
4,70
4,65
4,60
4,55
4,50
20
\Ч4
A\i:
28\Лу0
5
1
Не^сгпопчибая
^^ непоЭбижная
точка
%,
1|\\ ;7
\\25
it\^:i
14 .
-0,36 0 0,36
v;
ис. 3.18. То же, что на рис. 3.16 внутри устойчивости области.
Светлые кружки — устойчивые точки периода 2; треугольник —• неустойчивая непод-
неподвижная точка с сепаратрисой (сплошная кривая). Цифры показывают последовательность
движения по сепаратрисе (ср. рис. 3.10, б).
фуркаций устойчивых периодических точек с периодами 2 -> 4 ->
—>- 8 ->-16 и т. д. Этот процесс продолжается, пока М не достигнет
некоторого предельного значения, ниже которого все траектории
Отображения и линейная устойчивость 235
становятся неустойчивыми. В работе Лихтенберга и др. [72] под-
подробно описано поведение периодических точек k = 2 с изменением
М, включая бифуркацию 2 -> 4. Общая теория бифуркаций гамиль-
тоновых систем обсуждается в дополнении Б.
* 3.4д. Уравнения Гамильтона
Подобно тому как непрерывное движение динамической системы
можно описать разностными уравнениями на поверхности сечения
Пуанкаре, физическую задачу, сформулированную в виде отобра-
отображения, можно представить в форме уравнений Гамильтона. Это
позволяет использовать методы усреднения и резонансной теории
возмущений, рассмотренные в гл. 2. Как показано в п. 3.1в, раз-
разностные уравнения можно преобразовать в дифференциальные с по-
помощью периодической б-функции C.1.33). В случае отображения
C.4.6) получаем
du ? exp (t 2ял/) sini|;, C.4.24а)
dn iJ
J^^l^L, C.4.246)
dn и
где п играет роль непрерывной переменной времени. Уравнения
C.4.24) имеют гамильтониан
Н = 2пМ In и + 2 exp (I 2nnl) cos г|>, C.4.25)
где w и "ф — канонические переменные.
Усредненные уравнения. В области больших и (и > М) частота
колебаний частицы 2я велика по сравнению с у, т. е.
fob ib V9tt <f 1 И 4 ^fi)
В этом случае, как описано в п. 2.4а, гамильтониан C.4.25) можно
усреднить по па получить интеграл движения 2яЛ1 In «+
-f cos of = С. Однако область столь больших скоростей не пред-
представляет особого интереса. Вместо этого введем новые переменные,
как в резонансной теории возмущений (§ 2.4):
Ди = «—М1т, ф = а?>—2лтп, C.4.27)
где т — целое число. При условии Аи ^ иъ система уравнений
C.4.24) принимает вид
, exp (i 2nnl) sin ф , C.4.28а)
dn i
—-- = — Аи C.4.286)
dn U2
236 Глава 3
с гамильтонианом
^ ?osu. C.4.29)
Но это как раз и есть гамильтониан фазовых колебаний (п. 2.4а)
с учетом высокочастотных членов. Если движение в плоскости
(Аи, ф) считать медленным, т. е. если
(фп+1-фл)«2я, C.4.30)
то C.4.29) можно усреднить по п. В результате получаем усред-
усредненный гамильтониан
д//= _ ^Ш_ _(Д^_ +C0S~ = C) C.4.31)
и, 2
описывающий движение в окрестности неподвижных точек ф = 0;
я и Аи = 0. Максимум Аи соответствует сепаратрисе (С = -4- 1)
и равен [ср. B.4.31) ]:
(Ай)маКс = 2и1BяМГ1/2. C.4.32)
На рис. 3.12 и 1.14 инвариантные кривые системы C.4.31), показан-
показанные пунктиром, сравниваются с результатами численного модели-
моделирования. Отношение частоты малых фазовых колебаний [ср. B.4.30)]
C.4.33)
к частоте колебаний частицы 2яМ/и1 определяет гармонику вторич-
вторичных резонансов. Мы отложим эти вычисления, связанные с пере-
переходом к стохастическому движению, до гл. 4.
* § 3.5. Движение в окрестности сепаратрисы
Рассмотрим систему с двумя степенями свободы, близкую к интег-
интегрируемой. В окрестности резонанса гамильтониан такой системы
можно привести к стандартному виду
H = H0{J) + — Gp%—гР соэф, C.5.1)
используя резонансную теорию возмущений и производя усредне-
усреднение по быстрым фазам (см. § 2.4). Здесь медленное движение опи-
описывается интегрируемой системой уравнений маятника (см. п. 1.3а),
а быстрое движение описывается уравнениями:
J = const, C.5.2)
е = юо(У)^+ео. C.5.3)
Мы знаем, что такая картина движения не является полной, так
как взаимодействие между быстрыми (переменные в) и медленными
Отображения и линейная устойчивость
237
(переменная ср) колебаниями приводит к появлению вторичных ре-
зонансов и областей стохастичности. В окрестности же сепаратрисы
гамильтониана C.5.1) хаотическая компонента движения сохра-
сохраняется даже в пределе е -»- 0 (см. п. 3.2в).
а
j
1
1
1
1
I
— 7Г
7
Г
Рис. 3.19. Движение вблизи сепаратрисы маятника.
а — плоскость сечения (р, <р) (8 = const); б — плоскость сечения (J, 6) (ср = const).
Стохастическая траектория заполняет заштрихованную область вокруг невозмущенной
сепаратрисы (сплошная линия).
Гамильтониан C.5.1) был получен путем усреднения в окрест-
окрестности резонанса oVcoj = rls следующего гамильтониана [см.
B.4.9)]:
H = H0(J)-;- — Gp2 — eF coscp +
238 Глава 3
Л„, cos (-^<p--?-Q*+ &.,)• C.5.4)
где G, F, Л и % — функции переменной действия J, канонически
сопряженной быстрой фазе 9. Сравнивая C.5.1) и C.5.4), видим,
что медленное движение в переменных (р, ср) на поверхности се-
сечения 9 = const, описываемое гамильтонианом C.5.1), возмущено,
что приводит к появлению тонкого стохастического слоя вокруг
сепаратрисы. Этот слой схематически показан на рис. 3.19, а вместе
с невозмущенной сепаратрисой.
Можно также исследовать движение в переменных /, 6 на по-
поверхности сечения ср = const. В этих переменных невозмущенному
движению соответствует линия постоянного J. Под влиянием воз-
возмущения образуется стохастический слой, заштрихованный на
рис. 3.19, б. Видно, что в переменных /, 0 хаотическое движение
четко отделено от интегрируемого (тривиального) движения. По-
Построим поэтому отображение именно в переменных /, 6, выбрав
для удобства г) поверхность сечения ф»0.
*3.5а. Вынужденные колебания маятника
Прежде чем найти изменение переменной действия /, рассмотрим
более простую задачу. Дело в том, что при изменении J изменяется
также и частота сое (J). Более простая, но все еще интересная за-
задача получается, если считать частоту сое фиксированной. Это по-
позволяет развязать возмущенный маятник и остальную часть ди-
динамической системы. В таком случае фаза 0 просто пропорцио-
пропорциональна времени, а гамильтониан C.5.4) принимает вид 2)
Я — С^-е^созф + е^Л^соз^-ср 2-Q* + Xn?), C.5.5)
где G, F, Л, Q и % теперь постоянные, и мы опустили член Яо (/).
С точностью до членов порядка е гамильтонианы Н и Н полностью
эквивалентны. Это легко показать, если перейти к расширенному
фазовому пространству (п. 1.26) для гамильтониана C.5.5) с новыми
каноническими переменными J' = — Н' 10, и 0 = Ш и новым га-
гамильтонианом
Н' = Н + Ш'. C.5.6)
Сравнивая dJIdt из C.5.4) с dHldt из C.5.5), видим, что изменение
J пропорционально изменению Н:
AJ ~АН
C.5.7)
г) Выбор переменных J, 6 и сечения ф = 0 продиктован особенно-
особенностями действия возмущения вблизи сепаратрисы [см. ниже C.5.12)].—
Прим. ред.
2) Вместо этого можно просто пренебречь изменением частоты сое (J)
ввиду малости изменения /, как фактически и сделано ниже.— Прим. ред.
Отображения и линейная устойчивость 239
Вычисление А/. Проинтегрируем dH'dt, или, что эквивалентно,
dJ/dt по периоду невозмущенного движения маятника. Как будет
видно в дальнейшем, изменение AJ мало и экспоненциально зави-
зависит от отношения частот q.'r = Q,'coo- Предположим, что
wo=(eFGI/2CQ, C.5.8)
где соо — частота малых колебаний маятника. Так как амплитуды
Фурье Anq уменьшаются с ростом п и | q |, достаточно сохранить
лишь главный член с п = q = 1. Обозначив Л = Лп, получим
из C.1.31)
AJ = — ~ С dtsinl-ytf КО — -у (ш + е«I • C-5-9)
где для невозмущенного движения по сепаратрисе A.3.21) (см.
рис. 3.20, а) имеем
(es) — я, C.5.10)
a
8 = Q/ + 8n. C.5.11)
Величина % включена в постоянную 9„, равную фазе 0 в момент
n-го пересечения поверхности ф ?» 0. Переходя к переменной s =
= ®ot и учитывая, что вклад в интеграл дает только симметричная
часть подынтегрального выражения, получаем
д
АУ = е s4-{2r) (Qo) sinG,,. C.5.12)
Здесь функция
оо
^m(Q0)= i ds cos\~(f(s) — Qosj C.5.13)
называется интегралом Мельникова—Арнольда, а
есть отношение частот.
C.5.14)
Интеграл Мельникова—Арнольда. Интеграл C.5.13) является не-
несобственным и фактически не имеет определенного значения. Рас-
Рассмотрим интеграл
^m(Qo. s1) = 2[dscos\~-(f(s) — Qosj. C.5.15)
о
Как видно из рис. 3.20, в, при sx -> оо последний интеграл есть
сумма быстро осциллирующей части и некоторого среднего значе-
240
Глава 3
<t(s)
ния. Осциллирующая часть может быть велика по сравнению со
средним, но при усреднении по интервалу времени порядка пе-
периода колебаний вблизи
сепаратрисы вклад от нее
стремится к нулю. Сред-
Среднее значение ,9&'т опреде-
определяется областью s <C 1/Qo-
В этой области мгновенная
частота ф да 2соо (см. рис.
3.20, б) достигает наиболь-
наибольшего значения, макси-
максимально приближаясь к ча-
частоте возмущения Q. Это
и приводит к поведению,
изображенному на рис.
3.20, в. Ниже интеграл
в C.5.13) понимается в смы-
смысле своего среднего значе-
значения. Его оценка была
получена Мельниковым (см.
[70]) 1). Для целых т ин-
интеграл вычисляется точно
с помощью вычетов. При
-4 -3 -2 -1
Q0<;0 имеем
Осциллирующая
часть
реднее
_значение
( —Qo)exp(^Qo),
C.5.16)
:) Приведенные ниже экс-
экспоненциальные оценки были
впервые получены еще Пуан-
Пуанкаре [337, п. 226]. Поскольку,
однако, при Qo ~p 1 эффект экс-
экспоненциально мал, возникает
очень серьезная и трудная
проблема оценки точности это-
этого результата, которая до сих
пор обсуждается в литературе
(см., например, [197, 483,
484]). По существу вопрос был
решен уже в первых работах
Мельникова [298], который
показал, что все неэкспонен-
неэкспоненциальные поправки могут быть
оттрансформированы с помо-
помощью канонической замены пе-
переменных (см. также [314],
лемма 10.3). Тем не менее в некоторых специальных случаях, например, для
стандартного отображения, эффекты высших приближений приводят к появ-
появлению численного множителя порядка единицы, который пока не поддается
аналитической оценке (см. [70, § 6.1] и [485]).— Прим. ред.
Интеграл Мельникова — Ар-
Рис. 3.20.
нольда.
а — движение по невозмущенной сепаратрисе
<р (s); б — скорость движения ф' (s); в —интеграл
Мельникова — Арнольда равен среднему значе-
значению функции ^fm(S!).
Отображения и линейная устойчивость 241
эта величина обычно очень мала. Для Q0>0 получаем
C.5.18)
2лехр(л(?0/2)
sh(nQ0) v
и рекуррентное соотношение для /п>2 имеет вид
stm = 2Q°Mm-1 s4m.2. C.5.19)
(m— 1)
При Qo > т справедливо следующее асимптотическое представле-
представление:
Подробности вычисления этих интегралов можно найти в работе
[70].
Вернемся к соотношению C.5.12). Используя асимптотику
C*5.20) в виду того, что Qo ~ е~1/2, получаем первое уравнение
возмущенного отображения поворота C.1.13а) с функцией (г = 1)
/ = /osinen, C.5.21)
C.5.22)
* 3.56. Сепаратрисное отображение
Изменение фазы 0 между последовательными пересечениями по-
поверхности (г = 0 определяется полупериодом колебаний вблизи
сепаратрисы, который, согласно A.3.15), равен
Г = со-Чп-^-, C.5.23)
где величина
w(J)=-eF~QJ C.5.24)
.характеризует относительное смещение от сепаратрисы по энергии.
Изменение фазы 8 равно при этом просто QT. Отсюда число враще-
вращения во втором уравнении отображения поворота C.1.136) равно
2па = —In —. C.5.25)
Так как функция f считается независящей от /, то из C.1.16) еле"
дует, что можно положить g s 0, так что никакого дополнитель'
ного изменения фазы не происходит.
242
Глава 3
Оказывается, что более удобно перейти от J к переменной w,
определяемой формулой C.5.24). Тогда отображение принимает вид
wn+i = wn — сг>0 sin 9„, C.5.26а)
где
Q/o
= 8л/ —
C.5.266)
C.5.27)
Это и есть сепаратрисное отображение 170], которое описывает
движение в окрестности возмущенной сепаратрисы.
Неподвижные точки и их устойчивость. Мы не будем здесь рассмат-
рассматривать сепаратрисное отображение столь же подробно, как ото-
отображение Улама выше, а отметим лишь его наиболее характерные
особенности. Оба отображения очень похожи друг на друга, оба
относятся к классу явных отображений поворота и их можно пред-
представить в виде произведения инволюций (см. п. 3.16). Оба отобра-
отображения имеют нелинейность одного типа, которая приводит к уве-
увеличению фазового сдвига, а следовательно, и к стохастичности при
уменьшении переменной действия (w или и).
Неподвижные точки определяются из C.5.26) условием
32
Откуда
= ± 32 ехр /
2лт
= 2пт.
, где т—целое число, C.5.28а)
ех = О; я. C.5.286)
Устойчивость неподвижных точек определяется условием C.3.55)
Sp А | =
w1
C.5.29)
Следовательно, при а^Х) все неподвижные точки 6Х = О неустой-
неустойчивы, a 8j = я устойчивы при
C.5.30)
или
Qoexp
C.5.31)
Как и в случае отображения Ферми, можно ожидать, что величина
ws определяет важную границу перехода к сплошной стохастич-
стохастичности при
Отображения и линейная устойчивость 243
Сепаратрисное отображение играет чрезвычайно важную роль
в понимании хаотического поведения систем, близких к интегри-
интегрируемым. Как мы видели выше, резонансы в таких системах всегда
окружены сепаратрисами, а сепаратрисное отображение описы-
описывает движение в их окрестности, причем это движение является хао-
хаотическим при w ->¦ 0. Ввиду такой универсальности сепаратрисное
отображение интенсивно изучалось [70] с целью определения гра-
границы стохастичности wb, которая характеризует ширину стоха-
стохастического слоя вокруг сепаратрисы, а также для выяснения ста-
статистических свойств хаотического движения внутри этого слоя.
Результаты этих исследований представлены в гл. 4 и 5. Далее в
гл. 6 будет показано, что движение в окрестности сепаратрисы
лежит в основе анализа диффузии Арнольда, которая, вообще го-
говоря, всегда имеет место в системах с тремя и более степенями сво-
свободы.
Глава 4
ПЕРЕХОД К ГЛОБАЛЬНОЙ
СТОХАСТИЧНОСТИ
*§ 4.1. Введение
В гл. 3 мы видели, что в системах с двумя степенями свободы, близ-
близких к интегрируемым, вблизи сепаратрис резонансов возникают
области хаотического движения. Эти области сохраняются для
любого ненулевого возмущения е, хотя их площадь и стремится к
нулю при е -> 0. Следовательно, не существует резкого «перехода
к стохастичности» для какого-то критического значения е, и поэтому
смысл любого такого критерия должен быть определен более четко.
Одно из возможных определений состоит в измерении доли фа-
фазового пространства с хаотическим движением и в последующем
нахождении минимального значения е, для которого эта доля до-
достигает некоторого произвольно выбранного значения, скажем
1/10 или 1/2. Наличие подобной неопределенности приводит к тому,
что такой подход является в каком-то смысле качественным. Не-
Несмотря на это, он может в значительной степени способствовать
пониманию явления стохастичности. Для определения критерия
перехода к стохастичности использовались различные методы:
1) мгновенная скорость расходимости близких траекторий
[409, 44];
2) убывание корреляций [302, 401 ];
3) обмен энергией между степенями свободы [148];
4) фурье-спектр траекторий [318];
5) показатели Ляпунова [19];
6) КС-энтропия 170].
Первые три метода критиковались в литературе (см., напри-
например, [55, 59, 60]) как неспособные правильно различать регуляр-
регулярное и стохастическое движение *). С другой стороны, последние
три метода, как выяснилось, имеют большое значение и для ана-
анализа движения внутри хаотических областей, чему посвящена
гл. 5.
г) Хотя упомянутая выше критика и имеет некоторые основания, сле-
следует отметить, что эти методы успешно использовались в ряде работ, на-
например в [443] (первый метод) и в [127] (третий метод). Второй метод (при
правильном его применении) эквивалентен четвертому и особенно удобен
в реальных экспериментах, тогда как два последних метода больше подходят
для численного моделирования. Отметим также, что ссылки авторов при
перечислении методов носят случайный характер, более аккуратная библио-
библиография дана ниже, при описании некоторых из этих методов.— Прим. ред.
Переход к глобальной стохастичности
245
Более естественное определение «перехода к стохастичности»
вытекает из следующего наблюдения, характерного для различ-
различных систем с двумя степенями свободы: в фазовом пространстве
существует резкая граница между областями с узкими стохастиче-
Стохастическип
слой
Локальная
стохастичносгпь
Граница
стохастичности
Глобальная
стохастичносгпь
Граница
устойчивости
Рис. 4.1. Переход от локальной к глобальной стохастичности с ростом воз-
возмущения (Ми2).
скими компонентами движения, запертыми инвариантными поверх-
поверхностями, и областями сплошного стохастического движения. В пер-
первом случае изменение переменных действия ограничено шириной
сепаратрисы резонансов (см. рис. 4.1) и AJ/J ос -у/ г (п. 2.4а). Во
втором случае J изменяется хаотически в широких пределах, так
что AJ/J '-- 1. Ясно, что количественное определение перехода
от одного случая к другому дает важную информацию относительно
поведения системы. Будем называть эти две области соответственно
246 Глава 4
локальной (или изолированной, или слабой) и глобальной (или свя-
связанной, или сильной) стохастической областью, а сам переход —
границей стохастичности, или переходом к глобальной стохастич-
ности. Именно такой переход и рассматривается детально в этой
главе.
Как мы уже видели в задаче об ускорении Ферми (§ 3.4), гра-
граница стохастичности *) иь отделяет сплошную стохастическую ком-
компоненту при малых скоростях частицы от области со стохастиче-
стохастическими слоями вблизи сепаратрис резонансов при больших скоро-
скоростях (см. рис. 4.1, 1.14, и 3.15). Эта граница отличается от границы
устойчивости us, ниже которой все неподвижные точки соответст-
соответствующего отображения неустойчивы. Оказывается, что ub~>us,
откуда следует, что неустойчивость неподвижных точек достаточна,
но не необходима для глобальной стохастичности, т. е. это условие
является слишком сильным. Мы же ищем более эффективный кри-
критерий, которой был бы и необходимым, и достаточным. К сожале-
сожалению, чисто аналитического метода получения такого критерия не
существует. Поэтому приходится прибегать к различным правдо-
правдоподобным рассуждениям, подкрепленным численными эксперимен-
экспериментами. В этой главе мы рассмотрим пять методов, описанных качест-
качественно в п. 4.1а, каждый из которых дает свой вклад в понимание
рассматриваемой проблемы. В качестве модели для иллюстрации
этих методов мы используем стандартное отображение, свойства
которого обсуждаются в п. 4.16.
* 4.1а. Качественное описание критериев перехода
Первый критерий перехода к глобальной стохастичности, предло-
предложенный Чириковым [67] и позднее усовершенствованный им [70],
известен сейчас как критерий перекрытия. В своей простейшей
форме он постулирует, что последняя инвариантная поверхность
между двумя резонансами разрушается, когда невозмущенные се-
сепаратрисы этих резонансов касаются друг друга. Действительно,
интуитивно ясно, что касание стохастических слоев, которые, как
мы знаем, окружают сепаратрисы, должно приводить к разруше-
разрушению всех инвариантных поверхностей в этой области. Строго го-
говоря, критерий перекрытия не является ни необходимым, ни до-
достаточным. С одной стороны, последняя инвариантная поверхность
может разрушаться значительно раньше перекрытия рассматри-
рассматриваемых резонансов за счет взаимодействия других резонансов ме-
между ними. С другой стороны, возмущение может так исказить се-
сепаратрисы, что они фактически не будут перекрываться вопреки
предсказаниям по первому приближению. Фактически численное
моделирование показывает, что критерий перекрытия является
х) Напомним, что в этой задаче эффективное возмущение пропорцио-
пропорционально 1/и2.
Переход к глобальной стохастичности 247
чересчур жестким условием глобальной стохастичности. Он может
быть, однако, сделан более эффективным, если учесть ширину сто-
стохастического слоя сепаратрисы и некоторые из промежуточных
резонансов [70]. В таком виде критерий перекрытия рассматри-
рассматривается в § 4.2. Однако и в простейшем виде этот критерий дает гру-
грубую оценку для границы стохастичности и использовался в самых
различных задачах Чириковым [67—71], Фордом и сотр. [423],
Розенблютом и др. [349 ] и многими другими (более полную библио-
библиографию см. в работе [70]). Следует отметить, что в качестве гру-
грубого критерия стохастичности можно использовать также условие
потери линейной устойчивости периодических траекторий, которое
приводит к границе устойчивости us в примере § 3.4.
Используя аналогичную методику, Егер и Лихтенберг [212]
вычисляли размер вторичных резонансов между гармониками фа-
фазовых колебаний на основных резонансах и невозмущенными ко-
колебаниями. Они показали, что при перекрытии первичных резо-
резонансов параметр перекрытия вторичных резонансов, т. е. отношение
их размера к расстоянию между ними, сравним с параметром пе-
перекрытия для первичных резонансов и по индукции это же справед-
справедливо и для резонансов более высоких порядков. При этом локаль-
локальное число вращения для первичного резонанса вблизи его центра
равно а = 1/4, т. е. здесь возникает вторичный резонанс четвертой
гармоники. Изучение резонансной структуры со всей очевидностью
показывает, что простой критерий перекрытия является слишком
жестким. Численно было найдено, что когда параметр перекрытия
для первичных резонансов достигает 2/3 (при этом появляется
вторичный резонанс шестой гармоники), то этого достаточно,чтобы
разрушить последнюю инвариантную поверхность между первич-
первичными резонансами. Такой критерий применялся для многих за-
задач, как, например, ускорение Ферми [274] и циклотронный на-
нагрев [212, 275]. Отметим, что усовершенствованный критерий
перекрытия Чирикова также связан со вторичными резонансами,
но не в центре первичного резонанса, а вблизи его сепаратрисы.
Использование вторичных резонансов рассматривается в § 4.3. Со-
Соответствующая техника разложения, основанная на резонансной
теории возмущений, описана в § 2.4.
Третий метод определения границы стохастичности базируется
на анализе линейной устойчивости движения вблизи центра резо-
резонанса (его периодической траектории). Идея метода состоит в сле-
следующем. Поскольку потеря линейной устойчивости для резонан-
резонансов с наиболее низкой гармоникой (k = 1) является слишком жест-
жестким условием, более эффективным критерием может служить ли-
линейная устойчивость для тех резонансов на высоких гармониках k,
которые расположены вблизи некоторой инвариантной поверхно-
поверхности. Эта гипотеза была численно проверена и подтверждена Грином
[164, 165]. Более конкретно, гипотеза Грина состоит в том, что су-
существование инвариантной кривой с иррациональным числом вра-
248 Глава 4
щения а зависит от устойчивости соседних периодических точек,
рациональные числа вращения которых сходятся к а. Предпола-
Предполагается также, что эта устойчивость тем выше, чем хуже аппрокси-
аппроксимация а рациональными числами. Можно показать (§ 4.4), что на
отрезке @,1), т. е. между двумя целыми резонансами (k = 1), ирра-
иррациональным числом с наихудшей рациональной аппроксимацией
является так называемое золотое сечение х) ае = (^/Ъ— 1)/2. Поэ-
Поэтому можно ожидать, что последней инвариантной кривой, кото-
которая будет разрушена по мере роста возмущения, является именно
кривая с числом вращения а = ай. Это подтверждается и числен-
численными данными Грина 2). Таким образом, эффективный критерий
разрушения всех инвариантных кривых между целыми резонан-
резонансами сводится к исследованию асимптотической (k -*¦ оо) устойчи-
устойчивости периодических точек с а -»¦ ag. Для практической реализа-
реализации этого критерия требуется быстрая сходимость при k > 1, обес-
обеспечение которой облегчается следующим свойством периодических
точек при &—>-оо. Если возмущение близко к критическому для
некоторой инвариантной кривой, то в окрестности приближающих
ее периодических точек возникают вторичные резонансы с а = 1/6,
что соответствует приблизительно границе устойчивости периоди-
периодических точек. Этот факт связан с другим наблюдением (см. § 4.2),
что вблизи границы стохастичности такие же вторичные резонансы
появляются и внутри целых резонансов (k = 1).
Четвертый метод, предложенный Эсканде и Довейлом [17, 18],
также основан на анализе резонансов высоких гармоник в окрест-
окрестности некоторой инвариантной кривой. Однако в отличие от ме-
метода Грина это достигается путем последовательной ренормализа-
ции гамильтониана с сохранением его формы. Этот метод не столь
эффективен, как предыдущий, и в типичном случае приводит к зна-
значению границы стохастичности на 3-4-10% ниже фактического
согласно численным данным 3). Полученные этим методом резуль-
результаты относятся к более общему случаю двух резонансов произволь-
произвольной величины. При этом «последняя инвариантная кривая» не свя-
связана, вообще говоря, с золотым сечением. Метод и полученные с его
помощью результаты обсуждаются в § 4.5.
В заключение в § 4.6 кратко описан вариационный метод опре-
определения условий существования инвариантных торов. В гамильто-
новой форме он был развит Персивалем [328], а в лагранжевой —
Персивалем [330] и Клейном и Ли [228]. Используемая в послед-
последней работе техника весьма близка к описанной в п. 2.66 для нахож-
*) Таким же свойством обладают и все иррациональные числа вида
ag -f- m, где т — любое целое.
2) Но противоречит численным экспериментам, описанным в работе[76].
Обсуждение «золотой» гипотезы Грина см. в [76, 485].— Прим. ред.
3) Это расхождение (и даже его знак) может быть связано и с точностью
численного определения границы стохастичности при относительно корот-
коротком времени счета в [17, 18] (см. [70], D.49) и рис. 5.3).— Прим. ред.
Переход к глобальной стохастичности 21 <>
дения периодических траекторий и позволяет получить, как и ме-
метод Грина, эффективный критерий разрушения инвариантных
торов.
В § 4.7 приводится сравнение различных критериев перехода
к глобальной стохастичности и обсуждаются особенности их прак-
практического использования. Подчеркивается, что простой критерий
перекрытия дает оценку только по порядку величины, но его легко
применять в самых разных задачах. В качестве более эффективного
критерия в некоторых новых задачах можно отказаться от сложных
вычислительных процедур и прямо использовать уже полученные
решения, например результат Грина для стандартного отображе-
отображения, или вычисления Эсканде и Довейла. Все эти критерии приво-
приводят к правилу «двух третей», которое является достаточно эффек-
эффективным и удобным для использования *). Более подробное обсуж-
обсуждение возможностей различных критериев стохастичности и обшир-
обширную библиографию можно найти в обзорах Чирикова [70] и Табора
[401].
Если система имеет более чем две степени свободы, то резкой
границы стохастичности уже не существует. Это связано с тем, что
все стохастические слои резонансных сепаратрис в фазовом про-
пространстве связаны между собой. Возникающая при этом диффузия
Арнольда является, вообще говоря, очень медленной по сравнению
с диффузией в областях глобальной стохастичности. Поэтому в прак-
практическом отношении понятие границы стохастичности остается
содержательным и для многомерных систем.
*4.1б. Стандартное отображение
Для вычисления границы стохастичности используем в качестве
модели стандартное отображение C.1.22). Это позволит нам ана-
аналогично Чирикову и Грину исследовать переход к стохастичности
в терминах параметра стохастичности К- Мы уже видели в п. 3.16,
что стандартное отображение локально аппроксимирует более об-
общие нелинейные отображения. Покажем прежде всего, что это рас-
распространяется и на отображение Улама, и на сепаратрисное ото-
отображение.
Для удобства перепишем отображение Улама C.4.6) еще раз:
D.1.1а)
1. D.1.16)
Чтобы получить стандартное отображение, линеаризуем D.1.16)
*) Это правило справедливо только в случае перекрытия близких по ши-
ширине резонансов, см. рис. 4.12.— Прим. ред.
250
Глава 4
по переменной действия и вблизи неподвижной точки и = uv Со-
Согласно табл. 3.1, имеем
-^- = 2л/п, D.1.2)
где т — целое число. Подставляя ип = их + А«„ и сдвигая фазу
9Я = \|"п — л (—л<;9„ sg л), получаем стандартное отображение
/=/„-!-/? sin 9„, D.1.3а)
9я+1 = 9„ + /„+1, D.1.36)
где
/„ = ~ — D.1.4)
есть новая переменная действия, а
2яМ
D.1.5)
— параметр стохастичности. Следовательно, параметр К связан
со старой переменной действия их. Переход от отображения Ферми
к стандартному отображению иллюстрируется на рис. 4.2 для двух
значений ult приводящих к различным значениям К-
Проделаем то же самое с сепаратрисным отображением C.5.26):
ш„+1 = да„—ny0sin6n, D.1.6а)
32 D.1.66)
Неподвижные точки w = wx даются выражением
32
wx
D.1.7)
Подставляя wn — wx + Awn и линеаризуя по w, снова получим
стандартное отображение D.1.3), где
Q0Awn
In =
D.1.8)
QqWq
D.1.9)
Неподвижные точки. Неподвижные точки стандартного отображе-
отображения получаются из условия:
о а D.1.10)
91 = 0, л. v '
Для каждого целого числа т имеются две неподвижные точки.
Переход к глобальной стохастичности
251
Линеаризуя
вания:
1.1.3а), как и в п. 3.4в, получим матрицу преобразо-
-1
u
\±к)>
D.1.11)
отображение
-4тг
Рис. 4.2. Локальная аппроксимация отображения Улама стандартным ото-
отображением.
а — локальная стохастичность для малых К (исходное отображение линеаризовано в ок-
окрестности и,Л; б — глобальная стохастичность для больших К (линеаризация в окрест-
окрестности ulb).
252 Г.шва 4
где верхний знак соответствует 0Х = 0, а нижний Bj = я. При
этом det A= 1, как и должно быть для отображения, сохраняю-
сохраняющего фазовую площадь. Согласно C.3.55), условие устойчивости
зависит от следа матрицы А и имеет вид
B±#|<2. D.1.12)
Поэтому неподвижная точка &г = 0 всегда неустойчива 1), а эл-
эллиптическая точка &х ~ п превращается в гиперболическую с от-
отражением при
К>4. D.1.13)
В этом случае все неподвижные точки становятся неустойчивыми.
В общем случае отображение всегда периодично по фазе 8, но
не по /. Однако стандартное отображение периодично также и по /
D.1.36). Эта особенность приводит к существованию неподвижных
точек другого типа. С учетом периодичности по / соотношения
/4.1.10) нужно заменить теперь на следующие:
1и = 2ят, КйпВ11 = 2я1, D.1.14)
где т, I — целые числа.
«Неподвижные» точки с 1^=0 соответствуют на самом деле
ускорительным режимам движения [70], поскольку / увеличи-
увеличивается на 2л/ при каждой итерации. Условие устойчивостиD.1.12)
заменяется на
|2±/Ссоз91г|<2. D.1.15)
Отсюда и из D.1.14) следует, что с ростом / (и уменьшением
интервалы устойчивости существуют для сколь угодно больших
значений К- В отличие от этого для / = 0 имеется граница устой-
устойчивости /С<4. Это является любопытной особенностью именно
стандартного отображения, и поэтому не следует искать ускоритель-
ускорительные режимы в отображениях, которые лишь локально аппроксими-
аппроксимируются стандартным отображением.
Периодические точки. Чириков [70], Грин [165], Лихтенберг и др.
[272], а также Шмидт [363] исследовали различные семейства
периодических точек (?>1). Их можно разделить на два класса:
первичные, которые существуют и в пределе К -*¦ 0, и бифурка-
бифуркационные, которые возникают только выше некоторого порогового
значения К-
Остановимся подробно на периодических точках с периодом
k = 2. Такие точки образуют пары: (Iи Эх) и (/2, Э2). Итерируя
отображение дважды, получаем
D.1.16а)
D.1.166)
Считается, что К > 0.— Прим. ред.
Переход к глобальной стохастичности 253
D.1.16b)
GA
eJ
где гп1 и т.-, — целые числа. Условие устойчивости определяется
следом матрицы
1-h/CcoseJ
и приводится к виду
— 4<2K(cos61-cosG2)-:-K2cosG1cos92<0. D.1.18)
Если сложить D.1.16а) и D.1.16в), видно, что имеются два случая:
а) 62 = — 0! и б) 62 = 6Х—л, причем 0<С 9Х s? л. Для случая
«а» из D.1.16) следует соотношение
2лр — 461 = /Csine1, D.1.19)
которое определяет 6^ Это выражение при р = тг—т2 = 1 дает
первичные периодические точки, а при р>1 —бифуркационные.
Условие устойчивости D.1.18) принимает вид
— 4<KcosG1<0. D.1.20)
Первичные точки (/1>2 = 2л (т2 + 1/2); Gli2 = + л/2 при /С С 1)
неустойчивы для любых К., поскольку 6Х «^ л/2. Первые бифурка-
бифуркационные точки возникают при К = 4, когда неподвижная точка
(/2 = 2лт2, вх = я) становится неустойчивой, и остаются устой-
устойчивыми при 4«<ЛГ<;2л. Интервалы устойчивости имеются для
сколь угодно больших К., если при этом р достаточно велико.
В случае «б» из D.1.16) следует соотношение
2я(р— 1) = /Csin61, D.1.21)
которое определяет 6Ь а условие устойчивости принимает вид
K2cos2G1<4. D.1.22)
Здесь также имеются первичные точки /li2 = 2я (т2 + 1/2);
6i = я; 62 = 0, устойчивые при /С<2. Первые бифуркационные
точки для /7 = 2 возникают при К = 2л, когда аналогичные точки
в случае «а» становятся неустойчивыми. Для случая «б» точки устой-
устойчивы при 6,28<; ЛГ<6,59. Как и в случае «а», имеются интервалы
устойчивости для произвольно больших значений К'-
BлJ(р—lJ<K2<BnJ(p —1J + 4. D.1.23)
Отметим, что другие отображения могут и не иметь этого специфи-
специфического свойства [272]. Периодические точки большего периода
(k~>2) исследованы Шмидтом [363] и Шмидтом и Билеком [364].
Граница стохастичности. Численно легко получить сотни тысяч
итераций стандартного отображения D.1.3) и, таким образом, ис-
исследовать его динамику для различных значений К и начальных
254
Глава 4
условий. На рис. 4.3 показано изменение структуры фазовой пло-
плоскости с ростом К- При малом К ясно видны первичные эллиптиче-
эллиптические точки k = 1, 2, а также гиперболические точки с их стохасти-
in
2тг О
в
К = 0.5
в
А = 1,0
А' = 2,5
К = 4,0
Рис. 4.3. Фазовая плоскость стандартного отображения для разных К (по
данным работы [22]).
а — локальная стохастичность вблизи сепаратрис; вндны целый и полуцелый резонансы^
6 — глобальная стохастичность; в — полное разрушение полуцелого резонанса; виден
вторичный резонанс 4-й гармоники вокруг неподвижной точки; г — первичная непод-
неподвижная точка на пороге устойчивости; инвариантные кривые вытянуты по направлению
рождения двух бифуркационных точек.
ческими слоями. Переход от локальной к глобальной стохастич-
ности происходит между К = 0,95 и К = 1,00. Более детальные
численные исследования дают для границы стохастичности
Переход к глобальной стохастичности 255
К ~ 0,9716 (§ 4.4). С ростом К первичные точки периода 2, а за-
затем и периода 1 становятся неустойчивыми, однако, как видно из
рисунка, островки устойчивости существуют и при больших К-
Таким образом, стандартное отображение, в котором для любого
ненулевого значения К нет ни полной интегрируемости, ни сплош-
сплошного хаоса, является характерным представителем типичной га-
мильтоновой системы.
На рис. 4.4 показаны четыре траектории стандартного отобра-
отображения для К = 0,97, чуть ниже границы стохастичности. Две из
них лежат на инвариантных кривых, изолирующих стохастические
слои целого (k = 1) и полуцелого (k = 2) резонансов. Однако ре-
резонанс с k = 4 уже поглощен стохастическим слоем целого резо-
резонанса.
Гамильтониан. Аналогично отображению Улама (п. 3.4д) гамиль-
гамильтониан стандартного отображения получается с помощью периоди-
периодической б-функции и имеет вид
Я = — -f К cosB ? expBntmn), D.1.24)
2 m — — oo
где номер итерации п играет роль времени. Предположим, что
0 —- медленная переменная:
— «2я. D.1.25)
dn
Учитывая, что основной вклад дают члены с медленно меняющейся
фазой, оставим только слагаемые ся = 0иш = ±1:
Н = — + К cos 6 ~- 2К cos 0 cos 2nn. D.1.26)
Последний член в правой части будем считать возмущением, тогда
невозмущенный гамильтониан
#0 = — -f К cos9 D.1.27)
описывает маятник (п. 1.3а). Его фазовая плоскость показана на
рис. 1.4. Частота малых фазовых колебаний вблизи эллиптической
точки 0 = я равна:
@0 = K12, D.1.28)
а амплитуда колебаний по / есть
А/макс = 2К12. D.1.29)
Поскольку расстояние 81 между целыми резонансами равно для
стандартного отображения его периоду 2я, параметр перекрытия
резонансов имеет вид
2Д/Манс = 4/('/2 ^ D 1.30)
б/ 2я
256
Глава 4
Это отношение можно выразить через частоту малых фазовых ко-
колебаний D.1.28) или локальное число вращения а0 = соо/2я:
2Д/„
б/
= 4а0 = ¦
D.1.31)
Здесь Qo = 1/а0 — период малых колебаний, выраженный в числе
итераций отображения. Соотношение D.1.31), связывающее отно-
Рис. 4.4. Четыре траектории стандартного отображения для К = 0,97 (по
данным работы [165 ]).
Верхняя и нижняя группы точек принадлежат одной траектории.
сительный размер резонанса с его числом вращения, справедливо
для всех соседних резонансов любого порядка х). Например, из
того, что согласно численным данным граница стохастичности
приблизительно соответствует появлению вторичных резонансов
шестой гармоники (сц = 1/6), вытекает правило «двух третей»
2Д/„аКс/67 » 2/3.
*) Конкретный смысл этого «универсального» утверждения зависит от
величины б/, см. ниже конец п. 4.4а.— Прим. ред.
Переход к глобальной стохастичности 257
* § 4.2. Перекрытие резонансов
* 4.2а. Схема получения критериев
В этом параграфе, следуя работе Чирикова [70 ], мы получим
весьма эффективный количественный критерий перехода к гло-
глобальной стохастичности. Сначала, используя гамильтониан стан-
стандартного отображения, мы найдем условие касания сепаратрис
целых резонансов, что приведет к простейшему критерию пере-
перекрытия К, -- Jt2/4 яй 2,47. Далее, учтем полуцелый резонанс и най-
найдем более точное критическое значение К ~ 1,46. Это уже гораздо
ближе к численному результату [70], но все еще остается завышен-
завышенным. Наконец, учтем ширину стохастического слоя вблизи сепара-
сепаратрисы. (Чириков нашел, что резонансы третьей гармоники несу-
несущественны 1)). Для этого исследуем перекрытие вторичных резо-
резонансов вблизи сепаратрисы целого резонанса. Это может быть
сделано либо путем перехода от сепаратрисного отображения
(§ 3.5) к новому стандартному отображению, как в п. 4.16 выше,
либо путем непосредственного вычисления размера вторичных ре-
резонансов вблизи сепаратрисы, как в п. 4.36 ниже. Однако для по-
получения точного условия перекрытия вторичных резонансов не-
необходимо ввести те же поправки, что и для первичных и т. д. Можно
ожидать, что такой процесс сходится и дает правильный ответ.
Вместо проведения соответствующих довольно утомительных вы-
выкладок Чириков «замыкает» процедуру, вводя в отображение для
вторичных резонансов некоторый «корректирующий множитель» 2).
Это позволяет согласовать аналитические и численные результаты.
* 4.26. Вычисление критериев перекрытия
Простое перекрытие. Простейший критерий, как видно из
рис. 4.5, а, состоит в том, чтобы удвоенное значение А/Макс, вы-
вычисленное по D.1.29), было равно расстоянию между целыми ре-
зонансами 67 = 2я, откуда
4К1/2 = 2я ' D.2.1)
или
' " ' ' « 2,47. D.2.2)
1) Это не совсем так. С учетом замечания Кари критическое значение
понижается до К « 1,28 [70, с. 317].— Прим. ред.
2) На самом деле речь идет о чисто эмпирическом множителе R да 2,15,
который учитывает поправки к интегралу Мельникова — Арнольда C.5.22)
за счет отброшенных в D.1.26) высокочастотных членов. Аналитическую
оценку R пока получить не удалось. Замыкание же процедуры ренормали-
зации резонансов-производится элементарно [см. вывод D.2.23) ниже].—
Прим. ред. '
258
Глава 4
К = 2,47
I
\ма.кс
К = 1,46
2 макс
К = 1,2
т
Рис. 4.5. Схема перекрытия резонансов.
а -~ перекрытие (касание) целых резоиансов; б—перекрытие целых и полуцелого резо-
резонансов; в—перекрытие с учетом конечной ширины стохастического слоя целого ре-
резонанса (заштри ховано).
Переход к глобальной стохастичности 259
Поскольку это значение К слишком велико, мы уточним его, при-
приняв во внимание полуцелый резонанс, который расположен посе-
посередине между соседними целыми резонансами.
Перекрытие целого и полуцелого резонансов. Как показано на
рис. 4.5, б, касание сепаратрис этих резонансов приводит к усло-
условию
Д/l макс -f Д/Я макс = F/)и = Я, D.2.3)
где индексы 1 и 2 обозначают соответственно целый и полуцелый
резонансы.
Для вычисления ширины резонанса А/2 нужно учесть вторую
гармонику Фурье (§ 2.4). Для стандартного отображения эта гар-
гармоника появляется только во втором порядке теории возмущений,
поскольку исходное возмущение К sin 6 имеет только первую гар-
гармонику. Так как полуцелый резонанс максимально удален на фа-
фазовой плоскости от целых резонансов, то можно использовать стан-
стандартную теорию возмущений.
Чтобы получить новый гамильтониан Н до второго порядка
малости, используем метод Ли, описанный в п. 2.56. Гамильтониан
D.1.24) можно записать в виде
H = H0 + eHi = — + eK ? cos F— 2птп), D.2.4)
2 т]= — °°
где, как обычно, параметр е отмечает возмущение. Прежде всего
из уравнения Депри B.5.31а) первого порядка
д + I-!L)w1=*H1-H1 D.2.5)
дп dQ _
найдем производящую функцию Ли w1. Так как (Н^ = 0, где
скобки ( ) означают усреднение по невозмущенной траектории,
выберем Я] = 0 и решим D.2.5) относительно w^.
sin F — 2ятп) .. п „.
2пт— I
т
Поскольку полу целые резонансы расположены по / между целыми
резонансами, т. е.
/ = B/7 -f-1) п, D.2.7)
где р — целое число, то функция w1 не является сингулярной.
Преобразованный гамильтониан Н теперь вычисляется из уравне
ния Депри второго порядка
-Н2)-[шъ Hi + Hj], D.2.8)
где Н2 и Н1 равны нулю. Выберем Н2 так, чтобы среднее от правой
260 Глава 4
части D.2.8) обратилось в нуль:
772 = — ([wlt #!]>. D.2.9)
Раскрывая скобки Пуассона
D.2.10)
Я2
2 \ dlx dQ
и подставляя разложения для w1 и Ни получаем
у sin (e_2ron,n)v =
2 \^J Bят—
«2~
— ^2 / \^ cos[2n(m'—m)n] —cos [2В — 2я(т'+ т) п] \ ,.„..,
т, т'
При усреднении по невозмущенной траектории 6 = In первая
сумма обращается в нуль, за исключением членов т = т'. Послед-
Последние дают постоянное слагаемое, которое можно опустить. Во вто-
второй сумме остаются члены, для которых
2/ —2я(т' + т) = 0 D.2.12)
или с учетом D.2.7)
т + т' = 2р+\. D.2.13)
Для D.2.11) это дает
cos[26 — 2лBр+')п] ,4 2 14>
Bпу(т-р-
Сумма по т не зависит от р:
1
(
1
т — р
2
= я2. D.2.15)
Поэтому во втором порядке имеем
Я2=—-/-^-Vcos26, D.2.16)
где
ё = 6 — пBр+1)п D.2.17)
— медленная фаза. Из D.2.16) амплитуда колебаний / равна
А/2макс= —К. D.2.18)
Значение К, соответствующее перекрытию целых и полуцелых
Переход к глобальной стохастичности 261
резонансов, находим с помощью подстановки D.1.29) и D.2.18)
в D.2.3):
2К1/*+—К=л, D.2.19)
что дает К ж 1,46 [70]. Соотношение D.2.19) все еще завышает
критическое значение К- Дальнейшее улучшение этой оценки воз-
возможно путем учета резонансов более высоких гармоник (k~>2),
а также конечной ширины их стохастических слоев. Чириков сде-
сделал и то и другое и нашел, что наиболее существенным является
учет ширины стохастического слоя.
Ширина стохастического слоя. Будем исходить из отображения
D.1.6), которое описывает движение вблизи сепаратрисы резонанса:
wn+1 = wn — wosin<fn, D.1.6a)
-^- . D.1.66)
Здесь w — относительное отклонение энергии от ее значения К,
на сепаратрисе
w= -^-, D.2.20)
а ф — фаза внешнего возмущения [ф = 2лпв D.1.26)] в тот момент,
когда фаза колебаний на резонансе проходит эллиптическую точку;
<2о — отношение частоты внешнего возмущения к частоте малых
фазовых колебаний:
Qo=_^_. D.2.21)
к1/2
Как было показано в п. 4.16, линеаризация уравнения D.1.66)
по w приводит к стандартному отображению с параметром стоха-
стохастичности D.1.9). Используя для w0 выражение C.5.27), получаем
параметр стохастичности /С2 для вторичных резонансов вблизи
сепаратрисы в виде
D.2.22)
Подставляя в это выражение D.2.21) и требуя, чтобы на границе
стохастичности как для первичных, так и для вторичных резонан-
резонансов /С2 = К, получаем полуширину стохастического слоя:
4 BлL / —я2 \ ,. „ „о,
щ= —у-^ехр — ). D.2.23)
/E" V К'2 )
Теперь нужно связать w1 с полушириной стохастического слоя
A/s по переменной действия при 6 = я. Для маятника с гамиль-
гамильтонианом
Я= — + К cosB D.2.24)
262 Глава 4
энергия на сепаратрисе Н = К, а действие в точке 8 = я, согласно
D.1.29), равно /0 = 2Кт. Из D.2.20) для энергии
К + ЬН = К{\+Щ) D.2.25)
и фазы 6 = п из D.2.24) найдем
/2 = 27С B -Ь шх), D.2.26)
и если до ^ 1, то
/»2tfV*/i + -^Л • D.2.27)
Следовательно,
А1,= 1-10 = щ-^-. D.2.28)
Таким образом, уточненный критерий перекрытия (см. рис. 4.5, в)
можно записать в виде
2/с'/2 л. Л- = я. D.2.29)
Этот критерий означает, что ширина целого резонанса плюс ширина
его стохастического слоя плюс ширина полуцелого резонанса равна
расстоянию между центрами двух целых резонансов. Для полу-
получения критического значения К, определяющего границу глобаль-
глобальной стохастичности, нужно решить уравнение D.2.29) с wt
из D.2.23). В результате находим К = 1,2. С помощью дополни-
дополнительных эвристических соображений 1) Чириков [70 ] получил
К ж 1,06. Подробное численное исследование стандартного ото-
отображения [70 ] дало в качестве верхней границы близкое значение
К ж 0,99. В § 4.4 будет показано, что более тонкий критерий сто-
стохастичности приводит к значению К ~ 0,9716.
Ускорение Ферми. Задача об ускорении Ферми*приводится к стан-
стандартному отображению с К = 2пМ1и\ [см. D.1.5)]. Для исход-
исходного нелинейного отображения численно было найдено, что гра-
граница стохастичности находится при иь = 2,8 V'М (см. рис. 3.15).
Подстановка иь = и1 дает К « 0,8. Отличие от значения К » 1,0
для стандартного отображения можно легко объяснить тем, что
для этих двух случаев определение границы разное. Из рис. 1.14
видно, что иь « 28 = 2,8 -у/М. Но полученное таким путем зна-
значение иь является верхней границей стохастического движения
г) Главное из них —поправка к интегралу Мельникова—Арнольда; она
является по существу чисто эмпирической, см. примечание редактора на
с. 257.— Прим. ред.
Переход к глобальной стохастичности 263
и соответствует первой инвариантной кривой. Однако более пра-
правильно связать параметр стандартного отображения К со значе-
значением их в центре целого резонанса. Из рис. 1.14 видно, что иг =
= 25 = 2,5 л/М. Соответствующие этому значения К = 1,0 и
а = 1/6 согласуются с результатами для стандартного отображе-
отображения. Уменьшение возмущения К, (и) при увеличении и для отобра-
отображения Улама приводит к асимметрии, вследствие которой инва-
инвариантные кривые ниже резонанса разрушаются, а выше сохра-
сохраняются. Можно ожидать, что чем сильнее зависимость К (и), тем
больше отклонения от стандартного отображения г).
§ 4.3. Вторичные резонансы
В этом параграфе мы рассмотрим вторичные резонансы вынужден-
вынужденных колебаний маятника с гамильтонианом D.1.26). Вследствие
нелинейности свободных колебаний маятника в движении присутст-
присутствуют гармоники основной медленной частоты соо. Эти гармоники
могут оказаться в резонансе с быстрым внешним возмущением ча-
частоты 2я, который называется поэтому вторичным резонансом. По-
Поскольку исследование в общем виде является довольно громоздким,
мы рассмотрим отдельно вторичные резонансы вблизи центра пер-
первичного резонанса и вблизи его сепаратрисы.
4.3а. Центр резонанса
Особенности вторичных резонансов вблизи центра первичного ре-
резонанса (т. е. его эллиптической точки) детально исследованы в
п. 2.46. Переходя к переменным действие—фаза(/, ср)для маятника
с гамильтонианом
#0 = (- coo cos 6
и используя методы, описанные в п. 2.2а, получаем в первом по-
порядке теории возмущений новый гамильтониан [ср. с B.4.43) ]
Яо(/) = со0/--1—/2 D.3.1)
и частоту колебаний
со = со0 l-J. D.3.2)
8
Рассмотрим несколько более общий вид гамильтониана D.1.26),
введя амплитуду V и фазу 60 возмущения:
cosQt. D.3.3)
*) Помимо этого, точное положение границы стохастичности зависит от
расположения крайнего целого резонанса относительно критического ис,
где К (ис) — 1. Подробное обсуждение этого вопроса см. в работе [70,
§ 6.2].— Прим. ред.
264 Глава 4
В переменных /, ср
7?! = V cos Г l-~- \ 4i sin ф + во] cos (Qt). D.3.4)
Разложим Нг в ряд Фурье:
>0
D.3.5)
где т — целое^число,
D.3.6)
а У/ — функция Бесселя первого рода. Для укороченного стандарт-
стандартного отображения D.1.26) V = 2/С, Q^ = 2яге, 0О = 0 и остаются
только четные гармоники по ср.
Среднее от Нг по t отлично от нуля лишь вблизи резонансных
значений / = /0, для которых
/co(/o) = Q, D.3.7)
где со (/) — частота колебаний маятника. Поэтому, как и в п. 2.46,
можно использовать резонансную теорию возмущений, переходя
к медленной фазе
$ = /Ф—Ш D.3.8)
и сопряженной переменной
7=^-. D.3.9)
Преобразуя гамильтониан и разлагая его около резонансного зна-
значения J = /0, получаем
ЛЯ = (-^) -&?- -f- A, sin ф. D.3.10)
Здесь
cos 60; / = 2т,
й, согласно D.3.1) и D.3.9),
=_-^. D.3.12)
Гамильтониан D.3.10) описывает вторичные резонансы и имеет
Переход к глобальной стохастичности 265
ту же форму, что и гамильтониан D.1.27), описывающий первичные
резонансы. Расстояние между вторичными резонансами по частоте
равно
бсо = со (Л) —со (Jl+1)= —-y-^^-i-co. D.3.13)
Если присутствуют только четные или только нечетные гармоники,
то бсо = 2(о/1. Из D.3.2) и D.3.9) имеем
8(о = —18J. D.3.14)
8
Это означает, что расстояние по переменной действия равно
б/= 8m2?U) , D.3.15)
где tns = 1, когда симметрия отсутствует, и ms — 2, если имеется
четная или нечетная симметрия. Аналогично можно получить мак-
максимальную полуширину сепаратрисы:
AJWc = (-у-) (8Л,I/* D.3.16)
и частоту малых фазовых колебаний:
*. D.3.17)
Уравнения D.3.14) — D.3.17) дают параметр перекрытия
2Л,/макс 4 Ш; /4 3 1 Я)
6У ms
для вторичных резонансов.
Этот параметр обычно очень мал, если только параметр пере-
перекрытия для первичных резонансов не становится большим. На-
Например, для гамильтониана D.1.26) с ms = 2, V = 2/С, со « соо =
= К1/2 параметр перекрытия равен
2ДУмакс ,,9.^- /..\л1/„ /^ з т\
67
Наибольшее значение аргумента функции Бесселя % = л дости-
достигается на сепаратрисе первичного резонанса. Для I > я функция
Бесселя экспоненциально мала, и вторичные резонансы несущест-
несущественны. По этой же причине можно пренебречь и третичными и т. д.
резонансами.
Теперь мы можем оценить, при каком числе вращения вторич-
вторичные резонансы столь же важны, как и первичные. Приравнивая
параметры перекрытия D.3.19) и D.1.31) для одного и того же
266 Глава 4
числа вращения (Qo = /) и учитывая, что максимальный размер
вторичного резонанса достигается вблизи сепаратрисы первичного
при "/ = л, получаем
/4/,(я)=16. D.3.20)
Это соотношение приближенно выполняется для / = 4 и / = 6
(нечетные гармоники отсутствуют). Поэтому можно ожидать, что
взаимодействие вторичных резонансов будет столь же существенно,
как и для первичных резонансов при таком значении параметра
стохастичности К, когда в центре первичного резонанса появятся
вторичные резонансы с / = 4 и / = 6. По индукции то же справед-
справедливо и для резонансов всех уровней. В итоге мы приходим к сле-
следующему весьма существенному выводу: при достижении критиче-
критического числа вращения а « 1/5 для первичных резонансов резо-
резонансы всех уровней характеризуются тем же самым числом враще-
вращения и одинаковым значением параметра перекрытия. Такой вывод
о резком разрушении последней инвариантной кривой между резо-
резонансами является, таким образом, весьма правдоподобным с физи-
физической точки зрения *). Соответствующий этому переходу параметр
возмущения получается из D.1.28) и равен К = 1,2.
Численные исследования структуры вторичных резонансов
стандартного отображения отсутствуют. Однако они проделаны
для большого числа гамильтонианов с двумя степенями свободы,
поверхность сечения Пуанкаре которых похожа на фазовую пло-
плоскость стандартного отображения. Примером является задача о
движении частицы в магнитном поле и поле косой волны [383, 385]
(см. п. 2.26). Соответствующий гамильтониан в системе отсчета
волны имеет вид [см. B.2.67) ]
k2P2 °°
Н=-^--Ръ<о + РчЦ+ееФо 2 /«[*,Р (*>„)] sin (ф-тер).
D.3.21)
Выбрав Рф таким, чтобы f m было порядка единицы, авторы этих
работ исследовали несколько близких к резонансу гармоник. Их
результат для т — — 1, 0,1 приведен на рис. 2.10, б. Ясно виден
вторичный резонанс пятой гармоники внутри первичного резонанса
(в данном случае возмущение имеет нечетные гармоники). Видно
также, что между резонансами нет инвариантных кривых, поскольку
случайно разбросанные точки представляют одну траекторию, ко-
которая свободно блуждает между первичными резонансами.
х) К сожалению, эта красивая картина одновременного перекрытия ре-
резонансов на всех уровнях несправедлива даже качественно, поскольку при
перекрытии системы резонансов их центры остаются еще долго неразрушен-
неразрушенными. Для стандартного отображения, например, граница стохастичности
соответствует К = Кь » 1. а разрушение центра целых резонансов проис-
происходит только при К = Ks = 4. Формально, это связано с тем, что уравне-
уравнение D.3.20) не имеет решения при % 5^ 2, а при % = л оно несправедливо.—
Прим. ред.
Переход к глобальной стохастичности
267
4.36. Сепаратриса
Чтобы исследовать структуру вторичных резонансов вблизи се-
сепаратрисы, нужно сначала найти выражение для переменной дейст-
действия. Это можно сделать либо по теории возмущений, отправляясь
от движения по невозмущенной сепаратрисе, либо вычислить дейст-
действие прямо из точного решения для маятника вблизи сепаратрисы
(см. п. 1.3а). Хотя оба метода требуют довольно сложных вычис-
вычислений, выражение для переменной действия было найдено многими
авторами, и мы приведем полученные результаты, не вдаваясь в де-
детали самих вычислений. Ниже мы будем следовать работе Смита
[383] и Смита и Перейры [387], где действие было получено не-
непосредственно из точного решения.
Гамильтониан маятника D.1.27) можно записать в переменных
J, ф согласно A.3.10) и A.3.11). Для колебаний маятника имеем
где & и Ж
рода, и
, D.3.22)
полные эллиптические интегралы первого и второго
2к»=1+!
D.3.23)
откуда х = 1 при Н = ©о = К, т. е. на сепаратрисе. Частота ко-
колебаний маятника, согласно A.3.13), имеет вид
1
со (к) =
Ж (у.)
асимптотическое значение при х ->- 1 равно
1
In
D.3.24)
D-3-25)
Параметр перекрытия вторичных резонансов D.3.18) можно
записать в виде
V» l
2ЛД
= 2
dJ
О)
D.3.26)
где все величины берутся для резонансного значения /
/со(/) = 2я, D.3.27)
и /— четное число. Поскольку
da tto dx.
dJ
dx dJ
,, о <29
268
Глава 4
то из D.3.22) и D.3.23) получим после некоторых преобразований
dj
16
D.3.29)
Величина Л/ определяется из разложения Фурье для третьего
члена в D.1.26) с заменой 2К -> V и 9-> 6 (J, q>) из A.3.11). После
довольно громоздких вычислений Смит и Перейра нашли ([387],
приложение А):
D,&
ч =
12
I = 2m,
D.3.30a)
где
= ехр
X (У.) j
D.3.306)
Подставляя D.3.29) ?; и
D.3.30) в D.3.26), можно
получить параметр пере-
перекрытия 2А/макс/б/ в за-
зависимости от энергии Н.
Вблизи сепаратрисы
х2^ 1 и
ql 2 = ехр / -
Рис. 4.6. Относительная доля г фазового
пространства, в которой выполняется про-
простой критерий перекрытия, в зависимо-
зависимости от числа вращения се = 0)п/2л (по
данным работы [145]).
где Qo = 2п/соо — отноше-
отношение частоты возмущения
к частоте малых колеба-
колебаний маятника. Используя
D.3.30а) с V = 2К=
и опуская малое слагаемое (— qI, получаем
Подставляя это выражение вместе с D.3.29) в D.3.26), имеем
1б
Q§exp/--
67 J я - * \ 2
Из D.2.20) и D.3.23) находим соотношение
= I — х2.
1—X2
D.3.31)
D.3.32)
Переход к глобальной стохастичности 269
Введем параметр стохастичности К2 Для вторичных резонансов
с помощью условия перекрытия D.2.1) для стандартного отобра-
отображения
Приравнивая правые части D.3.31) и D.3.33), находим
Къ= - ° ехр ( _^L± \ D.3.34)
w \ 2 /
что в точности совпадает (при w — w±) с результатом D.2.22), по-
полученным из сепаратрисного отображения.
Фукуяма и др. [145] исследовали простой критерий перекрытия
вторичных резонансов в задаче о взаимодействии частицы с вол-
волной, используя эллиптические интегралы с некоторыми упроще-
упрощениями. На рис. 4.6 представлены их результаты для зависимости
относительной доли г фазового пространства, где выполняется про-
простой критерий перекрытия [параметр перекрытия D.3.26) равен
единице], от числа вращения
* I2n ~ 2л
Видно, что быстрый рост стохастической компоненты происходит
примерно при а да 0,2, т. е. при появлении вторичных резонансов
пятой гармоники. Это согласуется с приведенными выше данными.
*§ 4.4. Резонансы высоких гармоник
* 4.4а. Основы метода Грина
Рассмотрим развитый Грином [164, 165] метод, который позволяет
найти точную границу перехода к глобальной стохастичности. Этот
метод постулирует соответствие между двумя следующими свойст-
свойствами системы (рис. 4.7): 1) разрушение инвариантной кривой с ирра-
иррациональным числом вращения а и 2) потеря'устойчивости периоди-
периодических точек, число вращения которых rls ->- а при s -> оо (г, s —
взаимно простые числа).
Средний вычет. Для линеаризованного отображения, заданного
матрицей А вблизи периодической точки (см. п. 3.36), вычет опре-
определяется как
R=— B — SpA). D.4.1)
4
Сравнение с C.3.54) показывает, что для 0 sg R sc 1
D.4.2)
270
Глава 4
где а — сдвиг фазы на одну итерацию отображения. Поэтому пе-
периодическая точка устойчива при условии
0<Я<1. D.4.3)
Матрица А вычисляется с помощью C.3.43) и C.3.44) и для перио-
. •' M ''
,;v-'
у - /. .
:"¦ ,*3PtT
-..
u
:-•¦¦:¦. ¦
Рис. 4.7. К методу Грина.
Периодические точки 1 с <zn — r,'s E = 12) приближают инвариантную кривую 2 с ирра-
иррациональным числом вращения а.
дической точки с а = rls стандартного отображения ее можно
записать в виде
К cos Qi
D.4.4)
Из полученного выражения в принципе можно найти вычет R.
Однако более удобным методом нахождения вычета является пред-
представление его в виде детерминанта, как показано Хеллеманом и
Переход к глобальной стохастичности
271
Баунтисом [183]:
0 ¦ • ¦ —
R =
2 + i^cose,
D.4.5)
Соответствующая матрица размерности s X s является тридиаго-
нальной с дополнительными элементами — 1 в двух углах. Если
К велико, то R ее Ks. Грин показал, что это верно также и для
малых К, и на этом основании принял такую же зависимость и
для всех К' Следовательно, вычет экспоненциально зависит от
периода s. Для больших s значение R стремится к нулю в устой-
устойчивом случае и неограниченно возрастает в неустойчивом. Естест-
Естественно поэтому исследовать поведение величины
1 s
D.4.6)
которую Грин назвал средним вычетом. Постоянная |3 ~ 1 выби-
выбирается из условия быстрой сходимости при численном итерирова-
итерировании, что дает возможность получать надежные результаты для
относительно малых s. Условие устойчивости имеет вид: /<Г 1.
Золотое сечение. Можно показать (см., например, [227]), что наи-
наилучшим способом аппроксимации иррационального числа рацио-
рациональными является разложение первого в непрерывную дробь.
Для иррационального а на отрезке @, 1) такое разложение можно
представить в виде
а. —
D.4.7)
аЛ
«2 "Г
и символически записать как а = [а1г а2, а3, . . . ], где ап — по-
положительные целые числа. Значение аг равно целой части 1/а
272 Глава 4
и т. д.1). Разложение в непрерывную дробь единственно, а подхо-
подходящие дроби rn s,, = \аъ . . . , ап] -^i а„ наилучшим образом
аппроксимируют а в том смысле, что не существует других дробей
r;s, которые были бы ближе к а для s ^ sn. Можно показать, что
знаки последовательных разностей (а—rnisn) противоположны, a
сходимость
|а--^-|< ' D.4.8)
I s.i | snsn — l
является квадратичной по s для больших s. В качестве примера
возьмем число а — п—3 = 0,14159 ..., т. е. дробную часть л.
Разложение его в непрерывную дробь имеет вид
л — 3=[7, 15, 293, . . . ]. D.4.9)
Большие значения ап ясно указывают на быструю сходимость под-
подходящих дробей.
Можно ожидать, что инвариантная кривая, которая разру-
разрушается последней с ростом возмущения, имеет число вращения а,
которое хуже всего приближается рациональными числами, т. е.
разложение которого в непрерывную дробь содержит минимальные
ап- Очевидно, что таким является число 2)
ag = [l, 1,1,. . . ]= -^° ~' , D.4.10)
особые свойства которого были давно известны и которое полу-
получило название золотого сечения. Поэтому для определения границы
стохастичности нужно исследовать устойчивость периодических
точек с agn -> ag. Численные исследования стандартного отобра-
отображения, действительно, показывают, что последняя инвариантная
кривая имеет a « ag, подтверждая тем самым интуитивное пред-
предположение Грина 3). Любое отображение, которое можно локально
аппроксимировать стандартным отображением, будет обладать
этим же свойством. Однако резонансная структура стандартного
отображения весьма специфична (она является однородной по им-
импульсу). В более общем случае это уже не так [117]. Мы обсудим
этот вопрос в § 4.5.
При численном исследовании устойчивости сходимость улуч-
улучшается, если начальное значение R уже близко к предельному
1) Подобно тому как разложение в десятичную дробь (a = Sgrefe ";
k = 10) можно представить в виде отображения pn+i = k$n, modi; gn =
== [&PnL разложению в непрерывную дробь соответствует отображение:
Рп+1 — 1/Ря. modi; a,i=![i/P,j]. Оба отображения, кстати говоря, приводят
к хаотическому движению для почти всех а (см., например, [486], гл. 7 и
ниже).— Прим. ред.
2) Это «очевидное» заключение обманчиво. Например, если не ограничи-
ограничиваться положительными ап, то <Xg—1 = [—3, 3, —3, . . .].— Прим. ред.
3) В действительности ситуация как раз обратная: исходя из этого пред-
предположения, Грин исследовал устойчивость периодических точек только
для а = ag (см. п. 4.46 ниже).— Прим.* ред.
Переход к глобальной стохастичносги 273
при s-> оо. Грин численно показал, что в случае золотого сечения
для критического значения К = Кс вычет стремится к пределу
R(ag, Kc)=-~- D.4.11)
Поэтому при р = 1/4 в D.4.6) / становится ближе к единице, и
можно ожидать более быстрой сходимости. Это, действительно,
подтверждается численными данными.
Метод Грина позволяет также найти условия разрушения ин-
инвариантных кривых на фазовой плоскости. Наиболее устойчивой
будет инвариантная кривая с числом вращения вида
а = [аъ . . . , а„, 1, 1, . . . 1, D.4.12)
где аь . . . , а„ характеризуют определенную область фазовой
плоскости. Численные результаты показывают, что и в этом случае
вычет имеет тот же предел D.4.11), а значение р = 1/4 обеспечи-
обеспечивает быструю сходимость.
Помимо разложения в непрерывную дробь, можно использо-
использовать и другие аппроксимации а и соответствующие им системы
периодических точек. Например, Лансфорд и Форд [286 ] исполь-
использовали представление а = k± \ln, где k, n — целые числа,
причем п пробегает значения в интервале !<;«¦ =ё п0. Этот метод
оказался удобным, хотя и не очень точным. Еще один метод, осно-
основанный на фрактальных диаграммах, был предложен Шмидтом
и Билеком [364 ]. Мы сравним его с методом Грина в п. 4.46.
Другие результаты. В работе Грина [165] получены и другие
интересные результаты. Рассмотрим кратко некоторые из них.
Прежде всего из D.4.2) следует, что значение R = 1/4 соответст-
соответствует о = л/3. Это означает, что разрушение инвариантных кри-
кривых в какой-либо области фазового пространства соответствует
возникновению вторичных резонансов шестой гармоники вокруг
периодических эллиптических точек с большими s->oo. Но то
же самое происходит в стандартном отображении и для неподвиж-
неподвижной точки (s = 1), т. е. в противоположном пределе по s. Факти-
Фактически численные результаты Грина показывают, что все периоди-
периодические траектории с а = agn обладают этим свойством.
Другой результат Грина имеет большое практическое значе-
значение для проведения численных исследований. Он показал (подроб-
(подробнее см. § 5.5), что при численном счете траектории, лежащей на
инвариантной кривой, ошибки счета значительно больше вдоль
кривой, чем поперек 1). Поэтому численное определение самой ин-
инвариантной кривой можно производить на очень большом числе
итераций без существенного ее искажения.
Наконец, укажем, что метод Грина можно использовать для
проверки интегрируемости системы. Если R = О во всем фазовом
1 По этому поводу см. также работу [57].— Прим. ред.
274 Глава 4
пространстве, то собственные значения линеаризованного отобра-
отображения равны Х1 = Х2 = 1, а матрица отображения имеет вид
C.3.71). Это означает отсутствие резонансной структуры движения
и поэтому такая система является, по-видимому, полностью ин-
интегрируемой.
* 4.46. Численные эксперименты
Численный алгоритм. Схематически методика вычислений Грина
[164—166] сводится к следующему.
1. Приводим задачу к исследованию отображения, такого, на-
например, как стандартное отображение, или отображение
Улама. В общем случае для системы с двумя степенями сво-
свободы это может представлять некоторые трудности. По за-
заданному гамильтониану отображение можно получить ме-
методами теории возмущений (см. п. 3.16) или же с помощью
интегрирования уравнений движения на периоде отображе-
отображения. В некоторых случаях удобно использовать внутреннюю
симметрию системы, как это было сделано Грином [166]
в задаче Хенона—Хейлеса.
2. Находим точное положение эллиптических неподвижных
точек (k = 1) по возможности аналитически.
3. Численно находим зависимость а от расстояния до непод-
неподвижной точки вдоль линии симметрии. Для иррациональных
а это делается путем усреднения за большое число итераций
отображения, а для рациональных чисел а = rls — за s
итераций.
4. Выбираем последовательность подходящих дробей ап =
= rnlsn, сходящуюся к некоторому иррациональному числу а,
которое соответствует исследуемой инвариантной кривой.
Если мы интересуемся переходом к глобальной стохастич-
ности, то в некоторых системах, как, например, стандартное
отображение, в качестве а выбираем золотое сечение (а = ag).
5. Находим линеаризованное отображение А вблизи периоди-
периодических точек с ап = rjsn:
Xsn Xn =:z A • \Х Xn)i
где xs —значение х после sn итераций отображения, а
хп ¦— положение исследуемой периодической точки. Мат-
Матрица А находится обычно численно с помощью соотношений,
приведенных в п. 3.36.
Численные результаты. На рис. 4.4 показаны численные резуль-
результаты Грина для четырех траекторий стандартного отображения
с К = 0,97. Это значение К, по всей видимости, лишь немногим
ниже критического значения, разрушающего последнюю инва-
инвариантную кривую. Вследствие симметрии фактически существуют
Переход к глобальной стохастичности
275
две такие инвариантные кривые, которые расположены по обе сто-
стороны от полуцелого резонанса. Видно также, что траектория вблизи
сепаратрисы целого резонанса медленно диффундирует. Вследствие
конечного числа итераций неясно, существуют ли и другие инва-
инвариантные кривые, ограничивающие эту диффузию. Однако при
К = 0,9716 наблюдается совершенно иная картина для инвариант-
инвариантной кривой с а = ag, a при К, = 0,975 эта кривая уже, несомненно,
разрушена, поскольку траектории диффундируют в этом месте
фазовой плоскости, хотя и очень медленно.
Грин вычислил значения / для подходящих дробей золотого
сечения при К = 0,9716 и К = 0,9. Для сравнения эти резуль-
результаты сведены в табл. 4.1, из которой ясно виден переход от значе-
значений /< 1 при К = 0,9 к асимптотическому значению / л; 1 при
К = 0,9716. Обратим также внимание на резкое изменение асимп-
асимптотического значения R (для больших s) от ничтожно малого в устой-
устойчивом случае до R = 0,25 на границе стохастичности.
Таблица 4.1. Вычеты / и R в зависимости от r/s
к
rn'sn
2/3
3/5
5/8
34/55
55/89
89/144
144/233
=0,9
С
1
0,93896
0,919959
0,92775
0,92427
0,92409
0,92406
0,92401а)
К=0,9716
rnsn
1/1
1/2
2/3
3/5
377/610
610/987
987/1597
0,971635
0,971635
1,014042
0,993528
0,99999965
1,00000009
0,9999970
R
0,24291
0,23602
0,26068
0,24201
0,24995
0,25002
0,24988
а) Я=2,5-10-9.
Наглядную картину разрушения инвариантной кривой са = а{
можно получить, откладывая периодические точки для последова-
последовательных пар подходящих дробей. На рис. 4.8 сравниваются два слу-
случая: К = 0,95, для которого / (ag) » 0,977, и К = 0,9716, для
которого / (ag) « 1,000. Поскольку каждая последующая подхо-
подходящая дробь соответствует увеличению числа периодических то-
точек приблизительно в I/a раз, а на каждом из рис. 4.8 используется
пара подходящих дробей, ограничивающих значение а сверху и
снизу, горизонтальный масштаб последовательно растягивается
в (I/aJ раз для сохранения числа точек в выбранной области. Для
облегчения визуального анализа структуры периодических точек,
которые ограничивают инвариантную кривую с a = ag, вертикаль-
вертикальный масштаб на рис. 4.8 также растягивается в (I/aL раз. Из ри-
рисунка видно, что при К = 0,95 последовательные приближения
периодических точек равномерно сходятся к инвариантной кри-
276
Глава 4
вой. Напротив, при К = 0,9716 периодические точки обнаружи-
обнаруживают все новую и новую структуру на каждом последующем мас-
масштабе. Разумно заключить, что в этом случае инвариантная кривая
не существует *).
В заключение обсуждения метода Грина мы приводим на рис. 4.9
схематическую зависимость числа вращения а вблизи периодиче-
периодических точек от их периода s. Для а>1/2 периодические точки не-
5/
•
-
_ X
_
_
-
-
-
_
-
-
-
X
•
i 1
•
X
1
X
X
1
1
1
X
X
•
j 1
x/
/•
•
/
X
/
/
-
-•
-
-
X
X
* /x
tl u Растяжение х
9 X ^
1 1 1 1 1 1 1
se
X
v X •
• x • •
x«x x
<
M 1 | 1 M 1
X
1
1
-
1
-
~x
- X
-
-
1
1
1
1
x v
<
1
1
i «
X
•
X
X
X •
I 1 1
D
• xex
i i
X
•
1
x x
)
1
X
1
1
•
SB
1
-X
в
-
1
>
X
1
-
-
-
1
3
e
X
X
9
X
•
1 1 l
3
X
X
X
• •
X
1 1 1
e
x •
©
X
• •
A
i i
X
У
\
«9
|
•
l
X
«
X
1
X
1
X
j
X
о
1
1
б
Рис. 4.8. Периодические точки, соответствующие последовательным парам
подходящих дробей золотого сечения (по данным работы [165]).
а) К — 0,95; б) К = 0,9716.
устойчивы. При К С 1 а существенно меньше 1/6 даже для s = 1
(когда а = а) и экспоненциально убывает с увеличением s.
Последнее сохраняется для любого К <С 0,9716. Если же К =
= 0,9716, то, как следует из табл. 4.1, сГ= 1/6 (R = 0,25) для всех
достаточно больших s. В этом случае все периодические точки устой-
устойчивы, а отношение размера соответствующих им резонансов к рас-
расстоянию между последовательными резонансами (sn и sn+1) одина-
одинаково для всех п->оо. При /<Г>0,9716 величина а растет и при
достаточно большом s периодические точки оказываются неустой-
а) Конечно, это не более чем наглядные соображения. В этом отношении
данные табл. 4.1 более убедительны (см. также рис. 4.9).— Прим. ред.
Переход к глобальной стохастичност
277
чивыми. Таким образом, горизонтальная прямая а = 1.6 на рис. 4.9
соответствует как раз критическому значению К- Этот результат
подтверждается исследованиями Эсканде и Довейла [117, 118],
которые описаны в § 4.5.
Неустойчивость
К = 0,9716
Рис. 4.9. Схематическая зависимость числа вращения а вблизи периодиче-
периодических точек от их периода s.
Другой подход к исследованию системы резонансов высоких
гармоник связан с упорядочением соответствующих им периоди-
периодических точек на границе устойчивости с помощью фрактальных
диаграмм [364 ]. Основная идея состоит в разбиении всех периоди-
периодических точек на последовательные поколения по значению числа
вращения а. Первые два поколения соответствуют 1)
1
D.4.13)
п ±
т
х) Последовательные поколения дают разложение произвольного а =
= [п, т, . . .] в непрерывную дробь, для которой а; есть подходя-
подходящие дроби.— Прим. ред.
278
Глава 4
где п, т — любые целые (положительные и отрицательные) числа,
кроме нуля. С увеличением т периодические точки второго поко-
поколения приближаются к сепаратрисе одного из резонансов первого
поколения. Если же m = 1, то мы попадаем, очевидно, в первое
поколение. На рис. 4.10 показана зависимость критического зна-
значения параметра К {щ) (граница устойчивости) стандартного ото-
1,5
1,0
0,9
0,5
0°
л
о
о
о
АЛ
о
А
Ал
V
о
\ t
Л /
/
/л
\
л\
1 \ \
\
0,1
0,2
0,3
0,4
0,5
Рис. 4.10. Критические значения К для устойчивости трех поколений перио-
периодических точек стандартного отображения (по данным работы [364]).
Видна фрактальная структура функции К(а).
бражения для трех первых поколений периодических точек. За
исключением п = 1 (целый резонанс), значения /С(ах) для первого
поколения (кружки на рисунке) ложатся на гладкую кривую,
симметричную относительно аг = 1/2. Зависимости К (а) для вто-
второго и третьего поколений имеют аналогичную форму, но на бо-
более мелких масштабах по а. Подобная масштабная инвариант-
инвариантность характерна для фракталов (см. п. 7.1в).
Шмидт и Билек предположили, что максимальные значения
К (щ) в разных поколениях связаны соотношением
Ki - Ki
D.4.14)
Переход к глобальной стохастичности 279
где А; для больших / не зависит от /. Тогда из фрактальной диа-
диаграммы можно найти условия разрушения инвариантных кривых
между любыми резонансами по относительно небольшому числу
максимумов К {щ) первых поколений. Соотношение D.4.14) пред-
представляется правдоподобным по аналогии с последовательностью
бифуркаций как в диссипативных, так и в гамильтоновых системах
(см. п. 7.26 и дополнение Б). Шмидт и Билек сравнили предсказа-
предсказания существования нескольких инвариантных кривых на основе
фрактальной диаграммы на рис. 4.10 с прямым численным модели-
моделированием и получили хорошее согласие.
В заключение вкратце обсудим применение описанного метода
в других задачах. В простейшем виде этот метод был использован
еще Лансфордом и Фордом [286] в задаче Хенона и Хейлеса (см.
п. 1.4а). Они исследовали отображение на поверхности сечения
для полной энергии Е = 1/12 и Е = 1/8 (см. рис. 1.13, б и в), ис-
используя линию симметрии ру = 0, проходящую через основной
резонанс. Критерием устойчивости служило условие /<; 1, где сред-
средний вычет определяется как f = \ R \2/Q. Система резонансов вы-
высоких гармоник и их периодических точек задавалась соотноше-
соотношением
m±\ln sn
где целое m — фиксированное число, а п пробегает все целые по-
положительные значения больше 1. Поскольку такой выбор ап не
дает сходимости к какому-либо иррациональному значению а, ве-
величина / изменялась в широких пределах, принимая максимальные
значения вблизи целых резонансов, где 1/а„ — целое число. При
исследовании области вблизи резонанса пятой гармоники (а„ =
= 1/5) оказалось, что для Е = 1/12 величина / падает ниже 1.
В противоположность этому для Е = 1/8 величина / остается
больше 1, что означает разрушение инвариантных кривых в этой
области. Позднее Грин [166] установил, что разрушение инвари-
инвариантных кривых вблизи этого резонанса происходит при Е =
= 0,118<с 1/8. Мы видим, что даже такие трудные для аналитического
исследования задачи, как задача Хенона—Хейлеса, все же под-
поддаются решению описанным выше методом.
§ 4.5. Метод ренормализации для двух резонансов
Перейдем теперь к описанию метода [117, 118], позволяющего
исследовать разрушение инвариантных кривых между двумя про-
произвольными резонансами. Этот метод основан на изучении струк-
структуры фазовой плоскости вблизи инвариантной кривой на все более
мелком масштабе. При правильном выборе исследуемой инвариант-
инвариантной кривой можно определить таким путем переход к сильной
(или «глобальной») стохастичности.
280 Глава 4
Основой метода является последовательная ренормализация
исходного гамильтониана таким образом, что каждый новый га-
гамильтониан сохраняет свою форму, но при этом описывает резо-
нансы все более и более высокого порядка. На каждом этапе ре-
нормализации принимаются во внимание только два наиболее
важных резонанса, лежащие по обе стороны от исследуемой инва-
инвариантной кривой. Если параметр перекрытия этих резонансов стре-
стремится к нулю в процессе ренормализации, то инвариантная кривая
существует.
Следуя Эсканде и Довейлу, рассмотрим гамильтониан для ча-
частицы, взаимодействующей с двумя волнами:
— Vx cos (kxx—co^) — y2cos(fe2x —co20, D.5.1)
w
.и введем новые переменные
/= Pvm_vVl . D.5.2)
Q = k1(v2-v1),
где vl = ai1k1 и v2 = tt>2/^2 — фазовые скорости волн. В новых
переменных гамильтониан D.5.1) примет вид
/7!= /И cosij)—Pco?,k(§i — ilt), D.5.3)
2
где
к = —^- D.5.4)
равно отношению волновых векторов,
М= ^ D.5.5)
т (t'2 — fiJ
характеризует «основной» резонанс, а
Р = — D.5.6)
— возмущение. Гамильтониан D.5.3) описывает движение маят-
маятника, возмущенного волной с частотой Q. Именно такая форма
гамильтониана и будет сохраняться при ренормализации. Для не-
невозмущенной системы (Р = 0) с гамильтонианом Яо (J) перемен-
переменные действия / и фазы 8 определяются формулами A.3.10) и A.3.11),
а частота вращения со (J) — соотношением A.3.13). В предельном
случае равномерного вращения (М = 0)
со (/) = / = /.
Переход к глобальной стохастичности 281
Исследуем теперь условия существования инвариантной кри-
кривой с обратным числом вращения
— =<2 (•/)= —f- D.5.7)
а со (J)
в присутствии возмущения. При этом гамильтониан принимает вид
H = H0(J) — P cosk\i-(J, Q)-9J]. D.5.8)
В случае вращения
а|> = 9 + 5С(У,9),
где у, — периодично по 8 с периодом 2л и выражается через эллип-
эллиптические функции. Это позволяет разложить Н в ряд Фурье
оо
H = H0(J) — P 2 Un(J)cos[(k~n)e-kQt}. D.5.9)
я= — оо
Вторичные резонансы между гармониками частоты вращения со (Jп)
и основной частотой возмущения kQ, удовлетворяют условию
{k + n)(u(Jn)~ Ш = 0, D.5.10)
причем для них
Qn=-^T=k+n. D.5.11)
(О (J)
На рис. 4.11 приведен пример таких резонансов (k = 2) как в ис-
исходных переменных /, -ф, так и в переменных J, 9. Центр основного
М-резонанса расположен при Jm = 0, а режим вращения фазы гр
начинается выше его сепаратрисы для J>Jb =-- 4 у'М/л. Возму-
Возмущающий Р-резонанс (л = 0) расположен около Jр » / (точнее,
со (Ур) = Q). На рисунке также приведено несколько вторичных
резонансов с п > 1 [см. D.5.10)], гармоника которых по 8 равна,
Qn = k + n [см. D.5.9)].
Рассмотрим инвариантную кривую вблизи J — Уо, расположен-
расположенную между резонансами М и Р, с
^- D.5.12).
со (Jo)
Пусть"
Q>Jfe+l, D.5.13).
так что кривая лежит между вторичными резонансами п и п -- 1
(см. рис. 4.11), где п>-1 — целая часть
z = Q—k = n-\-bk, D.5.14)
a S? = (z}f — дробная часть 2. В дальнейшем нам будет удобнее
задавать п и б/г, а не Q.
') Если же Q < k + 1, то, переобозначив резонансы в D.5.1), получим
1,20 w
a-.;&-"v ^.w,..'^ *-'.v^:;:.-
-3,00 ~2,00 -1,00 0,0 1,00 2,00
t
a
1,Z0rr~
1,00
0,80 >'¦
J
0,60
i ? •"
0,20
¦•¦¦»•••¦
c. *¦
P
(n 0)
-3,00 2,00 -1,00 0,0 1,00 2,00
9
6
n--- !
С
n 2
n 3
n 4
i Вращрние
Колебания
M
Рис. 4.11. Поверхность сечения системы D.5.3) с двумя резонансами (М; Р) и параметрами X/Y = 1, S =- 0,4, А; =
= 2, Q = 1 (поданным работы [117]).
а — в исходных переменных /, -ф; б в переменных J, в; С — инвариантная кривая. Горизонтальная стрелка справа указывает
значение J .
Переход к глобальной стохастичности 283
Для получения ренормализованного гамильтониана, соответст-
соответствующего значению Q, пренебрежем в D.5.9) всеми вторичными ре-
зонансами, кроме п и п + 1. Так как рассматриваемая система не
вырождена, то изменение переменной действия мало (см. п. 2.4а),
и можно разложить Но по А/ = /—Jo до квадратичных членов
включительно:
Я» H0(J0) + ю (Уо) AJ- -LG(J0){Uy —
-РУп{Jo)cos[(k + n)Q—kQt] — PUn+1 (/„)cos\{k-a-]- \)Q—kQt],
D.5.15)
где G—обычный параметр нелинейности:
D516)
_
Выберем в качестве основного резонанса М наиболее близкий к Q
вторичный резонанс и обозначим оставшийся резонанс через Р.
Произведем каноническое преобразование к таким новым перемен*
ным /, я[), чтобы ренормализованный гамильтониан
Л=— Mcosi|j — Pcos?(\j; — Q-t) D.5.17)
принял вид исходного D.5.3). При этом
D.5.18)
(k + n + l-X)
(l_Ji_6ft)
z = n + bk =
k =
(8k —I)
. -•:- l — I)
(/г -'- п + Я)
D.5
D.5
D.5
D.5
.20a)
.206)
.20b)
.20r)
где снова п и бй—целая и дробная части
?=<?-?, D.5.21)
к(Щ — единичная ступенчатая функция:
к (Щ =
0, 8k-
^ 2
D.5.22)
284 Глава
Уравнения D.5.20) определяют ренормализационную группу 0~:
?T:(Sfe, n, /г, M, P)^(bk, л, ~k, М, Р),
т. е. отображение в пространстве параметров, которое допускает
последовательные итерации. Аналитическое исследование этого
пятимерного (негамильтонова) отображения связано с большими
трудностями. Эсканде и Довейл замечают, что bk и л зависят только
от bk, и исследуют неподвижные точки одномерного отображения
D.5.23)
bk / | ,
1 F* — X) Jf
которое получается из D.5.20а). Для неподвижных точек 8kn имеем
D.5.24а)
л) = [1, л, 1, п, . . .], D.5.246)
где скобки [ ] означают разложение в непрерывную дробь. В этих
неподвижных точках с
Q-<# = * + n-rton D.5.25)
отображение ?Г переходит в трехмерное отображение
Jl\:{k, X, У)-»(*. X, У),
где X = 2jV'М/й и F =[2 л/P/Q, имеют смысл относительной
полуширины резонансов. Отображение Ж%п имеет две притягиваю-
притягивающие точки: (/$, 0, 0) и (^, оо,оо) [117], где \tn — устойчивая не-
неподвижная точка одномерного отображения D.5.206). Подставляя
k = k = k\ в D.5.206) и используя D.5.24), получаем для устой-
устойчивого (положительного) корня:
kn = 8kn+l—l. D.5.26)
Если итерации отображения Жкп для начальных (k, X, Y) и выбран-
выбранного п (и соответствующего ему 1) сходятся к первой притягиваю-
притягивающей точке, то значения X и Y в процессе ренормализации стремятся
к нулю и инвариантная кривая должна существовать. Если же
итерации сходятся ко второй притягивающей точке, то инвариант-
инвариантная кривая, по-видимому, разрушена. На рис. 4.12 кривые Y (X)
показывают границу между двумя областями притяжения при фик-
Переход к глобальной стохастичностн
28 5
сированном k. При заданном отношении XIY эти кривые дают
максимальное (в зависимости от п и %, а следовательно, и от Q%)
значение параметра перекрытия резонансов S = X + Y, для ко-
которого между резонансами М и Р еще существует инвариантная
кривая. Цифры в скобках указывают значения п, для которых
1,00
0,80
0,60
0,40
0,20
0,0
0,20 0,40 0,60 0,80 1,00
X
Рис. 4.12. Зависимость Y от X для К = 1 и k — 1, 2, 3, 4 (по данным работы
[117]).
Числа в круглых скобках дают значения я.
достигается максимум S. Слева от крестов на каждой из кривых
величина Qn определяется согласно D.5.25), а справа резонансы
М и Р меняются местами, поэтому вместо D.5.25) имеем
Кривые Y (X) непрерывно зависят от k, например, кривая с k =
= 3/2 расположена примерно посередине между кривыми с k = 1
и k = 2. Можно показать, что (k, X, Y) и (Ilk, Y, X) определяют
одну и ту же систему. Поэтому рис. 4.12 представляет также слу-
286 Глава 4
чаи с k = 1/2; 1/3; 1/4. Для сравнения пунктирная прямая пока-
показывает правило двух третей 1): S = 2/3.
Эсканде и Довейл сравнили свои теоретические предсказания
для границы стохастичности с результатами численного моделиро-
моделирования системы D.5.3). Для X/Y в интервале 1—5 и k в интервале
1 ч-4 предсказанные критические значения 5 оказались на 3-f-10 %
ниже численных 2). Было проведено также сравнение с результа-
результатами Грина для стандартного отображения, гамильтониан кото-
которого можно записать в виде (k = 1; Q = 1):
Н=~_-^- У cos(i|>—/я*). D.5.27)
2 16 т=^оо
Критическое значение Грина К = 0,9716 соответствует S —
//л, = 0,6275. Если оставить только два резонанса, так что
^cos\|? — cos(\|p — 0, D.5.28)
16
cos\|?
16 Т 16
то из данных на рис. 4.12 (для X = Y и k = 1) получаем 5 = 0,70
или К = 1,21 при
2 ' Q 2 й
Это — одна из двух инвариантных кривых «золотого сечения»,-
найденных Грином. Как и ожидалось, критическое значение S
(или К) для двух резонансов больше, чем для отображения, кото-
которое имеет бесконечное число резонансов. Численное моделирова-
моделирование системы D.5.28) дает 5 = 0,74. Это не противоречит получен-
полученному на рис. 4.12 значению S — 0,70, если учесть, что точность
численного моделирования непрерывной системы значительно хуже,
чем для отображения.
Хотя описанный метод ренормализации и дает достаточно точ-
точное значение границы стохастичности, он является приближенным.
Основная погрешность связана с тем, что на каждом шаге ренорма-
ренормализации учитываются только два из бесконечного числа вторичных
резонансов. Это ясно видно из сравнения системы D.5.27) с беско-
бесконечным числом резонансов и D.5.28) с двумя резонансами. В этом
крайнем случае влияние дополнительных резонансов приводит
к заметному снижению критического значения с 5 = 0,74 до S =
= 0,63. Другие источники ошибок, такие, как разложение только
до квадратичных членов в D.5.15) или учет только некоторых зна-
значений Qn, менее существенны.
1) Существенно новый эффект, обнаруженный с помощью ренормализа-
ренормализации, состоит в значительном повышении критического параметра перекрытия
S при X > Y или X <^ Y. Это связано с «отталкиванием» слабого резонанса
сильным (подробнее см. в [117, 464]).— Прим. ред .
2) См. примечание редактора на с. 248.— Прим. ред.
Переход к глобальной стохастичности 287
Обобщение метода на автономные системы с двумя степенями
свободы и амплитудами М и Р, зависящими от импульсов, а также
на области внутри резонансов, является относительно несложным
[118]. Последнее обобщение позволит по-новому исследовать би-
бифуркации периодических траекторий.
§ 4.6. Вариационные методы
Опишем теперь вкратце предложенный Персивалем [328, 330, 331 ]
метод нахождения инвариантного тора, когда он существует. Ме-
Метод основан на некотором вариационном принципе, похожем на
примененный в п. 2.66 в случае периодических траекторий. Здесь
также удобно использовать уравнения Лагранжа [330, 331, 228].
Следуя Персивалю [331 ], рассмотрим лагранжиан L (q, q) ав-
автономной системы с N степенями свободы. Зададим инвариант-
инвариантный тор с помощью вектора частот о>, а траекторию на нем — с по-
помощью координат #ы (в), где в — угловые переменные на торе.
Тогда вариационный принцип можно сформулировать в виде
причем со при варьировании остается фиксированным. Здесь
ы-dq^/dQ = q, а символ ( ) означает усреднение по всем угло-
угловым переменным. Следует обратить внимание на близкое соответст-
соответствие между выражениями D.6.1) для инвариантного тора и B.6.25)
для периодической траектории. Выполняя варьирование, получаем
уравнения Лагранжа:
д / dL \ 3L п ,. п п.
(H D-6-2)
dq
Если q^ F) является решением D.6.2), то \qm (mt + 60) опреде-
определяет на торе траекторию с начальной координатой q^ (в0) и ско-
скоростью &-dq&!d%0.
При численном решении задачи разлагаем q(a в многомерный
ряд Фурье по угловым переменным
)) D.6.3)
и оставляем некоторое конечное число членов. Подставляя D.6.3)
в D.6.1) и проводя варьирование по коэффициентам Фурье, полу-
получаем систему алгебраических уравнений для Qm, которую можно
решить итерированием. Метод решения аналогичен описанному
в п. 2.66, и мы не будем его здесь повторять.
Этот метод применялся Персивалем и его учениками к некото-
некоторым нелинейным задачам молекулярной динамики, в частности
288 Глава 4
для вычисления квазиклассических колебательных уровней энер-
энергии многоатомных молекул [332, 333, 3291. Персиваль [331 ] также
использовал этот метод при нахождении перехода к глобальной
стохастичности для стандартного отображения. Он получил, что
инвариантная кривая с а = ag разрушается при К = 0,9716. При
этом критерием разрушения служила расходимость итераций для
коэффициентов Фурье. Хотя полученное им значение К находится
в прекрасном согласии с результатом Грина, Персиваль отмечает,
что расходимость итераций может объясняться и появлением ре-
резонансных знаменателей. Подробности этих исследований можно
найти в цитированных выше работах.
*§ 4.7. Заключение
В табл. 4.2 сравниваются различные критерии перехода от локаль-
локальной к глобальной стохастичности для стандартного отображения.
Критерии расположены в порядке возрастания их эффективности.
Поскольку не существует полной аналитической теории перехода
к стохастичности, то чем эффективнее критерий, тем более сущест-
существен в нем элемент численного анализа, необходимого для получе-
получения критического значения К- Поэтому все критерии представлены
также через более физическую характеристику — число вращения
а0 = 1/Qo Для целого резонанса 1), которое легко определяется
как численно, так и аналитически. Тот факт, что переход к глобаль-
глобальной стохастичности почти точно совпадает с а0 = 1/6, может по-
помочь более глубокому пониманию этого явления. Для стандарт-
стандартного отображения критерий а0 = 1/6 приводит с помощью D.1.31)
к критическому значению параметра перекрытия
2А/маКс ^ _2_ (А 7 П
Т[ —• D./Л)
Если перекрываются резонансы несколько разной ширины, как,
например, для отображения Улама, то «правило двух третей» D.7.1)
можно обобщить следующим образом:
(A/Mai<c)i -т~ (А/МаксJ ^ 2 .. - _.
u/i,2 3
Для отображения Улама численно найденная граница стохастич-
стохастичности на рис. 3.15 согласуется с условием D.7.2). Если же соседние
резонансы значительно отличаются по ширине, то оценки, полу-
полученные для стандартного отображения, неприменимы. В случае
J) Это утверждение спорно, поскольку а0 характеризует центр резонанса,
тогда как граница стохастичности определяется окрестностью сепаратрисы.
Приближенное совпадение критического К с Qo = 6 остается необъясненным
и справедливо, возможно, только для стандартного отображения. Во всяком
случае, при перекрытии двух резонансов (§ 4.5) Qo — 2k/X и изменяется
в широких пределах (см. рис. 4.12).— Прим. ред.
Переход к глобальной стохастичности
289
Таблица 4.2. Граница стохастичности для стандартного отображения
Критерий
1. Линейная устойчивость целых резонансов
2. Перекрытие целых резонансов
3. Уточненный критерий перекрытия
4. Перекрытие вторичных резонансов
5. Ренормализация для двух резонансов г) (a=ag)
6. Численные данные для стандартного отображе-
отображения и отображения Улама
7. Вариационный метод (a=ag)
8. Линейная устойчивость периодических точек с
4
(я/2J
1,2в)
1,2
1,2
1,0
0,9716
0,9716
2
3-4
5—6
5—6
5-6
6
6
6
б) Qo—номер гармоники вторичного резонанса;
cos Bn/QQ)=l—К12.
в) 1,06 с эвристическими поправками [70].
г) а—число вращения «последней» (самой устойчивой) инвариантной кривой между
целыми резонансами; a.g=(Yo—1)/2 — «золотое сечение».
двух резонансов достаточно эффективную оценку можно получить
графически из рис. 4.12. Из данных на рисунке можно найти также
число вращения а ^ (k + п) (вообще говоря, а Ф ag), а значит,
и значение J для последней инвариантной кривой.
Результаты, полученные для отображения Улама с двумя гар-
гармониками возмущения произвольной амплитуды [202] (см. 6.5.1),
показывают, что даже в случае значительной разницы амплитуд
правило двух третей «работает» удивительно хорошо. Критерий
двух резонансов (рис. 4.12) в этом случае также дает вполне хоро-
хорошие результаты. Однако, поскольку в системе имеется много раз-
различных резонансов, нужно очень аккуратно выбирать в интересую-
интересующей нас области фазового пространства два наиболее существенных
из них.
Глава 5
СТОХАСТИЧЕСКОЕ ДВИЖЕНИЕ
И ДИФФУЗИЯ
§ 5.1. Введение
В области глобальной стохастичности, где не существует ограни-
ограничивающих движение инвариантных поверхностей, полное описание
динамики системы, как правило, невозможно. В этом случае, од-
однако, можно использовать статистическое описание и исследовать
эволюцию средних величин, а не отдельных траекторий [62, 424].
Такой подход лежит в основе статистической механики (см., на-
например, [327]).
Методы статистического описания, обсуждаемые в этой главе,
существенно опираются на ряд математических результатов, рас-
рассмотрение которых выходит за рамки этой монографии. Однако
определенное представление об этих результатах все же необхо-
необходимо. Математическая сторона дела изложена в книге Арнольда
и Авеза [14] х). Мы же обсудим эти вопросы в более доступной
форме (§ 5.2). Там же кратко затронуты вопросы «случайности в де-
детерминированных системах» и влияния ошибок округления на ре-
результаты численного моделирования хаотического движения. В ка-
качестве физического введения в эту область можно рекомендовать
обзоры Форда [133], Берри [26] и Хеллемана [180] 2).
Перечислим некоторые основные вопросы, возникающие при ис-
исследовании стохастичности в динамических системах. Каким обра-
образом можно однозначно определить, что изолирующие интегралы
движения отсутствуют? Какие величины необходимы для описания
стохастического движения? Насколько численное моделирование
соответствует поведению реальной системы? При каких условиях
можно ограничиться изучением диффузии только в пространстве
действий? Какое влияние на диффузию оказывает внешний шум?
И наконец, как изменяются все эти свойства при увеличении числа
степеней свободы?
В течение главным образом последнего десятилетия эти во-
вопросы изучались рядом исследователей. Среди них Хенон и Хейлес,
Заславский, Чириков с сотр., Фрёшле, Форд с сотр., Гальгани
с сотр. и многие другие. В своей пионерской работе [188] по чис-
численному изучению стохастичности для двух связанных осциллято-
осцилляторов Хенон и Хейлес писали: «Проверка показала, что ... в области,
См. также [486].— Прим. ред.
См. также [340, 444, 481, 488].— Прим.
Стохастическое движение и диффузия 291
заполненной [инвариантными] кривыми, расстояние [между близ-
близкими траекториями] растет медленно, приблизительно линейно
[со временем], а ... в эргодической области это расстояние воз-
возрастает быстро, приблизительно экспоненциально». Дальнейшие
исследования подтвердили этот результат более строго, связав
экспоненциальную расходимость траекторий с энтропией Колмо-
Колмогорова и характеристическими показателями Ляпунова. Вычисле-
Вычисление этих характеристик движения стало стандартным методом
проверки на стохастичность. Эти вопросы будут гтодробно рассмот-
рассмотрены в § 5.2 и 5.3.
Для многих задач важной характеристикой движения является
функция распределения в пространстве переменных действия. Ис-
Исследование эволюции распределения значительно упрощается, если
ее описание удается свести к диффузионному уравнению. Такой
подход использовался Либерманом и Лихтенбергом [274 ] и дру-
другими авторами и будет описан в § 5.4.
Поправки к коэффициентам переноса, возникающие из-за на-
нарушения приближения хаотических фаз, можно учесть с помощью
представления Фурье (п. 5.4г). Воздействие внешнего шума на ди-
динамику системы рассмотрено в § 5.5.
§ 5.2. Основные понятия
* 5.2а. Эргодичность
Для отображения Т среднее по времени значение любой функции
/ (л:) в фазовом пространстве определяется следующим образом:
f(x) = lim -L t f(Tnx). E.2.1)
N-*<x> N n = 0
Можно показать, что для почти всех дг: а) функция / (л:) сущест-
существует; б) функция / является инвариантной, т. е. не изменяется
вдоль траектории:
и в) фазовые средние функций / (дг) и / (л:) совпадают. Фазовое
среднее определяется соотношением
</)= J f(x)dn, E.2.2)
м
где JC— фазовое пространство системы размерности М, а \х — ин-
инвариантная мера, т. е. ф, = Р (х) dMx, где Р (х) — инвариантное
распределение. Для гамильтоновых систем в канонических пере-
переменных х функция Р = 1. Метод получения инвариантных распре-
распределений в диссипативных системах описан в § 7.3. Динамическая
система называется эргодической, если для почти всех х
292 Глава 5
/(*) = </>. E.2.3)
Из этого определения ясно, что для эргодической системы среднее
по времени не может зависеть от х. Из произвольности функции
/ (дг) следует, что эргодичность имеет место только в том случае,
когда траектория попадает во все области фазового пространства,
т. е. подходит сколь угодно близко к. любой его точке бесконечное
число раз. Отметим, что обратное утверждение неверно х). Если,
например, система имеет инвариантные поверхности, то она не
является эргодической и называется обычно разложимой 2), хотя
у нее могут быть и стохастические области.
Свойство эргодичности зависит от того, на каком подпростран
стве оно определено. Так, автономная гамильтонова система не
может быть эргодической во всем фазовом пространстве из-за точ-
точного сохранения энергии. Однако можно говорить о ее эргодично-
эргодичности на энергетической поверхности. Если существуют и другие
интегралы движения, то система может быть эргодической только
на подпространстве, определяемом всеми этими интегралами. В не-
некотором смысле эргодичность оказывается универсальным свойст-
свойством, и основная задача сводится к определению подпространства,
на котором она существует.
Рассмотрим свойство эргодичности на примере движения на
торе, задаваемом отображением
Тфъ вя) = F1 + йI, Э2 + со2), mod 2л, E.2.4)
где а = coi;'co2 — иррациональное число. Покажем, что в этом
случае движение является эргодическим на торе. Для этого разло-
разложим временное среднее / (л:) в двойной ряд Фурье и сравним ко-
коэффициенты разложения функции / (дг):
а = I ex.p( — ik-x)f(x)diL
R к
и ее образа / (Тх):
Ьь— \ ехр [ — ik(x — со)] f(x)dn = exp{ik-(a)a ,
R к
где х = Тх. Из инвариантности функции / следует, что для любого
k ф О коэффициенты ак = bk = 0, если &а> Ф 0. Отсюда полу-
получаем, что для иррационального a (k(A ф 0) только а0 Ф 0, и функ-
функция / (л;) есть константа, как и требуется для эргодичности.
Физически отображение E.2.4) соответствует отображению по-
поворота на поверхности сечения 82 = const (индекс 1 опущен):
E.2.5)
г) Интересным примером подобных всюду плотных, но не эргодических
траекторий является диффузия Арнольда (см. п. 6.1а).— Прим. ред.
2) На эргодические компоненты (см. ниже).— Прим. ред.
Стохастическое движение и диффузия
Дв)
хохохохохо
6
Рис. 5.1. Эргодические свойства отображения поворота.
а — две периодические траектории (X и с) с рациональным числом вращения а (/) =
= 2/5; эргодичность иа инвариантной кривой / = const отсутствует; б — начальная
функция распределения f (в, 0), для которой временное среднее f (d.t) зависит от 6;
в — эргодическое движение иа инвариантной кривой с иррациональным числом враще-
вращения а, однако «серые» и «темные» траектории не перемешиваются.
294 Глава 5
Оно изображено на рис. 5.1, а для а = 1/5 (рациональное число)
и двух начальных условий (кружки и кресты). Выбрав / F), как
показано на рис. 5.1, б, легко видеть, что / = О для кружков и
/ = /0 для крестов. Таким образом, движение в этом случае не зрго-
дично. Для иррационального а траектория покрывает всю окруж-
окружность и / (л:) = (/) = /0;2, т. е. движение является эргодическим
на окружности.
Отображение E.2.4) соответствует движению интегрируемой
гамильтоновой системы на инвариантном торе (Qit 82). Можно
сказать, что это движение эргодично на торе, но не эргодично во
всем фазовом пространстве. Из рассмотренного примера квазипе-
квазипериодического движения ясно, что эргодичность еще не означает
стохастичность. С другой стороны, наше определение эргодичности
позволяет считать эргодическим стохастическое движение и в не-
некоторой ограниченной области фазового пространства, например
в стохастическом слое. Однако такое определение может оказаться
не очень удобным в том случае, когда область стохастичности со-
содержит много островков устойчивости *).
* 5.26. Характеристические показатели Ляпунова
Показатели Ляпунова играют важную роль в теории гамильтоно-
вых и диссипативных динамических систем. Они дают вычислимую-
количественную меру степени стохастичности. Помимо этого, су-
существует тесная связь между показателями Ляпунова и другими
характеристиками случайности, такими, как энтропия Колмого-
Колмогорова (п. 5.2в) или фрактальная размерность (п. 7.1в).
Грубо говоря, показатели Ляпунова характеризуют среднюю
скорость экспоненциальной расходимости близких траекторий.
Такая характеристика стохастичности была введена Хеноном и
Хейлесом [188] 2) и в дальнейшем исследовалась Заславским и Чи-
риковым [444], Фрёшле и Шейдекером [141—143] и Фордом [133].
Теория показателей Ляпунова [262] использовалась для ана-
анализа стохастического движения Оселедецем [323]. Связь показа-
показателей Ляпунова с энтропией Колмогорова рассматривалась Бенет-
Бенеттином и др. [19] и была установлена Песиным [334]. Метод вычис-
вычисления показателей Ляпунова развит Бенеттином и др. [20] и опи-
описан в § 5.3. Здесь же мы обсудим их свойства, следуя в основном
х) Все эти разнообразные случаи охватываются общим понятием эргоди-
ческой компоненты движения. Под эргодичностью же в физике понимается,
как показывает само название, эргодичность на энергетической поверхно-
поверхности.— Прим. ред.
2) Речь идет об использовании этого свойства в численных эксперимен-
экспериментах. Общие соображения о связи случайности с экспоненциальной неустой-
неустойчивостью движения высказывались еще Пуанкаре [489]; эта связь была
строго доказана в работах Хедлунда [490] и Хопфа [491] и"широко исполь-
использовалась Крыловым [241].— Прим. ред.
Стохастическое движение и диффузия
295
работам Бенеттина и др. [18—20]. Математические доказательства
можно найти в цитированной литературе.
Пусть динамическая система задана уравнениями
dt
M.
E.2.6)
Касссгпельное npocm
анстео
Характеристические показатели Ляпунова (по данным работы
Рис. 5.2.
[18]).
а — две близкие расходящиеся траектории; ги (t) = Ax (t) — касательный вектор; б —
касательное пространство, построенное на собственных векторах е± и е2 с показателями
Ляпунова <?! и <т2; для любого вектора w, непараллельного е2> G (w0) = ot, а для w, па-
параллельного е2, a (w0) = о2 < O"i.
296 Глава 5
Рассмотрим две близкие траектории с начальными условиями
х0 и х0 + Ajc0 (рис. 5.2, а). Их временная эволюция задает каса-
касательный вектор Ах (х0, t) с длиной
d(x0, t) = \Ax(x0, t)\.
Для удобства введем обозначение w = Ах. Динамику w можно
определить, линеаризуя уравнения E.2.6):
— =M(x(f))-w, E.2.7а)
dt
где
М = — E.2.76)
дх
— матрица Якоби для V. Введем среднюю скорость экспоненци-
экспоненциальной расходимости близких траекторий:
а (х0, w0) = lim -L- In 4гЩ' E'2'8>
t-+oo t d (jc0, 0)
d@)^0
Можно показать, что предел скорости а существует и она ограни-
ограничена. Далее, существует полная система М фундаментальных ре-
решений {е,-} уравнений E.2.7а), для каждого из которых скорость <т
имеет определенное (вообще говоря, различное) значение:
ot{x0) = o(x0, et). E.2.9)
Это и есть характеристические показатели Ляпунова. Они не за-
зависят от выбора метрики фазового пространства [323], и их можно
упорядочить по величине: аг > ст2 > . . . > ам.
В частном случае периодической траектории уравнения E.2.7)
задают некоторое линейное отображение на периоде т, которое
можно записать в виде
wn^ = k-wn. E.2.10)
Как было показано в § 3.3, матрица А имеет М собственных зна-
значений, вообще говоря, комплексных:
Обозначим соответствующие собственные векторы через в;. Тогда
для w0 = ei из E.2.10) следует
Wn = ^?et. E.2.11)
Отсюда, согласно E.2.8), получаем
o(et)= —ln\kt\ = ot. E.2.12)
Кроме того, из E.2.11) следует, что для
wo = ae1Jr ¦ ¦ . +смем
Стохастическое движение и диффузия 297
динамика вектора wn определяется первым ненулевым коэффици-
коэффициентом с,-. Если, например, сх Ф 0, то a (w0) = сгъ а если сх = О,
но с2 Ф 0, то a (w0) = о2ит. д. Иначе говоря, каждый показатель
Ляпунова определяет скорость а в некотором подпространстве
с размерностью на единицу меньшей, чем предыдущий. Следова-
Следовательно, для почти всех w значение а = ах. Это свойство иллюстри-
иллюстрируется на рис. 5.2, б.
Обобщение понятий собственных значений и собственных век-
векторов на непериодические траектории было дано Оселедецем [323].
Возможность такого обобщения связана с тем, что непериодические
траектории можно приближать периодическими с достаточно боль-
большим периодом.
Для любой непрерывной траектории, заданной дифференциаль-
дифференциальными уравнениями [например, E.2.6) ], по крайней мере один из
показателей Ляпунова, соответствующий собственному вектору
вдоль траектории, равен нулю. В случае гамильтоновой системы
показатели обладают следующей симметрией:
tf;= — G2N-1+1, E.2.13)
где 2N = М, а N — число степеней свободы. Для периодической
траектории это соотношение можно получить из симметрии собст-
собственных значений C.3.21). Отсюда вытекает, в частности, что у га-
гамильтоновой системы по крайней мере два показателя Ляпунова
равны нулю. Однако на энергетической поверхности (М = 2N—1)
один из них, соответствующий смещению перпендикулярно поверх-
поверхности, отсутствует.
Обобщенные показатели Ляпунова. Показатели Ляпунова для век-
векторов w называют также показателями первого порядка. Оселедец
[323 ] обобщил это понятие х) для описания средней скорости экс-
экспоненциального роста /7-мерного объема Vp, построенного на век-
векторах wlt . . . , wp (p < М). Тогда величина
а(р) (*0, Vp) = lim ~ v (*0> 0) E-2-14)
есть показатель Ляпунова порядка р. Оселедец [323], а также
Бенеттин и др. [20] показали, что а(р> (jc0, Vp) выражается через
сумму р показателей первого порядка. Аналогично тому как для
почти всех w справедливо соотношение а (х0, w) = ах (jr0), так
и для почти всех Vр величина а(р) определяется суммой р наиболь-
наибольших показателей
ct(p) = cTi + ct2t • • . +<V E-2.15)
Это соотношение используется для численного определения пока-
J) Обобщенные показатели Ляпунова использовались и ранее, см., на-
например, [378, 496].— Прим. ред.
298 Глава 5
зателей Ляпунова (см. § 5.3). При р = М получаем среднюю ско-
скорость экспоненциального роста фазового объема:
(Л1J E.2.16)
Для системы с инвариантной мерой (в частности, для гамильтоно-
вых систем)
м
в то время как для диссипативной системы эта сумма должна быть
отрицательной (см. § 7.1).
Отображения. В случае М-мерного отображения
xn+1 = F{xn) E.2.17)
выражение для аот получается из E.2.8) заменой t на п. Вместо
этого можно ввести собственные значения Х{ (п) матрицы
АЯ = [М(*Я)-М(.*Я_1). . . M(JCi)]u, E.2.18)
где М = dFldx — матрица Якоби для F. Тогда показатели Ляпу-
Ляпунова равны
аГ = liming,-(л) j. E.2.19)
гг->оо
Показатели Ляпунова для (М—1)-мерного отображения на по-
поверхности сечения Пуанкаре пропорциональны показателям, для
непрерывной траектории в М-мерном фазовом пространстве:
E.2.20)
где t = l М—1 («лишний» показатель для траектории равен
нулю). Коэффициент пропорциональности т равен среднему ин-
интервалу времени между последовательными прохождениями тра-
траектории через поверхность сечения. В случае автономной гамиль-
тоновой системы (М = 2N) размерность отображения есть М—2,
и, таким образом, исключаются оба нулевых показателя исходной
системы.
5.2в. Основные свойства стохастичности
Перемешивание. Понятие перемешивания является по существу
очень простым. Возьмем сосуд, содержащий, например, 20 % рема и
80 "о пепси-колы, причем вначале распределение рома в ессуде
произвольно, скажем, сплошной слой. Если теперь начать разме-
размешивать жидкость, то естественно ожидать, что после достаточно
длительного размешивания любой сколь угодно малый объем жид-
жидкости будет содержать «приблизительно» 20 % рома. Формализа-
Формализация подобного процесса и приводит к понятию перемешивания,-
Стохастическое движение и диффузия 299
Перемешивание подразумевает некоторое «огрубление» фазового
пространства, т. е. исследование его малых, но конечных областей *).
Можно показать [14], что перемешивание влечет за собой эрго-
эргодичность. Однако обратное неверно: из эргодичности не следует
перемешивание. Это сразу видно на примере отображения на торе
E.2.4), как показано на рис. 5.1, в. Разделим траектории на две
группы — «серые» и «темные». Ясно, что в процессе движения они
будут сохранять свое относительное расположение даже при ирра-
иррациональном а, когда каждая траектория покрывает весь тор. Это
и означает отсутствие перемешивания.
При t -> со система с перемешиванием приближается к равно-
равновесному состоянию: / (л:) -*~ (/). Покажем это на примере «отобра-
«отображения пекаря»
(Л 0<хп<\12,
Уп E.2.21)
Уп+iJ Bхп—\ \
L+W-. '**«•<'•
которое качественно обсуждалось в § 1.4. Следуя Форду [133] и
Берри [26], покажем, что «огрубленная» функция распределения
приближается к равновесной функции (константе). Из E.2.21)
получаем отображение для /:
Так как / быстро расслаивается по у, то для огрубления /„ проведем
усреднение по этой переменной:
1
gn(*)= Unix, y)dy.
о
Как мы увидим в § 5.4, это эквивалентно интегрированию по бьг
строосциллирующей фазе. Проведя усреднение для E.2.22), получим
1/2 1
1/2
') Понятие «огрубление» относится к функции распределения, а не к фа-
фазовому пространству, которое в классической механике является непрерыв-
непрерывным. Более того, эта непрерывность и есть источник случайности динамиче-
динамических траекторий (см. примечание редактора на с. 307). Правильнее было бы
сказать, что перемешивание является интегральным, а не локальным свойст-
свойством движения, которое формально определяется условием (см., например,
[486]): (f (Тпх) g (X) )->¦ (f (X) ) (g (X)) при п-*±оо, где f, g — любые
{неогрубленные) функции.— Прим. ред.
300 Глава 5
Таким образом, отображение для огрубленной функции g сводится
к усреднению g по двум половинам фазового квадрата. Это приво-
приводит в конце концов к однородной по х функции g, как и должно
быть при перемешивании *).
Интуитивно ясно, что рассматривавшиеся в предыдущих па-
параграфах стохастические системы являются перемешивающимися
(в пределах стохастической компоненты движения). Однако это
очень трудно строго доказать в конкретных случаях. Синаю [377]
удалось сделать это для системы твердых шариков (см. п. 1.4а). До-
Доказательство основано на рассеянии пучка траекторий при столк-
столкновении шариков (см. рис. 1.15, а). Хотя этот частный результат
и не доказывает наше предположение о перемешивании для типич-
типичной системы, близкой к интегрируемой, однако он оправдывает
подобные эмпирические обобщения, получаемые методом численного
моделирования.
К-системы. К-системы называются по имени Колмогорова, ко-
который ввел это понятие в работе [230 ]2). Эти системы имеют по-
положительную КС-энтропию (энтропию Колмогорова). КС-энтро-
КС-энтропия (по имени Крылова [241], Колмогорова [230] и Синая [376,
378 ]) определялась первоначально [230 ] посредством построения
специального разбиения фазового пространства. В момент времени
/ = 0 разделим пространство на множество {Л,- @)} малых ячеек
конечной меры и рассмотрим их эволюцию обратно по времени на
единичном временном интервале3). В результате получим новое
множество \Ai (—l)j. Каждый элемент пересечения этих двух
множеств В (— 1) = {At @) П А, (— 1)} имеет, как правило,
меньшую меру, чем элемент Л,- @). Продолжая этот процесс, по-
построим элементы множества
Я(-2)= И,@) П А,(-1) П Л*(-2)}
и т. д. Можно показать, что для того чтобы мера элемента В (— t)
экспоненциально уменьшалась при t-*-oo, должно выполняться
условие
1) Если переменные х канонические, что в данном примере выполняется.—
Прим. ред.
2) Сам Колмогоров назвал их квазирегулярными, имея в виду свойства
регулярного (типичного) случайного процесса. По поводу определения К-си-
К-системы, или К-свойства движения см. примечание редактора на с. 301.—
Прим. ред.
3) Эволюция крупноструктурной (огрубленной) функции распределе-
распределения Ai (t) назад по времени соответствует движению по траекториям вперед
по времени [ср. E.2.21) и E.2.22)].— Прим. ред.
Стохастическое движение и диффузия 301
где Rt — число элементов В (— /), а ц [Bi (— t) ] — мера эле-
элемента Bi. Величина hA имеет смысл средней скорости экспонен-
экспоненциального уменьшения |i (Bi). Тогда КС-энтропия h есть макси-
максимум (верхняя грань) hA по всем измеримым начальным разбиениям
фазового пространства г).
Так как КС-энтропия положительна только в случае экспонен-
экспоненциального уменьшения средней меры элемента В (назад по вре-
времени), то неудивительно, что она связана со средней скоростью
экспоненциальной расходимости близких траекторий (вперед по
времени), т. е. с показателями Ляпунова. Явное выражение для
этой связи было получено Лесиным [335 ], и его можно записать
в виде
E ot(x)]dj[. E.2.24)
I »° J
Здесь суммирование производится по всем положительным показа-
показателям Ляпунова, а интеграл берется по некоторой инвариантной
области фазового пространства. Вообще говоря, КС-энтропия по-
понимается как некоторая характеристика одной стохастической ком-
компоненты движения. В этом случае значения а,- не зависят от х и ин-
интеграл по Ж равен единице. Отсюда
А= I а{. E.2.25)
Oj.>o
Для автономной гамильтоновой системы с двумя степенями свободы
положительным может быть только alt откуда
h = o1. E.2.26)
При другой интерпретации [19] соотношение E.2.24) относится
ко всей (компактной) области фазового пространства. В этом слу-
случае для системы с двумя степенями свободы h определяет скорость
экспоненциальной расходимости близких траекторий, усредненную
по всей выбранной области фазового пространства. На регулярных
компонентах движения ах = 0. Положим для простоты, что на всех
стохастических компонентах ах одинаково и равно ах. Тогда из
E.2.24) получаем
h=№lt E.2.27)
где \xs — суммарная мера стохастических компонент. В § 5.3 мы
увидим, как использовать эти соотношения для численного опреде-
определения КС-энтропии, а также в качестве критерия стохастичности.
1) Если не только ft>0, но и hA > 0 для любого конечного разбиения
{Л,- @)}, то движение обладает К-свойством [378], которое оказывается,
таким образом, более сильным, чем положительность КС-энтропии. Грубо
говоря, К-система характеризуется однородностью процесса перемешива-
перемешивания.— Прим. ред.
302
Глава 5
Следует, однако, отметить, что, вообще говоря, разные стохастиче-
стохастические компоненты имеют различные значения аг. Поэтому, приме-
применяя соотношение E.2.24) к целой области фазового пространства,
надо брать правильное сред-
среднее значение av
Системы Аносова 1). Эти си-
системы введены и изучались
Аносовым [8, 9 ]. Они харак-
характеризуются линейным каса-
касательным пространством, кото-
которое разлагается на три ком-
компоненты:
1) составляющая вдоль
траектории с нулевым пока-
показателем Ляпунова;
•> 2) поперечное простран-
пространство, в котором траектории
расходятся экспоненциально
со скоростью, ограниченной
снизу равномерно по началь-
начальным условиям и времени;
3) поперечное простран-
пространство, в котором траектории
сближаются экспоненциально
со скоростью, ограниченной
х сверху, и тоже равномерно
по начальным условиям 2) и
времени.
Это очень сильные усло-
условия, и гамильтоновы системы,
близкие к интегрируемым,
никогда им не удовлетворяют.
Системы Аносова структурно
устойчивы [8], т. е. при дей-
действии малого возмущения
Рис. 5.3. Отображение Арнольда на то- они остаются системами Ано-
ре (по данным работы [14]). сова.
Область «кот» А трансформируется в ТА и PaCCMOTDHM СВОЙСТВЭ ЭТИХ
затем в Т*А.
1) В оригинале C-systems, т. е. (У-системы. Это менее распространенный
сейчас термин, который ввел Аносов — автор этих систем. Буква У происхо-
происходит от слова условия, которым должны удовлетворять эти системы; они
перечислены ниже в тексте.— Прим. перев.
2) Имеются в виду начальные условия как в касательном, так и в основ-
основном фазовом пространстве. В приведенном виде условия относятся только
к обратимым во времени системам, подробнее см. [8, 9, 14].— Прим. ред.
Стохастическое движение и диффузия 303
систем на простом, хотя и нефизическом примере, который
часто используется математиками. Следуя Арнольду, возьмем
отображение Т на торе вида
(Хп+Л_A 1 \ (Хп\
\Уп+1/ V 2 / \уп)
Отображение Т совпадает со своим касательным отображением А,
причем det А = 1, т. е. оба отображения сохраняют площадь. На
рис. 5.3, взятом из [14], показано преобразование тора вместе с
изображением знаменитого арнольдовского кота. Ясно видно рас-
расслоение фазового пространства и перемешивание. Используя ре-
результаты п. З.Зв, найдем собственные значения и векторы этого
отображения. Из характеристического уравнения
~Х 1 = 0
1 2-Я
получаем собственные значения
К 2= 3±^5 . E.2.29)
а из уравнения C.3.7) — собственные векторы
¦у),
E.2.30)
Растяжение происходит вдоль направления ?lt а сжатие — вдоль
ортогонального направления ?2. При этом, конечно, Хг = 1/Хг,
что следует просто из сохранения площади. Чтобы подчеркнуть
экспоненциальный характер растяжения, можно записать собст-
собственные значения в виде
К* = е±а, E.2.31)
где а = In [C + -\/5)/'2] одинакова для всех начальных условий.
Поэтому показатель Ляпунова о1 (х) = ст>0 и не зависит от х.
Следовательно, отображение E.2.28) является системой Аносова,
а значит [378 ], и К-системой. Его энтропия
Сдвиги Бернулли. В качестве заключительного примера рассмот"
рим системы, называемые бернуллиевскими. Пусть фазовое про"
странство разбито на М ячеек, каждая из которых помечена сеоим
символом щ и характеризуется вероятностью pt попадания в нее
траектории движения. Предположим, что состояние системы ые-
304 Глава 5
няется каждую секунду. Тогда динамическое движение описывается
некоторой последовательностью символов х). Рассмотрим теперь
такое отображение, которое сдвигает любую последовательность
на один элемент влево. Например, подбрасывая монету, мы полу-
получаем последовательность вида 2)
0 1110 11...,
где символы 0 и 1 соответствуют двум сторонам монеты. Для сдвига
Бернулли с числом символов М значение энтропии последователь-
последовательности длины п дается стандартным выражением 3)
лг
Максимум энтропии достигается для разбиения с pi = 1,'М и ра-
равен
Нт = п\пМ.
Сдвиг Бернулли можно задать простым отображением:
хп+1 = Мхп, mod 1.
При этом каждая итерация дает новый член последовательности
Бернулли. КС-энтропия этого отображения легко вычисляется и
равна h = In М, а Нт = hn. Таким образом, КС-энтропия опреде-
определяет скорость роста Нт со «временем» п. При п->-оо энтропия Нт
неограниченно возрастает.
Общая картина взаимосвязи между различными свойствами
случайного движения представлена на рис. 5.4. Стрелки между
прямоугольниками указывают направление импликации. Так, на-
например, К-системы обладают свойствами перемешивания и эргодич-
эргодичности4). Наиболее сильные статистические свойства динамической
1) Это —• так называемая символическая траектория.— Прим. ред.
2) Это не очень удачный пример, поскольку подбрасывание монеты
не является чисто динамическим процессом. Пример сдвига Бернулли в ди-
динамической системе см. ниже в тексте и E.2.32).— Прим. ред.
3) Это выражение заимствовано из теории вероятностей и справедливо
при условии, что попадания траектории в различные ячейки статистически не-
независимы. Динамическая система называется бернуллиевской, или сдвигом
Бернулли, если она обеспечивает выполнение этого условия для некоторого
определенного разбиения (фазового пространства), которое тоже называется
бернуллиевским. Хотя это свойство кажется на первый взгляд очень силь-
сильным (максимальным?), на самом деле это не совсем так из-за сингулярности
бернуллиевских разбиений в большинстве случаев (см. [497]).— Прим. ред.
4) В дополнение к связям на рис. 5.4 отметим, что система Аносова яв-
является также и бернуллиевской, точнее — всякий перемешивающий поток
Аносова с гладкой инвариантной мерой является бернуллиевским [498,
499].— Прим. ред.
Стохастическое движение и диффузия
305
случайности *) расположены в верхней части рисунка, а наиболее
слабые — внизу. Основная характеристика каждого свойства при-
приведена справа, а примеры соответствующих систем—слева.
Системы, близкие к интегрируемым, такие, как модели Хенона—
Хейлеса или ускорения Ферми, для которых характерно наличие
Отображение
Арнольда на торе
Прео^сазование пекаря
Геодезические на поверх-^
кг:mi: отрицательной
хпивизны
Равномерная \
экспоненциальная j
неистой чивость
Релаксация
к равновесию
Рис. 5.4. Взаимосвязь между различными статистическими свойствами слу-
случайного движения.
областей как регулярного, так и стохастического движения, не
обладают в полной мере ни одним из свойств, перечисленных
1) Согласно современной алгоритмической теории динамических систем
[448], которая кратко обсуждается ниже в п. 5.2г, свойство случайности
лежит как бы в другой плоскости. Формально алгоритмическая случайность
эквивалентна положительности КС-энтропии (h > 0), т. е. это свойство слабее
К-свойства (см. прим. ред. на с. 301). Однако оно обладает иным качест-
качеством: полностью исключает возможность динамического описания системы
ввиду принципиальной непредсказуемости отдельных траекторий.— Прим.
ред.
306 Глава 5
на рис. 5.4. Однако вблизи гомоклинных точек движение локально
эквивалентно преобразованию пекаря, что приводит к случайному
поведению типа сдвига Бернулли. Кроме того, как мы увидим
в §5.3, результаты численного моделирования убедительно показы-
показывают, что стохастические компоненты в таких системах (например,
стохастический слой) имеют положительную КС-энтропию, а сле-
следовательно, и определенные статистические свойства.
5.2г. Случайность и ее численное моделирование
Случайные последовательности. В каком смысле поведение детер-
детерминированной динамической системы может оказаться случай-
случайным? Прежде всего значительные усилия были направлены на
выяснение смысла самого понятия случайности [233, 338] (попу-
(популярное изложение см. в работе [61 ]) х). Интуитивно ясно, что слу-
случайная последовательность некоторых символов не должна под-
подчиняться никакой закономерности. Можно придумать различные
тесты, например на частоту появления определенных символов
в последовательности, пар символов и т. д., которые должна вы-
выдерживать случайная последовательность. В том случае, если по-
последовательность выдерживает все тесты, ее можно считать «слу-
«случайной»2).
Современное определение случайности основывается на том,
что информация, заключенная в случайной последовательности,
не может быть «сжата», т. е. представлена в более компактной форме.
Так, не существует правила вычисления случайной последователь-
последовательности, которое было бы существенно короче, чем просто ее копиро-
копирование. Эти идеи можно формализовать следующим образом. Опре-
Определим вначале минимальную длину программы (число бит) /Сс
вычисления N бит последовательности SN на некоторой ЭВМ. Ве-
Величина Кс зависит от ЭВМ, но ее можно представить в виде суммы
C N() + C,
где Сс > 0 зависит только от ЭВМ, но не от SN, а сложность f(N (S)
зависит только от последовательности SN. Ясно, что значение
сложности заключено между некоторой постоянной (любая про-
программа должна иметь хотя бы одну команду) и максимальным
когда ЭВМ просто копирует заданную последовательность.
х) См. также сборник [495], обзор [492] и популярную статью [449].—
Прим. ред.
2) Такое определение случайности по Мартин-Лёфу [493] (см. также
[492]) представляется слишком узким по крайней мере для теории динами-
динамических систем, поскольку оно включает в себя максимальные статистические
свойства, в частности полную независимость (бернуллиевость). Критику та-
такого определения случайности см. в работе [500].— Прим. ред.
Стохастическое движение и диффузия 307
Можно показать, что последовательности с максимальной слож-
сложностью действительно существуют х). Рассмотрим теперь некоторый
вычислимый тест на случайность. Тогда можно доказать следую-
следующую теорему: последовательность выдерживает все вычислимые
тесты на случайность тогда и только тогда, когда она имеет поло-
положительную сложность 2), т. е.
K(S)= lim
Сопоставим каждой последовательности точку на отрезке [0, 1 ].
Тогда меру множества последовательностей можно определить
как меру соответствующих действительных чисел 3). Можно до-
доказать, что по этой мере почти все последовательности случайны,
т. е. множество неслучайных последовательностей имеет меру
нуль 4).
Посмотрим теперь, как случайная последовательность возни-
возникает из детерминированного уравнения. Возьмем, например, сле-
следующее одномерное отображение на отрезке [0, 1 ]:
Xn+1=l0xn, mod 1 E.2.32)
¦с начальным условием
0<л:0<1.
Разделим «фазовое пространство» 0 ^ х0 < 1 на десять ячеек с но-
номерами а,: = 0, 1, 2, . . . , 9. Тогда, например, для начального
условия х0 = 0,157643 . . . отображение E.2.32) генерирует по-
последовательность
Ы = 1, 5, 7, 6, 4, 3. .
Является ли она случайной? Ответ зависит от того, случайно ли
начальное условие х0. Из упомянутой выше теоремы следует, что
почти все х0 случайны, а значит, и рассматриваемая последова-
последовательность почти наверняка случайна. Оказывается, что движение
вблизи гомоклинных точек в стохастическом слое случайно, а регу-
регулярное движение на инвариантных поверхностях не является слу-
случайным 5).
1) И даже составляют большинство из всех последовательностей данной
длины [231].— Прим. ред.
2) Это не теорема, а другое возможное (и более приемлемое для теории
динамических систем) определение случайности (см. примечание редактора
на с. 306). Впервые такое определение в эквивалентной форме было предло-
предложено Алексеевым (см. [501], с. 75, определение А и обзор [448]).— Прим.
ред.
3) То есть просто как длину на отрезке, или более формально, как меру
Лебега.— Прим. ред.
4) Подчеркнем, что возможность случайных траекторий в классической
механике связана, таким образом, с непрерывностью фазового пространства.
Заметим, что в квантовой механике и при численном моделировании это уже
не так (см. ниже и [77]).— Прим. ред.
5) Подобные заключения можно получить из теоремы Алексеева —
Брудно (см. [448, 494]), согласно которой упомянутая выше удельная слож-
сложность равна КС-энтропии: К (S) = h.— Прим. ред.
308 Глава 5
Ошибки округления. При исследовании гамильтоновых отображе-
отображений с их сложной структурой хаотического и регулярного движе-
движения широко используется численное моделирование, причем число
итераций отображения достигает многих миллионов. Возникает
вопрос: в какой степени численное моделирование с конечной точ-
точностью арифметических операций, ошибками округления и прочим
«шумом» соответствует реальной динамике системы? Существенное
влияние этих ошибок на такие характеристики движения, как рас-
распределение в фазовом пространстве, мера стохастической компо-
компоненты и другие, легко определить, изменяя точность счета. Фак-
Фактически такие проверки составляют неотъемлемую часть любого
численного эксперимента. Так, например, Грин [165] исследовал
влияние ошибок округления на определение границы стохастич-
ности и нашел, что оно пренебрежимо мало (см. п. 4.4а). Бенеттин
и др. [17] показали, что для систем Аносова численные ошибки
несущественны при вычислении временных средних, например,
показателей Ляпунова. Однако системы Аносова структурно
устойчивы, и вопрос о влиянии численных ошибок на другие си-
системы остается пока открытым1).
С другой стороны, конечная точность счета кардинально ме-
меняет некоторые свойства движения. Даже для регулярной траек-
траектории ошибка в начальных условиях растет, вообще говоря, ли-
линейно со временем, а для хаотических траекторий она растет экс-
экспоненциально быстро. Если мантисса чисел на ЭВМ имеет N дво-
двоичных разрядов, то начальные условия полностью забываются
через пт -— 2N итераций для регулярной траектории и всего через
nm ~ N итераций для хаотической траектории. В обоих случаях
система окажется далеко от своего начального положения, если
после пт итераций в одну сторону по времени сделать столько же
итераций в обратную сторону.
Более серьезная теоретическая проблема заключается в том,
что при этом смазывается четкое различие между хаотическими и
регулярными траекториями. Например, в случае двумерного га-
мильтонова отображения имеется конечное число состояний си-
системы М = 22N, и после п -< М итераций система обязательно
вернется в одно из предыдущих состояний. В результате все траек-
траектории такой системы оказываются периодическими. Это остается
справедливым и для диссипативных систем. В каком смысле можно
считать движение такой системы случайным?
Этот вопрос исследовался Ренно 1341], которая использовала
целочисленное отображение 2)
1) Структурная устойчивость здесь не помогает, поскольку ошибки ок-
округления не удовлетворяют требуемой гладкости возмущения (см. ииже по
тексту).— Прим. ред.
2) Следует подчеркнуть, что это отображение моделирует прежде всего
типичный эффект «экспериментальной установки» (ЭВМ), который отсутст-
Стохастическое движение и диффузия 309
¦и , ( m /1 2л i. \1 j
а,-+1 = а,- — Ь,- -I- ( 1 — cos bi) , mod m,
E.2.33)
/ . 2л . 2л \] ,
sin ai+i-pl — cos a;+1 , modm,
\ m m /J
2д \ /J
где [X J — целая часть X, К — параметр «стохастичности», а а
\\ Ъ — целые числа в интервале
-—т/2 < а, Ъ <т<2.
Это — взаимно-однозначное отображение М = т2 точек плоско-
плоскости (о, ft) на себя. Оно не содержит округления или каких-либо
других численных ошибок х). Для т, кратного 4, и /С<4 отобра-
отображение имеет две неподвижные точки: @, 0) и (— т/4, 0). Первая
устойчива при малых К., вторая неустойчива. Для К = 1,3 и я =
= 400 имеются 48 относительно коротких периодических траекто-
траекторий, заполняющих некоторую кольцевую область вокруг непод-
неподвижной устойчивой точки @, 0). Кроме того, имеются 9 очень длин-
длинных траекторий, которые довольно однородно покрывают большую
часть фазового квадрата и соответствуют, по-видимому, «хаотиче-
«хаотическому» движению. Для /С = 10 имеются только 12 (длинных) тра-
траекторий, представляющие «хаотическое» движение.
Ренно определила «случайность» периодических траекторий
следующим образом. Имеется всего М\ взаимно-однозначных ото-
отображений М точек на себя. Приписав одинаковую вероятность
\1М\ каждому из этих отображений, получим «случайное» отобра-
отображение 2). Такое отображение обладает следующими статистиче-
статистическими свойствами:
1. Вероятность траектории длины п, выходящей из данной
точки (а, Ь), равна ИМ и не зависит от п.
2. Средняя длина траектории равна (М + 1)/2.
3. Среднее число всех траекторий приблизительно равно
In М + у, где у = 0,577 ... — постоянная Эйлера.
Численное моделирование отображения E.2.33) при К = 1,3
и К = Ю с 300 :^ m < 800 подтвердило эти свойства «случайного»
вует в исходной динамической системе классической механики. Поэтому вво-
вводимые ниже понятия стохастичности и случайности для отображения E.2.33)
являются не более чем имитацией, которую нужно четко отличать от настоя-
настоящей случайности в непрерывном фазовом пространстве. Любопытно отметить,
что целочисленные отображения качественно моделируют некоторые кванто-
квантовые эффекты (см. [77]).— Прим. ред.
1) Точнее «ошибки» округления (взятие целой части) явно включены
в отображение.— Прим. ред.
2) В таком определении скрыта следующая эргодическая гипотеза: ста-
статистика траекторий для данного (типичного) отображения [например, E.2.33)]
приблизительно совпадает со статистикой всех М\ отображений.— Прим.
ред.
310
Глава 5
отображения. Эти результаты служат подтверждением того, что
хаотическое движение, наблюдаемое в гамильтоновых системах,
является следствием их динамики, а не конечной точности счета.
Последняя приводит, напротив, к периодичности движения. Чис-
Численные эксперименты, в которых точность счета изменялась, также
подтверждают этот вывод.
§ 5.3. Определение показателей Ляпунова и
КС-энтропии
Напомним (см. рис. 5.2) определение характеристического показа-
показателя Ляпунова а для траектории X (t) и близкой к ней х + w, где
.,и\ л w — касательный вектор:
= lim
d @)~,
о(х0, wo) =
d(t)
— In-
t d@)
E.2.8)
В системах, близких к инте-
интегрируемым, аналитический и
численный расчет показате-
показателей а (особенно максималь-
максимального о = стх) широко исполь-
используется в качестве критерия
стохастичности. Отметим
прежде всего [57 ], что в ин-
интегрируемых гамильтоновых
системах все а равны нулю.
Рассмотрим в качестве при-
примера движение на торе
{в проекции на плоскость (J, 0) см. рис. 3.1, а]:
J(t) = J0, E.3.1a)
J)t. E.3.16)
Рис. 5.5. Линейный рост расстояния
d (t) между близкими траекториями
в интегрируемой системе на примере
отображения поворота.
Как показано на рис. 5.5, траектории в этом случае представляют
собой окружности, а расходимость близких траекторий оказывается
максимальной, когда вектор w == (А/, 0), т. е. направлен вдоль
радиуса. Для двух близких траекторий имеем
91@=e0 + W, E.3.2а)
е2 (о = е0 + ©о* + «о4А E.3.26)
где ©о — производная по /. Расстояние между траекториями равно
= 4 (8,_ ехJ+<& = <% [(©о/оО2 +1] E-3-3)
Стохастическое движение и диффузия 311
и при больших t растет линейно со временем. Тогда из E.2.8) имеем
a1 = lim-^ln[(coo/00:?—l] =°- E.3.4)
t - -со 2/
С другой стороны, в хаотической области
d(t)^doe^(x)t, E.3.5)
lim-1-ln-u(- = G1>0. E.3.6)
5.3а. Аналитические оценки
Для достаточно простой динамической системы, в которой области
устойчивости занимают пренебрежимо малую часть фазового про-
пространства, максимальный показатель Ляпунова ах можно полу-
получить аналитически. Для стандартного отображения при больших
К это было сделано Чириковым [70 ]. Линеаризовав стандартное
отображение вблизи некоторой точки, не обязательно неподвиж-
неподвижной, получим из характеристического уравнения при больших К
наибольшее из двух собственных значений в виде
Я+ = /С | cos в |. E.3.7)
Так как вся фазовая плоскость считается стохастической, то ве-
величина а1 (и h) определяется просто усреднением In k+. В данном
случае это эквивалентно усреднению по 0 и дает
i 2fln|Kcos0 |d6 = ln— • E.3.8)
2
! fln|K |d
2я b 2
Этот аналитический результат сравнивался с численным значе-
значением ап, полученным для начальных условий на стохастической
компоненте. При К za 6, когда еще можно ожидать количествен-
количественного согласия с E.3.8), Чириков получил *) ап/а1 = 1,02.
Как мы видели в § 4.1, в стандартном отображении островки
устойчивости существуют при сколь угодно больших К- С увели-
увеличением К эти островки уменьшаются, но поскольку они могут су-
существовать вокруг периодических точек произвольно большого
периода, то возникает вопрос, не занимают ли они значительную
часть фазовой плоскости, что привело бы к неправильному значе-
значению КС-энтропии E.3.8) даже для больших К- Чириков исследо-
исследовал этот вопрос двумя методами. В первом квадрат 2л X 2я разде-
разделялся на 100 X 100 ячеек и вычислялась доля |j,s ячеек, в которые
попадала траектория с начальными условиями на стохастической
компоненте. Ясно, что такое «огрубление» может давать правиль-
правильные результаты только для относительно малых значений К, когда
х) Более полные аналитические и численные данные по КС-энтропии для
различных отображений приведены в работе [73J.— Прим. ред.
312
Глава 5
островки устойчивости достаточно велики. Во втором методе выби-
выбиралось некоторое число, скажем N = 100, траекторий со случай-
случайными начальными условиями и определялась доля цг тех из них,
для которых численное значение КС-энтропии близко к нулю. Ес-
Естественно ожидать, что [is + \x.r ж 1. Результаты этих численных
экспериментов представлены в табл. 5.1. Чириков пришел к за-
заключению, что мера устойчивых областей с увеличением /С стре-
стремится к нулю 1), так что при больших К возможно простое стати-
статистическое описание движения.
Таблица 5.1. Численное определение меры стохастической (ц5)
и регулярной (iir) компонент стандартного отображения (по данным
работы [70], табл. 5.3)
к
8,888
—
<ю-4
0
6,59
—
,0099
6,21
—
0,004
0
0
5
,98
,014
0
0
4
,92
,08
0
0
3
,89
,11
0
0
2
,79
,19
0
0
l
,44
,52
0.5
—
0,96
5.36. Численные методы
Удобным практическим критерием стохастичности в заданной об-
области фазового пространства служит численное определение пока-
показателей Ляпунова. Максимальный показатель о1 широко исполь-
использовался в качестве критерия стохастичности в ряде работ (см.,
например, 119, 41—43, 73, 133, 371 ]).
Вычисление at. Ранее было показано (п. 5.26), что а (х, w0) =
= а1(х) для почти всех касательных векторов w0. Поэтому для
вычисления а1 начальный вектор w0 можно выбирать произвольно.
Интегрируя совместно уравнения E.2.6) и E.2.7), находим вели-
величину
где для удобства принято dQ = d @) = 1. Трудности возникают
в том случае, когда | w | растет экспоненциально, что приводит
к переполнению и другим численным ошибкам. Чтобы изба-
избавиться от этих неприятностей, выберем определенный интервал
времени т, как показано2) на рис. 5.6, и будем перенормировывать
1) Согласно данным работы [73], \хг ~ ехр (— Сд/К), где С ~ const,
за исключением специальных значений К, близких к D.1.14).— Прим. ред.
2) Фактически на рис. 5.6 показан другой метод вычисления at — по
двум близким траекториям системы E.2.6), а не по одной траектории и ли-
линеаризованному уравнению E.2.7), как в тексте. Использование линеари-
линеаризованного уравнения имеет то преимущество, что его решение не зависит
от модуля | w |. Однако в некоторых специальных случаях удобнее интегри-
интегрировать две траектории (см., например, [470]).— Прим. ред.
Стохастическое движение и диффузия
313
I w I на единицу в конце каждого такого интервала х). Таким спо-
способом будем последовательно вычислять величины
dk = | Wk-i (т) |, E.3.9а)
= Wk-^x) , E.3.96)
где Wk (t) получается интегрированием E.2.6), E.2.7) на интервале
т с начальными значениями х {ki), Wk @). Если ввести величину
E.3.10)
пх
Гу„
Рис. 5.6. Схема вычисления максимального показателя Ляпунова (по дан-
данным работы [19]).
у = х + w, % — конечный интервал времени.
то из E.2.8) получаем
t = Hm сг„
E.3.11)
Для регулярного движения аг ~ 0, в то время как на стоха-
стохастической компоненте с^Х) и не зависит от х. Описанный метод
применим как для непрерывных траекторий, так и для отображе-
отображений.
Следуя работе Бенеттина и др. [19], проиллюстрируем исполь-
использование этого метода на примере модели Хенона—Хейлеса (п. 1.4а).
На рис. 5.7 приведена зависимость оп от пт для шести траекторий
с энергией Е = 0,125 (см. рис. 1.13). Три траектории A—3) нахо-
находятся, очевидно, в области устойчивого движения, тогда как три
другие D—6) — в широкой стохастической области, которая хо-
хорошо видна на рис. 1.13. Как и следовало ожидать, для первых тра-
траекторий с увеличением п величина сг„, очевидно, стремится к
х) То есть сокращать длину вектора w (| w \ -> da = 1), не изменяя его
направления (см. [73]).— Прим. ред.
314
Глава 5
нулю х), а для вторых, по-видимому,— к одному и тому же значе-
значению 2) ог.
Используя этот метод, Бенеттин с соавторами нашли зависи-
зависимость 0j от энергии Е в областях стохастического и регуляр-
регулярного движения (рис. 5.8). В последнем случае ап -> 0 (черточки
на оси абсцисс). Сплошная кривая соответствует подгонке значе-
значений О1'>0 к экспоненциальной зависимости. Используя соотно-
ю-' ~
10
-г _
Ю
-з -
Хаос
10г
пх
Рис. 5.7. Зависимость показателя ап от времени для траекторий на регу-
регулярной A—3) и стохастической D—6) компонентах (по данным работы [19]).
шение E.2.27) и зависимость 1—ц8 от Е, полученную Хеноном и
Хейлесом [188], Бенеттин с соавторами вычислили КС-энтропию
h (E) (пунктирная кривая на рис. 5.8). Они высказывают предпо-
предположение, что h(E)>0 для всех ?>0, что согласуется с нашими
общими представлениями о свойствах движения, хотя и не видно
из рис. 5.8 из-за различных приближений при вычислении о1. Это
указывает на некоторый присущий методу недостаток. Возможно,
например, что одна из траекторий на рис. 5.7, которая кажется
регулярной, на самом деле лежит в узком стохастическом слое.
Такую траекторию одинаково трудно обнаружить как непосредст-
непосредственно, так и при помощи настоящего метода, поскольку выход на
очень низкое плато о1 может оказаться за пределами фактической
1) Грубо говоря, как 1/лт [см. E.3.4)].— Прим. ред.
2) Вообще говоря, это не всегда так (см., например, [73], рис. 3). В дан-
данном примере близкие значения ап указывают на принадлежность всех трех
траекторий к одной и той же стохастической компоненте.— Прим. ред.
Стохастическое движение и диффузия
315
длительности счета 1). Мы вернемся к этим вопросам в гл. 6 при
обсуждении более сложного движения в многомерных системах.
Вычисление всех показателей Ляпунова 2). Следуя Бенеттину и др.
[20] 3), покажем, каким образом вычисляется полный набор по-
показателей Ляпунова в М-мерном фазовом пространстве. Ясно,
что любая попытка определить 02, 03 и т. д., выбирая касательный
вектор w вдоль векторов ег, ez и т. д. (см. рис. 5.2), обречена на
неудачу из-за неустойчивости этих
направлений, так что любые ошиб-
ошибки повернут в конце концов w (t)
вдоль е1. Вместо этого выберем
начальный базис из р ортонорми-
рованных касательных векторов
и численно определим р-мерный
объем Vp (t), заданный этими век-
векторами. Отсюда можно найти по-
показатель Ляпунова 0ip) порядка р
E.2.14). Проделав эту процедуру
для р = 1, 2, . . . , М, из E.2.15)
определим все показатели \ а1г
а2, . . . , ам. Здесь, однако, возни-
возникает следующая трудность. В про-
процессе движения углы между ка-
касательными векторами, вообще
говоря, экспоненциально умень-
уменьшаются и численные| ошибки рез-
резко возрастают. Поэтому в допол-
дополнение к перенормировке длины
векторов w необходимо также пе-
периодически ортогонализовать их.
0,15
0,10 f~
0,05
У
0,05
0,10
Е
0,15
Рис. 5.8. Зависимость максималь-
максимального показателя ах от энергии на
стохастической (крестики) и регу-
регулярной (черточки на оси абсцисс)
компонентах (по данным работы
[19]).
Сплошная кривая — экспоненциальная
интерполяция для О] > 0; пунктирная
кривая — КС-энтропия, пересчитанная
по or..
При этом новые векторы должны лежать в том же подпростран-
подпространстве, что и старые.
Оказывается, что такую процедуру одновременного вычисле-
вычисления всех р-мерных объемов можно свести к расчету эволюции М
векторов и их специальной ортогонализации по методу Грама—
J) Заметим, что хотя действительно таким методом нельзя установить
регулярность движения (интегрируемость) в некоторой области фазового
пространства, однако вполне можно обнаружить хаотическую (случайную)
компоненту движения, т. е. неинтегрируемость. В некотором смысле этот
численный метод дополняет аналитический метод обратной задачи рассеяния
(см. примечание редактора на с. 56), который позволяет, наоборот, доказать
только интегрируемость.— Прим. ред.
2) Заметим, что для критерия стохастичности нужен по существу только
максимальный показатель ах'ввиду неравенства h ^ а1 >- 0. Иначе говоря,
точное значение КС-энтропии h, которое требует знания всех показателей,
несущественно.— Прим. ред.
3) См. также [502].— Прим. ред.
316
Глава 5
Шмидта. Вспомним, что te>^_1 (т) — касательный вектор Wk~\ @)
через время т. Вычислим сначала для каждого временного интер-
интервала т следующие величины:
d^ = \w{klx(x)\t E.3.12а)
E.3.126)
4°
10
-г
10
Рис. 5.9. Все три положительных показателя Ляпунова для модели Конто-
пулоса (см. текст) (промежуточная область) (по данным работы [20]).
Затем для / = 2, . . . , М найдем последовательно величины
4-i (т) = «#Li (т)— ? (wlk' @)- w4U (т)) wf @), E.3.12в)
d^ = \u(Hi(-z)\, E.3.12г)
^@)= Uk-\-x) . E.3.12д)
Тогда в течение (k—1)-го интервала времени т объем Vp возрастает
в dk dk} . . . dip} раз. Отсюда, согласно E.2.14), получаем
ПТ ^
E.3.13)
Стохастическое движение и диффузия 317
Вычитая о[р~1) из о[р) и используя E.2.15), находим р-й показа-
показатель Ляпунова
ор = lim —!— V In d[p). E.3.14>
П-кх> ПХ J^j
Это соотношение фактически и используется при численном моде-
моделировании.
Бенеттин и др. [20] нашли таким способом все показатели Ля-
Ляпунова для нескольких гамильтоновых систем, включая 4- и 6-мер-
6-мерные отображения. Мы приведем их результаты для системы с тремя
степенями свободы, которая исследовалась Контопулосом и др.
[93]:
Движение этой системы ограничено при Ж0.097. Для Я = 0,09
фазовое пространство разделяется, грубо говоря, на три области:
большая область стохастичности с аг ж 0,03; а2 л; 0,008 и я3 » 0;
область регулярного движения (аг = 02 = о3 = 0) и промежуточ-
промежуточная область. На рис. 5.9 представлены результаты вычисления пер-
первых трех показателей Ляпунова для начальных условий в проме-
промежуточной области. Видно, что сходимость имеет место для
о, ж 3 X 10~3 и а3 = 0, соответствующего направлению вдоль
траектории. Поведение показателя а2 не вполне ясно.
Как мы увидим в § 6.2, эти результаты на самом деле обман-
обманчивы. Действительно, в системе с тремя степенями свободы первая
и третья области должны быть связаны слабой диффузией Ар-
Арнольда, благодаря которой траектория переходит из одной области
в другую. Поэтому, по-видимому, и для промежуточной области
с1 « 0,03, а а, « 0,008, что противоречит данным на рис. 5.9.
Это еще раз указывает на основную трудность численного опреде-
определения показателей Ляпунова: не существует априорного условия
для определения достаточного числа итераций п. Поэтому при чис-
численном моделировании необходимо использовать и другие методы,
такие, например, как метод сечения Пуанкаре1).
§ 5.4. Диффузия в пространстве действий
В областях фазового пространства, где движение полностью или
в основном стохастично (исключая небольшие изолированные ос-
островки устойчивости), его можно описывать с помощью функции
распределения, зависящей только от переменных действия (или
скоростей) 2). Эта задача представляет большой практический ин-
*) См. примечание редактора на с. 315.— Прим. ред.
2) Возможность усреднения по фазам при статистическом описании за-
зависит не только от стохастичности движения, но и от наличия в задаче двух
разных масштабов времени: быстрого перемешивания (по фазам) и медлен-
медленной диффузии (по переменным действия) (см. ниже по тексту). Такие масштабы
были введены Боголюбовым (см. [447], т. 2, с. 99).— Прим. ред.
318 Глава 5
терес. Так, например, в задаче Ферми основная цель заключалась
в нахождении возможного механизма ускорения космических лу-
лучей. При этом динамика фаз частиц по отношению к ускоряющим
их полям не представляет сама по себе интереса и требуется только
для определения среднего ускорения и энергетического распреде-
распределения. Аналогично и для электронного или нонно-циклотронного
резонансного нагрева плазмы физический интерес представляет
скорость нагрева и распределение по энергии.
В этом параграфе мы рассмотрим возмущенное отображение
поворота: =
unJrl = un^re[(un+1, %), E.4.1а)
+1, яр«). E.4.16)
где и, я|; — переменные действие — угол невозмущенного движе-
движения. В п. 5.4а дан вывод уравнения Фоккера—Планка для функции
распределения Р (и, п) и обсуждаются условия его применимости.
В п. 5.46 в приближении хаотических фаз вычисляются коэффи-
коэффициенты переноса. В качестве иллюстрации используются упро-
упрощенное и точное отображения Улама. В п. 5.4в получены стацио-
стационарная и нестационарные функции распределения. Корреляцион-
Корреляционные поправки к коэффициентам переноса рассмотрены в п. 5.4г.
* 5.4а. Уравнение Фоккера—Планка *)
Рассмотрим эволюцию функции распределения Р (и, «), ограничив-
ограничившись, естественно, областью сплошной стохастичности (без остров-
островков устойчивости). Примером может служить область и ,<С us (см.
п. 3.4а и б, рис. 1.14, 3.12 и 3.13) для упрощенной модели Улама:
E.4.2а)
mod0, E.4.26)
ип+1
где G — интервал периодичности по фазе A или 2л). Пусть эво-
эволюция Р (и, п) в такой области описывается как некоторый мар-
марковский процесс по и [424] 2):
Р{и, п + Ап) = $Р{и—Аи, n)Wt(u—Au, n, Аи,
E.4.3)
Здесь Wt (и, п, Аи, An) — вероятность перехода и -> и + Аи за
х) В отечественной литературе его чаще называют уравнением Фоккера—
Планка—Колмогорова (ФПК), поскольку строгий вывод этого уравнения,
условия его применимости и ковариантная формулировка даны в работах
Колмогорова [503, 504].— Прим. ред.
2) См. также [62, 505].— Прим. ред.
Стохастическое движение и диффузия " 319
«время» An. Предположим также, что An > 1 и Au<^P/(dP.'du),
т. е. существует такое An, что |для модели E.4.2) ]
2. E.4.4)
Тогда можно разложить PWf по первому аргументу. С точностью
до членов второго порядка по Аи получим
P(u — Au)Wt(u — Au) = P(u)Wt{u)~ d(PWt) Au +
ди
Подставляя это выражение в E.4.3) и учитывая нормировку
\Wt(u, n, Аи, An)d(Au)=l,
находим уравнение ФПК
— = _ — (ВР) + — J*-(DP), E.4.5)
дп ди 2 ди1
где средняя скорость 1)
¦lAuWt(u, n, Аи, An)d(Au), E.4.6)
An
а коэффициент диффузии
D(u) = —
An
(u, n, Аи, An)d(Au). E.4.7)
Соотношение между коэффициентами переноса. Следуя Ландау
1250], покажем, что для гамильтоновых систем2)
^ E.4.8)
2 du
1) Имеется в виду скорость изменения переменной и. В оригинале —
friction coefficient (коэффициент трения) — менее удачный термин, по-
поскольку такое «трение» существует и в гамильтоновых системах.— Прим.
ред.
2) Впервые соотношение такого рода было получено Эйнштейном в тео-
теории броуновского движения (см., например, [505], § 21). В работе Ландау
использовался принцип детального равновесия, который не всегда выпол-
выполняется даже и в автономной гамильтоновой системе (см. [506]). Вывод в
в тексте основан на независимости вероятности перехода от фазы ip (анало-
(аналогично работе Крылова и Боголюбова, см. [447], т. 2, с. 5). Поскольку и,
т|> — канонические переменные, то в последнем случае равновесное Р (и) =
= const, и E.4.8) сразу следует из E.4.5). Такой метод получения коэффи-
коэффициента В оказывается наиболее удобным (см., например, [505, 464]). Зна-
Значение соотношения вида E.4.8) состоит в том, что прямое вычисление В воз-
возможно только во втором порядке теории возмущений, в то время как для D
достаточно первого порядка.— Прим. ред.
320 Глава 5
Это позволяет записать уравнение ФПК в виде
дР д
I D дР \
\ 2 ди}'
дп ди
Для доказательства E.4.8) запишем изменение и с точностью до
членов, квадратичных по At:
• \
и (j _j- ДО = и @ + и At -\
2
где
и- Ш
• д2Н
и —
Из уравнений Гамильтона получаем
д2Н дН д*Н дН д2Н д / дН дН
и— 4- -f
ди ' дтрди Эгр ' dtydt д$ \ дЦ ди
д I дН V д I дН
1 ди \ д^р I Щ \ dt
Отсюда для Аи = и (t -f АО — u (О в0 втором порядке по А^
имеем
а
du \ dty I dip \ dip ди ' dt
Усредняя по 1|), получаем
Остальные члены исчезают из-за периодичности Н по if>. Анало-
Аналогично во втором порядке по А^:
(A uf = и2 (А/J = / — У (АО2.
\ dty I
Усреднение по гр дает
Сравнивая выражения для (Аи)^ и <(АиJ)ф, получаем соотноше-
соотношение E.4.8).
Условия применимости уравнения ФПК. Вероятность перехода Wt
зависит, конечно, не только от переменной действия и, но и от
фазы \\>. Однако при достаточно большом An > пс, где пс — время
Стохастическое движение и диффузия 321
релаксации функции распределения по фазе, можно усреднить
по у. Wt (и, я|>) -v Wt (и) = (Wt (и, Ц%.
Для выяснения условий такого приближения найдем прежде
всего направления собственных векторов системы E.4.2), исполь-
используя линеаризованное отображение (см. п. 3.36) с матрицей
\ — р 1—р/7
где р = QM'u2. Для собственных векторов получаем
(Д«, Дт|))сх(Г, ^,2-l), E.4.9)
где собственные значения даются выражением C.3.52). При
^i ~ I P/' I t> 1 собственный вектор растяжения направлен почти
по фазе (/' ~ 1). Последнее условие выполняется тем лучше, чем
меньше и по сравнению с us = F/W)I/2/2.
Для оценки пс предположим, что начальное распределение
сосредоточено в узком интервале Дар @), а Аи @) = 0. Тогда,
Ai|) (и) « kfAty @) « р"Дг|з @). Положив А\р (пс) ~ 9, найдем
с lnp v ;
т. е. нс слабо зависит от начального распределения. Напротив,
распределение по и остается локализованным в пределах Аи (пс) ~
•--• Q/Kx -~ (и/usJ « и. Поэтому можно ожидать, что при An ^> пс
эволюция распределения Р(и) описывается уравнениемФПК1) с коэф-
коэффициентами ВиОиз E.4.6) и E.4.7). Остаточные корреляции, однако,
сохраняются по крайней мере в течение одного периода отображе-
отображения. Их влияние будет рассмотрено в п. 5.4г.
Для a>«s существуют островки устойчивости, движение в ко-
которых не описывается уравнением E.4.5). Для стохастической
же компоненты, окружающей островки, простое усреднение по г))
уже неприменимо, поскольку при данном и допустимы не все зна-
значения фазы.
* 5.46. Коэффициенты переноса
Вычислим коэффициенты переноса E.4.6) и E.4.7) и сравним их
с результатами численного моделирования. Для отображения Улама
C.4.4) в простейшем случае2) п*==Ап — \, и в предположении
г) Фактически для этого нужно (см. примечание редактора на с. 317),
чтобы корреляционный масштаб времени пс был бы много короче диффу-
диффузионного масштаба tip ~ u2/D ~ и2 [D ~ /2 ~ 1, см. E.4.2)]. Поскольку
и sC us ~ М^2 и пс ~ 1, грубое условие диффузионного описания есть
М > 1.— Прим. ред.
2) Формально при этом нарушается первое условие E.4.4), однако оно
нужно только для перехода к дифференциальному уравнению E.4.5), но не
для вычисления D.— Прим. ред.
322
Глава 5
о равнораспределении по фазе получаем
В =
= О,
= \dty (АиJ =
12
о о
где Дм (г|э) = гр—1/2.
Этот результат, полученный в приближении случайных фаз J),
сравнивается на рис. 5.10 с численными данными по зависимости D
от п при различных начальных значениях скорости и. Значения D
0,6 -
0,4 -
0,2 -
0,0
и = 10, 20, 30,40
и = 60
100
200
Рис. 5.10. Зависимость коэффициента диффузии D от времени для отобра-
отображения C.4.4) (по данным работы [274]).
М= 10'; Ю3 траекторий с различными начальными условиями: сплошные кривые —
однородное распределение но фазе; пунктирная кривая — Дг|: =10 ; и = 30.
находились по 1000 траекториям отображения C.4.4) с М = 104,
что соответствует us = 50. Для и = 10, 20, 30, 40 и однородного
начального распределения траекторий по фазе вклад корреляций
1) Этот популярный, но неудачный термин означает на самом деле не
просто случайность фазы ty, но еще и полную статистическую независимость
ее последовательных значений т|> (п), что эквивалентно условию пс — 0.—
Прим. ред.
Стохастическое движение и диффц: ия 323
оказывается пренебрежимо малым, и D (и, п) --- D (и, 1) -- 1 12.
Однако для и = 50 корреляции существенно влияют на зависи-
зависимость D от п даже при н>200. При и = 60 наблюдается другой
эффект, связанный с тем, что часть траекторий оказывается в устой-
устойчивых областях и не дает вклада в диффузию. Наконец, в случае
неравномерного начального распределения по фазе наблюдается
некоторый переходный процесс, показанный пунктирной кривой
на рис. 5.10 для и = 30 и начальной ширины распределения
Aif = 10~3. Оценка E.4.10) дает в этом случае пс та 3, что соот-
соответствует по порядку величины данным рис. 5.10.
При учете смещения стенки величины и, г[; не являются канони-
каноническими переменными (п. 3.4а). Перейдем поэтому к каноническим
переменным Е, 0. Для функции распределения по «энергии» Е = и2
уравнение ФПК имеет вид
(ВР) л J
= - — (ВР) л- J ?— (DP), E.4.11)
дЕ 2 дЕ~
(ВР)
дп дЕ 2 дЕ~
где
В (Е) = —!- I AEWtd (AE), E.4.12)
An '
1 \(AEJWtd(AE); E.4.13)
An
здесь Wt — вероятность перехода (см. п. 5.4а). Из C.4.2а) и опре-
определения Е получаем (— F' = /; А/г = 1):
Для случайных и независимых значений канонической фазы 8
вероятность
Wtd(\E)=-^-,
1Л
а из C.4.2b)
2
Если, кроме того, функция / (г|эс) нечетна по грс,'_то
5=—"— |'2/2<%. E.4.14)
Аналогичные вычисления дают
D = —5- " D?/2 -f 3/4) dijv E.4.15)
^я —я
Для отображения C.4.4) / = 1|)с/2я, откуда В = 16 и О = Е/3 +
324 Глава 5
+ 3/80, что удовлетворяет соотношению E.4.8). Обратный пере-
переход к переменным и, г|з дает
Выражения В = B4ы)-х и D = 1/12 были получены впервые
Израйлевым и Ждановой [209 ] непосредственно из точного ото-
отображения C.4.1) *). Отметим, что соотношение E.4.8) в этом случае
не выполняется из-за неканоничности переменных и и г|х Более
детальное описание дано в работе Лихтенберга и др. [272].
* 5.4в. Стационарные и нестационарные решения
Для получения стационарного решения уравнения ФПК введем
полностью отражающие стенки при и = 0 и и = us. Буквально,
это, конечно, неправильно из-за проникновения траекторий в об-
область u~>us. Однако поскольку этот процесс происходит медленно,
то можно ожидать, что для значений и, достаточно малых по срав-
сравнению с us, решение с выбранными граничными условиями будет
близко к истинному. Положив в E.4.5) д/дп = 0, найдем решение
в виде
P(u)=P(uo)D(uo)D~1(u)ex.p \2B{u')D-1{u')du'. E.4.16)
"о
Для 5 = 0 и D = 1/12 распределение оказывается однородным
Р (и) = const, а для В ~ B4и)-х и D = l/12 — линейным: Р (и)=Си.
Эти результаты согласуются с численными экспериментами Либер-
мана и Лихтенберга ([274 ], рис. 12) и Израйлева и Ждановой,
([209], рис. 3). На рис. 5.11 представлены численные результаты
[274 ] для упрощенного (сплошная кривая) и точного (пунктирная
кривая) отображений Улама с / = г|э—1/2. Отклонения распреде-
распределений от ожидаемых в области u<us = М '2 ?а 16 связаны с не-
недостаточной для установления квазиравновесного состояния дли-
длительностью счета, а также с просачиванием траекторий в область
больших скоростей. С ростом и (ы>и5) островки устойчивости
быстро становятся преобладающими. Для точного отображения
при переходе к каноническим переменным Е, 9 получаем однород-
однородное распределение Р (Е) = Р (и) (duldE) = const.
В некоторых случаях можно также найти решение и нестацио-
нестационарного уравнения ФПК. Для упрощенного отображения Улама
D = 1/12, В = 0 и E.4.5) переходит в обычное диффузионное урав-
уравнение
^ LJ!^ E.4Л7)
дп 24 ди?
1) Небольшое различие между D = 1/12 и точным выражением D =
= 1/12 + 3/320 Е [см. E.4.15)] есть поправка второго порядка к скорости
диффузии опять-таки из-за неканоничности переменных и, г|> в C.4.1).
Обычно такая поправка не учитывается.— Прим. ред.
Стохастическое движение и диффузия
325
В случае точного отображения, подставляя в E.4.5) D = 1/12,
В = B4«)-\ получаем
— = —¦ — [« ^Г-( — I- E.4.18)
дп 24 ди [ ди \ и / J
Решение этого уравнения с начальным условием Р (и, 0) = б (и)
имеет вид
п. . 12и / 6и2
Р (и, п) = ехр ( —
п \ п
E.4.19)
Оно справедливо, конечно,
лишь до тех пор, пока тра-
траектории не начнут проникать
в область и>«5. Решение
полной задачи с учетом пе-
переходной области с остро-
островками устойчивости оказы-
оказывается очень сложным, и его
можно получить только чис-
численно.
Хотя рассмотренная за-
задача представляет сильно
идеализированную модель,
аналогичные результаты мож-
можно найти и для реальных
динамических систем. Приме-
Примером может служить задача
об электрон-циклотронном
нагреве в магнитных ловуш-
ловушках. Она подробно исследо-
исследована Егером и др. [212] и
Либерманом и Лихтенбер-
гом [275]. Было показано,
6-
с _
4-
з-
1-
ю
15
20
Рис. 5.11. Сравнение распределений по
скорости Р (и) (по данным работы [274]).
Сплошная кривая — упрощенное отображение
Улама C.4.4): пунктирная кривая — точное
отображение Улама C.4.1); Л1 = 10\
что нагрев можно приближенно описать системой уравнений, ана-
аналогичной C.4.8).
5.4г. Корреляционные поправки к коэффициентам переноса х)
В п. 5.46 коэффициенты переноса были получены в приближении
хаотических фаз на одной итерации отображения (An = 1). Од-
Однако, как было отмечено в п. 5.4а, уравнение ФПК справедливо
J) В оригинале — higher-order transport corrections (поправки высшего
порядка к коэффициентам переноса). Принятый в переводе термин более
явно отражает природу этих поправок.— Прим. перев.
326 Глава 5
только при An > пс, где пс — число итераций, за которое проис-
происходит перемешивание по фазе. Поэтому необходимо оценить по-
поправки к коэффициентам переноса за счет корреляций на интер-
интервале An — пс.
Впервые такие поправки были получены для стандартного ото-
отображения Речестером и Уайтом [345 ] и другим методом Речесте-
ром и др. [346]. Однако их техника использует введение допол-
дополнительного внешнего шума, и мы отложим ее обсуждение до сле-
следующего параграфа. Как показано в работе [3], эти же ме-
методы можно использовать и без введения шума.
Хотя такая техника применялась пока только к довольно про-
простым системам типа стандартного отображения, она является
весьма интересной, и мы изложим ее достаточно подробно, следуя
Абарбанелю. Он показал также [2], что этот же метод можно при-
применить к задаче о взаимодействии частицы с волной большой ам-
амплитуды (п. 2.26). Поскольку, как обсуждалось в п. 4.16 (см. также
[272]), стандартное отображение локально описывает широкий
класс систем, можно надеяться, что полученные для него резуль-
результаты будут качественно применимы и в более общем случае.
Представление Фурье. Для одной итерации стандартного отобра-
отображения
и коэффициенты
Г
переноса
F — '
2я
D
1 2
Д/1 = л sin
равны
|"а/^90-
1 2п
4л 0J
«о
о,
4
E.
E.4
E.4
4.20)
.21а)
.216)
Это приближение часто называют квазилинейным 1).
Для получения корреляционных поправок вычислим коэффи-
коэффициент диффузии
<(Л)8>/ , е
Dn = '±-2-. E.4.22)
2га
Введем вероятность W перехода /0, 60 -> /„, 6Я за п итераций. Тогда
Dn=-^-lW{In, 8„, п\10, 80, 0)(ln-I0JdIndQn. E.4.23)
*) Множитель 1/2 в уравнении ФПК E.4.5) включен здесь в определе-
определение квазилинейного коэффициента диффузии.
Стохастическое движение и диффузия 327
Нам потребуется свойство рекуррентности:
W(I, 9, n\I0, 90, Q) = ldI'dWW(I, 9, п\Г, 9', л-1)х
XW(I', 9', п—1|70, 60> 0), E.4.24)
где из уравнений отображения
tt"(/, 9, п\Г, в', п— 1) = б(/ — /' — Ksine'N(9 — 9'_ /'_ К sin в').
E.4.25)
Вычисление Dn непосредственно из E.4.23) — E.4.25) быстро
становится слишком громоздким. Такую процедуру можно про-
провести для п --= 2; она приводит к интересным осцилляциям D2
в зависимости от /0, хотя и не ясно, какое значение мог бы иметь
этот эффект. Для больших п необходимо найти метод, который
становился бы проще с ростом п. Как мы увидим, это можно сде-
сделать с помощью фурье-представления.
Представим W в виде ряда Фурье по 9 и интеграла Фурье по /:
W(I, 9, л|/0, е0> O)=^jdqexV(itnd + iqI)an(m, q), E.4.26)
m
где коэффициенты ап зависят также от /0 и 90.
Нас интересует значение Dn при больших п. Поскольку /„
растет как л]п, то для я» 1 в E.4.23) можно сохранить только
член с.1\:
Пп=^-\ dQdIPW (I, 9, п | /0,*.90) 0). E.4.27)
После подстановки E.4.26) в E.4.27) и интегрирования по 9 ос-
остается только член с т = 0. Замена /2 на — d2elgI/dq2 и двойное
интегрирование по частям (по q) приводит к выражению
Dn = ^-[ dqdleiql -5- [an @, q)}. E.4.28)
олучаем
E.4.29)
Интеграл по / дает 2лб (q). После интегрирования по q получаем
п 4я2 <9Чг@, q)
2n
9=0
Выведем теперь рекуррентное соотношение для а„, которое
потребуется нам для вычисления E.4.29). Из E.4.26)
an(m, q) = —!—jd9d/exp(—imQ—iqI)W(I, 9, n\I0, 90) 0).
BnJ
E.4.30)
Для n = 0 положим
W=8(I — /0)S(9—90), E.4.31)
exp(iqlirn%) E.4.32)
328 Глава 5
При п>0, подставляя E.4.24) в E.4.30), получаем
ап (т, а) = —Ц- J d6d/ exp (—imQ—iql) X
х Ш'(И'Ь{1 — /' — /С sin 9') б (9 — 6' — /' — /С sin 6') х
')а„-х{т', q'). E.4.33)
Интегрируя по 9 и /', находим
ап(т, q)= ' V j'dq'd<d'dlan_r{m'', q') x
хехр[— ш(9' + /) — iql-riq'(l — К sinQ') +im'Q']. E.4.34)
Интегрирование по / дает
2лб (—m—q — q'),
что позволяет взять интеграл по q'\
ап{т, q) = X \ dQ'an^(m', q) x
2л т> '
X exp [i (т! — т) 9' — t^K sin 0'], E.4.35)
где
q = q^m. E.4.36)
Используя разложение
оо
exp (iqK sin 9') = 2 // (i 4 \ К) exp (i/8' sgn (q)),
l=—ao
где sgn (.v) =- 1 для х > 0 и sgn (x) — — 1 для х<0, a fi — функ-
функция Бесселя, получаем после интегрирования по 9'
ап (т, q) = ?.i,?l(\q\K)bk{m'-m-l?,gnQ))an^{m\q). E.4.37а)
Здесь 6*. (т) = 1 при т = 0 и 6ft (т) = 0 при m Ф 0. Проведя
суммирование по т', находим рекуррентные соотношения:
ап{т„, qn) = '2i?in(\qn-i\K)an_-1(mn-1, qn^), E.4.376)
тп = тп-х—1п sgn (<7n_i) [из бй в E.4.37а)], E.4.38а)
qn = qn-i—mn [из E.4.36)]. E.4.386)
Итерируя E.4.376) я раз, получаем выражение для ап через а„:
ап{тп, qn)= 2 fin?ln-i- • • АаоК, ?о)- E.4.39)
'п 11
Фурье-траектории. Согласно E.4.38), набор п целых чи-
чисел |/„, . . . , /jj определяет некоторую траекторию на плоскости
Стохастическое движение и диффузия
329
Фурье (m, q). Из E.4.29) следует, что в коэффициент диффузии Dn
дают вклад только те из них, которые оканчиваются в точке т„ = О
и qn = 0. Типичная траектория показана на рис. 5.12, а.
Аргументы функций Бесселя равны К \qi \, и если qc Ф 0, то
при К -*- оо fi~ К~'~. Поэтому при больших К основной вклад
дают члены с qt —>¦ 0. Наибольший х) из них соответствует всем
/,- = 0. Согласно E.4.38), его фурье-траектория длины п является
неподвижной точкой вблизи начала координат (рис. 5.12, б). В этом
случае
an @, q) =
Bд)-
E.4.40)
@)
(-2)» --
"Ж,
(-3)
(-2)
Рис. 5.12. Фурье-траектории.
а — типичная траектория, оканчивающаяся в точке (т, q) = @, - 0); б — квазилиней-
квазилинейная неподвижная точка @, —0); в — траектория поправки порядка К~' 2; г -е — тра-
траектории поправок порядка К . Числа в скобках указывают значения / в соответствую-
соответствующих точках (т, q).
Подставляя это выражение в E.4.29) и разлагая /0 до квадратич-
квадратичных членов, получим при п > 1
д2
т. е. квазилинейный результат E.4.216) 2).
г) Это не очевидно заранее из-за взятия производной в E.4.29). Поэтому
необходимо проанализировать также члены с I = 1 и 1= 2 (см. ниже).—
Прим. ред.
2) Формально он не зависит от п, однако выражение E.4.29) получено
в предположении п > 1.— Прим. ред.
330 Глава 5
Для вычисления поправок к этому значению рассмотрим дру-
другие фурье-траектории. Главные поправки соответствуют траекто-
траекториям, наименее уклоняющимся от начала координат. Имеются две
траектории, возвращающиеся в начало координат через три шага *),
начиная с произвольного номера г. Из E.4.38) 2) имеем т1 + т% =0
или т1 = ± 1; т2 = + 1. Первая из траекторий показана на
рис. 5.12, в. Значения / для qr = 0+ получаются из E.4.38а) и
указаны на рисунке. Вклад этой траектории в величину ап опреде-
определяется из E.4.39):
[/о (WV-i (К \qr\)X
Учитывая, что \qr\ =\ qr+2 \ = q и \qr+11 = 1, получаем
-,. Bп?\ЫЩ\п-ЧГЛЩ]УЛК)е-1«'°. E 4.11)
Вторая траектория получается поворотом первой (рис. 5.12, б)
на 180° и дает точно такой же вклад в ап. Для больших п сущест-
существует 2п траекторий, соответствующих г = 1, 2, . . . , п0. Сумми-
Суммируя их вклады и оставляя в разложении E.4.41) по q только члены
с q2, находим
[ап @, q) = -^- ^- /2 (К). E.4.42)
Вместе с E.4.40) это дает
W2 Г 1 Т
E.4.43)
В пределе больших К и п второй член дает малую поправку к ква-
квазилинейному приближению. Действительно, из асимптотического
представления /2 (К)
видно, что поправка имеет порядок /("' 2.
Аналогичным образом можно найти траектории, дающие по-
поправки ~ ТС. К ним относятся траектории на рис. 5.12, г, д, е,
получающиеся из них поворотом на 180°. Окончательный резуль-
результат с точностью до поправок порядка К включительно имеет вид
E.4.45)
х) Из E.4.38) легко видеть,гчто возврат через два шага невозможен.—
Прим. ред.
2) Траектории с | f/гх | >- 1 дают меньшие поправки.
Стохастическое движение и диффузия
331
Он был получен Речестером и Уайтом [345] (без члена ftI)- За-
Заметим также, что разность /|—f\ имеет порядок К~2 и превышает
точность E.4.45).
Речестер и Уайт получили также численную зависимость ко-
коэффициента D50 от К по 3000 траекторий. Их результаты представ-
D
к
Рис. 5.13. Зависимость скорости диффузии D/D1 от параметра К стандарт-
стандартного отображения (по данным работы [345]).
Точки — численный эксперимент; кривая — теория.
лены на рис. 5.13. Точки соответствуют численным значениям D50,
нормированным на квазилинейный коэффициент диффузии /С2/4.
Сплошная кривая соответствует зависимости E.4.45) без слагае-
слагаемого 2) /|- Осцилляции в зависимости D (К) впервые были заме-
J) Эта ошибка была исправлена авторами в работе [346].— Прим. ред.
2) Для больших К основной эффект от этого члена сводится к неболь-
небольшому сдвигу кривой вверх. Отметим, что численный счет производился в при-
присутствии малого внешнего шума (см. § 5.5).
332 Глава 5
чены Чириковым [70]. Следует ожидать, что при /С<;4 роль обла-
областей устойчивости станет существенной и необходимо будет учи-
учитывать большее число фурье-траекторий. Для K<Z 1 стохастиче-
стохастические области ограничены и Dn —>¦ 0 при м->- оо. Чтобы сгладить
сингулярности, связанные со сложной структурой фазовой пло-
плоскости, Речестер и Уайт ввели небольшой внешний шум, влияние
которого мы рассмотрим в следующем параграфе. Можно надеяться,
что такой подход обеспечит сходимость суммы по всем фурье-тра-
екториям и позволит в принципе найти точное значение D. Здесь
возникает, однако, другая трудность. Карни и соавторы 1223 ]
показали, что D -> оо для тех значений К, при которых сущест-
существуют ускорительные режимы движения (см. п. 4.16). Связано это
с тем, что для некоторых начальных условий величина / изменяется
со временем монотонно, а не диффузионно, т. е. значительно быст-
быстрее, и соотношение E.4.45) становится неприменимым (см. также
[54 jI). В стандартном отображении ускорительные режимы по-
появляются при К > 2л. Их влияние видно на рис. 5.13 как повы-
повышение D вблизи нескольких первых максимумов. Аналогичные
результаты были получены Кари и Мейсом [53 ] для другого ото-
отображения.
§ 5.5. Влияние внешнего шума
5.5а. Введение
В § 5.4 было показано, что сильное перекрытие резонансов приво-
приводит к внутренней диффузии с такой же скоростью, как если бы
фазы возмущения были случайными. Это эквивалентно сильной
внешней диффузии, вызываемой посторонним по отношению к си-
системе источником шума. Для задачи о взаимодействии волна —
частица, например, это соответствует большому числу сильных
нескоррелированных волн, как предполагается в квазилинейной
теории. Таким образом, в пределе сильной стохастичности внутрен-
внутренняя и внешняя диффузии похожи друг на друга 2).
г) Асимптотический характер описанного метода (вычисления Dn при
п -> оо) обманчив. На самом деле реально [например, в E.4.45)] можно
учесть лишь несколько близких (п — 1) корреляций С (n) = (sin90 sin 6„).
Как показано в работе [54] (см. также [464]) прямым вычислением С (п),
соотношение E.4.45) включает фактически только две из них: С B) =,— /г/2
и С D) «/|/2 (С A) = 0; С C) = (f23—ff)/2 ~~ \КГ*). Вопрос об асимпто-
асимптотическом поведении С (п) при п -> оо является очень сложным. При наличии
границы стохастичности в фазовом пространстве (например, островки устой-
устойчивости) корреляции затухают очень медленно, как С (п) ос п~р\ р < 1. При
этом простое диффузионное описание может оказаться неприменимым, если
Dn -* оо при п -> оо. Сумма E.4.39) в этом случае расходится. Обсуждение
этих вопросов см. в работах [507, 508, 485] и в предисловии редактора пе-
перевода.— Прим. ред. «¦¦>
2) Наиболее существенное отличие между ними — сохранение энергии
в случае внутренней диффузии в автономной системе.— Прим. ред.
Стохастическое движение и диффузия
333
Однако в том случае, когда внешнее случайное воздействие мало
по сравнению с внутренним возмущением в самой системе, необ-
необходимо исследовать их совместное действие. Если, например, сла-
слабый внешний шум действует на систему в устойчивой области, то
траектория движения не останется, конечно, на гладкой инвариант-
инвариантной кривой. Однако скорость изменения интегралов движения бу-
будет определяться при этом, вообще говоря, лишь слабым шумом 1).
Такая устойчивость существенна как для реальных физических
систем, всегда подверженных действию шума, так и при числен-
численном моделировании с его неустранимыми ошибками счета.
Ав
г
AJ
Рис. 5.14. Расплывание фазовой ячейки для интегрируемой системы на при-
примере отображения поворота.
Линейный сдвиг происходит вдоль инвариантных кривых (пунктирные линии); ср.
рис. 5.5.
Описанная выше устойчивость основана на том, что малое воз-
возмущение приводит к расходимости близких траекторий в основном
вдоль, а не поперек инвариантных поверхностей. Покажем это на
примере отображения поворота C.1.8)
Jn+i=Jn, 6л+1 = 6Л + 2яа(Ул+1).
Пусть (рис. 5.14) близкие начальные условия равны J и J + AJ.
Тогда
Таким образом, продольный (по отношению к инвариантной кри-
кривой J = const) размер параллелограмма на рисунке
Эх (J + Д J) — 6Х (J) = 2ла' Д J
растет линейно с я, в то время как поперечный размер AJ остается
*) Вообще говоря, это не так, см. п. 6.36.— Прим. ред.
334
Глава 5
неизменным. Грин [165] получил аналогичный результат для дру-
другого примера, показав, что начальный круг ошибок преобразуется
в сильно вытянутый эллипс, большая ось которого направлена
вдоль инвариантной кривой.
f- 16 HiliiSliilb:
:;- 12 -
h^^^i^|^
?3 нИигзг ??|Ш?
Рис. 5.15. Фазовая плоскость (и, 4') Для отображения Улама со слабым внеш-
внешним шумом E.5.1) (по данным работы [274J).
Случайный скачок ф<гзьг Ai|' равномерно распределен в интервале [ А']' |
а — 10 210 итерации: б — !?0 480 итераций для одной траектории.
С 0,005; М = 10;
Стохастическое движение и диффузия 335
Указанное обстоятельство позволяет получать миллионы ите-
итераций отображения без значительной диффузии инвариантных кри-
кривых х). Тем не менее эта диффузия налагает некоторые ограничения
на точность определения границы стохастичности.
Для двумерных отображений Либерман и Лихтенберг [274 ]
численно исследовали медленную диффузию под действием шума
на примере упрощенного отображения Улама C.4.4):
"л+аНИп + ЧЬ—1/2|, E.5.1а)
i|'n+i = i|'n + M/«n+i-bAi|5, mod 1, E.5.16)
где Дя|> — дополнительный случайный сдвиг фазы. Если А\р при-
принимает любые значения во всем интервале [0, 1 ], то движение све-
сведется к случайным блужданиям независимо от динамического фа-
фазового сдвига М/ип+1. Именно это и наблюдалось при численном
моделировании. Для Дг|з < 1. что соответствует слабому случай-
случайному возмущению, области устойчивости также постепенно за-
заполняются траекторией. Это, однако, происходит значительно мед-
медленнее, чем само движение в этих областях. На рис. 5.15 показан
пример такого движения для—0,005-< AiJ>-<0,005. При таком слабом
шуме время диффузии в глубь островков устойчивости значительно
превышает период колебаний внутри них. Как видно из рис. 5.15,
мелкие островки почти заполнены траекторией, а крупные — лишь
немного деформированы. Интересно отметить, что более запол-
заполненные зоны возникают внутри устойчивых областей. Это является
следствием временного «захвата» траектории в этой области под
действием шума. Такие зоны повышенной плотности появляются
и в стохастической компоненте вокруг островков устойчивости.
На достаточно большом временном интервале, определяемом ста-
статистикой заполнения, все эти неоднородности должны исчезнуть.
5.56. Диффузия в присутствии резонансов
За достаточно большое время резонансы могут оказать сильное
влияние на диффузию даже под действием слабого шума. Так, на-
например, если в системе есть большие (неперекрывающиеся) резо-
резонансы, то малое внешнее возмущение может перевести траекторию
с нерезонансной инвариантной кривой на резонансную. Пусть время
между внешними «толчками» велико по сравнению с периодом фа-
фазовых колебаний. Тогда следующий толчок может произойти уже
1) Пример подобной диффузии вследствие ошибок округления приведен
в работе [73, §5]. Любопытно отметить, что скорость диффузии^оказалась
на два порядка меньше, чем для случайных ошибок той же величины.—
Прим. ред.
336 Глава 5
на другой стороне резонанса. При этом характерный коэффициент
диффузии в окрестности резонанса значительно возрастет 1):
D-(A/J/t, E.5.2)
где А/ — ширина резонанса, а т — время между двумя случай-
случайными толчками. Однако если значительные области фазового про-
пространства не содержат больших резонансов, то, как будет видно,
малая скорость нерезонансной диффузии существенно подавляет
глобальную диффузию.
Скорость диффузии. В присутствии слабого случайного возмуще-
возмущения скорость диффузии для стандартного отображения была полу-
получена аналитически Речестером и Уайтом [345 J и Речестером и др.
[346 ]. В последней работе был введен метод фурье-траекторий,
описанный в предыдущем параграфе. Покажем, как следует видо-
видоизменить метод п. 5.4г, чтобы учесть случайное возмущение. Вве-
Введем в стандартное отображение случайное изменение фазы |:
E.5.3а)
вя+1 = вп + 1п+1 + Ъ, E.5.36)
где ? имеет гауссово распределение с дисперсией а:
?-)• (ВА4)
Тогда вероятность перехода E.4.25) принимает вид
W(I, 9, п\Г, 9', л— 1) = J dip (?) 6 (/ — /'—/С sin 9') х
Хб(9 — 6'—/' — Ksine' —?). E.5.5)
Подставив это выражение в E.4.33) и проинтегрировав по 9 и /',
получим E.4.34) с дополнительным множителем
—яЛг). E.5.6)
В результате вместо E.4.376) приходим к следующему рекуррент-
рекуррентному соотношению:
ап (т„, qn) = \] fin (| qn-.x | /С) ехр / _-i-m2ncs
E.5.7)
J) Нижеследующее выражение в точности совпадает с оценкой Будкера
(см. [509], с. 50), который первым обратил внимание на такой механизм ди-
динамического усиления диффузии. Впоследствии это явление получило на-
название неоклассической диффузии, теория которой была развита Галеевым
и Сагдеевым [510].— Прим. ред.
Стохастическое Овижение и диффузия
337
Используя фурье-траектории, изображенные на рис. 5.12, б—е,
получаем коэффициент диффузии
А, = ^ \~ - П (К) е~° + ft (К) в'20 f 7\ (К) е'3а - /ЦК) г~Л ,
2 L 2
E.5.8)
который обобщает соотношение E.4.45), учитывая влияние внешнего
шума при К".:> 1 •
D
Pi
1
8
6
4
->
ю-2
8
6
4
ю-3
8
6
4
ю-4
:
-
; о= ю >
-
-
о=10-;
-
: 0=10-3^
-—"^
1 1 1
! 11 1 1
-^
J
1 1 1 1
/ -
п
III
-ггг
о = 0
Граница
Чирикоба
/К = 0,989
Г 1 1 1 1
0,1 0,2 0,4 0,6 1,0 2 4 6
Рис. 5.16. Зависимость скорости диффузии D/D1 от К для различных усло-
условий внешнего шума а (по данным работы [346]).
Сплошные кривые — метод фурье-траекторий; пунктирная кривая — оценка E.5.14);
кружки — численный счет (о = 10~2).
338
Глава 5
Более интересным является случай КС 1- Речестер и др. [346]
показали, что в низшем порядке по К вклад в коэффициент диффу-
диффузии дают только фурье-траектории с / — 0 и / ^ 1, причем для
Рис. 5.17. Фазовая плоскость стандартного отображения.
Стрелками показана типичная траектория, приводящая к усилению внешней диффузии
при К 4S; 1.
п ^> B//СJ эти траектории должны начинаться и заканчиваться
в точке т = 0, q = 0. В результате они получили
тН"Ш' E5-9)
где Di = /С2/4 — квазилинейный коэффициент диффузии. Для
определения поправок к Dn было проведено численное суммирова-
суммирование по многим фурье-траекториям. На рис. 5.16 эти результаты
(сплошные кривые) сравниваются с данными численного моделиро-
моделирования (кружки). Для малых К значения D сходятся к E.5.9), а
для больших К величина D не зависит от ст. Для нас представляет
интерес область /С с< 1, где инвариантные кривые препятствуют
развитию внутренней глобальной стохастичности.
Стохастическое движение и диффузия 339
Качественно эти результаты можно получить из следующих
простых соображений (рис. 5.17). Прежде всего заметим, что из-
изменение фазы 6 на величину I ^ 1 приводит, как это следует из
E.5.3), к изменению действия
6/ = |/mcos9|?. E.5.10)
Усреднение по распределению E.5.4) и по 8 дает
<F/)*) = -~ I2mo. E.5.11)
Принимая /,„ « /С/2, получаем коэффициент диффузии
= 4L^ E.5.12)
что совпадает при малых а и К с E.5.9) 1).
Вообще говоря, необходимо еще учесть усиление диффузии на
резонансах. Пусть, например, траектория попадает под действием
шума в стохастический слой целого резонанса в точке А, затем
идет вдоль слоя А ->¦ В (В') -> С и покидает резонанс в точке С.
Если полупериод фазовых колебаний Т C.5.23) мал по сравнению
с \'а (что справедливо для малых аи К ~ Т — 1), то область фа-
фазового пространства, в которой идет диффузия, сокращается на
ширину резонанса. Заметим, что диффузия траектории А —»- С
может идти либо наружу от резонанса, как рассмотрено выше,
либо внутрь резонанса. В последнем случае средняя скорость диф-
диффузии падает. Таким образом, имеются две группы траекторий:
быстрые, проходящие резонанс, и медленные, которые захваты-
захватываются в резонанс. В качестве простой оценки примем, что отношение
средних скоростей диффузии для двух групп траекторий обратно
пропорционально квадрату интервала диффузии
-^-—Г-Bл)* «-. E-5.13)
где, согласно D.1.29), ширина целого резонанса на рис. 5.17 равна
2/С1/2, и мы пренебрегаем влиянием других резонансов. Примем
далее, что половина траекторий, попадающих на границу резонанса
(в точке А), совершает полпериода фазовых колебаний (от А до С)
и половина из них выходит из резонанса (в точке С). Таким обра-
образом, четверть всех траекторий проходит резонанс и попадает в
группу быстрых траекторий. Эффективный коэффициент диффузии
равен
Dm = ~D? ^~DS. E.5.14)
4 4
Используя для Ds выражение E.5.12), получаем с учетом E.5.13)
результат, показанный на рис. 5.16 пунктирной кривой. Несмотря
на грубость оценки, она дает разумные значения даже для К > 1,
1) Приведенная оценка справедлива лишь по порядку величины, и ее
совпадение с E.5.9) случайно [см. ниже E.5.18)].— Прим. ред.
340 Глава 5
где внутренняя стохастичность становится глобальной. Связано
это с тем, что если К незначительно превышает критическое значе-
значение К, = 1, то средняя скорость диффузии по-прежнему опреде-
определяется шумом, поскольку внутренняя диффузия является очень
медленной. Другой более эффективный механизм усиления внеш-
внешней диффузии резонансами будет рассмотрен в п. 6.36.
Усреднение коэффициента диффузии. Согласно оценке E.5.14),
средняя скорость диффузии близка к медленной между резонан-
резонансами, если только они не занимают значительную часть фазового
пространства. Это связано с непрерывностью диффузионного потока,
так что градиент плотности больше там, где локальная скорость
диффузии меньше, и обратно. Рассмотрим некоторый стационарный
поток Г в области А/ с переменным коэффициентом диффузии.
В каждом небольшом интервале с постоянной скоростью диффузии
имеет место следующее соотношение для функции распределения Р:
E.5.15)
Последнее равенство определяет средние по области значения D
и dP/dl. Таким образом,
dP l /dP^ E.5.16)
(D) dl D (I) \ dl
и усреднение по интервалу Д/ дает
1 1 Г dP ,, I dP \ 1 Г dl
- Ul = <
(D) M ) dl \ dl I A/ J D (I)
ИЛИ
1 ' ' "' E.5.17)
(D) Д/
д/
Это соотношение показывает, что (D) определяется в основном
теми областями, в которых величина \ID максимальна, т. е. D (/)
минимальна.
Возвращаясь к оценке скорости медленной диффузии E.5.12),
мы видим, что ее можно сделать более аккуратно, если найти за-
зависимость /,„ (/) и усреднить по /:
1
2л
{Ds} 2я
— '2т(П о
E.5.18)
В заключение подчеркнем различие между усреднением диффу-
диффузии по различным траекториям и усреднением по фазовому про-
пространству. В первом случае усредняется сам коэффициент диффу-
диффузии D, а во втором — его обратное значение \ID.
Глава 6
МНОГОМЕРНЫЕ КОЛЕБАНИЯ
*§ 6.1. Резонанс многомерных колебаний
В системах, близких к интегрируемым, резонансы окружены, как
мы уже знаем, стохастическими слоями. Однако в случае двух сте-
степеней свободы сохранение энергии ограничивает движение вдоль
слоя. В поперечном же направлении слои изолированы друг от
друга инвариантными поверхностями.
Системы с тремя и более степенями свободы отличаются двумя
существенными особенностями:
1. Стохастические слои пересекаются друг с другом, образуя
в фазовом пространстве единую всюду плотную «паутину».
2. Сохранение энергии не препятствует движению вдоль слоев
в пределах энергетической поверхности. Поэтому за достаточно
большое время траектория, переходя от слоя к слою, охватывает
всю энергетическую поверхность, подходя сколь угодно близко
к любой ее точке.
Основной механизм внутренней диффузии вдоль стохастиче-
стохастических слоев называется диффузией Арнольда по имени открывшего
ее В. И. Арнольда [12]. Диффузия Арнольда является универсаль-
универсальной в том смысле, что не существует критической величины воз-
возмущения, необходимой для ее возникновения, хотя скорость диф-
диффузии стремится к нулю при уменьшении возмущения. Численные
исследования проведены во многих работах (см., например, [68,
139—143]); сравнение с теоретическими моделями в простейшем
случае взаимодействия трех резонансов обсуждается в работах
[68, 70, 146] х).
Хотя обычно диффузию Арнольда рассматривают в отсутствие
перекрытия резонансов 2) [70], похожая диффузия происходит
и при перекрытии группы резонансов, причем в последнем случае
скорость диффузии резко возрастает 3). Хорошей иллюстрацией
обоих режимов является модельная задача о колебаниях шарика
между плоской и периодически гофрированной в двух направле-
направлениях стенками. Эта система, похожая на отображение Улама с до-
дополнительной степенью свободы, была исследована Теннисоном
и др. [406].
х) См. также работу [475].-— Прим. ред.
2) Имеются в виду первичные резонансы.— Прим. ред.
) Однако она перестает быть универсальной, т. е. появляется порог по
возмущению (см. ниже п. 6.2г).— Прим. ред.
342 Глава 6
Примером диффузии вдоль слоя перекрывающихся резонансов
является модуляционная диффузия (п. 6.2г). В этом случае медлен-
медленные колебания одной из основных частот приводят к появлению
«боковых» резонансов, которые могут перекрываться в определен-
определенной области параметров. Эта диффузия не универсальна, т. е. су-
существует определенная величина возмущения, ниже которой бо-
боковые резонансы не перекрываются. Интересно отметить, что пере-
перекрытие возможно, даже если частота модуляции мала по сравнению
с модулируемой частотой. Этот результат, казалось бы, противоре-
противоречит интуитивному представлению об адиабатическом поведении
в таком случае *). Возможно, что модуляционная диффузия сущест-
существенна для динамики пучков в накопительных кольцах [211, 404] а).
Диффузия вдоль стохастических слоев может быть связана не
только с внутренней динамикой системы, но и с внешним шумом,
эффект которого значительно усиливается на резонансах (§ 6.3).
Подобная диффузия рассматривалась Чириковым [71 j и Теннисо-
ном [405]. Важным примером диффузии в многомерной системе
в присутствии шума является движение частиц в тороидальных
магнитных полях. Мы рассмотрим эту задачу в § 6.4 и проведем
сравнение теоретических выводов с результатами численного мо-
моделирования.
В § 6.5 кратко обсуждаются системы с очень большим числом
степеней свободы, среди которых есть примеры как регулярного,
так и стохастического поведения.
* 6.1а. Геометрия резонансов
Рассмотрим интегрируемую систему с N степенями свободы, га-
гамильтониан которой имеет вид
Яо =//„(/),
где /—Л'-мерный вектор переменных действия. Движение в 2АЛмер-
ном фазовом пространстве (/, 6) происходит по поверхности N-мер-
ного тора и определяется iV-мерным вектором фаз 6, канонически
сопряженным вектору /:
/(9 =/о, е(*) = ю(/)*+е01 F.1.1)
где со/ (/) = dHJdlj — невозмущенные частоты.
Пространство переменных действия. На рис. 6.1 представлено
«Химерное» пространство переменных действия. Невозмущенная
*) См. примечание редактора на с. 367.— Прим. ред.
2) Следует различать модуляционную диффузию вдоль резонансов много-
многомерной системы (п. 6.2г) от понижения порога перекрытия и последующей
диффузии поперек резонансов вследствие низкочастотной модуляции в си-
системе. Обе цитированные работы относятся именно ко второму (более про-
простому) эффекту, который рассматривался также в работах [68, 467]. —
Прим. ред.
Многомерные колебания
343
энергетическая поверхность определяется в этом пространстве
с помощью условия #0 (/) = а. Если, например,
#„ = ?//, F.1.2)
то эта поверхность является сферой.
Резонансе!
Рис. 6.1. Пространство переменных действия невозмущенного гамильтониана
F.1.2) (по данным работы [276]).
Показаны энергетические поверхности (сферы) и резонансные поверхности (плоское-щ!.
Определим (N—1)-мерную резонансную поверхность посредст-
посредством условия
i».©(/) = 0, F.1.3)
344 Глава 6
где т называется вектором резонанса и имеет целочисленные ком-
компоненты. Так как т может быть любым, то резонансные поверх-
поверхности всюду плотны в пространстве переменных действия. Для
квадратичного гамильтониана F.1.2) несколько резонансных по-
поверхностей показано на рис. 6.1.
Рассмотрим теперь влияние малого периодического по 6 воз-
возмущения:
= Н0A)-геН1([, 0),
F14)
где суммирование производится по всем т&. Уравнения Гамиль-
Гамильтона для / имеют вид
/=—дН/дд =—ie}mkVke . F.1.5)
Следовательно, каждая компонента возмущения возбуждает ко-
колебания / в направлении ти- Для большинства компонент коле-
колебания не будут резонансными, т. е. ntk-Q (t) Ф const, поэтому со-
соответствующая амплитуда колебаний / будет порядка е. Однако для
некоторых k = R возможен резонанс:
mR- 6 (t) = QR = const, F.1.6)
где QR — резонансная фаза. Тогда амплитуда колебаний в направ-
направлении тк имеет порядок е'/2 (§ 2.4).
В качестве примера на рис. 6.2 изображены некоторые из ре-
резонансных и энергетических поверхностей для гамильтониана
Я0 = /?-ьF/2J. F.1.7)
В этом случае, согласно F.1.3), резонансными поверхностями яв-
являются линии:
2 = 0. F.1.8)
Отметим, что так как при резонансе
mR.^~ = 0, F.1.9)
то вектор tnR лежит на невозмущенной энергетической поверхно-
поверхности. Вообще говоря, вектор mR не перпендикулярен резонансной
поверхности (см. пунктирный прямоугольник на рис. 6.2). Именно
в этом случае резонанс существенно усиливает действие внешнего
шума (§ 6.3). Из рис. 6.2 видно также, что резонансные поверхно-
поверхности не пересекаются на поверхности постоянной (ненулевой) энер-
энергии. Эта особенность типична для систем с двумя степенями сво-
свободы .
Многомерные колебания
345
Для трех и более степеней свободы резонансные поверхности,
вообще говоря, пересекаются, как показано на рис. 6.3, а для га-
гамильтониана F.1.2) с N = 3. Резонансными поверхностями яв-
являются здесь плоскости, проходящие через начало координат и пе-
пересекающиеся по прямым линиям. Они пересекают также сфери-
72
/66
//////
Ж
If//////'У ^*—"""
'/// /
/ 60 / 48
/54/4
/ / / /
V//
' //
/ 36
"А
6 !
»^г-
\ 1
Рис. 6.2. Линии резонансов (прямые) и линии постоянной энергии (эллипсы)
для гамильтониана F.1.7) (по данным работы [405]).
Числа на прямых — значения т, в F.1.8) при т2 = 1. Обведенная пунктиром область
показана в увеличенном виде на рис. 6.16.
ческие поверхности постоянной энергии Яо (/) = а и пересекаются
между собой на этих поверхностях. В местах пересечения возможны
переходы с одного резонанса на другой. Пересечения резонансов
с энергетической поверхностью образуют сложную единую сеть,
или паутину Арнольда, часть которой показана на рис. 6.3, б для
резонансов с \т;\ ^2.
В 2iV-MepHOM фазовом пространстве резонансы F.1.3)* образуют
BN—1)-мерные поверхности. Инвариантные же поверхности, оп-
определяемые соотношением / = const, являются /V-мерными. Уело-
346
Глава 6
Энергетическая
по&ерхность
Резонансы
Диффузия
ДрнальЭа
Рис. 6.3. Топология диффузии Арнольда.
а — диффузия (волнистая линия) переходит с одной резонансной погерхностн на другую по
линии пересечения их с энергетической поверхностью (по данным работы [276)); о—спау-
тина» Арнольда иа энергетической поверхности; показаны только некоторые из резо-
нансов (по данным работы [406]).
Многомерные колебания 347
вие пересечения стохастических слоев можно получить теперь гео-
геометрически. Если N > 3, то BN—1)-мерные резонансные поверх-
поверхности не изолированы друг от друга iV-мерными инвариантными
поверхностями (см. рис. 1.16). Схема стохастического слоя пред-
представлена также на рис. 1.17, где резонансная переменная IR — J г
характеризует фазовые колебания на резонансе, а остальные (N—1)
переменные действия представлены величиной J2 = Is и описы-
описывают движение вдоль слоя.
Особенность движения вдоль стохастического слоя можно по-
пояснить следующим образом. Пусть полная энергия сохраняется,
так что
причем для резонансной переменной
Д/Л~ е'/:. F.1.10)
Тогда для трех степеней свободы
Изменения переменных /s, и /Sa вдоль слоя могут быть большими
и ограничены [с учетом F.1.10)] только условием
В случае же двух степеней свободы (A/s2 = 0) из F.1.10) и F.1.11)
следует
A/S~e'%
т. е. смещение вдоль стохастического слоя мало.
* 6.16. Примеры диффузии Арнольда
Возможность неограниченного движения вдоль резонанса до-
доказана Арнольдом [12] на примере гамильтониана
Я = — (/д + /|) + е (cos QR — 1) A + И- si" ®s + И-cos 0-
При (i = 0 и е Ф 0 существуют два интеграла движения:
HR = — /д + е cos 8д = const,
причем последний из них описывает резонанс. Возмущение (ц =j? 0)
приводит к образованию стохастического слоя вокруг сепаратрисы
этого резонанса. Так как возмущение изменяет как IR, так и /s,
то возникает хаотическое движение вдоль стохастического слоя
(по /s). Роль третьей степени свободы играют здесь переменные t
и — Я (п. 1.26).
348 Глава 6
Арнольд высказал предположение, что движение вдоль резо-
нансов является типичным свойством многомерных нелинейных
колебаний, однако строгое доказательство этого отсутствует 1).
Недавно Холмс и Марсден [197], используя метод Мельникова
[299] (см. § 7.3 ниже), показали существование диффузии Арнольда
у большого класса гамильтоновых систем, близких к интегрируе-
интегрируемым.
Первые численные эксперименты по хаотическому движению
в многомерных системах были выполнены Фрёшле и сотр. 2). В ча-
частности, в работах Фрёшле [139, 140] исследовалось число изоли-
изолирующих интегралов движения в системах с тремя степенями сво-
свободы. Оказалось, что в зависимости от начальных условий сущест-
существуют либо два интеграла, либо ни одного (кроме энергии). Этот
результат находится в согласии с гипотезой Арнольда, что движе-
движение происходит либо по инвариантному тору, либо по стохастиче-
стохастическим слоям. Это значит, что в общем случае N степеней свободы
имеется либо N—1, либо ни одного интеграла движения, кроме
энергии. Аналогичные соображения высказывались Фрёшле [139]
и были подтверждены численными экспериментами [141—143]
для Лт = 3 и N = 4.
Модельная задача. Рассмотрим трехмерные колебания шарика ме-
между двумя упругоотражающими неподвижными стенками, одна
из которых плоская (z = h), а другая (г»0) — гофрированная
как по х, так и по у (рис. 6.4, а). Положение системы на четырех-
четырехмерной поверхности сечения задается значениями координат хп
и уп и углов а„ — arc tg (vx/vz) и р"„ = arc tg (vulvz) непосредст-
непосредственно перед п-м отражением от гофрированной стенки, где v —
вектор скорости шарика (рис. 6.4, б). Считая гофрировку слабой
(a h, ak <^ 1), можно записать упрощенное отображение (ср.
и. 3.4а) в явном виде
a«+1 = а* — 2axkx sin kxxn + pkxyc,
xn+1==xn + 2htgan+1, FЛ2а)
1) Основная трудность здесь — получение достаточно эффективных ана-
аналитических критериев неинтегрируемости, поскольку в полностью интегри-
интегрируемой системе диффузия Арнольда, конечно, отсутствует (см. примечание
редактора на с. 315). Одним из возможных критериев является пересечение
сепаратрис, которое было открыто и использовалось еще Пуанкаре [337,
и. 226] и интенсивно изучается в последнее время (см., например, [197,
479, 480, 483, 484, 511]). Однако использование этого критерия ограничено
в самом интересном (для диффузии Арнольда) случае очень слабого возму-
возмущения (см. примечание редактора на с. 240).— Прим. ред.
2) Это, конечно, не так. Достаточно вспомнить знаменитую работу Ферми,
Паста и Улама [127], в которой фактически наблюдалось и хаотическое дви-
движение (см. рис. 5—7), хотя основное внимание авторов было привлечено к ре-
регулярным колебаниям в многомерной нелинейной системе. Хаотический ас-
аспект этой задачи исследовался позднее во многих работах (см., например,
[135, 208]).— Прим. ред.
Многомерные колебания
349
= Р„ — 2ayky sin ^
F.1.126)
Здесь ус == sin (kxxn -f ^«), «а, йц — амплитуды гофрировки
только по х и только по у соответственно, а \л — удвоенная ампли-
амплитуда косой гофрировки, связывающей движение по х и у.
Гофрированная
стенка
ГлаЭкая стенка
Рис. 6.4. Модельная задача (по данным работы [406]).
¦а — колебания шарика между гладкой и гофрированной стенками; б — проекция дви-
движения на плоскость (х, г).
Если (-1 = 0, то отображение F.1.12) описывает независимее дви-
движение в плоскостях (х, z) и (у, г). На рис. 6.5 показаны различные
траектории на поверхности сечения (а, 6). Мы видим обычную кар-
картину для систем с двумя степенями свободы: резонансные и нере-
нерезонансные инвариантные кривые и стохастические области. Центр
целого резонанса при а = 0 = 0 соответствует устойчивым коле-
колебаниям шарика вдоль оси z в одном из минимумов «потенциальной
ямы» стенки. Инвариантные кривые вокруг этого центра соответст-
соответствуют «адиабатическим» колебаниям вдоль оси х, медленным по
сравнению с колебаниями по z. Имеются две основные стохастиче-
кие области. Толстый стохастический слой расположен в районе
350
Глава 6
а л; ± л,'2. Он возникает вследствие перекрытия целых резонан-
сов, при которых за один период колебаний по г траектория прохо-
проходит несколько периодов гофрировки по х, как показано на рис. 6.5.
Тонкий стохастический слой, отделенный при данных значениях
параметров от толстого слоя инвариантными кривыми, расположен
в окрестности сепаратрисы целого резонанса а — 0. Движение
„Толстый
слой"
ИнВариантны?
крибь'Е
-я/2
-7Г
Рис. 6.5. Фазовая плоскость (а, 6) модели F.1.12) (по данным работы [406]).
(X — 0; 6 -- kxx; отношение %х ; h : ах равно 100 : 10 : 2; ?. — 2л lix: 15 траеморнм
no 1 О1 итерации.
в нем происходит вблизи максимума потенциальной ямы гофриро-
гофрированной стенки и охватывает как колебания, так и пролет в сосед-
соседние ямы.
Типичный пример диффузии Арнольда в присутствии связи
показан на рис. 6.6. Четырехмерная поверхность сечения (а, х,
Р, у) представлена здесь двумя проекциями (а, х) и ф, у), которые
для удобства совмещены на рисунке. Начальные условия выбраны
внутри резонанса по х и в пределах тонкого стохастического слоя
по у. Численное моделирование показывает, что движение по у
остается внутри стохастического слоя, пока колебания по .v не до-
достигнут своей сепаратрисы. Последовательные стадии диффузии
по х под действием стохастических колебаний по у показаны на
рис. 6.6, б—г. Это и есть диффузия Арнольда, поскольку на поверх-
поверхности сечения она идет вдоль стохастического слоя резонанса по у.
При дальнейшем движении диффузия охватывает большую часть
Многомерные колебания
351
плоскости (а, х). В частности, наблюдались переходы диффузии
из одного стохастического слоя (у-резонанса) в другой (х-резо-
нанса), а также в толстый слой. Эти эффекты показаны на рис. 6.7
в проекции (а, |5) для х « у х 0. Траектория случайно блуждает
по тонким и толстым слоям, проводя большую часть времени в по-
последних.
сечения
I
X --= 3 5X106
а
х
л _ Начальные
условия
в = кхх, »=*v.y
Л; = 107
Рис. 6.6. Диффузия в тонком слое (по данным работы [406]).
.« h = 0,004; отношения %х : h : ох и Л : h : о„ равны 100 : 10:2.
Это, однако, еще не все. Вспомним, что система резонансных
поверхностей является всюду плотной в пространстве переменных
действия. Рассмотрим, например, резонанс связи
где о)х, ау — частоты колебаний, а тг, т2 — целые числа; на
рис. 6.7 показан резонанс, соответствующий т1 = —т2. Стохасти-
352
Глава 6
ческий слой этого резонанса также является составной частью
паутины Арнольда. Для начальных условий в этом слое и х да у да О
быстрые колебания шарика по оси z кажутся вначале устойчивыми.
Однако это не так. После достаточно большого числа отражений
мы можем обнаружить, что шарик движется почти вдоль стенок.
В типичном случае диффузия идет вначале по резонансу связи,
5 X 107
Толсглыи
слой
"OHKUU
слой
¦ ". ¦ ¦-'¦ . i
V
. •• .
: v
/ Начальные
/ условия "
/
*,-'¦
¦ <1>
4
W
'•, '...-¦'.
- ¦.; г
Ж
Тонкий слой
Толстый
слой
Рис. 6.7. То же, что и на рис. 6.6 в проекции на плоскость (а, C) (по данным
работы [276]).
А' — и ^ 0: 5 X 10" итераций.
затем по тонким стохастическим слоям и, наконец, по толстым
слоям. При этом шарик лишь изредка будет возвращаться в окрест-
окрестность начального положения вблизи х = у = 0, поскольку подав-
подавляющая часть паутины Арнольда состоит из толстых стохастиче-
стохастических слоев. Остальные же области вроде резонансов связи, где дви-
движение кажется регулярным, составляют пренебрежимо малую (но
всюду плотную!) часть стохастической паутины. Эта удивительная
картина является характерной для диффузии Арнольда.
Многомерные колебания 353
§ 6.2. Скорость диффузии вдоль резонансов
Первые теоретические оценки диффузии Арнольда были получены
Чириковым [68, 70 ] и его сотр. х). Теннисон и др. [406 ] и Либерман
[273 ] рассчитали скорость диффузии для модельной задачи, опи-
описанной в п. 6.16. Теоретический анализ основан на разделении ис-
исходной системы с тремя степенями свободы на две подсистемы, каж-
каждая из которых рассматривается в первом приближении незави-
независимо. Мы будем называть такой подход моделью стохастической
накачки 2) . В простейшем случае при этом учитывается взаимо-
взаимодействие только трех резонансов. Пусть, например, ведущий ре-
резонанс, вдоль которого идет диффузия Арнольда, связан, скажем,
со степенью свободы 2. Взаимодействие между степенями свободы.
1 и 2, описываемое гамильтонианом
Н± (/lt /2) еъ в,) « const, F.2.1)
приводит к интенсивному хаотическому движению поперек стоха-
стохастического слоя ведущего резонанса. Взаимодействие же между
степенями свободы 2 и 3 с гамильтонианом
Hi (It, /8, в., 63)~ const F.2.2)
вызывает более слабую диффузию Арнольда. Подсистемы F.2.1)
и F.2.2) рассматриваются последовательно. Сначала из F.2.1) на-
находятся величины 92 (t) и /2 (t), характеризующие движение в сто-
стохастическом слое. Затем они подставляются в F.2.2), что дает
возможность найти стохастическое изменение I3 (t), определяющее
диффузию Арнольда.
Основная трудность при использовании этого метода состоит
в выяснении, какие именно резонансы определяют диффузию вдоль
и какие-—поперек стохастического слоя. В случае трех резонан-
резонансов ведущим можно считать любой из них, что просто определяет
область начальных условий движения. Наиболее сильный из остав-
оставшихся задает диффузию поперек слоя, а более слабый вызывает
диффузию Арнольда 3).
* 6.2а. Расчет диффузии в модели стохастической накачки
Покажем, как оценить скорость диффузии Арнольда на примере
системы, описываемой отображением F.1.12). Мы рассмотрим три
различных режима диффузии с последовательно уменьшающейся
скоростью. Первый режим соответствует диффузии по а вдоль тол-
толстого стохастического слоя в плоскости (Р, у). Диффузия происхо-
происходит вследствие связи со случайным движением по у. Второй режим
х) См. работу [146].— Прим. ред.
2) Stochastic pump model. Этот механизм, по-видимому, впервые обсуж-
обсуждался кратко в работе [139].— Прим. ред.
3) Обсуждение такого «распределения ролей» между резонансами см.
в работе [70, § 7.2].— Прим. ред.
354 Глава 6
аналогичен первому, за исключением того, что диффузия по а идет
вдоль тонкого стохастического слоя {/-резонанса. Наконец, третий
режим отвечает диффузии вдоль резонанса связи.
Найдем прежде всего гамильтониан для отображения F.1.12).
Как и в п. 3.1в, преобразуем разностные уравнения F.1.12) в диф-
дифференциальные с помощью б-функции. В результате получаем не-
неавтономный гамильтониан с двумя степенями свободы:
Я (а, х, р, у, л) = — 2/ilncosa — 2/ilncosP — 281(п)С(х, у), F.2.3)
где
С(х, y) = axcoskxx + ayc.oskyy — {\l2)\LC.os{kxx + kyy), F.2.4)
6i(n)= S б("~=1 +2 ? cosBnn<7). F.2.5)
m=—оо <;=1
Диффузия в толстом слое. Выберем начальные значения $ и у вну-
внутри толстого стохастического слоя, а а и х вблизи центра целого
резонанса. При отсутствии связи между степенями свободы ([i = 0)
движение в плоскости (а, х) происходит по инвариантной кривой
(рис. 6.5). При включении связи происходит медленная диффузия
по а и х.
Перейдем к новым переменным ; Э = kxx, ц> = kyy, a = a/kx,
Р = §lky и представим гамильтониан Я в виде суммы Я = Нх -\-Ну,
где
Ну= — 2ftlncosp—2b1{n)aycosy, F.2.6а)
Нх х ha?—2ax cos 9 + \х cos F + q> (n)). F.2.66)
Здесь для удобства мы сохранили старые переменные а и |3 в но-
новом гамильтониане. В F.2.66) использовано приближение
— In cos a да a2/2 при a2 <^ 1, б, да 1 при со^ = 4ahk2 « 1, а (р
считается явной функцией п. Последнее допущение наиболее серь-
серьезно, поскольку при этом пренебрегается влиянием связи на дви-
движение по у. В результате мы получили два неавтономных гамиль-
гамильтониана с одной степенью свободы каждый х). Теперь можно ре-
решить уравнение движения независимой подсистемы F.2.6а) и найти
«стохастическую накачку» ф (п). Подставив ее в F.2.66), найдем
движение в плоскости (а, 8), которое и дает диффузию Арнольда.
В толстом слое, где имеется много перекрывающихся резонан-
сов, фаза ф хаотизуется за время порядка одной итерации отобра-
отображения 2). Поэтому с хорошей точностью можно считать, что после-
х) В этом случае говорят иногда о полутора степенях свободы.— Прим.
ред.
2) Дело не в перекрытии резонансов, а в масштабе времени релаксации,
в качестве которого можно принять грубо обратную величину КС-энтропии.
Последнюю легко оценить, поскольку подсистема F.2.6а) сводится локально
к стандартному отображению с параметром К = — ^k^a ft/cos2j3. — Прим.
ред.
Многомерные колебания 355
довательные значения фазы ср являются случайными и независимыми,
причем переход между ними имеет характер «скачка». Изменение Нх
определяется уравнением Гамильтона
йНх __ дНх
dn дп
Используя F.2.66), можно записать производную в виде
-^^ = -f- [fx cos (в + <р) I — ^x -^- sin [в + ф (п) ]. F.2.7)
an an on
Первый член в выражении справа описывает малые ограниченные
колебания. Считая колебания по 0 малыми
e = e0cos(©»n4-Xo), F.2.8)
где ах = 2п/Т = 2kx (axh)xl2, проинтегрируем второй член в урав-
уравнении F.2.7) по периоду отображения:
m+l
АНХ= I dniiQoax sin [ахп-\-х0] sin [Q-\-q>(n)].
m
При (йх < 1 подынтегральное выражение постоянно, поэтому
&НХ = \iQ0(dx sin [ахт + Хо] sin [9 + <р (m) ]. F.2.9)
Возводя это выражение в квадрат и усредняя как по %0, так и по ф,
получаем х)
1
)
В результате находим скорость диффузии в толстом слое
D1 = -L {(АНХ)*> = -i- F29oV*. F.2.10)
Z о
С изменением Нх в процессе диффузии параметры р. и и>х остаются
постоянными. Величина же 60 растет с Нх, а вместе с ней и скорость
диффузии.
На рис. 6.8, а—в теоретические значения Dt (сплошные линии)
сравниваются с результатами численного моделирования. Началь-
Начальные условия для 100 траекторий были одинаковыми в плоскости
(а, х) и случайными в пределах толстого слоя плоскости (|3, у).
Для каждой траектории просчитывалось 500 итераций отображе-
отображения. Вычислялись среднеквадратичные значения безразмерной
энергии (а2) = [h~2( (ЛЯ*J ) п]]/2, которые и сравнивались
1) Усреднение по фазе Хо. которая является постоянной интегрирования
в F.2.8), требует пояснения. На самом деле усреднять нужно по траектории,
т. е. по времени т. Для иррационального а>х при (йхт })> 1 это формально
эквивалентно усреднению по %0. Разумеется, диффузионный характер дви-
движения связан только с присутствием случайной фазы ф (т), иначе колебания
Нх были бы квазипериодическими.— Прим. ред.
356
Глава 6
с теорией. На рис. 6.8 каждый треугольник представляет резуль-
результат усреднения четырех независимых (по начальным условиям)
вариантов счета. Согласие с теорией достаточно хорошее, хотя она
Я несколько завышает систематически скорость диффузии. Это раз-
различие объясняется, возможно, тем, что значения фазы ф (т) не
полностью независимы.
-3
-4
-5
-6
-6
-5
-4
О
2,5
-3,5
1,2
1,5
-3
j_
2,0
2,5
3,0
б
3,5
Рис. 6.8. Диффузия в толстом слое (подданным работы [406]).
Сплошные линии — теория; треугольники — численные данные (статистический рагброо
для 100 траекторий лежит в пределах высоты треугольников); ц/h = 2 X l"~ ; n =500;
100 : 10 : 1; A,,
ay = 100 : 10 : 1,7
(кроме переменных величин).
Многомерные колебания 357
Диффузия в тонком слое. В этом случае начальные условия на пло-
плоскости (а, х) мы выбираем, как и в толстом слое, вблизи центра ре-
резонанса, а в плоскости (Р, у) — в тонком стохастическом слое ре-
резонанса. Как и в толстом слое, диффузия в плоскости (а, х) обуслов-
обусловлена слабой связью со стохастическим движением в плоскости
(Р, у). Однако скорость диффузии оказывается значительно меньше.
Действуя прежним методом, мы оставим теперь, однако, в функ-
функции бх (п) в F.2.6а) только члены с^ = 0и^=1из разложения
F.2.5) [ср. D.1.26)]. Используя, кроме того, приближение
— In cos р « |32/2, |32 ~ ciylh <^ 1, запишем гамильтониан F.2.6а)
в виде
Ну = ftp2—Ъху cos ф — Аау cos 2ял cos ср. F.2.11)
Здесь первые два члена определяют сепаратрису резонанса в пло-
плоскости (р, ?/), а третий приводит к образованию тонкого стохасти-
стохастического слоя в ее окрестности. Чтобы найти функцию ф (п) для
F.2.11), будем исходить из уравнения F.2.7), пренебрегая пер-
первым членом в его правой части:
¦^ = _H-^-sin[e + <p(/i)]f F.2.12)
dn dn
где 0 (п) определяется соотношением F.2.8). Примем, далее, что
на одном полупериоде фазовых колебаний ф (п) определяется дви-
движением по невозмущенной сепаратрисе (см. п. 1.3а) 1):
Фх (п) = 4 arctg (e<V) — я. F.2.13)
Обозначив s = (йуП, Qo — ах1а>и и записав фазу %0 в F.2.8) как
5Со = Qoso—я/2, получим из F.2.12)
=—(iBoQo J P(s)ds,
—оо
где
Р (s) = cos [Q0(s + s0) ] sin {90sin [Q0
При e0«l
P(s) = cos[Q0(s+So)lsin9, F.2.14)
и мы приходим к интегралу Мельникова—Арнольда (п. 3.5а):
j F.2.15)
о
который понимается в смысле его среднего значения по sx при
х) Поясним, что получаемое таким образом регулярное асимптотическое
решение фх (п.), которое только и используется ниже для вычисления ско-
скорости диффузии, не совпадает с решением ф (л) для подсистемы F.2.11). Раз-
Различие между ними сводится к хаотизации ф (я), которая учитывается в F.2.19)
неявно, со ссылкой на сепаратрисное отображение.— Прим. ред.
358 Глава 6
Sj-^oo. В рассматриваемом случае т = 2, и мы получаем
1 п „ ¦
-s4-2{—Qo)], F.2.16)
z
где, согласно C.5.18),
^2 (±Qo) = 4nQoe±IlQo 2 /sh (nQ0). F.2.17)
В результате находим
30Qo sin (Qoso) sh (itQ0/2)/sh (nQ0). F.2.18)
Из свойств сепаратрисного отображения (п. 3.56) мы знаем, что
величина Qoso хаотизуется на полупериоде фазовых колебаний Ту.
Усредняя по фазе Qoso, получаем
где
F(Qo) = Qo/4ch2(nQ0/2). F.2.20)
На рис. 6.9 приведен график функции F (Qo) с максимумом при
Qo л* 1,3 и довольно резким падением в обе стороны от максимума х).
Так, например, при изменении Qo в 4 раза скорость диффузии умень-
уменьшается на два порядка по сравнению с максимальной.
Для вычисления коэффициента диффузии необходимо найти
средний полупериод (Ту) колебаний в тонком стохастическом слое.
Вблизи сепаратрисы
32
где да = (Hy—HJ/HS 4^ 1, a Hs — 2ay — энергия на сепаратрисе.
Чириков [70] показал, что (Ту) можно найти, усреднив Ту (w)
по w в пределах стохастического слоя | w\ <; wx. Это дает
<7\,) = —llnf—Wll. F.2.21)
wy \_ \ w1 I J
При слабой связи [х 4^ ау для полуширины стохастического слоя wx
можно использовать соотношение D.2.23).
Коэффициент диффузии в тонком слое равен
D2 = (^,A^J>So F.2.22)
или с учетом F.2.19) и F.2.21)
D2 = 4n2[i2Q2QayF (Q0)/ln C26%). F.2.23)
*) При Qo С 1 полученные выражения справедливы лишь при дополни-
дополнительном условии Тиа>х > 2я, или sy = 0)y7V > 2n/Q0 (см. рис. 3.20, в), т. е.
только в очень тонком стохастическом слое шх <g 32 ехр (— 2n/Q0).— Прим.
ред.
Многомерные колебания
359
На рис. 6.10 эта теоретическая зависимость (сплошные линии)
сравнивается с результатами численных экспериментов (треуголь-
(треугольники). При счете использовалось 100 траекторий с одинаковыми
начальными условиями в плоскости (а, х) и слегка различными
в плоскости (|3, у) внутри тонкого стохастического слоя. Теорети-
Теоретические кривые строились по формуле F.2.23) с эмпирическим зна-
-1-1
9
т _
-4-
Go
Рис. 6.9. Функция F.2.20) для диффузии в тонком слое.
чением w1 = 0,191. Как и в случае толстого слоя, теоретические
значения лежат несколько выше численных. Возможно, что это
различие вызвано неполной хаотизацией ф (п) на полупериоде фа-
фазовых колебаний в стохастическом слое 1).
6.26. Диффузия по резонансу связи
Аналогичным образом можно было бы вычислить скорость диффу-
диффузии Арнольда и по резонансу связи, например &х = wy. Соответст-
Соответствующие довольно сложные расчеты были выполнены Либерманом
[273 ]. Здесь же, следуя работе Чирикова [70 ], мы рассмотрим
более простую модель, иллюстрирующую как диффузию по резо-
резонансу связи, так и взаимодействие многих резонансов [72 ]. Га-
Гамильтониан этой модели имеет вид
- exf (t),
F.2.24)
г) Существенное снижение скорости диффузии по сравнению с оценкой
F.2.23), особенно заметное на рис. 6.10, в, объясняется медленной диффу-
диффузией в относительно широкой периферической части стохастического слоя,
а также фазовыми корреляциями из-за конечной ширины слоя (см. ра-
работу [70], § 7.2 и 7.6).— Прим. ред.
360
Глава 6
о
3
Ь
-л
—2
-3
-4
-5
Г А д
' /
-6
-5 -4 -3 -2
а
-г
о
| -4
м -5
-б
-2
-3
-
-Г ? .
*^ д
1
^^
д
1
^-
д
1
2,0
2,5
3,0
3,5
4,0
4,5
Рис. 6.10. Диффузия в тонком слое (по данным, работы 406]).
Обозначения и параметры те же, что и на рис. 6.8, кроме п — 2000; К : Ь ! б_
100:
10 : 1,8.
Многомерные колебания 361
где t — время, а \\, и е — малые параметры. Эта система состоит
из двух нелинейных осцилляторов со слабой линейной связью
(параметр \х), причем на один из осцилляторов действует периоди-
периодическая внешняя сила &f(t). Нас будет интересовать окрестность
резонанса связи
а>х— ч>у^0, F.2.25)
где &х и &у — невозмущенные частоты нелинейных осцилляторов.
Переход к переменным действие—угол. Перейдем прежде всего
к переменным действие — угол невозмущенной системы (ц = е =0).
Невозмущенный гамильтониан
описывает два независимых осциллятора с сохраняющимися энер-
энергиями Ех и Еу. Выражение для переменной действия получается
обычным образом
м
где хм = D?'Л.I/| — амплитуда х-колебаний. Вводя новую пере-
переменную | = х/DЕх)'/', получаем
^ F-2.28)
где Ж A/-\/2) « 1,85 — полный эллиптический интеграл первого
рода. Соотношение F.2.28) устанавливает связь между переменной
действия / и энергией Е для каждого из осцилляторов^ ос //з).
Отсюда новый невозмущенный гамильтониан
Яо = Л (#+#), F.2.29)
где
А = / у^-. у^У3 « 0,87.
\ 41/2^0/1/2)/
Частоты колебаний равны
С/ х, у •J
Решение выражается через эллиптические функции (см., напри-
например, [70]) и имеет вид
cn(mA V
хм СП[а) Ж A/1/2) ^j ch [я (я-1/2I
п=1
362 Глава 6
r\ ne i i cos 3w< cos5wi /e o о,ч
« 0,95 cos &t A 4- 4- .... F.2.31)
t23 ^ B3)г т ч
Независимо от амплитуды колебаний вклад гармоник очень мал
и мы можем сохранить только первый член этого разложения.
Введя угловую переменную 0 = cat, запишем полный гамильто-
гамильтониан в виде
Н = А A^ + #)—iixM AХ) ум AУ) cos Qx cos 0F—
-8A;M(/X)cosexf@, F.2.32)
где
хи = (Ы)'и П° t ум = DA)'U Q F.2.33)
— амплитуды колебаний, полученные из сопоставления F.2.26)
и F.2.29).
Вблизи резонанса связи разность 6^.— Qy является медленной
функцией времени. Перейдем поэтому с помощью производящей
функции
к новым переменным:
%=е,—е„ ч>,=е,+е„. F.2.34а)
Тогда
^ /, = -^ = -/x + /2. F.2.346)
В окрестности резонанса связи 1Х « /у, так что /х < /г- Вы-
Выражая гамильтониан F.2.32) через новые переменные F.2.34) и
разлагая невозмущенную часть по 1Ъ получаем выражение для
нового гамильтониана
\^x^M (a) x
\f(t), F.2.35)
где
С(/2) = -А-Л/7\ F.2.36)
Ft / \ ,ъ v 11 \ ,, 11 \ /СО ОТЧ
2
Усреднение по быстрой фазе г|за дает
(/С) = 2Л/2/а + —G/?—Fcos^. F.2.38)
2
Отсюда видно, что /2 « const, со2 = 2W*, а переменные /ь я^
Многомерные колебания 363
совершают медленные колебания на резонансе связи с частотой
(для малых колебаний)
со! = У К? ос V^ F.2.39)
Взаимодействие трех резонансов. Пусть внешняя сила имеет вид
F.2.40)
причем обе частоты близки к резонансу и удовлетворяют нера-
неравенству
F.2.41)
т. е. частота (лх находится между Q± и Q2. Будем считать, что эти
два резонанса и определяют поведение системы, причем более силь-
сильный х) резонанс (с частотой Qx) возбуждает движение поперек
стохастического слоя, а более слабый (с частотой Q2) вызывает
диффузию Арнольда вдоль слоя. В этом случае диффузию Арнольда
удается рассчитать сравнительно просто (см. работу [70, § 7.5]).
Нелинейность приводит также к резонансам в высших порядках,
однако их вклад в диффузию очень мал. Опуская поэтому член
F cos ^2 в F.2.35), представим гамильтониан в виде суммы
где
K±= — GPl — Fcosipl—axM cos / *L±f^J cosSy, F.2.42)
-гхи cos / frffl + fr \ cosQit. F.2.43)
Эти выражения аналогичны соответственно F.2.11) и F.2.66), и
для определения скорости диффузии Арнольда по величине dK.\\ldt
можно использовать тот же метод. В результате находим [70 ]
D--**-. '-"% . F.2.44,
Q)X 1пC2е/ш)
где
Qo =
Для модельной задачи в п. 6.16 получается аналогичное выра-
выражение [273 ], хотя вывод его значительно сложнее. Скорость диф-
диффузии экспоненциально уменьшается с увеличением расстройки
(бю) и уменьшением связи (ft>i). Подчеркнем, что найденная ско-
скорость диффузии является локальной и изменяется в процессе диф-
диффузии.
1) Имеется в виду меньшая расстройка по частоте.— Прим. ред.
364
Глава 6
6.2в. Много резонансов
До сих пор при анализе диффузии Арнольда учитывались только
три резонанса. Пока возмущение не слишком мало, полученные
аналитические оценки хорошо согласуются с результатами числен-
численного моделирования. Однако для достаточно малого возмущения
о
i
-5-
-10-
-15-
V
\
ч • V
\
\
\
\
Три ___
резонанса
\
\
\
\
Рис. 6.11. Зависимость приведенной скорости диффузии'Арнольда D* от Qo
(по данным работы [72]).
Точки — численное моделирование; пунктирная линия — теория в приближении трех
резонансов.
теория значительно занижает скорость диффузии, поскольку в этом
случае существенно взаимодействие многих резонансов. Такой ре-
режим диффузии называется областью Нехорошева по имени совет-
советского математика, впервые получившего строгую верхнюю границу
для скорости диффузии Арнольда [314]. Однако его оценка сущест-
существенно завышает, вообще говоря, порядок действительной скорости
диффузии.
Взаимодействие многих резонансов исследовалось аналитиче-
аналитически [70 ] и численно [72 ] для модели F.2.24) с силой
/@ =
cos vt
1 — С cos vt
2е~
- cos mvt,
F.2.45)
где ох A—С2) <С 1. Чтобы выделить наиболее важную экспо-
Многомерные колебания 365
ненциальную зависимость, вычислялась приведенная [по F.2.44)]
скорость диффузии D*, согласно формуле 1),
9 9 9
Л xtfCuf
Уо*.
сох In
Зависимость lg D* от Qo в широком диапазоне показана на рис. 6.11
для (шх = (о у = 4,5 v и а = 0,1. Аналитическая зависимость
F.2.44) (пунктирная кривая) для трех резонансов (сох = 4v, сох =5v,
(ох = юь) хорошо согласуется с численными данными при малых
Qo, однако очень сильно занижает скорость диффузии для боль-
больших Qo.
Это расхождение можно объяснить влиянием резонансов вы-
высоких гармоник mv = kax, в частности, за счет следующих чле-
членов разложения F.2.31). Хотя их амплитуды малы, они располо-
расположены близко к резонансам сох = ооу = 4,5 v, т. е. для них рас-
расстройка б© = т\—Ых тоже мала и эффективное Qo — 1.
Приняв зависимость D* (Qo) в виде
1>* = Лехр(—5<$), F.2.46)
где А, В и у— подгоночные параметры, Чириков и др. [72] по-
получили из численных данных значение у « 1/2, т. е.—lg D ос ц~~ '.
Верхняя оценка Нехорошева [314 ] приводит к существенно мень-
меньшей величине у (см. [70]). Для гамильтониана общего вида с JV
степенями свободы
НA, в) = Я0(/) + |1Я(/, в),
где р. — малый параметр, а функция Но (I) при | /| -> 0 является
положительно определенной квадратичной формой 2), оценку Не-
Нехорошева можно записать в виде
|/|< |a>|.|/||iH-*exp(—l/|i<9, F.2.47а)
q(N) = ? . F.2.476)
v 3,N2— N + 8
Так как Qo ос l/o^ ос \Гхп, то у = 2q. Полагая в F.2.476) iV = 3,
находим у = 1/8. Это приводит к слишком медленному уменьше-
уменьшению скорости диффузии с \х и не согласуется с численными резуль-
результатами на рис. 6.11. По мнению Чирикова [70], более правильная
оценка соответствует3) q = UN. При N = 3 это приводит к зна-
значению у = 2/3, которое находится в разумном согласии с числен-
численными результатами.
*) В работе [72] использовалась несколько другая нормировка ?>*.—
Прим. ред.
2) Менее жесткое, но тоже достаточное условие состоит в том, чтобы энер-
энергетические поверхности Но (/) = const были всюду выпуклыми (см. [512]).
Примером может служить гамильтониан F.2.29).— Прим. ред.
3) Упрощенный вывод этого соотношения см. в работе [69].— Прим.
ред.
366
Глава 6
6.2г. Модуляционная диффузия
Обратимся теперь к модуляционной диффузии, при которой хао-
хаотическое движение происходит вдоль системы перекрывающихся
резонансов, вызванных медленной модуляцией возмущения. Сле-
Следуя Чирикову и др. [76], рассмотрим модельный гамильтониан
Я = — /?—/г cos (вц + Я sin Qt) + —1\—г cos (вх—в,), F.2.48)
Z, ?
Рис. 6.12. Схема резонансов при модуляционной диффузии.
где % и О, — амплитуда и частота фазовой модуляции соответст-
соответственно, а е — малый параметр связи. Используя разложение
оо
= E
F.2.49)
получаем мультиплет резонансов с центром в ю1 = /1 = 0 и эф-
эффективной шириной приблизительно 2Q, так как функции Бесселя
fn (К) быстро убывают при \п\ > К. Мультиплет показан на
рис. 6.12 в виде нескольких вертикальных линий на плоскости
частот @Ь ю2. Если резонансы мультиплета перекрываются, то
возникает широкий стохастический слой, по которому и идет мо-
модуляционная диффузия.
Многомерные колебания 367
Перекрытие в мультиплете. Движение внутри мультиплета опи-
описывается гамильтонианом
^ F.2.50)
Действуя, как и в п. 2.4а, получим G — 1 и F = k /„ (А,). Полная
ширина сепаратрисы для каждого из резонансов мультиплета оп-
определяется формулой B.4.31)
2А/Макс = 2Асомакс = 4 {FIG) ' = 4 ^F\fn (X) [. F.2.51)
Расстояние же между резонансами по частоте равно бсо = Q. Ис-
Используя правило двух третей (п. 4.16) х), запишем условие пере-
перекрытия
2Лсо^к^ J2_ F.2.52)
Q 3 к '
Подставляя F.2.51) в F.2.52) и принимая в качестве /„ (К) средне-
среднеквадратичное значение (пХ)~~1/2, приводим условие F.2.52) к виду
/e>Q2V^/20. F.2.53)
Если движение, описываемое гамильтонианом F.2.50), связано
с третьей степенью свободы, то неравенство F.2.53) есть также
условие модуляционной диффузии. Если же возмущение меньше
этой границы, то остается только диффузия Арнольда. Отметим
неожиданное следствие оценки F.2.53): чем меньше частота моду-
модуляции, тем ниже граница перекрытия по возмущению (k ее Q2).
На первый взгляд это противоречит нашей интуиции об адиабати-
адиабатических возмущениях, согласно которой с ростом отношения частот
влияние резонансов уменьшается 2). Это противоречие разрешается,
если принять во внимание, что стохастичность связана с прохожде-
прохождением резонанса, а это происходит только дважды за период моду-
модуляции 2я/Й. Поэтому при Q -> 0 скорость диффузии также стре-
стремится к нулю.
Отметим, что поскольку ширина мультиплета уменьшается
с уменьшением Q при заданном К, то при
/s>QV2/13> F.2.54)
ширина Ш<сАюмакс. В этом случае весь мультиплет сливается
в единый резонанс 3), а скорость диффузии по стохастическому
!) В данном случае это правило не улучшает точность оценки, поскольку
амплитуды и фазы соседних резонансов различны.— Прим. ред.
2) Эту интуицию следует подправить: при прохождении резонанса (вслед-
(вследствие модуляции), как и при прохождении частоты осциллятора через нуль,
адиабатичность всегда нарушается независимо от скорости прохождения.—
Прим. ред.
3) По этой причине оценка F.2.54) неточна — ширину слившегося ре-
резонанса следует определять по полной амплитуде возмущения k [см. F.2.48)],
а не по амплитуде гармоники kf n (к) [см. F.2.50)]. В результате получаем
k > Q42/16.— Прим. ред.
368
Глава 6
слою этого резонанса падает. Три режима *) движения в модуля-
модуляционном слое, определяемые неравенствами F.2.53) и F.2.54), схе-
схематически показаны на рис. 6.13.
Эти три режима были описаны Теннисоном [404 ] для модели
взаимодействия встречных протонных пучков в проекте накопи-
накопительного кольца Брукхейвенской лаборатории (США). В этой мо-
модели Теннисона использовалась модуляция частоты:
dt
¦=k
dt
cos Qt,
F.2.55)
2ХП
2ЛП
Рис. 6.13. Три режима движения внутри мультиплета в зависимости от ча-
частоты модуляции Q (по данным работы [276]).
а — большая частота Й, модуляционные резонансы не перекрываются, слабая диффузия
Арнольда вдоль отдельных стохастических слоев; б — промежуточная частота Й, ре-
резонансы перекрываются, сильная модуляционная диффузия вдоль широкого слоя; в —
очень малая частота Я, все резоиансы сливаются в один, диффузия Арнольда вдоль еди-
единого стохастического слоя.
тогда как в рассмотренной выше модели F.2.48) модулируется фаза:
-^_ = fcsin(e1 + A.sinQ0, -^- = /i. F.2.56)
Обе модели сводятся друг к другу путем замены переменных с про-
производящей функцией
F 7(
для
х) Существует также и четвертый, промежуточный, режим захвата
Многомерные колебания 369
причем % = K/Q. На рис. 6.14 показан эффект модуляции для стан-
стандартного отображения (при К = 0,007), что соответствует уравне-
уравнениям F.2.55), если заменить k на /Сбх (t), где 81 (t) — периодиче-
периодическая б-функция C.1.33). При X = 0 (рис. 6.14, а) имеется единст-
единственный резонанс с шириной 2A/MaKc = 4/A/2. При К = 0,63 и по-
последовательно уменьшающейся частоте Q на рис. 6.14, б виден муль-
типлет неперекрывающихся резонансов; на рис. 6.14,6 — частич-
частичное перекрытие резонансов; на рис. 6.14, г — полное перекрытие
резонансов.
Диффузия вдоль мультиплета. Вернемся к гамильтониану F.2.48).
Диффузию вдоль перекрывающихся резонансов мультиплета (по /2)
можно вычислить в модели стохастической накачки. Продольная
часть гамильтониана имеет вид
Отсюда [ср. F.2.7)]:
dH«. = _8 Л. cosFX—62) + е sin (9Х— 92) -
dt dt v x " " dt
Первый член приводит лишь к малым осцилляциям #ц, которыми
мы пренебрегаем. В результате получаем
АЯц «Л зтф-^-Л, F.2.58)
J dt
где фаза ф (f) = 0Х—92.
Для вычисления ф (t) нужно невозмущенное движение 9Х (t)
и 92 (t). Положив в F.2.57) е = 0, запишем решение в виде
%{t) = a2t — Хо— я/2. F.2.59)
Получить 6Х (t) из F.2.50) можно лишь приближенным методом.
Считая k малым параметром возмущения, запишем F.2.50) в виде
Яо = —1\ F.2.60а)
и
Я1= — fe2/n(^)cosF1 + nQ0- F.2.606)
п.
Используя каноническую теорию возмущений (п. 2.26) и замечая,
что (Hj) = 0, из B.2.44) получаем в первом порядке по k: Н = Яо,
1г = /0 = const, 0J = Iot, а для производящей функции — вы-
выражение [см. B.2.45) ]:
! fn(%)- sin^ + nQt). F.2.61)
ИЙ + /i
370
Глава 6
I 0-L.
а -я-
Рис. 6.14. Фазовая плоскость стандартного отображения при модуляции
К = 0,007. а — модуляция отсутствует; ч — г — частота модуляции «оследовательн»
Многомерные колебания
371
частоты.
уменьшается прн постоянной амплитуде.
372 Глава 6
Подставляя в F.2.606) 02 = 9Х = Iot и используя F.2.61), находим
F.2.62)
В качестве грубого приближения оставим в этой сумме один (наи-
(наибольший) член с п та X. Тогда
ф @ « (/о- Щ) t + Хо + я/2 + Л#/х (Я)/(/о + Щ* X
Xsin(/0 + A?)f, F.2.63)
где в подгоночном параметре 7? учитывается «эффективное» число
членов в сумме F.2.62). Выражение F.2.63) является основным
приближением при анализе движения в модуляционном слое.
Коэффициент модуляционной диффузии можно определить как
D(co2) = lim -±г{ [Atf, G)]2)v ^ F.2.64)
где усреднение *) по /0 производится по всей стохастической об-
области |/0|<Ш. Подставляя сюда F.2.58), получаем
X j йГа^ту{Г) ) . F.2.65)
—т I г„
Иепользуя F.2.63) и снова разлагая по функциям Бесселя, находим
апф@ = 24/(/о)со8{[(/+1)/0 + /т-юя]* + Хо}, F.2.66а)
У
где
1" ft/;^W 1F.2.666)
Интегрирование в F.2.65) по t" дает
dt" sin ф (t") = \ Aj (/0) cos Хо . б
F.2.67)
Интегрируя далее, сначала по /„, а затем по f, получаем
х) Усреднение по %0 требует пояснения. Фактически важна разность
фаз ф @) = Хо + я/2 [см. F.2.63)], которая, как и /0, не является на самом
деле постоянной вследствие стохастического движения при перекрытии ре-
зонансов в мультиплете.— Прим. ред.
Многомерные колебания 373
Здесь сумма по / ограничена б-функцией в F.2.67):
¦ ю2 — /„
/о + ХО "
При изменении /0 от — A.Q до Я-Q целое / изменяется от
до бесконечности. Аргумент функции Бесселя в F.2.666) обычно
мал 1), так что доминирующим является член с / = /. Опуская
остальные члены и усредняя по %0, получаем окончательный ре-
результат
С ростом со 3 величина / изменяется скачками, как это следует
из F.2.68). Соответственно график зависимости D(a>2) имеет вид
серии убывающих «плато» (рис. 6.15). Основное плато (/ = 0) со-
соответствует частотам О<со2<Ш, а остальные расположены в ин-
интервалах
B1— 1)Ш«о,<B*+1)Ш. F.2.70)
На основном плато f0 та 1 и коэффициент диффузии
D-f#- <6-2-7!>
Относительно большая скорость диффузии объясняется тем, что
внутри модуляционного слоя (см. рис. 6.12) выполняется условие
точного резонанса сох = /0 = со2.
На рис. 6.15 представлены численные значения приведенного
коэффициента диффузии
Д, = , F.2.72)
(е2со22/Дсо)
как функции (О2/Д(о. Здесь вместо Ш использована фактическая
полуширина модуляционного слоя Дсо « 1,ЗШ, X = 10, Q =
= 10~2, k = 5 х 10~4. Ясно видно основное плато со средним зна-
значением Dn = 1,6, что хорошо согласуется с величиной л/2 из
F.2.71). При со2>Д«в скорость диффузии резко падает, а затем,
с ростом со 2, уменьшается ступенчатым образом. Это как раз то,
что предсказывает теория F.2.69).
Для количественного сравнения с численными результатами
необходимо определить параметр R. Это было сделано путем под-
>) Если k ^ kx ~ Й2Х7/3 [см. F.2.69), f% (Х)~Х~1/3], что почти совпа-
совпадает с границей слияния резонансов мультиплета F.2.54).— Прим. ред.
374
Глава 6
гонки формулы F.2.69) к численным данным на краю двух послед-
последних плато A = 2, I = 3). Подставив найденное значение R ?» 5,3
в F.2.69), получим зависимость Dn (со2/Дсо), представленную на
рис. 6.15 сплошной линией. Если учесть, что в теории использова-
использовалось существенное упрощение F.2.63), согласие можно считать
0
-4
-8
-12
-16
-
—l—i i i i
\
I
' i '
1 il i > i I _
0,5
1,0
2,0 3,0 5,0
10,0
Рис. 6.15. Зависимость приведенного коэффициента диффузии Dn от вели-
величины оJ/До).
Точки — численные данные; сплошная линия — теория F.2.69); А, = 10; Q — 10 ;
k = 5 X 10~4; Ди = 1,3 ХЯ.
вполне удовлетворительным. Отметим, что теория предсказывает
резкий спад Dre(co2) после каждого плато и что все плато, кроме
основного (I = 0), имеют некоторый наклон. В пределах каждого
плато скорость диффузии спадает по закону
Многомерные колебания 375
где последнее выражение относится к / ^> 1. Все эти предсказания
находятся в разумном согласии с численными данными х).
§ 6.3. Внешняя диффузия
Рассмотрим движение системы, близкой к интегрируемой, под
действием внешнего шума. Резонансы в системе могут значительно
усиливать внешнюю диффузию. В п. 5.56 мы уже познакомились
с примером такого усиления классической диффузии за счет про-
прохождения резонанса (см. рис. 5.17).
Ниже мы рассмотрим усиление классических процессов пере-
переноса вдоль резонансов. Усиление возможно даже для автономной
системы с двумя степенями свободы в том случае, когда внешний
шум не сохраняет энергию, и система может двигаться вдоль ре-
резонансов. Такой процесс был исследован Теннисоном в работе
[405 ], основные результаты которой и представлены в п. 6.3а. Род-
Родственный процесс диффузии самого резонанса был рассмотрен Чи-
риковым [71 ] и Коэном и Раулэндсом [80] (п. 6.36) 2).
6.3а. Резонансное каналирование диффузии 3)
Геометрическая картина. Вернемся к гамильтониану F.1.7)
резонансные и энергетические поверхности (линии) которого по-
показаны на рис. 6.2. На рис. 6.16 в увеличенном масштабе изобра-
изображен участок рис. 6.2, ограниченный пунктиром. Введем резонанс-
резонансное возмущение
H1 = VR(I1, /2)cosF91-e2). F.3.1)
Вектор единственного резонанса mR = F, — 1) определяет на-
направление фазовых колебаний вдоль невозмущенной энергетиче-
энергетической поверхности, как показано на рис. 6.16. Пунктиром показана
полная ширина резонанса, ограничивающая максимальную ам-
амплитуду фазовых колебаний. Центр колебаний лежит на линии
резонанса в точке А.
х) Как и в случае диффузии Арнольда, здесь существует область Нехо-
рошева (п. 6.2в), в которой диффузия идет под действием комбинационных
резонансов высоких гармоник. Для модуляционной диффузии такой режим
наблюдался, по-видимому, в численных экспериментах [513].— Прим. ред.
2) Отметим также, что описанная выше модуляционная диффузия, и осо-
особенно диффузия Арнольда в тонком слое, становится практически интерес-
интересной только в присутствии (слабого) внешнего шума, который распространяет
такую диффузию на все начальные условия. Можно сказать также, что сред-
средняя скорость внешней диффузии резко возрастает за счет диффузии в стоха-
стохастических слоях (см. [70, § 7.7]).— Прим. ред.
3) Авторы используют термин «resonance streaming» (резонансное тече-
течение).— Прим. перев.
376
Глава 6
Рассмотрим теперь влияние не сохраняющего энергию внеш-
внешнего шума, который мы будем характеризовать мгновенным сме-
смещением системы из точки а в точку Ь на расстояние I (рис. 6.16).
При этом центр колебаний сдвигается вдоль линии резонанса из
точки А в точку В на расстояние
— l sin%
sin tp
F.3.2)
Ширина
резонанса
—^uZ?°nst . -—
_—- i
\
Колебания
после смешения
•г
1 в
& А
- /
Вектор
резонансо mj
1 ^ -—
-~""~\^——~~^-
Начальные
колебания
;
Рис. 6.16. Резонансное каналирование (по данным работы [405]).
Под действием внешнего шума система переходит из точки а в точку Ь, а центр фазовых
колебаний смещается из точки А в точку В.
Заемного случайных смещений среднее от sin2% будет порядка еди-
единицы, тогда как sin г|) =s const локально. В результате при гр <^ 1
скорость диффузии вдоль резонанса резко возрастает. Будем на-
называть такую диффузию резонансным каналированием. Определим
коэффициент диффузии вдоль резонанса формулой
где R — число случайных смещений системы в единицу времени.
Сравним это с классической диффузией по нормали к энергетиче-
Многомерные колебания 377
ской поверхности:
D±B = — R(Psm2x). F.3.3)
2
Отсюда
DKaH =——. F.3.4)
sin3 tp
Расчет диффузии. Если коэффициент внешней диффузии Do не за-
зависит от направления на плоскости (J\, /2), то D±E = Do и ?>ка„ =
= Do/sin2^. В случае анизотропной диффузии предположим, что
тензор внешней диффузии имеет вид
(Пх 0 \
т. е. оси 1Х и /2 совпадают с главными направлениями D. Тогда
начальное распределение в виде б-функции эволюционирует по
закону [62]
Ш
exp
f ^___A_Y F.3.5)
Введем новые переменные /j, /2, соответствующие повороту осей
на угол 8, так что ось Г2 направлена перпендикулярно энергетиче-
энергетической поверхности (рис. 6.16). Имеем
/,\ /cos0 — sin9\
Д .. F.3.6)
\sin 8 cos8y
Подставляя эго соотношение в F.3.5) и интегрируя по /J, получаем
где
sin2 26 + D-1 D~x cos2 29
?>-i cos2 6 -f D^ sin2 6
(Df + )
D~XE = — F.3.7)
i 2 6 D 2 6
— коэффициент диффузии по Г2. Зная D^E, из F.3.4) находим DKaH-
Другой метод состоит в выборе таких новых переменных /,
в которых тензор диффузии становится изотропным. Иначе говоря,
константы метрики g1' нового пространства действий выбираются
так, чтобы
Di! = Dog\ F.3.8)
где D1' — компоненты" исходного тензора внешней диффузии, а
378 Глава 6
Do — коэффициент изотропной диффузии. Если, например,
О Зб)' (б-3-9)
то новые элементы длины равны
Й = ,Л F.3.10)
После этого можно, но не обязательно, сделать формальное преоб-
преобразование к новым переменным
7i = /i, 72 = -^/2. F.3.П)
о
В обоих случаях диффузия будет изотропной. Эти преобразования
иллюстрируются на рис. 6.17 для невозмущенного гамильтониана
Но = /] + /! F.3.12)
и тензора диффузии F.3.9). В новых переменных F.3.11) невозму-
невозмущенный гамильтониан F.3.12) принимает вид
^ F.3.13)
Замена переменных соответствует производящей функции
Ft = 9J, + 66272, F.3.14)
откуда
5/i 5/г
Старое условие резонанса coj—-co2 = 0 заменяется новым
6@! —@2 = 0, F.3.15)
или в переменных действия
F.3.16)
6
Тем самым мы фактически пришли к модели невозмущенного га-
гамильтониана F.1.7). Используя F.3.13) и F.3.16), находим sin2i|) =
= 4D1D2/(D1 + D2J и соответственно величину коэффициента
диффузии центров колебаний в пространстве новых переменных
1 Окан (Di + D3)a _9д
sin2 г|> ?>0 4?>iDa
Скорость диффузии в исходных переменных получается с помощью
обратного преобразования переменных.
Многомерные колебания
379
Следуя Теннисону [405], рассмотрим пример резонансного ка-
налиррвания для гамильтониана
Я = 1\ + F/2J + VR cos F9X— 9,) F.3.17)
/•>
Тензор
дисрсрузии
J/,
Рис. 6.17. Изменение масштаба и преобразование переменных для перехода
к изотропной диффузии (см. текст).
Прямая линия — резонанс связи; пунктирная линия — линия постоянной энергии.
с VR = 10~5. Будем считать, что внешний шум вызывает периоди-
периодические (с периодом Т ~ 1) смещения Д/2 = 0, А/2 = Ю~5 sin г„,
где гп — случайные числа, равномерно распределенные в интер-
интервале @, 2л). На рис. 6.18 показаны последовательные положения
системы, усредненные по интервалам At = 500 и соединенные пря-
380
Глава 6
мыми линиями. Начальные условия (точка / на рис. 6.18) выбира-
выбирались на линии резонанса (пунктирная линия). В процессе диффу-
диффузии траектория в конце концов выходит из резонанса и оканчи-
оканчивается в точке F. Диффузия вдоль резонанса и есть резонансное
каналирование. Движение под острым углом к резонансной линии
связано с прохождением резонанса (ср. рис. 5.17). Оно идет почти
3,06
Рис. 6.18. Резонансное каналирование для модели F.3.17) (по данным ра-
работы [405]).
Ломаная линия — численные данные для траектории движения, усредненной на интер-
интервалах At к 500 к ЗТа, где То — период малых фазовых колебании; I, F — начальная
и конечная точки траектории; пунктирная линия — линия резонанса.
вдоль линии постоянной энергии. Наконец, вертикальное движе-
движение по обе стороны от точки F есть результат медленной классиче-
классической диффузии по /2 вдали от резонанса.
Резонансное каналирование возможно лишь для достаточно
сильного (широкого) резонанса, когда время внешней диффузии
поперек резонанса
Многомерные колебания 381
велико по сравнению с периодом фазовых колебаний
л. F.3.18)
Здесь AIR и D±R— полная ширина резонанса и скорость внешней
диффузии, перпендикулярная линии резонанса, а со^ — частота
фазовых колебаний. В примере Теннисона A/R ~ 3 X 10~3,
D R »'10~s, xD та 450, <»д « 0,03, так что условие 0>дТо «
«14>2я выполняется.
Резонансное каналирование при условии F.3.18) соответствует
так называемой банановой диффузии частиц в тороидальных маг-
магнитных ловушках при редких столкновениях. Такое название про-
происходит от формы инвариантных кривых внутри резонанса (см.
рис. 6.22, а) 1). С ростом уровня шума условие F.3.18) перестает
выполняться и происходит переход к режиму, при котором скорость
диффузии не зависит от величины шума,— к так называемому ре-
режиму плато2). Чириков [71] и Коэн и Раулэндс [80] исследо-
исследовали этот режим на модели, описанной в п. 6.36. Мы отложим
обсуждение этого режима до § 6.4, где рассматривается диффузия
частиц в тороидальных магнитных ловушках при наличии резо-
нансов. Наконец, при еще большей интенсивности шума резонанс-
резонансная структура уже не играет никакой роли, и возникает третий
режим чисто классической диффузии. В § 6.4 мы обсудим также
и этот режим. Средняя скорость диффузии в системе со многими
(неперекрывающимися) резонансами зависит также от доли фазо-
фазового пространства, занятого резонансами.
Резонансное каналирование имеет место и в многомерных си-
системах [405 ]. Внешняя диффузия усиливается вдоль резонансной
поверхности в направлении проекции на нее вектора резонанса3) mR.
Теннисон [405 ] полагает, что такого типа диффузия может быть
причиной «раздувания» встречных пучков в накопительных коль-
кольцах. Возможно также, что подобное усиление диффузии имеет ме-
место и в различных установках магнитного удержания и нагрева
плазмы. Теннисон отметил также, что в диссипативных системах
с затуханием по обеим степеням свободы резонансное каналирова-
каналирование может привести к быстрому увеличению одной из переменных
действия. Он сравнивает это с движением парусной лодки против
г) В отечественной литературе используется также термин «диффузия
Будкера», который первым предсказал и дал оценку такой диффузии (см.
примечание редактора на с. 336 и [71]).— Прим. ред. «t <
2) В отечественной литературе он называется также режимом Галеева—
Сагдеева, которые построили теорию диффузии в этих условиях [510, 71].
В рассматриваемой задаче такой режим имеет место только в случае многих
резонансов.— Прим. ред.
3) В отличие от двух степеней свободы усиление внешней диффузии воз-
возможно здесь, вообще говоря, и в том случае, когда внешний шум сохраняет
энергию, например, при рассеянии частицы (см. работу [405], рис. 8).—
Прим. ред.
382 Глава 6
ветра. Представим себе, что на рис. 6.16 лодка находится в точке а
и может двигаться только вдоль линии резонанса. Пусть плоскость
паруса параллельна вектору mR, а ветер, диссипативная сила,
давит в направлении от а к Ь. Тогда если наклон линии резонанса
отрицательный, то результирующая сила будет направлена от А
к 5, и лодка будет идти «на ветер» по /2, хотя при этом полная
энергия системы будет уменьшаться.
6.36. Диффузия резонанса
Модельное отображение. Рассмотрим явное отображение поворота
C.1.17)
/ / /()i0 F.3.19a)
ц), F.3.196)
где J, 6 — канонические переменные, а (л —- дополнительный па-
параметр. Вводя периодическую S-функцию, эти уравнения можно»
записать в форме гамильтоновых дифференциальных уравнений
типа C.1.34). Пусть теперь изменение параметра jx описывается
независимым уравнением
Н*+1 = Н« + In, F.3.20)
где t,n — случайная переменная. Тогда в системе F.3.19) с (i =
= |А„+1 возникает внешняя диффузия, аналогичная описанной
в п. 6.3а. Такой подход использовался Чириковым [71 ] и Коэном
и Раулэндсом [80 ] при исследовании процессов переноса в магнит-
магнитных ловушках.
Для упрощения анализа линеаризуем отображение F.3.19)
по переменным J и |i в окрестности ц = |л0 и неподвижной точки
(/„, 0О), положив 90 = 0 и определив Jo из уравнения а (/0, |i0) =kt
где k — целое число. В результате получаем расширенное стандарт-
стандартное отображение:
/„+! = /„ +К sine,,, F.3.21а)
n+l, F.3.216)
F.3.21b)
где
/п==2я-^-(У„-У0), F.3.22а)
Рп = 2я -^ (iin - цо), F.3.226)
ац0
^ F.3.23а)
F.3.236)
Многомерные колебания 383
Здесь К — параметр стохастичности; %п — нормированная слу-
случайная переменная: (|„) = 0 и (%2п) = 1, а
т= Bгаг-^ F.3.24)
\ дц0 I
— безразмерный параметр, характеризующий случайную вели-
величину ?„ ((&) = а2). Иначе говоря, т. равно числу итераций отобра-
отображения, за которое средний квадрат Р становится равным единице:
(Р2) = п/т. F.3.25)
Если К 2> 1, то резонансы перекрываются и диффузия по /
определяется приближенно квазилинейным выражением E.4.216):
Р1 = ((Д2/J) = -?-. F.3.26)
В этом случае фаза 8 является полностью стохастической, и диффу-
диффузия не зависит от внешнего шума по параметру ц. При т ^ 1 внеш-
внешний шум полностью хаотизирует 8 за одну итерацию отображения,
и скорость диффузии оказывается предельной F.3.26) независимо
от величины К- Нас, однако, интересует случай совместного дейст-
действия резонансов и внешнего шума (ср. п. 6.3а), который имеет место
при выполнении условий
/С« 1; т» 1. F.3.27)
В этой области изменения переменных / и Р за одну итерацию малы,
так что разностные уравнения F.3.21) можно аппроксимировать
следующей системой дифференциальных уравнений 1):
-^- = К sin 8, F.3.28а)
dn
=1 + Р, F.3.286)
dn
—^- =g/xVa. F.3.28b)
dn v
Диффузия резонанса. Уравнения F.3.28а) и F.3.286) имеют гамиль-
гамильтониан
tf = /2/2-fP(n)/ + /Ccos8, F.3.29)
описывающий «блуждающий» резонанс с центром'при / = — Р (п).
Используя F.3.25), получаем
= — • F.3.30)
v) В отличие от отображения F.3.21) уравнения^F.3.28) описывают един-
единственный резонанс / + Р = 0.— Прим. ред.
384
Глава 6
Локальный коэффициент диффузии внутри резонанса х) равен
D =J^L=-J—. F.3.31)
2га
2т
Линия
резонанса
Это выражение спра-
справедливо при условии, что
траектория остается вну-
внутри резонанса в течение
многих периодов фазовых
колебаний, т. е. что пара-
параметр
5 = (D0Td»l.
Л
1
Поборот
на угол В
5
Линия s
резонанса/^
/\ т
/^
F.3.32а)
Здесь соо — частота фазо-
фазовых колебаний, a xd —
время внешней диффузии
через резонанс. Поскольку
ширина резонанса <~ КVi r
то из F.3.30) получаем
оценку
Т^ — AT.
С другой стороны, частота
фазовых колебаний соода
да КХП, и условие F.3.32а)
принимает вид
Растяжение
по /г
6 ctgf раз
/
/ i
/Л 45°
F.3.326)
Фактически замена пере-
переменных
показывает, что S является
единственным параметром
уравнений F.3.28).
Рис. 6.19. Связь между резонансным ка- г) Точнее коэффициент
налированием (а) (п. 6.3а) и диффузией диффузии вместе с резонан-
резонанса (б) (п. 6.36). сом.— Прим. ред.
Многомерные колебания 385
Хотя локальный коэффициент диффузии представляет некото-
некоторый интерес и сам по себе, более важно знать среднюю скорость
диффузии. Ее можно найти следующим образом. Если пренебречь
диффузией вне резонанса (ср. п. 5.56) х), то средняя скорость диф-
диффузии пропорциональна доле времени, проводимого траекторией
внутри резонанса, которая в свою очередь пропорциональна фазо-
фазовой площади, занимаемой резонансом. Используя гамильтониан
F.3.29) и учитывая периодичность исходного отображения F.3.21)
по /, получаем для относительной фазовой площади резонанса
4BЛ')'/2 | A -cosQ)!4Q ,,
с о 4К /2
BяJ л2
Отсюда средний коэффициент диффузии
(D) = DTfr = -~ -^- • F.3.33)
Помимо диффузии вместе с резонансом происходит еще и диф-
диффузия внутри резонанса. Последний эффект был рассмотрен Коэном
и Раулэндсом [81 ], которые получили поправку к F.3.31) при
К С 1:
^/l) F.3.34)
Dr/lH
2т \ 2 — Л72
Неясно, однако, справедлива ли эта поправка в случае длительной
диффузии при многократном попадании в резонансы. Как бы то
ни было, эта поправка составляет всего около 50 %. По-видимому,
такого же порядка и другие ошибки, в частности, из-за приближе-
приближений вблизи сепаратрисы2). Поэтому можно принять выражение
F.3.33) в качестве разумной оценки средней скорости диффузии.
Связь с резонансным каналированием. Сравним расчет коэффици-
коэффициента диффузии вдоль резонанса Окгн в п. 6.3а с проведенным выше
расчетом Dr. Мы покажем, что при некоторых упрощающих пред-
предположениях эти задачи можно связать друг с другом.
Рис. 6.19, а напоминает схему расчета DKSH. Внешняя диффу-
диффузия с коэффициентом D±Е перпендикулярно энергетической по-
поверхности вызывает диффузию вдоль резонанса со скоростью
DKaH = D±?/sin2^. F.3.4)
*) Более подробно этот вопрос рассмотрен в работе [71].— Прим. ред.
2) По-видимому, имеется в виду нерезонансная диффузия вблизи ре-
резонанса. Согласно работе [71], эта поправка становится заметной только
при S > 108. С другой стороны, соотношение F.3.33) совпадает с точностью
лучшей 10 % с результатом Рютова и Ступакова [357], полученным ранее
другим методом. Поэтому поправка Коэна и Раулэндса остается проблема-
проблематичной. Если понимать ее как результат прохождения резонанса, то в рас-
рассматриваемом режиме Будкера (S > 1) прохождение является медленным,
и средний эффект многих прохождений близок к нулю (см. [467]).—
Прим. ред.
386 Г.шва 6
На рис. 6.19, б показано то же самое в новых переменных 1\, Г2,
так что внешняя диффузия с коэффициентом D Е идет теперь по
линии l'i, а вектор резонанса т направлен по 1\. При этом ве-
величина DXfi и угол tp не изменяются. Наконец, на рис. 6.19, в мы
еще раз переходим к новым переменным
что эквивалентно растяжению масштаба по Г2 в ctg \p раз.
Линия резонанса проходит теперь под углом 45°, а коэффици-
коэффициент внешней диффузии возрастает
Dp = Dx/rctg2ip. F.3.35)
Рассматривая Р как параметр и используя F.3.30), находим, что
компонента диффузии по / равна Dr = Dp. Сравнивая F.3.35)
и F.3.4), получаем
Dr = DKaH cos2 г|>. F.3.36)
Этим устанавливается соответствие между резонансным каналиро-
ванием и диффузией резонанса х).
Аналогичные соотношения можно получить и для многих сте-
степеней свободы, используя ортогональную метрику, описанную
Чириковым [70].
§ 6.4. Диффузия в тороидальных магнитных ловушках
Важным примером задачи о внутренней и внешней диффузии яв-
является задача об удержании плазмы в тороидальных магнитных
ловушках. Диффундировать могут как сами магнитные линии, так
и частицы поперек магнитного поля. Особый интерес представляет
диффузия частиц с учетом их столкновений или внешнего шума.
В зависимости от соотношения между шумом и динамикой частиц
диффузия может быть либо одномерной (аналогично п. 5.56), либо
типа резонансного каналирования (§ 6.3). В п. 6.4а рассматри-
рассматриваются основные резонансные процессы в тороидальных магнитных
ловушках. В п. 6.46 обсуждаются различные режимы внешней
диффузии. Проведено сравнение случаев неподвижных и диффун-
диффундирующих резонансов. В п. 6.4в приведен пример последнего слу-
случая, иллюстрирующий теорию, изложенную в п. 6.36. В п. 6.4г
кратко обсуждается самосогласованная задача, когда определяю-
определяющие движение частиц поля сами зависят от динамики частиц.
6.4а. Динамика магнитных линий
Различные конфигурации магнитного поля. Простейшее (торои-
(тороидальное) поле создается длинным прямолинейным проводником
х) Это соответствие является формальным и в общем случае несправед-
несправедливо. Если, например, внешний шум сохраняет энергию (скажем, упругое
рассеяние электрона на остаточном газе в магнитной ловушке), то Di? = 0,
тогда как Dr Ф 0.— Прим. ред.
Многомерные колебания
387
с током. В таком поле частицы дрейфуют поперек магнитных ли-
линий, поэтому оно не может служить для удержания плазмы. До-
Добавление азимутального тока приводит к появлению второй ком-
компоненты поля, так называемого полоидального поля (рис. 6.20).
Магнитные линии результирующего поля лежат на торе и напо-
напоминают фазовые траектории интегрируемой динамической системы
на рис. 3.1, а.
Для удержания плазмы были разработаны различные уста-
установки. Среди них система с жестким токонесущим проводником
Тсроибальное
¦^ поле
1
Большая
ось тора
Рис. 6.20. Геометрия тороидального магнитного поля.
вдоль малой оси тора г = 0 и аксиальным полем (левитрон), си-
система со спиральной обмоткой на торе г = а (стелларатор) и си-
система с тороидальным током в плазме (токамак).
Уравнения магнитных линий в таких системах можно записать
в гамильтоновой форме (см., например, [137, 307, 349 ]*)). В случае
азимутальной симметрии д1Щ = 0 (токамак и левитрон) полу-
получаются уравнения нелинейного осциллятора с одной степенью
свободы, а интегралом движения является магнитный поток, огра-
ограниченный магнитной поверхностью (см. ниже). Нарушение азиму-
*) Это связано с «несжимаемостью» магнитного потока (div В = 0), т. е.
сохранением «фазового объема» этой динамической системы, который в дан-
данном случае является просто трехмерным объемом в обычном пространстве.—
Прим. ред.
388
Глава 6
тальной симметрии приводит как бы к явной зависимости гамиль-
гамильтониана от «времениподобной» переменной г|з, а следовательно,
и к очень сложному движению. В частности, магнитные поверхно-
поверхности разрушаются, образуется магнитная резонансная структура
со стохастическими слоями в окрестности сепаратрис и в зависимо-
зависимости от величины возмущения возникает локальная или глобаль-
глобальная диффузия магнитных линий.
Магнитные поверхности. В тороидальной системе координат
(г, ф, г|)) (рис. 6.20) магнитные линии определяются уравнениями
u,s
0,6
0,4
0,2
0
-0,2
-0,4
-0,6
-0,8
1 1 1 1 1
-
г- Сепаратриса
/€ 1 1 (~\
I LL=2ir
1= ъ-1
1 1 1 1 1
1
-
-
\
1
г
-
-
1
dr
rdq>
Rdty
0,2
0,4 0,6 0,8
R
1,0 1,2 1,4
Рис. 6.21. Сечение магнитных поверхно-
поверхностей левитрона плоскостью ^ = const;
Ro = 1 (по данным работы [137]).
F.4.1)
где г и /? = /?0 + г cos <f —
малый и большой радиусы
линии поля; Вг и Вф— по-
лоидальные компоненты по-
поля, а Вф — тороидальная
компонента. Магнитное поле
в токамаке можно прибли-
приближенно представить в виде
[389]
Во
F.4.2)
, а вели-
COS ф ОПИ-
== /0
где Во = ?ф (
чина hs = 1 Н
сывает зависимость поля
от угла ф. В левитроне
для обеспечения равнове-
равновесия плазмы необходимо аксиальное поле, которое вносит допол-
дополнительную зависимость от ф, значительно более сильную, чем в
F.4.2). Пренебрегая последней, можно представить поле левитрона
в виде
Во
В = (Busin(f,
+ Bvcos(f, Bo
F.4.3)
где Bv— аксиальное поле (направленное вверх на рис. 6.20), а р =
= Iv/(IkR0) характеризует отношение аксиального /„ и азиму-
азимутального /^ токов. Аксиальное поле ослабляет полоидальное на
внутренней стороне тора, так что последнее обращается в нуль
(Вф = 0) в точке ф = л, г = В0/фВо). Магнитные линии полей
F.4.2) и F.4.3), определяемые уравнениями F.4.1), заполняют
магнитные поверхности, охватывающие малую ось тора и вложен-
вложенные друг в друга. Сечение магнитных поверхностей левитрона пло-
Многомерные колебания 389
скостью а|) = const показано на рис. 6.21. Обратим внимание на
магнитную поверхность типа сепаратрисы, которая содержит не-
неустойчивую периодическую траекторию с Вф = 0.
Как мы увидим ниже, единственным существенным параметром
невозмущенной магнитной поверхности является обычное число
вращения а, или угол «прокручивания» магнитной линии за один
оборот вокруг большой оси тора
2Я
0
= С ^L<ia|) = 2jTa. F.4.4)
В случае токамака hs ~ 1. Вводя переменную действия ? = г2/2,
приведем уравнения движения F.4.1) к виду
dty dip 2я
с гамильтонианом
1 .
Я„ @ = -М t (?) dl = const. F.4.5)
2я о
Аналогично, для поля левитрона F.4.3)
dz
F.4.6)
dz 2%
где z = г|)/2я, и принято, что Во = 1. Эти уравнения можно полу-
получить из гамильтониана
1п Г~Т^ V 2 1 + В« V2T cos ер.
V 2 1
Перейдем к переменным действие — угол (см. § 1.2)
2Я
/=-A-J УФ, F.4.7а)
2я о
dJ
где 5 — производящая функция. С точностью до членов, квадра-
квадратичных по /, получаем (см. § 2.2 или 2.5):
Яо= -L-\n(-*— — 2\ — 2Bfoj —Bttfj2. F.4.8)
Р V V 2
(-*— — 2\ — 2B
V V2/ /
Угол прокручивания i = dHJdJ определяет магнитную поверх-
поверхность. Подчеркнем, что при наличии азимутальной симметрии
390 Глава 6
(по г|)) гамильтониан магнитных линий описывает интегрируемую
систему с одной степенью свободы.
Резонансы. Рассмотрим модель возмущенного магнитного поля с га-
гамильтонианом
Я = Я0(/) + еЯ1(/, ф, Ц). F.4.9)
Разлагая вокруг невозмущенной траектории J = Jo + AJ и ф =
— гЬ -j- Аф, получаем уравнения
2л
2ix
О
21 Лт„соБ(тф—nty-\-%mn), F.4.10)
2я dJ
-AJ,
где Атп — амплитуды Фурье для
Рассмотрим резонансные невозмущенные магнитные поверх-
поверхности, для которых dq>/d^=^n/m. Переходя к резонансным перемен-
переменным (см. § 2.4)
ф= тф—nty,
находим следующий гамильтониан возмущенного движения:
Я= J?L-JL- (aj>* +гАтпсо&у, F.4.11)
2л dJ 2
где Д7 = AJ/m. Полуширина резонанса, согласно B.4.31), равна
1 макс —
m
еА,
(\/2n)di/dJ
V»
F.4.12)
В работе [137] произведен численный расчет магнитного поля
левитрона, возмущенного с помощью наклона кольцевого провод-
проводника. Для резонанса т = п = 1 (i = 2я) получено прекрасное
согласие с аналитическим выражением F.4.12), если только возму-
возмущение не превышает порог глобальной стохастичности. Для отно-
относительно больших возмущений наблюдалось образование вторич-
вторичных резонансов, как и предсказывает теория в § 2.4 и 4.3.
На рис. 6.22, а показано теоретическое (сплошная линия) и найден-
найденное численно сечение резонансной магнитной поверхности для не-
невозмущенного i = 2л. Локальное число вращения в центре ре-
резонанса а = 1/E,6), и поэтому вторичные резонансы не видны.
На рис. 6.22, б возмущение увеличено, так что а = 1/4 (вторич-
(вторичный резонанс на четвертой гармонике). Результаты численного
счета (кружки) теперь уже не ложатся на теоретическую кривую,
а соответствующая магнитная линия оказывается стохастической.
z о
-0,1 -
-0,2
г о -
-0,2
Рис. 6.22. Резонансы магнитных линий в левитроне при i = 2л (по данным работы [137]).
а — угол наклона кольцевого тока (возмущение) 6 = 0,25°; б — 6 = 0,5°; сплошные линии — теоретические инвариантные кри-
кривые; кружки — численный счет.
392 Глава 6
Теоретический анализ (см. п. 2.46) показывает, что вторичные ре-
зонансы с а = 1/4 и а = 1/5 перекрываются, что и приводит к на-
наблюдаемой стохастичности.
Аналогичные результаты для винтовой обмотки были получены
Розенблютом и др. [349] и Филоненко и др. [129]. Возмущения об-
общего вида в токамаках рассматривались Речестером и Стиксом [343 ]
и Финном [130]. В этих работах исследовались также перекрытие
резонансов и внутренняя диффузия 1). Во всех случаях рассматри-
рассматривалось возмущение и разрушение только магнитных поверхностей.
Принималось, что заряженные частицы двигаются точно вдоль
магнитных линий и конечный размер ларморовского радиуса не
играет роли. Поскольку мы рассматриваем задачи, эквивалентные
двум степеням свободы, то внутренняя диффузия возникает только
при перекрытии резонансов (гл. 5), тогда как диффузия влоль ре-
резонансов отсутствует.
6.46. Дрейфовые поверхности и диффузия _в статических полях
Дрейфовые поверхности. При учете конечного ларморовского радиуса
электрического поля и неоднородности магнитного поля оказыва-
оказывается, что частицы не следуют точно за магнитной линией, а мед-
медленно сдрейфовывают перпендикулярно ей. Траектории ларморов-
ларморовского центра заполняют дрейфовые поверхности. При этом могут
иметь место резонансы между гармониками неоднородности поля
и дрейфовым движением. Уравнения движения в дрейфовом прибли-
приближении в отсутствие токов имеют вид (см., например, [362], § 2.2) 2):
*L ??><* А F.4.13а)
F.4.136)
dt е В2 " В
dV\\ р AT) и
I, _ е aw ц
dt M ds M ds
где
В
— усредненная по ларморовскому вращению сила; |i =
= —Mv2±/B — магнитный момент; е — заряд частицы; М — ее
масса; Уц, v± —параллельная и перпендикулярная магнитному
полю компоненты скорости частицы; г — радиус-вектор ларморов-
ларморовского центра; s — координата вдоль магнитной линии; Ф — элек-
J) См. также работу [514].— Прим. ред.
2) См. также работы [515, 516].— Прим. ред.
Многомерные колебания 393
трический потенциал п с — скорость света. В дрейфовом прибли-
приближении [х является адиабатическим инвариантом и считается по-
постоянным (см. п. 2.36). Если В и Ф не зависят явно от времени,
то дрейфовое движение можно описать с помощью автономного
гамильтониана с двумя степенями свободы. В этом случае вместо
времени удобно использовать в качестве независимой переменной
величину s, причем ds/dt=v,,, где скорость и„ связана с интегра-
интегралами движения Е и (х соотношением
2 У/2(?-(х?)'/2, F.4.14)
М
а Е — полная энергия частицы. Получаемые в результате уравне-
уравнения дрейфового движения аналогичны уравнениям магнитной ли-
линии, описанным в п. 6.4а.
Нерезонансный дрейф. Рассмотрим сначала случай, когда дрейф
вызывается градиентом магнитного поля. Если магнитные поверх-
поверхности симметричны по <р (см. рис. 6.20), то сила F перпендику-
перпендикулярна магнитной поверхности и скорость дрейфа vD, согласно
F.4.13), направлена по касательной к магнитной поверхности.
Однако магнитное поле в системах с тороидальной геометрией типа
левитрона или токамака не обладает такой симметрией, что приво-
приводит к радиальной составляющей дрейфа частиц. Масштаб времени
такого дрейфа обычно велик по сравнению с временем оборота
вокруг большой оси тора. Поэтому в пренебрежении резонансами
высоких порядков радиальный дрейф можно описать автономным
гамильтонианом с одной степенью свободы, который является ин-
интегрируемым.
Дрейфовые траектории существенно зависят от отношения
vjv». В случае v,, <^ v± частицы оказываются захваченными
в некоторой области (по ф и ij?) с наружной стороны тора и совер-
совершают дрейфовые колебания, не попадая в область более сильного
магнитного поля с внутренней стороны тора. Проекция этого дви-
движения на плоскость i}> = const имеет форму «банана» (ср. рис. 6.22,а).
Амплитуда радиальных колебаний (при ф = 0) имеет порядок
Ar~(/?/a)V*Pt/i, F.4.15)
где pL — ларморовский радиус частицы. Подобные траектории для
захваченных частиц существуют и в других магнитных полях и не
зависят от резонансов между движением по ф и по ty (подробнее
см. в [389]).
Дрейфовая поверхность пролетных частиц х) повторяет форму
*) Пролетными называются частицы, которые совершают полный оборот
вокруг малой и большой осей тора, т. е. по ф и i|). Для поля токамака, на-
например, граница между пролетными и захваченными частицами соответст-
соответствует скорости у,, « v Br/R0I^2 при ф = 0.— Прим. ред.
394 Глава 6
магнитной поверхности, отклоняясь от нее на расстояние порядка
Pi./i. Можно сказать, что дрейфовой поверхностью в этом случае
является просто слегка возмущенная магнитная поверхность.
Дрейфовые резонансы. Если обе функции В и Ф зависят от ф и t|?,
то для пролетных частиц возможны резонансы. Однако из-за того,
что скорость дрейфа пропорциональна pL, размер дрейфовых ре-
резонансов мал по сравнению с размером резонанса самих магнитных
линий при том же возмущении магнитного поля. Если же присутст-
присутствует статическое электрическое поле, например, с потенциалом
вида
то возникают дрейфовые резонансы независимо от возмущения
магнитного поля. Возмущенный дрейф описывается в этом случае
системой уравнений вида F.4.10), причем амплитуды возмущения
еАтп ее р7,Фтя. Брамбилла и Лихтенберг [39] получили для про-
пространственной полуширины резонанса выражение, аналогичное
F.4.12):
RPiV/2 F4.16)
Т a di/dr
где Т — температура в энергетических единицах.
Диффузия в статических полях. Хотя размер резонанса F.4.16)
может быть велик по сравнению с амплитудой нерезонансных коле-
колебаний F.4.15), именно последние определяют обычно внешнюю
диффузию в статических полях. Причина этого состоит в следую-
следующем. В статическом случае положение резонанса (по г) опреде-
определяется условием (оф/(о,|, = dq/dty = п/т и не зависит от v.. или |х.
Внешняя диффузия за счет столкновений между частицами с из-
изменением и и и (х относится поэтому к типу, рассмотренному в п. 5.56.
Конечно, если дрейфовые резонансы перекрываются, то скорость
диффузии определяется глобальной стохастичностью движения.
Однако такое перекрытие возможно лишь в исключительных слу-
случаях, так как размер резонансов зависит от малого ларморовского
радиуса F.4.16). Поэтому в дальнейшем мы пренебрежем внутрен-
внутренней диффузией. Правда, резонансы несколько усиливают диффузию
даже в отсутствие перекрытия, однако средняя скорость диффузии
меняется при этом незначительно (п. 5.56).
В отличие от дрейфовых резонансов нерезонансные колебания
захваченных частиц F.4.15) существуют везде. Рассеяние частиц
изменяет их в и \i и может переводить частицы из захваченных
в пролетные, и наоборот. В результате частицы смещаются по ра"
диусу. В зависимости от частоты столкновений возможны три ре"
жима диффузии.
1. При низкой частоте столкновений захваченные частицы сме-
смещаются, в среднем, на величину Дг [см. F.4.15) за время пере-
Многомерные колебания 395
хода их в пролетные вследствие диффузии по v.,. Поэтому
скорость радиальной диффузии в этом режиме пропорцио-
пропорциональна частоте столкновений.
2. При промежуточной частоте столкновений захваченная ча-
частица переходит в пролетную раньше, чем она успевает со-
совершить полное колебание по радиусу, т. е. ее радиальное
смещение за один захват уменьшается по сравнению с F.4.15).
Однако при этом пролетные частицы с относительно малой
скоростью v.. также вносят существенный вклад в диффу-
диффузию, расширяя таким образом область (по v Л эффективного
радиального дрейфа. Учет всех этих эффектов приводит к
тому, что коэффициент диффузии перестает зависеть от ча-
частоты столкновений. Поэтому обычно этот случай называют
режимом плато.
3. При высокой частоте столкновений все частицы вносят вклад
в диффузию. Характерный масштаб радиального дрейфа ме-
между столкновениями равен р^/а, а коэффициент диффузии
снова пропорционален частоте столкновений.
Во всех трех режимах характерный масштаб радиального сме-
смещения пропорционален ларморовскому радиусу pL = vT/Q, так
что зависимость коэффициента диффузии от магнитного поля имеет
классический вид D ос р| ос 1/В2. Поэтому такую диффузию на-
называют неоклассической г). Подробная теория этой диффузии дана
в обзоре Галеева и Сагдеева [147]. Как отмечалось в п. 6.3а, ана-
аналогичные три режима диффузии существуют и в резонансном
каналировании.
6.4в. Диффузия в нестационарных полях
В нестационарных полях положение дрейфового резонанса уже за-
зависит от у.. (см. ниже), и резонансы возможны при любом г. По-
Поскольку ширина этих резонансов значительно превышает размах
радиальных колебаний запертых частиц F.4.15), то диффузия,
аналогичная неоклассической, будет определяться теперь резо-
нансами. Эта задача рассматривалась Геллом и др. [152] и, более
подробно, Невинсом и др. [316] 2).
Условие резонанса имеет вид
тсоф(/\ уи) + люф (г, ип) + /со = 0,
где <в — частота колебаний поля. Из этого условия (при заданных
1) Приставка «нео» здесь не очень оправдана, поскольку такой механизм
диффузии рассматривался Будкером еще в 1951 г. (см. [509], с. 50), хотя раз-
разработка полной теории этих процессов «несколько» задержалась [510].—
Прим. ред.
2) Эта задача впервые рассмотрена Погуце [525) для объяснения ано-
аномальной электронной теплопроводности в токамаке.— Прим. ред.
396 Глава 6
п, т и /) можно найти положение центра резонанса г = r(v,., со) г).
Если при этом имеет место внешняя диффузия частицы по v , то
резонанс диффундирует по г. Пример такой диффузии рассмотрен
в п. 6.36, а ее описание можно свести к отображению.
Рассмотрим переменное поле в виде плоской волны, фаза ко-
которой
Q = k-r — ®t, F.4.17)
где k — волновой вектор. В дрейфовом приближении скорость ча-
частицы параллельна магнитной линии, поскольку скорость дрейфа
считается малой по сравнению со скоростью частицы. Поэтому
скорость изменения фазы волны равна
-^--^(г)»,,-©, F.4.18)
где k.. — проекция волнового вектора на направление магнитного
поля.
Построение отображения. Будем использовать для простоты де-
картову систему координат, в которой х соответствует/" (см. рис. 6.23);
волновой вектор k = koy, а В (х) лежит в плоскости {у, z), причем
Ву = О при х = 0. Зависимость Ви (х) примем в виде
где Ls —• некоторая постоянная (для тороидального поля Li =
= {Rid) di/dr). Тогда
k^(x) = k±-f-, F.4.19)
где мы положили приближенно k0 = k±. Для потенциала волны
(D = (Docos0 F.4.20)
уравнения движения F.4.13) можно представить в виде
-^- = ^-cDosin0, F.4.21)
at t>
dV 0
= — ?nOosin0. F.4.22)
dt M
г) Обе частоты со и со. пропорциональны к., и при / Ф 0 положение
резонанса зависит от v ц. В статическом поле (со =0) Уц исключается из
резонансного условия, и резонанс, казалось бы, не может смещаться по г.
Это, однако, правильно, за исключением важного частного случая Уц =0,
когда условие резонанса автоматически выполняется при любом г. Факти-
Фактически в рассматриваемом ниже примере скорость диффузии F.4.40) вообще
не зависит от со (при S <<С 1). В частности, численные данные на рис. 6.25
относятся как раз к диффузии в статическом поле.— Прим. ред.
Многомерные колебания
397
Вместе с F.4.18) эти уравнения определяют возмущенное дви-
движение частицы в отсутствие столкновений. Из F.4.18) условие
резонанса с центром в точке х = х0 имеет вид
?Л-о> = 0, F.4.23)
Рис. 6.23. Конфигурация полей в модели дрегфовых резонансов.
где &..„ = &., (х0). Невозмущенное движение в центре резонанса
соответствует 9 = 0. Линеарлзуя уравнения движения по л; и в.,
получаем
F.4.24)
F.4.25)
dQ
dt
v,Ax + k,,Av,.,
F.4.26)
где Ax = x—xQ, Av^ = v,.—-v^0. В уравнение F.4.25) добавлено
случайное изменение скорости ?, которое учитывает столкновения
398 Глава 6
между частицами. Положим (?) = 0 и
d -o\
dt
F.4.27)
где vT — тепловая скорость частицы, а хс — среднее время между
столкновениями. Согласно F.4.23) и F.4.19), это приводит к сме-
смещению резонанса по х.
Преобразуем уравнения F.4.24) — F.4.26) к виду F.3.28). Для
этого исключим 9 из уравнений F.4.24) и F.4.25)
* ^^с) = е F.4.28)
dt v ^ k± *
и введем новую переменную
Y = Avn ^- Ах, F.4.29)
которая описывает только случайный процесс
Г = ?. F.4.30)
Выражая Au(j через К и Ах из F.4.29), подставляя в F.4.26), по-
получаем
х, F.4.31)
Параметр
S=J^ »_по_ FЛ32)
характеризует влияние поперечного градиента магнитного поля
(«шира»), которое существенно при S ^> 1. Путем изменения мас-
масштабов
I = —р~ Q A + S) Ах, F.4.33а)
P = kmY F.4.336)
система уравнений F.4.24), F.4.31) и F.4.30) приводится к стан-
стандартному виду F.3.28)
-^—= К sin 9, F.4.34а)
dt
-^- = / + Р, F.4.346)
dt K !
-^— =\, F.4.34b)
Многомерные колебания 399
где
К =klov2T (l+S)~?- , F.4.35a)
S = *uo? F.4.356)
и положено Т = Mv2T.
Скорость диффузии. Аналогично п. 6.36 коэффициент резонансной
диффузии по / определяется соотношением
?>r=.J-i-=-l-2- = J ^-^. F.4.36)
2< 2t 2 тс
Пренебрегая нерезонансной диффузией, получаем для средней ско-
скорости диффузии аналогично F.3.33):
(D) = Drfr, F.4.37)
где fr — доля резонансных частиц. Считая разброс Уц порядка
vT и, следовательно, согласно F.4.336), разброс/3 порядка k$ovT,
находим
fr f—, F.4.38)
k
что дает
iад V (^I//tc. F.4.39)
Переходя с помощью F.4.33а) к переменной Ах, имеем
Dx - -i ^ f-^f -?- ¦ F.4.40)
Этот результат был получен Невинсом и др. [316] более фор-
формальным методом, не раскрывающим механизма диффузии. Отме-
Отметим, что выражение F.4.40) не дает точного количественного значе-
значения коэффициента диффузии ввиду неопределенности оценки F.4.38).
Диффузию такого типа иногда называют псевдоклассической, так как
ее скорость F.4.40), как и для классической диффузии, пропорцио-
пропорциональна р|/тс, но зависит от амплитуды Фо резонансной гармоники
возмущения.
Сравнение аналитических и численных результатов. В работе Не-
винса и др. [316] проведено также сравнение с результатами чис-
численного моделирования, для которого использовались точные урав-
уравнения движения частицы, а столкновения учитывались по методу
Монте-Карло. В типичном случае для получения хорошей статисти-
статистики просчитывались траектории от 500 до 1000 частиц. Было по-
получено разумное согласие с теоретическими зависимостями от раз-
различных параметров. Мы приведем здесь два результата.
400
Глава 6
На рис. 6.24 численные данные (D*) сравниваются с аналити-
аналитическим выражением F.4.40) для Dx, в которое введен дополнитель-
дополнительный множитель. Подгонка дает D* = 0,8 Dx, т. е. согласие хорошее.
На рис. 6.25 показана зависимость скорости диффузии от эф-
эффективной частоты столкновений
Mvl
V,
¦фф
= v,
S)
F.4.41)
to2 -i
ю-
Рис. 6.24. Скорость дрейфовой диффузии D* в зависимости от параметра
шира S (по данным работы [316]).
°кл = pi'V еФп1Т = °'01' *ll'fc- = °'03; ш/* II о "Г = °-^ k±PL = 4'3 Х 10~3' Т°Ч"
ки—численные данные (с ошибками); сплошная линия —теоретические значения F.4.40)»
умноженные на 0,8 (подгонка, см. текст).
где vc = 1/тс. Видн плато и интересный переходный режим в
районе л>Эфф/соо = 1 где ю0 = K4i — частота фазовых колебаний
на резонансе 1). Скорость диффузии на плато можно определить,
х) Аналогичные результаты были получены для близкой, но более про-
простой модели в работе [517] (рис. 5).— Прим. ред.
Многомерные колебания
401
исходя из простого предположения, что при уЭфф>(о0 длина
дрейфа между столкновениями уменьшается с ростом vc таким об-
образом, что сохраняется отношение
уэфф/(о0^1. F.4.42)
Используя в F.4.42) w0 = К?12 из F.4.35а) и уэфф из F.4.41), на-
10 -
Рис. 6.25. Скорость дрейфовой диффузии в зависимости от частоты столкно-
столкновений (по данным работы [316]).
DQ =
= 0,08;
^/kx = 0,2; о) = 0; k±pL = 4,3 X И»
Точки — численные данные (с ошибками); сплошная линия — теоретические значении
F.4.40), умноженные на 1,3; пунктирная линия — плато F.4.43).
\одим vc и подставляем эту величину в F.4.40). В результате по-
получаем ::•> зависящий от vc коэффициент диффузии на плато1):
DY= -^—KvA -^-| pi. F.4.43)
?! Ч .
х) При А и ->¦ 0 эта оценка [как и в F.4.40)] становится неприменимой
в силу тех или иных ограничений. Если, например, рассматриваемая модель
справедлива при Дх si а, то амплитуда дрейфовых колебаний (kpjk .Лх
Х(еФ0/ГI/2^а и Daxn ^ pz vTkxn (еФ0/ГK/а.— Прим. ред.
402
Глава 6
Этот результат, полученный в пределе нулевого шира, отличается
от результата кинетической теории [358 ] лишь на числовой множи-
множитель, близкий к единице. Заметим, что, хотя соотношение F.4.42)
и является правдоподобным, оно не вытекает из рассматриваемой
теории *).
6.4г. Самосогласованная задача
Диффузия в тороидальных плазменных ловушках указывает на
очень важную особенность реальных физических задач, не рассмат-
0,
-0,8
-0,4
0
Рис. 6.26. Сечение магнитных поверхностей плоскостью ^ = const (числен-
(численные данные работы [48]).
Виден винтовой резонанс In = 2/1, окруженный тороидальным резонансом на третьей
гармонике.
риваемую явно в этой книге. Речь идет о самосогласованных по-
полях, которые, с одной стороны, определяют движение частиц, а
х) Это не совсем так. В работе [71] показано, что скорость диффузии на
плато дается квазилинейным выражением
DT « п
/Лео « (я/2) <?к\ф
Do,
которое совпадает с F.4.43) с точностью до числового множителя (см.
рис. 6.25).— Прим. ред.
Многомерные колебания
403
с другой — сами зависят от коллективных движении этих же ча-
частиц. При такой постановке задачи гамильтониан системы априори
неизвестен, а исследования проводятся обычно с помощью числен-
численного моделирования полной системы уравнений для частиц и поля.
Ниже кратко описан пример такой задачи.
0,8
0,4
0
-0,4
-0,8
I i ГТГ5 Г f
,>С7
те I
*У&<\
ч
1
V-
\
-
1 I
/ s
¦¦•¦'.' •
... .".
-¦ ¦¦ ¦''
it- '•
¦ .. ¦
\ V
1 1
J.-
¦ '
f
-¦(
•-¦у:
i
i
\
' \
у—
/
\
\
. |
t •-
"ч
у
¦¦I. 1
i
' • *¦*
\ '.' •
• ' - ¦ i
/ * -. *
¦¦¦"'¦-.
•r' i
.V
-.- . Д
', . Л '
' i;
i/
':¦ f ~^
/' -
|
-0,8 -0,4 0 0,4 0,8- -0,8 -0,4 0 0,4 0,8
t=1910rMU t.
1
-¦/
—.
I j -j,.:' г
'•'¦'• ' '•'"' .':' ¦"•'¦
»•.',. ¦ ' ¦¦..¦'-•.•'¦
'r'-t'.l
1
•-
¦ ,
i"
j _ i
.' v ¦'¦ '
•У""'';, '¦ ¦;:'
"¦ Г ' 1
1
'L
Jli '
II '
J_L
-0,8
-0,8 -0,4 0 0,4 0,8 -0,8 -0,4 0 0,4 0,8
t = 2060rM2 «=2116rMe
Рис. 6.27. To же, что и на рис. 6.26, но с учетом самосогласованного магнит-
магнитного поля для четырех моментов времени (численные данные работы [48]).
(' — характерное магнитогидродинамическое время.
Тиринг-моды и неустойчивости срыва в токамаках. В токамаке (см.
п. 6.4а) полоидальная составляющая магнитного поля возбуждается
азимутальным током частиц плазмы, движение которых считается
регулярным. Однако в плазме с конечной электропроводностью
возможна неустойчивость тиринг-моды (см., например, [48, 428])
с винтовым возмущением тока Aц>—mj) = const; I, n — целые числа).
404 Глава 6
Такое возмущение тока нарушает азимутальную симметрию маг-
магнитного поля и приводит к резонансам магнитных линий. В случае
цилиндрической симметрии одна винтовая мода приводит к обра-
образованию только одного резонанса, и конфигурация магнитного
поля остается регулярной. Однако с учетом тороидальности появ-
появляются новые резонансы. Например, винтовая мода с / = 2 и п = 1
приводит к образованию одного резонанса второй гармоники на
магнитной поверхности i = л. Тороидальность же добавляет к нему
резонанс третьей гармоники при i = 2я/3. В токамаках обычно
обе резонансные поверхности расположены в области, занятой
плазмой. Структура магнитных поверхностей в этих условиях,
полученная путем численного моделирования для стационарной
винтовой моды, показана на рис. 6.26. В данном случае область
стохастических магнитных линий оказалась незначительной. Од-
Однако если присутствует еще и винтовая мода с / = 2, п = 2, то об-
область стохастичности резко увеличивается. Результаты численного
моделирования эволюции двух этих мод путем решения самосогла-
самосогласованных уравнений для частиц и поля показаны на рис. 6.27 для
четырех моментов времени. На первом кадре ясно видны резонансы
с 1 = пи1 = 2я/3. На втором кадре виден результат взаимодейст-
взаимодействия между резонансами — большая часть магнитных линий в
в районе резонанса i = я стала стохастической. На третьем кадре
стохастичность распространяется и на область резонанса i = 2л/3.
И наконец, на четвертом кадре показана заключительная стадия
эволюции, которая привела практически к полному разрушению
магнитных поверхностей. Связанное с этим резкое изменение рас-
распределения тока по сечению камеры считается причиной неустой-
неустойчивости срыва в токамаках.
§ 6.5. Системы со многими степенями свободы
Исследования систем со многими степенями свободы всегда вызы-
вызывали большой интерес. Причиной этого является, с одной стороны,
желание понять поведение непрерывных систем, описываемых не-
нелинейными дифференциальными уравнениями в частных произ-
производных, а с другой — связь со статистической механикой. Геомет-
Геометрия многомерных резонансов рассматривалась в п. 6.1а, а также
в § 6.3 (более подробное описание можно найти в работе [70]).
С точки зрения резонансной структуры вопрос о поведении системы
с большим числом степеней свободы сводится к вопросу о том, воз-
возрастает ли плотность основных резонансов быстрее, чем умень-
уменьшается их ширина, по мере распределения энергии по многим
степеням свободы. Если это действительно так, то при N —>- оо сле-
следует ожидать перекрытия резонансов и сильной стохастичности
движения.
Чтобы как-то продвинуться в этом направлении, можно, напри-
Многомерные колебания 405
мер, обобщить модель ускорения Ферми на случай, когда движение
стенки является суперпозицией колебаний с несколькими часто-
частотами. Для случая двух частот это было сделано в работе Ховарда
и др. [202] для отображения J)
/tssins(pn + Arsmryn
«я+i = tin Л
ЫМ
^ (r + s)un+l
Здесь величина Л2 характеризует «энергию колебаний» соответст-
соответствующей частоты. Если считать полную энергию ?Л; = const и
i
возбудить колебания с N частотами, то ширина резонанса
Аи ос Л1/2 ос N~1/4. Считая распределение частот случайным,
можно ожидать, что максимальное расстояние между резонансами
6wMaKCoc (\nN)/N. Таким образом, параметр перекрытия резонансов
Дм д/3А
бймакс In N
F.5.2)
возрастает с N. Сравнивая результаты для одной и двух частот
в модели F.5.1), Ховард и др. [202] нашли, что эффект, по мень-
меньшей мере, порядка F.5.2). Однако они не исследовали зависимость
от N. Из оценки F.5.2) следует, что с ростом N при постоянной
полной энергии движение становится стохастическим во всем фа-
фазовом пространстве.
Такая упрощенная модель не является, конечно, адекватной
для всех многомерных систем. Так, например, она не описывает
солитонные регулярные решения, которые, как известно, сущест-
существуют для некоторых нелинейных дифференциальных уравнений
в частных производных (см., например, [240, 249, 438]J). Однако,
как мы увидим ниже, многие системы действительно оказываются
стохастическими при больших N.
Проблема Ферми—Паста—Улама. Одной из интересных моделей
является нелинейная цепочка, исследованная численно в работе
*) Для иррационального отношения rls (несоизмеримые частоты) можно
было бы говорить, в некотором смысле, о двух внешних степенях свободы
(см. работу [477]), как и предполагается ниже в основном тексте для произ-
произвольного числа N частот. Однако в цитируемой работе [202] г, s — целые
числа, и отображение F.5.1) описывает просто две гармоники одной частоты
(ср. [482, § 6], где исследовано аналогичное отображение с большим числом
гармоник). Отметим, что отображения вида F.5.1) с несоизмеримыми часто-
частотами естественно возникают в теории диффузии Арнольда [70, § 7.3]. —
Прим. ред.
2) См. также книгу [457].— Прим. ред.
406 Глава 6
Ферми, Паста и Улама [127]. Такую цепочку можно рассматри-
рассматривать как модель нелинейной струны, колебания которой описы-
описываются уравнением *)
ил ил I 1 | о о / "х \ I г\ /с с о\
Движение цепочки описывается системой нелинейных обыкновен-
обыкновенных дифференциальных уравнений (все массы приняты равными
единице):
*/ = (*/+! +*/-1 — 2*/)+ Р [(*/+! —*/)' — (*/ —*/-l)8ll F-5-4)
где / -- 1, 2, . . . , N и концы цепочки закреплены. Полное число
частиц было выбрано равным N = 64. Вопреки ожиданию энергия
не распределялась по различным модам колебаний, а система ре-
регулярно возвращалась к начальному состоянию2). Эти неожидан-
неожиданные результаты3) стимулировали многочисленные исследования
модели F.5.4) (библиографию по этой проблеме см. в работе [31 ]).
При аналитическом исследовании этой модели естественно ис-
использовать нормальные моды колебаний линейной системы ф = 0),
что было сделано в ряде работ (см., например, [135, 208]). С по-
помощью преобразования
ш4!**1-^- <б55>
6=1
Израйлев и Чириков при fi/8N <^ 1 нашли следующую приближен-
приближенную систему уравнений:
Щ- соьB—cof) a\\ = — 2 FkmcosQkm, F.5.6)
где coft = 2 sin {nkl2N), a 9Am = <s>km — частоты возмущения.
Используя критерий перекрытия резонансов, Израйлев и Чири-
Чириков после довольно громоздких вычислений получили следующее
условие стохастичности для низких мод:
^^-; k«N. F.5.7)
J) Для качественно правильного моделирования в правую часть уравне-
уравнения F.5.3) нужно добавить дисперсионный член (а2/12) д^х/дг*1, где а — рас-
расстояние между массами в цепочке. Решения же уравнения F.5.3) являются
сингулярными вследствие «опрокидывания» нелинейной волны.— Прим. ред.
2) Интересно отметить, что выдвинутая а работе [127] на основании этих
результатов общая гипотеза о существовании «квази-мод» (см. также [135])
была в тот момент уже доказана Колмогоровым [229] для широкого класса
гамильтоновых систем.— Прим. ред.
3) Первоначальное удивление было столь велико, что долгое время (до
работы [208]) случаи хаотических колебаний нелинейной цепочки в работе
1127] (см., например, рис. 5) оставались незамеченными.— Прим. ред.
Многомерные колебания 407
Они нашли, что эта оценка не противоречит имевшимся численным
данным. Это согласуется и с модельной оценкой F.5.2), которая
тоже предсказывает перекрытие резонансов при достаточно боль-
большом N. Однако так как при фиксированной энергии системы вы-
высокие моды будут иметь очень малую амплитуду, то не ясно, будет ли
хаотическая часть фазового пространства стремиться к нулю или
к единице с ростом N.
Аналогичные результаты были получены ранее Фордом и Уотер-
сом [135]. Они нашли, что существенный обмен энергией между
модами возможен только вблизи резонансов по невозмущенным
(линейным) частотам мод, и дали качественный критерий этого.
В соответствии с этим критерием они видоизменили модель Ферми—
Паста—Улама и численно продемонстрировали сильный обмен
энергией между всеми модами (для N = 5), который имел, по-ви-
по-видимому, стохастический характер.
Используя другой подход, Бивинс и др. [31] исследовали взаи-
взаимодействие нескольких мод в случае, когда одна из них имеет боль-
большую амплитуду и возбуждает соседние моды. Такой подход ох-
охватывает только относительно короткий интервал времени и ни-
ничего не говорит об асимптотическом поведении системы. Тем не
менее они наблюдали переход от регулярного обмена энергией
между модами при слабом возмущении к похожему [на хаотический
при более сильном возмущении х).
Модель притягивающихся листов. Для исследования зависимо-
зависимости стохастичности от числа степеней свободы Фрёшле и Шейдекер
A44) использовали модель в виде нескольких параллельных гра-
гравитационно-взаимодействующих листов, которая описывается га-
гамильтонианом
N N
Н{и, х)= — m2 M? + 4jtGm? |*/—*;|» F.5.8)
2 i=l />i
где т — масса листа, a G — гравитационная постоянная. Для
каждого счета начальные условия выбирались случайно при фиксиро-
фиксированной полной энергии системы. Уравнения движения интегрирова-
интегрировались аналитически до момента пересечения каких-либо двух листов.
В качестве критерия стохастичности использовалась локальная
х) Другое, более известное, решение проблемы Ферми—Паста—Улама
связывает регулярность колебаний некоторых видов нелинейной цепочки
с близостью их к полностью интегрируемым нелинейным системам при лю-
любой энергии (см., например, прекрасный обзор Забуского [518]). В частности,
уравнение F.5.3) с квадратичной нелинейностью ((дх/дгJ -> дх/dz) и дис-
дисперсией (см. примечание редактора на с. 406) имеет бесконечный набор не-
независимых интегралов движения и является, по-видимому, полностью ин-
интегрируемым. Хотя такое решение проблемы годится далеко не всегда ввиду
исключительности полностью интегрируемых систем, оно послужило толч-
толчком для развития мощных методов интегрирования нелинейных уравнений
(см., например, работы [457, 518]).— Прим. ред.
408
Глава 6
Таблица 6.1
N
(число листов)
2
3
4
. Модель F.5.8) притягивающихся
Число регу-
регулярных
траекторий
100
96
14
Число стохас-
стохастических
траекторий
0
4
86
Л7
(число^листов)
5
6
7
листов A00
Число регу-
регулярных
траекторий
1
0
0
траекторий]
Число стоха-
стохастических
траекторий
99
100
100
неустойчивость движения (§ 5.3). Полученные результаты приве-
приведены в табл. 6.1. Видно быстрое распространение стохастичности
по фазовому пространству с ростом числа листов N. Случай двух
листов является, как известно, интегрируемым.
Интерпретация этих результатов затруднительна, поскольку
сингулярность взаимодействия при пересечении листов нарушает
условие гладкости теоремы КАМ (п. 3.2а). Как мы знаем на при-
примере сингулярного отображения Улама C.4.4), это приводит к
глобальной стохастичности, а регулярные траектории сохраняются
только в островках устойчивости внутри резонансов. Если доля
этих островков уменьшается с ростом N, то можно ожидать бы-
быстрого возрастания числа стохастических траекторий, что согла-
согласуется с результатами [144].
Потенциал Леннарда-Джонса. Другим хорошо известным приме-
примером является система с потенциалом Леннарда-Джонса
V (гц) = 4е [(о/гцI2—(olrijf], F.5.9)
где гцд— расстояние между частицами i и /, а 0 — пространствен-
пространственный масштаб взаимодействия. Слабое притяжение при /¦*/> 0 сме-
сменяется сильным отталкиванием при гц<?.а. Гамильтониан системы
имеет вид
ipui
2 i=\ j<i
Гальгани и сотр. [148] исследовали эту задачу в простейшем слу-
случае одномерного движения частиц. Они обнаружили, что распре-
распределение энергии по невозмущенным (линейным) модам колебаний
увеличивается с ростом N. Эти результаты, однако, трудно интер-
интерпретировать с точки зрения стохастичности, поскольку обычные
критерии стохастичности в работе не использовались.
Стоддард и Форд [394] исследовали ту же задачу для двумерного
движения. Такая модель является сглаженным вариантом системы
твердых дисков, движение которых, как показал Синай, обладает
перемешиванием (см. п. 1.4а и § 5.2). В качестве критерия стоха-
стохастичности использовалась неустойчивость близких траекторий,
которая и была обнаружена для всех исследованных начальных
условий в системе из 100 частиц (N = 200). Этот результат пред-
Многомерные колебания 409
ставляется вполне естественным для сильно нелинейного взаимо-
взаимодействия Леннарда-Джонса.
Заключение. С ростом числа степеней свободы наблюдаются две
конкурирующие тенденции. С одной стороны, сетка резонансов
в фазовом пространстве становится все более плотной. С другой
стороны, ширина резонансов обычно уменьшается. В зависимости
от поведения усредненного параметра перекрытия движение си-
системы при N —>- оо может быть как полностью стохастическим,
так и полностью регулярным. Примером систем первого типа яв-
является газ Леннарда-Джонса, а второго — непрерывные си-
системы, такие, как нелинейная струна *). Хотя строгого критерия
разделения систем на эти два типа не существует, оценка перекры-
перекрытия резонансов позволяет, по-видимому, сделать правдоподобные
заключения о поведении системы при больших N.
') Последнее впечатление, по-видимому, обманчиво и связано с тем, что
наиболее известные примеры непрерывных систем относятся к очень спе-
специальному виду (слабо нелинейные волны), а их динамика исследована
только на относительно коротком масштабе времени и для узкого класса
начальных условий (небольшое число низкочастотных мод). По всем сущест-
существующим общим критериям граница стохастичности резко понижается с ро-
ростом N (см., например, работу [70], § 4.5 и 4.6), так что в типичном случае
при N -> оо хаос охватывает, по-видимому, практически все фазовое про-
пространство. Однако значение регулярной компоненты движения далеко не
исчерпывается занимаемым ею объемом фазового пространства (см. предис-
предисловие редактора перевода).— Прим. ред.
Глава 7
ДИССИПАТИВНЫЕ СИСТЕМЫ
§ 7.1. Простые и странные аттракторы
Диссипативные системы обладают той особенностью, что при их
движении фазовый объем сжимается к аттрактору более низкой
размерности, чем исходное пространство. При этом если какой-
либо параметр системы изменяется, то регулярное движение на
аттракторе может смениться хаотическим, и наоборот. Хотя наши
знания о хаотическом поведении диссипативных систем ни в коей
мере нельзя считать полными, все же к настоящему времени многие
особенности такого движения хорошо изучены. Разработаны также
методы теоретического анализа диссипативных систем.
В первом параграфе этой главы обсуждаются основные свойства
диссипативных систем, такие, как сжатие фазового объема и регу-
регулярное движение на простых аттракторах. Затем вводится понятие
странного аттрактора со стохастическим движением. В § 1.5 уже
приводился пример странного аттрактора. Здесь же обсуждаются
два других примера диссипативных систем со странными аттракто-
аттракторами: система Рёслера и отображение Хенона. Особое внимание
обращается на те свойства хаотического движения, которые свя-
связаны с возможностью перехода к одномерному отображению, а
также с геометрической структурой странного аттрактора. Эта
геометрия описывается в терминах канторовых множеств дробной
фрактальной размерности. Обсуждаются способы вычисления та-
такой размерности и ее связь с показателями Ляпунова.
В § 7.2 рассматривается динамика необратимых одномерных
отображений, начиная с их периодических точек, линейной устой-
устойчивости и структуры бифуркаций. Затем исследуется хаотическое
движение и его связь с показателями Ляпунова, асимптотическими
распределениями, спектром мощности, а также инвариантные свой-
свойства движения.
В § 7.3 рассматриваются двумерные обратимые отображения
и связанные с ними потоки. Показывается, что последовательность
бифуркаций удвоения периода, приводящая к хаотическому дви-
движению, аналогична найденной для одномерных отображений. Далее
описывается метод Мельникова для определения перехода от регу-
регулярного движения к стохастическому. Метод иллюстрируется на
примере вынужденных колебаний нелинейного осциллятора с за-
затуханием. Описан метод вычисления инвариантных распределений
с помощью уравнения ФПК.
Диссипативные системы 411
Наконец, в § 7.4 рассматривается переход к предельному слу-
случаю непрерывной среды. Приводится краткий вывод уравнений
Лоренца в задаче Рэлея—Бенара о движении подогреваемого снизу
слоя жидкости и обсуждаются условия применимости этих уравне-
уравнений. В заключение описываются различные модели перехода к тур-
турбулентности в жидкости и проводится сравнение с имеющимися
экспериментальными данными.
Хаотическому движению в диссипативных системах посвящено
большое число работ. В частности, одномерные отображения рас-
рассматриваются, например, в работах [82, 122, 123, 296] х). Имеются
также прекрасные обзоры [180, 194, 324, 340, 354, 368, 411 ]. Наше
изложение ниже основано главным образом на работах [180, 324,
368].
7.1а. Основные свойства
Рассмотрим движение, описываемое N дифференциальными урав-
уравнениями первого порядка
dx
dt
= V(x), G.1.1)
где х и V — ./V-мерные векторы, причем V не зависит явно от вре-
времени. Фазовое пространство такой системы характеризуется пере-
переменными xi (i = 1, N) и имеет размерность N. Если V— гладкая
функция, то решение для потока х (х0, t) существует при всех t.
Любая точка фазового пространства однозначно определяет состоя-
состояние системы G.1.1). В п. 1.26 уже показывалось, как построить
сечение Пуанкаре и соответствующее отображение Пуанкаре для
гамильтоновой системы. В диссипативных системах такие отобра-
отображения сохраняют некоторые, но не все свойства, присущие гамиль-
тоновым системам. Как видно из рис. 1.3, а, на котором изображена
поверхность сечения ?л, отображение Пуанкаре строится с по-
помощью интегрирования уравнений G.1.1) между двумя последова-
последовательными пересечениями траектории с ?л. Отображение имеет вид
xn+l = f(xn)t G.1.2)
где X и /—векторы размерности N—1. Если функция V (х) яв-
является гладкой, а вектор V нигде не касается ?л, то можно пока-
показать, что / (х) также гладкая функция. Более того, поскольку ре-
решение х(х0, t) существует для всех t, то функция / обратима,
т. е. уравнения G.1.2) можно однозначно разрешить относительно хп'-
Jfn = /-1(*«+i). G-1.3)
Это соответствует изменению знака времени и интегрированию
G.1.1) от хп+1 до х„.
См. также [526—529].— Прим. перев.
412 Глава 7
Сжатие фазового объема. По теореме Лиувилля (п. 1.26) при дви-
движении гамильтоновой системы ее фазовый объем сохраняется.
В противоположность этому в диссипативных системах фазовый
объем в среднем сжимается.
Вычислим изменение малого элемента объема Ат в точке х0:
Ат(х0, 0= ДА*, G.1.4)
где
Скорость изменения Ат равна
¦\,Х)-- ' rf(AT) _ V l rf(A^ G 16)
V ' Дт dt Zj Ax dt ' \ • ¦ )
i
Из G.1.5) имеем
Используя G.1.1) вблизи t = 0, для нормированного изменения
объема получаем из G.1.6) при ? —>-0:
^=divK. G.1.8)
дхс
Локальная величина Л зависит от х (t) и может быть как положи-
положительной (растяжение), так и отрицательной (сжатие). Однако под
диссипативными мы понимаем такие системы, для которых фазовый
объем в среднем сжимается. Записывая среднюю скорость сжатия как
In
Дт(Хо'°
Дт(х0, 0)
G.1.9)
потребуем, чтобы Л0<;0 для всех л:0.
Для Л/^-мерного отображения локальный объем Ат сжимается
за одну итерацию в | det М (х) | раз, где М — матрица Якоби для
отображения. Скорость сжатия равна
etM(Jf)|, G.1.10)
i
Дт dn
где п — число итераций. Усредняя эту величину вдоль траектории,
так же как и в G.1.9), получим Ло (л:0).
Общий случай диссипативных систем с произвольной зависи-
зависимостью Л (х) мало исследован. В большинстве известных задач
Л (х) = — с, где с — положительная постоянная, т. е. имеет ме-
место однородное сжатие всего фазового объема. Очевидно, что для
таких систем Ло = — с.
Диссипативные системы 413
Показатели Ляпунова. Среднюю скорость сжатия фазового объема
можно выразить через показатели Ляпунова, которые были опреде-
определены в п. 5.26 для гамильтоновых систем. То же самое определение
остается в силе и для диссипативных систем. Лля yV-мерного фазо-
фазового пространства имеется N показателей, которые можно упоря-
упорядочить следующим образом:
<*! > ст2 > • • • > aN>
где ах = амакс — наибольший показатель, а один из остальных
показателей, соответствующий смещению вдоль траектории, ра-
равен нулю. Используя E.2.14) и E.2.16), для средней скорости сжа-
сжатия получаем
Л'
Л„=2<т<. G.1.11)
Определение величины Ло согласно G.1.9) и G.1.11), равно
как и определение самих показателей Ляпунова, применимо как
для потоков, так и для отображений, включая отображение Пуан-
Пуанкаре, соответствующее исходному потоку. В последнем случае
Л*—1 показателей зг пропорциональны соответствующим показа-
показателям потока [см. E.2.20)], а нулевой показатель опускается.
Хаотическое движение, как и в гамильтоновых системах, свя-
связано с экспоненциальной расходимостью близких траекторий, т. е.
для хаотического движения зг >о. С другой стороны, фазовый
объем должен сжиматься. Из эти двух фактов следует, что хаоти-
хаотическое движение для одно- и двумерных потоков невозможно').
Для двумерного случая (N = 2) отображение Пуанкаре одномер-
одномерное (и обратимое), поэтому из G.1.11) следует, что Л0=сг1. Такое
отображение не может быть одновременно и диссипативным
(Л0<;0) и хаотическим (а1 >0). Поэтому наиболее простыми си-
системами с хаотическим поведением являются трехмерные потоки
или двумерные отображения. В последнем случае для хаотиче-
хаотического движения должно быть сг-,^0 и ах + а2<;0.
В некоторых предельных случаях из обратимых отображений
с N > 2 можно получить одномерные необратимые отображения.
Их поведение исследуется в § 7.2. Для таких отображений связь
растяжения фазового объема с расходимостью близких траекторий
нарушена, и при ах>0 возникает ограниченное хаотическое дви-
движение. Как будет показано, многие многомерные диссипативные
системы приближенно можно свести к одномерным отображениям.
Простые аттракторы. Так как фазовый объем в диссипативных
системах сжимается до нуля, то устойчивое стационарное движение
*) Фактически теорема Пуанкаре — Бендиксона утверждает, что хаоти-
хаотическое движение невозможно для любых двумерных потоков, как диссипа-
диссипативных, так и недиссипативных. Мы уже убедились в этом для гамильтоно-
гамильтоновых систем с одной степенью свободы (двумерное фазовое пространство).
414
Глава 7
в TV-мерной системе должно происходить на «поверхности» меньшей
размерности. Грубо говоря, такую поверхность и называют аттрак-
аттрактором. Более точно, мы будем называть аттрактором, следуя
Лэнфорду [254 ], такое подмножество X фазового пространства,
которое удовлетворяет следующим условиям:
1) X инвариантно относительно потока;
2) существует (открытая) окрестность X, которая сжимается
к А' под действием потока;
ПреЭельпып цикл Xz
Фок
Рис. 7.1. Простые аттракторы.
/—область притяжения фокуса X t; 2, 3 — область притяжения предельного цикла X,.
3) никакая часть X не является переходной х);
4) X нельзя разложить на два непересекающихся инвариантных
множества.
Областью притяжения аттрактора X является множество
состояний в фазовом пространстве, которые стремятся к X при
?—»-оо. Обычно для TV-мерного потока имеется конечное число
аттракторов Хъ . . . , Хм, хотя известны примеры и с бесконечным
числом аттракторов. С точностью до меры нуль все начальные со-
состояния лежат в области притяжения одного из М аттракторов
(см. рис. 7.1).
То есть траектория не уходит из нее при t -> оо.— Прим. ред.
Диссипативные системы
415
Для одномерных потоков единственными аттракторами являются
устойчивые неподвижные точки, или устойчивые фокусы (анало-
(аналогично точке Х1 на рис. 7.1). Например, для уравнения
~=V(x, ц),
at
ч
П\
\Х)
Рис. 7.2. Бифуркации в одномерных и двумерных потоках.
а — тангенциальная бифуркация; б — смена устойчивости; в—бифуркация удвоения;
г — обратная бифуркации удвоения; д — бифуркация Хопфа; е — обратная бифуркация
Хопфа. Случаи (а —г) типичны для одномерных потоков; случаи (с —г) — для двумер-
двумерных потоков. Сплошные кривые — устойчивые решения, пунктирные кривые —¦ неустой-
неустойчивые решения.
где V = (.1—х2, a fx —- некоторый параметр, положение неподвиж-
неподвижных точек получается из условия dxldt = 0 или V = — dUldx = О
и равно + VV Исследуя потенциал U (x, \i) вблизи неподвижных
точек, найдем, что точка х — +VV устойчива, а точка х =
= — |(i неустойчива. При ^i<;0 неподвижные точки для дейст-
действительных х отсутствуют. Появление двух неподвижных точек при
прохождении \х через нуль иллюстрируется на рис. 7.2, а и яв-
является примером тангенциальной бифуркации. Существуют би-
бифуркации и других типов. Так, для V = \лх—х2 происходит смена
устойчивости (рис. 7.2, б). Для V ~ уьх—х3 имеет место бифурка-
бифуркация удвоения г) (рис. 7.2, в), при которой вместо одного устойчи-
') В оригинале
Прим. перге.
pitchfork bifurcation (бифуркация типа «вилки»).—
416 Глава 7
вого фокуса возникают два. Возможна также и обратная бифур-
бифуркация удвоения (рис. 7.2, г). За исключением особых случаев, только
эти бифуркации и встречаются в одномерных потоках.
Для ограниченного двумерного потока на плоскости, согласно
теореме Пуанкаре—Бендиксона, имеются только два типа аттрак-
аттракторов: 1) устойчивые неподвижные точки, или устойчивые фокусы,
и 2) простые замкнутые кривые, или предельные циклы (кривая Х%
на рис. 7.1). Покажем, как образуется предельный цикл для си-
системы
-|-=(лг-Л G.1.12а)
— =<во>О, G.1.126)
dt
где г, в — полярные координаты. При |х<сО правая часть G.1.12а)
всегда отрицательная и траектория свертывается к фокусу г = 0.
Для [х>0 вблизи г = 0 скорость г положительна и неподвижная
точка г = 0 перестает быть притягивающей. Поскольку г>0 для
всех r<C[i и г<0 для г>ц, то траектория стремится к предель-
предельному циклу г (t) = fx, в (/) = (Dot -,- в0.
Превращение устойчивого фокуса в предельный цикл при про-
прохождении ju, через нуль (рис. 7.2, д) называется бифуркацией
Хопфа. Возможна также и обратная бифуркация Хопфа (рис. 7.2, е).
На рис. 7.2, а—е показаны все типичные бифуркации в двумерных
потоках х).
7.16. Примеры странных аттракторов
Наименьшая размерность фазового пространства, в котором воз-
возможен странный аттрактор, равна трем, как в модели Лоренца,
описанной в § 1.5. Еще более простая система была рассмотрена
Рёслером [350 ], и мы опишем ее ниже. Интересные свойства дву-
двумерного отображения со странным аттрактором будут рассмот-
рассмотрены на примере отображения Хенона [187].
Аттрактор Рёслера. Рассмотрим следующую систему нелинейных
дифференциальных уравнений [350]:
X=-(Y--Z),
Y = X+-^Y, G.1.13)
О
') В трехмерных потоках имеется аналог бифуркации Хопфа, когда
предельный цикл становится неустойчивым и переходит в «предельный тор».
Однако в общем случае притягивающие торы являются структурно неустой-
неустойчивыми относительно изменения параметра \i (см. работу [254]).
Диссипативные системы
417
Результат моделирования этой системы на аналоговой вычисли-
вычислительной машине для jx = 5,7 представлен на рис. 7.3, а [368], где
показана проекция странного аттрактора на плоскость X, Y (ср.
рис. 1.18, б). Рассмотрим сечение аттрактора по линии @,1), как
показано на рис. 7.3, а. Тогда последовательные значения Хп
в этом сечении определяются приближенно одномерным необрати-
необратимым х) отображением, представленным на рис. 7.3, б. Таким об-
образом, хаотическое движение на аттракторе Рёслера приближенно
описывается отображением для X.
СклпЭка
Рис. 7.3. Аттрактор Рёслера (по данным работы [368]).
а — проекция движения иа плоскость (X, У); б — одномерное отображение в плоскости
Y = 0.
Переход от трехмерного потока к одномерному отображению
является приближенным. Поэтому кривая на рис. 7.3, б должна
иметь конечную толщину, связанную с тонкой структурой слоя
в сечении Y = 0, который фактически содержит бесконечно много
отдельных листов. Однако для этого и многих других странных
аттракторов скорость сжатия фазового объема G.1.8) столь велика,
что при любом моделировании все листы кажутся слившимися в
один. Поэтому, вообще говоря, одномерное отображение представ-
представляет основные особенности поведения исходного потока 2).
Переход от простого к странному аттрактору иногда совершается
путем последовательных бифуркаций с удвоением периода, которые
сходятся по некоторому параметру к предельному значению. За
этим значением движение становится суперпозицией хаотического
*) В том смысле, что обратное отображение неоднозначно (двузначно).—¦
Прим. ред.
2) Вопрос о возможности описания трехмерного потока или двумерного
отображения с помощью одномерного отображения обсуждается в п. 7.3в.—
Прим. перев.
418
Глава 7
и периодического с обратными бифуркациями удвоения частоты.
На рис. 7.4, полученном Кратчфилдом и др. [97] с помощью ана-
аналогового моделирования системы G.1.13), эти бифуркации пока-
показаны, начиная с ц = 2,6 (а), когда аттрактором является простой
О 10 20 30 40 50
f, Гц
Рис. 7.4. Бифуркации удвоения периода для аттрактора Рёслера в проек-
проекции на плоскость (X, Y) (по данным работы [97]).
Ниже показана спектральная плотность мощности для Z (t): а) \л — 2,6; б) |i =3,5;
в) ц = 4,1; г) Ц = 4,23; д) ц = 4,30; е) |г = 4,60.
предельный цикл. При увеличении \i видны две первые бифурка-
бифуркации удвоения периода (бив). Показанный на рисунке спектр мощ-
мощности имеет в этих случаях вид острых пиков, характерных для
регулярного движения. Ясно видны последовательные удвоения
периода. Переход к хаотическому движению происходит при
liaa = 4,20. Возникающий для ju,>jli0o странный аттрактор
(рис. 7.4, г—ё) имеет вид полосы хаотического движения, которая
Диссшштивные системы
419
приближенно соответствует предельным циклам на рис. 7.4, а—в.
Соответственно спектр мощности представляет суперпозицию ши-
широкополосного шума хаотического движения и острых пиков
периодической компоненты. Ясно видны обратные бифуркации
удвоения частоты.
Переход к хаотическому движению через бифуркации удвое-
удвоения периода является, как мы увидим, характерным для широкого
класса диссипативных си-
систем как отображений,
так и потоков. При этом
зависимость бифуркаций от
параметра и форма спектра
оказываются универсаль-
универсальными вблизи перехода. Эти
вопросы будут рассмотрены
в § 7.2 и 7.3.
Топология аттрактора
Рёслера показана на рис.
7.5, а. Аттрактор представ-
представляет собой лист, который
растягивается по вертика-
вертикали, поперек траекторий
(стрелки), перегибается
вдоль траекторий, скла-
складывается, и, наконец, его
правый и левый края со-
соединяются друг с другом.
Аттрактор Лоренца устроен
более сложно (рис. 7.5,6).
Он состоит из двух листов,
которые растягиваются и
делятся на две части, при-
причем правый край каждого
листа соединяется с левы-
левыми краями обоих листов.
Можно представить се-
себе и другие топологические структуры странных аттракторов.
Хотя аттрактор Рёслера топологически проще аттрактора Ло-
Лоренца, однако соответствующее ему одномерное отображение
(рис. 7.3,6) имеет области, где производная | dXn+1/dXn |< 1.
Как показывается в § 7.2, в этом случае доказать хаотичность дви-
движения нелегко. Для аттрактора же Лоренца аналогичная произ-
производная всюду больше единицы. Доказано, что такие отображения
являются хаотическими.
Аттрактор Хенона. Слоистая структура аттрактора хорошо видна
на модели Хенона [187], которая описывается простым двумерным
Рис. 7.5. Топология аттракторов Рёслера
(а) и Лоренца (б).
Все отрезки, обозначенные одинаковыми буквами,
соединяются друг с другом.
420 Глава 7
квадратичным отображением:
Это отображение является обратимым, и его можно рассматривать
как отображение Пуанкаре для некоторого трехмерного потока.
Сокращение фазовой площади на одну итерацию определяется мно-
множителем
detM
d(xn+i,
Уп)
= 6. G.1.15)
Можно показать [187], что отображение G.1.14) является наибо-
наиболее общим квадратичным отображением с постоянным якобианом.
При достаточно большом х0 величина | хп \ -*¦ оо из-за квадратич-
квадратичного члена. Однако некоторая конечная область вблизи начала
координат стягивается к аттрактору. Отображение имеет две не-
неподвижные точки
G.1.16)
у+ = ох±
при условии, что
а>ао =
Легко проверить, что точка х_ всегда неустойчива, а точка х+
неустойчива при
3A— bf
При дальнейшем увеличении а>ах численное моделирование по-
показывает последовательность бифуркаций удвоения периода. Ат-
Аттрактор остается простым и представляет собой р = 2" точек;
р -у- оо при а^-аг. Далее для большинства значений а в интер-
интервале ai<Cu<c.a3 численные эксперименты определенно указывают
на существование странного аттрактора. И наконец, для а^>а3
большинство траекторий уходит на бесконечность.
Чтобы увидеть структуру аттрактора, Хенон выбрал относи-
относительно небольшое значение b — 0,3. В этом случае а0 » — 0,1225;
а1 « 0,3675; а2 ш 1,06; а3 я^ 1,55. На рис. 7.6, а показан странный
аттрактор для а = 1,4, полученный за 10* итераций отображения
с начальными условиями вблизи неустойчивой неподвижной точки.
Более детальная структура аттрактора видна на рис. 7.4, б—г,
представляющих собой последовательно увеличенные участки фа-
фазовой плоскости. Видно, что структура аттрактора при изменении
масштаба повторяется, т. е. имеет место масштабная инвариант-
Диссипативные системы
421
ность х). Это подобие соответствует структуре шнторова мно-
множества, которое будет описано в п. 7.1в. Экспоненциальная расхо-
расходимость близких траекторий, подтверждающая стохастичность
движения на аттракторе, численно получена в работах [99, 124,
375].
~!,5 -1,0 -0,5 0 0,5 1,0 1,5
10ч итераций
а
0,55 0,60 0,65 0,70
10s итераций
6
0,185
0,625 0,630 0,635 0,640
0,1889
0,6305 0,6310 0,6315 0,63Z0
10"
итерации
в
5x10'
итерации
г
Рис. 7.6. Слоистая структура аттрактора Хенона (по данным работы [187]).
а — траектория с начальными условиями в неустойчивой неподвижной точке; б—г —
последовательные увеличения малого участка фазовой плоскости (квадрат). Видна мас-
масштабная инвариантность структуры аттрактора.
Странный аттрактор существует не для всех значений а в ин-
интервале az<ia<.a3. Имеется много узких участков, в которых
движение является периодическим с периодами 3, 4, 5 ... и испы-
испытывает бифуркации удвоения периода [375]. Эти особенности дви-
движения рассматриваются в § 7.2.
*) Аналогичная структура аттрактора наблюдалась в работе [73] для
другого отображения (см. также [74, 530]).— Прим. ред.
422 Глава 7
Математически доказать стохастичность аттрактора Хенона
пока не представляется возможным. Ситуация значительно упро-
упрощается для разрывного отображения. Такой аттрактор с заменой х2п
на | хп | в G.1.14) был рассмотрен Лози [285], а доказательство его
хаотичности дано Мисюревичем [301 J.
7.1в. Геометрия странных аттракторов
Численные данные для отображения Хенона показывают, как мы
видели выше, что структура аттрактора повторяется на все более
и более мелких масштабах. Ее можно сопоставить с канторовым
множеством, свойства которого позволяют значительно лучше по-
понять природу странного аттрактора. Рассмотрим вначале размер-
размерность канторова множества. Для этого нам понадобится общее
определение фрактальной размерности. Затем мы рассмотрим
простой пример канторова множества и найдем его размерность.
И наконец, обсудим некоторые методы вычисления и измерения
фрактальной размерности странных аттракторов, уделяя основное
внимание ее связи с показателями Ляпунова. Наше изложение
следует частично обзорам Треве [411 ] и Отта [324].
Канторовы множества и фрактальная размерность. Примем сле-
следующее определение фрактальной размерности 1):
d(S)= lim-^^-, G.1.17)
V ; e+o In (We) V '
где 5 — некоторое множество в jV-мерном пространстве, а М (е) —
минимальное число Af-мерных кубов со стороной е, необходимых
для покрытия этого множества. При малых е из такого определения
следует, что
M(e)~Ke~d. G.1.18)
Размерность G.1.17) называют также емкостью. Для точки, линии
и области на двумерной поверхности фрактальная размерность
имеет обычные значения 0, 1, 2 соответственно. Действительно,
необходимое число квадратов со стороной е для покрытия точки
пропорционально 1/е°, для линии М ос lie1 и для двумерной об-
области М ос 1/е2.
Канторово множество является компактным, метрическим, нигде
не плотным, несчетным и может быть нулевой меры. Типичные кан-
канторовы множества имеют дробную размерность @<d<;l) и об-
обладают масштабной инвариантностью, т. е. при соответствующем
изменении масштаба подмножество «выглядит» так же, как и ис-
исходное множество. Известным примером канторова множества слу-
*) Такое определение размерности введено в работе [521]. Различные
понятия размерности и их взаимосвязь обсуждаются в обзоре [522] (см.
также [523]).— Прим. ред.
Диссипативные системы
423
жит так называемое «множество средних третей» (рис. 7.7), кото-
которое строится следующим образом. Возьмем закрытый отрезок [0, 1 ]
и выбросим из него открытый (без граничных точек) интервал A/3,
2/3). Затем из двух отрезков полученного множества 7\ аналогич-
аналогичным образом выбросим их «средние трети» и получим новое мно-
множество Т\. Повторяя эту процедуру бесконечное число раз, по-
получим множества Ти Т2, Т3, .... Канторово множество Т есть
пересечение всех Т„. Грубо говоря, это пересечение есть «предель-
«предельное Т„».
м
1
1/3
—I
2/3
I—
1/3
Т-,
1/9 2/9 1/3
2/3 7/9 8/9 1
1/9
Т3
Ml—I
Ht—I
1/27
Рис. 7.7. Построение множества Кантора.
М — число отрезков длины г, необходимое для покрытия множества Т
Из построения следует, что множество Тп состоит из М = 2"
разделенных интервалов длиной е = A/3)". Согласно G.1.17), фрак-
фрактальная размерность Т равна
d^mnJ^^Jna. 631.
П-^оо 1пЗ" 1пЗ
Множество Т имеет нулевую меру
Hm6/W=lim /-?-)" = 0.
Покажем, что множество Т несчетно. Для этого представим дейст-
действительное число х в интервале @, 1) в следующем виде:
424 Глава 7
где ai принимают, вообще говоря, три значения: 0, 1, 2. Однако,
для того чтобы х принадлежало Т, необходимо, чтобы все ас при-
принимали только два значения: 0 или 2 (см. рис. 7.7). И наоборот,
любая последовательность таких щ определяет х, принадле-
принадлежащее Т. Но тогда существует взаимно-однозначное соответствие
между канторовым множеством и множеством всех двоичных по-
последовательностей, которое представляет все числа в интервале
(О, 1). Последнее же, как известно, несчетно.
Связь между фрактальной размерностью и показателями Ляпунова.
Существует гипотеза [218], связывающая фрактальную размер-
размерность с показателями Ляпунова:
G.1.19)
где все показатели упорядочены обычным образом: а1 >
>а2 >-• - . ^>oN, а / — наибольшее целое число, для которого
Oi-r СГ2 + Г'. . + СУ/>0.
Рассел и др. [356] сравнили G.1.17) с G.1.19) для нескольких
двумерных отображений и трехмерных потоков. Для двумерных
отображений, у которых cJjX) >CTi 4- ст2, G.1.19) сводится к
d=l ^-- G.1.20)
Для трехмерных потоков с о^^О^сГд, сг2 = О Х) и О\ -\- ст3<;0
получим
d = 2 ^-. G.1.21)
Для непосредственного численного определения d, согласно G.1.17),
все пространство делится на ячейки со стороной 6. Затем отобра-
отображение итерируется до тех пор, пока не закончится переходной про-
процесс, после которого движение происходит на аттракторе. При по-
последующих итерациях помечаются те ячейки, в которые попадает
траектория. После достаточно большого количества итераций число
таких ячеек стремится к М (е). Из G.1.17) следует, что зависимость
In M от In e является линейной. Значение d можно определить с по-
помощью подгонки численных данных на эту прямую.
В табл. 7.1, взятой из работы Рассела и др. [356], срав-
сравниваются 2) значения d, полученные описанным прямым методом
J) Напомним, что для потока один из показателей всегда равен нулю.
2) Фрактальная размерность, которую использовали Каплан и Йорке
в своей гипотезе, является информационной размерностью. Было показано,
что она ограничена сверху емкостью G.1.17). В то же время Рассел и др.
[356] численно определяли емкость, которая, очевидно, очень близка к ин-
информационной размерности по данным табл. 7.1 (подробности см. в работе
Фармера [120]).
Диссипативные системы
425
и согласно G.1.19), для трех разных двумерных отображений и
трехмерного потока. Были выбраны отображения Хенона G.1.14),
(необратимое) отображение Каплана и Йорке:
Xj+1 — 2xj, mod 1,
G.1.22)
Уi +i = аУ7 + cos 4я^/
Таблица 7.1. Вычисление
Модель
Отображение Хенона
а=1,2; fe=0,3
Отображение Хенона
0=1,4; 6=0,3
Отображение Каплана—
Йорке
а=0,2
Отображение
Заславского
Г=3,0; е=0,3
v=400/3
Поток
фрактальной размерности
По показателям Ляпунова
G.1.19)
1,200+0,001
1,264+0,002
1,4306766
1,387+0,001
2,317+0,001
Прямое вычисление
G.1.17)
1,202+0,003
1,261 ±0,003
1,4316±0,0016
1,380+0,007
2,318+0,002
*) По данным работы [356].
и отображение Заславского:
Xj+1 = Xj-f- v A -f- \yyl) -f ev\i cos 2nx-h mod 1,
yi+1 = exp (— Г) (y; + e cos 2nxj).
G.1.23)
Для отображений Хенона и Заславского непосредственно вычис-
вычислялся только показатель Ляпунова alt а сг2 определялось из из-
известной скорости сжатия фазового объема G.1.10):
о1 + а2 = \п\ detM |,
G.1.24)
^ М равен—Ь для отображения Хенона и е — для отображе-
отображения Заславского. В случае отображения Каплана и Йорке аг =
= In 2 и <т2 = 1п а- И наконец, для потока ах + а3 находится ана-
аналитически, adj — численно. Во всех случаях наблюдается прекрас-
прекрасное согласие между G.1.17) и G.1.19). Использование гипотезы
G.1.19) гораздо проще, чем прямое вычисление по G.1.17), однако
эта гипотеза пока не доказана.
Другие способы определения фрактальной размерности обсуж-
обсуждались в работах Паккарда и др. [326], Фрёлинга и др. [138]
и Фармера [120].
426
Глава 7
§ 7.2. Одномерные необратимые отображения
7.2а. Основные свойства
Рассмотрим свойства одномерных отображений вида
xn+i = f(xn, С),
G.2.1)
где С — некоторый параметр. Как мы уже видели, к таким отобра-
отображениям сводятся более сложные диссипативные системы х). Они
возникают также и как самостоятельные простые модели некото-
некоторых систем. Например, переменная хп может описывать популя-
Рис. 7.8. Типичный пример одномерного необратимого отображения.
цию какого-то вида в л-й год, а / — влияние окружающей среды.
Пусть задана начальная популяция х0. Как будет изменяться эта
популяция? Как ее эволюция зависит от окружающей среды?
Ниже мы ограничимся функциями f некоторого определенного
вида. Если / — линейная функция, то решение G.2.1) тривиально.
В случае обратимой функции / (монотонная зависимость от х) дви-
движение также простое и не обладает хаотическими свойствами. Ста-
Стационарные состояния являются периодическими, а бифуркации
типа удвоения периода отсутствуют. Как будет видно ниже, хао-
х) Это справедливо, если исходная система имеет только один положи-
положительный показатель Ляпунова.
Диссипативные системы 427
тическое движение связано х) с областями вблизи /' (х) = 0. Поэ-
Поэтому мы ограничимся простейшим интересным случаем, когда f (х)
имеет единственный максимум (или минимум). Типичная / (х)
в этом случае схематически изображена на рис. 7.8. Для малых х
происходит увеличение х, а для больших — уменьшение. Такое
отображение может, например, моделировать окружающую среду,
в которой рост популяции ограничен запасами пищи и загрязне-
загрязнением окружающей среды.
Итерируя G.2.1), можно проследить за эволюцией х для лю-
любого заданного Л'о. Можно также исследовать поведение G.2.1) гра-
графически:
а) по х0 находим х1 = f (х0), двигаясь вертикально вверх (см.
рис. 7.8);
б) переводим х1 на ось х, двигаясь горизонтально до пересе-
пересечения с прямой f = х;
в) повторяя «а» и «б», находим х2, х3 и т. д. Из рис. 7.8 видно,
что отображение необратимо, поскольку одному и тому же
хх соответствуют два начальных состояния х0 и х'о. Поэтому
обратное отображение будет неоднозначным.
Для случая, изображенного на рис. 7.8, вне зависимости от
выбора х0 решение сходится к точке хХ1, которая является непо-
неподвижной точкой отображения:
xn = f(xn). [G.2.2)
Ясно также, что ххх — устойчивая (притягивающая) неподвижная
точка. Другая неподвижная точка х — 0 является неустойчивой
(отталкивающей).
Квадратичные отображения. Как уже упоминалось, переход к
хаосу для одномерного отображения с одним максимумом опреде-
определяется поведением отображения вблизи его экстремума. Для ти-
типичного случая, когда /' = 0, но /" Ф 0, отображение локально
квадратично. Разложение в ряд Тейлора вблизи экстремума при-
приводит к квадратичному отображению общего вида
zn+i=a+bzn + czl. [G.2.3)
Линейным преобразованием его можно привести к нормальной
форме, которую мы и будем называть квадратичным отображением:
*„+, = /(*„)' G-2-4а)
где
+ 2xl. G.2.46)
1) Это условие не является необходимым для хаоса, как показывает
рассмотренный ранее пример E.2.32), а также отображение Лоренца
(рис. 1.21). Напротив, области с f = 0 способствуют устойчивости (регу-
(регулярности) движения, так как они уменьшают показатели Ляпунова [см.
G.2.46)]. Поэтому рассматриваемая ниже теория бифуркаций удвоения пе-
периода в окрестности f (х) = 0 есть прежде всего теория сложного разруше-
разрушения такой устойчивости.— Прим. ред.
428
Глава 7
Представляют интерес две области параметра С. Для 0<С<2
интервал — C<ix<^0 переходит в себя, как показано на рис. 7.9, а
и б. Для — 1<С<1/2 переходит в себя интервал — 1/2-<*<
<; 1/2 — С (см. рис. 7.9, в—е). Отметим, что эти два интервала
значений С перекрываются (см. рис. 7.9, б и в), а движение в обоих
случаях аналогично и отличается только тем, какой отрезок х
переходит в себя. Особое значение имеет точка х* = — С72, в ко-
которой функция / экстремальна.
\-с
Чь/
//
t
\
\
\
\
\
-c /
/
1
1 у
/¦
у
Y
Уг.-е
— 1/, /
/
/
г
-xv
Рис. 7.9. Квадратичное отображение G.2.4) для различных значений пара-
параметра С.
Сплошная кривая показывает отрезок х, переходящий в себя. Случай I: — С <х < 0;
а) С >1/2; б) 0 < С < 1/2. Случай II: — 1/2 <х < 1/2 — С; в) 0< С < 1/2; г) С = 0;
д) — 1, 2 <С < 0; е) — 1 < С < — 1/2.
Другая удобная форма квадратичного отображения получается
путем замены х = — (fx/2) у и С = ja/2 в G.2.4). Это приводит к так
называемому логистическому отображению:
Уы-1 = МпA-Уп)- (^2-5>
Для 0<fi<;4 интервал 0<У<1 переходит в себя. Это соответст-
соответствует значениям С в интервале 0<С<;2 (рис. 7.9, а и б). Отображе-
Отображение G.2.5) использовалось как для изучения общих свойств одно-
одномерных отображений, так и в некоторых задачах популяционной
биологии. На рис. 7.10 показано отображение G.2.5) для двух зна-
значений }х. Оба отображения, G.2.4) и G.2.5), являются эквивалент-
эквивалентными представителями общего квадратичного отображения G.2.3).
Зеркальная симметрия. Квадратичные отображения обладают сим-
Диссипативные системы
ыетрией, которая приводит к одному и тому же поведению для двух
разных значений параметра. Действительно, производя в G.2.4)
линейную замену
L-C, G.2.6)
Рис. 7.10. Отображение G.2.5) для 0<ц<4.
Интервал 0 <i/ <]1 преобразуется сам в себя.
получаем
v O/"*v i O-v A О 7\
где новый параметр С равен
С=\— С. G.2.8)
Из сравнения G.2.7) и G.2.4) следует, что квадратичные отображе-
отображения с параметрами, равными С и 1—С, обладают одними и теми же
свойствами. Иначе говоря, отображение G.2.4) симметрично отно-
относительно С = 1/2. Аналогично, производя замену
у = A — (х) — A— 2|х~')у G.2.9)
в отображении G.2.5), получаем
I = \хуп A —Уп)г
где
т. е. отображение симметрично относительно \х = 1.
G.2.10)
G.2.11)
430 Глава 7
7.26. Периодическое движение
Рассмотрим неподвижные точки квадратичного отображения G.2.4)
и их линейную устойчивость. Неподвижные точки находятся из
условия:
, G.2.12)
которое соответствует пересечению кривой / (х), определяемой
G.2.46), и прямой / = х. Решение G.2.12) имеет два корня:
*ю = 0, *п = у —С G.2.13)
Устойчивость неподвижных точек определяется из линеаризован-
линеаризованного отображения (§ 3.3). Подставляя
Xn^x-L + Axn G.2.14)
в G.2.4) и удерживая только линейные члены, получаем
Д*п = А,«Д*0> G.2.15)
где собственное значение Xt = f (х,). Следовательно, хг — устой-
устойчивая (притягивающая) неподвижная точка, если l^l-c^l, и не-
неустойчивая (отталкивающая), если l^l^-l. Отсюда следует, что
точка 1И устойчива при
!/'Ы 1 = 1 2—2С|<1,
или для 1/2<С<3/2. Аналогично неподвижная точка х10 устой-
устойчива при
1П*юI = |2С|<1,
или для — 1/2<С<1/2.
Бифуркации. Рассмотрим устойчивость отображения при умень-
уменьшении параметра С, начиная с некоторого С>1/2, когда точка х1х
устойчива, а х10 неустойчива. При С0=1/2 точка х1г становится
неустойчивой, а х10 — устойчивой. При дальнейшем уменьшении С
вплоть до С = С\ = — 1/2 точка х10 остается устойчивой.
Чтобы понять, что происходит при С<с — 1/2, нужно рассмот-
рассмотреть периодические точки периода 2, которые находятся из усло-
условия:
))• G.2.16)
Это соответствует пересечению кривой
Ш = /(/=(*)) 17.2.17)
с прямой / = х, как показано на рис. 7.11, а и б для С> — 1/2
и С< — 1/2 соответственно. Если С> — 1/2, то оба пересечения
соответствуют неподвижным точкам х±1 ~ 1/2—С и х10 = 0, ко-
Диссипативные системы
431
торые, очевидно, удовлетворяют и G.2.16). В этом случае наклон
/2 (х) в нуле меньше единицы, так как
а | Хх |< 1 для С> — 1/2. Если же параметр С становится меньше
— 1/2, то наклон увеличивается и рождается пара неподвижных
точек отображения /2 (или периодических точек отображения /,
Рис. 7.11. Возникновение двух неподвижных точек х2 - с периодом 2 для
квадратичного отображения.
f 2 (х) =-- f (f (х)): а) О — 1/2; б) С < — 1/2.
рис. 7.11, б). Они удовлетворяют условиям
*2+= /(*»-) = />(*»+), G.2.18а)
xt- = f(x2+) = ft(xtj). G.2.186)
Позже мы получим явные выражения для Х2+ и х2_ как функций
параметра С.
Устойчивость хг± можно исследовать, как обычно, с помощью
замены х2]Я = х2± + Ах2>„ и линеаризации отображения. Для
точки х2- находим
где
Аналогично для х2+:
А2+ = /'(х2+)/'(х2_) = А2_. G.2.20)
Видно, что наклоны (собственные значения) одинаковы для обеих
точек. Как отмечено в п. 3.3а, для канонических отображений
432
Глава 7
это свойство является общим для неподвижных точек любого пе-
периода.
Из рис. 7.11, б следует, что если значение С чуть меньше С\ =
= — 1/2, то | Я, (х2-) | = | Я2 (Х2+) |< 1- Таким образом, как
только неподвижная точка периода 1 становится неустойчивой,
появляется пара устойчивых неподвижных точек с удвоенным пе-
периодом. Это явление иллюстрируется на рис. 7.12, где показана
Рис. 7.12. Положение неподвижных точек х10, х1г, х2+ и л;2_ в зависимости
от С.
Устойчивые неподвижные точки представлены сплошными линиями, неустойчивые —
пунктирными. Показан также экстремум f при х* = — С/2. А — бифуркация удвоения;
А' — зеркальная бифуркация удвоения.
зависимость координат неподвижных точек от параметра С. Сплош-
Сплошная линия обозначает устойчивость точки, а штриховая — неустой-
неустойчивость. Рождение пары устойчивых точек удвоенного периода
при С<— 1/2 является примером бифуркации удвоения (см. § 7.1).
На рис. 7.2, в показана также зеркальная бифуркация удвоения,
соответствующая зеркальному отображению G.2.7).
При дальнейшем уменьшении параметра С обе неподвижные
точки периода 2 становятся неустойчивыми. Поскольку в их ок-
окрестности отображение /2 (х) также квадратично, следует ожидать
аналогичной бифуркации, при которой возникают четыре непо-
неподвижные точки периода 4 и т. д. Означает ли это, что при любом
значении параметра имеется либо устойчивое решение, либо (устой-
(устойчивая) бифуркация? Оказывается, что нет. Последовательность
бифуркаций удвоения периода кончается, достигая бесконечного
периода при конечном значении параметра С = С,*,. За этим зна-
значением лежат области хаоса.
Диссипативные системы 433
Метод ренормализации. Для более глубокого понимания явления
последовательных бифуркаций рассмотрим ренормализацию ото-
отображения с одним максимумом при переходе от одной бифуркации
к следующей. Строгая теория ренормализации 183, 122], примени-
применимая к любым отображениям с одним максимумом, основана на
решении некоторых функциональных уравнений. Соответствующие
математические методы сложны и выходят за рамки этой моно-
монографии. Вместо этого, следуя Хеллеману [180—182], мы используем
более простой, хотя и менее общий, метод локальной аппроксимации
отображения с одним квадратичным максимумом. Это позволяет
построить приближенную теорию ренормализации на основе алге-
алгебраических, а не функциональных уравнений. Для квадратичного
отображения G.2.4), как мы видели выше, устойчивая неподвиж-
неподвижная точка х10 периода 1 возникает с уменьшением С при С =
= Со = 1/2, а устойчивые точки периода 2 — при С1 = — 1/2.
Последние получаются из G.2.18):
х2± = а±Ь, G.2.21а)
где
2а=—1/2 —С, G.2.216)
4&»=/с+—We— -J-), 6>0. G.2.21b)
Подставляя
в G.2.4), получаем
где
d = 2C + 4x2+, G.2.22)
е = 2С + 4х2_, G.2.23)
и начальные условия выбираются таким образом, чтобы при четных п
величина Ах была близка к х2+, а при нечетных — к х2_. Исклю-
Исключая Ахп+1 и удерживая члены по Ах до квадратичных включительно,
получаем для четных п
Ах =deAxn-{-2(e-srd2) Ах2п. G.2.24)
Путем изменения масштаба
х' = аАх G.2.25)
приводим G.2.24) к виду
434 Глава 7
где
С = de/2 = —2С2 + 2С + 2, G.2.27)
a = e+d2=1662 —126, G.2.28)
а 6 определяется согласно G.2.21в). Так как G.2.26) имеет тот же
самый вид, что и исходное отображение G.2.4), его неподвижные
точки испытывают бифуркацию удвоения периода при С = — 1 2.
С учетом G.2.27) это значение соответствует
да _ 0,72474,
при котором возникают неподвижные точки периода 4. Из G.2.21)
следует, что х2+ да 0,466 и х2_ да — 0,241 при С = С2. Отметим,
что точка х2+ лежит вблизи экстремума / при х* — — С/2; этот
факт мы используем ниже при нахождении закона подобия G.2.36).
Последовательность бифуркаций сходится к предельному зна-
значению С = С = Сю, которое находится из G.2.27):
отсюда
Сх= 1~л/17 да —0,781. G.2.29)
4
Численное моделирование дает С„о да — 0,78497, что находится
в хорошем согласии с результатом ренормализации.
Скорость сходимости С к Сое можно приближенно найти, пред-
предполагая, что асимптотически сходимость происходит по закону х)
С^даС^ + Лб-*. G.2.30)
Подставляя это выражение в G.2.27) и замечая, что k-я бифурка-
бифуркация по С соответствует (k + 1)-й по С, т. е.
получаем
б=— 40,0 + 2= 1 + У17 «5,12. G.2.31)
Численное решение точного уравнения ренормализации, найден-
найденное впервые Фейгенбаумом [122], дает для отображения с одним
квадратичным максимумом б да 4,6692. Закон подобия G.2.30)
можно представить в виде
Постоянная б не зависит от выбора параметра. Действительно,
!) Это предположение следует из G.2.27); см. ниже.— Прим. ред.
Диссипативные системы 435
введем новый параметр Р — g (С). Считая, что g—обратимая
функция, разложим Р (С) вблизи С»,:
Pk—Px = g'(Coo){Ck— C^). G.2.33)
Решая это уравнение относительно Ck и подставляя решение в
G.2.32), находим универсальное соотношение
Фактически из точной теории ренормализации следует, что б —
универсальная константа для всех отображений с одним квадратич-
квадратичным максимумом. Принимая, что асимптотический закон G.2.30)
справедлив и для k = 0 и k = 1, получаем полезную оценку для
предельного значения параметра (точки сгущения):
(РР) Р+\2ЦР~РО), G.2.34)
где использовано приближенное значение G.2.31) для б.
Наконец, перейдем к параметру подобия а, входящему в G.2.25).
Из G.2.28) и G.2.21b) при С = Сое [см. G.2.29) ]:
«=1662—126«— 2,24. G.2.35)
Точная теория ренормализации дает ах — 2,5029. Параметр а
определяет (асимптотически) изменение масштаба х при последо-
последовательных бифуркациях. Иначе говоря, при увеличении в а раз
вблизи х* = — С/2 очередная бифуркация будет выглядеть точно
так же, как и предыдущая. В частности, расстояние между непо-
неподвижными точками при последовательных бифуркациях вблизи х*
подчиняется закону подобия
- = а. G.2.36)
xk+i, -
Это соотношение справедливо для ветви, идущей от х^+.
Поскольку / локально квадратичная функция х, то для первых
итераций точек вблизи х* масштаб изменяется как а2. Отсюда
fAx*+)-fM = a\ G.2.37)
f ( ) f (x )
Полученное соотношение выполняется для значений ' xk на ветви,
идущей от xk~- Таким образом, для половины неподвижных то-
точек периода 2к масштаб изменяется как а, а для остальных —
как а2 [см. G.2.38) ].
Рис. 7.13 поясняет это поведение. На рис. 7.13, а отрезок Ахх
вблизи минимума отображения переходит в отрезок | Ах2 ^(Ах^2.
Однако затем Ах2 переходит в Ах3 снова вблизи минимума, причем
| Ах3 | ее | Ах21. При каждом отображении знак Ах изменяется.
На рис. 7.13, б показана полная структура неподвижных точек
436
Глава 7
Рис. 7.13. Иллюстрация масштабного преобразования по х для квадратич-
квадратичного отображения.
а — изменение начального &Xi вблизи экстремума; \хг ~ (Л*,J, но Ахг ~ Ах,; б —
три первые бифуркации удвоения; порядок движения по траектории периода 4 и 8 пока-
показан в круглых скобках.
Диссипативные системы
437
для трех первых бифуркаций. Цифры в круглых скобках показы-
показывают последовательность движения для траекторий с периодом 4
и 8, начиная с верхней точки. Отметим также, что расстояния ме-
между соответствующими ветвями, идущими от хь+ и от Xk-, отли-
отличаются в а раз.
При любом обратимом преобразовании от х к новой переменной
у соотношения G.2.36) и G.2.37) сохраняются. Следовательно,
0,67352673-
0,673526-
0,67352-
0,6735 -
0,673-
0,670 -
0,65-
0,5-
0 -
-1,0"
i* X
С„ С,
-0,784972822 -0,7849726 -0,78497 -0,7849 -0,7845 -0,780 -0,75 -0,5 0,5
Рис. 7.14. Последовательность бифуркаций удвоения периода для квадра-
квадратичного отображения в двойном логарифмическом масштабе (по данным
работы [417]).
По вертикальной оси отложены неподвижные точки х^ аттрактора периода 2 , который
образуется при С = С^ из аттрактора периода^ ~1. Видна неизменность скорости схо-
сходимости по С и по л; (константы б и а).
константа а также является универсальной, в том же смысле,
что и б.
Помимо последовательности бифуркаций, при уменьшении С
имеется зеркальная последовательность бифуркаций согласно
G.2.6) — G.2.8). Для нее С увеличивается, начиная с 1/2, и стре-
стремится к своей точке сгущения, которая определяется из G.2.8)
и G.2.29):
СОО = C + УТ7>4« 1,7808.
Для отображения G.2.5) зеркальная последовательность бифурка-
бифуркаций приходится как раз на обычно рассматриваемый интервал
0<Ср.<4. Используя G.2.8) и соотношение \i = 2С, находим, что
438 Глава 7
первая бифуркация наступает при yL± ~ 3, а точка сгущения равна
j"loo = C -f л/Т7)/2 да 3,5616,
что хорошо согласуется с численным значением [ix = 3,5700.
Существование бифуркаций удвоения очень большого периода
демонстрируется на рис. 7.14, полученном с помощью численного
моделирования квадратичного отображения [417]. Зависимость хи
от С отложена в двойном логарифмическом масштабе. Ясно видна
постоянная скорость сходимости по С и по х (с параметрами б и а
соответственно).
Спектральные свойства. При экспериментальном исследовании
сложного движения широко используется его спектр Фурье. Ниже
мы следуем анализу Фейгенбаума [123], который получил универ-
универсальный спектр одномерного отображения вблизи точки сгуще-
сгущения Соо.
Как известно, спектр периодического движения дискретный.
Когда происходит бифуркация удвоения периода, в спектре появ-
появляются субгармоники основной частоты отображения. Для даль-
дальнейшего анализа введем непрерывное время t и обозначим через
xtn) (t) решение после п-й бифуркации, а через Тп — его период.
Чтобы найти спектр, нам нужно общее соотношение для положе-
положения аттракторов. Из рис. 7.13, б и пояснений в тексте следует,
что ветви бифуркаций делятся на две группы, расстояния между
которыми удовлетворяют рекуррентному соотношению:
Г ' г—;
1
а
1
а2
G.2.38)
где t = 0 соответствует верхней неподвижной точке.
Для 1-й фурье-амплитуды имеем
п+1
Tn+i
С помощью сдвига на половину периода интегрирование можно
провести по периоду Тп:
G.2.39)
Диссипативные системы
439
Для четных I = 2k при п ^
[см. G.2.38) и рис. 7.13, б], и из G.2.39) получаем
2ft ~ Лк ¦ (/.J.4U)
Это означает, что фурье-амплитуда для данной частоты остается
неизменной при всех последующих бифуркациях. Для нечетных
/ = 2k + 1 подстановка G.2.38) в G.2.39) дает
dt
2Тп
— nilt
Сдвигая пределы во втором интеграле, имеем
х ехр —ш
. i t
Подставляя сюда разложение Фурье
ik't
получаем рекуррентное соотношение
2а
де
S =
— V L
/^ BА' + 1) - —
— Bft+ 1)
В пределе больших п, полагая 2k + 1 = \ и 2k!
меняя сумму в G.2.42) интегралом по |', находим
(л) /
S, G.2.41)
G.2.42)
1=|' и за-
G.2.43)
440 Глава 7
Поэтому для амплитудного спектра вблизи точки сгущения выпол-
выполняется универсальный закон подобия х):
X{n)
2
G.2.44)
где
?~' = —-—[2 {1+ а)]12. G.2.45)
Для приближенного значения G.2.35) для а имеем у = 5,79; точ-
точное значение а = — 2,5029 дает у = 6,57.
Согласно G.2.44), чтобы получить амплитуду новой гармоники
(вдали от точки бифуркации), появившейся в результате (п + 1)-й
бифуркации, нужно взять уменьшенное в 6,57 раза значение ам-
амплитуды гармоники, появившейся в результате я-й бифуркации.
Это теоретическое предсказание подтверждается экспериментально
(см. работу [123] и рис. 7.33). Мы обсудим эти экспериментальные
данные в § 7.4.
Другие периодические траектории. При уменьшении параметра С
от Со до Соо происходит бесконечное число бифуркаций удвоения.
При С <Соо также имеются области периодического движения.
Периодические траектории рождаются здесь парами (устойчивая
и неустойчивая) в результате тангенциальной бифуркации. В ка-
качестве примера2) рождения траектории с периодом 3 на рис. 7.15
отложена зависимость
/з(*)=/(/(/(*)))
для f (х) согласно G.2.46). Неподвижные точки периода 3 удовлет-
удовлетворяют уравнению
хз — /з \хз)-
Для С незначительно больше Cq3) это уравнение имеет только два
1) Приведенный вывод (взятый из работы [123], см. также [524]) яв-
является ошибочным. Во-первых, в данном случае нельзя заменять сумму ин-
интегралом, а во-вторых, неявно предполагаемая плавная зависимость ком-
комплексной амплитуды Х^ i j от k' явно несправедлива, хотя бы из-за фазо-
фазового множителя в G.2.41). Более естественным является предположение о
плавной зависимости модуля амплитуды и случайности ее фазы ввиду пере-
перехода при п -> оо к хаосу с непрерывным спектром. Тогда из G.2.41) и G.2.42)
можно получить у = 2а2 A + а2)~1/2= -\/2J3 « 4,65 [см. G.2.676)]. Точ-
Точная теория с использованием универсального отображения Фейгенбаума
дает для среднего по спектру параметра подобия значение (у) = 4,578 . . .
[540]. Небольшое различие между этими значениями объясняется, по-ви-
по-видимому, приближенным характером исходного закона подобия G.2.38). Со-
Соответственно изменяется и параметр C = 3,2375 ... в G.2.676). Последнее
значение приведено без объяснений в работе [205].— Прим. ред.
2) Согласно работе [261], «период 3 приводит к хаосу» (при другом зна-
значении параметра). Этот результат вытекает из более ранней теоремы Шар-
ковского [526] (см. также [547], с. 276).— Прим. ред.
Диссипативные системы
441
(действительных) корня, которые дают неподвижные точки пе-
периода 1 (рис. 7.15, а). Если же С<;Со3>, то уравнение имеет шесть
корней (рис. 7.15, б), которые соответствуют двум разным траек-
траекториям с периодом 3. Легко показать, что одна траектория устой-
устойчива (рис. 7.15, б, темные кружки), а другая—неустойчива (свет-
(светлые кружки). Критическое значение параметра Со3), при котором
рождаются эти траектории, равно
|3 — 0,9142.
Рис. 7.15. Рождение пары траекторий периода 3 при тангенциальной бифур-
бифуркации.
Темные кружки показывают устойчивую траекторию: светлые— пеустончиьую: а) С> С,,
б) С <С^ '. Пунктирная прямая f:, — х.
Поскольку вблизи неподвижных точек отображение /3 локально1
квадратично, то можно ожидать, что при дальнейшем уменьшении С
будут возникать бифуркации удвоения с периодами 3, 6, 12, 24 ....
Их точку сгущения С(® можно найти с помощью описанной выше
ренормализации или же путем численного моделирования. В по-
последнем случае С^ « — 0,92475. Существуют и зеркальные би-
бифуркации удвоения при С= 1—С.
Точно так же с помощью отображений /4, Д, /в, ¦ • • можно найти
устойчивые траектории с основным периодом п — 4, 5, 6, . . . . Для
каждой из этих траекторий существует своя последовательность
бифуркаций удвоения с начальной точкой Со"' и точкой сгущения
С?. Порядок, в котором появляются основные периоды при умень-
уменьшении параметра, является универсальным для всех отображений
с одним квадратичным максимумом. Например, первые шесть пе-
442
Глава 7
риодов упорядочены при уменьшении С следующим образом: 1, 6,
5, 3, 5, 6, 4, 6, 5, 6. Можно также найти и их общее число [296].
Например, имеются 202 основные траектории с периодом до 11
включительно; их упорядочение по параметру исследовано Метро-
полисом и др. [300]. Недавно Гейзал и Нирветберг [151 ] показали,
что для всех этих траекторий ренормализация имеет универсаль-
универсальную структуру.
7.2в. Хаотическое движение
Предельные циклы занимают конечную часть интервала по пара-
параметру. Для остальных значений параметра движение неустойчиво
и плотно покрывает конечный интервал по х при почти всех началь-
n^bt^=y±-—±:clf, (сжатие)
df2 (растяжение)
Рис. 7.16. Показатель Ляпунова равен среднему значению In \df/dx\ вдоль
траектории.
ных х0, а близкие траектории расходятся экспоненциально. Такое
движение получило название хаотического (см., например, [261,
297]). При его исследовании можно использовать некоторые ме-
методы, описанные в гл. 5 для гамильтоновых отображений. Особое
значение имеет показатель Ляпунова о и равновесное инвариантное
распределение Р (х).
Показатель Ляпунова. Для одномерного отображения имеется един-
единственный показатель Ляпунова [см. E.2.8)]:
N
а (х0) = lim — ) In
N-УСО N /_J
1=1
df
G.2.46)
Диссипативныс системы
443
Значение о положительно (см. рис. 7.16), если среднее по траекто-
траектории от \f \ больше 1. За исключением множества меры нуль, а
не зависит от выбора начального значения х0. При а>0 движение
хаотическое, а при a<zO существует предельный цикл. Зависимость
о от параметра С является обычно сложной. На рис. 7.17 представ-
о О
-0,5 -
-0,70 -0,75
0,95
-1,0
Рис. 7.17. Зависимость показателя Ляпунова сг от параметра С для квадра-
квадратичного отображения (поданным работы [368]).
Для G >0 движение хаотическое, а для о < 0 — периодическое. Сглаженная кривая
построена по 300 точкам с равномерным тагом по С.
лен пример такой зависимости 1368 ], полученной численным пу-
путем для квадратичного отображения. Значения а определялись
по формуле G.2.46) с N = 105 (число итераций) для каждой из 300
равномерно расположенных по С точек. Ясно видны относительно-
широкие интервалы по С с а<;0, которые отвечают периодическим
движениям с небольшим периодом. Для движения с большим пе-
периодом соответствующие им интервалы по С становятся меньше
расстояния между точками на рисунке и потому не видны. Хьюбер-
ман и Рудник [204 ] показали, что вблизи критического значения Сж
для хаотического движения о ее | С—Сх С, где r\ = In 2/ln 8 та
« 0,4498.
Показатель Ляпунова не зависит от (обратимой) замены пере-
переменных [323]. Действительно, пусть
G.2.47)
G.2.48)
где g' =A= 0. Тогда исходное отображение
хп +1 = / \Хп)
444 Глава 7
перейдет в отображение
у _i_i — ?Гг ) /7 9 4Q1
с показателем Ляпунова
N
о= lim— )
iv->.cx> N / ,
In
dxi+l
Согласно G.2.47), получим
dx,-, ,
G.2.50)
G.2.51)
dx,. (dgldx^dxi
откуда а = о.
Инвариантные распределения. Будем говорить, что Р (х) является
инвариантным распределением для отображения Т, если
Р (х) = ТР (х). G.2.52)
Другие названия — инвариантная мера г) или распределение ве-
вероятности. Примем, далее, что Р (х) нормировано на единицу:
\P(x)dx=l. G.2.53)
В общем случае отображение имеет много инвариантных распреде-
распределений. Из них выделенным является равновесное распределение,
которое получается итерированием отображения и для которого
среднее по времени равно фазовому среднему. Для предельного
цикла периода п распределение дискретно и представляет собой
сумму 8-функций в неподвижных точках с коэффициентом 1/п.
Для хаотического движения распределение Р (х) может быть раз-
разрывным, однако в типичном случае имеются конечные интервалы
по х с ненулевым Р (х).
Численно Р (х) можно получить из G.2.52). Для отображения
с одним максимумом в силу сохранения «числа траекторий» имеем
Р (х) dx— P (xx) dxj-f P (x2) dx2, G.2.54)
где точки хъ х2 — прообразы точки х (рис. 7.18). Записывая
dx'dx1 = [ df dx\X] и т. д., получаем
р (х) = P{Xl) + —-^- • G.2.55)
\df/dx\^ ^ \df:'dx\Xt
J) Существование инвариантной меры (сосредоточенной на аттракторе),
позволяющее распространить эргодическую теорию на диссипативные си-
системы, было доказано для широкого класса динамических систем Боголю-
Боголюбовым и Крыловым (см. [447], т. ), с. 411). Инвариантная мера единственна,
если существует только один аттрактор (одна «эргодическая компонента»
движения (ср. п. 5.2а), или «строгая эргодичность» [486], с. 43). Равновес-
Равновесным распределением ниже в основном тексте называется инвариантное рас-
распределение, сосредоточенное на одном аттракторе. Для него временные и фа-
фазовые средние совпадают в пределах области притяжения этого аттрактора.—
Прим. ред.
Диссипативные системы
445
Аналитически это функциональное уравнение решается в редких
случаях. Однако его можно решить численно по следующей схеме:
а) выбираем некоторое начальное Р[ — Рг (х);
б) вычисляем Л+1 по G.2.55) с Pi в правой части;
в) повторяем «б» до получения достаточной сходимости.
Этот метод иллюстрируется на рис. 7.19 [368] для отображения
G.2.5) с и = 4. Показаны первые три итерации Р,- с начальным рас-
распределением Рх (х) = 1. В данном случае имеет место быстрая схо-
сходимость к инвариантному распределению
i-l 2
Рис. 7.18. Построение инвариантного распределения Р (х).
«Число траекторий» на отрезке dx равно числу траекторий, пришедших из «прообразов»
dx\ и dx2.
которое будет получено аналитически ниже. Для \i = 3,8 и ц =
= 3,825 описанный метод дает инвариантные распределения, по-
показанные на рис. 7.20. В этих случаях движение, по-видимому,
также является хаотическим в некотором интервале по х. Знание
инвариантного распределения позволяет заменять усреднение по
времени усреднением по х. Например, можно вычислять показатель
Ляпунова по формуле:
G.2.56)
a=[dxP{x)\n
J
dx
При обратимой замене переменной х = g (x) новое инвариантное
распределение получается из условия
P(x)dx = P(x)dx. G.2.57)
446
Глава 7
In Р
4 !
Рис. 7.19. Численное определение инвариантного распределения Р (х) для
отображения G.2.5) с (х = 4 (по данным работы [368]).
Показано начальное распределение A) и его первые три итерации.
\пР
1
0
-1
у- = 3,825
Рис. 7.20. Численно найденное инвариантное распределение Р (х) для двух
значений ц отображения G.2.5) (по данным работы [368]).
Видны разрывы функции^/3 (х) и обратные бифуркации при увеличении ц.
Диссипативные системы
447
Треугольное отображение 1). В качестве примера рассмотрим про-
простое «треугольное» отображение (рис. 7.21). Оно имеет единствен-
единственный максимум / A/2) ¦= а, но не относится к квадратичным. Произ-
Производная /' равна + 2а в левой части и — 2а в правой части отобра-
отображения. Ясно, что движение является хаотическим для о>1/2,
поскольку все траектории расходятся экспоненциально (см.
рис. 7.16). Инвариантное распределение находится из G.2.55):
Р(х) =
2а
Р
2а
4- Р /1 —
О
О 4 I
Рис. 7.21. Симметричное треугольное отображение.
Для а = 1 имеется очевидное решение Р (х) = 1. Показатель Ля-
Ляпунова равен G.2.56):
Поскольку а>0, движение является хаотическим. Рассмотрим
теперь отображение
f(x) = 4x(l~x). G.2.58)
Введем новую переменную
*=(—)arcsin(V^)>
G.2.59)
1) В оригинале — tent map (отображение, похожее на палатку).—Прим.
перее.
448 Глава 7
тогда G.2.58) перейдет в треугольное отображение с а = 1:
G.2.60)
2х, 0<х<—,
2
2—2х, —
2
Из G.2.57) с Р (х) = I получим инвариантное распределение для
отображения G.2.58):
Р(х) = -— = — [хA — х)Г112, G.2.61)
dx л
которое можно сравнить с численными данными на рис. 7.19. По-
Показатель Ляпунова для отображения G.2.58) равен
^1 1
In | 4A — 2х)
¦— In О
,1 2
Отметим, что отображения G.2.58) и G.2.60) имеют одинаковую
величину о, поскольку она инвариантна относительно преобразо-
преобразования переменной. Соответственно любое обратимое преобразова-
преобразование квадратичного отображения G.2.4) сохраняет функцию о (С),
показанную на рис. 7.17.
Для отображения G.2.58) [и «зеркального» квадратичного ото-
отображения G.2.4) с С = — 1 ] точное решение имеет вид
хп = ± -± cos B"+1ф0) = sin2 B>0), G.2.62)
где ф0 определяется начальным условием х0. Статистические свой-
свойства отображения G.2.58) исследовались в работе [416]. Было по-
показано также, что движение является эргодическим и перемешиваю-
перемешивающим с экспоненциальной расходимостью близких траекторий 1).
Обратные бифуркации хаотического движения. При изменении па-
параметра С квадратичного отображения G.2.4) от Со = 1/2 до Сх =
^= — 0,78497 . . . возникает «дерево» бифуркаций, показанное на
рис. 7.14. Какова природа движения для С<Соо?
Эта область исследовалась Лоренцем [284 ], Колле и Экманом
[82] и Хеллеманом [182], ее качественная структура представлена
на рис. 7.22. Точки показывают хп в стационарном режиме
A000<«<;4000) для разных значений параметра С. Ясно видны
полосы с хаотическим движением (при С<^СХ). При уменьшении С
от значения С = Сж эти полосы сливаются и испытывают обратные
бифуркации в точках С = С*п. Видны также бифуркации предель-
J) Это вытекает, в частности, из свойств более простого отображения
фп+i = 2ф„, mod 2я для фазы в G.2.62) (см. конец п. 5.2в).—Прим. ред.
Диссипативные системы
449
ных циклов более длинного основного периода 6, 5 и 3, «разрезаю-
«разрезающие» хаотическую область. Для обратных бифуркаций хаотиче-
хаотических полос выполняется закон подобия с теми же константами б
и а, что и для бифуркаций предельных циклов при С>-Сх. Эти
результаты Гроссмана и Томае 1170] можно получить также из
описанной в п. 7.26 приближенной теории ренормализации [182].
г -с
-0,10
-0,50
-1,00 -0,95 / -0,90^-0,851 —0,80| | | -0,75
-ViC2' С* С*С_С3
-0,70 -0,65 —0,60
с, с
Обратные
бифуркации
ПоспеЭобагпельносгпь
бифуркаций
Рис. 7.22. Численное моделирование последовательности обратных бифур-
бифуркаций удвоения для квадратичного отображения (по данным работы [82]).
Для каждого значения С отложены 3000 значений xR A000 < п <4000). Видны полосы
хаотического движения для С <С00, которые сливаются при С — С^. Отмечены интер-
интервалы (по С) предельных циклов-. 1 — периода 3; 2 — периода 5; 3 — периода 6.
Спектр мощности. «Шумовое» движение в хаотическом режиме
можно охарактеризовать его спектром мощности Р (со, С), где о —
частота, а С — параметр. В отличие от таких свойств хаотического
движения, как показатели Ляпунова, спектр мощности легко из-
измерять экспериментально. В частности, представляет интерес вид
спектра при бифуркационных значениях Си вблизи критического Сх,
где происходит слияние полос хаотического движения. Движение
в этих полосах представляет собой суперпозицию периодических
колебаний и шума:
i
G.2.63)
450 Глава 7
Определим фурье-амплитуду посредством формулы
XN(<o, С) = -?-?хпе-Шп. G.2.64)
N ,2 = 1
Тогда спектр мощности равен
G.2.65)
Он состоит из острых пиков (периодические переходы между по-
полосами, аналогичные движению на предельном цикле при С^>СЖ)
и широкополосного шума (хаотическое движение внутри полос).
Следуя Хьюберману и Зисоку [205], получим сначала универ-
универсальный закон подобия для полной мощности в непрерывном
спектре G.2.68) для Ж (С). При С -— — 1 (см. рис. 7.22) движение
обладает перемешиванием2). Более того, как показано в работе
[170], корреляционная функция
m X
где
?
N-+0O N 1 = 1
является в этом случае «б-функцией», т. е.
W2, л = 0,
о, пфО. (?-2-66)
Это очень сильное статистическое свойство, означающее полное3)
х) Спектр «мощности» (точнее спектральная плотность), он же спектр
корреляционной функции ^ (п) (см. ниже), или просто спектр (в эргодиче-
ской теории) определяется как преобразование Фурье от Я7 (п):
Р (ш) = X ^ (n) cos (con).
2.JX/ л = — ОО
Для дискретного времени спектр определен по модулю 2я и обладает зеркаль-
зеркальной симметрией Р (ш)= Р Bл—ш). Переход к непрерывному времени со-
соответствует только интервалу частоты @, л) с независимыми фурье-компо-
нентами. Простое изложение спектрального анализа случайных процессов
см., например, в работе [519].— Прим. ред.
2) Это следует из положительности КС-энтропии (см. выше).— Прим.
ред.
3) Равенство нулю конкретной корреляционной функции не означает
«полное отсутствие корреляций. Существование определенных корреля-
корреляций следует просто из функциональной зависимости хп+г = f (хп).— Прим.
ред.
Диссшштивные системы 451
отсутствие корреляций уже через одну итерацию отображения1).
Величина W в G.2.66) есть среднеквадратичный размер единой
полосы хаотического движения при С = — 1. Каждая обратная
бифуркация удваивает число полос и уменьшает их ширину. В со-
соответствии с законом подобия G.2.36) и G.2.37) для половины по-
полос ширина уменьшается в а раз, а для остальных — в а2 раз.
Среднеквадратичная ширина одной полосы удовлетворяет закону
г* G-2'67а)
(k — номер бифуркации), или
Wk=Wop~k, G.2.676)
где
Заметим, что 2E = у [см. G.2.45) ]. Полная мощность в пределах
основной частоты отображения 2я равна
2я
JC (С) = |" do | г ((о, С) |2 = <$>, @), G.2.68)
о
где корреляционная функция ЯЗГ определяется только хаотической
частью движения [хп -+¦ гп, см. G.2.63) ]. Поэтому %?г @) = W\ и
jf(Cl) = jrof,-2k. G.2.69)
Но бифуркационные значения С^ сами удовлетворяют закону по-
подобия
Cl-Cn = (С*о —С») б-;г. G.2.70)
Исключая k, приходим к новому закону подобия
Л9 (С) ос (С» —C)tf, G.2.71)
где
21пр , _..
а = —-f« 1,544
In б
— универсальная постоянная. Хьюберман и Зисок [205] прове-
проверили этот результат путем численного моделирования отображения
G.2.5) и получили прекрасное согласие.
!) Заметим, что для многих систем с хаотическим движением корреля-
корреляции убывают совсем не так быстро, жюгда только как степень п [60]. [В ука-
указанной работе исследовались полностью интегрируемые системы и «убывание»
корреляций связано не с динамикой системы, а с методом вычисления корре-
корреляций. По поводу медленного убывания корреляций см. предисловие редак-
редактора перевода и цитированную там литературу.— Прим. ред.]
452
Г.щва 7
Спектральная плотность хаотического движения была найдена
в работе [434], следуя методу Фейгенбаума [123] (см. п. 7.26).
Полученный результат можно представить в виде
r(fo, Cl)=gk(A>)~rBka). G.2.72)
Здесь |г(со)|2— спектр движения при С ~ — 1, который можно
приближенно считать однородным (белый шумI). Фурье-ампли-
шумI). Фурье-амплитуды
2k
ftN=I^""" G-2.73)
Рис. 7.23. Спектр мощности при трех значениях С в обратной последова-
последовательности бифуркаций для квадратичного отображения (по данным работы
1434]).
Ломаная кривая — численные данные; плавная кривая, смещенная для удобства вниз,—
теория без учета дискретного спектра.
характеризуют систему хаотических полос шириной Wjk (/ = 1,
2, ... 2к) и находятся из рекуррентного соотношения2)
G.2.74)
г) См. G.2.66); заметим также, что значение частоты 2ka (в 7.2.72) бе-
берется по модулю 2я [см. G.2.68)].— Прим. ред.
2) При С -» Ссо этот закон подобия определяет масштабно-инвариантную
структуру как непрерывного (с \g0 i2 = 1), так и дискретного (c]gop =
= |Л0|.2б (ш)) спектра [кроме со = я (см. [520]), для которого справедливо
соотношение G.2.40)]. При переходе от спектральной плотности к ампли-
амплитудам гармоник (g> -> X^) правую часть G.2.74) нужно разделить на V 2
(интеграл отб Bш) равен 1/2). Обратим внимание, что законы подобия G.2.40),
G.2.44) и G.2.74) разные: в первом фиксирована частота, а во втором — но-
номер гармоники колебаний. Из G.2.74) следует также, что масштабный мно-
Диссипативные системы 453
причем, согласно G.2.72), g = 1. На рис. 7.23 показаны числен-
численные данные для спектра мощности при трех значениях параметра С.
Соответствующий универсальный спектр | gu |2, полученный с по-
помощью G.2.74), представлен сплошными линиями, которые сдви-
сдвинуты по вертикали для удобства сравнения. Согласие с численными
данными весьма хорошее. Напомним, что дискретный спектр в тео-
теорию не включен.
§ 7.3. Двумерные отображения и связанные с ними
потоки
Мы уже видели, что хаотическое движение может возникать в дис-
сипативных потоках с размерностью фазового пространства не
меньше трех, или в соответствующих этим потокам обратимых
отображениях Пуанкаре, размерность которых не менее двух.
В общем случае хаотическое движение имеет место лишь для узких
интервалов параметров. В этом существенное отличие от гамиль-
тоновых систем, где хаотическое движение сохраняется, как пра-
правило, в широком диапазоне параметров. Ниже описаны два крите-
критерия локальной стохастичности для диссипативных систем. В п. 7.3а
метод квадратичной ренормализации применяется к двумерным
обратимым отображениям и показывается сходимость последова-
последовательности бифуркаций удвоения периода и возникновение локаль-
локального хаотического движения. В п. 7.36 получен критерий перехода
к хаотическому движению вблизи сепаратрисы на примере вынуж-
вынужденных колебаний осциллятора с затуханием. Наконец, в п. 7.3в
рассмотрена модель ускорения Ферми с диссипацией и исполь-
используется описание хаотического движения с помощью уравнения ФПК.
Это уравнение позволяет получить первое приближение для инва-
инвариантного распределения на странном аттракторе.
7.3а. Бифуркации удвоения периода
Покажем, что последовательность бифуркаций удвоения является
тем механизмом, с помощью которого происходит переход от регу-
регулярного движения к хаотическому в широком классе двумерных
обратимых отображений. Более того, оказывается, что вблизи пе-
перехода движение системы можно локально описать одномерным
необратимым отображением. Эти результаты были получены на
основе точной теории ренормализации [83]. Однако мы будем по-
прежнему использовать приближенную теорию Хеллемана [180—
182].
житель у в G.2.44) является на самом деле сложной (фрактальной) функцией
частоты ш, а его среднее значение (с учетом множителя 1/V2) равно
\"?~^)~~ = 2а.2 A + а2)'2 и в точности совпадает с результатом для слу-
случайных фаз (см. примечание редактора на с. 440).— Прим. ред.
454 Глава 7
Рассмотрим последовательные бифуркации неподвижной точки1)
периода I некоторого двумерного отображения Т. После первой
бифуркации эта неподвижная точка становится неустойчивой. Раз-
Разложим отображение до квадратичных членов:
д л м „ I j I r г г II "п-п |. G.3.1)
где u, v — отклонение от неустойчивой неподвижной точки. При-
Примем, что якобиан этого отображения В = const<1, что, во всяком
случае, справедливо вблизи перехода.
Отображение G.3.1) можно привести к стандартному виду
n+nl + 2^n G.3.2)
следующим способом (см. [182], приложение А):
1. Переходим к переменным u', v', в которых матрица Л' диа-
гональна, а оба ее собственные значения Xlt X2 действительны,
поскольку неподвижная точка неустойчива; тогда Г пере-
переходит в Г".
2. Условие В = const дает возможность выразить все элементы
матрицы Г' через Гп, Г!з и собственные значения.
3. Переходим к новым переменным:
= и VrJi —о' Vri3.
4. Изменяем масштаб по s, вводя
Л —" " О,
В результате получаем G.3.2) с параметром
С= Xl + %2 . G.3.3)
2
В некоторых случаях стандартная форма G.3.2) находится
непосредственно. Например, отображение
(I. о. 4)
Vn+l = Vn + Un+l
сводится к G.3.2) с помощью замены х = Dv/2, С = B—б + А)/2
х) В случае периода k берем отображение Тк.
Диссипативные системы 455
и]В = 1—б. Отображение Хенона G.1.14) может быть сразу за-
записано в стандартной форме.
Квадратичная ренормализация. Исследуем, как и в п. 7.26, пове-
поведение вблизи неподвижной точки х10 = 0 при уменьшении С. Не-
Неподвижная точка устойчива, если
и неустойчива при
С<— LzA. G.3.5)
В результате бифуркации рождаются две устойчивые неподвижные
точки х2+ (см. рис. 7.12). Оба корня можно найти, записывая
х2± = а±Ь G.3.6а)
и итерируя G.3.2) дважды [ср. G.2.21) ]:
2а = — liA —С, G.3.66)
G.3.6b)
2
Подставляя х = х^ + Ах в G.3.2), получаем
Ах 4-ВАх 0 = еАх . + 2 (Ах Л2, G.3.7а)
J, G.3.76)
;n+1J. G.3.7b)
где d и е имеют вид [см. G.2.22) и G.2.23) ]:
d = 2C + 4xt+, G.3.8а)
-е = 2С + 4х2_. G.3.86)
При четных п траектория находится вблизи х2+, а при нечетных —
вблизи х2_. Умножая G.3.7а) на В, G.3.76) на ей складывая за-
затем с G.3.7в), получаем
Ахп+2 + В'Ахп_г = 2С'Ахп + 2е {Axnf + 2 [(Ах„+1J +
+ B(Axn_xJ], G.3.9)
где
В' = В2, G.3.10а)
!. G.3.106)
456 Глава 7
Член в квадратных скобках в G.3.9) пропорционален (Ах„J. Дей-
Действительно, вводя г = Ахп+1/ Axn_lt находим
(А ViJ+в (Ахп->У=с-2+в) <A*-i>'.-. <7-3-х *>
Пренебрегая квадратичным членом в G.3.76), имеем
(г + В) Ахп-г « dAxn. G.3.12)
Подстановка G.3.12) в правую часть G.3.11) дает
(Ахп+1у + В (А*,-!J « *{Г* + *} (Адся)8. G.3.13)
(/• + я)*
Вследствие квадратичной зависимости при бифуркации удвоения
г та 1, т. е. [ Лх„+1 [ близко к \Ахп^г\. Правая часть G.3.13) имеет
экстремум при г = 1 и поэтому слабо зависит от г при г« 1. От-
Отсюда
(Ахп+1У + В (Ахп^У « ^^ (Ах„J. G.3.14)
1 -г В
Подставляя G.3.14) в G.3.9) и переходя к переменной
х' = аДл:, G.3.15)
находим
х'п+2 + В'Х'п-2 = Ж'х'п + 2 КJ' G-3-16)
где
a^e+rTF' GД17)
Отображение G.3.16) имеет тот же вид, что и исходное G.3.2). Поэ-
Поэтому неподвижные точки нового отображения испытывают би-
бифуркацию при тех же значениях новых параметров В' и С [см.
G.3.5) ]. Последовательность бифуркаций, которые описываются
соотношениями G.3.10), сходится при значениях В' = В = В.» и
С = С = С». Для диссипативного отображения | В |< 1 и из
G.3.10а) следует, что Boo = 0. Поэтому все диссипативные отобра-
отображения вблизи перехода ведут себя локально как одномерные [ср.
G.3.16) с G.2.26) при В' = 0]. Неудивительно, что при подста-
подстановке В = В.» = 0 в G.3.106) условие С = С — Сх дает то же
самое значение
'V17 _ 0,781, G.2.29)
что и для одномерного случая. Бифуркационные значения С& схо-
сходятся к С» по тому же закону
С/с—С» л* АЬ
и с тем же множителем 6=1+ -\Л7 « 5,12, что и в одномерном
Диссипативные системы 457
случае. Параметр подобия ада — 2,24, определяемый формулой
G.3.17), также совпадает с G.2.35). Эти результаты указывают на
универсальный характер поведения всех диссипативных систем
вблизи перехода к хаотическому движению; они были проверены
численно для многих одномерных, двумерных и многомерных ото-
отображений. Однако следует подчеркнуть, что переход к стохастич-
стохастичности является локальным, т. е. относится только к данной непод-
неподвижной точке с ее последовательностью бифуркаций. В общем слу-
случае в диссипативной системе имеется много неподвижных точек,
каждая из которых должна претерпевать свою последовательность
бифуркаций, прежде чем возникает глобальный переход к хаоти-
хаотическому движению и странный аттрактор *).
В противоположность этому бифуркации двумерных гамильто-
новых отображений устроены более сложно. Из-за сохранения фа-
фазовой площади В' = В = Boo = 1 (если В = — 1, то можно взять
квадрат отображения; более подробно см. работу [182]). Поэтому
бифуркации удвоения гамильтонова отображения сохраняют дву-
двумерный характер даже вблизи точки сгущения (численные данные
см. в работе [36]). В результате, хотя масштабные факторы б и а,
а также параметр Сх и являются универсальными для всех дву-
двумерных гамильтоновых отображений, они имеют другие значения,
чем для диссипативных отображений. Более того, для гамильтоно-
гамильтоновых отображений имеется еще один универсальный масштабный
фактор Р, который вместе с а определяет преобразование фазовой
плоскости при бифуркациях. Определение р с помощью обобщения
описанного выше метода приводится в дополнении Б.
7.36. Движение вблизи сепаратрисы
В этом разделе мы рассмотрим метод Мельникова [299 ], позволяю-
позволяющий исследовать движение вблизи сепаратрисы системы, близкой
к интегрируемой. Этот метод позволяет получить критерий воз-
возникновения стохастичности в окрестности сепаратрисы при наличии
диссипации. Мы уже видели (см. п. 3.26 и рис. 3.4), что в типичной
гамильтоновой системе движение около сепаратрисы всегда хаоти-
хаотическое. Однако в присутствии диссипации это уже не так. Поэтому
важно найти условия, при которых возникает хаос.
Метод Мельникова использовался в теории динамических систем
Морозовым [305, 306], Мак-Лафлином [288, 289] и Холмсом [195,
196]. В частности, Морозов и Холмс исследовали этим методом
уравнение Дюффинга. Ниже мы следуем подходу Холмса (см.
[168]). В качестве примера рассмотрим простую двумерную авто-
*) Речь здесь идет о возможном слиянии хаотических аттракторов, воз-
возникающих из разных неподвижных точек.— Прим. ред.
458
Глава 7
номную систему с единственной гиперболической точкой под дейст-
действием периодического возмущения:
х = /о(х) + *Мх, *), G.3.18)
где х = (хъ л:а), а функция /х периодична по t с периодом Т. Не-
Невозмущенная система является интегрируемой и имеет гиперболи-
гиперболическую точку Хо с единой сепаратрисой х0 (t), так что
lim xo(t) = Xo.
в г
Рис. 7.24. Входящая и выходящая сепаратрисы гиперболической точки Хо-
а — интегрируемая система, обе сепаратрисы плавно переходят друг в друга; б — воз-
возмущенная система, выходящая сепаратриса окружает входящую; в — входящая сепара-
триса окружает выходящую; г — сепаратрисы пересекаются.
Схематически это показано на рис. 7.24, а, где в фазовом прост-
пространстве (х1г х2) системы изображены совпадающие в данном случае
входящая Xs (t) и выходящая хи (t) сепаратрисы. Внутри области,
охватываемой сепаратрисой, имеется, вообще говоря, эллиптиче-
эллиптическая неподвижная точка.
При включении возмущения фазовое пространство системы ста-
становится трехмерным (xlt x2, t), поэтому наиболее удобно рассмат-
рассматривать движение на поверхности сечения t = const (mod T). Как
показано в п. 3.26, в возмущенной гамильтоновой системе сепарат-
сепаратриса «расщепляется», т. е. входящая и выходящая сепаратрисы
уже не совпадают, а, вообще говоря, пересекаются между собой,
приводя к бесконечному числу гомоклинных точек и хаотическому
движению. В более общем диссипативном случае имеются три воз-
Диссипативные системы 459
можности [6611), показанные на рис. 7.24. Сепаратрисы либо
нигде не пересекаются, причем любая из них может полностью
охватывать другую (рис. 7.24, б и в), либо пересекаются в бесконеч-
бесконечном числе точек. Хаотическое движение возникает только в послед-
последнем случае.
Метод Мельникова. Чтобы найти условие пересечения, вычислим
по теории возмущений расстояние D между сепаратрисами в не-
некоторый момент времени t0. Для случая на рис. 7.24, б D<zO, а на
рис. 7.24, в D>0 при любом t0. И, только если для какого-либо t0
величина D меняет знак, возникает хаотическое движение2), по-
показанное на рис. 7.24, г.
Для вычисления D достаточно знать обе сепаратрисы Xs и х"
в первом порядке по е. Записывая
s, и ,, f\_ (f t\\Pjfs'u(t f\ f7 3 19)
где /0 — произвольный начальный момент времени, а х0 — единая
невозмущенная сепаратриса, и подставляя G.3.19) в G.3.18), по-
получаем в первом порядке
G.3.20)
где
dx\ "
dt
-М(хо)-х°-
I
М (х0) =
дхх
Р
дх2
<5/02
дх\ дхг
— матрица Якоби для вектора/0, взятая на невозмущенной траек-
траектории х0 (t—10). Нам нужно решение G.3.20) для Xs при t>t0
и для хи при t<z t0, такое, чтобы
lim .Vs = lim хи = Хр,
где Хр — возмущенное положение гиперболической точки. Эти
решения отличаются на вектор (е = 1)
d(t, to) = x\t, to) — xu(t, to) = x\(t, to)—x"(t, t0). G.3.21)
Расщепление сепаратрисы по Мельникову3) D (t, t0) определяется
как проекция d на нормаль iV к невозмущенной сепаратрисе х0
в момент времени t (рис. 7.25):
D(t, tQ) = N-d. G.3.22)
г) Все эти случаи рассмотрены Мельниковым [298].— Прим. ред.
2) Вообще говоря, это будет лишь так называемый переходной или вре-
временный хаос (см. ниже).— Прим. ред.
3) В оригинале — the Melnikov distance (расстояние Мельникова). —
Прим. перев.
460
Глава 7
Используя G.3.18) (при е = 0), определим вектор нормали как1)
N(t, *0) = Г!;Л*0)\ G.3.23)
V /oi Vе о) J
Вводя оператор 2)
G.3.24)
можно записать G.3.22) в виде
D(t, to) = fo/\d.
Рис. 7.25. Расщепление сепаратрисы D — Nd по Мельникову.
Пунктирной кривой показана невозмущенная сепаратриса гиперболической точки
которая под действием возмущения смещается в точку ЛГ
Чтобы найти явное выражение для D, представим его как
D = DS—DU, G.3.25а)
где
Ds' " (t, tg) = f0 Л xs{ ". G.3.256)
Дифференцируя по времени, имеем, например, для Ds:
\xl G.3.26)
г) Поскольку вводимый таким образом вектор Л' не является единичным,
величина D в G.3.22) не равна расстоянию между сепаратрисами и даже
имеет другую размерность. Для рассматриваемой здесь задачи об условии
пересечения сепаратрис это несущественно. С другой стороны, нормировка
Л' неоправданно усложнила бы нижеследующие уравнения для D, проще
сделать это в конце вычислений.— Прим. ред.
2) Действие этого оператора удобно представить в виде х/\у = &ikXiyk,
где &ik — единичная антисимметричная матрица (е12 = 1).— Прим. ред.
Диссипативные системы 461
Используя G.3.20) и jco = /o. получаем
D " = (М (лго) -/о) Л ^ + /оЛ (М (*„)' -*0 + /о Л Л. ("-3.27)
или
D s = Sp М (лго) /о Л ¦«? -;- /о Л Л = Sp М (*„) Ds + /0 /\ /ь
G.3.28)
где SpM = div/0. При интегрировании этого уравнения ограни-
ограничимся частным случаем, когда невозмущенная система является
гамильтоновой, т. е. SpM ^ 0 (см. п. 7.1а). Интегрируя G.3.28)
от t0 до оо и учитывая асимптотическое условие Ds (оо, t0) =
= /о (А"о) Л х\ = 0, находим
05й^о)=-]7оЛ/Д G.3.29)
Для D" аналогичным образом получаем
О"(/0, 'о)= f foAfidt. G.3.30)
— оо
Подставляя G.3.29) и G.3.30) в G.3.25а), окончательно имеем
D(t0, g=- I ЛЛ/Д G.3.31)
—оо
Полученная зависимость D от f0 определяет характер движения.
Если ?> (^0) меняет знак, то сепаратрисы пересекаются (рис. 7.24, г)
и движение в этой области является хаотическим.
Уравнение Дюффинга. Следуя Холмсу 1195], найдем условия пе-
перехода к хаотическому движению для уравнения Дюффинга
х—х-\-х3 = —гЬх -j- еу cos со/, G.3.32)
которое описывает колебания нелинейного осциллятора с малым
затуханием еб под действием периодической силы с амплитудой еу.
Перепишем G.3.32) в виде G.3.18):
x = v, G.3.33а)
v = x—xa-y-e[ycos(at—&v). G.3.336)
Линии постоянной энергии невозмущенного гамильтониана
Яо= —у2 -jc4 —^ • G.3.34)
2 2 4 '
показаны на рис. 7.26. Имеется единственная гиперболическая
точка х = v = 0 с единой сепаратрисой при Яо = 0. Чтобы найти
462
Глава 7
решение на сепаратрисе, выразим v (x) из G.3.34) и подставим
в G.3.33а). Имеем
откуда
dt
ft sh/
ch2/
G.3.35а)
G.3.356)
яп>о
Рис. 7.26. Кривые постоянной энергии невозмущенного гамильтониана
G.3.34).
Сравнивая G.3.33) и G.3.18), находим
= *— л:3;
— бо.
Отсюда
/о Л Л = v0 [у cos at — &v0],
и, согласно G.3.31),
G.3.36)
Подставляя G.3.356) в G.3.36) и заменяя переменную интегриро-
интегрирования (т = t—/0). запишем
= -v2vsincu/0
V '
sh т
ch2x
sin сот-f 26
' th2xdx
ch2x
Диссинативные системы 463
Второй интеграл вычисляется элементарно и равен 2 3, а первый
выражается через вычеты в точках тп = ni (п — 1,2). В резуль-
результате находим1)
7~~\ 14- 4- \ IC\ Sill шГп 40 ,-^ г\ Г)\
D(t0, /0) = у2 nyw ^—^— -f- —^—. (/.3.37)
ch
2
Хаотическое движение вблизи сепаратрисы возникает при условии
пересечения сепаратрис, т. е. когда D (t0) меняет знак. Из G.3.37)
следует, что это происходит, если
4 ch
Стационарное хаотическое движение. Нужно подчеркнуть, что ус-
условие пересечения сепаратрис G.3.38) является локальным крите-
критерием стохастичности и применимо только вблизи невозмущенной
сепаратрисы. Поэтому такой критерий ничего не говорит о появлении
странного аттрактора, который представляет стационарное хаоти-
хаотическое движение в большой области фазового пространства. Урав-
Уравнение Дюффинга без диссипации (б = 0) является гамильтоновым
и всегда имеет хаотические решения вблизи сепаратрисы. Мы знаем,
что хаотическое движение в этом случае происходит в узком слое
и ограничено инвариантными кривыми. Однако при 6>0 все ин-
инвариантные кривые разрушаются и траектория, хаотическая вблизи
сепаратрисы, может уйти далеко от нее и «захватиться» устойчи-
устойчивым фокусом или предельным циклом. Такое поведение наблюдал
Холмс [195] при аналоговом моделировании уравнения
Дюффинга2). Поэтому единственное, что можно ожидать при вы-
выполнении условия пересечения сепаратрис G.3.38), — это нерегуляр-
нерегулярное «блуждание» траектории в течение некоторого времени, пока
она не попадет на какой-либо аттрактор, простой или странный.
Фактически численное моделирование показывает, что появле-
появление странного аттрактора для уравнения Дюффинга, по всей ви-
видимости, связано с каскадом бифуркаций двух фокусов при х —
= ± 1; v = 0 (см. рис. 7.26). С помощью аналоговой вычислитель-
вычислительной машины Холмс исследовал поведение системы при фиксирован-
фиксированных б и со в зависимости от у. Его результаты приведены на рис.7.27.
При у<:0,76 наблюдалось только регулярное движение, показан-
х) Напомним, что расстояние между сепаратрисами находится делением
D (t0) на |ЛП = |/о! = W + х3 A-х2J]172 [для G.3.32)]. Вблизи гипербо-
гиперболической точки v, х -> 0, и расщепление сепаратрисы быстро возрастает,
а полученные приближенные оценки перестают быть спрайедливыми. В пре-
пределах их применимости, однако, это не влияет на условие пересечения се-
сепаратрис G.3.38) ниже.— Прим. ред.
2) Это явление «вырождения» хаоса, по-видимому, впервые было обна-
обнаружено в работе [274] и исследовалось в работах [73, 74, 530].—Прим. ред.
464 Глава 7
ное на рис. 7.24, в. В интервале 0,76<Су-<0,95 движение было
хаотическим в течение некоторого времени, а затем траектория
притягивалась к одному из двух фокусов. Далее, для 0,95<у< 1,08
происходит каскад бифуркаций обоих фокусов. И наконец, для
1,08<7<2,45 результаты моделирования указывают на присутст-
присутствие странного аттрактора, за исключением интервала 1,15<;т< 1.2,
где существует предельный цикл периода 5. Таким образом, хотя
как пересечение сепаратрис, так и каскад бифуркаций обоих фоку-
фокусов являются необходимыми условиями появления странного аттрак-
аттрактора1), они не являются достаточными.
' Точка
\ сгущения
1-ая Z-ая \ с-^—.
0 0,76 0,83 0,95 1,04 1,08 1,15 1,2 2,45
Пересечение * ¦ >v ¦ =-"
сепаратрис Бифуркации' Странный
усвоения аттрактор
периооа
Рис. 7.27. Поведение решения уравнения Дюффинга G.3.32) в зависимости
от амплитуды у внешней периодической силы заданной частоты w при по-
постоянном затухании 5.
/ — граница пересечения сепаратрис (численный результат); 2 — то же, теория G.3.38);
3 _ интервал существования предельного цикла периода 5.
Диссипативные отображения. Метод Мельникова можно исполь-
использовать и для изучения двумерных диссипативных отображений.
Рассмотрим, например, обобщенное стандартное отображение G.3.4)
(с заменой и и v на / и Э):
dn
G.3.39)
где 81 (п) — периодическая б-функция C.1.33). Если принять / =
= К sin 0, оставить только два члена в бх (п) « 1 -\- 2 cos 2лп
и ввести дополнительный малый параметр возмущения 8, то полу-
х) Ни бифуркации удвоения, ни пересечения сепаратрис не являются
необходимыми для хаотического аттрактора, как показывает классический
пример Лоренца (см. также конец п. 7.46). Тем более не требуется совпаде-
совпадения этих условий. Если, например, изменить знак линейной силы в уравне-
уравнении Дюффинга G.3.32), то сепаратрисы вообще не будет, а хаотический ат-
аттрактор останется [210].— Прим. ред.
Диссипативные системы 465
чим уравнения типа G.3.18):
Ksi
Kf e( — S/ + 2/Csin6cos2jm),
dn
G.3.40)
e
Невозмущенная сепаратриса этой системы имеет, как мы знаем,
вид [см. A.3.21)]:
G.3.41)
Подставляя G.3.41) в G.3.31), можно вычислить расщепление се-
сепаратрисы:
оо
D(no)= [ /0(м—п0) {— fi/0(n—no) + 2i<sin[8o(n—-n0)] cos2n;n} dn.
G.3.42)
Здесь первый интеграл берется элементарно, а второй сводится
к интегралу Мельникова—Арнольда (п. 3.5а). В результате полу-
получим
4я
Q
ch (nQo/2)
sin2nn0 —48 , G.3.43)
где Qo = 2я//С1/2. Поэтому условие пересечения сепаратрис имеет
вид
О3 1
4 сЬ(я(?о/2)
или для Qo ^>> 1
G.3.44)
Метод Мельникова можно обобщить и на многомерные системы
[196 ]. В частности, его можно использовать для изучения движения
вблизи сепаратрисы вторичных резонансов. Этот метод привел
также к важным математическим результатам в теории диффузии
Арнольда [197 ] х).
1) Речь идет о более аккуратном установлении самого факта существова-
существования диффузии в окрестности резонансных сепаратрис для широкого класса
гамильтоновых систем (гипотеза Арнольда [462]).— Прим. ред.
466 Глава 7
7.3в. Вычисление инвариантных распределений
Рассмотрим задачу о вычислении инвариантного распределения
Р (х) на странном аттракторе. Как упоминалось в п. 7.2в, Р (х)
удовлетворяет уравнению
Р{х) = ТР(х), G.3.45)
где Т — отображение в сечении Пуанкаре. В случае нескольких
инвариантных распределений мы будем понимать под Р (х) равно-
равновесное распределение, для которого среднее по времени на почти
любой траектории из области притяжения аттрактора равно фазо-
фазовому среднему, вычисленному с этим распределением х).
Пусть G (х) — некоторая функция в фазовом пространстве.
Ее временное среднее на траектории с начальными условиями х0
равно
G (х0) = lim — V G (Гх). G.3.46)
Для почти всех л:0 в области притяжения данного аттрактора G
не зависит от х0 и равно
G=\dxP{x)G(x), G.3.47)
где Р (х) — инвариантное распределение для аттрактора. Соотно-
Соотношение G.3.47) часто более удобно для вычисления G, чем G.3.46).
В частности, с помощью инвариантного распределения вычисляются
показатели Ляпунова (для одномерного отображения это описано
в п. 7.2в).
В случае гамильтоновой системы и канонических переменных х
равновесное распределение Р (х) = с, где постоянная с>0 на всей
хаотической компоненте движения и с = 0 вне ее. Если хаотиче-
хаотическая компонента заполняет почти все фазовое пространство, как,
например, в стандартном отображении C.1.22) при /С» 1. то
Р = 1/т, где т — объем произвольной области фазового простран-
пространства, по которой производится интегрирование в G.3.47). Однако
для диссипативных систем Р (х) априори неизвестно и его нужно
находить для каждого интересующего нас аттрактора2). Основной
метод определения Р (х) состоит в итерировании G.3.45)
Pv+l)(x) = TP{i)(x), G.3.48)
начиная с какого-либо начального распределения Р° (х) (предпола-
(предполагая, что вне области притяжения аттрактора Р{0) (х) = 0). Тогда 3)
') См. примечание редактора на с. 444.— Прим. ред.
2) При практических вычислениях средних обычно достаточно знать
крупноструктурное инвариантное распределение.
3) Этот предел существует, вообще говоря, лишь для хаотического ат-
аттрактора с перемешиванием.— Прим. ред.
Дисашативные системы 467
Сведение к одномерному отображению. Некоторое упрощение вы-
вычислений можно достигнуть по методу Бриджеса и Раулэндса [40].
Они исследовали двумерные отображения, которые можно описать
в некотором пределе с помощью одномерных отображений. Рас-
Рассмотрим отображение вида
x = F(x, у), G.3.49а)
y = bG(x, у), G.3.496)
где Ь — малый параметр. Полагая в нулевом порядке у — 0, по-
получаем одномерное отображение
x = F(x, 0) = F0(x). G.3.50)
Смещение аттрактора по у определяется уравнением G.3.496) при
у = 0. Решая это уравнение относительно х, находим
Подставляя х в G.3.50), в итоге получаем для аттрактора уравне-
уравнение нулевого порядка:
G.3.51)
Чтобы прийти к уравнению в следующем порядке, заменим х
и у в G.3.51) на х и у и решим его относительно у:
,, иг; Ip—1 (v\\ 11 Ч ^9\
У — C/vJo уj о \Х))' yl.o.oZ.}
Затем, подставляя это решение, как и раньше, в G.3.49а), получим
уравнение для аттрактора в первом порядке. Отображение Хенона
G.1.14) имеет вид G.3.49) с G (х, у) = х. Структура аттрактора,
найденная таким методом, удивительно хорошо совпадает с чис-
численными результатами.
Для получения инвариантного распределения методом итераций
возьмем начальное распределение в виде
Рт (х, у) = Рг (х) б (у-у (х)), G.3.53)
где Рг (х) — инвариантное распределение для одномерного ото-
отображения G.3.50), а у (х) определяется уравнением G.3.52). При
Ь <^ 1 это уже дает хорошее приближение для Р (х, у).
Трехмерные потоки приближенно описываются обычно с по-
помощью одномерных необратимых отображений, для которых и опре-
определяется численно инвариантное распределение [324, 368]. Мы уже
знаем два таких примера: аттрактор Лоренца (§ 1.5) и аттрактор
Рёслера(п. 7.16). Однако прямое сравнение действительного распре-
распределения и одномерного приближения проводится не часто. Израй-
лев и др. [210] сравнили полученные численным методом распреде-
распределение Рх (х) и распределение
y)dy
468 Глава 7
для трехмерного потока параметрически возбуждаемого нелиней-
нелинейного осциллятора и нашли хорошее согласие. Они указали также,
что малый параметр в G.3.49) связан с дробной частью фракталь-
фрактальной размерности df — aj\ a21:
6~exp[|a2|(uff— 1)] = ехр(а1 + а2). G.3.54)
Использование уравнения ФПК- Хорошим начальным приближе-
приближением Р@) инвариантного распределения может служить аналити-
аналитическое решение уравнения ФПК. Такой метод наиболее удобен
в случае малой скорости сжатия фазового объема (| аг -j- az \ & 0),
когда метод Бриджеса—Раулэндса неприменим. Этот случай можно
рассматривать как малое диссипативное возмущение гамильтоно-
вых отображений, для которых ax + сг2 = 0.
В качестве примера возьмем ускорение Ферми с диссипацией.
Используя упрощенное отображение Улама C.4.6), вводим дисси-
диссипацию посредством следующих формул:
G.3.55а)
G.3.556)
Здесь ип — приведенная скорость частицы, б <^ 1 — относитель-
относительная потеря скорости при столкновении с неподвижной стенкой,
\|з„ — фаза колеблющейся стенки в момент соударения с частицей,
а М > 1 пропорционально отношению расстояния между стенками
к амплитуде колебания стенки (п. 3.4а). Якобиан отображения
G.3.55) равен
R = д(""+" ЧУн) =1_б G.3 56)
д (Un, %)
При 6 = 0 отображение является гамильтоновьш и приводит к обыч-
обычной картине хаотического движения с островками устойчивости
(рис. 1.14).
Для 0-с^б <<;' 1 неподвижные точки в центрах областей устой-
устойчивости становятся притягивающими фокусами и можно ожидать,
что хаотическая компонента движения будет полностью разрушена.
Останется, однако, переходной хаос вблизи сепаратрис г), как опи-
описано в п. 7.36. Численное моделирование отображения G.3.55)
подтвердило эти представления. Например, при М = 100 для
0<б<;0,02, в том числе и для очень малых б ~ 10~6, наблюдался
переходной хаос. Полное разрушение стационарного хаотического
движения при малой диссипации является, по всей видимости,
типичным для таких систем. Исследование масштаба времени, в те-
:) При достаточно малом S переходной хаос охватывает практически всю
область стохастичности для 5 = 0 [73, 74, 531].— Прим. ред.
Диссипативные системы 469
чение которого сохраняется переходной хаос, проводилось, напри-
например, Чириковым и Израйлевым [73, 74 ]. Однако сейчас нас инте-
интересует стационарный хаос, т. е. образование странного аттрактора.
При М = 100 численные данные убедительно показывают, что
в интервале 0,03 ^ б ^ 0,3 (значения б>0,3 не исследовались)
имеется странный аттрактор г). Правда, при этом нельзя исключить
существование малых участков внутри этого интервала б с перио-
периодическим движением. На рис. 7.28, а показана поверхность сече-
сечения (и, 41) в интервале 4-<и<;7 после 4,5-105 итераций одной тра-
траектории. Хорошо видна слоистая структура аттрактора. Более
мелкая структура внутри слоев представлена на рис. 7.28, б, где
в увеличенном масштабе показан участок фазовой плоскости
4,4<и<;4,8. Этот участок состоит из 200-100 ячеек, а число ите-
итераций траектории составляет 3 ¦ 10е. Если просуммировать распре-
распределение Р (и, ур) по фазе г|з при постоянном и, то получается значи-
значительно более гладкое распределение Р (и). Согласно численным
данным, распределение Р (и) хорошо аппроксимируется распреде-
распределением Гаусса
Р (и) ос ехр(—оси2),
где а зависит от б, но не от М. Вычисление Р (и) производится так
же, как и в п. 5.46. Будем исходить из усредненного по фазе урав-
уравнения ФПК E.4.5). Коэффициенты трения В и диффузии D равны,
согласно E.4.6) и E.4.7):
1 2Я
В=—^- | dtyAu, G.3.57а)
2п 0"
1 2л
D = —— \ Л|)(ДыJ, G.3.576)
2л d
*) Образование хаотического аттрактора при достаточно сильной дисси-
диссипации, которое, по-видимому, наблюдалось также в работах [73, 74, 531],
связано с тем, что диссипация разрушает устойчивые области. Однако при-
приведенное в тексте критическое значение б = 0,03 вызывает сомнения. Для
образования хаотического аттрактора требуется по крайней мере, чтобы все
неподвижные точки отображения (см. рис. 1.14) стали неустойчивыми. Можно
показать, что это происходит при условии: б > B/я2М)^3 » 0,13 (М = 100),
что заметно превышает приведенное значение, и даже значение б = 0,1 в чис-
численном моделировании (рис. 7.28). Для данных на рис. 7.29 это же условие
имеет вид М > 203 (б = 0,1). Причина, по которой захват траектории в устой-
устойчивый фокус не наблюдается при численном моделировании, состоит, по всей
видимости, в том, что плотность равновесной функции распределения G.3.61)
в области захвата (8,7 5SJ и S^ 10 для данных на рис. 7.28) исчезающе мала
и соответственно время существования переходного хаоса огромно. В таком
случае вполне можно говорить о квазистационарном хаосе. Условие его
существования в данной модели, как можно показать, имеет вид: аМЬ > 1;
оно выполняется с запасом для всех численных данных на рис. 7.28 и 7.29.—
Прим. ред.
1-6
'11" 1 ii'11¦ jjJSмi¦''I!!!ш ',!,',
-5
- 4,8-
- 4,4-
М",:—,2?.,Г,
2»
4,4 i
0
2»
а Ф б *Р
Рис. 7.28. Фазовая плоскость для модели ускорения Ферми с диссипацией при М = 100 и й = 0,1.
а — одна траектория в интервале 4 < и <7; 4,5-10Г| итераций; б — то же в увеличенном масштабе по и; 3-Ю1' итерации, ЮОуЮО ячеек;
цифры пропорциональны логарифму числа попадгший в ячейку.
Диссипативные системы 471
где мы предположили равномерное распределение по фазе уже по-
после одной итерации. Из G.3.55а) имеем
Дм(ф)= — 6«J-sini|) G.3.58)
и
В=—Ьи, G.3.59а)
D= — -S2u2. G.3.596)
В стационарном состоянии и в отсутствие потока частиц уравнение
ФПК имеет вид
() G.3.60)
2 du
Опуская второй член в G.3.596) (см. ниже), получаем нормирован-
нормированное на единицу решение
/Л\12 . G.3.61)
На рис. 7.29 это решение (сплошная прямая) сравнивается с чис-
численными данными при 6 = 0,1 и различных М. При малых скоростях
все численные значения хорошо ложатся на теоретическую прямую
и не зависят от М. Однако при больших скоростях имеется систе-
систематическое отклонение. Очевидно, это связано с нарушением ус-
условия E.4.4) применимости уравнения ФПК, которое в данном слу-
случае принимает вид
р<°> du
или и2 С Dб)~2 = 6,25 при б = 0,1. Во всяком случае, G.3.61)
является хорошим первым приближением для инвариантного рас-
распределения, хотя в нем и полностью отсутствует слоистая струк-
структура, масштаб которой по и существенно меньше 1 (см. рис. 7.28, а).
Чтобы получить эту структуру, воспользуемся методом итера-
итераций, согласно G.3.48), взяв в качестве начального Р@> распределе-
распределение G.3.61). Записывая G.3.48) в явном виде, находим
P{i+l)(u, ij>) chuty = Pw (u, tydudty, G.3.62)
или
Pii+l) (п, ф) = RP{i) (и, $), G.3.63)
где
R = *<»¦ t\ G.3.64)
d(u, ip) V ;
— якобиан обратного отображения (Т~х)
и = и{и, ^), г|) = ^(п, -ф). G.3.65)
472
Глава 7
Для диссипативного отображения Улама G.3.55) R = A—б) из
G.3.56), а/-1 имеет вид
-г 2яМ
G.3.66)
и —
BnM/u)]
1-6
= 20
50
100
200
500
1000 -
10
Рис. 7.29. Сравнение численных данных для инвариантного распределения
с решением уравнения ФПК при S = 0,1 и различных значениях М.
По оси ординат отложена величина, пропорциональная интегралу функции распределе-
распределения по фазе ^.
Диссипативные системы
473
Подставляя G.3.66) в G.3.63) с Р{0) из G.3.61), получаем следующее
приближение для инвариантного распределения:
,12 1 Г 26j
РA)(«, 40 =
1-S
-ехр.
4,8-
G.3.67)
4,4
Рис. 7.30. Последовательные приближения при вычислении инвариантного
распределения (по данным работы [277]).
а) я(')(«, тр); б) Р'2)(и, г|>); начальное р(®Ни) из G.3.6!). Обозначение и параметры
те же, что и на рис. 7.28, б.
Это приближение показано на рис. 7.30, а, взятом из работы
Либермана и Цанга [277]. Его следует сравнить с численными дан-
данными на рис. 7.28, б. В обоих случаях использованы одинаковые
параметры модели и ее представления на фазовой плоскости. Гру-
Грубая слоистая структура Р хорошо согласуется с численными дан-
данными. Результат второй итерации G.3.63) — распределение Р{2) —
474 Глава 7
показан на рис. 7.30, б в тех же условиях. Согласие с численными
данными на рис. 7.28, б становится поразительно хорошим. Сле-
Следующие итерации дали бы еще более тонкую структуру аттрактора.
Для других значений 6, например 0,03, также имеется хорошее
согласие.
§ 7.4. Проблема турбулентности
Рассмотрим теперь связь исследованных выше конечномерных хао-
хаотических потоков с движением сплошной среды («жидкости») с бес-
бесконечным числом степеней свободы. Сначала мы обсудим вопрос,
в каком смысле конечномерные модели аппроксимируют жидкость,
а затем опишем некоторые механизмы перехода от регулярного
движения к турбулентному.
7.4а. Представление Фурье
Будем описывать поведение жидкости с помощью дифференциаль-
дифференциальных уравнений в частных производных вида
где Q — УИ-мерный вектор состояния жидкости [компонентами Q
могут быть, например, давление/? (х, t), скорость жидкости v(x, t),
плотность р (jc, t) и т. д. ], х — обычный радиус-вектор с компо-
компонентами х, у, z, а 3? (х) — независящий от времени нелинейный
дифференциальный оператор. Обычный метод изучения системы
G.4.1) состоит в переходе к представлению Фурье для вектора Q:
Q(x, t)^Zgk(t)eikx, G.4.2)
h
где
Подставляя G.4.2) в G.4.1) и используя ортогональность функций
ек'х , получаем уравнения движения в виде х)
Qk=Vk(qx. . .д„). G.4.4)
Если оставить в сумме G.4.2) N «наиболее существенных» мод, то
задача сведется к конечному числу (MN) обыкновенных диффе-
г) Такое представление годится, конечно, только для модельных задач
с простейшими граничными условиями. В более общем случае обычно ис-
используется разложение по собственным функциям соответствующего си-
системе G.4.1) линейного уравнения (см., например, книгу [534]).— Прим.
ред.
Диссипативные системы 475
ренциальных уравнений первого порядка, описывающих времен-
временную эволюцию этих мод. Такой метод называется приближением
Галёркина.
Рассмотрим в качестве примера задачу Рэлея — Бенара о теп-
тепловой конвекции (рис. 7.31, а). Слой жидкости толщиной h в поле
тяжести подогревается снизу при постоянной разности температур
AT = Т\—То. Движение жидкости описывается уравнениями
ШВШ1
о
g X Сила тяжести
Та
ъ
б
Рис. 7.31. Конвекция Рэлея—Бенара.
а — схема опыта; АГ= Г,- Го > 0; б — стационарная конвекция при ДГ>АГ..
Навье—Стокса. Ограничиваясь двумерным движением (d/'dz = 0),
введем функцию потока г|> (х, у, t), которая связана со скоростью
жидкости V (х, у, t) посредством формулы
г) = ухD). G.4.5)
Введем также функцию в (*, у, t), описывающую отклонение тем-
температуры Т (х, у, t) от линейной зависимости по у:
6 = 7—^! + -^- у. G.4.6)
В отсутствие конвекции в = 0. Для выбранных переменных за-
задача сводится к двум уравнениям в частных производных [283 ]:
476 Глава 7
дх ду ду дх / Л Зл;
Здесь v — кинематическая вязкость, g — ускорение силы тяжести,
а — коэффициент теплового расширения их — температуропро-
температуропроводность х). Примем граничные условия в виде 0 = я|з = Aij) == О
при у = 0 и у = h, что соответствует фиксированным То и 7\ и
свободной поверхности жидкости. При малых AT имеется устойчи-
устойчивое равновесное состояние гр = 6 = О, соответствующее покоя-
покоящейся жидкости и молекулярной теплопередаче. Еще лорд Рэлей
изучал линейную устойчивость этого состояния и показал, что
выше некоторого критического значения АТС оно становится не-
неустойчивым и в жидкости возникают циркулирующие потоки,
(рис. 7.31, б):
/ ) G.4.8а)
„ „ / пах \ . / яу \ ._ . о^.
6 = e0cos[ sini—^- , G.4.86)
\ h / \ h I
где параметр а характеризует периодичность движения по х. Вве-
Введем безразмерное число Рэлея, характеризующее разность темпе-
температур:
Ra=J*t^ G49)
Критическое значение числа Рэлея, определяющее возникновение
устойчивой конвекции, равно
Rc= A+а2K G.4.10)
а?
и принимает минимальное значение 27 л4/4 для а = \l-\Ji.
При дальнейшем увеличении Ra выше Rc регулярная конвек-
конвекция становится линейно неустойчивой. Эксперимент показывает,
что конвекция становится при этом нестационарной и нерегуляр-
нерегулярной. Для анализа этого случая, следуя Зальцману [359], разло-
разложим я|) и 9 в двойной ряд Фурье по х и у, так что коэффициенты
разложения будут зависеть только от t. Оставляя конечное число
членов, получаем представление движения в конечномерном фазо-
фазовом пространстве фурье-амплитуд. Зальцман численно нашел слу-
случаи хаотического движения 2). Лоренц [283] исследовал упрощен-
х) Величина со = — Д-ф характеризует вращение элемента жидкости
вокруг оси г и называется завихренностью (гсо = V X я).— Прим. ред.
2) См. благодарности в статье Лоренца [283].— Прим. ред.
Диссипативные системы 477
ную систему, в которой оставлены только три фурье-амплитуды:
а , /сГ v и\ ¦ I лах \ ¦ I ЯУ \
ж = V2 х @sin I sin / —— ,
х A + а») Т V W \ h ] \ h }
G.4.11)
A / I h
Здесь X — амплитуда конвективного движения, Y — разность
температур между восходящими и нисходящими потоками, a Z —
отклонение вертикального профиля температуры от линейного.
Подставляя G.4.11) в уравнение G.4.7), приходим к модели Ло-
ренца:
Х=— oX + oY, G.4.12а)
Y=—XZ + rX — Y, G.4.126)
Z = XY — bZ, G.4.12b)
где а = v/x — число Прандтля, г = RjRc — приведенное число
Рэлея, b = 4 A -г а2), а точка означает производную по безраз-
безразмерному времени т — л2/г~2 A + a2) xt.
Модель Лоренца и ее странный аттрактор уже рассматривались
в § 1.5 и выше в этой главе. Здесь же нас интересует вопрос: в ка-
какой мере эта модель представляет поведение жидкости в задаче
Рэлея—Бенара? На первый взгляд обе системы очень далеки друг
от друга, поскольку модель Лоренца является чрезвычайно упро-
упрощенной с ее всего лишь тремя модами для двух функций состояния
жидкости я|) и в. Увеличение числа мод до пяти, семи и даже че-
четырнадцати сохраняет некоторые черты поведения модели, включая
и образование странного аттрактора. Однако переход к хаотиче-
хаотическому движению может происходить при этом через разные после-
последовательности бифуркаций [98 ] (дополнительную библиографию
см. в работе [180]). Более того, численное моделирование двумер-
двумерной конвекции, согласно G.4.7), показывает отсутствие турбулент-
турбулентного движения х). В этом состоит существенное отличие от трехмер-
трехмерной конвекции Рэлея—Бенара, в которой турбулентность наблю-
наблюдается экспериментально.
В работе [131 ] было показано, что двумерные решения уравне-
уравнения Навье—Стокса можно описать асимптотически (при t —>¦ оо)
конечным числом мод N2. Этот результат был обобщен на трехмер-
трехмерные решения, причем N3ozj\fl [132]. Поэтому при фиксирован-
фиксированных параметрах системы и начальных условиях конечномерные
]) Это замечание непонятно. По поводу особенностей двумерной турбу-
турбулентности см., например, работы [542, 543].— Прим. ред.
478 Глава 7
модели с некоторым минимальным значением N2 (или N3) пред-
представляют все физически существенные свойства реального тече-
течения х). Треве [412] предложил численный метод проверки апосте-
апостериори, было ли выбранное число мод достаточным. Однако пока не
существует никакого метода определения необходимого числа мод
априори до численного моделирования2).
7.46. Переход к турбулентности
Обсудим теперь различные гипотезы относительно механизма пе-
перехода от регулярного течения к гидродинамической турбулентно-
турбулентности. За исключением самой ранней гипотезы Ландау [251 ], все
предложенные механизмы связаны с конечномерными моделями.
Имеющиеся экспериментальные данные не позволяют сделать оп-
определенного выбора между моделями, поскольку в опытах часто
присутствуют черты разных механизмов. Наше описание возник-
возникновения турбулентности базируется на обзорах Хеллемана [180 J,
Отта [324] и Экмана [112].
Хотя явление турбулентности известно уже сотни лет, деталь-
детальные измерения характеристик потока вблизи перехода были вы-
выполнены только в последнее десятилетие3). Возникновению тур-
турбулентного режима движения обычно предшествует возбуждение
') Точнее конечное число мод движения полностью определяет и все
остальные моды (см. также работу [545]). Физически это связано с сильным
затуханием высоких мод, которые, таким образом, просто повторяют с умень-
уменьшенной амплитудой колебания основных мод и имеют, в частности, тот же
тип спектра (дискретный или непрерывный). Иначе можно сказать, что дви-
движение на аттракторе вообще имеет конечное число мод, однако эти моды
не совпадают с невозмущенными модами приближения Галёркина. Отсюда
следует также, что движение имеет только конечное число положительных
показателей Ляпунова. Отметим, что конечномерность аттрактора (гипотеза
Хопфа [546]) доказана только для двумерного течения [131, 545], тогда как
в трехмерном случае это принимается в работе [132] в качестве гипотезы. —
Прим. ред.
2) Грубые априорные оценки получены в упомянутой работе [132] и их
можно представить в виде N^ ~ Re3 ~ N\'3, где Re — число Рейнольдса.
Однако эти оценки (как и критерий в работе [412]) являются лишь доста-
достаточными и, вообще говоря, весьма неэффективными. Например, в случае
однородной турбулентности они существенно превосходят естественную
оценку числа степеней свободы по Ландау и Лифшицу [539]: ./V2~Re3'2~./V3'3.
Это хорошо согласуется также с полученной недавно строгой оценкой снизу
(необходимой): N% ~ Re [560]. В любом случае такие оценки указывают
на существенный дефект используемых конечномерных моделей турбулент-
турбулентности, число степеней свободы которых фиксировано, а параметры изме-
изменяются.— Прим. ред.
3) Это краткое замечание представляет обширные многолетние исследо-
исследования турбулентности весьма однобоко (см., например, работы [535, 536]).
В последнее время, особенно после нашумевшей работы Рюэля и Тэкенса
[355], действительно были проведены некоторые специальные эксперименты,
иногда, кстати сказать, весьма поспешно (см. примечание редактора на
с. 483), по проверке ряда новых гипотез (см. ниже).— Прим. ред.
Диссипативные системы 479
колебаний одной или нескольких независимых частот и их гармо-
гармоник, а иногда и субгармоник. Основные эксперименты по деталь-
детальному исследованию перехода к турбулентности относятся к раз-
различным вариантам конвекции Рэлея — Бенара, а также вихрей
Тейлора, возникающих в слое жидкости между вращающимися
цилиндрами (так называемое круговое течение Куэтта). Эти при-
примеры мы и используем ниже при сравнении с различными гипоте-
гипотезами о механизме возникновения турбулентности.
Первоначальная картина возникновения турбулентности, пред-
предложенная Ландау, была основана на представлении об иерархии
неустойчивостей. При увеличении некоторого параметра, напри-
например числа Рейнольдса или числа Рэлея, нелинейные колебания
жидкости теряют устойчивость и появляются все новые и новые
независимые частоты движения а>1( а>2) а>3 . . . . При этом должно
наблюдаться квазипериодическое движение с одной, двумя, тремя
и т. д. основными частотами. Таким образом, мы приходим к по-
последовательности бифуркаций Хопфа, т. е. к движению по поверх-
поверхности некоторого тора возрастающей размерности. Движение вы-
выглядит все более и более сложным, однако непрерывный спектр
и хаотическое движение возникают лишь при бесконечном числе
бифуркаций. Модель Ландау представлена схематически в табл. 7.2.
Хотя в экспериментах и наблюдается до четырех [158] незави-
независимых частот, резкий переход к непрерывному спектру не согла-
согласуется с моделью Ландау 1). Помимо этого, теоретически было по-
показано (см. работу [112]), что последовательность бифуркаций
Хопфа, как и само квазипериодическое движение, не являются
типичными. Судя по рассмотренным выше примерам резкого 2)
возникновения непрерывного спектра, связанного с образованием
странного аттрактора, можно ожидать, что именно такой механизм
:) Поучительно отметить, что эта «квазипериодическая» модель турбу-
турбулентности была очевидно навеяна аналогиями с квантовой механикой. Вот
соответствующая цитата из оригинальной работы Ландау [251]:
«Задача об определении возможных значений «частот» Q при данных
граничных условиях движения представляет собой Eigenwert-проблему.
В результате ее решения должен получиться спектр «собственных частот» . . .
Можно предполагать, что частоты непрерывного спектра соответствуют
движениям г>! [возмущение], не затухающим на бесконечности [в простран-
пространстве], а частоты дискретного спектра —движениям, достаточно быстро за-
затухающим на бесконечности (подобно тому, как это имеет место во многих
других Eigenwert-проблемах) . . . Соответственно этому ниже мы можем рас-
рассматривать только «частоты» Q дискретного спектра».
В квантовой механике это действительно так.— Прим. ред.
2) Представление о «резком» переходе к хаотическому движению является
условным. Так, например, в механизме бифуркаций удвоения хаотический
аттрактор появляется в критической точке (С = Сое) лишь номинально, по-
поскольку мощность хаотической компоненты движения в этой точке равна
нулю и плавно возрастает в результате обратных бифуркаций (см., напри-
например, рис. 7.22).— Прим. ред.
480
Таблица 7
Модель
.2.
Модели
и механизмы
Глава 7
перехода
Механизм
к турбулентности
а) Ландау Неподвиж-
Неподвижная точка
Периодическая
траектория
б) Рюэль —
Тэкенс —
Ньюхаус
в) Фейгенбаум
г) Помо — Ман-
невиль
То же
То же
То же
(период Т)
То же
Бифуркация
удвоения
Обратная
тангенциальная
бифуркация
и послужит основой построения современной теории турбулентно-
турбулентности, как это и оказывается в действительности.
Рюэль и Тэкенс [355 ] предложили другой механизм возникнове-
возникновения турбулентности, согласно которому сначала происходят две
последовательные бифуркации Хопфа, как и в модели Ландау,
однако затем нелинейность разрушает трехчастотное движение
и образуется «странный» аттрактор (табл. 7.2). По первоначальной
гипотезе требовалась размерность потока не менее четырех. Пред-
Предположение о неустойчивости трехчастотного аттрактора в типичном
случае было позднее доказано, а минимальная размерность сокра-
сокращена до трех [317]х).
Модель Рюэля—Тэкенса исследовалась численно на примере
простого двумерного отображения [100]. Были обнаружены пере-
переходы от устойчивого фокуса к предельному циклу, затем к двух-
частотному движению и, наконец, к странному аттрактору. В этой
связи важно отметить, что в отличие от модели Лоренца с тремя
модами в модели конвекции Рэлея—Бенара, использующей 14 мод,
также обнаружен квазипериодический аттрактор на некоторой дву-
двумерной поверхности в 14-мерном фазовом пространстве [98].
х) Хотя работа [355] оказала фактически заметное влияние на развитие
как теоретических, так и экспериментальных исследований по турбулент-
турбулентности, предложенный ее авторами конкретный механизм хаоса, связанный
с резонансами высоких гармоник, представляется слишком «нежным» для
такого «грубого» явления, как гидродинамическая турбулентность. Что же
касается минимальной размерности потока, то этот вопрос был выяснен еще
в классической работе Лоренца [283] (см. также работу [533]).— Прим.
ред.
Диссипативные системы
481
Механизм
Квазипериоди-
Квазипериодическая траек-
траектория (две ос-
основные частоты)
То же
Бифуркация
Хопфа
Квазипериоди-
Квазипериодическая траек-
траектория (три ос-
основные частоты)
Странный
аттрактор
>¦ > Турбулент-
Бифуркации - г '
Хопфа ное
движение
Периодическая
траектория
(период 2 Т)
Хаотическое
движение с пе-
перемежаемостью
Периодическая
траектория
(период 4 X)
Бифуркации
удвоения
Странный
аттрактор
Некоторые экспериментальные данные, по-видимому, подтверж-
подтверждают модель Рюэля—Тэкенса. Так, в спектрах мощности появ-
появляется сначала одна, затем вторая и, возможно, третья независи-
независимая частота. На пороге появления третьей частоты внезапно воз-
возникает широкополосный шум, который свидетельствует о переходе
к хаотическому движению. Экспериментально исследовались как
вихри Тейлора в жидкости между вращающимися цилиндрами
[125], так и конвекция Рэлея—Бенара [5]. На рис. 7.32 из попу-
популярной статьи Суинни и Голуба [396 ] показаны спектры скорости
жидкости для течения Куэтта (слева) и для конвекции Рэлея—Бе-
Рэлея—Бенара (справа). В обоих случаях перед переходом к непрерывному
спектру наблюдается сначала одна, а затем две независимые ча-
частоты fx и /2. Однако это зависит, вообще говоря, от начальных
условий и иногда частоты/! и /2 оказываются синхронизованными *).
В другом эксперименте по течению Куэтта [158] наблюдались по
крайней мере четыре независимые частоты. Это указывает на то,
что переход к турбулентности происходит не всегда после двух би-
бифуркаций Хопфа, как в модели Рюэля—Тэкенса.
Третья модель перехода к турбулентности, предложенная Фей-
генбаумом, связана с последовательностью бифуркаций удвоения
периода [122]. Переход начинается с бифуркации Хопфа из устой-
устойчивого фокуса в предельный цикл с частотой /х. При дальнейшем
х) То есть отношение частот /i//2~ mln рационально (в пределах точно-
точности измерений ~ 10~4, см., например, работу [541]). Экспериментальная
независимость (несоизмеримость) частот определяется с той же точностью
для \т\, |га|<20.— Прим. ред.
482
Глава 7
увеличении параметра происходят последовательные бифуркации
удвоения, приводящие к периодическому движению с частотами
fi/2, /j/4, /1/8 и т. д. Эта последовательность сходится при некото-
некотором критическом значении параметра, при котором возникает
странный аттрактор (табл. 7.2). Механизм удвоения периода был
описан в § 7.2 и п. 7.3а, где показан его универсальный характер.
Существенно, что вблизи критической точки движение является
близким к одномерному (см. п. 7.3а).
ю1
_ ю-1
^7 ю-3
101
§ Ю-3
D
I
I 10
z
I 10-
" Течение
Куэтта
Г
и
A
Относительная
частота f/f0
0,15
Рис. 7.32. Спектры скорости жидкости между вращающимися цилиндрами
при трех значениях частоты внутреннего цилиндра /0 (слева), то же для трех
значений АХ в задаче Рэлея — Бенара (справа) (по данным работы [396]).
Модель Фейгенбаума хорошо подтверждается численными экс-
экспериментами на простых моделях. Как мы видели выше, бифурка-
бифуркации удвоения периода найдены и во многих динамических систе-
системах с малой размерностью, таких, как аттрактор Рёслера, отобра-
отображение Хенона, уравнение Дюффинга и др. Некоторые эксперименты
по конвекции Рэлея—Бенара обнаруживают эти бифуркации, а
также некоторые признаки их универсальности. Спектры скорости
высокого разрешения в эксперименте Рэлея—Бенара с водой, по-
показанные на рис. 7.33 [155, 157], демонстрируют некоторые из би-
бифуркаций удвоения. Было проведено также сравнение эксперимен-
экспериментальных значений амплитуд субгармоник с предсказаниями мо-
модели Фейгенбаума. Как показано в п. 7.26, отношение амплитуд
развитых субгармоник должно быть равным у ^ 6,6. На рис. 7.33,г
Диссипативные системы
483
расстояние между верхней прямой, проведенной по пикам гармо-
гармоник частоты /2/2, и нижней прямой соответствует множителю 6,6.
Видно, что большинство пиков гармоник частоты /2/4 примерно
ложатся на нижнюю прямую в соответствии с теорией х). В другом
z
S
10
10
0,0
Рис. 7.33. Бифуркации удвоения периода в эксперименте Рэлея—Бенара
(по данным работы [157]).
а — в — при увеличении числа Рэлея возникают субгармоники; г — хаотические полосы;
д — непрерывный спектр; е — при уменьшении Я появляется вторая частота /*.
эксперименте по конвекции Рэлея—Бенара в жидком гелии 1263]
наблюдались последовательные субгармоники flt /У2, /х/4, /х/8
и /У16 в спектре температуры. Отношение амплитуд последователь-
последовательных субгармоник также равно примерно 6,6 (см. работу [123]).
х) Сравнение экспериментальных данных на рис. 7.33, г для фиксиро-
фиксированного значения параметра С с законом подобия G.2.44) для разных С воз-
возможно вследствие того, что при бифуркации удвоения амплитуды прежних
частот (четные гармоники на рис. 7.33, г) остаются неизменными согласно
G.2.40). При сравнении необходимо, во-первых, учитывать, что масштабный
фактор 7 относится к амплитудам гармоник, а во-вторых, брать только не^
четные до бифуркации гармоники, т. е. только второй и шестой пики на
рис. 7.33, г. В результате среднее у яг 4,4 (см. примечание редактора на
с. 440).— Прим. ред.
484 Глава 7
Однако, как мы видели, другие эксперименты не подтверждают
эти свойства 1). Можно предположить, что причиной этого является
Внешний шум, который нарушает тонкую структуру спектра,
и в зависимости от условий эксперимента субгармоники то появ-
появляются, то пропадают. Такое поведение действительно наблю-
наблюдалось в численном моделировании Кратчфилдом и Хьюберманом
[96].
Рассмотрим, наконец, четвертый механизм возникновения тур-
турбулентности, лежащий в основе модели Помо и Манневиля [293 ]
и связанный с переходом к хаотическому движению с перемежае-
перемежаемостью. В этой модели при увеличении некоторого параметра пе-
периодическая траектория непосредственно превращается в хаоти-
хаотическую с перемежаемостью в результате обратной тангенциальной
бифуркации.
Следуя Экману [112], покажем, каким образом это происходит
на примере потери устойчивости предельного цикла периода 3 для
одномерного квадратичного отображения G.2.4). В п. 7.26 (см.
рис. 7.15 и пояснения к нему) было показано, что при С = Cq3) =
-= A—л/8I2 в результате тангенциальной бифуркации рождаются
устойчивая и неустойчивая траектории периода 3. Они сохра-
сохраняются в небольшом интервале значений С<С'о3). При С = Со3)
они сливаются и исчезают, рождая так называемое хаотическое
движение с перемежаемостью. Под этим понимается следующее:
можно показать, что хотя движение является хаотическим, однако
при малой разности С—Со3) — е типичная траектория будет на-
находиться в окрестности периодической траектории в течение ~ е~х1
итераций. При этом периодическая траектория
соответствует бифуркационному значению С = Со3). В течение
этого времени траектория выглядит как периодическая, а затем,
после выхода из этой области,— как хаотическая. Поэтому в мо-
модели Помо и Манневиля нерегулярное движение продолжается
в течение некоторого случайного промежутка времени, сменяясь
1 /о
периодическим со средней длительностью ¦—- | \i—\ic | , где \ic —
бифуркационное значение некоторого параметра ц.
Численное моделирование квадратичного отображения под-
подтверждает такое поведение [112]. Оно существует и для модели
Лоренца в некотором интервале параметров [293 ]. Подобный пе-
переход к турбулентности наблюдался во многих экспериментах,
включая конвекцию Рэлея—Бенара [273 ] и так называемую хи-
химическую турбулентность [352] (см. также дополнение А). Од-
Однако в этих случаях перемежаемость связана с переходом между
Речь идет, по-видимому, о данных на рис. 7.32. — Прим. ред.
Диссипативные системы 485
двумя квазиустойчивыми состояниями системы и остается неяс-
неясным, описывается ли такое поведение моделью Помо — Манневиля х).
Следует подчеркнуть, что единого механизма перехода к турбу-
турбулентности не существует 2). Если, например, система обнаружи-
обнаруживает бифуркации удвоения периода, то можно предсказать зависи-
зависимость этих бифуркаций от параметра. Однако пока неизвестно,
каким образом можно узнать заранее, в какой системе это будет
происходить. Отметим также, что все эти модели описывают только
возникновение турбулентности и ничего не говорят о свойствах
развитой турбулентности (см., например, 1295]).
х) Хотя термин «перемежаемость» появился недавно, подобные про-
процессы рассматривались уже довольно давно под более удачным, на наш
взгляд, названием — «структурная турбулентность» (см., например, работы
[537, 538], где имеется подробная библиография). В частности, появление
структур в хаотическом режиме простой диссипативной модели описано
в работе [530]. Такие флуктуирующие структуры часто встречаются и в га-
мильтоновых системах. Типичный пример —движение в узком стохастиче-
стохастическом слое сепаратрисы маятника (резонанса) (§ 3.5). Здесь имеются три
структуры (вращение в двух направлениях и колебания), между которыми
происходят случайные переходы.— Прим. ред.
2) См., например, работу [541].— Прим. ред.
Дополнение А
НЕКОТОРЫЕ ПРИЛОЖЕНИЯ
Во введении мы уже упоминали о некоторых применениях обсуж-
обсуждаемых в настоящей монографии методов. Поскольку наиболее
знакомой для нас областью является удержание и нагрев плазмы,
то большинство примеров в тексте относится именно к этому кругу
вопросов. Имеется, однако, много других областей, где рассматри-
рассматриваемая теория находит широкое применение: движение планет,
ускорение и накопление заряженных частиц, процессы в твердых
телах, молекулярная и химическая динамики, гидродинамика,
экология и т. д. Кроме того, близкие проблемы возникают при изу-
изучении квантовых систем, которых мы не касались. Чтобы частично
компенсировать указанный пробел, ниже дается краткая справка
о некоторых из перечисленных применений теории. Поскольку
круг обсуждаемых вопросов необычайно широк, мы даже и не пы-
пытаемся описать его полностью.
Многочисленные обзорные статьи и труды конференций помогут
читателю ориентироваться в этой области. Некоторые применения
теории в физике твердого тела (здесь не обсуждаемые) можно найти,
например, в трудах конференции [58 ] 1), а теория диссипативных
систем и ее приложения описываются в работе [81 ]. Весьма полезна
также обширная библиография в обзорах Чирикова [70 J и Хелле-
мана [180]; другие ссылки даются ниже.
А.1. Небесная механика
Самые ранние приложения обсуждаемых в настоящей монографии
методов, как и вообще применение самой гамильтоновой механики,
связано с попытками предсказать движение планет на достаточно
большом интервале времени. Именно к этой области относится зна-
знаменитая задача трех тел и ее упрощенный вариант, так называемая
ограниченная задача трех тел. Первая касается движения трех
произвольных гравитационно взаимодействующих масс. В более
простой «ограниченной задаче» масса одного из тел полагается
равной нулю и исследуется его движение в изменяющемся со вре-
временем гравитационном поле двух других тел. В 1904 г. Уиттекер,
х) Об одном интересном приложении стандартного отображения в физике
твердого тела см. работу [544] и цитированную там литературу.— Прим.
ред.
Некоторые приложения 487
обсуждая научные достижения того времени, отметил, что эта
проблема «вызвала исследования такого размаха, что с 1750 г. по
этой теме было опубликовано свыше 800 научных работ, многие из
которых носили имена величайших математиков».
Прежде всего Брунс [45] и Пуанкаре [337] показали, что все
изолирующие интегралы движения выражаются через известные
(классические) интегралы, такие, как энергия и импульс замкну-
замкнутой системы 1). Одновременно выяснилось, что ограниченная за-
задача трех тел содержит все существенные трудности общей задачи
и основные усилия были сконцентрированы на исследовании этого
упрощенного варианта.
Методы теории возмущений [337, 419] были вначале разрабо-
разработаны для получения приближенных решений задачи трех тел.
Затем они развивались с использованием новой техники асимпто-
асимптотических разложений, основанной на методе дополнительных
(к классическим) формальных интегралов Уиттекера [430]. Эти
методы были усовершенствованы Контопулосом и его сотрудни-
сотрудниками [86, 87], а также с использованием скобок Пуассона Мак-
Намарой и Уайтменом [292]. Другой способ, приводящий к тем же
результатам и развитый Густавсоном [171], заключается в преоб-
преобразовании гамильтониана с помощью рядов к нормальной форме.
Работы Хори [199], Гарридо [150] и Депри [102], в которых си-
систематически представлена техника преобразований Ли с исполь-
использованием скобок Пуассона, также появились в связи с проблемой
изучения движения планет.
Попытки решения задачи трех тел привели попутно к получе-
получению многих интересных математических результатов. Мы уже
обсуждали общую теорию периодического движения, связанную
с именами Пуанкаре [337 ] и Биркгофа [29 ], а также развитие тео-
теории КАМ. Изучение стохастичности тоже было обусловлено попыт-
попыткой понять хаотическое поведение траекторий вблизи гомоклин-
ных точек (см., например, [374, 310]). В одном из вариантов огра-
ограниченной задачи трех тел Ситников [379 ] и Алексеев [6 ] показали,
что в окрестности сепаратрисы (параболической траектории лег-
легкого тела) существуют траектории с произвольно большими и слу-
случайными временами возврата. Аналогичные результаты более аб-
абстрактного топологического характера были получены также Смей-
лом [381 ].
Для изучения движения на больших интервалах времени ис-
использовались различные численные (иногда в сочетании с аналити-
аналитическими) методы. Примером может служить задача Хенона и Хей-
*) Теорема Пуанкаре о несуществовании дополнительных аналитиче-
аналитических интегралов служила в течение длительного времени источником раз-
различных недоразумений, в частности, из нее делался неправильный вывод
об эргодичности движения. Вопрос был выяснен Колмогоровым [559] в связи
с созданием новой теории устойчивости, которая впоследствии получила на-
название теории КАМ.— Прим. ред.
488 Некоторые приложения
леса [188] (см. § 1.4). Обзор обширной литературы по этой плодот-
плодотворной задаче дан Чарчиллом и др. [78]. Контопулос и сотр. [88],
Форд и сотр. [423], Куммер [245], а также другие авторы с по-
помощью численных и аналитических методов изучали простые си-
системы связанных осцилляторов с целью выяснения общих свойств
нелинейных колебаний, существенных и для задачи трех тел. Как
отмечалось в предыдущих главах, эти исследования вместе с мате-
математическими результатами относительно поведения траекторий
вблизи гомоклинных точек и теорией КДМ привели (в том числе
и для ограниченной задачи трех тел) к сложной картине движения
в фазовом пространстве, подобно показанной на рис. 3.5 или 3.6.
Полная задача о движении планет с учетом их взаимных воз-
возмущений относится к очень специальной области, выходящей за
рамки этой книги. Хотя принято считать, что результаты изуче-
изучения простых моделей позволяют делать качественные предсказа-
предсказания о поведении более сложных физических систем, остается еще
много нерешенных вопросов по части устойчивости последних.
Для ознакомления с соответствующей обширной литературой сле-
следует обратиться к монографиям Уинтнера [433 ], Жебехели [400 ],
Зигеля и Мозера [374] и Хигихары [172, 173]. Недавние работы
в этой области обсуждаются Мозером [311 ] и Контопулосом [90].
Контопулос и сотр. [92] использовали упомянутые методы для
исследования других космических систем, в частности резонансов
в галактике.
Весьма интересный аспект проблемы длительной устойчивости
Солнечной системы связан с учетом ее многомерности, вследствие
чего инвариантные поверхности не являются изолирующими. Воз-
Возможно, что этим же объясняются и щели в кольцах Сатурна вблизи
резонансов с его внутренними спутниками. Чириков [68] изучал
подобную возможность для родственной проблемы «люков» в поясе
астероидов вблизи их резонансов с движением Юпитера х). Его пред-
предварительное заключение сводится к тому, что скорость диффузии Ар-
Арнольда достаточна для того, чтобы «очистить» люки за время жизни
Солнечной системы.
А.2. Ускорители и встречные пучки
Изучение динамики пучков в ускорителях и накопителях значи-
значительно содействовало пониманию адиабатических процессов и не-
нелинейных эффектов и дало ряд интересных примеров. Исследова-
Исследования начались здесь главным образом после открытия принципа
жесткой фокусировки [95]. К сожалению, многие результаты этих
1) Несмотря на некоторое внешнее сходство, первая задача является,
по-видимому, значительно более сложной из-за возможного влияния собст-
собственного гравитационного поля колец Сатурна (см., например, работу [553]),
тогда как динамика астероида — это типичная ограниченная задача трех
тел.— Прим. ред.
Некоторые приложения 489
работ появились в изданиях, известных лишь узкому кругу спе-
специалистов.
Первые исследования резонансов в сильнофокусирующих синх-
синхротронах были представлены на конференции в ЦЕРНе [160, 193].
Теоретический анализ обычно проводился в то время в линейном
приближении с использованием точного интеграла движения
(п. 1.36) и матричного формализма (§ 3.3) (см., например, [94,
258]) !).
Всегда присутствующие некомпенсированные нелинейности вы-
вызывают обычные искажения фазовой картины движения вблизи
основных резонансов. Эти нелинейности особенно существенны
в кольцевых фазотронах [398] 2). Пример исследования такого
резонанса с помощью нерезонансной (§ 2.2) и резонансной (§. 2.4)
теории возмущений содержится в обзоре Ласлета [255]. Обсуж-
Обсуждение этого круга вопросов можно найти также у Грина и Куранта
[162], Коломенского и Лебедева [232] и Лихтенберга [265].
Другой подход к ускорительным проблемам, имеющий лишь
косвенное отношение к предмету настоящей книги, связан с изу-
изучением динамики конечных областей фазового пространства, за-
заполненных большим числом частиц. Движение таких областей не
является квазипериодическим, а обладает свойством расслоения 3)
начальной области. При использовании крупноструктурной функ-
функции распределения это приводит к увеличению эффективного фа-
фазового объема частиц4). Некоторые аспекты этой проблемы изу-
изучались Херевордом и др. [189] и Лихтенбергом [264]. Сюда же
относится вопрос о многооборотной инжекции в кольцевой фазо-
фазотрон [399 ] и в накопительные кольца. Эти приложения и их связь
с различными системами транспортировки пучков заряженных ча-
частиц подробно рассмотрены Лихтенбергом [265].
Поскольку накопительные кольца должны удерживать частицы
на протяжении чрезвычайно большого числа оборотов и время
х) Линейные резонансы колебаний частицы в ускорителе, по-видимому,
впервые рассматривались Фурсовым и Будкером в 1947 г. (см. работу [509],
с. 230). Говард, Хайн и др. провели численное моделирование нелинейных
колебаний частицы в жесткофокусирующем синхротроне. Они фактически
наблюдали стохастические колебания и получили правильный эмпирический
критерий их возникновения.— Прим. ред.
2) В оригинале — Fixed Field Alternating Gradient Synchrotrons (син-
(синхротроны с постоянным полем и переменным градиентом). Мы используем
термин, принятый в отечественной литературе для ускорителей этого типа,
впервые предложенных Коломенским, Петуховым и Рабиновичем [549].—
Прим. перев.
3) В оригинале filamentation (нитеобразование).— Прим. перев.
4) Это означает, что спектр движения области является смешанным, т. е.
имеет как дискретную, так и непрерывную компоненты, даже если спектр
отдельной траектории является чисто дискретным. Отметим также, что изу-
изучение динамики области, точнее произвольной функции в фазовом простран-
пространстве, является одним из основных методов в эргодическои теории (см., напри-
например, работу [486] и § 5.2).— Прим. ред.
490 Некоторые приложения
жизни пучка составляет часы или даже дни, то успевают проя-
проявиться очень тонкие резонансные эффекты и, в частности, диффу-
диффузия Арнольда (см. гл. 6). Это обстоятельство может оказаться осо-
особенно важным в экспериментах на встречных пучках, когда ча-
частицы испытывают возмущение по крайней мере один раз за обо-
оборот при столкновении пучков (так называемые эффекты встречи).
Оценки скорости диффузии Арнольда для такого возмущения были
сделаны Чириковым [68 ], который показал возможность сущест-
существенного сокращения времени жизни пучка, особенно при наличии
связи с синхротронными колебаниями (см. также [207]). Другими
механизмами, исследованными в связи с попытками объяснить
уменьшение времени жизни пучка, являются модуляционная диф-
диффузия [404] и резонансное каналирование [405]. Проблема эффек-
эффектов встречи стимулировала численные исследования диффузии
Арнольда (см., например, [190]). Сокращение времени жизни пучка
действительно наблюдалось на электрон-позитронном накопителе,
но детального сравнения экспериментальных данных с теорией
пока не проведено. Поскольку число оборотов частиц в накопите-
накопителях превышает, как правило, 108, то обычное численное моделиро-
моделирование даже с использованием отображений оказывается практиче-
практически неосуществимым. Обзор современного состояния проблемы
эффектов встречи и ряд других интересных результатов содержатся
в трудах конференции [304].
А.З. Магнитные ловушки
Мы уже обсуждали значение задачи об удержании заряженной
частицы в магнитной ловушке для развития теории адиабатических
инвариантов нелинейных систем (§ 2.3). После пионерских работ
Альфвена [7 ] и Нортропа и Теллера [320 ], которые получили при-
приближенное решение для движения частицы в магнитном поле
Земли, был разработан ряд других методов асимптотического раз-
разложения, которые более точно учитывают геометрию реального
магнитного поля. Отметим здесь работы Лакины [247, 248] и Кри-
лина [236, 237 ] по аксиально симметричным магнитным ловушкам,
а также работу Драгта [106] по аксиально симметричному диполю.
Общие методы получения решений в любом порядке по параметру
разложения были разработаны Боголюбовым и Митропольским
[33] и Крускалом [238, 239]. Детальные вычисления во втором
порядке выполнены Нортропом и др. [321 ].
Однако, как выяснилось, получающиеся при таких разложе-
разложениях ряды оказываются расходящимися, а магнитный момент ча-
частицы изменяется на экспоненциально малую величину при каждом
отражении от магнитной пробки. Оценки такого изменения были
сделаны Хертвеком и Шлютером [191] и Чандрасекаром [53]1).
См. также работу [244].— Прим. ред.
Некоторые приложения 491
Более подробные расчеты выполнены Хастье и др. [176] и Ховар-
дом [201], которые использовали контурное интегрирование и ме-
метод перевала 2). Дальнейшее развитие этих методов, а также срав-
сравнение с результатами численного моделирования можно найти в ра-
работе Коэна и др. [81 ].
В случае аксиально симметричной магнитной ловушки задача
сводится к двум степеням свободы и, несмотря на изменение маг-
магнитного момента, возможно вечное удержание частицы 2). Это яв-
является следствием того, что инвариантные кривые изолируют при
малом возмущении стохастические слои резонансов между лармо-
ровским вращением и продольными колебаниями частицы, которые
рассматривались в работе [67]. Эти резонансы можно описать с по-
помощью отображения, как это было сделано Чириковым [68—70 ],
который исследовал условия адиабатичности движения. В некото-
некотором диапазоне параметров магнитный момент испытывает колеба-
колебания, значительно более медленные, чем продольные колебания ча-
частицы. Это явление было названо Розенблютом сверхадиабатич-
носпгью. Потеря сверхадиабатичности, что с физической точки зре-
зрения связано с исчезновением фазовых корреляций при последова-
последовательных прохождениях средней плоскости ловушки, эквивалентна
разрушению инвариантных кривых отображения.
Переход к глобальной стохастичности, когда частицы выле-
вылетают из ловушки, можно грубо определить с помощью численного
моделирования. Это было сделано Гарреном и др. [149] для ак-
аксиально симметричной прямой ловушки, Драгтом [106] для ак-
аксиально симметричного диполя и Сиамбисом [372 ] для несиммет-
несимметричной ловушки. Однако численное моделирование не может ре-
решить вопрос о длительном удержании частиц в ловушке. Поэтому
были поставлены специальные эксперименты в аксиально симмет-
симметричных ловушках при низкой плотности частиц, когда их взаимо-
взаимодействие пренебрежимо мало (см., например, [154, 338]). Эти экс-
эксперименты показали, что в достаточно сильном магнитном поле
время жизни частиц определяется классическим рассеянием на
остаточном газе3). Однако при умеренных полях имеется переход-
переходная область, где время удержания частицы все еще большое, но
зависит от поля. В последнем случае механизм потерь частиц оста-
оставался необъясненным. Наконец, при слабых полях сверхадиабатич-
ность нарушается и частицы быстро покидают ловушку. Обсуждая
*) Первые аккуратные вычисления экспоненциально малого изменения
магнитного момента частицы в ловушке были проведены в работе [550].—
Прим. ред.
2) Этот важный и строгий результат получен Арнольдом [11].— Прим.
ред.
3) Возможность длительного удержания частицы как в аксиально сим-
симметричной, так и в слабо асимметричной ловушке с достаточно сильным по-
полем была установлена в опытах Родионова [551 ] (см. также работу [552]).—
Прим. ред.
492 Некоторые приложения
результаты этих экспериментов, Чириков [68—70 ] предложил два
возможных объяснения: 1) существование слабой остаточной сто-
хастичности при возмущении, большем некоторой строгой границы
теории КАМ, но значительно меньшем, чем по критериям гл. 4;
2) наличие диффузии Арнольда вследствие слабой аксиальной
асимметрии или зависимости магнитного поля от времени. Оценив
скорость диффузии Арнольда, Чириков показал, что она достаточна
для объяснения наблюдаемого эффекта. Однако детальное сравне-
сравнение теории с экспериментом проведено не было. Мы согласны с за-
заключением Чирикова о том, что второе объяснение представляется
гораздо более правдоподобным, хотя вопрос и остается открытым.
Аналогичная задача возникает в связи с радиальной диффузией.
в амбиполярных ловушках с аксиально несимметричными проб-
пробками. Для аксиально симметричных систем сохранение углового
момента препятствует радиальной диффузии. Асимметрия, вноси-
вносимая стабилизирующими квадрупольными обмотками, нарушает
сохранение момента. Для амбиполярных ловушек этот эффект усу-
усугубляется наличием длинной центральной секции, что приводит
к возникновению резонансов низкого порядка между продоль-
продольным и дрейфовым движением и большим радиальным колебанием
частиц даже в отсутствие диффузии. В целом эта задача оказывается
весьма сложной и читателю следует обратиться к оригинальным
работам [79, 80, 357] *).
А.4. Нагрев плазмы
Взаимодействие двух резонансов, которое изменяет или разрушает
интегралы движения, можно ввести в систему специально для по-
получения желаемого эффекта, например для нагрева частиц. В элек-
электронном циклотронном резонансном нагреве (ЭЦРН) это дости-
достигается за счет резонанса между ларморовским вращением и элек-
электромагнитной волной. Один из методов расчета ЭЦРН в ловушке
заключается в определении величины изменения энергии при одно-
однократном прохождении резонанса, причем предполагается отсутст-
отсутствие корреляций фазы между последовательными прохождениями
[115, 161, 243]. Такой подход правилен выше порога стохастич-
ности и совершенно непригоден ниже его, как это описано в § 3.4.
Сейдл [367] впервые показал, что слабое резонансное электриче-
электрическое поле приводит к возникновению сверхадиабатических колеба-
колебаний, а не к стохастическому нагреву. Переход от адиабатического
движения к стохастическому с использованием метода Сейдла и
общего критерия перекрытия резонансов изучался Некрасовым
[315], Егером и др. [213], Либерманом и Лихтенбергом [275]. Не-
Недавно Бернштейн и Бэкстер [23 ] провели вычисление с учетом ре-
релятивистских эффектов. Численные исследования Спротта и Эд-
См. также работы [71, 517].— Прим. ред.
Некоторые приложения 493
мондса [390], а также эксперименты Уайеса и др. [435] и Бардета
и др. [15] дали результаты, неплохо согласующиеся с теорией. Ана-
Аналогичные расчеты перехода от сверхадиабатичности к стохастичности
были выполнены также в случае взаимодействия частицы в ловушке
с высокочастотным полем волн, возбуждаемых в самой плазме
[1, 348, 407].
Нелинейные взаимодействия описанных выше типов могут
иметь место даже в однородном магнитном поле. Возникающая
из-за конечной величины ларморовского радиуса нелинейность
приводит к появлению многих гармоник в спектре движения. Мы
уже рассматривали подобный пример в п. 2.4в. Отметим, что диа-
диапазон энергии частиц определяется гармониками, амплитуды ко-
которых достаточно велики. Детальное исследование ионного цикло-
циклотронного нагрева содержится в работах [220, 221 J.
Недавние эксперименты [257 ] по нагреву плазмы с помощью
двух волн разной частоты стимулировали теоретические разработки
в этой области. Ховард и др. [202] и Ронлин [347] показали, что
определяемый, согласно теории КАМ, порог нагрева по энергии
можно повысить примерно вдвое, если использовать волны одина-
одинаковой мощности. С физической точки зрения это объясняется, по-
видимому, образованием большего числа резонансов, перекрытие
которых возможно и при более высокой энергии. Было найдено,
что максимальный эффект достигается, когда разность частот срав-
сравнима с частотой продольных колебаний частицы. Важность резо-
резонанса с продольным движением отмечалась уже в работе Смита
и др. [384]. Другое объяснение эффективности нагрева двумя ча-
частотами было предложено Самеком и др. [360]. В случае одной ча-
частоты проходящие через резонанс частицы получают два быстро
следующих один за другим «толчка», которые могут компенсиро-
компенсировать друг друга. Введение второй частоты нарушает эту компен-
компенсацию и увеличивает достижимую энергию.
Во всех описанных выше случаях рассматривались не самосо-
самосогласованные волны в плазме. Для экспериментов по ЭЦРН такое
приближение, как правило, справедливо, если только плазменная
частота меньше электронной циклотронной частоты, что обычно
также имеет место. Однако для ионного циклотронного нагрева
это уже не так, что существенно ограничивает теоретический ана-
анализ. Кроме того, обычно не учитывается сложное пространствен-
пространственное распределение высокочастотного поля.
Эти трудности указывают на одну из фундаментальных проблем
теоретического подхода, в котором гамильтониан системы тре-
требуется знать заранее. Тем не менее был достигнут значительный
прогресс в согласовании теории стохастического ионного цикло-
циклотронного нагрева с экспериментами на токамаках [159].
Имеется ряд заслуживающих упоминания проблем, родствен-
родственных проблеме резонансного нагрева плазмы. Мы уже видели в
п. 2.5в (подробнее см. работы [51, 52, 312]), что пространственно
494 Некоторые приложения
неоднородное высокочастотное поле (а также высокочастотное поле
в пространственно неоднородном стационарном магнитном поле
[52 ]) действует на частицу с некоторой средней силой. Это может
быть использовано для высокочастотного удержания плазмы и сни-
снижения потерь частиц через магнитные пробки. Однако, как мы ви-
видели, движение частиц в этом случае не обязательно является адиа-
адиабатическим. Лихтенберг и Берк, изучая этот вопрос, показали, что
именно неадиабатичность определяет предел, который может быть
достигнут при высокочастотном удержании [268J. Аналогичные
вычисления были выполнены Хатори и Ватанабе [177] для лову-
ловушек со встречными пробками 1). Хотя высокочастотное поле вряд
ли можно использовать для удержания основной плазмы в термо-
термоядерных установках, оно может оказаться полезным для удержа-
удержания и нагрева теплой плазмы, необходимой для стабилизации плаз-
плазменных неустойчивостей. Задача о самосогласованном высокоча-
высокочастотном удержании рассматривалась также в работах [312, 425],
но не в той области параметров, где существенны стохастические
эффекты.
А.5. Химическая динамика
В § 7.4 отмечалось, что одной из основных целей изучения дисси-
пативных систем является гидродинамическая турбулентность.
Другая чрезвычайно интересная область связана с «турбулент-
«турбулентностью» в химических реакциях. Закон действующих масс, опреде-
определяющий временную эволюцию однородной химической системы,
приводит к нелинейным дифференциальным уравнениям первого
порядка 2). Каждому веществу соответствует одно уравнение, так
что для М веществ получается /И-мерный поток типа, рассмотрен-
рассмотренного в § 7.1. Поэтому неудивительно, что мы встречаем здесь все
виды движения, описанные в гл. 7, включая простые и странные
аттракторы.
На практике большинство однородных химических систем просто
релаксирует к стационарному состоянию (устойчивый фокус).
В 1958 г. Белоусов обнаружил периодические колебания в химиче-
химической реакции. Дальнейшие исследования были проведены Жабо-
тинским и сотр. [439], и эта реакция называется теперь реакцией
Белоусова—Жаботинского. Колебания цвета раствора с периодом
около минуты возникают в ходе реакции окисления лимонной кис-
кислоты бро.матом и могут продолжаться более часа, пока не будут
израсходованы исходные вещества. Сейчас известно много других
осциллирующих химических реакций (популярное изложение см.,
!) Cusp field — геометрия прямой магнитной ловушки, в которой маг-
магнитное иоле имеет противоположное направление в двух пробках.— Прим.
перев.
г) Подробнее см. книгу [554], где кратко описана также история воз-
возникновения химической динамики.-— Прим. ред.
Некоторые приложения 495
например, в работах [422, 432]) 1). Хотя первые модели реакции
Белоусова—Жаботинского включали одиннадцать химических ве-
веществ, Филд и Нойес [128] показали, что для описания достаточно
всего трех веществ, т. е. такую реакцию можно представить как
трехмерный поток в пространстве концентраций.
В гл. 7 обсуждалось возникновение странных аттракторов в
трехмерных потоках. Рюэль [353 ] предположил, что реакция Бе-
Белоусова—Жаботинского, как и другие химические реакции, мо-
может протекать хаотически (иногда это называется химической турбу-
турбулентностью). В настоящее время существование химической тур-
турбулентности надежно установлено как теоретически, так и чис-
численно [351, 410, 413]. Проведено также много экспериментов [101,
206, 365, 418, 426], которые со всей очевидностью выявляют этот
режим. Например, Вайдал и др. [418], измеряя фурье-спектр кон-
концентраций при возрастании скорости протекания реакции, на-
наблюдали бифуркацию удвоения периода, а затем и переход к хими-
химической турбулентности.
Еще более сложные и удивительные процессы происходят в не-
неоднородных системах Белоусова—Жаботинского. В тонком (около
2 мм) слое раствора спонтанно возникают окрашенные структуры
высокой степени сложности (спирали, дуги, окружности), которые
движутся вдоль слоя и исчезают при столкновениях [234, 432, 439 ].
При этом раствор в целом не движется, а изменяются концентра-
концентрации веществ вследствие реакций между ними и диффузии. Такие
реактивно-диффузионные системы должны описываться уравне-
уравнениями в частных производных, и изучение их намного сложнее,
чем однородных. Копель [233] аналитически установил существо-
существование плоских волн и разрывов, а также периодических во времени
и нерегулярных в пространстве решений простой модельной за-
задачи. Еще раньше хаотическое поведение было обнаружено в по-
подобной системе численно [246]. При этом выяснилось, что хаос
является следствием диффузии, тогда как в однородной системе
происходят только периодические колебания. Недавние экспери-
эксперименты [437], по-видимому, подтверждают, что именно диффузия
приводит к турбулентности. Переход к турбулентности выглядит
в экспериментах плавным без какой-либо резкой границы.
А.6. Квантовые системы
Как упоминалось во введении, появление квантовой механики дало
новый мощный импульс для развития классической теории возму-
возмущений [34 ]. С другой стороны, современные успехи в понимании
поведения классических динамических систем возродили интерес
к изучению квантовых систем в квазиклассическом приближении
h -v 0. Особенно важно установить соответствие между классиче-
См. работу [555].— Прим. перев.
496 Некоторые приложения
скими решениями (фазовые траектории) и квантовыми решениями
(волновые функции). Квантовую формулировку задачи можно по-
получить из классической х), однако квантовомеханическое решение
не следует непосредственно из классического. Неизвестно какое-
либо общее соответствие между обоими решениями, за исключе-
исключением полностью интегрируемых систем 2). В последнем случае дви-
движение по каждой из Л' степеней свободы является независимым как
в классической, так и в квантовой формулировке и правила квази-
квазиклассического квантования 3) хорошо известны (см., например,
[226, 329]). Каждая из N переменных действия принимает дискрет-
дискретные значения / = (п -\- ос/4) ft, где п и а — целочисленные век-
векторы квантовых чисел и индексов Маслова соответственно. Кван-
Квантовые уровни энергии Еп = Н (IЛ могут совпадать и пересекаться
при изменении параметров системы. Квазиклассическая волновая
функция имеет каустики в конфигурационном пространстве, соот-
соответствующие точкам поворота классического движения.
Для близких к интегрируемым классических систем, в ко-
которых регулярные и стохастические траектории сосуществуют в
сколь угодно малых масштабах, квантовые аналоги не ясны. Не-
Некоторое понимание достигнуто в отношении квантования класси-
классических систем с полностью стохастическим поведением (/^-систем).
Примерами являются отображение Арнольда [27 ] и бильярд Синая,
в частности «стадион», образованный двумя параллельными прямыми,
замкнутыми полуокружностями [59, 287 ]. Берри [24,25] и Заслав-
Заславский [440 ] предположили, что уровни энергии стохастической си-
системы должны отталкиваться, так что распределение расстояний
между ними имеет максимум при некотором конечном значении,
а не в нуле, как для интегрируемой системы4). Отталкивание на-
наблюдалось в численном моделировании для бильярда Синая и ста-
стадиона [27, 28, 59, 80, 287 ] и иногда принимается в качестве опреде-
определения квантовой стохастичности.
Ситуация с близкими к интегрируемым системами не так ясна.
Считается, что классическая иерархия резонансов с их стохасти-
стохастическими слоями и инвариантными торами «замазывается» при лю-
любом конечном /г. Квантовое фазовое пространство оказывается,
х) По-видимому, имеется в виду переход от классических величин к кван-
квантовым операторам.— Прим. ред.
2) Это не совсем так, см., например, работу [556].— Прим. ред.
3) В оригинале редко употребляемый термин — квантование по Эйн-
Эйнштейну—Бриллюэну—Келлеру [329]; общепринятое название — правило
квантования Бора—Зоммерфельда (см., например, книгу [557]).— Прим.
ред.
4) В указанных работах Берри этот вопрос не рассматривался; по-види-
по-видимому, имеется в виду статья [28]. В работе Заславского [440] (см. также
работу [442]) сделана попытка связать хорошо известное явление отталкива-
отталкивания уровней сложных атомов и ядер (см., например, книгу [558]) с динами-
динамическими характеристиками системы (обсуждение см. в работе 128})-— Прим.
ред.
Теория бифуркаций в гамильтоновых системах 497
таким образом, «крупноструктурным», так что можно пренебречь
почти всеми классическими областями (регулярными и стохасти-
стохастическими), размер которых много меньше h [329]. При этом кванто-
квантовое поведение может быть регулярным, даже если соответствующая
классическая система стохастична. Это подтверждается числен-
численными экспериментами Казати и др. [56] для квантового стандарт-
стандартного отображения и Маркуса [294 ] для квантовой задачи Хенона
и Хейлеса. Последний четко показал, что нестохастические кванто-
вомеханические состояния имеют место при таких значениях энер-
энергии, для которых классическое движение является существенно
стохастическим; он же дал обзор результатов применения обсуж-
обсуждаемых методов в молекулярной динамике. Еще одним следствием
крупноструктурности является то, что при конечном h инвариант-
инвариантные торы оказываются неизолирующими. Отт и др. [325] продемон-
продемонстрировали дифракцию волновой функции из классически регуляр-
регулярной области в стохастическую. Другие исследования обсуждаемой
проблемы представлены в работах Бермана и Заславского [21 ],
Чирикова и др. [77], Шепелянского [370], а также в трудах кон-
конференции [58]. Обзор этого направления дан Заславским [442] х).
Дополнение Б
ТЕОРИЯ БИФУРКАЦИЙ
В ГАМИЛЬТОНОВЫХ СИСТЕМАХ
Для гамильтонова отображения [В = 1 в G.3.2) ]
хп+1 + Хп-1 = 2Схп + 2х1 (Б.1)
соотношения G.3.5) — G.3.17) остаются справедливыми. Однако
из G.3.10а) следует
и, подставляя С = С = Сх в G.3.106), находим точку накопления
или
Со„ = C—У«Г)/4»— 1,2656. (Б.2)
Это близко к найденной численно величине5) — 1,2663 и отли-
отличается от значения для диссипативных отображений Соо » — 0,78.
Предполагая, что С& сходится к С«, по закону
Ck—Cx « АЬ~ ,
и подставляя это в G.3.106) при 5=1
х) См. также [488].— Прим. ред.
2) Точная теория ренормализации для двумерных гамильтоновых ото-
отображений [113] дает значения параметров подобия, которые очень хорошо
согласуются с численными результатами.
498
Теория бифуркаций в гамильтоновых системах
2°
Л = 1
С = -0,9 >\
/*.
21
= -1,10
21
А =
С =
21
С =
1
-1,02
1
-1,05
ч
No.
\
\
\
I = 5
' = -1,10
Л =5
С =-1,24
А = 5
С= -1,253
21
Л =5
С= —1,05
:
¦ ¦¦ Vv-;v
'/¦'¦ 'О_Г ..¦;-
Л =25
С = -1,253
\> V. -,7
Л = 100
С =-1,26
¦ - •" ¦ б
Рис. Б.1. Бифуркации удвоения периода (Т = 2ft, к = 0, 1, 2, 3, 4) для гамиль
Величина А указывает линейное увеличение масштаба. Буквы а, б я в я стрелки показывают
находим
9,06.
(Б.З)
Численное значение б ^ 8,72 для гамильтоновых отображений
отличается от параметра диссипативных отображений б « 4,66.
Теория бифуркаций в гамильтоновых системах
499
А = 100
С=-1,2632
/1 =200
С = -1,2636
-;<J-
A = 100
С = —1,2634
/1 =200
С = -1,264
•¦¦¦•$¦'
А = 200
С = —1,265
А =200
С = -1,266
ж
24
Л = 800
С = -1,266
тонова отображения (Б.1) на плоскости (хп+:, хп) (по данным работы[417]).
последовательность бифуркаций при уменьшении параметра С.
Наконец, параметр лподобия а в G.3.15) определяется выраже-
выражением G.3.17) при В = 1
Используя ей d из G.3.8), а"также а и b из G.3.6), находим
а"^—4,096, (Б.4)
500 Теория бифуркаций в гамильтпновых системах
тогда как численный результат а» — 4,018. Это значение а также
заметно отличается от величины а « — 2,5 для диссипативных
систем.
На рис. Б.1 представлена последовательность бифуркаций
отображения (Б.1) на плоскости (х„+1, х„) вблизи неподвижной точки
@, 0) при изменении параметра С. Величина А показывает увели-
увеличение масштаба соответствующей картинки. Ясно видны бифурка-
бифуркации с k = 1, 2, 3, 4.
Более подробное исследование двумерных гамильтоновых ото-
отображений обнаруживает дополнительный параметр подобия |3
[84, 167]. Следуя Грину и др. [167], мы покажем это, представив
(Б.1) в форме квадратичного отображения Вогелара
"' " ' (Б.5)
ft у rf 1 У I
где1) g = Cx -f Л'2. Такое представление отображения позволяет
выявить симметрию в бифуркациях. Неподвижная точка @, 0) в (Б.5)
становится неустойчивой при С = — 1, приводя к образованию пока-
показанного на рис. Б.2 бифуркационного дерева. Численно последо-
последовательные бифуркации сходятся по закону геометрической про-
прогрессии с показателем б « 8,72, что приближенно согласуется
с (Б.З); точка накопления С«, = — 1,2663 хорошо согласуется
с (Б.2).
Дополнительное измерение (по у) также должно иметь параметр
подобия. Это видно, например, из рис. Б.З. Здесь кружки пред-
представляют траекторию периода 2, возникающую при потере устой-
устойчивости неподвижной точки (квадрат); треугольники — траекто-
траекторию периода 4 и точки — траекторию периода 8. Нетрудно заметить
подобие в расположении периодических точек: картина вокруг
квадрата повторяется в уменьшенном масштабе вокруг левого
кружка (с отражением). Обе картины можно совместить, увели-
увеличив масштаб по оси хва» — 4,018 раза [что хорошо согласуется
с (Б.4)], а по оси у в Р « 16,36 раза. Фактически эти параметры
принимают точные значения лишь в ренормализационном пределе.
Оказывается, что при С = Сх подобие распространяется не только
на периодические точки, но и на все отображение Too, если приме-
применить его дважды и изменить масштабы [1671:
I оо — О " I со * О »
где
'а 0
О
1) В работе [167] исследовалось несколько иное отображение с функцией
g = Сх — A—С) х2, которое приводится к (Б.1) заменой — A—С) х -* х. —
Прим. ред.
Теория бифуркаций в гамильтоновых системах
501
Мы уже нашли выражения для Сх, б и а с помощью приближен-
приближенной квадратичной ренормализации. Аналогичным образом можно
вычислить и второй коэффициент подобия |3. Это было сделано
Мак-Кайем (см. работу [182], приложение С), и мы используем здесь
его метод. Представленное в форме Вогелара отображение (Б.1)
— Уп I W/iT^m
Уп+1= Хп
(Б.ба)
(Б.66)
Сое
-1,25
-1,20
С —1,15
—1,10
— 1.05
-1,00
к \ » *1/
„ \ i ¦ е It .
\ \ ^Ф d
- 47
. \
\
\
\
\
— \
\
\ь
\
N
|"
1-
1
а /
/
/
-0,4
-0,2
0,2
Рис. Б.2. Сечение бифуркационного дерева (в плоскости у — 0) для квадра-
квадратичного отображения Вогелара (по данным работы [167]).
Сплошные линии — устойчивые неподвижные точки; пунктирные линии — неустойчи-
неустойчивые.
имеет неподвижную точку х10 = у10 = 0. Возникающие из нее
точки периода 2 с координатами у2± = 0 и х3± определяются, как
и прежде, из G.3.6). Подставляя
х = х2 ±
в выражение (Б.6), находим
Axn+1=—Ai
^- Ахп + {Ахп)\
(Б.7а)
502
Теория бифуркаций в гамильтоновых системах
tjn+i = Ахп — Ахп+1—(Ахп+1J,
(Б.76)
где due по-прежнему определяются согласно G.3.8). После
однократной итерации (Б.7а) находим
(Б.8)
0,04
У 0
-0,04
-0,08
-
- t о
1
• А*
1
?
1
А
-
о
-
А
-0,4
-0,2
0,2
Рис. Б.З. Расположение (неустойчивых) неподвижных точек при С = С<х
(по данным работы [167]).
Вычитая (Б.8) из (Б.76), получаем
Ахп+2 =—Ахп+ еАхп+1 + 2 (Ахп+1)\ (Б.9)
Исключая Ахп+1 в (Б.9) с помощью (Б.7а) и удерживая линейные
члены Ахп, Ауп и квадратичный член (АхпJ, имеем
Ахп+г = — еАуп + С'Ахп + а (Д*„)% (Б. 10)
где
C' = -Lde — 1 (Б.11)
СПИСОК ОСНОВНЫХ ОБОЗНАЧЕНИЙ
Ниже приведены только обозначения, употребляемые на протя-
протяжении всей книги. Скалярные величины печатаются светлым кур-
курсивом, векторы — полужирным курсивом, а матрицы и тензоры —
прямым жирным шрифтом (рубленым).
А — векторный потенциал
А — матрица линейного
преобразования
s&m — интеграл Мельни-
Мельникова—Арнольда
В — магнитное поле
с — скорость света
D — коэффициент диффу-
диффузии
Е — энергия
& — полный эллиптиче-
эллиптический интеграл вто-
второго рода
F — производящая функ-
функция
9" — эллиптический интег-
интеграл первого рода
G — коэффициент нели-
нелинейности
h — КС-энтропия
h — постоянная Планка
Я — гамильтониан
#о — невозмущенный га-
гамильтониан
I — единичная матрица
/, J — переменные действия
f — функция Бесселя пер-
первого рода
k — волновой вектор
К — параметр стохастич-
ности
Ж — полный эллиптиче-
эллиптический интеграл пер-
первого рода
L — лагранжиан
L — оператор Ли
т, п — целочисленные век-
векторы
М — матрица Якоби
Ж — мера
N -— число степеней сво-
свободы
J? — мощность шума
р — импульс
Р — распределение веро-
вероятностей
г — радиус-вектор
t — время
Т — период
Т — эволюционный опера-
оператор Ли
и, v — скорость
U, V — потенциальная энер-
энергия
w — производящая функ-
функция Ли
W — вероятность перехода
х, у, z — координаты
X — матрица собственных
векторов
а — число вращения
е — параметр возмущения
Список основных обозначений
505
8 — вектор угловых пере-
переменных, канонически
сопряженных пере-
переменным действия
х — аргумент эллипти-
эллиптических функций
7. — собственное значение
1. — матрица собственных
значений
(.1 — магнитный момент
v — частота столкновений
р — ларморовский радиус
о — показатель Ляпунова
т — время
Ф. *Р — угловые переменные
Ф — электрический потен-
потенциал
со — частота колебаний
Q — ларморовская частота
I , ] — скобки Пуассона
знак порядка
ос — знак пропорциональ-
пропорциональности
х, е — орты
Т, L — операторы
det M — детерминант матрицы
Sp M — след матрицы
ЛИТЕРАТУРА
1. Aamodt R. E., Byers J. A.— Phys. Rev. Letters, 1972, v. 29, p. 1305.
2. Abarbanel H. D. I.— Physica, 1981, v. 4D, p. 89.
3. Abarbanel H. D. I., Crawford J. D.— Phys. Letters, 1981, v. 82A, p. 378;
Physica, 1982, v. 5D, p. 307.
4. Ablowitz M. J., Ramani A., Segur H.—i. Math. Phys., 1980, v. 21, p. 715.
5. Ahlers G., Behringer R. P.— Phys. Rev. Letters, 1978, v. 40, p. 712.
6. Алексеев В. М. — УМН, 1981, т. 36, № 4, с. 161.
7. Alfven H. Cosmical Electrodynamics.— Oxford: Oxford University Press,
1950. [Имеется перевод: Альфвен X. Космическая электродинамика.—
М.: ИЛ, 1952.]
8. Аносов Д. В.— ДАН СССР, 1962, т. 145, с. 707.
9. Аносов Д. B.— RAH СССР, 1963, т. 151, с. 1250.
10. Арнольд В. И.— УМН, 1963, т. 18, № 5, с. 13.
11. Арнольд В. И.— УМН, 1963, т. 18, № 6, с. 91.
12. Арнольд В. И.— ДАН СССР, 1964, т. 156, с. 9.
13. Арнольд В. И. Математические методы классической механики.— М.:
Наука, 1979.
14. Arnold V. /., Avez A. Ergodic Problems of Classical Mechanics.— N. Y.:
Benjamin, 1968.
15. Bardet R., Briand P., Dupas L. et al.— Nucl. Fusion, 1975, v. 15, p. 865.
16. Bellman R. Perturbation Techniques in Mathematics, Physics, and Engi-
Engineering.— N. Y.: Holt, Rinehart, and Winston, 1964.
17. Benettin G., Casartelli M., Galgani L., et al.— Nuovo Cimento, 1978,
v. 44B, p. 183; 1979, v. 50B, p. 211.
18. Benettin G., Galgani L.— in: Intrinsic Stochasticity in Plasmas/Eds. La-
Laval, Gressillon.— Orsay: Les Editions de Physique, Courtaboeuf, 1979,
p. 93.
19. Benettin G., Galgani L., Strelcyn J. M.— Phys. Rev., 1976, v. A14, p. 2338.
20. Benettin G., Galgani L., Giorgilli A., Strelcyn J. M.— Meccanica, 1980,
March, p. 21.
21. Berman G. P., Zaslavskiy G. M.— Physica, 1979, v. 97A, p. 367.
22. Berman R. H. Transition to Stochastic Behavior in a Deterministic Sys-
System.— Res. Lab. Elec. M. I. T. Report PRR 80/10, 1980.
23. Bernstein J. В., Baxter D. C— Phys. Fluids, 1981, v. 24, p. 108.
24. Berry M. V'.— Philos. Trans. R. Soc, 1977, v. A287, p. 237.
25. Berry M. V.— i. Phys., 1977, v. A10, p. 2083.
26. Berry M. V.— in: Topics in Nonlinear Dynamics/Ed. Jorna.— N. Y.:
American Institute of Physics, 1978, v. 46, p. 16.
27. Berry M. F.—in: Nonlinear Dynamics/Ed. Helleman.— N. Y.: Ann.
N. Y. Acad. Sci., 1980, v. 357, p. 183.
28. Berry M. Y.— Ann. Phys., 1981, v. 131, p. 163.
29. Birkhoff G. D. Dynamical Systems.— N. Y.: American Mathematical So-
Society, 1927. [Имеется перевод: Биркгоф Дж. Д. Динамические системы.—
М.: Гостехиздат, 1941.]
30. Birkhoff G. ?>.— Mem. Pont. Acad. Sci. Novi. Lyncaei, 1935, v. 1, p. 85.
Литература 507
31. Bivins R. L., Metropolis Л'., Pasta J. R.— J. Comput. Phys., 1973, v. 12,
p. 65.
32. Боголюбов H. H., Зубарев Д. Н.— Укр. мат. ж., 1955, т. VII, с. 5.
33. Боголюбов Н. Н., Митропольский Ю. А. Асимптотические методы в тео-
теории нелинейных колебаний.— М.: Наука, 1974.
34. Born M. The Mechanics of the Atom.— London: Bell, 1927. (Имеется пе-
перевод: Макс Борн. Лекции по атомной механике.— Киев: ГНТИ Укра-
Украины, 1934.)
35. Botintis Т. С. Nonlinear Models in Hamiltonian Mechanics and Statisti-
Statistical Mechanics, Ph. D. Thesis.— N. Y.: University of Rochester, Roches-
Rochester, 1978.
36. Bountis Т. С— Physica, 1981, v. 3D, p. 577.
37. Bountis T. C, Segur H., Vivaldi F.— Phys. Rev., 1982, v. A25, p. 1257.
38. Brahic A.— Astron. Astrophys., 1971, v. 12, p. 98.
39. Brambilla M., Lichtenberg A. J.— Nucl. Fusion, 1973, v. 13, p. 517.
40. Bridges R., Rowlands G.— Phys. Letters, 1977, v. 63A, p. 189.
41. Brillouin L.— Compt. Rend., 1927, v. 183, p. 24.
42. Brillouin L. Wave Propagation in Periodic Structures.— N. Y.: Dover,
1953. [Имеется перевод: Бриллюэн Л., Пароди М. Распространение волн
в периодических структурах.—М.: ИЛ, 1959.]
43. Brouwer D., Clemence G. M.— in: The Solar System III; Planets and Sa-
Satellites/Eds. Kuiper, Middlehurst.— Chicago: Chicago University Press,
1961, p. 31.
44. Brumer P., Duff J. W.— J. Chem. Phys., 1976, v. 65, p. 3566.
45. Bruns H.~ Berichte der Kgl. Sachs. Ges. der Wiss., 1887, pp. 1,55; Acta
Math., 1887, v. XI, p. 25.
46. Bunimovich L. A., Sinai Ya. G.— Commun. Math. Phys., 1980. v. 78,
p. 247.
47. Callen J. D.— Phys. Rev. Letters, 1977, v. 39, p. 1540.
48. Carreras В., Hicks H. R., Lee D. K— Phys. Fluids, 1981, v. 24, p. 66.
49. Cart/ J. R. Lie Transforms and Their Use in Hamiltonian Perturbation
Theory.— Lawrence Berkeley Laboratory Report 6350, 1978; Ph. D. The-
Thesis, University of California, Berkeley, California, 1979.
50. Cary J. R.— Phys. Reports, 1981, v. 79, p. 129.
51. Cary J. R., Kaufman A. N.— Phys. Rev. Letters, 1977, v. 39, p. 402.
52. Cary J. R., Kaufman A. N.— Phys. Fluids, 1981, v. 24, p. 1238.
53. Cary J. R., Meiss J. D.— Phys. Rev., 1981, v. A24, p. 2664.
54. Cary J. R., Meiss J. D., Bhattacharee A.— Phys. Rev., 1981, v. A23,
p. 2744.
55. Casati G.— Letters Nuovo Cimento, 1975, v. 14, p. 311.
56. Casati G., Chirikov B. V., Izrailev F. M., Ford J.— in: Stochastic Be-
Behavior in Classical and Quantum Hamiltonian Systems/Eds. Casati, Ford.—
N. V.: Springer-Verlag, Lectures Notes in Physics, 1979, v. 93, p. 334.
57. Casati G., Chirikov B. V., Ford J. — Phys. Letters, 1980, v. 77A,
p. 91.
58. Casati G., Ford J., (Eds). Stochastic Behavior in Classical and Quantum
Hamiltonian Systems.— N. Y.: Springer-Verlag, Lectures Notes in Physics,
1979, v. 93.
59. Casati G., Guarneri /., Valz-Gris F. On the Connection between Quanti-
Quantization of Nonintegrable Systems and the Statistical Theory of Spectra,
preprint.— Milano: Universita di Milano, 1980.
60. Casati G., Valz-Gris F., Guarneri /.— Physica, 1981, v. 3D, p. 644.
61. Chaitin G. J.— Sci. Am., 1975, May.
62. Chandrasekhar S.— Rev. Mod. Phys., 1943, v. 15, p. 1. [Имеется перевод:
Чандрасекар С. Стохастические проблемы в физике и астрономии.— М.:
ИЛ, 1947.]
€3. Chandrasekhar S.— in: The Plasma in a Magnetic Field/Ed. Landshof.—
Palo Alto: Stanford University Press, 1958.
508 Литература
64. Chandrasekhar S., Trehan S. K- Plasma Physics.— Chicago: University
of Chicago Press, 1960.
65. Chen F. Introduction to Plasma Physics.— N. Y.: Plenum Press, 1974.
66. Chillingworth D. R. J. Differential Topology with a View to Applica-
Applications.— London: Pitman, 1976.
67. Чириков Б. В.—Атомная Энергия, 1959, т. 6, с. 630.
68. Чириков Б. В. Исследования по теории нелинейного резонанса и сто-
хастичности.—Новосибирск: препринт ИЯФ СО АН СССР, № 267, 1969.
69. Чириков Б. В.— Физика плазмы, 1978, т. 4, № 3, с. 521.
70. Chirikov В. V.— Phys. Reports, 1979, v. 52, p. 265.
71. Чириков Б. В.— Физика плазмы, 1979, т. 5, № 4, с. 880.
72. Chirikov В. V., Ford J., Vivaldi F.— in: Nonlinear Dynamics and the
Beam — Beam Interaction/Eds. Month, Herrera.—N. Y.: American Iistitute
of Physics, AIP Conference Proceedings, 1979, v. 57, p. 323.
73. Chirikov B. V., Izrailev F. M. Colloques Internationaux du С N. R. S.,
N 229 (Toulouse, 1973).— Paris: С N. R. S., 1976, p. 409.
74. Chirikov B. V., Izrailev F. M.— Physica, 1981, v. 2D, p. 30.
75. Chirikov B. V., Izrailev F. M., Tayursky V. A.— Comput. Phys. Com-
mun., 1973, v. 5, p. 11.
76. Израйлев Ф. М., Чириков Б. В., Шепелянский Д. Л. Динамическая сто-
хастичность в классической механике.— Новосибирск: препринт ИЯФ
СО АН СССР, 80—209, 1980.
77. Израйлев Ф. М., Чириков Б. В., Шепелянский Д. Л. Переходная сто-
хастичность в квантовой механике.— Новосибирск: препринт ИЯФ
СО АН СССР, 80—210, 1980.
78. Churchill R. С, Pecelli G., Rod D. L.— in: Stochastic Behavior in Clas-
Classical and Quantum Hamiltonian Systems/Eds. Casati, Ford.— N. Y.:
Springer-Verlag, Lecture Notes in Physics. 1979, v. 93, p. 76.
79. Cohen R. H.~ Nucl. Fusion, 1979, v. 19, p. 1579.
80. Cohen R. H., Rowlands G.— Phys Fluids, 1981, v. 24, p. 2295.
81. Cohen R. H., Rowalnds G., Foote J. H.— Phys Fluids, 1978, v. 21, p. 627.
82. Collet P., Eckmann J. P. Iterated Maps on the Interval as Dynamical Sys-
Systems.— Basel: Birkhauser Verlag, Progress in Physics, 1980, v. 1.
83. Collet P., Eckmann J. P., Lanford О. Е.— Commun. Math. Phys., 1980,
v. 76, p. 211.
84. Collet P., Eckmann J. P., Koch H.— Physica, 1981, v. 3D, p. 457.
85. Collet P., Eckmann J. P., Koch H.— l. Stat. Phys., v. 25, p. 1. 1981.
86. Contopoulos G.~ Zeits. fur Astrophys., 1960, v. 49, p. 273.
87. Contopoulos G.~ J. Math. Phys., 1966, v. 7, p. 788.
88. Contopoulos G.— in: Dynamics of Stellar Systems/Ed. Hayli.— Int. Astr.
Union, 1975, p. 209.
89. Contopoulos G.— Cel. Mech., 1978, v. 17, p. 167.
90. Contopoulos G.— in: Stochastic Behavior in Classical and Quantum Ha-
Hamiltonian Systems/Eds. Casati, Ford.— N. Y.: Springer Verlag, Lec-
Lecture Notes in Physics, 1979, v. 93, p. 1.
91. Contopoulos G., Montsoulas M.— Astron. J., 1965, v. 70, p. 817.
92. Contopoulos G., Papayannopoulos Th. — Astron. Astrophys., 1980, v. 92,
p. 33.
93. Contopoulos G., Galgani L., Giorgilli A.— Phys. Rev., 1978, v. A18, p. 1183
94. Courant E. D., Snyder H. S.— Ann. Phys., 1958, v. 3, p. 1. 1Имеется
перевод в сб. «Проблемы современной физики», вып. 4, 1958.]
95. Courant E. D., Livingston M. S., Snyder H. S— Phys. Rev., 1952,,
v. 88, p. 1190. [Имеется перевод в сб.: Проблемы современной физики,
вып. 11, 1954.]
96. Crutchfield J. P., Huberman В. A.— Phys. Letters, 1980, v. 77A, p. 407.
97. Crutchfield J. P., Farmer D., Packard N. et al.— Phys. Letters, 1980,
v. 76A, p. 1.
98. Curry J. H.~ Commun. Math. Phys., 1978, v. 60, p. 193.
99. Curry J. H.— Commun. Math. Phys., 1979, v. 68, p. 129.
Литература 509
100. Curry J. #., Yorke J. A.— in: Lecture Notes in Mathematics 668, 1978,
p. 48.— Berlin: Springer-Verlag.
101. Degn H., Olsen L. F., Penan J. W.— Ann. N. Y. Acad. Sci., 1979, v. 316,
p. 625.
102. Deprit A.— Cel. Mech., 1969, v. 1, p. 12.
103. Derrido В., Gervois A., Pomeau V".—J. Phys., 1979, v. A12, p. 269.
104. De Uogelaere R.— in: Contributions to Theory of Nonlinear Oscillati-
Oscillations/Ed. Lefschetz.— New Jersey: Princeton University Press, Prince-
Princeton, 1958, v. 4, p. 53.
105. Dewar R. L.— i. Phys., 1976, v. A9, p. 2043.
106. Dragt A. J.— Rev. Geophys., 1965, v. 3, p. 255.
107. Dragt A. J., Finn J. M.— i. Geophys. Res.,'1976, v. 81, p. 2327.
108. Dragt A. J., Finn J. M.— J. Math. Phys., 1976, v. 17, p. 2215.
109. Дубинина A. #., Юдин Ю. Н.~ ЖЭТФ, 1968, т. 26, с. 707.
110. Dunnett D. A., Laing E. W., Roberts S. J., Robson A. E.~ Plasma
Phys. (J. N. E. Pt. C), 1965, v. 7, p. 359.
111. Dunnett D. A., Laing E. W., Taylor J. B.— i. Math. Phys., 1968, v. 9,
p. 1819.
112. Eckmann J. P.— Rev. Mod. Phys., 1981, v. 53, p. 643.
113. Eckmann J. P., Koch H., Wittwer P. A computer assisted proof of uni-
universality for area-preserving maps.— Preprint UGVA-DPT-1981/04-345,
Theoretical Physics, University de Geneve, 1981.
114. Эйнштейн А. К современному состоянию проблемы теплоемкости.—
Собр. научн. тр.—М.: Наука, 1966, т. 3, с. 277.
115. Eldridge О.— Phys. Fluids, 1972, v. 15, p. 676.
116. Eminhizer С. R., HellemanR. H. G., Montr oil E. W.— 3. Math. Phys.,
1976, v. 17, p. 121.
117. EscandeD. F., Doveil F.— J. Stat. Phys., 1981, v. 26, p. 257.
118. EscandeD. F., Doveil F.— Phys. Letters, 1981, v. 83A, p. 307; Phys.
Letters, 1981, v. 84A, p. 399.
119. Escande D. F.— in: Long-Time Prediction in Dynamics/Eds. Horton,
Reichl, Szebehely.— N. Y.: Wiley, 1983, p. 149."
120. Farmer J. D.— Physica, 1982, v. 4D, p. 336.
121. Farmer J. D., Crutchfield H., Froehling et al.— in: Nonlinear Dyna-
Dynamics/Ed. Helleman.— N. Y.: Ann.N. Y. Acad. Sci., 1980, v. 357, p. 453.
122. Feigenbaum M. J.— J. Stat. Phys., 1978, v. 19, p. 25; 1979, v. 21, p. 669.
123. Feigenbaum M. J.— Phys. Letters, 1979, v. 74A, p. 375.
124. Felt S. ?>.— Commun. Math. Phys., 1978, v. 61, p. 249.
125. Fenstermacher R., Swinney H. L., Gollub J. P.—J. Fluid Mech., 1978,
v. 94, p. 103.
126. Fermi E.— Phys. Rev., 1949, v. 75, p. 1169.
127. Fermi E., Pasta J. R., Ulam S. Studies of Nonlinear Problems. Los Ala-
Alamos Rept. LA-1940, 1955. [Имеется перевод: Энрико Ферми. Научные
труды.—М.: Наука, 1972, т. II, с. 645.]
128. Field R. J., Noyes R. M.— 3. Chem. Phys., 1974, v. 60, p. 1877.
129. Filonenko N. N., Sagdeev R. Z., Zaslavskiy G. M.— Nucl. Fusion, 1967,
v. 7, p. 253.
130. Finn J. M.— Phys. Fluids, 1977, v. 20, p. 1749.
131. Folas C, Prodi G.— Rend. Sem. Mat. Univ. Padova, 1967, v. 39, p. 1.
132. Foias C, Treve Y.— Phys. Letters, 1981, v. 85Л, p. 35.
133. Ford J.— in: Fundamental Problems in Statistical Mechanics, vol. 3/Ed.
Cohen.— North Holland, Netherlands, 1975.
134. Ford J., Lunsford G. H.— Phys. Rev., 1970, v. Al, p. 59.
135. Ford J., Waters J.—3. Math. Phys., 1963, v. 4, p. 1293.
136. Ford J., Stoddard S. D., Turner J. S.— Prog. Theor. Phys., 1973, v. 50,
p. 1547.
137. Freis R. P., Hartman С W., Hamzeh F. M., Lichtenberg A. J.— Nucl.
Fusion, 1973, v. 13, p. 533.
510 Литература
138. Froehling Н., Crutchfield J. P., Farmer D. et al.— Physica, 1981, v. 3D,
p. 605.
139. Froeschle C — Astrophys. Space Sci., 1971, v. 14, p. 110.
140. Froeschle C — Astron. Astrophys., 1972, v. 16, p. 172.
141. Froeschle C, Scheidecker J.-P.— Astrophys. Space Sci., 1973, v. 25,
p. 373.
142. Froeschle C, Scheidecker J. P.— Astron. Astrophys., 1973, v. 22, p. 431.
143. Froeschle C, Scheidecker J. P.—J. Comput. Phys., 1973, v. 11, 423.
144. Froeschle C, Scheidecker J. P.— Phys. Rev., 1975, v. A12, p. 2137.
145. Fukuyama A., Mamota H., Itatani R.— in: Proceedings, 3rd Sympo-
Symposium on Plasma Heating in Toroidal Devices/Ed. Sindoni.— Bologna:
Editrice Compositori, 1976; Phys. Rev. Letters, 1977, v. 38, p. 701.
146. Гадияк Г. В., Израйлев Ф. М., Чириков Б. В.— В сб.: Труды 7-й Между-
нар. конфер. по нелинейным колебаниям (Берлин, 1975).— Berlin: Aka-
demie-Verlag, 1977, Band II-l, S. 315.
147. Галеев А. А., Сагдеев P. 3.— В сб.: Вопросы теории плазмы/Ред- Леон-
тович.— М.: Атомиздат, вып. 7, 1973, с. 3.
148. Galgani L., Lo Vecchio G.— Nuovo Cimento, 1979, v. B52, p. 1.
.149. Garren A., Riddel R. J., Smith L. et al.— Proc. 2nd UN Conf. Peaceful
Uses Atomic Energy, 1958, v. 31, p. 65.
150. Garrido L. M.— J. Math. Phys., 1968, v. 10, p. 1054.
151. Geisal T-, Nierwetberg /.— Phys. Rev. Letters, 1981, v. 47, p. 1975.
152. Gell Y., Harte J., Lichtenberg A. J., Nevins W. M.— Phys. Rev. Letters,
1975, v. 35, p. 1642.
153. Giacaglia G. E. 0. Perturbation Methods in Nonlinear Systems. Appl.
Math. Sci. No. 8.— N. Y.: Springer-Verlag, 1971. [Имеется перевод
Джакалья Г. Е. О. Методы теории возмущений для нелинейных си-
систем.— М.: Наука, 1979).
154. Gibson G. W., Jordan W., Lauer E.,— Phys. Fluids, 1963, v. 6, p. 116.
155. Giglio G-, Musazzi S., Perini U.— Phys. Rev. Letters, 1981, v. 42, p. 243.
156. Goldstein H. Classical Mechanics.— Cambridge: Addison—Wesley Press,
Inc., 1951. [Имеется перевод: Голдстейн Г. Классическая механика.—
М.: Наука, 1975.]
157. Gollub J. P., Benson S. V., Steinman J.— in: Nonlinear Dynamics/Ed.
Helleman,— N. Y.: Ann. N. Y. Acad. Sci., 1980, v. 357, p. 22.
158. Gorman M., Reith L. A., Swinney H. L.— in: Nonlinear Dynamics/Ed.
Helleman.— N. Y.: Ann. N. Y. Acad. Sci., 1980, v. 357, p. 10.
159. GormezanoC, Hess W., IchtchenkoG. et al.— Nucl. Fusion, 1981, v. 21,
p. 1047.
160. Goward F. R.— in: Lectures on the Theory and Design of an AG Proton
Synchrotron.— Geneva: CERN, 1953, p. 19.
161. Grawe H.~ Plasma Phys., 1969, v. 11, p. 151.
162. Green G. K-, Courant E. D.— Handbuch der Physik, 1959, v. 44, p. 336.
[Имеется перевод в кн.: Ускорители/Ред. Яблоков.— М.: Атомиздат,
1962, с. 292.]
163. Green G.—Cambridge Philos. Trans., 1837, v. 6, p. 457.
164. Greene /.—J. Math. Phys., 1968, v. 9, p. 760.
165. Greene J.— S. Math. Phys., 1979, v. 20, p. 1183.
166. Greene J.— in: Nonlinear Dynamics and the Beam-Beam Interaction/Eds.
Month, Herrera.— N. Y.: American Institute of Physics, AIP Conference
Proceedings, 1979, v. 57, p. 257.
167. Greene J., MacKay R. S., Vivaldi F., Feigenbaum M. J.— Physica, 1981,
v. 3D, p. 468.
168. Greenspan В., Holmes P.— in: Nonlinear Dynamics and Turbulence/Eds.
Berenblatt, Looss, Joseph.— London: Pitman, 1981.
169. Grieger G., Ohlendorf W., Packer H. D. et al.— in: Proceed, of the IVth
IAEA Conf. on Plasma Phys. and Contr. Fusion.—Vienna: IAEA, 1971,
v. Ill, p. 37.
170. Grossmann S., Thomae S.— Z. Naturforsch., 1977, v. 32A, p. 1353.
Литература 511
171. Gustavson F.— Astron. J., 1966, v. 21, p. 670.
172. Hagihara Y.— in: The Solar System III; Planets and Satellites/Eds.
Kuiper, Middlehurst.— Chicago: Chicago University Press, 1961, p. 95.
173. Hagihara Y. Celestial Mechanics.— Cambridge: MIT Press. Massachu-
Massachusetts, 1970—1976.
174. Hall L. On the Existence of a Last Invariant of Conservative Mo-
Motion. Preprint UCID 18980, Lawrence Livermore Laboratory, Liver-
more, California.
175. Hastie R. J., Taylor J. В., Haas F. A.— Ann. Phys., 1967, v. 41, p. 302.
176. Hastie R. J., Hobbs G. D., Taylor J. В.— in: Proceed, of the 3rd IAEA
Conf. on Plasma Phys. and Contr. Fusion.— Vienna: IAEA, 1969, v. I,
p. 389.
177. Hatori Т., Watanabe Т.— Nucl. Fusion, 1975, v. 15, p. 143.
178. Helleman R. H. G.~ in: Statistical Mechanics and Statistical Methods/Ed.
Landman.— N. Y.: Plenum Press, 1977.
179. Helleman R. H. G.— in: Topics in Nonlinear Dynamics/Ed. Jorna.—
N. Y.: American Institute of Physics, 1978, v. 46, p. 264.
180. Helleman R. H. G.— in: Fundamental Ploblems in Statistical Mecha-
Mechanics, v. 5/Ed. Cohen.—Amsterdam: North Holland Publ., 1980, p. 165.
181. Helleman R. H. G. (Ed.). Nonlinear Dynamics.— N. Y.: Am. N. Y. Acad.
Sci., 1980, v. 357.
182. Helleman R. H. G.— in: Long-Time Prediction in Dynsmics/Eds. Hor-
ton, Reichl, Szebehely.— N. Y.: Wiley, 1983, p. 95.
183. Helleman R. H. G., Bountis T.— in: Stochastic Behavior in Classical
and Quantum Hamiltonian Systems/Eds. Casati, Ford.— N. Y.: Sprin-
ger-Verlag, Lectures Notes in Physice, 1979, v. 93, p. 353.
184. Helleman R. H. G., Montroll E. W.— Physica, 1974, v. 74, p. 22.
185. Henon M.— Q. Appl. Math., 1969, v. 27, p. 291.
186. Henon M.—Phys. Rev., 1974, v. B9, p. 1925.
187. Henon M.~ Commun. Math. Phys., 1976, v. 50, p. 69. [Имеется перевод
в сб.: Странные аттракторы/Ред. Синай, Шильников.— М.: Мир, 1981,
с. 152.]
188. Непоп М., Heites С— Astron. J., 1964, v. 69, p. 73.
189. Hereward H. G., Johnsen K-, Lapostolle P.— in: Proc. CERN Symp. on
High-Energy Accelerators.— Geneva: CERN, 1956, p. 179.
190. Herrera J. C, Month M., Peierls R. F.~ in: Nonlinear Dynamics and
the Beam-Beam Interaction/Eds. Month, Herrera.— N. Y.: American
Institute of Physics, A IP'Conference Proceedings: 1979, v. 57, p. 202.
191. Hertweck F., Schluter A.~—Z. Naturforsch., 1957, v. 12a, p. 844.
192. Hilderbrand F. B. Advanced Calculus for Engineers.— N. Y.: Prentice-
Hall, 1948.
193. Hine M. G. N.— in: Lectures on the Theory and Design of an A. G. Pro-
Proton Synchrotron.— Geneva: CERN, 1953, p. 69.
194. Holmes P. J.— Appl. Math. Modeling, 1977, v. 1, p. 362.
195. Holmes P. J.— Philos. Trans. R. Soc, 1979, v. 292, p. 41.
196. Holmes P. J.— SIAM J. Appl. Math., 1980, v. 38, p. 65.
197. Holmes P. J., Marsden J.— J. Math. Phys., 1982, v. 23, p. 669.
198. Holt С R. Construction of Integrable Hamiltonians. Ph. D. Thesis, Uni-
University of Colorado, Boulder, Colorado, 1981.
199. Hori G.— Astron. Soc. Japan, 1966, v. 18, p. 287.
200. Howard J. E.— Phys. Fluids 1970, v. 13, p. 2407.
201. Howard J. E.— Phys. Fluids, 1971, v. 14, p. 2373.
202. Howard J. E., Lichtenberg A. J. Lieberman M. A.— Physica, 1982,
v. 5D, p. 243.
203. Howland R. A.— Cel. Mech., 1977, v. 17, p. 327.
204. Huberman B. A., Rudnick J.— Phys. Rev. Letters, 1980, v. 45, p. 154.
205. Huberman B. A., Zisook А. В.— Phys Rev. Letters, 1981, v- 46, p. 626.
206. Hudson J. L., HartM., Marinko ?>.—-J.Chem. Phys., 1979, v. 71, p. 1601.
207. lzrailev'J. M.— Physica, 1980, v. ID, p. 243.
512 Литература
208. Израйлев Ф. М., Чириков Б. В.— ДАН СССР, 1966, т. 166, стр. 57.
209. Израйлев Ф. М., Жданова Т. А. К вопросу о статистическом ускорении
Ферми.—Новосибирск: препринт ИЯФ СО АН СССР, № 121, 1974.
210. Израйлев Ф. М., Рабинович М. И., Угодников А. Д. О приближенном
описании диссипативных систем со стохастическим поведением.— Горь-
Горький: препринт ИПФ АН СССР, № 17, 1981.
211. Израйлев Л. М., Мишнев С. И., Тумайкин Г. М. Численные экспери-
эксперименты по определению критерия стохастнчности при взаимодействии
встречных пучков (одномерная модель). — Новосибирск: препринт
ИЯФ СО АН СССР, № 77—43, 1977.
212. Jaeger F., Lichtenberg A. J'.— Ann. Phys., 1972, v. 71, p. 319.
213. Jaeger F., Lichtenberg A. J., Lieberman M. A.— Plasma Phys., 1972,
v. 14, p. 1073.
214. Johnston S., Kaufman A. N.— Phys, Rev. Letters, 1978, v. 40, p. 1266.
215. Jorna S. (Ed). Topics in Nonlinear Dynamics.— N. Y.: American Insti-
Institute of Physics, 1978, v. 46.
216. Кадомцев Б. Б.— Физика плазмы, 1975, т. 1, № 5. с. 710.
217. Kadomtsev В. В., Pogutse О. P.— Nucl. Fusion, 1971, v. 11, p. 67.
218. Kaplan J., Yorke J.— in: Lecture Notes in Mathematics.— Berlin:
Springer-Verlag, 1979, v. 730, p. 204.
219. Karney C. F. F. Stochastic Heating of Ions in a Tokamak by RF Power.
Ph. D. Thesis, 1977, MIT, Cambridge, Massachusetts.
220. Karney С F. F.— Phys. Fluids, 1978, v. 21, p. 1584.
221. Karney C. F. F.— Phys. Fluids, 1979, v. 22, p. 2188.
222. Karney C. F. F., Bers A.— Phys. Rev. Letters, 1977, v. 39, p. 550.
223. Karney С F. F., Rechester А. В., White R. В.— Physica, 1982, v. 4D,
p. 425.
224. Kaufman A. N.— in: Topics in Nonlinear Dynamics/Ed. Jorna — N. Y.:
American Institute of Physics, 1978, v. 46, n. 286.
225. Kaufman A. N., Cary J., Pereira N.~ Phys. Fluids, 1979, v. 22, p. 790.
226. Keller J., Rubinov S.— Ann. Phys. N. Y., 1960, v. 9, p. 24.
227. Хинчин А. Я- Цепные дроби.— M.: Физматгиз, 1961.
228. Klein A., Li С. Т.— J. Math. Phys., 1979, v. 20, p. 572.
229. Колмогоров А. Н.— ДАН СССР, 1954, т. 98, с. 527.
230. Колмогоров А. Я.—ДАН СССР, 1959, т. 124, с. 754.
231. Колмогоров А. Н.— Проблемы передачи информации, 1965, т. I, № 1,
с. 3.
232. Коломенский А. А., Лебедев А. Н. Теория циклических ускорителей.—
М.: ГИФМЛ, 1962.
233. Корей N.— in: Nonlinear Dynamics/Ed. Helleman.— N. Y.: Am. N. Y.
Acad. Sci., 1980, v. 357, p. 397.
234. Kopell N., Howard L. N.— Stud. Appl. Math., 1973, v. 52, p. 291.
235. Kramers H. A.— Z. Physik, 1926, v. 39, p. 828.
236. Krllin L.— Czech. J. Phys., 1967, v. B17, p. 112.
237. Krilin L.—Czech. J. Phys., 1967, v. B17, p. 124.
238. Kruskal M. D.— in: Proceedings of the 3rd Conference on Ionized Ga-
Gases.— Venice.: 1957.
239. Kruskal M. ?>.— Nucl. Fusion, 1962, Suppl., Pt 2, p. 775. [Имеется
перевод: Крускал М. Адиабатические инварианты.— М.: ИЛ, 1962.]
240. Kruskal M. D., Zabusky N. У.—J. Math. Phys., 1964, v. 5, p. 231.
241. Крылов Н. С. Работы по обоснованию статистической физики.— М.:
изд-во АН СССР, 1950.
242. Крылов Н. М., Боголюбов Н. Н. Введение в нелинейную механику.—
Киев: изд-во АН УССР, 1937.
243. Kuckes A. —Plasma Phys., 1968, v. 10, p. 367.
244. Kulsrud R. M.— Phys. Rev., 1957, v. 106, p. 205.
245. Kummer M.— Commun. Math. Phys., 1978, v. 55, p. 85.
246. Kuramoto Y., Yamada Г.— Prog. Theor. Phys., 1976, v. 56, p. 679.
247. Lacina J.— Czech. J. Phys., 1963, v. B13, p. 401.
Литература 513
248. Lacina J.— Plasma Phys. (J. N. E. Pt. C), 1966, v. 8, p. 515.
249. Lamb G. Elements of Soliton Theory.— N. Y.: Wiley, 1980. [Имеется
перевод: Лэм Дж.-мл. Введение в теорию солитонов.—• М.: МИР, 1983.]
250. Ландау Л. Д.— ЖЭТФ, 1937, т. 7, с. 203.
251. Ландау Л. Д.— ДАН СССР, 1944, т. 44, № 8, с. 339.
252. Lanford О. Qualitative and Statistical Theory of Dissipative Systems.
1976 SIME School of Statistical Mechanics.— Napoli: Liguori Editore,
1976.
253. Lanford 0.—in: Turbulence Seminar/Eds. Bernard, Rativ.— Springer
Lecture Notes in Mathematics 615, 1977, p. 114.
254. Lanford 0.— in: Hydrodynamic Instabilities and the Transition to Tur-
Turbulence/Eds. Swinney, Gollub.— N. Y.: Springer-Verlag, 1981. Chap-
Chapter 2.
255. Laslett L. J.— in: Focusing of Charged Particles/Ed. Septier.— N. Y.:
Academic Press, 1967, p. 355.
256. Laval G., Gresillon D. (Eds).— Intrinsic Stochasticity in Plasmas.—
Orsay: Les Editions de Physique, Coutraboeuf, 1979.
257. Lasar N., Barter J., Dandl R. et al.— in: Proceedings of the 2nd Works-
Workshop on Hot Electron Ring Physics/Ed. Uckan.— Oak Ridge: Oak Ridge
National Laboratory, Tennessee, 1980.
258. Lewis H. R., Jr.— Phys. Rev. Letters, 1967, v. 18, p. 510.
259. Lewis H. R., Jr.— i. Math. Phys., 1968, v. 9, 1976.
260. Lewis H. R., Leach P. G. L. A Generalisation of the Invariant for the
Time-Dependent Linear Oscillator. Preprint LA-UR 80-68, Los Alamos
Scientific Laboratory, Los Alamos, New Mexico, 1980.
261. Li T. Y., Yorke J. A.— Am. Math. Monthly, 1975, v. 82, p. 985.
262. Ляпунов А. М. Собрание сочинений, т. 1 и 2.— М.: изд-во АН СССР,
1954—1956.
263. Libhaber A., Maurer J.— J. de Physique, 1980, v. 41, pt. C3.
264. Lichtenberg A. J.— Rev. Sci. Instr., 1964, v. 54, p. 1196.
265. Lichtenberg A. J. Phase Space Dynamics of Particles.— N. Y.: Wiley,
1969. [Имеется перевод: Лихтенберг А. Динамика частиц в фазовом
пространстве.— М.: Атомиздат, 1972.]
266. Lichtenberg A. J.— in: Intrinsic Stochasticity in Plasmas/Eds. Laval,
Gressillon.— Orsay: Les Editions de Physique, Courtaboeuf, 1979, p. 13.
267. Lichtenberg A. J.— in: Stochastic Behavior in Classical and Quantum
Hamiltonian Systems/Eds. Casati, Ford.— N. Y.: Springer-Verlag, Lec-
Lectures Notes in Physics, 1979, v. 93, p. 18.
268. Lichtenberg A. J., Berk H. /.— Nucl. Fusion, 1975, v. 15, p. 999.
269. Lichtenberg A. J., Jaeger F. W.— Phys. Fluids, 1970, v. 13, p. 392.
270. Lichtenberg A. J,, Lieberman M. A. — Nucl. Fusion, 1976, v. 16, p. 532.
271. Lichtenberg A. J., Melin G.— Phys. Fluids, 1972, v. 16, p. 1660.
272. Lichtenberg A. J., Lieberman M. A., Cohen R. H.— Physica, 1980, v. ID,
p. 291.
273. Lieberman M. A.— in: Nonlinear Dynamics/Ed. Helleman.— N. Y.:
Am. N. Y. Acad. Sci., 1980, v. 357, p. 119.
274. Lieberman M. A., Lichtenberg A. J.— Phys. Rev., 1972, v. A5, p. 1852.
275. Lieberman M. A., Lichtenberg A. J.— Plasma Phys., 1973, v. 15, p. 125.
276. Lieberman M. A., Tennyson J. L.— in: Long-Time Prediction in Dy-
Dynamics/Eds. Horton, Reichl, Szebehely.— N. Y.: Wiley, 1983, p. 179.
277. Lieberman M. A., Tsang K-— Bull. Am. Phys. Soc, 1981, v. 26, p. 1013.
278. Lindstedt M.— Astron. Nach., 1882, v. 103, p. 211.
279. Liouville J.— i. Math. Pures Appl., 1837, v. 2, p. 16.
280. Littlejohn R. Lawrence Berkeley Laboratory Report UCID-8091, 1978,
Berkeley, California.
281. Littlejohn R.— J. Math. Phys., 1979, v. 20, p. 2445.
282. Littlewood J. E.— Ann. Phys., 1963, v. 21, p. 233.
283. Lorenz E. N.— 3. Atmos. Sci., 1963, v. 20, p. 130. [Имеется перевод
514 Литература
в сб: Странные аттракторы/Ред. Синай, Шильников.— М.: Мир, 198U
с. 88.]
284. Lorenz Е. N.— in: Nonlinear Dynamics/Ed. Helleman.— N. Y.: Am.
N. Y. Acad. Sci., 1980, v. 357, p. 282.
285. Lozi R.— J. Phys., 1978, v. 39, pt. C5-9.
286. Lunsford G. #., Ford J.— J. Math. Phys., 1972, v. 13, p. 700.
287. McDonald S. W., Kaufman A. N.—Phys. Rev. Letters, 1979, v. 42,
p. 1189.
288. McLaughlin J. В.— Phys. Rev., 1979, v. A20, p. 2114.
289. McLaughlin J. B.— 3. Stat. Phys., 1981, v. 24, p. 375.
290. McNamara В.—J. Math. Phys., 1978, y. 19, p. 2154.
291. McNamara В., Whiteman R. I. Invariants of Nearly Periodic Hamif-
tonian Systems. Culham Laboratory Report CLM Pill, 1966, Culham,
England.
292. McNamara В., Whiteman K. I.— J. Math. Phys., 1967, v. 8, p. 2029.
293. Manneville P., Pomeau Y.— Physica, 1980, v. ID, p. 219.
294. Marcus R. A.— in: Nonlinear Dynamics/Ed. Helleman.— N. Y.: Am.
N. Y. Acad. Sci., 1980, v. 357, p. 169.
295. Matthaeus W. H., Montgomery D.¦— in: Nonlinear Dynamics/Ed. Helle-
Helleman.— N. Y.: Am. N. Y. Acad. Sci., 1980, v. 357, p" 203.
296. May R. M.— Nature, 1976, v. 261, p. 459.
297. May R. M., Oster G. F.— Am. Natur., 1976, v. 110, p. 573.
298. Мельников В. К—ДАН СССР, 1962, т. 144, с. 747; 1963, т. 148, с. 1257.
299. Мельников В. К- — Труды Моск. мат. общ., 1963, т. 12, с. 3.
300. Metropolis N., Stein M. L., Stein P. R.— J. Combinatorial Theory,
1973, v. 15A, p. 25.
301. Misiurewics M.— in: Nonlinear Dynamics/Ed. Helleman.— N. Y.: Am.
N. Y. Acad. Sci., 1980, v. 357, p. 348.
302. Mo К- С— Physica, 1972, v. 57, p. 445.
303. Molchanov A. M.— Icarus, 1968, v. 8, p. 203.
304. Month M., Herrera J. C, (Eds.) Nonlinear Dynamics and the Beam-
Beam Interaction.— N. Y.: American Institute of Physics, AIP Con-
Conference Proceedings, 1979, v. 57.
305. Морозов А. Д.— Ж- вычисл. мат. и мат. физ., 1973, т. 13, № 5, с. 1134.
306. Морозов А. Д.— Диффер. уравнения, 1976, т. 12, № 2, с. 241.
307. Морозов А. И., Соловьев Л. С. Движение заряженных частиц в электро-
электромагнитных полях.— В кн.: Вопросы теории плазмы.— М.: Атомиздат,
1963, т. 2, с. 177.
308. Moser J.~ Nachr. Akad. Wiss. Gottingen. Math. Phys. Ю-, 1962, p. 1.
309. Moser /.— Ann. Scuola Normale Sup. Pisa Ser. Ill, 1966, v. 20, p. 499.
[Имеется перевод: УМН, 1968, т. 23, № 4, с. 179.]
310. Moser J. Stable and Random Motions in Dynamical Systems.— Princeton:
Princeton University Press, New Jersey, 1973.
311. Moser У.—Math. Intelligencer, 1978, v. 1, p. 65.
312. Motz H., Watson С J. H.— Adv. Electron Phys., 1967, v. 23, p. 153.
313. Nayfeh A. Perturbation Methods.— N. Y.: Wiley, 1973. [Имеется пе-
перевод: Найфэ А. Методы возмущений.— М.: Мир, 1976.]
314. Нехорошее Н. Н.~ УМН. 1977, т. 32, № 6, с. 5.
315. Nekrasov A. R.— Nucl. Fusion, 1970, v. 10, p. 387.
316. Nevins W. M., Harte J., Gell K.— Phys. Fluids, 1979, v. 22, p. 2108.
317. Newhouse S., Ruelle D., Takens F. — Commun. Math. Phys., 1978, v. 64,
p. 35.
318. NoidD. W., Koszykowski, Marens R. A.— i. Chem. Phys., J977, v. 67,
p. 404.
319. Northrop T. G. The Adiabatic Motion of Charged Particles.— N. Y.:
Wiley, 1963. [Имеется перевод: Hopmpon Т. Адиабатическая теория
движения заряженных частиц.— М.: Атомиздат, 1967.]
320. Northrop Т. С, Teller Я.— Phys. Rev., 1960, v. 117, p. 215.
Литература 515
321. Northrop Т. G., Liu С. S., Kruskal M. D.~ Phvs. Fluids, 1966, v. 9,
p. 1503.
322. Okuda H., Dawson J.— Phys. Fluids, 1973, v. 16, p. 2336.
323. Оселедец В. Я.—Труды Моск. мат. общ. 1968, т. 19, с. 179.
324. Ott Е.— Rev. Mod. Phys., 1981, v. 53, p. 655.
325. Ott E., Hanson J. D., Antonsen Т. М., Jr.— Bull. Am. Phys. Soc, 1981,
v. 26, p. 1013.
326. Packard N. H., Crutchfield J. P., Fanner J. D., Shaw R. S.— Phys.
Rev. Letters, 1980, v. 45, p. 712.
327. Penrose 0. Foundations of Statistical Mechanics.— Oxford: Pergamon
press, 1970.
328. Percival I. C.— i. Phys., 1974, v. A7, p. 794.
329. Percival I. C— Adv. Chem. Phys., 1977, v. 36, p. 1.
330. Percival I. C.— S. Phys., 1979, v. A12, L57.
331. Percival I. C.— in: Nonlinear Dynamics and the Beam—Beam Intera-
Interaction/Eds. Month, Herrera.— N. Y.: American Institute of Physics, AIP
Conference Proceed., 1979, v. 57, p. 302.
332. Percival !. C, Pomphrey N.— Mol. Phys., 1976, v. 31, p. 97.
333. Percival I. C, Pomphrey N.— Mol. Phys., 1978, v. 35, p. 649.
334. Песин Ю. Б.— ДАН СССР, 1976, т. 226, № 4, с. 774.
335. Песин Ю. Б.— УМН, 1977, т. 32, № 4, с. 55.
336. Poguste О. P.— Nucl. Fusion, 1972, v. 12, p. 39.
337. Poincare H. Les Methodes Nouvelles de la Mecanique Celeste. — Paris:
Gauthier-Villars, 1892. [Имеется перевод: Пуанкаре А. Новые методы
небесной механики, т. 1, 2. Избран, труды.— М.: Наука, 1971—1972.]
338. Пономаренко В. Г., Трайнин Л. Я-, Юрченко В. И., Ненецкий А. Н.—
ЖЭТФ, 1968, т. 55, с. 3.
339. Пустыльников Л. Д.— ДАН СССР, 1978, т. 241, № 5, с. 1035.
340. Рабинович М. И.— УФН, 1978, т. 125, вып. 1, с. 123.
341. Rannou F.— Astron. Astrophys., 1974, v. 31, p. 289.
342. Rechester А. В., Rosenbluth M. N.— Phys. Rev. Letters, 1978, v. 40,
p. 38.
343. Rechester А. В., Stix Т. Н.— Phys. Rev. Letters, 1976, v. 36, p. 587.
344. Rechester А. В., Stix T. H.-~ Phys. Rev., 1979, v. A19, p. 1656.
345. Rechester А. В., White R. В.— Phys. Rev. Letters, 1980, v. 44, p. 1586.
346. Rechester А. В., Rosenbluth M. N., White R. В.—Phys. Rev., 1981,
v. A23, p. 2664.
347. Rognlien T. D.~ in: Proceedings of the 2nd Workshop on Hot Electron
Ring Physics./Ed. Uckan.— Oak Ridge: Oak Ridge National Labora-
Laboratory, Tennessee, 1982, v. 2, p. 545.
348. Rosenbluth M. N.— Phys. Rev. Letters, 1972, v. 29, p. 408.
349. Rosenbluth M. N., Sagdeev R. Z., Taylor J. В., Zaslavskiy G. M.—
Nucl. Fusion, 1966, v. 6, p. 297.
350. Rossler O. E.— Phys. Letters, 1976, v. 57A, p. 397.
351. Rossler O. E.— Z. Naturforsch., 1976, v- 31a, pp. 259, 1168.
352. Roux J. C, Rossi A., BochelartS., Vidal C— Phys. Letters, 1980, v. 77A,
p. 391.
353. Ruelle D.— Trans. N. Y. Acad. Sci., 1973, v. 35, p. 66.
354. Ruelle Д.—Math. Intellegencer, 1980, v. 2, p. 126.
355. Ruelle D., Takens F.— Commun. Math. Phys., 1971, v. 20, p. 167.
[Имеется перевод в сб.: Странные аттракторы/Ред. Синай, Шальников.—
М.: Мир, 1981, с. 117.]
356. Russell D. A., Hanson J. D., Ott E.— Phys. Rev. Letters, 1980, v. 45,
p. 1175.
357. Рютов Д. Д., Ступаков Г. В.— ДАН СССР, 1978, т. 240, № 5, с. 1086.
358. Sagdeev R. Z., Galeev A. A. Nonlinear Plasma Theory.— N. Y.: Benja-
Benjamin, 1969. [См. также в сб.: Вопросы теории плазмы.— М.: Атомиздат,
1973, вып. 7, с. 205.]
359. Saltzman В.—J. Atmos. Sci., 1962, v. 19, p. 329.
516 Литература
360. Samec Т. К-, Hauss В. L., Guest G.— in: Proceedings of the 2nd Works-
Workshop on Hot Electron Ring Physics/Ed. Uckan.— Oak Ridge: Oak Ridge
National Laboratory, Tennesse, 1982, v. 2, p. 531.
361. Schmidt G.— Phys. Fluids, 1962, v. 5, p. 994.
362. Schmidt G. Physics of High Temperatupe Plasmas.— N. Y.: Academic
Press, 2nd ed.," 1979.
363. Schmidt G-— Phys. Rev., 1980, v. A22, p. 2849.
364. Schmidt G., Bia'lek J.— Physica, 1982, v. 5D, p. 397.
365. Schmits R. A., Graziani K- R-, Hudson J. L.— J. Chem. Phys., 1977,
v. 67, p. 3040.
366. Segur H. Lectures given at the International School of Physics (Enrico
Fermi), Varenna, Italy, unpublished.
367. Seidl M.— Plasma Phys. (J. N. E. Pt. C), 1964, v. 6, p. 597.
368. Shaw R.— Z. Naturforsch., 1981, v. 36a, p. 80-
369. Shenker S. J., Kadanoff L. P.— J. Stat. Phys., 1982, v. 4, p. 631.
370. Shepelyansky D. L.— Physica, 1983, v. 8D, p. 208.
371. Shimada /., Nagashima Г.— Prog. Theor. Phys., 1979, v. 61, p. 1605.
372. Siambis J. Guiding Center Motion of Charged Particles in Combined
Mirror Muitipole Cusp Magnetic Fields. Ph. D. Thesis, University of
California, Berkeley, California, 1965.1
373. Siambis J., Northrop T. G.— Phys. F uids, 1966, v. 6, p. 2001.
374. Siegel C. L., Moser J. Lectures on Celestial Mechanics. Grund. d. Math.
Wiss Bd. 187, Springer-Verlag, 1971. [Имеется сокращенный перевод
в кн.: Мозер Ю- Лекции о гамильтоновых системах.— М.: Мир, 1973.}
375. Simo С—J. Stat. Phys., 1980, v. 21, p. 465.
376. Синай Я- Г.— В кн.: Proceed, of the Intern. Congress of Mathemati-
Mathematicians, 15-22 August, 1962.— Uppsala: Almquist and Wiksells, 1963,
p. 540, Sweden.
377. Синай Я- /'•—ДАН СССР, 1963, т. 153, с. 1261-
378. Синай Я- Г— Изв. АН СССР, Сер. мат., 1966, т. 30, № 1, с. 15.
379. Ситников К- Н.— ДАН СССР, I960, т. 133, № 2, с. 303.
380. Slater J. С — Rev. Mod. Phys., 1948, v. 20, p. 473.
381- Smale S.— in: Differential and Combinatorial Topology/Ed. Cairns.—
Princeton: Princeton University Press, New Jersey, 1965.
382. Smale S.— Bull. Am. Math. Soc, 1967, v. 73, p. 747.
383. Smith G. R. Stochastic Acceleration by a Single Wave in a Magnetized
Plasma. Ph. D. Thesis, University of California, Berkeley, California,
1977 (Lawrence Berkeley Lab. Report LBL-6824).
384. Smith G. R., Byers J. A., LoDestro L. L.— Phys. Fluids, 1980, v. 23,
p. 278.
385. Smith G. R., Kaufman A. N.— Phys. Rev. Letters, 1975, v. 34, p. 1613.
386. Smith G. R., Kaufman A. N.~ Phys. Fluids, 1978, v. 21, p. 2230.
387. Smith G. R., Pereira N.~- Phys. Fluids, 1978, v. 21, p. 2253.
388. Solomonoff R. J.— Information Control, 1964, v. 7, p. 1.
389. Соловьев Л. С, Шафранов В. Д.— В сб.: Вопросы теории плазмы/Ред.
Леонтович.— М.: Атомиздат, 1967, вып. 5, с. 3.
390. Sprott J. С, Edmonds P. H'.— Phys. Fluids, 1971, v. 14, p. 2703.
391. Stern D.— J. Math. Phys., 1970, v. 11, p. 2771.
392. Stern D.— i. Math. Phys., 1970, v. 11, p. 2776.
393. Stix Т. Н.— Phys. Rev. Letters, 1973, v. 30, p. 833.
394. Stoddard S. D., Ford J.— Phys. Rev-, 1973, v. A3, p. 1504.
395. Stoker J. J. Nonlinear Vibrations.— N. Y.: Interscience, 1950. [Имеется
перевод: Стокер Дж. Нелинейные колебания в механических и элек-
электрических системах.— М.: ИЛ, 1953.]
396. Swinney H. L., Gollub J. P.— Phys. Today, 1978, v. 31 (August), p. 41.
397. Symon K- R—J. Math. Phys., 1970, v. 11, p. 1320.
398. Symon K- R-, KerstD. W., Jones L. W. et al.— Phys. Rev., 1956, v. 103,
p. 1837.
Литература 517
399. Symon К,- R-, Sessler A. M.— in: Proc. CERN Symp. High-Energy Acce-
Accelerators.— Geneva: CERN, 1956, v. l,p.44. [Имеется перевод в сб.: На-
Накопление релятивистских частиц/Ред. Лебедев.— М.: Атомиздат, 1963,
с. 48.]
400. Szebehely V. Theory of Orbits.— N. Y.: Academic Press, 1967.
401. Tabor M.— Adv. Chem. Phys., 1981, v. 46, p. 73.
402. Takens F.— Indag. Math., 1971, v. 33, p. 379.
403. Taylor J. В., Laing E. W.— Phys. Rev. Letters, 1975, v. 35, p. 1306.
404. Tennyson J. L.— in: Nonlinear Dynamics and the Beam-Beam Interac-
Interaction/Eds. Month, Herrera. — N. Y.: American Institute of Physics, AIP
Conferenae Proceedings No. 57, 1979, p. 158-
405. Tennyson J. L.— Physica, 1982, v. 5D, p. 123.
406. Tennyson J. L., Lieberman M. A., Lichtenberg A. J.— in: Nonlinear
Dynamics and the Beam-Beam Interaction/Eds. Month, Herrera.—
N. Y.: American Institute of Physics, AIP Conference Proceedings No.
57, 1979, p. 272.
407. Timofeev A. V.— Nucl. Fusion, 1974, v. 14, p. 165.
408. Toda M.— Prog. Theor. Phys. Suppl., 1970, v. 45, p. 174.
409. Toda M.— Phys. Letters, 1974, v. 48A, p. 335.
410. Tomita K-, Tsuda I.— Phys. Letters, 1979, v. A71, p. 489.
411. Treve Y.— in: Topics in Nonlinear Dynamics/Ed. Jorna.— N. Y.: Ame-
American Institute of Physics, 1978, v. 46, p. 147.
412. Treve Y.— J. Comput. Phys., 1981, v. 41, p. 217.
413. Tyson J. J.— J. Math. Biol., 1978, v. 5, p. 351.
414. Uckan N. A. (Ed). Proceedings of the 2nd Workshop on Hot Electron
Ring Physics.— Oak Ridge: Oak Ridge National Laboratory, Tennessee,
1982.
415. Ulam S. M.— in: Proceedings of the 4th Berkeley Symp. on Math. Stat.
and Probability. University of California Press, 1961, v. 3, p. 315. [Имеется
перевод в сб: Математика, 1963, т. 7, № 5, с. 137.]
416. Ulam S. M., Von Neumann J.— Bull. Am. Math. Soc, 1947, v. 53, p. 1120.
417. Van Zeijts J. B. J.— Internal D-l Report, Theoretical Physics Group,
Twente University of Technology, Enschede, Netherlands, 1980—1981.
418. VidalC, RouxJ.-C, BachelertS., Rossi A.— in: Nonlinear Dynamics/Ed.
Helleman.— N. Y.: Ann. N. Y. Acad. Sci., 1980, v. 357, p. 377.
419. Von Zeipel H.— Ark. Astron. Mat. Fys., 1916, v. 11, No. 1.
420. Waddell B. V., Rosenbluth M. N., Monticello D. A., White R. В.—
Nucl. Fusion, 1976, v. 16, p. 528.
421. Waddell B. V., Carreras В., Hicks H. R. et al.— Phys. Rev. Letters,
J978, v. 41, p. 1386.
422. Walker J.— Sci. Am., 1978, v. 239, No. 1, p. 152.
423. Walker J., Ford У.— Phys. Rev., 1969, v. 188, p. 416.
424. Wang M. C, Uhlenbeck G. E.— Rev. Mod. Phys., 1945, v. 17, p. 523.
425. Watari Т., Hiroe S., Sato Т., Ichimaru S.— Phys. Fluids, 1974, v. 17,
p. 2107.
426. Wegmann K-, Rossler O. E.— Z. Naturforsch., 1978, v. 33a, p. 1179.
427. Wentzel G.— Z. Phys., 1926, v. 38, p. 518.
428. White R. В., Monticello D. A., Rosenbluth M. N.. Waddell B. V.— in:
Plasma Phys. Contr. Nucl. Fusion.—Vienna: Int. Atom Energy Agency,
1977, v. 1, p. 569.
429. Whiteman K. J., McNamara В.—J. Math. Phys., 1968, v. 9, p. 1385.
430. Whittaker E. T. A Treatise on the Analytical Dynamics of Particles
and Rigid Bodies.— Cambridge: Cambridge University Press, 1964.
(Имеется перевод: Уитпгекер Е. Аналитическая динамика.— М.: ОНТИ,
1937.)
431. Wiedemann #.— in: Nonlinear Dynamics and the Beam-Beam Intera-
Interaction/Eds. Month, Herrera.— N. Y.: American Institute of Physics,
AIP Conference Proceedings, No. 57, 1979, p. 84.
432. Winfree A.— Sci. Am., 1974, v. 230, No. 6, p. 82.
518 Литература
433. Wintrier A. Analytical Foundations of Celestial Mechanics.— Princeton:
Princeton University Press, New Jersey, 1947.
434. Wolf A., Swift J.— Phys. Letters, 1981, v. 83A, p. 184.
435. Wyeth N. C, Lichtenberg A. J., Lieberman M. A.— Plasma Phys., 1975,
v. 17, p. 679.
436. Yamada Т., Kuramoto Y'.— Prog. Theor. Phys., 1976, v. 56, p. 681.
437. Yamazaki H., Oono Y., Hirakawa /(.— J. Phys. Soc. Jpn., 1978, v. 44,
p. 335; J. Phys. Soc. Jpn., 1979, v. 46, p. 721.
438. Zabusky N. J.— J. Math. Phys., 1962, v. 3, p. 1028.
439. Zaiken A. N., Zhabotinsky A. M.~ Nature, 1970, v. 225, p. 535.
440. Заславский Г. М.— ЖЭТФ, 1977, т. 73, № 12, с. 2089.
441. Zastavsky G. M.~ Phys. Letters, 1978, v. 69A, p. 145.
442. Zaslavsky G. M— Phys. Reports, 1981, v. 80, p. 157.
443. Заславский J'. M., Чириков Б. В.— ДАН СССР, 1964, т. 159, с. 306.
444. Заславский Г. М., Чириков Б. В.— УФН, 1971, т. 105, вып. 1, с. 3.
445. Заславский Г. М., Рачко X. Я-— ЖЭТФ, 1979, т. 76, № 5, с. 2052.
446. Zisook А. В., Shenker S. J.— Phys. Rev., 1982, v. A25, p. 2824.
ЛИТЕРАТУРА, ДОБАВЛЕННАЯ ПРИ ПЕРЕВОДЕ
447. Боголюбов Н. Н. Избранные труды.— Киев: Наукова думка, 1969.
448. Алексеев В. М., Якобсон М. В. Символическая динамика и гиперболи-
гиперболические динамические системы. Добавление в книге: Боуэн Р. Методы
символической динамики.— М.: Мир, 1979.
449. Ford /.— Physics Today, 1983, v. 36, No. 4, p. 40.
450. Гапонов-Грехов А. В., Рабинович М. И.— Природа, 1981, № 2, с. 54.
451. Синай Я- Г.— там же, № 3, с. 72.
-352. Чириков Б. В.— там же, 1982, № 7, с. 15.
453. Ландау Л. Д., Лифшиц Е. М. Механика.— М.: Наука, 1973,
454. Toda М.~ Phys. Rep., 1975, v. 18, p. 1.
455. Манаков С. В.—ЖЭТФ, 1974, т. 67, с. 543.
456. Gardner С. S., Greene J. M., Kruskal M. D., Miura R. M.— Phys. Rev.
Letters, 1967, v. 19, p. 1095.
457. Захаров В. Е., Манаков С. В., Новиков С. П., Питаевский Л. П. Тео-
Теория солитонов.— М.: Наука, 1980.
458. Hall L. S. A Theory of Exact and Approximate Configurational Inva-
Invariants.— Preprint UCRL-87094, Lawrence Livermore National Labo-
Laboratory, 1982.
459. Machankov V. G.— Phys. Rep., 1978, v. 35, p. J.
460. Ramani A., Dorizzi В., Grammaticos В.— Phys. Rev. Letters, 1982,
v. 49, p. 1539.
461. Bountis Т., Segur H. Logarithmic Singularities and Chaotic Behavior
in Hamiltonian Systems.—A. I. P. Conf. Proc, 1982, v. 88.
462. Арнольд В. И. Проблема устойчивости и эргодические свойства класси-
классических динамических систем.— Труды Международного конгресса ма-
математиков (Москва, 1966).— М.: Мир, 1968, с. 387.
463. Боголюбов Н. Н., Митропольский Ю. А., Самойленко А. М. Метод
ускоренной сходимости в нелинейной механике.— Киев: Наукова
думка, 1969.
464. Чириков Б. В. Динамика частиц в магнитных ловушках.— Вопросы
теории плазмы, вып. 13.— М.: Энергоиздат, 1983.
465. Эрдейи А. Асимптотические разложения.— М.: Физматгиз, 1962.
466. Чириков Б. В.— ДАН СССР, 1959, т. 125, с. 1015.
467. Чириков Б. В., Шепелянский Д. Л.— ЖТФ, 1982, т. 52, с. 238.
468. Ступаков Г. В.— Письма в ЖЭТФ, 1982, т. 36, с. 318.
469. Schoch A. Theory of Linear and Non-Linear Perturbations of Betatron
Oscillations in Alternating Gradient Synchrotrons.— Geneve: CERN
57-23, 1958.
Литература 519
470. Чириков Б. В., Шепелянский Д. Л.— Ядерная физика, 1982, т. 36,
с. 1563.
471. Чириков Б. В. Нелинейный резонанс.— Новосибирск: НГУ, 1977.
472. Wimtnel Н. К- Lagrangian Formulation of a Consistent Relativistic
Guiding Center Theory.— Preprint IPP 6/218. Garching bei MOnchen:
Max-Planck-Institut fur Plasmaphysik, 1983.
473. Vecheslavov V. V.— Physica, 1982, v. 5D, p. 387.
474. Menyuk C. R. Some Properties of the Discrete Hamiltonian Method.—
Physica D, в печати.
475. Chirikov В. V., Keil ?., Sessler A. M.— J. Stat. Phys., 1971, v. 3, p. 307.
476. Katok A.— Lecture Notes in Physics, 1983, v. 179, p. 47.
477. Чириков Б В, Природа и свойства динамического хаоса. Труды
международного семинара «Теоретико-групповые методы в физике
(Звенигород, 1982). —М.: Наука, 1983, т. II, с. 389.
478. Cushman R.— Trans. Amer. Math. Soc, 1978, v. 238, p. 45.
479. Зиглин С. Л.— ДАН СССР, 1980, т. 251, с. 786.
480. Козлов В. В. Методы качественного анализа в динамике твердого тела.—
М.: МГУ, 1980.
481. Заславский Г. М. Статистическая необратимость в нелинейных систе-
системах.— М.: Наука, 1970.
482. Чириков Б. В. Взаимодействие нелинейных резонансов.— Новосибирск:
НГУ, 1978.
483. Holmes P.— Physica, 1982, v. 5D, p. 335.
484. Sanders J. Л.—Celestial Mechanics, 1982, v. 28, p. 171.
485. Chirikov B. V.— Lecture Notes in Physics, 1983, v. 179, p. 29.
486. Корнфельд И. П., Синай Я- Г., Фомин С. В. Эргодическая теория.—
М.: Наука, 1980.
487. MacKay R. S. Renormalization in Area Preserving Maps. Thesis, Prin-
Princeton University, 1982.
488. Заславский Г. M. Стохастичность динамических систем.— М.: Наука,
1983.
489. Poincare H. Science et methode.— Paris: Flammarion, 1908. (Имеется
русский перевод: Пуанкаре А. Наука и метод.— Одесса, 1910.]
490. Hedlund G. A.— Bull. Amer. Math. Soc, 1939, v. 45, No. 4, p. 241.
491. Hopf ?.— Math. Ann., 1940, v. 117, p. 590.
492. Звонкий А. К-, Левин Л. А.— УМН, 1970, т. 25, № 6, с. 85.
493. Martin-Lot P.— Information and Control, 1966, v. 9, p. 602.
494. Брудно А. А.— УМН, 1978, т. 33, № 1, с. 207.
495. Машины Тьюринга и рекурсивные функции. — М.: Мир, 1972.
496. Былое Б. Ф., Виноград Р. Э., Гробман Д. М., Немыцкий В. В. Теория
показателей^Ляпунова.— М.: Наука, 1966.
497. Алексеев В. М. Символическая динамика.— Киев: Институт матема-
математики, 1976.
498. Бунимович Л. А.— Изв. АН СССР, сер. матем. 1974, т. 38, № 1, с. 213.
499. ОрнстейнЩД. Эргодическая теория, случайность и динамические си-
системы.— М.: Мир, 1978.
500. Schnorr С. P.— Math. Syst. Theory, 1971, v. 5, No. 3, p. 246. [Имеется
перевод в сб.: Сложность вычислений и алгоритмов.— М.: Мир, 1974.]
501. Алексеев В. М.— Мат. сборник, 1968, т. 76, № 1, с. 72.
502. Shimada /., Nagashima Т.— Prog. Theor. Phys., 1979, v. 61, p. 1605.
503. Kolmogoroo A. N.—Math. Ann., 1931, Bd. 104, s. 415. [Имеется пере-
перевод: УМН, 1938, № 5, с. 5.]
504. Kolmogorov A. N.— Math. Ann., 1936, Bd. 113, s. 766.
505. Лифшиц Е. М., Питаевский Л. П. Физическая кинетика.— М.: Наука,
1979.
506. Беляев С. Т. Кинетическое уравнение для разреженных газов в силь-
сильных полях.— В сб.: Физика плазмы и проблема управляемых термо-
термоядерных реакций.— М.: изд-во АН СССР, 1959, т. III, с. 50.
507. Катеу С. F. F.— Physica, 1983, v. 8D, p. 360.
520 Литература
508. Чириков Б. В., Шепелянский Д. Л. Статистика возвратов Пуанкаре
и структура стохастического слоя нелинейного резонанса.— В кн.:
IX Международная конференция по нелинейным колебаниям (Киев,
1981), т. П.— Киев: Наукова думка, 1983.
509. Будкер Г. И. Собрание трудов.— М.: Наука, 1982.
510. Галеев А. А., Сагдеев Р. 3.— ЖЭТФ, 1967, т. 53, с. 348.
511. Николаевский Е. С, Щур Л. К..— Письма в ЖЭТФ, 1982, т. 36, с. 176.
512. Нехорошее Н. Н. Метод последовательных канонических замен пере-
переменных.— Добавление в книге: Мозер Ю- Лекции о гамильтоновых
системах.—М.: Мир, 1973, с. 150.
513. Вивальди Ф., Форд Дж., Израйлев Ф. М., Чириков Б. В., Шепе-
Шепелянский Д. Л. Модуляционная диффузия в нелинейных колебательных
системах.— В кн.: IX Международная конференция по нелинейным
колебаниям (Киев, 1981), т. II — Киев: Наукова думка, 1983.
514. Чириков Б. В.— ДАН СССР, 1967, т. 174, с. 1313.
515. Сивухин Д. В.— В кн.: Вопросы теории плазмы. Вып. 1.— М.: Гос-
атомиздат, 1963, с. 7.
516. Морозов А. И., Соловьев Л. С.— В кн.: Вопросы теории плазмы.
Вып. 2.— М.: Госатомиздат, 1963, с. 177.
517. Kishinevskij М. E., Lysyanskij Р. В., Ryutov D. D. et al.— in: Plasma
Physics and Controlled Nuclear Fusion Research 1978. Vol. II.—Vienna:
IAEA, 1979, p. 411.
518. Zabusky N. J.— Journal of Computational Physics, 1981, v. 43, No. 2,
p. 195.
519. Харкевич А. А. Спектры и анализ.— M.: Физматгиз, 1962.
520. Thomae S., Grossmann S— Phys. Letters, 1981, v. 83A, p. 181.
521. Колмогоров А. Н., Тихомиров В. М.~ УМН, 1959, т. 14, № 2, с. 3.
522. Farmer J. D., Ott Е., Yorke J. A.— Physica, 1983, v. 7D, p. 153.
523. Штерн В. Н.— ДАН СССР, 1983, т. 270, с. 582.
524. Feigenbaum М. J.— Comm. Math. Phys., 1980, v. 77, p. 65.
ZSS-Jgggutse O. P.— Nucl. Fusion, 1972, v. 12, p. 39.
526. Шарковский А. И.— Укр. мат. журн., 1964, т. 16, с. 61.
527. Бунимович Л. А.— Мат. заметки, 1970, т. 8, вып. 2, с. 205.
528. Jakobson М. V.— Comm. Math. Phys., 1981, v. 81, p. 39.
529. Афраймович В. С, Быков В. В., Щильников Л. П.— Тр. Моск. мат.
общ-ва, 1982, т. 44, с. 150.
530. Израйлев Ф. М., Чириков Б. В.— В кн.: Труды совещания по програм-
программированию и математическим методам решения физических задач.—¦
Дубна: ОИЯИ, 1974, с. 266.
531. Израйлев Ф. М., Рабинович М. И., Угодников А. Д. Препринт ИЯФ
СО АН СССР, 82—70, Новосибирск, 1982.
532. Арнольд В. И. Дополнительные главы теории обыкновенных диффе-
дифференциальных уравнений.— М.: Наука, 1978.
533. Плыкин Р. В.— Матем. сб., 1974, т. 94, с. 243.
534. Ладыженская О. А. Математические вопросы динамики вязкой жидко-
жидкости.—М.: Наука, 1970.
535. Монин А. С, Яглом А. М. Статистическая гидромеханика.— М.: Наука,
1965 (ч. 1), 1967 (ч. 2).
536. Монин А. С— УФН, 1978, т. 125, с. 97.
537. Гольдштик М. А., Штерн В. Я.—ДАН СССР, 1981, т. 257, с. 1319.
538. Структурная турбулентность./Ред. Гольдштик.— Новосибирск, Инсти-
Институт теплофизики СО АН СССР, 1982.
539. Ландау Л. Д., Лифшиц Е. М. Механика сплошных сред.— М.: Гостех-
издат, 1953.
540. Neuenberg N.. Rudnik J.— Phys. Rev., 1981, v. B24, p. 493.
541. Gollub J. P., Benson S. V.— J. Fluid Mech., 1980, v. 100, p. 449.
542. Мирабель А. П., Монин А. С.— Успехи механики, 1979, т. 2, с. 47.
543. Kraichnan R. H., Montgomery D.— Rep. Prog. Phys., 1980, v. 43, p. 547.
544. Sinai Ya. G.— i. Stat. Phys., 1982, v. 29, p. 401.
Литератури 521
545. Ладыженская О. А.— ДАН СССР, 1972, т. 205, с. 318.
546. Hopf E.— Comm. Pure Appl. Math., 1948, v. 1, p. 303.
547. Ни В.— Physics Reports, 1982, v. 91, p. 233.
548. Бари Н. К- Тригонометрические ряды.— M.: Физматгиз, 1961.
549. Коломенский А. А., Петухов В. А., Рабинович М. С.— В сб.: Некото-
Некоторые вопросы теории циклических ускорителей.— М.: изд-во АН СССР,
1955, с. 7.
550. Дыхне А. М., Чаплин А. В.— ЖЭТФ, 1961, т. 40, с. 666.
551. Родионов С. Н.— Атомная энергия, 1959, т. 6, с. 623.
552. Gibson G., Jordan W., Lauer E.— Phys. Rev. Letters, 1960, v. 5, p. 141.
553. Кадомцев Б. 5.— Письма в ЖЭТФ, 1981, т. 33, с. 361.
554. Жаботинский А. М. Концентрационные автоколебания.— М.: Наука,
1974.
555. Шноль С. Э., Смирнов Б. Р., Задонский Г. Н., Ровинский А. Б.— Хи-
Химия и жизнь, 1982, № 7, с. 68.
556. Шнирельман А. И.— УМН, 1974, т. 29, № 6, с. 181.
557. Ландау Л. Д., Лифшиц Е. М. Квантовая механика.— М.: Наука, 1974.
558. Дайсон Ф. Статистическая теория энергетических уровней сложных
систем.— М.: ИЛ, 1963.
559. Колмогоров А. Н. Общая теория динамических систем и классическая
механика.— В кн.: Международный математический конгресс в Амстер-
Амстердаме 1954 г.—М.: Физматгиз, 1961, с. 187.
560. Бабин А. В., Вишик М. И.— УМН, 1983, т. 38, № 4, с. 133.
именной указатель
Аблоаиц (Ablowitz) 57
Авез (Avez) 199, 200, 290
Алексеев В. М. 307, 487
Альфвек (Alfven) 490
Аносов Д. В. 19, 302
Арнольд В. И. 15, 18, 186, 190, 199, 200,
290, 341. 364, 465, 491
Бардет (Bardet) 493
Баунтис (Bountis) 58, 171, 172, 174, 271
Белоусов Б. П. 494
Бенеттин (Benettin) 294, 295, 297, 308,
313, 315, 317
Берн (Berk) 494
Берман Г. П. 497
Бериштейи (Bernestein) 492
Берри (Веггу) 162, 290, 299, 496
Берс (Bers) 98, 139
Бивинс (Bivins) 407
Билек (Bialek) 253, 273
Биркгоф (Birkhoff) 14, 15, 104, 199, 487
Боголюбов Н. Н. 13, 104, 114, 115. 317,
319, 444, 490
Борн (Born) 92
Брамбилла (Brambilla) 394
Брахич (Brahic) 220, 221, 228
Бриджес (Bridges) 467
Брудно А. А. 307
Брунс (Brims) 487
Будкер Г. И. 336, 395, 489
Бэкстер (Baxter) 492
Вайдал (Vldal) 495
Ватанабе (Watanabe) 494
Галеев А. А. 336, 381, 395
Гальгани (Galgani) 408
Гаррен (Garren) 491
Гарридо (Garrido) 147, 487
Гейзал (Geisal) 442
Гелл (Qell) 395)
t--^ta,1u (Goldstein) 20
Голуб" luollub) 481
Грин (Green G.) 181, 247, 489
Грин (Greene J.) 194, 214, 220, 247, 252,
269. 273, 274, 279, 308, 500
Гроссман (Grossmann) 449
Густавсон (Gustavson) 65, 487
Депрн (Deprit) 147, 487
Джакалья (Giacaglia) 92, 104, 147, 154
Довейл (Doveil) 248, 277, 503
Драгт (Dragt) 199, 200, 490, 491
Дуннет (Dunnett) 122, 142
Дьюар (Dewar) 147, 149
Erep (Jaeger) 247, 325, 492
Жаботииский А. М. 494
Жданова Т. А. 324
Жебехели (Szebehely) 488
Забуский (Zabusky) 407
Зальцман (Saltzman) 476
Заславский Г. М. 220, 221, 294, 425, 496,
497
Зигель (Siegel) 488
Зисок (Zisook) 450, 451
Зубарев Д. Н. 114
Израйлев Ф. М. 324, 467, 469
Казати (Casati) 497
Кари (Сагу) 147, 164. 165, 332
Карий (Кагпеу) 98, 103, 139, 142, 332
Кауфман (Kaufman) 98, 139, 147
Клейн (Klein) 248
Колле (Collet) 448
Колмогоров А. Н. 15, 82, 162 168 186,
300, 318, 406, 487
Коломенский А. А. 489
Контопулос (Contopoulos) 190, 317 487
488
Копель (Kopell) 495
Коэн (Cohen) 375, 381, 382, 386, 491
Кратчфилд (Crutchfield) 418, 484
Крилин (Krilin) 490
Крускал (Kruskal) 13, 88, 104, 114, 490
Крылов Н. М. 13, 114. 319, 444
Крылов Н. С. 294, 300
Кулсруд (Kulsrud) 88
Куммер (Kummer) 488
Курант (Courant) 46, 489
Лакина (Lacina) 490
Ландау Л. Д. 20, 319, 478, 479
Лансфорд (Lunsford) 142, 190, 273, 279
Ласлет (Laslett) 489
Лебедев А. Н. 489
Левис (Lewis) 46
Лейнг (Laing) 142
Ли (Li) 248
Либерман (Lieberman) 111, 220, 221, 231,
291, 324, 325, 335, 353, 359, 473, 492
Линдштедт (Lindstedt) 82, 85
Литлджон (Littlejohn) 115, 147
Лифшиц Е. М. 478
Лихтенберг (Lichtenberg) 111, 126, 220,
221, 222, 231, 235, 247, 252, 291, 324,
325, 335, 394, 489, 492, 494, 503
Лич (Leach) 46
Лози (Lozi) 422
Лоренц (Lorenz) 19, 20, 76, 77, 79, 448,
476, 480
Лэнфорд (Lanford) 414
Ляпунов А. М. 294
Мак-Кай (МасКау) 501
Мак-Лафлин (McLaughlin) 457
Мак-Намара (McNamara) 65, 104, 142,
147, 148, 154, 160, 164. 487
Манневиль (Manneville) 484
Маркус (Marcus) 497
Марсден (Marsden) 348
Мартин-Лёф (Martin-Lof) 306
Мейс (Meiss) 332
Мельников В. К. 199, 240, 348, 457, 459
Метрополис (Metropolis) 442
Мцсюревич (Misiurewic7) 422
Мптропольский Ю. А. 13, 114
Мозер (Moser) 15, 162, 186, 190, 193, 199,
227. 488
Морозов А. Д. 457
Найфе (Neyfeh) 147
Невинс (Nevins) 395, 399
Некрасов А. К. 492
Нехорошев Н. Н. 73, 364, 365
Нирветберг (Nierwetberg) 442
Нойес (Noyes) 495
Нортроп (Northrop) 121, 154, 490
Оселедец В. И. 294, 297
Отт (Ott) 422, 478, 497
Паста (Pasta) 14, 56, 348, 406
Перейра (Pereira) 267, 268
Персиваль (Percival) 248, 287, 288
Лесин Я. Б. 294, 301
Петухов В. А. 489
Погуце О. П. 395
Помо (Pomeau) 484
Пуанкаре (Poincare) 13, 15, 16, 28, 82,
87, 90, 104, 197, 200, 240, 294, 348, 487
Пустыльников Л. Д. 221
Предметный указатель
523
Рабинович М. С. 489
Рассел (Russel) 424
Раулэндс (Rowlands) 375, 381, 382, 385,
467
Ренно (Rannou) 308
Речестер (Rechester) 326, 331, 336, 338,
392
Рёслер (Rossler) 416
Родионов С. Н. 491
Розенблют (Rosenbluth) 247, 392, 491
Ронлии (Rognlien) 493
Рудник (Rudnick) 443
Рютов Д. Д. 385
Рюэль (Ruclle), 19, 478, 480, 495
Сагдеев Р. 3. 336, 381, 395
Саймон (Syrnon) 46
Самек (Samec) 493
Сегур (Segur) 57
Сейдл (Seidl) 492
Снамбис (Siambis) 491
Синай Я. Г. 17, 71, 300, 496
Ситников К- Н. 487
Смейл (Smale) 199, 487
Смит (Smith) 98, 139, 267, 268, 493
Скайдер (Snyder) 46
Спротт (Sprott) 492
Стикс fStix) 392
Стоддард (Stoddard) 408
Ступаков Г. В. 385
Суиннн (Swinney) 481
Табор (Tabor) 249
Тейлор (Taylor) 142
Теллер (Teller) 490
Теннисон (Tennyson) 73, 341 34? 353
368, 375. 379, 381
Тода (Toda) 51
Томае (Thomae) 449
Треве (Treve) 422, 478
Тэкенс (Takens) 19, 193, 478, 480
Уайес (Wyeth) 493
Уайт (White) 326, 331, 336
Уайтмен (Whiteman) 65, 104 154 487
Уинтиер ^Wintrier) 488
Уиттекер (Whittaker) 20. 55, 154, 486, 487
Улам (Ulam) 14, 56, 68, 220. 348, 406
Уотерс (Waters) 407
Фармер (Farmer) 424, 425
Фейгенбаум (Feigenbaum) 20, 434, 438,
452, 481
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Адиабатический инвариант 13, 17, 31,
37, 88, 104, 124, 134, 154
— процесс 87, 111, 112, 349
Адиабатическое возмущение 106 107 154
367
Аносова системы 302 — 305, 308
Аттрактор, геометрия 74, 75, 78 417 — 422
— Лоренца 78 — 80, Н7
— область притяжения 414
— простой 19, 73, 74, 76 — 80 413, 414
440 — 442, 464
— странный (хаотический) 19, 20, 74 — 76,
78, 80, 416 — 425, 463, 464, 469
— — размерность 19, 74, 422 — 425
— Хенона 419 — 422
Бернулли свойство 304
— сдвиг 303, 304
— система 303—305
Ферми (Fermi) 14, 56, 68, 204, 220, 348.
4 06
Филд (Field) 495
Филоненко Н. Н. 392
Финн (Finn) 147, 199, 200, 392
Форд (Ford) 54. 190, 247, 273, 279. 294
299, 407, 408
Фрёлинг (Froehling) 425
Фрёшле (Froeschle) 294, 348, 407
Фукуяма (Fukuyama) 98, 139. 269
Фурсов В. С. 489
Xaruxapa (Hagibara) 488
Хастье (Hastie) 491
Хатори (Hatori) 494
Хаулэнд (Howland) 147, 164
Хедлунд (Hedlund) 294
Хейлес (Heiles) 54, 64, 290, 294, 314
Хеллеман (Helleman) 165, 171, 270, 290,
433, 448, 453, 478, 486
Хенон (Henon) 16, 54, 64, 204, 290. 294,
314, 416, 419, 421
Хереворд (Hereward) 489
Хертвек (Hertweck) 490
Ховард (Howard) 405, 491, 493
Холл (Hall) 56, 58
Холмс (Holmes) 348, 457, 461, 463
Хольт (Holt) 57
Хопф (Hopf) 294, 478
Хори (Hori) 147, 487
Хътоберман (Huberman) 443, 450, 451. 484
Цанг (Tsang) 473
Цейпелъ (Von Zeipel) 13, 87, 90
Чандрасекар (Chandrasekhar) 490
Чарчилл (Churchill) 488
Чириков Б. В. 17, 43, 68, 73, 111. 121,
122, 127, 164, 181, 193—195, 220.
221, 246, 247, 249, 252. 257, 262, 294,
311,332, 342, 353, 360, 365, 366, 375,
381, 382, 386, 469, 486, 488, 490, 491, 492,
497
Шарковский А. И. 440
Шейдекер (Scheidecker) 294, 407
Шепелянский Д. Л. 497
Шлютер (SchlQter) 490
Шмидт (Schmidt) 252, 253, 273
Штерн (Stern) 104, 154
Эдмондс (Edmonds) 492
Экман (Eckmann) 448, 478, 484
Эминицер (Eminhizer) 165
Эскгшде (Escande) 248, 277, 503
Бильярдная модель 348 353
Бифуркации 77, 78, 232, 415, 416, 430 —
432, 440, 442, 453
— обратные 416, 448, 449
— теория 415, 416, 433 — 438, 454 — 457,
497
Вырождение 126, 129, 130, 137, 138. 189 —
191
Вычет 269
— средний 271
Газ твердых шариков 70. 305
Галыпона доска 305
Гамильтониан автономный 23, 24, 59,
100, 148, 292, 298
— канонические преобразования 90—98,
132—134, 147, 180, 189, 259 — 261
— неавтономный 97, 98, ПО, 111, 154
184, 235, 236, 255, 259, 354
524
Предметный указатель
— переход к отображению 182, 183
— стандартный 43, 127, 236
— фурье-разложение 92, 95, 97, 98 12 3,
124, 132, 144 189, 235, 236, 281, 474 —
476
Гармонический осциллятор 36, 89, 129
— — медленно изменяющийся 87, 111,
119, 121, 156. 157
Гетероклинные точки 199 — 201
Гиперболические точки (траектории) 40,
196 — 201, 204, 206, 218 219, 230, 232,
254, 458 — 460, 462
Гомоклинные точки 198 — 201, 306, 307. 458
Грина критическое значение 275 — 277
Грубость см. Устойчивость структурная
Депри ряды 149, 239
Дисснпативные системы 73, 410
Диффузия Арнольда 18. 19, 59, 71—73,
249, 292, 317, 341, 346, 347, 350 — 352
357—365, 367
— внешняя 332, 337, 338, 375
— в пространстве действий 317
— модуляционная 18, 19, 342, 366
— неоклассическая 336, 395
— по резонансам 335, 353
— резонанса 382
— резонансное каналирование 375» 385.
386
— скорость 331, 337, 340, 353, 372, 373,
377, 378, 399 — 402
квазилинейная 326, 383
— тензор 377 — 379
— уравнение 291, 319 — 321
— частиц в ловушке 386
Золотое сечение см. Число вращения
Иерархия инвариантов 110, 111
— резонансов 62, 203, 204
Инвапдаит см. Интеграл движения
' пнв'ар'иантная кривая (поверхность) 17,
18, 33, 60 — 69, 72, 102, 103, 178, 185 —
200 .215, 231, 232, 247, 248, 272, 273,
279 — 281, 350
Инвариантное распределение (мера) 291,
444 — 448, 466
— — на аттракторе 444—448, 466
Интеграл действия 13, 20, 31
Интегралы движения 33, 34, 48, 55, 60,
98, 176, 203
— — адиабатические см. Адиабатический
инвариант
глобальные 38, 47. 52, 60, 98, 143 —
146
— — изолирующие 348, 487
— — инволюция 38
— — локальные 124, 200
К-системы 300, 301, 303, 305
Канторово множество 76, 422 — 424
Касательный вектор 295, 296
Квазипериодические колебания 35, 49,
74, 178, 294, 305
Компонента движения 232, 292, 294, 301,
311, 312, 314
Корреляции 332
— связь с коэффициентами переноса 321,
325, 326
— убывание 244, 332
Коэффициенты переноса 291, 319, 321, 325
Крупноструктурное разбиение («огрубле-
(«огрубление») 97, 299, 300
•Ляпунова показатели 244, 294, 301, 442 —
444, 448
— — вычисление 310
— — обобщенные 297
, 58
Теория возмущений
Магнитные ловушки 110, 111, 386, 490
Малые знаменатели си. Резонансные зна-
знаменатели
Марковский процесс 318
Матрицы 207 — 209, 214 — 220, 296
— снмплектическке 209 — 212
Маятник 39, 42. 93, 95, 152—154, 237
238, 263 — 269
— как модель резонанса 42, 127, 236, 255
— точное решение 39 — 42, 267
Мельникова—Арнольда интеграл 239 — 241
465
Метод Венцеля — Крймерса — Бриллюэна
(В КБ) 13
— Грина 247, 248, 269
— Дцннета—Лейнга—Тейлора (ДЛТ)
142 — 146
— касательных Ньютона 163, 181, 213
— Уиттекера конструирования интегри-
интегрируемых систем 55, 58
— усреднения см. ~
асимптотическая
— фурье-траекторий 326—332
Методы вариационные 287
— — в теории возмущений 168—174
Модель Контопулоса 316, 317
— Л еннарда- Джонса 408
— Лоренца 20, 57, 76, 77, 475 — 477, 484
— Ферми—Паста—Улама 14, 405 — 407
— Хенона—Хейлеса 16, 54, 58, 59, 63 —
67, 171—174, 313
Нелинейность колебаний 86,187 — 191
— — параметр 127, 189
— — умеренная 194, 195
Неподвижные (периодические) точки 125,
127, 130, 195, 214, 215, 228, 229, 232 —
234, 242, 250 — 253, 276, 277, 430
Непрерывная дробь 271—273, 277
Округления ошибки 290, 308, 309, 335
Отображение Арнольда 302, 305
— Вогелара 500, 501
— в сечении Пуанкаре 79, 179, 180, 238.
241, 242, 411
— гамильтониан 183, 184, 235, 236, 255, 256
— диссиггативное 464, 465. 468
— Заславского 425
— инволюции 181, 213, 214, 233, 242
— каноническое 179—182, 184, 228
— Ко.плана—Йорке 425
— квадратичное 204, 427—429
— линеаризованное 207, 214 — 220, 229,
296, 298. 321
— логистическое 428, 429, 447, 448
необратимое 76, 426
— обратимое 411
— одномерное 76, 79, 80, 233, 234, 426,
— поворота 179—182, 195, 204, 293, 333,
382
_ Пуанкаре 79, 179, 235, 238, 293, 348,
411, 453
— сепаратрисное 241, 250
— стандартное 181, 331,338, 382
— Улама 222 — 224, 227, 242, 249, 250,
321, 325, 334, 468
Параметры подобия 433 — 438, 451, 456,
457, 497 — 503
Пенлеве свойство 47 — 59
Перекрытие реэонансов 71, 257, 367 — 369,
405
критерии 17, 68, 246, 247, 289, 367
— — простое 257
_ _ улучшенное 258 — 262
Перемежаемость 484, 485
Переменные действие — угол (фаза) 31,
34 36, 37, 41, 90, 95, 107, 342, 361, 389
— дрейфовые 99, 100
Предметный указатель
525
— канонические 107, 178, 222, 223, 300,
323, 324
— обобщенные 22, 148, 154
— разделение 38. 115
— смешанные 147
Перемешивание 17, 70, 298—300, 305, 448
Переход к стохастичностн 245
— — турбулентности 478
Периодическая 6-функция 184, 235
Периодические траектории 60, 74, 125,
167, 178, 179, 207
Правило двух третей 256, 288
Предельный цикл 74, 416, 464, 480 — 482
Преобразование каноническое 95, 107,
123, 148, 149, 162, 354, 362, 378, 389
— пекаря (отображение) 71, 299, 305
Производящая функция 90, 182, 362, 378
Ли 25, 148. 180, 259
— — смешанных переменных 95, 123
фурье-разложенне 92, 95 — 98, 101,
109, 259, 369
Пространство действий 344—347
Пуанкаре сечение 15, 31—34. 53, 60, 61,
65 — 67, 69, 102, 103, 140, 141, 177, 411
Резонанс волна —частица 98—104, 135,
144—146, 161, 162, 280
— вторичный 61, 62, 130, 138, 139, 192,
202, 203, 205, 237, 263, 281
— высших гармоник 125, 269 — 274, 365
— — порядков 109
— дрейфовый 394—397
— многомерный 341
— первичный 61, 62, 126—130, 146, 186,
195, 200 — 205, 225, 228, 236, 237, 257 —
260
— прохождение 112, 113, 367
— связи 359, 375, 379, 390
— центр 127—129, 132, 134, 263, 397
Резонанса два 279 — 281
Резонансные знаменатели 83, 87, 89, 96,
98, 109, 187
— — устранение 123, 160
—¦ — — глобальное 142
— поверхности 343—346, 379
Резонансов взаимодействие 360, 364
— уровни 139, 168
Ренормализация 135, 248, 277 — 279, 433 —
438, 455 — 457, 501—503
— в стохастическом слое 257, 269
— Грина 269 — 277
— для двух резонансов 248, 279 — 287
— точыая'теория 433 — 435, 440, 453, 497
Рэлея— Бенара конвекция 20, 67, 475, 476
Сверхадиабатичность 491
Секулярные члены 82, 85
Сепаратриса 39, 41, 42, 49, 61 — 64, 67,
73, 128, 191, 197 — 200, 206, 234, 237, 267
Символическая траектория 304
Системы, близкие к интегрируемым 24,
36, 42, 59, 62, 89, 90, 180, 305, 310
— интегрируемые 38, 51, 54, 55, 70, 125,
176 — 180, 310, 315
— — конструирование 55
примеры 39, 51, 177
— квантовые 307, 309, 495
Сложность алгоритмическая 306, 307
Случайность 290, 294, 299, 305, 307
— связь со сложностью 306, 307
Случайные последовательности 306, 307
— фазы (приближение) 70, 71, 291, 322
Собственные векторы 207, 215 — 220, 296,
297, 303
— значения 207, 215 — 220, 230, 297, 303
Спектр мощности 79, 438 — 440, 449 — 453
Стохастическая накачка 353
Стохастический слой 61 — 63, 65, 71 — 73,
237, 238, 242, 243, 261—263, 347
— — мозуляцнонн ый 366 — 371
— — толстый 349 — 332. 351
— — тонкий 350—352, 357
Стохастичность глобальная 70, 71, 194,
215, 246, 248, 249, 254, 290
— граница 226, 231, 242, 246, 253 — 256
— критерии 200, 241. 246, 257, 291, 310
312, 315
— локальная 69, 245, 246, 254
— области 74, 201—206,245
— параметр 181, 249
— свойства 291, 298, 442, 449
Теорема Алексеева — Брудно 307
— Лаувилля 27, 412
— Пуанкаре—Бенднксона 413, 416
— Пуанкаре— Биркгофа 195
Теория возмущений асимптотическая 13,
87, 104, 105, 114—118, 203, 235, 236
— — вариационная с и. Вариационные ме-
методы
— — каноническая 81, 107, 369
— — классическая 89
Па 145
— — неканоническая 114
— — резонансная 17. 43, 121, 203 235,
262, 263, 390
— — сверхсходящаяся 82. 162
— Колмогорова—Арнольда — Мозера (КАМ)
38, 60, 68, 165, 184, 185, 203, 224
Тоды цепочка 47, 51—54, 57
Тор см. Инвариантная поверхность
Турбулентность гидродинамическая 474
— химическая 494
Удвоение периода 76, 430 — 432, 453 — 457,
498
Уравнение Дюффинга 461—465
— Фоккера — Планка — Колмогорова (ФПК)
318, 468 — 472
У-системы см. Аносова системы
Ускорение Ферми 59, 68, 69, 220, 262,
263, 468
Устойчивость движения, граница 231, 245
линейная 127—130, 207, 215, 228,
242, 247, 252, 253
островки 224, 225, 232, 245, 251 —
254, 469
— структурная 302, 308
Фазовая траектория 128, 129, 131, 178.
254, 414, 462
Фазовое пространство 18, 19, 25 — 27,
32, 58, 254, 255, 299, 307, 458
Разбиение 245, 246, 251, 300
— — расширенное 28 — 30, 95, 223
— — сокращенное 29, 33
фязовые колебания 130. 134, 226, 236
частота 136, 130, 236, 384
Фокус 74, 414—416, 463, 464, 468
Фрактальная размерность см. Аттракторы
Фрактальные диаграммы 277 — 279
Хаос см. Стохастичность, Случайность
Число вращения 179, 180, 241, 256. 281
— — золотое сечение 194, 272, 275 — 277
— — иррациональное 185
рациональное 195, 272, 279
Эллиптические точки (траектории) 39, 42,
197, 201, 204, 216 — 218, 224 232, 254
Энергетическая поверхность 292, 297,
343 — 346, 375, 376, 379, 385
Энтропия (КС-энтропня) 244, 300, 301,
303 — 305, 307, 513
— вычисление 301, 311, 315
—- связь с показателями Ляпунова 301
Эргодичность 14, 17, 70, 291, 299, 305,
487
ОГЛАВЛЕНИЕ
Предисловие редактора перевода 5
Предисловие 11
Глава 1. Общий обзор и основные представления 13
§ 1.1. Вводные замечания * 13
* § 1.2. Теория преобразований в механике 20
* 1.2а. Канонические преобразования 21
* 1.26. Движение в фазовом пространстве 25
* 1.2в. Переменные действие — угол 34
§ 1.3. Интегрируемые системы 38
* 1.3а. Одна степень свободы 38
* 1.36. Линейные дифференциальные уравнения 43
1.3в. Несколько степеней свободы 47
* § 1.4. Системы, близкие к интегрируемым 59
* 1.4а. Две степени свободы 59
* 1.46. Более чем две степени свободы 71
§ 1.5. Диссипативные системы 73
1.5а. Странные аттракторы 74
1.56. Модель Лоренца 76
Глава 2. Каноническая теория возмущений 81
§ 2.1. Введение 81
2.1а. Степенные ряды 84
2.16, Асимптотические ряды и малые знаменатели 87
2.1 в. Влияние резонансов 89
* § 2.2. Классическая теория возмущений 89
* 2.2а. Одна степень свободы 90
* 2.26. Несколько степеней свободы 95
§ 2.3. Адиабатическая инвариантность 104
* 2.3а. Введение и основные понятия 104
* 2.36. Каноническая адиабатическая теория 107
* 2.3в. Медленно изменяющийся гармонический осциллятор . 111
2.3г, Неканонические методы 114
§ 2.4. Резонансная теория возмущений 121
* 2.4а. Устранение резонансных знаменателей 123
* 2.46. Вторичные резонансы 130
* 2.4в. Резонансное взаимодействие волны и частицы 135
2.4г. Глобальное устранение резонансных знаменателей . . 142
§ 2.5. Метод преобразований Ли 146
2.5а. Общая теория 148
2.56. Ряды Депри 149
2.5в. Адиабатические инварианты 154
§ 2.6. Сверхсходимость 162
2.6а. Метод Колмогорова 165
2.66. Периодические траектории 167
2) Звездочкой отмечены параграфы и пункты, содержащие основной
материал.
Оглавление 527
Глава 3. Отображения и линейная устойчивость 175
* § 3.1. Гамильтоновы системы как канонические отображения . . . 176
* 3.1а. Интегрируемые системы 176
* 3.16. Системы, близкие к интегрируемым 180
* 3.1в. Уравнения Гамильтона и отображения 182
* § 3.2. Типичное поведение канонических отображений 184
* 3.2а. Иррациональные числа вращения и теория КАМ .... 185
* 3.26. Рациональные числа вращения и структура резонансов 195
* 3.2в. Полное описание нелинейного отображения 200
* 3.2г. Численный пример 204
§ 3.3. Линеаризованные уравнения 206
3.3а. Собственные значения и собственные векторы 207
* 3.36. Двумерные отображения 212
* З.Зв. Линейная устойчивость и инвариантные кривые .... 215
* § 3.4. Ускорение Ферми 220
* 3.4а. Физические задачи и их модели 221
* 3.46. Численное моделирование 224
* 3.4в. Периодические точки и их линейная устойчивость . . . 228
* 3.4г. Бифуркации 232
* 3.4д. Уравнения Гамильтона 235
* § 3.5. Движение в окрестности сепаратрисы 236
* 3.5а. Вынужденные колебания маятника 238
* 3.56. Сепаратрисное отображение 241
Глава 4. Переход к глобальной стохастичности 244
* § 4.1. Введение 244
* 4.1а. Качественное описание критериев перехода 246
* 4.16. Стандартное отображение 249
* § 4.2. Перекрытие резонансов 257
* 4.2а. Схема получения критериев 257
* 4.26. Вычисление критериев перекрытия 257
§ 4.3. Вторичные резонансы 263
4.3а. Центр резонанса 263
4.36. Сепаратриса 267
* § 4.4. Резонансы высоких гармоник 269
* 4.4а. Основы метода Грина 269
* 4.46. Численные эксперименты 274
§ 4.5. Метод ренормализации для двух резонансов 279
§ 4.6. Вариационные методы 287
* § 4.7. Заключение 288
Глава 5. Стохастическое движение и диффузия 290
§ 5.1. Введение 290
§ 5.2. Основные понятия 291
* 5.2а. Эргодичность 291
* 5.26. Характеристические показатели Ляпунова 294
5.2в. Основные свойства стохастичности 298
5.2г. Случайность и ее численное моделирование 306
§ 5.3. Определение показателей Ляпунова и КС-энтропии 310
5.3а. Аналитические оценки 311
5.36. Численные методы 312
§ 5.4. Диффузия в пространстве действий 317
* 5.4а. Уравнение Фоккера—Планка 318
* 5.46. Коэффициенты переноса 321
* 5.4в. Стационарные и нестационарные решения 324
5.4г. Корреляционные поправки к коэффициентам переноса . 325
§ 5.5. Влияние внешнего шума 332
5.5а. Введение 332
528 Оглавление
5.56. Диффузия в присутствии резонансов 335
Глава 6. Многомерные колебания 341
* § 6.1. Резонанс многомерных колебаний 341
* 6.1а. Геометрия резонансов 342
* 6.16. Примеры диффузии Арнольда 347
§ 6.2. Скорость диффузии вдоль резонансов 353
* 6.2а. Расчет диффузии в модели стохастической накачки . . . 353
6.26. Диффузия по резонансу связи 359
6.2в. Много резонансов 364
6.2г. Модуляционная диффузия 366
§ 6.3. Внешняя диффузия 375
6.3а. Резонансное каналирование диффузии 375
6.36. Диффузия резонанса 382
§ 6.4. Диффузия в тороидальных магнитных ловушках 386
6.4а. Динамика магнитных линий 386
6.46. Дрейфовые поверхности и диффузия в статических по-
полях 392
6.4в. Диффузия в нестационарных полях 395
6.4г. Самосогласованная задача 402
§ 6.5. Системы со многими степенями свободы 404
Глава 7. Диссипативные системы 410
§ 7.1. Простые и странные аттракторы 410
7.1а. Основные свойства 411
7.16. Примеры странных аттракторов 416
7.1 в. Геометрия странных аттракторов 422
§ 7.2. Одномерные необратимые отображения 426
7.2а. Основные свойства 426
7.26. Периодическое движение 430
7.2в. Хаотическое движение 442
§ 7.3. Двумерные отображения и связанные с ними потоки 453
7.3а. Бифуркации удвоения периода 453
7.36. Движение вблизи сепаратрисы 457
7.3в. Вычисление инвариантных распределений 466
§ 7.4. Проблема турбулентности 474
7.4а. Представление Фурье 474
7.46. Переход к турбулентности 478
Дополнение А. Некоторые приложения 486
АЛ. Небесная механика 486
А.2. Ускорители и встречные пучки 488
А.З. Магнитные ловушки 490
А.4. Нагрев плазмы 492
А.5. Химическая динамика 494
А.6. Квантовые системы 495
Дополнение Б. Теория бифуркаций в гамильтоновых системах . . . 497
Список основных обозначений ' • • 504
Литература §06
Именной указатель 522
Предметный указатель 523