Стохастические и хаотические колебания - Неймарк Ю.И., Ланда П.С.

Author: Неймарк Ю.И. Ланда П.С.

Tags: колебания акустика механика физика

Year: 1987

Similar

Основы теории колебаний.

Элементы теории колебаний

Теория колебаний

Сборник задач по теории колебаний. Часть 1

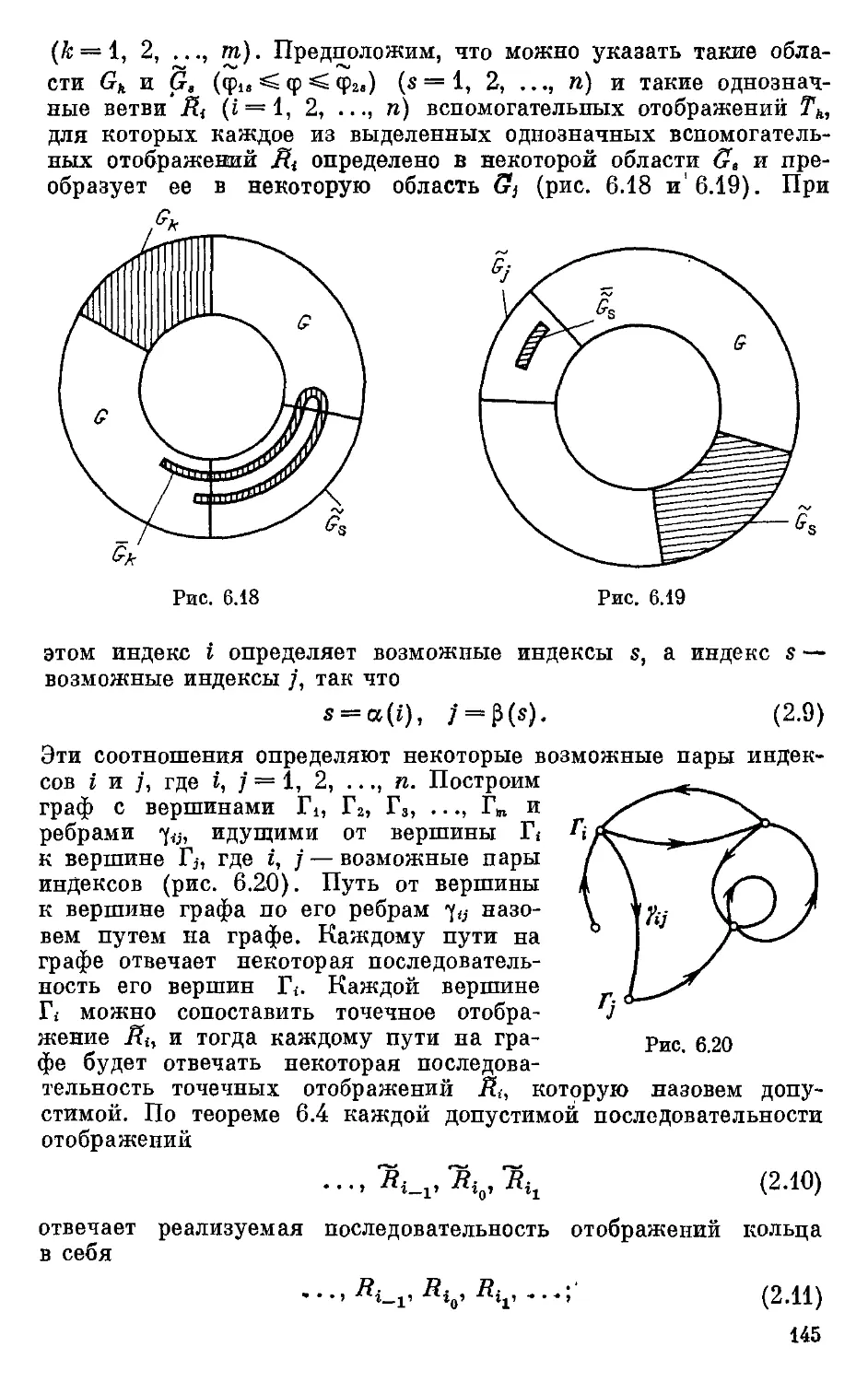
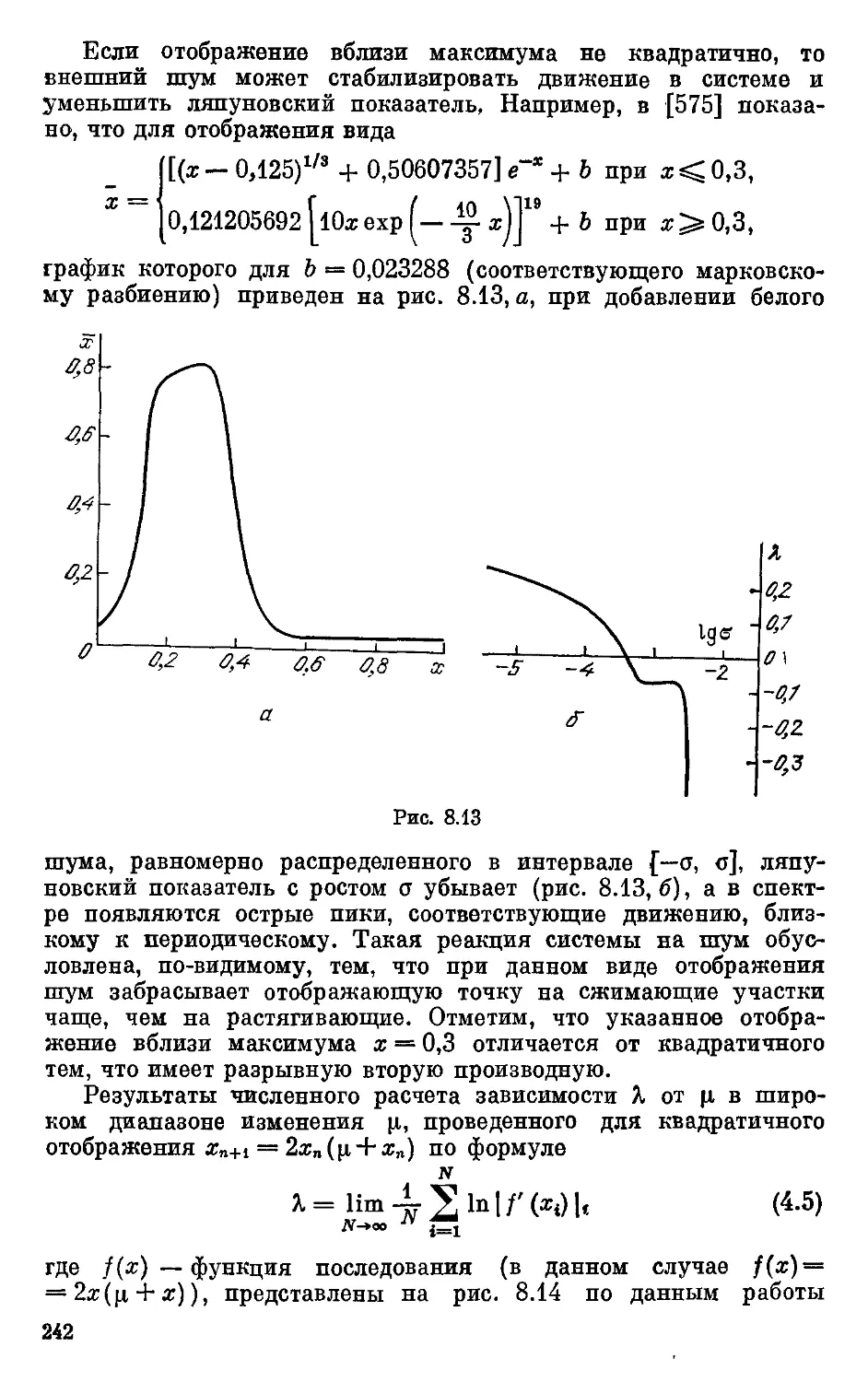
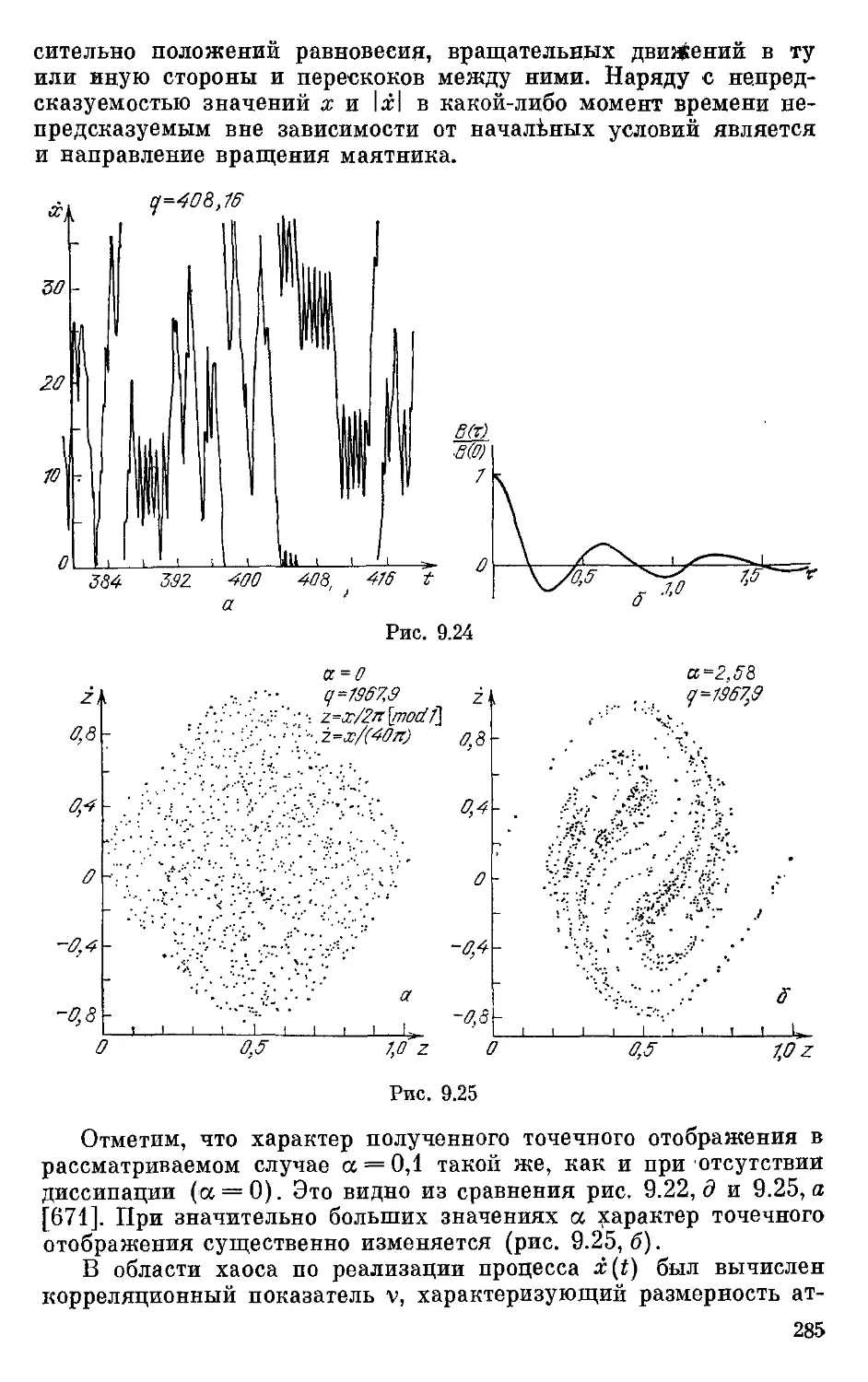
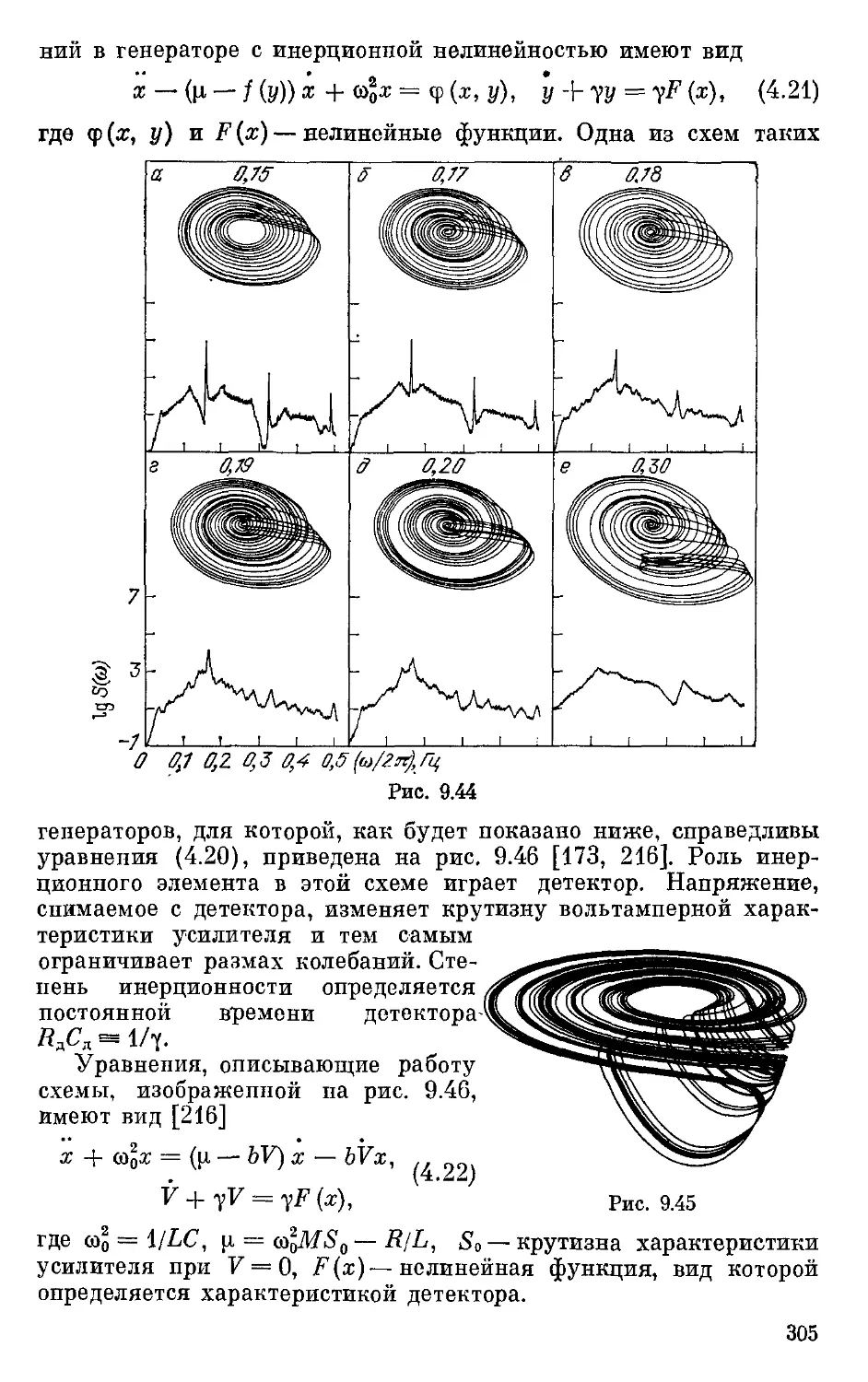
Text

Ю. И. НЕЙМАРК
П. С. ЛАНДА
СТОХАСТИЧЕСКИЕ
И ХАОТИЧЕСКИЕ
КОЛЕБАНИЯ
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1987

ББК 22.213
Н46
УДК 534
Н е й м а р к Ю. И., Л а н д а П. С. Стохастические и хаотические коле-
колебания.— М.: Наука. Гл. ред. физ.-мат. лит., 1987.— 424 с»
Излагается новый бурно развивающийся раздел теории нелинейных ко-
лебаний — стохастические и хаотические автоколебания в динамических си-
системах. Исследование этих проблем весьма актуально для многих областей
пауки, позволяет по-новому взглянуть на известные явления, например тур-
турбулентность в жидкости, газе и плазме, предсказывать возможность слож-
сложного поведения конкретных систем разпой природы. В книге приведено
множество примеров механических, физических, химических и биологиче-
биологических систем, в которых наблюдаются стохастические и хаотические ко-
колебания.
Для специалистов в области теории нелинейных колебаний, научных ра-
ботвиков, инженеров, аспирантов и студентов старших курсов, иптересую-
щихся указанными проблемами.
Табл. 18. Ил. 331. Библиогр. 693 назв.
Рецензент
доктор физико-математических наук В. М. Волосов
1703030000—>181 ^ Издательство «Наука».
Н пко/по\ Q7 76-87 ^© Главная редакция
Uoa(UiZ)-a/ ^ физикв-математичесьой
литературы, 1987

ОГЛАВЛЕНИЕ
Предисловие 5
Глава 1. Математические модели детерминированных дискретных
и распределенных динамических систем 7
§ 1. Простейшие типовые модели дискретных динамических си-
систем 8
§ 2. Хаотические движения детерминированных дхптмических си-
систем 22
§ 3. Простейшие математические модели распределенных дина-
динамических систем 27
§ 4. Дискретное описание распределенных динамических систем 33
§ 5. Модели локально активных сплошных сред 39
Глава 2. Порядок и хаос — две основные обшие тенденции в эволю-
эволюции динамических систем 41
§ 1. Порядок и хаос — устойчивость и неустойчивость ... 42
§ 2. Явления временной синхронизации 50
§ 3. Временной и пространственный порядок и хаос .... 53
Глава 3. Преобразователи, усилители п генераторы стохастичности 57
§ 1. Преобразователи стохастичности 57
§ 2. Усилители стохастичлости 61
§ 3. Генераторы стохастичности 68
§ 4. Настоящая ли стохастичность у стохастических и хаотиче-
хаотических движений детерминированных диламических систем? 76
Глава 4. Краткий обзор исследований, связанных с возникновением
проблемы хаотических и стохастических движений и теорией тур-
турбулентности 79
Глава 5. Локальные фазовые портреты простейших установившихся
движений и их бифуркаций 93
§ 1. Состояния равновесия 93
§ 2. Бифуркации состояний равновесия 99
§ 3. Фазовые портреты в окрестности периодических движений . 108
§ 4. .Бифуркации периодических движений 110
§ 5. Тороидальные иптегральные многообразия 119
Глава 6. Стохастические и хаотические аттракторы 124
§ 1. Вспомогательные отображепия и последовательности точеч-
точечных отображений 126
§ 2. Переход от «негатива» к «позитиву» и исследование типовых
ситуаций возликновеиия хаоса 136
§ 3. Условия возникновения хаотических и стохастических аттрак-
аттракторов 159
3

Глава 7. Бифуркации и пути возникновения хаоса и стохастичности 162
§ 1. Общее описание дерева возможных бифуркаций .... 164
§ 2. Серии бифуркаций 168
§ 3. Бифуркации и стохастический аттрактор в системе Лоренца 184
§ 4. Бифуркации и фазовый портрет осциллятора и ротатора с
параметрическим возбуждением 196
§ 5. О возникновении хаоса и стохастичпости в диссипативпых
динамических системах 209
Глава 8. Количественные характеристики стохастических и хаоти-
хаотических движений и некоторые универсальные закономерности при
переходах «порядок» — «хаос» и обратно 217
§ 1. Статистические характеристики , 217
§ 2. Ляпуновскне показатели. Размерность и энтропия стохасти-
стохастического аттрактора 227
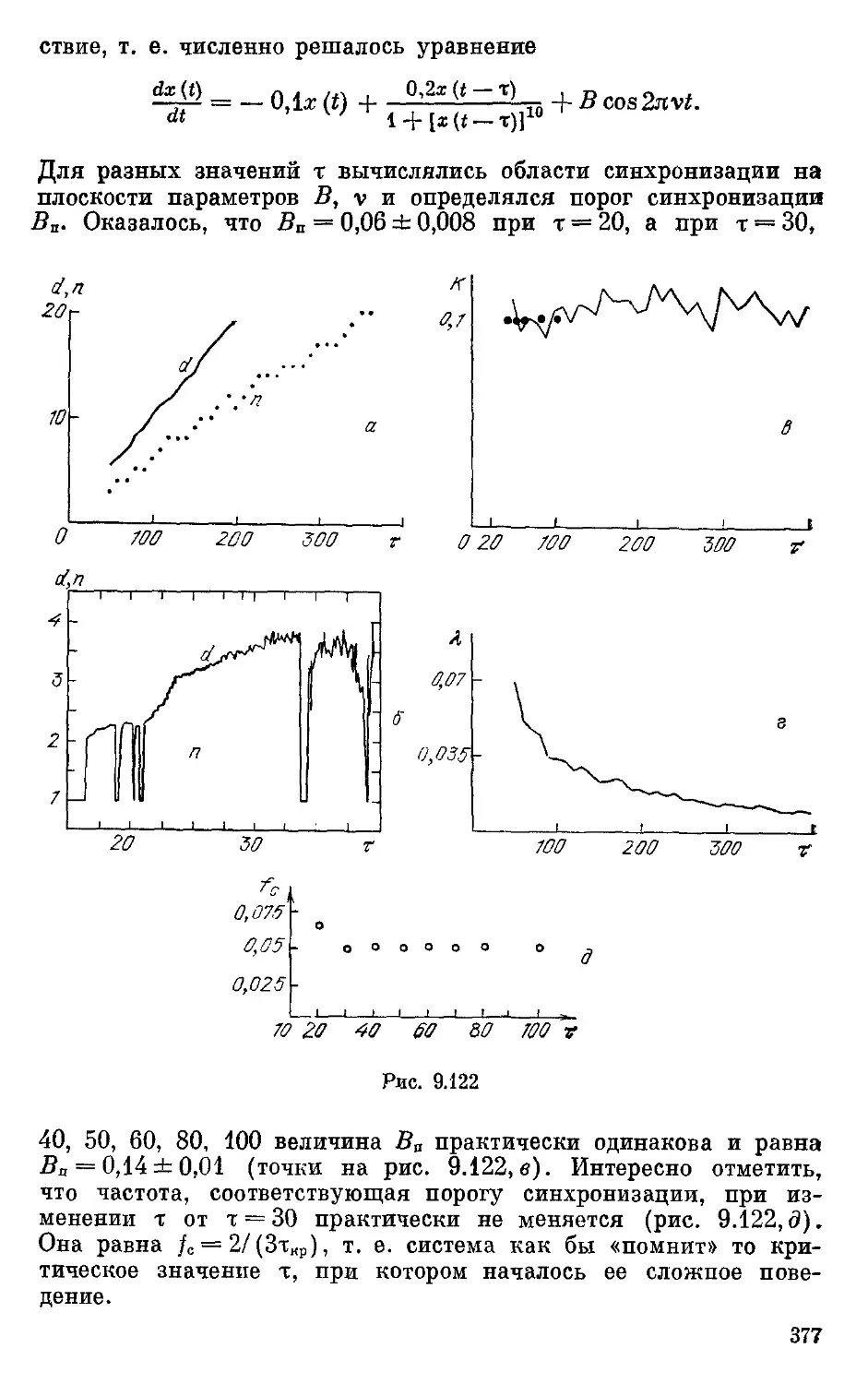
§ 3. Порог синхронизации как количественная характериствка
хаотических движений 237
§ 4. Некоторые универсальные закономерности при переходах «по-
«порядок — хаос» и аналогия с фазовыми переходами . . . 239
Глава 9. Примеры механических, физических, химических и биоло-
биологических систем, в которых возможны хаотические и стохастиче-
стохастические движения 262
§ 1. Нелинейный осциллятор с отрицательным трепием и удара-
ударами и другие системы с разрывными характеристиками . 262
§ 2. Генераторы на туннельных диодах 264
§ 3. Нелинейные осцилляторы с периодическим внешним воз-
воздействием 267
§ 4. Уравнения Лоренца и другие системы третьего порядка . 288
§ 5. Действие гармонической внешней силы на генераторы пе-
периодических и хаотических колебаний 313
§ 6. Взаимодействие генераторов колебаний различных типов 329
§ 7. Некоторые дискретные модели турбулентности .... 334
§ 8. Примеры моделей химической кппетики 342
§ 9. Систолы с запаздыванием и другие распределенные си-
системы 358
§ 10. Стохастичность в квантовых системах 383
Список литературы , 394

«Изучение природы есть наиболее продуктив-
продуктивный источник математических открытий.
Предлагая конкретную задачу, она дает пре-
преимущество исключения неясных задач и гро-
громоздких вычислений»
Ж. Фурье
Перед учеными стоит вопрос знакомый:
Порядок или хаос — что первичней,
Как днух начал соотнести законы3
Бессилен здесь, увы, подход привычный..»
В. ГолъОшмидт
(Отрывок из полыюго перевода
М. А. Гольдштика и В. Н. Штер-
Штерна |131] «Оды каскаду» В. Гольд-
шмидта [468])
«Если не грешить против логики, вообще не-
невозможно прийти к чему-либо»
А. Эйнштейн
ПРЕДИСЛОВИЕ
Открытие нерегулярных колебаний в детерминировапных ди-
динамических системах различной природы (физических, механи-
механических, технических, химических, биологических, экономических)
стало одной из крупнейших научных сенсаций последних лет,
вызвавшей громадный поток теоретических и экспериментальных
работ. Уже появилось немало обзоров и сборников статей (на-
(например [120, 122, 141, 143, 219, 257, 293, 313, 329, 339, 341, 413,
433, 484, 499, 525, 598, 665]), нескольких монографий [23, 157,
237, 336, 483, 655] и популярных работ [121, 168, 328, 626]. Соот-
Соответствующие разделы вошли в некоторые учебные пособия [100,
314, 317]. Для литературы по колебаниям и волнам характерно
разделение книг на общие и специальные. К книгам общего
плана можно отнести {15, 92, 96, 100, 111, 132, 243—245, 252,
269, 307, 314, 346, 352, 359, 360], а также [157, 237], посвящен-
посвященные главным образом гамильтоновым системам; к более специаль-
пым, в которых преимущественно рассматриваются системы кон-
конкретной физической природы,— [89, 90, 102, 103, 107, 116, 172,
174, 193, 194, 216, 217, 251, 318, 337, 340, 345, 347-350, 358].
Предлагаемая вниманию читателей книга, по мнению авторов,
имеет общий характер и посвящена стохастическим и хаотиче-
хаотическим колебаниям в диссипативных системах. В ной авторы дела-
делают попытку подвести некоторые итоги и выразить свое понима-
понимание проблемы.
Установление и признание того факта, что в сравнительно
простых системах без видимых случайных источников возможны
сложные непредсказуемые движения, названные впоследствии
стохастическими и хаотическими,— несомненпый успех прежде
всего теории колебаний. Он представляет собой такой же скачок
в понимании времепной и пространственной эволюции динами-

ческих Систем, как в свое время открытие регулярных автоко-
автоколебаний. О стохастических и хаотических движениях детермини-
детерминированных динамических систем естественно поэтому рассказы-
рассказывать с позиций теории колебаний, с точки зрения ее общих пред-
представлений и методов исследований. Наиболее эффективным
методом при изучении стохастических и хаотических движений
динамических систем является метод точечных отображений
[13, 15, 88, 100, 124, 259, 261, 267, 269, 287, 311, 312]. Он ши-
широко используется в книге. Поскольку рассматриваемые движе-
движения носят случайный характер, то важную роль играют также
статистические методы. В какой-то мере они также нашли от-
отражение в книге. Исследование хаотических и стохастических
движений конкретных систем, как правило, не может быть про-
проведено без привлечения современной вычислительной техники.
Алгоритмическое и программное обеспечение здесь играют дале-
далеко не последпюю роль (см., например, [283]), однако в книге
об этом пе говорится.
Особый интерес проблемы стохастических и хаотических ко-
колебаний состоит в том, что она объединяет усилия исследова-
исследователей разных специальностей — математиков, механиков, физи-
физиков, химиков, биологов.
Главы 1—7 написаны Ю. И. Неймарком, § 1 главы 8 —
П. С. Ланда и Ю. И. Неймарквм, § 2—4 главы 8 и глава 9 (кроме
§ 10) — П. С. Ланда, § 10 гл. 9 о стохастических движениях кван-
квантовых систем написан Б. А. Гришаниным.

Глава 1
МАТЕМАТИЧЕСКИЕ МОДЕЛИ
ДЕТЕРМИНИРОВАННЫХ ДИСКРЕТНЫХ
И РАСПРЕДЕЛЕННЫХ ДИНАМИЧЕСКИХ СИСТЕМ
Настоящая глава носит вводный характер. В ной описываются
простейшие математические модели детерминированных дипами-
ческих систем в виде дифференциальных уравнений, заданных
в фазовом пространство и определяющих временное изменение
фазового состояния. В плане фазовой трактовки движений дина-
динамических систем и колебательных явлений происходит первое
знакомство с хаотическими движениями детерминированных ди-
динамических систем.
Математическая модель играет в теории колебаний двоякую
роль: это и идеализированное описание реальных динамических
систем, и математическая модель, отображающая различные ко-
колебательные явления: гармонические колебания, нарастающие и
затухающие колебания, автоколебания, жесткий и мягкий режи-
режимы их возникновения, вынужденные колебания, резонанс, пара-
параметрическое возбуждение колебаний, стохастические и хаотиче-
хаотические колебания, различные волновые явления, бегущие и стоя-
стоячие волны, возникновение ударных волн, различные тины взаи-
взаимодействия волн и многое другое.
Мир динамических моделей стал поистине необъятным: по-
помимо астрономии, механики, физики и техники он охватывает
ныне и такие менее традиционные области, как, например, химия
[ИЗ, 152, 199, 309, 356], биология [112, 199, 319] и эконо-
экономика [135]. Все это неисчерпаемое разнообразие моделей не под-
поддается ни описанию, ни достаточно разумной классификации.
Тем не менее из бесконечного множества моделей можно выде-
выделить осповные простейшие и наиболее характерные модели.
Сколько-нибудь полный перечень даже простейших типовых мо-
моделей также достаточно обширен и заведомо различен у спе-
специалистов в разных областях науки. Приводимые ниже типовые
простейшие модели — пересечение этих перечней, т. е. модели,
необходимые и знакомые всем, кто занимается изучением коле-
колебаний и волн.

Помимо описания простейших типовых моделей, в этой главе
приводятся сравнительно новые, в некотором смысле более
сложные модели локально возбудимой среды и обсуждаются дис-
дискретные описания распределенных динамических систем, в связи
с чем вводятся понятия временного генератора и пространствен-
пространственного формирователя.
§ 1. Простейшие типовые модели дискретных
динамических систем
Гармонический осциллятор. Идеальными моделями гармони-
гармонического осциллятора являются груз массы тп иа пружине с жест-
жесткостью к (механическая модель) и электрический коптур с ем-
емкостью С и самоиндукцией L (электрическая модель) (рис. 1.1).
Явления диссипации энергии в обоих мо-
моделях не учитываются: нет потерь энер-
энергии в деформируемой пружине, сопротив-
сопротивления среды- движениям груза, сопротив-
сопротивления в проводах электрического кон-
контура, утечки заряда в конденсаторе, излу-
излучения электромагнитных волн. Энергия
Рис. 1.1 по рассеивается, она сохраняется и по-
постоянна.
Изменения положения х и соответственно заряда q в этих
идеальных моделях описываются линейным дифференциальным
уравнением второго порядка
£+0)^ = 0, A.1)
где величина ю равна соответственно 1/к/т и Yl/(LC). Задание
положепия x(ta) = Xo и скорости x(t!l) = xl в начальный момент
времени t = tu однозначпо определяет решение уравнения A.1):
х (t) = х0 cos w (t — t0) -f ^ sin ю (t — у, A.2)
и тем самым а; и ж в любой последующий момент времени t ^ t0.
Согласно A.2) измепопие х во времени при любых начальпых
условиях представляет собою гармонические колебания с одной
и той же частотой ю и разными амплитудами и фазами.
Фазовым пространством гармопического осциллятора является
двумерная плоскость х, х. Отдельные движепия A.2) на этой
фазовой плоскости х, х изображаются замкнутыми кривыми —
эллипсами (рис. 1.2). Точке ж = £ = 0, лежащей внутри этих
замкнутых кривых, отвечает состояние равновесия. Замкнутые
фазовые кривые рис. 1.2 вместе с состоянием равновесия образу-
образуют фазовый портрет гармонического осциллятора.
Отметим, что замкнутость фазовых траекторий этого фазового
портрета отражает факт сохранения энергии, выражаемый соот-

ношением
хг + (£>zx = const,
A.3)
которое получается интегрированием дифференциального урав-
уравнения A.1).
К дифференциальному уравнению A.1) приводит не только
рассмотрение колебаний груза на пружине или заряда конден-
конденсатора, замкнутого на самоиндукцию,
но и в том или ином приближении —
малых колебаний физического маятпи-
ка, строительных конструкций, машин
и мехапизмов, атомов, молекул и мно-
многих других систем.
Линейный осциллятор. Учет в меха-
механической и электрической моделях
(рис. 1.1) диссипации эпергии в виде
дополнительного члена в уравпении
A.1), линейпого по скорости движепия
груза или по току в контуре, приводит к несколько более общей
математической модели
i; + 26i + (йгх = 0, A.4)
получившей название линейный осциллятор.
Решение дифференциального уравнения A.4) при а2 — б2 =
= Q2 > О представимо в виде
х = e~S(f~fо) \х0 cos Q (t - 10) + *г +Q X" sin Q(t — у], A.5)
а при ю2 — б2 < 0 — в виде
'(г~'о), A.6)
Рис. 1.2
х = ■
к-к
где Xt,2 = — б ± Тб2 — о2, а х0 и х,, как и ранее, начальные значе-
значения х и х при £ = £о.
Член 26i в уравнении A.4) учитывает диссипацию энергии:
из уравнения A.4) следует, что
A.7)
Величина, стоящая в скобках,— это с точностью до постоянного
множителя полная эпергия осциллятора. Коэффициент б поло-
яштелен, поэтому со временем полпая эпергия уменьшается до
тех пор, пока х не обратится в пуль. Таким образом, линейный
осциллятор с б > 0 описывает затухающие колебания.
Однако коэффициент б может быть и отрицательным. При
б < 0 линейный осциллятор описывает нарастающие колебания
или пеколебательный уход от состояния равповесия.
В моделях, представленных на рис. 1.1, б<0 соответствует
так называемым отрицательному трению и отрицательному
9

сопротивлению. Отрицательность параметра б и вызываемая ею
раскачка системы обусловлены какими-то посторонними источ-
источниками энергии, какими-то механизмами ее подкачки. Этими ме-
механизмами могут быть падающие участки характеристики трения
или вольтамперной характеристики, например туннельного дио-
диода, а также клапанные механизмы подкачки энергии, происхо-
происходящей за счет направленных обратных связей, при которых дви-
движение осциллятора порождает силы, усиливающие это движение.
Таким образом, линейный осциллятор описывает как явление
затухания первоначального возмущения, так и явление его нара-
нарастания, как колебательный, так
и апериодический характер
этих затуханий и нарастаний.
£<в1 /!И1ГХ ^ \&>0 В первом случае состояпие рав-
равновесия х = х = 0 устойчиво,
а во втором — неустойчиво. Фа-
зовые портреты, отвечающие
\^__^^/ >^ этим двум разным случаям,
рис 13 ПРИ ®2 > ^>2 представлены на
рис. 1.3.
Консервативный осциллятор. Линейный осциллятор является
обобщением гармонического осциллятора, учитывающим процес-
процессы рассеяния и подкачки энергии и вообще любые процессы,
приводящие к экспоненциальному затуханию или нарастанию
первоначальных возмущений. Другим обобщением гармоническо-
гармонического осциллятора является консервативный осциллятор
В механической модели, представленной на рис. 1.1, это соответ-
соответствует учету нелинейной зависимости силы упругости пружины
от ее растяжения, а в электрической модели — учету зависимо-
зависимости емкости конденсатора от его заряда. При таком обобщении
гармонического осциллятора сохраняется замкнутость фазовых
траекторий, отражающая существование интеграла энергии:
|
-|_ + V (х) = const, A-9)
х
где F (*) = [
о
При Qx^> 0 и $@) = 0 фазовый портрет консервативного ос-
осциллятора имеет такой же вид, как и фазовый портрет гармони-
гармонического осциллятора. При функции Q{x) более общего вида фа-
фазовые портреты могут быть более сложпыми. Такие более слож-
сложные фазовые портреты при Q (х) = ах + Ьх3 изображены на
рис. 1.4.
Во времена Гюйгенса большой интерес вызывала задача об
изохронности колебапий, т. е. о независимости периода колеба-
колебаний от амплитуды. Уравнение A.8) описывает неизохронные
10

колебания, а уравнение A.1) — изохронные гармонические коле-
колебания. Поэтому консервативный осциллятор иногда называют
еще неизохронным или ангармоническим осциллятором.
Широко известным примером уравнения вида A.8) является
уравнение физического маятника
A.10)
" , mgl . n
ф + -у-этф = 0.
Его характерная особенность состоит в том, что функция @(ф) —
периодическая. Существенно также, что если раньше фазовое
Ь<0
а>0,Ь>0
Рис. 1.4
пространство было двумерной плоскостью х, х, то теперь это —
двумерный цилиндр (рис. 1.5). Цилиндричность фазового про-
пространства физического маятника обусловлена не только перио-
периодичностью функции Q(q>), но и цикличностью переменной х
(в данном случае х — это угловая переменная ф). Мыслим слу-
случай, когда х — не угловая переменпая, а периодичность функции
Q(x) связана с периодической структурой силового поля. На
рис. 1.6, а показан фазовый портрет физического маятника, а на
рис. 1.6,6 — фазовый портрет материальной точки, движущейся в
периодическом силовом поле вида Q (х) = со2 sin x. Ясно, что фи-
физически это разные системы. Чтобы различать их, отнесем фи-
физический маятник к консервативным ротаторам, под которыми
понимаются системы с цилиндрическим фазовым пространством,
описываемые уравнением вида A.8), в то время как консерва-
консервативный осциллятор, также описываемый уравнением вида A.8),
имеет в качестве фазового пространства двумерную плоскость.
В этой связи уместно подчеркнуть, что математическая модель
динамической системы определяется ее фазовым пространством и
11

оператором изменения ее фазового состояния [269, 286]. Опера-
Оператор изменения фазового состояния задан для любого состояния,
т. е. для любой точки фазового пространства, или, что то же,
он задан на фазовом пространстве. В случае консервативного ро-
ротатора функция Q(x) задана
на окружности, в случае ос-
осциллятора — на прямой. Один
оператор еще не определяет
динамической системы; необхо-
необходимо также указать, где этот
оператор определен, каково про-
пространство состояний системы.
Математическим образом
всех движений динамической
системы является ее фазовый
портрет. Фазовый портрет дает
пе только геометрическое изо-
Рис. 1.5 бражение отдельных движений,
состояний равновесия, перио-
периодических, хаотических и стохастических движений, но и опре-
определяет «логику» поведения динамической системы, его зависи-
зависимость от параметров.
Заметим, что в ^случае физического маятника и материальной
точки в периодическом силовом поле периодичность функции
Q (х) обусловлена совершенно различными причинами. В первом
а Рис. 1.6
случае — это следствие цикличности угловой переменной, задаю-
задающей положение маятника на окружности, во втором — следствие
периодичности силового ноля.
Позволим себе еще пояснить фазовый портрет физического
маятника, изображенный на рис. 1.6, а. Из дифференциального
уравнения физического маятника A.10) следует интеграл энергии
V2<P2 — «2 cos ф = h (со2 = gl/J).
A.11)'
12

Зависимость между ф и ф, определяемая соотношением A.11)'
с некоторым значением постоянной h, геометрически представ-
представляется кривой на фазовом цилиндре <р, <р. При всевозможных
значениях h мы получаем на цилиндре семейство фазовых кри-
кривых (рис. 1.6, я), представляющее фазовый портрет всевозможных
движений физического маятника. Фазовым кривым, вырождаю-
вырождающимся в точки О и О', отвечают нижнее и соответственно верх-
верхнее положения равновесия маятника. Кривым, охватывающим
точку О, отвечают всевозможные периодические колебательные
движения маятника; кривым, охватывающим цилиндр,— всевоз-
всевозможные периодические вращательные движения маятника. На
фазовом портрете видно, как переходят друг в друга различные
движения маятника при плавном изменении энергии h (пара-
(параметра h). Минимальному значению энергии h=—gl/J отвечает
нижнее равновесие маятника О.' С ростом h возникают колеба-
колебания возрастающей амплитуды (замкнутые фазовые траектории,
охватывающие точку О), значению h — gl/J отвечают три дви-
движения — верхнее положение равновесия О' и два движения S,
предельные к верхнему положению равновесия. При дальнейшем
росте h возникают вращательные движения в одну и другую
сторону.
Из фазового портрета физического маятника непосредственно
видно, что нижнее равновесие маятника устойчиво, а верхнее
неустойчиво. Это следует из того, что при значениях, близких
к —gUJ, маятник остается вблизи нижнего равновесия, а при
близких к gl/J маятник далеко уходит от верхнего равновесия.
Рассмотрим теперь изменения, вносимые диссипацией в дви-
движения и фазовый портрет консервативного осциллятора или ро-
ротатора. Речь идет о системе, описываемой уравнением
х + 28х + О{х) = 0. A.12)
Умножая это уравнение на х, находим, что
to* A.13)
где V(x) определяется, как и ранее в формуле A.9). Пусть фа-
фазовый портрет системы A.12) при 6 = 0 известен. Он состоит из
линий уровня функции W(x, x) = 42x2 + V(x). Согласно A.13)
фазовая точка (х, х) при б > 0 движется так, что переходит с
линий уровня с большим значением на линии уровня с меньшим
зпачением W(x, х),.
Это означает, что с появлением диссипации фазовые портреты
консервативных осцилляторов примут вид, показанный на
рис. 1.7, а фазовый портрет физического маятника (консерва-
(консервативного ротатора) — на рис. 1.8.
Осциллятор Ван-дер-Поля. Дифференциальные уравнения
A.1) и A.8) описывают периодические колебания, дифферен-
дифференциальное уравнение A.4)—экспоненциально нарастающие и
13

затухающие колебания. В качестве следующей типовой модели,
описывающей процессы возбуждения и установления периодиче-
периодических колебаний (автоколебаний) можно указать на осциллятор
Ван-дор-Поля
х-26хA-ах2)+а*х = 0. A.14)
Дифференциальное уравнение A.14) не инте^ируется в квад-
квадратурах и исследовалось обычными численными методами
а>0, Ь<0
а<0,Ь>0
a>0,b>o
Рис. 1.7
решения дифференциальных уравнений. В наиболее интересном
случае (б >0, а > 0) фазовый портрет уравнения Ван-дер-Поля
представлен на рис. 1.9. Из него видно, что перед нами автоко-
лебательпая система с одним единственным глобально устойчивым
>Ч
Рис. 18
Рис. 1.9
периодическим движением (предельным циклом). При ма-
малом б > 0 его исследование возможно известным методом Ван-
дер-Поля. При этом находится, что амплитуда автоколебаний
приближенно равна 1/21а, а частота равна со.
14

Осциллятор и ротатор. Естественным обобщением дифферен-
дифференциальных уравнений A.1), A.4), A.7), A.8), A.12) и A.14)
является уравнение вида
х + 26(х, x)x + Q(x) = 0. A.15)
При 6 (х, х) = 0 это — консервативный осциллятор, при б (х, х) =
= const и Q{x) = (a2x — это линейный осциллятор и при 8(х, х) =
= 26A — ах2) и Q(x)= (Л2х — это осциллятор Ван-дер-Поля. При
б (ж, i) = 0, Q (х) = со2 sin x и цялиндричности фазового простран-
пространства это — математическая модель физического маятника, частно-
частного случая консервативного ротатора.
Динамическую систему, описываемую уравнением вида A.15)
на двумерной фазовой плоскости, назовем осциллятором, а опи-
описываемую тем же уравнением на двумерном фазовом цилиндре —
ротатором. Отметим, что уравнение A.15) ■— это общее диффе-
дифференциальное уравнение второго порядка, поскольку любая диф-
дифференцируемая по х функция f(x, x) может быть записана в
виде
/(*, x) = f(x, 0)+[f(x, x)-f(x, 0)] = Q(x) + 28(x, x)x.
Неавтономные осциллятор и ротатор. Осциллятор и ротатор
A.15) являются автономными, не зависящими явно от времени,
динамическими системами. Неавтономный осциллятор и ротатор
описываются уравнением вида
х + 26(х, х, t)x + Q(x, *) = 0. A.16)
Частными случаями этого уравнения являются известные урав-
уравнения Дуффинга, Хилла и Матье, а также линейный осциллятор
под действием внешней гармонической силы. Такой же вид имеет
осциллятор Ван-дер-Поля с внешним гармоническим воздей-
воздействием.
Линейный осциллятор под действием внешней гармонической
силы
x+28x + a2x = Fcosxt A.17)
и уравнение Дуффинга
x + 28x + ax + bx3 = Fcosvt A.18)
описывают соответственно явления линейного и нелинейного ре-
зонансов. Кратко суть их состоит в следующем. Общее решение
уравнения A.17) представимо в виде суммы общего решения
соответствующего однородного уравнения, определяемого форму-
формулами A.5), A.6), и частного решения неоднородного уравнения
A.17), которое в комплексной форме можно записать в виде
При б > 0 именно это частное решение устанавливается спустя
достаточно длительное время; оно описывает установившиеся
15

вынужденные колебания линейного осциллятора и явление их
резонанса. Модуль комплексного числа A(v) — это амплитуда
выпужденпых колебаний, аргумент — их фаза. Явление резонан-
резонанса состоит в неограниченном возрастании максимальной ампли-
амплитуды вынужденных колебаний при б -*■ 0 (рис. 1.10). При этом
значение частоты v, соответ-
соответствующее максимальной ампли-
амплитуде, стремится к ю.
Вынужденные колебания
нелинейной системы, описыва-
описываемой уравнением Дуффинга,
исследовать столь просто не
удается. И поныне это уравне-
уравнение исследовано не полностью.
Без особого труда удается ис-
исследовать только случай малых
затуханий б и а > 0. Резонанс-
Резонансные кривые имеют при этом
вид, показанный на рис. 1.11,
и отличаются от резонансных
^ кривых линейного осциллятора
(рис. 1.10) наклоном «пика»
О
v=o>
Рис. 1.10
и появлением неодноднознач-
неодноднозначности. Наклон происходит вле-
влево или вправо в зависимости от знака величины Ъ в уравнении
Дуффипга A.18). Этим наклоном и неоднозначностью вызывает-
вызывается известное явление гистерезиса амплитуды вынужденных ко-
колебаний при медленном измепении частоты v внешней силы. Оно
состоит в скачках амплитуды и том, что эти скачки происходят
Рис. 1.11
при разных значениях v при монотоппом медленном возрастании
и убывании частоты v (рис. 1.11).
Исследование вынужденных колебаний нелинейпого осцил-
осциллятора Дуффинга обнаруживает еще одпу особенность: резонапс
возможен не только па частоте v = со, по и v = со/2, со/3, ...
(со2 = а). Это — так называемые субгармонические резонапсы.
Уравнения Матъе и Хилла. Уравнения Матье и Хилла опи-
описывают явление линейного параметрического возбуждения и ре-
16

зонанса гармонического осциллятора. Уравнение Хилла имеет
вид
x + \\i + <p(t)]x = 0, A.20)
где ф(£) — произвольная периодическая функция. Уравнение
Матье соответствует его частному случаю, когда периодическая
функция (p(£) = vsini. На
рис. 1.12 представлены области
(незаштрихованпые) парамет-
параметрического возбуждения колеба-
колебаний. При значениях парамет-
параметров ц и v из незаштриховапных
областей параметрического ре-
резонанса состояние равновесия
х = х = 0 неустойчиво, и уход
от него носит колебательный
характер с экспоненциально
возрастающей амплитудой. Су-
Существенно, что такое поведе- Рис. 1.12
пие, как видно из рис. 1.12,
возможно при сколь угодно малой величине амплитуды v пара-
параметрического изменения жесткости осциллятора
x + (\JL + vsint)z = O, A.21)
если только частота со = У\х связана целочисленным соотно-
соотношением
2со = п (п = 1, 2, 3, ...) A.22)
с частотой 1 гармонического параметрического воздействия.
Именно в этой возможности раскачки с помощью сколь угодно
малого параметрического воздействия при соблюдении одного из
условий A.22) и состоит явление параметрического возбуждения
и резонанса.
Явления нелинейного резонанса и хаотизации движений не-
нелинейного ротатора паходят отражение в дифференциальном пе-
автономном уравпешга второго порядка вида
х + 2Ьх + ((х + v sin t) sin x = М,
A.23)
которое описывает, в частности, колебания дисбалансного ротора
(физического маятника) па колеблющемся основании при нали-
наличии вращающего момента. Отметим, что и в осцилляторе Дуф-
фипга возможны хаотические вынужденные колебания. При этом
в обоих случаях изменения перемеппых х и х носят хаотический
и непредсказуемый характер. Фазовые пространства осциллятора
Дуффинга A.18) и уравнения дисбалансного ротора на гармони-
гармонически колеблющемся основании трехмерные. Если фазовые про-
пространства этих систем пересечь плоскостью, то движущаяся фа-
фазовая точка, пересекая ее, будет оставлять на ней следы в виде
точек. При периодическом движении фазовой точки таких точек
17

пересечения будет несколько, и через них фазовая точка будет
проходить периодически. При движении, асимптотическом к пе-
риодическому^ точек пересечения будет бесконечно много, но со
временем фазовая траектория начнет пересекать плоскость в не-
некотором числе точек, стремящихся к некоторым предельным по-
положениям. При хаотическом движении таких точек пересечения
бесконечно много, и они заполняют некоторые подчас очень
сложно устроенные множества. Пример такого множества то-
точек — облака точек пересечения секущей плоскости с фазовой
траекторией уравнения A.23) — приведен на рис. 1.13.
Xh
2'\
/-.
n
и
*
z-\
'■'':■"•.. . •••' ''•'•"•"'''•■.'''^•'•"■'
• '•**' V'" "'''.'.**-' * '''.''.'•'*
■.•"'.':" '.• ••'"■'.••"•' Vr."*::::\."
^■': "*'':■ ••■"' •^H:^'?i^-r
■■ ■ ■:■-...
•;. ..'■■•..«V:.w':'.i:
:••;:.••■:;•• "•j':;'i;i.1
•■;';• "xr.)' '.'
;•■•••.•'■•■ "•■■.'.•':-. •
Рис. 1.13
Уравнения Лоренца. Сравнительно недавно широкую извест-
известность приобрели дифференциальные уравнения Лоренца [563]
х = — а{х — у), y — rx — y — xz, £ = —bz + xy. A.24)
Они возникли как трехмодовое приближение уравнений двумер-
двумерной конвекции между параллельными горизонтальными стенками,
поддерживаемыми при постоянных, но разных температурах
(температура нижней стенки выше). '
Фазовое пространство такой системы — трехмерное евклидово
пространство. Все фазовые траектории входят в некоторую огра-
ограниченную область, где могут переплетаться самым причудливым
образом. Усилиями многих исследователей, использовавших ме-
методы качественной теории дифференциальных уравнений и чис-
численные эксперименты на современных вычислительных машинах,
было показано, что сложные движения фазовых точек в системе
Лоренца — хаотические. Вид одной из фазовых траекторий, со-
соответствующей такому сложному движению, показан на рис. 1.14.
Эта картинка получена на экране осциллографа путем высвечи-
высвечивания проекции фазовой точки через равные промежутки
времени.
15

Уравнения Лоренца A.24) после замены переменных х, у, z
к времени t на
т -
где е =(г — 1)~1/2, приводятся к виду [11]
13 «*-(?- 1)£ = 0, g = -609 + 8^5* A-25)'
g + 1 b о 2о-
a = р==
позволяющему трактовать их как нелинейный осциллятор с не-
нелинейной инерционной жесткостью. При е -*■ 0 инерционность
Рис. 1.14
жесткости осциллятора исчезает, а движение любой фазовой
точки подчиняется уравнению нелинейного консервативного ос-
осциллятора
ври некотором своем постоянном значении параметра q.
Система слабо взаимодействующих гармонических осцилля-
осцилляторов и система с быстровращающимися фазами. До сих пор все
приводимые нами модели дискретных динамических систем были
не более чем трехмерные. Ограничиться столь простыми моде-
моделями удается далеко не всегда. Если изучение моделей большей
размерности при сильных нелинейностях только начинается, то
при малых нелинейностях такие исследования достаточно про-
продвинуты, и здесь уже успели сформироваться некоторые типо-
типовые модели. В этой связи прежде всего можно указать на систе-
систему слабо взаимодействующих осцилляторов и роторов и на си-
систему с так называемыми быстровращающимися фазами.
19

Система п слабо взаимодействующих гармонических осцилля-
осцилляторов может быть записана в виде
xs -!- <a>lxs = e/s (хх, ...,хп; х17 ..., хп) (s = 1, 2, .. ., п), A .2'))
где е — малый параметр. При е = 0 она распадается на не взаи-
взаимодействующие гармонические осцилляторы и легко интегри-
интегрируется:
xs-=Ascos(wst + (fa). A.27)
При малом 8 решение также представимо в виде A.27), но при:
этом А, и ф8 уже не постоянные, а медленно меняющиеся функ-
функции времени. Скорость их изменения, т. е. As и ф«, порядка е.
Оцепим действенность влияний, которые могут оказывать
друг на друга осцилляторы. Их взаимодействия осуществляются
через правые части е/а уравнений A.26). Функции fs зависят от
£i, х2, ..., хп и Xi, x2, ..., хп, а каждое из переменных xs n xs
в первом приближении — гармоническое колебание с частотой со,.
В силу нелинейности зависимости /„ от Xi, . ■., хп и хи ..., хп
в ее спектральное представление, кроме частот (а{, ю2, ..., соэт,
войдут и их всевозможные целочисленные линейные комбинации
вида
• • • + тпап. A.28)
Амплитуды таких гармоник, вообще говоря, тем меньше, чем
больше числа т^ т2, ..., тп, поэтому основное внимание следует
обратить на первые комбинационные частоты. Разумно предпо-
предположить, что основную роль играют комбинационные частоты,
близкие к частотам осцилляторов coi, co2, ..., G>n. «Близкие» в
данном случае означает «отличающиеся на величину порядка е».
Так как параметр е сколь угодпо мал, то сильных эффектов при
сколь угодно 'слабых взаимодействиях следует ожидать только
при наличии в системе внутренних резонансов, т. е. целочислен-
целочисленных соотношений вида
to, = miCOi + яг2со2 + ... + тп&„.
Резонансные взаимодействия имеют место только при существо-
существовании целых чисел тп, Ф 0 и j Ф s. Только при этом условии /-й
осциллятор оказывает сильное воздействие на s-&.
Система дифференциальных уравнений вида
<р = со(х)-ЬеФ(ф, х), х = гХ(ф, х) A.29)
получила название дифференциальных уравнений с быстровра-
щающимися фазами. В этих уравнениях ф — вектор угловых пе-
переменных фь ф2, ..., фт, х — вектор w-мерного евклидова про-
пространства с компонентами хи х2, ..., хп, г — малый параметр,
функции Ф и X периодические по переменным <pt, ф2, ..., ц>т
с периодом 2я. К виду A.29) приводятся после замены перемеп-
20

ных хв = p8cos(j3, дифференциальные уравнения A.26). При этом
т = п и
w(;z) = ((»i, ©2, ..., ю„).
К виду A.29) приводится и более общая, чем A.26), система
дифференциальных уравнений
x. + Q,(x.)=efa(xlt ..., хп; х„ ..., хп), A.30)
соответствующая системе п слабо взаимодействующих нелиней-
нелинейных консервативных осцилляторов. При этом
(H(x) = (toi{x), (йг(х), . . ., (Ип(х)).
Гамилътоновы динамические системы. В задачах небесной
механики и теоретической физики значительную роль играют
гамильтоновые системы и близкие к ним при учете диссипатив-
ных эффектов. Система Гамильтона — это динамическая система,
уравнения движения которой записываются с помощью един-
единственной функции Гамильтона H(q, p) в виде
<?s = g, Р° = -Щ-В (» = *.2, ...,п). A.31)
Системы Гамильтона длительно и настойчиво изучались как
в аналитическом, так и качественном планах. Среди них есть и
очень простые (полностью интегрируемые) системы, и очень
сложные.
Сложность начинается уже с п ^ 2. Достаточно упомянуть
хотя бы знаменитую ограниченную проблему трех тел, задачу
о движении твердого тела с закрепленной точкой и многие другие.
Интегрируемая гамильтопова система с функцией Гамильто-
Гамильтона вида
Il A.32)
представляет собою набор невзаимодействующих консервативных
осцилляторов или ротаторов и совпадает с системой A.30) при
е = 0. Характерной особенностью фазового портрета такой систе-
системы является расслоение его на га-мерные интегральные торы
с квазипериодическими или периодическими обмотками. Урав-
Уравнения движения A.31) приводятся в этом случае к виду
а их решения q.(t, h,) при некоторых общих предположениях
являются периодическими функциями времени с периодами, за-
зависящими от постоянных интегрирования. Вопрос о сохранении
такой структуры при малых возмущениях функции Гамильтопа
был предметом рассмотрения в теории КАМ (по имени ее со-
создателей— Колмогорова, Арнольда и Мозера [255]). С ростом
возмущения эта структура, как правило, разрушается, и могут
возникнуть хаотические движения. Возможность такого разру-
разрушения числепно была подтверждена в работе Хенона и Хейлеса
21

1964 г. [501] для функции Гамильтона вида
н = 4" (р1 + р1) + -f Ы + яг)
где Нх = 9^3 — 1/з?2> а е — параметр возмущения. С ростом па-
параметра , е появляются хаотические траектории, образующие в
трехмерном подпространстве постояпной энергии весьма сложные
и запутанные клубки.
§ 2. Хаотические движения детерминированных
динамических систем
Просматривая перечень простейших типовых моделей дис-
дискретных детерминированпых динамических систем; нетрудно за-
заметить, что хаотические движения не встречались у двумерпых
систем, но появились, как только мы перешли к трехмерным.
Это не случайно: у двумерных гладких динамических систем —
автономных осцилляторов и ротаторов — хаотические режимы пе
существуют.
Единственно возможными установившимися движениями в
двумерпых системах являются устойчивые состояния равновесия
и периодические движения. Но при периодических силовых или
параметрических воздействиях на осциллятор или ротатор появ-
появляются хаотические движения. Они возникают и при автономных
инерционных изменениях параметров осциллятора или ротатора.
Примерами хаотизации движений осциллятора внешними пе-
периодическими возмущениями могут быть хаотические движения
в уравнении Дуффинга и осцилляторе Ван-дер-Поля. Пример
хаотизации периодическим параметрическим воздействием был
указан выше (уравнение A.23)). Был приведен и пример хао-
хаотизации при инерционпом изменении параметра (уравнения Ло-
Лоренца). Более подробное рассмотрение этих примеров и многих
других будет дано позднее — в гл. 7 и 9.
Размерность три — та наименьшая размерность, начиная с ко-
которой возможна хаотизация движепий в гладкой (дифференци-
(дифференцируемой) динамической системе.
Возможность существования непериодических установивших-
установившихся движений у системы третьего порядка была отмечепа еще в
1963 г. в работе Лорепца [563]. Однако широкую известность
этот факт получил только во второй половине 70-х годов.
Другим аналогичным и даже более ранним примерам повезло
значительно меньше: опи стали известпьт либо значительно позд-
позднее, либо остались в тени. Речь идет об исследованиях горьков-
ской школы теории нелинейных колебаний, проводившихся еще
в те времена, когда вычислительных машин не было и практи-
практически единственно возможный способ обнаружения хаотических
движений заключался в сведепии задачи к исследованию одпо-
мерного точечного отображения, а также о более поздпих работах
той же школы (теоретических исследованиях и эвристических
22

расчетах на современных ЭВМ), позволивших понять механизмы
возникновения хаотических движений и их общий характер.
Первоначальные примеры точечных отображений с весьма
сложными (как сказали бы сейчас, хаотическими) последователь-
последовательными преобразованиями возникли при рассмотрении конкретных
задач. В работах [3, 4] A952—1957 гг.) сложные режимы воз-
возникли в результате применения метода точечных отображений
для исследования работы двухпозиционцого регулятора темпе-
температуры с зоной опережения. Сложные движения были обнаруже-
обнаружены и при исследовании модели электромагнитного прерывателя
[354]. В работах [234, 235] A959—1960 гг.) уже исследовалось
произвольное кусочно-линейное отображение (из двух кусков)
прямой в себя. Необходимо также отметить работы [59, 60]
A906—1967 гг.), в которых с применением ЭВМ изучалось виб-
вибропогружение шпунта и движения дисбалансного ротора на ко-
колеблющемся основании.
Читая сейчас эти работы, необходимо иметь в виду, что тер-
термины «хаотические движепия» и «странный аттрактор» появи-
появились значительно позднее, а тогда такие движения назывались
непериодическими устойчивыми по Пуассону центральными дви-
движениями, или короче — движепиями, устойчивыми по Пуассону.
Эта терминология восходит к книге Д. Биркгофа «Динамиче-
«Динамические системы», переведенпой на русский язык в 1941 г., и кпиге
В. В. Немыцкого и В. В. Степанова «Качественная теория диф-
дифференциальных уравнений», вышедшей в 1947 г. Сам термин —
движение, устойчивое по Пуассону (в направлении возрастания
времени),— означает, что движение x(t) ограничено, и для лю-
любых ta и б > 0 существуют неограниченно возрастающие моменты
времени t0 < ti < t2 < ..., для которых
lb(*.)-a:(fe)ll<6 (я = 1, 2, 3, ...).
Укажем еще на работы [70, 269] A972 г.), где было численно
обнаружено, что хаотические движения возможны в трехмерной
диссипативной квазигамильтоновой системе, описываемой урав-
уравнениями вида
0=1,
где Н(х, у) = (х2 + у2J — 2а2(х2 — у2), а Ц, и v —малые парамет-
параметры. В этой работе исследовались некоторые статистические ха-
характеристики хаотических движений. «Облако» точек пересече-
пересечения хаотической фазовой траектории с секущей плоскостью 0 =
= 0 имело вид, показанный на рис. 1.15. Все соседние к этому
«облаку» точки притягивались «облаком», вовлекаясь в него.
Последнее утверждение следовало из теоретических соображений.
23

Доказать же теоретически экспоненциальную неустойчивость
по Ляпунову движений в «облаке» не удалось и пришлось
ограничиться численными результатами о непериодическом
или периодическом, но q очень большим периодом, характере
движений. Отметим, что в 1974 г. был построен аналогичный
Рис. 1.15
пример {271, 279] для негладкого точечного отображения, где
удалось установить теоретически оба факта: глобальное сжатие
и локальную неустойчивость. По существу, речь шла не о при-
примере, а о некоторой общей схеме, приводящей к таким примерам
и свидетельствующей об их общности и распространенности. Хао-
Хаотические движения^, обнаруженные в системе Лоренца, как вы-
выяснилось позднее в 1977 г. [276, 278, 280], укладываются в эту
общую схему.
Перечисленные примеры систем, в которых были обнаружены
хаотические движения, относятся к неконсервативным системам.
Для консервативных гамильтоновых систем примеры хаотических
движений были известны еще раньше — это движение без со-
сопротивления материальной точки по инерции в пространстве от-
отрицательной кривизны [363, 485, 498] и, в частности, по поверх-
поверхности, изображенной на рис. 1.16, и многие другие. Об этом
направлении будет рассказано в гл. 4.
Вернемся к упомянутым выше работам представителей горь-
ковской школы теории нелинейных колебаний А. С. Алексеева,
Н. Н. Леонова и 3. С. Баталовой.
В работе А. С. Алексеева [4] A955 г.) методом точечных
отображений исследование динамики двухпозиционного регуля-
регулятора температуры с зоной опережения сведено к исследованию
точечного отображения прямой в прямую, порождаемого отобра-
отображениями Ти Т2, i?i, В2, St и S2 полупрямых ut > 0, иг ^ 0,
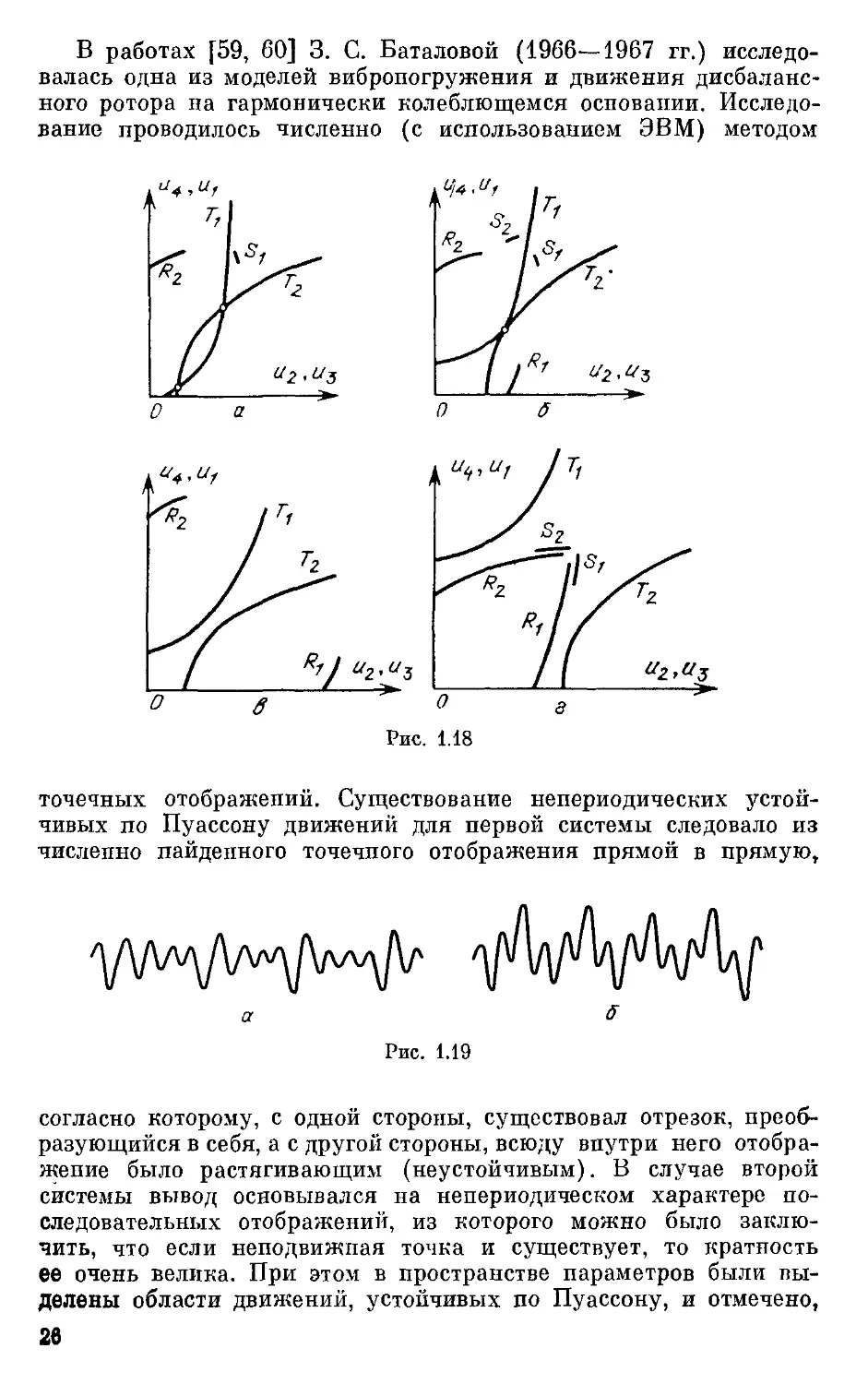
и3 > 0 и ut > 0 двулистной фазовой плоскости (рис. 1.17).
В зависимости от Значений параметров эти отображения мо-
могут иметь различный вид (рис. 1.18). Несмотря на сложность
такого отображения прямой в прямую, оно было детально изу-
изучено. Оказалось, что если случаю, изображенному на рис. 1.18, а,
соответствует единственное устойчивое периодическое движение,
то с переходом от рис. 1.18, а через рис. 1.18,6 и 1.18, в к
рис. 1.18, г возникают сложные периодические движения, в том
числе и несимметричные, несмотря на симметрию рассматривае-
рассматриваемой системы, причем эти сложные движения претерпевают бес-
24

конечное число бифуркаций, так что каждому из устойчивых
сложных режимов отвечает один из бесконечного числа интер-
интервалов на оси параметра, а дополнение к этим интервалам имеет
структуру канторова множества. Его точкам отвечают движения,
устойчивые по Пуассону (в направлении возрастания времени).
Рис. 1.16
Рис. 1.17
На рис. 1.19 показаны осциллограммы некоторых типов периоди-
периодических движений.
Если в работе А. С. Алексеева исследовалась конкретная
система автоматического регулирования, для которой были об-
обнаружены серии бифуркаций удвоения и явления, получившие
позднее название перемежаемости, то в работах [234, 235]
Н. Н. Леонова рассмотрения носят общий характер. В работе
[235] A960 г.) исследуется невзаимнооднозначное точечное ото-
отображение прямой в прямую вида
Тгх = а
0,
Т2х = Ъ + К2х, х > 0,
B-2)
зависящее от трех существенных параметров Я4, Я2 и Д = |аЬ~М.
Было найдено разбиение пространства параметров А,,, А2, А на
области, отвечающие различным типам многократных устойчи-
устойчивых неподвижных точек. Остальная часть пространства парамет-
параметров отвечает либо преобразованиям, приводящим к уходу в бес-
бесконечность, либо преобразованиям, устойчивым по Пуассону.
Области пространства параметров, отвечающие существованию
движений, устойчивых по Пуассону, были обнаружены и при
lXtl>l, |Я21 > 1, что по современной терминологии заведомо со-
соответствует наличию стохастического аттрактора. Пример такого
отображения показан на рис. 1.20. Получившее известность ото-
отображение Лоренца является его частным случаем, когда А = 1
(а = -Ъ) и Я, = Я2>1.
25

В работах f59, 60] 3. С. Баталовой A966—1967 гг.) исследо-
исследовалась одна из моделей вибропогружения и движения дисбаланс-
ного ротора на гармонически колеблющемся основании. Исследо-
Исследование проводилось численно (с использованием ЭВМ) методом
i
U1
I
7
1
О
0
Рис. 1.18
точечных отображений. Существование непериодических устой-
устойчивых по Пуассону движений для первой системы следовало из
численно лайденного точечпого отображения прямой в прямую,
Рис. 1.19
согласно которому, с одной стороны, существовал отрезок, преоб-
преобразующийся в себя, а с другой стороны, всюду внутри него отобра-
жепие было растягивающим (неустойчивым). В случае второй
системы вывод основывался на непериодическом характере по-
последовательных отображений, из которого можно было заклю-
заключить, что если неподвижная точка и существует, то кратпость
ее очень велика. При этом в пространстве параметров были вы-
выделены области движений, устойчивых по Пуассону, и отмечено,
26

что при изменении параметров в направлении к этим областям
происходит усложнение устойчивых периодических движений пу-
путем удвоения их периодов. ;
В теоретических исследованиях горьковской школы теории
нелинейных колебаний 1964—1970 гг. [262, 263, 266, 268, 288,
289, 370, 371, 374] было понята
роль гомоклинических и гетеро-
клинических кривых А. Пуан-
Пуанкаре в образовании непериоди-
непериодических устойчивых по Пуассону
движений, и тем самым выяс-
пены их общий характер и
важная роль, которую они
должны играть в теории нели-
нелинейных колебаний и временной
эволюции динамических систем.
Изложение этих исследований
будет продолжено в гл. 4, где
после некоторого знакомства с
существом вопроса они будут рис. 1.20
описаны в связи с исследова-
исследованиями и результатами других научных направлений, приведших
в конце 70-х — начале 80-х годов к взрыву всеобщего интереса
к стохастическим движениям динамических систем.
§ 3. Простейшие математические модели
распределенных динамических систем
Перейдем к описанию математических моделей распределен-
распределенных динамических систем. Разнообразие их столь велико, что
едва ли можно говорить о сколько-нибудь обозримом наборе ос-
основных типовых моделей. Все же некоторые из них стали пред-
предметом пристального внимания и позволили существенно продви-
продвинуться в вопросах исследования волновых и диффузиопных яв-
явлений, в изучении ламинарных и турбулентных гидродинамиче-
гидродинамических и конвективных течений жидкостей и газов.
В этом разделе мы бегло опишем некоторые из этих моделей
и придадим смешанным задачам математической физики фазо-
фазовую трактовку, при которой уравнения являются операторами из-
изменения фазового состояния. Такая трактовка позволяет с еди-
единой точки зрения рассматривать дискретные и распределенные
динамические системы, так как изменения фазового состояния
происходят и в тех, и в других, только в первом случае фазовое
состояние описывается точкой конечномерного пространства, а во
втором — точкой бесконечномерного пространства.
Уравнение диффузии. Изменение во времени плотности
р(х, у, z, t) вещества, диффундирующего в неограниченной про-
проницаемой одородной и изотропной среде, подчиняется параболи-
27

ческому уравнению в частных производных
- (зл>
Это уравнение позволяет по заданному начальному распределе-
распределению р(х, у, z, t0) найти распределение плотности в любой другой
момент времени t ^ t0. Так, если в начальный момент t = t0 все
вещество массы т сосредоточено в точке (ж„, Ун, £о), то из урав-
уравнения C.1) следует, что
р (х, у, z, t) =
/3
8„3/2 (f _ g3/2 д3/
Роль состояния в этом случае играет функция трех переменных
р(х, у, z, t) при фиксированном времени t, а пространства со-
состояний — множество всевозможных неотрицательных функций
трех переменных х, у, z с заданным значением общего количе-
количества вещества, т. е. с заданной величиной интеграла по всему
пространству.
В рассматриваемся случае с ростом времени плотность ве-
вещества р(х, у, z, t)-+0, поэтому все фазовые траектории фазо-
фазового портрета рассматриваемой системы стремятся к одной и
той же точке О, отвечающей функции р(х, у, z, t) = 0, которая
сама пе принадлежит фазовому пространству.
Пусть диффузия вещества происходит в ограниченной области
Q. Изменение плотности р(х, у, z, t) пусть по-прежнему удовлет-
удовлетворяет дифференциальному уравнению C.2), но теперь плот-
плотность р(х, у, z, t) не стремится к нулю с ростом времени. В чем
же отличие от предыдущей задачи? Отличие можно усмотреть,
сравнивая фазовые пространства. Новое фазовое пространство —
это множество всевозможных неотрицательных в области Q
функций р(х, у, z, t) с постоянным значением интеграла па
этой области
J р(.г, у, z, t)dxdydz = m, C.3)
а
равпым общей массе диффундирующего вещества т, и требова-
пием непроницаемости диффундирующего вещества через грани-
границу области Q, состоящем в равенстве нулю нормальной произ-
производной от плотности р(х, у, z, t) на границе области Q.
Последнее условие обычно рассматривается как граничное
условие, которое необходимо ввести дополнительно к уравнению
диффузии C.2), чтобы обеспечить полноту и единствеппость ре-
решения. Из сказанного выше следует, что это краевое условие
можно трактовать и как следствие определения фазового про-
пространства. При такой трактовке изменение состояния — плотно-
плотности вещества — подчиняется всегда одному и тому же уравне-
28

нию диффузии, но определенному на разных фазовых простран-
пространствах.
Общее линейное уравнение в частных производных. Продол-
Продолжим рассмотрение простейших математических моделей распре-
распределенных систем на примере уравнения в частных производных
4^ + 5^->-Си = 0, C.4)
где и — вектор-функция переменных х и t размерности п, Л, В
и С — квадратные матрицы пХп.
Решение этого уравнения будем искать в виде
и(х, t) = aeHat~m. C.5)
Подставляя C.5) в C.4), находим, что
C)aeHal-^ = O C.6)
и, следовательно,
(ia>A-ikB + C)a = O. C.7)
Итак, если выполняется условие C.7), то C.5)—решение урав-
уравнений C.4). Для выполнения условия C.7) (а¥=0) необходимо
и достаточно, чтобы выполнялось соотношение
O. C.8)
Уравнение C.8), называемое дисперсионным, определяет соот-
ношепие между временной частотой ш и волновым числом к
решения C.5). Оно определяет зависимость фазовой скорости
бегущей волны, равной ш//с, от ее временной частоты о>.
Рассмотрим подробнее, как связапы решения вида C.7) с
дисперсиоппым уравнением C.8). Для любого к, действительного
или комплексного, дисперсионное уравнение C.8) определяет п
соответствующих значений ш, (к), а2(к), ..., о>„(/с) и каждой
паре значений к и сла(к) отвечают некоторые а, определяемые
из уравнения C.7). При этом наряду с решением к, ш и а будет
решением и — к*, —ш* и а* (звездочка означает комплексно-со-
комплексно-сопряженное число). Это позволяет построить действительное ре-
шепие уравнепий C.4) в виде бегущей волны:
и (х, t) = аеНт-кх) + а*е-^*1~к*х\ C.9)
Формула C.9) задает гармоническую во времени и пространстве
бегущую волну, если ш и к действительные, и нарастающую или
затухающую во времени и в пространстве бегущую волпу при
комплексных о> и к.
Таким образом, выражение C.9), где ш, к и а определяются
уравнениями C.8) и C.7), задает многопараметрическое семей-
семейство решений уравнения в частных производных C.4). Из них
путем линейной суперпозиции могут быть сконструированы лю-
любые решения уравнения C.4). В этом и состоит их зпачение и
определяющая роль.
29

Суперпозиция волн C.9) не столь тривиальна, как аналогич-
аналогичная суперпозиция в линейных дискретных системах. Это связа-
связано с тем, что процессы во времени здесь связаны с простран-
пространственными изменениями. Ключевыми новыми понятиями здесь
являются групповая скорость и дисперсия [107, 132]. Эти две
величины описывают, как перемещается в пространстве и изме-
изменяется со временем волновой пакет, представляющий собой су-
суперпозицию гармонических волн в некотором небольшом интер-
интервале частот и соответствующих волновых чисел. Групповая ско-
скорость — это скорость перемещепия волнового пакета как неко-
некоторого образования. Дисперсия характеризует скорость расплы-
вания волнового пакета. При отсутствии дисперсии волповой
пакет не меняет своей формы, т. е. является бегущей волной
неизменной формы—так называемой стационарной волной. При
наличии дисперсии со временем происходит расплывание волно-
волнового пакета. Комплексное со влечет экспоненциальный рост или
уменьшение высоты пакета. Таким образом, групповая скорость
определяет скорость движения пакета, дисперсия — его расплы-
расплывание, а мницая часть (о — возрастание или убывание его высо-
высоты. Групповая скорость равна da/dk, а дисперсия определяется
величиной d2ti>fdk2.
Квазилинейная теория колебаний и волн. От линейных урав-
пений в частных производных C.4) перейдем к более общим
пелинеиным уравнениям
Л дм , г, дм , п е I дм дм\
А+ВСи *(и
Как изменяются с появлением нелинейности описанные выше
чисто линейные эффекты? При больших нелинейностях такая
постановка вопроса теряет смысл, так как линейные эффекты
полностью вытесняются нелинейными, но при малых нелиней-
нелинейностях можно говорить о некотором совокупном действии нели-
нелинейных и линейных эффектов и построить теорию, получившую
наименование квазилинейной теории колебаний и волн. В основе
этой теории лежит учет вызываемых нелинейностями отклонений
от принципа суперпозиции в силу взаимодействия и самовоздей-
самовоздействия волн, обусловливаемых правыми частями уравнений C.10),
которые содержат пе только основные частоты, но и (вследствие
нелинейности) всевозможные комбинационные частоты.
Для того чтобы сильное взаимодействие при слабых нелиней-
нелинейностях стало возможпым, как и в дискретном случае, необходимо
выполнение резонансных соотношений не только для частот (О,
но и для волновых чисел к, т. е. соотношений вида
+ ге2со2 + ... + пт(йт = 0,
у + п2к2 +... + пткт = 0.
Характер резопансного нелинейного взаимодействия волн суще-
существенно разный в отсутствие дисперсии и при ее наличии. Это
30

вызвано тем, что в отсутствие дисперсии наряду с парой а, к
дисперсионному/ уравнению удовлетворяют и пары so, sk (s =
= 2, 3, ...), что порождает резонансные соотношения C.11),
приводящие к перекачке энергии с низших гармоник в высшие.
При наличии дисперсии отсутствуют резонансные взаимодей-
взаимодействия, приводящие к перекачке энергии в более высокие гармо-
гармоники, и возникают условия, при которых возможно образование
небольших ансамблей волн (wi, &,), (ш2, к2), ..., (wm, km), удов-
удовлетворяющих условию синхронизма C.11), где пи щ, ..., пт —
пеболыпие отличные от нуля целые числа. Такие волны сильно
взаимодействуют друг с другом и образуют некоторую замкну-
замкнутую группу. Замкнутость или изолированность этого ансамбля
волн вызвана тем, что нет волн с частотой ю и волновым числом
к, для которых выполнялись бы условия синхронизма с волнами
этого ансамбля:
им + fiidii +... + пт(лт = О,
= 0 (ЗЛ2)
с п¥=0 и небольшими целыми значениями п, щ, п2, ..., пт.
Простейший из таких ансамблей могут образовывать три вол-
волны с соотношением синхронизма вида
о), + и2 - Из = 0, C.13)
Ь» —L- 1а _,„.., Та —. (Л
**'1 ' * ^^ "'З """"* '-'*
Уравнение простых волн. Нелинейное уравнение простых волн
?Ил.у(и)— = 0 C.14)
at / ох
рассматривается с времен Римана A860 г.). Оно описывает не-
нелинейные процессы в одномерной среде и допускает в качестве
решений так называемые простые волны:
и(х, t) = f(x-V(u)t). C.15)
Особенностью записи решения в виде C.15) является то, что
этот вид определяет и (х, t) неявным образом, как решение от-
относительно и уравнения C.15). Форма волн, т. е. и как функция
пространственпой координаты х, определяется уравнением C.15),
если в нем фиксировать время t. С изменением времени форма
волны меняется, и качественно проследить за этим изменением
можно, исходя из того, что V(u) имеет смысл скорости распро-
распространения участка волны с значением уклонения и. Характер
изменения формы волны существепно зависит от вида зависимо-
зависимости V(u). При V(u)~ const форма волн не меняется. При
dV/du > 0 происходит «опрокидывание» волны.
Уравнения Бюргерса и Кортевега-де Фриза. Учет лилейных
эффектов диссипации и дисперсии приводит к появлению в урав-
уравнении простых воли C.15) дополнительных членов, в результате
31

чего оно принимает вид
at ' v '
ди
8 и
C.16)
Это уравнение в частных производных объединяет известные
уравнения Кортевега-де Фриза (сс = О) и Бюргерса (^ = 0).
При F(u) = u и а = 0 решения этого уравнения изучены очень
подробно. В частности, изучены его решения типа бегущей вол-
волны. Возможные формы бегущих волн могут быть найдены как
решения некоторого обыкновенного дифференциального уравне-
уравнения. Подставляя
и = /A), l = x~ct C.17)
в уравнение C.16) при се = 0 и V(u) = u, приходим к обыкновен-
обыкновенному дифференциальному уравнению
РГ+(/-0/'=-о,
или после интегрирования
C.18)
Уравнение C.18) соответствует нелинейному консервативному
осциллятору. Фазовый потрет этого осциллятора изображен на
рис. 1.21, а. На этом фазовом портрете уединенной волне, кото-
которая в рассматриваемом случае оказывается солитоном, может
5с
Рис. 1.21
отвечать только одна фазовая кривая у, и то при условии, что
седловая точка О находится в начале координат, т. е. если h = 0.
Форма солитона изображена на рис. 1.21,6. Оп имеет вид одно-
одногорбой симметричной кривой с экспоненциально спадающими
краями.
Скорость распространения солитопа равна с. Как следует из
сказанного, каждой скорости распространения с отвечает солитоп
своей формы. Высота горба солитона равна Зс, т. е. чем «выше»
солитон, тем с большей скоростью он распространяется. Другим
фазовым траекториям фазового портрета рис. 1.21, а отвечают
32

бегущие волны других форм. Среди них солитон — единственная
уединенная волна с конечной энергией. Энергия всех остальных
волн бесконечна. Это, в частности, говорит о том, что из близо-
близости к фазовой кривой f существенно отличных от нее фазовых
траекторий нельзя сделать вывод о неустойчивости солитона.
Возмущение, отвечающее такому переходу, отнюдь не мало, оно
требует бесконечной энергии.
Солитоны являются частными решениями уравпепия Кортеве-
га-де Фриза, однако они играют очень важную, можно сказать,
определяющую роль: любое движение с конечной энергией спустя
достаточное время распадается на некоторое число солитонов,
каждый из которых имеет свою скорость и соответствующую ей
форму.
§ 4. Дискретное описание распределенных
динамических систем
Приведенные примеры математических моделей дискретпых
и распределенных динамических систем обнаружили значитель-
значительные различия между ними. Объясняется это тем, что описание
распределенной системы включает не только временную зависи-
зависимость, но и пространственное распределение. Особенно значи-
значительно различие между описаниями дис-
дискретных и распределенных систем при
волновой трактовке движений распреде-
распределенной системы. Но в основу описания
движений распределенной системы можпо
положить не только бегущие волны Да-
ламбера, но и стоячие волны Фурье. Ме-
Методы Фурье,, Ритца, Бубнова и Галеркина
не подчеркивают различия, а, наоборот,
сближают описания движений распреде-
распределенных и дискретных систем.
Выяснение возможностей и особенно-
особенностей фазовой трактовки движений распре-
распределенной динамической системы начнем
с рассмотрения конкретного примера одномерного конвектив-
конвективного течения жидкости в подогреваемой снизу согнутой в ви-
виде окружности трубе, расположенной в вертикальной плоскости
(рис. 1.22).
Пусть и (ф, t) — температура жидкости в трубе в месте ф
(ф — угол, отсчитываемый от вертикали) в момент времени t,
/(ф) — температура среды, окружающей трубу, а ю — скорость
течения жидкости в трубе.
Уравнение распространения тепла в трубе в одномерпой идеа-
идеализации запишется в виде
u(<p,t)
Рис. 1.22
ди
ди
D.1)
33

где А. — коэффициент теплопередачи от внешней среды к жид-
жидкости в трубе, a D — коэффициент диффузии1 тепла внутри жид-
жидкости.
Из теоремы об изменении момента количества движения по-
получаем
/со = — R*<§)gp sin ydy —ha, D.2)
где J — момент инерции жидкости в трубе, R — радиус закруг-
закругления трубы (рис. 1.22),
р = р (ф, t) = р0 [1 - хи (<р, t) ] D.3)
— плотность жидкости и х — ее температурный коэффициент
расширения.
Из уравнения D.1) и соотношений D.2) и D.3) непосред-
непосредственно ясны принятые упрощения и идеализация. В частности,
гидродинамическое течение и распределение температуры пред-
предполагаются одномерными, зависящими только от одной простран-
пространственной координаты ф. Жидкость считается несжимаемой, так
что угловая скорость ю не зависит от угла <р. Вместе с тем ее
плотность, р изменяется согласно D.3). Эти противоречивые тре-
требования отвечают известному приближению Буссинеска: передача
тепла принимается пропорциональной разности температур, теп-
теплоемкость жидкости — постоянной и при этом не учитывается
зависимость D.3) ее плотности от температуры.
Будем искать решение и(ф, t) уравнений D.1), D.2) и D.3)
в виде ряда Фурье [254, 258]
оо
и (ф, t) = и0 (t) + So, (t) sin st + b, (t) cos st. D.4)
s=l
Полагая, что /(ф) = /(—<р) и, следовательно,
/(ф) = /, cos ф + /2 cos 2ф +...,
после простых вычислений приходим к следующей системе обык-
обыкновенных дифференциальных уравнений относительно щЦ)г
eo(t), а,(О, МО, •••' М*)' М*)' •••:
тkRP ,
D.5)
as = sa>b3 — (Я, + s^D) as,
b\ = — sous — (h + s2D) bs -!- Я,/,.
Структуру связей между переменными щ, ю, а,, 6,, ... в полу-
полученных уравнениях D.5) можно изобразить в виде схемы, пока-
показанной на рис. 1.23. В прямоугольниках па этом рисунке стоят
34

взаимодействующие друг с другом группы переменных, стрелки
обозначают действие одних групп переменных на другие. В соот-
соответствии с этой схемой разобьем уравнение D.5) на части. Пер-
Первая часть — уравнение
D.6)
Из него следует, что с ростом времени и0 -*■ 0. Вторую часть
образуют уравнения
/со = ~- ог - ha,
а1 — (лЬ1 — (к -г D) Лц
bl = — сой^ — (Я, + D) Ь1
Уравнения D.6) с помощью замены
т = (К - D) t, х = 7^75, у =
хДР
2^ а+D)
—
Z
2А (X - Щ
гь, (х +
времени t и переменных ю, ai,.6i приводятся к уравнениям Ло-
Лоренца с коэффициентами 6 = 1
= г п^-пу Решения системы
Лоренца и, следовательно, урав-
уравнений D.6) могут быть очень
сложными, , стохастическими.
Наконец, s-я часть имеет вид
ая = sa>b3 — (К + s2D) as,
D.7)
—вый, — (К + s2D) bs + Xfs.
3-2, 3,4,...
Рис. 1.23
Из выражений D.7) непосредственно находим, что
~ (а! + Ы) = -(*-
- - As
Ь?) +
и поэтому через некоторое время точка (я„, fes) оказывается
внутри окружности с центром в начале координат и радиусом,
чуть большим, чем XfJA3. С ростом номера s радиусы таких
окружностей стремятся к нулю. Поведение точки (а8, Ь3) внутри
окружностей подчиняется уравнению D.7), где ю — некоторая
функция времени, определяемая дифференциальными уравне-
уравнениями D.6), эквивалентными уравнениям Лоренца. После заме-
замены времени t
A,t D.8)
35

уравнения D.7) приводятся к виду
as = —as + 'j-bs, bs = — bs~-ras + -r, D.9)
из которого следует (если учесть, что sAJ1 —>- 0 при s -*• оо и
U ~*~ 0 при s-*• то), что с ростом номера s влияние ш на перемен-
переменные as, b, уменьшается, и при очень большом s а, и Ь, близки
к нулю.
Теперь обратимся к представлению распределения м(<р, t)
теплового поля в виде ряда Фурье D.4). Согласно формуле D.4)
тепловое поле представляется в виде бесконечного числа стоячих
синусоидальных и косинусоидальных волн с амплитудами a, (t)
и bs(t) (s = l, 2, 3, ...). Напомним, что со временем щ(t)-* 0.
Если решения уравнений D.6) при s — 1 (т. е. уравнений Ло-
Лоренца) приближаются к состоянию равновесия, то и все осталь-
остальные амплитуды а„ и Ь, стремятся к постоянным значениям, и теп-
тепловое поле выходит на некоторое стационарное распределение.
Если зависимость от времени переменных а(, bt и ю стремится
к периодической, то к периодическим изменениям с тем же
периодом стремятся и все остальные переменные а., и Ья. Это со-
соответствует, согласно D.4), переходу с ростом времени к перио-
периодическому по времепи тепловому полю. Наконец, если изменения
«1, Ъ{ и со носят стохастический характер, то такой же характер
имеют и временные изменения теплового поля. При этом стоха-
стохастический характер изменения распределенного теплового поля
порожден стохастичностыю решений только системы трех диф-
дифференциальных уравнений, а само тепловое поле определяется
не только решением этой системы третьего порядка, но и реше-
решениями бесконечной системы уравнений, описывающей бескопеч-
ную последовательность стохастически возбуждаемых осцилля-
осцилляторов. Это обстоятельство влечет не только временную, но и про-
пространственную хаотичность. Чем медленнее с ростом s спад
амплитуд изменения переменных as и bs, тем ярче выражена эта
пространственная хаотизация.
Таким образом, рассмотренная система служит примером
распределенной системы, движения которой полностью определя-
определяются решениями системы обыкновенных дифференциальных
уравнений небольшой размерности. 13 какой мере этот частный
вывод может быть распространеп па другие распределенные си-
системы? Определенный и исчерпывающий ответ на этот вопрос
в пастоящее время дать трудно: качественно (по крайпей мере
в рамках квазилинейной теории) ситуация зависит от числа
степеней неустойчивости и степеней свободы с малым затухапи-
ем. В рассмотренной задаче одна степень неустойчивости (один
положительный показатель Ляпунова). Затухапия по остальпым
степеням свободы быстро растут. Как будет показано в дальней-
дальнейшем, именно с этим обстоятельством связана возможность по-
построения одномерной модели в виде точечного отображепия пря-
прямой в прямую, адекватно передающего особенности временного
36

поведения системы. Особенности же пространственного распре-
распределения требуют, учета значительно большего числа волновых
мод. В данном случае под волновой модой имеется в виду член
a, sin scp + ba cos scp,
входящий в представление одномерного теплового поля в виде
ряда Фурье D.4).
Таким образом, следует отличать число степеней свободы, не-
необходимое для приемлемого описания процессов временного из-
изменения, от числа мод, требуемых для пространственного описа-
описания. Для квазилинейных систем определяющая роль числа сте-
степеней линейной неустойчивости теоретически обоснована. Для
сильно нелинейных систем такое теоретическое обоснование от-
отсутствует, но все же можно думать, что и для них эта опреде-
определяющая роль в какой-то мере сохраняется. Что же касается чис-
числа учитываемых мод, то оно может быть очень большим, по-ви-
по-видимому, тем большим, чем меньше радиус пространственной кор-
корреляции. При описании турбулентных течений жидкости это
число может достигать очень больших значений.
Сказанное можно геометрически иллюстрировать схемой
рис. 1.24. Эта схема включает генератор временных изменений —
систему, вообще говоря, с большим числом степеней свободы,
возбуждаемую временным гене-
генератором, и формирователь про-
пространственно-временного описа-
описания. Это приближенная схема,
но для того чтобы она стала /
точной и полностью соответ- /
ствовала исходной распределен- |
ной математической модели, у
достаточно учесть в ней нали-
наличие обратного влияния возбуж-
возбуждаемой системы на временной
генератор. Из этого следует,
что построить такую упрощен- рис } 24
ную схему — это значит выде-
выделить времепной геператор, действием на который остальных
степеней свободы можно пренебречь. Такое выделение возможно
только после того, как сделан переход от описания распределен-
распределенной системы дифференциальными уравнениями в частных про-
производных к дискретному описанию, т. е. к описанию функций
и (х, t), где х — пространственные переменные, at — время, с по-
помощью рядов вида
Временной
зенератор
Возбуждаемая
подсистема
Лространст -
венно - времен -
ной формиро-
формирователь
и (х, t) = 2 в| (t) vs (х)
D.10)
и нахождению системы уравнений для «амплитуд» мод aB(t):
<Ц0=/.КХ ..-) E = 1,2,3,...). D.11)
37

Конечный результат, т. е. вид уравнений D.11), существенно
зависит от выбираемой системы пространственных мод va(x).
Здесь трудно дать общие рецепты. Но можно указать много удач-
удачных выборов в различных конкретных задачах. Впрочем, один
общий прием, реализация которого должна опираться на возмож-
возможности современных ЭВМ, указать все же можно. Он состоит в
следующем. Путем просчета на ЭВМ находится представительная
выборка интересующих нас решений иг(х, t) (£=1, 2, ..., N).
Затем по выборке иг(х, t}) (£ = 1, 2, ..., N; / = 1, 2, ..., Ж)
находится так называемый приспособленный базис v{(x),
v2(x), ..., vk(x). Приспособленный базис — это по возможности
небольшое множество ортонормированных функций таких, что
все функции выборки и (х, t,) приближенно представимы в виде
irx линейных комбинаций. Достаточно простые процедуры по-
построения такого приспособленного базиса известны [284]. Они
допускают уже сегодня практическую реализацию при MN « 105
и больше. После того как такой приспособленный базис vt(x),
..., vh(x) найден, отыскание уравнений D.11) осуществляется
по хорошо известным схемам [170, 253].
Дискретные модели распределенных динамических систем как
на уровне уравнений D.10), D.11), так и на последующей ста-
стадии выделения временного геператора и пространственного фор-
формирователя могут быть частными и общими. Частная модель —
это модель, допускающая рассмотрение не всех движений данной
распределенной системы, а только некоторых из них, определен-
определенного класса движений. Вопрос о том, для каких классов движе-
движений допустимо построение дискретных частных моделей, весьма
непрост. При попытке ответить на него необходимо иметь в ви-
виду естественное требование устойчивости (в том или ином смыс-
смысле) выделенного класса движений по отношению ко всем другим
близким к нему движениям. Это требование можно трактовать
как 'условие того, что выделяемый класс движений образует
устойчивое интегральное многообразие. Существует довольно раз-
развитая теория интегральных многообразий, однако она не позво-
позволяет реально выяснить устойчивость выделяемого частного клас-
класса движений распределенной системы, описываемой уравнениями
в частных производных.
Дискретная модель, получаемая с помощью приспособленного
базпса, может быть как общей, так и частной, в зависимости от
используемой при ее построении выборки движений. При этом
необходимость в проверке локальпой устойчивости отпадает и за-
заменяется естественно выполняемым требованием замкнутости
используемой частпой выборки движений.
В заключение отметим, что дискретные модели распределен-
распределенных систем устанавливают мостик между, казалось бы, столь
различными классами динамических систем. Если очень важные
волновые представления их разъединяют, то описание распре-
делепных систем с помощью времеппого геператора и простран-
пространственного формирователя их сближает, делая дискретную систе-
38

му частным случаем распределенной, когда она сводится к од-
одному временному генератору. Теория дискретных систем при
этом становится неотъемлемой частью теории распределенных
систем, в некотором смысле ее основой и ядром. Такой подход
вовсе не отметает волновые представления, он их только транс-
трансформирует, сводя к определенным особенностям пространствен-
пространственного формирователя.
§ 5. Модели локально активных сплошных сред
Изложенные выше общие соображения о движениях распре-
распределенной системы в значительной мере проникнуты квазилиней-
квазилинейной «идеологией», отводящей определяющую роль некоторому
небольшому набору мод примерно такого же вида, как в линей-
линейной системе. Вместе с тем мыслимы и возможны совершенно дру-
другие случаи. В нелинейных активных средах возникновение воз-
возмущений может носить локализованный и в некотором смысле
спонтанный характер. С подобной ситуацией мы сталкиваемся
при рассмотрении химических реакций в объемах или на поверх-
поверхностях при отсутствии перемешивания и при не очень быстрой
диффузии, в возбудимых и жизнедеятельных биологических сре-
средах (в сердечной мышце, в питательном субстрате с растущими
микроорганизмами). Аналогичные процессы могут происходить
и в среде, активное и возбудимое состояние которой поддержи-
поддерживается постоянной накачкой энергии из внешнего источника
энергии. Такая локализованная активность может приводить к
глобальной регуляризации движений сплошной среды, к тем или
иным упорядоченным ее движениям, но может порождать и хао-
хаотические и беспорядочные движения.
Простейшая математическая модель распределенной системы
обсуждаемого вида впервые, по-видимому, появилась в работах
[204, 455] и имеет вид
а
- = /(м)+Я_ E.1)
Затем возникли и рассматривались [1, 319, 354, 356] более
общие модели, описываемые системой уравнений
9£ = f(u,v)+DAu, % = g(u,v). E.2)
При D — 0 уравнения E.1) и E.2) вырождаются в конти-
континуальные, не связанные друг с другом системы одинаковых урав-
уравнений
и, соответственно, уравнений
ди , , „ ди
39

Это делает естественным наличие связей между решениями урав-
уравнений в частных производных E.1), E.2) и соответственно
обыкновенными дифференциальными уравнениями E.3), E.4).
Эта связь, в частности, проявляется в том, что неустойчивость
равновесий и автоколебательность систем E.3), E.4) соответ-
соответствует локальной возбудимости сред, описываемых уравнениями
E.1), E.2). Изучение моделей вида E.2) весьма сложно и очень
далеко от завершения. Но уже то, что уже известно, позволяет
обратить внимание на важную роль не только бегущих волн, но
и локализованных волн типа точечного источника, разрастающей-
разрастающейся вращающейся спирали и, возможно, некоторых других.
Распределенные модели с маломерным временпым генерато-
генератором и локальной возбудимостью можно рассматривать как пред-
представителей «чистых случаев». Очень сложные распределенные
модели гидродинамики являются по отношению к ним «смешан-
«смешанными случаями». Модель гидродинамики, описываемая уравне-
пием Навье — Стокса
g Vp + vAi;, divv = 0, E.5)
в зависимости от величины числа Рейнольдса может быть как
тгтпа, отвечающего маломерным временным генераторам, так и
тина локально-возбудимой среды. Первый тип характерен для
так называемых ламинарных течений и начальных фаз нару-
нарушения их устойчивости, второй — для развитой турбулентности.

Глава 2
ПОРЯДОК И ХАОС -
ДВЕ ОСНОВНЫЕ ОБЩИЕ ТЕНДЕНЦИИ
В ЭВОЛЮЦИИ ДИНАМИЧЕСКИХ СИСТЕМ
В предыдущей главе мы познакомились с простейшими ти-
типовыми моделями детерминированных динамических систем и
описываемыми ими движениями: состояниями равновесия, авто-
автоколебаниями, вынужденными колебаниями, различными типами
волновых движений, диффузионными процессами и хаотическими
движениями. Все это необычайное разнообразие движений мо-
может быть разделено на два основных типа, которые можно трак-
трактовать как порядок и хаос, регулярность и нерегулярность.
В случае дискретных систем разбиение движений на регуляр-
пые и хаотические характеризует только их временное поведе-
поведение. В случае распределенных систем речь может идти пе только
о временном, но и о пространственном порядке и хаосе, о перио-
периодичности и апериодичности, регулярности и нерегулярности не
только временной, но и пространственной структуры.
Если временное поведение динамической системы давно нахо-
находилось в центре внимания и представления о временном порядке
и хаосе обрели четкую математическую формализацию в явлени-
явлениях синхронизации и стохастичности, то различия между про-
пространственным порядком и хаосом, по существу, ранее не анали-
анализировались.
Как времепные, так и пространственные аспекты различий
между регулярным и хаотическим движением обсуждаются ниже.
Адекватным математическим образом временного порядка и
хаоса стали аттракторы, т. е. устойчивые состояния равновесия,
устойчивые периодические движения или автоколебания и, на-
копец, странные аттракторы. Адекватным математическим обра-
образом пространственного порядка и хаоса в двойственном представ-
представлении распределенной динамической системы оказались седловые
состояния равновесия, седловые периодические движения и бо-
более сложные сецловые инвариантные множества.
41

§ 1. Порядок и хаос — устойчивость и неустойчивость
Как уже говорилось, в настоящей главе речь пойдет об об-
общих характеристиках движений дискретных и распределенных
динамических систем, которые можно классифицировать как по-
порядок и хаос. Порядок во временном изменении — это уравнове-
уравновешенность взаимодействия, приводящая к устойчивому равнове-
равновесию, синхронность движений отдельных частей системы, влеку-
влекущая за собой периодическое движение всей системы в целом.
Хаос во временном изменении — это отсутствие регулярности,
нерегулярность, непредсказуемость и случайность. Простран-
Пространственные проявления порядка — это пространственная регуляр-
регулярность и согласованность. Пространственный хаос — это отсут-
отсутствие пространственной регулярности и рассогласованность.
Изменения в окружающем нас мире естественно делятся на
эти два класса. Смена дня и ночи образует регулярный времен-
временной ряд, в первом приближении периодический, но при более
внимательном рассмотрении — квазипериодический (двухперио-
дический), отражающий вращения Земли вокруг своей оси' и
вокруг Солнца. Волны на гладкой спокойной воде от брошенного
камня дают пример пространственно-временной регулярности.
Морские волны в сильный ветер или во время зыби могут слу-
служить примером хаоса, но иногда морские волны идут правильны-
правильными рядами друг за другом. Дни и ночи, лето и зима чередуются
периодически, а погода меняется весьма прихотливо, трудно пред-
предсказуемо, хотя и у погоды есть какие-то регулярные составляю-
составляющие, поскольку зимой не бывает +30°С, а летом 30°С.
Все эти примеры порядка и хаоса обыденны и привычны.
Они согласуются с нашими интуитивными представлениями о
порядке и хаосе. Но о какой непредсказуемости и случайности
может идти речь, когда мы рассматриваем вполне детерминиро-
детерминированное поведение решений дифференциальных уравнений, един-
единственность которых доказана?
Еще совсем недавно такого рода довод, опирающийся на тео-
теорему Коши о единственности решений дифференциальных урав-
уравнений, считался неотразимым и, казалось бы, исключал всякую
мысль о возможности случайных движений у детерминированных
динамических систем. Случайность, во всяком случае, в рамках
классических представлений, мыслилась чем-то привносимым из-
извне. Стохастические движения детерминированных систем рас-
рассматривались только как результат случайных воздействий из-
извне. И только в вопросах о природе стохастичности движений
молекул газа и вообще в вопросах статистической механики и
физики допускалась уступка, поскольку случайность была налицо.
Это несоответствие со временем стало привычным и списывалось
на громадные числа молекул, где все очень сложно.
Каково же было удивление, когда и в простых системах не-
неопровержимо обнаруживалась непредсказуемость, хаотичность и
стохастично сть.
42

Ниже, в гл. 4, события, которые привели к «прозрению», бу-
будут описаны подробнее, а сейчас мы только отметим и поясним
решающую роль в этом теории колебаний.
Далеко не все воспринимают теорию колебаний как науку
переднего края. Ее огромные успехи и влияние на формирова-
формирование принципа суперпозиции, спектрального подхода и линейной
теории, открытие и изучение автоколебаний, а сейчас — стохасти-
стохастических колебаний нередко «обезличиваются», утрачивают непо-
непосредственную связь с теорией колебаний, быстро становясь общим
достоянием. Наша книга — прежде всего о последних достиже-
достижениях теории колебаний, мепяющих наши фундаментальные есте-
естественно-научные представления, об открытии и исследовании
хаотических движений детерминированных автономных динами-
динамических систем, о возможности генерации такими системами сто-
стохастических колебаний, о новом, более широком взгляде на воз-
возможные движения динамической системы, о наличии двух про-
противоположных тенденций в эволюционировании динамической
системы — стремлении к порядку и стремлении к хаосу.
Тенденции к порядку и хаосу обусловлены устойчивостью и
неустойчивостью. Еще совсем недавно устойчивость рассматри-
рассматривалась как неотъемлемое требование физической реализуемости.
Казалось, что неустойчивые состояния равновесия и периодиче-
периодические движения физически нере-
ализуемы на протяжении про-
продолжительных интервалов вре-
времени и имеют значение лишь
в математических исследова-
исследованиях, поскольку играют важ-
важную роль в формировании гра-
границ областей притяжения ус-
устойчивых состояний равновесия
и периодических движений.
Роль неустойчивых состояний
равновесия и периодических
движений как границ областей
притяжения отражена на фазо-
фазовом портрете динамической
системы (рис. 2.1), которую
можно назвать триггером. Точ-
Точки Ot и О2 — устойчивые состояния равновесия (одно — типа фо-
фокуса, другое — типа узла). Точка О — неустойчивое состояние
равновесия типа седла. В него входят только две фазовых тра-
траектории Yi и ^2, и они разделяют устойчивые равновесия Ot и О2,
определяя возле каждого из них области притяжения Пг и П2.
Всякая фазовая точка области Пг стремится к точке Ои всякая
точка области Пг — к точке О2. Таким образом, в зависимости
от начальных условий система с таким фазовым портретом ока-
оказывается в одном из состояний равновесия (либо О4, либо Ог).
Перейти из одного из этих состояний равновесия в другое она
43
Рис. 2.1

может только в результате некоторого возмущения или толчка,
перебрасывающего ее из одной области притяжения в другую.
Такую систему можно назвать триггером, двоичным запоминаю-
запоминающим устройством, переключателем.
Однако роль неустойчивых движений в действительности зна-
значительно шире. Оказалось (и это было неожиданностью), что
именно неустойчивые движения порождают турбулентность и
сложные хаотические и стохастические движения динамических
систем. Тем самым два основных вида, две основные тенденции
эволюционирования — синхронизация (включая равновесие) и
стохастичность — представляют собой не что иное, как проявле-
проявления устойчивости и неустойчивости.
Механизм проявления устойчивости привычен и ясен, воз-
возможно, благодаря внедрению в наше сознание интуиции, опираю-
опирающейся на теорему Брауэра и принцип сжатых отображений Ба-
Банаха. Асимптотическая устойчивость всегда влечет за собой
устойчивые равновесия или устойчивые периодические движе-
движения. Асимптотически устойчивое ограниченное движение — это
либо устойчивое состояние равновесия или устойчивое периоди-
периодическое движение, либо движение, асимптотически приближаю-
приближающееся к одному из них. Механизм проявления неустойчивости
много сложнее и непривычнее. Для того чтобы его понять, нуж-
нужно прежде всего отбросить представление о физической реали -
зуемости движения как о требовании его устойчивости — сохра*
нения близости невозмущенной и возмущенной фазовых траек-
траекторий. Близость траекторий может не сохраняться, более того,
траектории могут локально экспоненциально разбегаться. Отдель-
Отдельные фазовые траектории при этом физически не реализуемы, но
они реализуемы как некоторая совокупность движений, облада-
обладающих определенной общностью. Представить себе все это не
просто, и, возможно, поэтому геометрический образ, состоящий
из таких фазовых траекторий, получил название «странный
аттрактор» — странное притягивающее множество.
Несмотря па сложность и необычность такого образования,
получившего название странного аттрактор*, условия его воз-
возникновения очень просты: сочетание глобального сжатия с ло-
локальной неустойчивостью. Конечно, остается неясным, возможно
ли такое сочетание, но если оно возможно, то неизбежно влечет
за собой существование странного аттрактора.
Как показывают конкретные примеры, такое сочетание дей-
действительно возможно. Более того, если оно возможно, то теорети-
теоретически устанавливается, что оно типично, т. е. что такая возмож-
возможность сохраняется и для всех близких динамических систем, не
разрушается малыми изменениями динамической системы. Ответ
на вопрос, как такое может быть, основывается на выявлении
роли так называемых гомоклипических структур. Гомоклиниче-
ские структуры мы рассмотрим в дальнейшем, а пока ограни-
ограничимся констатацией двух существенно разных вариантов пове-
поведения фазовых траекторий:
44

1) общее сжатие и локальная устойчивость;
2) общее сжатие и локальная неустойчивость.
Первая возможность приводит к устойчивым состояниям рав-
равновесия и устойчивым периодическим движениям, вторая — к сто-
стохастическим движениям, первая к порядку, вторая — к хаосу.
Таким образом, две основные, повсеместно наблюдаемые тенден-
тенденции в эволюционировании — порядок и хаос, соответствуют двум
общим возможностям поведения фазовых траекторий: с одной
стороны, общему сжатию и локальной устойчивости и общему
сжатию и локальной неустойчивости — с другой стороны.
Под общим сжатием понимается, что некоторая область G
фазового пространства переходит внутр_ь себя, т. е. спустя
некоторое время преобразеутся в область G <= G.
Под локальной неустойчивостью понимается разбегание очепь
близких вначале фазовых траекторий
такое, что в любой сколь угодно ма-
малой близости от невозмущенной тра-
траектории ч есть возмущенные траек-
траектории, которые со временем будут
отходить от нее на расстояние, боль-
большее некоторого е > 0. После того как
такая близкая фазовая траектория
•у' выйдет из е-окрестпости f, она
может снова в нее войти, но затем
в общем случае обязательно снова
выйдет и т. д.
Приведем простые примеры пер-
первого и второго типов поведения. На
рис. 2.2 изображен фазовый портрет, где глобальное сжатие со-
сочетается с локальной устойчивостью. При этом не только область
G переходит в лежащую в пей область G, но и любая малая об-
область g переходит в еще меньшую область g. Таким примером
может служить и система с фазовым портретом па рис. 2.1.
Рис. 2.2
Рис. 2.3
Перейдем к примерам второго типа, в которых общее сжа-
сжатие сочетается с локальной неустойчивостью. Возьмем торо-
тороидальную область G— «бублик» (внутренность двумерного тора),
45

вытянем его, утоньшим и изогнем так, чтобы он перешел в
тороидальную область G, лежащую в G, как показано на рис. 2.3
[332]. Это отображение G в G (назовем его Т) можно определить
аналитически. Для этого введем координаты х, у, т|з, как показа-
показано на рис. 2.4. При этом i|) — угловая переменная 0 «£ i|) < 2яг
а координаты х и у в области
G удовлетворяют неравенству
х2 + у2 <, \. Не опираясь на
рисунки, тороидальную область
G можно определить как мно-
множество точек (х, у, тM), для
которых тM — угловая перемен-
переменная, а х2 + у2 ^1, т. е. как
топологическое произведение
рис 2 4 окружности и круга. Отобра-
Отображение Т, переводящее область
G в область G, можно записать в переменных х, у, if в виде
х = qx + 0,5sin ф, у = qy + 0,5 cos ф, iM = 2г|?(то<12л), A.1)
где q < 1/2. Это отображение Т преобразует «бублик» G в лежа-
лежащий внутри него и дважды в нем оборачивающийся «бублик» G
(рис. 2.3). Действительно, при этом преобразовании A.1) всякое
сечение i|) = const области G — круг G^ единичного радиуса —
преобразуется в область £г$, лежащую внутри круга Gr
(рис. 2.5). Когда ф меняется от 0 до 2я, сечение G$ обегает
Рис 2.5
область G, а сечение G^ обегает ее дважды. При этом область
£г*, лежащая внутри бъ, «заметает» область G. Область G лежит
внутри G, поэтому происходит глобальное сжатие. Имеет место
и локальная неустойчивость, поскольку любые две близкие точки
с значениями координат -ф, различающимися на Ал|5, преобразу-
преобразуются в две другие точки с различием в координате -ф, равным
2Аф, т. е. вдвое большим.
Таким образом, отображение Т области G в G, изображенное
на рис. 2.3 и определяемое формулами A.1), глобально сжимаю-
сжимающее и локально неустойчивое. Рассмотрим его подробнее. 06-
46

ласть G преобразуется в область U, область U, в свою очередь,
таким же образом преобразуется в область G и т. д. Тороидаль-
Тороидальная область & лежит внутри тороидальной области G. Аналогич-
Аналогичным образом, в области G лежит область G и т. д. При этом
все время происходят сжатия по координатам х и у (q < 1/2)
и с каждым преобразованием число оборотов образа в области G
по координате i|) удваивается. Обла- _
сти G, U, G, ... неограниченно при- "
ближаются к некоторому предельно- п
му множеству /, которое инвариант-
инвариантно относительно отображения Т, т. е.
преобразуется под действием Т в
себя. На этом ^инвариантном мно-
множестве отображение Т для коорди-
координаты ф записывается в виде
A.2)
График отображения A.2) показан
на рис. 2.6. Это отображение A.2)
растягивающее: всякий малый от-
отрезок длины Лф оно преобразует
jb отрезок длины 2Лг|). Последовательные преобразования i|),
ф, i|), ... образуют периодическую последовательность, ес-
если i|) = 2л/с/B" — 1), где к и п — целые числа. Таких значений
•ф счетное множество и их лебегова мера равна нулю. Последо-
Последовательность i|), i|), ф, ... с значением i|), не принадлежащим этому
множеству, всюду плотно покрывает окружность 0 < i|) < 2я. Та-
Таким образом, отображение Т на инвариантном множестве / экс-
экспоненциально неустойчивое, растягивающее, и последовательные
преобразования любой его точки в общем случае всюду плотно
Рис. 2.7
покрывают /. На рис. 2.7 приведены последовательные значения
для 24 преобразований. Из рисунка виден их нерегулярный, хао-
хаотический характер. В заключение этого примера глобально сжи-
сжимающего и локально экспоненциально неустойчивого отображения
сделаем ряд общих замечаний.
47

Отображение Т взаимно однозначное, но на инвариантном
множестве / отображение переменной i|) не взаимно однозначное.
В приведенном примере отображение Т трехмерное. Его легко
обобщить на случай большей размерности, но построить анало-
аналогичные примеры с сохранением взаимной однозначности для
меньшей размерности нельзя.
Отображение A.1) — это простой пример взаимно однозначно-
однозначного глобально сжимающего и локально неустойчивого отображе-
отображения. Его последовательные итерации образуют в общем случае
хаотическую последовательность. Предельное множество этих по-
последовательностей образует некоторое инвариантное множество
/. С какой бы точностью ни была задана начальная точка х, у,
i|), ее достаточно далекие последовательные образы пе могут быть
найдены, так как с последовательными преобразованиями про-
происходит неограниченное и быстрое экспоненциальное нарастание
ошибки. В этом смысле достаточно далекие преобразования не-
непредсказуемы. Так, при первоначальной точности порядка 10~s
уже начиная с 20-го преобразования ошибка, вообще, порядка
единицы.
Этот пример трехмерного точечпого отображения может быть
легко трансформирован в пример динамической системы, описы-
описываемой дифференциальными уравнениями, но с четырехмерным
фазовым пространством. Для такой системы дифференциальных
уравнений точечное отображение Т будет отображением Пуанка-
Пуанкаре на секущей трехмерной плоскости.
Нечто аналогичное приведенному абстрактному примеру мо-
может происходить и в конкретных системах. Так, в фазовом про-
пространстве уравнений Лоренца A.24)
при 6 = 8/3, о = 10, г =24,4 после-
последовательные точки пересечения фа-
фазовых траекторий с секущей плос-
плоскостью z=r~ 1 приходят в очень
малую окрестность некоторой кривой
и J и остаются в пей, порождая тем
*" самым отображепие кривой / в се-
себя. Если вдоль этой кривой ввести
переменную и, то это отображение
имеет такой вид, как показано на
рис. 2.8. Оно всюду растягивающее,
причем типичные последовательные
значения и являются хаотическими.
Более подробно о системе Лоренца
и ее странном аттракторе будет рассказано в § 4 гл. 7.
Несколько другая ситуация, но также приводящая к хаоти-
хаотическим движениям, может иметь место па секущей плоскости
системы, приведенной в предыдущей главе.
Как и в случае системы Лоренца, па секущей плоскости, во
всяком случае, приближенно с большой точностью, последова-
последовательные точки преобразования, спустя некоторое их число, ложат-
48
7
Рис. 2.8

ся на некоторую кривую /, порождая на ней в случае уравнения
Лоренца отображение вида, показанного на рис. 2,8, а в случае
неавтономного ротатора A.23) предыдущей главы — отображе-
отображения, представленные па рис. 2.9, а—.г. Отображение рис. 2.8
очень похоже на отображение рис. 2.6: они оба всюду растяги-
растягивающие. Отображения рис. 2.9, а — г другие. Это отображения
Рис, 2.9
окружности в себя, и они не всюду растягивающие: у них всегда
есть участки, где коэффициент растяжения меньше единицы,
и даже точки, где он равен нулю. Рис. 2.9, а—г отвечают ряду
значений параметра v = 0; 0,7; 0,9; 1,32 и 2,2. Как можпО'
видеть из этих рисунков (например, если построить по ним по-
последовательные отображения при значепиях 0sSvsS2,2), воз-
возможны как однократные, так и многократные устойчивые непо-
неподвижные точки и хаотические последовательности. Первым от-
отвечают движения ротора, синхронные с частотой параметриче-
параметрического воздействия, второму — хаотические движения. С ростом
параметра v, как видно из рисунков 2.9, а — г, эти типы движе-
движений чередуются, причем зоны синхронизации по параметру v
с его ростом уменьшаются, а зоны хаотических движений рас-
расширяются. Более полное рассмотрение фазового портрета и его
изменений (бифуркаций) этой динамической системы содержится
в § 5 гл. 7.
Перейдем теперь к более подробным описаниям сначала яв-
явлений синхронизма, а затем временной и пространственной хао-
тизации. Напомним еще раз, что синхронизация, понимаемая
49-

как временная регулярность или временной порядок, является
проявлением общего сжатия и локальной устойчивости. Времен-
Временная хаотизация — проявление глобального сжатия и локальной
неустойчивости. Пространственную регулярность или хаос мож-
можно связать с особенностями структуры решений двойственного
дискретного представления движений распределенной системы.
§ 2. Явления временной синхронизации
С явлением .синхронизации человек встретился очень давно.
Вся его жизнь и жизнь окружающей природы были синхрони-
синхронизованы с временами года и сменами дня и ночи. Человек не
только наблюдал эти явления, но и активно стремился к возмож-
возможно лучшей синхронизации своих действий — действий охотника,
рыболова, скотовода, пахаря — со сменой времен года, дня и но-
ночи. Календарь и часы — результат этого стремления. Человек на-
наблюдал синхронизацию при массовых танцах и песнях, при пляс-
плясках и движениях под музыку или удары барабана.
Однако наука о синхронизации ведет свое начало с наблю-
наблюдения несравнимо более простых явлений.
Синхронизация колебаний маятников часов. Первое известное
описание такого простого явления синхронизации сделано Хри-
Христианом Гюйгенсом. До этого он изобрел и изготовил велико-
великолепные часы с очень точным ходом. Наблюдая свои часы, Гюй-
Гюйгенс обнаружил явление, которое необычайно его поразило,
и описал свое открытие следующим образом: «Маятник этих
часов имел длину 9 дюймов и груз полфунта. Механизм приво-
приводился в движение гирями, заключенными в ящик вместе с ме-
механизмом. Длина ящика была 4 фута. Внизу он был отягчен по
крайней мере 100 фунтами свинца, чтобы весь механизм воз-
возможно лучше сохранял на судне вертикальное положение. Двое
таких часов висели на одной и той же балке, покоящейся на
двух опорах. Оба маятника двигались всегда в противоположные
стороны, а колебания так точно совпадали, что никогда ни на
сколько не расходились. Тиканье обоих часов было слышно в од-
одно и то же мгновенье. Если искусственно нарушалось это сов-
совпадение, то оно само восстанавливалось в короткое время».
Синхронизация колебаний органных труб. Много позднее,
в XIX веке, явление синхронизации в акустических и электро-
электроакустических системах обнаружил Рэлей. Наблюдая две распо-
расположенные рядом органные трубы, он обнаружил, что при малой
их расстройке они звучат в унисон. Каждая из оргапных труб
представляет собой автоколебательную систему, генерирующую
звук с некоторой частотой со. Если эти частоты различаются ма-
мало, то обе трубы начинают издавать звук одной и той же частоты
и звучат в унисон. Иногда это звучание в унисон выражается
тем, что звук полностью исчезает: каждая из труб звучит, а вме-
вместе с тем никакого звука нет. Это соответствует тому, что трубы
50

генерируют звук точно одинаковых частот, но противоположных
фаз (фазы их колебаний различаются на я).
Синхронизация вращений электрогенераторов. Впервые явле-
явление синхронизации обрело значительное прикладное значение при
работе нескольких электрогенераторов переменного тока на одну
нагрузку — одну и ту же электрическую сеть. С появлением
первых электростанций нередко стали происходить разрушитель-
разрушительные аварии. Дело в том, что при работе на одну и ту же на-
нагрузку фазы генерируемых напряжений не совпадали, и вместо-
того чтобы совместно посылать ток в общую сеть, электрогене-
электрогенераторы пропускали его друг через друга и сжигали свои обмот-
обмотки. Чтобы этого не происходило, генераторы должны вращаться
с одной и той же частотой (совпадение частот должно выдержи-
выдерживаться очень точно) и одинаковыми (достаточно близкими) фа-
фазами. Как этого добиться, если генераторы приводятся во вра-
вращение разными турбинами? Даже самое точное регулирование
скоростей вращения турбин не может обеспечить полного совпа-
совпадения частот и фаз, поскольку при сколь угодно малой разности
Лсо ФО частот их вращения через время Т набежит разность
фаз, равная ЛшГ, и спустя время Г = я/Да> их фазы будут от-
отличаться на п.
В этой, казалось бы, безнадежной ситуации выручило явление
синхронизации. Оказалось, что при выполнении некоторых ус-
условий при не очень значительных расстройках частот электроге-
электрогенераторы сами синхронизируют друг друга и вращаются согла-
согласованно с очень большой точностью. '
Синхронизация при радиоприеме. Не менее важное приклад-
прикладное значение явление синхронизации получило в радиотехнике
и радиофизике. Без преувеличения можно сказать, что явление
синхронизации — синхронизации колебаний радиоприемника
внешним слабым радиосигналом — лежит в основе приема радио-
радиосигналов.
Основной математической моделью, которая рассматривалась
в прямой связи с возникшей задачей приема слабого радиосигна-
радиосигнала регенеративным приемником, было уравнение Ван-дер-Поля
с правой частью Е cos vt. Исследование этого уравнения обнару-
обнаружило, что синхронизация генератора Ван-дер-Поля может про-
происходить при сколь угодно малой амплитуде внешнего воздей-
воздействия, если только расстройка частот достаточно мала. При не-
недостаточно малой расстройке возникает двоякопериодический
режим.
Система фазовой синхронизации. Явление синхронизации ле-
лежит в основе разнообразных и многочисленных систем фазовой
синхронизации. Такие системы широко используются в связи и
измерениях.
Одна из задач фазовой синхронизации состоит в создании
мощных, весьма стабильных по частоте генераторов высокочас-
высокочастотных колебаний. Эта задача решается путем синхронизации
мощного источника колебаний с маломощным высокостабилънъгм
51

по частоте источником колебаний, например кварцевым гене-
генераторам.
Синхронизация механических вибраторов. Явление синхрони-
синхронизации находит значительные приложения во всевозможных уст-
устройствах вибротехники. Весьма эффективно явление синхрониза-
синхронизации используется при совместной работе многих механических
вибраторов, которые нужно заставить вращаться синхронно, не
соединяя друг с другом механически [89, 90].
Синхронизация движений планет и спутников. Явление син-
синхронизации используется для ориентирования в пространстве ис-
искусственных спутников Земли. Само по себе явление синхрони-
синхронизации движений небесных тел было замечено сначала у плапет
и спутников Солнечной системы в виде удивительных связей
между периодами обращений и вращений планет и спутников.
Объяснение этих связей оказалось очень непростым и в настоя-
настоящее время не завершено. Обнаруженные закономерности состоят
в наличии простых целочисленных соотношений между частота-
частотами орбитальных и собственных вращений планет и спутников
Солнечной системы вида [79, 256]
«!©! + Щ(д2 + . . . + ns(Os = 0, B.1)
где П|, пг, ..., п3 — пебольшие целые числа, a ©f, ©2, ..., <»s — ча-
частоты орбитальных или собственных вращений. Конечно, эти
удивительные соотношения могут быть и случайностью. Том бо-
более, что значения частот известны приближенно и указанные
между ними соотношения также не точные, а приближенные с
небольшими отклонениями. Но если это случайность, то очень
редкая: ее вероятность оценивается как величина порядка 10~".
Трудно поверить в осуществление события с такой ничтожной
вероятностью. Кроме того, некоторые из этих соотношений полу-
получили теоретическое обоснование.
Синхронизация сердечных сокращений. Ритмичным сокраще-
сокращениям нашего сердца мы обязаны синхронизации. Нарушение
нормальной синхронизации сокращений мышечных волокон серд-
сердца ведет к аритмиям, в том числе такой грозной, как фибрилля-
фибрилляция сердца.
Первая математическая модель синхронизации возбуждений
сердечных сокращений была предложена Ван-дер-Полем. Она
была навеяна изучавшимися в то время явлениями синхрониза-
синхронизации в радиотехнике и представляла собою три связанных между
собою генератора колебаний. С ее помощью удалось объяснить
многие аритмии и даже указать ряд новых, которые затем были
обнаружены. Однако для понимания причин возникновения фиб-
фибрилляций потребовалась более сложная модель проводящей воз-
возбуждаемой среды. Она объяснила причины и механизм возник-
возникновения фибрилляций сердца, при которых по сердечной мышце
начинают бегать беопорядочные волны сокращений мышц вместо
синхронных ритмичных их сокращений.
.52

§ 3. Временной и пространственный порядок и хаос
Несмотря па многообразие конкретных проявлений времен-
временной синхронизации, все они состоят в согласованных между со-
■бой изменениях отдельных подсистем динамической системы
с внешним периодическим воздействием, приводящих к периодич-
периодичности изменения состояния вне зависимости от того, дискретная
-эта система или распределенная. Явления пространственного по-
порядка исследованы гораздо меньше и используются не столь
широко, как явления временной синхронизации. Более того, если
явление временной синхронизации четко определено [89, 90], то
в отношении пространственного порядка такого определения нет
и все ограничивается относительно скромным набором конкрет-
конкретных, лишь отчасти, теоретически изученных, примеров: ячеек
Шелли-Холла и Бенара в конвективных течениях жидкости, вих-
вихрей Тейлора в вязкой жидкости между вращающимися цилинд-
цилиндрами и некоторых систем, в которых экспериментально наблю-
наблюдается четкая пространственная структура: устойчивых само-
самовозбуждающихся стоячих волн, вихрей Кармана за обтекаемым
жидкостью телом, сокращений возбудимой мышечной ткани
сердца, пространственно-временных перестроек ансамблей био-
биологических клеток и др. В последних случаях говорится не толь-
только о пространственном порядке, но и о наличии определенной
пространственной структуры и самоорганизации и в связи с этой
трактовкой о синергетике как новой науке о самоорганизации
[355, 356, 487].
Что же такое временной и пространственный порядки? Речь
идет, конечно, о распределенной системе. Воспользуемся ее дис-
дискретным представлением вида
as = /s(ax, a2, ...) (s = l,2, ...),
рассмотренном нами в гл. 1. Временной порядок с точки зрения
такого представления — это периодичность движений ее времен-
временного генератора или всей бесконечной системы для переменных
йч, а2, ... А что такое пространственный порядок? Под этим мож-
можно, например, иметь в виду периодичность и(х, t) no х при лю-
любом t или несколько более общую регулярность по х. Но эти
свойства функции и(х, t) достаточно сложно связаны с функция-
функциями v,, v2, .. . и аи а2, ... Поэтому мы перейдем от дискретного
представления движений распределенной системы в виде C.1)
к представлению вида
и(х, t) = 2М*) vs(x),
dvs C.2)
-& = g*(»u v* »з> • • ■) (* = 1, 2, ...),
которое назовем двойственным. Помимо уравнений C.2) функции
vi, Vt, v3, ... должны еще на границах пространственной области
53

удовлетворять некоторым краевым условиям, которые в одно-
одномерном случае можно записать в виде
JfiW 1*^ = 0, К2 (vt) \x=h = 0 (s = l,2,...). C.3)
Заметим, что в уравнениях C.2) v, — векторные функции не-
некоторой размерности т, а общее число кра&вых условий C.3)
равно т: р определяется первым условием и q — вторым
(p + q = ?n).
Ограничимся ради простоты конечным числом N функций
vu v2, ..., ^ и рассмотрим в соответствии с этим укороченную
систему C.2) и только соответствующую часть краевых условий
C.3) при s = l,2,...,N.
Рассмотрим сначала возможные решения системы уравнений
C.2) без краевых условий при всех х на бесконечном промежут-
промежутке — °о < х < +°° и построим ее «фазовый портрет». Построим
поверхности Ki и Кг размерностей qN и pN соответственно, отве-
отвечающие краевым условиям C.3). После этого задачу поиска ре-
решения уравнения C.2), удовлетворяющего краевым условиям
C.3), можно сформулировать как поиск отрезка фазовой траек-
траектории уравнения C.2), концы которого, отвечающие х = lt и
х = 1и лежат соответственно на поверхностях Ki и Кг.
Вопрос о возникновении пространственного порядка наиболее
интересен в случае, когда распределенная задача однородна
по х. Это соответствует тому, что в дифференциальные уравнения
C.2) переменная х явно не входит. Если трактовать перемен-
переменную как время, то система автономна. В этом случае для реше-
решения краевой задачи имеют значение не сами величины J, и 12,
точнее, не то, что краевые условия заданы при х = h и х = lz,
а то, каков промежуток между х = ^ и х —12. Обозначим этот
Рис. 2.10
промежуток через 1 = 1г — lt и рассмотрим решения, которые,
непрерывно меняясь с изменением I, существуют при I -*■ °°. Та-
Такие решения возникают, если в фазовом пространстве имеются
седловое состояние равновесия О и инвариантные многообразия
S+ и 5~, которые имеют непустые пересечения соответственно
с поверхностями Ki и К2. Эта ситуация поясняется на рис. 2.10.
54

Размерности поверхностей Kt и Кг должны быть согласованы
[334] с размерностями инвариантных многообразий S+ и S~,
в противном случае малейшее изменение положения поверхно-
поверхностей Kh К2, S+ или S~ может привести к исчезновению пересе-
пересечений Ж, с S+ и Кг с S~. В пределе при I -*- °° искомый отрезок
Z фазовой траектория составлен из двух отрезков *у+ и <у~ фазо-
фазовых траекторий, лежащих на S+ k S~. Отрезок у+ соединяет точ-
точку пересечения Kt с S+ с точкой О, а отрезок у~ — точку О с
точкой пересечения поверхностей S~ и isT2. При больших I иско-
искомый отрезок L фазовой траектории проходит последовательно
вблизи if+ и -у- (см. рис. 2.11, а). Все сказанное можно повторить
Рис. 2.11
и в случаях, когда вместо седлового равновесия имеется седловое
периодическое движение Г (рис. 2.11, б) или другое более общее
инвариантное седловое образование.
В изложенной ситуации естественно объясняется возникнове-
возникновение различных типов пространственных структур (равновесной,
периодической и хаотической) в зависимости от того, имеется ли
седловое равновесие О, седловое периодическое движепие Г или
седловое хаотическое движение /. Возникновение периодической
или хаотической пространственных структур аналогично возник-
возникновению периодических или стохастических автоколебаний, но с
той существенной разницей, что если раньше требовалась устой-
55

чивость, то теперь требуется седловой характер решения, согла-
согласованный с краевыми условиями. Согласование состоит в том,,
что суммы размерностей Kt и S+ и соответственно Кг и S~ долж-
должны быть не меньше размерности пространства mN. Отметим
еще, что для проявления в описанных ситуациях равновесной,
периодической или хаотической пространственных структур не-
необходимо еще, чтобы пространственная протяженность I была
достаточно большой.
Изложенное выше позволяет получить похожие и достаточно
естественные трактовки явлений временного и пространственного
порядка, а также противоположных им тенденций временного и
пространственного хаоса. По-видимому, помимо этих двух типов
эволюции динамических систем — синхронизации и стохастично-
сти — можно и целесообразно говорить и еще об одном типе эво-
эволюции — самоорганизации. Явления самоорганизации едва ли
следует сводить к временному и пространственному порядку.
По-видимому, следует, напротив, подчеркнуть тот новый смысл,
который она привносит,— возможность процессов, приводящих
к возникновению структур, устойчивых по отношению к более
или менее значительным и разнообразным изменениям внешних
условий и, наконец, структур, способных к росту и распростра-
распространению. Сводить самоорганизацию к той или иной временной и
пространственной упорядоченности, возможно, не следует еще
и потому, что в их основе лежат качественно разные механизмы.
Синхронизация — это проявление устойчивости во взаимодей
ствующих подсистемах, а самоорганизация — это проявление уп-
управляющих и организующих функций обратных связей, которые
целесообразно рассматривать с информационной точки зрения.
В заключение этой главы необходимо подчеркнуть, что разде-
разделение движений детерминированных динамических систем на
регулярные и хаотические в условиях, когда возможны промежу-
промежуточные случая, носит условный характер. Более того, всякое хао-
хаотическое движение в той или иной мере наделено некоторой ре-
регулярностью, некоторыми временными закономерностями и про-
пространственной структурой. Задача исследования хаотических дви-
движений — это в первую очередь обнаружение и описание их вре-
временных и пространственных закономерностей, носящих в одних
своих частях детерминированный характер, а в других — случай-
случайный. Хаотические движения песут в себе черты как регулярности,
так и стохастичности. Например, поток за обтекаемым толом при
достаточной его скорости носит в целом турбулентный, хаотиче-
хаотический характер, однако отрыв вихрей Кармана от обтекаемого тела
представляет собой явно регулярный периодический процесс.
Вместе с том скорости потока за обтекаемым телом — случайные
с более или менее выраженными периодическими составляющими.

Глава 3
ПРЕОБРАЗОВАТЕЛИ, УСИЛИТЕЛИ
И ГЕНЕРАТОРЫ СТОХАСТИЧНОСТИ
Выше все возможные движения детерминированной динами-
динамической системы были разделены па регулярные и нерегулярные,
на отвечающие порядку и хаосу. При этом нерегулярные хаоти-
хаотические движения представлялись как совместный эффект регу-
регулярных и случайных составляющих, как возмущение этой более
или менее выраженной регулярной составляющей некоторой слу-
случайной. В настоящей главе обсуждается природа случайной со-
составляющей нерегулярных хаотических движений.
§ 1. Преобразователи стохастичности
Пусть линейный осциллятор подвержен случайному воздей-
воздействию |(£) T&Ki что измепение его состояния х, х подчиняется
уравнению
(olx = l(t). A-1)
Решая уравнение A.1) при произвольных начальных условиях
х ==• х0, х = х0, при t = t0 находим, что
х (t) = е~6{1~'о) {х0cosQ(t — g + ~fisinQ (* — gj -f
t
+ 4" jV6((~T) 6 (t) sin Q (t — t) dx, A.2)
где Q2 = ml — б2 > 0. Пусть б > 0, тогда при t0 -*■ -°° из A.2)
следует, что
x{t)=-± J е-б"-т) I (т) sin Q (* - т) dr. A.3)
— оо
Согласно A.3) случайному воздействию |(£) отвечает случайное
же измепение x(t). Если |(i) — стационарный случайный про-
57

цесс с нулевым математическим ожиданием я заданной автокор-
автокорреляционной функцией Кц(х), то x(t)—также стационарный
случайный процесс с нулевым математическим ожиданием и ав-
автокорреляционной функцией
00 00
К ж (т) = -Ц f Г Кц (т — v + ц) e-6(v+ti) sin Qv sin Q|i dv d\i. A.4)
о о
Соответствующее A.4) соотношение между спектральной плот-
плотностью 5{{(©) случайного воздействия £(£) и спектральной плот-
плотностью 5«(©), как известно, имеет вид
Sxx И = к ) . A.5)
(й2— G)*J+46 AJ. х 7
Таким образом, линейный осциллятор с внешним случайным воз-
воздействием £(£) можно рассматривать как преобразователь слу-
случайного процесса |(£) в новый случайный процесс x(t). Форму-
Формула A.3) определяет реализации случайного процесса x(t) череа
реализацию случайного процесса £(£), а формулы A.4) и A.5)
устанавливают связи между автокорреляционными функциями и
спектральными плотностями в случае, когда £ (t) — стационарный
случайный процесс.
Формулы A.4) или A.5) позволяют найти дисперсию слу-
случайной величины x(t):
Dx = Kxx @) =-Ц Г Г Кц (ц - v) e-e<v+»> sin Qv sin Qfi dv d\i =
о о
If 8\\ <») d* A
Как и следовало ожидать, из обращения в нуль D\ следует об-
обращение в нуль Dx. Напомним, что из D\ = 0 следует, что
Кц(х)= 0, т. е. с исчезновением случайности в воздействии %{t)
исчезает и случайность в порождаемом им изменении координа-
координаты x(t) линейного осциллятора. В случае, когда случайное воз-
воздействие |(£) заменяется суммой некоторого заданного воздейст-
воздействия |о(£) и такого же, как и ранее, случайного воздействия |(£),
то с обращением в нуль случайной составляющей £ (t) выход
x(t) не обращается в нуль, но теряет свою случайность и стано-
становится детерминированным, т. е. случайность x(t), как и следова-
следовало ожидать, имеет своей причиной только случайность 1(£).
Сделаем еще замечание о характере преобразования случай-
случайной составляющей входного воздействия |(£) к выходной величи-
величине x(t), вытекающем из формулы A.6). Согласно этой формуле
преобразование спектра случайного воздействия £(£) в спектр
выходной величины x(t) происходит в соответствии с резонанс-
резонансными свойствами линейного осциллятора, с его резонансными
58

кривыми, изображенными на рис. 1.10. При этом далекие от ре-
резонанса случайные гармонические составляющие подавляются,
близкие, наоборот, усиливаются.
Пусть теперь случайное возмущение £B) воздействует не на
линейный осциллятор, а на осциллятор Ван-дер-Поля, так что
x-28x{l — x2)+(ozx = l(t). A.7)
Как и прежде, будем рассматривать |(£) как входное воздейст-
воздействие, a x\t)—как порожденный им выход. В противоположность
предыдущему случаю с обращением %{t) в пуль выход x(t) не
обратится в нуль, а, напротив, останется отличным от нуля
(б > 0) и с течением времени будет стремиться к некоторому
периодическому процессу х* (t). Мы видим, что, как и прежде,
случайность выхода исчезает вместе с исчезновением случайного
воздействия, но сам выход при этом вавсе не обращается в нуль.
В случае малости £(£) и малости величины б>0 поставлен-
поставленная задача допускает сравнительно простое приближенное ре-
решение. В новых переменных А и <р, связанных со старыми фазо-
фазовыми переменными х и х соотношениями
х = A cos(cl>£ + <p), х = (оА sin((ot + <р), A-8)
уравнения A.7) записываются в виде
А = 8А U — ~) - -i-1 sin ((at -i- <p), ф = - -~ i cos (©* + ф).
Фазовый портрет этих уравнений при % = 0 изображен на
рис. 3.1. К окружности Г, состоящей из состояний равновесий,
асимптотически приближаются все остальные фазовые точки, за
исключением точки неустойчивого равновесия О. Наличие малых
случайных воздействий (£ Ф 0) приводит к случайным блужда-
блужданиям фазовой точки в окрестности Г, т. е. амплитуда колебаний
А близка к двум, а фаза медленно меняется и может накапли-
накапливать свои изменения. В установившемся состоянии плотность ве-
вероятностей р(А, ф) не зависит от угла <р и изображается поверх-
поверхностью вида, показанного на рис. 3.2. Таким образом, входное
случайное воздействие % преобразуется в осцилляторе Ван-дер-
Поля в выходные флуктуации амплитуды колебаний и случай-
случайный дрейф фазы ф. Для отыскания соответствующей плотности
вероятностей может быть составлено широко известное уравне-
уравнение в частных производных Эйнштейна — Фоккера — Планка.
С помощью этого уравнения может быть найдено не только уста-
установившееся распределение вероятностей, т. е. уравнение изобра-
изображенной на рис. 3.2 поверхности, но и процесс ее установления,
а также плотности вероятностей перехода из одного состояния
А, ф в другое А, ф за ^время т [216, 310, 320, 342]. Эта плотность
вероятностей р{А, ф; А, ф; т) при т -^ °° имеет пределом устано-
установившуюся плотность вероятностей р{А).
59

Приведенные примеры иллюстрируют «преобразования слу-
случайности» в динамических системах: линейном осцилляторе w
осцилляторе Ван-дер-Поля. При этом внешняя случайность пре-
преобразуется в случайные изменения х и i или А и ф. До самого
последнего времени случайность в динамических системах только-
в таком плане и рассматривалась. Случайность в динамическую-
Р
Рис. 3.1
Рис. 3.2
систему привносилась извне в виде некоторого случайного воз-
воздействия, и только это случайное воздействие вызывало случай-
случайность изменения ее состояния и любых величин, определяемых
этим состоянием. Это позволяло представлять динамическую си-
систему как некий преобразователь случайных входов в случайные-
выходы. Такая точка зрения особенно естественна при рассмот-
рассмотрении сложных динамических систем в виде взаимодействующих
менее сложных подсистем. Каждая из выделяемых физически
или мысленно подсистем испытывает какие-то входные воздей-
воздействия и действует на другие подсистемы своими выходными воз-
воздействиями. Ранее считалось само собой разумеющимся, что слу-
случайность выходных воздействий обусловлена только случай-
случайностью входных воздействий, что каждая из подсистем — это
некий преобразователь случайности, преобразователь одних слу-
случайностей в другие, и что с исчезновением входной случайности,,
например стремлением к нулю ее дисперсии, случайность на вы-
выходе и ее дисперсия тоже исчезают. Выяснилось, однако, что
иногда при стремлении к нулю дисперсии входа дисперсия выхо-
выхода остается конечной. Объяснение и исследование того, как та-
такое может быть, составляет основную цель и содержание настоя-
настоящей книги. Оказалось, что помимо преобразователей стохастич-
ности (случайности) существуют динамические системы, кото-
которые являются генераторами стохастичности. Оказалось, что по
характеру связи выхода с входом динамические системы можно
разделить па преобразователи и генераторы стохастичности. Ог
преобразователей стохастичности генераторы стохастичности от-
отличаются тем, что на их выходе возможна стохастичность с ко-
60

нечной дисперсией при сколь угодно малой дисперсии входа. Это
грубое разделение целесообразно детализировать, введя еще не-
некоторый промежуточный случай, который назовем усилителем
стохастичности. Отличие преобразователя стохастичности от уси-
усилителя стохастичности не столь явное, как преобразователя сто-
стохастичности от генератора стохастичности. Так, усилитель стоха-
стохастичности с не очень большим коэффициентом усиления — это
преобразователь стохастичности, а усилитель стохастичности е
бесконечным или очень большим коэффициентом усиления — это
уже усилитель стохастичности, чем-то похожий на генератор сто-
стохастичности.
Таким образом, в соответствии со сказанным, по характеру
связи стохастичности входа со стохастичностью выхода будем
различать преобразователи стохастичности, усилители стохастич-
стохастичности и генераторы стохастичности [100, 272, 278, 280, 281].
О преобразователе стохастичности уже говорилось. Подводя итог,
отметим, что преобразователь стохастичности преобразует посту-
поступающее на его вход случайное воздействие в некоторое другое
случайное воздействие, причем так, что вероятностное описание
случайности выхода, по крайней мере, спустя некоторое время,
определяется вероятностным описанием случайности входа, и с
исчезновением стохастичности входа выход также теряет свою
стохастичность. Именно этот и только этот случай изучался до
последнего времени [104, 193, 194, 216, 299, 310, 320, 342]. Он
интенсивно исследовался при рассмотрении случайных колеба-
колебаний механических и радиотехнических систем. Таковы все при-
приведенные выше примеры. Основной задачей этих исследований
считалось отыскание характеристик и описание стохастичности
выхода по заданным характеристикам и стохастическим описа-
описаниям входа. В некоторых случаях эта задача решалась просто.
Так, в рамках корреляционной теории стационарных случайных
процессов спектральная функция выхода ^(со) линейной дина-
динамической системы связана оо спектральной функцией входа
S() соотношением вида
)\2Sl,((ii), A.10)
где K(ia>)—коэффициент передачи линейной системы. В ряде
случаев эти задачи приводятся к решению уже упоминавшегося
выше уравнения в частных производных Эйнштейна — Фокке-
ра — Планка.
§ 2. Усилители стохастичности
Усилитель стохастичности в принципе не отличается от пре-
преобразователя стохастичпости. Все дело в величине коэффициента
усиления. Если этот коэффициент очень велик, то стохастичность
выхода уже не поддается контролю, поскольку требует недоступ-
недоступной точности учета входных случайных воздействий. Простейший
пример такого типа — это пороговый элемент, вход ц которого
61

•связан с входом | зависимостью вида
[+1 при |>0,
О при |<0.
B.1)
Этот пороговый преобразователь сколь угодно малый случайный
процесс |(£) с МЪ, = 0 и Z)| < 1 преобразует в случайную после-
последовательность из +1 и 0. Другой пример — это консервативный
X
Рис. 3 3
осциллятор с фазовым портретом в виде вложенных друг в друга
замкнутых кривых (рис. 3.3, а). При сколь угодно малых слу-
случайных воздействиях фазовая точка начнет блуждать с одной
замкнутой фазовой кривой
на другую и ее общее пере-
перемещение со временем может
стать любым. Усиление ма-
малого случайного воздействия
до конечного и даже большо-
большого перемещения здесь проис-
происходит за счет эффекта «на-
«накопления возмущении». Ана-
Аналогичным усилителем стоха-
стичности является система,
фазовый портрет которой
есть двумерпый тор с перио-
периодической или квазипериоди-
квазипериодической обмоткой (рис. 3.3, б).
Пример, отличный от этих,
дает динамическая система
с фазовым портретом, пред-
представленным на рис. 3.4.
Рис. 3 4 Б отсутствие возмущений в
зависимости от начальпых
условий фазовая точка движется либо вдоль фазовых кри-
кривых Tfi и а, либо вдоль fi и 0, либо вдоль ^2 и а, либо, нако-
наконец, вдоль Y2 и р. С появлением сколь угодно малого возмущения
ситуация резко меняется: время от времени фазовая точка при
€2

своем движении вблизи точек О4 и О2 может совершить случай-
случайные переходы, продолжая движение либо вдоль fi, либо вдоль уг
и соответственно либо вдоль фазовой кривой а, либо вдоль |}.
Какое из движений она изберет, зависит от сколь угодно малых
случайных воздействий и поэтому случайно.
Приведенные примеры соответствуют особым и граничным
случаям. Появление малейшей зоны нечувствительности у поро-
порогового элемента коренным образом изменяет сказанное: величи-
величина | должна быть достаточно большой, превышающей порог. Фа-
Фазовые портреты в виде центра и периодических или квазиперио-
квазипериодических обмоток двумерного
тора вообще разрушаются при
сколь угодно малых неконсер-
неконсервативных добавках и являются
негрубыми по терминологии
Андронова — Понтрягина. В
этом смысле сами по себе при-
приведенные примеры могут ка-
казаться надуманными, отвечаю-
отвечающими только некоторым иде-
идеальным моделям и негрубым
системам. То же самое можно
было бы сказать и о следую-
следующем примере с фазовым порт-
портретом на рис. 3.4, поскольку
при малейших возмущениях
динамической системы сепарат-
сепаратрисы а, р, ^i и ^2 уже не будут
идти из одного седлового рав-
равновесия в другое и фазовый Рис 3.5
портрет может принять, напри-
например, вид, показанный на рис. 3.5. Теперь для аналогичных пере-
перескоков случайные воздействия должны быть не очень малы.
Хотя в этих примерах малейшие возмущения прекращают су-
шествование усилителя стохастичности с бесконечно большим
коэффициентом усиления, такие механизмы в несколько обоб-
обобщенном виде, как будет показано, могут порождать хаотические
движения динамической системы. При этом малые возмущения
только видоизменяют, но не разрушают ее способности к усиле-
усилению стохастичности.
Начнем с очень простого примера. Возьмем динамическую си-
систему, определяемую точечным отображением Т
™ Т'т
JU 1 *Ь
ах при
—у- а при —=■
— а (а: — 1) при
1-е
1 + е
1 + е
2
B.2)

отрезка [О, 11 в себя (рис. 3.6). В отображении B.2) а я г — па-
параметры (е — вообще говоря, малое положительное число,
1 ^ а < 2). Любая точка х0 отрезка [0, 1] после нескольких пре-
преобразований Т попадает на отрезок е, после чего преобразуется
циклически с периодом в N преобразований. Число N сложным
образом зависит от а и е, но, вообще говоря, с уменьшением е
Рис. 3.6
Рис. 3.7
неограниченно растет. При большом N точки периодической по-
последовательности Xi, х2, ..., Хх располагаются на отрезке [0, 1]
близко друг к другу и вперемежку (см. рис. 3.7). Возле каждой
точки этой последовательности можно построить окрестности
6i, б2, ..., 8N, переходящие в отрезок е. Возле точки xs эта
окрестность имеет ширину eu~n+s. Окрестности 6t, 62, •. •, б?г не
перекрываются, но лежат близко друг к другу и в общем случае
вперемежку. Среднее расстояние между этими окрестностями
порядка N~i, поэтому при большом ./V даже очень малые случай-
случайные воздействия нарушают последовательные переходы из 6t в б2,
из б2 в б3 и т. д. Нарушения этой последовательности переходов
начинают происходить, как только величина случайных воздей-
воздействий превосходит ea-JV, и по мере роста случайного воздействия
хаотизация переходов нарастает. Существенно подчеркнуть, что
пороговое значение амплитуды шума очень мало, например при
£ = Ю-2, а = 2 и N = 30 оно порядка Ю1.
С аналогичной ситуацией мы встречаемся и в случае извест-
известного и давно изучаемого точечного отображения
х=ахA — х) @<а<4), B.3)
график которого представлен па рис. 3.8. Роль окрестности е
в этом отображении играет малая окрестность точки, отвечающей
вершине параболы. Числа N у этого отображения могут быть
сколь угодпо велики. Более того, как известно, существует бес-
бесконечно много значений параметра а, при приближении к кото-
которым число N неограниченно возрастает. Эти возрастания проис-
происходят путем неограниченных серий удвоения числа N. На рис. 3.9
64

представлена диаграмма бифуркаций точечного отображения
B.3). На ней указаны два предельных значения для бесконеч-
бесконечных серий таких удвоений.
Уже эти примеры показывают достаточно общий характер
механизма хаотизации движений динамической системы, имею-
имеющей устойчивое периодическое движение с очень маленькой об-
областью протяжения. Размеры ее в самых узких местах в приве-
приведенном выше примере были порядка za~N, и именно малость этой
0,5,
а
3,0
Рис. "8.8
Г
5,5
Рис. 3.9
т
f
3.S3 I 5.8S
3,84
п
окрестности и значительность изменений движения после выхо-
выхода из нее обусловливают хаотизацию движений. Вместе с тем,
несмотря на эти случайные перескоки, последовательные преоб-
преобразования остаются в малой окрестности точек хи х2, х3, ..., xN,
образующих устойчивый W-кратный цикл неподвижных точек,
эти перескони только существенно нарушают циклический поря-
порядок перемещения по этим окрестностям и вызывают небольшие
размытия в каждой из окрестностей. При счете на ЭВМ (даже
с удвоенной точностью) необходимая точность счета для соблю-
соблюдения цикличности при больших N намного превосходит возмож-
возможности вычислительной машины, и это приводит к тому, что она
выдает хаотические последовательности вместо строго периоди-
периодических. Таким образом, хаотизация движений может возникать
в силу чрезвычайной узости области притяжения устойчивого
периодического движения, когда из-за этого происходят переско-
перескоки из одной части области притяжения в другую. Вместе с тем
эти переходы не должны полностью выводить фазовую точку из
всей области притяжения устойчивого движения. Иначе говоря,
с одной стороны, фазовая точка в силу узости области притяже-
притяжения под влиянием малых случайных воздействий переходит из
одной ее части в другую, а с другой стороны, она должна все
время оставаться в этой области притяжения, чтобы не перейти
в другую часть фазового пространства и не попасть в область
притяжения другого установившегося движения. Ясно, что поня-
65

тия «области» притяжения и «выхода» из нее требуют некоторо-
некоторого уточнения. Это уточнение состоит в необходимости различать
глобальную и локальную области притяжения. Глобальная об-
область притяжения П(Г) асимптотически устойчивого периодиче-
периодического движения Г — это множество фазовых точек, которые при
неограниченном возрастании времени имеют фазовую кривую Г
своим предельным множеством. Иначе говоря, для любой точки
¥еП(Г) фазовая траектория х(М, t), выходящая из точки М,
при t -+■ +°° асимптотически приближается к фазовой кривой Г,
так что
11тр(Г,*(М, *)) = 0. B4)
Область П(Г) можно получить путем обращения времени (при
t -*■ — оо) из достаточно малой окрестности Г. Под достаточно,
малой окрестностью можно понимать, например, настолько ма-
малую е-окрестность кривой Г, что для каждой ее точки М найдет-
найдется точка Мо на фазовой кривой Г такая, что при некоторых К и
одном и том же к при всех t > 0 (рис. 3.10)
р (х (М, t), х (Мо, t)) < Же-*р (М, Мо). B.5)
Точка Мо на фазовой кривой Г по точке М выбирается одно-
однозначно. Двух таких точек быть не может. Обозначим это одно-
однозначное отображение через F, так что M0 — F(M). Очевидно, что
F(M0) = Мо. Если за_время т
м точка М перейдет в Л/, а точ-
точка Мо — в_ Мо, то, очевидно,
F(M) = Мо. Для точек М,
достаточно близких к Г,
функция Т(М) непрерывна.
При удалении точки М от
Рис. 3.10 кривой Г возможны появле-
появления разрывов. Если МР — точка разрыва, то и все точки фазовой
траектории, выходящей из точки МР, соответствуют точкам раз-
разрыва, т. е. множество точек разрыва функции F состоит из фазо-
фазовых траекторий. В точке разрыва МР функция F не определена,
а при приближении точки М к точке МР величина К неограни-
неограниченно возрастает. При прохождении через точку разрыва точка
Мо = F(M) в общем случае изменяется скачком, например с
Мо на Мо. Это означает, что если раньше точка х{М, t) со вре-
временем оказывалась близкой к точке х{Мхь, t), то после точки
разрыва точка х(М, t) оказывается близкой к точке х{М\, t).
Таким образом, сколь угодно малое смещение точки М со време-
временем превращается в конечное смещение: в этом и состоит беско-
бесконечное усиление малых возмущений, если только они переводят
фазовую точку М через точку разрыва функции F. Сказанное
иллюстрируется рис. 3.11. На этом рисунке М' и М"— две близ-
близкие точки — «разделены» точкой разрыва МР. Несмотря на бли-
близость фазовых точек М' и М", выходящие из них фазовые траек-

тории сильна расходятся. Точкам М' и М" функция F ставит в
соответствие разные точки Mi и Мг на фазовой кривой Г.
Таким образом, для возникновения рассматриваемого меха-
механизма усиления стохастичности, с одной стороны, нужно, чтобы
почти все точки некоторой не очень малой окрестности асимпто-
асимптотически устойчивого периодического движения Г принадлежали
Рис. 3.11
его глобальной области притяжения П(Г), а с другой сто-
стороны, необходимо, чтобы точки МР< разрыва функции F(M)
содержались в очень маленькой окрестности фазовой кривой Г,
отвечающей периодическому движению. Второе требование всег-
всегда выполняется, если длина фа-
фазовой кривой Г велика и она
вся располагается в некоторой
конечной области. Заметим, что
важна длина замкнутой фазо-
фазовой кривой, а не период, за ко-
который ее обегает фазовая точ-
точка. Он, конечно, будет тоже ве-
велик, но само по себе это не
гарантирует большую длину
фазовой кривой из-за возможно-
возможности прохождения фазовой кри-
кривой Г вблизи седловых состоя-
состояний равновесия. Если эта
последняя возможность исклю-
исключается, то оба требования рав-
равнозначны.
Аналогичные механизмы
усиления стохастичности воз- Рис. 3.12
можны и в более общем случае
нескольких асимптотически устойчивых периодических движений
Г», Г2, Г3, ..., когда усиление возникает не только за счет «скач-
«скачков» вдоль Г„ но и за счет переходов с одних периодических
движений на другие (рис. 3.12).
67

Для минимального расстояния р точек разрыва МР до кривых
Г\, Г2, ... можно указать оценку вида
(—) ' B-6)
где V — общий объем, в котором находятся кривые 1\, Г2, ...,
L — общая их длина, с — некоторая постоянная, п — размерность
фазового пространства. Из этой оценки видно, что при неограни-
неограниченном возрастании L величина р убывает, стремясь к нулю. Эта
же оценка для минимального расстояния имеет место для каж-
каждой части фазовых траекторий 1\, Гг, ... общей длины L.
Таким образом, рассматривая динамическую систему как пре-
преобразователь стохастичности, можно выделить случай, когда это
преобразование происходит с бесконечно большим коэффициен-
коэффициентом усиления.
Назовем такие преобразователи стохастичности усилителями
стохастичности. Стохастические усилителя, обладая бесконечно
большим коэффициентом усиления, имеют некоторый порог, ко-
который в «идеальных» случаях может отсутствовать.
§ 3. Генераторы стохастичности
Генератор стохастичности качественно отличается как, от пре-
преобразователя стохастичности, так и от усилителя стохастичности.
Он похож на идеальный усилитель тем, что случайность его вы-
выхода не исчезает по мере уменьшения и исчезновения случайной
составляющей входа, и отличен от него тем, что стохастические
характеристики его выхода пренебрежимо мало зависят от до-
достаточно малых случайных входных воздействий и целиком опре-
определяются динамическими свойствами системы. В пределе при
стремлении случайных воздействий к нулю случайность выхода
не исчезает и вне зависимости от статистических характеристик
входа стремится к одному и тому же стохастическому выходу,
статистическое описание которого может быть найдено по опи-
описанию динамической системы.
Начнем с очень простого примера. Пусть состояние системы
меняется согласно уравнению
хп = 2хп-1 - [2хп^], C.1)
где [z] означает целую часть числа г. График этого точечного
отображения такой же, как на рис. 2.7. Устойчивых неподвиж-
неподвижных точек это отображение не имеет. Оно всюду неустойчиво и
растягивает в два раза любой отрезок. Весь отрезок [0, 1] отобра-
отображение C.1) преобразует в дважды покрытый отрезок [0, 1]. При
ж = 1/2 точечное отображение C.1) разрывно. Пусть начальное
значение х0 случайно и имеет произвольную гладкую плотность
вероятностей £о(|). Тогда согласно C.1) все последующие зна-
значения Xi, хг, х3, ... также случайны и их плотности вероятностей
68

, р2(|), ... связаны между собой соотношением [100]
г) ]•
Замечательным свойством преобразования C.2) плотности
вероятностей р„(|) в рп+1(|) является то, что независимо от на-
начальной плотности вероятностей />о(|)
т. е. предельная плотность вероятностей равномерная. Доказа-
Доказательство этого факта несложно. Действительно, дифференцируя
C.2) по |, имеем
откуда
max | рп (!) | < — max |
и следовательно, рп (|) -*• 0 при п-*■<». Но это означает, что
/>„(!) стремится к постоянной, которая в силу нормировки плот-
плотности вероятностей равна единице. Таким образом, плотность ве-
вероятностей состояния, которая устанавливается в рассматрива-
рассматриваемой системе, не зависит от начальной плотности вероятностей,
а определяется свойствами самой системы. Случайность может
быть привнесена в состояние случайным внешним воздействием.
Затем, если внешнее воздействие прекращается, то устанавлива-
устанавливается равномерное распределение. Если же случайные воздейст-
воздействия не прекращаются, но весьма невелики, то устанавливается
распределение, близкое к равномерному. То, что устанавливает-
устанавливается именно равномерное распределение,— особенность выбранного
нами простого примера, но сам факт установления предельной
плотности вероятностей, не зависящей от начального распреде-
распределения,— общий.
В качестве следующего примера возьмем линейный осцилля-
осциллятор с отрицательным трением и ударами, описываемый диффе-
дифференциальным уравнением вида [280],
ts), C.4)
где t, (s — 1, 2, 3, ...)—последовательные моменты времени,
в которые ж — 0 и ж>й>0. Параметры ю», б, р и а положи-
положительные, причем со2 = (Во — 62>0. Это автономная система вто-
второго порядка с двумерным фазовым пространством — фазовой
плоскости с разрезом вдоль луча х = 0, х > а и отождествленны-
отождествленными краями разреза, так что точка х = 0, х отождествляется
с точкой х = 0, х — р (рис. 3.13). Из вида фазового портрета,
изображенного на рис. 3.13, и из уравнения C.4) следует, что
последовательные значения х, и x,+i скорости непосредственно

после удара связаны соотношением
qxs при qxs<La,
Т.в _1_1 ==:= 1
ха+1
\qxs —
C.5)
при
где q = ехр 2Л6О). Соотношение C.5) можно рассматривать как
точечное отображение, преобразующее точку х, в точку xs+i. Воз-
Возможные существенно различные ви-
виды его графика изображены на
рис. 3.14. В случае рис. 3.14, о имеет
место неограниченная раскачка ос-
осциллятора. Амплитуда колебаний
его скорости х с некоторого момента
оказывается больше, чем рA — ?)~\
после чего монотонно и неограни-
неограниченно возрастает. Это имеет место,
когда точка М графика рис. 3.14, а
лежит выше точки N, т. е. когда
рA-д)-*<а. C.6)
При обратном неравенстве (рис.
Рис. 3.13 3.14, б) возможны два совершенно
разных типа поведения в, зависимо-
зависимости от начальных условий: при хо>рA — ?)~4 по-прежнему про-
происходят нарастающие колебания, при хо<рA— д) возникают
ограниченные хаотические колебания. Во втором случае после-
последовательные преобразования точки х0, хи #2, ... всюду плотно за-
заполняют отрезок / с концами a/q и aq — р* На отрезке / отобра-
х
жение C.5) — растягивающее, так что устойчивых неподвижных
точек (любой кратности) быть не может. Свойство растяжения
и общей ограниченности движений сближает этот случай с пре-
предыдущим примером: любое гладкое начальное распределение ве-
вероятностей значений, начальной скорости х0 с течением времени
70

стремится к некоторому предельному распределению, теперь уже
неравномерному. Поэтому описанный линейный неустойчивый
осциллятор с гасящими его колебания ударами является стоха-
стохастическим генератором. Осциллограмма изменения координаты х
этого стохастического генератора изображена на рис. 3.15.
Мы уже говорили о том, что размерность три — наименьшая
из тех, при которых динамическая система может иметь хаоти-
хаотические движения, а осциллятор с демпфирующими ударами дву-
двумерен и, тем не менее, может совершать хаотические колебания.
Рис. 3.15
В этом нет противоречия, так как утверждение о том, что три —
наименьшая размерность, относилось к гладким динамическим
системам, а у движений осциллятора с ударами возможны скач-
скачки фазовой точки. Вместе с тем заметим, что эти скачки можно
убрать, если сделать на плоскости х, х разрез по полупрямой
а: = 0, ж 5s а и затем левый берег этого разреза склеить вдоль по-
полупрямой х = О, ж 5s о — р с правым берегом разреза. По такой
фазовой плоскости с разрезом и отождествлением (склейкой) бе-
берегов разреза фазовая точка будет двигаться без скачков, но фа-
фазовое пространство, хотя оно и двумерно, не является более
плоскостью и этого оказывается достаточно для того, чтобы ста-
стали возможны хаотические движения.
Обратим внимание на характер перехода от хаотических дви-
движений к движениям, уходящим в бесконечность. Если точка М
графика рис. 3.14 лежит выше точки N, то имеют место только
движения с неограниченной раскачкой. При обратном соотноше-
соотношении происходят как движения с неограниченной раскачкой, так
и хаотические ограниченные колебания. Однако если точка М ле-
лежит чуть-чуть выше точки N, то в течение очень долгого време-
времени возможны хаотические ограниченные колебания, которые вне-
внезапно, в непредсказуемый момент времени переходят в нараста-
нарастающие колебания.
Рассмотрим двумерное отображение
[х = 2х - 1
<- 1,
при х^О, <- _
при х<0. C.7)
71

Точки 0iA, 1) и Ог{— 1, —1)~его седловые неподвижные точ-
точки. Квадрат G(|a:|<l, \y\ < 1) под действием отображения
C.7) преобразуется в себя — в две области G4 и G2, которые
являются соответственно отображениями областей 0 < х < 1,
\у\ ^ 1 и —1 < х < 0, \у\ ^ 1, составляющих квадрат G
yyy
У/////У/5г1
УЛаУ////;
0,
УУУУ/.
О? С-
221
Рис. 3.16
(рис. 3.16) в области d и G2. Каждая из областей G4 и G2 лежит
в квадрате G. Таким образом, для отображения C.7) имеет ме-
место глобальное сжатие — область G преобразуется в себя — и
локальная неустойчивость, поскольку отображение C.7)—растя-
C.7)—растягивающее по х (в два раза).
У отображения C.7) (назовем его Т) в области G не может
быть устойчивых неподвижных точек: любые две сколь угодно
близкие, по различающиеся координатой х точки при последо-
последовательных преобразованиях Т разбегаются на конечное расстоя-
расстояние, так что внутри G преобразование должно носить хаотиче-
хаотический характер. Чтобы лучше понять его, рассмотрим последова-
последовательные отображения области G. При однократном отображении
область G преобразуется в две области Gi и G2 (рис. 3.16, а).
При последующем преобразовании каждая из областей Gi и G2
переходит в две области, соответственно Gu, Gi2 и G2i, G23
(рис. 3.16, б). При этом имеют место включения
Gh^Gi, <312cG2, G21<=Gu G22cG2.
Аналогично каждая из областей Gxi (рис. 3.20, в) (г, / = 1, 2)
преобразуется в две области G,,! и G,j2, причем
G,H <= GlU Glj2 <= Gj2.
Продолжая эти преобразования, придем к всевозможным обла-
областям
при этом
Каждая яз прямоугольных областей (?$ i2 .jn по координате
72
C.8)
х

имеет ширину, равную 2, а по координате у ее ширина равна
3~". Из этого следует, что эти области в пределе при п -*■ °° стя-
стягиваются к некоторому множеству /, состоящему из континуума
отрезков прямых, располагающихся вдоль оси х. Предельное
множество / отображением Т переводится в себя, так что коор-
координата х подвергается преобразованию
\2х — 1 при х"> О,
Х \2х + 1 при х < О,
которое после замены х -*■ х — 1 может быть записано в виде уже
рассмотренного отображения C.1). Отметим еще, что отображе-
отображение, очень похожее на только что рассмотренное отображение
C.7), порождается фазовыми траекториями дифференциальных
уравнений Лоренца A.24) гл. 1 на двумерной секущей плоско-
плоскости z = г — 1.
Приведенные примеры можно продолжить; им полностью по-
посвящена последняя глава. А сейчас постараемся дать общий от-
ответ, в чем причина стохастического поведения рассмотренных
систем, каковы основные общие условия его возникновения. Как
уже отмечалось, при устойчивости генерация стохастичности не-
невозможна. Это обусловлено тем, что при устойчивости установив-
установившимися движениями могут быть только устойчивые состояния
равновесия и устойчивые периодические движения. В этих слу-
случаях даже при случайности начального условия в дальнейшем
со временем случайность исчезает, так как плотность вероятно-
вероятностей в пределе при t-*■<*> обращается в нуль всюду вне состоя-
состояния равновесия или вне замкнутой кривой, отвечающей периоди-
периодическому движению. В случае периодического движения некото-
некоторый след от случайности начального условия все же остается
в виде случайности фазы периодических колебаний. Но при этом
вероятностное описание этой фазы зависит от распределения ве-
вероятностей начального условия и им определяется. Таким обра-
образом, для генерации стохастичности необходима локальная не-
неустойчивость при общей ограниченности движений, лри некото-
некотором глобальном сжатии или, во всяком случае, отсутствии рас-
расширения.
На неустойчивость как причину непредсказуемости и слу-
случайности указывал еще А. Пуанкаре [608]. Более развитая аргу-
аргументация имеется у Н. С. Крылова [207] и М. Борна [410] и сво-
сводится к тому, что события, возникающие в результате неустой-
неустойчивых движений, непредсказуемы, так как сколь бы точно ни
были заданы начальные условия (а их точность практически
ограничена), спустя достаточно большое время малейшая ошиб-
ошибка приводит к весьма ощутимым различиям. Применительно к
долгосрочному прогнозу погоды эффект необычайно чувствитель-
чувствительной зависимости от малых возмущений был отмечен 9. Лоренцом
и назван «эффектом бабочки» по ассоциации с событиями одного
из рассказов Бредбери. Неустойчивость вносит неопределенность
в будущее эволюционирование динамической системы, делая его
73

в той или иной мере непредсказуемым. Меры ©той неопределен-
неопределенности были предложены А. Н. Колмогоровым, а также Р. Адле-
Адлером и А. Конхеймом (метрическая и топологическая энтропии).
Обе энтропии несколько по-разному характеризуют количествен-
количественную меру быстроты разбегания фазовых траекторий и величину
возникающей неопределенности. Итак, непредсказуемость и сто-
хастичность движений динамической системы порождается их
неустойчивостью при глобальном сжатии. Как же это фактиче-
фактически происходит и, в частности, как может сочетаться локальная
неустойчивость с глобальным сжатием?
Попытаемся ответить на этот вопрос, анализируя фазовый
портрет динамической системы. Пусть ч — фазовая траектория
и х0 и xt — ее точки. Предположим, что малая шаровая окрест-
окрестность б0 точки х0 через время t > 0 переходит к окрестность 8t
точки xt. В общем случае то, как будет меняться окрестность 6t,
пока она мала, определяется линеаризованными дифференциаль-
дифференциальными уравнениями относительно отклонений | от фазовой траек-
траектории ^
при исходных дифференциальных уравнениях
х = Х{х). (ЗЛО)'
По каким-то направлениям согласно линеаризованным уравне-
уравнениям происходят сжатия и по каким-то другим — растяжения.
В результате первоначально ша-
шаровая окрестность б0 преобразует-
преобразуется при больших t в эллипсоидаль-
эллипсоидальную окрестность б(, вытянутую
по одним осям и сжатую по дру-
другим (рис.3.17).Число осей эллип-
эллипсоида, по которым происходит
растяжение, равно числу степеней
Рис. 3.17 неустойчивости. Изменение объе-
объема эллипсоида с изменением
времени t определяется divX(;r). При divX(i)>0 эллипсоид
увеличивает свой объем, при обратном неравенстве —
уменьшает.
Каждый шар, лежащий в 6*, в свою очередь, с ростом време-
времени t преобразуется в вытянутый эллипсоид и т. д. В результате
первоначально шаровая окрестность б0 со временем будет все
более и более вытягиваться в направлениях неустойчивости и
сжиматься в направлениях устойчивости. Но вытягивающаяся
окрестность б, в силу глобального сжатия должна оставаться
в ограниченной области и, следовательно, не может не начать
изгибаться и как-то складываться. Для трехмерных гладких ди-
динамических систем, описываемых дифференциальными уравне-
уравнениями, единственным механизмом такого вытягивания, изгиба-
изгибания и,укладки является гомоклиническая структура. В гомокли-
74

нической структуре осуществляется последовательность преобра-
преобразований окрестности 6*, а затем ее частей- в окрестностях седло-
вых периодических движений и состояний равновесия. На
рис. 3.18 изображены метаморфозы, претерпеваемые первона-
первоначально шаровой областью, проходящей вблизи седлового равно-
равновесия и седлового периодического движения. Втягивание окрест-
окрестности в этот «преобразователь» происходит вдоль поверхности
S+, а выбрасывание — вдоль поверхности S~. После того как та-
такие втягивание и выбрасывание -совершились, весь процесс мо-
может повториться, как только какая-то часть выброшенной окрест-
окрестности попадает в зону захвата какой-нибудь поверхности S*
и т. д. Именно такая бесконечная серия преобразовавши может
иметь место в гомоклинической структуре.
Рассмотренное выше преобразование C.7) является простей-
простейшим примером, ъ котором осуществляется такая бесконечная по-
последовательность преобразований в окрестностях седловых не-
неподвижных точек Oi и Ог. Дальнейшее описание гомоклиниче-
ских структур и их роли в образовании хаотических движений
содержится в гл. 4 и 6, а в гл. 7 и 9 приводятся разнообразные
примеры их проявления.
75

Для динамических систем размерности, большей трех, отобра-
отображение A.1) гл. 2 дает другой пример неограниченного вытягива-
вытягивания и укладки. Характерной его особенностью является укладка
без складываний, которая требует для точечного отображения
размерности не меньше трех, а для соответствующей динамиче-
динамической системы, описываемой дифференциальными уравнениями,—
не меньше четырех. Уже этот факт говорит о возможностл су-
существенного отличия четырехмерных систем от трехмерных, а не
только трехмерных от двумерных. Насколько реально такое раз-
различие, в настоящее время сказать трудно в силу очень малой
изученности четырехмерных систем. Отметим тут же, что в че-
четырехмерных системах, как будет видно из дальнейшего, воз-
возможны бифуркации, которых нет в трехмерных системах. Весьма
правдоподобно, что отличие четырехмерных систем от трехмер-
трехмерных скорее всего окажется весьма значительным.
Как видно из сказанного, сложные преобразования в стоха-
стохастическом генераторе фазового пространства и связанная с этим
хаотизация движений не имеют своей причиной какие-то внеш-
внешние случайные возмущения. Все происходит в соответствии с де-
детерминированными уравнениями движения динамической систе-
системы и порождается ею самою. В этом отличие стохастического ге-
генератора от усилителя стохастчности, стохастичность которого
порождается и существенно зависит от малых случайных, воз-
возможно даже, не поддающихся учету возмущений. Вместе с тем
и в стохастическом генераторе нет никакой стохастичности, если
не предположить наличие каких-то случайных возмущений, хо-
хотя бы и неконтролируемо малых. Статистические характеристики
стохастического генератора не зависят от этих неконтролируе-
неконтролируемых случайных возмущений, но они необходимы, чтобы эта слу-
случайность была,— необходимы, хотя и могут быть сколь угодно
малыми. Трудно сказать, не является ли в действительности та-
такая трактовка заблуждением, но она — неизбежное следствие
наших сегодняшних представлений.
§ 4. Настоящая ли стохастичность у стохастических
и хаотических движений детерминированных
динамических систем?
В заключение настоящей главы необходимо затронуть очень
не простой вопрос о том, является ли стохастичность детермини-
детерминированных динамических систем «настоящей» стохастичностью,
той самой, изучением которой занимается теория вероятностей.
Такая постановка вопроса с самого начала требует уточнения.
Действительно, едва ли возможно отрицать, что стохастичность
окружающего нас мира — это стохастичность, порождаемая де-
детерминированными динамическими системами в флуктуирующем
квантовом микромире. Вопрос состоит в том, насколько, в какой
мере и в силу каких причин стохастичность макроскопических
детерминированных систем — систем классической физики — со-
76

ответствует канонизированной аксиоматике теории вероятностей.
Такая постановка вопроса чужда теории вероятностей, в кото-
которой наличие случайности и вероятности постулируется и вопрос
об их происхождении не ставится, возможно, потому, что эмпи-
эмпирическая база, на которой возникла теория вероятностей, не да-
давала никаких надежд на его решение. Сейчас, пожалуй, ситуа-
ситуация несколько иная. Более того, развитие теории нелинейных
колебаний и теории динамических систем вплотную подводит
к вопросам происхождения случайности и вероятности и откры-
открывает пути и подходы к решению возникающих проблем.
Случайные последовательности, генерируемые цифровыми
ЭВМ, принято называть квазислучайными. Так же нередко на-
называют и стохастические движения динамических систем. С пер-
первым можно согласиться: ЭВМ выдает при повторениях одну и
ту же последовательность, которая отражает определенные свой-
свойства случайной последовательности, но в полной мере ею не яв-
является. Обосновать столь же просто квазислучайность стохасти-
стохастических движений динамических систем не представляется воз-
возможным. Уточним условия функционирования и реализации сто-
стохастических движений динамической системы. Если их мыслить
такими же, как в случае ЭВМ, то стохастические движения ди-
динамической системы квазислучайны, но в том-то и дело, что они
не такие. Конечность разрядной сетки ЭВМ позволяет точно по-
повторить начальные условия, а малые помехи в силу этой конеч-
конечной разрядности не могут повлиять на результат счета. Для не-
непрерывной динамической системы и первое, и второе не так: на-
начальные условия повторены быть не могут и на движение дина-
динамической системы могут оказывать значительное влияние даже
очень малые помехи. В некоторой мере эти новые обстоятельства
можно отразить в математической модели вида
гх = f(x, у, 1), у = g(x, у), D.1)
где х и у — фазовые переменные динамической системы на уров-
уровнях разных масштабов, которые назовем микро- и макроописа-
макроописаниями, \ в интересующих нас случаях — очень малая случайная
величина, отражающая вероятностный характер движений в мик-
микромире, е — параметр, вообще говоря, очень малый, так что про-
процессы изменения х быстрые, а у — медленные. Таких различных
уровней быстроты изменения может быть и более двух.
В силу медленности изменения переменной у на небольших
промежутках времени ее можно считать постоянной. Примем, что
длительности этих промежутков постоянства у достаточно для
того, чтобы изменение переменной х успело принять установив-
установившийся характер. Тогда возникает плотность вероятностей вели-
величины х, зависящая от у. Если динамическая система, описываю-
описывающая изменение переменных х при постоянном у,— преобразова-
преобразователь стохастичпости, то действием § в силу малости можно
пренебречь. Напротив, если это усилитель или генератор стохас-
тичности, то такое пренебрежение недопустимо. Отметим, что во
77

втором случае, когда изменение х описывается стохастическим
генератором, установившаяся плотность вероятностей не зависит
от статистических характеристик случайной величины | и цели-
целиком определяется динамической системой
ei-/.(*, »,0) D.2)
при постоянном у.
Для значений времен порядка е изменение х носит детерми-
детерминированный характер; но в масштабе времен изменения у изме-
изменение х случайное. Можно предположить, например, что оно слу-
случайно уже на временах порядка Уе. Если это так, то во втором
уравнении системы C.11) х можно считать случайной величиной
с очень маленьким временем корреляции типа белого шума,
и тогда у — случайный марковский процесс, а компоненты у —
это случайные немарковские процессы. Это имеет место, если си-
система относительно у — преобразователь стохастичности. Но она
может быть и генератором стохастичности, и тогда ее стохастич-
ность другого типа, характеризуемая тем, что плотность вероят-
вероятности смены состояния является б-функцией. Подчеркнем, что
эта плотность вероятности является б-функцией в масштабе вре-
временных изменений переменных у при малых воздействиях х.
Какой же ответ предлагается на поставленный в этом пара-
параграфе вопрос? Стохастические и хаотические движения детерми-
детерминированных динамических систем — это и есть подлинная слу-
случайность окружающего нас мира. В этом новом аспекте ее
изучение только начинается, и этим началом мы обязаны «откры-
«открытию» стохастических и хаотических движений детерминирован-
детерминированных динамических систем.

Глава 4
КРАТКИЙ ОБЗОР ИССЛЕДОВАНИЙ, СВЯЗАННЫХ
С ВОЗНИКНОВЕНИЕМ ПРОБЛЕМЫ
ХАОТИЧЕСКИХ И СТОХАСТИЧЕСКИХ ДВИЖЕНИЙ
И ТЕОРИЕЙ ТУРБУЛЕНТНОСТИ
Еще совсем недавно все явления окружающего мира было
принято делить на детерминированные и случайные. Изучением
первых занималась теория дифференциальных уравнений, мате-
математическая физика, классическая механика и электродинамика,
изучением вторых — теория вероятностей, теория случайных про-
процессов, статистическая физика и квантовая механика. Такое чет-
четкое разделение казалось бесспорным и не вызывало сомнений,
хотя и были некоторые несообразности: вероятностный характер
законов классической статистической физики не имел четкого
обоснования и объяснялся ссылкой на очень большое число ча-
частиц и степеней свободы.
Однако оказалось, что даже движение одной частицы в рам-
рамках законов Ньютона может быть непредсказуемо и случайно.
Более того, выяснилось, что многие, даже самые простые детер-.
минированные автономные динамические системы могут иметь
стохастические движения. Современный научный мир, захлесты-
захлестываемый бурным потоком новых фактов и событий, воспринял эти
открытия как нечто незаурядное, затрагивающее наши глубин-
глубинные интуитивные представления.
Особенно остро вопрос о механизмах возникновения стоха-
стичности стоял в теории турбулентности жидкостей, газов и
плазмы. Возможно, что именно поэтому среди механиков и фи-
физиков, занимающихся теорией волн и турбулентностью, новое
понимание механизмов возникновения стохастичности было
встречено столь заинтересованно и бурно. Первое, несколько не-
неожиданное знакомство с новыми взглядами произошло на школах
по колебаниям и волнам 1972, 1973 и 1975 гг. [291, 292], на се-
семинаре по фазовой синхронизации в 1973 г. [273], на семинаре-
совещании по динамическим системам и процессам управления
в 1974 г. [271], на школе ученых-механиков в 1975 г. и на
школах по нелинейной теории гидродинамической устойчивости
79

в 1976 и 1978 годах. Началось оно с лекций [154, 270, 366] на
первой школе по колебаниям и волнам в марте 1972 г. Последу-
Последующие события нашли отражение в многочисленных публикациях.
Если раньше не замечали, что движения автономной динамиче-
динамической системы могут быть случайными, то теперь случайные дви-
движения стали обнаруживать всюду.
Аналогичное «знакомство» и последующая реакция несколько
позднее произошли и в ряде других стран. Можно указать на се-
семинары 1976—1977 гг. по турбулентности и уравнению Навье —
Стокса, семинар по точечным отображениям и их приложениям
1973 г. в Тулузе. Если на школах 1972—1973 гг. по колебаниям
и волнам основным стимулом послужили лекции, базирующиеся
на исследованиях горьковской школы теории нелинейных колеба-
колебаний (о них уже говорилось в гл. 1) и сибирской группы физиков,
представители которых впервые познакомились тогда друг с дру-
другом, то тематическим стержнем семинаров по турбулентности и
уравнению Навье — Стокса 1976—1977 гг. стали работа Лоренца
1963 г. [563] о непериодическом характере движений трех-
модовой модели конвективной турбулентности и работа Рюэля
и Такенса 1971 г. [627], содержавшая новые предположения
о природе турбулентности. Эти работы были переизданы
и именно вокруг них сконцентрировались многие из последу-
последующих работ.
До определенного времени проблемы исследования структуры
фазового портрета, возможных бифуркаций его, символической
динамики, эргодической теории и хаотизации и стохастизации
движений детерминированных динамических систем изучались
только узким кругом математиков и немногих специалистов по
теории колебаний.
Указанные выше и ряд других школ, съездов, конференций и
симпозиумов, частичная публикация прочитанных на них лекций
и докладов, а также ряд обзоров придали неизвестным ранее ра-
работам широкую огласку, и содержавшиеся в них новые идеи вы-
вызвали взрыв интереса к хаотическим движениям динамических
систем, породивший бурный поток научных работ (см. библио-
библиографию в конце книги). х
Такова внешняя сторона событий. Внутренняя их сущность
значительно сложнее. Событиям этого сравнительно короткого
периода предшествовали малоизвестные и не привлекавшие все-
всеобщего внимания исследования, проводившиеся в течение многих
лет. Об этих исследованиях, их внутренней мотивации и резуль-
результатах пойдет речь дальше. Мы кратко изложим их, сопоставив
прежнюю и новую точку зрения на детерминированность и слу-
случайность. Основная цель нашего изложения состоит в том, чтобы
показать внутреннюю связь проблемы стохастичности детермини-
детерминированных динамических систем с развитием теории колебаний,
топологической теории динамических систем, эргодической тео-
теорией и другими разделами современной математики, механики и
физики.
80

Естественно, что изложение этих вопросов в настоящей
книге не может быть подробным и полным. Оно по необходимо-
необходимости конспективно и схематично.
Прежняя точка зрения на природу случайного существенно
опиралась на нижеследующие представления.
1. Теория вероятностей допускает аксиоматическое построе-
построение, при котором существование вероятностей постулируется и
не ставится вопрос о том, откуда они берутся. Отметим, что гео-
геометрия, послужившая образцом такого аксиоматического построе-
построения науки, затем проявила интерес к своим основаниям, которые
были разработаны Н. И. Лобачевским, К. Гауссом, Б. Риманом,
Д. Гильбертом, Ф. Клейном.
2. Движения детерминированной динамической системы не
могут быть случайными, так как по теореме Коши однозначно
определяются начальными условиями.
3. Случайность окружающего нас мира, а для механиков и
физиков — объектов статистической физики, принято было «спи-
«списывать» на непостижимо большие числа частиц и степеней сво-
■ боды, на неполноту данных, наконец, на сложность и запутан-
запутанность движений.
4. Теории колебаний, качественной теории дифференциальных
уравнений и теории динамических систем удалось полностью ис-
исследовать лишь двумерные системы, а стохастические автоколе-
автоколебания возможны только у систем размерности, не меньшей трех.
Методы малого параметра А. Пуанкаре [243, 244] и асимптоти-
асимптотические методы Н. М. Крылова — Н. Н. Боголюбова [92], приме-
применимые к системам любой размерности, не позволяли обнаружить
стохастические движения, если их не было у порождающей
системы, что связано с нестепенным порядком малости обла-
областей существования стохастических движений по малому па-
параметру.
Мы видим, что в существовавших ранее общих представле-
представлениях о движениях детерминированных динамических систем не
было места хаотическим и стохастическим движениям.
Но дело, пожалуй, не только в этом. Примеры консерватив-
консервативных динамических систем с весьма сложным поведением фазо-
фазовых траекторий (тех самых, которые сегодня, не задумываясь,
назвали бы хаотическими и стохастическими) были известны до-
довольно давно, как и отдельные примеры неконсервативных си-
систем, сводимых к точечным отображениям с хаотическим пове-
поведением последовательных преобразований. Более того, Д. Бирк-
гоф [88] предложил общую классификацию движений динамиче-
динамических систем, включавшую эти сложные движения. Схема такой
классификации приводилась в работе А. А. Андронова «Матема-
«Математические проблемы теории автоколебаний» 1933 г. [12], где,
в частности, отмечалось, что совокупность всех движений может
образовывать сложную систему. Читая поистине пророческие
строки в работе А. А. Андронова и глядя на классификацию
Д. Биркгофа, трудно понять, что же собственно мешало сделать
81

еще один, казалось бы, совсем небольшой шаг к признанию хао-
хаотических и стохастических движений. Но причины, конечно же,
были. Хаотические движения воспринимались как нечто исклю-
исключительное и эфемерное, физически не реализуемое, нечто если и
возможное, то в другом, консервативном мире, мире звездной и
атомной динамики, а не грубых диссипативных систем.
Случайные движения — тоже объекты другого мира, отделен-
отделенного высоким барьером от мира детерминированных динамиче-
динамических систем. В качестве этого «барьера» выступает, казалось бы,
трудно опровержимый или игнорируемый довод — теорема
о единственности решения задачи Коши, гласящая, что решение
системы дифференциальных уравнений однозначно определяется
начальными условиями. «Следовательно», делали вывод привер-
приверженцы традиционных взглядов, ни о какой случайности не мо-
может быть и речи. С формальных позиций это простое соображе-
соображение — не только довод против стохастичности движений простых
динамических систем с небольшим числом степеней свободы, но
и неопровержимый довод против всей классической статистиче-
статистической механики и физики. Однако в статистической механике и
физике он не опровергается, а обходится с помощью уловки —
ссылки на очень большое число частиц, ссылки, оставляющей
чувство неудовлетворенности, но позволяющей как-то прими-
примириться с противоречием.
Новые взгляды на природу случайного опираются на следую-
следующие достижения современной математики.
1. Разработка зргодической теории и «наведение мостов» меж-
между детерминированным и стохастическим описанием динамиче-
динамических систем. Эргодическая теория ведет свое начало от гипотезы
эргодичности, выдвинутой еще Л. Больцманом. Согласно этой ги-
гипотезе в статистической механике усреднение по времени может
быть заменено усреднением по ансамблю [56]. Дальнейшие по-
попытки обоснования этой гипотезы привели к созданию сложной
и разветвленной эргодической теории, основные этапы развития
которой связаны с именами Д. Биркгофа, Дж. фон Неймана,
Э. Хопфа, М1 Морса, А. Я. Хинчина, А. Н. Колмогорова,
В. И. Арнольда, Ю. Мозера, Я. Г. Синая и др. Именно в рамках
этого круга идей возникли понятия полного перемешивания, тео-
теория Колмогорова — Арнольда — Мозера (КАМ) о наличии инте-
интегральных торов у гамильтоновых динамических систем, понятия
энтропии динамической системы и символическое описание ее
движений, топологической марковской цепи, открывающие пути
к статистическому описанию детерминированных динамических
систем.
Развитие эргодической теории естественно привело к чис-
численным исследованиям конкретных гамильтоновых динамиче-
динамических систем небольшой размерности и обнаружению у них слож-
сложных хаотических движений. Здесь в первую очередь следует ука-
указать работы М. Хенона и С. Хейлеса [501], Г. М. Израйлева,
Г. М. Заславского, Б. В. Чирикова [154—158, 160—164, 366, 418],
82

Г. Уокера и Дж. Форда [672], Дж. Форда и Г. Ландфор-
да [456] и др.
Решающую роль в переходе от систем статистической меха-
механики с числом частиц порядка 1023 к системам с небольшим чис-
числом степеней свободы, помимо работы Э. Ферми, Ж. Паста и
С. Улама [450], сыграли работы о движении свободной матери-
материальной частицы в римановом пространстве отрицательной кри-
кривизны (задача о геодезических линиях, ведущая свое начало от
работы Ж. Адамара 1889 г. [485]), а также так называемые
«бильярдные» задачи [88, 205, 326].
Бильярдная задача — это задача о движении материальной
частицы внутри области, ограниченной некоторой кривой, с упру-
упругими отскоками от границы как от идеально упругой стенки (вы-
(выпуклый бильярд — рис. 4.1, а, вогнутый — рис. 4.1, б). Выпуклый
Рис 4.1
бильярд был рассмотрен Д. Биркгофом на основе известной по-
последней геометрической теоремы А. Пуанкаре. Вогнутый бильярд
обладает совершенно другими свойствами: все его движения не-
неустойчивые, разбегающиеся, так как первоначально малое раз-
различие между движениями частицы с каждым отскоком от грани-
границы нарастает (рис. 4.1, б).
Последующими обобщениями такого бильярда можно считать
известную систему Синая из N идеально упругих шаров внутри
идеально отражающей сферы и бильярд типа «стадиона» [315].
В первом случае при N = 1 имеем выпуклый бильярд. Однако
уже при N = 2 и при любом N > 2 движения шаров уподобляют-
уподобляются тому, что имеет место в вогнутом бильярде. Это происходит
из-за взаимных столкновений, где каждый шар отталкивается от
«вогнутой границы» другого шара.
2. Разработка общей топологической теории гладких динами-
динамических систем. Основные принципиально важные результаты
здесь получены С. Смейлом и его последователями [6—9, 39—40,
175, 295, 330—332, 653]. В этих работах был выделен класс ди-
динамических систем типа Морса — Смейла, которые являются
прямым многомерным аналогом грубых систем в смысле Андро-
Андронова — Понтрягина [20]. Единственными их установившимися
движениями могут быть только состояния равновесия и периоди-
83

ческие движения. Напомним, что динамическая система
£-Х{х, у), y = Y(x, у) A)
называется грубой в смысле Андронова — Понтрягина, если она
и любая достаточно близкая к ней возмущенная система
х = Х(х,у)+р(х,у), y = Y(x,y)+q(x,y) B)
имеют топологически эквивалентные фазовые портреты. При этом
под малостью возмущений р(х, у) и q(x, у) имеется в виду не
только малость их самих, но и малость их частных производных
по х и у. Требование малости производных не может быть опу-
опущено, так как без него грубых систем вообще нет. Еще, пожа-
пожалуй, следует добавить, что фазовое пространство предполагается
компактным. Фазовая плоскость этому требованию не удовлетво-
удовлетворяет, и в случае двумерных систем необходимо вводить дополни-
дополнительное предположение о том, что рассматривается не вся фазо-
фазовая плоскость, а лишь некоторая ее ограниченная часть, внутрь
которой, пересекая границу, входят все фазовые траектории.
Топологическая эквивалентность означает существование вза-
взаимно однозначного и взаимно непрерывного отображения
х = 1{х, у), у = ц(х, у), C)
переводящего фазовые траектории невозмущенной системы D.1)
в фазовые траектории возмущенной системы D.2), или, короче,
преобразующего фазовый портрет невозмущенной системы в фа-
фазовый портрет возмущенной. К этому надлежит добавить требо-
требование" непрерывного обращения гомеоморфизма D.3) в тождест-
тождественный при неограниченном убывании (вместе с производными)
возмущающих добавок р(х, у) и q(x, у).
Определение грубой системы без сколько-нибудь существен-
существенных изменений переносится на многомерные системы. Сделаем
это, несколько геометризовав определение грубости. Пусть G —
пространство динамических систем
х = Х(х), D)
где х — многомерный вектор, а Х(х)—гладкая функция от х.
Под близостью в пространстве G понимается близость правых
частей Х(х) и их частных производных, т. е. матриц dX/dx. Ди-
Динамическая система, отвечающая точке Х(х) пространства дина-
динамических систем G, грубая, если она и все точки ее достаточно
малой окрестности имеют топологически эквивалентные фазовые
портреты. Необходимые и достаточные условия грубости двумер-
двумерных систем D.1) были сформулированы Андроновым и Понтря-
гйным. Аналогичные, но только достаточные условия для много-
многомерных систем были указаны С. Смейлом, а динамические си-
системы, удовлетворяющие этим условиям Смейла, названы систе-
системами Морса — Смейла. Как оказалось, грубыми многомерными
системами могут быть не только системы Морса — Смейла, но и
существенно более сложные, так называемые гиперболические
84

системы [175, 332]. Свойство гиперболичности означает неустой-
неустойчивость движений и выражается в том, что движущийся элемент
фазового объема в одних направлениях экспоненциально растя-
растягивается, а в других — сжимается. В качестве простого примера
гиперболической динамической системы можно указать систему
Рис. 4.2
на двумерном торе, определяемую точечным отображением вида
(рис. 4.2)
х = 2х + у (mod 1), у = х + г/(mod 1). E)'
Это — линейное отображение. Его характеристическое уравнение
2-Х 1
l l —:
= Я,2 — ЗХ +1 = О
имеет один корень, меньший .единицы (в соответствующем ему
направлении имеет место сжатие). В другом направлении, отве-
отвечающем второму корню, большему единицы, происходит растя-
растяжение.
Значительную известность получило гиперболическое точеч-
точечное отображение, названное впоследствии «подковой Смейла»,
которое является структурно устойчивым (грубым) и одновре-
одновременно имеет бесконечное множество различных седловых (не-
устсШчивых) неподвижных точек.
Динамические системы с гиперболическими структурами ана-
аналогичны системам, рассматриваемым и ранее символической ди-
динамикой [88, 588], и, в первую очередь, системам, описывающим
движение по инерции материальной точки в римановом простран-
пространстве отрицательной кривизны [363]. Однако при этом объем дви-
движущейся фазовой частицы не обязательно сохраняется: он мо-
может уменьшаться, и система может быть диссипативной.
Еще большей неожиданностью, чем существование в много-
многомерном случае совершенно новых типов грубых систем, было об-
обнаружение типичных негрубых систем, т. е. обнаружение обла-
областей негрубых систем [331].
Раньше казалось, что негрубые системы в пространстве пара-
параметров динамической системы — это лишь граничные случаи
между различными грубыми системами, т. е. поверхности кораз-
коразмерности единица и больше. После работ С. Смейла стало ясно,
85

что негрубые системы могут заполнять целые области простран-
пространства динамических систем, т. е. что для многомерных систем по-
понятие грубости Андронова — Понтрягина имеет ограниченную
применимость.
3. Исследование гомоклинических структур и выяснение их
роли в образовании сложных хаотических и стохастических дви-
движений детерминированных динамических систем. Кривые, на-
названные А. Пуанкаре гомоклиническими и гетероклиническими
[312], были обнаружены им в ограниченной проблеме трех тел —
задаче о движениях трех притягивающихся по закону Ньютона
материальных точек в предположениях, что это движение плос-
плоское и что одна из масс исчезающе мала и не оказывает влияния
на движение двух остальных. (Эта проблема и после Пуанкаре
неоднократно привлекала внимание многих исследователей.)
Гомоклинические ж гегероклиничеокие кривые привлекли вни-
внимание Пуанкаре потому, что возле них фазовые траектории, от-
отражающие движение системы, вели себя очень сложно и запу-
запутанно. Увидев это, Пуанкаре написал: «Если попытаться пред-
представить себе фигуру, образованную этими двумя кривыми и их
бесчисленными пересечениями, каждое из которых соответствует
двояко-асимптотическому решению, то эти пересечения образуют
нечто вроде решетки, ткани, сети с бесконечно тесными петлями:
ни одна из этих кривых никог-
никогда не должна пересечь самое
себя, но она должна навиваться
на самое себя очень сложным
образом, чтобы пересечь бес-
бесконечно много раз петли сети.
Поражаешься сложности этой
фигуры, которую я даже не
пытаюсь изобразить. Ничто не
является более подходящим,
чтобы дать нам представле-
представление о сложнбсти задачи трех
тел...» [312].
В 1967 г. эта сложная кар-
картина получила описание [263,
266]. Одновременно было отме-
отмечено, что некоторые сочетания
гомоклинических и гетерокли-
нических кривых могут образо-
образовывать структуры, порождающие весьма сложные движения сто-
стохастического характера, которые могут представить интерес для
описания турбулентности течений жидкостей ш газов. Сами эти
сложные образования были позднее названы гомоклиническими
структурами [268].
На рис. 4.3 и 4.4 изображены гомоклиническая f и гетерокли-
ничеокая f' фазовые траектории, Г и Г' — седловые периодиче-
периодические движения. Гомоклиническая фазовая траектория у при из-
Рис. 4.3

менении времени от —<» до +<» сматывается с Г и затем снова
на нее наматывается. Гетероклиническая фазовая траектория f'
при таком же изменении времени от —°° до +°° сматывается с Г
и наматывается на Г'. Пересечем Г секущей плоскостью S, как
Г
Рис. 4.4
это показано на рис. 4.5. Пусть Т — точечное отображение Пуан-
Пуанкаре, переводящее предыдущую точку пересечения секущей Е
с фазовой кривой в последующую точку пересечения. Точки пе-
пересечения с Г и Г' — это неподвижные точки преобразования Т.
Гомоклиническая и гетероклиническая фазовые траектории пере-
пересекаются с Е в некоторых бесконечных последовательностях то-
точек ... М-1, Мо, Мь ... Поскольку фа-
фазовая кривая у стремится к замкнутой
кривой Г при t -*■ —оо и t -*■ +о°, то
она лежит одновременно на интеграль-
интегральных многообразиях S+ и S~ седлового
периодического движения Г. Аналогич-
Аналогично, так как фазовая траектория "у'
асимптотически приближается к Г при
t -*■ —оо и асимптотически приближа-
приближается к Г' при t -*■ +оо, то она лежит
на интегральном многообразии S~ сед-
седлового периодического движения Г и
интегральном многообразии S+ седло- рис 4.5
вого периодического движения Г'. На
рис. 4 6 через S+ ж S~ обозначены следы пересечения поверхно-
поверхностей S+ и S~ с секущей поверхностью Е (изображены лишь
небольшие частя кривых S+ и S~). Продолжить их весьма не-
непросто: их продолжение — это и есть сложность, о которой гово-
говорил А. Пуанкаре. Вместо этого ограничимся схематическим
изображением (рис. 4.7 и рис. 4.8). С помощью таких весьма
упрощенных схем, показывающих только, как входят и как
87

выходят из окрестностей седловых периодических движений фазо-
фазовые траектории, можно дать представление о гомоклинической
структуре и порождаемых ею сложных движениях.
Схематически гомоклиническую структуру можно представить
в виде, показанном на рис. 4.8. Внутри областей D, находятся
седловые периодические движения Г.. В их окрестности элемен-
элементы фазового пространства
испытывают растяжения и
сжатия. Растяжения проис-
происходят вдоль поверхности S~
и сжатия — вдоль поверхно-
поверхности S+.
Фазовые траектории в ка-
какой-то части 3D? границы
(s, i = 1, 2) входят в об-
область D., а в какой-то дру-
другой части 8D7 границы вы-
выходят из D,. Стрелка f,j оз-
означает, что поток фазовых
траекторий, выходящих из
области D. через ее границу
dDTf входит затем через гра-
границу dDf в область Dj. Мо-
Может случиться, что при этом
нет фазовых траекторий, ко-
которые, выйдя из любой обла-
области D,, не оказались бы по-
рис. 4.6 том в одной из областей,
в которые ведут стрелки Чф
В этом случае каждая из фазовых траекторий, попавшая в одну
из областей D. через dDt' либо затем застрянет в одной из обла-
областей Dh либо будет все время переходить из одних областей
Du D2, ... в другие. Движение фазовой точки можно описать
последовательностью номеров областей Ds, которые она прохо-
проходит. В каждой из областей Dj она пребывает некоторое время,
двигаясь в окрестности седлового периодического движения Fj.
Это ее пребывание в окрестности Dj седлового периодического
движения Fj можно охарактеризовать числом оборотов п3, кото-
которое она делает в этой тороидальной окрестности. Таким образом,
движение фазовой точки можно описать последовательностью пар
чисел вида
• • •» /о» n?e» /и ni\* /г> rai2> »• • F)
Оказывается, что эта последовательность пар чисел — номеров
областей /, и чисел оборотов г г—однозначно определяет фазо-
фазовую траекторию и поэтому полностью задает ее. Далее можно
указать, какие последовательности возможны и какие невозмож-
невозможны, и в этом смысле дать полное описание фазовых траекторий,
88

не перестающих оставаться в областях D} ни при t -*■ +°°, ни
нри t -*• —о».
Осталось указать, в чем же состоит Случайность движений
фазовой точки. Она — в непредсказуемости ее движения, т. еУ
в непредсказуемости и случайности с некоторого момента чисел
Рис. 4.7
в
Рис. 4 8
последовательности F), случайности переходов из одной обла-
области Dj в другую и случайности времен пребывания (чисел обо-
оборотов) в каждой из этих областей. Подчеркнем еще, что фазовая
точка движется в каждой из областей Д вблизи седлового пе-
периодического движения, я поэтому ее движение неустойчиво,

первоначально близкие точки разбегаются и спустя некоторое
время движутся совершенно по-разному.
Напомнивд еще, что простой пример такого движения ужо
рассматривался и отмечалось, что именно гомоклиническая струк-
структура порождает стохастичность движений системы Лоренца
A.23) (гл. 1).
4. Тупики в завершении основ статистической механики и
разработке теории турбулентности. Статистическая механика и
физика основываются на ряде общих, ничем и никак не обосно-
ванных, но хорошо проверенных и эффективных постулатов. Го-
Говоря о необоснованности постулатов, мы имеем в виду, что они
должны были бы следовать из общих законов механики и физи-
физики; между тем еще никому не удавалось вывести их из первых
принципов. Эта ситуация существует давно, к ней привыкли, и с
точки зрения физика, не желающего «копаться» в основах, она
вполне приемлема. Подобная ситуация в каком-то смысле не
волнует и физика-теоретика по той простой причине, что класси-
классическая механика и физика — не более чем предельное прибли-
приближение квантовой теории, которая постулирует статистические за-
закономерности, хотя они никак не увязываются с проблемой сто-
хастизации детерминированных динамических систем. В силу
этого открытие стохастичности, хотя оно, возможно, и сулит не-
некоторое продвижение в проблеме обоснования классической ста-
статистической механики и физики, не вызвало сколько-нибудь за-
заметного энтузиазма.
Совсем иначе обстоит дело с проблемами гидродинамической
и плазменной турбулентности. Во-первых, теория турбулентно-
турбулентности, казалось бы, должна полностью основываться на классиче-
классических макроскопических уравнениях: уравнениях Навье — Стокса,
газодинамики, уравнениях магнитной гидродинамики, плазмы и
других, однако вывести основные характеристики турбулентного
движения из макроскопических уравнений пока не представляет-
представляется возможным и приходится прибегать к дополнительным сооб-
соображениям. Теория турбулентности необычайно разрослась, но
путь ее тернист и труден. Она вынуждена прибегать к полуэм-
полуэмпирическим и весьма сомнительным соображениям и до сих пор
не может разобраться даже в простейших типах течений, доволь-
довольствуясь весьма скудными теоретическими результатами о потере
устойчивости и численными расчетами, не подкрепленными хоро-
хорошей теорией. Такое неудовлетворительное положение сложилось
не только потому, что механика жидкостей и газов и ее уравне-
уравнения оказались очень сложными, а число степеней свободы удру-
удручающе велико, но и потому, что было совершенно пе ясно, в ка-
каком направлении надлежит двигаться, как, хотя бы в принципе,
может быть построена такая теория.
Новые воззрения на" стохастизацию движений динамической
системы (новые для механики жидкой среды представления тео-
теории нелинейных колебаний, теории динамических систем и тео-
теории бифуркаций) пробудили надежды на создание долгожданной
90

теории, на выход из тупика в решении ряда давно стоящих за-
задач. Столь радужные перспективы не могли не вызвать энтузи-
энтузиазма, который, как можно предвидеть, войдет в спокойное русло
после осмысливания возникающих колоссальных трудностей. Но
штурм начат и рано или поздно приведет к своим результатам.
До последнего времени в теории возникновения турбулентно-
турбулентности безраздельно господствовала гипотеза Ландау, высказанная
им в 1944 г. [230, 231]. В 1948 г. аналогичные соображения были
выдвинуты Хопфом [511]. Теория Ландау была, по существу,
первой попыткой объяснить турбулентность с тех пор, как
в 1883 г. Рейнольде обнаружил, что она возникает при увеличе-
увеличении параметра, названного впоследствии числом Рейнольдса
[613]. Теория Ландау связывает возникновение турбулентности
с неустойчивостью. Это безусловно верно, но то, как она это де-
делает, требует существенных уточнений. С точки зрения новых
воззрений теория Ландау не неверна, а не полна. Она указывает
лишь на один из возможных вариантов возникновения турбу-
турбулентности, причем, по-видимому, далеко не самый важный. Со-
Современная теория бифуркаций предлагает много других путей.
Некоторые из них в той или иной мере уже подтверждены экс-
экспериментами. Это новые, отличные от указываемых теорий Лан-
Ландау, пути хаотизации и стохастизации движения жидкости.
По Ландау возникновение турбулентности происходит в ре-
результате последовательной серии потерь устойчивости состоянием
равновесия, возникшим периодическим движением, появившимся
двоякопериодическим движением и т. д., в результате чего дви-
движение становится многопериодическим вида
1>@в/(«М, И,*, ..., (Umt), G)
где <в„ а>2, .-., сит — частоты, а функция /(<pt, <р, ..., <рт) как
функция переменных фь <р2, ..., <рт — периодическая по каждому
из них с периодом 2я. Рюэль и Такенс [627] обратили внимание
на то, что путь, указанный Ландау, не общий, что общая воз-
возможность — это образование странного аттрактора. Но как воз-
возникает странный аттрактор, они не исследовали. Идеи, выска-
высказанные Рюэлем и Такенсом в 1971 г., имеют свою предысторию.
Об автоколебательной природе турбулентности говорил еще в на-
начало 50-х годов Г. С. Горелик [217]. О возможной связи турбу-
турбулентности с гомоклиническими структурами и порождаемыми
ими сложными движениями говорилось в лекциях на пятой лет-
летней математической школе в 1967 г. [266].
Знакомясь сейчас с этими более ранними высказываниями,
нельзя пе заметить, что они претерпели значительные видоизме-
видоизменения в соответствии с общими представлениями и уровнем раз-
развития теории нелинейных колебаний и теории динамических си-
систем. Теория Ландау — прямой продукт современных ему пред-
представлений о генерации многопериодических колебаний. Выска-
Высказывание Г. С. Горелика — это следствие развившейся к тому вре-
времени теории автоколебаний А. А. Андронова. Высказывания
91

Ю. И. Неймарка о турбулентности — результат исследования им
гомоклинических структур, открытых еще А. Пуанкаре, новый
термин — странный аттрактор — и гипотеза Рюэля и Таккенса
о природе турбулентности непосредственно навеяны работами
С. Смейла.
Возможно, следует отметить еще одно забытое направление
попыток объяснения турбулентности, исходящих из отсутствия
теорем о существовании решений уравнений Навье — Стокса.
В них возникновение турбулентности трактуется как следствие
непродолжаемости по времени и разрушения их решений. Эти со-
соображения ведут свое начало от Лере [557] и были продолжены
в более поздних работах [633].
Что можно добавить ко всему этому? Прежде всего то, что все
приведенные выше высказывания исходят только от временной
трактовки движений динамической системы, от ее фазового порт-
портрета, а жидкость — это распределенная в пространстве среда,
и описание ее движения, помимо временной составляющей, вклю-
включает еще и пространственную. Турбулентность — не только вре-
временной хаос, -это еще и хаос пространственный. Конечно, вре-
временной и пространственный хаосы взаимосвязаны, но не сводят-
сводятся один к другому: вообще говоря, может быть временной хаос
и пространственный порядок, может быть временной порядок и
пространственный хаос. Турбулентность — это, вообще говоря,
и временной и пространственный хаос. На эту двоякую природу
хаоса при турбулентности обратил внимание в своем обзоре в
УФН А. С. Монин [257].
Вместе с тем, по-видимому, к турбулентности можно относить
и случаи только временного или только пространственного хаоса.
Временной хаос имеет своим адекватным геометрическим об-
образом странный аттрактор, пространственный хаос—согласован-
хаос—согласованное седловое (гиперболическое) инвариантное множество. Здесь,
по-видимому, необходимо дальнейшее уточнение.
Наконец, необходимо также заметить, что единственным гео-
геометрическим образом временного хаоса до недавнего времени бы-
было принято считать странный аттрактор. Сейчас уже ясно, что
это не так. Геометрическим образом временной турбулентности
может быть также одно или несколько устойчивых периодиче-
периодических движений с переходами за счет малых флуктуации с одного
на другое или на него же, т. е. турбулентность может быть
проявлением как геперации стохастичности, так и усиления
стохастичпости.

Глава 5
ЛОКАЛЬНЫЕ ФАЗОВЫЕ ПОРТРЕТЫ ПРОСТЕЙШИХ
УСТАНОВИВШИХСЯ ДВИЖЕНИЙ И ИХ БИФУРКАЦИЙ
В настоящей главе рассказывается о простейших установив-
установившихся движениях — состояниях равновесия и периодических
движениях. Излагается классификация состояний равновесия и
периодических движений, устанавливаются и исследуются основ-
основные типы их бифуркации. Рассматриваются не только устойчи-
устойчивые состояния равновесия и периодические движения, но и не-
неустойчивые седловые состояний равновесия и периодические дви-
движения. Если первые играют роль основных простейших устано-
установившихся движений, то вторые играют определяющую роль в
формировании границ их областей притяжения и в формирова-
формировании хаотических и стохастических движений, а также всего фа-
фазового портрета динамической системы.
§ 1. Состояния равновесия
Состояния равновесия — это решения дифференциального
уравнения
х = Х(х) A.1)"
вида х = х*, где х* — постоянный вектор, который находится
из условия
Х(х*) = 0. A.2J
В общем случае состояния равновесия образуют некоторое
множество' изолированных точек. В вырожденных особых слу-
случаях могут возникать многообразия состояний равновесия той
или иной размерности.
Вводя новую переменную 1 = х — х*, запишем дифференци-
дифференциальное уравнение A.1) в окрестности состояния равновесия
х = х* в виде
| Щх<1 + Д(Е), A.3)
где R(%)—не ниже второго порядка малости по 1< Отбрасывая
93

этот малый член jRA), приходим к линеаризованным в окрест-
окрестности состояния равновесия уравнениям движения вида
где А — некоторая постоянная квадратная матрица. В общем
случае, когда все собственные значения матрицы А — различ-
различные, как хорошо известно, существует невырожденная линейная,
вообще говоря, комплексная замена деременных
г) = £|, A-5)
после которой дифференциальное уравнение A.4) принимает вид
Л-Лть A.6)
где
Л = LAL-1
— диагональная матрица, диагональными элементами которой
являются корни характеристического уравнения
O. A.7)
Здесь Det означает определитель, а Е — единичную матрицу.
В скалярной форме дифференциальные уравнения A.6) запись^
ваются в виде
т|.-М. (в-1, 2, ..., в). A.8)
Корни Я, могут быть действительными и комплексными. В по-
последнем случае наряду с корнем Я, имеется и комплексно сопря-
сопряженный корень К+1 = К • Полагая К, = а, + ш„ \,+i = а, — ia,
и вводя новые действительные переменные
и> = т СП» + Tls+i), vs = ■%- (т|, — Tis+i)»
перепишем уравнения A.8) в виде
если
Я8
действительно, и
й. = о,м.
в
л.-
виде
Я.т]
У.
.,
= О)
.+
<78У„
A.9)
A.10)
если Я, = о, + ш, комплексно.
Дифференциальные уравнения A.9) и A.10) легко решаются,
так что
и
щ—е (Mj cos o>3^ — у" sm tt)si/,.
•//о- ,-u • Л' (U2)
vs = e (us sin (ost + ys cos (osr^t
где T)", и*t v° — начальные значения этих переменных при t = 0.
94

Исключим случаи к. — О и а, —0. Тогда согласно A.11) и
A.12) любая из переменных т)а, м8, у, с ростом времени либо не-
неограниченно возрастает, либо стремится к нулю. Вектор пере-
переменных первой группы обозначим через v, а второй — через и.
Для и и v могут быть записаны уравнения вида
и = Ли, v = 5v, A.13)
где А и В — матрицы. На диагонали матрицы А стоят либо отри-
отрицательные числа Я„ либо матрицы второго порядка вида
<°з\
\ )
A.14)
с отрицательным а„ на диагонали матрицы В аналогично либо
положительные числа к„ либо матрицы вида A.14) с положи-
положительными а,.
Пусть, р и q — размерности векторов и и v соответственно.
Тогда А — квадратная матрица р X р, а В — квадратная матри-
матрица qXq. Сумма р + q совпадает с общей размерностью п векто-
вектора х. Состояния равновесия с числами р и q корней Ки А,2, .. .Д„
слева и справа от мнимой оси будем обозначать через Ор-q.
Линеаризованные уравнения в форме A.13) замечательны
тем, что в них переменные и и v разделены и ведут себя по-раз-
по-разному: все компоненты вектора и стремятся к нулю при t -*■ +°°,
а все компоненты вектора v неограниченно возрастают при
t -*■ +оо. Итак, в окрестности состояния равновесия Ор> я при об-
общих предположениях уравнения движения A.1) могут быть за-
записаны в виде
)(")+F(u,v), A.15)
где функция F(u, v) не менее второго порядка малости по пере-
переменным u, v.
В уравнении A.15) в линейных членах переменные разделя-
разделяются, а в членах более высокого порядка в общем случае не раз-
разделяются. Спрашивается, в какой мере можно добиться такого же
разделения переменных и в членах более высоких порядков ма-
малости (чем линейные)? Как оказывается, ответ на этот вопрос
зависит от собственных значений Х±, Х2, ..., ^„. Имеет место сле-
следующая замечательная теорема, ведущая овое происхождение
от А. Пуанкаре. Ниже она приводится в формулировке А. Д. Брю-
но [95, 96].
Система дифференциальных уравнений вида
*. - К.х. + U (х) (в = 1, 2, ..., п), A.16)
где /, (х) — аналитические функции х не ниже второго порядка
по х, путем замены переменных вида
x. = y. + g.(y) (s = l, 2 п), A.17)
95

гДе £»(у) не ниже второго порядка по у, приводится к так назы-
называемому нормальному виду
2
где Q — вектор с компонентами qu g2, • •., qn, yQ = У\Уг • • - Уп\
а множество Ш$ определяется как множество всевозможных век-
векторов Q, для которых выполнены условия
qu q2, ..., q,-u q,+u ..., qn > 0, q, > — 1,
llQII-gi + g»+... + g»>l, A.19)
(Л, Q) = Xiql + Я2д2 + ... + Xnqn = 0,
и §sq — некоторые, вообще говоря, отличные от нуля коэффи-
коэффициенты. В этой тебреме речь идет о формальной возможности
преобразования к нормальному виду A.18). При этом ряды, оп-
определяющие преобразование, и сама нормальная форма, могут
расходиться. Нормализацию можно остановить на членах поряд-
порядка меньше iV. Тогда вместо нормальной формы A.18) получим
У* — КУ* + Уз S SsQyQ + YsNt, (i ОСП
где YsN — члены порядка не меньше N относительно у. После
этого вопросы о сходимости отпадут, а от правых частей потре-
потребуется дифференцируемость не более чем N + 1 раз. Условие
||Qll<iV—1 A.21)
совместно с неравенствами A.19) определяют не более чем ко-
конечное множество вектором Q:
Q1, Q2, Q3, ..., QL.
В множество Ша войдут только те из этих векторов, для которых
выполняется еще и последнее условие A.19). Поэтому множест-
множество Ш, будет пустым, если
(Л, Q')(A, Q2)...(A, QL)¥=0. A.22)
Из этого вытекает, что при общих предположениях о корнях %lf
Хг, ..., Кп множества Ш3 пустые, и следовательно, уравнения
A.20) в прежних действительных переменных и и v запишутся
в виде
и = Ли + /(и, v), v = 5v+,g(u, v), A.23)
где функции / и g не ниже N-то порядка малости.
Допустим теперь, что есть еще и нулевые и чисто мнимые
корни. Тогда, при общем положении остальных корней, выделяя
переменные w, отвечающие нулевым и чисто мнимым корням,
96

запишем дифференциальные уравнения A.22) в виде
u = .4u + /(u, v, w),
v = 5v + g(u, v, w), A.24)
w = Cw + wi?(w)+ h(u, v, w),
где по-прежнему функции /, g, h не ниже JV-го порядка по пере-
переменным u, v, w, a R (w) — полином от переменных w, обуслов-
обусловленный тем, что для чисто мнимых и нулевых корней выполня-
выполняются соотношения A.19) и A.21). Отметим, что выделение толь-
только линейных членов также приводит дифференциальные уравне-
уравнения A.1) к виду A.24) и при этом iV = 2.
Следующими полезными соображениями, которые могут быть
использованы для придания удобного вида дифференциальным
уравнениям A.24) в окрестности состояния равновесия, являют-
являются теоремы о существовании, гладкости и гладкой зависимости
от параметра интегральных многообразий дифференциальных
уравнений [264, 265, 269, 285]. Эти теоремы свое начало ведут
от работ Адамара и Перона. Согласно
им дифференциальные уравнения A.24)
в окрестности равновесия допускают два
интегральных многообразия £+(v = /*(w,
и)) и S~(u = g*(w, v)), пересечение ко-
которых образует интегральное многооб-
многообразие
/(u-tp*(w), v =
. A.25)
Для наглядного представления инте-
интегральных многообразий S+, S~ и 7 рас-
рассмотрим их сначала в случае, когда нет
чисто мнимых и нулевых корней и нели-
нелинейные члены отсутствуют. В этом случае
поверхности S+, S~ и 7 имеют соответст-
соответственно уравнения
v = 0, u = 0 и u = v = 0.
Рис. 5.1
Поэтому 7 — точка равновесия, S+ состоит из всех фазовых тра-
траекторий, стремящихся к 7 при t -*■ +°°, a S~ — из всех фазовых
траекторий, стремящихся к 7 при t -*■ — °° (рис. 5.1). При появ-
появлении нелинейных членов / и g в уравнениях A.24) поверхно-
поверхности S+ (v = 0) и S~ (u = 0) несколько деформируются, оста-
оставаясь касательными в точке 7 к многообразиям v = 0 и и = 0.
Точнее, имеет место не только касание, а соприкосновение поряд-
порядка не менее чем N— 1.
Пусть нелинейные члены отсутствуют, а корни на мнимой оси
есть. В этом случае интегральные многообразия S+, S~ и 7 имеют
соответственно уравнения v = 0, u = 0 и u = v = 0. Но теперь
многообразие 7 — не точка равновесия, а интегральное многооб-
97

разие размерности, равной числу корней характеристического
уравнения на мнимой оси.
При появлении нелинейных членов интегральные многообра-
многообразия £+, S~ п J деформируются и имеют соответственно с поверх-
поверхностями v = 0, u = 0 и u = v = О соприкосновения порядка не
меньше iV— 1. Фазовые траектории на многообразии подчиняют-
подчиняются, согласно последнему из уравнений A.24) и уравнением A.25)
интегрального многообразия /, дифференциальному уравнению
вида
w = Cw + wR (w) + h (ф* (w), ^* (w), w). A.26)
Тем самым полностью описано поведение фазовых траекторий на
многообразиях S+, S~ и /. Вне этих многообразий фазовые точки
приближаются к / вдоль S+ и затем удаляются от / вдоль S~.
Это в случае, когда р^О и q=£0. В случае р = 0 или q = О все
фазовые траектории уходят от многообразия / либо, напротив,
к нему приближаются. Особый интерес представляет случай
q = 0, когда многообразие S~ отсутствует, а многообразие S+
совпадает со всем фазовым пространством (некоторой окрест-
окрестностью точки равновесия Ор °) и фазовые траектории экспонен-
экспоненциально приближаются к интегральному многообразию /. Если
из этой малой окрестности при возрастании времени фазовые
траектории не выходят, то каждая из них экспоненциально при-
приближается к некоторой фазовой траектории на интегральном
многообразии /. Следовательно, асимптотическое поведение фа-
фазовых траекторий вблизи равновесия Ор ° определяется асимпто-
асимптотическим поведением фазовых траекторий только многообразия Jt
и в этом смысле фазовый портрет окрестности равновесия Ор °
определяется фазовым портретом окрестности Ор ° на многообра-
многообразии /. При p + ? = R и р^О и ?^0 состояние равновесия седло-
вого типа. При q = 0 оно устойчивое, а при р = 0 неустойчивое.
Поведение фазовых траекторий во всех этих случаях было опи-
описано выше, соответствующие фазовые портреты при одинако-
одинаковых р и q будем считать одинаковыми. Установлено, что такие
фазовые портреты топологически изоморфны, т. е. могут быть
преобразованы друг в друга с помощью взаимно однозпачного и
взаимно непрерывного преобразования.
В новых переменных
u = u — g*(vr, v), v = v —/*(w, u), w = w A-27)
дифференциальные уравнения A.24) запишутся в виде
и = Аи + и/ (и, v, w),
v = В\ + \~g (и, v, w), (I-28)
W = C\V -f~ WjR (w) + Wfe (u, V, W),
а интегральпыми многообразиями S+, S~ я J будут соответствен-

но v = 0, u = 0 и u = v = 0. Нелинейн_ые_ функции u/, vg и wh
по-прежнему останутся относительно u, v и w порядка малости
не меньше N — I, вид функции R не изменится.
Остался еще без ответа вопрос о роли членов в нормальной
форме, для которых выполнено условие A.19). Полного ответа
на этот вопрос нет. Можно лишь отметить, что, как будет по-
показано в § 2, в некоторых случаях эти, так называемые резонанс-
резонансные члены, весьма существенны.
§ 2. Бифуркации состояний равновесия
Ниже исследуется зависимость фазового портрета в окрест-
окрестности состояния равновесия от параметров динамической систе-
системы, т. е. от параметров ц, входящих в правые части описываю-
описывающей ее системы дифференциальных уравнений
i = X(x)fi). B.1)
Основным элементом такого исследования является прослежива-
прослеживание фазового портрета и его изменений при непрерывном изме-
изменении параметра р, вдоль некоторой кривой у в пространстве
параметров. Оказывается, что при прохождении некоторых точек
на этой кривой у происходит качественная перестройка фазового
портрета. Такие точки получили название точек бифуркации
фазового портрета, а отвечающие им значения параметров ц —
бифуркационных значений параметров. Через одну и ту же точ-
точку пространства параметров может проходить много различных
кривых f и заранее ниоткуда не следует, что изменение фазового
портрета не зависит от кривой, по которой меняются параметры.
Значит, понятие бифуркации зависит еще и от пространства па-
параметров, т. е. можно обнаружить, расширяя его, новые бифур-
бифуркации, сужая — какие-то бифуркации потерять. Выяснение того,
с каким именно случаем мы имеем дело при исследовании той
или иной динамической системы, требует уточнений.
Бифуркации можно рассматривать в пространстве всех ди-
динамических систем или какого-нибудь класса динамических си-
систем, например второго порядка с полиномиальными правыми
частями или описываемые уравнениями Гамильтона и т. д.
Точка ц* пространства динамических систем или простран-
пространства ее параметров называется точкой бифуркации, если в ее
сколь угодно малой окрестности найдутся точки, отвечающие
динамическим системам с качественно различными фазовыми
портретами. Это определение достаточно исчерпывающее, но оста-
остается пока неясным, что такое качественно различные фазовые
портреты. Обычно под качественно различными понимаются то-
топологически неэквивалентные фазовые портреты. Одпако в не-
некоторых случаях такое определение качественного различия
фазовых портретов может оказаться излишне детальным, это
может, например, иметь место в случае, когда бифуркационные
99

значения оказываются плотными, и тогда можно попытаться
определить качественное различие как-нибудь иначе.
При исследовании бифуркаций желательно, чтобы размерность
пространства параметров была как можно меньшей, а точки би-
бифуркации образовывали бы легко воспринимаемые геометриче-
геометрические образы. За счет чего и как можно этого добиться? Пусть
М — интересующее нас пространство параметров или динамиче-
динамических систем и пусть ц* — точка бифуркации в нем. Простейший
случай — это когда в малой окрест-
окрестности точки [г* есть точки, соответ-
соответствующие только двум качественно
различным фазовым портретам и в
этой окрестности возможен такой
выбор одного параметра ц, что раз-
разделяющая их поверхность есть ц = О
(т. е. для одного типа фазовых пор-
портретов (х > 0, а для другого ц < 0)
(рис. 5.2). В этом случае будем го-
говорить, что бифуркация в точке ц*
однопараметрическая, а бифуркаци-
онная поверхность \i = 0 по терми-
терминологии Андронова — Леонтович со-
соответствует системам первой степени негрубости*) [18, 19].
Возможен более сложный случай, когда в окрестности (х* есть
четыре типа фазовых портретов, разделяемых между собою дву-
двумя поверхностями. Выбирая параметры fx4 и (х2 так, чтобы эти
Рис. 5.2
а
Рис. 5.3
поверхности соответствовали fxt = 0 и (х2 = 0, а в четырех обла-
областях разных типов фазового портрета выполнялись соответствен-
соответственно неравенства fXi > 0 и fx2 > 0, \ку < 0 и fx2 > 0, \ii > 0 и [х2 < 0,
ц4 < 0 и \i2 < 0, приходим к двухпараметрическому описанию
бифуркаций в окрестности точки ц* (рис. 5.3, а). Окрестность
*) Другое изложение рассматриваемых вопросов, при котором понятия
грубости и степеней негрубости динамических систем не упоминаются,
можно найти в работе [43].
100

точки ц* может иметь и более сложный вид, например такой,
как показан на рис. 5.3, б. В этом случае в окрестности точки
ц* имеется не четыре, а только три области, отвечающие разным
типам фазового портрета. Они соответствуют следующим трем
комбинациям знаков параметров ^ > 0 и ц2 < 0, ц* > 0 и ц2 > О,
Hi < 0 и \i2 < 0. Таким образом, двухпараметрическое представ-
представление возможно и в этом случае. «Линия» пересечения бифур-
бифуркационных поверхностей [Дц == 0 и \лг = 0 во всех случаях отве-
отвечает негрубьщ системам второй степени негрубости.
Приведенные нами простые примеры позволяют дать общее
определение представимости бифуркаций с помощью г парамет-
параметров ць ц2, • ■., Цг- Именно, в окрестности бифуркационной точки
fi* пространства параметров или динамических систем М имеет
место представимость с помощью г параметров, если в этой'
окрестности возможен такой выбор г переменных, что каждый
пэ типов фазовых портретов соответствует одной или нескольким
комбинациям знаков этих параметров.
Теперь можно определить представимость бифуркаций не
только в окрестности трчки бифуркации, но и в некоторой обла-
области М пространства М. Бифуркации в области М представимы с
помощью параметров fil5 ц2, ..., fir, если существует конечное
или бесконечное множество кусочно-гладких функций /i(fii,
Иг, ..., fir), /2(^1, ..., fir), ... такое, что в любых двух точках
области М, отвечающих разным типам динамических систем (их
фазовых портретов), по крайней мере у одной из функций
/и /2, ... разные знаки. Подчеркнем, что фазовый портрет дина-
динамической системы и его разные типы могут рассматриваться гло-
глобально во всем фазовом пространстве или локально только в
некоторой его части, например в малой окрестности состояния
равновесия.
Теперь мы уже располагаем всем необходимым, чтобы дать
определение изолированной точки бифуркации fi*. Точка и* со-
соответствует изолированной бифуркации, если в достаточно малой
ее окрестности может обращаться в нуль не более чем конечное
число функций /i, /2, ... и в этой окрестности существует не бо-
более чем конечное число связных компонент различных типов
динамических систем. В противном случае точка неизолирован-
неизолированная и является точкой сгущения бесконечного числа областей,
отвечающих различным типам фазовых портретов. Это сгущение
вокруг точки бифуркации fi* может носить односторонний или
многосторонний характер.
Наличие точек сгущения впервые явно обнаружилось при
рассмотрении грубых отображений окружности в себя [242]. Дру-
Другие механизмы образования неизолированных точек бифуркации
были обнаружены в связи с изучением гомоклинических струк-
структур [262, 268]. В более поздних американских работах это явле-
явление названо Q-взрывом [295]. Как уже отмечалось, возможность
всюду плотного расположения неизолированных точек бифурка-
бифуркации была установлена С. Смейлом [331]. В последнее время
101

широкую известность получили бесконечные серии бифуркаций
^удвоений периода [444—448]. Все эти серии бифуркаций будут
рассмотрены в § 2 гл. 7.
Вернемся к дифференциальному уравнению B.1) и его со-
состояниям равновесия. Пусть О (х — х*) — одно из его состояний
равновесия и Xi, Xi, ..., Хп — корни его характеристического урав-
уравнения. Пусть М — пространство всевозможных гладких функций
Х(х) и ц* — точка в пространстве М, отвечающая рассматри-
рассматриваемой системе B.1),.
Теорема 5.1. Точка jx* не является точкой бифуркации состоя-
состояния равновесия О, если на мнимой оси нет корней Хи Х2, ■ • •, Хп-
Действительно, в этом случае состояние равновесия О сущест-
существует не только при ц = ц*, но и при всех ц, достаточно близких
к ц*, поскольку якобиан уравнения B.1), равный
отличен от нуля. Равенство нулю якобиана B.2) означало бы,
согласно A.7), что характеристическое уравнение имеет нулевой
корень.
При всех ц, достаточно близких к ц,*, состояние равновесия
не меняет своего типа, т. е. не меняет размерностей своих ин-
интегральных многообразий S+ и S~ и чисел р и q, и поэтому все
время остается типа Op'q.
Из теоремы 5.1 следует, что основными простейшими бифур-
бифуркационными точками состояния равновесия являются точки ц*,
для которых характеристическое уравнение имеет нулевой или
два чисто мнимых сопряженных корня. Каждому из этих случаев
в пространстве М отвечают поверхности yV0 и Na коразмерности
единица. Их уравнения могут быть записаны в виде
Deti£U = 0 B-3)
и соответственно в виде
Detl^
^_ш)£| = 0 @<со< + оо). B.4)
Уравнение поверхности Na имеет параметрическую форму.
Раскрывая определитель, запишем характеристическое уравнение
A.7) в виде
%(X) = к" + а,Хп-1 +... + пп-,% + а„ = 0. B.5)
Через его коэффициенты fli, а2, ..., а„, которые являются функ-
функциями параметра ц, уравнения бифуркационных поверхностей
No и Na могут быть записаны соответственно в виде
ап = 0 и An_! -=
°1
аз
аь
1
°2
0
ai
аз
0
1
0 ...
0 ...
°1 •••
= 0, B.6)
102

где Д„_! — предпоследний определитель Рауса — Гурвица урав-
уравнения B.5). Напомним, что последний определитель Рауса —
Гурвица An = впАп-i, так что обращение его в нуль определяет
обе бифуркационные границы iV0 и Na.
Пусть ц* е= NB. Уравнения движения при ц = ц* могут быть
записаны в виде A.28). Сосредоточим свое внимание на уравне-
уравнении для переменной w. При ц = ц* оно имеет вид
w = с* w2 + Cgiv3 + ... + h (u, v, w)
и при ц, близких к ц*, записывается в виде
c2wz
h(u, v, w), B.7)
где коэффициенты c0, cu c2, c3, ... и функция h гладко зависят
от ц и с0 = с4 == 0 при ц = ц*. В простейшем случае с2 = с* ф О
при ц = ц*, далее идет случай с2 = 0 и с3ф0. Рассмотрим
именно эти случаи. Малость члена h(u, v, w) в сочетании с не-
невырожденностью матриц А и В позво-
позволяет при отыскании состояния равно-
равновесия для значений параметра ц, близ-
близких к ii*, ограничиться уравнением
Со + ctw +
csw3
0. B.8)
Интересны решения этого уравнения,
обращающиеся в нуль при ц = ц,*. Па-
Параметр ц в общем случае имеет произ-
произвольную размерность. Поэтому для
упрощения рассуждений допустим, что
через точку |i*eM проходит произ-
произвольная прямая и v — параметр, ме-
меняющийся вдоль этой прямой и равный нулю в точке ц*
(рис. 5.4). Рассмотрим основные простейшие случаи:
Рис. 5.4
а) с0* = с* = 0, с0 = ^?
0,
0,
B.9)
б) с* = с* = с* = О, с'0ф0, С;=^0, с£
В первом случае согласно уравнению B.8)
„1/2 ,
w
-у-и
и во втором случае
B.10)
B.11)
Это соответствует графикам зависимости координаты w состоя-
состояния равновесия от параметра v, изображенным на рис. 5.5, а.
103

Для того чтобы эти графики стали бифуркационными диаграм-
диаграммами, на ветвях этих кривых следует указать еще типы соответ-
соответствующих им состояний равновесий. Из уравнения B.7) путем
подстановки в него найденных значений w находим все возмож-
возможные варианты существенно разных бифуркационных диаграмм,
изображенные на рис. 5.5, б.
В соответствии с изложенным имеет место следующая теорема.
Теорема 5.2. В случаях B.9) с точностью до направления
осей w и v имеют место бифуркационные диаграммы, представ-
представленные на рис. 5.6, где значения w как функции параметра v
определяются соответственно формулами B.10) или B.11).
На рис. 5.6 представлены изменения трехмерного фазового
портрета для первой и второй рассмотренных бифуркаций в пред-
предположении, что исходное состояние равновесия при v < 0 устой-
устойчивое, т. е. типа О3' °.
Пусть ц* е Na. В этом случае, в противоположность преды-
предыдущему, при изменении ц состояния равновесия сохраняется и
единственно в своей малой окрестности при всех ц, близких к ц*
(нет нулевого корня и якобиан отличен от нуля). Это позволяет
последнее из уравпений A.28) рассматривать на интегральном
многообразии u = v = 0. При этом оно превращается в уравнение
, 0, w) B.12)
на двумерном многообразии / (u = v = 0). Матрица С при jx = М-*^
имеет два чисто мнимых корня ±ico (ю Ф 0), а наинизпшй резо-
104

яансный член таков, что в компонентах уравнения B.12) запи-
записываются в виде
u?! = aw1 -<awt+g {w\ + wl)w1+ ...,
w2 = (ow1 + aw2 + g(w\ + ы£) a;2 + .. .f
где о = 0 при jii = ц*, а многоточия означают члены более высо-
высокого порядка малости по сравнению с любым из написанных
Рис. 5.6
членов. Умно»" ,ац цёрвйй уравнение на u?t, а второе на юг и скла-
складывая их, на? а0ДйМ, что
4 7/ («J + ^) = a {w\ + w§ + g (u;f + и;22J + ...,
или, вво; щ доййрную координату г и обозначая г2 через р, пере-
перепишем j долучйнное уравнение в виде
|p = a(v)P + g(v)p2+ ... B.13)
нг
, что а@) = 0 и полагая б = a'@)v +..., где о'(
, что в зависимости от знаков a'v^O и ^@)=5^0 имеет
один из фазовых портретов (рис. 5.7). При этом r = Vp
^уд колебаний) для периодического движения Г, устой-
устойчивого по переменным Wi и и>з. при o'v < 0, g > 0 и неустойчи-
105

вого по ним при o'v > 0, g<0, согласно B.14) порядка Vv,
точнее,
B.14)
где многоточия означают члены более высокого порядка малости
по v, чем vuz.
Пусть а'@)т^0 и направление измерения v выбрано так, что
о'@)>0, тогда при ^@)^0 согласно изложенному возможны
только два следующих случая.
Рис. 5.7
Теорема 5.3. При g@)>0 с возрастанием параметра v со-
состояние равновесия Ор-q переходит в Ор~г-9+2 и при зтом с со-
состоянием равновесия сливается периодическое движение Гр-1'9+2.
При g@)<0 состояние равновесия Орв переходит в Op~2-q+z, но
при этом от него отделяется периодическое движение Гр> 9+I.
Смысл чисел р и q в записи периодического движения ана-
аналогичен их смыслу при записи состояния равновесия и будет
уточнен в следующем параграфе.
По теореме 5.3 от устойчивого состояния равновесия Оп- °,
теряющего устойчивость при gr@)<0, происходит рождение
устойчивого периодического движения Г'1, а при ^@)>0 со-
состояние равновесия теряет свою устойчивость, сливаясь с не-
неустойчивым периодическим движением Г"~1>г.
106

Фазовый портрет в случае рождения устойчивого периодиче-
периодического движения Г3'' показан на рис. 5.8.
Теорема 5.3 впервые в двумерном случае была установлена в
работе А. А. Андронова и Е. А. Леонтович A939 г.) [16, 17]
и обобщена на произвольную
размерность в работах [259,
260]. В работе Хопфа [510]
4942 г. рассмотрен многомер-
многомерный случай, но ее результат
менее полный, так как не учтен
знак ляпуновской величины g.
Фактическое вычисление вели-
величины g для двумерных и трех-
трехмерных систем выполнено в ра-
работах [72, 73] и для многомер-
многомерных на основе [259, 260] —
в [351].
В заключение этого пара-
параграфа сведем полученные све-
сведения о бифуркациях состоя-
состояний равновесия в таблицу 1.
Под номерами 1—5 в этой таб-
таблице помещены бифуркации
устойчивых равновесий типа Оп> °. Формула, например, в первом
номере означает, что с состоянием равновесия Оп-а сливается сед-
ловое равновесие О"-1' *, и они оба исчезают. В следующем столб-
столбце указана коразмерность бифуркации (в общем случае это —
Таблица 1.
1
2
3
4
5
6
7
8
9
10
Формула бифуркации
0П,о _|_ 0П-1.1 ^0
0П,о_у0П-1,1_|_2оп,о
Оп-° + 2Оп~1Л -*• Оп~1Л
0П,О _>. 0«—2,2 1 рП,1
0П,О 1 рП—1,2 _^_ Qtl—2,2
0Р.9 4- 0P~1>9+1 -V0
0Р,9 _*. 0Р+1.9-1 _|- 2ОР'9
OP+i,9-i_2OP+i.*-i +
ОР,Я+ТР.Я+2^ОР-2,д+2
Коразмер-
Коразмерность
1
2
2
1
1
1
2
2
1
1
Пересекае-
Пересекаемая гра-
граница
No
No
No
Na
"a
No
No
No
"a
Характер
потери
устой-
устойчивости
жесткий
мягкий
жесткий
мягкий
жесткий
Фазовый
портрет
(рисунок)
5.6, а
5.6, б
5.7, вшб
5.7, г па
Теорема
5.2
5.2
5.2
5.3
5.3
5.2
5.2
5.2
5.3
5.3
107

число условий, которые должны выполняться для того, чтобы би-
бифуркация имела место). В следующем столбце указано, какая
бифуркационная граница пересекается. Далее идет столбец,
в котором приведен характер потери устойчивости, т. е. показа-
показано, что происходит с фазовыми точками, ранее близкими к точке
Оп- °, при потере ею устойчивости, когда параметр очень медлен-
медленно переходит через нулевое значение. Мягкий переход означает,
что фазовые точки мало меняют свое положение, так как от
ставшего неустойчивым равновесия отделяется устойчивое рав-
равновесие или периодическое движение. Напротив, жесткий пере-
переход означает значительный уход фазовых точек к какому-то
неизвестному другому установившемуся движению. Последпие
два столбца указывают на рисунки, изображающие в двумерном
или трехмерном случаях эти бифуркации и номера относящихся
к ним теорем.
§ 3. Фазовые портреты в окрестности
периодических движений
Рассмотрение фазового портрета, отвечающего дифференциаль-
дифференциальным уравнениям B.1), в окрестности замкнутой фазовой кривой
Г с помощью отображения Пуанкаре сводится к рассмотрению
точечного отображения
x=F(x, ц)
C.1)
в окрестности соответствующей неподвижной точки О (рис. 5.9).
Как и в случае состояния равновесия,- эти уравнения с исполь-
использованием линеаризации, теорем
о приведении точечного отобра-
отображения к нормальной форме и
теорем об инвариантных много-
многообразиях приводятся к виду
и = Аи + u/(u, v, w),
y = Bx + yg(u, v, w), C.2)
vv = Cw + wR (w) + w/i (u, v, w).
При такой записи инвариант-
инвариантные многообразия S+, S~ и /
имеют уравнения v = 0, и = О
рие 59 hu = v = 0 соответственно.
В полиноме i?(w), как и ранее,
собраны резонансные члены, отвечающие корням характеристи-
характеристического уравнения, лежащим на единичной окружности. Усло-
Условия резонанса, аналогичные условиям (Д.19), имеют вид
C.3)
108

где Хи Кг, ..., Кп — корни характеристического уравнения непод-
неподвижной точки О(х = х*):
{g|} 0. C.4)
Матрица А имеет собственные значения, по модулю меньшие
единицы, матрица В — большие единицы, а собственные значе-
значения матрицы С лежат на единичном круге.
Укажем еще общий вид клеток матриц А, В и С в формулах
C.2) в предположении, что эти матрицы приводимы к блочно-
диагональной форме.
Действительному корню К. на диагонали матриц А или В от-
отвечает элемент Ка. При Я,, = 0 в соответствующем месте на диаго-
диагонали матрицы С расположен элемент, равный нулю. Паре комп-
комплексных сопряженных корней ре±ир (р=5^1) отвечает на диагона-
диагонали матрицы А (р<1) или /?(р>1) матрица второго порядка
вида
/р cos ф — р sin ф
li ф р cos(p
При р = 1 блок C.5) располагается на диагонали матрицы С.
Тип простой неподвижной точки определяется числами р и
д корней характеристического уравнения C.4), лежащих внутри
и вне единичного круга; при этом предполагается, что корней,
лежащих на единичном круге, нет. Для неподвижной точки ОР: q
типа р, q инвариантные многообразия S+ и S~ имеют -соответст-
-соответственно размерности р и q и состоят из точек, стремящихся к точ-
точке Ор-q при неограниченном повторении отображений C.2) и
соответственно обратного отображения. Неподвижная точка OPi q
является точкой пересечения многообразий 5+ и S~ и в данном
случае совпадает с инвариантным многообразием 7. При наличии
корней характеристического уравнения, лежащих на единичной
окружности, инвариантное многообразие / имеет размерность,
равную числу корней на едичной окружности.
Качественное поведение отображения C.1) в окрестности не-
неподвижной точки О определяет поведение фазовых траекторий
вблизи замкнутой кривой Г, отвечающей периодическому дви-
движению. При этом точке О отвечает замкнутая фазовая траекто-
траектория Г, инвариантным многообразиям S+ и S~ размерностей р и q
неподвижной точки — интегральные многообразия S+ и S~ раз-
размерностей р + 1 и д+1 периодического движения Г. В соответ-
соответствии с этим числа р + 1 и q +1 определяют тип периодического
движения Г, что будет отмечаться записью вида Гр+1-в+1. По ин-
интегральным поверхностям S+ и S~ фазовые траектории асимпто-
асимптотически приближаются к Г при t -»- +°° и соответственно при
£-»-—<». Остальные фазовые траектории в окрестности Г прибли-
приближаются к Г вдоль S+ и затем удаляются вдоль S~.
109

§ 4. Бифуркации периодических движений
Тип неподвижной точки по его определению может ^изменить-
^измениться только при переходе одним из корней Xit Я2, ..., кп единич-
единичной окружности, поэтому бифуркационными могут быть только
те значения параметра ц, = ц,*, для которых имеется корень, ле-
лежащий на единичной окружности. В соответствии с этим основ-
основными простейшими бифуркационными поверхностями являются
поверхности N+i, N-t и NVt отвечающие соответственно одному
корню, равному +1 или —1, и двум комплексно сопряженным
корням е±щ.
Теорема 5.4. Точка ц*еМ является бифуркационной точкой
в том и только в том случае, когда уравнение C.4) имеет корень,
лежащий на единичной окружности, т. е. если точка ц* лежит
на одной из поверхностей N+i, N-i или Nv.
Если записать характеристическое уравнение в виде
X (К) = Г + аХ~1 + ... + й„_Д + ап = 0, D.1)
то бифуркационные поверхности N+i, JV_i и N* определяются со-
соответственно уравнениями
1 + а4 + а2 +... + а„ = 0, D.2)
1-о1 + о1-... + (-1)"о»-0, D.3)
D.4)
Уравнение последней поверхности Nv задается в параметриче-
параметрическом виде. Все поверхности N+l, N-i и iV, — коразмерности
единица.
Все сказанное до сих пор аналогично тому, что имело место
для состояния равновесия: бифуркационные поверхности N+l и
Л^ф неподвижной точки аналогичны бифуркационным поверхно-
поверхностям iV0 и №, состояния равновесия, а бифуркационная поверх-
поверхность N-t является новой. Однако возможные бифуркации перио-
периодического движения этим не исчерпываются. Бифуркация перио-
периодического движения Г возможна' еще за счет его исчезновения,
происходящего по трем сценариям: Г теряет замкнутость, уходя
в бесконечность, на Г появляется состояние равновесия, Г стя-
стягивается в точку. Других возможностей нет, точнее, нет других
возможностей прекращения существования периодического дви-
движения Г, не сопряженных с переходами через поверхности N+i,
N-i и Мр. Рассмотрим каждый из трех сценариев в отдельности.
Бифуркацию с уходом Г в бесконечность можно трактовать
как уход при изменении параметра ц некоторой точки Г в бес-
бесконечность.
Появление на Г состояния равновесия означает, что у этого
состояпия равновесия О появилась фазовая траектория 7. стре-
стремящаяся к нему как при t -*■ +оо; так и при t -*■ —°°. Следова-
Следовательно, эта кривая ^ есть пересечение интегральных поверхно-
поверхностей S+ и S~ состояния равновесия О. Таким образом, в этом
НО

случае бифуркация периодического движения Г состоит в пре-
превращении Г в двоякоасимптотическую кривую некоторого со-
состояния равновесия О, которая является кривой пересечения его
интегральных поверхностей S+ и S~.
При непрерывном изменении параметра ц и стягивании замк-
замкнутой кривой Г в точку эта точка должна быть состоянием рав-
равновесия, причем состоянием равновесия бифуркационным. Би-
Бифуркации состояний равновесия рассмотрены, и среди них име-
имеется бифуркация состояния равновесия, при которой с ним
сливается замкнутая фазовая кривая.
Это беглое рассмотрение возможных путей исчезновения замк-
замкнутой фазовой траектории Г в следующей главе будет продол-
продолжено, а сейчас мы вернемся к бифуркациям N+u AL, и Nv. Рас-
Рассмотрение бифуркаций, вызываемых переходом вдоль некоторой
кривой через поверхности N+i, N-i и Nm сводится к рассмотрению
точечного отображения C.2) только на инвариантном многооб-
многообразии /. Это отображение имеет вид
^"= Cw + wR (w) + wh @, 0, w). D.5)
В случаях только одного корня на единичном круге, равного +1
или —1, или только двух комплексно сопряженных корней е'ф и
е~щ это отображение D.5) принимает соответственно вид
w — w + a2w2 + a3w3 + ..., D.6)
w = — w + a3w* + a.ow5 -~ ..., D.7)
w = eivw + w 2 aq g Л*'2 +...., D.8)
«г». 12
где многоточия означают члены более высоких порядков мало-
малости, а возможные комбинации целых чисел дч и qz находятся
согласно C.3) из уравнения
где qi > -1, q2 > 0, q, + g2 ^ 1.
При ф, несоизмеримом с я, уравнение D.9) не имеет реше-
решений, отличных от qi = q2 = q 5s 1, поэтому отображение D.8)
записывается в виде
w = el(fw + a3u?w* + a-owzw*2 + ... D.10)
При ф = 2пк/т, где к и т — несократимые целые числа, помимо
написанных, появятся еще и другие резонансные члены. Они
находятся из уравнения
1-Г (?!-?.)= 0 (то<12я), D.11)
или, учитывая, что ф =И= 0, ф Ф п,
qi-qi=m, m = ±3, ±4, ... D.12)
111

При |/?г|=3 и |m|=4 добавляемые резонансные члены сущест-
венньь, при \т\ ^5 их можно при рассмотрении основного случая
а3 Ф 0 не учитывать. Первые два случая отвечают <р = 2л/3 и
ф = л/2, поэтому на бифуркационной поверхности Nv существуют
«линии» особых бифуркаций, отвечающих ф = 2л/3 и ф = л/2.
Рис. 5.10
Рис. 5.11
Коразмерность этих бифуркационных «линий» равна двум. На-
Наглядное схематическое изображение бифуркационных поверхно-
поверхностей N+i, N-i, Nv, Nia/s и Nx/z приведено на рис. 5.10. Отметим,
что на аналогичном рисунке для состояния равновесия есть толь-
только поверхности iV0 и Na (рис. 5.11).
Продолжим рассмотрение основного случая Nv. Формула D.10)
дает вид преобразования многообразия J при ц = ц.*. Так же,
как и в случае рассмотрения бифуркаций состояния равновесия,
введем параметр v и запишем возмущенное отображение D.10)
в виде
w = X{v)w + a{v)\w\zw + .. .=ВД[1 + a(v)\w\*]w + ..., D.13)
или, переходя к полярным координатам р, в, в виде
D.14)
Переменная р в этой записи с точностью до несущественных чле-
членов отделилась. Поэтому первое уравнение D.14) можно рас-
рассматривать как одномерное отображение, неподвижными точками
которого являются
v=o
V+
D.15)
Соответствующие возможные диаграммы точечного отображения
представлены на рис. 5.12.
Типы неподвижных точек pi и р2 (устойчивость и неустой-
неустойчивость) определяются величинами производных
р=р,
I , / . |2 dp
I Л \У) 1 > ,2
= 1—4-
р=р«
У v+ ... D.16)
112

Полагая ради определенности d\h(v)\/dv\4=0>0, приходим к би-
бифуркационным диаграммам рис. 5.13, а, где кружочки обозна-
обозначают устойчивость, а крестики — неустойчивость.
Рис. 5.12
.о"
>-*->< ххкхкх-
Рис. 5.13
Таким образом, нри переходе через бифуркационную поверх-
поверхность Л^ф в направлении образования двух новых корней харак-
характеристического уравнения C.4), по модулю больших единицы,
имеет место теорема [58, 260, 265, 629].
Теорема 5.5. Неподвижная точка Ор-" переходит в точку
Qp-г, 9+2 Одновременно с ней либо сливается инвариантная замк-
замкнутая кривая Г*'q+z, либо от нее отделяется инвариантная
113

кривая Гр- *+1. Первое имеет место при Re а @) > 0, второе — при
Rea@)<0.
Для соответствующего периодического движения в соответ-
соответствии с этой теоремой 5.5 имеет место
Теорема 5.5'. Периодическое движение Гр+1'я+1 переходит в
pp-i, 9+з Одновременно с этим, в зависимости от знака Rea@)!?5=0,
либо с ним сливается тороидальное инвариантное многообразие
Тр- 9+3, либо от него отделяется инвариантное тороидальное мно-
многообразие Г*+1.«+2 (рис. 5.13, б).
Особый интерес представляет частный случай теоремы 5.5,
когда р + 1 = п, q = 0, периодическое движение Гп-' теряет устой-
устойчивость и при этом одновременно рождается устойчивое двумер-
двумерное интегральное многообразие Г"-2. Это происходит при
Rea@)<0. При обратном неравенстве Rea@)>0 периодическое
движение Гп-' теряет устойчивость из-за слияния с неустойчивым
интегральным двумерным тором Гп~2>4. В отношении того, что из
себя представляют фазовые траектории на двумерных торах, тео-
теорема 5.5 ничего не говорит. Отметим только, что при v -*• 0 число
вращения Пуанкаре этих фазовых траекторий стремится к ф/2я.
При переходе через границу N+i в момент бифуркации ц, = ц*
точечное отображение имеет вид D.6), и его рассмотрение при-
приводит к результатам, полностью аналогичным тем, которые имели
место при исследовании бифуркации состояния равновесия с
переходом границы No. Справедлива следующая теорема [259].
Теорема 5.6. При переходе через границу N+i в основном слу-
случае az¥=0 в D.6) происходит либо слияние неподвижных точек
Ор-ч и Ор~к "+i и их исчезновение, либо рождение такой пары
неподвижных точек. '
Для периодического движения соответственно выполняется
следующая теорема.
Теорема 5.6'. При переходе через границу N+i в основном
случае az¥=0 происходит либо слияние периодических движений
jip+i, 9+i и р>, 9+2 c последующим их исчезновением, либо их одно-
одновременное рождение.
Случай а2 = 0, а3 ¥= 0 при ц, = ц,* аналогичен тому, который
имел место для состояний равновесия. Отметим, что особый слу-
случай «2 = 0, а3 =^= 0 может стать основным при наличии у рас-
рассматриваемой системы симметрии. Именно поэтому для него сде-
сделано исключение, и он рассматривается наряду с общим случаем.
В то время как бифуркации неподвижных точек при перехо-
переходах через границы N+i и Л^ф аналогичны бифуркациям состояний
равновесия при переходах через границы iV0 и N*, переход через
границу N-i сопровождается новым типом изменения, не имею-
имеющим аналогов у состояния равновесия [259, 260]. Рассмотрим
его подробнее. При ц = ц,* отображение одномерного многооб-
многообразия / имеет вид D.7). При значениях параметра ц,, близких
к |д*, рассматриваемая неподвижная точка Ov-" сохраняется (яко-
(якобиан, от которого зависит существование неподвижной точки,
обращается в нуль только на поверхности N+i), поэтому при
114

малых v отображение D.7) имеет вид
w = -a. (v) w + а2 (v) w* + а3 (v) w3 +..., D.17)
где а,@) = о2@) = 0 и ()
Повторим это отображение:
w= —ax(v) [— ax(v) и> + а2 (v)w2 + ...] +
+ а2 (v) [- аг (v) и; + а2 (v) ы;2 + .. .]2 +
+ а3 (v) [- а± (v) w + а2 (v) w2 + .. .]3 + ... =
= al(v)w+[-a1 (v) a2 (v) + а2 (v) a\ (v)] w2 +
+ [- ах (v) а3 (v) - 2a\ (v) aL (v)] w3 + ... =
= [1 + 2ai @) v] w - a3 @) w3 + ... D.18)
Дважды повторенное точечное отображение D.18) имеет три не-
неподвижные точки
^W... D.19)
Точка i^! является неподвижной и для исходного отображения
D.17), а неподвижные точки w2 и w3 отвечают циклу двукратных
неподвижных точек. Примем, что «i @) =#= 0 и что возрастание v
соответствует переходу корня через —1с убыванием аи так что
% < 0. Тогда в зависимости от знака а3 @) возможны следую-
следующие случаи, описываемые теоремами 5.7 и 5.7'.
Теорема 5.7. При пересечении бифуркационной границы N-u
когда неподвижная точка Ор-" теряет один корень характеристи-
характеристического уравнения, меньший единицы по модулю, и переходит в
неподвижную точку Ov~l •q+l цикл двукратных неподвижных то-
точек типа Ov-" или соответственно типа Op~ii q+i при at @) a3 @) > 0
от нее отделяется, а при % @) а3 @) < 0 с ней сливается.
Теорема 5.7'. При а!@)<0 и а3@)<0 периодическое движе-
движение Г'9+1 переходит в Гр> ?+2 и одновременно от него отделяется
периодическое движение Гр+1> 5+1 удвоенного периода. При % @) <
<0 и а3@)>0 при такой же смене Гр+1>в+1 на Tp-q+i проис-
происходит слияние с периодическим движением Гр> q+z удвоенного
периода.
Соответствующие бифуркационные диаграммы для точечного
отображения D.17) изображены на рис. 5.14. Последовательная
смена фазовых портретов в трехмерном случае при р = 2, q = 0
и а\ @) <0, а3@) < 0 изображена на рис. 5.15 и 5.16.
Выясним, почему у состояния равновесия отсутствует аналог
бифуркации ./V_i у неподвижной точки. Пусть ж = ж* — состояние
равновесия системы дифференциальных уравнений
х = Х(х) D.20)
115

v>0
Рис. 5.16

и x = f(t, Xo)—ее решение, удовлетворяющее начальному усло-
условию х@) = х0. Зафиксируем t — т и рассмотрим точечное отобра--
жение _
х = /(т, х). D.21)
Точка х* является его неподвижной точкой. Особенностью ото-
отображения D.21) является неотрицательность его якобиана, и по-
зтому характеристическое уравнение неподвижной точки не может
иметь нечетного числа отрицательных корней. Более того, при
т = 0 отображение D.21) — тождественное, и все корни его ха-
характеристического уравнения равны +1. Отметим, что между
корнями Я,1, Хг, ... характеристического уравнения состояния рав-
равновесия и корнями zu z2, ..., zn характеристического уравнения
соответствующей неподвижной точки точечного отображения име-
ют место соотношения zs = е , поэтому с ростом т однократный
корень —1 возникнуть не может. Что же означает корень —1
у характеристического уравнения отображения Пуанкаре с не-
неподвижной точкой О, отвечающей периодическому движению Г?
Для ответа на этот вопрос выясним, как связаны между собой
инвариантные многообразия / неподвижной точки точечного отоб-
отображения с таким же многообразием / у периодического движе-
движения Г. Ограничимся наглядным трехмерным случаем. Как видно
Рис. 5.17
из рис. 5.17, а, при z =+1 интегральное многообразие /—дву-
/—двусторонняя поверхность, а при z = — 1 (рис. 5.17, б) — односторон-
пий лист Мёбиуса.
При рассмотрении бифуркаций неподвижных точек и перио-
периодических движений были выделены, но оставлены без внимания
особые случаи типа Nv с значениями ф = 2я/3 и <р = я/2 кораз-
коразмерности 2. Рождение двумерного тора при общей бифуркации
типа Nv п бифуркация удвоения типа ALj (ф = я) были обна-
обнаружены в 1959 г. [259, 260]. Рассмотрение особых бифуркаций
117

Таблица 2
Формула бифуркации
Коразмер-
Коразмерность
Пересекае-
Пересекаемая гра-
граница
Характер
потери
устойчи-
устойчивости
Фазовый
портрет
(рисунок)
Бифуркации неподвижных точек
2Оп>°
Оп'° ->. О"~2.2 I р"Д
Оп'° 4- Г"'2 ->- О"-2
'9 4-
QP—2,9+2 _|. pp,g+l
1
2
2
1
1
1
1
1
2
2
1
1
1
Бифуркации периодических движений
жесткий
мягкий
жесткий
мягкий
жесткий
мягкий
жесткий
5.15, а
5.15, б
pw,l _^ -pTi—1,2 _i O'pWjI
pll,l _|_ 2рП-1,2 _,. рП-1,2
rn,l_^pn-2,3 + 7m,2
p»i,l _j_ yn-2,4 _>. рП-2,3
pn,l _^ ри—1,2 i pn,l
ртг,1 . pn—1,2 _^ рп—1,2
рр,9 4-гр-1-9+1-*0
ГР-9 -^ рР-1.9+1 4- 2ГР> *
рР,9_!_ 2рР-М+1_>рР-1.9+1
рР>9 _>. рР—2,?+2 1 уР,9+1
pPi? 1 ур—1,?+2 _^. рр—2,?+2
Гр'9 ~> рР-1,?+1 4- ГР>Я
1
2
2
1
1
1
1
1
2
2
1
1
1
1
No
N
Nl
N4>
N-i
N-i
No
N
№
N-i
»-i
жесткий
мягкий
жесткий
мягкий
жесткий
мягкий
жесткий
5.16
5.13
5.6'
5.6'
5.6'
5.5'
5.5'
5.7'
5.7'
5.6'
5.6'
5.6'
5.5'
5.5'
5.7'
5.7'
118

при ф == 2я/3 и ф == я/2 продолжается до настоящего времени и
не может считаться завершенным, несмотря на значительное чис-
число работ разных исследователей [42, 58, 195—197, 280, 290]. Это
объясняется невозможностью чисто аналитического исследования
и большим разнообразием и сложностью фазовых портретов, мо-
могущих возникнуть при пересечении границы 7УФ с ф = 2л/3 и
Ф = л/2. В зависимости от значений параметров здесь могут пред-
представиться случаи рождения как двумерных торов, так и периоди-
периодических движений седлового типа с пересекающимися инвариант-
инвариантными многообразиями S+ и S~, а также случаи, когда рождаются
устойчивые периодические движения утроенного и соответствен-
соответственно учетверенного периодов. Эти особые бифуркации могут при-
приводить к возникновению хаотических движений. Отметим, что
для случая ф = я роль бифуркации AL, в возникновении хаоти-
хаотических движений в значительной мере выяснена.
В заключение этого параграфа подытожим утверждения уста-
установленных в 'нем теорем, в таблице бифуркаций неподвижных
точек и периодических движений (см. табл. 2). Смысл формул
бифуркаций и данных ее столбцов аналогичен тому, что было
в приводимой ранее таблице бифуркаций состояний равновесия.
§ 5. Тороидальные интегральные многообразия
Интегральные двумерные тороидальные многообразия естест-
естественно возникают при бифуркации периодического движения с
переходом через поверхность Nv. Как следует из предыдущего
параграфа (теорема 5.5), при определенных условиях переход
через бифуркационную поверхность Nv сопровождается отделе-
отделением от периодического движения тороидального двумерного мно-
многообразия. Тороидальное двумерное интегральное многообразие
на своей поверхности может нести самые разнообразные фазовые
портреты, которые могут претерпевать бифуркации, не сопро-
сопровождающиеся разрушением несущего тора. Помимо этого, воз-
возможны бифуркации, при которых тор как гладкая интегральная
поверхность исчезает. Пути разрушения тора достаточно много-
многообразны. Среди них особый интерес представляют случаи, когда
тор разрушается как целое. Бифуркации тора как целого анало-
аналогичны бифуркациям периодического движения типов N+l, N-i
и Nv. Однако их исследование по образцу исследования бифурка-
бифуркаций периодических движений наталкивается на новую трудность,
поскольку приведение к нормальной форме уравнений в окрест-
окрестности тора предполагает приводимость линеаризованных уравне-
уравнений в окрестности тора к лилейным дифференциальным уравне-
уравнениям с постоянными коэффициентами. Возможен другой подход
к рассмотрению бифуркаций тора как целого. В основе его лежит
сведение задачи о бифуркациях двумерного тора к задаче о би-
бифуркациях инвариантной замкнутой кривой точечного отображе-
отображения. Для этого разрежем тор секущей поверхностью так, чтобы
в сечении получилась замкнутая кривая Г. Фазовые траектории
119

на торе и вблизи него порождают на Г и вблизи Г некоторое
точечное отображение. Примем, что это точечное отображение
в некоторой окрестности кривой Г представимо дифференциаль-
дифференциальными уравнениями, т. е. может рассматриваться как их отобра-
отображение сдвига. Возможность такого сколь угодно точного пред-
представления установлена для отображений, близких к тождествен-
тождественным [269]. Аналогичное представление имеет место и во многих
других случаях. Так обстоит дело для точечного отображения Т,
у которого нет пересечений инвариантных многообразий седловых
неподвижных точек и все инвариантные фазовые кривые асимп-
асимптотически стремятся к устойчивым и соответственно неустойчи-
неустойчивым неподвижным точкам. В случае двумерного отображения
соображения, обосновывающие это утверждение, сформулированы
в [100] и легко распространяются на многомерный случай.
Вернемся к двумерному интегральному тору Т, пересекаемому
секущей 2. Пусть на нем имеется квазипериодическая обмотка.
Тогда некоторая степень отображения Т секущей на замкнутой
кривой Г близка к тождественному преобразованию и> предста-
вима дифференциальными уравнениями на 2. Для этих диффе-
репциальных уравпений замкнутая фазовая кривая Г соответ-
соответствует периодическому движению, которое при изменении пара-
параметров может испытывать бифуркации типов iV+1, JV_t и Nv. Тем
самым вопрос о бифуркациях тора как целого сведен к уже рас-
рассмотренным бифуркациям периодических движений. Бифуркациям
типов N+u N-i и iVq, периодического движения Г соответствуют
бифуркации типов N+u N-i и Nq, двумерного тора как целого.
При этом соответственно происходит слияние устойчивого дву-
двумерного тора с неустойчивым и их исчезновение (N+l); потеря
устойчивости двумерным тором и либо одновременное рождение
нового устойчивого «удвоенного» тора, либо слияние с уже имев-
имевшимся «удвоенным» неустойчивым седловым тором (JV_i); потеря
устойчивости двумерным тором и рождение от него трехмерного
устойчивого тора либо слияние с трехмерным неустойчивым то-
тором. Выше предполагалось, что при изменении параметров сохра-
сохраняется квазипериодический характер движений на рассматривае-
рассматриваемом торе. Соблюдение этого требования осложняется тем, что
общий случай обмотки отвечает наличию одного или нескольких
устойчивых периодических движений, разделяемых неустойчивы-
неустойчивыми периодическими движениями. Какой из этих случаев будет
иметь место (квазипериодический или периодический), зависит
от числа вращения Пуанкаре. При рациональных значениях чис-
числа вращения им"еют место периодические движения и асимпто-
асимптотические к ним, разделяемые неустойчивыми периодическими
движепиями, при иррациональных числах вращения — квази-
квазипериодические движения. Число вращения Пуанкаре непрерывно
зависит от параметров, причем носит характер кусочно-постоян-
кусочно-постоянной функции при каждом рациональном значении. Обмотка тора,
отвечающая числу вращепия Пуанкаре вида p/q, где р и q — це-
целые несократимые числа и сумма \р\ + \q\ достаточно велика,
120

весьма близка к квазипериодической — близка, в частности, в том
смысле, что в направлениях, не касательных к тору, характери-
характеристические показатели Ляпунова лежащих на нем движений близ-
близки между собой. В случае квазипериодической обмотки все харак-
характеристические показатели Ляпунова равны. Такая же близость
имеет место и для корней характеристического уравнения не-
неподвижных точек отображения, порождаемого фазовыми траек-
траекториями на секущей поверхности 2. Это отображение в случае
трехмерной секущей 2 имеет такой вид, как показано на
рис. 5.18. Числа устойчивых и неустойчивых неподвижных точек
Рис. 5.18
на инвариантной кривой Г равны rq, где г — некоторое целое
число (обычно г=1, иногда г = 2).
Рассмотрим теперь, как меняются фазовые портреты точеч-
точечного отображения в окрестности замкнутой кривой Г при бифур-
бифуркациях типов iV+i, N-i и N<f. Сначала пренебрежем малым раз-
различием корней характеристических уравнений неподвижных то-
точек, принадлежащих разным циклам, а затем учтем его и оценим
вносимые изменения. При бифуркациях типа N+i происходит
слияние неподвижных точек на Г с неподвижными точками, ле-
лежащими вне Г, и их исчезновение. Это соответствует слиянию
устойчивого тора с неустойчивым и их исчезновению. При бифур-
бифуркации типа N-i по теореме 5.7 возможно либо отделение от каж-
каждой из неподвижных точек новых неподвижных точек удвоенной
кратности либо слияние с ними неподвижных точек удвоенной
кратности. Один из таких случаев представлен на рис. 5.19. Не-
Необходимо только иметь в виду, что эти случаи возможны только
при размерности исходного фазового пространства не меньше
четырех и соответственно размерности секущей 2 пе меньше
121

трех. Это ограничение размерности вызвано тем, что отрицатель-
отрицательных действительных корней должно быть четное число в свя-
связи с требованием положительности якобиана точечного отобра-
отображения.
При бифуркации типа N9, которая также требует размерности
исходного фазового пространства не меньше четырех, по теоре-
теореме 5.6 возможны два разных случая. В одном из них происходит
Рис 5.19
рождение трехмерного устойчивого тора (соответствующее рож-
рождению на секущей 2 от замкнутой кривой Г двумерного инва-
инвариантного устойчивого тора).
Все сказанное очевидно при квазипериодическом характере
движений на рассматриваемом двумерном интегральном торе.
Мало что меняется при больших р, q и точном совпадении мо-
моментов бифуркаций отдельных периодических движений на торе.
При их небольшом различии происходят изменения, показанные
для бифуркации типа N-t на рис. 5.19. При больших различиях
122

могут возникнуть изменения, не приводящие к появлению «уд-
«удвоенного» тора.
Аналогичные "рассуждения применимы и к трехмерному ин-
интегральному тору и приводят к его бифуркациям как целого
типов iV+i и N-i. Однако теперь уже с ростом размерности все
большую роль могут приобрести изменения на самом торе. Эти
изменения уже сами по себе могут вызывать хаотизацию и сто-
хастизацию движений при сохранении тора как устойчивого
многообразия. В случае двумерного тора они не могут хаотизи-
ровать движения на торе, но могут привести к его разрушению.
К таким бифуркациям следует отнести слияние и последующее
исчезновение устойчивого и неустойчивого периодических движе-
движений на торе (N+1). Эта бифуркация будет рассмотрена в следую-
следующей гл. 6. Следует иметь в виду, что она не всегда ведет к раз-
разрушению тора: все может ограничиться изменением числа вра-
вращения Пуанкаре фазовых траекторий на торе. Разрушение тора
могут быть следствием бифуркации отдельных периодических
движений на нем типов N-i и N9. Это Относится прежде всего к
случаям, когда испытывающее бифуркацию периодическое дви-
движение не покрывает тор достаточно густо. Бифуркация типа N,
может привести к последующему образованию гомоклинической
структуры через касание интегральных многообразий S+ и S~
седловых движений, ранее лежавших на торе.

Глава 6
СТОХАСТИЧЕСКИЕ И ХАОТИЧЕСКИЕ АТТРАКТОРЫ
Среди основных характерных особенностей динамической си-
системы важную роль играют ее установившиеся движения, к ко-
которым спустя некоторое время приходят любые другие ее дви-
движения. Установившееся движение — это предельное движение,
которое асимптотически устанавливается в динамической систе-
системе. При этом динамическая система изолируется от всех не-
неконтролируемых или случайных воздействий и рассматривается
как идеальная детерминированная динамическая система.
Всякое движение и всякая фазовая траектория, если она ог-
рапичена1), стремятся к некоторому предельному движению или
движениям. Точка хи— предельная для фазовой траектории x(t),
если можно указать бесконечно возрастающую последователь-
последовательность времен tu tz, t3, ... такую, что
Hmx (ts) = хш.
S-»oo
Нетрудно видеть, что множество предельных точек Хц, ограничен-
ограниченной фазовой траектории x(t) не пусто и состоит из фазовых
траекторий. Однако физически, т. е. с учетом неизбежных малых
возмущений, приближение фазовой траектории к предельному
множеству Ха будет наблюдаться лишь в том случае, когда Ха —
предельное множество не только для фазовой траектории x(t),
но и для всех других фазовых траекторий, близких к Хт. Если
множество Хи обладает этим свойством асимптотической устойчи-
устойчивости, то оно является аттрактором. Простейшие аттракторы —
это асимптотически устойчивые состояния равновесия и периоди-
периодические движения.
Принцип сжатых отображений Банаха позволяет рассматри-
рассматривать сжимаемость фазового пространства как причину существо-
существования устойчивого состояпия равновесия, а сжимаемость на се-
секущей поверхности — причину существования периодического
движения. Если фазовый объем D сжимается со временем в ле-
') Предполагается, что ограниченное множество компактно.
124

рис
жащий внутри него объем D и затем D сжимается в еще мень-
меньшую область D <=В и так далее, то интуитивно ясно, что область
D при t-++°° стягивается в точку, которая есть устойчивое со-
состояние равновесия. Эта сжимаемость воспринимается не только
как обоснование существования равновесия, но и как естествен-
естественная его причина. Аналогично, если область D на секущей пло-
плоскости 2 после повторного пересечения с ней фазовых траекторий
переходит в область D<=D, a D—внутрь себя и т. д. (рис. 6.1),
и если, как и ранее, имеет ме-
место сжатие, т. е. любые две точ-
точки после преобразования сбли-
сближаются, то внутри D есть един-
единственная неподвижная точка
(точка, преобразующаяся в се-
себя) и через нее проходит замк-
замкнутая фазовая траектория. И
снова сжатие воспринимается
как естественная причина су-
существования устойчивого пе-
периодического движения.
Эти наглядные и убедитель-
убедительные соображения имеют твер-
твердую теоретическую основу в
широко известных и широко
используемых теоремах Брауэра и Банаха и последующих их
обобщениях [206, 239].
Свойства динамической системы, например наличие в ней
диссипации энергии, также можно связывать со свойством сжи-
сжимаемости. Такого рода связи тоже достаточно прочно ощущаются.
Совершенно иная ситуация возникает, как только наряду со
сжатием появляется растяжение. Именно с такими не только
сжимающими, но и растягивающими отображениями неразрывно
связана стохастичность в динамических системах. Как уже го-
говорилось, стохастичность — следствие глобального сжатия при
локальной неустойчивости.
Последующее изложение метода вспомогательных отображе-
отображений позволяет сформировать новые наглядные представления,
которые могут служить основой для интуитивных представлений
и теоретического исследования несжимающих отображений. Они
позволяют единообразно и наглядно исследовать все известные
простейшие типовые ситуации, приводящие к хаотизации и сто-
хастизации движений детерминированной динамической системы.
Ниже таким путем исследуются простая гомоклиническая петля
А. Пуанкаре и петля с касанием, подкова Смейла, аттрактор Ло-
Лоренца, отображение кольца в себя, петля седлофокусного состоя-
состояния равновесия и седлоузла, петля особой седлоузловой непод-
неподвижной точки, гомоклиническая восьмерка и стохастический
синхронизм. Используемый при их исследовании аппарат вспо-
вспомогательных отображений и последовательностей точечных ото-
125

бражений разработан сравнительно недавно специально для ис-
исследования гомоклинических структур [262, 269, 282]. Перейдем
к его изложению, которое по необходимости будет кратким. До-
Дополнительные сведения можно почерпнуть в книгах [100, 269].
§ 1. Вспомогательные отображения
и последовательности точечных отображений
Начнем с очень простого примера. Точечное отображение
у = Ъу A.1)
преобразует квадрат С(Ы<1, |у|^1) в прямоугольник
<5(U1 «S1/2, lj/1^3), сжимая квадрат G вдоль оси х и растя-
растягивая вдоль оси у (рис. 6.2, а). В обла-
области пересечения квадрата и прямо-
прямоугольника обязательно есть единствен-
ная неподвижная точка. Для того что-
чтобы это стало очевидным, запишем ото-
отображение A.1) в виде
х = Чгх, у = Ч,у A.2)
и будем расаматривать его как отобра-
отображение точки с координатами х,у в точ-
точку с координатами х, у. При этом пря-
прямоугольник £(Ы<1, \y\ -S3) перей-
рис 6.2 Дет в прямоугольник G (| х | ^ 1/2,;
\у\ ^ 1) (рис. 6.2, б). Второй прямо-
прямоугольник лежит в первом, отображение сжимающее, и значит,
имеется единственная неподвижная точка х*, у*, переходящая
в себя. Но тогда эта же точка является неподвижной точкой и
исходного преобразования A.1).
Может показаться, что наличие этой неподвижной точки есть
следствие только пересечения областей О, и Е. Но легко убе-
убедиться, что одного пересечения недостаточно, а вот того, что
область G лежит внутри области G, уже достаточно.
Это простое рассуждение может быть обобщено на любое
отображение вида
a
fa
(u, v), v = g(u, v),
A.3)
сжимающее по переменным и и растягивающее по переменным v.
Разрешим второе из уравнений A.3) относительно v,
\ = g(u, v), A.4)
и подставим найденное значение v в первое уравнение A.3),
после чего получим
и-
= f(u, v).
A.5)
426

Будем рассматривать A.4) и A.5) как точечное отображение,,
переводящее точку (u, v) в точку (и, v). Исходное_отображение
было сжимающим по и, т. е. при переходе от и к и происходи-
происходило сжатие, и растягивающим по v, т. е. при переходе от v к v
происходило растяжение. Из этого следует, что точечное отображе-
отображение, определяемое формулами A.4) и A.5), является сжимающим
по_ обеим переменным и и у,-так как при этом и переходит в и,
a v в v. Следовательно, отображение A.4), A.5), если только он»
преобразует некоторую область G в область G czG, имеет един-
единственную неподвижную точку (u*, v*), для которой
u* = /(u*, v*), v* = |(u*, v*). • 'A.6)
По способу получения функций f и g из этих соотношений сле-
следует, что
u* = /(u*, v*), v* = g(u*, v*), A.7)
т. е. что точка (u*, v*) является неподвижной и для исходного
несжимающего отображения A.3).
Дальнейшее имеет целью развитие этих простых соображений
и их приложение к вопросам возникновения хаотических и сто-
стохастических движений и аттракторов как их геометрических об-
образов в фазовом пространстве.
1. Определение вспомогательного отображения и условия его-
сжимаемости. Пусть в области G(u, v), где и и v—г- и s-мер-
ные векторы, определено точечное отображение
(п, v) = 7>, v), A.8)
которое можно также записать в виде A.3), и пусть оно пре-
преобразует область G(u,v) в область G~ (u, v). _
Зафиксируем и и v и найдем все пары и и v, для которых
выполнялось бы соотношение A.8) или его другая запись A.3).
Возможные значения v при этом находятся из уравнения
v = *(u, v), A.9)
разрешаемого относительно v, после чего для каждого найденного
значения v соответствующее и находится из соотношения
п=/(и, v). A.10)
Отображение (возможно многозначное), определяющее все воз-
возможные пары u, v no u и v, назовем вспомогательным по отно-
отношению к отображению Т. Будем обозначать его через Т и запи-
записывать в одном из видов
(п, у) = Г(и,у) A.11)
или _ _
u = f(u,T), v = |(u, v). A.12)
По определению вспомогательного отображения, если оно ставит
127

точке (u, v) в соответствие точку (u, v), то точка (и, v) e G,
а точка (и, v)eff.
В случае, когда вспомогательное отображение Т конечнознач-
но или счетнозначно, его однозначные ветви будем обозначать
через Th j = 1, 2, 3, ...
Приведем пример, когда вспомогательное отображение дву-
двузначно. Отображение Т
п = -|-и, ~v = — 4 +г/4, A.13)
определенное в области G@<u=^l, 1у|^2), имеет двузначное
вспомогательное отображение
u = -g-«, v = ± Vv+ 4. A.14)
Каждая из однозначных ветвей Ту и Т2 определена в области
<7@=Su_=Sl, — A^v^O) и преобразует ее соответственно в об-
области Э1@<ы<1/2, 0<у<2) и §2@<м<1/2, — 2<у<0)
На линии v — —4 отображения Tt и Т2 совпадают, во всех осталь-
остальных точках области G они различны.
Можно думать, что двузначность вспомогательного отобра-
отображения Т связана с двузначностью обратного отображения Т~\
но это не так. Отображение
u, — uo + a(v — vo), v = Ъи + c(v — v0J A.15)
взаимно однозначно, но его вспомогательное отображение
— -ш / v — Ьи — -а / v — Ъи /л ла\
и = щ±ау —г-, v = v0 ± у —— A.16)
двузначно.
Назовем вспомогательное отображение сжимающим, если при
некотором О =S q < 1
ПбпН + H6vll < g («биИ + 116^11), A.17)
где 6u и 6v — малые изменения переменных_и и v, а би и 6v —
соответствующие им изменения переменных и и v, определяемые
по и и v согласно A.4) или A.5), так что в линейном при-
приближении ^
бп = 7u6u + 7;6v, 6v == iu6u + ]r^6v. A.18)
Знак II II, как обычно, обозначает норму. Это может быть евкли-
евклидова норма или норма по максимальному модулю одной из
компонент.
Сжимаемость вспомогательного отображения Т означает, что
исходное отображение Т—сжимающее по и и растягивающее
по v. Действительно, при 5v = 0 из A.17) следует, что ПбиП <
<gU6iill, а при би = 0 из A.17) следует, что 6v|>—Ц6у|.
128

Вспомогательное отображение сжимающее в смысле A.17), если
выполнено неравенство
max{||7'ull, 1й|1+тахЩ Ш1<9<1. A-19)
Пусть отображение Т вида
п = Ли + /(и, v), v = 5v + g(u, v), A.20)
где А ж В — линейные операторы такие, что
1Ш«£/>„ 115-МКрг, A.21)
функции / и g в области 6r(llull<a, llvll < а) удовлетворяют
условиям
тах{||/||,||^||}<^0, maxlll/uU/vU&U^}<^i A-22)
и постоянные Ко, Ки ри р2, а удовлетворяют условиям
К0<A-р)а, РгК±<1. A.23)
Тогда отображение Т имеет однозначное, определенное в области
ff(llull<a, llvll < а) вспомогательное отображение Т, которое бу-
будет сжимающим в смысле неравенства A.17), если
max
Доказательство этого утверждения содержится в [269]. Мы будем
многократно пользоваться теоремой о существовании вспомога-
вспомогательного отображения Т у отображения вида A.20). Важно, что
такое отображение Т существует и является сжимающим в до-
достаточно малой окрестности точки и = 0, v = 0, если только
отображение Т седловое, что отражается условиями A.21). Вы-
Выполнение всех остальных условий A.22) и A.23) обеспечивается
достаточной малостью окрестности этой точки.
2. Свойства вспомогательных отображений. Ниже приводятся
простые леммы о вспомогательных отображениях [269].
1. Отображения Т и Т имеют общие (простые) неподвижные
точки.
2. Неподвижные точки отображения TR находятся во взаим-
взаимно однозначном соответствии с неподвижными точками отбраже-
ппя ТК и совпадают с неподвижными точками отображения TR.
3. Если Т — сжимающее отображение, то его неподвижная
точка является седловой для отображения Т.
4. Если вспомогательные отображения Т и Л определены в
области {?(llull «£ a, llvll ^b), являются в ней сжимающими и пре-
преобразуют ее в область ff(llull^a, llvll ^6), то и отображение RT
определено, сжимающее и однозначное в области G и преобра-
преобразует ее в область G<= G.
9 Ю. И. Неймарк, П. С. Ланда 129

5. Пусть Т и Л — отображения, удовлетворяющие условиям
п. 4, и S определено в области G и удовлетворяет в ней условию
Липшица с константой К, причем
+a<1 2aK<t. A.25)
Тогда отображение RST имеет сжимающее в области G_вспомо-
гательное отображение RST и преобразует область G в G <=■ G.
3. Вспомогательные отображения и неподвижные точки. Пусть
отображение Т имеет вспомогательное отображение Т и одна из
однозначных ветвей этого вспомогательного отображения преоб-
преобразует некоторую область в себя. Тогда отображение Т, а следо-
следовательно, и отображение Т имеют неподвижную точку.
Неподвижные точки отображения Т, отвечающие неподвиж-
неподвижным точкам однозначных ветвей вспомогательного отображения,
заведомо будут разными, если образы областей определения этих
ветвей не пересекаются. Напротив, если вспомогательные ото-
отображения Т не имеют неподвижных точек, например области
определения отдельных однозначных ветвей не пересекаются со
своими образами, то и у, отображения Т их нет.
В случае сжимаемости вспомогательного отображения утверж-
утверждение о неподвижных точках допускает уточнение, состоящее в
утверждении не только существования или несуществования, но
и в случае существования — единственности. В дальнейшем сфор-
сформулированные выше утверждения о вспомогательных отображе-
отображениях и о связи неподвижных точек вспомогательных отображений
с неподвижными точками исходных отображений будут приме-
применяться в различных конкретных ситуациях. Ниже формулируются
теоремы для двух, в некотором смысле, крайних случаев.
Теорема 6.1. Пусть отображения^ Т{ (i = 1, 2, ..., п) имеют
однозначные в области ff (Hull < a, llvll «S Ъ) вспомогательные ото-
отображения Т„ каждое из которых преобразует область G в область
8 (II и 11^ а» II v ||^Ь). Тогда каждое отображение
TimTim-l ■ • • Vh* A-26)
где ii, iz, ..., im — произвольные числа от 1 до п, имеет в области
G(llulls£a, llvll ^ Ь) неподвижную точку ж^ im. Если вспомо-
вспомогательные отображения сжимающие, то эта неподвижная точка
единственная.
Теорема _6.2. Пусть Ти Т2, ..., Тп — определенные в области
G(llulls£a, llvll «£ Ъ) однозпачные ветви отображения Т, вспомо-
вспомогательного к отображению Т, и пусть любое из отображений Т,
преобразует область G в область Gs, лежащую внутри области
S flu К a, IMK&), причем области &Х,Э2, ...,Ъп попарно
не пересекаются. Тогда каждой последовательности чисел U, г2, ...
..., im (ls££ss£re) отвечает неподвижная точка х* i ...im ото-
130

бражения Тт, причем неподвижные точки х^ ...jm, отвечающие
разным последовательностям U, U, ..., im, разные.
Точка/а^ 12.,лт является неподвижной точкой отображения
TimTim-y -ifv где Tv Т Ч' • • •' Tim~ сужения отображения Т,
отвечающие однозначным ветвям вспомогательных отображений
7\> Ti2, .. .,Tim вспомогательного отображения Т. В случае
сжимаемости вспомогательных отображений Ти Т2, ..., Тп ото-
отображение Тт не имеет неподвижных точек, отличных от точек
Xixi ...iTOi и для каждого из отображений Tim ... Ti± это един-
единственная неподвижная точка.
4. Последовательности точечных отображений. В настоящем
разделе изложенные выше соображения о неподвижных точках
и вспомогательных отображениях обобщаются на бесконечные
в обе стороны последовательности точечных отображений.
Пусть
...,T-z,T-uT0,TuT2,... A.27)
— бесконечная в обе стороны последовательность точечных ото-
отображений, каждое из которых Т, определено в области Ga (llu,II <
< а„ llv.ll < Ь,), и пусть
..., (и-., v-0, К v0), (Ul, Vl), ... A.28)
— бесконечная в обе стороны последовательность точек, где каж-
каждая следующая точка (u,, v,) получается из предыдущей
(u,_i, v,_!) путем преобразования Т„ т. е. (рис. 6.3)
Г, (и...,, v._1) = (u«, v.). A.29)
С последовательностью точечных отображений A.27) можно
связать единственное отображение Т прямого произведения обла-
Рис. 6.3
стей ..., G-i, Go, Gu ..., которое точку (u, v), где и(..., _и_1:_ио,
иь ...)_и у_(.._., V-,, _уо> y_i, _^..)» преобразует в точку (и, v) =
= (..., и-,, и0, иц ...; v_,, v0, v,, ...), где
(uS)"v.) = 77.(u._1, v.-.). A.30)
131

Если имеет место A.29), то для всех s
и, = и„ v. = v.,
A.31)
A.28), явля-
и точка (u*, v*), отвечающая последовательности
ется неподвижной точкой отображения Т.
Таким образом, последовательности точек A.28), связанных
соотношениями A.29), отвечает неподвижная точка отображения
Т, и вопрос о существовании или несуществовании таких по-
последовательностей сводится к вопросу о существовании или не-
несуществовании неподвижных точек у отображения Т. Рассмот-
Рассмотрим это утверждение несколько подробнее, иллюстрируя его при-
применительно к фазовым траекториям динамической системы. Пред-
Предположим, что нас интересует, существует ли фазовая траектория,
которая все время переходит из области А в область В, яз обла-
области В в область С, затем возвращается в область А, после чего
все повторяется сначала. Пусть такое поведение фазовой траек-
траектории имеет место не только при возрастании времени, но и при
его убывании, т. е. при убывании времени фазовая точка из об-
области А переходит в С, из С в В, из В в А и т. д. Обозначим
через Tab, Твс и Тса отображения, пе-
переводящие фазовую точку соответствен-
соответственно из области А в В, из области В в С,
и из области С в А (рис. 6.4).
Простейший случай такого движе-
движения — периодическое движение, про-
проходящее последовательно через области
А, В и С. Если отображения ТАв, Твс и
ТСА сжимающие или если сжимающим
является произведение этих отображе-
отображений, то возможен только этот простей-
простейший случай. Если же эти отображения
несжимающие, то возможны и более
сложные случаи. Изложенное выше
позволяет их исследовать, во всяком
случае, тогда, когда вспомогательные
отображения ТАВ, ТВс и Тса или вспо-
вспомогательное отображение ТСаТвсТАв удовлетворяют условиям
одной из приведенных выше теорем.
При этом если вспомогательные отображения ТАв, Твс, Тса
(по крайней мере, два из них) многозначные, то наряду с раз-
различными седловыми периодическими движениями требуемым по-
поведением будут обладать и многие непериодические движения
(континуум таких движений).
Аналогичный вопрос можно поставить не только для перио-
периодически повторяющегося перемещения фазовой точки, но и для
перемещений ее по любой последовательности областей.
Многочисленные конкретные примеры использования этих со-
соображений мы приведем в следующем параграфе, а сейчас завер-
432
Рис. 64

шим рассмотрение последовательностей точечных отображений
A.27) и определенного на последовательностях A.28) отобра-
отображения Т.
Отображение Т определено в бесконечномерном нормирован-
нормированном пространстве последовательностей A.28). Норму в простран-
пространстве последовательностей можно определить как
|| (u, v) || = sup {|| (и,, vs)||}. A.32)
s
Перейдем от отображения Т к вспомогательному отображению Т.
Оно может быть сжимающим, так что при некотором 0 ^ q < 1
ll6vll<gr(ll6ull
A.33)
'S+7
В случае нормы A.32) это означает, что каждое из вспомога-
вспомогательных отображений Т, сжимающее. В общем случае, если ото-
отображение Т преобразует в себя некоторую выпуклую область G,
то отображение Т имеет в области G неподвижную точку. Если
дополнительно отображение Т еще и сжимающее, то эта непод-
неподвижная точка единственная и седлового (гиперболического) типа.
Область G, определяемая неравенствами
llu.-ilKa.-i, llv.lKb. (s = ...-l, 0, 1, ...), A.34)
— выпуклая. Отображением Т она преобразуется в себя, если
каждое из вспомогательных отображений Т, преобразует область
S'.(llu.-1ll<a,-i, Hv.lKb.)
в область &s(llws||<ae»
Jv._iK*»-i) (рис. 6.5).
Вспомогательное отобра-
отображение Т может быть по-
построено по вспомогатель-
вспомогательным отображениям Т„ по-
поскольку задание соотно-
соотношений
(и„ v._i) = f.(u.-1, v.)
A.35)
для всех s и есть опреде-
определение вспомогательного
отображения.
Подводя итог сказан-
сказанному, сформулируем тео-
теорему.
Теорема 6.3. Неподвижным точкам отображения Т, опреде-
определенного в области G, отвечает последовательность вида A.28),
для которой имеют место соотношения A.29).
Отображение Т существует, определено в области G и преоб-
преобразует ее в себя, если то же имеет место в отношении всех ото-
отображений Т,. Отображение Т сжимающее, если все отображения
Т. сжимающие.
"S+/
Рис. 6 5
133

В этой формулировке теоремы неявно предполагается, что все
вспомогательные отображения Та однозначные. Однако такое
предположение вовсе не обязательно и от него можно отказаться,
потребовав только, чтобы все однозначные ветви каждого много-
многозначного вспомогательного отображения Ts удовлетворяли тем же
требованиям, которое накладывались на однозначное отображе-
отображение Та. Многозначность вспомогательных отображений Т. делает
многозначным и отображение Т. Многозначность отображения Т
допускает возможность появления более чем одной неподвижной
точки у отображения Т даже при сжимаемости однозначных
ветвей многозначного отображения Т.
Появление более чем одной неподвижной точки у отображения
Т означает появление более чем одной последовательности A.28),
удовлетворяющей условиям A.29). Зафиксируем сказанное в ви-
виде теоремы.
Теорема 6.4. Пусть каждое из отображений Т, (s = ..., —1, О,
1, ...) имеет вспомогательное отображение Т, и Tajs (js = 1,
2,; ..., ma) —его однозначные ветви, a Tajs —отвечающее им суже-
сужение отображения Т„ Пусть каждое из вспомогательных отобра-
отображений T,js определено в области ^(llu.-JI <ав-и llv.ll < Ь.) и
преобразует ее в область Gs (|| us || <; as, | vs_x [| ^ 6s-i)- Тогда любой
последовательности отображений вида
...,r_lj_1, Г*,, Tlh, ... A.36)
отвечает по крайней мере одна последовательность точек
для которой при всех s имеют место равенства
Если в последовательности A.36) отображений TSjs все вспо-
вспомогательные отображения сжимающие, то последовательность
A.37), удовлетворяющая A.38), единственная.
Эта теорема по общности своей формулировки в отношении
существования требуемой неподвижной точки или последова-
последовательности охватывает все сказанное ранее. Однако она не содер-
содержит утверждений, позволяющих устанавливать отсутствие тех
или иных неподвижных точек или последовательностей. Вместе
с тем, как уже отмечалось, имеется и такая возможность. Имен-
Именно, если хотя бы одно из вспомогательных отображений ТSjs
отображения TSjs, входящего в последовательность A.36), пре-
преобразует область G, не в область Gs, а в область KSjs, не
пересекающуюся с областью €fs, то требуемая последовательность
точек A.37), удовлетворяющая соотношениям A.38), не суще-
существует.
134

В двумерном и трехмерном случаях переходу от исходных к,
вспомогательным отображениям можно придать наглядный гео-
геометрический характер. Чтобы подчеркнуть упрощение и облегче-
облегчение в понимании и исследовании структуры точечного отобра-
отображения, которые достигаются таким переходом, назовем его пере-
переходом от негатива к позитиву. При этом негатив — это исходное
точечное отображение, а позитив — соответствующее ему вспо-
вспомогательное [282]. Переходы от позитива к негативу удобно ис-
использовать для анализа различных типов ситуаций, возникающих
в фазовых портретах динамических систем. Ниже, в следующем
параграфе, они идут под номерами 1—10, а сейчас продемонст-
продемонстрируем переход от негатива к позитиву на гиперболическом
(седловом) отображении Т двумерного тора на себя вида
jc = 2z + #(modl), y=x + y{modl). A.39)
Отображение A.39) уже встречалось в гл. 4. Его негатив
изображен на рис. 4.2, согласно которому это линейное взаимно-
взаимнооднозначное отображение переводит квадрат /)@<ж<1, 0<
^= У < 1) с соответствующими отождествлениями сторон в себя
и так, что каждая его область De (s = 0, 1, 2, 3) переходит в
область D,. Записав это отображение в виде
<c = 2x + y-i, y = x + y-j, A.40)
найдем, что значения целых чисел i и / зависят от того, к какой
из областей Da принадлежит точка (х, у). Именно, при (х, у)е=
е-Д, j = / = 0; при (х, j)eB, г = 1, / = 0; при (х, г/)еД, г =
= 7 = 1 и при (х, y)^D3 i = 2,/ = 1.
Однозначные ветви вспомогательного отображения могут быть
записаны в виде отображений Ti и Т2. Отображение Ti предста-
вимо в виде
x=*=± + s, у=Ц*, A.41)
где s = 0 при х — у>0 и s = l при х — у <0, а ?2 — в виде
где s = 0 при х — у ^0 и s = l при х — у < 0. Вспомогательные
отображения 7\ и Т2— сжимающие (характеристические корни
1/2 ± г/2 по модулю равны 1/У2) и каждое из них преобразует
квадрат D @=£Л;<1, 0=£г/<1) в себя, причем их образы не
пересекаются. По теореме 6.4 любой последовательности отобра-
отображений
..;Tt_lt TiQ, fh, fh, ... A.43)
отвечает единственная последовательность точек
...; х-1, у-й ж0, Уо; хи у{; х2, у2; ..., A-44)'
135

связанных соотношениями
(*., у.)=Т(х,-1, у,.,). A.45)
Справедливо и обратное утверждение, т. е. любой последова-
последовательности A.44) точек, связанных соотношениями A.45), отве-
отвечает единственная последовательность вспомогательных отобра-
отображений A.43). Это дает полное описание всех фазовых траекто-
траекторий точечного отображения Т — как периодических, так и непе-
непериодических. Приведенное описание выдержано в духе так
называемой символической динамики.
Немного остановимся на нем. Будем изображать отдельные
куски последовательности A.43) буквами a, fi, f, ... Если по-
последовательность A.43) периодическая, т. е. вида ...осаа..., то
ей отвечает периодическая же фазовая траектория A.44). По-
Последовательностям вида
Рооа... и ... aacq
отвечают фазовые траектории, стремящиеся к ней при s -*■ +°° и
s ->—°° соответственно. Их множества образуют многообразия
S+ и S~ периодического движения ...aaaa... Фазовая траекто-
траектория, отвечающая последовательности вида . ..aa...afa.. .aa...,
является двоякоасимптотической к периодической траектории
... ааа... Фазовая траектория ... aa... оь^ЭЭ •..?••• асимптоти-
асимптотически приближается при s -*■ — <х> и s -*■ +<» к периодической
траектории .. .шга... и соответственно ... Pj}[}...
Пусть oti, <%г, ...— любое, в том числе и счетное, множество
периодов. Тогда нетрудно указать последовательности, отвечаю-
отвечающие фазовым траекториям, которые приближаются сколь угодно
близко к любой из периодических траекторий этого множества.
Можно показать, что почти все фазовые траектории всюду плотны.
Можно яодумать, что все это стройное множество движений
очень хрупко и отвечает только линейному отображению A.39).
Но это не т,ак. В действительности перед нами очень прочное
образование, и никаким малым и даже не очень малым возмуще-
возмущениям отображения A.39) его не разрушить. Это непосредствен-
непосредственно следует из того, что при таких возмущениях не нарушается
сжимаемость вспомогательных отображений 7\ и Т2, следствием
которой является вся сложная структура фазового портрета.
§ 2. Переход от «негатива» к «позитиву»
и исследование типовых ситуаций возникновения хаоса
Ситуация 1. Простая гомоклиническая петля А. Пуанкаре.
Рассмотрим гомоклиническую петлю А. Пуанкаре (рис. 6.6):
О — неподвижная точка, S+ и S~ — входящие в нее и выходящие
из нее инвариантные многообразия, М — их точка пересечения
(одна из точек пересечения кривых S+ и S~). В этой ситуации
отображение Т переводит после любого достаточного числа тп
преобразований- тонкую область А, расположенную вдоль линии
136

5+, в тонкую область Жт, располагающуюся вдоль кривой S~.
Далее, в силу пересечения кривых S~ и S+ в точке М, некоторая
область В после некоторого определенного числа т* преобразо-
преобразований Т переходит в область В, пересекающую область А.
Таково описание негатива. Что, собственно, можно извлечь из
него? Преобразований каких-нибудь областей в себя не видно,
сжимаемости нет. Разобрать-
Разобраться в этой ситуации не
просто.
Перейдем от негатива к
позитиву. Для большей на-
наглядности в этом переходе
изобразим отдельно отобра-
отображения областей А в Ат и В
в В (рис. 6.7). Отображение,
переводящее А в Ат,— это
Тт; отображение, преобразу-
преобразующее В в В,— это Тт*, обо-
обозначим его через L (т?г*фик-
сировано). На рис. 6.7 точки
а, Ь, О, с области А переходят в точки а, Ъ, О, с области А~тг
а точки d, е, /, g области В — в точки d, ё, J, g области Б. Коор-
Координаты и и v выбраны так, как показано на рис. 6.7 (вдоль
спрямленных кривых 5+ и S~ рис. 6.6).
Ат
\
У/,
Рис. 6.6
о 5
Рис. 6.7
Вспомогательное отображение Тт преобразует область At в
область Л™ (рис. 6.8). Это следует из того, что в силу сжимае-
сжимаемости, вспомогательного отображения Тт, _выбора области А в
числа тге, для нее мало М, а_для области Ат мало |и|. Одновре-
Одновременно для областей А и Ат переменные и и соответствен-
соответственно v меняются в конечных пределах. Вспомогательное ото-
отображение Тт при достаточно больших тге — сжимающее. Его
коэффициент сжатия стремится к нулю при wi-*-oof и ово

Рис. 6.8
однозначное. Таким образом, вспомогательное отображение Тт
преобразует область А,, в себя и является сжимающим с ко-
коэффициентом сжатия, стремящимся к нулю при т -*• °°. Точка
и = 0, у = 0 — его неподвижная точка. Таков позитив отобра-
отображения Тт.
Перейдем к позитиву для отображения L = Тт . Его негатив
изображен на рис. 6.7. Вспомогательное отображение преобразует
некоторую область Bi в область 2?t, ко-
которая лежит в области Аи если только
область А была выбрана достаточно
протяженной по и, а число т — доста-
достаточно большим. Вспомогательное ото-
отображение L однозначно в силу того,
что кривая S~ пересекается с кривой
S+ и имеет ограниченную константу
Липшица. Это непосредственно следует
из того, что образ линии и в области В
пересекается с линией v в области В
в одной точке, не касаясь. Таков пози-
позитив для отображения L (рис. 6.9).
Теперь совместим позитивы отобра-
отображений Тт и L и построим вспомога-
вспомогательное отображение LTm. Однако значительно проще построить
не вспомогательное отображение LTm (что вполне возможно), а
произведение отображений Тт и L: Тт преобразует область At
в область А™ и при этом сильно ее сжимает, Т, преобразу-
преобразует А™ как часть области Bi в область,
лежащую внутри Ви а следовательно,
и Ai. Поэтому для каждого пг^ m
отображение ZTm имеет неподвижную
точку, и согласно сказанному в преды-
предыдущем параграфе отображение Li =
_ у,тп*+т также имеет неподвижную
точку при любом m ^ m.
Вот к какому выводу приводит
принцип сжимаемости отображений
а для позитива: в окрестности точки М
" существует бесконечное множество
многократных неподвижных точек ото-
отображения Т, причем, начиная с неко-
некоторой кратности пг ~> тп* (здесь m* + m
заменено на пг*), они седловые и для
каждого m такая седловая многократная точка единственная.
Путем перехода к бесконечным последовательностям отобра-
отображений это утверждение может быть сформулировано как сущест-
существование для любой носледовательности чисел
Рис. 6.9
-1, /Ко,
m2,
(ш, > тп*)
B.1)
138

в окрестности точки М точек (us, v,) (s = 0, ±1, ±2, ...) та-
таких, что
("», у») =
B.2)
Рис. 6.10
Рассматриваемое точечное отображение Т можно интерпрети-
интерпретировать как точечное отображение на секущей, порождаемое фа-
фазовыми траекториями трехмерной динамической системы с фазо-
фазовым портретом, показанным на
рис. 6.10. На нем Г — седловое пе-
периодическое движение, ему на секу-
секущей плоскости отвечает неподвиж-
неподвижная точка О, f — двоякоасимптоти-
ческая фазовая кривая, приближаю-
приближающаяся к Г при t -*• +оо к t ->■ —оо.
Точка М на секущей — одна из то-
точек пересечения с ней двоякоасимп-
тотичеокой- фазовой траектории у.
Напомним, что ч — томоклипичеекая
кривая по терминологии А. Пуанка-
Пуанкаре. Выберем малую окрестность кри-
кривых Г и f. Согласно предыдущему
в этой окрестности есть всевозмож-
всевозможные фазовые кривые, оборачиваю-
оборачивающиеся вдоль Г некоторое число раз
и одновременно проходящие вдоль у.
В частности, есть седловая замкнутая фазовая траектория, обхо-
обходящая Гт> тп* раз и затем замыкающаяся вдоль f. Есть замк-
замкнутая седловая кривая, обходящая вдоль Г яь > тп* раз, затем
проходящая вдоль у, после чего снова идущая вдоль Г тп2 ~> тп*
раза, и, наконец, замыкающаяся вдоль f и т. д. Более того, для
любой бесконечной последовательности чисел вида B.1) сущест-
нует единственная фазовая траектория, проходящая вдоль Г
именно указанное число раз и одновременно проходящая вдоль f-
Все эти фазовые траектории вместе образуют седловое конти-
континуальное инвариантное множество /. Все это континуальное
множество / помещается в окрестности кривых Г и f. При увели-
увеличении тп* эти фазовые кривые размещаются все в меньшей и
меньшей окрестности б фазовых кривых Г и у. Через каждую из
фазовых кривых у m_1mQm1.. из множества / проходит два инва-
инвариантных многообразия S+ и S". Совокупность всевозможных
поверхностей S+ образует поток фазовых траекторий, входящих
в окрестность б и остающихся в ней при t -*• +оо. Всевозможные
поверхности S~ составлены из потока фазовых траекторий, вхо-
входящих в окрестность б и не выходящих из нее при t -*• — °°. Мно-
Множества всевозможных многообразий S+ и S~ отдельных фазовых
траекторий из / назовем многообразиями S+ и 5~ инвариантного
множества /. После этого нельзя не увидеть простой аналогии
седлового множества / и его многообразий 5+ и S~ с седло,вым

движением Г и его инвариантными многообразиями S+ и S~.
В частности, и в этом более общем случае все остальные фазовые
траектории входят в окрестность б вдоль S+, а выходят вдоль S~.
При этом по вхождении в окрестность б продолжительность пре-
пребывания и движения фазовой точки в ней может быть весьма
различной, весьма сильно меняющейся даже при очень малых
изменениях начального положения фазовой точки.
Все описанное происходит в окрестности б седлового периоди-
периодического движения Г и двоякоасимптотической к нему фазовой
траектории f. В частности, среди всевозможных фазовых траек-
траекторий, лежащих в этой малой окрестности Гну, есть всевозмож-
всевозможные двоякоасимптотические фазовые траектории для последова-
последовательностей чисел т, вида
оо, ти т2, ..., тк, «, B.3)
а также двоякоасимптотических фазовых траекторий f ш к любому
седловому периодическому движению Гш, соответствующему пе-
периодически повторяющейся последовательности чисел т, (s =
= ...—1, 0, 1,...) вида
Ш|, тщ, ..., тк B.4)
с любым периодом ш. В окрестности любых фазовых траекторий
Гш и 1<о, в свою очередь, имеется бесконечное множество фазовых
траекторий, подобных тем, которые есть в окрестности Г и |,
Аналогичная картина имеет место и в отношении седлового пе-
периодического движения Г и указанных всевозможных двояко-
двоякоасимптотических фазовых траекторий, отвечающих всевозможным
последовательностям вида B.3). Во всем этом нельзя не видеть
некоторой иерархии вложенных структур, когда одна и та же
структура некоторого общего вида вкладывается в предыдущую,
и так происходит бесконечное число раз.
Ситуация 2. Петля А. Пуанкаре с касанием. Эта ситуация от-
отличается от предыдущей тем, что кривые S+ и S~ не пересекают-
пересекаются, а касаются в некоторой точке М (рис. 6.11, а). Область А
выбираем так же, как и раньше. Образ Ат области А остается
таким же, как и в предыдущем случае. Так_жег как и раньше,
выбираем и область В, но теперь ее образ В после нескольких
преобразований Т касается кривой S+ в точке М (рис. 6.11).
Это влечет отличие позитива для отображения L. Вспомогатель-
Вспомогательное отображение L двузначло и определено в области Ви пре-
преобразуя ее в области В и и 2?12. Таков позитив для отображения L.
Фактически он уже встречался нам при рассмотрении одного из
примеров вспомогательных отображений.
Таким образом, отображение L преобразует область Bi в
Bi = Bi^\i B12, отображение ?"* преобразует область .Bi в об-
область В^ Серия этих областей для возрастающих m изображена
на рис. 6.12. По характеру приближения зтих областей В™ к точ-
точке О при m -*■ +оо можно различить два случая: прибли-
140

жение к точке О происходит вдоль оси ординат или вдоль
оси абсцисс. В первом случае, начиная с некоторого т, области
оказываются внутри области Ви напротив, во втором случае —
заведомо вне ее. Это означает, что в первом случае реализуются
всевозможные последовательности отображений вида
...,/%, Tn^LJs+1,..., B.5)
где ms > т*, /, = 1, 2 и ii означает сужение отображения L,
отвечающее одной однознач-
однозначной ветви L, а Ьг — другой.
Во втором случае таких по-
последовательностей для т, >
> т* заведомо нет. Если %
и v — корни характеристиче-
характеристического уравнения неподвиж-
неподвижной точки О, то, как легко
убедиться, первый случай
имеет место при kv < 1, а
второй — при %v > 1. Всевоз-
Всевозможные движения, отвечаю-
отвечающие последовательности B.5)
при Xv < 1, также образуют
некоторое множество /. На рИС- 6.12
границе, разделяющей обла- _
сти Вц и Вц, константа Липшица отображения L обращается
в оо, поэтому утверждение п. 5 о свойствах вспомогательного ото-
отображения для доказательства седлового характера последаватель-
141

ностей B.5) непосредственно не применимо. Но все же, смотря
на позитив рис. 6.12, можно думать, что они седловые. Более пол-
полное рассмотрение, подтверждающее эти интуитивные представле-
пия, содержится в [119, 137]. Это сближает ситуацию 2 с рассмот-
рассмотренной ранее ситуацией 1, так как в обоих случаях имеются кон-
континуальные седловые множества и их многообразия S+ и S~.
Однако между ними имеется существенное различие в глобаль-
глобальном поведении фазовых траекторий, о чем речь будет позднее.
Рассмотренная здесь ситуация является граничной между слу-
случаем двух близких пересечений кривых <S+ и S~ и отсутствия
a
i
С-
аа "
Щ
4*
в12
i
Рис. 6.13
их пересечения. На рис. 6.13 показаны позитивы, отвечающие
всем этим трем случаям.
Из них можно понять, как изменяются множество / и соот-
соответствующие ему допустимые последовательности преобразова-
преобразований, а также какая его часть отвечает седловым движениям. Эти
наглядные соображения будут подробно развиты в гл. 7.
Ситуация 3. Подкова Смейла. Подковой Смейла называется
отображение Т, преобразующее прямоугольную полосу abed в
подковообразно изогнутую полосу abed. Отображение прямоуголь-
прямоугольной полосы abed в подкову abed получается сжатием пря-
142

моуголышка вдоль сторон ad и be, вытягиванием его вдоль сторон
аЪ и ей и последующим изгибанием в виде подковы (рис. 6.14).
Можно заметить, что это отображение фактически уже знакомо.
Если рассматривать только одно из пересечений подковы с по-
полосой, то это ситуация 1, а если приподнять подкову так, чтобы
поворот подковы лежал в полосе,— это ситуация 2. Это сразу же
позволяет по негативу подковы Смейла нарисовать ее позитив.
а
ъ
\
d
\
с
/
1
b
1 ,.
с
щ
Рис. 6.14
О
I
Рис. 6.15
и,и
—>■
Он представлен на рис. 6.15: вспомогательное отображение Т
преобразует область G в две маленькие, лежащие внутри нее
области &J и G2, потому что отображение Т двузначное и сжи-
сжимающее. По позитиву непосредственно видно, что отображение
Т имеет две разные неподвижные седловые точки, Тг — четыре
неподвижные точки, Т3 — восемь и т. д. Этот случай подпадает
под действие теоремы 6.2. Пусть 7\ и Т2 — сужения отобра-
отображения Т, отвечающее однозначным ветвям вспомогательного ото-
отображения Т. В рассматриваемом случае — это отображение Т со-
соответственно в частях Gi и G2 области G (полосы abed). Отобра-
Отображение Т преобразует области Gt и G% в области Gi и G2. По
теореме 6.4 любой последовательности ..., i-u io, U, ч, ■■■ (is =
= 1, 2) отвечает единственная последовательность преобразуемых
отображением Т друг в друга точек, так что они последователь-
последовательно находятся в областях
••■'Сч- Gv Gv Gv ••• B-6)
Все неподвижные точки, отвечающие периодическим последова-
последовательностям областей B.6), седловые, как и все фазовые траекто-
траектории, отвечающие произвольным порядкам областей B.6).
Ситуация 4. Аттрактор Лоренца. Речь идет об отображении
Пуанкаре Т на секущей поверхности z = r— 1 уравнения Лорен-
Лоренца в момент возникновения странного аттрактора и после того,
как он возник. Соответствующие негативы изображены на
рис. 6.16. 0! и 02 — седловые неподвижные точки, SI, Si[ и
S2, S* — их инвариантные кривые, R — линия разрыва ото-
отображения, по обе стороны от нее отображение Т гладко и не-
143

прерывно продолжаемо на линию разрыва R. Негатив симмет-
симметричен относительно своего центра. Продолженное с разных сто-
сторон преобразование Т переводит линию R в точки Mt и Мг
соответственно. В согласии со сказанным области Gi и Gz, по-
показанные на рис. 6.16, отображаются в клинья G4 и G2. Негатив
описан.
Позитив представляет собой область &, преобразуемую в об-
области Gx и G2 (рис. 6.17) почти так же, как в случае подковы
о,
м,
OZ
Рис. 6.16
Рис. 6.17
Смейла, но с той существенной разницей, что области G1 и G2
примыкают к границам области &, а О4 и О2 — устойчивые не-
неподвижные точки вспомогательного отображения Т. Отсюда
непосредственно следует состав инвариантного множества /. Ос-
Осталось сказать, что в данном случае это седловое инвариантное
множество / и есть сечение странного аттрактора уравнений
Лоренца. Его особенностью является то, что его инвариантное
множество S~ содержится в /. Вдоль своего инвариантного мно-
множества S+ оно лритягивает к себе «соседние» фазовые точки.
Ситуация 5. Отображение кольца в себя. Если кольцо преоб-
преобразуется в себя и это отображение — сжимающее по радиусам,
то кажется естественным существование предельной замкнутой
кривой, к которой стягивается все кольцо. Однако это не всегда
так: предельное множество может быть и очень сложным, та-
такого же типа, как уже встречались в ранее рассмотренных си-
ситуациях 1—4. Чтобы в этом убедиться, как и ранее, перейдем
от негатива к,позитиву.
Пусть отображепие Т кольца G (r0 «S г «S i?0, 0^ф
в себя задано в виде
Ф = /(ф, г), 7~£(<р, г)
и пусть имеет место сжимаемость по радиусу, так что
B.7)
. B.8)
Обозначим через Тк отображения, вспомогательные к сужениям
отображения Т, определенным в областях Gh (ф1Л =£ ф < ф2Л)
144

(k — i, 2, ..., m). Предположим, что можно указать такие обла-
области Gk и G, (фи < ф < ф2.) (s = 1, 2, ..., га) и такие однознач-
однозначные ветви R{ (i = l, 2, ..., п) вспомогательных отображений Тк,
для которых каждое из выделенных однозначных вспомогатель-
вспомогательных отображений Л< определено в некоторой области G, и пре-
преобразует ее в некоторую область G) (рис. 6.18 и' 6.19). При
Рис. 6.18
Рис. 6.19
этом индекс i определяет возможные индексы s, а индекс s —
возможные индексы /, так что
^^ *™ \") » 1 — г \ / * \/
Эти соотношения определяют некоторые возможные пары индек-
индексов i и ;, где i, / = 1, 2, ..., п. Построим
граф с вершинами 1\, Г2, Г3, ..., ГЛ и
ребрами «(у, идущими от вершины Г(
к вершине Г3-, где i, j — возможные пары
индексов (рис. 6.20). Путь от вершины
к вершине графа по его ребрам ^у назо-
назовем путем на графе. Каждому пути на
графе отвечает некоторая последователь-
последовательность его вершин IV Каждой вершине
Г; можно сопоставить точечное отобра-
отображение й(, и тогда каждому пути на гра- рис 6 20
фе будет отвечать некоторая последова-
последовательность точечных отображений /?,, которую назовем допу-
допустимой. По теореме 6.4 каждой допустимой последовательности
отображений
...,%_1,%о,\ B.10)
отвечает реализуемая последовательность отображений кольца
в себя
-••> Я*_г #i0, Riv -•-;' B.11)
145

каждое Ris есть сужение отображения Т, отвечающее одно-
однозначному вспомогательному отображению Ris- Если множество
всевозможных путей на графе не сводится к конечному числу
замкнутых контуров или их периодическому повторению, то все-
всевозможным последовательностям отображений B.11) соответ-
соответствует сложное инвариантное множество Л Оно будет седловым,
если вспомогательные отображения й{ (i = 1, 2, ..., п)
сжимающие.
В заключение укажем пример точечного отображения кольца
в кольцо, изображенного па рис. 6.21, с нетривиальным инва-
инвариантным множеством J. На этом же рис. 6.21 изображен граф
допустимых последовательностей отображений. Отображение Т,
изображенное на рис. 6.21, преобразует область Gi в область G\.
Рис. 6.21
Вспомогательное отображение Ti трехзначно. Каждая его одно-
однозначная ветвь определена в области d и преобразует ее внутрь
области Gu лежащей внутри d- Из этого следует существование
сложного инвариантного множества /.
Отметим, что проведенное рассмотрение отображения двумер-
двумерного кольца в себя непосредственно обобщается на отображение
«-мерной тороидальной области G (Urll=£r0, 0^ф<2я), являю-
являющейся топологическим произведением (п — 1)-мерного шара
Ml ^г0 и одномерной окружности. Пример такого отображения
для п = 2 был рассмотрен в § 1 гл. 2.
Ситуация 6. Петля седлофокусного состояния равновесия.
В окрестности седлофокуса О2'1, в пренебрежении несуществен-
несущественными для дальнейшего нелинейными членами, уравнения дви-
движения фазовой точки и, v, z можно записать в виде
й = — аи — ©I?,
v = аи -аи,
B.12)
где а > 0, % > 0. Интегрируя эти уравнения на промежутке вре-
146

мени т, находим, что
п = е~" (и cos сот — v sin сот),
v = e~OT(MsincoT + i;cos сот), B.13)
Пересечем поток фазовых траекторий, приближающихся к точ-
точке О, секущей п+:
и2 + v2 = б2 @ *£ z s£ 6i), B.14)
а поток уходящих фазовых траекторий — секущей плоскостью
Q- (рис. 6.22):
z = е(М + Ы < e4). B-15)
Найдем связь между координатами точек пересечения (и, v, z)
z
Рис. 6.22
Рис. 6.23
и (и, v, z) фазовой траектории с секущими Q+ и От (рис. 6.23).
Учитывая B.14), положим
w = 6cos9, i; = 6sin(p. B.16)
Из последнего уравнения B.13), учитывая B.15), находим, что
1 , 8
Т = -г-In .
Л ^
Тогда из первых двух уравнений B.13) следует, что
B.17)
о/Х
1 Ч> 1 2
sin( Г1пт
При о > % и малых z это отображение сжимающее. Напротив,
при о<Я оно несжимающее. Разрешая уравнение B.17) отно-
относительно z и г?, запишем его в виде
2 = /»(й, ф), » = ftE, ф), (п, ф)еЛк, B.18)
147,

где Dh — кольцевые области вида, показанного на рис. 6.24, a Д
и gh — однозначные функции, о которых речь пойдет ниже.
С ростом к кольцевые области имеют все меньшую и меньшую
высоту. Считая п и ф заданными из первого уравнения, можно
найти z, пересекая кривую
- , z
ж = б|—
( а , z
cos — -у-In— +Ф
B.19)
прямой х = и (рис. 6.25).
Эти значения z = zk определяют функцию Д(м, ц>). Функция
gh{u, ф) получается подстановкой z = zk во второе уравне-
уравнение B.17).
Отображение B.18) будет сжимающим, если
max
ди
dv
ди
dz
B.20)
что имеет место при малых z вне малой окрестности верхней
Рис. 6.25
границы области Лк. Отображение B.18) является вспомога-
вспомогательным по отношению к отображению B.17). Обозначим од-
однозначную к-ю ветвь вспомогательного отображения через Тк.
Если точка (м, ф)еЛ, = Л,+1, но уже не принадлежит Ss+2,
то вспомогательное отображение в этой точке имеет s +1 обра-
148

зов, которые располагаются на плоскости z, v, как показано на
рис. 6.26. Это все при о < Я. При о > % отображение сжимающее
и само определяет позитив.
Допустим, что фазовая траектория "^ выходящая из точки
п = v = 0 секущей Q~, приходит в некоторую точку М секущей
Q+ (рис. 6.23). Фазовые траек-
траектории, близкие к у, порождают
точечное отображение L секущей
Q~ в секущую Q+. Это отображе-
отображение имеет вид
z = h(u,v), (f = k(u,v),
B.21)
где ft(Q, 0) = z0, к @, 0) = <р0 и z0,
Фо — координаты точки М на се-
секущей Q+.
Для построения позитивов отображения Т секущей Q+ в Q"
и отображения L секущей Q~ в Q+ отображение L следует за-
записать в виде
п = П(г, v), <р == A;(z, »). B.22)
Предположим, что это отображение однозначное и h'- @, 0) Ф 0.
Теперь все готово для построения позитива, изображенного на
ь
"8+7
-в-
Рис. 6.26
,z ъ
1 I
9
о
z
Рис. 6.27
рис. 6.27. На верхней части рис. 6.27 изображен позитив отобра-
отображения секущей Q+ в Й~, порождаемого фазовыми траектория-
траекториями, идущими вблизи седлофокуса. Отображение позитива мно-
многозначное, на оси п = 0 — бесконечнозначное, по мере удаления
от оси ц = 0 число образов отображения позитива уменьшается.
149

В нижней части рис. 6.27 показано отображение Г. Оно
преобразует окрестность точки (z0, 0) в окрестность точки (ф0, 0).
Из позитива видно, что если о < %, то в окрестности петли f
седлофокуса существует континуальное множество всевозмож-
всевозможных траекторий, образующих инвариантное множество J. При
и
Рис. 6.28
удалении точки z0 от оси z оно обедняется и исчезает. Это имеет
место при о < X. При о > X все значительно проще. Позитив для
этого случая совпадает с негативом и изображен на рис. 6.28.
Из него видпо, что если точка z0 достаточно близка к оси z, то
имеется устойчивое периоди-
периодическое движение, совмещаю-
совмещающееся с петлей f при обра-
обращении z0 в нуль и исчезаю-
исчезающее при z0 < 0.
Ситуация 7. Петля седло-
узла. Рассмотрим ситуацию,
аналогичную предыдущей
(рис. 6.29) с той разницей,
что состояние равновесия —
не седлофокус, а седлоузел
и описывается в линей-
линейном приближении уравне-
уравнениями
х = —Хх, у = ~-vy, z = \xz,
Рис 6.29 B.23)
где коэффициенты X, v, ц положительны и ради определенности
v > %. Секущие поверхности Q+ и Q~ имеют уравнения х = б
и z = е. Точечное отображение Q+ в Q~ записывается в виде
\|X/V
-(тГ
150

При ц > v это отображение сжимающее и совпадает со своим
вспомогательным. При ц. < v за вспомогательное принимается
отображение
y = (-j) У, * = e(-f) • B-25)
Это отображение в силу v > \i и X > ^ при малых а; сжимающее.
Как и ранее, отображение £2+ в &~ обозначим через Т,
а отображение Й"вЙ+ — через L.
Позитивы для отображений Т и L изображены на рис. 6.30.
Через г/о, z0 обозначены координаты точки М пересечения кри-
кривой S~ с секущей Q+. Из этих позитивов видно, что при возра-
возрастании z0 от значения z0 = 0 происходит возникновение периоди-
периодического движения вблизи первоначальной петли, что при р. > v
это периодическое движение устойчивое, а при ц, < v — седловое.
Сравнивая ситуации с петлей в случаях седлофокуса и седло-
узла, обнаруживаем, что при а>Х и n>v в обоих случаях
возникают устойчивые периодические движения, а при о < К и
\а < v — седловые движения, но в случае седлоузла — это перио-
периодическое движение, а в случае седлофокуса — сложное инвари-
инвариантное множество.
Ситуация 8. Петля особой свдлоузловой неподвижной точки.
Рассматриваемая ситуация относится к точечному отображению,
которое может возникнуть па секущей поверхности. При этом
в фазовом пространстве системы, пересекаемом секущей, име-
имеются слившиеся устойчивое и седловое периодические движения.
При дальнейшем изменении параметров, отвечающем пересече-
пересечению бифуркационной поверхности N+i, возникшее в результате
слияния сложное седлоузловое периодическое движение исчез-
151

нет. На секущей плоскости имеется сложная седлоузловая не-
неподвижная точка О, возникшая в результате члияния седловой
и узловой неподвижных точек. Кроме этого, предполагается, что
инвариантная кривая S~, выйдя из точки О, потом снова к ней
возвращается, образуя петлю. Это приближение может проис-
происходить по-разному: путем гладкого вхождения в точку О
(рис. 6.31, а), изгибаясь, как показано на рис. 6.31,6, и пере-
пересекаясь с кривой S+ и изгибаясь (рис. 6.31,б). В последнем
Рис. 6.31
случае не совсем уместно говорить, что кривая S~ возвращается
к точке О, скорее она пересекается с S+ и образует петлю
Пуанкаре, с той особенностью, что точка О теперь — особый
седлоузел, который от малейшего изменения параметров может
исчезнуть или снова раздвоиться на седловую и узловую непод-
неподвижную точки. Рассмотрение всех трех случаев сводится к ис-
исследованию точечного отображе-
отображения кольца в себя. Как выбира-
выбирается это кольцо, видно из
рис. 6.32. При этом предполагает-
предполагается, что такое кольцо может быть
выбрано достаточно тонким для
того, чтобы некоторая степень
рассматриваемого отображения Т
преобразовывала его в себя. Ото-
Отображение кольца в себя рассмат-
рассматривалось в ситуации под номе-
номером 5. К второму и третьему
случаю могут быть применены
изложенные там соображения,
которые приводят к существо-
существованию сложного инвариантного
множества. Первый случай приводит к существованию в кольце
инвариантной гладкой замкнутой кривой, возникающей из замк-
замкнутой петли S~ при исчезновении особого седлоузла. На рис. 6.33
.изображены негативы, отвечающие второму и третьему случаям
непосредственно после исчезновения особой седлоузловой непод-
152
Рис. 6.32

вижной точки. В негативе область G преобразуется после до-
достаточного числа повторений преобразования в область П, при
этом вначале происходит ее сжатие и растяжение в направле-
направлениях S+ и S~. После этих растяжений и сжатий область G пе-
переходит в область U, которые пересекаются, как доказано на
Рис. 6.33
рис. 6.33. Эти пересечения приводят по аналогии с уже встре-
встречающимися ситуациями к существованию сложного седлового
инвариантного множества.
Ситуация 9. Восьмерка. Восьмеркой назван фазовый портрет
точечного отображения плоскости в плоскость с неподвижной
седловой точкой О и двумя петлями сепаратрис S~ = S+
(рис. 6.34). При малейшем возмущении точечного отображения
восьмерка разрушается и мо-
могут возникнуть касания или
пересечения инвариантных
кривых S~ и S+ (рис. 6.35).
Отдельные петли этой вось-
восьмерки уже рассматривались
в ситуациях 1 и 2, поэтому
известно, какие движения Рис. 6.34
могут быть возле каждой из
нетель. В частности, при касаниях очень важной характеристи-
характеристикой оказалась седловая величина Kv. Сложное инвариантное
множество есть внутри петель только при Xv < 1. Однако, кроме
движений вблизи каждой из петель, у восьмерки возможны дви-
движения возле каждой из петель с переходами от одной петли
к другой. Цель дальнейшего состоит в рассмотрении этих дви-
движений, включающих в себя движение возле каждой из петель
как частный случай.
Это рассмотрение, естественно, не будет таким подробным,
как при первоначальном рассмотрении ситуаций 1 и 2. В част-
частности, мы не будем изображать позитивы и негативы отдельных
153

преобразований, а вместо этого изобразим их общую схему.
Введем области Аи Ви Си Di и Аг, В2, С2, D2, как показано на
рис. 6.36. Отображения, переводящие А^ в В,, is в D2, С4 в Di
и Сг в Б2,— это некоторые степени отображения Т, например
Тк, Т\ Тт и Г". Числа к, I, т, п — произвольные и большие не-
некоторого N (для того чтобы все эти области можно было счи-
считать тонкими и сжатия вспомогательных отображений Т", Т', Тт
и Тп — достаточно сильными). Прл некоторых степенях преоб-
преобразования Т, выделенные штриховкой на рис. 6.37 части обла-
областей Bi U B2, Di U D2, переходят в «изогнутые» области Bi U В2 и
Di U Z?2. Преобразования, с помощью которых это осуществляет-
осуществляется, обозначим через L и М. Теперь можно изобразить общую
схему этих преобразований так, как это показано на рис. 6.38.
154

Переход от этой схемы преобразований, соответствующей нега-
негативу, к схеме преобразований, отвечающей позитиву,— это толь-
только замепа отображений на вспомогательные и соответствующее
переименование областей, причем новые области уже будут пре-
преобразовываться друг в друга, а отображения в конечном счете
будут сжимающими, так что
эта схема становится схемой до-
допустимых последовательностей
преобразований или различных
обходов вдоль каждой из петель
и переходов от обходов одной
петли к обходу другой. Всевоз-
Всевозможные последовательности
отображений, осуществляющие
эти переходы, соответствуют
всевозможным путям на графе,
изображенным на рис. 6.38.
Ситуация 10. Стохастический
синхронизм. Синхронизмом на-
назван фазовый портрет точечного
отображения, представленный
на рис. 6.39. Точки О„ О2, ..., Ор жО[, О'.2, ...,О'Р при преоб-
преобразовании Т циклически переходят друг в друга, так что точка
с номером i переходит в точку с номером /' по формуле
/ = i + g(modp), B.26)
где ряд — взаимно простые числа. Отсюда следует, что все
точки Ои О2, ..., Ор и О1, О2, ...,ОР—неподвижные кратно-
кратности р; р-кратные неподвижные точки Ои О2, ..., Ор— седловые,
Рис. 6.36
Рис. 6.37
Рис. 6.38
и их инвариантные многообразия могут либо пересекаться, либо
не пересекаться, а в граничном случае касаются друг друга. На
рис. 6.39 ради простоты они изображены совпадающими, малые
изменения этого случая могут привести к любой из перечислен-
перечисленных возможностей.
155

При пересечениях и при касаниях или случаях, близких
к касанию, но без пересечений, может возникнуть сложное сед-
ловое инвариантное множество. Возникновение такого сложного
инвариантного множества имеет место при пересечениях и
в двух остальных случаях, если седловая величина Xv < 1. Об-
Общая роль седловой величины будет
выяснена в дальнейшем.
Пусть фазовый портрет синхро-
синхронизма относится не к точечному ото-
отображению, а к дифференциальным
уравнениям. Его в этом случае легко
дополнить до двух основных про-
простейших вариантов, которые показа-
показаны на рис. 6.40. При этом точки
0i, 02, ..., Ор — седловые состоя-
состояния равновесия, и поэтому для
придания сходства этим фазовым
портретам дифференциальных урав-
уравнений и точечного отображения сле-
следует вместо отображения Т рассматривать Тр. Но и после этого
между фазовыми портретами останутся различия. Так, для диф-
дифференциальных уравнений кривые 5+ и S~ пересекаться не
могут. Напротив, для точечного отображения пересечение воз-
возможно. В случае фазового портрета рис. 6.40, а внутри каждой
Рис. 6.39
Рис. 6.40
из петель помещается устойчивое равновесие, а внутри петель
фазового портрета рис. 6.40, б — неустойчивое. Интересно заме-
заметить, что в первом случае седловая величина больше единицы,
а во втором меньше. Понять, что это именно так, легко из смыс-
смысла седловой величины как величины якобиана преобразования Т
вблизи седловых неподвижных точек.
156

Из предыдущего ясно, что в окрестности неподвижных точек
Ои О2, ..., Ор и их инвариантных кривых в случае точечного
отображения могут существовать сложные седловые инвариант-
инвариантные множества. В случае дифференциальных уравнений анало-
аналогом такого множества могут быть только совпадающие попарно
кривые S+ и S~. При разрушепии этого слияния могут возник-
возникнуть либо внутри петель, либо вне их устойчивые периодические
движения. Такой же фазовый портрет для точечного отображе-
отображения на секущей поверхности отвечал бы появлению тороидаль-
тороидальных интегральных многообразий у исходной системы, в кото-
которой взята эта секущая. Вносит ли что-нибудь новое в эту кар-
картину возможность возникновения сложного седлового инва-
инвариантного множества? Оказывается, вносит. Чтобы придать
конкретный смысд этому различию, будем рассматривать пере-
переменные на секущей плоскости как разность фаз с неким внеш-
внешним периодическим воздействием и результирующую амплиту-
амплитуду колебаний, возникающих в результате этого внешнего воз-
воздействия. При этом переход к дифференциальному уравнению
можно трактовать, например, как результат использования мето-
метода усреднения. Если речь идет о фазовом портрете дифферен-
дифференциального уравнения, то возможные общие случаи — это либо
синхронизм фаз и постоянство амплитуды (устойчивые состоя-
состояния равновесия), либо периодическое изменение разности фаз и
величины амплитуды.
При наличии сложного инвариантного множества, если бы
фазовая точка могла оставаться в его малой окрестности, или,
еще лучше, к нему асимптотически приближаться, появляется
новая возможность хаотического изменения разности фаз и,
в соответствии с этим, амплитуды колебаний. Такой синх-
синхронизм естественно назвать стохастическим синхронизмом.
Стохастичность его проявляется на фазовом портрете ото-
отображения Тр в медленном хаотическом блуждании фазовой
точки в окрестности точек Ои О2, ..., Ор и кривых S~ и S+
(рис. 6.41).
Все рассмотренные выше ситуации допускают непосредствен-
непосредственные многомерные обобщения. Их рассмотрение мало чем отли-
отличается от приведенного, но, конечно, теряет в наглядности.
Отметим, что принимаемые при этих рассмотрениях упрощенные
записи некоторых отображений пе снижают их общности, по-
поскольку основываются на свойствах вспомогательных отображе-
отображений, не нарушаемых пренебрегаемыми нелинейными членами.
Вместе с тем, следует иметь в виду, что существуют ситуации,
приводящие к сложным седловым инвариантным множествам,
которые могут быть реализованы только при размерности то-
точечного отображения, большей двух. Одна из таких сутуаций
была описана в гл. 2. Заметим, что если не требовать взаимной
однозначности преобразования, то она реализуема даже при
размерности единица. При исследовании этой ситуации также
может быть применен переход от негатива к позитиву.
157

Вернемся к отображению A.1) гл. 2. Его сжимающее вспо-
вспомогательное отображение двузначно, и однозначные его ветви
записываются в виде
5\: х = qx + 0,5 sin -£■, г/ = qy + 0,5 cos -f-» i|j = -^-;
- - - B-27)
?2: a; = qx — 0,5 sin -^-, у = да — 0,5 cos^-, ij; = -y+n.
Каждое из этих отображений Ti и ?*2 преобразует в себя
область G (ж2 + г/2<1, 0<г|)<2я), причем образы ТД и TZG
Рис. 6.41
не пересекаются. Отсюда следует, что каждой из последователь-
последовательностей отображений вида
-••> U_v Un, i»., Th, ... (», = 1, I) B.28)
отвечает единственная последовательность точек
..., (ж-j, г/-1, -ф-i), (ж0, г/0, т|з0), («1, г/i, i
такая, что
ф,),-.. B.29)
B.30)
Множество всевозможных последовательностей C.29) — фазовых
траекторий отображения Т — образует сложное инвариантное
седловое множество /. Это множество седловое, так как каждая
из последовательностей точек C.29), в силу сжимаемости вспо-
вспомогательных отображений Г4 и Тг, седловая.
158

Выше единообразным образом путем перехода от негатива
к позитиву были рассмотрены различные ситуации, приводя-
приводящие к нетривиальному седловому множеству. Среди них есть
как открытые сравнительно давно еще А. Пуанкаре, так и от-
открытые совсем недавно, немногим более десяти лет назад. Мно-
Многие из них затем неоднократно переоткрывались. Это относится,
например, к ситуации с петлей сложного седлоузла, интерпре-
интерпретируемой впоследствии то как перемежаемость, то как возник-
возникновение хаотичности при разрушении двумерного интегрального
тора. Первые три сутации следует считать идущими от А. Пуан-
Пуанкаре. Простую петлю изучал Д. Биркгоф. Он установил наличие
в ее малой окрестности бесконечного числа периодических дви-
движений. Этот результат был обобщен на многомерпые системы
в работе [372]. Дальнейшие результаты получены на основе
метода вспомогательных отображений в работах [263, 266, 275].
Начало рассмотрения петли с касанием анонсировано в обзорном
докладе [262] и затем завершено в работах [100, 117, 119, 137].
Подкова Смейла естественно рассматривалась им самим.
Петля седлофокусного равновесия рассматривалась в рабо-
работах [262, 288, 370]. Петля особой седлоузловой неподвижной точ-
точки имеет длинную историю, восходящую к работам А. А. Андро-
Андронова и А. А. Витта [14], А. А. Андронова и Е. А. Леонтович
[16], где возник и был впервые рассмотрен ее аналог для диф-
дифференциальных уравнений. Затем этот случай исследовался
в работах [49, 50, 236, 271]. О восьмерке уже говорилось в § 2
гл. 1. Стохастический синхронизм как своеобразный аналог обыч-
пого синхронизма, но со случайно буждающей фазой, впервые
отмечен в работе [273].
Наконец, заметим, что приведенное выше рассмотрение всех
перечисленных ситуаций основывается на лекциях £282].
§ 3. Условия возникновения хаотических
и стохастических аттракторов
Когда сложное седловое множество /, которое, как было по-
показано, возникает во многих разных ситуациях, может быть
притягивающим и оказаться странным аттрактором? Ясно, что
для этого прежде всего необходимо, чтобы характеристические
показатели движений множества / обеспечивали сжатие фазо-
фазового объема. Это, несомнеппо, необходимое условие, но его мало.
В окрестности отдельного седлового движения может происхо-
происходить сжатие фазового объема и даже очень сильное, и все же
отдельное седловое движепие не может быть аттрактором: фа-
фазовые точки сначала подходят к нему, а затем уходят. (Воз-
(Возможность приближения по поверхности S+ пе в счет, поскольку
ее мера равна нулю.) Заметим, что достаточным признаком
сжатия фазового объема для динамической системы, описывае-
описываемой дифференциальным уравнением
к = Х(х), C.1),
159

является
divX(x)<0. C.2)
При этом, если
divX(x)s£6<0,
то за время т фазовый объем V превращается в объем, не
больший, чем Ve6x. Так для уравнений Лоренца A.24) гл. 1
§ = —0-J-K0 и сжатие фазового объема происходит очень
быстро и сильно: за единицу времени oir уменьшается примерно
в 103—105 раз. Несмотря на сжатие фазового объема, одно изо-
изолированное седловое периодическое движение аттрактором быть
не может, хотя оно, конечно, может ускорить процесс сжатия
фазового объема другими устойчивыми и мало сжимающими
фазовый объем периодическими движениями. Иначе говоря, воз-
возможна такая своеобразная «взаимопомощь»: седловые движения
уменьшают фазовый объем и далее этот уменьшенный фазовьШ
объем поглощается «слабенькими» устойчивыми движениями
с очень маленькими областями всестороннего сжатия, имеющего
место лишь в малой их окрестности. Такое может быть и часто
бывает, но седловые движения и сами могут образовать аттрак-
аттрактор, нужно только, чтобы их было много. Что так может быть,
показывает аттрактор Лоренца. Существуют и другие примеры.
Хотелось бы понять охватывающую их общую схему. Напри-
Например, возможно, что каждое из седловых движений некоторого
множества приближает и удаляет от себя элементы фазового
объема, уменьшает их объем и после этого передает другому
седловому движению. То, в свою очередь, сжимает фазовый
объем поступившей к нему фазовой частицы и передает ее
другому седловому движению и т. д. Для того чтобы такая схе-
схема реализовалась, инвариантные поверхности S~ всех седловых
движений должны входить в их же состав. Вспомним, что имен-
именно с такой ситуацией мы встречались в аттракторе Лоренца,
что и отмечалось при его рассмотрении. Достаточно ли такого
требования, т. е. требования S~ <= /? По-видимому, да, если
учесть, что после каждого прохода возле седлового движения
расстояние фазовой точки от поверхности S~ уменьшается и они
все ближе и ближе подходят к множеству S~, а коль скоро
S~ <= /; то и к множеству /. Итак, страпныи аттрактор — это ин-
инвариантное седловое мпожество /, для которого многообразие
S~ принадлежит ему самому и для движений которого седловая
величина о < 1. Такой странный аттрактор будем называть сто-
стохастическим аттрактором. Наряду с этим возможны «странные
аттракторы», состоящие как из седловых, так и устойчивых
движений, в своеобразной взаимопомощи сжимающих фазовый
объем и «аннулирующих» его на «слабых» устойчивых движе-
движениях, которые играют роль стоков фазового объема. Такое тоже
может быть. Откуда берутся эти слабые устойчивые движения
в массе сжимающих фазовый объем седловых? Один из меха-
механизмов образования таких слабых устойчивых движепий можно
160

указать — это касание или очень близкое расположение инва-
инвариантных кривых 5+ и S~. Если касание есть, то наличие «сла-
«слабых» устойчивых движений неизбежно. Причина их образования
понятна из рассмотрения ситуации 2 в предыдущем параграфе
и вызвана обращением в бесконечность производной от вспомо-
вспомогательного отображения, обозначенного там буквой L, па неко-
некоторой линии. Более детально этот вопрос мы рассмотрим в сле-
следующей гл. 7, а сейчас ограничимся тем, что обратим внима-
внимание на возможность существования таких симбиозных странных
аттракторов, подчеркнем необычайную малость локальных ок-
окрестностей притяжения, входящих в них устойчивых периоди-
периодических движений и дадим им название хаотических аттракторов.
Сказанное в отношении аттракторов в условиях, когда возможно
и естественно либо уменьшение фазового объема, либо его уве-
увеличение, требует существенных дополнений в случае гамильто-
новой системы. У гамильтоновых систем фазовый объем сохра-
сохраняется, у них не может быть ни увеличения фазового объема,
пи его уменьшения, так как
^0. C.3)
Если бы для гамильтоновой системы выполпялось условие S~ cr
<=/, то, так как седловая величина о = 1, доказать приближение
фазовых точек было бы нельзя, но зато ничто не мешало бы
инвариантному множеству / иметь меру, отличную от нуля, что
раньше было невозможно, так как мера множества / должна
была бы меняться. Таким образом, структура инвариантного
седлового множества в гамильтоновом случае существенно дру-
другая. Гамильтопов странный аттрактор — это инвариантное сед-
ловое множество с лебеговой мерой, отличной от нуля. Вместе
с тем, как и в случае негамильтонового диссипативпого аттрак-
аттрактора, должно выполняться условие S~ <= /. Замена времени t на
—t пе меняет гамильтопового характера динамической системы,
по при этом инвариантные множества S+ и S~ меняются места-
местами. Это пе может пе натолкнуть па мысль, что для гамильто-
гамильтоновых систем S+ cr /, Это действительно так, ибо в прртивном
случае множество / могло бы втягивать в себя внешний фазо-
фазовый объем, что невозможно без его выбрасывания.

Глава 7
БИФУРКАЦИИ И ПУТИ ВОЗНИКНОВЕНИЯ
ХАОСА И СТОХАСТИЧНОСТИ
В предыдущей главе были рассмотрены простейшие типовые
ситуации, приводящие к существованию сложных нетривиаль-
нетривиальных седловых инвариантных множеств /. Если такое сложное
инвариантное множество / еще и притягивающее, то оно —
странный аттрактор, обладающий свойством локальной неустой-
неустойчивости, по устойчивый в целом. Наряду с таким «статическим»
изучением сложных седловых множеств / представляют интерес
и исследования, выясняющие, как они возникают в динамике —
при изменении параметров. Сочетание «статического» и «дина-
«динамического» подходов позволяет не только полнее исследовать
стохастические и хаотические движения, но во многих случаях
облегчает их обнаружение и изучение.
Обычно динамическая система зависит от параметров, с их
изменением ранее устойчивое равновесное состояние становится
неустойчивым, и лишь затем наступает хаотизация движений.
Последующее поясняет то, как это может происходить. Здесь
возможна как физическая трактовка, так и более опосредство-
опосредствованный подход, основанный на геометризации динамики системы
в виде ее фазового портрета. Каждая из трактовок имеет право
на существование. Они не исключают, а дополняют друг друга.
Физическая точка зрения исходит из анализа причин воз-
возникновения локальной неустойчивости, ведущих к нарастанию
колебаний, и причин, которые могут затормозить это нарастание
и привести в конечном счете к эффекту глобального сжатия.
Специфика условий возникновения хаотических и стохастиче-
стохастических колебаний, в отличие от условий возникновения периоди-
периодических колебаний, состоит в различии механизмов глобального
сжатия. Для периодических автоколебаний — это плавное огра-
ограничение колебапий, а для хаотических автоколебаний — относи-
относительно резкий их сброс или переходы па другие режимы дви-
движения. Причины же неустойчивости могут быть одпи и те же
в случае возникновения как периодических, так и стохастиче-
стохастических колебаний.
Геометрическая точка зрения, опирающаяся на рассмотрение
фазового портрета и его измепений, фиксирует свое внимание
на его бифуркациях, или, как сейчас стали говорить, катастро-
162

фах. В основе такого подхода лежит представление о том, что
качественные изменения фазового портрета происходят не путем
плавных изменений, а путем скачкообразных изменений при
отдельных значениях параметров, их бифуркационных значени-
значениях. В последние годы представления о возможных бифуркациях
сильно изменились. Ранее считалось, что бифуркации изолиро-
изолированы друг от друга, что на фазовом портрете они имеют лока-
локализованный характер. Все оказалось значительно сложнее. Точки
бифуркаций могут сгущаться и образовывать сложные множе-
множества, а соответствующие им изменения фазового портрета могут
захватывать целые области фазового пространства. Бифуркации
не независимы, так что о сериях или множествах бифуркаций
можно говорить как о некоторой новой, сложной бифуркации.
Оказалось целесообразным изучать зависимость фазового порт-
портрета не только от одного параметра, а от целых групп парамет-
параметров. Сам по себе этот факт не новый, и такой подход для по-
получения более полных картин возможных бифуркаций исполь-
использовался и раньше при решении различных конкретных задач.
Однако за последнее время подверглись уточнению представле-
представления о наименьшей группе параметров, с изменением которых
связана рассматриваемая бифуркация, о чем была речь в пре-
предыдущей пятой главе.
Вместе с тем, несмотря на все эти усложнения, осповпую
роль по-прежнему играют бифуркации состояний равновесия,
периодических движений и их интегральных многообразий 5+ и
S~. В дополнение к четким законам бифуркаций состояний рав-
равновесия и периодических движений обнаружились новые законы
серий бифуркаций и их связи с так называемыми вложенными
структурами, с касаниями инвариантных многообразий S+ и S~,
с особым характером зависимости числа вращения Пуанкаре от
параметров.
В лекциях Р. Фейнмана [353] есть очень образное описание
возникновения турбулентности с ростом числа Рейпольдса.
Нарисованная там картина и ее возросшая сложность по срав-
сравнению с более ранними описаниями как нельзя лучше соответ-
соответствует параллельно и независимо идущему процессу усложнения
представлений теории бифуркаций. Последующее изложение име-
имеет целью прояснить все возможные метаморфозы фазового порт-
портрета, которые могли бы отвечать переходу ламипарпого
течения в турбулентное и вообще устойчивого равновесного
состояния в хаос. Ото изложение не посит исчерпывающего ха-
характера, оно лишь в общих чертах описывает картину. После
описания дерева возможных бифуркаций более подробно рас-
рассматриваются серии бифуркаций. Затем описываются бифурка-
бифуркации в двух конкретных и достаточно детально изучепных ди-
динамических системах — системе Лоренца и нелинейпом парамет-
параметрически возбуждаемом осцилляторе и ротаторе. Эти примеры
позволяют достаточно подробно проследить пути возникновения
порядка и хаоса.
163

§ 1. Общее описание дерева возможных бифуркаций
Пусть вначале имеется устойчивое состояние равновесия О"- °.
Потерять свою устойчивость при непрерывном изменении па-
параметров или исчезнуть оно может лишь вполне определенными
описанными в гл. 5 тремя способами:
1) стать неустойчивым, превратиться в состояние равновесия
типа О"'22 с одновременным отделением устойчивого периоди-
периодического движения ГП|' или слиянием с неустойчивым периодиче-
периодическим движением Г"~''2;
2) потерять устойчивость и превратиться в состояние равно-
равновесия типа On~1'l с одновременным отделением двух устойчи-
устойчивых состояний равновесия типа Оп< ° или слиянием с двумя не-
неустойчивыми состояниями равновесия типа О"1;
3) исчезнуть, слившись с седловым состоянием равновесия
типа О"-1'».
При отделении от состояния равновесия Оп-" устойчивого
периодического движения или устойчивых состояний равновесия
прЪисходит мягкий переход от прежнего установившегося дви-
движения (состояния равновесия) к новым установившимся дви-
движениям (устойчивому периодическому движению или одному из
устойчивых состояний равновесия). Напротив, при слиянии с со-
состоянием равповесия Оп- ° неустойчивого периодического движе-
движения, неустойчивого равновесия или равновесий переход к новому
установившемуся движению носит жесткий характер. К какому
именпо новому установившемуся движению происходит жесткий
переход, локальная теория бифуркаций не указывает. Это мо-
может быть равновесие, периодическое, хаотическое или стохасти-
стохастическое автоколебание. Это может быть и уход в бесконечность.
Отметим, что общими являются только бифуркации 1 и 3, би-
бифуркация 2 является общей только при часто встречающейся
симметрии динамической системы. Подчеркнем, что все эти
бифуркации были уже рассмотрены в гл. 5. Теперь они собра-
собраны вместе и представлены на дереве возможных бифуркаций,
изображенном на рис. 7.1. Они соответствуют переходам через
бифуркационные границы No и N».
Далее, если -в результате описанных бифуркаций вновь воз-
пикает устойчивое состояние равновесия, то с ним, естественно,
могут произойти опять только такие же бифуркации. Поэтому
далее описываются только бифуркации устойчивого периодиче-
периодического движения ГП| \
Опишем теперь основные возможные при непрерывном изме-
изменении параметров бифуркации устойчивого периодического дви-
движения ГП| 1.
1. Периодическое движение Тп-i исчезает, сливаясь с седло-
седловым периодическим движением Г'2.
2. Периодическое движепие Г"'1 теряет устойчивость, отде-
отделяя от себя устойчивое же периодическое движепие удвоенного
периода или сливаясь с неустойчивым периодическим движением
164

удвоешюго периода. В обоих этих случаях исходное периоди-
периодическое движение Г"' * превращается в периодическое движение
типа Г"-2.
3. Периодическое движение !""■i теряет устойчивость, отде-
отделяя от себя устойчивое двумерное тороидальное многообразие
Тп-2 или сливаясь с неустойчивым двумерным тороидальным
многообразием Тп~к 3.
Эти бифуркации отвечают переходам в пространстве пара-
параметров через бифуркационные поверхности iV+i, N-t и Nv с зна-
значениями ф, ОТЛИЧНЫМИ
от 0, я, 2я/3 и я/2. Зна-
Значения ф = 0 и ф = я
отвечают бифуркациоп-
пым поверхностям iv+1
и N-x.
Значения ф = 2я/3 и
Ф = я/2 отвечают осо-
особым резопансным слу-
случаям потери устойчиво-
устойчивости исходным периоди-
периодическим движением Ги>'.
Особые резонансные
случаи исследовались
в большом числе работ
[42, 43, 58, 195-197,
274, 280, 290]. Отметим
только, что при резо-
резонансной потере устой-
устойчивости возможно отде-
отделение от теряющего
устойчивость периоди-
периодического движения ГП|'
устойчивых периодиче-
периодических движений утроен-
утроенного и учетверенпого периодов, а также хаотических движений.
К перечисленным бифуркациям периодического движения
Г"-', вызванным переходами через бифуркационные поверхности
N+i, N-i и Nv, следует добавить бифуркации, при которых замк-
замкнутая фазовая кривая, отвечающая периодическому движепию
Гп' \ стягивается к состоянию равновесия или на ней появляется
состояние равновесия, и она превращается в петлю, идущую из
этого состояния равновесия в него же. О первой бифуркации
уже говорилось — это бифуркация 1 состояния равновесия, вто-
вторая бифуркация рассматривалась в гл. 4 в ситуации «петля сед-
лоузла» под номером семь. Укажем еще па возможный уход
фазовой траектории, отвечающей периодическому движению,
в бесконечность.
Выше мы описали основные бифуркации, отвечающие бифур-
бифуркационным грапицам коразмерности 1. При симметрии динами-
N
\
Рис. 7.1
165

ческой системы основной может быть и бифуркация, при кото-
которой устойчивое периодическое движепие Г"' * превращается в сед-
ловое Г"'2, отделяя от себя одновременно два новых устойчи-
устойчивых периодических движения типа Г''. Эта бифуркация про-
происходит при пересечении границы N+1.
Потеря устойчивости периодическим движением или его ис-
исчезновение вызывают смену установившегося движения. Смена
установившегося движения может быть мягкой или жесткой.
При мягкой смене установившегося движения вместе с плавным
изменением параметров происходит и плавная и постепенная
смена установившегося движения. При жесткой смепе устано-
установившегося движения, напротив, несмотря па плавное изменение
параметров, смена установившегося движения происходит
скачком.
Участки бифуркационных границ, отвечающих мягкой смене
установившегося движения, можпо называть безопасными, а от-
отвечающие жесткой смене — опасными. Понятие мягкого и жест-
жесткого возникновения автоколебаний было введепо А. А. Андро-
Андроновым. Понятие опасных и безопасных границ было введено
Н. Н. Баутиным [72, 73] для границ областей устойчивости со-
состояния равновесия. Дальнейшее обобщение этих понятий на
периодические движения связано с работой [259], на основе
которой можно дать общее определение и описать общую кар-
картину мягкой и жесткой смены установившегося движения.
Пусть /—установившееся движение, т. е. состояние равпове-
сия, периодическое или стохастическое движение, точнее, пе са-
само движение, а его геометрический образ в фазовом простран-
пространстве. Установившееся движение / имеет область притяжения
П(/), внутри которой находится /. При непрерывном изменении
параметра и. динамической системы меняется как установившее-
установившееся движение, так и его область притяжения ПG). Возможны
два различных случая: первый — когда при бифуркационном
значении параметра ц. = ц* существуют сколь угодпо малые е-ок-
рестности /, которые со временем преобразуются строго внутрь
себя, и второй — когда та'ких окрестностей нет, и любая доста-
достаточно малая е-окрестность / преобразуется в область, у которой
есть точки, лежащие вне этой е-окрестности. При этом отбро-
отброшена возможность граничного случая, когда существуют сколь
угодно малые окрестности /, преобразующиеся в себя. Первый
случай соответствует мягкому режиму смены установившегося
движения, второй — жесткому. В первом случае вновь возникаю-
возникающее установившееся движение отделяется от прежнего устано-
установившегося движения /, а его область притяжения непрерывно
возникает из области притяжения прежпего установившегося
движения /. Во втором случае, напротив, прежнее установив-
установившееся движение / теряет устойчивость или исчезает, и фазо-
фазовые точки из его окрестности с ростом времепи переходят к но-
новому установившемуся движению, которое, как правило, суще-
существовало и до рассматриваемой бифуркации установившегося
166

движения /. На дереве возможных бифуркаций (рис. 7.1) би-
бифуркации установившихся движений, сопровождающиеся жест-
жесткой сменой, отмечены черными кружочками. При мягкой смене
установившегося движения локальная теория бифуркаций ука-
указывает, каково новое установившееся движение. Напротив, при
жесткой смене новое установившееся движение не указывается.
Но здесь есть исключения, когда теоретически возможны нело-
нелокальное рассмотрение и выяснение этого нового режима. Это —
бифуркация устойчивого состояния равновесия через сложный
седлоузел при наличии петли и попарное исчезновение устой-
устойчивого и седлового движения через их слияние на устойчивом
двумерном торе. Обе эти бифуркации фактически были рассмот-
рассмотрены в предыдущей главе в ситуациях 6, 7 и 8.
Перейдем к описанию бифуркаций устойчивого двумерного
тора Тп-2. Бифуркации устойчивого двумерного тора можно раз-
разделить на собственно бифуркации тора как инвариантного ус-
устойчивого многообразия, на бифуркации фазового портрета на
торе и, наконец, бифуркации отдельных периодических движений
на торе. Если размерность фазового пространства, в котором на-
находится двумерный устойчивый тор, больше трех, то возможны
его бифуркации (так же, как и периодического движения) ти-
типов N+u N-i и Nv. В трехмерном фазовом пространстве возмож-
возможны только бифуркации N+i. При бифуркации N+i устойчивый
тор Тп-2 сливается с седловым Tn~l-3 и исчезает. При бифурка-
бифуркации N-t устойчивый тор «удваивается», и одновременно от него
отделяется седловой тор Тп~1-3. При бифуркации Nv устойчивый
тор Тп-2 переходит в неустойчивый и одновременно от пего отде-
отделяется трехмерный устойчивый тор или устойчивый тор Тп~ \ ста-
становясь неустойчивым, сливается с трехмерным седловым тором.
Бифуркации на двумерном торе могут быть вызваны измене-
изменением числа вращения Пуанкаре его обмотки. При рациональном
числе вращения обмотка тора периодическая, точнее, на торе
есть устойчивые периодические движения, а остальпые фазовые
траектории к ним приближаются, за исключением такого же
числа неустойчивых периодических движений, которые играют
роль разделяющих границ локальных областей притяжения ус-
устойчивых периодических движений. При иррациональном числе
вращения обмотка двумерного тора квазипериодическая. Число
вращения Пуанкаре как функция параметра в общем случае ку-
кусочно-постоянная, при всяком ее изменении происходят бифур-
бифуркации обмотки тора — фазового портрета на торе. Бифуркации
отдельных периодических движений на торе ничем не отлича-
отличаются от описанных уже бифуркаций периодических движений.
Дерево бифуркаций (рис. 7.1) описывает только бифуркации
состояний равновесия, периодических движений и двумерных
торов. Помимо этих относительно хорошо изученных бифуркаций,
к появлению хаотических и стохастических движений могут
привести изменения относительно расположения интегральных
многообразий S+ и S~ . седловых равновесий и периодических
167

движений, пе связанные непосредственно с бифуркациями устой-
устойчивых состояний равновесия или периодических движений.
Именпо так, например, возникает странный аттрактор в системе
Лоренца A.16) гл„ 1 при возрастании параметра г.
§ 2. Серии бифуркаций
Как уже отмечалось, представление о множестве точек би-
бифуркации как о некоторых поверхностях в пространстве пара-
параметров оправдалось далеко не полностью. Следующим естествен-
естественным усложнением это*! примитивной картины является представ-
представление о сериях бифуркаций, о бесконечных множествах поверх-
постей, накапливающихся к некоторой предельной поверхности,
или поверхностям, которые, в свою очередь, также образуют
бесконечные множества. Настоящий параграф посвящен рассмот-
рассмотрению некоторых из таких серий.
1. Серии бифуркаций, связанные с числом вращения Пуан-
Пуанкаре. По-видимому, первым объектом, разрушившим прежние
представления о бифуркационном множестве, было взаимоодно-
взаимооднозначное точечное преобразование окружности в себя вида
0 = /@)(mod2n), B.1)
где /(9) — гладкая периодическая с периодом 2я функция угло-
угловой переменной G, для которой /'(9)>0.
Пусть 0о, 0i, 02, ...— бесконечная последовательность преоб-
преобразующихся друг в друга точек
в»+1 = /F») (А = 1, 2, 3, ...) B.2)
и Д0Й — величина дуги, соединяющей точки Qk с Gft+1. А. Пуан-
Пуанкаре установил, что предел
и-1
существует и не зависит от начальной точки 90 [311]. Именно
этот предел со и получил название числа вращения Пуанкаре.
Из доказательства видно, что число вращения Пуанкаре пред-
представляет собой топологический инвариант, т. е. остается неизмен-
неизменным при любой взаимнонепрерывной замепе угловой перемен-
переменной 0. Много позднее А. Г. Майер установил [242], что число
вращения Пуанкаре непрерывно зависит от параметра, т. е. если
функция /@) непрерывно зависит от параметра ц, то и числе
вращений со является непрерывной функцией параметра ц..
Далее А. Г. Майером был выяснен вопрос об общих видах
отображения окружности в окружность. Еще Пуанкаре устано-
установил, что при иррациональном со отображение B.1) не имеет
периодических точек и что если у отображения B.1) есть пе-
периодические точки, то со рационально (причем если со = p/q, где
р и q — взаимно простые целые числа, то периодические точки
168

отображения B.1) имеют кратность q). Оказалось, что грубыми,
а тем самым общими, могут быть только отображения окружно-
окружности с рациональными значениями чисел вращения и, т. е. с и
вида p/q. Эти грубые общие отображения при ю = p/q имеют
в общем случае 2г (г=1, 2, ...) циклов неподвижных точек
кратности q, из которых rq устойчивых и rq неустойчивых. Не-
Неустойчивые неподвижные точки разделяют устойчивые. На
рис. 7.2 изображепы фазовые портреты точечного отображения
Рис. 7.2
и
г=1; р = 3, <? =
B.1) соответственно при р = 3, q =
г = 1 и, наконец, р = 3, ? = 1 и г = 2.
Пусть теперь отображение B.1) непрерывно зависит от па-
параметра ц, так что
0 = /@, ц) (mod 2л), , B.4)
и пусть со(ц) — его число вращения Пуанкаре. Естественно счи-
считать общим случаем тот, когда значениям со(ц) вида p/q отве-
отвечают отображения общего
вида. В этом случае любое
равенство со (\i) —p/q сохра-
сохраняется для некоторого ин-
интервала значений парамет-
параметра ц, и следовательно,
функция со(ц), будучи не-
непрерывной, имеет интер-
интервал постоянства при каж-
каждом (х, для которого со (ц.) =
—p/q. Некоторое представ-
представление о такой функции да-
дает график рис. 7.3. Этот
2/5\
7/31 .,
„
j>wc
график соответствует не-
непрерывной функции, и поэтому co(fx) принимает все промежуточ-
промежуточные значения, а из этого следует, что на любом промежутке изме-
изменения числа вращения (о(\х) содержится бесконечное мпожество
бифуркаций, счетное число которых отвечает бифуркациям циклов
неподвижных точек. Такова не очень простая картина бифуркаций
169

при изменении параметра ц. Обнаруживается она уже у точечного
отображения вида хB.4), которое возпикает на секущей окруж-
окружности 2 двумерного тора, т. е. все сказанное имеет прямое отно-
отношение к бифуркациям этой обмотки тора. Значениям числа вра-
вращения (о(ц), несоизмеримым с 1, отвечают непериодические
квазипериодические обмотки, напротив, при <a(\i) = p/q на торе,
вообще, имеется г устойчивых и г неустойчивых периодических
движений, при обегаиии каждого из которых секущая окруж-
окружность оказывается пересечепной q раз, а тор — обойденным
р раз. Этот тор может быть, в частности, двумерным устойчи-
устойчивым тором в n-мерпом пространстве, на котором находятся г
(г=1, 2, ...) устойчивых периодических движений типа Г' и
г седловых типа Г"'2.
Выше говорилось о бифуркациях обмотки двумерного инте-
интегрального тора, порождаемых изменением числа вращения Пу-
Пуанкаре. В частности, эти бифуркации могли происходить на торе,
который рождается от периодического движения при изменении
параметров, приводящем к переходу через бифуркационную
поверхность N^ коразмерности единицы. В момент рождения
тора число вращепия фазовых траекторий на нем равно <р/2я и
в дальнейшем может меняться. При этом рождение тора носит
изолированный характер, т. е. оно происходит при некотором
значении параметра \х = (i* и при \х, близких к ц*, по отличных
от [i*, отделений или слияний торов с периодическим движе-
движением нет. Однако в особых случаях и, в частности, для гамиль-
тоновых систем, рождение интегральных торов от периодических
движений может носить совсем другой, «непрерывный» харак-
характер [61]. Это связано с особенностями гамильтоновых систем и
в первую очередь с тем, что при наличии у нее периодического
движепия только с двумя комплексными корнями последние
обязательно имеют вид е±щ и при изменении параметров воз-
возможны только следующие случаи:
щ) эти корни непрерывно перемещаются по единичной окруж-
пости, оставаясь комплексными;
б) обращаются в двойной корень, равный +1, и после этого
становятся действительными, один больше, а другой меньше
единицы;
в) обращаются в двойной корень, равный —1, и затем ста-
становятся действительными, один больше, а другой меньше —1.
В первом случае точечное отображение в окрестности непод-
неподвижной точки представимо в виде
.) B.5)
и после замены р на ер — в виде
р = р + ер2(...), ф = ф + 2я<а (ер, ц)+ер(...), B.6)
где е — искусственно введенный малый параметр, а ц — пара-
параметр рассматриваемой системы. При е = 0 система имеет непод-
■170

вижную точку типа центр, окрестность которой заполнена замк-
замкнутыми инвариантными кривыми р = const. На каждой из этих
инвариантных кривых определено точечное отображение окруж-
окружности в себя с числом вращения Пуанкаре, равным о (ер, ц).
Пусть е = 0 и меняется параметр ц. При ю^сйр < 0 с возраста-
возрастанием |я происходит рождение от неподвижной точки р = 0 новых
инвариантных кривых р = const с
новыми значениями числа вращения,
а при о)ро),1 > 0, напротив, погло-
щение имеющихся (рис. 7.4) [61].
Так будет происходить при е = 0.
При малом е > 0, а число е может
быть выбрано тем меньше (чем
меньшая окрестность неподвижной
точки рассматривается) некоторые
из инвариантных кривых мало изме-
изменятся и останутся замкнутыми ин-
инвариантными кривыми, а некоторые,
отвечающие w = p/q, изменятся су- Рис. 7.4
щоственпо, превращаясь в синхро-
синхронизмы. Эти выводы о сохранении замкнутых кривых основыва-
основываются на теории КАМ, созданной в трудах Колмогорова, Арноль-
Арнольда и Мозера. Рождение из резонансного уровня, отвечающего ра-
рациональному числу вращения вида p/q, синхронизма, составлен-
составленного из Ъг циклов g-кратных неподвижных точек, следует из уп-
упрощенных соображений теоремы Пуанкаре — Биркгофа о со-
сохраняющем площадь отображении кольца в себя. Теоретически
значение г может быть любым, но практически встречаются чаще
всего г = 1 и иногда г = 2. Таким образом, мы приходим к вы-
выводу, что в окрестности неподвижной точки типа центр у сохра-
сохраняющего площадь отображения с изменением параметра |я про-
происходят серии бифуркаций в соответствии с изменением величин
Ф и зависимостью © от р. Будут ли наблюдаться такие серии
бифуркаций при движении по бифуркационной поверхности Nv
общей динамической системы? У общей динамической системы
серии бифуркаций наблюдаться не будут. Бифуркации будут про-
происходить только при переходе через значения ф = я/2 и ф =
= 2лУЗ (и, конечно же, при ф = 0, п), а также при смене знака
аналога ляпуновской величины (знак которой в этом критиче-
критическом случае определяет устойчивость неподвижной точки).
Прежде чем перейти к рассмотрению следующих возможно-
возможностей, отметим, что приведенные выше общие соображения о рож-
рождении из неподвижной точки замкнутых кривых и синхронизмов
могут быть повторены и для новых родившихся в синхронизмах
неподвижных точек типа центр и т. д., в результате чего мы при-
приходим к бесконечной иерархии вложенных структур, красноречи-
красноречиво говорящей о необычайно сложном устройстве окрестности не-
неподвижной точки типа центр. Рассмотрение закономерностей
этой иерархии структур для конкретных систем проводилось
171

численными методами с использованием ЭВМ в работах
[61, 63—67]. О результатах этих работ еще будет речь в связи
с дальнейшим рассмотрением в этой главе нелинейного парамет-
параметрически возбуждаемого ротатора.
При превращении комплексных корней егф и е"'ф в двойной
корень +1 или двойной корень —1с последующим переходом в
два различных действительных корня (один корень, больший по
модулю, больше, другой меньше единицы), неподвижная точка
типа центр превращается в седловую неподвижную точку и од-
одновременно из нее рождаются либо две однократные точки типа
Рис. 7.5
Рис. 7.6
центр, либо две двукратные точки типа центр, образующие цикл
двукратных неподвижных точек (рис. 7.5). Это — одна из воз-
возможностей. Вторая возможность состоит в том, что в момент об-
образования двукратного корня +1 или —1 происходит слияние с
рассматриваемой неподвижной точкой двух неподвижпых точек
типа седла, однократных в случае двойного корня +1 и двукрат-
двукратных в случае двойного корня —1 (рис. 7.6). Таковы возможные
бифуркации неподвижной точки, отвечающие двум последним из
описанных выше движений корпей характеристического уравне-
пия. Отметим, что при обратном движении корней соответствую-
соответствующие обращения этих бифуркаций описывают бифуркации седло-
вой неподвижной точки.
2. Серии бифуркаций и вложенные структуры. Рассмотрение
взаимно однозначного отображения окружности на себя привело
к понятию числа вращения Пуапкаре и сериям бифуркаций, вы-
вызываемым особым характером зависимости числа вращения от
параметра. Аналогично исследование гладкого однозначного, но
не взаимно однозначного отображения прямой в прямую
х = /(х,ц) B.7)
привело к открытию серий бифуркаций удвоения. Широкую из-
172

вестность эта серия бифуркаций обрела после работ Феигенбау-
ма, обнаружившего у этой серии бифуркаций замечательную
универсальную закономерность, носящую теперь его имя. Сама
серия бифуркаций удвоения наблюдалась много раз и ранее при
исследовании конкретных систем, ее существование непосред-
непосредственно следует из замечательного порядка сосуществования не-
неподвижных точек преобразования прямой в прямую, открытого
А. Н. Шарковским еще в 1967 г. [368]. Согласно этой закономер-
закономерности неподвижные точки разных кратностей могут сосущество-
сосуществовать лишь при соблюдении порядка, определяемого последова-
последовательностью
3<5<7<...<3-2<5-2<...<3-22<5-22<...
...<... <23<22< 2 <1, B.8)
которая означает, что если есть неподвижная точка какой-нибудь
из указанных в этой последовательности кратностей, то обяза-
обязательно есть неподвижные точки всех последующих в этом ряду
кратностей. В частности, согласно последовательности B.8), ес-
если есть трехкратная точка, то ей должны предшествовать все
точки кратностей 2, 22, 2\ ..., 7 • 2\ 5 • 2\ 3 • 2\ ... 7 • 22, 5 • 22,
3 • 22, ..., 7, 5, 3, причем обязательно в указанном порядке, т. е.
сначала точки кратности 2, затем точки кратности 22, затем —
кратности 23 и т. д., наконец, точки кратностей 7, 5 и 3.
Закон универсальности Фейгенбаума относится к последова-
последовательным значениям [1и |Яг, |Яз, ..., параметра ц, при которых воз-
возникают неподвижные точки кратностей 2, 22, 2", ... Для этих
последовательных значений параметра утверждается существо-
существование предела
lim ^^i+1 = 4,6692 ..., B.9)
одного и того же для всех преобразований общего вида прямой
в прямую, т. е. существование некоторой универсальной копстан-
ты 4,6692 .. . Наличие этой универсальной закономерности позво-
позволяет, в частности, по нескольким первым значениям \it, ц2,
указать приближенно предельное значение
|1 B.10)
с достижением которого завершается бесконечная серия бифур-
бифуркаций удвоения кратности неподвижной точки.
Этот факт подтвержден многочисленными численными экспе-
экспериментами, проведенными как Фейгепбаумом, так и многими дру-
другими авторами. Вместе с тем нолное теоретическое обоснование
универсальности Фейгепбаума отсутствует, хотя пути его прове-
проведения ясны и «мешают лишь вычислительные трудности».
В 1984 г. вышел обзор работ по универсальности Фейгенбаума
[115]. В нем универсальность и ее изучение связывается с мето-
методом ренормализационной группы, хорошо известным в теории
173

фазовых переходов второго рода в статистической механике. Од-
Однако универсальности можно придать и песколько другой аспект,
связывающий теорию бифуркаций удвоения, по-видимому, с об-
общим свойством вложенности структур фазового портрета дина-
динамической системы [198]. Свойство вложенности структур обна-
обнаруживается не только в связи с сериями бифуркаций увеличения
кратности неподвижной точки, но и в гомоклинических структу-
структурах, в расположении синхронизмов гамильтоновых систем [65],
в неоднократно отмечаемой канторовой структуре странных ат-
аттракторов.
Если б — область фазового пространства,, в которой у вектор-
векторного поля нет никаких особенностей, то некоторая ее часть б
гомеоморфна ей. В этой части б, в свою_очередь, можно указать
еще меньшую часть б, гомеоморфную б, а следовательно, и б,
и т. д. до бесконечности, т. е. фазовый портрет без особенностей
такой же, как фазовый портрет его сколь угодно малых частей.
Аналогично, если б — окрестность состояния равновесия или не-
неподвижной точки, то фазовый портрет в ней такой же, как и у сколь
угодно меньших других окрестностей этого состояния равновесия
или неподвижной точки. Таким образом, в обоих этих случаях
можно говорить, что фазовый портрет допускает бесконечные
серии вложенных друг в друга одинаковых (гомеоморфных) фа-
фазовых портретов. Это утверждение представляется тривиальным.
Но давайте зададимся таким же вопросом по отношению к не-
несколько более сложной структуре фазового портрета, например
к восьмерке, изображен-
изображенной на рис. 7.7. Для того
чтобы построить такую
же серию вложенных друг
в друга однотипных фазо-
фазовых портретов, можно в
одну из петель восьмерки
или в обе петли вложить
Рис 77 восьмерку, затем в каж-
каждую из новых восьмерок
вложить снова восьмерку и т. д. до бесконечности. Это очень похо-
похоже на вложение друг в друга до бесконечности матрешек. Рас-
Раскрывая одну матрешку, мы неизменно получаем «такую же»
матрешку, как и была. От °° отпять единицу — остается та же
бесконечность. Матрешка уменьшилась в размере и только, но
осталась гомеоморфна исходной.
Дадим формальное, несколько более общее определение вло-
вложенной структуре и выясним условия ее существования. Пусть
ц — некоторый гомеоморфизм, преобразующий окрестность б в
окрестность ti6, лежащую внутри окрестности б. Тогда ri26 — ок-
окрестность, лежащая внутри окрестности т]б, т]3б, лежит внутри
-Т12б и т. д. (рис. 7.8). Пусть теперь в окрестности б определено
точечное отображение Т. Отображение Т в окрестности б эквива-
174

лентно отображению Тт (т — некоторое целое число) в окрест-
окрестности ti6, если
п-1Г"т1 - Т. B.11)
Действительно, от точки хеб к точке Тх можно, согласно
B.11), перейти, преобразовав точку х в точку у ^цх^г\8, при-
применив к ней затем преобразование Тт и вернувшись обратно в
Рис. 7 8
Рис 7.9
окрестпость б с помощью преобразования т] (рис. 7.9). А зто
и означает эквивалентность отображений ГиГв окрестностях
6 и, соответственно, т]6.
Рассмотренные ранее примеры вложенных структур и «мат-
«матрешка» соответствовали т = 1. Новое, формальное определение
несколько более общее. Согласно этому более общему определе-
определению для вложенности структур с т > 1 должен существовать
гомеоморфизм ц, преобразующий окрестность б в лежащую внутри
нее окрестность г\8, такой, что выполняется соотношение B.11).
Исключим неопределенность, связанную с выбором гомеомор-
гомеоморфизма т], и покажем, что ц можно считать обычным преобразо-
преобразованием подобия, например х -»- ах, где 0 < а < 1; г\ — гомеомор-
гомеоморфизм, преобразующий шаровую окреснтость б в ее часть т)б, по-
поэтому он эквивалентен отображению подобия, т. е. существует
гомеоморфизм | такой, что
Т1 = Г%1, B.12)
где £ — преобразование подобия. После подстановки в B.11)
имеем
i-'s-'&zt'k = т, или s-'sr-r's = m-\
или, накопец,
S-'JfS = Я, B.13)
где R = \Т\~1 — отображение, гомеоморфное Т. Таким образом,
для того чтобы отображение R, эквивалентное Т, допускало вло-
вложенные структуры, должно выполняться условие B.13), где £ —
отображение подобия:
£х = ах @<а<1). B.14)
175

Это означает, что решение уравнения B.13) относительно R при
всевозможных 0 < а < 1 дает все с точностью до эквивалентно-
эквивалентности отображения, допускающие вложенные структуры с задан-
заданным числом т.
Решение R* уравнения B.13) можно рассматривать как не-
неподвижную точку отображения
Л = 3?R = l-lRml, B.15)
определенного в пространстве всевозможных допустимых отобра-
отображений R.
Таким образом, вопрос о вложенных структурах свелся к воп-
вопросу о неподвижных точках отображения Я?, определенного в
пространстве отображений.
Пусть #~ — поверхность бифуркаций отображения R, отвеча-
отвечающих рождению то-кратной неподвижной точки, так что после
пересечения этой поверхности для некоторой точки i*s8
Rmx* = x*. B.16)
Для преобразования R = S~^R согласно B.15) имеем
R - ГгЩ, или Rm = Г1^,
и поэтому согласно B.16)
#mV = £x*. B.17)
Следовательно, точка £х* является то2-кратной неподвижной точ-
точкой отображения R, точка £2х* является »г3-кратной точкой ото-
отображения R = 2?~XR = 2?~ZR и так далее. Из этого вытекает сле-
следующий важный вывод. Если ST — бифуркационная поверхность,
па которой происходит рождение то-кратпой неподвижной точки,
то поверхность SJ~1^" является бифуркационной поверхностью
рождения т2-кратной неподвижной точки, поверхность 3?~гЗг —
бифуркационной поверхностью рождения ?га3-кратной неподвиж-
неподвижной точки и так далее. И поэтому серия бифуркаций, при которой
последовательно рождаются m-кратные неподвижные точки, за-
затем пгг-кратпые, »г3-кратные и т. д., соответствует последователь-
последовательным пересечениям поверхностей 2Г, i?^, 3?~г5Г, ... Поведение
последовательности поверхностей
У, g-'g', S-ZT, &-*&-, ... B.18)
существенно зависит от вида неподвижной точки отображения
3?~\ от .ее инвариантных многообразий S+ и S~ и их расположе-
расположения относительно бифуркационной поверхности ЗГ. Здесь можно
выделить случай, когда поверхность #~ пересекает одномерное
инвариантпое многообразие S~, а многообразие S+ имеет кораз-
коразмерность 1 (рис. 7.10). В этом случае последовательность поверх-
поверхностей B.18) имеет инвариантную поверхность S+ своей пре-
предельной поверхностью. Это не означает, что у нее нет других
предельных точек, но инвариантная поверхность
176

Рис. 7.10
предельных точек поверхностей B.18) и они приближаются к по-
поверхности S+ упорядоченно, «поверхность за поверхностью»
(рис. 7.10). Так происходит потому, что вдоль поверхности S+
отображение 3?~* растягивающее, а вдоль S~ сжимающее.
Рассмотренный случай интересен еще и тем, что предельное
множество бифуркационных поверхностей содержит многообра-
многообразие коразмерности единица,
и это делает достаточно ес-
естественным и частым пере-
пересечение с ней одномерных
кривых, отвечающих изме-
изменению какого-нибудь одного
скалярного параметра дина-
динамической системы, т. е. в
пространстве параметров ди-
динамической системы рас-
рассматриваемой серии бифур-
бифуркаций отвечает поверхность
коразмерности 1. Теперь уже
довольно очевидно, что для
последовательности бифур-
бифуркационных значений пара-
параметра, отвечающих пересече-
пересечениям с поверхностями B.18),
имеет место закоп Фойгенбаума. При этом ясно, что константа
Фейгенбаума равна единственному большему единицы корню
характеристического уравнения неподвижной точки отобра-
отображения 9?.
Таково возможное объяснение возникновения серий бифур-
бифуркаций удвоения. Ни для одномерного, ни тем более для много-
многомерного отображения описанная картина те получила полного
доказательства, хотя она хорошо подтверждается численными
вычислениями неподвижной точки отображения 2', возмож-
возможностью приближенного определения числа а и собственного зна-
значения, большего единицы, и нескольких других, меньших еди-
единицы. Наличие и характер пересечения кривой S~ и поверхности
ЗГ не выяснялся.
Помимо серий удвоения, можно ожидать серии бифуркаций
утроепия [197] и учетверепия, а также другие серии бифуркаций,
отвечающие другим вложенным структурам.
В заключение на рис. 7.11 наглядно представлена вложенная
структура для отображения прямой в прямую при т = 2 — би-
бифуркация удвоения кратности неподвижпой точки. На рис. 7.11
изображены графики отображения Т и Г2. График отображения
Т в квадрате Di подобен графику отображения Т2 в квадрате Dz.
Однократная неподвижная точка х2 отображения Tz соответ-
соответствует однократной точке xi отображения Т, но для отображе-
отображения Т точка х2 является двукратной неподвижной точкой.
177

.T I
Рис. 7.11
3. Серии бифуркаций при касании инвариантных многообра-
многообразий S+ и S~. Описываемые в этом разделе серии бифуркаций бы-
были обнаружены в работах [117—119, 137, 262]. Они возника-
возникают в процессе сближения и касания интегральных многообразий
седловых равновесий или седловых периодических движений. Ка-
Касания инвариантных многообразий S+ и S~ приводят к возник-
возникновению гомоклинических структур
или их изменениям как на уровне
исходных инвариантных многообра-
многообразий, так и новых, возникающих в
гомоклинической структуре. Эти се-
серии бифуркаций состоят в попар-
попарном рождении периодических дви-
движений разных типов, например Г2'2
и Г3'1, и последующем трансформи-
трансформировании периодического движения
Г3'1 по типу серии бифуркаций удвое-
удвоения периода. В результате возника-
возникает как бы двойная серия бифурка-
бифуркаций рождения пар и последующих
удвоений одного из движений в каж-
каждой паре. Рождение «из ничего» пар периодических движений,
по существу, уже было описано в главе 6 в ситуациях 2, 3 и 6.
Проводимое там рассмотрение следует лишь несколько продол-
продолжить с точки зрения происходящих в этих ситуациях бифур-
бифуркаций.
Вернемся к пегативу ситуации 2, в которой имеет место каса-
касание многообразий S+ и S~ седловой неподвижной точки, но вве-
введем теперь параметр е так, что при е > 0 касания нет, при е = О
происходит касание и при е < 0 — пересечение. Соответствующие
этим случаям негативы отображений Тт (т—1, 2, . ..) и ото-
отображения L, которое тоже равно некоторой степепи отображения
Т, изображены на рис. 6.11, б. Отображение Тт преобразует об-
область А в область А, а отображение L — в область В в В. Пози-
Позитив, отвечающий этим отображениям, показан на рис. 6.13. Здесь
отображение L преобразует область Вх в область В,. Это отобра-
отображение двузначно, в соответствии с этим область В^ состоит из
двух областей Вп и B,z. Отображение Тт преобразует область Bt
в область 5™. Если 5™ попадает внутрь области Ви то это оз-
означает существование двух неподвижных точек у отображения
TmL. При достаточно большом т в зависимости от величины па-
параметра е область В™ находится либо вне области Ви либо внут-
внутри нее. Входит она в область Вх через ее границу Ь, на которой
происходит рождение двух однозначпых ветвей отображения
Е, и константа Липшица отображепия £ обращается в бесконеч-
бесконечность. Пусть для конкретности отображепия Т и L представимы
в виде
T-L п = Ли@<Л<1), f = v»(Kv<»), B.19)
L; п = — a(v — 1)+ bu + 1, v = е + c(v — 1J + du.
178

При е =0 точка @, 1) на инвариантной,кривой S~ преобразует-
преобразуется отображением L в точку A, 0) на инвариантной кривой S+,
а кривая S~ преобразуется в кривую _S~, касающуюся в точке
A, 0) кривой S+. При е > 0 кривые 5~ и S+ не пересекаются,
а при е<0 пересекаются (рис. 7.12). Вспомогательные отобра-
отображения Т и Е записываются согласно B.19) в виде
L: и = —yv — du — е, ,у = 1-| j=yv-—du — в.
Ус Ус
Из B.20) следует, что граница Ъ области Вг в этом конкретном
случае определяется уравнением
v-du-г^О. B.21)
После этих пояснений вернемся к прерванному рассмотрению.
При убывании е область 5™ через границу Ъ попадает в область
В{. При этом «из ничего» рождаются две неподвижные точки, ко-
которые, как известно, должны быть
разных типов. Но затем с убывани-
убыванием параметра в по мере удаления об- /, >
ласти В™ от границы Ъ обе ветви
вспомогательного отображения TmL
становятся сжимающими, и обе по-
появившиеся неподвижные точки ото-
отображения — седловыми одного ти-
тина. Это означает, что одна из по-
появившихся точек претерпела какие-
то бифуркации, в результате чего рис 7.12
типы обеих точек стали одинаковы-
одинаковыми. Обратим внимание на одну деталь. Области В™ при возра-
возрастании тп уменьшаются и в зависимости от того, будет ли \Х < 1
или уХ > 1, приближаются к точке О (гг = у = О) по-разному.
При уХ < 1 приближение происходит вдоль оси v, а при vX > 1 —
вдоль оси п. В соответствии с этим неподвижные точки отобра-
отображения TmL возникают при малых в > 0 или только при в < 0.
Таким образом, по мере удаления от границы Ъ области В™
возникающие неподвижные точки отображения ТШЬ претерпева-
претерпевают бифуркации, после которых они становятся однотипными. При
этом ни одна из возникающих точек не может исчезнуть, и не
могут появиться новые оддократные неподвижные точки, по-
поскольку якобиан отображения TmL обращается в нуль только на
кривой Ъ. Это достаточная подсказка для того, чтобы понять, что
происходит с одной из родившихся простых неподвижных точек:
она меняет свой тип и отделяет от себя двукратную неподвиж-
неподвижную точку того же типа.
Проследим, как это происходит на конкретном примере ото-
отображений B.20). Отображение TmL можно записать в виде
м = Хт [—a{v — 1) + йи+ 1], v — vm [в + с (у — IJ + du]. B.22)
179

Из B.22) находим, что координаты и*, v* неподвижных точек
находятся из соотношений
adXm .._„,] ,_.* лч .-m . dXm
с {v* _ 1J + _
— v-mj(i;* — I) — v~"
1-ЬХт
f8 = 0, B.23)
i-ЬХ71
— ЪХ71
Запишем еще характеристическое уравнение этих неподвижных
точен:
%{z) = zz - [ЪХт + 2cvm(v* - l)]z +
+ Xmvm [ad - 2bc (у* - 1) ] = z2 + xz + ц = 0. B.24)
Критическое значение е = e*, при котором происходит рождение
пары неподвижных точек, определяется согласно B.23) усло-
условием
adXT'
1-ЬХ
— V
-4с _
1-ЬГ
+ е* = 0. B.25)
При этом значении е = е* один из корней характеристического
уравнения B.24) равен единице,
так что
1 + т + ц = 0, B.26)
где т и ц определяются, как вид-
видно из характеристического урав-
уравнения B.24), формулами
x = -bKm-2cvm(v*-l),
B.27)
На рис. 7.13 показано разбиение
плоскости параметров т, ц харак-
характеристического уравнения B.24)
Рис. 7.13 н& области D(s), отвечающее s
корням внутри единичного круга
и 2 — s вне его. Границами разбиения па этой плоскости явля-
являются Л'+1, N-i и JV,. При е = е* точка (т, ц) лежит па бифурка-
бифуркационной границе N+1. При большом т в зависимости от того,
какое из неравенств Ал> < 1 или A/v > 1 выполняется, она распо-
располагается вблизи оси т либо, напротив, весьма далеко от нее.
Пусть, ради определенности, Xv < 1. Точка М соответствует не-
неподвижной точке в момепт ее рождепия. При дальнейшем умень-
уменьшении е (е < е*) появляются две неподвижные точки, каждой
из которых отвечают свои значения т и v. Это приводит к раз-
раздвоению точки М на две точки Ж, и Мг. При уменьшении е от
значения е* после раздвоения одна из точек на плоскости т, м-
180

смещается налево, а другие направо. Сначала они попадают в об-
области -D(l) и -0B), поэтому им соответствуют неподвижные
точки типов О1-1 и О20. При дальнейшем уменьшении параметра
е точка, смещающаяся направо, достигает бифуркационной гра-
границы iV_, и пересекает ее. При этом неподвижная точка О2'0
превращается в неподвижную точку типа Ql>1 и одновременно
от нее рождаются две двукратные неподвижные точки типа О2'0.
Приведенный пример можно сделать еще прозрачнее, если за-
заметить, что все написанные формулы упрощаются с обращением
коэффициента d в нуль. Более того, в этом случае отображение
TmL сводится, согласпо B.22), к одномерному хорошо знакомому
отображению вида
F = vmE + c(i;-1)V\ B.28)
Его график представлен на рис. 7.14. С уменьшением е парабола
графика отображения спускается вниз. При е = е* возникает кри-
критическая неподвижная точка, которая
затем разбивается на две неподвижных
точки иг и v2. Сначала одна из них
устойчива, а другая — неустойчива. Не-
Неустойчивая и при дальнейшем убыва-
убывании параметра е остается неустойчи-
неустойчивой, а устойчивая точка становится не-
неустойчивой, претерпевая бифуркацию,
соответствующую границе iV_,. При
этой последней бифуркации рождает-
рождается двукратная устойчивая точка, с ко-
которой происходит такая же бифурка-
бифуркация и т. д., пока устойчивая точка не
исчезнет и не останутся в бесконеч-
бесконечном числе одни неустойчивые точки.
Выше были рассмотрены только серии бифуркаций непод-
неподвижных точек отображения TmL при всевозможных т > т*.
. Аналогичным образом могут быть рассмотрены' и серии бифурка-
бифуркаций отображений более общего вида
Ы L ... L L (Z.Zy)
и даже бесконечных в обе стороны последовательностей отображе-
отображений вида
Гт1т Tm^T TmsT /9 ЧП\
Li I 1-t ... 1 Zv... [tZ.GU)
«Ключом» к рассмотрению таких последовательностей отображе-
отображений является позитив отображения TnLTm, т. е. вспомогательное
отображение TnLTm.
Последующие рассуждепия носят вполне общий характер.
Однако ради конкретности они будут проводиться па примере
отображений Т и L вида, определяемого формулами B.19). В этом
181
Рис. 7.14

случае отображения TnLTm и TnLTm представимы в виде
v = vn [е + с (vmv - lJ + Л"ц],
и = 1п\ ±= Vv~nv-dlmu - s + Ыти + ll, B.31)
у = v L уь ^v y ~"dA и ~Е + т
Вспомогательное отображение TnLTm преобразует свою область
определения G в некоторую область G. Чем больше целые чис-
числа иг и га, тем меньше область G. Одной из границ области опре-
определения является линия
v-"» - dkmu - е = 0, B.32)
на которой происходит ветвление на две однозначные ветви вспо-
вспомогательного отображения TnLT^, так что область G может быть
определена неравенствами вида
OsSwsSa, O^v<b, v~nv - dXmu -s>0. B.33)
Область G, согласно B.33), пе больше области, определяемой
при некотором К^ неравенствами
\U ~ ^ iTJ^t" ТХAЕГ i'i!r,»,V« ' 1/2V B-34)
I у у~ ^с }£ v~ шах (\ б I 5l v~ j
и лежит внутри области G, если выполнепы условия
v-"-m - dkn+m - е> К2тах(Кп+т, v-"-m)max(lel1/2, Г/2, v~n'2).
B.35)
Напротив, область G лежит заведомо вне области G при выполне-
выполнении условия
B.36)
Области значений тип, определяемые неравенствами B.35) и
B.36), разделены очень узкой щелью
-К2тахAп+т, v-n-m)max(lE|l/2, Kn'\ v"m/2)<
<.v-"-m-dXn+m-e<K2max(lm+n, v-n-m)max(l8l1/2, Xn/2, v"m/2).
B.37)
Применяя теорему, сформулированную в гл. 6, приходим к сле-
следующему выводу.
182

Последовательность отображений вида
B.38)
реализма, если все пары чисел пг, тв удовлетворяют услови-
условиям B.35), и нереализуема, если хотя бы одна такая пара удов-
удовлетворяет условию B.36).
Необходимо иметь в виду, что в этой последовательности каж-
каждое из отображений L можно трактовать либо как сужение Lu
отвечающее одной однозначной ветви двузначного вспомогатель-
вспомогательного отображения Е, либо как сужение L2, отвечающее другой
однозначной ветви вспомогательного отображения. При больших
положительных е ни одно из условий B.35) при ns, ms> N вы-
выполняться не может. Напротив, при больших отрицательных 8
всевозможных последовательностей вида B.38) появляется бес-
бесконечное континуальное множество.
Выясним условия сжимаемости отображений TnLTm. Из (8.31)
непосредственно находим, что
где
6u =
du
du
du
du
0Л
8u +
n+m
du
dv
a
?,
8v,
JJA
8v =
n+m
dv
du
8u
dv
So,
aknv~n n
2
^ = -4v—D,
Ус ]/v-nv— d\mu — e
Для сжимаемости достаточно выполнения неравенств
du dv du dv _ ^. ,
du du ' g'v g~v
или неравенств
B.39)
> К3 max(Km+n,
n), Ып+т < q. B.40)
Эти неравенства обеспечивают седловои характер последо-
последовательностей отображений вида B.38). С уменьшением е они
обязательно выполняются, если ранее были выполнены нера-
неравенства B.35).
Теперь можно подвести итог. При уменьшении е происходит
счетное множество бифуркаций рождения пар неподвижных то-
точек отображений вида B.31) и континуальное множество пар
последовательностей вида B.38). Кроме того, с одной из непод-
неподвижных точек каждой родившейся пары происходит бесконечная
серия бифуркаций удвоения кратности. Нечто подобное проис-
происходит и с последовательностями вида B.38). После завершения
183

этих серий удвоения остаются только седловые неподвижные точ-
точки. Это заведомо имеет место при выполнении неравенств B.40).
Все сказанное описывает бифуркации только в одной из ок-
рестпостей гомоклинической структуры, а таких окрестностей в
гомоклинической структуре может быть очень много. Сколько-
нибудь полпое рассмотрение этого вопроса достаточно запутано
и сложно, поэтому мы ограничимся сделанным замечанием.
Ситуация, аналогичная описанной, имеет место и при про-
прохождении через петлю седлофокуса, т. е. при образовании и ис-
исчезновении двоякоасимптотической замкнутой фазовой траекто-
траектории, идущей из седлофокуса в него же. Эта петля есть необщее
(пегрубое) пересечение интегральных многообразий S+ и S~ сед-
седлофокуса. Наличие серий бифуркаций уже отмечалось при рас-
рассмотрении ситуации 6 в гл. 6. Более подробное рассмотрение
проводится по изложенному образцу.
§ 3. Бифуркации и стохастический аттрактор
в системе Лоренца
Как уже говорилось, дифференциальные уравнения Лоренца
возникли как трехмодовое дискретное приближение в задаче
о тепловой конвекции между горизонтальными плоскостями.
В гл. 1 было показано, что уравнения Лорбпца с параметром
Ъ = 1 являются основпыми в описании конвективной циркуляции
жидкости в замкнутом круговом контуре. Наличие в них непе-
непериодических установившихся движений было установлено в
1963 г., но достаточно полпое исследование было выполнено
только в 1976—78 гг. сразу в нескольких работах [46, 68, 69,
276—278, 280, 539, 551, 552, 679], среди которых можно выделить
два направления: одно, идущее от «подковы Смейла», и второе —■
от гомоклинических структур А. Пуанкаре.
Гомоклипическая структура, обнаруженная в системе Лоренца,
сравнительно очень проста. В ней нет той непостижимой сложно-
сложности, о которой писал А. Пуанкаре, и в этом смысле она уникаль-
уникальна. Упрощение вызвано особенностями структуры трехмерного
фазового портрета, находящими отражение в наличии линии раз-
разрыва точечного отображения на секущей плоскости, и возмож-
возможностью разделения неременных, о чем вкратце уже говорилось.
Ниже дается более подробное изложение результатов исследова-
исследования системы Лоренца
х = — ах + оу, у = rx — y — xz, z = — bz + xy, C.1)
анализируются перестройки ее фазового портрета и бифуркации
при возрастании параметра г. Параметры о, Ъ и г предполага-
предполагаются положительными. Наиболее полные численные исследова-
исследования относятся к случаю о = 10, Ъ = 8/3 и г < 150, по рассматри-
рассматривались и другие случаи.
Перейдем к непосредственному исследованию системы Лорен-
Лоренца C.1), разбив его на пункты.
184

1. Замена переменных х, у, z на —х, —у, z не меняют вида
уравнений C.1), и поэтому фазовый портрет симметричен от-
относительно оси z.
2. Все фазовые траектории системы C.1) идут внутрь
сферы
V = x2 + y2+(z-o-ry = K2{o + rJ C.2)
с центром в точке х = у = 0, z = о + г и радиусом К (а + г). Дей-
Действительно, согласно C.1) производная по времени от фупкции
V = х2 + yz+(z-a-rJ
равна
Поэтому сделанное утверждение будет иметь место, если сфера
C.2) лежит вне эллипсоида, определяемого уравнением V = О,
что заведомо имеет место, если
3. При возрастании времени имеет место повсеместное сжатие
фазового объема, поскольку для уравнений C.1)
div(x, у, г) = -1-Ь-а<0. C.3)
4. Точка О (х = у = z = 0) является состоянием равповесия
при всех значениях параметров Ъ, о и г. Его характеристическое
уравнение имеет вид
(Л + Ъ)[Х2 +(о + 1)Л + оA - г)]= 0. C.4)
Из C.4) следует, что при г < 1 имеет место состояние равно-
равновесия типа О30, а при г> 1 — типа О2'1, т. е. соответственно ус-
устойчивый узел и седлоузел, а бифуркация происходит при пере-
переходе через границу No.
5. При г > 1, кроме описанного состояния равповесия О
(x = y = z = O), имеется еще два состояния равновесия О, и О
с координатами х = у = ±УЪ(г— 1) и z = г — 1. Они возникают
при потере устойчивости состоянием равповесия О при г = 1 и
расположены симметричпо относительно оси z. В силу симмет-
симметрии их типы одинаковые и определяются корнями характеристи-
характеристического уравнения
Х3+(а + Ь+ i)V + b(o + r)K + 2bc(r-i) = 0. C.5)
Согласпо этому уравнению C.5) при возрастании г от зпачепия
г = 1 эти состояния равновесия Oi и О2 являются последователь-
последовательно устойчивыми узлами типа О\л и О\л, затем устойчивыми
фокусами и при
2
седлофокусами 6V и О2' .
185

6. Смена устойчивости состояний равновесия Oi и О2 проис-
происходит при переходе через границу iVm и поэтому сопровождается
либо влипанием в них неустойчивых седловых периодических дви-
движений, либо рождением устойчивых периодических движений.
Что именно произойдет, зависит от знака ляпуновской величины.
Ее подсчет дает, что имеет место влипание неустойчивого перио-
периодического движения. При Ъ — 8/3 и о = 10 потеря устойчивости
состояниями равповесия и одновременное влипание в них неус-
неустойчивых седловых периодических движений Т\'г и Г^'2 соглас-
согласно C.6) происходит при г = 24,74.
Для того чтобы понять, откуда взялись периодические движе-
движения Г4 и Г2, будем уменьшать параметр г от бифуркационного
значения г = 24,74 и численно прослеживать периодические дви-
движения Г4 и Г2. При г = 13,92 периодические движения 1\ и Г2
превращаются в петли инвариантных кривых Si и S2 седло-
вого состояния равповесия О2'1 (рис. 7.15).
7. Теперь можно описать фазовые портреты при 0 < г < 1 и
при 1 < г < 13,92. В первом случае состояние равновесия О гло-
глобально устойчиво, и к нему стя-
стягиваются все фазовые траек-
траектории. Когда параметр г, воз-
возрастая, переходит через бифур-
бифуркационное значение г = 1, со-
состояние равновесия О 'теряет
свою устойчивость и из него
появляются два новых устой-
устойчивых равновесия Ot и О2. Все
фазовые траектории стремятся
к одному из них. Разделяющей
их границей является инвари-
инвариантная поверхность состояния
равновесия О (рис. 7.16). При
возрастании параметра г от
Рис. 7.15 г = 1 следует проследить изме-
изменения двух' инвариантных кри-
кривых iS7 и £Г, выходящих из точки О. При г= 13,92 они превра-
превращаются в гомоклинические петли и оказываются на двумерной
инвариантной поверхности S+ состояния равповесия О (рис. 7.15).
8. Прослеживание дальнейших изменений фазового портрета
при возрастании г удобнее проводить, используя секущую плос-
плоскость 2 с уравнением z = г — 1 (рис. 7.17).
При г = 13,92 на секущей плоскости z = г — 1 фазовый порт-
портрет точечного отображения имеет такой вид, как показано на
рис. 7.18. На рис. 7.18 линия R — след пересечения интегральной
поверхности S+ состояния равновесия О с секущей S, О4 и Ог —
состояния равновесия, которые оказываются па секущей плоско-
плоскости z = г— 1. Точки Mi и Ni (Д#2 и iV2) — последовательные точ-
точй й Si (S^) с секущей
ки
186
пересечепия инвариантной кривой

плоскостью S. Из рис. 7.17 можно представить вид фазового
портрета точечного отображения на секущей 2 при значениях г,
несколько меньших бифуркационного значения г = 13,92. Точки
Ми Nu ... и М2, N2, ... — последовательные точки пересечения
S^ и iS7 с секущей. Кривая R разбивает секущую плоскость на
Рис. 7.16
Рис. 7.17
/У,
две части, каждая из которых, является областью притяжения
одного из устойчивых состояний равновесия О4 или О2, которые
на секущей являются устойчивыми неподвижными точками.
Линия R разделяет области притяжения неподвижных точек
#1 и О2, и на ней отображение Т секущей Е разрывно; близкие
точки, расположенные по разные стороны от линии R, преобра-
преобразуются в далеко отстоящие друг от друга точки. Разрывность
преобразования секу-
секущей вызвана тем, что
при приближении к ли-
линии R время движения
фазовой точки до сле-
следующего пересечения
секущей 2 неограничен-
неограниченно возрастает. Фазовая
траектория, начинаю-
начинающаяся в точке М, близ-
близкой к линии R, дви-
движется вблизи поверхно-
поверхности S+ к точке О, за-
затем вдоль кривой S~[ или S^ в зависимости от того, с какой сто-
стороны от кривой R расположена точка М. Двигаясь вблизи S~[ или
SJ, она вновь пересекается с секущей S в точке М, близкой к
Mi, или соответственно М2. При приближении к кривой R с ка-
какой-нибудь ее стороны точка М в пределе совпадает с Mi или Мг.
Таким образом, отображения Т с каждой из сторон кривой R
187
Рис. 7.18

могут быть непрерывно продолжены на кривую R. Продолжен-
Продолженные отображения будут непрерывными с каждой из сторон кри-
кривой R, включая саму кривую R. Однако одно продолженное ото-
отображение будет преобразовывать ее в точку Mi, а другое — в точ-
точку Мг (рис. 7.17).
На рис. 7.17 изображен общий вид фазового пространства и
секущей 2 при значениях параметра г, несколько меньших 13,92.
Напомним, что остальные параметры о и Ъ предполагаются ради
определенности фиксированными: о = 10, Ъ = 8/3. При возраста-
возрастании г вплоть до значения г = 13,92 вторые точки пересечения iV,
и N2 интегральпых кривых <ST и £<Г с секущей плоскостью 2
приходят на линию разрыва R. Это соответствует появлению у со-
состояния равновесия О двух петель 5^ и SJ, показанпых на
рис. 7.15. Напомним, что эти петли лежат на интегральной по-
поверхности S+ состояния равновесия О, а точечное отображение
на секущей плоскости 2 при этом имеет вид, условно изображен-
изображенный на рис. 7.18 (условно в том смысле, что на рис. 7.18 пред-
представлен отдельный его фрагмент, а не глобальная картина, кото-
которая в целом достаточно сложна). На рис. 7.18 по разные стороны
от кривой R определены разные отображения 7\ и Т2. Они сим-
симметричны. Кривые Pi и Р2 они преобразуют в кривую R, а кри-
кривую R в точки М, и М2, которые, в свою очередь, преобразуются
в точки Ni и N2 кривой R. Области, лежащие между кривыми Pt
и R, Р2 и R, стягиваются соответственно к неподвижным устой-
устойчивым точкам О, и О2. Сказанное означает, что любая внутрен-
внутренняя точка этих областей при после-
последовательных преобразованиях асимп-
асимптотически приближается соответствен-
соответственно к неподвижной точке либо Oh
либо О2.
9. При дальнейшем увеличении па-
параметра г сверх г == 13,92 от каждой из
замкнутых петель интегральных кри-
кривых S^ и S^ рождается неустойчивое
седловое периодическое движение 1\ и
соответственно Г2. Эта бифукация рож-
рождения периодических движений от пе-
петель седлового равновесия рапее была
рассмотрена в гл. 5. На секущей по-
поверхности этой бифуркации отвечает
отделение от точек iV, н N2 двукрат-
двукратных пенодвижных точек, которые мы обозначим теми же бук-
буквами Г\ и Г2, что и соответствующие им периодические движе-
движения. Точки пересечения N{ и N2 интегральпых кривых S~ и S^
состояния равновесия О с секущей S с возрастанием г переме-
перемещаются, пересекая линию R при г = 13,92. Фазовый портрет на
секущей S пепосредственпо после перехода параметром 'г через
значение 13,92 изображен на рис. 7.19. На следующем рис. 7.20
188
о—
i
*;
г2
\
2.
R
"" О
Рис. 7.19

показан общий вид основных элементов трехмерного фазового
портрета. Новыми являются периодические движения Tt и Г2 и
их двумерные интегральные многообразия 57* и Sf, S2 и52, Сле-
Следы пересечения с секущей плоскостью 2 периодческих дви-
движений и их интегральных многообразий на рис. 7.19 обозна-
обозначены также через Г\, Г2, S^, S^, Si и S2 • При г, не-
немного превышающем 13,92, точки Г\, Г2, iVi и N2 близки к
Рис. 7.20
линии R (при г-»- 13,92 они стремятся к линии R). Как показы-
показывает численный счет *), взаимное расположение точек Nt и Л~2
и инвариантных кривых Sf и' S£ неподвижных точек Г, и Г2
именно таково, как показано на рис. 7.19. С дальнейшим ростом
параметра г их взаиморасположение изменится и примет вид, по-
показанный на рис. 7.21. Изменение их взаимного расположения
происходит при г = 24,06. При этом бифуркационном значении
параметра г = 24,06 точки N< и iV2 лежат соответственно на ин-
инвариантных кривых S~i и 52 .
Рассмотрим фазовые портреты на секущей плоскости S
(z = г — 1), изображенные на рис. 7.19, 7.21 и фазовый портрет
рис. 7.22, соответствующий граничному бифуркационному слу-
случаю. На всех этих портретах имеются две седловых неподвижных
точки и соответствующие им интегральные многообразия S+ и S'.
На рис. 7.19 опи пересекаются и образуют гомоклиническую
структуру. На рис. 7.21 этого пересечения нет, рис. 7.22 — гра-
граничный.
*) При малых превышениях г над 13,92 такое расположение согласу-
согласуется с теоретическими выводами.
189

Таким образом, гомоклиническая структура у уравнений Ло-
Лоренца возникает при г = 13,92. Наличие гомоклинической струк-
структуры означает существование бесконечного множества / всевоз-
всевозможных седловых, в том числе и всевозможных периодических,
движений. Однако при 13,92 «S г < 24,06 они не образуют ат-
аттрактора. Это следует хотя бы из того, что инвариантпые кривые
О,
о
2.
1
в, >
к,
R
о,
г,
Рис. 7.21
Рис. 7.22
Sx и S2 выходят за пределы множества /, поскольку они вы-
выходят за пределы полосы между инвариаптными кривыми St и
S£, где находится множество / (рис. 7.19).
Дальнейшие изменения с ростом параметра г включают ин-
инвариантные многообразия £Г и S7 в множество инвариантных
седловых движений /. Происходит это при г > 24,06 (рис. 7.22
и 7.21). Ближайшее следующее изменение фазового портрета
происходит при г == 24,74: периодические движения Г4 и Г2 сли-
сливаются соответственно с состояниями равновесия Ог и О2. На се-
секущей плоскости этому соответствует слияние неподвижных то-
точек Y, и Г2 с точками О{ и О2. Таким образом, при г = 24,06 воз-
возникает стохастический аттрактор. Он уже рассматривался в § 2
гл. 6 (ситуация 4). Дополним теперь это рассмотрение выясне-
выяснением вида предельного множества / при г = 24,06 и доказатель-
доказательством возможности сведения преобразования секущей плоскости
2 в себя к преобразованию прямой в прямую, о чем кратко уже
говорилось в гл. 4. Обратим внимание на то, как все точки фазо-
фазового пространства (за исключением, конечно, неустойчивых рав-
равновесий) «поглощаются» стохастическим аттрактором, и на то,
что аттрактор при возрастании параметра возникает из «ничего»
жестко. Жесткое возпикповение стохастического аттрактора про-
проще всего проследить на соответствующем отображении прямой
в прямую.
10. На рис. 7.22 изображен фазовый портрет точечного отобра-
отображения Т на секущей плоскости при г = 24,06. При преобразова-
преобразовании Т четырехугольник Г^ГгЛ^ преобразуется в себя так, что
190

область Di .преобразуется в Т)и a D2 — в £J (рис. 7.23). При этом
области Ki и К2 (рис. 7.22), лежащие вне четырехугольника
TtNiTiNi, попадают внутрь этого четырехугольника. Такое «по-
«поглощение» фазовых точек четырехугольником NiTiN2T2 происхо-
происходит с каждым преобразованием Т. Четырехугольнику NiTiN2Ti
в трехмерном фазовом пространстве отвечает некоторая область
G. Она преобразуется в себя так, что за каждую единицу време-
времени ее объем V уменьшается до объема Ve~l~"~b, а освободивший-
освободившийся объем в области G заполняется фазовым объемом, приходя-
приходящим извне. Это в конечном счете приводит к приходу всех то-
точек фазового пространства в область G, за исключением, конеч-
конечно, точек неустойчивых равновесий Ot и О2.
Что же происходит в самой области G? Вернемся к секущей
плоскости._Области Z)t и D2 преобразование Т переводит^ в обла-
области Di и D2. В свою очередь, ^аждая. из областей DA и Б2 преоб-
преобразуется в две области Dn, D^2 и D2U D22, лежащие в областях
%
sz
D.. D,
я, hi
Рис. 7.23
Di ж D2. Каждая из областей Dv, преобразуется в две области Din
и Dtj2, лежащие в областях DH и D32 соответственно. Этот про-
процесс преобразования областей можно продолжать неограниченно,
при этом область
\ч..лп C.7)
преобразуется в две области
Dhir..ini и Dhh...in2. C.8)
Первая иа них лежит в области D,2,3...,ni, вторая—внутри области
23n
К этому следует добавить, что каждый раз при преобразова-
преобразовании Т происходит сжатие в направлении кривых S+ и растяже-
пие вдоль кривых S~. Предельное множество этих вложенных
друг в друга областей (число их растет как 2") и есть стохасти-
стохастический аттрактор. Он состоит из континуума предельных кривых,
каждой из которых можно присвоить некоторую бесконечную
191

последовательность номеров iit i2, is, ••■, так что кривая ^i^i^..
есть предел вложенных друг в друга областей
Dh гэ Dhh гэ Dl3hh гэ Л Wl ^ ... C.9)
11. Перейдем теперь к вопросу о сведении точечного отобра-
отображения Т двумерной секущей 2 к одномерному точечному отобра-
отображению. Сведение понимается в следующем смысле: если подхо-
подходящим образом выбрать на секущей плоскости переменные и и v,
то отображение Т в пих запишется в виде
й =■/(»), v=g(u, v), C.10) .
где gv(u, v) <<7<1. Запись в таком виде означает, что координат-
координатные линии и = const преобразуются друг в друга и последова-
последовательные координаты преобразований v стремятся к некоторой по-
последовательности значений vu i>2, ..., определяемой только после-
последовательностью значений щ, и2, ... Искомые координатные ли-
линии и строятся последовательно следующим образом. Отображе-
Отображение Т разрывно па линии R и разбивается на два отображения
7\ и Т2, совпадающих с Т по разные стороны от линии разрыва R.
В качестве первой серии координатных линий и примем ли-
линии 7\ 1Л и Т2 1i?(s1 = l, 2, ...), в качестве второй — линии
Т^2Тг$1В и T2hTihR (s2 = 1, 2, ...), в качестве третьей — линии
Т~$3Тг°2тГхП и Т^тТЧ^Я (», = 1,2,...)нт. д. Эти линии не
пересекаются и образуют всюду плотное заполпение области D.
Согласно этому построению выбор координатных линий и един-
единствен. Напротив, в выборе координатных линий v имеется неко-
некоторый произвол. Преобразуя область D в прямоугольник так, что-
чтобы координатные линии и были прямыми, вх качестве линий v
можно, например, выбрать систему прямых, ортогопальных ли-
линиям и. В выбранных таким образом переменных отображение Т
записывается в виде C.10), поскольку под действием отображе-
отображения Т координатные линии и переходят друг в друга, а по пе-
переменной v имеет место сжатие.
Рассмотрим теперь отображение прямой в прямую, опреде-
определяемое первым соотношением C.10). При г = 24,06 оно имеет
вид, показанный па рис. 7.24. На графике точечного отображе-
отображения точки Ni и iV2 отвечают разным сторонам линии разрыва R,
а точки Ft и Г2 — таким же точкам на секущей. График точеч-
точечного отображения симметричен относительно начала координат,
и точки Ni и Г\ и соответственно, N2 и Г2 при г = 24,06 имеют
одинаковые координаты п. Самое незначительное уменьшение
параметра г опускает точку 1\ ниже точки Nz, и странный ат-
аттрактор исчезает, поскольку все точки отрезка (+1, —1) оказы-
оказываются за его пределами. Напротив, при г = 24,06 или немного
больше этого значения (рис. 7.25) точка 1\ лежит выше' точки
Л^2, отрезок J преобразуется в себя, и к нему стягиваются точки
отрезка (+1, —1). Это говорит о скачкообразном, жестком воз-
102

никновении стохастического аттрактора при переходе параметра
г через критическое значение г* = 24,06. Критическое значение
г* зависит от параметров о ж Ъ, входящих в уравнение Лоренца.
При а = 10 и Ъ = 8/3, как уже указывалось, оно равно 24,06. За-
Зависимость г* от о при Ъ = 8/3 представлена на графике рис. 7.26.
Вернемся немного назад к рис. 7.23, а и б. Эти рисунки схе-
схематические, не соответствующие реальным масштабам. На самом
Рис. 7.24
Рис. 7.25
деле области D± и ZJ очень тонкие, и характерные размеры обла-
областей DiU Bl2, D2i, D22 отличаются от нуля лишь в третьем знаке.
Сказанное означает, что последовательные преобразования секу-
секущей плоскости 2 после небольшого числа преобразований попа-
попадают в окрестность некоторой кривой. Так, при рассматриваемых
ниже значениях параметров круг хг + уг < 10 после одного пре-
преобразования превращается в полос-
полоску не шире 0,5, а после двух-трех
преобразований — в полоску не шире
10~3. Эти очень топкие полоски на
рис. 7.27 изображены линиями Л и /2.
Естественно, что на этих линиях нахо-
находятся неподвижные точки Ot, O2, 1\ и
Г2. Пренебрегая толщиной этих полос и
рассматривая их как линии /t и /2, мы
тем самым приводим отображение Т
двумерной секущей 2 в себя к отобра-
отображению кривой в кривую. Вводя на
этой «кривой» координату и, получа-,
ем одномерное отображение
u = f(u), C.11)
приближенно описывающее асимптотическое поведение отобра-
отображения секущей плоскости 2. С точностью до сделанных прибли-
приближений оно совпадает с таким же по описанию отображением пря-
прямой в прямую, к которому свелось отображение на аттракторе /.
193
70
70 20
Рис. 7.26
30 0

На рис. 7.27 кривые /t и Л, найденные численно, показаны для
серии значений параметра г. При изменении г меняется и одно-
одномерное отображение C.11). При значительном возрастании г опо
перестает быть всюду растягивающим. Более того, на графике
точечпого отображения появляются точки с горизонтальной ка-
касательной, как это имеет место у неоднократно упоминавшегося
преобразования
х = ахA — х),
что также приводит к появлению устойчивых многократных не-
неподвижных точек, а у системы Лоренца — устойчивых периоди-
периодических движений. В частпости, при г = 100 такое устойчивое
Рис. 7.27
периодическое движение было найдено численно [68]. Оказалось,
что оно существует в интервале изменения параметра г [99, 98;
100,06].
С помощью преобразования прямой в прямую C.11) поведе-
поведение фазовых траекторий уравнения Лоренца можно отобразить
в виде серии точечных отображений прямой в прямую, показан-
показанных на рис. 7.28. Первый рис. 7.28, а отвечает устойчивости со-
состояния равновесия О @<г<1), второй рис. 7.28,6 — появле-
появлению двух устойчивых состояний равновесия О, и О2, третий
рис. 7.28, в — рождению неустойчивых периодических движений
Г± и Г2 и появлению разрыва непрерывности, четвертый
рис. 7.28, г — возникновепию стохастического аттрактора, пятый
рис. 7.28, д — влипанию периодических движений 1\ и Г2 в со-
состояния равновесия ft и О, и последний 7.28, е — появлению
у графика точечного отображения горизонтальных касательных и
в связи с этим устойчивых неподвижных многократных точек.
Мы видим, что в этой интерпретации возникновение стохастич-
ности в системе Лоренца похоже на то, как возникает стохастич-
ность в неустойчивом осцилляторе с отрицательным трением и
ударами, рассмотренном в гл. 3.
194

Рис. 7.28

§ 4. Бифуркации й фазовый портрет осциллятора
и ротатора с параметрическим возбуждением
В этом параграфе рассматриваются уравнения вида
Ф = со, со = М — hu> +(v + \i sin t)sin ф, D-1)
где ф — угловая переменная, а М, h, v и \i — параметры. Такие
дифференциальные уравнения описывают, например, движение
дисбалансного ротора или маятника на колеблющемся основании,
движение заряженной частицы в поле синусоидальной волны и
многое другое. В системе, описываемой уравнениями D.1), воз-
возможны как явления синхронизации, так и хаотизации движений.
При M~h — O система D.1) представляет собой неавтономную
гамильтонову систему, которая при замене этф на ф превраща-
превращается в широко известное уравнение Матье, описывающее явле-
явления линейного параметрического возбуждения и резонанса. При
v = 0 уравнения D.1) имеют прямое отношение к задачам син-
синхронизации вибраторов, находящихся на общем основании, и ис-
исследовались в 1967 г. в работе [60], где были обнаружены как
различпые типы сипхронизмов, так и непериодические движения,
устойчивые по Пуассону, а по современной классификации — ха-
хаотические движения. Более детальпо случай v = 0 исследовался
в работах [62, 65, 67]. Отдельно и весьма подробно изучались
случаи I = /i = 0hI = v = 0 [6.3, 64, 66].
Неавтономная система D.1) с помощью новой угловой пере-
переменной G может быть записана в виде автономной системы треть-
третьего порядка вида
Ф = со, 0 = 1, со = М — hat — (v + [a sin e)sin<p, D 2)
фазовое пространство которой трехмерно и цилиндрично по пе-
переменным ф и G. Двумерный цилиндр G = 0 является для урав-
уравнений D.2) секущей поверхностью, на которой фазовые траек-
траектории порождают отображение Т. К изучению его сводится изу-
изучение движений и фазового портрета трехмерной динамической
системы D.2).
Дифференциальные уравнения D.1) содержат четыре пара-
параметра М, h, v и \i, в связи с чем рассмотрение зависимости фазо-
фазового портрета от них целесообразно разбить на частные случаи:
случай М = h = 0, дополненный последующим выяснением зави-
зависимости от параметра h, и случай v = 0, дополненный рассмот-
репием малых и больших h. Роль параметров М, h, v, ц в форми-
формировании фазового портрета и его бифуркаций различна в соот-
соответствии с их физическим смыслом: h — параметр величины дис-
диссипации, |j, — параметрического внешпето воздействия, М — внеш-
внешнего постоянного воздействия, v — возвращающей к равновесию
силы упругости.
196

1. Случай М = h = 0. Выпишем ради удобства в этом случав
уравнения D.1) отдельно в виде
8 = 1, (p+(v + nsine)sincp = O. D.3)
Будем исследовать точечное отображение Т на секущем цилиндре
8 = 0 путем численного счета на ЭВМ по специальным програм-
программам исследования точечного отображения [283], включающим про-
программу численного отыскания неподвижных точек, корней их ха-
характеристических уравнений и их инвариантных кривых S+ и S~.
Ключом к исследованию фазового портрета и его зависимости от
параметров является выделение синхронизмов Гр, и построение их
инвариантных кривых S+ и S~.
Синхронизм Гр, — это периодическое решение ф = ф(£), для
которого выполняется соотношение
D.4)
где р и q — целые числа (р — 1, 2, ..., q = 0, ± 1, ± 2, ...), при-
причем целое число р Ф 0 не может быть уменьшено. Период этого
периодического движения равен 2пр, a 2nq имеет смысл общего
изменения угла ф при обегании фазовой точкой замкнутой фазо-
фазовой кривой, отвечающей синхронизму ГРв. Поэтому синхронизм
с q = 0 отвечает колебательному движению, а синхронизм с
с/ Ф 0 — вращательному. Синхронизму Гр, на секущей 8 = 0 отве-
отвечает цикл р-кратных неподвижных точек, который мы также обо-
обозначим через Гр,.
Так как рассматриваемая система гамильтонова, то при дви-
движении фазовых точек сохраняется фазовый объем, и отображение
Т секущей 6 = 0 сохраняет площадь. Следовательно, характери-
характеристическое уравнение любой неподвижной точки точечного отобра-
отображения секущей G = 0 в себя имеет вид
р2 + Лр+1 = 0, D.5)
и его корни pt и р2 либо действительные и такие, что ptp2 = 1, ли-
либо они комплексно сопряженные: pt = ре1ф и р2 = ре~'ф. В первом
случае при I pir2 f Ф 1 мы получаем неподвижную точку типа седла,
во втором — типа центра. Бифуркации неподвижной точки воз-
возможны только при р4 = р2 = 1 или pi = р2 = — 1, т. е. при А = — 2
и А = 2. Схематически все возможные простейшие осповные би-
бифуркации представлены на рис. 7.29, аи б. При каждой из этих
четырех бифуркаций либо одна неподвижная точка превращается
в три, либо три неподвижные точки — в одну. Различие в случаях
Pi = р2 = 1 и pt = р2 = — 1 состоит в том, что неподвижные точки
ГР, заменяются неподвижными точками удвоенной кратности
Ггргд, что соответствует удвоению периода соответствующих пе-
периодических движений.
Опишем синхронизмы Гр, систем D,3). Начнем с значений па-
параметров \i = v = 0. При этих значениях дифференциальные урав-
уравнения D.3) интегрируются, и
Ф + а>г, D.6)
197

где ф и со — начальные значения ф(£) и ф(£) при t = 0. Этим на-
начальным условиям отвечает синхронизм Yvq при условии, что
D.7)
т. е. когда со = q/p и значение ф — любое. Синхронизмам ГРа на
Рис. 7.29
секущем цилиндре 6 = 0 отвечают неподвижные точки, для кото-
которых со = q/p и ф — любое. Множество этих неподвижных точек об-
образует окружность (рис. 7.30). Фазовая траектория, выходящая
из любой точки (ф, со = q/p), пересекает цилиндр
последовательно в точках
Ф + 2~, со
ф +
-£-, со), ..., U+2nq?—-s со
Рис. 7.30
и, наконец, снова в точке (ф, со), обежав q раз
вокруг цилиндра G = 0, в положительном направ-
направлении при q > 0 и в отрицательном — при q < 0.
Значению со = 0 (9 = 0) отвечают состояния
равновесия.
Обратим внимание на то, что синхронизмы
Грд на цилиндре 8 = 0, а следовательно, и в фа-
фазовом пространстве, всюду плотны. Можно ду-
думать, что наибольшее значение имеют синхро-
синхронизмы с малыми значениями чисел р и q. Во всяком случае,
только они могут сохраняться с появлением сил диссипации в
виде НФО. Общее доказательство этого факта содержится в ра-
работе [i42].
От тривиального случая v = \i = 0 перейдем к простому слу-
случаю р, = 0, т. е. к уравнению
Ф + v sin ф = 0. D.8),
198

Это уравнение также интегрируется, и его первый интеграл
имеет вид
£_ _ v cos ф = Я. D.9)
Фазовый портрет точечного отображения на цилиндре 6 = 0, сов-
совпадающий по виду с фазовым портретом автономного консерва-
консервативного ротатора D.8), изображен на рис. 7.31. Точки Oi и О2 —
неподвижные точки типа центр и седло; S — замкнутые кривые,
2п
Н
Рис. 7.31
Рис. 7.32
изображающие совпадающие инвариантные кривые S+ и S~ сед-
ловой неподвижной точки О2. Точке Ot соответствует Н = — v,
а точке О2 соответствует Н = v. Остальным фазовым кривым от-
отвечают значения Н > — v, причем при —v < Н < v — это замкну-
замкнутые фазовые кривые, охватывающие точку Ot и изображающие
периодические колебательные движения, а при Н > v — замкну-
замкнутые кривые, охватывающие цилиндр и изображающие периоди-
периодические вращательные движения. Период т этих движений зави-
зависит от у ж Н. При Н -*■ — v он стремится к 2л/Уу, при Н -*■ v не-
неограниченно возрастает, а при #-*■<» стремится к нулю. Каче-
Качественный вид графика зависимости периода т от Н показан на
рис. 7.32. При v ->- 0 фазовый портрет рис. 7.31 переходит в фа-
фазовый портрет рис. 7.30. При этом область колебательных дви-
движений, заключенная между линиями S, переходит в линию
со = 0, так что каждое колебательное движение системы D.8)
стягивается к состоянию равновесия ф = ср = 0. Каждое враща-
вращательное движение TPi {q Ф 0) системы D.8) возникает из соот-
соответствующего вращательного движения ТРд системы D.8) при
v = 0, непрерывно меняясь с изменением параметра v. Напротив,
колебательные синхронизмы Гр0 при возрастании параметра v
отделяются от точки Ot (ф = со =0), причем синхронизм Гро си-
системы D.8) отделяется от точки Ot при v = q2/p2, где q — число
колебаний за период 2пр. Синхронизмы ГРа пересекают цилиндр
199

G = 0 по замкнутым кривым, и поэтому образуют в исходном
трехмерном пространстве двумерные тороидальные поверхности
с периодической обмоткой и числом вращения Пуанкаре q/p. Ос-
Остальным замкнутым кривым на секущей G = 0 также отвечают
тороидальные интегральные многообразия, но с квазипериодиче-
квазипериодической обмоткой.
От случая [х = 0, непрерывно меняя параметр ц, переходим
к случаю [х Ф 0. Проследим за тем, что происходит с синхрониз-
синхронизмами Tvq. С непрерывным изменением параметра \х от нуля в ок-
окрестности каждой кривой на секущем цилиндре 6 = 0, отвечаю-
отвечающей синхронизмам YPq, возникает г синхронизмов Ypq, отвечаю-
отвечающих 2г циклам р-кратных неподвижных точек, г из которых —
типа центр и г — типа седло. Каждая из седловых неподвижных
точек имеет свои инвариантные кривые S+ и S~. Все это вместе
образует фазовый портрет вида, представленного на рис. 7.33
(г=1 ир = 4). Он несколько упрощен, поскольку на самом де-
деле, как правило, кривые S+ и S~ пересекаются, образуя гомокли-
ническую структуру, ранее названную стохастическим синхрониз-
синхронизмом. На рис. 7.33 упрощенно представлены и окрестности непод-
неподвижных точек типа центр, о чем ниже будет сказано.
Фактическое построение фазовых портретов, возникающих с
изменением параметра [х от каждого синхронизма ГР„ или, что
то же, от соответствующего резонансного уровня уравнения D.8),
Рис. 7.33
Рис. 7.34
требует численного счета на ЭВМ. На рис. 7.34 показаны некото-
некоторые из таких вычисленных фазовых портретов синхронизмов при
v = 0 и |х = 0,185. Под Т(р, q, r) имеются в виду циклы непод-
неподвижных точек Гра типа центр и седло, число которых равно 2г,
совместно возникшие из соответствующего резонансного уровня.
Подчеркнем, что «фазовый портрет» па рис. 7.34 включает только
неподвижные точки и инвариантные кривые. Проведение вычис-
вычислений позволило обнаружить, что при р и q нечетных г = 1, а ес-
если числа р и q разной четности, то г == i или г = 2 в зависимо-
200

сти от того, в какой из двух некоторых областей находятся зна-
значения параметров v и [х.
Таким образом, с увеличением параметра и. от нуля каждый
резонансный уровень уравнения D.8) порождает соответствую-
соответствующий синхронизм Г (р, q, r) как совокупность 2г циклов непод-
неподвижных точек, отвечающих отдельным синхронизмам Г„д, поло-
половина из которых — типа центр, а половина — типа седла. Таких
синхропизмов Г (р, q, r) возникает счетное множество, и возника-
возникают они из всюду плотного множества резонансных Уровней синхро-
синхропизмов Tpq уравнения D.8). Однако сложность фазового портрета
системы D.3) при и. Ф 0 этим не исчерпывается. Области, возник-
возникшие внутри каждого из синхронизмов возле его неподвижных точек
типа центр, в свою очередь, порождают счетное множество синхро-
синхронизмов, каждый из которых, в свою очередь, таким образом по-
порождает новые синхронизмы и так далее. Таким образом, возни-
возникает сложнейшая бесконечная иерархия «вложенных структур».
Численно в этой иерархии вложенных структур обнаруживаются
четкие закономерности, однако сколько-нибудь полное теорети-
теоретическое изучение закономерностей их следования в настоящее
время отсутствует. То, что известно, выяснено численно в конк-
конкретных системах на основе изложенных выше в § 2 этой главы
соображений о рождении синхропизмов при изменении парамет-
параметра из неподвижной точки типа центр. Именно эти соображения
приводят к пониманию общей картины вложенных структур и
являются путеводными при численном исследовании.
Следующие полезные сведения дает общая теорема о конечно-
конечности числа синхронизмов при наличии диссипации. Численпый
счет позволяет выявить, как происходит исчезновение синхрониз-
синхронизмов и какие синхронизмы остаются. У сохраняющихся сипхро-
низмов неподвижные точки типа центр становятся устойчивыми
фокусами, седла сохраняют свой тип, а их инвариаптные мно-
многообразия могут образовывать сложные гомоклинические струк-
структуры.
В описапной иерархии структур с каждым из синхронизмов
при изменении параметров могут происходить бифуркации, кото-
которые были описаны выше и изображены на рис. 7.29. В частности,
эти бифуркации могут приводить к тому, что «устойчивые» син-
синхронизмы, отвечающие неподвижным точкам тина центр, будут
удваивать свои периоды, одновременно порождая все новые и
повые седловые неустойчивые синхронизмы и приводя к возник-
возникновению гомоклипических структур и хаотизации движений. Этот
процесс, как показывают конкретпые численные исследования,
начинается с синхронизмов низких рангов, доходит до высших,
охватывая всю иерархию вложепных структур. Под рапгом сип-
хронизма [61, 65] понимается его порядковый номер в иерархии
вложенных структур. Нулевой ранг имеют синхронизмы, рожда-
рождающиеся от резопансных уровней. Первый ранг имеют синхрониз-
синхронизмы, рождающиеся из неподвижных точек типа центр синхрониз-
синхронизмов нулевого ранга. Второй ранг имеют синхронизмы, рождаю-
201

\
щиеся от неподвижных точек типа центр синхронизмов первого
ранга и так далее. На рис. 7.35 показана область, где все синхро-
синхронизмы иерархии структур оказываются седловыми из-за завер-
завершения серий бифуркаций удвоения периода с синхронизмами
всех рангов. Это не исключает возможности неседловых точек за
счет бифуркаций прикосновений инвариантных кривых S+ и S~,
которые не всегда удается
обнаружить при численном
счете. На рис. 7.36 изобра-
изображены 2 • 103 итераций при
]х = 2, v = 0. Как пересека-
пересекаются в этом случае инвари-
инвариантные кривые S+ и S~
лишь нескольких седловых
неподвижных точек, показа-
показано на рис. 7.37.
Как уже отмечалось, вся
эта великолепная картина —
фазовый портрет иерархии
вложенных структур, при-
примеры которой представлены
на рис. 7.38, исчезает с по-
появлением демпфирования.
Исчезновение начинается с
Рис. 7.35 синхронизмов высоких ран-
рангов, так что сколь угодно
малое демпфирование оставляет лишь конечное число синхрониз-
синхронизмов. Всякий оставшийся синхронизм типа центр демпфирование
превращает в устойчивый фокус, седло же остается седлом. П07
этому после того,' как процесс перевода синхронизмов типа центр
в синхронизмы удвоенного периода закончен и остались только
седловые синхронизмы, можно думать, что достаточно малое
демпфирование не разрушит хаотичности движений.
Случай v =■ 0. Уравнение D.1) в этом случае принимает вид
ю, 9 = 1, а — М -1- ha — \х sin 9 sin ф.
D.10)
Здесь можно выделить подслучай h> M, замечательной особен-
особенностью которого является сжатие всего фазового трехмерного про-
пространства ф, 9, и в очень малую окрестность некоторой двумер-
двумерной поверхнбсти. На секущем цилиндре 8 = 0 эта поверхность
оставляет след в виде кривой /, как показано на рис. 7.39. Тем
самым рассмотрение поведения фазовых траекторий приближен-
приближенно сводится к точечному отображению окружности в себя (топо-
(топологически кривая / — окружность).
При ц = 0 уравнения D.10) интегрируются, так что
202

Рис. 7.36
Рис. 7.37
a.

Фазовый портрет точечного отображения секущей 9 = 0 в соот-
соответствии с D.11) имеет очень простой вид, показанный на
рис. 7.40. Все фазовые траектории при t -*■ + оо асимптотически
экспоненциально приближаются к окружности и = M/h. На этой
окружности / имеет место отображение
Ф = Ф + 2л ^-(mod 2л). D.12)
Проследим теперь, как меняется это отображение D.12) окруж-
окружности в себя с ростом параметра ц. Пусть для определенности
М = 0,1 и h = 1. Тогда при значениях \i,
равных соответственно 0,0; 0,5; 0,7; 0,94;
1,1; 1,32; 1,9; 2,2; 3,5 и 4,3, точечные
отображения окружности / в себя вы-
выглядят так, как показано на рис. 7.41.
Рис. 7.39
Рис. 7.40
Мы видим, что при малых ц, < 0,92 имеют место либо квазипе-
квазипериодические движения, либо синхронизм высоких порядков. При
\х « 0,92 возникает касание графика функции точечного отобра-
отображения с биссектрисой, а затем сначала две, потом четыре точки
пересечения. Это означает появление сначала одного, а затем
двух устойчивых периодических движений периода 2я. При даль-
дальнейшем росте параметра ц- они теряют устойчивость, но взамен
появляются устойчивые периодические движения периода 4л.
Уже при ц = 1,44 устойчивые неподвижные точки численно не
обнаруживаются, и движения системы посят хаотический харак-
характер (естественно, в малой окрестности некоторой тороидальной
поверхности, пересекающейся с секущим цилиндром 8 = 0 по
замкнутой кривой J). При дальнейшем увеличении параметра \х
возникают новые пересечения графика точечного отображения с
биссектрисой, т. е. вновь, но уже для очень узкого промежутка
значений параметров возникают устойчивые периодические дви-
жепия периода 2л, 4л и т. д. Затем наступает хаос. При дальней-
дальнейшем увеличении параметра ц картина повторяется, но с каждым
разом области существования устойчивых периодических движе-
движений периодов 2я, 4л, ... по параметру \l становятся меньше и
меньше. При больших значениях параметра \х они практически
исчезают, и движения приобретают хаотический характер. Инте-
204

/г-0
/1=0,34
р-7,9
ресно отметить, что хотя с ростом и вновь и вновь возникают
устойчивые периодические движения периода 2л, все опи различ-
различных типов. При первом воз-
никповепии это — синхро-
синхронизмы Гю, втором — Гц,
третьем — Г12.
Таковы выводы, которые
непосредственно следуют из
серии графиков рис. 7.41,
получеппых при числепном
счете на ЭВМ. Вместе с тем,
ото описание все же не-
несколько огрублено. Ему бы-
было бы легко придать точный
смысл, если бы у системы
D.10) имелся асимптотиче-
асимптотически устойчивый двумерный
тор и кривая / была бы сле-
следом его пересечения с се-
секущей 8 = 0. Но так дело
обстоит не при всех значени-
значениях параметра \l. С появлени-
появлением двузначности обратного
отображения окружности
в себя кривая / не может
быть следом пересечения ин-
интегрального двумерного то-
тора с секущим цилиндром
0 = 0. Неоднозначность воз-
возникает оттого, что / являет-
является следом пересечения с се-
секущей 8 = 0 некоторого тон-
тонкого тороидального слоя, в
котором движепия фазовых
точек зависят не только от
координаты и вдоль кривой
J, но и от малых попереч-
поперечных отклонений от кривой /.
Фактически мы имеем то-
точечное отображение в себя
тонкого кольца, которое
приближенно заменено ок-
окружностью /. Отображение
кольца в себя было рассмот-
рассмотрено в § 2 гл. 6 (ситуа-
(ситуация 5). Как следует из это-
этого рассмотрения, наличие
сильной сжимаемости отображения в поперечном к кольцу на-
направлении, т. е. по его радиусам, пе препятствует отсутствию
205
У)
А
л

инвариантной гладкой кривой внутри кольца и хаотичности дви-
движений в нем. Сформулированные там достаточные условия хао-
хаотичности используют только наличие растяжений вдоль кольца
и то, как преобразуется координата (назовем ее и) вдоль кольца.
Эти сведения и дает отображение окружности в себя на рис. 7.41.
Для того чтобы отображение кольца приобрело хаотический ха-
характер, согласно этим условиям у точечного отображения окруж-
окружности в себя должны быть участки растяжения, а само отобра-
отображение должно быть неоднозначно обратимым.
Выше было рассказано о результатах численного исследования
уравнения D.10) при М = 0,1; h = 1. Однако, как показали
аналогичные численные исследования, такие же результаты по-
получаются и при других значениях параметров М и h, если только
h> М. При несоблюдении этого условия и h < М возможность
сведения к точечному отображению окружности в себя исчезает,
и необходимо исследовать точечное отображение двумерного ци-
цилиндра в себя. Общая схема изменений фазового портрета ока-
оказывается следующей. При малых \х возникают устойчивые вра-
вращательные синхронизмы, области притяжения которых разделя-
разделяются сепаратрисами S+ и S~ седловых неподвижных точек.
С ростом параметра ц число их возрастает, и вместе с этим воз-
возникают пересечения сепаратрисных кривых седловых неподвиж-
неподвижных точек, отвечающих разным синхронизмам. Это приводит к
усложнению вида областей притяжения устойчивых синхрониз-
синхронизмов. Дальпейшее увеличение параметра и- сопровождается появ-
появлением новых пересечений сепаратрис и возникновением гомо-
клинических структур, содержащих циклы. При этом характер
приближения фазовых точек к устойчивым синхронизмам носит
весьма сложный немонотонный характер: фазовая точка то при-
приближается к нему, то удаляется и, лишь попав в достаточно ма-
малую его окрестность, стремится к нему. В соответствии с этим
области притяжения устойчивых синхронизмов имеют сложпый
и тонкий характер. При дальнейшем росте параметра \i начина-
начинаются бифуркации удвоения периодов устойчивых синхронизмов
с одновременным образованием новых седловых синхронизмов,,
которые ведут к еще большей хаотизации движений и утоныпе-
нию областей притяжения устойчивых синхронизмов. При ни-
ничтожно малых возмущениях фазовая точка блуждает по поверх-
поверхности секущего цилиндра, не попадая в малые окрестности устой-
устойчивых синхронизмов.
Ниже приводится более полное описание фазовых портретов
и их изменений для М = 0,1; h = 0,05 м 0<ц< 1,8. При ц, = О
фазовый портрет имеет такой же вид, как на рис. 7.40. Первая
существенная бифуркация с ростом параметра ц происходит при
[А = 0,11. При этом возпикает сложная неподвижная точка типа
седлоузел, которая с дальнейшим ростом и- распадается на устой-
устойчивую узловую неподвижную точку А+ и неустойчивую седловую
В+. Затем с ростом параметра ц в интервале 0,12 < ц < 1,43 ус-
устойчивая узловая точка А+ становится устойчивым фокусом, от-
206

вечающим синхронизму типа Гц. Отметим, что в момент рож-
рождения синхронизма при \i = 0 его число вращения Пуапкаре рав-
равнялось двум, а для этого устойчивого синхронизма оно равно еди-
единице.
На рис. 7.42 показан общий вид фазового портрета при
ц = 0,25. Все фазовые точки приближаются либо к синхронизму
/, либо к синхронизму А+.
При |j, — 0,301 возникает новая сложная седлоузловая непод-
неподвижная точка, которая, как и предыдущая, распадается на устой-
устойчивую узловую А+ и седловую
В~. Опи отвечают синхрониз-
синхронизму типа Г,-!.
На рис. 7.43 изображен фа-
фазовый портрет при \л = 0,35.
Рис. 7.42
Рис. 7.43
На нем, как и на предыдущем рис. 7.42, отмечены разными щтри-
ховками и отсутствием штриховки области притяжепия разных
синхропизмов.
Несмотря на сложный вид фазового портрета, его общая струк-
структура очень проста: цилиндр 9 = 0 разбивается на три области
притяжения синхронизмов А+, А~ и J. Это соответствует разбие-
разбиению трехмерного исходного фазового пространства на три области
притяжения трех устойчивых синхронизмов. При дальнейшем
росте параметра ц- возникают сначала касания, а затем и пере-
сечепия сепаратрисных кривых 5+ и S~ не только различных,
но и одних и тех же синхронизмов. Это приводит к образованию
гомоклинических структур, содержащих циклы. Фазовый портрет
207

необычайно усложняется, поскольку появляется бесконечное мно-
множество синхронизмов седлового типа. Области притяжения устой-
устойчивых синхронизмов усложняются и становятся очень тонкими.
Фазовая точка может долго хаотически двигаться, прежде чем
начнет приближаться к одному из устойчивых синхронизмов
А+, А~ и /. На рис. 7.44 приведен упрощенный фазовый портрет
точечного отображения на се-
секущем цилиндре 9 = 0 при \i =
= 1,15. Сепаратрисные инвари-
инвариантные кривые седловых не-
неподвижных точек В+ и В~ об-
образуют довольно сложную сеть
взаимопересечений. На рис. 7.44
оставлены только первые точ-
точки пересечения кривых 5+ и
S" седловых синхронизмов
В+ и В-.
Дальнейший рост парамет-
параметра ц приводит к исчезновению
спачала устойчивого синхро-
синхронизма /, а затем через бифур-
бифуркации типа N+i происходит
смена устойчивости синхрониз-
синхронизмов А+ и А~.
Исчезповение устойчивого синхронизма / происходит при «пе-
«перехлесте» сепаратрис S+ и S' седла В+. Эта бифуркация имеет
место при \х = 1,205. После нее фазовый портрет приобретает
вид, показанный на рис. 7.45. Обе бифуркации синхронизмов А+
и А~ типа iV+i происходят при изменении параметра от 1,39 до
Рнс. 7.44
Рис. 7.45
Рис. 7.46
1,40. Каждая такая бифуркация приводит к появлению двух но-
новых устойчивых синхронизмов того же типа. При fj, = 1,5 соот-
соответствующий портрет показан па рис. 7.46. При дальнейшем уве-
увеличении параметра ц- с новыми устойчивыми синхронизмами,
появившимися из А+ и А', происходят бифуркации удвоепия пе-
208

риодов. Вновь возникшие устойчивые синхронизмы удвоенных
периодов типов Г22 и Г2-2. Можно думать, что при дальнейшем
возрастании параметра ц устойчивые синхронизмы с удваиваю-
удваивающимся периодом исчезают, однако утверждать, будто устойчивые
синхронизмы полностью отсутствуют, после этого нельзя, так как
они могут появляться вследствие все новых и новых касаний
инвариантных кривых 5+ и S~ седловых синхронизмов, число
которых бесконечно. Вместе с тем, области притяжения этих
устойчивых синхронизмов настолько тонки, что попытки их пря-
прямого численного обнаружения обычно ничего не дают.
§ 5. О возникновении хаоса и стохастичности
в диссипативных динамических системах
Подведем краткий итог соображениям о причинах и путях
возникновения хаоса и стохастичности в диссипативных динами-
динамических системах. Приводимые выше примеры системы Лоренца
и ротатора с параметрическим возбуждением будут существенно
пополнены в гл. 9, содержащей описания и анализ конкретных
систем, допускающих стохастические и хаотические колебания.
Общей причиной хаотизации и стохастизации движепий ди-
динамической системы являются потеря ими устойчивости и экспо-
экспоненциальное разбегание близких фазовых траекторий, сочетаю-
сочетающиеся с их общей ограниченностью и некоторым их общим сжа-
сжатием. Простейшей моделью экспоненциальной неустойчивости в
сочетании е общим сжатием может служить экспоненциальное
нарастание отклонения с последующим его сбросом. Эту воз-
возможность можно представить себе как на физическом уровпе, так
и на уровне преобразований фазового пространства, отображаю-
отображающих реальные движения физической системы. В фазовом про-
пространстве ей соответствует наличие области G, в которой фазо-
фазовые траектории экспоненциально разбегаются и затем покидают
ее. После того как фазовые траектории покидают область G, ха-
характер движепия изменяется, и дальнейшее движение фазовых
точек приводит к их возврату в исходную область G. Этот воз-
возврат в область G и есть фаза сброса возпикшего отклонения. За-
Затем все повторяется. Такова простейшая модель. Ее можпо фор-
формализовать в виде двух последовательных преобразований Т и S
фазового пространства видов, показанных на рис. 7.47. С первой
фазой связывается возбуждение, вызванное неустойчивостью,'
подкачкой энергии, более или менее бурным развитием процесса,
со второй — возвращение к исходному состоянию за счет каких-
то перестроек, протекающих в системе процессов, изменения их
характера. Простейшим примером таких фаз может служить
описанный выше неустойчивый осциллятор с демпфирующими
ударами, когда парастание колебапий сменяется их умепъшепи-
ем в результате удара. Нечто подобное в движениях системы Ло-
Лоренца представляют собой раскачки возле неустойчивых цирку-
циркуляции, результатом которых является переброс к другой сим-
209

метричпой циркуляции, раскачка возле нее и переброс к.преж-
к.прежней и т. д. Нечто подобное представляют и движения маятника
на колеблющемся основании, где смена ситуации — это измене-
изменение соотношения фаз колебаний маятника и точки подвеса.
Подобные общие соображения могут быть развиты для систем,
г __
а
77/f///////////ТТТ>ь
Рис. 7.47
описываемых далее в гл. 9. Конечно, это всего лишь качествен-
качественные общие представления о механизмах стохастизации и хаоти-
зации движений динамических систем.
Недостаточны они уже потому, что и периодические автоко-
автоколебания — также результат противоборства двух тенденций не-
неустойчивости и раскачки системы и ограничения этой раскачки.
При этом причины неустойчивости и раскачки могут быть одни
и те же, а различие заключается в характере ограничения: в пер-
первом случае это замедление и ограничение нарастания, а во вто-
втором — сброс. Но что такое ограничение и что такое сброс? Како-
Каковы модели и как поточнее охарактеризовать эти различия и их
механизмы?
Дальнейшее продвижение требует изучения точечных ото-
отображений Т и R, описывающих разбегание и соответственно сброс.
Для многих случаев это было сделано в гл. 6 при рассмотрении си-
ситуаций 1—10. Сейчас это рассмотрение будет продолжено в более
общем плане.
Наиболее явно нарастание и сброс видны у преобразования
вида
хп+1 = qxn — [qxn],
где q > 1 и [z] означает целую часть z.
Фаза нарастания — это преобразование вида
Фаза сброса — это переход от уп+1 к xn+i по формуле
Жп+1 = Уп+1 — [Уп+l],
E.1)
E.2)
E.3)
после которого av+i опять становится меньше* единицы.
Сравним теперь преобразование E.1) с преобразованием
/Л | f-f / /Л \ /V» I ^ /Л
Хп+1 Q\Xn)Xn, \д.4:)
где q(xn) — убывающая функция от х„, так что для некоторых а
и Ъ (a<b) q(a)>l и
210

В этом случае при некотором а<х* < Ъ q(x*) = 1. При хп <
< х* последующее значение xn+i > х„, но по мере приближения хп
к х* разность хп+1 — хп убывает. Более того, при х„ > х* эта раз-
разность отрицательна.
Приведенные примеры можно рассматривать как простейшие
модели, поясняющие механизмы плавного ограничения нараста-
нарастания и его сброса. Почему же в первом случае имеют место не-
непредсказуемость и случайность, а во втором этого пет? Различие
состоит в том, как очень отдаленные значения хп зависят от на-
начального а-о или, вообще, как х„ зависит от хт при п, много боль-
большем т. Во втором случае для того, чтобы найти х„ с точностью
е, необходимо задать х0 с точностью г/К, где К — некоторое,
может быть, и большое, но одно и то же число для всех п. В пер-
первом случае дело обстоит совсем иначе: для того чтобы найти
хп с точностью е, необходимо знать ха с точностью не меньшей,
чем е/q". С ростом п эта требуемая точность нерграничеппо окс-
поненциально растет, и именно эта неограниченная потеря точ-
точности делает значения х„ для больших п непредсказуемыми, в то
время как во втором случае они все предсказуемы с точностью
е, если только точность задания х0 не меньше е/К. Факт неогра-
неограниченной потери точности преобразованием E.1) можно видеть
еще и в том, что значения х„ с ростом номера п определяются все
более и более далекими десятичными разрядами записи началь-
начального значения х0. Особенно наглядно это при q = 10, поскольку
в этом случае хп — просто число, десятичная запись которого по-
получается отбрасыванием первых п знаков в десятичной записи
числа ха.
Этот характер зависимости последующих значений х„ от пре-
предыдущих является общим для стохастических движений, он сле-
следует из так называемой символической записи движений детер-
детерминированной динамической системы.
Обоснованием такой символической за-
записи могут служить теоремы гл. 6 о су-
существовании и единственности тех или
иных последовательностей точечных
отображений. Так, для точечного ото-
отображения Т прямой в прямую, изоб-
изображенного на рис. 7.48, обратное,отоб-
ражепие сжимающее и двузначное.
Примем его однозначные ветви за
вспомогательные отображения Tt и Т2-
Сужением Ti и Тг исходного отобра-
отображения Т, отвечающим однозначным
ветвям Tt и Тг вспомогательного ото-
отображения, является отображение Т,
определенное соответственно только на отрезке [0, 1/2] и от-
отрезке [1/2, 1].
Возьмем произвольную точку х0 ^ [0, 1]. Ее последовательные
преобразования xt = Тх0, хг = Txt, ..., xs+i — Txs, ... соверша-
Рис. 7.48
211

ются либо с помощью сужения Ти если соответствующее х3 е
е[0, 1/2], либо с помощью Г2, если ха^{\/2, 1]. Каждой точке х0
отвечает некоторая последовательность чисел
£о> Ч) 1г, • • •, is, ■ ■ ч \Э.э)
каждое из которых либо 1, либо 2. По теоремам о последователь-
последовательностях точечных отображений для любой такой последовательно-
последовательности из единиц и двоек найдется точка х0, которой она соответ-
соответствует. Такая точка единственная, поэтому соответствие между
точками х0 отрезка [0, 1] и всевозможными последовательностя-
последовательностями E.2) взаимно однозначное. Взаимная однозначность следует
из растягивающего характера отображения Т. Действительно,
если таких точек две, х0 и х0, то при любом п
\г — т \ — 2\х л—х , I = ~2п\х — х \<:\
что невозможно.
Таким образом, точки х0 отрезка [0, 1] и всевозможные после-
последовательности E.5) находятся во взаимно однозначном соответ-
соответствии, а последовательности E.5) можно
трактовать как некоторую обобщенную
двоичную запись числа х0. Для отображе-
отображения рис. 7.48 это обычная двоичная
запись числа х0. Если отображение
рис. 7.48 заменить на отображение
рис. 7.49, то- взаимная однозначность
сохранится, но последовательность E.5)
уже не будет обычной двоичной записью
числа х„.
Посмотрид!, как выглядит отображе-
пие Т, если воспользоваться записью чис-
Рис. 7.49 ла хо в виДе последовательности4 E.5).
Непосредственно ясно, что числу Xi =
= Тх0 будет отвечать последовательность iu г2, г3, •.., числу
хг = Txi — последовательность i2, h, ii, ■ ■ ■ и т. д. Поэтому мож-
можно записать, что
T(is, i.+l, ...)="(«.+., «.+., •••)• E-6)
Это и есть символическая запись точечного отображения Т. За-
Заметим, что она одна и та же для отображения как рис. 7.48, так
и рис. 7.49. Опа одинакова не только для этих отображений, но
и для любого отображения Т многомерной области G в себя,
если только это отображение имеет сжимающее двузначное об-
обратное отображение Т, распадающееся па две однозначные ветви
f\ и Тг. Сказанное переносится на случай многозначного сжима-
дощегося обратного отображения. Для пего также возможна
запись в виде E.6) с тем лишь различием, что теперь последова-
последовательности E.5) состоят не из единиц и двоек, а большего набора
чисел или символов ©t, ft>2, ..., ©m.
212

Сказанное легко переносится на произвольное точечное ото-
отображение Т с мпогозначным сжимающим вспомогательным ото-
отображением Т. Но теперь в случае седлового отображения Т не-
необходимо считать последовательности E.5) бесконечными в обе
стороны вида
..., г_2, i-x, i0, г'х, i2, ■. . E.7)
Последовательность E.7) с отмеченным символом £0 взаимно од-
однозначно связана с точкой х0. При пребразовании Т отмеченный
символ U заменяется на it. При s-кратном применении преобра-
преобразования он переходит в символ is. Сама же бесконечная после-
последовательность E.4) остается без изменений. С помощью записи
отображения Т в виде E.6) или, в более общем случае, в виде
Т (..., £_ь £0, £х, ...) = (..., £_х, £0, £1? i2, ...), E.8)
где стрелками указаны отмеченные символы, можно объяснить,
почему последующее движение фазовой точки с течением време-
времени определяется все более и более далекими разрядами десятич-
десятичных записей компонент начального ее положения. Множество
точек, отвечающих всевозможным последовательностям E.7) с
заданными символами г_„ . .., i0, iu .. ., £s, составляют некоторую
область, которая стягивается в точку при s -»- °°. Из этого следу-
следует, что задание нескольких первых десятичных разрядов может
определить только конечные числа символов справа и слева от
отмеченного. Вместе с тем положение точки Т'пх0 при достаточ-
достаточно больших тп определяется симво-
символами, расположенными слева и спра-
справа от нового отмеченного символа
к записи хт, которые при т > s за-
зависят от более далеких десятичных
разрядов точки х0.
Выше речь шла о некотором иде-
альпом сочетании нарастания и раз-
бегания с последующим сбросом.
Однако нередко наряду с растяже-
растяжениями имеются и сжатия. Харак-
Характерным примером может служить
отображение прямой в ирямую, изо-
изображенное на рис. 7.50. Оно всюду
растягивающее, кроме малых участ-
участков возле точек Ми Мг, ... — экст-
экстремумов графика точечного отобра-
отображения рис. 7.50. Хаотизация движений имеет при этом другую
природу. Она обусловлена не неустойчивостью, а недостаточной
устойчивостью имеющихся периодических движений. Эта недо-
недостаточность заведомо имеет место, если устойчивые периодиче-
периодические движения располагаются в ограниченной области фазового
пространства и изображаются фазовыми кривыми достаточно
213
Рис. 7.50

большой длины. При этом даже очень слабые возмущения при-
приводят к случайным перескокам фазовой точки при ее движении
с одних участков периодических движений на другие. С физи-
физической точки зрения и с точки зрения моделирования на ЭВМ
здесь, как и в первом случае полной неустойчивости, наблюдает-
наблюдается хаотизация движений.
Вместе с тем для отдельных значений параметров и такие
отображения могут обладать настоящей локальной неустойчи-
неустойчивостью, хотя эта неустойчивость, если можно так выразиться,
эфемерна (негруба) и может исчезнуть от сколь угодно малых
изменений параметров. Тем не менее для «точных» значений
параметров она существует. В качестве примера приведем уже
встречавшееся нам отображение
х = ахA — х)
при а = 4. Замена переменных х = — A — cos 2я0) приводит его
к виду [9, 143, 534]
= 29 — f20],
совпадающему с E.1) при q = 2.
Перейдем теперь к вопросу о том, как сочетаются в фазовом
пространстве разбегание и сброс. Как сочетаются нарастание и
ограничение нарастания, хорошо известно, и на этом мы оста-
останавливаться не будем. Нас будут интересовать только нараста-
нарастание и сброс, приводящие к хаотизации и стохастичности.
В основе возникновения стохастических и хаотических дви-
движений лежат гомоклинические структуры, именно они порожда-
порождают сочетание неустойчивости, локального разбегания и общего
сжатия. Вместе с тем переход от устойчивости к неустойчивости
требует исчезновения устойчивых состояний равновесия и устой-
устойчивых периодических движений или достаточно большого увели-
увеличения их периодов, точнее, длин соответствующих фазовых кри-
кривых. Устойчивые периодические движения и состояния равнове-
равновесия могут потерять устойчивость или исчезнуть лишь несколь-
несколькими вполне определенными способами. В этом смысле можно
говорить о различных путях перехода к хаосу и стохастичности.
Эти возможные пути были описаны в § 1 этой главы. Позволим
себе их вкратце перечислить.
1. Устойчивое состояние равновесия пли периодическое дви-
движение сливается с соответствующим неустойчивым движением,
и оба состояния исчезают.
2. Состояние равновесия или периодическое движение теря-
теряет устойчивость, одновременно порождая устойчивое периодиче-
периодическое движение или соответственно устойчивое двумерное торои-
тороидальное многообразие с периодической или квазипериодической
обмоткой.
3. Устойчивое периодическое движение либо стягивается в
точку, порождая устойчивое равновесие, либо сливается с рав-
214

новесием, порождая у него двоякоасимптотическую кривую как
пересечение свбих интегральных многообразий S+ и S~.
4. Периодическое движение теряет устойчивость, но одно-
одновременно появляется устойчивое периодическое движение удво-
удвоенного периода. Эта последняя трансформация может повторять-
повторяться много раз, образуя бесконечную серию бифуркаций удвоения
периода.
В результате перечисленных бифуркаций устойчивое состоя-
состояние равновесия или периодическое движение либо исчезает, ли-
либо оставляет после себя устойчивый двумерный интегральный
тор. Этот устойчивый интегральный тор, в свою очередь, может
потерять устойчивость или исчезнуть несколькими разпыми пу-
путями. Здесь можпо различать случаи преобразований тора как
целого и преобразований периодических движений па торе, в ко-
печном счете также ведущих к его разрушению. Двумерный ус-
устойчивый тор как целое может слиться с неустойчивым двумер-
двумерным тором и исчезнуть, может стать неустойчивым, породив
устойчивый «удвоенный» двумерный тор (только при размерности,
большей трех), наконец, может стать неустойчивым при одно-
одновременном появлении устойчивого трехмерного тора. Трехмерный
тор, в свою очередь, может испытать подобные измеиепия. При
этом следует иметь в виду, что по мере роста размер-
размерности устойчивого тора появляется новая возможность хаотиза-
хаотизации движений на торе, не сопровождающаяся его разрушением.
Это краткое описание необходимо пополнить бифуркациями
периодических движений в резонанспых случаях 1 :, 3 и 1:4,
а также резонансными бифуркациями тора.
С периодическими движениями на торе могут произойти все
бифуркации, возможпые для периодических движений. При этом,
опять-таки, следует различать случаи, когда бифуркации проис-
происходят на торе и вне его.
Таковы возможные пути исчезновения устойчивых движе-
движений — леобходимой предпосылки хаотизации и стохастизации дви-
движений динамической системы. Сами по себе они еще не приво-
приводят к хаотизации движений, но необходимы для ее возникнове-
возникновения. Более того, в областях, где нет устойчивых состояний равно-
равновесия и периодических движений, хаотизация может возпикнуть
и без этой «предварительной подготовки», не в результате под-
подмены простого аттрактора хаотическими движениями. Хаотиче-
Хаотические движения могут жестко возникнуть в области притяжения
состояния равновесия или периодического движения.
Хаотические движения порождаются гомоклинической струк-
структурой, которой обусловлены разбегание и последующая «упаков-
«упаковка» разбежавшихся фазовых траекторий. Конкретных видов
гомоклинических структур очень много и, как правило, они не-
необозримо сложпы, если иметь в виду их достаточно полное опи-
описание. Но можно ограничиться и упрощенным, сокращенным
описапием. Гомоклиническая структура включает в себя бесконеч-
бесконечное число седловых неподвижных точек всевозможных кратно-
215

стей и их инвариантных многообразий S+ и S~, сложнейшим
образом пересекающихся друг с другом. (Могут пересекаться
только многообразия S+ с S~. Многообразия S+ с мпогообразия-
ми S+, так же, как и многообразия S~ с многообразиями S~, пе-
пересекаться пе могут.) В этой запутанной сложнейшей сети пере-
пересечений есть значительная взаимообусловленность. Она состоит,
в частности, в том, что пересечения многообразий >S+ и S~ ка-
какой-нибудь одной или нескольких седловых неподвижных точек
влечет за собой существование бесконечного множества других
седловых неподвижных точек большей кратности и пересечения
их многообразий S+ и S~. Она состоит и в том, что наличие од-
одних пересечений многообразий >S+ и S~ приводит к другим пере-
пересечениям, которые, в свою очередь, порождают следующие пере-
пересечения и т. д. Естественно, возникает некоторая иерархия седло-
седловых неподвижных точек возрастающей кратности и все более
и более мелких и усложняющихся пересечений ипвариантных
многообразий S+ и S~. В отой иерархии, по-видимому, можно
видеть некоторое подобие вложенных структур. Именно с ней
связаны неизбежность и естественность иерархии гомоклиниче-
ской структуры и ее общий характер. В значительной мере
она характеризуется своим верхним уровнем, т. е. непод-
неподвижными точками наименьших кратностей и «первыми» пересе-
пересечениями их инвариантных многообразий S+ и S~. Примерами:
могут служить упрощенпые изображения гомоклинических
структур на рис. 7.44—7.46.
Сравнительно простые гомоклинические структуры возникают
при преобразовании прямой в прямую и в системе уравнений
Лорепца.
После того, как хаос возник, организующая его гомоклини-
ческая структура может перестраиваться и повлечь за собой пе-
перестройки типа «хаос — хаос». Таких перестроек необозримое
множество. Однако на уровне упрощенного описания гомоклипи-
ческой структуры они легко обозреваются и могут состоять либо
в появлении новых или исчезновении прежних пересечений меж-
между инвариантными многообразиями S+ и S~ уже существующих
седловых неподвижных точек, либо в возникновении новых сед-
седловых неподвижных точек и новых пересечений инвариантных
многообразий S+ и S~, либо в обратном процессе исчезновения пе-
пересечений S+ и S~ и седловых неподвижпых точек. Перестройки
верхнего уровня приводят к бесчисленным перестройкам нижних:
уровней гомоклипической иерархии или подготавливаются ими.
Эти перестройки сопровождаются бесконечным множеством би-
бифуркаций слияния и исчезновения неподвижных точек и бифур-
бифуркациями удвоения периода, о чем рассказывалось в § 2 этой
главы. При этом устойчивые неподвижные точки также рожда-
рождаются и исчезают. Если периоды этих рождающихся и существу-
существующих устойчивых периодических движений достаточно велики,
то это но приводит к нарушению хаотического характера движе-
движений дипамической системы.

Глава 8
КОЛИЧЕСТВЕННЫЕ ХАРАКТЕРИСТИКИ
СТОХАСТИЧЕСКИХ И ХАОТИЧЕСКИХ ДВИЖЕНИЙ
И НЕКОТОРЫЕ УНИВЕРСАЛЬНЫЕ ЗАКОНОМЕРНОСТИ
ПРИ ПЕРЕХОДАХ «ПОРЯДОК — ХАОС» И ОБРАТНО
Для количественного описания стохастических и хаотических
движений используют такие понятия, как распределение веро-
вероятностей, корреляционная функция, спектральная плотность, ля-
пуновские показатели, размерпость и энтропия стохастического
множества. Некоторые из этих величин легко измерить экспе-
экспериментально (например, спектральную плотность), другие мож-
можно определить только на основе численного анализа. В ряде
случаев указанные величины удается вычислить аналитически.
§ 1. Статистические характеристики
В гл. 4 говорилось о том, что одним из основных возраже-
возражений против существования стохастических решений дифферен-
дифференциальных уравнепий в свое время была теорема единственности.
Действительно, при постановке задачи Коши решение должно
быть единственным, полностью определяемым начальными ус-
условиями и, следовательно, вполне предсказуемым. Как же может
возникнуть непредсказуемость? Оказывается, что при исследова-
исследовании стохастических решений постановка задачи Коши неправо-
неправомерна. Она никогда не соответствует условиям эксперимента (на-
(натурного или численного), поскольку пачальные условия прин-
принципиально не могут быть заданы абсолютно точно. Поэтому име-
имеет смысл формулировать задачу на статистическом языке. Пусть
в начальный момент времени задано пекоторое распределение
вероятностей, близкое к б-образному. Если в последующие мо-
моменты зто распределение по крайней мере не уширяется, то мож-
можно с самого начала считать его б-функцией и рассматривать
задачу Коши. Решение при этом будет регулярным и предска-
предсказуемым. В противном случае, когда первоначально заданное рас-
распределение вероятностей расплывается и приобретает конечную
ширину даже при стремлении начального распределения к
217

6-образному, решение является стохастическим (или хаотиче-
хаотическим, если указанное расплывание происходит за счет малых
случайных возмущений). Из такой постановки задачи сразу сле-
следует, что стохастические движения в динамических системах
представляют собой особый тип случайных процессов, и для их
описания удобно пользоваться обычными статистическими ха-
характеристиками: распределением вероятностей, корреляционной
функцией, спектральной плотностью и т. п. Особенность этих
процессов заключается в том, что в отсутствие случайных воз-
возмущений вероятность перехода для них всегда является 6-функ-
цией, и поэтому корреляционная функция выражается через
одномерное распределение вероятностей').
Для дипамических систем, описываемых экспоненциально не-
неустойчивым разрывным отображением отрезка в себя, существо-
существование предельной плотности вероятностей строго доказано [553].
Поясним качественно, почему такая плотность вероятностей су-
существует. Рассмотрим растягивающее отображение п — Ти и
выберем в качестве начальной точку и0. Тогда ut = Ти0, иг =
= Tiii, . .. Если предположить, что точка и0 может быть задана
абсолютно точно, то эта последовательность однозначно опреде-
определена и ни о каком статистическом ее описании не может быть
и речи, поскольку нет никакой случайности и неопределенности.
Неопределенность может быть внесена либо за счет задания
некоторого начального распределения вероятностей для значе-
значения и0, либо за счет каких-то неконтролируемых помех, нару-
нарушающих точное выполнение преобразования Т. Из-за растяги-
растягивающего характера последнего даже при сколь угодно узком
начальном распределении вероятностей и при сколь угодно ма-
малых помехах в последовательности точек м0, и,, и2, ... должна
возникнуть случайность, причем случайность, статистическое
описание которой не зависит от вида начального распределения
и помех. Следовательно, при такой трактовке стохастичность
динамической системы — это стохастичность, порождаемая сколь
угодно малыми флуктуациями и замечательная тем, что опа не
зависит от этих флуктуации, а определяется самой динамиче-
динамической системой.
Расчет предельной плотпости вероятностей для динамических
систем в общем случае представляет собой непростую задачу
и требует применения ЭВМ. В некоторых наиболее простых
случаях этот расчет удается провести аналитически. По-видимо-
По-видимому, впервые пример такого расчета приведен в работе Улама
и фон Неймана [670], где рассмотрено квадратичное отображе-
отображение х — 1 — цх2 и показало, что при ц. = 2 существует предель-
предельная плотность вероятностей, равная w(x)= 1/(яУ1 — хг). Рас-
') Именно этим стохастические движения в детерминированных дина-
динамических системах отличаются от «истипно» случайных, вызванных, напри-
например, случайной внешней силой (данный факт был отмечен Р. Л. Стратоно-
вичем).
218

чет основан на том, что заменой переменной х — —cos (пу) ука-
указанное квадратичное отображение при \i = 2 сводится к линей-
линейному у = 2у на отрезке О *S у *S 1. Поскольку для линейного
отображения распределение вероятностей w(y) равномерно,
после перехода к переменной х сразу получается приведенная
выше формула. Ниже будут приведены два других примера рас-
расчета предельного распределения вероятностей. В качестве пер-
первого примера рассмотрим линейный осциллятор с отрицатель-
пым трением и демпфирующими ударами, описываемый урав-
уравнением C.4) гл. III. Для такого осциллятора точечное отобра-
отображение переменной у = ж|х=о+ легко вычисляется и имеет вид
C.5) гл. III. Для того чтобы в фазовом пространстве рассмат-
рассматриваемого осциллятора имелось предельное стохастическое мно-
множество / (странный аттрактор), величины р и q должны удов-
удовлетворять условию a(q— l)< р < а.
Стационарное распределение w(y) для переменной у, опи-
описываемой точечным отображением y = f(y), должно удовлетво-
удовлетворять следующему уравнению:
A.1)
Используя свойства б-функции, из A.1) получаем линейное
функциональное уравнение
w (у) = 2 w (у\ (у)) Ву\ (y)lDy, A.2)
г=1
ГДе y'i(y) — i-ii корень уравнения f(y')=y, Dy'i(y)/Dy— якобиан
преобразования от у к у'. Решая точно или приближенно урав-
уравнение A.2), можно найти и>(у), а по нему вычислить распре-
распределение вероятностей во всей области странного аттрактора. Для
рассматриваемой системы при определенных соотношениях меж-
между параметрами удается использовать более простые приемы
[227, 228].
Все фазовые траектории в пространстве х, у, пересекающие
ось у в интервале /0 = [г/4, г/о], где yl — a, yo = qa, будут испы-
испытывать скачок. Предположим, что выполняются условия
l_gr«e?-*(l_?-«)( p = qa(l-q-"), A.3)
где к и т — любые целые числа. Эти условия означают, что
при скачке один элемептарпый интервал 10 переходит в т эле-
элементарных интервалов /fe+m-i = [yk+m, Ун+m-i], ■ ■'., h = {Ук+т, yh],
где yh = yoq~k, т. е. точки у0, у и ..., ук+т образуют марковское
разбиение отрезка [ук+т, у о] C25]. При условиях A.3) стацио-
парное распределение вероятностей w(y) удается рассчитать ана-
аналитически {227, 228]. Одновременно можно вычислить стацио-
стационарное распределение w (у) для значений у при х = О— Резуль-
219

таты расчета можно записать в следующем виде:
Cqa (a =0,1, ...,fc-l),
ci_qa.+ l-h-m
(a = к — 1, к, ..., к + т — 1),
C(l-8ao)qa (a = 0, 1, ...,fc),
1 _ gOC-h-m
A.4)
(a = fe, к+ 1, ..., к + т— 1),
где а — номер интервала, в который входит соответствующее
значение у, т. е. у е /а, бт„ — символ Кронекера.
Зависимости w(y) и w{y), построенные на основе формул
A.4) для т = 3, & = (>
(g = l,171, jj/a = 0,717),
представлены на рис. 8.1.
Ыи)\ > ' ~г Постоянная С, содер-
"'\ П?>г-/,\ ^—[ w(y) жащаяся в формулах
A.4), определяется из ус-
условия нормировки и равпа
Рис. 81
[
+q(k-mq-<h+m))]-1.
Отметим, что найденное распределение вероятностей пол-
полностью определяется динамическими свойствами рассматривае-
рассматриваемой системы, поэтому такая система представляет собой гене-
генератор стохастических колебаний.
В качестве второго примера рассмотрим кусочно-линейное
отображение [125]
J— ц + A + ц) и при и > О,
" = ( ц + A + Ц) и при и < 0. ( ' '
График отображения A.5) приведен па рис. 8.2. Отображение
A.5) имеет такой же общий вид, как и одномерное отображе-
отображение для системы Лоренца, и во многих случаях может быть
получено из последнего подходящим выбором переменной и.
Легко видеть, что отображение A.5) при 0 < ц. < 1 преоб-
преобразует отрезок [—1, 1] в себя и является растягивающим с ко-
коэффициентом растяжепия 1 + ц.. Из рис. 8.2 видно, что предель-
предельное мпожество / занимает отрезок [— ц., ц].
Пусть wo(u) — произвольная гладкая плотность вероятностей
на отрезке [—1, 1]. При преобразованиях A.5) она изменяется
по рекуррентной формуле (см. уравнение G.45) в [100]):
<u.). A.6)
Предполагается, что в формуле A.6) все точки и, (u + \i)/(l +
+ ц.), {и — ]и)У A + ц.) отличны от нуля, т. е. от точки разрыва
220

точечного отображения A.5). Точки (и + ц)/A + ц), (ы —ц.)/
/A + ц) представляют собой обратные преобразования точки и,
т. е. (и±ц)/A + ц)=Т~1и.
Рассмотрим последовательные точки щ = ц, Ui = Tu0, и2 =
= Ти,, и3 = Тиг, ... Пусть при некотором целом m TmUt> = 0.
К точкам и„, и,, п2, .. ., ит = О добавим еще точки um+i = — ц,
Мт+2 -/ ^тп+1, • • v Him ^
= Tu2m-i = 0. Множество Л/
точек и0, и,, ..., игт обладает /-
теми свойствами, что содер-
содержит точку разрыва и = 0, и
каждая из точек us пре-
преобразованием Т переводится
в точку us+l Ф 0, если s Ф
Фтп—1, 2т— 1, и в точку
и = 0, если s = m — 1 и
2т-1.
Рассмотрим произволь-
произвольный интервал Д4 = \щ, и,],
не содержащий других то-
точек множества М. Отобра-
Отображением Т он преобразуется
в интервал А = [u,+i, uJ+i],
длипа которого в A + ц)
раз больше длины исходно-
исходного интервала. Поэтому интервал А заведомо может содержать
в себе йрутие точки множества М. Таким образом, точки ы0,
ии .. ., и2т определяют па отрезке [—ц, ц] такое его разбиение
на интервалы [ы„ uj, при котором каждый из них преобразу-
преобразуется в один или несколько таких же интервалов. Указанное раз-
биепие отрезка [—ц, ц] называется марковским по отпошению к
отображению Т [8, 325]. При наличии марковского разбиения ни
одна из точек и & М не может обратным преобразованием Т~1
перейти в точку uh e M, и поэтому для таких начальных точек
и в соотношениях A.6) никогда не встретится точка разрыва
отображения Т. В силу этого для указанных начальных точек и
соотношения A.6) справедливы при всех п. Дифференцируя
A.6) по ы, находим
Отсюда следует, что
A-гЮ
A.8)
и поэтому на каждом интервале гладкости, т. е. на каждом ин-
интервале \и„ щ] марковского разбиения, при условии 2/A + ц.J<
< 1, т. е. при
ц>У2-1, A.9)
предельная плотпость вероятностей постоянна.
221

Эта кусочно-постоянная плотность может быть легко найде-
найдена из соотношений A.6), поскольку они приводятся к системе
линейных уравнений для определения предельных плотностей
* * *
вероятностей wx; U72, ..., w2m на интервалах марковского раз-
разбиения. Действительно, точки и0, ии ..., щт образуют 2т ин-
интервалов марковского разбиения Д,, А2, ..., А2т, па которых
плотности вероятностей при п-й итерации соответственно равны
Wi" * Щ; > • • •» и>2т- Согласно A.6) они преобразуются в неко-
некоторые новые постоянные плотности w" , w\ , ..., Щт J «
связанные со старыми соотношениями вида
2т
A.10)
где
f 1/A +
Рн = I 0,
), если А{с: ГА,-,
если А{ П TAj = ф.
Графики предельных плотностей w*(u), вычисленных для
ряда значений ц, соответствующих марковским разбиениям,
и
приведены на рис. 8.3. Отметим, что численные расчеты подтвер-
подтвердили, что при \i < У2 — 1 марковские системы являются перио-
периодическими, а при ц> У2 — 1 — эргодическими [125].
Вернемся к анализу сделанного ранее предположения о том,
что при некотором целом т
Ггац, = 0. A.11)
Решая это уравнение относительно параметра р. при различных
т, мы найдем значения ц, при которых имеется марковское
222

разбиение. При малых т такие значения ц могут быть найдены
аналитически. Покажем, что множество корней уравнений A.11)
при всевозможных т всюду плотно на отрезке [0, 1]. Действи-
Действительно, из A.5) получаем
где е3 = —signGls~1u), ео = 1. Допустим, что па некотором ип-
тервале [ц, ц] нет ни одного из корней уравнений A.11). Тогда
при всех ц е [ц,, ц] величины еь е2, . .., е,т одинаковы и
\етц + 8т—»цA + M.)+... + eou(l + (j,)™| =£1 ц.
Последнее означает, что при любом т
1 1
Из A.13) следует, что сходящийся при и.>0 степенной ряд
е _1 g 1
0 J1 + И 2 A + цJ
тождественно равен нулю на интервале [ц, и], и поэтому все
его коэффициенты е0, 6i, ... должны быть нулями, чего не
может быть. Значит, на любом отрезке [|ti, ц] имеются корни
уравнений A.11). Последнее означает, что марковские разбие-
разбиения отрезка [— ц, ц] по отношению к отображению A.5) всюду
плотны по параметру jn.
Другие примеры расчета стационарного распределения веро-
вероятностей для систем, описываемых одномерным и двумерным
(вида C.10) гл. 7) точечными отображениями, приведены в ра-
работах [481, 532, 536].
Как уже отмечалось, знание предельного распределения ве-
вероятностей w(x) для динамической системы, описываемой век-
вектором х, позволяет в принципе вычислить корреляционную
функцию процесса x(t) и связанную с ней теоремой Хипчина
[362] спектральную плотпость. Для стохастических движений
корреляционная функция с ростом времени т спадает. В неко-
некоторых случаях такой спад является экспоненциальным [99, 343,
422]. Однако часто он имеет степенной характер [97].
Спектральные плотности S(о) являются простейшими и до-
достаточно информативными количественными характеристиками
стохастических движений динамических систем. Измеряя их
экспериментально или вычисляя с помощью ЭВМ, можно доволь-
довольно четко выделять момент начала хаотизации, а также проис-
происходящие бифуркации при плавном изменепии параметров. Так,
в случае периодического движения спектр состоит из ряда эк-
эквидистантных линий на частотах м, 2м, Зм, . .. (см., например,
рис. 8.4, а, где изображены экспериментальные спектры скоро-
скорости при 'тепловой конвекции в слое воды, полученпые в работе
22а

[469]; R — число Рэлея, Rc — критическое значение R, при кото-
котором возникает конвекция, /2 = (й/2л). При бифуркациях удвое-
пия периода появляются дополнительные линии на частотах
<а/2, 3<й/2, 5«в/2, .... (рис. 8.4,6), «а/4, Зсо/4, 5«в/4, ...
(рис. 8.4, в). При переходе к квазипериодическому движению,
10
10
ff,3f,ni
кроме основной частоты coi, появляется вторая несоизмеримая
с ней частота м2, а также их линейные комбинации (см., па-
пример, рис. 8.5, где представлены эксперимептальные спектры
температуры при тепловой копвекции в ртути [443] (/ = са/2л).
При хаотизации сначала наряду с дискретным спектром появ-
появляется фон, который постепенно усиливается, и паконец, спектр
приобретает сплошной характер (рис. 8.4, г, д). Изменепие ха-
характера спектра подчиняется определенным закономерностям,
часть из которых будет обсуждена ниже. Много копкретных
примеров спектров при переходах к хаосу и в режимах хаоти-
хаотических и стохастических колебаний будет приведено в следу-
следующей главе.
В заключение рассмотрим влияние случайных возмущений на
предельную инвариантпую плотность вероятностей. Будем пред-
предполагать, что отображение Т переводит точку х в точку х,
а случайное возмущение заменяет точку х точкой у с плот-
плотностью вероятностей f(x, у). Тогда последовательпые плотности
224

вероятностей w,\x) и iv,+i{y) связаны соотношением
= 2 J^tf1-1*) |т?
/ (х, у) dxt
где суммирование производится по всем значениям обратного
20,000
en
см
-50,000
250,00
20,000
£0
ел
-50,000
■Г, МГц
Рис. 8 5
250,00
отображения Т~\ а интегрирование — по области определения
отображения Т, преобразуемой им в себя.
Согласно этой формуле предельная плотность вероятностей
w* (х) зависит как от точечного отображения Т, так и от плот-
плотности вероятностей помех f(x, у). Однако согласно изложенному
ранее характер этой зависимости может быть существенно раз-
разным в соответствии с тем, имеет ли место случай преобразова-
225

ния, усиления или генерации стохастичности. Ниже приводятся
данные математического эксперимента, проведенного И. С. Гель-
фер, с отображениями, отвечающими усилителям и генераторам
стохастичности, которые описываются формулами
х=ахA — х) и х = |xsigna; +A + ц)х.
Плотность вероятностей f(x, у) была выбрана в виде
при | х — у\ <Ch,
при \x — y\^h,
где v и h задаются, a f определяется из условия нормировки.
Математический эксперимент состоял в последовательных вы-
вычислениях, согласно приведенной выше формуле, плотностей ве-
вероятностей Wi{x), Wz(x), w3(x), ... для указанных выше пре-
преобразований Т и функций f(x, у) с последующей обработкой
т б „ . получаемых данных. При этом
л и ц а ' отличие вычисляемых плотно-
плотностей вероятностей от пре-
предельной w*{x) оценивалось ве-
величиной
Р« = JI Щ (х) — w* (х) | dx.
При проведении расчетов об-
обнаружилось, что р, » ае~х*. Зна-
Значения а и и при указываемых
значениях параметров а и соответственно \i приведены в таб-
таблице 8.1. Для тех же отображений Т и значений параметров а
и ц в таблице 8.2 помещены величины расхождений
г
и, = 0,618
и, = 0,839
а = 3,92
а = 3,98
а
0,03
0,09
0,32
0,2
к
0,57
0,5
0,29
0,3
р = J | w* (х) — w* (х) | их
предельных плотностей вероятностей w*(x) и w*(x) в отсут-
отсутствие и при наличии случайных возмущений. Величина случай-
случайного возмущения в этой таблице характеризуется его диспер-
дисперсией D.
Таблица 8.2
A=0,618
D
0,2.10"»
0,2-10-*
0,5-10-2
Р
0,0036
0,027
0,11
A=0,839
D
0,3-10-»
0,8-10-6
0,2-Ю-8
Р
0,003
0,013
0,089
а=3,92
D
ю-'
0,5.10
0,5.10"*
Р
0,13
0,22
0,32
а=3,98
D | р
ю-'
0,5-10-»
0,5.10"*
0,12
0,20
0,29
Из таблицы 8.2 видно, сколь сильно различаются интенсив-
интенсивности шумов, вызывающие значительные изменения предельной
плотности вероятностей. Эти различия могут быть и большими,
так как при машинном счете неизбежно присутствуют «свои
собственные возмущения».
226

§ 2. Ляпуновские показатели. Размерность
в энтропия стохастического аттрактора
Поскольку, как уже неоднократно говорилось, все траекто-
траектории, образующие стохастический аттрактор, неустойчивы по Ля-
Ляпунову, они должны иметь хотя бы один положительный ляпу-
новский показатель. Наличие положительного ляпуновского по-
показателя является одним из основных критериев стохастичности
движения.
Ляпуновские показатели определяются следующим образом
[101, 240, 297]. Пусть задана динамическая система, описывае-
описываемая уравнением
x-F(x), B.1),
где х — вектор с компонентами хи х2, ..., хп. Рассмотрим две
близкие траектории x(t) и Xi(t), исходящие из точек х0 и х10,
и пусть y(t) = xi(t)~ x(t) (y(O) = x,o —х0). Если траектории
близки, то эволюцию вектора y(t) можно описать линеаризован-
линеаризованным уравнением
где д¥/дх — матрица с элементами dFJdx,. Известно, что систе-
система уравнений B.2) имеет п фундаментальных частных реше-
решений y»(f) = e{(i) таких, что для каждого из них величина
B.3)
существует и имеет вполне определенное, в общем случае от-
отличное от остальных, значение. Эти значения Xi(x0) называются
ляпуновскими показателями [240]. Легко убедиться, что для лю-
любого начального вектора общего положения у@) величина
равна Ki(x0) —максимальному показателю. Ляпунова.
Непосредственный расчет показателей Ляпунова по формуле
B.3) для систем с экспоненциальной неустойчивостью траекто-
траекторий практически невозможен в силу того, что даже при очень
малом 1у@I величина 1у(£I с ростом t неограниченно возра-
возрастает, что приводит к переполнению регистров ЭВМ и суще-
существенным ошибкам. Чтобы избежать этих трудностей, Бенетти-
ным и др. [397—400] был предложен следующий алгоритм вы-
вычисления ляпуновских показателей. Прежде всего остановимся
на расчете максимального показателя Ляпунова A,t. Для этого
выберем некоторую траекторию x(t) на интервале O^t^T, явля-
являющуюся решением уравнения B.1) и плотно покрывающую весь
аттрактор. Будем решать уравнение B.2) совместно с уравне-
уравнением B.1) в окрестности этой траектории при некотором
227

начальном условии у0 таком, что 1уо1 = 1. Через некоторое
заданное время т вектор y(t) примет значение У1 = у(т). Дли-
Длину вектора yt обозначим dt. Далее решение уравнения B.2)
продолжим с другого начального условия у10 = yi/dt. Значение
y(t) в момент времени
f^J ->& t = 2x обозначим у2,
а длину вектора у2 —
— d2. В результате мно-
многократного примене-
применения описанной проце-
процедуры (рис. 8.6) полу-
получим последовательность
чисел d(, где г =
х5
Рис. 8.6
= 1, 2,
равен
, д
т — Г/т. Максимальный показатель Ляпунова
i = lim ^Г 2 ln di-
B.4)
Заметим, что для траекторий, лежащих на аттракторе, величины
Х{ не зависят не только от начальной точки х0 на выбранной
траектории (что следует из произвола в выборе начала отсчета
времени), но и от самой траектории.
Чтобы вычислить другие ляпуновские показатели, в работах
[397—400, 647] предлагается использовать аналогичную про-
процедуру, но с обязательной ортогонализациеи по методу Грама —
Шмидта. Поясним это на примере вычисления следующего по
величине ляпуновского показателя К2 ^ Я,4. Обозначим вектора
Yi и yjdt, вычисленные при счете Ки через w^J) и Vj1* соответ-
соответственно (vj1* = wpVdj). В качестве начального для уравнения B.2)
зададим вектор v£ , ортогональный вектору Vq » т. е. удовлетво-
удовлетворяющий условию (vo^Vq1*) = 0. Через время т вектор v@2) перей-
дет в вектор wx . Составим линейную комбинацию векторов
ia) i^ так, чтобы она была ортогональна вектору v^. Для
( i i1, где ^ — неопределенный множи-
множитель, и потребуем, чтобы (ui^vi1') = 0. Отсюда находим (S =
= — (v?i Vi ). В качестве начального вектора для второго шага
возьмем вектор vAi) = Uj2)M2)r где ^i2) = |u(i2)|- Поступая
аналогичным образом на каждом г-м шаге, вычислим 4г)
Ляпуновский показатель Я,2 определяется выражением
об он
этого положим u(x = wi +
B.5)
Чтобы вычислить /-й ляпуновский показатель, нужно на каж-
каждом г-м шаге проводить операцию ортогонализации по отноше-
228

нию к векторам v£x\ \f\ ...,vf J). Для этого образуем вектор
„<'> = wl;) + р>^ + Р2у({2) + ... + pj-iv^" и потребуем, чтобы
(„Pvi") = О, („?МЯ)) = 0, ..., (u?)vii-1)) = 0. Отсюда находим
р-А = _ (w"Vf«). Следовательно, и^ = w</> - *2 (w?>vi*>) у?\
Ляпуновский показатель Я^ определяется по формуле
т
где di;) = |uiJ)|. Таким способом можно вычислить последова-
последовательно или одновременно все п ляпуновских показателей1).
Перейдем теперь к определению энтропии и размерности сто-
стохастического аттрактора. Прежде всего введем понятие тополо-
топологической энтропии [380]. Топологическая энтропия динамической
системы, описываемой дифференциальными уравнениями, опре-
определяется следующим образом. Предположим, что мы можем раз-
различать точки фазового пространства, отстоящие друг от друга
на расстояние, превышающее некоторую величину е > 0. Рас-
Рассмотрим пучок траекторий, выходящих из окрестности началь-
начальной точки радиуса е, т. е. в начальный момент не различимых.
Число различимых траекторий в некоторый момент времени t
обозначим N(e, t). Топологической энтропией называется ве-
величина
h = lim lim In (iV (e, t))/t.
e-»o t-»oo
Топологическая энтропия характеризует степень разбегания
близких фазовых траекторий. Если траектории со временем не
разбегаются либо разбегаются недостаточно сильно (например,
по степенному закону), то h = 0. В противном случае h > 0.
Такие количественные характеристики стохастических движе-
движений, как размерность и метрическая энтропия, которые будут
описаны ниже, строго говоря, относятся только к генераторам
стохастических колебаний. В какой-то мере их можно использо-
использовать и для усилителей стохастичности с пренебрежимо малым
порогом хаотизации при условии фиксированных малых случай-
случайных воздействий.
Как уже указывалось, для процесса х(£), описывающего ко-
колебания стохастического генератора, должна существовать пре-
предельная плотность вероятностей w(x). Покроем аттрактор куби-
кубиками с ребрами длины е, < е. Пусть число этих кубиков равно
N(e). Обозначим i-й кубик символом г{. Вероятность нахождения
изображающей точки в кубике е* равна
pi= \ w (x) dx.
') Отметим, что обоснованием описанного способа является теорема
Оселедца об обобщенных показателях Ляпунова [297].
229

Согласно Шеннону [642] энтропия системы равна
Я(е) = - inf 2 Рг log2Pi. B.7)
ег 1=1
Величина #(е) характеризует неопределенность нахождения
изображающей точки в кубиках е(. При измельчении покрытия
значение энтропии #(е) неограниченно возрастает. Однако мо-
может существовать предел
а = lim H (e)/log2 e-i. B.8)
е-» о
Величина о получила название информационной размерности ат-
аттрактора [440, 442, 473, 474, 476, 477, 502, 610], или размерно-
размерности Реньи [689]. В том случае, когда предел B.8) не суще-
существует, вводят понятия нижней информационной размерности
а = lim inf (H (e)/log2 е) и верхней а = lim sup (Я (e)/log2 e).
е-»о ^ е-*о
Энтропия #(е) достигает наибольшего значения при равен-
равенстве вероятностей ру = рг = ... = pN = 1/N(e), которое равно
loga iV(e). В этом случае величина о достигает своего макси-
максимального значения
d = lim log2 N (e)/log2 e-i, B.9)
e>o
e->o
которое получило название фрактальной размерности, или емко-
емкости, аттрактора D42, 570, 604, 688, 689]. Иногда величину d
называют также энтропийной размерностью [365]. В случае не-
несуществования предела B.9) аналогично сказанному выше вво-
вводят понятия нижней емкости d и верхней 3.
В случаях, когда аттрактором является точка, линия или дву-
двумерная поверхность, значение d соответственно равно 0, 1 и 2.
Однако при сложном виде аттрактора величина d может быть
нн нн ни ни ни ни ни ич
Рис. 8.7
дробной. Так, для одномерного канторова множества, способ по-
получения которого ясен из рис. 8.7, е=A/3)", N(e)=2n и, сле-
следовательно,
d = lim log2 2n/log23" = log2 2/log2 3 = 0,6309...
7l-»oo
230

Подчеркнем, что мера расположенного на прямой канторова мно-
множества равна нулю, а емкость отлична от нуля и равна дроб-
дробному числу.
Определенные выше информационная и фрактальная размер-
размерности не являются единственными. Значительную известность
получила размерность Хаусдорфа [493], определяемая следую-
следующим образом. Пусть в w-мерном пространстве задано множество
точек. Покроем его w-мерными кубиками с ребрами длины
6,<ei определим величину 1ц= lim Id (е), где ZD (е) = inf 2ei •
е-»о г
Хаусдорф показал, что существует критическое значение D,
выше которого lD = 0, а ниже lD = °°. Критическое значение
D = dH, при котором величина Id, называемая мерой Хаусдорфа,
конечна, называется размерностью Хаусдорфа. Легко показать,
что dH ^ d. Действительно, если выбрать кубики с одинаковы-
одинаковыми длинами ребер е, то Id(z)!=N(s)sd> ld(e) (вследствие опе-
операции inf). При е -*■ 0 согласно B.9) ГДе) -> 1, и поэтому
Zd<l. Отсюда сразу следует, что d^dH. (В общем случае
d>d>dH.)
Непосредственный расчет хаусдорфовой размерности и даже
емкости аттрактора по формуле B.9) с ростом числа степеней
свободы динамической системы сильно усложняется [480]. При
этом значительно проще оказывается вычисление так называемой
корреляционной размерности v [473, 474, 476, 477, 479, 502,
610]'). Величина v определяется через корреляционный интеграл
N
С (г) = lim * ^ * (е - I * -*Л BЛ0)
N-*oo -/V j j
где ■& (z) — функция Хевисайда, х( — вектор, описывающий поло-
положение изображающей точки в фазовом пространстве в момент
времени ta + ix, т — некоторый заданный промежуток времени,
Af—число выборок. Величина С (г) определяет относительное
число пар точек, расстояние между которыми не больше е. При
малых е корреляционный интеграл С(е)~ ev. Отсюда следует, что
v= Hm[lnC(e)/lne].
е-»о
В работе [474] обращено внимание на то, что размерности
о, d и v являются частными значениями так называемой обоб-
обобщенной размерности
dq = lim Iq (б)/1п e—1,
е-»о
JV(e)
где /g(e) = A/A — q)) In 2 p\ — энтропия Реньи порядка q [612].
Нетрудно видеть, ччо d= dq\g==0+, o=limd9, v=de|9=2. Поскольку
для q>0 Iqf^Iq/ при q > q', то v<o<d. Таким образом,
') Иногда величипу v называют поточечной размерностью.
231

значение v может быть использовано для оценки фрактальной
размерности аттрактора снизу.
Для определения величины v достаточно знать лишь одну
реализацию процесса x^t), вследствие чего она легко поддается
численному счету и очень удобна для обработки результатов
экспериментальных исследований. Более того, в работах [459,
475, 479] показапо, что величину v можно вычислить и в том
случае, когда на динамическую систему действует слабый шум,
несколько искажающий ее поведе-
поведение. При этом оказывается, что
для малых е, сравнимых с дис-
дисперсией шума, С(е)~е", где
п — размерность фазового прост-
пространства, а при е, превышающем
Lr . дисперсию шума, С(е)~е\ где
v < п. Характерная зависимость
1пС(е) от In e в этом слу-
случае имеет вид, показанный на
рис. 8.8.
Кроме введенных выше, часто
используют размерности, вычис-
вычисляемые через ляпуновские пока-
показатели %„ %2, •••, ^п. Формула
Рис. 8.8
Каплана — Йорке [540, 554], определяющая так называемую
ляпуновскую размерность, имеет вид
3
B.11)
где все А,< расположены в порядке убывания %i > Я2 ^ ... ^ Я„,
а / определяется из условий Xt + Х2 + ... + %} > 0, Xt + Я2 + ...
.. , + Xi + h+i < 0. В трехмерной автономной диссипативной си-
системе только один ляпуновскии показатель может быть поло-
положительным, поскольку другой равен нулю, а сумма всех трех
должна быть отрицательной. Поэтому для трехмерной системы
формула B.11) принимает вид
db = 2 + Xi/\kl\. B.12)
В силу сказанного выше \%3\ > ^i и 2 < dL < 3. Если скорость
сжатия фазового объема во всех точках пространства одинакова
и равна divx = —а, то Х± — 1Л.31 = —ее. В этом случае для при-
применения формулы B.12) достаточно знать лишь один положи-
положительный ляпуновскии показатель A,i.
В работах [688, 689] предложена еще одна формула для
оценки размерности аттрактора, также содержащая ляпуновские
показатели:
где к — число неотрицательных показателей. В этих работах
232

показано, что DLK d *£ d «£ dL. Легко видеть, что для трехмер-
трехмерных систем или систем, описываемых двумерными точечными
отображениями, формула B.11') совпадает с B.12) и, следова-
следовательно, Dv = d = d = dL. Это подтверждается также данными
работы [628], где проведено численное сравнение величин dL и d
на примерах отображений Хенона [500]:
cos
= Уп + 1 — а,х\,
Каплана — Йорке [540]
xn+l = Zxn {mod 1>, z/n+i = ауп
Заславского с учетом диссипации [690]
\ц cos 2nxn]{mod 1),
, где ц = A — ехр(-Г))/Г;
а также уравнений Рабиновича — Фабриканта [315] (см. D.31)
гл. 9). Результаты сравнения приведены в таблице 8.3.
Таблица 8.3
Система
Хенон
а = 1,2, 6 = 0,3
а = 1,4, 6= 0,3
Каплан и Йорке
а = 0,2
Заславский
Г = 3,0, е = 0,3, v = 400/3
Рабинович — Фабрикант
1,200±0,001
1,264±0,002
1,4306766
1,387±0,001
2,317±0,001
d
1,202±0,003
1,261 ±0,003
1,4316±0,0016
1,380±0,007
2,318±0,002
Формула Мори [586] определяет величину
I
1
B.13)
где к — число неотрицательных ляпуновских показателей, т и
I — соответственно числа положительных и отрицательных по-
показателей. В общем случав dM^DL^ dL, а для трехмерных си-
систем du = dL. Для бесконечномерных систем dM = К т. е. совпа-
совпадает с числом направлений неустойчивости [439].
Знание размерности аттрактора весьма существенно для мно-
многих физических задач. Прежде всего, размерность позволяет оце-
оценить минимальное число динамических переменных, которым в
принципе может быть описано движение на аттракторе, что
особенно важно для распределенных систем. Как правило, хаус-
дорфова размерность аттрактора для распределенных систем ко-
конечна [51, 165, 489, 571]. Известно [571], что любое компактное
множество, имеющее конечную хаусдорфову размерность dH, мо-
может быть взаимно однозначно спроектировано на гиперплоскость
233

размерности, не большей, чем 2dH + 1. Кроме того, в некоторых
случаях размерность типа хаусдорфовой непосредственно вхо-
входит в выражения для измеряемых физических характеристик.
С этим, по-видимому, впервые столкнулся Л. Ричардсон при"
попытке измерить длину береговой линии Англии, которая силь-
сильно изрезана [614]. Заменив береговую линию ломаной с длиной
звена е, Ричардсон обнаружил, что длина ломаной Lt = Ne при
уменьшении е неограниченно растет. Оказалось, однако, что при
этом неизменной остается величина X = Nsd, где d > 1 [57, 570].
Таким образом, Можно записать Lt = Ae'~d. Если взять два уча-
участка побережья с длинами аппроксимирующих ломаных Lu и
L2t, то отношение LiJLZe = lkj%2, т. е. не зависит от е. Следо-
Следовательно, разные участки побережья можно сравнивать между
собой по величине Я, имеющей смысл меры Хаусдорфа. Величи-
Величина d при этом имеет смысл размерности Хаусдорфа. Для по-
побережья Англии d=l,24, для Австралии — d= 1,13. Другим
примером является рассмотренная А. М. Дыхне задача об опре-
определении эффективной проводимости объемной анизотропной сре-
среды с хаотически расположенными направлениями максимальной
и минимальной проводимостей, но так, что в среднем среда
изотропна. Наконец, знание размерности часто помогает иден-
идентифицировать характер движения в системе и переходы от одного
вида движения к другому.
Метрическая энтропия К [205], введенная А. Н. Колмого-
Колмогоровым [202, 203] и Я. Г. Синаем [324], определяется выражением:
e-o
К = lim lim lim (-1 J /i & iN) In p (fx iN)}, B.14)
где p (iif i2, ..., In) — вероятность того, что точка х (t = 0), при-
принадлежал типичной фазовой траектории на аттракторе, лежит
в кубике е^, х (t — т) — в кубике е^, ..., х (t — (N — 1) т) — в ку-
кубике eijy. Метрическая энтропия является частным случаем энт-
энтропии Реньи порядка q, равной
Kq = lim lim lim J /_ In 2 P* &. • • •' '»))•
B-15)
Можно показать, что выражение B.14) является пределом вы-
выражения B.15) ири q ->- 1. Отметим, что метрическая энтропия
К никогда не превышает топологическую энтропию h [382, 426].
Для расчета метрической энтропии удобно использовать фор-
формулу, связывающую ее с ляпуновскими показателями. Я. Б. Пе-
синым [301] установлено, что энтропия К на аттракторе равна
сумме положительных ляпуновских показателей, т. е.
К = 2 &|\ B.16)
i=l
где т — число положительных ляпуновских показателей.
234

Для систем большой размерности, в том числе бесконечно-
бесконечномерных, отыскание численных значений показателей Ляпунова,
как и непосредственное вычисление величин a, d и К, является
сложной задачей. Поэтому представляет интерес сравнительно
простая вычислительная процедура, которая позволяет оценить
ляпуновские показатели, размерность аттрактора и метрическую
энтропию, зная реализацию лишь одной из координат фазового
пространства. Эта процедура была предложена Паккардом [600]
и Такенсом [657]. Использование такой процедуры особенно
удобно при обработке экспериментальных результатов для рас-
распределенных систем, где знать весь бесконечномерный вектор
x(t) просто невозможно [681].
Пусть xit #2, . • -., х„ — последовательные значения одной из
координат фазового пространства системы x(t) через промежут-
промежутки времени т, т. е. х{ — х(Н). Из этих значений можно скон-
сконструировать новую динамическую систему размерности тп, взяв
в качестве иго значения вектора у(т), описывающего положение
точки в новом фазовом пространстве, у Г ={а:4, a:i+1, ..., xi+m-i}.
Теорему Такен'са можно сформулировать следующим образом.
Для почти любых наблюдаемой реализации x(t) и времени за-
задержки т аттрактор сконструированной динамической системы
размерпости тп будет иметь те же свойства (например, ту же
размерность и тот же спектр ляпуновских показателей), что и
исходный, если только тп 5* 2dH + 1, где dH — хаусдорфова раз-
размерность исходного аттрактора. Эта теорема является следствием
теоремы Манье [571].
Отметим, что вместо переменных xt, xi+l, ..., a:,+m-i можно
взять x(t), x(t), x(t), ..., xim-l)(t).
Для каждого тп тем или иным способом можно вычислить
размерность аттрактора и энтропию сконструированной дина-
динамической системы. Вначале с ростом тп размерность будет уве-
увеличиваться, а энтропия как-то изменяться, а затем они достиг-
достигнут постоянных значений, которые можно принять за размер-
размерность и энтропию аттрактора исходной системы.
При применении этой процедуры особенно удобными оказыва-
оказываются оценки размерности аттрактора с помощью корреляционного
показателя v и метрической энтропии — с помощью энтропии
Репьи второго порядка [478]. Для вычисления v на основе реали-
реализации одной из координат фазового пространства x(t) конструи-
конструируются описанным выше способом динамические системы разных
размерностей тп и вычисляются корреляционные интегралы
JV-»oo
Сп (в) - Ню J ' Цг -1 уГ- уП )• B-17)
Величину m следует увеличивать до тех пор, пока наклон
зависимостей 1пСт(е) от lne не достигнет насыщения.
23S

Для оценки величины энтропии К2 следует при достаточно
больших т вычислить несколько иные корреляционные интегра-
интегралы, а именно
Сй> (е) - Нт 2 4" П * (в -1 уЩ - У$& | )• B.18)
JV-»ooJ>i=1 N ft=o
Легко видеть, что Сот\е) = 2 Рг(н> h> • ••» *«)> где p(U, i2, ...
..., i.) — вероятности, входящие в выражение B.15). Отсюда
и из B.15) следует, что
С&' (е) = ехр (- пК?* (г)), B.19)
где К? (г) JL in 2 Р2 (h, *„..., is).
ij.ij,...,!,
Записав аналогичное выражение для Cm (e) и учитывая,
что при достаточно больших s К^ (г) = К%+1) (г) « К2, получаем
23
73
75
7/
■-0,008 ±0,001
B.20)
Как показывают численные расчеты, проведенные в [478,
479], с ростом s величина Ки вначале уменьшается, а затем
стремится к константе, которую
можно отождествить с энтропией
К2 (см. рис. 8.9, где изображена
зависимость К2, от s для системы
(9.3), (9.21) гл. 9 при т = 23
[478]). Из выражений B.14) и
B.15) следует, что К2^К, поэто-
поэтому положительность К2 может
служить надежным критерием сто-
хастичности движений.
Другой способ оценки размер-
размерности аттрактора на основе проце-
, , дуры Паккарда — Такенса (обоб-
20 24 s щенной на случай нескольких из-
измеряемых переменных) предложен
в работе [238]. При этом в каче-
качестве размерности п, названной авторами размерностью вложения,
предлагается использовать число переменных, однозначно
определяющих состояние системы на аттракторе. Пусть в каче-
качестве фазовых переменных сконструированной на основе указан-
указанной выше процедуры динамической системы выбраны значения
У(™^—{хи ач+ь • • • > xi+m-i}- Тогда п определяется следующим обра-
образом. Если т^п, то переменная xi+m должна быть функцией пре-
предыдущих m переменных, т. е.а:{+п,=/(у(/™)). Если же тп<п, то
xi+m не будет функцией этих переменных. В [238] предлагается
использовать следующий критерий функциональной зависимости.
236
72 76
Рис. 8.9

В пространстве векторов у^ выберем сферу радиуса е с центром
в точке ■уо) и рассмотрим все точки фазовой кривой, попавшие
внутрь этой сферы при достаточно больших i. Если для этих
точек переменная xi+m оказывается отстоящей от значения хт
на расстояние, не превышающее некоторой величины d(e),
уменьшающейся вместе с уменьшением е, то считается, что Х{+т
зависит от переменных yim). В случае отсутствия зависимости ве-
величина d(e) не должна зависеть от е. Как показали численные
расчеты [238], размерность вложения п, как и следовало ожи-
ожидать, всегда больше фрактальной размерности d. Так, для пре-
предельного цикла получено п =• 2, для двумерного тора — п = 3.')
В работе [681] описаны алгоритмы для вычисления спектра
ляпуновских показателей на основе обработки временной реали-
реализации процесса согласно процедуре Паккарда —Такенса2).
§ 3. Порог синхронизации как количественная характеристика
хаотических движений
Как показано в ряде работ [28, 76, 78, 151, 214, 215, 223,
428], при воздействии гармонической внешней силы на автоколе-
автоколебательную систему, работающую в хаотическом режиме, возмо-
возможен переход от хаотических колебаний к периодическим с пе-
периодом, кратным периоду внешней силы, т. е. возможно явление
синхронизации. Существенно, что как бы ни менялась частота
воздействия, такой переход воз-
возникает только начиная с не-
некоторого критического значения
амплитуды воздействия (см.,
например, рис. 8.10, где изоб-
изображены области синхронизации
в лампе обратной волны [78],
на которую действует внешний
гармонический сигнал). В свя-
связи с этим имеет смысл опре-
определить понятие порога синхро-
синхронизации как минимального
значения амплитуды гармони-
0,02-
0,0/-
Л
-
1
-0,08 -0,04
Рис. 8.10
ческого воздействия, при кото-
котором на какой-либо частоте наступает синхронизация. Наличие
ненулевого порога синхронизации для хаотических автоколеба-
автоколебательных систем связано с тем^ что стремление к упорядочению
движения (к синхронизации) в таких системах происходит на
') О близком по идее способе оценки размерности вложения п и рецеп-
рецепте конструирования динамической системы по данным эксперимента см.:
В г о о m h e a d D. S., King G. P. Extracting Qualitative Dynamics from
Experimental Data // Physica D.—1986.—V. 20, № 2, 3.—P. 217—236.
2) См. также: Dimensions and Entropies in Chaotic Systems.— Springer-
Verfag Berlin Heidelberg, 1986.
237

фоне противоположной тенденции к хаосу. Синхронизация на-
наступает тогда, когда первая тенденция начинает превалировать
над второй. Если сихронизуемая система работает в периодиче-
периодическом режиме, то порог синхронизации равен нулю [89, 90]. По-
Поэтому отличие от нуля порога синхронизации может служить
критерием хаоса в динамических системах.
Естественно предположить, что порог синхронизации связан
с такой количественной характеристикой стохастических движе-
движений, как метрическая энтропия Колмогорова. Такая гипотеза
была проверена и подтверждена численным счетом для целого
ряда конкретных систем [214, 215, 224]. Оказалось, что зависи-
зависимость между порогом синхронизации Ва и энтропией К достаточ-
достаточно хорошо аппроксимируется формулой
Вп = СК\ C.1)
где С — величина, зависящая от выбора масштабов динамиче-
динамических переменных и времени, а % примерно одинаково для всех
исследованных систем и равно х = 0,33 ± 0,10 ').
Для трехмерных систем энтропия отождествлялась с поло-
положительным ляпуновским показателем Х+, который вычислялся
на основе алгоритма Бенеттина. Зависимость C.1) при % — 0,33
и найденные численно точки для всех исследованных трехмер-
трехмерных систем представлены на рис. 8.11. (На этом рисунке v0—
частота внешнего воздействия, соответствующая порогу синхро-
синхронизации, Ct = Cvq). Постоянная С определялась по минимуму
среднеквадратичного отклонения BJC от К%. С точностью до
Рис. 8 И
ошибок численного эксперимента, обусловленных в основном по-
погрешностью в определении порога синхронизации, найденные
точки за редким исключением соответствуют зависимости C.1).
') Отметим, что порог синхронизации, по-видимому, следует определять
по началу сложного поведения систем при выходе из области синхрониза-
синхронизации, например по появлению бифуркаций удвоения периода.
238

Чтобы убедиться в том, что в формулу C.1) входит именно
энтропия, а не максимальный ляпуновский показатель, в работе
[224] была исследована синхронизация хаотических колебаний
в системе Маккея—Гласса (см. уравнения (9.3), (9.21) гл. 9).
Эта система, описываемая уравнением с запаздывающим аргу-
аргументом, замечательна тем, что для нее, начиная с некоторого
значения времени запаздывания т, максимальный ляпуновский
показатель с ростом т уменьшается, а энтропия остается при-
примерно постоянной. В B24] получено, что в этой области значе-
значений т порог синхронизации практически не меняется, что ука-
указывает на его связь именно с энтропией.
Конкретный вид исследованных систем и более подробные
результаты будут рассмотрены в следующей главе.
§ 4. Некоторые универсальные закономерности
при переходах «порядок — хаос» и аналогия
с фазовыми переходами
В настоящее время в литературе часто встречаются утверж-
утверждения об аналогии между переходами динамических систем от
движений одного типа к движениям другого типа (например,
от состояния равновесия к периодическому движению, от регу-
регулярного движения к хаотическому, от одних хаотических режи-
режимов к другим и т. п.) и известными в статистической физике
фазовыми переходами второго рода [56, 106, 127, 232, 241, 298,
309, 327, 338, 339, 355, 356]. Действительно, между этими яв-
явлениями формально имеется много общего, что проявляется,
в частности, в степенной зависимости некоторых величин, име-
имеющих смысл параметра порядка (или беспорядка), от разности
между бифуркационным параметром и его критическим значе-
значением. (В статистической физике роль бифуркационного парамет-
параметра играет температура.) Особо важным является тот факт, что
показатель' степени, называемый критическим индексом, универ-
универсален для целого класса систем, совершающих фазовый переход.
Идея такой аналогии ведет свое начало от работы Г. Хакена
[486J, в которой он обратил внимание на аналогию фазовых пе-
переходов и переходов через порог возбуждения в генераторах с
мягким возбуждением. Критический индекс для зависимости амп-
амплитуды колебаний вблизи порога от превышения над порогом
возбуждения равен 1/2. В дальнейшем указанная аналогия была
развита Ю. Л. Климонтовичем [191, 192], рассмотревшим влия-
влияние шума на генератор вблизи порога, т. е. в критической обла-
области. В отличие от фазовых переходов в равновесных системах,
рассматриваемых в статистической физике, переходы, связанные
с бифуркациями в динамических системах, принято называть
неравновесными фазовыми переходами [355, 487]. Хотя, как уже
указывалось, аналогия между переходами «порядок — порядок»,
«порядок — хаос», «хаос — хаос» и фазовыми переходами носит
во многом формальный характер, она весьма полезна, так как
239

позволяет для анализа этих явлений с успехом использовать хо-
хорошо развитые методы теории равновесных фазовых переходов,
например методы скейлинга и ренормализационной группы
[106, 115, 237, 241, 298, 327, 513].
Прежде всего, остановимся на переходе от порядка к хаосу,
сопровождающемся бесконечной последовательностью бифурка-
бифуркаций удвоения периода в соответствии с законом Фёйгенбаума
[444, 445, 447, 448]. Такой переход характерен для систем, дви-
движение которых точно или приближенно описывается одномер-
одномерным точечным отображением с гладким максимумом. Если вбли-
вблизи максимума, который без ограничения общности можно счи-
считать расположенным в точке х = 0, функция последования за-
записывается в форме
/(z)=l-jilz|', D.1)
где z > 1, ц — бифуркационный параметр, то обобщенный закон
Фёйгенбаума можно записать в виде [430, 494, 513, 514, 516,
541]')
|*»-|i« ~ б"", D.2)
П-»оо
где цп — значение параметра \ь, при котором происходит га-я би-
бифуркация удвоения периода, ц«, = lira \in, б — константа, зави-
п-»оо
сящая от показателя степени z в выражении D.1). Значения 6
Таблица 8.4
Z
1,0
1,5
2,0
2,5
3,0
3,5
4,0
б
2
3,8004
4,6692
5,4127
6,0847
6,7053
7,2851
а
оо
3,8889
2,5029
2,1368
1,9277
1,7895
1,6903
z
5,0
6,0
7,0
8,0
9,0
10,0
11,0
б
8,345
9,31
10,18
10,98
11,72
12,48
13,15
a
1,556
1,468
1,405
1,35
1,32
1,29
1,27
при разных значениях z приведены в табл. 8.4 i[516]. Из таб-
таблицы видно, что величина б монотонно растет с ростом z. Кон-
Константой Фёйгенбаума обычно называют значение б = 4,6692...,
соответствующее z = 2. В дальнейшем, если не будет специаль-
специальных оговорок, мы будем понимать под символом б именно это
значение.
Закон Фёйгенбаума можно записать и в другой форме [663,
664]:
()\
') В работе [541] рассмотрен более сложный вид отображения вблизи
его максимума и введены еще две универсальные константы.
240

где ю„ = 2л/Т„ = 2л/(Г-2п), v = In 2/ln б = 0,4498.... Действи-
Действительно, из D.2) следует, что при больших п
1п(ц,«. — Цп)" = — vn In б + const =
= —re In 2 + const = In (on — In «o + const.
Потенцируя это равенство, получаем D.2*). Записанный в фор-
форме D.2*) закон Фейгенбаума аналогичен закону изменения па-
параметра порядка ю„ для фазового перехода второго рода с кри-
критическим индексом v. Отметим, что
»n->V-oo
(Н'оо — Рп
1-V
■ ОО.
По другую сторону перехода, когда jx>jioo, в качестве пара-
параметра беспорядка можно принять либо величину положительного»
ляпуновского показателя X, либо топологическую энтропию к
[303], либо порог синхронизации Вш. Хотя для систем, описы-
описываемых одномерным точечным отображением с гладким максиму-
максимумом, при jx, большем JX», почти
везде существуют устойчивые пре-
предельные циклы [576], расчеты, про-
проведенные, например, в [518, 643,
663, 664], показали, что из-за неиз-
неизбежного присутствия малого шума
эти циклы, как правило, не прояв-
проявляются и вблизи значения и»,
D.3)
Рис. 8.12
где v — тот же критический индекс,
что и в D.2*). При наличии мало-
малого внешнего шума интенсивности аг ляпуновский показа-
показатель А, может стать положительным при (д, = цс < Ц» D24, 427,.
651]. В [651] показано, что для квадратичного отображения
ц» - цс ~ о", где р = In б/lnB0) = 0,8217...,
• • Ч D.4)
— универсальная константа, связанная со второй константой
Фейгенбаума, а = 2,5029... Заметим, что значение константы аг
как и б, зависит от показателя степени z в выражении D.1).
Приведенное значение соответствует z = 2. Значения а при дру-
других z приведены в табл. 8.4. Из таблицы видно, что константа
а при возрастании z от 1 до °° монотонно убывает от со до 1.
Качественные зависимости % от ц при ц- ~ \1„ для квадра-
квадратичного отображения без шума (сплошная линия) и при на-
наличии малого шума (штриховая линия) приведены на рис. 8.12.
') Более точное значение: р = 3,2375...
241

Если отображение вблизи максимума не квадратично, то
внешний шум может стабилизировать движение в системе и
уменьшить ляпуновский показатель, Например, в [575J показа-
показано, что для отображения вида
[[(г-0,125I/3 + 0,50607357]е~* + Ъ при ж<0,3,
Х = [0,121205692 [l0* ехр (- Щ- *)]" + Ъ при ж> 0,3,
график которого для Ь - 0,023288 (соответствующего марковско-
марковскому разбиению) приведен на рис. 8.13, а, при добавлении белого
0,2 0,4 0,0 0,8 х
а
-0,1
'0,3
Рис. 8.13
шума равномерно распределенного в интервале [-о-, о], ляпу-
н^ский показатель с ростом с убывает (рис. 8.13,6), а в спект-
спектре появляются острые пики, соответствующие движению, близ-
близкому к периодическому. Такая реакция системы на шум обус-
обусловлена, по-видимому, тем, что при данном виде отображения
шум забрасывает отображающую точку на сжимающие участки
чаще чем на растягивающие. Отметим, что указанное отобра-
отображение вблизи максимума х = 0,3 отличается от квадратичного
тем что имеет разрывную вторую производную.
Результаты численного расчета зависимости % от ц в широ-
широком диапазоне изменения ц, проведенного для квадратичного
отображения xn+i = 2xn(\i + xn) по формуле
где fix) - функция доследования (в данном случае /(*) =
-2*(ц + *)Гщ>вДОтавлены на рис. 8.14 по данным работы
242

[643]. Области отрицательных зачений К соответствуют обла-
областям существования устойчивых периодических решений неболь-
небольшого периода. Вблизи значения ц = \1„ — —0,78497... зависи-
зависимость А, от ц определяется формулой D.3) и имеет вид, по-
показанный на рис. 8.12.
Поскольку, как уже говорилось в предыдущем параграфе,
порог синхронизации Ва связан с ляпуновским показателем X
-0,70 -0,7$ -0,80 -0,85 -0,90 -0,95 /л
Рис. 8.14
соотношением Ва ~ Xх, то из D.3) получаем, что вблизи ц„
fln~(|i-n-)e, D.6)
где а = xv.
Другими параметрами беспорядка после перехода к хаосу
могут служить интенсивность сплошного спектра N и ширина
пиков спектра Доз. В [519, 680] для
./V получена следующая зависи- >
мость:
iV(|i)~(|i-|i-)c, D.7)
где 5 = 2 In рЛп б = 1,5184... При-
Приведем вывод этой зависимости. Ин-
Интенсивность Сплошного спектра из-
изменяется с ростом параметра ц при
слиянии отдельных слоев аттракто-
аттрактора в области обратных бифуркаций
удвоения [344, 421, 425, 448, 564].
Иллюстративная схема прямых и обратных бифуркаций уд-
удвоения показана на рис. 8.15 [564]. Рассмотрим отображение
x=f(x), и пусть xm = fn(x0). Величина хт определяется как
периодическими переходами между слоями, так и хаотическим
перемещением внутри самого слоя. Поэтику хт можно предста-
243

вить в виде
хт = 2 Aj exP (icOjTO) -f- n (то), D.8)
з
где п (то) — шумовой член. В соответствии с D.8) спектральная
плотность для процесса хп при некотором значении бифуркаци-
бифуркационного параметра ц равна
S (со, ц) = 214 (ц) |2 б (со - coj) + | л(ш, ц) |2, D.9)
т. е. представляет собой суперпозицию дискретных линий *) и
шумового фона. Интенсивность сплошного спектра N(\i) равна
2Л
), D.10)
где С(^i И1) = 1™ ~дГ Zn^+^c)"(m, n) — корреляционная
IV-.» JV
функция шума. Поскольку шум обусловлен случайным блужда-
блужданием внутри каждого слоя, то очевидно, что 5@, n)=PP(jx),
где W(n) — средняя ширина слоя при данном значении пара-
параметра ц. В соответствии с законом подобия, установленным
Фейгенбаумом, при переходе через бифуркационное значение
параметра половина слоев уменьшается в а раз, а другая поло-
половина — в а2 раз. Поэтому среднеквадратичная ширина одного
слоя при (х = jXm+i, где (Xm+1 — значение параметра ц, соответ-
соответствующее (иг+1)-й обратной бифуркации удвоения, равна
wm+1 = j/JE+5]w*s т w*» DЛ1)
где р определяется выражением D.4). Из D.10) и D.11) сле-
следует, что _ _
. D.12)
Так как для больших значений п цп — ц» = const fi~n, то из
D.12) следует формула D.7). Действительно, логарифмируя
D.7), получаем
InNQ,n)= 2(ln p/ln 5)ln(]in — ц.)+ С = -In In p + С„
In N(iin+i) = — 2 (re + l)ln p + Ct.
Эти равенства эквивалентны D.12).
Как уже говорилось, после перехода к хаосу в результате
бесконечной последовательности бифуркаций удвоения периода
спектр состоит из узких линий, обусловленных сменой слоев ат-
') На самом деле эти линии имеют конечную ширину, о чем будет ска-
сказано ниже.
244

трактора и шумового фона, вызванного случайными блуждания-
блужданиями вдоль каждого слоя. При удалении от точки перехода шири-
ширина узких спектральных линий Дю, как и интенсивность шумово-
шумового фона, растет. В работах [305, 438] показано, что Доз ~
~((х-ц=„)р, где р = In 2|371n б = 1,9745 ... по данным [438] и
р = 2,426... по данным [305].
Другими универсальными характеристиками перехода Фей-
генбаума являются отношение интенсивностей появляющихся
субгармоник при ге-й и (п+ 1)-й бифуркациях удвоения периода
и изменение формы сплошного спектра при обратных бифурка-
бифуркациях. В работе [446] Фейгенбаум получил, что при п -*■ «>
Sn+xBk)nSn(k), Sn+iBk+i)=r*SAk + m), где f = 2p =
= 4а7У2A + а2)« 6,57, Sn(к)— интенсивность к-ш гармоники ос-
основной частоты <а„ = 2п/Тп вдали от ге-й бифуркации удвоения.
Полученные соотношения означают, что огибающая спектра рож-
рожденных при (ге+1)-й бифуркации субгармоник (вдали от точки
бифуркации) должна лежать ниже огибающей спектра рожден-
рожденных при n-й бифуркации субгармоник на 20 lg f « 16,35 дБ. Од-
Однако, как показано в [593], Фейгенбаум_ошибся при вычислении
величины у. В действительности у = У2р = 4,5785 ..., что соот-
соответствует разности между огибающими спектров в 13,214... дБ.
Этот результат неоднократно подтвержден как в физических, так
и в численных экспериментах (см., например, [535, 658]). Форма
сплошного спектра после перехода к хаосу подчиняется анало-
аналогичным закономерностям. В работе [680] получено, что спект-
спектральная плотность при(ге+1)-й обратной бифуркации (Sn+i(a))
связана со спектральной плотностью при n-й бифуркации (£„((о))
соотношением
Sn+1 (со) = ±A+а?-2а cos соГ) Sn B©). D.13)
При этом 50(й) в интервале от 0 до 2л/Т считается константой
(белый шум). Формула D.13) хорошо согласуется с непосредст-
непосредственными численными расчетами спектральной плотности для
квадратичного отображения, выполненными в [680]. Результаты
сравнения приведены на рис. 8.16, где кривые 1 соответствуют
численным данным, а 2 — теории без учета дискретных составля-
составляющих спектра (кривые 2 для удобства смещены вниз).
В системах, описываемых двумерным и n-мерным точечными
отображениями, зависящими от одного параметра, при бифурка-
бифуркациях удвоения периода имеют место аналогичные универсальные
закономерности [420, 693]. Так, на примере двумерного ото-
отображения
хп+1 = 2{г (хп + xl) — уП1 уп+1=Вхп @<5<1) D.14)
в работе [693] показано, что значения параметра ц, при которых
происходят бифуркации удвоения периода, подчиняются законо-
закономерности типа Фейгенбаума, но с другой константой, зависящей
245

от величины коэ
иента связи В:
D.15)
где BiJl) = Bin. Зависимость б„ (В"), вычисленная на ЭВМ при
0,5
Q. О
со
-0,5
_
7 ЬГ
. I iff! S^
*,_^/i
л/2
со
-7,5
-2ft
-2,5
-3,5
-4,o,
-
f
1/
A
t 1
] 1
i 1 i
достаточно большом, но конечном значении п, показана на
рис. 8.17. При В = Ве = 0, б„ E^п)) ► 4,6692..., а при В =
П-*ОО
7 -
8,7210...
Хотя при любом В < 1 lim В™ = 0 и, следовательно,
бп (Б?) = 4,6692...,
практических расчетах для В,
близких к единице, можно
получить существенное отли-
отличие от константы Фейгенбау-
ма. Отметим, что параметр В
имеет смысл параметра дисси-
диссипации, причем значение В =
= 1 соответствует случаю от-
отсутствия диссипации, т. е. га-
мильтоновой системе (произве-
#2 ' ~fl4 ~Off ~O8 ~317'> Дение мультипликаторов непод-
неподвижных точек отображения рав-
Рис. 8.17 но единице). Поэтому получен-
полученный результат можно тракто-
трактовать следующим образом. В диссипативных системах, описывае-
описываемых двумерным точечным отображением, каскад бифуркаций
удвоения периода вблизи точки сгущения происходит так же,
246

как и в системах, описываемых одномерным отображением.
В гамильтоновых же системах с двумерным отображением кон-
константы перехода получаются другими: б = 8,7210..., а =
= 4,018... [237].
1 Как уже отмечалось, кроме бесконечной последовательности
бифуркаций удвоения периода, в принципе возможна такая же
последовательность бифуркаций утроения периода. Она также
должна подчиняться ряду универсальных закономерностей [130,
516]. Для систем, описываемых одномерным точечным отображе-
отображением с функцией последования вида D.1), эти закономерности
подобны закономерностям Фейгенбаума, но с другими константа-
константами. Зависимость констант б и а от показателя степени z в выра-
выражении D.1) для последовательности бифуркаций утроения пери-
периода продемонстрирована в табл. 8.5 [516]. Интересно отметить,
Та
Z
1,5
1,6
1,7
блица i
б
73,12
63,71
59,02
S.5
а
30,10
20,80
15,81
2
1,8
1,9
2,0
б
56,64
55,55
55,26
а
17,75
10,72
9,28
г
2,1
2,2
3,0
б
55,50
56,10
66,99
а
8,21
7,38
4,37
что с ростом z константа а монотонно убывает, как и в случае
удвоений периода, а константа б вначале убывает, достигает ми-
минимума при z = 2 и лишь затем начинает расти. Такое поведение
константы б существенно отличается от случая последовательно-
последовательности бифуркаций удвоения периода. Кроме того, значения кон-
констант б и а при бифуркациях утроения значительно больше, чем
при удвоениях, что практически не позволяет наблюдать больше
одной такой бифуркации.
В работе [210] получены некоторые универсальные закономер-
закономерности при малом внешнем периодическом воздействии на систе-
систему, описываемую одномерным точечным отображением типа
параболы. Показано, что с ростом величины воздействия значе-
значения бифуркационного параметра цп, соответствующие ге-й бифур-
бифуркации удвоения периода, монотонно растут. (В случае нерезо-
нерезонансного воздействия найденные значения ц„ соответствуют би-
бифуркациям удвоения квазипериода тора.) Отметим, что распро-
распространение полученных результатов на область хаоса, возможно,
позволит объяснить наличие порога синхронизации и его связь с
положительным ляпуновским показателем.
При переходе к хаосу, сопровождающемся так называемой пе-
перемежаемостью, также существует ряд универсальных законо-
закономерностей, аналогичных закономерностям при фазовых переходах
второго рода. Для систем, описываемых одномерным точечным
отображением, такие закономерности выявлены в . работах [229,
304, 435, 503, 504, 572, 573, 577, 609]. Вблизи перехода через пе-
247

ремежаемость одномерное отображение можно представить в ви-
виде, показанном на рис. 8.18. В момент перехода устойчивая не-
неподвижная точка отображения М сливается с неустойчивой
точкой М' и исчезает. Такая бифуркация часто называется каса-
касательной. Примем значение бифуркационного параметра е в мо-
момент касания отображения с биссектрисой за нуль. Тогда при
/
/
/
1 ОС
1
Рис. 8.18
достаточно малых е и небольших |ж,|, хг (рис. 8.18) участок /
отображения можно аппроксимировать следующим образом:
xz + e, D.16)
где г — четное число. Когда отображающая точка движется по
участку /, движение системы при достаточно малых е > 0 будет
близким к периодическому («ламинарная» фаза). Длинные участ-
участки почти регулярного поведения системы будут перемежаться
короткими нерегулярными всплесками («турбулентные» фазы),
соответствующими переходам отображающей точки на участок
отображения // и обратно. Отсюда и название «перемежаемость».
В работах [504, 515] методом ренормализации показано, что дли-
длительность «ламинарной» фазы т при .малых е > 0 пропорциональ-
пропорциональна е~A~1/г). Такой же результат получен в [503] путем замены
разностного уравнения D.16) дифференциальным уравнением и
его интегрирования.
В этих же работах, а также в [304, 435] рассмотрено влияние
внешнего шума на поведение системы и показано, что в случае
е = 0 средняя длительность «ламинарной» фазы т пропорцио-
пропорциональна g-w-wi'+v, Где g2 — интенсивность шума. Чтобы полу-
получить этот результат, авторы работ [304, 503] переходят от урав-
уравнения Ланжевена к соответствующему уравнению Фоккера —
Планка. Однако решение этого уравнения получено в [304, 503]
при граничных условиях, не соответствующих рис. 8.18. Соот-
Соответствующие граничные условия получены в работе [229], резуль-
результаты которой будут изложены ниже.
248

Наличие внешнего шума можно онисать дополнительным чле-
членом в уравнении D.16):
х = z + x + axz + g\, D.17)
где множитель g выбран так, чтобы <£>2 = 1. Предположим, что
шум | является некоррелированным и имеет нулевое среднее
значение, т. е. <£> = 0, <|п£п'> = дпп>, где 8пп>— символ Кронеке-
ра, п, п' — номера итераций.
При достаточно малых е, g и ах\л уравнение D.17) можно
заменить дифференциальным уравнением, разделив обе его час-
части на некоторое малое At. Масштаб времени удобно выбрать так,
чтобы At = 1. Тогда соответствующее дифференциальное уравне-
уравнение примет вид
*L=B + .az' + &(t), D.18)
где <Е@>—О, <Б(*Ж*')>(О
Если размеры участков отображения, на которых происходит
обмен отображающих точек между кривыми / ж II, малы (усло-
(условия малости имеют вид е + ах\, к(е + ах\) <г2 — хг, где к —
тангенс угла наклона участка //, аппроксимируемого от-
отрезком прямой), то уравнению D.18) можно сопоставить следу-
следующее уравнение Фоккера — Планка для плотности вероятности
w(t, x) [342]:
4
Прежде всего рассмотрим стационарное решение уравнения
D.19)- Для его получения достаточно задать одно граничное ус-
условие и условие нормировки. Поскольку все точки, достигшие
границы хг, уходят из рассматриваемого интервала, то
ю(«,) = 0. D.20)
Стационарное решение уравнения D.19) с граничным усло-
условием D.20) при х е [xi, хг] имеет вид
D.21)
где Ge — значение потока вероятности G = (е + ахг) w —%-irr в
интервале [xt, хг\ При х < х^ поток вероятности равен нулю, и
поэтому
w (х) =
D.22)
249

Заметим, что при удалении влево от точки Xi величина w(x)
быстро убывает, причем тем быстрее, чем меньше интенсивность
шума g1. При g = 0 w(x)= 0 для х < xt.
Постоянная Go определяется из условия нормировки при ин-
интегрировании по всем значениям а; от —°° до х2, т. е.
+
В наиболее простом случае, когда g
непосредственно следует, что
Тех
*i
да g =
Г
L
= 0,
2
из
( «y*+1
уравнения
)]'
D
D.
.23)
19)
0 при х<.хг.
Величину Go в формуле D.24) удается вычислить в явном виде
для достаточно малых значений е, когда е «С ах\л. При этом
)l/2- D-25>
Из D.24) видно, что при z = 2 распределение вероятностей
при отсутствии шума имеет форму лоренцевской линии с макси-
максимумом в точке г = 0и шириной Уе/а.
При наличии шума малой интенсивности, когда g2 < e, фор-
форма распределения вероятностей, описываемая выражениями
D.21), D.22), близка к D.24), но максимум несколько смещен в
сторону отрицательных значений х. Как показали численные
расчеты, при gz ^ e функция w (ж) очень слабо зависит от е. Гра-
Графики функции w(x), построенные по результатам этих расчетов
для различных значений параметров, приведены на рис. 8.19.
Вычислим теперь среднюю длительность «ламинарной» фазы
т. Согласно результатам гл. XVIII книги [342]
t = G0-\ D.26)
где Go — поток вероятности на интервале [a;lf x2], определяемый
выражением D.23). При g = 0 ne<Caa:i,2 из D.26) и D.25) име-
имеем т~е~A~1/г), что совпадает с результатами работ [503, 504,
515]. В другом крайнем случае, когда е = 0, но g Ф 0, имеем
т = 2"-1)/(г+1> ((z + ±)/ауь+»г*1-"'1*+1)В, D.27);
250

где
2 *
В = J exp (u*+i) J ехр (— vz+1) dvdu +
ui u
+ J exp(u*+i)duj ехр (—v*+i) dv,
и
2a \i/(z+D
При g8 «a|z,i2|*+1 можно положить ut«"—°°, u, = <», и величи-
величина J5 не будет зависеть от g. При этом из D.27) следует, что
т ~ £-*(*-»>/(*+i>t Полученная зависимость т от g совпадает с ре-
результатами работ [435, 503, 504, 515].
В>(Х)
О 0,07
Рис. 8.19
0,013!
251

Зависимости т от g2, вычисленные по формулам D.26), D.23^
при различных значениях остальных параметров, приведены на
рис. 8.20. Как и w{x), значения т при g% > e практически не
зависят от е, о чем свидетельствуют данные, приведенные
в табл. 8.6,
Вычислим далее ляпуновский показатель % для рассматривае-
рассматриваемого отображения, используя в качестве исходной формулу D.5).
При этом существенным может
оказаться следующий член разло-
разложения отображения на участке /,
содержащий нечетную степень z.
f, xz=0,D2>
,z~2
Таблица 8.6 г =
-ff
-4
Рис. 8.20
10
ю-»
10
10
e
0
10"»
10
0
10
10-6
0
10
0
lO
t
25,32
25,30
25,08
23,11
54,55
54,50
51,12
9,30
9,28
2,208
2,207
С учетом этого члена зададим отображение на участке / в виде
х = г + х + ах' + bxz+i + gt, D.28)
а на участке // — в виде
х=х1 + к(х-хг).
D.29)
Подставляя D.28) и D.29) в формулу D.5), получаем
[N
2 In (l + azxl'1 + b(z + l)xl)+Qln\k\\, D.30)
где Q — число переходов отображающей точки с участка / на
участок // за N + Q итераций. Очевидно, что при больших N
Q = Nh < N. В силу эргодичности процесса на участке / выра-
выражение D.30) можно записать так:
1 = j w (x) In A + azx*-1 + b (z + 1) x1) dx + ^j-ln | к \, D.31)
где w(x)—стациоларное распределение вероятностей, форма ко-
которого близка к вычисленной ранее, поскольку член bx2+i мал.
Последнее видно из рис. 8.21, где приведена зависимость w(x)
при g2 — 10~в и b = 30 (остальные параметры те же, что и на
рис. 8.19, а). Эта зависимость почти точно совпадает с кривой 2
на рис. 8.19, а.
252

При g = 0, e<g.azli2 можно положить w (х) =* Go/(е + ах*-h
+ bxz+i), где Go приближенно определяется выражением D.25).
В этом случае при условии az | аг1J Г + Ь (z 4- 1) х\,2 <С 1 интеграл
в выражении D.31) легко вычисляется. В результате получаем
г sin (re/z)
2л
In -pL + Л. (ж, _
In | fc |j. D.32>
•750
-0,07
О
0,02 х
Отсюда видно, что % > О, т. е. движение стохастическое, если
выражение в фигурных скобках в D.32) положительно. В про-
противном случае после перехо-
перехода возникает периодическое
движение с большим перио-
периодом. При этом поведение си-
системы может быть хаотиче-
хаотическим в указанном в гл. 3
смысле. Отметим, что аттрак-
аттрактор в фазовом пространстве
системы, соответствующий
ее хаотическому поведению,
в работах [45, 381] был на-
назван квазиаттрактором, хотя
более» точно его следовало
бы назвать квазистранным
аттрактором.
В случае стохастического
движения после перехода
ляпуновский показатель %
плавно нарастает по закону
Д, ~ 8(»-»/«) несмотря на то,
что рассматриваемый переход является жестким. Зависи-
Зависимости Я от е без шума (сплошная линия) и при наличии
шума интенсивности g2 = 10~6 (штриховая линия), вычисленные
с помощью ЭВМ по формуле D.31), показаны на рис. 8.22. В от-
отличие от перехода Фейгенбаума, при рассматриваемом переходе
в случае не очень больших \к\ шум оказывает стабилизирующее
влияние на систему, поскольку забрасывает отображающую точку
в область сжимающего участка отображения1). При достаточно-
больших \к\ основную роль играет уменьшение т за счет шума,
что приводит к увеличению ляпуновского показателя с ростом
интенсивности шума, т. е. к дестабилизации движения.
Следует заметить, что выражение D.31) определяет величину
ляпуновского показателя весьма приближенно, поскольку основ-
основной вклад в интеграл дают далекие от нуля значения х, при ко-
которых ошибка, возникающая при переходе от разностного урав-
уравнения к дифференциальному, больше, и следовательно, значения
w{x) вычислены менее точно.
Рис. 821
Х\, 2
]) Этот эффект не учтен в работе [304] из-за того, что в ней положено-
±
253

В работах [218, 606] рассмотрен другой тип перехода к хаосу
•через перемежаемость, когда отображение имеет вид, показанный
на рис- 8.23. В момент перехода устойчивая неподвижная точка
М сливается с двумя неустойчивыми точками М' и М" и стано-
становится неустойчивой. За счет участков отображения // и //' ото-
отображающая точка всегда возвращается в область вблизи точки
М. При небольшом х0 уча-
участок / отображения мож-
можно аппроксимировать сле-
следующей формулой:
х=A + е + ахг)х, D.33)
где z — четное число. Мо-
Момент перехода соответст-
соответствует е = 0. При достаточ-
достаточно малых е отображаю-
отображающая точка длительное
время будет находиться
вблизи точки М, т. е. дви-
движение будет близким к
периодическому («лами-
(«ламинарная» фаза). Участки
такого движения будут
перемежаться короткими
Рис. 8.22 «турбулентными» всплес-
всплесками, соответствующими
переходам в области отображения //, //' и обратно.
С учетом внешнего шума отображение D.33) имеет вид
D.34)
где <%> = 0, <%2> = 1. При lei, g, az(j<l уравнение D.34) может
«быть заменено дифференциальным уравнением
^- = (е + axz) x + gl (t), D.35)
где <
b
Рис. 8.23
254

Рассмотрим для простоты случай полностью симметричного
отображения, как это показано на рис. 8.23, и будем считать,
что участки обмена отображающих точек между областями /, //
и //' малы. Соответствующие условия малости легко записать
аналогично тому, как это было сделано раньше. При этом участ-
участками обмена вблизи точек ^х0 в силу их малости можно прост»
пренебречь, тогда как участок [—Ь, Ь] (рис. 8.23) вблизи точки
х = О необходимо учитывать ввиду нахождения в нем неподвиж-
неподвижной точки М. (При стремлении Ъ к нулю распределение вероят-
вероятностей в точке х — О получает особенность.)
В областях й^ \х\ <:Х0 уравнению D.35) можно сопоставить
уравнение Фоккера — Планка без источника:
£--£Кв + «О*»]+-££. D.38>
Граничные условия для уравнения D.36) в точках х — ±х0 в со-
соответствии с D.20) имеют вид
*=0. D.37>
В области — Ъ < х < Ь в уравнение . D.36) следует добавить
источник, вид которого можно вычислить. Однако ради просто-
простоты в силу малости величины Ъ этот источник можно считать
постоянным и равным некоторой неизвестной величине R. Зна-
Значение R определяется из условий непрерывности плотности и
потока вероятностей в точках i = 0 и at = ±Ь.
Стационарное решение уравнения D.36), удовлетворяюще»
условиям D.37), следующее:
<4.38>
(В силу симметрии достаточно рассмотреть только область по-
положительных значений х.)
Из условия dw/dxlx*.,, = 0, вытекающего из симметрии плот-
плотности вероятностей при положительных и отрицательных зна-
значениях х, и выражения для потока вероятностей в точке х — О
находим R = GJb. С учетом этой связи между R и Go решение
уравнения D.36) с постоянным источником R в области 0 ^ х ^
< Ь, удовлетворяющее условиям непрерывности в точке х = br
имеет вид
D.39>

Из условия нормировки находим Go
-1.
• <4-40>
В предельном случае g = 0 непосредственно иэ уравнения
<4.36) имеем
где
(/)
Iг = J <fy/(l + У1)-
О
При z = 2 /2 = arctg (Уа/еЬ), при z = 4
В случае е -»- 0 h -»- я/2, /t -*- У2я/4
Графики функции и? (ж) при а = 30, х0 = 0,01, е = 10~',
■fe = (А;/2) (е + axl)x0 — ЪЛ0~ и различных значениях парамет-
параметров z и g* приведены на рис. 8.24. Как следует из результатов
численного счета, при g2^g2,(z), где g2~ 10~7 для z = 2 и 10~8
для z = 4, распределение вероятностей практически перестает
зависеть от g2. Кроме того, при g2 ^ 10~7 оно почти одинаково
для z = 2 и z = 4 (сравните кривую 3 на рис. 8.24, а и кри-
кривую 2 на рис. 8.24, б).
В силу сделанного выше предположения о малости величины
Ъ по сравнению с х0 для вычисления средней длительности ла-
ламинарной фазы можно по-прежнему считать, что поток вероят-
вероятности постоянен и равен Go. Тогда с учетом того, что отобра-
отображающая точка находится в области г>0 с вероятностью 1/2,
имеем
т = G2. ч D.43)
При ^ = 0 и достаточно малых е из D.43) и D.42) имеем
т = /2/(йа1/ге(*-1)/г). D.44)
256

Отсюда видно, что т ~ г-и-*/г> при малых е, как и в ранее рас-
рассмотренном случае. В частности, т ~ е~1/а при z = 2, что совпа-
совпадает с результатами работы [606].
Оценим зависимость т от g2 в предельном случае 8 = 0. По-
Полагая в D.40) u = Ba/(z + 2)£2I/(z+24 получаем
D.45)
где
В = j ехр (ц*+2) j ехр (— vz+2) dvdu +
о «
"о ьо
+ -L j* ехр (u*+2) j (у — 60) ехр (- уг+2) dwut,
2a Ni/B+2)
2a
При g2 < аЬг+2 можно положить и0 = °° и й0 = °°. Тогда
со оо
В я* у- Г ехр (wz+2) j и ехр (— vz+*) dvdu ~ g*lb+z\
0
Следовательно, т ~ g-2^-1
w (я) 10
т. е. предельная зависимость т
wto)
400-
Z-4
-Off/
-дОд
0,01 -0,01
Рис. 8.24
-6ОЬ
от g2 при 8 = 0 тоже совпадает с ранее рассмотренным случа-
случаем. (При z = 2 она также совпадает с результатами работы
[606], хотя эти результаты получены не вполне корректно.)
Численные расчеты, проведенные по формулам D.40), D.43)
при а = 30, 6 = 3-10~4, Хо = 0,01 показали, что при g2 ?э 10~"
257

зависимость т от g2 практически не зависит от е, а при g2 > 10 в
и от z. Ее вид продемонстрирован на рис. 8.25. На том же ри-
рисунке штриховой линией показана асимптотическая зависимость
т от g2 при 8 = 0, z = 2.
Величину ляпуновского показателя для рассматриваемого
отображения можно вычислить по формуле, аналогичной D 31):
*о
К = 2 \ w (x) In A + е + a (z -f 1) хг) dx + -~- In | к |, D.46)
где А; — тангенс угла наклона участков отображения // и //'.
При g = 0, е + a(z + 1)^о <Cl с учетом D.41), D.43) получаем
Рис 8 25
Из D.47) видно, что в этом случае ляпуновский показатель
может быть положительным даже при достаточно малых Iftl.
Это связано с тем, что при
е > 0 весь участок отобра-
7^ч\~~""--. 119Х жеиия / является растя-
растягивающим. При достаточно
малых е, как следует из
D 47) и D.44), величина Я,
с ростом е нарастает про-
порциопалыю еA~1/г). Зави-
Зависимости 1 от е при различ-
различных значениях g2 (а) и от
gl при е = 0 (б) показаны
на рис. 8 26. Отметим, что в
отличие от ранее рассмот-
рассмотренного случая внешний шум
дестабилизирует поведение системы, существенно увеличивая
ляпуновский показатель. Это отличие также связано с тем, что
при е > 0 отображение в области / не имеет сжимающих
участков.
Из полученных здесь и выше результатов следует, что пере-
переход к стохастичности через перемежаемость аналогичен фазово-
фазовому переходу второго рода, причем в качестве параметров беспо-
беспорядка можно рассматривать либо Я, либо т~1. Для обоих пара-
параметров критические индексы получаются одинаковыми и зави-
зависящими лишь от показателя степени z, т. е. от характера ото-
бражепия вблизи точки касания или точки перегиба.
Отметим, что жесткое возникновение стохастического режи-
режима, не сопровождающееся перемежаемостью (как в системе Ло-
Лоренца при малых значениях параметра г [686]), аналогично фа-
фазовому переходу первого рода, поскольку при таком переходе
258

ляпуновский показатель % и энтропия К нарастают скачком с
характерным для жестких переходов гистерезисом (рис. 8.27).
Переходы к хаосу, сопровождающиеся возникновением и
разрушением тора, также должны характеризоваться рядом уни-
универсальных закономерностей, но пока опи изучены слабо. Неко-
А 70
торые закономерности, имеющие место при разрушении тора,
кроме уже описанных, выявлены в работах [24, 50, 167, 390,
416, 417, 463, 615]. Кое-что известно и для случая, когда перед
разрушением тора возникают бифуркации удвоения его квази-
квазипериода [37, 389, 537, 538]. Так, в работах [537, 538] на примере
системы, описываемой двумерным точечным отображением вида
s sin 2nynt, yn+1 =
ехп
D.48)
где С — константа, имеющая смысл числа вращения Пуанкаре,
показано, что число бифуркаций удвоения тора, происходящих
при изменении параметра А, ко-
конечно и определяется парамет-
ром связи е. Этот вывод следует
из диаграммы, демонстрирующей
области существования тора с
квазипериодом 2п X Т на плоско-
плоскости параметров А, е. Вид такой
диаграммы для С = (У5 — 1)/2
показан на рис. 8.28. На этом
рисунке А „ — критическое зна-
значение параметра А, при котором
в случае 8 = 0 закапчивается
каскад бифуркаций удвоения
периода цикла. Из приведенной диаграммы можно построить
зависимость от е числа удвоений тора I при переходе к хаосу
(рис. 8.29). Из рисунка видно, что максимальные или минималь-
минимальные здачения е, соответствующие данному значению I, прибли-
25
Рис. 8.27

женно ложатся на прямую, уравнение которой имеет вид
lg 2' = const — a lg e, D.49)
где а = 1/3.
Ряд закономерностей, устанавливающих порядок смены ре-
зонапсов на двумерном торе, получен в работах [449, 597, 611,
644] на примере двумерного отображения вида
6п+1 = 6„ + Q + Ъгп - (К/2п) sin 2л6п,
D'50)
гп+1 = Ъгп - (tf/2rc)sin 2я9п.
Соответствующий отображению D.50) двумерный тор характе-
характеризуется числом вращения Пуанкаре W = lim (8n — 90)/п. При
тг-»оо
резонансе на торе W — p/q, где р и q — целые числа- Число
вращения W равно p/q, если и только если существуют такие
2
то
70~г Я?'3 70~4 ,„
A„,-A (Aoo = 7,407757...)
Рис. 8.28
70
-S
70'
Рис. 8.29
10
-з
80 и Го, что 9, = 80 + р, г, = г0. Каждое иррациональное значе-
значение W — W можно представить как продел последовательности
рациональных чисел Wt = p,/q,, т. е. W = lim Wt. В цитирован-
пых выше работах рассматривается значение И^ = (У5 — 1)/2
(золотое сечение). При этом Wt = F,/F,+i, где Fx — так называ-
называемые числа Фибоначчи, удовлетворяющие рекуррентному соот-
соотношению F,+i = F% + F,_4 с начальными условиями Fo = 0,
Fi = 1. В [644] для случая Ъ — 0 показано, что последователь-
последовательность разностей чисел QX(K), соответствующих значениям W%
(W(K, Q,(K))=Wi) при достаточно больших i образует геомет-
геометрическую прогрессию, знаменатель которой, вообще говоря, зави-
зависит от К:
D.51)
При 0<_К<1 б (К) =—W~2 = — 2,61803 ..., а при К=1
б(K) = -W~v = -2,83360 ..., где у = 2,16443 ... Легко видеть,
что формула D.51) аналогична закону Фейгенбаума с констан-
константой Ь(К). В указанной работе определяется и другая константа,
260

аналогичная константе Фейгенбаума а: а (К) = lim щ {К), где
i-too
щ (К) = dj-i/dj, di — 6g._1 — 60 — /?{_! при $ = Qt (К). Величи-
Величина а {К) равна — W~x = —1,61803 ... при 0 < К< 1 и — W~* =
= -1,28857 ... при Я = 1 (х = 0,52687 ...).
В остальных цитированных выше работах отображение
D.50) рассматривается при 0 < Ъ < 1. Оказывается, что законо-
закономерность D.51) справедлива и в этом случае, только 8(К) =
= -W~2 при 0*£К<Ке< 1 и 6(^) = -ТГ-1' при Я = ЯС. Для
Ъ = 0,5 Яс = 0,9788 ...
В работе [531] на примере отображения D.50) с Ъ = 0 пока-
показано, что при критическом значении К, равном единице, обла-
области значений Я, где W = p/q, образуют канторовское множества
с фрактальной размерностью d = 0,87.

Глава 9
ПРИМЕРЫ МЕХАНИЧЕСКИХ, ФИЗИЧЕСКИХ,
ХИМИЧЕСКИХ И БИОЛОГИЧЕСКИХ СИСТЕМ,
В КОТОРЫХ ВОЗМОЖНЫ ХАОТИЧЕСКИЕ
И СТОХАСТИЧЕСКИЕ ДВИЖЕНИЯ
В настоящее время известно большое количество реальных и
модельных механических, физических, химических и биологиче-
биологических систем, в которых происходящие процессы имеют хаоти-
хаотический характер. Поскольку аналитическое исследование таких
систем, как правило, невозможно, то вывод о наличии хаотиче-
хаотических или стохастических движений делается на основе анализа
результатов численных или натурных экспериментов. Подобных
результатов уже накопилось очень много. Некоторые из них
будут изложены ниже, причем основное внимание будет уделе-
уделено результатам численного эксперимента.
§ 1. Нелинейный осциллятор с отрицательным трением
и ударами и другие системы с разрывными характеристиками
Как уже отмечалось, одним из самых простых и наглядных
примеров стохастических генераторов является осциллятор с от-
отрицательным трением, колебания которого ограничиваются за
счет ударов, уменьшающих скорость осциллятора на величину р
и производимых в моменты времени £„, в которые х = 0 и х ^
> а > 0 [150, 280]. Таким осциллятором может служить, напри-
например, маятник Фроуда [15, 216, 345]. Считая трение слабо нели-
нелинейным, запишем уравнение осциллятора в виде
х — 26 A — сеж2) x + <i>2ox = —p'2l8(t — ts). A.1)
s
Анализ возможных решений зтого уравнения при а = 0 прове-
проведен в § 3 гл. 3. Поэтому ниже мы рассмотрим случай а¥=0.
В этом случае точечное отображение y = f(y), где у — х,
аналитически вычислено быть не может (по крайней мере, точ-
точно). Однако его характер легко представить. В зависимости от
параметров это отображение может иметь один из видов, пока-
262

занных на рис. 9.1 [150]. В случае а при любых начальных ус-
условиях в системе возбуждаются периодические колебания, соот-
соответствующие устойчивой неподвижной точке Л/2. В случае б в
зависимости от начальных условий возбуждаются либо периоди-
периодические колебания, либо стохастические, т. е. в фазовом прост-
пространстве системы имеются два аттрактора — предельный цикл и
У
У
J
J
Рис. 9.1
странный аттрактор. Наконец, в случаях в ж г при любых на-
начальных условиях возможны только стохастические колебания.
Области значений г/, соответствующие установившимся стохасти-
стохастическим колебаниям, на рис. 9.1 выделены жирными линиями и
обозначены буквой /. Переход от случаев а и б к случаям в ж г
происходит в результате слияния устойчивого и неустойчивого
предельных циклов (на рис- 9.1 неустойчивому предельному
циклу соответствует неустойчивая неподвияшая точка Mi).
В зависимости от того, произойдет ли это слияние ниже точки
А или выше ее, переходы оказываются различными. В первом
случае до перехода странный аттрактор отсутствовал, а сущест-
существовала лишь непритягивающая гомоклиническая структура.
Слияние устойчивого и неустойчивого предельных циклов про-
происходит как раз в области этой структуры, которая после слия-
слияния становится притягивающей и образует стохастический ат-
аттрактор. Поэтому возникновение стохастичности после такого
нерехода сопровождается перемежаемостью. Сказанное хорошо
263

иллюстрирует график точечного отображения на рис. 9.1, г, со-
соответствующий описанному переходу к стохастичности. Как уже
говорилось в предыдущей главе, при удалении от точки перехо-
перехода длительность «ламинарных» фаз сокращается, а «турбулент-
«турбулентных» увеличивается, и в результате «ламинарные» фазы ис-
исчезают.
Во втором случае, когда слияние устойчивой и неустойчивой
неподвижных точек происходит выше точки А, странный ат-
аттрактор существовал и до перехода наряду с устойчивым пре-
предельным циклом- Поскольку слияние устойчивого цикла с неус-
неустойчивым происходит вне области аттрактора, перемежаемости
не возникает. При изменении параметра в обратную сторону
должен наблюдаться гистерезис, характерный для жестких пе-
переходов.
В работе [184] исследовано движение твердого тела па плос-
плоскости под действием силы пружины, конец которой перемещает-
перемещается с постоянной скоростью. Уравнение движения имеет вид
тх + к(х— vt) = FTp(i).
Предполагается, что при х Ф 0 FTp (х) — —Fo sign х, а при х = О
сила трения по модулю не превосходит некоторой величины
F(x), зависящей от времени т неподвижного контакта между
телом и плоскостью, причем при т = О F = Fo, а при т -*■ °° F
стремится к некоторому конечному значению Fi. В соответствии
с зтим зависимость F(x) задается в виде
F{x) = F1-(F1-Fo)e-°\
Аналитически показано, что при определенных значениях Fi, б
и v в системе возникают стохастические автоколебания, описы-
описываемые кусочно-линейным растягивающим отображением от-
отрезка в себя.
§ 2. Генераторы на туннельных диодах
Другими достаточно простыми примерами стохастических ав-
автоколебательных систем являются различные типы генераторов
с туннельными диодами [190, 314, 607, 682]. Рассмотрим снача-
сначала один из них, схема которого представлена на рис. 9.2, A90,
314, 607]. Уравнения такого генератора в предположении, что
характеристика усилителя линейна, имеют вид
й = -и + ^1я Cru + i{u)=I% B.1)
где i(u)—ток через туннельный диод Д, Ci — паразитная ем-
емкость туннельного диода, S — крутизна характеристики усили-
усилителя. Вольтамперная характеристика туннельного диода качест-
качественно имеет вид, показанный на рис 9.3, а.
Уравнения B.1) удобно записать в безразмерных пере-
переменных:
х = 26а: + у — gz, у - — х, zz = x — /(z), B.2J
264

— %~п "С1* точка оз-
начает дифференцирование по безразмерному времени т.
Рис. 9.2
О
/ z
Рис. 9.3
7
Вид функции /(z) показан на рис. 9.3, б. При достаточно
малых е движение системы в фазовом пространстве будет сос-
состоять из медленных раскручивапий относительно состояния
равновесия х = 0, у = 0 на поверхно-
поверхности малых z, соответствующих левой
ветви функции f(z), и быстрых пере-
перескоков на правую ветвь функции f{z)
и обратно. При обратном перескоке на
поверхность малых z величина у ока-
оказывается малой, т. е. происходит ее
быстрый сброс. В этом отношении дан-
данный генератор аналогичен рассмотрен-
рассмотренному в предыдущем параграфе.
Вид точечного отображения для си-
системы B.2) в приближении идеализи-
идеализированной характеристики туннельного
диода (рис. 9.4) показан на рис. 9.5, а [607]. Временная реали-
реализация процесса y{t), полученная экспериментально [190, 314,
265
/ z
Рис. 9.4

Рис. 9.5
-—F--1
i №—J
Рис. 9.6
0,90
70
w
-z
0,90 (
Г,00 iA2 O,O
Vac. 9.7
_J | 1_
0/ 0J2 0,3 f

607J при g = 2,4, е = 4,8 • 10~s представлена на рис. 9.5, б. Она
очень похожа на осциллограмму колебаний маятника с отрицатель-
отрицательным трением и демпфирующими ударами, приведенную на рис. 3.15.
В работе [682] рассмотрена схема генератора с двумя тун-
туннельными диодами (рис. 9.6). Численное решение уравнений
такого генератора показало, что в определенной области пара-
параметров колебания оказываются стохастическими, причем соот-
соответствующее точечное отображение является разрывным и экс-
экспоненциально неустойчивым (рис. 9.7,а), а спектр колебаний —
сплошным (рис. 9.7,6). Интересно отметить, что точечное ото-
отображение на рис. 9.7, а полностью совпадает с приведенным на
рис. 3.14, б.
§ 3. Нелинейные осцилляторы с периодическим
внешним воздействием
Колебательные системы с одной степенью свободы, находя-
находящиеся под действием внешних сил, имеют трехмерное фазовое
пространство, где третьей координатой является время. В та-
таких системах хаотические колебания возможны даже при пери-
периодических внешних воздействиях. Подобные колебания наблю*
дались как в численных, так и в физических экспериментах.
Прежде всего рассмотрим нелинейный осциллятор, описыва-
описываемый уравнением Дуффинга и находящийся под действием гар-
гармонической внешней силы, содержащей, в общем случае, посто-
постоянную составляющую:
х + ах + кх + ух3 = Во + В cos at. C.1)
Исследованию уравнения C.1) посвящено большое число ра-
работ. Рассмотрены различные виды упругих характеристик: мяг-
мягкая (к>0, f<0) [153, 419, 436, 517], жесткая (к>0, ^>0)
[208], с нулевой (fc = 0, 4 > 0) [394, 495, 496, 542] и отрица-
отрицательной (fc<0, т>0) [З86> 506i 508> 585] линейной жест-
жесткостью. Отметим, что путем сдвига начала координат уравнения
с 1с < 0 и So ^ 0 сводятся к виду
у + ау + ку + № + чу3 = В cos at, C.2)
где к > 0, т. е. к уравнению нелинейного осциллятора с несим-
несимметричной упругой характеристикой и симметричным внешним
воздействием.
Как при мягкой, так и при жесткой упругой характеристике
хаотические колебания существуют при достаточно большой
амплитуде внешней силы в интервале частот &>, где соответст-
соответствующая амплитудно-частотная характеристика неоднозначна
(область бистабильности). Как показали численные эксперимен-
эксперименты, эти колебания возникают путем последовательности бифур.-
каций удвоения периода. Области таких бифуркаций и хаотиче-
хаотических колебаний для к = 1; f = —4; а = 0,4; В = 0,115; -В0 = 0
получены в [517] с помощью АВМ. Критическое значение час-
267

тоты ш, при котором наступает хаос, равно ©«, = 0,5567. Даль-
Дальнейшее уменьшение частоты и приводит снова к периодическим
колебаниям, причем их амплитуда соответствует нижней ветви
резонансной кривой.
Численное моделирование уравнения C.1) при к = 1, ^<0,
Bd = 0, В = 1 [153] показало, что при значениях параметров,
соответствующих [517] (а = 0,4; ^ = —0,0529), бифуркации уд-
удвоения периода и переход к хаосу не наблюдаются. Эти явления
происходят лишь при больших значениях 1^1 A^1 > 1^1 *=
=■ 0,058), что соответствует большим значениям амплитуды
внешней силы. Так, например, при f =» —0,061 (а = 0,4) первая
30-
20
10
I It I , 1—.——1 1—*-
О{> 0,583
OJ 0,8 0,9 7,0 о>
Рис. 9.8
•бифуркация удвоения наблюдалась при (Oi = 0,5904, вторая —
при и2 = 0,5898, третья — при и» = 0,5897 и т. д. Каскад бифур-
бифуркаций удвоения заканчивался при ю.» = 0,5896, после чего на-
наступал хаос.
-268

В области хаоса наблюдаются узкие окна, где колебания яв-
являются периодическими с периодом, равным трем, пяти и семи
периодам внешней силы. Такое поведение является характер-
характерным для систем, описываемых одномерным точечным отображе-
отображением с гладким максимумом [576]. При уменьшении частоты
ниже сод = 0,585 решение сис-
системы уходило на бесконеч-
бесконечность.
Полученные результаты
представлены па рис. 9.8, где
сплошными линиями показаны
периодические режимы, а ко-
косой штриховкой — область хао-
хаоса. Горизонтальными линиями
внутри области хаоса показан
режим утроения периода, а вер-
вертикальными — упятерения. За-
Зависимости области бифуркаций
и хаотических колебаний от
параметра i для ряда значе-
значений а показаны на рис. 9.9,
жа которого видно, что при
увеличении ■у область сложно-
сложного поведения системы смеща-
смещается в сторону более высоких
частот. Штриховой линией на
рис. 9.9 показана граница
рождения гомоклиническои
структуры для случая а = 0,4,
построенная на основе крите-
критерия В. К. Мельникова [250,
507, 580] по формуле "укр =
= Bа79) (shx/xJ, где х =
= яю/У2. Тот факт, что эта
граница не совпадает с грани-
границей хаоса, означает, что суще-
существует область значений -у и ю,
где имеется гомоклиническая
структура, но она не является
притягивающей. В этой обла-
области должен наблюдаться хао-
хаотический характер переходных
процессов.
В случае жесткой упругой характеристики хаос возникает
при значительно больших значениях амплитуды внешней силы.
Гак, для а = 0,2; к=*1\ у = 1;50 = 0 он наблюдался при 5 = 50
в области частот 1,5 < и < 2 [208]. В качестве иллюстрации на
рис. 9.10 показано распределение точек на секущей плоскости
>t = 0 [mod 2я/о»] при и = 1,9. На этом рисунке выделены обла-
269

сти 1, 2, 3, для которых были определены относительные часто-
частоты р попадания отображающей точки в эти области при разных
начальных условиях. Оказалось, что с ростом числа итераций
эти частоты стремятся к предельным значениям, определяющим
предельную вероятность нахождения отображающей точки в
указанных областях (для области 1 — р « 0,05, для 2 — р «
«0,26, для 3 — />«0,10). Однако осталось невыясненным, ха-
характеризует ли зта вероятность внутреннюю динамику системы
или внешний шум.
Для осциллятора с несимметричной упругой характеристи-
характеристикой (или с несимметричным внешним воздействием) хаотиче-
хаотические решения имеют место в широком диапазоне значений ам-
амплитуды и частоты внешней силы. Так, для а = 0,05; к = 0;
«2
-0,2
1
1
•
J
r
t
4-
-0,8 -0,4-
Численное решение
0,4 л
-0,8 -0,4 О 0,4- я
Экспериментальные результаты
Рис. 9.11
7 = 1; 50 = 0,04; и = 1 хаос наблюдался при В > 0,12 [496, 542].
Точечное отображение на секущей плоскости t = 0 [mod 2я/&>]
для В = 0,14 показано на рис. 9.11.
Структура аттрактора на секущей плоскости t = 0 [mod 2л]
для уравнения C.1) с Л = —1, ^ = 1, © = 1, В0 = 0 и различных
значений а ж В исследована
в [508]. В работе [585] для
подобного случая (^ = —к —
= 1/2; © = 0,833; 5 = 0,16;
Во = 0) оценена фракталь-
фрактальная размерность d в зависи-
зависимости от коэффициента за-
затухания а. Оказалось, что
при малых а величина d
близка к трем, тогда как
0,04 0,06 0,Т2 0,1$ О,2О 0,14а.
Рис. 9.12
при увеличении а она пада-
падает до двух (рис. 9.12).
Переход к хаосу в осцил-
осцилляторе, описываемом урав-
уравнением C.1) при к < 0, у > 0, Во = 0, наблюдался эксперимен-
экспериментально в работе [386]. Масштабы были выбраны так, что fc = —1;
7 = 4; а = 0,154. При частоте внешней силы &> = 1,253 переход
270

к хаосу с ростом амплитуды внешней силы В происходил путем
последовательности бифуркаций удвоения периода. Начиная с не-
некоторого значения В на фазовой плоскости х, х наблюдался
хаотический аттрактор, охватывающий (в зависимости от на-
начальных условий) одну из особых точек автономного осцилля-
осциллятора (±1/2, 0). При этом спектр колебаний становился сплош-
сплошным, по сильно заваленным в области низких частот
O,S
Рис. 9.13
(рис. 9.13, а)- При увеличении амплитуды В возникали редкие
случайные перескоки с этого аттрактора на другой, охватываю-
охватывающий другую (симметричную) особую точку. Из-за наличия пе-
перескоков спектр существенно расширяется в низкочастотную
область (рис. 9.13, б). При дальнейшем увеличении В каждый
из аттракторов начинает охватывать обе особые точки. Между
этими аттракторами также имеются случайные перескоки, приво-
приводящие к наличию низкочастотной части спектра, изменяющейся
по закону 1// (рис. 9.13, в). Вид временной реализации, соответ-
соответствующей такому режиму, показан на рис. 9.13, г. По мнению
авторов [386], описанное явление может служить некоторой мо-
моделью фликкер-шума. Более общая картина возникновения шума,
подобного фликкерному, за счет перескоков между различными
аттракторами обрисована в [385]').
') Совершенно иная попытка объяснения природы фликкер-шума на
основе динамического хаоса предпринята в работе [94].
271

В работах [529, 562, 603, 658] приведены эксперименталь-
экспериментальные результаты для нелинейного колебательного контура, опи-
описываемого уравнением
LCV + RCV + V = Vo sin Bя/0,
где C = C0(l + F/0,6I/2, Со = 300 пФ, L = 10 мГн, R = 28 Ом.
При увеличении Уо в такой системе возникает последователь-
последовательность бифуркаций удвоения периода, после чего наступает хаос.
Область хаоса несплошная. В ней имеются «окна», в которых
колебания являются периодическими с различными периодами.
Об этом свидетельствуют данные, приведенные в табл. 9.1
Тг
Пери-
Период
2
4
8
16
32
Хаос
12
24
6
12
i6
лица
0,639
1,567
1,785
1,836
1,853
1,856
1,901 1
1,902 j
2,073 1
2,074 j
9.
I
Г
\
1
Бифуркационные
значения
Начало хаоса
Окно
Окно
Пери-
Период
5
10
7
14
3
6
12
24
9
18
2,353
2,363
2,693
2,696
3,081
3,338
3,711
3,821
4,145
4,154
}
\
/
1
[
j
}
Окно
Окно
Широкое окно
Окно
[658], где указаны граничные значения Vo, соответствующие об-
областям периодических режимов («окнам»). Последовательность
найденных периодических решений очень напоминает порядок
смены кратностей неподвижных точек для одномерного отобра-
отображения, установленный А. Н. Шарковским [368]. Переход к хао-
хаосу из разных окон периодичности происходит по-разному: либо
через последовательность бифуркаций удвоения периода [562,
658], либо через перемежаемость [603], либо жестко с типичным
для такого перехода гистерезисом [529].
Решения, аналогичные изложенным выше и более сложные,
получены также для уравнения физического маятника с внеш-
внешним воздействием [139, 140, 401, 408, 432, 482, 543]
Ф + аф + sin ф = Во + В cos (at
и уравнения [548]
ф + аф + sin ф + [}ф = Во + В cos
C.3)
C.3*)
В определенных приближениях эти уравнения описывают по-
поведение фазы волновой функции в контакте Джозефсона, вклю-
включенном в цепь переменного тока [139, 140, 401, 408, 482, 548],
272

а также систему фазовой синхронизации [82—87, 432] *). В ка-
качестве иллюстрации приведем полученные экспериментально в
}4ozJ для системы фазовой синхронизации, описываемой уравне-
уравнением C.3), бифуркационную диаграмму на плоскости парамет-
параметров 5, со (рис. 9.14), а также эволюцию фазового портрета
0,25 0,50
Рис. 9.14
0,75
(а — е) и спектра колебаний (ж — к) при увеличении В и фик-
фиксированном значении и-0,67 (рис. 9.15). Из рисунка (9.15)
^чТ'/о™' пОнпеРвых' Фазовый портрет симметричной системы
@.6) (В0 — 0) может быть несимметричным (рис. 9.15, б — е),
во-вторых, переход к хаосу происходит путем бифуркаций удво-
удвоения периода, а при дальнейшем увеличении В наблюдаются
обратные бифуркации (рис. 9.15, г и ж). При еще больших В
появляются островки периодических движений. Так, например,
на рис. 9.15 3 и и изображены фазовый портрет и спектр дви-
движения с утроенным периодом.
Возникающий хаос, по мнению авторов [432], обусловлен
случайными переходами изображающей точки в фазовом прост-
пространстве из области вблизи одного неустойчивого цикла в близко
расположенную область вблизи другого неустойчивого цикла
Численные результаты, полученные в [543] для уравнения
\д.б) при #о = 0; а = 0,2; со = 0,6, несколько отличаются от
приведенных выше, поскольку являются более детальными. Так
в табл. 9.2 приведены различные типы решения, возникающие
при изменении параметра В с достаточно малым шагом Вслед-
Вследствие быстрой смены типов решения, они, естественно, не мог-
могли быть замечены при эксперименте и отражены на диаграмме
рис. У.14. Наиболее интересным отличием является то, что при
n4fif9b7QM£UI°M изменении В от значения 0,61278 до значения
u,oi^/y происходит переход от периодического решения к хао-
хаотическому, не сопровождающийся удвоениями периода. Этот
и показана роль гомоклипических структур.
273

В=0,50
-100
I I I 1 i i i
о
о
В=0,68
•1ПГ)\ I I 1 I 1 I I
О 1 о> 2
О
-100
в-oje
ЦДч
i i i I i I i
о
1 to 2
О
ес=0,25; В0=0
К-помехи на частотах,
кратных SO Гц -100
3=1,94-
I I I I I I t
<у Z
Рис. 9.15

скачок авторы объясняют сменой характера симметрии реше-
решения. Хаотический режим, в свою очередь, довольно быстро сме-
сменяется периодическим режимом с периодом 7.
В отличие от C.1), уравнения вида C.3) и C.3*) допуска-
допускают решения, соответствующие регулярным и нерегулярным вра-
вращениям маятника в ту или иную сторону. Такие решения полу-
получены численно в [543] и наблюдались экспериментально в [432].
Таблица 9.2
в
0,61278
0,61279
0,62
0,626
0,63465
0,64
0,65
0,66
0,67-0,71
0,72
0,725
0,73
0,7309
0,74-0,76
Тип решения
период 1
хаос
хаос
период 7
период 14
хаос
период 7
хаос
период 1
период 2
период 4
хаос
период 5
хаос
Б
0,7607—0,77
0,77—0,80
0,81
0,82
0,83
0,84-0,89
0,90
0,91
0,92
0,93-0,96
0,97
0,98
0,99
1,0
Тип решения
последовательность 2X2
хаос
период 2
период 16
период 2
хаос
период 3
период 3
период 6
хаос
период 3
хаос
период 3
хаос
На бифуркационной диаграмме (рис. 9.14) они характеризуют-
характеризуются числом п, равным числу оборотов за период внешней силы.
В области хаоса число оборотов и направление вращения от пе-
периода к периоду могут изменяться.
Бифуркации удвоения периода и переход к хаосу при воз-
воздействии гармонической внешней силы были обнаружены также
в таких простых системах, как линейный маятник, упруго уда-
ударяющийся о стенку, и кусочно-линейный осциллятор. Уравне-
Уравнения движения таких систем можно записать в виде
и
где k(x)=ki при х > 0, к(х)=к2 при х < 0. Эти уравнения
интересны тем, что в принципе допускают точное аналитиче-
аналитическое решение. Исследование первого уравнения проводилось в
работе [659] при ц = 4,5, а второго — в [639] при А;, =Bя/1,1J
и кг =Bл/4,5J. В качестве бифуркационного был выбран па-
параметр h. В работе [639] удалось проследить за шестью бифур-
бифуркациями удвоения периода. Соответствующие этим бифуркаци-
бифуркациям значения hn и величины 8„ — (hn — hn-i)/(hn+i — hn) приве-
приведены в табл. 9.3.
275
х + A/4т]2)а; =(l/r]2)sin *, х > 0
х + 2hx + к(х)х = sinBrt£ + ф),

Хаотизация колебаний происходит и при периодическом воз-
воздействии на нелинейные осцилляторы, описываемые более слож-
сложными уравнениями [496, 497], и систему связанных нелинейных
осцилляторов [123, 211, 583]. Этим явлением пытаются объяс-
объяснить возникновение некоторых болезней сердца, например,
Таблица 9.3
п
к1
в»
1
0,5889
2
0,6479
3
0,65546
7,80
4
0,657038
4,79
5
0,6573748
4,69
6
0,65744680
4,68
аритмические сокращения сердечной мышцы [466, 530], наблю-
наблюдаемые экспериментально [467]. Работа [497], в которой числен-
численно моделировались уравнения
х + hx + A/8) Cyz + хг)х = В cos t,
Зх* + у2)у = В C'4)
при kt = кг = 0,5; В„ = 0,03 и изменении параметра В, особенно
интересна тем, что в ней, по-видимому, впервые наблюдались
бифуркации удвоения квазипериода тора. Об этом свидетельст-
свидетельствует рис. 9.16, где изображена эволюция инвариантной кривой
на проекции секущей плоскости Пуанкаре t = 0 [mod 2л]. Как
видно из рисунка, авторы наблюдали, по крайней мере, две би-
бифуркации удвоения (б и в), после чего возникал хаотический
аттрактор (г).
До сих пор мы рассматривали внешние воздействия, входя-
входящие в уравнения движения аддитивно (внешние силы). При
параметрических внешних воздействиях на нелинейные осцил-
осцилляторы наблюдаются не менее интересные эффекты. Возможные
наборы бифуркаций и хаотических режимов для таких осцилля-
осцилляторов описаны в § 4 главы 7 (в основном по материалам работ
[60, 62—67]). Здесь мы остановимся на результатах других ра-
работ и обратим особое внимание на качественные стороны пове-
поведения системы и спектральные характеристики колебаний.
Уравнение физического маятника с колеблющейся осью подвеса
имеет вид
/ф + Яф + mb(g + av20 sin vot) sin ф = 0,
C,5)
где / и т — момент инерции и масса маятника, Ъ — расстояние
от центра масс до оси подвеса, Яф — момент сил трения, g — ус-
ускорение силы тяжести, а и v0 — амплитуда и частота колебаний
оси подвеса. Путем изменения масштаба времени и сдвига его
начала отсчета уравнение C.5) можно привести к виду
cos
276

В области основного параметрического резонанса (v0 = 2) это
уравнение подробно исследовано в [546, 547, 559, 560, 581). При
малых а граница устойчивости состояния равновесия для урав-
уравнения C.6) определяется условием q = qa «* а. При q > q0 в си-
системе возникают периодические колебания с периодом Т = 2я.
У
г
0
-1
\ (■
1 .
) 1
У
X
Рис. 9.16
Эти колебания остаются устойчивыми вплоть до некоторого зна-
значения q = qt, зависящего от а. Так, qt = 0,713 ±0,012 для а =
= 0,2. При этом значении q становятся возможными два различ-
различных вращательных движения маятника с периодом, равным пе-
периоду колебаний оси подвеса л:
одно — по часовой стрелке, другое —
против. При дальнейшем увеличе-
увеличении q каждое из этих движений ис-
испытывает бифуркации удвоения пе-
периода. Бифуркационные значения q
приведены в таблице 9.4. В конце
каскада бифуркаций удвоения в фа-
фазовом пространстве системы образу-
образуются два хаотических аттрактора, со-
соответствующих нерегулярным вращениям маятника в ту или иную
сторону (в зависимости от начальных условий). При з = 1,045
направление вращения маятника начинает изменять знак. Сред-
277
Т а б л в
Т/к
1
2
4
8
16
гц а 9.4
•
0,7925±0,0025
0,984±0,010
1,01975±0,00025
1,03075±0,00025
1,03275±0,00025

няя частота перемены знака растет с ростом q. При этом хао-
хаотические аттракторы располагаются все ближе к неустойчивым
многообразиям, проходящим через точки х = ±я, х = О на секу-
секущей поверхности t = 0 [mod я] (рис. 9.17). При q = l,58 происхо-
происходит обратный переход от хаотических к периодическим движени-
движениям, соответствующим устойчивым вращениям в ту или иную
4,00
, •" -
• • •
у**
• *
* •
3J4 -2,35 -7,57 ~0,73 0
~T,00
•72,ff0
* ' * ф
г
bar _
—i 1 ;—i
7,57 Z35 л
» •
•
Рис. 9.17
сторону с периодом л. При уменьшении коэффициента трения а
картина качественно не меняется, но все бифуркационные зна-
значения параметра q несколько уменьшаются.
Вне областей параметрического резонанса поведение решения
уравнения C.6) исследовалось в работах '[91, 93, 109, 171, 423,
671] и др. Из теории уравнения Матье известно (см. также [91,
93, 171]), что при достаточно больших значениях частоты и ам-
амплитуды колебаний оси подвеса (v0 > 1, q > ?i) верхнее положе-
положение равновесия маятника становится устойчивым (при этом ниж-
нижнее положение равновесия также остается устойчивым). Анали-
Аналитически оценку границы устойчивости верхнего положения рав-
равновесия удобно произвести, если пренебречь затуханием а и за-
записать уравнение C.6) при малых % = х — л в виде
|
C.7)
где т = vot, е = l/v0 — малый параметр, с = q/vo. Как мы увидим
ниже, на границе устойчивости величина с имеет порядок
единицы.
278

Решение уравнения C.7) на временах т, меньших или поряд-
порядка единицы, будем искать в виде ряда по малому параметру е:
1 = #„ + еу, + егу, +... C.8)
Подставляя C.8) в C.7) и приравнивая члены при одинаковых
степенях е, найдем у0, уи г/2, ... Ограничиваясь членами второго
порядка малости, получаем
Г /т3 ч
I = CJt —2ceBsiiiT —tcost) + е2 f-jj ^-c2sin2t —
_^+£!l^x)] + C2[l + 2CscoST + s2(^-cV + £l^)]i
C.9)
£ = d [l — 2ce (cost + tsin t) + e2 (y - -|-c2 cos 2т - с2т2 —
—с2т sin 2т)] + C2r[- 2ce'sin т + e2 (т — 2с2т - с2 sin 2т)],;
где Ci, Cz — произвольные постоянные, определяемые из началь-
начальных условий.
Для нахождения границы устойчивости согласно теории Фло-
ке [359] достаточно энать два фундаментальных частных реше-
решения уравнения C.7) при т = 2я. Обозначим эти частные реше-
решения |i(t) и 12(т). Если решение |i(t) удовлетворяет начальным
условиям gi@)=l, li@) = 0, а 12(т) — начальным условиям
|2@) = 0, |2@)=1, то условие устойчивости состояния равнове-
равновесия имеет вид [359]
р^1. C.10)
При этом мультипликаторы определяются выражением
Из C.9) следует, что |1Bя) = 12Bя)= 1 + 2л2е2A-2с2). От-
Отсюда и из C.10) находим условие устойчивости: с2 > 1/2, т. е.
q^ qi = vo/l/2. При этом условии и а = 0 маятник при малом от-
отклонении от верхнего положения равновесия будет совершать не-
незатухающие квазипериодические колебания с частотами v0 и Q =
= У2с2 — 1 (рис. 9.18). (Выражение для частоты Q следует из
C.11).) Если а =7^0, то колебания затухающие и положение рав-
равновесия асимптотически устойчивое.
С ростом q «собственная» частота Q колебаний маятника от-
относительно верхнего положения равновесия растет, и когда она
достигает значения vo/2, вновь возникает неустойчивость (муль-
(мультипликаторы проходят через значение —1). Оценку верхней гра-
границы устойчивости <7* можно произвести, если положить в урав-
уравнении C.7) c = q*/v0 и g = 4sin(T/2) + £sinCT/2). Тогда для
279

q* и отношения В/А получаем выражения: q* = (к 117 — 9)vJ/8,
В/А == (У 117 — 9)/18 » 0,1. Численные расчеты, проведенные
Т. С. Ланда, дали следующие результаты: при а = 0,1; vo = 9,5;
<7i = 6,9; <7* = 21,5; при vo = 20 и том же а — дч = 14,15; д* =
= 91,70. Эти значения близки к теоретическим при а = 0: qt —
= 6,72; g* = 20,49 для v0 = 9,5; ql = 14,14; g* = 90,83 для v0 = 20.
Аналогичным образом происходит потеря устойчивости ниж-
нижнего положения равновесия. «Собственная» частота колебаний
Рис. 9.18
маятника относительно нижнего положения равновесия, как лег-
легко показать, равна Я = У2с2 + 1. Когда она достигает значения
vo/2, устойчивость теряется. Поскольку при соответствующих по-
потере устойчивости значениях q (v0 > 1) сила тяжести сказывает-
сказывается незначительно, то граничное значение q приблизительно сов-
совпадает с вычисленным ранее значением q*.
При g > д* в зависимости от начальных условий маятник
может совершать незатухающие периодические колебания с пе-
периодом 4jt/vo относительно нижнего либо верхнего положения
равновесия. Кроме того, возможны режимы регулярного враще-
вращения, когда за период колебаний оси подвеса маятник соверша-
совершает один оборот в ту или иную сторону. Проекция фазового порт-
портрета на плоскость х, х при а = 0,1; л>0 = 20; q — 95,92, получен-
полученная на ЭВМ, представлена на рис. 9.19, а [225]. Вид реализации
процесса x(t), его спектральная плотность и форма предельного
цикла, соответствующие колебаниям относительно верхнего поло-
положения равновесия, при тех же значениях параметров показаны
на рис. 9.19, б, в ж г. Отметим, что области притяжения предель-
предельных циклов снаружи являются довольно узкими. При сравни-
сравнительно небольших отклонениях от этих циклов маятник перехо-
переходит во вращательный режим.
Как уже отмечалось, при v0 > 1 и q~^> q* влияние силы тяже-
тяжести является несущественным, поэтому уравнение C.6) можно
записать в виде
x + ixx + 2qcos v<,tsinx= 0. C.12)
Заметим, что к уравнению C.12) приводят исследования движе-
движения частицы в поле двух волн [109, 225, 671], колебаний стрелки
280

компаса в переменном магнитном поле, направленном перпенди-
перпендикулярно оси компаса [423] и др.
Чтобы оценить размах колебаний при малых q — q*, положим
в уравнении C.12) а = 0 и разложим sin# в ряд около значения
х = 0 (или х = я), ограничиваясь кубическим членом разло-
разложения:
х + 1q cos vot (x —>ж76) = 0.
Подставляя сюда x = Asin(v0t/2) (амплитуды третьей и более
27,7 2?,9 22,1 22,Ъ 22,
высоких гармоник вблизи границы неустойчивости малы), нахо-
находим Аг = 6A — q*/q). Эта зависимость хорошо соответствует чис-
численным расчетам (точки на рис. 9.20).
Начиная с некоторого значения q — qz (q2 да 98,47 при v0 = 20)
устойчивые предельные циклы вокруг верхнего и нижнего поло-
положений равновесия сливаются с неустойчивыми и исчезают. В ре-
результате остаются лишь режимы регулярного вращения. Для
таких режимов выполняются следующие условия: x(t+ 2jtre/v0) —
— 2nm=x(t), x(t+2nn/v<,) = x(t), где п — 1, 2, ..., m = ±l,
±2, ... (синхронизмы типа re, m, как они были названы в гл. 7).
281

А
Указанные условия означают, что, во-первых, скорость вращения
маятника изменяется периодически с периодом, в п раз большим
периода внешнего воздействия, во-вторых, за п периодов внешне-
внешнего воздействия маятник совершает т оборотов. Области сущест-
существования режимов, соответствующих различным значениям вига,
рассчитаны в [65, 66]. Ниже
будет идти речь только о та-
таких режимах вращения, для
которых за один период ко-
колебаний оси подвеса маятник
совершает один оборот, т. е.
т = п. При q<q% наблюда-
наблюдались режимы, соответствую-
соответствующие п = т = 1. При этом
спектр скорости имеет вид,
показанный на рис. 9.21, а.
0,2-
9/
дз
S5 97
Рис. 9.20
99
у Интересно отметить, что ча-
стота v0 в спектре скоро-
скорости не наблюдается, что
связано с практической равноправностью верхнего и нижнего
положений равновесия. После исчезновения предельных циклов,
соответствующих колебательным режимам {q>qz), в спектре
скорости вращения х появляется частота vo/2 (рис. 9.21,6), т. е.
т = п = 2. В этом проявляется своего рода память системы о ко-
колебаниях с частотой vo/2. Соответствующее точечное отображе-
отображение на секущей плоскости t = 0 [mod 2jt/v0] и вид участка про-
проекции фазового портрета показаны на рис. 9.22, а и 9.23, а. При
увеличении q возникает бифуркация удвоения периода, т. е.
в спектре появляется частота vo/4, а затем эта частота и частота
vo/2 исчезают и точечное отображение становится таким, как на
рис. 9.22, б. Этот режим соответствует т = п = 1. Он существует
при 124,44 < q < 173,40. При q = 173,40 в спектре скорости по-
появляются частоты 2vo/3 и 4vo/3 (рис. 9.21, в), т. е. возникает
режим с т = п = 3. Соответствующие этому режиму точечное
отображение и проекция фазового портрета показаны на
рис. 9.22, в и 9.23, б. Указанный режим устойчив при 173,40 <
< q < 189,72. Далее он теряет устойчивость, и возникает движе-
движение с удвоенным периодом. Следующая бифуркация удвоения
периода происходит при q — 190,10. На этом цепочка бифурка-
бифуркаций удвоения обрывается, и при q = 190,70 снова возникает ре-
режим вращения с т = п = 1 (рис. 9.22, г).
При q « 204 существовавшая до этого гомоклиническая струк-
структура (о ее существовании можно судить по хаотическому харак-
характеру процессов установлепия) становится притягивающей, и в
системе, кроме регулярных аттракторов, соответствующих перио-
периодическим вращениям, рождается еще один аттрактор — хаотиче-
хаотический. Его область притяжения растет с увеличением q, а области
притяжения регулярных аттракторов уменьшаются. При q « 306
мультипликаторы циклов, соответствующих регулярным враще-
282

С/=408,76
Рис. 9.21
tf| tj = 102,04 A
• • •
ZOV 20
i i i i i i '
0 4rt &n 72ЛХ
(?=178,57
qT 753, Off
i i t ' i i
= 408,15
20
20
T 1 T T t I
x
г"
-50Y
<?L
1 1 I Т 1 I
<?я- /2Д1 Д? " 4rt 87t 1Zn
Рис. 9.22

виям, проходят через значение +1, после чего эти циклы исче-
исчезают. В системе остаются только хаотические аттракторы. При
Ч > ?нР «* 306 режимы регулярных вращений не наблюдались
[225]. (Из результатов работы [65] следует, что при а = 0 регу-
регулярные режимы вращений должны исчезнуть при д>355.) Со-
Согласно критерию Б. В. Чирикова о перекрытии резонансов [418],
tj =102,04
а-178,57
Рис. 9.23
справедливому при а = 0, хаос должен наступить при q ~ Jtv0 л;
«1257, т. е. при значении q, существенно большем qKV.
В области хаоса спектральная плотность процесса x(t), то-
точечное отображение и проекция фазового портрета показаны на
рис. 9.21,г,5, 9.22,5 и 9.23, в соответственно. Зависимость x(t)
(а) и вид корреляционной функции для случайного процесса
x(t) (б) при тех же значениях параметров приведены на
рис. 9.24. Из рис. 9.23, в видно, что в хаотическом режиме движе-
движение маятника состоит из участков колебательных движений отно-
284

сительно положений равновесия, вращательных движений в ту
или иную стороны и перескоков между ними. Наряду с непред-
непредсказуемостью значений х и \х\ в какой-либо момент времени не-
непредсказуемым вне зависимости от начальных условий является
и направление вращения маятника.
q=4O8,7ff
ZO
ЩИ
■8@)
7
384
0,8
0,4
О
-0,4
-0,8
33Z 400 408, 416 t
а
Рис. 9.24
.::..■•■■■■ q■ =1367,9
■■■■ •'••:.:..::'.'-•: z=x/2n\modf\
'■'■ ■■■:.■ ■■:-У-.±-х/D0п)
а
J I I
0,5
1,0 z О
Рис. 9.25
2
0,8
0,4
0
-0,4
-0,8
г '
£.,■: ;Л
»■'■'■'
!'V. V " %
• '■ '•'. I
"•
1 1 1 1
i]-1367,9
"•к •,
:■! .-■'''
W ^У ■'
•'.•■■■ s
'•"■■:'
i i t i L
0,5
1.0 z
Отметим, что характер полученного точечного отображения в
рассматриваемом случае а = 0,1 такой же, как и при отсутствии
диссипации (а = 0). Это видно из сравнения рис. 9.22,5 и 9.25, а
[671]. При значительно больших значениях а характер точечного
отображения существенно изменяется (рис. 9.25,6).
В области хаоса по реализации процесса x(t) был вычислен
корреляционный показатель v, характеризующий размерность ат-
285

трактора. Результаты расчета при а = 0,1; v0 = 20 приведены в
табл. 9.5. Как и следовало ожидать, с ростом q размерность ат-
аттрактора увеличивается.
Бифуркации удвоения периода и переход к хаосу наблюда-
наблюдались в [47, 161, 526, 528] для уравнения
)x + xi = 0. C.13);
Показано, что в области хаоса точечное отображение сводится к
одномерному, имеющему гладкий максимум. В работе [47] при
фиксированном значении q и измене-
изменении а обнаружены переходы от одного
вида аттрактора к другому. Один из
таких переходов наблюдался при v0 =
= 2, q = 50 и уменьшении а до значе-
значения а* = 0,4576. При а < а* происхо-
происходило резкое увеличение фрактальной
размерности аттрактора d, а также средней мощности N и
спектральной плотности колебаний S{a) (рис. 9.26).
К уравнениям нелинейного осциллятора с внешним воздей-
воздействием (как параметрическим, так и силовым) сводятся в одно-
модовом приближении уравнения для амплитуды напряженности
V
т
а б л и
306
1 2'4
ца
9.5
408
2,6
510
2,7
поля в газовом лазере, находящемся во внешнем модулированном
световом поле [683] или в постоянном поле, но при модуляции
накачки [636], а также уравнения для интенсивности поля и раз-
разности населенностей рабочих уровней в твердотельном лазере
при периодической модуляции потерь [248, 249, 527]. Последние
имеют вид
x = gez(n — I — ficosQt), п — в[а — п(х+1)], C.14)
где х — безразмерная интенсивность поля в лазере, п — относи-
относительная разность населенностей рабочих уровней, а — относи-
относительная разность населенностей в отсутствие поля, задаваемая
накачкой, g = Дйр/^ > 1 — произведение ширины полосы резона-
286

У- Д- >У- ■/*•
\„ -/
t
/3~0,ОО7
i
/3-0,01
0,018
v -/Ц^ у
0,0535
Рис. 9.27

тора Д©р на время установления разности населенностей f~l,
е =g~l(a— I) < 1, [} и Q — амплитуда и частота модуляции
потерь. Эволюция характера колебаний и вида фазового портре-
портрета для типичных параметров твердотельного лазера, Q = 0,4 и
изменении [J показаны на рис. 9.27 [249]. Из рисунка видно, что
переход к хаосу в этой системе происходит путем последователь-
последовательности бифуркаций удвоения периода. Подобный переход наблю-
наблюдался экспериментально в [387] для СО2-лазера и в [357, 544]
для твердотельного лазера на гранате с неодимом.
§ 4. Уравнения Лоренца и другие системы
третьего порядка
По существу, первой динамической системой, в которой чис-
численно были обнаружены и исследованы стохастические автоколе-
автоколебания, как уже говорилось, является система уравнений Лорен-
Лоренца [563], описывающая в трехмодовом приближении конвектив-
конвективное движение в слое жидкости,
подогреваемом снизу [217, 414].
Она имеет вид
У
Ktueffa-
олемент
X
Инерцион-
Инерционный
элемент
Усили-
Усилитель
-Ах
~XZ, 2, = -
D.1),
Рис. 9 28
Уравнения Лоренца относятся
к классу автоколебательных си-
систем с инерционным самовоз-
самовозбуждением [52, 53, 391]. В таких
системах, структурная схема которых показана на рис. 9.28, воз-
возникновение генерации происходит за счет инерционности цепи
обратной связи, приводящей к так называемому инерционному
взаимодействию между динамическими переменными. В про-
простейшем случае соответствующие уравнения колебаний име-
имеют вид
х + 2Ьх + а20х = — ку + / (х, х, у),
У
= ах+ф(я, х, у),
где б — коэффициент трения, f — параметр инерционности, к и
а — коэффициенты линейной связи между переменными, / и ф —
нелинейные функции, не содержащие линейных членов').
Условие самовозбуждения для системы D.2) следующее:
ak^28(al + 28Y + y2). D.3)
Отсюда видно, что колебания могут возбудиться лишь при f ^
<ЧкР, где уКр = — б + ]/о2 + ак/28— «э^, т.е. при достаточной
инерционности цепи обратной связи.
') Более общий случай рассмотрен в работе [55].
288

Систему уравнений Лоренца D.1) можно свести к виду D.2),
если исключить переменную Y и положить х = Х — V6(r— 1),
/ (х, у) = - ^-j- <s>ax + 4р
■ = &, а = Bа-Ь)соо, D.4)
, ф (х) = (а — 6/2) ж2.
Уравнения Лоренца допускают чисто механическую модель,
предложенную С. И. Злочевским и состоящую из двух твердых
Z/
Рис. 9.29
тел: несущего и носимого осесимметричного ротора (рис. 9.29).
Эта система тел обладает следующим свойством: при движении
ротора относительно несущего тела распределение масс в про-
пространстве не изменяется. Следовательно, тензор системы остает-
остается постоянным. Такая система твердых тел называется гироста-
гиростатом. Предполагается, что центр масс гиростата (точка О) непод-
неподвижна и эллипсоид инерции гиростата имеет форму эллипсоида
вращения. Ротор вращается относительно несущего тела с по-
постоянной угловой скоростью Q вокруг своей оси симметрии, ко-
которая неподвижно закреплена на несущем теле и перпендику-
перпендикулярна оси симметрии гиростата. К гиростату приложен внешний
момент М, зависящий от угловой скорости <а вращения несущего
тела вокруг неподвижного центра масс.
Уравнения движения гиростата в проекциях на связанные с
несущим телом оси координат, которые выбраны так, что ось ОХ
совпадает с осью симметрии гиростата, а ось OZ параллельна
оси вращения ротора, имеют вид
1хЫх + haY = Мх,
IaY + (Ix — I) <Bxtt>z — hax = Mr,
Iaz + (/ — Ix) aY(i>x = Mz.
Здесь ах, ©у, ©z — проекции мгновенной угловой скорости а на
289

оси координат OXYZ; Ix — осевой момент инерции гиростата, / —
экваториальный момент инерции гиростата, h = JQ — относитель-
относительный кинетический момент ротора, J — его осевой момент инер-
инерции, Q = const.
Если Мх = My = Мг = 0, со Ф 0 и Q Ф 0, то гиростат, как из-
известно [108], совершает периодические колебания либо находится
в перманентном вращении. В пространстве скоростей траектории
движения изображающей точки — полодии — расположены па
эллипсоиде энергии несущего тела гиростата
1х®х + I (ш| + со|) -=2Т — const.
Если Мх, MY, Mz отличны от нуля и равны
Мх = (а + h)aY — аах, MY = — сму, Mz = — daz,
то уравнения движения гиростата можно записать в виде
и* = -£- (coy— со.*:),
1х
h IX~I
юу = у ах j—
Полагая
X = (Ix~I)ax/c, Y*=(Ix-I)ar/c, Z = (IX
x=(c/I)t, a = al/clx, r=hl/clx, b = d/c,
получаем уравнения Лоренца в стандартной форме D.1).
О свойствах системы уравнений Лоренца говорилось уже
очень много (см. § 3 гл. 7). Она исследовалась также в большом
числе работ. Кроме тех, которые уже были указаны, отметим
следующие: [10, И, 81, 98, 233, 302, 308, 321, 375, 384, 458, 460,
556, 567, 572, 578, 579, 625, 635, 648-650, 655, 662, 686]. Неко-
Некоторые результаты этих работ, представляющие собой существен-
существенное добавление к сказанному ранее, будут изложены ниже.
В области стохастичности спектр колебаний в системе Лорен-
Лоренца является сплошным и достаточно широким (рис. 9.30), что
свидетельствует о наличии сильного перемешивания [441]. При-
Приближенный расчет спектра выполнен в работе [567]. Емкость
аттрактора Лоренца близка к двум. Так, при Ъ — 4, о = 16, г = 40
она равна d = 1,98 ± 0,02 [578, 579] (ляпуновская размерность,
вычисленная по формуле Каплана — Йорке, dL = 2,06 [587]). За-
Зависимость максимального ляпуновского показателя от параметра
г для указанных значений Ъ и о, на основе которой в [587] вы-
вычислялась ляпуновская размерность, приведена на рис. 9.31 [686].
Интересно отметить, что в области значений г вблизи гкр » 33,45
эта зависимость имеет такой же вид, как на рис. 8.28. Штрих-
пунктирная кривая на рис. 9.31 соответствует метастабильпому
хаосу.
290

Остановимся далее на поведении системы уравнений Лоренца
при больших значениях параметра г. Известно, что при доста-
достаточно больших значениях г (г> 313) решение уравнений Лорен-
Лоренца всегда является периодическим. Форму и размеры предельно-
предельного цикла при этих значениях г удается приближенно рассчитать
аналитически [52, 53, 308, 375, 391, 648}. Для этого удобно про-
произвести замену переменных, использованную в [375, 648, 649].
Исключим из уравнений
D.1) величину У и введем
новые переменные т ==
= Va(r-l)t,
l = [2a(r-l)]-X,
T)=(Z-.X72o)/(r-l).
В этих переменных уравне-
уравнения D.1) можно записать в
виде
D.5)
где 1 ()()
малый параметр. Первое
уравнение D.5) описывает
колебания нелинейного ос-
осциллятора с частотой, мед-
медленно меняющейся согласно
второму уравнению. Метод
усреднения для систем та-
такого класса разработан
В. М. Волосовым [111].
0,1 0,3
Рис. 9.30
0,4- ы/2те
При ц, —0 уравнения D.5) имеют периодическое решение
I = I(-4i Л, Ф), Л = const, D.6)
где ! = о) (Л, т))т + ф, со (А, т1) = 2я/Г(Л, т,), Т(А, л)-период
колебании в пулевом приближении по ц, А — максимальное зна-
значение 1. Решение D.6) должно удовлетворять системе первых
интегралов уравнений D.5) при ]х = 0:
2
= т _
D.7)
D.8)
где Е, т0 — постоянные, имеющие смысл энергии и начала отсче-
отсчета времени, НЦ, |, г)) — функция Гамильтона.
291

Следуя методу усреднения Волосова, удается получить урав-
уравнения для медленных переменных без знания явного вида реше-
решения D.6) с использованием лишь первых интегралов D.7), D.8).
Выберем в качестве одной из медленных переменных величину
~2\ ! 3i 1 L
4
0 7 20 го 40 50 700
200 300
Рис. 9.3 i
А, которая связана с энергией Е соотношением
Из D.7) следует, что усредненное уравнение для энергии име-
имеет вид
D.9)
Вычисляя подынтегральное выражение с учетом D.5) и D.7),
находим
дН l дН ■• дН ■
= 101-1N + Is] Ъ - I [(-Л — 1) I + Is + Л] -
D.10)
Принимая во внимание, что, как следует из D.8),
йг = dl/[2E-(n-l)V- I42\i/Z
и
Г А
= 4 f F(l)dH[2E - (ц - 1) E2 -
292

получаем из D.9) и D.10)
где
|J С f [Bа — Ъ) f — Ъ
А
2'
А
I, (А, Л) = A. J [22? - (ц - 1) I2 - !V2]1/2 dg, D.12)
. о
А
Т (А, ц) = 4 j d|/[2£ - (т) - 1) |2 - 6«/2]1/а.
о
Усредненное уравнение для медленной переменной т] имеет вид
r\ — ~ ]i[br\ — Bа— Ь)/3]/(о+ 1), D.13)
где
А
2£Г — (т, — 1) S2 — g4/2]1/2 '
В стационарном режиме решение уравнений D.11), D.13)
определяется из следующей системы трансцендентных урав-
уравнений:
11(А,г])=12(А,г]), г1=^-Ь/3(Л)Л). D.14)
Содержащиеся в ней интегралы Л, /2, /3 и Т выражаются через
полные эллиптические интегралы 1-го и 2-го рода К (к) и Е(к)
[133]. Подставляя эти выражения в D.14) и учитывая связь
между модулем эллиптических интегралов к и амплитудой А,
получаем систему уравнений для определения стационарных
значений к, Аг, ц и Т:
3Bо-Ъ)ЕЦк)-1(о+ 1) A-2&2)+ 2Bа- Ъ) B- к*)]Е(к)К(к) +
= 0, D.15)
Л = Я2A —2Аг2)+ 1, Т =
где Аг = АЧ2к\
Уравнения D.15) легко могут быть решены численно или
графически. Например, для б = 10, Ъ = 8/3 находим кг ~ 0,9;
Az ~ 0,35; г\ ~ 0,84; Т ~ 23,4. Подставляя найденные значения
4zt|B уравнение D.8) с учетом связи между А2 и Е, определя-
определяем форму колебаний переменной |: |(т) = 0,59 сп @,44т, 0,95).
Вид функции | (т) и проекция фазового портрета на плоскость
■ц = 0,84 показаны на рис. 9.32, а ж б. Координаты особых точек
О, О' и О" следующие: О(| = | = п = 0), О'A =-0,36, 1 = 0,
ц = 0,871, 0"A = 0,36, 1 = 0, т) = 0,87)..
293

Обратим внимание на то, что при увеличении параметра г
размах колебаний переменной X увеличивается как Уг^а период
колебаний в исходном времени t уменьшается как 1/Уг.
При уменьшении параметра г найденное периодическое реше-
решение теряет устойчивость и порождает периодическое решение с
удвоенным периодом. Последнее снова теряет устойчивость
Рис. 9.32
и т. д., т. е. возникает бесконечная последовательность бифур-
бифуркаций удвоения периода. Дальше оцять появляется область
устойчивости периодического решения, которое, в свою очередь,
также испытывает бифуркации удвоения периода. Известны, на-
например, следующие области таких бифуркаций [460]: последова-
последовательность бифуркаций начинается при г = 233,5 и заканчивается
при г — г„ = 210 или начинается при г =
= 148,4 и заканчивается при г„ = 145.
В области 148,4 < г < 166,07 решение
уравнений Лоренца является периодиче-
периодическим. При увеличении г от значения г =
= га = 166,07 происходит переход к хаосу
*и через перемежаемость [572], причем сред-
средняя длительность «ламинарной» фазы до-
достаточно точно подчиняется закономер-
закономерности т ~ (г — ra)"in. Именпо при рас-
рассмотрении этого перехода и было в [572]
установлено само понятие «перемежае-
«перемежаемость». Таким образом, в области боль-
больших значений параметра г система уравнений Лоренца ве-
ведет себя подобно динамической системе, описываемой одномер-
одномерным точечным отображением с гладким максимумом. Возмож-
Возможность перехода к хаосу через перемежаемость хорошо видна из
графика точечного отображения, приведенного на рис. 0.33 для
о =16, 6 = 4, г= 140 [662].
Зависимость поведения решений уравнений Лоренца от пара-
параметров о и Ь исследована мало. В работе [655] показано, что при
294
Рис. 9.33

фиксированном значении о = 10 весь диапазон изменения пара-
параметра Ъ имеет смысл разделить на три качественно различных
области: область / — 0 < Ь < Ъ*, где 2 < Ъ* < 8/3, область // —
Ь* <Ъ < Ъг, где Ьг = 14,5, область /// — Ъ>Ъг. В. области // ха-
характер решений качественно такой же, как и при Ъ = 8/3 (прав-
(правда, при b>bi = о~1 = 9 особые точки Ot и Ог всегда устойчи-
устойчивы). В области / картина бифуркаций и топология аттрактора
более сложны, чем в области II. Наконец, в области ///, наобо-
наоборот, все просто и потому не представляет интереса. Область //
подробно исследована в '[635]. В работе [308] аналитически ис-
исследована эволюция решения при изменении параметра о и фик-
фиксированном достаточно большом значении параметра г, позволя-
позволяющем использовать асимптотические методы.
К уравнениям Лоренца сводятся уравнения для медленных
амплитуд напряженности поля, поляризации и разности населен-
ностей в лазерах и мазерах в одномодовом приближении при ну-
нулевой расстройке частоты генерации от центра линии усиления
[134, 296, 308, 356, 592, 692]. Однако реальные параметры этих
приборов, как правило, таковы, что стационарное решение все-
всегда является устойчивым, т. е. стохастические режимы не воз-
возникают1). При ненулевой расстройке получается система урав-
уравнений пятого порядка, которая легко может быть сведена к комп-
комплексным уравнениям Лоренца, изученным в [457] и имею-
имеющим вид
± = -а(х-у), y = rx~y-xz, z = -bz + xy* + x*y, D.16)
где о, г, х и у ■— комплексные, Ь и z — действительные величины.
В работе [533] исследуется другая форма комплексных урав-
уравнений Лоренца, эквивалентная шести уравнениям первого поряд-
порядка и имеющая вид
х = -а(х-у), y = rx-y-x*z, z = -bz + xy, D.17)
где г, х, у и z комплексны, а ср и Ъ действительны. Эти уравне-
уравнения, как указывают авторы, в определенном приближении опи-
описывают волны магнитного поля Солнца.
В отличие от обычной системы Лоренца D.1), в системах
D.16) и D.17) переход к хаосу может происходить через рожде-
рождение и последующее разрушение тора. Так, для системы D.17)
при 6 = 0,5; о = 1; г=2Ш, где D — действительный бифуркаци-
бифуркационный параметр, схема бифуркаций выглядит следующим образом
[533]. При 0<D<i система D.17) имеет единственное устой-
устойчивое решение д: = г/ = z = 0. В области D > 1 это решение ста-
становится неустойчивым, но имеется устойчивый предельпый цикл,
который существует до D = 2,07. При этом значении D пара
') В работе [545] сообщается, что в лазере на парах аммиака, накачи-
накачиваемом излучением СОг-лазера, экспериментально достигнут такой одномо-
довый режим, при котором стационарное решение становится неустойчивым
и возникает стохастичность.
295

комплексно сопряженных мультипликаторов цикла выходит на
единичную окружность, и рождается двумерный тор. Проекция
этого тора на плоскость Re у, Re z для D — 3 показана на
рис. 9.34, а. Проекция секущей поверхности Пуанкаре Re x = О
на ту же плоскость приведена на рис. 9.34, г. При D = 3,47 про-
происходит рождение трехмерного тора, проекции которого па ту же
плоскость и соответствующее сечение Пуанкаре показаны на
рис. 9.34,6 и д (.0 = 3,6). Наконец, при Z) = 4,0 тор разрушается
и возникает хаотический аттрактор, вид которого в тех же про-
проекциях при1/) = 8 продемонстрирован на рис. 9.34, в и е.
Как уже отмечалось, уравнепия Лоренца легко приводятся к
виду D.2), где нелинейные функции / и ф определяются выра-
выражениями D.4). При других, более .простых видах нелинейных
функций / и ф уравнения D.2) исследовались в работах [54, 220,
392]. Были рассмотрены два случая:
/(*, y) = ~gxy, <p(x) = lx\ D.18а)
j{x) = -nx\ у{х) = -1хг-кх\ D.186)
В первом случае физический механизм быстрого сброса энер-
энергии, необходимого для возникновения хаоса, такой же, как у си-
системы Лоренца, и обусловлен модуляцией частоты колебаний
переменной х колебаниями переменной у. По зтой причине та-
такой механизм назван в [54, 220, 392] параметрическим. В отли-
отличие от него механизм сброса энергии во втором случае назван
силовым [54, 392]. В обоих случаях система уравнений D.2) яв-
является диссипативной, поскольку div{x, х, у) = — B6 + ч)< 0.
В работах [54, 220, 392] численным моделированием показа-
показано, что существуют области параметров, где решение уравнений
D.2), D.18) является нерегулярным, корреляционная функция
резко спадает, спектр является сплошным, энтропия Колмогорова
положительпа, а точечное отображение, по крайней мере при-
ближепно, сводится к одномерному. Характерные примеры реа-
реализации процесса x(t), корреляционной функции В(х), спект-
спектральной плотности S(f) и точечного отображения в случае а по-
показаны на рис. 9.35, а—г. Как видно из рисупка, при данных
значениях параметров точечное отображение является близким
к разрывному и па начальном участке сильно растягивающим.
Размерность аттрактора, оцененная по формуле Каплана — Йор-
Йорке, в области хаоса изменяется в пределах 2,05—2,30. Типичный
вид аттрактора показан на рис. 9.35, д.
Переход от периодических колебаний к хаотическим при из-
изменении параметров в случае а может происходить как путем
бесконечной последовательности бифуркаций удвоения периода,
так и жестким образом [54, 222, 392]. Первый тип перехода на-
наблюдался, папример, при 26 = 1,1; к = 1,73; a = co0 = Z = l; f =
= 0,27 и увеличении параметра g. Получилась следующая по-
последовательность бифуркационпых значений g; g = {15,66; 24,07;
25,50; 25,80; 25,86}, которая приводит к следующей последова-
296

1 1 1
;
-
-
-
и*
.:.
*. ;
"Л*
i i
\' t
i i
i i i
;
-
-
-
i i t
35

S®k
70 x
0,6
Г
0,4-
0,Z
-
£>
л
A
1 1 ! !
4г 0,4
/
/
h Л.
чл
ff,6
е
2fi-
•
i t
0,8
Рис.
'f,f
*2S,S
i _i_
W
9.35

тельности чисел 8) = (gJ+i — g,)/{g,+i — gj+t): Sj = E,88, 4,767,
4,761}. Можно предположить, что эта последовательность сходит-
сходится к константе Фейгенбаума б = 4,6692... Вид точечного отобра-
отображения вблизи границы перехода к хаосу показан на рис. 9.35, е.
При дальнейшем увеличении параметра g максимум отображе-
отображения резко возрастает, а падающий участок становится все круче.
В результате отображение принимает такой вид, как на
рис. 9.35, г.
Жесткий переход к хаосу происходил, например, при 26 = 1,1;
а = сйо = /,= 1; f = 0,5; g = 30 и увеличении параметра к. При
к<ки где ki » 1,91, в фазовом пространстве системы имеется
лишь один аттрактор — устойчивая особая точка в начале коор-
координат. При /с = &, возникает еще один аттрактор — странный,
который сосуществует с первым до к = к2, где к2 = 2,06 — значе-
значение к, при котором устойчивая особая точка в начале координат
теряет устойчивость. Общий вид точечного отображения при
к<кг показан на рис. 9.36, а. Оно имеет две неподвижные точки
\х\
Рис. 9.36
О ж А, причем точка О соответствует устойчивой особой точке в
начале координат, а А — неустойчивому предельному циклу. При
к < ki точка А лежит выше точки В (рис. 9.36, б), и поэтому
при любых начальных условиях отображающая точка попадает в
точку О. При ki<k< кг, наоборот, точка А расположена ниже
точки В (рис. 9.36, в) и в системе имеются два аттрактора. При
299

к = кг точки А и О сливаются, и в фазовом пространстве систе-
системы остается только один аттрактор — странный. Участок отобра-
отображения вблизи начала координат при к~^> к2 показан на
рис. 9.36, г. Из-за того, что точка В расположена ненамного выше
точки О, в области значений к, близких к кг, возникает явление,
похожее на перемежаемость. Попав на участок вблизи начала
координат, отображающая точка остается на нем достаточно дол-
долго, что соответствует большому числу малых колебаний с мед-
медленно нарастающей амплитудой. Выйдя из области этого участка,
точка снова на него возвращается. Характерный вид реализации
процесса x(t) при к = 2 показан на рис 9.37.
А
\J
Рис. 9.37
В случае б вид аттрактора и характер точечного отображения
существенно отличаются от случая а (рис. 9.38). Зависимость х
от х, построенная нэ основе точечного отображения на секущей
плоскости х~— 0,13 (рис. 9.38,6) по форме близка к параболе
(рис. 9.38, в). Переход от периодического режима к хаотическому
при изменении параметров наблюдался только путем бифуркаций
удвоения периода. По сравнению со случаем а спектр колебаний
в режиме хаоса является более узким, а корреляционная функ-
функция спадает медленнее (рис. 9.39).
Система уравнений, легко приводящихся к виду D.2),, была
рассмотрена также в работе [148]. Ее численное исследование
проводилось при ©о = 1; 6 = 0,05; & = 1; f — 0,5; а — In M — 0,5;
f(x, х, уИ_0; ч(х.)={0,Ц1-еху{-х(х-2ПпМ)]) + хПпМ}Х
Х(х — УЫМ) — 2х2Т/ЫМ. Параметр М варьировался. При указан-
указанных значениях параметров система имеет три особые точки с ко-
300

ординатами 01={х, х, #) = @, О, 0), 02={1пЛ/, 0, —InM), Os =
= B In it/, 0, —2 In M). Как и в системе уравнений Лоренца, точки
0j и 03 расположены симметрично относительно точки 0%. При
М > 1 особая точка О2 неустойчива, а точки О4 и О3 устойчивы
при М< Mo ~ 1,88 и колебательно неустойчивы при М>Ма.~
При М = Мо вокруг особых точек О4 и О3 рождаются устойчивые
предельные циклы, которые при дальнейшем увеличении М те-
теряют устойчивость, претерпевая бифуркации удвоения периода,
приводящие к хаосу. Области хаотических и периодических коле-
колебаний по параметру М чередуются.
-Наряду с системой Лоренца значительную известность полу-
получила система уравнений, предложенная Рёсслером [618]:
D.19)
где е, f и (X — параметры. В отличие от уравнений Лоренца, урав-
уравнения D.19) в зависимости от параметров либо вообще не имеют
301

особых точек, либо имеют две особые точки с координатами
Отсюда видно, что особые точки существуют лишь при ц > 2Уё/.
Первая из этих точек всегда апериодически неустойчива, а вто-
вторая может быть устойчивой. При некотором значении \\ начинает
Рис. 9.39
выполняться условие колебательной неустойчивости второй осо-
особой точки, и в системе возбуждаются автоколебания. Их харак-
характер зависит от величины ц, (при фиксированных значениях
остальпых параметров).
Система уравнений D.19) исследовалась численно в работах
[425, 618] при е = / = 0,2. В этом случае условие колебательной
неустойчивости второй особой точки совпадает с условием ее
рождения. При не очень больших значениях ц, колебания явля-
являются периодическими. Им соответствует в фазовом пространстве
однооборотпый цикл (рис. 9.40, а). Начиная со значения \х = 3,5
возникает последовательность бифуркаций удвоения периода
(рис. 9.40,6, виг). Критическое значение \х равно ц» = 4,20.
Затем в фазовом пространстве системы возникает хаотический
аттрактор, имеющий слоистую структуру (рис.. 9.40, д, е, ж).
Слоистая структура пропадает при м, = 4,60 (рис. 9.40, з). При
302

этом уровень сплошного спектра существенно возрастает. Бифур-
Бифуркационная диаграмма, соответствующая рис. 9.40, показана на
рис. 9.41 [425]. Вид аттрактора в стереопроекции для р, = 5,7
О 10 2030 40 5&(ы/2тГ),Гц
Рис. 9.40
I
I
продемонстрирован на рис. 9.42 [618]. Такого рода аттрактор
Рёсслер впоследствии назвал «спиральным» (см. ниже па
стр. 353).
При \х < ц„о система уравнений D.19) не имеет положитель-
положительных ляпуновских показателей, а при ц — ц» такой показатель
появляется. Зависимость макси-
максимального отличного от нуля ляпу-
новского показателя К от пара-
параметра (х не является монотонной
(рис. 9.43) [618]. По своему ха-
характеру она очень напоминает
аналогичную зависимость для од-
одномерного квадратичного отобра-
отображения (ср. с рис. 8.14).
При больших зпачениях \х ха-
характер аттрактора и спектра ко-
колебаний существенно изменяется.
Так, при ц = 8,5, / == 0,4 и изме-
изменении е от 0,15 до 0,30 эволюция
аттрактора и соответствующие спектры колебаний показаны на
рис. 9.44. Из рисунков видно, что при е = 0,3 в спектре колеба-
колебаний полностью отсутствуют дискретные составляющие. Такой
303
Рис. 9.41

характер спектра авторы [441] объясняют появлением на аттрак-
аттракторе вместо «складки» (рис. 9.42) «воронки» (рис. 9.45). Нали-
Наличие «воронки» говорит о том, что фазовые траектории непрерыв-
непрерывно переходят из окрестности седлового цикла в окрестность
седлового состояния равновесия и обратно.
Рис. 9.42
0,7
'0,1
А
i i i / ■ i I i
V
i
f
(
i
3,0
4,0
Рис. 9.43
5,0
Еще одной детально исследованной системой третьего поряд-
порядка является система /
Х^цХ+Y-XZ, t^-X, Z=^^[b{X)T-Zl D.20)
где Ь (X) — функция Хевисайда, (а, — превышение над порогом
генерации, f — параметр инерционности. Система D.20) описы-
описывает одну из схем так называемых генераторов с инерционной
нелинейностью. Такой термин впервые был введен К. Ф. Тео-
дорчиком в 1945 г. [347]. Он относится к автоколебательным си-
системам, в которых самовозбуждение колебаний происходит за
счет безынерционной положительной обратной связи, приводя-
приводящей к отрицательному сопротивлению, а их ограничение — за
счет нелинейного инерционного взаимодействия между динами-
динамическими переменными. В простейшем случае уравнения колеба-
304

ний в генераторе с инерционной нелинейностью имеют вид
i'— (I* — / (У)) i +ео;* = <р(*, у), y + yy = yF(x), D.21)
где ц>(х, у) и F{x)— нелинейные функции. Одна из схем таких
0,7ff
0,77
0,20
30
О 0,1 0,1 0,3 0,4 0,5(ы/?.л),Гц
Рис. 9.44
генераторов, для которой, как будет показано ниже, справедливы
уравнения D.20), приведена на рис. 9.46 [173, 216]. Роль инер-
инерционного элемента в этой схеме играет детектор. Напряжение,
снимаемое с детектора, изменяет крутизну вольтамперной харак-
характеристики усилителя и тем самым
ограничивает размах колебаний. Сте-
Степень инерционности определяется
постоянной времени детектора-^
Уравнения, описывающие работу
схемы, изображенной па рис. 9.46,
имеют вид [216]
-2~ = (ц. — 6F) ж — bVx,
х +
D.22)
Рис. 9.45
V+yV = yF(x),
где <а0 = i/LC, ц, = (alMS0 — R/L, So — крутизна характеристики
усилителя при F = 0, F(x)— нелинейная функция, вид которой
определяется характеристикой детектора.
305

Подставляя в первое уравнение D.22) выражение для t из
второго уравнения, получаем уравнения вида D.21), где y = bV,
f(y) = U, ф(#, у)~"{ху — '{ЪхР{х). Полагая далее х = Х, х~цх +
+ xy = Y, y=Z, coo = 1, bF(x) = $(x)x\ получаем уравнения
D.20).
Система, описываемая уравнениями D.20), численно и экспе-
экспериментально исследовалась в работах [22, 23, 27—35, 44]. Было
Рис. 9.46
обнаружено [27, 29, 31], что в некоторой области значений [х и у
колебания в системе имеют нерегулярный характер, причем их
вид зависит от начальных условий.
Аналогичные результаты получены и в натурном эксперимен-
эксперименте (рис. 9.47). При фиксированном значении одного параметра
Рис. 9.47
(например, -{) и увеличении другого (ц) хаос возникает путем
последовательности бифуркаций удвоения периода в соответствии
с закономерностью Фейгенбаума. Об этом свидетельствуют дан-
данные табл. 9.6 [31], где приведены расчетные и эксперименталь-
экспериментальные бифуркационные значения параметра ц при i = 0,3 и соот-
соответствующие им значения б, = (цг-1 — (х,-2)/(jxt — Цг-i). При £ = 5
значение 6, практически совпадает с константой Фейгепбаума.
306

i
1
2
3
4
5
Та
блица 9.6
•Ч раоч
0,770
1,020
1,0713
1,08216
1,08449
M*i эксп
0,77
1,02
1,07
1,08
6г раоч
4,873
4;724
4,66896
"расч
= 1,08512, ц0
= 1,09
При небольшом отклонении параметра и от значения и°°
(а именно при Hi = 1,10112) в фазовом пространстве системы
рождаются еще два двухоборотных предельных цикла Г2 и Т'%,
один из которых устойчивый, а другой — седловой [32]. Это хо-
хорошо видно из графика на
рис. 9.48, на котором приве-
приведены мультипликаторы (т)
двухоборотных циклов Г2,
Г2 и Г2 (Г2 — двухоборот^"
ный цикл, который возник
при \х = 0,770, соответствую-
соответствующем первой бифуркации
удвоения периода). Из
рис. 9.48 следует, что в об-
области n'i < \i < (x'2, где ц'г =
= 1,31902, в системе сущест-
существует по крайней мере одно
устойчивое периодическое решение, соответствующее циклу Г2.
Если, оставаясь на этом цикле, уменьшать параметр ц, то при
И = Hi, как показывают численные расчеты, происходит переход
к хаосу через перемежаемость. Эволюция спектра для такого
перехода продемонстрирована на рис. 9.49. Частота /0 соответству-
соответствует циклу Г2, частота f{ пред-
представляет собой характерную ">
частоту хаотического аттрак-
аттрактора, возникшего в результа-
результате цепочки удвоений цикла 2
Г2. Обратим внимание на то,
что в спектре отсутствуют
линейные комбинации ча-
частот /о и /j, что характерно
для спектров при перемежа-
перемежаемости.
Кроме этого вида переме- ~7
жаемости, в системе D.20)
обнаружена перемежаемость -2
тина «хаос — хаос» [22]. Это
явление исследовано при f =
= 0,097 и изменении пара-
параметра и- При увеличении
И возникает последовательность бифуркаций удвоения цикла
основного периода То, заканчивающаяся при н = M-i ~ 2,39. После
этого в фазовом пространстве возникает хаотический аттрак-
аттрактор /i. С увеличением и область, занимаемая этим аттрактором,
увеличивается. С другой стороны, в точке и= 2,31 из сгущения
траекторий рождается пара трехтактных циклов, один из которых
устойчивый, а другой — седловой. Устойчивый трехтактный цикл
о -«
Рис. 9 48
307

с ростом и. также претерпевает последовательность бифуркаций
удвоения периода, заканчивающуюся в точке [X = ц2 = 2,35 и при-
приводящую к рождению хаотического аттрактора /2. В области
2,40 < (х < ц*, где (о,*«2,445, независимо существуют оба
/1=7,10772
/х 4,7070
=7,700ff
Рис. 9.49
аттрактора Л и /2, зоны притяжения которых в фазовом про-
пространстве разделены сепаратрисной поверхностью. При \i = ц*
сепаратрисная поверхность разрушается и аттракторы сливают-
сливаются, образуя объединенный аттрактор /0. Однако при (Л ^ ц* изо-
изображающая точка длительное время находится в области аттрак-
аттрактора Л. Переход с /, на /2 происходит нерегулярно во времени и
носит характер коротких всплесков. Среднее время т пребывания
изображающей точки в области Л при малых ц — \х* подчиняет-
подчиняется такой же закономерности, как и при перемежаемости «перио-
«периодическое движение — хаос», а именно т = С([х — ц*)~1/2, где С==
= 18. При увеличении ц — ц* средняя энергия колебаний растет,
спектр становится более равномерным, смещаясь в область низ-
низких частот, а автокорреляционная функция сужается (рис. 9.50).
При выводе уравнений D.20) характеристика усилителя пред-
предполагалась линейной. Если учесть нелинейность характеристики,
308

т. е. заменить в D.22) So на So — Stx2, то уравнения D.20) при-
примут вид
X=\iX+Y-XZ-dX3, Y = -X, 2-]
1'де d = alMS^ Как показали численные и физические экспери-
эксперименты [33], увеличение безынерционной нелинейной диссипации,
характеризуемой параметром d, приводит к разрушению хаоса и
О
\\ч>(дг)\
=2,55
0,5
О
Z5
50 Лг
Рис. 9.50
установлению периодического движения, причем это разрушение
происходит путем бесконечной последовательности бифуркаций
«уполовинивания» периода.
К системам уравнений третьего порядка приводят некоторые
модели нелинейного взаимодействия волн. Так, резонансное вза-
взаимодействие трех квазигармонических волн в нелинейной среде с
учетом только квадратичной нелинейности описывается уравне-
уравнениями [429]
^ % */. D-23)
309

где Ah — комплексные амплитуды волн, 6 = со, — <а2 — со3 — рас-
расстройка, (Оь — частота k-ii волны, т — коэффициент нелинейной
связи. При выводе уравнений D.23) предполагается, что по про-
пространственным координатам волны являются синусоидальными.
В работах [676, 677] рассматривается случай, когда одна из
волн (первая) неустойчива, т. е. Ч1>0, а остальные две устой-
устойчивы, т. е. ■уг, з < 0. Вводя безразмерные время, амплитуды и фа-
фазы волн по формулам
t == у^\, Ак = у^тГ1^ ехр {i (щ — aht)}
и разделяя действительные и мнимые части, получаем
а, = а, + а2а3 cos ф, D.24)
а2- з = — Г2, s#2, з — ЯА, г cos ф, D.25)
in ф, D.26)
где ф = ф1 — <р2 — фз, А = 6/^1, Г2, з= 1 "Уз, з I/Ti» точка над символом
означает дифференцирование по т. Если Г2 == Г3 = Г, то из урав-
уравнений D.25) следует, что d (al— a^/dx = — 2Г(а|— <4), т. е.
разность интенсивностей второй и третьей волн со временем стре-
стремится к нулю. Поэтому в стационарном режиме можно положить
а3 = а2. Тогда уравнения D.24) —D.26) примут вид
а 1 — ai + alcos Ф» а2 = — Га2 — ахаг cos ф,
/ а\\ D-27)
Ф = А + \2а1 sin ф.
Полагая далее Х = а, соэф, Г = а1зтф, Z = а\, получаем сле-
следующие уравнения:
£ = X-kY + Z-2Y\ Y = AX+Y + 2XY, Z = -2TZ-2XZ.
D.28)
Уравнения D.28) исследовались в [676, 677] при А = 2 и из-
изменении Г от 1 до 25. При меньших значениях Г нарушается ус-
условие сжатия фазового объема (div{X, Y, 2} = 2A — Г)), необхо-
необходимое для того, чтобы значения X, Y, Z оставались конечными.
Поэтому такие значения Г не имеют физического смысла. Были
найдены области периодических и хаотических режимов, а также
значения Г, при которых происходят бифуркации удвоения и
утроения периода. Показано, что точечное отображение для си-
системы D.28) приближенно является одномерным.
В работах [313, 315] рассмотрено резонансное взаимодействие
трех волн в среде с кубической нелинейностью. Для комплекс-
310

ных амплитуд этих волн Ак имеем уравнения
dA
—i = yA + 2imAlA2Ase~m + imA1 (| A1|2 + 2 \A2 |2 + 2 \A3|2),
D.29)
% ^{2 \AX |2 + | Л2,3|2 + 2| Л3,2|2),
где 8 = 2o)( — oJ — ciK — расстройка. Как и раньше, будем счи-
считать, что Yi > О, Уг, з < 0. Полагая в D.29)
t = 77гт, 4* = l/7i/21 т | а* ехр {г (ср* — coft0
получаем
а1аз г
/ °Ч 2 а9 2\ 2
Ф = А + I 2а2а3 — т^- % — ^- ai cos cp — ах
2 3
где Г2,»= Iy*. sl/fi» Ф = Bф1 — ф2 — 93)signm, A = F/Yi)sign m.
Если Г2 = Г3 = Г, то, как и в предыдущем случае, разность ин-
тенсивностей второй и третьей волн стремится со временем к
нулю. При этом для а^ 2 и <р получаем уравнения
«1 = ai + «ia2 sin ф, a2 = — Га2 — (fl?a2/2) sin ф,
D.o(J)
Ф = А + Bа2 — a2) cos ф — а\ 4- al-
Полагая X = ai соз(ф/2), Y = aiSin((p/2), Z = a2/2, преобра-
преобразуем уравнения D.30) к следующему виду:
X - X - {-У1 + Г (Z + X2), Г= Г+ -|-X +
Z = - 2FZ — 2ZFZ. D.31)
Как и раньше, физический смысл имеют только значения
Г > 1, при которых фазовый объем системы сжимается. Числен-
Численное исследование уравнений D.31) при этих значениях Г по-
показало, что в некотором диапазоне параметров решение имеет
хаотический характер, его корреляционная функция спадает,
а точечное отображение плоскости Z = const в себя сильно вы-
вытянуто вдоль оси Y и, следовательно, приближенно может быть
сведено к одномерному. Вид точечного отображения, временная
реализация процесса и характер аттрактора для А = 2,3, Г = 1,26
показаны на рис. 9.51.
Несколько иная модель трехволнового взаимодействия, опи-
описывающая комбинационное рассеяние света в диэлектрике, ис-
исследована в [584]. Уравнения для комплексных амплитуд волн
при соотношении частот 2o)t = ш2 +0)з, где u»i — частота волны
накачки, ш2 и со3 — частоты волн антистоксовой и стоксовой
311

компонент, имеют вид [388]
-Из1)А,
Кг = Ъ*Къ + Р2,з ( Hi I2 Л2,з + Л21<2)-
Вводя действительные амплитуды и фазы, т. е. полагая 4ft =
= aAexp(£(pft), получаем
«1 = ТА + Pi (аг ~ аз) аи
«2,3 = Г2,3О2,3 + Р2,3 («2,3 + «3,2 COS ф) of,
)
D.33)
где ш = 2ф! - ф2 - ф3. В [584] положено ф {t) ^ 0 и задано Ya = *.
^t_,==-!, р, = 5, р2 = -9, 0з = 1. Для этих значений параметров
100
Рис. 9.51
312

переменные ah изменяются хаотически, максимальный ляпунов-
ский показатель положителен и точечное отображение прибли-
приближенно сводится к одномерному.
В работе [555] рассмотрена задача о движении твердого тела
с линейной цепью обратной связи, предназначенной для стаби-
стабилизации движения. Эта задача приводит к уравнениям
1^-0/iX+Y+lOYZ, t-~X-0,AY+5XZ, Z^aZ
D.34)
получающимся из уравнений Эйлера с учетом цешг обратной свя-
связи. Численное решение уравнений D.34) при а = 0,175 показало,
Рис. 9.52
что в фазовом пространстве системы имеются два хаотических
аттрактора (рис. 9.52): один из них соответствует случайным
перескокам между особыми точками @,2390; 0,0308; 0,2103) и
(-0,2390; 0,0308; 0,2103), второй —между точками @,0315;
-0,1224; -0,1103) и (-0,0315; 0,1224; -0,1103).
§ 5. Действие гармонической внешней силы на генераторы
периодических и хаотических колебаний
Периодическая внешняя сила может оказывать двоякое воз-
воздействие на генератор: с одной стороны, она может привести к
хаотизации периодических колебаний [141, 147, 173, 216, 428,
472, 669], с другой — к синхронизации хаотических колебаний
[28, 36, 37, 54, 76, 78, 151, 214, 215, 223, 428]. Ниже мы рас-
рассмотрим оба этих эффекта.
Эффект хаотизации колебаний при воздействии внешней силы
на генератор с инерционной нелинейностью, по-видимому, впер-
впервые был подмечен Л. Н. Капцовым [173] при численном моде-
моделировании укороченных уравнений для амплитуды и фазы ко-
313

гут
7000 -
лебаний и напряжения на детекторе. Последние имеют вид [216]
а — -х- A — bV) а — а0Ас sin ф,
E-1)
Ф = А Ас cos ф, V = — yV + уКа,
где по — 1/ЬК—амплитуда колебаний автономного генератора.
Хаотизация колебаний в генераторе с инерционной нелиней-
нелинейностью может происходить и при параметрическом воздействии
внешней силы с частотой по-
порядка частоты процесса уста-
установления колебаний [216].
Это явление эксперименталь-
экспериментально и численно исследовано
в работах [74, 75].
При экспериментальном
исследовании использовалась
схема генератора с детекто-
детектором (рис. 9.45). Параметри-
Параметрическое воздействие U =
= Uo cos 2nvt подавалось на
усилитель / и складывалось
с напряжением V, снимае-
снимаемым с детектора. Наличие
параметрического воздейст-
воздействия приводит к модуляции
амплитуды генератора. При
малых значениях £/0 глуби-
глубина модуляции амплитуды
максимальна, если частота
воздействия близка к частоте
процесса установления [216],
определяемой превышением
над порогом генерации ц и
постоянной времени детек-
Рис. 9.53 тора ВЯСД = ■у-1. В силу не-
нелинейности зависимость ам-
амплитуды модуляции от частоты имеет гистерезисный характер,
что приводит к возможности скачков.
На диаграмме, приведенной на рис. 9.53, изображены области
существования различных режимов модуляции амплитуды. Ли-
Линия / соответствует скачку амплитуды модуляции от малой (сле-
(слева) к большой. Заштрихованные области соответствуют регуляр-
регулярной модуляции. В областях 1, 2, 3, 4 частота модуляции соответ-
соответственно равна v, v/2, v/3, v/4. (Области синхронизмов более
высокого порядка, чем 1/4, на диаграмме не изображены.) В не-
заштрихованных областях модуляция является нерегулярной.
Выход из областей регулярной модуляции при исследованных
значениях параметров происходил путем бесконечной последова-
314

тельности бифуркаций удвоения периода. Так, например, при
частоте v = 3 кГц, близкой к частоте процесса установления,
и увеличении амплитуды воздействия Uo в диапазоне, отмечен-
отмеченном на рис. 9.53 вертикальной чертой, эволюция временной реа-
реализации сигнала с генератора показана на рис. 9.54.
Для определения границ перехода к хаосу и оценки степени
хаоса использовался порог синхронизации. Для этого па иссле-
исследуемый генератор с инерционной нелипейностью, работающий в
Рис. 9 54
режиме хаотической модуляции амплитуды, подавался сигнал с
дополнительного генератора на частоте, близкой к частоте авто-
автоколебаний исследуемого генератора (/=130 кГц). При этом
оказывалось, что начиная с некоторого критического значения
амплитуды дополнительного генератора В модуляция амплитуды
исследуемого генератора становилась регулярной. Частота воз-
воздействия каждый раз варьировалась таким образом, чтобы кри-
критическое значение В было минимальным. В результате строилась
зависимость этого минимального критического значения В (ко-
(которое, согласно данному в § 3 гл. 8 определению, мы называем
порогом синхронизации Вп) от величины [/„ при фиксированном
значении частоты v. Вид таких зависимостей для трех значений
v (v = 2,0 кГц, v = 2,8 кГц и \>=4,0 кГц) показан на рис. 9.55,
а—в. Более детально зависимость Вш от £/„ вблизи границы пере-
перехода к хаосу при v = 3 кГц показана на рис. 9.55, г. Эта зави-
зависимость имеет степенной характер, о чем свидетельствует ее гра-
график, построенный в логарифмическом масштабе на рис^ 9.56. На
этом же рисунке приведены аналогичные зависимости для двух
других значений частоты v. Показатель степени г в зависимости
Вш = (U0 — Uoa>)r оказался неодинаковым для разпых значений
частоты v (при v = 2,5 кГц /- = 0,5, при v = 3 кГц г = 0,4, при
315

v — 3,9 кГц г = 0,3). Каково происхождение этого различия, сви-
свидетельствующего об отсутствии универсальности, осталось не-
невыясненным.
Численное моделирование процессов в исследуемом генераторе
проводилось в рамках укороченных уравнений для амплитуды
«« 0*8
v -4000
X
0,5
\_О,1
v =3000 Гц
L/
80 120 160 200[/0,mBW,8 20 20,2 20,4 Ц„мв
6 е
Рис. 9.55
и напряжения на детекторе, имеющих вид
а = -1- [т] - аа2 - Ъ (V + Uo cos 2nvt)] a, V = —yV + yKax E.2)
где а — коэффициент, характеризующий безынерционную нели-
нелинейность усилителя. Эти уравнения решались при следующих
значениях параметров: г\ = 2,5 • 106, а = 100, Ъ = 106, 7 = 180,
if-1,3.
Характер решения уравнений E.2) качественно соответство-
соответствовал наблюдаемым экспериментально явлениям перехода к хаосу.
В области хаоса для системы E.2) на основе алгоритма Бенет-
тина вычислялся положительный ляпуновский показатель Я. За-
Зависимость Я от Uo при v — 2,8 • 103 показана на рис. 9.57. Ка-
Качественно она повторяет зависимость порога синхронизации Вп
316

от Uo для соответствующего значения частоты v. Таким образом,
результаты физического и численного экспериментов подтверж-
подтверждают гипотезу о том, что порог синхронизации может служить
удобной и информативной характеристикой хаотических дви-
движений.
В работе [669] проведено численное и экспериментальное ис-
исследование автоколебательной системы, описываемой уравнением
х— jxA — х2)х + х3 = 5cos cat. E.3)
В автономном режиме (В = 0) колебания такого генератора
являются периодическими с частотой со0 = 1,617 и амплитудой
А = 1,824. При В Ф 0 в зависимости от +
частоты со возможны как синхрониза-
синхронизация различных порядков, так и квази- 77
периодические колебания, соответству-
соответствующие в фазовом пространстве дву-
двумерному тору. В области достаточно
7 -
v=2,8 кГц
Рис. 9.56
0,05 0,1 вгОгв
Рис. 9.57
больших В колебания могут иметь хаотический характер.
Так, например, при со = 4 и 5 = 1 в системе имели место
квазипериодические колебания, которым на секущей по-
поверхности t ~ 0 [mod 2л/со] соответствует замкнутая инвариант-
инвариантная кривая (рис. 9.58, а). Спектр таких колебаний содержит
четыре составляющих на частотах coi, 4o>i — со, со и Зсо4, где
©! = 1,614 « ©о (рис. 9.58, б). При увеличении В колебания
становятся хаотическими. Вид точечного отображения на секу-
секущей плоскости t = 0 [mod 2л/со] и соответствующий ему спектр
для случая В = 17 показаны на рис. 9.58, в и г. В работе [669]
приведены и другие наборы значений В и со, при которых коле-
колебания имеют хаотический характер. Отмечено, что наличие ку-
кубического члена в уравнении E.3), отличающего его от уравне-
уравнения Ван дер Поля с внешним воздействием, при малых значениях
|Л существенно для хаотизации колебаний.
При больших \i, соответствующих релаксационному режиму
работы автономного генератора, хаотизация возможна и в обыч-
317

ном генераторе Ван дер Поля с внешним воздействием, описы-
описываемом уравнением [141, 147, 472]:
х — ц A — х2)х + х = В cos со*.
E.4)
Так, хаотическое решение уравнения E.4) было обнаружено в
[147] при ц = 3; В = 2,5; со = 2,7.
Более общий случай рассмотрен в работе [149], где с помощью
аналогового и численного моделирования исследовано уравнение
х — цA — хг)х + х + %х3 = В cos mt.
Показано, что в широкой области параметров ц, |, В и со это
а:
3
2
7
О
-1
.*••"*"
-3 -2 -/ О
а
г з х
so»
70
-f
70
-2
0,01
О 7,0 2,0 3,0 4,0 v
уравнение имеет хаотические решения с широким спектром, при-
причем хаос возникает в результате образования и разрушения дву-
мерпых торов.
Переход к хаосу через возникновение и разрушение квази-
квазипериодических режимов наблюдался также при гармоническом
внешнем воздействии на систему Лоренца [428] и генератор с
инерционной нелинейпостью [-28, 34—36]. Внешнее воздействие
318

в [428] задавалось параметрически, т. е. исследовалась система
X = a(Y~X), Y =-Y + (г + а сов vtt)X-XZ,
где а = 10, & = 8/3. Параметр г варьировался вблизи значения
гп = 166,06, соответствующего порогу перемежаемости автоном-
автономной системы, а частота со — вблизи удвоенной частоты колебаний
в ламинарной фазе (со « 11). Выше порога перемежаемости (при
г = 166,07) внешнее воздействие с амплитудой а — 1 в узком ин-
интервале частот вблизи 11,02 синхронизовало хаотические колеба-
колебания, а вне этого интервала приводило к перемежаемости типа
«тор — хаос» (рис. 9.59, а, б, в, г). При г < гп (г = 166), со = 10
*itailiiii«iiih
Рис. 9.59
и малых амплитудах воздействия наблюдались квазипериодиче-
квазипериодические колебания (рис. 9.59, д), которые при увеличении а выше
критического значения акр « 0,05775 разрушались и становились
хаотическими. Переход к хаосу также имел характер переме-
перемежаемости типа «тор — хаос» (рис. 9.59, е).
319

Воздействие гармонической внешней силы на генератор с
инерционной нелинейностью численно и экспериментально ис-
исследовано в [28, 34, 35] в рамках следующей модели (сравните
с D.20)):
XX+YXZ + Bt, Y =-X,
При перезопансном воздействии (со =И= 1) и малых значениях р,,
при которых в автономном генераторе устойчив основной перио-
периодический режим, возникают биения, соответствующие в фазовом
Рис. 9.60
пространстве двумерному тору (рис. 9.60 (физический экспери-
эксперимент) и 9.61, а (численный эксперимент)). Если частоты не-
несоизмеримы, то обмотка тора является квазипериодической
(рис. 9.60, а), в противном случае — периодической (рис. 9.60,6
и в). Характерный вид реализации процесса X(t) при со < 1 и
со > 1 показан на рис. 9.62 (физический эксперимент). При уве-
увеличении ц начинаются бифуркации удвоения квазипериода тора
(рис. 9.63, а и б (физический эксперимент), 9.61, б (численный
эксперимент)) и возникает хаотический аттрактор (рис. 9.63, в
320

и 9.61, б). Аналогичные результаты имеют место и при увели-
увеличении амплитуды воздействия В. В работе [35] показано, что при
фиксированном В число удвоений тора до' его разрушения ко-
конечно и определяется амплитудой воздействия В: чем меньше В,
-1,0
0,5
-2 -7
'•••••• .о
-■2 .-/ 2 А
7,5
:'<••
3 Y
r,o\:-:
'oJ'"*y.
-50-
Y \§S,a5
5l
••"•v.v. :;•-.-.,:-
~/ 2 3 *Y~50
1§S,AB
-50
-2 "/ О 1 2 3 4 Y
Рис. 9.61
fO f
тем число удвоений больше. Спектр ляпуновских показателей
для аттрактора, соответствующего рис. 9.63, в, следующий-
Х= @,03196; 0; -0,00523; -0,228). На основе отих данных
321

Рис. 9.62
Рис. 9.63

вычислена ляпуновская размерность по формуле Каплана —
Йорке с^ = 3,117.
Иная картина наблюдалась при уменьшении параметра ц от
значений, соответствующих двумерному тору. Этот режим в фи-
физическом эксперименте достигался следующим образом. В отсут-
отсутствие внешнего воздействия параметр ц увеличивался до тех пор,
пока в системе не возникал устойчивый двухтактный цикл (на-
(например, р. = 1,4; "у = 0,3). Затем вводилась внешняя сила, обес-
обеспечивающая устойчивую синхронизацию на основной частоте.
Далее амплитуда В плавно уменьшалась до рождения устойчи-
устойчивого двумерного тора и при дальнейших измерениях поддержи-
поддерживалась постоянной. Затем плавно уменьшался параметр ц. При
Рис. 9.64
зтом происходило жесткое разрушение двумерного тора с обра-
образованием хаотического аттрактора (рис. 9.64). Это явление уве-
уверенно наблюдалось в интервале значений параметра f от 0,1
до 0,5.
В работе [36] гармоническое внешнее воздействие подавалось
на систему двух связанных генераторов с инерционной нелиней-
постыо. При этом в определенной области параметров наблюдал-
наблюдался переход к хаосу через возникновение и разрушение трехмер-
трехмерного тора.
Обратный эффект периодизации хаотических колебаний при
гармоническом внешнем воздействии наблюдался в работе [28].
Было обнаружено, что в случае, когда автономный генератор
работал в хаотическом режиме (например, при ц = 1,45; f =
= 0,21), а частота внешней силы близка к собственной (ю = 1),
при В > So * 1,14 наступала синхронизация, при которой период
колебаний совпадал с периодом внешней силы. Области синхро-
синхронизации для уравнений E.5) при f = 0,3 и ряде значений ц
323

вычислены в дипломной работе Г. Г. Шаталовой1). Пример та-
такой области приведен на рис. 9.65, а.
Аналогичные явления наблюдались и при внешнем воздейст-
воздействии на систему Лоренца. Исследование синхронизации колеба-
колебаний в системе Лоренца, по-видимому, впервые было проведено в
7,5
0.5
80-
II II I ^
I I
0,72 0,73 0,74 0J5v=b>/2n 7,5 2,0 v
Рис. 9.65
работе [151] при помощи АВМ. Моделируемые уравнения имели вид
3D
20
/О
2 = Z + J3cosBnvf),
где а = 10, Ъ = 8/3, г = 55. Области синхронизации на плоскости
параметров В и v, полученные в [151], изображены на рис. 9.66.
В области / период синхронизован-
I ж ных колебаний Т совпадает с перио-
периодом внешнего воздействия То = 1/v,
а в области II — Т вдвое больше Т„.
I ^ Существенным является наличие по-
1 I рога синхронизации по амплитуде
2 2,6 3»тц воздействия. ^
Синхронизация колебании в си-
Рис, д.бб стеме Лоренца при силовом внеш-
внешнем воздействии исследовалась
Г. Г. Шаталовой. Для этого уравпения Лоренца были записаны
в форме D.2) и в первое уравнение была введена гармоническая
внешняя сила. Таким образом, моделировалась (численно)- сле-
следующая система уравнений:
( 3 х2 \
х + 28х + ©«ж = — ад — Иг ©ож + -о- + У )х + в cos Bnvt), E.6)
у
7 1,3
') Шаталова Г. Г. Явление синхронизации в хаотических системах
при внешнем периодическом воздействии: Дипломная работа.— М ' Физфак
МГУ, 1985.
324

где 26 = 0+1 11, й>о1Ь(г1), Ь 8/3, а ю0BоЬ)
*=E2/3)ю0. Одна из областей синхронизации для г = 40 пока-
показана на рис. 9.65, б.
Более детальное исследование синхронизации хаотических
колебаний проведено в [223] на примере системы с инерционным
самовозбуждением вида D.2) с нелинейными функциями вида
D.186). Исследуемые уравнения имели следующий вид:
26ж
cos Bn\t)t
У + ТУ = ах — 1Х% —
E:7)
Рис. 9.67
Система E.7) моделировалась на ЭВМ при следующих значениях
парнметров: 26=0,75, щ — *( = a = Z = fc = 1, /с = 20, га =17,5.
Вычисленные области синхрониза-
синхронизации для этой системы показаны
нат>ис.9.67. В областях-синхрони-
областях-синхронизации хаотический аттрактор,
имеющий для автономной си-
системы вид, показанный на
рис. 9.38, а, изменяется в зависи-
зависимости от значений В и v на
двух-, трех-, четырех- или шести-
оборотные циклы. Вид двухобо-
ротного и трехоборотного циклов
показан на рис. 9.68, а и б. Об-
Области трех и шестиоборотных
циклов на рис. 9.67 заштрихо-
заштрихованы. Отметим, что переход внутри областей синхронизации от
двухоборотных к четырехоборотным и от трехоборотных к шести-
оборотным циклам сопровождается бифуркациями удвоения пе-
периода. Двухоборотный и трехоборотный циклы в области / со-
соответствуют синхронизации на основной частоте внешней силы
(период колебаний равен периоду внешней силы), а в области
// — синхронизации на второй субгармонике (период колебаний
вдвое больше периода внешней силы). Чтобы составить .пред-
.представление о переходах от одного вида циклов к другому при из-
изменении частоты внешней силы v, были построены бифуркацион-
бифуркационные диаграммы, показывающие зависимость от v координаты х
циклов при пересечении ими сверху плоскости х = —0,2 для двух
фиксированных значений амплитуды В (рис. 9.69). Из диаграмм
видно, что при В = 2 вблизи границ области синхронизации про-
происходит каскад бифуркаций удвоения периода, приводящий к
хаосу. Бифуркации удвоения внутри областей синхронизации не
дают начала серии таких бифуркаций и, следовательно, не при-
приводят к хаосу.
Как показали численные расчеты, переходы из областей син-
синхронизации в область хаоса происходят по-разному в зависимости
от амплитуды внешнего воздействия. При малых значениях В эти
325

переходы происходят через режим биений, т. е. квазипериодиче-
квазипериодических колебаний. Проследим один из них для случая 5 = 1 в об-
области частот v от 0,249 до 0,255. При уменьшении частоты v до
B-2, 2-0,39
Рис. 9 68
значения v4 = 0,2535, соответствующего выходу из области син-
синхронизации, в системе возникают биения, что приводит к появ-
появлению пиков в низкочастотной части спектра на частотах fm =»
(т = 1, 2, 3, ...) и вблизи частоты внешней силы на
х
7,0
0,5
А
8-7
0,5
[0,25 0,3 0,5
3=2
O,ff» 0,35 0,4 0,45 0,5 »
Рис. 9.69
частотах /n = v + nve (n = ±l, ±2, ±3, ...) (рис. 9.70,а). При
уменьшении v число различимых частот растет, а частота ve не-
незначительно увеличивается. При v = v2 = 0,2504 происходит
бифуркация удвоения квазипериода тора (rT = l/v6), в резуль-
результате чего в спектре появляются частоты т\6/2 и v 4- п\ь/2. При
v = vs = 0,24903 спектр становится практически сплошным, хотя
на его фоне имеются пики на частотах V и 2v (рис. 9.70, б).
При дальнейшем уменьшении v эти пики исчезают.
326

При В > Вкр » 1,3 переход иа области синхронизации в об-
область хаоса происходит путем последовательности бифуркаций
удвоения периода цикла. Так, для случая В = 2 удалось просле-
проследить первые три такие бифуркации (см. рис. 9.69). Фазовый
портрет цикла после первой бифур-
бифуркации удвоения E = 2, v = 0,38) •*
показан на рис. 9.71. 3
Как уже говорилось в § 3 гл. 8,
в работах {214, 215] была высказана
гипотеза о связи порога синхрониза-
\SCf)
»-0,2S$
Рис. 9.71
ции с метрической энтропией Колмогорова, совпадающей в слу-
случае трехмерных систем с положительным ляпуновским показа-
показателем. Эта гипотеза была проверена на примерах систем E.5),
E.6), E.7), а также системы D.2) с нелинейными функциями
вида D.18а). С учетом внешней силы последняя имеет вид
х + 2бж + т\х = — ку — gxy + В cos cat,
У + УУ = ах + №-
E.8)
Численное исследование системы E.8) проводилось при сле-
следующих значениях параметров: ^=0,27; а0 = а — I = 1; А; = 1,73;
26 = 0,5 и 1,1. Примеры областей синхронизации при 28 = 0,5;
g= 12,2 и 26 = 1,1; g = 30 показаны на рис. 9.72.
327

Зависимость порога синхронизации от энтропии К, равной
положительному ляпуновскому показателю, для всех исследован-
исследованных систем показана на рис. 8.11 (А — для системы E.5), X —
E.6), О_ E.7), •— E.8)). На рис. 9.73 показаны зависимости
5
0,03
0,07
E5)
+ 7,09 7,70 7,77/г:
A i \
0,4
О,2
0,7
70
Zff-0,5
ff-72,2
0,25
(S.S)
30 50 70 90 Г
-
-
IV
1
г
/—+
Г
i i i
E8)
/ '-"
/^1~~2?=0,5
1 1 ^
'78 20 22 24 2ff к 70
Рис. 9.73
20 ЭО 40 50
А,+ от соответствующих параметров. На эти зависимости нанесе-
нанесены точки — значения А,+, вычисленные по формуле C.1) гл. 8 на
основе измеренных значений Вп. С точностью до ошибок числен-
численного эксперимента, обусловленных в основном погрешностью в
определении порога синхронизации, эти точки за редким исклю-
исключением ложатся на указанные зависимости.
328

§ 6. Взаимодействие генераторов колебаний-различных типов
При взаимодействии генераторов периодических и хаотиче-
хаотических колебаний также возможны либо их периодизация, либо
хаотизация. Покажем зто прежде всего на примере двух связан-
связанных генераторов, один из которых описывается уравнениями
D.2), D.186), а другой — уравнением Ван-дер-Поля [223J. Урав-
Уравнения, описывающие взаимодействие этих генераторов, имеют вид
F.1)
s*<V
0,7 0,2 6>3 0}4 0,5 0,6 Г
Х + Ш-
y + ЧУ — ax - 1хг — hx3,
U — \i(l — u2)u + co2w = тпгх.
При численном моделировании уравнений F.1) были заданы
следующие 'значения параметров: 26 = 0,75; А; = 20; га = 17,5;
Юо==„==а = ^ = й=1; ц = 0,1. Остальные параметры варьирова-
варьировались. Случай тп2 = 0 эк-
эквивалентен рассмотренно-
рассмотренному в предыдущем пара-
параграфе, причем /n-i = 1 со-
соответствует В = 2. Зафик-
Зафиксируем rrti = 1, (в = л и
проследим за поведением
системы при изменении
mt. При тпг< топор *** 1,2
решение уравнений F.1)
является периодическим с
периодом, вдвое большим
периода колебаний авто-
автономного генератора Ван
дер Поля, т. е. Т = 4. Это
означает, что происходит
синхронизация хаотиче-
хаотических колебаний первого
генератора периодически-
периодическими колебаниями второго.
При тпг > Отпор синхрони-
синхронизация разрушается и воз-
возникают биении; т. е. ква-
квазипериодические колеба-
колебания. Область их сущест-
существования занимает малый
участок по параметру ш2. рис д.74
При дальнейшем увеличе-
увеличении тп2 первый генератор переходит в режим хаотических колеба-
колебаний и, в свою очередь, навязывает свои чаетвты генератору
Ван-дер-Поля, тем самым его хаотизуя. Спектры колебаний обоих
генераторов и взаимная корреляционная функция при mz — о
показаны на рис. 9.74. Отметим, что взаимная корреляционная
329
,Т~ 0,2 0,3 0,4 0,5 Of f
Аг

функция имеет максимум при т = 0, равный 0,5. При еще боль-
больших значениях тп2 спектры обоих генераторов сближаются по
ширине и расположению пиков, а максимальное значение взаим-
взаимной корреляционной функции возрастает.
В случае, когда частота автономного генератора Ван-дер-Поля
ю расположена вне зон синхронизации первого генератора при
тпг = 0, уже при малых значениях т2 происходит существенное
расширение спектра генератора Ван-дер-Поля и его хаотизация.
При дальнейшем увеличении тг ширина спектра генератора Ван-
дер-Поля увеличивается до ширины спектра первого генератора
в автономном режиме.
Интересные явления наблюдаются также при взаимодействии
двух генераторов хаотических колебаний. В качестве первого
примера рассмотрим два связанных генератора, описываемых
уравнениями D.2) с нелинейными функциями D.18а) и D.186)
[223]. Система уравнений, описывающая взаимодействие таких
генераторов, имеет вид
хг + 261г1 + <а\х1 = — кху1 — пх\ + т^,
Vi + У1У1
262а;2 + ®\х2 = — к2у2 — gx2y2
У 2
Уравнения F.2) моделировались при следующих значениях
параметров: 2б4 = 0,75; /1 = 17,5; к{ = 20; ^i = ai = li = h = (h =
= Z2 = @i = co2 = 1; 2б2 = 0,5; ^2=0,1; &2 = 10; ^ = 20; ml — m2 =
=-т. В отсутствие связи (т = 0) колебания обоих генераторов
являются хаотическими и не коррелированными между собой.
Спектры колебаний имеют разную ширину и расположение пич-
ков (.рис. 9.75, а). При увеличении связи т ширины спектров
выравниваются, а пички располагаются на близких частотах.
В этом смысле можно говорить о взаимной синхронизации гене-
генераторов хаотических колебаний. Для примера на рис. 9.75, б
представлены спектры процессов xt(t) и x2(t) для случая т = 1.
Из сравнения рис. 9.75, а и б видно, что при т = 1 спектр вто-
второго генератора существенно смещен в низкочастотную область,
а его ширина существенно меньше, чем при т=0. На рис. 9.76
показана взаимная корреляционная функция процессов xt(t) и
xz(t). Ее первый максимум расположен при тт^О, что указывает
па некоторый «фазовый сдвиг» между колебаниями обоих гене-
генераторов.
В качестве другого примера рассмотрим взаимодействие двух
одинаковых генераторов хаотических колебаний. Соответствую-
Соответствующие уравнения имеют вид
х1Л + 2S;rli2 + ю2£1>2 = — kylt2 — пх\л + тх2>1,
F.3)
г/1,2 + УУ1,2 = axlt2 — lx\t2 — hx\>2%
330

где 26 = 0,75; fc = 20; п=17,5; ю — if =*a*=l = h= 1. В отсут-
отсутствие связи (m = 0) при несовпадающих начальных условиях
корреляция колебаний обоих генераторов отсутствует. При т Ф 0
5(Г)
а
0,5
S(f)
О 0,5 1 Г
Рис. 9.75
происходит синхронизация генераторов в описанном выше смыс-
смысле. При этом пички спектров смещаются в низкочастотную об-
область (рис. 9.77, а). Взаимная корреляционная функция колеба-
колебаний обоих генераторов при т = 3 приведена на рис. 9.77, б.
Аналогичные эффекты наблюдаются и при взаимодействии
генераторов хаотических
колебаний, описывав- o,ff-
мых уравнениями D.2),
D.18а).
В работе [34] числен-
численно исследовано взаимо-
взаимодействие двух индуктив-
индуктивно связанных генераторов
с инерционной нелиней-
нелинейностью. Если параметры
генераторов одинаковы,
-0,5
Рис. 9.76
то
- F) Xli2 =
Ylt2 -
где 0 «£ Г < 1 — коэффициент индуктивной связи.
уравнения модели имеют вид
1г2г1>2 + Г OiX2>1 + У2Д - X2tlZ2>1),
, F.4)
331

Несмотря на полную идентичность генераторов, в такой си-
системе при увеличении параметра ц и фиксированных значениях
1 и Г A = 0,3, Г = 0,3) возникают квазипериодические колеба-
колебания с основными частотами /0 и /i (эти колебания возникают при
А.
О 0,1 0,2 as 0,4 0,5 0,6 0,7 f О
Рис. 9.77
^ 2,0^2,4"?
ц — (x* = 1,58). Соответствующий спектр показан на рис. 9.78, а.
Несмотря на то, что /i«B/5)/0, процесс является квазипериоди-
квазипериодическим, т. е. обмотка соответствующего двумерного тора является
незамкнутой. Об этом свидетельствует спектр ляпуновских по-
показателей, содержащий два нулевых значения. При дальнейшем
увеличении ц квазипериод тора удваивается (рис. 9.78, б), и ко-
колебания становятся хаотическими (рис. 9.78, в). Наблюдавшееся
число удвоений тора конечно и тем меньше, чем больше коэф-.
фициент связи Г. Этот факт согласуется с результатами работы
[538]. Возникающий после разрушения тора хаотический аттрак-
аттрактор является несимметричным, т. е. выполняется по крайней
мере одно из неравенств: Zt Ф Х2, Yt Ф У2, Zt Ф Z2. Представляет
интерес тот факт, что спектр хаотических колебаний, возникаю-
возникающих таким путем, не содержит ярко выраженных пиков и яв-
является весьма широким.
На рис. 9.79 показаны зависимости от ц ляпуновской размер-
размерности dL и метрической энтропии К, вычисленных на основе
спектра ляпуновских показателей. Видно, что размерность хаоти-
хаотического аттрактора больше трех, как и в случае воздействия
внешней гармонической силы на один генератор (см. § 5),
а энтропия монотонно растет с ростом ц.
Хаотизация колебаний может происходить и тогда, когда
взаимодействующие генераторы в отсутствие связи совершают
периодические колебания. Примеры такого рода рассмотрены в
работах 1[169, 322, 323]. В {322, 323] исследована система уравне-
уравнений, моделирующая взаимодействие двух нейронных популяций,
каждая из которых состоит из двух типов нейронов, возбуждаю-
возбуждающих (х3) и тормозных (ys) [322]. Эта система имеет вид
Xt = -xt + th(Ui 4- h^ ~ byt)~\-1 (x2 -xy),
у i = — eyt + e ih(v
— Xi + th(u2
— Ьу2)-¥-1 (Xi — xz),
F.5)
где щ = u<l-hi+b,v =
332
l-p (/ = 1, 2).

Рис. 9.78
ACM аттрактор
X-70'
7,4 7,ff iff
1,7 IS fi
333

Численное исследование уравнений F.5) проводилось при
фиксированных значениях параметров uo = O,8; 'v0 = 4; 6=0,5;
р = 5; е = 0,005; f =*= 0,01; А2 = 1,141 и варьировании параметра
hi в диапазоне 1,11< hi < 1,16. При указанных > значениях пара-
параметров каждая из популяций в отсутствие связи A = 0) нахо-
находится в режиме автоколебательной активности, т. е. соответст-
соответствующие уравнения описывают генератор периодических колеба-
колебаний. При hi = hi генераторы идентичны, и связанная система
также совершает периодические колебания. Хаотизация колеба-
колебаний происходит при hi ¥= h2. Оказалось, что, если hi < 1,1225, си-
система имеет устойчивый трехоборотный цикл. При ht» 1,1225
этот цикл сливается с таким же неустойчивым циклом и исче-
исчезает. В результате возникает перемежающаяся стохастичность.
Вблизи этого перехода точечное отображение на секущей поверх-
поверхности Пуанкаре приближенно сводится к одномерному разрыв-
разрывному отображению.
В работе [169] рассмотрена система связанных через емкости
генераторов с инерционной нелинейностью, которые в автоном-
автономном режиме совершают периодические колебания, близкие к ре-
релаксационным. Численно и экспериментально показано, что за
счет связи колебания хаотизуются.
§ 7. Некоторые дискретные модели турбулентности
Как уже говорилось, система уравнений Лоренца является
простейшей (трехмодовой) моделью конвективной турбулентно-
турбулентности. В классической задаче о плоском слое жидкости, подогревае-
подогреваемом снизу, эта система выделяется из более полной системы
уравнений, если ограничиться первыми пространственными гар-
гармониками компонент скорости, нулевыми, первыми и вторыми
пространственными гармониками температуры [217]. Очевидно,
что вследствие этих ограничений система Лоренца справедлива
лишь вблизи порога возникновения конвективных валов, т. е.
при значениях г, близких к единице. При больших г надо учи-
учитывать более высокие пространственные гармоники, и уравнения
типа Лорепца становятся неадекватными. Такой учет произведен
в работе [574], где показано, что характер решения существенно
зависит от числа учитываемых мод.
Кроме системы уравнений Лоренца, в литературе рассматрива-
рассматривается еще ряд дискретных моделей уравнения Навье — Стокса.
В работах [409, 462] описана пятимерная модель, в [461] — семи-
семимерная, а в [463] ■— двенадцатимерная. Результаты, полученные
для моделей разных размерностей, существенно отличаются друг
от друга. Так, в случае пятимерной модели переход к хаосу при
увеличении числа Рейнольдса происходит только путем бифурка-
бифуркаций* удвоения периода. При этом точечное отображение на секу-
секущей поверхности сводится к одномерному. В случаях же семи-
семимерной и двенадцатимерной моделей переход к хаосу происходит
через возникновение и последующее разрушение квазипериоди-
334

ческих режимов, которым в фазовом пространстве системы со-
соответствуют двумерные торы.
Существенное изменение результатов при увеличении размер-
размерности модели показывает, что они плохо описывают решение ис-
исходного уравнения Навье — Стокса. Однако изучение этих моде-
моделей интересно и полезно с точки зрения общей теории динамиче-
динамических систем, исследования их сложного поведения и возможных;
путей перехода к хаотическим режимам.
Покажем, как получаются уравнения для этих моделей. Рас-1
смотрим двумерное течение несжимаемой жидкости под дейст-
действием пространственно периодической внешней силы f, которую'
можно представить в виде конечного числа членов ряда Фурье
* = 2 (Mk|)/kexp(ikx), G.1)
где х = {хи xj, к = iht, hj — волновой вектор с целыми компо-
компонентами, кх = (hz, —ht}, L — множество 27V векторов таких, что
если k e L, то и —к е L. Коэффициенты ft удовлетворяют ус-
условию
fk=---f-k. G.2)
Такое движение жидкости описывается уравнением непрерыв-
непрерывности
divU = 0 G.3)
и уравнением Навье — Стокса
£H
G.4)
где U = iu, v) — вектор скорости, v — кинематическая вязкость,
р — давление.
Решение уравнений G.3), G.4) в соответствии с G.1) можно
искать в виде
U(х) = 2 (kx/1 k|)Vkexp (&х), G.5).
k~L
где 7к — —Т-к- Решение G.5) автоматически удовлетворяет
уравнению G.3). Подставляя G.5) и G.1) в уравнения G.4) и
исключая давление р, получим
У
( }
Пусть L —множество векторов ki=(l, 1), k2 = C, 0), k3=*»
-B, -1), k4 = (l, 2), k,-@, 1), ke = B, 2), kr-(l, -2), а сила
f не зависит от времени и содержит лишь одну пространствен-
пространственную гармонику с волновым вектором к3, т. е. f = (к3±/|к31)!к х
хехр(гк3х). В этом случае уравнения G.6) имеют частное
335

Тк3 =
решение вида
_Укл = аХь% Yke =
где а = 10уУ2, Хи Xz, ..., -X, — действительные величины, удов-
удовлетворяющие уравнениям
X, = -2Х, + 4У5ХгХ3 + 4УХ4Х5,
G.7)
7, X, = -5Х7
где точка означает дифференцирование по времени х = vt,
R — /k jo. — аналог числа Рейнольдса.
Уравнения пятимерной модели [409, 462] получаются из G.6),
если в множестве L ограничиться пятью волновыми векторами
ki, k2, k3, k4 и k5. Для получения же двенадцатимерной модели
нужно взять двенадцать волновых векторов.
Ограничимся изложением результатов исследования семимер-
семимерной модели G.7), выполненного в работе [461]. При R^Ro'"
«227,1 четыре симметрично расположенных в фазовом прост-
пространстве предельных цикла становятся неустойчивыми и превра-
превращаются в четыре двумерных тора с частотами /t (частота цикла)
и /2 = i/TT, где Гт — квазипериод тора. Проекция на плоскость
хв, #з инвариантной кривой на секущей гиперплоскости Xi = 0,
соответствующей одному из таких торов, а также спектральные
плотности отображения Пуанкаре для х3 и потока для Xi{x) при
R = 269 показаны на рис. 9.80, а. При R = Д., где 275 <Rt< 276,
возникает первая бифуркация удвоения квазипериода тора
(рис. 9.80, б), а при Л = Л2, где 294<R2<294,5,— вторая
(рис. 9.80, в). Третья бифуркация удвоения тора в [461] обнару-
обнаружена не была. При увеличении R от значения Л2 инвариантная
кривая становится все более нерегулярной (рис. 9.81). Хаос на-
''0,5 1,0 7,5 2,0 2,5 Xs 0,5 7,0 7,5 2,0 2,5 Хе 0,5 7,0 7,5 2,0 2,5 Хв
Рис 9.81
337

ступает при R = Л3, где Rt ~ 299,25. На рис. 9.82 показана эво-
эволюция отображения Пуанкаре и спектра отображения при изме-
изменении R от 300 до 310. Из рисунка видно, что при R = 300 основ-
основной в спектре отображения является частота /2/4, при R = 304 —
частота /2/2, а при R = 310 — частота /2. Такая эволюция спектра
аналогична той, которая наблюдается при рождении хаоса через
последовательность бифуркаций удвоения периода цикла (см.,
например, [221, 344, 564]). При увеличении R до 325 хаотиче-
хаотический аттрактор непрерывно увеличивается в размерах, но сохра-
сохраняет свою структуру. При R > 325 структура аттрактора изме-
изменяется. Так, при R = 326,25 отображение Пуанкаре имеет вид
замкнутой кривой, описывающей три петли (рис. 9.83, а). По-
Поскольку в спектре отображения (рис. 9.83, б) кроме острых пи-
пиков имеется сплошной фон, такой аттрактор все еще является
хаотическим. Пики соответствуют частотам nf, где /' « Д/3. При
R > Л4, где Л4 ** 326,25, возникают области синхронизации, со-
соответствующие различным рациональным числам вращения Пуан-
Пуанкаре p = /7/i. Зависимость р от R в диапазоне 325<Д<347
приведена на рис. 9.84. На этом рисунке ясно видны области
синхронизации различных порядков. Наконец, при Л>Л5, где
347 < Rs < 348, структура аттрактора становится похожей на ту,
что была при R < 325 (рис. 9.85).
Ляпуновская размерность аттрактора dL, вычисленная по фор-
формуле Каплана — Йорке, в диапазоне R,< R< 300 оказывается
несколько больше двух. С ростом R она увеличивается и при
R > 300 становится несколько больше трех. В области R^<R<
< Rb величина dL снова уменьшается до значений, незначительно
превышающих двойку. При R>Rb ляпуновская размерность
опять возрастает, становится больше трех и непрерывно растет
с ростом R. Однако этот рост медленный и при R = 500 все еще
<k = 3,28.
В отличие от [409, 461—463], где рассматриваются маломер-
маломерные модели уравнения Навье — Стокса, в работе [300] *) иссле-
исследована многомерная модель, получающаяся при решении этого
уравнения методом конечных разностей с граничными условиями,
соответствующими течению в плоском прямолинейном канале
(течению Пуазейля) [217]. Если исключить из уравнений G.3),
G.4) давление р, положить f = 0 и ввести функцию тока г|з, так
чтобы и = dty/ду, v = —dty/dz, то для tf» получим следующее урав-
уравнение [217]:
Здесь х и у — безразмерные координаты соответственно вдоль и
поперек канала, отнесенные к ширине канала h, t — безразмерное
*) См. также: Генкин М. Д., Добровольский В. А., Перми-
н о в С. М. Анализ крупномасштабных структур течения вязкой несжимае-
несжимаемой жидкости в плоском прямолинейном канале.— Препринт № 155 ИОФ
АН СССР, Москва, 1986.
338

время, отнесенное к h/щ, где и0 — скорость жидкости в центре
канала при ламинарном течения, R = uoh/v — число Рейнольдса.
Течение моделировалось на участке канала с безразмерной дли-
длиной I *= 6,28. Была выбрана сетка, содержащая 129 X 129 элемен-
элементов. Шаг по времени выбирался равным 10~3. Граничные усло-
условия на входе канала соответствовали профилю скорости в случав
-07-
0,0 0,7 1,4 2,7 2,8 Х6
а
-9,0
0,00 0,75
Рис. 9.83
t,50
2,25
-7/23
5/ГГ6
4/93
3/70
5/777
7/764
5/778
3/77
4/9S
5/179
е/кэ
330
335
Рис. 9.84
340
345 R
ламинарного течения, т. е. м@, у, t) = 4y(l — y), г@, у, t) — 0.
В качестве начальных условий был задан такой же профиль ско-
скорости во всем канале, но с малым возмущением (не более 1%).
Вследствие наличия возмущения при достаточно больших числах
Рейнольдса {RKp == 5780 [217]) задаваемый профиль скорости
разваливался, и в канале устанавливалось неламинарное тече-
течение, характеризуемое наличием крупномасштабных, нерегуляр-
нерегулярных по пространству, но периодически по времени рождающихся
вихрей. При R «= 6500 период рождения вихрей в указанном
безразмерном времени равен Г = 3,65. Время установления такого
течения норядка 200. На рис. 9.86 изображены линии тока при
340

3,3 Хв -1,5 -O,5 O,5 7,5 2,5 3,5 4,5 Xs
JjP$x3M R~400M
ы
0,00 0,84 f,58 2,52 ы
5
Рис. 9.85
Рис. 9.87

R '= 6500 в мрмент времени t = 300. Из рисунка видно, что вихри
зарождаются и существуют только у стенок канала. О периодич-
периодичности рождения вихрей свидетельствует наличие хотя и слож-
сложного по форменно замкнутого цикла в фазовом пространстве
сконструированной на основе процедуры Паккарда — Такенса
динамической системы с координатами Ui (£)., v± {t), Ui (t + т),
»i(* + t), bi(* + 2t) и vi(t + 2t), где ut(t)-uE; 0,48; *), i>i(*) =
= uE; 0,48; t), t = 0,07. Проекция этого цикла на плоскость
Ui(t), ut(t + 2х) изображена на-рис. 9.87, а.
Авторы работы [300] отмечают, что получающийся после про-
процесса установления профиль скорости близок к экспериментально
наблюдаемому (отклонение не превышает 8%). Близким к экспе-
эксперименту оказывается и турбулентное сопротивление (разница
порядка 12%).
Несмотря на периодический по времени характер течения,
частицы жидкости в потоке экспоненциально разбегаются, т. е.
происходит перемешивание. Разбегание частиц можно характе-
характеризовать величиной К, аналогичной ляпуновскому показателю
где d(t) — расстояние между частицами в момент времени t,
угловые скобки означают усреднение по всем точкам канала. При
R = 6500 получено К = 0,36.
Периодичность рождения вихрей нарушается даже при слабом
внешнем воздействии на течение. Так, при небольшой вибрации
стенок канала (v(x, 0, t) — v(x, I, t) = 0,01 sin 2nt) фазовый порт-
портрет приобретает вид, показанный на рис. 9.87, б, т. е. возникает
хаотический аттрактор. Корреляционная размерность этого ат-
аттрактора в указанном выше шестимерном фазовом пространстве
оказалась равной 3.7. Коэффициент разбегания частиц % при на-
наличии вибрации стенок увеличивается и становится равным 0,6
(разброс для разных точек канала порядка 0,15). Аналогичные
явления наблюдаются и при периодической модуляции скорости
на входе канала.
§ 8. Примеры моделей химической кинетики
В 1920 г. Лотка [565] предложил гипотетическую химическую
реакцию, в которой возможны колебания концентраций реаги-
реагирующих веществ. Уравнения этой реакции выглядели следующим
образом:
Аналогичная модель в дальнейшем была использована Вольтерра
для объяснения колебаний численности конкурирующих видов
животных и растений [114]. Эта модель получила название «хищ-
«хищник— жертва».
342

В 1951 г. колебательная химическая реакция в гомогенной
системе была открыта экспериментально Б. П. Белоусовым. Од-
Однако его результаты были опубликованы лишь в 1959 г. {80].
Затем такие реакции были детально исследованы А. М. Жабо-
тинским [152]. С тех пор возможность существования колебатель-
колебательных химических реакций (в частности, в гомогенных системах)'
уже не подвергается сомнению. В настоящее время известно
довольно много периодических реакций [1, 152, 199, 319, 356].
Для лучшего' их понимания разработаны некоторые простые ма-
математические модели. Наибольшую известность получили модели,
называемые брюсселятором и орегонатором [356]. Брюсселятор
описывает следующую химическую реакцию между веществами
Л, X, Y, В, D, Е:
А^Х, B + X^Y + U, 2Х+7^3Х, X-+E. (8.1)
Название модели обусловлено тем, что эта реакция была иссле-
исследована в Брюсселе И. Пригожиным с сотрудниками [129, 294,
595]. Обозначая концентрации реагирующих веществ в (8.1) теми
же буквами и считая А и В заданными, получим уравнения брюс-
селятора, представляющие собой частный случай системы, пред-
предложенной Тьюрингом в 1952 г. [666]:
X = A-(B+l)X+X2Y, ? = BX-X*Y. (8.2)
При В>1 + А2 уравнения (8.2) имеют устойчивое периодическое
решение [217]. Если концентрация вещества А промодулирована
со временем по гармоническому закону, т. е. А=А0 + а cos cot,
то колебания концентраций X и Y могут стать хаотическими
[491, 535]. В этом случае уравнения (8.2) описывают нелиней-
нелинейный осциллятор с гармоническим внешним воздействием. На при-
примере системы (8.2) с промодулированной величиной А в [535]
была численно подтверждена закономерность, установленная в
[519] и показывающая, как зависит
суммарная интенсивность сплошного
спектра от параметра после перехо-
перехода к хаосу в результате бесконечной
цепочки бифуркаций удвоения пе-
периода (см. § 4 гл. 8). При числен-
численном моделировании были выбраны
следующие значения параметров:
Л0 = 0,4, 5=1,2, а = 0,05. При этом
частота автоколебаний автономной
системы равнялась со0 = 0,375. Би-
Бифуркации удвоения периода и пере-
переход к хаосу наблюдались при увеличении частоты модуляции о.
Последовательность бифуркаций начиналась при со = 0,712, а за-
заканчивалась при со = Юоо = 0,7877. После этого с ростом со ин-
интенсивность сплошного спектра росла так, как это показано на
рис. 9.88. Линейный участок зависимости (сплошная линия) хо-
343

рошо соответствует установленной в [519] формуле ЛГ(со)==
-JV,(©-©.)«, где I = 1,5247...
Роль модуляции концентрации вещества А, приводящей к хао-
хаосу при реакции (8.1), может играть дополнительное вещество Z,
концентрация которого изменяется вместе с изменением кон-
концентраций X и Y и, в свою очередь, влияет на их изменение.
Рассмотрим, например, следующую схему реакции [217]:
X->Z, Z+Y + X. (8.3)"
Соответствующие уравнения для изменения концентраций имеют
вид [217]
Х=*А -E+ 1)Х+ X2Y + YZ,
Y = BX-X2Y~YZ, (8.4)'
2 = r(X-YZ).
Отметим, что система, описываемая уравнениями (8.4), относится
к классу автоколебательных систем с инерционным самовозбужде-
самовозбуждением [52, 53, 391]. Действительно, введя новые переменные х =
= Х+У-Х„-7„, y~Z-Z, + r(l + Zt)x, z = X-X0, где Х0 = А,
Y0=(B— 1)/A, Zo = А2/(В — 1) — стационарные значения кон-
концентраций X, Y, Z, преобразуем уравнения (8.4) к виду
(х, у, z), (8.5J
z =—28z + «fix + ку — f (х, у, z),
где Т = Г(Я-1)М, a = r[r(B-l + A*)/A-A2/{B-\)l 26 =
=*А2В/(В- 1)-В + 3, со* = А2В/(В— i) — r(B—l + A*)/A, к =
= E-1)Л4, <р(*, у, z)=-r(x-z)iy-r(B-l+A2)x/(B-l)l
f(x, у, z) = -(x~z)[y + z* + 2Az-r(B-l + A2)x/(B-l)]-
— (В— ijzf/A. Исключая из уравнений (8.5) переменную z, по-
получим уравнения вида D.2), описывающие колебания в -систе-
-системах с инерционным самовозбуждением.
Хотя система (8.4) численно еще не исследована, можно ожи-
ожидать, что в некоторой области параметров изменения концентра-
концентраций X, Y, Z будут иметь хаотический характер.
В работах [631, 637, 638] рассмотрена система из двух свя-
связанных брюсселяторов вида (8.2)
■^1,2 = А1>2 (-Dl,2 + 1) -^1,2 + Xli2Ylt% + Сх (X2>i ^Ll,2)>
Yi,2 — Blt2Xlt2 7—Xlt2Ylt»-\-Cy (Y2,i — Yltt)t \ * '
где Сх, Су — константы связи. При численном моделировании
уравнений (8.6) в [631] было задано: ^i = l,6, Вг = А\ + 2 (i==
— 1, 2), Сх~Су = С. Параметры А2 и С варьировались. При ма-
малых С колебания переменных Хиг и Ylti в общем случае были
344

квазипериодическими с отношением частот р, определяемым
параметром А2. Такие квазипериодические колебания с р =
= 0,61791 и спектром ляпуновских показателей @, 0, —1,081;
—1,997) наблюдались, например, при С =0,01, Аг = 0,84896. При
увеличении С наблюдались как резонансы различных порядков,
так и переходы от квазипериодических режимов к хаотическим.
Эти переходы контролировались по спектру ляпуновских показа-
показателей. Так, например, при С = 0,125; Аъ — 0,5550 получался сле-
следующий спектр ляпуновских показателей: @,037; —0,002; —0,616;
— 1,591). Наличие положительного ляпуновского показателя го-
говорит о том, что наблюдаемый режим являлся хаотическим.
В работах {637, 638] брюсселяторы полагались идентичными,
а коэффициенты Сх и Су — разными. При этом было выбрано:
Ai=*A2 = A = 2, CJCV = q = 0,1. Параметры Сх и В = В1=*В2
варьировались. Оказалось, что при малых Сх переход к хаосу
происходит через образование и разрушение тора [637], а при
больших — через последовательность бифуркаций удвоения пе-
периода цикла :[638]. Чтобы продемонстрировать эти переходы,
Таблица 9.7
Сх
0,05247
0,05245
0,05242
0,05239
0,05238
0,0523
0,0522
0,0521
0,000
0,000
0,000
0,000
0,009
0,043
0,068
0,075
X,
0,000
-0,010
0,000
0,000
0,000
0,000
0,000
0,000
и
-0,011
—0,010
-0,034
—0,049
—0,063
—0,172
-0,42
-0,58
—2,684
—2,681
-2,677
-2,673
-2,671
-2,658
—2,57
—2,47
2
1
2
2
2,143
2,250
2,162
2,129
В = 5,5
Таблица 9.8
Сх
1,20
1,21
1,26
U
0,078
0,107
0,200
0,00
0,00
0,00
и
-2,68
—2,69
—2,82
-30,87
-30,67
-32,17
2,029
2,040
2,071
В = 5,9
приведем табл. 9.7 и 9.8, где указаны спектры ляпуновских по-
показателей и ляпу,новская размерность1 аттрактора в зависимости
от параметра Сх при фиксированном значении В. В интервале
Схе [0,05246; 0,05244] E = 5,5), где размерность аттрактора рав-
равна единице, наблюдался резонанс на торе с соотношением частот
3:1. При Ск<={0,9; 1,1933] E = 5,9) было зафиксировано не-
несколько устойчивых и неустойчивых периодических движений,
причем при увеличении Сх период устойчивых движений удва-
удваивался. Значения Сх в таблице 9.8 выбраны в области хаоса.
345

Другой известной моделью колебательной химической реакции
является так называемый орегонатор [105, 141, 246, 356, 452].
Впервые эта модель была предложена Филдом и Нойесом-[452]
иэ Университета штата Орегон в Юджине (отсюда и название
«орегонатор»). Она представляет собой сильно упрощенный ва-
вариант более сложной модели, предложенной в 1972 г. [451] для
описания основных особенностей реакции Белоусова — Жаботин-
Жаботинского. Схема реакции, называемой орегонатором, выглядит сле-
следующим образом:
А + Г-♦ X + Р, X + Y-^2P, А + X -^ 2Х + 2Z.
где А = [ВгОГ], Х = [НВгО2], 7 = [Bri, Z = [Ce4+], P =
= [НОВг]. Единицы измерения концентраций X, Y, Z и масштаб
времени можно выбрать так, что уравнения реакции (8.7) бу-
будут иметь вид [452]
X = a(Y-XY+X-gXz),
Y = a~i(-Y-XY + fZ), (8.8)
где а ~ 102, ii ~ Ю-1 -5-10, g ~ 10"» - 10, / ~ 1. Известно [141t
246, 452], что орегонатор отражает основные черты автоколеба-
автоколебательной реакции Белоусова — Жаботинского. Форма колебаний
концентраций X, У, 2 и проекции соответствующего предельного
цикла, полученные в [452] при а = 77,27, ц, = 0,1610, g =
= 8,375 • 10~в, / = 1, показаны, на рис. 9.89 (цифры указывают
моменты времени). Еще в 1973 г. Рюэлем [624] было высказано
предположение, что в реакции Белоусова — Жаботинского коле-
колебания концентраций могут быть не только периодическими, но и
хаотическими. Далее это предположение было подтверждено ка-
качественным исследованием [661, 668], аналоговым [660] и числен-
численным [667] моделированием, а также экспериментально [437, 520,
616, 617, 623, 634, 652, 656, 673].
Тайсоном [668] были предложепы схема и уравнения моди-
модифицированного орегонатора:
X+P, X+Y^2P,
2Х-+А + Р, X + Z-*hY+Q;
X = a(Y-XY+X-EXZ-gX2),
= a~l(-Y-XY + fZ), (8.9)
где e « 2 • 10~5. Несмотря на то, что уравнения (8.9) отличаются
от (8.8) малыми членами &XZ, они имеют качественно отлич-
отличные решения.
346

Другая модификация орегонатора, рассмотренная в [667], за-
заключается в том, что в схеме (8.7) допускается протекание ре-
реакций в обоих направлениях. Скорости реакций в обратном на-
направлении обозначаются k-i, А-2, ..., &_5 соответственно. Урав-
Уравнения такой модели с учетом того, что реакция осуществляется в
IgX
5,0
3,0
7,0
00
IgX
lg/
igZ
'\
rt
-'F
4v
2-
0-
[бг] критическая концентрация-
i
j
50 700 750 200 250 300 t
a
~2,0 00 2,0
-2,0
0,0
2,0
Ig/
Рис. 9.89
проточном реакторе, удобно записать в следующем виде:
% = Wi — w2 + w3 — 2iVi — X/r,
Y =—Wt — w 2 + w5 — Y/r,
2 — w3—w5 — Zfx,
P = wl + 2w2 + wi — wi — P/x,
где
= kzAX - k-3X% w, = k.X2 - k-J.P,
(8.10)
т — время реакции, равное отношению объема реактора к ско-
скорости потока. Уравнения (8.10) исследовались численно в [667]
347

при различных значениях т и ki — 1,34, k-t = 104, к2 = 1,6 • 10',
fc_2 = 5-10-5, к, = 8-10* к-3=>4$-101\ А4 = 4-10\ Л_*-
= 1,6 • Ю-10, А, = 90, fc_» - 1Q-S, A = 0,06.
В работах [333, 654} предложена использовать в качестве
удобной модели химической реакции Бедоусова — Жаботинского
систему уравнений Н. Н* Баутина £15, 71], замечательную тем,
что для нее известно точное решение. Эта система уравнений
имеет вид
lX-X'-XY*, Г =-аХ+E2Y - Y3 - УХ2. (8.11J
В [333, 654] приводятся варианты модифицированной системы
Баутина. В частности, рассмотрена неавтономная система, полу-
получающаяся из (8.11) заменой постоянных параметров Еи Ег и а
на переменные: Ei (t) = е4 — ezt sin at, E2{t) = e2 + ez2 sin at, a (t) =
= a0 + e sin at. В такой системе, по-видимому, возможны слож-
сложные нерегулярные режимы автоколебаний.
Первые эксперименты, в которых наблюдались хаотические
колебания концентраций реагирующих веществ в реакции Бело-
усова — Жаботинского, проводимой в поточном реакторе, изложе-
изложены в [520, 623, 634]. Для объяснения экспериментов Хадсона
[520] в работе [605] была предложена следующая модель:
х = hx + у + 0,lz, у = —х,
(812^
где е — малый параметр. Численное решение уравнений (8.12)
при е "= 0,1 и различных значениях h качественно соответствует
экспериментальным данным Хадсона, полученным для различ-
различных значений скорости потока g мл/мин. Это соответствие про-
продемонстрировано на рис. 9.90 [605], где в левой колонке приве-
приведены экспериментальные данные Хадсона, а в правой — решения
уравнений (8.12) (z(t)).
Более детальные исследования проведены Роуксом и Суинни
с сотрудниками {105, 616, 617, 652, 656, 667]. При определенных
значениях скорости потока ими наблюдался переход от периоди-
периодических колебаний концентраций (рис. 9.91, а) к хаотическим
(рис. 9.91,6). Здесь слева показаны колебания потенциала бро-
бромид-ионов, в середине — соответствующие спектральные плотно-
плотности, а справа—двумерные аттракторы в координатах B(tk) и
B(th+ т), построенные по алгоритму Паккарда — Такенса. От-
Отметим, что вид двумерного аттрактора существенно зависит от
времени задержки х, Его деформация при изменении т для слу-
случаев, показанных на рис. 9.91, а и б, представлена на рис. 9.92
и 9.93 соответственно. На основе трехмерного аттрактора в коор-
координатах В(t{), B(f,+ т), B(tt+2x), проекция которого изобра-
изображена на рис. 9.94, а, в [652] построено точечное отображение на
секущей плоскости, перпендикулярной рис. 9.94, а и проходящей
через штриховую линию- (рнс. 9.94, б). Поскольку все точки ото-
отображения расположены на одной прямой, оно является одномер-
348

ным. Зависимость последующего значения координаты X вдоль
этой прямой от предыдущего показана на рис. 9.94, в. Эта
зависимость хорошо аппроксимируется формулой Xn+i =
= аХ„ехр(—ЬХ„).
В работе [616] экспериментально обнаружено, что переход к
хаосу в реакции Белоусова — Жаботинского в зависимости от
|rt|«|iW|*MI
Рис. 9.90
параметров может происходить различными путями: путем бес-
бесконечной последовательности бифуркаций удвоения периода, че-
через перемежаемость и путем разрушения квазипериодического
движения. Этим лишний раз подчеркивается универсальность пу-
путей перехода к хаосу в системах различной природы и сложности.
Кроме реакции Белоусова — Жаботинского, в настоящее вре-
время известно много других колебательных химических реакций,
в которых также возможны хаотические изменения концентра-
концентраций реагирующих веществ. Так, в работе [596] описаны обнару-
обнаруженные авторами хаотические изменения концентраций кислоро-
кислорода в реакции окисления субстрата NADH при участии в качестве
349

дн' вноп-дшоау юпьмшоу

10 /\
"A
20 A
Vi
V
Рис. 9.92
Рис. 9.93

катализатора фермента пероксидазы. В работе [367] проведено
численное исследование уравнений химической реакции взаимо-
взаимодействия водорода с кислородом на металлических катализато-
катализаторах. Показано, что эти уравнения также могут иметь решение в
Рис. 9.94
виде хаотических колебаний. В работяг [415, 640] найдены слож-
сложные режимы колебаний в открытых биохимических системах, мо-
моделируемых тремя уравнениями первого порядка; в {393] рас-
рассмотрено хаотическое поведение системы, свяаанвых химических
осцилляторов.
Рёсслером [619—622] предложен ряд моделей, гипотетических
химических реакций, при которых изменения концентраций реа-
реагирующих веществ могут иметь хаотический характер. Эти мо-
модели таковы:
(8.13)
352

Соответствующие уравнения для концентраций реагирующих ве-
веществ имеют вид [619—622]
kzX — —g \ д.4 X,
X
где к2 = к'г — к5 — к7, к3 — к'ае0. Вид аттрактора в стереопроекции
(о), проекции его на плоскости XY, XZ, ZY (б) и временные
3
t
X Z
1,
it ■
1 1
1
Рис. 9.95
реализации процессов X(t), Y(t), Z{t) (в) в области хаоса по-
показаны на рис. 9.95. Такой тип хаоса Рёсслер назвал «спираль-
«спиральным» или «амплитудным».
355

2J
(8.15)
Реакция (8.15) описывается уравнениями [621]
X = к 4- к X— к ХУ
. ' " *Х + К' . (8.16)
j: — к^л. — кьх + к6х l, l — к7 — к6х z,
где к2 = к2 — fe4- Как и (8.14), уравнения (8.16) в определенной
области параметров имеют хаотические решения. Пример такого
решения показан на рис. 9.96. Возникающий здесь тип хаоса
Рёсслер назвал «винтовым» [620].
3) Кроме (8.13) и (8.14), Рёсслер предложил модель гипоте-
гипотетической химической реакции, описываемой системой дифферен-
дифференциальных уравнений четвертого порядка. Она имеет следующий
вид [622]:
Вид хаотического аттрактора для этой модели в стереопроекции
и временная реализация процесса Z(t) показаны на рис. 9.97.
Система (8.17) интересна тем, что в ней два ляпуновских пока-
показателя положительны. Такой тип хаоса Рёсслер назвал «гипер-
«гиперхаосом,» .
Если химические реакции протекают в протяженных объемах,
то существенную роль играет диффузия веществ [319, 666]. По-
Поэтому соответствующие уравнения будут содержать частные про-
производные [217, 319, 356, 453, 666]. Диффузия может способство-
способствовать, появлению хаоса [306]. Так, в работе [550] численно было
установлено, что в системе вида
которую вблизи порога самовозбуждения можно записать в фор-
форме одного уравнения с комплексными коэффициентами [549,
684]
д-~ = [1 + ic0 - A + ic2) | w I»] w + A + ic,) Aw,
хаос является именно следствием диффузии, так как в однород-
однородной системе, описываемой двумя дифференциальными уравне-
уравнениями первого порядка, возможны только периодические коле-
354

бания. Об этом же говорят и эксперименты, проведенные в ра-
работе {685].
К задачам химической кинетики тесно примыкают экологи-
экологические задачи о взаимодействии различных видов животных и
1-ис. 9.96
растений. Классической моделью подобного взаимодействия яв-
является модель Лотки — Вольтерра [114, 566]
£
(8.18)
где щ — численность i-й популяции (i = 1, 2, ..., т). В работе
[664] отмечается, что в такой модели при т = 3 и изменении
одного из параметров может возникнуть последовательность би-
бифуркаций удвоения периода, приводящая к хаосу.
355

В качестве примера рассмотрим модель экологической систе-
системы, состоящей из двух нар «хищник — жертва». Схема взаимо-
взаимодействия видов в такой модели представлена на рис. 9.98 [5,
383]. Растения Mt и М\ (жертвы) в процессе жизнедеятельности
Рис. 9.97
L M*
»,
1
X
м'ж
J
Mi
\
Рис. 9.98
(например, путем фотосинтеза) потребляют какое-то вещество
М„ (биоген), запасы которого в окружающей среде ограничены.
Расход вещества Мо компенсируется за счет распада растений
Mi и М'\ и животных М^ и М2 после их гибели. Животные М2
и Мг (хищники) поддерживают свое существование, поедая ра-
растения. Уравнения модели имеют вид
XX.
| ^З^З Уз /
4+&V
(8.19)
Ч + ах*
356

где Si — коэффициенты смертности, ^ — коэффициенты потреб-
потребления, р( — коэффициенты фотосинтеза, а и Ъ — коэффициенты
насыщения, х0 — количество биогенного элемента Мо, xi и х3 —
содержание биогена в жертвах Mt и Ми хг и ж4 — содержание
биогена в хищниках М2 и Мг- Полное количество биогенного
элемента остается постоянным, т. е.
4
2 х^ = М = const. (8.20)
При определенных ограничениях па параметры система урав-
уравнений (8.19), (8.20) допускает стационарное решение, соответ-
соответствующее отличному от нуля содержанию биогена во всех взаи-
взаимодействующих видах. При значениях параметров et = е2 = (Ji =
= Рз = ^2 = Y4 = 1) ез = £д — Ti = Ъ — 2, Ь = а, которые были вы-
выбраны при численном моделировании системы (8.19), (8.20), об-
область существования этого решения па плоскости параметров
0,7 0,2
Рлс. 9.99
0,3
а и М лежит выше кривой ABC (рис. 9.99) [383]. Области устой-
устойчивости- этого решения заштрихованы косыми линиями. При
переходе через бифуркационные кривые DB п FH происходит
мягкое возбуждение периодических колебаний. Размер предель-
предельного цикла в фазовом пространстве при удалении от бифурка-
циопных кривых монотонно растет до тех пор, пока не достигает
границ пространства. Заметим, что фазовое пространство систе-
системы (8.19), (8.20) ограничено и представляет собой четырехмер-
четырехмерную пирамиду, образованную координатными гиперплоскостями
4
х, = 0 (г = 1, 2, 3, 4) и гиперплоскостью х0 = 0, т. е. 2 х% = 0-
i=i
357

При достижении границ цикл начинает изгибаться и претерпе-
претерпевать бифуркации. Численно обнаружены бифуркации удвоения
цикла, приводящие к хаосу. Области хаоса на рис. 9.99 заштри-
заштрихованы горизонтальными линиями. На рис. 9.100 приведены при-
примеры сложного предельного цикла (а) и хаотического аттрактора
Рис. 9.100
(б). На том же рисунке показаны реализация (в) и спектр (г)
процесса xs(t) в хаотическом режиме. Интереспо отметить, что
несмотря на то, что исследуемая система имеет четвертый поря-
порядок, ни при каких значениях а и М в ней не наблюдались квази-
квазипериодические движения.
§ 9. Системы с запаздыванием
и другие распределенные системы
Хаотические колебания в системах, с запаздыванием, являю-
являющихся частным случаем распределенных систем, к настоящему
времени изучены достаточно широко. Здесь прежде всего следует
выделить большой цикл работ, посвящепных численному и экс-
экспериментальному исследованию геператоров, главным образом
СВЧ-диапазона, с запаздывающей обратной связью [21, 26, 37,
76-78, 128, 144-146, 176-183, 186-189, 209, 212, 226]. В этих
358

работах показано, что в таких генераторах, могут возбуждаться
мощные хаотические колебания в широком диапазоне парамет-
параметров. В. Я. Кисловым с сотрудниками был разработан и построен
первый геператор подобного рода — шумотрон, созданный на базе
лампы бегущей волны с линией задержки в цепи обратной свя-
связи [188]. Блок-схема такого генератора представлена на рис. 9.101
Нелинейный
актибнь/й
элемент
Линия
задержки
Фильтр
Рис. 9.101
Рис. 9.102
[21, 176, 177, 183]. Она содержит нелинейный активный эле-
элемент — лампу бегущей волны, резонанспый фильтр и линию за-
задержки. Резонансный фильтр с добротностью /0/А/ = 200 ограни-
ограничивает полосу усиления А/ активного элемента и позволяет плав-
плавно перестраивать центральную частоту /0. Число собственных
мод - генератора, попадающих в полосу усиления, составляет
Д/т ~ 10, где т — время задержки. Детальное исследование тако-
такого генератора проведено в [176—183].
При увеличении глубины обратной связи % = 10 lg {Рт/Рвых),
где Р„ и Рвы% — мощность волны на входе и выходе активного
элемента, в системе возникают периодические автоколебания, по
форме близкие к гармоническим, на некоторой частоте /, соот-
соответствующей моде с максимальным линейным инкрементом. На-
Начиная с некоторого значения X = %i этот режим сменяется авто-
автомодуляционным режимом с периодом модуляции 2т. Характерной
особенностью этого режима является наличие в спектре огибаю-
огибающей большого числа гармоник основной частоты /i = 1/2т. В оп-
определенной области расстроек о = т(/0 —/) дальнейшее увеличе-
увеличение X сопровождается последовательным появлением в спектре
огибающей еще двух частот /2 и /3 и их линейных комбинаций
mifi + rrizfz + msfs (рис. 9.102, где в скобках указаны значения
ти тг, ms). При Я==Х„Р дискретпые составляющие спектра скач-
скачком размываются и одновременно появляется «шумовой пьеде-
пьедестал», который увеличивается вместе с уширением пиков с ро-
ростом Я. Переход к хаосу через режим трехчастотной модуляции
проиллюстрирован на рис. 9.103, где в левом столбце показаны
спектры сигнала модуляции, в среднем — сигнал модуляции на
входе активного элемента (верхние кривые) и на его выходе
(нижние кривые), в правом — проекции фазового портрета.
359

Режим трехчастотной квазипериодической модуляцяда наблю-
наблюдается лишь в узкой области расстроек о и частот рабочей моды
/. Для большинства фиксированных значений / при изменении
а рождение частоты /3 не наблюдается. В этом случае периоди-
периодическая автомодуляция (рис. 9.104, а) с ростом Я сменяется ква-
квазипериодической с двумя несоизмеримыми частотами /4 и /2
Рис. 9.103
(рис. 9.104,6). Переход от двухчастотыой квазипериодической
модуляции к хаосу с ростом "К происходит через режим синхро-
синхронизации (резонансы па торе). В зависимости от величины о этот
переход выглядит по-разному. В одном случае возникает резо-
резонанс с соотношением частот /4//2 = 7/3 (рис. 9.104, в). Появле-
Появление этого резонанса сопровождается гистерезисом по параметру
X, что говорит о его «жестком» происхождении. При увеличении
% до Я,кр модуляция скачком становится хаотической (рис. 9.104, г).
В другом случае после возникновения квазипериодической моду-
360

яяции два соседних пика на частотах Д и Л — Д с ростом Я
сближаются и при некотором значении Х = Х, «схлопываются» в
один узкий пик на частоте fJ2, что соответствует резонансу на
торе с соотношением частот Д/Д = 2/1 (рис. 9.105,6). Далее про-
происходит цепочка бифуркаций удвоения периода цикла
Рис. 9.104
'(рис. 9.105, в, г), заканчивающаяся образованием хаотического ат-
аттрактора. При дальнейшем увеличении X возникает последователь-
последовательность обратных бифуркаций в спектре хаотических колебаний
(рис. 9.105,5 — з). Таким образом, в этом случае возникновение
хаоса происходит по сценарию Фейгенбаума.
В некоторой области значений о и / переход к хаотической ав-
автомодуляции происходит через перемежаемость. В зависимости от
этих параметров в эксперименте зафиксированы переходы к хаосу
через перемежаемость от режимов стационарпой генерации
(рис. 9.106,а), периодической (рис. 9.106,6) и квазипериодиче-
квазипериодической (рис. 9.106, е) автомодуляции.
361

Рис. 9.105
Рис. 9.106

Область хаоса не является однородной. В ней при изменении
параметра А, наблюдаются бифуркационные переходы трех типов:
1) Рождение в фазовом пространстве из сгущения траекто-
траекторий устойчивого и неустойчивого предельных циклов и возник-
возникновение в связи с этим «окна устойчивости».
2) Жесткое разрушение хаотической модуляции и установ-
установление режима стационарной генерации на частоте соседней моды.
3) Перемежаемость типа «хаос — хаос» между двумя различ-
различными режимами хаотической модуляции. Этот переход проил-
проиллюстрирован на рис. 9.107, где показаны фазовый портрет, спектр
Рис. 9.107
и распределение вероятностей для одного из хаотических аттрак-
аттракторов (а) и для слияния двух хаотических аттракторов (б),
а также вид сигнала модуляции (в).
Наличие нелинейной запаздывающей обратной связи приво-
приводит к возможности генерации хаотических колебаний даже в та-
такой простой системе, как линейный колебательный контур
(рис. 9.108) [146]. Уравнение колебаний в таком контуре имеет
вид
x + 2fa + efc = Bf[x(t-T)], (9.1)
где 26 = R/L, «о = 1/LC, Б = K/LC. В работе [146] уравнение
(9.1) заменялось соответствующим разностным уравнением, ко-
которое решалось с помощью ЭВМ. Были рассмотрены два случая:
1) f(x) = smx при х^[0, я] и f(x) = O при х Ф [0, я], т. е. функ-
функция f(x) не меняет знака, 2) f(x) = s'mx, т. е. f(x)—зпакотгере-
363

менная функция. Обнаружено, что в обоих случаях при увели-
увеличении коэффициента усиления К периодические колебания с
дискретным спектром переходят в хаотические, имеющие сплош-
сплошной спектр. Однако ширина сплошного спектра и его интенсив-
интенсивность во втором случае оказались существенно больше, чем в
первом.
Хаотизация возбуждаемых колебаний может происходить и
при введении дополнительной запаздывающей обратной связи в
R
| 1_
L
}
Блок
задержки
Нелинейный
усилитель
Рис. 9.108
автоколебательную систему, например в генератор Ван-дер-Поля
с нелинейной собственной частотой [226]. Уравнение такого ге-
генератора с учетом запаздывающей обратной связи имеет вид
х - (х A - х*) х + tog [1 + / (х)] х = <аЦех (* — т (t)), (9.2)
где [х > 0, ©о — линейная часть собственной частоты генератора,
f(x)—нелинейная функция, не содержащая линейного члена,
к — коэффициент запаздывающей обратной связи, x(t)— время
задержки, которое в общем случае может быть функцией време-
времени t. Уравнение (9.2) может служить простейшей моделью доп-
плеровского автодина, применяющегося в системе ближней ра-
радиолокации [364]. Если скорость движения объекта постоянна,
то т = То + at, где т0 = 2LJc, а — 2v/c, Lo — расстояние до объекта
в момент времени t = 0, v — скорость объекта, с — скорость света.
Введя безразмерное время t' = co0f, получим для величин
|а' и То следующие выражения: |х' = [а/ш0, То = юото — 4jiL0/^
где Я — длина волны радиолокационного сигнала. Отсюда видно,
что в реальных условиях величина т0 очень велика, а а — мала.
В силу этого большой практический и теоретический интерес
представляет исследование поведепия решений уравнения (9.2)
при а = 0. При числепном моделировании уравнения (9.2) пола-
полагалось ш<,= 1, |л = 0,1, f(x)=Gx2, T = To + fltf. Параметры G, к,
т0, а варьировались. Прежде всего рассмотрим результаты реше-
решения уравнепия (9.2) при а = 0. Если зафиксировать значения
параметров G и т0 (G = 0,l» то = ЗО) и изменять коэффициент
дополнительной обратной связи к, то решение эволюционирует
следующим образом. При малых к @ < к < ка « 0,09) оно явля-
является периодическим с частотой /0 = 0,17 « 1/2л, примерно равной
частоте колебаний генератора без дополнительной обратной свя-
364

зи. При к = к0 это решение становится неустойчивым и возни-
возникает устойчивое квазипериодическое решение с основными ча-
частотами /о и Д = 0,029 « I/to. Спектр такого решения при к =■
= 0,4 изображен на рис. 9.109, а. При дальнейшем увеличении к
наблюдаются бифуркации удвоения квазипериода тора. Первая
Рис. 9.109
бифуркация происходит при к = ki » 0,42. Спектр колебаний ге-
генератора после первой бифуркации показан на рис. 9.109, б. Вто-
Вторая бифуркация удвоения происходит при к = к2& 0,75. При
к = к3 « 1,3 наблюдается картина, похожая на третью бифурка-
бифуркацию удвоения квазипериода тора. Однако с уверенностью этого
утверждать нельзя, поскольку амплитуды возникающих субгар-
субгармоник сравнимы с уровнем шумового фона. При дальнейшем
увеличении к (к>к^.«1,7) шум резко возрастает, что свиде-
365

тельствует о возникновении хаоса. Вид спектра при к = 4 пока-
показан на рис. 9.109, в.
Отметим, что при изменении параметра к частоты /0 и Д
изменяются незначительно. Частота /4 определяется в основном
временем задержки т0, о чем свидетельствует график, приведен-
приведенный на рис. 9.110.
Аналогичное описанному выше поведение системы наблюда-
наблюдается и при других значениях времени задержки т0 и параметра
A
7,0 -
0.5
70 20 30 40 f0
Рис. 9.110
20 30 40
Рис. 9.111
нелинейности G. Однако конкретные значения коэффициента к,
при которых происходят бифуркации рождения тора и удвоения
его квазипериода, существенным образом зависят от этих пара-
параметров. При увеличении времени задержки соответствующие би-
бифуркационные значения коэффициента к уменьшаются, о чем
свидетельствует рис. 9.111, на котором приведены зависимости
от то значений к0, &4 и кг (при G —0,1). При увеличении пара-
параметра нелинейности G бифуркационные значения коэффициента
к также уменьшаются. Об этом
говорят данные, приведенные
в табл. 9.9 для т0 = 40.
Характер перехода к хаосу
качественно сохраняется, если
в качестве бифуркационного
параметра взять т0 или G. От-
Отличие состоит лишь в том, что
при изменении т0 существенно изменяется частота /t (рис. 9.110),
а при изменении G в основном изменяется частота /0.
Чтобы определить влияние параметра а, было проведено ре-
решение уравнения (9.2) при достаточно большом, заведомо не-
нереальном значении а, а именно при а = 10~2. В этом случав
переход к хаосу происходил не так, как при а = 0. Рассмотрим
этот переход для случая G = 0,{, то = 2О и увеличении парамет-
параметра к. Уже при малых значениях к в системе генерируются ква-
випериодические колебания с двумя основными частотами /0 =
= 0,17 и /о = 0,002 « а/о, где fD — допплеровское смещение ча-
частоты. В фазовом пространстве системы этим колебаниям соот-
366
Та
G
0,1
1,0
блица
ft.
0,03
0,003
9.9
ft,
0,3
0,025
ft*
0,6
0,045

ветствует двумерный тор. При к = к,.«0,3 двумерный тор те-
теряет устойчивость и возникает трехмерный тор, соответствующий
квазипериодическим колебаниям с тремя основными частотами
/о, /в и /i = 0,05 « 1/то. При дальнейшем увеличении коэффици-
коэффициента к квазипериодические колебания скачком сменяются хаоти-
хаотическими, о чем свидетельствует резкое увеличение шумового фо-
фона в спектре.
Наблюдаемые переходы к хаосу можно характеризовать на-
наряду со спектром изменением размерности аттрактора. Для этого
на основе реализации процесса x{t) по методике Паккарда — Та-
кенса конструировались динамические системы разных размер-
размерностей s. Для них определялась корреляционная размерность v,,
которая при увеличении s быстро стремилась к постоянному зна-
значению v. Это значение v принималось за размерность аттрактора.
•
О,ОГ" 7 5 !О
Рис. 9.112
К
V
/?
/ .
17777
vLtt
О
1
Р
i
/ ->
Рис. 9.113
Пример зависимости v от к показан на рис. 9.112. Как и следо-
следовало ожидать, в области периодических колебаний v = 1, в обла-
области квазипериодических, соответствующих двумерному тору, v =■
= 2, в области хаоса величина v плавно нарастает с ростом к,
начиная от значения, равного двум.
Большое количество работ посвящено численному и экспери-
экспериментальному исследованию систем, описываемых уравнением вида
-bxA) + f(x(t-T)). (9.3)
К такий системам относится, например, кольцевой оптический
резонатор с нелинейной поглощающей средой, в который посту-
поступает внешнее световое поле [465, 521—523] (рис. 9.113). Выве-
Выведем уравнение (9.3) для такой системы, считая, что поле в по-
поглощающей среде описывается уравнениями полукласспческой
теории для двухуровневых атомов с однородным упгаренпем ли-
линии [185]. Эти уравнения имеют вид [110]
dt2
с2 °-4 + 4л ^4 = 0,
dz2 at2
(9.4)
367

где <В — напряженность светового поля в среде, 9* — поляриза-
поляризация, N — разность населенностей, £2 — частота атомного перехода,
d — дипольный момент, y« — величина, обратная поперечному
времени релаксации, ч — величина, обратная продольному време-
времени релаксации, z — координата вдоль резонатора, No — разность
населенностей в отсутствие поля. Перепишем уравнения (9.4)
в переменных £ = t — z/c и z:
£***+ **£* = о,
(9.5)
Решение уравнений (9.5) будем искать в виде
& (i, z) = 4-
4 я (s + т-'z) e~iQ° +к-
где E(l + z/c, z), P(| + z/c, z) —медленно меняющиеся комплекс-
комплексные функции % и z. Разность населенностей 7V(g + z/c, z) также
будем считать медленно меняющейся функцией. Подставляя
(9.6) в (9.5) и оставляя только члены первого порядка малости,
получаем
§ || ^ (9.7)
где к = а/с — волновое число, б = ш — Q — расстройка между ча-
частотой падающего света и частотой атомного перехода.
При условиях Yi > 7, c/L, которые обычно выполняются для
твердотельных поглотителей, поляризацию Р из уравнений (9.7)
можно исключить:
Я id2NE idzNE , , -Xv /o o\
Подставляя (9.8) в первое уравнение (9.7) и интегрируя его,
получим
Е (g + z/c, z) = £ (|, 0) exp [29W (g, z) (Й + Yi)/(S2 + 7i)l»
z
где 8 = ndzk/%, W (g, z) = J iV (| + z'/c, z') dz'. Подставим теперь
о
(9.8) и (9.9) в третье уравнение £9.7) и проинтегрируем его по
368

f— Т(^-ад-^F,0){exp(^£)-ij, (9.10)
z от 0 до z. Тогда получим следующее уравнение для W{\, z):
f
где 5( )(S )
Перейдем в уравнении (9.10) к старым переменным t n z,
положим z = l и обозначим cp(t) = W(t~ т, l)/Nol, где % — Ь/с —
время обхода резонатора. Уравнение для cp(t) примет вид
(9.11)
Чтобы получить уравнение для E(t, 0), запишем граничное
условие, которое сразу следует из рис. 9.113:
Е (t, 0) = ]/Т^Тй Е{ (t) + ReikLE (t — i-=±, l). (9.12)
Подставив в (9.12) выражение (9.9), получим
E(t,O) =
+ ReihLE (t-x, 0) exp [2QNnl(i8 + Yl) ф/(б2 + Ti)]- (9-13)
Система уравнений (9.11) и (9.13) определяет амплитуду поля
в точке z — 0 и функцию ф (t).
Вводя безразмерные переменные t' — yt, %' = ^т
= - х (t) + [1 - 5» (х @)/Д2] 1у(« —т) |2, (9.14)
= Л + 5 (х (*)) у (* - т)
х (f) = 28ЛУ8 [Ф (Г) -
у (f) = (d/fc) [8/2у (бг + у\)]112 Е (Г, 0)
и опуская штрихи, получаем для переменных x(t) и y(t) сле-
следующие уравнения:
где
В случае достаточно слабого внешнего поля и достаточно длин-
длинной поглощающей среды, когда A — R)E\<^in%ykl\N0\, ве-
величина ф близка к единице и функция В(х) изменяется слабо.
Если к тому же выполняется условие kl \ No \ ;§> % (б2 + 7i)/2^d2Ylt
то 5<1 (поскольку ^"^О), и уравнение (9.15) можно
369

решить методом последовательных приближений. В первом при-
приближении по В имеем
y(t — x) = A + AB(x(t — <c)) в*(*(<-т)+*о)# (9 16)
Подставляя (9.16) в (9.14) и пренебрегая членами порядка Вг,
получаем замкнутое уравнение Для х, содержащее члены с за-
запаздывающим аргументом:
^ = - х (t) + А* {1 + 2В (х (t - т)) cos [х (t-x) + x0}}. (9.17)
Уравнение (9.17) имеет вид (9.3), в котором 6 = 1, f(x) =
A*[l + 2B()( + )]
Стационарное решение уравнения (9.17) определяется из
трансцендентного уравнения
хс = А2 [1 + 2В (хв) cos (xc + х0)]. (9.18)
Это уравнение легко решается графически.
Отметим, что даже при слабой зависимости В от ж величи-
величину В, вообще говоря, нельзя считать постоянной, так как dB/dx =
= (f1/6)B. Только при нерезонансном воздействии на среду,
когда 6 > ifi, можно положить В = const, что и сделано в рабо-
работах [522, 523]. Ниже будет
рассмотрен именно этот
случай.
Для исследования ус-
устойчивости решения (9.18)
положим в (9.17) х-
Х X X X X X "'
0,5
7 2тг
5 г
xxxxxxxxvxxxxxxxx
Рис. 9.114
и линеаризуем по £:
—2А2В sin(zc + х0) t[t — т).
(9.19)
Отсюда получаем харак-
характеристическое уравнение
) ,
(9.20)
где С = АгВsin(xc +х0). Используя метод D-разбиений [280],
построим области устойчивости стационарного решения (9.18)
на плоскости параметров Сит (рис. 9.114). Из рисунка видно,
что при |С|<0,5 стационарное решение (9.18) всегда устойчи-
устойчиво. При С < —0,5 решение апериодически неустойчиво при лю-
любом времени задержки т. Наконец, при С > 0,5 решение устой-
устойчиво при малых т (т<т*(С)) и колебательно неустойчиво
прит>т*(С).
В работе [522] показано, что при переходе через границу ко-
колебательной неустойчивости вначале возникают периодические
колебания функций x(t) и y(t), а затем хаотические
370

(рис. 9.115,а и в). Соответствующие спектральные плотности
процесса \y(t)\ приведены на рис. 9.115,6 и г. Интересно от-
отметить, что в режиме хаотических колебаний происходит пере-
перекачка энергии в устойчивые моды, для которых Re p < 0.
В работе [523] уравнение (9.3) исследовалось численно при
Ъ — \, т = 40, j{x) = лцA — sin ж), где ц — бифуркационный па-
параметр. График, из которого
можно найти стационарное зна-
значение ха для этого случая,
приведен на рис. 9.116. Из
этого графика видно, что хс <
< я/2, т.е. С = 0,5я[А cosxc>0.
Это означает, что потеря ус-
устойчивости стационарного реше-
решения в такой системе может про-
происходить только колебательным
образом. Из характеристическо-
характеристического уравнения (9.20) следует,
\y(t)\z
е
5
О
S(b>)
70
ЛЛААААЛЛЛ
0,001
\y(t)\z
70
5
20
60 А-2,17
?
/и
(И
0,5
\Ш
lift
7
л! Я
\Щ
7,5
Л
ш
J 1
ы/2п
ш
60 а-2,85-
что на границе устойчивости,
когда р = т, должны удовлет-
удовлетворяться следующие уравнения:
и = —tg сот, 2С = — 1/cos сот. По-
Поскольку О 0 и т > 1, то ре-
решением этих уравнений явля-
являются следующие значения и:
0,5 7 1,5 ы/2Я
; г=3,5;
Рис. 9.115
ft)i « л/т, (Оз да Зл/т, (о5 * 5л/т и т. д. Соответствующие зна-
значения С равны: С4 » 1/2 + л74т2, Cs « 1/2 + 9л74т2, С5 ^
« 1/2 + 25я74т2 и т. д. Отсюда и из (9.18) следует, что первая
мода с частотой (о4 теряет устойчивость при ц = ц4 = 0,376, при-
причем на границе устойчивости ха = 0,557. Следующая (третья)
мода с частотой (os теряет устойчивость при ц3 = 0,387 (хс =»
= 0,565), пятая —при ц5 = 0,407 (хс = 0,579), седьмая —при
ц7 = 0,437 (хс = 0,599) и т. д. Численное исследование показа-
показало, что периодические колебания с периодом То « 2т, возникшие
при ц = Ца = р.», при некотором значении ц теряют устойчивость,
после чего происходит каскад бифуркаций удвоения периода,
заканчивающийся при ц = цг«0,696. После этого решение
371

-1
www
t 1
in
J
приобретает хаотический характер, однако до ц = цв «0,777
средняя частота колебаний по-прежнему равна ю0«я/т
(рис. 9.117,а). При ц>|хв возникает последовательность пре-
превращений другого типа: средняя частота колебаний при
увеличении ц изменяется
скачками (<о0 -*- Зо)о -*■ 5ю9 -+■
-+■ 7(о0) (рис. 9.117,6, в, г).
При уменьшении параметра
ц процесс идет в обрат-
обратную сторону, но при этом
имеет место гистерезис
(рис. 9.118,а). Наличие ги-
гистерезиса говорит о том, что
в системе одновременно су-
существуют два или несколь-
несколько аттракторов, разделенных
некоторой сепаратрисной по-
поверхностью.
Аналогичные результаты
получаются при фиксиро-
фиксированном значении ц и
увеличении параметра т
(рис. 9.118, б).
Описанное выше поведе-
, ние системы наблюдалось
экспериментально в работах
[465, 512].
— Уравнение (9.3) описыва-
описывает также изменение амплиту-
амплитуды генерируемого сигнала в
замкнутой в кольцо цепочке
из резонансного фильтра, линии задержки и нелинейного уси-
усилителя с амплитудной характеристикой ABUZ = f(ABX) в предполо-
предположении, что собственная частота одной из мод замкнутой цепочки
7-я гармоника
ff-я аармоника
/1=0,82
-
- ~*3-я
гармоника
^-'
77-я
<\Л75--Я
73-я
б
1 L,
7 -_ ___^
О ,4 0.5 0,6 0,7 0,8 р О 20 40 60 80
Рис. 9.118
совпадает с резонансной частотой фильтра и что фазовая нели-
нелинейность усилителя отсутствует [182,186, 335]. При численном мо-
моделировании этого уравнения в [182] было выбрано: f(x) = ц, — х2,
372

a
4 8 72 7& t/r
-/.30
С
4T
1=7,55
x(t-t)
Рис. 9.И9

bx — ib. Результаты приведены на рис. 9.119. Из рисунка видно,
что при изменении ц от 1,65 до 1,80 средняя частота колебаний
увеличивается втрое. Этот переход аналогичен рассмотренному в
[523], однако детально не исследован.
В работе [568] уравнение вида (9.3) с
(9.21J
используется в качестве математической модели процесса реге-
регенерации белых кровяных шариков у больных хронической лей-
лейкемией. Из медицинских данных известно, что у таких больных
число белых кровяных шариков изменяется со временем хаоти-
хаотически (рис. 9.120, а [568]). Численное исследование уравнений
600
700
ZOO WO 400
Время, сутки
Рис. 9.120
500
еоо
(9.3), (9.21) показало, что при определенном выборе парамет-
параметров, а именно при Ь = 0,1 сут~\ а = 0,2 сут~\ п —10 и т =
= 10 сут, решение имеет хаотический характер и зависимость
концентрации кровяных шариков х от времени t (рис. 9.120,6)
очень похожа на приведенную на рис. 9.120, я. При меньших
значениях т величина x(t) изменяется периодически. Переход
от периодического решения к хаотическому при увеличении т
происходит путем последовательности бифуркаций удвоения
периода.
Более детально уравнения (9.3), (9.21) при Ь = 0,1, а = 0,2,
п=10 и различных значепиях т исследовались численно в ра-
работах [224, 439, 477, 610]. При т<4,53 устойчивым является
стационарное решение х = х0 = 1. В диапазоне 4,53 < т < 13,3
x(t) изменяется перодически с периодом Г = 3т. При т = ткр =
= 13,3 начинается каскад бифуркаций удвоения, заканчиваю-
374

t'Vt
АлЛлЛлЛллл
Pec. 9.121, a

щийся при т = 16,8. Эволюция временных реализаций процесса
x(t) и спектральной плотности колебаний при увеличении t от
т = 14 показана на рис. 9.121, а [224, 439]. Соответствующая
эволюция вида аттрактора в проекции на плоскость x(t), x{t — x)
приведена на рис. 9.121, б. С ростом времени задержки т фрак-
фрактальная размерность аттрактора d и число положительных ля-
Рис. 9.121, б
пуновских показателей п в среднем увеличиваются (рис. 9.122, а).
Вместе с тем существуют области значений т, где решение яв-
является периодическим и размерность падает до единицы
(рис. 9.122,6). Несмотря на рост размерности аттрактора, ме-
метрическая энтропия Колмогорова К остается примерно постоян-
постоянной (рис. 9.122, е), что объясняется уменьшением с ростом х
максимального ляпуновского показателя (рис. 9.122, г). Спектр
ляпуновских показателей, размерность аттрактора и энтропия
вычислялись для дискретной динамической системы, составлен-
составленной по рецепту Паккарда — Такенса, о котором уже не раз го-
говорилось ранее. На примере системы (9.3), (9.21) в работах
[439, 477, 610] проводилось сравнение различных размерностей
аттрактора. Результаты сравнения приведены в таблице 9.10.
В работе [224] с целью исследования синхронизации на си-
систему (9.3), (9.21) подавалось гармоническое внешнее воздей-
376

ствие, т. е. численно решалось уравнение
Для разных значений т вычислялись области синхронизации на
плоскости параметров В, v и определялся порог синхронизации
В*. Оказалось, что Вп = 0,06 ± 0,008 при т==20, а при т = 30,
d,n
20г
10
к
200 300
0 20 /ОО 200 дОО
А,
0,07
0,035
30
0,075
0,05
0,025
700
200
о о о о о о
i i i l__l L ! I I »_
70 20 40 60 80 700 V
Рис. 9.122
40, 50, 60, 80, 100 величина Ва практически одинакова и равна
Вв = 0,14±0,01 (точки на рис. 9.122,в). Интересно отметить,
что частота, соответствующая порогу синхронизации, при из-
изменении т от т = 30 практически не меняется (рис. 9.122,5).
Она равна /с = 2/Cткр), т. е. система как бы «помнит» то кри-
критическое значение т, при котором началось ее сложное пове-
поведение.
377

В работах [200, 201, 646J исследовались системы двух урав-
уравнений Лотки— Вольтерра с запаздыванием:
(9>22)
Система (9.22) описывает динамику популяций двух конкури-
конкурирующих видов с учетом насыщения. В [646] полагается е, > 0,
Таблица 9.10
т
17
23
30
100
V
1,95
2,44
3,00
7,50
dM
2
2
3
6
d
2,13
2,76
2,84
2,10
2,82
3,58
10
v — корреляционная размерность, dM — размер-
размерность, вычисленная по формуле Мори, d — фракталь-
фрактальная размерность, вычисленная непосредственно по оп-
определению, dL — ляпуновская размерность, вычислен-
вычисленная по формуле Каплана — Йорке.
Хаотическое
решете
а«>0, а«>0, т«= х{, т« = 0. Рассмотрены два случая: 1) в, = 1,5,
82 = 2, вц = я22 — 1, di2== 1, Й21 == 2; 2) 8i — 82 =г 2, йц = я22 == 2,
я12 = a2i = 1. В первом случае состояние равновесия, соответ-
соответствующее стационарному существованию обоих видов (iV4 = 0,5,
N2 = 1), при т< = 0 неустой-
неустойчиво. Во втором случае со-
соответствующее состояние
равновесия (Nt — N2 = 2/3)
при tf = 0 устойчиво. В ра-
// боте детально исследуется
//Хаотическое именно второй случай. Ре-
// решение зультаты исследования сле-
следующие. При увеличении
т4 и т2 стационарное состоя-
состояние теряет устойчивость и
возникают периодические
колебания численности ви-
видов. При дальнейшем уве-
увеличении Ti и т2 возникают
области хаотических режи-
режимов, причем переход к хаосу
происходит путем последовательности бифуркаций удвоения
периода (рис. 9.123). Так, например, при Ti = 16, и уве-
увеличении т2 каскад бифуракций удвоения периода начи-
начинается при т2»0,77. После его завершения возникает хаоти-
378

ческий аттрактор, показанный в стереопроекдии на рис. 9.124, а.
Одновременно с ним в фазовом пространстве системы сущест-
существует устойчивый предельный цикл. В зависимости от началь-
начальных условий колебания численности будут либо периодическими,
Рис. 9.124
либо хаотическими. При увеличении т2 этот цикл бифурцирует
и рождает другой хаотический аттрактор (рис. 9.124,6).
В работе [201] система (9.22) используется для описания
динамики развития насекомых, имеющих две активные стадии
жизни: личинок и имаго (имаго — взрослые насекомые, способ-
способные размножаться и расселяться по территории). В этих урав-
уравнениях Ni — численность имаго, iV2 — численность личинок,
8i>0, е2 —0, a,i>0, a«<0, тн = ъ — среднее время жизни по-
популяции имаго, т22 = 0, т12 — т2 — время между появлением ли-
личинок и имаго, т21 = 1 — т2—время между появлением имаго и
личинок. Если le21|iVi»8i, то производной ft* во втором урав-
уравнении (9.22) можно пренебречь, и его решение при a22=|a2Jl
принимает вид
Подставляя (9.23) в (9.22), получаем
ffi(t) = [е - atN(t- т)+ ajf(t-
где 8 = 8!, т = Xi, ui = аи, a2— la12l.
4
(9.24)
Уравнение (9.24) решалось на ЭВМ при е = 3, т = 0,125г
a1 = 3/(l — a), где a^=ajau Параметр а варьировался. Стацио-
Стационарное решение N = 1 теряет устойчивость при а « 0,506, после
чего рождается устойчивый предельный цикл, амплитуда кото-
379

рого резко растет с ростом а, а период примерно постоянен и
равен 1,1. При а = 0,665 начинается каскад бифуркаций удвоения
периода, заканчивающийся при а = 0,730. При а » 0,587 появля-
появляется еще один устойчивый периодический режим с периодом
примерно вдвое меньше предыдущего (Г « 0,55). При а = 0,64
этот режим переходит в режим биений, а затем в хаотический.
Последний в некотором смысле представляет собой сочетание
двух описанных выше периодических режимов: на временной
оси имеются интервалы с расстоянием между пиками ~0,55 и
интервалы с расстоянием ~1,1. При дальнейшем увеличении
а возникают окна, где имеются периодические режимы с боль-
большим периодом. Так, при а — 0,71 период примерно равен 38.
В отличие от систем с запаздыванием, исследования распре-
распределенных систем, описываемых уравнениями в частных произ-
производных, чрезвычайно ограничены. Здесь можно указать лишь
работы [51, 165], в которых аналитически произведена оценка
размерности аттрактора для некоторых типов уравнений в част-
частных производных, работы [25, 38, 41, 123, 213, 306], в которых
исследуются цепочки, моделирующие одномерные диссипативные
среды, а также немногочисленные работы, в которых были обна-
обнаружены хаотические режимы при численном решении уравне-
уравнений в частных производных. Об одной из таких работ уже го-
говорилось в § 7 [300]. К ним относятся также [687], в которой
решались уравнения, подобные уравнению Кортевега-де-Вриза,
и [396, 406, 509, 524], в которых моделировалось уравнение си-
синус-Гордона с затуханием и внешней силой. Имеется, правда,
сравнительно большое количество экспериментальных работ, по-
посвященных наблюдению и исследованию хаотических колебаний
в гидродинамике (см., например, {395, 411, 469, 470, 561, 569]),
в лазерах [376—378, 488, 492, 505, 525, 592, .674, 675], нелиней-
нелинейной оптике [431, 454, 525, 591, 594] и некоторых других систе-
системах [2]. Однако большинство из этих работ еще требует осмыс-
осмысливания.
Работы [395, 411, 569] интересны тем, что в них, по-видимо-
по-видимому, впервые убедительно показано, что размерность аттрактора
в некоторых гидродинамических системах может быть весьма
небольшой. В указанных работах использовалась методика обра-
обработки данных эксперимента согласно процедуре Паккарда — Та-
кенса. В [411] рассмотрено течение жидкости между двумя вра-
вращающимися концентрическими цилиндрами с отношением ра-
радиусов 0,875. Виды аттрактора в координатах V(t), V(t + x),
где V(t) — радиальная составляющая скорости жидкости, и
соответствующие сечения Пуанкаре для ряда значений R/Rc
(R — число Рейнольдса, пропорциональное угловой скорости
вращения внутреннего цилиндра, R с— критическое число Рей-
Рейнольдса, при котором возникают вихри Тейлора) показаны на
рис. 9.125, а и б (сечения Пуанкаре получены пересечением фа-
фазовых траекторий в трехмерном пространстве V(t), V(t + x),
F(£ + 2t) с плоскостью, параллельной оси V(t + 2x) и проходя-
380

щей через штриховую линию на рис. 9.125,а). В [411] вычисля-
вычислялись как емкость аттрактора d, так и корреляционный показа-
показатель v. Как видно из рис. 9.126, эти величины оказались близки
друг к другу.
В работе [395] исследовалось течение Куэтта между двумя
сферами с соотношением радиусов (г» —г4)/г1 = 1,006 и радиусом
R/Pc=10,1
R/Rd=15,2
I-
V. '
V "
V -"
i
1
i
I
p
7
1
*■■**.■ ' -
Рис. 9.125
наружной сферы r2 = 150,16 ± 0,03 мм. Вращалась только внут-
внутренняя сфера. В широком диапазоне чисел Рейнольдса R =
= Qri/v0, где £2 — угловая скорость вращения внутренней
сферы, vo — кинематическая ^ ^
вязкость, измерялись спектры
скорости и вычислялась размер-
размерность аттрактора сконструиро-
сконструированной по Паккарду — Такенсу
динамической системы. Полу-
Получено, что при увеличении R
размерность аттрактора в сред-
среднем увеличивается, но остается
сравнительно малой.
В [569] исследовалось кон- 3
вективное движение жидкости
при нагревании и при сильной
униполярной инжекции ионов. /
Оказалось, что размерность аттрактора, оцененная на осно-
основе вычисления корреляционного показателя -v, в первом слу-
случае при Ra/Rac = 235 равна 2,8 ± 0,1, а во втором случае
при U/Uc = 5£ (Uc = 50 В — критическое значение потенциа-
381
7
а
i
a g
Рис.
7-
9.126
а
Д
1
4-
-d

'- -в — о--4 о
ла, при котором возникает конвекция)—5,1 ±0,3. Зависи-
Зависимости v от размерности фазового пространства сконструирован-
сконструированных на основе процедуры Паккарда — Такенса динамических
систем для рассмотренных двух случаев B, 3) и для белого шу-
шума A) продемонстрированы на рис. 9.127. Как видно из ри-
рисунка, для белого шума то-
тоже наблюдается небольшое
насыщение размерности с
ростом п, которое связано
с ограниченностью числа вы-
выборок, но не столь явное,
как для экспериментальных
реализаций исследуемых про-
процессов.
В работе [2] исследова-
исследовались нерегулярные бегущие
страты в низкотемпературной
плазме, получаемой в поло-
положительном столбе тлеющего
газового разряда [217J. На
границе самовозбуждения
страты имеют во времени синусоидальную форму, а затем, по
мере удаления от границы, их спектр обогащается и становится
сплошным. Пример зависимости от времени интенсивности бо-
бокового свечения разряда, характеризующей форму страт в дан-
данной части трубки, показан на рис. 9.128, а. Спектр этого свече-
свечения приведен на рис. 9.128,6. Обработка полученных сигналов
Рис. 9.127
70 S
Рис. 9.128
с помощью процедуры Паккарда — Такенса и использование ме-
методики вычисления корреляционного показателя v, позволили
оценить размерность соответствующего аттрактора. Для периоди-
периодического режима величина v оказалась близкой к единице
(рис. 9.129,а,в), а для режима, соответствующего рис. 9.128,
v » 5,5 (рис. 9.129, б, г). На рис. 9.129, в ж г показано измене-
382

0
8
с
-70
-20
-4
l
м
I
-3
/
/
-2
i
S-/7
а
-7 0
i i
ins 0 -5" -^ -з -г -;
Ins
7,5"
-/2-
-/<?-
1
1-2
! 1
х/
хХ х
<' /
X X
/ /
X х^
/ ii
< 3''4
t
>
х'
к' /
X )
х>
//
/
/
1
<
/-5
2—s
5-5
-4
-В
=14
=/6
2-? з
ние величины v в зависимости от размерности сконструирован-
сконструированной системы для периодического (в) и хаотического (г) ре-
режимов.
§ 10. Стохастичность в квантовых системах1)
В отличие от классических систем, движение которых может
быть как полностью детерминированным, так я стохастическим
или хаотическим, в квантовых системах детерминизм, как из-
известно, невозможен по самому определению квантовых случай-
случайных величин, описываемых некоммутирующими операторами.
Если состояние квантовой системы таково, что какой-то набор
коммутирующих переменных имеет детерминированный харак-
характер, то другие ее переменные, не коммутирующие с указанными,
будут иметь существенную статистическую неопределенность.
Наиболее простые границы для минимальной неопределенности
в системе некоммутярующих переменных устанавливаются не-
неравенством Гейзенберга. В квантовых системах классические
') Написан Б. А. Гришаниным.
383

стохастические или хаотические движения всегда происходят на
фоне квантового индетерминизма, приводящего к неопределенно-
неопределенности понятия классической траектории. Квантовыми стохастиче-
стохастическими системами принято называть системы, стохастические в
классическом пределе h-*-0 [156, 691]'). В квантовом случав
ограничиваются рассмотрением только гамилыоновых систем,
поскольку для негамильтоновых классических систем квантова*
ние, заключающееся в сопоставлении каноническим импульсам
и координатам операторов р, q со стандартными коммутацион-
коммутационными соотношениями qips — pjqt = Ъ8ц, не однозначно.
Первая трудность, возникающая при попытке обобщения
классических результатов теории хаотических и стохастических
систем на квантовый случай, связана с различием традиционных
математических форм классической и квантовой механики. Если
в классической механике система с п степенями свободы опи-
описывается уравнениями для числовых переменных qit ..., qn,
Pi, ..., рп, то в шредингеровском представлении квантовой
механики аналогичная система описывается уравнением Шредин-
гера для волновой функции iH<7i, • • -, <Zn, Pi, • •-, Рп, t). Установле-
Установление соответствия между квантовыми и классическими уравнения-
уравнениями на основе этого представления является затруднительным.
Традиционным приемом в этом случае является рассмотрение
квазиклассического приближения, которое связывает волновую
функцию с квазиклассическими траекториями. Однако эта
связь является простой лишь для полностью интегрируемых си-
систем, для которых осуществляется независимое квантование
функций действия, соответствующих разделяющимся перемен-
переменным, по правилам, отвечающим квантованию стационарных ор-
орбит по Бору — Зоммерфельду [247]. В случае - же систем, в ко-
которых в классическом пределе возможны стохастические движе-
движения, простого соответствия между стационарными волновыми
функциями и классическими траекториями не существует.
Несмотря на это, предпринят ряд попыток связать стохастич-
ность квантовых систем в классическом пределе со свойствами
стационарного энергетического спектра в квазиклассическом
приближении. В работах [601, 602] показано, что стохастическо-
стохастическому движению классической системы можно сопоставить нерегу-
нерегулярность энергетического спектра квантовой системы. В [155] на
основе аналогии с классическими бильярдами выводится закон
расталкивания случайных энергетических уровней в виде рас-
распределения вероятностей для расстояния между ближайшими
уровнями АЕ:
p(AE)~\AE\const/ln\ A0.1);
где к — безразмерный параметр такой, что при к > 1 соответ-
') См. также: Касати ЗК. О свойствах квантовых систем с хаотиче-
хаотическим классическим пределом // Проблемы нелинейных и турбулентных про-
процессов в физике. Ч. 2. Тр. II Межд. раб. группы/Под ред. А. С. Давыдова,
В. М. Черноусенко.— Киев: Наукова думка, 1985.— С. 50—56.
384

ствующая классическая система является стохастической. Из
A0.1) следует, что при /с>1 и АЕ ->- 0 вероятность р(Д£)->-0.
Указанные критерии стохастичности подтверждены рядом чис-
численных экспериментов. При этом отмечается [160], что статисти-
статистические свойства движения определяются не только структурой
энергетического спектра, но и свойствами собственных функций.
Более ясное качественное представление о соответствии между
классической и квантовой теориями достигается при их изло-
изложении в идентичной форме. Такая возможность связана с ис-
использованием взамен уравнений Шредингера эквивалентных гей-
гейзенберговских уравнений движения для динамических перемен-
переменных, которые совпадают по форме с классическими уравнениями
Гамильтона, отличаясь от них операторным характером и не-
некоммутативностью канонических импульсов и координат. Еще
большее сближение формализма достигается при описании кван-
квантовых динамических переменных числовыми функциями клас-
классических фазовых переменных X — (q, p). Это возможно после
введения линейного базиса е(Х) в пространстве квантовых ди-
динамических переменных на основе представления
А = J / (X) 1 (X) dX, A0.2)
ставящего каждому А в соответствие свою функцию /(X). Наи-
Наиболее наглядно использование базисов, которые в классическом
пределе^ %-*-0 соответствуют б-функциям: в (X) -»- б (X — X),
Х = (?, р). Таким широко используемым представлением являет-
является представление Вигнера [678]. Важно отметить, что с учетом
конечности размерности гильбертова пространства, отвечающего
конечному фазовому объему Q (N — Q/{2rih)r, где г—число
степеней свободы), операторы, представляемые функциями
/о(Х), равными нулю вне Q, имеют вид квадратных NXN мат-
матриц и требуют для своего описания конечного числа базисных
элементов. Это означает, что континуальный набор базисных
элементов е(X), где XeQ, является переполненным. Предель-
Предельный переход Q ->- °° делает очевидной переполненность базиса
е(Х) и в неограниченном фазовом объеме. Это обстоятельство
означает возможность неоднозначного представления Л-»-/(Х),
которая устраняется после выбора соответствующего наи-
наиболее простого правила: в представлении Вигнера /(Х) =
= BяЙ)гТг1е(Х) [136].
С использованием представления Вигнера изменение как
квантовых переменных, так и классических (также характери-
характеризуемых функциями /(X)), описывается уравнением
где 3? — линейный оператор, называемый оператором Лиувилля
385

(«лиувиллианом»). В квантовом случав он задается вигнвровским
представлением квантовой скобки Пуассона, т. е.
S - f И[Я (Х+1 о £) - Ж (X _ « о ji,)], A0.4)
где гйо — коммутационная матрица канонических переменных,
N — символ упорядочения, расставляющий операторы д/дХт пра-
правее умножения на переменные X. В классическом пределе, т. е.
при Ъ -*• 0, 9? = 3?0, где 3?* — классическая скобка Пуассона:
q? баб О 6J6 О б<7@ О
Преобразование /(X) под действием 2% сводится, в силу пер-
первого порядка этого дифференциального оператора, к движению
начальных значений X по классическим траекториям. В кван-
квантовом случае для нелинейных систем 3? — 3?о — ■S'd Ф 0, и дви-
движение сопровождается дополнительной квантовой диффузией,
описываемой оператором S'd, разложение которого по степеням
5/5Х содержит только нечетные степени, начиная с третьей. Эта
диффузия носит обратимый характер: 2>+ = — 2?, т. е. 3? — ан-
антиэрмитов оператор. Собственные значения оператора 3? чисто
мнимые, т. е. Я, = ia, а собственные функции удовлетворяют ус-
условию /_ш (X) = /ш (X). Если гамильтониан Ж не зависит от
времени, то эволюция к моменту времени t описывается опера-
оператором S(t) = exp(.2?£), и ее обратимость означает, что возврат
к начальному состоянию может быть достигнут также путем
динамической эволюции с лиувиллианом 2?+ = —S.
Оператор временной эволюции S (t) — Т exp I J &дХ I можно
' \о /
представить в виде S(t) = SD(t)Su(t), где St описывает движение
по классическим траекториям, а
p-
Lo
SD (t) - Т exp J So (т) ^dSo1 (t) dx A0.6)
— дополнительную квантовую диффузию, обусловленную ангар-
монизмом системы. Это представление делает наглядным основ-
основные закономерности динамики квантовых систем, стохастических
при Ъ -*■ 0. Квантовая диффузия приводит к замазыванию дета-
деталей стохастического движения с ростом времени t вплоть до
полного подавления стохастичности. Этот механизм, обусловлен-
обусловленный квантовой дифракцией со стохастических траекторий, ис-
исследовался в [490, 599]. Он определяет нижнюю временную гра-
границу прекращения стохастического движения.
Как отмечено выше, непрерывный характер оператора 3? и
функций /(X), представляющих динамические переменные, в
квантовом случае является фикцией вследствие переполненно-
переполненности базиса е(Х). Это влечет за собой дискретность и ограничен-
386

ность спектра собственных значений оператора & при движений
в конечной области фазового пространства системы со стацио-
стационарным гамильтонианом. Соответственно движение, описываемое
оператором S(t), будучи составленным из конечного числа гар-
гармонических составляющих, является квазипериодическим, воз-
возвращаясь сколь угодно близко к первоначальному состоянию.
Стохастичность в квантовых системах, таким образом, принци-
принципиально носит «переходной» характер [164, 402—405, 412, 645].
Это проверялось рядом численных расчетов, в частности, для
модели плоского ротатора с периодическими толчками, завися-
зависящими от угла поворота. При этом, в отличие от классических
систем, для которых численный расчет стохастического движения
после некоторого времени t в обратном направлении из-за ошибок
округления не приводит к возвращению системы в начальное
состояние, в квантовом случае такой возврат имеет место из-за
конечности числа квантовых состояний, если ошибки округления
достаточно малы [164].
Изменение состояния системы во времени как в классическом,
так п в квантовом случае может описываться двумя эквивалент-
эквивалентными способами: либо посредством изменения переменных, ха-
характеризующих физические величины, либо посредством изме-
изменения распределения вероятностей, характеризующего состоя-
состояние системы. В квантовом случае два указанных способа описа-
описания временной эволюции называются соответственно представ-
представлением Гейзенберга и представлением Шредингера. Выше было
описано представление Гейзенберга. Переход к представлению
Шредингера производится заменой Z ->- 3?+, где &+ в описан-
описанном представлении Вигнера сводится просто к замене д/дХ-*-
-*—5/5Х, поскольку д/дХ — антиэрмитовы операторы.
Квантовое распределение вероятностей в представлении Виг-
Вигнера задается разложением матрицы плотности р по базису
BяЙ)гГ(Х):
р =
Вводимая таким образом функция и>(Х) имеет размерность
плотности вероятностей в фазовом пространстве, вещественна и
нормирована на единицу. Она называется вигнеровской плот-
плотностью (вероятностей).
С помощью функции w(X) средние значения физических
переменных, представленных согласно A0.2) функциями /(X),
вычисляются по классической формуле
В отличие от классической плотности вероятностей, вигне-
ровская плотность не обязательно положительна, хотя реально
это имеет место практически во всех случаях, где использование
представления Вигнера технически удобно. Более существенно
следующее квантовое свойство функции w(X): она не может,
387

в отличив от классических распределений, быть локализованной
в сколь угодно малой области фазового пространства, т. е. иметь
вид 6(Х —Хо), соответствующий детерминированному состоя-
состоянию с фазовыми переменными, в точности равными Хо. Для
любой матрицы плотности р вигнеровская плотность w(X) та-
такова, что корреляционная матрица канонических переменных
Ж = J XKTw (X)
удовлетворяет матричному неравенству Гейзенберга [136]. Не-
Невозможность детерминированных состояний связана с опреде-
определением канонических переменных как некоммутирующих опе-
операторов X.
Рассмотрим наиболее простой пример квантовой стохастиче-
стохастической системы, изучавшийся во многих работах [237]. Это плоский
ротатор, подвергающийся периодическим б-образным толчкам,
во время которых ему сообщается обобщенный импульс (момент
количества движения) F@), зависящий от угла поворота 8. Га-
Гамильтониан такой системы имеет вид
где р, 0 — операторы обобщенного импульса и координаты, / —
момент инерции, At (t) = ^b(t — nt0) — периодическая последо-
последовательность б-функций, описывающих мгновенные толчки.
В вигнеровском представлении лиувиллиан, описывающий
изменение вигнеровской плотности, согласно A0.4) представля-
представляется выражением
[( + ££)-г(е-Щ (Ю.7)
При этом ввиду кинематической симметрии системы, а именно
периодичности по углу 0 функции V@) и неразличимости зна-
значений 0, отличающихся на целое число 2я, гильбертово про-
пространство состояний представляется набором бизисных функций
г|5т@)=ехр(гт0)/У2я. Соответствующий этой структуре наибо-
наиболее общий вид вигнеровской плотности определяется выраже-
выражением
" (Р, 6) = 2 2 -к Ртпе«т~т6 (р - П 1±Л.\ A0.8)
2 2 -к Ртпе6 (р П 1
п т. \ '
где pmn — элементы неотрицательно определенной нормированной
B Pmn = l) эрмитовой матрицы, описывающей матрицу плот-
плотности р в базисе функций г|зт. Состояния, соответствующие точ-
точно определенным импульсам, описываются впгперовской плот-
плотностью
wm(p, 0) = 8(р — %т)/2п.
Эти состояния полностью неопределенны по углу.
388

Пример некоторого вигнеровского распределения подобного
рода (для плоского ротатора) приведен на рис. 9.130. Объем,
в котором локализована огибающая вигнеровской плотности, не
менее величины 2лЪ, т. е. объема заштрихованной полоски. Рас-
Распределение по импульсам локализовано на значениях %{т + п)/2г
wfp$)
Рис. 9.130
т. е. квантовано порциями Ъ/2. Эта структура с учетом перио-
периодичности F@) в A0.7) инвариантна относительно соответствую-
соответствующего преобразования S*(t). Действительно, разложив V(Q) по
функциям ехр(гпгв), убеждаемся, что второе слагаемое в A0.7),
определяющее изменение по импульсу, соответствует комбина-
комбинациям сдвигом на Ъ.т/2, поскольку &*ц>[±т%/2)д/др] является
оператором сдвига по р на величину ±т%/2.
Перейдем к безразмерным переменным: p'—ptjl, t' = t/t0,
u(8)= F(8)/F0, где Fo — максимальная величина передаваемого
обобщенпого импульса. В этих переменных & -»- 2"t0,
(t) -> Д (Г) = 2 6 (Г - п),
, 6) =
= WJL,
Л(т-п)в(
Таким образом, роль постоянной Планка играет теперь безраз-
безразмерный показатель степени квантовости |, определяющий вели-
чипу объема квантования фазового пространства.
Опуская штрихи, для оператора 9?* в безразмерных пере-
переменных из A0.7) получаем выражепие
где К = VotJI — максимальный безразмерный передаваемый
импульс.
Для случая i>@) = cos0 из A0.10) имеем
l[expD|j_exp(-l^)]. A0.10*>
389-

Поскольку рассматриваемые функции вида A0.9) сингуляр-
сингулярны по импульсам р, то в операторах A0.10), A0.10*) их не-
неограниченный характер, обусловленный квантованностью им-
импульсов, существен и не позволяет непосредственно перейти
к квазиклассическому приближению. Действительно, ни при ка-
каких значениях | оператор (|/2) д/др нельзя считать малым и
разлагать по нему оператор сдвига ехр[(|/2M/5р]. Однако можно
поступить следующим' образом. Изменение истинной сингуляр-
сингулярной функции w{p, 6) можно описать некоторой непрерывной
функцией w(p, 6), по которой просто и однозначно может быть
восстановлена исходная функция w(p, 8) вида. A0.9). Наиболее
естественной и общепринятой является следующая процедура
замены w-+w. Функция A0.9) имеет структуру
где
">j(9)= 2 глГ Pmn exp tf (тге — n)Q].
Размажем каждую из функций 8(р — 1%/2) на интервал по-
порядка |, т. е. заменим 8(р — 1%/2) непрерывной функцией /;(р)
такой, что
U(P) dp = J 6 (р — Zg/2) dp = 1.
В качестве функции fi{p) можно выбрать, например, fi(p)
= sin [л Bр - Zl)/1] /я (р -11/2). Тогда
и> (Р, е) = 2 Щ (9) sin [я Bр - Zg)/£]/n (р - 1Ц2).
В точках р = 1\12 функция w{p, 0) равна 2од@)/|. Очевидно,
что функция w(p, 0) удовлетворяет условию нормировки, как
это требуется для вигнеровской плотности.
Под действием 2?+ функция w(p, 0) преобразуется таким
образом, что соответствующие ей значения Wi(Q) выражаются
сами через себя, так что после восстановления функции ю(р, 0)
последняя всегда имеет структуру A0.9). Если шг(в) мало из-
изменяется при переходе от I к 1 + 1, то функция w(p, 0) плавно
меняется в масштабах порядка 5- Поэтому в классе функций
ги(р, 0) можно выделить функции, соответствующие квазиклас-
квазиклассическим состояниям, для которых (%/2)д/др является малым
оператором.
Разделяя оператор 2*1", определяемый выражением A0.10*),
на классическую часть вида A0.5) и квантовую добавку к ней,
получаем
2* = - рд/дв -Kk(t) sin вд/др, A0.11)
3>t = ~ Kb it) sin 0 { [2 sh D ±] - I A]. A0.12)
390

Составляющей A0.11), описывающей классическое движение,
за один период времени от t = п + 0 до t = n +1 + 0, вклю-
включающий скачок импульса на Xsin0 в момент £ = п+1, соответ-
соответствует оператор перехода
S% = Т exp f [ - К sin в б (т— п) д/др — рд/дв] dx .
I п+о J
Учитывая, что д/др и д/дВ являются операторами инфинитези-
мального сдвига по соответствующим переменным (т. е. сдвига
на бесконечно малую величину dx), после разложения экспо-
экспоненты на сомножители в соответствии со стандартной формулой
перехода к представлению взаимодействия получаем:
St = T~(^K sin0) 7~(- р). A0.13)
В выражении A0.13) Та($) = ехр($д/да)— оператор сдвига по
переменному, стоящему в индексе, на величину, указанную в
аргументе; 0, р — значения переменных 9 и р в момент времени
t = п + 0, 0, р — соответствующие значения в момент t = п + 1 + 0.
Оператор Г§-(— р) описывает свободное движение ротатора до
момента толчка. При этом 0 = 0 + р, а импульс не меняется. Опе-
Оператор Т~(— К sin 9)^ наоборот, описывает скачок импульса в
момент толчка, при котором угол 0 не меняется, а р =
Оператору St соответствует суперпозиция указанных преоб-
преобразований, которая называется стандартным отображением и
хорошо изучена д классической теории [157, 237].
Полный квантовый оператор перехода, соответствующий сум-
сумме инфинитезимальных операторов A0.11) и A0.12), можно
представить в виде S+ = SkT~(—р), где
St = exp {tf sin ffi- Щ- i) - Т^Щ] A0.14)
— оператор преобразования состояния w(p, 0) за время толчка.
При | -*• 0 оператор Sk на множестве квазиклассических со-
состояний вырождается в оператор сдвига Г~(—if sin0).
Выделяя в A0.14) классический и квантовый сомножители
в соответствии с A0.12), для чисто квантового вклада вида A0.6)
имеем
Sj = S£2~(ffsinej. A0.15)
В отличие от Sk — Sr>T~(— KsinQ) операторы St и
Т~(—if sin 9) по отдельности не сводятся к суперпозиции сдви-
сдвигов Т~ (± |/2) и поэтому нарушают изображенную на рис. 9.130
391

квантовую структуру плотности w(p, 0), соответствующей
tv(p, 9). Правильное квантовое преобразование, справедливое не
только для квазиклассических, но и для любых плотностей
iv(p, 9), представляется лишь суперпозицией этих операторов.
Для выяснения пределов применимости квазиклассиче-
квазиклассического анализа достаточно в A0.14) удержать в показателе
экспоненты члены разложения операторов сдвига Т~(± 1/2) =
е= ехр [± (|/2) д/др] по | до третьего порядка включительно. Пос-
После подстановки полученного выражения для Sk в A0.15) по-
подучаем
St = ехр [(Z|2/24) gin вд3/др3 + О (|4)], (ЮЛ6)
где вир изменяются от одного момента времени t = n до друго-
другого в соответствии с классическим стандартным отображением.
Очевидно, что степень квантовости движения благодаря на-
наличию в выражении A0.16) оператора д/др существенно зави-
зависит от скорости изменения по переменной р функции w(p, 0).
Последняя определяется масштабами описываемых деталей дви-
движения: только в этих масштабах допустима нелокальность
функции w(p, 0), неизбежно вытекающая из соотношения неоп-
неопределенности. Чем меньше масштаб описываемых деталей, тем
больше величина д/др в выражении A0.16) и жестче условия,
накладываемые па параметр | < 1 применимостью квазикласси-
квазиклассического описания.
Пусть, например, Д»|— характерный размер по переменной
р островка устойчивости на фазовой плоскости. Тогда масштаб
локализации w(p, 0), необходимый для качественно правильного
■описания движения, должен быть не меньше Д. Поэтому вели-
величина д/др — по меньшей мере порядка 1/Д, если внутри области
Д нет более тонкой структуры зависимости движения от коор-
координат. За время t > 1 оператор квантового вклада определяется
суперпозицией операторов A0.16). Полагая, что показатели экс-
экспонент в каждом таком операторе можно рассматривать как не-
независимые случайные величины, имеющие одинаковый порядок
по абсолютному значению, и разлагая все экспоненты в ряд,
получаем для отклонения результирующего преобразования от
•единичного оператора следующее выражение:
Полагая % ~ 1, получаем отсюда оценку для масштаба времени
потери устойчивости за счет квантового перехода в область сто-
хастичности:
.3 \2/
Аналогичным образом может происходить переход из области
стохастичпости в область устойчивости.
392

В рассмотренном примере неавтономной системы ее гамиль-
гамильтониан не гарантирует движения в ограниченной области фазо-
фазового пространства и неизбежно вытекающей отсюда необходи-
необходимости квазипериодичности^ движения. В классическом случае при
КЖа» 0,97164 должен происходить переход к неограниченной
диффузии по импульсу [237]. Квантовый же характер движения,
становящийся существенным на достаточно больших временах,
приводит, согласно численным экспериментам, к подавлению этой
диффузии. Если бы система была автономной с ограниченным
фазовым объемом^ то такое подавление являлось бы очевидным
следствием квантования фазового пространства. Отметим, что
анализ эволюции вигнеровской плотности для рассматриваемого
примера, качественно правильно описывающий характер ее из-
изменения на больших временах, содержится также в рабо-
работе [404].
В заключение авторы хотят поблагодарить А. П. Крылову
за помощь в подборе литературы, В. В. Алексеева, В. С. Ани-
щенко и Д. И. Трубецкова за предоставленные фотографии ре-
результатов экспериментов.

СПИСОК ЛИТЕРАТУРЫ
1. Автоволновые процессы в системах с диффузией: Сб. научных трудов.—
Горький: Ип-т прикладной физики АН СССР, 1981.
2. Александров Б. П., Ланда П. С, Швилкин Б. Н. Метод определения
числа степеней свободы по экспериментальным данным на примере бе-
бегущих страт II Физика плазмы.—1986.—Т. 12, № 1.—С. 120—123.
3. Алексеев А. С. Электронная модель двухпозиционного регулятора тем-
температуры с зоной опережения / ДАН СССР.—1952.—Т. 87, № 3.—
С. 393—396.
4. Алексеев А. С. Двухпозиционный регулятор температуры с зоной опе-
опережения / Памяти А. А. Андронова.—М.г Изд-во АН СССР, 1955.—
С. 45—76; Тр. Горьк. физ.-техн. ин-та и радиофака ГГУ, Мученые запис-
записки.—1957.—Т. 35.—С. 105—201.
5. Алексеев В. В., Корниловский А. И. Автостохастические процессы в
биофизических системах / Биофизика.— 1982.—- Т. 27, вып. 5.— С. 890—
894.
6. Алексеев В. М. Квазислучайные динамические системы, I, II, III /
Мат. сб.—1968.—Т. 76, № 1.—С. 72—134; 1968.—Т. 77, № 4—С. 545—
601; 1969.—Т. 78, № 1.—С. 3—50.
7. Алексеев В. М. Квазислучайные колебания и качественные вопросы
небесной механики // Тр. IX летней мат. школы.— Киев: Ин-т матема-
математики АН УССР, 1972.— С. 212—341.
8. Алексеев В. М. Символическая динамика // Тр. XI мат. школы.— Киев:
Ип-т математики АН УССР, 1976.
9. Алексеев В. М., Якобсон М. В. Символическая динамика п гиперболи-
гиперболические системы. (Добавление к книге Р. Боуэна «Методы символиче-
символической динамики») — М.: Мир, 1979.—С. 196—240.
10. Лндрейчиков И. П., Петровская Н. В., Юдович В. И. Бифуркации и сто-
стохастические движения в некоторых гидродинамических системах /
ВИНИТИ.— М., 1981.— Деп. в ВИНИТИ, № 3485—80.
11. Лндрейчиков И. П., Юдович В. Я./Численный анализ бифуркаций пре-
предельных циклов системы Лоренца / ВИНИТИ.— М., 1981.— Деп. в
ВИНИТИ, № 3630—80.
12. Андронов А. А. Математические проблемы теории автоколебаний //
Собр. тр.—М.: Изд-во АН СССР, 1956.—С. 84—124.
{Ъ. Андронов А. А. Теория точечных преобразований Пуанкаре — Брауэ-
ра — Биркгофа и теория нелинейных колебаний // Вестник АН СССР.—
1944.— №6.
14. Андронов А. Л., Витт А. А. К теории захватывания Ваи-дер-Поля //
Собр. тр. Л. А. Апдропова.—М.: Изд-во АН СССР, 1956.—С. 51—64.
15. Андронов А. А., Витт А. Л., Хайкин С. Э. Теория колебаний.—М.: Физ-
матгиз, 1959; М.: Наука, 1981.
16. Андронов А. А., Леонтович Е. А. Некоторые случаи зависимости пре-
предельных циклов от параметров // Ученые записки ГГУ.— 1939.— В. 6,
№ 3.- С. 3-33.
394

17. Андроцов А. А., Леонтович Е. А. Рождение предельных циклов из не-
негрубого фокуса или центра и от пегрубого предельного цикла //
Мат. сб.- 1956.- Т. 40, № 2.— С. 179-234.
18. Андронов А. А., Леонтович Е. А. Динамические системы первой степепи
негрубости на плоскости // Мат. сб.— 1965.—< Т. 68, № 3.— С. 328—372.
19. Андронов А. А., Леонтович Е. А., Гордон И. И., Майер А. Г. Теория
бифуркаций динамических систем на плоскости.— М.:'Наука, 1967.
20. Андронов А. А., Понтрягин Л. С. Грубые системы // ДАН СССР.—1937.—
Т., 14, № 5.—С. 247—250.
21. Анисимова Ю. В., Дмитриев А. С, Залогин Н. Н., Калинин В. И., Кис-
Кислое В. Я., Панас А. И. Об одном механизме перехода к хаосу в систе-
системе электронный пучок — электромагнитная волна // Письма ЖЭТФ.—
1983.— Т. 37, № 8 — С. 387—389.
22. Анищенко В. С. Взаимодействие странных аттракторов (СА), переме-
перемежаемость типа «хаос —хаос» Ц Письма ЖТФ.— 1984.—Т. 10, вып. 10.—
С. 629-632.
23. Анищенко В. С. Стохастические колебания в радиофизических систе-
системах. Ч. 1, 2.— Саратов: Изд-во СГУ, 1985; 1986.
24. Анищенко В. С. Разрушение квазипериодических колебаний и хаос в
диссипативных системах // ЖТФ.— 1986.— Т. 56, № 2.— С. 225—237.
25. Анищенко В. С, Арансон И, С, Постное Д. Э., Рабинович М. И. Прост-
ранствеппая синхронизация и бифуркации развития хаоса в цепочке
связанпых генераторов // ДАН СССР.—1986.—Т. 280, ЛЬ 5.—С. 1120—
1124.
26. Апищенко В. С, Астахов В. В. Экспериментальное исследование сто-
хастизации автоколебаний в усилителях с внешней обратной связью /
Лекции по электронике СВЧ и радиофизике, кн. 5.— Саратов: Изд-во
СГУ, 1980.—С. 118—133.
27. Анищенко В. С, Астахов В. В. Экспериментальное исследование-меха-
исследование-механизма возникновения и структуры страпного аттрактора в генераторе
с инерционной нелипейностью II Радиотехника и электроника.— 1983.—
Т. 28, МЬ 6.— С. 1109-1115.
28. Анищенко В. С, Астахов В. В. Бифуркационные явления в автостоха-
автостохастическом генераторе при внешнем регулярном воздействии // ЖТФ.—
1983.—Т. 53>ып. 11,—С. 2165—2170.
29. Анищенко В. С, Астахов В. В., Летчфорд Т. Е. Многочастотпые и сто-
стохастические автоколебания в генераторе с инерционной нелиней-
нелинейностью II Радиотехника и электропика.— 1982.— Т. 27, № 10.— С. 1972—
1978.
30. Анищенко В. С, Астахов В. В., Летчфорд Т. Е. Стохастический аттрак-
аттрактор в модели генератора с инерционной нелинейностью // Вопросы
электроники СВЧ.— Саратов: Изд-во СГУ, 1983.— С. 31—44.
31. Анищенко В. С, Астахов В. В., Летчфорд Т. Е., Сафонова М. А. О би-
бифуркациях в трехмерпой двупараметрической автономной колебатель-
колебательной системе со странным аттрактором Ц Изв. ВУЗов, Радиофизика.—
1983.—Т. 26, № 2.—С. 169—176.
32. Анищенко В. С, Астахов В. В., Летчфорд Т. Е., Сафонова М. А. К во-
вопросу о структуре квазигиперболической стохастичности в инерцион-
инерционном автогенераторе // Изв. ВУЗов. Радиофизика.— 1983.— Т. 26, № 7 —
С. 832—842.
33. Анищенко В. С, Летчфорд Т. Е., Сафонова М. А. Влияние диссипатив-
ной пелинейности на бифуркации в автостохастичоских системах //
Радиотехника и электроника.— 1984.—Т. 29, №7.— С. 1355—1361.
34. Анищенко В. С, Летчфорд Т. Е., Сафонова М. А. Разрушение квазипе-
квазипериодического движения за счет удвоений и стохастичность в системе
связапных генераторов Ц Изв. ВУЗов. Радиофизика.— 19S4.— Т. 27,
№ 5.- С. 565—575.
35. Анищенко В. С, Летчфорд Т. Е., Сафонова М. А. Эффекты синхрони-
синхронизации и бифуркации синхропных и квазипериодических колебаний
в неавтономном генераторе / Изв. ВУЗов. Радиофизика.— 1985.— Т. 28.—
№ 9.-С. 1112—1125.
395

36. Анищенко В. С, Летчфорд Т. Е., Сафонова М. А. Критические явления
при гармонической модуляции двухчастотных колебаний. Переходы к
хаосу через трехмерный тор / Письма ЖТФ.—1985.— Т. 11, вып. 9.—
С. 536-541.
37. Анищенко В. С, Постное Д. Э. Переходы к стохастичности в инерци-
инерционном генераторе с запаздыванием. Проблема конечномерпого описа-
описания // ЖТФ.— 1985.— Т. 55, Л"» 1.- С. 162—167.
38. Анищенко В. С, Постное Д. Э., Сафонова М. А. Размерность и физиче-
физические свойства хаотических аттракторов в цепочке связанных генера-
генераторов I/ Письма ЖТФ.— 1985.—Т. 11, вып. 24.—С. 1505—1509.
39. Аносов Д. В. Грубость геодезических потоков на компактных римано-
вых многообразиях отрицательной кривизны // ДАН СССР.—1962.—
Т. 145, № 4.— С. 707—709; Эргодические свойства геодезических пото-
потоков на замкпутых многообразиях отрицательной кривизны // ДАН
СССР.—1963.—Т. 151, К° 6.—С. 1250—1252.
40. Аносов Д. В. Геодезические потоки па замкнутых римаповых многооб-
многообразиях отрицательной кривизны ^Тр. мат. ин-та им. В. А. Стеклова.
Т. 90.— М., 1967.
41. Арансон И. С, Рабинович М. И., Старобинец И. М. Переходы в хаосе Ц
Проблемы нелинейных и турбулентных процессов в физике. Ч. 2. Тр,
II Междунар. рабочей группы/Под ред. А. С. Давыдова, В. М. Черно-
усеико.— Киев: Наукова думка, 1985.— С. 3—15.
42. Арнольд В. И. Потеря устойчивости автоколебаний вблизи резопапса й
версальные деформации эквивариантных векторных полей / Функцио-
Функциональный анализ.— 1977.— Т. 11, № 2.— С. 1—10.
43. Арнольд В. И. Дополнительные главы теории обыкновенных дифферен-
дифференциальных уравнений.— М.: Наука, 1978.
44. Астахов В. В. Исследование динамических процессов в автоколебатель-
автоколебательных системах с инерционной нелинейностью // Вопросы электроники
СВЧ.— Саратов: Изд-во СГУ, 1983.— С. 45—50.
45. Афраймович В. С. Принцип кольца и квазиаттр'акторы // Тр. IX Мешд.
копф. по нелин. колеб., т. 2,— Киев: Наукова думка, 1984.— С. 34—36;
Страппые аттракторы и квазиаттракторы / Проблемы нелинейных и
турбулентпых процессов в физике. Ч. 2. Тр. II Междунар. рабочей груп-
группы/Под ред. А. С. Давыдова, В. М. Черноусенко.— Киев: Наукова дум-
думка, 1985.— С. 21—24.
46. Афраймович В. С, Быков В. В., Шилъников Л. П. О возникновении
и структуре аттрактора Лорепца / ДАН СССР.— 1977.— Т. 234, № 2.—
С. 336—339.
47. Афраймович В. С, Рабинович М. И., Угодников А. Д. Критические точ-
точки и «фазовые переходы» в стохастическом поведении неавтономного
ангармонического осциллятора / Письма ЖЭТФ.— 1983.— Т. 38, вып. 2.—
С. 64-67.
48. Афраймович В. С, Шильников Л. П. О малых периодических возмуще-
пиях автопомпых систем II ДАН СССР.— 1974.— Т. 214, № 4.— С. 739—
742.
49. Афраймович В. С, Шильников Л. П. О некоторых глобальных бифур-
бифуркациях, связанных с исчезновением неподвижной точки седло — узел Ц
ДАН СССР.— 1974.—Т. 219, № 6.—С. 1281—1284.
50. Афраймович В. С, Шилъников Л. П. Инвариантпыо двумерпые торы, их
разрушение и стохастичность // Методы качественной теории диффе-
дифференциальных уравнепий.— Горький: Изд-во ГГУ, 1983.— С. 3—26.
51. Бабин А. В, Вишик М. И. Аттракторы эволюционных уравнений с
частными производными и оценки их размерности Ц УМН.—1983.—
Т. 38, вып. 4.— С. 133—187.
52. Бабицкий В. И., Лапда П. С. Автоколебания в системах с инерцион-
инерционным возбуждением / ДАН СССР.—1982.—Т. 266, № 5.—С. 1087—
1089.
53. Бабицкий В. И., Ланда П. С. Автоколебательные системы с инерциоп-
ным возбуждением Ц Динамика систем.— Горький: Изд-во ГГУ, 1983.—
С. 147—181.
396

54. Бабицкий В. И., Ланда.П. С, Ольховой А. Ф., Перминов С. М. Стоха-
Стохастическое поведение автоколебательных систем с инерционным само-
самовозбуждением II Динамика систем.— Горький: Изд-во ГГУ, 1985.—
С. 14—49.
55. Бабицкий В. И., Ланда П. С, Перминов С. М. Колебания в машинах с
учетом инерционности регулятора скорости вращения двигателя Ц Ма-
Машиноведение.— 1985.— Л» 2.— С. 31—35.
56. Балеску Р. Равновесная и неравновесная стохастическая механика.—
М.: Мир, 1968.— Гл. 9, 10.
57. Баренблатт Г. И. Подобие, автомодельность, промежуточная асимпто-
асимптотика.— Ленинград: Гидромстеоиздат, 1982.
58. Барсук Л. О., Белослудцев Н. М., Неймарк Ю. И., Салганская Л. М. Ус-
Устойчивость неподвижной точки в критическом случае и некоторые осо-
особые бифуркации I/ Изв. ВУЗов. Радиофизика.— 1968.— Т. 11, Л1 11.—
С. 1632-1641.
59. Баталова 3. С. Изучение вибропогружепия пшупта при лобовом сопро-
сопротивлении грунта II Инж. журнал, механика твердого тела.—1966.—
№ 2.- С. 165-173.
60. Баталова 3. С. О движениях ротора под влиянием внешней гармони-
гармонической силы II Инж. журнал, механика твердого тела.— 1967.— № 2 —
С. 66-73.
61. Баталова 3. С. О рсзопанспых уровнях гамильтоновых систем / Ди-
Динамика систем, вып. 19.— Горький: Изд-во ГГУ, 1980.— С. 60—79.
62. Баталова 3. С, Безденежных А. Н., Неймарк Ю. И., Ромашова И. Б.
О бифуркациях, приводящих к хаотизации движения ротора // Дина-
Динамика систем. Вып. 19.—Горький: Изд-во ГГУ, 1980.—С. 110—125.
63. Баталова 3. С, Белякова Г. В. О колебательных движениях маятника
с вибрирующей точкой подвеса // Динамика систем (оптимизация и
адаптация).—Горький: Изд-во ГГУ, 1982.—С. 145—170.
64. Баталова 3. С., Белякова Г. В. О структуре фазового пространства урав-
уравнений движения маятника с колеблющейся точкой подвеса/ВИНИТИ,—
М., 1984.— Деп. в ВИНИТИ, Л» 3539—84.
65. Баталова 3. С, Бухалова Л. В. Иерархия структуры фазового прост-
пространства уравнения движений маятника с колеблющейся осью враще-
вращения I/ Динамика систем,— Горький: Изд-во ГГУ, 1983.— С. 85—111.
66. Баталова 3. С, Бухалова Н. В. Динамика маятника с колеблющейся
вертикальной осью вращения.— Препринт/НИРФИ.— Горький, 1984.—
№ 187.
67. Баталова 3. С, Бухалова Л. В., Неймарк Ю. И. Бифуркации фазового
портрета дисбалапсного ротора на гармонически колеблющемся осно-
основании, приводящие к хаотизации его движений Ц Динамика систем
(численные методы исследования динамических систем).— Горький:
Изд-во ГГУ, 1982.-С. 112-126.
68. Баталова 3. С, Дубровина И. А , Неймарк Ю. И., Орлова Е. Е. Числеп-
ное исследование решений дифференциальных уравнений конвектив-
конвективной турбулентности Лоренца // Динамика систем, вып. 16.— Горький:
Изд-во ГГУ, 1979.— С. 59—81.
69. Баталова 3. С, Дубровина И. А., Неймарк Ю. И., Орлова Е. Е. О струк-
структуре фазового пространства и бифуркациях в дискретпой модели кон-
конвективной турбулентности Лоренца Ц ПММ.—1981.— Т. 45, вып. 4.—
С. 637—644.
70. Баталова 3. С, Неймарк Ю. И. Об одной динамической системе с гомо-
клииической структурой // Теория колебаний, прикладная математи-
математика и кибернетика, в. 1.—Горький: Изд-во ГГУ, 1973.—С. 131—147.
71 Баутин Н. Н. К теории синхронизации // ЖТФ.— 1939.— Т. 9, Л» 6.—
С. 510—513. /
72. Баутин И. Л. О поведении дипамических систем при малых наруше-
нарушениях условий устойчивости Рауса — Гурвица // ПММ.— 1948.— Т. 12,
№ 5.— С. 613—632.
73. Баутин Н. Н. Поведение дипамических систем вблизи грапицы обла-
области устойчивости.—Изд. 2-е, перераб. и доп.—М.: Наука, 1984.
397

74. Везаева Л. Г., Капцов Л. Н., Ланда П. С. Исследование хаотической
модуляции колебаний в генераторе с инерционной нелинейностью при
параметрическом внешнем воздействии / Радиотехника и электрони-
электроника.— 1987.— Т. 32, № 3.— С. 647—650.
75. Безаева Л. Г., Капцов Л. Н., Ланда П. С. Порог синхронизации как
критерий стохастичности в генераторе с инерционной нелинейностью Ц
5КТФ.— 1986.- Т. 56, Л"° 9.- С. 1849—1853.
76. Безручко Б. П., Булгакова Л. В., Кузнецов С. П., Трубецков Д. И. Экс-
Экспериментальное и теоретическое исследование стохастических автоко-
автоколебаний в лампе обратной волны // Лекции по электронике СВЧ и ра-
радиофизике, кн. 5.— Саратов: Изд-во СГУ, 1980.— С. 25—77.
77. Безручко Б. П., Булгакова Л. В., Кузнецов С. П., Трубецков Д. И: Сто-
Стохастические автоколебания и неустойчивость в лампе обратной вол-
волны II Радиотехника и электроника.—1983.—Т. 28, № 6.—С. 1136—
1139.
78. Безручко Б. П., Кузнецов С. П., Трубецков Д. И. Экспериментальное
наблюдение стохастических автоколебаний b's динамической системе
электроппый пучок — обратпая электромагнитная волна // Письма
ЖЭТФ.— 1979.- Т. 29, вып. 3.- С. 180-184.
79. Белецкий В. В., Хентов А. А. Вращательные движения намагниченно-
намагниченного спутника.— М.: Наука, 1985.
80. Белоусов Б. П. Периодически действующая реакция и ее механизм: Сб.
рефератов по радиационной медицине.— М.: Медгиз, 1959.— С. 145—
148; Химия и жизнь.— 1982.— № 1.— С. 65—68.
81. Белых В. Н. О бифуркациях сепаратрис седла системы Лоренца / Диф-
Дифференциальные уравнения.— 1984.— Т. 20, № 10.— С. 1666—1674.
82. Белюстина Л. И., Белых В. Н. О неавтономной фазовой системе урав-
уравнений с малым параметром, содержащей инвариантные торы и грубые
гомоклинические кривые / Изв. ВУЗов. Радиофизика.—1972.— Т. 15,
№ 7.— С. 1039—1048.
83. Белюстина Л. П., Белых В. И. О глобальной структуре | разбиения фа-
фазового пространства одпой неавтономной системы / Дифференциаль-
Дифференциальные уравнения.— 1973.— Т. 9, № 4.— С. 595—608.
84. Белюстина Л. П., Белых В. Н. Гомоклинические структуры, порождае-
порождаемые простейшей моделью фазовой автоподстройки Ц Фазовая синхро-
синхронизация.— М.: Связь, 1975.— С. 97—106.
85. Белюстина Л. И., Кивелева К. Г., Фрайман Л.' А. Качественно-числен-
Качественно-численный метод в исследовании трехмерных нелинейных систем фазовой
синхронизации // Системы фазовой синхронизации.— М.: Радио и
связь, 1982.— С. 21—45.
86. Белюстина Л. Н., Отрокова И. Н. Исследование возникновения гомо-
клинической структуры качественно-численным методом / Динамика
систем (математические методы теории колебаний).— Горький: Изд-во
ГГУ, 1979.— С. 82-94.
87. Белых В. Н., Максаков В. П. Качествепное исследование разрывного
отображения цилиндра из теории фазовой синхронизации Ц Методы
качественной теории дифференциальных уравнений.— Горький: Изд-во
ГГУ, 1982.- С. 135-149.
88. Биркгоф Дж. Д. Динамические системы.— М.: Гостехиздат, 1941.
89. Блехман И. И. Синхронизация динамических систем.— М.: Наука, 1971.
90. Блехман И. И. Синхронизация в природе и технике.— М.: Наука, 1980.'
91. Боголюбов Н. Н. Теория возмущений в нелинейной механике Ц Сб. Ин-
та строит, механики АН УССР.—1950.— Т. 14.— С. 9—34.
92. Боголюбов Н. И., Митр о польский Ю. А. Асимптотические методы в те-
теории нелинейных колебаний.— М.: Наука, 1974.
93. Болотин В. В., Воробьев В. И., Семенов В. А., Чернов В. К. О парамет-
параметрической стабилизации неустойчивых форм равновесия механических
систем // МТТ.- 1979.— № 1— С. 36—44.
94. Бонч-Бруевич В. Л. Стохастические автоколебания как один из возмож-
возможных источников шума 1// / ДАН СССР.— 1984.— Т. 278, № 2.— С. 335—
339.
398

95. Брюно А. Д. Аналитическая форма дифференциальных уравнений /
Тр. Моск. мат. об-ва.-1971.-Т. 25.-С. 119-262; 1972.-Т. 26.-С. 199—
239; Множества аналитичности нормализующего преобразования.— Пре-
принт/ИИМ АН СССР.— М., 1974.— Л° 93.
96. Булгаков Б. В. Колебания.— М.: Гостехиздат, 1954.
97. Бунимович Л. Л. О скорости убывапия корреляций в динамических
системах // Проблемы нелинейных и турбулентных процессов в физи-
физике: Тр. II Междупар. рабочей группы. Ч. 2./Под ред. А. С. Давыдова,
B. М. Чериоусенко,— Киев: Наукова думка, 1985.— С. 28—30.
98. Бунимович JI. А., Синай Я. Г. Стохастичпость аттрактора в модели Ло-
Лоренца Ц Нелинейные волны.— М.: Наука, 1979.— С. 212—226.
99. Бунимович Л. А., Синай Я. Г. Скорость убывания корреляций в одно-
одномерных экологических моделях // Термодинамика и кинетика биологи-
биологических процессов.—М.: Наука, 1980.—С. 226—235.
100. Бутенин Н. В., Неймарк Ю. И., Фуфаев Н. А..Введение в теорию нели-
нелинейных коле'йаний.— М.: Наука, 1976.
101. Былое Б. Ф., Виноград Р. д., Гробман Д. М., Немыцкий В. В. Теория
показателей Ляпунова и ее приложения к вопросам устойчивости.— М.:
Наука, 1966.
102. Вайнберг Д. В., Писаренко Г. С. Механические колебания и их роль
в технике.— М.: Наука, 1965.
103. Ван-дер-Полъ Б. Нелинейная теория электрических колебаний.— М.:
Связьиздат, 1935.
104. Вентцель А. Д., Фрейдлин М. И. О малых случайных возмущениях ди-
динамических систем / УМН.—1970.—Т. 25, в. 1.—С. 3—55.
105. Видалъ К. Динамические неустойчивости, наблюдаемые в системе Бело-
усова — Жаботинского Ц Синергетика/Под ред. Б Б. Кадомцева,— М.:
Мир, 1984.- С. 109-125.
106. Вильсон К. Дж. Ренормализационная группа и критические явления II
УФН.- 1983.-Т. 141, вып. 2.-С. 193-220.
107. Виноградова М. Б., Руденко О. В., Сухорукое А. П Теория волн.—М:
Наука, 1979.
108. Виттенбург Й. Динамика системы твердых "тел.— М.: Наука. 1982.
109. Власова О. Ф., Заславский Г. М. Влияние диссипации на образование
хаоса при перекрытии двух резонапсов.— Препринт/СО АН СССР.—
Красноярск, 1983.— № 245Ф.
110. Волновые и флуктуациопныо процессы в лазерах/Зейгер С. Г., Кли-
монтович Ю. Л., Ланда П. С, Лариопцев Е. Г., Фрадкин Э. Е.— М.: На-
Наука, 1974.
111. Волосов В. М., Моргунов Б. И. Метод осреднения в теории нелинейных
колебательных систем.—М.: Изд-во МГУ, 1971.—С. 249—277.
112. Волъкенштейн М. В. Биофизика.— М.: Наука, 1981.
113. Вольтер Б. В., Сальников И. Е. Устойчивость режимов работы химиче-
химических реакторов.—М.: Химия, 1981.
114. Волътерра В. Математическая теория борьбы за существование.— М.:
Наука, 1976.
115. Вул Е. В., Синай Я. Г., Ханин К. М. Универсальность Фсйгенбаума и
термодинамический формализм Ц УМН.— 1984.— Т. 39, вып. 3.— С. 3—
37.
116. Вулъфсон И. И., Коловский Ш. 3. Нелинейные задачи динамики ма-
машин.— М.: Машиностроение, 1968.
117. Гаврилов Н. К. О трехмерных динамических системах, имеющих негру-
негрубый гомоклипический контур Ц Мат. заметки.—1973.— Т. 14, № 5.—
C. 687—696.
118. Гаврилов Н. К. О бифуркациях периодических движений вблизи внут-
внутреннего резонанса 1:3 Ц Исследования устойчивости и теория колеба-
колебаний.—Ярославль, 1977.—С. 192—199.
119. Гаврилов П. К., Шилъников Л. П. О трехмерных дипамических систе-
системах с негрубой гомоклипической кривой, I, II // Мат. сб.—1972.—
№ 8.—С. 475-492; 1973.—Л» 1.—С. 139-156.
399

120. Гапонов-Грехов А. В., Рабинович М. И. Мандельштам и современная
теория нелинейных колебаний / УФН.— 1979.— Т. 128, вып. 4—С. 579—
624.
121. Гапонов-Грехов А. В., Рабинович М. И. Хаотическая динамика простых
систем / Природа.—1981.— № 2.— С. 54—65.
122. Гапонов-Грехов А. В., Рабинович М. И. Нелинейная физика. Стохастич-
ность и структуры.— Препринт/ИПФ АН СССР.— Горький, 1983.—
№ 87 I/ Физика XX века: Развитие и перспективы.— М.: Наука, 1984.—
С. 219—280.
123. Гапонов-Грехов А. В., Рабинович М. И., Старобинец И. М. Динамиче-
Динамическая модель пространственного развития турбулентности Ц Письма
ЖЭТФ.— 1984.- Т. 39, вып. 12.- С. 561—564.
124. Гаушус Э. В. Исследование динамических систем методом точечных
преобразований.— М.: Наука, 1976.
125. Гелъфер И. С, Неймарк Ю. И. Плотности вероятностей, соответствую-
соответствующие кусочно-линейным отображениям с марковским разбиением Ц Ди-
Динамика систем. Устойчивость, синхронизация и хаотичность.— Горький:
Изд-во ГГУ, 1983.— С. 52—85.
12£. Гидродинамические неустойчивости и переход к турбулентности/Под
ред. X. Суиппи, Дж. Голлаба.— М.: Мир, 1984.
127. Гилмор Р. Прикладная теория катастроф. Т. I.—M.: Мир, 1984.
128. Гинзбург Н. С, Кузнецов С. П. Периодические и стохастические авто-
модуляционныо режимы в электропных генераторах с распределенным
взаимодействием Ц Релятивистская высокочастотная электроника.—
Горький: ИПФ АН СССР, 1981.- С. 101—144.
129. Гленсдорф П., Пригожин И. Термодинамическая теория структуры, ус-
устойчивости и флуктуации.— М.: Мир, 1973.
130. Гольберг А. И., Синай Я. Г., Ханин К. М. Универсальные свойства для
последовательности бифуркаций утроения периода // УМН.—1983.—
Т. 38, № 1.— С. 159—160.
131. Голъдштик М. А., Штерн В. П. Структурная турбулентность в диссипа-
тивных системах.— Препринт/ИТФ СО АН СССР.— Новосибирск, 1981.—
№ 74-81.
132. Горелик Г. С. Колебания и золны.— М.: Физматгиз, 1959.
133. Градштейн И. С, Рыжик И. М. Таблицы интегралов, сумм, рядов и
произведений.— М.: Наука, 1971.— С. 259—262.
134. Грасюк А. 3., Ораевский А. Н. Переходные прбцессы в молекулярном
генераторе // Радиотехника и электроника.—1964.— Т. 9, № 3.— С. 524—
532.
135. Гринберг А. И. Динамические модели народного хозяйства.— М.: Эко-
Экономика, 1985.
136. Гришанин Б. А. Квантовая электродинамика для радиофизиков.— М.:
Изд-во МГУ, 1981.
137. Груздев В. Г., Неймарк Ю. И. Символическое описание движений в ок-
окрестности негрубой гомоклинической структуры и его изменение при
переходе к близким системам // Динамика систем, вып. 8.— Горький:
Изд-во ГГУ, 1975.— С. 13—33; Символическое описание движений в ок-
окрестности негрубой гомоклинической кривой // Укр. мат. журнал.—
1976.— Т. 28, № 6.— С. 723—734.
138. Горбиков С. П., Неймарк Ю. И. Основные режимы движения при виб-
вибротранспортировании с подбрасыванием // Изв. АН СССР. Механика
твердого тела.—1981.— № 4.— С. 39—50.
139. Губанков В. И., Зиглин С. Л., Константинян К. И., Кошелец В. П., Ов-
Овсянников Г. А. Стохастические колебания в туннельных джозефсонов-
ских переходах // ЖЭТФ.—1984.— Т. 86, вып. 1.— С. 343—351.
140. Губанков В. И., Константинян К. И., Кошелец В. П., Овсянников Г. А.
Хаотическая неустойчивость в туннельных дягозефсоновских перехо-
переходах II Письма ЖТФ.—1982.—Т. 8, № 21.—С. 1332—1335.
141. Гуккенхеймер Дж. Неустойчивости и хаос в негидродинамических си-
системах II Гидродинамические неустойчивости и переход к турбулент-
пости/Под ред. X. Суинни, Дж. Голлаба.—М.: Мир, 1984.—С. 317—335.

142. Гуртовник А. С, Неймарк Ю. И. О синхронизации динамических сис-
систем / ПММ.—1974—Т. 38, № 5.-С. 800—809.
143. Динамические системы.— 1, 2. Сер. Современные проблемы математи-
математики, фундаментальные направления.— М.: ВИНИТИ, 1985.
144. Дихтяр В. Б. Стохастические автоколебания в системе связанных авто-
автогенераторов с запаздыванием Ц Радиотехника и электроника.—1982.—
' Т. 27, № 2.— С. 310—320.
145. Дихтяр В. Б., Кислое В. Я. Стохастические колебания в резонансных ав-
автогенераторах с запаздыванием // Нелинейные волны. Стохастичность
и турбулентность.— Горький, 1980.— С. 37—45.
146. Дихтяр В. Б., Старков С. О. Автостохастизация колебаний в генерато-
генераторах, описываемых нелинейным разностным уравнением, сводящимся
к дифференциальному уравнению второго порядка с запаздывающим
аргументом // Радиотехника и электропика.—1982,— Т. 27, № 12.—
С. 2457-2463.
147. Дмитриев А. С, Кислое В. Я. Странный аттрактор в неавтономном
уравнении Вап-дер-Поля // Радиотехника и электроника.— 1982.— Т. 27,
№ 12.— С. 2454-2456.
148. Дмитриев А. С, Кислое В. Я. Стохастические колебания в автогенера-
автогенераторе с инерционным запаздыванием первого порядка / Радиотехника
и электроника.— 1984.— Т. 29, № 12.— С. 2389—2398.
149. Дмитриев А. С, Кислое В. Я., Спиро А. Г. Хаотические колебания в
неавтономном генераторе с реактивной нелинейностью / Радиотехни-
Радиотехника и электроника.— 1983.— Т. 28, № 12.— С. 2430—2439.
150. Дружиловская Т. Я., Неймарк Ю. И. Стохастические автоколебания не-
нелинейного осциллятора с ударным поглотителем энергии // ПММ.—
1982 — Т. 46, вып. 6.— С. 924—930.
151. Дудник Е. Н., Кузнецов Ю. И., Минакова И. И., Романовский Ю. М.
Синхронизация в системах со странным аттрактором / Вестник МГУ.
Сер. 3.— 1983.— Т. 24, Лг 4.— С. 84-87.
152. Жаботинский А. М. Концентрационные автоколебания.— М.: Наука, 1974.
153. Желудев Н. И., Макаров В. А., Матвеева А. В., Свирко Ю. П. Струк-
Структура хаоса при возбуждении нелинейного осциллятора гармонической
внешней силой // Вестник МГУ.— Сер. 3.—1984.— Т. 25, № 5.— С. 106—
109.
154. Заславский Г. М. Стохастические волновые процессы.— Препринт/
НИРФИ.—Горький, 1973.—№ 41.
155. Заславский Г. М. Статистика энергетических уровней при разрушении
интегралов движения // ЖЭТФ.—1977.—Т. 73, вып. 6A2).—С. 2089—
2097.
156. Заславский Г. М. Стохастичность квантовых систем // Нелинейные вол-
пы. Самоорганизация.— М.: Наука, 1983.—С. 96—106; Статистическая
необратимость в нелинейных системах.— М.: Наука, 1970. (Современ-
(Современные проблемы физики.)
157. Заславский Г. М. Стохастичность динамических систем.— М.: Наука,
1984.
158. Заславский Г. М., Чириков Б. В. Стохастическая неустойчивость нели-
нелинейных колебаний // УФН.—1971.—Т. 105, вып. 1.—С. 3—39.
159. Зельдович Я. В., Соколов Д. Д. Фрактали, подобие, промежуточная асим-
асимптотика II УФН.—1985.— Т. 146, вып. 3.— С. 493—506.
160. Израйлев Ф. М. Распределение расстояний между уровнями квази-
квазиэнергии для квантовых систем в классическом пределе.— Препринт/
ИЯФ СО АН СССР.—Новосибирск, 1984.—№ 84—63.
161. Израйлев Ф. М., Рабинович М. И., Угодников А. Д. О Приближенном
описании диссипативных систем со стохастическим поведением.— Пре-
принт/ИПФ АН СССР.— Горький, 1981.— № 17.
162. Израйлев Ф. М., Чириков В. В. Статистические свойства нелинейной
струны / ДАН СССР.— 1966.— Т. 166, № 1— С. 57—59.
163. Израйлев Ф. М., Чириков В. В. Стохастичность простейшей динамиче-
динамической модели с разделенным фазовым пространством.— Препринт/ИЯФ
СО АН СССР.— Новосибирск, 1968.— № 191.
401

164. Израйлев Ф. М., Чириков Б. В., Шепелянский Д. Л. Переходная стоха-
стичность в квантовой механике.— Препринт/ИЯФ СО АН СССР.— Но-
Новосибирск, 1980.—№ 80—120.
165. Илъяшенко Ю. С. О размерности аттрактора К-сжимающих систем в
бесконечномерном пространстве // Вестник МГУ. Сер. 1.— 1983.— Т. 24,
№ 3.- С. 52-59.
166. Йорк Дж. А., Йорк Э. Д. Хаотическое поведение и гидродинамика /
Гидродинамические неустойчивости и переход к турбулентности/Под
ред. X. Суинни, Дж. Голлуба.—М.: Мир, 1984.—С. 101—123.
167. Йосс Ж., Джозеф Д. Элементарная теория устойчивости и бифурка-
бифуркаций.— М.: Мир, 1983.
168. Кадомцев В. В., Рязанов А. И. Что такое синергетика? / Природа.—
1983.—№ 8.—С. 2—11.
169. Кальянов Э. В., Лебедев М. И. Стохастические колебания в системе свя-
заппых генераторов при наличии инерционности // Радиотехника и
электроника.—1985.—Т. 30, № 8.—С. 1570—1576.
170. Канторович Л. В., Крылов В. И. Приближенные методы высшего анали-
анализа.— М.— Л.: Гостехиздат, 1949.
171. Капица П. Л. Динамическая устойчивость маятника при колеблющей-
колеблющейся точке подвеса // ЖЭТФ.—1951.—Т. 21, вып. 5.—С. 588—597.
172. Капранов М. В., Кулешов В. Н., Уткин Г. М. Теория колебаний в ра-
радиотехнике.— М.: Наука, 1984.
173. Капцов Л. Н. Возникновение пичкового режима в неавтономном гене-
генераторе с инерциоппой нелинейностью // Радиотехника и электроника.—
1975.— Т. 20, вып. 12.— С. 2496—2499.
174. КарпманВ. И. Нелинейные волны в диспергирующих средах.— М.: На-
Наука, 1973.
175. Каток А. В. Динамические системы с гиперболической структурой: Тр.
IX летней мат. школы.—Киев: Ин-т математики АН УССР, 1972.—
С. 126-211.
176. Кац В. А. Стохастизация структур и переходы в хаосе в автогенерато-
автогенераторе с запаздыванием // Лекции по электропике СВЧ и радиофизике,
кн. 2.— Саратов: Изд-во СГУ, 1983.— С. 49—64.
177. Кац В. А. Переходы в хаосе, инициированные внешним гармоническим
воздействием, в распределенном автогенераторе с запаздыванием (экс-
(эксперимент).—Там же.— С. 65—68.
178. Кац В. А. Экспериментальная демонстрация .универсальных свойств
последовательности бифуркаций удвоения Фейнгепбаума при переходе
к хаосу в распределенном генераторе с запаздыванием // Письма
ЖТФ.— 1984.— Т. 10, № П.— С. 684—689.
179. Кац В. А. Переход к «развитому хаосу» в модели распределенного гене-
генератора с запаздыванием // Некоторый вопросы современной физики.
Ч. 1.—Саратов: Изд-во СГУ, 1984.—С 31—37.
180. Кац В. А. Механизм возникновения хаоса в распределенном генераторе
обратной волны // Там же, Ч. 2 — С. 28—33.
181. Кац В. А., Кузнецов С. Л. Переход к хаосу через бифуркации удвое-
удвоения периода в модели генератора с запаздывающей обратной связью.
Численпый эксперимент // Там же.— С. 45—48.
182. Кац В. А. Возпикповсние и эволюция хаоса в распределенпом генерато-
генераторе с запаздыванием // Изв. ВУЗов. Радиофизика.—1985,— Т. 28, № 2.—
С. 161—176
183. Кац В. А., Трубецков Д. И. Возникновение хаоса при разрушении ква-
квазипериодических режимов и переходе через перемежаемость в распре-
распределенном генераторе с запаздыванием Ц Письма ЖЭТФ.— 1984.— Т. 39,
вып. 3.— С. 116—119.
184. Кащеневский Л. Я. Стохастические автоколебания при сухом тре-
трении II Инженерпо-физический журнал.— 1984,— Т. 47, № 1,— С. 143—
147.
185. Квантовая радиофизика, т. I, II.— М.: Сов. Радио, 1972.
186. Кислое В. Я. Теоретический анализ пгумоподобных колебаний в элект-
электронно-волновых системах и автогенераторах с запаздыванием // Лек-
402

ции по электронике СВЧ и радиофизике, кн. 5.—Саратов: Изд-во СГУ,
1980.— С. 25-77.
187. Кислое В. Я., Залогин Н. Н., Мясин Е. А. Исследование стохастических
автоколебательных процессов в автогенераторах с запаздыванием /
Радиотехника и электроника.—1979.—Т. 24, № 6.—С. 1118—1130.
188. Кислое В. Я., Мясин Е. А., Богданов Е. В. Генератор СВЧ широкополос-
широкополосных колебаний.— Заявка Кг 964513/19—09 от 31.07.68.
189. Кислое В. Я., Мясин Е. А., Залогин Н. Н. О нелинейной стохастизации
автоколебаний в электронно-волновом генераторе с задержанной обрат-
обратной связью И Радиотехника и электропика.—1980.— Т. 25, № 10.—
С. 2160—2168.
190. Кияшко С. В., Пиковский А. С, Рабинович М. И. Автогенератор радио-
диапазопа со стохастическим поведением // Радиотехника и электро-
электропика.—1980.—Т. 25, Ко 2.—С. 336—343.
191. Климонтович Ю. Л. Броуновское движение в автоколебательных систе-
системах и при фазовых переходах Ц Термодинамика и кинетика биологи-
биологических процессов.— М.: Наука, 1980.— С. 100—118.
192. Климонтович Ю. Л. Статистическая физика.— М.: Наука, 1983.— С. 330—
333, 521—553.
193. Кляцкин В. И. Статистическое описание динамических систем с флук-
флуктуирующими параметрами.— М.: Наука, 1975.
194. Кляцкин В. И. Стохастические уравнения и волны в случайно-пеодпо-
родных средах.— М.: Наука, 1980.
195. Коган В. П. Потеря устойчивости неподвижной точки в окрестности
резонанса 1 :3.— Деп. в ВИНИТИ, № 8068—84.
196. Коган В. П. Бифуркации неподвижных точек двумерпых отображений
в окрестности резонанса 1 : 3.— Деп. в ВИНИТИ, 1985, № 3882—85.
197. Коган В. П., Неймарк Ю. И. Бифуркации фазового портрета в окрест-
окрестности неподвижной точки при резонансе 1:3/ Динамика сис-
стем (оптимизация и адаптация).— Горький: Изд-во ГГУ, 1982.—
С. 115-144.
198. Коган В. п., Неймарк Ю. И. Серии бифуркаций и вложенные структу-
структуры Ц Динамика систем (устойчивость, автоколебания и стохастич-
ность).— Горький: Изд-во ГГУ, 1981.—С. 78—89.
199. Колебательные процессы в биологических и химических системах: Тр.
Всесоюзного симпозиума по колеб. процессам в биол. и хим. системах,
т. 1.— М.: Наука, 1967; т. 2.—Пущино-на-Оке: ОНТИ НЦБИ АН СССР,
1971.
200. Колесов Ю. С. Математические модели экологии // Исследования по
устойчивости и теории колебаний.— Ярославль: Изд-во ЯГУ, 1979.—
С. 3-40.
201. Колесов 10. С, Кубышкин Е. 77. Некоторые свойства решений диффе-
ренциально-разпостных уравнений, моделирующих динамику измене-
изменения численности популяций насекомых // Исследования по устойчиво-
устойчивости и теории колебаний.— Ярославль: Изд-во ЯГУ, 1983.— С. 64—86.
202. Колмогоров А. Н. Новый метрический инвариант транзитивных дина-
динамических систем и автоморфизмов пространств Лебега // ДАН СССР.—
1958,—Т. 119.—С. 861-864.
203. Колмогоров А. Н. Об энтропии на единицу времени, как метрическом
инварианте автоморфизмов II ДАН СССР.—1959.— Т. 124.— С. 754—
755.
204. Колмогоров А. Н, Петровский Г. И., Пискунов В. С. Изучение уравне-
уравнения диффузии с источником вещества и его приложение к биологиче-
биологическим проблемам. // Бюлл. МГУ. Математика и механика.—1937.—Т. 1,
в. 6.— С. 1—26; Вопросы кибернетики, в. 12.— М.: Изд-во АН СССР,
1975.— С. 3; Колмогоров А. Н. Избранные труды. Математика и механи-
механика.— М.: Наука, 1985.— С. 221—246.
205. Корнфельд И. П., Синай Я. Г., Фомин С. В. Эргодическая теория.— М.:
Наука, 1980.
206. Красносельский М. А. Топологические методы в теории нелинейных
интегральных уравнений.— М.: Гостехиздат, 1956.
403

207. Крылов И. С. Работы по обоснованию статистической физики,— М.— Л.:
Изд-во АН СССР, 1950.
208. Крюков Б. И., Середович Г. И. О «странном» поведении решений урав-
уравнения Дуффипга И ДАН СССР.—1981.—Т. 258, № 2.—С. 311—314.
209. Кузнецов С. П. Сложная динамика генераторов с запаздывающей обрат-
обратной связью (обзор) / Изв. ВУЗов. Радиофизика.— 1982.— Т. 25, № 12.—
С. 1410—1428.
210. Кузнецов С. П. О воздействии периодического внешнего возмущения
па систему, демонстрирующую переход порядок — хаос через бифур-
бифуркации удвоения периода // Письма ЖЭТФ.—1984.— Т. 39, вып. 3.—
С. 113—116.
211. Кузнецов С. П.,1 Колосова Г. М. Об одном типе универсального поведе-
поведения связанных систем // ЖЭТФ.—1984.— Т. 86, вып. 3.— С. 998—
1004.
212 Кузнецов С. П., Перельман А. П., Трубецков Д. И. Автомодуляционные
и стохастические режимы в клистроне бегущей волны с внешней об-
обратной связью / ЖТФ.— 1983,— Т. 53, вып. 1.— С. 163—166.
213. Кузнецов С. П., Пиковский А. С. Универсальность бифуркаций удвое-
пия периода в одномерной диссипативной среде // Изв. ВУЗов. Радио-
Радиофизика.— 1985.— Т. 28, № 3.— С. 308—319.
214. Кузнецов 10. И., Ланда П. С, Ольховой А. Ф., Перминов С. М. Порог
синхронизации как характеристика фазового перехода «хаос — поря-
порядок».— Препринт/Физический факультет МГУ.— М., 1984.— № 9/1984.
215. Кузнецов Ю. И., Ланда П. С, Ольховой А. Ф., Перминов С. М., Связь
между амплитудным порогом синхронизации и энтропией в стохастиче-
стохастических автоколебательных системах // ДАН СССР.— 1985.— Т. 281, № 2.—
С. 291—294.
216. Ланда П. С. Автоколебания в системах с конечным числом степеней
свободы.— М.: Наука, 1980.
217. Ланда П. С. Автоколебания в распределенных системах.— М.: Наука,
1983.
218. Ланда П. С. О влиянии шума на переходы к хаосу через перемежае-
перемежаемость // Вестник МГУ. Сер. 3.—1987.—Т. 28, № 5.—С. 25—27.
219. Ланда П. С, Неймарк Ю. И. Хаотические колебания в неравновесных
физических и химических системах: Тр. Института нефтехимического
синтеза АН СССР.— М.: Наука, 1987.
220. Ланда П. С, Ольховой А. Ф., Перминов С. М. Исследование стохастиче-
стохастических автоколебаний в физических системах с инерционным самовозбуж-
самовозбуждением II Изв. ВУЗов. Радиофизика.—1983.—Т. 26, К° 5.—С. 566—572.
221. Ланда П. С, Ольховой А. Ф., Перминов С. М. Эволюция спектров авто-
автоколебаний в зоне стохастичности Ц Вестник МГУ. Сер. 3.— 1984.— Т. 25,
№ 3.— С. 74-77.
222. Ланда п. С, Перминов С. М. Пути возникновения стохастических авто-
автоколебаний в системах с инерционным самовозбуждением / Вестник
МГУ. Сер. 3.— 1985.— Т. 26, Л» 2.— С. 27—30.
223. Ланда П. С, Перминов С. М. Взаимодействие периодических и стохас-
стохастических автоколебаний / Изв. ВУЗов. Радиофизика.—1985.— Т. 28,
№ 4.— С. 424-427.
224. Ланда П. С, Перминов С. М. Сипхропизация хаотических колебаний
в системе Маккея — Гласса // Изв. ВУЗов. Радиофизика.— 1987.— Т. 30,
№ 3.— С. 437—439.
225. Ланда П. С, Перминов С. М. Хаотические колебания нелинейного ос-
осциллятора с параметрическим воздействием // ВИНИТИ.— М., 1986.—
Деп. в ВИНИТИ, № 7098—86.
226. Ланда П. С, Перминов С. М., Шаталова Г. Г., Дамгов В. Н. Стохасти-
Стохастические автоколебапия в генераторе с дополнительной запаздывающей
обратной связью Ц Радиотехника и электроника.— 1986.— Т. 31, Л» 4.—
С. 730-733.
227. Ланда П. С., Стратонович Р. Л. Расчет стационарного распределения ве-
вероятностей для одного из простейших странных аттракторов // ДАН
СССР.— 1982.— Т. 267, № 4.— С. 832—836.
404

228. Ланда П. С, Стратонович Р. Л. Вероятностные характеристики стохас-
стохастических колебаний регулируемого маятника // МТТ.—1984.— № 4.—
С. 26—31.
229. Ланда П. С, Стратонович Р. Л. К теории перемежаемости / Изв. ВУЗов.
Радиофизика.— 1987.— Т. 30, № 1.— С. 65—69.
230. Ландау Л. Д. К проблеме турбулентности / ДЛН СССР.— 1944 — Т. 44,
№ 8.— С. 339—342.
231. Ландау Л. Д., Лифшиц Е. М. Механика сплошных сред.— М.: Гостех-
издат, 1953; Гидродинамика ■—М.: Наука, 1986.
232. Ландау Л. Д., Лифшиц Е. М. Статистическая физика.—М.: Наука, 1964.
233. Леонов Г. А. О глобальной устойчивости системы Лоренца / ИММ.—
1983.—Т. 47, вып. 5.—С. 861—863.
234. Леонов П. II. О точечном преобразовании прямой в прямую // Изв.
ВУЗов. Радиофизика.— 1959.—Т. 2, № 6.—С. 942—956.
235. Леонов Н. Н. К теории разрывного преобразования прямой в прямую //
Изв. ВУЗов. Радиофизика.— I960.— Т. 3, Кг 5.— С 872—886.
236 Леонтович-Андронова Е, А., Неймарк Ю. И. Об одной особой бифурка-
бифуркации динамической системы в трехмерном пространстве, связаниой с ис-
исчезновением периодического решения: В сб. докл. политехи, ип-та.—
Ташкент, 1964.— С. 132—139.
237. Лихтенберг А., Либерман М. Регулярная и стохастическая динамика.—
М.: Мир, 1984.
238. Лукащук С. И., Предтеченский А. А., Фалькович Г. Е., Черных А. И.
О вычислении размерностей аттракторов по экспериментальным дан-
данным.— Препринт/СО АН СССР.— Новосибирск, 1985.— Кг 280.
239. Люстерник Л. А., Соболев В. И. Элементы функционального анализа.—
М.: Наука, 1965.
240. Ляпунов А. М. Собр. соч., т. 1, 2.— М.: Изд-во АН СССР, 1954—1956.
241. Ма Ш. Современная теория критических явлений.— М.: Мир, 1980.
242. Майер А. Г. Грубое преобразование окружности / Уч. зап. ГГУ.—
1939.— Вып. 12.— С. 215—230.
243. Малкин И. Г. Методы Ляпунова и Пуанкаре в теории нелинейных ко-
колебаний.—М.: Гостехиздат, 1949.
244. Малкин И. Г. Теория устойчивости движения.— М.: Наука, 1966.
245. Мандельштам Л. И. Собр. трудов, т. IV; Лекции по колебаниям A930—
1932 гг.).— М.: Изд-во АН СССР, 1955.
246. Марсден Дж., Мак-Кракен М. Бифуркация рождения цикла и ее при-
приложения.— М.: Мир, 1980.
247. Маслов В. П., ФеЬорюк М. В. Квазиклассическое приближение для урав-
уравнений квантовой механики.— М.: Наука, 1976.
248. Маторин И. И., Пиковский А. С, Ханин Я. И. Мультистабильность и
автостохастичность в лазере с инерционной активной средой при пе-
периодической модуляции потерь // Квантовая электроника.—1984.— Т.
11, № 10.—С. 2096—2103.
249. Маторин И. И., Ханин Я. И. Автостохастические явления в лазерах //
Лекции по электронике СВЧ и радиофизике, кн. 2.— Саратов: Изд-во
СГУ, 1983.— С. 23—31.
250. Мельников В. К. Устойчивость центра при периодических по времепи
возмущениях // Тр. Московского мат. об-ва.— 1963.— Т. 12.— С. 3—52.
251. Жигулин В. В., Медведев В. И., Мустель Е. Р<, Парыгин В. Н. Основы
теории колебаний.— М.: Наука, 1978.
252. Митрополъский Ю. А. Метод усреднения в нелинейной механике.— Ки-
Киев: Наукова думка, 1971.
253. Михлин С. Г. Вариационные методы в математической физике.— М.:
Наука, 1970.
254. Мишенков Ф. М, Моторов В, М., Моторова Э. А. Устойчивость естест-
естественного тепломассопорепоса.— М.: Атомиздат, 1976.
255. Мозер Ю. Лекции о гамильтоновых системах.— М.: Мир, 1973.
256. Молчанов А. М. О резонансной структуре солнечной системы // Совре-
Современные проблемы небесной механики и астродинамики.— М.: Наука,
1973.— С. 32-41.
405

257. Ионии А. С. О природе турбулентности / УФН.— 1978.— Т. 125, в. 1.—
С. 97—122; Гидродинамическая неустойчивость II УФН.—1986.— Т. 150,
в. 1.-С. 61-105.
258. Моторова Э. А., Неймарк 10. И. Об устойчивости нелинейной распреде-
распределенной модели естественной циркуляции // Автоматика и телемеха-
телемеханика.— 1974, № 3,— С. 28—36.
259. Неймарк Ю. И. Метод точечных отображений в теории нелинейных ко-
колебаний. I, II, III I/ Изв. ВУЗов. Радиофизика.— 1958.—-.Ш 1.—С. 5—6,
41-66; № 2.- С. 95-117; № 5-6.- С. 146-165.
260. Неймарк Ю. И. О некоторых случаях зависимости периодических дви-
движений от параметров / ДАН СССР.—1959.—Т. 129, Л"» 4.—С. 736—739.
261. Неймарк Ю. И. Метод точечных отображений в теории нелинейных ко-
колебаний: Тр. Междунар. симп. по нелин. колеб., т. 2.—Киев: Изд-во
АН УССР, 1963.— С. 268—307.
262. Неймарк Ю. И. Некоторые методы исследования динамических систем:
Тр. 2-го Всес. съезда по теор. и прикл. мех., вып. 2.— М.: Наука, 1965.—
С. 97—111.
263. Неймарк Ю. П. О движениях, близких к двоякоасимптотическому дви-
движению / ДАН СССР.—1967.—Т. 172, № 5.—С. 1021—1024.
264. Неймарк Ю. И. О существовании и грубости инвариантных многообра-
многообразий точечных отображений / Изв. ВУЗов. Радиофизика.— 1967.— Т. 10,
№ 3.- С. 311-320.
265. Неймарк Ю. И. Интегральные многообразия дифференциальных урав-
уравнений.—Изв. ВУЗов. Радиофизика.—1967.—Т. 10, № 3.— С. 321—334.
266. Неймарк Ю. И. Структура движений динамической системы в окрестно-
окрестности гомоклинической кривой: Тр. V летней мат. школы, 1967.— Киев:
Ип-т мат. АН УССР, 1968.— С. 400—433.
267. Неймарк Ю. И. Метод точечных отображений в теории нелинейных ко-
колебаний / Механика в СССР за 50 лет.—М.: Наука, 1968.—С. 137—156.
268. Неймарк Ю. И. Об одном классе динамических систем: Тр. Междунар.
симп. по нелин. колеб., т. 2.—Киев: Изд-во АН УССР, 1970.—С. 363—
376.
269. Неймарк Ю. И. Метод точечных отображений в теории нелинейных ко-
колебаний.— М.: Наука, 1972.
270. Неймарк Ю. И. Стохастичпость в динамических системах // Теория ко-
лебапий, прикладная математика и кибернетика.— Горький: Изд-во
ГГУ, 1973.—С. 3—11.
271. Неймарк Ю. И. Стохастические движения динамических систем / Ди-
Динамика систем, вып. 7.— Горький: Изд-во ГГУ, 1974.— С. 3—50.
272. Неймарк Ю. И. О возникновении стохастичности в динамических систе-
системах / Изв. ВУЗов. Радиофизика.—1974.— Т. 17, № 4.— С. 602—607.
273. Неймарк Ю. И. Синхронизация и стохастичпость Ц Фазовая синхрони-
синхронизация.—М.: Сбязь,'1975.— С. 64—82.
274. Неймарк 10. И. Гомоклинические структуры и резонансы // Динамика
систем, в. 9.— Горький: Изд-во ГГУ, 1976.— С. 53—59.
275. Неймарк Ю. И. Символическая динамика, порождаемая гомоклипиче-
скими структурами // Дифференциальные уравнения.—1976.— № 2.—
С. 256—262.
276. Неймарк Ю. И. Особые интегральные многообразия и возникновение
сто*астичности в дипамических системах: Тр. конф. памяти Н. Г. Че-
таева (Иркутск, 1977).—Новосибирск: Наука, 1979.—С. 128—134.
277. Неймарк Ю. И. Инвариантные многообразия и стохастические движе-
движения динамических систем // Проблемы асимптотической теории нели-
нелинейных колебаний.— Киев: Наукова думка, 1977.— С. 160—168.
278. Неймарк Ю. И. Теория нелинейных колебаний и стохастические движе-
движения динамических систем II Динамика систем, вып. 12.— Горький: Изд-
во ГГУ, 1977.— С. 74—95.
279. Неймарк Ю. И. Синхронизация и стохастичность: VII Intern Konf. tiber
nichtlineare Schwingungen, b. 1, 2.— Berlin: Academie, 1977.— S. 133—146.
280. Неймарк Ю. И. Динамические системы и управляемые процессы.— М.:
Наука, 1978.
406

281. Неймарк Ю. И. О возникновении стохастичности в динамических систе-
системах: Тр. Всес. конф. Асимптотические методы в теории нелинейных
колебаний.—Киев: Паукова думка, 1979.—С. 133—141.
282. Неймарк Ю. И. Хаотические и стохастические автоколебания // Качест-
Качественные методы исследования дифференциальных уравнений и нели-
нелинейных колебаний.—Киев: Ип-т мат. АН УССР, 1981.—С. 99-115.
283. Неймарк 10. И., Баталова 3. С, Белякова Г. В., Ежевская Н. Е., Ко-
Коган Л. В., Ходова А. Ф. Алгоритмы и программы численпого исследо-
исследования динамических систем.— Горький: Изд-во ГГУ, 1983.
284. Неймарк 10. И., Баталова 3. С, Васин Ю. Г., Брейдо М. Д. Распознава-
Распознавание образов и медицинская диагностика.— М.: Наука, 1972.
285. Неймарк 10. И., Коган В. П., Гуртовник А. С. О гладкости по перемен-
переменным и параметру инвариантных поверхностей точечных отображений
в банаховом пространстве // Динамика систем, оптимизация и адапта-
адаптация, вып. 14.— Горький: Изд-во ГГУ, 1978.—С. 115—142.
286. Неймарк 10. И., Коган Н. Я., Савельев В. П. Динамические модели тео-
теории управления.— М.: Наука, 1985.
287. Неймарк Ю. И., Фуфаев II. А. Метод точечных отображений и его при-
приложения к исследованию динамических систем / Успехи механики.—
1980.— Т. 3, вып. 4.— С. 23—53.
288. Неймарк Ю. И., Шилъников Л. П. Об одном случае рождения периоди-
периодических движений И ДАН СССР.—1965.— Т. 160, А» 6.— С. 1261—1264.
289. Неймарк Ю. И., Шилъников Л. П. Об одном случае рождения периоди-
периодических движений II Изв. ВУЗов.— Радиофизика.— 1965.— Т. 8, №. 2.—
С. 330-340.
290. Нейштадт Л. П. Бифуркации фазового портрета одной системы, возни-
возникающей в задаче о потере устойчивости автоколебаний вблизи резонан-
резонанса 1 :4 // ПММ.—1978.— Т. 48, вып. 5.- С. 830-840.
291. Нелинейные волны // Изв. ВУЗов. Радиофизика.—1974.—Т. 17, №4.
292. Нелинейные волны // Изв. ВУЗов. Радиофизика.—1976.—Т. 19, № 5, 6.
293. Нелинейные волны. Стохастичпость и турбулентность.— Горький: ИПФ
АН СССР, 1980.
294. Николис Г., Пригожий И. Самоорганизация в неравновесных системах.—
М.: Мир, 1979.
295. Нитецки 3. Введение в дифференциальную динамику.— М.: Мир, 1975.
296. Ораевский А. Н. Мазеры, лазеры и странные аттракторы Ц Квантовая
электропика.—1981.—Т. 8, № 1.—С. 130—142.
297. Оселедец В. И. Мультипликативная эргодическая теорема. Характери-
Характеристические показатели Ляпунова динамических систем // Тр. Моск.
мат. об-ва.—1968.—Т. 19.—С. 179—210.
298. Наташинский А. 3., Покровский В. Л. Флуктуационпая теория фазовых
переходов.— М.: Наука, 1982.
299. Первозванский А. А. Случайные процессы в нелинейных системах.— М.:
Физматгиз, 1962.
300. Перминов С. М., Добровольский В. А., Аникеев Г. И., Генкин М. Д. Про-
Процесс перемешивания жидкости в плоском канале Ц ЖТФ.—1987.—
Т. 57, № 1.— С. 171—173.
301. Лесин Я. Б. Характеристические показатели Ляпунова и гладкая эрго-
эргодическая теория / УМН.—1977,—Т. 32, № 4.—С. 55—112.
302. Петровская Н. В., Юдович В. И. Гомоклинные петли системы Зальцма-
Зальцмана — Лоренца/ВИНИТИ.- М., 1980.- Деп. в ВИНИТИ, № 2380—79.
303. Пиковский А. С. О статистических свойствах простейшей модели сто-
стохастических автоколебаний / Изв. ВУЗов. Радиофизика.— 1980.— Т. 23,
№ 7.— С. 883—884.
304. Пиковский А. С. О влиянии флкутуаций па переход к перемежающей-
перемежающейся стохастичпости.— Препринт.— Горький, 1981.— № 39.
305. Пиковский А. С. О поведении спектра странного аттрактора в критиче-
критической точке. / Изв. ВУЗов. Радиофизика.— 1982.— Т. 25, № 7.— С. 846—
848.
306. Пиковский А. С. Хаотические автоволпы / Письма ЖТФ.—1985,—Т. 11,
вып. П.—С. 672—675.
407

307. Плисе В. А. Нелокальные проблемы теории колебаний.— М.: Наука, 1964.
308. Покровский Л. А. Решение системы уравнений Лоренца в асимптоти-
асимптотическом пределе большого числа Рэпея // Теор. и мат. физика.—1985.—
Т. 62, № 2.- С. 272-290.
309. Полак Л. С, Михайлов А. С. Самоорганизация в неравновесных физи-
физико-химических системах.— М.: Наука, 1983.
310. Понтрягин Л. С, Андронов А. А., Витт А. А. О статистическом рассмот-
рассмотрении динамических систем / 5КЭТФ.— 1933.— Т. 3, вып. 3.— С. 165—
180; Собр. соч. А. А. Андронова.— М.: Изд-во АН СССР, 1956.— С. 142—
160.
311. Пуанкаре А. О кривых, определяемых дифференциальными уравнени-
уравнениями.— М.— Л.: ОГИЗ, 1947.
312. Пуанкаре А. Избр. труды, т. И.— М,: Наука, 1972.
313. Рабинович М, И. Стохастические автоколебания в. радиофизике и гид-
гидродинамике. Эксперименты и модели Ц Нелинейные волны. Стохастич-
ность и турбулентность.— Горький: ИПФ АН СССР, 1980.— С. 5—23Ч
314. Рабинович М. И., Трубецков Д. И. Введение в теорию колебаний и
волн.—М.: Наука, 1984.
315. Рабинович М.Й., Фабрикант А. Л. Стохастическая автомодуляция волн в
неравновесных средах // ЖЭТФ.— 1979.— Т. 77, вып. 2(8).— С. 617—629.
316. Риман Б. Сочинения.— М.: Гостехиздат, 1948.
317. Рихтмайер Р. Принципы современной математической физики, т. 2.—
М.: Мир, 1984.
318. Розенвассер Е. Н. Колебания нелинейных систем.— М.: Наука, 1969.
319. Романовский Ю. М., Степанова Н. В., Чернавский Д. С. Математическая
биофизика.— М.: Наука, 1984.
320. Рытое С. М. Введение в статистическую радиофизику.— М.: Наука, 1966.
321. Рэнд Д. Топологическая классификация аттракторов Лоренца // Стран-
Странные аттракторы.— М.: Мир, 1981.— С. 239—251.
322. Сбитнев В. И. Стохастичность в системе двух связанных вибраторов Ц
Нелинейные волны. Стохастичность и турбулентность.— Горький: ИПФ
АН СССР, 1980.— С. 46—56.
323. Сбитнев В. И. Стохастичность в системе связанных осцилляторов: Тр.
IX Межд. конф. по нелин. колеб., т. 3.— Киев: Наукова думка, 1984.—
С. 477—479.
324. Синай Я, Г. О понятии энтропии динамической системы // ДАН СССР.—
1959.— Т. 124, № 4.— С. 768—771.
325. Синай Я. Г. Марковские разбиения и У-диффеоморфизмы // Функц.
анализ и его приложения.— 1968.— Т. 2, Л"» 1.— С. 64—89.
326. Синай Я. Г. Динамические системы с упругими отражениями // УМН.—
1970.— Т. 25,-№ 2.— С. 141—192.
327. Синай Я. Г. Теория фазовых переходов.— М.: Наука, 1980.
328. Синай Я. Г. Случайность неслучайного II Природа.—1981.— № 3.—
С. 72-80.
329. Синергетика/Под ред. Б. Б. Кадомцева.— М.: Мир, 1984.
330. Смейл С. Структурно устойчивые гомеоморфизмы с бесконечным чис-
числом периодических точек: Тр. Междунар. симп. по нелип. колеб.— Ки-
Киев: АН УССР, 1963.— С. 365—366.
331. Смейл С. Структурно устойчивые системы пе всюду плотны // Матема-
Математика.— 1967.— Т. 11 : А — С. 107—112.
332. Смейл С. Дифференцируемые динамические системы / УМН.—1970.—
Т. 25, № 1.—С. 113—185.
333. Смоэс М. Химические волны в колебательной системе Жаботипского.
Переход от временной организации к пространственно-временной //
Синергетика/Под ред. Б. Б. Кадомцева.—М.: Мир, 1984.—С. 139—163.
334. Соболев С. А. О смешанных задачах для уравнений в частных произ-
производных с двумя независимыми переменными / ДАН СССР.—1958.—
Т. 122, № 4.- С. 555—559.
335. Солнцев В. А., Андреевская Т. М. Условия амплитудной автомодуляции
в автогенераторе с запаздыванием / Радиотехника и электроника.—
1983.— Т. 28, № 3.— С. 561-568.
408

336. Сонечкин Д. М. Стохастичность в моделях общей циркуляции атмосфе-
атмосферы.— Л.: Гидрометеоиздат, 1984.
337. Старжинский В. М. Прикладные методы нелинейных колебаний.—М.:
Наука, 1977.
338. Стенли Г. Фазовые переходы и критические явления.— М.: Мир, 1973.
339. Стенли, X., Канильо А., Клейн У., Наканиси X., Реднер С, Рейнольде П.,
Шли-фер Г. Критические явления: прошлое, настоящее и «будущее» //
Синергетика/Под ред. Б. Б. Кадомцева.— М.: Мир, 1984.— С. 41—63.
340. Стокер Дж. Нелинейные колебания в механике и электрических систе-
системах.— М.: ИЛ, 1952.
341. Странные аттракторы/Под ред. Я. Г. Синая и Л. П. Шильникова.— М.:
Мир, 1981.
342. Стратонович Р. Л. Избранные вопросы теории флуктуации в радиотех-
радиотехнике.— М.: Сов. Радио, 1961.
343. Стратонович Р. Л. Корреляторы процессов в простейших системах со
страдными аттракторами // ДАН СССР.—1982.—Т. 267, № 2.—С. 355—
344. Стратонович Р. Л., Николаевский Е. С. О последовательности бифурка-
бифуркаций движения странных аттракторов при их дроблении в случае про-
простых систем // ДАН СССР.— 1984.— Т. 276, № 2.— С. 363—366.
345. Стрелков С. п. Введение в теорию колебаний.— М.: Наука, 1964.
346. Стрэтт Дж. (Рэлей). Теория звука.— М.: Гостехиздат, 1955.
347. Теодорчик К. Ф. Автоколебательные системы.— М.: Гостехиздат, 1952.
348. Тимошенко С. П. Теория колебаний в инженерном деле.— М.: Физмат-
гиз, 1959.
349. Тондл А. Нелинейные колебания в механических системах.—М.: Мир,
1973.
350. Тондл А. Автоколебания механических систем.— М.: Мир, 1979.
351. Труженикова В. Н. Условия рождения периодического движения из
состояния равновесия Ц Изв. Вузов. Радиофизика.— 1962.— Т. 5, № 2.
352. Уизем Дж. Линейные и нелинейные волны.— М.: Мир, 1977.
353. Фейнман Р. Ф., Лейтон Р., Сэндс М. Фейнмановские лекции по физике.
Т. 7 (Физика сплошной среды).— М.: Мир, 1966.
354. Фуфаев Н. А. Теория электромагнитного прерывателя: Памяти А. А. Ан-
Андронова.— М.: Изд-во АН СССР, 1955 — С. 334—382.
355. Хакен Г. Явления перехода и переходные процессы в нелинейных си-
системах / Синергетика/Под ред. Б. Б. Кадомцева.— М.: Мир, 1984.—
С. 7—17.
356. Хакен Г. Синергетика.— М.: Мир, 1980; Синергетика. Иерархии неус-
тойчивостей в самоорганизующихся системах и устройствах.— М.: Мир,
1985.
357. Хандохин П. А., Ханин Я. И. Автостохастический режим генерации
твердотельного кольцевого лазера с низкочастотной периодической мо-
модуляцией потерь II Квантовая электроника.—1984.— Т. 11, № 7.—
С. 1483-1487.
358. Харкевич А. А. Автоколебапия.— М.: Гостехиздат, 1953.
359. Хаяси Т. Нелинейные колебания в физических системах.— М.: Мир, 1968.
360. Хейл Дж. Колебания в нелинейных системах.— М.: Мир, 1966.
361. Хентов А. А. Синхронизация спутников // Динамика систем.— Горький:
Изд-во ГГУ, 1974.—С. 51—102.
362. Хинчин А. Я. Теория корреляции стационарных стохастических про-
процессов / УМН.— 1938.— Вып. 5.— С. 42—51.
363. Хопф Э. Статистика геодезических линий на многообразиях отрицатель-
отрицательной кривизны II УМН.— 1949.— Т. 4, вып. 2.— С. 129—170.
364. Хотунцев Ю. Л., Тамарчак Д. Я. Синхронизованные генераторы и ав-
автодины на полупроводниковых приборах.— М.: Радио и связь, 1982.
365. Четаев А. Н. Нейронные сети и цепи Маркова.— М.: Наука, 1985.
366. Чириков Б. В. Стохастические волновые процессы.— Препринт/
НИРФИ.— Горький, 1973.- № 42.
367. Чумаков Г. А., Слинько М. Г. Кинетическая турбулентность (хаос) ско-
скорости реакции взаимодействия водорода с кислородом на металличе-
409

ских катализаторах / ДАН СССР.—1982.—Т. 266, № 5,—С. 1194—1198.
368. Шарковский А. Н. Сосуществование циклов непрррывного преобразова-
преобразования прямой в себя II Укр. мат. журнал.— 1964.— Т. 26, № 1.— С. 61— 71.
369. Шилъников Л. П. Некоторые случаи рождения периодических движений
от особых траекторий ff Мат. сб., 1963.—Т. 61 A04), № 4.—С. 433—446.
370. Шилъников Л. П. Об одном случае существования счетного множества
периодических движений ff ДАН СССР.—1965.— Т. 160, № 3.— С. 558—
561.
371. Шилъников Л. П. О рождении периодических движений из траектории,
идущей из состояния равновесия типа седло — седло в него же / ДАН
СССР.—1966.—Т. 170, Л» 1.—С. 49—52.
372. Шилъников Л. П. О существовании счетного множества периодических
движений в окрестности гомоклинической кривой / ДАН СССР.—
1967.—Т. 172, № 2.—С. 298—301.
373. Шилъников Л. П. Об одной задаче Пуанкаре — Биркгофа ff Мат. сб.—
1967.—Т. 74 A16), № 3.—С. 378—397.
374. Шилъников Л. П. К вопросу о структуре окрестности гомоклинической
трубы инвариантного тора ff ДАН СССР.—1968.— Т. 180, № 2,— С. 286—
289.
375. Юдович В. И. Асимптотика предельных циклов системы Лоренца при
больших числах Рэлея/ВИНИТИ.— М., 1979.—Деп. в ВИНИТИ,
№ 2611-78.
376. Abraham N. В. A New Focus on Laser Instabilities and Chaos ff Laser
Focus.— 1983.— No 5.— P. 73—81.
377. Abraham N. В., Dangoisse D., Glorieux P., Mandel P. Observation of Un-
Undamped Pulsations in a Low-Pressure, Far-Infrared Laser and Compari-
Comparison with a Simple Theoretical Model ff J. Opt. Soc. Amer. В.— 1985.—
V. 2, No 1 — P. 23—34.
378. Abraham N. В., Lugiato L. A., Mandel P., Narducci L. M., Bandy D. K.
Steady-State and Unstable Behavior of a Single-Mode Inhomogeneously
Broadened Laser.— Ibid. P. 35—46.
379. Aceves A., Adachihara H., Jones C, Lerman J. C, McLaughlin D. W.,
Moloney J. W., Newell A. C. Chaos and Coherent Structures in Partial
Differential Equations ff Physica D.—1986.—V. 18.—No 1—3.—P. 85—
112.
380. Adler R. L., Konheim A. G., McAndrew M. H. Topological Entropy /
Trans. Amer. Math. Soc—1965.—V. 114, No 2.—P. 309—319.
381. Afraimovich V. S., Sil'nikov L. P. On Strange Attractors and Quasi-At-
tractors ff Nonlinear Dynamics and Turbulence.— Boston — London —
Melbourn, 1983.— P. 1—34
382. Alekseev V. M., Yakobson Щ. V. Symbolic Dynamics and Hyperbolic Dy-
Dynamic Systems / Pbys. Rep.— 1981.— V. 75, No 5.— P. 290—325.
383. Alekseev V. V., Kornllovsky A. N. Ecosystems Stochasticity Model ff Eco-
Ecological Modelling— 1985 — V. 28.— P. 217—229.
384. Andrade R., Rauh A. Nonlinear Stability Analysis of the Lorenz Model
Lyapunov's Direct Method / Z. Phys,—1983.—B. 50. No 2.—S. 151—159.
385. Arecchi F. Т., Badti R., Politi A. Low-frequency Phenomena in Dynami-
Dynamical Systems with Many Attractors ff Phys. Rev. A.—1984.— V. 29, No 2,—
P. 1006-1009.
386. Arecchi F. Т., Lisi F. Hopping Mechanism Generating 1// Noise in Non-
Nonlinear Systems / Phys. Rev. Lett.— 1982.— V. 49, No 2.— P. 94—98.
387. Arecchi F. Т., Meacci R., Pnccioni G., Tredicce J. Experimental Evidence
of Subharmonic Bifurcations, Multistability and Turbulence in a Q-swit-
ched Gas Laser / Phys. Rev. Lett.—1982.—V. 49, No 17.—P. 1217—1220.
388. Armstrong J. A., Bloembergen N., Ducning I., Pershan P. S. Interactions
between Light Waves in a Nonlinear Dielectric ff Phys. Rev.—1962.—
V. 127, No 6.— P. 1918—1939.
389. Arneodo A., Coullet P. H., Spiegel E. A. Cascade of Period Doublings of
Tori // Phys. Lett— 1983- V. 94A, No l.-P. 1—4.
390. Aronson D. G., Chory M. A., Hall G. F., McGehee R. P. Bifurcations from
an Invariant Circle tor Two-Parameter Families of Maps ot tne Plane: a
410

Computer-Assisted Study // Comm. Math. Phys.—1982.—V. 83, No 3.—
P. 303—354.
391. Babitzky V. I., Landa P. S. Auto-oscillation Systems with Inertial Self-
Excitation // ZAMM.— 1984 — B. 64, No 8 — S. 329—339.
392. Babitzky V. I., Landa P. S., Olhovoy A. F., Perminov S. M. Stochastical
Behavior of Auto-Oscillation Systems with Inertial Self-Excitation /
ZAMM.— 1986.— B. 66, No 2.— S. 73—81.
393. Bar-Eli K. On the Stability of Coupled Chemical Oscillators // Physica
D.— 1985 — V. 14, -No 2.— P. 242—252.
394. Beiersdorjer P., Wersinger J. M. Topology of the Invariant Manifolds of
a Period-doubling Attractors for Some Forced Nonlinear Oscillators //
Phys. Lett.— 1983.— V. 96A, No 6.— P. 269—272.
395. Belyaev Yu. N, Monakhov A. A., Scherbakov S. A., Yavorskaya I. M. So-
Some Routes to Turbulence in Spherical Couette Flow // LaminaT— Turbu-
Turbulent Transition. IUTAM Symp. Novosibirsk 1984.—Berlin — Heidelberg:
Springer, 1985.—P. 669—676.
396. Benett D., Bishop A. R., Trnllinger S. E. Coherence and Chaos in the Dri-
Driven, Damped Sine-Gordon Chain // Z. Phys. В.— 1982.— В. 47, No 3.—
S. 265-277.
397. Benettin G., Froeschle C, Scheidecker J. P. Kolmogorov Entropy of a Dy-
Dynamical System with an Increasing Number of Degrees of Freedom /
Phys. Rev. A.—1979.—V. 19, No 6.—P. 2454—2460.
398. Benettin G., Galgani L. Lyapunov Characteristic Exponents and Stochas-
ticity /I Intrinsic Stochasticity in Plasmas /Ed. by G. Laval, D. Gressi-
lon.— Orsay: Les editions de physique courtaboeuf, 1979.— P. 93—114.
399. Benettin G., Galgani L., Giorgilli A., Strelcyn J. M. Lyapunov Characteris-
Characteristic Exponents for Smooth Dynamical Systems and for Hamiltonian Sys-
Systems; a Method for Computing All of them. P. 1, 2 // Meccanica.— 1980.—
V. 15, No 1.— P. 9—20, 21—30.
400. Benettin G., Galgani L., Strelcyn J. M. Kolmogorov Entropy and Numeri-
Numerical Experiments // Phys. Rev. A.—1976.—V. 14, No 6.—P. 2338—
2342.
401. Ben-Jacob E., Goldhirsch I., Imry Y., Fishman S. Intermittent Chaos in
Josephson Junctions // Phys. Rev. Lett— 1982.— V. 49, No 22 — P 1599—
1602.
402. Berman G. P., Iomin A. M., Zaslavsky G. M. Method of Quasiclassical Ap-
Approximation for C-number Projection in Coherent States Basis // Physi-
Physica D.— 1981.— V. 4D, No i, 2 — P. 113—121.
403. Berman G. P., Kolovsky A. R. Correlation Function Behavior in Quantum
Systems which are Classically Chaotic II Physica D.—1983.—V. 8D,
No 1, 2 —P. 117-141.
404. Berman G. P., Kolovsky A. R. Dynamics of Classically Chaotic Quantum
Systems in Wigner Representation /I Physica D.— 1985.— V. 17D, No 2.—
P. 183—197.
405. Berman G. P., Zaslavsky G. M. Quantum Mappings and the Problem of
Stochasticity in Quantum Systems // Physica A.— 1982.—V. 111A, No 1.—
P. 17—44.
406. Bishop A. R., Fesser K., Lomdahl P. S,, Trullinger S. E. Influence of So-
litons in the Initial State on Chaos in the Driven Damped Sine-Gordon
System /I Physica D — 1983.— V. 7D, No 1—3.— P. 259—279.
407. Bishop A. R., Lomdahl P. S. Nonlinear Dynamics in Driven, Damped Si-
Sine-Gordon Systems // Physica D.— 1986.— V. 18D, No 1—3.— P. 54—66.
408. Bohr Т., Bak P., Jensen M. H. Transition to Chaos by Interaction of Re-
Resonances in Dissipative Systems. II Josephson Junctions, Charge-Density
Waves, and Standard Maps II Phys. Rev. A.—1984.— V. 30, No 4.—
P. 1970—1981.
409. Boldnghini C, Franceschini V. A Five-Dimensional Truncation of the Pla-
Plane Incompressible Navier-Stokes Equations U Comm. Math. Phys.—
1979.—V. 64, No 2.—P. 159—170.
410. Born M. Vorhersagbarkeit in der klassischen Mechanik // Z. Physik —
1958.— B. 153, No 3— S. 372—388,
411

411. Brandstdter A., Swift J., Swinney H. L, Wolf A. Low-Dimensional Chaos
in a Hydrodynamic System II Phys. Rev. Lett.— 1983.— V. 51, No 16.—
P. 1442-1445.
412. Casati G., Chirikov B. V., Israilev F. M., Ford J. Stochastic Behavior of a
Quantum Pendulum under a Periodic Perturbation // Lect. Notes in
Phys.— Berlin: Springer.— 1979.— V. 93.— P. Э34—352.
413. Chaos and Statistical Methods/Ed. Y. Kuramoto.— Berlin: Springer,
1981
414. Chandrasekhar S. Hydrodynamic and Hydromagnetic Stability.— Oxford:
Clarendon Press, 1961.
415. Chay T. R. Chaos in a Three-Variable Model of an Excitable Cell / Phy-
sica D.— 1985.— V. 16D, No 2.— P. 233—242.
416. Chenciner A., looss G. Bifurcations de Tores Invariants II Arch. Rat. Mech.
Anal — 1979- V. 69, No 2 — P. 109-198.
417. Chenciner A., looss G. Persistance et Bifurcation de Tores Invariants /
Arch. Rat. Mech. Anal—1979.—V. 71, No 4.—P. 301—306.
418. Chirikov B. V. A Universal Instability of Many-Dimensional Oscillator
Systems // Phys. Rep.— 1979.— V. 52, No 5.— P. 263—379.
419. Chni S. Т., Ma К. В. Nature of Some Chaotic States for Duffing's Equati-
Equation / Phys. Rev. A.— 1982.— V. 26, No 4.— P. 2262—2265.
420. Collet P., Eckmann J. P., Koch H. Period Doubling Bifurcations for Fa-
Families of Maps on Rn I/ J. Stat Phys.—1981.— V. 25, No 1.— P. 1—14
421. Collet P., Eckmann J. P., Lanford О. Е. Universal Properties of Maps on
a Interval // Comm Math. Phys.—1980.—V. 76, No 3.—P. 211—254.
422. Crawford J. D., Cary J. R. Decay of Correlations in a Chaotic Measure-
Preserving Transformation II Physica D.— 1983.— V. 6D, No 2.— P. 223—
232.
423. Croquette V., Poiton C. Cascade of Period Doubling Bifurcations and Lar-
Large Stochasticity in the Motions of a Compass II 1. Physique.—1981.—
V. 42, No 24 — P. 537—539.
424. Crntchfield J. P., Farmer J. D., Haberman B. A. Fluctuations and Simple
Chaotic Dynamics / Phys. Rep.—1982 —V. 92, No 2.—P. 45—82.
425. Cratchfield J. P., Farmer J. D., Packard N., Shaw R., Jones G., Donne-
ly R. J. Power Spectral Analysis of a Dynamical Systems /'Phys. Lett.—
1980.— V. 76A, No 1.— P. 1—4
426. Cratchfield J. P., Packard N. II. Symbolic Dynamics of One-Dimensional
Maps: Entropies, Finite Precision and Noise II Int. J. Theor. Phys.—
1982— V. 21, No 6-7.— P. 433-446.
427. Cratchfield J. P., Packard N. H. Symbolic Dynamics of Noisy Chaos I/
Physica D.— 1983.— V. 7D, No 1—3.— P. 201—223.
428. Dadio H. Resonance and Intermittent Transition from Torus to Chaos in
Periodically FoTced System near Intermittency Threshold // Progr. Theor.
Phys. Japan.— 1983.— V. 70, No 3.— P. 879—882.
429. Davidson R. C. Methods in Nonlinear Plasma Theory, ch. 6.— N. Y.: Aca-
Academic, 1972.
430. Derrida В., Gervois A., Pomeau Y. Universal Metric Properties of Bifur-
Bifurcations of Endomorphisms II J. Phys. A.— 1979.— V. 12, No 3.— P. 269—
296.
431. Destine M. W., Gibbs H. M., Hopf F. A., Kaplan D. L. Bifurcation Gap in
a Hybrid Optically Bistable System // Phys. Rev. A.—1982.—V. 26,
No 6.—P. 3720—3722.
432. D'Hamieret D., Beasley M. R., Haberman B. A., Libchaber A. Chaotic Sta-
States and Routes to Chaos in the Forced Pendulum II Phys. Rev. A.—
1982 — V. 26, No 6.— P. 3483—3496.
433. Eckmann J.-P. Roads to Turbulence in Dissipative Dynamical Systems /f
Rev. Mod. Phys.—1981.—V. 53, No 4, P. 1.—P. 643—654. (Имеется пере-
перевод: Экман Ж.-П. Переход к турбулентности в диссипативных динами-
динамически системах // Сипергетика/Иод ред. Б. Б. Кадомцева.— М.: Мир,
1984 —С. 190—219.)
434 Eckmann J.-P., Ruelle D. Ergodic Theory of Chaos and Strange Attrac-
tors II Rev. Mod. Phys.— 1985.— V. 57, No Э, P. 1.— P. 617—656.
412

435. Eckmann J.-P., Thomas L., Wittwer P. Intermittency in the Presence of
Noise // J. Phys. A.— 1981.— V. 14A, No 12.— P. 3153—3168.
436. Elgin J. N., Forster D. Mechanism for Chaos in the Duffing Equation //
Phys. Lett—1983 —V. 94A, No 5.—P. 195-197.
437. Epstein 1. R. Oscillations and Chaos in Chemical Systems ff Physica D.—
1983.—V. 7D, No 1—3.—P. 47—56.
438. Farmer I. D, Spectral Broadening of Period-Doubling Bifurcation Sequen-
Sequences / Phys. Rev. Lett.— 1981.— V. 47, No 3.— P. 179—182.
439. Farmer J. D. Chaotic Allractor of an Infinite — Dimensional Dynamical
System // Physica D.— 1982.— V. 4D, No 3.— P. 366—393.
440. Farmer J. D. Information Dimension and the Probabilistic Structure of
Chaos /I Z. Naturforsch.—1982.—В. 37а, Н. 11.—S. 1304—1325.
441. Farmer J. D., Crutchjield J., Frochling II., Packard TV., Shaw R. Power
Spectra and Mixing Properties of Strange Attraclors ff Ann.— N.— Y.
Acad. Sci — 1980.— No 357.- P. 453-472.
442. Farmer J. D., Ott E., Yorke J. A. The Dimension of Chaotic Attractors //
Physica D.— 1983.— V. 7, No 1—3.— P. 153—180.
443. Fauve S., Libchaber A. Rayleigh — Benard Experiment in a Low Prandtl
Number Fluid, Mercury ff Proc. Intern. Symp. on Synergetics at Schloss
Elmau, Bavaria, I981./Ed. H. Haken.— Berlin — Heidelberg.— N. Y.: Sprin-
Springer.— 1981.— P. 25—35. (Имеется перевод: Фове С, Либхабер А. Экспе-
Эксперимент Рэлея — Венара в ртути — жидкости с низким числом Прандт-
ля / Синергетика.— М.: Мир, 1984.— С. 234—247.)
444. Feigenbaum Ж. J. Quantitative Universality for a Class of Nonlinear
Transformations // J. Stat. Phys.— 1978.— V. 19. No 1.— P. 25—52.
445. Feibenbaum M J. The Universal Metric Properties of Nonlinear Trans-
Transformations // J. Stat. Phys.— 1979.— V. 21, No 6.— P. 669—706.
446. Feigenbaum M. I. The Onset Spectrum of Turbulence ff Phys. Lett.—
1979.— V. 74A, No 6.— P. 375—378.
447. Feigenbaum M. J. The Transition to Aperiodic Behavior in Turbulent
Systems ff Cornm. Math. Phys.— 1980.—V. 77, No 1.—P. 65—86.
448. Feigenbaum M. J. Universal Behavior in Nonlinear Systems / Los Alamos
Sci.— 1980.— V. 1, No 1.— P. 4—27 (имеется перевод: Фейгепбаум М.
Упиверсальпость в поведении нелипейных систем / УФН.—1983.—
Т. 141, В. 2.-С. 343-374); Physica D— 1983.— V. 7D, No 1—3.—P. 16—
39.
449. Feigenbaum M. J., Kadanoff L. P., Shenker S. J. Quasiperiodicity in Di3-
sipative Systems: a Renormalization Group Analysis ff Physica D.—
1982.— V. 5D, No 2, 3 —P. 370-386.
450. Fermi E., Pasta I., Ulam S. Studies of Non-Linear Problems.— Los Alamos
Scient. Lab. Report LA —1940, 1955. (Имеется перевод: Ферми Э. Науч-
пые труды, т. II.—М.: Наука, 1972.—С. 645—656.)
451. Field R. J., Kbros E., Noyes R. M. Oscillations in Chemical Systems. II.
Thorough Analysis of Temporal Oscillation in the Bromate — Cerium —
Malonic Acid System // J. Amer. Soc— 1972.— V. 94, No 25.— P. 8649—
8664.
452. Field R. J., Noyes R. M. Oscillations in Chemical Systems. IV. Limit Cyc-
Cycle Behavior in a Model of a Real Chemical Reaction Ц J. Chem. Phys.—
1974— V. 60, No 5.— P. 1877—1884.
453. Fife P. C. Mathematical Aspects of Reacting and Diffusing Systems ff
Lect. Notes in Biomath. No 29.— Berlin: Springer, 1979.
454. Firth W. /., Wright E. M. Oscillation and Chaos in a Fabry — Perot Bi-
Bistable Cavity with Gaussian Input Beam // Phys. Lett.—1982.— V. 92,
No 5.— P. 211—216.
455. Fischer R. The advance of advantageous genes // Ann. of Eugenics.—
1937.— V. 7.— P. 355-369.
456. Ford J., Lanford G. H. Stochastic Behavior of Resonant Nearly Linear Os-
Oscillator Systems in the Limit of Zero Nonlinear Coupling / Phys. Rev.—
1970.- V. 1A, No 1 — P. 59—70. ,
457. Fowler A. C, Gibbon J. D., McGuinness M. J. The Complex Lorenz Equ-
Equations // Physica D.- 1982 —V. 4D, No l.-P. 139-163.
413

458. Fowler А. С, McGuiness M. J. Hysteresis in the Lorenz Equations / Phys.
Lett— 1982.— V. 92A, No 3.— P. 103—106.
459. Franaszek M. Effect of Random Noise on the Deterministic Chaos in a
Dissipative System // Phys. Lett—1984.—V. 105A, No 8.—P. 383—386.
460. Franceschini V. A Feigenbaum Sequence of Bifurcations in the Lorenz
Model // J. Stat. Phys— 1980.— V. 22, No 3.— P. 397—406.
461. Franceschini V. Bifurcations of Tori and Phase Locking in a Dissipative
System of Differential Equations / Physica D.—1983.— V. 6D, No 3.—
P. 285-304.
462. Franceschini V., Tebaldi C. Sequences of Infinite Bifurcations and Tur-
Turbulence in a Five-Mode Truncation [I J. Stat. Phys.—1979.— V. 21,
No 6.- P. 707-726.
463. Franceschini V., Tebaldi C. Breaking and Disappearance of Tori ff Comm.
Math. Phys.— 1984.— V. 94, No 2.— P. 317—329.
464 Froscfi H., Buttner H. Tmo Coupled Impact Oscillators / Z. Phys. B: Con-
denced Matter.— 1985.— B. 58, No 4.— S. 323—328.
465. Gibbs H. M., Hopf F. A., Kaplan D. L., Shoemaker R. L. Observation of
Chaos in Optical Bistability II Phys. Rev. Lett.— 1981.— V. 46, No 7.—
P. 474—477.
466. Glass L., Guevara M. R., Shrier A. Bifurcations and Chaos in a Periodical-
Periodically Stimulated Cardiac Oscillator II Physica D.— 1983.— V. 70, No 1—3.—
P. 89-101.
467. Goldberger A. L., Bhargava V., West B. J., Mandell A. J. Nonlinear Dyna-
Dynamics of the Heartbeat I/ Physica D.—1985.—V. 17D, No 2.—P. 207—214.
468. Goldschmidt V. M. Turbulent Transport: Some General Comments // Lect.
Notes in Phys. V. 76.—Berlin: Springer, 1978.— P. 1—21.
469. Gollnb J. P., Benson S. V., Steinman J. A Subharmonic Route to Turbu-
Turbulent Convection / Ann. N. Y. Acad. Sci.— 1980.— No 357.— P. 22—27.
470. Gollub J. P., Meyer C. W. Symmetry-Breaking Instabilities on a Fluid
Surface // Physica D- 1983— V. 6D, No 3- P. 337-346.
471. Gorman M., Widmann P. J. Nonlinear Dynamics of a Convection Loop:
a Quantitative Comparison of Experiment with Theory // Physica D.—
1986.— V. 19D, No 2.— P. 255—267.
472. Grasman J., Nijmeijer #., Veling E. J. M. Singular Perturbations and a
Mapping on an Interval for the Forced Van-der-Pol Relaxation Oscilla-
Oscillator // Physica D.— 1984.— V. 13D, No 1, 2.— P. 195—210.
473. Grassberger P. On the Hausdorff Dimension of Fractal Attractors // J. Stat.
Phys.— 1981.— V. 26, No 1.— P. 173—179.
474. Grassberger P. Generalized Dimension of Strange Attractors // Phys.
Lett- 1983.- V. 97A, No 6 — P. 227-231.
475. Grassberger P., Ben-Mizrachi A., Procaccia I. Characterization of Expe-
Experimental (Noisy) Strange Attractors II Phys. Rev. A.—1984.— V. 29,
No 2.— P. 975—977.
476. Grassberger P., Procaccia I. Characterization of Strange Attractors /
Phys. Rev. Lett.— 1983.— V. 50, No 5.— P. 346—349.
477. Grassberger P., Procaccia I. Measuring the Strangeness of Strange Attrac-
Attractors / Physica D.— 1983 —V. 9D, No 1.—P. 189—208.
478. Grassberger P., Procaccia I. Estimation of the Kolmogorov Entropy from
a Chaotic Signal // Phys. Rev. A.—1983.—V. 28, No 4.—P. 2591—2593.
479. Grassberger P., Procaccia I. Dimensions and Entropies of Strange Attxac-
tors from a Fluctuating Dynamics Approach // Physica D.— 1964.— V. 13,
No 1, 2.— P. 34—54.
480. Greenside H. S., Wolf A., Swift J., Pignotaro T. Impracticality of a Box-
Counting Algorithm for Calculating the Dimensionality of Strange Attrac-
Attractors I/ Phys. Rev. A.—1982.— V. 25, No 6.— P. 3453—3456.
481. Grossman S., Thomae S. Invariant Distributions and Stationary Correla-
Correlation Functions of One-Dimensional Discrete Processes // Z. Naturforsch.—
1977— B. 32a, H. 12 — S. 1353—1363.
482. Gubankov V. N., Konstantinyan K. I., Kosheletz V. P., Ovsyannikov G. A.
Chaos in Josephson Tunnel Junctions / IEEE Trans. Mag.—1983.—
V. 19, No 3 — P. 637-639.
414

483. Guckenheimer J. M., Holmes Ph. Nonlinear Oscillations, Dynamical Sys-
Systems, and Bifurcation of Vector Fields.—N. Y.— Berlin — Heidelberg —
Tokyo: Springer, 1983.
484. Gumowski. I., Mira C. Recurrences and Discrete Dynamic Systems //
Lect. Notes in Math. No 809.— Berlin: Springer, 1980.
485. Iladamard J. // Bull. Soc. Math. France.— 1901.— V. 29.— P. 224—228.
486. Haken 11. Cooperative Phenomena in Systems Far from Thermal Equi-
Equilibrium and in N'onphysjcal Systems / Rev.<Mod. Phys.—1975.—V. 47,
No 1.—P. 67—121.
487. Haken 11. Synergetics—a Field Beyond Irreversible Thermodynamics /
Lect. Notes in Phys. V. 81— Berlin: Springer, 1978.— P. 140—168.
488. Halas II. J., Liu S-N., Abraham N. B. Route to Mode Locking in a Three-
Mode He —No 3.39 \im Laser Including Chaos in the Secondary Beat
Frequency // Phys. Rev. A.— 1983.— V. 28A, No 5.— P. 2915—2920.
489. Hale J. Infinite Dimensional Dynamical Systems // Lect. Notes in Math.—
V. 1007.— Berlin: Springer, 1983.— P. 379—400.
490. Hanson J. D., Ott E., Antonsen Т. М. Influence of Finite Wavelength on
the Quantum Kicked Rotator in the Semiclassical Regime // Phys. Rev.
A.— 1984.— V. 29A, No 2 — P. 819—825.
491. Hao Bai-lin, Zhang Shu-yu. Subharmonic Stroboscopy as a Method to Stu-
Study Period-Doubling Bifurcations II Phys. Lett.— 1982.— V. 87A, No 6.—
P. 267-270.
492. Намек R., HolUnger F., Weber II. Chaotic and Periodic Emission of High
Power Solid State Lasers / Opt. Comm.— 1983.— V. 47, No 2.— P. 141—
145.
493. Hausdorff F. Dimension und AuCeres Mafl // Math. Ann.— 1918.— B. 79,
H. 2.— S. 157—179.
494. Hauser P. R., Tsallis C, Curado M. F. Criticality of the Routes to Chaos
of the 1 — a | x \z Map II Phys. Rev. A.—1984.—V. 30A, No 4.—P. 2074—
2079.
495. Hayashi C. The Method of Mapping with Reference to the Doubly Asymp-
Asymptotic Structure of Invariant Curves II Int. J. Non-Linear Mech.—1980.—
V. 15, No 415!— P. 341—348.
496. Hayashi C, Abe M., Oshima K., Kawakami H. The Method of Mapping
as Applied to the Solution for Certain Types of Nonlinear Differential
Equations // Tp. IX Междунар. конференции по нелинейным колебаниям
(Киев, 1981), т. I.—Киев: Наукова думка, 1984.—С. 40—44.
497. Hayashi С, Kawakami H. Bifurcations and the Generation of Chaotic Sta-
tes in the Solutions of Nonlinear Differential Equations / Теор. и прикл.
мех. 4-й Нац. копгр.; Варна, 1981. Докл. Кп. I.—София, 1981.—С. 537—
542.
498. Hedlund G. A. The Dynamics of Geodesic Flows // Bull. Amer. Math.
Soc— 1939.— V. 45, No 4.—P. 241—260.
499. Helleman R. H. G. Self-Generated Chaotic Behavior in Nonlinear Mecha-
Mechanics II Fundamental Problems in Statistical Mechanics. V. 5./Ed. E. G.
D. Cohen.— Amsterdam.— N. Y.: North-Holland, 1980.— P. 165—233.
500. Henon M. A Tvvo-Dimensional Mapping with a Strange Attractor // Comm.
. Math. Phys.— 1976.— V. 50, No 1.— P. 69—77. (Имеется превод: Хенон М.
Двумерное отображение со странным аттрактором / Странные аттрак-
аттракторы.—М.: Мир, 1981.—С. 152—163.)
501. Henon M., Heiles С. The Applicability of the Third Integral of Motion;
Some Numerical Experiments I/ Astron. J.— 1964.— V. 69, No 1.— P. 73—
79.
502. Hentschel H. G. E., Procaccia I. The Infinite Number of Generalized Di-
Dimensions of Fractals and Strange Attractors // Physica D.—1983.—
V. 8D, No 3.— P. 435—444.
503. Hirsch J. E., Huberman B. A., Scalapino D. J. Theory of Intermittency /
Phys. Rev. A.— 1982.— V. 25A, No 1.— P. 519—532.
504. Hirsch I. E., Nauenberg M., Scalapino D. J. Intermittency in the Presence
of Noise: a Renormalization Group Formulation II Phys. Lett.— 1982.—
V. 87A, No 8.— P. 391-393.
415

505. Hoffer L. M., Chyba Т. H., Abraham N. B. Spontaneous Pulsing, Period
Doubling, and Quasi-Periodicity in a Unidirectional, Single-Mode, Inho-
mogeneously Broadened Ring Laser // J. Opt. Soc. Amer. В.—1985.—
V. 2, No 1.— P. 102-107.
506. Holmes P. Nonlinear Oscillator with a Strange Attractor // Phil. Trans.
Roy. Soc. London.— 1979.— V. 292, No 1394— P. 419—448.
507. Holmes P. J. Averaging and Chaotic Motions in Forced Oscillations /
SIAM J. Appl. Math.— 1980.— V. 38, No 1 — P. 65—80.
508. Holmes P., Whitley D. On the Attracting Set for Duffing's Equation /
Physica D.—1983.—V. 7D, No 1—3.—P. 111—123.
509. Holyst J. A., Zagorski A., Sukiennicki A. On the Possibility of Determi-
Deterministic Chaos in a Driven Damped Heisenberg Chain // Phys. Status So-
lidi.- 1985 — B. 127, No 1.— S. 29-32.
510. Hopf E. Abzweigung einer periodischen Losung von einer stationaren
Losung eines differential Systems: Ber. Math.— Phys. Sachsische Akade-
mie der Wissenschaften. B. 94.— Leipzig, 1942.— S. 1—22.
511. Hopf E. A Mathematical Example Displaying the Features of Turbulen-
Turbulence // Comm. Pure Appl. Math.— 1948.— V. 1.— P. 303—322.
512. Hopf F. A., Kaplan D. L., Gibbs H. M., Shoemaker R. L. Bifurcations to
Chaos in Optical Bistability II Phys. Rev.—1982.— V. 25A, No 4—
P. 2172—2182.
513. Ни, В. Introduction to Real-Space Renormalization-Group Methods in Cri-
Critical and Chaotic Phenomena II Phys. Rep.—1982.— V. 91, No 5.—
P. 233-295.
514. Ни В., Mao J. M. Period Doubling: Universality and Critical Point Or-
Order / Phys. Rev. A.— 1982.— V. 25A, No 6.— P. 3259—3261.
515. Ни В., Rudnick J. Exact Solutions to the Feigenbaum Renormalization-
Group Equations for Intermittency // Phys. Rev. Lett.—1982.— V. 48,
No 24.— P. 1645—1648.
516. Ни В., Satija I. I. A Spectrum of Universality Classes in Period Doub-
Doubling and Period Tripling / Phys. Lett— 1983.— V. 98A, No 4— P. 143—
146.
517. Huberman B. A., Crutchfield J. P. Chaotic States of Anharmonic Systems
in Periodic Fields I/ Phys. Rev. Lett.—1979.—V. 43, No 23.—P. 1743—
1747.
518. Huberman B. A., Rudnick J. Scaling Behavior of Chaotic Flows // Phys.
Rev. Lett.— 1980.— V. 45, No 3.— P. 154—157.
519. Huberman B. A., Zisook A. B. Power Spectra of Strange Attractors //
Phys. Rev. Lett.— 1981.— V. 46, No 10.— P. 626—632.
520. Hudson J. L., Hart M., Marinko D. An Experimental Study of Multiple
Peak Periodic and Nonperiodic Oscillations in the Belousov — Zhabotins-
ky Reaction / J. Chem. Phys.— 1979.— V. 71, No 4 — P. 1601—1606.
521. Ikeda K. Multiple-Valued Stationary State and Its Instability of the
Transmitted Light by a Ring Cavity System // Opt. Comm.—1979.—
V. 30, No 2.— P. 257—261.
522. Ikeda K., Daido H., Akimoto O. Optical Turbulence: Chaotic Behavior of
Transmitted Light from a Ring Cavity II Phys. Rev. Lett— 1980.— V. 45,
No 9.— P. 709—712.
523. Ikeda K., Rondo K., Akimoto O. Successive Higher-Harmonic Bifurcations
in Systems with Delayed Feedback / Phys. Rev. Lett.—1982.— V. 49,
No 20 — P. 1467—1470.
524. Imada M. Chaos Caused by the Soliton — Soliton Interaction // J. Phys.
Soc. Japan.—1983.—V. 52, No 6.—P. 1946—1956.
525. Instabilities in Active Optical Medium II J. Opt. Soc. Amer.—1985.—
V. B2, No 1.
526. Ho II. Successive Subharmonic Bifurcations and Chaos in a Nonlinear
Mathieu Equation II Progr. Theor. Phys. Japan.— 1979.— V. 61, No 3.—
P. 815-824.
527. Ivanov D. V., Khanin Ya. I., Matorin I. I., Pikovsky A. S. Chaos in a So-
Solid-State Laser with Periodically Modulated Losses /I Phys. Lett.— 1982.—
V. 89A, No 5.— P. 229—230.
416

528. Izrailev F. M., Rabinovich M. I., Ugodnikov A. D. Approximate Descrip-
Description of Three-Dimensional Dissipative Systems / Phys. Lett.—1981.—
V. 86A, No 6, 7 — P. 321—325.
529. Leffries C, Perez J. Direct Observation of Crises of the Chaotic Attractor in
a Nonlinear Oscillator / Phys. Rev. A.— 1983.— V. 27, No 1.— P. 601—603.
530. Jensen J. H., Christiansen P. L., Scott A. C. Chaos in the Beeler — Reu-
ter System for the Action Potential of Ventricular Myocardial Fibres //
Physica D.— 1984 — V. 13, No 1, 2.— P. 269—277.
531. Jensen M. H., Bak P., Bohr T. Complete Devil's Staircase, Fractal Dimen-
Dimension, and Universality of Mode-Locking Structure in the Circle Map //
Phys. Rev. Lett.— 1983.— V. 50, No 21.— P. 1637—1639.
532. Jensen R. V., Oberman C. R. Calculation of the Statistical Properties of
Strange Attractors // Phys. Rev. Lett.— 1981.— V. 46, No 24.— P. 1547—
1550.
533. Jones C. A., Weiss N. O., Cattaneo F. Nonlinear Dynamos a Complex Ge-
Generalization of the Lorenz Equations Ц Physica D.—1985.— V. 14D,
No 2.— P. 161—176.
534. Kadanoff L. P. Roads to Chaos // Physics Today.— 1983.— V. 36, No 12.—
P. 46—53. (Имеется перевод: Каданов Л. П. Пути к хаосу // Физика
за рубежом. 85.— М.: Мир, 1985. С. 9—32.)
535. Кси Т. Universality of Power Spectra of a Dynamical System with an In-
Infinite Sequence of Period-Doubling Bifurcations // Phys. Lett.—1981.—
V. 86A, No 5.— P. 263—266.
536. Kai Т., Tomita K. Statistical Mechanics of Deterministic Chaos // Progr.
Theor. Phys. Japan.— 1980.— V. 64, No 5.— P. 1532—1550.
537. Kaneko K. Doubling of Torus / Progr. Theor. Phys. Japan.—1983.—
V. 69, No 6.— P. 1806—1810.
538. Kaneko K. Oscillation and Doubling of "Torus / Progr. Theor. Phys.
Japan.- 1984.— V. 72, No 2.— P. 202-215.
539. Kaplan J. L., Yorke J. A. Preturbulence: a Regime Observed in a Fluid
Flow Model of Lorenz.— Research supported by NSF Grant NCS76—24432,
1977.—P. 1—49.
540. Kaplan J. L., Yorke I. A. Chaotic Behavior of Multi-Dimensional Differen-
Difference Equations // Lect. Notes in Math.—1979.—No 730.—P. 204—227.
541. Kawai H., Туе S.-H. H. Approach to Chaos: Universal Quantitative Pro-
Properties of One-Dimensional Maps // Phys. Rev. A.— 1984.— V. 30, No 4.—
P. 2005—2023.
542. Kawakami H. The Bifurcation Pattern of Periodic Solutions Observed in
tiuffing's Equation // Tp. IX Междунар. конф. по нелинейным колеба-
колебаниям (Киев, 1981).—Киев: Наукова думка, 1984.—С. 162—165.
543. Kerr W. С, Williams M. В., Bishop А. Д., Fesser К, Lomdahl P. S., Tral-
linger S. E. Symmetry and Chaos in the Motion of the Damped Driven
Pendulum // Z. Phys. B: Condensed Matter.—1985.—B. 59, No 1.—
S. 103-110.
544. Khandokhin P. A., Khanin Ya. I. Instabilities in a Solid-State Ring La-
Laser // J. Opt. Soc. Amer. В.— 1985.— V. 2, No 1.— P. 226—231.
545. Klische W., Weiss С. О. Instabilities and Routes to Chaos in a Homoge-
Homogeneously Broadened One- and Two-Mode Ring Laser // Phys. Rev. A.—
1985- V. 31, No 6.— P. 4049—4051.
546. Koch B. P., Leven R. W. Subharmonic and Homoclinic Bifurcations in a
Parametrically Forced Pendulum // Physica D.— 1985.— V. 16D, No 1.—
P. 1—13.
547. Koch B. P., Leven R. W., Ротре В., Wilke C. Experimental Evidence for
Chaotic Behavior of a Parametrically Forced Pendulum // Phys. Lett.—
1 1983.- V. 96A, No 5.— P. 219—224.
548. Kornev V. K., Semenov V. K. Chaotic and Stochastic Phenomena in Su-
Superconducting Quantum Interferometers / IEEE Trans. Mag.—1983.—
V. 19, No 3- P. 633-636.
549. Kuramoto Y., Tsuzuki T. On the Formation of Dissipative Structures in
Reaction — Diffusion Systems II Progr. Theor. Phys. Japan.—1975.—
V. 54, No 3.- P. 687-699.
417

550. Kuramotd Y., Yamada T. Turbulent State in Chemical Reactions }/ Progr..
Theor. Phys. Japan.— 1976.—V. 56, No 3.—P. 679—681.
551. Lanford О. Е. An Introduction to the Lorenz System // Papers from the
Duke Turb. Conf. A976), Paper No 4, p. 1—21.
552. Lanford О. Е. Computer Pictures of the Lorenz Attractor // Lect. Notes in
Math., No 615.— Berlin — Heidelberg — N. Y.: Springer. 1977.—P. 113—116.
553. Lasota A., Yorke J. A. On the Existence of Invariant Measures for Pie-
cewise Monotonic Transformations II Trans. Amer. Math. Sot— 1973.—
V. 186- P. 481-488.
554. Ledrappier F. Some Relations Between Dimension and Lyapunov Expo-
Exponents I/ Comm. Math. Phys.—1981.—V. 81, No 2.—P. 229—238.
555. Leipnik R. B. Double Strange Attractors in Rigid Body Motion with Li-
Linear Feedback Control // Phys. Lett.—1981.— V. 86A, No 2.— P. 63—67.
556. Leonov G. A'., Abramovich S. M., Bunin A. I. Global Stability of the Lo-
Lorenz System /I Nonlinear and Turbulent Processes in Physics. V. 3.—
N.—Y.: Gordon and Breach, Harwood Academic Publishers, 1984.
557. Leray J. Sur le mouvement d'un liquide visqueux emplissant l'espace /
Acta Math.— 1934.— V. 63.— P. 193—248.
558. Levandowsky M.. Childress W. S., Spiegel E. A., Hutner S. H. A Mathe-
Mathematical Model of Pattern Formation by Swimming Microorganismos // 1.
Protozool.— 1975.— V. 22, No 2.— P. 296—306.
559. Leven R. W., Koch B. P. Chaotic Behavior of a Parametrically Excited
Damped Pendulum // Phys. Lett.— 1981.— V. 86A, No 2.— P. 71—74.
560. Leven R. W., Ротре В., Wilke C, Koch B'. P. Experiments on Periodic
and Chaotic Motions of a Parametrically Forced Pendulum // Physica D.—
1985.— V. 16, No 3.— P. 371—384.
561. Libchaber A., Fauue S., Laroche С Two-Parameter Study of the Routes
to Chaos / Physica D.— 1983.— V. 7D, No 1—3.— P. 73—84.
562. Linsay P. S. Period Doubling and Chaotic Behavior in a Driven Anhar-
monic Oscillator // Phys. Rev. Lett.—1981.— V. 47, No 19.— P. 1349—
1352.
563. Lorenz E. N. Deterministic Nonperiodic Flow // J. Atmos. Sci.— 1963.—
V. 20, No 2.— P. 130—141. (Имеется перевод: Лоренц Э. Детерминиро-
Детерминированное непериодическое течепие Ц Странные аттракторы.— М.: Мирт
1981 —С. 88—116.)
564. Lorenz E. N. Noisy Periodicity and Reverse Bifurcation Sequences Ц Ann.
N. Y. Acad. Sci.- 1980.- V. 357.- P. 282-291.
565. Lotka A. J. Undamped Oscillations Derived from the Law of Mass Acti-
Action // J. Amer. Chem. Soc- 1920- V. 42, No 8.- P. 1595-1599.
566. Lotka A. J. Elements of Physical Biology.— Baltimore, 1925.
567. Liicke M. Statistical Dynamics of the Lorenz Model // J. Stat. Phys.—
1976- V. 13, No 6.- P. 455-475.
568. Mackey M. C, Glass L. Oscillation and Chaos in Physiological Control
Systems // Science — 1977.- V. 197, No 4300.— P. 287-289.
569. Malraison В., Atten P., Berge P., Dubois M. Dimension of Strange Attrac-
Attractors: an Experimental Determination for the Chaotic Regime of Two Con-
vective Systems ff J. Physique Lettres.— 1983.— T. 44, No 22.— P. 897—
902.
570. Mandelbrot В. В. Fractals: Form, Chance and Dimension.— San Francis-
Francisco: Freeman Сотр., 1977.
571. Mane R. On the Dimension of the Compact Invariant Sets of Certain Non-
Linear Maps // Lect. Notes in Math.—1981.—V. 898.—P. 230—242.
572. Manneville P., Pomeau Y. Intermittency and the Lorenz Model / Phys.
Lett.- 1979 — V. 75A, No 1-2.- P. 1-2.
573. Manneville P., Pomeau Y. Different Ways to Turbulence in Dissipative
Dynamical Systems // Physica D.—1980.—V. 1, No 2.—P. 219—226.
574. Maschke E. K., Saramito B. On the Transition to Turbulence in Magneto-
Hydrodynamic Models of Confined Plasmas Ц Physica Scripta.— 1982.—
V. T2: 2.— P. 410—417.
575 Matsumoto K., Tsuda I. Noise-induced Order / J. Stat. Phys.— 1983.—
V. 31, No 1 — P. 87-108.
418

576. May R. M. Simple Mathematical Models with Very Complicated Dyna-
Dynamics / Nature.— 1976.— V. 261, No 6.— P. 459—467.
577. Mayer-Kress G., Haken H. Intermittent Behavior of the Logistic System //
Phys. Lett.— 1981.— V. 82A, No 4— P. 151—155.
578. McGainness M. J. The Fractal Dimension of the Lorenz Attractor II Phys.
Lett— 1983.— V. 99A, No 1.— P. 5-9.
579. McGuinness M. J. A Computation of the Limit Capacity of the Lorenz At-
Attractor И Physica D.— 1985.— V. 16D, No 2.— P. 265—275.
580. McLaughlin J. B. Stochastic Behavior in Slightly Dissipative Systems //
Phys. Rev. A.— 1979.—V. 20A, No 5.— P. 2114—2119.
581. McLaughlin J. B. Period — Doubling Bifurcations and Chaotic Motion for
a Parametrically Forced Pendulum // J. Stat. Phys.— 1981.— V. 24, No 2.—
P. 375-388.
582. McLaughlin J. В., Martin P. C. Transition to Turbulence in a Statically
Stressed Fluid System // Phys. Rev.— A.— 1975.— V. 12A, No 1.— P 186—
203.
583. Miles J. Resonantly Forced Motion of Two Quadratically Coupled Oscil-
Oscillators // Physica D.- 1984 — V. 13D, No 1, 2,— P. 247-260.
584. Mdonni P. W., Ackerhalt J. R., Galbraith H.W. Chaos and Nonlinear Op-
Optics: a Chaotic Raman Attractor / Phys. Rev. A.— 1983.— V. 28A, No 2.—
P. 887—891". \
585. Moon F. C, Hi G.-X. The Fractal Dimension of the Two-Well Potential
Strange Attractor // Physica D.—1985.—V. 17D, No 1.—P. 99—108.
586. Mori II. Fractal Dimensions of Chaotic Flows of Autonomous Dissipative
Systems // Progr. Theor. Phys. Japan.— 1980.— V. 63, No 3.— P. 1044—
1047.
587. Mori H., Fujisaka H. Statistical Dynamics of Turbulence / Lect. Notes
in Phys. V. 132.— Berlin: Springer, 1980.— P. 181—197.
588. Mors E., Hedlund G. A. Symbolic Dynamics. I, II // Amer. J. Math.—
1938.— V. 60.— P. 813-866; 1940.— V. 62.
589. Myrberg P. J. Iteration von Quadratwurzeloperationen // Ann. Acad. Sci.
Fennica. Ser. A.— 1958.—V. 259.—P. 1—10.
590. Myrberg P. J. Iteration der reellen Polynome Zweiten Grades / Ann.
Acad. Sci. Fennica. Ser. A.—1958.—V. 256.—P. 1—10; 1959.—V. 268 —
P. 1—10; 1963.— V. 336.— P. 1—10.
591. Nakatsuka H., Asaka S., Itoh H., Ikeda K., Matsuoka M. Observation of
Bifurcation to Chaos in an All — Optical Bistable System Ц Phys. Rev.
Lett— 1983.— V. 50, No 2.— P. 109—112.
592. Narducci L. M., Sadiky H., Lugiato L. A., Abraham N. B. Experimentally
Accessible Periodic Pulsations of a Single-Mode Homogeneously Broade-
Broadened Laser (the Lorenz Model) // Opt. Comm.—1985.—V. 55, No 5.—
P. 370—376.
593. Nauenberg M., Rudnick J. Universality and the Power Spectrum at the
Onset of Chaos / Phys. Rev. В.— 1981— V. 24B, No 1.— P. 493—495.
594. Neyer A., Voges E. Dynamics of Electrooptic Bistable Devices with De-
Delayed Feedback // IEEE J. Quant. Electr.—1982.—V. QE-18, No 12.—
P. 2009—2015.
595. Nicolis G. Stability and Dissipative Structures in Open Systems Far from
Equilibrium / Advances in Chemical Physics. V. 19./Ed. I. Prigogine,
S. A. Rice.— N. Y.— L.— Sydney — Toronto: Wiley — Intersci., 1971.—
P. 209—324.
596. Olsen L. F., Degn H. Chaos in a Enzyme Reaction / Nature.— 1977.—
V. 267, No 5607.— P. 177—178.
597. Ostlund S., Rand D., Sethna J., Siggia E. Universal Properties of the Tran-
Transition from Quasi-Periodicity to Chaos in Dissipative Systems Ц Physi-
Physica D— 1983.— V. 8, No 3 — P. 303—342.
598. Ott E. Strange Attractors and Chaotic Motions of Dynamical Systems //
Rev. Mod. Phys — 1981.— V. 53, No 4., P. 1.— P. 655—671.
599. Ott E., Hanson J. D., Antonsen Т. М. The Influence of Diffraction on Wa-
Waves with Ergodic Ray Trajectories / Bull. Amer. Phys. Soc.—1981.—
V. 26, No 7.— P. 1013.
419

600. Packard N. H., Crutchfield J. P., Farmer J. £>., Shaw R. S. Geometry from
a Time Series // Phys. Rev. Lett,— 1980.— V. 45, No 9.— P. 712—716.
601. Percival I. C. Regular and Irregular Spectra // J. Phys. B: Atom, and Mo-
lec. Phys.— 1973.— V. 6, No 9.— P. L229—232.
602. Percival I. C. Semiclassical Theory of Bound States / Advances in Che-
Chemical Phys. V. 36./Ed. I. Prigogine, S. A. Rice.— N. Y. London — Sydney —
Toronto: Wiley — Intersci, 1977.— P. 1—61.
603. Perez J., Jeffries C. Direct Observation of a Tangent Bifurcation in a Non-
Nonlinear Oscillator // Phys. Lett.— 1982.— V. 92A, No 2.— P. 82—84.
604. Pesin Ya. B. On the Notion of the Dimension with Respect to a Dynami-
Dynamical System II Ergod. Theory and Dyn. Systems.— 1984.— V. 4, No 3.—
P. 405-420.
605. Pikovsky A. S. A Dynamical Model for Periodic and Chaotic Oscillations
in the Belousov —Zhabotinsky Reaction II Phys. Lett.—1981.—V. 85A,
No 1.— P. 13-16.
606. Pikovsky A. S. A New Type of Intermittent Transition to Chaos // J.
Phys. A. Math. Gen.—1983.—V. 16.—P. L. 409—112.
607. Pikovsky A. S., Rabinovich M. I. Stochastic Oscillations in Dissipative
Systems // Physica D,— 1981.— V. 2, No 1 — P. 8—24.
608. Poincare H. Calcul des Probabilites.—Paris: Gautier — Villard, 1912.
609. Pomeau Y., Manneville P. Intermittent Transition to Turbulence in Dissi-
pative Dynamical Systems II Comm. Math. Phys.— 1980.— V. 74, No 2.—
P. 189-197.
610. Procaccia I., Grassberger P., Hentschel H. G. E. On the Characterization
of Chaotic Motions Ц Lect. Notes in Physics.—No 179.—Berlin: Sprin-
Springer, 1983.— P. 212—221.
611. Rand D., Ostlund S., Sethna J., Siggia E. D. Universal Transition from
Quasiperiodicity to Chaos in Dissipative Systems // Phys. Rev. Lett.—
1982.— V. 49, No 2.— P. 132—135.
612. Renyi A. Probability Theory.— Amsterdam: North-Holland, 1970.
613. Reynolds O. An Experimental Investigation on the Circumstances which
Determine whether the Motion of Water shall be Direct or Sinuous, and
of the Law of Resistance in Parallel Channals // Phil. Trans. Roy. Soc—
1883.— V. 174.— P. 935.
614. Richardson L. F. The Problem of Contiguity: an Appendix of Statistics
of Deadly Quarrels // General Systems Yearbook.— 1961.—V. 6.— P. 139—
187.
615. Riela G. Loss of Stability and Disappearance of Two-Dimensional Inva-
Invariant Tori in a Dissipative Dynamical System // Phys. Lett— 1982.—
V. 91A, No 5.— P. 203-204.
616. Roux J. С Experimental Studies of Bifurcations Leading to Chaos in the
Belousoff — Zhabotinsky Reaction // Physica D.— 1983.— V. 7D, No 1—
3.- P. 57-68.
617. Roux J. C, Simoyi li. H., Swinney H. L. Observation of a Strange Attrac-
tor / Physica D.— 1983.— V. 8, No 1—2.— P. 257—266.
618. Rossler О. Е, An Equation for Continuous Chaos // Phys. Lett.— 1976.—
V. 57A, No 5 — P. 397-398.
619. Rossler O. E. Chaotic Behavior in Simple Reaction Systems.— Z. Natur-
forsch.— 1976.— B. 31a, II. 3/4.— S. 259—264.
620. Rossler О. Е. Chemical Turbulence: Chaos in a Simple Reaction-Diffusion
System // Z. Naturforsch.—1976.—B. 31a, H. 10.— S. 1168—1172.
621. Rossler О. Е. Chaos in Abstract Kinetics Two Prototypes.— Bull, of Math.
Biol.— 1977.— V. 39, No 2.— P. 275—289.
622. Rossler O. E. An Equation for Hyperchaos // Phys. Lett.— 1979.— V. 71A,
No 2, 3.— P. 155—157.
623. Rossler O. E., Wegmann K. Chaos in the Zhabotinsky Reaction // Natu-
Nature.— 1978. V. 271.— P. 89—90.
624. Ruelle D. Some Comments on Chemical Oscillations // Trans. N. Y. Acad.
Sci.— 1973.— V. 35, Ser. II, No 1.— P. 66—71.
625. Ruelle D. The Lorenz Attractor and the Problem of Turbulence / Lect.
Notes in Math. No 565.— Berlin: Springer, 1976.— P. 146—158.
420 ,

626. Ruelle D. Strange Attractors // Math. Intellengencer.—1980.— V. 2,
No 3 — P. 126—137.
627. Ruelle D., Takens F. On the Nature of Turbulence // Comm. Math. Phys.—
1971.—V, 20, No 2.—P. 167—192.
628 Rassel D A., Hanson J. D., Ott E. Dimension of Strange Attractors Ц
Phys. Rev. Lett —1980—V. 45, No 14-P. 1175-1178.
629. Sacker R. Invariant Surfaces and Bifurcation of Periodic Solutions of Or-
Ordinary Differential Equations.—N. Y.: Courant Institute of Mathematical
Sciences, 1964.
630. Saltzman B. Finite Amplitude Free Convection as an Initial Value Prob-
Problem / J. Atmos. Sci.— 1962.— V. 19, No 4.— P. 329—341.
631. Sano M., Sawada Y. Transition from Quasiperiodicity to Chaos in a Sys-
System of Coupled Nonlinear Oscillators // Phys. Lett.—1983.— V. 97A,
No 3.— P. 73—76.
632. Savage С. М., Walls D. F. Optical Chaos in Second-Harmonic Generati-
Generation /I Opt. Acta.— 1983.— V. 30, No 5.— P. 557—561.
633. Scheffer V. Geometric Fractale do la Turbulence Equations de Navier —
Stokes et Dimension de Hausdorff // С R. Ac. Sci., Paris.— 1976, P. 121—
122.
634. Schmits R. A., Graziani K. R., Hudson J. L. Experimental Evidence of
Chaotic States in the Belousov — Zhabotinsky Reaction ff J. Chem. Phys.—
1977- V. 67, No 7.— P. 3040-3044.
635. Schmutz M., Rueff M. Bifurcation Schemes of the Lorenz Model Ц Phy-
sica D.— 1984.—V. 11D, No 1, 2.—P. 167—178.
636. Scholz H. J., Yamada Т., Brand II., Graham R. Intermittency and Chaos
in a Laser System with Modulated Inversion // Phys. Lett.—1981.—
V. 82A, No 7 — P. 321-323.
637. Schreiber I., Marek M. Transition to Chaos via Two-Torus in Coupled
Reaction — Diffusion Cells // Phys. Lett,— 1982.— V. 91A, No 6— P. 263—
267.
638. Schreiber I., Marek M. Strange Attractors in Coupled Reaction — Diffu-
Diffusion Cells I/ Physica D.— 1982.— V. 5D, No 2+3.— P. 258—272.
639. Schulman J. N. Chaos in Piecewise-Linear Systems // Phys. Rev. A.—
1983 — V. 28, No 1.— P. 477—479.
640. Schulmeister Th., Sel'kov E. E. Folded Limit Cycles and Quasi-Stochastic
Self-Oscillations in a Third-Order Model of an Open Biochemical Sys-
System / Studia Biophysica.— 1978.— B. 7.2, H. 2.— S. 111—112.
641. Seydel R. Attractors of a Duffing Equation.— Dependence on the Exciting
Frequency.— Physica D, 1985, V. 17D, No 3.— P. 308—312.
642. Shannon С. Е. A Mathematical Theory of Communication. P. I—III /
Bell. System Techn. J.—1948.—V. 27, No 3.—P. 379—423; No 4.—
P. 623—656.
643. Shaw R. Strange Attractors, Chaotic Behavior, and Information Flow /
Z. Naturforsch.—1981.—V. 36a, H. 1.—S. 80—112.
644. Shenker S. J. Scaling Behavior in a Map of a Circle onto Itself: Empiri-
Empirical Results / Physica D.— 1982.— V. 5, No 2+3.— P. 405—411.
645. Shepelyansky D. L. Some Statistical Properties of Simple Classically
Stochastic Quantum Systems // Physica D.—1983.— V. 8D, No 2.—
P. 208—222.
646. Shibata A., Saito N. Time Delays and Chaos in Two Competing Species //
Math. Biosciences.— 1980.— V. 51, No 3/4.— P. 199—211.
647. Shimada I., Nagascima T. A Numerical Approach to Ergodic Problem of
Dissipative Dynamical Systems / Progr. Theor. Phys. Japan.—1979.—
V. 61, No 6.—P. 1605—1616.
648. Shimizu T. Analytic Form of the Simplest Limit Cycle in the Lorenz Mo-
Model / Physica A.— 1979.— V. 97, No 2.— P. 383—398.
649. Shimizu Т., Morioka N. Transient Behavior in Periodic Regions of the
Lorenz Model // Phys. Lett.— 1978.— V. 69A, No 3.— P. 148—150.
650. Shimizu Т., Morioka N. Period-Doubling Bifurcations in a Simple Mo-
Model I/ Phys. Lett.- 1981 —V. 83A, No 6.-P. 243-250.
421

651. Shraiman В., Wayne С. E., Martin P. С Scaling Theory for Noisy Period-
Doubling Transitions to Chaos / Phys. Rev. Lett.— 1981.— V. 46, No 14—
P. 935—939.
652. Simoyi R. H., Wolf A,, Swinney H. L. One-Dimensioaal Dynamics in a
Multicomponent Chemical Reaction II Phys. Rev. Lett.—1982 — V. 49,
No 4 — P. 245—248.
653. Smale S. Dynamical Systems and Turbulence // Lect. Notes in Math.
No 615.— Berlin: Springer, 1977.
654. Smoes M.-L. Period of Homogeneous Oscillations in the Ferro-in-catalized
Zhabotinskii System / J. Chem. Phys.—1979.—V. 71, No 11.—P. 4669—
4679.
655. Sparrow С The Lorenz Equations: Bifurcations, Chaos and Strange Afr-
tractors / Appl. Math. Sci. V. 41.— Berlin: Springer, 1982.
656. Swinney H. L. Observations of Order and Chaos in Nonlinear Systems /
Physica D.—1983.—V. 7D, No 1—3.—P. 3—15.
657. Takens F. Detecting Strange Attractors in Turbulence / Lect. Notes in Math.
No 898.—Berlin —Heidelberg—N. Y.: Springer, 1981.—P. 366—381.
658. Testa J., Perez J., Jeffries С Evidence for Universal Chaotic Behavior
of a Driven Nonlinear Oscillator // Phys. Rev. Lett.—1982.— V. 48,
No 11 — P. 714—717.
659. Thompson J. M., Graffari R. Chaotic Dynamics of an Impact Oscillator //
Phys. Rev. A —1983.—V. 27A, No 3 — P. 1741-1743.
660. Tomita K., Tsuda I. Chaos in the Belousov — Zhabotinsky Reaction in a
Flow System // Phys. Lett,—1979.—V. 71A, No 5, 6,—P. 489—492.
661. Tomita K.', Tsuda I. Towards the Interpretation of Hudson's Experiment
on the Belousov — Zhabotinsky Reaction // Progr. Theor. Phys. Japan.—
1980—V. 64, No 4.-P. 1138-1160.
662. Tomita K., Tsuda I. Towards the Interpretation of the Global Bifurcation
Structure of the Lorenz System / Progr. Theor. Phys. Suppl. (Japan).—
1980. No 69 —P. 185-199.
663. Tresser C, Coallet P. Iterations d'endomorphismes et groupe de renorma-
lisation // С R. Acad. Sci. Paris.—1978.—T. 287A, No 7.—P. 577—584.
664. Tresser C., Coullet P. Critical Transition to Stochasticity // Intrinsic Sto-
chasticity in Plasmas/Ed. G. Laval, D. Grassilon.— Orsay: Les editions de
physique courtaboeuf, 1979.— P. 365—372.
665. Turbulence and Chaotic Phenomena in Fluids/Ed. T. Tatsumi.—Amster-
Tatsumi.—Amsterdam: North Holland, 1984.
666. Turing A. M. The Chemical Basis of Morphogenesis II Philos. Trans. Roy.
Soc— 1952.— V. B237, No 641.- P. 37-72.
667. Turner J. S., Roux I.-C, McCormick W. D., Swinney II. L. Alternating
Periodic and Chaotic Regimes in a Chemical Reaction — Experiment and
Theory // Phys. Lett.— 1981.— V. 85A, No 1.— P. 9—12.
668. Tyson J. J. On the Appearance of Chaos in a Model of the Belousov — Re-
Reaction / J. Math. Biol.— 1978.— V. 5, No 4.— P. 351—362.
669. Veda Y., Akamatsu N. Chaotically Trancitional Phenomena in the Forced
Negative — Resistance Oscillator II IEEE Trans, on Circuits and Sys-
Systems-1981—V. CAS —28, No 3.-P. 217-223.
670. Ulam S. M., von Neumann J. On Combination of Stochastic and Determi-
Deterministic Processes // Bull. Amer. Math. Soc—1947.— V. 53, No 11.—
1 P. 1120.
671. Vlasova O. F., Zaslavsky G. M. Dissipation Effect on Chaos Onset in a
Two-Resonance Overlap Case /I Phys. Lett.—1983.— V. 99A, No 9.—
P. 405—410.
672. Walker G. H., Ford J. Amplitude Instability and Ergodic Behavior for
Conservative Nonlinear Oscillator Systems // Phys. Rev.—1969.— V. 188,
No 1.— P. 416—432.
673. Wegmann K., Rossler О. Е. Different Kinds of Chaotic Oscillations in the
Belousov — Zhabotinsky Reaction II Z. Naturforsch.—1978.— B. 33a,
H: 10.— S. 1179—1183.
674. Weiss C. O., Godone A., Olafsson Л.-Routes to Chaotic Emission in a CW
He-Ne Laser / Phys. Rev. A— 1983.- V. 28A, No 2- P. 892—895.
422

675. Weiss С. О., King H. Oscillation Period Doubling Chaos in a Laser ff
Opt. Gommun.— 1982.— V. 44, No 1.— P. 59—61.
676. Wersinger J. M., Finn J. M., Ott E. Bifurcation and «Strange» Behavior
in Instability Saturation by Nonlinear Three-Wave Mode Coupling //
Phys. Fluids.—1980.—V. 23, No 6.—P. 1142—1154.
677. Wersinger J. M., Finn^J. M., Ott E. Bifurcations and Strange Behavior in
Instability Saturation by Nonlinear Mode Coupling // Phys. Rev. Lett.—
1980.— V. 44, No 7.— P. 453—456.
678. Wigner E. P On the Quantum Correction for Thermodynamic Equilibri-
Equilibrium // Phys. Rev — 1932.— V. 40, No 5.— P. 749—759.
679. Williams R. F. The Structure of Lorenz Attractors Ц Lect. Notes in Math.
No 615.—1977.—P. 94—112. (Имеется перевод: Странные аттракторы.—
М.: Мир, 1981.—С. 58—72.)
680. Wolf A., Swift ]. Universal Power Spectra for the Reverse Bifurcations
Sequence // Phys. Lett.— 1981.— V. 83A, No 5.— 184—188.
681. Wolf A., Swift J. В., Swinney H. L., Vastano J. A. Determining Lyapunov
Exponents from a Time Series / Physica D.—1985.— V. 16, No 3.—
P. 285—317.
682. Yamada T. Chaotic State in an Electronic Circuit Analysis of Gollub et
al's Experiment / I. Phys. Soc. Japan.— 1982.—V. 51, No 11.—P. 3423—
3430.
683. Yamada Т., Graham R. Chaos in a Laser System under a Modulated Exter-
External Field I/ Phys. Rev. Lett.— 1980.— V. 45, No 16.— P. 1322—1324.
684. Yamada Т., Kuramoto Y. A Reduced Model Showing Chemical Turhulen-
ce I/ Progr. Theor. Phys. Japan.—1976.— V. 56, No 2.— P. 681—683.
685. Yamazaki H., Oono Y., Hirakawa K. Experimental Study on Chemical
Turbulence / J. Phys. Soc. Japan.—1978.—V. 44, No 1.—P. 335—336;
1979.— V. 46, No 2.— P. 721—728.
686. Yorke J. A., Yorke E. D. Metastable Chaos: The Transition to Sustained
Chaotic Behavior in the Lorenz Model // J. Stat. Phys.—1979.—V. 21,
No 3 — P. 263-277.
687. Yoshimura K., Watanabe S. Chaotic Behavior of Nonlinear Evolution Equ-
Equation with First Order Dispersion // J. Phys. Soc. Japan.— 1982.— V. 51,
No 9.- P. 3028-3035.
688. Young L.-S. Capacity of Attractors // Ergod. Theory and Dyn. Systems.—
1981.—V. 1, P. 3.—P. 381—388.
689. Young L.-S. Dimension, Entropy and Lyapunov Exponents // Ergod. The-
Theory and Dyn. Systems.— 1982.— V. 2, P. 1.— P. 109—124.
690. Zaslavsky G. M. The Simplest Case of a Strange Attractor Ц Phys. Lett.—
1978.— V. 69A, No 3.— P. 145—147.
691. Zaslavsky G. M. Stochasticity in Quantum Systems // Phys. Rep.— 1981 —
V. 80, No 3.— P. 159—250.
692. Zeghlache H., Mandel P. Influence of Detuning on the Properties of La-
Laser Equations Ц J. Opt. Soc. Amer.—1985.— V. B2, No 1.— P. 18—22.
693. Zisook A. B. Universal Effects of Dissipation in Two-Dimensional Map-
Mappings I/ Phys. Rev. A.— 1981.— V. 24, No 3.— P. 1640—1642.

Юрий Исаакович Неймарп, Полина Соломоновна Ланда
СТОХАСТИЧЕСКИЕ И ХАОТИЧЕСКИЕ КОЛЕБАНИЯ
Редакторы Ю. А. Данилов, И. М. Бокова
Художественный редактор Т. Н. Колъченпо
Технический редактор В. Н. Кондакова
Корректоры Т. С. Родионова, И. Я. Кришталъ
ИБ № 32417
Сдано в набор 23.03.87. Подписано в печать 05 11.87. T-20I86. Формат 6
мага офсетная. Гарнитура обыкновенная. Печать высокая. Усл. печ. ;
кр.-отт. 26,5. Уч.-изд. л. 28,15. Тираж 5100 экз. Заказ 753. Цена 4 р. 50 к.
Ордена Трудового Красного Знамени издательство «Наука»
Главная редакция физико-математической литературы
117071 Москва Б-71, Ленинский проспект, 15
4-я типография изд-ва «Наука»
630077 г. Новосибирск-77, ул. Станиславского, 25