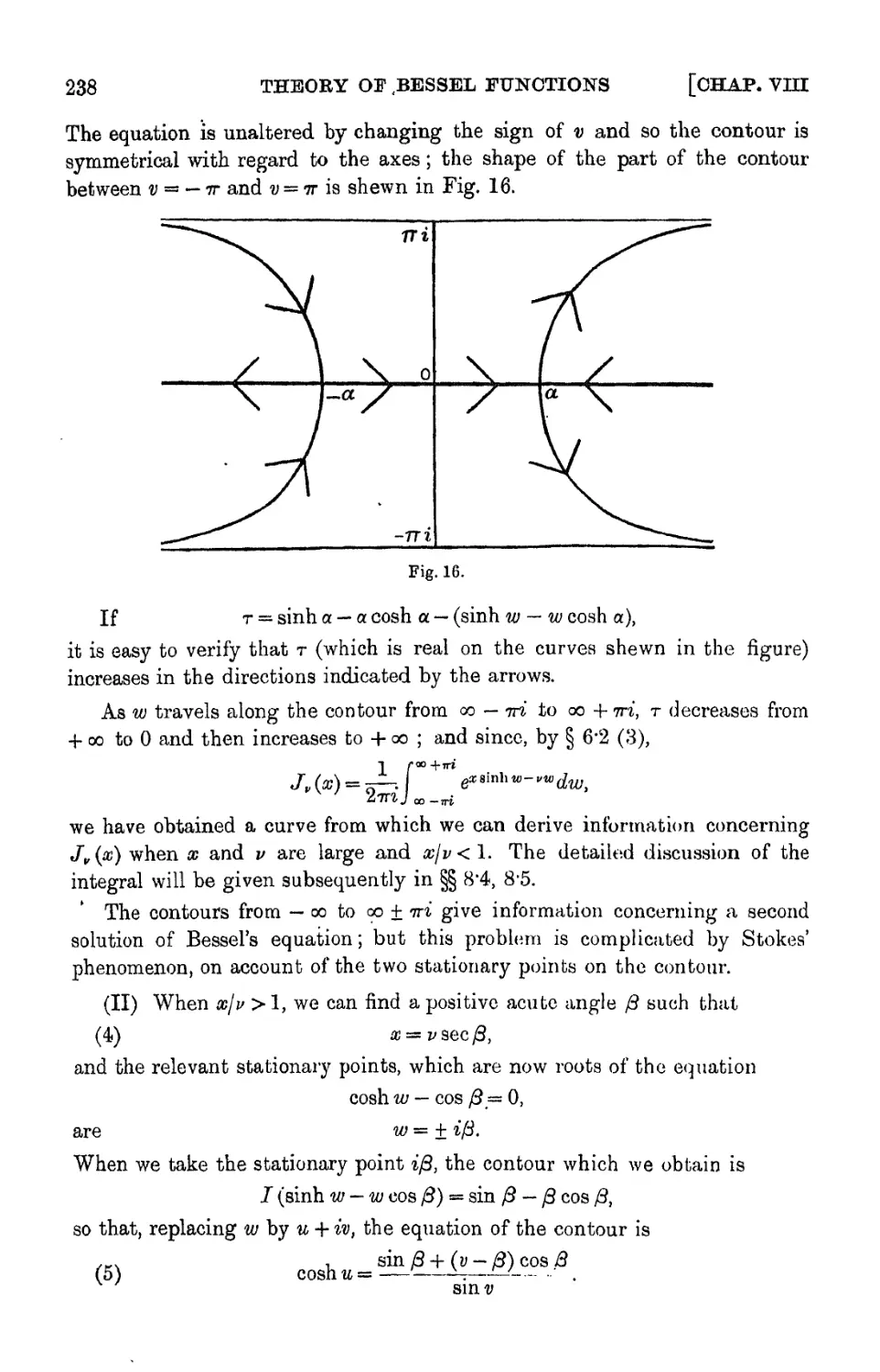
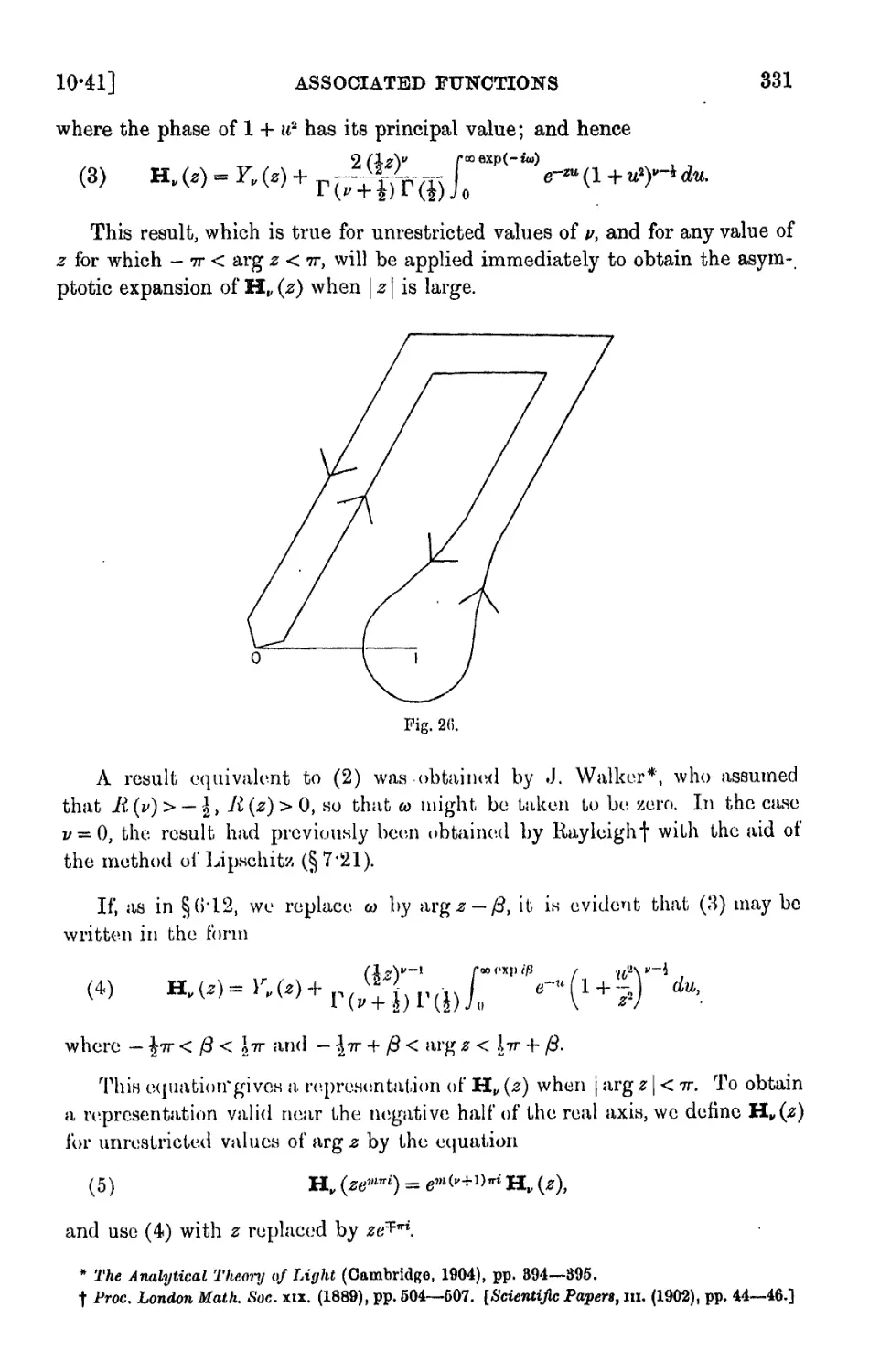
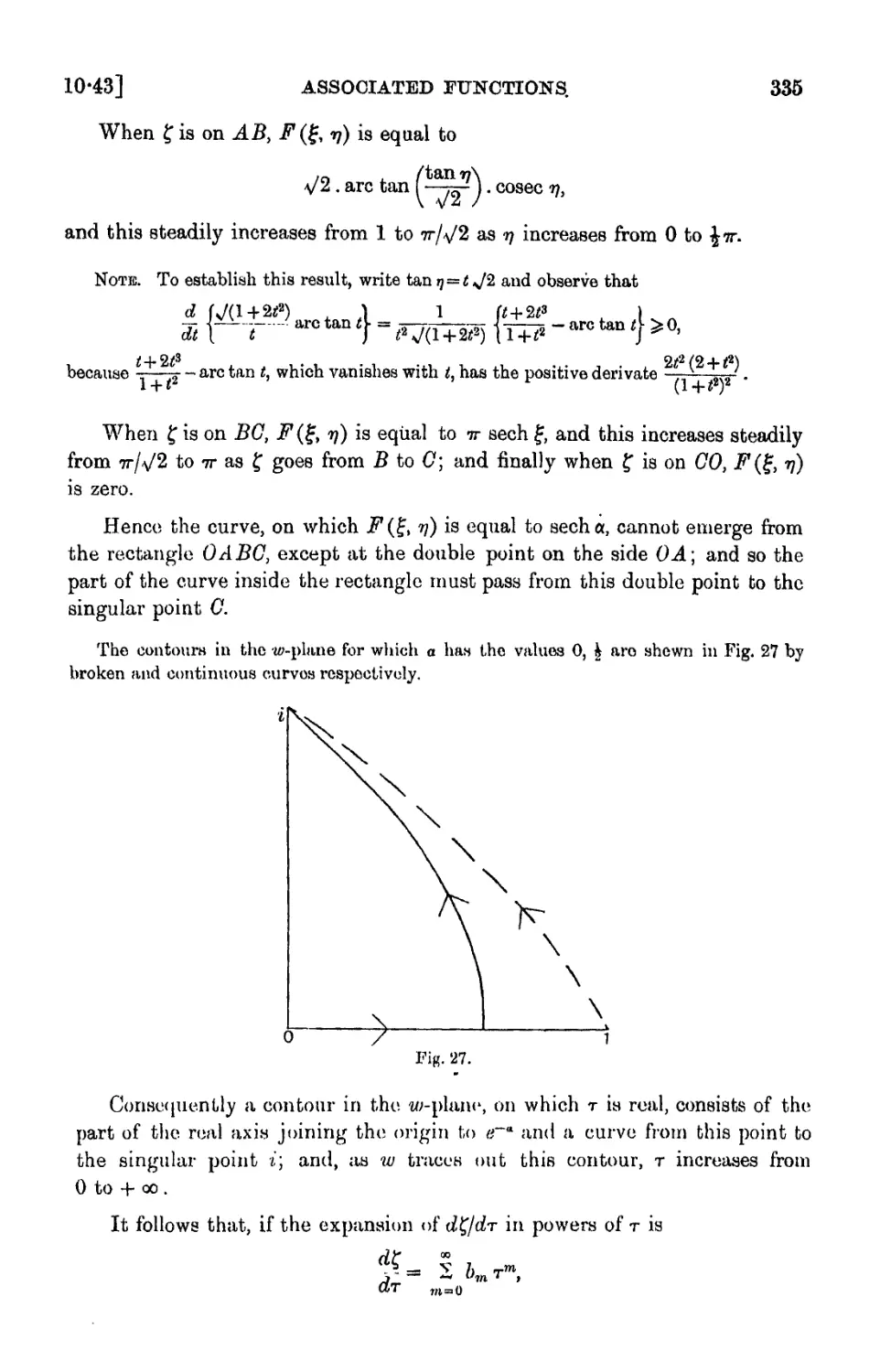
Similar
Text
A TREATISE ON THE
THEOEY OF
BESSEL FUNCTIONS
BY
G. N". WATSON, Sc.D., F.RS. .
PROFESSOR OF PUBE MATHEMATICS IN THE UNIVERSITY OF BIRMINGHAM
LATELY FELLOW OF TRINITY COLLEGE, CAMBRIDGE
SECOND EDITION
CAMBEIDGE
AT THE UNIVERSITY PRESS
1<L4
hirst Edition 1 U'22
Second Edition KMi
IN OW3.VT UIUTAIN
PREFACE
book has heen designed with two objects in view. The first is the
development of applications of the fundamental processes of the theory of
functions of complex variables. For this purpose Bessel functions are admirably
adapted; while they offer at the same time a rather wider scope for the appli-
application of parts of the theory of functions of a real variable than is provided by
trigonometrical functions in the theory of Fourier series.
The second object is the compilation of a collection of results which would
be of value to the increasing number of Mathematicians and Physicists who
encounter Bessel functions in the course of their researches. The existence of
such a collection seems to be; demanded by the greater abstruseness of properties
of Bessel functions (especially of functions of large order) which have been
required in recent years in various problems of Mathematical Physics.
While my endeavour has been to give an account of the theory of Bessel
functions which a Pure Mathematician would regard as fairly complete, I have
consequently also endeavoured to include all formulae, whether general or
special, which, although without theoretical interest, are likely to be required
in practical applications; and such results are given, so. far as possible, in a
form appropriate lor these purposes. The breadth of these aims, combined
with the necessity for keeping the size of the book within bounds, has made
it necessary to be as concise as is compatible with intelligibility.
Since, the hook is, for the most part, a development of the theory of func-
functions as expounded in the Course of Modern Analysis by Professor Whittaker
and myself, it has been convenient to regard that treatise as a standard work
of reference for general theorems, rather than to refer the reader to original
.sources.
It is desirable to draw attention here to the function which I have regarded
as the canonical function of the second kind, namely the function which was
defined by Weber and used subsequently by Schltifli, by Graf and Gubler and
by Nielsen. F\>r historical and sentimental reasons it would have been pleasing
to have felt justified in using Hank el's function of the second kind; but three
considerations prevented this. The; first is the; necessity for standardizing the
function of the second kind; and, in my opinion, the authority of the group
of mathematicians who use Weber's function has greater weight than the
authority of the mathematicians who use any other one function of the second
kind. The second is the parallelism which the use of Weber's function exhibits
between the two kin<Is of Bessel functions and the two kinds (cosine and sine)
VI PREFACE
of trigonometrical functions. The third is the existence of the device, by which
interpolation is made possible in Tables I and III at the end of Chapter XX,
which seems to make the use of Weber's function inevitable: in numerical work.
it has been my policy to give, in connexion with each section, references
to any memoirs or treatises in which the results of the section have been
previously enunciated; but it is not to be inferred that proofs given in this
book are necessarily those given in any of the sources cited.* The bibliography
at the end of the book haw been made as complete as possible, though doubtless
omissions will be found in it. While I do not profess to have inserted every
memoir in which Bessel functions are mentioned, I have not consciously omitted
any memoir containing an original contribution, however slight, to the theory
of the functions; with regard to the related topic of Riccati's equation,! have
been eclectic to the extent of inserting only those memoirs which seemed to
be relevant to the general scheme.
In the case of an analytical treatise such as this, it is probably useless to
hope that no mistakes, clerical or other, have remained undetected; but the
number of such mistakes has been considerably diminished by the criticisms
and the vigilance of my colleagues Mr C. T. Preece and Mr T. A. Luaisden,
whose labours to remove errors and obscurities have been of the greatest
value. To these gentlemen and to the staff of the University Press, who have
given every assistance, with unfailing patience, in a work of great typographical
complexity, I otter my grateful thanks.
O. N. W.
Auguaf&\, 102-2.
PREFACE TO THE SECOND EDITION
To incorporate in this work the discoveries of the last twenty years would
necessitate the rewriting of at least Chapters XII—XIX; my interest in
Bessel functions, however, has waned since 1922, and I am consequently not
prepared to undertake such a task to the detriment of tny other activities.
In the preparation of this new edition 1 have therefore limited myself to the
correction of minor errors and misprints and to the emendation of a few
assertions (such as those about the unproven character of Bourget's hypo-
hypothesis) which, though they may have been true in 1922, would have been
definitely false had they been, made in 1941.
My thanks are due to many friends for their kindness in informing me of
errors which they had noticed; in.particular, I cannot miss this opportunity
of expressing my gratitude to Professor J. R. Wilton for the vigilance which
he must have exercised in the compilation of his list of corrigenda.
G. N. W.
March 31, 1941.
CONTENTS
CHAP. 1'ACiK
T. BESSEL FUNCTIONS BEFORE 182E 1
I!. THE HESSE L COEFFICIENTS M
III. 15ESSEL FUNCTIONS 38
IV. DIFFERENTIAL EQUATIONS ... ... 85
V. MISCELLANEOUS PROPERTIES OF BESSEL FUNCTIONS . J32
VI. INTEGRAL REPRESENTATIONS OF BESSEL FUNCTIONS . 160
VII. ASYMPTOTIC EXPANSIONS OF BESSEL FUNCTIONS . . 194
VIII. BESSEL FUNCTIONS OF LARGE ORDER ...... 225
IX. POLYNOMIALS ASSOCIATED WITH BESSEL FUNCTIONS . 271
X. FUNCTIONS ASSOCIATED WITH BESSEL FUNCTIONS . . 308
XL ADDITION THEOREMS 358
XII. DEFINITE INTEGRALS 373
XIII. TNFINITE INTEGRALS .... .... 383
XIV. MULTIPLE INTEGRALS 450
XV. THE ZEROS OF BESSEL FUNCTIONS 1 477
XVI. NEUMANN SERIES AND LOMMEL'S FUNCTIONS OF TWO
VARIABLES 522
XVII. KAPTEYN SERIES 551
XVIII. SERIES OF FOURIER-BESSEL AND DINI 576
XIX. SCHLOMILCH SERIES 618
XX. THE TABULATION OF BESSEL FUNCTIONS . . . 654
TABLES OF BESSEL FUNCTIONS 065
BIBLIOGRAPHY 753
INDEX OF SYMBOLS 789
LIST OF AUTHORS QUOTED 791
GENERAL INDEX 796
To stand upon every point, and go over things at largo, and to bo cu
particulars, belongeth to tho first author of tin* story : but to ti.se*
and avoid much labouring of tho work, is to bo granted to him t
make an abridgement.
•2 Maccaiikks ii. :io,
CHAPTER I
BESS EL FUNCTIONS BEFORE 1820
l'l. Riccati's differential equation.
The theory of Bessel functions is intimately connected with the theory of
a certain type of differential equation of the first order, known as Riccati's
equation. In fact a Bessel function is usually defined as a particular solution
of a linear differential equation of the .second order (known aw Bcssel's equation)
which is derived from Riccati's equation by an elementary transformation.
The earliest appearance in Analysis of an equation of Riccati's type occurs
in a paper* on curves which was published by John Bernoulli in 1004-. Tn
this paper Bernoulli gives, aw an example, an equation of this type and states
that he has not solved it"f\
In various letters']; to Leibniz, written between 101O and 1704, James
Bernoulli refers to the equation, which he gives in the form
dy — yydx + tnvdx,
and states, more than once, his inability to solve it. Thus he writes (Jan. 27,
1097): " Vellum porro ex To so ire mini ot hanc. tent.averis dy = yydx-\- ,r.vd,r.
Ego in mille formas transmutavi,sed ope ram meam improhuin Problema per-
pettio lusit." Five years later he succeeded in reducing the equation to a linear
equation of the second order and wrote§ to Leibniz (Nov. 15, 1702): " (a)ua
occasione recordor aequationes alias memoral.ae dy~yydx-\-x"du: in qua nun-
quarn separare potui indeterrninatas a se invieem, sicut aequatio maneivt
simpliciter differential is: sed separavi i 1 las reducendo aequationem ad haue
differentio-differentialem|| ddy: y = — ,ra dx"."
When this discovery had been made, it was a simple step to solve the last
equation in series, and so to obtain the solution of the equation of the first
order as the quotient of two power-series.
* Ada F. nidi toy inn publicatu Lipxian, 1(>94, ]ip. 4;{.r)—4H7.
t " K«to proposita aequatio differential in luicc xulx-]- y-d.r ~a"ilij (inac an pur Hcparationcin
indctormiiiataruni conHtrui poKnit nondum tcntavi" ([). 4,!J()).
X Sec faibnizem getiamellte Werkt, J^iitto FoIrb (Mathonmtik), in. (Hallo, lH,r>r>), pp. /i0—H7.
§ Ibid. p. 615. Bernoulli's procedure wuh, eiTcctivuly, to take a new variable a defined by tho
formula
1 du
u dx
=y
in the equation di/[(lx = x"-\-y1i, and then to replaee it by y.
|| The connexion between this equation and a special form of Bessel'n equation will bo seou
in §4-3.
W. B. F. 1
2 THEORY OF BESSEL FUNCTIONS [CHAP. I
And, in fact, this form of the solution was communicated to Leibniz by
James Bernoulli within a year (Oct. 3, 1703) in the following terms*:
"Reduco autem aequationem dy^yydx+ocxdx ad fracfcionem c-ujus u torque,
terminus per seriem exprimitur, ita
, ,
347811 8478111215
3.4.7 3.4.7.8.11 8.4.7.8.11.12.15 3.4. 7.8. 11 . 12. 10. JU. ll>
y" , ^ , * *" , ^"^ ~
3.4 + 3.4.7.8 3.4.7.8.11.12 T 3.4. 7. 8. U . 12. 15 . Hi
quae series quidem actuali divisione in unam conflari possunt, hc<1 in qua
ratio progressionis non tam facile patescat, scil.
_ a* x> 2a;11 _ 13a?16 „
y ~ 3 + 3.3.7 + 3.3.3.7.11 + 3.373.' 3. 5. 7 . 7 .31 °"
Of course, at that time, mathematicians concentrated their energy, so tar
as differential equations were concerned, on obtaining solutions in 'finite terms,
and consequently James Bernoulli seems to have received hardly the full credit
to which his discovery entitled him. Thus, twenty-two years later, the pa per f,
in which Count Riccati first referred to an equation of the type which now
bears his name, was followed by a notej hy Daniel 'Bernoulli in which it, was
stated that the solution of the equation^
axn dx + uudx — bdu
was a hitherto unsolved problem. The note ended with an announcement, in
an anagram of the solution: "Solutio problematis ab 111. Kiecato propu.sito
characteribus occultis involuta 24a, %, 6c, 8d, 33e, 5/* 2//, 47>, ',YM, HI, 21 ni,
26n, 16o, 8p, oq, 17r, 16s, 2St, 32u, 5x, 3y, +, -, ——, +, =, -I-, 2, 1."
The* anagram appears never to have been solved; but Bernoulli published
his solution|| of the problem about a year after the publication of the anagram.
The solution consists of the determination of a set of values of n, namely
— 4w/Bm ± 1), where m is any integer, for any one of which the equation in
soluble in finite terms; the details of this solution will be given in $ 4f 1, \-1 1.
The prominence given to the. work of Riccati by Daniel Bernoulli, combined
with the fact that Riccati's equation was of a slightly more general type than
• See Leibnizem gesavidlic Werke, Dritte Folge (Miithematik), lit. (Hallo, lH5.r>), p. 7,">.
¦\ Acta Eruditorum, Suppl. vin. A724), pp. 06—73. The form in which lUcoali look tho
equation was
xmdq — du + uu dxiq,
where q=xn.
t Ibid. pp. 73—75. Daniel Bernoulli mentioned that solutions had been obtained by thn-o
other members of his family—John, Nicholas and the younger Nicholas.
§ The reader should observe that the substitution
hdz
u= — -
z dx
gives rise to an equation which is easily soluble in series.
|| Exercitationes quaedam mathematicae (Venice, 1724), pp. 77—80; Ada Eruditorum, 172C
pp. 465—473.
1*2] BESSEL FUNCTIONS BEFORE 1826 3
John Bernoulli's equation* has resulted in the name of Riccati being associated
not only with the equation which he discussed without solving, but also with
a still more general type of equation.
It is now customary to give the namef Riccati's generalised equation to
any equation of the form
where P, Q, R are given functions of x.
It is supposed that neither P nor 11 is identically zero. If 22=0, the equation is linear;
if P=O, the equation is reducible to the linear form by taking \\y as a new variable.
The last equation was studied by Euler J; it is reducible to the general
linear equation of the second order, and this equation is sometimes reducible
to Bessel's equation by an elementary transformation (cf. §§ 3*1, 4#3, 4*31).
Mention should be made here of two memoirs by Euler. In the first§ it
is proved that, when a particular integral yx of Riccati's generalised equation
is known, the. equation is reducible to a linear equation of the first order by
replacing y by yx + l/u, and so the general solution can be effected by two
quadratures. It is also shewn (ibid. p. 59) that, if two particular solutions are
known, the equation can be integrated completely by a single quadrature; and
this result is also to be found in the second|| of the two papers. A brief dis-
discussion of these theorems will be given in Chapter iv.
12. Daniel Bernoulli's mechanical problem.
In 1738 .Daniel Bernoulli published a memoiriT containing enunciations of
a number of theorems on the oscillations of heavy chains. Thu eighth ** of
these is as follows: " De fiyura catenae uniformiter oscillantis. Sit catena AG
uniformiter gravis ot perfects flexilis suspensa de puncto A, eaque oscillationes
facere uniformes intelligatur: porvenorit catena in situm AMF; fuoritque
longitudo catenae = 1: longitudu cujuscunque partis FM — x, sumatur n ejus
valorisff ut fit
_ L JL _ l* il _ —A"
+ 4~4.9n3+479.16ft4 4".~9.16.25ns +
* See James Bernoulli, Opera Omnia, u. (Geneva, 1744), pp. 1054—1057; it is stated that the
point of liiccati'ti problem is the determination of a solution in finite terms, and a solution which
rt'Rerubles the solution by Daniel Bernoulli is given.
t Thu term ¦ lliceati's equation ' was used by D'Alembert, ItiBt. de VAcad. R. dea Sci. de Berlin,
xix. A7C8), [published 1770], p. 242.
X Institutiones Calculi Intefjraliii, n. (Petersburg, 1769), §881, pp. 88—89. In connexion with
the reduction, see James Bernoulli's letter to Leibniz already quoted.
§ Novi Comm. Acad. Petrop. vin. A760—1761), [published 1763], p. 82.
|| Ibid. rx. A7E2—1763), [published 1764], pp. 163—164.
IF " Theoremata de osoillutionibus oorporurn filo flexili oonnexorum et catenae verticaliter
BUspenBae," Comm. Acad. Sci. Imp. Petrop. vi. A732—3), [published 1738], pp. 108—122.
** Loc. cit: p. 116.
ft The length of the simple equivalent pendulum is n.
4 THEOBY OF BESSEL FUNCTIONS [CIIAL\ I
Ponatur porro distantia extrerai puncti Fab linea'vertical! = 1, (lieu fore
distantiam puncti ubicunque assumpti M ab eadem linea verticali aequalem
1'" n + 4^ ~ 479^ + OTfen4 "* 479.1G. 25/in
He goes on to say: "Invenitur brevissimo calculo n = proxime IHiiW /....
Habet autem littera n infinitos valores alios."
The last series is now described as a Bessel function* of order zero and
argument 2*J(xjv); and the last quotation states that this function has an
infinite number of zeros.
Bernoulli published^ proofs of his theorems.soon afterwards; in theorem
vin, he obtained the equation of motion by considering the forces acting on
the portion FM of length x. The equation of motion was also obtained \>y
EulerJ many years later from a consideration of the forces acting on an element
of the chain.
The following is the substance of Euler's investigation :
Let p be the line density of the chain (supposed uniform) and let. T lie. the ten.sinn u\
height x above the lowest point of the chain in its undisturbed position. The unit inn lieini;
transversal, we obtain the equation 8T=gp8;c by resolving vertintllv l«»r an element <<f
chain of length 8x. The integral of the equation is T=g/).v.
The horizontal component of the tension is, effectively, T(dijjdx) where >/ i.s the Imrt
zontal) displacement of the element; and so the equation of motion \»
9
If we substitute for T and proceed to the limit, we find thai,
(Fy_ d ( dy\
d~>~(Jd\Vd)
If / is the length of the simple equivalent pendulum for any one normul viUrat inn, \vi-
write
where A and ? are constants ; and then II (x/f) is a solution of tlio ('(juatiDn
d ( do\ o .
dx \ ax) f
If a?//=u5 we obtain the solution in the form of Bernoulli's .series, namely
1 1.4 1.4.9+1.4.9.16 ¦"¦
* On the Continent, the functions are usually called cylinder fuuriioiiH, or, oowumnuilly, func-
functions of Fourier-Bessel, after Heine, Journal fur Math. lxix. A808), p. V2.H- hcc iiIho Muth Ann
in. A871), pp. 609—610.
+ Comm. Acad. Petrop. vn. A734-5), [published 1740], pp. 162—17D.
t Ada Acad. Petrop. v. pars 1 (Matliematica), A781), [published 1784], pp. 1.-57 177. Kuler
took the weight of length e of the chain to be E, and he defined ,j to he the iiuuihiuo of tlu-
distance (not twice the distance) fallen by a particle from rest under gravity in a mioond. KuIit'h
notation lias been followed in the text apart from the significance of g and tho introduction of
p and 8 (for d).
1*3] BESSEL FUNCTIONS BEFORE 1826 5
The general solution of the equation is then shown to be Di' + Ov I - 2, where C and
I) are constants. Since y is finite when A'=0, 0 must l>e zero.
If a is the whole length of the chain, y=0 when x=a, and so the equation to dofcermine / is
By an extremely ingenious analysis, which will be given fully in Chapter xv, Eulot
proceeded to shew that the three smallest roots of the equation in a/faVQ l*44-79.r>, 716Gf>K
and 18-63. [More accurate values are l-44f»79fl."), 7'017Hlf)fi and 18-7217517.]
In the memoir* immediately following this investigation Euler obtained the general
solution (in the form of series) of the equation ,- («¦,-) + r~0, but his statement of the
v ' l du \ dwj '
law of formation of .successive coefficients is rather incomplete. The law of formation had,
however, been stated in his Institutions* Calct'li [nttufwlix^, it. (Petersburg, 17C!)), ? iO7,
pp. 233-235.
1. Eiders mechanical problem..
The vibrations of a stretched membrane were investigated by Euler} in
L764. He arrived at the equation
1 d-z tf-s 1 dz 1 d'-z
e'1 dt~ dr" r dr r'2d<fr'
where z is the transverse displacement, at time t at the point whose polar
coordinates are (r, <f>); and e is a constant depending on the density and
.tension of the membrane.
To obtain a normal solution he wrote
z «= it sin (at. + A ) sin (fi<j> + li),
where a, A, ft, H are constants and u is a function of r; and the result of
substitution of this value of ^ is the differential equation
dru , J dit fa" ft-\ .,
dr- r dr ¦ e- r-J
The solution of this equation which is finite at the origin is given on p. 2a(i
of Euler's memoir; it is
,. _ rp j i a 7 i. ... a f . . ._ i.
where n has been written^ in place of 2/0+ T.
This differential equation is now known as Bessel's equation lor functions
of order ft; and ft may have || any of the values 0, 1,2, ....
Save for an omitted constant factor the series is now called a liessel
coefficient of order ft and argument ar/e. The periods of vibration, "IttJol, of a
* Artn Actul. J'etnrp. v. pars 1 (Mnlhi'iiuitica), A7H1), [published 17H-1], pp. 17H—11H.
+ See also §§085, 91W (p. 1H7 ft. ssq.) ibr tho nolutitm of an utmocialiul onuation which will Ir-
dificusHed in jj 3-52.
X Novi Comm. Actul. Petvop. x. A70i), [publlshod 1700], pp. 218—42<j().
^ Thu reason why Euler made this change of notation in not obvioua.
|| If p were not an integer, the displacement would not be a one-valued function of position,
in viuw of the faotor sin ((Sij> + fi).
6 THEOBY OF BESSBL FUNCTIONS [CHAP. T
circular membrane of radius a with a fixed boundary* are to be determined
from the consideration that u vanishes when r = a.
This investigation by Euler contains the earliest appearance in Analysis of
a Bessel coefficient of general integral order.
14. The researches of Lagrange, Carlini and Laplace.
Only a few years after Euler had arrived at the general Bessel coefficient.
in his researches on vibrating membranes, the functions reappeared, in an
astronomical problem. It was shewn by Lagrangef in 1770 that, in the elliptic,
motion of a planet about the sun at the focus attracting according to the law
of the inverse square, the relations between the radius vector r, the mean
anomaly M and the eccentric anomaly E, which assume the forms
M - E «- e sin E, r - a A - e cos E),
give rise to the expansions
E = M + 2 An sinnM, - * 1 + ie2 + S Bn cos vM,
«=i a " n~i
in which a and e are the semi-major axis and the eccentricity of the orbit and
2'l+2'rt m! (</t + m)\
Lagrange gave these expressions for n = 1, 2, 3. The object of the expansions
is to obtain expressions for the eccentric anomaly and the radius vector in
terms of the bime.
In modern notation these formulae are written
J.n = 2/n(ne)/n, Bn = - 2 («/») Jn' (tw).
It was noted by Poisson, Connaissance des Terns, 1836 [published 1833], p. <i that,
n _ 6 (lAn
a memoir by Lefort, Journal de Math. XI. A846), pp. 142—152, in which an orror nmdc ly
Poisson is corrected, should also be consulted.
A remarkable investigation of the approximate value of A n when n is large
and 0< e< 1 is due to Carlini^; though the analysis is not rigorous (and it
would be difficult to make it rigorous) it is of sufficient interest for a brief
account of it to be given here.
* Cf. Bourget, Am. Sci. de VEcole norm. tup. ra. A866), pp. 55-95, and Clin-o, Quarterly
Jovrnat. xxi. A886), p. 298.
t Hilt, de VAcad. R. des Sci. de Berlin, xxv. A769), [publiahed 17711, pp. 20-1—231*. Weuvrei
in. A869), pp. 113—138.]
% JRicerche sulla convergenza delta Krie che servo, alia soluzione del problema di KfiUem
(MUan, 1817). This work was translated into German by Jaoobi, A*tr. Nach xxx. AH50)
col. 197-254 [Werke, vn. A891), pp. 189-245]. See also two papers by ScheiW datod '
reprinted in Math. Amu xvu. A880), pp. 531—544, 545—560.
1'4] BESSEL FUNCTIONS BEFORE 1826 7
It is easy to shew that An is a solution of the differential equation
••'*»-" + .'•?•—0-1 A-a
Define u by the formula All = 2nn~'i f/Ulk/nl and then
e2 (~ + iCl \ + tu- w2 A - e2) = 0.
Hence when ii is large either u or «2 or dujde must bo largo.
If u = 0(na) we should expect ul and rfrt/^e to bo 0(?i!Jo) and O(«a) respectively; and
on considering the highest powers of n in the various terms of the last differential equation,
we find that a = 1. It is consequently assumed that u admits of an expansion in descending
powers of n in the form
where ii0, Uy, u.^, ... are independent of n.
On substituting thi.s .series in the differential equation of the first order and equating to
zero the coefficients of the various powers of ?i, wo find that
wliere u^dujde ; so that v()— ± , ?<i -- "--„, and therefore
f Udf = U JHr __ ; ^ _ ^ + v/( I - C2) + 1 j _ J log ( 1 _ ,2) _,_ ... }
and, since the value of An shews that \udi -«log he whefi « i.s small, tho upper .sign must
be taken and no constant of integration is k> bo added.
From Stirling's formula it now follows at onco that
and this is tho result obtained by Carlini. This method of approximation has been carried
much further by Meissel (see § 8*11), while Uauchy* has also discussed approximate
formulae for An in the ease of comets moving in nearly purabolu: orbits (soo § 8-42), for
which Carlini's approximation is obviously inadequate.
The investigation of which an account has ju.st been given is much more
plausible than tho arguments employed by Laplacef to establish the corre-
corresponding approximation for Bn.
The investigation given by Laplace is quite rigorous and the method which
he uses is of considerable importance when the value of Bn is modified by
taking all the coefficients in the series to be positive—or, alternatively, by
supposing that e is a pure imaginary. But Laplace goes on to argue that an
approximation established in the case of purely imaginary variables may be
used ' sans crainte ' in the case of real variables. To anyone who is acquainted
with the modern theory of asymptotic series, the fallacious character of such
reasoning will be evident.
* Comptes Rendus, xxxviri. A854), pp. 900—993.
f Mtcanique Cileste, supplement, t. v. [first published 1827]. Oeuvres, v. (Paris, 1882),
pp. 486—489.
8 THEORY OF BBSSEL FUNCTIONS [CHAP. I
The earlier portior of Laplace's investigation is based on the principle
that, in the case of a series of positive terms in which the terms steadily in-
increase up to a certain point and then steadily decrease, the order of magnitude
of the sum of the series may frequently be obtained from a consideration of
the order of magnitude of the greatest term of the series.
For other and more recent applications of this principle, see Stokes, Proc. Camb. Phil.
Soo. vi. A889), pp. 362—366 [Math, and Phys. Papers, v. A905), pp. 221—225], and Hardy,
Proc. London Math. Soo. B) n. A905), pp. 332-^-339 ; Messenger, xxxiv. A905), pp. 97—101.
A statement of the principle was given by Borel, Ada Mathematica, xx. A897), pp. 393—
394.
The following exposition of the principle applied to the example considered
by Laplace may not be without interest: *-
The series considered is
~ «=o 2n + 2m m! (ra + m)! '
in whioh n is large and e has a, fixed positive value. The greatest tonn i« that for which
«is=/i, where /z is the greatest integer such that
V(n + p) (n + 2/x - 2) < (n + 2/z) n*e8,
and so p is approximately equal to
Now, if um denotes the general term in Bn^\ it is easy to verify by Stirling's theorem
that, to a first approximation, -4±±.' ~ qt\ where
U
Hence BnW^u^ {I + 2q +
since* q is nearly equal to 1.
Now, by Stirling's theorem,
««-' exp {
and so
{1+^A+6*)}" ¦
The inference which Laplace drew from this result is that
B - f2
This approximate formula happens to be valid when e<l (though the reason
for this restriction is not apparent, apart from the fact that it is obviously
necessary), but it is difficult to prove it without using the methods of contour
* The formula l + 2S(/{ ~\/['irl{l-q)\ may be inferred from general theorems on series;
cf. Bromwioh, Theory of Infinite Series, § 51. It is also a consequence of Jacobi's transformation
formula in the theory of elliptic functions,
M0h) = (-'>)-Hn@|-T-i);
see Modern Analysis, § 21-51.
1*5] BESSEL FUNCTIONS BEFORE 1826 9
integration (cf. § 8-31). Laplace seems to have been dubious as to the validity
of his inference because, immediately after his statement about real and
imaginary variables, he mentioned, by way of confirmation, that he had
another proof; but the latter proof does not appear to be extant.
1. The researches of Fourier.
In 1822 appeared the classical treatise by Fourier*, La Theorie analytique
de la Chal&iir; in this work Bessel functions of order zero occur in the dis-
discussion of the symmetrical motion of heat in a solid circular cylinder. It is
shewn by Fourier (§§ 118—120) that the temperature v, at time t, at distance
x from the axis of the cylinder, satisfies the equation
dv _ K /d2v 1 dvy
It ~ Ul) [d:rn- + x t
where K, G, J) denote respectively the Thermal Conductivity, Specific Heat
and Density of the material of the cylinder; and he obtained the solution
where (j = mC])/K and m has to be so chosen that
hv + K (dv/dx) = 0
at the boundary of the cylinder, where h is the External Conductivity.
Fourier proceeded to give a proof (§§ 307—309) by Rolle's theorem that
the equation to determine this values of ni hasf an infinity of real roots and
no complex roots. His proof is slightly incomplete because he assumes that
certain theorems which have been proved for polynomials are true of integral
functions; the defect is not difficult to remedy, and a memoir by HurwitzJ
has the object of making Fourier's demonstration quite rigorous.
It should also be mentioned that Fourier discovered the continued fraction
formula (§313) for the quotient of a Bessel function of order zero and its
derivatc; generalisations of this formula will bo discussed in §§ 5'6, 965.
Another formula given by Fourier, namely
a.'2 a* ft" I
1 + +
had been proved some years earlier by Parseval§; it is a special case of what
are now known as Hessel's and Poisson's integrals (§§ 2*2, 2'3).
" This urcal.tii- pint of Vouimpi-'h veHcaroliiin wuh contained in a memoir dopoeifcod in the archives
of the Freud) InntiUite on HcpL liH, 1H11, and crowned on Jan. G, 1812. This memoir ia to be
found in the Mvm. de VAcud. tics ScL, iv. A819), [published 1824], pp. 185—56C; v. A820),
| published lHUH], pp. lM—'24E.
I Thin i« n ^'ciU'raliHation of Bernoulli's Htatoment quoted in § 1.
:'. Math. Ann. xxxin. A889), pp. '240—2E0.
8 Mvm. den xttvanx Gtrtintjerts, t. A805), pp. E39—048. .This paper also contains the formal
Htali'iuntt df thn the.oroni on Fourier conntantB which is sometimes called Pareeval's theorem;
another j»a])(!i' l»y thm little known writer, Mf.m. den savaiu strangers, i. A805), pp. 379—398, con-
tainH a Kenoral Holution of Laphice'H equation in a form involving arbitrary functions.
10 THEORY OP BESSEL FUNCTIONS [CHAP. I
The expansion of an arbitrary function into a series of Bessel functions of
order zero was also examined by Fourier (§§ 314—320); he gave the formula
for the general coefficient in the expansion as a definite integral.
The validity of Fourier's expansion was examined much more recently by Hankel,
Math. Ann. vm. A875), pp. 471—494; Schlafli, Math. Ann. x. A876), pp. 137—142; Dini,
Serie di Fourier, i. (Pisa, 1880), pp. 246—269; Hobson, Proc. London Math. Sue. B) vn.
A909), pp. 359—388; and Young, Proc London Math. Soc. B) xvin. A920), pp. 163-200.
This expansion will be dealt with in Chapter xvin.
1*6. The researches of Poisson.
The unaymmetrical motions of heat in a solid sphere and also in a solid
cylinder were investigated by Poisson* in a lengthy memoir published in 1823.
In the problem of the. sphere f, he obtained the equation
d?R n(n + l)
where r denotes the distance from the centre, p is a constant, n is a positive
integer (zero included), and R is that factor of the temperature, in a normal
mode, which is a function of the radius vector. It was sheAvn by Poisson that
a solution of the equation is
rn+1 cos (rp cos to) sin2U+1 todco
Jo
and he discussed the cases n — 0, 1, 2 in detail. It will appear subsequently
(| 3*3) that the definite integral is (save for a factor) a Bessel function of
order n + ^.
In the problem of the cylinder (ibid. p. 340 et seq.) the analogous integral is
Jo
cos (hX cos &)) sin2n co dco,
where n= 0,1, 2,... and X is the distance from the axis of the cylinder. The
integral is now known as Poisson's integral (§ 2'3).
In the case n = 0, an important approximate formula for the last integral
and its derivate was obtained by Poisson (ibid., pp. 350—352) when the variable
is large; the following is the substance of his investigation:
LetJ t70(i)=- I cos (? cos w) da>, Jo' (k)= I cos a sin (k cos «) i«.
"¦ J o it J o
Then Jo (k) is a solution of the equation
* Journal de Vficolc R. Poly technique, m, (cahier 19), A823), pp. 249—403.
+ Ibid. p. 300 et seq. The equation was also studied by Plana, Mem. della Ji. Accad. delle Sci.
di Torino, xxv. A821), pp. 532—534, and has since been Btudied by numerous writers, some of
whom are mentioned in § 4-3. See abo Poisson, La ThSorie Mathtmatique de la Chaleur (Paris,
' 1835), pp. 366, 369.
$ See also Rdhrs, Proc London Math. Soc. v. A874), pp. 136—137. The notation Ja(k) was
not used by Poisaon.
1] BESSEL FUNCTIONS BEFORE 1826 11
When k is large, 1/DP) may be neglected in comparison with unity and so we may expect
that Jo (k) s/k is approximately of the form A cos ? + 2? sin k where A and B are constants.
To determine A and B observe that
cos k.J0 (X-)-sin k.J6' (k)=- I * {cosH<w cos BAsin2?co) + sinHw cos B& cos2 ?co)} da.
"¦ J o
Write 7T - <u for <w in the latter half of the integral and then
cos k. J{) (k) - sin k. J{{ (k) = — I cos2 \<a cos Bk sin2 %a) da>
f j o
and similarly sink../<, (k)+cosk. J({ (k) = —~r \ A -~ )" si
[ VBfc) / ;?2\2 COS /*°°COS
But hm I (i_ __ ) . a>2.^=| . .r2. ota?=-i J(i7r),
fc-^oo Jo \ 2k J sm Jo sm - ¦*
by a well known formula*.
[Note. It is not easy to prove rigorously that the passage to the limit is permissible;
the simplest procedure is to appeal to Bromwich's integral form of Tannery's theorem,
Bromwich, Theory of Infinite Series, § 174.]
It follows that
cos k ../,, (k) - sin /-. Jo' (k) = . A + tk),
<in k. JK) (k) + cos k. •/,,' (k)= -rr—r-: A i-yk),
where <*-*-<) and rjk-»~O as k-»-tx>; and therefore
Jo (k) = -j—.v [A + «*) cos /t + A + r)k) sin -{.•],
It was then assumed by Poisson that Ju(k) is expressible in the form
+ + % + ...
k kl
where ;i = /i=l. The series are, however, not convergent but asymptotic, and the validity
of thin expansion was not established, until nearly forty years later, when it was investi-
investigated by Lipschitz, Journal filr MatL i-vi. A859), pp. 180—196.
The result of formally operating on the expansion assumed by Poisson for the function
tfl 1
J0(k) -JGrk) with the operator -¦ + 1 +/m 'a
,[<¦!. ].ff-;M , 2.2^'-A.2 + jr)yl' . 2 . SB'"-B. 3 + j-) A" , 1
* Cf. WatBon, Complex Integration and Cauchy's Theorem (Camb. Math. Tracts, no. 15,1914),
p. 71, for a proof of these results by using contour integrals.
12 THEORY OF BESSEL FUNCTIONS [CHAP. I
and so, by equating to zero the various coefficients, we find that
«-g5, A"=-^-^A, A'"- ^—i?, ...
1 a »« 9 a T>>" 9'25 A
and hence the expansion of Poisson's integral is
^ * 9 . 9-25
/ 1 9 9.25 \ . . ~|
v +m ~ 2: 8*#" otpz* + • • •;sm J ¦
But, since the series on the right are not convergent, the researches of Lipschitz and
subsequent writers arc a necessary preliminary to the investigation of the significance of
the latter portion of Poisson's investigation.
It should "be mentioned that an explicit formula for the general term in the expansion
was first given by W. B. Hamilton, Trans. K. Irish Acad. xix. A843), p. 313; his result
was expressed thus:
- f I cosB/3sin a) rf«= —^- 2 [0]"» ([--|]»J D/3)~)l cos ^-\i,n -±n),
and he described the expansion as serai-convergent; the expressions [O]~"and [ —i}" arc
to be interpreted as Ijn ! and { — i) (— §)... (-
A result of some importance, which was obtained by Poisson in a subsequent,
memoir*, is that the general solution of the equation
is y = j4^ J e~hxaosu>da) + 5^ I e~hxcosu log (a; sin- «¦>
Jo Jo
where J. and 5 are constants.
It follows at once that the general solution of the equation
d*if 1 dy 7, _
ace- x ax °
is
— A\ e~hxcos<° dco + B \ e-hxcoato\og {x sin-ca) g5gu.
.'o Jo
This result was quoted by Stokesf as a known theorem in 1850, and it is
likely that he derived his knowledge of it from the integral given in Poisson's
memoir; but the fact that the integral is substantially due to Poiswon has
been sometimes overlooked^.
* Journal de.. V&co\e R. Poly technique, xn. (eahier 19), A823), p. 476. The corresponding
general integral of an associated partial differential equation was given in an earlier memoir,
ibid, p. 227.
t Cavib. Phil. Trans, ix. A856), p. [38], [Math, and Phys. Papers, in. A901), p. 42].
? See Encyclopgdie des Sci. Math. n. 28 (§53), p. 213.
1'7] BESSEL FUNCTIONS BEFOKE 1826 13
1'7. The researches of Bessel.
The memoir* in which Bessel examined in detail the functions which now
bear his name was written in 1824, but in an earlier memoir^ he had shewn
that the expansion of the radius vector in planetary motion is
- = 1 + ? e2 + 2 Bn cos nM,
where Bn = sin u sin (nu — ne sin u) clu \
nir J o v
this expression for Bn should be compared with the series given in § 1'4.
In the memoir of 1824 Bessel investigated systematically the function IJl
defined by the integral J
Ikh = Ty coa (hit — k sin u) du.
lit
He took h, to bo an integer and obtained many of the results which will be
given in detail in Chapter ii. Bessel's integral is not adapted for defining the
function which is most, worth study when h is not an integer (see §10*1); the •
function which is of most interest for non-integral values of h is not I//1 but
the function defined by Loinmcl which will be studied in Chapter ill.
After the time of Bess<>l investigations on the functions became so numerous
that it seems nmvenie.nt at this stage to abandon the. chronological account
and to develop the theory in a systematic and logical order.
An hiatoiMcal jKn-.ount. of lnsouivhen from the time of KouruM1 to 1858 lias boon compiled
l>y Wagner, livni Mitthcil'uinfrn, 18!M, pp. 20-l--2(i(i; a briefer account of the early history
wan given by Rlag»i, Atti <icUa li. Av.cud. <h-i Lined, (Transmit!), (:i) iv. AH80), pp. 2.r>{)—ii\\\.
* lirrlhwr Abh. lH'2-1 [nublishod 1HUE|, pp. 1—52. The date o? this incmuir, ''UntcrsachuiiK
ilc.H TlicilH dcf iiluiH'turisclK'ii Htorungcn, w<;lchei- aus der BewcKunj; <lcr Sount' ontsteht," is
.Ian. li'.t, 1K24.
•|- lin-hnvr Abh. 1KH1- 17 [published 181<)J, ])p. 4il—.">/>.
;[: This integral occurs in the cxnunnion of thu ocw.ntric anomaly; with the uolatiou oE § 1-4,
"'lJt '* JU' '
a foiiuulii u\vvn by I'oi.smin, Cunnamance den Tern*, 1825 [publishod 1R2*2], p. 3H3.
CHAPTER II
THE BESSEL COEFFICIENTS
21. The definition of the Bessel coefficients.
The object of this chapter is the discussion of the fundamental properties
of a set of functions known as Bessel coefficients. There are several ways of
defining these functions; the method which will be adopted in this work is to
define them as the coefficients in a certain expansion. This procedure is due
to Schlomilch*, who derived many properties of the functions from his defi-
definition, and proved incidentally that the functions thus defined are equal to the
definite integrals by which they had previously been defined by Bessel f. It
should, however, be mentioned that the converse theorem that Bessel's inte-
integrals are equal to the coefficients in the expansion, was discovered by Hansen|
fourteen years before the publication of Schlb'milch's memoir. Some similar
results had been published in 1836 by Jacobi (§ 2*22).
The generating function of the Bessel coefficients is
.KH).
It will be shewn that this function can be developed into a Laurent series,
qua function of t\ the coefficient of tn in the expansion is called the Bessel
coefficient of argument z and order n, and it is denoted by the symbol Jn (z),
so that
A) eKH)-. I t»Jn(z).
• «= —90
To establish this development, observe that eizt can be expanded into an
absolutely convergent series of ascending powers of t; and for all values of t,
with the exception of zero, e~*elt can be axpanded into an absolutely conver-
convergent series of descending powers of t: When these series are multiplied
together, their product is an absolutely convergent series, and so it may be
arranged according to powers of t; that is to say, we have an expansion of the
form A), which is valid for all values of z and t, t = 0 excepted.
* Ztittchrift fiir Math; wnd Phys. n. A857), pp. 137—165. For a somewhat similar expansion,
namely that of ezC0B9t 8ee Frullani, Mem. Soc. Ital. {Modena), xvni. A820), p. 503. It muat be
pointed out that Sbhldmiloh, following Haneen, denoted by Jlhn what we now write as JnBz);
but the definition given in the text is now universally adopted. Traces of Hanson's notation
are to be found elsewhere, e.g. Sohlafli, Math. Ann. m. A871), p. 148.
+ Berliner Abh. 1824 [published 1826], p. 22.
X Ermittelung der Absoluten Stdrungen in Ellipses von beliebiger Excentricit&t und Neigung,
i. theil, [Sohriften der Sternwarte Seeburg: Gotha, 1843], p. 106. See also the French transla-
translation, Mimoire »ur la determination des perturbations absolues (Paris, 1845), p. 100, and Leipziger
Abh. n. A855}, pp. 250—251.
2*1, 2*11] THE BESSBL COEFFICIENTS 15
If in A) we write — 1/t for t, we get
rt" —oo
on replacing n by — n. Since the Laurent expansion of a function is unique*,
a comparison of this formula with A) shews that
B) /-(*)« <-)»./»(*),
whore n is any integer — a formula derived by Bessel from his definition of
Jn (z) as an integral.
From B) it is evident that A) may be written in the form
C) ek*(t-iit) = Jo (Z) + v {p + (-.)«t-n] Jn (*).
«-i
A nummary of elementary results concerning «/„ B) has been given by Hall, The Analyst,
1. A874), pp. 81-—84, ami an account of elementary applications of these functions to
problems of Mathematical Physics has been compiled by Harris, American Journal of
Math, xxxiv. A912), pp. 3i)l—420.
The function of order unity has been encountered, by Turriere, Nouv. Ann. de Math. D)
IX. A1H5)), pp. 133—411, in connexion with the steepest curves on the surface z=-y E.i>2 -y*).
21. The ascending series for Jn(z).
An explicit expression for Jn (z) in the form of an ascending series of powers
of z is obtainable) by considering the series for exp(J^) and exp( — ^zjt), thus
Wlu'ii n is u po.sit.ivo integer or zero, tho only term of the first series on the
right which, when associated with the general term of the second series gives
rise t,o a term involving tn is the term for which r = n + m; and, since ?i ^ 0,
then4 is always one (,enn for which r has this value. On associating these
terms for all the values of m, we see that the coefficient of tn in the product is
3 (I*)'11- (-\z)m
wif 0 (n + m) \ m \
We thei'efore have the result
* For, if not, zero oouhl hv. oxpandod into a Laurent Heries in (, in which some of the
coufliciuntH (nay, in inirticular, that of /"') woro uoL zero. If wo then multiplied the expansion by
t-m-i anfl iulegrated it round a circle with oentru at the origin, we should obtain a contradiction.
ThiH roBult was uotiood by Cauohy, Comptes Rendus, xm. A841), w. 911.
16 THEORY OF BESSEL FUNCTIONS [CHAP. II
where n is a positive integer or zero. The first few terms of the series are
given by the formula
B) M»)—$r-
In particular
?2 z4 z°
To obtain the Bessel coefficients of negative order, we select the terms in-
involving t~n in the product of the series representing exp (\zb) and exp(— Izjt),
where n is still a positive integer. The term of the second series which, when
associated with the general term of the first series gives rise to a term in t~n
is the term for which m = n + r ; and so we have
~ ).==() f ! (n + v)! '
whence we evidently obtain anew the formula § 2*1 B), namely
J-n{z) = (-)nJn(z).
It is to be observed that, in the series A), the ratio of the (m + l)th term
to the mth term is — \z"J\in (n + to)), and this tends to zero as on -*• oo , for all
values of z and n. By D'Alembert's ratio test for convergence, it follows that
the series representing Jn(z) is convergent for all values of z and n, and so it
is an integral function of z when n ~ 0, + 1, + 2, + 3,
It will appear later (§ 4'73) that Jn (z) is not an algebraic function of z
and so it is a transcendental function; moreover, it is not an elementary
transcendent, that is to say it is not expressible aa a finite combination of
exponential, logarithmic and algebraic functions operated on by signs of
indefinite integration.
From A) we can obtain two useful inequalities, which are of some import-
importance (cf. Chapter XVI) in the discussion of series whose general term in a
multiple of a Bessel coefficient.
Whether z be real or complex, we have
and so, when n 5s 0, we have
This result was given in substance by Cauchy, Comptes liendus, xm. A841), pp. 687,
854; a similar but weaker inequality, namely
was given by Neumann, Theorie der BesseVschen Functionen (Leipzig, 1867), p. 27.
2*12] THE BESSBL COEFMCIENTS 17
By considering, all the terms of the series for Jn (z) except the first, it is
found that
E) jn(z)J&f
where 6 <exp ±A—=• - 1
It should be observed that the aeries on the right in § 21 A) converges uniformly in
tiny bounded domain of the variables z and t which does not contain the origin in the
Z-plano. For if 8, A and It are positive constants and if
the terms in the expansion of exp (^zt) exp (felt) do not exceed in absolute value the corre-
corresponding terms of the product exp (?/2A) oxp (^/2/&), and the uniformity of the convergence
follows from the test of Weierstrass. Similar considerations apply to the series obtained
by term-by-term differentiations of the expansion 2tn Jn (z), whether the differentiations be
performed with respect to z or t or both z and t.
2*12. The recurrence formulae.
The equations*
A) Jll_l(z) + Jn+1(z)^Jn(z)>
B) Jn_1B)-/n+1(^) = 2/w'(^),
which connect three contiguous functions are useful in constructing Tables of
Bessel coefficients; they are known as recurrence formulae.
To prove the former, differentiate the fundamental expansion of § 2-l,
namely
,»*«-*">= i FJn{z),
n- -so
with respect to t; we get
i«(l + l/P)e**('/0« 2 nt^Jn(z),
ho that
Jsa + l/P) 5 lnJn(z)= 5 ntn-\r»{z).
?l= — oo »= — oo
If the expression on the left is arranged in powers of t and coefficients of tn~x
are equated in the two Laurent series, which are identically equal, it is evident
that
| z {./¦„_, (z) + /?H, (*)} = nJn (z),
which is the first of the formulaef.
* Throughout the work primes are used to denote the derivate of a function with respect to
its argument.
f Differentiations are permissible because (§ 2*11) the resulting series ar? uniformly convergent.
The equating of coefficients ie permissible because Laurent expansions are unique.
w. u. p. 2
18 THEOBY OF BESSEL FUNCTIONS [CHAP. II
Again, differentiate the fundamental expansion with respect to z; and then
{t~xm= 2 t*Jn'(z),
so that K*-V<) ^ tnJn{z)= t tnJnr(z).
By equating coefficients of tn on either side of this identity we obtain formula
B) immediately.
The results of adding and subtracting A) and B) are
C) sJn' (z) + nJn (z) = zJn_, 0),
D) zJn 00 - nJn (z) = - z Jn+1 (z).
These are equivalent to
E) j?{*M*)} = *J»-i{*),
F) §-z{z-nJn(z)} = -2~nJn+dz)-
In the case n=0, A) is trivial while the other formulae reduce to
G) Jo'(*) = -/,(*).
The formulae A) and D) from wbich the others may be derived wore discovered by
Bessel, Berliner Abh. 1824, [1826], pp. 31, 35. The method of proof given here is due to
Schltimilch, Zeitschrift fur Math, und Phys. ir. A857), p. 138. Schlmnilch proved A) in
this manner, but he obtained B) by direct diflerentiation of the scries for r/u (z),
,A. formula which Sehlomilch derived (ibid. p. 143) from B) is
(8) 2r^#= 2 (-TrCm.Jn-m(z),
where rQm is a binomial coefficient.
By obvious inductions from E) and F), we have
(9) ()
A0) [~) (r* Jn E)} = (-rz-»-™Jn+m (,),
where n is any integer and in is any positive integer. The formula A0) is due
to Bessel (ibid. p. 34).
As an example of the results of this section observe that
zJx (z) - 4/2 (z) - zJs (z)
= 4/2 (z) - SJt (z) + zJ, (z)
2
n=l
= 4 t (~-y-*nJm(z),
n-i
since zJiN+i (z)-*-0 as N-+ oo , by § 211 D).
2-13, 2-2] THE BESSEL COEFFICIENTS 19
The expansion thus obtained,
A1) */,<*)« 4 2 {-f-'nJ^iz),
is useful in the developments of Neumann's theory of Bessel functions (§37).
2*13. The differential equation satisfied by Jn(z).
When the formulae § 2'12 E) and F) are written in the forms
the result of eliminating* Jn-\ (z) is seen to be
that is to say
-n ^ <*J + „,-« Jn (Z)\ = - *.-«/„ (*),
dz )
and so wo have Bessel's differential equation*
A) ^'Q + ^W + v-^J.^o.
az~ az
The analysis i.s simplified by using ihi; oponitur ^ denned as z(d\d.z\
Thus the recurrence formulae are
(S + a) Jn (Z) = zJw (Z), (Sr - W + 1) ,/"„_, («) = - Zjn (z),
and ho
(^ - n + 1) [2~l (^ + ;«) ./„ (z)] = - ^,/u (a),
that is
an<l the equation
reduces at once to Bcssel's (Mjuation.
Corollary. The .same differential equation i.s obtained if',/,,.,.,(.:) i.s eliminated from the
formulae
D + H+l) ./n + 1 {Z) = Z,ln B), (.9 - ») ./„ B)= -*J1I+ ,B).
2'2. Bessel'.s integral for the Bessel coefficients.
Wo shall now prove that
A) -/„ 0) = .-,1 I "' cos {n6-z sin 0) rf^.
This cfjuation waa taken by Bessolf as the definition of Jn (z), and he
derived the other properties of the functions from this definition.
* Berliner Abh. 182J.[publi«lu'd 1820], p. H4; see also Frullani, Mem. Soc. ItaL.(Modeaa), xxm.
AH20), p. 504.
f Ibid. pp. 22 und 35.
2—2
2Q THEORY OF BBSSEL FUNCTIONS [CHAP. II
It is frequently convenient to modify A) by bisecting the range of in-
integration and writing 2ir—8- for 6 in the latter part. This procedure gives
1 f*
(o\ Jn {z) = - cos {nd - z sin 6) dd.
W 7T Jo
Since the integrand has period Irr, the first equation may be transformed
into
C) Jn{z)-n~ \ cos (rtd — z sin 6) dd,
v ' . 67? J a
where a is any angle.
To prove A), multiply the fundamental expansion of §21 A) by t~n~l and
integrate* round a contour which encircles the origin once counterclockwise.
We thus get
The integrals on the right all vanish except the one for which w = n; and
so we obtain the formula
Take the contour to be a circle of unit radius and write t = e~i0, so that 0
may be taken to decrease from 2n + a to «. It is thus found that
E) Jn{z)** ^- I ^V"*-"*') d6,
a result given by Hansenf in the case a = O.
In this equation take a = — tt, bisect the range of integration and, in the
former part, replace 0'by —6. This procedure gives
and equation B), from which A) may be deduced, is now obvious.
Various modifications of Bessel's integral are obtainable by writing
1 f* 1 /'"¦
Jn (z) = — I cos nd cos (z sin d) dd + - sin nd sin (z sin 0) dd.
TT JO ^ JO
If 6 be replaced by tt- ^ in these two integrals, the former changes sign when
n is odd, the latter when n is even, the other being unaffected in each case ;
and therefore
Jn {z) — — sin nd sin (z sin d) dd j
F) Vrl («0dd)>
7T
sin nd sin (^ sin 6) dd
* Term-by-term integration ia permitted because the expansion is uniformly convergent on the
contour. It is convenient to use the symbol J<a+) to denote integration round a contour encircling
the point a ouce counterclockwise.
t Ermittehuig der ahsoluten Stirrungen (Gotha, 1843), p. 105.
2-21] THE BUSSEL COEFFICIENTS 21
1 <<jr
~ I cos n$ cos (z sin 6) d6 I
"I1" J 0
G) y° ^ (»even).
= — / cos w# cos (z sin 0) eft?
If 6 be replaced by \tr— jj in the latter parts of F) and G), it is found that
2 f*""
(8) Jn (z)= -(-)*(»-1) cos in] sin (z cos rj) drj (n odd),
T Jo
2 r ^ir
(9) «/M(s) =-(-)*« cos m?7 cos(z cos97) c??7 (?i even).
The last two results are due substantially to Jacobi*.
[Note. It was shewn by Parseval, Mem. des savans Strangers, I. A805), pp. 639—648,
that
1 /•«•
•... = I cos (a sin x) dx,
IT J 0
?2. 4a 22. 42 6Z
and ho, in the special caBe in which « = 0, B) will be described as Parseval's integral. It
will be seen in § 2*3 that two integral representations of Jn (z), namely Bessel's integral
and Poisson's integral l>ecorno identical when n—O, so a special name for thi« case is
justified.]
The reader will find it interesting to obtain (after Bessel) the formulae § 2'12 (I) and
S 2-12 D) from Bessol's integral.
2*21. Modifications of Parseval's integral.
Two formulae involving definite integrals which aro clo.sely connected with Parseval's
integral formula are worth notice. The first, namely
A) t/o {\/{z2 — '/a)f — - I #''coa cos B sin 6) dB,
IT J (I
is due to Bcsael +. The simplest method of proving it is to write the expression on the
right in the form
1 f*
/ /ill COB 0 \-lZ Bill 0 (JA
lir J -n
expand in powers of y cos d + iz sin 6 and use the formulae
j.n1GH u>1 ' J-tt '/COfcJ u>i r(«+i) v
the formula then follows without difficulty.
The other definite integral, due to Catalan \, namely
B) Jo Bi s/z) = - / " e«i-i-«) cob 0 COH {A - z) Hin 0} dd,
ir J 0
ia a special caso of A) obtained by .s\ibstitutitfg 1 —2 and 1 +z for 2 and y respectively.
* Journal fUr Math. xv. A336), pp. 12—18. [Gen. Math. Werke, vi. A891), pp. 100—102]; the
integrals actually given by Jacobi had limits 0 and v with factors 1/w replacing the factors 2/w.
See also An^er, Neueste Schriften der Naturf. Ges. in Danzig, v. A855), p. 1, and Oauohy,
Comptes Ite.ndus, xxxvui. A854), pp. 910—913.
+ Berliner Abh., 1824 [published 1826], p. 37. See sIho Anger, Neueate Schriften der Naturf.
Ges. in Danzig, v. A855), p. 10, and Lomrael, Zeitschrift filr Math, mid Phys. xv^A870), p. 161.
% Bulletin de VAcad. R. de Belgique, B) xli. A870), p. 988.
22 THEORY OF BESSEL FUNCTIONS [CHAP. II
Catalan's integral may be established independently by using the formula
l 1 [to+)
m! 2*u J
m
so that
m »m r @ +)
2
so gin 1 m »m r
by taking the contour to be a unit circle; the result then follows by bisecting the range of
integration.
2'22. Jacobi's expansions in series of Bessel coefficients.
Two 'series, which are closely connected with Bessol's integral, were dis-
discovered by Jacobi*. The simplest method of obtaining them is to write
t = ±ei$ in the fundamental expansion § 2*1 C). We thus got
CO
tt=l ~
= Jo (*) + 2 2 J2n(z)cos Zn6 ± 2i 2 J.ill+1 {z) sin Bn. + 1H.
n=l n=0
On adding and subtracting the two results which are combined in this formula,
we find
00
A) cos(zsin6) = Jo(z) + 2 2 Jm(z) cos
B) sin 0 sin 0)= 2 2 Jm+l(z)xi
Write \tt — 7/ for 6, and we get
C) COS (Z COS 7]) = Jo (z) + 2 2 (-)n Jon (z) COS 2/G7,
GO
D) sin (z cos 97) = 2 2 (—)" «/2n+I B) cos B» + 1)?;.
The results C) and D) were given by Jacobi, while the others weni obtained later by
Angert. Jacobi's procedure was to expand com B cos 7) and sin (z t:os 17) into a series of
coBines of multiples of rj, and use Fourier's rule to obtain the coedficionts in the form of
integrals which are seen to be associated with Bessel's integrals.
In view of the fact that the first terms in A) and C) arc nob formed
according to the same law as the other terms, it is convenient to introduce
Neumann's factor I en, which is defined to be equal to 2 when a is not zero,
and to be equal to 1 when n is zero. The employment of this factor, which
* Journal filr Math. xv. A836), p. 12. [Ges. Math. U'erke, vi. A891), p. 101.]
t Ncueute Schriften der Naturf. Gvs. in Danzig, v. A855), p. 2.
X Neumann, Theorie der BesseVschen Functianen (Leipzig, 18G7), p. 7.
2*22] THE BESSEL COEFFICIENTS 23
will be of frequent occurrence in the sequel, enables us to write A) and B) in
the compact forms:
GO
E) cos B sin 6) = 2 em J2n {z) cos 2nd,
00
F) sin B sin 6) = X e2n+1 Jm+1 B) sin Bn +1) $.
If we put 6 = 0 in E), we find
(') I — Z emjm{2).
If we differentiate E) and F) any number of times before putting 6 — 0, we
obtain expressions for various polynomials as series of Bessel coefficients. We
shall, however, use a slightly different method subsequently (§ 2'7) to prove
that zm is expansible into a series of.Bessel coefficients when m is any positive
integer. It is then obvious that any polynomial is thus expansible. This is a
special case of an expansion theorem, due to Neumann, which will be investi-
investigated in Chapter xvr.
For the present, we will merely notice that, if @) be differentiated once
before 6 is put equal to 0, there results
(8) 2= § ea»+iB/i + l)./an+100,
n-o
while, if 0 be put equal to lir after two differentiations of E) and (C), then
@) 2 sin 2 = 2 |22 J, (z) - 42 J, (z) + Gu J, (z) - ...},
A0) z com z = 2 11a J, B) - 3a ./„ \z) + 5- Jt B)-...}.
These results are due to Lommel*.
Notk. The expression exp \\z(t- l/t)\ introduced in $ 2-1 is not a generating function
in the strict .Mcn.se. The generating functiont associated with enJn(z) is 2 fui"i/n(^)-
If thi.s expression l>e called A', by using the recurrence formula $ 2*12B), wo have
?-JH)*+i(iH7
If we .solve thi.s differential ('([nation we get
I / I \ f~
A1) • =es +2 [t+ ty- j j> '«Wu
A result equivalent to this was given hy Brenke, Bull. American Math. Sac. xvi. A910),
pp. 2ii.r;—230.
* Studlen ilher di<< Be.tseVnc.hen Functional (Leipzig, 1868), p. 41.
t It will be seen in Chapter xvi. that this is a form of " Lommcl's function of two variables."
24 , THEOEY OP BESSEL FUNCTIONS [OTIAP. II
23. Poisson's integral for the Bessel coefficients.
Shortly before the appearance of Bessel's memoir on planetary perturbations,
Poisson had published an important work on the Conduction of Heat *, in the
course of which he investigated integrals of the typesf
cos (z cos 6) sinm+1 Odd, \ cos (z cos 6) sinan 0*M<
o Jo
Avhere n is a positive integer or zero. He proved that these integrals are
solutions of certain differential equations^ and gave the investigation, which
has already been reproduced in § 1, to determine an approximation to the
latter integral when z is large and positive, in the special case d — 0.
We shall now prove that
['
Jo
and, in view of the importance of Poisson's researches, it seems appropriate to
describe the expressions on the right§as Poisson's integrals lor Jn (c). In tho
case n= 0, Poisson's integral reduces to Parseval's integral (§ -"-).
Ifc is easy to prove that the expressions under consideration aiv (Mjual to
Jn(z)] for, if we expand the integrand in powers of j and then integrate
term-by-term||, we have
- 5 ^—r [corf"" ^siir" 0<W
7Tm=0 Bm)! Jo
^2m 1^3. 5...B/; - l).l .:5..r) ...
and the result is obvious.
* Journal de I'ficole R. Poly technique, xn. (cahier 19), A823), pp. '249—10:5.
t Ibid. p. 293, «t seq.; p. 340, et seg-. Integrals equivalent to thorn had proviouHly l«'»n
examined by Euler, List. CaZc. I7(«. i/. (Petersburg, 1769), Ch. x. S 1036, but 1'oinmm'H foniiH ant
more elegant, and bis Btudy of them i8 more eyBtematic. See also § ,'J\S.
J E.g. on p. 300, he proved that, if
R =rn+1 I cos (rp eos w) sin271 w </w,
Jo
then B satisfies the differential equation
dra ,.2 Ji ~ ~ ^ «¦
§ Nielsen, Handbuch der Theorie der Gylinderfunktionen (Leipzig, 190-i), p. 51, oallH them
Basel's second integral, but the above nomenclature seems preferable.
II The series to be integrated ia obviously uniformly convergent; the procedure adopted is duo
to Poisson, ibid. pp. 814, 340.
2-3, 2-31] THE BESSEL COEFFICIENTS 25
Poisson also observed* that
j eizam0 sin2n 0d6 = f * cos (z cos 6) sin2Jl Odd;
JO JO
this is evident when we consider the arithmetic mean of the integral on the
left and the integral derived from it by replacing 6 by tt — 6.
We thus get
B) J (z\ = -*' pizcosO qin
A slight modification of this formula, namely
has suggested important developments (cf. § 61) in the theory of Bessel
functions.
It should also bo noticed that
fir n-ir
D) cos(seoH0)sin2n0d0 = 2 co
Jo Jo
= 2 cos(>sin0)cos2n0cZ0,
jo
and each of those expressions gives rise to a modified form of Poisson's integral.
An interesting application of Besael's and Poisson's integrals was obtained
by Lommelf who multiplied tho formula
= 1 (-) ¦ - - ~«--x-,—-— -—smim6
Bnt)!
by iH)H(zci)Hd) and integrated. Ii^thua follows that
231. Kes&el'x invedigutum of Poisson's integral.
'Vho. proof, i.hat ,/„ (z) is ocjual to Poisson's integral, which was given bj'
BcHHcl.}, in HOinewhai/ elaborate; it is substantially as follows:
it is scon on diltbrentiation that
' , cos 6 sin-" 6 com (z cor 0) — n " , »in8M+I 0 sin (z cos 6)
A0 \_ J 2n + I J
= Bm - 1) .sin8"-1-1 6 - In sin*1 ^ + 0~- —1 sinan+2 <9 cos (z cos 0),
* PuiHKon ftfitimlly mado the statement (p. 293) concerning the integral whioU contains
Hina"'¦' 0; but, as ho pointn out on p. MO, odd powers may be replaced by oven powers throughout
hiH unalysiH.
•j- Studien ilber die Iie»geV»rhen Functianen (Leipzig, 1868), p. 30.
+ lirrliner Abh. 1824 [published lH2fi], pp. 30—1O. Jacobi, Journal filr Math. xv. A886), p. 13,
[Gen. Math. Werke, vi. AS(.J1), p. 102], when giving his proof (§ 2-32) of Poisson's integral formula,
objected to Hie artificial character of Bg8ho1'b domonfltration.
26 THEOEY OF BESSEL FUNCTIONS [CHAP. II
and hence, on integration, when ?i > 1,
Bn -1) I"*" cos (z cos 0) sin291 Bdd - 2n \ cos (z cos 0) sin™ 6d0
Jo Jo
+ , z _ ("cos@cos0)sinBl+a0^0 = 0.
ZW + I J o
If now we write
iifZ1 f ™* /• rtrt«» /)\ sinm Q^Q - ^ (?,);
the last formula shews that
z<f) (n - 1) - 2ncj6 (to) + s<f> (n + 1) = 0,
so that <jb(?i) and «/n(^) satisfy the same recurrence formula.
But, by using Bessel's integral, it is evident that
6 (I) = - (""" cos (z cos 0) sin2 6dd = -^ I' -%. {sin {z cos 0I sin
¦jrJo ttJo fto ( ]
If".
= - sin {z cos 0) cos Odd = — t/0' (z) = </, (^),
ttJ o
and so, by induction from the recurrence formula, wo have
4>{n) = Jn(z),
when n = 0,1, 2, 3, ....
2'32. Jacohi's investigation of Poissons integral.
The problem of the direct transformation of Poisson's integral into Bossel's
integral was successfully attacked by Jacobi*; this method necessitates the use
of Jacobi's transformation formula
dn-i BJnan-! Q 1.3.5... B?i - 1) . Q
¦—-j-rri—=(-)n~1 --- 'sinw^,
where /u. = cos 0. We shall assume this formula for the moment, and, .since no
simple direct proof of it seems to have been previously published, we shall
give an account of various proofs in §§ 2*321—2-323.
If we observe that the-first n~ 1 derivates of A — /x8)'1"*, with inspect to
fi, vanish when /u,= ± 1, it is evident that, by n partial integrations, we have
zu I * cos (z cos 0) sinm Odd = zn ! cos (zft). A - /Aa)tt-l dp
J0 J -1
J
l
COS EM -
* Journal fiir Math. xv. A8S0), pp. 12—13. [Ges. Math. Werke, \i. A801), pp. 101—102.] See
also Journal de Math. i. A836), pp. 195—196.
2-32, 2-321] THE BESSEL COEFFICIENTS 27
If we now use Jacobi's formula, this becomes
cos (za —
= 1.3.5... Bn — 1I cos (z cos 0 - %mr) cos ndcW
Jo
()()
by Jacobi's modification of § 22 (8) and (9), since cos(scos0 — ?n7r) is equal
to (—)*'* cos {z cos 6) or (-i)**11) sin B cos 0) according as n is even or odd; and
this establishes the transformation.
2*321. Proofs of JacohPs transformation.
Jacobi's proof of tho transformation formula used in § 2'Zi consisted in deriving it
as a special case of a formula due to Laoroix*; but the proof which Laeroix gave of
his formula is open to objection in that it involves the use of infinite scries to obtain
a result of an elementary character. A proof, based on the theory of linear differential
equations, wan discovered by Liouville, Journal de Math. vi. AB41), pp. 69—73; this
proof will be given in § 2-U22. Two yearn after Liouville, an interesting symbolic proof
was published by Boole, i'anib. Math. Journal, in. AB43), pp. ^IC—22-1. xVn elementary
proof by induction wan given by Gruniirt, Arc/do dor Math, und Plum. iv. A844), pp. 104—
109. This proof consists in shewing that, if
tlion B,,,., — A — u2) -- ' — yjtuG,, — n Ui — \) I 9,. da.
<? J i
and that ( - )" "' 1 . li. f> ... ('¦In — I) (win nS)jn satisfies the same recurrence formula.
Other proof's of this character have boon given by Todhunter, Differential Calculus
(London 1H71), Oh. xxvm., and Orawford r, Proc. ICdinburgh Math. AW. xx. A902),
pp. 11 IT), but all these proofs involve complicated algebra.
A proof depending on the use of contour integration in due to Scbliifli, Ann. di Mat. B)
v. (IK73), pp. 201—202. The contour integrals arc of the. type used in establishing
Lagrange'.s expansion; and in vj ii*3lW we shall give the modification of Schliifli's proof,
iii which the use of contour integrals is replaced by a use of Lagrauge's expansion.
To prove Jambi'n formula, differentiate by Leibniz' theorem, thus:
- 2 ( - )'" >iuC,m , i (sin \0)-m '1 (cos kdf'1'-- ~ '
m (i
• sin ('In x kfl),
and this is tin1 transformation required];.
"¦ Tntitr du Ciilr. Dijl'. i. (Paris, IKK), 2nd edition), pp. 1H2—1HU. Sen also a note written by
Catalan in 1H0H, MtUu. dc la Soc. It. den Sri. dr. Urge, B) xn. A8H.r)), j>p. IJ12—31tt.
I Crawford iittribntoK tin; formula to Kodriguen, posHibly in couHotjuenoc of an incorrect state-
statement by I'rdiK't, Herne11 d' Kxercivra (I'ai-iH, lK<iG), p. id, that it i« ^iven in EodriguoB' diBsertation,
Currrxp. mi- PKcolc It. Poll/technique, in. AK14—1H1C), pp. :ilil—:iH.r).
:[ I owe this proof to Mr C. T. I'roeco.
28 THEORY OF BBSSEL FUNCTIONS [CHAP. II
2*322. LiouvUle's proof of Jacobtfs transformation.
The proof given by Liouville of Jacobi's formula is as follows:
(l~fi2)w~* and let D be written for dfdfn then obviously
Differentiate this equation n times; and then
A - j*2) D>l+1y-fiD»y+n*Dn-1y=O:
so that (? + iA Z>"-1?/=0.
Hence * Dn~1y=A sn\n9 +Bcoan9>
where A and D are constants ; since Dn~1y is obviously an odd function of 6, B is zero.
To determine A compare the coefficients of 6 in the expansions of Dll~1y and A sinjitf in
ascending powers of 0. The term involving 6 in Da~ly is easily seen to be
^"-M-)"-1 B»- 1) B»- 3) ... 3.1. A
so that wyl = (-)»-1l .3.5... Bn-l),
and thence we have the result, namely
d*-isin«»-i0 .1.3.5...Bw-
()"~l
2*323. ScklqflCs proof of Jacobi's Iran* formation.
We first recall Lagrango's expansion, which is that, if z~/x + kf (z), then
*(•) = * 00 + | ? ^
so that </,' («) ^ = 1 ^ ^1
subject to the usual conditions of convergence*.
Now take / («)a ~fc A -«•), 0'(«Ks/(l-a«),
it being supposed that </>' B) reduces to ^A -/a2), i.e. to sin 6 when A-»-0.
The singularities of z qua function of h are at A = e±ffl; and so, when 6 is real, tho ex-
expansion of a/A — s2) in powers of h is convergent when both | h \ and | z \ are less than unity.
NOW 2 = {l-v'(l
I \n-l (jjn - 1 ojn 27i - 1 Q
Hence it follows that ¦ \ ¦; ^r-r = = is the coefficient of A"-1 in tho ex-
2n.(n-l)! dfin~l
pansion of *j{\ — z1). (Cz/d/i) in powers of h. But it ia evident that
in A dz (l~heie)-i-(l-he-i6)^ ? 1.3.5... B^-1) enie - ni0
in A ?
and a consideration of the coefficient of A11 in the last expression establishes the truth of
Of. Modern Analysis, § 7*32.
2-322-2-33] THE BESSEL COEFFICIENTS 29
2*33. An application of Jacobi's transformation.
The formal expansion
r fir oo
/ (cos x) cos vxdx — 2 (—)mamf{n+m) (cos x) dx,
.1A iiikH
/
. 0 .'0 j>i-0
in which <xm is the coefficient of Pl+im in the expansion of Jn (t)/J0 (t) in as-
ascending powers of t, has been studied by Jacobi*. To establish it, integrate
the expression on the left n times by parts; it transforms (§ 2'32) into
W (cos m) sin
and, when sin2na; is replaced by a series of cosines of multiples of x, this becomes
1 /¦"¦ ,. w x T- 2» ft 2n(rt-l) , "I 7
Q , ,. 7H—: /(n) (cos «) 1 —7 cos 2« + ¦'- -—y--r cos 4a; - ... dx.
2.4.f)... Bn).'o L " + 1 (n+l)(n+2) J
We now integrate/(n)(cosa;) cos 2tf, /"" (cos a;) cos 4>x, ... by parts, and by
continual repetitions of this process, we evidently arrive at a formal expansion
of the type stated: When /(cos a;) is a polynomial in cos#, the process
obviously terminates and the transformation is certainly valid.
To determine the values of the coefficients a,,^ in the expansion
I /(cos x) cos nxdx =f S (-)mam/"i+9in) (cos as) dx
thiiH obtained, write
/(cok a;) = (-)*" cos (t cos x), (—)*'«-J> sin (t cos x),
according as n is even or odd, and we deduce from § 2-2 (8) and (9) that
./„(«)- 2 (-ra^*" {(-)»¦/,@},
so that am has the value stated.
It has been stated that the expansion is valid when /(cos x) is a poly-
polynomial in cok;/:; it can, however, be established when /(cos x) is merely re-
restricted to be an integral function of cos x, say
J bn co.s" x
v
provided that lirn a/| btl \ is less than the smallest positive root of the equation
J0(t) = 0 ; the investigation of this will not be given since it seems to be of
no practical importance.
# Journal Jilr Math. xv. AHH6), pp. 25—2E [Ges. MaiA. IFerfce, vi. A891), pp. 117—118]. See
uluo Jacobi, A«tr. Narh. xxvin. AB49), col. 94 [Ges. Math. Werke, vn. A891), p. 174].
30 THEORY OF BESSEL FUNCTIONS [CHAP. II
24. The addition formula for the Bessel coefficients.
The Bessel coefficients possess an addition formula by which Jn (y + z)
may be expressed in terms of Bessel coefficients of y and z. This formula,
which was first given by Neumann* and Lommeli", is
(l) Jn(y + *)« 2 J
in- -oo
The simplest way of proving this result is from the formula § 2*2 D), which
gives
1 f@+)
Jn (# + *) = 21 r"~1 e*l2/+Z1 tt'*' dt
¦|0+) oo
t Jm.{y)\ V"-*-*eM
m^-a> J
oo
= 2 Jm {y) Jn~m (z),
TO- -co
on changing the order of summation and integration in the third line of the
analysis; and this is the result to be established.
Numerous generalisations of this expansion will be given in Chapter xr.
2'5. Hansen's series of squares and products of Bessel coefficients.
Special cases of Neumann's addition formula were given by Hanson J as
early as 1843. The first system of formulae is obtainable by squaring the
fundamental expansion § 21 A), so that
By expressing the product on the right as a Laurent series in t, and equating
the coefficient of tn in the result to the coefficient of tn in the Laurent ex-
expansion of the expression on the left, we find that
In particular, taking n = 0, we have§
A) JoBs) = Jf (z) + 2 ? (-Y Jr»(z) = ? (-)'• er J*(z).
* Theorie der BcsseVgchen Functionen (Leipzig, 1867), p. 40.
t Studienilber die BesseVschen Functionen (Leipzig, 1868), pp. 26—27; see also Sohlafli, Math.
Ann. in. A871), pp. 135—137.
t Ennitteluvg der dbsoluten St'drungen (Gotha, 1843), p. 107 et seq. Hansen did not give D),
and he gave only the special case of B) in which n=l. The more general formulae are due to
Loramel, Studien ilber die BesseVschen Functionen (Leipzig, 1868), p. 33.
§ For brevity, J,,2 (z) is-written in place of {Jn («)}2.
2-4-2-6] THE BESSEL COEFFICIENTS 31
From the general formula we find that
B) Jn B*) - 2 Jr (z) Jn-r (*) + 2 2 (~)r Jr (z) Jn+r (z),
when the Bessel coefficients of negative order are removed by using § 2*1 B).
Similarly, since
{rJ JrM*)}{j2 JL-y*v*J»(*)}
= exp [\z (t - 1/0} exp [\z (- i + 1/0]
it follows that
00
D) 2 (-)'1 Jr (Z) J*n-r (*) + 2 2 Jr (z) Jm+r (z) = 0.
Equation D) is derived by considering the coefficient of tin in the Laurent
expansion ; the result of considering the coefficient of tm+1 is nugatory.
A very important consequence of C), namely that, when x is real,
E) IJ.^I^l, |./r(*Oh
where r = 1, 2, 3, ..., was noticed by Hansen.
2. Neumann's integral for </na (z).
It is evident from § 2*2 E) that
and so
JH* (z) = - - -¦ I"" I eni^ ¦» e-wisi»0H-si" +j d0dcji.
To reduce this double integral to a single integral take new variables defined
by the equations
0 2 0f 2
? % f
so that
It follows that
" V ' 27T*
where the field of integration is the square for which
Since the integrand is unaffected if both y and ylr are increased by w, or if y
is increased by it whilo yfr ia Himultaneously decreased by ir, the field of inte-
integration may evidently be taken to be the rectangle for which
7T.
32 THEORY OF BESSEL FUNCTIONS [ <%" A I1. 11
Hence
THEORY
V J 27T
_ 1
IT-.
OF
¦!'
2io
J
Jo
BESSEL
1 0ini\jj—a
i-rr
an, v,^^ COS
FUNCTIONS
izsin*cosx c^^
If we replace % by ?71- + 0, according as^ is acute or obtiiNr. we nbt.-tiit th»
result
J) ^n2(*) = - f** Jm Bz sin 6) dO.
This formula may obviously be written in the form
2> Jn {z) = - f V^ B* si
which is the result actually given by Neumann*. It was <lt-rivc-tl by him t»y
some elaborate transformations from the addition-theorem winch will"},, ,av,-n
v.Z- F°Of Which has Just been Siven is sugcttHlecl l>v l.h.« i»r,.«.f ..f
that addition-theorem which was published by Graf and CJublci-f
JVe obtain a different form of the integral if we-pcribrin Mir mt,Kr:i.i,.,,
*lth r6SpeCt t0 * msfcead of wi^ respect to +. This pruccchuv Kiv,.s
/n2 (*)»" in- ( «^o B« sin -Jr) e2"^ ^,
so that J-'r
C) Jn* (Z) = — I ^ jo ^z sb
-1 f*
- ~ Jo •/. B« sin f)
a result which SchlafliJ attributed to Neumann.
2'61. Xeumunn's series for J 2 (*)
2'61, 2-7] THE BESSEL COEFFICIENTS
This result was written by Neumann in the form
33
where
B)
271
7",=
w + 1) Bn + 3)
Bn + 2) (In + 4)'
,p B7i + 1) Bw + 3) Bn + 5)
This expansion is a special case of a more general expansion (due to
Schlafli) for the product of any two Bessel functions as a series of powers with
comparatively simple coefficients (§5-41).
27. JSchlomilch's expansion of zm in a series of Bessel coefficients.
Wu shall now obtain the. result which was .foreshadowed in §2*22 con-
concerning the expansibility of zm in a series of Bessel coefficients, where m is any
positive integer. The result for in = 0 has already been given in §2*22 G).
In the results §2-22A) and B) substitute for cos 2nd and sin Bn + 1N
their expansions in powers of sina 8. These expansions are*
? l
The results of substitution are
(.,,q /> oiT, A)\ - / /"*\ 4. 9 V f
sin (z sin ^) = ^ J.,tl+, h
J
JJ' B sin ,).,j ,
Tf we rearrange the series on the right as power series in sin 6 (assuming
that it is permissible to do so), we have
2 (-)• B sin
= i, --~ -¦¦-
:, (n-s)\
* Cf. Hobson, Plane Trigonometry A918), §§80, 82.
"W. IJ. I<\
34 THEORY OF BESSEL FUNCTIONS [CHAP. II
If we expand the left-hand sides in powers of sin 0 and equate coefficients,
we find that
n=l
_ ?
The first of these is the result already obtained; the others may be com-
combined into the single formula
A) (?s)m = 2 * ^ - /TO+2rl D (m = 1, 2, 3, ...)
, The particular cases of A) for which w = 1, 2,3, were given by Schlomilch *.
He also shewed how to obtain the general formula which was given explicitly
some years later by Neumann f and LommelJ.
The rearrangement of the double series now needs justification; the rearrangement ia
permissible if we can establish the absolute convergence of the double series.
If we make use of the inequalities
in connexion with the series for sin (z sin S) we see that
oo I 9 oJn a [28 + 1
2 1 sin g ' . | ^ |28 +1 exp
s=o Bs + l)! '2 ' t
= siuh (| z sin 01) exp (^ 12 j2),
and so the series of moduli is convergent. The series for cos (z sin 6) may be treated in
a similar manner.
The somewhat elaborate analysis which has just been given is avoided in
Lommel's proof by induction, but this proof suflPers from the fact that it is
supposed that the form of the expansion is known and merely needs verifica-
verification. If, following Lornmel, we assume that
\2) _ ^1
* Zeitschriftfilr Math, und Phys. n. A857), pp. 140—141.
f Theorie der BesseVschen Functionen (Leipzig, 1867), p. 38.
X Studien ilber die BesseVschen Functionen (Leipzig, 1868), pp. 35—36. Lommel's investigation
is given later in this section.
2-71] THE BESSBL COEFFICIENTS 35
[which has been proved in §2*22 (8) in the special case m — 1], we have
l (m+n—l)\)
L+ }
+ 2n).(m + n)\ r
!
»=0
Since (m + n)\ Jm+2n {z)fn\-*~ 0 as n -*- oo , the rearrangement in the third
line of the analysis is permissible. It is obvious from this result that the in-
induction holds for m = 2, 3, 4,
An extremely elegant proof of the expansion, diu> to A. 0. Dixon*, is as follows:—
Let t be a complex variable and lot u Iks defined by the equation u=.. —;,, no that when
t describes a small circuit round tho origin (in.sido the circle 11 \~ 1), u does the wame.
We then have
7I ¦ f *(l' *
= 2^TT—z- I oxl
when we calculate the sum of the residues at the origin for the last integral; the inter-
interchange of the order of summation and integration is permitted because the series converges
uniformly on the contour; and the required result is obtained.
F-Ki tin • 1 duni . ; , , , , d lot»- u ~1
Notic. When m is zero, -¦• , has to be replaced by - - ,° .
1 titi (to (X f I
2 1. ScJdihnilch's ex^)a7isions of the type 2?i''«/M (-)•
The formulae
A) 2 Bnfr>J^{z)^ I /'I*'"*-,
d') S (t&nJr lY^'"* Jn (z)— 2 /J ''^ z'im +'
n=o m—(i
in which p is any positive integer [zero included in B) but not in A)] and 1^ i.s a numeri-
numerical coefficient, are evidently very closely connected with the results of § 2-7. The formulae
* Messenger, xxxn. A903), p. 8; a proof on the Banie lines for the case ?«=1 had been pre-
previously given by Kapteyn, Nieuw Archie/ voor Wiskunde, xx. A893), p. 120.
3—2
36 THEORY OF BESSEL FUNCTIONS [CHAP. II
were obtained by Schlomilch, Zeitsohrift fiir Math,, und Phys. 11. A857), p. 141, and he
gave, as the value of
where wCfc is a binomial coefficient and the last term of the summation is that for which h
is bn -1 or ?(m-1). To prove the first formula, take the equation § 2-22 A), differentiate
2p times with respect to 8, and then make 6 equal to zero. It is thus found that
o Bm)! J^o"
The terms of the series for which m > p, when expanded in ascending powers of 6,
contain no term in tf2*, and so it is sufficient to evaluate
o Bm)! J6=o m=
m=0
since terms equidistant from the beginning and the end of the summation with respect to
k are equal. The truth of equation A) is now evident, and equation B) is proved in a
similar manner from § 2*22 B).
The reader will easily establish the following special cases, which were stated by
Schl5milch:
113 Jx<Ls) + 33 Jz
v2.3.4J3B) + 4. 5. 6J6(«)-i-6. 7. 8^7(«)+. .. = ^3.
2*72. Neumann's expansion of z* as a series of squares of Bessel coefficients.
From Schlbmilch's expansion (§ 27) of z*71 as a series of Bessel coefficients
of even order, it is easy to derive an expansion of zim as a series of squares of
Bessel coefficients, by using Neumann's integral given in § 2-6.
Thus, if we take the expansion
O) 2
and integrate with respect to $, we find that
so that (when m > 0)
Bm)! ?0
2*72] THE BESSEL COEFFICIENTS
This result was given by Neumann*. An alternative form is
37
and this is true when m = 0, for it then reduces to Hansen's formula of § 2'5.
As special cases, we have
C)
= ~ 2 ett. 4M2 D^ - 22) Jn2 (z),
•5 . 4 ,i=2
' f'
fH • 4«2 D»ia - 22)
n* B),
4. 5.6 n=
If we differentiate A), use § 2T2 B) and thou rearrango, it is readily found that
an expansion whoac exiatenco was indicated by Neumann.
* Leipziger Berichte, xxi. A869), p. 226. [Math. Ann. in. A871), p. 585.]
CHAPTER III
BESSEL FUNCTIONS
3*1. The generalisation of Bessel's differential equation.
The Bessel coefficients, which were discussed in Chapter II, are functions
of two variables', z and n, of which z is unrestricted but n has hitherto been
required to be an integer. We shall now generalise these functions so as to
have functions of two unrestricted (complex) variables.
This generalisation was effected by Lommel*, whose definition of a Bessel
function was effected by a generalisation of Poisson's integral; in the course
of his analysis he shewed that the function, so defined, is a solution of the
linear differential equation which is to be discussed in this section. Lommel's
definition of the Bessel function Jv (z) of argument z and order v wasf
B cos e) ^ m<
and the integral on the right is convergent for general complex values .of v
for which R(v) exceeds —\. Lommel apparently contemplated only real
values of v, the extension to complex values being effected by Hanked;
functions of order less than — \ were'defined by Lommel by means of an ex-
extension of the recurrence formulae of § 2'12.
The reader will observe, on comparing § 3 with § 1*6 that Plana and
Poisson hadinvestigated Bessel functions whose order is half of an odd integer
nearly half a century before the publication of Lommel's treatise.
We shall now replace the integer n which occurs in Bessel's differential
equation by an unrestricted (real or complex) number^ v, and then define <i
Bessel function of order v to be a certain solution of this equation; it va of
course desirable to select such a solution as reduces to Jtl(z) when v assumes
the integral value n.
We shall therefore discuss solutions of the differential equation
which will be called Bessel's equation for functions of order v.
* Studien iiber die BesseVschen Fwictionen (Leipzig, 1868), p. 1.
+ Integrals resembling this (with v not necessarily an integer) were studied byDuhamel, Coma
cCAnalyse, ii. (Paris, 1840), pp. 118—121.
% Math. Ann. i. A869), p. 469.
§ Following Lommel, we use the symbols v, y. to denote unrestricted numbers, the symbols
n, m being reserved for integers. This distinction iB customary on the Continent, though it has
not^yet come into general use in this country. It has the obvious advantage of shewing at a
glance ¦whether a result is true for unrestricted functions or for functions of integral order only.
3-1] BESSEL FUNCTIONS 39
Let us now construct a solution of A) which is valid near the origin; the
form assumed for such a solution is a series of ascending powers of z, say
y= 2 cmS
where the index a and the coefficients cm are to be determined, with the pro-
proviso that c0 is not zero.
For brevity the differential operator which occurs in A) will be called V,,
so that
B) vrS5. *+*? + ,._,*
dz- dz
It is easy to see that*
V, 2 cmza+m = 2 cm[(a + my-vl}g*+m + 2 cmz«+w+\
The expression on the right reduces to the first term of the first series,
namely c{) (<xa — v~) za, if we choose the coefficients cm so that the coefficients of
corresponding powers of 2 in the two series on the right cancel.
This choice gives the system of equations
/c, {(a + 1)9-!/8} =0
c,\(a + 2y-v~\+c0 =0
c!,j(a+3)a-vaj-r-e, =0
C)
Cm {(a + niy -1/"} + Ck-2 = 0
If, then, these equations are satisfied, we have
D) V, X cw3ft+m=Cb(a»-i/J)*\
wt - 0
From this result, it is evident that the postulated series can be a solution
of A) only if a= ±p; for c0 is not zero, and za vanishes only for exceptional
values of z.
Now consider the with equation, in the system C) when wi> 1. It can be
written in the form
cm (a — v + m) (a+i/ + m) + cm_u = 0,
and so it determines cm in terms- of cTO_2 for all values of m greater than 1
unless a— v or a+ v is a negative integer, that is, unless — 2v is a negative
integer (when a = — v) or unless 2v is a negative integer (when a — v).
We disregard these exceptional values of v for the moment (see §§ 3*11,
3), and then (a + m)a — i/* does not vanish when m = l, 2, 3, .... It now
* When the conutants o and cm have been determined by the following analysis, the series
obtained by formal processes jh easily Been to be convergent and differentiate, so that the formal
procedure actually produces a aolution of the differential equation.
40 THEORY OF BESSEL FUNCTIONS [CHAP. Ill
follows from the equations C) that ol — ci = cs-= ... =0, and that cm is ex-
expressible in terms of c0 by the equation
<*» (a~ v + 2)(a- v + 4>) ... (oi-v
The system of equations C) is now satisfied; and, if we take a = v, we see
from D) that
is a formal solution of equation A). If we take a = — v, we obtain a second
formal solution
In the latter, c0' has been written in place of c0, because the procedure of
obtaining F) can evidently be carried out without reference to the existence
of E), so that the constants c0 and c0' are independent.
Any values independent of z may be assigned to the constants c0 and c</ '>
but, in view of the desirability of obtaining solutions reducible to Jn {z) when
v -*• n, we define them by the formulae*
G) Co==2'T(i; + l)> Cd' = 2-T(-i/ + 1)'
The series E) and F) may now be written
In the circumstances considered, namely when 2v is not an integer, these series
of powers converge for all values of z, {z = 0 excepted) and so term-by-term
differentiations are permissible. The operations involved in the analysisf by
which they were obtained are consequently legitimate, and so we have obtained
two solutions of equation A).
The first 'of the two series defines a function called a Bessel function of
order v and argument z, of the first kind%; and the function is denoted by
the symbol Jv (z). Since v is unrestricted (apart from the condition that, for
the present, 2v is riot an integer), the second series is evidently J_v (z).
Accordingly, the function Jv(z) is defined by the equation
(8) J<~\- 1 ()m(i^+2m
It is evident from § 2'11 that this definition continues to hold when v is a
positive integer (zero included), a Bessel function of integral order being
identical with a Bessel coefficient.
* For properties of the Gamma-function, see Modern Analysis, eh. xn.
+ Which, up to the present, has been purely formal.
X Fuuctions of the second and third kinds are denned in §§ 3-5, 354, 3-57, 3«6.
3*11] BESSBL FUNCTIONS 41
An interesting symbolic solution of Bessel's equation has been given by Cotter* in the
form
where D^.djdz while A and B are constants. This may be derived by writing successively
[zD - 2v + D~xz] z"y = -!
zD (z
z- y
which gives Cotter's result.
3*11. Functions whose order is half of an odd integer.
In § 3*1, two cases of Bessel's generalised equation were temporarily omitted
from consideration, namely (i) when v is half of an odd integer, (ii) when v is
an integer^. It will now be shewn that case (i) may be included in the general
theory for unrestricted values of v.
When v is half of an odd integer, let
*» = (r + *)>,
where r is a positive integer or zero.
If we take a — r +•Iin the analysis of § 31, we find that
.lBr + 2) =0,
ami so
( \i
/\ 0 = __ ___ S LJ!?
K } am 2.4... Bm). Br + 3) Br + 5)... Br 4- 2m + 1)'
which is the value of c»tn given by § 3'1. when a and v are replaced by r + ?.
If we take
1
we obtain the solution
which ih naturally denoted by the symbol Jr+i(z), so that the definition of
§ 3-1 (8) is still valid.
If, however, we take a = — r — |, the equations which determine cm become
(cl.l(-2r) =0, , >
( } \cm. m (m - 1 - 2r) + c^ => 0. {m }'
As before, cx, cs, ...,csr-i are all zero, but tho equation to determine c^+i is
ctr?ci ^/m* equation is satisfied by an arbitrary va/we of <ha-+u when to > r, cm+1
is defined by the equation
2m+1 Br + 3) Br + 6)... Bm + 1). 2 . 4 ... B?« - 2r)"
* Proc. It. Irish, dead. xivn. (A), A909), pp. 157—161.
f The oases combine to form the cane in which 2v is an integer.
42 THEORY OF BBSSEL FUNCTIONS [CHAP. Ill
If /„ (z) be defined by § 3-1 (8) when v = -r - \% the solution now con-
constructed is*
c0 2-^ r A - r) J-r-i 0) + W2** r (r + f) Jr+h (z).
It follows that no modification in the definition of Jv (z) is necessary when
v = ±(r + ?); the real peculiarity of the solution in this case is that the
negative root of the indicial equation gives rise to a series containing two
arbitrary constants, c0 and c2r+1, i.e. to the general solution of the differential
equation.
3*12. A fundamental system of solutions of BesseVs equation.
It is well known that, if yx and y2 are two solutions of a linear differential
equation of the second order, and if y-[ and yi denote their derivates with
respect to the independent variable, .then the solutions are linearly inde-
independent if the Wronskian determinant^
yl yi
does not vanish identically; and if the Wronskian does vanish identically,
then, either one of the two solutions vanishes identically, or else the ratio of
the two solutions is a constant.
If the Wronskian. does not vanish identically, then any solution of the
differential equation is expressible in the form cx yx + c2 y2 where Cy and ca are
constants depending on the particular solution under consideration; the
solutions yx and y% are then said to form a fundamental system.
For brevity the Wronskian of yx and, y^ will be written in the forms
the former being used when it is necessary to specify the independent variable.
We now proceed to evaluate
OR {J, (*),/_<*)}.
If we multiply the equations
Vv /_„ {z) = 0, Vr Jv (z) = 0
^ by Jv (z), J^v {z) respectively and subtract the results, we obtain an equation
which may be written in the form
* In connexion with series representing this solution, see Plana, Mem. della R. Accad. delle
Sci. di Torino, xxvi. A821), pp. 519—538.
| For references to theorems concerning Wronskians, Bee Eneyclopedie des Sci. Math. 11. 1&
(§ 23), p. 109. Proofs of the theorems quoted in the text are given by Forayth, Treatise on
Differential Equations A914), §§72—74.
32] BESSEL FUNCTIONS 43
and hence, on integration,
(l) »{./„<*), J-Az)] = -,
Z
where G is a determinate constant.
To evaluate G, we observe that, when v is not an integer, and \z\ is small,
we have
Jv (*} = r'(^l){l + 0 {z% J: {2)=Pp){l + 0 {z^
with similar expressions for J-V(z) and J'-v(z); and hence
j. w .r , w - j-, w/; w=1 \
2 sin vtr ,, . .
= - + 0 (s).
7T2T '
If we compare this result with A), it is evident that the expression on the
right which is 0(z) must vanish, and so*
A) /¦()) 2sini'7r
B)
TTZ
Since .sin vn is not zero (because v is not an integer), the functions Jv{z),
J~v(z) form n fundamental system of solutions of equation § 3 A).
i'ii i/ is an integer, «, we have seen that, with the definition of § 2*1 B),
and when v is inude equal to —n in § 3'1 (8), we find thai
r (z, _ y (-)"(l*y-*+-
vSmce the first n terms of the last series vanish, the series is easily reduced to
(—)n <l,i{z), so that the two definitions of ./_M(s) are equivalent, and the
function.s >fn{z), J-n(z) do nut form a fundamental system of solutions of
Vessel's equation for functions of order n. The determination of a fundamental
system in this case; will be investigated in § 3E3.
To sum up, the function Jv{z) is defined, for all values of v, by the
expansion of § IV1 (8); and J,,(z), so defined, is always a solution of the equation
V,,y— 0. When v is not an integer, a fundamental system of solutions of this
equation is formed by the functions <lv{z) and J-V{z).
A generalisation of the Beasel function has been effected by F. li. Jackson in his
researches on " ba-sio numbers." Briefly, a bawic number [u] is defined iis--——, where piib
the base, and the basic (Umtiiti function r,,(") is defined to .satisfy the recurrence formula
The basio BoHHel function \n then defined by replacing the numbers which occur in the
series for the BenHel function by basic numbera. It haH been shown that very many theoreniH
* This refuilt is due to Loramnl, Math. Ann. iv. A871), p. 104. He derived the value of C by
making z -*- oo and using the approximate formulae whioh will be inveatigated iu Chapter vii.
44 THEORY OF BESSEL FUNCTIONS [CHAP. Ill
concerning Bessel functions have their analogues in the theory of basic Bessel functions,
but the discussion of these analogues is outside the scope of this work. Jackson's main
results are to be found in a aeries of papers, Proc. Edinburgh Math. Soc. xxi. A903), pp.
65-72; xxn. A904), pp. 80—85; Proc. Royal Soc. Edinburgh, xxv. A904), pp. 273—276;
Trans. Royal Soc. Edinburgh, xli. A905), pp. 1—28, 105—118, 399-408; Proc. London
Math. Soc. B) I. A904), pp. 361—366; B) II. A905), pp. 192—220; B) ill. A905), pp. 1—23.
The more obvious generalisation of the Bessel function, obtained by increasing the
number of sets of factors in the denominators of the terms of the series, will be dealt with
in § 4. In connexion with this generalisation see Cailler, Mem. de la Soc. de Phi/s. de
Genhve, xxxiv. A905), p. 354; another generalisation, in the shape of Bessel functions of two
variables, has been dealt with by Whittaker, Math. Ann. lvil A903), p. 351, and Peres,
Gomptes Rendus, clxi. A915), pp. 168—170.
313. General properties of Jv (z).
The series which defines Jv{z) converges absolutely and uniformly* in any
closed domain of values of z [the origin not being a point of the domain when
R (v) < 0], and in any bounded domain of values of v.
For, when lvl ^ JV and \z\ -$ A, the test ratio for this series is
m (v + m)
whenever m is taken to be greater than the positive root of the equation
m? - mN - I As = 0.
This choice of m being independent of v and z, the result stated follows from
the test of Weierstrass.
ifencef Jv (z) is an analytic function of z for all values of z (z = 0 possibly
being excepted) and it is an analytic function of v for all values of v.
An important consequence of this theorem is that term-by-term differen-
differentiations and integrations (with respect to z or v) of the series for Jv (z) are
permissible.
An inequality due to Nielsen \ should be noticed here, namely
where j 6 \ < exp {|^j^j} -1,
and | vq+1 I is the smallest of the numbers j v\-\ j, (v+2), | v+3|, ....
This result may be proved in exactly the same way as § 2*11 E); it should be com-
compared with the inequalities ¦which will be given in § 3.
Finally, the function z", which is a factor of Jv (z), needs precise specifica-
* Bromwich, Theory of Infinite Series, % 82.
+ Modern Analysis, § 5-3.
% Math. Ann. iai. A899), p. 230; Nyt Tidsskrift, rx. B A898), p. 73; see also Math. Ann. ly.
A902), p. 494.
3-13, 3*2] BESSEL FUNCTIONS 45
tion. We define it to be exp (v log z) where the phase (or argument) of z is
given its principal value so that
— 7r < arg z % 7r.
When it is necessary to "continue" the function Jv{z) outside this range of
values of arg z, explicit mention will be made of the process to be carried out.
3*2. The recurrence formulae for Jv (z).
Lommel's generalisations* of the recurrence formulae for the Bessel co-
coefficients (§ 2*12) are as follows:
A) J^(z) + Jv+l(z) = ^Jv(z)
B) Jv^(z)-Jv+1{z)^^JJ(z),
C) zJv'(z) + vJ,.(z) = zJv^(z),
D) zJ: (z) -vJv{z) = - zJv+l(z).
These are of precisely the same form as the results of § 2'12, the only difference
being the substitution of the unrestricted number v for the integer n.
To prove them, we observe first that
- 12* r (z\\ - — vKJl
d ' K h
dz ' "K h dz „,=„ 2"+2j" . m \V(v + m -t 1)
oo ( \m ^v—\ +2»n.
= nZo 2"-i+«" \ m\'V"(v~+'m)
When we differentiate out the product on the left, we at once obtain C).
In like manner,
dz " dz ,M*l!() 2"+2m. m! F (y + m + 1)
v . _L— .—
» / \m-\ l ^aw+i
= ,,,t«, 2^"^'"+r."mTT"r(V+ wi + 2)
whence D) is obvious; and B) and A) may be obtained by adding and sub-
subtracting C) and D).
• StUdien ilber die tkascV»chen Fnnctionen (Leipzig, 1868), pp. 2, 6, 7. Formula C) waa given
when v is half of an odd integer by Plana, Mem. delta R. Accad. ddle Sai. dl Torino, xxyi. A821),
p. 538.
46 THEORY OF BESSEL FUNCTIONS [CHAP. Ill
We can now obtain the generalised formulae
F)
by repeated differentiations, when m is any positive integer.
Lommel obtained all these results from his generalisation of Poisson's
integral which has been described in § 3*1.
The formula A) has been extensively used* in the construction of Tables
of Bessel functions.
By expressing JV-i (s) ^nd J^v (z) in terms of J±v (z) and J'±v B) by C)
and D), we can derive Lommel's formula f
G) J, 0) /,_„ (,) + /_, {z) Jv_x (z) = 2 -^
from formula B) of § 3'12.
An interesting consequence of A) and B) is that, if Qv {?) ¦= Jv2 B), then
(8) Q»-i(*)-&+i(*)-y<2;(*);.
this formula was discovei'ed by Lommel, who derived various consequences of it, Studien
ilher die BesseVschen Functionen (Leipzig, 1868), pp. 48 et seq. See also Neumann, Math.
Ann. hi. A871), p. 600.
3*21. Bessel functions of complex order.
The real and imaginary parts of the function Jv+i^ (%), where 1/, /u, and x
are real, have been discussed in some detail by Lommel+, and his results were
subsequently extended by B6cher§.
In particular, after defining the real functions KPiflL(x) and Sv>flL(x) by the
equation ||
Lommel obtained the results
,,,,
B) ^>(«)
C) fifr+1,M («) = iSf
* See, e.g. Lomnael, Milnchener Abh. xv. A884—1886^, pp. 644—647.
t Math. Ann. tv. A871), p. 105. Some associated formulae are given in § 3-03.
$ Math. Ann. m. A871), pp. 481—486.
§ Annals of Math. vi. A892), pp. 137—160.
|| The reason for inserting the factor on the right ia apparent from formulae which will be
established in § 3-8.
3*21, 3'3] BESSEL FUNCTIONS 47
with numerous other formulae of like character. These results seem to be of
no great importance, and consequently we merely refer the reader to the
memoirs in which they were published.
In the special case in which v — 0, Bessel's equation becomes
solutions of this equation in the form of series were given by Boole* many
years ago.
3'3. LommeVs expression of Jv(z) by an integral of Poissons type.
We shall now shew that, when 11 (v) > - ^, then
A) ,/„ 0) = r - .j*^--. JJcOS (* COS 6) BUL»0d0.
It was proved by Poissonf that, when 2v is a positive integer (zero in-
included), the; expression on the right is a solution of Bessel's equation; and
this expression was adopted by Loininel;J; as the definition of J,,(z) for positive
values of v + ?.
Lommel subscquontly proved that tins function, no defined, is a solution of Bessel's
generalised equation and Unit it satisfies tlie recurrences formulae of § 32; and he then
defined ./„ (z) for value* of v in the intervals (— J, — i|), ( —ij, - &), (-¦•?, -I), ¦¦• by suc-
successive applications of ^ 3-2 A).
To deduct' A) from UuMlefinition of Jv{z) adopted in this work, we trans-
transform the general term of the series for ./",, (z) in the following manner:
m\
9.2m- r 1
Bm)!V
provid<>d that R (v) > - |.
Now when R(v)^{, the series
conve.rgOH unifonuly with respect to t throughout the interval @, 1), and writ
may be. integrated tenn-by-torm; on adding to the result the term for which
* I'hil. Trans, of tin1 Roijul Km. 1814, p. SJIJS). See also 11 question set in the Mathematical
Tripon, 1K<M.
f Journal do. I'ikole U. l'olijtechnique, xn, (cahicr 19), A823), pp. 300 et seq., 340 et seq.
Strictly Kponkmg, Poimion shewed that, when l2» is an odd integer, the expression on the right
multiplied by Jz is a solution of the oquation derived from Besael'a equation liy the appropriate
ohange of depondont variable.
:|: Nlmlien iJber din Jieneel'nefien h'unctioncn (Leipzig, 18G8), pp. 1 et seq.
48 THEORY OF BESSEL FUNCTIONS [ <11! A T. IU
m = 0, namely I tv-^(\-t)~^dt, which is convergent, we find (hat. wh.it
im=o yzm). i
whence the result stated follows by making the substitut ion / sin- 0 .it
using the fact that the integrand is unaffected by writing ir — 0 in ]il;u-r «>i
When -|<JS(i/)<|, the analysis necessary to establish the lunt. <«<|imti<.n i-« a \<.:\
more elaborate. The simplest procedure seems to be to take the .series with fh«- in .! •
terms omitted and integrate by parts, thus
m.2 Bm)! j0 • m=2V + %- Bm)T
U=2
d
1 v-l I K ( — V'1 »2 I
o U=2 Bm)! A~° J '"<
on integrating by parts a second time. The interchain nt tv, i
integration in the second line of analysis is permtibl o f' ;" 1:iIIIIIIiml l'
convergence of the aeries. On adding the inteLT 0I^ ^«>unt .,( ,1,,. „,,„•,.,.,„„_,
which are convergent), we obtain totZ^T"*^"* *° thl> tl<P" '" "''' *
It follows that, when R („) > _ ^ then
,w. rt(:+«r («•'•sin
-W.>t»?vahd only when
3*31] BESSEL FUNCTIONS 49
An expansion involving Beraoullian polynomials has been obtained from D) by Nielsen*
with the help of the expansion
in which <fin(f-) denotes the nth. Bernoullian polynomial and a=izt.
[Note. Integrals of the type C) were studied before Poisaon by Plana, Mem. della It.
Aecad. dellc Sci. di. Torino, xxvi. A821), pp. 519—538, and subsequently by Kumrner,
Journal filr Math. xn. A834), pp. 144—147; Lobatto, Journal fiir Math. xvn. A837), pp.
3E3—371; and Duhamcl, Cours W Analyse, n. (Paris, 1840), pp. 118—121.
A function, substantially equivalent to ./„ B), denned by the equation
r\
e/(/x, x) = I A — ifiy* eo.s ox. di>,
J 0
was investigated by Lommel, Archh> dcr Math, und Phys. xxxvii. A861), pp. 349—360.
The converse problem of obtaining the differential equation satisfied by
zK [P c'Uv-aT-Uv-BY-'dv
(
was also discussed by Lommcl, Arc/uv der Math, und Phys. xl. A863), pp. 101—126. In
connexion with llii.s integral see also Euler, Inst. Gale. Int. ir. (Petersburg, 1769), § 1036,
ami Petzval, Integration der linearen Dijfcrentialgleichungen (Vienna, 1851), p. 48.]
3*31. Inequalities derived from PoLsson's inte<j7'al.
From § 3'3 ((J) it follows that, if v bo real and greater than — •?, then
(I) '.r,(z)\-;
By using the recurrence formulae § ^A) and D), we deduce in a similar
manner that
B)
By using the expressionf {2/(ttz)Y cos z for t/_j (z) it may be shewn that
A) in valid when i> = —,}.
These inequalities should be compared with the less stringent inequalities
obtained in §«J"ltt. When v is complex, inequalities of a more complicated
character can be obtained in the same manner, but they are of no great im-
importance.
* Math. Ann. lix. A<JO4), p. 108. The notation used in the text is that given in Modem
Analysis, § 7'2; Nielsen uhob a different notation.
t The reader nhould have no difficulty in verifying this result. A formal proof of a more
general theorem will be given in § 'S-l.
W. H. V. 4
50 THEORY OF BESSEL FUNCTIONS [CHAP.
3*32. Gegenbauer's generalisation of Poissoris integral.
The integral formula
in which 0/ (i) is the coefficient of an in the expansion of A - ?<xt + a'2) * in
ascending powers of a, is due to Gegenbauer*; the formula is valid when
R (v) > - $ and n is any of the integers 0,1, 2, .... When n = 0, it obviously
reduces to Poisson's integral.
In the special case in which v — §, the integral assumes tfye form
B) Jn+i (z) = (-i)n (j-j* jVcos 9 Pn (cos 6) sin 6 dd;
this equation has been the subject of detailed study by Whittakerf.
To prove Gegenbauer's formula, we take Poisson's integral in the form
and integrate n times by parts; the result is
Now it is known thatj
whence we have
and Gegenbauer's result is evident.
A symbolic form of Gegenbauer's equation is
} "
this was given by Rayleigh§ in the special case v = \.
The reader will find it instructive to establish C) by induction with the ciid of the
recurrence formula
¦ Wiener SiUuvgsberichte, lxvii. B), A873), p. 203; txx. B), A875), p. 15.. See also Bauer,
¦Milnchener Sitzungsberickte, v. A875), p. 262, and 0. A. Smith, Giornale di Mat. B) xn. A905),
pp. 365—373. The function Cn" (t) has been extensively studied by Gegenbauer in a series of
memoirs in the Wiener Sitzungsberichte; some of the more important results obtained by him are
given in Modern Analysis, §15-8.
+ Proc. London Math. Soc. xxxv. A903), pp. 198-206. See §§ 6*17, 10'5.
t Cf. Modern Analysis, § 15-8.
§ Proc. London Math. Soc. rr. A873), pp. 100, 263.
3-32,3*33] BESSEL FUNCTIONS 51
A formula which is a kind of couverse of D), namely*
in which /*"** denotes a generalised Legendre function, is due to Filon, Phil. Mag. F) vr.
A903), p. 198; the proof of this formula is left to the reader.
33. Gegenbauer's double integral of Poisson's type.
It has been shewn by Gegenbauei-j- that, when R (v) > 0,
C) Jv (V) = \T\ \ exp [iZ cos 9 - iz (cos <f> cos $ + sin <f> sin Q cos tlr)]
7rl \v) J oJ o
sin2"-1 -\Jr sin12" Od-yjrdO,
where ot2 = Z- + z* - 2 Zz cos <^> and Z, z, <j> are unrestricted (complex) variables.
This result was originally obtained by Gegenbauer by applying elaborate in-
integral transformations to certain addition formulae which will be discussed in
Chapter XI. It is possible, however, to obtain tho formula in a quite natural
manner by means of transformations of a type used in the geometry of the
sphere;]:.
After noticing that, when z = 0, the formula reduces to a result which is
an obvious consequence of Pokson's integral, namely
,fv <Z) = VV ¦— eix™* sin2" 0.
v I ()'
sin2
I (i').'o
we proceed to regard -v/r and 6 as longitude and colatitude of a point on a
unit sphere; we denote the direction-cosines of the vector from the centre to
this point by (I, m, n) and the element of surface at the point by dco.
We then transform Poisaon'a integral by making a cyclical interchange of
the coordinate axes in the following manner§ :
.T\ If e Hina* 6 .sin8*-1
trl {JJ
i-"-} dw
TtI {V)J '«>()
= &?)\ [ "f"" e'^"'"9*""*cos8' ^sin Od^dd.
TTl (v).'o .'()
' It is supiioscd Unit
f Wiener SitzitMtjsberichtr, lxx.iv. B), AH77), pp. 128—121).
X Tliis method in offoolive in proving nmnerouH formulau of which analytical piools wore
ivon by (Sugcnlumtsr ; uml it Hemns not unlikely that he discovered those funuulne by tho method
i qUQHlion; of. SS Vl-12, 12-14. 'fho device* ih used by Boltrauii, Lombardn Jlcndlconli, (*i) xnt.
1«HO), p. !$2rt, for n fathor dilTorent iniriioso.
§ The symbol jj,,,^ moans that tho integration extends over the Riirfaco of the hemipphore on
'liich vi ifi positive.
4—i
52 THEORY OF BESSEL FUNCTIONS [CHAP. HI
Now the integrand is an integral periodic function of ifr, and so the limits of
integration with respect to ^ may be taken to be a and a + 2tt, where a is an
arbitrary (complex) number. This follows from Cauehy's theorem.
We thus get
Jv(ib)- ("»'ar)> j | *'eivr sin 6cos* cos*y-i0sm6dylrd6
TlT (v) J o J a
= (i™)" I *I ^i-orsinecos (*+a)cos2"8sin 8d<Ard8.
ttT(v))o Jo
We now define a by the pair of equations
ta cos a = Z -¦ z cos <?, tsr sin a = z sin <?,
so that
jv ( o ) „ iW! I* f 2irexp [i (? __ ^ cos </>) sin 0 cos ^ - tar sin <? sin f sin #]
wl (v) Jo Jo „ . ... ,„
cob2" 8 sin vdty dv.
The only difference between this formula and the formula
J» («) = ^S^ f * r exP [»w sin ^ cos ^1 c03'" e sin ^d^rf^
ttI (y)Jo Jo
is in the form of the exponential factor; and we now retrace the steps of the
analysis with the modified form of the exponential factor. When the steps are
retraced the successive exponents are
i{Z — zcos (f>)l — izsin <j). m,
i(Z — z cos <?) n — iz sin <f>. I,
i{Z—z cos </>) cos 6 — iz sin <f> cos ty sin 6
The last expression is
iZ cos 8 — iz (cos </> cos 8 + sin <? sin 8 cos \Jr),
so that the result of retracing the steps is
AJ.jjjAv fir fir
? /-; ' exp [iZ cos 5 — i^ (cos <f> cos 9 + sin A sin 0 cos a!tI
^r(j/)JoJo
sin2" aJt sin2
and consequently Gegenbauer's formula is established.
[Note. The device of using transformations of polar coordinates, after the manner of
this section, to evaluate definite integrals seems to be due to Legendre, M4m. de VAcad. des
ScL, 1789, p. 372, and Poisson, Mem. de VAcad. des Sci. in. A818), y. 126.]
3*4. The expression of J±(»+j) (z) in finite terms.
We shall now»deduce from Poisson's integral the important theorem that,
when v is half of an odd integer, the function Jv(z) is expressible infinite terms
by means of algebraic and trigonometrical functions of z.
It will appear later (§ 4*74) that, when v has not such a value, then /„ {z)
is not so expressible; but of course this converse theorem is of a much more
recondite character than the theorem which is now about to be proved.
3-4] BESSEL FUNCTIONS 53
[Note. Solutions in finite terms of differential equations associated with Jrn+i 00 were ob-
obtained by various early writers; it was observed by Euler, Misc. Taurinensia, ill. A762—
1765), p. 76 that a solution of the equation for e^t/^.,., (z) is expressible in finite terms; while
the equation satisfied by ^Jn+Az) was solved in finite terras by Laplace, Conn, des Tan*.
1823 [1820], pp. 245—257 and Mecavique Celeste, v. (Paris, 1825), pp. 82—84 ; by Plana, Mem.
della It. Accad. delle Sci. di Torino, xxvi. A821); pp. 533—534; by Paoli, Mem. di Mat. e
di Fis. (Modena), xx. A828), pp. 183—188; ami also l>y Stokes in 1850, Trans. Camb. Phil.
Soc. ix. A856), p. 187 [Math, and Phis. Papers, n. A883), p. 350], The investigation
which will now be given is based on the work of Lommel, Studien ilher din BesseVschen
Functionen (Leipzig, 1868), pp. 51—56.]
It is convenient to restrict » to bo a positive integer (zero included), and
then, by § 3'3 D),
;,
di*
when we integrate by parts 2». + I times; since (I - f)n is a polynomial of
degree 2n, the process then terminates.
To simplify the last expression we observe that if dr(l — t2)n/dtr be cal-
calculated from Leibniz' theorem by writing A — t-)n = A — t)n(l +t)n, the only
term which does not vanish at the upper limit arises from differentiating n
times the factor A —t)n, and therefore from differentiating the other factor
/• — ii times; so that we need consider only the terms for which r^n.
and similarly '¦ | = (—)r ".,.<?„.«!-¦
It follows that
m\i\ hence
A) ./„+
This result may bi>. written in the form*'
B) ¦^(
2r+ 1)
* A compact nicUiod of obtaining Huh formiiln \a (Ljivcn by do la Valk'e Pons.iin, Ann. de Iu
Soc. Set. df llriiMllsH, xxix. (li)O.V, j>p. 1 -10—14:-t.
54 THEORY OF BESSEL FUNCTIONS [CHAP-
In particular we have
the former "of these results is also obvious from the power series for Jj. (z).
Again, from the recurrence formula we have
anfl hence, from AK
e ,.r0 rT(n- r)! (Siy ,.r0 r\{n-r)l B*)"
But, obviously, by induction we can express
as a polynomial in 1/s multiplied by e±iz, and so tue must have
±iz % (±i)'-»(
for, if-not, the preceding identity would lead to a result of the form
where fa {?) and $%(z) are polynomials in \\z; and such an identity is obviously
impossible*.
Hence it follows thatf
o r 1 (n - r)! B«)r ^
r=o r 1 (n - r)! B«)r ^o r t (n - r) 1 B^)r
zdz) z
Consequently
D) J n ,(
* Of. Hobson, Squaring the Circle (Carabtidge, 1913), p. 51.
t From the series
"* U r A)
it is obvious that J, (e) = (—\
3*41] BESSEL FUNCTIONS 55
and hence
E) /_,_, W = (_j [cos (. ^A^/
,„ ( )(
In particular, we have
F) /_,(,)- (^) cos,, •/_,(,)_(_)(____„„,)
We have now expressed in finite terms any Bessel function, whoso order is
half of an odd integer, by means of algebraic and trigonometrical functions.
The explicit expression of a number of these fimutioas can be written down from
numerical results contained in a letter from Hcrmite to Giordan, Journal fur Math, lxvi.
A873), pp. 303—311.
31. Notations for functions whose order is half of an odd integer.
Functions of the types ./.i-oHj) C2) occur with such frequency in various
branches of Mathematical Physics that various writers have found it desirable
to denote them by a special functional symbol. Unfortunately no common
notation has been agreed upon and none of the many existing notations can
be said to predominate over the others. Consequently, apart from the summary
which will now be given, the notations in question will not be used in this work.
In hi.s researches on vibrating spheres .suitouihWI by a gas, Stokes, Phil. Trans, of the
llo<f<d Soc. ciA'in. (IH()8), p. 4.01 [Math, and Phys. Papers, iv. A901), p. 300], made use of
the series
n (Wjf 1) (it-!)«(» + !)(»+ 2)
+ SS.iW a. 4. (/«»•)*
which in annihilated by the operator
frJ .„. d ii (n+l)
dr* dr /•"
This series Stokes denoted by the symbol /„(?") and he wrote
where »S'H and *S',,' are zonal .surface harmonics; so that \^,, i.s' annihilated by tho total
operator
d~ 'A d ,, /' (/i -f-1)
- -)- -)- in- — ,
dr- r dr r-
and by the partial operator
¦ .,+ - + - • ., -,* {Hill fK-:
In this notation Stoker wan followed by Haylei;^h, I'rov. London, Math. >So<\ IV. ^1^73),
pp (jn—io;}, 2."i3 '283, and ugniu /Vof. //»?/<// Sor. i.xxir. (HKK), pp. -10—11 \Sricntijlc
y'f//ic/'.S v. (l!)l'2), pp. 112 -114|, aj)art iVotu the csomparatively trivial change that Haylcigh
would have written/„ (imr) where Stokes wrote/,,(r).
56 THEORY OF BESSEL FUNCTIONS [CHAP. Ill
In order to obtain a solution finite at the origin, Bayleigh found it necessary to take
#n'= (- )"+1 Sn in the course of his analysis, and then
It follows from § 3-4 that -—&& > = (i -4- ) — ,
° rn+l \^ rcrJ r '
and that
In order to have a simple notation for the combinations of the types e*u' ftl (± w*) which
are required for solutions finite at the origin, Lamb found it convenient to write
in his earlier papers, Proc. London Math. Soc. xni. A882), pp. 51—66; 189—212; XV.
A884), pp. 139—149; xvi. A885), pp. 27—43; Phil Trans, of the Royal Soc. clxxiv. A883),
pp. 519—549; and he was followed by Bayleigh, Proc. Royal Soc. lxxvii. A, A906),
pp. 486—499 [Scientific Papers, v. A912), pp. 300—312], and by Love*, Proc. London
Math. Soc. xxx. A899), pp. 308—321.
With this Dotation it is evident that
-(-)• »• 3¦ 5 ...
Subsequently, however, Lamb found it convenient to modify this notation, and accord-
accordingly in his treatise on Hydrodynamics and also Proc. London Math. Soc. xxxn. A901),
pp. 11—20, 120—150 he used the notation t
* fcw_i_ [~1 *2 ,
ywW 1.3.3... Bn + l)L 2B»+3)^2.4Bn
(d \n e~iz
- —j- I = ^n B) - ityn (z),
zcLzJ z
sothat *„(«), g)t+^ * , «M*)- -S+-J-"- •
while Bayleigh, Phil. Trans, of the Royal Soc. ccni. A, A904), pp. 87-110 [Scientific Papers,
v. A912) pp. 149—161] found it convenient to replace the symbol fn{z) by Xniz)- Love'
Phil. Trans, of the Royal Soc. ccxv. A, A915), p. 112 omitted the factor (-)" and wrote
while yet another notation has been used by Soramerfeld, Ann. der Phytik und Chemie, D)
xxviii. A909), pp. 665—736, and two of his pupils, namely March, Ann. der Phy&ik und
Chemie, D) xxxvu. A912), p. 29 and Rybczynaki, Ann. der Physik und Chemie, D) xi.r.
A913), p. 191 ; this notation is
d \n sin2
)
Ca B) = faz? [Jn + j B) + ( -)» iJ_n _ j B)],
and it is certainly the best adapted for the investigation on electric waves which was the
subject of their researches.
* In this paper Love defined the function En{z) as (-)n.l .3 ... Bn-l) ( — j — , but, as
stated, he modified the definition in his later work.
t This is nearer the notation used by Heine, Handbuch der Kugelfunctionen, 1. (Berlin, 1878),
p. 82 ; except that Heine defined $n(z) to be twice the expression, on the right in his treatise, but
not in his memoir, Journal fur Math. lxix. A869), pp. 128—141.
3*5] BESSEL FUNCTIONS 57
Somiuerfeld's notation is a slightly modified form of the notation used by L. Lorenz, who
used vH and vn + ( - )n iwn in place of \0>tt and fn; see his memoir on reflexion and refraction
of light, K. Danake Videnskobernes Sehkabs Skrifter, F) vi. A890), [Oeuvres scientifiques, I.
A898), pp. 405—502.]
3*5. A second solution of BesseVs equation for functions of integral order.
It has been seen (§ 3*12) that, whenever v is not an integer, a fundamental
system of solutions of Bessel's equation for functions of order v is formed by
the pair of functions Jv (z) and ./_„ (z). When v is an integer (= n), this is no
longer the case, on account of the relation »/_„ (z) = (-r-)n Jn (z).
It is therefore necessary to obtain a solution of Bessel's equation which is
linearly independent of Jn (z); and the combination of this solution with Jn (z)
will give a fundamental system of solutions.
The solution which will now be constructed was obtained by Hankel*;
the full details of the analysis involved in the construction were first published
by Bocherf.
An alternative method of constructing Hankel'n solution was discovered hy Forsyth;
his procedure, is based on the general method of Frobonius, Journal fiir Math, lxxvi. A874),
pp. 214—235, for dealing with any linear differential equation. Forsyth's solution was
contained in hi.s lectures on differential equations delivered in Cambridge in 189-1, and it
has since been published in his Theory of Differential Equations, iv. (Cambridge, 1902),
pp. 101—10*2, -mid in his Treatise on Differential Equations (London, 1903 and 1914),
Chapter vi. note 1.
It is evident that, if v be unrestricted, and if n be any integer (positive,
negative or zero), the function
/,(*)-(_)«./¦_(,)
is a solution of Vessel's equation for functions of order v\ and this function
vanishes when /> = /(.
Consequently, so long as v ? v, the function
J,,(z) -(-)»./-„ {z\
v — n
is also a solution of Bessel's equation for functions of order v; and this function
assumes an undetermined form* when v — v.
We shall now evaluate
,im/.w.-<::>¦_•(.-? W,
,. -*. rt v - n
and we shall shew that it is a solution of Bessel's equation for functions of
* Math. Ann. i. A8(i<)), pp 4fi!) -472.
t A ninth of Math. vi. A892), pp. 8/5—DO. See aim Niemoller, Zeituchriftfilr Math, und Phys.
xxv. <1HHO), pp. (i.r) - 71
:\: The crhcucc of Hiuikcl's invuBtigatiou is the construction of an expression which satisfies
the equation when v in not an integer, which assumes an undetermined form when v is equal to
the integer n and which han a limit when v-*-u.
58
THEORY OF BESSEIr FUNCTIONS
[CHAP. Ill
order n and that it is linearly independent of Jn{z)) so that it may be taken
to be the second solution required*.
It is evident that
Jv(z) - H" J- (z) _ Jv jz) - Jn(z) XnJ__v(z)-J_n(z)
: z ~~ "" z :—\ j :
v — n
as v-^n} since both of the differential coefficients existf..
Hence
v
n
exists; it is called a Bessel function of the second land of order n.
To distinguish it from other functions which are also called functions of
the second kind it may be described as Hankel's function. Following Hankel,
we shall denote it by the sym"bolj Y?l<V) so that
n (z) = lim
n
and also
B)
^ }
v~n
dv x ' dv
It has now to be shewn that YOT (z) is a solution of Bessel's equation.
Since the two functions J±v (z) are analytic functions of both z and v, the
order of performing partial differentiations on J±v(z) with respect to z and v
is a matter of indifference §. Hence the result of differentiating the pair of
equations
with respect to v rnay be written
w. o.
When we combine the results contained in this formula, we find that
v.
* The reader will realise that, given & solution of a differential equation, it is not obvious that
a limiting form of this solution is a solution of the corresponding limiting form of the equation.
t See § 8*1. It is conventional to write differentiations with respect to z as total differential
coefficients while differentiations with respect to v are written as partial differential coefficient-.
Of course, in many parts of the theory, variations in v are not contemplated.
X The symbol Y%(z), which was actually used by Hankel, is used in this work to denote a
function equal to 1/w times Hankel's function (§ 3*54).
§ See, e.g. Hotson-, Functions of a Real Variable A921), §§ 312, 318.
3-51]
so that
~dJv(z) , ,n
dv { }
BESSEL FUNCTIONS
dJ-v (z)'
dv
dJv (z)
dv
)J-V(z)'
dv
59
Now make z^ ~^n. All the expressions in the last equation are continuous
functions of v, and so we have
dJv{z)
— (
-v (z)
= 0,
where v is to be made equal to n immediately after the diiferentiations with
respect to v have been performed. We have therefore proved that
\ *-* / It, If, \ / v )
so that YnB") is a solution of BesseVs equation for functions of order n.
It is to be noticed that
J?^ B,\ 7TT 1 1 1 11 ^ ' /
V -*¦ — n V -j- 11
_
—— ii I ii
n
whence follows a result substantially due to Lonnnel*,
Again,
dv
while, because Jv(z) is a monogenic function of v at v = 0, we have
dv
V =30
dJv{
a (— z^)_
)ws that
— ^
a^
~dJv (z)~
dv
E)
A result equivalent to this Vas given by Duhamelf as early as 1840.
3*51. The expansion oJ"Y0(z) in an ascending series.
Before considering the expansion of the general function Y,^), it is con-
convenient to examine the function of order zero because the analysis is simpler
and the resulting expansion is 'more compact.
We use the formula just obtained,
* Studien iiber die HeaseVachen Functional (Leipzig, 1868), p. 87. Lommel actually proved
thiH reault for what is sometimes called Neumann's function of the second ldnd. See § 3'58 (8).
t Court d'Analyse, n. (Paris, 1840), pp. 122—124.
60 THEORY OF BESSEL FUNCTIONS [CHAP. ITI
and the result of term-by-term differentiation is
Y(,(V) = 2 ? — -J, /¦ Jloei" (¦k-z) — s- log F (v + m ¦+ 1) [
\_m*omW(v + m+1) { ° dv ° j_
v-0
where ty denotes, as is customary, the logarithmic derivate of the Gamma-
function*.
Since 0 <\^ (m +1) < m when ?n = l, 2, 3, ... the convergence of the series for Yo(z)
may, be established by using D'Alembert's ratio-test for the series in which ^(w+1) is
replaced by m. The convergence is also an immediate consequence of a general theorem
concerning analytic functions. See Modern Analysts, § 5*3.
The following forms of the expansion are to be noticed :
A) Y0(z
»i=0 K'''' ¦)
r oo (—)™(XzYm 1
B) Yo(*)= 2 log(**).«/,(*)- S V , ,* t(m + 1)h
L »«=o \m ¦) J
C) Yo (z) = 2 [7 + log (\z)} Jo (z) - 2 JS (~r (^^r A ' l ¦ ¦ 1]
The reader will observe that
is a solution of Bessel's equation for functions of order- zero. The expansion of
this function is
(log*) 2 (-V^} 2 ( I V 7 + 5 + -+-[-
This function was adopted as the canonical function of the second kind of order zero by
Neumann, Theorie der Bessel'sohen Functionen (Leipzig, 1867), pp. 42—44; see § 3-57.
But the series was obtained as a .solution of Bessel's equation, long before, by Euler f.
Eulor's result in his own notation is that the general solution of the equation
xx cdy + x dx cy + gxny ex2 — 0
_2yliy n GAg- 2 '22Ag3 3n 100%4
W V~ HFX ~ 1. 8a*X" + 1.8.W *"" " r8.27.'64M» +
«/i" 1 . 4w' ' 1.4.9%°' 1.4.9.l6ns"
+ a «naf+1.4»i*-1! 1.4.»»«lC +1.4.9.
* Modern Analysis, Gh. xn. It is to be remembered that, when m is a positive integer, then
"/'A)=-7, ^(m + l)=\ + h + ••• +--7,
where 7 denotes Eider's constant, 0-5772157
t Imt. Gale. Int. 11. (Petersburg, 1709), §977, pp. 233—235. See also Ada Acad. Petrop. v.
A781) [published 1784], pars 1. Mathematics, pp. 186—190.
3*52] BESSEL FUNCTIONS 61
where A and a are arbitrary constants. He gave the following law to determine successive
numerators in the first line:
6 = 3.2-1.0, 22=5.6-4.2, 100 = 7.22-9.6,
548 = 9 .100-16 . 22, 3528 = 11. 548-25 . 100 etc.
this law is evidently expressed by the formula
3'52. The expansion of Yn (z) in an ascending series and the definition of
We shall now obtain Hankel's* expansion of the more general function
Yn(z), where n is any positive integer. [Cf. equation D) of § 3'5.]
It is clear that
dv
when v-^-»?, where ?? is a positive integer. That is to say
The evaluation of [dJ_v {z)ldv\-n is a little more tedious because of the pole
of yjr (- v 4- m 4-1) at i> = n. in the terms for which m = 0,1, 2, ..., n — 1. We
break the series for «/_„ (z) into two parts, thus
,
M( ) »! T(- v +m 4-
and in the former part we replace
1 , F (v — m) sin (v — m) it
Now, when 0 ^ m < n,
3 \(\ z)~v+*m F (v — w) sin (j» - m) ir
)
v — m) sin (v—mOr 4- cos (v—in) ir —ir~l log (^) sin (v—inOr}]v»n
F (n - m) cos (n - nt) 7r.
* itfat/j. Ann. i. A869), p. 471.
62 THEORY OF BESSEL FUNCTIONS [CHAP. Ill
Hence
'?. — m)
dv La,, m~o ml
that is to say
Wl -( ^(n-m-l)! -
when we replace wi by ?? + m in the second series.
On combining A) and B) we have Hankel's formula, namely
(8) Y(i)— s ( )'a ( ]}**>
x
! Ill 1 )
^ 2 ^ <>-^ w "*" 1 ^ 2 ?(+mf
In the first terra (m = 0) of the last summation, the expression in { } is
1 1 1
=-+5 + ... +-.
12 n
It is frequently convenient (following Lommel*) to write
D) %(z)J^-Jv
so that
when i/ is a negative integer, ^v (z) is defined by the limit of the expression
on the right.
We thus have
F) Yn (*) = 2 Jn (z) \ogz + <$n @ + (-)« 3_7( (*).
The complete solution of x -rK + ay=O was given hi the form of a series (part of which
contained a logarithmic factor) by Euler, Inst. Cede, Int. II. (Petersburg, 1769), 4^§ 935,
936; solutions of this equation are
#* Jx BaM), ** Yt BaU'i).
Euler also gave (ibid. §§ 937, 938) the complete solution of %$ — + ay=O; solutions of
this equation are
Studicn ilber die Be&seVschen Functional (Leipzig, 1868), p. 77.
3-53,3-54] BESSEL FUNCTIONS 63
3-53. The definition o/Yv (z).
Hitherto the function of the second kind has been defined only when its
order is an integer. The definition which was adopted by Hankel* for un-
unrestricted values of v (integral values of 1v excepted) is
A) Y^)
This definition fails both when v is an integer and when v is half of an
odd integer, because of the vanishing of sin 2v7r. The failure is complete in
the latter case; but, in the former case, the function is defined by the limit
of the expression on the right and it is easy to reconcile this definition with
the definition of § 3*5.
To prove this statement, observe that
,. __ ,, v f ire'* v-n Jv(z)cos vir-«/"_„0I
hm Y,, (z) = hm . . —-- z±-*
,,-».n ,,-*.)! [cos vk sin vrr v — n J
v-n
~ , . , • |"(-)n COS I»7T - 1 T . /]
= Yn (z) + Inn > -' Jv{z)
i'-*-n L V — n J
and so we have proved that
B)
It is now evident that Y^^), defined either by A) or by 1' limiting form
of that equation, is a solution of Bessel's equation for functions of order v both
when (i) v has any value for which 2v is not an integer, and when (ii) v is an
integer: the latter result follows from equation B) combined with § 3*5 C).
The function Y,, (z), defined in this way, is called a Bessel function of the
second kind (of Hankel's type) of order v; and the definition fails only when
v +1 is an integer.
Notb. The reader should bo careful to observe that, in wpito of the change of form, the
function Yv (z), qua function of v, is continuous at v = n, except when z ia zero; and, in
fact, Jv {?) and ~Yv(z) approach thoir limits ¦/„ B) and Yn (z), aw u-*-n, uniformly with
respect to z, except in tho neighbourhood of 2 = 0, where n in any intogor, positive or negative.
3'54. The Weber-Schldfii function of the second kind.
The definition of the function of tho second kind which was given by
Hankel (§ 33) was modified slightly by Webcrf and SchlafliJ in order to
avoid the inconveniences produced by tho failure of tho definition when the
order of the function is half of an odd integer.
* Math. Ann. 1. A869), p. 472.
¦\ Journal fUr Math, lxxvi. A873), p. 9; Math. Anv. vi. A873), p. 148. These papors are
dated Sept. 1872 and Oct. 1872 respectively. In a paper written a few months before these,
Journal filr Math. lxxv. A873), pp. 75—105, dated May 1872, Weber had used Neumann's
function of the second kind (see §§ 8-57, 3-58).
% Ann. di Mat. B) vn. A875), p. 17 ; thiH paper is dated Oot. 4, 1872.
64 THEOBY OF BESSEL FUNCTIONS [CHAP. Ill
The function which was adopted by Weber as the canonical function of the
second }rind is expressible in terms of functions of the first kind by the formula*
Jv (z) cos viT — J.,, (z)
sin vtt
(or the limit of this, when v is an integer).
Schlafli, however, inserted a factor \tr\ and he denoted his function by
the symbol K, so that, with his definition,
Jv(z)cosvrr-J-V(z)
Jti v (Z) — ?7T : .
x ' - sinv7r
Subsequent writers, however, have usually omitted this factor %-ir, e.g. Graf
and Gublerin their treatisef, and also Nielsen, so that these writers work with
Weber's function.
The symbol K is, however, used largely in this country, especially by
Physicists, to denote a completely different type of Bessel function (§ 3-7),
and so it is advisable to use a different notation. The procedure which seems
to produce least confusion is to use the symbol Yv(z) to denote Weber's function,
after the manner of Nielsen}, and to adopt this as the canonical function ol
the second kind, save in rare instances when the use of Hankel's function of
integral order saves the insertion of the number tt in certain formulae.
We thus have
A) Yv {z) = jvWcoBiHr-J.,,^ = cosj^r
v ' s ' sin vw ire'1
B) Fn<*)« Km ^(^tt-J.^I
[Note. Schlafli's function has been used by B6cher, Annals of Math. vi. A892),
pp. 85—90, and by McMahon, Annals of Math. vm. A894), pp. 57—61; ix. A895),
pp. 23—30. Schaf heitlin and Heaviside use Weber's function ¦with the sign changed, ho
that the function which we (with Nielsen) denote by Yv (z) is written as - Yv B) by
Schaf heitlin § and (wheu v — n) as -Gn{z) by Heaviside||.
Gray and Mathews sometimesif use Weber's function, and- they denote it by the
symbol Yn.
* Weber's definition was by an integral (see §6-1) which is equal to this expression; the
expression (with the factor \v inserted) was actually given by Sohlatli.
t Einleitung in die Theorie der Bestel'schen Funhtionen, 1. (Bern, 1898), p. 34 et xeq.
% Nielsen, as in the case of other functions, writes the number indicating the ordoi- as an
index, thus Y"(z), Handbuch der Thearic der Cylinderfunktionen (Leipzig, 190-i), p. 11. There
are obvious objections to suoli a notation, and we reserve it for the obsolete function used by
Neumann (§3-58).
§ See, e.g. Journal filr Math. cxiv. A895), pp.31—44, and other papers; also Die Theorie der
BesscV'schen Funktionen (Leipzig, 1908).
|| Proc. Royal Soc. liv. A893), p. 138, and Electromagnetic Theory, 11. (Loudon, 1899), p. 255;
a change in sign has been made from hifi Electrical Papers, n. (London, 1892), p. 445.
If A Treatise on Bessel Functions (London, 1895), pp. 65—66.
3-55] BESSEL FUNCTIONS 65
Lommel, in his later work, used Neumann's function of the second kind (see § 3f57), but
in his Studien iiber die Bes&eVschen Functionen (Leipzig, 1868), pp. 85—86, he used the
function
\* rn (z)+{i (n+4)+log 2) jn (z),
where YH(z) is the function of Weber. One disadvantage of this function ia that the
presence of the term \js (n + $) makes the recurrence formulae for the function much more
complicated; sec Julius, Archives JV&erlandaises, xxvni. A895), pp. 221—225, in this
connexion.]
3*55. Heine's definition of the function of the second hind.
The definition given by Heine* of the function of the second kind possesses
some advantages from the aspect of the theory of Legendre functions; it
enables certain generalisations of Mehler's formula (§ 6*71), namely
lim Pn (cos 6In) = Jo F),
n-*- ¦¦*>
to be expressed in a compact form. The function, which Heine denoted by
the symbol Ktl B), is expressible in terms of the canonical functions, and it is
equal to — ^irYn{z) and to — ?Yrt(.s); the function consequently differs only
in sign from the function originally used by Schlafli.
The uso of Heine's function aeeniH to have died out on the Continent many years ago ;
the function was occasionally used by Gray and Malhews in thoir treatise+, and they term
it (/„ B). In this form the function has boon extensively tabulated first by Aldis:|: and
Airey§, and mibscquontly in British Association Reports, 1913, 1914 and 1916.
This revival of the uko of Hoino'a function acorns distinctly unfortunate, both on account
of the existing multiplicity of functions of the second kind and also on account of the fact
(which will become moro apparent in Chapters vi and vn) that the relations between the
functions ./„ B) and Yn{z) present many points of resemblance to the relations between the
cosine and sine; mo that the adoption|| of Jn{z) and (.?n(z) a.s canonical functions is com-
comparable to the use of cosz and -\tth\i\z as canonical functions. It must also be pointed
out that the symbol On(z) ban boon uwed in .senaes other than that just explained by at least
two writera, namely Ileaviaide, I'roo. Royal Hoc. uv. A893), p. 138 (as was stated in § 34),
and Dougall, Proc. Edinburgh Math. Sac. xvni. A900), p. 3E.
Notb. An error in sign on p. 245 of Ileme'w treat mo has been pointed out by Morton,
Nature, r,xni. A901), p. 29; the error ia equivalent to a change in the sign of y in formula
§ 351 C) supra. It was also stated by Morton that thi.s error had apparently boon copied
by various other writers, iuoluding (as had been previously noticed by Gray IT) J. J. Thomson,
Recent Researches in Electricity and Magnetism (Oxford, 1893), p. 2G3. A further error
* Handbuch der Kuyelfunctionen, 1. (Berlin, 1878), pp. IRS—218.
t A Treatise on Basel Functions (London, 1B'.M), pp. 5I, 147, '242.
I 1'rvc. Royal Soc. lxvi. A900), pp. 32—43.
§ Phil. Mag. (C) xxn. A011),.pp. 658—608.
II Erotn the historical point of view there in something to bo said for using Hankel's function,
and alno for using Neumann's function; but Heine's function, boing more modern than either,
has not oven thia in its favour.
II Nature, xlix. A894), p. 359.
w. b. F. 5
66 THEOBY OF BESSBL FUNCTIONS [CHAP. Ill
noticed by Morton in Thomson's work seems to be due to a most confusing notation employed
by Heine; for on p. 245 of his treatise Heine uses the symbol Ko to denote the function
called -?*rF0 in this work, while on p. 248 the same symbol Ko denotes -?tt (Fo- iJ0).
3* 56. Recurrence formulae for Yv (z) and Yv {z).
The recurrence formulae which are satisfied by Yv (z) are of the same form
as those which are satisfied by Jv (z); they are consequently as follows:
A) 7^l(z)+7^(z)^7p(z),
B) YP^(z)-Yv+l(z) = 27/0),
C) zY9'{z) + v7,{z)-z7,-l(z),
D) ZY;(z)-vYv(Z) = -zYv+l(z),
and in these formulae the function Y may be replaced throughout by the
function Y.
To prove them we take § 3'2 C) and D) in the forms
jz [zv Jv (*)} = ** J~ (*) > jz \*v J- (*)} = -*v J-v+i 00;
if we multiply these by cot vir and cosec vrr, and then subtract, we have
whence C) follows at once. Equation D) is derived in a similar manner from
the formulae
^ [z- Jv («)} = - s- Jv+1 (z), ^ [z-* «/_„ (^)] = z-" /_,_, (*>.
By addition and subtraction of C) and D) we obtain B) and A).
The formulae are, so far, proved on the hypothesis that v is not an integer ;
but since Yv (z) and its derivatives are continuous functions of v, the result of
proceeding to the limit when v tends to an integral value n, is simply to
replace v by n.
Again, the effect of multiplying the four equations by ire™ sec vtt, which
is equal to ire{v±'vOri sec [y ± 1) v, is to replace the functions Y by the functions
Y throughout.
In the case of functions of integral order, these formulae were given by Lommol,
Stud-ten iiber die Bessel'schen Functionen (Leipzig, 1868), p. 87. The reader will find it
instructive to establish them for such functions directly from the series of § 3-52.
Neumann's investigation oonnected with the formula D) will be discussed hi § 3'58.
3-56,3*57] BBSSEL FUNCTIONS 67
3*57. Neumanns function of the second kind.
The function which Neumann* adopted as the canonical function of the
second kind possesses the advantage that it is represented more simply by
integrals of Poisson's type than the functions of the second kind which have
been hitherto discussed; but this is its only merit.
We first define the function of order zerof, which will be called F(o) (z).
The second solution of Bessel's equation for functions of order zero being
known to contain logarithms, Neumann assumed as a solution the expression
Jo (z) log z + w,
where w is a function of z to be determined.
If this expression is to be annihilated by V0) we must have
VoW^-Vo {./,(*) log*}
= -2*Jr0'(s).
Bat, by §212 A1),
- 2z /„' 0) = 2z J, (z) = 8 2 (-)»-' n Jm (z);
and so, since Vo Jin {z) = 4n2 J.M (z), we have
the change of the order of the operations ? and Vo is easily justified.
Hence a possible value for w is
2S(-^4(«)/«,
and therefore Neumann's function F@) (z), defined by the equation
A) F« (*) = Jo (*) log z + 2 I (-)»->J^ ,
n-1 n
is a solution of Bossel's equation for functions of order zero.
Since w -*- 0 as z ¦*¦ 0, (the series for w being an analytic function of z near
the origin), it is evident that /„ (z) and Ym (z) form a fundamental system of
solutions, and hence Yo (z) is expressible as a linear combination of Jo (z) and
Ym(z); a comparison of the behaviours of the three functions near the origin
shews that the relation connecting them is
B) Y* {z) = ?Yo (*) + (log 2 - 7) Jo {t).
* Theovie der Bessel'schenFunctionen (Leipzig, 18E7), pp. 42—14. "Neumann calla this function
Iiessel's associated function, and he doscriboa another function, On{z), fts the function of the second
kind (g 9-1). But, because O)l(z) h not a solution of BqshcI'h equation, this dcnci-iplion is un-
undesirable and it has not survived.
+ Neumann's function is distinguislied from the Webei'-Sohlafli function by the position of the
suilix which indicates the order.
5—2
68 THEORY Oi1 BESSEL FUNCTIONS [CHAP. Ill
3*571. The integral of Poissoris type for Y& (z).
It was shewn by Poisson* that
is a solution of Bessel's equation for functions of order zero and argument x;
and subsequently Stokes obtained an expression of the integral in the form of
an ascending series (see § 3*572).
The associated integral
2 ft*
- cos (z sin 0). log Dz cos2 0) d0
Tf j 0
was identified by Neumannt with the function 7<°> (z); and the analysis by
which he obtained this result is of sufficient interest to be given here, with
some slight modifications in matters of detail.
From § 2-2 (9) we have
(-)">/"»»(*) = A f 4rrcos (z cos 6) cos 2n6dO,
and so, if we assume that the order of summation and integration can be
changed, we deduce that
o v (-)" Jm (*) 4.. f ** . m 2 cos 2n0 ,a
2 X ^_i—?i-v_/ — _ cos u cos q\ 2 do
2
2 [l*
— I cos (z cos 6). log D sin2 8) dd;
from this result combined with Paxseval's integral (§ 2'2) and the definition of
Y(o) (^t), we at once obtain the formula
A) F«°» 0) = - f ^cos (* cos 0). log Da sin2 (9) dd,
from which Neumann's result is obvious.
The change of the order of summation and integration haa now to be examined,
because 2n~1 cos 2nd is non-uniformly convergent near 6=0. To overcome this difficulty
we observe that, since 2 ( -)» J2n (z)jn is convergent, it follows from Abel's theorem J that
2 (-}n^2nB)/n= Km 2 (-)*a*/*.(*)/»« lim - 2 I
* Journal de. v?cole B. Polytechnique, xn. (cahier 19), A823), p. 476. The solution of an
associated partial differential equation had been given earlier [ibid. p. 227). See also Dnhamel,
Cours d?Analyse, n. (Paris, 1840), pp. 122—124, and Spitzer, Zeitschrift filr Math, und Phys. n.
A857), pp. 165—170.
•j- Theorie der Bessel'tchen Functionen (Leipzig, 1867), pp. 45—49. See also Niemoller, Zeit-
Zeitschrift Jilr Math, und Phys. xxv. A880), pp. 65—71.
X Cf. Bromwich, TJieory of Infinite Series, § 51.
3-571,3-572] BBSSEL FUNCTIONS 69
Now, since a is less than 1, 2 (a'v coa 2nd)/n does converge uniformly throughout the
range of integration (by comparison with 2an), and so the interchange is permissible; that
is to say
2 S
- 2
" / As a* COS 2nd JA 2 /"I* . » a1lcos2%(9 ,.
cos (a cos 8) dd«=- I cos (z cos 0) 2 dd
' n it J 0 n.t ?i
1 /i*
= - - I cos B cos 0) log A - 2a cos 2(9 + a2) dd.
"^ / 0
Hence we have
~YJ (z)
1 /"i
lim _
We now proceed to shew that*
(YJ (z) 1 /i
2 S_i—aw = _ lim _ 008 ^ cos Qj log (x _2a oos 26 + a2)
=«l n w y
lim I
*l-0 J 0
lim
0 J 0
It isevidont that 1 -2acos 25 + a'2-
and so log A - 2a cos 20 -fa2) ^ log Da sin2 d).
Hence, if A he the upper bound + of | cos (z cos8) \ when 0^0 ^7r, we have
I (*" co.s (z cos (9) (log (I-2a cow 2(9 + a2) - log Da sin2 (?)} dd
J
* {log A - 2a coh 2(9 + a2) - log Da sin2 d)} dd
0
0
torin-by-torin integration being permissible .since a<l. Hence, when a<l,
I cos (z cos 6) {log (l-2a cos 28 -I- a'J) - log Da sin'2 d)) dd < Jinvl log (l/a)-»-O,
as «-^l -0; and this is the result to bo proved.
Consequently
I (~ )nJ'*1 ^ = - lim - I ^ cos (z cos (9). log Da sin2 (9) dd
JI---1 W a-*-l-07r y ()
- __ / cos (zoos(9).log Dsin2(9)^,
"¦ J o
and tlie interchange is finally justified.
The reader will find it interesting to deduce this result from Poisson's intogral for Jv{s)
combined with § 3*5 (B).
3'572. Stokes' scries for the Poisson-Neumann integral.
Tho differential oquation considered by Stokes J in 1850 was -A + - j-'ni2y=O, where
m is a constant. This is Bosael's equation for functions of ordor zero and argument imz.
Stokes statod (presumably with reference to Poisson) that it was known that the general
•solution waH
y =, f n {C+ Dibg (z sin2 d)} cosh (tu cos (9) dd.
J o
* The value of this limit was assumed by Neumann.
t If z is real, 4 = 1; if not, A =$ oxp {| 2 (z) |}.
t Tram. Camb. Phil. Soc. ix, A856), p. [38]. [Mathematical rtn& Physical Papers, in. A901),
p. 42.]
70 THEORY OF BESSEL FUNCTIONS [CHAP. Ill
It is easy to see that, with Neumann's notation, the value of the expression on the right
iir {0-2) log Dm,)} Jo (imz)+faDri°) (xmz).
The expression was expanded into a series by Stokes; it is equal to
z) Jo {imz) + 22) 2 V^r cos2n 6 log 8in ddd>
71=0 (*«,} ' J 0
and, by integrating by parts, Stokes obtained a recurrence formula from which it may be
deduced that
3#58. Neumann's definition of F(n> (z).
The Bessel function of the second kind, of integral order n, was defined by
Neumann* in terms of F(o) (z) by induction from the formula
A) z dYfa^-
which is a recurrence formula of the same type as §2*12D). It is evident
from this equation that
B) F<»> <*) = (-*)» (^ f<°>
Now F@) (z) satisfies the equation
j
and, if we apply the operatorf —j- to this equation n times, and use Leibniz'
zdz
theorem, we get
C) * (l)"+! rm¦<*>+Bn+2)
and so
z*(J^j [z-"YW (z)) + Bn + 2) (~~\ \z-nY™ {»)) + z-*Y*> (z) = 0.
This equation is at once reducible to
D) *srw(«)-0,
and so F(n) (z) is a solution of Bessel's equation for functions of order n.
Again, C) may be written in the form
{-*1 F<n+1> ()} - B» + 2)#-n-i F^1)(*) + z~nF<w> (*) = 0,
* Theorie der Bessel'schen Funclionen (Leipzig, 1867), p. 51. The function is undefined when
its order is not an integer.
t The analysis is simplified by taking i«2=f, bo that
d _d
zdz *~df
3-58,3-581] BESSEL FUNCTIONS 71
so that
z
whence we obtain another recurrence formula
E) z ~jf^ + nYW (z) = *F^' («>
When avc combine A) with E) we at once deduce the other recurrence
formulae
F) F' (*) + F««+1> (z) = — F<«> (*),
z
G) F<w-]> (*) - F"l+1J (*) = 2
Consecjuently F(Jl) B^) satisfies the same recurrence formulae as ./„ {?), Yn
and Yn (*). It follows from § 3'57 B) that
(8) YM (z) = ^7rYn(z) +(log 2 -
A solution of the equation V,t(y) = 0 in the form of a definite integral, which reduces'to
the integral of § 3'571 when « = U, has boon constructed by Spitzor, Zeitschrift filr Math,
und Phys. ill. A858), pp. 244-246; of. {} 3-583.
3*581. Neumann's expansion of Y{n) (z).
The generalisation of the formula § 3-57 A) has been.given by Neumann*;
it is
u -1 cjrn—m—t ^ J T I v\
+ s —
111 1
where sn — T + ^ + -tz -t- ... 4- - , so — ().
12 3 n
To establish this result, we first define the functions Ln (z) and Un (z) by
the equations
C) f/,,w=s,,/),w+ I (r)^^
so that F'°)(^) = X0^)-f70D
We shall prove that Ln(z) and CTn^) satisfy the recurrence formulae
D) ?M+1 (*) = - /-»' (*) + (n/z) Ln (*), ff,*, (*) = ~ l/»' <*) + (n/a) 0^ («),
and then A) will be evident by induction from § 3*58 B).
* Theorie der Bessel'schen Functional (Leipzig, 1867), p. 52. See also Lommel, Studien ilber
die BesseVschen Functioncn (Leipzig, 1868), pp. 82—84; Otti, BernMittheilungen, 1898, pp. 31—35;
and Haentzschel, Zeitschrift/Ur Math. undPhrja. xxxi. A886), pp. 25—38.
72 THEORY OF BESSEL FUNCTIONS [CHAP. Ill
It is evident that
1[ T
and the first part of D) is proved. To prove the second part, we have
dz\ zn ] ndz\ zn
J (z) 1 °°
^ + J
and the second part of D) is proved. It follows from §358B) that .
Y»*> (z) - Ln+1 (z) + Un+1 (z)_ d[ If* (z) - Ln (*) + U« (z)\
zn dz\
and since the expression on the right vanishes when n = 0, it is evident by
induction that it vanishes for all integral values of n. Hence
and the truth of equation A) is therefore established.
3*582. The power series for Un (z),
The function Un (z), which was defined in § 3-581 C) as a series of Bessel
coefficients, has been expressed by Schlafli* as a power series with simple
coefficients, namely
( Y A
To establish this result, observe that it is true when n — 0 by § 3*51 C) and
§3*57 A); and that, by straightforward differentiation, the expression on the
right satisfies the same recurrence formula as that of § 3*581 D) for Un (z);
equation A) is then evident by induction.
Note. It will be found interesting to establish this result by evaluating the coefficient
of (?s)n+2m in the expansion on the right of § 3-581 C).
* Math. Ann. in, A871), pp. 146—147.
3-582-3-6] BESSEL FUNCTIONS 73
The reader will now easily prove the following formulae:
<*) 3» (*) = G - log 2} Jn (z) - Un (z),
C) • F<») (z) = Ln (z) + 3, (z) + (log 2 - 7) Jn (z),
D)
3-583. The integral of Pomon's type for F('») (z).
The Poisaon-Neumann formula of § 3-571 for F(°) (z) was generalised by Lommel,
Shidien ilber die BesseVsehen Functionen (Leipzig, 1868), p. 86, with a notation rather
different from Neumann's; to obtain Lommel's result in Neumann's notation, we first
observe that, by differentiation of Poisson's integral for Jv (z), we have
G^F^)f 6 (kg (* cos2 Q-
and so, from § 3-582 C),
*"cos (*ain
and hence, since ^ (^) = ^ A) — 2 log 2 = - y - 2 log 2, we have the formula
A) n»)(z) = -T1&I lhirco
1 [n + -%) 1 {it) J 0
{*<+i)K4)}n()+M),
in which it is to bo remembered that Ln B) i« expressible as a finite combination of Bessel
eoeflieiontu and powers of z.
3. Functions of the third kind.
In numerous developments of the theory of Bessel functions, especially
those which are baaed on Hankel's researches (Chapters VI and vii) on integral
representations and asymptotic expansions of Jv {z) and Yv (z), two combina-
combinations of Beasel functions, namely ./„ (z) ± i Yv (z), are of frequent occurrence.
The combinations also present themselves in the theory of "Bessel functions
of purely imaginary argument" (§ 3'7).
It has consequently seemed desirable to Nielsen* to regard the pair of
functions Jv{z) ±iYv(z) as standard solutions of Bessel'a equation, and he
describes them as functions of the third, hind; and, in honour of Hankel,
Nielsen denotes them by the symbol //. The two functions of the third kind
are defined by the equations^
A) Bll\z) = Jv(z) + iYv{z), Hf\z) = Jv{z)-iYv{z).
From these definitions, combined with § 3'54 A), we have
B) a...w_-r_-A>Y=>rniz®, /,<»w.l-M-r1.*®..
v ' v v ' % sin vk " —iB}nv7r
When v is an integer, the right-hand sides are to be replaced by their limits.
Since Jv{z) and Y,,(z) satisfy the same recurrence formulae (§§3, 3*56),
in which the functions enter linearly, and since the functions of the third kind
* Ofversigt over det K. Damke Videmkabernen Setekabs Forfiandlinger, 1902,. p. 125. Hand-
buck der Theorie dcr Cylinderfunktioiien (Leipzig, 1904), p. 16.
f Nielsen uses the symbols ^(z), H^{z).
74 THEORY OF BESSEL FUNCTIONS [CHAP. Ill
are linear functions (with constant coefficients) of Jv (z) and Yv (z), it follows that
these same recurrence formulae are satisfied by functions of the third kind.
Hence we can at once write down the following formulae:
C) I
<*) *
<„ .f^
F) ,f^
G) <<
(8) V,tt
Note. Kayleigli on several occasions, e.g. Phil. Mag. E) xliii. A897), p. 266 ; F) xiv.
A907), pp. 350—359 [Scientific Papers, rv. A904), p. 290; v. A912), pp. 410—418], has used the
symbol Dn (z) to denote the function which Nielsen calls $niH®' (z).
* 3*61. Relations connecting the three kinds of Bessel functions.
It is easy to obtain the following set of formulae, which express each
function in terms of functions of the other two kinds. The reader will observe
that some of the formulae are simply the definitions of the functions on the
left.
A) J,{M)
B) J^ (*)
(to Y (.w^(
E) g^M^^
F) h B) (*). *"
From E) and F) it is obvious that
G) H™ (z) - e- If ?» (*), if (_8i (z). e
r.
sin
sin
2»
v{z)-e
sin
VTT
VK
)-e-"
-viti y
VTT
ml Y (
>
w
3-61-3-63] BBSSEL FUNCTIONS 75
3*62. Bessel functions with argument — z and zemni.
Since Bessel's equation is unaltered if z is replaced by — z, we must expect
the functions J±v(— z) to be solutions of the equation satisfied by J±v(z).
To avoid the slight difficulty produced by supposing that the phases of
both of the complex variables z and — z have their principal values*, we
shall construct Bessel functions of argument zemiT\ where m is any integer,
arg z has its principal value, and it is supposed that
arg (zemni) — nnr + arg z. .
Since Jv {z)\zv is definable as a one-valued function, it is obviously con-
convenient to assume that, when the phase of z is unrestricted, Jv(z) is to be
denned by the same convention as that by which zv is defined; and accordingly
we have the equations
A) Jv(z(Fwi)*=emv*iJv(z)>
B) J_v(zemvi)^e-mvjriJ^v(z).
The functions of the second and third kinds will now be defined for all
values of the argument by means of the equations § 3*54 A), § 3*6 A); and
then the construction of the following set of formulae is an easy matter:
C) Yv (zemH) = e- mvni Yv (z) + 2i sin mv-ir cot vtt Jv (z),
D) Y_,, (ze"lwi) = e~mynt F_„ (z) + 2i sin mm cosec vn Jv (z),
E) II {t\ze»™) = e--- JffW (*) - 2e--* ^^ J? (z)
= !Ea rjate? h<1) (z) - e—*6in™^ H«(z\
BinvTT " sini;7r "
ainQ tw^5 B) sin "^ w (z)
sini>7r
Of theao results, C) was given by Hauled, Math. Ana. vm. A875), p. 454, in tho special
case when m— 1 and i» is an integer. Forniulao equivalent t» E) and F) were obtained by
WolKjr, Math. Ann. xxxvn. A890), pp. 411, 412, when ?»=1; sco § 6*11. And a memoir
by («raf, Zeitichrift fiir Math, und Phya. xxxvm. AH93), pp. 116—120, contains tho general
formulae.
3*63. Fundamental systems of solutions of Bessel's equation.
It has been seen (§ 3*12) that Jv (z) and «/_„ (z) form a fundamental system of
solutions of Bessel's equation when, and only when, v is nob an integer. We shall
now examine the Wronskians of other pairs of solutions with a view to deter-
determining fundamental systems in the critical case when v is an integer.
• For Arg(-z) = Argitt, according as I(z) $ 0.
76 THEOBY OF BESSEL FUNCTIONS [CHAP. Ill
It is clear from § 3'54 A) that
m [Jv (*), Tv (z)} - - cosec m. Mi [Jv (*), J-v (*)}
vz'
This result is established on the hypothesis that v is not an integer; but con-
considerations of continuity shew that
A) «{/,(*).*,(*)}-2/(t*),
whether v be an integer or not. Hence Jv(z) and Yv(z) always form a funda-
fundamental system of solutions.
It is easy to deduce that
B) ?l
and, in particular*,
C)
When we express the functions of the third kind in terms of Jv (z) and
Yv {z\ it is found that
D) Oft {H ^ (*), H? (z)} = - 2t m {Jv (z), Yv (*)} = - 4i/M,
so that the functions of the third kind also form a fundamental system of
solutions for all values of v.
Various formulae connected with A) and C) have been given by Basset, Proc. London
Math. Soc. xxi. A889), p. 55; they are readily obtainable by expressing successive differ-
differential coefficients of Jv(z) and Yv{z) in terms of Jv{z), Jv' (z\ and Yv(z\ Yv' (z) by re-
repeated differentiations of Bessel's equation. Basset's results (of which the earlier ones
are frequently required in physical problems) are expressed in the notation used in this
work by the following formulae:
E) Jv (z) Yv" {z)-Yv {z)Jv" (»)« - Ij,
F) JJ (z) JV' (*)- F/ (*) J» (*) =
G) Jv (z) Y,'» (e) - Yv (z) JJ" (•)-! (^~-1)
(8) j; (») Yy"' (z)- f; (z)Jv'" (?)=
A0) Jv (t)
A1) j;W
Throughout these formulae Yv may be replaced by J_v if the expressions on the right
are multiplied by -sim/ir; and Jv> Yv may be replaced by E^\ H^ throughout if the
expressions on the right are multiplied by - 2i*.
¦ Of. Lommel, Math. Ann. tv. A871), p. 106, and Hankel, Math. Ann. vm. A875). p. 457.
3-7] BESSEL FUNCTIONS 77
An associated formula, due to Lommol*, Math. Ann. iv. A871), p. 106, and Hankel,
Math. Ann. vin. A875), p. 458, is
A2) •/¦„(*) rr+1@-J,+tw f,(Z)=-^.
This is proved iu the same way as § 3*2 G).
3'7. Bessel functions of purely imaginary argument.
The differential equation
which differs from Bessel's equation only in the coefficient of y, is of frequent
occurrence in problems of Mathematical Physics; in such problems, it is usually
desirable to present the solution in a real form, and the fundamental systems
Jv (iz) and /_„ (iz) or Jv (iz) and Yv (iz) are unsuited for this purpose.
However the function e-»"Tri Jv (iz) is a real function of z which is a solution
of the equation. It is customary to denote it by the symbol Iv(z) so that
When 2 is regarded as a complex variable, it is usually convenient to define
its phase, not with reference to the principal value of argi.gr, as the consideration
of the function Jv {iz) would suggest, but with reference to the principal value
of arg z, ho that
/„ (z) = e~*"ni Jv (ze*vi), (— 7r < arg z ^ \it),
/„ (z) = e*"ni Jv (ze~^% (^7t < arg z ^ it).
The introduction of the symbol Iv (z) to denote "the function of imaginary
argument" is due to Bassetf and it is now in common use. It should be men-
mentioned that four yeans before the publication of Basset's work, Nicolas+ had
suggested the use of the symbol l<\ (z), but this notation has not been used by
other writers.
Tho rohitive positions of I'ure and Applied MathoinaticH on tlio Continent as compared
with thia country are remarkably ilhmlralud by tho fact that, in Nielsen's standard
troatiNO^, neither tho function Iv B), nor the aocond solution Ky(z), which will bo defined
immediately, i« even mentioned, in npito of their importance in physical applications.
The function I~v{z) is also a solution- of A), and it is easy to prove (cf.
§8-12) that
' C) 2^
* Lommel gavi! the correHponding formula for Neumann'H function of the second kind.
I Proc. Cam!). Phil. Sac. vi. A889), p. 11. LTm's paper wa« first published in 1880.] Basset,
in this puper, defined the funotion of integral order to be ?+n Jn (iz), but ho subsequently changed
it, in his Hydrodynamics, 11. (Uambridgo, 1H88), p. 17, to that given iu the text. The more
recent definition in now universally used.
X Ann. tici. de VJ&cole norm. sup. B) xi. A882), eupplement, p. 17.
§ Handbuch der Theorie. der Cylinderfunktionen (Leipzig, 1904).
78 THEOEY OF BESSEL FUNCTIONS [CHAP. Ill
It follows that, when v is not an integer, the functions /„ (z) and /_„ (z) form
a fundamental system of solutions of equation A).
In the case of functions of integral order, a second solution has to be con-
constructed by the methods of §§ 3*5—3'54
The function Kn (z), which will be adopted throughout this work as the
second solution, is denned by the equation
An equivalent definition (cf. § 3'5) is
It may be verified, by the methods of § 3^5, that Kn (z) is a solution of A) when
the order v is equal to n.
The function Kv(z) has been defined, for unrestricted values of v, by
Macdonald*, by the equation
F) JT.W-^W-^W
and, with this definition, it may be verified that
G) Kn(z) = Mm Kv(z).
It is easy to deduce from F) that
(8) ' Kv (z) = iTrt'e^ Hl? (iz) = ^ie"^ H^l (iz).
The physical importance of the function Kv(z) lies in the fact that it is a
solution of equation A) which tends exponentially to zero as z-+.<x> through
positive values. This fundamental property of the function will be established
in § 7-23.
The definition of Kn(z) is due to Baaaot, Proc. Gamb. Phil. Soc. vi. A889), p. 11, and
his definition is equivalent to that given by equations D) and E); the infinite integrals by
which he actually defined the function will be discussed in §§ 6-14, 6*15. Basset subse-
subsequently modified his definition of the function in his Hydrodynamics, n. (Cambridge, 1888),
pp. 18—19, and his final definition is equivalent to ^-—. —^—^ ~^-
2n+1|_ ov dv Jv~n
In order to obtain a function which satisfies the same recurrence formula© as Iv (z),
Gray and Mathews in their work, A Treatise on Beisel Functions (London, 1895), p. 67,
omit the factor l/2n, so that their definition is equivalent to
2J_ dv Ov
The only simple extension of this definition to functions of unrestricted order is by the
formula
K, iz) s \v cot V* {/_„ (z) - Iv («)},
* Proc. London Math. Socxxx. A899), p. 167.
3*71] BESSEL FUNCTIONS 79
(cf. Modern Analysisy § 17*71) but this function .suffers from the aerioua disadvantage that
it vanishes whenever 2i» is an odd integer. Consequently in this work, Macdonald's
function Will be used although it has the disadvantage of not satisfying the same recur-
recurrence formulae as Iv (z).
An inspection of formula (8) shews that it would have been advantageous if a factor \rr had
been omitted from the definition of Kv(z); but in view of the existence of extensive tables
of Macdonald's function it is now inadvisable to make the change, and the presence of the
factor is not so undesirable- as the presence of the corresponding factor in Schliifli's function
($ 3*54) because linear combinations of Iv (z) and K„ (z) are not of common occurrence.
3*71. Formulae connected with Iv{z) and Kv{z).
We shall now give various formulae for Iv(z) and Kv(z) analogous to
those constructed in §§ 3*2——3*6 for the ordinary Bessel functions. The proofs
of the formulae are left to the reader.
o,. 9j>
A) /,_, (*) - /„+, (z) = L} L (*), Kv-r (z) - Kv+i (*) = ~^Kv(z),
z z
B) /,_! (z) + /,.H 0) = 2/; (z), Kv-X (z) + Kv+l (z) = - 2KV' (g),
C) zlj (z) + vlv (z) = zlv^ (z), zK; (z) + vKv (z) = - zK^ (z),
D) zi; (z) - vlv (z) = zl,+l (z), zK; (z) - vliv (z) = - zKy+1 (z),
d V" (/,.<*)) _ frim(z) ( d \»<KP(*)\ _, ^K^(z)
G) V(*) - 11 (a), ^.' (*) = ~ Ar, («),
(8) /_„ {z) = /„ (^), Ar_, (^) = 7C (^).
The following integral formulae are valid only when R(v +• \) > 0 :
:o.sh (z cos 0) wii
•1
V m C0Hh (^ cos
"*cosh
80 THEORY OF BBSSEL FUNCTIONS [CHAP. Ill
These results are due to Basset. We also have
A0) 1 n+i (*) - -—j \t ^ -1 (n _ r), B0)r
(n) r ,_x - ,^v (~Y(n + r)\
-* ^
A4) iT0 (*) = - log (\z) . /. (z) + 2 ^ f (tn + 1),
A5) ^.W-gS, m, (i^-»
m
A6) Z"o(*) = -^ f
Iv (zemvi) = e"^ I
A8) Zv (^e-) = e-™** Kv (z) - iri ^^ Iv (z),
sm vtt
A9) »(!,(«), ^r(*)}—1/*,
B0) i9 oo zv+1 (*> + /„_,! (*) jr, (o = \\z.
The integral involved in A6) has been discussed by Stokes (cf. § 3-572).
The integrals involved in (9) and the series in A4) were discussed by Riemann in his
memoir "Zur Theorie dev Nobili'schen Farbenringe," Ann. der Pkysik und Chemie, B) xcv.
A855), pp. 130—139, in the special case in which v=0\ he also discussed the ascending
power series for 70 B).
The recurrence formulae have been given by Basset, Proc. Camb. Phil. Soc. vi. A889),
pp. 2—19; by Macdonald, Proc. London Math. Soo. xxix. A899), pp. 110—115; and by
Aichi, Proc. Phys. Math. Soc. of Japan, C) n. A920), pp. 8—19.
Functions of this type whose order is half an odd integer, as in equations A0) and A2),
were used by Hertz in his Berlin Dissertation, 1880 [Qes. Werke, 1. A895), pp. 77—91];
and he added yet another notation to those described in § 3*41.
3-8] BESSEL FUNCTIONS 81
3'8. Thomson's functions ber (z) and bei (z) and their generalisations.
A class of functions which occurs in certain electrical problems consists of
Bessel functions whose arguments have their phases equal to \ir or ? it.
The functions of order zero wore first examined by W. Thomson*; they
may be defined by the equationf
A) ber (a:) + i bei (x) = Jn (ari \Ji) = /„ {x ^i),
where x is real, and ber and bei denote real functions. For complex argu-
arguments we adopt the definitions expressed by the formulae
B) ber (z) ± i boi (z) = /„ (zi V+ i) = Jo (* V ± »)•
Hence we have
(8) ber (,)-!-«?<$
Extensions of these definitions to functions of any order of the first, second and
third kinds have been effected by llusscllj: and Whitehead§.
The functions of the second kind of order zero were defined by Russell by
a pair of equations resembling B), the function /„ being replaced by the
function Ko, thus
E) kcr (z) ± i kei (z) - Ko (z«/± i).
Functions of unrestricted order v were defined by Whitehead with reference
to Bessel functions of the first and third kinds, thus
F) ber,, (z) ± i bei, (z) •¦= ./„ (ze'iiri),
G) her,, (z) ± i hoi, (z) = //„"> {ze^ni).
It will be observed that||
(8) ker {z) = - hrr hei {z), kei (z) = ^ir her (z),
in consequence of § ^(8).
The following Heries, due to Russell, are obtainable without difficulty:
(<)) ker 0) = - log D*). ber (z) + \tt bei (z)
* Preflidentiiil AddrcH« to the Instituto of Kloofcrioul Enp;inoei'u, IH80. [Math, and Plnjs.
PapiTH, in. A8»O), p. 4<J. ]
f In the caao of Eunctiona of zoro ordor, it iH ciiHtonmry to omit tho anflix which indicates
the order.
X Phil. Mag. @) xvn. A909), pp, 524—r>82.
§ Quarterly Journal, xui. A911), pp. 31C—342.
|| Integrals equal to ker B) and koi (z) oocnr in a memoir by Hertz, Ann. der Physik und Chemie,
C) xxii. A884), p. 450 [Gem. Werke, 1. A89G), p. 2891-
w. b. if. 6
82 THEORY OF BBSSEL FUNCTIONS [CHAP. HE
A0) kei (z) = - log (\z). bei (z) - \ir ber (z)
It has also been observed by Russell that the first few terms of the expansion of
ber2 B)+bei2 {z) have simple coefficients, thus
but this result had previously been obtained, with a different notation, by Nielsen (cf.
§ 5-41); the coefficient of (%s)irn in the expansion on the right is l/[(m !J. Bm)!].
Numerous expansions involving squares and products of the general
functions have been obtained by Russell; for such formulae the reader is
referred to Russell's memoir and also to a paper by Savidge*.
Formulae analogous to the results of §§3*61, 362 have been discussed by
Whitehead; it is sufficient to quote the following here:
A2) ber_v (z) = cos wr. ber,, (z) — sin wrr. [heiv (z) — bei,, (z)],
A3) bei_v (z) = cos vrr. beiv (z) + sin vrr. [herv (z) — ber,, (z)],
A4) her_v (z) =* cos vir. herv (z) — sin vrr. heik (z),
A5) hei_v (z) = sin vjt . herv (z) + cos vir. heiv (z).
The reader will be able to construct the recurrence formulae which have
been worked out at length by Whitehead.
The functions of order unity have recently been examined in some detail
by B. A. Smithf.
3*9. The definition of cylinder functions.
Various writers, especially SonineX and Nielsen§, have studied the general
theory of analytic functions of two variables ^v (z) which satisfy the pair of
recurrence formulae
913
A) ».-»(*)+ ».**(*)« 7 *,(*),
in which z and v are unrestricted complex variables. These recurrence formulae
are satisfied by each of the three kinds of Bessel functions.
Functions which satisfy only one of the two formulae are also discussed by
Sonine in his elaborate memoir; a brief account of his researches will be given
in Chapter x.
* Phil. Mag. F) xix. A910), pp. 49—58.
f Proc. American Soc. of Civil Engineer^ xlvi. A920), pp. 375—425.
t Math. Ann. xvi. A880), pp. 1—80.
§ Handbuch der Theorie der Cy UnderfunktiantH. (Leipzig, 1904), pp. 1, 42 et seq.
3'9] BESSEL FUNCTIONS 83
Following Sonine we shall call any function 9Bv{z), which satisfies both of
the formulae, a cylinder function. It will now be shewn that cylinder functions
are expressible in terms of Bessel functions.
When we combine the formulae A) and B), we find that
C) z<®J (z) + v<@v (z) = *$Lx (z),
D) zc@; (z) - v<$v (z) = - zK+l {z),
and so, if & be written for z (d/dz), we deduce that
E) (* + *) #,(*)-*«•_,(*),
F) (^-^K(z)^-z%,+1(z).
It follows that
#,(),
that is to say
G) V^rE)-0.
Hence <#„ (z) = <*„/„ (z) + &„ K, (*),
where a,, and bv are independent of z, though they may depend on v. When
we substitute in C) we find that
«„«/„_, 0) + hvYv^ (z) = a,,-!J,._i (z) + by-iYr-i (z),
and so, since ./„_! (z)/ Yv_t (z) i.s not independent of z, we must have
Hence a,, and bv must be periodic functiiona of v with period unity; and,
conversely, if they arc. such functions of v, it is easy to see that both A) and
B) arc satisfied.
Hence the general solution of A) and B) is
(8) #'„ (z) = or, („) J,. (z) + «r2 (v) Yv (z),
whore, ¦n-i(v) and ¦nry(r) arc arbitrary periodic functions nf v with period unity.
It may be observed that an equivalent solution is
(9) K (z) = W| (,) //„<" B) + flr4 (») ^<4' («).
A difference oquutioii, which is more general thiin A), him been cxatuiiied by
Messenger, xxxiv. A905), pp. 52—71 ; in cortnin circuin.stancoa the solution i.s expressible
by BeaMol functious, though it UHiially involves hyporgeoinotric functions.
Notk. The name cylinder function i.s used by Nielsen to denote Jv (s), \\, (i), //,,<') (:">
and i/v('i|) (z) sus well as the more general function.s diweuHaed in thin section. This procedure
ia in accordance with the principle laid down by Mittag-Lefflor that it irt, in general,
undesirable to associate functioim with the names of particular mathematicians.
The name cylinder function in derived from the fact that normal solution* of Laplaoc'«
equation in cylindrical coordinates are
(cf. § 4"8 and Modern Analysis, § 18'5).
THEORY OE BESSEL FUNCTIONS [CHAP. Ill
writers*, following Heinet who called Jn{z) a Fourier-Bessel function, call Jn(z)
• function.
>ugh Bessel coefficients of any order were used long before the time of Bessel
3, 1*4), it seems desirable to associate Beasel's name with them, not only because
:come generally customary to do so, hut also because of the great advance made by
a the work of his predecessors in the invention of a simple and compact notation
functions.
Bessel's name was associated with the functions by Jacobi, Journal fiir Math. xv.
A836), p. 13 [Qes. Math. Werke, vi. A891), p. 101]. "Transcendentium /** naturam varios-
que usus in determinandis integralibus definitis exposuit ill. Bessel in commentatione
celeberrima."
A more recent controversy on the name to be applied to the functions is to be found in
a series of letters in Nature, lx. A899), pp. 101, 149, 174; lxxxi. A909), p. 68.
* E.g. Nicolas, Ann. Sci. de VEcole norm. sup. B) xi. A882), supplement,
f Journal fur Math. lxix. A868), p. 128. Hoine also soems to be responsible for the term
cylinder function.
CHAPTER TV
DIFFERENTIAL EQUATIONS
4*1. Daniel Bernoulli's solution of Riccati's equation.
The solution given by Bernoulli* of the equation
A) %-a.-+by
consisted in shewing that when the index )i has any of the values
0; -f-*; -8,-5; -V. -V-; -?,-?; •••>
while a and 6 have any constant vainest, then the equation is soluble by
means of algebraic, exponential and logarithmic functions. The. values of vi
just given are comprised in the formula
4w
<2> " " - 2,,,. ± I •
where m is zero or a positive integer.
Bernoulli's method of solution is as follows : Tf u bo called the index of the
equation, it is first proved that the general equation'! of index n is transformable;
into the general equation of index N, where
C) N=- " ;
and it is also proved that the general equation of index n is transformable
into the general equation of index v, where;
D) v = - h - 4.
The liiccati equation of index zero is obviously inUigrable, because the
variables are separable*. Hence,by D), the e'.epialiem of ineicx — [< is inU'-grabh1.
Hence by (tf), the eejuation of itidesx — 1j is integrabl«\ If Liu's pn»ec;ss be con-
continued by using the transformat.iems C) and D) alternately, we1 arrive1 at I.be
set of soluble cases given above1, and it is eiasy te> see1 thai, these ease's ;in>
comprised in the general lonnula B).
* lixercitationcs quaeiiam nuithematicar (Yemen, 1721), pp. 77- -Hi); Act<i fr'.nidilonnn, 17'Ji5,
pp. 473—47E. The notation us«d by Bernoulli Han Ixiun uliKlitly modified; and in this unalyaia
n ta uot reatricteel to be an integer.
+ It ia assumed that neither a nor b in zero. If oithor were zoro tho vaviahlcm would obviuuHly
be separable.
$ That is, the eejuation in which a ami h havu arbitrary viUuoh.
86 THEORY OF BESSEL FUNCTIONS [CHAP. IV
4*11. Daniel Bernoulli's transformations of Riccati's equation.
Mow that the outlines of Bernoulli's procedure have been indicated, we
proceed to give the analysis by which the requisite transformations are effected.
Take § 4'1 A) as the standard equation of index n and make the substitutions
n+l ' * 7
[Note. The substitutions are possible because -1 is not included among the values of
n. The factor n+1 in the denominatoi was not inserted by Bernoulli; the effect of its
presence is that the transformed equation is more simple than if it were omitted.]
The equation becomes
1 dY h
that i
is
where N — — nj(n + 1); and this is the general equation of index JV.
Again in § 4'1 A) make the substitutions
The equation becomes
d% V'
where v = — n — 4; and this is the general equation of index v.
The transformations described in § 4*1 are therefore effected, and so the
equation is soluble in the cases stated. But this procedure does not give the
solution in a compact form.
4*12. The limiting form of Riccati's equation, with index —2.
When the processes described in §§41, 4'11 are continually applied to
Riccati's equation, the value to which the index tends, when m -*- qo in
§ 4*1 B), is - 2. The equation with index ~ 2 is consequently not soluble by
a finite number of transformations of the types hitherto under consideration.
To solve the equation with index — 2, namely
write y — v/z, and the equation becomes
dv . , „
z -j- — a + v + bv2;
dz '
and this is an equation with the variables separable. •
Hence, in this limiting case, Riccati's equation is still soluble by the use
of elementary functions.
4-11-4-13] DIFFERENTIAL EQUATIONS 87
This solution was implicitly given by Euler, Inst. Calc. Int. n. (Petersburg, 1769), § 933,
p. 185. If we write (cf. § 4-14) y = —j-rri the equation which determines y is
which is homogeneous, and consequently it is immediately soluble.
Enler does not seem to mention the limiting case of Riccati's equation explicitly,
although he gave both the solution of the homogeneous linear equation and the transforma-
transformation which connects any equation of Riccati's type with a linear equation.
It will appear subsequently (§§ 4*7—4*75) that the only cases in which
Riccati's equation is soluble in finite terms are the cases which have now been
examined; that is to say, those in which the index has one of the values
0; -f -*; -§, -|; .... -2,
and also the trivial cases in which a or b (or both) is zero.
This converse theorem, due to Liouville, is, of course, much more recondite
than Bernoulli's theorem that the equation is soluble in the specified cases.
4*13. Eider's solution of Riccati's equation.
A practical method of constructing a .solution of Riccati's equation in the
soluble cases was devised by Euler*, and this method (with some slight changes
in notation), will now be explained.
First transform Riccati'a equation, § 4*1 A), by taking new variables and
constants as follows:
A) yss — Tf/b, ab — ~dl, ?i = 2<7-2;
the transformed equation is
B) ^ + r? - c'z2"-* = 0 ;
and the soluble cases are those in which l/q is an odd integer.
Define a new variable w by the equation
C) ,-^+1*?,
so that the equation in w is
D) ^ + 2c**-1 dy + (q - 1) czi-'w = 0.
A solution in series of the last equation is
r-0
provided that
A (M + G ^lKV ±<1~ 1)
* Nov. Comm. Acad. Petrop. vm. A700—1701) [1703], pp. 'A—03 ; and ix. A762—1768)
[1764], pp. 154—169.
88 THEORY OF BESSEL FUNCTIONS [CHAP. IV
and so the series terminates with the term Amz~qm if q has either of the values
± l/Bm + 1); and this procedure gives the solution* examined by Bernoulli.
The general solution of Riccati's equation, which is not obvious by this method, was
given explicitly by Hargreave, Quarterly Journal, vn. A866), pp. 256— 258, but Hargveave's
form of the solution was unnecessarily complicated; two years later Cayley, Phil. Mag. D)
xxxvi. A868), pp. 348—351 [Collected Papers, vii. A894), pp. 9—12], gave the general solu-
solution in a form which closely resembles Euler's particular solution, the chief difference between
the two solutions being the reversal of the order of the terms of the series involved.
Cayley used, a slightly simpier form of the equation than B), because he took constant
multiples of both variables in Riccati's equation in such a way as to reduce it to
E) ^+^_^-2=0.
4" 14. Gayley's general solution of Riccati's equation.
We have just-seen that Riccati's equation is reducible to the form
dz
given in § 4)*13 B); and we shall now explain Cayley'sf method of solving
this equation, which is to be regarded as a canonical form of Riccati's
equation.
When we make the substitution| v) = d(\ogv)/dz, the equation becomes
A) g_c2^-aw==0;
and, if Uj, and U2 are a fundamental system of solutions of this equation, the
general solution of the canonical form of Riccati's equation is
where Cj and <72 are arbitrary constants and primes denote differentiations with
respect to z.
To express Ux and U3 in a finite form, we write
v = w exp (czQjq),
so that the equation satisfied by w is § 4-13 D). A solution of this equation
in w proceeding in ascending powers of & is
(g-PCg-P
and we take Ux to be exp (czQ/q) multiplied by this series.
• When the index n of the Biccati equation is - 2, equation D) is homogeneous.
t Phil. Mag. D) xxxvi. A868), pp. 848—351 [Collected Papers, vn. (-1894), pp. 9—12]. Of. also
the memoirs by Euler which were cited in § 4*13.
t This is, of course, the substitution used in 1702 by James Bernoulli; cf. § l-l;
4-14] DIFFERENTIAL EQUATIONS 89
Now equation A) is unaffected by changing the sign of c, and so we take
and both of these series terminate when q is the reciprocal of an odd positive
integer. Since the ratio f/j : 272 is the exponential function exp Bc2q/q)
multiplied by an algebraic function of 2$, it cannot be a constant; and so
Uu Us form a fundamental system of solutions of A).
If q were the reciprocal of an odd negative integer, we should write
equation A) in the form
whence it follows that
where yx and y» are constants, and
The series which have now been obtained will be examined in much greater
detail in §§ 4*4—4'42.
The reader .should have uo difficulty in constructing the following solutions of Ricoati's
equation, whon it is soluble in finite terms.
(i)
(iii)
(i)
(ii)
(iii)
Equation
(drjjdz) +7,2=1
(drfjdz)+7,2 => z ~ yb
Equation
(drjIdzW-Z-*
(drj^+rj^Z-W
Values of f/1( C/2
exp (±z)
A + r>21('6 + Xtf-apfi) exp (+ bzm)
Values of Vif V%
z exp (+ \jz)
z(l + 32-'/3)exp(±32-1/3)
2.(!!5.::.!.!?.a:!'.):i^.±6.::r.)
It is to be noticed that the series Dlf U^ (or Vlt V2, as the case may be) are BUpposed
to terminate with the term before the first term which has a zero factor in the numerator;
see § 4*42 and Glaishor, Phil. Trans, of the Royal Soc. olxxii. A881), p. 773.
90 THEORY OF BESSEL FUNCTIONS [CHAP. IV
Among the writers who have studied equation A) are Kummer, Journal fUr Math. xn.
A834), pp. 144—147, Lobatto, Journal par Math. xvn. A837), pp. 363—371, Glaisher (in
the memoir to which reference has juist been made), and Suchar, Bull, de la Soc. Math, de
France, xxxn. A904), pp. 103—116; for other references see § 4-3.
The reader will observe that when ?=0, the equation A) is homogeneous and imme-
immediately soluble; and that the second order equation solved by James Bernoulli (§ 1*1) is
obtainable by taking 2=2 in A), and so it is not included among the soluble cases.
• 4*15. Schlafli's canonical form of Riccati's equation.
The form of Riccati's equation which was examined by Schlafli* was
This is easily reduced to the form of § 413B) by taking -t~ala as a new
independent variable.
To solve the equation, Schlafli wrote
dloi
and arrived at the equation
the general solution of the equation in y is
y = c1F(a> t) + G»t-*F (- a, t).
The solution of A) is then
= <hV**F (a + l>t)+c2F(-a-1, t)
U ~ ClF(a, t) + c2t~aF (- a, t)
The connexion between Riccati's equation and Bessel's equation is thus
rendered evident; but a somewhat tedious investigation is necessary (§ 4*43)
to exhibit the connexion between Cayley's solution and Schlafli's solution.
Note. The function <? : s, denned as the series
1+2 + 1 °2 . 1 ^l +
z+2" 2(z+l)T2. +
which is evidently expressible in terms of Schlafli's function, was used by Legendre,
Mdments de Odometrie (Paris, 1802), note 4, in the course of his proof that n ia irrational.
Later the function was studied (with a different notation) by Clifford; see a posthumous
fragment in his Math. Papers (London, 1882), pp. 346—349.
• Ann. di Mat. B) i. A8B8), p. 232. The reader will see that James Bernoulli's solution in
series (§ 1*1) ia to be associated with Schlafli's solution rather than with Cayley's solution,
f Tais notation ahould be compared with the notation of § 4*4.
4*15,4-16] DIFFERENTIAL EQUATIONS 91
It is obvious that Jv (z)=(\z)» F (v, - ?z2),
and it has recently been suggested* that, because the Schlafli-Clifford notation simplifies
the analysis in the discussion of certain problems on the stability of vertical wires under
gravity, the standard notation for Bessel functions should be abandoned in favour of a
notation resembling the notation used by Schlafli-Cliftbrd :—a procedure which seems com-
comparable to a proposal to replace the ordinary tables of trigonometrical functions by tables
of the functions
4*16. Miscellaneous researches on Riccatts equation.
A solution of Riocati's equation, which involves definite integrals, was given by Murphy,
Trans. Camb. Phil. Soc. in. A830), pp; 440—443. The equation which he considered is
~ + Au* = Blm,
at '
and, if a be written for l/(m+2) and A~l d (log y)/dt for u, his solution (when ABa?**!) is
A-» [(f> (A) exp (^//z) +e/> (I/A) exp (A*1/")] dh,
where d> (h) = ehh~a P e-^ha~l dh= 2 *"
rv ; Jo «»0a
If \jh be written for h in the second part of tho integral, then the last expression given
for y reduces to irit multiplied by tho residue at the origin of h~l (p (h) oxp (tl'ajh), and the
connexion between Murphy's solution and Schliifli's solution (§ 4'15) is evident.
An investigation w.-is published by Clmllis, Quarterly Journal, vil. A806), pp. 51—58,
which shewed how to connect two equations of tho type of § 4-13 B), namely
in one of which lfq is an odd positivo integer, and in tho other it is an odd negative
integer. This investigation is to be associated with the discovery of the two types of
solution given in § 4-14.
mi • du an , ., „ ,.
The equation -,- + —h 6z" uz - czm~0,
1 dz z
which is easily transformed into <ui equation of Riccati's type by taking 2»-« + 1 and z?u na
new variables, was investigated by Ruwsou, Messenger, vn. A878), pp. 69—72. Ho trans-
transformed it into the equation
ctz
by taking bu*=czaly; two such equations are called cognate Riccati equations. A somewhat
similar equation wan reduced to Riccati's typo by Bimsinne, Journal de Muth. XVI. A851),
pp. 255—256.
The connexions between the various types of equations which different writers have
adopted as canonical forms of Riccati's equation havo been set out in a paper by Greenhill,
Quarterly Journal, xvi. A879), pp. 294—298.
* Greenhill, Engineering, cvn. A1I9), p. 334; Phil. Mag. F) xxxvin. A919), pp. 601—528;
see also Engineering, oix. A920), p. 851.
92 THEOBY OF BESSEL FUNCTIONS [CHAP. IV
The reader should also consult a short paper by Siaoci, Napoli Rendiconti, C) vn.
A901), pp. 139—143. And a monograph on Riccati's equation, which apparently contains
the majority of the results of this chapter, has been produced by Feldblum, Warschau
Univ. Nach. 1898, nos. 5, 7, and 1899, no. 4.
4*2. The generalised Riccati equation.
An obvious generalisation of the equation discussed in § 4*1 is
A) ^
where P, Q, R are any given functions of z. This equation was investigated
by Euler*. It is supposed that neither P nor R is identically zero; for, if
either P or R is zero, the equation is easily integrable by quadratures.
It was pointed out by Enestrom, Encyclopddie des Soi. Math. n. 16, § 10, p. 75, that a
special equation of this type namely
nxx dx - nyy dx+xx dy=xy dx
was studied by Manfrediua, De constructione aequationwn differentialum primi gradus
(Bologna, 1707), p. 167. "Sed tamen haec eadem aequatio non apparet quomodo construi-
bilis sit, neque enlni videmus quomodd illam integi-ernus, nee quomodo indeterminatas ab
invicem separemus."
The equation A) is easily reduced to the linear equation of the second
order, by taking a new dependent variable u denned by the equation f
The equation then becomes
1 dR\ du
Conversely, if in the general linear equation of the second order,
/A\ dhb du n
(where pQ, p1} p2 are given functions of z), we write
E) u=ebldz,
the equation to determine y is
dz p0 p0J y'
which is of the same type as A). The complete equivalence of the generalised
Riccati equation with the linear equation of the second order is consequently
established.
The equations of this section have been examined by Anisimov, Warschau Univ. Nach.
1896, pp. 1—33. [Jakrbuch fiber die Fortschritte der Math. 1896, p. 256.]
* Nov. Gomvi. Acad. Petrop. vni, A760—1761) [1763], p. 32; see also a short paper by W. W.
Johnson, Ann. of Math. m. A887), pp. 112—115.
f This is the generalisation of James Bernoulli's substitution (§1*1). See also Euler, Inst.
Calc. Int. n. (Petersburg, 1769), §§ 831, 852, pp. 88,104.
4-2,4-21] DIFFERENTIAL EQUATIONS 93
4*21. Eiders theorems concerning the generalised Riccati equation.
It has been shewn by Euler* that, if a particular solution of the
generalised Riccati equation is known, the general solution can be obtained
by two quadratures; if two particular solutions are known the general
solution is obtainable by a single quadrature f. And it follows from theorems
discovered by Weyr and Picard that, if three particular solutions are known,
the general solution can be effected without a quadrature.
To prove the first result, let y0 be a particular solution of
and write y = yo+ \/v. The equation in v is
dv
dz
of which the solution is
v exp [f(Q + 2Ry0) dz} + JR exp {J(Q + 2%,) dz}. dz = 0,
and, since v = 1/B/ —yo), the truth of the first theorem is manifest.
To prove the second, let yQ and yx be two particular solutions, and write
~ y - yi'
The result of substituting (yiW — yo)/(w — 1) for y in the equation is
(w — 1 )a (^ w — 1 rf^ w - 1 ^2 w - 1 \ w -1
and, when we substitute for (dyjdz) and (dyo/dz) the values P + Qy^ + Ry^
and P+ Qyo + -Z2y,,2, the last equation is reduced to
1 dw tv n
- -y- = lv?/o — iit/i,
so that w = c exp j/Giy0 - i^i) <i*j,
where c is the constant of integration. Hence, from the equation defining w,
we set; that y in expressed as a function involving a single quadrature.
To prove the third result, let ;</„ and y, bo the solutions already specified,
let 2/a be a third solution, and let c' be the value to be assigned to c to make
y reduce to y... Then
and this is the integral in a form free from quadratures.
* Nov. Comrn. Ac.ad. Petrop. vni. A760—17C1) [1763], p. 32.
t Ibid. p. 59, and rx. A76-2—1763) [1764], pp. 163—164. See also Minditig, Journal fiir
Math. xr,. A850), p. 361.
THEORY OF BESSEL FUNCTIONS [CHAP. IV
It follows that the general solution is expressible in the form
Hence it is evident that, if jfc, ytl y,, jfc be any four solutions, obtained by
giving G the values 0» Ct, Q%, d respectively, tAen *te crow-rofro
is independent of z; for it is equal to
In spite of the obvious character of this theorem, it does not seom to havo
been noticed until some forty years ago*.
Other properties of the generalised Riccati equation may be derived from
properties of the corresponding liDear equation (§ 4-2). Thus Raffy \ has gi von
two methods of reducing the Riccati equation to the canonical form
these correspond to the methods of reducing a linear equation to its normal
form by changes of the dependent and independent variables respectively.
Various properties of the solution of Riccati's equation in which P, Q, ft arc rational
functions have been obtained by C. J. D. Hill, Journal filr Math. xxv. A843), pp. 23 - 37 ;
Autoune, Comptes Rendus, xcvi. A883), pp. 1354—1356; cxxvin. A899), pp. 410—412 ; ami
Jamet, Comptes Rendut de VAssoc. Frangaise (Ajaccio), A901), pp. 207—228 ; Ann. dr la
Fac. des Sci. de Marseille, xn. A902), pp. 1—21.
The behaviour of the solution near singularities of P, Q, R has been studied by Kulkon-
hagen, Jfieuw Archief voor Wiskunde, B) vi. A905), pp. 209—248.
The equation of the second order whose primitive is of the type
where eu c2, c% are constants of integration (which is an obvious generalisation of the
primitive of the Riccati equation), has been studied by Vessiot, Ann. de la Fac. dc* Sci. dr.
Toulouse, ix. A895), no. 6 and by Wallenburg, Journal fiir Math. exxt. A900), pp. 210 217;
and Comptes Rendus, exxxvn. A903), pp. 1033—1035.
• Weyr, Abh. bnhm. Ges. Wm. F) vin. A875-1876), Math. Mem. x. p. 30 ; Pioanl ^nn Sri
de VEcole uorrn. tup. B) vi. A877), pp. 342-343. Picard's thesis, in which the result -j» con-
contained, « devoted to the theory of sui-faces and twisted curves-a theory in which Hicoali'H
equation has various applications.
t Nouv. Ann. de ilpth. D) n. A902), pp. 529—545.
4'3] DIFFERENTIAL EQUATIONS 95
4*3. Various transformations of Bessel's equation.
The equations which we are now about to investigate are derived from
Bessel's equation by elementary transformations of the dependent and inde-
independent variables.
The first type which we shall consider is*
,n d'u p(p+l)
A) _?_cHt = /!-iL__u, •
where c is an unrestricted constant. The equation is of frequent occurrence
in physical investigations, and, in such problems, p is usually an integer.
The equation has been encountered in the Theory of Conduction of Hoat and the
Theory of Sound by Poisson, Journal de V&cole Poly technique, xn. (cahier 19), A823),
pp. 249—403; Stokes, Phil Trans, of the Royal Soc. 1868, pp. 447—464 [Phil. Mag. D)
xxxvi. A868), pp. 401—421, Math, and Phys. Papers, IV. A904), pp. 299—324]; Rayleigh,
Proc. London Math. Soc. iv. A873), pp. 93—103, 25S--283 [Scientific Papers, I. A899).
pp. 138, 139]. The special equation in which p = 2 occurs in the Theory of the Figure of
the Earth; see Ellis, Camb. Math. Journal, u. A841), pp. 169—177, 193—201.
Since equation A) may be written in the form
Q d? (fur*) d (usr*) , ., „ , ..., . rt
aW + Z" dz " ^ + (P + &) 1 • uz = °-
its general solution is
B) u = z*%H{ciz\
Consequently the equation is equivalent to Bessel's equation when p is
unrestricted, and no advantage is to be gained by studying equations of the
form A) rather than Bessel's equation. But, when p is an integer, the solu-
solutions of A) nre expressible "in finite termsf" (cf. § 3 4), and it is bhen
frequently desirable to regard A) as a canonical form. The relations between
various types of solutions of A) will be examined in detail in §§ 4*41—4>'4>'].
The second type of equation is derived from A) by a transformation of
the dependent variable which makes the indicial equation have a zero root.
The roots of the indicial equation of A) are p + 1 and -p, and so we write
u = vz~p; we arc thus led to the equation
C) __^__c2w:=0,
of which the general solution is
D) fl = ^+K^,+i(cu).
* See Plana, Mem. della II. Acctid. delle Sci. di Torino, xxvi. A821), pp. 519—538, andPaoli,
Mem. di Mat. e di Fis. della Soc. ltaliana delle Sci. xx. A828), pp. 183—188.
t This was known to Plana, who studied equations A) and E) in the paper to whioh referenoe
has just been made. ,
96 THEORY OF BESSEL FUNCTIONS [CHAP. IV
Equation C), which has been studied in detail by Bach, Ann. Sci. de Vtlcole norm. sup.
B) in. A874), pp. 47—68, occurs in certain physical investigations; see L. Lorenz, Ann.
der Physik und Chemie, B) xx. A883), pp. 1—21 [Oeuvres Scientifiques, I. A898), pp. 371—
396]; and Lamb, Hydrodynamics (Cambridge, 1906), §§ 287—291. Solutions of equation C)
in the form of continued fractions (cf. §§ 5-6, 9 5) have been examined by Catalan, Bulletin
de I'Acad. R. de Belgique, B) xxxi. A871), pp. 68—73. See also Le Paige, ibid. B) xli.
A876), pp. 1011—1016, 935—939.
Next, we derive from C), by a change of independent variable, an equation
in its normal form. We write z — fijq, where q—l/Bp +1), the equation then
becomes
E) ~
and its solution is
F) v-
When a constant factor is absorbed into the symbol 9B, the solution may be
taken to be
Equation E), which has already been encountered in § 4-14, has been studied by Plana,
Mem.della R. Aocad. delle Sci. di Torino^ xxvi. A821), pp. 519—538; Cayley, Phil. Mag.
D) xxxvi. A868), pp. 348—351 [Collected Papers, vh. A894), pp. 9—12]; and Lommel,
Studien itber die BesseVschen Functioned (Leipzig, 1868), pp. 112—118.
The system of equations which has now been constructed has been dis-
discussed systematically by Glaisher*, whose important "memoir contains an
interesting account of the researches of earlier writers.
The equations have been studied from a different aspect by Haentzschel f
who regarded them as degenerate forms of Lame's equations in which both of
the invariants g2 and g3 are zero.
The following papers by Glaiaher should also be consulted: Phil. Mag. D) xmr. A872),
pp. 433—438; Messenger, via. A879), pp. 20—23; Proc. London Math. Soc. ix. A878),
pp. 197—202.
It may be noted that the forms of equation A) used by various writers are as followa:
(Glaisher).
Equation E) has been encountered by Greenhill J 5n his researches on the stability of a
vertical pole of variable cross-aection, under the action of gravity. When the oroas-section
is constant, the special equation in which y=| is obtained, and the solution of it leads to
Bessel functions of order +•?.
* Pl\il. Trans, of the Royal Soc. clxxh. A881), pp. 759—828; see also a paper by Curtis, Cam-
Cambridge and Dublin Math. Journal, xx. A854), pp. 272—290.
t Zeitschriftfilr Math, und Phy*. tlxxl. A886), pp. 25—33.
t Proc. Catnb. Phil. Soc. iv. A883), pp. 65—73.
4'3l] DIFFERENTIAL EQUATIONS 97
4#31. Lommel's transformations of Bessel's equation.
Various types of transformations of Bessel's equation were examined by
Lommel on two occasions; his earlier researches* were of a somewhat special
type, the laterf were much more general.
In the earlier investigation, after observing that the general solution of
is
B) y = z"%\,{z\
Lommel proceeded by direct transformations to construct the equation whose
general solution is z^v~°-%'v (yz1*), where a, /3, 7 are constants. His result,
which it will be sufficient to quote, is that the general solution of
C) z* ~ + Ba - 2/3v + l)z j- + (#V^a + « (« - 2?i/)} u = 0
is
D) tt = ^"-«K(Y23)-
When # = 0, the general solution of C) degenerate's into
anil when 7 = 0, it dogonerutcs into
unlo.s.s fiu i.s zero.
The .solution of C) wan given explicitly by Lomnuil in numerous special eases. It will
be .sufficient to quote the following for reference:
(f>) d?l + - -d- + 4 ^ - ?,J u = 0 ; a = %'v (f).
, ^ dru du
(«) + +
(8)
@)
A1) (d^±ZU~()' u =
An account of Stokes' researches on the solutions of equation A1) will be given in
§§ 6-4, 10-2.
* Studien ilher die BcaseVachen Functionen (Leipzig, 1868), pp. 98—120; Math. Ann. in.
A871), pp. 475—487.
t Math. Ann. xiv. A879), pp. 510—586.
W. B. F. 7
98 THEORY OF BESSEL FUNCTIONS [CHAP. IV
Lommel's later researches appeared at about the same time as a memoir
by Pearson*, and several results are common to the two papers. Lommel's
procedure was to simplify the equation f
of which the solution is (§ 4*3)
A2) *-*
On reduction the equation becomes
.
Now define the function <jf> (z) by the equation
It will be adequate to take
A4) *(*)«
If we eliminate %(^), it is apparent that the general solution of
4 ^j
IS
As a special case, if we take <? (z) = 1, it is seen that the general solution of
is
A8) y
Next, returning to A3), we take ^ («) = {-^r (z)}*-", and we find that the general
solution of
IS
B0)
Messenger, ix. A880), pp. 127—131. j- The inactions x («) and ^(z) are arbitrary.
4-32] DIFFERENTIAL EQUATIONS 99
The following are special cases of A7):
B1) g + (^_^),/ = 0; y = <&,(#),
B2) d+ /y = 0] y-'^W
The independent researches of Pearson proceeded on very similar lines
except that he started from Bessel's equation instead of t from the modified
form of it. The reader will find many special cases of equation A7) worked
out in his paper.
A partial differentialjequation closely connected with G) and (8), namely
has been investigated by Kcpinski, Math. Ann. r,xi. A906), pp. 397—405, and Myller-
Lebedcfif, Math. Aim. lxvi. A909), pp. 325—330. • The reader may verify that Kepinski's
formula
—r j oexp x r } &\ t
is ii .solution, whon/(w) denotes an arbitrary function of w.
The special case of the equation when v= — 1 wa« also investigated by Kepinski, Bull,
int. de I'A cad. den Svi. de Uracovie, lUOfl, pp. L9H—2iM.
4'32. Malnmti'n's differential equation.
Twenty year.s before Lnnmicl published Iuh rosenrehes on traiisformation.s of Bessel's
equation, Malin.steu* investigated conditions for the integrability in finite terms of the
equation
d~ it r d>j
which is obvioimly a gonerali.sation of Be-ssol's equation ; and it is a special case of § 4'31
A5).
To reduce the equation, Malmston chone new variables defined by the formulae
*-CJ, .'/=--«?"¦',
where p and q are constants to be suitably chosen.
Tlie transformed equation is
We ehoo.se p and q so that this may reduce to the equation of § 4%3 A) considered by
Plan a, and therefore we tako
2pq - q +1+ q>' = 0, (m + 2) q - 2,
so thatp= -hr-\m.
The equation then reduces to
de u^+aI1 *c J'
* Camb. and Dublin Math. Journal, v. A8.10), pp. 180 — 182. The oase in which « = 0 had been
previously considered by MalmBt6n, Journal fUr Math, xxxix. A850), pp. 108—115.
7—2
100 THEORY OF BESSEL FUNCTIONS [CHAP. IV
By § 4*3 this is integrablc in finite terms if
¦where n is an integer; so that
The equation is also obviously integrable in the trivial cases A=0 and m— - 2.
notation of Pochhammer for series of hypergeometric type.
A compact notation, invented by Pochhammer* and modified by Barnes f,
is convenient for expressing the series which are to be investigated. We shall
write now and subsequently
(«)„ = a (a + 1) (a + 2) ... (a + n - 1), (aH = 1.
The notation which will be used is, in general,
(«i)» (g«)n • • • Mn n
In particular,
„ n . ~\ _ ? (i)» («)n Mn n
pt, ..., pq, Z)= X . 7~y Z .
n=0 "! \Pi)n\PQ)n ••• \Pq)n
i (p; ^) =
The functions defined by the first three series are called generalised hyper-
hypergeometric functions.
It may be noted here that the function & (a; p\ z) is a solution of the
differential equation
and, when p is not an integer, an independent solution of this equation is
*1-<\1JP1(a-p + l; 2 -p; z).
It is evident that
Various integral representations of functions of the types xJ^, ^F^ 0i^3 have been studied
by Pochhammer, Math. Ann. xli. A893), pp. 174—178, 197—218.
* Math. Ann. xxxvi. A890), p. 84 ; xxxvm. A891), pp. 227, 586, 587. Cf. § 4-15.
t Proe. Londmi Math. Soc. B) v. A907), p. 60. The modification due to BarneB is the insertion
of the suffixes p and q before and after the F to render evident the number of sets of factors.
4*4,4*41] DIFFERENTIAL EQUATIONS 101
4*41. Various solutions in series.
We shall now examine various solutions of the equation
d-u „ p(p + 1)
dz1 z-
and obtain relations between them, which will for the most part be expressed
in Pochhammcr's notation.
It is supposed for the present that p is not a positive integer or zero,
and, equally, since the equation is unaltered by replacing p by — p— 1, it is
supposed that /) is not a negative integer.
It is already known (§ 4*3) that the general solution* is ?*r^+i (caV), and
this gives rise to the special solutions
^ • o*\ G> + 8; i e1*9); r-P. 0Ft (* - p; } <W).
The equation may be written in the forms
dz* ~ * dz z'2
which are suggested by the tact that the functions ei:CZ are solutions of the
original equation with the right-hand side suppressed.
When ^ is written for z (d/dz), the last pair of equations become
(S - p - 1) ($ + p). (ue*n) ± 2cz% (m*cz) = 0.
When we solve these in series we an: led to the following four expressions for u:
jt^ (p + i; 2p + 2\ - -2cs); z~i'6RZ. ,Ft(~p; -2p; -2cz);
z ^ (p + i . 2p + 2; -2c2); • z~ve~u .Jt\{-p; - 2p; Icz).
Now, by direct tnultiplication of series, the two expressions on the left are
expansible in ascending series involving z>'+\ zp+l\zp+i, .... And the expressions
on the right similarly involve z~>', z^~l't z""l\ Since none of the two sets of
powers are the same when 2p is not an integer, we must have
A) ew.,/'', 0> + 1 i 2p + 2 ; - 2cz) = er" .J<\(}> + 1; '2p + 2 ; 2cz)
B) <?¦'. tF, (- p ; - 2p ; - 2cz) = <?-«. ,F, {-p\ - 2;>;
= n^,(i-;»; i^2;-
Those formulae are due to Kuminerf. When (I) has been proved for general
/alues of p, the truth of B) is obvious otv replacing p by — p — 1 in (I).
We now have to consider the cases when 2p is an integer.
* It follows Jrom § 3*1 that a special investigation is also neoosnary when ]> is hall of an odd
nteger.
t Journal filr Math. xv. A830)), pp. 18b—111.
102 THEORY OF BESSEL FUNCTIONS [CHAP. IV
When p has any of the values $,$,$,..., the solutions which contain z~p
as a factor have to he replaced by series involving logarithms (§§ 3'51, 3'52),
and there is only one solution which involves only powers of z. By the
previous reasoning, equation A) still holds.
When p has any of the values 0,1, 2, ... a comparison of the lowest powers
of z involved in the solutions shews that A) still holds; but it is not obvious
that there are no relations of the form
-p; -2p; -
x{~p\ ~2p;
where ku kz are constants which are not zero.
We shall consequently have to give an independent investigation of A)
and B) which depends on direct multiplication of series.
Note. In addition to Rummer's researches, the reader should consult the investiga-
investigations of the series by Cayley, Phil. Mag. D) xxxvi. A868), pp. 348—351 [Collected Papers,
vn. A894), pp. 9—12] and Glaisher, Phil. Mag. D) xliii. A872), pp. 433—438; Phil.
Trans, of the Royal Soc. clxxii. (] 881), pp. 759—828.
4*42. Relations between the solutions in series.
Th-3 equation
ecziF1 (p + 1; 2p + 2; -2cz) = e-^F,(p + l; 2p + 2; 2cz),
which forms part of equation A) of § 4*41, is a particular case of the more
general formula due to Kummer*
(i) i^(«; p; O = «^(p-«; p; -?),,
which holds for all values of a and p subject to certain conventions (which will
be stated presently) which have to be made when a and p are negative integers.
We first suppose that p is not a negative integer and then the coefficient of
?n in the expansion of the product of the series for e$ and lJP1 (p — a; p ; — ?) is
if we first use Vandermonde's theorem f and then reverse the order of the factors
in the numerator; and the last expression is the coefficient of ?w in & (a; p; ?)•
The result required is therefore established when a and p have general complex
values j.
* Journal filr Math. xv. A836), pp. 138—141; see also^Baoh, Ann. Sci. de'l'ficole norm. sup. B)
in. A874), p. 55.
t See, e.g. Chrystal, Algebra, n. A900), p. 9.
X Another proof depending on the theory of contour integration has been given by BarneB,
Tram. Camb. Phil. Soc. xx. A908), pp. 254—257.
4*42] DIFFERENTIAL EQUATIONS 103
When p is a negative integer, equation A) is obviously meaningless unless
also a is a negative integer and | a \ < \ p j. The interpretation of A) in these
circumstances will be derived by an appropriate limiting process.
First let a be a negative integer (= — N) and let p not be an integer, so
that the preceding analysis ia valid. The series ^ (— iV; p; f) is now a
terminating series, while XF{ (p + N ; p; — ?) is an infinite series which con-
consists of JV+ 1 terms followed by terms in which the earlier factors p + N,
p 4- N + 1, p + N + 2, ... in the sequences in the numerators can be cancelled
with the later factors of the sequences p, p -f 1, p -f- 2, ... in the denominators.
When these factors have been cancelled, the aeries for ^(-iV; p ; ?) and
xFi (p ¦+ N; p ; — ?) are both-continuous functions of pne&v p = — M, where
M ia any of the integers iV, N +1, N + 2, ....
Hence we may proceed to the limit when p -*• — M, and the limiting form
of A) may then be written*
B) ^(-if; -1/; C)-i=flflJf'l(tf-.3f;-4f;-?I,
in which the symbol ~] means that the series ia to stop at the term in ?A', i.e.
the last term in which the numerator doos not contain a zero factor, while
the symbol 1 moans that the sories is to proceed normally as far as the term
in ^'w~iV, and then it is to continue with henna in ^i1/+l, %'v+ii ...,the vanishing-
factors in numerator and denominator being cancelled as though their ratio
were one of equality.
With this convention, it is easy to see that
C) lFl(-N\ -M- ?I=i*U-*V; -#;?)!
NUM- N)\
When we replace N by M - N and ? by — ?", we have
D) ^(N-M- -M; -fI -^(N-M; -i)/;
As an ordinary case of A) we have
,F,{M-N^ 1; J/+2; f) = e^Fx (N + 1; M + 2; - ?)>
and from this result combined with B), C) and D) we deduce that
E) xF^-N; -M- ^^e^Fx{N-M- -M;-ZI.
This could have been derived directly from A) by giving p — a (instead of a)
an integral value, and then making p tend to its limit.
*' Cf. Cayloy,Messenger (old series), v. A871), pp.77—8'2 [Collected Papent,viu. A895),pp.458—
462], and Glaishor, Messenger, vni. A879), pp. 20—23.
104 THEORY OF BESSEL FUNCTIONS [CHAP. IV
We next examine the equation
F) fl-^Cp + l; 2p + 2; - Zcz) = «/x(p +1; ?<?*«),
which forrn9 the remainder of equation A) in § 4*41, and which is also due to
Kummer*.
If we suppose that 2p is not a negative integer, the coefficient of (cz)n in
the product of the series on the left in F) is
c,m
m)\
Now — t 2m. nGm (p + l)m (- n - 2p -1)^ is the coefficient of tn in the
expansion of A - 2t)-*-1 A - t)n+w+\ and so it is equal to
1 f(o+) 1 /¦(»+)
?p\ A - 2?)-p-1 A - t)n+2P+1 ir^1 dt = ~\ A - v?)-?-1 u-n~l du,
where u = t/(l — t) and the contours enclose the origin but no other singularities
of the integrands. By expanding <the integrand in ascending powers of u, we
see}that the integral is zero if n is odd, but it is equal to ,, > |?t when n is
even.
Hence it follows that
and this is the result to be proved.
When we make p tend to the value of a negative integer, — N, we find by
the same limiting process as before that
lim 1F1{p + l; 2p + 2] -2cz)^1F1(l-N\ 2-2F; -2c*) 1
N
It follows that
0*\(f-i\r; &**) = &*.Mil-N; 2-2iV; ~2czI
f—WrAr—1M AT'
If we change the signs of c and 2 throughout and add the results so obtained,
we find that
G) 2.^x(t-iV; ic^2)=e«.1F1(l-iV; 2-2ZV; ~2czI
* Journal filr Math. xv. A836), pp. 138—141. In connexion with the proof given here, see
Barnes, Trans. Camb. Phil. Sac. zx. A908), p. 272.
4*43] DIFFERENTIAL EQUATIONS 105
the other terms on the right cancelling by a use of equation A) This is, of
course, the expression for J_#+j {icz) in finite terms with a different notation.
For Barnes' proof of Rummer's formulae, by the methods of contour inte-
integration, see § 6.
4 3. Sharpe's differential equation.
The equation
A> 'g + g + C' + ^-o.
which is a generalisation of Bessel's equation for functions of order zero,
occurs in the theory of the reflexion of sound by a paraboloid. It has been
investigated by Sharpe*, who has shewn that the integral which reduces to
unity at the origin is
rftn
B) y = C cos (z cos d + A log cot ?0) dd,
J 0
where
C) 1 = C f "cos (A log cot hd) dd.
Jo
This is the appropriate modification of Parseval's integral (§ 2'3). To in-
investigate its convergence write cos d = tanh <j>, and ib becomes
D) tf~wJ0 cosh</>
It is easy to sec from this form of the integral that it converges for (complex)
values of A for which 11 (A)' < 1, andf
2
C— - cosh hirA.
7T
The integral has been investigated in great detail by Sharpe and he has
given elaborate rules for calculating successive coefficients in the expansion of
y in powers of z.
A simple form of the solution (which was not given by Sharpe) is
The reader should have no difficulty in verifying this result.
* Messenger, x. A881), pp. 174—185 ; xn. A884), pp. 66—79; Proc. Camb. Phil. Soe. x. A900),
pp. 101—136.
t See, e.g. Wataon, Coviplex Integration and Cauchy}s Theorem A914), pp. 64—65.
106 THEORY OF BESSBL FUNCTIONS [CHAP. IV
4*5. Equations of order higher than the second.
The construction of a differential equation of any order, which is soluble
by means of Bessel functions, has been effected by Lommel* ; its possibility
depends on the fact that cylinder functions exist for which the quotient
^v iz)\^_v (z) is independent of z..
Each of the functions Jn (z) and Yn (z), of integral order, possesses this
property [§§ 231, 3*5]; and the functions of the third kind Hv® (*), Hv® (z)
possess it (§ 3'61), whether v is an integer or not.
Now when § 3*9 E) is written in the form
Am.
A) ^^ G Vf> = {h)m^(v-m) #-» G V*),
the cylinder function on the right is of order — v if m = 2v.
This is the case either (i) if v is an integer, n, and m = 2n, or (ii) if
v = n +¦ ^ and m = In +1.
Hence if <$n denotes either Jn or Yn, we have
From this equation we obtain Lommel's result that the functions zin Jn G \/z),
n(y \/z) are solutions off
\*)
fern zn 1
where 7 has any value such that <ym— (—)nom, so that
7 = ic exp (rvi/n). (r = 0, 1, 2, ..., n - 1)
By giving 7 all possible values we obtain 2n solutions of B), and these
form a fundamental system.
Next, if ^n+i. denotes H{1]n+h we have (^-{n+h) = e(n+^ni%lH> so that
and hence ^in+lJffA>n+j G *Jz) is a solution of
where 7 has any value such that 72n+1 = c27l+1 e-'"*^**, so that
7 = - io exp {r7ri/(n + \)), (r = 0, 1, % ..., 2w)
and the solutions so obtained form a fundamental system.
* Studien ilher die Bessel'schen Functionen (Leipzig, 1868), p. 120; Math. Ann. 11. A870),
pp. 624—635.
f The more general equation
has been diacussed by Molina, Mem. de I'Acad. de* Sd. de Touloute, G) thi, A876), pp. 167—189.
4-5]
DIFFERENTIAL EQUATIONS
107
For some applications of these results, see Forsyth, Quarterly Journal^ xix. A883),
pp. 317—320.
In view of A), which holds when m is an integer, Lotnmel, Math. Ann. n. A870), p. 635,
has suggested an interpretation of a "fractional differential coefficient." Thus he would
interpret (^-) oxp (±y Jz) to mean ($o(yijz). Tho idea has been developed at some
length by Heaviside in various papers.
Lommel's formulae may be generalised by considering equation C) of
§ 4'31, after writing it in the form
C» + a) (»• + a - 2l3v) u = - ^fs^u,
the solution of the equation being tt = z^v-a(&v{ryzfi). For it is easy to verify-
by induction that, with this value of u,
II (^ + a - 2r/3) (^ + a - 2/3v - 2r/3) a = (-)'l/92)l(
and so solutions of
w-l
4) II (? + a - 2r/3) (^ + a - 2/3v - 2r/3) u = (-)n/3m<
are of the form u = z$v~a<$v {^},
where 7 = cexp (vTri/n). (r = 0, 1, ..., n — I)
By giving 7 these values, we-obtain "In solutions which form a fundamental
system.
In the special case in which n = 2, equation D) reduces to
($¦ + a) (S- + a - 2?) (^ + a - 2^v) (^ + a - 2/9v - 2/8) it = /9JcJ^ m.
This aiiuation reseinblns an equntion which has been encountered by Nicholson* in tho
investigation of tho shapes of Spongo Hpiculon, namely
* U*"|
@)
that is to aay 3C
If we identify this with tho special form of D) we obtain the following four distinct sets
of values for a, #, /x, v :
a
0
s
»
-I
p
1
*
-A
0
1
*
3
V
\
1
10
* Proc. Royal Soc. xam. A A917), pp. 50E—619. See also Dendy and NicholHon, Proc. Royal
Soc. lxxxix. B A917), pp. 573—587; the special oases of E) in which ,u, = 0 or 1 had been solved
previously by Kirchhofl, Berliner Monatsherichte, 1879, pp. 815—828. [Ann. der Physik und
Chemie, C) x. A880), pp. 501—512.]
1Q6 THEORY OF BESSEL FUNCTIONS [CHAP. IV
These four cases give the following equations and their solutions:
F) ^=«; «
(9) 37
These seem to be the only equations of Nicholson's type which are soluble with the aid
of Bessel functions; in the case y*=2, the equation E) is homogeneous. Nicholson's general
equation is associated with the function
/3,-2M 2 + 2;* 1+2^ z*"^ \
0 3 \4-3j*' 4-2j*' l-2/i' D-2/*O"
4*6. Symbolic solutions of differential equations.
Numerous mathematicians have given solutions of the equation § 4'3 A)
namely
in symbolic forms, when p is a positive integer (zero included). These forms
are intimately connected with the recurrence formulae for Bessel functions.
It has been seen (§ 4*3) that the general solution of the equation is
and from the recurrence formula § 39 F) we have
Since any cylinder function of the form ^j (oiz) is expressible as
where a and /3 are constants, it follows that the general solution of A) may
be written
A modification of this, due to Glaisher*, is
C) u{)
where a' == a/c, ft'——/3/c. This may be seen by differentiating oc'ef:!:+ft'e~cz once.
* Phil. Trans, of the Royal Soc. clxxh.. A881), p. 813. It was remarked by Glaisher that
equation C) ib substantially given by Earnahaw, Partial Differential Equations (London, 1871),
p. 92. See also Glaisher, Quarterly Journal, xi. A871), p. 269, formula (9), and p, 270..
4-6] DIFFERENTIAL EQUATIONS 109
Note. A result equivalent to B) was set by Gaskin as a problem* in the Senate House
Examination, 1839; and a proof was published by Leslie Ellis, Camb. Math. Journal, II.
A841), pp. 193—195, and also by Donkin, Phil. Trans, of the Royal Soc. oxlvii. A857),
pp. 43—57. In the question as set by Gaskin, the sign of c2 was changed, so that the solu-
solution involved circular functions instead of exponential functions.
Next we shall prove the symbolic theorem, due to Glaisherf, that
\zdz) -*p+4v dz)
In operating on a function with the operator on the right, it is supposed
that the function is multiplied by 1/z2p~'- before the application of the
operators z* (d/dz).
It is convenient to write
and then to use the symbolic formula
E) /(*). (e"°Z) = ea0 ./(* + a) Z,
in which a is a constant and Z is any function of 2.
Tho proof of this formula presents no special difficulties when /'(.!)) is a polynomial in
3, as is the caso in tho present investigation. See, o.g. Foi\syth, Treatise on Differential
Equations A5I4), $ 33.
It is easy to see from E) that
zdz
2p + 2) C> - '2p + 4) (^ - 2p + 6) ... S,
when we bring the successive functions e""-0 (beginning with those on the left)
past the operators one at a time, by repeated applications of E).
We now reverse, the orderJ of the operators in tb<; last result, and by a
reversal of the previous procedure we. got
^ + 2^ - 2) (^ + 2p - 4)... (^ + 2) ^
dz
" Tho problom wa« tlie Hecond pjirt of qucHtion ft, Tuonday aftornoon, Jan 8, 1839; Hec tho
Cambridge. University Calendar, 1SB9, p. 315).
f Nuuvelle Coir. Muth. n. A870), pp. 240—243, iM'J—!iC0 ; mid Phil Trans, of the Royal Soc
olxxii. A881), pp. HOB—805.
f. It waa remarked by Ctvyley, Quarterly Journal, xn. A872), p. 132, in a footnote to a paper by
Glaishor, that differential operators of the form a"*1 yz~a, i.o. ^-a, obey the commutative law.
110 THEORY OF BESSEL FUNCTIONS [CHAP. IV
and this is the result to he proved. If we replace p by p •+• 1, we find that
When we transform B) and C) with the aid of D) and F), we see that
the general solution of A) is expressible in the following forms:
The solutions of the equation
d* z dz cv~°'
[C) of §4-3], which correspond to B), C), G) and (8) are
A different and more direct method of obtaining G) is due to Boole, Phil. Trans, of the
Royal Soc. 1844, pp. 251, 252 ; Treatise on Differential Equations (London, 1872), ch. xvn.
pp. 423—425; see also Curtis, Cambridge and Dublin Math. Journal, ix. A854), p. 281.
The solution (9) was first given by Leslie Ellis, Camb. Math. Journal, n. A841), pp. 169,
193, and Lebesgue, Journal de Math. xr. A846), p. 338; developments in aeries were
obtained from it by Bach, Ann. Sci. de I'jtcole norm. sup. B) in. A874), p. 61.
Similar symbolic solutions for the equation -7-5 — cizi<1~iv=0 were discussed by Fields,
CtZ"
John Hopkins University Circulars, vi. A886—7), p. 29.
A transformation of the solution (9), due to Williamson, Phil. Mag. D) xi. A856),
pp. 364—371, is
A3) i>=c2p (I -Y (o^+pfl—).
This is derived from the equivalence of the operators -*-,--, when they operate on
functions of cz.
We thus obtain the equivalence of the following operators
it being supposed that the operators operate on a fuuction of cz; and Williamson's formula
is then manifest.
4*7] DIFFERENTIAL EQUATIONS 111
4*7. Liouville's classification of elementary transcendental functions.
Before we give a proof of Liouville's general theorem (which was mentioned
in § 4-12) concerning the impossibility of solving Riccati's equation "in finite
terms " except in the classical cases discovered by Daniel Bernoulli (and the
limiting form of index — 2), we shall give an account of Liouville's* theory
of a class of functions known as elementary transcendental functions] and we
shall introduce a convenient notation for handling such functions.
For brevity we write j"
, Jx (*) = *(*) slog*, l,(z)=>l(l(z)), h(*)= I &(*)), ...,
ex (z) = e (z) = ez, e., (z) = e (e (z)), e3 (z) = e (e2 (*)),
}, «,/(*)-5 {«,/(*)}
A function of z is then said to be an elementary transcendental function^
if it in expressible as an algebraic function of z and of functions of the types
lr<f>(z), e,.ty(z), <s,xB)> whore- the auxiliary functions 4>(z), ^fr(z), x(~) ar<-1
expressible in terms of z and of a second set of auxiliary functions, and so on;
provided that there exists a finite number n, such that the »ith set of auxiliary
functions are all algebraic functions of z.
The. order of an elementary transcendental function of z is then defined
inductively as follows:
(I) Any algebraic function of z is of order zero§.
(II) Tf fr{z) denotes any function of order r, then any algebraic function
of functions of the types
lf.(z)y ef.{z), 9/,(s), /,(,), /r_, <*)..../.(*)
(into which at least one of the first three enters) is said to be of order r + 1.
(III) Any function is supposed to be expressed as a function of the lowest
possible order. Thus elfr(z) is to be replaced by f,-(z), and it is a function of
order ¦/•, not of order r + 2.
In connexion with Uiin and tho following Hoct.ions, tin*, render should study Hardy,
Ordiws of fv/ini(i/ (Cunl). Mulli. Trncts, no. 12, 1910). The function.s ili.scuascd by Hardy
wcro of ¦: uli^lit.ly moru restricted cliamct.or hhan those now under i-onsidonitimi, Hinca, 1'ur
]»i.H pui'pones, l,h(! symliol v is not required, and also, for liin purposes, it is oonvuniont to
po.s1ul.ite the reality of thu functions which ho. investigates.
It may be noted that Liouville did not study properties of the. Hynibol s in detail, but
merely remarked that it had many properties akin to tho.se of the .symbol I.
* Journal, tie Math. n. A837), pp. 5E—105 ; in. A838), pp. 523—547 ; iv. A839), pp.423—456.
t It is supposed that the integrals aro all indefinite.
X "Une fonction iiuio exylioito."
§ For the purposoH of this invoHtigatiou, irrational powers of z, such us z*, of course inu«t
not be regarded as algebraic functions.
112 THEORY OF BESSEL FUNCTIONS [CHAP. IV
4*71. Liouville's first theorem* concerning linear differential equations.
The investigation of the character of the solution of the equation
A) 3?-«*(*)>
in which % (z) is a transcendant of orderf n, has been made by Liouville, who
has established the following theorem :
If equation A) has a solution which is a transcendant of order m + 1, where
m^n, then either there exists a solution of the equation which is of order], n,
or else there exists a solution, u1} of the equation expressible in the form
B) u1 = <jili(z).efli(z))
where fy.{z) is of order fx, and the order of ^^(z) does not exceed fxy and /u. is
such that n ^ /* ^ m.
If the equation A) has a solution of order m + 1, let it be /m+1 (z) ; then
fm+i (z) is an algebraic function of one or more functions of the types lfm (z)y
qfm (z), efm (z) as well as (possibly) of functions whose order does not exceed
m. Let us concentrate our attention on a particular function of one of the
three types, and let it be called 6, ^ or © according to its type.
(I) We shall first shew how to prove that, if A) has a solution of order
m + 1, then a solution can be constructed which does not involve functions of
the types 6 and ^.
For, if possible, let /,,l+1 (z) = F(z, 6), where F is an algebraic function of 8;
and any function of z (other than 6 itself) of order m+1 which occurs in F
is algebraically independent of 6.
Then it is easy to shew that
m *?.-F W,) = ^+ 2 d^(z) d*F
W dz, *-X W - dz2 +fm(z) dz
\fm{z) dz \ d6> \_dz\fm(z) dz
it being supposed that z and 8 are the independent variables in performing
the partial differentiations.
The expression on the right in C) is an algebraic function of 6 which
vanishes identically when 6 is replaced by lfm(z). Hence it must vanish
identically for all values of 6 \ for if it did not, the result of equating it to
zero would express lfm{z) as an algebraic function of transcendants whose
orders do not exceed m together with trans^endants of order m+1 which are,
ex hypothesi, algebraically independent of 8.
* Journal de Math. iv. A839), pp. 435—442.
t This phrase is used a8 an abbreviation oi " elementary transcendental function of order m."
¦f Null solutions are disregarded; if u were of order less than n, then , would be of order
U uZ
less than n, which is contrary to hypothesis.
4*71] DIFFERENTIAL EQUATIONS 113
In particular, the expression on the right of C) vanishes when 8 is replaced
by 0 + c, where c is an arbitrary constant; and when this change is made the
expression on the left of C) changes into
d"F(z, 0 + c) „, A x , .
^i -FB,e + c).x (*),
which is therefore zero. That is to say
When we differentiate D) partially with regard to c, we find that
dF(z, 6 + c) &F (z, 6 + c)
dc ' dc2 > •••
are solutions of A) for all values of c independent of z. If we put c = 0 after
performing the differentiations, these expressions become
dF(z,6) d*F(z,6)
d6 ' d&> ' '"'
which are consequently solutions of (I). For brevity they will be called
Fo> Fee, ••••
Now either F and Fe form a fundamental system of ¦solutions of A) or
they do not.
If they do not, we must have*
where A is independent both of z and 9. On integration we find fchat
where <1> involves transcendants (of order not exceeding m + 1) which are
algebraically independent of 0. But this is impossible because eA0 is not an
algebraic function of 6; and therefore F and Fe form a fundamental systein
of solutions of A).
Hence F90 is expressible in terma of F and Fe by an equation of the form
Fee = AFe + BF,
where A and B are constants. Now this may be regarded as a linear equation
in 6 (with constant coefficients) and its solution is
F = <l\ea0 + ^eW or F= e*° {<!>, + <J>a0},
where <PX -and ^ are functions of the same nature as <X>, while a and ft are
the'roots of the equation
a?-Ax-? = 0.
The only value of F which is an algebraic function of 9 is obtained when
a = ft — 0 ; and then F is a Linear function of 0.
Similarly, if /,»+, (z) involves a function of the type 'S-, we can prove that
it must be a linear function of ^.
* Since F mint involve 0, Fe cannot be identically zero.
w. B. v. 8
114 THEORY OF BESSEL FUNCTIONS [CHAP. IV
It follows that, in so far as fm+x (z) involves functions of the types 0 and S-,
it involves them linearly, so that we may write
f^) = $ei(z)O2(z)...ep(z).%(z)%(z)...\(z).fp,q(z),
where the functions ^p,q(z) are of order m +1 at most, and the only functions
of order m +1 involved in them are of the type 0.
Take any one of the terms in /m+iC?) which is of the highest degree, qua
function of 8U 9.,,...%,%, ..., and let it be
Then, by arguments resembling those previously used, it follows that
9 9 9 9 i
d$i dO2 ddp d^i 9^2 9^q
is a solution of A); i.e. typ,Q B) is a solution of A).
But typtQ (z) is either a function of order not exceeding m, or else it is a
function of order m+1 which involves functions of the type © and not of
the types 6 and ^r.
In the former case, we repeat the process of reduction to functions of lower
order, and in the latter case we see that some solution of the equation is an
algebraic function of functions of the type ©.
WTe have therefore proved that, if A) has a solution which is a transcendant
of order greater than n, then either it has a solution of order n or else it has a
solution which is an algebraic function of functions of the type ef,j.{z) and
</>m (¦&)» where /M (z) is of order /u, and 4v (z) is of an order which does not exceed /a.
(II) We shall next prove that, whenever A) has a solution which is a
transcendant of order greater than n, then it has a solution which involves
the transcendant ef^z) only in having a power of it as a factor.
We concentrate our attention on a particular transcendant © of the form
e/M(^), and then the postulated solution may be writter in the form G(z} ©),
where G is an algebraic function of ©; and any function (other than © itself)
of order ft 4-1 which occurs in G is algebraically independent of ©.
Then it is easy to shew that
/KX dG n /x dG , ««,,
E) -& - G. X W - W + 28/,
The expression on the right is an algebraic function of © which vanishes
when © is replaced by ef^(z), and so it vanishes identically, by the arguments
used in (I). In particular it vanishes when © is replaced by c ©, where c is
independent of z. But its value is then
4*71] DIFFERENTIAL EQUATIONS 115
so that
<Pg(*,o6)
When we differentiate this with regard to c, we find that
dG (z, c©) &G (z, c©)
OC 00
are solutions of A) for all values of c independent of z. If we put c = 1, these
expressions become
Hence, by the reasoning used in (I), we have BO© — AG or else
where A and B are constants.
In the former case G = <t>©/1, and in the latter (r has one of the values
where cl:>, (l>i, 4>2 are functions of ^ of order fi + 1 at most, any functions of
order yu +1 which are involved being algebraically independent of B; while
7 and 8 are the roots of the equation
*(*- I)- Ax- B = Q.
In any case, G either contains B only by a factor which is a power of (F1) or else
G is the sum of two expressions which contain H only in that manner. In tin;
latter case*,
G (z, (;©) - c*V (*, H)
is a solution of (I) which contains © only by a factor which is a power of (H).
By repetitions of this procedure, we see that, if ©,, ^X, ... ©r are all the
transcendants of order fi + 1 which occur in the postulated solution, we can
derive from that solution a sequence of solutions of which the sth contains
©i) ^a> ••• ^« only by factors which are powers of H,, (»\, ... <*)„; and the rth
member of the sequence consequently consists of a product of powers of
<F)U CwJ) ... Hr multiplied by a transcendant which is of order fx, at most; this
solution is of the form
which is of the form <^ {z). ef^ (z).
* If <I>1 is not identically zero; if it ia, then %QS ia a solution of the specified type.
8—2
n6 THEORY OF BESSEL FUNCTIONS |_CHAP. IV
4-72. LiouvilWs second theorem concerning linear differential equations.
We have just seen that, if the equation
d?u_ . .
A) 'dz2~U^
[in which %{z) is of order n] has a solution which is an elementary tran-
transcendant of order greater than n, then it must have a solution of the form
where fi>n. If the equation has more than one solution of this type, let, a
solution for which p has the smallest value be chosen, and let it be called «|.
Liouville's theorem, which we shall now prove, is that, for this solution, the
order of d (log u^/dz is equal to n.
Let
d log «i _ t
and then t is of order /* at most; let the order of t be N, where iV <: p.
If N=n, the theorem required is proved. If N>nt then the equation
satisfied by t, namely
B) -+*2= (z)
has a solution whose order iV is greater than n.
Now t is an 'algebraic function of at least one transcendant of tin; types
[ts-i(z), sfx-\(z\ efs-\{z) and (possibly) of transcendants whose order docs
not exceed JV- 1. We call the first three transcendants 8, Sv, H respectively.
If ? contains more than one transcendant'of the type 0, we concentrate
our attention on a particular function of this type, and wo write
¦* TP / *. Z)\
t =" X* ( Z) U j.
By arguments resembling those used in § 4-71, we find that, if N > tt, then
is also a solution of B). The corresponding solution of A) is
and this is a solution for all values of c independent of z. Hence by
differentiation with respect to c, we find that the function u2 defined as
is also a solution of A); and we have
.so that
diu diu
lhdz Un-dI-u*F'-
4*72,4-73] DIFFERENTIAL EQUATIONS 117
But the Wronskian of any two solutions of A) is a constant*; and so
vrh\ = C,
where C is a constant.
If C = 0, F\s independent of 6, which is contrary to hypothesis ; so G ^ (), and
Hence ux is an algebraic function of 6 ; and similarly it is an algebraic function
of all the functions of the typos 6 and S- which occur in L
Next consider any function of the type H which occurs in t; we write
t = G (z, 0),
and, by arguments resembling those used in §4-71 and those used earlier in
this section, we find that the function u. donned as
i ~]
- cxp [(} (z, c:B) dz
fa Jr-l
is a solution of A)-; and we have
so that
dil-x dllx »r\/t
This Wronskian is a constant, C\, and .so
Consequently vt, is an algebraic function, not only of all the transcendants of
the types 0 and ^, but also of those of type M which occur ini; and therefore
?/, is of order N. This is contrary to the hypothesis that ux is of order (i+ 1,
where /* ^ iVr, if Ar > n.
The contradiction shews that JV cannot be gn^ater than n\ hence the order
of rf(log u^/dz is n. And this is the theorem to b<» established.
4*73. Liouville's theorem ~f that Besnel's equation has no algebraic integral.
We shall now shew that the equation
dz" dz
has no integral (other than a null-function) which is an algebraic function of z.
We first reduce the equation to its normal form
by writing y-uz~l, p = ±v — \.
* See e.g. Forsyth, Treatise on Differential Equations A914), § 65.
t Journal dc Math. iv. A839), pp. 429—435 ; vi. A841), pp. 4—7. Liouvillo's first investigation
was concerned with the general caao in •which x B) iR any polynomial; the application (with
various modifications) to B<?88eFs equation was given in his later paper, Journal de Math. vi.
A841), pp. 1—13, 3C.
118 THEORY OF BESSEL FUNCTIONS [CHAP. IV
This is of the form
dht , .
d?=lL*>{2)>
where
If possible, let Bessel's equation have an algebraic integral; then A) also
has an algebraic integral. Let the equation which expresses this integral, u,
as an algebraic function of z be
C) cS0(u,s)*O,
where ?& is a polynomial both, in u and in z; and it is supposed that ?#¦ is
irreducible*.
Since u is a solution of A) we have
D) MuvM? - ZS€uz<s4uMz + Mzz -S4U* + MuX (*) = 0.
The equations C) and D) have a common root, and hence all the roots
of C) satisfy D).
For, if not, the left-hand sides of C) and D) (qua functions of u) would
have a highest common factor other than S€ itself, and this would be a
polynomial in u and in z. Hence &4> would be reducible, which is contrary to
hypothesis.
Let all the roots of C) be Wj, u^, ... u3I. Then, if s is any positive integer,
is a rational function of z; and there is at least one value of s not exceeding
M for which this sum is not zerof.
Let any such value of s be taken, and let
m=l
M /(\u \r
Also let Fr=s(s-l)..,(s-r + lJC7 ,
m = \ \ (iZ )
where r = 1, 2, ... s. Since u1} uit... un are all solutions^ of A), it is easy to
prove that
E) g
dW
F) -jf-'Wr+i + ris-r + VxWWn, (r = 1, 2,... s- 1)
G) ^
* That is to say, ?4> has no factors whicli are polj'nomials in u or in z or in both w and z.
f If not, all the roots of C) would be zero.
+ Because D) is satisfied by all the roots of C), qua equation in u.
4*73] DIFFERENTIAL EQUATIONS 119
Since Wo is a rational function of z, it is expressible in partial fractions,
sothafc W-2AP+2 —"•»
n= - k n,q \" ^q)
where An and Bn<q are constants, « and A are integers, n assumes positive
integral values only in the last summation and aq=f= 0.
Let the highest power of l/(z - aq) which occurs in Wo be \\{z - aq)p.
It follows by an easy induction from E) and F) that the highest power of
l/(z - aq) in Wr is I/O - a(J)p+r, where r = 1, 2,... s.
Hence there is a higher power on the left of G) than on the right. This
contradiction shews that there are no terms of the type Bn>q {z — aq)~n in Wo
and so ,„ A .
We may now assume that A\ j= 0, because this expression for Wo must
have a last term if it does not vanish identically.
From E) and F) it is easy to see that the terms of highest degree in z
which occur in Wu, Wlt Wo, W3, ... are*
AKz\ \AK2*-\ AKsz\ \/lACs-2)^-\....
By a simple induction it ia possible, fco show that the term of highest degree
in W,r is ylA^ . 1 . 8 ... Br-]).s (s- 2) ... (s- 2r + 2).
An induction of a more complicated nature is then necessary to shew that the
term of highest degree in W.ir+X is
\Ai*-l2.4,...{2r).(8-l)(8-S)...(8-2r + l).aF1{h,-l*'> 4 - i* ; l)r+i,
where the suffix r + 1 indicates that the first r + 1. terms only of the hyper-
geometric series are to be taken.
If s is odd, the terms of highest degree on the left and right of G) are
of degrees X — 2 and A, respectively, which is impossible. Hence TF0 vanishes
whenever s is odd.
When s is even, the result of equating coefficients of z1"'1 in G) is
XAi.sl^-XA^.s}^^, -?s; i-k; l)i8.
That is to say \AK. s\ ,F, (i ,-^s; ? - ±s; 1) = 0,
and so, by Vandermonde's theorem,
The expression on the left vanishes only when A, is zerof.
* It is to be remembered that the term of highest degree in x(^) ia - !•
•|- Tho analyais given by Liouville, Journal de Math. vi. A841), p. 7, seems to fail at this
point, because he apparently overlooked the possibility of \ vanishing. The failure seoms in-
inevitable in view of the fact that J^+. (z) + </'in_i (^) is an algebraic function of z, by § 3-4. The
subsequent part of the proof given liore is based on a suggestion made by Liouville, Journal de
Math. iv. A889), p. 435; see also Genocchi, Mem. Accad. delle Sci. di Torino, xxni. A866),
pp. 299—362; Comptes Rendus, lxxxv. A877), pp. 391—394.
120 THEOEY OF BESSEL FUNCTIONS [CHAP. IV
We have therefore proved that, when 5 is odd, WQ vanishes, and that, when
s is even, Wn is expressible in the form
where AQ)8 does not vanish.
V A z~n
n=0
From Newton's theorem which expresses the coefficients in an equation
in terms of the sums of powers of the roots, it appears that M must be even,
and that the equation ?4 (u, z) = 0 is expressible in the form
(8) uM+ 2u*-
where the functions "$r are polynomials in \\z.
When we solve (8) in a series of ascending powers of ljz} we find that
each of the branches of u is expressible in the form
m=0
where n is a positive integer and, in the case of one branch at least, c0 does
not vanish because the constant terms in the functions ^r are not all zero.
And the series which are of the form
CmZ
ttl=0
are convergent* for all sufficiently large values of z.
When we substitute the series into the left-hand side of A), we find that
the coefficient of the constant term in the result is c0, and so, for every branch,
c0 must be zero, contrary to what has just been proved. The contradiction
thus obtained shews that Bessel's equation has no algebraic integral.
44. On the impossibility of integrating Bessel's equation in finite terms.
We are now in a position to prove Liouville's theoremf that Bessel's
equation for functions of order v has no solution (except a null-function)
which is expressible in finite terms by means of elementary transcendental
functions; if 2v is not an odd integer.
As in § 4*73, we reduce Bessel's equation to its normal form
A) 3?-"*<*>»
where x(JS)=z~^JrP.(P + *)/*2 an(*P = ± v~\-
Now write d (log u)jdz = t, and we have
B) . *+,+¦!_?<?+!> _o.
* Gcmrsat, Goun d'Analyse, n. (Paris, 1911), pp. 273—281. Many treatises tacitly assume the
convergence of a series derived in this manner from an algebraic equation,
t Journal de Math. vi. A841), pp. 1—13, 36.
4*74] DIFFERENTIAL EQUATIONS 121
Since ^(z) is of order zero, it follows from § 472 that, if Bessel's equation
has an integral expressible in finite terms, then B) must have a solution
which is of order zero, i.e. it must have an algebraic integral.
If B) has an algebraic integral, let the equation wnich expresses this
integral, t, as an algebraic function of z, be
C) ?€(t,z) = O,
where S€ is an irreducible polynomial in t and z.
Since t is a solution of B), we have
D) 642+{x(z)-t*}at = 0.
As in the corresponding analysis of § 4*73, all the branches of t satisfy D).
First suppose that there are more than two branches of t, and let three
of them be called tlt t>, ts, the corresponding values of m (denned as exp jtdz)
being ult t^, us. These functions are all solutions of A) and so the Wronskians
dus du% dux dus dv2 dux
dz dz dz dz dz dz
are constants, which will be called 0,, C», Ca.
Now it is easy to verify that
n _ du:i d'iu _ .
and t3 — ti is not zero, because, if it were zero, the equation C) would have a
pair of equal roots, and would therefore be reducible.
Hence 6\ ^ 0, and so
Therefore u.zu3 (and similarly u3ux and uxu2) is an algebraic function of z.
But Wi
and therefore uy is an algebraic function of z. This, as we have seen in§4'73,
cannot be the cane, and so t has not more than two branches.
Next suppose that t has two branches, so that t9^ (t, z) is quadratic in t.
Let the branches be U ± \/ V, where U and V are rational function^ of z. By
substituting in B) wo find that
Let V be factorised so that
where A is constant, tcq and \ are integers, and Kq and«a9 are not zero.
122 THEOBY OF BESSEL FUNCTIONS [CHAP. IV
From the second member of E) it follows that
tj •< kq
and then by substituting into the first member of E) we have
Now consider the principal part of the expression on the left near aq. It
is evident that none of the numbers rcq can be less than — 2, and, if any one
of them is greater than — 2 it must satisfy the equation
^+4^ = 0,
so that Kq is 0 or — 4, which are both excluded from consideration. Hence all
the numbers Kq are .equal to — 2.
Again, if we consider the principal part near oo, we see that the highest
power in V must cancel with the — i in ^ (z), so that \ = — 2 kq.
q
It follows that *JV is rational, and consequently ?? (t, z) is reducible, which
is contrary to hypothesis.
Hence t cannot have as many as two branches and so it must be rational.
Accordingly, let the expression for t in partial fractions be
A
Bn<,
*- 2 4n*»+2
where An and Bn> q are constants, k and. \ are integers, n assumes positive
values only in the last summation and aq ^ 0.
If we substitute this value of t in B) we find that
»=»-« 11,9(^ — 09) U--IC (z-aq)n) z2
If we consider the principal part of the left-hand side near aq we see that
lj(z — aq) cannot occur in t to a higher power than the first and that
¦B1)9~-B2li9=0,
so that jBlt9= 1.
Similarly, if we consider the principal parts near 0 and 00, we find that
Since p = + v — \, we may take A^ = -p without loss of generality.
It then follows that
Accordingly, if we replace u by z~pe±izw in A), we see that the equation
must have a solution which is a polynomial in 2, and the constant term in
this polynomial does not vanish.
4*75] DIFFERENTIAL EQUATIONS 123
When we substitute 2 cmzm for w in G) we find that the relation connecting
successive coefficients is
m (m — 2p — 1) cm ± 2icm_! (m — p — 1) = 0,
and so the series for w cannot terminate unless m—p — \ can vanish, i.e. unless
p is zero or a positive integer.
Hence the hypothesis that Bessel's equation is soluble in finite terms leads
of necessity to the consequence that one of the numbers + v — \ is zero or a
positive integer; and this is the case if, and only if, 2v is an odd integer.
Conversely we have seen (§ 3*4) that, when 2v is an odd integer, Bessel's
equation actually possesses a fundamental system of solutions expressible in
finite terms. The investigation of the solubility of the equation is therefore
complete.
Somo. applications of this theorem to equations of the types discussed in § 4 have
been recorded by Lebesguc, Journal de Math. xr. A846), pp. 338—340.
4*75. On the impossibility of integrating Riccati's equation infinite terms.
By means of the result just obtained, wo can discuss Riccati's equation
dz
azn + bii-
with a view to proving that it is, in general, not integrable in finite terms.
It has been seen (§ 4'21) that the equation in reducible to
where ?i=2<y —2; and, by § 4-3, the last equation is reducible to Bessel's
equation for functions of order l/Bg) unless q = 0.
Hence the only possible cases in which liiccuti's equation is integrable in
finite terms are those in which q is zero or \/q is an odd integer; and these
are precisely the cases in which n is equal to — 2 or to
(m = 0, 1, 2, ...)
2??;, ± I"
Consequently the only cases in which Riccati's equation is integrable in finite
terms are the classical cases discovered by Daniel Bernoulli (cf. § 4*1 i) and the
limiting case discussed after the manner of Euler in §4*12.
This theorem was proved by Liouville, Journal de Math. vt. A841), pp. 1—13. It
seoms impossible to establish it by any method which is appreciably more brief than the
analysis used in the preceding sections.
124 THEORY OF BESSEL FUNCTIONS [CHAP. IV
4*8. Solutions of Laplace's equation.
The first appearance in analysis of the general Bessel coefficient has been
seen (§ 1*3) to be in connexion with an equation, equivalent to Laplace's
equation, which occurs in the problem of the vibrations of a circular membrane.
We shall now shew how Bessel coefficients arise in a natural manner from
Whittaker's* solution of Laplace's equation
v ; 3a; dy* dz2
The solution in question is
B) V=\ f(z + ix cos u + iy sin n, u) die,
J — ir
in which / denotes an arbitrary function of the two variables involved.
In particular, a solution is
(n ¦ • •
ek (i + izGOBU + iysinu) cos mu du>
— IT
in which k is any constant and in is any integer.
If we take cylindrical-polar coordinates, defined by the equations
x — p cos <?, y = p sin </>,
this solution becomes
= 2ekz eikpC0*v cos mv cos vi6 dv,
J o
= 2trim e*z cos m<p. Jm (kp),
by § 2'2. In like manner a solution is
f ""
gk B+wcoBtt + iysinM) sin mU(lU)
J —W
and this is equal to i-iri™ ekz sin m.(j>. Jm (kp). Both of these solutions are
analytic near the origin.
Again, if Laplace's equation be transformed^ to cylindrical-polar coordi-
coordinates, it is found to become
* Monthly Notices of the R. A. S. lxh. A902), pp. 617—620; Math. Ann. lvii. A902),
pp. 883—341.
t The simplest method of effecting the transformation is by using Green's theorem. See
W. Thomson, Camb. Math. Journal, iv. A845), pp. 33—42.
4*8,4*81] DIFFERENTIAL EQUATIONS 125
and a normal solution of this equation of which ekz is a factor must be such that
is independent of <f>, and, if the solution is to be one-valued, it must be equal
to — m% where m is an integer. Consequently the function of p which is a
factor of V must be annihilated by
da Id
and .therefore it must be a multiple oiJm{kp) if it is to be analytic along the
line p - 0.
We thus obtain anew the solutions
^l^mf.Jnikp).
olll
These solutions have been derived by liobsou* from the solution e^'J^^p) by Clerk
Maxwell's method of differentiating harmonics with respect to axes.
Another solution of Laplace's equation involving Besael functions has been obtained by
Hobson (ibid. p. 447) from the equation in cylindrical-polar coordinates by regarding 8/82
as a symbolic operator. The solution ho obtained is
sin
where/(s) is an arbitrary function; but the interpretation of this solution when <$m involves
a function of the second kind is open to queution. Other solutions involving a Bessel
function of an oporator acting on an arbitrary function havo been given by Hobson, Proc.
London Math. Hoc. xxiv. A893), pp. 55 -A7 ; xxvi. A895), pp. 4<J—494.
4*81. Solutions of the equations of wave motions.
We shall now examine the equation of wave motions
A) "?+--%-v=1.~^,
in which t represents the time and c the velocity of propagation of the waves,
from the same aspect.
Whittaker'sf solution of this equation is
B) V = f{n; sin u coh v + ymnu sin v + z cos u + ct, u, v) dudv,
J -IT J 0
where /denotes an arbitrary function of the three variables involved.
In particular, a solution is
V=\ I eikix»i"ut''mi'+y«UluaU>v+zrwu+el)F(u, u)dudv,
J -vJ 0
where F denotes an arbitrary function of u and v.
* Proc. London Math. Hoc. xxn. A892), pp. 431—449.
t Math. Ann. uvu. A902), pp. 342—345. See also Havelock, Proc. London Math. Soc. B) n.
A904), pp. 122—137, und Watson, Messenyer, xxxvi. A907), pp. 98—106.
126 THEORY OP BESSEL FUNCTIONS [CHAP. IV
The physical importance of this particular solution lies in the fact that it
is the general solution in which the waves all have the same frequency kc.
Now let the polar coordinates of («, y, z) be (r, 9, <?), and let (a>, -f) be the
angular coordinates of the direction (u, v) referred to new axes for which the
polar axis is the direction @, tp) and the plane >Jr = 0 passes through the
2-axis. The well-known formulae of spherical trigonometry then shew that
cos co = cos 0 cos it + sin 9 sin u cos (v — <?),
sin u sin {v — </>) = sin a> sin -x/r.
Now take the arbitrary function F (u, v) to be Sn {u, v) sin u, where Sn de-
denotes a surface harmonic in {u, v) of degree n; we may then write
Sn (u, v) = 8n,@, ?; », "f),
where Sn is a surface harmonic* in (o>, \Jr) of degree n.
We thus get the solution
Vn = eilcet r T eikra0Hw ^n (9, (/>; w, -Jr) sin o> rf«d-^r.
J -irJ 0
Since Sn is a surface harmonic of degree n in (&>, i|r), we may write
S« {0, +; a), t) = A» F>, <f>). PM (cos a))
+ S {^n
l
where jln @, ^>), Jln(m) @, <f>) and J5n<m> @, </>) are independent of w and •x/r.
Performing the integration with respect to ty, we get
Vn = 27reifceJ^lw @, ^>) (^-«»B-Pn (cos «) sin
by § 3-32,
Now the equation of wave motions is unaffected if we multiply x, y, z and
t by the same constant factor, i.e. if we multiply r and t hy the same constant
factor, leaving 6 and </> unaltered; so that An @, </>) may be taken to be in-
independent^ of the constant "k which multiplies r and t.
Hence lim (k~n Vn) is a solution of the equation of wave motions, that is
to say, rnAn(9, <?) is a solution (independent of t) of the equation of wave
motions, and is consequently a solution of Laplace's equation. Hence An @, ?)
This follows from the fact that Laplace's operator is an invariant for changes of rectangular
+ This is otherwise obvious, because Sn may be taken independent of k.
axes.
4-82] DIFFERENTIAL EQUATIONS 127
is a surface harmonic of degree n. If we assume it to be permissible to take
An @, cp) to be any such harmonic, we obtain the result that
eihctr~ijn+i (kr) P,™ (cos 6)C™ mcf>
is a solution of the equation of wave'motions*; and the motion represented by
this solution has frequency Ice.
To justify the assumption that An(d, $) may be any surface harmonic of degree n, we
construct the normal solution of the equation of wave motions
3 / „ i V\ 1 5 / . . c V\ 1 . ?fl V r* 32 V
[ n*ZI J/ (l fj 1
3 / „ i V\ 1 5 / . . c V
_ [ n*Z I «J_, / (Jill fj
r V dr ) + ain & d6 \ d6
_ [ «J_, fj 1-1- . — -_
dr V dr ) + ain & d6 \ d6 ) + am* 6 dp ~ cl dt
which has factors of the form eikel .' md>. The factor which involves 6 must then be of
8111
the form Pnm(con 6); and the factor which involves r is annihilated by the operator
dr \ dr)
ao that if this factor in to bo analytic at the origin it inu.st be a multiple of </rt.(.j {kr)l*Jr.
4182. Theorems derived from solutions of the equations of Mathematical
Physics.
It in possible to prove (or, at any rate, to render probable) theorems con-
concerning Bossel functions by a comparison of various solutions of Laplace's
equation or of the equation of wave motions.
Thus, if we take the function
ekzJ0 [k*/{f? + a9 - 2ap cos $)},
by making a change of origin to the point (a, 0, 0), we see that it is a solution
of Laplace's equation in cylindrical-polar coordinates. This solution has ekz as
a factor and it is analytic at all points of space. It is therefore natural to
expect it to be expansible in the form
r oo "I
ekz \ Ao Jo (kp) + 2 2 (Am cos m<f> + Bm sin m<f>) Jm(kp) .
Assuming the possibility of this expansion, we observe that the function under
consideration is an even function of (f>, and so Bm — 0; and, from the symmetry
in p and a, Am is of the form cmJm(/ca), where cm is independent of p and a.
We thus get
oo
Jo )/cV(pa + a" ~ 2ap cos </>)} = 2 emcmJm{kp) Jm(ka) cos m<f>.
If we expand both sides in powers of p, a and cos <j>, and compare the
coefficients of {k-pa cos <?)m, we get
Cf. Bryan, Nature, lxxx. A909), p. 309.
128 THEORY OF BESSEL FUNCTIONS [CHAP. IV
and so we are led to the expansion*
00
Jol&vV + a2 - 2ap cos </>)) == 2 emJm(kp) Jm(ka) cos m<j>,
of which a more formal proof will be given in § il*2.
Again, if we take eifc(ct+z\ which is a solution of the equation of wave motions,
and which represents a wave moving in the direction of the axis of z from
+ oo to - oo with frequency he and wave-length Zirjk, we expect this expression
to be expansible! in the form
where cn is a constant; so that
gifcrcosfl __ I \ ^ q i"
If we compare the coefficients of (At cos 0)w on each side, we find that
(n + |)" 2». (n\y'
and so cn = n +1; we are thus led to the expansion^:
\fer/ ,l=o
of which a more formal proof will be given in § 11'5.
4*83. Solutions of the wave equation in space of p dimensions.
The analysis just explained has been extended by Hobson§ to the case of
the equation
dxf + Zxf + " * + datf " ca dt- '
A normal solution of this equation of frequency kc which is expressible as a
function of r and t only, where
must be annihilated by the operator
9 .JP13 ,
9?2 r 8r
and so such a solution, containing a time-factor eiict, must be of the form
* This is due to Neumann, Theorie der BeaeVichen Functionen (Leipzig, 1867), pp. 59—65.
t The tesBeral barmonicB do not occur because the function is symmetrical about the azie of z.
J ThiB expansion is due to Bauer, Journal filr Math. vn. A859), pp. 104, 106.
§ Proc. London Math. Soc. xxv. A894), pp. 49—75.
4-83] DIFFEEENTIAL EQUATIONS 129
Hobson describes the quotient W\(p-.>i)(k?')/(Jcr)klp~s) as a cylinder function
of rank p ; such a function may be written in the form
By using this notation combined with the concept of ^-dimensional space,
Hobaon succeeded in proving a number of theorems for cylinder functions of
integral order and of order equal to half an odd integer simultaneously.
As an example of such theorems we shall consider an expansion for
/ j/l *j(r- + a" — 2a/1 cos <?) j p),
where it is convenient to regard c/> as being connected with xp by the equation
Xp — r cos cj>. This function multiplied by eikct is a solution of the wave equation,
and when we write p — r sin 0, it is expressible as a function of p, (ft, t and of
no other coordinates.
Hence
eikotJ [/.' VO'" + «"" - 2a?1 cos <f>) \ p]
is annihilated by the operator
dp- p op aXy
that is to say, by the operator
d* p-l d (/)-2)cos0 d I 3» ,2
„ -t- ¦— ^ -t ~'~ ; " -, ¦" "T ., x~.- -T it> ¦
or- r or r- sm <p d<p r- <)<p-
Now normal functionH which are annihilated by this operator are of the form
where JJn (cos 0 ¦ p) is the coefficient* of an in the expansion of
A - 2a cos </> + cpy-b'.
By the reasoning used in § 4*82, we infer that
J \/c V(/"'J +- a2 — 2(W cos <?) | p\
Now uxy)and all the JBes.se 1 functions and equate the coefficients of
(k'-ar cos <j>)"- on each side; we find that
so that /ln=2^-'(;? + ^-l)r(iy>-- 1).
* So that, in Ge^enbauer's notation,
W. B. l'\
130 THEORY OP BESSEL FUNCTIONS [CHAP. IV
We thus obtain the expansion
'2 + a2 - 2ar cos <f>)}
+ a2 - 2ar cos
?i=0
An analytical proof of this expansion, which holds for Bessel functions of
all orders (though the proof given here is valid only when p is an integer), will
be given in § 11*4.
4*84. Batemav's solutions of the generalised equation of wave motions.
Two systems of normal solutions of the equation
3F 3F VV &V IPV
*¦ ' daf dxj dxi dccf ~ c2 dt2
have been investigated by Batenlan*, who also established a connexion between
the two systems.
If we take new variables p, or, %, -^ denned by the equations
xx = p cos ^, sc3 = <t cos i/r,
xz — p sin x, #4 = cr sin i/r,
the equation transforms into
A normal solution of this equation with frequency kc is
/M (kp cos O) Jv (ho- sin ^>) ei b»x+f*+*<?Oj
where <l> is any constant.
Further, if we write
p = r cos (j>, <r=r sin ^>,
so that (r, %, ^3 <^>) form a system of polar coordinates, equation B) transforms
into
3r2 r dr 2
r dr r2 8</J + 'r2
cos2 ^ dx2 + r2 sin2
Now normal solutions of this equation which have e*0*x+">H-*<rf> as a factor
are annihilated by the operator
Meuenger, xxxni. A904), pp. 182—188; Proc. London Afatfc. ^oc. B) m. A905), pp. 111—123.
4-84] DIFFERENTIAL EQUATIONS 131
and since such solutions are expressible as the product of a function of r and
a function of <f> they must be annihilated by each of the operators
dr2 r dr
32 . . , , , ,, 9 . ,. /. . , s v? v2
^.; 4-(cot(D —tan
5y + 4\ (X + 1) - -—-r-r-r ,
dty d<f> K cos'</> sin3 <^
where X, is a constant whose value depends on the particular solution under
consideration. The normal solutions so obtained are now easily verified to be
of the form
(kr)'1 JA+l (kr) cos^ sin"<f>
2 2
It is therefore suggested that
J^ (A;?1 cos <f> cos •$) /v (A:r sin <? sin
is expressible in the form
2 aK (kr)~x J.d\+i (/c?') cos'4^) sin" 6 . ojP, (^—^r X, -—
where the summation extends over various values of X, and the coefficients
depend on X and <t>, but not on r or 0. By symmetry it is clear that
+\ + 1; v + l; sin-<J>V
where b\ is independent of <J>.
It is not difficult to see that
and Bate man has proved that
We shall not give Bateman's proof, which is based on the theory of linear
differential equations,*but later (§ 11/6) we shall establish the expansion of
J,, (kr cos <j> cos <1>) Jv (kr sin <j> sin <t>) by a direct transformation.
9—2
CHAPTER V
MISCELLANEOUS PROPERTIES OF BESSEL FUNCTIONS
5'1. Indefinite integrals containing a single Bessel function.
In this chapter we shall discuss some properties of Bessel functions which
have not found a place in the two preceding chapters, and which have but
one feature in common, namely that they are all obtainable by processes of a
definitely elementary character..
We shall first evaluate some indefinite integrals.
The recurrence formulae § 3"9 E) and F) at once lead to the results
. A)
B) j z~"+} <@v (z) dz = -
To generalise these formulae, consider
jV»/(*) #,(
let this integral be equal to
where A (z) and B (z) are to be determined.
The result of differentiation is that
z"^f(z)<$v(z) = z»» U*(z)<@v(z) + A(zJ^±1^V(Z)-A(z)^v+1 (z)
I z
+ «•+» \B' (z) <@v+1 (z) 4 B (z) <@v (*)}.
In order that A (z) and B(z) may not depend on the cylinder function, we
take A (z) = B' (z), and then
f{z)~ A' (z) + ^±-2 A(z) + B{z).
z
Hence it follows that
C) JV+1 \b"{z) + 2-?±l B' (z) + B («)| K (z) dz
= z^ [B1 {z) <@v (z) + B (e)%sv+, (z)}.
This result was obtained by Sonine, Math. Ann. xvi. A880), p. 30, though an equivalent
formula (with a different notation) had been obtained previously by Lominel, Studien ihber
di-e Bessel'schen Funclionen (Leipzig, 1868), p. 70. Some developments of formula C) are
due to Nielsen, Nyt Tidsskrift, ix. A898), pp. 73—83 and Ann. di Mat. C) vi. A901),
pp. 43—46.
For some associated integrals which involve the functions ber and bei, see Whitehead,
Quarterly Journal^ xlii. A911), pp. 338—340.
5-1, 5-11] MISCELLANEOUS THEOREMS 133
The following reduction formula, which is an obvious consequence of C),
should be noted:
D) |**+*c@v(z) dz = -<ji*- v-)\z»~lK(z) dz
5*11. Lo-mmel's integrals containing two cylinder functions.
The simplest integrals which contain two Bessel functions are those
derived fr6m the Wronskian formula of § 312 B), namely
r , •. T,, •. 2 sin vv
irz
which gives
dz v «/_„ (z)
A)
]
z,T*{z) 2sinj77r Jv(z) '
'¦ dz it J^v(z)
z'Jjz) J~-*(z)= ~ 2 sin w g Tv{z) '
and similarly, from § 3'6:i A),
: (h _7T YAS)
zJ;- (z) ~ 2 </„ \z)'
-, ~ dz v Jv(z)
(o) I sY/(z) = ~2 r:V)'
The reader should liave no difficulty in evaluating the .similar integrals which contain
any two cylinder functions of the mune order in the denoiuinator. The formulae acLunlly
given are duo to Lommel, Math. Ann. lv. AH71), pp. J03—11(>. The reader should compare
C) with the result duo to Euler which wan quoted iu ij 1 -52.
Some more interesting results, also due to Lommel*, are obtained from
generalisations of Bessel's ucjnation.
It is at once verified by differentiation that, if y and 77 satisfy the equations
then
* Math. Aim. xtv. A879), pp. 520—5315.
134 THEORY OF BESSEL FUNCTIONS [CHAP. V
Now apply this result to any two equations of the type of § 4*31 A7). If
^»> ^ denote any two cylinder functions of orders fi and v respectively, we have
where <f) (z) and >/r (z) are arbitrary functions of z.
This formula is too general to be of practical use. As a special case, take
$ (z) and sfr (z) to be multiples of z, say kz and Iz. It is then found that
G) JS j(# - P)z - ~^\ K (kz) tv {lz)dz
(Jfc.8) tv («*) - ^ (^) ^v+1 (^)) -(ji-v) %\ (kz) *@v (Iz).
The expression on the left simplifies still further in two special cases (\)(jl=v,
)ife=.«.
If we take fi = v, it is found that
(8) f . % (fa) *, (U) iz =
& — t
This formula maj'.be verified by differentiating the expression on the right.
It becomes nugatory when k — l, for the denominator is then zero, while the
numerator is a constant.
If this constant is omitted, an application of l'Hospital's rule shews that,
when l-^k,
(9) I*z^.(kz)<$»(kz)dz = -~ {kz<^+:(kz)t/ (A?*)
.- luV^{he) W^Xkz) - ^ (kz) %\+, (kz)}.
The result of using recurrence formulae to remove the derivates on the
right of (9) is
A0) je^ikz)'^ (kz) dz = \e* {2^M (kz) ^M (kz) - ^ (kz) r#M+1 (kz)
5-11] MISCELLANEOUS THEOREMS 135
Special cases of these formulae are:
A1) J'z ^ (kz) dz = \z* [<@* (kz) - %Vi (&*) K+i (kz)}
l ~ ^) Vj (kz) + V <&
v fS — — —
A2) ?<$„. {kz) %% {kz) dz - \z> [2<&n (kz) r$_M (kz) + <$„_, {kz) c$-»-x (kz)
J
the latter equation being obtained by regarding e~tL1ticS ^(kz) as a cylinder
function of order — /j,.
To obtain a different class of elementary integrals take k = I in G) and it
is found that
A3) W (kzW (kz) d- = - kZ W'+l {kz)
J *^ ^ z
z f
fi + v
The result of making v -*-/x in this formula is
A4) j ^M (&») ^v(/^) = 2
The last equation is also readily obtainable by multiplying the equations
1 *yCAi / \ *j
by "" a ' "^mC^) respectively, subtracting and integrating, and then re-
placing z by kz.
As a special case we have
A5) J ^Vfa)" = ^{^I(^)^(fa)-^(fa)^I(fo))+-~^»(A»).
An alternative method of obtaining this result will be given immediately.
Results equivalent to A1) are as old as Fourier's treatise, La Th&orie Analytique do la
Chaleur (Paris, 1822), §§ 318—319, in the case of functions of order zero ; but none of the
other formulae of this section seem to have been discovered before the publication of
Lommel's memoir.
Various special cases of the formulae have been worked out in detail by Marcolongo,
Napoli Rendiconti, B) in. A889), pp. 91—99 and by Chessin, Tram. Acad. Sci. of St Louis,
xii. A902), pp. 99—108.
136 THEORY OF BESSEL FUNCTIONS [CHAP. V
52. Indefinite integrals containing two cylinder functions; Lommel's
second method.
An alternative method has been given by Lomnael* for evaluating some
of the integrals just discussed. By this method their values are obtained in a
form more suitable for numerical computation.
The method consists in adding the two results
~ {z» ^(z) %\ (*)} = - z> [% (z) Wv+1 (z) + <g?M+1 (*) %\ (z)}
(z) %,+1 (*)} = z» (#„ (*) K+l (z) + fy+l (z) %\ (z)}
^.(p-fM-v-2) zo-i ^ {z) W,,+l (z),
so that
= z' [^ (z) Wv (g) + Y^+l (z) (SJv+l (z)},
and then giving special values to p.
Thus we have
A)
B)
As special cases of these
C) /**-*-» ff Vh 00 dz = - 5— [Vf (z) + ^ fl 00},
D) j z^ W (z) dz = 4— _ {^
Again, if p be made zero, it is found that
(/* + v)J K(*)®,@ --Qi + v+2)j r<fM+1 (z) %°v+l (z) -Z-
so that, by summing formulae of this type, we get
= r^ (z) @y (z) 4- 2 "S VM+m (Z) r&v^n 0) + %+n (Z) &v+n (Z).
m=l
* Math. Ann. xiv. A879), pp. 530—536.
z
5-12-5-14] MISCELLANEOUS THEOREMS 137
In particular, if /x = v = 0,
_ A?
F) J (
= - i [V. (*) $. 0) + 2W?1 ^ (*> $„ <*) + % (,)
where n — 1, 2, 3, .... But there seems to be no simple formula for
For a special case of A) .see Rayleigh, Phil. May. E) xi. A881), p. 217. [Scientific Papers,
I. A899), p. 516.]
53. Soni.ne'a integrals containing two cylinder functions.
The analysis of $ Tr\ has been extended by Souine, Math. Ann. xvi. A880), pp. 30—33,
to the disc:iiHnion of conditions that
J f(z) r$ W* B)} *$'*• W' iz)\ dz
may be expressible in tho form
A iz) Vr'a {</> B)} 'fi> v ty (z)} + B (z) Y/>'M+\ {</* (z)) ((" v tyi2))
+ o B) '{/'•'in {'P (z)\ 'ft 1/+1 fy (i)' ¦+¦ d (z) '^v+i '*/* B)i' r^v4i 'iV' C)}'
but the reaultH aru too complicated and not. sufficiently important to justify their insertion
here.
5'14. Schaflieitlvn's reduction formula.
A reduction formula for
which is a natural extension of the formula § 51 D), has been discovered by
Schafheitlin* and applied by him to discuss the rate of change of the zoros of
c@v{z) as v varies (§ 15).
To obtain the formula we observe that
5} *r.
%\ (z) Wv'(z)] + * [zwtf,1* (z) + (fi + l) z»+l %', (z) '<C {z)} dz.
Now, by a partial integration,
jjl + 3) f V+9(&V* {z) dz = [^ +:t '$;* (z)]
+ 2
* Berliner Sitmngsberichte, v. A906), p. 88.
138 THEORY OF BESSEL FUNCTIONS [CHAP. V
and so
0* + 1) | V+2 ^/2 (*) dz = |>+8 ^/2 (*)] + 2 J V+1 (*2 - *2) #„ (*) #/ 0) dz.
Hence, on substitution,
(fi + 1) f V O2 - v2) ^/ (*) d?
(«) dz + {(jjl + If - 2v2j [V+1^, («) ^'(^ dz
0)
By rearranging we find that
+ 2) f
and this is the reduction formula in question.
5*2. Expansions in series of Bessel functions.
We shall now discuss some of the simplest expansions of the type ob-
obtained for Qz)m in § 2-l7. The general theory of such expansions is reserved
for Chapter XVI.
The result of § 2*7 at once suggests the possibility of the expansion
A) (W..i(?±*^»>
which is due to Gegenbauer* and is valid when fi is not a negative integer.
To establish the expansion, observe that
is a series of analytic functions which converges uniformly throughout any
bounded domain of the s-plane (cf. § 3*13); and since
d*lva '
it is evident that the derivate of the series now under consideration is
w] -o.
¦ TFicner Sitzungsberichte, lxxiv. B), A877), pp. 124—130.
5-2,5*21] MISCELLANEOUS THEOREMS 139
and so the sum is a constant. When we make z -*-0, we see that the constant
is unity; that is to say
wr0 n! (W-^m«(*)- I-
and the required result is established.
The reader will find that it is not difficult to verify that when the expansion on the
right.in A) is rearranged in powers of gt all the coefficients except that of #¦ vanish; but
this is a crude method of proving the result.
5*21. The expansion of a Bessel function as a series of Bessel functions.
The expansion
X ,~0 n\ T(v + l-fi- n)f(v'+ n + 1)
is a generalisation of a formula proved by Sonine* when the difference v — ju,
is a positive integer; it is valid when /a, v and v — n are not negative
integers.
It is most easily obtained by expanding each power of z in the expansion
of {^zy~vJv(z) with the aid of § 5, and rearranging the resulting double
series, which is easily seen to be absolutely convergent.
It is thus found that
r{? + m+ n)
r (u+w) r (y + i
= .* »ff (, +! - m-• i) r\
by Vanderrnonde's theorem; and the result is established.
If we put v = fx -f m, we find that
which ia Sonine's form of the result, and is readily proved by induction.
* Math. Ann. xvi. A880), p. 22.
140 THEORY OF BESSEL FUNCTIONS [CHAP. V
By a slight modification of the analysis, we may prove that, if k is any
constant,
x gi^j Qi + n, -n\ v + 1; k-) (fi + 2n) JM+an(z).
This formula will be required in establishing some more general expansions
in § 11-6.
5*22. Lommel's expansions of (z + li)±)svJv [>J(z + ^)}-
It is evident that (z + h)~^vJv {\J(z + h)}, qua function of z 4- h, is analytic
for all values of the variable, and consequently, by Taylor's theorem combined
with | 3-21 F), we have
oo Uiri Jm
A) (z + h)~*J,y(z +h)} « 2 "~ %- \z-*Jv (V*)}
Again, (z 4- h) VJV {\J(z + h)} is analytic except when z+ h = 0; and so,
provided that | h \ < I 2}, we have
B) "
f „ (v)
These formulae are due to Lommel*. If we take v = ~\ in A) and »' = ^- in
B) we deduce from § 3'4, after making some slight changes in notation,
C)
D)
equation D) being true only when |?|<?J3|. These formulae are due to
Glaisherf, who regarded the left-hand sides as the generating functions
associated with the functions whose order is half of an odd integer, just as
exp [\z (t — Ijt)} is the generating function associated with the Bessel co-
coefficients.
Proofs of C) and D) by direct expansion of the right-hand sides have
been given by Glaisher; the algebra involved in investigations of this nature
is somewhat formidable.
* Studien iiher die liesseVschen Functionen (Leipzig, 1868), pp. 11—16. Formula A) was given
by Bessel, Berliner Abh. 1824 [1826], p. 35, for the Bessel coefficients.
+ Quarterly Journal, xti. A873), p. 136 ; British Association Report, 1878, pp. 469—470. Phil.
Trans, of the Royal Soc. clxxii. A881), pp. 774—781, 813.
5-22] MISCELLANEOUS THEOREMS 141
We shall now enumerate various modifications of A) and B).
In A) replace z and h by z- and Icz'2, and then
E) Jv {W(l + k)) = A + A)*' 2 U
7/1 = 0
and, in particular,
If we divide E) by A -f &)*" and then make & -*. — 1, we find that
^ r(v + l)"m:(> m! l/v+JttW
In like manner, from B),
(8) Jv [z*J{\ + /,;)} = A + k)-*> % ^'CZf- J_n (z),
¦m.~o i*1-
provided that J Ic \ < 1.
If we make A- -*- — 1 + 0, we find, by Abel's theorem,
Jim [A +k)*J, {WO +^I] = S ^-^.^_WI(A
provided that, the series on the right i.s convergent. The convergence is obvious
when v is an integer. If v is not an integer, then, for large values of ?»,
t^""./_ (,) - t-^JK^'"-'_>„!„ (,„ _ ,), „
Hence the condition for convergence! is H(v)>0, and if the condition i.s
satisfied, the convergence i.s absolute. Consequently, when A'(V)>0, and also
when v is any integer,
(9) 2 S---?-.lf*> J,_.w,.(^) = 0.
,„ _ i, //A !
In like manner, if R(i>) > — 1, and also when v is any integer, we have
A0) J,(*V2) = 42-J" % V*'T-*-**{*)•
It should be observed that functions of the second kind may be substituted
for functions of the first kind in A), B), E) and (8) provided that i h. \ < j z ,
and | h \ < 1; sfo that
A1) (« +A)"*' Yv W(* + h)} - S ^"^')Wi8-^+»> F^Cvfc),
00 ( 1 /
w=0 7
142 THEORY OF BESSEL FUNCTIONS [CHAP. V
These may be proved by expressing the functions of the second kind as a
linear combination of functions of the first kind; by proceeding to the limit
when v tends to an integral value, we see that they hold for functions of
integral order.
By combining A1)—A4) with the corresponding results for functions of
. the first kind, we see that we may substitute the symbol "gf for the symbol
Y throughout. .
These last formulae were noted by Lommel, Studien, p. 87. Numerous generalisations
of them will be given in Chapter xi. It has been observed by Airey, Phil. Mag. F) xxxvr.
A918), pp. 234—242, that they are of some use in. calculations connected with zeros of
Besael functions.
When we combine E) and A3), and then replace \/(l + k) by X, we find
that, when |X2-1|<1,
A5) ff. (\z) = X" 2 U {* U*«i <#v+m (s),
and, in particular, when X is unrestricted,
These two results are frequently described* as multiplication theorems for
Bessel functions.
It may be observed that the result of treating A4) in the same way as (8) is that
(when v is taken equal to an integer n)
(H) -(»-l)! B/*)»«,r 2 m^ *»-«(*).
m=0 m •
An alternative proof of the multiplication formula has bee.n given by Bbhiner, Berliner
Sitzungsberichte, xin. A913), p. 35, with the aid of the methods of complex integration;
see also Nielsen, Math. Ann. lix. A904), p. 108, and (for numerous extensions of the
formulae) Wagner, Bern Mittheilungen, 1895, pp. 115—119; 1896, pp. 53—60.
[Note. A special case of formula A), namely that in which v = l, was discovered by
Lommel seven years before the publication, of his treatise; see Archiv der Math, xxxvn.
A861), p. 356.
His method consisted in taking the integral
— M cos (?r cos 6 + yr sin 6) d? dr)
over the area of the circle ?2+»j2=l, and evaluating it by two different methods.
The result of integrating with respect to rj is
-^ j cos frcoa 6)via U(l-?). rain
?
See, e:g. Sohafheitlin, Die Th?orie der Besselschen Funktimen (Leipzig, 1908), p. 83.
5*23, 5*3] MISCELLANEOUS THEOREMS 143
and the result of changing to polar coordinates (p, (p) is
=- I I cos {rp cos (cp — 9)} pdpdcp = — I j cos (rp cos <p) pdpd<p
Alt J -ir J o &1T J —V J 0
= i- J J cos (?r) (*?<*, = ^ ? a - |*)icos (?r) rff-J^ (r)/r.
If we compare these equations we obtain A) in the case v = \ with z and h replaced by
?-2 cos2 0 and r2sin20.]
5'23. The expansion of a Bessel function as a series of Bessel functions.
From formula § 5 22 G), Lommel has deduced an interesting series of
Bessel functions which represents any given Bessel function.
If fx, and v are unequal, and //, is not a negative integer, we have
The repeated series is absolutely convergent; consequently we may re-
rearrange it by replacing p by m — n, and then we have
and hence, by Vandermonde's theorem,
A) </,(-)= ^---^^r^^
m!
Thia formula was given by Loinmcl, Studien ubar die Bes&efschen Functionen (Leipzig,
1868), pp. 22—23, in tho wpecial caso fx = O; by differentiating with respect to v and then
putting 1^ = 0, it is found that
B) M'o(*Wo(*)l"g(^)-rr(f+V ^ ^fenCW-^^+.W •
and, when f*=0, we liave Lommol'a formula
C) ^Y0(z) = .r0(z).{y+\og(hz)}+ 2
2 .
=l "* • '*»•
This should be compared with Neuinann'B expansion given in § 3'57.
5*3. An addition formula for Bessel functions.
An extension of the forraula of § 2 to Bessel functions of any order is
A) Jv(z + t)= 2 Jv-
where | z\ < 111, v being unrestricted. This formula is due to Schlafli* ; and
the similar but more general formula
B) %\(z + t)= X <$v-
is due to Sonine-f.
* Math. Ann. in. A871), pp. 135—137. f Ihid- XVI- A880), pp. 7—8.
144 THEORY OF BESSEL FUNCTIONS [CHAP. V
It will first be shewn that the series on the right of A) is a uniformly
convergent series of analytic functions of both z and t when
z | < r, R «; j t \ ^ A,
where r, R, A are unequal positive numbers in ascending order of magnitude.
When m is large and positive, Jv-m(t)Jm(z) is comparable with
sin vir. {\R)V. (r/R)m ~^
and the convergence of the series is comparable with that of the binomial
series for A — rjKy. When m is large and negative (= — n), the general
term is comparable with
T(v'+n-hl).nl
and the uniformity of the convergence follows for both sets of values of m by
the test of Weierstrass.
Term-by-term differentiation is consequently permissible*, so that
•" 7ft= -00
1 "
-5 X J",_m (t) (/w_i (ar) - «/¦,„+! {z)\,
" in = - oo
and it is seen, on rearrangement, that all the terms on the right cancel, so
that
00
Hence, when | z \ < \t\, the series 2 Jv_m (t) Jm (z) is an analytic function
7tt= -00
of 2- and ^ which is expressible as a function of z + t only, since its derivates
with respect to z and t are identically equal. If this function be called
F {z +1), then
TO=—00
If we put 2 = 0, we see that F(t)=J?(t), and the truth of A) becomes
evident.
Again, if the signs of v and m in A) be changed, we have
m= —oo
and when this result is combined with A), we see that
C) 5
1»= -CO
* Cf. Modern Analysis, § 5*3.
5'4] MISCELLANEOUS THEOREMS 145
When this is combined with A), equation B) becomes evident.
The reader will readily prove by the same method that, when | z \ < i t |,
D) Jv{t-z)= I Jv+m{t)Jm{z),
7I= — 00
E) #„(*-*)= S %\+m{t)Jm{z),
»)! = —00
F) Yv{t-z)= S F,+
Of these results, C) was given by Loinmcl, Studien uber die BesseVschen Functionen
(Leipzig, 1868), when v is an integer; while D), E) and (G) were given* explicitly by Graf,
Math. Ann. xliii. A893), pp. 141—142. Various generalisations of these formulae will be
given in Chapter xi.
5*4. Products of Bessel functions.
The ascending series for the product J^ (z) Jv (z) has been given by various
writers; the expansion is sometimes stated to be clue to Schonholzerf, who
published it in 1877, but it had, in fact, been previously published (in 1870)
by SchlarliJ. More recently the product has been examined by Orr§, while
Nicholson]j has given expansions (cf. § 5-42) for products of the forms
M*)Y*(z) and Ym(z)Yn(z).
In the present section we shall construct the differential equation satisfied
by the product of two Bessel functions, and solve it in series. We shall then
(§ 541) obtain the expansion anew by direct multiplication of scries.
Given two differential equations in their normal forms
if y denotes the product vw, we have
y" = v"w + 2v'iv' + vw"
where primes indicate differentiations with respect to z.
* See also Epstein, Die vicr Rechnungtoperationen mil Beasel"when Fimctionen (Bern, 1894),
[Jahrbuch iiber die l'ort»chritte tier Math. 1H93-181I, pp. 845—846].
t Ueber die Auxwerthung he.atimmterlntegrale.init Iliilfc von Veriindettmgendea Integrutionsioeyes
(Bern, 1877), p. 13. The authorities who attribute the expansion to Schonholzer include Graf and
Guhler, Einlcihtng in die Thcorie tier HeaaaVacheii Funktioncn, u. (Bern, 15H0), pp. 85—87, and
Nielsen, Ann. Sci. dc vAcole norm. sup. C) xvm. A901), p. 50; Handbuch der Theoric der Gyliu-
dcrfunktionen (Leipzig, 1904), p. (JO. According to Nielsen, Nouv. Ann. de Math. D) n. A902),
p. 3'J6, MeiBael obtained some series for products in the Iserlohn Progmmm, 18G2.
X Math. Ann. in. A871), pp. 141—142. A trivial defect in Schlafli's proof is that lie uscb a
contour integral which (as he points out) converges only when
§ Proc. Camb. Phil. Soc. x. A900), pp. 93—100.
|| Quarterly Journal, xuir. A912), pp. 78—100.
w. B. F.
146 THEORY OF BBSSEL ITJNCTIONS [CHAP. V
It follows that j!~ [y" + (I + J)y} = 2v"w' + 2v w"
and hence y'" + 2 (/ + J) ?/ + (I' + /') y = (/ - /) (vfw - vw').
Hence> in the special case when I = J,y satisfies the equation
but, if J *fc J, it is easy to shew by differentiation that
B) *L W—
This is the form of the differential equation used by Orr; in connexion with A), see
Appell, Comptes Rendw, xoi. A880), pp. 211—214.
To apply these results to Bessel's equation, the equation has to be reduced
to a normal form; both Orr and Nicholson effect the reduction by taking
z ^v(z) as a new dependent variable, but, for purposes of solution in series, it
is simpler to take a new independent variable by writing
so that (~ni$ + (e29 - v*) Jv (z) = 0.
atf
Hence the equation satisfied by J^ (z) Jv (z), when ft? ^ v2, is
that is to say
C) O4 - 2 O2 + v2) Sa + (m2 - v*f] y + 4e2S (^ +1) (% + 2) y = 0,
and the equation satisfied by Jv (z) J±v (z) is
D) ^(^-4^
Solutions in series of C) are
m=0
where a — + p + v and
4 (a 4- 2m -1) (a + 2m) cm-\
m~ (a+ ijl + v + 2m) (a + /Lt — v + 2m) (a — /t + 7/ + 2m) (a - /a — v + 2w/) '
If we take a = /u + v and
we obtain the series
00
2 -
v + m+ 1)T (/t + m + 1)T (v + m+ 1)'
and the other series which are solutions of C) are obtained by changing the
signs of either fi or v or both /x and v.
5-41J MISCELLANEOUS THEOREMS 147
By considering the powers of z which occur in the product J^ (z) Jv (z) it
is easy to infer that, if 2/z, 2v and 2 (fx + v) are not negative integers and if
/a2 j= n8, then
In like manner, by solving D) in series, we find that, when 2v is not a
negative integer, then
and, when 7/ is not a negative integer, then
By reasoning which resembles that given in § 4*42, it may be shewn that
F) holds when v is half of an odd negative integer, provided that the quotient
F Bv + 2m + 1)/F Bv + in + 1) is replaced by the product Bv + m + l)m.
5*41. Products of series representing Bessel functions.
It is easy to obtain the results of § 5-4 by direct multiplication of series.
This method has the advantage that special investigations, for the cases in
which /xa= v2 and those in which j^ + v is a negative integer, are superfluous.
The coefficient of (-)"l(^y+"+2»l in the product of the two absolutely
convergent series
2 (-) H)
) r\T(
2 v
mfo m! r (/* + »i + 1) nr0n\T(v+n +
is i
n=0«! r (" + « + 1) • (»« - n)! I" (/* + W - M + 1)
m! r C/jl + m + 1) T (p + m + 1)
(fjL + v+m + 1 )m
~ m! T (/u, + m + 1) P {y + to 4-1)'
when Vandermonde's theorem is used to sum the finite series.
Hence, for all values of /x and v,
a,nd this formula comprises the formulae E), F) and G) of § 5*4.
10—2
148 THEORY OF BESSEL FUNCTIONS [CHAP. V
This obvious mode of procedure does not seem to have been noticed by any of the
earlier writers; it was given by Nielsen, Math. Ann. lii. A899), p. 228.
The series for J0(z) cos z and J0(z)a'mz were obtained by Bessel, Berliner Abh. 1824,
[1826], pp. 38—39, and the corresponding results for Jv{z) cos z and Jv(z) aim were
deduced from Poisson's integral by Lonimel, Studien iiber die Bessel'sohen Functionen
(Leipzig, 1868), pp. 16—18. Some deductions concerning the functions ber and bei have
been made by Whitehead, Quarterly Journal, xlii. A911), p. 342.
More generally, if we multiply the series for /M (az) and Jv (bz), we obtain
an expansion in which the coefficient of (-)m a* 6" (\zy+v+m is
3on\ r(i/ + ?i + l).(m -n)! F(> + m-n + l)
_ a2m BF, (- m, - ji - m; y + 1; 67a2)
"" m! r(fi + m + l)T(v + l)
and so
B) ^M^F,) = (i^M"
1 (-) (|oa)8w afi (- m, - /Ji - m; v + 1; 6'/
and this result can be simplified whenever the hypergeometric series is
expressible in a compact form.
One case of reduction is the case b — a, which has already been discussed ;
another is the case b — ia, provided that fj? == v-.
In this case we use the formula*
and then we see that
/ N r / \ V (~)W (\CLZ)-V^m COS
C)
iW=o w! r (y + m + 1) I> + 2m + 1)'
DA / ( )I ( \- 5 (~)m (j^Jm cos (\v - ^m)
00
(~\ T / \7" / \ *C*
If we take a = e^ in C) we find that
F) ber,2 (z) + bei,2 («) = S — (^)a>+4m
m=o ml 1 (v + w + 1) F (» + 2m + 1)'
an expansion of which the leading terms were given in § 3-8.
* Cf. Kutnmer, Journal fUr Math. xv. A836), p. 78, formula E3).
•5-42] MISCELLANEOUS THEOREMS 149
The formulae C), D), E) were discovered by Nielsen, Atti delta R, Accad. dei Lincei, E)
XV. A906), pp. 490—497 and Monatshefte fiir Math, und Phys. xix. A908), pp. 164—170,
from a consideration of the differential equation satisfied by Jv{az) J±v{bz).
Some series have been given, Quarterly Journal, xli. A910), p. 5ft, for products of the
types Jj,3 (z) and J^ (z) «/_„ («), but they are too cumbrous to be of any importance.
By giving fi the special values + \ in B), it is easy to prove that
G) e"°->/,_ i « {g ( i t* ?
The special case of this formula in which 2v is an integer has been given
by Hobson*.
5'42. Products involving Bessel functions of the second hind.
The series for the products «/)»(z) Yn (z), Jm (z) Yn (z), and Ym (z) Yn (z)
have been the subject of detailed study by Nicholsonf; the following is an
outline of his analysis with some modifications.
We have
irJ,(z) Yn (z) = 1 [J,(z) Jv («)} - (-)»I [J, (z) J_v (,)},
where v is to be made equal to n after the differentiations have been performed.
Now
and
^ {J, (Z) J_ {Z)\ = - log QZ). J. (Z) J-v (Z)
- " +"»"' + l)'r'O* + r +1)'!1 (- v + r + 1)
n-l
We divide the last series into two parts, 2 and % . In the former part we
have
* Proc. London Hath. Soc. xxv. A894), p. G6; see also Cailler, M6m. de la Soc. de Phys. de
Genlve, xxxiv. A902—1905), p. 310.
f Quarterly Journal, xvau A912), pp. 78—100. The expansion of J0(z) Yq(z) bad been given
previously by Nielsen, Handbuch der Theorie der Cyliiiderj'unktionen (Leipzig, 1904), p. 21.
150 THEORY OF BESSEL FUNCTIONS [CHAP. V
while in the latter part there is no undetermined form to be evaluated. When
r is replaced in this part by n + r, it is seen that
ttJ.(z) Yn(z) = - 2o rlTOi +
| (-)rg
!(
x {g(?) ^(/
--^(/ju + n + r + l)- a//(> + r +1)
- ^ (ft + r + 1) - i|r (r + 1)}.
The expression on the right is a continuous function of //, at //, = in where
m— 0,1, 2, ..., and so the series for irjm{z) Yn(z) is obtained by replacing /j,
by m on the right in A).
The series for Tm (z) Yn (z) can be calculated by constructing series for
in a similar manner. The details of the analysis, which is extremely laborious,
have been given by Nicholson, and will not be repeated here.
5 3. The integral for Jp{z)Jv(z).
A generalisation of Neumann's integral (§ 2*6) for Jn2 (z) is obtainable by
applying the formula*
to the result of § 5*41; the integral has this value when m —0,1,2,..., provided
that R(jm + v)>-1.
It is then evident that
J()J() 2
so tha.t.1 when JR (/a + v) > — 1,
2 f*
A) JMB)JV(^) = -
7T J 0
the change of the order of summation and integration presents no serious
difficulty.
* This formula is due to Cauchy; for a proof by contour integration, see Modern Analysis,
p. 263.
5-43-5-51] MISCELLANEOUS THEOREMS 151
If n be a positive integer and R (ji — n) > — 1, then
B) j; (z) Jn (z) = -fc? ( */„_» B* cos 0) cos (i* + n) 0d0,
T Jo
and this formula is also true if yu and w are &otf/i integers, but are otherwise
unrestricted.
Formula A) was given by SchltiBi, Math. Ann. in. A871), p. 142, when p±v are both
integers; the general formula ia due to Gegenbauer, Wiener Sitzungsberichte, oxi. Ba),
A902), p. 567.
5*5. The expansion oftyzY*" os a series of products.
A natural generalisation of the formulae of Neumann (§2*7) and Gegenbauer
(§ 5-2) is that
Ml-0 "i!
The formula is true if /a and v arc not negative integers, but the following
proof applies only if R(/x +u + l)> — 1.
From § 5-2 we have
1 ^±"+2«)^+"±^/,+^,, B,003^).
If we multiply by cos (/j, — v) 6 and integrate, it is clear from § 5'43 that
^ + „ + 2m) T (/* + v + m)
J
^ cos (/x — vNdd= S
o m-0 Wl
X
and the result follows by evaluating the integral on the left; for other values
of fx and v the result may be established by analytic continuation.
The formula in at once deducible from formulae givon by Gegeubauer, Wiener Sitzungs-
berichte, lxxv. B), A877), p. 220.
5*51. Lommel's series of squares of Bessel functions.
An expansion derived by Lommel* from the formula
z dz
so that
1 f
-, (z) dz = [ ^ (v + 2n) /»
* The results of this seotion will be found in Math. Ann. h. A870), pp. 632—633; xiv. A878),
p. 532 ; MUnchener Abh. xv. A886), pp. 548—549.
152 THEORY OF BESSEL FUNCTIONS [CHAP. V
Hence, by § 511 A1), we have
A) \* \.1\_, (if) -</„_, E) Jv (z)} = I (v + 2n) J\+m (*),
n-0
on taking zero as the lower limit when R(v)>0; by adding on terms at the
beginning of the series, it may be seen that the restriction R,(v) > 0 is super-
superfluous.
If we take in turn v — \, v = f, and add and subtract the results so obtained,
we have (§ 3*4)
B) -= X
T 71=0
sin 2# °°
{6) —x = -^ \—) l
Jinr n~o
while, by taking v = l, we see that
D) \z* {«/02 (z) + Jf (z)} = 2 Bh 4-
Another formula of the same tvpe is derived by differentiating the series
for it is evident that
5 c 7"s /»\_9 V c T (AT' (A
~t~ & cji o fi^.n x*1) — •" *-i en <J v+n \") " v+n \*/
00
— S e T fr\ \ T (v\ T /iy\\
and so,, when R(v) >0, we obtain a modification of Hansen's formula (§2-5),
namely
E) 2 e»A^(*)~2J J,2@t-
«=o Jo t
An important consequence of this formula, namely the value of an upper
bound for j Jv(%) j, will be given in § 1342.
By taking v-\, it is found that
~[ ^t
Jo
0
F)
2
" Z
dt
sin2i
. o t
and so
»=0
where, as usual, the symbol Si denotes the "sine integral." This result is given
by Lommel in the third of the memoirs to which reference has been made.
5-6] MISCELLANEOUS THEOREMS 153
5*6. Continued fraction formulae.
Expressions for quotients of Bessel functions as continued fractions are
deducible immediately from the recurrence formula given by §3*2A); thus,
if the formula be written
Jv(z) \z\v
it is at once apparent that
\ ) 7 7~T\ = t
This formula is easily transformed into
B) Jv^ 1 1 - -1 «/m+«l±i(?)
. W ' J?_x (z) 1v\z - 2\v +1)/z - ... - 2 {v + mjlz - j;,+m (z) "
These results are true for general values of v; A) was discovered by
Bessel* for integral values of v. An equivalent result, duo to Schlomilchf, is
that, if Q,, {z) = Jv+l(z)/\}jZ Jv (z)}, then
KP) V, W - „ +1 _ J7+ 2 -7+8 - ... - v + m - 4 '
Other formulae, given by Lommel^, are
Jv+l(z) z z2 z" z" *J,+m+i(z)
D)
Jv(z)
W; Jv (z) + 2 (i; + 1) - 2 (v + 2) - ... - 2 (iJ + m) - ^,,+m B) "
The Bessel functions in all these formulae may obviously be replaced by any
cylinder functions.
It was assumed by Bessel that, when in -*• co, the last quotient may be
neglected, so that
J.(z) _\z\v \s*l\v(v+l)) \z*l[(v
JZJ—r
F)
r- 1
* Berliner Abh. AS'24), [18'2()]t p.})]. Formula B) neeron not to have been given by the earlior
writers; soo Encyclopedic den Sci. Math. n. 28, § .38, p. 217. A slightly different form is used by-
Graf, Ann. di Mat. B) xxin. A895), p. -17.
•(• Zeitschrift fttr Math, und Phys. 11. A857), p. 142 ; Schlouiilch considerud integral values of
v only.
% Studien tibev die Be&seVxchcn Functionen (Leipzig, 18C8), p. 5 ; see also Spitzer, Archiv der
Math, und Phys. xxx. A858), p. 332, and Giinther, Archiv der Math, und P/iys. Lvr. A874),
pp. 292—297.
154 THEORY OF BESSEL FUNCTIONS [CHAP. V
It is not obvious that this assumption is justifiable, though it happens'to
be so, and a rigorous proof of the expansion of a quotient of Bessel functions
into an infinite continued fraction will be given in § 9*65 with the help of the
theory of " Lommel's polynomials."
[Note. The reason why the assumption is not obviously correct is that, even though
the fraction pm\iw. tends to a limit as m-*-oo, it is not necessarily the case that n^m w+*
tends to that limit; this may be seen by taking
The reader will find an elaborate discussion on the representation of Jv (z)/Jv-i (z) as a
continued fraction in a memoir* by Perron, Miinchener Sitzungsberichie, xxxvu. A907),
pp, 483—504; solutions of Riccati's equation, depending on such a representation, have
been considered by Wilton, Quarterly Journal, xlvi. A915), pp. 320—323. The connexion
between continued fractions of the types considered in this section and the relations con-
connecting contiguous hypergeometric functions has been noticed by Heine, Journal filr
Math. lvii. A860), pp. 231—247 and Christoffel, Journal filr Math, lviii. A861),
pp. 90—92.
5*7. Hansen's expression for Jv{z) as a limit of a hypergeometric function.
It was stated by Hansenf that
A) J,(,)- lim -
/l
We shall prove this result for general (complex) values of v and z when X and
H tend to infinity through complex values.
If X —1/5, n = 1/rj, the (m + l)th term of the expansion on the right is
This is a continuous function of 8 and 7); and, if S0,t]0 are arbitrary positive
numbers (less than 2 | z I), the series of which it is the (m + l)th term con-
conrH.
| I ( )
verges uniformly with respect to 8 and 7} whenever both | 8 | <S0 and 1771 )
For the term in question is numerically less than the modulus of the (w + 1 )th
term of the (absolutely convergent) expansion of
and the uniformity of the convergence follows from the test of Weierstrass.
Since the convergence is uniform, the sum of the terms is a continuous
* This memoir is the subject of a paper by Nielsen, Miinchener Sitzungsberichte, xxxvm.
A908), pp. 85—88.
+ Leipziger Abh. 11. A855), p. 252 5 see also a Halberstadt dissertation by F. Neumann, 1909.
[Jakrbuch Uber die Fortsehritte der Math. 1909, p. 575.]
5-7,5*71] MISCELLANEOUS THEOREMS 155
function of both the variables (B, rj) at @,0), and so the limit of the series is
the sum of the limits of the individual terms; that is to say
lim (**} - F (l 1 • v + 1 • - Z*
\n — o/
and this is the result stated.
5'71. Bessel functions as limits of Legendre functions.
It is well known that solutions of Laplace's equation, which are analytic
near the origin and which are appropriate for the discussion of physical
problems connected with a sphere, may be conveniently expressed as linear
combinations of functions of the type
rnPn (cos 0), rnPnm (cos 0) °°S m <j>;
Sill
these are normal solutions of Laplace's equation when referred to polar
coordinates (r, 0, <f>).
Now consider the nature of the structure of-spheres, cones and planes
associated with polar coordinates in a region of space at a great distance from
the origin near the axis of harmonics. The spheres approximate to planes and
the cones approximate to cylinders, and the structure resembles the structure
associated with cylindrical-polar coordinates; and normal solutions of Laplace's
equation referred to such coordinates are of the form (§ 4'8)
e-ikzJm(kp) . vi(b.
r sin ^
It is therefore to be expected that, when r and n are large* while 9 is small
in such a way that r sin 0 (i.e. p) remains bounded, the Legendre function
should approximate to a Bessel function; in other words, we must expect
Bessel functions to be expressible as limits of Legendre functions.
The actual formulae by which Bessel functions are so expressed are, in
effect, special eases of Hanson's limit.
The most important formula of this type is
A) lim Pn (cos-)=/„(*).
This result, which hccuis to have been known to Neumannt in 1862, has been investi-
investigated by Mohlor, Journal fur Math. Lxvm. A868), p. 140; Math. Ann. v. A872), pp. 136,
141—144; Heine, Journal fur Math. lxix. A869), p. 130; Raylcigh, Proc. London Math.
Soo. ix, C1878)> 1>P- 61—64 ; Proc. Royal Hoc. xcn. A, A916), pp. 433—437 [Scientific Papers,
i. A899), pp. 338—341 ; vi. A920), pp. 393—397]; and Giuliani, Giorn. di Mat. xxn. A884),
pp. 236—239. The result ban been extended to generalised Lcgundre functions by Heine
and Raylcigh.
It has usually been assumed that n tends to infinity through integral
values in proving A); but it is easier to prove it when n, tends to infinity as
a continuous real variable.
* If ?i were not large, the approximate formula for Pnm (cos 6) would be (8him0)/»il.
+ Cf. Journalfilr Math. lxii. A863), pp. 36—49.
156 THEORY OF BESSEL .FUNCTIONS [CHAP. V
We take Murphy's formula
Pn (cos zjn) = aFj (- n, «• +1; 1; sin'2 \zjn);
and the reasoning of the preceding section is applicable with the slight
modification that we use the inequality
when j z | ^ 2 | n \, and then we can compare the two series
2F, (- n, n + 1; 1; sin2 \z\n\ .F, A/fi,, l/*0 +1; 1; ^8021 z |«),
where So is an arbitrary positive number less than § | z \~x dnd the comparison
is made when \n\> l/80. The details of the proof may now be left to the reader.
When n is restricted to be a positive integer, the series for Pn (cos z/n)
terminates, and it is convenient to appeal to Tannery's theorem * to complete
the proof. This fact was first noticed by Giuliani; the earlier writers took for
granted the permissibility of the passage to the limit.
In the case of generalised Legendre functions (of unrestricted order m),
the definition depends on whether the argument of the functions is between
¦f1 and — 1 or not; for real values of cg (between 0 and tt) we have
n ™ cos - ) = -. . :,¦ 2^i (— ft) w +1; m + 1; sin3 ? cc n),
\ 11/ F(m + 1) v
so that
B) lim »»Pn-« (cos ^ = /m (a;),
but otherwise, we have
Pn~m (cosh ~) = ta^2^^ oFi (- n, n +1; m + ¦ 1 ; - sinh2 \ z/n),
so that
C) lim nmPn-m (cosh -) = Jm («).
The corresponding formula for functions of the second kind may be deduced
from the equation which expresses! Qnm in terms of Pnm and Pn~m; it is
D) lim 2n(m + ri)nr $"* V°sh n) = Km(^)-
This formula has been given (with a different notation) by Heine:};; it.is most
easily proved by substituting the integral of Laplace's type for the Legendre
function, proceeding to the limit and using formula E) of § 6'22.
* Cf. Brornwich, Theory of Infinite Series, § 49.
+ Cf. Barnes," Quarterly Journal, xxxix. A908), p. 109 ; the equation is
in Barnes' notation, which is adopted in this work.
t Journal fUr Math. lxiz. A868), p. 131.
5-72] MISCELLANEOUS THEOBEMS 157
Another formula, slightly different from those just discussed, is
<«> Km P.
this is due to Laurent*, and it may be proved by using the second of Murphy's
formulae, namely
Pn (cos 0) — cos'1 \0. ^ (- n, - n; 1; - tan2 \6).
[Note. The existence of the formulae of this section must be emphasized because it
used to be generally believed that there was no connexion between Legendre functions and
Bessol functions. Thus it was stated by Todliuntor in his Elementary Treatise on Laplace's
Functions, Lame's Functions and BcsseVs Functions (London, 1875), p. vi, that " these
[i.e. Bessel functions] are not connected with the main subject of this book."]
5*72. Integrals associated luith Melder's formula.
A completely different method of establishing the formulae of the last
section was given by Mehler and also, later, by Bayleigh ; this method depends
on a use of Laplace's integral, thus
1 fn
1\ (cos 6)-- (cos 8 + i sin 6 cos 6)n d6
1 f"
— _j
7T .' 0
Since
n log (cos (z/n) +¦ % sin (z/n) cos (f>) -*- iz coa §
uniformly as n ¦->- oo when 0 ? 0 < 7r, we have at once
lim Pn (coa zjn) - f eizcos¦ dej) = Jo {2).
Heinej" and de Ball;]: have made similar passages to the limit with integrals
of Laplace's type for Legend re functions. In this way Heine has defined
Bessel functions of the second and third kinds; reference will be made to his
results iu § (r22 when we deal with integral representations of Yv(z).
Moliler ha.s also given a proof of his formula by using the Mchlor-Dirichlct integral
1 n (OOH 0) _ -¦ j ^ -
If ?«/>=>!/¦, it may be wliewn that
but the pa-saago to the limit })resci)tH some little difficulty bccau.se the integral is an im-
improper integral.
Various formulae have been given recently which exhibit the way in which
* Joumal </e Math. C) 1. A875), pp. 384—385; the formula actually given by Laurent is
erioneous on account of an arithmetical error.
t Journal fiir Math. lxix. }18G8), p. 181. See also Sharpe, Quarterly Journal, xxtv, A890),
pp. 383—386.
X Asir. Nacli. exxvni. A891), col. 1—4.
158 THEORY OF BESSEL FUNCTIONS [CHAP. V
the Legendre function approaches its limit as its degree tends to infinity.
Thus, a formal expansion due to Macdonald* is
A) Pn-™(cos0)
«(n+?rm (cos \ey™ [Jm («)
+ sin4 \6 {^x J^+a(x) - Jm+2 (a) +$xr1 Jw+1 (a?)} + ...],
where a? = Bn +1) sin \0.
Other formulae, which exhibit an upper limit for the error due to replacing
a Legendre function of large degree by a Bessel function, aref
B) Pn (cos 7}) ± iir~l Qn (cos rj)
= V(sec tf). «±(»+««i-tM,) ryo {(n + ^ tan*/} + %Y0 {(n +1) tan ^J]
v)
D) Qn (cosh ?) = e-(^+i)<f-tanh « ^(sech ^ . ^o ^(n + $ tann |j
where, in B), 0 ^ rj < ^ir, and, in C) and D), f ^ 0; the numbers 9Xl 62, 6% are
less than unity in absolute magnitude, and n may be complex provided that
its real part is positive. But the proof of these results is too lengthy to be
given here.
5' 73. The formulae of Olbricht
The fact that a Bessel function is expressible by Hansen's formula as a
limit of a hypergeometric function has led OlbrichtJ to investigate methods
by which Bessel's'equation is expressible as a confluent form of equations
associated with Eiemann's P-functions.
If we take the equation
of which a fundamental system of solutions is the pair of functions
and compare the equation with the equation defined by the scheme
!a, b, c, \
«, A 7, *[.
«'. 0, 7. >
* Proc. London Math. Soe. B) xm. A914), pp. 220—221; Borne associated results had been
obtained previously by the same writer, Proc. London Math. Soc. xxxi. A899), p. 269.
+ Watson, Trans. Gamb. Phil'. Soc. xxn. A918), pp. 277—308; Measenrjer, xlvu. A918),
pp. 151—160.
X Nova Acta Caes.-Leop.-Acad. (Halle), 1888, pp. 1—48.
5-73] MISCELLANEOUS THEOREMS 159
namely
fry | fl-tt-tt^ 1 -fi-fi' ^ l-Y-y|dy
|
— a 2 — 6 z — c ) dz
x \act'(a-b)(a-c) | ffff F - c) F ~ a) t 77' (c - a) (c -
{ -2 — a z — b z — c
(z - a)(z— b) (z — c) '
we see that the latter reduces to the former if
a = 0, a— v — fi, a' = — v — p,
while b, c, fi, fi', 7, 7' tend to infinity in such a way that fi + fi' and 7 H- 7'
remain finite (their sum being 2/j. + 1) while fifi' =77' = \b* and b + c — O.
We thus obtain the scheme
f 0, 2ifi, -2ifi, j
liin Pi v-fi, fi, 7, z\,
l-z/-/i, -fi, 7', J
where 7, 7' = /i + ^ ± ^{0"- + ?)a + /3al-
Another similar scheme is
{0, ifi, 00, )
v-fi, fi, 7, z\
-v-fi, -fi, <y', J
with the same values of 7 and 7' as before.
A scheme for Jv (z) derived directly from Hansen's formula is
( 0, oo, -4a/9, >,
(aAZZ) [-\V) fi-\v, v+l-a-fi. J
Olbricht has given other schemes but they are of no great importance and
those which have now been constructed will be sufficient examples.
Note. It has been observed by Haentzsohcl, Zeitschrift fiir Math, und Pkys. xxxi.
A886), p. 31, that the equation
du*
whoee solution (§ 4-3) is k^ (Aw), may be derived by confluence from Lamp's equation
when the invariants g2 and ^3 of the Weierstrassian elliptic function arc made to tend to
zero.
CHAPTER VI
INTEGRAL REPRESENTATIONS OF BESSEL FUNCTIONS
6*1. Generalisations of Poisson's integral.
In this chapter we shall study various contour integrals associated with
Poisson's integral (^ 23, 3'3) and Bessel's integral (§ 2*2). By suitable choices
of the contour of integration, large numbers of elegant formulae can be obtained
which express Bessel functions as definite integrals. The contour integrals will
also be applied in Chapters vii and viii to obtain approximate formulae and
asymptotic expansions for Jv (z) when z or v is large.
It happens that the applications of Poisson's integral are of a more
elementary character than the applications of Bessel's integral, and accordingly
we shall now study integrals of Poisson's type, deferring the study of integrals
of Bessel's type to § 6*2. The investigation of generalisations of Poisson's
integral which we shall now give is due in substance to Hankel *.
The simplest of the formulae of § 3'3 is § 3*3 D), since this formula contains
a single exponential under the integral sign, while the other formulae contain
circular functions, which are expressible in terms of two exponentials. We
shall therefore examine the circumstances in which contour integrals of the type
eiztTdt
are solutions of Bessel's equation; it is supposed that T is a function of t but
not of z, and that the end-points, a and b, are complex numbers independent
of z.
The result of operating on the integral with Bessel's differential operator
Vti denned in § 3\L, is as follows:
V, \zv \ eizt Tdt\ = zv+* \ elzt T{\-12) dt + Bv + l)izv+>
[ J a ) J a J
eizi Ttdt
* Math. Ann. i. A869), pp. 473—485. The discussion of the corresponding integrals for Iv(z)
a&d Kv{z) is due to Sohlafli, Ann. di Mat. B) i. A868), pp. 232—242, though Schlafli's results
are expressed in the notation explained in § 4-15. The integrals have also been examined in great
detail by Gubler, Zurich VierteljahrsschrLft, xxxm. A888), pp. 147 —172, and, from the aspect of
the theory of the linear differential equations which they satisfy, by Graf, Math. Ann. xlv. A894),
pp. 235—262; lvi. A903), pp. 432—444. See also de la Vallee PouBBin, Ann. de la Soc. Sci. de
BruxelUs, xxix. A905), pp. 140—143.
6-1]
INTEGRAL REPRESENTATIONS
161
by a partial integration. Accordingly we obtain a solution of Bessel's equation
if T, a, b are so chosen that
%j\T(?- 1)} =- Bz/ +1) Tt, IV* T(V - 1I* = 0.
The former of these equations shews that T is a constant multiple of
(t' — iy-i, and the latter shews that we may choose the path of integration,
either so that it is a closed circuit such that eizt(t" —1)" + * returns to its
initial value after t has described the circuit, or so that efat(i2- 1)" + * vanishes
at each limit.
A contour of the first type is a figure-of-eight passing round the point
t = 1 counter-clockwise and round t = — 1 clockwise. And, if we suppose
temporarily that the real part of z is positive, a contour of the second type is
one which starts from + ooi and returns there after encircling both the points
— 1, + 1 counter-clockwise (Fig. 1 ami Fig. 2). If we take a, b = ± 1, it is
Pig. 2.
necessary to suppose; that. R(v -\- !,)>(), and we merely obtain Poisson's
integral.
To make the many-valued function (?'- — 1 )"""* definite*, we take, the phases
of i — 1 and t+1 to vanish at the point A when? the contours cross the real
axis on the right of t-1.
We therefore proceed to examine the contour integrals
•(l-h ( )
zv etzt (i9 -])"-* dt, zv
J A J +• c
eizt
f - I)"~J dt.
* It is supposed that y has not one of the vuIuoh \, %, J, ... ; for then the intugrands &vcanalytic
at ±1, and both integrals vanish, by Canohy's theorem.
w. u. if.
11
162 THEORY OF BESSEL FUNCTIONS [CHAP. VI
It is to be observed that, when R (z) > 0, both integrals are convergent,
and differentiations under the integral sign are permissible. Also, both
integrals are analytic functions of v for all values of v.
In order to express the first integral in terms of Bessel functions, we
expand the integrand in powers of z, the resulting series being uniformly
convergent with respect to t on the contour. It follows that
ro=O '"¦:
Now tm (t2 — II""* is an even or an odd function of t according as m is even
or odd; and so, taking the contour to be symmetrical with respect to the origin,
we see that the alternate terms of the series on the right vanish, and we are
then left with the equation
zv I ' 4gtCP — l)w-*dt*=2 ? , Z 1 &**(&— ly^dt
Ja • «-o Bm)! Jo
= 2
m-o Bm)! Jo
on writing t = \/u; in the last integral the phases of u and u — 1 vanish when
u is on the real axis on the right of u = 1.
To evaluate the integrals on the right, we assume temporarily that
R(v + ^)>0; the contour may then be deformed into the straight line
from 0 to 1 taken twice; on the first part, going from 0 to 1, we have
u—l-=(l~u)e~tri, and on the second part, returning from 1 to 0, we have
u — 1 = A — u) e+ni, where, in each case, the phase of 1 — u is zero.
We thus get
Now both sides of the equation
-l(» - I)-* du = Kcos„
o
are analytic functions of v for all values of v\ and so, by the general theory of
analytic continuation*, this result, which has been proved when i2 {v + •?) > 0,
persists for all values of v.
* Modern Analysis, § 5-5. Tue reader will also find it possible to obtain the result, when
R (" + ?) <0, by repeatedly using the recurrence formula
Jo U ' v+n+b Jo U
which is obtained by integrating the formula
the integral is then expressed in terms of an integral of the same type in which the exponent of
m- 1 has a positive real part.
6-1] INTEGRAL REPRESENTATIONS 163
Hence, for all * values of v,
= 2" +l I T (i) r (V + |) COS V7T . Jv (z).
Therefore, if v + $ is not a positive integer,
A)
and this is Hankel's generalisation of Poisaon's integral.
Next let us consider the second type of contour. Take the contour to lie
wholly outside the circle \t\ = 1, and then (t-— I)"-* is expansible in a series
of descending powers of t, uniformly convergent on the contour; thus we have
v ; m=o rn ! 1 (| - i')
and in the series the phase of t lies between — %tt and +• 4-tt.
Assuming! the permissibility of integrating term-by-tcrm. we have
But
r<o-B
<*> (ixj) la
where a is the phase of z (between ± A77-); and, by a well-known formula*, the
last integral equals - 2tti/V Bhi — 2v -f 1).
Hence
,'(-! + , 1+) <*
when we use the duplication fonnula§ to express V Bm — 2y -H i) in terms of
r(h ~ v + m) and V (—/'+- in + 1).
* If v - \ is a negative integer, the BnnpleKl wuy of evaluating the intcynil in to ouloulute tho
residue of the integrand at m = 1.
t To justify the tcrm-by-term integration, obuerve that 1 ' | eizt dt \ ibcouvur^cul; lot
J 00 i
ita value be A". Siuce the expansion of (t*-l)"~l converges uniformly, it follows that, when wo
are given a positive number e, we cau find an integer Mo independent of t, Huoh that tho remainder
after M terms of the expansion does not exceed efK in absolute valuo when M 5: Jl/0. Wo then
have at once
ooi
aud the required result follows from the definition of the Bum of an infinite serios.
% Cf. Modern Analysis, § 12-22. § Cf. Modern Analysis, § 12-1».
11—2
164 THEOBY OF BESSEL FUNCTIONS
Thus, when B (z) > 0 and v + \ is not a positive integer,
[CHAP. VI
This equation was also obtained by Hankel.
Next consider
J ooiexp(-t«>)
where &>is an acute angle, positive or negative. This integral defines a function
of z which is analytic when
— \tr + ax arg z < \tt + <o)
and, if z is subject to the further condition that | arg#| < ^ir, the contour can
be deformed into the second of the two contours just considered. Hence the
analytic continuation of j-v{z) can be defined by the new integral over an
extended range of values of arg z\ so that we have
P/l_ ,A pvvi A ~
C)
e*{r-iy-*dt,
V
i 1 {%) J ooiexp(-ia.)
, where arg z has any value between — ^ir + a> and \ir + oo.
By giving « a suitable value*, we can obtain a representation of «/_„ (z)
for any assigned value of arg z between — it and tt.
When R (z)>0 and R (v + ?) >0 we may take the contour to be that ahewn in Fig. 3,
\/
/\
in which it is supposed that the radii of the circles are ultimately made indefinitely small.
By taking each straight line in the contour separately, we get
i) A -py-l dt
- t2y-l dt
+
1
-fiy-idt .
* If | w | be increased in a series of stages to an appropriate value (greater than
sentation of J-v (z) valid for any preassigned value of arg z may be obtained.
a repre-
repre6-11]
INTEGRAL REPRESENTATIONS
165
On bisecting the third path of integration and replacing t in the various integrals by it,
—/, ±t, t, it respectively, we obtain a formula for J_v(z), due to Gubler*, which corre-
corresponds to Poisson's integral for Jv(~); the formula is
D) J-^s^Tjv2+lfr(ii) [>Sinr („ e~J'
and, if this be combined with I'oisaon's integral, it is found that
E) Yv (z) = r (^? ^) [ J' sin (zt). A -««)*" 4 dt -
a formula which was also discovered by Gubler, though it had been previously stated by
Weber t in the case of integral values of v.
After what has gone before the reader should have no difficulty in obtaining a formula
closely connected with A), namely
F) Jv{z) = l
in which it is supposed that the phase of t'2 — 1 vanishes when t is on the real axis on the
right of t — \.
6*11. Modifications of Ilankel's contour integrals.
Taking R(z) > 0, let us modify the two contours of §6 into the contours
shewn in Figs. 4 and 5 respectively.
Fig. 4. Fit?. <r).
By making those portions of the contours which are parallel to the real
* Zurich Vicrtcljnhraschrift, xxxur. A88H), p. 155). Hue also Graf, ZciUchriJl fiir Hath, und
Phys. xxxviii. A803), p. 115.
f Journal filr Math, lxxvi. A873), p. 9. Cf. Hayashi, Nyt TUlsskrift for Malh. xxnr. n, (li)J^),
pp. 8G—(J0. The formula was examined in tho cuso ^ = 0 by Esohorioh, Moiiutshe/tc. filr Math,
und Phys. m. A892), pp. 142, 231.
166 THEOBY OF BESSEL FUNCTIONS [CHAP. VI
axis move off to infinity (so that the integrals along them tend to zero), we
obtain the two following formulae:
eizt (p _ ] y-j dt + eizt (t2 - 1)"-J dt
1+ooi ' J -1+ooi J
U(l+) f(-l+) _
efe« ^_ iy-h dt
l+ooi .'-1 + ooi
In the first result the many-valued functions are to be interpreted by taking
the phase of t2— 1 to be 0 at J. and to be + v at B, while in the second the
phase of t- — 1 is 0 at A and is —tt at B.
To avoid confusion it is desirable to have the phase of t" - 1 interpreted
in the same way in both formulae; and when it is supposed that the phase of
ir — 1 is + 7T at B, the formula A) is of course unaltered, while B) is replaced by
/qx T (,\ r <*-">•(*«)'
r r
L J
J-1+ooi
In the last of these integrals, the direction of the contour has been reversed
and the alteration in the convention determining the phase of i2 —1 has
necessitated the insertion of the factor e-2(K-sOrt
On comparing equations A) and C) with § 3'61 equations A) and B), we
see that
unless v is an integer, in which case equations A) and C) are not independent.
We can, however, obtain D) and E) in the case when v has an integral
value (n), from a consideration of the fact that all the functions involved are
continuous functions of v near v = n. Thus
¦#«A) (*) - Km HJu (z)
and similarly for Hn{2) (z).
6'12] INTEGRAL REPRESENTATIONS 167
As in the corresponding analysis of § 61, the ranges of validity of D) and
E) may he extended by swinging round the contours and using the theory of
analytic continuation.
Thus, if — -|7r < co < f 7r, we have
F) #„<» (,)
while, if — f 7r < « < \tt, we have
G) HM.T3JZIU f
provided that, in both F) and G), the phase of z lies between — \ir + <o and
\rr + o).
Representations are thus obtained of //„"> (z) when arg z has any value
between — it and 2tt, and of Hv® (z) when arg s has any value between
— 2-7T and rr.
If co be increased beyond the limits .stated, it i.s necessary to make the contours coil
round the singular points of the integrand, and numerical errors are liable to occur
in the interpretation oi' the integrals unless great eare ia taken. Weber, however, him
adopted this procedure, Math. Ann. xxxvn. A890), pp. 'Ill—412, to determine the for-
formulae of § 3-62 connecting IIv(l)(-z), IIvV)(-z) with //„<>>(s), HvW(z).
Notk. The formula l2iYv(z) = HvM{z) — IIvV)(z) makes it possible to oxpress Yv(z)'m
terms of loop integrals, and in this manner Ilankel obtained the scrioH of § 3\r>2 for
Yn (z); this investigation will not be reproduced in view of the greater simplicity of
Hankel'a other method which has been described in fcj 3-52.
6#12. Integral representations of functions of the third kind.
In the formula §6*1"J ((i) suppose that the phase of z has any given value
between — it and 2ir, and define /3 by the equation
arg z = <y + ft,
so that — \ir < ft < \ir.
Then we shall write
t- L = e-J^s-i (- u),
so that the phase of — n increases from — it + ?? to vr + ft as t describes the
contour; and it follows immediately that
A) //,<- 00 = 1LLLJ^2 • ( r« (_ tt)-» (i +1) dn,
where the phase of 1 + \iujz has its principal value. Again, if ft be a given
acute angle (positive or negative), this formula affords a representation of
Hv{1} (z) valid over the sector of the .z-plane in which
- \ir + ft < arg z<\tca- ft.
168 THEORY OF BBSSBL FUNCTIONS [CHAP. VI
Similarly*, from §611 G),
B) ? ^ ^
where ^9 is any acute angle (positive or negative) and
- 17r + ft < arg z < \tt + ?.
Sincef, by § 3-61 G), #_„« (s) = e"« jffrW (*), it follows that we lose nothing
by restricting v so that R (v + \) > 0; and it is then permissible to deform
the contours into the line joining the origin to oo expi/3, taken twice; for the
integrals taken round a small circle (with centre at the origin) tend to zero
with the radius of the circle |.
On deforming the contour of A) in the specified manner, we find that
C) #<»(,)
where /? may be any acute angle (positive or negative) and
R(v + \)>0, - \tt + 13 < arg z < |tt + J3.
In like manner, from B),
TTZj V(v + $) Jo V 1Z)
where ft may be any acute angle (positive or negative) and
R (v + |) > 0, - f 7T + j3 < arg z < \tr + /3.
The results C) and D) have not yet been proved when 2v is an odd positive integer.
But in view of the continuity near v=n + % of the functions involved (where » = 0, 1,2, ...)
it follows, as in the somewhat similar work of § 6*11, that C) and D) are true when v = \,
f, |, .... The results may also be obtained for such values of v by expanding the integrands
in terminating series of descending powers of z, atid integrating terni'by-term; the formulae
so obtained are easily reconciled with the equations of § 3'4.
The general formulae C) and D) are of fundamental importance in the
discussion of asymptotic expansions of J±v{z) for large values of \z\. These
applications of the formulae will be dealt with in Chapter vii.
A useful modification of the formulae is due to Schafheitlin§. If we take
arg z = /3 (so that arg zt is restricted to be an acute angle), and then write
u — iz cot 6, it follows that
rin^tf
* To obtain this formula, write
f There seems to be no simple direct proof that
is an even function of v.
X Cf. Modern Analysis, § 12*22. § Journal fur Math. cxrv. A894), pp. 31—44.
6'13] INTEGRAL REPBESENTATIONS 169
and hence that
•sin (*r
**
These formulae, which are of course valid only when iJ (v + |) > 0, were
applied by Schafheitlin to obtain properties of the zeros of Bessel functions
(§§ lS't^i—15*35). They were obtained by him from the consideration that the
expressions on the right are solutions of Bessel's equation which behave in the
appropriate manner near the origin.
The integral I e~uz «""& A + ?«)M~* dti, which is reducible to integrals of the types
J o
occurring in C) and D) when /j. — v, htx» been studied in soiho detail by Nielsen, Math. Ann.
lix. A904), pp. 89—102.
The integrals of thia section are alao discussed from the aspect of the theory of asymp-
asymptotic solutions of differential equations by limjtzew, Warschau Polyt. Inst. Nach. 1902,
nos. 1, 2 [Jahrbuch ilber die Fortschritte der Math. 1903, pp. 575—077].
6" 13. The geneudised Mehler-flonine integrals.
Some elegant definite integrals maybe obtained to represent Bessel functions
of a positive variable of a suitably restricted order. To construct them, observe
that, when z is positive (= w) and the real part of v is less than -|, it is per-
permissible to take co = \tr in § (M] ((>) and to take w = — \tt in § 611G), so
that the contours aro those shown in Fig. 0. When, in addition, the real part
of v is greater than — \, it is permissible to deform the contours (after the
manner of § 612) so that the first contour consists of the real axis from + ]
to + oo taken twice, while the second contour consists of the real axis from
— 1 to - oo taken twice.
1'ig. 6.
We thus obtain the formulae
^ 9 A - e*) fV' (t* - 1 )»-* dt,
P (a) = - rA~.-~l;-^- (I - e2'"-^) ffl-** (t* -1)""* dt,
7T-41 (^) ,'l
the second being derived from § 6*11 G) by replacing t by -1.
170 THEORY OF BESSEL FUNCTIONS [CHAP. VI
In these formulae replace v by — v and use the transformation formulae
given by § 3*61 G). It follows that, when x > 0 and - \ < R (v) < |, then
A) H" (*) -^j—j^jj-^j j i — ^,
so that
- v) r
Of these results, C) was given by Mehler, J/aitA.. Ann. v. A872), p. 142, in the special
case v-=0, while Sonine, Math. Ann. xvi. A880), p. 39, gave both C) and D) in the same
special case. Other generalisations of the Mehler-Sonine integrals will be given in §• 6*21.
6'14. Symbolic formulae due to Hargreave and Macdoncdd.
When R (z) > 0 and R (v + §) > 0, it ia evident from formula § 6'11 F) that
tr(i)/^— \iz)" j fii*tC\—ti'V-idt
r(v+t)T(t) J l+cci
where the phase of 1 — ft lies between 0 and — \n.
If D denotes (dfdz) and/is any polynomial,-then
and so, when v+^ is a positive integer, we have
JM
When i/ + ^ is not a positive integer, the last expression may be regarded as a symbolic
representation of HJM B), on the understanding that / (D) (e±«/s) is to be interpreted as
Consequently
M
and similarly
so that
C)
D\ Y (z) {W (I l D^-h ~
6-14,6-15] INTEGRAL REPRESENTATIONS 171
The series obtained from D) by expanding in ascending powers of D does not converge
unless it terminates; the series obtained in a similar manner from C) converges only
when R(v)>\.
The expressions on the right of C) and D), with constant factors omitted, were given
by Hargrcave, Phil. Trans, of the Royal Soc. 1848, p. 36 as solutions of Bessel's equation.
The exact formulae are duo to Macdonald, Proc. London Math. Soc. xxix. A898), p. 114.
An associated formula, valid for all values of v, is derivable from § 6*11 D). If n is any
positive integer, we see from tho equation in question that
J i+*«
71111 ('*)
so that
A similar equation hold.s for the other function of the third kind, and so
This result, proved when R(z)>i), is easily extended to all values of z by the theory of
analytic continuation; it was discovered by Sonino, Math. Ann. xvi. A880), p. 66, when
v = ?i, and used by Stein thai, Quarterly Journal, xvm. (L882), p. 338 when v = n+h; in the
case when v = n + i the result was givon slightly earlier (without the use of the notation
of Beasel functions) by Glaisher, Proc. Cavih. Phil. Soc. m. A880), pp. 269—271. A proof
basod on arguments of a physical character has boon given by llavclock, Proc. London
Math. Soe. B) n. A904), pp. 124—125.
6*15. Sclddjii's* integrals of Poissoti's type for Iv{z) and Kv{z).
If we take co = \ir in § 6*1 C) and then replace z by iz, wo find that, when
! arg * | < \ir,
r (% ) i (l
and the phase of t2 — 1 at the point where t crosses the negative real axis is — 2tt.
Fig. 7.
If we take R(v +^)>0 to secure convergence, the path of integration
may be taken to be the contour of Fig. 7, in which the radii of the circles
may be made to tend to zero. We thus find the forraulaf
J_p (z) = liizi^l^-. [A _ <r—0 ( V< (f - 1)-* dt
+ t (e-"^ + e~avni) [ e-zt A - i3)""* dt ,
* Ann. di Mat. B) i. A8E8), pp. 239—241. Schliifli obtained the results A) and B) direofcly
by the method of § 6-1. t Cf. Serret, Journal de Math. ix. \1844), p. 204.
172 THEORY OF BESSEL FUNCTIONS [CHAP. VI
in which the phases of t2 — 1 and of 1 — t2 are both zero. Now, from § 3*71 @),
we have
B) /»=
T^Twii) r.r(l - ^*¦
and so
C) /_ (.) -1. (,) - ?&=&??" W />- (' - 1^ *
that is to say*
D) Kv 0) = ~$^j^ jV« (*> - 1)-* <ft,
whence we obtain the formula
E) 7C (*) = rr
a result set by Hobson as a problem in the Mathematical Tripos, 1898. The
formulae are all valid when R(v + J)>0 and ;arg.2J< \tr. The reader will
find it instructive to obtain D) directly from § 611 F).
6*16. Basset's integral for Kv (xz).
When x is positive and z is a complex number subject to the condition
| arg z j < \tt, the integral for H{^v{xze^1) derived from § 611 F) may be written
in the form
Now, when R(v)~^ — \, the integral, taken round arcs of a circle from p to
p giitri-iargz^ ^en(js ^0 Zero as p -*» oo , by Jordan's lemma. Hence, by Cauehy'a
theorem, the path of integration may be opened out until it becomes the line
on which R (zt) — 0. If then we write zt = iu> the phase of — (uPfz2) — 1 is — tt
at the origin in the u-plane.
It then follows from § 3'7 (8) that
TV / \ 1 * — JL utr» TT (I.1 / A-rvV \
e~xzt dt
ar(t)
_r(-v+i-).B^
and so we have Basset's formula
valid when R (v + |) > 0, « > 0, | arg z\<\ir The formula was obtained by
Bassetf, for integral values of v only, by regarding K0(x) as the limit of
* The integral on the right was examined in the case f=0 by Riemann, Ann. der Phy-uk und
Chemie, C) xcv. A855), pp. 130—139.
t Proc. Camb. Phil. Soc. vi. A889), p. 11; Hydrodynamics, n. (Cambridge, 1888), p. 19.
6'16, 6*17] INTEGRAL REPRESENTATIONS 173
a Legendre function of the second kind and expressing it by the corresponding
limit of the integral of Laplace's type (Modern Analysis, § 15'33). The formula
for Kn (xz) is obtainable by repeated applications of the operator —j-.
zctz
Basset also investigated a similar formula for /„ (xz), but there is an error
in his result.
The integral on the right in A) was studied by numerous mathematicians before Basset.
Among these investigators were Poisson (ace § 6'32), Journal de I'ltcole Folgtechniqne, IX.
A813), pp. 239—241; Catalan; Journal de Math. v. A840), pp. 110—114 (reprinted with
some corrections, Mem. de la Soc. R. des Sci. de Liege, B) xn. A885), pp. 26—31); and
Serret, Journal 'de Math. vni. A843), pp. 20, 21; ix. A844), pp. 193—210; Schlomilch,
Analytischen Stvdien, n. (Leipzig, 1848), pp. 96—97. These winters evaluated the integral
in finite terms when v + A is a positive integer.
Other writers who must be mentioned are Malra.stdn, A'. Svcnstcn, V. Akud. Handl. lxii.
A841), pp. 6f> —74 (see $ 7'23); Svanbcrg, Nooa Ada Reg. Soc. Sui. Upsala, x. A832), p. 232 ;
Leslie Ellis, Trans. Ca/u.b. Phil. Sue, vni. A849), pp. 213-210; Euuepor, Math. Ann. VI.
A873), pp. 360—30;") ; Glaisher, Phil. Trans, of the Royal Soc. clxxii. A881), pp. 792—
815; J. J. Thomson, Quarterly Journal, xvur. A882), pp. 377—381; Coate.s, Quarterly
Journal, xx. A885), pp. 2f>0—2(iO; and Oltmmare, Comptcs Jtendus de VAxsoo. Fmnpaise,
xxiv. A895), part u. pp. 167—171.
The laat named writer proved by contour integration that
j
cos .nt .dii _ (-)"-' 7T
Jk* + z*? " 2^' .'{n- I)!
•"-'(l+zO".
The. former of these results may be obtained by differentiating the equation
.da Tre~'rs^v
and the latter is tlion obtainable by using Lagrang«'s expansion.
6*17. Wlnttdker'fi* yenerulisations of llavkel's integrals.
Formulae of the type contained in § 32 suggest that solutions of Bessel's
equation should be constructed in the form
zi ( V' Tdt.
It may be shewn by the methods of § (y I that
and so the integral is a solution if Tin a solution of Lcgondre's equation for
functions of order v— \ and the values of the integrated part are the same at
each end of the contour.
* Proc. London Math. Soc. xxxv. A903), pp. 198—20G.
174 THEORY OF BESSEL FUNCTIONS [CHAP. VI
If T be taken to be the Legendre function Qp_j (t), the contour may start
and end at +ooiexp(— ia>), where co is an acute angle (positive or negative)
provided that z satisfies the inequalities
— %ir + co <argz<\tc + co.
If T be taken to be Pv_j(<), the same contour is possible; but the
logarithmic singularity of Pv~i (t) at t~ — 1 (when v~\ is not an integer)
makes it impossible to take the line joining — 1 to 1 as a contour except in
the special case considered in §8*32; for a detailed discussion of the integral
in the general case, see § 10'5.
We now proceed to take various contours in detail
First consider
/¦(
J o
where the phase of t is zero at the point on the right of t = 1 at which the
contour crosses the real axis. Take the contour to lie wholly outside the circle
1*1 = 1 and expand Q „_$(?) in descending powers of t. It is thus found, as in
the similar analysis of § 6*1, that
(hz)* g40W (+,+)
17 L (?) ' octexp(-tui)
and therefore
B) /_, (z) = ^^tk- ** Q-,-i @ dt
If we combine these formulae and use the relation* connecting the two
kinds of Legendre functions, we find that
C) Hy'2> («) = ^4.
Again, consider
, ra+)
z*\ e^Qy^(t)dt;
J ooiexp(—fio)
this is a solution of Bessel's equation, and, if the contour be taken to lie on the
right of the line R(t) — a, it is clear that the integral is 0 [z* exp(— a\z\)} as
z—~ + <x>i. Hence the integral is a multiple of #„<•) (z). Similarly by making
z -*~ — oo i, we find that
J o
ooiexpt— iu)
* Tibe relation, discovered by Schlafli, iB
cf. Hobson, Phil. Trans, of the Royal Soc. cixxxyu. A896), p. 461.
6-2] INTEGRAL REPRESENTATIONS 175
is a multiple of Hv('l) (z). From a consideration of A) it is then clear that
Bs^<?--iO'+iW* "A+)
D)
i cxp(~iu>)
lri f(-1+>
<t* Q._ * it) dt,
¦ *i cx)()
Bz
E) 2T,« (*) - ^
and hence, by§ 3'61 combined with Schliifli's relation,
w w wl
w wl ($) cos y i«!»(/«)
this is also obvious from C).
The integral which differs from (G) only by encircling the point 4-1 instead
of — 1 is zero since the integrand is analytic iiuside such a contour.
In E) and (G), arg (t + 1) vanishes where the contour crosses the real axis
on the right of" — 1, and, in E), arg {t — L) is — tt at that point.
6*2. Generalisations of Bessel's integral.
We shall next examine various representations of Bessol functions by a
system of definite integrals ami contour integrals due to Sonine* and
Schlaflif. The fundamental formula which will be obtained is easily reduced
to Bessel's integral in the case of functions whose order i« an integer.
We take Hankel's well-known generalisation} of the second Eulerian
integral
1 i r (o-i-)
— _.__ I f-v-m-i A ,]f
(v+m + l) l2,7nJ-M
in which the phase of t increases from — nv to tt as i describes the contour, and
then
Consider the function obtained by interchanging the signs of summation
and integration on the right; it is
•(on , g,\
.-4*
This is an analytic function of z for all values of z, and, when expanded in
ascending powers oi' z by Maclaurin's theorem, the coellicients may be obtained
by differentiating with regard to z under the integral sign and making z zero
after the differentiations^. Hence
r'-'expu- .¦[ dt— y, —¦ •-
* Mathematical Collection, v. (Moscow, 1870) ; Math. Ann. xvi. A880), pp. 0—29.
t Ann. di Mat. B) v. A873), p. 204. His memoir, Math. Ann. in. AH71), pp. 134—149, should
also be consulted. In addition, see Graf, Math. Ann. lvi. A003), pp. -123—432, and Chexain, Johnx
Hopkins University Circulars, xiv. A895), pp. 20—21.
t Cf. Modern Analysis, § 12-22. § Of. Modern Analysis, §§ 5-32, 4-44.
176 THEOEY OP BESSEL FUNCTIONS [CHAP. VI
.and so we have at once
This result, which was discovered by Schlafli, was rediscovered by Sonine;
and the latter writer was the first to point out its importance.
When | arg z\<\ir, we may swing round the contour about the origin until
it passes to infinity in a direction making an angle arg z with the negative
real axis.
On writing t — \zu,y we then find that, when | arg z j < \nr,
This form was given in Sonine's earlier paper (p. 335).
Again, writing u = ew, we have
i roo+7rt
C) . /„(*) = «—. eZBiabw~vw dw,
Z7TI J oo—wi
valid when | arg 2 | <\ic. This is the first of the results obtained by Schlarli.
In this formula take the contour to consist of three sides of a rectangle, as
in Fig. 8, with vertices at oo — iri, — iri, tri and x + iri.
ni \
-171
Pig. 8.
If we write t + iri for w on the sides parallel to the real axis and ± id for w
on the lines joining 0 to + in, we get Schlafli's generalisation of BesseVs integral
1 f IT ' /* OO
D) /„($) = — cos{yQ - zsin &)dd — e~vt~zsinht dt,
7T J 0 IT Jo
valid when j arg z \ < \ir.
If we make arg z -*- + \tt, the first integral on the right is continuous and,
if R (v) > 0, so also is the second, and /„ (z) is known to be continuous. So D)
is still true when z is a pure imaginary if R{y) is positive.
The integrals just discussed were examined methodically by Sonine in his
second memoir; in that memoir he obtained numerous definite integrals by
appropriate modifications of the contour. For example, if \|r be an acute angle
(positive or negative) and if
6'21] INTEGRAL REPRESENTATIONS 177
the contour in C) may be replaced by one which goes from oo — (ir — ty) % to
oo + (tt + y!jf)i. By baking the contour to be three sides of a rectangle with
corners at oo — (rr — -v/>) i, — (tt — yfr) i, (ir + yfr) i, and oo + (nv + yfr) i, we obtain,
as a modification of D),
E) /, (z) = e—^ r e"81"*008"cos (v$-zcosyjr sin d) dd
7T J o
^ Jo
Again, if we take ^ to be an angle between 0 and ir, the contour in C) may
be replaced by one which passes from oo — (|-7r -f yfr) i to oo + (|tt 4- ty) i, and
so we find that
1 fJf
F) /, (z) = - cos (j/0 - ^ sin
^ C0S ^ - 1 w - Vty) dt,
_ j
"VJu
provided that | arg z\ is less than both -^ and nr — yfr.
When R(i') > 0 and z is positive (=#)> we niay take\^ = O in the last
formula, and get*
G) Jv(x)= - cos{yS — a;sin ^)dd + tf'^Hin (xuoaht — \vrr)dt.
Another important formula, derived from A), is obtained by spreading out
the contour until it is parallel to the imaginary axis on the right of the origin;
by Jordan's lemma this is permissible if lt(v) > — 1, and we then obtain the
formula
in which c may have any positive value; this integral is the basis of many of
Sonine's investigations.
Integrals which msnmblc those given in this section nro of importance in tho investiga-
investigation of the diffraction of light by a prism; hoo (Jarnlnw, Proc. London Math. Soc. xxx.
A899), pp. 121--] ill ¦ W. 11. Jackson, Proc. London Math. Soc B) I. A904), pp. 393—414;
Whipple, Proc. London Math. Soc. B) xvr. A917), pp. 94—111.
6*21. Integrals which represent functions of the second and third kinds.
If we substitute Schliirli's integral § 62 D) for both of the Bessel functions
on the right of the equation
Yv (z) = Jv (z) cot vtr — »/_„ (z) cusec vn,
we find that
rrr Trr
7r Yv (z) — cot vnv \ cos(vd — z&\T\6)d6-coseci>'Tr\ cos(r0 +sain 6)dd
h) Jo
- cos vir f*e~vl-zs[nh'¦dt-l evt-zahlhldt
Jo. i»
* Of. Gubler, Math. Ann. xlix. A897), pp. 583—584.
W. B. V. 12
178 THEORY OF BESSEL FUNCTIONS [CHAP. VI
Eeplace 6 by tt - 6 in the second integral on the right, and it is found on re-
reduction that
A) Yv (z) = - ("sin (z sin 0 - v6) d9-~ [*\evt + e~vt cos v-rr) e~zainht dt,
a formula, practically discovered by Schlafli (who actually gave the correspond-
corresponding formula for Neumann's function), which is valid when | argz\< ^tt.
By means of this result we can evaluate
irij _oo
when | arg z \ < -J-tt ; for we take the contour to be rectilinear, as in Fig. 9, and
ni
X o
Fig. 9.
write — t, id, t + iri for w on the three parts of the contour; we then see that
the expression is equal to
1 f« ] fit
±_l 6vt-zsmht(lt + _ ei
TTtJo TTJO
O
and this is equal to Jv (z) + iF,(z) from formula A) combined with §6D).
Hence, when | argz\<^tt, we have
B) H,® (z) = —.
•TTl
_«,
1 rao-m"
C) H® (z) = - —.A gisinh«-,« ^w>
T^J -oo
Formulae equivalent to these were discovered by Sommerfeld, Math. Ann. xlvii. A896),
pp. 327—357. The only difference between these formulae and Sommerfeld'a is a rotation
of the contours through a right angle, with a corresponding change.in the parametric
variable; see also Hopf and Sommerfeld, Archiv der Math, und Phys. C) xvm. A911),
pp. 1-16.
By an obvious change of variable we may write B) and C) in the forms
D) H,W (z) = —. tt-»-i exphe (u--)\ du,
1 f«> exp(—iri) ( / 1 \ ^
E) Hv& (z) - - -U «--i exp hi (u -~)\ du;
6*21] INTEGRAL REPRESENTATIONS ' 179
the contours are those shewn in Fig. 10, emerging from the origin and then
bending round to the left and right respectively; results equivalent to these
were discovered by Schlafli.
Fig. 10.
[Note. There is no difficulty in proving these results for integral values of v, in view
of the continuity of the functions involved ; cf. § Gil.]
We proceed to modify the contours involved in D) and E) to obtain the
analytic continuations of the functions on the left.
If co is an angle between — ir and tt such that | w — arg21 < \tt, we have
F)
and
1 roooxp
V J TTiJoexp/o
' exp hz[u--)\ du,
oxp
the contours being those shewn in Fig. 11 and Fig. 12; and these formulae
give the analytic continuations of the functions on the left over the range of
Fig. 11. Fig. 12.
values of z for which to — ^nr < arg#< «o 4- \tt\ and co may have any value
between * - nv and ir.
'' If | w I were iucreased beyond these limita, diflSculties would arise in the interpretation of
the phase of u.
12—2
180 ' THEOBY OF BESSEL FUNCTIONS [CHAP. VI
Modifications of B) and C) are obtained by replacing w by w ± \tri; it is
thus found that*
g—J VTtl I" CC •
(8) Hv^ (Z) = r-
eiz cosh w (josh vW,dw,
0
(9) W W—S-j.
provided that |argz\<\ir.
Formulae of special interest arise by taking z positive (=%) in F) and G)
and -1 < E {v) < 1. A double application of Jordan's lemma (to circles of
large and small radius respectively) shews that, in such circumstances, we may
take co= \ir in F) and w = — \ir in G). It is thus clear, if u be replaced by
+ iel, that
^ 7T» J_oo Tti JO
A1) iLW (a;) = - ^-^ ( e~i^oaht-vt fa _ f_ I g-tecosht cosh ^ . dt,
and hence, when x > 0 and — 1 < E (i/) < 1, we have
2 /*°°
A2) ,/„ (x) = - sin (a; cosh t — •jU7r) •cosn v^> • dt,
A3) Fv (x) = I cos (# cosh i — -J ptt) . cosh vt.dt\
TT J 0
and, in particular (cf. §63),
when we replace cosh t by i.
The last two formulae are due to Mehler, Math. Ann. v. A872), p. 142, and Sonine,
Math. Ann. xvi. A880), p. 39, respectively; and they have also been discussed by Basset,
Proc. Camb. Phil. Soc. vni. A895), pp. 122—128.
A slightly different form of A4) has been given by Hardy, Quarterly Journal, xxxn.
A901), pp. 369—384; if in A4) we write a? = 2 J(ab), xt = au+blu, we find that
A6) f" sin («« + -) ^ = Wo {2 J{ab)}.
Note. The reader will find it instructive to obtain A4) from the formula
n . .. 2 fw sin
combined with the formula § 5*71 A). This was Mehler's original method.
* Cf. Coates, Quarterly Journal, xxi. A886), pp. 183—192.
6-22] INTEGRAL REPBESENTATIONS 181
6*22. Integrals representing Iv{z) and Kv(z).
The modifications of the previous analysis which are involved in the dis-
discussion of Iv (z) and Kv (z) arc of sufficient interest to be given fully; they are
due to Schlafli*, though he expressed his results mainly in terras of the
function F (a, t) of §415.
The analysis of § 6 is easily modified ho as fco prove that
and hence, when | argz | < \nr,
C) IA z) = --}-. f" "e*11"'
The formulae B) and C) are valid when arg z = ± |7r if R (v) > 0.
If in C) the contour is taken to be three; sides of a rectangle with corners
at oo — iri, — 7ti, 7ri, oo + 7ri, it is found that
D)
so that
and hence,
E)
j
when
\i\rgz\
ezlimOcoHi'0d6
IT
|<.\7T,
e~ZC0Hlw cosh vt. dt,
Jo
^conhvt.dt,
(
Jo
a formula obtained by Schlaflif by means of somewhat elaborate transforma-
transformations.
From the. results just obtained, we can evaluate
when i arg^ \< lir. For it is easily seen that
ZTTl J - oo
* /(nn. di Mat. B) v. A873), pp. 190—205.
f Ann. di Mat. B) v. A873), pp. 109—201; tins formula was lined by Heine, Journal fur
Math, i.xix. A868), p. 131, aa the definition to whioh reference waa made in § 5'72.
182 THEORY OF BESSEL FUNCTIONS [CHAP. VI
and hence
2tsini/ir
Again, we may write E) in the form
G) Kv{z) =
and hence, by the processes used in § 6'21,
(8) Kv (z)=t vr«-> exp - \z (u + -) du,
when — 7r < «< 7r and — \tt + a>< arg ^ < \ir + <o.
Similarly
(9) e™ /_, (*) - e-"« Jv (^) = =^' m-"-1 exp U^ (i* + -) \du;
7T JOexp(-w+o,)i (V W/J
this is valid when 0 < w< 27r and — \ir + &>< arg ^ < |7r + w.
The contours for the formulae'(8) and (9) are shewn in Figs. 13 and 14
respectively.
Pig. 13. Fig. 14.
Further, when z is positive (= x) and — 1 < R (v) < 1, the path of integra-
integration in (8) may be swung round until it becomes the positive half of the
imaginary axis; it is thus found that
ri | v-"-1 exp {- \ix [v - -) \ dv,
Jo (. \ v/)
Kv (a) = |e-}
so that
A0) Kv(x) = %e-*v»ir e-ixa™ht~vt dt,
J
and, on changing the sign of v,
A1) Kv{x) =
6*23] INTEGRAL REPRESENTATIONS 183
From these results we see that
A2) 2coa$vir.Kv(a)) = l e-ixainht cosh vt.dt,
so that
1 f00
A3) Kv (x) = r— / cos (x sinh t) cosh vt. dt,
7 cosfvirJo
and these formulae are all valid when x > 0 and — 1 < R(v) < 1.
In particular
A4) Ko (x) = cos (.-«sinh 0 d« = -775-jriV>
.'o Jo v(" + J)
a result obtained by Mehler* in 1870.
It may be observed that if, in G), we make tho substitution hzel = T, we find that
A5) *„(*) = $ (i«)^exp {-r— } ~
provided that /i(s'-)>0. The integral on the right has been studied by numerous mathe-
mathematicians, among whom may be mentioned Poianon, Journal de VEcole Polytechniqne, ix.
(cahier 16), 1813, \\ 237; Ulaisher, British Association Report, 1872, pn. 15—17; Proc.
Camb. Phil. Sue. in. AH80), pp. 5—12; and Kaptoyn, Bull, des Sci. Math. B) xvr. A892),
pp. 41—44. Tho integrals in which v has the special values ? and \ wore discussed by
Euler, Inst. Gala. Int. iv. (Petersburg, 1794), p. 415; and, when v is half of an odd
integer, the integral has been evaluated by Legcndro, Exercicxs de Catcul Integral, I. (Paris,
1811), p. 366; Cauchy, Rvercires des Math. (Paris, 1826), pp. 54—56; and Schlomilch,
Journal fllr Math. xxxm. A84fi), pp. 2C8—280. Tho integral in which tho limits of inte-
integration art) arbitrary has boon examined by Binct, Co tuples Ilendun, xn. A841), pp. 958—
962.
6*23. Hardy s formulae for integrals of Du Bois Reyinond's type.
The integrals
TOO ?.2 F JO rfO.
sin t. sin — . t"~x dt, cos t. cos — . tv~l dt,
Jo t Jo t
in which x > 0, — 1 < R{v) < 1, have been examined by Hardyf as examples
of Du Bois Reyinond's integrals
I™ f(tfmt.t^dt,
Jo cos
in which f(t) oscillates rapidly as t -*- 0. By constructing a differential equation
of the fourth order, Hardy succeeded in expressing them in terms of Besael
functions; but a simpler way of evaluating them is to make use of the results
of §§6'21, 6-22.
* Math. Ann. xvnt. A881), p. 182.
+ Messenger, xl. A911), pp. 4=4—51.
184 THEORY Or BESSEL FUNCTIONS [CHAP. VI
If we replace t by o?e{, it is clear that
Too g,1 reo
sin t sin —. tv~l dt = x" sin (xel) sin (aer*). evt at
JO t J _oo
fe2ia;cosh« _|_ e~Uxcos\it _ giixuinht _ g-2issinhtj Qvt fit
— 00
^[ Bx) - Trie*"* i/(_2)r Ba-)
„ ()
and hence we have
A) I™ sintsin^ .tv-'dt = -r-~~i- [
Jo < 4sm|i/7rL
and similarly
B) [" v.os«cos j. t"-> dt - ^[V7r W-u B«) - ^ Ba?) + /_ Ba;) - /, Ba;)].
When v has the special value zero, these formulae become
C) rBin«sin?.^ = i
Jo t t
D) f °° cos t cos ^. ^ = - \nr Yo Ba?) + J5f0
Jo it
6'24. Theisinger's .extension of BesseVs integral.
A curious extension of Jacobi's formulae of § 2-2 has been obtained in the case of «/0 (x)
and Jx(x) by Theisinger, Monatshefte fur Math, und Phys. xxiv. A913), pp. 337—341; wo
Bhall now give a generalisation of Theisinger's formula which is valid for functions of order
v where - \ < v < |.
If a is any positive number*, it ia obvious from PoiBson's integral that
2 fi-'c"I' fi"
J (x) = ——v»*/ , , <?-aEsin 8 cos (x cos 6) sin2" 6dd
r(v+^)r(^) Jo v
+ r(p2,(!fwiv I ' (l-e-**««<>)cos(d
Now 2 I " A— e~c
Jo ¦
IT 1 _ g—OIBillfl
o sinh (a? Bin 6)
z-ljzy dz
-2 •. ,"Vi .-/--,ti sinh (-ta;?).
where the contour passes above the origin. Take the contour to be the real axis with an
indentation at the origin, and write z— ±tan faf> on the two parts of the contour; we thuB
find that the last expression is equal to
/i^l-expC-a.wcotrfI) . . . ... ,_. ,„„ , d
.-. - — . Y sin (x tan id>). eVWl cot2" d> -r
o sin(a;cot^>) ^ ~^ ^si
. f iv 1 - exp (axicot d>) .
+ i J r-~s
J a si
cos (i^ cot $-v1r)s
sm
= 4 f ** sin (i
Jo
* In Theisinger's analysis, a is au even integer.
6-24-6-31] INTEGRAL REPRESENTATIONS 185
and therefore
A) lii^iilii) Jv (A.) „/"*"¦ c-«x«in0 COH (,v coa 0) Hjn* flrffl
+ 2 fi\sin(tocot0)co3(^o(,t</,-^)Sin(A>-tan^c«)t^0 ^- .
Jo " ' sin (a?cot<]!>) ' Bin <j>
The transformation fails when v^?, because the integral round the indentation does
not tend to zero with the radius of the indentation. The form given by Theiainger in the
case v = l differs from A) beoau.se he works with ij 3*3 G) which gives
r (v—&) r CA'i Hir
B) —XTTTr-i 'h 0») = I " e-ax»in• .sin (.r cos 8) sin2" 0 cos 8d6
. . P17 . ,, , .> ,, . , . sin2(^tan-i0) ,,„ ., , dd>
+ i I sin (mx cot (i) cos (ifw.1 cot d)-vir) - ---= r-fr^ cot2" c/> -r—J-v,
Jo sin (#uot (/>) 'Hin2))!)
provided that §<d<$.
6'3. TAe equivalence of the integral representations of Kv{z).
Three different types of integrals which represent Kv{z) have now been
obtained in §§6M5D), 0-22E) and 010A), namely
_. I e-z™»htcosh vt.dt,
Jo
/r r (w 4-!}). {2z)v r* coh a,™. dtt
"(K)" x'V(\) Jo («» + *')•'+*•
The equality of the first and necond was directly demonstrated in 1871 by
Schliirli*; but Poishou proved the equivalence of the second and third as early
as 1815-1, while M alms ten gave a less direct proof of the equivalence of the
second and third in IK41. We proceed to describe the three transformations
in question.
61. tSchldflVs tranafonnufioH.
Wo first give an abstract of the analysis used by Schliifli, Ann. di Mat. B) v. A873),
pp. 19?)--201, to provo the relation
1\w)'(-,2?" t' «"s( (<2 - 1)"- * <it = [ " e~"™uo cosh v6d6
1 (" + 2) J ) Jn
which arises from a comparison of two of the- integral rnpresontationw of Kv (z), and which
may be established by analysis resembling that of $ 2'323.
We have, of course, to suppose that li (z) >0 to secure convergence, ami it is convenient
at first to tal<e+ - i < li (v) < 1.
* An earlier proof is duo to Kmntnor, Journal fiir Math. xvn. A837), pp. 228—242, but ifc h
much more elaborate tlian Schliiili's invusUgation.
I The result is established for larger values of R (i>) either by the theory of analytio continua-
continuation or by the use of rocurreuoo formulae.
186 THEORY OF BESSEL FUNCTIONS [CHAP. VI
Now define S by the equation
where x^l; and then> if t—x — (# -1) it, we have
"I f w [r,— \S\ v~i
«->(l-n)"-Hl 1
o
/"
Jo
on expandingthe last factor of the integrand in powers of u and integrating term-by-term.
Replacing x by cosh 6, we see that
so that, by a partial integration,
r(i) Jo vr(i) Jo
z
r(i-v)JO
dudt
-*' /""«-f«(*a-
the inversion of the order of the integrations presents no great theoretical difficulty, and
the transformation is established.
6'32. Poisson's transformation.
The direct proof that
is due to Poisson*, Journal de VEcole Polytechnique, ix. A813), pp. 239—241. The equation
is true when \axgz\<\ir, x>0 and R(p)> — ?, but it is convenient to assume in the
course of the proof that R (v) > \ and j arg z \ < {ir, and to derive the result for other values
of z and v by an appeal to recurrence formulae and the theory of analytic continuation.
If we replace t by a new variable defined by the equation v=<s"e~vi, we see that it is
sufficient to prove that
* See also Paoli, Mem. di Mat. e di Fit. della Soc. Italiana delle Sci. xx. A828), p. 172.
6-32,6-33] INTEGRAL REPRESENTATIONS 187
Now the expression on the left is equal to
/o jo (v* + zy+\"dtdu==]0 j0 s"~i Q^V {-H^2 + z2)}cos.vu.dsdu
= I I {exp (- sm2) cos #?t. du} .nv~\ exp (— sz2) ds,
Jo Jo
when we write t=s <>2+-22) and change the order of the integrations*.
Now / exp (- m'2) cos xu. du=\T (i) s- i exp (- %x*/s),
and so we have
which establishes the result.
[Note. It is evident that s^^ve-'/z^lvV/z. Tho only reason for modifying
1 fM
A J —00
by taking »asa parametric variable in to obtain an integral which is ostensibly of the
«anie form as the integral actually investigated by Poisson ; with his notation the integral is
I exp (— ./.•" - a*.v~ ") dx.]
Jo
6'33. Mulmslen's transformation.
Tho method employed by Malmstcnt in proving that, when fi{z)>Q and R(v)> -i,
then
P"r(i")J, {u*+z*y + h- r(,+i) J,
is not ko direct as the analysis of $$ 6*31, G-32, ina.sruuch an it involves an appeal to the
theory of linear differential equations. It is first shewn by Malnistdn that the three
expressions
cos (xu) du f" _ tl 2 _ 2, „ _. . /¦x ?(, . _ 2
a functions of .r, arc annihilated { by the opemtor
and that as %-*- +oo, the third is ^(e11) while the first and second are bounded, provided
that R (v) > 0. It follows that the .second and third expressions form a fundamental system
of solutions of the equation
Cf. Bromwioh, Theory of Infinite Series, § 177.
K. Srenska V. Akad. Handl. lxii. A841), pp. Co—74.
The reader should have no difficulty in supplying a proof of this.
188 THEORY OP BESSEL FUNCTIONS [CHAP. VI
and the first i8 consequently a linear combination of the secoud and third. In view of the
unboundednesB of the third as #-*-+<»> it is obvious that the first must be a constant
multiple of the second bo that
f °
jo
c _
where 0 is independent of x. To determine C, make x-*~0 and then
so that
aud the required transformation follows, when R(v)>0, if we use the duplication formula
for the Gamma function.
f '*" cos xu . du
An immediate consequence of Malmsten's transformation is that / -.- a'—r.r.n
J 0 \U -\-Z~)
expressible in finite termB; for it is equal to
IS
method of evaluating the integral is simpler than a method given by Catalan,
Journal de Math. v. A840), pp. 110—114; and his investigation is not rigorous in all its
stages. The transformation is discussed by Serret, Journal de Math. vni. A843), pp. 20,
21; IX. A844), pp. 193—216; Bee also Cayley, Journal de Math. xn. A847), p. 23E
{Collected Papers, I. A889), p. 313.]
6*4. Airy's integral.
The integral
r°°
cos (t3 ± at) dt
Jo
which appeared in the researches of Airy* "On the Intensity of Light in the
neighbourhood of a Caustic" is a member of a class of integrals which are
expressible in terms of Bessel functions. The integral was tabulated by Airy
by quadratures, but the process was excessively laborious. Later, De Morgan f
obtained a series in ascending powers of a? by a process which needs justification
either by Stokes' transformation (which will be explained immediately) or by
the use of Hardy's theory of generalised integrals^
* Trans. Gamb. Phil. Soc. vi. A838), pp. 379—402. Airy used the form
Cos \tr (m3 - mw) dw,
f
Jo
0
but this is easily reduced to the integral given above.
t The result was communicated to Airy on March 11, 1848; Eee Trans. Comb. Phil. Soc. vm.
A849), pp. 595—599.
J Quarterly Journal, xxxv. A904), pp. 22—66; Trans. Camb. Phil. Soc. xxi. A912), pp. 1—48.
6'4j INTEGRAL REPRESENTATIONS 189
Stokes observed* that the integral satisfies the differential equation
d"v . .
and he also obtained the asymptotic expansions of the integral for large
values of x, both positive and negative.
As was observed by Stokes (loc. cit. p. 187), thin differential equation can be reduced
to Bessel's equation ; cf. § 4*3 E) with 2q = 3. The expression of Airy's integral in terms of
Besael functions of ordorst + ^ was published first in a little-known paper by Wirtinger,
Berichtc des natur.-med. Vereins in .Innsbruck, xxm. A897), pp. 7—15, and later by
Nicholson, Phil. Mag. F) xvn. A909), pp. 6—17.
Subsequently Hardy, Quarterly Journal, xu. A910), pp. 226—240, pointed out the con-
connexion between Airy's integral and the integrals discussed in ^ 0*21, 6*22, and ho then
examined various generalisations of Airy'a integral (§§.10*2—10*22).
To evaluate Airy's integral+, we observe that it may be written in the form
- I exp (i7,:l + iirt) dt.
^ J -co
Now consider this integrand taken along two arcs of a circle of radius p with
centre at the origin, the arcs terminating at p, pe^1 and pe1"', pe*1 respectively.
The integrals along these arcs tend to zero asp -*¦ cc , by Jordan's lemma, and
hence, by Cauchy's theorem, we obtain Stokes' transformation
[ f co exp Jiri
foo [ fooexpjiri
cos (f ± xt) dt = ~\ exp (if ± irt) dt
J() ? J 00 HXp JtT1
I f [e^[ exp (- t-1 ± e^xr) + e *w exp (- r1 ± e" ^xr)} dr]
the contour of the second integral consists of two rays emerging from the
origin and the third integral is obtained by writing re^vl, re^vl for t on these
rays.
Now, since the resulting scries are convergent, it may be shewn that§
w - 0 m ¦
* Trim*. Ctnufi. J'/iil. Svc. ix. A8011), pp. IGli—187. [Math, mid PIiijh. Pn^-rx, n A883),
pj). 32U—349.] Hce also Stokes1 letter of May 1'2, 1848, to Airy, Sir (!. G. Stokcx, Memoir and
Scientific Correa-pondcnce, i\. (Cambrid^o, 1007), pp. 15'J—100.
t l-'or other occurrences of theso t'unctiouB, see Bayleigh, Phil. May. (G) xxvni. A914),
pp. 609—619; xxx. A915), pp. 829—388 [Scientific Papers, vi. A920), pp. 266—275; 341—349]
on stability of motion of a viscous fluid; also Weyl, Math. Ann. i-xviu. A910), p. 267, and, for
approximate formulae, §8*4*3 infra.
X The integral is convergent. Cf. Hardy, he. cit. p. 228, or de la Valloo Poubbiu, Ann. de la
Soc. Set. <te Jinixelles, xvt. A892), pp. 150—180.
§ Bromwich, Theory of Infinite iSeries, § 176.
190 THEOBY OF BESSEL FUNCTIONS [CHAP. VI
and so
f
m-o m\ Jo
= 5 5 (
_ r
This is the result obtained by De Morgan. When the series on the right
are expressed in terms of Bessel functions, we obtain the formulae (in which
x is to be taken to be positive) due to Wirtinger and Nicholson:
6*5. Batoned integral representations of Bessel functions.
By using integrals of a type introduced by Pincherle* and Mellinf, Barnea+
.has obtained representations of Bessel functions which render possible an easy
proof of Kuramer's formula of § 4-42.
Let us consider the residue of
- T Bm - s). (izy
at s = 2m 4- r, where r - 0,1, 2,.... This residue is (-)r (iz)im+rlr\, so the sum
of the residues is (—)mzlme~iz.
Hence, by Cauchy's theorem,
^T^T^ + mTTi) *'
if the contour encloses the points 0, 1, 2, .... It may be verified, by using
Stirling's formula that the integrals are convergent.
Now suppose that JR (*»)> — \, and choose the contour so that, on it,
R (v + s) > — ?. When this last condition is satisfied the series
? r Bm - s)
is convergent and equal to
* Eend. del E. Ittituto Lombardo, B) xix. A886), pp. 559—562 ; Atti della II. Ace ad. dei
Lineei, ser. 4, Efindtconfi, iv. A888), pp. 694—700, 792—799.
f Mellin has given a summary of hia researcheB, Math. Ann. lxviii. A910); pp. 305—337.
{ Camb. Phil. Tram. xx. A908), pp. 270—279. For a bibliography of researches on integrals
of this type, see Barnes, Proc. London Math. Soc. B) v. A907), pp. 59—65.
6*5] INTEGRAL REPRESENTATIONS 191
by the well-known formula due to Gauss. If therefore we change the order
of summation and integration * we have
r (\ -iz-SML f@+)r(-s)rp, + s + ?).(^)g^
Jv{z)e ~ a** L
T(v + i« + i)r(v + i* +1)•
The only poles of the integrand inside the contour are at 0, 1, 2, When
we calculate the sum of the residues at these poles, we find that
so that
A) J, (t) e-» =
which is Kummer's relation. In like manner, we find that
B) J, (z) e« = Y^T)liPl (V + *; 2i; + X
These formulae, proved when jK (v) > — \, are relations connecting functions
of v which are analytic for all values of v, and so, by the theory of analytic
continuation, they are universally true.
It is also possible to represent Bessel functions by integrals in which no
exponential factor is involved. To do this, we consider the function
qua function of 5. It has poles at the points
5 = 0, 1, 2, ...; - v, - v + 1, - v 4- 2, ....
The residue at s = m is
sin vir ' ?n\ V (v + m + 1)'
while the residue at s = — v + m is
sin vir' vi! V (v + in + 1)'
so that
C) vre-i^+n-t #„«) (Z) = - — I r (- v - s) V (- s) {\iz)v+w ds,
j&TT'l J
and, in like manner,
D) -/re*<"+'»« Hv<" (z) = - ^. f r (- v - s) r (- «) (- Iizy+°-» ds,
where the contours start from and return to + oo after encircling the poles of
the integrand counter-clockwise. When | arg iz \<\ir in C) or | arg (— iz) j < \ir
in D) the contours may be opened out, so as to start; from ocu and end at
— oo i. If we reverse the directions of the contours we find that
E) 7re-*("+1>« ff,121 0) = =i-. rc+c°V (- v - s) V (- s) (|»>)-+M rf»,
Z7TI J -c-aoi
* Cf. Bromwich, Theory of Infinite Series, § 170.
192 THEOEY OF BESSEL FUNCTIONS [CHAP. VI
provided that J arg iz I < \ir; and
F) 7rei<"+1)« H® (z) = ~ f""""""V (- v - s) T (- a) (- ^V)v+28 (fa,
provided that j arg (-iz) !<?•""> and, in each integral, c is any positive number
exceeding R (v) and the path of integration is parallel to the imaginary axis.
There is an integral resembling these which represents the function of the
first kind of order v, but it converges only when R(v) > 0 and the argument
of the function is positive. The integral in question is
G). ,(M
and it is obtained in the same way as the preceding integrals; the reader
will notice that, when j s | is large on the contour, the integrand is 0 (| s I""").
6*51. Barnes' representations of functions of the third kind.
By using the duplication formula for the Gamma function we may write
the results just obtained in the form
a) j (z)«.*»
Consider now the integral
in which the integrand differs from the integrand in A) by a factor which is
periodic in 5. It is to be supposed temporarily that 2v is not an integer and
that the path of integration is so drawn that the sequences of poles 0,1, 2, ...;
— 2v, 1. — 2v, 2 — 2v, ... lie on the right of the contour while the sequence of
poles — v — \, —v — \% -v — §, ... lies on the left of the contour. In the first
place, we shall shew that, if | arg iz j < f 7r, the integral taken round a semi-
semicircle of radius p on the right of the imaginary axis tends to zero as p -*¦ oo ;
for, if s — p ei9t we have
and, by Stirling's formula,
g
~ peie log Biz) - (v + p&*) (log p + id) + pei6 - % log Bir) ;
and the real part of this tends to — co when — %ir<6<lTr, because the dominant
term is - p cos 6 log p. When 6 is nearly equal to ± \ir, \ sin sir | is comparable
with \ exp [prr \ sin 61] and the dominant term in the real part of the logarithm
of s times the integrand is
p cos 8 log j Iz \ - p sin 8. arg 2iz - p cos 6 log p + p8 sin 8 + p cos 8- Ipir | sin 01,
and this tends to — <x> as p -*• co if j arg iz \ < §7r.
6*51] INTEGRAL REPRESENTATIONS 193
Hence s times the integrand tends to zero all along the semicircle, and so
the integral round the semicircle tends to zero if the semicircle is drawn so as
to pass between (and not through) the poles of the integrand.
It follows from Cauchy's theorem that, when j arg iz \ < §tt and 2v is not an
integer, then
may be calculated by evaluating the residues at the poles on the right of the
contour.
The residues of
r (- s) r (- 2u - s) r (v+s + d . {lizy
at s — m and s = — 2v 4- m are respectively
7T r (v + m +1). Biz)m _ 7T r (~v +m ¦+-\). Biz)~*v+m
sin tvrv m! V Bv + m + 1) ' sin Ivir m\ V (— tv + m + 1)
and hence
r' r (- *) r (- iv - «> r (v +«+ j>. B«)« <is
J -w1-
"- snT^-'¦r(i-2v)-^(i'1 l~2"; 2">
It follows that, when | arg is | < ilir,
B) i/,w(^) = e"ltt"VirI""u/l"n'li ^>ftV
7T-!
cri
and similarly, when ! arg (— w) j < I ir,
("^N H w(A— e~ ((>s f;7r '
x ["' r (~«) r(-2v-s) V(v+s + l).(~lizyds.
- OC (
The restriction that vis not to bo an integer maybe removed in the usual
manner by a limiting process, but the restriction that 2i> must not be an odd
integer cannot be removed, since then poles which must be on the right of the
contour would have to coincide with poles which must be on the left.
w. b. p.
13
in
cases
CHAPTER VII
ASYMPTOTIC EXPANSIONS OF BESSEL FUNCTIONS
7-1. Approximate formulae for Jv (z).
In Chapter in various representations of Bessel functions were obtained
the form of series of ascending powers of the argument z, multiplied in sonic
by log z. These series are well adapted for numerical computation when
^ is not large compared with 4(i/ + l), 4(i/ + 2), 4(i/ + 3), .... since the series
converge fairly rapidly for such values of z. But, when | z \ is large, the series
converge slowly, and an inspection of their initial terms affords no cluo to the
approximate values of Jv{z) and Yv(z). There is one exception to this .state-
.statement; when v + ? is an integer which is not large, the expressions for J±v (~)
in finite terms (§3-4) enable the functions to be calculated without difficulty.
The object of this chapter is the determination of formulae which render
possible the calculation of the values of a fundamental system of solutions of
Bessel's equation when z is large.
There are really two aspects of the problem to be considered ; (.lie invest.i-
gation when v is large is very different from the investigation when v i.s neH.
large. The former investigation is, in every respect, of a moro recondite
character than the latter, and it is postponed until Chapter vm.
It must, however.be mentioned that the first step towards the. solution ol'
the more recondite problem was made uy Carlini* some years before Poi.sson'.s-f-
investigation of the behaviour of JQ(x), for large positive values of .r, was
published.
The formal expansion obtained by Poisson was
/„(*)« — cos(tf-J-7r).-M—i-i?_ + i • 6 •& • ' _ I
\-7rx) I K i J \ 2!(8a;)« 4!(8«L "")
("I2 12 '¦}- <V~ l "
+ sm (a; - M. -V - —~-~ + I
V ? ; |l!8a: 3! (8a;)8 +'"*J '
when x is large and positive. But, since the series on the right are not con-
convergent, and since Poisson gave no investigation of the remainders in t,h<>
series, his analysis (apart from his method of obtaining the dominant term) is
to be regarded as suggestive and ingenious rather than convincing.
! C°niuer9enza ddla serie ch* «"« «fl« ooluzione delproblema di Keplero (Milan,
1617). An account of these investigations has already been given in § 1-4
t Journal de VEcole Poly technique, xu. (cahier 19), A823), pp. 350-
see
Functions (London, 1895), pp. 34—38.
7*1] ASYMPTOTIC EXPANSIONS 195
It will be seen in the course of this chapter that Poisson's aeries arc asymptotic; thin
has been proved by Lipschitz, Hankel, Sehlafli, Weber, Stioltjos and Barnes.
It must be mentioned that Poisson merely indicated tho law of formation of Hiioeessivo
terms of the series without giving an explicit expression for the gunoml tonn ; such an
expression was actually obtained by W. R. Hamilton* (cf. § 1'6).
The analogous formal expansion for Jy (x) is due to HaiiHo.nf; and a few
years later, Jacobij obtained the more general formula which is now usually
written in the form
Jn (#) ~ ( —) cos (x — -|n 7r — I rr)
yrrxJ [_
J Dna - 1«) D?i2 - 3") Dn9 - I") Dn9 - 3a) Dw« - 5*) D/ia - 7a)
( 2!"('8i)a + 4!(8^ "
- sin (^ -
These expansions i'orJ0(x) and ./, (.v) wm; uwjd by llan/stiu for purpowm of nunuirioal
computation, and a comparison of the results so obtained for isolated values of .v with Mje
results obtained from the ascending norioH 1<><1 Hanson to infer that tlid expansions, nltliough
not convergeut, could safely be used for purposes of computation §.
Two years before the publication of .Jacobi's c.x])ansion, PlanaH luid din-
covered a-method of transforming Paiwval'.s inLcgral which placed thcicxpan.sioii
of Ja(x) on a much more, satisfactory busi.sH. Hi.s work was followed by l.lw1
researches of Lipschitz**, who gave the first rigorous invcstigalion of I,lie
asymptotic expansion of J^[z) with the aid of \\\v. theory of contour integra-
integration; Lipschitz also briefly indicated how his results could Unapplied l.o ./„ (;),
The general formulae for J,.(z) and Yv{z), where /' haw any assigned (com-
(complex) value and z is large and complex, were obtained in the great memoir by
Hankel ft. written in 1868.
* Some information concerning W. It. HiitiiiUoii'H rorfoarohoH will \w found in Sir (Senriit'
Gabriel Stokes, Memoir and Scientific Correspondcnrt', i. (CamliridKO, M)(O), pp. 1110- ¦ I ilfi.
t Krmittelung tier absolutcn Stiirunijen [Schriftni tier Stornwurte Svrlninj], ((iol.liu, IHl.'t),
pp. ny—123.
%A8tr.Na.ch. xxvin. A849), col. «L. [O«. Math. lVeriw, vir. (lH')l), p. 17-1.1 Jmiol.i'n rtmiilt
is obtained by making the Bubatitutions
J2 . nin (* - 4«7r - |tt) = ( - lL»(»l-l)Hin x _ ( _ i jin(n- i; C()H ^
in the form quoted.
§ See n, note by Niemoller, Zeitschrift fUr Math, wid Phye. xxv. A8H0), pp. .]1- -4H.
II Mem. delta R. Accad. delle Sci. di Torino, B) x. (lB-ii)), pp. 275—292.
If Analysis of Plana's type wan used to obtain the aaymptotio oxpanmonH of J,, (z) and IV (s) l)y
ilcMahon, Annals of Math. via. A894), pp. 57—E1.
** Journal fttr Math. lvi. A859), pp. 189—19G.
tt Math. Ann. i. A869), pp. 467—501.
13—52
196 THEORY OF BESSEL FUNCTIONS [CHAP. VII
The general character of the formula for Yn(z) had been indicated by Lommel, Studien
iiber die Bessel'schen Functionen (Leipzig, 1868), just before the publication of Haukol'a
memoir; and the researches of Weber, Math. Ann. vi. A873), pp. 146—149 must also be
mentioned. •
The asymptotic expansion of Kv{z) was investigated (and proved to be
asymptotic) at an early date by Kummer*; this result was reproduced, with
the addition of the corresponding formula for /,, (z), by Kirchhoff f; and a little-
known paper by Malmst6n| also contains an investigation of the asymptotic
expansion of Kv (z).
A close study of the remainders in the asymptotic expansions of Jo (.?), Yo G^X ^ (x)
and Kd(%) has been made by Stieltjes, Ann. Sci. de VEcole norm. sup. C) in. A886),
pp. 233—252, and parts of his analysis have been extended by Callandreau, Bull, des &ci.
Math. B) xiv. A890), pp. 110—114, to include functions of any integral order; while
results concerning the remainders when the variables are complex have been obtained by
Weber, Math. Ann. xxxvn. A890), pp. 404—416.
The-expansions have also been investigated by Adamotf§, Petersbtirg Ann. Inst. polyt.
1906, pp. 239—265, and by Valewink|| in a Haarlem dissertation, 1905.
Investigations concerning asymptotic expansions of Jv (z) and Yv (z), when
\z\ is large while v is fixed, seem to be most simply carried out with the aid
of integrals of Poisson's type. But Schlaflill has shewn that a large number of
results are obtainable by a peculiar treatment of integrals of Bessel's typo,
while, more recently, Barnes** has discussed the asymptotic expansions by
means of the Pincherle-Mellin integrals, involving gamma-functions, which
were examined in §§ 6*5, 6*51.
7'2. Asymptotic expansions of H^ {z) and Hv® (z) after Hankel.
We shall now obtain the asymptotic expansions of the functions of the
third kind, valid for large values of \z\\ the analysis, apart from some slight
modifications, will follow that given by Hankelff.
Take the formula § 612 C), namely
valid when - \ir < j3 < \-rr and - \tr + /3 < arg z < |tt + /3, provided that
The expansion of the factor A + ^iujz)v-^ in descending powers of z is
* Journal filr Math. xvii. A837), pp. 228—242. + Ibid, xlviii. A854), pp. 348—370.
$ K. Svenska V. Akad. Handl. ixn. A841), pp. 65—74.
§ See the Jahrbuck iiber die Fortschritte der Math. 1907, p. 492.
II I6W.190S, p. 328. IT Ann. di Mat. B) vi. A875), pp. 1—20.
** Tram. Camh. Phil. Soc. xx. A908), pp. 270—279.
ft Math. Ann. i. A869), pp. 491—495.
7-2]
ASYMPTOTIC EXPANSIONS
197
but since this expansion is not convergent all along the path of integration,
we shall replace it by a finite number of terms plus a remainder.
For all positive integral values of p, we have*
It is convenient to take p so large that R (v — p — |) ^ 0; and we then choose
any positive angle 8 which satisfies the inequalities
The effect of this choice is that, when 8 is given, z is restricted so that
- 7T + 28 < arg z < 2-n- - 28.
When the choice has been made, then
ut
2iz
sin 8,
<7T,
for the values of t and u under consideration, and so
say, where Ap is independent of z.
On substituting its expansion for A + ^iujz)v'^ and integrating terra-by-
term, we find that
2\> .. , ,
Hto(z\-BY
" ^ ; \-irz)
where
{ fo<i - ^ * r
where jBp is a function of v, p and $ which is independent of z.
Hence, when R (v — p — |) < 0 and # (v + |) > 0, we have
(i) ff«•> W = (AI ^.-w-
when z is such that — tv + 2S ^ arg z <2ir — 2B, 8 being any positive acute
angle;,and the symbol 0 is the Bachmann-Landau symbol which denotes a
function of the order of magnitude f of z~v as | z \ -*¦ oo.
The formula A) is also valid when R (v — p — |) > 0; this may be seen by
* Of. Modern Analysis, § 5-41. The use of this form of the binomial expansion seems to bo
due to Graf and Gubler, Einhitung in die Theorie der BesseVschcn Funktionen, I. (Bern, 1898)»
pp. 86—87. Of. Whittaker, Modern Analysis (Cambridge, 1902), §161; Gibson, Proc. Edinburgh
Math. Soc. xxxvni. A920), pp. 6—9; and MaoRobert, ibid. pp. 10—19.
t Of. Modern Analysis, § 2-1.
198 THEORY OF BESSEL FUNCTIONS [CHAP. VII
supposing that R(v- $>-%)> 0 and then taking an integer q so large that
R(v-q-%)<0; If the expression which is contained in [ ] in A) is then
rewritten with q in place of p throughout, it may be expressed as p terms
followed by q -p +1 terms each of which is 0 (*-*) or o (*"*); and the sum
of these q — p + 1 terms is therefore 0 (z~v).
In a similar manner (by changing the sign of i throughout the previous
work) we can deduce from § 6*12 D) that
provided that R (v + %) > 0 and that the domain of values of z is now given
by the inequalities
-2?r + 28^args^7r-2&.
If, following Hankel, we write
_ {4>v* - I2} {<k»* - 32)... {4i/a - Bm - I)'2}
2«».m!
these expansions become
For brevity we write these equations thus:
E) Bfi W
F) jr.-w
Since (»/, m) is an even function of v, it follows from the formulae of
§ 3*61 G)j> which connect functions of the third kind of order v with the corre-
corresponding functions of order — v, that the restriction that the real part of v
exceeds - \ is unnecessary. So the formulae A)—F) are valid for all values
of v, when z is confined to one or other of two sectors of angle just less than 37r.
In the notation of generalised hypergeometric functions, the expansions are
G) i« w~(i)'«<-¦•*-»¦>. jr
(8)
of which G) is" valid when — w < arg * < 27r, and (8) when - 27r < arg ^ < tt.
7*21] ASYMPTOTIC EXPANSIONS 199
7'21. Asymptotic expansions o/Jv(z), J-V(z) and Yv(z).
If we combine the formulae of § 7'2, we deduce from the formulae of § 3*01
(which express Bessel functions of the first and second kinds in terms of
functions of the third kind) that
/ 2
(i) JW(
<„ ,.w()[
+¦ COS (z ~ } 2<7T - } 7r) . i - »¦ ¦ -, ¦ ,
m-o V-~y J
D) F_rW~f2y V
+ cos (z + }, vir - }tt) . i, - --' •-- ¦--,-
and (in the casi; of funct-ions of integral order u onlij),
These formalin* arc all valid for largv values of j z \ provided thai j arg z\<ir\
and the error dm1, to stopping at any term is obviously of the order of magni-
magnitude of that term multiplied by \\z. Actually, however, this factor \\z may
be replaced by i/z-; this may be. seen by taking the expansions of IIJ^ (z) and
HJd (z) to two terms further than the. last term required in the particular
combination with which we have to deal.
As has been seen in § 7-2, the integrals which are dealt with when
H(v)>-1 represent-, H® (z) and H®(z\ but, whe.n lt(v)<-l, the integrals
from which the asymptotic expansions are derived are those ¦which represent
HM-,(z) and H®-r(z). This difference in the mode of treatment of Jv{z)
and Yv(z) for such values of v seems to have led some writers to think* that
formula A) is not valid unless lt[v) > — \>
* Cf. Sheppard, Quarterly Journal, xxm. A889), p. 223 ; Searle, Quarterly Journal, xxxix.
A908), p. 60. The error appears to have originated from Todhunter, An Elementary Treatise on
Laplace's Functions, Lam^n Functions and BesneVs Function* (London, 1875), pp. 312—Blii.
200 THEORY OF BESSEL FUNCTIONS , [CHAP. VII
The asymptotic expansion of J0(z) was obtained by Lipschitz* by inte-
integrating e*** A - i2)~J round a rectangle (indented at ± 1) with corners at ± 1
and ± 1 + oo i. Cauchy's theorem gives at once
f eizt A - #)-* dt + e$™ re^-w tr* B + tu)-* du
J-i .'o
TOO
- eiwi e~{i+u)z u~* B - iu)~* du ==¦ 0,
.0
and the analysis then proceeds on the lines already given; but in order to
obtain asymptotic expansions of a pair of solutions of Bessel's equation it
seems necessary to use a method which involves at some stage the loop
integrals discussed in Chapter vi.
It may be convenient to note explicitly the initial terms in the expansions
involved in equations A)—D); they are as follows:
« (-)m . (v, 2m) _ Dya
~ ~ B)» "
wo () 118*
The reader should notice that
- I2 (^2jri!)J4il^) (^ _?)
~3T(87
a formula given by Lomuiel, Studien, p. 67.
Note. The method by which Lommel endeavoured to obtain the asymptotic expansion
of Yn{z) in his Sticdien, pp. 93—97, was by differentiating the expansions of J±v(z) with
respect t?> v; but of courae it is now known that the term-by-term differentiation of an
asymptotic expansion with respect to a parameter raises various theoretical difficulties.
It should be noticed that Lomrael's later work, Math. Ann. iv. A871), p. 103, is free from
the algebraical errors which occur in his earlier work. These errors have been enumerated
by Julius, Archives Neerlandaises, xxviii. A895), pp. 221—225. The asymptotic expansions
of Jn(z) and Tn{z) have also been studied by McMahon, Ann. of Math. vrn. A894),
pp. 57—61, and Kapteyn, Monatshefte fiir Math, und Phys. xiv. A903), pp. 275—282.
A novel application of these asymptotic expansions has been discovered
in recent years: they are of some importance in the analytic theory of the
divisors of numbers. In such investigations the dominant terms of the ex-
expansions are adequate for the purpose in view. This fact combined with the
consideration that the theory of Bessel functions forms only a trivial part of
the investigations in question has made it seem desirable merely to mention
the work of Voronoif and WigertJ and the more recent papers by Hardy §.
* Journal fiir Math. lvi. A859), pp. 189—196.
t Ann. Sci. de VEcole norm. sup. C) xxi. A904), pp. 207—268, 459—534; Verh. des Int.
Math. Kongresses in Heidelberg, 1904, pp. 241—245.
% Ada Mathematica, xxXvu. A914), pp. 113—140.
§ Quarterly Journal, xlvi. A915), pp. 263—283; Proc. London Math. Soc. B) xv. A916),
pp. 1—25.
7-22] ASYMPTOTIC EXPANSIONS .201
7*22. Stokes' phenomenon.
The formula § 721 A) for Jv{z) was established for values of z such that
| arg z | < 7T. If we took arg z to lie between 0 and 2tt (so that arg ze~vi lies,
between — it and ir) we should consequently have
so that, when 0 < arg z < 2tt,
-2)
- sin (« + 1-.V7T + ,|tt) ^ V^^'
and this expansion is superficially quite different from -the expansion of
§ 7*21 A). We shall now make a close examination of this change.
The expansions of § 7 21 are derived from the formula
and throughout the sector in which — tt < arg z < 2tt, the function Hv^ (z) has
the asymptotic expansion
The corresponding expansion for 11 v^ (z), namely
(!) ^(^
is, however, valid for the sector - 2-7T < arg z < tt. To obtain an expansion
valid for the sector 0 < nrgz < 2ir we use the formula of § 3'62F), namely
IIW (z) = 2 cos vir. H,® (ze-**) + evrti Hv^ (ze^1),
and this gives
Wz
The expansions A) and B) are both valid when 0<arg^<7r; now the
difference between them has the asymptotic expansion
and, on account of the factor eiz which multiplies the series, this expression is
of lower order of magnitude (when \z\\s large) than the error due to stopping
THEOBY OF BESSEL FUNCTIONS [OHAP.
at any definite term of the expansion A); for this error is 0 (e'iz *r*~*)
we stop at the pth term. Hence the discrepancy between A) and (-), wluc ^
occurs when 0<arg*<ir, is only apparent, since the series in A) has to I
used in conjunction with its remainder.
Generally we have
where the constants c,, c2 have values which depend on the domain of valuos
assigned to arg z. And, if arg .2 is continually increased (or decreased) whil<<
\z\ is unaltered, the values of c, and c2 have to be changed abruptly at various
stages, the change in either constant being made when the function wliie.U
multiplies it is negligible compared with the function multiplying the other
constant. That is to say, changes in d occur when I (z) is positive, whil^
changes in c2 occur when I(z) is negative.
It is not difficult to prove that the values to be assigned to the constant*
cx and c-2 are as follows:
|2p(+i)>ri) [Bp _ l) 7t < arg z < B/> + 1) tt],
i)" [2p7T < arg « < ( 2p + 2) 7r'|,
where p is any integer, positive or negative.
This phenomenon of the discontinuity of the constants was discovered by
Stokes and was discussed by him in a series of papers. It is a phenomenon
which is not confined to Bessel functions, and it is characteristic of integral
functions which possess asymptotic expansions of a simple type*.
The fact that the constants involved in the asymptotic expansion of the arudytic function
Jv (z) are discontinuous was discovered by Stokes in (March?) 1857, and the discovery wuh
apparently one of those which are made at three o'clock in the morning. Seo Sir Uvonje
Gabriel Stokes, Memoir and Scientific Correspondence, i. (Cambridge, 1907), p. (W. Th<>.
papers in which Stokes published his discovery are the followingt: Trans. Camb. Phil.
Soc. x. A864), pp. 106—128; XI. A871), pp. 412—425; Ada Math. xxvi. A902), pp. »i>3 ¦
397. [Math, and Phys. Papers, IV. A904), pp. 77—109; 283—298; v. A905), pp. 283- iW7. J
The third of these seems to have been the last paper written by Stokes.
7*23. Asymptotic expansions of Iv (z) and Kv{z).-
The formula §7*2E) combined with equation §3*7(8), which coime<U,s
Kv (z) and H^ (iz), shews at once that
* Cf. Bromwich, Theory of Infinite Series, § 133.
t Stokes illustrated the change with the aid of Bessel fnnctions whose, orders are 0 and
the latter being those associated with Airy's integral (§ 6-4).
7-23, 7*24] ASYMPTOTIC EXPANSIONS 203
when | argz j < § ir. And the formula /„ (z) = e*vrri Jv {e~^vi z) shews that
provided that — \ir < arg 2 < |7T.
On the other hand, the formula Iv(z) = e~^vniJv (<?**' z) shews that
(d) "( } ~ B^7)* ^« ~2^r + 12^)T Mto BFr '
provided that — §7r < arg 2; < \tt.
The apparent discrepancy between B) and C) when z has a value for
which arg z lies between —\tt and |tt is, of course, an example of Stokes'
phenomenon which has just been investigated.
The formulae of thi.s section wore ntated explicitly by Kummer, Journal filr Math. XVII.
A837), pp. 228—242, and Kirchhnff, Journal fur Math, xlviii. A854), pp. 348—376, except
that, in B) and C), the negligible second series is omitted. The object of the retention of
the negligible scries is 1,0 make A) and C) formally consistent with $3'7(G).
The formulae are also given by Rictnann, Ann. der Pkysik und C/temie, B) xcv. A855),
p. 135, when v = 0. Proofs are to bo found on pp. 49E—498 of Hankel's memoir.
A number of extremely interesting symbolic investigations of the formulae are to be
found in Heaviaide's* papers, but it is difficult to decide how valuable such researches are
to be considered when modern standards of rigour are ado])ted.
A remarkable memoir is due to Malmste'rif, in which the formula
cos ax. dx -we~a
xfBa)n + nG\(n+l).Ba)*-1 +nGa(n+ l)(n+2).Ba)M~2+ ...]
is obtained (cf. § 6'3). This formula is written symbolically in the form
(m cos ax. dx _ Trcra ( I )n
the [ ] denoting that [n]" is to bo replaced by (/<)_,„, and this, in Malmsten's
notation, means
It will be observed that this notation is different from the notation of § 4*4.
7'24. The asymptotic expansions of her (z) and bei B).
From the formulae obtained in §§ 721, 7*23, the asymptotic expansions of
Thomson's functions ber (z) and bei (z), and of their generalisations, may be
written down without difficulty. The formulae for functions of any order have
been given by WhiteheadJ, but, on account of their complexity, they will not
* Proc. Eoyal Soc. mi. A893), pp. 504—529; Electromagnetic Theory, n. (London, 1899). My
thanks are due to Dr Bromwich for bringing to my notice the results contained in the latter work.
+ K. Svemka. V. Akad. Handl. lxii. A841), pp. E5-74.
$ Quarterly Journal, xlii. A911), pp. 829—338.
204 THEORY OF BESSEL FUNCTIONS [CHAP. VII
be quoted here. The functions of zero order had heen examined previously by
Russell*; he found it convenient to deal with the logarithms^ of the functions
of the third kind which are involved, and his formulae may be written as follows:
lber & - exPaO)cos a (A
{~ z) sin "w
(~g) cos o /
j() V(/tt) sin' K
where
" z 1 25 13
0) +
384a8 V2 128s4
7T 1 1 25
The ranges of validity of the formulae are | axgz | < \ir in the case of A) and
| arg z | < \<k in the case of B).
These results have been expressed in a modified form by Savidge, Phil. Mag. F) xix.
A910), p. 51.
7*25. Hadamard's modification of the asymptotic expansions.
A result which is of considerable theoretical importance is due to
Hadamard^; he has shewn that it is possible to modify the various asymptotic
expansions, so that they become convergent series together with a negligible re-
remainder term. The formulae will be stated for real values of the variables, but
the reader should have no difficulty in making the modifications appropriate
to complex variables.
We take first the case of Iv{x) when v > — \. When we replace sin \6 by
u, we have
the last result being valid because the series of integrals is convergent.
We may write this equation in the form
where 7 denotes the "incomplete Gamma-function" of Legendre§.
¦ Phil. Mag. F)'xvn. A909), pp. 531, 537.
t Cf. the similar procedure due to Meissel, which will be explained in § 8-11.
X Bull, de la Soc. Math, de France, xxxvi. A908), pp. 77—85. § Cf. Modern Analysis, § 16-2.
7-25, 7*3] ASYMPTOTIC EXPANSIONS 205
For large values of x, the difference between
is O(xv+n+h e~2x) which is o(l) for each integral value of n.
In the case of the ordinary Bessel functions, we take the expression for
the function of the third kind
/ 9 \i oi&— iwir—Jir) Too / o'tj\"~i
V \7T^.' l(l/ + $) Jo V 2xJ
\) J „
so that
B> //,<¦)(«) - (A)! ^^.-1., 5 (^1"'Vr(»+-';iti^+o(
7 \7ra7 „,-(, I (y+J). w!B?a')'n x
and similarly
S" 'r
From these results it is easy lo dcrivo convergent scries for the functions
of the first and .second kinds.
Hadaimiril guvc. tho formulae, for fuiuitioii.s of order /.iv.r»> only ; but t.ho extension to
ftmotioriH of any order oxcoeding - I in obvimi.s.
7*3. Formulae for the remainders in the (tsi/)ii}ttotic expansions.
In §7'2 we gave an investigation which shewed that the remainders in
the asymptotic expansions of Hvw {z) and H^ {z) are of the same order of
magnitude as the first terms neglected. Jn the case of functions of the first
and second kinds, it is easy to obtain a more exact and rather remarkable
theorem to the effect that when v is real* and x is positive the remainders
after a certain stage in the asymptotic expansions of J±v (x) and Y±v (x) are
numerically less than the first, terms neglected, and, by a slightly more re-
recondite investigation (§ 72), it can be proved that the remainders are of the
same sign as the first terms neglected.
Let us write
* We may take v^O without losing generality.
206 THEORY OF BESSEL FUNCTIONS [CHAP. VII
so that
— ) [cos (x + \vtt -\-n) P (x, v) - sin (x + \v-rr - \tt) Q (x, v)],
IT 00/
B) Y±v (x) = (J~) [sin{x + %vk-\ir) P {x, v) + cos (x + \vtt - \ir) Q(x, v)].
Now 7(i') = 0 and, in the analysis of §7*2, we may take 8 to be %tt since
the variables are real, and so Aip — 1.
It follows that, if p be taken so large that 2p > v — \, there exists a
number 6, not exceeding unity in absolute value, such that
± 2x) mto ml \2i»/ Bp)! V2^/
and, on adding the results combined in this formula, we hav.e*
+2/ ^V 2a?; mt0 Bm)! UW + Bp)\
where | ^01 ^ 1; and, since ^Q is obviously real, -1 ^ ^0< 1.
It follows on integration that
1 {X, V) —
i
and since
I <90 e~u u"+2^-i du
Jn
= V (v + 2p
we see that the remainder after p terms in the expansion of P (%, v) does not
exceed the (p + l)th term in absolute value, provided that 2p > v — \.
From the formula
ml
2; B
we find in a similar manner that the remainder after p terms in the expansion
of Q (x, v) does not exceed the (p + l)th term in absolute value, provided that
2p$* v — |.
These results were given by Hankel, Math. Ann. i. A869), pp. 491—494, and were
reproduced by Gray and Mathews in their Treatise on Bessel Functions (London, 1895),
p. 70, but small inaccuracies have been pointed out in both investigations by Orr, Trans.
Camb. Phil. Soc. xvn. A899), pp. 172—180.
In the case of Kv (x) we have the formula
( + rJ **•
* Thi9 result was obtained in a rather different manner by Lipschitz, Journal fUr Math. lvi.
A859), pp. 189—196.
7*31] ASYMPTOTIC EXPANSIONS 207
and
and, when j)^v— ?, the last term may be written
where 0 < ^ •§ 1, and so, on integration,
v
where 0 < #2 -S ] when p ^ v — \.
This is a more exact result than those obtained for P (.r, v) and Q(x,v)
by the same methods; the reason why the greater exactness is secured is, of
course, the fact that A + \ at/r)v~i'~* is positive and does not oacilhite in sign
after the manner of A + \iut!xY~v~* ± A - \iiitjx)v~P-^.
71. The researches of titieltjes on </„(.<"), Vu(x) and A"o (.•*:).
The results of § 7"<S were put into a more precise form by Sticltjes*, who
proved not only that the remainders in the asymptotic expansions associated
with Jo (.'/;), Yn (:v) arid Ar0(a;) are numerically less than the first terms neglected,
but also that the remainders hare the tianw- si(/n as those terms.
Sticltjcs also examined /(i(.r), but, his result is complicated and wo shall not reproduce
it+. It i.s only to be expected that /„ (.r) is intractable because in the dominant expansion
the toruiH all have the same, sign whereas in the other throe asymptotic expansions the
terms alternate in si^n.
It i.s evident from the definitions of §7%'J that
T (a; 0) = ^:'' I i' -"* ir k- \{ I + Jr«)-* + A - \in) *} dti,
Q(-'\ 0)- i~ I & "¦*¦»/"* ((I +J/m)-!-(! -\iu)¦'}(/».
In these formulae rejilace A + lji<)~- by
2 '*"¦ d(j>
W. o !• ± i?" sina</>
* ylnn. 6Yct. (Z« VEcole norm. sit}). C) in. (lHfi()), pp. 233—2f>'2.
t The function Iv(x) has alfio been oxamined by Sclial'hcitlin, Jahresbericht tier Deulschen
Math.-Vereinigwig, xix. A930), pp. 120—129, but he appears to use Lagrange's form for the
remainder in Tajlor'a thoorom when it is inapplicable.
208 THEORY OF BBSSEL FUNCTIONS [CHAP. VH
It is then evident that
(**{1 \? i* / + + (y-1 (im2 sin4
- \v? sin* </> + ...+ (-y-1 (im2 sin4 tf)*'-1
in4
)/( i 2 sin
where p is any positive integer (zero included).
Now, obviously,
sin.
o l+i^sm8^ ^ Jo
0 h'es between 0 and 1; and hence
If we multiply by the positive function e~wa: u~h- and integrate, it is evident
that
Bp-2)!(&»)ap~a
+( - + ^ > 2)
where 0 < 6i < 1, and p is any positive integer (zero included); and this is
result which had to be proved for P(x, 0).
Similarly, from the formula
^ |i
we find that
where 0 < ^2 < 1> and p is any positive integer (zero included); and this is the
result which had to be proved for Q (%, 0).
In the case of K»{x)y Stieltjes took the formula
Ko(x) = ~ I" e~™it-*A+ \u)~Hu,
v^ Jo
I
and replaced A + \u)~i by - | -— ^. - ; the procedure then follows the
J 7rJo 1+fusina<f> *
method just explained, and gives again the result of § 7'3.
By an ingenious device, Callandreau* succeeded in applying the result of Stieltjea to
obtain the corresponding results for functions of any integral order; but we shall now explain
a method which is eftective in obtaining the precise results for functions of any real order.
* Bull, des Sci. Math. B) xiv. A890), pp. 110—114.
7-32] ASYMPTOTIC EXPANSIONS 209
7*32. The signs of the remainders in tlie asymptotic expansions associated
with Jv (x) and Yv (x).
It has already been seen that /„ (%) and Yv (x) are expressible in terms of
two functions P(x,v) and Q(x,v) which have asymptotic expansions of a
simpler type. We shall now extend the result of Stieltjes (§7-31) so as to
shew that for any real value* of the order v, the remainder after p terms of
the expansion of P (x, v) is of the same sign as (in addition to being numerically
less thanf) the (p + l)th term provided that 2p > v — \\ a corresponding result
holds for Q (a, v) when 2p > v — $. The restrictions which these conditions lay
on p enable the theorem to be stated in the following manner:
In the oscillatory parts of the series for P {x, v) and Q (x, v), the remainders
are of the same sign an, and numerically less than, the first terms neglected.
By a slight modification of the formulae of § 7*3, we have
P )
Q {x'v)=2~i
and, exactly as in § 7 3, we may shew that
l _ typ- It{{[+1 iuty-:P-H _ A _ ?lltT-^ i-ij dt
The reader will see that we can establish the theorem if we can prove that,
when 2p > v — |, the last term on the right is of fixed .sign and its sign is that of
It is clearly sufficient to shew that
. -— -. f \\ -tfi'~* \i 1A + JwtO"-*+i-(L -iittO'-^"-*} dt
Zp — v—^'o
is positive. Now this expression is equal to}
* As in § 7*3 we may take v^:0 without loss of generality,
t This has already been proved in § 7'3.
i Since |sinD\u«) |^\u/, the condition 2p>v-^ secures the absolute convergence of the
infinite integral.
w. B. F. 14
210 THEORY OF BESSEL FUNCTIONS [CHAP. VH
Now A — ?)^-2 is a monotonic decreasing function of t\ and hence, by the
second mean-value theorem, a number ?, between 0 and 1, exists such that
I (I- tyv* sin (\\ut) eft = [ sin {\\ut) dt > 0.
Jo Jo
Since T Bp - v +1) is positive, we have succeeded in transforming
i _ typ-^i {A + |iu*)"-*H-(l -\iut)v^^) dt
into an infinite integral in which the integrand is positive, and so the expression
under consideration ic positive.
That is to say,
,~o Bm)l +* Bp)!
where 0>O when 2p> v — \. And it has already been seen (§7'3) that in
these circumstances | 01 ^ 1. Consequently 0 ^ 6 $ 1; and then, on multiplying
the last equation by e~uxuv~^ and integrating, we at once obtain the property
stated for P {x, v).
The corresponding property 'for Q (x, v) follows from the equation
the details of the analysis will easily be supplied by the reader.
Note. The analysis fails when ~^<v<-| if we take p=0, but then the phase of
(l±im)"-4 lies between 0 and ±%(v-%)tt, and so J {(l-j-^'u)"-4 + (l - }iu)v-l} has the
same sign as unity, and, in like manner, i{(l-t-?m)"~4-(l -^i«)"~4}/i has the same sign as
i(v-|-)M, and hence P(#, v) and <2 (^> ") have the same sign as the first terms in their
expansions, so the conclusions are still true; and the conclusion is true for Q(x> v) when
7*33. Weber's formulae for the remainders in the expansions of functions
of the third kind.
Some inequalities which are satisfied by the remainders in the asymptotic
expansions of Hvll) (z) and Hv® (z) have been given by Weber*. These inequali-
inequalities owe their importance to the fact that they are true whether z and v are real
or complex. In the investigations which we shall give it will be supposed for
simplicity that v is real, though it will be obvious that modifications of detail
only are adequate to make the mode of analysis applicable to complex values
* Math. Ann. xxxvn. A890), pp. 404—416.
7-33]
ASYMPTOTIC EXPANSIONS
211
of v. There is no further loss of generality in assuming that v^0, R(z)^0.
We shall write | z \ = r, and, since large values of | z | are primarily under con-
consideration, we shall suppose that 2r^ v — \.
If v -1 > 0, we have*, by § 6'12 C),
(z) | -
— "tw—7 n e uv * l + o-
w*/ r(l/ + f) .'o \ 2*
—) p,- --f
' 2 \iel'(*~*'"r~i'r)l
Jo V ZrJ
du
v —
i du
i / o \t
\\irz)
i
!
If 0 ^ v < •?, we use the recurrence formula
and apply the inequality just obtained to each of the functions on the right.
It is thus found that
and similarly
wheret
C)
G = 1 -
2r
The results may be called Weber's crude inequalities satisfied by HV{1) (z)
and Hv{"] (z). By an elegant piece of analysis, Weber succeeded in deducing
more refined inequalities from ihiun in the following manner:
Take the first /) terms of the series involved in Hankel's two expansions
and denote them by the. symbols ^,,A) (z; -p), S,,'2' (z; p), so that
7 (—\m (v
It is easy to verify that
We regard this as an equation to be-solved by the method of variation of para-
parameters; we thus find that
2,ll) {*; p) = Q**? e-<^i'-4-) {il («) jyrw (z) + j5 E)
* In the third lino of analysis the inequality ex^ 1 + x (x^O) haB been used,
t When k i we take 2r ¦> v + S.
14—2
212 THEORY OF BESSBL FUNCTIONS [CHAP. VII
where A (z) and B (z) are functions of z so chosen that
(A' (z) Hvw (z) + B' (g) #„<»(z) = 0,
\a'(z) ^H* (,)+*'(*)?B.» (z) - - (*»*)-*rf«M--w_?ifc^.
It follows that
and so
where ^1 is a constant.
We obtain a similar expression for B (z), and hence it follows that
tj]) (z; p) = {AHvw (z) + BHV® (z)} D 7r^)i e-«-(*-^*-i*)
By considering the behaviour of both sides of this equation'as z -*- + oo , it
is not difficult to see that A = 1 and i? = 0.
Hence we may write Hankel's formulae in the forms
rw (z) = (—) 6««-i-»-l») {S/» (z;p) + RpV],
\7rz/
where the remainder itlj,111 may be defined by the equation
Sinee R (z) > 0, we have \z + t\^ a/(^2 + ^2)» and so, by using the crude
inequalities, we see that the modulus of the last integrand does not exceed
(
Hence
», p) | f (r2 + f )-i<p+D dt,
J o
f
J o
and so, when p > 1, we have
and similarly
These are the results obtained by Weber; and it will be observed that in
the analysis no hypothesis has been made concerning the relative values of v
and p; in this respect Weber's results differ from the results obtained by
other writers.
7*34] ASYMPTOTIC EXPANSIONS 213
7-34. Approximations to remainders in tite asymptotic expansions.
When the argument of a Bessel function is not very large*, the asymptotic
expansion is not well adapted for numerical computation because the smallest
term in it (with the remainder after the smallest term) is not particularly
small; at the same time the argument may be .sufficiently large for the
ascending series to converge very slowly.
An ingenious method for meeting these numerical difficulties was devised
by Stieltjesf; we shall explain the method in detail an applied to the function
K0(x) and state the results which were obtained by Stieltjes by applying the
method to Jo {%) and Yo (x).
We apply the transformation indicated in § 7"81 to the formula §0*15D),
so that
p—X TOO p—XU //,,
o .' o «*(? -t- jvt sin- 0)
-
v
o Jo u* (I + luHin20) J
That is to say,
where
Now the value of m for which @, •/n)/B.r)m is Uiast in nearly e<]iial Ui 2./-
when .* is large; accordingly, in order U> c.(Hisi(itT l.ho ronmindor al'tior the
smallest term of the series for Ar,( (.-/.•). wo ^Iioohi' ^ ho that
x = lp + a,
where a is numerically less than unity; and then
ri Too /V «--/U
7TSJo Jo ?/>(! -I- JftHin*^)
Now, as u increases from 0 to oo , \ ue~ *" iiiereaHcs from 0 up U) a maxinium
?-1 (when m = 2) and then decreases t<j z(M-u ; ho we write
where f increases from — oo to oo, and, for similar reaaoiiH, we? write
sin2 6 — e~i\
* The range of valueB of x uuder contempliilion for tho function.1! Jn(.r), 1 '0 (x) and A'«(.rJ in
rom about 4 to about 10.
t Ann. Sci. dc I'Ecole norm. avp. (8) m. A886), pp. 241—252.
214 THEORY OF BESSBL FUNCTIONS [CHAP. VIl
The domain of integration becomes the whole of the (?, n) plane; and it is
found that
where
o«.| o-ix c°° r °° ( °° ^
7T* J-ooJ-oo |r,*=0 J
by some rather tedious arithmetic. It follows* that the dominant terms of
the asymptotic expansion of Rp for large values of p are
so that
B)
0, 2 "f ,0
It is easy to verify by Stirling's theorem that
Ba;)" v ; *
so that the error due to stopping at one of the smallest terras is roughly half of the first
term omitted.
In like manner Stieltjes proved that, if P (x, 0) and Q (x, 0) are defined as
in § 7'3, then
where
provided that ^) is chosen so as to be nearly equal to x, and t is defined to
be x — jp.
Results of this character are useful for tabulating Bessel functions in the critical range;
some similar formulae have been actually used for that purpose by Airoy, Archiv der Math,
und Phys. C) XX. A913), pp. 240—244-; C) xxn. A914), pp. 30—43 ; and British Association
Reports, 1913, 1914.
It would be of some interest to extend the results, which Stieltjes has established for
Bessel functions of zero order (as well as for the logarithmic integral and some other
functions), to Bessel functions of arbitrary order.
* Of. Bromwich, Theory of Infinite Series, §§133, 137, and 174, or the lemma which will be
proved in § 8-3,
7*35, 7'4] ASYMPTOTIC EXPANSIONS 215
7*35. Deductions from SchafheiUin's integrals.
If we replace u by 2 tan 6 in the formulae of § 7'32, we deduce that
** sin"-* 6 cos (v-\)Q
which resemble Schafheitlin's integrals of §6'12,
It is obvious from these results that
P(x,v)>o, (-i<"<4)
Q (a, v)>0, (? < v < f)
Q (#, v) < 0. (— \ < v < \)
An interesting consequence of these results is that we can prove that
Q{x,v)IP{xtv)
is an increasing function of x when — ?< v <\ and that it is a decreasing
function of x when | < v < f.
For we have
Q' (x, v) P (x, v) - F (x, v) Q (x, v)
_ . o .'o
where
jp (ut (j))= - - -'- - (tan v — tan (?) coa {v — \) a sin {v —
so that
----- (tan 6 — tan ^>) sin (| —r v) |
If we interchange the parametric variables 6, <j> in the double integral and
add the results ho obtained wo, set! that, when —\<v< •§, the double integral
has the same sign as \ — v ; and this proves the result.
7*4. Schlo-Jii's investigation of the asymptotic expansions of JBessel functions.
In a memoir which seems hardly to have received the recognition which
its importance deserves, Schliifli* has given a very elegant but soincwKat
elaborate investigation of the asymptotic expansions of the functions of the
third kind.
The integral formulae from which lie derived these expansions are
generalisations of Bessol's integral; although Bessel's integral is not so well
adapted as Poisson's integral for constructing the asymptotic expansion of
* Ann. di Mat. B) vi. A875), pp. 1—20. The only standard work oa Beasol functions in which
the importanco of this memoir is reoognised is the trisaUne by Graf and G-ubler.
216 THEORY OF BBSSBL FUNCTIONS [OHAP. VII
/„ (z) when z is large and v is fixed, yet Schlafli's method not only succeeds
in obtaining the expansion, but also it expresses the remainders in a neat and
compact form.
Schlafli's procedure consisted in taking integrals of the type
=—.-. vr"'1 exp \ + h'eia (u + - ] \ du,
27TIJ f f2 V WJ
and selecting the contour of integration in such a way that, on it, the phase* of
lreia (m - 2 + lju)
is constant. He took two contours, the constants for the respective contours
being 0 and rr; and it is supposed that r is positive and a is real.
(I) Let us first take the phase to be tt; write
u = l +pei\
where p is positive and 6 is real, and then
reiap2e2ie/(l + peie)
is negative, and is consequently equal to its conjugate complex.
Hence we have
/i\ sin (a+ 20) sin 6 .,„,,,
Next choose a new parametric variable <? such that
<f> = 20 + a - ir,
and then
/o\ _ cos i (a ~ <?) id, . to, (u — IJ __ —r sin2 0
» cos \(a + 0) w cos ? (a — <?) cos |(a + <j>)'
Now, as <j> varies from — Gr — a) to Gr — a), u traces out a contour emerging
from the origin at an angle — (ir - a) with the positive real axis and passing to
infinity at an angle (tt — a) with the positive real axis, provided that 0 < a < 2tt.
If this restriction is not laid on a the contour passes to infinity more
than once.
We shall now lay this restriction on a; and then the contour is of the type
specified for formula § 6'22 (9), provided that we give a> and arg z the same
value a, as is permissible.
It follows that
eV7liI-v(reia)-e~vH Iv(reia-\- 1 r"~a
ZT-—= — — « : I U~"~1 exp
1% sin vtt 2*rn J _(„._,») x
where u is defined in terms of (f> by equation B).
* The reader will find it interesting to compare the general methods of this section with the
"method of steepest descents" which in applied to obtain various asj'mptotic expansions in
Chapter vm.
7*4] ASYMPTOTIC EXPANSIONS 217
Changing the sign of $ is equivalent to replacing u by 1/u, and so, replacing
the expression on the left by its value as a function of the third kind, we have
"I fir—a C / 1 \ > f] \f\cf 11
C) ei"H Hvu (*•«'«—»*>) = —. (irv + w) exp \ W» U + - H. —?- d<b.
rrt J o (. \ wj a<p
From B) it follows that — reia(u — iy/u increases steadily* from 0 to + co
as cf> varies monotonically from 0 to tt — a.; and, if we write
- reia (u - Vfju ~ t,
so that t is positive when u is on the contour, we have
du dt _ dt
u ^ - 7'ei<r(u -I/it) = F*(^-«)» (m* + t
the range of values of arg u being less than ir.
Next, by Cauchy's theorem,
it is convenient to take the point ?=1 inside the contour, but ? = 0 must be
outside the contour because the origin is a branch-point.
It follows that
)
Hence
Now it is evident that
where p ia any positive integer (zero included). It will be convenient subse-
subsequently to suppose that -p exceeds both R(v— \) and R(— v — ^).
On making this substitution in the laat integrand and observing that
27rtJ C (G U tK~r(i/-w+i).Bm!) Bw)! '
(with the notation of §7), we deduce that
where
t«+,if) e-\t tP
J
„. d sin2 <f> _ sin </> A + 2 ooa a cos </> + cob2 <p)
d<f> cos a + cos <f> ~ (cos a+ oos </>J
218
THEOBY OF BESSEL FUNCTIONS
[CHAP. VH
First consider
1 /•(«+, 1/M+, 1
Whenp is so large that it exceeds both R(v — {) and ?(— v — %), we take the
contour to be as shewn in Fig. 15; and when the radii of the large and small
circles tend to oo and 0 respectively the integrals along them tend to zero.
If now we write
on the two rays (which are all that survives of the contour), we find that
_ (~)p cos v-w f1 .vP-"-i A - x)P+"
T~ 1 T^~T^
Fig. 16.
Now the numerator of the integrand is positive (when v is roal), and the
modulus of the denominator is never less than 1 when {it < a < -jtt ; for other
values of a it is never less than | sin a |.
Therefore
where | 0O | is 1 or | cosec a | according as cos a is negative or positive. When v
is complex, it is easy to see that
G)
-V
COS VTT
cos R (vrr)
7*4] ASYMPTOTIC EXPANSIONS 219
Hence, finally, when — $tt < arg z < $rr,
)e
where | 0! | does not exceed 1 or | sec (arg z) \ according as I(z) is positive or
negative, provided that v is real and p + ? > | v \. When v is complex, the modi-
modified form of the remainder given by G) has to be used.
Since R {1 -te(l -a;)j$reia)} 2s 0 when R(e-ill)$Q, we see that, in (8),' Bx
has its real part positive when v is real and I(z) ^0.
If z be replaced by iz in (8) we find that, when | arg 2 | < 7r,
and, when v is real,
(i) 72 @a) > 0 and | 03 \ < 1, if R {z) > 0,
(ii) j #a I < I coscc (arg z) \, if R (z) < 0.
The modifications necessary for complex values of v are left to the reader.
(II) We next discuss the consequences of talcing the phase of
to be zero. As before, we write
u = 1+ pei0,
and then reu p~ e"!<>/( I -\-pei0) is positive, and therefore equal to its conjugate
complex, so that we obtain anew equation (I). We then diverge from the
preceding analysis by writing
so that
I (a + <p) ., . (a—I)" rsin2^
„=i@)e..i,,. reia (y=_.^
sin .J (a - ^>) ' « sin
Now, as <f> varies from — a to a, u traces out a contour emerging from the
origin at an angle a with the positive real axis and passing to infinity at an
angle —a with the positive real axis, provided that a lien between —tt and tt.
The contour is then of the type specified for formula § (r22 (8) if, aa is per-
permissible, we give o> and argxr the same value a.
It follows that, when — 7r < a. < it,
Kv (reia) = }2 cos vir \ w"" exp 1 - }2 reia lu+ ¦) I ? d(j>,
where ii is defin<id as a function of <j> by equation A0); and therefore
A1) //„« (re'<«-»">) = w^.l-\\u-v + u")exp|^~^reia fu + ^1 -
220 THEORY OF BESSEL FUNCTIONS [CHAP. VII
and hence, if now
t = reia(u-'iy/u,
we find that
(lto H <* (reiW) - ^ 6XP t^3 IK rA"t+) *—*- ^'"*ifH.1)^
A2) i/,>(t«i ;)_——-^^ JJ (S-~Ty-&Kreu) '
We have consequently expressed a second solution of Besael's equation in a
form from which its asymptotic expansion can be deduced; and the analysis
proceeds as in the case of Hv[l) (z), the final result .being that, when
where | #2 j does not exceed 1 or | sec arg^ | according as I {z) ^0 or I(z) ^ 0,
provided that v is real and p + \ > | v \; and R ($») ^ 0 when / (z) ^ 0. If v is
complex the form of the remainder has to be modified, just as in the case of (8).
It should be observed that, since the integrands in C) and A1) are even
functions of v, it is unnecessary in this investigation to suppose that R (v)
must exceed — \, as was necessary in investigations based on integrals of
Poisson's type.
7*5. Barnes' investigation* of asymptotic expansions of Besnel functions.
The asymptotic expansions of functions of the third kind follow immediately
from Barnes' formulae which were obtained in §§6'5, 651. Lot us consider
V (- s)V (- 2v - s)T (v + s + l)(- 2iz)° ds
—001— V-p
If | arg (— iz) | ^ f it - B, we have
-s + v+p)V(-s~v+p) r(s~
coi
aai
^ \T (- s + v + p) V (- s - v + p) r(s~p + %)e^-Vslih ,
J -oai
and the last integral is convergent and so the first integral of all is
0 [(- 2u)-"-*'}.
But, by the arguments of §6-51, the first integral is -2iri times the sum
of the residues at the poles on the right of the contour, and so it is equal to
- 7T- Hvu B)/!>l"(z-J"r) cos v-nB*)"] plus - 2iri times the sum of the residues at
s = _j/_.i.)-.I,_|j .,, t _ „ _p _|_ ?. The residue at - v - m - ^ is
* Trans. Camb. Phil. Soc. xx. A908), pp. 273—279.
7*5, 7-51] ASYMPTOTIC EXPANSIONS 221
and so, when j arg (— iz)
and this is equivalent to the result obtained in § 7*2. The investigation of
HJ® (z) may be constructed by replacing i by - i throughout.
The reader should notice that, although the determination of the order of
magmtude of the remainders by this method is transparently simple, it is not
possible to obtain concrete formulae, concerning the magnitude and the sign
of the remainders, which are ultimately supplied by the methods which have
been previously considered.
7*51. Asymptotic expansions of products of Bessel functions.
It does not seem possible to obtain asymptotic expansions of the four
products J±n(z) J±v{z) in which the coefficients have simple forms, even
when yu,= v. The reason for this is that, the products /I/' (z) H^ (z) and
H^w (z) Hvw (z) have asymptotic expansions for which no simple expression
exists for the general term; the leading terms in the two expansions are
7TZ
1 q: +
4
The products H^ (z)!!^ (z) and ///> (z)Hvil)(z),however, do possess simple
asymptotic expansions; and from them we can deduce asymptotic expansions
for
M*)M*) + YMYM
and for JM (z) Yv (z) - Yh (z) Jv (z).
The simplest way of constructing the expansions is by Barnes' method,
just explained in § 7. A consideration of series of the type obtained in
§ 5*41 suggests that we should examine the integral
the contour is to be chosen so that the poles of F Bs + 1) lie on the left of the
contour and the poles of the other four Gamma functions lie on the right of
the contour; and it is temporarily supposed that /*, v and fi±v are not
integers, so that the integrand has no double poles. The integral is convergent
provided that | arg(w) | < §7r.
222 THEOBY OF BESSEL FUNCTIONS [CHAP. VII
First evaluate the integral by swinging round the contour to enclose the
sequences of poles which lie to the right of the original contour; the expression
is equal to minus the sum of the residues at these poles, and the residue at
m + |(/i + v) is
9r»e*iH-')** r (fi + v + 2m + 1) ¦ (-)m (%zy+v+zm
sin fiir. sin vrr. sin (/* + v)ir'm! V(fi + m + 1) F (v + m +1) V (/jl + v + m +1)'
It follows that
_v(z)
sin fnr sin vrr \ sin (fx + v) it sin (jm-
_v (z)
_
sin (v — fi) ir sin (fi + v) ir
sinGt +v)tt ^^'^ **w J "w<
>™ {2 cos fj,7T cos vrr +i sin (/* + v)
- cot 10* - v) tt {J. {z) Yv (z) - Y. (z) Jv {z)\ ]
By writing —i for i throughout the analysis we deduce that, if both
|argiz| and |arg(— iz) \ are less than f 7r, i.e. if |argz\<tt, then
7*51] ASYMPTOTIC EXPANSIONS 223
and
<2> t
tan i (^ - ») 7T. (/„ («) T. (z) - Y
r (--"'* - s) r (- ^p - *) sin 57r. (*,)¦ a.
These results hold for all values of /a and v (whether integers or not)
provided that, in the case of the former fi+v and fi — v are nofc even integers,
and. in the case of the latter /x + v and fj, — v are not odd integers.
We now obtain the asymptotic expansions of the functions on the left of
A) and B) after the manner of § 7'5.
We first take p to be an integer so large that the only poles of the in-
integrands on the left of the line R (s) = —p — \ are poles of FB6* + 1); and then
J -<X>< ./ - X/-J)- J
(when either integrand is inserted) is equal to 2?n' times the sum of the
residues at the poles between the contours. Since
we deduce that the asymptotic expansions, when |arg2l< it, are
C) [Jh (z) Jv (z) + V. (z) \\ (,) j - cot \(p-v)ir. [J. (z) Yv <*) - Jv (z)
. U + V
Sill -t- - 7T
—^—x
7tz2 sin $((A — v) 7r V 2 2 2 2 2 z-j
and
D) [/M(z) Jv (z) + TM(z) Yv (z)} + tan \(n-v)ir. [Jh(z) Yv (z) - ./, (z) Y^z)]
ttzcos i (/a — v)rrr"i \ 2 ' 2 ' 2 ' 2 ' 2' 07
THEORY OF BESSEL FUNCTIONS [OHAP. VII
In the special case when /a = p, the last formula reduces to
E) JS(*)+YS(*)~§-g ? A.3.5...Bm-l))^,
and, in particular,
Formula E) seems to have been discovered by Lorenz, K. Danske VidensL Sehkabs
Skrifter, F) vi. A890). [Oeuvres seientifiques, l. A898), p. 435], while the moro general
formulae C) and D) were stated by Orr, Proe. Camb. Phil. Soc. x. A900), p. 99. A proof
of E) which depends on transformations of repeated integrals was given by Nielsen, Hand-
biich der Theorie der Cylinderfunktionen (Leipzig, 1904), pp. 245—247; the expansion E)
is, however, attributed to Walter Gregory by A. Lodge, British Association Report, 1906,
pp. 494—498.
It is not easy to estimate exactly the magnitude or the sign of the re-
remainder after any number of terms in these asymptotic expansions when this
method is used. An alternative method of obtaining the asymptotic expansion
of JJ* (z) + IV {z) will be given in § 135, and it will then be possible to form
such an estimate.
CHAPTER VIII
BESSEL FUNCTIONS OF LA RUE ORDER
8*1. Bessel functions of large order.
The subject of this chapter is the investigation of descriptive properties,
including approximate formulae, complete asymptotic expansions, and in-
inequalities of various types connected with Bessel functions; and the pro-
properties which will Le examined are of primary importance when the orders of the
functions concerned are large, though many of the results happen to be true
for functions of all positive orders.
We shall first obtain results which arc. of a purely formal character,
associated with Carlini's formula (§ 1*4). Next, we shall obtain certain
approximate formulae with the aid of Kelvin's* "principle of stationary
phase." And finally, we shall examine the contour integrals discovered by
Debyef; these will be employed firstly to obtain asymptotic expansions when
the. variables concerned are real, secondly, to obtain numerous inequalities of
varying degrees of importance, and thirdly, to obtain asymptotic expansions
of Bessel functions in which both the order and the argument are complex.
In dealing with the function ./,, (./;), in which v and x are positive, it is
found that the problems under consideration have; to he divided into three
classes, according us u-jv is less than, nearly equal to, or greater than unity.
Similar sub-divisions also have to be made in the corresponding theorems
concerned with complex variables.
The trivial problem <>f determining the asymptotic. expansion of Jv [z\ when v i.s largo
and z in fixed, may he noticed here.
It. is evident, l>y applying Stirling's theorem to the expansion of i^ 3*1, that
Jv (z)~exp [>' + .< log (kz) -(.'-hi) log •'} • <\> + '' +'; + -.. ,
L " »'* J
when* rns=\i\lBTr); this result lion heen pointed out hy Horn, Math. Ann. I.II. AH99),
p. 3.W.
[No'i'K. For physical applications of approximate formulae for functions of largo order,
the following writers niiiy l>e consulted: Maedonald, Proo. ttvynl Soc. i,xxi. A903), pp. 251—
2fi8 ; LXXti. A004), pp. r>!> -UH ; x.<\ A A9M), pp. fH—(il; Phil. Trans, of the Royal Sue. CXX. A
(li)lu), pp. 113—111; Dehye, Ann. dor 1'kysik it/td (Jhnnie, Dj xxx. A1H9), pp. &7—130"';
March, Aim. der l'/rt/xik and dhemic, D) xxxvn. A912), pp. 20—f>0; Rylxayriski, A-itv, der
* Phil. May. (R) xxm. AHH7), pp. 252—255. [Math, and Phys. Pupero, iv. A'JlO), pp. 803—806.]
In connexion witli tlio principle, hoo Htoken, Trtiwt. Vamb. I'hil. Sov. ix. A85A), p. 176 footnote.
[Math. undPhys. Poper*, u. AHH3), p. IMl.J
i1 Math. Ann, i.xvii. (l'.IOi)), pp. t~>'.l5—558; Milnchencr Hitzuvgsderichte, xh. [5], A910)..
W. H. P. 15
228 THEORY OF BESSEL FUNCTIONS [CHAP. VIII
where*
A) P,=?^Dsec2/3 + sec</3)
Sf^Li. C2 sec2 ft + 288isec* /3 + 232 sec" ft 4 13 sec8 ft)
2^ + 4128° sec4^+14884 seC/3 +17493 sec8/3
+ 4242 sec10 ft + 103 sec13 /3)
B) ^==p
A6 -1512 sec2 ft - 3654 sec4 ft - 375 sec8 /3)
8
B56 + 78720 sec2/3 + 1891200 sec4/3 + 4744640 secB/3
322560j/b
4-1914210 sec8/3 + 67599 sec10 ft)
To determine Jv {v sec ft) in terms of these expansions, we take ft to tend
to ^tt, and compare the results so obtained with the expansions of Hankel's
type given in § 7*21; we see that, as ft-^-^Tr,
and we infer that
cot
C) ^
D) Hvv (vsec/8) =
It follows that
E) Jv (v sec ft) = . / f J . e'1'" cos (Qv
/a\ v / o\ //2cot/3\ _„ . n
(o) xv{vsecp) = A/ I ).e ^"sin(y^
where P^ and Q,, are defined by A) and B). It will appear subsequently
(§ 8'41) that these formulae are actually asymptotic expansions of Jv (v sec /3)
and Yv (y sec ft) when v is large and ft is any assigned acute, angle.
Formulae which are valid for small values of ft, i.e. asymptotic expansions
of Jv (z) and Yv (z) which are valid when z and y are both large and are nearly
equal, cannot easily be obtained by this method; but it will be seen in § 8*2
that, for such values of the variables, approximations can be obtained by
rigorous methods from SchlafU's extension of Bessei's integral.
* The reader will observe that the approximation has been carried two stages further than in
the corresponding analysis of § 8*11.
8-2] FUNCTIONS OF LARGE ORDER 229
Note. The dominant terms in the expansions E) and (t>), which may be written in the
form
G) Jv {x)=Mv cos (Q, - iff), Yv (x)*=Mv sin (Qv - ?*¦),
where ^
Qv "" iJifP ~ V<1) ~ hV7T + '' arC Sm ("/¦*')>
had been obtained two years before the publication of Meisaol's paper by L. Lorenz in a
memoir on Physical Optics, K. Danske Videnskab&rnes Selskahs Shifter, F) vi. A890).
[Oeuvres Seimtifiques, i. A898), pp. 421—436.]
The procedure of Lorenz was to take for granted that, as a consequence of the result
which has been proved in § 7*51,
2 .j;2 2.4
and then to use the exact equation
(8) dQ^- 2
which is easily deduced from the Wron.skian formula of $ 3*63 A), to provo that
J [
[rr.vMv~
whence the approximation stated for Qt, follows without difficulty.
Subsequent roHoarchoH on the linen laid down by Loronz are duo to Macdonald, Phi/.
Trans, of the. Jtoi/af Soc. ccx. A A!IO), pp. 131- HI, and Nicholson, Phil. Mag. (G) xiv.
A907), pp. 697—707 ; («) xix. (MHO), pp. ±}H- d-IS); r»I(J -r>37; Proc. London Math. Soo. {i)
IX. A911), pp. G7—HO; B) xi. (IMS), pp. KM--I2C. A romilt conooming Qv.,x- Qu, wliich
in closely connected with (H), haa been publi.shod l>y A. Lodge, liritixh Association Report,
1906, pp. 494—498.
8. The principle of stationary phase. Hessel functions of equal order
and argument.
The principle of stationary j)ha.s(i was formally enunciated by Kelvin* in
connexion with a problem of Hydrodynamics, though the. essence of the principle
is to be found in .some much earlier work by Stokesf on Airy'.s integral (§ ()*4)
and Parseval's integral (§ 2), and also in a posthumous paper by Riemann.|.
The problem which Kelvin 'propounded wan to find an approximate) expression for the
integral
•«==¦ I cos \m {.>•- tf(m)\] dm,
which exj>ressos the effect at place and time (x, t) of an impulnivo disturbance at place and
time @, 0), when /(?«) is the velocity of propagation of two-dimensional waves in water
corresponding to a wave-length 2ir/m. The princ'plo of intorforonce set forth by Stokes
* Phil. Mag. F) xxm. A887), pp. '252—255. [Math, and Phys. Papers, iv. A910), pp. 803—306.]
t Camh. Phil. Trans, ix. A85E), pp. 175,183. [Math, and Phys, Payerr, II. A888), pp. 341, 851.]
% Ges. Math. Werhc (Leipzig, 1870), pp. 400—400.
230 THEORY OF BESSEL FUNCTIONS [CHAP. VIH
and Rayleigh in their treatment of group-velocity and wave-velocity suggested to Kelvin
that, for large values of x—tf(m), the parts of the integral outside the range (fi -a, p + a)
of values of m are negligible on account of interference if p is a value (or the value) of m
which makes
In the range (/x-a, /i+a), the expression m {x-tf(m)} is then replaced by the first
three terms of its expansion by Taylor's theorem, namely
^{x-tf (ji)} + 0. (m - fx) - ?* {fif" (/i) + 2/' (/*)} (m - /02,
and it is found that, if*
\/2
then
In the last integral the limits for <r, which are large even though a be small, have been
replaced by - oo and + oo .
It will be seen from the foregoing analysis that Kelvin's principle is, effectively, that in
the case of the integral of a rapidly oscillating function, the, important part of the integral is
due to that part of the range of integration near which the phase of the. trigonometrical
function involved is stationary^.
It has subsequently been noticed| that it is possible to give a formal
mathematical proof of Kelvin's principle, for a large class of oscillating functions,
by using Bromwich'a generalisation § of an integral formula due to Pirichlet.
The form of Bromwich/s theorem which will be adequate for the applica-
applications of the principle to Bessel functions is as follows :
Let F(x) be a function of x which has limited total fluctuation when cc^Q;
let yhea function of v which is such that py-^oo as v-*¦ co . Then,if—\<\x,<\>
v" Paf~xF(as)sinvx. dx — F(+ 0) f* t"~lsint.dt=F(+ 0) V (fi) sin \/nr;
Jo Jo
and, ifO<fi< 1, the sines may be replaced by cosines throughout.
The method which has just been explained will now be used to obtain an
* This is the appropriate substitution when m {x-tf (m)\ has a minimum at m=/u.; for a
maximum the sign of the expression under the radical is changed.
t A persistent search reveals traces of the use of the principle in the writings of Cauahy. See
e.g. equation A19) in note 16 of his Theorie de la propagation ties Ondex, crowned Sept. 1815,
M6m.pr4se.nt6s par divers savants, I. A827). [Oeuvres, A) i. A882), p. 280.]
$ Proc. Camh. Phil Soc. xix. A918), pp. 49—55.
§ Bromwioh, Theory of Infinite Series, § 174.
8-2] FUNCTIONS OF LARGE ORDER 231
approximate formula for Jv(v) when v is large and positive. This formula,
which was discovered by Cauchy*, is
A) Jv{
2* . 3^ 7TP^
This formula has been investigated by means of the principle of stationary phase, com-
comparatively recently, by Nicholson, Phil. Mag. (G) xvi. A909), pp. 276—277, and Rayleigh,
Phil. Mag. F) xx. A910), pp. 1001—1004 [Scientific Papers, v. A912), pp. 617—620]; see
also Watson, Proe. Camb. Phil. Soo. xix. A918), pp. 42—48.
From § 62 D) it is evident that
Jv (v)- I cos {v F - sin 6)\ dd - —— e-^+sinh*) dt,
TT J 0 TT Jv>
and obviously
sin vir I00 • , •> If
— -¦it lit, ^ — i o no = u \ i / v).
7T • 0 TTJi)
Hence
,/„ („) = l- ("cos [v {d - ain d)\ d6 + 0 (l/v).
TT J I)
Now let 0 = 0 — ain #, and then
/ cos [v F — urn d)\ d0 = I y '^-^d<}>.
But lim = -9,
0 -*.()! — COH ^ 6 *
and hence, i/ </>7A — cos 6) has limited total fluctuation in the interval @, v),
it follows frmn Bromwich's theorem that
"" coa vd> 2 f00 _ i .
aw <^j „ j <p 3 coh v<bd(b
and then A) follows at once.
It still has to bo proved that (/^/(l -coh 0) ha.s limitud total Iliiotuation ; to establish
this result wo observe that
d % ^
where </ (tf) - 2 ^ T ^-^ - 3 F - sin 0),
til 11 U
so that // @) = 0, g (tt - 0) = + oo ,
(f @) = A - coa ^)»/(l -hcoH 6) > 0,
and therefore, by integration, g(8)^Q when O^^^rr. Consequently <j)*/(l-cos 8) i»
monotonic and it is obviously bounded. The result required is therefore proved.
* Comptes Jtendus, xxxvm. A854), p. 998. [Oeuvres, A) xn. A900), p. 608.] A proof by
Cauchy's methods will be given in § 8'21.
232 THEORY OF BBSSBL FUNCTIONS [CHAP. VIII
By means of some tedious integrations by parts*, it is possible to obtain
a second approximation, namely
B) /rW
and it may also be proved that
C) ^(,)
an associated formula is
The asymptotic expansions, of which the.se results give the dominant
terms, will be investigated with the aid of more powerful analytical machinery
in § 8-42.
8*21. M&isseV-s third expansion.
The integral just discussed has been used by Cauchy f and Meissel + to
obtain the formal asymptotic expansion of /„ (n) when n is a large integer.
It will now be explained how this expansion was obtained by Cauchy and (in
a more complete form) by Meissel; the theoretical justification of the pro-
processes employed will be investigated in § 8*42.
Taking the formula
Jn (n) = - fcos [n F - sin 0I dd,
T J 0
let us write 0 — sin 0 — ^ts; it then follows that, for sufficiently small values of t,
and Xo = 1j
It follows that
1 P7 (
Jn(n) = -\
e, $nt3 is larg
Jn(n) ~ - i Bm + 1) \m. # I °° «2m cos (%nts) dt,
IT «i=0 .' 0
\ ( )
.'0 ( wi=0
When n is large, $nt3 is large at the upper limit, and Meissel inferred that
* SeeProc. Cam6. Phil. Soc. xix. A918), pp. 42—48.
t Comptes Rendus, xxxvm. A854), pp. 990—993, 1104—1107. [Oeuvres, A) xii. A900),
pp. 161—164, 167—170.]
t Astr. Nach. cxxvn. A891), col. 359—362; cxxvm. A891), col. 145—154. Concerning
formula A), Meisael stated "Sehon vor dreissig Jahren war ich zu folgenden Formel gelangt."
8*21,.8-22] FUNCTIONS OP LABGE ORDER 233
where Q is the sign indicating a "generalised integral" (§ 6'4); and hence, by
integrating term-by-term and using Euler's formula, Meissel deduced that
1 OC
A) ./»(n)~- 2 A™ F(§m+
Meissel also gave an approximation for Xnl, valid when m is large; and this approxima-
approximation exhibits the divergent character of the expansion A).
The approximation is obtainable) by the theory developed in tho memoir of Darboux,
"Sur ^approximation dea functions dc tres granda nombrea," Journal de Math, C) iv. A878),
pp. 5—56, 377—416.
We consider the singularities of 8 qua function of t; the singularities (where 6 fails to
be monogenic) are the points at which 6 = 2rjr and C = A2nr)", where ?• = +1, +2, +3, ...;
and near* t— ±.{\%tys the dominant terms in the expansion of 6 arts
By the theory of Darboux, an approximation to Am in the sum of the coefficients of
fim + i }n fc]J0 expansions of the two function!-, oompri.sed in the last formula ; that is to way
that
Am~2. (.ion-)!* v»rri
Bjw + 1)! (I^tt)"'"'1 ¦»
and so, by Stirling's formula,
(IH)i r(Ji)(H»+il)*(ia7r)'m'
Thi.s is Moiasel'.s a]))»r<>ximnt,ioii; an approximation of the name character was obtained
by Cauchy, lor. cit., p. 1 IO(>.
8*22. The ajqriimtion of Kelni-n's principle tu /
The principle of Ht.atioiifiry jjlianu ha.s 1k:c>ii applied by Ray]eight to obtain
an approximate formula for ,/,. (/> sec /3) where ^ is a fixed positive acute angle,
and v is large. \.
As in § S'2 we have
Jv(v s»;c /8) = -1- Tcos {vF-se.c j3 .sin tf)} <W + 0 (IIv),
W . 0
and # — seC/S sin ^ ia stationary (a minimum) when 6 = /?.
Write 0 — ace /3 sin 9 — ft — tan ft -{¦ (f>, ho that </> decreases to zero as # in-
increases from 0 to ft and then increases as # increases from /3 to 7r.
• These are the HinKularitios whioh are uoaroat to tho origin,
t Phil. Mag. («) xx. A910), p. 1004. [Hcievtijic Papers, v. A012), p. 620.]
X See also MacdonaliJ, Phil. Trans, of the Royal Soc. cox. A A910), pp. 181—144; and Proc.
EoyalSoc. lxxi. A908), pp. 261—258; i.xxn. A904), pp. 59—68.
234 THEORY OF BESSBL FUNCTIONS [CHAP. VIII
Now
cos {vF — sec /3 sin 6)} dO
In
cos \y (<f> + ^8 — tan f3)\ -5-7 a<^>,
Jo J a9
-K
0 rir-p + tan/5"]
tan/3-/3 Jo
and
<20
1
as 6
VB tan ?)
Hence, if <ft (ddjd<j)) has limited total fluctuation in the range 0 ^ 0 ^ ir, it
follows from Bromioictis theorem that
cos [v (8 — sec y3 sin 8)} d& ^ 2 cos [v (9 + p — tan /3)}
Jo Jo
and so
T cos {1/ (tan fl-&)- \tt]
The formula
B) Yv (v sec /3) <^ sl-
is derived in a similar manner from § 6*21 A).
The reader will observe that these are the dominant terms in Meissel's
expansions § 8*12 E), F).
To complete the rigorous proof of these formulae we have to shew that </>- (d8/d<f>) has
limited total fluctuation.
Now the square of this function, namely <fi (dBjdcf))'*, is equal to
0 - sec j3 sin 6 -18 + tan fl _ , ..
(l-secpcostfJ"" W)
say. But
,,. . _ cos fl coseo 6 A - see ft cos 6f - 2 {6 - sec>.Jj sin 6 - j3 + tan |Q)
cos j3 coaec ^ A -
The numerator, h{$\ of this fraction has the differential coefficient
— cos /3 cos 6 cosec2 6 A - sec /3 cos 6)*,
and so kF) decreases steadily as 6 increases from 0 to -im-, and then increases steadily
as 8 increases from ^n to n; since k(9) = 0 when d = p<$n, it follows that A'(8)^0
when 0^0</3 and /i'@) changes sign once (from negative to positive) in the range
Hence | Jh F) j is monotpnie (and decreasing) when 0^ 6</3, and it has one stationary
point (a minimum) in the range /3 < 8 < jt ; since | ^A (^) | is bounded and continuous
when 0 ^ 0 ^v it consequently has limited total fluctuation when 0 ^ 6 ^ n, as had to be
proved.
8*3] FUNCTIONS OF LARGE ORDER 235
8*3. The method of steepest descents.
A development of the theory of contour integration, called the method of
steepest descents*, has been applied by Debyef to obtain integral representa-
representations of Bessel functions of large order from which asymptotic expansions are
readily deduced. If, in general,, we consider the integral
in which j v | is supposed to be large, the contour is chosen so that it passes
through a point w0 at which f'(w) vanishes ; and the whole of the contour is
then determined by the assumption that the imaginary part of f(w) is to
be constant on it, so that the equation of the contour may be written in
the form
//(W) =//(<>.
To obtain a geometrical conception of the contour, let w — u + iv, where u, v
are real; and draw the surface such that the three coordinates of any point
on it are
u, v, Rf(w).
If Rf\w) — z, and if the s-axis be supposed to be vertical, the surface has no
absolute maxima or minima except where f{w) fails to be monogenic; for, at
all other points,
du? dv-
The points [ui)y v0, Kf(wn)] are saddle points, or passuH, on the surface, so that
the contour of integration is tin; plan of a curve on the, surface which goes
through one of the passes on the surface. Thi.s curve possesses a further
property derived from the equation of the contour; for the rate of change of
f(w), at any given value of w, haw a definite modulus, since f(w) is supposed
to be monogenie ; and since I/{w) does not change as w traverses the contour,
it follows that Rf(w) must change, as rapidly us possible; that is to Kay, that
the curve is charactermed by the property that its direction, at any point of
it, is so chosen that it is the steepest curve through that point and on the
surface.
It may happen that we have, a freedom of choice in selecting a pass and
then in selecting a contour through that pass; our choice is to be determined
from the consideration that the curve must descend on both sides of the pass;
for if the curve ascended, Rf{u>) would tend to + oo (except in very special
cases) as w left the pass, and then the integral would diverge if R(v) > 0,
* French "Mcthode du Col," Gorman "Methotlo der Suttelpunkte."
t Math. Ann. lxvii. A009), pp. 535—558; MUnchener SitzuntjKbcrichte, XL. [6], A910). The
method is to be traced to a posthumous paper by Riemaim, Werke, p. 405; and it has recently
been applied to obtain asymptotic expansions of a variety of funotions.
236 THEOEY OF BESSEL FUNCTIONS [CHAP. VIII
The contour has now been selected* so that the integrand does not
oscillate rapidly on it; and so we may expect that an approximate value of
the integral will be determined from a consideration of the integrand in the
neighbourhood of the pass: from the physical point of view, we have evaded
the interference effects (cf. § 8*2) which occur with any other type of contour.
The mode of derivation of asymptotic expansions from the integral will be
seen clearly from the special functions which will be studied in §§ 8*4—8*43,
8*6, 81; but it is convenient to enunciate at this stage a lemmaf which will
be useful subsequently in proving that the expansions which will be obtained
are asymptotic in the sense of Poincare.
Lemma. Let F{r) be analytic when \ r J ^ a + 8, where a > 0, 8 > 0; and let
m-l
when | t | ^ a, r being positive; also, let \F (r)\< Kebr, where K and b are
positive numbers independent of r, when r is positive and r^a. Then the
asymptotic expansion
f00 00
e~vrF{r) dr~ S amT (m/r) v~mlr
Jo m = l
is valid in the sense of Poincare when \v\is sufficiently large and
arg v [ ^ \tt — A,
where A is an arbitrary positive number
It is evident that, if M be any fixed integer, a constant 7ij can be found
such that
M-l
whenever t ^ 0 whether t ^ a or t > a; and therefore
e-"r^(T)d;T= 2 e-VTamT{m/r)~ldr + RM,
JO m-\ J 0
/"*
where " | RM j < I I e~VT I. K, r{Mlr]~x e&T dr
Jo
provided that R (y) > 6, which is the case when j v j > b cosoc A. The analysis
remains valid even when b is a function of v such that R (v) — b is not small
compared with v. We have therefore proved that
f er^F (t) dr = Mt \m Y (m/r) v~™* + 0 (v~
JO m-l
f
O
and so the lemma is established.
* For an acoount of researches in which the contour is the real axis Bee pp. 1343—1350 of
Burkhardt's artiole in the Encyclopddie der Math. Wiss. u. 1 A916).
+ Cf. Proc. London Math. 8qc. B) xvn! A918), p. 133.
8-31] FUNCTIONS OF LAItGE ORDER 237
8*31. The construction of Debyes contours* when the variables are real.
It has been seen in §§ 6'2,6'21 that the various types of functions associated
with Jv (%) can be represented by integrals of the form
taken along suitable contours. On the hypothesis that v and so are positive,
we shall now examine whether any of the contours appropriate for the
method of steepest descents are of the types investigated in §§ 6*2, 6'21.
In accordance with the principles of the method of steepest descents, as
explained in § 8*3, we have first to find the stationary points of
x sinh w — viu,
qua function of w, i.e. we have to solve the equation
A) x cosh w — v =¦ 0;
and it is at once seen that wo shall have three distinct cases to consider,
in which xjv is less than, greater than, or equal to 1, respectively. We con-
consider these three cases in turn.
(I) When x\v < 1, we can find a positive number a such that
B) x — l/.sech a,
and then the complete solution of A) is
iv — ± a + 2
It will be sufficient to confine our attention to the stationary pointsf ± a; at
these points the imaginary part of a; sinh w — my i.s zero, and so the equation
of the contour to be discussed is
/ (.v sinh w — vw) — 0.
Write w =. a +iv, where it, v are n«il, and this equation becomes
cosh u .sin v — v cosh a = 0,
so that v = 0, or
, v cosh a
C) cosh u = - .
v ' sm v
The contour v = 0 gives a divergent integral. We therefore consider the
contour given by equation C). To values of v between 0 and rrr, corre-
correspond pairs of values of u which are equal but opposite in sign; and as v
increases from 0 to 7r, the positive value of u steadily increases from a to 4- oo .
* The contours investigated in thiH section are thofio which were diaousacd in Debye's earlier
paper, Math. Ann. i.xvn. A1H9), pp. 585—558, except that their orientation is different; cf. § 01.
t The effect of taking stationary points other than ±a would be to translate the oontour
parallel to the imaginary axiB.
238
THEORY OF ,BESSEL FUNCTIONS
[CHAP. VIII
The equation is unaltered by changing the sign of v and so the contour is
symmetrical with regard to the axes; the shape of the part of the contour
between v = — ir and v = tt is shewn in Fig. 16.
TTi
-7TI
\
Fig. 16.
If t = sinh a —a cosh a — (sinh w — w cosh a),
it is easy to verify that r (which is real on the curves shewn in the figure)
increases in the directions indicated by the arrows.
As w travels along the contour from oo — nri to oo + wi, r decreases from
+ oo to 0 and then increases to + oo ; and since, by § 6-2 C),
1 f«>+7rt
J/,v.\ I pxs'mhw—vw,!,,,,
we have obtained a curve from which we can derive information concerning
Jv(x) when x and v are large and x\v< 1. The detailed discussion of the
integral will be given subsequently in §§ 8, 8'5.
The contours from — oo to oo ±nri give information concerning a second
solution of Bessel's equation; but this problem is complicated by Stokes'
phenomenon, on account of the two stationary points on the contour.
(II) When xjv > 1, we can find a positive acute angle ft such that
and the relevant stationary points, which are now roots of the equation
cosh w — cos /3 = 0,
are w = + ift.
When we take the stationary point ift, the contour which we obtain is
I (sinh w — w cos ft) = sin ft — ft cos ft,
so that, replacing w by u + iv, the equation of the contour is
, sin. ft+(v- ft) cos B
cosh ii=—-——.—¦—'-- • .
E)
sin?;
8-31] FUNCTIONS OE LARGE ORDER 239
Now, for values of v between 0 and rr, the function
sin ft + (v — ft) cos ft — sin v
has one minimum (y = ft) at which the value of the function is zero ; for other
values of v between 0 and it,
sin ft + (v — ft) cos ft > sin v.
Hence, for values of v between 0 and tt, equation E) gives two real values
of u (equal but opposite in sign), and these coincide only when v — ft. They
are infinite when v is 0 or it.
The shape of the curves given by equation E) is as shewn in the upper
half of Fig. 17 ; and if
r — i (sin ft — ft cos ft) — (sinh w — w coh /3),
it is easy to verify that t (which is ival on the curves) increases in the
directions indicated by the arrows. As w travels along the contour from — oo •
to oo + 7rt, t decreases from + oo to 0 and then increases to + oo and so we
Fig. 17.
have obtained a curve from which |§ EL D)j we can derive information con-
corning IIVU) (a:) wluin ./¦ and v are large and xjv > 1. The detailed discussion
of the integral will be given in $ S'41, 1;V8.
If we had taken the stationary point ~ift, we should have obtained the
curves shewn in the lower half of Fig. 17, and the curve going from — oo to
oo — Tri gives an integral associated with Hv['iy{x); this also will be discussed
in § 8'41. The two integrals now obtained form a fundamental system of
solutions of Bessel's equation, so that there is a marked distinction between
the case xjv < 1 and the case oojv > 1.
240
THEORY OF BBSSEL FUNCTIONS
[CHAP. VHI
(III) The case in which v=*x may be derived as a limiting case either
from (I) or from (II) by taking a or ft equal to 0. The curves now to be con-
considered are v — 0 and
F) cosh u = w/sin v,
and they are shewn in Fig. 18.
Fig. 18.
We obtain information concerning H}^ (v) and HJ'2] (v) by considering the
curves from — oo to oo + iri, while information concerning Jv (v) is obtained
from the curve which passes from oo — tt% to oo + iri. The detailed investiga-
investigation will be given in §§ 8'42, 8*53, 8#54.
8*32. Geometrical properties of Debye's contours.
An interesting result which will be found to be important in dealing with zeros of
Besael functions (§ 15 "8), and which is also used in proving certain approximate formulae
which will- be stated in § 83, is assooittted with the second of the three contours just dis-
discussed (Fig. 17 of § 8'31). The theorem in question is that the dope* of (he branch from
— oo to oo + Tti is positive and does not exceed */2.
It is evident that, for the curve in question,
(v — /3) cos o cos ,3
. , du sin (v —
sinh u -7- = ^ 0
av sm'v
But sin (y — /3) sec v - (v - /3) cos /3 has the positive derivative coa j3 tan2 v, and hence it
follows that
sin (v — 3) — (v — /3) cos v cos ?f
has the same signt as v—/3. Therefore since v — /3 and v are both powtive or both negative
for the curve under consideration, dvjdu is positive.
* Proc. Camb. Phil. Soc. xix. A918), p. 105. Since, in the limiting case (Fig. 18) in whioh
C=0, the slope is 0 on the left of the origin and is ^3 immediately on the right of the origin, no
better results of this type exist.
t This is obvious from a figure.
8'32, 8*4] FUNCTIONS OF LARGE ORDER 241
Again, to prove that dv\du does not exceed JS, wo write
and then it is sufficient to prove that
.•ty'2(v)-%p(v) + 1^0.
Now the expression on the left (which vanishes when v—fi) has the derivate
0-*(«)]
¦ ; u--- \(v — B) {sin2 w+ 3 cos2 v) cos)9-|-siuiJj;sm/9 — 3 cos v sin (v-8)\
sin3 v L ^ K/J
" 3 coa*sin (t> ~ ^
,i -i.- j • A 4 sin4 »cos/S .......
has the positive denvato .— -.,— . a j v,, and so, since it is positive when v~0, it is
^sin v -p o cos vj
positive when 0 < v < tt. Therefore, sinco ^' (v) has the same sign as v - /9, it follows that
has the same sign as ?' - /3, and consequently
has y = )9 for ita only minimum between v=0and v~ir; and therefore it is not negative.
This proves the result stated.
8. The asymptotic expansion* of Jv (v scch a).
From the results obtained in §8*31 wo shall now obtain the asymptotic
expansion of the function of the first kind in which the argument is lesa than
the order, both being largo and positive;.
We retain the notation of § 8'31 (J); and it is clear that, corresponding to
any positive value of t, there are two values ofw," which will be called w-^ and
m,; the values of wx and w.2 differ only in the sign of their imaginary part, and
it will be supposed that
I(wl)>0, I(w,)<0.
We then have
f,v (timll a-«) fee (,/,,,, fill))
Jv {v sech a) = -¦ . e~XT < -, , (It,
2.7TI J o ( (IT (IT )
where x = v sech a.
Next we discuss the expansions of ?/;, and w% in ascending powers of t.
Since r and dr/dw vanish when w — a, it follows that the expansion of t in
powers of w — a begins with a term in (w — a)a; by reverting this expansion,
we obtain expansions of the form
wl-a= S --^ Ti(mfl)> w»-«= 5 (-)'»+' -^-Ti^1),
,»=(,m+l »0o wi + 1
* The aaymptotio expansinnH contained in thiB Beotion and in §§ 8'41, 8*42 were established
by Debye, Math. Ann. lxvii. (l<H<)), pp. 535—55H.
w. B. V. 16
242
THEORY OF BESSEL FUNCTIONS
[CHAP. VIII
-xnd, by Lagrange's theorem, these expansions are valid for sufficiently small
'allies of j r j. Moreover
1
2iri
*+> dw
l(m+i) *
The double circuit in the T-plane is necessary in order to dispose of the
ractional powers of r; and a single circuit round a in the w-plane corresponds
o a double circuit round the origin in the T-plane. From the last contour
ntegral it follows that am is the coefficient of l/(w — a) in the expansion of
,-j-{m+i) in ascending powers of w — a; we are thus enabled to calculate the
?oefficients am.
Write w — a = W and we have
t = — sinh a (cosh W - 1) — cosh o (sinh W — ^Y)
vhere c0 = — | sinh a, Ci = — $• cosh a, c2 = - fa sinh a,.... Therefore am is the
coefficient of Wm in the expansion of (c0 + c, H^ + c2 F2 + ...j-1 ("l+>).
The coefficients in this expansion will bo called ao(?n), a^m), a,o(?)i), ....
ind so we have
1)
m + 1 c2 (^ + l)B» + 3) cf
' 2.1! "ci,4" 2s!"" " "cV2
ra + 1 c;t (m + l)(m + 3) 2c, c2
(wi +1) (m + 3) (m +J3)
^) (m + 3) (w + 5) 3(j,aca
v.. , 1)(//t+ 3)(w4-5)G)
c,*j
2)
jn substitution we find that
ao = ao @) = 4- (-1 sinh a)-*,
aj = a, A) = - (- | sinh a) {? coth a],
a2 = a2 B) = - (- | sinh a)~» {? - ^ coth2 a],
a3 = a3 C) = — (— \ sinh a) {-^ coth a — ^47 coth3 a},
a4 = a4 D) = 4- (- i sinh «)-«{T|H - ^ coth2a 4 $& coth*a}
8*4] FUNCTIONS OF LAEGE ORDER 243
JNow j -= 2, a«mrm*
dr w -0 "
when I t 1 is sufficiently small; and since
-7— = cosh a — cosfh w,
aw
it follows that d {wx — w^/dr tends to zero as t tends to + 00 .
Hence the conditions stated in the lemma of § 8'3 are satisfied, and so
Jo \dr dr)
asymptotic expansion
y u2w F (m + |)
is large.
Since ar# {(a/, - a)/r* 1 -*¦ J ir as t -*- 0, it follows that, in B), the phase of a0
has to be interpreted by the convention arg «„ = + l-rr, and hence.
C) J",(i/secha)~ - e v L (»* + *>. Al» ..
7 ^irv tanh a) Ul _0 F(|) (Ji/tanha)™'
where
(A „ = 1, ^4, = ? - 5^ coth" a,
^* = 1 !i r - rtVfl coth'J a + ^ c»th* a,
The formula C) givc^H th(^ afl>'niptoti(^ oxpatiHion of •/„(!>secha) valid when
a is any fixed positive number and i/ is largo and positive.
The corresponding expansion for Uiu function of tlio hccoikI kind, obtained by taking a
contour from -oo to oo ±niy is
(V r (V**ha)~- ""(n"tmiha) ^ r(m+4) (-)»'.'i,(,
The position of the singularities of d(wx — w^jdr^ qua function of the
complex variable r, should be no tied. Tlu\so singularities correspond to tho
points where w fails to bo a tnonogenic function of t, i.e. the points where
dr/div vanishes. Hence the singularities correspond to the values ±a.-h%nri
of w, ho they are the points when;
r = Imri cosh a, r = 2 (sinh a- a cosh a) + 2'H.tti cosh a,
and ?h assumes all integral values.
It in convenient to obtain a formula for dwjdr in tho form of a contour integral; if
(w0, t0) bo a pair of corresponding valuon of (w, r), then, by Oauchy's theorem,
/dw\ 1 [(*»+) dw dr 1 F(«>o+) dw_
\drjo"^2iri J drr-m" 2jrt J r-tq'
wliero the contour includes no point (except wQ) at which r haa the value r().
10—2
244 THEORY OF BESSEL FUNCTIONS [CHAP. VIII
8*41. The asymptotic expansions of Jv (v sec /3) and Yv (v sec /3).
In § 8 we obtained the asymptotic expansion of a Bessel function in
which the argument was less than the order, both being large; we shall now
obtain the asymptotic expansions of a fundamental system of solutions of
Bessel's equation when the argument is greater than the order, both being large.
We retain the notation of § 8-31 (II); it is clear that, corresponding to any
positive value of t, there are two values of w lying on the contour which
passes from — oo to co + tri; these values will be called Wj and w2, and it will
be supposed that
B (wO > 0, R (w2) < 0.
We then have
v sec 8) « : e~xr \ -j1 - -j- \ dr,
^ in Jo [dr dr)
where x—vsec/3. The analysis now proceeds exactly on the lines of §8*4
except that a is replaced throughout by i/S, and the Bessel function is of the
third kind.
It is thus found that
dwj
[* _w(^ dwj
e {—? ?—r
Jo [dr dr\
To determine the phase of a0, that is of (— \i sin /3)~*, we observe that
arg {(iVx — ift)fr} -*- + ? 7r as t -*- 0, and so
Consequently
A) H a> (v sec 8)
In like manner, by taking as contour the reflexion of the preceding contour
in the real axis of the w-plane, we find that
B) JT
In these formulae, which are valid when fi is a fixed positive acute angle
and v is large and positive, we have to make the substitutions:
If we combine A) and B), we find that
D) Jv (v sec ft) ~
8-41,8-42] FUNCTIONS OF LARGE ORDER 245
E) F,(»secj8)«»
Tain (v tan 8 vB
Utan#
The dominant terms in these expansions are those obtained by the principle
of stationary phase in § 8'21.
8*42. Asymptotic expansions of Bessel functions whose order and argument
are nearly equal.
The formulae which have been established in §§ 8'4, 8#41 obviously fail
to give adequate approximations when a (or /?) is small, that is when the
argument and order of the Bessel function concerned are nearly equal. It is,
however, possible to use the same method for determining asymptotic ex-
expansions in these circumstances, and it happens that no complications arise by
supposing the variables to be complex.
Accordingly we shall discuss the functions
where z and v are complex numbers of large modulus, such that | z — v \ is
not large. It will appear that it is necessary to assume that z — v = o(z^), in
order that the terms of low rank in the expansions may be small.
We shall write
i'«*(l-e),
and it is convenient to suppose temporarily that
iarg2'< |tt.
We then have
^ roo-l-iTi
A) Hv{l) (z) — ¦ . exp \z (.sinh w - w) -f- sew) dw,
where the contour is that shown in Fig. 1<S; on this contour sinh^w — w is real
and negative.
Wo write
r = w — si nh w,
and the values of w corresponding to any positive value of r will be called wx
and ?-y2. of which ?«, is a complex number with a positive real part, and w., i*
a real negative number.
We then have
B) HJn 0) = —-. | e~M \exp (««/,) -4^ - exp (z€W2) -~\ dr.
v/ 7rc J o [ wr ar)
246
THEORY OF BESSEL FUNCTIONS
[CHAP. VIII
The expansion of t in powers of w begins with a term in vfi, and hence we
obtain expansions of the form
exp\zewi) -j— — t z* omrs ,
ex
CubU
2
= t~3 2 6* {m+i) H bm t*"»,
wi=O
and these are valid when | r \ is sufficiently small.
To determine the coefficients bm we observe that
__Lf
" tori]
@+)
As in the analogous investigation of § 8*4, a single circuit in the r-plane
is inadequate, and the triple circuit is necessary to dispose of the fractional
powers of t; a triple circuit round the origin in the r-plane corresponds
to a single circuit in the w-plane.
It follows that bm is equal to leiim+l)rri multiplied by the coefficient of wm
in the expansion of
exp (zew). {(sinh w — w)/w3}~^m+1).
The coefficients in this expansion will be called bo(vv), 6j(w), b.2(m),... so that
It is easy-to shew that
C)
For brevity we write
8*42]
so that*
FUNCTIONS OF LARGE ORDER
247
B, (ez) =
B, {ez) = ? eV
We then have
exp (zeWjj
exp
//.111 OO
and [exp (zeiv). (dw/dr)] satisfies the conditions of the lemma of § 8'3.
It follows from the lemma of §8*3 that
E) #.«<*) — .?. 5 e^^iBm(ez)sm j (wi + 1O
and similarly
F) //„« (*) ~ - .^ J^-I«»-h)« /iw(€5)Hin i (wi -f-1) 7T.
We deduce at onc<^ l.hab
r
From the C'auchy-Mci.sHc.l formula §S'2l B), it is to be inferred that, when
in is large,
(-)» «,„ («,) ™,. j (»+1)».
but there seems to lie no very simple approximate formula for Iitll(ez).
Tin; dominant terms in G) were, obtained l>y Me.iH.s«l, in »i Kin? Pnn/rammi, 1892;
and .some similar results, which neein to roHOtnblo thowc stated in ^ H*43, woro obtained by
Ivoppe in a Merlin Prayramm :|, 1H!)O. 'M\u\ dominant teruiH in (H) as well aw in G) woro
-also investigated by Niehol.son, Phil. May. ((>) xvi. A«K)H;, j>p. 271—279, shortly bofore tho
appearance of Debyo'H nioinoir.
* Tho vnlnoH of /?„(()), /'u(O), .../*io@) word ^ivon by MoibhuI, AMr. Nach. oxxvn. A891),
col. 351>—362; apart from tho uhc of tho dontourH MriiHHel'H analywiH (of. § H-21) iH HtiliBtnntially
the (same ah the analymH Rivmi in thin Hoction. The object of iiBhi« tho mothoda of contour
integration in to evado the diffiuultiuH produced by UHing gencraliHcd integrala.
The vnlueH of 11^ ('~)> lh (ez) an<' "o iez) w'" b*1 found in a paper by Airoy, Phil. Mag. ((i) xxxi.
A91E), p. fi'i-t.
t See tlie Jahrbuch illter die Forttchntte. der Math. 1R92, pp. 47E—478.
% Sec the Jahrbuch ilber die FartHchritte der Math 1899, pp. 420, 421.
248 THEORY OF BESSEL FUNCTIONS [CHAP. VIII
We next consider the extent to which the condition | arg#| < |7r, which
has so far been imposed on formulae E)—(8), is removable.
The singularities of the integrand in B), qua function of t, are the values
of t for which wx (or w2) fails to be a monogenic function of t, so that the
singularities are the values of t corresponding to those values of w for which
dr/dw = 0.
They are therefore the points
T = 2W7TI,
where n assumes all integral values.
It is consequently permissible to swing the contour through any angle r/
less than a right angle (either positively or negatively), and we then
obtain the analytic continuation of Hvin (z) or Hv{i) (z) over the range
— |7r - t) < arg?<?7r — 7}. By giving 77 suitable values, we thus find that
the expansions E)—(8) are valid over the extended region
— ir < arg z < it.
If we confine our attention to real variables, we see that the solution of the problem is
not quite complete; we have determined asymptotic expansions of Jv (x) valid when ,r and
v are large and (i) xjv <1, (ii) xfv> 1, (iii) | x — v \ not large compared with x\ But there
are transitional regions between (i) and (iii) and also between (ii) .and (iii), and in theho
transitional regions xjv is nearly equal to 1 while | x — v \ is large. In these transitional
regions simple expansions (involving elementary functions only in each term) do not exist.
But important approximate formulae have been discovered by Nicholson, which involve
Bessel functions of orders ± \. Formulae of this type will now be investigated.
8*43. Approximate formulae valid in the transitional regions.
The failure of the formulae of §§ 8*4—842 in the transitional regions led
Nicholson* to investigate second approximations to Bessel's integral in the
following manner:
In the case of functions of integral order n,
J,i(#) = - cos (nd — x sin 6) dd.
it Jo
and, when x and n are nearly equal (both being large), it follows from Kelvin's
principle of stationary phase (§ 8*2) that the important part of the path of
integration is the part on which 6 is small; now, on this part of the path,
sin 6 is approximately equal to 6 — \6%. It is inferred that, for the values of-
x and n under consideration,
Jn (*) ~ - f cos (nd -%0 + \xdz) dd
if
¦ Phil. Mag. F) xix. A910), pp. 247—249; see also Emde, Archiv der Math, und Phys. C)
xxiv. A916), pp. 239—250.
8*43] FUNCTIONS OF LARGE ORDER 249
and the last expression is one of Airys integrals (§6*4). It follows that,
when as < n,
()
' it
and, when x > n,
/9\ t / \ 1 f 2 (a; — n
B) JOOj
where the arguments of the Bessel functions on the right are ? {2 (cc-
The corresponding formula for Yn (x) when x > n was also found by
Nicholson ; with the notation employed in this work it is
C) r.(.)~
The chief disadvantage of these formulae is that it seems impossible to
determine, by rigorous methods, their domains of validity and the order of
magnitude of the errors introduced in using them.
With a view to remedying this defect, Watson* examined Debye's
integrals, and discovered a method which is theoretically simple (though
actually it is very laborious), by means of which formulae analogous to
Nicholson's are obtained together with an upper limit for the errors involved.
The method employed is the following:
Debye's integral for a Bessel function whose order v exceeds its argument
*'(= v sech a) may be written in the formf
Jv (v sech a) = —s—r— / e~XTdw,
where t = — sinh a (cosh w — 1) — cosh a (sinh w — w),
the contour being chosen so that t is positive on it.
If t is expanded in ascending powers of w, Carlini's formula is obtained
when we approximate by neglecting all powers of w save the lowest,
-|w2sinha; and .when a = 0, Cauchy's formula of §8 2A) is similarly ob-
obtained by neglecting all powers of w save the lowest, - $w3.
These considerations suggest that it is desirable to examine whether the
first two terms, namely
— \w"sinh a- iws cosh «,
may not give an approximation valid throughout the first transitional region.
The integral which we shall investigate is therefore
e~xrdW,
where r = — -| W2 sinh a. - \ W3 cosh a,
* Proc. Camb. Phil. Soc. xix. A918), pp. 96—110.
t This is deducible from §8-31 by making a change of origin in the ir-plane.
250
THEORY OF BESSEL FUNCTIONS
[CHAP. VIII
and the contour in the plane of the complex variable W is so chosen that r is
positive on it. If W = U -f- iV, this contour is the right-hand branch of the
hyperbola
and this curve has contact of the third order with Debye's contour at the origin.
It therefore has to be shewn that an approximation to
i
e~XTdiv is
is
These integrals differ by
j/\J-
[J ao JO
dW) ,
-j- \dr,
dr
and so the problem is reduced to the determination of an upper bound for
{d(w—W)/dr}\. And it has been proved, by exceedingly heavy analysis
which will not be reproduced here, that
\d(w-W)
d
<
sech a,
and so
/>/,"
Hence
dw dW\
' dr j
"ooexp(j7rO
(
exp (-!«•;
where | Qx \ < 1.
To evaluate the integral on the right (which is of the type discussed in
§ 6*4), modify the contour into two lines starting from the point at which
W = - tanh a and making angles ± $tt with the real axis.
If we write W= - tanh a + f-e^™ on the respective rays, the integral becomes
elm exp (^v loxfcz aj / exp j_ ^vf& _ ^v^e^i tanh2 a} dg
Jo
— e"!^ exp (|y .tanh1'' a) exp j— I v%3 — | v%e~^ tanh2 a} d%.
Expand the integrands in powers of tanh2 a. and integrate term-by-term—a
procedure which is easily justified—and we get on reduction
§ 7ri tanh a exp (^v tanh3 a). [/"_ j (-|y tanh3 a) — /j (^ tanh3 a)],
and hence we obtain the formula
D) Jv (v sech a) = - -— exp [v (tanh a -f ^ tanh3 a - a)} ifj (?i> tanh8 a)
+ 3^r-lexp {i/(tanh a-a)},
where | 021 < 1. This is the more precise form of Nicholson's approximation A).
8'43] FUNCTIONS OF LARGE ORDER 251
It can be shewn that, whether \.v tanh3 a be small, of a moderate size, or
large, the error is of a smaller order of magnitude (when v is large) than the
approximation given by the first term on the right.
Next we take the case in which the order v is less than the argument
x (= v sec ft).
We then have
gvi(tanj3-/3) ,-oo+zGr-/3)
Hvw (v sec ft) = :— I e~aT dzv,
TTl J _ a, -ip
where T = — i sin 13 (cosh w — 1) — cos ft (sinh xu — w),
the contour being so chosen that r is positive on it.
The process of reasoning already employed leads us to consider the integral
je-^dW,
where T = - $»' Tf2 sin ? - \W3 cos /3,
and the contour in the plane of the complex variable W is such that t is
positive on it. If W= U+iV, this contour is the branch of the cubic
(?/-F2)tan/3 + ?FCtf3- V*) = 0
which passes from — go — itan/3 through the origin to oo exp^7n".
It therefore has to be shewn that an approximation to
e~xrdw is j e~XTdW.
The difference of these integrals is
and it has been proved that, when* ft ? \ir, then
- W)
< 127r sec 6
dr
Hence it follows that
4>d
e~XTdW+ ,
To evaluate the integral on the right, modify the contour into two lines
meeting at W= — i tan ft and inclined at angles .$ tt and 7r respectively to the
real axis. On these lines, write
W = - i tan ft - f, - i tan ? + ?eK
* The important values of /S are, of course, small values. If /S if" not small, Debye's formulae
of § 8-41 yieli effective approximations. The geometrical property of Debye's contour which was
proved in § 8*32 is used in the proof of the theorem quoted.
252 THEORY OF BESSEL FUNCTIONS [CHAP. VIII
expand the integrands in powers of tan* & integrate term-by-term, and it is
found that
e~XT dW = $iri tan 0 exp (- ? vi tan3 0)
J — co— itan/3
x [e~ J-* J_ j (? v tan8 ?) + «** Jj ($ i> tan8 0)]
exp (_ jOT- tan3 0) FjW (|» tan8
V3
On equating real and imaginary parts, it is at once found that
E) Jv (v sec 0) = ?tan 0 cos {» (tan 0 - ?tan3 0-0)}. [J- j + Jj]
+ 3 -* tan /S sin (i; (tan )9 - i tan3 ? - 0)}. [J. j - J{] + 2402/i/,
F) Yv(vsec/?) = ?tan0sin {»(tan0-$tan80-0)}. [J-j + Jj]
- 3"* tan /8 cos [v (tan ? - ? tan3 ? - ?)}. [J_ j - /j] + 24^,/»,
where the argument of each of the Bessel functions J±j on the right is
?i>tans/3; and | 6^\ and | 6t\ are both less than 1. These are the more precise
forms of Nicholson's formulae B) and C); and they give effective approxima-
approximations except near the zeros of the dominant terms on the right.
It is highly probable that the upper limits obtained for the errors are
largely in excess of the actual values of the errors.
8*5. Descriptive properties* of Jv (vx) when 0 < x ^ 1.
The contour integral, which was obtained in § 8*31 (I) to represent
Jv (v sech a) was shewn in § 8-4 to yield an asymptotic expansion of the function.
But the contour integral is really of much greater importance than has hitherto
appeared; for an integral is an exact representation of a function, whereas an
asymptotic expansion can only give, at best, an approximate representation.
And the contour integral (together with the limiting form of it when x — 1)
is peculiarly well adapted for giving interesting information concerning Jv(vx)
when v is positive.
In the contour integral take v to be positive and write
so that u = log r, v — 9.
With the contour selected,
x sinh w — w
is equal to its conjugate complex, and the path of integration is its own re-
reflexion in the real axis. Hence
1 Too +ni
Jv (vx) = jr—A ev iXBinh w~w) dw
27nJoc-,rJ
r
-If,
* The results of this section are investigated in rather greater detail in Proc. London Math. Soc.
B) xvi. A917), pp. 150-174.
8*5] FUNCTIONS OF LARGE ORDER s 253
Changing the notation, we find that the equation of the contour is
r 1 _ 26
r x sin 6'
so that
and, when this substitution is made for r, the value of (w — x sinh w) is
log =—f. cot 6, VC^2 — *'2 sm2 6).
° x sin u '
This last expression will invariably be denoted by the symbol* F{6, x)}
so that
(.1) Jv{vx) =
and by differentiating under the integral sign (a procedure which is easily
justified) it is found that
This is also easily deduced from the equation
JJ (vx) ^^r—.r Vle»(*^v>-w sinh wdw.
Before proceeding to obtain further results concerning Bessel functions, it
is convenient to set on record various properties f of F{6ix). The reader will
easily verify that
D)
so that
E)
h F (*¦ •) - Srrjzs
and also
Next we shall establish the more abstruse property
G) FF, x) 2s F@, x) + \ (& - x2 sin2 0)f»J(l + a?).
To prove it, we shall first shew that
\ 0 - a? sin 0 cos 6
* This function will not be confused with Schlafli's function defined in § 4'15.
¦\ It is supposed throughout the following analysis that 0<;e<1,
254 THEORY OF BESSEL FUNCTIONS [CHAP. VIII
It is clear that
so thatj if gF,x), qua function of d, attained its greatest value at 0 or tr,
that value would be less than V(l + *2)* I? however, g F, sc) attained its
greatest value when 0 had a value 60 between 0 and tt, then
0o)__
@o"-a!sBinB0o)* (df-tfsirfO,)* ~
and therefore
g (9, as) $ g @O, as) = V(l - & cos 20O)
so that, no matter where g{9,x) attains its greatest value, that value does
not exceed V(l + °^)-
Hence
and so
ffl^(^) Z"9<9-x2sin
whence G) follows at once.
Another, but simpler, inequality of the same type is
(8) F@, a) > F(Q, x) + ^02 J(\ - a?).
To prove this, observe that
- * sin2 d)
and integrate; then the inequality is obvious.
From these results we are now in a position to obtain theorems concerning
Jv {yx) and JJ (vx) qua functions of v.
Thus, since
the integrand being positive by E), it follows that Jv(vx) is a -positive de-
decreasing function of v\ in like manner, «/„' (vx) is a positive decreasing function
ofv.
Also, since
3 \evF(H,Z) T AJT\\ 1 [t
97^ ^r I
the integrand being positive by E), it follows that e"*1'0-*) Jv (vx) is a decreasing
function ofv; and so also, similarly, is evFifi>x) Jv' (vx).
8-51] FUNCTIONS OF LARGE ORDER 255
Again, from (8) we have
p—vF@, X) /•«•
"ic
T JO
0,x) r<
I n
7T Jo
so that
e-vF @,*)
(9) Jv (vx) < {1 -
The last expression is easily reduced to Carlini's approximate expression
(§§ T4, 8*11) for Jv(vx); and so Carlini's expression is always in error by
excess, for all* positive values of v.
The corresponding result for JJ (vx) is derived from G). Write
and replace 0 F, x) by G for brevity.
Then
e-vF@,x) roo
IT 7(|
and so
A0) xJJ (vx) < e~" W- *) A + .x-2)V<\/B7ri/).
The absence of the factor \/(l —a;2) from the denominator is remarkable.
It is possible to prove the formulaf
[j(vtut~ ?L -
Joi/lrWdtBwv»)*(l-a?)* {1 + ^/A-«¦))-
in a very similar manner.
This concludes the results which we shall establish concerning a single
Bessel function whose argument is less than its order.
8'61. Lemma concerning F@,x).
We shall now prove the lemma that, when 0 ^a;^: 1 and 0 ^0 <;ir, then
A) *Z#_-> _ lm «, - F @, ,)| t-*™?™* > 0.
The lemma will be used immediately to prove an important theorem con-
concerning the rate of increase of ,/„ (vx).
* It i8 evident from Debye'B expansion that the expression is in error by exooas for sufficiently
large values of v.
f Cf. Proc. London Math. Soc. B) xvi. A917), p. 157.
256 THEORY OF BBSSEL FUNCTIONS [CHAP. VIII
If V@2 - «* sin2 0) s 27@, a), we shall first prove that
dF@,x) idH@,x)
dd I dd
is a non-decreasing function of 0 ; that is to say that
A-0 cot 0J + 02-x- sin2 0
0~-a? sin 0 cos 0
is a non-decreasing function of 0.
The differential coefficient of this last function of 6 is
@ - x* sin 0 cos 0)~2 [@2 cosec2 0 - 1 - ? sin2 0) A - a;2)
-f 2 @2 cosec2 0 - 0s cot 0 cosec2 0 - | sin2 0) A - x*)
+ 2za A-0 cot 6) @ cosec 0 - cos 0J + sin2 0 A - a-2K],
and every group of terms in this expression is positive (or zero) in consequence
of elementary trigonometrical inequalities.
To establish the trigonometrical inequalities, we first observe that, when 0 < 0 $ n,
(i) 8+'sin 0 cos 6 - 20-x sin2 0^0,
(ii) 8+s'm 8cos 6-282cot 6^0,
(iii) sin 0 - 8 cos 8 - $ sin3 8^0,
because the expressions on the left vanish when 0=0 and have the positive differential
coefficients
(i) 2 (cos8-6~x sin8f, (ii) 2 (cos 8-8 cosec 8)'\ (iii) sin 8{8-sin 8 coa0),
and then
62 cosec2 (9 - (9s cot 8 cosec2 0 - \ sin2 0
= (<92 cosec2 8 -1) A - 8 cot (9) + cosec (9 (sin 0 - 8 cos (9 - ? sin3 8) ^ 0,
<92cosec20-l-Jsin20
=8 cosec2 0 @ + sin 8 cos (9 - 20~l sin2 0) + cosec 0 (sin 0 - 0 cos 0 - ? sin3 0) > 0>
so that the inequalities are proved.
It has consequently been shewn that
where the. variables are understood to be 6 and x, and primes denote differ-
differentiations with regard to 0. It is now obvious that
d \F'H F)ffd (F*)
deXHr-F) = HT0\n]
and, if we integrate this inequality from 0 to 0, we get
Since F' and H/H' vanish when 0 = 0, this inequality is equivalent to
and the truth of the lemma becomes obvious when we substitute the value
of H @, x) in the last inequality.
8-52] FUNCTIONS OF LARGE OEDEE 257
8*52. The monotonic property of Jv (vx)jJv (v).
We shall now prove a theorem of some importance, to the effect that, if x
is fixed, and 0 < x < 1, then. Jv {vx)jJv (v) is a non-increasing function of v, when
v is positive.
[The actual proof of the theorem will be valid only when 8^x%l, (where S is an
arbitrarily small positive number), since some expressions introduced in the proof contain an
x in their denominators; but the theorem is obvious when 0 ^ x ^ 5 since e^fo.*) Jv {vx) and
e~vF{o, x)/jv (v) are non-increasing functions of v when x is sufficiently small; moreover, as
will be seen in Chapter xvir, the theorem owes its real importance to the fact that it is
true for values of x in the neighbourhood of unity.]
It will first be shewn that
m T (&lJ(VX) dJ(vx)dJ{vx)
Ovdx ox dv
To establish this result, we observe that, with the usual notation,
Jv(vx)= -
dJv{vx)_ v
dx
and, when we differentiate under the integral sign,
{0 w .)]-* !i?ff..')rf», de
l v ' /J dd
if we integrate by parts the former of the two integrals.
Hence it follows that
Jv{vx)*{>(»*)_ VA™) dJ>W=_i^
' dvdx dx dv 27r
where
by using the inequality F(yfr, x) ^F(Q, x) combined with the theorem of § 8*51.
w. b. f. 17
258 THEORY OF BESSEL FUNCTIONS [CHAP. VIII
Since ?1 @, -ty) is not negative, the repeated integral cannot be negative;
that is to say, we have proved that
7-/ ,d'2Jv(vx) dJv{vx)dJv{vx)
Jv (yx) ——-= ^ — ^ U
dvox ox ov
so that
dv I "v
Integrating this inequality between the limits x and 1, we get
so that
dJv(vx) I _ . dJv(v) I T
Since Jv(yx) and Jv(y) are both positive, this inequality may be written
in the form
and this exhibits the result which was to be proved, namely that Jv(vx)IJv{v)
is a non-increasing function of v.
83. Propeviies of Jv(v) and Jv'(v).
If, for brevity, we write F@) in place of FF, 1), so that
A) F ($) = log - —-i^7lS1-- - cot 9J(&Z- sin* 0),
° 8in0
the formulae* for Jv{v) and Jv'(v) are
B) jv(u)=i
The first term in the expansion of F (d) in ascending powers of 6 is
403/(9 ^3); and we shall prove a series of inequalities leading up to the
result that F (d^O3 is a non-decreasing function of 6.
We shall first shew that
To prove this we observe that
^ . #$ + ^ ^ _ rin.
<k It is to be understood that J"v' (v) means the value of dJv (x)/dx when x haa the particular
value v.
8'53] FUNCTIONS OF LARGE ORDER 259
and that
A. f* ~0c°t0) _ fl2cosec2fl-f-flcotfl-2
_ (^cosec» (9 + 6 cot fl - 2) sin»- 9
Hence it follows that
d (F'@)) 0-sin0cos<9 . „ n
\ = e>W-^rW( sec2 e + ecot 6~2)
by inequalities proved in § 851.
Consequently
C) 6F"F)-2
that is to say A (^' (^) _ ZF @)} > 0.
If we integrate this inequality from 0 to 0 we get
D) dF'(ff)-3F(d)>0,
and this is the condition that F(8)/03 should be a non-decreasing function of 6.
It follows that
F{e, i) > lim F(d) 4
and therefore
2*3*^*'
so that Cauchy's approximation for /^ (i/) is always in error by excess.
An iueqnality which will be required subsequently is
E) 2 F* - sin2 6) F' F) -3F- sin 6 cos 6) F{6) > 0.
The truth of this may be seen by writing the expression on the left iu the form
(ff*-2sin2d+tf sin6cos 6) F' F) + F -sin 6cos 0) {0/"@)-3FF)},
in which each group of terms is positive (cf. § 81).
[Note. A formula resembling those which have just been established is-
r\ i ^
F) / Jv(vt)dt~±-
Jo *»> 3
.see Phil. Mag. f&j&xv. A918), pp. 364—370.]
260 THEOBY OF BESSEL FUNCTIONS [CHAP. VIII
8'54. Monotonic properties of Jv (v) and Jv' (v).
It has already been seen (§ 8#5) that the functions Jv (v) and JJ (v) are
decreasing functions of v. It will now be sKewn that both v*Jv (v) and v%Jv'(v)
are steadily increasing* functions of v.
To prove the first result we observe that
_ t rF(d) e~VF (., de
?- ^ [6F' F) - SF@)} e~"F^ dO
o7T J o
since the integrated part vanishes at each limit and (§ 8*53) the integrand is
positive.
Hence v$ Jv (v) is an increasing function of v; and therefore
A) v*Jv{v)< lim \v\Jv{v)} =r(i)/B'3M = 0-44731.
In connexion with this result it may be noted that
^A) = 0-44005, 2.78 (8) = 0-44691.
To prove the second result, by following the same method we find that
by § 8*53 E), and so v* Jv' (v) is an increasing function of v.
Hence
B) v* JJ (v) < lim {v* JJ (v)} = 3^ T (^)/B*tt) = 0-41085.
It is to be noted that
J{ A) = 0-32515, 4JV (8) = 0-38854.
8'55. T/ie monotonic -property of v*JJ (v)/Jv(v).
A theorem which is slightly more recondite than the theorems just proved
is that the quotient
WW + WMv)}
is a steadily increasing function of v.
* It is not possible to deduce these monotonic properties from the aBymptotic expansions. If,
aB»»-*-oo, J'(p)~(f>(»), and if <p(v) is monotonic, nothing can be inferred concerning monotonic
properties of/(v) in the absence of further information concerning/^).
8-54, 8-55] FUNCTIONS OF LARGE ORDER 261
To prove this result we use the integrals already mentioned in §§ 8'53,
8 4 for the four functions
(v),
Taking the parametric variable in the first and third integrals to be -f in
place of 0, we find that
[, (v)) 7P J o J 0
where
- sin> 0) -
-FW\
- sin2
+ ^sin5cos ^ - 2sin2 (9)
by §8-51. The function Cl^O,^) does not seem to be essentially positive
(cf. § 8-52); to overcome this difficulty, interchange the parametric variables
S and i|r, when it will be found that
? {??! ^ ff(n, (tf.
IV [V*jv{v)) 7TZJ o J 0
Now, from the inequality just proved,
^ J-_1JC_
yjr2 + ty sin yfr cos ^ — 2 sm2 -^ ,, ^ „, ,^ _
— sin2
Since. 0-i V(^ - sin2 0) and J 0JT@) - ,P@) are both (§ 8-68) increasing functions
of 0, the factors of the first term in the sum on the right are both positive or
both negative; and, by §§8-51, 8-53, the second and third terms are both
positive. Hence Ox @, ^) +- H, M e) is positive, and therefore
which establishes the result stated,
262 THEOEY OF BESSEL FUNCTIONS [CHAP. VIII
8*6. Asymptotic expansions of Bessel functions of large complex order.
The results obtained (§§8'31—82) by Debye in connexion with /„(&•)
and Yv (x) where v and x are large and positive were subsequently extended*
to the case of complex variables. In the following investigation, which is, in
some respects, more detailed than Debye's memoir, we shall obtain asymptotic,
expansions associated with «/„ (z) when v and z are large and complex.
It will first be supposed that | arg z\<\rtr, and we shall write
v — z cosh 7 = z cosh (a + ift),
where a and ft are real and 7 is complex. There is a one-one correspondence
between a + ift and v/z if we suppose that ft is restricted to lie between f 0
and 7r, while a may have any real value. This restriction prevents z\v from
lying between — 1 and 1, but this case has already (§ 8*4) been investigated.
The integrals to be investigated are
TTlJ-
~ nl e-'fi*» dw = - --. [" e**^ dw,
7TI.I _«, TTlJ -oo+rti
where f(w) = w cosh 7 — sinh w,
A stationary point of the integrand is at 7, and we shall therefore in-
investigate the curve whose equation is
If we replace w by u + iv, this equation may be written in the form
(v - ft) cosh a cos /? + (u — a) sinh a sin /3 — cosh u sin v + cosh a sin /8 = 0.
The shape of the curve near (a, /3) is
{(u - «J ~(v- ftJ} cosh a sin ft + 2 (u - a) (v - ft) sinh a cos ft = 0,
so the slopes of the two branches through that point are
\ tr + ^arc tan (tanh a cot ft),
— ? 7r + ^arc tan (tanh a cot ft),
where the arc tan denotes an acute angle, positive or negative; Rf(tu) in-
increases as w moves away from 7 on the first branch, while it decreases as w
moves away fro.m 7 on the second branch. The increase (or decrease) is steady,
and Rf(w) tends to + 00 (or - 00 ) as w moves off to infinity unless the curve
has & second double-point J.
* Miinchener Sitzungsherichte, xl. [5], A910); the asymptotic expansions of Iv(x) and Kv(x)
were Btated explicitly by Nicholson, Phil. Mag. F) xx. A910), pp. 938—943.
f That is to say 0</3<tt.
X As will be seen later, this is the exceptional case.
8*6,8-61] FUNCTIONS OF LARGE ORDER 263
If (i) and (ii) denote the whole of the contours of which portions are
marked with those numbers in Fig. 19, we shall write
Svw (*) = --. ! e-*-»> dw, Sv® (z) = - —. I e»/<«> dw,
and by analysis identical with that of § 8'41 (except that i/8 is to be replaced
by y)> it is found that the asymptotic expansions of SV{1} (z) and 8V® (z) are
given by the formulae
S
B)
where arg (— ? j/7rt tanh 7) = arg z + arg (— 1 sinh 7),
and the value of arg (— i sinh 7) which lies between — f 7r and |tt is to be taken.
Fig. 19.
The values of Ao, A1} Ai} ... are
'Ao = 1, Ai - % — s\ coth2 7,
7 + i^fffV cothJ 7,
C)
It remains to express ?TVA' (^) and Hv® (z) in terms of 8VW (z) and /S,,1-' B);
and to do this an intensive study of the curve on which
//(«;) «//(y)
is necessary.
8*61. The form of Debyes contours when the variables are complex.
The equation of the curve introduced in the last section is
A) (v — /3) cosh a cos ft + (u — a) sinh a sin y8
— cosh u sin v + cosh a sin /S = 0,
where («, u) are current Cartesian coordinates and 0< y8< 7r.
Since the equation is unaltered by a change of sign in both u and a, we
shall first study the case in which a ^ 0; and since the equation is unaltered
when 7r — v and ir - y8 are written for a and 0, we shall also at first suppose
that 0 < /3 <^7r, though many of the results which will be proved when # is
an acute angle are still true when [3 is an obtuse angle.
THEORY OF BESSEL FUNCTIONS [CHAP. VIII
For brevity, the expression on the left in A) will be called <?(w, v). Since
??0*j1) = sinh a sin ? - sinh u sin v,
ou
it follows that, when v is given, dcji/du vanishes for only one value of u, and so
the equation in u,
<j> (% v) - 0,
has at most two real roots; and one of these is infinite whenever v is a multiple
Of 7T.
When 0 < v< tt, we have*
<f>(~ 00,1)) =-OO, <f>(+CC ,V) = ~ CO ,
'(f> (a, v) = cosh a {(» - j3) cos /3 - sin v + sin 0} > 0,
and so one root of the equation in u,
(j> (u, v) — 0,
is less than a and the other is greater than o, both becoming equal when v = /?.
By considering the finite root of the equations
<? (u, 0) = 0, (f> (u, it) = 0,
it is seen that, in each case, this root is less than a, so the larger root tends
to + oo as v tends to + 0 or to it - 0, and for values of v just less than 0 or just
greater than tt the equation <? (it, v) = 0 has a large negative root. The shape
of the curve is therefore roughly as shewn by the continuous lines in Fig. 20.
Next consider the configuration when v lies between 0 and — tt.
v-
)
-r
TTi
f
\
— TTi
0
\
y-2iri
Fig. 20.
Wh6n v is - ft d(f> (u, v)/du vanishes at u - '- a, and hence 0 (u, - /3) has a
minimum value
2 cosh a sin /3 A — /3 cot /3 — a tanh a)
at u = — a. There are now two cases to consider according as
1 — /3 cot /3 — a tanh a
is (I) positive or (II) negative.
* Since d<f> [a, t;)/9u=cosha (cos j3-cosv), and this has the same sign as v-/3, <f> (a, t>) has a
minimum value zero at v=j9.
8-61]
FUNCTIONS OF LARGE ORDER
265
The domains of values of the complex 7 = a -f i@ for which
1 — ft cot ft — a tanh a
is positive (in the strip O^ft^-rr) are numbered 1, 4, 5 in Fig. 21; in the
domains numbered 2, 3, 6a, 66, 7 a, 76 the expression is negative;, the cor-
corresponding domains for the complex vjz = cosh (a 4- iff) have the same numbers
in Fig. 22.
6b
TTi
—¦—^>
7b
la
^
5
v
3
A
V
0
Fig. 21.
4
2
^_p_-_—-—•
6b
6a
Fig. 22.
(I) When 1 — ft cot ft - a tanh a is positive, (f> (u, — ft) is essentially positive,
so that the curve never crosses the line v = -ft. The only possibility therefore
is that the curve after crossing the real axis goes off to — 00 as shewn by the
upper dotted curve in Fig. 20.
(II) When 1 -/Scot /3- a.tanh a is negative, the equation <?(-a, w) = 0
has no real root between 0 and ft - 2ir, for
50 (— a, v)/dv = cosh a (cos ft — cos v).
Therefore <?>(--a, v) has a single maximum at -ft, and its value there is
negative, so that $ (— a, v) is negative when v lies between 0 and /3 — 2ir.
Also 4>(u,ft— 2-77-) has a maximum at u = a, and its value there is negative,
so that the curve $ (u, v) = 0 does not cross v = ft—2ir; hence, after crossing
the real axis, the curve must pass off to 00 - iri, as shewn by the dotted curve
on the right of Fig. 20.
This completes the discussion of the part of the curve associated with
&V]) (z) when a > 0, 0 < ft ^ \ir.
Next we have to consider what happens to the curve after crossing the
line v t= + 7r.
Since $ (a, v) — cosh a {(v - /3) cos ft — sin v + sin ft],
and the expression on the right is positive when v > ft, the curve never crosses
the line u = a; also
<j> (u, mr) = (u — a) sinh a sin ft + (mr — ft) cosh a cos ft + cosh a sin ft,
266
THEORY OF BESSEL FUNCTIONS
[CHAP. VIII
and this is positive when u > a, so that the parts of the curve which go off to
infinity on the right must lie as shewn in the north-east corner of Fig. 23.
When l-«tanha + Gr-/3)cot/3>0,
i.e. when (a, /3) lies in any of the domains numbered 1, 2 and 3 in Fig. 21, it is
found that the curve does not cross v = 2nr — /3, and so the curve after crossing
v = 7r passes off to — oo + iri as shewn in Fig. 23 by a broken curve.
We now have to consider what happens when (a, /3) lies in the domain
numbered 6a in Fig. 21. In such circumstances
1 - a tanh a + (tt - ?) cot y8 < 0;
and </> (— a, v) has a maximum at v ~ 2ir — fi, the value of <j> (- a, 2tt - /S) being
negative. The curve, after crossing v = tt, consequently remains on the right of
u = — a until it has got above v «= 2-tt — #.
Now $ (— a, v) is increasing in the intervals
(/S,27r-y8), Btt + /S, 4tt-/9), D7T + /9, 6-rr-?),
let the first of these intervals in which it becomes positive be
Then <? (w, 2Mir + 2ir — /3) has a minimum at u — — a, at which its value is
positive, and so the curve cannot cross the line v=> 2Mw + 27r-/3; it must
therefore go off to infinity on the left, and consequently goes to
-oo +BJf+lOri;
it cannot go to infinity lower than this, for then the complete carve would
meet a horizontal line in more than two points.
i*6l] FUNCTIONS OF LARGE ORDER
When (a, ft) is in 6a, the curve consequently goes to infinity at
26'
~oo
¦/here M is the smallest integer for which ] — a tanh a + {(M + 1) tt — ft] cot /?
s positive.
We can now construct a table of values of the end-points of the contours
or SyM (z) and Sv® (z), and thence we can express these integrals in terms o'
/vA> (z) and Hv® (z) when (a, ft) lies in the domains numbered 1, 2 and 6a it.
Jig. 21; and by suitable reflexions we obtain their values for the rest of th<-
•omplete strip in which 0 <ft< nr. The reader should observe that, so far ar
he domain 1 is concerned, it does not matter whether ft is acute or obtuse.
If M is the smallest integer for which
1 - a tanh a + {(M + l)ir-/3] cot /3
s positive when cot /3 is positive, and if JV is the smallest integer for which
1 - a tanh a - (Ntt + ft) cot ft
^s positive when cot/3 is negative, the tables of values of Svm(z) and Sv® (z
xre as follows:
Regions
1,3,4
2,6a
5,76
66
7a
End-points
— oo , oo + ni
oo — ni, co -f ni
— oo, — oo.+ 2tti
-oo - 2Nni,co + ni
-oo,oo + BJ/+l)m
2./, B)
2e-»«iJ_v(z)
fiAW#,,(i)(8<.-AM)
Regions
1,2,5
3, la
4, 66
6a
76
End-points
- oo + ni, oo
— oo + iri, — oo — ni
oo + 2ni, oc
-oo + BJ/ + l)»t, oo
— oo-f Trt, oo- 2Nni
2 J, («)
2e"Ti /_ „ (z)
eMvni ffjp) (zeMri)
e-Nnri ffvm (zeNH)
From these tables asymptotic expansions of any fundamental system o~
;ojiutions of Bessel's equation can be constructed when v and z are both arb-
rarily large complex numbers, the real part of z being positive. The range o
'alidity of the expansions can be extended to a somewhat wider range of values
»f arg z by means of the device used in § 8*42.
268 THEORY OF BESSEL FUNCTIONS [CHAP. VIII
The reader will find it interesting to prove that, in the critical case j8=^7r, the contours
pass frojn — oo to co 4- nri and from - oc + iri to co , so that the expansions appropriate to
the region 1 are valid.
Note. The differences between the formulae for the regions 6a and 6b and also for the
regions la and lb appear to have been overlooked by Debye, and by Watson, Proc. Royal
Soc. xcv. A, A918), p. 91.
8*7. Kapteyn's inequality for Jn (nz).
An extension of Carlini's formula (§§ 8'11, 8) to Bessel coefficients in
which the argument is complex has been effected by Kapteyn* who has
shewn that, when z has any value, real or complex, for which z- — 1 is not
a real positive numberf, then
znex-p{n\/(l — z*
A) \Jn(nz]
This formula ia less precise than Carlini's formula because the factor Btt?i) - A —z2)* does
not appear in the denominator on the right, but nevertheless the inequality is sufficiently
powerful for the purposes for which it is required J.
To obtain the inequality, consider the integral formula
Jn (nz) = ^—. I t1'1 exp [\nz (t - 1/t)} dt,
in which the contour is a circle of radius eu, where u is a positive number to
be chosen subsequently.
If we write t = eu+{a, we get
Jn (nz) = 5- [" exp [n [%z (euei9 - e-"le~i6) -u- id}] dO.
AIT J —n
Now, if M be the maximum value of
| exp [\z (eueie - e-ue~i9) - u - id] |
on the contour, it is clear fchat
But if z = peia-, where p is positive and a is real, then the real part of
\z(euei9 - e~ue-ie) -u~i6
is %p{eu cos(a+ 6) — e~u cos (a - 6)} — u,
and this atfain$ its maximum value when
tan 6 — — coth u tan a,
and its value is then
p V(sinh8 u + sin2 a) —' u.
* Ann. Set. de VEcole norm sup. C) x. A893), pp. 91—120.
f Since both sides of A) are continuous when z approaches the real axis it follows that the
inequality is still true when z- -1 ia positive: for such values of z, either sign may be given to the
radicals according to the way in which z approaches the cuts.
% See Chapter xvn.
8-7]
FUNCTIONS OF LARGE ORDER
269
Hence, for all positive values of u,
| Jn (npeu) j ^ exp [np «/(sinh2 u + sin2 a) — mo].
We now choose u so that the expression on the right may be as small as
possible in order to get the strongest inequality attainable by this method.
The expression
p V( sinh2 it + sm2 ot) — u
has a minimum, qua function of u, when u is chosen to be the positive root of
the equation*
sinh n cosh u 1
V(sinh2 u + sin2 a) p'
With this choice of u it may be proved that
2 V(l — z*) • sinh u cosh u = ± (cosh 2t* — e-ia),
and, by taking ^ to be real, it is clear that the positive sign must *be taken in
the ambiguity. Hence
2 A + a/A — z2)} sinn u cosh u = em — eM"a,
and so
log
_ i
and it is now clear that
n (m) |
sinh2 u 4- sin2 a
sinh u cosh w
p V(sinh2 u + sin2 a) — w,
J^ exp V(l — ¦s;2)]
An interesting consequence of this inequality is that j Jn (nz) | ^ 1 so long
as both j z 11$ 1 and
!*expVO-_5»): -,
To construct the domain in which the last inequality is satisfied, write as
before z — peia, and define u by the equation
sinh u cosh u 1
V(sinh2 u + sin2 a) p'
The previous analysis shews at once that, when
z exp
then
/? \/(sinh2 w 4- sin2 a) — u = 0.
* This equation is a quadratic in sinha u with oue positive root.
270
THEORY OF BESSEL FUNCTIONS
[CHAP. VIII
It follows that
2u
sinh 2w'
sin2 a = sinh u (u cosh u — sinh u).
As u increases from 0 to 1-1997 ..., sin2a increases from 0 to 1 and p de-
decreases from 1 to* 0-6627434.... It is then clear that i V*** ffi "" f?
1 + y(l ~ z)
inside and on the boundary of an oval curve containing the origin. This curve
Fig. 24. The domain in which j fn (nz) | certainly does not exceed unity.
is shewn in Fig. 24; it will prove to be of considerable importance in the
theory of Kapteyn series (Chapter xvn).
When the order of the Bessel function is positive but not restricted to be an integer wo
take the contour of integration to be a circle of radius eu terminated by two rays inclined
±ir — arc tan (coth u tan a) to the real axis. If we take [ t | = ev on these rays, we get
iSinvjr /"* P i cosh (u+v) — cos 2a cosh (v-u) ~] ,
x — ' - vv \ dv
and so
3inv7r| f- . . ...\
~V l^exp{-«/('y-M)}rfv|
* This value is given by Plummer, Dynamical Astronomy (Cambridge, 1918), p. 47.
CHAPTER IX
POLYNOMIALS ASSOCIATED WITH BESSEL FUNCTIONS
9*1. The definition of Neumann's polynomial 0n(t).
The object of this chapter is the discussion of certain polynomials which
occur in various types of investigations connected with Bessel functions.
The first of these polynomials to appear in analysis occurs in Neumann's *
investigation of the problem of expanding an arbitrary analytic function f(z)
into a series of the form XanJn (z). The function 0n (t), which is now usually
called Neumann's polynomial, is defined as the coefficient of enJn (z) in the
expansion of l/(t — z) as a series of Bessel coefficients!, so that
A) -i- = Jo (*) 00 (t) + 2,7, (*) 0, @ + 2/2 (z) 0, (t) + ...
b "~ Z
From this definition we shall derive an explicit expression for the function,
and it will then appear that the expansion A) is valid whenever \z\< \t\.
In order to obtain this expression, assume that | z \ < \ 11 and, after expanding
1/D - z) in ascending powers of z, substitute Schlomilch's series of Bessel
coefficients (§27) for each power of z.
This procedure gives
1 1 °° z"
- _ — _ -I- V _
t-z t sfi t*+1
2" f (a + 2m).(a + ml)! r I
1 ^ ^ () f •
)
Assuming for the moment that the repeated series is absolutely convergent J,
* Theorie dor Bessel'schen Functional (Leipzig, 18E7), pp. 8—15, 'Hi; sec also Journal fiir
Math, lxvii. A867), pp. 310—314. Neumann's procedure, after assuming the expansion A), iH to
derive the differential equation which will be given subsequently (§ 9#12) and to solvo it in
series.
t In anticipation of § 1611, we observe that the expansion of an arbitrary function is obtained
by substituting for l/(t - z) in the formula
% Of. Pineherle's rather more general investigation, Rcndiconti R. 1st. Lomhardo, B) xv. A882),
pp. 224—225.
272 THEORY OF BESSEL FUNCTIONS [CHAP. IX
we effect a rearrangement by replacing s by n — 2m, and the rearranged series
is a series of Bessel coefficients; we thus get
n=l
()
*> 11=1 {m-O
Accordingly the functions On (t) are denned by the equations
(8)
It is easy to see that
D) ««0»@BS-^r
and the series terminates before there is any possibility of a denominator factor
being zero or negative.
We have now to consider the permissibility of rearranging the repeated series for
\ftt — z). A sufficient condition is that the series
T
should be convergent. To prove that this is actually the case, we observe that, by § 2-11
D), we have
< 2 D | * |)«+** {exp (i 1
0
Hence
_ 1 z | exp (fr ! z P)
The absolute convergence of the repeated series is therefore established
under the hypothesis that \z\ < \ t j. And so the expansion A) is valid when
'^rj<|i|, and the coefficients of the Bessel functions in the expansion are
defined by B) and C).
It is also easy to establish the uniformity of the convergence of the ex-
expansion A) throughout the regions 111 >R, \z\^r, where R >r > 0.
9-1] ASSOCIATED POLYNOMIALS 273
When these inequalities are satisfied, the sum of the moduli of the terms does not
exceed
J - (s + 2m).(s + m-l)\ (?rI+aw exp (|r2)\ exp (frr2)
U2o" w! * "¦ (* + 2m)!' J * S-r ''
Since the expression on the right is independent of z and t, the uniformity of the
convergence follows from the test of Wcierstrasa.
The function 0n(i) was called by Neumann a Bessel function of the second
kind*; but this term is now used (cf. §§ 3*53, 3'54) to describe a certain solution
of Bessel's equation, and so it has become obsolete as a description of Neumann's
function. The function On (t) is a polynomial of degree n + 1 in 1/t, and it is
usually called Neumanns polynomial of order n.
If the order of the terms in Neumann's polynomial is reversed by writing
|n-mor \{n — \) — m for m in B), according as n is even or odd, it is at
once found that
/k\ n ^ 1 *4 n. (In + m -1)\ , ,
~~t + !?+ I6 + t7 '
0n (t) = 4 J? ^^jyp^ (» odd)
These results may be combined in the formula
The equations E), F) and G) were given by Neumann.
By the methods of § 2'11, it is easily proved that
(») I c« 0n {t) U J • (n!) • (| 111)"" exp (J |
where | 0 j ^ [exp (? | * |2) - l]/B« - 2).
From these formulae it follows that the series %a.nJn(z) 0n(t) is convergent
whenever the series 1an(z]t)n is absolutely convergent; and, when z is outside
the circle of convergence of the latter series. <tn Jn(z) 0n(t) does not tend to
zero as n -+¦ oo , and so the former series does not converge. Again, it is easy
to prove that, as n -+¦ oo ,
en Jn {*) On (t) -~l{l~ ^ + 0 («-) j ,
* By analogy with the Legendre function of the second kind, Qn (t), which is such that
-i-= 2 (in + l) Pn(z)Qn(t).
l~Z 71=0
Cf. Modern Analysis, % 15-4.
W. B. F. 18
274 THEORY OF BESSEL FUNCTIONS [CHAP. IX
and hence it may be shewn* that the points on the circle of convergence at
which either series converges f are identical with the points on the circle at
which the other series is convergent. It may also be proved that, if either
series is uniformly convergent in any domains of values of z and ?, so also is
the other series.
Since the series on the right of A) is a uniformly convergent series of
analytic functions when |z \ < \ t \, it follows by differentiation| that
^ g r
where p, q are any positive integers (zero included).
It may be convenient to place on record the following expressions:
02 (t) = l/t + 4/i3, 08 (t) = 3/P +
04 (t) = l/t + 16/?» + -192/i8, OB (t) = 5/P +
The coefficients in the polynomial 0n (t), for w=0, 1, 2, ... 15, have been calculated by
Otti, Bern Mittheilungen, 1898, pp. 4, 5.
9*11. The recurrence formulae satisfied by 0n{t).
We shall now obtain the formulae
A) (n -1Hn+1@ + (n +1) Qn-^0-gfo^±> On(t) =
B) 0^(t)- 0n+1 @ = 20n'(t),
C) _01(*)=Oo/@-
The first of these was stated by Schlafli, Math. Ann. in. A871), p. 137, and proved by
Gegenbauer, Wiener Sitzungsberichte, lxv. B), A872), pp. 33—35, but the other two were
proved some years earlier by Neumann, Theorieder BessePschen Functionen (Leipzig, 1867),
p. 21.
Since early proofs consisted merely of a verification, we shall not repeat
them, but give in their place an investigation by which the recurrence for-
formulae are derived in a natural manner from the corresponding formulae for
Bessel coefficients.
Taking \z \ < 11 \, observe that, by § 91 A) and § 2*22 G),
00 CO
(t-z)l enJn (z) 0n (t) = 1 = 2 en cos2 \rnr. Jn (z),
n=0 »=0
* It is sufficient to use the theorems that, if Zbn is convergent, so also is 2bjn, and that then
S6K/n2 is absolutely convergent.
t This was pointed out by Pincherle, Bologna Memorie, D) ni. A881—2), p. 160.
+ Cf. Modern Analysis, § 5*33.
9'11] ASSOCIATED POLYNOMIALS 275
and hence
z I enJn (z) On (t) = I enjn E) {tOn (f) - cos* \n-rr)
n=0 n=0
= 2 enJn (z) [tOn (t) - COS2 |W7TJ,
n=l
since tOa(t)= 1. If now we use the recurrence formula for J7i(z) to modify
the expression on the right, we get
I enJn (z) On (t) = 2 (J^ (*) + /„+, 0I [tOn (t) - cos2 %mr)ln.
If we notice that Jn+l(z)[tOn(t) — co82^inr)/n tends to zero as n-*-oo, it
is clear on rearrangement that
Jo E) {00 («) - *0, @1 + ^ (*) {20, (t) - \tO, (t) +1}
a) tOn+'{t) tOn-'{t) + 2n sin2 *
Now regard z as a variable, while t remains constant; if the coefficients of
all the Beasel functions on the left do not vanish, the first term which does
not vanish can be made to exceed the sum of all the others in absolute value, by
taking \z\ sufficiently small. Hence all the coefficients vanish identically*
and, from this result, formula A) is obvious.
To prove B) and C) observe that
\dt dzj t — z '
and so, \z\ being less than \t\, we have
2 €»/„ (*) On' (t) + 1 enJn (*) 0n (t) = 0.
n - 0 n - 0
By rearranging the series on tbo left we find that
1 enJn E) On' («) = /, («) 00 («) - 2 |^., <5> - /M+1 E>| On (t)
n=0 n=l
= - Jo (Z) 0, @ - 2 -/„ (Z) @n+1 @ - On-, (*)}.
that is to say,
¦/o («) {Oo' (t) + 0, (t)} + 2 Jn(z) [Wn (t) + Ott+l (t) - On_, («)} S 0.
On equating to zero the coefficient of J,x(z) on the left, just as in the
proof of A), we obtain B) and C).
* This is the argument used to prove that, if a convergent power series vanishes identically,
then all its coefficients vanish (cf. Modern Analysis, §3-73). The argument ie valid here because
the various series of Bessel coefficients converge uniformly throughout a domain containing z = 0.
18—2
276 THBOBY OF BESSEL FUNCTIONS [CHAP. IX
By combining A) and B) we at once obtain the equivalent formulae
D) ntOn-j (t) - (to2 - 1) 0n (t) = (n - 1) tOn' (t) + n sin2 \n-rr,
E) ntOn+1 (t) - (n2 - 1) On (t) = - (n + 1) tOn' (t) + n sin2 \n-K.
If & be written for t (d/dt), these formulae become
F) (n - 1) (^ + n + 1) 0n (t) = n \tOn^ (t) - sin2 \n-rr),
G) (n +1) (^ - n + 1) 0w («) = -» {tOn+1 (t) - sin2 |wtt} .
The Neumann polynomial of negative integral order was defined by Schlafli*
by the equation
(8) 0-(*)-<-)" ?«@-
With this definition the formulae A)—G) are valid for all integral
values of n.
9*12. The differential equation^ satisfied by On(t).
From the recurrence formulae §9'11 F) and G), it is clear that
(S + n + 1) O - n +1) On (t) = r (fc + » + 1) {- ntOn+i (t) + naina Jtittj
fit
= —.- (^ + n + 2) On+1 (t) + n sin2 %nir
= — t {tOn (t) — cos2 \n7r) + n sin2 \nir,
and consequently On(t) satisfies the differential equation
(^ + IJ On (t) + («2 - TO2) On (t) = t COS2 ^UTT + W Sin2 \fiir.
It follows that the general solution of the differential equation
d'*y 3 dy f n2 —1\ _cos2-|-n7r nsin2|//7r
is ^OnW + r^ntf),
and so the only solution of A) which is expressible as a terminating series
is On{t).
It is sometimes convenient to write A) in the form
where
(neven)
i2. (nodd)
* Jtf«tfe. ^«n. m. A871), p. 138.
t Neumann, Theorie der BesseVschm Funetionen (Leipzig, 1867), p. 13; Journal fur Math.
ixvh. A867), p. 314.
9*12, 9'13] ASSOCIATED POLYNOMIALS 277
Another method of constructing the differential equation is bo observe that
andso
2 <nJn(z)On(t)= 2 <nri>Jn
n=0 „=(,
{t-zf ' it-zf^ t-z
Now 1 = 2 BnJ2n (z), 2= 2 e2n +! (in +1) Jin +1 (z),
k=o n=o
and hence t+z=t2 S en,<7n («) ./„ C).
71=0
Therefore
^2Fn,/n (*) 1^1^ ^ +3< - + 1 + *2 - »»| 0n (<) - t*ffn (OJ 350.
On equating to zero the coefficient of Jn (z) on the loft-hand aide of this identity, just
as in § 9*11, we obtain at once tho differential equation satisfied by 0n(t).
9' 13. Neumanns contour integrals associated with On{z).
It has been shewn by Neumann* that, if G be any closed contour,
A) I 0m CO 0n (z) dz ~ 0, {in = n and m j= n)
J c
B)
C) f Jn
J a
where k is the excess of the number of positive circuits of the contour round
the origin over the number of negative circuits.
The first result is obvious from Cauchy's theorem, because the only singu-
singularity of Om{z) On{z) is at the origin, and the residue there is zero.
The third result follows in a similar manner; the only pole of the inte-
integrand is a simple pole at the origin, and the residue at this point is l/en.
To prove the second result, multiply the equations
V«y« (*) = 0, Vn [z0n (z)\ - *gn (*)
by z0n{z) and Jm {z) respectively,and subtract. If U{z) be written in place of
Jm{z) dz Z°n{Z) "dz '
the result of subtracting assumes the form
*• TJ'{z)+zU{z) + {m* - n2)zJm{z) On{z) = z3gn{z) Jm{z)>
* Theorie der BetseVtchcn Functionen (Leipzig, 1867), p. 19.
278 THEOBY OF BBSSEL FUNCTIONS [CHAP. IX
and hence
[zU(z)]c+(m*-n*)[ Jm{z)On{z)dz = \ z*gn(z)Jm(z)dz.
Jo Jo
The integrated part vanishes because U(z) is one-valued, and the integral
on the right vanishes because the integrand is analytic for all values of z; and
hence we deduce B) when m* ^ n8.
Two corollaries, due to Schlafli, Math. Ann. in. A871), p. 138, are that
D)
The first is obtained by applying B) and C) to the formula § 2-4 A), namely
and the second follows by making an obvious change of variable.
9*14. Neumann's integral for On(z).
It was stated by Neumann * that
a) cm - r|u+V(" l
J
0
We shall now prove by induction the equivalent formula
B) On (z) = \\ [[t + V(l + t2)}n + {W(l + *2)}n] e~« dtt
Jo
where a is any angle such that | a + arg z \ < \ir; on writing ? = u/z, the truth
of A) will then be manifest.
A modification of equation B) is
C) On (z) = l ^ *Ve + {-ye-1*6) fi-*«w»» cosh 0d0.
Jo
To prove B) we observe that
("Mexpta faa expta
Jo Jo
and so, by using the recurrence formula § 9*11 B), it follows that we may write
(• oo exp ia
0B(*)- <f>n(t)e-*dty
Jo
where
D) <?n+1 (t) - 2«^n 00 - ^ (t) = 0,
and
E) *.(«)«
* Theorie der BesseVsehen Functionen (Leipzig, 1867), p. 16; Journal filr Math. lxvu. A867),
p. 312.
9*UJ ASSOCIATED POLYNOMIALS 279
The solution of the difference equation D) ia
<j>n (t) = A{t + V(«2 + l)}n + B [t - V(l + *2)}n,
where A and B are independent of n, though they might be functions of t.
The conditions E) shew, however, that A = B = \; and the formula B) is
established.
This proof was given in a symbolic form by Sonine*, who wrote <j>n (Z>). A/z) where we
/°o expia
<\>n @ e""zt dt, D standing for (djdz).
0
A completely different investigation of this result is due to Kapteynf,
whose analysis is based on the expansion of § 91 A), which we now write in
the form
When j ^I < I z |, we have
if p be so chosen that
It follows that
(fa 1 ,
= M S /*•/« (S) \
z .'0 (»=-«, J
.' 0 L»= -»
We shall wow shew that tho interchange of summation and integration ia justifiable; it
will be sufficient to shew that, for any given values of ? and z (such that | f | < | z |),
m r
n=N-\-\ Jo
z
can be made arbitrarily small by taking N sufficiently large J ; now
amlso
(O\ f
Jo
* Math. Ann. xvi. A880), p. 7. For a similar symbolic investigation aee § 6-1-1 supra.
t Ann. Sci. de I'ticole norm. slip. C) x. A893), p. 108.
X Cf. Bromwich, Theory of Infinite Seriea, § 176.
280 THEORY OF BBSSEL FUNCTIONS [OHAJP. IX
Therefore, since | i j < | z |, we have
M r
n=N+\ J 0
and the expression on the left can be made arbitrarily small by taking iV sufficiently large
when 2 and ? are fixed.
Hence, when | ? j < j z |, we have
JL I p^l
L I
where On (z) is defined by the equation
e du,
and it is easy to see that 0n(z), so denned, is a polynomial in 1/z of degree
?i+ 1.
When the integrand is expanded* in powers of z and integrated term by
term, it is easy to reconcile this definition of On(z) with the formula § 9'1 D).
9*15. Sonine's investigation of Neumann's integral.
An extremely interesting and suggestive investigation of a general type
of expansion of l/(a — z) is due to Soninef; from this'general expansion,
Neumann's formula (§9'1) with the integral of § 94 can be derived without
difficulty. Sonine's general theorem is as follows:
Let yjr (w) be an arbitrary function of w; and, if -ty (w) = %, let w = ^ {°°)>
so that 41 is the function inverse to ty.
Let Zn and An be defined by the equations%
Then — = S ZnAn,
a — z „=_«,
it being assumed that the series on the right is convergent.
Suppose that for any given positive value of x, \ w \ > \ -fa («) | on a closed
curve C surrounding the origin and the point z, and | w \ < \ ^ (a) \ on a closed
* Cf. Hobson, Plane Trigonometry A918), § 264.
t Mathematical Collection (Moscow), v. A870), pp. 323—382. Sonine's notation has been
modified slightly, but the symbols \p and ^ are his.
X This is connected with Laplace's transformation. See Burkhardt, EneyclopSdie der Math.
Wiss. ii. (Analysis) A916), pp. 781—784.
9-15,9*16] ASSOCIATED POLYNOMIALS 281
curve c surrounding the origin but not enclosing the point z. Then
oo -I ao rm /•
2 ZtlAn = ~ S e^w
w
dwdx
W —
= (
Jo
()
o
provided that i? (z) < R (a); and the result is established if it is assumed
that the various transformations are permissible.
In order to obtain Neumann's expansion, take
yjr (¦«/) = -| O - 1/w), 4- (*) = * ± V(*'J + 1),
and then
>* «
n0
Since
An + (-)» ^l_rt = ("e--* [{« ± .v/(al2 + l)}n + (-)B {a ± *J(a? + l)}~n] dx,
J o
we at once obtain Neumann's integral.
Sonine notes qj. 328) that
Jn (z) ~ {\zYJn!, <rt 0B («) ~ n ! (i«)-»,
so that the expansion of l/(a —2) converges when |a|<|a|; and in tile later part of hiw
memoir he gives further applications of his general expansion.
9'16. The generating function of 0n (s).
The series 2 (-)nentn0n(z), which in a generating function associated with 0n(z),
does not converge for any value of t except zero. Kaptoyn*, however, haa "summed" the
series after the method of Borel, In the following manner:
nJ~Y (ntn°n B)=«- + nl, »i (i"-ttin)T(i«)^~t
_ v " (w +i) • (n+m) ' P" '"'
2 (»+i).(»+»«)i^-^1
1 » Bm)! ^"/ _
* Nieuw Archiefvoor Wiskunde B), vi. A905), pp. 49—55.
282 THEOBY OF BESSEL FUNCTIONS [CHAP. IX
/"> e~udu
is convergent so long as A - f) zjt is not negative.
There is no great difficulty in verifying that the series 2 ( — )nfntn0n(z) is an asym-
ptotic expansion of. the integral for small positive values of t when | arg z | < n, and so the
integral may be regarded as the generating function of 0n (z). Kapteyn has built up much
of the theory of Neumann's function from this result.
9'17. The inequality of Kapteyn's type for 0n(m).
It is possible to deduce from Neumann's integral an inequality satisfied
by On{nz) which closely resembles the inequality satisfied by Jn (m) obtained
in § 8-7.
We have
the path of integration being a contour in the w-plane, and so
where that value of the radical is taken which gives the integrand with the
greater modulus.
Now the stationary point of
\w + V(w2 + «*)} e~w
is V(l — 22), and so
A) I On(nz) I < ^ |L±^^pj| (W + W + *•)} 6-1.1 cZti; |,
where the path of integration is one for which the integrand is greatest at the
stationary point.
If a surface of the type indicated in § 8-3 is constructed over the w-plane,
the stationary point is the only pass on the surface; and both w = 0 and
w — + oo are at a lower level than the pass if
Hence, since a contour joining the origin to infinity can be drawn when B) is
satisfied, and since the integral involved in A) is convergent with this contour,
it follows that, throughout the domain in which B) is satisfied, the inequality
is satisfied for some constant value of A ; and this is an inequality of the same
character as the inequality of § 8'7.
9*17, 9-2] ASSOCIATED POLYNOMIALS 283
9*2. Gegenbauer's generalisation* of Neumann's polynomial.
If we expand zvj{t — z) in ascending powers of z and replace each power of
z by the expansion as a series of Bessel functions given in § 5, we find on
rearrangement that
zv _ « z"+'
_ Z 2"+* { 5 (y + < + 2m). T (y + s + m) }
the rearrangement has been effected by replacing s by n — 2m, and it presents
no greater theoretical difficulties than the corresponding rearrangement in § 9'].
We are thus led to consider Gegenbauer's polynomial A1hv(t), defined by
the equation
(i) AnAi)^
this definition is valid whenever v is not zero or a negative integer; and when
| z\< \t\, we have
B) .— = 2 An>v(t)Jv+n(z).
t — z n^o
The reader should have no difficulty in proving the following recurrence
formulae:
C) ^v + 7l)i1]
n +
E) (i;
F) (i/ + «) ^n+l, „ @ - {v + n +
G) AM(*)-
* Wiener Sitzungsberichte, lxxiv. B), A877), pp. 124—130.
284 THEOBY OF BESSEL FUNCTIONS [CHAP. IX
The differential equation of which AniV(t) is a solution is
<8> 5? +
where
(9) 9nAt)=
The general solution of (8) is J.n, „ @ + tv~l c$v+n (t).
Of these results, C), D), (8) and (9) are due to Gegenbauer; and he also
proved that
A0) ~. Jl0+) An, „ @ «« <*i = 2" »* r (j/). (v + n) Gn" (z),
where Gnv (z) is the coefficient of an in the expansion of A — 2az + a*)~"; this
formula is easily proved by calculating the residue of (izt)m An> v (t) at the origin.
The corresponding formula for Neumann's polynomial is
1 rio+)
A1) — -. 0H (t) eizt dt = i11 cos {n arc cos z\.
The following formulae may also be mentioned :
A2) I Am y (z) An v (z) dz = 0, (m = n and m j= n)
J c '
A3) f z~" Jv+m(z) An<v{z) dz = 0, (m2^n2)
¦I G
f
A4) *-" Jv+n (z) An „ (z) dz = 2irik,
.' c
where G is any closed contour, n — 0,1, 2, ..., and h is the excess of the number
of positive circuits over the number of negative circuits of (J round the origin.
The first and third of these last results are proved by the method of § 9*13 ;
the second is derived from the equations
V,+w Jv+m (z) = 0, Vu+n [zl~v An> „ (*)} = s?-* gn> „ (z),
whence we find that
(m - n) Bv + m + n) I z~v Jv+m (z) An, v (z) dz = I z-~v gn „ (z) Jv+m (z) dz = 0.
Jo J c
9'3. Schldfli's polynomial Sn (t).
A polynomial closely connected with Neumann's polynomial On (t) was
investigated by Schlafli. In view of the greater simplicity of some of its
properties, it is frequently convenient to use it rather than Neumann's poly-
polynomial.
9-3] ASSOCIATED POLYNOMIALS 285
SchlaflTs definition* of the polynomial is
<bt (lit _ im — 1 \\
A) flf»@ = 2 (ll-^L_l)j(^)-n+,W) (n ^ 1}
B) S,@-0.
On comparing A) with § 9'1 B), we see at once that
C) \n Sn (t) = tOn (t) - cos2 \mc.
If we substitute for the functions 0n (t) in the recurrence formulae. § 91 A)
and B), we find from the former that
D) Sn+i (t) + ?n-i (t) - 2nt~l SH (t) = 4* cos'J 1- nir,
and from the latter,
| (n - l)8n^ (t) - | (n + 1) Sn+1 (t) = nSn' (t) - ntr' 8n (t) - 2t~l cos2 frnr.
If we multiply this by 2 and add the result bo D), we got
E) Sn_1{t)-Sn+l(t) = 2Sn/(t).
The formulae D) and E) may, of course, be proved by elementary algebra
by using the definition of Sn(t), without appealing to the properties of
Neumann's polynomial.
The definition of Schlafli's polynomial of negative order is
F) <8Ln(*)-(-)n+1&@,
and, with this definition, D) and E) are true for all integral values of n.
The interesting formula, pointed out by Schliifli,
G) fifM_, CO+ iSll+1 @-40B(«),
is easily derived from C) and D).
Other forms of the recurrence formulae which may be derived from D)
and E) are
(8) t8n-i @ - nSn @ - t8n' (t) = 2 cos2 \ wir,
(9) tSn+l (t) - nSn (t) + tS.n' (t) = 2 cos91 mr.
If we write Sy for t (d/dt), these formulae become
A0) (S + n) Sn @ = t$n-i @-2 cos" I nir,
A1) (^ - n) Sn @ = - tXn+i @ + 2 Gon*$nir.
It follows that
(^2 - >r) Sn (t) = t (Sr + 1 - m) Sn_, @ + 2/i cos2 ^nvr
= - Pfin (t) + 2t sin2 \ nir + 2//. cos" \ nir,
and so *Sn@ is a solution of the differential equation
A2) t* -f- + t -j + {t* - ?<a) y = 2« sin21 nir + 2n cos'^ ? nvr.
Cot" C^6 •
* Math. Ann. in. A871), p. 138.
286 THEORY OF BESSEL FUNCTIONS [CHAP. IX
It may be convenient to place on record the following expressions :
5,@-2/*, ?2(?) = 4/?a,
St (t) = 2jt + 16/?, S4 (t) = 8/t* + 96/t\
S6 (t) = 2jt + 48/?3 + 768/P, SC) (t) = 12/t2 + 384/f* + 7680/*8:
The general descending series, given explicitly by Otti, are
_2n 2n(w!»-2') 2n (»s - 22) (it8 - 42)
~t2+ P ~+ t6
- ? 2 (?t2 - I2) 2 (h2 - I2) (w2 - 32)
~1+ ? + i5 +'""
The coefficients in the polynomial Sn (t), for n — 1, 2, ... 12, have been calculated by Otti,
Bern Mittheilungen, 1898, pp. 13—14; Otti's formulae are reproduced (with some obvious
errors) by Graf and Gubler, Einleitung in die Theorie der BesseVschen Funktionen, n. (Bern,
1900), p. 24.
9*31. Formulae connecting the polynomials of Neumann and Sc/ddfli.
We have already encountered two formulae connecting the polynomials of
Neumann and Schlafli, namely
\n Sn (t) = t0n (t) - cos2 -|?i7T,
of which the former is an immediate consequence of the definitions of the
functions, and the latter follows from the recurrence formulae. A number of
other formulae connecting the two functions are due to Crelier*; they are
easily derivable from the formulae already obtained, and we.shall now discuss
the more important of them.
When we eliminate cos2-|->wr from § 9*3 C) and either § 9*3 (8) or (9), we
find that
A) Sn_l(t)~Sn'(t) = 2On(t),
B) S»+,@+5«'@-2OB@.
Next, on summing equations of the type § 9*3E), we find that
<D»-D
C) #„(<) = -2 2 S'n-2m-i(t) + sin2 imr.SAt),
and hence
D) Sn (t) + Sn^ (t) = - 2 "?2 S'n.m-i (t) + Sx (t).
¦m=0
* Covyptes Rendw, cxxv. A897), pp. 421—423, 860—863; Bern Mittheilungen, 1807, pp. 61—96.
9*31,9-32] ASSOCIATED POLYNOMIALS 287
Again from § 9'3 G) and E) we have
4 {()„_: (t) + 0B+1 (*)} = ?n~2 @ + %Sn (t) + Sn+i (t)
= <A-2 (*) - Sn (t)} - {Sn (t) - Sn+2 («)} 4,Sn (t)
so that
E) Sn" (t) + Sn (t) = 0n_x @ + 0M+1 (i).
This is the most interesting of the formulae obtained by Crelier.
Again, on summing formulae of the type of §911 B), we find that
< 4G1-1)
F) 0n(t) = -2 2 O'^-i(*) + sin?\mr . O1 (t) + cos2\mr.Oo(t),
JM=*O
and hence
G) 0n (t) + 0n-, (t) = - 2 ^ O'n^-x («) + 0, («) + 0Q (t).
9*32. Grafs expression, of Sn (z) as a sum.
The peculiar summatory formula
A) Sn(z) = 7T i [Jn(s)Ym(s)-Jm(z)Yn(z)}
m— —n
was stated by Graf* in 189&, fchc proof being supplied later in Graf and
Gubler's treatisef. This formula is most readily proved by induction; i% is
obviously true when ?i = 0, and also, by §3*63A2), when n—\. If now the
sum on the right be denoted temporarily by <j>n{z), it is clear that
<?n+1 (z) + <?„_, (z) - Bn/s) <fin {z)
m+1 n+l
= irjn+1(z) s rm(«)-«-yw(«) 2 ./„(*)
m=-7i-l m=-?i-l
+ ^M(*) ^ Y^W-irY^z) ^ Jm(z)
m=— n+l m= — n+l
-{2mriz)Jn{z) I Fm(^) + Bn7r/^) Yn(z) 2 JwD
m=—w »t=-n
Now modify the summations on the right by suppressing or inserting terms
at the beginning and end so that all the summations run from -nton; and
we then see that the complete coefficients of the sums XJm(z) and 2 Ym(z)
vanish. It follows that
<f>n+i (*) + (f>n-i (*) - Bn/s) <?„ 0)
- wJW (*) (y.+» (*) + F_n_, (^} - 7T Fw (Z) [Jn+1 (Z) + /.n-x (Z)\
- »/»., (*) {Yn(») + Y_n (z)} + irYn^ («) {./w (*) + JLn (^)j
= - 7T {1 + (- 1)W1 {Jn-i (Z) Yn (Z) - Jn {Z) IV* (*)}
= 4^~1COS2^W7T,
by §363A2); and so 4>nB) satisfies the recurrence formula which is satisfied
by Sn(z), and the induction that <$>n{z) = Sn(z) is evident.
* Math. Ann. XLin. A893), p. 138.
t Einleitung in die Theorie der BesseVschen Funklionen, n. (Bern, 1900), pp. 34—41.
288 THEORY OF BESSEL FUNCTIONS [CHAP. IX
9*33. Crelier's integral for 8n(z).
If we take the formula §914B), namely
r oo exp ta
On («) = * [{t + V(l + *2)jw +{t~ V(l + *2)}Jl] «' dt,
and integrate by parts, we find that
On(z) = i
JITT ft
+
Hence it follows that
This equation, which was given by Schlafli, Math. Ann. in. A871), p. 146, in the form
B) Sn(z) = Jo {«•*-(-)»« «fl}e 'i-nhfldfl,
is fundamental in Crelier'a researches*, of which we shall now give an outline.
We write temporarily
and then
so that
T
rn — """ /yi ; rp >
¦in J- 71/ J n—l
and therefore
the continued fraction having n elements. It follows that T?H.i/7'n is the
quotient of-two simple continuants-\ so that
Tn+i __ iTB^ 2^, ...,2^^
Tn
the suffixes w, n — 1 denoting the number of elements in the continuants.
It follows that^: Tn(KBt)n-\ is independent of n; and since
yi = 2V(l + <»),
we have
* Comptet Rendus, cxxv. A897), pp. 421—423, 860—863; Bern Mittheilunyen, 1897, pp. 61—96.
t Chrystal, Algebra, n. A900), pp. 494—502.
$ Since all the elements of the continuant are the same, the continuant may be expressed by
this abbreviated notation.
9-33,9*34] ASSOCIATED POLYNOMIALS 289
and hence
r« oxpio
C) ?*(*)= 2 K{2t)n^e~^dt.
J n
From this result it is possible to obtain all the recurrence formulae for
8n(z) by using properties of continuants.
9*34. Schl&fli's expansion of Sn(t + z) as a series of Bessel coefficients.
We shall now obtain the result due to Schlafli* that, when \z\<\t ,
Sn (t + z) can be expanded in the form
A) 8n(t + z)= 2 Sn_m{t)Jm(z).
VI ~ — 00
The simplest method of establishing this formula for positive values of n
is by induction f. It is evidently true when n — 0, for then both sides vanish :
when n — 1, the expression on the right is equal to
Sx(t)J0(z)+ 2 [S^
2
111 = 1
= 2 2 *mOm(t)Jm(-z)
= 2/0 + z) = 8, (t + z),
by §9-1 (I) and §9-3 G).
Now, if we assume the truth of A) for Schlafli's polynomials of ordens
0, 1, 2, ... n, we have
Sn+l (t + z) = Sn^ (t + z)~ 2Sn' (t + z)
= t 6'n_.,rt_x (t)Jm(z)~2 t S'n^n(t)Jm(z)
= ? /SfB+1_m(O«/mCs),
Mi = — r>
and the induction is established; to obtain the second line in the analysis,
we have used the obvious result that
* Math. Ann. in. A871), pp. 139—141; the examination of the convergence of the aeries is
left to the reader (cf. § 9-1).
+ The extension to negative values of n follows on the proof for positive value?, by § 9-3 (G).
W. B. F. 19
290 THEOBY OF BESSEL FUNCTIONS [CHAP. IX
The expansion was obtained by Schlafli by expanding every term on the right of (I) in
ascending powers of z and descending powers of t. The investigation given hero is due to
Sonine, Math. Ann. xvi. A880), p. 7; Sonine's investigation was concerned with a more
general class of functions than Schlafli's polynomial, known as hemi-cylindrical functions
(§ 10-8).
When we make use of equation § 9*3 G), it is clear that, when | z \ < 11 \,
B) On(t + z)= ? On.m{t)Jm{z).
TO = —oo
This was proved directly by Gegenbauer, Wiener Sitzungsberichte, lxvi. B), A872),
pp. 220—223, who expanded 0n (t+z) in ascending powers of z by Taylor's theorem, used
the obvious formula [cf. § 9*11 B)]
and rearranged the resulting double series.
It is easy to deduce Grafs* results (valid when [ z I < i t ]),
D) Sn{t-z)= 1 8n+m(t)Jm(z),
E) 0H(«-*)- 5 OW,(«)J.(«).
9-4. TAe definition of Neumanns polynomial ?ln (t).
. The problem of expanding an arbitrary even analytic function into a,
series of squares of Bessel coefficients was suggested to Neumannf by the
formulae of § 2*72, which express any even power of z as a series of this type.
The preliminary expansion, corresponding to the expansion of l/(t — z)
given in § 91, is the expansion of l/(?2—.z2); and the function D.n (t) will
be defined as the coefficient of en Jn{z) in the expansion of \j{tl — 22), so that
A) n~Z~* = ^°2 (*) ^° (*)+ '^i ^) ^! (*)+ 2^2 (*) ^MO + ¦ • •
= i enjn2B)nw(i).
To obtain an explicit expression for Cln(t), take xz\ < \t |, and, after ex-
expanding l/(?2 — z2) in ascending powers of z, substitute for each power of z the
* Math. Ann. xliii. A893), pp. 141—142; see also Epstein, Die vier Rechnung<operationen
mit BesseVschen Functionen (Bern, 1894). [Juhrbuch liber die Fortschritte der Math. 1893—1891,
pp. 845—846.]
t Leipziger Berichte, xxi. A869), pp. 221—256. [Math. Ann. in. A871), pp. 581—610.]
9-4]
ASSOCIATED POLYNOMIALS
291
series of squares of Bessel coefficients given by Neumann (§ 2*72). As in
§ 91, we have
1 ? z™
5=0
1 2
T "
t/i!
fl 4-
when we rearrange the series by writing n — s for in; this rearrangement
presents no greater theoretical difficulties than the corresponding rearrange-
rearrangement in § 9.
Accordingly the function Cln @ is defined by the equations
C) O0 @ = l/?2.
On reversing the order of the terms in B) we rind that
D) n.(o- i I n^ - V-fe"^!1' ¦ (» > i)
while, if B) be written out in full, it assumes the form
.2.3 4NaD?r-22)Dn--4")
. _2- _1_
4 t* 4.5.0
Also
2-n(n!K
I 2n
where
2n ' * 2hBh-2)
Bn-l)Bw-3)Bn-5)
nB«-2)B»-4) '
^ m 2»Bw-2j...2 '
Since 0 < ©2n< 1, it is easy to shew by the methods of § 211 that
(8) j en Hn (t) | < 2-'1111-2»-" (n!)'J exp (|
and, when n > 0,
(9) ennn (t) = 2"" «-^-'J («!)• A + tf),
where | 6\ $ (exp|i|2 - l}/B»i- 1).
19—2
292 THEOBY O!F BESSEL FUNCTIONS [CHAP. IX
By reasoning similar to that given at the end of § 9*1, it is easy to shew
that the domains of convergence of the series 1.an Jn* (z) Xln (t) and %an (zftf"
are the same.
The reader should have no difficulty in verifying the curious formula, due
to Kapteyn*,
91. The recurrence formulae for Hn (t).
The formulae corresponding to § 9*11 B) and C) are
B)
C) B/0 n; (t) = - 2n, («) + 2n0 (*).
There seems to be no simple analogue of § 9*11 A). The method by which
Neumannf obtained these formulae is that described in § 9'11.
Take the fundamental expansion § 9*4 A), and observe that
and that, by Hansen's expansion of § 2'5,
2Ji(m)J,'(*)--z 2 {J*n-i{z)-<K+i(z)\ln.
n = l
We find by differentiations with regard to t, and with regard to z, that
n=0
- *aJ = 2 Jo (*) Jo' (z) Ho («) + « 2 (JV: (*) - JVi (*)} ^n (*)
On comparing these results, it is clear that
*-> t enjn>(z)nn'(t)+ 2 (jrv,(*)-^a»+i(«)}.{«n(*)-/
On selecting the coefficient of Jna(z) on the left and equating it to zero
(cf. § 91), we at once obtain the three stated formulae.
* Ann. Sei. de I'Acole norm, xup. (8) x. A893), p. 111.
t Leipziger Beriehte, xxi. A869), p. 251. [Math. Aim. in. A871), p. 606.]
9*41, 9*5] ASSOCIATED POLYNOMIALS 293
9*5. Gegenbauer's generalisation of Neumanns polynomial On (?).
If we expand z** j{t — z) in ascending powers of z and replace each power
of z by its expansion as a series of products of Bessel functions given in § 5,
we find on rearrangement (by replacing s by n — 2m) that
efl -{- V oo ~u. ¦+• v 4- &
_ 5? ^ ) ? ¦*¦ \A" i 2'
«r<) i8+1 (»i=o r(/ti + j/+s+l) w!
x
00
^>
?h— am + i
(At+1/ + n) r(fj. + bi-m+l)V (v + In -m + l)T(fi + v + n - wt)
wi! r((tt + i/ 4- n — 2//i + 1 j
it is supposed that | 21 < 111, and then the rearrangement presents no greater
theoretical difficulties than the corresponding rearrangement of § 9'1.
We consequently are led to consider the polynomial Bn.ylK)V(t)t denned by
the equation
~^r.,-ln — m + l)V(v + %H—m + \)r(fjL + v + n — m)n .wn
X ,Mt0 w !~T (/* + w + w - 2//i + 1) ^'
This polynomial waa invostigated by Gegenbauer*; it satisfies various
recurrence formulae, none ol which arc of a simple character.
It may be noted that
The following generalisations of Gogenbauer's formulae are worth placing
on record. They are obtained by expanding the Bessel functions in ascending
series and calculating the residues.
] <o-f-)
<3> .A '"'
D) 5^-.|"'+)r»./.B«sin
x J<\(- w,^ + 1, fM + v + n; %f* + ±v + {, \fi + \v + 1; sina
In the special case in which (jl^v, this reduces to
E)
This formula may be still further specialised by taking </> equal to \ir or ^tt.
¦ Wiener Sitzungsberiehle, lxxv. B), A877), pp. 218—222.
294 THEORY OF BBSSEL FUNCTIONS [CHAP. I
9*6. The genesis of Lommel's* polynomial Rm<„ (z).
The recurrence formula
may obviously be used to express Jv+m(z) linearly in terms of Jv{z) anc
Jv~i(z); and the coefficients in this Hnear relation are polynomials in \\:
which are known as Lommel's polynomials. We proceed to shew how t<
obtain explicit expressions for them.
The result of eliminating Jv+l (z), Jv+i (z),... Jv+m-i (z) from the system o'.
equations
Jv+p+i (z) - B (v + p)l*\ Jv+P (z) + Jy+p-i (z) = 0, (p = 0,1, ... to - 1
is easily seen to be
l), 1, 0
0, 1, -22-1(i/ + m-2), 0
0, 0, 1, 0
0, 0, 0, 1
J?{z), 0, 0, -fc-^+
Jv-l(z)-Bpjz)Jv(z), 0, 0, 1
By expanding in cofactors of the first column, we see that the cofactor o"
Jv+m (z) is unity; and the cofactor of (—)w*~1 /„ (z) is
1,
o,
1,
-22 (v+m-3K
o,
o,
o,
0
0
0
0, 0, 0, -2«-1(i' + l), 1
0, 0, 0, " 1, -<2z-1v
The cofactor of (—)m~l Jv^ B) is this determinant modified by the suppressioi
of the last row and column.
The cofactor of (—)m~lJv(z) is denoted by the symbol (—)m Rm>„ (z); anc
Rm,v(z)> thus denned, is called Lommel's polynomial. It is of degree m in 1/r
and it is also of degree m in v.
The effect of suppressing the last row and column of the determinant by
which Rm>v(z) is defined is equivalent to increasing v and diminishiag m b}
unity ; and so the cofactor of (-)9M~1 Jv-.x (z) is (-)m~1 Rm_it,+1 (z).
Hence it follows that
Jv+m (z) ~ J* (*) Rm, v (z) + J*-i (z) Rm-h v+, (z) = 0,
* Math. Ann. iv. A871), pp. 108—116.
9-6,9*61] ASSOCIATED POLYNOMIALS 295
that is to say
A) Jv+m 0)« Jv (z) Rm, „ (z) - /„_! (z) Rm-it v+1 (z).
It is easy to see that* Rm>v(z) is the numerator of the last convergent of
the continued fraction
(v ± m — \\
The function Rm>v{z) was defined by Lotnmel by means of equation A).
He then derived an explicit expression for the coefficients in the polynomial
by a somewhat elaborate induction; it is, however, simpler to determine the
coefficients by using the series for the product of two Bessel functions in the
way which will be explained in § 9'61.
It had been observed by Bessel, Berliner Abh., 1824, p. 32, that, in consequence- of the
recurrence formulae, polynomials An.l (z), #n_i (z) exist such that
where [cf. § 92 (8)]
It should be noticed that Graft nnd CrelierJ use a notation which differs from
Lommel's notation ; they writo equation A) in the form
9" 61. The series for Lommel's polynomial.
It is easy to see that {—)mJ-v-m {z), qua function of the integer m, satisfies
the same recurrence formulae as Jv+m(z)\ and hencu the analysis of § 9"E also
shews that
A) (~)m/_,_M(*) =./_,(*)Rm>v(z) + J_VH(*) /iw_lir+I (z).
Multiply this equation by ./„_, (z) and § 9*6 A) by J-v+l (z), and add the results.
It follows that
B) Jv+m (z) J_,+l (z) + (-)- /_v_m («) /r_, (*)
= Rm<v{z) \J,(b) J-v+l (z) + J_v(z)./,_, (z)}
* Of. Chrystal, Algebra, n. A900), p. 502.
t Ann. di Mat. B) xxm. A896), pp. 45—05; Einleitung in die Theoric tier BeaaeVtclien Funk-
tionen, n. (Bern, 1900), pp. 98—109.
t Ann. di Mat. B) xxiv. A896), pp. 131—163.
296 THEORY OF BESSEL FUNCTIONS [CHAP. IX
by § 3 G). But, by § 51, we have
(A T t,\-l (-F(
+>n{Z)J-v^{Z)~ Z\r( +
fi-o n! r(- p - w + n + 1) r (v + n)
when we replace n in the last summation by m + p + l. Now it is clear
that
(m+p+l)\ p\ (m + p + iji! p\ '
and so, when we combine the series for the products of the Bessel functions, we
find that
2 sin VTT n . , '» (~)m+n(_ m . n\ (X2\-m+m-i
sin vk <*•
V nt() 71! (ill - inj\ V(v + 71) '
the terms for which n>\m vanish on account of the presence of the factor
(—m + n)n in the numerator.
When v is not an integer, we infer that
n=o >i! (?/i - 2n)! F (V + w)
n=0 r(i/ + ?i) x^ 7
But the original definition of Rm<v(z), by means of a determinant, shews
that R,^(z) is a continuous function of i, for all values of v, integral or not •
and so, by an obvious limiting process, we infer that C) is a valid expression'
tor Rm<v{z) even when „ is an integer. When „ is a negative integer it may
be necessary to replace the quotient
*> t™ -JL> bv r-V" ^ W-T w + !>
r(i;+W) '^ rT-i;-«iT#7Ti)
in part of the series.
The herie,, C; wa.s giveu by Lommel, Math. Ann. iv. A871), pp. 108-111- a
An interesting result, depending on the equivalence of the quotients just
mentioned, was first noticed by Graf*, namely that
D) R
Ann. di Mat. B) xxm. A895), p. 56.
9*62] ASSOCIATED POLYNOMIALS 297
In the notation of Pochhammer (cf. §§ 4*4, 4*42), we have
E) B,w>v{z) = {v)m{\z)-m.J\{\-lm, -|m; v,-m, \-v-m; -*»).
Since RM,v{z)/z is a linear combination of products of cylinder functions of
orders v + hi and v — 1, it follows from § 5'4 that it is annihilated by the operator
O4 - 2 {(w + in)- + (v - l)-j ^J + {0 + m)B ~(v-l )8]-] + 4s" (V + 3^ + 2) ;
where <& = z(d/dz); and so Rwv(z) is a solution of the differential equation
F) [O + w) O + 2v + vi - 2) O - 2i/ - »i) (S - wt - 2)] y
An oiiuatiou equivalent to this was stated by llurwitz, Math. Ann. xxxiil. A889),
p. 251; ami a lengthy proof of it waa given by Nielsen, ^1?^?^. di Mat. C) VI. A901),
pp. 332—334; a .simple proof, differing from the proof just given, may be obtained from
formula E).
9'62. Various properties of Loinmel's polynomial.
We proceed to enumerate .some theorems concerning Rmt,(z), which were
published by- Lomiwel in his memoir of 1871.
In the first place, § (J'u' A) holds if the Bessel functions are replaced by any
other functions satisfying the same recurrence formulae; and, in particular,
A) Yv+m{z) = K(z) RMtv (*)- F,..., (*) Rm.hv+1 (z),
whence it follows that
B) Y,,,.M B) /„_., (s) - JVTin B) }•;_, (z)
= R,,,,v{z) 1 Yv{z)./,_, E) - Jv(z) F,,_1(.2))= - mm>v(z)l(irz).
Next, in §9"C1B), takevn to be an even integer; replace in by 2m, and
v by v - vi. The equation then becomes
C) Jv+m{z)Jm+,_v(z) + «/_„_„, (*),/_,„_,+„(*) = 2 (-) sin vir. Jttm,?^,i(e)/(irz),
and, in the .special case v—\, we get
D) J',^.i (z) + J*- w_i {z) = 2 (-)« iiam, i,,H («)/M,
that is to say
This is the special case of the asymptotic, expansion of § 751 when the
order is half of an odd integer.
In particular, we have
F)
225
298 THEORY OF BESSEL FUNCTIONS [CHAP. IX
Formula E) was published in 1870 by Lommel*, who derived it at that time by a
direct multiplication of the expansions (§ 3'4)
followed by a somewhat lengthy induction to determine the coefficients in the product.
As special cases of § 9'6 A) and § 9-61 A), we have
2\* . ^ . , / 2
B \^ / 2 \^
—) sinz.Rmii(z)~ I —) cos*.2^,9(e),
TTZ/ XnZ)
(-r J-m-i (*) = [^f cos *. Rm> i (*) + (j^)* sin z. Rm
By squaring and adding we deduce from D) thatf
(8) R\n,i(z) +J?Ml|W»(-r^H.W
Finally, if, in § 9*61 B), we replace m by the odd integer 2m + 1 and then
replace v by v — m, we get
(9) Jv+m+1 (z) J_v+m+1 [z) — J_|/_m_1 {z) Jv.-m-\ \z)
= 2 (-)m sin virRzn^v_m (*)/(ir*).
An interesting result, pointed out by Nielsen, .4?mi. di Mat. C) v. A901), p. 23, is that
n
if we have any identity of the type 2 >fm (z) Jv + TO (z) = 0, where the functions fm (z) are
m=0
algebraic in z, we can at once infer the two identities
S /mCL,,(#0, 2 AWClhiW^O,
m=o m=0
by writing the postulated identity in the form
2 /„ (*) {Jv (z) Hm, v iz) - Jv-1 (?) An-i, ,+1 (*)}s0,
and observing that, by § 474 combined with § 3*2 C), the quotient Jv-i(z)lJv («) is not an
algebraic function. Nielsen points out in this memoir, and its sequel, ibid. C) vi. A901),
pp. 331—340, that this result leads to many interesting expansions in series of Lommel's
polynomials; some of these formulae will be found in his Handbuch der Theorie der
Cylinderfunktionen (Leipzig, 1904), but they do not seem to be of .sufficient practical
importance to justify their insertion here.
9*63. Recurrence formulae for LommeVs 'polynomial.
In the fundamental formula
replace m and v by m +1 and v — 1; on comparing the two expressions for
Jp+m (z), we see that
* Math. Ann. n. A870), pp. 627—632.
t This result was obtained by Lommel, Math. Ann. iv. A871), pp. 115—116.
9*63] ASSOCIATED POLYNOMIALS 299
Divide by /„_! (z), which is not identically zero, and it is apparent that
A) Rmr*.*i 2(l71}
To obtain another recurrence formula, we replace m in § 92 B) by m + 1
and m — 1, and use the recurrence formula connecting Bessel functions of
orders v + m — 1, v + m and v + m + l; it is then seen that
\&) J^ni-l v \z) + -"-m+i i/ B) = - -",rt v \z)>
and hence, by combining A) and B),
Again, write § 92 B) in the form
— Z~m~* Rm< „ B) = [Z~"~m Jv+m \z)\ \Zv~l J „_! (z) j — [z~"~m Yy+m \Z)] \ZV 1 */t^-i \Z)\,
and differentiate it. We deduce that
D) R\n> „ (s) = /2m, „ (z) + Rm+lt v_j (*) - 2i!w+li „ («),
z
and so, by C), A) and B),
/k\ 7?' (A — — 7—Ti (z\4-'R (tA—R (A
F) ii!',n „ (z) = —-+-OT ^ „ (*) - /i,n_1,+, (z) - Rm+l v (z),
G) Rm,p(z)=- V m~ Rm,v{z)+Rm+\,*-i{*) + -Rm-\,v{*)'
The majority of these formulae were given by Lomrnel, Math. Ann. IV. A871), pp. 113—
116, but F) is duo to Nielsen, Ann. di Mat. C) vi. A901), p. 332; formula B) haa boon UHod
by Porter, Annals of Math. B) in. A901), p. EE, in discuHsing the zoroa of llm< v («)•
It is evident that B) may be uaod to define Rmv(z), when bho parameter
m is zero or a negative integer; thus, if B) is to hold for all integral valuew
of wi, we find in succession from the formulae
jl> / 4i/(j» + 1) „ . . 2v
that
and hence generally, by induction,
(9) R v (z) = (—)W~J Rrn-2 v(z)-
This formula was given by Graf, Ann. di Mat. B) xxni. A895), p. 50.
If we compare (9) with Graf's other formula, § 9*61 D), we find that
When the functions of negative parameter are defined by equation (9), all the
formulae A)—G) are true for negative as well as positive values of m.
300 THEORY OF BESSEL FUNCTIONS [CHAP. IX
9'64. Three-term relations connecting Lommel polynomials.
It is possible to deduce from the recurrence formulae a class of relations
Avhich has been discussed by Crelier*. The relations were obtained by Crelier
from the theory of continued fractions.
First observe that § 9*63 B) shews that Jv+m (z) and Rm„ (z), qua functions
of m, satisfy precisely the same recurrence'formula connecting three contiguous
functions; and so a repetition of the arguments of § 9*6 (modified by replacing
the Bessel functions by the appropriate Lommel polynomials) shews that
A) J^m+n,v \z) — -t^m, v\z) Rn,v+m \Z) ~ R-m—\v \z) -"-«—i.v+m+i \Z)-
Next in §98B) replace m by m — 1 and v by v+l, and eliminate
2 (in + v)\z from the two equations; it is then seen that
Rm, v iz) Rm, v+i (z) — i?m+i, v (?) Rm-i, v+i (z)
= Rm-\, v (z) ¦fim-l.t+i (z) — Rm, v (z) Rm-1, v+\ (z),
and so the value of the function on the left is unaffected by changing m into
m — 1. It is consequently independent of m; and, since its value when m — 0
is unity, we have Crelier's formula
B) Rm>v (z) Rm< u+1 (z) —'Rm+i,v (z) Rm-i, *+i (z) = 1)
a result essentially due to Bessel (cf. §96) in the special case v = 0.
More generally, if in § 9*63 B) we had replaced m by m — n and v by v -f n,
we should have similarly found that
¦"wi, v \Z) J^"m— n+i,v+n \Z) J-hn+i,» \Z) -t^m—n^+h \Z)
— -tlm—i, v \Z) Hrn—n,v-\-n \Z) J-hn,v \Z) tlm—n—i, v+n \Z),
and so the value of the function on the left is unaffected by changing m into
m — 1. It is consequently independent of m ; and since its value when m = n
is Rr-i,A*), we find from § 93 A0) that
C) Kmtv \Z) Hm—n+i,v+n \Z) Rtn+i,v \z).Mm—n,v+n \Z) — -K"tu-i,v \2)>
a result given in a different form by Lommel+.
Replace m and n by m — 1 and n + 1 in this equation, and it is found that
D) Hm-.itV\Z) tiyn—n—\, v+n+\ \Z) — ¦tlm,v \z) ¦K"m-n—2,v+n+i \z) == -t^n,v \Z)-
If we rewrite this equation with p in place of n and eliminate Rm^1>v(z) be-
between the two equations, we see that
Rn, v (z) Rm-p-i,v+p+\ (z) — Rp< „ (z) Rm-n_h v+n+1 (z)
— Rm,v\Z)[Rm—p-2,v+p+i \z) Rm-n-i,v+n+\ \z) — Rra—n-i,v+n+i \Z) R7n—p—ilV+p+i \z)]
— Rm,v \Z) i^n-p—\,v+p+i \z)y
by C). If we transform the second factor of each term by means of § 9'63 A0),
we obtain Crelier's result (loc. cit. p. 143),
E) Rn>v (z) JBp_m_1) v+m+i (z) — RPt v (z) Rll—m-h v+m+i (z)
~ -^m,c \z) -"jj—n—\,v+n+\ \z)-
* Ann. di Mat. B) xxiv. A896), p. 136 et seq. f M"th> Ann- IV-
9-64] ASSOCIATED POLYNOMIALS 301
This is the most general linear relation of the types considered by Crelier; it
connects any three polynomials Rm<v(z), Rni/(z), Rp>v{z) which have the same
parameter v and the same argument z. The formula may be written more
symmetrically
(o) J^n,v \?) Rp-m~i,v+m+i \z) + Rp,v \z) Rm~n-\,v+n+i \z)
"T -tim, v \z) -»''«—p—\, v+p+i \z) = ">
that is to say
0) . 2 Rn,v(z)Rp-m-i,i>+m+i(z) = 0-
in, n, p
A similar result may be obtained which connects any three Bessel
functions whose orders differ by integers. If we eliminate Jv+m-\ (z) between
the equations*
)" v-\-n \z) ~ " v+m \z) -"ji—»h,h-»i \z) " v+m—l \z) ¦^/n—m—x,v-i-m+i \z)i
"v+p \z) ~ *Jv+m \z) ¦lip—m,i>+iii \z) ~~ J v+m—i \z) -^p—m-i.v+m+i \z)>
we find that
" v+n \Z) ?*>p—m—\,»+m+\ \z) ~~ •'v+p \z) J?,i—>n—\,i>+m+i \z)
~ " v+m \z) l^n—7n,v+in \z) l*p—in—i, v J-?/t-t-i \z) -"^i—m, *+m \z) ^*?i—w—i,?H-m+i \z)\
— Jv+m \z) J^p-n-^.v+n+i \z) \
the last expression is obtained from a special case of E) derived by replacing
m, n, p, v by 0, n — m, p — m, v -f- m respectively.
It follows that
(8) ? Jv+n (z) Rp-m-i, v+m+i (z) = 0,
m, n, p
and obviously we can prove the more general equation
(9) S f^+»U)^p-m-i.v+fn4i(^) = 0.
where *2f denotea any cylinder function.
The last two forrnulao aecin nevor to have, licon previously statod explicitly, though
Graf and Gnhlcr hint at the. oxi.stonoc of sucli oqiiation.s, h'inleitunf/ in die. Theorie dor
Besset'scheri Funktionen, n. (JJcni, 1!)(K)), jtp. 108, 105).
[Note. If we eliminate «^_i B) from the equations
and use B) to nininlify the resulting equation, wo find that
•A-B)= -'A. + m(z) /'»-!,nl (?)+./^ + M_iB) /("„,-!, •-+ l(^),
and ho, replacing «< hy v-w, wo have.
«/v_„, B) = - ./„ (z) Rm _ jj, v _ m M C) + ./v _ ! (c) Rm - lt v_m + 1 B)-
By using § 9-G3 A0), we deduce that
./„-,„ {*)~>h (z) li.w,„ (z) -•/,.-, (s) A'.-,,,-,, n . B),
that is to say that the equation $ 9fj A), which has hitherto beon ewnsidored only for
positive values of the parameter m, in atill true for negative values.]
* It ifl supposed temporarily that m is tho Hinallest of the intern in, m, j); but since the final
result is symmetrical, this restriction may be removed. See also the note at the end of tho Hootion.
302 THEORY OF BESSEL FUNCTIONS [CHAP. IX
9*65. Hurwitz' limit of a Lommel polynomial.
We shall now prove that
A) J1* -J(*>
This result was applied by Hurwitz, J/a^A. Ann. xxxin. A889), pp. 250—252, to discuss
the reality of the zeros of Jv{z) when v has an assigned real value (§ 15-27). It has also
been examined by Graf, Ann. di Mat. B) xxin. A895), pp. 49—52, and by Crelier, Bern
Mittheilungen, 1897, pp. 92—96.
From 19-61 C) we have
y (m-2n)! T(» + m+1)"
Now write
(m-n)\T(u + m-n + 1) .
(m-2n)\V(v + m + l) ~tf^m>n)>
so that
dim n)=
v ' ; (v + m)(v + m-l) ...(v + m-n + l)'
If now N be the greatest integer contained in \v\, then each factor in the
numerator of 0(m, ri) is numerically less than the corresponding factor in the
denominator, provided that n > N.
Hence, when n > N, and m > 2N,
\6(m,n}\<l,
while, when n has any fixed value,
lim 6 (m, n) = 1.
Since 2 ¦ fJ(* }
is absolutely convergent, it follows from Tannery's theorem* that
7T
and the theorem of Hurwitz is established.
00 ( — )n (iz)v + 2n
Again, since the convergence of 2 - ,¦ ¦¦ r is uniform in any bounded domain t
o«! T{v + n+\) J
of values of z (by the test due to Weierstrass), it follows that the convergence of
to its limit is also uniform in any bounded domain of values of z.
* Cf. Bromwich, Theory of Infinite Series, § 49.
t An arbitrarily small region of which the origin is an internal point must obviously be
excluded from this domain when E (v) ^ 0.
9*65, 9'7] ASSOCIATED POLYNOMIALS 303
From the theorem of Hurwitz it is easy to derive an infinite continued
fraction for /„_] (z)/Jv (z). For, when </„ [z) ^ 0, we have
~f-^- = lira
= lim L^-l/^-^-,
by § 9'63 A). On carrying out the process of reduction and noticing that
we find that
iW (>).,_.__ 1 I 1_
iC,,+, (^) 2 (i/ + 1) z-1 - ~i(v + 2) s-1- ... - 2 (./+ »i) i-- '
and hence
,2\ •/.^.^)=9^-1 1 . l .
K) Jv{z) 2 (i/+I)*-2A'+ 2) *-'-...
Thi.s procedure avoids the necessity of proving directly that, when «i-*-oo, the lust
element of the continued fraction
,/, B) 2 (v+1 )i::l -...
may bo neglected; the method is due to (huf, Ann. di Mat. (~1) xxni. A Ht)T>), p. .">2.
9*7. The modified notation for IjOiumel polynomials.
In order to discuss properties of the zeros of Lonnnel polynomials, it i.s
convenient to follow Hurwitz by making a change in the notation, for the
reason that Lomrnel polynomials contain only alternate powers of the variable.
Accordingly we define the modified Lonnnel polynomial </,„,,{z) by the
equation*
<*'* p (-)» I1 (r + wi - u + I) ^
A) </lll<v{z)-^m-n^n r(|/ + n+l)
.so that
B) ^l,,H^)=(br"ii/M,1-({4
By making the requisite changes in notation in §§ (Witt, 9"(>4, the i'(>ader
will easily obtain the following formulae:
C) gm+l%?(z) = (p + vl+\)gm,,(z) -zgm.,,„(z), [§ i)'O3 B)]
(*) //m+i.,-1 («) = vgm.Az) - Zf/m-i,^! B), [§ 9'()S A)]
E) ^--I^{*|l^,(*)H^m-...(*)+^,,.H1 >-!(*). [§»
(«) *w« ^ l^" flr«,, (*)} = ^h-,,-! (*) -«/*+,,, (z), [§ 9-68 D)]
[A special case of § 9'64 E).J
* This notation differs in unimportant detailn from the notation used by llurwit/,.
304 THEORY OF BESSEL FUNCTIONS [CHAP. IX
These results will be required in the sequel; it will not be necessary to write
down the analogues of all the other formulae of §§ 9'6—964.
The result of eliminating alternate functions from the system C) is of
some importance. The eliminant is
(v + m) gm+2i v (z) = cm (z) gm> „ (z) - (v + m + 2) z*gm_^ „ (z),
where cin (z) = (v + m + 1) {(v + m)(v + m + 2) — 2z\,
We thus obtain the set of equations:
' 0 + 2)gitV (z) = c%(z)g%v(z) -(v + 4>) z*g0>v {z),
(v + 4>)gs>v(z) = c4 (z) gi>v {z) - (v 4- 6) z2gi>v {z),
(v + 2s) ^+2i, (z) = Ca, {z) gUiv (z) - (v + 2s + 2) z^g^^„ (z),
(v + 2m-2) g^,, v {z) = cm^ («) gm_2> „ («) - (i; + 2m) ^m
(8)
9*71. TAe reality of the zeros of gimv{z) when v exceeds — 2.
We shall now give Hurwitz' proof of his theorem* that when v > — 2, the
zeros of gm,,v(z) are aM f^al; and also that they are all positive, except when
— l>v>-2,in which case one of them is negative.
After observing that gwitV{z) is a polynomial in z of degree m, we shall
shew that the set of functions gimtV{z), g-M^viz), ... g-iiV(z), gn,v(z) form a set
of Sturm's functions. Sufficient conditions for this to be the case are (i) the
existence of the set of relations § 9*7 (8), combined with (ii) the theorem that
the real zeros of g-im-^vi2) alternate with those of gzmv(z).
To prove that the zeros alternate, it is sufficient to prove that the quotient
gim,t>(z)l9vm-2,i>(z) is & monotonic function of the real variable z, except at the
zeros of the denominator, where the quotient is discontinuous.
We have f^ (z) ±
dz
where Wir,» = 9r,v(*) g\,„ (z) - g,t„(z)g'r%„(*);
and. from § 9'7 C) it follows that
R (V + 2m) Kft
(v + 2m - 2)g
so that
m-l
2I2a2m,2w-2 = 5'22m-2,,(^+(^ + 2m) 2 (v + 2r)fzrhv(),
r=l
and therefore, if m > 1, 5EKami!!nir-2 is expressible as a sum of positive terms
when v > — 2.
* Afaift. Ann. xxxin. A889), pp. 254—256.
V71, 9-72]
ASSOCIATED POLYNOMIALS
305
The monotonic property is therefore established, and it is obvious from a
jraph that the real zeros of gmi-v, v (^) separate those of g.m< v (z).
It follows from Sturm's theorem that the number of zeros of gmv(z) on
my interval of the real axis is the excess of the number of alternations of sign
n the set of expressions g^,lt„ (z), g^-^„(z)> ...,go>v(z) at the right-hand end of
he interval over the number of alternations at the left-hand end.
The reason why the number of zeros ia the excess and not the deficiency is that the
inotient g2mi v{z)/ffim-2, v B) 'a & decreasing function, and not an increasing function of z,
-.s in tho usual version of Sturm's theorem. Sec Burnsido and Panton, Theory of Equations,
. A918), § 9Q.
The arrangements of signs for the set of functions when z has the values
- ^ 0, oo are as follows:
-oo
0
oo
2?/j
+
±
2w - 2
+
±
2m - 4
+
±
2
+
±
-
0
+
+
+
.; urmer or lower signs are to be taken according as y + 1 is positive or
yaiive; and the truth of Hurwitz' theorem is obvious from an inspection
i this Table.
9'72. Negative zeros- of g.an<v(z) when v < — 2.
Let v be less than — 2, and let the positive integer s be defined by the
nequalities
- 2,v > v > - 2,s- - 2.
It will now be shewn that*, when v lies between — In and— 2s - 1, g^^z)
iasno negative zero; but that, ivhen v lies between. — 2s—I and — 2s — 2, gwn,iV(z)
i,as one negative zero. Provided that, in each case, m is taken to be so large
hat v + 2m is positive.
It will first be shewn that the negative zeros (if any) of g&n<v(z) alternate
vith those of g<t,n-%v(z)-
* This proof differs from the proof given by Hurwitz; Beo Proc. London Math. Soc. B) xix.
1921), pp. 266—272.
W. B. F. 20
306 THEORY OF BESSEL FUNCTIONS [CHAP. IX
By means of the formulae quoted in § 9*7, it is clear that
() ± i
= (v +
= (y + 2m) g
provided that v + 2m is positive and z is negative. Therefore, in ,the circum-
circumstances postulated, the quotient
is a decreasing function, and the alternation of the zeros is evident.
The existence of the system of equations § 9*7 (8) now shews that the set
of functions
form a set of Sturm's functions.
The signs of these functions when z is — oo are
+,+, .... +, +,->+> .-., (-)',
and there are s alternations of sign. When z is zero, the signs of the
functions are
the upper signs being taken when —2s>v> — 2s— 1, and the lower signs
being taken when — 2s- I > v> — 2s- 2; there are s and s + 1 alternations
of sign in the respective cases. Hence, when —2s>v>-2s — 1, ffm.,vB) hfls
no negative zero; but when - 2s - 1 > v'> - 2s - 2, g2m,iV(z) has one negative
zero. The theorem stated is therefore proved.
9*73. Positive and complex zeros ofg2m>v(z) when v< — 2.
As in | 9*72, define the positive integer s by the inequalities
-2s>p>~2s-2.
It will now be shewn* that when v lies between - 2s and - 2s — 1, gWttlV{z)
has m — 2s positive, zeros; but that, when v lies between — 2s — 1 and — 2s — 2,
gm,v(z) has m — 2s—\ positive zeros. Provided that, in each case, m is so large
that m+ v is positive.
* This proof is of a more elementary character than the proof given by Hurwitz; see the
paper cited in § 9*72.
9'73j ASSOCIATED POLYNOMIALS 307
In the first place, it follows from Descartes' rule of signs that, in each case,
9zm,Az) cannot have more than the specified number of positive zeros. For,
when v lies between - 2s and —25 — 1, the signs of the coefficients of
1, z, z\ ..., z\ z**\ z*+\ z^\ ...,zm in gWt?(z)
are +, +, +, ..., +, -, +, -, ..., (-)»;
and since there are m — 2s alternations of sign, there cannot be more than
m — 2.s% positive zeros. When v lies between — 2s — 1 and — 2s — 2 the corre-
corresponding set of signs is
_ i / \m •
> } > • ••> > » ~i > "•> \ ) j
and since there are m — 2s — 1 alternations of sign there cannot be more
than m — 2s — 1 positive zeros.
Next, we shall prove by induction from the system of equations § 9*7 (8)
that there are as many as the specified number of positive zeros.
When v lies between - 2s and — 2s — 1, the coefficients in g^tV{z) have no
alternations of sign (being all +) and so this function has no positive zeros.
On the other hand
9*»+*,u@) > 0, gu+,,v(+ M ) = - oo ,
and so gi8+iiV(z) has one positive zero, o^, say; and, by reasoning already given,
it has no other positive zeros. Next, take gM+ilV(z); from § 9'7 (8) it follows
that its signs at 0, ahl, + oo are +,—, + ; hence it has two positive zeros, and by
the reasoning already given i t has no others. The process of induction (whereby
we prove that the zeros of each function separate those of the succeeding
function) is now evident, and we infer that <j.,m>v{z) has m— 2.9 positive zeros,
and no more.
Again, when v lies between — 2s — 1 and — 2.s' — 2, the coefficients in
#48+2,v{z) have no alternations in sign (being all —), and so this function ha.s
no positive zeros. On the other hand
<7«+4,.(O) < 0, gu+4,A+ oo ) » + oo ,
and so gmi>v{z) has one positive zero, and by the reasoning already given it
has no other positive zero.
By appropriate modifications of the preceding reasoning we prove in suc-
succession that .<7«+fll„(.?), g4n+n,v(z), ••• have 2, 3, ... positive zoroa, and in general
that g-2m)V{z) has 7n - 2.v — 1 positive zeros.
By combining these results with the result of § 972, we obtain Hurwitz'
theorem, that, when v < — 2, and in is so large that in + v is positive, //?,>,,,„(?)
has 2s complex zeros, where s is the integer such that
-2s>v>- 2s - 2.
20—2
CHAPTEE X
FUNCTIONS ASSOCIATED WITH BESSEL FUNCTIONS
10*1. The functions 3v{z) and E,(^) investigated by Anger and H. F.
Weber.
In this chapter we shall examine the properties of various functions whose
definitions are suggested by certain representations of Bessel functions. Wo
shall first investigate functions defined by integrals resembling Bessel's inte-
integral and Poisson's integral, and, after discussing the properties of several
functions connected with Yn (z) we shall study a class of functions, first defined
by Lommel, of which Bessel functions are a particular case.
The first function to be examined, Jv(z), is suggested by Bessel's integral.
It is defined by the equation
A) J, (z) = - I "cos (v6 - z sin 6) dO.
7T Jo
This function obviously reduces to Jn (z) when v has the integral value n.
It follows from § 6'2 D) that, when v is not an integer, the two functions are
distinct. A function of the same type as Jv(z) was studied by Anger*, but
he took the upper limit of the integral to be 2-7r; and the function J^(^) is
conveniently described as Anger's function of argument z and order v.
A similar function was discussed later by H. F. Weberf, and he also
investigated the function E,, (z) defined by the equation
B) E, (z) = - ["sin {v6 - z sin 0) d0.
7T J 0
In connexion with this function reference should also be made to researches by Lommel,
Math. Ann. xvi. A880), pp. 183-208.
It may be noted that the function — / cos (i/0 —asin 8) dd which was actually dia-
ln J 0
cussed by Anger is easily expressible in terms of JV (z) and 13, (z); for, if we replace 8 by
2rr — 8 in the right-hand half of the range of integration, we get
\ fin 1 fn 1 [k
— I cos(v0-z3in0)o?0 = r- I cos(vQ ~ZH\nd)dd + -cr cosBvtt-v& + z sin 0) dfi
in J o ^tt J o «jo
= cos2j/»r . Jp B) +sin vtt cos vn. E,, B).
* Neueste Schriften der Naturf. Ges. in Danzig, v. A855), pp. 1—29. It was shewn by PoiRson that
Vv I cos (vd - z sin 6) dO = (z - u) sin vir,
Additions a la Conn, des 1 emps, 1836, p. 15 (cf. § 10*12), but as he did no more it seems reasonable
to give Anger's name to tbe function.
t ZUrich Vierteljahrmhrift, xxiv. A879), pp. 33—76. Weber omits the factor l/rrjn his defi-
definition of Ev (a).
10'1] ASSOCIATED FUNCTIONS 309
To expand Jv {z) and E,, (z) in ascending powers of z, write \nr + <f> for 6
in the integrals and proceed thus:
• [ln
a\nm 6 sin vd dO = I cosm <? sin (\vrr + vcf)) dj>
J - Jt
= 2 ain \vir cosm <?> cos v<bd<b
'o
.'o
. mlsin
by a formula due to Cauchy*.
In like manner,
sin1'1 ^ cos v6d6 = r r~TT
o 2wr(Awj-4»'+1)
But, evidently,
1 oo /_\m »!ttn Ttt 1 oo /_\m 2-m+l
JAz)=- ^ --,;--Tr sin"»l^cosy(9^+ - ^ ,-/"-i\7
'w 7rm=0 (-2m)! Jo 7rma.0B?»+l)I
so that
oo (—)m(if2)-
IS) Ju (Z) = COS >rl'7r Jw rr;; 7~ ¦" , .", > / \ ~,~tX
oo / \7«
+ ainii'7r ^ -tS-; - , -
and similarly
oo i )m (irz\''n
D) ¦.W-HinW^p^^^^/f^^^^
,„.,() I1 {m — |v + ij) 1' (>il + kv + |)
These results may be written iu the alternative forms
* r~ *i i h 1
, „. M , . mil vir I _ z z &
sin j'7t f ^ ^3 2D
F) 1^,,- -w- .
1 + cos vir
Results equivalent to the.se were given by Anger and Weber.
Tho formula corresponding to E) was given by Anger (boforo tho publication of his
memoir) in a lotter to Cauchy which was communicated to the French Academy on July
17, 1854; soe Comptes Rendun, xxxix. A854), pp. 128—135.
* Mem. sur les intigrales difinies (Paris, 1825), p. 40. Cf. Modern Analysis, p. 263.
310 THEORY 6F BESSBL FUNCTIONS [CHAP. X
For a reason which will be apparent subsequently (§ 10*7), it is convenient
to write
/•7\ , /Vi= — ?l 4. fL
V) VW-ii^ A2A)C22) (P3)C22)E2^) "•'
(8) «->,*(*) = - -2 + y2 ^2. _ „«) ~ v* B2 _ „«) D,9 - „«)+ •';»
and, with this notation, we have
(9) J, (a)
0>„ ()
IT 7T
/ia\ « / \ 14-COSV7T 1/A — COS I/7r)
A0) E, (a) = : So, „ (z) - -+ } *_,, „ (z).
It is easy to deduce the following formulae from these results:
A1) cos v6 . cos {z sin 6) dO = — v sin vrr. s_, v (^),
Jo
tic
A2) sin v^ . cos (z sin 0) d# = — v A — cos vir). 5_j v (^),
Jo '
A3) I sin v6. sin (a sin 6) dO — sin vir . s0 v (z),
Jo
r-rr
A4) I cos v6 . sin B; sin 0)d^ =A + cob vrr). s0 v (z),
Jo •
A5) cos v(j>. cos B; cos </>) d^> = — 1/ sin \vk . 5_j ^ (z),
Jo
A6) cos vcp. sin (z cos </>) d<^> = cos ^7r. s0 v (z).
Jo
Integrals somewhat resembling the integrals discussed in this section, namely
fe™»°?*(nO-coad)ddt
J sin
have been examined by Unferdinger, Wiener Sitzungsberichte, lvii. B), A868), pp. 611—620.
Also, Hardy, Messenger, xxxv. A906), pp. 158—166, has investigated the integral
f °° dd
\ a\n(v6-zwine) ~-.
Jo o
and has proved that, when v is real, it is equal to in- 2 rjnJn (z), where »;„ is 1, 0 or - 1
n= -00
according as v — n is positive, zero, or negative.
10*11. Weber's formulae connecting his functions with Anger's functions.
It is evident from,the formulae § 101 (9), A0), A5) and A6) that
/i\ - / % „ / \ 4 COS il/7T /"i7r , ,
A) Jv (z) 4- J_,, (z) = — I cos v<fi cos (
B) Jv (^) - J_v (z) = ^— cos v<f} si
IT JO
(z cos
10-11,10-12] ASSOCIATED FUNCTIONS 311
C) e,(,) + e_(,)»-!~!±!![ [*"cosp<}>Bin(zcos<f>)d<b,
IT .' 0
D) Ey (z) - E_y (z) = S1 ^t/7r cos vrf» cos (s cos <?) dd>.
7T .' 0
It follows on addition that
J, (a) = \ cot Jvtt (E, (z) - E_, (*)} -1 tan Jw {E, (*) + E_v (a)},
so that
E) sin i»7r. Jv (z) = cos V7r . Ev (z) - E_v (z),
and similarly
F) sin vtr . Ev (^) = J_v (z) — coa vtt . J,, (z).
The formulae E) and F) are due to Weber.
10*12. Recurrence formulae for Jv (z) and Ep {z).
The recurrence formulae which are satisfied by the functions of Anger and
Weber have been determined by Weber.
It is evident from the definite integrals that
J,-! (z) + J,+1 (z) - 2v Ju (z) = -? f * (coa d--) cos (vd - z sin 6) dd
Z IT JO \ Z/
in 0)}de
J
TTZ I o dd
2 Hill I/7T
and
2i/_ , . 2 f'r
2v 2 f'7 v\
E,,_, B) + E,+, E) - — E, (z) - - I f cos 0 - - J sin (v6? -2 sin 0) d0
2 r-^ ,
2A — cos vrr)
It i.s also very easy to prove that
From these results we deduce- the eight formulae
/1 \ T / \ . -r 1 \ 2v _ , x 2 sin vtt
A) J_, (^ -t- JH.t (z) = -JM(^) ,
Z TTZ
B) J^1(*)-Jr+1E)«2Jr/(*)l
C) (^ + v) J, (z) = ^J,_, (*) + (sin vrr)/w,
D) (^ - v) Jv (z) = - zJv+1 (z) - (sin wr)/
312 THEORY OF BESSEL FUNCTIONS [CHAP. X
-2vT (A
= — *» \z>
F) Bv-1(«)-Bv+,W = 2Er (*),
G) (^ + v) Ev (Z) =^EM (z) + A - COS V7r)/7T,
(8) O - v) E, (z) = - *E,+1 (z) - A - cos V7r)/7r,
where S, as usual, stands for z(d/dz).
Next we construct the differential equations; it is evident that
(e) = (*-v) {zJv^ (z) + (sin vjr)/ir}
— (v sin i>7r)/7r
(z) + (z sin w7r)/7r - (v sin vjr)f7r,
so that
We also have
(W - v2) B, (z) = (%-v) {zE^ (z) + A - cos i«r)/ir}
=>z(& + l-v) Ev_j (?r) ~ i/A - cos V7r)fir
= — Z2 E,, (^) — ? A + COS l/7r)/7T — 1/ A — COS V7r)/TT,
so that
A0)
7T
Formulae equivalent to (9) and A0) were obtained by Anger, Neueste Schriften tier
Naturf. Ges. in Danzig, v. A855), p. 17 and by Weber, Zurich Vierteljahrssckrift, xxiv.
A879), p. 47, respectively; formula (9) had been discovered earlier by Poisson (of. § 101).
KV13. Integrals expressible in terms of the functions of Anger and
H. F. Weber.
It is evident from the definitions that
A) Jv(z)±iEv(z) = - J"exp {± i(V0 -zsin Q)\ dd.
By means of this result, combined with formulae obtained in §§ 6'2—622, it
is possible to express numerous definite integrals in terms of the functions of
Bessel, Anger and Weber. Thus, from § 6'2 D) we have
B) I fl-^-nh* dt « JL^ {J, (,) _ Jv {z)]>
when |arg0|<|7r; the result is valid when \oxgz\=-\ir, provided that
R (v) > 0.
Again, we have
10-13, 10* 14] ASSOCIATED FUNCTIONS 313
so that, when we combine B) and C),
D) |" *-*»»"»>«cosh vt dt= h-rr tan Ji/tt {J, (s) - Jv{z)} - \tr {E,(z) + F,(«)},
E) |M <r"iHl1' sinh ^ d« = |tt cot Jwr {/„ (z) - Jv (z)) - ?tt {E, (z) + Yv {z)\.
The integral g-zcoshf ^g^ vifa ^as already been evaluated (§6-3); but
j o '
I™ e-zcoalxtsinhvtdt
h
does not appear to be expressible in a simple form; its expansion in ascending
powers of z can be obtained from bhe formula of § 6*22 D),
0) = - f^^ocos v$dO + 2 S1--y7r re-z™»usinhi/i
bub, since
fn «> z^i /i //i (~)w win V7r CT / i/ + m _ v + m
J. C0S " C0S •*«" " W(, + ») ¦<Fl (- "¦ -»- ; a - • g ; -
the integral under consideration cannot be evaluated in any simple form*.
The formulae B)—E) are nugatory when v is an integer, but from §§ 6*21,
9-33 we have
F) I" 0»'-»l»" ' d< = \ [Sn (Z) - 7TEn (Z) - 7T YH (Z)},
J (I
G) (" e-'"-"i"i" dt = i (-)» '•' |»SY(, (a) + ttE71 (z) + nr \\ (z)\.
Jo
Tho asH(K;iat,(^i intcgraLs
./ ii niii Jo mn
have been nnticftri by (loiitiw, Quarterly Journal, xx. AHH5), p. 2(!0.
VarioiiH integrals of tho.so types occur in rCHoarchcs on dittraction by a prism; noe, e.g.
Whipplo, Prw.. London Math. ,%<:. B) xvi. A1I7), p. 101$.
10*14. Asymptotic expansions of Anger- Weber functions of large argument.
It follows from § KM3 B) that, in order to obtain the asymptotic expansion
of J±v(z) when \z\ is large and |arg^|<^7r, it is sufficient to obtain the
asymptotic expansion of the integrals
fjT-vt—znh\h t (]f
ll
To carry out this investigation we shall first expand cosh vi/cosh t and
sinh j>?/cosh t in a series of ascending powers of sinh t.
* See Anding, Sechsxtelliye Tafeln der lictmcliicheii b'unktionen imaifiniiren Arguments (Leipzig,
1911) [Jahrbuch ilber die Fortschrilte der Math. 1911, pp. •11K—494], and Tukeuchi, TShokuMath.
Journal, xvtn. A020), pp. 295—296.
314 THEORY OF BESSBL FUNCTIONS [CHAP. X
If eil = u, we have, after the manner of § 7*4,
so that
cosh vt J flu+> 1/M+<1+)
J
~ 27riJ (C- l)a - 4fsi
cosh« (C
(?-lJp-i {(?_ I)* _4? sinh2
Now
7T * Bm)!
and, if we take p so large that R(p +^±%v)>Q, and then take the contour
to be that shewn in Fig.'15 of § 7*4, we find that
7T Jo
If v and t are real, the last expression may be written in the form
(-)pcosfri
where 0^.6x^1, since 1 + 4a; A — a>) sinh21 > 1.
It follows that, when R (p + fr + fr v) > 0, we have
cosh y< = cos i wr T^1 (-ynT{m + \ + \v)Y(m ±}Z\v)
coshtf 7r |_m=0 Bm)!
)r(fH-W B sinh
.2W
For complex values of v and t this equation has to be modified by replacing
the condition 0 < 6X < 1 by a less stringent condition, in a way with which the
reader will be familiar in view Qf the similar analysis occurring in various
sections of Chapter vii.
Similarly we have
/"(-!«+, 1/M + ) ( 1 1
10*14] ASSOCIATED FUNCTIONS 315
so that
sinh^_ 1 /•(«+. i/«+,i+) g»df
whence it follows that, if we take p so large that R (p + 1 + \v) > 0, then
sinh vt sin i v
cosh* 7T |_TO==o Bm+ 1)!
/(" j"JlH1^ B sinh t)*+l I .
On integrating these results, it follows that
r
J0
I
m=0
s (-
If v is real and 2 is positive, these asymptotic expansions possess the
property that the remainder after p terms is of the same sign as, and is numeri-
numerically less than, the (p + l)fch term when p is so large that R (p + I + \ v) > 0.
It follows from §§ 1013 B) and C) combined with § 1011 @) that
A)
sin vtt
TTZ
V V B- - li") M B* - I'") Da - l/J)
e
¦.
1 - cos vtt \v _ j/ Bs - i/a) 7/ B- - z/'J) Da - v'J) _
-wz [z z* zn
TIiohc rosults wore .stated without proof by Wc.bcr, Zurich Yie.rtolju/irm'.hi'ift, xxiv.
A870), p. 48 and by Lommel, Math. Ann. xvi. A880), pp. 180— 1H8. Tlioy wore proved tin
.special casos of much more goncrul formuku by Nieln(!n, llandlmch de.r Theorio. der
Cylindarfunktionen (Leipzig, 1904), p. 228. Tho proof of thin action doiw not hcohi to have
been given previously.
Since the only singularities of coah vt/couht and ainh vtjcon\\t, qua functions
of sinh^, arc at sinh t = ± i, it is possible to change the contours of integration
into curves in the i-plane on which arg (ainh t) ia a positive or negative acute
angle; and then we deduce in the usual manner (cf. §6'1) that the formulae
A) and B) are valid over the sector | arg z \ < it.
316 THEORY OF BESSEL FUNCTIONS [CHAP. X
10*15. Asymptotic expansions of Anger- Weber functions of large order and
argument.
We shall now obtain asymptotic expansions, of a type similar to the
expansions investigated in Chapter viii, which represent J,, (z) and Ev (z)
when | v | and \ z j are both large.
In view of the results obtained in^ § 1013, it will be adequate to obtain
asymptotic expansions of the two integrals
1 /""
_ / gTW-zsinht^
TTJO
As in Chapter viii, we write
v — z cosh (a + i/9) = z cosh 7,
where 0 ^ ft ^ 7r and 7 is not nearly equal* to ttx.
(I) We first consider the integral
1 f° 1 r*>
— I e~vt~zainhtdt=: — I g-ztfcosh y-fsinh t) fy
TTJO T J 0
in which it is supposed temporarily that v\z is positive. When cosh 7 is positive,
t cosh 7 + sinh t steadily increases from 0 to 00 as t increases from 0 to 00 ; wo
shall take this function of t as a new variable t.
It is easy to shew that t is a monogenic function of t, except possibly when
t = Bw +¦ lOrt cosh y± sinh y + y cosh y,
where n is an integer; and, when coshy is positive, none of these values of r is a real
positive number; for, when y is real, B?i + 1) tricosh y does not vanish, and, when y is a pure
imaginary ( = i/3), the singularities are on the imaginary axis and the origin is not one of
them since y is not equal to iri.
The expansion of dt/dr in ascending powers of t is
where
and so am is the coefficient of 1/t in the expansion of r in ascending-
powers of t. In particular we have
_ 1 1 _^~ cosn 7
1+cosh 7' 1 2 A -f cosh 7)*1 2 24 A + cosh <yf '
_ 225 — 54 cosh <y + cosh2 7
as ~ 720A +cosh7I0 "
From the general theorem of § 8'3, we are now in a position to write down
the expansion
A) ^
Expansions valid near y=xi are obtained at the end of this section.
10*15] ASSOCIATED FUNCTIONS 317
This expansion is valid when v/z is positive; it has, so far, been established
on the hypothesis that | arg z j < \ir, but, by a process of swinging round the
contour in the T-plane, the range of validity may be extended to cover the
domain in which | arg z\< it.
Next, we consider the modifications caused by abandoning the hypothesis
that cosh 7 is real. If we write t — u + iv, the curve on which t is real has
for its equation
u sinh a sin /3 + v cosh a cos /9 ¦+ cosh u sin v = 0.
The shape of this curve has to be examined by methods resembling those
of § 81. For brevity we write
u sinh a sin j3 + v cosh « cos /3 4- cosh a sin v = <t> (u, v).
Since 4> (w, v) is unaffected by a change of sign of both u and a, we first
study the curve in which a ^ 0. It is evident that the curve has the origin as
its centre.
Since d<$> (u, v)ldu = sinh a sin /3 + sinh u sin v,
it follows that, when v has any assigned value, d<i>/du vanishes for only one
value of u, and so the equation in u
cfc (u, v) = 0
has, at most, two real roots; and one of these is infinite whenever v is a
multiple of it.
When 0 > v > — it, we have
<I> (— oo ,¦?;) = — oo , <t> (+ oo , v) = — oo ;
and, when v = ft — 7r, the maximum value of ^((t, w), qua function of a, is at
u = a, the value of <1? (u, ?;) then being
- cosh a sin /9 {1 — a tanh a + (ir - /3) cot ^j.
If this is negative, the equation <1> (u, /9 — rr) = 0 has no real loot, and ho the
contour does not meet the line v = $ — it or (by symmetry) the line
V — ir — jS.
Hence provided that the point (a, /?) lies in one of the domains num-
numbered I, 2, :i in Fig. 21 of § 8#(I, the contour <t> (u, v) = 0 lies as in Fig. 25,
the continuous curve indicating the shape of the contour when a is positive
Fig. 25.
and the broken curve the shape when a is negative; the direction in which t
increases is marked by an arrow.
318 THEORY OF BESSEL FUNCTIONS [CHAP. X
It follows that the expansion A) is valid when (a, ft) lies in any of the
domains 1, 2, 3.
Next, we have to consider the asymptotic expansion when («, ft) does not
lie in any of these domains. To effect our purpose we have to determine the
destinations of the branch of the curve <J> (u, v) = 0 which passes through the
origin.
Consider first the case in which a is positive and ft is acute. The function
<t> (a, v) has maxima at v = Bn •+• 1) ir — ft and minima at v = B?? + 1) tr + ft,
each minimum being greater than the preceding; and since <f> (a, ft — tt) is now
positive, it follows that <j> (a, v) is positive when v is greater than — it.
Hence the curve cannot cross the line u = a above the point at which
v — - w, and similarly it cannot cross the line u - — a below the point at which
v=ir. The branch which goes downwards at the origin is therefore confined
to the strip — a < u < a until it gets below the line v — — 2Ktt + rrr — #, where
K is the smallest integer for which
1 - a tanh a + {Bif + 1) 7T -/9} cot ? >0.
The curve cannot cross the line v = — BK + 1) 7T+./3, and so it crosses the
line u = a and goes off to infinity in the direction of the line v = — IKtt.
Hence, if o is positive and $ is acute, we get
while, if a is negative and /9 is acute, we get
By combining these results with those obtained in § 861, we obtain the
asymptotic expansions for the domains 6 a and 7 a.
If, however, C is obtuse and a is positive, the branch which goes below the
axis of u at the origin cannot cross the line u = a below (a, ir — @) and it does not
cross the M-axis again, so it must go to — oo along the line v = — BL + 1) 7r,
where L is the smallest integer for which
1 - a tanh a - {BX + 1) it + /3\ cot /3 > 0.
Hence, if a is positive and ft is obtuse, we get
while, if a is negative and ft is obtuse, we get
co+BL+l)»ri
1 r-
E) -
TTJu
10'15] ASSOCIATED FUNCTIONS 319
By combining these results with those obtained in § 8*61, we obtain the
asymptotic expansions for the domains 4, 5, 66 and 76.
Since formula A) is the only one which is of practical importance, we shall
not give the other expansions in greater detail.
An approximate formula for a^, when m is large and y is zero, namely
was obtained by Cauchy, Comptes Rendus, xxxvin. A854), p. 1106.
(II) Next consider the integral
1 /ta0 1 f
_ I evt-zain\it fa _ _ I e-z(-tcoshy+B\nht) fa
ttJo ttJo
The only difference between this and the previous, integral is the change in
the sign of cosh 7; and so, when 7 lies in any of the regions numbered 1, 4,
5 in Fig. 21 of §8-61, we have
where aOT' is derived from aw by changing the sign of cosh 7; so that
,_
1-cosh 7' -(I-cosh 7)*' ^ 24A -ooah^O'
This expansion fails to be significant when 7 is small, just as the previous ex-
expansion A) failed when 7 was nearly equal to iri.
To deal with this case we write
v = z A — e), 'r — t — sinh t,
after the method of § 8*42. It is thus found that
i r°° 1 f~°° dt
t gct-zsinht dt — - e?r e~'zt j- dr
7rJ0 7rJo <ZT
1 r-00 00
and hence
A result equivalent to this has been given by Airoy, Proc. Royal Soc. xciv. A, A918),
p. 313.
320 THEORY OF BESSEL FUNCTIONS [CHAP. X
10*2. Hardy's generalisations of Airy's integral.
The integral considered by Airy and Stokes (§ 6*3) has been generalised
by Hardy* in the following manner:
If s = sinh (j>, then
f 2 cosh 2<jb = 4s2 + 2
I 2 sinh 3</> = 8s3 + 6s
I
[ 2 sinh o<f> = 32sB + 40s3 + 10s,
and generally
2 l™l n<j> = Bs)\F, (- *«, i - in; 1 - n; -1
the cosh or sinh being taken according as n is even or odd.
Now write
Tn(t,ot) = tn.,Fl(-^n,^~^n;l-n-)
so that
( T2(i,a) = i2 + 2a
T3<?, a) = t* + %at
T, (t, a) = t4+ 4ai2 + 2a2
Then the following three integrals are generalisations! of Airy's integral:
A) Ci»(o)= I™cos Tn(t, a)dt,
J o
B) Sin(a) = j sin Tnit, a) dt,
C) ^"n («) = f exp {- Tn (t, a)} dt.
Jo
It may be shewnj that the first two integrals are convergent when a is
real (whether positive or negative) if n — 2, 3, 4,.... But the third integral
converges when a is .complex ; and it is indeed fairly obvious that Ein{oi) is
an integral function of a.
When n is an even integer, the three functions are expressible in terms
of Ressel functions; but when n is odd, the first only is so expressible, the
other two involving the function of H. F. Weber.
Before evaluating the integrals, we observe that integral functions exist
which reduce to Cin (a) and Sin (a) when a is real; for take the combination
Gin («) + iSin (a) = f" exp [iTn(t, a)} dfc
JO
* Quarterly Journal, xli. A910), pp. 226—240.
t The sine-integral in the case n=3 was examined by Stokes, Camb. Phil. Trans, ix. A856),
pp. 168—182. [Math, and Phys. Papers, n. A883), pp. 332—349.]
X Hardy, loc.cit., p. 228.
10*2, 10-21] ASSOCIATED FUNCTIONS 321
By Jordan's lemma, the integral, when taken round an arc of a circle of
radius jR with centre at the origin (the arc being terminated by the points
with complex coordinates jK, Re*™1*1), tends to zero as R-*-oo.
And therefore
roooxp(J«7«)
Cin (a) + iSin (a) = exp {* Tn (t, a)} dt
Jo
= eW» | °°exp {- Tn (t, ae~Hln)} dr,
Jo
where t = te~^iriln; and the last integral is an integral function of a. The
combination Gin(a) — iSin(a) may be treated in a similar manner, and the
result is then evident.
10*21. The evaluation of Airy-Hardy integrals of even order.
To evaluate the three integrals Gin(a), Sin(a), Ein(a) when n is even, we
suppose temporarily that a is positive, and then, making the substitution
t = 2a* sinh (u/ri)
in the integrals, we find that, by § 6'21 (.10),
n J o
2«1 f
Gin («) + iSin (a) = — 0XP Bain i cosh u) cosh (u/n) du
n J o
u Bai?t),
that is to say
Gin(a) + iSin(a) = .™h ~{flW/« J_xlnBa»»)- er™* JVn
H Hill yTTl'lt)
If we equate real and imaginary parts, we have
In a similar manner,
2a^ f
Eh, (a) = exp (— 2a*71 cosh w) cosh (ajn) du,
so that, by §(J-22E),
C) Kin(a) = B<*/n)KlhgBa**).
These results havo. been obtained on the hypothesis that a is positive; and
the expressions on the right are the integral functions of a which reduce to
Cin (a), Sin (a) and Ein (a) when a is real, whether positive or negative. Hence,
when a is negative the equations A), B), C) are still valid, so that, for example,
we have
(H <a\= - * J V (-)»O"«
nV } 2nain(i/n)Ut m!f(m+li/»)
whether a be positive or negative.
w. b. f. 21
322 THEORY OF BESSEL FUNCTIONS [CHAP. X
Hence, replacing a by — ft, we see that, when ft is positive and n is even,
then
D)
E)
F)
O»(-/8)-
&in(-ft) =
Ein(-ft) =
(/-„„ W - /„. B/3-)],
It follows from § 4'31 (9) that, when n is even, the functions Cin (a) and
8in (a) are annihilated by the operator
and that Ein (a) is annihilated by the operator
In the case of the first two functions it is difficult to obtain this result*
directly from the definitions, because the integrals obtained by differentiating
twice under the integral sign are not convergent.
10*22. The evaluation of Airy-Hardy integrals of odd order.
To evaluate Cin(a) when n is odd, we suppose temporarily that a is
positive, and then, by § 6'22 A3),
2a* r
Gin (a) = — cos Ba*71 sinh u) cosh (uln) du
n Jo
7b
That is to say,
A)
Using the device explained in § 1021, we see that, when /9 is positive,
It follows that the equation § 10'21 D) is true whether n be even or odd;
and, whether n be even or odd, Oin(a) is annihilated by the operator
dl (_)nnt «-2
for all real values of a.
* It has been proved by Hardy, loc. cit., p. 229, with the aid of the theory of "generalised
integrals."
10'22] ASSOCIATED FUNCTION 323
Next we evaluate Ein (a) when a is positive; making the usual substitution,
we find that, by § 1013 D),
2a* f"
Ein (a) = — exp (— 2a*n sinh u) cosh (u/n) du
w J o
= ~ {tan (WO Ji/n B«»») - B1/n Ba*-)]
+ -^7r-~-r- {JL^ Ba*») - J1/n Ba*-)}.
n sin (tr/n)l ' v 7 ' v /J
Hence the series which represents Ein (a) when n is odd and a may have
any value is
J n ~ n cos (\Tr/r\)m=0 F (m + f —1/%) F (?ft + -| + ^-/w)
~- f oo / \m «tnti co / \m nmn \
+ J 51 .l—iL.W „ V _A~J__I L
w sinX7r/«) (mt0 m! F (m + 1 - l/?i) m^0 w! F (?» + 1 + l/n)J '
and hence it follows that
D) — + n>or-*\ EiH («) = ^a*1
(da j
Next consider Cin(a) + i Sin(a), where a is temporarily assumed to be
positive. From § 103 D) we deduce that
2gj /•*>
Gin (a) + i >S'in (a) = — exp Ba*.n i sinh ?^) cosh (u/n) du
{tan (^Tr/n) J1/n (- 2a*'lt) - E1/u (- 2a»«t)}
«
n cos (^tt/«) m r (w + | - i/n) F (w + f +
™* F*«/» /_1/n Ba*-) - e-*-V« /
r/J!I
and therefore
whence it follows that, when /9 > 0,
y ±ZL-.ii
n-o F (to + & — ^/u) F Gfi •
21—2
324 THEORY OF BESSEL FUNCTIONS [CHAP. X
and hence, for all real values of a,
G) 1-^L - nB an-*\ Sin (a) = - nob <»-»>.
(da2 )
This equation was given by Stokes in the case n =¦ 3.
It should be noticed that
(8) 8in(a) + (-)*«n+D Ein(a) = nf?*v/n) {sin <**/
Wit
{sin (iw/n)+ (-!)»*+"}
where /9 = — a, and a and /9 are real.
The formulae of the preceding three sections are due to Hardy, though
his methods of obtaining them were different and he gave some of them only
in the special case n = 3.
10*3. Conchy's numbers.
In connexion with a generalisation of Bessel's integral which was defined
by Bourget, and subsequently studied by Giuliani (see § 10'31), it is convenient
to investigate a class of functions known as Cauchy's nawhers.
The typical number, JV_nijt|W, is defined by Cauchy* as the coefficient of
the term independent of t in the expansion of
H)K)*
in ascending powers of t. It is supposed that n, k, and in arc integers of which
the last two are not negative.
It follows from Cauchy's theorem that
A) 2
2'n+A: jm r-n
2m+ktfn r
1*4 {e~ni0 + (~)m enie] cos* 8 sin OdB
Jo
IT Jo
It is evident from the definition that N-.n>ktm is zero if — n + k + m is odd or
if it is a negative integer.
* Comptes RenduK, xi. A840), pp. 473—475, 510—511; xn. A841), pp. 92—93; xnr. A841),
pp. 682—687, 850—854.
10'3] ASSOCIATED FUNCTIONS 325
From A) it is seen that
C2~\ AT , — (—\m AT , — (-\n-k i\r ,
V-6/ -iv — n,k,m— V / xv«,J:,m— \ ) -ivM,Jk,m-
These results, together with recurrence formulae from which successive
numbers may be calculated, were given by Bourget*.
The recurrence formulae are
C) -ZV-m,k, in, = -"->i+-i, Jfc-i,m + -N-n-\,k-i,m >
and they are immediate consequences of the identities
rn (t +1 /tf (t -1 ft)m = v~n(t + i /t)k~i (t -1 /t)m + rw-x (t + i/tf-1 (t - i/t)m,
t~n (t + i/tf (t - i/om = t1-* (t + i/t)k (t - i/t)m~i - t-n~i (t + i/t)k (t - i/t)m-\
By means of these formulae any Cauchy's number is ultimately expressible in
terms of numbers of the types i\T_njti0, iV_wom.
A different class of recurrence formulae, also due to Bourget, owes its
existence to the equation
4
"dtV-t
It follows that
@+)
by a partial integration. On performing hhe differiitifciatiou we see that
E) (in + I) N-n,k, m = *'^-«,*-i, rn li ~ (^ ^
and similarly
F) (^ -I- 1) JV-«,it,hi = nN_Kk+liin_! - (m -
Developments duo to (JhcHsiu, Annals of Math. x. AH05---<>), j)p. I—2, aro
I- 0
(«) iV _ n, ,. 1(i = s (-)'' A-. N . ui. _.,,, ,, ,„ ..,.
r-l)
Theso may bo deduced by induction from C) and (-1).
Another formula due to (Jh<\snin is
(9) ff-n,*, .»=» 2 ( -)rtCp..r.mCr,
whore p — \ (k+m — n). Thiw i« proved by .selecting the coufficiuut of tn in the product
(<+l/0*x(«-l/0Bl.
* Journal de Math. B) vi. A861), pp. 88—54.
326 THEORY OF BESSEL FUNCTIONS [CHAP. X
10*31. The functions of Bourget and Giuliani.
The function Jn<k(z) is defined by the generalisation of Bessel's integral
where n is an integer, and k is a positive integer.
It follows that
o T eXP {- * (n6 - Z Sin 6)\ • B C0S 6f d6>
Z7T J -.„
and therefore
B) «7n * CO = - T B cos e)k <=os (n& ~ z sin 0) de>
7T .1 o
The function Jn,k(z) has been studied by Bourget, Journal de Math. B) vi. A861),
pp. 42—65, for the sake of various astronomical applications; while Giuliani, Giornale di Mat.
xxvi. A888), pp. 151—171, has constructed a linear differential equation of the fourth
order satisfied by the function.
[Note. An earlier paper by Giuliani, Giornale di Mat. xxv. A887), pp. 198—202,
contains properties of another generalisation of Bessel's integral, namely
1 /¦"¦
- / coa (n6 - 2" sin" 6) de,
it J a
but parts of the analysis in this paper seem to be incorrect.]
If we expand the integrand of A) in powers of z, we deduce from § 10'3 that
C) /«,*(*)= 2^f # ;
and it is evident from A) that
D) Jn<a(z) = Jn(z).
Again from § 10B) and C) it is evident that
E) J-n,k(*) = (-Y^kJn,*(*).
F) Jn,k (z) = /„-,,*_, (*) + «/¦„+,,*_, B);
and, if we take Ic— 1 in this formula,
G) ^,..W-v^(').
z
These results were obtained by Bourget; and the reader should have no
difficulty in proving that
(8) 2J'M <*) - J*-i,k (*) - /.+,,*(*)•
Other recurrence formulae (due to Bourget and Giuliani respectively) are
(9)
A0) 4J"n,*_a E) . Jn>, («) - 4J^ (z).
10-31] ASSOCIATED FUNCTIONS 327
The differential equation is most simply constructed by the method used
by Giuliani; thus
1 f"¦ d
Vn Jn k (z) = - -ja {— (n + z cos 0) sin (nB - z sin 0)] B cos Of dd
' "".'(> **C7
2& P1
= (w + 2 cos 0) sin (n0 - z sin 0) B cos 0)*-1 sin 0d0
T Jo
2k f* (d )
w t B) + — i ja cos (w^ - z sin 0) f B cos d)k~l sin 0d0
TT .!(, [atf j
'n fc B) cos (n0 - z sin 6) ~ {B cos 0)*-1 sin 01 ^0,
7T J 0 wC
7T J 0
and so
d*
Operating on this equation by -^- + 1, and using A0), it follows that
n Jn'k{Z) + 2kzJ'n'k& + ^J^(z)\ = k(k~ l) JnA*)>
and hence we have Giuliani's equation
A1) *J\k(g) + Bk + 5)zJ'\k(g) + [2z* + (k + 2Y -n2} J\k(z)
+ B/c + 5) gJ\ fc (g) + (z* + k + 2 - na) Jnt k (z) = 0.
It was also observed by Giuliani that
A2) e'*Bi"oBcos0)*= 25 €.mJ.zn>k(z)cou2nd
71 = 0
00
+ i % em.HJm+l<k(z)ainBn+l)d;
this is verified by applying Fourier's rule (of. § 2*2) to the function on the
right.
A somewhat similar function J(z\ v, k) ban boon utudiod by Bruna, A»tr. Nach. CIV.
A883), col. 1—8. Thitt function is duiined by tho aoricn
00 i' _ <ni /jL-»\»' + afc+aT»i. 9.,
The most important property of this function is that
A4) /(,,., *)-/(.;
¦whence it follows that
328 THEORY OF BESSEL FUNCTIONS [CHAP. X
10'4. The definition of Struve's function I3.v{z).
Now that we have completely examined the functions defined by integrals
resembling Bessel's integral,, it is natural to investigate a function defined by
an integral resembling Poisson's integral. This function is called Struve's
function, although Struve investigated* only the special functions of this
type of orders zero and unity. The properties of the general function have
been examined at some length by Siemonf and by J. Walker ?
Struve's function lrLv{z), of order v, is denned by the equations
sin2" Odd,
provided that R(v) > - \.
By analysis similar to that of § 3'3, we have
? f tf^1 A - <2)"~i ^^
M J o
H.W-,7^
r (v +1) r (J) w.o Bm + 1)!
so that
The function Hv(,z) is denned by bhis equation for all values of v, whether
R(u) exceeds — f or not. It is evident that Hv (z) is an integral function of v
and, if the factor (\z)v be suppressed, the resulting expression is also an in-
integral function of z.
It is easy to see [cf. §§ 211 E), 3121 A)] that
where
and | vo + f | is the smallest of the numbers 11> +f|,
* Mim. de VAcad. Imp. des Sci. de St Pitersbourg, G) xxx. A882), no. 8; Ann. der Physik,
C) xvn. 11882), pp. 1008—101G. See also Lommel, Archiv der Math, und Phys. xxxvi. A861),
p. 399.
t Programm, Luisenschule, Berlin, 1890. [Jahrbuch iiber die Fortschritte der Math. 1890,
pp. 340—342.]
X The Analytical Theory of Light (Cambridge, 1904), pp. 392—395. The results contained in
this section, with the exception of C), D), A0) and A1), are there given.
10-4] ASSOCIATED FUNCTIONS 329
We can obtain recurrence formulae thus:
d_ ,
d \Z
and similarly
= ~
^+1 T (w + f) r A/ + m + $
^^a"r (m +1) r (i; + m +
On comparing these results, we find that
E) "SS-v-i {z) + Hv+1 (z) = — Hv B) + p V
F) EU (*) - Hr+I (*) = 2H/ (jr) {
G) (^ + ,)H,B) = Ah(^
(8) (* - „) Hv {z) = r(-J^
In particular we have
(9) A{*HI(*)} = *H0(*)) 1{H
Again, from G) and (8), we have
(*» - v>) H, (*) - (Sr -1,) {^
so that H,,B) satisfies the diflferential equation
A0) V, Hv (*) = p^-^y i^jy •
Tho function Lv (s) which boars the Hamo rolation to Struve's function aa Iv (z) bears
to Jv{z) haw been studied (in tho caso v=0) by* Nicholnon, Quarterly Journal, XLIL A911),
p. 218. This function is denned by the equation
(U) U («)= ^fSTrF
the integral formula being valid only when R(v)> — \.
The reader Bhould have no difficulty in obtaining the fundamental properties of this
function.
* See also Gubler, Zilrich Vierteljahrmchri/t, xi.vii. A902), p. 424.
330 THEORY OP BESSEL FUNCTIONS [CHAP. X
10*41. The loop-integral for M.v (z).
It was noticed in § 1O4 that the integral definition of Hv(z) fails when
U(v)<-$, because the integral does not converge at the upper limit. We
can avoid this disability by considering a loop-integral in place of the definite
integral.
Let us take
(P - 1)"-* sin zt. dt,
Jo
where the phase of i2 -1 vanishes at the point on the right of t = 1 at which
the contour crosses the real axis, and the contour does not enclose the point
If we suppose that R(v) > — ?, we may deform the contour into the seg-
segment @, 1) of the real axis, taken twice, and we find that
/¦(i+) f1
(t2 - 1)"-* sin zt.dt** % cos vrr\ A - i2)""* sin zt. dt,
Jo Jo
where the phase of 1 -1 is zero.
Hence, when R (v) > — ?, we have
Both sides of this equation are analytic functions of v for all * values of v;
and so, by the general theory of analytic continuation, equation A) holds for
all values of v.
From this result, combined with § 61 F), we deduce that
B) j. (z) + iav (z) = r (* ~l\'r^ f1+) «* («2 -1)-* dt
To transform this result, let a> be any acute angle (positive or negative),
and let the phase of z lie between — \tt + to and \ir + a>. We then deform
the contour into that shewn in Fig. 26, in which the four parallel lines
make an angle — « with the imaginary axis. It is evident that, as the lines
parallel to the real axis move off to infinity, the integrals along them tend to
zero. The integral along the path which starts from and returns to 1 + oo ie~iu>
is equal to Hvw (z); and on the lines through the origin we write t = iu, so
that on them
(f -1)--4 = eT (»-i)« (i + u*y-l.
It follows that
jv (z)+iuv (z) - H* (z) + r^ffr (i) i e~m A + uiy~k du>
* The isolated values }i $,$,... are excepted, because the expression on the right is then an
undetermined form.
10*41] ASSOCIATED FUNCTIONS
where the phase of 1 + u2 has its principal value; and hence
331
This result, which is true for unrestricted values of u, and for any value of
2 for which - it < arg z <ir, will be applied immediately to obtain the asym-,
ptotic expansion of Hv (z) when | z | is large.
Fig. 2A.
A result equivalent to B) was obtained by J. Walker*, who assumed
that 11 (v)> — I, Ji(z)>0, so that to might be taken to be zero. In the case
v—0, the result had previously been obtained by Rayloighf with the aid of
the method ol' Lipschita (§ 7*21).
If, as in §(M2, we replace w by arg 2-/3, it is evident that C) may be
written in the form
> ex}) «
where — \ir < y8 < iir and - \rr + /3 < arg z < In + /3.
This equation*gives a representation of Hv (^) when j arg z \ < tv. To obtain
a representation valid near the negative half of the real axis, we define H,,(.z)
for unrestricted values of arg z by the equation
E) H,, (zemni) = e» ("+*>** Hv (,?),
and use D) with z replaced by ze^vi.
* The Analytical Theory «/ Light (Cambridge, 1904), pp. 894—395.
t Vroc. London Math. Soc. xix. A889), pp. 504—507. [Scientific Papers, in. A902), pp. 44—46.]
332 THEORY OP BESSEL FUNCTIONS [CHAP. X
If vie write z**ix in C), where x is positive, we see bhat, when R(v)<i,
and, by considering imaginary parts, we deduce that
a result given by Nicholson, Quarterly Journal, xlii. A911), p. 219, in the special case in
which i»=O.
10*42. The asymptotic expansion of Hv {z) when \z\is large.
We shall now obtain an asymptotic expansion which may be used for tabu-
tabulating Struve's function when the argument z is large, the order v being fixed.
Since the corresponding asymptotic expansion of Yv (z) has been completely
investigated in Chapter vn, it follows from § 10*41 D) bhat it is sufficient to
determine the asymptotic expansion of
L
As in | 7'2, we have
We take p so large that i? (v -p — |) <0, and bake 8 bo be any positive angle
for which
so that if is confined to the sector of the plane for which
- it + 28 < arg z^tt — 28.
We then have
so that
t'tfc.
^ sin h,
I(Sin
say, where Ap is independent of z.
It follows on integration that
> OXp tK
where
0 (-BTV).
a exp i|3
10-42, 10-43] ASSOCIATED FUNCTIONS 333
We deduce that, when j arg z | < ir and | z j is large,
provided that R (p — v + .]) ^ 0; but, as in § 7*2, this last restriction may be
removed.
This asymptotic expansion may also be written in the form
B) H. (,)- Y. W + I?F(, + [^;(}>y^ + 0 (*>—).
It may be proved without difficulty that, if v is real and z is positive, the
remainder after p terms in the asymptotic expansion is of the same sign
as, and numerically less than the first term neglected, provided that
R (p + I- —v)> 0. This may be established by the method used in § 7-32.
The asymptotic expansion* was given by Rayloigh, Proc. London Math. Soc. XIX. A888),
p. 004 in the cawe v = 0, by Struve, Mem. de I'A cad. Imp. das ScL de St Petersbourg, G)
xxx. A882), no. 8, p. 101, and Ann. der Pkys. und Okemie, C) xvn. A882), p. 1012 in the
case i> = 1; the result for general valuer of v was given liy J. Walker, The Analytical
Theory of Light (Cambridge, 1904), pp. 31L—395.
If v has any of the values ?, '•},, ..., then A + iP/z1)"'* i.s expressible as a
terminating series and Yv(z) i.s also expressible in u finite form. It follows
that, when v is half of an odd positive integer, Ht.(z) is expressible in terms
of elementary functions. In particular
10'43. The asymptotic expansion of Ntrave's functions of large order.
We shall now obtain asymptotic expansions, of a type, similar to the
expansions investigated in Chapter Viti, which represent Struvc'.s function
Hv (z) when | v \ and | z \ are both largo.
Am usual, we, shall write
v = z cosh (a + i/9) = z cosh 7
and, for simplicity, we shall confine (he investigation to the special case in
which cosh 7 is real and positive. The. more general case, in which cosh 7 is
complex may be investigated by the methods used in § <S-(i and § 1015, but it is
of no great practical importance and it involves some rather intricate analysis.
* For an asymptotic; expansion of the. HHHOi'.iutiul inti^'al
„ ( 1 -I- j ) du,
see Raylcigh, Phil. Mag. ((i) vm. (l!H4), pp. 481—487. [Scientific Papas, v. A912), pp. 200—211.]
334 THEORY OP BESSEL FUNCTIONS [CHAP. X
The method of steepest descents has to be applied to an integral of Poisson's
type, and not, as in the previous investigations, to one of Bessel's type.
In view of the formula of § 10*41 C), we consider the integral
dw
which we write in the form
f „ dw
where r = w- cosh 7. log A + w3).
It is evident that r, qua function of tv, has stationary points where w = e**,
so that, since 7 is equal either to a or to ift, two cases have to be considered,
which give rise to the stationary points
(I) e±a, (II) e±l*.
Accordingly we consider separately the cases (I) in which z/v is less than 1, and
(II) in which z/v is greater than 1.
(I) When 7 is a real positive number a, r is real when w is real, and, an w
increases from 0 to 00 , t first increases from 0 to e~a — cosh a. log (J + e~2a),
then decreases to ea — cosh a. log A + e211) and finally increases to + 00 .
In order to obtain a contour along which r continually increases, we. suppose
that w first moves along the real axis from the origin to the point e~a, and
then starts moving along a certain curve, which leaves the real axis at right
angles, on which t is positive and increasing. '
To find the ultimate destination of this curve, ..it is convenient to make a
change of variables by writing
?= % + iy, e~a = sinh ?0,
where ?, 77 and ?0 are real.
The curve in the ?-plane, on which r is real, has for its equation
cosh f sin <r\ = 2 cosh a arc tan (tanh f tan ?/),
and it has a double point* at ?„.
We now write
v 1 y \ _ 2 arc tan (tanh ? tan rj)
~ cosh ? sin y
and examine the values of F(%, 17) as ? traces out the rectangle whose corners
0, A, B, C have complex coordinates
0, arc sinh 1, arc sinh "I + J tti, I iri.
As ?goes from 0 to A, F(t;, rj) is equal to 2 sinh f/cosh8 ^, and this .steadily
increases from 0 to 1.
* Except when a = 0, in which case it has u triple point.
10-43] ASSOCIATED FUNCTIONS.
When ? is on AB, F(t;, rj) is equal to
V2.arc tan [—jcr)• cosec %
335
and this steadily increases from 1 to tt/^/2 as r) increases from 0 to \tr.
) j2 and observe that
arc tan *\ "
Notb. To establish this result, write tan t)
d
It
T
because
- arc tan «, which vanishes with i, has the positive derivate
When ? is on J?C, i^1 (f, i;) is equal to 7r sech |, and this increases steadily
from 7r/V2 to it as ? goes from B to 0; and finally when ?" is on GO, F(j;, rj)
is zero.
Hence the curve, on which F (?, if) is equal to sech a, cannot emerge from
the rectangle OABG, except at the double point on the side CM; and so the
part of the curve inside the rectangle must pass from this double point to the
singular point G.
The contours in the w-plane for which a ha,s the values 0, \ are shewn in Fig. 27 by
broken and continuous curves respectively.
Fig. '27.
Consequently a contour in the w-phuu', on which t is real, consists of the
part of the real axis joining the origin to e~a and a curve from this point to
the singular point /'; and, aa w traces out this contour, r increases from
0 to + oo .
It follows that, if the expansion of d^jdr in powers of r is
dt °°
ar w=o
336 THEORY OF BESSEL FUNCTIONS [CHAP. X
then
(V™ A + w2)"-* duo =
and hence, by 10*4 A), we have
(i) H.w-.j.w
It is easy to prove that
b0 = 1, &x = 2 cosh 7, 52 = 6 cosh2 7 — \, b3 = 20 cosh3 7 — 4 cosh 7, ....
(II) When 7 is a pure imaginary (= i/9), t is real and increases steadily
from 0 to 00 as w travels along the real axis from 0 to 00; and so
/•oo foo f I
JO JO (\/(l+
Hence, from § 10-41 C) it follows that
provided that j arg z \ < \ir. This result can be extended to a somewhat wider
domain of values of arg z, after the manner of § 8*42.
From the corresponding results in the theory of Bessel functions, it is to be
expected that these results are valid for suitable domains of complex values
of the arguments.
In particular, we can prove that, in the caae of functions of purely imaginary argument,
C) lip (vx) ~ /„ (vx)
when I v I is large, | arg v \ <^n-, % is fixed, and the error is of the order of magnitude of
times the expression on the right.
[Note. If in (I) we had taken the contaur from w—0 to w=e~a and thence to w— -i,
we should have obtained the formula containing %JV (z) in place of - i,fv (z). This indicatcn
that we get a case of Stokes' phenomenon as y crosses the lino # = ().]
10*44. The relation between Hn (z) and En (z).
When the order n is a1 positive integer (or zero), we can deduce from
§ 10*1 D) that En (z) differs from - Hn (z) by a polynomial in z; and when n
is a negative integer, the two functions differ by a polynomial in 1/z.
10-44, 10*45] ASSOCIATED FUNCTIONS 337
For, when n is a positive integer or zero, we have
and
_
and therefore, since Jw B) = ./„ (z), we have
n q\ {m-1) iri A ^yt-Trt.
E'1 ^*>=tx r (f- w r (« +1 •} ~ H &
that is to say
A) B,w^ rlM! »,\
In like manner, when — n is a negative integer,
B) B_,(*)- ^
10*45. !/V<e sign, of Struve's function.
We shall now prove the interesting result that !!„(&¦) is positioe when x is
positive and v has any positive value greadisr than or (ujual to \, This result,
which was pointed out by St.ruve* in the caso u=l, is derivable from a
definite integral (which will be established in § 115*47) which is of con-
considerable importance in the Theory of Diffraction.
To obtain the result by an elementary method, we integrate § H)-4(l) by
parts and then we see that, for values of v exceeding1 \,
r (J¦ +1) v (i
ck ri r™""
- Bi/ - I) I cos (j; cos 6) m\"v-20 cos 0d0\
r4ir
— (w —I) <'.oh (."¦ ctis (^) sui""""*^ c<
Jo
is^jl -cos(.eco«^)J (^
since the integrand is positive.
* A"«»i. <'c VAcad. Im\i. den Sri. de St Pctcrdwurif, G) xxx. AB82), no. 8, pp. 100—101. The
proof given here is the natural (ixtension of NtnivcV proof.
w. ». v.
338 THEORY OF BESSEL FUNCTIONS [CHAP. X
When v is less than h, the partial integration cannot be performed ; and, when i/ = A, we
have
and the theorem is completely established.
A comparison of the asymptotic expansion which was proved in § 1O42 with that of
Yv (x) given in § 7 1 shews that, token x is sufficiently large and positive, H,, (.«) is positive
if i>>? and that Hv (x) is not one-signed when v <\; for the dominant torm of tho
asymptotic expansion of H,, (x) is
according as v > \ or v < ^. The theorem of this section proves the more extended result
that Struve's function is positive for all positive values of x when v >-J and not meroly
for sufficiently large values.
The theorem indicates an essential difference between Struve's function and Bessel
functions; for the asymptotic expansions of Chapter vn shew that, for sufficiently large
values of x, Jv (x) and Yv (x) are not of constant sign.
10*46. Theisinger's integral.
If we take the equation
\ j
= / jhn e-*™o log
J -h*
log
1 + hdz
and choose the contour to be the imaginary axis, indented at the origin*, and then write
z— ±ttan^</>, we find that
and so
7" Vo (X)-I*o (.*)} = / cos (x cot <f>) log tan (|tt+J0) -j-^,
A) /0 (a?) - Lo (a1) = -5 I ^ cos («tan 0) log-cot (^) -^ ,
it j o coscp
a formula given by Theisinger, Monatshefte fiir Math, und Phys. xxiv. A913), p. 341.
If we replace x by asintf, multiply by win (9, and integrate, we find, on changing the
order of the integrations in the absolutely convergent integral on the right,
/ "Ei (> tan <p) log cot (?cp) -^- = J ( *" {/„ (a; sin (9) - Lo (.« aiu 6)\ sin fldd
J o cos <p 2 J o
cos <p
so that
B) f **?!(*tan 0)lqgoot A0) ^ = | .1~'"*,
y 0 COS ^5 ¦" '<-
on expanding the integrand on the right in powers of x. This curious roault is also due to
Theisinger.
* The presence of the logarithmic factor ensures the convergence of the integral round the
indentation.
10-46,10*5] ASSOCIATED FUNCTIONS 339
10. Whittakers integral.
The integral
l
which is a solution of Bessel's equation only when 2v is an odd integer, has
been studied by Whittaker*.
It follows from § 617 that, for all values of v,
A) V, L* [X e^iVj (t) dt\ = - lim |>*e&« A - &) P'.-M)]
I .'-l J f-*--i+o
= — cos vir.
IT "
If we expand the integrand (multiplied by eiz) in ascending powers of z and
integrate term-by-term + it is found that
(A\ 1 I ~'-i It /.\ 7. r» 1 _."«»» \m1iti) • I/O i
The formula of § 3*32 suggests that we write
and then it is easy to verify the following recurrence formulae, either by using
the series B), or by using recurrence formulae for Legendre functions:
2v f
C) Wv_, {z) + Wv+1 (z) = - \WV (z) -
D) Wv_, (s) -
-v z~i e~iz
2»r) r (|-
F) (» _ „) W. (,) — ,ww (,)
An asymptotic expansion of W, {z) i'or large values of | z | may be obtained by
deforming the path of integration after the manner of Lipschitz (§ 71).
* Proc. London Math. Soc. xxxv. A903), pp. 198-200.
t By a uso of Legondre'H equation tho recurrence formula
j_{(i + 0* ^-i @'"=(-M- +?-t J_t (i + 0«- /Vi @ ^
/I 2
P^, («)d(=———\-p75i v by expand hit,'
-1 I ($ +V) L [ft V)
F (i - vi i + v > 1» i - 4*) iQ ascending powers of 1 - t, and integrating torm-by-term.
22—2
340 THEORY OF BESSEL FUNCTIONS [CHAP. X
The function is thus seen to be equal to
Now it is known that*, near t= 1,
Py-iit^tFiQ-v^ + v, 1; J-iO.
cos
x {log f ---) -
{ \ A J
{g f ) ty ( + l) + f (m- v
{ \ A J
and since
we obtain the asymptotic expansion
G) Wr(«)~lJ5T,«(*)
fir+i*) cosi/tt f « (v, rn)
1)— log 25 — ?7™} .
Some functions which satisfy equations of the same general type as A) have been
noticed by Nagaoka, Journal of the Coll. of Sci. Imp. Univ. Japan, iv. A891), p. 310.
10*6. The functions composing Yn{z).
The reader will remember that the Bessel function of the second kind, of
integral order, may be written in the form (§ 3*52)
w=0 «l!
The series on the right may be expressed as the sum of four functions, each of
which has fairly simple recurrence properties, thus
A) irYn(z)=2{\og(lz)-f(l)}Jn(z)-Sn(z) + rn(z)-2Un(z),
* Cf. Barnes, Quarterly Journal, xxxix. A908), p. 111.
10*6] ASSOCIATED FUNCTIONS • 341
where
B) Tn (z) = - 'S1 (n -^rJ* (.b)-n+2w
and (cf. § 3-582)
C) Un (z) = S {JU?J^ {+ (n + m +1) - f A)}.
m=0
The functions 7'nB) and Un(z) have been studied by Schlafli, Math. Ann. in. A871),
pp. 142—147, though he used the slightly dift'erent notation indicated by the equations
Sn(z)=-2Gn(z), 7;B)=2//MC), Un(z)=-En(z);
more recent investigations are clue to Otti* and to Oraf and Gublert.
The function Tn (z) is most simply represented by the definite integral
D) Tn (z) = - r$nr - 6) sin {z sin 6 - nd) dd.
To establish this result, observe that
m> in-i r (m + L+«) r (n + m -I-1 - e)
J
t)n+4i»i \og_t .
_ 2 r* ^ e"l0(-?:^in^y^^._(^_:-|7r)
¦""'i J o m> -l,i -1 "(n + 2m)!
where i has boon replaced by ei"r)i.
It follows that
S (- ^ .sin 6IH im _ (cosh (- iz sin ^) (?i even)
V
Now
m>-in-i \n + 2w)! Vsinh (— iz sin t9) (?i odd)
and so
Tn (a) = --. F - W) U»w-f*Hhi« + eMi(«-^)-»-i*Bia«j ^t
7TtJo
* i/er« MittheilunriP.n, 1898, pp. 1—56.
t Einleitung in die Theork der Bessel'schen t'uaktionen, n. (Born, 1900), pp. 42—69. Loramel'B
treatise, pp. 77—87, should also be consulted.
342 THEORY OF BESSEL FUNCTIONS [CHAP. X
If 6 is replaced by it — 6 in the integral obtained by considering only the
second of the two exponentials, the formula D), which is due to Schlafli, is
obtained at once.
The corresponding integral for Un (z) is obtained by observing that
n (a-- [I 5 (-)w(^)n+2
n W " |> m-o -m! r (n +
and so, from § 6 D), we deduce that
E) ff»(*) = {16g(i«)-*(l)}/n(*)
+ - f "(9 sin (n0 - z sin 0) <20 + (-)» f °
vr Jo Jo
10*61. Recurrence formulae for Tn{z) and Un{z).
From § 10-6 D) we see that
- 0) sin 0 sin 0 - w0). B cos 6 - 2n/z] d6
?7r - ^) ^ (cos (*sin Q-v^de
= -cos2|??.7r-- Jn(z),
z z
on integrating by parts and using Bessel's integral.
Thus
A) T,» (z) + Tn+1 (t) = Bn/*) Tn (z) + 4 [cos^nTr - Jn (z)}/z.
Again Tn' (z) = - ['(W - d) sin 0 cos (s sin 6 - w0) d0,
7T Jo
and so
B) Tn_1(z)-Tn+l(z) = 2Tn'(z).
From these formulae it follows that
C) O + n) Tn (z) - ^f^ (z) - 2 cos21-Mr + 2J« (^),
D) (* - n) Tn {z) = -z Tn+1 (z) + 2 cos2 \ nrr - 2Jn (z),
and hence (cf. § 1012) we find that
E) Vn Tn (z) = 2\z sin2 \rnr + n cos2 \mr\ - 4m- Jn (z).
10*61, 10*62] ASSOCIATED FUNCTIONS 343
With the aid of these formulae combined with the corresponding formulae
for Jn{z)t Yn(z) and Sn (z), we deduce from § 10*6A) that
F) U-x (z) + Un+1 (z) - {2n/z) Un (z) -B/*) Jn {z),
(?) Un.x (z) - Un+1 (z) = 2Un' (z) - B/*) Jn(*),
(8) (* + n) Un (z) = zUn^ (z) 4- %TH (z),
(9) (^-n)Un(z) = -zUn+1 (z), [cf. §§358A), 3'58B)]
i I IM \/ / / ( c \ —*• ..i, / v I I o'x
ixvi M **^ "ft V*1/ ~~ **& *J 9t-|-i I *• /•
The reader may verify these directly from the definition, § 10*6 C).
It is convenient to define the function T_n (z), of negative order, by the
equivalent of § 10 D). If we replace 0 by ir — 6 in the integral we find that
T_n (z) = • - ['(<? vr - d) sin (z sin <9 + n^) dd
7T Jo
7T J {)
and so
(ii) r_nB) = (-y^Tn(z).
We now define U_n(z) by supposing § 10'fi A) to hold for all values of n ;
it is then (bund that
A2) tf_B(*) = (-)" \Un(z) - Tn(z) + Stt(z)\.
10-62. Series for Tn(z) and Uu(z).
We shall now shew how to derive the expansion
A) T (z) = 1& \J ., (z) — J .. (z)\
from § 10'G D). The method which we shall use is to substitute
. .. ", sin imO
i, 7T — G = i - - -
m\ I'1
in the integral for Tn(z), and then integrate tenn-by-torm. This procedure
needs justification, since the Fourier series does not converge uniformly near
0 = 0 and 0 =¦ tt, and, in fact, the equation just quoted is untrue for those two
values of 0.
To justify the procoHS*, let ft and € be arbitrarily (small positive numbers. Since the
series convergeH uniformly when fi <; 6 %n — S, wo cyui ihid an integer m0 such that
M sin 2>»0
(\n-6)- 2 - - j<«>
* The analysis immediately following is duo to D. Jook?on, Palermo Rcndiconti, xxxh. A911),
pp. 257—202. The value of the constant A is r8fjl(.)....
344 THEORY OF BESSBL FUNCTIONS [OHAP. X
throughout the range fi < 6 <tt- S, for all values of M exceeding m0. Again, for all values
of 6 between 0 and ir, we have
r-6~ 2 S1
f
Jo
fb" sin BM+l)t t ,
t am ?
dt=lnr I — dx
for some value of ^ between 5 and ^7r, by the second niean-vulue theorem, .since i/sln t is
a monotonic (increasing) function.
By drawing the graph of .r~lsina; it is easy to sec that the last expression cannot
exceed It I —-dx in absolute value ; if this be called Ik A, we have
"Jo *'
Tn(z)A $
s?
9 f /"S /"ir-8 /"t
rr (Jo J & t J tt-
m=\ m )
.| .sin B .sin 6-iid)\dd
where 5 i.s the upper bound of 18in [z sin 6 - nd) |.
Since 2(^L5 + eMis arbitrarily small, it, follows from the definition of an
infinite series that*
2 (*"
tin (ztin 6-11
oo ]
= ^ -- {Jn+Bm (Z) ~ Jn-M (z)\,
and the result is established.
It will be remembered that Un (z) has already been defined (§ 3-581) as a
series of Bessel coefficients by the equation
and that, in § 3'582, this definition was identified with the definition of Un (z)
as a power series given in § 10'6 C).
10*63. Graf's expansion of Tn (z +1) as a series of Bessel coefficients.
It is easy to obtain the expansion
A) Tn(z+t)= S Tn_m(t)Jm(z),
m= -oo
* This expanaion was diacovered by Schliifli, Math. Ann. in. A871), p. 146.
10-63, 10*7] ASSOCIATED FUNCTIONS 345
for, from § 10*6 D), it is evident that
Tn (z + t) = 2 1\\tt - 6) sin (t sin 8 - nd + z sin 6) d6
0) ? Jm(z) {ei(t*™<>-n9+m9) _ e-Wmx9-n8+m0)} &Q
= - | "(fa - 6) 2 «/",„(^) sin [t sin 0-()i- wi) 0} d0,
by using § 2*1; since the scries under the integral sign is uniformly con-
convergent, the order of summation and integration may be changed, and the
result is evident.
The proof of the formula given by Graf, Math. Ann. xi-iii. A893), p. 141, is more com-
complicated ; it depends on tho use of the series of § 1OT>2 combined with § 2'4.
There sooms to bo no equally simple expression for Un (z + t).
10*7. The genesis of Lmnmel's functions 8,,.tV(z) and Sp.,v(z)-
A function, which includes an special cases the polynomials zOn (z) and
Sn (z) of Neumann and Schliilii, was derived by Lommel, Math. Ann. ix. A870),
pp. 425—444, as a particular integral of the equation
A) Vl/;// = /,:^+1,
where k and (j, are constants. It- is easy to shew thai, a particular integral of
this equation, proceeding in ascending powers of z beginning with z**1, is
C2) / ~ z
K
For brevity the expressions on the right are written in the form
The function .s'Mi>,(^) is evidently undefined when either of the numbers
fi ± v is an odd negative integer*. Apart from this restriction the general
solution of (I) is evidently
C) // = '(>'• „ (z) + /»'.s'Mi „ (z).
In like manner the general solution of
d"i/ n dit
D) jit + L
* The solution of kho equation for such values of fi and v is discussed in § 10*71.
346 THEORY OF BESSEL FUNCTIONS [CHAP. X
Next let us consider, the solution of A) by the method of "variation of
parameters.33 We assume as a solution*
y= A(z)J?(z) + B{z)J-v(z),
where A (z) and B(z) are functions of z determined "by the equations
Jv(z)'A'{z) + J-A*) &{*)**<>>
J'v (z) A' (z) + /'_, (*) B' (z) = hr-\
On using § 312 B), we see that
Aw.^_fVj_(z)dz, aw-J?-JVj,(,>a*.
v ' 2 sin vtt J & sm yir j
Hence a solution f of A) is
F) y = n ^ Fjv (z) f V J-v (z).dz - J-v (*) f V Jv (z) dz ,
x ' v 2 sin vk [_ J J J
where the lower limits of the integrals are arbitrary.
Similarly a solution of A) which is valid for all values of vt whether
integers or not, is
G) y = \Tctv \YV (z) j*z* Jv (z) dz - Jv (z) jZz» Yv (z) dz\ .
It is easy to see that, if both of the numbers fi ± v + 1 have positive real
parts, the lower limits in F) and G) may be taken to be zero. If wo expand
the integrands in ascending powers of z, we see that the expression on' the
right in F) is expressible as a power series containing no powers of z other
than z»+\ z*+s, z^+i, .... "Hence, from C), it follows that, since neither of the
numbers fi±v is an odd negative integer, we must have
In obtaining this result it was supposed that v is not an integer ; but, if
we introduce functions of the second kind, we find that
(9) s^v @) = \v \yv 0*) JV Jv (z) dz - Jv (z) J* * Yv (z) dz~\ ,
and in this formula we may proceed to-the limit in making v an integer.
It should be observed that, in Pochhammer's notation (§ 4'4),
A0) *,„(*) = ^
7^9 =.
(fl - V + 1) (fl + V + 1)
* Cf. Forsyth, Treatise on Differential Equations A914), §66; it is supposed temporarily that
v is not an integer.
f The generalisation of this result, obtained by replacing zn+i in A) by an arbitrary fvmotion
of 2, was given by Chessin, Comptes Rendus, exxxv. A902), pp. 678—679; and it was applied by
Mm, Coviptes Rendus, cxxxvi. A903), pp. 1124—1126, to solve a sequence of equations resembling
Bessel's equation.
10*71] ASSOCIATED FUNCTIONS 347
The associated function $Mi „ (z) is derived from a consideration of a solution
of A) in the form of a descending series. We now proceed to construct this
solution and investigate its properties.
10*71. The construction of the function S^v(z).
A particular integral of the equation § 10'7 A), proceeding in descending
powers of z} beginning with z*~\ is
A) y =
i ..... .+
This series,however,does not converge unless it terminates; but if it terminates,
it is a solution of § 10*7 A), and it will be called JcS^^z).
The series terminates if n — v is an odd positive integer, or if /j, + v is an
odd positive integer, and in no other case.
In the former case we write /x = v + 2p + 1, and then we have
8 (z)_ „-, « (iTr(if*zkti)r<i * tJ" t 4)
v (-
= (-)»• 2"-> r (it* - \v +1) r a/*
When jjl — v — 2p + 1, the function
vanishes, and so, when /j, — v is an odd positive integer, we have
x Ml v ' Mt v ' sin ;^7r
X [cos l(fi— v)tt. ./_„ (^r) — cos I (/x -(- v) 7T. ./„ B)].
Since both sides of this equation are even functions of vt the equation is
true also when /ul + v is an odd positive integer, ho that it holds in all cases in
which Slxv{z) has, as yet, been defined. We adopt it as the general definition
of SlltV(z), except that, when v is an integer, we have to use the equivalent form
C) ?;,.,(*) = «„,,(*) + 2*- r(j/i- \v +1) rdfi + \» +1)
x [sin \ (/ul — v) 7r. «/„ (z) — cos \(fx — v) tt . Yv (z)].
It will be shewn in § 10*73 that #MI,(,2) has a limit when /x+ v or fi — v
is an odd negative integer, i.e. when s^v (z) is undefined ; and so, of Lommel's
two functions sIA.v(z) and 8hv(z)} it is frequently more convenient to use the
latter.
348 THEORY OF BESSEL FUNCTIONS [CHAP. X
It will appear in § 10*75 that the series A), by means of which S^u (z) is
defined when either of the numbers fi ± v is an odd positive integer, is still
of significance when the numbers fi ±v are not odd positive integers. It
yields, in fact, an asymptotic expansion of $Mi „ (z) valid for large values of
the variable z.
10'72. Recurrence formulae satisfied by Lommel's functions.
It is evident from § 10*7 B) that
that is to say
(i) s^w
Again, it is easy to verify that
7 0
J-Z [z" «m, , (Ot = O + v - 1) z" S|1_i. „_, 0),
so that
B) s'n ,„ (z) + (v/z) s^v(z) = (/j, + v -1) v^-i (z),
and similarly
C) *'m.* (*) ~ {viz) *Mf „ (z) = (jl - V - 1) V-l, M-l BV
On subtracting and adding these results we obtain, the formulae
D) Bv/«)^„(^) = (yu, + v- 1)sM_2i„_,(z)~(fi~v- l)s^hv+,{z),
E) 2«V,, («) = (/¦* + v - 1) *^_,, ,-i («) + (/* - v - 1) v-i,^+1 D
The reader will find it easy to deduce from § 10*71 B) that the functions of
the type s^v(z) may be replaced throughout these formulae by functions of
the typ^ S^ v (z); so that
F) S^,v{z) = *+> - {0* + IJ- *»} 8^(s),
G) S'»>v (z) + (v/z) S^iz) = (ix + v- l)S^v_, (z),
(8) &„(,) - (v/z) Sh>v(z) = (fM-v-l) SIhh., (*),
(9) Bv/z)ShtV(z) = (im + v- 1)S^^(z)-(p-v- \)8^ltv+1 (z),
A0) 28f,<v («) = (> + v -.1) ?,_,,„_, (*) + 0*" v -1) i8U.liHa D
These formulae may be transformed iu various ways by using A) and F). They are
due to Lornmel, Math. Ann. ix. A876), pp. 429—432, but his methods of proving them were
not in all cases completely satisfactory.
10*73. Lommel's functions Sll<v(z) when fi + v is an odd negative integer.
The formula § 10*71 B) assumes an undetermined form when fx — v or //, + v
is an odd negative integer*. We can easily define Sv_2p-.hv(z) in terms of
8y-i,u{z) by a repeated use of § 10*72 F) which gives
w=o
* Since SMl v B) is an even function of v, it is sufficient to consider the case in which /u. - v ia an
odd negative integer.
10*72, 10*73] ASSOCIATED FUNCTIONS 349
We next define Sv^liV(z) by the limiting form of § 1072 F), namely
The numerator (which is an analytic function of fi near /ul = v — 1) vanishes
when ft = v — 1, and so, by L'Hospital's theorem*
8 (z\ - — \zv loe- z - 9'Sm-2- "
*V-i.*W-2j,[*log, -^-
Now it is easy to verify that
9/* l
X B log 2r + ^ A) + yjr (y + 1) - ^ (w + 2) - yjr (v + m + 2)j.
Also
= 2" r (i; + 1) Sin i»7T {log 2 + | -^ A) + -^i|r (i; + 1)+ 17T COt i/7r},
and
and hence it follows that
-2"-27rr(;/) Yv(z),
and this formula, which appears to be nugatory whenever v i« a negative
integer, is, in effect, nugatory only when v =0; for when v — — n (where n 18
a positive integer) we define the function by the formula
?>—it—I,— n \Z) ~ &—n— 1,n \^h
in which the function on the right ia defined by equation § 10*73 (I).
To (littcuBB the cdHO in which v=0, wo biko tho formula
which given S-.,, 0 (*) = ^ [|a {^ '' - *S'M + 2,0 (,)j
Since *^.(.)-^»
' > {r (i^ + i!)}2 {°0N iM^ • iro B) -sin fan . JQ B)},
it follows, on reduction, that
D) -Sf_,f0(*)=4 ^ (~?#-i.{]"K(^)-V'(^+l)P-
* Cf. Brorawich, Tfteory 0/ Infinite Series, § 152.
350 THEORY OF BESSBL FUNCTIONS [CHAP. X
10*74. Functions expressible in terms of LomtneVs functions.
From the descending series given in § 10*71 A) it is evident that Neumann's
polynomial On(z) is expressible in terms of LotnineFs functions by the equations
A)' O.2l)l{z)-(l/«) S^iz), O,,)l+1 (z) = {Bm + 1)/*} S0|SW+1 (z),
and Schlafli's polynomial Sn (z) is similarly expressible by the equations
B) S2m (z) = 4m &.liJin (z), Sim+1 (z) = 2^SOi2Jft+) (*).
It is also possible to express the important integrals
rz rz
z* Jv (z) dz, I z» Yv (z) dz
J J
in terms of Lommel's functions; thus we have
T {*" Jv(z).z1-'S^lt„_!(z)} = zJv^(z)S^lt„_!(z)+(p-v-l)zJv(z)aV2)„(z),
(LZ
jz {z*~> Jv.x (z). Z-* Shi, (z)) = - zJv (z) S.iV(z) + (n + v-l) z^ (z) 8^ ,_x (z).
On eliminating S^hv-i(z) from the right of these equations, and using
110-72 F), we find by integrating that
C)
and proofs of the same nature shew that
D) |Vi;(i)(fc-0' + »-l)*7,(«)^llM(')-«FH(«MM(«)J
and, more generally,
E) I"z*<@v{z)dz = {n+v-l)zV?{*)S^K,_, (z)-zK-i(*)S»,v (z).
Special cases of these formulae are obtained by choosing /x and v so that
the functions on the right reduce to Neumann's or Scfelafli's polynomials, thus
F) J *#to(z) dz = *• |2jn _ x %ln(z) O2TO_t (jt) - <9Wr.1 (z) O2m (
(z)}.
Of these results, A), C), D) and F) are contained in Lommel's paper, Math. Ann. ix.
A876), pp. 425—444; F) and G) were given by Nielsen, Handbuch der Theorie der
Cylinderfunktionen (Leipzig, 1904), p. 100, but his formulae contain aome misprints.
It should be noticed that Lommel's function, in those cases when it is
10*74, 10-75] ASSOCIATED FUNCTIONS 351
expressible in finite terms, is equivalent to Gegenbauer's polynomial of § 9*2.
The formulae connecting the functions are*
(8)
A
lib; ?>
2-h p{y + m +1) v
III •
It follows that the most general case in which the integral E) is expressibje
in terms of elementary functions and cylinder functions is given by the formula
W v+2)ji—1 \Z) ¦"¦•itn,v \Z)
v + 2m
The function defined by the series
haw \)een .studied in groat dotail by W. H. Voungt; this function possesses many properties
analogous to those of Bessel functions, but. the increase of simplicity over Lommel'a more
general function seemsainnufficient to justify an account of them here.
Tlio integral v \ -'— -¦ .dt has Iwjen .studied (when v is an integer) by H. A. Webb,
Messenger, xxxnr. A904), p. 58; and ho stated that, when i/=?i, its value is ()u(z). This in
incorrect (as was pointed out liy Kaptoyn); and the value for general values of v isj
when A' (j>) > 0 and | arg ( - z) \ < n.
10*75. The asymptotio expansion of >S'Mi „ {z).
We shall now shew by Barnes1 method^ that, when fi ±v arc not odd
positive integers, then $^,,(,2) admits of the asymptotic expansion
(i) sr,. w ~ *
when \z\is large and |argz \ < tr.
Let us take the integral
The contour is to be drawn by taking p to be an integer so large that the
only poles of the integrand on the left of the contour are poles of cosecs7r, the
poles of the Gamma functions being on the right of the contour.
* Gegenbauer, Wiener Sitzungubenchte, lxxiv. B), A877), p. 126.
t Quarterly Journal, xlui. A911), pp. 161—177.
X Of. (Jubler, Ziirich Vierteljahmchrift, xi.vn. A902), pp. 422—428.
§ Proa. London Math. Soc. B) v. A907), pp. 59—118; cf. §§ 6-5, 7-5, 7'51.
352 THEORY Or BESSEL FUNCTIONS [CHAP. X
The integral is convergent when {arg z | < nr, and it may be seen without
difficulty that it is 0 (z»-2P).
It may be shewn from the asymptotic expansion of the Gamma function
that the same integrand, when integrated round a semicircle, of radius R with
centre at — p — fr, on the right of the contour, tends to zero as R -*- oo, provided
that R tends to infinity in such a manner that the semicircle never passes
through any of the poles of the integrand.
It follows that the expression given above is equal to the sum of the
residues of
at the points
0,-1,-2, ...,-(.p-l),
1,2,3,....
When we calculate these residues we find that
z
— v + m)
+ p 17r x '* + »tf 7 **^ 2 pj = 0(z*-*?),
so that
sini/7r
X [COS ^ (/A - l/) 7T . «/_„ (^) - COS fr (fJb + v) 7T . Jv (z)] = 0 (
and so, by § 10*71 B), we have the formula
and this is equivalent to the asymptotic expansion stated in A).
10-8] ASSOCIATED FUNCTIONS 353
10'8. Hemi-cylindrical functions.
Functions Sn (z) which satisfy the single recurrence formula
A) SM_1B)-Sn+1B)-2S?l'(^)
combined with
B) S^*) —S,'(*)
have been studied in great detail by Sonine*. They will be called hemi-
cylindrical functions.
It is evident that Srt (z) is expressible in the form
Sa(*)=/„(.D). S»,(*),
where D = d/dz and /„ (D) is a polynomial in D of degree n; and the polynomial
fn (?) satisfies the recurrence formula
combined with
It follows by induction (cf. § <)i4) that
and therefore
C) s,lB) = U!-/-)
If it is supposed that (I) holds for negative values of n, it is easy to see that
D) S_n(.) = (-rSn(*).
To obtain an alternative expression to C), put ? = sinh?, and thenf
(" wen)
« (,M)dd)
1 + 2, r +~ ''^j1-- ?' + ••• (m even)
Hence
(S(, (z) -I- J- So" (*) + -" ¦ " ~ " S((lv (z)+... (/i even)
It is to be noticed thabO,, {z), Tn (z) and E,,(s) an- henii-cylindrical functions,
but >SnB), Un(z) and H7l(^Van^ not hemi-fylindrieal functions.
It should be remarked that the single recurrence formula
gives rise to functions of no greater intrinsic interest than Lominel's polynomials.
* Math. Ana. xvr. A8H0), pp. 1—!), 71—HO.
t See e.g. HoLhuu, J'lune Tritionoiartrii ASJ1H), §2(M.
w. a. if. 23
354 THEORY OF BESSEL FUNCTIONS [CHAP. X
10*81. The addition theorem for hemi-cylindrical functions.
We shall now establish Sonine's important expansion*
A) S1Jf (* + <)= I fn(t)Sm.n(z)',
w=-oe
the expansion is valid when z +1 lies inside the largest circle, whose centre is
at the point z, which does not contain any singularity of the hemi-cylindrical
function under consideration.
Take as contour a circle C with centre z such that So(?) has no singularity
inside or on the circle. Then
The series converges uniformly on the contour, and so we have
5
2
= S €nJn(t)fn(-^-)sm{z)dz
But it is easy to verify that
f) -/«-«(f) + (")V-+« (I).
so that
whence Sonine's formula is obvious.
It should be noticed that, if Sn B) denotes a function of a more general
type than a hemi-cylindrical function, namely one which merely satisfies the
equation
S^l(*)-Sn+l(*)«2S»/(*),
luithout satisfying the equation Sj {z) = — So' B), we still have
fn {- -?) Sm {z) = Sm_n (^) + (-)» SOT+n D
and so the formula A) is still valid. We thus have an alternative proof of
the formulae of §§ 5'3, 91, 9'34 and 10-63.
* Math. Ann. xvi. A880), pp. 4—8. See also K8nig, Math. Ann. v. A872). pp. 810—840; ibid.
xvii. A880), pp. 85—86.
10*81, 10*82] ASSOCIATED FUNCTIONS 355
10*82. Nielsen's functional equations.
The pair of simultaneous equations
A) JPr_, (z) - Fv+l E) - 1FJ (z) - 2/, {z)/z,
B) Fv.x (z) + ^+1 E) - B*/*) J1, (*) = 2g. (z)/z,
where fv (z) and gv (z) are given arbitrary functions of the variables v and z,
form an obvious generalisation of the pair of functional equations whereb}"
cylinder functions are defined. It has been shewn by Nielsen* that the
functions /„ (z) and gv (z) must satisfy the relation
/,_, (*) +/,+, (*) - Bv/z)fv (z) = gv.x (z) - gv+l (z) - 2gv' (z);
and it has been provedf that, if this relation is satisfied, the system can be
reduced to a pair of soluble difference equations of the first order.
For brevity write
/, @ + 9v @ = «-< (*)> A(z) ~ !J» (z) = Pv B),
and the. given system of equations is equivalent to
C) (* + v) Fv (z) = zi\-x (z) - «„ (z),
D) («V - v) h\ (z) = - zFu+i (z) - & {z).
It is now evident that
(*a - n») Fv {z) = (V> - v) [zF^ {z) - <xv (z)\
= - tfb\ {z) - z^v_, {z) - (* - v) <xv (z),
so that VVFV (z) = - zfiv_x (a) - (Vi - v) av (z).
Again
(^ - S) K (z) = (^ + v) [- zFv+x (z) - 0, (*)J
= - ^V (*) + ?«„ + , B) - (^ + V) & B).
We are thus led to the equation
E) V,F?(t)=z1*,(*).
where
F) znsv (z) = - *#„_, B) - (^ - v) av {z),
G) ^tsr, (z) = + ^.H (r) - (^ -I- «;) /9, («).
On comparing these values of cxv(^), we are at once led to Nielsen's
condition
(8) fv.x (z) +fv+1 (z) - {Zvjz)fv (z) - //v_, (z) -g?tl(s)- 2gv' (z).
It now has to be shewn that Nielsen's condition is sufficient for the exist-
existence of a solution of the given system. To prove this, we assume (8) to bn
* Ann. di Mat. C) vi. A901), pp. 61—5'.).
f Watson, Messenger, xLvni. A919), pp. 41)—53.
23—2
356 THEOBY OF BBSSBL FTTNCTIONS [OHAP. X
given, and, after defining .. (,) by F) and G), we solve E) by the method
of variation of parameters. The solution is
(9) F. (z) = /„ (*) L - \ir \*a Y* («) *>> @ dt]
+ Yv (z) \dv + \ir JV, (t) sr, (t) dt^ ,
where a and b are arbitrary constants; and cv and dv may be taken to be
independent of z, though they will, in general, depend on v.
It remains to be shewn that c and dv can be chosen so that the value of
Fv {z) given by (9) satisfies A) and B), or (what comes to the same thing)
that it satisfies C) and D). If C) is satisfied, then
*/,„ (*) jc - \ir J S Yv (t) *v (t) dt\ - hirz Jv (z) Yv {z) vv (z)
(*) \dv + \ir I* J,"@ nr,, («) dti + frrz Yv (z) Jv(z) vrv(z)
= zJ-i (z) jc^x - \tr |* 7^ @ -or,-! @ d«
+ 27,_, B) ] (?,_, + \ir Jy-i (t) -av-x (t) dt\ —av (z),
I J b )
that is to say,
zJv_x (z) L - cr_, - \ir j" {7, («) w, @ - y^, @ w,., («)} d«l
r -s -i
+ ^7^(*) d,-d^ + |tt {/„(i)gt,(«)- /,_,(t) w^(«)} (Z« ho,(*) = 0.
L 6 J
But it is easy to verify that
^ l#rl («) ^ (*) - ^ (z) av (z)) = tr, (*) ^ (^) - wr., (z) %Vi («),
since F) and G) are satisfied; and so C) is satisfied if
zJ^ (z) j c - c,, - |tt 7^ (z) ?_, («) - 7, («) a, («)]*].
and this condition, by § 3-63-A2), reduces to
zJv.x (z) {cv - o^ + \tt [ 7^ (a) /S^ (a) - 7r (a) a, (a)]]
+ 5 7^ (z) [dv - d,_: - fr [J^ (b) pv__x (h) _ jp (&) ftif F)-j| = 0
Consequently, so far as C) is concerned, it is sufficient to choose c, and dv
to satisfy the difference equations
f A0) c, - (v_x = - |tt {F« (a) /3^ (a) - Yv (a) a, (a)},
1A1) dv - d^ = Itt f J^ F) /S^ E) _ j; F) a>/ F)|.
10*82] ASSOCIATED FUNCTIONS 357
and the reader will have no difficulty in verifying that, if these same two
difference equations (with v replaced by v+ 1 throughout) are satisfied, then
the value of Fv (z) given by (9) is a solution of D).
These difference equations are of a type whose solutions may be regarded
as known*; and so the condition (8) is a sufficient, as well as a necessary,
condition for the existence of a solution of the given pair of functional equa-
equations A) and B).
If, as z -*¦ oo ,
fv(z) = 0(zl-s), gv(z) = O(zl~*),
where S > 0, then we may make a -*¦ oo , 6 -*- oo , and we have
cv — cv—i, dv — «„_!,
so that the general solution may be written
A2) Fv (z) = Jv (z) Itt, (v) + |tt p Yv (t) uv (t) dtl
f"
where ^G^) and ir2(v) are arbitrary periodic functions of 1/ with period unity.
Note. Some interesting properties of functions which satisfy equation B) only are to
be found in Niolscu'a earlier paper, Ann. di Mat. C) v. A901), pp. 17—31. Thus, from a
set of formulae of the type
it is easy to deduce that
A3) Fv + n(z) = Fv(z) /<
711 ---II
the first two terms on tho right are the complotnontary function of the diflbrenee equation,
and the series is the particular integral.
* An account of various memoirs dealing with suoli aquations ia given by Barnes, Proc. London
Math. Snc. B) 11. A004), pp. 438—460.
CHAPTER XI
ADDITION THEOREMS
11-1. The general nature of addition theorems.
It has been proved (§ 4*73) that Bessel functions are not algebraic functions,
and it is fairly obvious from the asymptotic expansions obtained in Chapter vii
that they are not simply periodic functions, and, a fortiori, that they arc not
doubly periodic functions. Consequently, in accordance with a theorem due
to Weierstrass*, it is not possible to express Jv (Z+z) as an algebraic function
of JV{Z) and Jv(z). That is to say, that Bessel functions do not poisons
addition theorems in the strict sense of the term.
There are, however, two classes of formulae which are commonly doncribed
as addition theorems. In the case of functions of order zero the two cIjihsch
coincide; and the formula for functions of the first kind is
Jo {V(# + z* - 2Zzcos <?)} = S emJm (Z) Jm (z) cos rncf>,
m-0
which has already been indicated in § 4*82.
The simplest rigorous proof of this formula, which is due to Neumann f,
depends on a transformation of Parseval's integral; another proof is due to
Heine \, who obtained the formula as a confluent form of the addition theorem
for Legendre functions.
11*2. Neumanns addition theorem^.
We shall now establish the result
00
(!) Jn(w)- 2 emJm(Z) Jm (z) cos m</>,
m-0
where, for brevity, we write
«¦ = V(?2 + z* - 2Zz cos <f>),
and all the variables are supposed to have general complex values.
* The theorem was stated in §§ 1—3 of Schwarz' edition of Weierstrass' lectures (Berlin,
1893); see Phragmen, Acta Math. vn. A885), pp. 33—42, and Forayth, Theory <•/ Functions A918)',
Ch. xiii for proofs of the theorem.
t Tkeorie der Bessel'schen Functional (Leipzig, 1867), pp. 59—70.
XHandbuch der Kugelfunctioncn, i. (Berlin, 1878), pp. 340—343; of. § 5-71 and Modern
Analysis, § 15'7.
§ In addition to Neumann's treatise cited in § 11-1, see Beltrami, Atti delta R. Accad. di Torino
xvi. A880—1881), pp. 201—202. '
11-1—11-3] ADDITION THEOREMS 359
We take the formula (Parseval's integral)
itT J _„ *TT J -n
which is valid for all (complex) values of vr and a, the integrand being a periodic
analytic function of 6 with period 2-7T. We next suppose that o is defined by
the equations
ts sin a = Z — z cos (f>, ¦& cos a = z sin <?,
and it is then apparent that
1 [IT
Ju (ot) = s~- I exp [i(Z — z cos </>) sin 6 + iz sin </> cos 0} e20
/7T Ht= _
2 .AWI (^
the interchange of the order of summation and integration following from
the uniformity of convergence of the aeries, and the next step following from
the periodicity of the integrand.
If we group the terms for which the values of m differ only in nign, we
immediately obtain Neumann's formula.
The corrcs{)onding formulae, for BcshcI functions of ordo.r ±h wore, obtained l>y Clebsi'h,
Journal filr Math. lxi. A8E3), pp. 224—2*27, tour yem\s before tho publication of Ncuinaiui'n
formula; see $ 1T4.
11*3. Graf's generalisation of Neumanns formula.
Neumann's addition theorem has bee.n extended to functions of arbitrary
order v in two different ways. The extension which seems to be. of more
immediate importance in physical applications is due to Graf*, whose
formula is
A) J. (W). jl-l^*}*" = J /,-,« (Z) Jin (z) e^'K
and this formula is valid provided that both of the numbers |^e:tt'*| are less
than \Z\.
* Math. Ann. xliii. A893), pp. 142—144 and Verhandlungen der Schweiz. Naturf. Gen. 1890,
pp. 59—61. A special case of the result hat) also been obtained by Nielsen, Math. Ann. mi. A899),
p. 241.
360 THEOEY OF BESSEL FUNCTIONS [CHAP. XI
Graf's proof is based on the theory of contour integration, but, two years after it was
published, an independent proof was given by G. T. Walker, Messenger, xxv. A896), pp. 76—
80; this proof is applicable to functions of integral order only, and it may be obtained
from Graf's proof by replacing the contcmr integrals by definite integrals.
To prove the general formula, observe that the series on the right in A)
is convergent in the circumstances postulated, and so, if arg^=a, we have
jTTI m-—co J -OOGXp(-
dt
( f \\\
exp \\Z [t--\
—ia) {. \ «/J
vf, x\ * ft
there is no special difficulty in interchanging the order of summation and
integration *.
Now write
(Z — ze~ '*) t = vru, (Z — ze^/t = vrju,
where, as usual, ¦or = *J(Z2 + 22 — 2Zz cos ^>),
and it is supposed now that that value of the square root is taken which makes
¦m ~*~ + Z when z -*¦ 0.
For all admissible values of z, the phase of mjZ is now an acute angle,
positive or negative. This determination of -or renders it possible to take the
w-contour to start from and end at — oo exp (— i/3), where /3 — arg vr.
We then have
(Z) /„ W *» = i , f2^^)" f"'+' exp jj. (« - 1I ^
27T?. V W / ./-ooexp(-?i3) (V M/J «
by § 6-2 B); and this is Grafs result.
If we define the angle -^ by the equations
Z — Z COS <jf> = •nr COS -v/r, ^ sin j) — ts sin •\Jr,
where i|r -*- 0 as ^ •-*• 0 (so that, for real values of the variables, we obtain the
relation indicated by Fig. 28), then Graf's formula may be written
B) e"*/„(*-)= 5 Jv+m(Z)Jm(z)e™*,
m — ~ oo
and, on changing the signs of <? and yfr, we have
C) c-**J?(v)= 2 J«
* Of. Bromwi'ch, Theory of Infinite Series, § 176.
11-3]
whence it follows that
D) /„(>
ADDITION THEOREMS
361
(JLJ
Fig. 2H.
If, in this formula, we. change the signs of v and -in, we readily deduce from
§ 3-54 that
E) )r (V)C0S vt]r= ^ Y (Z) J l-)Cmvi6
sm ,,l = _ jo sin
and so
Sill
-a
)»=— oo
cos
Tho formula E) was given by Neumann in his treatise in tho special cane v—0; hoc
also Sommerfeld, Math. Ann. xi,v. A894), p. 27(i; ibid, xi.vn. A85H), p. 3.r><>. Somo physical
applications of the formulae arc duo to ttuhwanwuhild, Math. Ann. i.v.(l!H2), pp. 177—247.
If we replace Z, z and •nr in these equations by iZ, is and its respectively,
it is apparent that
sin mi ——oo sin
(8) l\.v\vx) . pyfr = Z/ J'-v+in (•") *m {.&) • 'Mtp-
sm HJ---00 H"'
Of those resultw, G) was stated by Beltrami, Atti delta It. Anuid. di Torino, xvi. A880—
1881), pp. 201—202.
The following special results, obtained by taking </) = ^7r, should be noticed :
do)
where
- 2
1I - — 00
< | Z \.
Z — ct cos -v/t, ^ = w sin -v^ and
For the physical interpretation of these formulae tho. reader is referred to
the papers by G. T. Walker and Schwarzschild ; it should be observed that, in
the special case in which v is an integer and the only functions involved are
of the first kind, the inequalities | zeM<i> \<\Z\ need not be in force.
362 THEORY OF BESSEL FUNCTIONS [CHAP. XI
11*4. Gegenbauer's addition theorem.
The second type of generalisation of Neumann's addition theorem was
obtained by Gegenbauer* nearly twenty years before the publication of
Graf's paper.
If Neumann's formula of § 111 is differentiated n times with respect to
cos (f>, we find that
) d11 cos (to + n) <j>,
This formula was extended by Gegenbauer to functions of non-integral order
by means of the theory of partial differential equations (see § 11'42); but
Soninef gave a proof by a direct transformation of series, and this proof we
shall now reproduce; it is to be noted that, in A), z is not restricted (as in
§ 113) with reference to Z.
We take Lommel's expansion of § 5*22, namely
and replace f and h by Z* + z* and — 2Zz cos <jj respectively; if we write
in place of Jv (nr)/-5r" for brevity, it is found that
s s (-)9^+2gcosy</) Jv+p+q (Z)
-,to,=o 29.pl ql Z^ '
by a further application of Lommel's expansion with ? and h replaced by Z2
and z\
But, by § 5-21,
Jv+p+g(Z) A q\ v+p+2k
Zv k^k\{q-k)l
and so
\" )>
(-)9 (v + p + 2k) r {v + p + k) zp+*i cos? <j> Jv+p+2k (Z)
) "Z"
the triple series on the right being absolutely convergent, by comparison
with
oo co a
f y y
A* j-< -t-i
p-Og-OA-0
\ m ^ _ ?)l r („ + p + 2k) V(v +p + q + k +
* Wiener Sitzungsberichte, LXi. B), A875), pp. 6—16.
t Math. Ann. xvi. A880), pp. 22—23.
11-4, 11-41] ADDITION THEOEEMS 363
But, for an absolutely convergent series,
oo q oo oo
5=0 &=0 fc=0n=0
and so
rt- I ? I (-)fc+?t(y + f + 2*)rQ> + p + A?)***""cos*0 Jv+p+ik
p-o*ro»-o 2s*+a»p!&!n!I> + p+2& + n+l) ?'
?," (-)* 2^ (» + p + 2/c) r (i; + p + A?) cos? <jb /,^
= 5 V H* 2"+»'~2* A; + m) r (i> + ffl - fc) cos^-^
*-o»it2jfc (wi-2^)!)fcl
1 ^ (-)fc 2"+wt-2fc (y + w) T A/ + m - k) cos"-^
XT <*•» (-)* 2«"a* r (v + m - fc) cos"-* 0 „
N°W ,?0 (m-8ib)libir(y) = °
where, as in § 3*32, Cm" (cos $) denotes the coefficient of am in the expansion
of A — 2a oos (f> + a2)"" in ascending powers of a. We have therefore obtained
the expansion
B) '%} = 2" T(v) 2 (V + m) ^ (*) '^» <*) Cm- (cos *),
which is valid for all values of Z, z, and <?>, and for all values of v with the
exception of 0, — 1, — 2, ....
In the special case in which v --1, we have
C) S-^-w . , S (m + 1) % <*> . /»"/ ^ i'. («* «.
tar w_0 /,/¦" \/2>
Thia fonnuln is due to (Jlobsuh, Journal fttr Math. lxi. (IH03), p. 227; it i.s nlso
given l>y Hc.ino, Journal fur Math. lxtx. A8E8), p. 133, and Neumann, Lcip;u;cr Iteriehte,
1886, pp. 7f> —82. The formula in which 2i/ is a poHitivo integer has been obtained by
Hobson, I'rnc. London Math. Soc. xxv. A8})-l), p}). (J0--(il, from a conHidcration of solutions
of Laplaott's e([uation for space of 2i/+Si diinensionn.
An extension of fcho expansion B) haw Leon given by Wcndt, Monat»hvftc far Math, itnd
Phys. xr. A!)()()), pp. 125—131 ; the effect of her generalisation is to express
as a weries of Besaol functioiiH in which the cooflicients are .somewhat complicated
determinants.
11*4]. The modified form of Gec/enbauer's addition theorem.
The formula
A) Lz"JL -/ = 2" T(v) X (—)m(v + m) ~^~r/v -• —-'I ¦ ¦ C,,," (cos (f>)
may be established in the same manner as the Gegcnbauer-Sonine formula of
§ 11-4. This formula does not seem to have been given previously explicitly,
364 THEOEY OF BESSEL FUNCTIONS [OHAP. XI
though it is used implicitly in obtaining some of the results given subsequently
in this section.
Unlike the formulae of § 11*4, the formula is true only when \z\ is so
small that both the inequalities | zeii4> \<\Z\ are satisfied; but, in proving the
formula, it is convenient first to suppose that the further inequalities
\2Zzcos<j)\<\Z2 + zo*\, \z\<\Z\
are satisfied.
We then use Lommel's expansion of § 5*22 B) in the form
p P
which is valid when j h \ < | ?|.
It is then found by making slight alterations in the analysis of § 11*4 that
=&) = ? t
{
os^
_ ? v V (~)P+I(v +p + 2k)T(- v-p-q-k)z****cos^ <f> J-v-p^(Z)
-lOZu^' &p\k\(q-k)\r(i-v-p-k) - ?"
" + P + 2/g) r (~ V - V - 2/g - ?t) P+ik+in P f
v-p-k) Z»
(-)p+k2v+P(p+p + 2k)T(v + p + k) cosy 0 /_,_y_2fe(^) Jv+p+2k (z)
p\k\ Z" zv
~ fc) C0S '""^ ^ ^-m (^) Jv+m (z)
- 2" r (V) I (-r(v+m) J—;}Z) %^ a,/ (cos ^,
so the required result is established under the conditions
|, \z\<\Z\.
Now the last expression is an analytic function of z when z lies inside the
circle of convergence of the series*
| Q + m) If-2"-™ zm Cmv (cos 0)
9,to"rA -v-m)t{l+v+ m) '
and this circle is the circle of convergence of the series
2 {-A
Hence the given series converges and represents an analytic function of z
provided only that | ze*'* \<\Z\; and, when this pair of inequalities is satisfied,
/_„{¦m)'jisv is also an analytic function of z.
* Cf. § 5-22.
11-41] ADDITION THEOREMS 365
Hence, by the theory of analytic continuation, A) is valid through the
whole of the domain of values of z for which
ze*
<\z\.
If in A) we replace v by — v we find that
B) ^jL-2-r(-V) 2
w=o
Again, if we combine A) with § 114 B), we see that, for the domain of
values of z now under consideration,
and so, generally,
2' r (*) 5 (v + m) %/*> J^L CJ (cos #
0 /j *
?H-0
If in C) we make z> -*- 0 and use the formulae
Co° (cos <f>) = 1, lim {r (i/) (i; + wt) CM" (cos (/>)) = 2 cos m$, (m ^t 0)
we find that
E) Fo («*) - 2 em K« (Z) 7« (*) cos m 0.
The formulae A) and B) havo not been given pro.viou.sly; but (tt) m due to (ii
and («r)) was given by Neumann in bin treati.se (.savo that tlie 1'unutionn Ym were replaced
by the functiouw }r()). The formula C) with v eijiml to an integer lm.s also been examined
by Heine, Handlmch dor Kwjdfitnctionen, i. (Berlin, 1H7H), pp. 403—¦104. Home develop-
developments of D) are due to Tgnatowsky, Arc/iiv dcr Math, mid Phys. C) xvm. A911), pp. 322—
327.
If we replace iT, z and txt by iZ, iz and its in the. formulae of § 11*4 and
this section we find that
F) h G}=2" r (,) s (-r {v+m) %-JZ) Iv+;}2) cv (^ $),
G) 7-"G> = 2^ r (,) 5 (-r(v + mS-j}^Iv-r1 cv(cos 0),
(8) —---= 2" F (i>) S (v + vi)—~—- - Gmv (cos <f>).
•or*' »»=o ¦""" ¦2"
Of these formulae, (8) is due to Macdonald, Proc. London Math. Soc. xxxn. A900),
pp. 156—157; while (G) and G) were given by Neumann in tho special caao v = \.
36? THEOEY OF BESSEL FUNCTIONS [OHAP. XI
The formulae of § 11*4 and of this section are of special physical importance
in the case i/ = *. If we change the notation by writing ka, kr and $ for Z,
z and <j> we see that the formulae become
sin k ^(rM^^2arcos^)
¦ a? — 2ar cos 6)
cos fc VCr2 + a- - 2ar cos (9)
'(r2 + ^ ~ 2ar cos ^)
>»=o
exp ¦[- feV(r8 + a9- 2ar cos g)}
' " " (^ + a2 - 2ar cos ^>
= t Bm + 1) " v ' -q±i-i-' Pm (cos 6).
These formulae are of importance in problems in which pulsations omanato from a
point on the axis of harmonics at distance a from the origin, in presence of a sphere whowo
centre is at the origin. Cf. Carslaw, Math. Ann. lxxv. A914), p. 141 et saq.
The following special cases of D) were pointed out by Gegonbauor, and
art- worth recording:
If (i> = 7T, we have
If <b=z\nr, we have
13» '*'}?? t/)] = 2- 2 (-)« (p + 2m)
If Z= z. $ - 0, and % is taken to be /„,
a formula already obtained (§ 5'5) by a different method; in this connexion
th«- ivadt-r should consult Gegenbauer, Wiener Sitzungsberichte, lxxv B)
rl!s77), p. 221. ' ' v h
More generally, taking Z=z, <}>±Q, <®? = J?i we have
r, te. at. gives also special cases of this formula, obtained by taking
11-42] ADDITION THEOREMS 367
Again, it can be shewn that*, ii R(v)> — %,
(=0 0>i^p)
I sin2" <f> Gm" (cos </>) 0/ (cos </>) dqb < ?r r By + »t) ,
l~ 2^>"+ to). »ii[r (!/)}• (w ~ p)
and so, provided that R (v) > — ?,
and, more generally,
Jo (Z" + Z- — V/tZ COS </>)*" T
= 7T r Bi/ + m) ^+M (Z) J,+Az)
2—1.m)r(v) ~ZV >
A simple proof of this formula+, in the special ca.se in which m-0 and the cylinder
functions arc functions of the fir.st kind, was given by Sonine, Math. Ann. xvi. A880),
p. 37. Another direct proof for functions of tho first kind is duo to Kluyvoi', Pror. Section
of ScL, K. A cad. van Wat. te Amsterdam, xi. A009), pp. 749—755. An indirect proof,
depending on $ liH3(l\ is duo to Gcgenbauor, Winner Sitzimgsberichte, lxxxv. B), A882\
pp. 491—502.
[Note. An interesting consequence of D), which was noticed by (Jegonbauer, Wiener
Sitzungsbericlite, lxxiv. B), A877), p. 127, is that, if | :a±i'1' j < | Z \ throughout the contour
of integration, then (of. $ 9*2)
H[)ecial cases of this formula, resembling the results of ^ SY% arc obtainable by taking <j)
oqual to, 0 or n."]
11 2. (ietfenbauer'ii inoestujutwn of the addition theorem.
The method used by (Jegonlmuer, Wiener RUzuntjdmruihtc, i.xx. B), A875), pp. (>—1E,
to obtain the addition theorem of §11 is not quite so easy to justify as Sonine's
transformation. It consists in proving that Q. is a solution of tho partial differential
equation
d-Q 2./-H dQ I (fia 2i/cot </> dG
?z- z az z* (H- zl d<\> '
and assuming that $2 can be expanded in tho form
Q= 2 Iim. Vmv (cos <f)),
m--<)
where BM is independent of <?, and 6'm" (con <]>) is a polynomial of degree m in costj!); it,
follows that
* Gegenbauer, Wiener Sitzuityauerichte, t.xx. B), A875), pp. 4S3—445), and Batoman, Proc.
London Math. Hoc. B) iv. A006), p. 472; cf. also BnrnoB, Quarterly Journal, xxxix. A908), p. 189;
Modern Analysis, § 15-51 and Proc. London. Math. Uoc.ki) xvn. A919), pp. 241—246.
•(• Formula(lO) has been given in the special onriov = 0by Heaviaido, Electromagnetic Theory, in.
(London, 1912), p. 207, in a somewhat disguised form.
368 THEOEY OF BESSEL FUNCTIONS [CHAP. XI
is a constant multiple of 4/(cos0), and so Cm'(ooB*) may be taken to be the ^f^
of a- in the expansion of (l-2«eos 0 + a*)-". And then ^3 qua fcnotion of * «atu.fio» tho
differential equation
so that Bm is a multiple of z~>Jv+m (*), the other solution of this differential equation not
being aualytic near the origin.
From considerations of symmetry Gegenbauer inferred that Bm qua function of Z, i.s
a multiple of Z-yJy+n(Z), so that
o-
where 6m is a function of «/ and m only; and bm is determined by comparing coeHioionts of
zmZmco8m<p in Q and in the expression on the right.
A similar process was used by Gegenbauer to establish § 11-4i C), but tho analy«i.s
seems less convincing than in the case of functions of the first kind.
11*5. The degenerate form of the addition theorem.
The formula
A) e*cos* = (?)* ? B» + 1) i» Jn+i (*) Pn (cos 0)
was discovered by Bauer* as early as 1859; it was generalised by Gegcnbauurf,
who obtained the expansion
B) efcco.# = 2" T (v) 2 (v + m) i™ ^-(~} 6V (cos <f>);
m=0
Bauer's result is obviously the special case of this expansion in which v = 4.
In the limit when n-*•(), the expansion becomes the fundamental expansion
of §2-1.
Gegenbauer's expansion is deducible from the expansion of § 11'41 D) by
multiplying by ?"+* and making Z-*. oo ; it is then apparent from § 11 -41 @)
and A0) that the physical interpretation of the expansion is that it; gives
the effect due to a train of plane waves coming from infinity on tho axis of
harmonics in a form suitable for the discussion of the disturbance produced
by the introduction of a sphere with centre at the origin.
A simple analytical proof of the expansion consists in expanding zv eitvm*
in powers of z and substituting for each power the series of Bessel functions
supplied by the formula of § 5-2; we thus find that
?
»=o n\
JournalfUr Math. lvi. A859), pp. JL 106
S^iSH2)'A874)'pp- 355-367; "S1V-B)' A877»- "¦
11-5] ADDITION THEOREMS 369
If we rearrange the repeated series by writing n — m — 2k, we deduce that
+vi) r(v + »i-Jc)Jv+llt (z)
»t=OA=0 lc- \m
2"I» 2 (v
and this is Gegcnbauer's result.
Modified forms of this expansion, also due to Gegenbauer, are
C) e*cos* = 2" r (w) 2 (i; + wt) ^±^ Cm" (cos <?),
7I = 0 ^
D) «-*«»* = 2r r (y) V (_)m . („ + m) -i"+"tL_> Cw- (COS </)),
E) cos (i cos 0) = 2" r (v) 2 (-)«. (* + 2m) t/-+^>> C'V (cos (/.),
m=0 ^
F) ain(scoa<J>) = 2"r(iO 2 (-). (P + 2w + I) -t2!5P^ (>2Jrt+1 (cos </)),
m=() ^
The last is a generalisation of Poisaon's integral, which was obtained by a
different method in §3*32. It is valid only when li{») > — k-
Those formulae are to bo found on pp. 3({3--3(>f> of the lirnt of Uogenbauer'.s memoirs
to which reference haa just been made.
Equation A) was obtained by Hobnon, I'roc. London Math. So<\ XXv. (IH9-1), p. .r>!>, by a
consideration-of solutions of Laplace's equation in Hpai-o of %i> +• 2 dimensions, 2i> + 'l being
an integer.
A more general set of formulae may be derived from B) by replacing
cos (p by cos <p cos 0' + sin (/> sin 0' cos a/t, multiplying by sin2" -\|r, and inte-
integrating with respect to \jr. The. integral*
I Cw"(cos (f) cos <f>' -|- sin <f) sin <h' cos ty) sin-"~' ¦fyd-ty-
= " ,' Cm''(cos(i)(.(l/(ci)s(i'),
1 Bi'+//i)
which is valid when It (v) > 0, shews that
I exp['i^(coa $ cos 0' + sin <?> sin <f>' cos ^JjHin*" -^rdyjr
Jo
w-o I1Bt'4-/'i) -"
* Cf. Gegenbauer, Wiener SUzuntisberichte, lxx. B), A874), p. i:S3; en. Ba), A898), p. 912.
w. B. i\ '^
370 THEORY OF BESSEL FUNCTIONS [CHAP. XI
and so
(9) / • . ¦ .flV exP [**cos 0cos01
v y (zsin^sin^'I""*
z* °m (C0S *> °m (C°S 0)-
The integral used in the proof converges only when R (v) > 0, but the final
result is true for all values of v, by analytic continuation.
This result was given by Bauer, Miinchener Sitzungsberichte, v. A875), p. 263 in the
case v=\; the general formula is due to Gegenbauer, Monatshefte fur Math, und Phys. x.
A899), pp. 189—192; see also Bateman, Messenger, xxxin. A904), p. 182 and a letter from
Gegenbauer to Kapteyn, Proc. Section of Sci, K. Acad. van Wet. te Amsterdam, iv. A902)
pp. 584—588.
Interesting special cases of the formula are obtained by taking <f>' equal to 0 or to ^tt ;
and, if we put <f>' equal to ?tt, multiply by elZcas^ sin2" <f> and integrate, we find that
A0) -L J
Jv_ j B sin
= 2" H2ir) 2 (
w!
so that the expression on the left is a symmetric function of z and Z\ this formula also
was given by Bauer in the case v=\.
11 . Bateman's expansion.
We shall now establish the general expansion
A) \zJp.{z cos <? cos <b)Jv{z sin <f> sin <?•)
co
= cos*1 (]E> cos*1 $ sin" </> sin" <t> 2 (-)n(/A +
0
x a^ (- n, ix + v + n + 1; v + 1; sin2 <?>),
which is valid for all values of fi and v with the exception of negative integral
values.
Some of the results of § 11*5 are special cases of this expansion, which was
^discovered by Bateman* from a consideration of the two types of normal
solutions of the generalised equation of wave motions examined in § 4*84.
We proceed to give a proof of the expansion by a direct transformation.
* Messenger, xxxni. A904), pp. 182—188; Proc. London Math. Soc. B) in. A905), pp. 111—123.
11*6] ADDITION THEOREMS 371
It is easy to deduce from the expansion (§ 5*21) of a Bessel function as a
series of Bessel functions that
\zJp(z cos <f> cos <i>) Jv (z sin <f> sin <E>)
5 (-)m (heY+7m+x (cos <f> cos <&>+»» . .
= ^ , n . ¦ —-r— Jv (z sin 6 sin cl>)
m-0
so f( \>n Qog" A COS"
= cos" <b cos" <E> sin" A sin" <?> 2 , „ ,—
2, +
; sin'- $ sin'- <?>) i
«, r
= cos'4 </> cos" <1> sin" (^ sin" * 2 (/* +1> + 2»i + 1) JrM+,+.,,H.1 B)
?t~o L
x oFj (wi — n, fi + v 4- in + n + l; 7/ + 1 ; sin2 ^ ain2
_jp + w + l; /x 4-1, v + I; t'«>H- ^t> cos- <l>, .sin- <j> sin'- ^
where Jp4 donotes the fourth type of Appell'.s* liypcrgcomotric i'uncliions of
two variables, defined by the equation
We now have to transformf Appcill's function into a product of hyper-
geometric functions in order to obtain equation A); in effecting the trans-
transformation we assume that R (/x) > 0, though obviously this restriction may
ultimately be removed by using the theory of analytic continuation.
The transformation is a consequence of the. following analysis, in which
.series are rearranged, and a free use is made of Vandermonde's theorem:
. Jpj (- n, ji+v + n + 1; /u. + I, v -I- I ; co.s" (/> cos2 (I>, sin- <? sin- <I\)
s v <-
r-o <t
r! (y + l)r Co <! (« - 0: »to «! (/x 4-
* Comptes ltendits, xc. A8H0), pp. 296, 731.
•[¦ This ti-ansformutioa Iuih not been previouHly notiood t() «;xist oxcopt iu the sjiucial caso in
which 'l> = 't>, eeo Appell, Journal dc Math. C) x. AH8-1), pp. 407—i^H ; bquio aBsociated rosoarclies
are dne to Tissurand, Annalvs (Mdmoirna) dc COlmervatoire (Pai'in), xvin. A88;5), rn<$m. C.
372 THEORY OF BESSEL FUNCTIONS [CHAP. XI
= » »-»• r+s « (- n)y+8 (/a + y + n + 1 )r+s (-)t+u sin8' </> sin2" 4>
,r0 ,r0 «-r «.,. r! A/ + l)r (t - r)! (r + * - <)! (u - r)! (ji + l)r+g_M
= | v 2 V (~ nVf«(^ + y + n + !)>•+« (~)t+M sin2t <f> sin
| 2 V
<-o «^0 r-0 a-i-r »*! (v + l)r (t - r) ! (r + S - t)\ (ll, - r)\ ((I + l)r+«-M
t Q +1 + u + l)n_t (-)n+Msin2t <jb sin2" <
= 22^
<-o «-o rto r! (v +1),. (< - r)! {u - r)! (^ + 1)M_M
x ^ (- (i — n, v + n + 1; v + 1; sin2 <E>)
x gj?1! (- n, a* +1> + n + 1; v +1; -sin2 <E>).
Hence we at once obtain the result
zJp,{zcos <?cos<3>) ./„(^sin </> sin <3>)
= cos* 9 cos* $ am- <? Bin' $
+ 1; " + 1; sin2</»)
x a^ (- n, n + v + n + 1; v + 1; sin2 <?),
from which Bateman's form of the expansion is evident.
CHAPTER XII
DEFINITE INTEGRALS
12*1. Various types of definite integrals.
In this chapter we shall investigate various definite integrals which contain
either Bessel functions or functions of a similar character under the integral
sign, and which have finite limits. The methods by which the integrals are
evaluated are, for the most part, of an obvious character; the only novel feature
is the fairly systematic use of a method by which a double integral is regarded
as a surface integral over a portion of a sphere referred to one or other of
two systems of polar coordinates. The most interesting integrals are those
discussed in §§ I2—121, which are due to Kapteyn and Bateman. These
integrals, for no very obvious reason, seem to be of a much more recondite
character than the other integrals discussed in this chapter; their real sig-
significance has become apparent from the recent work by Hardy described in
§ 12*22. The numerous and important types of integrals, in which the upper
limit of integration is infinite, are deferred to Chapter xm.
The reader may here be reminded of the vory important integral, due. to
Sonine and Gegenbauor, which has already been established in § 11*41, namely
cos cf>)} n
*- 2* cob *)*? C
12" 11. So nine's first finite integi al.
The formula
A) J^ (*) = -2^~~+ f) [**^(* sin V) sin»+l 6 cufi**' Odd,
which is valid when both It(//,) and R(v) exceed - I, expresses any Bossel
function in terms of an integral involving a Bessel function of lower order.
The formula was stated in a slightly different form by Sonine*", Rutgersf
and Schafheitlin j, and it may be proved quite simply by expanding the inte-
* Math. Ann. xvi. A880), p. 36; see also Gegonbauev, Wien&r Sitzwnysberichte, lxxxvhi. ('2),
A884), p. 979.
t Nieuw Archiefvoor Wiskunde, B) vi. A905), p. 370.
J Die Theorie der Bessel'schen Funktionen (Leipzig, 1908), p. 31. Sohafkeitlin Heema to have
been unaware of previous researches on what he desoribes as a new integral.
374 THEORY OF BESSEL FUNCTIONS [CHAP. XII
grand in powers of z and integrating term-by-term, thus
f *
o ¦ TV/" i\ f J* (* sin B)sinM+1 e cosBH"x
lv 1 (v + 1) Jo
= 2 -V
and the truth of the formula is obvious.
It will be observed that the effect of the factor sin*1"*6 in the integrand
is to eliminate the factors F (/a + m 4-1) in the denominators. If we had taken
sin1"^ as the factor, we should have removed the factors ml. Hence, when
R (v) > — 1 and /x is unrestricted, we have
B) J*VM (z sin 6) sin-" 6 cos"" Odd
In particular, by taking j; = -|)we have
C) f-W V^(*sintfW"'10B0 = 11^(*).
\7T/ J Q
A formula* which is easily obtained from A) is
D) f inJ» (z sin 6) Iv (z cos 6) tan *+1 Odd = VJ^~\^^ Jv (z),
JO I (f V + $fA+ i)
f » ( ) ( ) J^
when R(v)>R(fj,)> — l. This may be proved by expanding /„ (z cos 0) and
integrating term-by-term, and finally making use of Lommel's expansion
given in § 5*21.
The functional equation, obtained from A) by substituting functions to be determined,
Fix and Ftl+v+ly in place of the Bessel functions, has been examined by Sonine, Math. Ann.
Lix. A904), pp. 529—552.
Some special cases of the formulae of this section have been given by Beltrami,
htituto Lombardo Rendiconti, B) xiil A880), p. 331, and Rayleigh, Phil. Mag. E) xn. A881),
p. 92. [Scientific Papers, I. A899), p. 528.]
It will be obvious to the reader that Poisson'a integral is the special case of A) obtained
by taking /*=-?• •
For some developments of the foromlae of this section, the reader should consult two
papers by Eutgers, Nieuw Archie/voor Wiskunde, B) vi. A905), pp. 368—373; B) vn. A907),
pp. 88—90.
12'12. The geometrical proof of Somite's first integral.
An instructive proof of the formula of the preceding section depends on
the device (explained in § 3'33) of integrating over a portion of the surface of
a unit sphere with various axes of polar coordinates.
If {I, w, n) are the direction cosines of the line joining the centre of the
* Due to Rutgers, Nieuw Archief voor Wishmde, B) vn. A907), p. 175.
12*12] DEFINITE INTEGRALS 375
sphere to an element of surface d<o whose longitude and co-latitude are </> and
0, it is evident from an application of Poisson's integral that
+1) V (?) (\z)v^ f "jp(z sin 6) sin*+16 cosa"+1 6d8
Jo
* I %fc« i Q cos2"*1 8 sin2" 6d6d8
o .'o
l dco
m>0,rt>0
m
a"+1
n
Jo
and the truth of Sonine's formula is obvious.
An integral involving two Bessel functions which can be evaluated by the
same device* is
o
in which, to secure convergence, ll(v) > — J.
If we; write
¦or" = ain1^ + cos18 - 2 Hina0 cos28 cos c/> = I - sin* 2^ co.s2
and use 111*41 A0), we sec. that the integral in equal to
fin
,/"„(* sin 0) si
rio
sin 6) sin"+1 (9 cos2v 8d6,
so that finally, by 112*11 (I),
A)
* This integral haB been evaluated by a different method by Butgers, Nieuw Archie/ voov Wis-
kunde, B) vn. A907), p. 400; cf. also § 12-22.
376 THEORY OF BESSEL FUNCTIONS [CHAP. XII
Some integrals which resemble this, but which are much more difficult to evaluate,
have been the subject of researches by Bateman, Kapteyn and Rutgers; see § 12-2.
As a simple example of an integral which may be evaluated by the same device, the
reader may prove that, when M(v)> — •&,
B)
by writing the integral on the left in the form
2"+1 T \) I
This formula was given (with v — Qi) by BScher, Annals of Math. viii. A894), p. 136.
12*13. Sonine's second finite integral.
The formula
A) f^(«m0)^(?cos0)8m^^
which is valid when both R(/x) and R(v) exceed — 1, is also due to Sonine* ;
and, in fact, he obtained the formula of § 12*11 from it by dividing both sides
of the equation by Zv and then making Z -^0.
A simple method of proving the formula is to expand the integral in powers of z and Z
and to verify that the terms of degree n+i/ + 2mon the left combine to form
in'.
The proof by this method is left to the reader.
We proceed to establish Sonine's formula by integrating over portions of
the surface of a unit sphere. Under the hypothesis that R(fj.) and R(v)
exceed — |-, we see that, with the notation of § 12A2, we have
Jo
o . o J o
fn fin firr
JO- 0 J -Jir
O- 0 J -Ji
zi) miv C0S2m ff a
0 J. m>0
ei sin 9 (zl+Zm) tfv
o >o
2>
\
o Jo o
* Math. Ann. xvi. A880), pp. 35—36
12*13] DEFINITE INTEGRALS 377
Now the exponential function involved here is a periodic analytic function of
ty with period 27r, and so, by Cauchy's theorem, the limits of integration with
respect to yjr may be taken to be a and 2-n- + a, where a is defined by the
equations
vr cos a = z, vr sin a = Z,
and vr = sl{Zn- + z"). If we adopt these limits of integration, and then write
¦\/r + a for y\r, the triple integral becomes
Jo Jo Jo
and this integral may also be obtained from its preceding form by replacing
z by vr and Z by zero. On retracing the steps of the analysis with these
substitutions we reduce the triple integral to
(v + 1)
"/ ir
and we obtain Sonine's formula by a comparison of the initial and final
expressions
Sonine'.s own proof of thia formula was based on tho use of infinite dis-
discontinuous integrals, and the procewa of making it; rigorous would be long and
tedious.
The formula may be extended to the domains in which — * ^. R (/x) > — 1,
and — \ ^ 7? (v) > — 1, by analytic continuation.
In Sonine'a formula, replace Z by ^(Z'^ + t;2—2Z?cos(f>), multiply by
min <f>/(Z*+ ?>-2Z?unii<f>)iv,im<\ integrate. It, follows from § 11-41 A6) that
B) i n Jy. {2.sin 6)JV(Zcoh d)J*(ScoH^)Hin'1+1 d cos Odd
° = z*&_? f' ,/wl{^ + ^+r-2^cos^)}
provided thab
Thia rcsxilt is also due to Sonino, ibid. p. 45. In connexion with tho formulae of this
section the rcador should consult Macdonald'a memoir, Proc. London Math. Soc. xxxv
A903), pp. 442, 443.
378 THEORY OF BESSEL FUNCTIONS [CHAP. XII
12* 14. Gegenbawr1 s, finite integral.
An integral which somewhat resembles the first of Sonine's integrals,
namely
fir QQg
I . (z cos 6 cos ylr) Jv_x {z sin 6 sin ylr) 0/ (cos 6) b'mv+idd6,
Jo sin
has been evaluated by Gegenbauer*; we shall adopt our normal procedure of
using the method of integration over a unit sphere.
It is thus seen that
eiz cob e cos * Jv_^ (jg gjn Q Qln ^ Qv (cos 0) gin*** Q d()
= tttt™t- f * f * e?a (cosB °os *+sin e 9in * cos*) °rv (cos (9) sin2" (9 sin2" A d<f> dO
A W •«•(?) Jo Jo
= -^tt^-TvT eiz &hl6co*<-'i>-*) C/ (sin 6 cos 6) cos2"6 sin (9rf<6 rf(9
1 W1 (f) Jo -o
i* r*"'/'2"
eiz sin'cos * Cv" (sin 0 cos (<^> + f)} cos2" (9 sin (9 <*4> dO,
J 0 J 0
since the penultimate integrand is -a periodic analytic function of <j!> with
period 2tt.
If we retrace the steps of the analysis, using the last integral instead of its
immediate predecessor, we find that the original integral is equal to
[ eizl Gvv (lcosf-7n sin i|r) n2"-1 do*
J«>o
= (if^JJil? f'rGr^^^/(cos^ooa 0 - sin^sin (9cos <?) si
i I1') A ii) -Ioh
Now, by the addition theoremf for Gegenbauer's function,
0/ (cos yjr cos ^ — sin •x/r sin ^ cos <?)
+^ .^^
v+p
X 0^ (COS tf) C^_l (COS ^r) (?;-* (COS <?).
* Wiener Sitzungsberichte, lxxv:.B), A877), p. 221 and lxxxv. B), A882), pp. 491—502.
t This -was proved by Gegenbauer, Wiener Sitzungsberichte, lxx. B), A874), p. 433; cn. Ba)
A893), p. 942.
12-14, 12-2] DEFINITE INTEGRALS 379
When this is multiplied by sin2" ^ and integrated, all the terms of the integral
of the sum vanish except the first which is
r\rBv) „ , nKr% , /¦«¦ .
Jok
We thus find that
and hence, by § 3 3 2,
Jo
= — I I' Sin" *y C,v (COS yjr) Jv+r (z).
()
\ z J
If we equate real and imaginary parts, we obtain Gegenbauer's formulae
B) com (zQoa 6 cos ylr)^fl,_i{z am 6 sin f) C/(coh 9) Hinv+i 6 dO
Jo
j(-)ir B7r) sin""* V G>" (cos ^r),/,.,.,. B), (?• even)
|o ' (/-odd)
and
C) I sin («cos 6 cos -v^) Jv_j (z.sin 0 sin •v/r) Cr» (o.s 0) Min"+*^ci!(9
J 0
{(), (?• even)
(_)*(!-» /M 8in"-i ^ C'/ (cos f) Jv+r(z). (r odd)
12*2. Integrals deduced from Bateman's expansion.
In Bateman's expansion of § 1 Hi, write ^ = <jf>; and then, noting Jacobi's
formula*
j,^, (-n, (i + v+n+1; v+l; sin- ^>)
.(/* + 1/ + 2n + 1) I10* + v + ?i + 1) r (v + n + 1)'
we deduce that, when itl(yLt) and i2(y) both exceed —1,
^1 Jh(z cos2 <f))Jv(z sin2 d>) sin <j!> cos ^ rf<^> = 2 (—)M t/M+v+wl+1 (
Jo »=o
Journal filr Math. lvi. A859), pp. 149—175 [IFer/ce, vi. A891), pp. 184—202].
380 THEOEY OF BESSEL FUNCTIONS [CHAP. XII
that is to say
B) rjll(t)Jp{z-t)dt^2 2 (-)n
J o »=o
An important deduction from this result is that, when R (ji) > 0 and R (v) > — 1,
i]f [z
, (t) Jv(z~t)~ = {/,_, @ + /M+1 @} J, (* - *) dt = 2J^V (z),
o t Jo
so that
(d) J»(t)Jv(z-t)-- = — .
.'o t fi
This formula is due to Bateman*; some special cases had been obtained
independently by Kapteynf, who considered integral values of /x and v only.
It will be observed that we can deduce from B), combined with § 2*22 B),
that
rz n
D) Jy.(t)J-,,C?-1)dt = sinz, I J,l
Jo Jo
when — 1 < R (/x) < 1, and when — 1 < R (/*) < 2 respectively.
By interchanging /j, with y and ? with z —t in C), we see that, if
and R (v) are both positive, then
dt( +
t ' z-t \fi
It seems unnecessary to give the somewhat complicated inductions by
which Kapteyn deduced C) from the special case in which fi = v = l, or to
describe the disquisition by Rutgers^ on the subject of the formulae generally.
12'21. Kapteyn's trigonometricalintegrals§.
A simpler formula than those just considered is
rz
A) cos (z-t)J0(t)dt=zJ0(z).
Jo
' To prove this, we put the left-hand side equal to u, and then it is easily
verified that .
d%u T , .
and therefore
u = zjo (z) + A cos z + B sin z,
where A and B are constants of integration.
* Proc. London Math. Soc. B) in. A905), p. 120. Some similar integrals occurring in the theory
of integral equations are examined by the s^me writer, ibid. B) iv. A90G), p. 484.
t Proc. Section of Sci., K. Akad. van Wet. te Amsterdam, vn. A905), p. 499; Nieuw Archie/
voor Wiskunde, B) vn. A907), pp. 20—25; Alton, de la Soc.R. des Sci. de Ltige, C) vi. A906), no. 5.
X Nietav Archiefvoor Wiskunde, B) vn. A907), pp. 385—405.
§ Mem. de la Soc. R. des Sci. de LiSge, C) vi. A906), no. 5.
12-21] DEFINITE INTEGRALS 381
Now, when z is small,
u = z + o (z*y
and so A — B = 0, and the result is established.
It follows from A) by differentiation that
B) f sin (z-t). J{) (t) dt = zJx (z),
Jo
and, by a partial integration,
fz
C) Bin (z - t).Ji(t)dt = am z-zJ0(s).
Jo
The formula
D) sin (* - 0 *lJf> dt = t v (_)» JM+Win Wf
which is valid when 2^(/a) >(), ia of a more elaborate character, and the result
of the preceding section is required to prove it.
We write v = [* Jo (z -1) J^ (t) dl,
J o
and then we have
d! ¦! +«= f" i-A," (- - 0 -i-./«(- -1)\ J. (t) dt + j; (z)
A2~ o
by § 12'2.
By the method of variation of parameters (of. §7'JW), we deduce that
t
v = A eos j + // sin z '+ fi I sin (r; - /) ¦
and, since i'= ," + 0(z'l*:1),
when z is small, it follows that, when Ji(fi)>0,
A = 7* = 0.
Hence we obtain the required result.
By differentiating D) with respect to z we find that
E) eos (z — t) -M— (/1 = i (—)" en •/M+...« (/).
. o t /* m-.o
382
THEORY OF BESSEL FUNCTIONS [CHAP. XII
12*22. Hardy's method of evaluating finite integrals.
As a typical example of a very powerful method of evaluating finite integral* wo almll
now give a proof of the formula (cf. § 12%12)
which is valid when R(/*)> -§ and R{v)>~\,
The method is more elaborate than any other method described in this chapter, booauso
it involves the use of infinite integrals combined with an application of Lerch'n theorem +
on null-functions.
Let /"** JM (zr2sin2d) Jv O2cos20) r^**"*^™***18 co$2v+1 ddd^fi (r),
By changing from polar coordinates (?•, 5) to Cartesian coordinates (x, if) und u.sing
^ 13*2 E) we see that, whenever t>\I(z)\, then
f3°exp(-r20./i(J')rfr= f exp(-a;20Jv{za^3fl"*^dx j
Jo Jo J
and hence, by an obvious modification of Lerch's theorem, /j(r) is identically equal to
fi if); and this establishes the truth of the formula.
12*3. Chessin's integral for Yn («).
A curious integral for Yn B) has been obtained by Chessin, American Journal, xvi.
A894), pp. 186—187, from the formula
1.1. 1
if we substitute this result in the coefficients of the ascending sories for Y,, (z), wo obtain
the formula in question, namely
dt.
• I must express my thanks to Professor Hardy for communicating the method to in« before
the publication of his own developments of it. The method was used by Eamanujan to evaluate
many curious integrals; and the reader may use it to evaluate the integrals examined earlier in
.this chapter.
t Acta Mathematica, xxvn. A903), pp. 339-352. The form of the theorem required hero ia
that, if/fr) is a continuous function of r when r > 0, such that
for all sufficiently large positive values of t, theu/(r) is identically zero.
CHAPTER XIII
INFINITE INTEGRALS
13*1. Various types of infinite integrals.
The subject of this chapter is the investigation of various classes of infinite
integrals •which contain either Bessel functions or functions of a similar character
under the integral sign. The methods of evaluating such integrals are not
very numerous; they consist, for the most part, of the following devices:
(I) Expanding the Bessel function in powers of its argument and inte-
integrating terrn-by-term.
(II) Replacing the Bessel function by Poisson's integral, changing the order
of the integrations, and then carrying out the integrations.
(III) Replacing the Bessel function by one of the generalisations of Bessel's
integral, changing the order of the integrations, and then carrying out the
integrations; this procedure has been carried out systematically by Sonine*
in his weighty memoir.
(IV) When two Bessel functions of the same order occur as a product
under the integral sign, they may be replaced by the integral of a single
Bessel function by Gegenbauer's formula (cf. § 12-1), and the order of the in-
integrations is then changed f.
(V) When two functions of different orders but of the .same argument
occur as a product under the integral sign, the product may be replaced by
the integral of a single Bessel function by Neumann's formula (§ 53), and
the order of the integrations is then changed.
(VI) The Bessel function under the integral sign may be replaced by the.
contour integral of Barnes' type (§ 6'5) involving Gamma functions, and the
order of the integrations is then changed ; this very powerful method has not
previously been investigated in a systematic manner.
Infinite integrals involving Bessel functions under the integral sign are
not only of great interest to the Pure Mathematician, but they are of extreme
importance in many branches of Mathematical Physics. And the various bypes
are so numerous that it is not possible to give more than a selection of the
most important integrals, whose values will be worked out by the most suitable
methods; care has been taken to evaluate several examples by each method.
In spite of the incompleteness of this chapter, its length must be contrasted
unfavourably with the length of the chapter on finite integrals.
* Math. Ann. xvi. A880), pp. 33—60.
t This procedure has been carried out by Gegenbauer in a number of papers published in the
Wiener Sitzungnberichtc.
384 THEORY OF BESSEL FUNCTIONS [CHAP. XIII
13-2. The integral of Lipsckitz, with BanheVs generalisations.
It was shewn by Lipschitz* that
0)
where R (a) > 0, and, in order to secure convergence at the upper limit of in-
integration, both the numbers R (a ± ib) are positive. That value of the square
root is taken which makes | a + V(a2 + b*) \ > \ b \.
The simplest method of establishing this result is to replace the Bessel
coefficient by Parseval's integral (§ 2) and then change the order of the in-
integrations—a procedure which may be justified without difficulty. It is thus
found that*
i r°° /*"¦
- e~at elhtao66 dddt
Tio Jo
1 f* dO
7r ] o a — ib cos 0
and the formula is proved.
Now consider the more general integral
This integral was first investigated in all its generality by Hankelf, in a
memoir published posthumously at about the same time as the appearance of
two papers by Gegenbauer%. These writers proved that, if R (//, + v) > 0, to
secure convergence at the origin, and the previous conditions concerning a
and b are satisfied, to secure convergence at infinity, then the integral is
equal to
F ffi+v p + v+l , 6a
To establish this result, first suppose that b is further restricted so that
J b | < j a \. If we expand the integrand in powers of 6 and integrate term-by-
term, we find that
/"oo co (—\m fl A\«+2»n. Too
e-at Jv (bt) tr-1 dt= S ¦ \ ~ , 2 vr ^+"+-™-> e~at dt
Jo •m=i)W! r(i/ + m + l) jo
_ v (-)m(kb)v+*m T((M+v + 2m)
* Journal filr Math. lvi. A859), pp. 191—192.
t Math. Ann. vin. A875), pp. 467—468.
X Wiener Sitzungsberichte, lxx. B), A875), pp. 433—443; ibid, lxxii. B), A876), pp. 343—344.
In the former, the special case fi-=v + l was investigated by the integral given in §3*32; in the
latter, Gegenbauer obtained the general result by substituting Poisson's integral for Jv(bt).
13*2] INFINITE INTEGRALS 385
The final series converges absolutely, since | b | < | a |, and so the process of
term-by-term integration is justified*. Hence
B) re~at
Jo
The result has, as yet, been proved only when R (a) > 0 and j b \ < j a |;
but, so long as merely
R (a + ib) > 0 and R (a - ib) > 0,
then both sides of B) are analytic functions of b; and so, by the principle of
analytic continuation, B) is true for this more extensive range of values of b.
Again, by using transformations of the hypergeometric functions, B) may
be written in the following forms:
C)
J
„ ffi + v l-fji + v.
The formula B) has been used by Gegcnbaucr-j- in expressing toroidal
functions as infinite integrals; special cases of B) are required in various
physical researches, of which those by Lamb J may be regarded as typical.
By combining two Bessel functions, it is easy to deduce that
D) j e-niY?{bt)l!L-ldt
Jo
= cotK7r ,, > 2^11 v~> —--¦ — ; v+1; —
(ui + lrf^-v) r (v+l) \ 2 ' 2 aJ +
provided /t(n)> | /i'(i') j ami R(a±ib) > 0; special cases of this fonuula are due to Hobson,
Proc. London Math. Sue. xxv. A8JJ), p. 7.r>, and Heaviside, Electromagnetic Theory^ in.
(London, 1912), p. 85.
It is obvious that interesting special cases of the fornmlao so fur discuswed may be
* Cf. Bromwieh, Theory of Infinite Series, § 176.
t Wiener Sitzuntjuberichte, c. (), AHU1), pp. 7<i5—7C6; (legenbuuur also expressed Horiee,
¦whose general termB involve toroidal functions and Beseel functions, as iutegruls with Bessel
functions under the integral Hign.
t Proc. London Math. Soc. xxxiv. A902), pp. 276—281; B) vir. A909), pp. 122—1-11. See
also Macdonald, Proc. London Math. Soc. xxxv. A903), pp. 428—413 and Busset, Proc. Camb.
Phil. Soc. v. A880), pp. 425—433.
w. B. P. 25
386 THEORY OF BESSEL FUNCTIONS [CHAP. XIII
obtained by choosing y. and p so that the hypergeometric functions reduce to elementary
functions. Thus, by taking /* equal to p+1 or p + 2, we obtain the results
E)
F)
provided that R(v)> -?, R (v) > -1 respectively.
These formulae were obtaiued by Gegenbauer, Wiener Sitzungsberichte, lxx. B), A875),
pp. 433—443; they were also noticed by Sonine, Math. Ann. xvi. A880), p. 45; and Hardy,
Trans. Camb. Phil. Soc. xxi. A912), p. 12; while Beltrami, Atti della R. Accad. delle Sci.
di Torino, xvi. A880—1881), p. 203, and Bologna Memorie, D) n. A880), pp. 461—505, has
obtained various special formulae by taking /x = l and p to be any integer.
Other special formulae are
f° dt
G) e~atJjbt)---
Jo t
[Note. It was observed by Pincherle, Bologna Memorie, D) vm. A887), pp. 125—143,
that these integrals are derivable from the generalised form of Bessel's integrals (§ 6'2) by
Laplace's transformation (cf. § 9-15). This aspect of the subject has been studied by
Macdonald, Proc. London Math. Soc. xxxv. A903), pp. 428—443, and Cailler, Me'm. de la
Soc. de Physique de Genlve, xxxiv. A902—1905), pp. 295—368. The differential equations
satisfied by E) and F), qua functions of a, have been examined by Kapteyn, Archives
Nderlandaisea, B) vi. A901), pp. 103—LI6.]
The integral I —r-—- J0(bt)tdt was obtained by Neumann, Journal fur Math, lxxii.
A863), p. 46, as a limit of a series of Legendre functions (cf. § 14*04). The integral does
not seem to be capable of being evaluated in finite terms, though it is easy to obtain a
series for it by using the expansion
71=0
A series which converges more rapidly (when b is large) will be obtained in § 13*51.
Some integrals of the same general type are given by Weber, Journal fur Math. lxxv.
A873), pp. 92—102; and more recently the formula
(9) rJv(bt)t"dt_{%)vY{p+\) » 1
Jo «rt-l J-K ~ ¦«=i(ns*2 + 68)>'+*'
which is valid when R (v) > 0 and | I(b) | < tr, has been obtained by Kapteyn, Mem. de la
Soc. R. des Sci.de Ltige, C) vi. A906), no. 9.
13*21. The Lipschitz-Hankel integrals expressed as Legendre functions.
It was noticed by Hankel that the hypergeometric functions which occur
in the integrals just discussed are of the special type associated with Legendre
functions; subsequently Gegenbauer expressed the integrals in terms of toroidal
. functions (which are known to be expressible as Legendre functions), and a
little later Hobson* gave the formulae in some detail.
* Proc. London Math. Soc. xxv. A893), pp. 49—75.
13*21] INFINITE INTEGRALS 387
To obtain the fundamental formulae* of this type, we shall change the
notation by writing
a — cosh a, b = i sinh a,
where a is a complex number such that
-&7r</(a) ^^tt;
we thus obtain the formula
A) r%-<cwh« /„ (t sinh a)Pdt = T(ji + v+l) P~" (cosh a),
Jo
provided that JR (/j, + v) > — 1.
The special cose of this formula in which v=0 hud been given by Callandreau, Bull, des
Sci. Math. B) xv. A891), pp. 121—124, two years before Hobson published the general
formula.
It follows at once from A) that
B) [V'coah. Rv(t sinh a) fl*dt = -,-i^L-- YU-v+l) Q/ (cosh a),
Jo sin(^ + i/)Tr
provided that 11 (fi + 1) > | R (v) |.
The modification of A) which has to be used when the argument of the
Legendre function-}* is positive and less than 1 is
C) ["e-tcos? jv (t 8jn 0) p dt = V (jj, + p + I) iV"' (cos /3),
Jo
and hence we find that
Bin(/4 + I/OT 7T
x [Q/ (cos j8 + (){) e*w' + y/ (cd.s 0 - Ot) e-*''«].
Some special cases of this formula have been given by Ilobson, loc. cit. p. 7«"), and by
Heaviside, Electromagnetic Theory, in. (London, 1912), p. 8!").
An apparently different formula, namely
has been studied by Stein thai.}. This ibnmila is connected with formulae' of
the previous type by Whipple's§ transformation of Legendiv functions, which
* Since, by a change of variable, the integrals arc exiireawible in tttrms of the ratio of b to a, no
generality ia lost. The various exprosflioriK for Legondre functions as bypergeometric series which
are required iu this analysis are giveu by Barnes, Quarterly Journal, xxxix. (lyOfcJ), pp. 97—20-1.
f The reader will remember that it i8 customary to give a different definition for the Legeudre
function in such circumstances; cf. Hobson, Phil. Trans, of the Royal Soc. clxxxvii. A, A896),
p. 471; and Modern Analysis, §§ IS'5, 15-0.
X Quarterly Journal, xvni. A882), pp. 337—340.
§ Proc. London Math. Soc B) xvi. A917), pp. 301—314.
388 THEOBY OF BESSEL FUNCTIONS [CHAP. XIII
expresses a function of cosh a in terms of a function of coth a. The more
general formula of the same type is
/¦go cos vk Q"~\ (cosh a)
In these formulae, E (/x + v) > 0 and R (cosh a) > 1.
On replacing v by — v in F), we find that
G) J^z(^v(^)r()r^)^
and this formula is valid when R (/*) >\R(v)\ and R (cosh a) > — 1.
If we take cosh a=0, we deduce that
(8)
a result given by Heaviside* in the case v =0.
When p=l, G) becomes
(9) r,-i«n.jrr@A—r2-fc,
K ' Jo w sinvw sinho '
and hence, if v~0,
j
air t*\j* arcsinh «,/(a2-l) arc sin J(l - a2) arc cos a
If we replace a by + z'fc, we find that
and so, when 11 (b) \ < 1,
A0) [08F1
Jo
A1) fsin(^ —' arCSiah&
Jo
The former of these is due to Basset, Hydrodynamics, n. (Cambridge, 1889), p. 32.
[Note. Various writers have studied the Lipschitz-Hankel integrals from the aspect of
potential theory; to take the simplest case, if (p, <f), z) are cylindrical coordinates, we have
It is suggested that, since e~<>t Jo (zt) is a potentnxl function, the integral on the left is a
potential function finite at all points of real space except the origin and that ont the plane
2=0 it is equal to 1/p, and so it is inferred that it must be the potential of a unit charge at
the origin. But such an argument does not seem to preclude the possibility of the integral
being a potential function with a complicated essential singularity at the origin, and so
this reasoning must be regarded as suggestive rather than convincing.
* Electromagnetic Theory, in. (London, 1912), p. 269.
t On the axis of z, the integral is equal to a constant divided by | z |.
13*22] INFINITE INTEGRALS 389
For various researches on potential theory with the aid of the integrals of this section,
the reader may consult Hafen, Math. Ann. lxix. A910), pp. 517—537. For some develop-
developments baaed on the potential function
J
see Bateman, Messenger, xli. A912), p. 94.]
13*22. Applications of the addition formula to the Lipschitz-Hankel integrals.
It is easy to deduce from the results of the preceding sections combined
with § 11-41 A6) that, if all four of the numbers R(a±ib±ic) are positive
and R(fi + 2v) > 0, while or is written in place of VFS + ca - 26c cos </>), then
A) fe-atJv(bt)Jv(ct)t^dt
JO'
The hypergeometric function reduces to an elementary function if fx = 1 or 2;
and so we have
The case //. = 2 may be derived from this by differentiation with respect to ft.
Thebo formulae, or special cases of them, havo boon examined by tho following writers:
Beltnuni, Bologna Memorie, D) n. AHH0), pp. 401—r>05; Atti ddla R. Accad. dell'e Sri. di
Torino, xvr. AHR0—1881), pp. 201 — 205; Summerfeld, Konigsberg Dissertation, 1391;
Gegenlmuer, Moiiatshaftc fiir Math, und Phys. v. A894), p. f>5; and Macdonald, Proc.
London Math. Soc. xxvi. A893), pp. 2fO— 200.
V>y taking /x= — 1, v = l in A), we liud that.
? dt = I. ( W {J(a* + 2-2 cos <j>) - a} A -! -nn <f>) def,,
so that the integml on the left, which wan encountered by Rayleigh, PhiL Mag. (")) xlii.
AH!)U), p. 1!);j [Scientific Papers, iv. (lOOl), p. 2A0], i.s expressible as an elliptic: integral.
[
J it
An integral which may be associated with A) ia
dd
f00 fl
C) COS at Io (U) Iu (Ct) dt =
This was discovered by Kirchhoft'* as early as 1853; the reader should havo
no difficulty in deducing it from § 13-21A0) combined with §11*41A0); it
is valid if all the numbers
R(c±b± ia)
are positive.
* Journal filr Math, xlviii. A854), p. 364.
390 THEORY OF BBSSEL FUNCTIONS [CHAP. XIH
A somewhat similar result, namely
D) r e~attfL-vJl,(bt)Jv(ct)dt
Jo
f
jo
Bin* 0 rift
which is valid when R (a±ib±ic)>Q and R(n)> -^, is due to Gegenbauer, Wiener
Sitzungsberichte, lxxxviii. B), A884), p. 995. It is most easily proved by substituting
integrals of Poisson's type for the Bessel functions. In the memoir cited Gegenbauer has
also given a list of cases in which the integral on the right is expressible by elementary
functions (cf. § 13-23).
13*23. Gegenbauer s deductions from the integrals ofLipschitz and Hankel.
A formula due to Gegenbauer, Monatshefte fur Math, und Phys. iv. A893),
pp. 397—401, is obtained by combining the results of §13*2 with the integral
formula of § 53 for the product, of two Bessel functions; it is thus possible to
express certain exponential integrals which involve two Bessel functions by
means of integrals of trigonometrical functions*. The general result obtained
by Gegenbauer is deduced by taking the formula
2 /"*"¦
Jy, (bt) Jv(bt) = —\ JM+V (%t cos <f>) cos (/j,-v)(f> dcf>,
multiplying it by e~iat iP+v and integrating from 0 to oo ; it is thus found that,.
if R(a)>\I(b)\ and RQjl + v)>-1, then
[V2at j;(bt)Jv(bt) t*+v dt=- I" f V2a*J»+p Bbt cos<i>) ^+veos (u -v)A.d<bdt
Jo TJOJ»
f I atJ^v Bbt cos (j>)t*+v cos (fi-v)<f>.dtd(f>
= - f I
cos
The inversion of the order of the integrations presents no great theoretical
difficulties; hence
A) re-*atJfl(bt)Jv(bt)tr+''dt
Jo
_ F (fi + v +-|) b*+v fl" cos't+'/ <fr cos (im-v)<f> .
tt3 Jo (a2 + b> cos2 $Y+*+l *'
This result, in the special case in which /i=v = 0, had been obtained previously by
Beltrami, Atti delta R. Aocad. delle Sci di Torino, xvi. A880—1881), p. 204.
As particular cases of A) take /x = l and v equal to 0 and to — 1. It is found that
B)
* See also an earlier note by Gegenbaaer, ibid. pp. 379—380.
13-23, 13-24] INFINITE INTEGBALS 391
where the modulus of the complete elliptic integrals K and Bis 6/N/(a2+62). Beltrami's
corresponding formula is
Replacing b by ib, we deduce from B) that
where R (a) > \ R F) |, arid the modulus kx of the elliptic integrals is bja. The formulae C)
and D) may be modified in a similar manner.
It was stated by Gegcnbauer that tho integrals in B), C) and E) are expressible by
means of elliptic integrals, but he did not give tho results in detail; some forrmilae
deducible from the results of this section were given by Meisscl, Kiel Programm, 1890.
[Jahrbuch liber die Fortschntte der Math. 1890, pp. 521—522.]
13*24. Weber s infinite integral, after Schafheitlin.
The formula
Jv(t)dt _ Ia(?a0
in which 0 < R (w) < R(v) + |, was obtained by Weber* for integral values of
v. The result was extended to general values of v by Soninef; and the com-
completely general result was also proved by SchafheitlinJ.
Tho formula is of a more recondite type than tho exponential integral formulae given
in § 13*2; it may be established as a limiting case of these formulae, for, since the conditions^
of convergence are satisfied, we have by § 13-2 C)
. I» U W + 2.". +1.
2" r (p +1)' a ! \2' 2 ' '
whence the formula is at once obtained.
A direct method of evaluating tho integral is to substitute Poisson's integral for tho
Bessel function, and then change the order of the integrations; this is tho method used by
Schafheitlin, but the analysis is intricate because the result is established first for a
limited range of values of n and v and then extended by tho uso of recurrence formulae
and partial integrations.
Analytical difficulties are, to a large extent, avoided by using contour
integrals instead of the definite integrals of Schafheitlin. If we suppose that
* Journal fUr Math. lxix. A868), p. 230. Tho apodal case in which v = 0 was set by Stokes as
a Smith's Prize question, Jan. 29, 18E7. [Math, and Phyx. Papers, v. A905), p. 347.]
t Math. Ann. xvi. A880), p. 39.
% Math. Ann. xxx. A887), pp. 157—161.
§ Of. Bromwioh, Theory of Iitfinite Series, § 172.
392 THEOBY OF BESSEL FUNCTIONS [CHAP. XIII
R(fi)<0 and R(v)> ~\, we then have (the integrals being absolutely con-
convergent)
— 2i sin ju,7
By the theory of analytic continuation, this result is valid when ju, and v are
subjected to the single restriction R(fx)<R (v +§).
When R (p) > 0, we deform the contour into the positive half of the real
axis taken twice, and we at once obtain the Weber-Schaf heitlin formula.
The integral*
may be treated in exactly the same manner; the only difference in the
analysis is that cos (t cos 6) has to be replaced by — sin (t cos 6), and so, by
Euler's formula (adapted for contour integrals), the factor cos %firrr has to be
replaced by — sin Ifnr.
It is thus found that
provided' that R (/i) < R (v + f) and R (/a) ^ 0.
When R(fi) > — 1, the contour may be deformed into the positive half of
the real axis taken twice, so that
provided that -1 <R(/j.)^0 and R(ji)<R(v) + %.
If we take fi = 0, v — 1, we see that
This result, combined with the asymptotic formula
Bt) dt _2/ 1 1 \ _ cosBx+%tt)
was used by Struvo, Ann. der Physik und Chemie, C) xvn. A882), p. 1014, to tabulate
, B0 dt
1 /"H^
for both small and large values of x. The last integral is of importance in the Theory of
Diffraction.
* Generalisations obtained by replacing Besael functions by Lommel's functions (§ l0'7) in
the integrals of this section and in many other integrals are discussed by Nielsen, K.
Videnskabernea Sehkabs Skrifter, G) v. A910), pp. 1—37.
13*3] INFINITE INTEGRALS 393
[Note. By differentiating A) under the integral sign we obtain Weber's result
D) I J0(t)\ogtdt=-y-\og2;
J o
this formula has also been investigated by Lerch, MonaUhefte fiir Math, und Phys. I.
A890), pp. 105—112.
The formula for functions of the second kind, corresponding to A), is
Yv (t) dt r (^|x) r (htM — p) cos (ifj, — v)tr
provided that | R(v)\<R(fi-p)<$. This result hcis been given by Heaviside, Electro-
Electromagnetic Theory, in. (London, 1012), p. 273, when v = 0.]
13*3. Weber's first exponential integral and its generalisations.
The integral formula
A) Jo Jo (at) exp (-pH-) -tdt=2p2 exp (-
was deduced by Weber* from his double integral formula which will be
discussed in § 14*2. This integral differs froin those considered earlier in the
chapter by containing the square of the variable in the exponential function.
It is supposed that | argp | < \tt to secure convergence, bub a is an unrestricted
complex number.
It is equally easy to prove Hankd'af more general formula,
B) j™ Jv (at) exp (-p*&). t*-1 dt
o«
by a direct method. To secure convergence at the origin, ifc must now be
supposed that:]:
7? (p + v) > 0.
To obtain the result, we observe that, since (by § 73)
f /,„, (| a 11). | exp (- pH1) |. 11*-1 j dt
is convergent, it is permissible^ to evaluate the given integral by expanding
Jv(at) in powers of ? and integrating term-by-term.
* Journal fiir Math. lxix. A8G8), p. 227. Weber also evaluated B) in the case n — p + 2, v being
an integer.
t Math. Ann. vin. A875), p. 409. See also G'j^enbauer, Wiener Sitzungsberichte, lxxii. B),
A876), p. 346.
X This restriction may be disregarded if we replaoe the definite integral / by the contour
J o
/"@+)
integral
§ Cf. Bromwich, Theory of Infinite Series, § 176.
394 THEORY OF BESSEL FUNCTIONS [CHAP. XIII
It is thus found that
h
1
w=o m! r (v + m +1)' 2
arid this is equivalent to the result stated.
If we apply Kummer's first transformation (§ 4*42) to the function on the
right in B), we find that
C) p Jv (at) exp (-ft*). P'1 dt
and so the integral is expressible in finite terms whenever fi — v is an even
positive integer.
In particular, we have
D)
provided that R(v)> — 1. This integral is the basis of several investigations
by Sonine, Math. Ann. xvi. (^p80), pp. 35—38; some of these applications are
discussed in § 13*47.
In order that the hypergeometric function on the right in B) may be
susceptible to Kummer's second transformation (§4>42)J we take fi~l; and,
if we replace v by 2v, we then find that
E) |V.W«p(-^.4- ^«p (-?) .1
a result given by Weber in the case v=-\.
If we replace v by — v, it is easy to see that
F) Yw (at) exp (- ft*) dt
J o
Vtt / a? \ f r / a2 \ . 1 v I a2 \ 1
=x~j— exp - vr-- Jv rr- tan V7T + - A „ 5-: SeC V7T ,
when | JS (v) j < '¦?; and, if we make p -*- 0, (a being now positive), we find that
G) fr.Mif-'^,
Jo a
when | R (v) \ < ^, by using § 7*23; and, in particular,
(8)
13*31] INFINITE INTEGBALS 395
Formulae E) and F) were given (when v=0) by Heaviside, Electromagnetic Theory', ill.
(London, 1912), p. 271.
Another method of evaluating the integral on the left of C) is suggested by Basset,
Proc. Camb. Phil. Soc. vm. A895), pp. 122—128; the integrals have also been evaluated
with the help of Laplace's transformation by Macdonald, Proc. London Math. Soc. xxxv.
A903), pp. 428—443; see also Curzon, Proc. London Math. Soc. B) xm. A914), pp. 417—
440; and Hardy, Trans. Camb. Phil. Soc. xxi. A912), pp. 10, 27, for formulae obtained by
making p'2 a pure imaginary.
For some applications of the integrals of this section to the Theory of Conduction of
Heat, see Rayleigh, Phil. Mag. F) xxn. A911), pp. 381—396 [Scientific Papers, vi. A920),
pp. 51—64].
13*31. Weber s second exponential integral.
The result of applying the formula §11'41A6) to the integral just dis-
discussed is to modify it by replacing the Bessel function under the integral
sign by a product of two Bessel functions of the same order.
If •sr = V(«2 + b* — 2ab cos <f>) and if R (v) > — \, R Bv + fx) > 0, | argjp | < \ir,
we thus deduce that
exp (- p*P) Jv (at) Jv (bt) ir~l dt
exp (— pH2)' - -v • tv+>L~* sin'2" ^d^dt
The hypergeomctric function reduces to unity when /x = 2; so that
exp (- fit) J. (at) J. (bt) tdt = ^r^f 'm />xp (- |.) ei
(\ab}pl)v ( aa + &a\ f* fab cob 6
(„ +1)r(i)cip ( T^) J M *p' )sin
If we expand the exponential under the integral sign, we find that
A) J o exp (- jW) Jv (at) J? (bt) tdt = A. exp (- -1^9 ) /„ (^) .
This formula is valid if R (v) > — 1 and | arg p | < ^v.
Like the result of § 13'3, thia equation m duo to Weber, Journal filr Math. lxix. A868),
p. 228; Weber gave a different proof of it, as also did Hankcl, Math. Ann. vm. A875),
pp. 469—470. The proof given here is duo to Gogenbaucr, Wiener Sitzimgxberichte, lxxii.
B), A876), p. 347. Other investigations are duo to Sonino, Math. Ann. xvr. A880), p. 40;
Sommerfeld, Konigsberg Dissertation, 1891; Macdonald, Proc. London Math. Soc. xxxv.
A903), p. 438; and Cai'ller, Mem. de la Soc. Phys. de Geneve, xxxiv. A902—1905), p. 331.
Some physical applications are due to Carslaw, Proc. London Math. Soc. B), vm. A910),
pp. 365—374.
396 THEORY OF BESSEL FUNCTIONS [CHAP. XIII
13*32. Generalisations- of Weber's second exponential integral.
When the Bessel functions in integrals of the type just considered are
not of the same order, it is usually impossible to express the result in any
simple form. The only method of dealing with the most general integral
f * J* (at) Jv (bt) exp (- pH*) t*-'1 dt
Jo
is to substitute the series of § 11 6 for the product of Bessel functions and
integrate term-by-term, but it seems unnecessary to give the result here.
In the special case in which \ = v — jn, Macdonald* has shewn that the integral
is equal to
aaY~v ft" ,,„,,/,. ,4.,/jr fab sin 0\ ( 62+ a2sin20\ JQ
-^_i cos2**-2"-1 6 sinv+a 6IV o . exp -r- dd,
p2V (fi - v) J n V 2pJ j r V 4p2 /
by a transformation based on the results of §§ 12'11, 13*7.
An exceptional case occurs when a — b ; if R (\+ fi + y) > 0, we then have
(at) exp (- ft')«- dt = ^,-
by using the expansion of § 5 41. Some special cases of this formula have
been investigated by Gegenbauerf.
13*33. Struve's integral involving products of Bessel functions.
It will now be shewn that, when R (yu, + v) > 0, then
Jo
,
r
This result was pbtained by Struve, Mem. de VAcad. Imp. des Sci. de St Pitersbourg, G)
xxx. A882), p. 91, in the special case ^i = v = l; the expression on the right is theu equal
to 4/Cir).
In evaluating the integral it is first convenient to suppose that R (/*) and
R (v) both exceed \. It then follows from § 3-3 G) that
f00 /¦*"¦ /^""sin (t sin 0) sin (i sin <?>) „ „ ,, , ,. • ^ • , 7/1 7, 7,
—^ i i zl cosn-n.-a ^ cos2p <f> sin 8 sin cj)ddd<pdt.
J 0 J 0 J 0 t2
* Proc. Lontioji il/atA. Soc. xxxv. A903), p. 440.
t Wiener Sitzungsberichte, lxxxviii. A884), pp. 999—1000.
13*32,13-33] INFINITE INTEGRALS 397
In view of the fact that ?"~2 sin it sin 6) sin (t sin <?) does not exceed numeri-
numerically the smaller of 1/t- and sin 6 sin <f>, the repeated integral converges
absolutely, and the order of the integrations may be changed.
Since *
I0 sin (t sin 0) sin (t sin <?•) , _ Utt sin 6, @ ^ <?)
Jo t (?7r sm<p, (a ^ <p)
we find that the triple integral is equal to
Att I I cos2'4 0 cos2" 6 sin2 0 sin 6d6dd>
J o J o
-r- ^tt I I cos2* 6 cos2" </> sin 6 sin2 <?rf<jf>dd.
J 0 J 0
But, by a partial integration, we have
fjir ( /•* )
Bi/ - 1) cos2"-2 6 sin </> cos2* ^ sin2 0rf^^ <i<f>
Jo (Jo J
= - cos2" $ I cos2* 6 sin2 6d0\ + j cos2" </>. cos2* </> sin2 <6d0
L Jo Jo J o
The other integral is evaluated in the same manner, and so we have
- J, (t\ jv (t) r (jl + v -1) r (•]) {B/i -1) + B* -1)}
o P+* 2^" V(jj.+ v + i) V (jl + i) r (i; + *) '
whence the result stated is evident. The extension over the range of values
of ft and v for which merely R (jn + v) > 0 is obtained by the theory of analytic
continuation.
It may be shewn in a wimilar manner that, when R (p + v) is positive, then nlwo
B) fH,(QH,(Qit.
Jo t^v 2^
This result was also obtained by Struve (ibid. p. 104) in the case /*¦=»< = 1.
By using § 10*45 we find that, when R (/*) and R (v) exceed \,
J o <*+"
B/*-l)Bv-l) I" fiir /"i7r {I-cok (< sin ^)} {1 - eon (< win </>))
2f*-t-"-;J7rp (p+^Y (y-\-\) J 0 Jo Jo t'1
X cos2* 5 cos'2"-'2 0 sin ^ sin <jid8d<fidt.
Now, if a and $ are positive, it appears from a consideration of
—- dz
z*
This result is easily proved by contour integration.
398 THBOBY OF BESSEL FUNCTIONS [CHAP. XIII
round a contour coasting of the real axis and a large semicircle above it, that
A - cos (ami- cos Q8Q> fff_ f00 sin (at) sm (fit) d(
f
Jo
Hence the triple integral under consideration is equal to the triple integral evaluated in
proving A), and consequently B) is established in the same way as A).
The reader will prove in like manner that, if R ¦» and R (v) both exceed \, then
r
and this may be extended over the range of values of /i and v for which R(v)>\ and
fl (/*+»)> 1.
The integrals Jq — ^+7+2~ *> Jo "~>+v+i at
may he evaluated in a similar manner, but the results are of no great interest*.
13-4. The discontinuous integral of "Weber and Schaflieitlin.
The integral
J,(at)Jv(bt)
"&-' " '
in which a and b are supposed to be positive to secure convergence at the
upper limit, was investigated by Weber, Journal fur Math. lxxv. A873),
pp. 75—80, in several special cases, namely,
(i) X = /u = 0, i/=l, (ii) \ = -?, /* = 0, v=±\.
The integral was evaluated, for all values of X, /x and v for which it is convergent, by
Soninet, Math. Ann. xvi. A880), pp. 51—52; but he did not examine the integral in very
great detail, nor did he lay any stress on the discontinuities which occur when a and b
become equal. Some years later the integral was investigated very thoroughly by Schaf-
heitlin %, but his preliminary analysis rests to a somewhat undue extent on the theory of
linear differential equations.
The special case iu which X=0 was discussed in 1895 by Gubler$ who used a very
elegant transformation of contour integrals ; unfortunately, however, it seems impossible
to adapt fiubler's analysis to the more general case in which X =? 0. The analysis in the
special case will be given subsequently (§ 13*44).
* Some related integrals have been evaluated by Siemoa, Programm, Luisemchule, Berlin,
1890 [Jahrbuch ilber die Fortschritte der Math. 1890, p. 341].
t See also § 13-43 in connexion with the researches of Gegenbauer, Wiener Sitzungsberichte,
lxxsviii. B), A884), pp. 990—991.
+ Math. Ann. xxx. A887), pp. 161—178. The question of priority is discussed by Sonine,
Math. Ann. xxx. A887), pp. 582—583, and by Schafheitlin, Math. Ann. xxxi. A888), p. 156.
§ Math. Ann. xlviii. A897), pp. 37—48. See also Graf and Gubler, Einleltung in die Theorie
der BesseVschen Funktionen, n. (Bern, 1900), pp. 136 148.
13*4] INFINITE INTEGRALS 399
The first investigation which we shall give is based on the results of § 13'2.
The conditions for convergence are*
fR (fi + v + 1) > R (\) > - 1, )
\R(fjL+v+l)>R(\)>0> (a = b)
it being supposed, as already stated, that a and b are positive.
We shall first suppose that the former conditions are satisfied, and we
shall also take b < a. The analysis is greatly shortened by choosing new
constants a, /3, 7 defined by the equations
{2a =
{
7 = v + 1, [v - 7 — 1.
It will be supposed that these relations hold down to the end of § 13-41.
It is known that
J **¦
since the integral on fcho loft is convergent; now, when c has any assigned
positive value, the integral on the right is convergent for complex values of b;
we replace 6 by z and the. resulting integral is an analytic function of z when
R (e) > 0 and \I(z)\< c.
Now e~u ——J dt
U-o
tm-\ ja I /J i -jm-
m-0 ">¦ 1 Ky+'H
provided thatf
th-O '///J T G+ 7M) Jo ' ^V
is absolutely convergent; and it is vaxy to shew that this is the case when
z\<c.
Hence, when j z \ < c,
r _(, Ja-p (at) ,/7_, (zt) ... _ « (-)'" (k) ^-'"-1 (hiY -i' VBa 4- 2///)
I $ ' ,. ¦ (tit ~~ *-rf III/ ' j •' "\J I1 /3 1 \
x .7'1! (a + 7n, I- — /3 — hi. ; a — C + 1; .,
\ it' "T" C
* It follows from the asymptotic exuanuiunH of the Hokhc.1 functions that the conditions
are sufficient to secure convergence when a — b, provided that fi -v in an odd integer.
t Cf. Bromwich, Theory of I»finite Series, § 17(J.
400 THEOBY OF BESSEL FUNCTIONS [CHAP. XIH
and the hypergeometric function on the right may be replaced by*
Now the moduli of the terms in the expansion of
9Jl1(« + OT,i-/Q-m; \\ as)
do not exceed in absolute value the alternate terms in the expansion of
A — \Jx)~A~%m, where A is the greater of | 2a | and | 2/3 — 11; and, similarly, the
moduli of the terms in.the expansion of
aFl(a+m + ^, l-/8-»i; f; x)
do not exceed in absolute value the alternate terms in the expansion of
(i - v#)~'1~2w~7Vtf.
Hence the terms in the infinite series which has been obtained do not
exceed in absolute value the terms of the series
where % = c2/(a2 + c2). But this last series is absolutely convergent when
\z\< \l(a? + c2) — c, and it represents an analytic function of z in this domain.
Hence, by the general theory of analytic continuation,
b « + 2m)
o m! f (y + m)(a2 + c2)a+w r(a- 0 +1)
\ a ¦+¦ c /
provided that z satisfies the three conditions
Now take 0 to be a positive number so small that
6<V(a2+C2)-G,
and take 0 < c $ G, so that also
6<v/(»2 + c2)-c.
* Gf. Forsyth, Treatise on Differential Equations, A914), § 127.
13*4] INFINITE INTEGRALS 401
Then in the last integral formula we may take z = b, and when this has been
done, if we use fonctions majorantes just as before, we find that the resulting
series has its terms less than the terms of an absolutely convergent series
! f G + m) (a-+ C*)a+TO _ (
r (-
where X = Ci/(a* + C*).
Hence, by the test of Weierstrass, the original series converges uniformly
with respect to c when 0 -g c $ C, and therefore the limit of the series when
c -*¦ 0 is the same as the value of the series when c = 0.
We have therefore proved that
c + oJo
and therefore
- (_)m bv+am-i r Ba + 2m.) T (I)
= z
TO=0 ml r G + m) 2--"+Y+awi-1 a,a+^ ^m V A - ^ - -m) T (a + m + |;
It has therefore been shewn that
Jo
that is to say
f/M + v-X+1 V-X-/J.+ 1 b'\
provided that 0 < b < a, and that the integral is convergent. This is the result
obtained by Sonine and Schafheitlin.
If we interchange a and b, and also /u, and v, throughout th/? work, we find
that, when 0 < a < b and the integral is convergent, then
C) ,o ¦ #—„¦ "—zt—n^-mviv-ayria-,
x J?; (a, a -7 +1; a - /3 + 1; |.) .
W. B. F.
26
402 THEORY OF BESSEL FUNCTIONS [CHAP. XHI
Now it so happens that the expressions on the right in A) and C) are not
the analytic continuations of the same function. There is consequently a
discontinuity in the formula when a = b; and it will be necessary to examine
this phenomenon in some detail.
13*41. Tiie critical case of the Weber-Schafheitlin integral.
In the case of the integral now under consideration, when a = b, we have,
as before,
f- J,(at)J,{id) dt_ lim rc-etJ»{at)Jv(at) ^
Jo t c-++oio t
assuming that R (n + v +1) > R (A.) > 0, to secure convergence.
Now consider
tJa-fi
e
where z is a complex variable with R (z) positive.
When R (z) > 2a we may expand the integrand in ascending powers of a
and integrate term-by-term, this procedure being justified by the fact that
the resulting series is convergent.
We thus get, by using § 5'41,
2m) ,
o ty a p
00 I
= S
M-oJ
o m! r(a-/8 + m + 1) TG+ wi)T (a-/8 +7 +m)
(~)w (lay-^^771-1 T Ba + 2m) T (a - /3 + 7 + 2m)
Now the integral on the left is an analytic function of z when R (z) > 0,
and so its value, when z has the small positive value c, is the analytic con-
continuation of the series on the right.
But, by Barnes' theory *, the series on the right and its analytic continua-
continuations may be represented by the integral
27riJ_oci^+t«r(a-/y + s + l)rG + s)r(a-/3 + 7+^ C S) *'
and this integral represents a function of z which is analytic when | arg z \ < ir.
It is supposed -that the contour consists of the imaginary axis with loops to
ensure that the poles of V (— s) lie on the right of the contour, while the poles
of T Ba + 2s) and of T (a - /3 + 7 + 2s) lie on the left of the contour.
When \z \ < 2a we may evaluate the integral by modifying the contour so
as to enclose the poles on the left of the contour and evaluating the residues
* Proc. London Math. Soc. B) v. A9o/), pp. 59—118. See also §§ 6'5, 6-51 supra.
13'41] INFINITE INTEGRALS 403
at them. The sum of these residues forms two convergent series proceeding
in ascending powers of z; hence, when R (z) > 0 and | z \ < 2a,
™-1s»" T G - a - g -m)T(ct+ \
2 mt0 ml T A - 0 - hjn) V G - a - ?/H) T G - ? - ??u)
1 » (-)m (|o)-«-' ^-q-3+m r (a + ? - 7 - w) r (^a + J7 - jff +
Now R G — a — /3) > 0, and so, when we make 2 assume the positive value
c and then make c-*-0, we deduce that
fV^(ot)^(at) , (la)*—*-1 rG -0-/8)
v ; J ~" ^-^ 2r(i4)rGa)rG
provided that R (a) > 0, R G - a - ft) > 0.
From the Gaussian formula for J^or, /3; 7; 1);there is therefore no discontinuity
in the value of the integral, though there is a discontinuity in the formula which
expresses that value as b increases through the. value a.
The result may be written in the alternative form
2P (.
provided that R (n + v + 1) > R (X) > 0.
If /I — v is an odd integer the integral converges when 0 > R (A.) > — 1 ;
this case next demands attention.
We shall make a change in notation by writing a + p and a — p— 1 in
place of/a and v in the preceding analysis ; if R(\)> 0, we then find that
e~zt
Jo
|ar+M- r Bot+ 2n) V Ba + 2,s- - X)
-A r (a + p + s + 1) P (a -p + s) T Ba + s) ( <S'} S>
w f (- X- m) V(ct
2 nZi m! r (p-
2G—2
404 THBOBY OF BESSEL FUNCTIONS [CHAP. XIII
and hence
unless X = 0. This should be compared with the more general formulae
obtained from § 13'4, namely that, when b < a,
J ^
Jo
tK
and, when & > a,
E)
Since X ^ 0, the functions on the right in D) and E) do not tend to limits
when a -*- b.
On the other hand, when X is zero, the contour integral becomes
J_ f "* da)*"*2*-1 {r Ba + 2^)}a r (- s)
2iri J -ooi 22a+2* r (a + p + s +1) T (a - p + s) T Ba + s) '
and the residue at s = — a is (—)i3/Ba).
It follows that
F) Ja+P(at) Ja-^-a(&«) dt=\, , f(9 ,
J 0 V~V/\za7>
according as b < a, 6 = a, b > a. Since
it is evident that ?/ie yaZue of the integral when b —a is the mean of its limits
when b = a - 0 and b = a + 0.
The result of taking X —1 in B) is
/\ [°° r i ^ r i *\<h 2 sini(j/-u)»r
G) I Jn(at)Jv{at) — = ^—p—,
» Jo t ir v* — n*
which is also easily obtained by inserting, limits in § 5'11 A3); this formula has been
discussed in great detail by Kapteyn, Proc. Section of Sci., K. Akad. van Wet. te
Amsterdam, iv. A902), pp. 102—103; Archives N&rlandaises, B) vi. A901), pp. 103—
116.
13*42]
INFINITE INTEGRALS
405
13*42. Special cases of the discontinuous integral.
Numerous special cases of interest are obtained by giving special values
to the constants X, //,, v in the preceding analysis. To save repetition, when
three values are given for an integral, the first is its value for b < a, the second
for b - a, and the third for b > a ; when two values only are given, the first is
the value for b^a, the second for b^a; and the values are correct for all
values of the constants which make the integrals convergent.
The following are the most important special cases*:
A) ' — rl+— ) J
B)
C)
sin bt^
Olt
(at) cos bt
r00
D) JM (aO sin bt. dt =
Jo
-2]
cos (/x arc sin (b/<i)}
fM Hill hfJ-TT
Special cases of preceding results are
F)
r r
Jo (at) sin bt .dt= ¦
Jo
f
Jo
Jo (at) cos bt. dt =
0,
0.
These two formulae, which wore given by Wolmrt, Journal fiir Math. i,xxv. A873),
p. 77, are known as Weber's discontinuous factors; they arc jiSHoei.-itcd with the problom of
determining the potential of an electrified circular disc];.
* Numerous other speoial cases are given by Nielsen, Ann. <U Mat, C) xiv. A908), pp. 82—90.
The integrals in D) and E) diverge for certain values of fi when a = I».
t The former was known to Stokes many years earlier, and was, in fact, set by him as a
Smith's prize examination question in Feb. 1853. [Muth. ahd fhys. Papers, v. A905), p. 319.]
JCf. Gallop, Quarterly Journal, xxi. A880), pp. 230—231.
406 THEORY OP BBSSEL FUNCTIONS [CHAP. XIII
Another special formula is ^
(o;
and if we put /*- 1, we obtain Weber's result (ibid., p. 80),
[l/b.
The result of putting ,-* - (8) « known as i)^^ **«*««<< jtotor; see tho
article by Voss, Encyclopadie der Math. Wm. n. A), A916), p. 109.
Some other specfal formulae have been found useful in the theory of Founer senes by
W H Young, Ldpdger Berichte, Lxm. A911), pp. 369—387.
'Another method of evaluating E) has been given by Hopf and Sommerfeld, Arc/uv der
Math, vmd Phy*. C) xvnr. A911), pp. 1-16.
A consequence of formula A) must be noted. When , > 0, we have, by § oT»l (o),
«(*)
0
= 1,
and so
A0) W*)I<1, I^hW
provided only that v be positive; this is an interesting generalisation of Hansen's inequality
(§ 2-5) which was discovered by Lommel, Miinchener Abk. xv. A886), pp. 548—fL9.
The reader may find it interesting to deduce Bateman's integral *,
/no @
A1)
from the Weber-Schafheitlin theorem.
13*43. Qegenbauer's investigation of the Weber-Schafheitlin integral.
In the special case in which the Bessel functions are of the same order,
Gegenbauerf found that by his method Weber's integral could be evaluated
in a simple manner.
If R Bv + 1) > R (X> > R (v + ?) we have
J o
2«6 cos
sin
2^ T(v +1) r (i) r (|X + ^) J0 (aa + 62 - 2a& eos /)
* Metienger, xu, A912), p. 101; for a proof of the formula by another method, see Hardy,
Messenger, xui. A913), pp. 92—93.
t Wiener Sitzungsberichte, lxxxviii. B), A884), p. 991.
13-43] INFINITE INTEGRALS 407
by § 13*22. When b< a, the expression on the right is
Now from the recurrence formulae
J* {A -z>)-i»Cn»-(z)} = (n + 2
^ {A -
we see that
(n + l)p (l
= (n + 2^- 2i/ - 1) f 2 A - a8)'-*
i -l
so that
I
jo
(cos *>sin
By+n+i)grny Jo
Hence it follows that
and this agrees with the result of § 13.
The method given here is substantially the same as Gegenbauer's; but
he used slightly more complicated analysis in order to avoid the necessity of
apjjealiiig to the theory of analytic continuation to establish the result over
the more extended range R Bv + 1) > R(\) > — 1.
By expanding the finite integral in powers of cos </>, we obtain the formula
dt - (abYr(v
A) | Jv(at)Jv ^2,{a, + lfr
+ 1 - \ 2v f 3 - X
which is valid whether a > b or a < b. This result was given by Gegenb'auer,
and with this form of the result the discontinuity is masked.
The reader will find it interesting to examine the critical case obtained
by putting b = a in the finite integral.
408 THEORY OF BESSEL f "UNCTIONS [CHAP. XIII
13*44. Gubler's investigation of the Weber-Schafheitlin integral.
The integral
I J,,{at)Jv{bt)dt
Jo
will now be investigated by the method due to Gubler*. It is convenient,
first bo consider the more general integral
.' 0 tK
even though this integral cannot be evaluated in a simple manner by Gubler's
methods. It is first supposed that R(v) >0, R(X) >\, R(/x~\)>—l; and,
as usual, a and b are positive, and a > b.
From the generalisation of Bessel's integral, given by § 6*2 B), it is evident
that the integral is equal to
o r@+) ( / i\)
- s-'-^exp \lbt\z~ - \\dzdt.
J -00 ( \ ZJ)
We take the contour as shewn in Fig. 29 to meet the circle i z \ = 1 and the
Fig. 29.
line R(z), = 0 only at z — ± i; and then, for all the values of z and t under
consideration,
and the repeated integral converges absolutely, since
| z~v~x dz |
is convergent. The order of the integrations may therefore be changed, and
we> have
Jo ^ 2inJ .oo Jo tK
If we write
* Math. Ann. XLvra. A897), pp. 37—48.
13-44] INFINITE INTEGRALS 409
and suppose that that value of ? is taken for which | ? | ^ 1, we have, hy § 13,
Jo ^
•<"+»
i + l; F+>)
by Rummer's transformation*.
Next consider the path described by ? when 2 describes its contour. Since
the value of ? with the greater modulus is chosen, the path is the curve on
the right of the circle in Fig. 29; and the curve is irreducible because different
branches of z, qua function of ?, are taken on the different parts of it. The
curve meets the unit circle only at eliu>, where a> is the acute angle for which
6 = ttsin«u.
Now both the original integral and the final contour integral are analytic
functions of X when R (X) > — 1, so long as a ± b. Hence we may takef X =0,
provided that R (/a) > — 1; and then we have?
Next write ?= zr and then
^n _ In + a . , _ t (In + a)
~ t (fir -+- 6)' (ir + b '
and the t contour is that shewn in Fig. SO; it sl.arts from — b/u, encircles the
origin clockwise, and returns to —b/n; where Lhe contour crosses the positive
half of the real axis, we have argr = 0.
Q. dz _ 1 adr
s A + f8) 2 t{I>t + a)
we find (on reversing the direction of the contour) that
JM (at) Jv (bt) dt = o . tH^-m-d (/>t + (,.)-i(H-M+D (ar + 6I <"+"-¦> dr
J 0 ^7I"i J -/>/«
„ w
a-
* Journal far Math. xv. A88G), p. 7H, formula E7). See also Barnes, Quarterly Journal, xxxix.
A908), pp. 115—119.
t If \=jfcO, the bypergoometriu function does not in general reduce to an elementary function,
and the analysis becomes intractable.
m THEORY OF BESSEL FUNCTIONS [CHAP. XIII
If we expand in ascending powers of b>/a> and substitute the values of the
Euler-Pochhammer integrals, then Gubler's result
\ 2 2
is manifest.
Fig. 30.
13*45. A modification of the Weber-Schafheitlin integral.
The integral
which converges if R (a) > 11 (b) j and R (v+ 1 - X) > | R (fi) |, is expressible in
terms of hypergeometric functions, like the Weber-Schafheitlin integral, but
unlike that integral it has no discontinuity when a = b.
To evaluate it, expand Jv (bt) in powers of b, assuming temporarily that
i b j < j a i in order that the result of term-by-term integration may be a
convergent series. By using § 131 (8) it is found that
i/-X-
and, in particular,
B) f K,(at)Jr(bt)*+**dt =
Jo
a-
(aa + bty+'+1
provided that JB (v +1) > | R Qj) | and iE (a) > 11 (&) |.
Formula A) was given by Heaviside* when p » v = 0 and X is 0 and - 1.
* Electromagnetic Theory, in. (London, 1912), pp. 249, 268, 275.
13-45,13-46] INFINITE INTEGRALS 411
13'46. Generalisations of the Weber-Sclwfheitlin integral.
To obtain the values of integrals containing three Bessel functions under
the integral sign, take the integral
/*oo T /™f\ T /hj.\
I U n^Clbj d v[Ol) j
Jo Jk dt>
replace 6 by ^(b* + c" — 26c cos <p), where b and c are positive, multiply by
sin2" <?/F2 + c2 - 26c cos </>)*" and integrate. It is thus found that
f» ,/M(at) Jv(bt) Jv(ct) , _ (\bc)v /"- r*/^ (at) Jv (tsrt) . . ,J±J±
Jo **+"" r(y + j)r(i)J0 Jo—-;?--*nrmte>
where tsr — VF2 + c2 — 26c cos ^>); and the integral on the right is absolutely
convergent if
R (v) > - |, R (fi + v + 2) > R (X + 1) > 0.
Change the order of the integrations on the right; then the result of the
integration with respect to t is an elementary function of -or if X -t- v + 1 = ± fi,
by the formulae
It follows that
A) r ,L (at) Jv (bt) Jv (ct) t1-* dt
J<>
l)T(i) /> - *" -
in which the value of ^1 is
6a + c2 - ft2
0, arc cos _r , tt
according as a2 is less than, between, or greater than the two numbers
provided that both R ({/,) and R (v) exceed — \-
In particular
B) /; ./,+1 (at) J. (U) J. (ct) * = .--pig--^^ /; sin
Multiply by av+[ and differentiate under the integral sign with respect to
a\ and we then obtain the interesting result that, if R{v) > — I,
C) | M)MU)JW
when «, 6, c are the sides of a triangle of area A; but if a, b, c are not sides
of a triangle, the integral is zero.
This formula in due to Sonine, Math. Ann. xvi. A880), p. 46; other aspects of it have
been investigated by Dougall, Proc. Edinlmrgh Math. Soc. xxxvu. A919), pp. 33—47.
412 THEORY OF BESSEL FUNCTIONS [CHAP. XIII
It has been observed by Macdonald* that the integral on the left in A) is
always expressible in terms of Legendre functions. The expression may be
derived from the integral on the right in the following manner:
When a, b, c are the sides of a triangle, by the substitution
sin \j> = sin §A sin 6
we have
rA
(a2 - 6* - c- + 2be cos (fry-1 sin'2" <f> d<j>
.' o
A
= Bbcy~"-1 (cos </> - cos Ay~v~l sin2" (f>d<j>
Jo
= 2^-z»-i (bey-'-1 sin**-1 % A . I "A-sin214 sin2 0)*-* sin2" 0 cos2"-2"-16d6
Jo
and therefore, if R (/a) and R (v) exceed — \, and a, b, c are the sides of a
triangle, we have
D) J /M (at) Jv (bt) Jv (at) t^ dt - FC)'2^7'A ^(cos A ).
If, however, a2 > (b + cf, and we write
a? ~ 62 - c2 = 26c cosh ?4,
we have
(a2 - b" — c- + 2/>c cos (jb)^-"-1 sin2" 6dd>
Jo
= Bbcy-''~1 (cosh ?€ + cos ^b)'1-''-1 sin21'
(».+i)?<*)
so that, when ct2 > F + c)'J, we have
/~\ I™ t / *\ r n*\ t / 4.\*\ ,ji (&c)'*~1cosi'7r.sinh'1itp^r.i-iii/
(o) «/„(«0 /„ F«) /„(c«)i1"/1 dt =^—^ .- Q (c
Jo (j77 L ft^ "~-
In like manner, we deduce from § 13*45 B) that
F) Ck, (at) Jv(bt) Jv (ct) t^ dt = - -%J^-^^l)l*r.V Q^k; (X),
y Jo • B7r)^Fc)'i+1sin(/i, + yOr K"-i v y
where 26c X = a- + b" + c2; and in this formula a, b, c may be complex,
provided only that the four numbers
R (a ± ib ± ic)
are positive; this result is also due to Macdonald.
* Proc. London Math. Soc. B) vn. A909), pp. 142—149.
13*46] INFINITE INTEGRALS 413
[Note. The apparent discrepancy between these formulae and the formulae of Mac-
donald'.s paper is a consequence of the different definitions adopted for the function Qnm;
see § 5*71.]
Other formulae involving three Bessel functions may be obtained by taking
formula § 11'6 A), replacing z by x, multiplying by
2,
and integrating.
It is thus found that
G) Jh (x cos $ cos <t>) Jv {co sin $ sin <1>) Jp (a; cos 6) —-
J 0 *'
</> cos^ <1> sin1' </> sin"<f> cosp 6
»-o
+ p A. p X fx v _
x 2^1 ¦¦¦- a;¦¦ + n +1> .) • ~ n'> P +!; cos
x ....Pi(- w, yu- + v + n + 1; v + l\ sin'2</>)
x 9J?\(-?i, ^ + v + « + 1; v+l; sin- <J
when R(fj, + v + p + 2)> R(X)>-1
and cos d is not equal to ± cos (A> + ^f>).
Some special cases of this result have been given by Gogonbauor in a letter to Kaptcyn,
Proc. Section of Scz., K. Acad. oan Wet. te Amsterdam, iv. A902), pp. 684—f>H8.
Some extensions of formula («S) have been given recently by Nicholson*.
If (Xj, a»,... am are positive numbers arranged in descending order of magnitude
it is easy to shew that, if
•m
a, > 2 am, R(v) >—1,
then
(8)
the simplest method of establishing this result is by induction, by .substituting
Gegenbauer's formula of § 11-41 [on the assumption that R(v)> — |] for
Jv(am-xt) Jv{amt), and then changing the order of the integrations.
When al} a^,... am are such that they can be the lengths of the sides of
a polygon, the integral is intractable unless m — 3 (the case already considered),
or m = 4.
* Quarterly Journal, xlviii. A920), pp. 831—329. Some associated integrals will be discussed
in §13-48.
414 THEORY OF BBSSEL FUNCTIONS [CHAP. XIII
When Oj, a2, a3, <x4 can form the sides of a quadrilateral, we write
= IT
so that A is the area of the cyclic quadrilateral with sides ^,0^, a3, a4.
The integral can be evaluated in a simple form only* when v = 0; but
to deduce its value, it is simplest first to obtain an expression for the integral
when R(v) >\, and deduce the value for v = 0 by analytic continuation; the
value of the integral assumes different forms according asf
i.e. according as A2 ^ a! as a3 a4.
We write •or2 = a,/ + a82 — 2^ as cos <][>, and replace Jv(a2t) Jv(aAt) by
Gegenbauer's formula, so that
where the lower limit is given by ta =aa — a4 and the upper limit by w = ax + a4
or ctz + On, whichever is the smaller.
We write
so that the upper limit for # is 1 or &.j*J(a1a.,a*a4): this expression will be
called 1/Jfc.
We now carry out the process of analytic continuation (unless a, + a4=a» J- aa,
when the integrals diverge at the upper limit if v — 0), and we get
f 0Q 4
II JQ(ant)tdt
0 7V = 1
~ ~5 [K^i "t" a4' "" CT } l^3 ~ (ai "" a4/j {'SJ'2 — (ft2 ~ OaJ} f(^a "I" aaJ ~ <BJ'2t] 'WCt'or
7T .1
1 rl or 1/fc ^7^.
1 v (
7T2A ^ I
Hence
(9) n J0{ant)tdt =
.' 0 M = l
where K denotes the complete elliptic integral of the first kind, and that one
whose modulus is less than unity is to be taken.
* For other values of v it is expressible as a hypergeometric function of tliree variables,
f We still suppose that al'^a.i'^a3^ai.
13*47] INFINITE INTEGRALS 415
Nicholson has also evaluated
when R (v) > 0 and a > 0. The simplest procedure is to regard the integral as
a special case of the last, so that it is equal to
and hence*
13*47. The discontinuous integrals of Sonine and Gegenbaner.
Several discontinuous integrals, of a more general character than the Weber-
Schafheitlin type, have been investigated by Sonine I and GegenbauerJ; some
modifications of these integrals are of importance in physical problems.
The first example§ which we shall take is due to Sonine, namely
A) Jo {ti + z)h
(a < b)
@,
{If-
To secure convergence, a and b are taken to be positive and R(v)>R(fi)>~-l;
if a— b, then we take R (v) > R (p + 1) > 0. The number z is an unrestricted
complex number, and the integral reduces to a case of the Wober-Schafheitlin
integral when z is zero.
The integrals involved being absolutely convergent||, we see from § 6'2 (8)
that, if c> 0, then
Ju.ibt)' v\°' . * '' P+1dt
I I JM (bt) t^1 u~"~l exp Ua (u - -•
J 0 .' r-cot 1. V 'j
ij. I'e+ooi [^(ci1 63) M ft22~l
* An arithmetical error in Nielioleon'H work has been corrected. The result for values of B [v)
between 0 and ? is obtained by analytic continuation.
t Math. Ann. xvi. A880), p. 38 et snq.
X Wiener Sitzungsberichte, lxxxviii. A8ft4), pp. 990—1003.
§ This formula is also investigated by Cailler, Mdm. de. la Soc. de 2>'ij/». de Geneve, xxxiv.
A902—19Q5), pp. 348—349.
H The convergence is absolute only when Ji (v) --2J (m + 1)>0; for values of v not covered by
this condition, the formula is to be established by analytic continuation.
THEORY OF BESSEL FUNCTIONS [CHAP. XIII
When a < b the contour involved in the last integral may be deformed into an
indefinitely great semicircle on the right of the imaginary axis, and the
integral along this is zero; but, when a^b, we have to apply § 6'2 (8), and
then we obtain the formula stated*.
A related integral
may be evaluated in a similar manner.
We suppose that a and b are positive f, and that R (/*)> — 1; in evaluating
the integral it is convenient to suppose that \&rgz\<\tt, though we may
subsequently extend the range of values of z to \&rgz\<^7r by analytic
continuation.
From § 6-22 (8) it follows that the integral on the left of B) is equal to
Jr(bt) ^+1 u-"'1 exp [- la (u + ——)] dudt
\_ ~ \ u J^
2a
by § 62 (8); and this is the result stated.
Now make arg z -*¦ f \it. If we put z = iy, where y > 0, we find that
{<!(<*+ *))j* {J ( V('6>)) F {y V(a2
provided that B(v) <1; and it is supposed that the path of integration avoids
the singularity t—y by an indentation above the singular point, and that
interpretation is given to V(<2 - 2/2) which makes the expression positive when
t>y.
If we had put z = ~ iy, we should have had the indentation below the real
axis and the sign of i would have been changed throughout C).
In particular
where the upper or lower sign is taken according as the indentation passes
above or below the axis of y.
* For physical applications of this integral, see Lamb, Proc. London Math. Soc. B) vn. A909),
pp. 122—141.
t With certain limitations, a and b may be complex.
13-47] INFINITE INTEGRALS 417
The last formula (with the lower sign*) has been used in physical investigations by
Sommerfeld, .4?*?*. da- Phy&ik und C/iemie, D) xxvm. A909), pp. 6S2—683; see .also
Bateman, Electrical and Optical Wave-Motion (Cambridge, 1915), p. 72.
If in A) we divide by If- and make b-*-(), we obtain Sonine's formula
provided that a ^ 0 and R {\ v — \) > R (/a) > — 1; this might have been
established independently by the same method.
Similarly, from B) we have
if a> 0 and It fa) > -I.
In E) replace v by 2v, a by 2 sin 0 and integrate from 8 = 0 to 8= ^tt. It
follows that
w i U r <A* + 1) |'*' ^-^-. B« sin
,, (
this is valid when R (v - i) > R (/*) > - 1.
The integral on the right, is easily expansible in powers of z\ but the only
case of interest is when 2i< = 2/x + 3, and we then have
so that
(9) |z ^('•-^¦'^-^M^H-ca*);
and these are valid if R(v)>l. The last formula was established in a
different manner (when i'=l)by Struvef; and from it. we deduce the important
theorem that}, when v>\ and «:>0, H,,(.-/;) is positive. Struve's integral is
of considerable value in the Theory of Diffraction.
Sonic variations of Sonine's discontinuous integral arc obtainable by
multiplying by 6M-+1 and then integrating with respect to b from 0 to b.
It is thus found that
the upper limit in the last integral being b or a, whichever is the smaller.
* My UmnkH are due to I'vofi/Ksor Love for pointing (int to me the desirability of emphasizing
the ambiguity of f%'n.
+ Ann, der l'luj»ik mid Chcmie, C) xvn. A882), pp. 1010—1011.
t OF. § 10-45.
w. b. P. 27
418 THEORY OF BESSEL FUNCTIONS [CHAP. XIII
If b < a, the integral on the right seems intractable, but, when b > a, we
put u =s a sin 6 and deduce that
provided that R (v +1) > R (p) > - 1; this is one of Sonine's integrals.
If we replace a by u in A) and then take a^b and integrate with respect
to u from a to oo after dividing by uv~\ we find that, when z is restricted to be
positive,
V-* Jv^x (yz) dv
_ a1'-16* I
~ zv-*-lJo ( )
2a" &1" r°° r°°
= r^yF^ io Jo r~l v""" Jv-*~1 {vz) exp {~* (v'z + J2I dvdt
ty-y+i a"-1 b*
by § 13*3 D), and thence we see that
provided that a < 6 and it! (v -f 2) > it! (/j,) > - 1; the restriction that z is
positive may now be removed.
Formula A0), which may be written in the form
where R(v + 2)> R (/*)> 0 and b>a, has been generalised in two ways by
Gegenbauer*, by the usual methods of substituting Neumann's integral and
Gegenbauer's integral (cf. § 13'1) for the second Bessel function.
The first method gives
A3) jo
= -f !b Ju (bt) r.^^-^zx^^jjuj ji-i cos (X -
IT JO J Q
provided that b > 2a and R (v + X + f) > R (/x) > 0.
* Wiener Sitzung&herichte, lxxxviii. B), A884), pp. 1002—1003.
13-48] INFINITE INTEGRALS
If «r = V(a2 + c2 — 2ac cos <f>), the second method gives
JH (ot) '
0
/;
(a*)
if 6>a+c and
By induction it follows that, if b > Sa,
A5)
where the product applies to n values of a, and
_R (wp + In + I) > R (ft) > 0.
If the induction of the second method is uned aftor applying the first method once, we
find still fui'ther generalisations.
The special case of A5) when 2-*-0 is
A6)
JO
a vr a, \_l \v -f 1;J
this has been pointed out by Kluyver, Proc. Section of Sci., K. Akad. van Wet. te Amster-
Amsterdam, xi. A909), pp. 749—755.
13" 48. The problem of random flights.
A. problem which was propounded by Pearson * (in the case of two-dimen-
two-dimensional displacements) is as follows :
" A man starts from a point 0 and walks a distance a in a straight line ;
he then turns through any angle whatever and walks a distance a in a second
straight line. He repeats this process n times.
"I require the probability that after these n stretches he is at a distance
between r and r + Sr from his starting point, 0."
The generalised form of the problem, in which the atretches may be taken
to be unequal, say al} a2,..., an, has been solved by Kluyverf with the help of
the discontinuous integrals which were discussed in § 13-42; and subsequently
Rayleigh.]: gave the full details of the analysis of the problem (which had been
examined somewhat briefly by Kluyver), and then obtained the solution of the
corresponding problem for flights in three dimensions.
If svl is the resultant of a,, a2,..., am (m = 1,2,,.., n — 1), and if 6m is the
* Nature, lxxii. A905), pp. 294, 842 (see also p. 318); Drapers' Company Research Memoirs,
Bioraetrio Series, in. A906).
jProc. Section of Set., K. Akad. van Wet. te Atnsterdavi, vin. A900), pp. 841—850.
%Phil. Mag. F) xxxvn. A919), pp. 321—847. [Scientific Papers, vi. A920), pp. 604—626.]
27—2
420 THEORY OF BESSEL FUNCTIONS [CHAP. XIII
angle between sm and am+1, then, in the two-dimensional problem, all values of
the angle 6m between — ir and it are equally probable.
Now let P)X\r\ au a.2) ..., an) denote the probability that after u stretches
the distance from the starting point shall be less than r, so that the probability
that the distance lies between r and r + hr is
dPn(r; au a3, ...,an)gr
dv
It is then evident that
P«(r;olfat,...,aB)«-5-i— f ["" ... T id$n-lden_2...d02dei,
\&7r) J -n J -7T J -n J
where 0u d.2,..., 9n_2 assume all values between — tr and ir, while dn^ is to
assume only such values as make*
sn ^ r,
for each set of values of 8X, 62,..., 0n-z-
Now(§13-42)
and so, if this discontinuous factor is inserted in the (n — 1 )-tuple integral, the
range of values of 6n^ may be taken to be (— tt, it).
We change the order of the integrations with respect to dn^x and t, and,
remembering that
S"n =: ^ w—a T" ^"n ^®n~\ ^hi COS un~.i.
we get •
r\ I J, (rt) Jo (sn t) dt 46^ = 2-rrr \°° J, (rt) Jo (sn^t) Jo (ant) dt
J -J o Jo
by § 11-41 AG). We next make the substitution
s2,!-! = sV2 + aVi - 2s;i_2 an_! cos 0?l_2)
and perform the integration with respect to 0n_2. By repetitions of this pro-
process we deduce ultimately that
r=o n
Pn (r ; ax, a2, ..., a») = r Jj (-rt) II /0 (am<) d«,
Jo m-\
and this is Kluyver's result.
We shall now consider the corresponding problem for space of p dimensions.
In this problem it is no longer the case that all values of 8m are equally likely.
If generalised polar coordinates (in which 6m is regarded as a co-latitude) are
used, the element of generalised solid angle contains 6m only by the factor
sinl'~* 6mddvli and 8m varies from 0 to it. The symmetry with respect to the
polar axis enables us to disregard the factor depending on the longitudes.
* It is to be remembered Jiat «,„ is a function of the variables 0\, 82, ..., 0m-1.
13*4:9] INFINITE INTEGRALS 421
LfPn(r; alta2, ...,an\p) denotes the probability that the final distance is
less than-r, we deduce, as before, that
Pn(r; alta2, ...,an\p)
T rr
.' o JoJm~i
where the integration with respect to 0M_, extends over the values of 0W_]
which make sn < r.
The discontinuous factor: which we now introduce is
and then, since by § 11*41 A6),
Jo a»*P1
we infer that
Pn(r; a,, a, ...,au|p) = r
When the displacements au u,2, ..., an arc all equal to a, and n is large, we may
approximate to the value of the integral by Laplace's* process. The important
part of the integrand is the part for which t is small, and, for such values of t,
so that (§ 13-3)
Pn(r;a,a,...,a\ p) ~ p ^ J^ (^O*"-' JiP (rt) uxp ^- ^ J
This process of approximation has been carried much further by Rayleigh in
the cases p = 2, p — 3, while Pearson has published various arithmetical tables
connected with the problem.
13*49. The discontinuous integrals of Gallop and Hardy.
The integral
]dt
is convergent if a and b are positive and R (/jl + i>)> — 1; when a = b the last
condition must be replaced by Ii(/J, + v)> 0.
The special case of the integral in which /x = 0, v = ? has been investigated by Gallop,
Quarterly Journal, xxi. \188G), pp. 232—234; and the case in which a=b has been
investigated by Hardy, Proc. London Math. Soc. B) vn. A90!)), pp. 469. The integral is
obviously to be associated with the discontinuous integrals of Weber and Schafheitlin.
* La tMorie analytique des ProbabilitS* (Paris, 1812), chapter m. The process may be
recognised as a somewhat disguised form of the method of steepest descents.
422 THEORY OF BESSEL FUNCTIONS [CHAP. XIII
To evaluate the integral in the general case, the method discovered by
Hardy is effective; suppose that a^b, and at first let us take R{v)> — ¦&,
R (fi) > ^} so that Poisson's integral may be substituted for the second
Bessel function and all the integrals which will be used are absolutely con-
convergent. Write t in place of t + ?,and let z—^—Z, so that the integral to be
evaluated becomes
2 (hbY f00 [WJ (at)
f00 [WJ (at)
*JL cos Q& cos <?) cos F^cos <?) sin2" <f>dc})dt
cos* ^cos
by a special case of § 13*4 B).
This integral is expressible in a simple manner only when /* = ?, a case
considered by Gallop, or when a = 6, the case considered by Hardy.
We easily obtain Gallop's two results
A) f Sbla{* + t)J0{bt)dt = 'rrJ0{bz),
facosi*s.dM
and Hardy's formula
C) pjA<z+»»»>z^r}idt.
x -
The reader will find it interesting to obtain A) by integrating
round the contour formed by the real axis and an indefinitely great semicircle above it; it
has to be supposed that there is an indentation at — z when z is real.
The integral
f
J — c
Z -tv
has also been considered by Gallop. To evaluate it, we observe that
z+t'
13*5] INFINITE INTEGRALS 423
and so the integral may be written in the form
I {- sin a (z +1)} Jo (bt) dt+ f sin a(z + t) JQ (bt) dt
J -oo JO
Jo
r oo fafa0
= 2 cos az sin at Ja (bt) dt + z\ cos w (# +1) JQ (bt) dtdu
Jo . 0 .' -oo
ra r<*>
— 2# cos'ii(^r + i) J0(bt)dtdu
.0 .'()
r oo /*a Too
= 2 cos ttz sin at JQ (bt) dt + Sz I I sin ^2 sin ut Jo (bt) dt du.
.' o J o J o
o J o J o
Hence, when a > 6,
sin B& cosh 0) &$>
V(«-6) Jo
but, when a < 6,
i, \f(u> -b*)
are cosh
r
J
13*5. Definite integrals evaluated by contour integration.
A large number of definite integrals can be evaluated by considering
integrals of the forms
\f %;Fa) H,<» (az) dz,
f <
taken round suitable contours; it ia supi)oscd that 0 (z) is an algebraic
function, and that a is positive.
The appropriate contours aro of two types. We take the first type when
<f> (z) has no singularities except poles in the upper half-plane; the contour is
taken to be a large semicircle above the real axis with its centre at the origin,
together with that part of the real axis (indented at the origin) which joins
the ends of the semicircle.
We take the second type when 0 (z) has branch points in the upper half-
plane; the contour is derived from the first type by inserting loops starting
from and ending at the indentation, one loop passing round each branch point,
so that the integrand has no singularity inside the contour.
A more powerful method (cf. § 131) which is effective in evaluating
integrals with Bessel functions under the integral sign is to substitute for the
Bessel function one of the integrals discussed in § 6'5, and change the order of
424 THEORY OF BESSEL FUNCTIONS [CHAP. XIII
the integrations; since the integrand in §6 G) is 0 (%v~s), qua function of a?,
where $ is an arbitrarily small positive number, the double integral usually
converges absolutely when the original integral does so, and the interchange
produces no theoretical difficulties.
13*51. Hankel's integrals involving one Bessel function.
Before Hankel investigated the more abstruse integrals which will be
discussed in Chapter xiv, he evaluated a large class of definite integrals * by
considering
1 lr+HJ»{as),
(
taken round the first type of contour described in § 135. In this integral, a
is positive, m is a positive integer (zero included), r is a complex number with
positive imaginary part, and
The first inequality secures the convergence of the integral when the radius
of the indentation tends to zero; and (as a consequence of Jordan's lemma)
the second inequality ensures that the integral round the large semicircle
tends to zero as the radius tends to infinity.
The only singularity of the integrand inside the contour is the point r. It
follows that
J. p a? {?>> (ax) - e^HJ* (aa^Q) , _ 1 ffr+) z^Hu (az)dz
_1_ (A )m ;rP-2 H B (ar
It follows from § 3-62 E) that
A) jo [A + eO-*) J»(ax) +1 A -
2m.ml\rdrJ { v /J
This result can be expressed in a neater form by writing r = ik, so that
R (A?) > 0. It is thus found thatf
B) |o [cos i(p-1;OT. Jr(a«) + sin
.m\\
* Hankel's work was published posthumously, Math. Ann. vm. A875), pp. 458—461. A partial
investigation of the integral with e=n, p = 2n + 2, m=2n was given by Neumann, Theorie der
BeiseVschen Functionen (Leipzig, 1867), p. 58.
•)• The evaluation of integrals of this oharacter which contain only one of the two Bessel
functions is effected in § 13 *G.
13*51] INFINITE INTEGRALS 425
The reader should notice the following special cases of this formula:
/o\ f° t r / \ v i \i xx~vdx amKv.,u(ak)
C) I {cos vk . •/„(ax)- sm vn-. Yv(ax)}-r-r.—j^-.—r-. — * , -J-,
Jo Jl(x2 + k-)m + 1 2»l.m\ ku + m
. f^x^1 Jyjflx) dx _ «»'?"-"¦ Kv_m{ak)
W Jo (.«»+iti>)«+"»"""" 2».m!
The former is valid when - 2m - -il < R (v) < 1, and the latter when - 1< It (v) < 2?«,4-1.
For an extension of D) to the case when m in not an integer, see § 13'6 B).
The special formula
...
E)
has been pointed out by Mehler, Math. Ann. xvm. A881), p. 194, and Basset, Hydro-
Hydrodynamics, ii. (Cambridge, 1889), p. 19; while Nicholson, Quarterly Journal, xlii. A911),
p. 220, has obtained another special formula
r Y0(ax)dx_ A'0(ai)
(b} jn ~2"+F~~~' "it-" '
by a complicated transformation of repeated integrals.
Some integrals resembling those just given may be established here,
though it is most convenient to prove them without using Cauchy's theorem.
Thus, Nicholson has observed that
r J0(ax)dx _2f ft" cos (ax cos 6)
J 0 a? + k1 7T J o U) x- + k-
1 /**"¦
akcos0d6
by § 10*4 A1), provided that a and 72 (k) are both positive; so that
G)
More generally, if ii (v) > -1, we have
and since, by a special form of B),
provided that R (v) < 2 and a is positive, it follows that
/a-" f" ^ (aa?) -t- t'Hy (ax) j
— ~— / [A'+ elnri) J* {ax) + * A — evri) Hv (cw?)] ¦
426 THEORY OF BESSEL FUNCTIONS [CHAP. XIII
and so we have the formula
(8) ! [cos \im. Jv (ax) + sin \w. Hp (ax)] ^-~j^ T fk ^" ^ "L" ^^'
0
where a> 0, R(k) > 0 and - ? < R(v)< 2. The change in the order of the
integrations presents no great theoretical difficulties.
A somewhat similar integral is
xvKv (ax) dx
o x- •+¦ k*
which converges if R (v) > -f and R (a) > 0.
If we choose k so that R (k)> 0, we have, by § 616 A),
ix T(v + ^) f°° [°° Ba)vcos%u. dudx
"""TTiT Jo Jo (&
*) f" (?a)? ervl° du
= **!?L |H_,(a/c) - 7_, (ale)),
4COSV7T1 V V J
when we use § 10*41 C). Hence, when R (v) > — \,
(9) r1-^— = -. {H_,, (ak) - F
v J .o ic2 + A;2 4cosi/7Tl v y
and therefore, when 72 (v) < f,
o x2 -H A;2 a;" 4«1/+1 cos v7r l
These formulae (when v — 0) are due to Nicholson, and the last has also
been given by Heaviside.
m* • . i f00 Jv(ax) dx
The integral „ / —
5 Jo xt + fc x"
has been investigated by Gegenbauer*. To evaluate it, we suppose that
R(v)> — \ and that a and R(k) are both positive; we then have
J ^ + /g2 ^= IVi7+T) r"O)J / C0S^+°^ siQ2"^^^
and so
Jv(ax) dx
* Wiener Sitzungsberichte, lxxh. B), A876), p. 349. Gegenbauer's result is incorrect because
he omitted to insert the term - Iip (ah); and consequently the results which he deduced from his
formula are also incorrect. A similar error was made by Basset, Proc. Comb. Phil. Soc. vi. A889),
p. 11. The correct result was given by Gubler, Zurich Vierteljahnachrift, axvii. A902),
pp. 433.-424.
13*52] INFINITE INTBGEALS 427
The condition R (v) > — ? may now be replaced by the less stringent
condition R (v) > -&, by analytic continuation.
An integral which may be evaluated in the form of a aeries by this method is
J o sinh tt.v v K ' '
which is a generalisation of Neumann's integral described in § 13*2; it is supposed that
|/2(a)| + |7(&)|<*r and R(v)> -1.
By taking ¦=—.¦. I —-v— HJV (bz)
J b 2vi J sinh itz
round the contour used in this section, we find that the definite integral is id times the
sum of the residues of
sinh az TT „. ...
__ —¦ ffvM(bz)zv + l
Hinh vz
at the points i, 2i, 3i, .... It follows that
A2) f sm|iaf J tbx)as'*1da: = - 2 (-)»-in?+1 am net. Kv(nb).
The series converges rapidly if b in at all largo.
An integral expressible au a nimilar series was investigated by Rieinann, Ann. der Physik
und C/temie, B) xcv. A855), pp. 132—135.
13*52. The generalisation of Hankel's integral.
Let us next consider the integral
dz
_1_ fzP~1Hl/^(az)
This differs from Hankel's integral in containing the (complex) number fi
in place of the integer m. The conditions for convergence (with the second
type of contour specified in § 13'5) are*
The contour is chosen with a loop to exclude the point ik, as shewn in
Fig. 31, and then there are no poles inside the contour; and the integral round
the large semicircle tends to zero as the radius tends to infinity. Hence
, j
Now -1-
• As in § 18-51, we take R(k)>0.
428
THEORY OP BESSEL FUNCTIONS [CHAP. XIII
Hence, when we expand .fly11 (az) in ascending powers of z, we find that
sin V7r.
and therefore
1)
msQ m! T (v + m + 1) T (hp + \v - /x + m)
A) I [cosQ-p — |-1/ — /iOr. Jv(ax) + sin (-ij-p —?i> —^)ir. Yv{axy\j~n—^
Fig. 81.
It is natural to enquire whether the integral of this type which contains
a single Bessel function cannot be evaluated; it seems that the only effective
method of evaluating it is the method which will be explained in § 136.
13*53. HankeVs integrals involving a product of Bessel functions.
Integrals resembling those of §13*51, except that they contain a product
of Bessel functions instead of a single Bessei function, have been investigated
by Hankel* by applying Cauchy's theorem to the integral
f
in which a > b > 0, m is a positive integer, r is a complex number with a
positive imaginary part, ^ denotes any cylinder function of order /u,, and
Math. Ann. vm. A875), pp. 461—467.
13'53] INFINITE INTEGRALS 429
[When #m is a Lcssel function of the first kind, j It (fi) j may be replaced by —R(ij.) in
this inequality.]
When a = b, the presence of a non-oscillatory term* in the asymptotic ex-
expansion of the integrand shews that we must replace 2m+ 4 by 2?n + S in the
inequality in order to make the integral, when taken round a large semicircle
above the real axis, tend to zero as the radius telids to infinity.
The contour to be taken is that of §13'52; and if we proceed in the
manner of that section, we find that
Numerous special cases of this result are given by Hankel.
It must be pointed out. that, \\'hen.p = 2w, + 3 and a — b, the integral round the large
semicircle tends to a non-zero limit as tho radius tends to infinity; and, if
^ (cm) = cx //„<»> (az) + c2 //M<2> (a*),
we then obtain the new formula
1 / »/
^"'+1. m\ \rdr
The particular case of A) in which p = 2, m = 0 and V?> is a Beswel function
of the first kind deserves special mention; it is
C) J,,, {b:v) [cos l(fi-vOr.Jv (ax) + sin ^ (/a - v) ir. Yv (ax)] \ .,
-' o " •*"""~7"
= ? iri e* <"-m) wi /„ Fj-) ^o (ar)(
provided that a > b > 0 and ft (/t) > | R (v) | - 2.
If we take /a = v and A' (i») > - I, we see that
D) JA)V() , ..
V ; J :tr - '/-
according as a. 5 />.
The existence of (.he discontinuity in the expression for this integral was
pointed out by Hankel.
If we modify formula C) we see. that, if a^b> 0 and /? (k) > 0, then
r.. *r i« -a» (M [c°s 4 (/* - ^ *¦ • ^ (
J o .ir + /c
= I
* Since /7M<-» («x;) //„<" («z) ~ -'-, ci('*"I'Ori when | z | is large.
430 THEORY OP BBSSEL FUNCTIONS [CHAP. XHI
More generally, taking equation A) with ra = 0 and ^ = J^ we have
,-v)tt.Jv(ax) + sin \(p + p- v)tr. Yv(ax)]dx
0 X"
In this result replace p by p -f v, a by \J(al + ca ~ 2ac cos 0), where a ~ c> b,
multiply by sinSl'^/(a2 + ca — 2ao cos #)*", and integrate with respect to 6 from
0 to tt; we find from Gegenbauer's formula, § 11*41 A6),
G) I ^-Ti2 v —[cos?(p +/*)tt Jv(ax) + sin?(p + /xOrYv(ax)] dx
= - IM (bk) Iv (ck) Kv (ak) h>~*.
This process may be repeated as often as we please; and we find that, if
a > b + So, then
(8)
~ 1) v) 7T. F,
n Iv (cjc). Kv (ak).
l
Again, by considering
round the contour previously used, where both b and fi differ in the different
factors of the product, we obtain the slightly more general result
(9) Jo" ^mT2 [n J»{bx)] •[cos*{p + Xfl'v) v •Jv{CIX)
+ sin | (p + 2/4 - v) 7T. Yv (ax)] dx = - [II /^FA;)] /i „ (a/c) fa1
provided that a > 21R (b) \ and 72 {p + 2 (/a)] > | E (j/) |.
If p + S/x — i/ is an even integer, the integral on the left involves functions
of the first kind only; a result involving the integrals of products of functions
of the first kind of this type was given by Gegenbauer, who overlooked the
necessity for this restriction (cf. §13*51).
An extension of Hankel's results is obtained by considering
1 f
m J
2m J (f + ?»)** (z2 - r2)w+1
round the contour, where a ^ b > 0, m is a positive integer, and
It follows that
1 (AX*\ iMH+^h H
13-54]
and, in particular,
INFINITE INTEGRALS
431
a result obtained in a much more elaborate manner by Sonine, Math. Ann.
xvi. A880), pp. 56—60.
13*54. Generalisations of Nicholson's integral.
An interesting consequence of Mehler's integral of § 13'51 E) is due to
Nicholson*, namely that, when a and k are positive,
f» JQ(ax)xdx
A) Jo W
The method by which this result is obtained is as follows:
Ko (ale) Ja (ale) = r —v f--,->- ->¦¦ dp
Jo p + fC"
If00/"" P
_ _ I -j-~-T- Jo [a
7T .' 0 J o p" + A:"
^2 — 2p/«f cos
This repeated integral may be regarded aa an absolutely convergent double
integral, since the integrand is O(p~'i) when p is large. Now make a change
of origin of the polar coordinates by writing
p c<>s </> = k + r coa 6, p sin <? = r sin ^,
and we have;
fx J0{«r)rdr
J
and this is the result to be .established.
To generalise the result consider
taken round the contour shewn in Fig. 32.
It is supposed that a is positive, and, to ensure convergence,
Quarterly Journal, xlii. A1I1), p. '2'14.
432 THEOEY Or BESSEL FUNCTIONS [CHAP. XIII
It is also supposed that | arg k | < ?77% and the loops in the contour surround
the points
By analysis resembling that of § 1352, the reader will find that
~~^ dec
B) |o [cos(\p- \v- 2^)tt . Jv(ax) + sin(\p~\v-2fi)ir. Yv(ax)]
(at+W)*-
+ ^v + -^m) p+ v—4s/jb+2m
)C0S 4
p _ v _ 4^ 4. 2m
7T
If the series on the right are compared with those given in § 51, it is seen
that the former is expressible as a product of Bessel functions ifp — 2 = i/=/x + ?
or if p — 4 = v = fj, + I, while the latter is so expressible ifp— 2 = — v = /a + |-
orifp — 4 = — j/ = /x + |.
The corresponding integral which contains a single Bessel function will be
considered in § 13-6.
13'55. Sonine's integrals.
A number of definite integrals, of which special forms were given by
Sonine, Math. Ann. xvi. A880), pp. 63—66, can be evaluated by the method
of contour integration.
The most general contour integral to be taken is
2-7rt J (z + k)m+1 ^ v
round a contour consisting of the parts of the circles
I z I = 8, I z I = R,
terminated by the lines arg (— z) = + it, and the lines which join the extremities
of these circular arcs*.
It is supposed that m is an integer and k is not a negative real number.
The:nintegral round | z \ = B tends to zero as S-^0, provided that R (p) > | R (v) |,
and the integral round | z j = R tends to zero as R-*- 00 , provided that
R(p)< m + §.
By Cauchy's theorem we have
1 f g*(z"i"^) ( Vre g1^ dm
i J (z + k)™*1 ^ " ~~ m! dkm ••
* Cf. Modern Analysis, § 6*2; or § 7'4 supra.
13*55] INFINITE INTEGRALS 433
and thus we have
1 foe J(x+k\ gv-i
2ttiJo (* + A)m+l1
\ (v J-T^+l tt/" («) lSil1 (P + ") ""¦ + 2i C0S *"•" C0S P71"}
+ iF,, («;) sin (p — i/) 7r] dx.
In particular, taking m = 0, we get
1 roo ei(a;+A-) «p-i
B) ^-»//,,fl) (/„•) = - —-- - [/, (x) (sin (p + v) 7r + 2i cos vtt cos ott
7T .' () X + /C
+ i F,, (a;) sin (p — v) tt] (io,
If we con.sider the integral
1 t
we find that
\ [<a &~i[X-\rk) ,
C) /C //„<*» (k) = - 'r - - [/„ (ar) (sin (p + v)ir- 2i cos i/7r cos p7r|
— iF, (./:) sin (p — i/) 7r]
If we tako p = 1, v = 0, wo got
D) ./„(/<;)= - - >¦•- J0(.v)dx,
tr . o x -r It
/k\ \r ,i\ 2 [meoa(x + k) r .
The last two results arc due to Hotline*.
More generally, taking p = v -\- I and — | < R (i>) < |, we get
(«) M • . J,(x)dx = +-.c-¦ ~ k~{J,(k)±iYv(k)},
IT J o X + k 2t COS VTT l
a result also due to Sonine.
By writing ('°'S (;/; | h) = - -T - f sin t (x + k) dt,
J b x + k x + k Jo v
and using the formulae (fl) and G) of § 13*42, Sonine deduced from E) that
G) Ko (k) = - 2 f* Jl) (*} dx + - I^ sin (k cos 0) d0t
and hence from §§ 3T)()B), fH I B),
(8) Yn (k) = - 2 r ^n (* + *) «AO) rf* + 2 f *"sin (/l*CO8 ^ - i 'i7r)C0H n6;rW*
""".'() 7** .' 0
* See also Lerch, Monatshefte fUr Math, ttitd Phije. i. A8t>0), pp. 105—112.
W. I). V. ^
434 THEORY OF BESSEL FUNCTIONS [CHAP. XIII
13*6. A neiv method* of evaluating definite integrals.
We shall now evaluate various definite integrals by substituting for the
Bessel function, under the integral sign, the definite integral of § 6*5, and
reversing the order of the integrations.
As a first example consider the integral of Hankel's type
ax)j
o (^ + &2)"+1 '
in which it is at first supposed that
R(v)>0, RBfj, + 2)>R(p + v)>0;
and a is a real (positive) number, in order that the integral may converge.
The integral is equal tof
27rtJo
x (i«). ik^* ds
1 (/4 4- 1)
When this is evaluated (by swinging round the contour so as to enclose the
poles on the right of the contour) we find that
f." a;P~l Jv (ax) dx
' 2
4
The hypergeometric'functions on the right are reducible to Bessel functions
in certain circumstances; the former if p — v + 2 or p =¦ v 4- 2/x 4- 2, the latter
if p = 2 ± i;.
By the principle of analytic continuation A) is valid when
In particular, taking p = v+2, we find that
B) Jo (*+*y+* "FFo^Ij'"-^ }>
a formula obtained by auother method by Sonine, Math. Ann. xvi. A880), p. 50; it is
valid when
* This method is due to Lerch, Rozpravy, v. A896), no. 23 [Jahrbuch iiber die FortschritU der
Math. A896), p. 233]; he shewed that
but no other use has been made of the, method.
t The change of the order of the integrations may be justified without difficulty.
13-6]
INFINITE INTEGRALS
435
A formula of some interest is obtained by making p = 1, /j, — — |, the
hypergeometric functions then reducing to squares or products of Bessel
functions; and another such formula is found by making p — 1 — v, yu, = v — \.
It is thus deduced that (cf. § 5*41)
provided that R (v) > — 1; and that
a; B«/*-)" V(v +
./,(</&¦) (fa
provided that li (v) > ~ |.
Next consider
in which a > 0 and j arg /c j < :[ tt. It ih first, to be supposed that
The integral is equal fco
x (Jrt)
sin
x con (^-p +• j- y — yu- + \in) it
2m + 3) 1' B/x - Jp - |»/ + 2-w + 3)J '
This expanHion is a repr<isentatiion of the integral when the conditions to bo
laid on /n, v and p are
Now take the cases in which the rirnt series reduces to a product of Bessel
functions, namely
p — 2 = v = ^,+ | or p — 4< ~ v = ft + \.
By §5*41 we then obtain the formulae
a;-+»,/, (ax) dx __ (lay Vvr .
" ^~ )- r c;+1) ^(a/l) Av((d)'
Jo («
2¦.
r ^
The former of these is valid when R (»)>-%, the latter when R(v) >?,and,
in both, a > 0 and | arg k\< \ ir.
•J8 - 2
436 THEORY OF BESSEL FUNCTIONS [CHAP. XTII
Finally, as an example suggested by § 13*55, we shall consider
af~* Jv (ax) dx
./ o o + ky+i '
in which a > 0 and | arg k \ < tr. It is first to be supposed that
R(v)>0, R(/j, + l)>
The integral is equal to
T(-s) ar-HlaxY** , ,
>
(-)» {\ak)v+im V (p + v + 2m)
sin (p + v-/*)ir. (/ ) [m
_ ? (|a/g>+1~P+w r (/z + m + 1) sin ^ (p + v - ^ - m) tt
The first series reduces to Jv (ak) when /j, = 0, and the second series is then
expressible by Lommel's functions (cf. § 10'7). In particular we have
v y Jo x+k 2cosvttl v • v /J
provided that — \ < R (v) < |.
The reader will find that a large number of the integrals discussed in this
chapter may be evaluated by this method.
13*61. Integrals involving products of Bessel functions.
If an integral involves the product of two Bessel functions of the same
argument (but not necessarily of the same order), it is likely that the integral
is capable of being evaluated either by replacing the product by Neumann's
integral (§ 5'43) and using the method just described, or else by replacing the
product J^ (x) Jv (x) by
27T'tJ -
r
in which the poles of Y(—s) are on the right of the contour while those of
F (/m + v + 2,9 + 1) are on the left; this expression is easily derived from § 5'41
by using the method of obtaining §6.
The reader may find it interesting to evaluate
vp~^ ,7^ (a.v) Jv (ax) dx
by these methods. The result is a combination of two functions of the type •iF4, and the-
final element in each function is a2?2.
13*61] INFINITE INTEGRALS 437
Another integral formula, obtainable by replacing Jv (bjx) by an integral, is
A) f Z'1 J^ {ax) Jv {blx) dx
Jo
Tp + i)"t' 3 V + ' " "+1" ~~+1> 167
This is valid when a and & arc positive and
The general formula was given by Haimmanta Rao, Messenger, xlvii. A918), pp. 134
137; special cases had been given previously by Cailler, Mdnu de la Sue. de Phi/s. de Geneve,
xxxiv. A902—1905), p. 352; Bateman, Truns. Gamb. Phil. Soc. xxi. A912), pp. 185, 186;
and Hardy, who discussed the caso of functtiouH of orders + i, (sec $ 0'23).
An interesting example of an integral* which contains a product is
D* °° dx
e x-p (— if a;2) Jv (a1) Jx-V (a:) ;,'
s x"
+ &?lrh)l^2 l(lg ^ - ^ ("+1) - ^ B -")
which may bo written in the form
r°° / ¦. »\ f r / \ r / \ .l^'Hini'TT I dx
j o exp (-Fx>) \JV (,,) Jt_ (x) - ;-/7(T -~v) | r.
HID Z/7T
It is easily proved that
f °° { r r 'i'7' H'n ''
cxp (-p'*x") \JV (*¦) J,_v(x) — -
_M17(s + i)TG+ .v +i)T(iji;+«) B/>)«
= 1 ^ _ Bn + 1)!B/>)--w
~ 4. h^i »•(n"+ 1) ! T (i/ + •/* + 1) T B - ;> + w)'
and this series is an integral function of l/p.
To obtain an asymptotic r(>})n.isentation of the. integral, valid when | p J is
small and | argp |< ^ir, we observe that the last integrand has double poles
at 0 and — 1, and simple poles at - §, — 2, - |, — 3, ....
* This integral was brought to my notice by Mr 0. G. Dur.vin, who encountered it in a
problem of Diffusion of Salts in a circular cylinder of liquid.
438 THEORY OF BESSEL FUNCTIONS [CHAP. XIII
Hence we find
ds
A - 2v)sin vtt 2 » (-)nBy)nT(ln)
~2irv{l-v) P + Hr3 2»(n- 2) V (v + 1 - $n) FB~u- -|-n). (n- 2)!
and so
B) lim ^(poc)Jv{x)J,_v(x)
5-^-1- 0 L- « X
+ 2 ^
In the special case v = 0, we find that
l?(
1 -T "^^to -tt2 Bm + IJ Bm + 3). Bm + 1)!'
13. Integral representations of products of Bessel functions.
From Gugenbauer's formula of § 11 1 A6) an interesting result is obtain-
obtainable by taking the cylinder function to be of the first kind and substituting
the result of § 6*2 (8) for the function under the integral sign.
This procedure gives
= SiJ. J^.,sm *¦' expr
and if we change the order of the integrations, we find that
This result is proved when R (v) > — | and \z\< \Z\\ but the former restriction
may obviously be replaced by R (v) > — 1, and the latter may be removed on
account of the symmetry in z and Z. It is also permissible to proceed to the
limit by making | z \ -*-1 Z |.
13-7, 13*71] INFINITE INTEGRALS 439
By using the results of § 6*21 D) and E), we find in the same way that
provided that R (v) > — 1 and | z \ < | Z j.
The. formula A) was obtained by Macclonald, Proc. London Math. Sol. xxxii. A900),
pp. lf>2—155, from the theory of linear differential equations, and he deduced Gegcnbauer's
integral by reversing the uteps of the analysis whioh we have given. The formulae B) and
C) were given by Macdnnald, though they are also to be found in a modified form in
Soninc's memoir, Math. Ann. xvr. AHH0), p. Gl.
A further modification of the integrals on tlio right in B) and C) wns given by Sonine,
the object of the change1 being to remove the exponential functions.
For physical applications of those integrals, see Maedonald, Proc. London Math. Soc.
B) xiv. A01.0), pp. 410—127.
13*71. The expression of A",, (Z) Kv(z) as <ui integral.
We shall next obtain a formula, due to Macdonald*, which represents I ho.
product KV(Z)Kv{z) as an integral involving a single function of the. type
A',,, namely
A) hlf(Z)K?(z)= I exp -,- A,. .
This formula is valid for all values of v when
; arg Z \ < -rr, \ arg z \ < nr and | arg (Z + z) j < .} tt]
but it is convenient to prove it, when Z, z have positive values A", ,r, and
to extend it by the theory of analytic continuation; the formula, which is
obviously to be associated with \ 1 l'-tl (l(i), is of some importance- in dealing
with the zeros of functions of the typo K,.(z). It is possible to prove the formula
without the rather elaborate transformations used in proving § 11*41 AE);
the following proof, which differs from Macdonald's, is on the lines of § 2"(j.
By §0-22G) we have
1 ['* (<jn
X) A',, (.r) = 4 J ^ j ^ c-"(/-l-")- • (;oB • /~-ri'os'
f<-2i<r/' -.vcosh(rf ?/)-!•<¦.inIk v- f/i (UJdT.
¦ ¦ — x •' - c
If (XeT-\- xe~'r)eu be. taken as a new variable r, in the integral
| Q-XcoshG'-|-U)-xcosh(T- U) ftU>
J -it,
* Proc. London Moth. Sw. xxx. (lHi)O), pp. Ifi9—171.
440 THEOBY OF BESSEL FUNCTIONS [CHAP. XIII
dv
it becomes J^ exp ^- ^ |« +}J
and so we have
and, on performing the integration with respect to T, we at once obtain
Macdonald's theorem when, the variables X and x are positive.
13*72. Nicholsons integral representations of products.
We shall now discuss a series of integral representations of Bessel functions
which are to be associated with Neumann's integral of § 5*43.
The formulae of this type have been developed by Nicholson*, and the
two which are most easily proved are
,0O
A) Kp. (z) Kv (z) = 2 K^v Bz cosh t) cosh (fi-v)t dt
Jo
.CO
= 2 K^v Bz cosh t) cosh (p +• v) t dt,
.'0
when j arg z \ < \ir, while /a and v are nnrestricted.
To obtain these formulae we use § 6'22 E) which shews that
K^(z)Kv(z) = -\ ( e~s{cosh^+c<>8h«)cosh fdcosh vu dtdu.
The repeated integral is absolutely convergent, and it may be regarded as a
double integral. In the double integral make the transformation
t + « = 2T, t-u=W,
and it is apparent that
Kll(z)Kv(z)^l [ ^ e-^osh70oshtrCOSn/[iB1+ U)codxv(T- U)dTdU.
*> J —oo J —oo
But 2 cosh /j.{T+U) cosh v (T - U)
= cosh (fi + v) T cosh (fi-v) U+ cosh (/j, - v) T cosh (p + ;<) U
+ sinh (fx + v)T sinh (/n~v) U + sinh (/a - r) 7' sinh (yu, + jv) U.
The integrals corresponding to the last two of these four terms obviously
vanish; and, if we interchange the parametric variables T and fin the integral
corresponding to the second of the four terms, we obtain the formula
K^{z)Kv{z)^\\ [ e-a* eoshT coshercoah (H. + V)Tcosh (fx-v)UdTdU.
^J —00 J -00
If we integrate with respect to U we obtain the first form of A), and if we
integrate with respect to T we obtain the second form of A).
* Quarterly Journal, xlii. A911), pp. 220—223.
13*72, 13*73] INFINITE INTEGRALS 441
. The formula
B) JM (z) Iv {z) = - [** /,+„ Bz cos 6) cos {n-vN d0,
which is valid when 11 (/j, + v) exceeds — 1, is at once deducible from Neu-
Neumann's formula.
If we take /j, = 0 and change the sign of v, we find that
7T
C) /„ (z) Kv (*) = - I'"" Kv B» cos 0) cos vQ d0.
7T 'o
More generally, if we take /j, — ~m and then replace fi and v by m and — v,
we find that, if j 11 (v — m) j < 1, then
D) Im{z)Kv(z)= 2(^)
If we combine C) with § G'K) A) we find that
provided that — I < R(v) < i; and in particular
Jn(u)du
a result of which a more general form lias binui given in ^ 13, lurmula (^3).
13-73. Nicholson's integral* for ,// (s) + 17B).
The integral, corresponding to those just discussed, which represents
Jj(z) + Yv~ (z) is diHicult to eatahlish rigorously. It is first necessary l,o
assume that the argument is positive (~x), and it is also necessary to appeal
to Hardy'a theory of generalised integrals, or some such principle, in the course
of the proof.
Take the formula (§ (>-21)
From the manner in which the integrand tends to zero as jiuj-»-gc on
the contour, it is clear that when an exponential factor exp (— \w"\ is inserted,
the resulting integral converges uniformly with regard to \, and so it is a
continuous function of \. Uuncef
i •oo+ni
(>x]> {- Xw"\ extiifow-vio ^v/r.
|.() TTl .
- fjU
* Phil. Mag. (G) xix. (I'.)IO), p. 234; Quartcrli/ Journal, xui. A911), p. ii'21.
t Hardy, Quarterly Journal, xxxv. A5H4), pp. 22—66; Trans. Camh. Phil. Sac. xxr. (l'Jl'2),
pp. 1—48. In this integral (us distinguiRhod from tboae which follow) the sign lim is commuta-
commutative with the integral sign.
U2. THEORY OF BESSEL FUNCTIONS [CHAP. XIII
By Cauchy's theorem, the contour may be deformed into the line.
/ (u>) = |7r, so long as X has an assigned positive value; writing t + \tri for w,
we get
' ffMM (a?) = lim e—^- f° exp {- \ (t + iTrtW &°<*»M-* dt
X+0 T* J
7TI J_co
in Hardy's notation. In like manner
HJ$ (as) = - e~^- 0 I" e-«coai» u-,« ^i6>
with an implied exponential factor exp {— X,(u — \iriy).
Since the requisite convergence conditions are fulfilled when A, > 0, we may
regard the product of the two integrals
x [
(in which e^t) and e2(u) stand for the exponential factors) as a double
integral
) I ex (t) e, (u) eix^0>ih'~cosh«>-•¦«+«)(dtdu).
Wo thus find that
Tr^if,"! (a;) Hvw (x)=G I
with the implied exponential factor
exp {- A. (t + \irif — \(u — |7riJ}
Make the substitution t + u=2T,t — u*=2U and then
-Itt- {JJ(x) + F,2 (x)} = g
with an implied exponential factor
—X, J —W
exp {-
In view of the absolute convergence of the integral, it may be replaced by
the repeated integral in which the integration with respect to U is performed
first, so that
|tt2 [J* (x) + Yj- (x)} = g\ rr e2^81'rsinh l'-ivT d UdT
J 0 J - TO
with an implied exponential factor in each case equal to
exp {
13-73] INFINITE INTEGRALS 443
We first consider the integral
roo
exp {— 2X(U + l77"i'J) etosinhTsinhudU,
J —00
in which T is positive.
When T is positive, the tT-path of integration may be deformed into the
contour / ( U) ~ \ir) if we then write U- v + liri, where v is real, the integral
becomes
j exp {- 2X (v -t- TriJ} e-te»Jnh *«»»»» rfu
J -CC
= 2 exp BX7T2) I exp (~ 2Xv2) cos 47rXv. <r te8inh 2'CO9h v dv
Jo
= 2 exp BX7T2) e-to8lnh 2'coshl' dv
— 2 exp BX7T2) (I — exp(- 2Xw2) cos 47rX?;l e~txsinh rc08h vdu.
.mi
To approximate to the latter integral when X is small, we use the
inequalities
0^1— exp (— 2X?/) cos 4<7rXi>
= 1 — exj) (— 2Xwa) -|- 2 exp (— 2X?r) sin- 27tX?j *S 2X?;- + H7r"X"v'\
so that, for some value of 0 between 0 and 1,
rco
exp [~2\(U+ hirif] e2"smhT8inh/;dU
J _« "
r[a> r"
= Z exp (ZXtt") I 6 "' dv — (ZA. -\~ i>7r~X~) u v~c
L'o -'o
= 2 exp BX7r) KoBa:ainh 7') - BX + HttuX") 0 \J /v' B.-i;sinh 7')[
If we treat the integral
f " exp {- 2X (U + I tti)8} c"ateHinh '/'siTlh''<i U
J -co
in a similar manner, we find it equal to
2/fu B.;; sinh 71) - 2X0, -L^., ArM B.v si nh 2')| ,
where O^^^l, provided that T is positive.
On collecting the results and remembering l.hal. means the same thing
. 0
as lim I , we find that
= lim lim / expBX7rB)i{'0Ba;Hinh T)
- B\ + Htt^4) 6 exp B\tt<j) 1^, A^B.t-sinh T
+ lim lim f0 r/foB«sinh2')-2X6'1{^-/^B^sinhT)l
444 THEORY OF BESSEL FUNCTIONS [CHAP. XHI
Now', qua function of T,
•f|l A^ B* sinh T)\ = 0 {(log sinh T)%
[OUT Jji-o
when T is small, and so we may proceed at once to the limit by making B4-*- 0,
since the integral is convergent; and, since the integrals
f X I— K^ Bx sinh T)\ e^T dT
Jo (d/*" J^-o
are convergent, the result of making X -*-0 is
i 7T2 {Jv- (a) +17. («)} = f" iT0 Ba? sinh 7) (<r 2"T + e*vT) dT.
Jo
It is therefore proved that, when a? > 0,
J",2 (*) +17 (.r) = -o !n Z"o Ba; sinh T) cosh
7T" J
If we replace X by ^, both sides of this equation become analytic functions
of z, provided that R (z) > 0. Hence, by the theory of analytic continuation,
we have the result
A) Jw*(z) + IV (z) = -2 r Ko Bs sinh t) cosh 2vtdt,
TT Jo
provided that R (z) > 0.
Another integral formula which 'can be established by the same method* is
B) /„ (z) dI^ - Yv (z) ^ = - ? f" ^ B, sinh«) e— (ft.
To prove this formula, we first suppose that z is a positive variable (which
we replace by so), and then
= 11H »
2i( "
i r00 rM
- or-- G1 (« - * - Tri)
^7T"l j —a>J -co
= - 4-- G r r B [/" + Trt) e2tesinh rsinl1 ^ e-2"r. (dTd U)
= - 4~- <^ f °°f °° BlT+iri)e*ix8inhTsinho-e-2,tdjjdy
f (W+Tri)e~*ix8inhTsinhue^TdUdT.
J-oo
11 For the full details of the analysis, see Watson, Proc. Royal Soe. xciv. a, A918), pp. 197
202.
13-73] INFINITE INTEGRALS 445
Now, T being positive, we have
TOO
BU + Trt) exp (- 2X(U+ 17rO2} e*-VHinhTa'inh udll
. •- co
Too
= 2 (v + 7Ti) exp {- 2X (v + tti)-} e-'2xa[nh Tcosh*dv
J -00
and, since ve~ix^nhTaoiihv is an odd function of v, it may be proved that the
last integral is
2iri e-2*<rinh r
where fche constant implied in the symbol 0 (X.) is a function of T such that
its integral with respect to T from 0 to x> is convergent.
In like manner,
H [2U + TTi)exp [~2\(U+l 7rt")"] e-'M*sillh*'sillhudU
.' — 00
= 2v exp (- 2\v")e-~x*inhT™^»dv = 0.
J -00
Hence it follows thai
Jv{x) ar;("';)_ Yv{x)dJ'{x) = -
<h> up
= -|
7T.0
The extension to the casts in which the argument of the Bessel functions is
complex with a positive real part is made as in A).
It should be mentioned that formula B) is of importance in the discussion
of descriptive properties of zeros of Bessel functions.
Tho mulcr may liiul it interesting to provo that
¦¦':;'¦•» r(;)'v;
and hence that.
C) ./„'(.) ? VJ (S> - JV W "^ {S)* - -"', /"'"(^o»sh 27'- ,/-'; AV±«
Other I'onnnlfio which may he eHbililishod by the niothoils of thi.s section aro
D) ./M(-")./,W+ IV (.')}',(=)
= 4, f A'v_^(;Hinhi!)-{t'"x + l')' + "-('x"H'Kc0S(M-I')T
71" J()
thoHu are valid when R(s)>0 and | tf (M-i») |<1; thoy do not appear to have been
previously published.
446 THEORY OF BBSSBL FUNCTIONS [CHAP. XIII
13'74. Deductions from Nicholsons integrals.
Since ifo(?) is a decreasing* function of ?, it is clear from § 13-73 A) that
Jv*(as)+YS(x)
is a decreasing function of x for any real fixed value of v, when x is positive.
Since this function is approximately equal to 2/Gnc), when x is large, we
shall investigate
and prove that it is a decreasing function of x when v>\, and that it is an
increasing function of a; when v< ?.
It is clear that
Btc sinh T) + 2x sinh TKQ' Bx sinh Z^cosh 2vTdT
-9 Ko Bx sinh T) tanh Tcosh 2vT
7T I JO
K<, Bx sinh 71) cosh 2vT — -r™ {tanh Tcosh i
l_
on integrating the second term in the integral by parts. Hence
= -8-2 (*" .fiTo B« sinh 21) tanh Tcosh 2vT {tanh T - 2^ tanh 2i/T} dT.
Now XtanhA-T is an increasing function of \ when A,>0, and so the last
integrand is negative or positive according as 2v > 1 or 0 < 2v < 1; and this
establishes the result.
Next we prove that, whsn x ^ v ^ 0,
is an increasing function of x.
If we omit the positive factor S(x2 — i^)~i/7r2 from the derivate of the ex-
expression under consideration we get
{xK« Bx sinh t) + 2 (*9 - v2) sinh *. Ko' {2x sinh t)} cosh 2v< d«,
Jo
and to establish the theorem stated it is sufficient to prove that this integral
is positive.
* This is obvious from the. formula
13*74] INFINITE INTEGRALS 447
We twice integrate by parts the last portion of the second term in the
integral thus
2vl \°°sinh t Ko' Bxsinh t) cosh 2vt dt
J o
["ioo f° d
v sinh t sinh 2vtKa' Bx sinh t) \ - v I -j- [sinh tKo' Bx sinh 01 sinh 2vtdt
Jo Jo at
Too ^
= — v \ -r fsinh tK0' Bx sinh t)\ sinh 2vtdt
./ o ?W
= — v \ 2x sinh t cosh i JT0 Ba; sinh t) sinh 2^^d!^
.'o
= - a; sinh t cosh tK0 Bx sinh i) cosh 2vt
+ x I t- [sinh t cosh tf ifu Ba; sinh t)] cosh 2j;i dt
J 0 ""
- I '.[as cosh 2*^0 Ba; sinh t) + 2x" sinh «cosh2tK0' Bx sinh i)] cosh 2vt dt:
the simplification after the second step is produced by using the differential
equation
The integral under discussion consequently reduces to
[— 2a; sinh" t A",, Ba; sinh t) — 2a;2 sinh31Ko' Bx sinhi)] cosh 2vt dt
.'o
x sinh3 < ;r /o . , , .
, , 7v 0 Ba; sinh 0 cosh Ivt
coshi Jo
+ a; KQ Bx sinh t)\—2 sinh21 cosh 2i^ + ,, | . ¦' cosh 2vf [
Jo [ a< (uosh i ) J
a; Ko B.?: sinh <) [tanh2«co.sh 2i/« + 2i/ sinlr11 such i sinh 2vt] dt,
' o
and this is positive because the integrand is positive; hence the differential
coefficient of
(%*-vi)i{Jv*(x)+ F,,2 (.r) j
is positive, and the result is established.
Since the limits of both the functions
x \JS(x)+ Y/(x)\, (tf - p»)» («/,•(*)+ >?(.r)}
are 2/tt, it follows from the last two results that when x^v^l,
An elementary proof of tho last inequality (with various related inequalities) was
deduced by Sehafhcitlin, Berliner tiitzungsberichte, v. A906), p. 8E, from the formula
(of. § 5-14)
where ^ (x) s aJv (x) + b Yv (x).
THEORY OF BESSBL FUNCTIONS [CHAP. XIII
The next consequence which we shall deduce from the integrals of § 13*73
is that, when v is positive,
To obtain this result, we observe that the expression on the left may be
written in the form
— — — f0OJK'0Bv sinh T) e^vT dT
— |~1 - [V«KaBvsinh?.) dt] .
But, for each positive value of t, 2vsinh(^tfv) is a decreasing function of v,
and so, since Ka(x) is a positive decreasing function of its argument, we see that
o
o \
is a decreasing function of v, and therefore
by using the asymptotic expansions of § 8*42 ; and this establishes the result
stated.
13*75. The asymptotic expansion of Jj* (z) + Yv2 (z).
It is easy to deduce the asymptotic expansion of /v2 (z) + F,,2 (z) from
Nicholson's formula obtained in § 13'73, namely
Jv2 (z) + Yv2 (z) = —2 Kz Bz sinh t) cosh 2vtdt\
for we have, by § 7*4D),
it,, cos vk n! I (R (v) v) I
cosxfc(i»7r) Bp)!
and, when v is real and p is so large that p + \ > v, Rp lies between 0 and
13-75, 13-8] . INFINITE INTEGRALS 449
We at once deduce the asymptotic expansion
./„» (z) + IV (*) ~ -. 2 ml%'?) 2» f * K\ Bzu) tt™ d«,
¦"""iji-o (^»i)! Jo
tliat is to say, by § 13l (8),
A) ^H^)-^ 5 ll.3...Bm-n;(^;
this is proved when R(z)>0, but it may be extended over the wider range
I arg z j < 7r; and, if v is real and z is positive, and p exceeds v — \, the remainder
after p terms is of the same sign as, and numerically less than, the (p+ l)th
term.
13*8. Raman ujan's integrals.
Some extraordinary integrals have been obtained by Raman 11 j an* from an
application of Fourier's integral theoremf to Cauehy's well-known formula
which is valid if R(fx + p)> 1. The application shewn that
0, (I i'i > tt),
where t is any real number.
By expanding in ascending powers of .•/; and //, and then applying this
formula, it is seen that
^ e"(" m) ^[v[2 c°s ^ {/i
if — tt< i< 7r; for other real values of i, the integral is zero.
In particular
B)
In view of tho rcH<»irohes of iMarcli, Ann. tier Phifnih mid t'/n'inie, (-1) xxxvii. (li)lii),
pp. 29—50 and Rybczyn.ski, Ann. der P/u/sik mid C/ienuc, (¦[) xi.i. (l»13j, l>l»- 11*1—208, it
seems (juito likely that, in unite of the. erroneous character of tlin analysis of the.se: \vribern},
these integrals evaluated l>y Kamanujan may prove to be of the highest importance in the
theory of tho traiiNmiflNion of Electric. Waves.
* Quarterly Journal, xlviii. A920), pp. 2'J'i—rflO.
f Cf. Modern AnalytiK, §§ St'7, ll'l.
t Cf. Lovo, Phil. Tram, of the Royal .S'oc.ccxv. a, A915), pp. 123—12-1.
w. B. v. . 29'
CHAPTER. XIV
MULTIPLE INTEGRALS
14'1. Problems connected with multiple integrals.
The difference between the subjects of this chapter and the last is more
than one of mere degree produced by the insertion of an additional integral sign.
In Chapter xiii we were concerned with the discussion of integrals of perfectly
definite functions of the variable and of a number of auxiliary parameters; in
the integrals which are now to be discussed the functions under the integral
sign are to a greater or less extent arbitrary. Thus, in the first problem which
will be discussed, the integral involves a function which has merely to satisfy the
conditions of being a solution of a partial differential equation, and of having
continuous differential coefficients at all points of real three-dimensional space.
In subsequent problems, which are generalisations of Fourier's integral
formula, the arbitrary element has to satisfy even more general restrictions
such as having an absolutely convergent integral, and having limited total
fluctuation.
14*2. Weber's infinite integrals.
The integrals which will now be considered involve Bessel functions only
incidentally; but it seems desirable to investigate them somewhat fully
because many of the formulae of Chapter xiii may easily be derived from
them, and were, in fact, discovered by Weber as special cases of the results of
this section.
Weber's researches* are based upon a result discovered by Fourierf to the
effect that a solution of the equation of Conduction of Heat
du _ &u dhi d^u
dt ~ dx> dy3 + d?
is
~
x exp j_ (x* + F2 + Z*)\ dXdYdZ,
where CI> is an arbitrary function of its three variables.
Weber first proved that, if <$> (x, y, z) is restricted to be a solution of the
equation
* Journal fur Math, lxijc. A868), pp. 222—237.
t La Thiorie Avalytiqve de la Chaleur (Paris, 1822), § 372. The simpler equation with oaly
one terra on the right had previously been solved by Laplace, Journal de VKcole poly technique,
vm. A809), pp. 235—244.
14-1, 14*2] MULTIPLE INTEGRALS 451
then
B) u = exp (- kH) <S> (x, y, z),
provided that <I> has continuous first and second differential coefficients, and
the integral converges in such a way* that transformations to polar coordinates
are permissible.
The method by which this result is established is successful in expressing
a more general triple integral as a single integral [cf. equation D) below].
If we change to polar coordinates by writing
2ZVi = ?'sin0eos</>, 2Y Jt = r sin d sin (f>, 2Z^/t = rcosO,
we get
1 f °° f"" [n
u — j-A——i <I> (ob + r sin 9 cos 6, y -f ?• sin 6 sin (p, z + r cos 0)
{'b-TTty Jo Jo J-7T
x exp ( — v>) t2 sin 6 d<f>dOdr.
Now consider the function of r, vr (r), defined by the equation
or (r) =1 <3> (x + r sin 6 cos <t>, y + r sin 6 sin <fi, z + r cos 6) sin 6 d6d6.
JO J-7T
It is a continuous function of r, with continuous first and second differential
coefficients when r has any positive value; and the result of applying the
operator
1 d ( „ d\
r1 dr \ drj
to -ex (r) is
. 0 .' -7T {,' VI \ VI / )
We proceed to shew that the last integral is zero. If we make use of the
differential equation A), which 4> satisfies, we find that
._\ mjl 4(sin,») + i8in
7* JJ [sin0 d0 \ ad/ sin2^ Oft)
To avoid the difficulty! caused by the apparent singularity of the last inte-
integrand on the polar axis, we consider the integral taken over the surface of a
sphere with the exception of a small cap of angular radius 8 at each pole;
since the integrand on the left is bounded at the poles, the integrals over the
caps can be made arbitrarily small by taking & sufficiently small.
If we perform the integration of the second term on the right with respect
* A sufficient condition is that * should be bounded when the variables assume all real values,
infinite values of the variables being included. Cf. the corresponding two-dimensional investigation,
Modern Analysis, § 12-41.
t This difficulty was overlooked by Weber.
29—2
452 THEORY OF BESSEL FUNCTIONS [CHAP. XIV
to $, we see that its integral vanishes because 33>/9<? is supposed to be a one-
valued function of position. The first term on the right gives
sin 6 -j^- d<j>,
and this can be made arbitrarily small by taking S sufficiently small since
a$/(sin d dO)
is continuous and therefore bounded.
rr 1 d ( octar(r)\ , ,„ , ,
Hence — -=- [r- —~^ + k2w (r)
r-2 dr \ dr J v J
can be made arbitrarily small by taking 8 sufficiently small, and therefore it
is zero.
Consequently
,. . , , A sin kr 4- B cos kr
so that nr (r) — ,
r
where A and B are constants; since or (r) and its derivate are continuous for
all values of r, A and B must have the same constant values for all values
of r.
If we make r-*-Q, we see that
B ~0, A = 47r<t> (on, y, z)Jk.
Hence*
exp (" Ssin kr -rdr=exp ("kH) *(a;> y> z)>
and this establishes Weber's result.
A similar change to polar coordinates shews that, if 4> (x, y. z) is a solution
of A) of the type already considered, and if f{r) is an arbitrary continuous
function of r, then
D)
— OO .' — 00 J — 00
\ >J> f (r) sm &r. rdr.
k .'o
The reader will have no difficulty in enunciating sufficient conditions
concerning absoluteness of convergence, to make the various changes in the
* This integral is moat easily evaluated by differentiating the well-known formula
f° ( r2\
I exp( - — JcoB/cr. dr=Ay(irt)exp(-ft2t)
with respect to k.
14-3] MULTIPLE INTEGRALS 453
integrations permissible. One such set of conditions is that <t> should be
bounded as the variables tend to infinity, and that
f(r) = O(r-P), (r^O); /(r) = 0 (r-«), (r * oo ),
where p < 3, q > 1.
A somewhat simpler formula established a,t about tho same time by Weber* is that,
if u(r, 6) is a function of the polar coordinates (r, 6) which has continuous first and second
differential coefficients at all points such that O^r^a, whose value at the origin is u0,
and which is a solution of the equation
/¦t
then / ?i (r,
J -7T
when 0 < r < a. The proof of this is left to the reader.
14*3. General discussion of Neumann's integral.
The formula
A) f^udu f° P F(R, ^). Jo [u
JO J 0 J -7T
was given by Neumann in his treatisef published in 1862. In this formula,
F (R, <$?) is an arbitrary function of tho two variables (R, ct>), and fchc in-
integration over the plane of the polar coordinates G?,, <T>) i.s a double integration.
In the special case in which the arbitrary function ia independent of <L>, we
replace the double integral by a repeated integral, and then perform the in-
integration with respect to <D; the formula reduces to
B) I"" udu rV(ii) Jo (uR) Jo (ur) lidR = F(r),
Jo Jo
a result which presents a closer resemblance to Fourier's integral{' than A).
The extension of B) to functions of any order, namely
C) ["tidy, (""VCR) /,(uR) Jv (ur) RdR = F(r),
Jo Jo
was effected by Hankel§. In this result it ia apparently necessary that v^ — \,
though a modified form of the theorem (§§ 145 —14'52) is valid for all real
values of v; when v—±\, C) is actually a case of Fourier's formula.
The formulae B) and C) are, naturally, much more easy to prove than A);
and the proof of C) is of precisely the same character as that of B), the
• Math. Ann. i. A869), pp. 8—11.
t Allgemeine L'omng des Problemes ilber den sLatioiiflren Temperaturzustmul emeu homogenen
K'6rper8, welcher von zioei nichtconcetitrisciien Kageljliichen beyrenzt wird (Hallo, 1862), pp. 147—
151. Cf. Gegenbaoer, Wiener Sitziuigsberichte, xcv. B), A887), pp. 409—410.
% Cf. Modern Analysis, §9*7.
§ Math. Ann. viii. A875), pp. 476—483.
454 THEORY OF BESSEL FUNCTIONS [CHAP. XIV
arbitrariness of the order of the Bessel functions not introducing any additional
complications.
Following Hankel, many writers* describe the integrals B) and C) as
"Fourier integrals" or "Fourier-Bessel integrals."
On account of its greater simplicity, we shall give a proof of C) before
proving A); and at this stage it is convenient to give a brief account of the
researches of the various writers who have investigated the formulae.
As has already been stated, Hankel was the first writerf to give the
general formula C). He transformed the integral into
lira rRF(R)dR [ Jv{uR)Jv{ur).udu
= lim FRF(R)[RJV+1(\R) Jv(\r)-rJv+1(\r) JV(\R) -——,
A-».oo JO It" ~ 7
and then applied the second mean-value theorem to the integrand just as
in the evaluation of Dirichlet's integrals. Substantially the same proof was
given by Sheppardj. who laid stress on the important fact that the value
of the integral depends only on that part of the i2-range of integration which
is in the immediate neighbourhood of r, so that the value of the integral is
independent of the values which F(R) assumes when R is not nearly equal to r.
A different mode of proof, based on the theory of discontinuous integrals,
has been given by Sonine§, who integrated the formula (§ 13-42)
after multiplication by F(R)RdR, from 0 to oo, so as to get
r»+i f" rjv+1(Ur) Jv(uR)F(R)RdRdu = f R"
Jo Jo Jo
and then, by differentiating both sides with respect to r, formula C) is at once
obtained; but the whole of this procedure is difficult to justify.
A proof of a more directly physical character has been given by Basset||,
but, according to Gray and Mathews, it is open to various objections.
A proof depending on the theory of integral equations has been constructed
by Weyll
The extension of Hankel's formula, which is effected by replacing the
* See e.g. Orr's paper cited later in this section.
t A statement of a mode of deducing C) from A) when v is an integer was made by Weber,
Math. Ann. vi. A878), p. 149, but this was probably later than Hankel's researches, since it is
dated 1872, while Hankel's memoir is dated 1869.
X Quarterly Journal, xxm. A889), pp. 223—244. ' § Math. Ann. xvi. A880), p. 47.
|| Proc. Camb. Phil. Soc. v. A886), pp. 425—133. Sea Gray and Mathews, A Treatise on Bessel
Functions (London, 1895), pp. 80—82.
II Math. Ann. lxvi. A909), p. 324.
14*3] MULTIPLE INTEGRALS 455
Bessel functions by arbitrary cylinder functions, was obtained by Weber*, and
it will be discussed in §§ 14'5—1452.
An attempt has been made by Orf to replace the Bessel functions by any
cylinder functions, the w-path of integration being a contour which avoids the
origin; but some of the integrals used by him appear to be divergent, so it is
difficult to say to what extent his results are correct. The same criticism
applies to the discussion of Weber's problem in Nielsen's treatise. It will be
shewn (§ 14'5) that if, as Nielsen assumes, the two cylinder functions under
the integral sign are not necessarily of the same type, the repeated integral is
not, of necessity, convergent.
It should be stated that, if r be a point of discontinuity of F(R), the
expressions on the right in B) and C) must be replaced byj
l[F(r-0)+F{r+0)},
just as in Fourier's theorem.
For tho moro recent researche.s by Neumann, the reader .should consult his troati.se
Uebcr die nacli Kreis-, Kugel- and Ct/liitder-functionen fortschreitenden Entwickelwigen
(Leipzig, 1881).
Neumann's formula A) was obtained by Mehler§ as a limiting case of a
formula involving Legendre functions; in fact, it was apparently with this
object in view that ho obtained the. formula of § 5'71,
lim /*„ [cos (s//i)| =*/«(*),
but it does not seem easy to construct a rigorous proof on these lines (cf.
§144). A more direct method of proof is given in a difficult memoir by
Du Bois Reyrnond|| on the general theory of integrals resembling Fourier's
integral. The proof which we shall give subsequently (§§ 14"O et seq.) is based
on these researches.
Subsequently ErmakorHF pointed out that the formula is also derivable
from a result obtained by Du Boi.s Keymond which is the direct extension to
two variables of Fourier's theorem for one variable, namely
Ermakoff deduced the formula by changing to polar coordinates by means of
the substitution
a = u cos w, ft — u sin m,
and effecting the integration with respect to u>.
* Math. Ann. vi. A873), pp. 140—161.
t Proc. Royal Irish Acad. xxvn. a, A(JO9), pp. 205—24H.
% Tho value of the integral ab a point of rliaoonliiniiity lias been examined with some care by
Cailler, Archives des Sci. (Soc. HelvStiquc), D) xiv. A902), pp. ;J47—350.
§ Math. Ann. v. A872), pp. 135—137.
|| Math. Ann. iv. A871), pp. 3«2—390. 1f Math. Ann. v. A872), pp. 639—C40.
456 THEORY OF BESSEL FUNCTIONS [CHAP. XIV
If (r3 <?) and (R, <E>) be the polar coordinates corresponding to the Cartesian
coordinates (w, y) and (X, Y) respectively, the formal result is fairly obvious
when we replace SP (X, Y) by F(R, <t>); but the investigation by this method
is not without difficulties, since it seems to be by no means easy to prove that
the repeated integral taken over an infinite rectangle in the («, j3) plane may
be replaced by a repeated integral taken over the area of an indefinitely great
circle.
If the arbitrary function F (R, <E>) is not continuous, the factor F(r, <?)
which occurs on the right in A) must be replaced by the limit of the mean
value of F (JR, <i>) on a circle of radius 8 with centre at (r, <?) when 8 ->-0.
This was, in effect, proved by Neumann in his treatise of 1881, and the proof
will be given in §§ 14'6—143. The reader might anticipate this result from
what he knows of the theory of Fourier series.
A formula which is more recondite than C), namely
D) I fJ J^u-r)^^ F(R)dudR~F(r\
has been examined by Batcman, Proc. London Math. Soc. B) iv. A906), p. 484; cf. § 12'2.
14'4. Hankel's repeated integral.
The generalisation of Neumann's integral formula which was effected by
Hankel (cf. § 14-3) in the case of functions of a single variable, may be formally
stated as follows:
Let F (R) be an arbitrary function of the real variable R subject to the
condition that
exists and is absolutely convergent; and let the order v of the Bessel functions
be not* less than — %. Then
A) \*udu pV(fl) /„ (uR) Jv (vr) RdR = UF(r + 0) + F(r - 0)},
.' o J o
.' o J o
provided that the positive number r lies inside an interval in which F(R) has
limited total fluctuation.
The proof which we shall now give is substantially Hankel's proof, and it
is of the same general character as the proof of Fourier's theorem; it will be
set out in the same manner as the proof of Fourier's theorem given in Modern
Analysis, Chapter ix. It is first convenient to prove a number of lemmas.
* It seems not unlikely that it is sufficient for v to be greater than -1; but the proof for the
more extended range of values of v would be more difficult.
14-4, 14*41] MULTIPLE INTEGBALS 457
14#41. The analogue of the Riemann-Lebesgue lemma.
A result, which resembles the lemma of Riemann-Lebesgue* in the theory
of Fourier series, and which is required in the proof of Hankel's integral
theorem is as follows :
rb
Let~f I F(R)\/R.dR exist, and (if it is an improper integral) let it be
¦ a
absolutely convergent; and let v^ — \. Then, as X -*- oo ,
It is convenient to divide the proof into three parts; in the first part it is
assumed that F(R)\/R is bounded, and that b is finite; in the second part
the restriction that b is finite is removed; and in the third part the restriction
that F(R)*JR is bounded is also removed.
(I) Let the upper bound of \F(R)»JR\ be K. Divide the range of in-
integration (a, b) into n equal intervals by the points xu x,z, ... xn^ (xa= a,
con — b), and choose n so large that
2 ( Um - Lm) (a:m - #,H_i) < e,
in-i
where e is an arbitrarily small positive number and Ulth and Lm are the upper
and lower bounds of F(R) \/R in the ?uth interval.
Write V (It) \JR = F(Rm^) ViC-i + &>w (R), so that, when ./? lies in the with
interval, | tom (R) \ •$ Um — Lm. Now, when v^—l, both of the functions of a;,
are bounded when x >= 0, even though the integral is not convergent as x -*¦ oo .
Let A and B be the upper bounds of the moduli of these functions. It is then
clear that
! [ F(R)Jv(\R)RdR
n
m = 1
+ 2 f'" (om(R)J,(\R)^/R.dR
m~\ .' %m-\
n i F(R _ ) iJR _ I i [Xx™ I " F
2 -- , - ''l I Jv (x) ^jx. dx i + 2 I
2?
* Cf. Modern Analysis, §9-41.
t The upper limit of the integral may be iniiniko ; und a^O. Tho apparently irrelevant faotor
E preserves the analogy with § 14-3 C).
458 THEORY OF BESSEL FUNCTIONS [CHAP. XIV
By taking X sufficiently large (n remaining fixed after € has been chosen) the
last expression can be made less than 2AeJ\J\) and so the original integral
is o A/-A).
(II) If the upper limit is infinite, choose c so that
\F(R)\y/R.dR<e,
J c
and use the inequality
fWF(R)JJ\R)RdR ^ \° F(R)Jv(\R)RdRl + 4rr\F(R)\\/R-dR>
Ja Ja I V^Jc
then, proceeding as in case (I), we get
F(R)Jv(\R)RdR
J
The choice of n now depends, on € through the choice of c as well as by the
mode of subdivision of the range of integration (a, c); but the choice of n is
still independent of \ and so we can infer that the integral (with upper limit
infinite) is still o(l/*J\).
(Ill) If F(R) hJR is unbounded*, we may enclose the points at which it is
unbounded in a number p of intervals 8 such that
r .
& J 8
By applying the arguments of (I) and (II) to the parts of (a, b) outside these
intervals, we get
¦ 1 VI T>\ T f\ T>\ DJD ^ LJjft \p T" i.) it OXx€
I.' a A,* y K
where K is now the upper bound of | F (R) \ Vi2 outside the intervals 8. The
choices of both K and n now depend on e, but are still independent of \ so
that we can still infer that the integral is o (l/\/\).
14*42. The inversion of HankeVs repeated integral.
We shall next prove that, when v^ — \, and j F(R)\/R .dR exists and
Jo
is absolutely convergent, then
o Jo
= lim rF(R) \ IV, (uR) Jv {ur) udu] RdR,
A.-*-oo J 0 {J 0 )
provided that the limit on the right exists.
* Cf. Modern Analysis, § 9-41.
14*42, 14*43] MULTIPLE INTEGRALS 459
For any assigned value of \, and any arbitrary positive number e, ex
hypothesi there exists a number yS such that
where A is the constant defined in § 14*41.
If we write FB2) Jv (uR) Jv (ur) uR = <f> (R, w),
it is clear that*
\ \ <f> (R, u) du\ dR - \ 6(R, u) dR [ du
.' o (.' o J J o (.' o J
i f00 f fA ) /"A ( f° )
= \ \\ cf> (R, u) du\ dR - I 1 6(R,u)dR\du
Jn [Jo J Jo [. p )
•$ M <M#, w)|d«*[d22+ j '(/>(«, w) | dK
J/s(Jo j J o I .' /s )
r f ^ \F(R)\ JR.dRdu,
o Jp \l">"
J p .'o Vr
< e.
Since this result is true for arbitrarily small values of e, we infer that
' 0 J 0
the integral on the left existing because the integral on the right is assumed
to exist. If the integral oxi the left has a limit as X -*- oo, it is evident from
the definition of an infinite integral that
udu\ F (R) Jv (uR) Jv (ur) R dR
.' 0 •' 0
= lim ruduTF(K)Jv(uR)Jv(ur)RdR
A -* oo J 0 -' 0
= lim IV B2) \Tj, (uR) Jv {ur) udu\ RdR,
A-*x ' 0 [Jo )
() \T, () v {) \
A-*x .' 0 [Jo )
and this is the inversion formula which had to bo proved.
14'43. The relevant part of the range of integration in Hankel's repeated
integral.
Next we shall prove that, in Hankel's integral, the only part of the 22-range
of integration which contributes anything to the value of the integral is the
.part of the path in the immediate vicinity ofr, provided merely that F(R) >JR
has an absolutely convergent integral.
* The justification of the inversion of the order of integration for & finite reotangle whose sidea
are X and /3 presents no great theoretical difficulties.
THEORY OF BESSEL FUNCTIONS [CHAP. XIV
10 effect this, it is sufficient to prove that, if r is not a point of the
interval* (a, 6), then
( udu \ F (R) Jv (uR) Jv (ur) RdR = O.
Jo J a
We invert the order of the integrations, as in § 14*42, and we find that, if
the limits on the right exist,
I udu I F B2) Jv (uR) Jv (ur) RdR
J 0 J a
= lim \hF(R)\rjv('uR)Jl,(ur)ud%i\ RdR
X -* oo .' a [JO )
= lim ¦ -.-_.. . . \.BdR
A.-* oo
= lim \J, (\r) f ^
- lim \rJv+1 (Xr) f *
Since both the integrals
a .
are exhypothesi absolutely convergent, it follows from the generalised Riemann
Lebesgue lemma (§ 14*41) that the last two limits are zero; and so
F (R) Jv (uR) J, (ur)
provided that r is not such that a % r < b.
14*44. The boundedness of I Jv(uR)Jv(ur)uRhdudR.
J a JO
It will now be shewn that, <xs X -»- oo ,the repeated integral
( f V, (uR) Jv (ur) uRh dudR
J a J 0
remains bounded, provided that a and b have any (bounded) positive values. It
is permissible for a and b to be functions ofX of which one (or both) viay tend
to r as \ -*- oo.
Let us first consider the integral obtained by taking the dominant terms
of the asymptotic expansions, namely
—r / cos (uR - \vtt - W) cos (ur - Ivnr — ±ir) du dR
it \jr J a .' o 4
1 [b ("sin X B2 - r) cos {X (R + r) — vir] — cos pit] ,„
= —— I — _ djj,
it </rJal R-r R+,r J
1 f r*»->0 sin x , fA(H-f) cos (a. _ V7r\ j + ri
= —r; —~dx- i i dx + cos j/ttlog —¦— .
* It is permissible for I to be infinite.
14*44] MULTIPLE INTEGRALS 461
The first integral is bounded because I dx is convergent; and the
J -00 *"
second integral is bounded because I ^T— dx is convergent; and so
the integral now under consideration is bounded, and its limit, as X -*¦ oo , is
the limit of
-¦. I - - dx + cos vrr log ,
T \'r U \(n-r) '" ' ~
provided that this limit exists.
But we may write
Jv (uR) J,, (ur) uR- dudR
0 rb r°°
7rVt'J« Jo
— cos (k/2 — \vir — \tt) cos (ur —
I \)?iruJv (uR) Jv (ur) \/(Rr)
— cos (uR— \vrr — \ir) cos (ur — \vir — \ti)\ dudR
2 ['' fx
H T cos («jK - J-i/7r — ;}7r)cos (ur— h tt — \ir) dudR.
tt \Jr J a J o
Now, of the integrals on the right, the. first, is the integral with respect to
R of an integral (with respect to u) which converges uniformly in any positive
domain of values of R and r, and so it is a continuous (and therefore bounded)
function of /¦ when r is positive and bounded.
The third integral has been shewn to be bounded, and it converges to a
limit whenever
) sin x
[
J \
dx
'A(rt-r) *
does so.
The second integral may be written in the form
4jj/! _ \ rb /*<» r j
— ¦ —r- -f. sin (uR, — Ivtt — |7r)cos (nr— Ivir — \tt)
1
H cos (uR— \vir — l7r) sin (ur — \vn — \"tr) 4- 0 (I/2'2) dudR
ur
where ^ (A.), </>a (X) aud ^>3 (X) are functions of X and 7i! which tend uniformly
to zero as A. -*- oo .
462 THEORY OF BESSEL FUNCTIONS [CHAP. XIV
Hence, for all bounded positive values of a, b, r, the integral
[ f Jv{uR)Jv{ur)uRldwdR
Ja JO
is bounded as A. -*¦ oo ; and it converges to a limit whenever
5Ei? dx
does so.
14*45. Proof of Hankel's integral theorem.
Now that all the preliminary lemmas have been proved, the actual proof
of Hankel's theorem is quite simple.
Since F (R) has limited fluctuation in an interval of which r is an internal
point, so also has F{R) \/R; and therefore we may write
where %x (R) and ^2 (R) are monotonic (positive) increasing functions.
After choosing a positive number e arbitrarily, we choose a positive number
S so small that F(R) has limited total fluctuation in the interval (r — 8, r + 8)
and also
%1 (r + S)- %1 (r + 0)< e| %1(r-0)-%1(r-S)<|
Xa(r+S)-368(r + O)<ej ' %2 (r- 0)- x,(r- 5) < e(
If we apply the second mean-value theorem, we find that there exists a
number ? intermediate in value between 0 and 8 such that
rr+s rK
Xl{R)Jv(vR)J,{ur)u JR.dndR
= xi (r + 0) f" /, («B) J, (ur) u V^ • dudR
J r .0
i 0' ) x )
J r+f ^ 0
Since
Jo
as x __ oo , 8 remaining fixed, it follows from § 14#44 that the first term on the
right tends to a limit as X -*¦ oo while S remains fixed. And the second term
on the right does not exceed Ce in absolute value, where C is the upper bound
of the modulus of the repeated integral (cf. § 14-44<).
Hence, if
lim f f h
A-».oo J r JO
it follows that
lim I' (K
\-»-oo J r JO
exists and is equal to (?,%] (r + 0)/*Jr.
14*45] MULTIPLE INTEGRALS 463
We treat %2(J?) in a similar manner, and also apply similar reasoning to
the interval (r — 8, r); and we infer that, if
lira /' I Jv{uR)Jv(:iir)iLRhdudR = G.il»Jr)
\-*.«> J r-& .'0
rr+s r\ +
then lim F(R) Jv(uR)Jv(ur)uRdudR
\ ->. oo .' r -S J 0
exists and is equal to
ClF(r+0) + CiF{r-0).
We now have to evaluate G, and C^ By the theory of generalised
integrals*, we have
n roo rr+S ,
ip. = JAuR) Jv (ur) uR* dRdu
Vr id J r
= lim I exp(-p2?t'J)(' J,(uR)Jv(ur)ultitdRdti
ji-»o Jo -' »•
= lim *exp (- p*tts) ,/¦„ (jj^) ,/„ (ur) uR* chidR
;.-»-().'/• .0
= lim ~-i exp \ - A/2? . /„
by §13-31A).
Now, throughout the range of intugratitm,
as p + Q.
Hence (\ = lim - -- oxp \-K ' ,, [ <{R
p^.o Ip \'7r. ,. ( 4p~ j
1 rwi>
= lim —¦ I exp (-./;¦'') d.r = ^,
and similarly
• 1 f<>
C. = lim -. • exp (—./;'-) dx = A.
7,_».o vtJ -!«//>
We have therefore .shewn that
•r-l-6
.' »—6 J 0
exists and is equal to
lim /' '* PF(R).Jv(uK)'!Aitr)uRdudli
-»-oo .' r-6 JO
* Hardy, Quarterly Journal, xxxv. (li)O-l), pp. 2'2—OG. For a different method of calculating
C, and Co, se« §l-i-52.
464 THEORY OF BESSEL FUNCTIONS [CHAP. XIV
But, if this limit exists, then, by § 142,
t" udu j°° F(R) Jv (uR) Jv(ur) RdR
Jo Jo
also exists and is equal to it; and so we have proved Hankel's theorem, as
stated in § 144.
The use of generalised integrals in the proof of the theorem seems to be due to
Sommerfeld, in his Konigsberg Dissertation, 1891. For some applications of such methods
combined with the general results of this chapter to the prohlhne des moment* of Stieltjes,
see a recent paper by Hardy, Messenger, xlvii. A918), pp. 81—88.
14*46. Note on Hankel's proof of Ms theorem.
The proof given by Hankel of his formula seems to discuss two points somewhat
inadequately. The first is in the discussion of
lim I f F{R)Jv(iiR)Jv{v,i')idldudR,
a-*« J o J o
which he replaces by
lim
In order to approximate to this integral, he substitutes the first terms of the asymptotic
expansions of the Bessel functions without considering whether the integrals arising from
the second and following terms are negligible (which seems a fatal objection to the proof),
and without considering the consequences of \R vanishing at the lower limit of the path of
integration.
The second point, which is of a similar character, is in the discussion of
rr+8 r\
lim Jv{uR)Jv(ur)uRdudR;
A-».» J r+f J 0
after proving l>y the method just explained that this ifa zero if ? tends to a positive limit
and is ? if ?=0, he takes it for granted that it must be bounded if ?-*-() us A-*-oc ; and
this does not seem prima facie obvious.
14*5. Extensions of Hankel's theorem to any cylinder functions.
We shall now discuss integrals of the type
f" udu r F(R)r$v(uR) f@v {ur) RdR,
in which the order v of the unrestricted cylinder function f6"v(z) is any real*
number. The lower limits of the integrals will be specified subsequently,
since it is convenient to give them values which depend on the value of v.
For defmiteness we shaH suppose that
9ov (z) = a (cos a. Jv (z) ¦+ sin a. Yv (z)],
where a and a are constants.
* The subsequent discussion is simplified and no generality is lost by assuming that p^Q.
H-46-H-51] MULTIPLE INTEGKALS 465
The analogue of the Riemann-Lebesgue lemma (§ 14-41), namely that
f'F(R) Vv (\R) RdR = o A/V\),
J a
pro vided that f' F (R) K/R. dR
exists and is absolutely convergent, may obviously be proved by precisely the
methods of § 14-41, provided that a <: b < x , and
f« >0 if.0^<?,
\a>0 if v>\. [>
The theorem of § 14-44 has to be modified slightly in form. The modified
theorem is that the repeated integral
f /An (uR) <(K (nr) n JR. dudR
J H J T
is bounded as A.-*-oo while t remains fixed; us in §14*44, a and b may be
functions of X which have finite limits as X — dc, The number t is positive,
though it is permissible for it to be zero when Q^v^^.
Also the repeated integral and the integral
''-'"> sin.?; ,
— d.c
A(n-r) ¦*'
both converge or both oscillate as A, ¦* x,
[Note. If the two cylinder functions in the repeated integral were not of the sanift
type, i.e. if we considered the integral
/ ' ( *K ("/l>) '0"v
J a J t
it would be found that the convergence of thin integral nece.s.sitafce.s the cunveryenco. (if the,
integral
fj-r) 1 -et)H,r ,
A(«-r) •'¦'
and so, if X F — r)-*-oo aa X-*-oc , the repeated integral is divergent*.]
14-51. The extension of Hankel's theorem when i) <rv%l.
Retaining the notation of §§ 14'4—14-5, we .shall now prove the following
theorem.
Let I F(R)\/R.dR exist and be an absolutely convergent Integral, and
J o
let 0 ^ v-^l. Then
A) I" uduf* F (R) % (uR) (<$v (ur) RdR
* This point was overlooked by Nielsen, HaiuUnich tier Thcorie tier Cijlinderfunhtionen
(Leipzig, 1904), p. 865, in his exposition of Hankel's theorem.
W. B. F. 30
m THEORY OF BESSEL FUNCTIONS [CHAP. XIV
promded that the positive number r lies inside an interval in which F{R) has
limited total fluctuation.
As in 514-42, we may shew that
udu
o .'o
= lim r F (R) \ ^ <®, (uR) % (ur) uRdtt dR,
provided that the limit on the right exists.
But now we observe that
= —-— \uR <@?+l (uR) c@v (ur) - ur %Vi-i (ur) %'v (uR)
Rt _ r21_ tu x ' J
= ^__ [R %^+1 (xR) <@v (xr) - r r$v+1 (Xr) &1, (XR)']
2o-2 sin a sin (a + v-rr) R2v - r-v
I
Hence we infer that, if r is noi a point of the interval (ci, b), then
F(R) j <$v (uR) <@v {ur) uRdudR
v y 7rsmv7r J JS"r"(R2/•") v y
as X -*¦ oo ; and so the last repeated integral has a limit when X -*- oo .
Now choose an arbitrary positive number e, and then choose S so small
that F (R) has limited total fluctuation in the interval (r — 8,r+ 8) and ho that
j | F(R) - F(r + 0) | < e if r < R < r + 8,
\\F(R)-F(r-0)\<e if r-8*R<r.
Now take f"F(R) I*<@v(uR)%dv(ur)ududR,
Jo Jo
and divide the J?-path of integration into four parts, namely
@, r - 8), (r - 8, r), (r, r + 8), (r + 8, oo ).
Apply the second mean-value theorem as in § 14*45, and we find that
T F(R) f % (uR) <@v (ur)uRdudR
Jo Jo
_ 2o-2 sin a sin (a + vrr) f f r~&
+ F(r + 0) Vr. |* [^ ^ (MJ?) ^ (Ur) u&dudR
+ F(r-0)</r.tr !K <@v (UR) <®, (ur) uRUudR
J r-sJ0
U-51] MULTIPLE INTEGRALS 467
where | rj | has an upper bound which is independent of X and which is
arbitrarily small when e is arbitrarily small.
The integrals on the right converge to limits when X ->¦ oo, and so, by
making e -*¦ 0 after X -*- oo , we infer that
I" udu r F(R) K (uR) <@v (ur) RdR
Jo Jo
is convergent and equal to
) /"» R^jzf
Jo R»->r»(R«-^
/•oo fr+S
+ F(r + 0) vV. lim <@v (uR) % (ur) uRURdu
fi-*00 .'r
+ F(r -0)*Jr. lim ( Ir@v (uR) rSv (ur) uR>dRda,
«-*-() .'0 Jr-S
provided that the limits on the right exisb.
To prove that the limits exist and to evaluate them simultaneously, take
F(R) = R" when r < R < r + 8 and F(R) = 0 for all other values of R.
We thus find that
•oo [r+8
m
= lim r frl" rtfv{uRy&v(w)uRv+ldRdu,
J) J
/•oo [r+8
im <@v(uR)%
-j-lWO Jr
•provided that this repeated limit exists; and similarly
f+Uim f°° (r r&v(uR)%\(ur)uRtdRdu
= lim f" fr K (uR) %\ (ur
S-*-0 Jo Jr-S
For brevity we write h in place of r -I- 8. We then have
[*' f % (uR) %\ (ur) uRv+> dRdu
JO Jr
== f* {bv+l r$\+, (ub) - r"+' %°v+, (ur)} %\ (ur) da
Jo
since the second of these throe integrals is convergent, and the third is abso-
absolutely convergent when 0 < p < 1 — v.
Now the last expression can be replaced by a combination of the four
integrals of the types
/ 7s 4., r / \i Jv(ur) du
-hi(ub) - r"+1JMv+1)(ur)} j_^u\ • ^»
30—2
468 THEORY OF BESSEL FUNCTIONS [CHAP. XIV
and these are all absolutely convergent. They may be evaluated as cases of
Weber's discontinuous integral of § 13*4, and hence we find that
{ (ub) - r"+> <@v+l (ur)} <@v (ur)%
. o u
_ o-sr1' sin (a + prrr) sin (« + vn). T (v +1 — p)
~ 2^ sin pir sin vir. V (v + 1)T (p~+Tj
a-r " sin a sin (a + pir + vtr). V A — p)
2^ sin {pir + vie) sin vtr. T A - v) V (v + p + 1)
¦>¦* f (i i r\
The limit of this expression, when p -*• 0, is reducible to
o-2r"sinasin(a+vt
7r sin V7r
i _ + 2 log _ JF (i _ „; 1 - i/; t
+ \ir cot a - ^7r cot (a + vir) — yjr A) + ty (—v) ,
after some algebra; and the limit of the-last expression, when b-*r + 0, is
simply -Icrr*.
In like manner it may be shewn that
lim [* r <@v
S~*-+OJ 0 J r-S
and so we have proved that
udu
provided that 0 $ v % \, F(R) is subject to the conditions stated in § 14s and
c&v (z) ~ a- {cos a Jv (z) + sin aYv (z)};
and this is the general theorem stated at the beginning of the section.
142. Weber's integral "theorem.
Too
It is evident from § 14-51 that, if F(R) *JRdR exists and is absolutely
J a
convergent, where a > 0, then
A) lim J" F(R) [R <$v+1 (XR) % (Xr) - r<$v+1 (Xr) % (XR)] ^^2
provided that r lies inside an interval in which F{R) has limited total
fluctuation and F(R) is defined to be zero when 0 < R < a, if the order of the
cylinder functions lies between — ? and \.
14*52] MULTIPLE INTEGRALS 469
We shall now establish the truth of this formula for cylinder functions of
unrestricted order.
Let [R9^ (XR) <&, (Xr) - rrtfv+1 (Xr) <@v (XR)] ^-^ = ®,(R,r; X).
It is an easy deduction from the recurrence formulae that
<?„ B2, r; X) - ^ (R, r; X) = -—-^ [^(X22)<@v(Xr) + <@v_, (Xr) <@v (XR)],
and so, by the analogue of the Riemann-Lebesgue lemma. (§ 14*41), we have
B) lim P [<PV B2, r; X) - $„_, B2, r; X)] RF B2) dfl = 0.
Hence, by adding up repetitions of this result,
C) lim p [<&„ B2, r; X) - 4>,,±« B2, r; X)] 22^B2) d22 = 0,
K J
K-*-oo J a
Vfhere n is any positive integer.
Choose n so that one of the integers v±n lies between + \, and then from A)
lim P <bv±n B2, r; x) 222^B2) rf22 = \^ [F (r + 0) + F (r - 0)},
and so, for all real values of v, we deduce from C) that «,
D) lim r<Pr(R,r; X)RF(R)dR =*lo*[F(r + 0) + F(r- 0)}.
This result is practically due to Weber*, and it was obtained by the method
indicated in § 14*46.
To obtain the result in Weber's form, let
, (,) = Fr (r) /, E) - /, (r) 7, (*),
, 00 s Fr B2) j; (z) - Jv (R) Yv (z).
Then
u
^
and the expression on the left is also equal to
u [RWv+l (uR) % (ur) - r%+1 (ur)^v (uR)]
= uRlYvB2) Jv+1 (uR) - Jv(R) Yv+l(uR)][Yv(r) Jv(ur)- Jp(r) Yv(ur)]
-ur[Yv (r) Jv+1 (ur) - Jv (r) Yv+1 (ur)) [ Yv (R) Jv (uR) - Jv B2) Yv (uR)]
= uYv B2) Yv (r) [RJV+1 (uR) Jv (ur) - rJv+1 (?»•) /, (w.22)J
+ iw {J, B2) Yv (r) - Jv (r) Yv B2)} [22 Jv+1 (uR) Yv (ur) ~ RYv+1 (uR) Jv (ur)
- r Yv+1 {ur) Jv (uR) + rJv+l (ur) Yv (uR)]
-$u{Jy B2) 7, (r) + Jv (r) Yv B2)} [RD,+l (uR)Dv (ur) - rDv+1 (ur)Dv (uR)
- RDy+1 (uR) Dv (ur) + rDv+x (ur) Dv (uR)]
- iiJy(R) Jv (r) [RYV+X (uR) Yv(ur) - rYv+{(ur) Yv(uR)],
where
* Math. Ann. vi. A873), pp. 146—161.
470 THEORY OF BESSEL FUNCTIONS [CHAP. XIV
Now suppose that
r f(R)RdR
J a
exists and is absolutely convergent; and consider
Km Pf(R)
Carry out the integration with respect to u, and replace the integrated part
by the sum of the four terms written above, divided by Ri — r*.
Since Jv(R)Y>(r)-Jv(r)Yv(R)
R3 — r-
is bounded near r, and has limited total fluctuation in any bounded interval
containing r, it follows that the integrals corresponding to the second group
of terms tend to zero as X -*¦ oo, by the generalised Riemann-Lebesgue lemma.
Corresponding to the third group of terms we get a pair of integrals which
happen to cancel.
When we use A), we are therefore left with the result that
lim f" f(R)f ^,O)f „ (uR) uR . dudR
= M^20') + >V(r)
that is to say
F) [°° udu r f(R)c^,,(ur)^v(uR)RdR
in which the cylinder functions are defined by (o), and r lies inside an interval
in which f(R) has limited total fluctuation.
Apart from details of notation, this is the result obtained by Weber in the
case of functions of integral order.
14*6. Formal statement of Neumann's integral theorem.
We shall now state precisely the theorem which will be the subject of
discussion in the sections immediately following. It is convenient to enunciate
the theorem with Du Bois Reymond's* generalisation, obtained by replacing
the Bessel function by aay function which satisfies certain general conditions.
The generalised theorem is as follows :
(I) Let ^(X, Y) be a bounded arbitrary function of the pair of real
variables (X, Y), which is such that the double integral
exists and is absolutely convergent.
* Math. Ann. iv. A871), pp. 383—390. Neumann's formula (cf. § 14-8) is obtained by writing
q{t)sJ0(t), and the conditions (I)—(III) are substantially those given in Neumann's treatise
published in 1881.
14-6, 14*61] MULTIPLE INTEGRALS 471
(II) When NP (X, Y) is expressed in terms of polar coordinates, let it be
denoted by F (R, <J>), and let F (R, <E>) have the property that (for all values
of Q between ± ir), F(R, <J>), qua function of R, has limited total fluctuation in
the interval @, oo ); and let this fluctuation and also F(+ 0, <X>) be integrable
functions of 4>.
(III) // SI (R, <1>) denote the total fluctuation of F (R, <?>) in the interval
(± 0, i?), let Cl(R, 4>) tend to zero uniformly with respect to $> as R-^0,
throughout the tvhole of the interval (— it, it), with the exception* of values of <3>
in a number of sectors the sum of whose angles may be assumed arbitrarily
small.
Since \F(R, <J>) - F(+ 0, <t>)| ^0,(R, <t>), this condition necessitates that
F (R; <!>) -*¦ F (+ 0, <3>) uniformly except in the exceptional sectors.
(IV) Let g(R) be a continuous function of the positive variable R, such
that g (R) *JR is bounded both when R-*~0 and when R -*¦ oo .
i fa
Let g (t) tdt — 0 (R), and let G (t) — be convergent.
Jo Jot
g () (
Jo Jo
Then ^ udu f" f" ? {X, 7). g {u V(Xa + P)]. (dXdY)
JO J ~aoJ ~x>
is convergent, and is equal to
r°° fit
27r.[iM*T(+0)<I>)] O(t)~,
Jo "
where $HF(+ 0, c^) meansf
Before proving the main theorem, we shall prove a number of Lemmas,
just as in the case of Hankel's integral.
14*61. The analogue of the Riemann-Lebeague lemma.
Corresponding to the result of § 14'41, we have the theorem that if T is
an unbounded domain^ surrounding the origin, of which the origin is not an
interior point or a boundary point, then, as X -*- oo ,
* The object of the exception is to ensure thnt the reasoning is applicable to tho case (which
is of considerable physical importance) in which * {X, Y) is zero outside a region bounded by one
or more analytic curves and is, say, a positive constant inside tho region, the origin being on tho
boundary of the region.
t The discovery that the repeated integral is equal to an oxpresnion involving the mean value
of F(R, *) when the origin is a point of discontinuity of F(R, <I>) was made by Neumann, Veber
die tiaehKreis-, Kug?l- und Cylindcr-functionenj'prtHchreitenden Entwickelungen (Leipzig, 1881),
pp. 130—181.
t For instance T might be the whole of tho plane outside a circle of radius 5 with centre at the
origin.
472 THEORY OP BESSEL FUNCTIONS [CHAP. XIV
It will be observed that this is a theorem of a much weaker character than the
theorem of § 14-41, in view of hypothesis (II) of § 14*6. The reason of this is the fact that
G (\R) may be* 0 (J\) for certain values of R, and this seems to make arguments of the
type used in § 14#41 inapplicable.
To prove the lemma, suppose first that T is bounded. Then, for any value
of 4>, F(R, 4>) may be expressed as the difference f of two (increasing) mono-
tonic functions %: (R, <3>), ^2 (R, <I>), whose sum is the total fluctuation of
F(R, 3>) in the interval @, jR).
If Ro and jR] are the extreme values of R for any particular value of <3>, it
follows from the second mean-value theorem that, for some value of Rz between
jR0 and Ry,
Xl (R, *) 0 (\R) -p- = %! (-Ro, ®) 0 (*J2) -n- + %a (Ri, ®) G QJt) -«-
CKR* dt C*R\ fit
= XiA2,,*) G(t)j + K(Ru$) G(t)^.
Since G(t)-— is convergent, if e is an arbitrary positive number, we can
J t
choose X so large that
G(t)T,<e,
for all values of f not less than the smallest value of Ro. Also
and similarly
whence it follows that
R
and, since ^(+ 0, <E>) is bounded, this can be made arbitrarily small by taking
e sufficiently small, and it is independent of the outer boundary of T. Hence
we may proceed to the limit when the outer boundary tends to infinity.
* This is the case when g (R) — Jo (R); then G (R)~RJl (R). It is by no means impossible that
some of the conditions imposed on I*1 (/?, 3>) are superfluous.
t Cf. Modern Analysis, §3'64.
14'62] MULTIPLE INTEGRALS 473
We infer that, if T has no outer boundary, the modulus of
can be made arbitrarily small by taking \ sufficiently large; and this is the
theorem to be- proved.
14*62. The inversion of Neumann's repeated integral.
We shall next prove that the existence and absolute convergence of the integral
{dXdY±~
r r y(X
J-J- K *
are sufficient conditions that
fucki!"
o J — oo .' -co
= lim f r ¦V(X>Y)\Kg{u>J(X*+Y'i))udu{dXdYI
\-*.x J - <x>J—oo JO
provided that the limit on the right exists.
For any given value of X. and any arbitrary positive value of e, there exists
a number /? such that
f[ JJj F B2, cD) | 22* (dRd*) <
where A is the upper bound of | (jr (u) \ V«.
We then have
C0 PF(.R, V)g(uR) udu. R (dRdty
-JT J 0 JO
- r r r F(R, <I>) g (uR) R (dJKd*) udu '
J Q J -it J 0 j
-wJti J 0
_ fA f r F(R,<t>)g(idt)R(dRd<&)udi
JO J -K J ft
J -irJ ft Jo '
< e.
Since this is true for arbitrarily small values of e, we infer that
[Wr I™F(R,Q>)g(uR)R(dRd<P)udu
J 0 J -WO
= lim f I" P F(R,®)g(uR)udu.R(dRd<P),
the integral on the left existing because the limit on the right is assumed to
exist.
J0
474 THEORY OF BESSEL FUNCTIONS [CHAP. XIV
Hence it follows that, if the limit on the right exists, then
' F(R,&)g(uR)R(dBd&)
fir /"oo
= lim! I
X-»» 00 J —IT J 0
14*63. The proof of Neumann's integral theorem.
We are now in a position to prove without difficulty the theorem due to
Neumann stated in § 14. We first take an arbitrarily small positive number
e and then choose the sectors in which the convergence of ?1 (R, <I>) to zero is
uniform, in such a way that the sum of their angles exceeds 2tt— e. We then
choose 8 so small that >Q (R, <E>) < e in these sectors whenever R $ B; and we
take the upper bounds of
du
and
to be B and C.
G(u) —
e u
We then apply the second mean-value theorem. We have
/7 7?
- Xl
S /7 7?
^ G (KB) ~
= Xi(+0,
where 0 < ? ^ 8.
Now
Hence
[*
Jo -ti j a
where 11) \ is less than 2eG inside the sectors in which convergence is uniform,
and is less than 1BC in the exceptional sectors.
Hence it follows that
u
J -nJ 0
J q
2ir.2eC+e.2BC
Hence, for large values of X,
i r r
1 J —ir J 0
that is to say
lim
J -it J 0
14-63, U'64] MULTIPLE INTEGEALS 475
Now the expression on the loft is independent of e; and so since e is arbitrarily
small, we infer that the limit is zero. That is to say,
exists and is equal to
"Jo T ' u
Applying the result of § 14C2, we see that Neumann's theorem has now
been proved.
In the special case in which g (u) = Ja(u), we have
ru
Jo
so that G (a) = uJx (u),
and (' Villldu' = (*(_/; (,,)> da = i:
J 0 " .' 0
Hence we have
A) udu xlr(X, 1 ) .J0[u*J(X"+ Y'-)}.(dXdl )
J() / _a J -co
= 2tt ifilM' (+ 0 . cos 4), + 0 . sin *).
If we change the origin, we deduce that
Jo J -a: J -a.
= 2tt J-KW' (.'• 4- 0 cos fb, // + 0 sin (l>),
and finally, changing to polar coordinates,
C) ruduT r
J() J -it J -a
where fflXF(r, <f) now means the mean of the values of F(R, <?>) when (R, <I>)
traverses the circumference of an indeiinitely small circle with centre (r, </>)
14*64. M elder's investigation of Neumanns integral.
Neumann's integral has been deduced by Mehler* from the formula
by a limiting process; in this formula
cos 7 = cos 6 cos 6) + sin 6 sin 6 cos (<? — <?).
The formula is obtainedf by constructing a solution of Laplace's equation,
valid inside a sphere of radius k, "which has an assigned value f{6, <p) on the
surface of the sphere.
* Malh. Ann. v. A872), pp. 135—137 ; cf. Lamb, Proc. London Math. Soc. B) n. A905), p, 381.
t Of. Modern Analysis, § 18*4.
476 THEORY OF BESSEL FUNCTIONS [CHAP. XIV
The limiting process used by Mehler is that suggested by the result of-
§ 571; the radius of the sphere is made indefinitely large, and new variables
jR, r are defined by the equations
r =
so that R, r are substantially cylindrical coordinates of the points with polar
coordinates («, ®, 4>), (/c, 0, (/>); the function of position /(@, <E>) is then de-
denoted by F(R, <E>), and Pn(cosy) becomes approximately equal to Jo (invite),
where
w2 = Ri +¦ r2 - 2Rr cos (<? - (j>).
We are thus led to the equation
F{r, rf>)= hm 2 --; F(R, $U0(nW« —— d<&.
K-*.oo «=0 W Jo J-i «
If now we write u\k ¦== u, and replace the summation by an integration (taking
\Jk as the differential felement), we get
F (r, 4>) = l^ [" w^M J" J" .P (,R, 3>) Jo (unr) RdRd®,
which is Neumann's result.
But this procedure can hardly be made the basis of a rigorous proof, be-
because there are so many steps which require justification.
Thus, although we know that
is a potential function (when r< k), which assumes the value fF, $) on the
surface of the sphere, the theorem that we may put p = k in the series
necessitates a discussion of the convergence of the series on the surface of the
sphere; and the transition from the surface of a sphere to a plane, by making
k ¦*• oo y with the corresponding transition from a series to an integral, is one
of considerable theoretical difficulty.
It is possible that the method which has just been described is the method
by which Neumann discovered his integral formula in 1862. Concerning his
method he stated that "Die Methode, durch welche ich diese Formel so eben
abgeleitet habe, ist nieht vollstandig strenge."
CHAPTER XV
THE ZEROS OF BESSEL FUNCTIONS
15*1. Problems connected with the zeros of Bessel functions.
There are various classes of problems, connected with the zeros of Bessel
functions, which will be investigated in this chapter. We shall begin by proving
quite general theorems mainly concerned with the fact that Bessel functions
have an infinity of zeros.and with the relative situations of the zeros of different
functions. Next, we shall examine the reality of the zeros of Bessel functions
(and cylinder functions) whose order is real, and discuss the intervals in
which the real zeros lie, either by elementary methods or by the use of Poisson-
Schaf heitlm integrals. Next, we shall consider the zeros of ./„ (z) when v is not
necessarily real, and proceed to represent this function as a Weierstrassian
product. We then proceed to the numerical calculation of zeros of functions
of assigned order, and finally consider the rates of growth of the zeros with
the increase of the order, and the situation of the zeros of cylinder functions of
unrestrictedly large order. A full discussion of the applications of the results
contained in this chapter to problems of Mathematical Physics is beyond the
scope of this book, though references to such applications.will be made in the
course of the chapter.
Except in §§ 154—15'54, it is supposed that the order v, of the functions
under consideration, is real.
The zeros of functions whose order is half an odd integer obviously lend
themselves to discussion more readily than the zeros of other functions. In
particular the zeros of ——--7lii_._2i have been investigated by Schwerd
and by Rayleigh*; and more recently Hermitef has examined the zeros of
Jn+l(a:). The zeros of this function have also been the subject of papers by
Rudski} who used the methods of Sturm; but it has been pointed out by
Porter and by Schafheitlin§ that some of Rudski's results are not correct, and,
in particular, his theorem that the smallest positive zero of Jn+i (x) lies
between ? (n -"- 1) it and \ (n + 2) it is untrue. Such a theorem is incompatible
with the inequality given in §15'3 E) and the formulae of §§ 15*81, 1583.
* Schwerd, Die Beugungserscheinunyen (Mannheim, 1835); cf. Verdet, Lecons d'Optique
Physique, i. (Paris, 1869), p. 266; Bayleigh, Proc. London Math. Soc. iv. A873), pp. 95—103.
t Archiv tier Math, und Phys. C) i. A901), pp. 20—21.
% M6vi. de la Soc. R. des Sd. de LUge, B) xvnr. A895), no. 3. See also Prace Matematyczno-
Fizyczne, in. A892), pp. 69—81. [Jahrbuch ilher die Fortschritte der Math. 1892, pp. 107—108.]
§ Porter, American Journal of Math. xx. A898), p. 198; Sohafheitlin, Journal fiir Math. oxxn.
A900), p. 804.
478 THEORY OF BESSEL FUNCTIONS [CHAP. XV
15*2. The Bessel-Lommel theorem on the zeros of Jv (z).
It was stated by Daniel Bernoulli* and Fourierf that /0 (z) has an infinity
of real zeros; and a formal proof of this result by an analysis of Parseval's
integral is due to Bessel \. It was subsequently observed by Lommel § that
Bessel's arguments are immediately applicable to Poisson's integral for Jv{z),
provided that — \ < v ^ \. A straightforward application, of Rolle's theorem to
x±vJv(x) is then adequate to prove Lominel's theorem that Jv{z) has an
infinity of real zeros, for any given real value of v.
The Bessel-Lommel investigation consists in proving that when — \ < v < \y
and x lies between mrr and (m 4-1) ir, then Jv (x) is positive for even values
of m, @, % 4, ...), and is negative for odd values of m, A, 3, 5, ...). Since
Jv(x) is a continuous function of x when x^O, it is obvious that Jv(x)
has an odd number of zeros in each of the intervals (\rr, ir\ (§v, 2tt),
Some more precise results of a similar'character will be given in §§ 15*32—15-36.
To prove Lominel's theorem, let x = (in + \6) it where 0 ^ 0 ^ 1; then, by
obvious transformations of Poisson's integral, we have
cos
. Bm + ey ] 0
f,m+0
gn^ ,Bot
Now the last integral may be written in the form
f,m+0 CQg 1^^
and so agn J.(«) = sgn^ ,Bot + ^m>|<,,*l
where (-)' vr = f ™^? du,
=fW+e
cos i7"* du
If now we write u = 2r — 1 + U, and then put
{Bm + Of - Br - 1 + f/"J}"-* - {Bm 4- 0K -Br -1 -
it is clear that
sin
and, since |j v^$,fr(U) is a positive increasing If function of ?\
* Comm.*icad. Sci. Imp. Petrop. vi. A732—8) [1738], p. 116.
t La Thiorie Analytique de la Ghaleur (Paris, 1822), §803.
X Berliner Abh., 1824, p. 39.
§ Studien liber die Bessel'schen Functional (Leipzig, 1868), pp. 65—67.
|| This is the point at whioh the condition v ^\ is required; the condition v > - \ ensures the
convergence of the integral.
IT The reader will prove this -without any difficulty by regarding r as a continuous variable and
then differentiating/,.(U) with respect to r.
15-2-15-22] ZEROS OF BESSEL FUNCTIONS 479
It follows that
and so
sgn /„ (m-rr + \0ir) = sgn [(-)m {vj -H (vm - t*^) + (v.m_2 - *>«_,) + ...}]
since vmr is obviously not negative.
That is to say, when — -| <y ^ \,
+, (w = 0,2,4,...)
(•m-1,3,5,...)
and from this result Lommel's theorem follows in the manner already stated.
The zeros of Ji(x), as well as those of ,/0 (*•), have been investigated by Baehr, Archives
Nkrlandaises^vu. A872), pp. 351—358, with the help of a method which resembles the
Bcssel-Lonmiel method. Baehr's result for Jt (.v) is that the function is positive when x
lies in the intervals @, tr), (ffrr, Sir), (§«-, 5tt), ..., and that it is negative when x lies in
the intervals ($ir, 2n-), (§ir, iir), (Qrr, Qtt), .... The function Jt(x) has also been investi-
investigated in this way by G. N. Moore, Annals of Math. B) ix. A908), pp. 156—162.
The results just stated are of a leas exact nature than the results obtained with the aid
of slightly more refined analysis by Solmfheitlin (§8 1533—15*35).
It was noted by Whewell, Traits. Gumb. Phil. »S'oc. ix. A85G), p. 156, that «/0 (;)•) has a
zero between 2 and 2 N/2, fuid that the fuuetion Ho (z) has some real zeros.
15*21. The non-repetition of zeros of cylinder functions.
It is easy to prove that $'„ (z) has no repeated zeros, with the possible ex-
exception of the origin*. For,if '$;.(?)and Yov'(z) vanished simultaneously, it would
follow, by repeated differentiations of the differential equation V1/r^(^)=0,
that all the differential coefficients of c&v (z) would vanish at the common zero of
(i$v (z) and r$J (z), and then, by Taylor's theorem,('(j!v (z) would be identically zero.
15*22. The interlacing of zeros of Bessel functions.
It will now be shewn that if jvA, j,>2, ••• are the positive zeros of JP{x);
arranged in ascending order of magnitude, then, if v > — 1,
This result is sometimes expressed by saying that; the positive zeros of ./„(*•)
are interlaced with those of /„+, (&•).
To prove the result we use the recurrence formulae
¦- 'ar'J (x)) = - ar'J (x) -- jaf+> /„ (a)} - x^ Jv (,v) *
dxl " ' ' "+1 dx v+1 '
the first of these shews that between each consecutive pair of zeros of
x~" Jv (x) there is at least one zero of x~" Jv+1 (x), and the second shews that
between each consecutive pair of zeros of xv+x Jr+i (x) there is at least one zero
of %v+lJv(a)); and the result is now obvious.
* This is a special case of a theorem proved by Sturm, Journal de Math. i. A836), p. 109.
480 THEORY OF BESSEL FUNCTIONS [CHAP. XV
If v^—1, the zeros are obviously still interlaced but the smallest zero of Jv + i(.r) is
nearer the origin than the smallest zero of Jv (x).
The result concerning interlacing of positive zeros is obviously true for any real
cylinder function* c@v (x) and the contiguous function ^v+l (>?')•
This fundamental and simple property of Bessel functions appears never
to have been proved until about a quarter of a century agof, when four
mathematicians published proofs almost simultaneously; the proof which has
just been given is due to Gegenbauer^ and Porter §; the other proofs, which
are of a slightly more elaborate character, were given by Hobson|| and
van VleckiT.
It has been pointed out by Porter that, since
at any positive zero of Jv (x) the functions /v+1 (x) and /„+» (*) have the
same sign: but at successive zeros of Jv (x) the function Jv+l (x) alternates in
sign, and so there are an odd number of zeros of Jv+2 (x) between each con-
consecutive pair of positive zeros of/„(#); interchanging the functions Jv+» (x) and
Jv (x) throughout this argument, we obtain Porter's theorem that the positive
zeros of Jv+2 (x) are interlaced with those of Jv (x).
15*23. Dixon's theorem on the interlacing of zeros.
A result of a slightly more general character than the theorem of § 15'22
is due to A. C. Dixon**, namely that, when v> — l, and A, B, G, D are
constants such that ADj* BG, then the positive zeros of AJv(x) + BxJv'(x) are
interlaced with those of GJV (x) + DxJy' (x), and that no function of this type
can have a repeated zero other than x = 0.
The latter part of the theorem is an immediate consequence of the formula,
deducible from §5-11 A1),
Jv (x), xjv' (x)
J* (t) tdt = -^x d [Jv(as)} d \xJv' (x
dx ' dx
for the integral is positive when x is positive and the expression on the right
would vanish at a repeated zero of AJv(x) + BxJv'(x).
* A real cylinder function is an expression of the form
a.Jv(x)+pYv{x)
in which a, /3 and v are real, and x is positive.
t Of. Gray and Mathews, A Treatise on Bessel Functions (London, 1895), p. 50.
X Monatshefte fiir Math, und Phys. vm. A897), pp. 383—384.
§ Bulletin American Math. Soc. iv. A898), pp. 274—275.
I! Proc. London Math. Soc. xxvm. A897), pp. 372—873.
IT American Journal of Math. xix. A897), pp. 75—85.
** Messenger,xxxxi. A903), p. 7; see also Bryan,Proc. Gamb. Phil. Soc. vi. A889), pp. 248—264.
15-23, 15-24] ZEROS OF BESSEL FUNCTIONS 481
To prove the former part of the theorem, we observe that, if
, ._CJ,(x)+_Dx_Jv/(x)
^^ ~ AJ~(x)+'Bxj;\x)}
then ?{m)^
and so # (x) is monotonic. The positive zeros of <p (x) are therefore interlaced
with the positive poles, and ffom this result the former part of the theorem
is obvious.
If the function Jv{x) is replaced by a real cylinder function <xJv (x) -\-CYv(x),
we have
' < \ , 2vfi (a sin vir + /3cos vir)
d_6v(x) d{x^{x)} + -^^^r '
dx ' dx
provided that — 1 < v < 1; and so the theorems concerning non-repetition and
interlacing of zeros are true for A%(x) + Bxr$v'(x) and Cc@v{x) + DxrtfJ (x)
provided that /3 (a sin vir + /3 cos vir) is positive.
Again, since
v' ' ~~dx'""
the theorem is true for zeros exceeding + *Jv2, whether v lies between — 1
and 1 or not.
The result of § 15*22 is tho special case of Dixon's theorem in which
15*24. The interlacing of zeros of cylinder functions of order v.
Let (Wv{x) and f6''v{x) be any distinct cylinder functions of the same order ;
we shall prove that their positive zeros are interlaced*.
If ($,, (x) = uJu
then K (x) WJ (,'/;) - %°v (x) <&,' (x) =
irx
Now it is known that, at consecutive positive zeros of ($v (a1), %J» (x) has opposite
signs, and therefore, from tho last equation, $'„(&•) has opposite signs; that is
to say f$v{x) has an odd number of zeros between each consecutive pair of
positive zeros of (&\{x)\ similarly r@?(x) has an odd niuuber of zeros between
each consecutive pair of positive zeros of %'v (x); and so the zeros must be
interlaced.
If we take one of the cylinder functions to be a function of the first kind,
we deduce that all real cylinder functions have an infinity of positive zeros.
* Olbrioht, Nova Ada Caes.-Leop.-Acad. (Halle), 1888, pp. 43—48, has given an elaborate dis-
discussion, of this result with some instructive diagrams.
W. B. F. 31
482 THEOBY OF BESSBL FUNCTIONS [OHAP. XV
15-25. Lommel's theorem on the reality of the zeros of Jv (s).
An extension of a theorem due to Fourier*, that the function J9 (z) has no
zeros which are not real, has been effected by Lommelf. The extended theorem
is that, if the order v exceeds -1,'then the function Jv(z) has no zeros which
are not real.
To prove Lommel's theorem, suppose, if possible, that a is a zero of /„(*)
which is not real. It follows from the series for Jv(z) that a is not a pure
imaginary, because then
would be a series of positive terms.
Let a0 be the complex number conjugate to a, so that a« is also a zero of
Jv(z), because Jv(z) is a real function of z.
Since v > — 1, it follows from § 511 (S) that
o tJv (at) Ju fat) dt = —- [ J, (ax) —^- - J. fax) d;v J ,
and so, since a2 ^ a02,
t\jv(cLt)J,,(aot)dt = Q.
Jo
The integrand on the left is positive, and so we have obtained a contradiction.
Hence the number a cannot exist, and the theorem is proved.
Similar arguments J may be used to shew that, if A and D arc rcvil sunl i» > — 1, the
function AJV (z) + BzJv' (z) has all its zeros real, except that it has two purely imaginary
zeros when (AjB) + v<0.
These results follow from the series for -=- {zAlB Jv B)} combined with the formula
P*Jr1,C3Q.7'l,G8b0*=O,
Jo
which is satisfied if j8 and /30 are any zeros of AJv(z) + BzJv' (z) such that /3a=?/V-
15*26. The analogue of Lommel's theorem for functions of the second kind.
It is not possible to prove by the methods of § 15-25 that§ Yv (z) has no
complex zeros in the region|| in which | arg^ | < ir. But it has been proved
by Schafheitlinl that Y0(z) has no zeros with a positive real part, other than
the real zeros.
* La Theorie Analytique de la Chahur (Paris, 1822), § 308; see also Steam, Quarterly Journal,
xvn. A880), p. 98.
t Studien iiber die Bessel'schen Functionen (Leipzig, 1868), p. 69.
J See A. C. Dixon, Messenger, xxxn. A903), p. 7.
§ Or, more generally, <$„ (z).
I, When arg2=±,r, Yv (z)=e*'"ri Yv(-z)±2i cos ,VJV{- z), and hence, by §3-03 A), !'„(*)
cannot vanish unless v is half of an odd integer. This type of reasoning is clue to Macdounld,
Proc. London Math. Soc. xxx. A899), pp. 165—179.
T Archiv der Math, und Phys. (8) i. A901), pp. 133-137. In this paper Schafheitlin also sub-
subjects the complex zeros of Tj {z) to a similar treatment.
15'25-15-27] ZEROS OE BESSEL FUNCTIONS 483
For let j3 be a complex zero of Y0(z), and let /30 be the conjugate complex,
so that ft is also a zero of Yo(*). Then, by §§ 511 (8) and 351 A),
and so, if j3 = pe*", we have
and the expression on the left is positive while the expression on the right is
negative when a> is an acute angle.
15*27. The theorems of Surwitz on the zeros of Jv{z).
The proof which was given by Fourier that the zeros of Jo (z) are all real
was made more rigorous and extensive by Hurwitz*, who proved (i) that when
v >~l, the zeros of Jv(z) are all real, (ii) that, if s is a positive integer or
zero and v lies between — Bs+ 1) and —Bs+2), Jv(z) has 4s +2 complex
zeros, of which 2 are purely imaginary, (iii) that, if s is a positive integer and
v lies between — 2s and — Bs + 1), Jv (z) has 4s complex zeros, of which none
are purely imaginary. To establish, these results, we use the notation of § 9.
We take the function g2m,v{K) which has, in the respective cases (i) in
positive zeros, (ii) m — 2s — 1 positive zeros, 1 negative zero and 2s complex
zeros, (iii) m — 2s positive zeros and 2s complex zeros.
We now prove that, if/„(?) = ? rJ7 , TT\>then the function/„(?)
n=i) n\ I \v + n -\- i)
has at least as many complex zeros as gm<y(t). After Hurwitz, we write
i / y \ _ gsmi+i, v \ b ) 9^1, v \ b ) ~ ff'-in+l, v \ b ) flam, v ( b )
where f, t) are real and ?=t; + iv> K' = ? — iv- The terms of highest degree in
Qm (^,v) ar© easily shewn to be
\m (m + 1) {v + m) (v + m +1) {(v + m) Bm +1) + m - 1} (f24- v2)m~l I
and since g^^ is a" real function, it follows that if ? is a complex zero of
(?)< so a^so is ?' > an(l therefore the complex zeros satisfy the equation
Again, it is not difficult to deduce from the recurrence formulae (§ 9'7) that
* Math. Ann. xxxiii. A889), pp. 246—266; cf. also Segar, Messenger, xxir. A893), pp. 171—181,
for a discussion of the Bessel coefficients. The analysis of this section differs in some respects from
that of Hurwitz; see Watson, Proc. London Math. Soc. B) xix. A921), pp. 266—272.
31—2
484 THEORY OF BESSEL FUNCTIONS [OHAP. XV
Hence, for sufficiently large values of m (i.e. those for which v + 1m is positive),
the curve <j>m(%,v) = Q lies in the finite part of the plane, and 4>w{M,y)™
negative when ^TO+1 (ft 17) is zero so the curve tf>m+i (ft 1?) = 0 lies whollywmcte
one or other of the closed branches which compose the curve cf>m (?, ??) - 0.
Hence as m- 00, the complex zeros of g^ (?) He in bounded regions of
the ?-plane, and consequently have limit-points.
Now, since, by §§965, 9'7,
can be made arbitrarily small in any bounded domain of the ?-plane, by taking
vi sufficiently large, it follows from Lagrange's expansion* that the number of
zeros off, (?) in any small area is at least equal to the number of zeros of #»„,»(f)
in that area when m is sufficiently large; and so /„ (?) has 2s complex zeros.
None of these zeros is real, for if one of them were real it would be a limit
point of two conjugate complex zeros of gim<v{^), and so it would count as a
double zero of/v(^); and/v(?) has no double zeros.
Again, from the series for/v (?) it is seen that, when v lies between — Bs + 1)
and - Bs + 2),/,, (?) must have one negative zero, and it cannot have more than
one negative zero, for then gw,t „(?) could be made to change sign more than once
as % varied from 0 to — oo [since g»H,p(^) can be made to differ from fv{?) hy
an arbitrarily small number], and this is impossible.
For similar reasons /„(?) cannot have more than 2s complex zeros.
If we replace ? by \z-, so that negative values of ? correspond to purely
imaginary values of z, we obtain the results stated in the case oi Jv (z).
For a discussion of zeros of Besscl functions in association with zeros of polynomial**
based on father different ideas, the reader should consult Lindner, Sitz. dar Berliner Mat/i.
Ges. xi. A911), pp. 3—5. It may be mentioued that Hurwitz has extended his* ronultH to
generalised Bessel functions in a brief paper, Hamburger AfUtkeihrngen, 11. AHDO),
pp. 25—31.
158. Bourget's hypothesir.
It has been conjectured by Bourgetf that, when v is a positive integer
{zero included), the functions Jv{z), Jv+m{z) have no common zeroa, other
than the origin, for all positive integral values of m.
It seems that this theorem was not proved before 1929, except in some
simple special cases, such as m = 1 and m— 2 (cf. § 15-22).
The formula
Jv^n (s) = Jv {?) Rm „ (Z) - Jv_x
* Cf. Modem Analysis, §7*32.
t Ann. Sci. de VEcole norm. sup. in. A866), pp.55—95.
15-28, 15*3] ZEROS OF BESSEL FUNCTIONS 485
shews that, since Jv (z) and Jv^ (z) have no common zeros, the common zeros
of Jv (z) and Jv+m (z) must satisfy fche equation
i.e. they must be algebraic numbers.
It has, however, been proved by Siegel* that Jv{z) is not an algebraic
number when v is a rational number and z is an algebraic number other than
zero; hence follow theorems which include Bourget's hypothesis as a special case.
"When v is half of an odd integer, it is easy to shew that </„ (z) and Jy+m iz)
have no common zerosf; for such zeros are algebraic numbers and it is known
that no algebraic number % can satisfy the equation
since the right-hand side is algebraic in z when v is half of an odd integer.
The proof I given by Lambert and Legendre that 7r is irrational may be
applied to § 5*6 F) to prove that Jv (z) has no zero whose square is rational
when v is rational; an inspection of the polynomial Rm^t v+i(z) now immediately
yields an elementary proof of Bourget's hypothesis in the cases m — 3 and w = 4.
15*3. Elementary properties of the zeros of Jv (x).
It is possible to acquire a considerable amount of interesting information
concerning the smallest zeros of Jv{x) and related functions, when v is positive,
by a discussion of fche differential equation satisfied by Jv (x) together with
the recurrence formulae; we shall now establish the truth of a selection of
theorems concerning such zeros.
Tho reader will Hnd a more systematic investigation^ of these theorems in various
papers by Schafhcitlin, notably Journal fiir Math. exxn. A900), pp. 299—321; Archiv
der Math, und Pkys. C) 1. A901), pp. 133—137; Berliner Sitzungsberichte, ill. A904),
pp. 83—85.
For brevity, the smallest positive zeros of Jv(oc), JJ (x), Jv"(%), ... will be
called jv, jv', jv", .... The smallest positive zeros of Yv(x), YJ (x), Yv" (x), ...
will similarly bo called yv, yj, yv"
We first prove that
A) jv>v, jJ>v.
It is obvious from the power series for Jv{x) and /„' (.r) that these functions
' Abhqndlungcn A kail. Berlin, 1929, pp. 1—70. This abstruse and important memoir contains
numerous applications of Siegel's fundamental theorem.
t This was noticed by Porter, American Journal of Math. xx. A99-i), p. 208.
J Cf. Hobson, Squaring the Circle (Cambridge, 1913), pp. 44, 51—53.
§ Some related results are due to Watson, Proc. London Math. Soc. B) xvi. A917), pp. 165—
171.
486 THEORY OF BESSEL FUNCTIONS [CHAP. XV
are positive for sufficiently small positive values of x; and, from the differential
equation
it is evident that, so long asa<v and /„ (a?) is positive, xJvr (x) is positive and
increasing, and so Jv (oc) increases with x.
Therefore, so long as 0 < x < v, both /„ (oc) and xJv' (x) are positive increasing
functions so thatj,, and^V cannot* be less than v.
- Again, from the differential equation
and so J" (x) has become negative before x has increased to the value v from
zero. Hence, whent v>l,
B) jj'<v.
Next, since
the expression on the right is positive so long as x < v + 2. Now, if _;'„' were less
than *J{v (v •+ 2)), the expression on the right would be negative when x is equal
to jv' (which, from a graph, is obviously less than jv), and this is not the case.
Therefore
C) o Jv'>*J{
Now, from § 15*22 it follows that
and, as has just been stated,
so that Jv(jJ) and Jv+*(jJ) are both positive. If now we put x=jj in the
formula
it is obvious that
D) jv'
Similarly, by putting x =jv in the formula
(v + 3) Jv (x) + 2 (* + 2) jl - 2^ + 1jt(t/ + 3)| jv+i (X) + („ + l) J,+4 (x) = 0,
we deduce that
and therefore
E) VK"+2
* Cf. Riemann, Partielle Differentialgleichungen (Brunswick, 1876), p. 269.
t When 0-cv < 1, JV" (*) is negative for sufficiently small values of x.
15*3] ZEEOS OF BESSEL FUNCTIONS 487
In like manner, we can deduce from the formulae
and J'v+l («) - - „ |i - ?zlj J, (*) - („ + l) JJ' (X)
that
F) VK"-l)}<j/'<V(*a-l).'
Some rather better inequalities than these are obtainable by taking more
complica,ted formulae; thus, from the equation
Jv+0 (x) - Jv+i (x) ROi p+1 (x) - Jv (x) BiyV+2 (x),
Schafheitlin* deduced that
JV+i (j*) > 0>
i.e. Sjv* - 16 {v + 2) (y + 4)>a + 16 (y + 1) (v + 2) (v + 4) (v + 5) > 0.
Since jv* is certainly less than § (v + 2) (v + 4), by results already proved, jv
must be less than the smaller positive root of the equation
3aJ - 16 (v + 2) 0 + 4) a3 +16 (y + 1) (v + 2) (v + 4) (y + 5) = 0,
and hence, a fortiori,
G) i,
Similarly, from the equation
Schafheitlin deduced that
(8) j/WM' + S)}.
and, when v > 4,
(9) j/>VK" + 3)},
these inequalities being derived from the consideration that jv' lies between
the positive roots of the equation
a* - 3 (v + 2J x2 + 2v {v + 1) (v + 3) (i; + 4) - 0.
The discussion of yv requires slightly more abstruse reasoning. We use
the result that
¦/,'(*) +17 (*)
,is a'decreasing function of x; this is obvious from §1373. Hence it follows
that Yji(x) decreases through the interval @,jv'), and so ;/„ exceeds jv'\ again,
in this interval Yv{x) is negative, and it follows from §3"G3A) that Y,,(jv)is
positive, since Jv'(jv) is obviously negative.
Hence
A0) j/<y,<>.
This inequality (with jvf replaced by v + ?) was established by Schafheitlinf
with the aid of rather elaborate analysis.
* Berliner Sitzungsberichte, in. A904), p. 83.
t Journal ftlr Math. oxxn. A900), pp. 317—321.
488 THEORY OF BESSEL FUNCTIONS [CHAP. XV
15*31. Stationary values of cylinder functions*.
It has already been seen that the cylinder function Jv (%) cos a — Yv (x) sin a,
or 9BW (%), has an infinite number of positive zeros, and so there are an infinite
number of positive values of x for which it is stationary. Such values of x
which exceed the order v (supposed positive) will be called fiy, fi», p,s, ..., where
We shall now study some of the simpler properties of the sequence
The first theorem which we shall establish is that
l#.M!>l#,0t,)|>l#.(/K.)l>....
To prove this, observe that the function A (x) defined as
has the negative derivate
and so A(fr)> A(/a2) > A(fis)> ....
Since A (/j.n) — c<@? (/a,,.), the truth of the theorem is now evident.
A more interesting result is suggested by Hankel's asymptotic formula
(§7-21)
l
This indicates the possibility of proving inequalities consistent with
Avhon /xn is large.
It can in fact be shewn that
(I) The values assumed by (%~— v2)^\ c@v{x)\ when x takes the values filf fa,
/j,3, ...form an increasing sequence ivhose members are less than VB/7r).
(II) The values assumed by x^\^v{x)\ when x takes the values /j,r, /JLr+i,
f^r+2, ••• form a decreasing sequence whose members are greater than \/BJtt)
provided that.
(i) />?V3, (ii) ^>vi {4i/B + 4 + VD8v8 + 13)]/Dz/2~ 3).
Consider the function
A (x) <@* (x) + 2B (x) % {x) <@v' (x) + G {x) <$:* {sb) s 6 {x),
where A (x), B(x), G{x) are to be suitably chosen. We have
©'(a?) = {A'{a) - 2(«2 - v2) B{ay)jxi) <@* (x)
+ 2{& (x) + A(x)-B {x)jx -(&- u>) G (x)lx*} % (x) <$„' (x)
+ {C (x) + 2B {x) - 2G{x)/x} ^v'2 (x)
^D{xYSJ"{x\
where D {x) = C (x) + 2B (x) - W (x)/x,
* Cf. Proc. London-Math. Soc. B) xvi. A917), pp. 170—171.
15*31, 15*32] ZEROS OF BESSEL FUNCTIONS 489
provided that A (as) is chosen arbitrarily and that B(x) and C(x) are then
defined by the equations
C (x) - x" {Bf (a) + A (w) - B (x)/x}/(x- - v*\
(I) If A (a:) ~ (x-- v% then
W (x) (.«* - ifi)% = a? Ca- + 14«;V + 4^) > 0,
arid mo ® (x) is an increasing function of x which is therefore less than
lim ®(«) = 2/w.
Since <") (/*„) = (^ift8 - i/s)l 'gf,2 (/in) we see that when ?i assumes the values
1, 2, .... then the numbers (/v - y2)^ r$v((in)\ form an increasing sequence
lews than VB/7r).
(II) If .4 (a?) = x, then
2X» (as) (a;'J - v»)* = - a? [D^- - 3).«' - 8z/= (v* +1) a? + y4 Dj/2 -1)}
provided that 4i;a > 11 and .•*; exceeds the greatest root of the equation
(<k-'J - 3) ./-4 - 8i>a (i/1-1 + 1)x- + vl D>v" - 1) = 0. ,
In thi.s ciaHr (H) (,r) is a decreasini/ function and we can apply arguments; similar
to those lused in theorem (I), to deduce the truth of theorem (II).
152. Sahafheitiin's investigation of the zeros of J<s(x).
By means of l,hu integrals which have been given in §6'123 it has been
shewn l>y Schafheitlin* that the only positive zeros of J6(x) lie in the intervals
(mir-V Jvr, -nnr +Itt) and the only positive zeros of F0(ap) lie in the intervals
(•imr + \ir) imt + '^ir), when; >u= 0, 1, 2, —
We shall first give Schafheitlin's investigation for J0(x), with slight
modifications, and then we shall prove similar results for cylinder functions
of the type
J,, (oc) cos a — Yv (x) sin o
(where v lies between - i and §), by the methods used by Schafheitlin.
Schafheitlin's investigations were confined to the values 0 and \ir of o.
From an inspection of the formula of §E*12 G),
2 Ojy)
it is obvious that, when vnr <x< mw + f rr,
and so sgn Jo (x) = sgn (- l)m.
Consequently Jo («?) has no zeros in the intervals (mir, mir + |?r).
* Journal filr Math. cxiv. A894), pp. 31—44.
490 THEORY OF BESSEL FUNCTIONS [CHAP. XV
To prove that J0(x) has no zeros in the intervals (rrnr + ^tt, mir + tt), write
00
and then JM- 2J=
7r
The last integrand is negative or positive according as
0 < 0 < 2(f> or 2(f> < 0 < \ir.
Since 0 < ^ir, the second of these intervals is the longer] and the function
.—23 cote
sin 0 Vcos 0
is an increasing function* of 6 when x >\nr and 6 is an acute angle.
Hence to each value of 9 between 0 and 20 there corresponds a value
between 2<f> and |tt for which sin (^0>— <f>) has the same numerical value, but
has the positive sign, and the cofactor of sin(|0 — <?) is greater for the second
set of values of 6 than for the first set. The integral under consideration is
consequently positive, and so J0(x) cannot have a zero in any of the intervals
(rMr + ^TT, mir + ir). Therefore the only positive zeros of JQ{x) are in the
intervals (mir + f ir, mir +17r).
15*33. Theorems of Schafheitlin's type> when — ^ < v ^ \.
We shall now extend Schafheitlin's results to functions of the type
$*„ (x) = «/„ (%) cos a — Yv (x) sin a,
where 0 < a < ir and — \ < v < \.
We shall first prove the crude result that the only positive zeros of <i$v (a?)
lie in the intervals
(mir 4- f 7T + \vit — a, rrnr + tt — a)
where m — 03 1, 2,.... This result follows at once from the formulae of § 6*12,
which shew that
for, when mir — a < x < mir + f ir + ^y-n- — a,
we have sgn[sin (x + a — v0 + \0)~\ = sgn (— l)w,
and so, for such values of x, ^v (x) is not zero. Consequently the only zeros
of 9BV (x) lie in the specified intervals, and there are an odd number of zeros
in each interval, with the possible exception of the first if a > f ir + ? vir.
Next we obtain the more precise result that the only positive zeros of *$„ (x)
lie in the intervals
(mir+ f7r + \vvr— a, mir + |7T + \vir — a)
* Its logarithmic derivate is
Bz - Bin 6 cos 8) cosec2 0 + % tan 6.
15-33,15*34] ZEEOS OF BESSEL FUNCTIONS 491
where m = 0, 1, 2, ..., except that, if a is sufficiently near to ir, there may be
zeros* in the interval
ty'ir + \vtt — a, "" — «)•
We shall prove this result by proving that (WV (x) has a fixed sign throughout
each of the intervals f
(mir + ^7r + \ vtt — a, mrr + w — a).
Write oc = (m+lOr-a-(l-2v)(fi,
where <f> is an angle between 0 and ^ir.
With this value of x,
a? f* cos-»g sin {A - 2,) (|fl - 0)} t.
To each value of 0 between 0 and 2<? there corresponds a value between 2<jE>
and \nr for which sin {A — 2v)(\0 — ^>)} has the same numerical value, but
has the positive sign.
Again e~*x cot B cos""* ^/sin2"+10
is an increasing function of 6 provided that
2x > max [*Bi/ +1) sin 0 cos 0 + (v - \) ^|~j,
and this condition is satisfied when oc>\ since v^\.
Hence, if x > \ and
mrr + lir + {vtt — a. < % < mir + ir — or,
we have sgn r$v (x) = sgn (- l)m+\
and this proves the more precise theorem.
15-34. Theorems of Schafheitlin's type, when % < v < f.
We next consider the function
c(ov (x) = Jv (x) cos a — Yv (x) sin a,
where 0 < a < ir, as before, in which it is now supposed that ? < v < $.
We shall first prove the crude result that the only positive zeros of %\ (x)
lie in the intervals
(witt — a, rmr — \tt + \vtt — a)
where j m — 0,13 2,.... This result follows at once from the formulae of § 6*12,
which shew that
fi>rcotf-*gsin(a?+ «-y0 + ^) cote ,, .
1 e
for when rmr— \tt+ \vrr— a<x< (m + 1) ir-a,
* By taking as an alternative function J\v\ (x) and applying the theorem of § 15*24, we see that
there cannot be more than one such zero.
t If x < \ and m = 0, the reasoning fails when |7r + |i/7r-o<J.
X If a>(i»'-i)w, the interval for which m=0 is, of course, to be omitted.
492 THEORY OF BESSEL FUNCTIONS [CHAP. XV
we have sgn [sin (cc + a. - vO + \ 6)] = sgn (- 1)™,
whence the theorem stated is obvious.
Next we obtain the more precise result that the only positive zeros of 9BV (x)
lie in the intervals
(w7r — ^7r •+ ^ vrr — a, nvn — \tt + \ vrr — a),
where m = 0, 1, 2, ..., except that, if a is sufficiently near to 7r, there may be
a 2ero in the interval @, J vir — \ir — a), and there may be one in the interval
Gr — a, \7r + \vir — a).
We use the same notation and reasoning as in § 15'33; only now, if
g-2a;cot0 cos""^ 0/sin2"^16 ^.fF}
f{6) is-not necessarily an increasing function of 6; but it is sufficient to prove
that, when 0 < ty < 20, then
To obtain this result, observe that
l
{cosec2 B0 + V^) + cosec2 B0 — \j/)}
,T v-\ 2^ + 1 1
4(f) ? J ,
|_cos B<f)-\--y) cos B0 — \j/) Bin B0 + \j/) sin B0 - y)J
But [cosec2 B0 + ^) + cosec2 B0 - ^)] ain B0 + ^) sin B0 -1^)
is an increasing function of i^, and therefore, a fortiori,
[cosec2 B0 + \fr) + cosec2 B0 - ^)] cos B0 + ^) cos B0 - ty)
is an increasing function, since this function exceeds the former by an increasing function
because 40 is an acute angle; and so jr Iog'>^-J7—-jl is always positive if it m positive
when ^ = 0, i.e. if
\x > {(v - \) tan2 20 + Bk +1)} sin 40,
and this is the case when x> f i/ + J.
Hence, when \<v<§, the only zeros of ^„(x), which exceed f v + ^, lie in
the intervals
(mir — Itt + ^vrr — a., rtitr — \ir + \vnr — a).
The method seems inapplicable for larger values of v on account of the
oscillatory character of sin {x + a — v9 + \9) as 6 increases from 0 to \tt \ a
method which is effective for these larger values will now be explained.
15*35. Schafheitlin's investigations of the zeros of cylinder functions of
unrestrictedly large order.
We shall now prove that, if v >\, those zeros of the cylinder function
Jv (oc) cos a — Yv (x) sin a
which exceed Bz/+ 1) Bv + 3)/?r lie in the intervals
(mir — a + \wr + \fr, mnr — a ¦+• \vrr + f 7r)
where m assumes integer values.
15-35] ZEEOS OP BESSEL FUNCTIONS 493
The method used to obtain this result is due to Schafiieitlin.*; but he
considered the case of functions of the first kind and of integral order only, and
his reasoning is made lengthy and obscure by the use of arguments equivalent
to the use of the second mean-value theorem when the explicit use of that
theorem is obviously desirable.
As in the preceding analysis, write
r@v [so) = Jv (x) cos a — Yv {sc) sin a,
so that
2"+I^ fi7rcos'-*0 8in(* + ave + W te
4
Now cot2 0. e~2xcot0 increases as 8 increases from 0 to 02 and then decreases
as 6 increases from 0,, to I-it, where 6* — arc tan—'—?.
v + •§¦
It will be observed that 02 is nearly equal to ^tt when x is large compared
with v.
Now suppose that x lies between
inir — a + |-7r (v — \) and mrr — a + \rr (v — \) 4- |-7r,
and then choose 01 so that
X + a — (v + |) 0j = W7T.
It is easy to verify that
so that ^! is a positive angle less than 0,, provided that
V + A 7T
arc tan - - - < --
4y 4- 6 '
We suppose now that
/
so that 0i is certainly less than O.z.
Then, by the second mean-value theorem, there exists a number 0O, between
0 and 0!, such that
,, *"¦ cos""* 0 sin (cc + a - v6 +16) n
Journal filr Math. oxxn. A900), pp. 299—321.
494 THEORY OF BESSEL FUNCTIONS [CHAP. XV
Now qua function of 6,
cos (as + a - v6 - \ 0)/cos"+* 0
is stationary when sin (% + a — v0 + ^O) = 0, and for such values of 6 the
fraction is equal to + l/cos""* 6.
_, cos(<a5 + a-y0o--&0o)
Hence —i -rr^—-—
COSV+* 0O
cannot exceed numerically the greatest value of l/cos"~* 6 in the interval @, #i),
and therefore
fcosQnTT+
SgQ1 cos'+M,
Therefore, since the sign of sin (a + a— v9 + \6) is the sign of (— l)m when 6
lies between #t and \tt, we see that, for the values of x under consideration,
Hence, when x exceeds Bv+ 1) Bv + 3)/7r, c$v(%) has no zeros in intervals of
the type
(m7T — a + ^ v7r —-^tt, mtr — a + ^ i/7r + |7r),
and so the only zeros of ^ («?) which exceed Bv +1) Bi> + 3)/7r lie in intervals
of the type
(mm— a + $vtt + ^7r, wi7T — a + \vn + ?ir),
and this reduces to Schafheitlin's result* when a = 0 and v is an integer.
The reader will observe that this theorem gives no information concerning
the smaller zeros of ^v{x) when v is large ; it will be apparent in § 15'8 that
there are a large number of zeros less than Bj>+ l)By+ 3)/7r, and that
interesting information can be obtained concerning them by using Debye's
integrals.
15*36. Bdcher's theorem-f on the zeros
A result of a slightly different character from those just established was
discovered by Bdcher from a consideration of the integral formula § 11*41 A6).
The theorem in question is that ^0 (x) has an infinite number of positive zeros,
and the distance between consecutive zeros does not exceed 2;0 where j0 is the
smallest positive zero of Jo (cc).
To establish this result, write v = 0, z=j0 in § 11*41A6), and then
.'o
f H d<f> = <*<$„ (Z) Jo (j0) = 0.
'o
Hence $*„ (•») cannot be one-signed as <f> increases from 0 to -it, i.e. as «r
increases from Z— j9 to Z-+jn; and so ^(nr) must vanish for at least one
value I of or in the interval (Z- j0, Z+j0). Since Z is an arbitrary positive
number (greater than j0), Bocher's theorem is now evident.
• Schafheitlin gives Bj<+3) Bv+S]\tv as the lower limit of the values of x for which the zeroB
lie in the specified intervals.
t Bulletin American Math. Soc. v. A899), pp. 385—388.
t Of. Modern Analysis, §3-63.
15'36, 15-4] ZEROS OF BESSEL FUNCTIONS 495
[Note. By a form of Green's theorem,
f dv , f du .
I u~ as = | v — as,
J Ov J cv
where u, v are two solutions of r-s + r~b + k = 0 with continuous second differential
coefficients inside the closed curve a, and d/dv indicates differentiation along the normal.
By taking v-Ja {s/(.r2+y2)} and the curve to be ?2+g2=jo\ Weber* deduced that u
must vanish at least twice on any circle of radius jti.
Bocher inferred from this result that since %n (r) cosnd satisfies the requisite conditions
except at the origin, if a circle of radius j0 is drawn with centre on the axis of x and
subtending an angle less than ir/n at the origin, r$n (»;) must vanish somewhere on the
circle. Hence the positive zeros of r$n (¦>') are such that consecutive zeros are at a distance
apart less than 2;'o, and the distance from the origin of the smallest of them does not
exceed j0 \ 1 +cosec ?- \.
(_ •in)
These results are of interest on account of the extreme simplicity of the methods used
to prove them.]
15*4. On the number of zeros of Jv(z) in an assigned strip of the z-plane.
We shall next give the expression for /„ (z) as a Weierstrassian product,
and then develop expressions involving quotients of Bessel functions in the
form of partial fractions; but as a preliminary it is convenient to prove the
following theorem, which gives some indication as to the situation of those zeros
of /„ (z) which are of large modulus. In this investigation it is not supposed
that v is restricted to be a real number, though it is convenient to suppose
that v is not a negative integer. When v is real the results of § 15'2 to some
extent take the place of the theorem which will now be proved.
Let C be the rectangular contour whose vertices are
+ iB + {iril{y), ±iB + mir + \vtt + \tt,
where B is a (large) positive number.
We shall shew that when m is a sufficiently large integer the number of
zeros of z~v Jv(z) inside G is precisely equalf to m.
Since z~v Jv(z) is an integral function of z, the number of its zeros inside
0 is
1 /' dlog {w~"Jv{w)) J_ f Jr+l (w)
2TrtJc dw 2tti J c J * (tu)
* Math. Ann. i. A869), p. 10.
t When v is a real negative number (and for certain complex values of v) there may be pairs
of zeros on the imaginary axis; in such circumstances the contour C has to be indented, and each
pair of zeros is to be reckoned as a single zero.
496 THEORY OF BESSEL FUNCTIONS [CHAP. XV
We now consider the four sides of C in turn. It is first to be observed that
on all the sides of G,
P^fe* »-*^-W {1 + Vl<„(w)\,
Hv® (w)
where r)lt „ (w) and tJi v (w) are 0 A/w) when j w | is large.
Now, since the integrand is an odd function*, we have, as B -*¦ oo ,
_ J_ f"iB+*^'(l'>i±ji?i>dw- -L f *+i"(
-*• ~—. I idw=\il(y).
2iTT% J ' 7? 1 * 77
Next take the integral along the upper horizontal side of C; this is equal to
2-7T
iw Jv {W)
T+iir A i-
as 5 -*• oo.
Similarly the integral along the lower side tends to the same value, and
so the limit of the integral along the three sides now considered is m + \v 4- i»
Lastly we have to consider the integral along the fourth side, and to do
this we first investigate the difference
which, when | w \ is large, is equal to
W
Now
and so
~2~iJ J( {
Hence the limit of the integral round the whole rectangle is m + 0 A/m).
* Allowance is made for the indentations, just specified, in the first step of the following analysis.
15-41] ZEROS OF BESSEL FUNCTIONS 497
If we take m sufficiently large, we can ensure that the expression which
is 0 A/m) is numerically less than 1; arid since the integral round the rectangle
must be an integer, it is equal to m.
That is to say, the number of zeros of z~vJv(z) between the imaginary axis
and the line on which
{
is exactly m.
Note. The approximate formulae quoted for the functions of the third kind shew
that the large zeros caunot have a large imaginary part; and so all the zeros of Jv(n) lie
inside a strip whose sides are parallel to the real axis and at distances from it which are
bounded when | v | is bounded.
15*41. The expression of Jv{z) as an infinite product
It is possible to express Jv(z) as a product of 'simple factors' of
Weierstrassian type, each factor vanishing at one of the zeros of Jv(z). In
order to express Jv(z) in this form, it is convenient first to express the
logarithmic derivate of z~vJv(z) as a series of rational fractions by Mittag-
Leffler's theorem*.
The zeros of z~vJv{z) are taken to be ±jV|i, + jv,2, ±>,s, ••• wheref
-& O'x.n) > 0 and j 72 ( jv§1) j $ | R (>f3) \^\R (>,*) U • • •, the values of jvA, /„.,,,
jv<i, ... .being all unequal (§15'2l). We draw a (large) rectangle D, whose
vertices are ±A± iB, where A and B are positive, and we suppose that ±jv>ln
are the zeros of highest rank which are inside the rectangle.
We now consider
±[ ? dm
2iri J j) w (w — z)' Jv (w)
where z is any point inside the rectangle, other than a zero of Jv (iu), and v is
not a negative integer.
The only poles of the integrand inside the rectangle are z, ±jv<i, ± jvr>, ...,
— J", in '¦
The residue at z is Jv+I(z)/Jv(z) and the residues at ±jv n are
^Jv,n Jv.n)
since JJ (z) = - Jv+1 (z) when z « + jv>n, by § 3-2.
It follows that
v,n
2tt% j d w (w — z)' Jv (w)
* Acta Soc. Scient. Fennicae, xi. A880), pp. 278—293. Cf. Modern Analysis, § 7-4.
t If JR(±%/I,)n)=O for any value of n, we choose^ n to have its imaginary part positive.
W. a F. 32
498 THEORY OF BESSEL FUNCTIONS [CHAP. XV
We next shew that, by giving A and-B suitable sequences of values which
increase without limit, Jv+i(w)/Jv(w) can be taken to be bounded on D.
Since this function is an odd function of w, it is sufficient to consider the
right-hand half of D.
We take A = Mir + R (%v +I) rr, where M is a positive integer; and then
we take M to be at least so large that M = m, which is possible by § 15-4<, and
also to be so large that we can take the functions rjVtl(w), 77VJ(w), defined in
§15-4, to be less than, say, ? in absolute value.
Then Jv+1 {u))jJv(w) is bounded whenever
I g2t (W—Jen—{n) I
is* less than \ or greater than 2; and when the expression does not lie within
these limits, I(vf) is bounded and w is not arbitrarily near a zero of Jv(w) ;
so that, from the asymptotic expansion of §7*21, Jv+l (w)/Jv (w) is bounded on
the part of the rectangle within, this strip.
That is to say Jv+1 (w)jJv{w) is bounded on the whole of the perimeter of
the. rectangle D as B and M tend to infinity.
Hence
and therefore f
n=l l*-ji».* jv.nj n=l U+jv.n jv,n
When we integrate, we find that
expJ_ rJ^dtU 5 |(i_4-)expD-)
r( Jo J*(t) j »=ilV JV,J l \JV,J) «=i
and hence
This is the expression of Jv (z) in the specified form.
The formula may also be written in the modified form
C) ^(*>
This formula was assumed by Euler, Acta Acad. Petrop. v. pars ], A781) [1784], p. 170,
when v = 0, and subaequently by various writers for other values of v; cf. §§ 15-5, 15*51.
The analysis of this section is due in substance to Graf and Qubler, Einleitung in die
Theorie der Bessel'schen Funktionen, i. (Bern, 1898), pp. 123—130, and it was given
explicitly by Kapteyn, Monatshefte fUr Math, und Phys. xiv. A903), pp. 281—282.
* Because ¦¦ ~ * > _,
t If we take the rectangle to have its vertices at A±iB, -A'±iBt we see that the two aeries
on the right converge separately.
15*42] ZEROS OF BESSEL FUNCTIONS 499
The expansion on the right of A) is evidently expansible in a power series; the
coefficients in such a series have been expressed as determinants by Kapteyn, Proc. Section
of Sci., K. Acad. van ]Yet. te Amsterdam, viir. A905), pp. 547—549, 640—642; Archives
Nderlandaises, B) xi. A906), pp. 149—168. Some associated formulae have just been
published by Forsyth, Messenger, l. A921), pp. 129—149.
15*42. The Kneser-Sommerfeld expansion.
A.n expansion which, in some respects, resembles the partial fraction
formula obtained in § 151 is as follows:
v,n)jv,n
in which % and X are positive numbers such that
while z and v are unrestricted (complex) numbers, except that it is convenient
to take E (z) > 0.
The expansion was discovered in the case i/=0, as a special form of an expansion
occurring in the theory of integral equations, by Kneser, Math. Ann. lxiii. A907), pp. 511—
517. Proofs of this and of related expansions for integral values of v were published
later by Sommerfeld, Jahresberioht der Deutschen Math. Verei?iigu?ig, xxr. A913), pp. 309—
353, but Sommerfeld's method of proof has been criticised adversely by Carslaw, Proc.
London Math. Soc. B) xm. A914), p. 239.
It may bo noticed that the expansion has some connexion with the ' Fourier-Bessel'
expansions which will be discussed in Chapter xvni.
To obtain a proof of the expansion, consider the integral
1 f #„<» (Xw) Hv® (w) - Hv® (Xw) #„<•> (w) Jv (xw) .
K 1 _ * \ i - _ ____________ rfyj
in which the path of integration is a rectangle with vertices ± Bi, A ± Bi, and
it is supposed that the left side of the rectangle is indented at the origin.
The integral round the indentation tends to zero with the radius of the
indentation, whether v be an integer or not; and the integrals along the two
¦parts of the imaginary axis cancel.
Also, when x and X satisfy the specified inequalities, the function
[Hvu (Xw) #,,« (w) - #,(a| (Xw) #„<•> («/)} Jv (xw)(Jv (w)
remains bounded on the other three sides of the rectangle when B -*- oo and
when A -»-oo through the values specified in §15*41.
Hence the limit of the integral round the rectangle is zero, anct so the
limit of the sum of the residues of the integrand at the poles on the right of
the imaginary axis is zero.
Now the residue at z is
32—2
15*5] ZEROS OF BESSEL FUNCTIONS 501
multiply out the product on the right, and equate coefficients of the various
powers of z in the identity; we thus obtain the system* of equations
•1 _ i
~ TIT = ** -
whence
- ^6 - o-b + l<7i - n
+
Since 0 < o^ < a2 < a3 < ..., it is evident that
l/a,m < crm, crOT+1 < o^/
and so o-^-1/" < ^ < a-mfam+l
By extrapolating from the following Table:
1
2
3
4
5
6
1-000 000
1-414 213
1 -442 250
1-445 314
1-445 724
1-445 785
ffmlffm+i
2-000 000
1 -500 000
1-454 545
1 -447 368
1-446 089
Euler inferred that a2 = 1*445795, whence
l/«: = 0-691661, 2 V«i = 2-404824.
By adopting this value for a^, writing
X I/On™ = crm',
and then using the inequalities
l(a2m < a'm, «/,„+, < cr'm/a,,
Euler deduced that a2= 7-6658, and hence that ^=18-63, by carrying the
process a stage further.
These results should be compared with the values
ax= 1-445796, a2=7-6178, a3 = 18-72,
derived from the Tables of Willson and Poirce, Bulletin American Math. Soc. in. A898),
pp. 153—155.
The value of ax is given by Poissout. as 1-446796491 (misprinted as 1-46796491);
according to Freeman I this result was calculated by Largeteau for Poisaon by solving the
quartic obtained by equating to zero the first five terms of the series for Jo B Klz); the
magnitude of the sixth term is quite sufficient to account for the error.
* This system is an obvious extension of Newton's system for an algebraic equation,
t M€m. de VAcad. R. des Sci. xn. A833), p. 330.
t Proc. Camb. Phil. Soc. ra. A880), pp. 875—377. Of. Freeman's translation of Fourier's La
Th€orie Analytique de la Ghaleur, p. 310, footnote.
502 THEORY OF BESSEL FUNCTIONS [CHAP. XV
15-51. RayleigKs extension of Eider s formula.
The method just described .vas used independently by Rayleigh * to calcu-
calculate the smallest positive zero of Jv (z).
Taking the formula (§ 15'41)
T,, (l»Y nil- —
S 1
and writing ^ ~nr
° n=lj v,n
we find, after Rayleigh, that
—
f2JO+3)(^ + 4)'
O- |5J =
+ 2Y(v + 3H + 4>)(v + 5)
The smallest positive zeros of Jt(z) and Jx{z) are deduced to be 2-40482G
and 3-831706.
Immediately afterwards Cayley f noticed that crvW can be calculated rapidly when r ia
a power of 2 by a process which he attributed to Encke %, but which is more usually known
as Graeffe's § method of solving an equation.
The method consists in calculating avM when r is a power of 2 by starting with tho
given equation and forming from'it a sequence of equations each of which has for its roots
the squares of the roots of its predecessor; and o-^r) then rapidly tends to a ratio of
equality with l//2rv,i.
Cayley thus found trp'8) to be
429p& + 7640i>« + 53752»>3 + 185430y2 + 311387^ + 202738
216 (,, + 1)8 („ + ?)* (k + 3J (v + 4J (j» + 6) (»+6) (k + 7) (»+B)'
It was observed by Graf and Gubler|| that the value of <rv(r> can easily be checked by tho
formula
where Br is the rth Bernoullian number; this formula is an evident consequence of tho
equation
Extensions of some of these results to the zeros of zJJ (z) + kJv (z), whero h is a constant,
have been made by Lamb, Proc. London Math. JSoc. xv. A884), p. 273.
The smallest zero of Jv {z), for various values of v between 0 and 1, has recently been
tabulated by Airey, Phil. Mag. F) xli. A921), pp. 200—205, with the aid of the Raylcigh-
Cayley formulae.
* Proc. London Math. Soc. v. A874), pp. 119—124. [Scientific Papers, i. A899), pp. 190—195.]
t Proc. London Math. Soc. v. A874), pp. 123—124. [Collected Papers, n. A896), pp. 19—20.]
t Journal fur Math. xxn. A841), pp. 193—248.
§ Die Aufl'osung der hoheren numerischen Qldichungen (Zurich, 1837).
|| EinUitung in die Theorie der Benel'sclien Funktionen, i. (Bern, 1898), pp. 130—131.
15-51,15-52] ZEROS OF BESSEL FUNCTIONS 503
[Note. The procedure of calculating the sum of the rth powers of the roots of an
equation in order to obtain the numerical value of its largest root seems to be due to
Waring, Meditationes Analytical (Cambridge, 1776), p. 311; other writers who were
acquainted with such a method before Graeffe are Euler (cf. § 15-5); Dandelin*, Mdm. de
I'Acad, R. des Sci. de Bruxelles, ill. A826), p. 48; Lobatschevsky*, Algebra, or Calculus
of Finite* (Kazan, 1834), § 257.]
15*52. The large zeros of JQ(x).
The most effective method of calculating the large zeros of cylinder
functions (when the order v is not too large) is, in substance, due to Stokes^,
though subsequent writers have, to some extent, improved on his analysis.
Stokes' method will be sufficiently illustrated by his own example % /0(a:)>
whose zeros are the roots of the equation
with the notation of § 7*3. It will be remembered that the asymptotic
expansions of P (x, 0) and Q (x, 0) are
1.9 1.9.25.49
For sufficiently large values of x, P (x, 0) is positive, Q (x, 0) is negative
and the quotient Q(w, 0)/P(x,0) is a negative increasing § function of x.
The function cot(# — ^tt) is a decreasing function which vanishes when
x — nir — J-7T, and so it is obvious from a graph of cot (x-\ir) that there
exists a positive integer N such that when n > N, JQ (x) has precisely one zero
in each of the intervals (utt — \tt, mr + \tt), and that the distance of the zero
from the left-hand end of the interval tends to zero as n —- oo .
Again, if ur, v,. denote the (r+ l)th terms of P(x, 0) and Q(x, 0) we may
write
m-l m-1
P{x, 0)= S ur + 6un, Q(^,0)= $vr\-exvm,
r=0 r-0
where 6 and 6l are certain functions of x and m which lie between 0 and 1.
* I owe these two references to Professor Whittaker.
t Camb. Phil Trans, ix. A856), pp.,182—18d. [Math, and Phye. Papers, n. A883), pp. 350—
353.]
X Stokes also considered Airy's integral (§ 6-4) and J\ (x), for the purpose of investigating the
position of the dark bands seen in artificial rainbows.
§ The reader may verify, by § 3-63, that its derivate is
{l-2*-QS}/ja|
where P, Q stand for P (x, 0), Q {x, 0); and, by the asymptotic expansions, this is ultimately
positive.
504 THEORY OF BESSEL FUNCTIONS [CHAP. XV
Now consider the equation
m-l
2 ur+ 8um
r=0
in which it is temporarily supposed that 6 and 01; instead of having their actual
values, are any numbers which lie between 0 and 1.
The equation now under consideration involves no functions more compli-
complicated than trigonometrical functions. If x were supposed complex, there
would be a number of contours in the a-plane each of which enclosed one of
the points wrr — \tt and on which | cot (x -r \ir) \ exceeded the modulus of the
quotient on the right.
By Biirmann's theorem* the modified equation would have one root inside
the part of the contour which surrounds mr — \ir, and this root can be ex-
expanded in descending powers of mr — \ir.
We thus obtain an expansion for the root of the equation in the form
^ = (n7r|7r)+!^r
v 4 } rr=0 (nir - \iryr+1'
in which the coefficients fr F, di) are independent of n but depend on 9 and 0j;
and it is readily perceived that the first m of the coefficients are actually
independent of 9 and 61, so that, when r < m, we may write
fr@, 00=/,..
Now the sum of the terms after the mth is a bounded function of 6 and 6X
as 8 and 9r vary between 0 and 1; and it is clear that the upper bound of the
modulus of the function in question is 0{n~%m~l) as n -*¦ oo . Hence, when 6
and 0t are given their actual values which they have at the zero under con-
consideration, the sum of the terms after the mth is still 0 (n").
That is to say, it has been proved that there exists one zero (nearly equal
to mr — J-7r),-and its value may be written
m-l f
— («r- W + So (w-4^« + 0(«-»-).
Hence the asymptotic expansion of the -zero is
00 X
% ~~
xr^nir — \tt + z,
i*=0
It remains to calculate the first few of the coefficients/.. If
_ Q (x, 0)
where ^ ->¦ 0 as x -** so , then
^JL__33. 3417
Cf. Modern Analysis, § 7-31.
15*53] ZEROS OF BESSEL FUNCTIONS 505
, 1 25 1073
sot at ^""fcTssIS + siSa?"""
and therefore the equation to be solved assumes the form
, , 1 25 1073
The result of reverting the series is
, , , 1 31 3779
X = {nir - I jr) + r— - oo-jrj~- \—3 +
This series is adequate for calculating all the zeros of Jo (&•), to at least five
places of decimals, except the smallest zero, for which n — 1.
15*53. The large zeros of cylinder functiov^.
It is easy to see that the large zeroa of any cylinder function,
Jv (z) cos a — Yv (z) sin a,
where v and a are not necessarily real, may be calculated by Stokes' method
from a consideration of the equation
cot (z - \vir - \ir + a) = pTjA•
It seems unnecessary to prove the existence of such zeros (with large
positive real parts) or the fact that they may be calculated as though the
•series for P (z, v) and Q (z, v) were convergent, because the proof differs from
the investigation of the preceding section only in tedious details.
The expression for the large zeros of a cylinder function of any given order
was calculated after the manner of Stokes by McMahon*; but the subsequent
memoirs of Kalahnef and Marshall}' have made the investigation more simple
and have carried the approximation a stage further with no greater expendi-
expenditure of work in the calculation.
Following Marshall we define § two functions of z, called M and ^, by the
equations
M COS yfr = P(z, v), M sin yjr ==- Q(z, v),
on the understanding that M -*- +1 and yjr -*- 0 as z -*- + 00 .
It is then clear that
( 2 \*
Jv (z) cos a - Yv (z) sin a = f — J if cos (z - \vir — \ir + a — yjr).
* Annals of Math. ix. A895), pp. 23—25; see also Airey, Proc. Phys. Soc. 1911, pp. 219—224,
225—232.
+ ZeitschriftfiirMath. und Phys. uv. A9Q7), pp. 55—86.
X Annals of Math. B) xi. A910), pp. 153—160.
§ Of. Nioholson, Phil. Mag. F) xix. A910), pp. 228—249.
506 THEORY OF BESSEL FUNCTIONS [CHAP. XV
Again
Yv{z)
arc tan < ,". :! = z — \vn — \ir —
and, when we differentiate this equation, and use § 363 C), we find that
dyjr __ 2/('irz)
so that,, by §7-51,
dz
When the expression on the right is expanded as far as the term involving
1/z9, we find that
1 dyfr^ ft-1 (ft-1) (ft—25) (ft-l)(fta-11V+ 1073)
(fj. -1) Eft3 ± 1535ft2 + 54703ft - 375733)
in this equation ft has been written in place of" 4i>2 for brevity. It follows, on
integration, that
+1073)
+ 54703/^ - 375733)
+ 7.2lsz7
and so the equation to be solved is*
-25)
2>e 3.2V
If /3 = (n + \v - \) ir — a, the result of reversion is
2r*R- ^—^ (ft -1)Gft - 31) (ft- 1)(83ft2 - 982ft + 3779)
Z™ 23j8 ~ 3.27/3s 15.210/3°
_ (ft -1) F949ft8 - 153855ft2 + 1585743ft - 6277237) _
105.2ls/37 "~ ""
Therefore the large zeros of /„ (z) cos a — Yv (z) sin a are given by the
asymptotic expansion
* This equation (in the case v = l) was given by Gauss in his notebook with the date Oct. 16,
1797, but no clue is given concerning the method by which he obtained it. [Cf. Math. Ann:
lvii. A902), p. 19.]
15-54, 15-6] ZEROS OP BESSEL FUNCTIONS
507
[Notk Tho fact that JJQ + Y*{z) has a simple asymptotic expansion shortens the
alyaiH m a manner which was not noticed by Marshall; he used the equations
and he w>lved the latter by assuming a descending series for M.)
15-54. Zeros of functions related to cylinder functions.
The method of Stokes is, of course, applicable to functions other than
those just investigated. Thus McMahon* has calculated the large zeros of
V v {z) and of - _•--—<-' when the cylinder function is a Bessel function of
the first or second kind.
Tho general formula for the large zeros of ^J {z) is
8 - ft±l _ V + 82^-9 _
where B1 = (n, + ^v + \)ir — a, while the corresponding formula for the large
+ 154/4+95
zeros ot l *\ /i lg
dz
Tho zeros of j; (a) 7, (fo) - Yv {z) Jv (kz),
whwo k \» coriHtant, ami of
Jv'(z)Yv'(kz)-Yv'(z)Jv'(h)
havo. Ikmmi treated in a aimilar manner by McMahon. Kaliib.ne+ has constructed tables of
tho zciroH of the former function when k has tho values 1*2, To, 2'0 and v is 0, -^, 1, f, 2, # ;
whiles it him l>con proved by Carslaw, Conduction of Heat (London, 1922), p. 128, that these
/.oro,s arc all real vvhou v and h are real. The zeros of JJ (z) Yv (h) - YJ (z) Jv (Jcz) have
b«cn oxamined by Sasaki, T6hoku Math. Journal, v. A914), pp. 45—47.
15 6. T/ie mode o/ variation of the zeros of a cylinder function when its
order is varied.
The equation in z
has an infinite number of roots, the values of which depend on v; since Jv(z)
ia an analytic function of both z and v, so long as z±0, it follows that each
root of the equation is (within certain limits) an analytic function of v. A
Himilar statement holds good when the function of the first kind is replaced
by any cylinder function of the type J,(*)eosa- F,(*)sina, where « is any
constant.
If j denotes any particular zero of Jv (*), the rate of change of j, as v varies,
i» given by the ordinary formula of partial differentiation
* AnnaU of Math. ix. A895), pp. 26—29.
+ Zeitschrift/Ur Math, und Phys. liv. A907), pp. 55—86.
508 THEORY OP BESSEL FUNCTIONS [CHAP. XV
Since Jv (j) = 0, it follows that /„' (j) = - Jv+1 (j) ± 0, so long as j is not
zero, and hence, from §511 A5), when M(v)> Q,
This formula shews that when v is positive, the positive zeros of J\ {x) in-
increase as v is increased.
Equation B) was stated without proof by Schlafli, Math. Ann. x. A876), p. 137 ; and the
deduction from it was established in a different manner by Gegenbauer*, M4m. de la Soc.
B. des Sci. de Liege, C) 71. A900), no. 3, in the case of the smallest zero of Jv (x).
We proceed to extend the results already obtained to the positive zeros of
c@v (z) = Jv(z) cos a~Yv (z) sin a,
where v is an unrestricted real variable, and a is constant (i.e. independent of v).
The extended theorem is as follows:
Any positive zero, c, of rSv (z) is definable as a continuous increasing function,
of the real variable v.
To prove this theorem we observe that c is a function of v such that
arc tan \ r ; !
is constant, so that
dc[d . \Yv{z)Y] T9 * \Yv{z)Y\
¦j- k- arc tan \ T ; (\ + U-arc tan \-r-r-x M =0,
and therefore
Hence, by § 13-73 B), we have
fir f00
C) ~ = 2c Ka Bc sinh t)
av Jo
Since the integrand is positive, this formula shews that c is an increasing
function of v.
A less general theorem, namely that, if c is a zero which is greater than
the order v (supposed positive), then c is an increasing function of v, has been
proved by Schafheitlin | with the aid of very elaborate analysis.
It will be observed from the definition of Yv (z) that c tends to zero only
when v tends to any negative value which satisfies the equation
sin (a - wit) - 0.
* The reader should note that the analysis in the latter part of Gegenbauer's memoir is
vitiated by hiB use of Eudski's erroneous results (§ 15'JL).
t Berliner Sitzungtberichte, v. A906), pp. 82—93 ; Jahresbericht der Deutschen Math. Vereini-
gung, xvi. A9Q7), pp.272—279.
15-6] ZEROS OP BESSEL FUNCTIONS . 509
It should be noticed that C) shews that, when v is taken to be a complex
number and c is a (complex) number, with a positive real part, then c is an
analytic function of v; and so, as v varies, the zeros of c@v {z) vary continuously,
and they can only come into existence or disappear when c fails to be an
analytic function of v, i.e. when c = 0.
It folloAvs that the positive zeros of c@v (z) are derived from those of $$ (z)
by a process of continuous variation as v varies, except that one positive zero
disappears whenever v passes through one of the specified negative values.
If we now choose a so that* 0^a<7r,' we see that, as v varies from \
to any value exceeding (cl/tt) — 1, no zeros disappear during the process of
variation of v, and so in the case of zeros which are so large that the formula
of Stokes' type (§ 15'53) is available, the formula
. , 4i>3-l
gives the nth positive zero, when the positive zeros are regarded as arranged
in order of magnitude.
If, however, v has varied so that it finally lies between (ot/m-) — k and
(a/rr) — k — 1, where k is a positive integer, k zeros have disappeared, and so
the formula just quoted gives the (n — k)th positive zero.
This type of argument is due to Macdonald, Proc. London Math. Soc. xxix. A898),
pp. 575—584; it was applied by him to the discussion of the zeros of Bessel functions of the
first kind of order exceeding - 1.
If we draw the curve rSx{y) — §> it evidently consists of a number of
branches starting from points on the negative half of the #-axis and moving
upwards towards the right, both x and y increasing without limit on each
branch.
If we take any point with positive coordinates (p0, ya) and draw from it a
line to the right and a line downwards terminated by the a-axis, it is evident
that the curve (^'x(y) = 0 meets each of the lines in the same number of
points. It follows that the number of zeros of rS„ (t/0), qua function of v, which
exceed va is equal to the number of positive zeros of (gfI,0 (y) qua function of y
which are less than ya. This is a generalisation of a theorem due to Macdonald f,
who took Vq = 0 and the cylinder function to be a function of the first kind.
Fig. 33 illustrates the general shape of the curves Jx (y) = 0, the length
of the sides of the squares being 2 units. A much larger and more elaborate
diagram of the same character has been constructed by Gasser|, who has also
constructed the corresponding diagram for Yx(y)=>0. The diagram for
<$x (y) = 0 is of the same general character as that for Jx (y) — 0, except that
* Tim does not lead to any real loss of generality.
t See a letter from Macdonald to Carslaw, Proc. London Math. Soc. B) xin. A914), p. 239.
t Bern Mittheilungen, 1904, p. 135.
510
THEOBY OF BESSEL FUNCTIONS
[CHAP. XV
the portions of the curves below the axis of x consist merely of a number of
isolated points on the lines on which 2a? is an odd integer.
V
Fig. 33.
[Note. The reader will find it interesting to deduce from § 13-73 C) that, if c' is a zero
of $V (*), then
D) T-"~!T~\ (c'2eosh2*-,,2)Jff0B?>'8inh*)e-M<ft,
and hence, if the variables are real and c' > | v \ > 0, then c' increases with v.
The sign of ddjdv has also been discussed (by more elementary methods) by Schaf heitlin,
Jahresbericht der Deutschen Math. Vereinigung, xvi. A907), pp. 272—279; but the analysis
used by Schafheitlin is extremely complicated.]
15*61. The problem of the vibrating membrane.
The mode of increase of the zeros of Jv (x) -when v is increased has been
examined by Rayleigh* with the aid of arguments depending on properties of
transverse vibrations of a membrane in the form of a circular sector. If the
membrane is bounded by the lines 0 — 0 and 6 *» irjv (where v > \), and by
* Phil. Mag. F) xxi. A911), pp. 53—58 [Scientific Papert, n. A920), pp. 1—5]. Of. Phil. Mag.
F) xxxn. A916\ pp. 544—546 [Scientific Papers, vi. A920), pp. 444—446].
15*61, 15*7] ZEROS OF BESSEL FUNCTIONS 511
the circle r = a, and if the straight edges of the membrane are fixed, the dis-
displacement in a normal vibration is proportional to
Jv (rp/c) sin v6 cos (pt + e),
where c is the velocity of propagation of vibrations. If the circular boundary
of the membrane is fixed, the values of apjc are the zeros of «/„ (x), while if
the boundary is free to move transversely they are the zeros of JJ (oc).
The effect of introducing constraints in the form of clamps which gradually
diminish the effective angle of the sector is to increase v and to shorten the
periods of vibration, so that p is an increasing function of v, and therefore
(since a and c are unaltered) ap/c is an increasing function of v. That is to
say, the zeros of Jv (%) and JJ (%) increase with v.
By using arguments of this character, Rayleigh has given proofs of a
number of theorems which are proved elsewhere in this chapter by analytical
methods.
15*7. The zeros of Kv(z).
The zeros of the function Kv (z), where visa given positive number (zero
included), and z lies in the domain in which | arg^ | < |tt, have been studied
qualitatively by Macdonald *.
From the generalisation of Bessel's integral, given in § 6*22, it is obvious
that Kv(z) has no positive zeros; and it has been shewn further by Macdonald
that Kv(z) has no zeros for which | args \^\ir. This may-be proved at once
from a consideration of the integral given in § 13'71; for, if z — reia were such
a zero (r> 0, — \ir< ck^tt), then z — re~i<K would be another zero ; but the
integral shews that
rr , • \ rr , • x 1 f" f v racos 2a) rr /r3\ dv
Kv (rela) Kv (re~la) - » exp ] — s \KV — I —
v ' v 2 Jo ( 2 v J \vj v
which is contrary to hypothesis.
If a is equal to ± |-7r, we have
| Kv (re**) | = \w V{/va ('') + YJ> (r)},
and so Kv (z) has no purely imaginary zeros.
Next we study the zeros for which R(z) is negative, the phase of z lying
either between \tr and 7r or between —\ir and — tr.
It may be shewn that the total number of zeros in this pair of quadrants
is the even integerf nearest to v — \, unless v — \ is an integer, in which case
the number is v — \.
.In the first place, there are no zeros on the lines argz — ± ir, unless v-\
* Proe. London Math. Soe. xxx. A899), pp. 165—379.
t This is not the number given by Macdonald.
512 THEORY OF BESSEL FUNCTIONS [CHAP. XV
is an integer; for Kv{re±vi) = e^v1ti Kv{r) + ttc I,,(r), and, if both the real and
the imaginary parts of this expression are to vanish, we must have
cos vrr. Kv (r) — 0, sin vtt . Kv (?•) -I- ir /,, (r) = 0.
Since the Wronskian of the pair of functions on the left of the equations is
Gr/r)cos v7r, they cannot vanish simultaneously unless cos \nr — 0.
Now consider the change in phase of zv Kv (z) as z describes a contour
consisting of arcs of large and small circles terminated by the lines arg z = ± ir,
together with the parts of these lines terminated by the circular arcs.
(Of. Fig. 15 of §7-4.)
If the circles be called V and 7, their equations being | z | = R and | z | = 8,
it is evident that the number of zeros of Kv(z) in the pair of quadrants under
consideration is equal to the number of zeros of zv Kv (z) inside the contour,
and this is equal to l/B7r) times the change in phase of z" Kv (z) as z traverses
the contour.
Now the change in phase is
arg \zv Kv (z)\ - arg [zv Kv (z))
L Jr L Jy
|_ JJlexpiri |_ J
As R-*-oo and 8~*-0, the first two terms* tend to 2ir(v — ?) and 0
respectively, because when | z | is large or small on the contour,
Zv Kv (Z) rsj Zv-h~Z V(iir), Z" K, (Z) ~ 2" T (j/)
respectively!.
The last two terms become
r of + tr cos vir. I Jr) 1R
hm 2 arc tan T-r . , :—¦> r / s .
Now if„ (r) is a positive decreasing function of r while /„ (?•) is a positive
increasing function, and so the last denominator has one zero if sin vnr is
negative, and no zero if sin vjt is positive.
If therefore we take the inverse function to vanish when r-»0, its limit
when r->oo is are tan (cot vtt), the value assigned to the inverse function
being numerically less than two right angles and having the same sign as the
sign of cos vrr.
Hence the total number of zeros of Kv(z) in the pair of quadrants\ in which
JR (z) is negative and | arg z \ < it is
v — ? + - arc tan (cot vrr),
7T
* This is evident from the consideration that the asymptotic expansion of § 7*23 is valid when
| arg z | ^ ir.
t The second of these approximate formulae requires modification when v=0.
X The two zeros of K^ (z) are not very far from the points - 1-
15*8] ZEROS OP BESSEL FUNCTIONS 513
and the reader will find it easy to verify that this number is the even integer
which is nearest toi»-|.
When v — \ is an integer, Kv (z) is a polynomial in z multiplied by a
function with no zeros in the finite part of the plane, and so the number of
zeros for which R (z) < 0 is exactly v-%.
Next consider the portion of the plane for which ir < oxgz ^ 2ir.
If we write z = ?e*wi, we have
Kv (z) = - \tre-*™ [ Yv @ +1 A + 2e*™) Jv (?)],
and so Kp (z) has a sequence of zeros lying near the negative part of the
imaginary axis. The zeros of large modulus which belong to this sequence
are given approximately by the roots of the equation
tan (?- \vtr - ?tt) = - i A + 2e2l"ri);
it may be verified that they are ultimately on the right or left of the imaginary
axis in the ^-plane according as cos2^7r is less than or greater than \\ i.e.
according as v differs from the nearest integer by more or less than \. The
sequence does'not exist when e2viti = — 1, i.e. when v is half of an odd integer.
There is a corresponding sequence of zeros near the line arg z — — f 7r.
15*8. Zeros of Bessel functions of unrestrictedly large order.
The previous investigations, based mainly on integrals of Poisson's type,
have resulted in the determination of properties of zeros of Bessel functions,
when the order v is not unduly large. This is, of course, consistent with the
fact that Hankel's asymptotic expansions, discussed in Chapter vn, are
significant only when v" is fairly small in comparison with the argument of
the Bessel function.
The fact that Debye's integrals of § 8*31 afford representations of functions
of large order suggests that these integrals may form an effective means of
discussing the zeros of Bessel functions of large order; and this, in fact, proves
to be the case*. Moreover, the majority of the results which will be obtained
are valid for functions of any positive order, though they gain in importance
with the increase of the order.
We shall adopt the notation of § 8*31, so thatf
p vi (tan/3—/3) roo + wi-iP
Hvu (v sec 8) = . - e-vrdw,
where — t = sinhtu —w +i tanC(cosh w — 1), and the contour in the plane of
the complex variable w is chosen so that t is positive on it.
* Watson, Proc. Royal Soc. xoiv. a, A918), pp. 190—206.
f We shall use the symbols x and vseo/3 indifferently when x^v.
w. B. F. 33
514 THEORY OP BESSBL FUNCTIONS [OHAP. XV
If w = u 4- iv, where u and v are. real, u and v both increase steadily as w
describes the cqntour, so that
fa> rir-j5
e~vr du, e~VT dv
J -00 J -P
are both positive.
Hence, if we regard ft as variable, and define
raa+vi-ip
arg e~VT dw
J -w-i/3
to be a positive acute angle when j3 = 0, and to vary continuously with j8, it
will remain a positive acute angle for all values of j8 between 0 and \tr\ and,
moreover, by § 8*32, it cannot exceed J?r, since dvjdu^.\J'&.
This positive acute angle will be called %, and then ^ will be defined by
the equation
V = v (tan /3 - j3) + % - \ir.
It is then evident that
where J?l is positive (not zero); and
/„ («) = iW cos V, Yv (a?) = jffl sin ^.
If 9BV (a) = «/v (a) cos a - F,, (a?) sin a,
it is clear that the only zeros of c(s>v (%), gi'eater than v, are derived from the
values of W which make "^ + a equal to an odd number of right angles.
It is easy to shew that Nf increases with x, when v remains constant. For
we have
HT = arc tan , ; ;, -r- = T—-{x—' „- -.-^ > 0.
Jv{x) doc Jv2(x)+ Yv-(x)
Hence, as x increases, ^V increases steadily, and so, to each of the values
of M?" for which
¦ty = (to + 1) it - a,
corresponds one and only one positive zero of 9BV (x).
Next we shall prove that % is also an increasing function of x. This is a
theorem of a much deeper character, since the result of §13<I74 is required
to prove it; we thence have
d (tan j3 - /3) 2/(ttx) _ V(a;2
% __ _
d~~d V
>
dx~dx V Tx JJJxJ+Yj'ix) x
From Hankel's asymptotic expansion it is clear that
lim x ~ h'm \x — |vn — \tt — \f(a? — v2) + v arc cos (vjx) + \tr +
%-*• w
and so arc tan -j—y / \\ < X < i7r>
in which the expression on the left is a positive acute angle.
15-8] ZEROS OP BESSEL FUNCTIONS 515
To form an estimate of the value of % when v is large, we write
/„ (v) — — Yv (v) tan %;
hence, from § 8*42, we have
lim yv =
r(t)
and, when v is large,
tan yv = ~j^ \ 1 — -
V3l 210 r (*).(*!¦)
so that, when v is large, yv is an increasing fuiicbion of v.
The following Table gives the sexagesimal measure (to the nearest half
minute) of the angle whose circular measure is 7,,; it exhibits the closeness of
yv to its limit, even when v is quite small:
V
0
0
i
28° 39'
1
29°23i'
29° 38'
2
29° 45'
3
29°51'
4
29° 54'
6
29°56i'
8
29°57i'
10
29" 58'
12
.29° 58V
00
30°
The table suggests that 7,, is an increasing function of v for all positive
values of v\ to prove that this is the case we need the theorem that
v dv " dv 3
and this inequality has already been established in §13*74.
We are now in a position to infer that ?ov (v sec /3) has a zero for which
v (tan # — j3) + % = mir — a,
where m is any positive integer (unity possibly excepted); and therefore at
the positive zeros of (S\ (v sec yS), with the possible exception of the first,
v (tan /3 — j8) has a value between
(m — I) 7r — a and mir — yv — a,
and the difference of these expressions (when v is not small) slightly exceeds T^7r.
From the result of § 15*3 A0), it follows that the phase of #„<»» (Ar) eia
increases from a — ^ir to ^faasX increases from 0 to any value exceeding v,
and so, if 0 < a < -rr, the number of zeros of c@v (X) in the interval @, x) is the
greatest integer contained in (M/" + oc)/7r + \.
A simple theorem which may be noted here is that, when j>2> ?, it follows from § 13*74
that, if S is any positive number, I ^^* decreaaes as S is increased. This result
shews that the interval between consecutive zeros of c@v (x) decreases when the rank of the
zeros is increased.
A different proof of this theorem is due to Porter; cf. § 15-82.
33—2
516 THEORY OF BESSBL FUNCTIONS [CHAP, XV
15*81. The smallest zeros of Jv (x) and Yv (as).
It has been seen (§ 15'3) that Jv (cc) and Yv(x) have no zeros in the interval
@, v), when v is positive, and it is fairly obvious from the asymptotic formulae
obtained in § 8'42 that they have no zeros of the form v + o (»>*) when v is large.
The asymptotic formulae which were quoted in § 8*43 shew that, with the
notation of § 15"8,
where the inverse tangent denotes a negative acute angle.
Hence, at the smallest zero of Jv (a?),
As 0 increases from 0 to \ir) the expression on the left increases from
1 + 0 (l/*/v), while the expression on the right decreases from 0'2679 to 0; the
smallest root occurs for a value of 0 for which v (tan 0 — 0) lies between \vr
and \ 7r, so that
v (tan 0 - 0) = \v tan8 0 + 0 (*-*).
Hence, if we solve the equation
tan (f-f7r)=-Q(?,J)/P (?,?),
the value of f so obtained is the value of ^i/tan3^ at the zero with an error
which is 0 (v~ty. The value of ? is approximately 2*383447, and hence the
smallest positive zero of Jv (x) is
v + v*x 1-855757 + 0A).
In like manner, by solving the equation
of which the smallest root is approximately f =0*847719, we find that the
smallest zero of Yv (x) is
v + vi x 0-931577 + 0A).
The formula for the smallest zero of Jv (x) has been given by Airey, Phil. Mag. F)
xxxiv. A917), p. 193. Airey's formula was derived by using Debye's asymptotic expansion
of § 8*42 for Jv (x) when x has a value such that
For such values of the variables, it has not been proved that Debye's expansion is valid,
and although Ajlrey's method gives the two dominant terms of the smallest zero of Jv (xi)
correctly, the numerical result which Airey gives for the smallest zero of JJ {x) is not the
same as that of § 15-83. The reason why Airey's method gives correct results is that «/„ (v + ?)
is expansible in powers of <*¦ so long as f is o(v), and in this expansion it is permissible to
substitute Debye's formulae for Jv(v), Jv' (i>), Jv" (v), ....
A formula for the smallest zero of J^v{x) was given by Airey. This zero may lie any-
anywhere between 0 and the smallest zero of Jv (x), according to the value of v.
15*81, 15-82] ZEROS OF BESSEL FUNCTIONS 517
It does not seem to be possible to make further progress by the methods used in this
section. We shall now make a digression to explain the methods of Sturm (which have
been applied to Bessel's equation by various mathematicians), and we shall then give an
investigation which leads to the fascinating result that the two expressions which, in this
section, were proved to be 0A) are in reality 0 {y~^)> so that approximations are obtained
for the smallest zeros of Jv (x) and Tv{x) in which the errors are 0(v~^)} i.e. the errors
become negligible when v is large.
[Note. An elementary result concerning the smallest zero of Jv (%) has been obtained
from the formula of § 5*43 by Gegenbauer, Wiener Sitzunqsberichte, cxr. Ba), A902), p. 571;
if (i — v +1 where 0 < e < 1, then the smallest zero of Jiv + e (x) is less than twice the smallest
zero of Jv (jki\ because, for the latter value of x the integrand cannot be one-signed.]
15*82. Applications of Sturm's methods.
Various writers have discussed properties of Bessel functions by means of
the general methods invented by Sturm* for the investigation of any linear
differential equation of the second order. The results hitherto obtained in
this manner are of some interest, though they are not of a particularly deep
character, and most of them have already been proved in this chapter by
other methods.
The theorem which is at the base of the investigations in question is that,
given a differential equation of the second order in its normal form
in which the invariant / is positive, then the greater the value of I, the more
rapidly do the solutions of the equation oscillate as x increases.
As an example of an application of this result, we may take a theorem due to Sturm
{ibid. pp. 174—175) and Bourget, Ann. sci. de Vticoh norm. sup. in. A866), p. 72, that, if
v2 - ? be positive and c be any zero of <@v {%) which exceeds v/( - i), then the zero of <@v (x)
which is next greater than c does not exceed e
This result follows at once from the consideration of the facts that the function
#*<gp,, (#) is annihilated by the operator (§ 4*3)
— +
i/2 —
and that, when x ^ c, 1 %
> f.
C
A slightly more abstruse result is due to Porter, American Journal of Math. XX. A898),
pp. 196—198, to the effect that, if vl >? and if the zeros of $>„ (x), greater than V(v2-?),
in ascending order of magnitude are c1? c2» cs? ••• then cn+\-an decreases as n increases.
This has already been proved in § 15'8 by another method.
Other theorems of like nature are due to Bocher, Bulletin American Math. Soc. in.
A897), pp. 205—213; vn. A901), pp. 333—340; and to Gasser, Bern Mittheilungen, 1904,
pp. 92—135.
* Journal de Math. i. A836), pp. 106—186; an account of recent researches on differential
equations by Sturm's methods is given in a lecture by Bficher, Proc. Int. Congress of Math. i.
(Cambridge, 1912), pp. 163—195..
518 THEORY Off BESSEL FUNCTIONS [CHAP. XV
15*83. Applications of Sturm's methods to functions of large order.
We proceed to establish a number of results concerning cylinder functions
of large order which are based on the following theorem of Sturm's type :
Let u^ (x) and u% (x) be solutions of the equations
such that, when x = a,
«i (a) = u2 (a), W (a) = < (a),
and let Ix and /2 be continuous in the interval a^x^b, and also let u-?(x) and
u2' (x) be continuous in the same interval.
Then, if 11'^I2 throughout the interval*, 1^(^I exceeds \u1(x)\ so long as
x lies between a and the first zero of ux (x) in the interval, so that the first zero
ofu-l{x') in the interval is on the left of the first zero of uz(x).
Further, if u/ (a) has the same sign as ux (a), the first maximum point of
| u-y (ac) | in the interval is on the left of the first maximum point of \ u2 (x) j, and,
moreover
max | ux (x) | < max | u2 (x) |.
To prove the theorem f, observe that, so long as ux(x) and u2(x) are both
positive,
d2u2 d2^ ,,
and so, when we integrate,
L dx dxja
Sihce. the expression now under consideration vanishes at the lower limit,
we have
Hence we have
dx
and therefore
that is to say,
B)
(x) ^ Ux (a)
* To simplify the presentation of the proof of the theorem, it is convenient to change the signs
of ux (x) and u2(x), if necessary, so that ^{x) is positive immediately on the right of ? = a; the
signs indicating moduli may then be omitted throughout the enunciation.
t The theorem is practically due to Sturm, Journal 4e Math. i. A836), pp. 125—127,145—147.
15-83] ZEEOS OF BESSEL FUNCTIONS 519
It follpws that just before ux(x) vanishes for the first time ih(ai) is still
positive, and it has remained positive while x has increased from the
value a.
The first part of the theorem is therefore proved.
Again, if w/(a) is positive, as well as «: (a), then Ui(x) must have a maximum
before it vanishes, and at this point, /xl5 we have from A)
so that -Ma' (fij is positive and u.2' (%) must be positive in the interval @, /u-j).
Therefore the first maximum point yu2 of w2(#) must be on the right of /v
Finally we have
max wx (x) = Wj (/^) ^ u2 (fix) ^ xu (fa) = max tta (#)>
and the theorem is completely proved.
When two functions, ux (cc) and w2 (*)»are related in the manner postulated
in this theorem, it is convenient to say that ux(x) is more oscillatory* than
¦w2 (x) and that «2 (#) is ^ss oscillatory than lij (a;).
We shall now apply the theorem just proved to obtain resultsf concern-
concerning Jv(x) and Yv(x) when v is large and ai — v is 0(i>*). Our procedure will
be to construct pairs of functions which are respectively slightly less and
slightly more oscillatory than the functions in question.
In the first.place we reduce Bessel's equation to its normal form by writing
x — veB; we then have
A function which is obviously slightly less oscillatory than ^v(vee) for
small positive values of 6 is obtainable by solving the equation
D) [+2^1 it-0,
since e20 -1 ^ 26 when 0 > 0;
The general solution of D) is
and the constants implied in this cylinder function have to be adjusted so
that u and its differential coefficient are equal to $'„ (ve°) and its differential
coefficient at d = 0.
* The reason for the use of these terms is obvious from a consideration of the special case in
which Ix and I2 are positive constants.
t These results supersede the inequalities obtained by Watson, Proc. London Math. Soc. B)
xvi. A917), pp. 166—169.
520 THEORY Off BESSEL FUNCTIONS [CHAP. XV
It follows that a function which is (slightly) less oscillatory than <WV (x),
when x > v, is
B0)*
We now endeavour to construct a function which is (slightly) more oscil-
oscillatory than 9$v (x), in order that we may have $*„ (x) trapped between two
functions which are more easily investigated than <WV (os).
The formula for the less oscillatory function, combined with the result
stated in § 8*43, suggests that we should construct a function of the type*
where yjr F) is a function of 6 to be determined. It might be anticipated
from § 8'43 that the suitable form for ¦xjr F) would be ? tan3 ft where sec /3 = e6;
but it appears that this function leads to a differential equation whose solution
is such that its degree of oscillation depends on the relative values of v and 0,
and we are not able to obtain any information thereby.
The invariant of the equation determined by
is known to be (§ 4'31)
and it is requisite that this should slightly exceed v2 (e20 — 1). It is consequently
natural to test the value of ty @) which is given by the equations
by determining whether^ for this value of >fr (d),
wig 3 Mr"(*))', 5 w
'0 41} +l
When we replace e0 by sec /S, we find that
^•'@) - tan ft ^@)
4 cos
r" F) = sec j8 cosec ft ty" (8) =
tan /3 sin2!
and hence we have to test the truth of the inequality
Now -.
a
is negative when tana /3 < V24 - 3, and it is positive for greater values
of tan2 ft
* The multiple of the cylinder funotion is taken so that the product satisfies a differential
equation in its normal form; cf. § 4*31 A7).
15*83] ZEROS OF BESSEL FUNCTIONS 521
Hence, since E) is true when j8 = 0, it is true when 0 < /3 ^ ft, where ft
is a certain angle between arc tan ^{^24 — 3} and %rr The sexagesimal
measure of ft is 59° 39' 24"-27.
Proceeding as in the former case, we find that the function
s/{3 A-/3 cot 0)}. [r (f) (H* ff. (?) J-h [v (tan 0 - /3)}
+ T (i) ft*I #,' (v) Jh [v (tan ? - 0)}]
is slightly more oscillatory than Jv (v sec #), so long as* 0 ^ # < ft.
We can now obtain an extremely important result concerning the smallest
zero of rSv (cc) which is greater than v; for let ^ V be the smallest value of ?
which ma^es
r (!) {W v* (*) J-h @ + r a) (*w (.) Ji (f)
vanish. Then 6o^A of the equations
2(9 = X,,2/^ v (tan /3 —/3) = & V
give a; = v + |\,,V + 0 (it*).
Since, by Sturm's theorem, the zero of ^v [x) lies between two expressions of
this form, we see that the value of the zero of 9ov (a?) which is next greater than v
is expressible in the form
y + $\,M+0(i/-l).
When %\ (&•) is equal to Jv (x) it is easy to verify from a Table of Beasel
functions of orders ± $ that
>,„= 1-926529 + 0(*H),
and so the smallest zero of Jv (x), when v is large, is
v + i/*x 1-855757+ 0(v-l).
In like manner, the smallest zero of Yv (x) is
i/ + i/*x 0-931577+ 0(*r*).
The first maximum of Jv (%) may be obtained in a similar manner, by differ-
differentiating f the two expressions constructed as approximations.
The result is that if 1/mvs is the smallest value of ? which makes
vanish}, then the first maximum of iTv(x) is at the point
v + i^V + 0 (*-»),
i.e. at the point
v + v* x 0-808618 + 0 (*H).
The first maximum of the function Yv ix) cannot be treated in this manner because its
first maximum is on the right of its first zero; this follows at once from § 15*3, because
Yv (x) increases from - co to 0 as x increases from 0 to the first zero.
For an investigation of the maximum value of Jv(x) qua function of v the reader
should consult a paper by Meissel, Astr. Nach. oxxvill. A891), cols. 435—438.
* This restriction is trivial because we have to oonsider values of ? for which p/93 is bounded;
i.e. small values of /S.
+ The permissibility of this follows from the second part of Sturm's theorem just given.
% This value of ? is approximately 0-685548.
CHAPTER XVI
NEUMANN SEKIES AND LOMMEL'S FUNCTIONS OF TWO VARIABLES
16*1. The definition of Neumann series.
The object of this chapter and of Chapter xvn is the investigation of
various types of expansions of analytic functions of complex variables in series
whose general terms contain one or more Bessel functions or related functions.
These expansions are to some extent analogous to the well known expansions
of an analytic function by the theorems of Taylor and Laurent. The expansions
analogous to Fourier's expansion of a function of a real variable are of a much
more recondite character, and they wil-1 be discussed in Chapters xvill and xix.
Any series of the type
2 anJv+n(z)
n=0
is called a Neumann series, although in fact Neumann considered * only the
special type of series for which v is an integer; the investigation of the more
general series is due to Gegenbauer j".
To distinguish these series from the types discussed in § 16-14, the description 'Neu-
'Neumann series of the first kind' has been suggested by Nielsen, Math. Ann. lv. A902), p. 493.
The reader will remember that various expansions of functions as Neumann
series have already been discussed in Chapter v. It will be sufficient to quote
here the following formulae:
where to-2 = Za + z2 - 2Zz cos <j>.
We shall first discuss the possibility of expanding an arbitrary function
into a Neumann series; then we shall investigate the singularities of the
analytic function defined by a Neumann series with given coefficients; and
finally we shall discuss the expansions of various particular functions.
For a very general discussion of generalisations of all kinds of series of Bessel functions,
the reader may consult memoirs by Nielsen, Journal fiir Math, oxxxii. A907), pp. 138—
146; Leipziger Berichte, lxi. A909), pp. 33 —61.
* Thearie der BetseVschen Functionen (Leipzig, 1867), pp. 33—35.
+ Wiener Sitzungtberichte, txxiv. B), A877), pp. 125—127.
16-1, 16-11] NEUMANN SERIES 523
Various expansions of types which resemble Neumann's (othe,- than those given in this
chapter) are due to H. A. Webb, Phil. Trans, of the' Royal Soc. cciv. A905), p. 487 and
Nielsen, Atti delta R. Accad. dei Lined, E) xv. A906), pp. 490—497.
16*11. Neumanns expansion* of an arbitrary function in a series of Bessel
coefficients.
Let f(z) be a function of z which is analytic inside and on a circle of
radius R with centre at the origin. If G denotes the contour formed by this
circle and if z is any point inside it, it follows from Cauchy's theorem that
Now, by § 9*1,
-i-= 2 en0n(t).Jn(z)-3
and this expansion converges uniformly on the contour. It follows at once
that
A) /(*)= 2 anJn{z),
where
B) an
and this is Neumann's expansion.
If the Maclaurin expansion off(z) is
/O)= S bnzn,
we see that
On=^-.[ On(t)\ ibm
tm On (t) dt
and so
This result shews that the Neumann series corresponding to a given function
assumes a simple form whenever a simple expression can be found for the sum
The construction of the Neumann series when the Maclaurin expansion is
given is consequently now merely a matter of analytical ingenuity.
* Theorie der BesseVschen Functionen (Leipzig, 1867), pp. 33—35. See also Konig, Math. Ann.
v. A872), pp. 338—340.
524 THEORY Off BBSSEL FUNCTIONS [CHAP. XVI
16*12. Neumann's* analogue of Laurent's theorem.
Let f(z) be a function of z which is analytic and one-valued in the ring-
shaped region defined by the inequalities
Let C and c be the contours formed by the circles
\z\ = R, \z\*=r,
both contours being taken counter-clockwise; then, if z be a point of the region
between the circles, we have
o t-z 2iriJc *-t
- 5 ?=-**<*){ f(t)On(t)dt+t ~On{z)\ f(t)Jn(t)dt
n=0 Am Jc n = 0*iri Jo
Consequently f(z) is expansible in the form
A) /(*) =H4{z) + $ <On(z), .
where
If the Laurent expansion oif{z) in the annulus is
we have, as in §16*11,
/(»)- 2 &,* + 2 i,
«=0 n=l *
16*13. Gegenbauer's generalisation of Neumann's eaypansion.
By using the polynomial j4n>1,(?) defined in §9*2, Gegenbauerf has
generalised the formula given in §16*11.
If f(z) is analytic inside and on the circle | z j = R, and if C denotes the
contour formed by this circle, we have
and so
A)
»=o
* Theorie der BesseVtchen Functionen (Leipzig, 1867), pp. 36—39.
t Wiener Sitzungsberichte, ixxiv. B), A877), pp. 124—130. See Wiener Denkschriflen,
A884), pp. 293—316 for some special cases of the expansion.
16* 12-16* 14] NEUMANN SERIES 525
where
B) a^~
provided only that v is not a negative integer.
If, as in §16*11, the Maclaurin expansion of/B) is
/<*)- t bnz»,
then
/o\ \^n V(v-\~n — wi)
\& ) afi'=s\v *t*n) aj ?i ". ™* vi)r— 2wi•
Neumann's expansion of § 1612 may be generalised in a similar manner.
16*14. The Neumann-Gegenbauer expansion of a function as a series of
squares or products.
From the expansion of § 9*5, namely
-—= 2 Bn.lj.iV(t)Jl,Jr)irl.{z)Jv^n{z)i
C — Z M=o
which is valid when | z \ < \ 11, we can at once infer that, if f(z) is analytic
when | z \ «$ r, then the expansion
A) ^+"/(^)= t a»
71 = 0
is valid when | ? | < r, and the coefficients are given by the formula
B) an
C being the contour formed by the circle | z \ = r. This expansion is due to
Gegenbauer*', an expansion closely connected with this, namely that
C) /(*)= I OhVs»(*),
where
D) an' = ^-.jctf(t)nn(t)dt}
and Cln(t) is Neumann's second polynomial (§9'4), is valid provided that f(z)
is an even analytic function; this expansion was obtained by Neumann f.
Gegenbauer's formula has been investigated more recently by Nielsen, Nouv. Ann. de
Math. D) II. A902), pp. 407—410.
A type of series slightly different from those previously considered is
derived from the formula of §5*22G) in the form
* Wiener Sitzungsberichte, lxxv. B), A877), pp. 218—222.
t Math. Ann. in. A871), p. 699.
THEORY OF BESSEL FUNCTIONS [CHAP. XVI
winch shews that
E) 5 bn**« = I an (**)» <>+»> JHv+n) (z),
n=0 n=0
where
Expansions of this type have been the topic of a detailed investigation by
Nielsen*.
16*2. Pincherle's theorem and its generalisations.
00
Let 2 an Jv+n (z) be any Neumann series, and let the function defined by
71=0
this series and its analytic continuations be called/^).
Let also
The function defined by f(z)N and its analytic continuations will be called
the associated power series off(z).
The Neumann series converges throughout the domain in which
lim %\{anJv+n(z)}\<l,
and this domain is identical with the domain in which
n-*-oo V
by Horn's asymptotic formula (§8*1).
It follows that a Neumann series has a circle of convergence, just like a
power series, and the circles of convergence of a Neumann series and of the
associated power series are identical.
The theorem that the convergence of a Neumann series resembles that of
a power series is due to Pincherlef; but it is possible to go much further,
and, in fact, it can be proved that/(z) has no singularities which are not also
singularities oif{z)N.
To prove this theorem, we write
* Nyt Tidsskrift, ix. (b), A898), pp. 77--79.
f Bologna Memorie, D) in. A881), pp. 151—180; see ako Nielsen, Math. Ann. lv. A902),
pp. 493—496.
16-2, 16-3] NEUMANN SERIES 527
and then, inside the circle of convergence*,
From the theory of analytic continuation it follows that, if (f> B) is analytic
for any value of z, so also is f(z), provided that the path of integration is suitably
chosen; and so all the singularities of f(z) must "be singularities of (f> (z).
Now the series defining <p (z) may be written in the form
an
and a theorem due to Hadamard f states that, if
F^z)** ? bnz>\ Fn_(z)= 5 onz\ F,(z)= ? bncnzn,
n=0 n=0 n = 0
then all the singularities of Fs (z) are expressible in the form By, where /3 is
some singularity of i^j (z) and y is some singularity of F.2 (z).
Since the only finite singularity of the hypergeometric function
)
is at the point z — 1, it follows that all the singularities of $ (z) are singularities
of/(zXv; and therefore all the singularities of f(z) are singularities of/(s)jy;
and this is the theorem which was to be proved.
The reader should have no difficulty in enunciating and proving similar
theorems\ connected with the other types of expansions which are dealt with
in this chapter.
16'3. Various special Neumann series.
The number of Neumann series, in which the coefficients are of simple
forms, whose sums represent functions with important analytical properties is
not large; we shall now give investigations of some such series which are of
special interest.
By using the expansion
(V - W cos 26 + I)"* = 1 t-m-zPn (cos 26),
H = 0
* It is assumed that R{v-\-\) is positive; if not, the several series under discussion have
to be truncated by the omission of the terms for whioh R(v + n + %) is negative, but the general
argument is unaffected.
t Acta Math. xxn. A899), pp. 55—64; Hadamard, La Strie de Taylor (Parih, 1901), p. 69.
X For such theorems oonoerning the expansion of § 16*14, see Nielfien, Math. Ann. lii. A899),
p. 230 et seq.
528 THEORY OF BESSEL FUNCTIONS [CHAP. XVI
Pincherle* has observed that
1 f
-»¦ cob 20 + 1) '
where the contour lies wholly outside the circle 111 = 1.
If now we write \ (t — 1/t) — w, so that the contour in the w-plane is a
(large) closed curve surrounding the origin, we find that
S Jan-H U)Jrw(COS 20) =
and so we obtain the formula
A) S J2n+i (*) P» (cos 20) = ~ e-«MM dlu «-^ e-iZ8in e snu du,
where the modulus of the elliptic function is sin 6.
The interesting expansion
t 24
f
.to 2.4..7
has been given by Jolliffej*, who proved that the series on the right satisfied
the same differential equation as Jv* (%z). This expansion is easily derived as
a special case of § 11*6 A), but the following direct proof is not without
interest:
By Neumann's formula (§ 5*43) we havej
and, if we expand J2v {z \/t) into the series
x 2FX (- m, %v + m + 1; 2v + 1; t) «/^+2m+1 (z),
we find on integration that
m=0 *
* Bologna Memorie, D) vm. A887), pp. 125—143. Pincherle used elliptic functions of modulus
coseo 6 in his result.
t Messenger^ xlv. A916), p. 16. The corresponding expansion of z$ Jv-^ (Jz) Jv (^z) was obtained
by Nielsen, Nyt Tidsukrift, ix. b, A898), p. 80.
% If R {v + J) < 0, we use loop integrals instead of definite integrals.
16*31] NEUMANN SERIES 529
where
am = 7T ml V(^l) /o'""*^ ~ t]~iiFl (~m>2v + m + l^v + l; t)dt
Jin ffiv+m 11 Am)
by m partial integrations.
It follows that am is the coefficient of hm in the expansion of
in ascending powers of h ; and this expansion ia absolutely convergent when
|A|<1.
u we write t = -——-.—-,
1-hu
we find that
S a,wAw = - [1T* A - A A - t)}~»-i A
m = 0 7T JO
«1 f U"-i (l _ u)-i (l _ A2w)~* du.
t Jo
It is now evident that a2n+i = 0 and that
v
tt" wi...Bn) r(v + n + l) '
and this formula at once gives JoUiffe's form of the expansion.
16'31. The Neumann series summed by Lommel.
The effects of transforming Neumann series by means of recurrence
formulae have been studied systematically by Lommel*; and he has suc-
succeeded by this means in obtaining the sums of various series of the type
%anJv+n(z)
in which an is a polynomial in n.
Take the functions
v,n (z) =1 (v + 2n + 1)/9M(v + 2n+l) Jv+,n+l (z),
n=0
,() (
where fm (y) is a function to be determined presently.
* Studien Uber die BesaeVschen Functionen (Leipzig, 1868), pp. 46—49.
W. B. F. 34
THEORY OF BESSEL FUNCTIONS [CHAP. XVI
Sy the recurrence formula we have
A) - ?4,,m CO = 2 /m 0 + 2w + 1) [Jv+m (z) +
Z w=0
'provided that fm (v) satisfies the equation of mixed differences
fzin(v + 2n + 3)+fM(v + Zn + l)=2(V+2n
A solution of this equation is
We adopt this value of fm(v) and then it is found by the same method that
B) - JU (*) - -/m-i (y) J^ B) + 2?4v>m-i (*).
z
Hence it follows that
S4v,m 0) = W™ (v + 1) Jv (z) - ^fzm^ (v) Jv+1 (z)
m
and so <s4,,m (z) = ^ S [\z™fm (v + 1) /, (z)
-?~^fm-x{v) Jv+i («)} + a"B+8^,-i 0).
Therefore, since
If*
) = 5 / «/v («) di,
^^0
we have
C)
)
and similarly, from the expression for 3v>m(z),
* Recent applications of Neumann series to the solution of equations of mixed differences are
due to Bateman, Proc. Int. Congress of Math. i. (Cambridge, 1912), pp. 291—294.
16*32] NEUMANN SERIES 531
The potentialities of the other recurrence formula
were also investigated by Lommel, but the results are uot so interesting. As examples of
his expansions the reader may notice that
These results were given by Lommel, though his formulae contain numerical errors.
16*32. The Neumann series summed by Kapteyn.
The sum of the series
2 n/, <*)./» (a)
is expressible as the integral
, faJx(z~v) T . w
lz I ..-Li .' JQ (a — xi)dv\
J0 2~V
the sums of the alternate terms of the series have been expressed by Kapteyn*
in the form of integrals from which this integral may be deduced, and
conversely Kapteyn's formulae may be deduced from this integral.
We proceed to establish thF result by a simplified form of Kapteyn's
methods.
The series may be written in the formf
\z 2 [Jn-i {z) + Jn+\ {z)\ Jn («) — J2~ni j ¦? (^"'l "•" ?~"~~2) U~n~X
exp \fc (t--) + |a (it. - - j [ dudt
x
o+j
where the contours may be taken to be the circles \u\ = l, \t\ = A >1.
Now, let
I-a—: ,-—t exp Ha. [u—)y du.
Then, if m = \{t — \jt), we have
dl
Archie/ voor Wiskunde, B) vn. A907), pp. 20—25; Proc. Section of Sci., K. Aknd.
van Wet. te Amsterdam, vn. A905), pp. 494—500; Kapteyn has subsequently summed other series,
ibid. xiv. A912), pp. 962—969.
t The interchange of summation and integration is permissible so loug ab | jii|>l, where t, it
are any points on the contours.
34—2
532 THEORY OF BESSEL FUNCTIONS [CHAP. XVI
Therefore, on integration,
1 pa
&: o
where G is independent of a. By taking a = 0, we see that C = 1/t.
Hence we have
+1 [ Jexp {*(,-«+!)(*- j)| {«/, («)- /a (v)} dv
= 1 [/<>(*-a+'*>) +1/", (* —a+
"* Jo
the majority of the terms having a zero residue at t =0.
Consequently
S nJn («) Jn (a) = 5 | 1V / Jo (w) dv,
that is to say
A) S nJn (*) Jn (a) = I f ° ^^?> Jo (a - v) d».
If we select the odd and even parts of the functions of z on each side of
this equation, we find that
B) 2 Bn+l)Jm+1(z)Jm+1(a)
w=0
Z fa f Ja (ar - n) J,(g+v)} T , . j
= I 1-^ +-LX-i J\ J9(a-v)dv,
*Jo [ Z-V 2 +V ) X
which is one of Kapteyn's formulae; and
2nJ (t\J (^-Z\Jl
z-cl
_ , f- iJ^z-v) _ Jlil±»)) _ dy
4Jo ( z-v z + v J v 7
- ? fa f^i?±!L) + ii^'JJi Jo (« _ ,) dv>
when we integrate by parts.
Hence it follows that
().()! ffl+
n=l 4Jo Jo ( 2+« Z — V
which is the other of Kapteyn's results.
16-4] NEUMANN SERIES 533
The reader should have no difficulty in proving by similar methods that,
when R (v) > 0.
.., S , . r , , r , v (v — l)z[a /„_! (z - v) T , . ,
D) %(v + n) Jv+n(*) J*+n(«) = ~—y~~ Io - z_v J»(a~«)^v
vz [a Jp(z — v) T . j
2 Jo z-v v y
16*4. jTAe Webb-Kapteyn theory of Neumann series.
Neumann series have been studied from the standpoint of the theory of
functions of real variables by H. A. Webb*. His theory has been developed
by Kapteynf and subsequently by BatemanJ. The theory is not so im-
important as it appears to be at first sight, because, as the reader will presently
realise, it has to deal with functions which must not only behave in a
prescribed manner as the variable tends to ± qo , but must also satisfy an
intricate integral equation. In fact, the functions which are amenable to the
theory seem to be included in the functions to which the complex theory is
applicable, and simple functions have been constructed to which the real
variable theory is inapplicable.
The result on which the theory is based is that (§ 132)
("j (t)J (t)dt-i° (m*n)>
J o ^ {t) Jm+1 {t) 1 " {l/Dn +2) (m = n),
so that, if an odd function f{x) admits of an expansion of the type
CO
/(#)= 2 a2n+1 Jm+1 (x),
and if term-by-term integration is" permissible, we have
" w t
We are therefore led to consider the possibility that
A) /(a) = JoDn + 2)/2n+1(*)
and we shall establish the truth of this expansion under the following
conditions:
(I) The integral
exists and is absolutely convergent.
jXf(t)dt
Jo
* Messenger, xxxm. A904), p. 55.
t Messenger, xxxv. A906), pp. 122—125.
% Messenger, xxxxu A907), pp. 31—37.
534 THEORY OF BESSEL FUNCTIONS [CHAP. XVI
(II) The function f(t) has a continuous differential coefficient for all
¦positive values of the variable which do not exceed x.
(III) The Junction f(t) satisfies the equation
B) 2/' @ = J" ^ {/(„ +1) + f(v -1)} dv
when t does not exceed x.
We now proceed to sum the series
S=l Dn + 2) Jm+1 (x) I" ^f^ f(t) dt,
n=0 JO I
and we first interchange the order of summation and integration. It is evident
that
2 Jm+1 (x) {Jm (t) + «/¦„„+, (t)}
tt=0
converges uniformly with respect to t for positive (unbounded) values of t,
since | J2n @ I < * and S j Jm+1 (x) | is convergent. Hence, since fit) possesses
an absolutely convergent integral, we may effect the interchange, and then,
by § 16-32,
? - f(t) 2 Dn + 2) J2n+1 (x) J2n+1 (t) ~
io U=o J *
+ fV. (e - v) (Vf(v -1) ^P dtdv.
Jo Jo t
We now transform the last integral by using § 12*2, and then we have*
o j o
= I" IUJ0 (u - t)f(x - u) J±P- dtdu
J OJ 0 t
rx
— \ J\ (")/(* — w) du
Jo
rx
~fix) ~ Jo (u)f (x — u) du.
JO
* The first transformation is effected by writing
16-4] NEUMANN SERIES 535
Hence
oo
C) 2 Dn
Now write
f (v) — - —~ {f(t + v) -+f(t -*«)} d* = F(v)>
* 'o t
so that jP (v) is a continuous function of v, since Jx (t)/t has an absolutely
convergent integral.
If then we are to have S—f(x) when x has any value in such an interval
as @, X), we must have
[X
J0(x~v) F(v)dv = O,
Jo
throughout this interval; and, differentiating with respect to oc,
F(x)=\XJx(x~v)F(v)dv.
Jo
Since j Jx (x — v) j ^ 1/V2, it follows by induction from this equation, since
where A is the upper bound of | F{x) \ in the interval and n is any positive
integer.
If we make n -*¦ x>, it is clear that F(x) = 0, and so the necessity of equation
B) is established.
The sufficiency of equation B) for the truth of the expansion* is evident
from C).
It has been pointed out by Kapteyn that the function sin (x cosec«) is
one for which equation B) is not satisfied; and Bateman has consequently
endeavoured to determine, general criteria for functions which satisfy equation
B); but no simple criteria have, as yet, been discovered.
[Note. If J'{x) is not an odd function, we expand the two odd functions
${/(*)-/(-•*¦)}, k{/(*)+/(-•*>!
separately; and then it is easy to prove, by rearranging the .second expansion, that
)- 2
where a0 = - f /(*) /, (| x I) dx,
A J _oo
f 00 Am
J -00 I •*
provided that the appropriate integral equations are .satisfied.]
* The sufficiency (but not the necessity) of the equation was proved by Kapteyn.
536 THEORY OF BESSBL FUNCTIONS [CHAP. XVI
16*41. Cailler'8 theory of reduced functions.
The Webb-Kapteyn theory of Neumann series which has just been ex-
expounded has several points of contact with a theory due to Cailler*. This
theory is based on Borel's integral connecting a pair of functions. Thus, if
/(*)-! cnz\
ra=0
then the function f(z)g denned by the series
00
f(z)B = 2 cn.n\zn,
tt=O
supposed convergent for sufficiently small values of \z\, may be represented
by the integral
Jo
The function f{z)R maybe termed the reduced function (la rdduite) off(z).
If the Neumann series which represents f{z) is
00
/(*)- 2 anJn(z),
n=0
then we have, formally,
w=0 JO
Now put
and we see that
Hence, if the Neumann series for f(z) is 2 anJn (z), then the generating
function of 2 anfn is
provided that this function is analytic near the origin-
More generally, if f(z) has a branch-point near the origin of such a nature
that
A) /W=U
then
* M6m. de la 8oc. de Phys. de Geneve, xxxrv. A902—1905), pp. 295—368.
16*41,16-5] LOMMEL'S FUNCTIONS 537
In like manner, if
00
C)
then
D) 5
n.
[Note. If eta*fAnbz—'2anJn(z),
¦n=i
then I a ,*-
This result, which is immediately deducible from Cailler's theory, was set as a problem
in ttie Mathematical Tripos, 1896.]
16*5. Lomtnel's functions of two variables.
Two functions, which are of considerable importance in the theory of
Diffraction and which are defined by simple series of Neumann's type, have
been discussed exhaustively by Lommel* in his great memoirs on Diffraction
at a Circular Aperture and Diffraction at a Straight Edge.
The functions of integral order n, denoted by the symbols Un (w, z) and
Vn (w, z), are defined by the equations
00 /?/A M+2*"'
A) Un{w,*)= 2 (-)m(-
\ZJ
oo >w\ -n-tm,
B) K« <«/,*)- 2 (-r(^) J-n
It is easy to see from §2*22 C) that
C) i/M(^^)-F_M+2(M;^)= S (-fF
»l=-00 \* '
'w z*
= COS<2+^
T)'
D) Un+1 (w, z) - F_M+, (w, z) = sin ^-
The last equation may be derived from the preceding equation by replacing
n by n + 1.
There is no difficulty in extending A) to define functions of non-integral
order; for unrestricted values of v wr write
E) Uv(w,z)= 1 (-
w=o
* ^l&A. dcr matfe. p/tj/s. C/a«se d<rr k. b. Akad. der Wist. (Miinchcn), xv. A886), pp. 229—328,
529—664. The first memoir deals with functions of integral order; and the definition of Vn (w, z)
in it differs from that adopted subsequently by the factor (- l)n. Much of Lommel'e worlc is repro-
reproduced by J. Walker, The Analytical Theory of Light (Cambridge, 1904). The occurrence of Lommel's
functions in a different physical problem has been noticed by Pocklington, Nature, lxxi. A905),
pp. 607—608.
THEORY OF BESSEL FUNCTIONS [CHAP. XVI
The expression on the right is an integral function of z, and (when the
factor i0y is removed) an integral function of w.
The corresponding generalisation of B) gives a series which converges
only when v is an integer. And consequently it is convenient to define
Vv (w, z) for unrestricted values of v by means of the natural generalisation of
C), namely
F) Vv(W} z) - cos (| + ~ + ~) + U.v+2 (w, z).
It is evident that
G) Uv (w, z) + IU («, *)
(8) V. (w, z) + Vv+, (w, z) = (?y /_, (z).
As special formulae, we deduce from § 2*22 that
(9) Z70 (*,«) = Fo(«, *) - i {/0 (*) + cos *),
A0) C/(^^) = -F1(^^) =
and hence, by G) and (8),
A2) Uan+l (z, z) = ~. Vm+1 (z, z) = \ {-y {sin z - Y (-)»e2)rt+1
provided that n^l in A1), and n^O in A2).
It is also to be observed that, as a generalisation of these formulae,
A3) Vn{w,z) = {-yUn(z*lw,z).
" .si n "
The functions 2 md.Jm(z), 2 8\n(m+$)d.Jm + i (z),
m=0 CfjS m=0
which are closely associated with Lommel's functions, have been studied by Kapteyn,
Proc. Section of Sci., K. Akad. van Wet. te Amsterdam, vn. A905), pp. 375—376, and by
Hargreaves, Phil. Mag. F) xxxvi. A918), pp. 191—199, respectively.
16'51. The differential equations for Lommel's functions of two valuables.
It is evident by differentiating § 16*5 A) that
A)
and hence
and consequently
z2 1
Uv (w, z) = -2 Uv+2 (w, z)-- Uv+, (w, z),
16*51, 16-52] 'LOMMEL'S FUNCTIONS 539
It is now evident that Uv (w, z) is a particular integral of the equation
B) & +
OZ2 Z 02 W2
Since the complementary function of this equation is
z- 22
A cos jr- + B sin r-,
2w 2w
where A and J5 are independent of z, it is clear from § 165 F) that V_v+2 (w,z)
is also a particular integral. Therefore Vv (w, z) is a particular integral of
These equations are due to Lomnael, Milnchener Abh. xv. A886), pp. 561—563.
16*52. Recurrence formulae for LommeVs functions of two variables.
We have just obtained one recurrence formula for Uv(w, z), namely
A) ^Uv(™,z) = -^Uv+1(w,z).
To obtain other formulae, we observe that
•_9- Uv(w,z)= 2 (-)m(v+2m){w/zy+^Jv+2m(z)jz
OW m=o
= \ 5 (-)- (w/zY+™-> {/„+,,»_, (z) + Jv+.im+1 (z)},
^ wi=0
and so
B) 2 1 Uv (w, z) = 17^., (w, z) + (z/wf ff,+1 (w, *).
Again, by differentiating § 16'5 F) we deduce that
C) lvv(w,z)=-^V^(w,z),
D) 2 A F, (w, ^) = FM+1 (w, z) + (jsjwf V^ (w, z).
If now we take w = cz, where c is constant, we deduce that
E) 2 ~- Uv (cz, z) = ctr^ (c«, ^) - A/c) ?7,+I (w, 2r),
clz
F) 2 ~ F, (cz, ^) = cF,+1 @8, z) - A/c) F^ (w, z).
CLZ
Hence we get
4 ~ Uv{cz, z) = c3 U,-*(cz, z)-2Uv(cz, z) + A/c2) Uv^(cz, z)
= c"J^ (z) + C~*JV (z) - (c + 1/cJ Uv (cz, z).
540 THEORY OF BESSEL FUNCTIONS [CHAP. XVI
Hence it follows that Uv (cz, z), and similarly V_v+2 (cz, z), are particular
integrals of the equation
The particular case in which s= 0 is of some interest; we have
(8) uv(w,o)= 2 ^/;f;xn,
and so Uv (w, 0) and F_,,+2 (w, 0) are expressible in term's of Lommel's functions
of one variable by the equations
(9) g.(«.0)-
A0) F^(«,0)-
Of these results, (l)-r—(8) were given in Lommel's memoir.
The following formulae, valid when n is a positive integer (zero included),
should, be noticed:
coslw- 2L_ym_ 1
A2) ?W, (W, 0) = (-)« [sin ^ -js^Llil^-.. J ,
A3) ?/_n (w, 0) = cos {\w + \nir).
Hence it follows that
FO(W,O) = 1, Fn+I(w,0)-0,
A5) 7_ (w, 0) = (-)« 2 U
i»=0
n /_
p.**.,(«,o)=(-r t(/
16*53. Integral representations of Lommel's functions.
The formulae
A) Uv (w, z) = —x Jv_! (zt). cos (| w A — t2)). t"dt,
z Jo
which are valid when JB (i/) > 0, may be verified immediately by expanding
the integrands in powers of w and then using the result of § 12*11 A) in
16-53] LOMMEL'S FUNCTIONS 641
performing term-by-term integrations. For other values of v, they may be
replaced by the equations
C) Uv (w, z) = - ^-jj-j-j-g- j ^ Jv_x (- zt). cos \lw A - **)} • (- ty dt,
-,(-*«).sin
in which the phase of — t increases from — ir to nr as t describes the contour.
It is clear that, when R (v) > 0,
E) Uv (w, z) ± iUv+1 (w, z) = —-x\ Jv-i (zt) exp {+ \iw A - V)\. ^ di.
* Jo
By modifying this formula we can obtain integral representations of Vv (w, z)
valid for positive values of w and z. Let us consider
-^ T J,-: (^) exp [± \iw A -««)}. t" dt.
z Jo
The integral converges at the lower limit when R (v) > 0 and at the upper
limit when R (v) < f, if w and z are restricted to be positive.
To evaluate the last integral, swing the contour round until it coincides
with the ray arg t= + \ir, this ambiguity in sign being determined by the
ambiguity in sign in the integral; such a modification in the contour is
permissible by Jordan's lemma.
When we expand the new integral in ascending powers of z, as in § 13*3,
we find that
^ I ^ /„_, (zt) exp [± \iw A - *)). V dt
w e\ (_(z
2" w=ow!l {v+m)J0
iw ™ (-On {\zf
that is to say
F) ^ fV,., (^) exp {+ \iw A - *•)}. ^ A = exp (± -| ± ^
f
When we combine the results contained in this formula, we see that, if w>0,
z>0, and 0 < R(v) < |, then
G) ^ Jo /,_, (zt) cos (|W A - *)} .t»ctt = cos (_ + — -. -j ,
(8) -T-i /_, (rf) sin [\w A - *)} . t" dt = sin (T) + ^ -
* .'o
542 THEORY OF BESSBL FUNCTIONS [CHAP. XVI
It follows at once from A) and B) combined with § 16*5F) that
(9) Vz_v (W| *) = - — I Jv_x (zt) cos {\w A - V)). V dt,
A0) F,_v (w, z) = --,., Jv-, (zt) sin [\w A -t*)}. V dt.
2 J l
Since convergence at the origin is now unnecessary, the theory of analytic
continuation enables us to remove she restriction It (v) > 0.
Changing the notation, we see that
aV—1 Too /7/
A1) Vv («/, z) = - ?- ^ ^_r (rt) cos (iw A - *)) ^2,
A2) 7^^^)^ ^-.(^sinl^a^)},
provided that w and z are positive and i2(i/)> \.
The following special formulae are worth mention :
A3) Um(z,z)
f Jm-z {zt) sin \\
|
fl
= I Jm-i (zt) sin {|a A - t2)}. t2n dt.
Again, from F), we see that
and, in particular,
wco8\2ii>y'
The last results should be compared with § 13*3; see also Hardy, Trans. Camb. Phil.
Soc. xxi. A912), pp. 10, 11.
The formulae of this section (with the exception of the contour integrals) arc all to be
found in one or other of Lommel's two memoirs.
16*54. Lommel's reciprocation formulae.
It is evident from § 165A3) that functions of the type Ut,(z2/w, z) are
closely connected with functions of the type Uv (w, z) provided that v is an
integer.
16-54, 16-55] LOMMEL'S FUNCTIONS 543
To appreciate the significance of such relations observe that
d P fz~ \ iz* \~\
-7- cos (\wf). Uv [ —, zt) + sin (hvf). Uv+1 (— , zt)
dt\_ v<s \w J v<: \w I \
r iz- \ 'z*- \i
= sin {\wtx).\-wtUJ- , zt) -wtUv+2l-,zt)\
= — zJv (zt) sin (jfawt2). (wtjzY~v.
On integration we find that
(!) -~\ \ J* (zt) sin (\w&) t1-" dt
— — cos \w. Uv (—, 2 j — sin \w. Uv+1
and, similarly,
B) ~
Hence it follows that
C) ~ /,_, (rf) cos {J«; A - t*)}. P dt
Z J o
and
D) ,/,_„ (,*) sin {Jw A - P)\. t" dt
z Jo
G~ \ fz" \ (z* \
~->A- cos hw • tfi-r I ~w . °J + sin ^w. U^v [ —, OJ ,
and these integrals differ from the corresponding integrals of the preceding
section only in the sign of the order of the Bessel function.
The reader will find some additional formulae concerning Lommel's functions in a,
paper by Schafheitlin, Berliner Sitzungsberichte, viii. A909), pp. 62—67.
16*55. Pseudo-addition formulae for functions of orders ^ and |.
Some veiy curious formulae have been obtained by Lommel, which connect
functions of the type Uv (w, z) with functions of the same type in which the
second variable is zero, provided that v is equal to \ or f.
When we wribe v — \ in § 16-53 E), we get
(ni) \\ /"I
~j J exp {+ % {\w -zt- \wt*)\ dt
w
exp {+ % (\w + zt- Jw??)} eft.
7 Jo
544 THEORY OF BESSEL FUNCTIONS [CHAP. XVI
Now write
_ (w 4- zf . _ (w - zJ
and we find that
U±(w, z) ±iU$(w, z) = 0T«r _ exp {+cri(l — f2)} df
+ «**« (^) J _v{22/Bw5)texP i±Bi C1 - ?2I d^>
where ^ = i — j Ii + — L (ox) (^ )
in the respective integrals, and V0", VS are io 6e interpreted by the conventions*
Hence we have
U (w, z)±iUi(w, z) = \e** {UkBo-, 0) ± iU%B<r, 0)}
-)
7T/ Jo
exp ±«(l-p) df.
When we take <r?2and S|2 as new variables in the last two integrals respectively,
these integrals are seen to cancel; and so we have the two results combined
in the formula
A) Ui(w, z) ± %Uk{w,z) * ^{^B0-, 0) ± iU^ic, 0)|
and, as a corollary,
B) Uk {z, z) ± iUi (z, z) = \e^ {Uh Da, 0) ± t C79 Da, 0)}.
These formulae are due to Lommel, Milnckener Abh. xv. A886), pp. 601 —605 ; they are
reproduced by Walker, The Analytical Theory of Light (Cambridge, 1904), pp. 401—402.
16'56. Fresnel's integrals.
It is easy to see from § 16'53 A) and B) that, when R(v)> 0,
Uv (w, 0) - g^rf^) J 0 **~l cos t*w A - ^ dt>
Uv+1 (w, 0) = 2v_7F{v) Jo ^"-l sin few A - ?)j dt,
so that
W o>-ir«/ \ *a" cos (W) di - ^ (w' °) cos Iw + ^+i (w, 0) sin % w,
6 1 \V) JO
B) v i2" sin (Jwf) d« = 17., (w, 0) sin \w - Uv+1 (w, 0) cos \w.
* These are not the same as tbe conventions used by Lommel.
16*56] lommel's functions 545
If we take v = \ and modify the notation by writing \w — z = \rrru?, we
see that
= [ Uh Bz, 0) cos z + Ui Bz, 0) sin *]/^2 -
> °)sin * + 7J B*> °)cos *]W'2>
and
D)
j o
= [ tfj B*, 0) sin z-Ui {2z, 0) cos *]
= i - [ ^i B«, 0) cos * - F3 B2) 0) sin s]/V2.
We thus obtain ascending series and asymptotic expansions for Fresnel's
integrals*
ru
t, ail
Jo
cos (-| Trf2) (ft, ( sin
o J
The ascending serios, originally given by Knockenhaucr, Ann. dcr Physik und Chemie,
B) xlt. A837), p. 104, are readily derived from the (/-Heries, namely
while the asymptotic expan.sions, duo to Cauchy, Comptes Rendus, xv. A842), pp. 554, 573,
are derived with equal ease from the K-ncries, namely
,„. rr ,a x /4*\4 [\ 1.3 1.3. ,1.7
Tables of Fresnel'H integrals wore constructed by Gilbert, jJ/c'/ji. courounees da I'Acad.
It. des Sci. de liruxellcs, xxxi. (L863), pp. 1—52, and Lindatedt, Ann.der Physik and Chemie,
C) xvii. A882), p. 720; and by Loinmel in hi.s second memoir.
Lommel has given various representations of Fresnel's integrals by series
which are special cases of the formulae"j"
(9) \~J.(t)dt = 2 2 /,+,»+,(*)
J 0 n=0
~n=o(^+T)"G+H).
A0) [-/.(I)*- i (' + i)(^ + 3) ,,(L+_2.-l)
Jz «=o a
* Jl/cwt. rfe Z'/itv«Z. den Sci. v. A818), p. 339. [Oeuvres, i. A86C), p. 176.]
t It is supposed in (9) that 11 (*-)> -1.
w. a p. 35
546 THEORY OF BESSEL FUNCTIONS [OELAP. XVI
These are readily verified by differentiation. Other formulae also due to
Lommel are
(ii) (V.
+ 21 sin 1*1 5 (-)»•/„+•, A*) ,
U=0 J
A2) !2 J* (t) dt = 2« sin ^ I I (-)» Jn+i (t*)l
Jo L»-o J _ _.
r oo |
— 2* cos \z ? (—)n J"n+j (|^) .
L«=0 J
These may also be verified by differentiation.
16*57. Hardy's integrals for Lommel's functions.
The fact that the integrals
f00 / x b\ dt f00 . / . b\ tdt
f cos [at —) z , I sin I at — j ^—
Jo \ t J X. -T t Jo \ 6/ i T t
are expressible in terms of elementary functions* when a and b are positive
suggested to Hardyf the consideration of the integrals
r i ^\dt r ' t b]tdt
and he found them to be expressible in terms of Lommel's functions of two
variables of orders zero and unity respectively. This discovery is important
because the majority of the integrals representing such functions contain Bessel
functions under the integral sign.
If 1/i be written in place oi't, it is seen that
P* ' ( t -\ d- - f" (it aN\ dt
/o\ f" '• ( ¦ .b\ tdt r . ( . b\dt f°- . /,. . a\ tdt
B) | sin
and since, by § 6'13 C),
it is suflficient to confine our attention to the case in which b <a.
We now write
c = */(b/a), so = 2sj{ab), 6 - |A - c2)/c,
* Hardy, Quarterly Journal, xrxn. A901), p. 374. "When the lower sign is taken it is supposed
that the integrals have their principal values.
+ Messenger, xxxvm. A909), pp. 129—132.
16-57] lommel's functions 547
and then the"substitutions t — ceu and coshw=T shew that
/;
b\ dt f°° cos (x cosh u) du
at + 7
f°° f 1 1 )
cos (x cosh m) \ ——r-77—- 4- —,.-—¦ . [ du
Jo /\ceu + l/(ceu) ce~u + l/(c*rM) j
cos (a'"
Now consider
eixrrdr
where Y is a contour consisting of the real axis and a large semicircle above
it, the real axis being indented at t = + 1.
The only pole of the integrand inside the contour is at id, and so
?~-\
As the radius of the large semicircle tends to infinity, the integral round
it tends to zero by Jordan's lemma, and hence
cob(xt). rdr 1 f1 sin(a;T). rdr _ ire~xB
^1) + 2 J _! '(^T
Thus we have
f00 / b\ dt 7r€~{a~b) a + b {* sin (a cos (f>). cos (j>d(f>
But
Jo r
cos cf) 4c
and so we find that
C) | cos (at -f
Jo \ i/ i-fv & w=i
Similarly it is found that*
D) sin I a<+7),¦•¦¦= ^ tt S <
and
E) Pj%c
F) P\ &m [at +-\ -—- = —|-7rcos(a+6) —7T 2 (—)m-lti*mJili
The details of the analysis will bj9 found in Hardy's paper.
35—2
548 THEOBY OF BESSEL FUNCTIONS [CHAP. XVI
The last two results may be written in the form
. 2
(8) U, (», ,) + 7. (», «) —- - * Jo »n (:2- + g) ^,
provided that 0 < w < x.
16*58. Integrals of Gilbert's type for Lommel's functions.
An obvious method of representing Uv(w, z) and Vv(w, z) by integrals is
to substitute the Bessel-Schlafli integral of §6*2 for each Besscl function in
the appropriate series. We thus get
When the contour is so chosen that it lies wholly outside the circle on
which 111 = \ | w |, we may change the order of summation and integration
and get
,,v T7 , , 1 /•(«+. i^+.-^)+) (*w/i)"
A) ^^ ^> = &S J.. 1 + i4^
Now the residues of the integrand at + \ivj are
and so
Making a slight change in the notation, we deduce that
B) 7'<W'*)-S
and, in this integral, the points + iw lie outside the contour.
In general it is impossible to modify the contour in B) into the negative
half of the real axis taken twice, in consequence of the essential singutarity of
the integrand at the origin. The exception occurs when 2=0, because then
the essential singularity disappears, and
and hence
D) Vv (w, 0) = -TT-T- du>
(TT Jo 1 + U2
provided that R(i>)>0 and a is an acute angle (positive or negative) such
that
550 THEORY OF BESSEL FUNCTIONS [CHAP. XVI
It is evident from § 16*5 F) that the corresponding formulae for Uv (w, z)
are
C)
D) *7,,(w, ^)~c| ^V|
m=0
These results were given by Lommel*, but he did not investigate them in.
any detail.
The asymptotic expansion of Vv(cx, x), when v is 0 or 1 and c is fixed, while
x is large and positive, has been investigated by May all f.
The dominant term for general (real) values of v greater than — \ is
readily derived from § 16*53 A2) which shews that
7V (ex, at)~- — j (—J cos {set + \vir - \tt) sin [\ ex A - f~)} — .
Now, if c>l, the functions $cx(l — ti)±(xt + ^vrr — \ir) vary monotonically
as t increases from 1 to oo, and hence it may be verified by partial integra-
integrations that
E) Vv (CX, X) ~ ^ —j ^2 i COS {X + \V7T~\ 7T),
j
the next term in the asymptotic expansion being 0 (x~%).
If, however, c<l, then ^cx(l - P) + (cct + \vtt — \ir), qua function of t,
has a maximum at 1/c; and hence, by the principle of stationary phase (§ 8*2),
it follows that
F) Vv {ex, x) ok -^ cos \^x (c + - ) 4- ^vtt [.
Finally, when c=l, the maximum-point is at one end of the range of
integration, and so the expression on the right in F) must be halved. We
consequently have
G) Vv (x, x) ~ \ cos (x + \vtt).
This equation, like E) and F), has been established on the hypothesis
that v> — {-; the three equations may now be proved for all real values of v
by using the recurrence formula § 16*5 (8).
* Mlnchener Abh. xv. A886), pp. 540, 572—573.
+ Proc. Camb. Phil. Soc. ix. A898), pp. 259—269.
CHAPTER XVII
KAPTEYN SERIES
17*1. Definition of Kapteyn series.
Any series of the type
on
in which * v and the coefficients an are constants, is called a Kapteyn series.
Such series owe, their name to the fact that they were first systematically
investigated, qua functions of the complex variable z, by Kapteyn j" in an
important memoir published in 1893. In this memoir Kapteyn examined the
question of the possibility of expanding an arbitrary analytic function into
such a series, and generally he endeavoured to put the' theory of such series
into a position similar to that which was then occupied by Neumann series.
Although the properties of Kapteyn aeries are, in general, of a more
recondite, character than properties of Neumann series, yet Kapteyn series
are of more practical importance; they first made their appearance in the
solution of Kepler's problem which was discovered by Lagrange.j; and redis-
rediscovered half a century later by Bohso1§; and related series are of general
occurrence in a class of problems concerning elliptic motion under the inverse
square law, of which Kepler's problem may be taken as typical. More recently,
in the hands of Schott|| they have proved to be of frequent occurrence! in the
modern theory of Electromagnetic Radiation.
The astronomical problems, in which all the variables concerned are real,
are of a much more simple analytical character than the problems investigated
by Kapteyn; and in order to develop the theory of Kapteyn series in a simple
manner, it seems advisable to begin with a description of the series which
occur in connexion with elliptic motion.
17*2. Kepler s problem and allied problems discussed by Bessel.
The notation which will be used in this section in tho discussion of the
motion in an ellipse of a particle under the action of a centre of force at the
focus, attracting the particle according to the inverse .square law, is as follows:
The semi-major axis, semi-minor axis, and the eccentricity of the ellipse
are denoted by a, b, and e. The axes of the ellipse are taken as coordinate
* It will, fur the most part, be assumed that v is zero,
t Ann. 8ci. de VEcole norm. sup. (8) x. A893), pp. 91—120.
t Hist, de VAcad. R. des Sci. de Berlin, xxv. A769) [17703, pp. '204—'2153. [Oeuvren, in. (ISM),
pp. 113—138.]
§ Berliner Abh. 1816—7 [1819], pp. 49—55.
II Electromagnetic Radiation (Cambridge, 1912).
17-2] KAPTEYN SERIES 553
In particular e sin E is an odd periodic function of M, and so, for all real
values of E> it is expansible into the Fourier sine-series
00
esinE= S An sin nM,
n = l
where An= I esin EainnMdM
7T Jo
f 2e sin Ecos nM~]« 2 f"- ,.d(esini?) TIJ.
+ — cos nil/ —i—rjrr—idif
2 f* ,rdE-dM
— — I cos nM
2_
Mr
= \jn(ne).
Hence it follows that
E) E = M+ I -
— i n
and this result gives the complete analytical solution of Kepler's problem con-
concerning the eccentric anomaly. The series on the right is a Kapteyn series which
converges rapidly when e < 1, and it is still convergent when e = 1; cf. §§ 8,8*42.
The radius vector is similarly expansible as a cosine series, thus
™ 00
- = Bo + S Bn cos nM,
2 C"
= — cos nM.dE
firrr I «.
where B{) = - I (l-€CosE)dM
A-e cos Ef dE
7T./o
while, when n j* 0,
2
Bn = —
ir
A - € cos i?) cos nMdM
J o
r2(l-ecos^)sinrLflflB 2 /"» . d(ecos^) ,,
= — H / am nM -—j~m—-dM
L W7T Jo W7TJ0 MM
— sin E sin (n^ — ne sin JS1) diE1
nir Jo
so that
F) - = 1 + ^e2 - 2 - //(ne) cos nM.
554 THEORY OF BESSEL FUNCTIONS [CHAP.
The expansion of the true anomaly is derived from the consideration that
vj — M is an odd periodic function of M, and so
00
w — M — ? Gn sin nM,
71 = 1
2 I*""
where G.n = - (to — Jlf) sin nMdM
ir Jo
f 2(w-Jlf)cosnJf'lir 2 f1 ,, (dw .\ ,u
L W7T Jo rnrJo \dm )
2 V(l — e2) fv cos (nE — ne sin
f cos (??? - n6 sin ??) , „
— — I -— (XxJf.
nrr J 0 1 — e cos ?r
This expression is not such a simple transcendent as the coefficients An
and Bn. The most effective method of evaluating it is due to Bessel*, who
used the expansion
= l + 2/ cos E + 2/2 cos 2E + 2/8 cos ZE +¦ • • •,
where / =
On making the substitution, we find at once that
>»=i
17*21. Expansions associated with the Kepler-Bessel expansions.
A large class of expressions associated with the radius vector, true anomaly
and eccentric anomaly, are expansible in series of much the same type as those
just discussed. Such series have been investigated in a systematic manner by
Herzf, and we shall now state a few of the more important of th^m; they are
all obtainable by Fourier's rule, and it seems unnecessary to write out in
detail the analysis, which the reader will easily construct for himself.
First, we have
a A - e2) - r
r cos w = x—ae — ,
so that
_ |e + 5 ? jh* (ne) cob nM)
& tt=l W
and next
,0, rsinw b . ^ V(l-e2) ? 2 r , . . 1/f
B) = -smA= z± 2 - /„ (ne) sin nM,
a a e w=1 n K
* Berliner Abh. 1824 [1826], p. 42.
+ Astr. Nach. cvn. A884), col. 17—28. Various expansions had also been given by Plana, Mem.
della R.Accad. delle Sci.di Torino, B) x. A849), pp. 249—332. In connexion with their convergence,
Bee Cauchy, Comptes Rendus, xvin. A844), pp. 625—643. [Oeuvres, A) vm. A893), pp. 168—188.]
17-21,17-22]; KAPTEYN SERIES 555
while
C) cos E = -— = - | e + % - Jn' (ne) cos nM.
ae w-i«
Next, if m is any positive integer*,
00 J
D) cos mE - m 2 - [Jn-m (ne) — Jn+rn (ne)} cos nM,
71 = 1 H.
°° 1
E) sin mE = m 2 - {Jn.-™ (we) + Jn+m (ne)) sin ti#.
The expansion of a/r is particularly simple, namely,
F) - = 1+2 2 Jn (ne) cos nM.
t »=i
The expansions of cos w and sin w are
1 _ 62 «j
G) cosw = — e H 2 2/„ (ne) cos nM,
e »=
(8) sin w = V(l - e'2) 1 2 /„' (ne) sin nM.
The expansions of cos w/r2, sin w;/r3 are of a simple form, namely
a2 °°
(9) -3cos?^/= 2 2nJn'(ne)coanM,
a2 \/ A — e2) °°
A0) — sin w = -^ % 2n Jn (ne) sin nM.
[Note. It is pointed out by Plumnaer, Dynamical Astronomy (Cambridge, 1918), p. 39,
that these are readily derived from the Cartesian equations of motion in the form
cftx as cos w _ dPy a3 sin w
combined with A) and B).]
17*22. $wms o/ special Kapteyn series.
The reader will observe that, in the case of the expansions of even functions
of M, the results simplify when we take the particle to be at one of the ends
of the major axis, because then the three anomalies are all equal to 0 or to 7r,
while the radius vector is equal to a A — e) or to a A + e). From the results
of the last section we thus obtain the following formulae, which were given by
Herz in the paper already quoted:
B) **- - 2 Jn(ne), -Mr-* (-)n~'Mne),
\i-~c) n=\ \x-rej fie
* It is seen from C) that, when m is equal to 1, the expansion D) has to be modified by the
insertion of a oonetant term. These two formulae were given by Jaoobi, Astr. Nach. xxvm. A849),
col. 69. [Get. Math. Werke, vn. A891), p. 149.]
THEORY OF BESSEL FUNCTIONS [CHAP. XVII
More generally we find by differentiating § 17*21 F) that
(- )m~l
W 2
I—
Since -j-vj = =. -r^. the expressions on the left in D) and E) can
dM 1 - e cos E dE ^ v ' v
be calculated for any positive integral value of m, with sufficient labour.
Again, if we regard e and M as the independent variables, it is easily
seen that
1 ] cos# dE
8e (sin E A - e cos E)\ sin2 E A - e cos E) de
—•—etti rrr, \ — cos E + e sin E ,-r-
sin E A — e cos 2?J [ 3e
~ dM\ - e cosE'
so that, by § 17-21 F)
d ( 1 )
^ = - 2 S
{sin E (I—e gos, E)) Ma=1 v
and therefore, if we integrate with e = 0 as the lower limit,
1 1 °° /*e
F) ——rm 7k -•—»*¦ = — 2 % n sin nM A Jn (nx) doc.
v ' sinEA-e cos Z?) smif tt=1 Jo
If we differentiate with respecb to M, we find that
,_. cosjE1 cosilf e
sina E A - e cos ^J sin2 M A - e cos i?K
= 2 Stf cos nil/. I Jn (nx) da:.
n = l ^0
The last two expansions do not appear to have been published previously.
Expressions resembling those on the right of F) and G) have occurred in the researches
of Schott, Electromagnetic Radiation (Cambridge, 1912) passim.
Thus, as cases of D) and E), Schott proved (ibid. p. 110) that
« e2 n 4.^ oo fe <3
(8) SnV^SnO-IX 4' 2n' j2n{2nx)dx=6A e«V
The last of these may be obtained by taking M equal to 0 and v in G).
17-23] KAPTEYN SERIES 557
17*23. Meissel's expansions of Kapteyn's type.
Two extremely interesting series, namely
2 S J*»-
2,1 - iy + p i« + p (l* + p) C» + f)
+ . ^ _ +
cia+ei)Ca+ta>E-j+r)
have been stated by Meissel* who deduced various consequences from them ;
it is to be supposed at presentf that 0 < e ^ 1, and ? is real.
The simplest method of procedure to adopt in establishing these ex-
expansions is to take the Fourier seriesJ
« cos inM _tt cosh (tt~2M)^ 1
»ti V + f" ~" " ' 2? sinh Trf " 2f'
(which is valid when 0 ^ M <; tt), replace M by /i1 - e sin E, and integrate from
0 to 7r. It is thus found that
« J9n B»e) _ L r (tt coah (tt - 2A1 + 2e sin K) % 1 )
»«i 'r + r ttJo (. §Rinh7rf f-J
1 /' *«¦ (tt cosh B5 + 2e cos 5) f 1
= \-
2 f 4* (tt cosh 1PB . cosh Bef cos 6) 1
Now the last expression is an even integral function of e, and hence it is
expansible in the fonn§
v . I " » _ rlfj
i l'Aiii.\) I.. sinh wP
\'_ turn—2-'2»;i
by a formula due to Cauchy||; and the truth of Meissel's first formula is now
evident.
The second formula follows in like manner from the Fourier series
? cos Bwj-_l)J/'_7T sinh {\tt - MJJ
* ylstr. Nach. exxx. A892), col. 363—H68.
t The extension to complex variables is made in § 17"81.
J See Legendre, Exercices de Gale. Int. n. (Parie, 1817), p. 166.
§ It is easy to see that the term independent of e vanishes.
|| M6m. sur les integrates difiniea (Paris, 1825), p. 40. Cf. Modern Analysis, p. 263.
558. THEORY OF BESSEL FUNCTIONS [CHAP. XVII
Now, since the series obtained from A) and B) by differentiations with
respect to ?2 are uniformly convergent throughput any bounded domain
of real values of ?, we may differentiate any number of times and then make
We thus deduce that
are polynomials* in. e; the former is an even polynomial of degree 2m, and
the latter is an odd polynomial of degree 2to — 1.
The values of the former polynomial were given by Meissel in the cases m=l, % 3, 4, 5;
the values for m= 1, 2, 3 are
2V2~8'2~32+72'
The values of the latter polynomial for m=l, 2, 3 are
e e es e 5«3 f5
2' 2~18' 2~8i 450*
Meissel also gave the values of the latter polynomial for m— 4, 5.
Conversely, it is evident that every even polynomial of degree 2m is
expressible in the form
oc
»=0
and that every odd polynomial, of degree 2m — 1, is expressible in the form
2 W»-i[Bn-l)€],
where an and bn are even polynomials in 1/n and l/Bn—1) respectively, of
degree 2m.
17*3. Simple Kapteyn series with complex variables.
It was stated in § 17*1 that, in general, Kapteyn series are of a more
recondite character than Neumann series, and we shall now explain one of
the characteristic differences between the two types of series.
In the case of Neumann series it is, in general, possiole to expand each of
the Bessel functions in the form of a power series in the variable, and then to
rearrange the resulting double series as a power series whose domain of con-
convergence is that of the original Neumann series.
* It is to be noted that the coefficients of e2 and e2"* in the respective polynomials are not
zero; they are
1 ; .... and
2.1a.3!4...Bm-l)!'*
17-3] KAPTEYN SERIES 559
The corresponding property of Kap'teyn series is qaite different; for the
Kapteyn series
HJ{
is convergent and represents an analytic function (cf. § 87) throughout the
domain in which
< lim
while the double series obtained by expanding each Bessel function in powers
of z is absolutely convergent only throughout the domain in which
and the latter domain is smaller than the former; thus, when the limit is 1,
the first domain is the interior of the curve shewn in Fig. 24 of § 8'7, in
which the longest diameter joins the points + 1, while the shortest joins
the points ±ix 06627434; while the second domain* is only the interior of
the circle J z | = OG627434.
Hence, when we are dealing with Kapteyn series, if we use the method of
expansion into double series we succeed, at best, in proving theorems only for
a portion of the domain of their validity; and the proof for the remainder of
the domain either has to take the form of an appeal to the theory of analytic
continuation or else it has to be effected by a completely different method.
As an example of the methods which have to be employed, we shall give
Kapteyn'sf proof of the theorem that
A) ~--«l+2 5/nH,
provided that z lies in the open domain in which
z exp V(l
1 +VA -
This domain occurs so frequently in the following analysis that it is con-
convenient to describe it as the domain if; it is the interior of the curve shewn
in Fig. 24 of § 87.
Formula A) is, of course, suggested by formula B) of § 17'22.
To establish the truth of the expansion, we write
1+2 I Jn(nz) = S(z),
« = i
and then it has to be proved that S(z)= 1/A — z).
Since J(nz)-1 P+TeXp ^ {t~ 1/t)]Tdt
bince ^W-^J [- ¦ t J * >
* For an investigation of the magnitude of this domain, see Puiseux, Journal de Math. xiv.
A849), pp. 33—39, 242—246.
t Nieuw Arcniefvoor Wiskunde, xx. A893), pp. 123—126; Ann. set, de VKcole norm, sup, C)
i. A893), pp. 96—102.
560 THEORY OF BESSEL FUNCTIONS [CHAP.,XVn
we see that, if we can find a circle T with centre at the origin of such a radius
that on it the inequality
exp {fr (*-!/*)} .
B)
is true, then
i r
t
w ^ ; 2iri J (r+) 1 - r1 exp
To investigate B), we recall the analysis of § 87. If z - peia, t = eu+ie,
where p, u, a, 6 are all real (p and u being positive), then B) is satisfied for
all values of 6 if
p \/(smh2 u + sin8 a) — u < 0 ;
and when w is chosen so that the last expression on the left has its least
value, this value is (§ 87)
which is negative when 2 lies in the domain K. Hence, when z lies in the
domain K, we can find a positive value of u such that the inequality B) is
satisfied when 11 j = eu.
Again, if we write ljt in place of t in C) we find that
+) 1 -1 exp {- \z
where 7 is the circle \t\— e~u.
When we combine C) and D) we find that
2S(z) = JL
and so 28 (z) is the sum of the residues of the integrand at its poles winch lie
inside the aunulus bounded by V and 7.
We next prove that therp is only one pole inside the annidus*, and, having
proved this, we notice that this pole is obviously t = 1.
For the number of poles is equal to
If d log [1 - t~l exp \\z {t - 1/0}]
dt
I f rflog[l-riexp{^(*-l/Q)]^
, 1
Air% J (r+) at
1 f d\og[l-t&y[-k*{t-l/t)}]Jt
2m J (r+) dt
iri J {r+) dt
L. f
dt
The corresponding part of Kapteyn's investigation does not seem to be quite so convincing
as tbe investigation given in the text.
17-31] KAPTEYN SERIES 561
Now the first of these integrals vanishes; for, if we write
then 1171 < 1 on F, and so the expression under consideration may be written
in the form
\
and the integral of each term of the uniformly convergent series involved is
zero.
Hence the number of zeros of 1 - t~J exp [\z (t - l/t)) in the annulus is
equal to
It follows that 28 (z) is equal to the residue of
at t= 1; and this residue is easily calculated to be 2/A — z).
It has therefore been shewn that /Sv(.s) is equal to 1/A — z) throughout the
domain K, i.e. throughout the whole of the open domain in which tho, series
defining >S(z) is convergent.
[Note. It is possible to prove that. *S (z) eonverges to the .sum 1/A — ~) on the boundary
of K, except at 2 = 1, but tho proof requires an appeal to be nuuKs to theorems of an Abelian
typo; cf. § 17-K.]
17*31. The extension of Meissel's expansions to the case of complex: variables.
We rfhall now shew how to obtain the expansions
which are valid when z lies in the domain K and ? is a complex variable
which is unrestricted apart from the obvious condition that & must not be an
integer in A) nor an odd integer in B). Those: results arc. the obvious
extensions of MeisHel's formulae of § 17 23.
[Notk. Tho oxpan.sioiiH when f i.s a pure imaginary havo to be established by a limiting
process by making ? approach the imaginary axi.s ; since the functions involved in A) and
B) are all oven functions of (, no generality i.s lost by assuming that It (?) i.s positive.]
w. u. V. 3G
562 THEORY OF BESSEL FUNCTIONS [CHAP. XVII
In order to establish these formulae, it is first convenient to effect the
generalisation to complex variables of the expansion of the reciprocal of the
radius vector given by § 17-21 F). That is to say, we take the expansion
1 + 2 % Jn (nz) cos «</>,
which we denote by the symbol jS(s, </>), and proceed to sum it by Kapteyn's
method (explained in § 17'3), on the hypotheses that <? is a real variable and
that z lies in the domain K. We define a complex variable f by the equation
<j)=sTfr — z sin ^.
The singularities of ^, qua function of </>, are given by cos f = l/z, that is
0 = arc sec z — \/(z2 — 1).
None of these values of 0 is real* if z lies in the domain K; and, as </> in-
increases from 0 to oo through real values, ty describes an undulating curve
which can be reconciled with the real axis in the -^-plane without passing
over any singular points-
It follows that if, for brevity, we write
then
*( ANLf
J If* t
with the notation of § 17. By the methods of that section wo have
1-ff2dt
> (f>)~2<7ri!<
[
<x+>y-)l-2Ucos<f>+U* t '
and so 2S (z, (f>) is equal to the sum of the residues of the integrand at those of
its poles which lie inside the annulus bounded by T and y.
We shall now shew that there are only two poles inside the annulus, and,
having proved this, we then notice that these poles are obviously t = e±f*.
By Cauchy's theorem, the number of poles is equal to
1 f cnog(l-2ffcos</>+ Z73)J4
; I -j7 at
ztn ' (r+,y-) OK
c? log A - 2 Z7 cos gt> -f- C72)
¦ — ctt
dt
l)<i \~
() Ln0 J dt
= 2,
* It is easy to shew that such values of <j> satisfy the equation
so that | a*1* | <1.
17-31] KAPTEYW SERIES 563
the integral of each term of the uniformly convergent series vanishing, just
as in §17-3.
Now the residues of
1-^ _ 1
at tf = e*** are bofch equal to 1/A-^ cos ^); and therefore we have proved that
1 °°
C) z ,r = 1 + 2 2 Jn (nz) cos rub,
l — zcos-ylr 1 x / r>
in the circumstances postulated; and the series on the right is a periodic
function of cb which converges uniformly in the unbounded range of real
values of <j6.
Hence, when R (f) > 0, we may multiply by e~& and integrate thus:
/•oo oo /-oo roo Q—&
I e~^ dd> + Z X Jn (nz) e~& cos ncbddi— I — dd>.
Jo «=i Jo J0l--s:cos^r
That is to say,
D) f e-«+~°8i»¦><ty - i + 2
+ 2 2 &,
b n = l W + <9
where the path of integration is the undulatory curve in the i/r-plane which
corresponds to the real axis in the </>-plane; and, by Cauchy's theorem, this
undulatory curve may be reconciled with the real axis.
Now, when the path of integration is the real axis, the integral on the left
in D) is an integral function of z; and this function may be expanded in the
form
no zmt">n C°°
m-o ml Jo
By changing the sign of z throughout the work we infer the two formulae
»-i \_ZV7-— 1; -r t, w=i V-i«i — J-ji Jo
which are now established on the hypotheses that z lies in the domain K and
thatJB(f)>0.
By dividing the paths of integration into the intervals @, tt), (tt, 27r),...
and writing \tt + 8, §7r + 6,... for ty in the respective intervals, we infer thab
erS* sin2"*y\rd<r = -™^—r ( "cosh %Q. cos3™
o r T sinh^-TT^Jo
1
36—2
J64 THEORY OF BESSEL FUNCTIONS [CHAP. XVII
and that
sin2'" -bd-fr = ,\ •„[""cosh ?0.cos2
By substitution in E) and F) and writing 2^ for f in E) we at once infer the
truth of A) and B) when R (?) > 0; and the mode of extending the results to
all other values of K has already been explained. The required generalisations
of Meissel's expansions are therefore completely established.
17*32. The expansion of zn into a Kapteyn series.
With the aid of Meissel's generalised formula it is easy to obtain the
expansion of any integral power of z in the form of a Kapteyn series. It is
convenient to consider even powers and odd powers separately.
In the case of an even power, zm, we take the equation given by § 17'31 A)
in the form
m 1 f
{ } 2iri]
2iri} M=i"r{m+ 1 +i?) V(m+ 1 — it) " s .
where the contour of integration is the circle | f | =n + \. Since both series
converge uniformly on the circle, when z lies in the domain K, term-by-term
integrations are permissible.
Consider now the value of
When in <n, there are no poles outside the contour, and so the contour may
be deformed into an infinitely great circle, and the expression is seen to be
equal to uniby; but when in >t\, the poles ±im are outside the circle and the
expression is equal to unity minus the sum of the residues of the integrand
at these two poles, i.e. to
(m + n)!
viM+v. (m — n— 1)! '
The expression on the left of A) is therefore equal to
Next wo evaluate
r (m + 1+ »f> r (m + 1 -
17*32] KAPTEYN SERIES 565
When m ^ n, the origin is the only pole of the integrand, and, if we take the
contour to be an infinitely great circle, the expression is seen to be equal to 1.
But, when m >n, there are no poles inside the circle j ?| = n + %, and the
expression is zero.
Hence we have
B) 2I/
m-1
If we replace n by n — 1 and subtract the result so obtained from B), we
find that
ri# <m —n— 1)!
and so
{ OI & — <w i it *w
If n= 1, equation C) is at once deducible from equation B), without the
intervening analysis.
When we have to deal with an odd power, z'ai'\ we take the equation
given by § 17'*31 B) in the form
D)
x Ji (fM-Wi^+n ••• 1B^- i)v
and we deduce in a similar manner that
(.,) „ ^1B*1-1)*} -w^(i (w_iy«.<WL_w_j
Hence
The formulae C) and F) may be combined into tho single formula
which is obviously valid throughout the domain K when n has any of the
values 1, 2, 3, —
This formula was discovered by Kapteyn *; the proof of it which has
just been given, though somewhat artificial, seems rather less so than Kapteyn's
proof.
* Ann. 8ci. de V&cole norm. mp. C) x. A893), p. 103.
566 THBOEY OF BESSEL FUNCTIONS [CHAP. XVII
17*33. The investigation of the Kapteyn series for zn by the method of
induction.
We shall now give an alternative method* of investigating the expansion
of zn as a Kapteyn series, which has the advantage of using no result more
abstruse than the equations
A) i = 1+2 2 /,„ (mz), = = 1+2 2 (—)m Jm (mz),
which were proved for real variables in § 17'22 and for complex variables in
§ 17'3; it is, of course, supposed that, if z is real, then — 1 < z < 1, and, if z is
complex, then z lies in the domain K.
The induction which will be used depends on the fact that when the sum,
00
f(z), of the Kapteyn series 2 amJm(mz) is known, then the sum F(z) of the
series X m ma—- can be obtained by two quadratures, if the former series
m—i m
converges uniformly. To establish this result, observe that, by term-by-term
differentiations,
, tfc -J> \Z) (IJP \Z) v f 9 T /; / v / I \ T I / \1
* —j 2 • + z —,—- = 2, am p Jm ymz) + {zjm) Jm {mz)\
00
so that (z j-) F (z) — A - zi)f(z);
it follows at once that F(z) can be determined in terms off(z) by quadratures.
Now, from A), we have
oo 1 qS,
*9 T ft) \ — *
M4 = 1 1 ~~ &
and so, if F(z)^lJ^Z\
then . f z ¦
Therefore, in the domain K,
where J. and 5 are constants of integration. If we make ^^-0, we see that
Consequently
B) *-2 I J'«»(amir).
* Watson, Messenger, xlvi. A917), pp. 150—157.
17-33] KAPTEYN SERIES 567
In like manner, we deduce from A) that
r»=0
and hence that
The expansions of ^n when w is 1 or 2 are therefore constructed.
Now assume that, for some particular value of n, zn is expansible in the
form
¦»-l
and consider the function <j> (z) defined by the equation
00 «o2 __ *j2
By the process of differentiation already used, we have
On integration we deduce thai
It is obvious that A' = B' = 0 from a consideration of the behaviour of
near the origin.
Hence the expansion of znJr<1 is
, m2 — w2,
where oTOi 7l+2 = —-—— om> n.
It follows at once by induction that
h
m>3>
and so * »-n«^(-^_7^rr (w _n + T)•
That is to say
~ ^ .t.tn"** r(m -n + 1) '
and this is equation C) of §1732. The expansion of z™'1 is obtained in the
same way from the expansion of z; the analysis in this case is left to the
reader.
568 THEORY OF BESSEL FUNCTIONS [CHAP. XVII
We therefore obtain the expansion
(to (lzY
TOt0 (n + 2m)"+1. m!
which is the expansion obtained by other methods in §17*32; and the ex-
expansion is valid throughout the domain K.
Since the series
mZQ (n + 2m)«+x. ml
is absolutely convergent (being comparable with % 1/m2), the expansion D)
converges uniformly throughout K and its boundary. The expansion is there-
therefore valid (from considerations of continuity) on the boundary of K, and in
particular at the points z = ± 1, as well as throughout the domain K.
17*34. The expansion of l/(t — z) in a Kapteyn series.
From the expansion of zn, obtained in the two preceding sections, we can
deduce, after Kapteyn*, the expansion of 1/B —z) when z lies in the domain
K and t lies outside a certain domain whose extent will be defined later in
this section.
Assuming that \t\ > j z |, we have
l
<
= | ^ | |
t-z <+ttti«n+1 < „-! <n+J «-o (n + 2m)n+I.ml
Now, if
the repeated series is expressible as an absolutely convergent double series if
the double series
is convergent. But the terms in this series are less than the terms of the
double series
| | 2«T«+!!W _ 2FexpF2
provided that U|>2F.
Hence, when
z exp V(l -
rearrangement of the repeated series for \/(t - z) is permissible, and, when we
arrange it as a Kapteyn series, we obtain the formula
(!) -—- = <^0@ + 2 i <&n(t)Jn(nz),
* Ann. sci. de I'ticole norm. sup. C) x. A893), pp. 113—120.
17-34,17-35] KAPTEYN SERIES 569
where*
B) ©„(*)«= 1/tf,
t (^-
From the last formula we may deduce a very remarkable theorem discovered
by Kapteyn; we have
i "v" (w_~ m ~].)! = 1 ^ (ft-2mJ. (w- m-J.)!
and therefore, by § 9'1 B),
"n'tlit \JJJ7 71, \ t I "™
so that, by § 9-12A),
D) <&n (t) = n A - ?2) 0?l (w«) 4- sina |mtt + t cos2 Jtott
when n = 1, 2, 3, ....
Kapteyn s polynomial Cn (t) is therefore expressible in terms of Neumanns
polynomial 0n (nt).
It is now possible to extend the domain of validity of the expansion A);
for, by § 8*7 combined with § 917, it follows that the series on the right of
A) is a uniformly convergent series of analytic functions of z and t when z
and t lie in domains such that
E) 12 (z) < n(t) ?l(z)<?l(\)
. _ . z exp V(l -z'*)
wheiv 12 (z) = ¦ ¦ l -
The expansion A) is therefore valid throughout the domains in which both
of the inequalities E) are satisfied.
[Notk. This result gives a somewhat more extensive domain of values of t than was
contemplated by Kapteyn; he ignored the theorem proved in {$ S>* 17, and observed that
(since the coefficients in the series for <©„(<!) are positive) when j t \ ^ 1,
by D); so that Kapteyn proved Lhiit A) in valid when
O(a)<O(l), UI^L]
17*35. Alternative proofs of the expansion of l/(t - z) into a Kapteyn series.
Now that explicit expressions have boon obtained for the cocfficientH in the expansion
1 =.©„(*)+ 2 2 ^n(t)J,t(m),
t — Z jj = i
it ia possible to verify this expansion in various ways. Thus, if <8>n (t) be defined as
w A - t'z) 0n (nt) H-sin2 \nn +1 cos'2 hnir,
the reader will find it an interesting analysih to take the series
+ ^ + 2 A ««) ?n On (nt) Jn (nz),
Cf. Kapteyn, Nieuw Archie/voor Wiskunde, xx. A893), p. 122.
THEORY OF BESSEL FUNCTIONS [CHAP. XVII
. _jstitute suitable integrals for the Bessel coefficients and Neumann polynomials, and
reduce the. result to lj(t—z) after the manner of §9*14.
Or again, if we differentiate the expansion twice with respect to z we find that
z2 z ~\ °°
and then, dividing by 1 —z2, and making use of § 17*3 A), we find that
2i!2 t(t2+3)
(f _ 1J (f-zf " (<* -1K (t-zf
whence the differential equation for ©n (t) is easily constructed in the form
and hence it follows that
©n (t)=n A -1!2) 0n (nt) + sinH»7r +1 cos2 %nir + fx {An Jn {nt)+Bn Yn (nt)},
where An and Bn are independent of t; but it does not seem easy to prove that An = Bn=0.
17'4. The expansion of an arbitrary analytic function into a Kapteyn
series.
We shall now prove the following expansion-theorem:
Let f(z) be a function which is analytic throughout the region in which
fl(z)^a, where a^l.
Then, at all points z inside the region,
CO
A) /(^) = O0+2 2
n-l
where
B) cfc-
and the path of integration is the curve oti which fl (t) = a.
This result is obvious when we substitute the uniformly convergent
expansion
®0(t) + 2 5 ®n(t)Jn(ns)
for lf(t— z) in the equation
t-z '
since ?l(t) = a on the contour, while both Q(z)<l and H {z) < H (t) when z
is inside the contour.
This theorem is due to Kapteyn.
17-4, 17-5] KAPTEYN SEKIES 571
It is easy to deduce that, if the Maclaurin series for f(z) is
/(*)- 2 anzn,
then
C) «o=afl,
D} « = - ^ ^
m.\
17*5. Kapteyn series in which v is not zero.
The theory of Kapteyn series of the type.
m=-0
in which v is not zero or an integer, can be made to depend on the ex-
expansion of zv. The result of § 17*33 suggests that it may be possible to
prove that
throughout the domain K.
It is easy enough to establish this expansion* when \z\< 0*6627434; but
no direct proof of the validity of the expansion throughout the remainder of
the domain K is known, and the expansion has to be inferred by the theory
of analytic continuation.
To obtain the expansion throughout the interior of the specified circle,
expand the series on the right in powers of z. The coefficient of zv+9r is
(_y-m („ + 2m)"+ar
?k=o (v + 2m)v+1. ra!' 2v+2r (r — m) I F A/ +
_ r (u) ^ (—)^-w A/ + 2m,yr~i r (v + in) r (v +
When r>l, the last series is a polynomial in v of degree 3?—1 which is
known to vanish identically whenever v is an integer. It therefore vanishes
identically for all values of v. The expansion A) is therefore established
(inside the circle) by a comparison of the coefficient of zv on each side of the
equation.
From this result, we can prove that, under the conditions specified in § 17*4,
B) .— = ? an,„ (*) J,+n {(v + n) z\,
t — z n=0
where
* This was done when |z|<0-659 by Nielsen, Ann. xci. de Vticole norm. sup. C) xvni. A901),
pp. 42—46.
572 THEORY OF BESSEL FTnTOTIOITS [CHAP. XVII
It is not difficult* to express Mn,v{t) in terms of Gegenbauer's polynomial
¦A.n,»(nt+ hvt), defined in §92.
And the reader will easily prove that iff(z) satisfies the conditions specified
in § 17-4, then
D) z"f{z) = 2 an< „ Jv+n \{v + n)z],
where
E) «nilf
in which the contour of integration surrounds the origin ; and hence
/fiN _ 1 <^n (v + n — 2mJ F (v + n — m) an_2m
2 m=0 (%v + n)v+n~'im+1. m! '
where a0, a^ ... are the coefficients in the Maclaurin series for/(^).
[Note. Jacobi in one of his later papers, Astr. Nach. xxvin. A849), col. 257—270 [Cfes.
Math. Werke, vu. A891), pp. 175—188] has criticised Carlini for stating that certain
expansions are valid only when \z\ < 0*663 But Carlini had some excuse for hin state-
statement because the expansions are obtained by rearrangements of repeated scries which are
permissible only in this domain, although the expansions are actually valid throughout the
domain K.~\
17*6. Kapteyn series of the second kind.
Series of the type
have been studied in some detail by Nielsenf. But the only series of this
type which have, as yet, proved to be of practical importance ?. are some
special series with /a = i>, and with simple coefficients. The results required in
the applications just specified are obtainable by integrating Meissel's expansion
of § 17*31 A) after replacing z by 2sin0. It is thus found that, throughout
the domain K,
so that
and hence we deduce that 2,Jn1(nz)/ri-m is a polynomial in 22 of degree m;
while the sum of series of the type %n2mJ^{nz) may be found in a similar
manner from the corresponding expansion %n'imJm{1nz).
* Cf. Nielsen, Ann. sci. de I'Ecole norm. sup. B) xviii. A901), p. 60.
t Ann. sci. de I'Ecole norm. sup. C) xviii. A901), pp. 39—75.
% Cf. Schott, Electromagnetic Radiation (Cambridge, 1912), Chapter vin.
17-6, 17*7] KAPTEYN SEBIES 573
Thus Schott* has shewn that
C) 2 »Vn2(,w)» -A4+.'J
.1 = 1 16 A -^)^ •
A general theory resembling that of § 1614 is deducible from the ex-
expansion
which is easily derived from § 17'5 A) and is valid throughout K; but it
seems unnecessary to go into details which the reader should have no difficulty
in constructing, in the unlikely event of his requiring them.
17*7. Kapteipi series which converge outside the domain K.
If iim \y/an\= 1,
tt-i-ao
we have seen that the Kapteyn series %anJn{nz) represents an analytic-
function throughout the domain K. But since, when x is real, \Jn(nx)\< 1,
the series may converge along the whole of the real axis, although when I z \ > 1,
the scries does not converge at points which are not on the real axis.
The behaviour of such a Kapteyn series may he summed up-|- by saying
that it resembles a power-series throughout tin; domain K and that it re-
resembles a Fourier series on the. real axis outside K.
As an example, let us consider the series
o= v /n (»'«)
It is evident that, if 0 = -yfr — x sin ty, then
1
S — \ „
J n
since, the Fourier series is uniformly convergent.
Now, when .r>l, (/> decreases as yfr increases from 0 to areeos(l/.r) and
then increases to ir as \^ inenjuses from arc cos (I/a;) to rr. If in he the integer
such that the minimum value of 0 lies between — 2-niir and — 2 (m + l)rrr, let
the values of yfr corresponding to the values
0, - 27T, - 4tT, ..., - 2/U7T, - 2W17T, .... - 2tT, 0
of ^> be 7o, 7., ... 7m. 8,,,, K,-i, -.. Si, So, and then
* Electromagnetic Radiation (Cambi-idKC, 1912), p. 120.
I1 The HUggeation of tlioae annlogiea wau made by rroi'CBfior Hardy.
574 THEORY OF BESSEL FUNCTIONS [CHAP. XVII
Now when yjr lies in the intervals G,., yr+J) and (8r, Sr+1) the sum of the
series under the integral sign is
1 <?2 - %7r<f> + ?tt2 + r (r + 1) 7T2 + (r + 1) tt<j>,
and, since
I (
— se sin yfr) dty = ^Tp + % cos \jr,
- 00 sin ^ff dty — ^ty* 4- 2% (^ cos yjr — sin -\^) + J &2 (^ - sin -v/r cos i/r),
it may be shewn without much difficulty that
? = ?a? + $a? + i {? (S,2 - 7r2) + «(cos 8r - cos 7r)} + 2tt S r (8#'. - 7,.).
0
The reader will see that a large class of Kapteyn series may be summed by
this method*.
17*8. The convergence of Kapteyn series on the boundary of the domain K.
With the exception of the points ± 1, the boundary of K presents no
features of special interest; because, by means of Debye's asymptotic expansion
the consideration of the convergence of the Kapteyn series ~%an Jv+n {(v + n) z\
is reducible to that of the power series
1 + V(l - O
and that of two similar seriesf with ^Jn5, \fnn written for *Jn.
The points ± 1 present more interest, because the ordinary asymptotic
expansions fail. But the lacuna thereby produced is filled, for real values of v,
by the following theorem of an Abelian type:
The convergence of
is sufficient to ensure both the convergence qf%anJv+n{v -\-n) and the continuity
of 1 <xnJv+n {(v •+¦ n) x\ throughout the interval^ 0 $ cc ^ 1.
Since San/n" converges and {n/(v + n)}* is monotonic, with a limit as n -* 00 ,
it follows§ that 2 <xnj{v +ny converges; and since, by § 8*54, (v + n)» Jv+n (v + n)
is monotonic, with a limit as n-*oo, ifc follows that SctnJv+n(v + n) converges.
* In this connexion the researches by Nielsen, Oversigt K. Danske Videmkabernes Selskabs,
1901, pp. 127—146, Bhould be consulted,
t If an/N/w does not tend to zero the series cannot converge; and if it does tend to zero
2an/>/n5 is absolutely convergent, and so, if we replace eachBessel function by the first two terms
of the asymptotic expansion with a remainder term, the series of remainder terms is absolutely
convergent.
X Due allowance has to be made for the origin if e<0.
§ Bromwich, Theory of Infinite Series, % 19.
17-8] KAPTEYN SERIES 575
A • • Jv+n\(v + n)x\
Again, since _1^.'1H_ LJ.
s Ju+n (v + n)
is a 'function of n which does not increase as n increases, for all values of as
in the interval 0^#<l, it follows from the test of Abel's type for uniformity
of convergence* that
t anJ»+n {(v + n) nc\
is uniformly convergent (and therefore continuous) throughout the interval
0 ^ x ^ 1; and this proves the theorem.
By reversing the reasoning, it may be shewn that if 2 anJv+n (v + n) con-
converges, so does 2«n/» , so that the convergence of 2a?l/n3 is both necessary
and sufficient for the theorem to be true; the theorem is therefore the best
theorem of its kindf.
* Bromwicb, Theory of Infinite Series, § 44.
f This wrh pointed out by Profoasor Hardy. Of. WatBon, Proc. London Math. Soc. B) xvi.
A917), pp. 171—174.
CHAPTER XVIII
SERIES OF FOURIER-BESSEL AND DINI
18'1. Fourier's formal expansion of an arbitrary function.
In his researches on the Theory of Conduction of Heat, Fourier* was led
to consider the expansion of an arbitrary function f(x) of a real variable of .•/,¦
in the form
A) f(®)= 2 a.mJQ(jmx),
where juj^js, ••• denote the positive zeros of JQ(z) arranged in ascending
order of magnitude.
The necessity of expanding an arbitrary function in this manner arises
also in Daniel Bernoulli's problem of a chain oscillating under gravity and in
Euler's problem of the vibrations of a circular membrane with an initial arbi-
arbitrary symmetrical displacement (§§ 13, 1).
In order to determine the coefficients am in the expansion, Fourier multi-
multiplied both sides of (l)by x J0(jma) and integrated between the limits 0 and ].
It follows from § 5'11 that
J o (,$«/i Uwi)> 7il = n,
and hence Fourier inferred that
B) am « yA-- f' tf(t) Jo (jmt) dt.
If we now change the significance of the symbols jmi so thatf j\,J2>j*> •••
denote the positive zeros of the function Jv (z), arranged in ascending order
of magnitude, then
C) /(»)= 2 a»J.(j««),
where
D) am = w~rrr f tf(t)Jv (jmt) dt.
) J 0
This more general result was stated by LommelJ; but, of course, neither
in the general case nor in the special case v = 0 does the procedure which has
been indicated establish the validity of the expansion; it merely indicates how
the coefficients are to be determined on the hypothesis that the expansion
exists and is uniformly convergent.
* La TMorie'Analytique de la Chaleur (Paris, 1822), §§316—319.
+ The omission of the suffix v, associated with jlt j-2> hi •••> should cause no confusion, and it
considerably improves the appearance of the formulae.
X Studien iibev die Bessel'scken Functionen (Leipzig, 1868), pp. 69—73.
18*1] FOURIER-BESSEL SERIES 577
In fact the simplicity of the procedure is somewhat deceptive; for the
reader might anticipate that, if the function f(x) is subjected to appropriate
restrictions, the expansion would be valid for all values of v for which the
integral
I tJv(jmt)Jv(jnt)dt
J o
is convergent, i.e. when v ^ — 1.
Dini, however, remarked that he was unable to deal with the range
- \<v< — -^and limited himself to the range v^— h. Several subsequent writers,
while proving theorems for the latter range, asserted that the extension to the
former range was merely a matter of detail; but it was not until after 1922 that
anyone took the trouble to supply the detail which is tedious and of no great
interest. In the exposition given here, it will be supposed that v~^-\.
The first attempt at a rigorous proof of the expansions A) and C) in
contained in some notes compiled by Hankel* in Ib69 and published post-
posthumously. A more complete investigation was given by Schlaflif a year
after the publication of Hankel's work; and an important paper by HarnackJ
contains an investigation of the expansion C) by methods which differed
appreciably from those of earlier writers.
A few years after the appearance of the researches of Hankel and Schlafli,
the more general expansion
E) ./»= t /;,„./„ (X,,,r),
VI"- 1
where \x, Xa, X.,, ... denote the positive zeros (in ascending order of magnitude)
of the function
z-"[zJu'{z)^lUv{z)\,
when v^. — \ and // is any given constant, was investigated by l)ini§.
The coefficients in the expansion an; given by the formula
F) \{\u;-,/») J,8(X,,,) + \,,*JV"' (Xm)\ bM = 2\,,r f tj @ Jv(\mt) dt.
Jo
The mode of determination of the numbers X,,t subjects f(oo) to what is
known as a 'mixed boundary condition,' namely that f'(x)+Hf(a:) should
formally vanish at x = 1.
The expansion E) was examined by Fourier (when v— 0) in the. problem
of the propagation of heat in a circular cylinder when heat is radiated from
the cylinder; in this problem the physical significance of // is the. ratio of the
external conductivity of the cylinder to the internal conductivity.
* Math. Ann. vm. A875), pp. 471 -491. In tho courHo of this paper, Hankel obtained tho
integral formula of § 14M. na a limiting cane of C).
t Math. Ann. x. A876), pp. 1.H7 -14'2.
J Leipzit/er fierichte, xxxix. A887), pp. 15I-—214; Math. Ann. xxxv. A88',)), pp. 41—62.
§ Serie di Fourier (Pisa, 1880), pp. 1D0—277.
W. B. F. 37
578 THEORY OP BESSEL FUNCTIONS [CHAP. XVIII
It was pointed out by Dini that the expansion E) must be modified* by
the insertion of an initial term when H + v — 0; and, although Dini's analysis
contains a numerical error, this discovery seems to make it advisable to
associate Dini's name rather than Fourier's with the expansion.
The researches which have now been described depend ultimately on a set
of lemmas which are proved by Cauchy's theory of residues. The use of com-
complex variables has, however, been abandoned, so far as possible, by Kneser f
and HobsonJ, who have constructed the expansion by using the theory of
integral equations as a basis.
On aesthetic grounds there is a great deal to be said for, this procedure,
because it seems somewhat unnatural to use complex variables in proving
theorems which are essentially theorems concerning functions of real variables.
On the other hand, researches based on the theory of integral equations are
liable to give rise to uneasy feelings of suspicion in the mind of the ultra-
orthodox mathematician.
The theory has recently been made distinctly more complete by the
important memoir of W. H. Young§, who has thrown new light on many
parts of the subject by using modern knowledge of the theory of functions of
real variables in conjunction with the calculus of residues. An earlier paper
by Filon|| which makes some parts of the analysis appreciably less synthetic
must also be mentioned here.
The question of the permissibility of term-by-term differentiation of the
expansion which represents a function as a series of Bessel functions has been
discussed by Fordif, who has obtained important results with the help of
quite simple analysis (cf. § 18'4).
More recondite investigations are due to C. N. Moore**, who, after studying
the summability of the expansion by Cesaro's means, has investigated the
uniformity of the convergence of the expansion in the neighbourhood of the
origin, and also the uniformity of the summability of the expansion (when
not necessarily convergent) in this neighbourhood.
The reason why the uniformity of the convergence (or summability) of
the expansion in the neighbourhood of the origin needs rather special con-
consideration is that it is necessary to use asymptotic formulae for Jv (Xmx) which
are valid when \nx is large; and, as % approaches zero, the smallest value of
to, for which the asymptotic formulae are significant, is continually increasing.
* Details of necessary modifications when H+v ^0 will be given in § 18'3. The modification
was also noticed by Kirchhoff, Berliner Sitzungsberichte, 1883, pp. 519—524.
t Archiv derNath.undPhys. C)vn. A903),pp. 123—133; Math. Ann: lxiii. A907), pp. 477—5'24-
X Proc. London Math. Soc. B) vn. A909), pp. 359-—388.
§ Ibid. B) xvm. A920), pp. 163—200.
|| Ibid. B) iv. A906), pp. 396—430. Cf. §§ 19-21—19-24.
IT Trans. American Math. Soc. iv. A903), pp. 178—184.
** Ibid. x. A909), pp. 391—435; xu. A911), pp. 181—206; xxi. A920), pp. 107—15G.
580 THEOBY OF BESSEL FUNCTIONS [CH.AP. XVIII
and a Fourier series in which the coefficients are expressed as integrals,
1 I*17 1 /"*¦
am = — /(?) cos mtfcfa, 6W = - / /(?) sin mtdt.
It is necessary to make a similar distinction* between the types of series
which will be dealt with in this chapter; any series of the type
00
m=l *
in which the coefficients am merely form a given sequence of constants, will
be called a series of Bessel functions.
If, however, the coefficients in this series are expressible by the formula+
2 i'1
a™ = 15—7T~\ %f (*) Jr" C™ *)dt>
the series will be called the Fourier-Bessel series associated withf{x).
And if, further, the series converges to the sum f(x) for any point x of
the interval @, 1), the series will be described as the Fourier-Bessel expansion
of f(x\
In like manner, the series
00
S bmJv(\mx),
where \, \, \3,... are the positive zeros of
will be called Bini's series of Bessel functions.
If the coefficients bm are determined by the formula^:
{(\mz- v*) J*(\m) + Xm2J/4(\m)} bm = 2Xm« P tf {t) Jv(Knt)dt,
J o
the series will be called the JDini series associated withf(x).
And if, further, the series converges to the sum/(«;) for any point x of the
interval @, 1), the series will be described as the Dini expansion of f(x).
Some writers have been inclined to regard Fourier-Bessel expansions as
merely a special case of Dini expansions, obtainable by making H-*-cc; but
there are certain distinctions between the two expansions which make this
view somewhat misleading (cf. §§ 18-26, 18-34, 18-35).
18*12. Special cases of Fourier-Bessel and JDini expansions.
There are very few expansions of simple functions in which the coefficients
assume a simple form.
One function whose expansion has simple coefficients has already been
* The greater part of the terminology is due to Young, Proc. London. Math. Soc. B) xvin.
A920), pp. 167—168.
t It is Bupposed that the integral is convergent for all positive integral values of Jft.
X It is supposed that the series is modified, as in § 18-34, when S + v ^0.
18-12, 18*2] FOURIER-BESSBL SERIES 581
investigated in § 15-42. Another is xv, which gives rise to the formal expansions
m=l
It will be seen subsequently that A) is valid when 0 <# < 1, and B) when
, if # + y>0. Cf. §§ 18-22, 18-35.
The reduction formula
K? I' *" + 2n + 1 Jv (Xw<) *=(v+2n) /„ (Xm)-Xm,/-; (X,n) - 4rc (v+n) 1V + *«-'J,,(
jo ; o
is easily established, so that the Dini expansion of xv+2'1 may bo determined when v is any
positive integer. The Dini expansion of a.'" + 2ll + 1 may similarly be determined; in this
case the general coefficient is expressible in terms of known functions and
/M
I t"Jv(X,nt)dt.
Jo
In order to calculate this when v is an integer, McMahon* has proposed to tabulate the
function
Jo (t) dt» Jx (*) + 'h (x)+Ju (.r) +...,
whinh is a special form of one of Lommel's functions of two variables (t$ 16-.r>, lti'.^fi).
18*2. The methods of Hankel and Schlafli.
The earlier investigations which were described in § L!Si are based on the
analysis used by Dirichletf in his researches on trigonometrical aeries of
Fourier's type; this method of proceeding is obviously suggested by the
fact that the trigonometrical series are special cases of the Fonrier-Bessel
expansion, obtained by giving v the values + \.
In the case of Fourier's theorem, to provo that
oo
f(x) — \ao + 2 (am. cos via: + b,n sin mx),
wt-l
where am = / / (t) cos mtdt, bm = - f(t)»mmtdt,
it is sufficient to prove that
1 f
/(x) = lim — / {? + cos(x-t) + cos 2 («? -t) + ... + cosn{x -1)\ f(t) dt,
,,, that /W=^2
* Proc. American Assoc. 1900, pp. 42—43. The tabulation ih most simply effected by using
§ 10'74C) in conjunction with Table I. (pp. 666—E97); see Table VIII.
t Journal fUr Math. iv. A829), pp. 167—169.
582 THEORY OF BESSEL FUNCTIONS [CHAP. XVHI
In the case of the general Fourier-Bessel expansion, the corresponding
limit to be evaluated is
lim l^iff
n-*.oo <j>i=l«' v+\\Jm)
and so it is necessary to investigate the behaviour of the sum
¦m=l J2v+\ (jm)
when n is large-; and it is in this investigation that the use of the calculus of
residues is more than desirable.
In the case of Dini's expansion, the corresponding sum which needs
examination is
m-l (W ~ **) J
An application of the calculus of residues which will be described in §§ 18*3—
18'33 shews that the difference of the two sums is readily amenable to dis-
discussion, and so we are spared the necessity of repeating the whole of the
analysis of the Fourier-Bessel expansion with the modifications appropriate
to the more general case of the Dini expansion.
18*21. The Hankel-Schlafli contour integral.
We shall now begin the attack on the problem of Fourier-Bessel expansions
by discussing properties of the function Tn (t, x), defined by the equation
m T (* «.\ v j
{*¦) J-nKt,OS)= *, Yi TT~\ '
m-l v v+i \Jm)
where 0<ic^l, O^i^l, and the order v is real and is subject to the condition
The method which will be used is due to Hankel* and Schlaflif, though
many of the details of the analysis are suggested by Young's J recent memoir.
The function Tn (t, x) is obviously as fundamental in the theory of Fourier-
Bessel expansions as is the function
sm(n + ^)(x-t)
sin ? (x — t) '
in the special theory of Fourier series.
In order to obtain the formulae connected with Tn{t, x) which are sub-
subsequently required it is necessary to express the wth terra of the sum for
Tn (t, x) as the residue at jm of a function, of the complex variable w,
which has poles at jlt j2, js, ...jn. When this has been done, we express
* Math. Ann. vm. A875), pp. 471—494.
t Ibid. x. A876), pp. 137—142.
% Proc. London Math. Soc. B) xvra. A920), pp. 163—00.
18-21] FOURIER-BESSEL SERIES 583
Tn (t, #) as the integral of this function round a rectangle of which one of the
sides lies along the imaginary axis while the opposite side passes between
jn and jn+1. The sides parallel to the real axis are then moved off to infinity
in opposite directions, so that, in order to secure the convergence of the integral,
it is necessary to prescribe the behaviour of the integrand as | / (w) | -*• oo.
There are three integrands which we shall study, namely
B) 2 [tj,(sow) Jv+1 (tw) - xJv(tw) Jv+l{am)}/[(f - x*)Jv*(w)},
C) 7TW {/„ (w) Yv (xw) - Jv (ww) Yv (w)} Jv (tw)/Jv (w),
D) irw [Jv (w) Yv (tw) - Jv (tw) Yv (w)} Jv (xw)JJv (w).
The first of these was the integrand studied by Schlafli; the other two are
suggested by the work of Kneser and Carslaw which was described in § 15*42.
A study of the asymptotic values of these integrands indicates that B) is
suitable for discussions in \vhich xj*t and 0 < oo +1 < 2; C) when* 0 ^t<%<\',
and D) when 0 <$# < t < 1.
We proceed to verify that the integrands all have the same residue, namely
1JV (jm®) Jv (jmt)IJ\+i(jm),
at w =jm. In the case of B), we define the functionf g (w) by the formula
E) g (w) = «3^ {tJ* (nw) ^+1 (tw) - nJv (tw) J»+i (*w)}.
and then, if w = jm + 6, where 6 is small, we have
Jv (W) = 0JJ( jm) + i & Jv" ( jm) + ...,
so that
W J.' (W) = ffijm JJ* (jm) + &J; (jm) {jmJ :' (jm) + JJ (jm)\ + ¦ ¦..
It is easy to verify, by using Bessel's differential equation, that the coeffi-
coefficient of 83 on the right vanishes; and hence the residue of g (w)j[wJjt(w))
atjmis
and this is easily reduced to
%Jv(jmX)Jv(jv
by using recurrence formulae.
In the case of C), the residue at jm is
wjwi {Jv (jm) Yv (jmx) - Jv (jmx) Yv (jm)} Jv (jmt)/Jv' (jm)
= - irjmj, (jmx) Jv (jmt) Yv (jm)/Jv' (jm)
~ 2J* (jm°c) Jv (jmfyJJ* (jm),
by §3'63, and this is the expression required; the integrand D) is dealt with
in the same way.
* This is most easily seen by writing the integrand in the form
\itiw {HyM {w) 7^B) (xu>) - HA) (xw) HvW (w)} Jv (tw)\Jv (w).
| T,he results obtainable by using the integrand B) are discussed in great detail by Graf and
Gubler, Einleitung in die Theorie der Bessel'schen Funktioven, i. (Bern, 1898), pp. 131—139.
584 THEORY OP BESSBL FUNCTIONS [CHAP. XVIII
We next take the contour of integration to be a rectangle with vertices
at ± Bi, An ± Bi, where B will be made to tend to oo, and An is chosen so
that jn< An<jn+1. When it is desired to assign a definite value to An, we
shall take it to be equal to (n + $ v + \) ir, which lies between jn and jn+z when
n is sufficiently large (§ 15'53).
Now it is easy to verify that the three integrands are odd functions of w,
and so the three integrals along the left sides of the rectangles vanish*.
Again, if w — u + iv, it may be verified that when v is large, and either
positive or negative, while u > 0, then the three integrands are respectively
0 (e~^-x-^% 0 (<r(a;-{> l°i)> O(e~ll-x)W),
and so, for any assigned value of An, the integrals along the upper and lower
sides of the rectangle tend to zero as B -*• oo when x and t have the relative
values which have already been specified.
We thus obtain the three formulae
~ SKI 1 An-*i Jo )
@<x+t<2;
G) Tn {t, «) = I. fAn+<*1 w \JV (w) Yv (xw) - Jv (xw) Yv (w)} Jv
(8) Tn(U) = ^.fil>+Mtw {Jv(w) Yv (tw)- Jv (tw) Yv (w)} J>SppJ™.
From equation F) it is easy to obtain an upper bound for | Tn (t, x) \; for
it is evident from the asymptotic expansion of § 7*21 that, when v + \ is posi-
positive (or zero) and bounded, there exist positive constants cx and c2 such that
when w is on the line joining An— cc i to An + oo % and t > 0, provided that n
exceeds a value which depends on v. Hence
so that
A0) \T (tx\\< —
1 nK' n^TTC.2*\t*-x*\B-x-t)</(xt)'
This inequality gives the upper bound in question.
* It is necessary to make an indentation at the origin, but the integral round the indentation
tends to zero with the radius of the indentation.
18*22] FOTJRIER-BESSEL SERIES 585
It is also easy to see that
[tt"+*Tn(t,x)(#-x*)dt
Jo
?»+l rAn-jr co i diV
— r \ [tJv {XW) Jv+2 (tw) — xJv+l (tw) Jv+1 (XW)} T ... ,
71% J A,, — oo> WJu~\W)
f rAn+ooi
—r I
and hence
[Note. Theorems obtained by a consideration of integrals involving Besael functions
of the first kind only can usually be made to cover the origin, in view of the fact that the
constant Cj in equation (9) is independent of t in the interval 0 <2 ^ 1. Thus A1) may be
written
valid whon 0<#^l, O^i^l. This extension ib not so easily effected when integrals
involving functions of the second kind have been used because the simplest inequality
oorres[»ouding to (9) ia
I Yv (tw) | < o{ {| tw | - " log | tw | +1 tw |" *} oxp {| / (tw) |},
and it is a somowhat tedious matter to obtain a wimple upper bound to the integrand in
(8) from this inequality.]
Equation ((>) was used by Schltifli to prove fchat, when n is large, then
m (t a l _ [^S^Al^ZJ10) _ ain A n (t + a;)"]
(t K> } " 2 */(xt) Lain &tt (tI-x) ain i v(t + x)\ '
but, since the order of magnitude of the error in this approximation is not
evident, we shall next evaluate some integrals involving Tn (t, x) by means of
which difficulties caused by the unknown error may bo evaded.
18*22. integrals involving T,n (t, x).
The two fundamental formulae which we shall now obtain are as follows:
A)
B)
From
these
it
Inn
ft -*. 00 J 0
lim 1
/t-*-00 J 0
is obvious that
lim ( t"+l Tn (t, x) dt = a*, @ < x < 1)
ft -*- 00 J 0
C) lim ! tv+l Tn (t, x) dt = lx". @ < x < 1)
n-»-oe J a;
In the course of proving A) it will be apparent that
«* f F+lTn(t,x)dt-~x*+l
JO
uniformly as ?i -* oo when «; lies in the interval
0^a;<l -A,
where A is any positive number.
586 THEORY OF BESSEL FUNCTIONS [CHAP. XVIII
We shall also investigate the boundedness of
ft
Jo
in the interval in which 0 < t < 1.
Of these results, A) was given by Young, Proc. London Math. Soc. B) xvm. A920),
pp. 173—174? and the proof of it, which will now be given, is his. Formula B) seems to be
new, though it is contained implicitly iu Hobson's memoir.
It is evident that
(w (,) f?n\
0 m=ljm" M-l \Jm)
When we transform the sum on the right into a contour integral after the
manner of § 18*21, we find that it is equal to
_1_ f °°* 2Jv(xw)dw _ _1_ M«+°°* 13v (xw) dw
27riJ_oot- wJv.{w) Ziri J An-«,i wJv{w)
In the former of these two integrals, the origin has to be avoided by an
indentation on the right of the imaginary axis.
Since the integrand is an odd function of w, the value of the first integral
reduces to tzi times the residue of the integrand at the origin, so that
'o tTnJAn-aoi Wjv(w)
Now
!i 2 J, (aw) dw
JAn-*
exP (- A
c2.4.n A —x)*Jx'
and, from this result, A) is evident; it is also evident that
at ! f+lTn(t,ao)dt-xv+i
Jo
tends uniformly to zero as n -*¦ oo so long as 0 ^ x ^ 1 — A.
It will be observed that the important expansion
D I 2J(y)
which was formally obtained in §18*12, is an immediate consequence of A).
Formula B) can be proved in a somewhat similar manner (though the
details of the proof are rather more elaborate) by using an integrand involving
functions of the second kind It ia easy to s.ee that
J
>?,((,«)*= i
o
An+Bi
x*+i rAn+Bi
= km -5J- J, (w) Yv (xw) - Jv {cm) Y? (w)}
B-^oo a* J AK-Si
18*22] FOURIER-BESSEL SERIES 587
Now take 0 < a? < X in the last integral and substitute for the Bessel functions
the dominant terms of their respective asymptotic expansions, valid when | w
is large (§7-21). The error produced thereby in the integrand is, at most,
0 A/w2) when 0 < x ^ 1; and, as n ->- oo, we have
Mn+
JAn-
_2L
Now the result of substituting these dominant terms is
xv rAn+Bi sin «/A —a?) sin (#«; — ¦?• i>7r — ;|7r)
— lim . I - - — t r —-. -cLw
J ($$)
_ .. x" M»+/'1'cos(w — \vir~\tt)-q,<}§{%xw-w — \vitr- \ir) ,
— nm ^r . I • ¦ • - ¦-¦ —div
J { $ ^ )
nm ^r . I
B-+-«> ZTTl J An-Bi IV COS {W — $VJT- ^ 7f)
COS B«W — W — 1 vtt — I -
CAn+JJi
= *«"- lim
B-^ooJ An-Bi
We shall have to discuss, almost immediately, several integrals of this general
type; so it is convenient at this stage to prove a lemma concerning their
boundedness as n -*¦ oo .
Lemma. T/ie integral
(An+m U0H (XW " ^"Tr" ^ dm
$ \)
lira (An+
mil i
«-»«, J An-
is 0 A/w.), as n->- oo, if - 1 < X < 1; and the integral is bounded if 0 < X < 1.
If we put w—An±iv, whore An, as usual, stands for (w + ^i' + ?) w, tho expression under
consideration may bo written in the form
nT . .. ,. . f° coshXv.rfi; . /s .. . P j;HinliX«.o?w ~I
|_ n K Jo (Ani+vi)cosh v v Jo (A^ + ir) coah wj
When — 1 < X < 1, the modulus of thin iIoob not exceed
2 f °° cosh \v. dv 2 f°° v\ainhXv\dv
An J o coali w -4n27o cosh v '
and the first part of the Lemma is obvious.
Again, if 0 ^X < 1 and v A — X) = ?, we have*
0 < v A - X) sinh Xv = ? Binh (v — ^)< cosh v,
so the integral to bo considered does not exceed (in absolute value)
and the second part of the Lemma is proved.
It follows immediately from the Lemma that
V+I Tn (t, co) dt = \xv + 0 A/n),
I"
JO
0
when 0 < x < 1; and this is equivalent to B).
* The function f sinh(»-?) has one maximum, at ?0 say. and its value there is equal to
sinh2 (i; - ?0) / cosh (v - fo) which is less than sinh (v - f0) •
588 THEORY OP BESSEL FUNCTIONS [CHAP. XVIII
Moreover, if we close the range of values of x on the right so that 0 < # < 1,
we infer from the Lemma that the integrals
[ V1 Tn (t, x) dt, ( V+> Tn (t, x) dt
Jo J(\
are bounded as n -*¦ oo when 0 < ,c ^ 1.
Lastly we shall consider
-'0
and we shall prove that, when 0 < t ^ 1 and 0 < x *$ 1, this integral in a bounded
function of n, x and t, as '»¦ -*¦ oo.
It is easy to shew by the methods which have just been used that, when
l, i.e. when t "* x, then
f t"+lTn(t,ce)
Jo
dt
nt=l Jm"~v+i(jm)
= lim ^ f "n+iJl' {/„ («,) yp (aw) - J, (ow) F, («,)} ^L^'] du;
sin(«ty-ii/Tr-^_) ,
1 \"~
~j— I — Lim —i—r I ~7~~~—i 1
AJ B — x'ffWFJ.u-Bi w cos (w-%vir-$ir
1\ v i"+- [A*+Bi COS (OCIV + tlU - •/;• - -i I'TT -
AJ B^. oo 27rtap J ^n_w «y cos (tf - ^ i/tt - J ir)
J
r-J i ?_ _.^tt,i
W;* J ^n_?t W COS (W — ^7T — -4 7T)
These integrals are of the type examined in the Lemma given earlier in this
section; and so the original integral is bounded when — 1 <x + t— 1^1
and — l<l + t — x^l, i.e. when 0< t^.x^ 1.
To prove that the integral is bounded when 0 < x ^ t ^ 1, we first shew that
f tv+lTn(t,w)dt
= lim ' [J? (W) Yv+1 (tw) - Jv+l (tw) Yv (w)} ~J^ ,
An-Bi
and then apply the arguments just used in order to approximate to the
integral on the right; the details of the analysis are left to the reader.
It has therefore been proved that, if A be o,n arbitrary positive number, then
j [ f+'Tn(t,x)dt
|Jo
ivhere U is independent of n, x and t when
18*23] FOTTRIER-BESSEL SERIES 589
These results constitute the necessary preliminary theorems concerning
Tn (t, x), and we are now in a position to discuss integrals, involving Tn (t, x),
which occur in the investigation of the Fourier-Bessel expansion associated
with an arbitrary function/(a1).
18*23. The analogue of the Riemann-Lebesgue Lemma*.
We shall now prove that, if (a, b) is any part of the closed interval @,1),
such that x is not an internal point or an end point of (a, b), then the existence
and the absolute convergence of
l"t*f(t)dt
are sufficient to ensure that, as n -*- go ,
[" tf(t)Tn(t,x)dt = <>(!),
J a
where'f 0 < x ^ 1.
The reader will observe that this theorem asserts that the only part of the
path of integration in
\\f(t)Tn(t,x)dt
which is of any significance, as n -*- oo , is the part in the immediate vicinity of
the point a.
It is convenient to prove the theorem in three stages. Tt i.s first supposed
that tff(t) is bounded and that the. origin is not an end point of (a, b). In
the second stage we remove the restriction of boundedness, and in the third
stage we remove the restriction concerning the origin.
(I) Lot t-"f(t) = F(t)(&-:/?),
and let the upper bound of \F(t)\ in (a, b) be K. Divide (rr, b) into p equal
parts by the points tx, L,... tp..u (t0 = a, tp = b); and, after choosing an arbitrary
positive number e, take p to be so large that
p
where Um and Lm are the upper and lower bounds of F(t) in (im_,, tm).
Let F(t)=LF(tm^)+(om{t),
so that | <om(t) | ^ Um-Lm in (tm^, tm).
It is then evident that
'b p
tf(t)Tn(t,x)dt= ^ F(tm.
i m -1
f
wl=l J tm-\
* Cf. Modern Analysis, §9-41.
t If i = l, it is, of course, supposed that 6>cl.
590
THEORY OF BESSEL FUNCTIONS [CHAP. XVIII
and hence, by the inequalities A0) and A1) of § 18*21,
rb 8c1aKp
\\f{t)Tn(t,x)dt
J a
— x — b)\/oc
4c2
that is to say
4-e
Now the choice of e fixes p; when e (and therefore p) has been chosen, we
are at liberty to choose An so large that An > 2Kp/e. That is to say, by a
suitable choice of An, we may make the integral on the left less than
TTGi B - X - E) Vtf '
which is arbitrarily small. Consequently the integral is o A) as An -»- oo , and
this is the theorem to be proved.
(II) When F(t) is not bounded throughout (a, b), let it be possible to
choose r intervals /t, such that F(t) is bounded outside these intervals and.
such that
2 f \F(t)\dt<e.
When t lies in one of the intervals fx we use the inequality
and hence, if K is the upper bound of 1^D)! in the parts of (a, b) outside the
intervals ft, by applying (I) to each of these parts, we have
If we take e sufficiently small (thus fixing K) and then take An to be
sufficiently large, we can make the expression on the right (and therefore also
the expression on the left) arbitrarily small, and this is the result which had
to be proved.
rb
(III) If $f(t)dt exists and is absolutely convergent, we can choose rj
Jo
so small that
t2 - a4
j dt < e,
and then, since we have
\ntf{t)Tn{t3x)dt
Jo
ttc22.B - as - b) V
*»/(*)
dt.
18-24] FOURIER-BESSEL SERIES 591
it follows from (II) that
\r.™™*\<zm*hv*?rT'+$l
where K is the upper bound of | F (t) j in (t), b) when the intervals /u, are
omitted.
Hence it follows that the expression on the left can be made arbitrarily
small by taking n sufficiently large, and so the analogue of the Riemann-
Lebesgue Lemma is completely proved.
1824. The Fourier-liessel expansion.
We shall now prove the following theorem*, by means of which the sum
of the Fourier-Bessel expansion associated with a given function is determined:
Let f(t) be a function defined arbitrarily in the interval @, 1); and let
I tl-f(t) dt exist and (if it is an improper integral) let it be absolutely convergent.
J 0
Let am= Ti -r-r j tf(t)Jv{jmt)dt,
*J k+1 \Jm) ¦! 0
where v + \ ^ 0.
Let x be any internal point of an interval (a, b) such that 0 < a< b < 1 and
suck thatf(t) has limited total jiiwtuation in (a, b).
Then the series 2 amJv(jmx)
is convergent and its sum is $ \f(x + 0) +f(x — 0)}.
We first observe that, by §§ 18-21, 18-22,
2 a,nJv(jmw) = iltf(t)Tn(t,x)dt,
m=-l JO
4 {/(* - 0) +/(* + 0I = li «""/(* - 0) f «"+I Tn (t, x) dt
+ lim x~»f(x + 0) IV1 Tn (t, x) dt.
Hence, if
8n(x) ~ \Xt"+> [t~"f(t) - x-"f(x - 0)) Tn (t, x) dt
x-"f(x + 0)} Tn(t,x)dt,
it is sufficient to prove that 8n(x)-*.{) as n-*oc in order to establish the
convergence of
2 OmJ^Um*)
to the sum \ [f(x + 0) +f(as - 0)\.
* Hobaon, Proc. London Math. Soc. B) vn. A909), pp. 387—388.
THEORY OF BESSEL FUNCTIONS [CHAP. XVIII
.¦ e now discuss
V x-vf{x + 0)} Tn(t,as)dt
in detail, and the reader can then investigate the other integral involved in
Sn (x) in precisely the same manner.
The function t~v f(t) — x~vf(x + 0) has limited total fluctuation in (x, b),
and so we may write*
r •/ (t) - x-"f(x + o) = %1 (*) - %2 (*),
where Xi @ an<^ %2 00 are bounded positive increasing functions of t in (x, b),
such that
Hence, when an arbitrary positive number e is chosen, there exists a
positive number 8 not exceeding b — x, such that
0 $#(*)< 6,
whenever x^.t^x + &.
We then have
fV+1 {t-vf(t)-x~"f(x+0)} Tn(t,x)dt
J X
rx+s rx+&
+ t"+> Xl (i) Tn (t, x)dt-\ «h-i %2 (^ yn (t, x) dt.
We now obtain inequalities satisfied by the three integrals on the right.
It follows from the analogue of the Biemann-Lebesgue lemma that the
modulus of the first can be made less than e by taking n sufficiently large.
Next, from the second mean-value theorem it follows that there is a number
f between 0 and 8 such that
rx+S rx+S
f" Xi (t) Tn (t, x) dt = Xi (a + 8) i"+1 Tn (t, x) dt,
J X Jx+I;
and, by § 18-22, the modulus of this does not exceed 2?7e; and similarly the
modulus of the third integral does not exceed 2 Ue. By treating the integral
between the limits 0 and x in a similar manner, we deduce that, by taking n
sufficiently large, we can.make the difference between
2 a>mJAjmX) and ?{/(« + 0) +f(x - 0)}
numerically less than (8U + 2) e; and this is arbitrarily small.
Hence, by the definition of an infinite series, we have proved that, in the
circumstances postulated, ? amJv(jmx) is convergent and its sum is
m-l
i {/(a+ 0)+/(«-<>)};
and this is the theorem to be proved.
* Cf. Modem Analysis, § 3-64.
18-25] FOURIER-BESSEL SERIES 593
18*25. The uniformity of the convergence of the Fourier-Bessel expansion.
Let/(?) satisfy the conditions enunciated in §18*24, and also let f(t) be
continuous (in addition to having limited total fluctuation) in the interval (a, b).
Then the Fourier-Bessel expansion associated withf(t) converges uniformly to
the sumf(x) throughout the interval (a + A, b — A) where A is any positive number.
This theorem is analogous to the usual theorem concerning uniformity of
convergence of Fourier series *; the discussion of the uniformity of the con-
convergence of the Fourier-Bcssel expansion near x = 1 and near x = 0 requires
rather more careful consideration, in the first place because formula § 18'22 A) is
untrue when a'=1, and in the second place because it is not practicable
to examine the bounds of
0
when x and t are small, without using approximations for Bessel functions of
the second kind.
The difficulties in the case of the neighbourhood of x — 1 are. easy to over-
overcome (cf. § 18*26); but the difficulties in the case of the neighbourhood of
the origin are of a graver character; and the discussion of them is deferred
to § 18-55.
We shall prove, the theorem concerning uniformity of convergence through-
throughout (ci+ A, 6 —A) by a recapitulation of the arguments of the preceding section.
In the first place, since continuity involves uniformity of continuityf, the
choice of 8 which was made in § 18*24 is independent of x when ./; lies in
(u + A, b- A).
Next we discuss such an integral as
-1
Since 8 is independent of x, it follows from the proof of the Riemann-
Lebesgue lemma (^ 18-23) that this integral tends to zero uniformly as n -*-cc ,
provided that
[t~*j\t)-x-\f(x))dt
f11 <*/¦(<) \dt + \ x-"f(.r) | fl i"+* dt,
Jo'' JO
¦x+t
is a bounded function of x.
Now
i
.rl-S
and this is bounded in (a + A, b — A) since fix) is continuous and therefore
bounded in this interval.
* Cf. Modern Analysis, § 9-44.
t Cf. Modern Analysis, § 361. It is now convenient to place an additional (trivial) restriction
on 5, namely that it should be less than A, in order that the interval (x-d, x + 5) may lie inside
the interval (a, b).
W. n. p. 38
594 THEORY OF BESSEL FUNCTIONS [CHAJP. XVIII
Similarly the other integrals introduced in § 18-24 tend to zero uniformly,
and so
n
tends to zero uniformly as n-*oo, and this proves the theorem stated.
18*26. The uniformity of the convergence of the Fourier-Bessel expansion
near x = l.
It is evident that all the terms of the Fourier-Bessel expansion vanish at
the point x — 1, so that, at that point, the sum of the terms of the expansion
is zero.
Since uniformity of convergence of a series of continuous functions involves
the continuity of the sum, it is evident that the condition
is necessary in order that the convergence of the Fourier-Bessel expansion
associated with/(#) may be uniform near x — \.
We shall now prove that the conditions that f{x) is to be continuous in
(a, 1) and that /(I) is zero, combined with the conditions stated* in § 18'24,
are sufficient for the convergence to be uniform throughout (a + A, 1).
The analysis is almost identical with that of the preceding section; we take
(V1 [t-of(t)-X-"f(x)} Tn(t,x)dt,
J 0
just as before, and we then divide the interval @, 1) either into three parts
@, x — 8), (x — B,x+ 8), (co + 8, 1), if x ^ 1 — 8, or into two parts @, x — 8),
{x — 8, 1),. if x > 1 — 8. And we then prove that the three integrals (or the two
integrals, as the case may be) tend uniformly to zero.
Again, when /(I) = 0, we can choose Zx so that
| «-/(*?) | <«, i/(«)|<e
when 1 — 8X ^ x ^ 1.
Then the expression
f(x)-x-"f(x)!\"^Tn(t,x)
Jo
dt
tends uniformly to zerof as n-»-oo when" # lies in (a + A, 1— 8X), and the
expression does not exceed (Z7+l)e for any value of n when x lies in
* The interval (a, b) is, of coarse, to be replaced by the interval (a, 1).
t Because the integral involved tends to as" uniformly throughout (A, 1 - 8{), by § 18-21.
18*26,18-27] FOTTRIER-BESSEL SERIES 595
Hence we can make
/ (x) - x-" f (*) [ V+1 Tn (t, x) dt
Jo
arbitrarily small for all values of a; in (a + A, 1) by a choice of n which is
independent of x; and this establishes the uniformity of the convergence of
t\f(t)Tn(t,x)dt
Jo
to the sum/(i») in (a + A, 1) in the postulated circumstances.
18*27. The order of magnitude of the terms in the Fourier-Bessel series.
It is easy to prove that, if t*f(t) has limited total fluctuation in (a, b),
where (a, b) is any part (or the whole) of the interval @, 1), then
as \-»-oo.
From this theorem we at once obtain Sheppard's result* that
*l v+i\Jm) J
when 0<a?^l; this equation, of course, has a well-known parallel in the
theory of Fourier series.
We first observe that, as a consequence of the asymptotic expansion of § 7*21,
*¦
0
where c is a constant, independent of t when t lies in the interval @, oo ).
Now write t^f(t) = fii^ — ^it), where i|r, (t) and ^(t) are monotonic
in (a, b); and then a number f exists such that
r,(a) ! t>< Jv (Xt) dt + -f, (/,) f 'ti J, (Xt) dt
J a J ?
A similar result holds for ^a(?), and hence the theorem stated is evident.
If it is known merely that
rbt*f(t)dt
exists and is absolutely convergent, then aU that can be proved is the
theorem that
Quarterly Journal, xxnr. A889), p. 247.
38—2
18-a] DINI SERIES 597
where H and v are real constants, and
The coefficients bm are to be determined by the formula
hm \ tJ* (X,nt) dt = [ltf(t) ./"„ (Xmt) dt
Jo Jo
so that
ltf{t)Jv(kmt)dt
0
r \hjjij "T" A^jg, t/y ( A/j^y
Before proceeding further, we shall explain a phenomenon, peculiar to certain
Dini expansions, which has no analogue in the theory of Fourier-Bessel
expansions.
The investigation of Dini expansions is based on properties of a function
which has poles at the zeros of
and, when H + v = 0, this last function has a zero at the origin.
Further, if H + v is negative, the function has two purely imaginary zeros.
It is only to be expected that these zeros should contribute to the terms
of the series, and such a contribution in fact is made.
If H+ v = 0, an initial term
J o
has to be inserted on account of the zero at the origin.
If H + v is negative and the purely imaginary zeros arc ±'iXfl, then an
initial term
\ / / \ '**~ ' "*i\ r~'» /a V * " •» t >~> i ^ \ I / \ ^ " \^*u^/ ^*'k
y A.|)" "p V j 1 v" i f\*Q/ ~~ A,|j"i|, " ( A.(( J J (j
must be inserted on account of the zeros ± iX,,.
These initial terms in the resp(;ctive cases will bo. denoted by the common
symbol /$o(•'•')> 'so ^la^p ^^c series which will actually be considered is
.¦#0(a:)+ - I'mJAKi*),
wt-l
where ;$Q(x) Ls zero when H + v is positive and is defined as the expression
A) or B) in the respective cases H + u = 0, // + v < 0.
[NoTii. The fact that an initial term must l>o iiiMM-toci when // + v ¦•-•¦-() was noticed by
Dini, iSerie di Fourier (Pisa, 1HHO), p. '2G8, but Dini j^ive it.s vahic. inairructlv, t.ho factor
.('' being omitted. Dini's formula was misquoted by Nielsuu, IJttndbucli der Theorie der
Gylinderfwiktionen (Leipzig, 11H4), p. 354. For eorroctions of these errors, see Bridgoinan,
Phil. Mag. @) xvi. A908), pp. 947 -048; C'hree, Phil. Mug.,{i>) xvu. A009), pp. 329-331;
and C. N. Moore, Trans. American Math. Hoc. x. A909), pp. -119--420.]
598 THEORY OP BESSEL FUNCTIONS [CHAP. XVIII
"We now consider the function
(xw) Jv (tw)
Jv {w) {wJJ (w) + HJV (w)}'
This function has poles at juj^ja, • • • > *-i> ^*> ^*> • • • > @ or + %\0).
The residue of the function at jm is
The residue at \m is
The residue at the origin when H 4- v — 0 is
-4<(i/+l)a;>'^.
The residues at ± i\0 when if + v is negative are both equal to
Now let !>„ be a number, which lies between A™ and Xn+1, so chosen that
it is not equal to any of the numbers jm; and let j^ be the greatest of the
numbers jm which does not exceed Dn.
= S
m=l
where ?40(a;, t) is defined to be 0, 2 (v + 1) a?"?" or
(V + y4) /> (X,) - V A'
according as if +1/ is positive, zero or negative.
Then, evidently,
-V n ri
2 awJ,,(jmtf)-^0(tf)- X ftm/^X^a?)*/ tf(t)Sn(t,x]H)dt.
wi-l m=l Jo
We shall now prove a number of theorems leading up to the result that, when
0 < x < 1, the existence and absolute convergence of
Jo
are sufficient to ensure that, as n -*¦ oo,
18:31, 18-32] DINI SERIES 599
This equation enables us to deduce the properties of Dini's series in respect
of convergence* from the corresponding properties of the Fourier-Bessel
series.
18'31. The contour integral for Sn (t, x; H).
It is evident from Cauchy's theory of residues that
+™i 2w Jv (xw) Jv (tw) dw
2th J-co.
(xw) Jv (tw) dw
Jv (w) \wJJ (w) + HJV (w)}'
where the symbol P denotes Cauchy's c principal value.' The integrand being
an odd function of w, the second integral vanishes, and so we have
n ^x'n)' 2-rri] nn. . ? Jv (w) [wJJ (w) + HJV («,)} *
An immediate consequence of this formula (cf. § 1821) is that
where cs is independent of n, x and t.
Also
(V> <7 (t a
and hence
where c4 is independent of ?i, a1 and t.
18*32. The analogue for Sn{t, x; H) of the Jtiemann-Lebesgue lemma.
We shall now prove the theorem that, if (a, b) is any part {or the whale)
of the interval @, 1), then the existeiice and absolute convergence of
are sufficient to ensure that, as n -- oo ,
l
J a
provided that 0 < a: < 1. And, if b< 1, the theorem is valid when 0 < x % 1.
The proof has to be divided into three stages just as in the corresponding
theorem (§ 18*23) for Tn(t, x). We shall now givo the proof of the first stage,
when it is supposed that t^f(t) is bounded and a > 0. The proofs of the re-
remaining stages should be constructed by the reader without difficulty.
* Except at tbo point x—1.
600 THEORY OF BESSEL FUNCTIONS [CHAP. XVIII
Let t
and let the upper bound of | F(t) j in (a, b) be K.
Divide (a, b) into p equal parts by the points tx, t2i..., tv_x (to = a, tp — b),
and, after choosing an arbitrary positive number e, take p to be so large that
2 {Um-Lm)(tm-tm-i)<e,
m—1
where Um and Lm are the upper and lower bounds of F(t) in (?m_i, tm).
Let FtysFit^J + atnit).
so that | <om (t) \<Um — Lra, in (tm_1} tm).
Then
()j t»«8n(t%x;H)dt+i f* t'+i a>vl(t)8n(t, x\ H)dt.
m=l J tm~\. »=1 •> <i»_i
Hence, by §18-31,
and if we now take n so large that Dnec3> 2Kp cif we have
[ tf{t)8n(t>x;H)dt
J a
B - x - b) \/x'
and the expression on the right is arbitrarily small. Hence the integral on
the left tends to zero as n—-co.
When the reader has removed the restrictions concerning boundedness
and the magnitude of a by the method of § 18*23, the theorem is completely
proved.
As a corollary, it should be observed that
b
tf(t)8n(t,x',H)dt
tends uniformly to zero as n -*¦ oo when 0^?<$lif&<l, and when 0 < x ^ 1 — A
if 6 ^ 1, where A is an arbitrary positive number.
18' 33. Dini's expansion of an arbitrary function.
An immediate consequence of the result of the preceding section is that
the existence and absolute convergence of the integral
are sufficient to ensure that the Dini expansion associated with f(x) behaves
¦ in the same manner, as regards convergence (or summability), as the Fourier-
Bessel expansion throughout the interval @ < x < 1).
18*33] . DINI SERIES 601
For it is evident that
n N
,%(x) + 2 bmJv(\mx)~ 2 amJv(jmx)
m~l m-1
tends to zero as % -^-qo when 0 < a- < 1; and this sum (multiplied by \/#) tends
uniformly to zero when 0 ^ x ^ 1 — A.
Now, since the numbers \m and jm which exceed | v | are interlaced
(§ 1523), it follows that Dn may be choseu so that n — iV has the same value
for all values of n after a certain stage.
Therefore, since
»
a& X amJv(jmx)-<~0,
uniformly throughout @,1), we have proved that
2
tends to zero, as ri-*-oo , uniformly throughout @,1 — A).
That is to say, the .series
is uniformly convergent throughout @,1 — A) and its sum is zero.
It follows from the 'consistency theorems' concerning convergent aeries*
that, when the series is 'summed' by Cesaro's means, or ?my .similar method, it
is (uniformly) summablo and its ' sum ' is zero.
Hence, if, for any 'particular value of x in the interval @, 1 —A), the series
X x*amJv(jMx),
in - i
associated urith f(x), is convergent (or is sumniable by some 'method), than the
series
00
xK%(x)+ 2 utbmJv(\nx)
m -•¦ 1
y'.s' conve?-gent {or is sumrnable by the same method) and the two series have the
same ' sum.'
And if, further, the Fourier-Bessel series (multiplied by \Ar) *-s< uniformly
convergent (or uniformly summable) throughout an interval (a, b), where
<)<«.<&< 1,
then also the Dini series (multiplied by *Jx) is uniformly convergent (or uni-
uniformly summable) throughout (a, b).
In particular, if/(#) has limited total HuctuaLion in (a, b) where
0 <a <b^l,
* Cf. Bromwioh, Theory of Infinite Series, § 100.
602 THEORY OF BESSEL FUNCTIONS [CHAP. XVIH
then the series
00
converges to the sum
(« + <>)+/(«-0)} .
at all points x such that a + ?mx%b-&, where A is arbitrarily small; and
the convergence is uniform if f(x) is continuous in (a, b).
18*34. The value of Dini's series at a: = 1.
We shall now complete the investigation of the value of the sum of Dini's
series by considering the point x = 1; and we shall prove the theorem, due to
Hobson *, that, iifix) has limited total fluctuation in the interval (a, 1), the sum
of the Dini expansion at x = 1 is /(I — 0).
We first write
Tn(t}x- H) = Tn(t,x)-8n(t,x; H)
s
and then we have
1 f ¦Dn+c0 * w <f> (w, x) ,/„ (tw) dw
n
V 2™ J D^ni W JJ (W) + BJV
where
2t™ J D^ni W JJ (W) +
<f> (w, x)~tt [{wJJ {w) + HJV{w)\ Yv (xw) - [w Yv' (w) + HYV («/)} J„ (xw)].
The former representation of Tn {t,x; H) is valid when 0 < t < x ^ 1, the
latter when 0 < x < t ^ 1.
[Note. These representations of TH (t, x; H) are strictly analogous to the representa-
representations of Tn (t, x) given by § 18-21 G) and § 18-21 (8); the fact that there is no formula for
Tn (t, x; S) analogous to § 18*21 F) is the reason why Dini series were discussed in § 18-33
with the help of the theory of Fourier-Beasel aeries.]
Now consider the value of
f tv+> Tn(t,l; E) dt
J o
when 0 < t < 1. We have
b-*«
iJi)n-jsi wJ>,'(w) + HJv(w)
-rri
Proc. London Math. Soc. B) vn. A909), p. 388.
18*34] DINI SERIES 603
For any given positive value of B, it follows from § 18'21 that this is a
bounded function of t in the interval (8,1). When B < t^ 1 -S,it is 0 A/Dn).
And when t = 1, it has the limit 1 when n-*oo.
It follows that
,() v()
m = 1
Since t~"f(t) —/(I — 0) has limited total fluctuation in (a, 1) we may
write it in the form Xi @ - %a @> where %j (f) and ;\;2 (?) are bounded positive
decreasing functions of t such that
Hence, given an arbitrary positive number e, we can choose a positive
number B, not exceeding 1 — a, such that
whenever 1 — 8 <; t % 1.
We then have
f V+1 [t-"f(t) -/(I - ())} Tn {t, 1; H) dt
Jo
= P~ V+> [t- f(t)-f{\. - 0)] Tn(t, 1; //) d,t
Jo
+ P tv+1 %i @ 2'n («, I; //) (it-I t • Xa («) Tn (t, 1; //) dt.
Jl-S Jl-S
By arguments similar to those used in § 184, the first integral on the
right is o(l) as n-*co ; and neither the second nor the third exceeds
2ehm\ f't"^ Tn(ttl; H)dt
in absolute value (cf. § 18-24), and this expression is arbitrarily small.
It follows that
lim /V+1 [t-"f(t)-f(l-O)}Ta(t,l)H)dt = Q,
and ao we have proved that, in the circumstances postulated at the beginning
of this section,
converges to the sum / A — 0).
This discrepancy between the behaviours of Dini series and of Fourier-
Bessel series (§ 1826) is somewhat remarkable.
604 THEORY OF BESSEL FUNCTIONS [CHAP. XVHI
18*35. The uniformity of the convergence of Dini's expansion in an inies^val
extending to w — 1.
Because Dini series do not vanish identically at x = 1, it seems not unlikely
that/the condition that f(x) is continuous* in (a, 1), combined with the
existence and absolute convergence of
(\if(t)dt,
Jo
and the condition that f(x) has limited total fluctuation in (a, 1), may be
sufficient to ensure the \miformity of the convergence of the Dini expansion
in (a + A, 1).
We shall prove that this is, in fact, the case.
The reason for the failure in the uniformity of the convergence of the
Fourier-Bessel expansion (§ 18*26) near x = 1 was the fact that
\
Jo
does not converge uniformly to x" in (A, 1), as was seen in § 1822. We shall
prove that, on the contrary,
f tv+*Tn{t,x; H)dt
Jo
does converge uniformly to xv in (A, 1), and the cause of the failure is
removed.
A consideration of § 1826 should then enable the reader to see without
difficulty that the Dini expansion converges uniformly in (a + A, 1).
It is easy to see, from § 18'34, that
is the sum of the residues of
irt^ [{wJv' O) + HJV (w)} Yv+1 (tw) - [w YJ («,) + HYV (w)} Jv+i (tw)]
x Jv (xw)l[wJv' (w) + HJV (w)},
at A.J, Xo, ..., \n, plus half the residues at 0 or + i\> if H + v^ 0.
Hence | p+i Tn(t,x; H)dt
is the sum of the residues of
-B/w) (H + v) Jv(xw)l{wJv' iw) + HJv(w)),
and hence, when 0 < x ^ 1,
_ooj- w {wJv (w)
* Without restriction on the value of/ A-0).
18*35, 18-4] DINI SERIES 605
and the integrand on the right* is of the order of magnitude of
and so the integral on the right converges uniformly to zero like l/(Dn*J%)
when A ^ x < 1. That is to say
converges uniformly to x" in (A, 1); and we have just seen that this is a suf-
sufficient condition lor the uniformity of the convergence of the Dini series
associated with/(?) to the snmf(x) in (a + A, 1) under the conditions postu-
postulated concerning
18*4. The differentiability of Fourier-Bessel expansions.
In the earlier part of this chapter we obtained an expansion which, when
written in full, assumes the form
A) /(«) = ~ OmJ?{jmt?x).
tn-l
We shall now study the circumstances in which, given this expansion, it
is permissible to deduce that
( 2) /' (x) = t (Imjm, v JJ (jm, * «)•
m = l
This problem was examined by Fordf, and his investigation is analogous
to Stokes' researches on the differentiability of Fourier series;];.
Ford also iuveHtigated the diffcraitiability of Dini's expansion when H— — v, but his
method ia not applicable to other values of II.
It is evident that we can prove the truth of B) if we can succeed in
proving that
v °°
^ 1M-1
and the numbers jmiV are the positive zeros of
z-^{zJ'tl+i(z) + (v + l)Jl,+l(z)}.
Now we know thatf'(x) — (n/x)f(x) admits of the Dini expansion
00
inside any interval in which Lhe function has limited fluctuation, provided that
exists and is absolutely convergent.
* The term in wJv' (w) is more important than the term in ,Tv(w) except in the limit when H
is infinite; this shews clearly the reason for the difference in the behaviour of the Dini expansion
from that of the Fourier-Bessel expansion (cf. § 18-26).
t Trans. Avierican Math. Soc. rv. A908), pp. 178—184. % Of. Modern Analysis, § 9*31-
606 THEORY OF BESSEL FACTIONS [OHAP. XVIII
The coefficients bm are given by the formula
2 JV- fV'<*) ~ "/(*)} J"^ Um,vt) dt
J ft
fc.-
v+l U
iy\J2,
T73^
Jrn,,vm,i
provided that tf(t) /v+1 (jw> „ ?) =0.
Sufficient conditions that this may be the case are
(i) ?"+2/(?)--0 as t-*>0,
(ii) /(l-0) = 0,
(iii) f(t) is continuous in the open interval in which 0 < t < 1.
These conditions combined with the existence and absolute convergence of
are sufficient to ensure the truth of B) in any interval in which
has limited total fluctuation.
18*5. The summability of Fourier-Bessel series.
A consideration of the values of the coefficients in the Fourier-Bessel
series associated with f(x), combined with the expression of Tn (t, x) as a contour
integral, suggests that it is no easy matter to discuss by direct methods the
question of the summability,by Cesaro's means, of the Fourier-Bessel expansion.
It is, however, very easy to investigate the summability when the method
of Riesz* is used to 'sum' the series, and then the suramability @1) can be
inferred with the help of quite elementary analysis.
The expression which will be taken as the 'sum' of the series by the
method of Riesz is
Urn I (l-hL\amJv(jmX);
and when this limit exists, the Fourier-Bessel series will be said to be sum-
mable (B).
It is evident that
A) I ^)U) \
* Cf. Hardy, Proc. London Math. Soc. B) nn. A910), p. 309.
18-5,18*51] FOUKIER-BESSEL SEBIES 607
where
and so it will be convenient to dispuss the properties of Tn (t, a; | jR) after the
manner of § 18*22 before we make further progress with the main problem.
18*51. Theorems concerning Tn(t, x \ R).
When Tn (t, x\R) is defined by equation B) of § 18*5, it is a symmetric
function of t and x, and so we shall proceed to establish the properties of the
function on the hypothesis that 0 < t^ x ^ 1, and we can then write down the
corresponding properties when 0 < x < t ^ 1 by interchanging t and x in the
results already obtained.
We first observe that Tn (t, x | R) is the sum of the residues of
My) Yv{xw)-Jv{xw) Yv(w)\ Jjt&>
For brevity we; write
w [Jv (w) Yv (xiu) - Jv (xw) Yv (w)} = & (w, x),
and then it is obvious that, when* t<x,
If"' ^/ .
2iAnJ _«,»
Jv(w)
since <P(w,x)Jv(tvj)fJv(w) is an odd function of w.
We shall now obtain some upper bounds for
<b (w, x) Jv {tw)IJv (w) |
both when w is on the line joining An — oo i to An + oo r, and when w is on the
imaginary axis; the formulae which will be discussed are valid when 0 %x % 1
and 0 •$ t% 1, the sign of x — t being immaterial.
To obtain these inequalities, we shall use series of ascending powers of w
when | w\ is not large, and inequalities derived from the formulae of Chapter vn
when | w \ is not small.
* Wheu t 5; x, the integrals taken along the linen joining ± iB to An ± W do not tend to zero
as B -*¦ oo . There is uo need to make au indentation at the origin, because 4> (w, x) is analytic at
the origin.
THEORY OF BESSEL FUNCTIONS [CHAP. XVIII
We first deal with the factor Jv(tw)jJv(w). We observe that*
Jv (tw)
A)
Jv(w)
when w *is on either contour; this follows from inequalities of the type
§ 18-21 (9) when | w \ is not small, and from the ascending series when | w | is
not large (i.e. less than jm).
We next consider <t> (w, x), which is equal to
\iw {Evw (w) Hv{% (xw) — Hv[1) (xw) HJi] (w)};
it is convenient to make two investigations concerning this function, the
former being valid when — \4.v^\, the second when v^\.
(I) The first investigation is quite simple. It follows from §3*6 and
§ 7*33 that
for all the values of w and x under consideration when — ? ^ v % {. Hence
C) |*(»,*)|<^erp{(l-aJ)|/(ii;)|}.
(II) When v^\ and \w\ is not large, it is easy to deduce from the
ascending series for Jv (w), Yv (w), Jv (xw) and Yv (xw) that
D) | $ (w, x) | < k31 w | or".
If | w I is not small, we use the inequalities (deduced from § 7-33)
together with the inequalities
,,* (xw) | < k4 {\ xw j-* + | xw
Hv® (xw) | < kA \\ xw \-i + j xw |
It follows from § 3'6 and § 7*33 that the inequalities F) are true whether
| xw j is large or not. Hence,
G) 1 $ (w, a?) | < k2k, far* + x~v \ w |*-'} exp {A - a;) j / (w) \},
when v > | and | to | is large, whatever be the magnitude! of | xw \.
If we now combine the results contained in formulae C), D) and G) we
deduce that, whether — \^v *z,\ ox v^\,
(8) | * (w,x)\ < k6(x-t 4-af-v)exp {A - #) \I(w)\},
* It is supposed that the numbers kls k2, fc3,... are positive and independent of w, a; and «;
their values may, however, depend on the value of v.
t Provided of course that
18-51] FOURIER-BESSEL SERIES 609
when w is any point of either contour and 0 < x <$ 1. Henc •, by A), it follows
that
(9) 4> (w,x) J-j^ < k0r* (x-i + x~") exp {-(x~t)\I(w)\},
when 0 < x ^ 1 and 0 ^ t^ 1.
We now return to the integral formula for Tn (t, x \ R). If we replace w by
An ± iv and + iv in the first and second contour integrals respectively, we
deduce that, when 0 < t < % ^ 1,
We have consequently proved the two inequalities
do) ir.ft.uQK^.^ (o^ <,,i),
It is to be remembered that ka is independent of .•/.• and t, so that wo may
make | x — 11 tend to zero, if we desire to do so.
One other pair of inequalities is required in order to discuss the behaviour
of T.n(t, x | R) when x and t are nearly equal. To obtain them, we write;
/ ,Jv(t;w)dw
when O^i<;.'/;^1; in this integral the contour ia taken to be a rectangle with
vertices + iAn, An ± %An.
It is easy to see that (9) is satisfied whether w be on the horizontal aides
or on the vertical sides of this rectangle; and the; factor 1 — (io/An) does not
exceed V2 in absolute value at any point of the contour.
Consequently the modulus of the integrand does not exceed
ke <-* (or* + or") V2 ;
and since the length of the contour is QAn, we infer that, when
A2) \Jn(t,w\R)\<
and similarly, when ()%.$ <; t < I,
The last four inequalities are sufficient to enable us to discuss adequately
the summability (R) of Fourier-Besscl series. The reader will observe that
the consideration of small values of a; has increased the length of the analysis
to an appreciable but not to an undue extent.
w. b. f. 39
610 THEORY OF BESSEL FUNCTIONS [CHAP. XVIII
18*52. The analogue of Fejera theorem.
We can now prove that the existence and the absolute convergence of
[
o
are sufficient to ensure that the Fourier-Bessel series associated with f (t) is
summable (R) at all points x of the open interval @,1) at which the two limits
f(cc±O) exist. And the sum (R) of the series is
H/(« + Q)+/(*-<>)}.
This theorem is obviously the analogue of Fejer's theorem* concerning Fourier
series.
Sincei" a series which is convergent is summable (JR), it follows from § 18*35
that, when 0<«<l,
lim \XtvJ*Tn(txx\R)dt= lim \\
= \xv.
Hence it follows that, when the limits f(x ± 0) exist, then
lim rtv+*Tn(t,x\R)ar''f(x-Q)dt+ lim fV+1 Tn{t,x\R)x'vf{x+O)dt
4{/ 0)/(>0)}
We are now in a position to consider the sum Sn(x\ R), defined as
I (l~?) am Jv (jmx) - f V* Tn (t, x i R) x~"f(x - 0) dt
- f tv+1 Tn (t, x | R) xrvf{x + 0) dt,
J x
and we shall prove that it can be made arbitrarily small by taking n sufficiently
large.
The sum 8n (x \ R) is equal to
f V* {i-" f{t) - x-"f(x - 0)} Tn (t, x\R)dt
Jo
+ f i"+1 {irvf(t) - x~"f(x + 0)} Tn (t, x | R) dt.
Now, on the hypothesis that the limits f(x ± 0) exist, if we choose an arbitrary
positive number e, there exists a positive number]: 8 such that
f|tr»f{t)-x-»f(x + 0)|< e, (x^t^x+h),
II ^"/@ ~ *¦"/(« ~ 0) | < e, (x S* t> x - S).
We now choose a positive function of n, say <r (w), which is less than 8 for
sufficiently large values of n, and divide the interval @,1) into six parts by
the points x ± B, x ± c (n), x.
* Of. Modern Analysis, § 9-4. t Cf. Modern Analysis, § 8-43.
X It is convenient to take 5 less than x and 1 - x.
18*52] FOTTRIER-BESSEL SERIES 611
In the intervals (O,a:-S), (x-$, x-o-(n)) and also in the intervals
(x + a (n), x + 8),(x+S,l) we use inequalities of the form given in § 18*51 A0)
and A1); and in the intervals (x- <r(n), oc), (x, x + ar(n)) we use inequalities
of the form given in % 18*51 A2) and A3).
It is thus found that | Sn (x \ R) I does not exceed
A
!x+s
!x+s JL
For any given value of e (and therefore of 8), the first and last terms in this
expression can be made arbitrarily small by taking >i sufficiently largo, on
account of the convergence of
J [)
The remaining terms do not exceed
2k,e(&s-* + ar1')( 1 3/lnso*(w)|
An W(n)+ V2 }
and, if we take <r(n) = l/An, this is independent of n, and it can be made as
small as we please by taking e sufficiently small initially.
We can therefore make the intermediate terms in the expression for
i ISn(w\ R)\ as small as we please by taking e sufficiently small, and when this
has been done, the first and last terms can be made as small as we please by
taking n sufficiently large.
That is to say, \8n(oc\R)\ can be made arbitrarily small by taking v
sufficiently large, so that *
lim 8u(ic\R) = 0.
Hence
lim 2 (l - ?r) amJv (jmx) = x->f(w - 0) lim f V' Ta (t, x \ R) dt
+ w-"f(x+0) lim
since the limits on the right exist.
31)—2
612 THEORY OF BBSSEjL FUNCTIONS [CHAP. XVIII
Since each of the limits on the right is equal to \oovt it has now been
proved that
2 amJv(jmx)
is summable (R) with sum I {f(x + 0) +f(x — 0)[ provided that the limits
f(x ± 0) exist; and this is the theorem to be established.
As a corollary, the reader should be able to prove without difficulty that, if/(<) is
continuotis in (a, b), the summability (R) is uniform throughout the interval in which
fr-A, where A is any positive number. Cf. § 18*25.
18*53. Uniformity of summability of the Fourier-Bessel series near the
origin.
We shall now examine the uniformity of the summability (R) of the
Fourier-Bessel expansion throughout an interval of which the origin is an
end-point. It will be supposed that the expansion is modified by being mul-
multiplied throughout by »Jx, and it will then be proved that, if t~"f(t) is con-
continuous in the interval @,b), then the modified expansion is uniformly summable
throvghout @, b — A), where A is any positive number.
Given e, we can now choose 8 (less than A) so that
whenever x — S^.t^.x + 8 and t>0, provided that x lies in @,b — A).
Since continuity involves uniformity of continuity, this choice of S may be
taken to be independent of x.
We now write
Sn(xI R) = [ t"+1 \t~vf(t)-x-"f{x)\ Tn(t,x\R)dt
Jo
and then examine | x*Sn (x\R)\ after the manner of § 18*52.
We express a$Sn{x\R) as the sum of six integrals (some of which are to
be omitted when x< 8), and we see that jx^Sn(x\R)\ does not exceed
-<rln'> dt
J ( dt
A L J J
An LV2 J* J,+,W(«-
In this formula any of the limits of integration which are negative are supposed
to be replaced by zero.
18*53, 18-54] FOURIER-BESSEL SERIES 613
Now this upper bound for | a$8n (oc | R) | does not exceed
and, since x~"f(x) is bounded (because it is continuous), this can be made
arbitrarily small by a choice of n which is independent of x.
Consequently #*$„(#\ R) tends to zero uniformly as n-*- oo.
Now it has already been shewn (§ 18'22) that
f ir"Tn(t,x)dt
Jo
is uniformly convergent in @,1 — A), and so, since uniformity of convergence
involves uniformity of summability,
«*"*/(«)[ t"+lTn(t,x\R)dt
Jo
tends uniformly to #*/(#) in @, b — A).
Hence, since a?Sn{w\R) tends to zero uniformly,
«* f tf(t) Tn (t, x | R) dt
Jo "
tends uniformly to «*-"/(*) f t"+lTn (t, x | R)dt, i.e. to *•*/(«) in @, b - A).
Jo
It has therefore been proved that
S OmatJrijmX)
is uniformly summable (ii) in @, 6 — A) with sum x\f(:r), provided that
exists and is absolutely convergent, and that t~"f(t) is continuous in @,6).
18'54. Methods of' summing' Fourier-Bessel series.
We shall now investigate various methods of summing the Fourier-Bessel
series*
on Che hypotheses (i) that the limits/(.r ± 0) exist, (iij that
exists and is absolutely convergent, and (iii) that the series is summablo (li).
It conduces to brevity to write/,,, (x) in place (jiamx!!Jv(jmx), so that/w (x)
lends uniformly to zero (§ 187) as m-*-oo when ar lies in @, 1).
"' The faotor x^1 is inserted merely in order that the disouBskm may cover the investigation of
uniformity of sumroability near the origin.
614 THEORY OF BESSEL FUNCTIONS [OHAP. XVJII
Consider first the limit
lim I (l-*)/•<*)
which gives the most natural method (of Riesz' type) for summing the senos.
Since (jnlAn)^l, it is evident that
lim I (
?
lim ? (lM
exists and is equal to
Again, since/n(a?) = o(l), it is easy to see that
n
2 fm(*) = o(n),
so that
and therefore
lim X {l-^)fm(oc)= lim I (l -
the limit on the right exists in consequence of the hypotheses made at the
beginning of the section.
Again, since
whether m be o (n) or 0 (n), it follows that
and so
lim
Consequently the hypotheses that the limits f{x ± 0) exist @ < x < 1) and
tjiat the integral
exists and is absolutely convergent are sufficient to ensure that
is'summable (C1) wrata «ttm !«;*¦ {/(a; + 0) +/(# — 0)].
3y the same reasoning, if/(«) is continuous in (a, b), the summability (C1)
is uniform in (a•+ A, 6 - A); and, if a = 0 and t~vf(t) has a limit as ? -* 0, the
summability (G1) is uniform in @, & — A),
5, 18-56] FOURIER-BESSEL SERIES 615
L8'55. Uniformity of convergence of the Fourier-Bessel expansion near the
in.
We can now prove, by using Hardy's convergence theorem*, that, iff
limited total fluctuation in @, b), while/(i) is also subject to the conditions
18-53, then
00
2 aVha$Jv(jmw)
niformly convergent in @, b — A) with sum o$ f{x).
Let h{t) be an auxiliary function denned to be equal to f{t) in @, b) and
al to zero in {b, 1); and let the Fourier-Bessel series associated with h(t) be
«t=l
00
Then, by § 18*54, 2 amx^Jv {jmx) is uniformly summable (G1) throughout
> —A) with sum x\f(x), and, by Sheppard's theorem (§18*27), am/^jm is
./m), while (jmx)^Jy(jmx) is a bounded function of x and m. Hence, by
•dy's convergence theorem,
2 amx*Jy(jmx)
niformly convergent throughout @, b — A), with sum x^f(x).
Again
« ri
x" 1/1 — ft \ SPm I I '\ W 1 •—— 0fl3l / / i"f\ I // I*1 I il /
m=\ Jb
. this tends uniformly to zero in @, b — A) as w-»-oo by an analogue of the
mann-Lebesgue lemma (§ 18-23).
n
Hence X amx* Jy ( jmx) tends uniformly to the sum x\f(x) in @, b — A) as
-30 ; and this is the theorem to be established.
1856. Summability of Dini series.
Except when x = 1, the aumrnability (G1) of the Dini series associated with
) may be inferred by combining the results of § 18*33 and §§ 18-51—18f53.
The summability (G1) may, however, be established independently! for
points x such that 0 < x $ 1 by replacing An and the functions Jv (w) and
(w), which occur in § 18*5, by Dn and the functions wJJ (w) + HJV (w) and
V (w) + HYV (w) respectively; the details of the analysis may be left to the
,der, and he will find that when x = 1 the expression \ [f{x + 0) +f(x- 0I
ist be replaced by/(I — 0).
* Cf. Moder. Analysis, §8'5.
t Of course on the hypotheseB ooncerning f(t) whioh wore assumed in § 18-53.
616
THEOEY OF BESSEL FUNCTIONS [CHAP. XVIII
of convergence was dealt with in §§ 18-33,18-35.
The stability of Dini series (and of Fourier Bessel ser^).
cation of Abel's method is of some physical importance Thus ^
problem of the Conduction of Heat in an infinite solid cylinder of radius unity,
the temperature v at distance r from the axis satisfies the equation
dv
dv, )
\drn- rdr]'
with the boundary condition
\i+Bv'\ =0,
if the initial distribution of heat is symmetrical.
Normal solutions of the differential equation satisfying the boundary
condition are
and so the temperature v is given by the series f
5 bmJo(Kir)exV(-k\mH),
where the coefficients bm are to be determined from the consideration that
m=l
is the Dini series associated with the initial temperature f(r). It is evident
that the initial temperature is expressible as
lim 2
/-*-+0 m-l
and this limit exists when the Dini series is summable (R).
18. The uniqueness of Fourier-Bessel series and Dini series.
It has been shewn by YoungJ that the existence and the absolute con-
convergence of
are sufficient to ensure that if all the coefficients am of the Dini series (or tlw
Fourier-Bessel series) associated withf(t) are zero, then the function f (t) must
be a null-function.
* La Thiorie Analytique de la Chaleur (Paris, 1822), §§ 306—320. Cf. Rayleigh, Phil. Mag. {6)
xii. A906), pp. 106—107 [Scientific Papers, v. A912), pp. 338—339] ; and Kirohhoff, Berliner
Sitzungsbericltte, 1883, pp.519—524.
t In this physical problem, H > 0, and so there is no initial term to be inBerted.
: Proc. London Math. Soc. B) xvm. A920), pp. 174—175.
18-6] FOURIEB-BESSEL SERIES 617
To prove this theorem we observe that, when p — 0,1, 2, ..., we may write
{j)
where the coefficients am are determined by the formula
71 P tv
and the series on the right converges uniformly in @, 1 — A) and oscillates
boundedly in A — A, 1). It is therefore permissible to multiply the expansion
by t*f(t) and integrate term-by-term.
It follows that
= 0.
5 amjltf(t)Jv(jmt)dt
w=o Jo
=
Since all the integrals
1f**+lf(t)dt (p-1,2,3,...)
o
are zero, it follows that t"f(t) is a null-function, by Lerch's theorem*, and
the theorem stated is proved for Fourier-Bessel series. The theorem for Dini
series can be proved in precisely the same way, and it is theoretically simpler
because the* Dini series associated with ?"+!# does not fail to converge uni-
uniformly in A — A, 1).
It is possible to construct a theory of series of Bessel functions of the types
oc oo
2 a,mJv(jmac), 2 bmJv(\mx),
(where the coefficients am and bm are any constants) which resembles Riemann's
theory of trigonometrical seriesf.
Such a theory is, however, more directly associated with Schlomilch's
series of Bessel functions, which will be discussed in Chapter xix; and it
seems convenient to defer the examination of the series
00 OO
2 amJv(jmx), 2 bmJy(\m,<v)
m—l *»—1
by Riemann's methods to § 19'7, when the discussion of the series forms a simple
corollary to the discussion of Schlbmilch series.
* Leroh, Ada Mathematica, xxvii. A903), pp. 345—347; Young, Messenger, xl. A910),
pp. 37—43. Cf. § 12-22.
t Cf. Modern Analysis, §§ 9-6—9-632.
CHAPTER XIX
SCHLOMILCH SERIES
19*1. Schlomilch's expansion of a function of a real variable.
In Chapter xvm we dealt with the expansion of a function f(x) of the
real variable oc in the form
CO
/(#)= 2 amJv(jmx),
where jm is the mth positive zero of Jv (z), so that, for large values of m,
That is to say, the argument of the Bessel function in a term of high rank in
the series is approximately proportional to the rank of the term.
In this chapter we shall discuss the series in which the argument of the
Bessel function in each term is exactly proportional to the rank of the term.
By choosing a suitable variable, such a series may be taken to be
00
2 amJv(mas).
m=l
It will appear subsequently that it is convenient to add an initial term
(§19%11; cf. §18'33); and the analysis is simplified by making a slight modi-
modification in the form of the coefficients in the series (§ 19*2).
Series of this type were first investigated by Schlomilch*. They are not
of such great importance to the Physicist as Fourier-Bessel series, though
Rayleighf has pointed out that (when v = 0) they present themselves
naturally in the investigation of a periodic transverse vibration of a two-
dimensional membrane, if the vibration is composed of an unlimited number
of equal one-dimensional transverse vibrations uniformly distributed in direction
through the two dimensions of the membrane.
Apart from applications the series present various features of purely
mathematical interest; and, in particular, it is remarkable that a null-function
can be represented by such a series in which the coefficients are not all zero
(§19-41).
In some respects the series are more amenable to analysis than Fourier-
Bessel series, but the two types of series have many properties in common;
and the reader will be right when he infers from a comparison of the
arguments jmx and mx that the relevant range of values of x is @, tt) for
Schlomilch series, corresponding to the range @, 1) for Fourier-Bessel series.
* Zeitsehrift filr Math, und Phys. n. A857), pp. 155—158; Sohlomiloh oonsidered only the
special caseB »=0 and ?=1.~
. f Phil Mag,~(b) xxi. A911), pp. 567—571 [Scientific Papers, vi. A920), pp. 22—25].
19*1, 19-11] SOHLOMILCH SERIES 619
19*11. Schlomilch's eaypansion in a series of Bessel functions of order
zero.
We now state and prove the expansion theorem discovered by Schlb'milch.
The theorem is concerned with the expansion of an arbitrary function f(x)
of the real variable x, and, with modern terminology, it is to the following
effect:
Letf(x) be an arbitrary function, with a derivate f (x) which is continuous
in the closed interval @, ir) and which has limited total fluctuation in this
interval.
Thenf{x) admits of the expansion
oc
A) /(a?) = |«o + 2 am Jo (™#)
where
ao = 2/(O)+ I I uf (u sin (j>)d(f>du,
B) vhJo
I 2 fn [l*
i a = - / / uf (u sin <b) cos mu d<bdu: (in > 0)
I IT Jo Jo
and this expansion is valid, and the series is convergent, throughout the closed
interval @, it).
Schlomilch's investigation is based on a discussion of the integral equation
C) /(«)= 2 f 7/0 sin 6)d6,
wJo
of which he proved that a continuous solution is
D) g (x) =/@) + x [V (x sin 0) d<f>.
Jo
We proceed to verify that the function g(x) defined by D) actually is a
solution of C); wo substitute the value given by D) in the expression on the
right of C), and then we see that
2 /•*"¦
7T
"g (x sin 6)dO=2 f* 1/@) + x sin 0 I f (x sin 0 sin <j>) d<j>\ d0
o i" J o ,L -' o " J
Lx [ '7r /'ir
7T Jo Jo
Now replace 0 by a new variable % defined by the equation
sin v = sin 0 sin 6
620 THEORY OF BESSEL FUNCTIONS [CHAP. XIX
and change the order of the integrations. We deduce that
- I g(xsin 9) dd -/@) = — I I /'(x sin 0 sin <?) sin 0 d<j>d0
- - f** f f (x sin v) s™eG0SXd%dd
sin 0
W
\% ft*»,, • xT • /cos 0\li7r
— f (x sin v) - arc sin cos
IT J o |_ \COS %/ J x
f tar
Jo
and so, when g (x) is denned by D), g (x) is a solution of C).
Now it is easy to verify from D) that, when/'(«) is a continuous function
with limited total fluctuation in the interval @, 7r), so also is g{os)\ and
therefore, by Fourier's theorem, g (x) is expansible in the form
; aw cosm«,
w-1
where
am = - I # («) cos rnudu
2 f* r r*• i
= - I /@) + m I /' (u sin ^>) d<^> cos mudu,
*"" J 0 (_ Jo' J
and this series for g (x) converges uniformly throughout the interval @, tt).
Hence term-by-term integrations are permissible, and so we have
2 r*""
f(x) = - I g (x sin 0) dd
= — I -<-J(X0 -h S aTOcosGn«sin^)[- dd
^Jo ( w=i j
ao
= |ao4- 2 amJ0(mx),
m=l
and this is the expansion to be established. It is easy to verify that the
values obtained for the coefficients am are the same as those given by
equation B).
When the restriction concerning the limited total fluctuation of f (x)
is removed, the Fourier series associated with g (x) is no longer necessarily
convergent, though the continuity of f(x) ensures that the Fourier series
19*2] SCHLOMILCH SERIES 621
is uniformly summable @1) throughout @, ir); and bonce, by term-by-term
integration, the series
00
^ao+ % amJ0(mx)
is uniformly summable @1) throughout @, tt), with sum /(#); an application
of Hardy's convergence theorem* then shews that the additional condition
is sufficient to ensure the convergence of the Schlomilch. series to the sum
f(ai) when x lies in the half-open interval in which 0 < x ^ ir.
For further theorems concerning the summability of Schlomilch series,
the reader should consult a memoir by Chapman \.
[Note. The integral equation connecting /(a?) and g (x) is one which was solved in 1823
by Abel, Journal fur Math. i. A826), p. 153. It has subsequently been investigated | by
Beltrami, 1st. Lombardo Rendiconti, B) xni. A880), pp. 327, 402 ; Volterra, Ann. di Mat.
B) xxv. A897), p. 104 ; C. E. Smith, Trans. American Math. Soc. vni. A907), pp. 92—106.
The equation
— I*"" I ^f (x sin 6 sin 0) sin 6 d<j>d6 -/(a?) -/@)
is most simply established by the method of changing axes of polar coordinates, explained
in § 3-33 ; this method was used by Gwythor, Messenger, xxxnr. A904), pp. 97—107, but
in view of the arbitrary character of f(x) the analytical proof given in the text seems pre-
preferable. In connexion with the changes in the order of the integrations, cf. Modern Analysis,
§4-51.
19. The definition of Schlomilch series.
We have now investigated Schlomilch's problem of expanding an arbitrary
function into a series of Besscl functions of order zero, the argument of the
function in the (m + l)th term being proportional to m; and the expansion is
valid for the range of values @, ir) of the variable.
Such series may be generalised by replacing the functions of order zero by
functions of arbitrary order v; and a further generalisation may be effected by
taking the general term to contain not only the function Jv (vise) but also a
function which bears to the Bcsael function the same kind of relation as the
sine does to the cosine. The latter generalisation is, of course, suggested by
the theory of Fourier series, an$ we are thus led to expect the existence of
expansions valid for the range of values (— ir, tt) of the variable.
The functions which naturally come under consideration for insertion are
* Cf. Modern Analysis, § 8\5.
t Quarterly Journal, xliii. A911), p. 34.
X Some interesting applications of Fourier's integral theorem to the integral equation have
been made by Steam, Quarterly Journal, xvn. A880), pp. 90—104.
622 THEORY OF BESSEL FUNCTIONS [CHAP. XIX
Bessel functions of the second kind and Struve's functions; and the types of
series to be considered may be written in the forms*:
iK | amJy(mx)+bmYv(mx)
I an ? O"in Jv {mx) + bm H,, (mx)
P(w+T) +m=i Jfmxy
Series of the former type (with v- 0) have been considered by Coatesf;
but his proof of the possibility of expanding an arbitrary function f{x) into
such a series seems to be invalid except in the trivial case in which f(x) is
defined to be periodic (with period lir) and to tend to zero as x -*- oo .
Series of the latter type are of much greater interest, and they form a
direct generalisation of trigonometrical series. They will be called generalised
Schlomilch series.
Two types of investigation suggest themselves in connexion with general-
generalised Schlomilch series. The first is the problem of expanding an arbitrary
function into such a series; and the second is the problem of determining the
properties of such a series with given coefficients and, in particular, the
construction of analysis (resembling Riemann's analysis of trigonometrical
series) with the object of determining whether a generalised Schlomilch
series, in which the coefficients are not all zero, can represent a null-function.
Generalised Schlomilch series have been discussed in a series of memoirs by Nielsen,
Math. Ann. Lil. A899), pp. 582—587 ; Nyt Tidsskrift, x. B A899), pp. 73—81 ; Oversigt
K. Danske Videnskabernes Selskabs, 1899, pp. 661—665 ; 1900, pp. 55-^-60 ; 1901, pp.
127—146 : Ann. di Mat. C) vi. A901), pp. 301—329.
Nielsenj has given the forms for the coefficients in the generalised
Schlomilch expansion of an arbitrary function and he has investigated with
great detail the actual construction of Schlomilch series which represent
null-functions, but his researches are of a distinctly different character from
those which will be given in this chapter.
The investigation which we shall now give of the possibility of expanding
an arbitrary function into a generalised Schlomilch series is based on the
investigation given by Filon§ for the case v = 0 in his memoir on applications
of the calculus of residues to the expansions of arbitrary functions in series of
functions of given form. It seems to be of some importance to give such an
investigation|| because there is no obvious method of modifying the set of
* The reason for inserting the factor xv in the denominators is to make the terms of the second
series one-valued (cf. § 1921).
t Quarterly Journal, xxi. A886), pp. 189—190.
X See e.g. his Handbuch der Tkeorie der Cyiinderfunktionen (Leipzig, 1904), p. 348.
§ Proc. London Math. Soc. B) iv. A906), pp. 396—430.
|| It has to be assumed that - \ < v < \. The results which will be proved in §§ 19-41—19>62
suggest that it is only to be expected that difficulties should arise for other values of v.
SCHLOMILCH: SERIES 623
Tv (mx), Hv (mx) so as to obtain a set which is a normal orthogonal
interval (— ir, tt); and consequently there is no method of obtaining
ents in a Schlomilch expansion in so simple a manner as that in which
.ents in a Fourier-Bessel expansion are obtained (§ 18'1).
vestigation, which forms the latter part of the chapter, concerning
entation of null-functions by generalised Schlomilch series, is of
e same character as the exposition of Riemann's researches on
:rical series given in Modern Analysis, §§ 9'6—9632.
The application of the calculus of residues to the generalised
i expansion.
all now explain the method* by which it is possible to discover the
the coefficients in the generalised Schlomilch expansion which
> an arbitrary function f{oc), when the order v of the Bessel functions
sen — | and ?. When this has been done, we shall not consider the
f the processes by which the discovery has been made, but we shall
jctly that the Schlomilch series in which the coefficients have the
values actually does converge to the sum f(x).
analogous to the procedure which is adopted in Dirichlet's proof of Fourier's
in the expansion
f{x) = \a<i+ 2 (a.wOOsma? + j3OTsin7H#)
of the coefficients are discovered by multiplying the expansion by cos mx and by
i integrating, so that the values of a,n and /3,n are taken to bo given by the
am=- I f(t) co&mtdt, (im=- - I f(t)m\mtdt.
vJ-w' nJ -*'
ake the series in which the coefficients have these values, namely
,y- | f(t)dt+- 2 j f(t)coam(x-t)dt,
A-K J -„ Tm=i J -„
that it actually converges to the sum f(x).
tiduces to brevity to deal with the pair of functions
Jv (mx) ± i Hp (mx)
H'mloy '~ '
)f with the pair of functions
Jv (rux)/(^mx)v, H,, (mx)j(^mx)v.
1 write
t from details of notation, the following analysis is due to Filon; it was given by him,
noir just cited, for the special case v=0, but the extension to values of v between ±\
o difi&culty.
62i THEORY OP BESSEL FUNCTIONS [CHAP. XIX
so that* <pr(z) is analytic and uniform for all finite values of the complex
variable z\ and evidently
We now observe that (—)m ^(w) is the residue at z — m of the function
where m = 0, ±1, ±2, ...; and so we shall consider the integral
sinvrz
in which the contour C is a circle, of radius M + \, with its centre at the
origin, and M is an integer whioh will be made to tend to infinity.
The function F(z) is assumed to be one-valued throughout the 2-plane,
and to be analytic at infinity (cf. §19#24); its only singularity in the finite
part of the plane is an essential singularity at the origin.
By Jordan's lemma, the integral tends to zero as M tends to infinity,
provided that v> — \.
It is evident, by calculating residues, that
2 (-)m [F (m) </>„ (mx) +F(- m) </>„ (- mx)}
is equal to the residue at the origin of
F(z)f
sin vz '
that is to say
B) ? (-) {F (m) 4>v (mx) + F(~m) <f>v (- mx)}
= --—. F(z) —P^—- dz.
zvi J x ' sin nrz
The problem of expanding an arbitrary function f(x) into a generalised
Schlbmilch series is consequently reduced to the determination of the form of
F(z) in such a way as to make
27ri J N ' sm nrz
differ by a constant from f(x).
* The insertion of the factor ($z)v in the denominator makes <pv(z) amenable to Cauchy's
theorem when the contour of integration completely surrounds the origin.
19-22] SCHLOMILCH SERIES 625
19*22.. The construction of the function F(z).
We now take the contour integral
and, in order to calculate it in a simple manner, we shall suppose that F(z) is
expansible in a series of Filon's type*
where ^n (z) denotes the sum of those terms in the expansion of ir~l sin irz
whose degree does not exceed n, and the coefficients pn will be defined later.
The reader will observe that
With this definition of F(z), it is evident that, for small values of \z\,
p
SU17TZ n^i [
1 wrn+l cos \n-ir + 0 (z)
, . .
\ sinirz J r v 7
It follows immediately that
v 7 sin7rz
/o^ t ^M *¦- cos t
}i
i Bti r a
and consequently we proceed to identify
with /(«) — /@). For this purpose we have to assume temporarily that/(.x-)
has differential coefficients of all orders at the origin, and then w^ define the
coefficients pn by the equation
We next transform this equation defining pn in such a way that the sum
of the series, by which F{z) is defined, is expressible in a compact symbolic
form; the transformation of the series for F{z) can be effected by expressing
* This type of series is fundamental in Filon's theory, and is not peculiar to Scblomilch
expansions; thuB, in his work on Fourier-Bessel series, sin irz is replaced by z~vJv (z) and \f/n (z)
denotes the sum of the terms whose degree does not exceed n in the expansion of that function.
"W. B. P. 40
626 THEORY OF BESSEL FUNCTIONS [CHAP. XIX
the coefficients pn in a form which involves n only as an exponent. For this
purpose we make use of Eulerian integrals of the first kind, and, in order
that they may be convergent, we shall find that it is necessary to suppose that
— \<v<\. We then have
@)/oA" eri"
l JM=0
and so we obtain the symbolic formula
where 2) stands for d/du.
Now, if we arrange the series
in descending powers of ?, it is easy to verify that
and therefore
Again, a consideration of B) shews that we need to sum the series
% pn 7TW COS \ 717T
and we are able to effect our purpose by making use of formula D), whence
we find that
We have now obtained symbolic expressions for all the coefficients in the
generalised Schlomilch expansion of /(«), but it is necessary to transform
these expressions into more useful forms, by finding the significance to be
attached to the symbolic operator —jj-\—^» both f°r general values of z and
for the value zero of z.
19-23] SCHLOMILOH SERIES 627
19*23. The transformation of the symbolic operators in the generalised
Schlomileh expansion.
We proceed to obtain an interpretation* of the symbolic expression
The usual interpretation of ~—r f(tu) is
\ e~izr>f{tv)dv,
J a.
where a is a constant of integration; and therefore
sinh ttD ... x sinh7r
7T
Now, by the symbolic form of Taylor's theorem, we have
where ^ (u) is an arbitrary function of u; and hence it follows that
1_7T (D - IZ)J V 'J^o L ^ J* J«-0
= ~- I e™ IU+" e-^fitv) dv
Ja Jtt-0
that is to sayf
cos
ET
t sin 7T2
H—
[/'+?""] «-*•/<«»)*«•
2tt
The second term on the right has simple zeros at all the points at which
^O, ±1, +2, ....
Therefore, so far as the calculation of residues of
smirz
* The interpretations of numerous expressions involving symbolic operators of the types under
consideration have been discussed by Gregory, Cambridge Math. Journal, i. A839), pp. 22—32 and
by Boole, Differential Equations (London, 1872), chapters xvi and xvn.
+ The expression for F (z) which is derived from this formula doeB not appear to have a
singularity at the origin unless a is infinite or is a function of z; but it seems unreasonable to be
perturbed by this when we consider the nature of some of the analysis which has already been
used in the course of this investigation.
40—2
628 THEORY OF BESSEL FUNCTIONS [CHAP. XIX
at 0, ± 1, ± 2. ... is concerned, we may omit the second term on the right in A),
and calculate the residues of
Sin 7TZ
where F(z) is defined by the formula
Again, from § 19-22 (G) and equation A) of this section we have
1 /7/2V
The first term on the right in C) is equal to T (v + l)/@), except when*
v — 0; when v = 0, the value of the term in question is zero.
We thus obtain the expansion
D) f{x) = </>„ @) P @) 4- 1 (-) [F (m) <?„ (mx) + F (- m) ^, (- nwc)].
In the special case in which v - 0, the modified form of C) shews that an
additional term /@) must he inserted on the right in D).
"When we change the notation to the notation normally used for Bessel
functions and Struve's functions, the expansion becomes
mx) + 6TOHr (w.x)
wheref
-7-I «"" I r(t»)COS
¦ ¦" sin
This is the generalised form of Schlotnilch's expansion.
19-24. The boundedness of F(z), as j z \ -*- ao.
We shall now prove that, when the function f(x) is restricted in a suitable manner,
the function F{z) is bounded when |z|-»-oo, whatever be the value of argz. The reader
will remember that the assumption that F{z) is bounded waa made in § 19*21 to secure
the convergence of the contour integral.
We take the series of § 19-22 A), by which F(z) was originally denned, namely
* When v ia negative it is necessary to use a modified expression for the integrals; cf. § 19*3.
t When v=0, the expression for a0 has to be modified by the insertion of the term 2/@), in
consequence of the discontinuity in value of the expression on the right of C).
19-24, 19-3] SCHLOMILCH SERIES 629
and divide it into two parts, namely the first. iV terms and the remainder of the terms,
where N is the integer such that
When ns$iVr, the terms of i^rt(z) do not exceed nn~l\z\n/n !, and therefore, \vh<*-n n$N,
nir"~* I ?. \nl(i>. n tt»—i
.71+1
When «¦ ^ N, we have 1i^,, (z)! < n--1 sinh n-1 z |, and therefore
!*L=i (n-l)l n\z\»+l n=0 \z
t,. ninhn-lzl
Since -,—;->r '. -
tends to zero as |z|-*-a>, it is evident that a sufficient condition for F{z) to be bounded
us I ? j -*- x is that the series
11-1
should be convergent; and this i.s the ca.se if/(*') is such'that
2 nv + i | /"(") @) |
h=i
is convergent.
19'3. The expayision of an arbitrary function into a generalised Schlomilch
series.
Now that the forms of the coefficients in'the generalised Schlomilch
expansion have been ascertained by Filon's method, it ia an easy matter to
specify sufficient conditions for the validity of the expansion and then to
establish it.
The theorem which we shall prove* in as follows:
Let v be a number such that — \ < v < |; and letf{x) be. defined arbitrarily
in the interval (-it, tt), subject^ to the following conditions:
(I) The function h(x), defined by the equation
exists and is continuous in the closed interval (— tt, rr).
(II) The function h(;t:) has limited, total fluctuation in the intervtxl (—ir, tt).
(III) If ii is negative I the integral
is absolutely convergent when A is a (small) number either positive or negative.
* The expansion is stated by Nielsen, Handbuch der Theorie dor Cylinderfuvktionen (Leipzig,
JilOJ), p. 348; but the formulae which he gives for the coefficients in the expansion seem to be
quite inconsistent with those given by equation B).
1 The effect of conditions (I) and (II) is raeroly to ensure the uniformity of the convergence
of a certain Founer series connected with /; (.c).
+ If v is positive, this LipschiU condition is satisfied by reason of (II).
630 THEORY OF BESSEL FUNCTIONS [CHAP. XIX
Thenf{x) admits of the expansion
n\ ft \- K , S amJv(mx) + IH, (true)
A) J^-TjTvT^Jti W^T
where
m > 0; ?&$ to?«0 o/ a0 «'s obtained by inserting an additional term
on the right in the first equation of the system B).
We shall base the investigation on a discussion of the integral equation
it will be proved that a continuous solution is given by the formula
D) g(x) = T(v + l)f@)
^ /^ sec"*1 <» ^ [sin* <? [f{x sin <f>)
[Note. The (absolute) convergence of the integral contained in this formula is secured
by condition (III). It should be observed that the aggregate of terms containing /@) in
equation D) may be omitted when v is positive in view of the formula
which is valid only when v is positive.]
We proceed to verify that the function g (x) defined by D) actually is a
solution of C), by taking g (x) to be defined by D), substituting in the.expres-
sion on the right of C), and reducing the result tof(x).
The result of substitution is
2 COS W9T /"i* r^" (J
—-^- \ J cos3" 9 sec8"" <? ^ [sin2" <f> {f(x sin 6 sin <f>) -/@)}] d<}> dd
Hence we have to prove that
^—^ [^ f ^cos2" 9 sec2-+1 <j> ^j [sbs- <f> {f(x sin 6 sin <f>) -/@)}] d(f>d6
Replace <^> on the left by a new variable % defined by the equation
sin x = sin # sin <f>,
change the order of the integrations in the resulting absolutely convergent
integral, and then replace 0 by a new variable yfr defined by the equation
cos 8 = cos x a'n fy
19*3] SOHLOMILCH SERIES 631
j
We thus deduce that
cos«*^8ec»>'+1^^T[siii
rjir re sjn Q COS2" 6 d
- j, J. (iiS^ii^ipi d-^-xt/
/•*»/•*"¦ sin 0 cos2" 0 dr. f
= io ix (co^~-cos^r^[Sm2^{/
=/o 7!*tan2" * d*' 4[sin2"x [f{x sin
and hence the formula to be established is evident; and so, when g(x) is
denned by D), then equation C) is satisfied.
Now, by Fourier's theorem,
00
g(ac) — \a(>+ 2 {am cos mcc + bm sin wmj),
TO—1
where
&m = <7 (w) cos mudu,
bm= j g(u) sin mudu;
and it is easy to verify that when f(x) is a continuous function with limited
total fluctuation in the interval (— 7r, 7r) so also is g (x), and therefore the
expansion for g (&•) is uniformly convergent when - it + 8 < x <$ ir — 8, where 8
is an arbitrarily small positive number.
Replace # by # sin 0 in the expansion of g {%), multiply by cos"" 6, which
has an absolutely convergent integral, and integrate term-by-term; wo deduce
at once that
and this expansion converges uniformly when — ir+ B^x ^ir — B.
The values of am and 6m given by formula E) are easily reconciled with
those given by formula B).
It should be noticed that, by the Riemann-Lebesgue lemma, am and bm
are both 0 (l/m) when m ia large. This seems to be connected with the fact
that when we come to deal with any Schlb'milch series (§ 19#62) we are
unable to make any progress without assuming that S6m/m is convergent (or
some equivalent hypothesis); this assumption will appear in § 192 to be
necessary because the differential equation which Struve's function satisfies
is not homogeneous, so that Struve's function is not of a type which occurs in
solutions of Laplace's equation or the wave equation; there would conse-
632 THEORY OF BESSEL FUNCTIONS [CHAP. XIX
quently seem to be reasons of a physical character for the limitations which
have been placed on f(x) in order to ensure the existence of the Schlb'milch
expansion.
[Note. Just.as in § 19*11, if condition (II) concerning the limited total fluctuation of
•Zvf(x) + xf'(x) is not satisfied, then all statements made in this section up to this point
about convergence of series have to be replaced by statements about summability (Cl).]
There is one important consequence which follows from the fact that am
and bm are both 0 A/m) when 2vf(x) +xf (x) has limited total fluctuation
in (— ir, rr), namely, that in the neighbourhoods of — ir and ir, the general
term of the Schlomilch expansion is 0 (l/mv+%), and so the expansion repre-
represents a continuous function; hence the expansion converges (uniformly) to
the sum f(x) throughout the interval (—ir, ir).
19*4. Special functions represented by Schlumilch series.
There are a few problems of Mathematical Physics (other than the problem
mentioned in § 19*1) in which Schlomilch series occur in a natural manner,
and we shall now give an account of various researches in which Schlo'milch
series are to be found.
b A very simple series is
1+ 1 «r™V0(mp);
this series is convergent when p and z are positive, and, if p and z denote
cylindrical-polar coordinates, it is a solution of Laplace's equation at all points
of space above the plane z — 0.
Various transformations of the series have been given by Whittaker *;
thus, by changing to Cartesian coordinates (x, y, z) and using § 2-21, we have
oo
(l) i+S^/()
w i
2tt J _„ 1 - exp {- (z + ix cos u + %y sin u)\
When x2 + y2 + z2 < 1, the integrand may be expanded in ascending powers
of z 4- ix cos u + iy sin u.
If this is done, we getf
» 1 fir
B) 1+2 e~™Ja {mp)« ±
ixcosu+iysmu 2
/_\wi-i g
Bm)!
(z + ix cos u + iy sin uJm~l du
1 1
where (r, &) are the polar coordinates corresponding to the cylindrical-polar
coordinates (p, z), and Bx, B.2) Bs, ... are Bernoulli's numbers.
* Math. Ami. lvii. A903), pp. 341—342.
I Cf. § 4-8 and Modern Analysis, §§ 7-2, 18-31.
19*4] SCHLOMILCH SERIES 633
Another transformation of the series, also given by Whittaker, is obtained
from the expansion for 1/A —e~l) in partial fractions; this expansion is
1_ = 1 1 f 1
1 - e~l t 2 w~i(? — 2miri j5
whence we deduce that
C) 1+ 2 €T
I ]
wMri - sK + a3 + y")J
ixi' + y1] V[(
It follows that the series represents the electrostatic potential due to a
set of unit charges (some positive and some negative) at the origin and at a
set of imaginary points.
The reader may find it interesting to discuss the. Lipschitz-FIankel integral
of § 13*2 as a limiting form of a series of Whittakcr's type.
Some other series have been examined by Nagaoka* in connexion with a
problem of Diffraction. One such series is derived from the Fourier series for
the function which is equal to l/v'(l — .*•-) in the interval (—1, 1).
The Fourier1 series in question is
1 1 v
s/{\ - 'a?) ~ *7r *u~\' " """" U>b m7r'''
and it converges uniformly throughout the interval (— 1 + A, I —A), when' A
is any positive number.
Multiply by eaxi and integrate, and we then obtain the formula, (also due
to Nagaoka)
. a cos 'imr,r — wiri sin m7ra.'~|
1 f* eaxidx ieaxi f~l n ^ r
7tJ a/A — *) 2 |_a „, i
The series on the right hi E) converges uniformly throughout the interval
(— 1, 1) and so we may take — 1 and 1 as limits of integration.
Hence, for all values (real and complex) of a,
F) J.(a)-\l+2a>t?!!].
a [_ ,„._-! a-— m-ir- J
A more general result, valid when R (v + ij) > 0, is
* Journal of the Coll. of ScL, Imp. Univ. of Japan, iv. A891), pp. 301—822. Some of Nagaoka's
formulae are quoted by Cinelli, Nuovo Gimento, D) i. A895), p. 152.
634 THEORY OF BESSEL FUNCTIONS [CHAP. XIX
This expansion is also obtainable by expressing - --% as a sum of partial
fractions*.
Various representations of the integral on the left of E) were obtained by Nagaoka;
the formula quoted seems to be the most interesting of them.
Finally we shall give the formulaf
This is deducible from the Fourier series
S cosBm-l)a? vr .
by replacing a? by a? sin 6 and integrating with respect to 0 from 0 to \tt.
As an example of the calculation of the sum of a Schlbmilch series when
the variable lies outside the interval (— nr, it), we shall take ir<x<2tt, and
then, if/(#) denotes the sum of the Fourier series, we see that
{Bm-Da} 2 f* . a. ,a
.1 Bm -1)
Tare sin (vr/x)
( rare sin (irlx) rk ^
If + \f(<vsin O)d0
so that, when it < ar < 27r, we have
f= V(" "'}"^~'arccosU + T•
19*41. Null-functions expressed as Schlomilch series.
We shall now prove the remarkable theorem that
(i) 1+ 2 (~r j.(wwb)-o,
4 m-l
provided that 0 < a? < 7r; the series oscillates when x = 0 and diverges to
+ oo when x-=-t>.
This theorem has no analogue in the tneory of Fourier series, and, in fact,
it is definitely known J that a Fourier cosine-series cannot represent a null-
function throughout the interval @3 ir).
* Cf. Modern Analysis, § 7.
t This was set as a problem in the Mathematical Tripos, 1895.
+ Cf. Modern Analysis, §§ 9-6—9'632.
19*41] SCHLOMILCH SERIES 635
It is easy to prove A) by using Parse val's integral; when M is a large
integer, we have
1 M 2 (** A M
=r + 2 (-)m Jo (mx) = - i o + s (-)
f
Jo
fxco
J o
7r Jo cos (%x sin
_{-)^_ fxcos(M + J)w
7T J o COS
=0A),
cos ("** sin
,
as M-*¦ oo, by the Riemann-Lebesgue lemma*, which is applicable because
the integral
f* du
Jo cos %u.\/(x2- ita)
exists and is absolutely convergent when 0 < x < it.
Hence we have proved that
lim \\+ f (-)mJ0(mx)\=0
M-
when 0 < x < it ; and this is the theorem stated.
It is easy to prove in a similar manner that
(i) when — \ < v < \ and 0 < x < 7r, (ii) when v>\ and 0 < x ^ it.
By using Poisson's integral we have (since v> — \)
1 )lf / \ «*» T / \
JL ifL I . ,,. \lib i I ffYi 1* I
? - + 2 v-^—^v—^
cos (if +?)« _ t d
as M -*¦ oo , provided that the integral
f* (xa - u*Y-i 7
f^—- ^
J o COS f M
exists and is absolutely convergent; and this is the case when x and v satisfy
the conditions stated.
The truth of B) is now evident.
If n is a positive integer, and if v is so large that v — 2n > — \, the operator
d f d | 2J
xdx\ dx J
* Cf. Modern Analysis, § 941.
636 THEORY OF BESSEL FUNCTIONS [CHAP. XIX
may be applied n times to equation B). The effect of applying the operator
once to the function /„ (mxVX\™xY ia to multiply the function by - m3; and
therefore, when 0 < x < 7r,
that is to say,
C) •? fi~»-lJn ®>
provided that either
(i) - \ < v - 2» ^ \ and 0 ^ as < ir, or (ii) v-*Ln>\ and 0 ^ x ^ ir.
The formulae given in this section are due to Nielsen*, Math. Ann. \,u. A899),
pp. 582—587; two other papers by Nielsen on this subject were published at about t,h«
same time, Nyt Tidsshift, x. B A899), pp. 73—81; Ooersigt K. Danske Yidenskabernes
Sehkabs, 1899,' pp. 661—665. In the first two of these three papers integral values of v
only were considered, the extension to general values of v being made in the third paper.
Shortly afterwards + Nielsen gave a formula for the sum of the aeries in B) when x > * ;
this formula is easily obtained from the integral of Dirichlet's type
J o COS §11
by considering the behaviour of the integrand at w=tt, 3v, 5ir,
It is thus found that, when x is positive and q is the integer such that
then
J
The importance of Nielsen's formulae lies in the fact that they make it
evident that, when a function f(x) is denned for the interval (— tt, it), if the
function can be represented by a Schlomilch series throughout the interval
(except possibly at a finite number of points) the representation is not unique
and there are an unlimited number of Schlb'milch series which are equal to
the function/(a;) throughout the interval, except at a finite number of points,
namely the points already specified together with the origin and (when
- i < v ^ \) the end-points + it.
The converse theorem, that the only Schlomilch series with non-vanishing
coefficients which represent null-functions at all points of the interval
-Tr<x<tr, (when\ -? < v ^\) except the origin are constant multiples of
_i | (~)mJv{mx)
I>4-1) ™=1 Qmwy '
* Formula A) was rediscovered by Gwyther, Messenger, xxx.ni. A904), p. 101.
t Oversigt K. Danske Videnskabernes Selskabs, 1900, pp. 55—60; see also a later paper by
Nielsen, Am. di Mat. C) \i. A901), pp. 301—329 for more complicated results.. Of. § 19-4(9).
X The theorem is nntruewhen i»g; cf. formula C). It would be interesting to know whether
any Schlomilch series other than the one given can represent a null-function when 4,
;v<i\.
19*5] SCHLOMILCH SERIES 637
is, of course, of a much deeper character, and it seems that no proof of it has
yet been published. We shall now discuss a series of propositions which lead
up to this theorem; the analysis which will be used resembles, in its main
features, the analysis*, due to Riemann, which is applicable to trigonometrical
series.
19*5. Theorems concerning the convergence of Schlomilch series.
We shall now discuss the special type of Schlomilch series in which v = 0,
and in which Struve's functions do not appear; the object of taking this par-
particular case is to avoid the loss of clearness due to the greater complication
in the appearance of the formulae in the more general case. With a few
exceptions, the complications in the general case are complications in detail
only; those which are not matters-of detail will be dealt with fully in
§§19'6—19-62.
The series now to be considered is
oo
A) i«0+ 2 am J (nix),
in which the coefficients am arc arbitrarily given functions of m.
We shall first prove the analogue of Cantor's lemma f, namely that the
condition that am Jo (nix) -*- 0 as m -*- oo , at all points of any interval of values
of x, is sufficient to ensure that
am = o (V'»0-
[Note. If the origin is a point of the interval in question, then the theorem that
am-o(l)
is obviously true.]
Take any portionJ of the interval which does not contain the origin, and
let this portion be called I1. Let the length of/j be Lx.
Throughout I, wo have (cf. § 7'3)
I r 2 \
am Jo (mas) -am./[ ). [P (ma:, 0) cos (rnx - ?7r)-Q (mar, 0) sin (mx - Jtt)] ;
A' ytllTTXj
and, as in -*- oo ,
P (mx, 0) ¦*• 1, Q (mx, 0) — 0.
Hence, for all sufficiently large values of to, (say all values exceeding m0)
\
at all points of /,.
Now suppose that am is not o (Vm) \ w© have to shew that this hypothesis
leads to a contradiction.
* Cf. Modern Analysis, §§ 9-6—9-632. •+ Ibid. § 9'61.
J Since <70 (ma;) is an even function of x, the portion may be supposed to be on the right of
the origin without loss of generality.
638 THEORY OF BBSSEL FUNCTIONS [CHAP. XIX
If am is not o (>Jm), a positive number « must exist such that
whenever m is given any value belonging to a certain unending sequence*
rth, m2, in,,.... Let the smallest member of this sequence which exceeds both
m0 and 1tt\Lx be called m{.
Then cos (mi x - \ir) goes through all its phases in Ilt and so there must
be a portion f of Iu say /2) such that
| cos (mi x - \ir) | > ? J3, | sin (mix - \tt) j < ?
at all points of I2. If L2 is the length of i2, then L2 - Iv/mi.
Next let the smallest member of the sequence mr which exceeds both mi
and 27r/?2 be called m^.
Then cosGna'a?-^7r)goes through all its phases in 72, and so there must
be a portion of /2) say I3, such that
| cos (m^x — ^7r) I > ^- ^3, | sin (wj'a? — ^7r) | < ^~
at all points of /s. If L3 is the length of 73, then Z8 == $Tr/m2'.
By continuing this process, we obtain a sequence of intervals Iu I2, Ta,...
such that each is contained in its predecessor; there is therefore a point X
which lies inside all these intervals, and at this point we have
| cos (mX — \ir) j ^ ^ \/3, | sin (mX — \Tr) \ ^ \,
when m has any of the values mi, mj} m*',
For such values of m we consequently have
2
and this is inconsistent with the hypothesis that am Jo (mcc) tends to zero at
all points of /x.
The contradiction which has now been obtained shews that am must be
The next theorem which we shall prove is that, if the Schlomilch series
converges throughout any interval, then the necessary and sufficient condition
* It is supposed that mi<m
t There are, in fact, at least two euoh portions ol Ii; in order that I2 may be uniquely deter-
determined, we take I2 to be that portion which lies on the left of the others.
19*51] SCHLOMILCH SERIES 639
that the series should converge for any positive value of x (whether a point of
the interval or not) is that the series
2 am. I ( 1. cos (mx — \ir) + -— sin (mx — hr)
m»i V KfrnrxJ |_ #™# J
should be convergent for that value of x.
This theorem is evident from the fact that the general term of the
trigonometrical series differs from amJ0(mx) by a function of m which is
0 (amm~V)i'= o (m~3); and 5o(m~a) is a convergent series.
19*51. The associated function.
Let the sum of the series
00
?ao+ % amJ0(mx),
at any point at which the series is convergent, be called /(#).
Let
«/ n i , ? amJ0(mx)
A)
m=l
Then F(a?) will be called the function associated with the Schlomilch
series whose sum is/(#).
It is easy to see that, if the series defining f(x) converges at all points
of any interval, then the series defining F(#) converges for all real values
of x.
For am J0(nix)-*-0 as m-^oo at all points of the interval, and therefore
(§19-5)
Again, by § 2*5 E), for all real values of x
\Jn(mx)\^l>
and consequently
a^J^tnx)^ A
Since
is convergent, it is obvious that the series on the right in A) must be
convergent.
It is evident, moreover, not only that the convergence is absolute, but also
that it ia uniform throughout any domain of values of the real variable x.
640
THEORY OF BESSEL FUNCTIONS [CHAP. XIX
19*52. Lemma I.
We shall now prove that, if V(x) is the function associated with the
Schlomilch series whose sum isf(x), and if
A) G (?,«) =
then
B) lira G (x, a) = xf(x)
at any point x at which the series defining f(x) is convergent, provided that'
It is easy to deduce from A) that
Cr (x, a) = %aox — 2
x [(x + a) Jo (»m + 2ma) + (a? - a) J,, (m# - 2ma) - 2a? Jo
and, from l'Hospital's theorem, it follows that
Km . ; [(« + a) J"o (ww + 2ma) + (« - a) J"o (wwc - 2ma) -
4m2a2
= lim -zr—- \JQ (mso + 2wa) — Jo (mx — 2ma)
+ 2m (x + a) Jof (mx + 2ma) - 2m (a; — a) /„' (mx — 2ma)]
= a; Jo" (ma;) + «/"„' (mx)[m
Consequently the limits of the individual terms of the series defining G(a;,«)
are the individual terms of the series defining xf(x).
It is therefore sufiScient to prove that the series for &(x,a) converges
uniformly with respect to a in an interval including the point a — 0 when x
has any value such thab the series for/(#) is convergent.
It may be assumed, without loss of generality, that x is positive^, and we
shall then take | a j so small that it does not exceed \x; we shall now prove
that the series for G (x, a) converges uniformly when — \x ^ a $ \x.
By observing that
x ± a - Vl« (x + 2a)) = -~- --
and that the series
« am Jo (mx ± 2ma)
m-1 m2 [as ± a + V [a (x
* Since we are not assuming more than the convergence of / (a:) at a single point, it is not
permissible to infer from § 19-5 that om muBt be o (,/m).
t The functions tinder consideration are even functions of *; and Bince a @, a)=0, the special
case in which 2=0 needs no further consideration.
19*52] SCHLOMILOH SERIES 641
is uniformly convergent (upper or lower signs throughout being taken), we
see that & (x, a) differs from
wi=i 4m* a?
(mx + 2raa) + \/(x — 2a). JQ (mx — 2ma) — 2 V#. Jo (ma?)]
by the sum of two series, each of which is uniformly convergent.
It is therefore sufficient to establish the uniformity of the convergence of
the last series which has been written down.
Now take the general term of this series, namely
- ^^ y{x + 2a). Jo (mx + 2ma) + s/(x - 2a). Jo (mx - 2ma) - 2 V*. Jo (mx)],
and write it in the form
2x\ F , .sin (mx- |*r) /sin?na\2
—- I cos(««p — iir) +—~5 =—-
2a; \ cos (mx — ^7r) sin 2ma
V \
/
V V
' 8to (a?2 - 4a2) "
2a? \ sin (mx — \ir) cos 2ma.
ma?) — <I> (ma? + 2ma) — <l> (m« — 2ma)
where ^ (y) is defined by the formula
* C/) = (P B/, 0) - 1} cos (y - i,r) - |i + Q B/, 0)| sin (y -
The general term is thus expressed as the sum of four terms, and we
proceed to prove that each of the four series, of which these terms are the
general terms, is uniformly convergent.
The first two series are proved to be uniformly convergent, in connexion
with the theory of trigonometrical series*; and the third is obviously
uniformly convergent from the test of Weierstrass.
To deal with the fourth series, we observe that, by the first mean-value
theorem, numbersf 8 and Qx exist such that
* Cf. Modern Analysis, §§9*62, 9-621. It ba's been the general (but not invariable) custom to
obtain various properties of the series without establishing the uniformity of their convergence.
The convergence of the aeries for f(x) is required to deal with the first series; the second series
can be dealt with in consequence of the less stringent hypothesis that am=o (>Jm).
t The number 0 is a function of a variable t which will be introduced immediately.
W. B. P. 41
642 THEORY OF BESSEL FUNCTIONS [OHAP. XIX
for which
2<S> (mx) - <*> (mx + 2ma) - <?> (mx - 2nw)
= 2ma I {<?' (ma; - 2mat) - <&'(mx + 2mat)} dt
Jo
= - 2ma f 4??ia? *" (mx - 2ma6t) dt
Jo
= — 4m2 a2 <t>" (wia; - 2mad1).
Since <?" (y) = 0 (Iff) when y is large, it is evident that
5 ^"(ma!~2ma6i)
m=l
is uniformly convergent with respect to a.
Hence Gr (x, a) is expressed as the sum of six series each of which converges
uniformly with respect to a when — \x<ol< \x; and therefore
lim Gr (x, a)
a-M)
is equal to the sum of the limits of the terms of the series for Gr(x, a), i.e. it
is equal to xf(x), provided that the series for f(x) is convergent; and this is
the lemma to be proved.
19-53. Lemma II.
We shall next prove that, with the notation o/§§ 19*51,19'52, the condition
that a,,, = o (*Jm) is sufficient to ensure that
V (x + *)F (x + 2q) + (& - «) F (a? - 2a) - 2a?F (a) _ n
IX 111 " - ~ — — ¦¦¦¦"¦ — ~— . . . - __. yj
a-HD ft
for all values of x.
As in § 19*52, we need consider positive values of x only; and we express
the series for a Gr (x, a) as the sum of six series each of which is easily seen to
be uniformly convergent when —\x< a< \x, by applying the theorems con-
concerning trigonometrical series which were used in § 19*52.
Hence
lim [a Gr (a;, a)]
0
+ (x~a) Jq (mac - 2ma) — 2.eJ0 (mx)\
and this is the lemma to he proved.
19-54. The analogue of Riemann's theorem* on trigonometrical series.
We can now prove that, if two Schlb'milch series of the type now under
consideration (i.e. with v = 0, and with Struve's function absent) converge
* Cf. Modern Analysis, §'J-63.
19*53, 19*54:] SOHLOMILOH SERIES 643
and have the same sum-function throughout the interval @, it), then corre-
corresponding coefficients in the two series are equal. The formal statement of
the theorem is as follows:
Two Schlomilch series, of the special type, which converge and are equal at
all points of the closed interval @, ir), with the possible exception of a finite
number of points, must have corresponding coefficients equal, unless the end-
points 0 and ir are both exceptional points.
If these points are exceptional points, the two series may differ by a constant
multiple of the series
%+ 2 (~)™J0(mx).
m-l
Let the difference of the two series be
00
|ao+ 2 amJ0(mx),
m-l
and let the sum of this series be f(x), so that /(a?) converges to zero for all
values of x between 0 and ir, except the exceptional values.
Let %i> ft be any points (except the origin) of the interval @, ir), such
that there are no exceptional points inside* the interval (ft, ft).
We proceed to prove that, if F(#) is the function associated with the
Schlomilch series for f(x), then F (x) is a linear function of log x in the
interval (ft, ft). This is the analogue of Schwarz' lemma-f-.
If 0 = 1, or if 0--1, and if
4> (x) = 6 [f <«) - F (ft) - |°|((^|> {F (ft) - F (ft)) ]
then (f>(x) is continuous when ft^^^ft, and
If the first term of <f> (x) is not zeroj throughout the interval (ft, ft), there
will be some point c at which it is not zero. Choose the sign of 6 so that the
first term of <)E> (c) is positive at c, and then choose h so small that (p (c) is
still positive.
Since <)E> (a?) is continuous in (ft, ft), it attains its upper bound which is
positive since </>(c) is positive. Let it attain its upper bound at c,, so that
h<Ci< ft.
Now by Lemma I (§ 19-52)
- 2a) - 2c,
* The points ?n |2 themselves may be exceptional points,
f Cf. Modern Analysis, § 9-631.
X If it is zero throughout (^, &J, then P (a;) is obviously a linear function of log x.
41—-2
644 THEORY OF BESSEL FUNCTIONS [CHAP. XIX
But <j> (cj + 2a) ^ </> (ex), <? (cx - 2a) ^ $ (Cl), so the limit on the left must be
negative or zero. This contradiction shews that the first term of <f> (%) must
be zero throughout (&, ?2), that is to say that F(a?) must be a linear"
function of log x; and this is the theorem to be proved.
Hence the curve whose equation is y — T (x) consists of a set of segments
uf logarithmic curves with equations of the type
y = A log x + B.
Now, by § 19-51, F (x) is continuous in @, tt), and so these logarithmic curves
are connected at the exceptional points; and the curve y=>V(x) cannot have
an abrupt change of direction at an exceptional point, because, by Lemma II,
even when f is an exceptional point; that is to say
Hence the constants A and B cannot be discontinuous at the exceptional
points, and so they have the same values for all values of x in the
interval @, tt).
Consequently, when 0 < x < ir,
Make x -*- 0; the series on the left has a limit, namely
because it is uniformly convergent. Therefore A log x + 5 has a limit when
x-*¦ 0, and so Aia zero.
Consequently, when 0 < x % tt,
» amjn(mx)
m = \ ''I'
and the series on the left converges uniformly throughout @,7r), so integrations
term-by-term are permissible.
Replace a? by a? sin 9, multiply by sin 9, and integrate from 0 to \-rr. Then,
by §12-11,
i
_ ^ dm, sm rax
Hence, when 0 < x < rr,
wt=l
19*6] SOHLOMILOH SERIES 645
Multiply by sin mac and integrate from 0 to ir; it is then evident that
m _. / sTO (ttOo fffi
2m9 V - |_2™8 wi J "
Since am is given to be o (\/m), this equation shews that
Hence we must have
fft=l
From the results contained in § 19*41 concerning the behaviour of the
series on the right at x = 0 and at &•= ir, it is evident that f(x) cannot be a
convergent Schlomilch series at either point unless aQ is zero; and this proves
the theorem stated at the beginning of this section.
19. Theorems concerning the convergence of generalised Schlomilch series.
We shall now study briefly the series
We shall first prove that, when v<\, the condition that the (w+ 1)th term of
the series tends to zero as m -*• oo at all points of any interval of values of x
is sufficient to ensure that
[Note. If the origin is a point of the interval in question, then the theorem that
aw=o(l)
is obviously true.]
Since the series under consideration is unaffected by a change in the sign
of x if the signs of all the coefficients bm are also changed, no generality is
lost by considering an interval on the right of the origin.
We call this interval /,; and, at all points of/,, we have, by § 1041 D),
amJv{moc) + bm'H.v(mx) cm rTJ. . , , i • \
_™_1V. L... ™_ V /_ ™ -[P (mj:,v) cos (ma:-fair-l-ir-rin)
(\mx)v (?ma:)I'+Vff
— Q {mx, v) sin (via: — \vnr — |tt — vm)] + bm . 0 (m~l),
where am = cm cos vm, bm = cm sin t}m.
We now suppose that am and bm are not both o(m"+i); we have to shew
that this hypothesis leads to a contradiction.
If am and bm are not both o (m"+*), a positive number € must exist such
that
cm>€ra"+*
whenever m is given any value belonging to a certain unending sequence
646 THEORY OF BESSEL FUNCTIONS [CHAP. XIX
We now prove, exactly as in § 19*5, that, at some point X of I1} the
inequalities
I cos (mX — \vir — \ir — rj^) | ^ \ *J3, | sin (mX — \vtt — \tt —'
are satisfied whenever m has any value belonging to a sequence (m/) which
is a sub-sequence of the sequence (mr).
For values of m which belong to this sub-sequence we have
- e. 0 (W-*),
and, since v — \ is negative, the expression on the right cannot be arbitrarily
small. This is the contradiction which is sufficient to prove that am and b.m
must both be o (?«."+¦) if the (m + l)th term of the Schlomilch series tends to
zero at all points of J^
The reader may now prove (as in § 19) that, when v<\,if the generalised
Schlomilch series converges throughout any interval, the necessary and sufficient
condition that it may converge for any positive value of x (whether a point of
the interval or not) is that the series
Smx K a * '
should be convergent for that value of x.
19*61. The associated function.
Let us take — \ < v < ^, and let the sum of the series
\ a0 ? am Jv (mos) + bm H,, (moc)
at any point at which the series is convergent be called fv (x).
Let
Then Pv (x) will be called the function associated with the Schlomilch series
whose sum is fv(oc).
It is easy to prove that, if the series defining fv (x) converges at all 'points
of any interval, then the series defining Tv(x) converges for all real values of x.
The only respect in which the proof differs from the analysis used in
§ 19'51 is that the additional theorem that H.v(so)/xy is a bounded function of
the real variable x has to be used.
648 THEORY OF BBSSEL FUHCTIONS [CHAP. XIX
and the exceptional points (if any) are not internal points of the interval, then
Fv(x) is a linear function* of a;" in the interval. It may then be shewn
that the exceptional points do not cause any discontinuity in the form of Fr (%),
and hence we deduce that
where A, B, A\ B' are constants.
Now take the equation
_ , vaoofS amJv(mx) + bmHv(mx)
replace x by x sin 0, multiply by sin*"+1 0/cos2* 0, (which has an absolutely
convergent integral) and integrate from 0 to ?tt. The series for Fr(a?sin0)
converges uniformly in this interval of values of 0, so term-by-term integra-
integrations are permissible.
It is thus found that
I*
Jo
'.Cima;)* " cos2"<9
— v) * amsinma?+6w,A—
When we substitute for Fv (a; sin ^) we deduce that
* o^ sin mx + bm A - cos mx) aoa? Ax1-*" V (
A> i ^ = l~
when 0 < x ^ rr ; and a similar equation may be obtained when 0 ^ a? > — it.
Since am and 6m are both o (m"+*), it is permissible to differentiate A) twice
term-by-term when 0 > v > - \; but it may only be differentiated once if
If we differentiate, twice or once as the case may be, the resulting series
on the left tends to a limit as x-^-0, but the resulting expression on the right
fails to do so unless A is zero.
We infer that .4 = 0, and in like manner A' must be zero; the continuity
of Fr (x) at the origin then shews that B and B must be equal.
It now follows from A) that
/o\ v »msinma; + 6w(l-coswa;) a0^ _ _ .
B) ^ --jg.-.Rrr
when — 7r ^ x ^ ir.
* When v is zero ar1^ has to be replaced by log x.
19*7] SCHLOMILCH SERIES 64#
Multiply B) by cos ma? and integrate from — 7r to 7r; and then
C) &m = 0.
Again, multiply by sin mx and integrate; and then
(_)m am = aQ + w2 {2BV (v + 1) - ?ao7r2}.
This equation is inconsistent with the fact that am is o (ra"+*) unless
2BT (»/ + 1)
and then am = ( — )'«¦ a0.
Hence the series for fv (x) must reduce to
L J"
Now at least one of the points 0, it, — tt is not an exceptional point; and
the series for/„(«?) cannot converge at that point unless a0 is zero, so that am
is also zero.
We have therefore proved that, if the series % bm/m is convergent all the
coefficients am and bm must vanish; that is to say, the two Schlo'milch series
with which we started must have corresponding coefficients equal. And this
is the theorem to be proved.
We have therefore established for Schlomilch Heries in which — \ < v < \
theorems analogous to the usual theorems concerning the representation of
null-functions by trigonometrical scries.
19*7. Theorems of Riemanns type concerning series of Bessel functions and
Dini's series of Bessel functions.
We shall now give a very brief sketch of the method by which the series
discussed in Chapter xviii, namely
00 U3
2 Oni Jv(jmV), S bmJv(\mx),
m=l to-1
(in which v > — ^) may be investigated after the manner of Ricmann's investi-
investigation of trigonometrical series.
The method is identical with the method of investigation of Schlomilch
series just given in §§ 19 6—19*62, though there are various points of detail*,
which do not arise in the case of Schlomilch series, due to the fact that jm
and Xm are not linear functions of m.
* These points of detail are very numerOuR and there is no upecial difficulty in discussing any
of them; but it is a tedious and lengthy process to set them out in full, and they do not seem to
be of sufficient importance to justify the use of the space which they would require. The reader
who desires to appreciate the details necessary in such investigations may consult the papers by
C. N. Moore, Trans. American Math. Soc. x. A909), pp. 391—435; xn. A911), pp. 181—206;
xxi. A920), pp. 107—156.
650 THEORY OF BESSEL FUNCTIONS [CHAP. XIX
In the first place, it is easy to prove by the method used in § 19'5 that
if the series
00 00
t OmJyiJna), 2 bmJv(\mCc)
converge throughout any interval of values of x> then
dm = o @a), bm = o (V*»).
Next we consider the associated function; we write
CO
/(«)= t amJv(jmoc),
m=l
and then the function associated with/(#) is defined by the equation
A 5
m-ljm 'V
It may be proved that, when x has any positive value for which the series
defining f(x) is convergent, and if the expression
r-jKa? + 2va + a) F(x + 2a) - 2x F{x) + (x - 2i*t -<t)F(x- 2a)]
is arranged as a series in which the mth term has am for a factor, then the
latter series is uniformly convergent with respect to a in an interval containing
the point a = 0, and that its limit when a-^0 is —xl~''f(x).
It may also be proved that, whether the series for f{x) converges or not,
the condition that am — o {*jin) is sufficient to ensure that
i
— [(a; -f 2vol + a) F (x + 2a) - 2x F (x) + (a - 2va - a) F (as - 2a)]
tends to zero with a.
The proofs of these theorems depend on a number of lemmas such as the lemma* that
is a bounded function of a; proofs of the lemmas cau be constructed on the lines of the
proofs in the special (trigonometrical) ease in which v=*\.
It now follows in the usual manner (cf. § 19*54) that, when f(x) is a null-
function throughout the interval @, I), then F(x) satisfies the differential
equation
and sot F (x) = A + Bar*",
where A and B are constants. This equation is valid when 0 < x
* Cf. Modern Analysis, § 9-62.
t When v=0, F{x) =A +B' logx.
19-7] SOHLOMILOH SERIES 651
Now since v> — %, J*{jm%)l(jm®)v is bounded when O^x^l whatever
be the value of m; and so, when* v < \, the series
converges uniformly when 0 ^ x ^ 1, by the test of Weierstrass.
Hence F(x) is a continuous function of x in the closed interval and so B
is zero when v is positive; and E is zero in the case v = 0.
For any assigned value of n multiplying the series for F(x) by xp+1 Jv(jn x)
does not destroy the uniformity of its convergence; and, when we integrate,
we find that
n
an ¦ J* On) = in (Axv + Bx~") x J,. (jnte) dx
J o
Now, when n is large,
and so the formula just obtained for an is inconsistent with the equation
an = o (s/n) when v > - | unless both ^L + J? and 7? are zerof; and then an is
zero.
Hence a series of Bessel functions (in which v> — \) cannot converge to
the sum zero at all points of the interval @,1), with the possible exception of
a finite number of points (the origin not being an exceptional pointy when
v > ?), unless all the coefficients in the series are zero.
We infer that two series of Bessel functions, in which v > — \, cannot
converge and be equal at all points of the interval @, 1), with the. possible
exception of a finite number of points, unless corresponding coefficients in the
two series are equal.
Dini's series §
QO
f(x)= % bm
may be dealt with in the same manner. The associated function is defined
by the equation
m = l ^m &
* When v-%.\, the convergence of the series for f(x)lxv at.r = 0 is sufficient to ensure the
uniformity of the convergence.
t An exception might occur when v - 1 = - \ ; but this is the trigonometrical case.
X The series divided by xv then has to converge at the origin.
§ It is supposed for the present that J7+i>>0, so that no initial term is inserted.
652 THEORY QF BESSEL FUNCTIONS [CHAP.
and it is inferred that when /(#) is a null-function throughout @, 1), then
constants A and B exist such that
bn Ml - ?-2) /,« (X.) + JJ* (X»)| - V? (A*
- X.
and 5 = 0 when v ^ 0.
Now, when n is large
so that, if
and this is inconsistent with the equation
bn = o (s/n),
since v > — $.
Hence 5 is zero, and therefore
;a (Xn)l «^lxwJ,
This equation is inconsistent with the equation
bn=o (Vn)
unless A is zero, since Jv+l (X^) is not zero; and then bn is zero.
We next consider what happens when H + v is zero or negative ; in these
cases Dini's series assume the forms
00
w=l
00
bolv(\ox)+ 2 bmJv(\mso\
m=l
respectively.
In the second of the two cases the previous arguments are unaffected by
the insertion of an initial term; the ftrst of the two cases needs more careful
consideration because the initial term to be inserted in the associated
function is
and hence, when n > 1,
bnJS (X») = Xn2 J ^ 4^Laf + 4° + J?ar-H nJv (\nx) dx
j
19*7] SCHLOMILCH SERIES 653
Since bn = o (\M) we infer first that 5 = 0, by considering the term in
(| Xw)", and then that b0 = 0; and so bn = 0 for all values of n.
We infer also that, as in the limiting case of series of Bessel functions,
Dini's series of Bessel functions cannot represent a null-function throughout
the interval @, 1), and that if two of Dini's series (with the same v and H)
converge and are equal at all points of the interval @,1), with the exception
of a finite number of points, then corresponding coefficients in the two series
are equal.
CHAPTER XX
THE TABULATION OF BESSEL FUNCTIONS
201. Tables of Bessel Functions and associated functions.
It is evident from a consideration of the analysis contained in Chapters vii,
vin and xv that a large part of the theory of Bessel Functions has been con-
constructed expressly for the purpose of facilitating numerical computations
connected with the functions. To the Mathematician such computations are
of less interest and importance* than the construction of the theories which
make them possible; but to the Physicist numerical results have a significance!
which formulae may fail to convey.
As an application of various portions of the Theory of Bessel Functions,
it has been considered desirable to insert this Chapter, which contains an
historical account of Tables.of Bessel Functions which have been previously
published, together" with a collection of those tables which seem to be of the
greatest value for the present requirements of the Physicist.
The reader will not be concerned with the monotony and technical irrele-
irrelevance of this Chapter when he realises that it can be read without the efforts
required to master the previous chapters and to amplify arguments so ruth-
ruthlessly condensed.
The first Tables of Jo (x) and Jy (x) were published by Bessel himself in
his memoir on Planetary Perturbations, Berliner Abhandlunyen, 1824 [1826],
pp. 46—52. These tables give the values of /0 (as) and Jx (x) to ten places of
decimals for a range of values of oo from cc = 0 to x — 320 with interval 0*01.
A short Table of J»{x) and J?(x) to four places of decimals was constructed
by Airy, Phil. Mag. C) xviii. A841), p. 7; its range is from x = 0 to x « lOO
with interval 0-2. AiryJ had previously constructed a Table of 2J\ (x)/x, of
the same scope.
The function Jx(x)jx was subsequently tabulated to six places of decimals by Lommol,
Zeittchrift fur Math, und Phys. xv. A870), pp. 164—167, with a range from x-.-Q to #=.20'0
with interval 0-1; tHs Table, with a Table of ^(x)^, was republiahcd by Lomrnol,
Munchener Abkandlungen, xv. A886), pp. 312—315.
* Cf. Love, Proc. London Math. Soc. B) xiv. A915), p. 184.
t Gf. Lord Kelvin's statement " I have no satisfaction in formulas unless I feel their arithmetical
magnitude-at all events when formulas are intended for definite dynamical or physical problems. •'
Baltimore Lecture* (Cambridge, 1904), p. 76.
: Tram. Camb. Phil. Soc. v. A835), p 291. A Table of fij, («)/* and its square, to four or five
places of decimals, in which the range is from 0 to the circular measure of 1125° (with interval 15°),
was given by Schwerd, Die Beugungserscheinungen (Mannheim, 1835), p. 146.
20*1] TABULATION OF BESSEL FUNCTIONS 655
In consequence of the need of Tables of Jn(x) with fairly large values of
n and x for Astronomical purposes, Hansen constructed a Table of Jo (x) aud
Ji (x) to six places of decimals with a range from x — 0 to x — 10 with
interval 0*1; this was published in his Ermitteliutg der absokiten Stiirungen
in Ellipsen von beliebiger Excentricitdt and Ntigung (Gotha, 1843). Hansen's
Table was reprinted by Schlbmilch* and also by Lommelf who extended ifc
to x = 20.
These tables, however, are superseded by Meissel's great Table of J0(x)
a,ndJ1(x) to twelve places of decimals.']:, published in the Berliner Abliand-
lungen, 1888; its range is from x — 0 to x =15-50 with interval O'Ol.
Meissel's Table was reprinted in full by Gray and Mathews, A Treatise
on Bessel Functions (London, 1S95), pp. 247—266, and an abridgement of it
is given in Table I infra, pp. 666—697.
A Table of Jo (*) and /, (x) to twenty-one places of decimals, from x — 0
to #=6'0 with interval O'l, has been constructed by Aldis, Proc. Royal ISoc.
lxvi. A900), p. 40.
A Table of J{){nn) to six places of decimals forn=l, 2, 3, ..., 50 has been computed by
Nagaoka, Journal of the Coll. of Sti. Imp. Univ. Japim, iv. A891), p. 313.
The value of «/|,D0) was computed by W. R. Hamilton from the. ascending series, Phil.
Mag. D) xiv. A857), p. 375.
A Table of J\{oo) to six places of decimals from #=201 to # = 41 with interval 01 or
0'2 has been published by Stoiner, Math, and Natvnoiss. Bcrir.hte cam Unyurn, xi. AH!L),
pp. 372—373.
The earliest table of functions of the .second kind was constructed by
B. A. Smith, Messenger, xxvi. A896), pp. 98—101; this is a Table to four
places of decimals of Neumann's functions ]r'0) (x) and VT(I) (x). Its range is
from x — 0 to a = r00 with interval 0 01 and from .;¦•= 1*0 to ,r = 10'2 with
interval 01.
A more extensive table of these functions is given in the British Asso-
Association Report, 1914, pp. 76—82; this is a Table to six places of decimals
whose range is from x = 0 to x— 150 with interval 0'02; a year later a table
was published, ibid. 1915, p. 33, in which the values of Y m (*c) and F'n (a:)
were given to ten places of decimals for a range from ,r = 0 to .r = 6 with
interval 0*2 and from x = (i'O to x— 16'0 with interval 0*5.
Shortly after the appearance'of Smith's Table, an elaborate table was con-
constructed by Aldis, Proc Royal Soc. lxvi. A900), p. 41, of Heine's functions §
Ga(x) and Gx(x) to twenty-one places of decimals; the reader should be
* Xeitschrift jilr Math, und Phyx. n. A867), pp. 15H—lGo.
f Sludien iiber die Dessel'xchen Functioneu (Leipzig, 18C8), pp. 127—135.
X Meissel's Table contains a misprint, the correct value of «/0@62) being +0-90G1K..., not
+ 0-905l8.... An additional misprint was made in the reprint of the Table by Gray and Mathews.
§ These functions were also tabulated by B. A. Smith, Phil. Matj. E), xi.v. (lti'JH), pp. Vl'l—
12b; the scope of this table is the same as that of Iiis Table of 1*(°) (x) and YW (.c).
656
THEOEY OF BESSEL FUNCTIONS [CHAP. XX
reminded that these functions are equal to -$iryo(«) and - %ir Ya (x) re-
respectively. The range of Aldis5 Table is from so» 0 to as = 6'0 with interval 0*1.
Another table of these functions with a smaller interval was published in
the British Association Report, 1913, pp. 116—130; this table gives the
functions to seven places of decimals for a range from x = 0 to x~ 16'00 with
interval 0-01. The Report for 1915, p. 33, contains a table to ten places of
decimals from x — 6'5 to x = 15*5 with interval 0*5.
The functions Fo (x) and Y1 (x) are tabulated to seven places of decimals
in Table I infra; this table has an appreciable advantage over the British
Association Tables*, in that the auxiliary tables make interpolation a trivial
matter; in the British Association Tables interpolation is impracticable.
By means of the recurrence formulae combined with the use of the tables
which have now been described, it is an easy matter to- construct tables ot
functions whose order is any integer. Such tables of</,»(#) were constructed
by Hansen and reprinted by Schlomilch and Lommel after their Tables of
Jo(x) and Jx (a1). Subsequently Lommel, Mtinchener Abhandlungen, XV. A886),
pp. 315—316, published a Table of Jn{x) to six places of decimals, in which
n = 0, 1,2,..., 20, and x =0,1, 2,..., 12; this Table is reprinted in Table IV
infra, pp. 730—731. A Table of Jn (x) of practically the same scope was also
published by Meissel, Astr. Nach. cxxviii. A891), col. 154—155.
A much more extensive Table of Jn(x) was computed by Meissel, but it
seems that he never published it. He communicated it to Gray and Mathews
for publication in their Treatise, pp. 267—279. This table gives Jn(cc) to
eighteen places of decimals when n =0, 1, 2,... , 60, and a = 0, 1, 2, ..., 24.
Some graphs of Jn (so) were constructed, with the help of the last-mentioned
table, by Hague, Proc. Phys. Soc. xxix. A917), pp. 211—214.
The corresponding Tables of functions of the second kind are not so ex-
tensive.
The British Association Report, 1914, pp.83—86 contains Tables of Gn(x)
to five places of decimals forf n = 0, 1, 2, ...,13 for the range x = 0 to 6#0
with interval 0*1 and x = 60 to 16 with interval 0*5.
Similar Tablesf of F("> (x) to six places of decimals (with the intervals
in the earlier part equal to 0'2) appeared in the Report for 1914, pp. 34—36.
Some values of Hankel's function Yn(x) had been given previously by
Nicholson, Proc. London Math. Soc. B) xi. A913), pp. 113—114.
A Table of Yn(x) to seven (or more) significant figures is contained in
Table IV infra. This has been computed from Aldis' Table of <?0 (x) and Gx (cc).
•In the course of computing Table I, a small part of the British Association Table of Go (x\
mi (,, (,) was checked, and the last digits in it were found to be unreliable in about 5 °l of thi
f Lines checked. •
* For the larger values of n the functions are not tabulated for amall values of x.
20*1] TABULATION OF BESSEL FUNCTIONS 657
Tables of \og10[^(%Trx). \ jHV1'(#) | ] to eight significant figures are given
in the British Association Report, 1907, pp. 94—97. The values assigned
to v are 0, \, 1, 1J,..., 6?, and the range of values of x is from ar= 10 to 100
(interval 10) and 100 talOOO (interval 100). For this range of values of x,
the asymptotic expansion (§ 7*51) gives so rapid an approximation that the
Table is of less value than a table in which the values of x and the intervals
are considerably smaller. *
Functions of the first kind with imaginary argument have been tabulated
in the British Association Reports. The Report for 1896, pp. 99—149, con-
contained a Table of Io (x) to nine places of decimals, its range being from x = 0
to x — 5100 with interval 0001. A Table of 7j (as) of the same scope had been
published previously in the Report for 1893, pp. 229—279; an abridgement
of this (with interval 0'01) was given by Gray and Mathews in their Treatise,
pp. 282—284.
Tables of /„(#) and It (x) to twenty-one places of decimals have been con-
constructed by Aldis, Proc. Royal Soc. lxiv. A899), p. 218. The range of these
Tables is x = 0 to x-Q-0 with interval O'l; Aldis also gave (ibid. p. 221) the
values of /„(#) and Ir(x) for x = 7, 8, i), 10, 11.
Extensive tablet? connected with 70 (,v) and /, (x) have been published by
Andin g,Sec}isstelUge Tafeln der Bessel'achen FunMionenimagintiren Arguments
(Leipzig, 1911). These tables give log,,, /„ (x) and log,,, {Ix {x)fx\ from ,r™0
to x— lO'OO with interval 001. They also give the, values of the functions
VB7nc). e~* Iu (x), VBwa:) . e~xlv (x), logi0 [V* . h (¦'¦)} »» l«ff»« W* ¦ I> (>'•)]
for values of as from .r=l()-() to a? = 50*0 (interval 01), x = 50 to .r=00
(interval 1), x — 200 to x= 1000 (interval 10), and for various larger values of.-/;.
Table II infra, pp. 698—713, gives the values of e xIl}(x) and e~x Iv (//•);
these have been computed, for the most part, by interpolation in Aldis' Table.
The earliest tables of functions of the type Kn(x) were constructed by
Aldis, Proc. Royal Sue. lxiv. A899), pp. 219—221. These give Ku(a-) and
Ki(x) to twenty-one places of decimals for values of .¦/; from ,r=0 to ,-r = ()-0
with interval O'l, and also to between .seven and thirteen significant figures
from x- 50 to a; = 12t() with interval 0*1.
The values of exKa{nc) and e^Kx (x) in Tuble II infra, were computed with
the help of Aldis' Table, like the values of e~~xf0 (x) and e~xIx(iv).
By means of recurrence formulae, /„(&•) has been tabulated to twelve sigiii-
ficant figures for n = 0, 1, 2,..., 11 over the range of values of x from x = 0
to as = 60 with interval 0-2. These Tables of In(x) were published in the
British Association Report, 1889, pp. 29—32, and reprinted by Gray and
Mathews in their Treatise, pp. 285—288. An abridgement (to five significant
figures) of these Tables has been given by Isherwood, who added to them
w. b. p. 42
658 THEORY OF BESSEL FUNCTIONS [CHAP. XX
Tables of Kn(x) to five significant figures for n = 0,1, 2,..., 10 over the range
of values of x from x = 0 to x = 6'0 with interval 0-2. Isherwood's Tables were
published in the Mem. and Proc, Manchester Lit. and Phil. Soc, 1903—1904,
no. 19.
Tables of e~xIn(x) and Kn{x) to seven places of decimals are given in
Table IV infra, pp. 736—739.
The earliest Tables of Bessel functions of large order were constructed by
Meissel, who has calculated Jm(n) to twelve significant figures for n = 10,
11,..., 2l,Astr. Nach. cxxix. A892), col. 284; Meissel also calculated ^A000)
to seven significant figures for w = 1000, 999, ..., 981, ibid, cxxviii. A891),
col. 154—155. The values of Jn(n), J^n), Y™(n), Y^-^(n), Gn(n), G«-i(«)
to six places of decimals for values of ?i from n=l to n = 50 (interval 1),
n=50 to n=100 (interval 5), w = 100 to n = 200 (interval 10), n = 200 to
n = 400 (interval 20), n=400 to w=1000 (interval 50), n = 1000 to n = 2000
(interval 100) and for various larger values of n, are given in the British
Association Report, 1916, pp. 93—96.
Tables of Jn(n), J«'(w), Yn(n), Yn'(n) to seven places of decimals are given
in Table VI infra, pp. 746—747.
The functions ber (a?), bei (as), ker (x) and kei (x) have been extensively
tabulated on account of their importance in the theory of alternating currents.
A brief Table of ber (a?) and bei(#), computed by Maclean, was published
by Kelvin, Math, and Phys. Papers, in. A890), p. 493. Tables of J0(x\/i)
and v'2. J\ (oa *Ji) to twenty-one places of decimals have been constructed
by Aldis, Proc. Royal Soc. lxvi. A900), pp. 42—43; their range is from
cc — Q to a; =6*0 with interval 0*1. These are extensions of the Table of
J0(x«Ji) to nine places of decimals for the range from oc = O to x— 6 0 with
interval 0-2 published in the British Association Report, 1893, p. 228, and
reprinted by Gray and Mathews in their Treatise, p. 281.
Tables of ber (ob), bei (x), ker (x) and kei (a--) to four significant figures for
x= 1, 2, 3,..., 30, have been published by Savidge, Phil Mag. F) xix. A910),
p. 53.
The functions ber (x), bei (x)y ber' (x) and bei' (x) are tabulated to nine
places of decimals, from x = 0 to x = 10*0 with interval 01 in the British
Association Report, 1912, pp. 57—68; and a Table of ker (x), kei (x), ker' (at)
and kei' (x) of the same scope (except that only six or seven significant figures
were given) appeared in the Report for 1915, pp. 36—38. Tables of squares
and products of the functions to six significant figures from # = 0 to x — 10'0
with interval 0*2 were given in the Report for 1916, pp. 118—121.
The functions /±(w+i)(#) have been tabulated to six places of decimals by
Lommel, Miinchener Abh. XV. A886), pp. 644—647, for n = 0, 1, 2,..., 6 with
x ~ \, 2,..., 50, and (in the case of functions of positive order) n = 7, 8,.... 14
20-1] TABULATION OF BESSEL FUNCTIONS 659
with x = 1, 2,..., 20, and n = 15..... 34 with smaller range-* of values of x; see
Table V infra, pp. 740—743. A Table of the same functions to four places of
decimals with n =0, 1, 2 and from a; = 0 to a: = 80 with interval 0*2 is given
by Dinnik, Archiv der Math, und Phys. C) XX. A913), pp. 238—240.
Functions related to J±(n.+i) (x) have recently been tabulated in the British
Association Reports. The notation used is
) • Jn+t, («) = Sn (as), (-)n V(W). J_n^(x) = Cn (x),
and the functions tabulated are Sn(x), Cn(x), En2(x), Sn'(x), Cn'(x), En'-(x),
and their logarithms. In the Report for 1914, pp. 88—102, the functions are
tabulated to seven significant figures for n~0,1,2,..., 17 and .* = 1,2,3, ..., 10,
and in the Report for 1916, pp. 97—107, for n = 0, 1, 2,..., 10 and x= 1-1,
1-2, ...,1-9.
Functions of order + |, + |, have been tabulated by Dinnik, Archiv der
Math, und Phys. C) xvni. A91.1), pp. 337—338, to four places of decimals;
the functions tabulated are F A + \ )J± $ (x), F(l + $) J±$(x) from &• = () to
x = 8*0 with interval 0*2; and Dinnik has also tabulated /±i(a;), I.hi(x), ibid.
C) xxii. A914), pp. 22E—227 and J±k(x), J±i(x), ibid. C) xxi. A913),
pp. 324—326. All these tables have the range x = 0 to x = 80 with interval
0'2. The Tables of F(l ± \)J±\(<r) are leaa extensive than Table III infra,
pp. 714—729 ; but, with the exception of Dinnik's tables, there exist no
tables of functions of orders §, { and ?.
In connexion with functions of order + \, Airy's Table of his integral
I
Jo
cos ? 7r (vf — rnw) dw
o
must be mentioned; Airy calculated by quadratures and by ascending scries
the values of this integral for values of -m from -515 to +5E with interval
0'2; a seven-figure Table from m = — 4 to ?n = 4 is given in the Trans. Camb.
Phil. Soc. VI. A838), p. 402, and a five-figure Table from w = - 5-E to m = 5'tt,
ibid. viii. A849), p. 599.
Apart from the work of Euler described in § 15*5 the earliest computation
of the zeros of J0(x) and Jx (x) is due to Stokes, Trans. Camb. Phil. 8oc. ix.
A856), p. 180 [Math, and Phys. Papers, n. A883), p. 355]. Stokes gave the
values of the first twelve zeros (divided by tt) of J0(v) and Jx (x) to four places
of decimals. In the same memoir he gave the first fifty zeros of Airy's integral,
and the first ten stationary points of this integral.
The first nine zeros of J0(x), Ji(x), ..., /5(«) were computed by Bourget,
Ann. sci. de VlZcole nonn. sup. ill. A866), pp. 82—87. Bonrget's results are
given to three places of decimals; some corrections in his Tables have recently
been made by Airey*.
* Pliil. Mag. ((>) xxxii. A016), pp. 7—1-1.
4a- 2
660 THEORY OF BESSBL FUNCTIONS [CHAP. XX
Bourget's Tables have been reprinted so frequently that their authorship has-been
overlooked by the writers of the articles on Bessel Functions in the Encyclopadie der
Math. Wiss. and the Encyclopedia des Sci. Math.
The first five zeros of .f, (x) and J2(x) were given to six places of decimals
by Lommel, Zeitschrift fiir Math. und. Phys. xv. A870), p. 167 and Munchener
Abhandlungen, xv. A886), p. 315.
The first ten zeros of Jo (x) were computed to ten places of decimals by
Meissel, Berliner Abhandlungen, 1888.
The first fifty zeros (and their logarithms) of J0{x) were given to ten places
of decimals by Willson and Peirce, Bulletin American Math. Soc-. ill. A897),
pp. 153—155; they also gave the values of J^(x) and log 1 Ji(«0 | at these
zeros to eight and seven places of decimals respectively.
The first fifty zeros of Ji (x) and the corresponding values of Jo («0 were
computed to sixteen places of decimals by Meissel*, Kiel Programon, 1890;
this Table is reprinted by Gray and Mathews in their Treatise, p. 280.
Tables of roots of the equation
Jn (x) Yn (kx) - Jn (fee) Yn (x) = 0
have been constructed by Kalahne, Zeitsohrift fur Math, und Phys. liv. A907),
pp. 55—86 ; the values taken for k are 12, 1-5 and 20, while n is given the
values 05 *, 1, f, 2, \.
Dinnik in his Tables of functions of fractional order mentions the values
of a few of the zeros of each function, while Airey, PhiL Mag. F) xli. A921),
pp. 200—205, has computed the value of the smallest zero of Jv(x)'for small
fractional values of v by Euler's method.
Rayleigh, Proc. London Math. Soc. x. A878), pp. 6—7 [Scientific Papers,
l. A899), pp. 363—364], has calculated that
has a maximum when x* — 0'4858.
Airey, Archiv der Math, und Phys. C) xx. A913), p. 291, has computed
the first ten zeros of 3xJQ(%) - 2/, (x) and of 1xJ0(x) - Jj(x) to four places
of decimals.
In his memoirs on Ditfraction, Milnchener Abhandlungen, xv. A886),
Lommel has published tables connected with his functions of two variables,
but these tables are so numerous that a detailed account of them will not be
given here. His Table of Fresnel's integrals (p. 648) to six places of decimals
from x = 0 to x = 50'0 with interval 0*5 (with auxiliary tables for purposes
of interpolation) must, however, be mentioned, and with it his Table of the
first sixteen maxima and minima of these integrals.
* Jahrbuch iiher die Fortschritte der Math. 1890, p. 621. In consequence of the inaccessibility
of Meissel's table, the zeros of J\ (x) were recomputed (to ten places of decimals) for insertion in
Table VII, p. 748.
20-2] TABULATION OF BESSEL FUNCTIONS 661
Lommel's form for Fresnel's integrals was
o
a different form was tabulated earlier by Lindstedt, Ann. der Physik und
Chemie, C) xvn. A882), p. 725.
Defining the functions M (x) and N (x) by the equations
cos t2dt — M (%) cos x1 — N (a) sin x\
f
J a
sin t2dt = M (x) sin x2 + N (as) cos x\
and writing x — {(y+ %)tt} , Lindstedt tabulated M{x) and N (x) to six places
of decimals from y = 0 to y — 9*0 with interval 0*1.
The function I(x) defined as
has been tabulated to four places of decimals by Struvc, Ann. der Physilc und
Ghemie, C) xvn. A882), pp. 1008—101E, from x = 0 to 4'0 (interval 01), from
f =40 to 7-0 (interval 02) and from x = 7*0 to 110 (interval 0'4).
A table of values of the integral
in which the limits are consecutive zeros (up to the forty-ninth) of Jt (x), has
been published by Steiner, Math, und Naturwiss. Barichte aits Ungarn XI.
A894), pp. 366—367; this integral occurs in the problem of Diffraction by
a Circular Aperture.
No Tables of Struve's functions- seem to have been constructed before the
Table of Ho {x) and Hx (x) which is given on pp. 666—697.
20*2. Description of the Tables contained in this book.
Preliminary considerations on the magnitude and character of the tables
to be included in this book led to the following decisions :
(I) That space, did not usually admit of the inclusion of more than seven
places of decimals in the tables.
(II) That the tables should be so constructed as to minimise the difficulty
of making interpolations. In particular, it was decided that a table with a
moderately large interval (such as 0'02), together with an auxiliary table to
facilitate interpolation, would be more useful than a table with a smaller
interval (such as 0'01), occupying the same space as the first table and its
auxiliary, in which interpolation was impracticable.
662 THEORY Or BESSBL FUNCTIONS [CHAP. XX
(III) That in computing tables, calculations should be carried to ten
places of decimals in order to ensure that the number of cases of inaccuracy
in the last figure of the published results should be trivial*. This does not
apply to the auxiliary tables of angles which are entered in Tables I and III.
In order to obtain seven-figure accuracy, it is not sufficient to tabulate to
tenths of a second of arc, because the differences per minute of arc in a seven-
figure table of natural sines may be as large as 00002909; on the other hand,
an error of a hundredth of a second does not affect the value of the sine by
more than 0#00000005. Hence, for seven-figure accuracy, it was considered
adequate to compute to nine places of decimals the sines (or cosines) of the
angles tabulated and then to compute the angles from Gifford's Natural Sines
(Manchester, 1914); these are eight-figure tables with an interval-J- of 1".
The angles tabulated may consequently frequently be in .error as to the
last digit, but, in all probability, the error never exceeds a unit (i.e. a
hundredth of a second of arc).
We now proceed to describe the tables in detail.
Table I consists primarily of Tables of JQ (x), Y{) («), Ja (a?) and F, (x) from
«=»0 to 16*00 with interval of 0'02. The values of JQ(x) and J,{x) up to
15-50 are taken from Meissel's Table j, while the values of Y0(x) and F, (so)
were computed partly by interpolation in Aldis' Table of GQ (x) and G^ (x) and
partly from the asymptotic expansions of /02 (x) + Yo- (x) and Ji> (x) -b F,2 (a)
given in § 7'51.
The auxiliary tables § give the values of I #nA> (a?) | and arg Hn(l) {x) for
n — Q and n — 1. In these tables the first differences are sufficiently steady
(except for quite small values of x) to enable interpolations to be effected
with but little trouble on the part of the reader; thus, when x is about 10
the second differences of | iT0«> (x) j do nob exceed 0-0000009.
The values || of | Hnll> (x) \ and arg Hn(l) (x) can consequently be computed
by the reader for any value of x less than 16, with the exception of quite
small values. The corresponding values of Jn(oc) and Yn(x) can then bo
calculated immediately by the use of seven-figure logarithm tables.
* The tables -were differenced before removing the last three figures, and it was found that the
ten-figure resultB -were rarely in error by more than a unit in the tenth place; so it is hoped that the
number of errors in the last figure retained does not exceed about one in every thousand entries.
t No tables with a smaller interval have been published; the uRe of any tables with a larger
interval and a greater number of decimal places would have very greatly increased the labour of
constructing the auxiliary tables of angles, and the increased accuracy so obtained would be of no
advantage to anyone using the auxiliary tables for purposes of interpolation.
J I must here express my cordial thanks to the Preussische Akademie der Wissensohaften zu
Berlin for permitting me to make use of this Table.
§ The idea of constructing the auxiliary tables grew out of a conversation with Professor Love,
in the course of which he remarked that it was frequently not realised how closely Bessel functions
of any given order resemble circular functions multiplied by a damping factor in which the rate
of decay is slow.
|| The remarks immediately following of course presuppose that a is 0 or 1.
20-2] TABULATION OF BESSEL FUNCTIONS 663
The relation between the various functions tabulated may be expressed
most briefly by regarding | Hn{l) (x) \ and arg Hn{1) (x) as the polar coordinates
of a point in a plane; then the Cartesian coordinates of this point are Jn(%)
and Yn (x). Thus, from the entry for x — 8*00,
+ 01116508 = 0-2818259 cos 412° 28' 40"'60,
+ 0-2235215 = 0-2818259 sin 412° 28' 40"-60.
Table I also contains the values of Struve's functions Ho(#) and H^1).
These functions are included in Table I, instead of being contained in a
separate Table, to facilitate interpolation; by § 10-41 D), the difference
Hw (x) — Yn (x) is a positive monotonic function, and it varies sufficiently
steadily for interpolation to be easy when oc is not small.
The Tables of Struve's functions were computed by calculating the values of Ho(#)
and Ho'(.ff) directly from the ascending series when x — \, 2, 3,..., and then calculating
Ho" (a?), Ho'" (#),... for these, values of a: from the differential equation $ 10-4A0) and the
equations obtained by differentiating it.
¦ A few differential coefficients .are adequate to calculate H0(.r) and Ho' (.x) by Taylor's
theorem for the values 0-5, O6, 0-7, ... <-f .v. Interpolation to fiftieth* of the unit is then
effected by using Taylor's theorem in the same manner. This process, though it seems at first
sight to be complicated and lengthy, is, in reality, an extremely rapid one when a machine*
is used. It is very much moro effective than the use of asymptotic expansions or the
process suggested in the British Association Ilrport, 1913, p. 11E. As an example of tho
rapidity of the process, it may bo stated that the values of <'~xIn (*¦) and e~x Ix (.v) in Table f I
took less than a fortnight to compute; of course the time taken over this tabulation was
appreciably shortened by the usu of Aldis' Table as a framework for interpolation.
Table II consists of Tables of er*I0(x)t e~xI\(x\ e? KQ(a), and ex AT, (./•),
and a Table of ex is inserted, in case the reader should require the values of
the functionsf /„(&¦), lA^), ^"oC/;) an(l ^i(A'M tne functions arc tabulated
from 0 to 16-00 with interval 002.
Interpolation by differencing is easy in the case of the first four functions
throughout the greater part of the range.
The Table of ez was constructed with the help of Newman's Table of e~r,
Trans. Camb. Phil. Soc. XIII. A883), pp. 145—241. Unlike the other Tables
in this book, the Table of ex is given to eight significant figures^, and care
has been taken that the last digit given is accurate; in every entry. Interpo-
Interpolation in this Table is, of course, effected by multiplying or dividing entries
by exponentials of numbers not exceeding 0*01; such exponentials can be
calculated without difficulty.
* The machine on which the calculations were carried out is a Marchant Calculatiug Machine,
10 x 9 recording to 18 figures.
t These functions were not tabulated because tableH of them are uusuited for interpolation.
X Nine figures are given in parts of the Tuble to avoid spoiling its appearance.
664 THEORY OF BESSEL FUNCTIONS [CHAP. XX
Newman's Table gives e~x to a large number of places of decimals, but the actual
number of significant figures in the latter part of the Table is small; and less than half of
the Table of & was constructed by the process of calculating reciprocals; the rest was con-
constructed from Newman's Table by using the values of e13 and em given by Glaisher*, and
the value of e~15-° given by Newman in a short table of e~x with interval 0*1. These ex-
exponentials were employed because the tenth significant figures in all three and the eleventh
significant figures in the first and third are zero.
Table III consists of Tables of J{{x), F4(x), j H^ (x)| and | arg#V" O)I
of the same scope as Table I, and interpolations are effected in the manner
already explained. A Table of e K^ (x) is also included. These Tables are
of importance in dealing with approximations to Bessel functions of large
order (§ 8-43), and also in the theory of Airy's integral.
The reader can easily compute values of J_j (a?) from this table by means
of the formula
J_j (x) = | H^ (x) | cos {60° + arg H^ (#)}•
Table IV gives the values of Jn {as), Yn (x), <r*In (x) and Kn (x) for various
values of x and n. The values of Jn (x) are taken from Lotnmel's Tablet, with
some corrections, but the remainder of Table IV, with the exception of some
values of En(x) taken from Isherwood's Table f, is new; they have been con-
constructed in part by means of Aldis1 Tables of functions of orders zero and unity.
Table V is Lommers Tablet of J±(n+i){x) and Fresnel's integrals with
some modifications and corrections.
Table VI gives the values of Jn(n), Yn(n), Jn'(n), Yn'(n) and n*Jn(n),
n* Yn (n), n* Jn' (n), n* Yn' O) for n = 1, 2, 3,... 50. Interpolation in the tables
of the last four of the eight functions is easy.
Table VII gives the first forty zeros of Jn(x) and Yn(x) for various values
of ft; part of this Table is taken from the Tables of Willson and Peircet-
Forty zeros of various cylinder functions of order one-third are also given.
Table VIII gives the values of
[*•/.(*) eft, if* F.(«) A,
-'o Jo
from x — 0 to 50 with interval 1, together with the first sixteen maxima and
minima of the integrals. The former table of maxima and minima can be
used to compute the coefficients (c? § 1812) in certain Fourier-Bessel aeries
for which v — 0.
* Trans. Gamb. Phil Soc. xiii. A883), p. 245.
11 must here express my cordial thanks to the Bayerische Aiademie der Wissenschaften zu
Miinchen, to the Manchester Literary and Philosophical Society, and to the American Mathe-
Mathematical Society for permitting me to make use of these Tables. The non-existence of adequate
trigonometrical tables of angles in radian measure has made it impracticable to check the last
digits in the entries in the greater part of Table V.
TABLES
OF
BESSEL FUNCTIONS
666
TABLES OF BESSEL FUNCTIONS
Table I. Functions of order zero
O-O2
0-04
0-06
0-08
o-io
O-I2
0-14
0-16
0-18
O-2O
O-22
0-24
O-26
O-28
0-30
0-32
o-34
0-36
0-38
0-40
0-42
0-44
0-46
0-48
0-50
0-52
°-54
0-56
0-58
o-6o
0-62
0-64
o-66
o-68
0-70
072
074
076
078
o-8o
0-82
0-84
o-86
o-88
0-90
0-92
o-94
0-96
0-98
I-OO
+ I-OOOOOOO
+ 0-9999000
+ 0-9996000
+ 0-9991002
+ 0-9984006
+ 0-9975016
+ 0-9964032
+ 0-9951060
+ 0-9936102
+ 0-9919164
+ 0-9900250
+ 0-9879366
+ 0-9856518
+ 0-9831713
+ 0-9804958
+ 0-9776262
+ 0-9745634
+ 0-9713081
+ 0-9678615
+ 0-9642245
+ 0-9603982
+ 0-9563838
+ 0-9521825
+ O-9477955
+ 0-9432242
+ 0-9384698
+ o-9335339
+ 0-9284179
+ 0-9231233
+ 0-9176518
+ 0-9120049
+ 0-9061843
+ 0-9001918
+ 0-8940292
+ 0-8876982
+ 0-8812009
+ O-S74539I
+ 0-8677147
+ 0*8607300
+ 0-8535868
+ 0-8462874
+ 0-8388338
+ 0-8312284
+ 0-8234734
+ 0-8155711
+ 0-8075238
+ O-7993339
+ 0-7910039
+ 07825361
+ O7739332
+ 0-7651977
554
2-1219006
1-8626264
1-6780254
I-5342387
1-4161969
1-3158701
1-2284710
1-1509166
1-0811053
- 0-9591221
- 0-9050133
- 0-8545676
- 0-8072736
- 0-7627204
- 07205732
- 0-6805558
~ 0-6424376
- 0-6060246
- 0-5711520
- 0-5376789
- 0-5054836
- 0-4744608
- 0-4445187
- 0-4155768
- 0-3875642
- 0-3604182
- 0-3340833
- 0-3085099
- 0-2836537
- 0-2594751
- 0-2359383
- 0-2130113
- 0-1906649
- 0-1688729
- 0-1476114
- 0-1268587
- 0-1065950
- 0-0868023
- 0-0674640
- 0-0485651
- 0-0300917
- 0-0120311
+ 0-0056283
+ 0-0228974
+ 0-0397860
+ 0-0563032
+ 0-0724576
+ 0-0882570
2-7520297
2-3455622
2-1136647
1-9525811
1-8299993
17315984
1-6497727
1-5800007
I
59377
1-4659257
I-4I824I4
1-3752907
1-3362914
1-3006375
1-2678500
1-2375444
1-2094070
1-1831788
1-1586436
1-1356190
1-1139500
1-0935036
1-0741648
I8
1-0384231
1-0218560
1-0060645
0-9909884
0-9765738
0-9627727
O'94954i7
0-9368418
0-9246378
0-9128976
0-9015920
0-8906945
0-8801807
0-8700283
0-8602168
0-8507273
0-8415424
0-8326455
0-8240231
0-8156598
O<8o75434
07996618
07920038
O784559O
O7773I77
07702706
-900
- 68° 41' 42*16
6° 6' ''
- 56°
10*79
o K 44
52° 54 7-85
51° 2 0^32
49o 14 37*05
47 3i 4*89
45° 5o
44° *3
42 37
41 4
39° 32
44-63
o-4i
46-9I
27*57
53-32
38° 2 5I-54
36° 34 I2*42
35° 6 47-25
33 4° 28*14
32° 15' 8*97
3O° 50; 44*27
29 27 9-25
28° 4'-19*71
260 42' 11*96
25° 2O' 42*72
23° 59' 49*07
220 39' 28*42
21° 19' 38*41
2O° O' 16*94
180 4i'22*10
17° 22' 52*16
l6° 4 45-55
14° 47 0*82
130 29' 36*67
120 12' 31*88
IO° 55; 45*35
9 39 16*05
8° 23 3*o5
7: 7 5*48
5° 51 22*51
4° 35; 53*41
3° 20 37*48
2 5 34*o6
°° 5o 42*55
o 23' 57*61
i° 38' 26*96
2° 52' 45-99
4° 6; 55*16
S° 20' 54*92
34 45''67
o-ooooooo
+ 0-0127318
+ 0-0254603
+ 0-0381819
+ 0-0508934
+ 0-0635913
+ 0-0762722
+ 0-0889328
+ 0-1015097
+ 0-1141796
+ 0-1267590
+ 01393046
+ 0-1518131
+ 0-1642813
•I- 0-1767056
+ 0-1890829
+ 0-2014099
+ 0-2136834
+ 0-2258999
+ 0-2380565
+ 0-2501497
+ 0-2621765
+ 0-2741336
+ 0-2860180
+ 0-2978265
+ 0-3095559
+ 0-3212033
+ 0-3327655
+ 0-3442396
+ 0-3556226
+ 0-3669114
+ 0-3781032
+ 0-3891950
+ 0-4001841
+ 0-4110675
+ 0-4218424
+ 0-4325061
+ 0-4430558
+ 0-4534^888
+ 0-4638026
+ O-4739944
+ 0-4840616
+ 0-4940018
+ 0-5038124
+ o5i
+ 0-5324422
+ 0-5417103
+ 0-5508368
+ 0-5598197
+ 0-5686566
O*O2
O-O4
o-ob
0-08
o-io
O-I2
O-lA
O'lO
0-18
O-2O
O-22
0-24
O-26
O-28
0-30
0-32
o-34
0-36
0-38
0-40
0-42
0-44
0-46
0-48
0-50
0-52
O4
0-56
0-58
o-6o
0-62
0-64
O-66
o-68
0-70
0-72
074
0-76
0-78
o-8o
0-82
0-84
o-86
o-88
0-90
0-92
0-94
0-96
0-98
l-OO
TABLES OF BESSEL FUNCTIONS
Table I. Functions of order unity
667
O-OOOOOOO
+ 0-0099995
+ 0*0199960
+ 0-0299865
+ 0-0399680
+ 0-0499375
+ 0-0598921
+ 00698286
+ 0-0797443
+ 0-0896360
-h 0-0995008
+ o-1093358
-I- O-T IOI381
-I- o-1289046
-f- O-T386--J2S
I 0-1483x88
+ 0-1579607
I- 0-1675553
I 0-1770997
-f- 0-186591 I
+ 0-1960260
+ 0-205403.1
I- 0-2147188
I- 0-2239699
f 0-2331540
-f- 0-2422685
I- 0-2513105
h 0-2602774
¦I- 0-2691665
¦I- 0-2779752
-I- 0-2867010
-t- 0-2953412
I- 0-3038932
+ 0-3123547
+ 0-32072^0
+ 0-3289957
-I- 0-3371705
+ 0-3452448
i 0-35321^4
h 0-3610829
h 0-3688420
\- 0-3764916
-(- 0-3840292
+ 0-3914529
+ 0-3987603
+ 0-4059495
+ 0-4130184
-I- 0-4199649
+ 0-426787!
+ 0-4334829
•+¦ 0-4400506
31-8598128
15-9643089
10-6757892
8-0376696
6-4589511
5-4094402
4-6619853
4-1030547
3-6696037
3-3238250
3-0416730
2-8071277
2-6091059
2 -439^71
2-2931051
2-1649866
2-0520233
I-051 <>372
1-8617949
1-7808720
1707554O
1-6407704
I'579^33l
- 1-4714724
- I 4233094
- 1-3784737
- 1-3365858
- 1-2973191
- I 2603913
- 1-2255572
- 1-1926026
- 1-1613400
- 1-1316043
- 1-1032499
- 1-0761476
- 1-0501828
- 1-0252532
- 1-0012677
- 0-9781442
o-934I97°
O-9I32475
0*8929069
0-8731266
0-8538622
0-8350735
0-8167241
0-7987806
0-7812128
31-8598144
15-9643214
10-6758314
8-0377690
6-459I44I
* 5-4O977I7
4-6625082
4-1038295
3-6706983
3-3253140
3-O436375
2-8096347
2-6122083
4433
2-2978968
2-I7O74I5
2-0588527
1-9596561
1-8711218
1-7916282
1-7198647
1-6547603
1-595432O
1-5411449
1-4912830
I-4453258
1-4028308
6
33493
1-3267657
1-2925880
1-2606415
1-2307120
1-2026122
1-1761767
1-1512595
1-1277312
1-1054763
1-0843920
1-0643861
1-O453758
1-0272864
1-0100507
0-9936077
0-9779022
0-9628837
0-9485066
9
0-9215120
0-9088223
0-8966259
arg
-90°
- 89° 58' 556
- 89° 55' 41-64
- 890 50' 20*64
~ f9° 42; 54-34
- 890 33 25*29
- 890 21' 56*38
- 890 8' 30*73
-88° 53'ii*6g
- 88° 36' 2'-65
-88° 17' 7*17
- 870 56' 28*81
-87°34'ii*n
- 870 io' 17*63
- 86° 44'51*87
-86° 17'57*28
- 850 49' 37*22
- 85° 19' 55*00
- 84° 48' 53*80
- 840 16' 36*72
-«3°43' 6*78
- 830 8' 26*86
- 820 32' 39*76
- 8i° 55' 48*18
-81° 17; 54*69
- 8o° 39' 1*79
- 790 18' 27*16
- 78° 36' 49-Qo
- 77 54 22*18
- 770 ii' 5*99
- 760 27' 3*26
- 75° 42' 15*81
- 74° 56 45''4i
- 74° 10 33?73
- 73° 23 42?3»
- 720 36' I2"87
- 710 48' 6*68
- 7°° 59' 25^22
- 700 10' 9*80
- 690 20' 21 3
- 68° 30' 2*20
- 670 39' i2'-39
- 66° 4/ 53-42
- 650 56 6*35
- 65 3 52i
- 640 11' 11 -'97
- 630 18' 6*57
- 620 24' 36^89
- 6i° 30' 43^79
- 6O° 36' 28?IO
o-0000000
+ 0-0000849
+ 0-0003395
+ 0-0007638
+ 0-0013575
+ 0-0021207
+ 0-0030528
+ 0-0041539
+ 0-0054232
+ 0-0068607
+ 0-0084657
+ 0-0102377
+ O-OI2I7O2
+ 0-0142806
+ 0-0165502
+ 0-0189843
+ O-O2I582O
+ 0-0243427
+ 0-0272652
+ 0-0303489
+ 0-0335925
+ 0-0369952
+ 0-0405559
+ 0-0442733
+ 0-0481463
+ O-O52I737
+ 0-0563542
+ 0-0606865
+ 0-0651691
+ 0-0698006
+ 0-0745797
+ 0-0795046
+ 0-0845739
+ 0-0897860
+ 0-0951392
+ 0-1006317
+ O-IO626I9
+ O-II2O279
+ O-II79279
+ O-I23960I
+ O-I3OI225
+ 0-1364131
+ 0-1428299
+ O-14937'IO
+ 0-1560343
+ O-I628I75
.+ 0-1697186
+ 0-1767354
+ 0-1838656
+ 0-1911070
+ 0-1984573
O-O2
0-04
O-O6
0-08
o-io
O-I2
0-14
o-io
0-18
O-2O
O-22
0-24
0-26
0-28
0-30
0-32
0-34
0-36
0-38
0-40
0-42
0-44
0-46
0-48
0-50
0-52
o-54
0-56
0-58
o-6o
0-62
0-64
o-66
O-68
0-70
0-72
0-74
0-76
0-78
O'OO
0-82
0-84
o-86
o-88
0-90
0-92
0-94
0-90
0-98
l-OO
668
TABLES OF BESSEL FUNCTIONS
Table I. Functions of order, zero
X
1-O2
1-O4
i-ob
l-o8
I-IO
1-12
X'H
x'xi
1-18
1-2O
1-22
I-2A
1-26
1-28
I-3O
I-32
i-34
1-36
1-38
1-40
1-42
1-44
xm4'
i-48
i-5o
1-52
1-54
1-56
1-58
1-6o
1-62
1-64
1-66
1-68
1-70
1-72
174
176
178
i-8o
1-82
1-84
1-86
1-88
r-9O
1-92
1-94
1*96
1-98
2-OO
/.w
+ 0-7563321
+ 07473390
4- 07382212
+ 07289813
+ 07196220
4- O-7IO146I
4- O7OO5564
4- 0-6908557
4- O-68IO469
+ O-671I327
4- o-66in63
+ 0-6510004
4- 0-6407880
+ 0-6304822
+ 0-6200860
+ 0-6096023
4- 0-5990343
+ 0-5883850
+ 0-5776576
+ 0-5668551
+ 0-5559807
+ 0-5450376
+ 0-5340289
+ 0-5229579
+ 0-5118277
+ 0-5006415
+ 0-4894026
+ 0-4781143
+ 0-4667797
+ 0-4554022
+ 0-4439850
+ O-4325313
4- 0-4210446
+ 0-4095280
+ 0-3979849
+ 0-3864185
+ 0-3748321
+ 0-3632292
+ 0-3516128
+ 0-3399864
+ 0-3283532
+ 0-3167166
+ 0-3050797
+ 0-2934460
4- 0-2818186
+ 0-2702008
+ 0-2585959
+ 0-2470071
+ 0-2354376
+ 0-2238908
+ 0-1037085
+ 0-1188188
-1- 0-1335943
+ 0-1480406
+ 0-1621632
+ 0-1759670
+ 0-1894567
+ 0-2026367 1
+ 0-2155111 !
+ 0-2280835
+ 0-2403577
+ 0-2523369
+ 0-2640243
+ 0-2754228
+ 0-2865354
+ 0-2973645
+ 0-3079127
+ 0-3181824
+ 0-3281758
+ 0-3378951
+ 0-3473424
+ 0-3565195
+ 0-3654285 |
4. 0-3740710
+ 0-3824489
+ 0-3905639
+ 0-3984176
4- 0-4060116
+ 0-4133476
+ 0-4204269
+ 0-4272512
+ 0-4338219
+ 0-4401404
+ 0-4462083
4- 0-4520270
+ 0-4575979
+ 0-4629223
+ 0-4680019
+ 0-4728378
+ 0-4774317
+ 0-4817849
+ 0-4858909
+ 0-4897751
+. 0-4934149
+ 0-4968200
+ 0-4999917
+ 0-5029315
+ 0-5056411
+ 0-5001220
+ 0-5103757
O-7634O92
O-7567255
O75O2I2O
O-74386I4
O-7376671
O-7316228
O-7257225
O-71996O6
O7I433I7
0-7088309
O-7O34533
O-6981944
O-693O499
0-6880157
O-683O879
O-678263O
O-6735372
O-6689O73
O-66437OI
O-6599226
O-65556I8
O-65I285O
O-647O895
O-6429728
O-6389325
O-6349662
O-63IO7I7
0-6272469
0-6234898
O-6I97983
O-6l6l7O6
6-6I26O49
O-6O9O994
O-6O56526
O-6O22'627
O-5989282
O-5956477
O-5924I98
O-5892429
O-586II59
O-583O374
O-58OO06I
O-577O2IO
O'574O8O9
O-571I845
O-56833IO
O-5655IQ2
O-562748I
O-56OOI68
O-5573243
ai
7°
10
n°
12°
13°
15°
•16°
17°
18°
19°
21°
22°
230
24°
26°
27°
20°
29°
3O0
31°
33°
34°
36°
37°
39°
41 =
43C
45'
46
47
4»
49
52
53
54
55
56
58
59
6c
61
61
6-
6'
6?
p ff ix\
0 0 \ 1
48' 27*80
2' 1*68
15' 27*64
28' 46*01
41' 57*10
55' 1*20
7' 58*58
20' 49*49
33' 34*20
46' 12*92
58' 45*88
11' 13^30
23' 35-37
35' 52-28
48' 4*22
0' n''36
12' 13-86
24' n*88
36' 5?57
47 55*08
59' 4°''54
II' 22*o8
22' 59*82
34' 33*9°
46 4*43
57' 3r°
8' 55-24
20' 15*74
31' 33-io
42' 47*42
' 53' 58'-77
3 5 7*26
» 16' 12*95
3 27' 15*94
3 38' 16*30
0 49'14*10
0 o' 9*41
0 11' 2-31
0 21' 52*85
0 32' 41*11
0 43' 27*14
° 54' n'-oo
0 4'52-75
15 32'-45
° 26' iC'14
° 36' 45^88
° 47' 19;73
0 8' 21*89
)° 18' 50*32
+ O-5773455
+ 0-5858842
+ 0-5942706
4- 0-6025028
4- 0-6105787
+ 0-6184965
+ 0-6262544
+ 0-6338504
+ 0-6412828
+ 0-6485500
+ 0-6556502
4- 0-6625819
+ 0-6693434
+ O-6759334
+ 0-6823503
+ 0-6885928
+ 0-6946595
+ 07005492
4- 07062606
+ 0-7117925
+ 0-7171439
4- 0-7223136
+ 0-7273008
+ 0-7321043
+ 0-7367235
+ O-74II573
+ 0-7454051
4- 0-7494662
+ O-7533398
+ O-757O255
+ O76O5226
+ O76383O6
+ O7669493
+ O769878I
4- O7726168
+ O-775-I652
+ O-777523O
4- O77969O2
+ O7OI6666
+ 0-7834523
4- O785O474
+ 0-7864512
+ O7876658
+ O7886897
+ 0-7895236
4- O-79OI68O
+ O79O623;
+ 0-790889^
4- O79O9681
+ O79O8588
X
I-O2
1-04
i-o6
1-08
I-IO
1-12
I-I4
I-IO
I-IO
I-2O
1-22
1-24
1-26
1-28 '
1-3°
1-32
i-34
1-36
1-38
1-40
1-42
1-44
1-46
1-48
1 50
152
1-54
1-56
1-58
l-6o
1*62
1-64
1-66
1-68
170
1-72
174
1-76
178
i-8o
1-82
1-84
1-86
1-88
1-90
1-92
1-94
1-96
1-98
2*OO
TABLES OF BESSEL FUNCTIONS
Table I. Functions of order unity
669
X
I-O2
i-od.
I-OO
1-08
I'lO
I'I2
I-I4
I'lO
1-18
I-2O
1-22
1-24
I«2O
1-28
1-3O
1-32
1-34
1-36
1-38
1-40
1-42
1-44
1-46
1-48
150
1-52
i\54
1-56
1-58
i-oo
1-62
1-64
1-66
1-68
1-70
1-72
1-74
1-76
1-78
i-8o
1-82
1-84
1-86
1-88
1*90
1-92
1-94
1-96
I-98
2'OO
Jli*)
+ 0-4464882
+ 0-4527939
+ 0-4589660
+ 0-4650027
+ 0-4709024
+ 0-4766634
+ 0-4822840
+ 0-4877629
+ 0-49^0984
+ 0-4982891
+ 0-5033336
+ 0-5082305
+ 0-5129786
+ 0-5175766
+ 0-5220232
+ 0-5263174
+ 0-5304580
+ 0-53^4439
+ 0-5362741
+ O-54I9477
+ 0-5454638
+ 0-5488215
+ 0-5520200
+ 0-5550586
+ O-5579365
+ 0-5606532
+ 0-5632079
+ 0-5656003
+ 0-5678298
+ O-5698959
+ 0-571798^
+ O-5735368
+ O-575IIO8
+ 0-5765204
+ 0-5777652
+ O-5788453
+ 0-5797604
+ 0-5805107
+ 0-5810962
+ 0-5815170
+ O-58I773I
+ 0-5818649
+ 0-5817926
+ 0-5815566
+ 0-5811571
+ 0-5805946
+ 0-5798695
+ 0-5789825
"*" O-577934I
+ 0-576724?
Yi(*)
- 0-7639930
- 0-7470959
- 0-7304984
- 07141794
- 0-6981196
- 0-6823011
- 0-6667078
- 0-6513248
- 0-6361385
- 0-6211364
- 0-6063070
- 0-5916398
- 0-5771253
- 0-5627546
- 0-5485197
- O-5344I33
- 0-5204287
- 0-5065597
- 0-4928008
- 0-4791470
- 0-4655936
- 0-4521367
- 0-4387723
- 0-4254973
- 0-4123086
- 0-3992036
- 0-3861800
- 0-3732356
- 0-3603688
- o-347578o
- 0-3348619
- 0-3222194
- 0-3096498
- 0-2971522
- 0-2847262
- 0-2723716
- 0-2600881
- 0-2478757
- 0-2357345
- 0-2236649
- 0-2116671
- 0-1997416
- 0-1878091
- 0-1761102
- 0-1644058
- 0-1527766
- 0-1412236
- 0-1297478
- 0-1183504
- 0-1070324
O-8848938
O-8735987
O-8627I54
O-85222O5
O-842O92O
O-8323II7
O-822859I
O-8I37I78
O-8O487I5
O-7963O55
0-7880056
O-7799589
O-772I533
O-7645772
O-75722OO
O-75OO7I7
O-743I229
O-7363647
O-7297888
O-7233873
O-7I71528
O-7IIO785
O-7O5I576
O-699384O
0-6937518,
0-6882554
0-6828896
0-6776493
0-6725298
0-6675267
0-6626355
0-6578524
0-6531734
0-6485948
0-6441131
0-6397250
0-6354274
0-6312171
0-62*70914
0-6230473
0-6190823
0-6151939
0-6113796
0-6076371
0-6039642
0-6003588
0-5968189
O-5933424
0-5899276
0-5865726
arg
-59°o
-58°
-57°
-55°
-55°
-54°
-53°
-52°
-51°
- 5O°
-49°
-48°
- 47
-460
- 45°
-44°
-43°
-42°
-400
- 39
-38=
-37
-36C
-35°
-34
-33
-32C
— 3T
-3O;
- 29'
- 28(
-27
- 26
-25
-24
-23
- 22
- 21
- 19
— l8
-.11
- 15
-I4
" 13
- 12
- II
- IO
<
41'
46;
59
3'
7',
13'
15'
18'
2O'
22'
23'
25
26'
27'
2i,
28'
28'
28'
28'
28'
28'
27'
27'
2b'
25'
24
3 22
3 21
'19
17
3 10
314
3II
I 9
7
4
3 2
I*9
M
50*60
52;O3
54*55
5 6 "99
41*07
7-4O
16^56
9'-io
45-57
6-48
12'33
3-58
40*70
4^12
14^26
n'-54
56'-34
29 -03
49 "98
59-54
58^03
45-7»
23*11
50-30
7"°5
15-44
13-93
3'r39
44-O5
' if/'17
', 39I9Z
' 3'-52
3*7O
' 56-4I
' 4i'-o5
' 2O'-2I
;5i'^68
' 163
' 34*63
a 56' 46^45
1 5°
°47
°.44
o41
I 37
°34
52^04
/ 5i;57
' 33*oi
; 15-22
51-93
' 23-27
' 49'3«
+
+
+
+
+
+
+
+
-t-
-t-
+
+
+
-h
+
+
+
+
+
+
+
+
-1-
+
+
+
4
-1
4
H
-t
-\
-)
H
-
0-2059142
0-2134753
0-2211382
0-2289005
0-2367597
°*?447i33
0-2527589
0-2608939
0-2691157
0-2774218
0-2858095
0-2942761
0-3028191
O-3114357
0-3201231
0-3288788
0-3376999
0-3465837
O-3555273
0-3645280
o-373583o
0-3826894
0-3918443
0-4010450
0-4102085
0-4195719
0-4288924
0-4382471
o-447633o
O-457O472
- 0-4664869
¦ 0-4759490
- o-48543Of
- 0-4949288
- 0-5044407
- 0-5139633
L 0-5234937
h 0-5330289
-1- 0-542566!
H
h 0-5521021
h 0-5616342
+ ¦0-5711594
l- 0-5806748
1- 0-5901775
1- 0-5996045
t- 0-6091329
t- 0-6185800
I- 0-6280027
I- 0-6373982
H 0-6467637
X
I-O2
I-O4
I-OO
1-08
I-IO
I-I2
1-14
l-i6
1-18
I-2O
1-22
1-24
1-26
1-28
I-3O
1-32
1-30
1-38
I-^O
I'42
1-44
1-46
1-48
1-5°
1-52
i'-5t
1-58
I-OO
1-62
1-64
1-66
1-68
1-70
1-72
174
1-76
178
i-8o
•1-82
1-84
i-86
1-88
1-90
1-92
1-94
1.96
1-98
2-OO
670
TABLES OF BESSEL FUNCTIONS
Table I. Functions of order zero
I
X
2*O2
2-04
2-Ob
2*08
2*10
2*12
2*IA
2*10
2-18
2-2O
2-22
2-24
2*26
2-28
2-3O
2-32
2*34
2*30
2*38
2*40
2*42
2-44
2*46
2*48
2*50
2*52
2-54
2*56
2*58
2*OO
2-62
2-64
2*66
2-68
2-70
2-72
2-74
2-76
2-78
2*8O
2-82
2-84
2*86
2*88
2-90
2*92
2*94
2*96
2*98
3.00
/o(*)
+ 0*2123697
+ 0-2008776
+ 0-1894177
+ 0-1779931
+ 0-1666070
+ 0-1552625
+ 0-1439626
+ 0-1327106
+ 0-1215095
+ 0-1103623
+ 0*0992720
+ 0-0882416
+ 0-0772742
+ 0-0663726
+ 0-0555398
+ 0-0447786
+ 0-0340921
+ 0*0234828
+ 0*0129538
+ 0*0025077
- 0*0078527
- 0*0181247
- 0*0283057
- 0-0383929
- 0-0483838
- 0-0582758
- 0-0680664
- 0-0777531
- 0-0873334
- 0-0968050
• - 0-1061654
- 0-1154123
- 0-1245434
- 0-1335565
- 0-1424494
- 0-1512198
- 0-1598658
- 0-1683852
- 0-1767759
- 0-1850360
- 0*1931636
- 0*2011568
- 0*2090137
- 0*2167325
- 0*2243115
- 0*2317491
- 0-2390434
- 0*2461931
- 0*2531964
- 0*2600520
1
+ 0*5124038
+ 0-5142080
+ 0-5157900
+ 0-5171513
+ 0-5182937
+ 0-5192190
+ 0-5199289
+ 0-5204252
+ 0-5207097
+ 0-5207843
+ 0-5206508
+ 0-5203112
+. 0-5197675
+¦ 0-5190215
+ 0-5180754
+ 0-5169311
+ 0-5155908
+ 0-5140565
+ 0-5123304
+ 0-5104147
+ 0*5083116
+ 0*5060233
+ 0-5035522
+ 0-5009004
+ 0-4980704
+ 0-4950645
+ 0-4918851
+ 0-4885347
+ 0-4850157
+ 0-4813306
+ 0-4774820
+ 0-4734724
+ 0-4693043
+ 0-4649805
+ 0-4605035
+ 0*4558761
+ 0-4511009
+ 0*4461806
+ 0*4411181
+ 0-4359160
+ 0-4305772
+ 0-4251045
+ 0-4195008
+ 0-4137689
+ 0*4079118
+ 0-4019323
+ 0*3958334
+ 0*3896181
+ 0-3832893
+ 0-3768500
0*5546698
O-5520523
0-5494710
0-5469250
O-5444I37
0-5419362
O-5394917
O-537O796
O-534699I
O-5323496
0-5300304
0-5277408
0-5254803
0*5232482
0-5210439
0-5188670
0-5167167
0-5145926
0*5124942
0-5104209
0-5083723
0-5063478
°-5?4347i
0-5023696
0-5004149
0-4984826
0*4965722
0-4946834
0-4928157
0*4909688
0-4891422
O-4873357
0-4855488
0-4837812
0-4820325
0-4803025
0-4785907
0-4768970
0-4752209
O-4735621
0-471920.*
0-470295'
0*4686871
0-4670950
0-4655187
0-4639582
0*4624131
0-460883
0-459368
0*457867
arg H^{x)
67° 29' I7'*O2
68° 39' 42-05
69 5°' 5'44
710 0' 27*23
720 io' 47*47
730 21' 6'-"i8
740 31' 23*41
75° 4i\ 39;i9
78° 52' 5h553
790 12' 18*15
8o° 22' 28*45
8i° 32' 37'*46
820 42' 45*20
83° 52' 51*71
850 2' 57*01
86° 13' 1*12
87° 23' 4*08
88° 33' 5;9O
890 43 6*62
9o° 53' 6*25
920 3' 4'-83
930 13' 2*36
940 22' 58*88
95° 32' 54*40
960 42' 48-94
97° 52' 42*52
99° 2'35-17
ioo° 12' 26'-go
1OI° 22' 17*74
1O2° 32' 7*69
103° 41' 56*77
104° 51' 45 1
1060 i' 32-41
107° n' ig'*oo
108° 21' 4*79
109° 30' 49*80
no 40' 34'-04
iii° 50' 17*53
113° o' o'*27
114° 9'42*29
115° 19'23*59
iib° 29' 4*20
117° 38' 44*12
1180 48' 23*36
119° 58' 1*94
121° 7' 39*86
122° 17' 17*15
1230 26' 53*82
124° 36' 29*87
H.W
+ 0-7905626
+ 0-7900800
+ 0*7894119
+ 0-7885590
+ 0-7875222
+ 0-7863025
+ 07849006
+ 0-7833178
+ 0-7815550
+ 0-7796135
+ 07774943
+ 0-7751986
+ 0*7727279
+ 0*7700834
+ 0*7672665
+ 0-7642787
+ 0-7611214
+ 0-7577962
+ 07543047
+ 07506485
+ 07468293
+ 0-7428488
+ 07387088
+ O7344112
+ 0*7299577
+ 0*7253504
+ 0-7205912
+ 07156821
+ 07106251
+ 0-7054223
+ 07000759
+ 0-6945880
+ 0-6889609
+ 0-6831967
+ 0-6772977
+ 0-6712664
+ 0-6651050
+ 0-6588160
+ 0-6524017
+ 0-6450646
+ 0-6392073
+ 0-6324323
+ 0-6255420
+ 0-6185392
+ 0-61-14264
+ 0-6042062
+ 0-5968814
+ 0-5894546
+ 0-5819286
+ 0-5743061
X
2*O2
2-O4.
2-OO
2*Oo
2-IO
2-12
2*14
2*l6
2*Io
2*2O
2-22
2*24
2*2O
2-2o
2*3°
2-32
2-34
2-36
2-38
2-40
2*42
2-44
2*46
2*48
2*50
2*52
2-54
2-56
2-58
2*60
2-62
2-64
2*66
2-68
2*70
272
274
276
2-78
2-80
2-82
2-84
2-86
2-88
2*90
2-92
2-94
2*96
2*98
3.00
TABLES OF BESSEL FUNCTIONS
Table I. Functions of order imny
671
X
2-O2
2-O4
2'OD
2-o8
2-IO
2-12
2-14
2-16
2-18
2-2O
2-22
2*24
2-20
2-28
2'3°
2-32
2-34
2-36
2-38
2-40
2-42
2-44
2-46
2-48
2-50
2-52
2-50
2-58
2-60
2-62
2-64
2-66
2-68
2-70
2-72
274
276
278
2-80
2-82
2-84
2-86
2-88
2-90
2-92
2-94
2-96
2-98
3-00
JM
+ O'5753554
+ 0-5738267
+ 0-5702942
+ 0-5682921
+ 0-5661342
+ 0-5638212
+ 0-5613543
+ 0-5587345
+ 0-5559630
+ 0-5530410
+ 0-5499696
+ 0-5467502
+ o-5433»4i
+ 0*5398725
+ 0-5362170
+ 0-5324190
+ 0-5284801
+ 0-5244016
+ 0-5201853
+ 0-5158327
+ 0-5113456
+ 0-5067256
+ 0-5019745
+ 0-4970941
+ 0-4920863
+ 0-4869528.
+ 0-4816957
+ 0-4763168
+ 0-4708183
+ 0-4652020
+ 0-4594700
+ 0-4536245
+ 0-4476676
+ 0-4416014
+ 0-4354281
+ 0-4291500
+ 0-4227693
+ 0-4162882
+ 0-4097092
+ 0-4030346
+ 0-3962667
+ 0-3894079
+ 0-3824607
+ 0-3754275
+ 0-3683108
+ 0-3611130
+ 0-3538368
+ 0-3464846
+ 0-3390590
Yx{x)
- 0-0957951
- 0-0846398
- 0-0735677
- 0-0625801
- 0-0516786
- 0-0408645
- 0-0301393
- 0-0195045
- 0-0089616
+ 0-0014878
+ 0-0118422
+ 0-0220999
+ 0-0322594
+ 0-0423191
+ 0-0522773
+ 0-0621324
+ 0-0718828
+ 0-0815267
+ 0-0910627
+ 0-1004889
+ 0-1098039
+ 0-1190059
+ 0-1280934
+ 0-1370647
+ 0-1459181
+ 0-1546522
+ 0-1632654
+ 0-1717560
+ 0-1801226
+ 0-1883635
+ 0-1964774
+ 0-2044627
+ 0-2123179
+ 0-2200416
+ 0-2276324
+ 0-2350890
+ 0-2424099
+ 0-2495937
+ 0-2566393
+ 0-2635454
+ 0-2703106
+ 0-2769339
+ 0-2834140
+ 0-2897497
+ 0-2959401
+ 0-3019839
+ 0-3078802
+ 0-3136281
+ 0-3192264
+ 0-3246744
I<WI
0-5832757
0-5800353
0-5768497
O-5737I74
0-570637°
0-5676071
0-5646262
0-5616930
0-5588064
0-5559650
0-5531678
0-5504135
0-5477011
0-5450295
O-5423977
0-5398047
O-5372496
O-53473I5
0-5322494
0-5298025
0-5273901
0-5250111
0-5226650
0-5203509
0-5180682
0-5158160
O-5I35938
0-5114009
0-5092366
05071003
0-5049913
0-5029092
0-5008534
0-4988232
0-4968182
0-4948378
0-4928816
0-4909490
0-4890395
0-4871528
0-4852883
0-4834456
0-4816243
0-47982-40
0-4780443
0-4762847
O-4745449
0-4728245
0-4711232
0-4694406
arg H{\\x)
- 9° 27' 10*37
- 8° 23' 26*38
- 7° 19' 37-51
- 6° 15 43*88
-5° ii'45*59
- 40 7' 42*76
- 3° 3' 35-49
- 1° 59 23*88
- 0° 55' 8*03
o° 9' 11*98
1° 13' 36*04
2° 18' 4*07
3° 22' 35*97
4° 27 11*68
5° 31' 51*10
6° 36' 34*16
70 41' 20*77
8° 46' 10*86
9° 5i' 4'37
10° 56' 1*21
12° 1' 1*31
13° 6' 4*62
14° ii n*o6
15° 16' 20*57
16° 21' 33*IO
17° 26' 48*57
18° 32' 6*93
19° 37' 28*12
20° 42' 52*08
21° 48' 18*76
22° 53' 48*11
23° 59' 20*07
25°, 4 54-6o
26° 10 31*65
27° 16' 11*16
28° 21' 53*09
29° 27' 37*39
30° 33 24*03
31 39 12*95
32° 45' 4*11
33° 5O' 57*48
34 56 53'-oi
36° 2' 50*66
37° 8'50*39
38° 14' 52*17
39° 20' 55*96
40° 27' 1*72
4i°33 9'42
42° 39 I9"O2
43° 45' 3O*5O
+ 0-6560964
+ O-6653933
+ 0-6746517
+ 0-6838688
+ O-693O4I8
+ O-7O2I68O
+ 07II2445
+ 0-7202688
+ 0-7292381
+ 0-7381496
+ 0-7470008
+ O-755789O
+ 0-7645117
+ 0-7731661
+ O7817498
+ 0-7902603
+ O798695O
+ 0-8070514
+ O-8I53272
+ 0-8235198
+ 0-8316270
+ 0-8396463
+ 0-8475755
+ O-8554I22
+ 0-8631542
+ 0-8707993
+ 0-8783453
+ 0-8857900
+ 0-8931314
+ 0-9003674
+ 0-9074958
+ 0-9145148
+ 0-92I4224
+ 0-9282167
+ 0-9348957
+ O-94I4577
+ 0-9479OO8
+ O-9542233
+ O-96O4235
-1- 0-9664998
+ 0-9724504
+ 0-9782739
+ 0-9839687
+ O-9895333
+ 0-9949663
+ I-OOO2663
+ I-OO543I8
+ I-0IO46I7
+ 1-0153547
+ 1-0201096
X
2-O2
2-O4
2-OO
2-08
2-IO
2-12
2-I4
2-16
2-18
2-2O
2-22
2-24
2-26
2-28
2-3O
2-32
2-34
2-36
2-38
2-40
2-42
2-44
2-46
2-48
2-50
2-52
2-54
2-56
2-58
2-60
2-62
2-64
2-<>b
2-()8
2-70
2-72
2-74
2-76
2-78
2-80
2-82
2-84
2-86
2-88
2-90
2-92
2-94
2-96
2-98
3-00
672
TABLES OF BESSEL FUNCTIONS
Table I. Functions of order zero
X
3'°2
3-04
3-06
3-08
3-10
•3-12
3;i6
3-20
3 2
3'24
3-26
3-28
3-30
3-32
3-34
3-36
3-38
3-40
3-42
3H4
3-4O
3-48
3-50
3-52
3-54
3-56
3-58
3'6o
3-62
3'64
3'66
3-68
3.70
372
374
3.76
378
3-oo
3-82
3-8/
3-86
3-88
3-90
3.92
3-94
3:9'
3-98
4«oo
- 0-2667583
- 0-2733140
— O'2797I78
- 0-2859683
- 0-2920643
- 0-2980048
- 0-3037884
- 0-3094142
- 0-3148811
- 0-3201882
- 0-3253345
- 0-3303193
- 0-3351416
- 0-3398009
- 0-3442963
- 0-3486272
- 0-3527931
- 0-3567934
- 0-3606277
- 0-3642956
- 0-3677967
- 0-3711306
- 0-3742972
- 0-3772963
- 0-3801277
- 0-3827914
- 0-3852873
- 0-3876155
- 0-3897760
- 0-3917690
- O-3935947
- 0-3952533
- 0-3967452
- 0-3980707
- 0-3992302
- 0-4002242
- 0-4010532
- 0-4017178
- 0-4022187
- 0-4025564
- 0-4027318
- 0-4027. 56
- 0-4025986
- 0-40229^8
- 0-4018260
- 0-401202'
- 0-400421?
- 0-3994854
- 0-398394-
- 0-3971498
4- 0-3703033
+ O-3636522
+ 0-3568997
+ 0-3500489
4- O-343IO29
4- 0-3360648
+ 0-3289376
4- O-32I7245
+ 0-3144287
4- 0-3070533
4- O-2996OI3
+ O-292O76O
4- 0-2844806
4- O-2768l82
•+- O-2O9O92O
+ O-26I3052
+ O-25346O9
+ O-2455624
4- 0-2376128
4- O-2296I53
•+- O-22I5732
4- 0-2134896
+ O-2O53678
4- O-I972IO8
+ O-I89O2I9
+ O-I8O8O43
+ 0-1725612
+ 0-1642956
+ O-I56OIO9
+ O-I477IOO
4- O-I393962
+ 0-1310727
+ O-I227424
+ 0-1144086
+ 0-I0O0743
4- O-O977426
4- 0-0894167
4- O-O8IO994
' + 0-0727939
4- 0-0645032
4- 0-0562303
+ 0-0479782
+ 0-0397498
+ O-O3I5481
+ O-O233759
+ O-OI52362
+ O-OO7I3I9
- 0-000934;
- 0-008959.
- 0-0169407
!«?(*)!
0-4563820
0-4549104
0-4534520
0-4520090
0-4505787
0-4491618
0-447758;
0-4463673
0-4449893
0-4436239
0-4422708
0-4409300
0-4396011
0-4382841
0-4369787
0-4356849
0-4344023
0-4331310
0-4318706
0-4306210
0-4293822
0-4281539
0-4269360
0-4257283
0-4245308
0-4233432
0-4221655
0-4209974
0-4198389
0-4186898
0-4175501
0-4164195
0-4152980
0-4141855
0-4130817
0-4119867
0-4109003
0-4098223
0-4087528
0-4076915
0-4066383
0-4055933
0-4045561
0-4035269
0-4025054
0-4014915
0-4004853
0-3994865
0-3984951
O-3975HO
arg
1250
126°
1280
129°
130°
131°
132°
133'
135°
1360
137°
I3»°
139°
1400
1410
143°
1440
145°
1460
147°
1480
150°
1520
153°
154°
155°
157°
158°
159°
i6oc
i6ie
I62C
i63c
l65<
I66C
167'
168'
169"
170
172
173
174
175
176
177
178
180
181
182
46;
55'
5
14
24
33'
43
52
2'
II'
21'
3°'
40'
49;
59'
8'
18'
27'
37
46'
56'
5
14'
24'
33
43'
52'
1'
ii'
20'
29'
39
57'
7'
16'
;25;
;44;
'53'
I 3
3 12
3 21
9 30
3 40
in
158
0 8
c ^7
0 26
\x)
5*31
4O'-i6
i4'-42
48'-ii
21*23
53''80
25*82
28*27
58?7i
28*65
58-08
27''02
55-47
23-45
5O-95
18*00
44''59
*o*74
36-44
1*71
26*56
50*98
15*00
38*61
1*82
24*63
47'O5
9*10
3o/-77
52*06
12''99
33 6
53''78
I3''65
33"i7
52-36
11*21
29*74
47*93
5-8i
23-37
40-63
57*57
14*22
30*56
'46*60
' 2*36
; 17*86
'33-05
XT lv\
4- 0-5665900
+ O-5587829
+ O-55O8877
4- O-5429O73
+ O-5348444
4- 0-526702!
+ 0-5184831
+ O-5IOI9O5
4- 0-50I827O
+ O-4933957
+ 0-4848996
+ 0-4763415
+ 0-4677245
+ 0-4590516
+ 0-4503257
+ 0-4415499
4- 0-4327272
+ 0-4238607
+ 0-4149532
4- 0-4060080
4- 0-3970279
4- 0-3880161
+ 0-3789757
4- 0-3699095
+ 0-3608208
+ O-35I7I24
+ 0-3425876
+ O-3334492
+ 0-3243003
+ 0-3151440
+ 0-3059833
4- O-29682II
4- 0-2876605
4- 0-2785044
+ O-2693559
+ O-26O2I79
+ O-25IO933
4- 0-2419852
+ 0-2328964
4- 0-2238298
+ 0-2147883
4- O-2O57749
4- 0-1967923
+ 0-1878435
+ 0-1789312.
4- O-I7OO582
+ 0-1612273
+ O-I5244I2
+ O-I437O27
+ O-135OI46
X
3-02
3-04
3-06
3-08
3-10
3-12
3-14
3-16
3-18
3-20
3-22
3-24
3-26
3-28
3-3°
3-32
3-34
3-3O
3*38
3-4°
3-42
3-44
3-46
3'48
3-5O
352
3-54
3-56
3-58
3-60
3-62
3'^4
3-60
3-68
3.70
372
I?i
378
3-80
3-82
3'84
3-86
3-88
3-90
3-92
3'94
3-96
3-98
4-00
TABLES OF BESSEL FUNCTIONS
Table I. Functions of order uray
673
X
3*O2
3-O4
3*o6
3-08
310
3-12
3'i4
3*i6
3'i8
3'2O
3-22
3-24
3-26
3-28
330
3-32
3-34
3-36
3-38
3-4°
3-42
3*44
3-46
3-48
3-5O
3-52
3-54
3-56
3-58
3o
3-62
3-64
3 -66
3-68
3-7O
372
3-74
3-76
378
3'8o
3:|2
3-8^
3-88
3-90
3-92
3-94
3-96
3-98
400
4-
+
4-
4-
4-
+
4-
4-
+
4-
4-
4-
4-
+
4-
4-
4-
4-
4-
4-
4-
4-
+
4-
+
4-
4-
4-
4-
4-
+
4-
4-
4-
4-
4-
4-
4-
4-
4-
4-
-
—
-
—
_
-
—
-
AM
0*3315626
0-3239979
0*3163677
0*3086746
0*3000211
0*2931100
0*2852440
0*2773257
0-2693579
0-2613432
0-2532845
0-2451844
0-2370457
0-2288711
0-2206635
0-2124255
0-2041599
0-1958696
0-1875574
0-1792259
0-1708779
0*1625163
0*1541439
0-1457634
O-I373775
0*1289892
O-I2O6OIO
0-1122159
0-1038365
0-0954655
0-0871059
0-0787602
0-0704312
0-0621215
0-0538340
0-0455712
0-0373359
0-0291307
0-0209582
0*0128210
0*0047218
0*0033369
o*oi13524
0*0193223
0-0272440
0-0351151
0-0429330
0-0506953
0-0583995
0*0660433
4-
4-
4-
4-
+
4-
4-
4-
4-
4-
+
4-
4-
+
+
4-
4-
4-
4-
4-
4-
4-
4-
4-
4-
+
+
4-
4-
+
+
+
4-
4-
4-
4-
4-
4-
4-
4-
4-
4-
4-
+
4-
4-
4-
4-
4-
4-
0*3299712
0-3351158
0*3401076
O-3449457
0-3496295
O-354I583
O-35853I4
0-3627483
0-3668084
0-3707113
O-3744565
0-3780436
0-3814723
0-3847421
0-3878529
0-3908045
O-3935966
0-3962292
0-3987021
0-4010153
0-4031689
0-4051628
04069973
0-4086724
0-4101884
0-4115455
0-4127440
O'4i37843
0-4146667
0-4153918
o-4J59599
0-4163716
0-4166275
0-4167282
0-4166744
0-4164668
0-4161062
°-4x 55934
0-4149293
0-4141147
0-4131506
0-4120381
0-4107780
O-4O937I7
0-4078200
0-4061243
0-4042858
0-4023056
0-4001851
O-3979257
0-4677763
0-4661301
0-4645016
0-4628904
0-4612963
o-4597x9o
0-4581582
0*4566135
0*4550847
0*4535716
0*4520738
0-4505911
0-4491233
0-4476701
0-4462312
0-4448064
O-4433955
0-4419983
0-4406145
O-4392439
0-4378863
O-43654I5
0-4352093
0-4338895
0-4325819
o-43i28(L
0-4300026
0-4287305
0-4274699
0-4262206
0-4249824
O-4237552
0-4225387
0-4213329
0-4201376
0-4189527
0-4177779
0-4166131
0-4154582
0-414313^
0-4131776
0-4120516
0-4109349
0-4098274
0-4087290
0-4076396
0*4065590
0-4054871
0*4044238
0-4033691
arg H{
4< 5i;
45° 57
47 4
48° 10'
49° 16'
500 23'
51° 29'
52° 36
53° 42
54 49
55° 55'
57° 2
58° 8
59° 15
6o° 21'
6i° 28'
62° 35'
63 41
64° 48'
65° 55'
67° I'
68° 8'
690 15'
700 22'
71° 29'
72° 35'
73° 42
74° 49,
75° 56
77° 3'
78° 10'
79° 17'
8o° 24'
81° 31'
820 38'
83° 45'
84° 52;
85° 59
87° 6'
88° 13'
890 20'
900 27'
9i° 34'
92° 42'
93° 49'
94° 56'
96° " 3;
970 10'
98° 18'
99° 25'
43-8i
58*93
15 '-82
16*83
4°;52
32-76
1-25
31''29
2 "86
35-92
10 5
46-43
23J84
2 5
42-85
2 4''40
7*28
5I-48
36-98
•23'75
n-77
1 -04
51V51
4 3 '• 18
36*04
30-05
•25*21
2l'-5O
18*89
i7'-38
16*94
T7''57
19-23
21 ''94
2 5''66
30*37
36*07
4 2'-75
50*38
58*96
* 8*47
18*89
30*22
42*44
55-54
24-33
4-
4-
+
4-
4-
+
4-
4-
+
+
4-
4-
4-
+
+
4-
4-
4-
4-
4-
+
4-
4-
4-
4-
4-
4-
+
4-
4-
4-
4-
4-
4-
4-
4-
4-
4-
4-
4-
4-
"I"
4-
4-
4-
4-
4-
4-
4-
4-
I-O24725I
I-O292OO3
I-O33534O
I-O377252
I-O4I773O
1*0456765
I-O494347
I-O53O469
I-O565I24
I-O5983O3
I-O63OOO1
I-O66O211
I-O688928
I-O7I6I47
I-O74I863
I-O766O72
I-O78877O
I-O8O9955
I-O829624
1-0847774
I-O8644O6
1-0879516
1 -08931 O6
I-O9O5I7 5
I-OCJI5723
I-O924752
I-O932264
I-O93826O
1-O942743
I-O9457I6
1-O947183
I-O947I47
I-O94 56I .
I-O942589
1-0938077
I-O932O84
T-092 4617
I-O9I5683
I-O9O5J:89
I -0893444
I-O88OI56
1-O865434
I-O849288
1-0831727
I-O8*12762
1*0792403
1-O77O662
1-°74755 J
1*0723082
1-0697267
X
3*02
3-04
3-06
3-o8
3*10
3-12
3-14
3-16
3-18
3'2O
3-22
3-24
3-26
3-28
3'3O
3-32
3-34
3-36
3-38
3-4°
3'42
3-44
3-46
3-48
3-5O
3-52
3-54
3-56
3-5«
3-60
3-62
3-64
3*60
3-68
3-7°
372
3'7-1
376
3-7»
3-80
3-82
3-84
3-86
3-88
3-9O
3-92
3'94
3-96
3-98
4-00
W. B. P.
43
674
TABLES OF BESSBL FUNCTIONS
Table I. Functions of order zero
X
4'O2
4'°4
4-06
4-08
4-10
4-12
4-14
4-16
4-18
4-20
4-22
4'24
4-26
4-28
4-30
4-32
4-34
4#36
4-38
4-40
4-42
4'44
4-46
4.48
4-5O
4*52
4-54
4-56
4-58
4-60
4-62
4-64
4-66
4-68
4-70
472
474
4:7|
4-80
4-82
4-8*
4-86
4-88
4-90
4-92
4-94
4-96
4-98
5-00
/o(*)
- 0-3957530
- 0-3942053
- 0-3925079
- 0-3906622
- 0-3886697
- 0-3865318
- 0-3842500
- 0-3818259
- 0-3792610
- O-376557I
- O-3737I57
- 0-3707386
- 0-3676276
- 0-3643845
- 0-3610111
- O-3575O93
- 0-3538810
- 0-3501281
- 0-3462527
- 0-3422568
- 0-3381424
- 0-3339116
- 0-3295666
- 0-3251095
- 0-3205425
- 0-3158678
- 0-3110877
- 0-3062045
- 0-3012204
- 0-2961378
- 0-2909591
- 0-2856866
- 0-280.3228
- 0-2748700
- 0-2693308
- 0-2637076
- 0-2580029
- 0-252219^
- 0-2463592
- 0-2404253
- 0-2344201
- 0-2283462
- 0-2222062
- 0-2160027
- 0-2097383
- 0-2034158
- O; 1970377
- cl906067
- 0-184125'
- 0-1775968
- 0-0248755
- 0-0327610
- 0-0405944
- 0-0483732
- 0-0560946
- 0-0637561
- 0-0713550
- 0-0788889
- 0-0863551
- 0-0937512
- 0-1010748
- o#io832'34
- 0-1154947
- 0-1225863
- 0-1295959
- 0-1365213
- 0-1433602
- 0-1501104
- 0-1567699
- 0-1633365
- 0-1698081
- 0-1761827
- 0-1824583
- 0-1886330
- 0-1947050
- 0-2006723
- 0-2065332
- 0-2122859
- 0-2179287
- 0-2234600
- 0-2288780
- 0-2341813
- 0-2393683
- O-2444376
- 0-2493876
- 0-2542172
- 0-2589248
- 0-2635093
- 0-267969;
- 0-2723038
- 0-2765116
- 0-2805915
- 0-2845427
- 0-2883640
- 0-2920546
- 0-2956136
- 0-2990401
- 0-3023333
- 0-3054928
- 0-3085176
I<WI
0-3965340
O-3955643
0-3946015
O'3936457
0-3926967
O-39I7546
0-3908191
0-3898903
0-3889680
0-3880522
0^871428
0-3862397
0-3853428
0-3844522
0-3835676
0-3826891
0-3818166
0-3809499
0-3800891
0-3792341
0-3783848
.0-3775411
0-3767030
0-3758705
0'375O434
0-3742217
0-3734053
O-3725943
0-3717805
0-3709878
0-3701923
0-3694018
0-3686164
0-3678359
0-3670603
0-3662896
0-3655237
0-3647625
0-3640061
0-3632543
0-3625071
0-3617645
0-3610265
0-3602920
O-3595637
0-3588389
0-3581185
0-3574023
0-3560904
0-3559828
183° 35' 47'r96
184 45 2-62
185° 54' 16*99
187° 3'31*11
1880 12' 44*96
1890 21' 58*54
190° 31' 11*87
1910 40' 24*95
192° 49' 37-78
193 58 50*36
1950 8' 2*71
196° 17' 14*81
197° 26' 26*67
198° 35' 38*31
199° 44' 49*71
2OO° 54' O*88
2O2° 3' 11*83
2030 12' 22*56
204° 21' 33*08
205° 30' 43?37
2060 39' 53*45
207° 49 3?33
2080 58' 12*99
210° 7' 22*45
2110 16' 31*70
212° 25' 40-76
213° 34' 49-62
214° 43' 58*28
215° 53' 6*75
217° 2' 15*03
218° ii' 23*12
2190 20' 31*03
22O° 29' 38*75
221° 38' 46*29
222° 47' 53*65
223° 57' 0*83
225° 6' 7*84
226° 15' 14*68
227° 24' 21*34
228° 33' 27%
229° 42' 34*17
230° 51'40*33
232° o' 46*33
233° 9' 52*17
2340 l8' 57*85
235° 28' 3*37
236° 3^ 8*74
238°'55' i9*oi
240° 4 23*93
+ 0-1263794
+ 0-1177998
+ 0-1092784
+ 0-1008179
+ 0-0924208
4- 0-0840896
+ 0-0758269
4- 0-0676351
+ 0-0595166
+ 0-0514740
+ 0-0435095
+ 0-0356255
4- 0-0278243
+ 6-O2OIOOI
+ 0-0124793
+ 0-0049399
- 0-0025077
- 0-0098616
- 0-0171197
- 0-0242798
- 0-0313400.
- 0-0382984
- 0-0451530
- 0-0519019
- 0-0585433
- 0-0650755
- 0-0714966
- 0-0778050
- 0-0839990
- 0-0900771
- 0-09603.76
- 0-1018790
- 0-1075998
- 0-1131987
- 0-1186742
- 0-1240251
- 0-1292500
- 0-1343477
- 0-1393170
- 0-1441567
- 0-1488659
- 0-1534435
- 0-1578884
- 0-1021997
- 0-1663760
- 0-1704182
- 0-1743238
- 0-1780925
- 0-1817237
- 0-1852168
X
4-02
4-04
4-06
4-08
4-10
4-12
4-14
4-16
4-18
4-20
4-22
4-24
4-26
4-28
4-30
4-32
4-34
4-36
4-38 -
4-40
4-42
4-44
4-46
4-48
4-5O
4-52
4*54
4'5O
4-58
4-60
4-62
4-64
466
4-68
47°
4-72
4-74
4-76
4-78
4-80
4-82
4-84
4-86
4-88
4-90
4-92
4-94
4.96
4-98
5-00
TABLES OF BBSSEL FUNCTIONS
Table I. Functions of order unity
675
X
4'O2
4-04
4-08
4-10
4-12
4-14
4«i6
4-18
4-20
4-22
4-24
4-26
4-28
4*30
4*32
4'34
4-3O
4-38
4-40
4-42
4'44
4-48
4*5°
4-52
4-54
4-56
4-58
4-60
4-62
4-64
4-66
4-68
4-70
472
474
476
4-78
4-80
4-82
4-84
4-86
4-88
4-90
4-92
4-94
4-96
4-98
5-00
Jii*)
- 0-0736243
- O'o8ii4oi
- 0-0885884
- 0-0959669
- 0-1032733
- 0-1105054
- 0-1176609
- 0-1247378
- 0-1317339
- 0-1386469
- 0-1454750
- 0-1522160
- 0-1588679
- 0-1654287
- 0-1718966
- 0-1782695
- 0-1845457
- 0-1907233
- 0-1968005
- 0-2027755
- 0-2086467
- 0-2144125
- 0-2200710
- 0-2256209
- 0-2310604
- 0-2363882
- 0-2416027
- 0-2467026
- 0-2516864
- 0-2565528
- 0-2613006
- 0-2659284
- 0-2704352
- 0-2748196
- 0-2790807
- 0-2832174
- 0-2872280
- 0-2911133
- 0-2948707
- 0-2984999
- 0-3019999
- 0-3053702
- 0-3086098
- 0-3117182
- 0-3146947
•- 0-3175386
- 0-3202495
- 0-3228269
- 0-3252702
- 0-3275791
Yt(*)
+ 0-3955287
4- 0-3929956
4- 0-3903277
4- 0-3875267
+ 0-3845940
4- 0-3815313
4- 0-3783401
4- 0-3750222
+ 0-3715792
4- 0-3680128
4- 0-3643248
4- 0-3605171
+ O-35659I4
4- 0-3525497
+ 0-3483938
4- 0-3441256
+ O-3397472
+ 013352606
4- 0-3306677
+ 0-3259707
4- 0-3211716
4- 0-3162725
+• 0-3112757
+ 0-3061832
+ 0-3009973
4- 0-2957202
4- 0-2903542
4- 0-2849015
4- 0-2793644
+ 0-2737452
4- 0-2680464
4- 0-2622702
4- 0-2564190
4- 0-2504952
+ O-2445OI3
4- 0-2384397
4- 0-2323128
4- 0-2261230
4- 0-2198730
4- 0-2135652
4- 0-2072020
4- 0-2007860
4- 0-1943198
4- 0-1878058
4- 0-1812467
4- 0-1746449
4- 0-1680031
4- 0-1613238
4- 0-1546097
4- 0-1478631
0-4023226
0-4012845
0-4002545
0-3992325
0-3982185
0-3972123
0-3962138
0-3952229
0-3942396
0-3932638
0-3922953
0-3913340
0-3903799
0-3894328
0-3884928
0-3875596
0-3866333
0-3857136
0-3848007
0-3838942
0-3829943
0-3821008
0-3812136
0-3803327
0-3794579
0-3785893
0-3777267
0-3768700
0-3760193
O-375I744
O-3743352
0-3735018
0-3720740
0-3718517
o-37IO35°
0-3702237
0-3694177
0-3686171
0-3678218
0-3670317
0-3662467
0-3654068
0-3646919
0-3639221
0-3631571
0-3623971
0-3616418
0-3608913
0-3601456
O-3594O45
argH(;
IOO°
IOI°
IO2°
103°
IO5°
106°
1070
io8°
1090
IIO°
iii°
112°
114°
115
1160
1170
1180
1190
I2O°
121°
123°
124°
125°
120°
127°
128°
129°
130°
132°
I33U
134°
136°
137°
i38c
139'
T A T
142°
143'
144
I45C
H6;
I4o":
I5OC
151'
152'
153
154
155
32'
39.
47
54
1
9'
16'
23'
31
38'
46'
53
0'
8'
15'
23'
30
38'
45'
53
o'
8'
15'
23'
30'
38'
45,
53
o'
8'
16'
23'
31
39;
46'
54;
2'
9'
17'
25'
32'
4O'
A ^
' 55'
' 3'
3 11'
'19'
3 26'
'34;
'42'
40*00
56-49
13*81
31-94
50-87
10'-59
3i'-o8
52-34
14-36
37ri 2
0-62
24-85
49-79
15 -45
41 "80
8^84
36-56
4 "96
34'r°2
3'74
34'-io
5'-io
36-73
8-99
41 "80
15*34
49*42
24"o<)
59-35
35*18
11*59
48-50
20 9
4" 17
4 2 "80
21 '•<)b
1 5
41*87
22"(H
3 "85
45i
27*87
10 2
53-80
37-59
21''79
6;47
51*01
37*22
23*28
+
4-
4-
4-
+
+
4-
4-
4-
4-
4-
4-
4-
4-
+
4-
4-
+
+
4-
+
4-
4-
4-
+
¦1-
4-
•1-
+
H-
4-
+
+
+
+
+
4-
+
4-
4-
-i-
-(-
+
4-
+
-1-
4-
4-
4-
+
aw
1-0670119
1-0641653
1-0611881
1-0580818
1-0548479
1-0514880
1-0480034
I-O443959
1-0406671
1-0368186
1-0328522
1-0287695
1-0245724
1-0202627
1-0158422
1-0113128
1-0066764
1-0019350
0-9970906
0-9921451
0-9871006
0-9819591
0-9767229
O-97I3939
O-9059744
0-9604664
o-954b724
o-<)i](ji94^]
O-9434347
O-9375956
0-9316703
0-9250883
o-c)ig(t2.\(j
0-9134914
0-9072901
0-9010230
0-8946941
0-8883042
0-8818503
0-8753528
0-8087963
o-802i8cjr
0-8555338
0-8488330
0-8420890
0-8353045
0-8284820
0-8216241
0-8147332
0-8078119
4'
V
02
4-04
4'
4'
4"
4-
4-
4*
4-
4'
4'
4-
4-
r|-
4-
4-
4'
4"
4
4*
4
4
4
4
06
08
10
12
\l
18
20
22
It
28
30
32
34
36
38
40
42
44
46
48
4-50
4
4
4
4
4
4
4
4
4
4
52
54
56
58
Oo
•62
•04
•00
•08
•70
4-72
4
4
4
4
4
• 4
4
4
4
4
4
4
5
74
-70
II
•82
•84
•80
•88
•90
•92
•94
•96
•98
•00
43—2
676
TABLES OF BESSEL FUNCTIONS
Table I. Functions of order zero
X
5"O2
5*04
5-06
5-o8
5-io
5-12
5'i4
5-i6
5.18
5-20
5-22
5-24
5-26
5-28
5-3O
5-32
5-34
5-36
5-38
5-4O
5H2
5-44
5-46
5-48
5-5O
5-52
5-54
5;56
5-60
5-62
5-64
5-66
5-68
57O
572
574
576
5-78
5-80
5-82
5-88
5-9O
5-92
5-94
5-96
5-98
6-oo
M*)
- 0-1710232
- 0-1644075
- 0-1577524
- 0-1510606
- 0-1443347
- 0-1375776
- 0-1307919
- 0-1239803
- 0-1171456
- o-i 102904
- 0-1034176
- 0-0965297
- 0-0896293
- 0-0827198
- 0-0758031
- 0-0688822
- 0-0619598
- 0-0550386
- 0-0481211
- 0-0412101
- 0-0343082
- 0-0274180
- 0-0205422
- 0-0136833
- 0-0068439
- 0-0000266
+ 0-0067661
+ 0-0135315
+ 0-0202673
+ 0-0269709
+ 0-0336398
+ 0-0402716
+ 0-0468638
+ 0-0534141
+ 0-0599200
+ 0-0663792
+ 0-0727894
+ 0-0791482
+ 0-0854533
+ 0-0917026
+ 0-0978937
+ 0-1040245
+ 0-1100928
+ 0-1160964
+ 0-1220334
+ 0-1279015
+•0-1336987
+ 0-1394230
+ 0-1450725
+ 0-1506453
- 0-3114072
- 0-3141609
- 0-3167784
- 0-3192590
- 0-3216024
- 0-3238083
- 0-3258764
- 6-3278063
- 0-3295978
- 0-3312509
- 0-3327654
- O-334I4I3
- o-3353785
- 0-3364772
-O-3374373"
- 0-3382591
- 0-3389428
- 0-3394886
- 0-3398969
- 0-3401679
- 0-3403021
- 0-3402999
- 0-3401619 1
- 0-3398886
- 0-3394806
- 0-3389385
- 0-3382631
- O-337455O
- 0-3365151
- O-3354442
- 0-3342432
- 0-3329130.
- 0-3314545
- 0-3298689
- 0-328157,1
- 0-3263203
- 0-3243597
- 0-3222763
- 0-3200715
- 0-3177464
- 0-3153025
. -0-3127411
- 0-3100636
- 0-3072714
- 0-3043659
- 0-3013488
- 0-2982215
- 0-2949856
- 0-2916428
- 0-2881947
0-3552793
O-3545799
0-3538847
oi353i934
0-3525062
0-3518230
O-35II437
0-3504684
O'3497968
0-3491291
0-3484652
0-3478051
0-3471487
0-3464959
03458469
0:3452^014
O-3445595
0-3439212
0-3432863
0-3426550
0-3420271
0-3414027
0-3407816
0-3401639
O-3395496
0-3389385
0-3383307
O-3377262
0-33712.19
0-3365267
O-33593I7
O-3353399
O-33475"
O-334I655
O-3335828
o-333°°33
0-3324267
o*33l853O
0-3312824
0-3307146
0-3301498
0-3295878
0-3290286
0-3284723
0-3279188
0-3273681
0-3268201
0-3262749
0-3257324
0-3251925
241° 13' 28*68
2420 22' 33*30
243° 31' 37;76
244 40 42-09
245° 49' 46*28
246° 58' 50*32
248° 7' 54-22
249 16 57-98
250° 26' i'-6i
25i°35' 5"«
252^44' 8^47
253 53 1170
255° 2' 14*80
256° 11' 17*76
257° 20' 20*60
2580 29' 23*32
239o 38; 2**91
260° 47' 28*37
2610 56' 30*72
263° 5'32'-95
264° 14' 35"°5
265° 23' 3T-o<{
266° 32' 38*91
267° 41' 40*66
268° 50' 42*30
269° 59' 43-83
2K 8 45-24
272° 17 46/-54
273° 26' 47/73
274° 35' 48*81
275° 44' 49-79
276 53 50*65
278° 2' 51*41
279° 11' 52*07
2800 20' 52*62
281° 29' 53*07
2820 38' 53*42
283° 47' 53-07
284° 56' 53-82
28§° 5'53-87
287° 14' 53-83
288° 23' 53'<68
289° 32' 53'44
290° 4i'53'-n
291 ° 50 52-68
292° 59' 52-16
294° 8' 51*54
295 17 50-84
296 26' 50*0 <
297° 35' 49:i6
- 0-1885712
- 0-1917864
- 0-1948618
- O-I977971
- 0-2005919
- 0-2032458
- 0-2057586
- 0-2081301
- 0-2103600
- 0-2124483
- 0-2143949
- 0-2101998
- 0-2178630
- 0-2193846
- 0-2207647
- 0-2220035
- 0-2231013
- 0-2240583
- 0-2248740
- 0-2255513
- 0-2260882
- 0-2264860
- 0-2267451
- 0-2268062
- 0-2268499
- 0-2266969
- 0-2264079
- 0-2259836
- 0-2254249
- 0-2247327
- 0-2239078
- 0-2229512
- 0-2218639
- 0-2206469
- 0-2193014
- 0-2178284
- 0-2162291
- 0-2145048
- 0-2126567
- 0-2106861
- 0-2085942
- 0-2063827
- 0-2040527
- 0-2016058
- 0-1990435
- 0-1963672
- 0-1935787
- 0-190679,4
- 0-1876711
- 0-1845553
X
5-02
5-04
t)-o6
_ _o
5-00
5-10
5-12
5-i4
5-16
5-18
5'2O
5-22
5-24
5-26
5-28
5'3°
5-32
5-34
5-36
5-38
5'4°
5-42
5-44
5-4f
5-48
5-5°
5-52
5-54
5«
5-58
5-60
5-62
5-68
57°
572
574
5'7§
578
5.80
5-82
5-84
5-86
5-88
5-9O
5-92
5-94
5-96
5-98
o-oo
TABLES OF BESSEL FUNCTIONS
Table I. Functions of order unity
677
X
5-O2
5-04
5-o6
5-o8
5-io
5-12
5-14
5"i6
5-i8
5-20
5-22
5-24
5-26
5-28
5-3O
5-32
5-34
5-36
5-38
5-4O
5-42
5-44
5-46
5-48
5-5O
5-52
5-54
5-56
5-58
5-60
5*62
5-64
5-66
5-68
5-7O
5-72
574
576
5-7«
5-80
5-82
5"§4
5-86
5-88
5-9O
5-92
5-94
5-96
5-98
6-oo
M*)
- 0-3297533
- 0-3317925
- 0-3336963
- 0-3354646
- 0-3370972
- 0-3385940
- 0-3399550
- 0-3411802
- 0-3422695
- 0-3432230
- 0-3440409
- 0-3447234
- 0-3452707
- 0-3456831
- 0-3459608
- 0-3461043
- 0-3461140
- 0-3459903
- O-3457337
- 0-3453448
- 0-3448242
- 0-3441725
- o-3433<)O5
- 0-3424788
- 0-3414382
- 0-3402696
- 0-3389739
- 0-3375518
- 0-3360045
- O-3343328
- 0-3325379
- 0-3306208
- 0-3285826
- 0-3264245
- 0-3241.177
- 0-3217534
- 0-3192429
- 0-3166176
- 0-3138787
- 0-3110277
- 0-3080661
- 0-3049952
- 0-3018166
- 0-2985318
- 0-2951424
- 0-2916501
- 0-2880563
- 0-2843629
- 0-2805715
- 0-2766839
+ 0-1410869
4- 0-1342835
4- 0-127^556
4r O-I2O6O57
4-O-II37364
4- 0-1068504
4- O-O9995O2
+ 0-0930384
+ 0-0861176
4- O-O79I9O3
4- 0-0722592
4- O-O653269
4-0-0583958
+ 0-0514685
4- 0-0445476
4- 0-0376356
4- 0-0307351
4- 0-0238485
4- 0-0169784
4- O-O1OI273
4- 0-0032975
~ 0-0035083
- O-OIO2879
- 0-0170386
- 0-0237582
- 0-0304443
- 0-037094.4
- 0-0437062
- 0-0502774
- 0-0568056
- 0-0632886
- 0-069724!
- O-O76IO99
- O-O824437
- 0-0887233
- 0-0949466
- o-ioiiir5
- 0-1072157
- 0-1132573
- 0-1192341
-- 0-1251442
- 0-1309855
-- 0-1367560
- 0-1424539
- 0-1480772
- 0-1536240
- 0-1590925
- 0-1644809
- 0-1697874
- 0-1750103
0-3586680
0-3579362
0-3572088
0-3564859
0-3557675
0-3550534
O-3543437
0-3536383
O-352937I
0-3522402
O-35I5474
0-3508587
0-3501742
O-3494936
0-3488171
0-3481446
O-3474759
0-3468112
0-3461503
O-3454933
0-3448400
0-3441904
0-3435445
0-3429024
0-3422638
0-3416288
O-34O9975
o-3403696
O-3397452
0-3391243
0-3385069
O-3378928
0-3372821
0-3366748
0-3360708
O-33547OO
O-334O725
0-3342782
0-3336871
O-333O99I
o-3325i43
O-33I9326
o-33i354°
0-3307784
0-3302059
0-3296363
0-3290697
0-3285061
O-3279453
0-3273875
156° 50' 9*80
157° 57' 56-75
159 5 44?I5
160" 13'31*99
1610 21' 20*26
1620 29' 8*96
163° 36' 58*08
164° 44' 47*61
165° 52 37-56
167 0' 27*92
.168° 8' 18*68
1690 16' 9*84
170° 24' 1*40
I7i°3i'53''34
172° 39 45-6^
!73° 47' 38-39
174°55 31-49
1760 3' 24*96
177° 11' 18*80
178° 19' 13*00
1790 27' 7*56
180° 35' 2*49
181° 42 57*78
182° 50'53*41
183 5S 49-39
185° 6'45*72
1860 14' 42*38
187° 22' 39*38
i88° 30' 36*72
1890 38' 34'-39
190° 46' 32*39
191" 54' 3071
193 2' 29'-35
1940 10'28*30
195° 18' 27*57
196° 26' 27*15
197° 34' 27"O4
I980 42' 27'-23
199° 50' 2T-J2.
200° 58' 282
2O2° ()' 29'-(H
203° 14' 30*98
2O40 22' 32*fM
2050 30' 34*01
206° 38' 36*85
2070 46' 39*37
208° 54 42*17
210° 2 45-25
211° IO' 48*60
212° l8' 52*23
H.M
4- O-8OO8629
+ O-7938886
4- O7868916
+ O7798745
4- 0-7728398
+ 0-7657902
+ 07587281
4- 0-7516562
+ 0-744577°
+ O-737493O
4- 0-7304068
4- O-72332II
4- 07162382
4- O7O916O7
4- O7O2O912
4- 0-6950321
4- 0-6879861
+ 0-6809555
+ 0-6739428
4- 0-6669506
4- 0-6599812
4- 0-6530372
4- 0-6461209
+ O-6392347
4- 0-6323810
4- O-62S5623
4- 0-6187809
4- O-6I2O39O
4- O-6O5339I
+ 0-5986835
-t- 0-5920743
+ 0-5855138
4- 0-5790044
+ O-572548I
4- 0-5661472
4- 0-5598038
+ O-55352O1
+ 0-5472981
+ 0-5411399
+ 0-535047A
4- O-529O2 3I
4- 0-5230685
+ 0-5171858
4- 0-5113768
4- 0-5056434
4- 0-4999876
+ 0-4944111
4- 0-4889157
4- 0-4835031
+ O-478I753
X
5'O2
5-O4
5-06
5-o8
5-10
5*12
5-14
5-i6
5-18
5-20
5-22
5*24
5-26
5-28
5*30
5.32
5-34
5-30
5-38
5*40
5-42
5-44
5-46
5-48
5-5O
5-52
5-54
5-56
5-58
5-60
5-62
5-64
5-66
5-68
5-7O
5-72
574
5-76
5-?8
5-80
5-82
5-84
5-86
5-88
5-go
5-92
5'94
5-96
5-98
6-oo
678
TABLES OF BBSSEL FUNCTIONS
Table I. Functions of order zero
6-O2
6-O4
6-o6
6-o8
6-io
6-12
6-14
6-l6
6-l8
6-2O
6-22
6-24
6-26
6-28
6-30
6-32
6*34
6-36
6-38
6-40
6-42
6-44
6-46
6-48
6-50
6-52
6*54
6-50
6-58
6-6o
6-62
6-64
6-66
6-68
6-70
6-72
6-74
6-76
678
6-8o
6-82
6-84
6-86
6-88
6-90
6-92
6-94
6-96
6-98
7-00
4- 0-1561393
4- 0-1615527
4- 0-1668837
4- 0-1721306
4- 0-1772914
4- 0-1823646
4- 0-1873484
4- 0-1922411
4- 0-1970413
4. 0-2017472
4- 0-2063574
4- 0-2108705
4- 0-2152848
4- 0-2195991
4- 0-2238120
4- O-2279222
4- 0-2319283
4- 0-2358292
4- 0-2396237
4- 0-2433106
4- 0-2468888
4- 0-2503573
4- 0-2537151
4- 0-2569612
4- 0-2600946
4-0-2631145
4- 0-266020:
4- 0-2688106
4- 0-2714853
4- 0-2740434
4- 0-2764843
+ 0-2788074
4- 0-20IOI22
4- 0-2830981
4- 0-2850647
4- 0-2869117
4- o-'2886385
4- 0-2902449
4- 0-2917307
4- 0-2930956
4- O-2943394
4- 0-2954620
4- 0-2964633
4- 0-2973434
4- 0-2981020
4- 0-2987395
+ O-2992557
4- 0-2996510
4- 0-2999254
4- 0-3000793
" 1
Yo(*)
- 0-2846430
- 0-2809093
- 0-2772356
- 0-2733835
- 0-2694349
- 0-2653917
- 0-2612556
- 0-2570287
- 0-2527128
- 0-2483100
- 0-2438221
- 0-2392513
- 0-2345996
- 0-2298691
- 0-2250617
- 0-2201798
- 0-2152253
- 0-2102005
- 0-2051075
- 0-1999486
- 0-1947259
- 0-1894417
- 0-1840982
- 0-1786977
- 0-1732424
- 0-1677348
- 0-1621770
- 0-1565714
- 0-150920,4
- 0-1452262
- 0-1394913
- 0-1337179
- 0-1279085
- 0-1220655
- 0-1161911
- 0-1102879
- 0-1043582
- 0-0984043
- 0-0924287
- 0-0864339
- 0-0804221
- 0-0743958
- 0-0683573
- 0-0623092
- 0-0562537
- 0-0501933
- 0-0441303
- 0-0380671
- 0*0320062
- 0-0259497
O-3246553
O-324I2O8
O-3235889
O-323O596
O-3225328
O-322OO87
0-3214870
O-32O9679
O-32O45I3
o-319937 !
0-3194255
0-3189162
0-3184094
0-3179050
0-3174029
0-3169032
0-3164059
0-3159109
0-3154182
0-3x49278
0-3144396
0-3139537
0-3134701
0-3129887
0-3125094
'0-3120324
o-3575
0-3110848
0-3106143
0-3101458
0-3096795
0-3092152
0-3087530
0-3082929
0-3078348
O-3O73788
0-3069248
0-3064727
0-3060227
O-3O55746
0-3051285
0-3046843
0-3042421
0-3038017
0-3033633
0-3029268
0-3024921
0-3020593
0-3016283
0-3011992
2980 44' 48*19
299° 53' 47**3
3010 2'45*98
3020 ii' 44*74
3030 20' 43*43
3040 29' 42*03
305° 38' 42*54
3°6! 47, 38*97
307 56' 37*32
309 5 35*59
310° 14' 33*77
3110 23'31*88
312° 32' 29*90
313° 41' 27*85
3140 50' 25*73
315° 59' 23*52
317° 8'21*24
3180 17' 18*88
3190 26' 16*44
3200 35' 13*94
32i° 44' 11*36
322° 53' 8*71
3240 2' 5*98
3250 11' 3*18
3260 20' 0*31
327° 28'57*38
328° 37' 54*37
329° 46' 51*29
33O° 55 48-14
332° 4 44r93
333° *3'41 5
3340 22' 38*30
335° 3i 34*88
3360 40' 31*40
337° 49' 27*36
3380 58' 24*25
3400 7'20*58
3410 16' 16*84
3420 25' 13*0,
343 34 9*i8
3440 43' 5*26
3450 52' 1*27
347° 0'57*22
348° 9'53*12
3490 18' 48*95
35o° 27' 44*73
351° 36 4O*45
352° 45' 36*io
353° 54' 3i*7O
355° 3 27*25
Hov»
- 0-1813339
- 0-1780085
- 0-1745809 •
- 0-1710529
- 0-1674264
- 0-1637033
- 0-1598854
- O-I559746
- 0-1519730
- 0-1478824
- 0-1437050
- 0-1394427
- 0-1350977
- 0-1306719
- 0-1261676
- 0-1215867
- 0-1169310
- 0-1122043
- 0-1074071
- 0-1025422
- 0-0976117
- 0-0926181
- 0-0875634
- 0-0824500
- 0-0772802
- 0-0720564
- 0-0667807
- 0-0614556
- 0-0560834
- 0-0506605
- 0-0452073
- 0-0397080
- 0-0341711
- 0-0285990
- 0-0229940
- 0-0173587
- 0-0116953
- 0-0060063
- 0-0002941
4- 0-0054389
4- O-OIIigoj
4- 0-0169576
4- 0-0227386
4- 0-0285306
+ 0-0343315
4- 0-0401386
4- 0-0459497
4- 0-0517624
, 4- O-O57574-
4- 0-0633830
6-O2
6-04
6:06
6-o8
6-io
6-12
5-14
r O
6-18
6-20
6-22
6-24
6-26
6-28
6-30
6-32
6'34
6-^6
^-0
6-38
6-40
6-42
6-44
6-46
6-48
6-50
6-52
6-54
6-56
6-58
6-6o
6-62
6-64
6-66
6-68
6-70
6-72
6'74
6-76
6-78
6-8o
6-82
6-84
6-86
6-88
6-90
6-92
6-94
6-96
6-98
7-00
TABLES OF BESSBL FUNCTIONS
Table I. Functions of order unity
679
Y^x)
\H{\\x)\
- 0-2727017
- 0-2686269
- 0-2644612
¦ O-26O2O66
• 0-2558648
¦ O-25I4378
¦ 0-2469275
0-2423358
¦ 0-2376649
0-2329166
• 0-2280930
• 0-2231961
0-2182281
0-2131910
0-2080869
0-2029180
0-1976865
0-1923944
0-1870440
0-1816375
0-1761771
0-1706650
0-1651035
o-I594949
0-1538413
0-1481451
0-1424086
0-1366341
0-1308238
0-1249802
0-1191054
0-1132019
0-1072720
0-1013179
00953421
0-0893469
0-0833346
0-0773076
0-0712681
0-0652187
0-0591615
0-0530989
0-0470332
0-0409669
0-0349021
0-0227866
0-0167404
0-0107051
0-0046828
• 0-1801479
- 0-1851985
¦ 0-1901605
- 0-1950322
• 0-1998122
¦ 0-2044989
¦ 0-2090908
¦ 0-2135865
• 0-2179846
¦ 0-2222836
0-2264824
0-2305796
0-2345740
0-2384643
0-2422495
0-2459284
0-2494998
0-2529629
0-2563166
0-2595599
0-2626920
0-2657119
0-2686190
0-2714123
0-2740913
0-2766551
0-2791032
0-2814349
0-2836498
0-2857473
0-2877269
0-2895883
0-2913310
0-2929548
0-2944593
0-2958444
0-2971098
0-2982554
0-2992811
0-3001869
0-3009727
0-3016385
0-3021846
0-3026109
0-3029176
0-3031051
O-3O3I734
0-3031230
0-3029541
0-3026672
0-3268325
0-3262804
0-3257311
0-3251846
0-3246409
0-3240999
0-3235616
0-3230261
0-3224932
0-3219630
0-3214354
0-3209104
0-3203880
0-3198682
O-3I935O9
0-3188362
0-3183239
0-3178142
0-3173069
0-3168020
0-3162996
O-3I57996
0-3153020
0-3148067
0-3143138
0-3138232
O-3I3335O
0-3128490
0-3123653
0-3118839
0-3114047
0-3109277
0-3104529
0-3099804
0-3095099
0-3090417
0-3085756
0-3081116
0-3076497
0-3071899
0-3067322
0-3062765
0-3058229
O-3O537I3
0-3049217
0-3O44741
0-3040285
o-3O35849
0-3031432
0-3027035
2130 26' 56*12
2140 35' 0*27
215° 43' 4*69
2i6°5i' 9*37
2170 59' 14*31
219° 7' 19*50
22O° 15' 24*94
221° 23' 30*64
222° 31' 36*59
223° 39' 42*78
224° 47' 49-21
225° 55' 55-89
227° 4' 2*8l
'228° 12' 9*97
229° 2O' 17*35
2300 28' 24*98
231° 36' 32*83
2320 44' 40*91
233° 52' 492
235° o'57*75
236° c/ 6*51
238° 25' 24*68
239° 33' 34-O9
240° 41 '43-72
241° 4?' 53*56
242°58' 3*61
244° 6' 13*86
245° 14' 24-33
2460 22 35-00
2480 38' 56*96
249° 47' 8*24
250 55 19'71
252° 3'3i8
253°«; 43*25
254° !9 55-31
255° 28' 7*56
256° 36' 20*01
257° 44' 32-64
258° 52' 45*45
260 o 58-45
261° 9' 11*64
262° 17' 25*01
2630 25' 38*56
264° 33' 52*29
265° 42' 6*19
266° 50' 20*27
267° 58' 34-53
269° 6' 48*96
+ 0-4729337
+ 0-4677800
+ 0-4627160
4- 0-4528629
+ 0-4480769
+ 0-4433866
+ 0-4387935
+ 0-4342988
+ 0-4299040
+ 0-4256104
+ 0-4214192
+ 0-4173317
+ 0-4133490
+ 0-4094724
+ 0-4057028
+ 0-4020415
+ 0-3984894
+ 0-3950474
+ 0-3917166
+ 0-3884978
+ 0-3853919
+ 0-3823996
+ 0-3795218
+ 0-3767591
+ 0-3741123
+ 0-3715819
+ 0-3691685
+ 0-3668728
+ 0-3646951
+ 0-3626360
+ 0-3606958
+ 0-3588749
+ O-357I737
+ 0-3555923
+ 0-3541310
+ 0-3527901
+ 0-3515696
+ 0-3504696
+ 0-3494901
+ 0-3486313
+ 0-3478930
+ 0-3472751
+ O-3467775
+ 0-3464001
+ 0-3461426
+ 0-3460047
+ 0-3459862
+ 0-3460867
+ 0-3463057
6-O2
6-04
6-o6
6-o8
6-io
6-12
6-14
6-16
6-1-8
6-2O
6-22
6-24
6-26
6-28
6-30
6-32
6-34
6-36
6-38
6-40
6-42
6-46
6-48
6-50
6-52
6-5<>
6-58
6-DO
6-62
6-64
6-66
6-68
6-70
6-72
6-74
6-76
6-78
6-8o
6-82
6-84
6-86
6-88
6-90
6-92
6-94
6-96
6-98
7-00
680
TABLES OF BESSEL FUNCTIONS
Table I. Functions of order zero
YQ(x)
HoW
7'O2
7>O4
7-06
7-08
7«io
7-12
7-14
7-16
7-i8
7*20
7.22
7-24
7*20
7-28
7-32
7'34
7-3&
7-38
7-40
7*42
7-44
7'4|
7-48
7-5O
7-52
7-54
7-58
7-60
7-62
r6A
.7-66
7-68
7.70
7*72
774
7*8o
7-82
7-8'
7-88
7.90
7-92
7'94
7.96
7-98
8-oo
4- 0-3001128
4- 0-3000264
4- 0-2998204
+ 0-2994953
4- 0-2990514
+ 0-2984893
+ 0-2970096
4- 0-2970128
4- 0-2960996
4- 0-2950707
+ 0-2939268
4- 0-2926686
+ 0-2912970
+ 0-2898128
+ O-2882I69
4- 0-2865103
4- 0-2846939
+ 0-28276:
4- 0-28073
+ 0-2785962
+ 0-2763512
+ 0-2740018
4- 0-2715492
+ 0-2689947
4- 0-2663397
4- 0-2635853
4- 0-2607329
+ 0-2577839
4- 0-2547397
+ 0-2516018
4- 0-2483717
4- 0-2450508
4- 0-2416407
4- 0-2381429
+ 0-2345591
4- 0-2308910
4- 0-2271400
4- 0-2233081
4- 0-2193967
4- 0-2154678
4- O-2II343O
4- 0-2072042
4- O-2O29932
4- 0-1987118
4- 0-1943618
4- 0-1899452
4- 0-1854639
4- 0-1809198
4- 0-1763147
4- 0-1716508
- O-OI99OO2
- 0-0138600
- 0-0078314
- 0-0018167
4- 0-0041818
4- O-OIOl6l7
4- 0-0161208
+ 0-0220568
4- 0-0279674
4- 0-0338504
4- 0-0397036
4- 0-0455247
+ 0-0513115
4- 0-0570620
4- 0-0627739
4- 0-0684451
4- 0-0740734
4- 0-0796569
4- 0-0851934
4- 0-0906809
4- 0-0961173
4- 0-1015007
4- O-IO68292
4- O-II21OO7
4-0-1173133
4- 0-1224652
+ O-I275545
4- 0-1325793
+ O-I375379
4- 0-1424285
4- 0-1472494
4- 0-1519980
4- 0-1566751
4- 0-1612765
4- 0-1658016
4- 0-1702488
4- 0-1746164
4- 0-1789029
4- 0-1831070
4- 0-1872272
4- O-I9I262O
4- O-I952IOI
4- 0-199070!
4- 0-2028408
4- 0-2065209
4- O-2IOIO93
4- 0-2136046
4- 0-2170058
4- 0-2203118
4- 0-2235215
0-3007719
0-3003464
0-2999227
0-2995008
0-2990806
0-2986622
0-2982456
0-2978307
0-2974175
0-2970060
0-2965962
0-2961881
0-2957817
0-2953769
0-2949738
0-2945724
0-2941726
O-2937743
0-2933777
0-2929827
0-2925893
0-2921975
0-2918072
0-2914185
0-2910313
0-2906457
0-2902616
0-2898790
0-2894979
0-2891183
0-2887401
0-2883635
0-2879883
0-2876146
0-2872424
0-2868715
0-2865021
0-2861341
0-2857676
0-2854024
0-2850386
0-2846763
0-2843152
0-2839556
0-2835973
0-2832404
0-282884$
0-2825305
0-2821776
0-2818259
356° 12' 22*74
3570 2i' 18*17
358° 30' 13*54
359°. 39 8*86
3600 48' 4'-i2
361* 56; 59*33
363 5 54'49
364° 14' 49-59
365° 23'44-'64
3660 32' 39*63
41' 34-57
50' 29*46
59' 24*30
8' 19*09
17' 13*83
37
368'
369;
371
372'
8*52
?6
373° 26
374 35,
375° 43: 57-75
376° 52
378° 1
52*2C
46*7*
3790 10' 41*22
3800 19' 35*61
3810 28' 29*96
3820 37' 24*26
3830 46' 1 §'-52
3860 54' X6^8
387° 13 1*00
3880 21'55*07
3890 30' 49*09
3900 39' 43*07
391° 48' 37*00
392° 57 3o-
394° 6'24*74
3950 15' 18*54
3960 24' 12*30
397° 33' 6*02
398° 41' 59*70
399° 50' 53-33
4000 59' 46*9
4020 8' 40*4,
403° 17' 33*98
404 26 27*45
4°5° 35' 20*87
4060 44' 14*26
407° 53' 7
4090 2 0*92
4100 io' 54*19
411° 19' 47*41
4120 28' 40*
4- 0-0691861
4- 0-0749812
4- 0-0807662
+ 0-086538^
4- 0-0922958
4- 0-0980360
4- 0-1037565
+ 0-1094553
4- 0-1151299
4- 0-1207782
4- 0-1263979
4- 0-1319868
+ 0-1375427
4- 0-1430634
4- 0-1485467
+ O-I5399O5
+ 0-1593927
4-0-1647511
+ 0-1700638
+ 0-1753286
4- 0-1805435
4- 0-1857066
4- 0-1908158
4- 0-1958692
4- 0-2008648
4- 0-2058008
4- 0-2106753
4- 0-2154865
4- 0-2202325
4- O-2249II5
4- O-2295219
4- 0-2340620
4- 0-2385299
4- 0-2429241
4- 0-2472429
4- 0-2514848
4- 0-2556482
+ 0-2597315
+ 0-2637334
4- 0-2676524
4- 0-2714870
4- 0-27^2358
4- 0-2788977
4- 0-2824711
4- 0-2859549
4- 0-2893479
4- 0-29264
4- 0-2958566
4- 0-29897OO
4- 0-3019881
7-02
7'°4
7-06
7-08
7-10
7-12
tia
7-16
7-18
7-20
7-22
7-24
7-26
7-28
7-3O
7.32
7-34
7-3|
7-38
7-40
7-42
7'44
7-4O
7-48
7.50
7-52
7-54
7-56
7'58
7*60
7-62
7-66
7-68
77o
7.72
7-74
7-76
7.78
7-80
7.82
7-84
7-86
7-88
7-90
7-92
7-94
7-96
7-98
8-oo
TABLES OF BESSEL FUNCTIONS
Table I. Functions of order unity
681
X
7*O2
7*04
7*o()
7-08
7-10
7*12
7*14
7-10
7*t8
7-20
7*22
7*24
7-2O
7-28
7-3"
7-}2
7\\\
7*3C)
7' i**"
7*40
7--H
7-44
7'4'»
7-4-S
7<>
7-5-
7".'L
7-5fl
7\vs
7-00
7-1.2
7-<H
7-OH
7-70
7-72
7*74
77"
7.78
7-80
7-82
7-84
7-80
7-88
7*90
y-()Z
7'(H
7-96
7-98
8-oo
4-
4-
+
4-
+
4-
4-
+
4-
4-
+
+
-
4-
4-
4-
4-
4-
4-
t-
•1-
4-
4
4-
4-
•1
¦1-
•1
f
1
1
1-
1-
4-
1-
-1
+
1-
4-
4-
1
¦1
4-
4
4
4-
4-
+
JM
0-0013241
O-OO73I34
0-0132828
0*0192302
0-0251533
0*0310498
0-0*369177
0-0427547
0-0485586
O-O543274
0-0000589
0-0657511
0-0714.017
0-0770089
0-0825704
0-0880844
o-o<K5488
0-0989017
0-1043211
O-1O<)(J5I
0-1148718
0-1200593
0-1251857
0-1302494
0-1352484
0*1401811
o-145045A
0-1498404
o-1545O3O
0-1592138
o-1037892
0-1682883
0-1727096
0-1770510
0-1813*127
o* 1854916
0-1895868
o- 1035970
O-KO52O8
0-2013569
0-205104 r
0-2087011
0-2123267
0-215*7999
0-2191794
0-2224642
O-22SO533
0-2287457
0-2317403
0-2346363
Yx(x)
- 0-3022627
- 0-3017411
- 0-3011029
- 0-3003486
- 0-2994789
- 0-2984943
- 0-2973957
- 0-2961837
- 0-2948590
- 0-2934226
- 0-2918752
- 0-29021*77
- 0-2884511
- o-2865>63
- 0-2845944
- 0-2825063
- 0-2803132
- 0-2780161
-- 0-2756103
- 0-2731149
- 0-2705132
- 0-2678124
- 0-2650138
- 0-2621187
- 0-2591285
- 0-2560446
- 0-2528084
- 0-2490015
- 0-246245*1
- 0-2428010
- 0-2392706
- 0-2356555
- 0-2319574
- 0-2281778
- 0-2243185
- 0-2.203810
- 0-2163672
- 0-2122788
- 0-2081175
- 0-2038851
- o-1995834
- 0-195-2143
- 0-1907797
- 0-1862813
- 0-1817211
- 0-1771010
- 0-1724229
- 0-1676888
- 0-1629007
- 0*1580605
0*3022656
0*3018297
0-3013957
0*3009636
0-3005333
0-3001049
0-2996784
0-2992536
0-2988307,
0-2984096
0-2979903
0-2975727
0-2971569
0-2967429
0-2963306
0-2959200
0-2955112
0-2951041
0-2946986
0-2942948
0-2938927
0-2934923
0*2930935
0-2926963
0-2923007
0*2919068
0*2915145
0-2911237
0-2907345
0-2903469
0*2899609
0*2895764
0-2891935
0-2888120
0*2884321
0-2880537
0-2876768
0-2873014
0-2869274
0-2865549
0-2861839
0-2858143
0-2854462
0-2850795
0-2847142
0-2843503
0-2839878
0-2836267
0-2832670
0-2829087
argH(
270°
271°
272°
273°
274°
275°
277°
278°
279°
280°
281°
282°
283°
285°
286°
287°
288°
289°
2900
291°
293°
294
295°
296°
297°
298°
299°
3000
302°
3030
3040
305
306
307°
3O8C
3ioc
3iic
312°
313^
1
3i|c
318
319
320
321
322
323
324
326
15'
2K
39'
Q/
56'
4'
12'
21'
29'
37'
45'
54'
to.
IO'
19'
27'
35'
43'
52'
0'
8'
17'
25'
33'
42',
5°
58'
• 6'
15'
23'
31
40
48'
56'
5;
13
21'
3O
38
;46
55
3
s 11
3 20
D 28
3 36
'45
53
0 2
Io"
33;
3''
19*
34;
6"
22-
38'*
55'-
11*
28"
45'
2'
19'
36^
54'
11'
29'
47'
5'
23'
42'
0'
19'
37
56
33
27
37
65
08
69
45
37
45
69
09
65
36
22
23
4°
1
17
78
54
'00
'46
'07
'82
56-70
15
34
54
13
33
52
72
'87
*'i6
'58
¦13
•82
12*63
32
52
12
33
53
14
34
,55
' 16
;37
58
' 20
' 41
' 3
¦58
¦65
•85
2
•20
'^89
;7i
•72
^90
0
'•62
''16
4- 0-3466429
4- 0-3470978
4- 0-3476699
+ 0-3483585
+ 0-3491631
4- 0-3500830
4- 0-3511175
4- 0-3522659
+ O-3535275
+ O-3549OI3
+ 0*3563867
+ 0-3579825
+ 0*3596880
4- 0-3615021
4- 0*3634239
+ O-3654523
4- 0-3675862
4- 0-3698244
4- 0-3721659
4- 0-3746094
+ O-377I537
+ O-3797976
+ 0-3825396
+ 0-3853786
4- 0-3883131
4- 0-3913417
4- 0-3944630
+ 0-3976756
4- 0-4009779
4- 0-4043684
4- 0-4078456
4- 0-4114078
4- 0-4150535
4- 0*4187811
4- 0-4225888
4- 0-4264750
4- 0-4304379
4- 0-4344758
+ 0-4385870
4- 0-4427696
4- 0-4470219
+ 0-4513419
+ 0-4557279
4- 0-4601780
4- 0-4646902
4- 0-4692627
4- 0-4738934
+ 0-4785806
.+ 0-4833221
+ 0-4881160
X
7*O2
/
7'°4
7*06
7*08
7*10
7*12
7*14
7*16
7.18
7*20
7*22
7-24
7-26
7-28
7-30
7.32
7-34
7-36
7-38
7-40
7-42
7-44
7-46
7-5O
7-52
7-54
7-56
7 *5^
7-60
7-62
7*64
7-66
7-68
7.70
7.72
774
7-7§
7.78
7-80
7-82
7-84
7-86
7-88
7-90
7-92
7-94
7-96
7-98
8*oo
682
TABLES OF BESSEL FUNCTIONS
Table I. Functions of order zero
X
8-O2
8-O4
8-o6
8-o8
8-io
8-12
8*i6
8-i8
8-2O
8-22
8-24
8-26
8-28
8-30
8-32
2*3*
8-36
8-38
8-40
8-42
8-44
8-46
8-48
8-50
8-52
8-54
8-50
8-58
8-6o
8-62
8-64
8-66
8-68
8-70
8-72
f-74
8-76
8-78
8*8o
8-82
8-84
8-86
8-88
8-90
8-92
8*94
8-96
8-98
9-00
JM
+ O-I669299
+ O-I62I542
+ P-I573255
+ 0-1524459
+ O-I475I75
+ 0-1425423
+ O-I375223
4- 0-1324598
4- O-I273568
4- O-I222I53
+ O-II7O375
+ O-III8256
4- 0-1065816
+ O-IOI3O77
+ O'O96oo6l
+ 0-0906789
+ O-O853282
+ 0-0799563
+ 0-0745652
+ 0-0691573
+ O-0637345
+ 0-0582992
+ 0-0528534
+ 0-0473994
+ 0-0419393
+ 0-0364752
+ 0-0310094
+ 0-0255440
+ O*O2Oo8l2
+ 6-0146230
+ 0-0091717
+ 0-0037293
- O-OOI7OI5
- O'OO7I2OO
- O-OI25227
- O-OI79O8I
- 0-0232739
- 0*0286182
- 0*0339388
- 0*0392338
- O-O445OII
- 0-0497387
- CO549445
- 0*0601167
-. 0*0652532
- 0*0703522
- O-O754II6
- 0-0804295
- 0*085404!
- 0-0903336
nw
+ 0*2266339
+ 0-2296480
+ 0*2325628
+ 0*2353776
+ 0*2380913
+ 0*2407033
+ 0-2432126
+ 0*2456187
4- 0-2479207
+ 0-2501180.
+ 0-2522101
4- 0-2541963
+ 0-2560762
+ 0-2578492
+ 0-2595150
+ 0-2610730
+ 0-2625230
4- 0-2638647
4- 0-2650977
+ 0-2662219
+ 0-2672370
+ 0-2681430
+ 0-2689397
+ 0-2696271
+ 0-2702051
+ 0-2706738
+ 0-2710333
+ 0-2712837
+ 0*27142*51
+ 0-2714577
+ 0*2713818
+ 0*2711977
+ 0*2709056
+ 0*2705060
+ 0*2699992
+ 0*2693857
4- 0-2686660
4- 0*2678405
+ 0-2669100
4- 0*2658749
+ 0*2647360
+ 0-2634939
+ 0-2621493
+ 0-2607030
+ 0-2591558
+ 0-2575085
+ 0-2557620
+ 0-2539172
+ 0-2519741
+ 0-2499367
0-2814756
O-28II266
0-2807789
0-2804324
0-2800873
O-2797434
0-2794007
0-2790594
0*2787192
0*2783803
0-2780427
0-2777062
0-2773710
0-2770370
0*2767042
0-2763725
0-2760421
0-2757128
O-2753847
0-2750578
0-2747321
0-2744075
0-2740840
0-2737617
O-27344O5
0-2731204
0-2728025
0-2724836
0-2721669
0-2718513
0-2715368
0-2712233
0-2709109
0-2705996
0-2702894
0-2699803
0-2696722
0-2693651
0-2690591
0-2687541
0*2684502
0-2681473
0-2678454
0-2675445
0-2672446
0-2669458
0-2666479
0-2663510
0-2660552
0-265760;
axgH^{x)
413° 37' 33''75
414 46 26*87
4I5° 55' i9'-94
417° 4' 12*98
4180 13' 5'-g8
4I90 2l' 58^95
420° 30;;.51 "87
421° 39' 44-76
422° 48 37*62
423 57 3o'-43
4250 6' 23*21
4260 15' i5'-96
427° 24' 8*67
428° 33' 1*35
429 41 53''99
43°° 5°' 4°"*59
431° 59/ 39-16
433° 8'31*70
434° 17 24*21
4350 26' i6?68
436° 35' 9-i 1
437 44 1*51
438° 52' 53*88
4400 1 46*22
4410 io' 38*53
4420 19' 30*80
443° 28' 23*04
444° 37 15-25
445 46' 7*43
446° 54' 59?58
448° 3' 51*69
449° 12' 43*77
4500 21' 35*83
4510 30' 27*85
45 20 39' 19*84
4530 48' 11*80
454° 57', 3;73
457° 14' 47*51
458° 23' 39*35
459° 32' 3I*I7
4600 41' 22*95
4610 50' 14*71
4620 59' 6*44
464? 7' 58*14
4650 16' 49*81
466° 25' 41*45
467° 34 33-07
4680 43' 24*66
4690 52' 10*22
+ 0-3049098
+ 0-3077342
+ 0-3104602
+ 0-3130870
+ 0-3156137
+ 0-3180394
+ 0-3203635
+ 0-3225852
+ 0-3247036
+ 0-3267183
+ 0-3286286
+ 0-3304339
+ 0-3321337
+ 0-3352147
+ 0-3365952
+ 0-3378684
+ 0-3390341
+ 0-3400920
4- 0-3410418
+ 0*3418834
+ 0-3426166
+ 0-3432414
+ 0-3437576
+ 0*3441653
4- 0*344^644
+ 0*3446550
+ 0-3447373
+ 0-3447114
+ O-3445775
+ O-3443357
+ 0-3439865
+ 0-3435301
4- 0-3429669
+ 6-3422972
4- 0-3415216
4- 0*3406404
+ 0-3396543
4- 0-3385638
+ O-3373694
4- 0-3360719
4- 0-3346718
+ 0-3331700
+ 0-3315672
4- 0-3298642
4- 0-3280617
4- 0*3261608
4- 0-3241622
4- 0-3220669
4- 0-3198760
X
8-O2
8*04
8*oo
8*o8
8-io
8-22
8-14
8-16
8*i8
8*20
8-22
8-24
8-20
8-28
8-30
8-32
8*34
8-36
8-38
8-40
8-42
8-44
8-46
8-48
8-50
8-52
.8-54
8-50
8-58
8-6o
8-62
8-64
8-66
8-68
8-70
8-72
8-74
8-76
8-78
8-8o
8*82
8-84
8-86
8-88
8-90
8*92
8-96
8-98
9*00
TABLES OF BESSEL FUNCTIONS
Table I. Functions of order unity
683
X
8-O2
8*04
8«o6
8*o8
8-io
8-12
8-14
8-i6
8-i8
8-2O
8-22
8-24
8-26
8-28
8-30
8.32
§*32
8-36
8-38
8-40
8-42
8-44
8-46
8-48
8-50
8-52
f5i
8-56
8-58
8-60
8-62
8-64
8-66
8-68
8-70
8-72
!"?*
8-76
8-78
8*8o
8-82
8-84
8-86
8-88
8-90
8-92
8-94
8-96
8-98
9-00
+ 0-2374329
+ 0-2401291
+ 0*2427241
+ 0-245217-}
+ 0-2476078
+ 0-2498950
+ 0-2520782
+ 0-254157°
+ 0-2561306
+ 0-2579986
+ 0-2597605
+ 0*2614159
+ 0-2629644
+ 0-2644050
+ 0-2657393
+ 0-2669651
+ 0-2680829
+ 0-2690924
+ 0-2699936
+ 0-2707863
+ 0-2714704
+ 0-2720460
+ 0*2725131
+ 0-2728717
+ 0-2731220
+ 0-2732640
+ 0-2732981
+ 0-2732244
+ 0-2730432
+ 0-2727548
+ 0*2723596
+ 0-2718580
+ 0-2712504
+ 0-2705372
+ 0-2697190
+ 0-2687964
+ 0-2677699
+ 0-2666402
+ 0*2654079
+ 0*2640737
+ 0-2626384
+- 0-2611028
+ 0-2594677
+ 0-2577339
+ 0*2559024
+ 0-2539740
+ 0-2519497
+ 0-24983O6
+ 0-2476176
+ 0-2453118
Yt(x)
- 0-1551702
- 0-1482318
- 0-1432475
- 0-1382191
- 0-1331488
-r 0-1280386
- 0-1228906
- 0-1177069
- 0-1124896
- 0-1072407
- 0-1019624
- 0-0966569
- 0*0913261
- 0*0859723
- 0*0805975
- 0*0752040
- 0-0697937
- 0-0643690
- 0-0589319
- 0-0534845
- 0-0480290
- 0-0425676
- 0*0371023
- 0-0316353
- 0-0261687
- 0-0207046
- 0-0152452
- 0-0097926
- 0*0043488
+ 0-0010840
+ 0-0065038
+ 0-0119084
+ 0-0172950
+ 0*0226640
+ 0*0280110
+ °-°333346
+ 0-0386328
+ 0*0439037
+ 0-0491453
+ 0-0543556
+ 0-0595326
+ 0-0646744
+ 0*0697790
+ 0-0748447
+ 0-0798694
+ 0-0848513
+ 0-0897886
+ 0-0946795
+ 0-0995220
+ 0-1043146
0-2825517
0-2821961
0*2818419
0-2814889
0-2811373
0-2807871
0-2804381
0-2800905
0-2797441
0-2793991
0-2790553
0-2787128
0*2783716
0*2780316
0-2776929
O-2773554
0-2770191
0-2766841
0-2763503
0*2760177
0*2756864
O-275356?
0-2750272
0-2746994
0-2743728
0-2740473
0-2737230
0-2733998
0*2730779
0-2727570
0*2724373
0-2721187
0*2718012
0-2714849
0-2711696
0-2708555
0*2705424
0*2702305
0-2699196
0-2696098
0-2693011
0-2689934
0*2686868
0*2683813
0*2680768
0-2677733
0-2674709
0*2671694
0*2668691
0*2665697
,T(i). .
arg H x (x)
327° 10' 24*81
328° 18' 46*58
329° 27' 8?46
33O° 35' 3o'-46
33i 43 52*57
332° 52' 14-79
334° o'37*12
335° 8'59*56
336° 17' 22*11
337° 25' 44'-78
338° 34' 7r55
3390 42 30-42
34° 5°'53v4O
341 59' l6'-49
343° 7'39''69
3440 16' 2'igg
345° 24' 26*39
346° 32' 49"9O
347° 41' I3*5i
348° 49' 37?22
349° 58' 1-O3
351 6' 24*94
352° 14' 48*95
353 23' 13*05
354 3i' 37-26
355° 40' 1*56
356° 48' 25*97
357° 56' 50*46
359° 5'i5-o6
360° 13' 39'--74
361° 22' 4*52
362° 30' 29*39
363° 38' 54*35
364° 47 I9*4i
365 55' 44-57
367° 4' 9*81
368° 12' 35'' 14
369° 21' 0*57
370° 29' 26*08
37i°37'5i8
372° 46' 17^36
373 54 43"i4
375° 3' 9-oo
376° 11'34^95
377° 20' 0^98
3780 28' 27"io
379° 36'53-3O
380° 45' 19*59
381° 53 45-96
383° 2'12^41
+ 0-4929604
+ 0-4978531
+ 0-5027922
+ 0-5077756
+ 0*5128012
+ 0-5178671
+ 0*5229711
+ 0-5281111
+ 0-5332850
+ 0-5384907
+ 0*5437262
+ 0*5489893
+ 0-5542779
+ 0-5595898
+ 0-5649229
+ 0-5702752
+ O-5756443
+ 0-5810283
+ 0-5864249
+ 0-5918321
+ 0-5972476
+ 0-6026694
-1- 0-6080953
+ 0-6135232
+ 0-6109510
+ 0-6243764
+ 0-6297975
+ 0*6352120
+ 0*6406180
H- 0-6460132
+ O-65I3957
+ 0-6567633
-I- 0-6621130
+ 0-6674455
+ 0-6727561
+ 0-6780436
+ 0-6833000
+ o-68»54i3
+ 06937475
+ 0-6989226
+ 0-7040647
+ 0-7091718
+ 0-7142420
+ 0-7192734
+ 0-7242641
+ 0*7292122
+ 07341159
+ 0*7389734
+ 0*7437828
+ 07485424
X
8*02
8-04
8-o6
8-o8
8-io
8-12
8*14
8*16
8-18
8-2O
8*22
8*24
8*26
8*28
8*30
8*32
8-34
8-36
8-38
8-40
8-42
8-4^
8-46
8-/|8
8-50
8-52
8-54
8-56
8-58
8-6o
8-62
8-64
8-66
8*68
8-70
872
Pi
8*76
878
8-8o
8-82
•8-84
8-86
8*88
8*90
8*92
§•94
8*90
8-98
9-00
684
TABLES OF BESSEL FUNCTIONS
Table I. Functions of order zero
X
9'O2
9-04
9-06
9-08
9-10
9-12
9-14
9-16
9-18
9-20
9-22
9-24
9-26
9-28
9'3O
9-32
9-34
9-36
9-38
9-40
9-42
9-44
9.46
9-48
9-5O
9-52
9'54
9-56
9-58
9-60
9-62
9-64
9-66
9-68
9-70
9-72
9-74
9-76
9-78
9-80
9-82
9-8a
9-86
no
9-88
9-90
9-92
9-94
9-96
9-98
io-oo
- 0-0952160
- 0-1000496
- 0-1048325
- 0-1095629
- 0-1142392
- 0-1188596
- 0-1234224
- 0-1279258
- 0-1323684
- 0-1367484
- 0-1410642
- 0-1453143
- 0-1494972
- 0-1536113
- 0-1576552
- 0-1616274
- 0-1655265
- 0-1693511
- 0-1730999
- 0-1767716
- 0-1803648
- 0-1838783
- 0-1873109
- 0-1906615
- 0-1939287
- 0-1971117
- 0-2002092
- 0-2032202
- 0-2061437
- 0-2089787
- 0-2117244
- 0-2143797
- 0-2169439
- 0-2194161
- 0-2217955
- 0-2240814
- 0-2202730
- 0-2283698
- 0-2303710
- 0-2322760
- 0-2340844
- 0-2357955
- 0-2374090
- 0-2389243
- 0-2403411
- 0-2416590
- 0-2428777
- 0-2439968
- 0-2450163
- o-245935c
t
+ 0-2478029
+ 0-2455748
+ 0-2432536
+ 0-2408402
+ 0-2383360
+ 0-2357420
+ 0-2330595
+ 0-2302898
+ 0-2274341
+ 0-2244937
+ 0-2214700
+ 0-2183644
+ 0-2151782
+ 0-2119130
+ 0-2085701
+ 0-2051510
+ 0-2016573
+ 0-1980905
+ 0-1944522
+ 0-1907439
+ 0-1869673
+ 0-1831240
+ 0-1792157
+ 0-1752440
+ 0-1712106
+ 0-1671174
+ 0-1629659
+ 0-1587580
+ 0-1544955
+ 0-1501801
+ 0-1458137
+ 0-1413982
+ 0-1369352
+ 0-1324268
+ 0-1278748
+ 0-1232810
+ 0-1186475
+ 0-1139760
+ 0-1092686
+ 0-1045271
+ 0-0997535
+ 0-0949498
+ 0-0901178
+ 0-0852597
+ 0-0803773
+ 0-0754727
+ 0-0705477
+ 0-0656045
+ 0-0606450
+ 0-0556712
I«™WI
0-2654663
0-2651734
0-2648814
0-2645904.
0-2643003
0-2640112
0-2637230
0-2634358
0-2631495
0-2628641
6-2625796
0-2622961
0-2620135
0-2617318
0-2614510
0-2611711
0-2608921
0-2606140
0-2603368
0-2600604
0-2597850
0-2595104
0-2592367
0-2589638
0-2586918
0-2584206
0-2581503
0-2578809
0-257612^
O-2573445
0-2570775
0-2568114
0-2565461
0-2562816
0-2560180
O-255755I
O-255493I
0-2552318
0-2549714
0-2547117
0-2544529
0-2541948
0-2539375
0-2536810
0-2534253
0-253170
0-252916
0-252662
0-252410
0-252158
arg
7Io
72
73°
474°
475°
476°
477°.
479°
.80°
.81 °
482°
483°
484°
485°
487°
488°
489°
490°
491°
4920
493°
495!
496C
497°
498°
499C
5°°
5O2c
5°3C
504'
5O5
506
507
508
5n
512
513
514
515
5i6
518
519
520
521
522
523
524
52?
527
HW(x)
i'
9'
18'
27'
36'
45'
54,
3'
11'
20'
29'
38'
47'
56'
5'
13'
22'
31'
4O;
49'
58
7
15
24
33
42
„_
> 0
' 9
j
= 26
= 35
44
3 53
0 2
°I0
I19
°28
°.37
:^
©,
°3<
4i
7 75
59*26
50*73
42*18
33'-6o
25*01
16-39
73
59"O5
50'-35
41*62
32*86
24*08
15*28
6*44
5 7 9
48''70
39''00
30*87
21*92
12*95
, 3 "94
54-92
'36*80
'27*70
'18*58
' 9?44
' 0*28
'51*08
'41*87
'32*65
23*40
' 14*12
' 4*82
'55-49
46*15
'36*79
'27*40
18*00
' 8*57
'59-12
.'49*65
'40*1'
)' 30*6^
)'21*11
y 11*56
°57' 1*99
0
°i;
5 52*39
^'42*78
H.W
+ O-3I759O4
+ O-3I52III
+ O-3I27393
+ O-3IOI76I
+ O-3O75226
+ O-3O478OO
+ O-3OI9495
+ O-299O324
+ O-296O3OO
+ O-2929435
+ O-2897743
+ 0-2865238
+ O-283I934
+ 0-2797845
+ 0-2762985
+ O-272737O
+ O-2691OI4
+ O-2653933
+ O-26l6l43
+ O-2577659
+ 0-2538498
+ O-249867S
+ 0-2458208
+ O-24I7II2
+ O-23754O6
+ O-2333IO7
+ O-229O23I
+ 0-2246796
+ O-22O282I
+ O-2I58322
+ O-2II33I9
+ O'2O67829
+ O-2O2I87I
+ 0-1975464
+ O-I881375
+ O-I833732
+ 0-17857X5
+ O-I737344
+ O-I688637
+ O-I6396I5
+ O-I59O296
+ O-I54O7OO
+ 0-1490847
+ O-I44O757
+ O-I390449
+ O-I339943
+ 0-1289259
+ 0-1238417
+ 0-1187437
X
9-02
9-O4
9-00
9-08
9-10
9-12
9-14
9-16
9-18
9*20
9-22
9'24
9-26
9-28
9-30
9-32
9-34
9-36
9-38
9-40
9-42
9-44
9.46
9-48
9-5O
9*52
9-54
956
9-58
9-60
9-62
9-64
9-66
9-68
9-7O
9.72
974
9.76
978
9-80
9-82
9-84
9-86
9-88
9-90
9-92
9*94
9-96
9-98
IO-OO
TABLES OF BESSEL FUNCTIONS
Table I. Functions of order unity
685
X
g-02
9-04
9-06
9-08
9-10
9'12
9-14
9'i6
9-18
9-20
9-22
9*24
9*26
9-28
9-3O
9-32
9-34
9-36
9-38
9-40
9-42
9-44
9-46
9-48
9-5O
9'52
9'54
9-56
9-58
9'6o
9-62
9-64
9-66
9-68
97°
9-72
974
976
9-78
9-80
9-82
9-84
9-86
9-88
9-90
9-92
9-94
9-96
9-98
IO-OO
4- 0-2429143
4- 0-2404263
4- 0-2378489
+ 0-2351833
4- 0-2324307
4- 0-2295925
4- O-2266698
4- 0-2236640
4- 0-2205765
4- 0-2174087
+ 0-2141618
4- 0-2108375
4- 0-2074370
4- O-2O3962O
4- 0-2004139
+ 0-1967943
4- 0-1931047
4- 0-1893468
4- 0-1855221
4- 0-1816322
4- 0-1776789
4- 0-1736637
4- 0-1695884
+ 0-1654548
4- 0-1612644
4- 0-1570192
4- 0-1527208
4- O- [48371 T
4- 0-143^718
4- 0-1395248
4- 0-13503x9
4- 0-1304950
4- 0-1259159
4- 0-1212965
4- 0-1166386
4- 0-1119443
4- 0-1072154
4- 0-1024537
4- 0-0976613
4- 0-0928401
4- 0-0879920
4 0-0831189
4- 0-0782229
4- 0-0733059
+ 0-0683698
4- 0-0634167
4- 0-0584484
+ 0-0534670
4- 0-0484745
4- 0-0434727
Y^x)
4- 0-1090553
+ 0-1137425
+ 0-1183744
4- 0-1229495
4- 0-1274659
4- 0-1319221
4 0-1363164
4- 0-1406474
+ 0-1449133
4- O-I49II28
+ O-I532443
4- 0-1573063
4- 0-1612974
4- 0-1652162
+ 0-1690613
4- 0-1728314
4- 0-1765251
4- 0-1801413
4- 0:1836785
+ 0-1871357
4- 0-1905116
4- 0-1938050
+ 0-1970150
4- 0-2001403
1- 0-2031799
4- 0-2061329
4- 0-2089982
-I- 0-2117749
4- 0-2144621
4- 0-2x70590
4- 0-2195646
4- O-22I9783
4- 0-2242992
4- 0-2265267
4- 0-2286600
4- 0-2306986
-1- 0-2326417
4- 0-2344889
4- 0-2362395
4- 0-2378932
4- 0-2394495
4- 0-2409079
4- 0-2422681
4- 0-2435297
4- 0-2446924
4- 0-2457560
4- 0*2467203
4- 0-2475850
+ 0-2483501
4- 0-2490154
I*?WI
0-2662713
0-2659740
0-2656776
0-2653823
0-2650879
0-2647945
0-2645021
0-2642107
O*26392O2
0-2636307
0-2633421
0-2630545
0-2627679
0-2624.822
0-2621974
0-2619135
0-2616306
0-2613486
0-2610675
0-2607873
0-2605080
O-26O2297
O-2599522
0-2596756
0-2593990
0-2591250
0-2588511
0-2585780
0-2583058
0-2580344
0-2577639
O-2574943
0-2572255
0-2569576
0-2566904
0-2564242
0-2561587
0-2558941
0-2556303
O-2553673
0-2551052
0-2*548438
o- 2545833
0-2543235
0-2540646
0-2538064
0-2535491
0-2532925
0-2530367
0-2527816
arg
3840
386°
387
388°
389°
39i°
392°
393°
394°
395°
396°
397°
399°
400°
401°
402°
403°
4°5°
406°
408°
4090
4100
411°
*\2l
414°
416°
417°
418°
4190
420°
421°
422°
424°
•125
426
4 27°
428°
429^
43^°
433°
434
435°
436
«Zo
438°
440
10'38'.
19' 5-
27'32*
35'59-
44 25 •
52^52;
9' 46 •
18'14'
26'41'-
35; 8;-
52; 3;
8' 58'
17'26'
25'54'
34 22*
42 50'
51'18'
59' 46'
8' 14'
16'42'
25' 10'
33'30'
42' 7'
50 36'
59' 4'
7-33
16' 1'
24' 30
32 5()
4 1' 28
A(>' 57
58' 26
6' 55
15'24
2 Y 54
32'23
4(>'52
49' 22
57 52
6'21
14'5°
23'20
31' 50
40'20
48' 49
57'J9
5 49
94
56
26
04
9O
84
86
95
12
37
70
59
7S5
49
27
13
06
06
zi
28
50
79
15
58
08
'64
'28
'99
'76
'61
• 52
'49
•53
•'64
•'82
•06
•3"
•73
*i6
"¦(>(>
"•'12
'•84
*52
*27
*oo
;95
-88
*87
+
4-
4-
4-
+
+
4-
4-
4-
+
+
4-
4-
4-
+
+
4-
4-
4-
4-
+
4-
4-
4-
+
4-
4-
4-
¦(-
4-
+
'1-
4-
4-
4-
+
4-
4-
-1
-1-
4-
4-
4-
4-
+
+
4-
4-
4-
+
O-75325O4
O7579O5I
0-7625048
O767O477
0-7715322
O-7759567
0-7803195
0-7846192
O788854O
07930226
0-7971234
O-8OII549
0-8051156
0-8090043
0-8128195
0-8165598
O-82O224O
0-8238107
0-8273187
0-8307469
0-8340939
O-8373587
0-8405401
0-8436371
0-8466485
0-8495735
0-8524110
0-8551601
0-8578198
0-8603894
0-8628679
0-8652546
0-8675487
0-8697495
0-8718563
0-8738685
O-8757855
0-877(^066
o-B^ttH
o-88o95<L
0-8824901
0-8839230
0-8852579
0-8864944
0-8876322
0-8886710
0-8896106
0-8904508
0-8911914
0-8918325
X
9-02
9-O4
9-06
9-08
9*lo
9-12
9-14
9-16
9-18
920
9-22
9-24
9-26
9-28
9-30
9-32
9'34
9-36
9-38
9-4°
9-42
9-44
9-46
9-48
9-50
9-52
9-54
9-56
9-58
9-60
9-62
9-64
9-66
9-68
97°
9-72
9-74
976
978
9-80
9-82
9-8.1
9-86
9-88
9-90
9-92
9-94
9-96
9-98
io-oo
686
TABLES OF BESSEL FUNCTIONS
Table I. Functions of order zero
arg
IO-O2
IO-O^
IO-Of
io-o8
IO-IO
IO-I2
IO*I,<
IO*I(
10-18
IO-2O
10-22
10-2^;
I0-2t
IO-28
IO-3O
O-32 I -
io-3(o
IO-38
10-40
10-42
10-4/
io-4f
IO-
10-50
10-52
10-54
10-56
10-58
io-6o
10-62
10-64
io-6<:
io-68
10-70
10-72
10-74
10-76
io-
IO-«O
10-82
IO'
io-86
io-88
10-90
10-92
10-94
10-96
10-98
II'OO
0-2467551
0-2474743
0-2480931
0-2486116
0-2490297
• 0-2493474
• 0-24951
- 0-2496822
• 0-2496996
- 0-2496171
- 0-2494350
- 0-2491536
- 0-2487732
- 0-2482942
- 0-2477108
0-2470416
0-2462690
0-2453994
O-244433'
0-243371?
0-2422148
0-2409635
0-239617?
0-2381792
0-2366482
0-2350255
0-2333120
• 0-231508=
¦ 0-229615?
- 0-2276350
- 0-2255670
- 0-2234127
- 0-2211732
- 0-2188495
- 0-2164427
- 0-2139539
- 0-2113843
- 0-2087349
- 0-2060071
- 0-2032020
- 0-2003208
- 0-1973650
- O-I943357
- 0-1912343
- 0-1880622
- 0-1848208
- 0-1815115
- 0*1781356
- 0-1746947
- 0-1711903
+ 0-0506850
+ 0*0456886
+ 0-0406838
+ 0-0356728
+ 0-0306574
+ 0-0256397
+ 0-0206210
+ 0-0156052
+ 0-0105924
+ 0-0055852
+ 0-0005856
- 0-0044044
0-0093830
- 0-0143481
- 0-0192978
0-0242303
0-0291435
0-0340355
0-0389045
6-0437486
• 0-0485659
• 0-0533546
• 0-0581128
- 0-0628386
¦ 0-0675304
- 0-0721862
- 0-0768043
- 0-0813830
- 0-0859205
- 0-0904152
- 0-0948652
- 0-0992689
- 0-1036247
- 0-1079309
- 0-1121859
0-1163881
0-1205360
0-1246281
0-1286627
OM 326384
0-1365537
0-1404073
0-1441977
0-1479234
0-1515832
O-I55I757
• 0-1586996
¦ O-I62I537
• 0-1655367
¦ 0*1688473
0-2519069
0-2516564
0-2514068
0-2511578
0-2509096
O-25O6622
0-2504154
0-2501694
0-2499241
0-2496795
O-2494357
0-2491925
0-2489501
0-2487084
0-2484674
0-2482270
0-2479874
0-2477484
O-2475IO2
0-2472726
0-2470357
O-2467995
0-2465640
0-2463291
0-2460949
0-2458614
0-2456285
0-2453963
0-2451648
O-2449339
0-2447037
0-2444741
0-2442451
0-2440168
0-2437891
0-2435621
O-2433357
0-2431099
0-2428847
0-2426602
0-2424363
0-2422130
0-2419903
0-2417683
0-2415468
0-2413260
0-2411057
0*2408861
0-2406671
0-2404486
528°
529°
532
50
['13*82
'54''4i
534° 7'44*68
535 *6 34*93
536025'25*16
537° 34' I5''37
538°43' 5*56
539°5i'55''73
541 o'45*88
5420 9'36*02
5430 18'26*13
5440 27'16*23
545°36' 6*31
546°44'56*37
547°53 46*41
549° 2'36*44
550011'26*44
551020'16*43
552029' 6*41
553°37'5k-36
5540 46' 46*30
555 55'30'22
4'26-12
'13'16*00
»2o' 5'"8l
'39'45*55
562°48;35*37
5650 6'14*95
566015' 4*71
567023'54*46
5680 32'44*20
569°41'33*91
570050'23*61
573q
2*97
574°16 52*62
575° 25'42*26
576034'31*88
577 43 21*48
578052'11*07
5800 1' 0*6.
581 ° 9 50*21
582° 18'39*7.
583°27'29*2
584°36'18*7
0-1136338
0-1085142
0-1033807
0-0982533
0-0931162
0-0879771
0-0828382
¦ 0-0777014
¦ 0-0725687
- 0-0674420
- 0-0623234
- 0-0572148
- 0-0521181
- 0-0470353
- 0-0419684
- 0-0369192
h 0-0318896
h 0-0268817
h 0-0218972
h 0-0169381
I- 0-0120062
t- 0-0071034
t- 0-0022315
- 0-0026077
- 0-0074123
- 0-0121806
- 0-0169108
- O-O2I6OI2
- 0-0262499
- 0-0308553
" 0-0354157
- 0-039929
- 0-044394
- 0-0488103
" 0-0531741
- 0-0574847
- 0-0617406
- 0-0659402
- O-O7OOO2I
- 0-0741646
- 0-0781864
- 0-0821461
- 0-0860421
- 0-0898731
- 0-0936378
~ 0-0973349
- 0-1009630
- 0-1045209
- O-IO8OO73
- O-III42IO
IO-O2
IO-O4
IO-O8
IO-IO
IO-I2
IO-IA
10-16
10-18
IO-2O
IO-22
IO-24
IO-26
IO-28
I0-3O
IO-32
10-34
1036
10-38
10-40
10-42
10-4
10-4
10-48
1050
10-52
10-54
10-56
10-58
io-6o
IO-62
10-64
io-66
io-68
10-70
1072
10-74
10-70
10
10
10-82
10-84
10-86
io-88
10-90
10-92
10-94
10-91
10-9
II-Oi
TABLES OF BESSEL FUNCTIONS
Table I. Functions of order unitv
687
X
IO-O2
io-OA
io-oo
io-o8
IO-IO
IO-I2
IO-I4
IO-IO
io-i8
IO-2O
IO-22
IO-24
IO-26
IO-28
1O-3O
IO-32
10-34
10-36
10-38
10-40
10-42
10-44
10-46
10-48
10-50
10-52
10-54
10-56
10-58
io-6o
10-62
10-64
10-66
10-68
1070
10-72
10-74
10-76
10-78
1000
10-82
10-84
io-86
io-88
10-90
10-92
IO-94
10-96
10-98
II-OO
Jx(*)
4 0-0384638
+ 0-0334497
4 0-0284322
+ 0-0234135
4 0-0183955
4 0-0133801
+ 0-0083694
4 0-0033652
- 0-0016305
- 0-0066157
- 0-0115886
- 0-0165471
- 0-0214895
- 0-0264137
- 0-0313178
- O-O362OOI
- 0-0410586
- 0-0458914
- 0-0506967
" 0-0554728
- 0-0602176
- 0-0649296
- 0-0696068
- 0-07^2475
- 0-0788500
- 0-0834125
- 0-0879333
- 0:0924107
- 0-0968431
- O-IOI2287
- 0-1055659
- 0-1098532
- 0-1140889
- 0-1182715
- 0-1223994
- O-I2647II
- 0-1304852
- 0-1344401
— 0*1383343
- 0-1421666
- O-I459354
- 0-1496394
- 0-1532774
- 0-1568479
- 0-1603497
- 0-1637815
- 0-1671422
- 0-1704305
- 0-1736452
- 0-1767853
4 <
+
4
+
+
4.
4
4
4
-(-
4
+
4
+
+
4
4-
4
4
+
+
+
4
+
+
4
4-
4
+
4
4
4
+
+
+
+
+
4-
+
4
+
3-2495809
3-2500465
3-2504122
3-2506782
3-2508444
0-2509111
0-2508783
0-2507464
0-2505154
0-2501858
O-2497578
0-2492319
0-2486082
0-2478874
0-2470699
0-2461562
0-2451468
0-2440423
0-2428434
0-2415506
0-2401646
0-2386862
0-2371162
0-2354552
0-2337042
0-2318640
0-2299355
0-2279195
0-2258171
0-2236293
0-2213570
0-2190013
0-2165633
0-2140441
0-2114448
0-2087666
0-2060107
0-2031783
0-2002707
0-1972891
0-1942349
+ 0-1911093
+
+
+
+
4
4
+
4-
0-1879138
0-184.6498
0-1813185
0-1779215
0-1744602
0-1709362
0-1673507
0-1637055
!«¦:'« 1
0-2525274
0-2522739
0-2520212
0-2517692
0-2515180
0-2512676
0-2510179
0-2507690
0-2505208
0-2502733
0-2500266
0-2497806
0-2495353
0-2492907
0-2490469
0-2488038
0-2485614
0-2483197
0-2480787
0-2478385
0-2475989
0*2473600
0-2471218
0-2408843
0-2466475
0-2464114
0-2461760
0-2459412
0-2457071
0-2454736
0-2452409
0-2450088
0-2447773
0-2445465
0-2443164
0-2440869
0-2438581
0-2436299
0-2434024
0-2431755
0-2429492
0-2427236
0-2424.986
0-2422742
0-2420505
0-2418273
0-2416048
0-2413829
0-2411616
0*2409410
axg
441°
442°
443°
444
445°
4460
448°
449°
45°:
451°
452°
453:
456°
457°
458°o
459°
4600
461 °
4620
464°
465°
4660
467°
4680
469°
47O°
472°
473°
474°
475!
476°
4Z
480°
48ic
482°
4.83C
485C
486
488
489
490
491
492
493
494
496
497
«>
14'19*
22'50'
3l'2O*
39'50"
48' 20''
5-5'5i"
5'2I«
I351"
22' 22*
3o'53'
39'23^
47'54'
56'25'-
4 55'
13 26"
3O'28'
38'59'
47 3O"
56' 1'
4' 33'
23' 4'
30; 3|
47' 9*
55'4I'
4 12
12'44'
21'16'
29'47'
38'19
93
04
21
44
73
08
49
95
48
06
69
39
94
80
72
69
71
79
93
12
36
65
00
40
85
35
91
'52
18
'89
'65
46'51T46
55' 23
3'55
12'27
20'59
29'3T
'38' 3
'46'35
\S5'e 7
3,39
12 12
>20^44
°37'49
32
•'23
•'ig
•20
'25
'36
•51
'•71
"96
•26
1
•00
•43
0 46'21r92
°54'54
3 27
•45
?O3
°n'59r65
4.
4*
4
t
4
+
+
4-
+
4
4
+
+
+
4-
4
+
+
4
+
4
+
+
4
+
4
4
+
4
4
4
+
4-
4
+
+
4
+
4
+
4-
4
4
+
4-
4
4
4
HlW
O-8923738
O-8928I55
0*8931574
O-893399O
O-8935423
O-8935856
O-8935295
O-8933744
O-893I2O4
0-8927679
O-8923I72
0-8917685
O-89II224
O-89O3793
O-8895395
O-8886O36
O-8875722
0-8864459
O-8852252
O-8839IO7
O-8825O33
O-88IOO35
O-8794I22
O-87773OI
O-875958O
0-8740969
O-872I475
O-87OIIO9
0-8679879
O-8657796
0-8634870
o-86iiiio
0-8586529
0-8561136
0-8534944
0-8507964
0-8480208
0-8451689
0-8422418
0-8392408
0-8361673
0-8330226
0-8298080
0-8265250
0-8231749
0-8197592
0-8162792
0-8127366
0-8091327
0-8054691
X
I0'02
IO-OA
io-oo
10-08
IO-IO
IO-I2
10-14
IO-IO
10-18
IO-2O
IO-22
IO-24
IO-26
IO-28
IO'3O
IO-32
10-34
IO-36
10-38
10-40
10-42
10-44
10-46
10-48
1050
10-52
10-54
10-56
10-58
io-6o
10-62
10-64
IO-66
IO-68
10-70
10-72
10-74
10-76
10-78
1O-5O
1O-82
10-84
io-86
io-88
10-90
10-92
10-94
10-96
10-98
II-OO
688
TABLES OF BESSEL FUNCTIONS
Table I. Functions of order zero
X
II-O2
H-O4
II'OO
n-o8
11*10
11*12
11-14
ii-i6
II-I8
11-20
11-22'
11-24
11-26
11-28
11-30
11-32
n-34
11-36
11-38
11-40
11*42
11*44
11-46
11-48
11*50
II*52
n-54
11*56
11-58
n-6o
11*62
11-64
ii*66
ii*68
11-70
11-72
11-74
11*76
11-78
ii*8o
n-8
n-8
11-8
n-8
n-9
n-9
n-9
n-9
n-9
I2-O0
Jd*)
- 0*1676238
- 0-1639968
- 0*1603109
- 0-1565675
- 0-1527683
- 0-1489149
- 0*1450089
- 0*1410520
- 0*1370458
- 0-1329919
- 0*1288922
- 0-1247483
- 0-1205018
- 0*1163346
- 0-1120685
- 0-1077650
- 0-1034261
- 0*0990535
- 0-0946491
- 0-0902145
- 0-0857517
- 0-0812623
- 0-0767484
- 0-0722117
- 0-0676539
- 0-0630771
- 0*0584830
- 0*0538735
- 0-0492505
- 0-0446157
- 0-0399711
- 0-0353184
- 0-0306597
- 0-0259967
- 0-0213313
- 0-016665;
- 0-0120006
- 0-0073391
- 0-0026825
+ 0-0019672
+ 0-0066082
+ 0-0112388
+ 0-0158571
4- 0-0204612
+ 0-025049,:
+ 0-0296200
+ 0-0341710
+ 0-038700
4- 0-043207
+ 0-047689;
Yd*)
- 0-1720845
- 0*1752470
- 0-1783338
- 0-1813437
- 0*1842758
- 0-1871289
- 0-1899021
- 0-1925944
- 0-1952050
" 0*1977329
- 0-2001772
- 0-2025372
- 0-2048121
- 0-2070011
- 0-2091034
- 0-2111185
- 0-2130457
- 0-2148843
- 0-2166338
- 0-2182937
- 0-2198634
- 0-2213425
- 0-2227306
- 0-2240273
- 0-2252321
- 0-2263449
- 0-2273652
- 0-2282930
- 0-2291278
- 0-2298697
- 0-2305185
- 0-2310740
- 0-2315362
- 0-2319050
- 0-2321806
- 0-2323629
- 0-2324520
- 0-2324481
- 0-2323513
- 0-2321618
- 0-231879*
- 0-2315056
- 0-2310396
- 0-2304820
- 0-2298332
- 0-2290937
- 0-228263!
- 0*227344
- 0*226335
- 0-2252373
ihYmi
0-2402308
0-2400135
0-2397968
0-2395807
0-2393652
0-2391503
0-2389359
0-2387222
0-2385090
0-2382963
0-2380843
0-2378728
0-2376618
0-2374514
0-2372416
0-2370323
0-2368236
0-2366155
0-2364078
0-2362008
0-2359942
'0-2357882
0-2355828
0-2353779
0-2351735
0-2349696
0-2347663
0-2345635
0-2343612
0-2341595
0-2339582
0-2337575
0-2335573
0-2333576
0-2331584
0-2329598
0-2327616
0-2325639
0-2323668
0-2321701
0-2319740
0-2317783
0-2315831
0-2313884
0-2311942
0-2310005
0-230807;
0-2306146
0-230422;
0-2302306
arg
585°
5860
5880
5°9o
59O
59i:
592°
593°
594°
596°
597°
598°
599°
6oo°
6oi°
6020
604°
605°
6060
6070
6080
6090
6io°
612°
6130
6140
615°
616°
6xjc
619°
62Oc
62IC
622C
623'
624
625
627
628
629
630
631
632
633
635
636
637
638
639
640
641
T-f
45'
53
2'
II'
2O'
29'
38
46'
55'
4'
13'
22
31'
39;
48'
57'
6'
15'
23'
32'
41'
5°'
,"w
8''29
57'77
47-23
36-69
26-13
i5;55'
4*96
54-35
43 T73
33-O9
22 '-44
11-78
1 Tio
50*41
39-7O
28*98
18*25
7'-51
56-75
45-97
35-iS
24*38
59'13''56
8'
16'
25'
34'
43'
52'
0
9
18
27
36
45
'53
' 2
311
D 20
'29
°3l
° 55
0 4
oi3
°22
2-73
51*89
41*04
3°"r7
19*28
8*39
5 7 8
46-56
24*68
13*72
' 2*75
'51*76
'4O*77
' 29''75
' 18*73
' 7*70
'56*65
'45*59
34''52
'23*44
'12*34
' 1*24
030'50*12
°39
4*
38*99
' 27''84
'16*69
H „(*)
- 0*1147608
- 0*1100257
- 0-1212144
- 0-1243200
- 0-1273593
- 0-1303133
- 0-1331870
- 0-1359795
- 0-1386899
- 0-1413173
- 0-1438608
- 0-1463196
- 0-1486929
- 0-1509799
- 0-1531801
- 0-1552926
- 0-1573169
- 0-1592522
- 0-1610982
- 0-1628541
- 0-1645196
- 0-1600942
- 0-1675773
- 0-1689687
- 0-1702681
- 0-1714749
- 0-1725891
- 0-1736163
- 0-1745384
- 0-1753731
- O-I76H44
- 0-1767622
- 0-1773163
- 0-1777760
- 0-1781436
- 0-1784169
- 0-1785968
- 0-1786832
- 0-1786765
- 0-1785768
- 0-1783843
- 0-1780994
- 0-1777222
- 0-1772532
- 0-1766928
- 0-1760413
- 0-1752992
- 0-1744669
- 0*1735451
- 0-1725341
X
ii*
ii-
ii-
ii-
ii-
ii-
ii-
ii-
ii-
ii-
ii-
ii-
ii*
ii*
ii-
11
11
11
11
11
11
11
11
11
11
11
11
11
11
11
11
11
11
11
11
11
11
11
11
11
11
11
11
11
11
11
11
11
11
12
02
04
06
08
10
12
14
16
18
20
22
24
26
28
30
32
34
36
38
40
42
44
4<>
48
5°
52
56
58
60
•62
•64
¦66
•68
•70
•72
•74
•7S
•78
•80
•.82
•84
•86
•88
•90
•92
•94
•96
•98
•00
TABLES OF BESSEL FUNCTIONS
Table I. Functions of order unity
689
X
II-O2
H-O4
II-00
n-o8
II-IO
11-12
II-I4
11-16
ii-i8
II-2O
11-22
11 -24
11-26
11-28
II-3O
11-32
n-34
11-36
11-38
11-40
11-42
n-44
11-46
11-48
11-50
11-52
J1*54
11-56
11-58
ii-6o
11-62
11-64
H-66
11-68
11 -70
11-72
n-74
11-76
11-78
ii-8o
11-82
11-84
n-86
n-88
11-90
11-92
H-94
11-96
11-98
I2-OO
- 0-1798496
- 0-1828371
- 0-1857467
- 0-1885774
- 0-1913283
- 0-1939984
- 0-1965868
- 0-1990926
- O-2OI5I5O
- 0-2038531
- O-2O6IO63
- 0-2082738
- 0-2103549
- 0-2123488
- 0-2142550
- 0-2160729
- O-2I78OI9
- 0-2194415
- O-22O99I2
- O-22245O6
- 0-2238192
- 0-2250966
- 0-2262825
- 0-2273766
- 0-2283786
- 0-2292883
- O-23OIO55
- 0-2308300
- 0-2314617
- O'232OOO5
- 0-2324463
- 0-2327992
- 0-2330591
- O-233226I
- O-2333OO2
- 0-2332817
- 0-233X707
- 0-2329674
- 0-2326720
- 0-2322847
- O-23I8O6O
- 0-2312361
- 0-2305754
- 0-2298243
- 0-2289832
- O-228O528
- 0-2270334
- O-2259255
- 0-2247299
- 0-2234471
+ o-1600021
+ 0-1562419
+ 0-1524266
+ 0-1485578
+ 0-1446371
+ O-I4O666I
4- 0-1366465
4- 0-1325799
4- 0-1284681
4- 0-1243127
-1- 0-1201154
+ 0-1158779
4- O-IIl6O2I
+ 0-1072896
4- O-IO29422
4- 0-0985617
4- 0-0941498
4- 0-0897083
+ 0-0852391
4- 0-0807440
+ 0-0762247
4- 0-0716830
4- 0-0671209
4- 0-0625402
4- O-O579425
+ 0-0533299
4- 0-0487042
4- 0-0440671
4- 0-0394206
4- 0-0347665
4- 0-0301065
4- 0-0254427
+ 0-0207768
4 0-0161106
4- 0*0114460
4- 0-0067849
-I- O-OO2I2O9
- 0-0025199
- 0-0071598
- 0-0117890
- 0-0164057
- O-O2IOO0I
- 0-0255944
- 0-0301628
- 0-0347115
- 0-0392388
- 0-0437430
- 0-0482223
- 0-0526749
- 0-0570992
O-24O72O9
O'24O5OI4
O-24O2826
O-24OO643
0-2398466
O-2396296
O-2394I3I
O-239I972
.O-23898I9
O-238767I
O-238553O
O-2383394
O-238I264
O-2379I4O
O-2377O2I
O-23749O9
O-23728OI
O-237O7OO
O-23686O4
0-2366513
0-2364428
0-2362349
0-2360275
0-2358207
0-2356144
0-2354086
0-2352034
0-2349987
02347946
0-234.5910
0-2343879
0-2341854
O-2339833
0-2337818
0-2335809
0-2333804
0-2331804
0-2329810
0-2327821
0-2325837
0-2323858
0-2321884
0-2319915
0-2317951
0-2315993
0-2314039
0-2312090
0-2310146
0-2308207
0-2306273
rrU). .
arg H1 (x)
498020'32*32
4990 29' 5'-o3
500°37'37*79
501°46 10*59
5020 54'43*4.4
504° 3'16*34
505°11'49*27
5060 20'22*25
507° 28'55*20
508037'28*35
5og°46' 1*46
510° 54'34*61
512° 3' 7*81
5I3°ii'4i*O5
514°20'14*33
515° 28' 47*65
516037'21*01
517° 45'54*42
518° 54'27*8^7
52O° 3' 1*36
521° II'34*89
522° 2O' 8*46
5230 28'42*07
524° 37'I5''72
525 45 49-41
526°54'23*14
5280 2'56*91
529°11'30*72
53O°2O' 4*58
531°28'38*47
532°37'12*39
533° 45 46*36
534-54 20*37
5360 2'54*41
537° 11'28*49
5380 20' 2*6l
539°28'36*77
540 37 10*96
5410 45' 45*19
542° 54'I9?46
544° 2'53-77
545011'28*11
5460 20' 2*49
547° 28' 36*91
548037'11*36
549° 45' 45 "85
55O°54 20*37
552° 2'54*93
' 553°11'29-53
554 20' 4*16
4- 0-8017474
4- O7979691
4- 07941357
4- 0-7902489
4- 0-7863103
4- 0-7823215
4- O7782842
+ O7742OOI
4- O77OO7O7
4- 0-7658979
4- 0-7616832
4- 0-7574286
+ O7531356"
4- 07488060
4- O7444416
+ 0-7400442
+ 0-7356155
+ 0-7311573
+ O72667I5
4- O7221598
+ 0-7176241
4- 0-7130601
+ 07084877
-1- 07038907
4- 0-6992769
+ 0-6946483
4- O-69OOO66
+ 0-6853536
+ 0-6806913
4- 0-67602x5
+ 0-6713459
4- 0-6666665
4- 0-6619851
+ 0-6573035
+ 0-6526236
+ 0-6479472
+ 0-6432761
4- 0-6386122
+ 0-6339572
4- 0-6293131
4- 0-6246815
4- 0-6200643
4- 0-6154633
4- O-6IO88O2
4- 0-6063169
4- 0-6017751
+ 0*5972565
4- 0-5927628
4- O-5882959
+ 0-5838573
X
II-OL
II-O*
II-OC.
n-ot
II-IC
Il-Ii
II'I*
II-IC.
ii-ii
II-2'
11-2".
II-2*
II-2C
II-2fc
II-3C
11-31
11-3*.
ii-3c
11-3^
11-4-.
n-4^
11-4*
11-4c
r i*4ir
ii-5c
It-JC
II-5-
11-51
n*5i
11-6c
il-6i
IX-6,
ll-6(
n-6fc
11-70
11-72
1174
11-76
11-78
11-So
IT-82
II-84
n-86
n-88
1190
11-go
n-94
11-96
11-98
I2-OO
W. B. F.
44
690
TABLES OF BESSEL FUNCTIONS
Table I. Functions of order zero
X
12*02
I2-OA
I2*OO
12-68
I2-IO
*2'I2
I.2-IA
12-10
I2-I8
I2-2O
12-22
I2-2A
12-20
12-28
I2-3O
I2-32
12-34
12-36
12-38
12-40
12-42
12-44
12-46
12-48
12-50
12-52
12-54
12-56
12-58
12-60
12-62
12-6^
12-66
12-68
12-70
12-72
12-74
12-76
12-78
12-80
12*82
12-84
12-86
12-88
12-go
12-92
12-9^
12-96
12-9
13-00
+ 0-0521447
+ 0-0565718
+ 0-0609690
+ 0-0653346
+ 0-0696608
+ 0-0739640
+ O-O782245
+ 0-0824460
+ 0-0866292
+ 0-0907701
+ 0-0948680
+ 0-0989212
+ 0-1029283
+ 0-1068877
+ 0-1107980
+ 0-1146576
+ 0-1184651
+ 0-1222191
.+ 0-1259182
+ 0-1295610
+ 0-1331462
+ 0-1366724
+ 0-1401382
+ 0-1435426
+ 0-1468841
+ 0-1501615
+ O-I533737
+ 0-1565195
+ O-I595977
4- 0-1626072
+ 0-1655471
+ 0-1604160
+ 0-1712131
+ 0-1739374
+ 0-1765879
+ 0-1791636
+ 0-1816637
+ 0-1840872
4- 0-1864334
+ 0-188701,
+ 0-1908904
+ 0-1929997
4- 0-1950281
4- 0-1969764
+ 0-198842,
+ 0-2006261
¦+• 0*2023269
+ 0-2039441
+ 0-2054773
+ 0*2069261
v.w
- 0*2240513
- 0-2227778
- 0-2214173
- 0-2199706
- 0-2184384
- 0-2168214
- 0-2151204
- 0-2133362
- 0-2114698
- 0-2095218
- 0-2074933
- 0-2053852
- 0-2031985
- 0-2009341
- 0-1985931
- 0-1961765
- 0-1936855
- 0-1911210
- 0-1884844
- 0-1857766
- 0-1829990
- 0-1801527
- 0-1772390
- 0-1742591
- 0-1712143
- 0*1681060
- 0-1649354
- 0-1617040
- 0-1584131
- 0-1550641
- 0-1516585
- 0-1481976
- 0-1446830
- 0-1411161
- 0-1374984
- 0-1338314
- 0-1301168
- 0-1263559
- 0-1225504
- 0-1187019
- 0-1148120
- 0-1108823
- 0-106914=
- 0-102909?
- 0-098870,:
- 0-0947977
- 0-090693^
- 0-0865592
- 0-0823968
- 0-0782079
0-2300393
0-2298485
0-2296581
0-2294682
0-2292788
0-2290899
0-2289014
0-2287134
0-2285259
6-2283388
0-2281522
0-2279660
0-2277803
0-2275950
0-2274102
0-2272258
0-2270419
0-2268585
0-2266754
0-2264928
0-2263107
0-2261290
0.2259477
0-2257669
0-2255865
0-2254065
0-2252270
0-2250479
0-2248692
0-2246909
0-2245131
0-2243357
0-2241587
0-2239821
0-2238059
0-2236302
0-2234548
0-2232799
0-2231054
0-2229313
0-2227576
0-2225843
0-222411^
O-222238C
O-222O668
0-2218951
0-2217238
0-2215529
0-221382.
0-22I2I2-
arg
643°
644°
645°
6460
6470
648°
649°
6510
652°
653°
654°
655°O
6560
658°
659°
66o°
66i°
6620
663°
6640
666'
6670
668°
6690
6700
6710
672
67<
676°
67/
678'
679'
680'
682'
683
684
685
686
687
688
690
691
692
693
694
695
697
698
699
" 0
6'
14'
23'
32
41'
52'
58'
7'
16'
25'
34'
43'
51
0'
9'
18'
27'
35'
44
53'
2'
11'
19'
28'
37'
46'
55'
3'
12'
21'
30
>39
> . Q
^ 56
J 5
'14
3 23
32
W
5-52
54*35
43*16
31*96
20*74
9*52
58*29
47''°4
35*78
24*51
13*23
1*94
50*64
39 *3 2
28*00
16*67
5*32
53 "96
42*60
31*22
19*83
8*43
45*6o
34**7
22*73
11*28
59*82
48*35
36*86
25*37
13*87
'50*84
'39-3O
'27*76
'16*21
' 4*65
'4o'53"o8
3 49
3 58
° 7
ol6
°24
°33
0 4.2
0 51
0 0
0 8
•17
41-50
'29^91
'18*31
' 6-70
'55 8
'43?45
'31*81
'20*16
' 8*51
'56-85
45*17
- 0-1714348
- 0-1702475
- 0-1689731
- 0-1676121
- 0-1661654
- 0*1646336
- 0-1630175
- 0-1613180
- O-I595359
- 0-1576720
- 0*1557274
- 0-1537028
- 0-1515994
- 0-1494180
- 0-1471598
- 0*1448257
- 0-1424169
- 0-1399344
- O-I373794
- 0-1347532
- 0-1320567
- 0-1292914
-'0-1264583
- 0-1235588
- 0-1205943
- 0-1175659
- 0-1144750
- 0-1113230
- 0-I08lII2
- 0-1048412
- 0-1015142
- 0-0981318
- 0-0946953
- 0-0912064
- 0-0876664
- 0-0840769
- 0-0804395
- 0-0767556
- 0-0730269
- 0*0692549
- 0*0654413
- 0*0615876
- 0*0576954
- 0-0537665
- 0*0498024
- 0-0458049
- 0*0417755
- 0-0377160
- 0-0336280
- 0-0295133
X
12*
12-
12-
12-
12-
12-
12*
12-
12-
12*
12*
12-
12
12
12-
12
12
12
12
12
12
12
12
12
12
12
12
12
O2
04
OO
08
IO
12
14
16
18
2O
22
24
26
28
3°
32
34
36
38
40
42
44
46
48
50
52
54.
•50
I2-58
12
12
12
12
12
12
12
12
12
12
12
12
12
12
12
12
12
12
•60
62
•64
•66
•68
•70
•72
•76
78
•80
•82
•s±
•86
•88
•90
•92
•94
I2-96
12
13
¦98
•00
TABLES OF BESSEL FUNCTIONS
Table I. Functions of order unity
691
X
I2-O2
I2-O4
I2-O0
I2-O8
I2-IO
12-12
12-14
12-16
12-18
I2-2O
12-22
12-24
12-20
12-28
I2-3O
I2'32
12-34
12-36
12-38
12-40
12-42
12-44
12-46
12-48
12-50
12-52
12-54
12-56
12-58
I2-6O
12-62
1264
12-66
12-68
12-70
12-72
12-74
12-76
12-78
12-80
12-82
12-84
12-86
12-88
12-90
12-92
12-94
12-96
12-98
1300
Jl(*)
- 0-2220777
- 0-2206225
- 0-2190821
- 0-2174574
- 0-2157490
- 0-2139578
- 0-2120846
- 0-2101303
- 0-2080958
- 0-2059820
- 0-2037900
- 0-2015206
- 0-1991749
- 0-1967540
- 0-1942588
- 0-1916907
- 0-1890506
- 0-1863397
- 0-1835591
- 0-1807102
- 0-1777942
- 0-1748122
- 0-1717656
- 0-1686557
- 0-1654838
- 0-1622513
- 0-1589594
- 0-1556097
- 0-1522036
- 0-1487423
- 0-1452276
- 0-1416606
- 0-1380431
- 0-1343765
- 0-1306622
- 0-1269019
- 0-1230971
- 0-1192494
- 0-1153604
- 0-1114316
- 0-1074646
- 0-1034612
- 0-0994229
- 0-0953513
- 0-0912483
- 0-0871153
- 0-0829541
- 0-0787603
- 0-0745538
- 0-0703181
Yx(x)
- 0-0614935
- 0-0658561
- 0-0701853
- 0-0744794
- 0-0787369
- 0-0829561
- 0-0871355
- 0-0912733
- 0-0953682
- 0-0994184
- 0-1034226
- 0-1073791
- 0-1112866
- 0-1151435
- 0-1189484
- 0-1226999
- 0-1263966
- 0-1300372
- 0-1336202
- 0-1371444
- 0-1406084
- 0-1440111
- 0-1473511
- 0-1506272
- 0-1538383
- 0-1569831
- 0-1600606
- 0-1630696
- 0-1660091
- 0-1688779
- 0-1716752
- 0-1743998
- 0-1770509
- 0-1796274
- 0-1821280
- 0-1845534
- 0-1869012
- 0-1891710
- 0-1913621
- O-I934738
- 0-1955054
- 0-1974561
- 0-1993253
- 0-2011125
- 0-2028170
- 0-2044382
- 0-2059758
- 0-2074291
- 0-2087978
- O'2ioo8i4
0-2304343
0-2302419
0-2300499
0-2298584
0-2296674
0-2294769
0-2292868
0-2290973
0-2289082
0-2287195
0-2285313
0-2283436
0-2281564
0-2279690
0-2277833
0-2275974
0-2274120
0-2272270
0-2270425
0-2268585
0-2266749
0-2264917
0-2263090
0-2261267
0-2259449
0-2257635
0-2255826
0-2254020
0-2252220
0-2250423
0-2248631
0-2246843
0-2245059
0-2243280
0-2241505
0-2239734
0-2237967
0-2236204
0-2234446
0-2232092
0-2230942
0-2229196
0-2227454
0-2225716
0-2223982
0-2222253
0-2220527
O-22I88OS
0-2217080
0-2215374
argif'J'w
555°28'38*83
556°37'13*53
557 45 4»?27
558° 54 23*<>4
560° 2'57*84
.561°ii'32*68
562° 20' 7*55
5630 28'42*46
564° 37'17-4O
565°45 52-38
566° 54'27*39
568° 3 2*43
569°ii'37*50
5700 20'12-61
571°28'47^75
572°37'22^93
573 45 58*13
574°54 33-37
576° 3 8*64
577 11'43"95
578°2o' 19-28
5790 28'54*65
580° 37'3o*os
581°46' 5*48
582054'40*94
5840 3'16*43
5850 11' 51-95
5860 20'27*51
587°29' 3-09
588° 37' 38*71
589046'14*35
59O°54'50*03
592° 3'25*74
593° 12' 1*47
5940 20'37*24
595° 29' 13*04
596°37'48*86
597° 46; 24*72
59«°55 0*60
6oo° 3'36i
6oi° 12' 12*45
6O2°2O'48*43
6030 29' 24*43
6o4°38' 0*46
605046'36*51
6o6°55'l2o
608° 3 48*71
609012'24*85
6lO°2l' I*O2
611029'37*22
Hx(*)
+ 0-5794489
+ 0-5750722
+ 0-5707290
+ 0-5064209
+ 0-5621495
+ 0-5579164
+ O-5537234
+ 0-5495718
+ 0-5454634
+ 0-5413995
+ 0-5373819
+ o-5334ii9
+ 0-5294911
+ 0-5256209
+ 0-5218027
+ 0-5180381
+ 0-5143282
+ 0-5106746
+ 0-5070786
+ 0-5035415
+ 0-5000646
+ 0-4966492
+ 0-4932964
+ 0-4900076
+ 0-4867839
+ 0-4836265
+ 0-4805365
+ o-4775i5i
+ 0-4745632
+ 0-4716820
+ 0-4688725
+ 0-4661356
+ 0-4634724
+ 0-4608838
+ 0-4583706
+ O-4559337
+ 0-453574°
+ 0-4512923
-t- 0-4490893
+ 0-4469659
+ 0-4449226
+ 0-4429602
+ 0-4410794
+ 0-4392807
+ O-4375647
+ 0-4359320
+ 0-4343830
+ 0-4329183
+ 0-4315383
+ 0-4302435
X
I2-O2
12-04
I2-O0
12-O8
I2-IO
12-12
12-I4
12-10
12-18
I2-2O
12-22
12-24
12-20
12-28
I2-3O
12-32
12-34
12-36
12-38
12-40
12-42
12-44
12-46
12-48
12-50
12-52
12-54
12-56
12-58
12-60
12-62
12-64
12-66
12-68
12-70
12-72
12-74
12-76
12-78
12-80
12-82
12-84
12-86
12-88
12-90
12-92
12-94
12-96
12-98
13-00
44—2
692
TABLES OF BESSEL FUNCTIONS
Table I. Functions of order zero
/<>(*)
Y9{x)
arg
I3O2
13-04
I3o6
13-08
13-10
13-12
13-18
13-20
13-22
1324
13-26
13-28
13-30
1332
13-34
1336
13-40
13-42
13-44
13-46
13-48
I3-5O
13-52
13-54
I3-56
I3-58
13-60
13-62
13-66
13-68
1370
I3'72
1374
1376
1378
13-80
13.82
13-84
13-86
13-88
13-90
13-92
13-94
13-96
13-98
14-00
+ 0-2082899
+ 0-2095684
+ O-2IO76I2
+ 0-2118679
+ O-2I28882
+ O-2I382I9
+ 0-2146687
+ 0-2154284
+ O-2I6IOO9
+ O-2I66859
+ 0-2171835
+ O-2I75935
+ O-2I79I59
+ O-2t8l5O8
+ 0-2182981
+ 0-2183579
+ 0-2183304
+ 0-2182156
+ C2180I38
+ O-2177252
+ O-2I73499
+ 0-2168884
+ 0-2163409
+ 0-2157076
+ 0-2149892
+ 0-2141858
+ 0-2132981
+ 0-2123263
+ 0-2112712
+ 0-2101332
+ 0-2089128
+ 0.2076107
+ 0-2062276
+ 0-2047641
+ 0-2032208
+ 0-2015986
+ 0-1998982
+ 0-1981203
+ 0-1962659
+ O-I943356
+ 0-1923305
+ 0-1902515
+ 0-1880993
+ 0-1858751
+ 0-1835799
45
+ 0-1787801
+ 0-1762777
+ 0-1737085
+ 0-1710735
- 0-0739941
- o-o697573
- 0-0654990
- O-o6l22II
- 0-0569253
- 0-0526132
- 0-0482867
- 0-0439475
- 0-0395973
- O-O352379
- 0-0308710
- 0-0264983
- O-O22I2I7
- 0-0177428
- 0-0133634
- 0-0089853
- 0-0046101
- O-OOO2396
+ 0-0041244
+ 0-0084802
+ O-OI28262
+ 0-0171605
+ 0-0214816
+ 0-0257876
+ 0-0300770
+ 0-0343480
+ 0-0385990
+ O-O420282
+ 0-0470341
+ O-O5I2I5O
+ 0-0553693
+ 0-0594954
+ 0-0635916
+ 0-0676565
+ 0-0716883
+ 0-0756856
+ 0-0796469
+ 0-0835705
+ 0-0874551
+ O-O9I299O
+ 0-0951009
+ 0-0988593
+ O-IO25727
+ 0-1062398
+ 0-1098592
+ 0-1134294
+ O-II09492
+ O-I2O4I72
+ 0-1238321
+ 0-1271926
C22IO426
O-22O8732
0-2207043
0-22O5357
0-2203676
O-22OI998
O-22OO324
0-2198654
0-2196987
O-2I95325
0-2193666
O-2I92OIO
0-2190359
O-2I887II
0-2187067
0-2185427
O-2I8379O
0-2182158
0-2180528
0-2178903
0-2177281
q-2 175662
0-2174047
0-2172436
0-2170829
0-2169225
0-2167624
0-2166027
0-2164434
0-2162844
0-2161257
0-2159674
0-2158095
0-2156519
0-2154946
0-2153-
0-2151;
0-2150249
0-2148690
0-214713.
0-214558:
0-214403;
0-214248:
0-214094.
0-213940'
0-213787
0-213633'
0-213481
0-213328
0-213176
oo° 26'33*48
¦oi0 35'21*79
020 44' 10*08
O3°o52;5f7
¦05° 1'46*65
06010'34*92
'07° 19'23-18
'08° 28'11*43
'09° 36' 59''68
no° 45' 47*91
711°54'36*14
713° 3 24*35
714012'12*56
715021' 0*76
716029'48*96
7° 38' 37*14
347 25*31
719°56'13*47
7210 5' 1*63
722°13'49*78
724°31'26*05
725°40 14*17
726 49 2*29
727°57' 5O*39
7290 6'38*49
730°15'26*58
731024'14*66
732° 33' 2*73
733 4i'5o*8o
734°50'38*86
735°59 26*90
737° 8 14*9.
738°17' 2*9
739 25'51*00
740°34'39*02
741 43 27*
742°52'15*03
744 1 3; _
745 9 51*01
746°i8'38*99
747°27'26*96
748°36^14*92
75O°53'50*82
752° 2;38*76
753°11'26 .
754°20'14*63
755°29' 2*5
756° 37 5o'-45
0-0253735
- 0-0212104
- 0-0170257
- 0-0128211
- 0-0085984
- 0-0043592
- 0-0001054
+ 0-0041614
+ 0-0084393
+ 0-0127268
+ 0-0170219
+ 0-0213229
+ 0-0256282
+ 0-0299359
+ 0-0342443
+ 0-0385517
+ 0-0428564
+ 0-0471565
+ 0-0514504
+ 0-0557363
+ 0-0600126
+ 0-0642775
+ 0-0685292
+ 0-0727662
+ 0-0769866
+ 0-0811889
+ 0-0853714
+ 0-0895324
+ 0-0936702
+ 0-0977832
+ 0-1018698
+ 0-1059283
+ 0-1099573
+ 0-1139550
+ 0-1179199
+ 0-1218505
+ 0-1257452
+ 0-1296025
+ 0-1334209
+ 0-1371989
+ 0-1409350
+ 0-1446278
+ 0-1482758
+ 0-1518777
+ 0-1554320
+ 0-158937
+ 0-1623925
+ 0-1657960
+ 0-1691466
+ 0-1724429
13-02
13-04
13-06
13*08
13-10
3-12
13-16
13-18
13-20
13-22
13-24
13-26
13-28
13-3°
13-32
13-34
13-36
I3-38
13-40
13-42
I3;4
I3-48
I3-5O
I3-52
I3-5-
I3-
13-
13-6
13-6
13-66
13-68
I3-7O
13-72
13-7
13-76
13-82
13.84
13-86
13-88
I3-9O
13-9
13-94
13-96
13-9
14-0
TABLES OF BESSEL FUNCTIONS
Table I. Functions of order unity
693
Ji{*)
Yx(*)
arg
H{\\x)
I3-O2
1304
13-06
13-08
13-10
13-12
I3-I4
13-16
13-18
13-20
13-22
13-24
13-26
13-28
13-32
1334
13-36
I3-38
13-40
13-42
13-46
13-48
13-50
13-52
13-54
I3-5O
I3-58
13-60
13-62
13-64
13-66
13-68
13-70
I3-72
13-74
I3-7O
I3-78
13-80
13-82
13-84
13-86
13-88
13-90
13-92
13-94
13-96
13-98
14-00
- 0-0660609
- 0-0617841
- 0-0574892
- 0-0531781
- 0-0488525
- 0-0445140
- 0-0401645
- 0-0358056
- 0-0314391
- 0-0270667
- 0-0226902
- 0-0183113
- 0-0139317
- 0-0095532
- 0-0051775
- 0-0008063
+ 0-0035587
+ 0-0079157
+ 0-0122630
+ 0-0165990
+ 0-0209219
+ 0-0252301
+ 0-0295218
+ 0-0337954
+ 0-0380493
+ 0-0422817
+ 0-0464911
+ 0-0506758
+ 0-0548341
+ 0-0589646
+ 0-0630655
+ 0-0671353
H- 0-0711725
+ 0-0751755
+ 0-0791428
+ 0-0830728
+ 0-0860640
+ 0-0908150
+ 0-0946243
+ 00983905
+ O-IO2II2I
+ 0-1057877
+ O-IO94l6O
+ o-i 129955
+ 0-1165249
+ O-I2OOO29
+ O-I234282
+ O-I267995
+ O-I3OII56
+ O-I333752
O-2II2796
O-2I2392O
0-2134183
O-2I43582
O-2I52II5
O-2I5978O
O-2166575
O-2I72499
O-2I7755I
O-2l8l729
0-2185034
0-2187466
0-2189025
O-2I897I2
0-2189527
0-2188473
O-2I8655O
0-2183761
0-2180108
0-2175595
0-2170223
0-2163997
0-2156920
0-2148996
0-2140229
0-2130625
0-2120188
0-2108924
0-2096838
0-2083936
0-2070225
0-2055711
0-2040400
0-2024302
0-2007421
0-1989768
0-1971349
0-1952173
0-1932249
0-1911585
0-1890191
0-1868077
0-1845252
0-1821726
0-1797510
0-1772613
0-1747048
0-1720824
0-1693954
0-1666448
0-2213665
0-2211959
0-2210257
0-2208559
0-2206866
0*2205176
0-2203490
0-2201807
0-2200129
0-2198455
0-2196784
0-2195117
O-2I93454
0-2191795
0-2190139
0-2188487
0-2186039
0-2185195
0-2183555
0-2181918
0-2180285
0-2178655
0-2177029
0-2175407
0-2173788
0-2172174
0-2170562
0-2168954
0-2167350
0-2165750
0-2164153
0-2162559
0-2160969
0-2159382
0-2157799
0-2156220
0-2154644
0-2153071
0-2151502
0-2149936
0-2148374
0-2146815
0-2145260
0-2143708
0-2142159
0-2140614
0-2139072
0-2137533
0-2135998
0-2134466
612°38'13*45
613°46'49-71
6i4°55 25*99
6i6° 4' 2*30
617°12'38*63
618°21^14*99
620° 38' 27*80
621°47' 4-24
622°55'40*71
624° 4'17*21
626 21'30*28
627°30' 6^85
628° 38' 43 '-45
6290 47' 2o'-o8
630°55'56-73
632° 4 33?4r
633 13 10*12
634021'46-85
635° 3°' 23''6O
636°39' 0*38
637° 47'37''19
638 56'14*02
640° 4'50*87
641° 13' 27*75
642 22 4*66
645° 47'55-52
646°56'32-52
648° 5' 9-55
649 13 46*60
6500 22'23*67
651°31' 0*77
652°39'37"89
653°48'15*04
654°56'52-2i
650° 5 29'-41
6570 14' 6*62
658°22'43*86
6590 31'21*12
66o° 39'58*41
661 ° 48' 35*72
662°57'13*05
664° 5'5O-4O
665°14'27-78
666°23' 5-18
667°3i'42''6o
668° 40' 20*04
+ 0*4290341
+ 0-4279106
+ 0-4268732
+ 0-4259222
+ 0-4250579
+ 0-4242805
+ 0-4235900
+ 0-4229868
+ 0-4224709
+ 0-4220422
+ 0-4217010
+ 0-4214472
+ 0-4212807
+ 0-4212014
+ 0-4212094
+ 0-4213044
+ 0-4214062
+ 0-4217547
+ 0-4221096
+ 0-4225507
+ 0-4230776
+ 0-4236901
+ 0-4243876
+ 0-4251699
+ 0-4260365
+ 0-4269869
+ 0-4280206
+ 0-4291371
+ 0-4303358
+ 0-4310161
+ 0-4329775
+ 0-4344191
+ °-43594°4
+ O-4375400
+ 0-4392190
+ 0-4409748
+ 0-4428071
+ 0-4466981
+ 0-4487550
+ 0-4508850
+ 0-4530871
+ 0-4553603
+ 0-4577036
-l- 0-4601160
+ 0-4625965
+ 0-4651439
+ 0-4677571
+ 0-4704350
+ 0-4731766
13-02
I3-O4
13-06
13-08
13-10
13-12
13-16
13-18
13-20
13-22
13-24
13-26
13-28
I3-3O
I3-32
13-34
I3-36
I3-38
13-40
13-42
13-46
13-48
I3-52
13-54
X3-56
I3-58
13-60
13-62
13-64
13-66
13-08
13-70
13-72
13-74
13-76
13-78
13-80
13-82
13-84
13-86
13-88
1390
13-92
13-94
13-96
13-98
14-00
694
TABLES OF BESSEL FUNCTIONS
Table I. Functions of order zero
Y0(x)
arg
Ho(*)
14-02
14-04
14-06
14-08
14-10
14-12
14-14
14-16
14-18
14-20
14-22
14-24
14-26
14-28
14-30
14-32
14-34
14-36
14-38
14-40
14-42
14-44
14-46
14-48
14-50
14-52
14-54
14-56
14-58
14-60
14-62
14-66
14-68
1470
14-72
14-74
14-76
14-78
14-80
+ 0-1683739
+ 0-1656108
+ 0-1627855
+ 0-1598991
+ 0-1569529
+ 0-1539481
+ 0-1508861
+ 0-1477681
+ 0-1445954
+ 0-1413694
+ 0-1380914
+ 0-1347629
+ 0-1313851
+ 0-1279596
+ 0-1244877
+ 0-1209709
+ 0-1174107
+ 0-1138085
+ 0-1101658
+ 0-1064841
+ 0-1027650
+ 0-0990100
+ 0-0952206
+ 0-0913984
+ 0-0875449
+ 0-0836617
+ 0-0797504
+ 0-0758127
+ 0-0718500
+ 0-0678641
+ 0-063856^
+ 0-0598288
+ 6-0557827
+ 0-0517198
+ 0-0476418
+ 0-0435503
+ 0-039447
+ °'O353334
+ 0-0312113
+ 0-0270823
14-82
14*84
14-86
14-88
14-90
14-92
14-94
14-96
14-98
15-00
+ 0-022948
+ 0-018810
+ 0-014670,
+ 0-010530
+ 0-006391
+ 0-002255
- 0-001875
- o-006000
- 0-010117
- 0-014224
0-1304974
O-I337454
O-I369354
0-1400660
0-1431362
+ 0-1461449
+ 0-1490909
O-I5I973I
+ 0-1547905
+ O-I57542I
+ 0-1602268
+ 0-1628437
+ 0-1653919
+ 0-1678704
+ 0-1702783
+ 0-1726147
+ 0-1748790
+ 0-1770701
+ 0-1791875
+ 0-1812302
+'0-1831977
+ 0-1850893
+ 0-1869042
+ 0-1886420
+ 0-1903019
+ 0-1918835
+ 0-1933862
+ 0-1948095
+ 0-1961530
+ 0-1974163
+ 0-1985989
+ 0-199700
+ 0-2007208
+ 0-201659
+ 0-2025163
+ 0-2032910
+ 0-203983
+ 0-2045933
+ 0-2051206
+ 0-2055652
+ 0-2059270
+ 0-20O2OOC
+ O-2O64O2
-f- 0-206515
+ 0-206546
+ 0-2064941
+ 0-206360
+ O-2O6I43'
+ 0-2058^4
+ 0-205464
•2130243
•2128727
•21272I4
1-2125705
I-2I24I9O
O-2I22695
0-2121195
2II9699
0-2118205
O-21I67I5
O-2II5227
0-2113743
0-2112262
0-2110784
0-2109310
0-2107838
0-2106369
0-2104904
0-2103441
0-2101982
0-2100525
9-2099072
0-2097621
0-2096174
0-2094729
0-2093288
0-2091849
0-2090414
0-2088981
0-2087552
0-2086125
0-2084701
0-2083280
0-2081862
0-2080447
0-2079035
0-2077626
0-2070219
0-2074816
0-2073415
0-2072017
0-2070622
0-2069229
0-2067841
0-2066453
0-206506'
0-206368!
0-2062309
0-2060934
0-20595
57°46'38*36
58*55 26*25
7600 4'14*14
761013' 2*02
762021'49*89
63030'37*76
7640 39/ 25*62
65°48;'13*47
66° 57' i'-32
68° 5'49*16
769014'36*99
770023'24^81
[° 32'12*63
772°4i' 0*44
773°49'48-24
774058'36*03
776 7'23''82
777016'11*60
778024'59*38
779 33'47**5
780042'34*91
781051'22*66
7830 o'10*41
784° 8'58*16
785017'45*89
786026'33*61
787°35;21<33
791 ° I'44*46
7920 10'32*15
7930 19' I9''84
794°28; 7'52
795°36[55 20
796045'42*87
797°54'3O*53
7990 3'18*19
8oo°i2' 5*8
8020 29'41*12
803°38^28*75
8o5°56' 3*98
8070 4'51*60
8080 13'39*21
809022'26*8l
8io°31'14*40
811°40' 1*99
812048'49*57
+ 0-1756839
+ 0-1788681
+ O-I8I9944
+ 0-1850617
+ 0-1880687
+ 0-1910143
+ 0-1938974
+ 0-1967169
+ 0-1994718
+ O-2O2IOIO
+ 0-2047836
+ 0-2073385
+ 0-2098248
+ O-2I224I6
+ 0-2145880
+ O-2I68632
+ 0-2190663
+ 0-2211964
+ O-223253O
+ O-225235I
+ O-227I42I
+ O-2289733
+ 0-2307281
+ 0-2324058
+ 0-2340059
+ 0-2355279
+ 0-2369710
+ 0-2383350
+ 0-239619^
+ 0-2408236
+ 0-2419474
+ 0-2429903
+ 0-2439521
+ 0-2448324
+ 0-2456309
+ 0-2463475
+ 0-2469820
+ 0-2475341
+ O-24.8OO38
+ 0-2483909
+ 0-2486955
+ 0-2489173
+ 0-2490565
+ 0-2491132
+ 0-2490872
+ 0-2489788
+ 0-2487881
-t- 0-2485152
+ 0-2481604
+ 0-2477238
14-02
14-04
14-06
14-08
14-10
14-12
14-14
14-16
14-18
14-20
14-22
14-24
14-26
14-28
14-3°
I4-32
14-34
14-36
I4-38
14-40
14-42
14-44
14-46
14-48
14-50
I4-52
14-54
14-56
14-58
14-60
1462
M-64
14-66
14-68
14-70
1472
14-74
14-76
14-78
14-80
14-82
14-84
14-86
14-88
1490
14-92
14-94
14-96
14-98
15-00
TABLES OF BESSEL FUNCTIONS
Table I. Functions of order unity
695
X
14-02
14-04
14-06
14-08
14-10
14-12
14-14
14-16
14-18
14-20
14-22
14-24
14-26
14-28
14-30
14-32
14-34
14-36
14-38
14-40
14-42
14-44
14-46
14-48
14-50
14-52
14-54
I4-5|
14-58
14-60
14-62
14-64
14-66
14-68
14-70
14-72
14*74
14-76
14-78
14-80
14-82
14-84
14-86
14-88
14-90
14-92
14-94
14-96
14-98
15-00
Jx{*)
+ 0-1365770
+ 0-1397201
+ 0-1428030
+ 0-1458248
+ 0-1487844
+ 0-1516805
+ 0-1545122
+ 0-1572785
+ 0-1599783
+ 0-1626107
+ 0-1651747
+ 0-1676695
+ 0-1700940
+ O-I724475
+ 0-1747291
+ 0-1769380
+ 0-1790734
+ 0-1811346
+ 0-1831209
+ 0-1850317
+ 0-1868661
+ 0-1886237
+ 0-1903038
+ 0-1919059
+ 0-1934295
-t 0-1948740
+ 0-1962389
+ 0-1975240
+ 0-1987287
+ 0-1998527
+ 0-2008956
+ 0-2018572
+ 0-2027371
+ 0-2035352
+ 0-2042513
+ 0-2048851
+ 0-2054365
+ 0-2059054
+ 0-2062918
+ 0-2065956
+ 0-2068167
+ O-2O69553
+ 0-2070113
+ 0-2069849
+ 0-2068762
+ 0-2066853
+ 0-2064124
+ 0-2060577
+ 0-2056215
+ 0-2051040
- 0-1638320
- 0-1609579
- 0-1580240
.- 0-1550314
- 0-1519813
- 0-1488752
- 0-1457142
- 0-1424998
- 0-1392332
- 0-1359159
- 0-1325491
- 0-1291344
- 0-1256731
- 0-1221607
- 0-1186166
- 0-1150243
- 0-1113912
- 0-1077189
- 0-1040089
- 0-1002626
- 0-0964816
- 0-0926076
- 0-0888219
- 0-0849462
- 0-0810421
- 0-0771111
- 0-0731549
- 0-0691749
- 0-0651730
- 0-0611506
- 0-0571093
- 0-0530509
- 0-0489769
- 0-0448890
- 0-0407888
- 0-0366779
- 0-0325580
- 0-0284307
- 0-0242978
- 0-0201607
- O-OI6O2I2
- O-OII88O9
- 0-0077415
- 0-0036045
+ O-OOO5283
+ 0-0046553
+ 0-0087750
+ 0-0128857
+ 0-0169858
+ O-O2IO736
0-2132937
0-2131411
0-2129889
0-2128370
0-2126855
0-2125342
0-2123833
0-2122327
0-2120824
0-2119325
0-2117828
0-2116335
0-2114845
0-2113358
0-2111874
0-2110394
0-2108916
0-2107442
0-2105971
0-2104502
0-2103037
0-2101575
0-2100116
0-2098660
0-2097207
0-2095757
0-2094310
0-2092866
0-2091425
0-2089987
. 0-2088552
0-2087120
0-2085691
0-2084265
0-2082842
0-2081422
0-2080004
0-2078590
0-2077178
0-2075769
0-2074363
0-2072960
0-2071560
0-2070163
0-2068768
0-2067377
0-2065988
0-2064602
0-2063219
0-2061838
669°48'57-51
670°57 35-oo
672° 6 12*51
673°14'50*04
674°23'27*60
675° 32' 5'ri7
676°40'427
677 49 20*39
678° 57'58^03
68o° 6'35*69
681°15'13*38
682°23'51*08
683° 32'28*81
684°41' 6*55
685°49'44*32
686°58'22'^ii
688° 6'59*92
689°i5'37''75'
690° 24 15''60
69i°32'53-47
692° 41' 31 ''37
693°5O' 9'r28
694° 58' 47*22
696° 7'25-18
697 16 3'-i6
698° 24'41 4
699°33'i9':i5
700°41'57*18
7°i°5° 35-23
7O2°5y'i373i
7°4° 7'5i*4°
705°16'29^51
706°25' 7*64
707°33 45-8o
70S042'23*97
709° 51' 2'-i6
710°59'40*36
712° 8'18*59
7i3°i6/56^84
714 25'35*10
715°34'13^39
716°42'51-69
7i7°5i'3o'oi
719° 0' 8-36
720° 8'46*72
721°17'259
722° 26' 39
723° 34'41''90
724°43'20*33
725 5i 58*79
Hx(*)
+ 0-4759804
+ 0-4788455
+ 0-4817705
+ 0-4847542
+ 0-4877954
+ 0-4908927
+ 0-4940449
+ 0-4972506
+ 0-5005085
+ 0-5038172
+ 0-5071753
+ 0-5105814
+ 0-5140341
+ 0-5175320
+ 0-5210736
+ 0-5246575
+ 9-5282821
+ 0:5319460
+ 0-5356477
+ o-5393«57
+ 0-5431583
+ 0-5469642
+ 0-5508016
+ 0-5546691
+ 0-5585651
+ 0-5624879
+ 0-5664361
+ 0-5704080
+ 0-5744019
+ 0-5784163
+ 0-5824496
+ 0-5865001
+ 0-5905662
+ 0-5946463
+ 0-5987387
+ 0-6028418
+ 0-6069539
+ 0-6110734
+ 0-6151987
+ 0-6193280
+ 0-6234599
+ 0-6275926
.+ 0-6317244
+ 0-6358538
+ 0-6399791
+ 0-6440987
+ 0-6482109
+ 0-6523142
+ 0-6564068
+ 0-6604873
X
14-02
14-04
14-06
14-08
14-10
14-12
14-14
14-16
14-18
14-20
14-22
14-24
14-26
14-28
14-30
14-32
14-34
14-36
14-38
14-40
14-42
14-44
14-46
14-48
14-50
14-52
14-54
14-56
14-58
14-60
14-62
14-64
14-66
14-68
14-70
14-72
14-74
14-7,6
1478
14-00
14-82
14-84
i4-8g
14-88
14-90
14-92
14-94
14-96
14-98
15-00
696
TABLES OF BESSEL FUNCTIONS
Table I. Functions of order zero
15-02
15-04
15-06
15-08
5-10
5-12
5-14
5-i6
5-i8
15-20
15-22
I5-24
15-26
15-28
I5-3O
I5-32
I5-36
I5-38
15-40
I5-42
x5-44
15-46
15-48
15'5°
I5-52
15-54
i5-5f
15-60
15-62
15 '6A
15-66
15-68
15-70
1572
1574
15-76
15-78
15-80
15-82
8
15-
15-90
15-92
15-94
15-96
15-98
16-00
0-0183207
0-0224042
0-0264732
0-0305263
0-0345619
0*0385782
0-0425738
0-0465472
0-0504967
• 0-0544208
- 0-0583180
- 0-0621868
- 0-0660256
- 0-0698330
- 0-0736075
- 0-0773477
- 0-0810521
- 0-0847192
- 0-0883477
- 0-0919362
- 0-0954833
- 0-0989876
- O-IO24478
- 0-1058626
- 0-1092307
- 0-1125507
- 0-1158215
- 0-1190418
- 0-1222103
- 0-1253260
- 0-1283875
- 0-1313938
- O-I343438
- 0-1372363
- 0-1400702
- 0-1428446
- 0-1455583
- 0-1482104
- 0-1507998
- O-I533257
- 0-1557872
- 0-1581832
- 0-1605130
- 0-1627757
- 0-1649705
- 0-1670966
- 0-1691532
- 0-1711396
- 0-1730551
- 0-1748991
+ 0-2050021
+ 0-2044585
+ 0-2038339
+ 0-2031287
+ 0-2023432
+ 0-2014779
+ 0-2005332
+ 0-1995096
+- 0-1984076
+ 0-1972277
+ O-I9597°5
+ 0-1946367
+ 0-1932268
+ 0-1917415
+ 0-1901815
+ 0-1885475
+ 0-1868403
+ 0-1850007
+ 0-1832093
+ 0-1812872
+ 0-1792950
+ 0-1772338
+ 0-1751045
+ 0-1729078
+ 0-1706449
+ 0-1683167
+ 0-1659242
+ 0-1634685
+ 0-1609506
+ 0-1583715
+ 0-1557325
+ o-i53°346
+ 0-1502790
+ 0-1474668
+ 0-1445992
+ 0-1416775
+ 0-1387029
+ 0-1356766
+ 0-1326000
+ 0-1294742
+ 0-1263006
+ 0-1230805
+ 0-1198153
+ 0-1165064
+ 0-1131550
+ 0-1097626
+ 0-1063305
+ 0-1028603
+ 0-0993533
+ 0-0958110
0-2058191
0-2056823
0-2055459
0-2054097
0-2052737
0-2051381
0-2050027
0-2048675
0-2047327
0-2045981
0-2044638
0-2043297
0-2041959
0-2040624
0-2039291
0-2037961
0-2036633
0-2035308
0-2033986
0-2032666
0-2031349
0-2030034
0-2028722
0-2027412
0-2026105
0-2024801
0-2023499
0-2022199
0-202090:
o- 2019607
0-2018315
0-2017026
0-2015739
0-201445
0-2013172
0-2011892
0-201061
O-2OO934
0-200806
0-200679;
0-2005531
0-200426.
0-200300
0-200174
0-200048
0-199922
0-199797
0-199672
O-I99547
0-199422
6'24*71
;2359^3
° 32'47'3§
°4i'34^93
820050'22*47
82i°59'io''oi
8230 7'57?54
824016'45^06
825° 25'32''57
8260 34'20*08
827°43' 7^58
828051'55*08
8300 o'42*58
8310 9'30*07
832° 18'17*55
833°27' 5-O3
834°35 52-50
835 44 39-96
836053'27-42
8380 2'14*87
839°II' 2*32
840° 19' 49*76
i°28'37*20
842° 37'24*63
843° 46' I2''o6
844°54'59-48
8460 3'46*89
847°12'34*30
88°''
849° 30' 9*11
850038'56*50
851° 47'43%
852°56'31*27
854° 5'i8?6
855° 14' 6"o_
856°22'53*39
857 31 4O-75
858040'28*11
859° 49' 15H6
86o°58' 2
8620 6'5O
863°15'37*38
864024'24*81
86°'"
866°41'59-46
867° 50'46*78
868° 59' 34'-o
870° 8' 21*31
8°' 8*6
+ 0-2472058
+ 0-2466066
+ 0-2459265
+ 0-2451659
+ 0-2443252
+ 0-2434048
+ 0-2424052
+ 0-2413268
+ 0-2401701
+ 0-2389357
+ 0-2376242
+ 0-2362361
+ 0-2347721
+ 0-2332329
+ 0-2316191
+ 0-2299315
+ 0-2281707
+ 0-2263377
+ 0-2244331
+ 0-2224578
+ 0-2204127
+ 0-2182987
+ 0-2161166
+ 0-2138674
+ 0-2115520
+ 0-2091715
+ 0-2067269
+ 0-2042191
+ 0-2016493
+ 0-1990185
+ 0-1963278
+ 0-1935784
+ 0-1907714
+ 0-1879079
+ 0-1849893
+ 0-1820166
+ 0-1789911
+ 0-17591
+ 0-1727868
+ 0-1696105
+ 0-1663866
+ 0-1631163
+ 0-1598009
+ 0-1564420
+ 0-1530407
+ 0-1495986
+ 0-1461170
+ 0-1425972
+ 0-1390409
+ 0-1354493
15-02
15-04
15-00
15-12
I5-I4
15-16
15-18
15-20
15-22
15-24
15-26
15-28
15-3°
I5-32
15-34
15-36
I5-38
15-4°
I5-42
15-48
15-52
15-58
I5-6O
15-62
I5't
15-68
15-70
1572
1574
15-76
15-80
15-82
15.&
5
15-90
15-92
15-94
15-96
15-98
16-00
TABLES OF BESSEL FUNCTIONS
Table I. Functions of order unity
697
arg
15-02
15-04
15-06
15-08
15-10
15-12
I5'i4
15-16
15-18
15-20
15-22
15-24
15-26
15-28
15-30
15-32
15-34
I5-3&
I5-38
15-42
15-44
15-46
15-48
15-50
I5-52
15-54
15-58
15-60
15-62
15-64
15-66
15-68
15-70
15-72
15-74
15-70
i5'78
15-80
15-82
15-84
15-86
15-88
15-90
15-92
15-94
15-96
15-98
16-00
+ 0-2045057
+ 0-2038267
+ 0-2030675
+ 0-2022280
+ 0-2013102
+ 0-2003130
+ 0-1992373
+ 0-1980838
+ 0-1968530
+ O-I955454
+ 0-1941618
+ 0-1927027
+ 0-1911688
+ 0-1895608
+ 0-1878794
+ 0-1861255
+ 0-1842998
+ 0-1824032
+ 0-1804363
+ 0-1784003
+ 0-1762958
+ 0-1741239
+ 0-1718855
+ O-1695816
+ 0-1672132
+ OT647812
+ O-I622868
+ O-15973IO
+ 0-157114c;
+ 0-1517062
+ 0-1489160
-I- 0-1460700
-I- 0-1431695
+ 0-1402157
+ 0-1372099
+ 0-1341533
+ 0-1310471
+ 0-1278927
+ 0-1246913
+ 0-1214444
+ 0-118x532
+ o-1148192
+ 0-1114436
+ 0-1080279
+ 0-1045735
-1- 0-1010818
+ O-O975542
+ 0-0939922
-t- 0-0903972
+ 0-0251476
+ 0-0292062
+ 0-0332478
+ 0-0372707
+ 0-0412735
+ 0-0452546
+ 0-0492124
+ 0-0570521
+ 0-0609309
+ 0-0647803
+ 0-0685990
+ 0-0723853
+ 0-0761378
+ 0-0798551
-1- 0-0835358
+ 0-0871785
+ 0-0907816
+ 0-0943440
+ 0-0978042
4- 0-1013409
i- 0-1047727
+ 0-1081584
+ 0-1114966
-l- 0-1147861
+ 0-1180258
-l- 0-1212142
+ 0-1243503
+ 0-1274329
+ 0-1304608
+ 0-1334329
+ 0-1363480
+ 0-1392052
+ 0-1420033
+ 0-14^7413
+ 0-1474181
-l- 0-1500329
+ 0-1525847
+ 0-1550724
-I- 0-1574953
+ 0-1598524
+ o-1621429
+ 0-1643659
+ 0-1665207
+ 0-1686064
+ 0-1706224
+ 0-1725680
+ 0/1744424
+ 0-1762450
+ 0-1779752
0-2060460
0-2059085
0-2057713
0-2056344
0-2054977
0-2053613
0-2052252
0-2050893
0-2049537
0-2048184
0-2046834
0-2045486
0-2044141
0-2042798
0-2041459
0-2040121
0-2038787
0-2037455
0-2036125
0-2034799
0-2033475
0-2032153
0-2030834
0-2029518
0-2028204
0-2026892
0-2025584
0-2024278
0-2022974
0-2021673
0-2020374
0-2019078
0-2017784
0-2016493
0-2015204
0-2013918
0-2012634
0-2011353
0-2010074
0-2008798
0-2007524
0-2006252
0-2004983
0-2003717
0-2002452
0-2001190
O-I999931
0-1998674
0-1997419
0-1996167
727° o'37'-25
728° 9'15*74
729*17 54*25
730026'32*77
732°43'49*87
733 52'28*45
735° 1' 7*<>4
736° 9'45*05
737018'24*28
738=27' 2*93
739 35 4i*59
740 44 2O'-27
741°52'58*97
743 1 37*69
744° 10'16*42.
745°i8'55'-i7
746°27'33*94
747°36'12-72
74«°44 5I-52
749°53'3or34
7510 2 Cil17
752010 48-02
7530 it)'26*89
754? ^' 5*77
755° 3<>'44*67
756° 45 -23*59
757°54' 2*52
759° 2'41*47
7600 11 20*43
761°19'59*41
762028'38*41
763°37'I73
764 45 56*4t>
765 54'35-5°
767° 3'I4-56
768011'53*64
769°20'32*73
77o°2t) 11*84
77^° 37'5O*9f»
772°46'30*10
773°55 9*25
775° 3 48-42
776 12 27-61
777021' 6*81
7782946O3
779°38'25*26
7»o°47' 4*50
781055'43*76
7830 4'23*04
+ 0-6645540
+ 0-6686052
+ 0-6726395
+ 0-6766552
+ 0-6806508
+ 0-6846246
+ 0-6885753
+ 0-6925011
+ 0-6964006
+ 0-7002724
+ 0-7041148
+ 0-7079263
+ 0-7117050
+ O-7I545I2
+ 0-7191616
+ 0-7228353
+ 0-7264711
+ 0-7300674
+ 0-7336229
+ 0-7371363
+ 0-7406061
-1- 0-7440312
+ 0-7474101
-1 0-7507416
+ 0-7540245
+ 0-7572574
+ 0-7604392
-l- 0-7635687
•l- 0-766644 7
-1- 0-7696660
-l- 0-7726316
+ O-77554O2
+ 0-7783909
+ 0-7811825
•1- 0-7839140
+ 0-7865845
-l- 0-7891929
+ 0-7917383
+ 0-7942197
+ 0-7906362
-1- 07989870
•l- 0-8012712
-1- 0-8034880
+ 0-8056365
+ 0-8077161
+ 0-8097259
+ 0-8116653
+ 0-8135336
+ 0-8153300
+ 0-8170541
15-02
15-04
15-06
15-08
15-10
15-12
15-14
15-16
15-18
15-20
15-22
15-24
15-26
15-28
15-30
I5-32
15-34
15-30
I5-38
15-40
I5-42
15-44
15-46
15-48
I5'5°
I5-52
15-5-1
I5-56
I5-58
15-60
15-62
15-64
15-66
15-68
15-70
15-72
15-78
15-80
15-82
5
15-
15-90
15-92
I5-94
15-96
15-98
16-00
N '^VOOO O N tj"VOOO O N "!HO 00 O N tJ-vOOO O N ^f"vO00 O N ''i^OOO O N ^hvOOO O N *<J"VO00 O N ^"VOOO O N ^"VOOO O
9 9. O w WWWHN N N N N CO co CO CO CO ^" ^t" "^* "^ "^ 'O *O *O IO lOtO VO vO VO VO C^ t^ C^ t^ C^OO 00 00 00 00 Os Os Os OS Os O
ooooo ooooo ooooo ooooo 60666 66666 66666 66666 66666 6 6 6 6 w
1
I
rooo "~>w O>
w OvO t-~O
O w cooo t~»
N0O0O N M
O O M CO«O
N -<*-vO00 O
OOOO
Osco O
vO COO tN
OS t^W W O
¦*N ION <*¦
ro r
r
N
t^N MO0O0
<?> OsO OsOO
tfCN
fON O
OmhOO
O COOS
N ^
OOO
t^vO WOO00
N O SfOH
OOOOh
OOO
w ^- 00 w tO00
O
COO
woo
O
t-t-M
^o Q>co
O dO
Of
00 VO
O
OOOOw whwwn N N N coro CO "*$" "st" "^ ^J" to^OVOvOvO vo t^t^C^OO 00 00 Os Os O 6 O w
00 3
COO jO
VO Tf-00 O O>
o>oot«o
N
o t^cnoo co
O O Os co
O CO
Os W CO O >O
vOooirt
Oio omo>
-5j-Os<Mt^fO
-<i-cococ^t^
vOOsOs COVO
OsOO OOvOOO
O^O
Oh o
OXONNO
inio fvoo w
OOsOOOOs
noos3co
(NvOOsOmh
qohocoh
NhVO OsO
h QiO 1
omhnco c»osTfOsw -<i-<M pooo «n
OsOsOsWO «n<MOs OsOO iO Os COO PO
utonn m t-»Tt-c* pooo O\oo onio
Tfw00«OCs Os <J~> u->DO en OM N^m
hO O")N oowOOW ""jOO co OsvO
rtoOMOH 00 iOW OsvO co O oo w. en
O OOOOtt t fO O O
N 9 w COOO ro OsvO cow Ost^tOCON w O OsCO t^ VO<0«0^-CO rONNWw OOOsOsOs OOOOOpt^t^ t^ r~»vp vO vO
OsOO t>.vO >O >O ^ ^^ ^t" CO rococo CO
0NOC
CO00 fOO N
vOCO-5t-0«0
IOH NtfIN
OOOvOvOVO
O N>n(OH
«O t ^ ^ ^
tOOOt
N00N00CO
OsOfOMN
O> O t^w M
NON*O
O>00 VO Ko
h tM N
N O
ONC0 Nff)
w rJ-00 w O
N00 ¦«> «
-^Os<nH00
m OsOO t~~u->
ONN
N oi« t
O 1O t--vO CO
N tHO rovO
N O -*aO m
1ONO00N
tKon O Os
NN
O0 O Ko OO O
rorOPOrOCO CONNNN (NNNNw wmhmm
tOvO t^-N^" H0OO»NW NvOwwvO ^hOsNwN t"»vO t~» COOO N COVO vO ^ w tJ- h <O O f~»vO t~»>O^ t~~OscONiO wvOOOCO'*"
N Os u~) ij oo w "^* Os Os CO N vO VO O t^ t^ t^ t^*CO CO ^4* ^"O*vO O Os l^O "^ ^ ^O w00 Os O CO Tf"VO COCO *O C^CO O VO O CO O*M O
O W VO *O Os M O 00 C"nOO h 5^*00 *O t^ f^ *O N OsvO ^ "^"VO N N *O ^" Os OsvO O N M Os t^ CO OS *O N Os 00 00 O *O w w COOO 00 w
OONNOsN COOCO'^'N 00OO00CO VO t^O Nt~» O h OW * OOwiNNW 0>i00 COVO 00OO00C~-Tf h N(ONh Tf-vO t~0O. O>
Os OsOO VO»0 COw00«ON 00<OWVON NN NNO wiOOsNVO Os COVO OsN 'tNON t vOOOON^i- VOt^OsON CO^" >OvO .t^-
O w N ro ^t* *OVO vO t^OO OO O^ O O w w N N CO ro ^4" "^" *^t" *O ^O *OVO vO vO t*^- t^* t^OO 00 00 CO 00 O*0s0s OsOsOsOO OOOOO
O ^S ^S ^K ^S f\ f. f\ f\ f\ ?"» Q |j |t fc^ L.J Lj |^j 1J l^. L^. Li LJ 1J ^i y^A 1^. j^ ^i Li Li ^J tj LJ LJ ^J LJ LJ ^ LJ U ^f W PJ M f*l M M M M
66666 66666 66666 66666 66666 66666 66666 66666 66666 66666
t*"joo co Os Os
VO CON COO vO COVO OsOO
OsO H N O
t~^M <O00 VO
00 vO t^Os O
>O OS covO 00
n oo <o
)VO ¦'tf-N O Oit^tO'tf-N H
>osOsosos ooooop.oocp op
66666 66666 66666
OOOOO
vpOOOO>ro iowcOwN
w 1O ^f"H f-^iOf^-
N -^-co Os w t^00 N
. -WO>0 co Q 00 Osco
vO >O "o rf- ir> v>vO vo l^- Os
00 t^vo lO Tl- CO N W O Os
vOvOvOvOvO vOvOvovO to
66666 66666
N C0«0f0>0
vO tot^vO <O
OsOO 00 O\0
00 vO vOOO CO
N ^O Os
iO
o>vooo o os
00 O tfOOO
O O
O t
CON t--w O
00 OsvO vO ro
CO00 OsiOVO
VO N O O w
t lOOCO
00 1O0000V©
N M ri-00 OS
won r-o
KSO COOs t-^
t VO O >O
00 00 ttO
OOOOO OOOOO OOOOO OOOOO
N -<J-\O00 O N t}-vO00 O N rj-vOOO O
OOOOw wwwwn NNNNro
OOOOO OOOOO OOOOO
N Tt-vOOO O
co co co co ^}~
6 6 6 6 6
OOOOO OOOOO
N tHOOO O
6 6 6 6 6
N ^\OO0 O N ¦^OOO O N Tt-vOOO O
f^r^f^t^-00 O00000CO Os OsOsOsOsO
OOOOO OOOOO OOOOw
<O oooooooo
o 000*4*- to
COMMMM
O 00 <?¦-&• tO
On 4* 4»- 4* -fi
O O0Ov4». tO
WtOtOtOtO tOHMWW ^ 6 6 6 O
O OOOO*. tO O COO\4>- to O COGN4* to
OOOOO OOOOO
O M H M H
00O W4* <7>
On Ca>00 tO tO
O O0O-&. to
OOO to 00 00
UOO hk
WOJWWW
H 10 M to to
OOO M-H Oi
to tOOJOn <7>
•?- O OOO O
OJOj HU O
tO 00O O0M
OOOOO
oouioJoJoo
ooooo ooooo
00 MWU 00
OOH41.M O
Hln OM VO
OOJOJ OOJ
OooO
4». 4». 4*. 4*. on
O tOOn OOO
On O4=>- O Cy
mm CO-t^
On OOOOQiUi
M 10 MM 10
OOOOO
OJOJOJOJ OJ
00 00 00O vo
OJ CTiCW O>
OWM tO 00
G\ OOOOOn O
tO COOn OM-l
H 00
ooooo ooooo ooooo
ooooo
to li N Ki M
ooooo ooooo
to to to to to to to to to to
ooooo ooooo
to to to to to tototototo
ooooo ooooo ooooo ooooo ooooo
tototototo tototototo tototototo tototototo to to to to to
OOO
hU Com to
00 00 00 00 00
Ui O^^l OOO
Oi^J OOOOC^l
tO^J^J M 00
OOUi to tOO
OOOO O
ooooo
CTOO
O 00 00 00 00
O O COM O* UW H OOOi
OJ OOO O O O tO H M O
O O O4* OJ M4»- to tO O
H CO O**OJ VO H 00
O
t O HNJ
O 0"»0 OOOJ
HI OOJO
u( 0000
to H OO CO
tO4* O*M CO
On OJ O**0n O O ^* 4*- vO "**4
O*OJ 00 COOo H O M H O
05
I
s
4
OOOOO
co coco co 6o
ooooo
do cooo oooo
ooooo
CO 00 00 OOO
OOOOO O O
00 tOM M O\ M
OOOJ 004*. H
JiOMOOto OJOOn OOn
O»to to to co
ooooo
ooooo
O HI M tO tO
O O
tO O"»O"» H H-
ooooo
ooooo
04^
4
O O> hi
O IO<_n
^ O ©
O
CO4P
OU COCO tO
ooooo
ooooo
too
H(?H OC^I
O MO OOO
ooooo
OOO O O h
ooooo
tO44
^ OM<
M OO
O C4
to to to coui
OOOOO Ohmmm
Ui O>^5 OOOO O O M WU>
)UW O C4 OO4
CO4 OlOi4
OJ O OOJ-O
OJOOOOOi
OOO^OM
M
00
CO
OOOOO OOOOO himmmw mmmmm Mtotototo tOtOtvtOto OJ OJ U> U> U> U> U> U> 4». 4^- 4». 4». 4>-4>-Oi
OJ 4i 4^ <J\ <y* C~^<! 00 OOO O m tO to U> 4»- Oi G^ 00 OOmmOJ 4=>-Cji O1^! 00 Oh MUOi O> OOO MtO 4^<-nMOM C
OJ 6 C^OJ O M* HiOv) A W OOM C~4^ U) toto i-iMWrthj U*Us) OD HW COU) O>H ^H O tO O O"^ tO M O M t0U>
4*. OMUi4i 4»- O^O-^ O CCXl^l O-*>. O COM O tv 00 On G\-D -t^- mm4^O00 OOiOJOiO O N O h 00 004i- OtOOi ^OmOO^
OW OO M MUiMU)^. OtOOUL=>- O) hvjuO C~Oi M to m C?M Oi tO CO Ui 4^ DU M OOO to CO O O O H COW O M O HI CO
(?.H^ O O OAUislO U OUi OO Ot04^UJOi -Ovl^AiO OiUivJLo^ OJtO O^M to \)OUMW -^ h tO^ 00 U»4^4»-U>M
OOChOOO OO O-f>NfH * hOi CC4w 10 U) CCOl 4». OiCOmOO O NUOhO VJOOO1U1 U>O00t00O OlO O O> tO CO M C7»Oi -v3
3
03
OJ tO O O CO O"'0n 4=^ to m 6 O
004»- OOn to OOOn MOM 4^ Ki
OtoOOOO OnOoOJC^Hi OO
OMOJMO OOOnMOn 00
On4&. lOOnOn O OOoOJOi
CT>OJM M 00 ^^ C\.QOCO
m O H OOn 4^O COOJ4=>-
OJLn
. On M CO
O^OO O
- O
O 00M O*Ji
O1U1 On OM
OJ4^. 004* 10
O O COUi 10
OJ '_n to O to
tOUl M O'-n
4^ OOtOOJ tv
4=^ OoOJ Ki m OO 00 COM
COO OtoOJ 0nMOH4».
H tOOn OM On4* O^OOJ
OiO i?> <3^ n
004»-On O to
04 O
O0n O'-n O
HMln 004^-
tOO m
O O** t
O mOJOJ m
O UO^
4
0O MOn 00
O O^O^0nM
to ON*. ^ m
OOJ tO w CO
O^O MOJM
MMOnOiM
OJ to m m O
tOOn COM O\
O? O Ot
O? O Ot
HW OS1 00
MMOJ O>0n
O^-iji 004*.
O 4
OO 00OOM
O-t* OOtOM
4»4 OOOJ
O>OJ N M
OiMM HO
OV© Hvl^.
OOlOOOO
OOOOO O CO 00 CO 00
¦ • o co on*, to
O C0ON4»- tO
QOMMMM M C!^C^C^O^
O 000*4*- tO O OOO* tO
4*- OJOJOJOJ
O O4 N
700
TABLES OP BESSEL FUNCTIONS
Table II. Functions of imaginary argument, and ex
X
2-O2
2-O4
2O6
2-08
2-IO
2-12
2-14
2-16
2-I8"
2-20
2-22
2-24
2-20
2-28
2-3O
2*32
2-34
2-36
2-38
2-40
2-42
24
2-46
2-48
2-50
2-52
2-54
2-56
2-58
2-60
2-62
2-64
2-66
2-68
2-70
2-72
2-74
2-76
2-78
2-8o
2-82
2-84
2-86
2-88
2-90
2-92
2-94
2-96
2-98
3-oo
0-3066592
0-3048408
0-3030525
0-3012935
0-2995631
0-2978606
0-2961855
0-2945369
0-2929144
0-2913173
0-2897451
0-2881970
0-2866727
0-2851715
0-2836930
0-2822366
0-2808018
0-2793881
0-2779951
0-2766223 .
0-2752693
0-2739356
0-2726209
0-2713246
0-2700464
0-2687860
0-2675429
0-2663168
0-2651072
0-2639140
0-2627367
0-2615749
0-2604285
0-2592970
0-2581801
0-2570776
0-2559892
0-2549146
0-2538534
0-2528055
0-2517706
0-2507484
0-2497387
0-2487412
O-2477557
0-2467820
0-2458198
0-2448690
0-2439292
0-2430004
e-^hix)
0-2149779
0-2146797
0-2143750
0-2140643
0-2137477
0-2134256
0-2130983
0-2127660
0-2124291
0-2120877
0-2117422
0-2113927
0-2110396
0-2106829
0-2103230
0-2099600
0-2095941
0-2092256
0-2088545
0-2084811
0-2081055
0-2077279
0-2073485
o-2069674
0-2065846
0-2062005
0-2058151
0-2054285
0-2050408
0-2046523
0-2042628
0-2038727
0-2034820
0-2030907
0-2026991
0-2023071
0-2019148
0-2015224
0-2011299
0-2007374
0-2003450
O-I999527
0-1995606
0-1991688
0-1987773
0-1983862
O-I979955
0-1976053
0-1972157
0-1968267
ex K0(x)
0-8377564
0-8339966
0-83028^5
0-8266281
0-8230172
O-8I94537
0-8159366
0-8124650
0-8090377
0-8056540
0-8023128
0-7990133
0-7957545
07925350
0-7893561
07862149;
07831112
0-7800443
O-777OI35
0-7740181
07710575
07681308
0-7652376
07623771
07595487
07567518
07539859
07512504
O7485447
07458682
0-7432205
0-7406011
07380094
O7354449
0-7329072
O-73O3957
0-7279102
0-7254500
0-7230148
07206041
0-7182176
0-7158548
O7I35I54
0-7111989
07089050
07066333
07043834
0-7021551
0-6999479
0-6977616
e*Kx(x)
1-0270373
1-0207097
1-0144909
1-0083780
1-0023681
0-9964584
0-9906463
0-9849292
0-9793046
0-9737702
0-9683236
0-9629626
0-9576851
0-9524890
0-9473722
0-9423329
O-9373692
O-9324793
0-9276613
0-9229137
0-9182347
0-9136228
0-9090764
0-9045941
0-9001744
0-8958159
0-8915172
0-8872771
0-8830942
0-8789673
0-8748952
0-8708767
0-8669107
0-8629961
0-8591319
0-8553169
0-8515502
0-8478308
0-8441577
0-8405301
0-8369469
0-8334074
0-8299106
0-8264557
©•.8230420
0-8196687
0-8163349
0-8130399
0-8097830
0-8065635
7-5383249
7-6906092
7-8459698
8-0044689
8-1601699
8-33H375
8-4994376
8-6711377
8-8463063
9-0250135
9-2073308
9-3933313
9-5830892
9-7766804
9-9741825
10-1756743
10-3812306
10-5909515
10-8049029
11-0231764
11-2458593
11-4730407
11-7048115
• 11-9412644
12-1824940
12-4285967
12-6796710
12-9358173
13-1971382
13-4637380
I3-7357236
14-0132036
14-2962891
14-5850933
14-8797317
15-1803222
15-4869851
15-7998429
16-1190209
16-4446468
16-7768507
I7-H57655
17-4615269
17-8142732
18-1741454
18-5412875
18-9158463
19-2979718
19-6878167
20-0855369
X
2-O2
2-O4
2-06
2-08
2-IO
2-12
2-14
2-16
2-18
2-2O
2*22
2-24
2-26
2-28
2-3O
2-32
2-34
2-36
2-38
2-40
2-42
2-44
2-46
2-48
2-50
2-52
2-54
2-56
2-58
2-60
2-62
2-64
2-66
2-68
270
272
2-74
2-76
2-78
2-8o
2:82
2-84
2-86
2-88
2-90
2-92
2-94
2*96
2-98
3*oo
4*-CO CO CO CO COCOCOCOCO COCOCOCOCO COCOCOCOCO COCOCOCOCO COCOCOCOCO COCOCOCOCO COCOCOCOCO COCOCOCOCO COCOCOCOCO
O O O O O
O GO^ «0
00 CO CO 00
to
O C- O> On On
O Ot 10
OnCji Cn Cn Cn
O Co Owfa. 10
4^ CO Coco U<
O GOC-&. tO
Co to to to to
O OOOwP>- to
>0 M M M M
tO
O CoCM^ K>
OOOOO OOOOO OOOOO OOOOO OOOOO OOOOO OOOOO OOOOO OOOOO OOOOO
tototototo totototoio to to to to to to tv to to to to to to to to to to to to to tototototo tototototo tototototo
00000 Ommmm mmmmm mmmmm MtOtOtOtO tototototo tototototo COCOCOCOCO COCOCOCOCO
O O OO OOO OOmmio toco4i4-.Cn C CnO CCOO OOOMtO tO CO 4*. 4*- Cn CO O COO OMMtOCo -ji. Cn Cn CO
001 HslO) 004*. OOnIO O Cn hi o 4*. O CnCo C On Co O O 4*- O COCn tO O On 4^ m O C4*^ to O 00 C4^ tO O O O On
O C-P>- m O COOOO CO Om4^00 +\OA Qs| 4»- to O O O OMCoCnO CoOCoOC 4*. Co COCO 4*. COCO 004*-
M O m 00 O O O CO O O 00 to 10 00 O 0>O O 4*- 04^ CoOO to 4*. to 00 M m O 4*- O 00 COCn O + sl COO COO Cn
O CO Cn CCn Cn C COCo O mOOOnm 4^ CXhOi tOCoOOCO 4*- O Oi to m 4*. tO C CoO O tO CO COCn Co M Cn m m
to to to to to
Co Co 4i. 4i. 4i.
OOVO O H tO
Cn Co tO M O
w OOO-O CO
t0vO-O4>- to
CTivO tOCn tO
OOOOO OOOOO OOOOO OOOOO OOOOO OOOOO OOOOO OOOOO OOOOO OOOOO
oo-^
jo co
OOO O v?> O
O O4
Cn CO i
O O >
COCO >
i.O O
-ICO C
-ICO O
COCOCOCOCO
O O M M M
H4>. Co tO C
m Co O^Cn Cn
O to O hi O
00 00 CO Co Co
to to tococo
H-fkS) H^k
O (-n vC 4*. 00
O OCn m O
On^O On On m
CO CO 00 00 00
CO 4-^ 4*. 4-^ Cn
coMCn ooto
Co COCO O4*-
o ooO to c
vO O OvA *"J
00 00 00 00 00
CnCn C
COO
OOi (¦
toO-^
TiCO
J CO
1OO
to tO4i O CO
00 00 00 00 CO
OO 000000
4*-O M4*. CO
o c to o c
OCO 004* m
04^- to M4*.
00 CO COO O O O O vO vO
OOOOO MMMtOtO
tO Cn vO Co *^J O 4*. 00 to Cn
to OO 4*- M O C4*. to O
OOOtOCn OCntOOOO
- - - - , tooco o oo
O O OOO OOOOO
to Co Co 4*. -4^ 4^ Cn Cn C On
OCOO hOi Ooto CO4*-
O Cn 4*- to O O O CCn CO
CoO M 4*. O tOOCOOCO
C4*- tO O On m Cn O CCO
OOOOO t? O O O O OOOOO OOOOO OOOOO OOOOO OOOOO OOOOO OOOOO OOOO
CTt CTi O"> O1 CTi
O O tOCOCn
»0 O M OMi
O4>- O COCT-
O COO M +
vJ4v OVA O
CT- C^ CTi O^ On
0>COO M to
OiH On tOO
Cn 0*0 O4*-
O h(O Co hi
Wsl H COO
toco
IO O
to 004* O C
OCn to m o
M 10 C M 00
CO m tOCn
On CTi CTi O> O>
CO CO CO CO CO
tOCoCnO 00
to CO4*- h»j
H^sl to CO
0004^ to to
hi MO HiCn
O tOCoCnO
4 hi cocn tO
Cn4>-4i-Cn CO
On toco On4^
OO OO &
OlLW
to COOiCOCO
CMOtOOO
CoCoOOCn
CTiO>0>OCTi
CnCnONCTi0\
OOHicoCn
OO Owfi-CO
Cn 00 to CO CTi
tOtOOOCTi
Coco CoO O
COOCOS
d O^O O O
O4
.CCCCOn COnCCC
O O 00 00 00 00 COO O O
COOOCoCn OO MCoCn
tOMOOO OOOOO Mtoco4*-Cn
Cn CO COO OO00MC COMtOCnO
O 004* Msl Cn O tO Co Co m CO+. OCn
tOO COO Co m mO Com m mCO m CO
OOOOO OOOOO OOOOO OOOOO OOOOO OOOOO OOOOO OOOOO OOOOO OOOOO
On On On On On
00 00 00 00 CO
MCoCnO O
CnCnCnCnCn
sl-t>- CocoCn
Cn OnCO CoO
O OnO 10 CO
On On
O O
O O O O O
MCOCnO O
Cn OnO OOO
OCn Co toco
COCn OCo4i.
COCn K> tOCn
o o o o o _ _ , _
00001-1 MMMWtv
t04^O000 COCnoOtO
OtOCoCnO OtOCnCCHi
Cn m COO O O Cn tO m tv
4* Co to Q 00 CCn 4*. Cn O
Cn HU O O
Coco4i4>.4*. 4^-CnCnCnCn CC CO O OOCOOOOo OOOOO
4*. C-C m-U C" CO m Co C O m 4^. CO tOCnO OCO CO tO Cn O M4*.-vj o Co
+. OOhU O 4^O4*.OCn OOnIOOC CoOOo C4^ tOMOOO OOMtOCo
C-mO-Cm CCoCoCnO O CnO 4*-m tOCnMOtO 00 CO MO O 4*- to Co CO
O C-P>. CnO OO'-fiCnM toOtOtOO 4^~J CoO O OmCooCO CoCntocoO
O CnMQCnO h O 10 N* COCOO CO COCOCCCO 004^-00
CnCnCnCnCn 4^ 4^ -li-li 4^- 4^4^4^ 4^-4^ 4*.C0CoCoCo COCOCOCOCO COCOCOCOCO tototototo tototototo tototototo tototototo
4*. CO tO M Q O COO CCn 4^CototOHi OOOc Co-O CCn Cn4^co COKimmO OOCo OOO O C CnOi Cn 4u.4»cocotO KimmOO
Hji khUi OCoOfOQ-N MCnOCnO CnOCnMC M-
CnCn4*.4*.4*. 4*.4*.4^CnC O CoO O to
OmOimO OtOCtOO Om4*.oCn
COO OOOO KJ4i.CnCn4i MC COO 4^
M OCO C-f*- 4i.tOCo4i.tO m04*.OCo
CnCot0O4*. 4*-MCnOO 004* tO O O
O 4^- On m Cn O Cn m 4^ CO 4*. 10 C O 4^-
4*- Cn COOCO
4i 4i CO Co
O C Hi (-4 O
CoCo Co COCn
004»-CO C-
4 00
OOCCnCO MCnMCOC O--J COm c
COCO CO C4^ CnO CCO 4*- O O O O
t0CnMO4>- 4*-0004^- mommco
CO4i.OH.t0 CntOOCnM OOOtOOl
4*. MOO CO tO too COCn O M mo m
O
O4C tO
tOCn OCO OO
ONOCno M
COOCO tO tO
OCOO tO O
OCn to O O
to COCO C O COOCn M
CnOCn COCO O4*. Cn tO tO
CoCnOONCO CnOCn4*.vO
O-P* CXO O M tOOCO tO
I
4>-COCOCOCO CO LOCO CO CO
CO CO CO CO CO
cooooo
O CC4
COCOCOCOCO LOCO CO COLO
CO CO CO CO CO
O COC-f1- tO
CO Co Co Co Co
4^ Co Co Co CO
O COP
COCOCOCOCO
COCOCOCOCO COCOCOCOCO
tOMMMM MOOOO
O COC4*. tO O COC4*. tO
O C d C C
0 CoC-?. to
702
TABLES OF BESSEL FUNCTIONS
Table II. Functions of imaginary argument, and ex
X
4*02
4'°4
4o
4-08
4-10
4*12
4*14
4-16
4-18
4-20
4*22
4*24
4-26
4-28
4-30
4-32
4*34
4-36
4-38
4-40
4*42
4-44
4-46
4-48
4-5O
4-52
4-54
4-56
4'5°
4-60
4-62
4-64
4-66
4-68
4-70
4.72
4-74
4-76
4.78
4-80
4-82
4-84
4-80
4*88
4*90
4-92
4*94
4*96
4.98
5-00
0'2064393
O'20588l2
O*2053278
0*2047789
O-2042345
0'2036945
O-203I589
0*2026275
0*2021003
0-2015774
O-2O1O585
O-20O5438
O*20O033O
O*I995262
O*I99O233
O*I985242
O-I98O29O
O-I975375
0*1970497
0*1965656
0*1960851
0*1956081
0*1951347
0*1946648
0*1941983
O'x937352
0-1932754
0-1928190
0-1923658
0-1919159
0*1914692
0-1910256
0-1905851
0-1901478
0-1897134
0-1892821
0-1888538
0-1884283
0-1880058
0-1875862
0-1871694
0-1867554
0-1863442
0-1859357
0*1855300
0*1851269
0*1847265
0*1843287
0*1839335
0*1835408
O-I784228
O'I78O96l
O-I7777O9
O-I77447O
O-I77I245
O'I768O33
CI764836
0*1761652
0*1758482
0-1755325
O*I752l82
O-I749O53
O-I745937
O-I742835
O-I739746
0-1736671
O-I7336O9
O-I73O56O
O-I727525
O'I7245O2
O-I72I493
O-I7I8497
O-I7I55I5
O-I7I2545
O-I7O9588
0-1706644
O-I7O37I3
O-I7OO795
0*1697890
O-I694997
O-I692II7
O'l68925O
O-I686395
O-I683553
O-I68O723
O-I6779O5
O-I675IOO
O-I6723O7
O*l669526
O-I666757
O*l664000
O*l66l256
0-1658523
O-I655802
O-I653093
O*l65O396
O*l6477IO
0*1645036
O-I642374
O-I639723
O-6O78573
O-6O6427O
0-6O50069
O*6O35968
O-6O2I965
O-6OO8O6O
O-5994251
0-5980537
O-59669I7
O-595339O
O-5939955
0-5926611
O-59I3357
0-5900192
0-5887114
0-5874124
0-5861220
0-5848400
0-5835665
0-5823013
0-5810443
0-5797954
O-578554O
0-5773218
0-5760968
0-5748796
0-5736701
0-5724683
0-5712740
0-5700872
0-5689078
O-5677357
0-5665708
0-5654131
0-5642625
0-5631189
0-5619823
0-5608525
O-5597295
0-5586133
0-5575038
0-5564008
O-5553O45
0-5542145
0-5520539
0-5509830
0-5499184
0-5488599
0-5478076
O-67962I9
0-6776840
O-6757623
0-6738564
O-67I9662
O-67OO914
O-66823I8
0-6663872
O-6645575
O-6627424
O-66O94I8
O-659I553
O-6573830
O-6556246
O-6538798
O-652I486
O-65O43O8
0-6487262
O-647O346
O-6453559
O-6436899
0-6420364
O-64O3953
0-6387665
O-637I498
O-635545O
O-633952I
O-6323708
O-63O8OIO
O-6292426
O-6276955
O-626I595
O-6246345
0-6231203
O-62l6l69
O-62OI24I
O-6l864l8
O-6I7I699
O-6I57O82
O-6I42566
O-6l28l5I
O-6II3834
O-6O996lO
O*6O85494
O-6O7I468
O-6O57537
O-6043699
O-6O29955
O-6OI6301
O-6OO2739
ex
55-701106
56-826343
57-974311
59-145470
60-340288
61-559242
62-802821
64-071523
65-365853
66-686331
68-033484
69-407852
70-809983
72-240440
73-699794
75-188628
76-7O7539
78*257134
79-838033
81-450869
83-096285
84-774942
86-487509
88-234673
• 90-017131
9I-835598
93-690800
95-583480
97-514394
99-484316
101-494032
103-544348
¦ 105-636082
107-770073
109-947172
112-168253
114-434202
116-745926
119-104350
121-510418
123-965091
126-469352
129-024202
131-630664
134-289780
137-002613
139-770250
142-593796
I45-474382
148-413159
X
4*02
4-04
4*06
—0
4*08
4*io
4-12
4-14
4-16
4*18
4-20
4*22
4-2^
4-26
4*28
4*3°
4-32
4-34
4-36
4-38
4*40
4*42
4'44
4-46
4-48
4-5O
4-52
4-54
4-56
4-58
4*60
4*62
4*64
4-66
4-68
4-70
4-72
4'74
4-76
4-78
4*80
4*82
4-84
4-86
4-88
4-90
4*92
4"94
4*96
4*98
5*00
ONOi OjOiOi OjOjOjOiOi OlOiOiOiOi Ol Ol Oi O* Oi Oi Oi Oi Ol Ol Ol Ol Oi Oi Oi Ol Oi Ol Oi Ol Ol Ol Oi Ol Ol Ol Ol Oi Oi Ol Oi Ol Oi Oi Oi
OOOOO O CO CO 00 00 COO O O O O On On ON On CTiOi Oi Oi Ol oi * * * * 4^OJOJOJOJ OJ 10 10 to tO 10MWHM h 6 6 6 6
O COON* 10 O 00 O>* to O 00 On* to O 00 On* to O MCM^ tO O COON* 10 O CO O\* tO O COON* tO O 00O4> 10 O Co On* tO
ooooo ppppp ooooo ppppp ppppp ppppp ppppp ppppp ppppp oppop
On On On On On On On On On On O^ ONO O o O O O o o O o o o *o O O o O o o O o O o o o o o o o 00 00 00 00 00 00 00 00 Co
On OnO OO CO CO OOO O OvOOOO hhhHH tOO>OJOJ4^ 4>-4i.O>OiOi OnOn ONO; -O si CD OOvO O OOOOw HMtOWOJ
OnO tOOiOO M4>.OOOJ OnO tOOiO tOOiOOHOi COm^OOH 4>-OOH4^0o MOiOOtOOi OtOONOOJ 0;i-i4^00tO OnOOJ-vJ m
O>Oi^4^OJ OJOJ4i4i.Oi Ol ON^l OO tOOJOiOOO tOOiOOM4». OOHOiO^i. COOJ COOJ CO 4>-OOiH00 + H 00 ONOJ MOO ONOi
•OO-KOOO vlOOMU O COO OOMOi mvOOOOJ vO OnOi Oi 00 OJ O COO m OnOJ h to Oi O COO OOJ ID OOOOHSl O1O1 COOJ O
4^. OJ 00CO-?- slvn O HO 4^. ONOi 1-1 4>- Oi4^ M OnO m h OO On Oj O Oi wo OJ M COO-O O WO4^0J Oi O"^l COOJ wOJ O WO
ppppp ppppp ppppp ppppp ppppp ppopp ppppp ppppp ppppp ppppp
O1O1O1O1O1 O1O1O1O1O1 O1O1O1O1O1 O1O1O1O1O1
O 10 4^. ONO M OJONQOOtO Uvlvp
to
to to to to to
O 10-li- O^vO
Ln O OovO w
H CM0vO-<»
O O CTO tO
Oi
to
OOHLkl
W OJ ON OOO 10
H-^ M 0 tO OnO
O OJ M O vO O i-*
M vo ON tO COOJ 00
|
to o>
O
Ul Oi Oi Ln t^i
•0-0 000000
•<J vO «-*>• G>
OWM H CTi
HVO OOOOO
OOJ OO
O1O1O1O1O1 OnOnONONON OnONOnONOn OnOnONOnOn
OOO OOO OOOOM HHHMN tOtOOJOJOJ
O MOJ On CO MOJ ONCOI-I OJ ON0Ot-<4^ ONO n4^"O
O*vOU) 00 tO-O tO-OOJ C00JO4>- O ON tO 004>- O
10 ono'-" to vo ooooooo um to cooi ojojojOi 00
COOJ 004^ 00 4*. OJ 10 tOOJOi VOOJ OOOiOJ
net
ions
r
GO
O
w
CO
CO
OOOOO
Oi OiOiOtOi
ooooo
bOO^O
ooooo ooooo ooooo ooooo ooooo ooooo ooooo ooooo ooooo
1 CCO m
HOJ vO vO
O
ooooo
Oi O>"^1 OOVO
vO-<» O%-f>. tO
4 O|
Oi Ol Oi Oi Oi O1O1O1O1O1
O O >-< tOUJ
H vO OOO^vji
io-<i to Co*-
Oi^ COOtvJ
ooooOoi-ii.
OOO Oh tO
w OOOiOJ M M O O O M
4 O OO
O^ tOOJ vo O
O^ O
Oj 10 M O O
tO-|i- ON CO tO
4 o o
OnOJ O Oi O ON to O vO
OiOiOiOiOi
10 tO iOOjOJ
•<1 OovO O M
vO OOOO-^l-O
Oi vO-^ vOOi
O1O1O1O1O1
ojojojojoj
toOJ-I^Oi On
~J On ON ON ON
M OOOlOJ M
•O^.-vI0i 00
OOJ O OOi
9 9 9 9
OnOiOiOiOi
000 o
ON ON ON ON On . - _
O O O O H OJO» OOtO ON
»<l M HM CO Ol OOONO H
4^ OOiOOJ
?
ooooo
Oi O1O1O1O1
iooj.ji.Oi on
M M M 10 tO
•O «sj' 00 O tO
Oi vO OOOJ-fi
O OOO to
ooooo ooooo
OlOiOiOiOi
4i4^OiOi
COO O 11
too>OJ?
Oi Oi Oi Oi Oi
O1O1 Oi Oi Oi
tOOJ-*>- Oi ON
4LU O
Oi OOt-i ON M
O 10 OOJ to
OJ M-O h4i
4LU
Cniovo
•O OO
CTlO
ppppo
Oi O1O1 O1O1
O1O1 On ON On
-J OOO H N
OOO OHIO
oj to tooj4>-
4>- OsOi O t-t
OOO OJ OOJ
OOOOO
Oi O1O1O1O1
On On On ON O*-
OJ-*k Oi On-vJ
OJ-Ji. OVO 00
Oi OOi-tOi vO
OO4 10 On
M On
OOOOO
Oi O1 <J\ Oi Oi
4 O»4
OOONMOJOJ
O tOOi OOOJ
ppppp
Oi O1O1O1O1
•O--J
. _ 000
O H OJ Ol *O
O O O H tO
OOJOiOJ vO
O OOOO O
OOOOO
O4 Oi
OnO w O 00
ppppp
Oi O1O1O1 Oi
OOOOOOVOVO
"<1 OOVO w tO
M4>--vI OOJ
OOOiOJ 10 tO
OOVO OOOl M
O44 ON w
ppppp
OiOiOi Oi Oi
O O v© vO O
OnO tOOi O
tOOJOi OOtO
OrO COCOON
s
10^
000
•OOJ
OJOJOJOJOJ ojojojojoj
OnOi Oi4>.OJ OJtOMMO
Oi-O OOJ On
tototototo toioioioto
HOi OOi O4>- O
O 0
OJ O
O
lOslOJ OO
OOi 4* ON 0
tO'MOJO OiwOJ-t^O
10
OOVO H^ &
OM4^ ONOO
OOIOVO
OW
to to to to to
JvWWOJ tO
-K vOOi OOi
to to 10 to to
tO M M O O
MM tO 004*
OvOvO OOOO
O ON tO CO4>.
on
^. O OOO. ON
10-0 to-ooj
ON M tO OOOl
*». 0000 o
N OO H H+> O+.
On OOO* 00 -. _ .
o4>-o4^"O o 10 ton 00
H ONO NO On tO 4^ »0 OJ
OO;* w m * 10OO OO
OJ H tO OOtO 10 OOOl M CO
OJOJ* OnO tO ON MOOJ
OJONCOOOJ OCOONHOJ
ONO HO* 10
0000* HH 10
H OOVO 0 00 *
O1
^ O O M
vO OOi OOJ
H 0M0 W 0
OnOi O1O1O1 O1O1O1O1O1 O1O1O1O1O1 O1O1O1O1O1 O1O1O1O1O1 O1O1O1O1O1 O1O1O1O1O1 O1O1O1O1O1 O1O1O1O1O1 O1O1O1O1O1
OvpvOOO OCOCOCoCp COO OOO OOnCn6nOn OU OiOiOi Oi***4^ *OJOJ<jJOJ OJtOtOtOlO JOH-y^1^ HO*"*
O OoO>* to O CoCn* tO O COC~>* 10 O COON* 10
44
O 0OGN4* 10
o
O 00O\4»- tO O 00ON4>- 10 O 00
ON4* to
704
TABLES OF BESSEL FUNCTIONS
Table II. Functions of imaginary argument, and e-"
X
6-02
6-04
6-o6
6-o8
6-io
6-12
6-14
6-16
6-i8
6-2O
6-22
6-24
6-26
6-28
6-30
6-32
6'34
6-36
6-38
6-40
6-42
6-44
6-46
6-48
6*50
6-52
6'54
6-56
6-58
6-6o
6-62
6-64
6-66
6-68
6-70
6-72
f'74
6-76
6-78
6-80
6-82
6-84
6-86
6-88
6-90
6-92
6-94
6-96
6-98
7-00
e-*I0(x)
0-1663661
0-1660763
0-1657880
0-1655012
0-1652159
0-1649321
0-1646498
0-1643089
0-1640894
0-1638114
0-1635348
0-1632596
0-1629858
0-1627134
0-1624424
0-1621727
0-1619044
0-1616374
0-1613717
0-1611073
0-1608443
0-1605825
0-1603220
0-1600628
0*1598048.
0-1595481
0-1592927
0-1590385
0*1587855
O-I585337
0-1582831
0-1580336
0-1577854
O-15753O4
0-1572925
0-1570477
0-1568042
0-1565617
0-1563204
0-1560802
0-1558411
0-1556031
0-1553662
0-1551304
0-1548956
0-1546619
O-I544293
0-1541978
0-1539672
O-I537377
e-xIx{x)
0-1518372
0-151-6237
0-1514111
0-1511994
0-1509885
0-1507784
0-1505691
0-1503607
0-1501531
O-1499463
0-1497403
0-1495351
O-14933O7
0-1491271
0-1489243
0-1487223
0-1485211
0-1483206
0-1481209
0-1479220
0-1477238
0-1475264
0-1473297
0-1471338
0-1469386
0-1467442
0-1465505
0-1463576
0-1461653
O-I459738
0-1457830
O-I45593O
0-1454036
0-1452149
0-1450270
0-1448397
0-1446532
0-1444673
0-1442821
0-1440976
0-1439138
0-1437306
o-i43548i
0-1433663
0-1431852
0-1430047
0-1428248
o-1426457
0-1424071
0-1422892
e*KQ(x)
0-5010588
0-5002584
0-4994618
0-4980689
0-4978799
0-4970946
0-4963130
O-495535I
0-4947608
O-49399O2
0-493-2232
0-4924597
0-4916998
0-4909434
0-4901905
0-4894411
0-4886950
0-4879524
0-4872132
0-4864773
0-4857448
0-4850156
0-4842896
0-4835669
0-4828474
0-4821312
0-4814181
0-4807082
0-4800014
0-4792978
0-4785972
0-4778997
0-4772053
0-4765138
0-4758254
0-4751400
0-4744575
O-4737779
0-4731013
0-4724276
O-47I7567
0-4710887
0-4704235
0-4697612
0-4691016
0-4684449
0-4677908
0-4671395
0*4664910
0-4658451
exK1(x)
0-5411776
0-5401848
0-5391973
0-5382151
0-5372382
0-5362666
O-5353OOI
o-5343387
O-5333825
O-53243I3
0-5314851
O-53O5438
0-5296075
0-5286761
O-5277494
0-5268276
0-5259105
0-5249982
0-5240905
0-5231874
0-5222889
0-5213950
0-5205056
0-5196207
0-5187402
0-5178642
0-5169925
0-5161251
0-5152620
0-5144032
0-5135486
0-5126982
0-5118520
0-5110099
0-5101719
0-5093380
0-5085080
0-5076821
0-5068602
0-5060421
0-5052280
0-5044178
0-5036114
0-5028088
0-5020099
0-5012149
0-5004235
0-4996359
0-498851.9
0-4980716
ex
411-57860
419-89303
428-37544
437-02919
445-85777
454-86469
464-05357
473-42807
482-99196
492-74904
502-70323
512-85851
523-21894
533.78866
544-57191
555-57299
566-79631
578-24636
589-92771
601-84504
614-00311
626-40680
639-06106
651-97095
665-14163
678-57839
692-28658
706-27169
.720-53933
735-09519
749-94510
765-09499
780-55094
796-31911
812-40583
828-81751
845-56074
862-64220
880-06872
897-84729
915-98501
934-48913
953-36707
972-62636
992-27472
1012-31999
1032-77021
i°53-63356
1074-91837
1096-63316
X
6-02
6-04
6-o6
6-o8
6-io
6-12
6-14
6-16
6-18
6-2O
6-22
6-24
6-26
6-28
6-30
6-32
6-34
6-36
6-38
6-40
6-42
6-44
6-46
6-48
6-50
6-52
6-54
6-50
6-58
6-6o
6-62
6-64
6-66
6-68
6-70
6-72
6-74
6-76
678
6-8o
6-82
6-84
6-86
6-88
6-90
6-92
6-94
6-96
6-98
7-00
TABLES OP BESSEL PTJNCTIONS
Table II. Functions of imaginary argument, and ex
705
X
7-02
7-04
7-06
7-08
7-10
7*12
7-14
7'i6
7-18
7-20
7'22
7-24
7'2O
7-28
7-30
7'32
7-34
7'36
7-38
7'4°
7-42
74
7-46
7-48
7-50
7-52
7'54
7'5<>
7-58
7-60
7-62
7-64
7-66
7-68
7-70
772
774
776
7-78
7-80
7-82
7-84
7-86
7-88
7-90
7-92
7-94
7.96
7-98
8-oo
O-I535O93
0-1532819
O-I53O554
0-1528300
0-1526056
0-1523822
0-1521597
0-1519382
0-1517177
0-1514982
0-1512796
0-1510620
0-1508453
0-1506295
0-1504147
0-1502007
0-1499877
0>I497756
0-1495644
O-I49354I
0-1491447
0-1489362
0-1487285
0-1485218
0-1483158
0-1481x08
o-1479066
0-1477032
0-1475007
0-1472990
0-1470981
0-1468981
0-1466988
0-1465004
0-1463028
0-1461060
0-1459100
0-1457148
0-1455203
0-1453267
0-1451338
0-1449417
0-1447503
0-1445597
0-1443099
0-1441808
0-143092*
0-1438048
0-1436179
0-1434318
er-I^x)
0-1421120
0-1419354
0-1417594
0-1415840
0-1414093
0-1412352
0-1410617
0-1408889
0-1407166
0-1405450
O-I4O3739
0-1402035
0-1400337
0-1398644
0-1396958
O-I395277
0-1393603
O-I39I934
0-1390271
0-1388613
0-1386962
0-1385316
0-1383076
0-1382041
0-1380412
0-1378789
0-1377171
O-I375559
O-I373952
0-1372350
O-I37O754
0-1369164
0-1367579
0-1365999
0-1364424
0-1362855
0-1361291
O-I35973-2
0-1358179
0-1356630
o-i355o87
O-T353549
0-1352016
0-1350488
0-1348965
O-I347447
O-I345934
0-1344426
0-1342923
0-1341425
e>>K0{x)
0-4652019
0-4645614
0-4639235
0-4632882
0-4626556
0-4620255
0-4613980
0-4607731
0-4601507
O-45953O8
0-4589134
0-4582985
0-4576861
0-4570761
0-4564686
0-4558634
0-4552607
0-4546604
0-4540625
0-4534669
0-4528736
0-4522827
0-4516941
0-45x1077
0-4505237
0-4499419
0-4493624
0-4487851
0-4482101
0-4476372
0-4470665
0-4464981
O-44593I7
O-4453076
0-4448056
o-4442457
0-4436879
0-4431322
0-4425786
0-4420271
0-4414776
0-4409302
0-4403848
0-4398414
0-4393001
0-4387607
0-4382234
0-4376880
0-437*545
0-4366230
0-4972948
0-4965217
O-495752I
0-4949860
0-4942235
0-4934644
0-4927087
0-4919565
0-4912077
0-4904623
0-4897202
o-48898i4.>
0-4882459
O-4875I37
0-4867848
0-4860591
0-4853365
0-4846172
0-4839010
0-4831880
0-4824780
0-4817712
0-4810674
0-4803667
< 0-4796689
0-4789742
0-4782825
o--1775937
0-4769079
0-4762249
O-4755449
0-4748678
0-4741935
0-4735220
0-4728534
0-4721876
o-47x5245
0-4708642
0-4702066
0-4695518
0-4688997
0-4682502
0-4676034
0-4669593
0-4663178
0-4656789
0-4650426
0-4644089
O-4637777
0-4631491
1118-7866
1141-3876
1164-4452
1187-9685
1211-9671
1236-4504
1261-4284
1286-9109
1312-9083
I339-43O8
1366-4891
1394-0940
1422-2565
1450-9880
1480-2999
1510-2040
1540-7121
1571-8366
1603-5898
1635-9844
1669-0335
1702-7502
1737-1481
1772-2408
1808-0424
1844*5673
1881-8300
1919-8:155
1958-6290
1998-1959
2038-5621
2079-7438
2121-7574
2164-6198
2208-3480
2252-9596
2298-4724
2344-9046
2392-2748
2440-6020
2489-9054
2540-2048
2591-5204
2643-8726
2697-2823
2751-7710
2807-3605
2864-0730
2921-9311
2980-9580
X
7-02
7-04
7-06
7-08
7-10
7-12
7-14
7-16
7-i8
7-20
7-22
7-24
7-26
7-28
7-3O
7-32
7-34
7-3"
7-38
7-40
7-42
7-44
7-40
7-48
7-5O
7-52
7-54
7-50
7-58
7-60
7-62
7-64
7-60
7-68
7-70
772
774
776
778
7-80
7-82
7-84
7-86
7-88
7-90
7-92
7-94
7-96
7.98
8-oo
W, B. V.
45
vo coCooooo cpooooqooo qocooooooo oooooooooo oooooooooo oaqooooooo oooooooooo oooooooooo oooooooooo oooooooooo
6v6v6v6vO' VOOOCOOOCO O°cr*j -^j-vj-vj •*J6acV>6a6a Ono\ oi O> O> Oi A A A A AoJOJOJOJ oititOtOlO K)Mmmm m 6 6 6 O
O CO OAA to O CO OAA to O 00 CM-. tO O OOOAA tO O OOOAA >0 O OOOA @ O CO OAA »0 O OOOAA >0 O OOOAA «0 O OOO^A to
OOOOO OOOOO OOOOO OOOOO OOOOO OOOOO OOOOO OOOOO OOOOO OOOOO
OJOJOJOJOJ WWWWW WWWWW OJOJOJOJOJ OJOJOJOJOJ WWWWW OjAAAA AA-AAA -AAAAA AAAAA
A Oi Oi Oi Oi Oi Oi ON On On OA OA OA"*0 *<1 M M M M M CO 00 CO 00 00 O O O O O OOOOO OOmmm- m m m to to tOtOtO OJ OJ
0 m to A Oi M oo O to Oj Oi OA Oo O m OJ oi Oa OoO m OJ A Oa Co o m OJ Oi On Co O to OJ Oi M Co O to A On*~0 O m w Oi oa Oo O to
wi hvj io 00 OJOOiM-vj OJOOiW-O AO OAOJ VD OAOJ O OAOJ O"<1AhiCO OitOO"<lA t0O-<lOiOJ OOO OAA to Ht O "O OAA
OAOOAtO 0-~JOiAOJ OJAOiOnOO MOi COLO 00 AO^JOiOJ mmmmOJ -A^JOAOO OJO oSOJ' O O 00 00 OOO HJivJ H O\
01 Oi O O OA -vj A OAA *-J O>H HM>O -<100AOi to OAOl On OOtOtOCOO OA OAA 00 VOM H (OvO AOlOJ COO COA MM*
o
OS
i
O O O O O
to »o to to to
OOOOO OOOOO
to to to to to
sj O0O30Q00
OOO m tooj
OA O OJ C^O
mOO vDOOMtO
o to oo bo to o hi cAoi o
OOOOO
to to to to to
OOOOO OOOOO OOOOO OOOOO OOOOO OOOOO
to to to to to
00 00 CO COO _____
Oi OV-J O O M OJ A Oi -vj
tOOl OOtOOl OOtOOlO tO
A OnvD tOOl lOWM tO 00
O*>M 10 tO Ol
K)OJOJ(->JOJ
lO O O O O
COO M
CTOO
OJOJOJOJOJ OJOJOJOJOJ OJOJOJOJOJ
OOOOhi mmmmm Mtotototo
Oi O> OOO HI t00JOiC\00 OOtoOoOi
AOOtOOAO A00t0O\M OlOOJ 00 JO
VjD *^J OnOi Oi Oi Oi On 00 O JO Oi 0010 On
AMOi-OOJ AOOOJM AI0AMI0
OJOJOJOJOJ OJOJOJOJOJ
tOtOtOOJOJ OJOJOJOJOJ
On OO^O m tO ^- Oi O^ OOvO
¦^4 hi Q\ O Oi O A O A O
OOi HvJW O OOOnAOJ
OOOOOJOJ CO M HOW »
w
F
o
w
OOOOO OOOOO OOOOO OOOOO OOOOO
t tooi
tO-O M O>O
vD4i vO4^ vO
Oi 10 M WU>
O O O
to to to
COOO OO O O hi
COtO-vJtOON mOmhOiO
W O OMO vO
Oi COCTiO O
to to to to to
m to to tooj
Oi O-P- vO-P*
to O OOCTiOi
COvJ <J\ Cow
vO hi OOtOOJ
OOOOO
to to to to to
OOOOO OOOOO OOOOO OOOOO
to to to to to
Oi On On'vI "vl OO
_ . _ . 00 W COOJ COOJ
OJ to M OO 0(Klsls)si
> to O O M A O OnA A
ONWM 00
OJ
OM
O
tototoojw wojojojoj Ojojojwoj
OOO OOO MMtOtOW W-AOiOiOn
OOW COW O A O A O A O Oi O Oi O
•<1 CO OOVD O HMWUisl OmA OnvO
On O Oi tO hi tO Oi vO ON-A H^ On O Oi OJ
OAW --0OO s(J> OOMW AWM OOOl
OOOOO
WWW W W
>OA 0>vO w
OlOl^J M--J
K3A A OJ M
OOOOO OOOOO OOOOO OOOOO OOOOO OOOOO OOOOO OOOOO OOOOO
slvj oo COO OOOwtO I0WOJAA OiOi ON-~J M 00 OOO VOO WMtOIOW AAOiOiCTn
to *vj OJ OOOo vO h vO Oi O OA m *^J to 00 OJ vO Oi O On to *^J OJ vO Oi O On to OOA* O On 10 "vl OJ
A-JOWM MOiOWOO tOsJ M OOW O Oi M -<1 A hi OOOt WO OO OnOi W to M O O O O
AAOiOA MMtOOiO 00M OOhi-vJ AAOiOOl WWOiOM OiMOOiW WC>m 0o~O
COW OotOON OmWCJnCO OfOOtCotO ON»0 ooOi A AOiOOJO vOOAOOO OWOmA
oa-o cocoo o b hi hi to
O On to Ot>A O On to COOi
OOOMtO AOfvJOtO
O W O COO W O OoO W
to OJ "M OnvO O^J OJ h^ O
OP
0
I
00--J •<! •<! •<!
mvO-O OvA
OA OOOJ 00
OJ tOU> M O
•O-O-O O>Ch
OJ M O vO-vl
OJ COA O C\
m O>A A Co
O^ C\ Ci CT> C7>
G~it-n OJ W M
OJ O"<l-f- M
O^Oi Oi t_n Ln
O OOO O>'-Ji
O OoOXjiA
AO
AWWWOJ WWWWW WWWWW
A OO to M O O OO^J C^Oi A OJ to M m O O OCrO ~J OnOt AAW IOIOmmO
WIOmmm HHIitoW AOi'MO-O tOACACOM A CnO W On O to C' O A
M A COOi A -^v] 10 COCl --JOtO OOOi OJ A C\O A OOOOOOOM AOOitvM
O OAOJ m O
COOJOl VO 00
OJ tO-J-O vO
O HlJl M tO
A O M
•OVO OOO OA
OJ O to tOA
OTvl •<! CT> OA
O tO CYO M
O OOiOJOJ
m A OJ to 00
to OA-N O OA
to OA-vJ COA
OA M C'OJ O
<-n O COAOi
vOOi m A OJ
OAOi to A CO
-O A OOiO
OAAOiOi O
COO COU>OJ
COO O OOi
O O O O m
OA O O COOA
OACOA O O
'^O COV) o
COM OOiOi
~j sO vO A O
A O to
A
O COM vO 6
Oiuooh ki
OA OA-O O
W} O
A »0 tO CA m
OAOJ O M-vJ
COOJ 0WM
Hi to H tOOJ
I
vp oo Oo co Co cocooooooo oooooooooo oocoooooco oooocoooco oo Co oooo oo oooooooooo oooooooooo oooooooooo oooooooooo
vo (iioocboa
o
0 OvO vO vO
O OC7t
cococococo
OAvJi <Ji <J\ <Ji
o coc-j*. to
CO CO CO 00 00
OnA A A A
O
oooooooooo
A OJOJ OJOJ
O COQAA to
oooooooooo
OJ 10 tO t-i 10
O OOC-A to
qocooooooo
10MMMM MOOOO
O OOCTiA @ O OOC-A >0
TABLES OF BESSEL FUNCTIONS
Table II. Functions of imaginary argument, and ex
707
X
9-02
9-04
9-06
9-08
9-10
9'12
9-14
9-16
9-18
9-20
9-22
9-24
9-26
9-28
9-3O
9-32
9-34
9-36
938
9-40
9-42
9'44
9-46
9-48
9-50
9-52
9-54
9-56
9-58
9-60
9-62
9-64
9-66
9-68
9-70
9-72
9*74
9-70
9-v8
9-80
9-82
9-84
9-86
9-88
9-90
9-92
9-94
9-96
9-98
lo-oo
0-1348051
0-1346512
0-1344978
O-I34345O
0-1341927
0-1340409
0-1338896
0-1337388
0-1335885
0-1334388
0-1332895
0-1331408
0-1329925
0-1328447
0-1326975
0-1325507
0-1324044
0-1322586
0-1321133
0-1319684
0-1318240
0-1316801
0-13153^7
0-1313938
0-1312513
0-1311092
0-1309677
0-1308266
0-1306859
O-I3O5457
0-1304060
0-1302667
0-1301278
0-1299894
0-1298514
0-1297139
0-1295768
0-1294401
0-1293039
0-129x681
0-1290328
0-1288978
0-1287633
0-1280292
0-1284955
0-1283623
0-1282294
0-1280970
0-1279650
0-1278333
e-I^x)
0-1270971
0-1269697
0-1268426
0-1267159
0-1265895
0-1264636
0-1263380
0-1262127
0-1260879
0-1259634
0-1258392
0-1257154
0-1255920
0-1254689
0-1253462
0-1252239
0-1251018
0-1249802
0-1248589
0-1247379
0-1246173
0-1244970
0-1243771
0-1242575
0-1241382
0-1240193
0-1239008
0-1237825
0-1236646
0-1235470
0-1234298
0-1233128
0-1231962
0-1230800
0-1229640
0-1228484
0-1227331
o-1226181
0-1225034
0-1223891
0-1222751
0-1221613
0-1220479
0-1219348
0-1218220
0-1217096
0-.I2 I5974
0-1214855
0-1213739
0-1212627
O'4Il8497
O-4II4O53
O-4IO9623
O-4IO52O7
O-4IOO8O6
0-4096419
0-4092045
0-4087686
0-4083341
O-4O79OIO
0-4074692
0-4070388
0-4066098
O'4o6i82i
O-4O57558
0-4053308
0-4049071
0-4044848
0-4040638
0-4036441
0-4032257
0-4028087
0-4023929
0-4019784
0-4015651
0-4011532
0-4007425
0-4003331
0-3999249
0-3995180
0-3991123
0-3987078
0-3983046
0-3979026
O-3975OI8
0-3971023
0-3967039
0-3963067
o-3959i67
O-3955I59
0-3951223
0-3947299
O-3943386
O-3939485
O-393559C)
0-39317*7
0-3927851
0-3923996
0-3920152
0-3916319
0-4341069
O-43359O4
O-433O758
0-4325629
0-4320519
o-43I5427
0-4310352
0-4305295
0-4300256
0-4295234
0-4290230
0-4285243
0-4280273
0-4275321
0-4270385
0-4265467
0-4260565
0-4255680
0-4250811
0-4245960
0-4241124
0-4236305
0-4231502
0-4226716
0-4221945
0-4217x91
O-.J212452
0-4207730
0-420^023
0-4198332
0-4193656
0-4188996
0-4184351
0-4179721
0-4175107
0-4170508
0:4165924
0-4161355
0-4156801
0-4152261
O-4M7737
0-4143227
0-4*38731
0-4134250
0-4129784
0-4125332
0-4120894
0-4116471
0-4112061
0-4107666
ex
8266-7771
§4337771
8604-1507
8777-9660
8955-2927
9136-2016
9320-7651
9509-0571
9701-1528
9897-1291
10097-0643
10301-0386
10509-1333
10721-4319
10938-0192
11158-9819
11384-4082
11614-3885
11849-0148
12088-3807
12332-5822
12581-7169
12835-8844
13095-1865
i*335972(J8
13629-6112
139O4-947f)
14185-8462
14472-4193
147O4781O
15063-0499
15367-3437
15677-7847
1599-1 *49<>9
16317-0072
16647-2447
101)83-5414
17326-0317
17670-0529
18033-7449
18398-0507
18709-7100
i<)i48-8894
19535-7227
I993O-37O4
20332-9906
20743-7443
21162-7957
21590-3125
22026-4658
X
9-02
9.04
9-06
9-08
9-10
9-12
9-14
9-16
9-18
9-20
9-22
9-24
9-26
9-28
9-30
9-32
9-34
936
9-38
9-40
9-42
9-4.4.
9-46
9-48
9-5O
9-52
9-54
9'5u
9-58
9-60
9-62
9-64
9-66
y-68
9-70
9-72
9-74
97O
978
9-80
9-82
9-84
9-86
q-88
9--9O
9-92
9-94
9-96
9-98
IO-OO
45—2
708
TABLES OF BBSSEL FUNCTIONS
Table II. Functions of imaginary argument, and ex
X
IO-02
IO-O4
IO-OO
10-08
IO-IO
10-12
10-14
IO-IO
10-18
IO-2O
IO-22
10-24
10-26
10-28
10-30
10-32
10-34
10-36
10-38
10-40
10-42
10-44
10-46
10-48
10-50
10-52
10-54
10-56
10-58
io-6o
10-62
10-64
io-66
io-68
10-70
10-72
1074
10-76
10-78
io-8o
10-82
10-84
io-86
io-88
10-90
10-92
10-94
10-96
10-98
11-00
e~xh[x)
0-1277021
0-1275713
0-1274409
0-1273109
0-1271813
0-1270521
0-1269233
0-1267948
0-1266668
0-1265392
0-1264119
0-1262850
0-1261585
0-1260324
0-1259067
0-1257813
0-1256563
0-1255317
0-1254075
0-1252836
0-1251601
0-1250369
O-I249I4I
.0-1247917
0-1246697
0-1245480
0-1244266
0-1243056
0-1241850
0-1240647
0-1239448
0-1238252
0-1237059
0-1235870
0-1234685
0-1233503
0-1232324
0-1231149
0-1229977
o-i2288o8
0-1227642
0-1226480
0-1225322
0-1224166
0-1223014
0-1221865
0-1220719
0-1219577
0-1218438
0-1217302
0-1211517
0-1210411
0-1209307
0-1208206
0-1207109
0-1206014
0-1204922
0-1203833
0-1202747
0-1201664
0-1200584
0-1199506
0-1198432
0-1197360
0-1196292
0-1195226
0-1194162
0-1193102
0-1192044
o-1190990
0-1189938
0-1188888
0-1187842
0-1186798
0-1185757
0-1184718
0-1183682
0-1182649
0-1181619
0-1180591
0-1179566
0-1178544
0-1177524
0-1176507
0-1175492
0-1174480
0-1173471
0-1172464
0-1171459
0-1170458
0-1169458
0-1168462
0-1167467
0-1166476
0-1165487
0-1164500
0-1163516
0-1162534
0-1161554
0-1160578
exK0(x)
0-3912498
0-3908688
0-3904889
0-3901101
0-3897324
O-3893558
0-3889803
0-3886059
0-3882325
0-3878603
0-3874891
0-3871189
0-3867498
0-3863818
0-3860149
0-3856489
0-3852841
0-3849202
O-3845574
0-3841956
0-3838348
0-383475°
0-3831163
0-3827586
0-3824018
0-3820461
0-3816913
o-38i3375
0-3809848
0-3806330
0-3802821
O-3799323
O-3795834
O'37923<54
0-3788884
0-3785424
O-3781973
O-3778532
0-3775100
0-3771677
0-3768264
0-3764860
0-3761465
O-3758O79
0-3754702
O-375I335
O-3747976
0-3744627
0-3741287
0-3737955
ePK^x)
0-4103284
0-4098917
0-4094563
0-4090223
0-4085897
0-4081584
0-4077285
0-4073000
0-4008727
0-4064468
0-4060223
O'4O5599O
0-4051771
0-4047565
0-4043372
0-4039191
0-4035024
0-4030869
0-4026728
0-4022598
0-4018482
0-4014378
0-4010286
0-4006207
0-4002140
0-3998085
0-3994043
0-3990013
O-3985995
0-3981989
O-3977995
0-3974013
0-3970043
0-3966084
0-3962137
0-3958202
0-3954279
0-3950367
0-3946467
o-3942578
0-3938701
O-3934835
0-3930980
0-3927137
0-3923305
0-3919484
o-39i5673
0-3911874
0-3908086
0-3904309
ex
22471-430
22925-383
23388-506
23860-986
24343-009
24834-771
25336-466
25848-297
26370-467
26903-186
27446-666
28001-126
28566-786
29143-874
29732-619
30333-258
30946-030
31571-181
32208-961
32859-626
33523-434
34200-652
34891-551
35596-408
36315-503
37049-124
37797-566
38561-128
39340-114
40134-837
40945-615
41772771
42616-637
43477-55O
44355-855
45251-903
46166-052
47098-668
48050-124
49020-801
50011-087
51021-378
52052-078
53103-600
54176-364
55270-799
5638y343
57526-443
58688-554
59874-142
X
IO-O2
I0-O4
10-06
10-08
IO-IO
IO-I2
10-14
10-16
10-18
I0-2O
10-22
IO'24
10-26
IO-28
IO30
IO-32
10-34
10-36
10-38
10-40
10-42
10-44
10-46
10-48
10*50
10-52
io-54
10-56
10-58
io-6o
10-62
10-64
10-66
io-68
10-70
10-72
io-74
10-76
10-78
io-8o
10-82
10-84
io-86
io-88
10-90
10-92
10-94
10-96
10-98
II-OO
TABLES OF BESSEL FUNCTIONS
Table II. Functions of imaginary argument, and ex
709
X
II-O2
11-04
Ii-o6
n-o8
II-IO
II-I2
11-14
H-l6
II-I8
11-20
11 '22
11-24
11-20
11-28
II-3O
11-32
n-34
11-36
11-38
11-40
11-42
H-44
11 -40
11-48
11-50
11-52
u-54
11-56
11-58
n-6o
11-62
11 -64
n-66
n-68
11-70
11-72
1174
11-76
11-78
11-8o
11-82
11-84
n-86
n-88
11-90
11-92
11-94
11-96
II-98
I2-0O
e-xI0(x)
0-1216169
0-1215039
0-1213912
0-1212789
0-1211669
0-1210551
0-1209437
0-1208326
0-1207218
0-1206113
0-1205011
0-1203912
0-1202817
0-1201724
0-1200634
0-1199547
0-1198463
0-1197382
0-1196303
0-1195228
0-1194156
0-1193086
0-1192020
0-1190956
0-1189895
0-1188837
0-1187782
0-1186729
0-1185680
0-1184633
0-1183589
0-1182548
0-1181509
0-1180473
0-1179440
0-1178410
0-1177382
0-1176357
°-I][75335
O-II743I5
0-1173298
0-1172284
0-1171272
0-1170263
0-1109256
0-1168252
0-1167251
0-1166252
0-1165256
0-1164262
e~*Ix{x)
0-1159603
0-1158631
0-1157662
0-1156694
O-II5573O
0-1154767
0-1153807
0-1152849
0-1151894
0-1150941
0-1149990
0-1149042
0-1148096
0-1147152
0-1146211
0-1145272
O-H44335
0-1143401
0-1142468
0-1141538
0-1140610
0-1139685
0-1138762
0-1137841
0-1136922
0-1136005
0-1135090
0-1134178
0-1133268
0-1132360
0-1131454
0-1130551
0-1129649
0-1128750
0-1127852
0-1126957
0-11260*64
0-1125173
0-1124284.
0-1123398
0-1122513
0-1121630
0-1120750
0-1119871
0-1118995
0-H18120
0-1117248
0-1116378
0-1115509
0-1114643
e*K0(x)
O-3734632
O-373I3I9
0-3728014
0-3724717
0-3721430
0-3718151
0-3714881
0-3711619
0-3708367
0-3705122
0-3701886
0-3698659
0-3695440
0-3692229
0-3689027
0-3685833
0-3682648
O-367947O
0-3676301
0-3673140
0-3669987
0-3666843
0-3663706
0-3660578
O-3657457
O-3654344
0-3651240
0-3648143
0-3645054
0-3641973
0-3638900
o-3635834
o-3632777
0-3629727
0-3626684
0-3623650
0-3620623
0-3617603
0-3614591
0-3611587
0-3608590
0-3605600
0-3602618
O-3599643
0-3596676
O-3593716
0-3590763
0-3587818
0-3584880
o-358i949
+ Kx(x)
0-3900543
0-3896788
0-3893043
0-3889309
0-3885586
0-3881873
0-3878171
0-3874480
0-3870799
0-3867128
0-3863468
0-3859818
0-3856178
0-3852548
0-3848929
0-3845320
0-3841721
0-3838132
0-3834553
0-3830984
0-3827425
0-3823875
0-3820336
0-3816806
0-3813286
0-3809775
O'38o6275
0-3802783
O-37993O2
O-379583O
0-3792367
0-3788914
O-378547O
0-3782035
0-3778610
O-3775I94
0-3771787
0-3768389
0-3705001
0-3761621
03758251
0-3754890
"•3751537
O'3748i94
O'3744859
O-374I533
O-37382K)
0-3734908
0-3731608
0-3728318
ex
61083-680
62317-652
63576*552
64860-883
60171-160
67507-906
68871-656
70262-956
71682-362
73130-442
74607-775
76114-952
77652'576
79221-262
80821-638
82454-343
84120-031
85819-368
87553-O35
89321-723
91126-142
92967-012
94845-070
96761-068
98715771
100709-962
102744-438
104820-013
106937-518
IO9O97-799
111301-721
113550-165
115844-030
118184-235
120571-715
123007-425
125492-340
128027-453
r ^0013-780
i33-J5'J353
135944-229
i386<)o-48.5
14l4<J'2Io
M435°'55i
147260-625
150241-608
15 3 276-690
156373-085
I59532-O3I
162754-791
X
II-O2
II-O4
II-OO
ii-o8
II-IO
11-12
11-14
II-IO
ii-i8
II-2O
11-22
11-24
11-26
11-28
II-30
11-32
11-34
11-36
11-38
11-40
11-42
11-44
11-46
11-48
11-50
11-52
n-54
11-56
11-58
ii-6o
11-62
11-64
1 r-66
n-68
11-70
11-72
1174
11-76
11-78
ir-8o
11-82
11-84
i r -86
n-88
11-90
11 -92
11-94
11 -96
11-98
I2-O0
N Tf-vO 00 O N ^"VO 00 O N "^O 00 O N ^J"VO 00 O N t(-vO 00 O N "^O 00 O N ^-vO 00 O N rf-O 00 O N tfvC 00 O N 'tf-vO 00 O
NNNNN NNNNN NNNNN NNNNN NNNNN NNNNN NNNNN NNNNN NNNNN NNNNCO
vO rf- OnvO vO m tNfUO >O <OOnOvNOn tJ- to CO N. N Tt- Tf- CO u"> O> vO - •<*- H r~- to to N vO O TOOvO >O CON COOC ON CO Tf- w N
vO On On m 00 VO to lOOO M OnOO to C^- On wOiNOOvO iO tovO 00N O CO CO CO to +flNO d 00 to C^- O •**" O-CC N + H ""
N V0 00 O M to N **4" N On tJ~ m m to to ^4" M m CO M vO O *O CO Is** 00 00 O VO 00 On m V0 00 O» 00 CO Tt~ IO C^» ^t" ON to to N On OAvO CO CO
t|-Onh h N O M On ¦O00 O O00 tM3> COO OOOnO O m i-i n co tOOO COOO to "^vO On to t|- vO N M •<*- H coOnhOOm
O CO00 CO00 IO N OnOO I~» 00 CJ^O COVO M vO N OnOO O. t~-CO O CO t^ N OnvO IO U">vO 00 N N COmOON to OnvO CO CO COvO OVO Tt"
Q\ CO Is** O *<30 N vO M IO O\ "^"OO CO C^» N C^ N t^ COOO CO OS ^* O VO N OO Tf" M l~^ Tt" m OO to N OnvO tJ~ N O 00 vO " ~ ~ ~
OOOOOnOnOn OOMmm NNCOCO"^ "^t-iO lOvO VO t^- C-~O0 O>Oi OOMNN CO^t""^" tovO vO t^OO <J< O
MMMMM NNNNN NNNNN NNNNN NNNNN COCOCOCOCO COCOCOCOCO COCOCOCOtI-
g
M
I
03
CO
ft
O
COVO
o
iO M 00 V) W 00 ^O 04 O^ *O
M M M OOO^O^
co co co co co cococococo
66666 66666
H N WOO CO
vO Tf* CO t-f C^ 00 vO
04 **^^Q cO ^Tv ^.f^i cO O
C^ooooco i>* ...
•O vO vO vO *O 'OO^OO O
CO CO CO CO CO CO CO CO CO CO
I>«I>«100 CO
00 i-i lOO
vO vO
.h m o*
-OC\
CO
m co to ^i" co
tJ" CO CO CO CO COCOCOCOCO
O O»^t"M00 to N ONvO CO O
.... Th t|- CO CO CO CON NNM WMOOO O.,_ _
VO vO vO vO VO vOvOvOvOvO vOvOvOvDvo vOvOvOvOvO vO to to to to
COCOCOCOCO COCOCOCOCO COCOCOCOCO COCOCOCOCO COCOCOCOCO COCOCOCOCO
0000
ooooo ooooo ooooo ooooo ooooo ooooo ooooo ooooo
COM
>ooo
o m «'n ^- tovb"t>i» b
O^vO CO O O» ^t" m 00 to CO
O» C^» t>« C^vO vO vO to *O to
iO to to to to *O to to tO to
COCOCOCOCO COCOCOCOCO
OOOOO OOOOO
vO O> QtvO O
O.N00 tOCO
M CO Tj-VOOO
to -<i- -^- Tt- co
COCOCOCOCO COCOCOCOCO
66666 66666
t(- t(-m to
1-1 CO
O N . _ _
N O>vO COO
M H H H H
votOiOiOtO
COCOCOCOCO COCOCOCOCO
MOO N M vO
¦"*-•-< O O>00
¦too N lOO
OOOOO OOOOO
CO CO CO CO CO
6 6 6 6 6
CO CO CO CO CO
6 6 6 6 6
CO CO OOCOCO
6 6 6 6 6
COCOCOCOCO
6 6 6 6 6
C^-w C^Thco tOOO COO O\ O co 00 to CO covO O vO COCO •<*¦ OO CO OOO On m iohOO N oomOvNO Om •$¦0*^0 ¦<+¦ "+-VO O> ¦<*¦
W* 00 COOO COOO rt-0»ON00 T|-M00tON OO-iOCOM O>00 VO lOTl" ^tTKON M NCOCO"<MO vO tvOO (?H CO to O- O< N
O m CO ^hvO C^-OO N -^t-tot>-CO O N CO<or-» On O CS t(-vO t^O>w CO to C^. CT> w CO to C^-Onh CO to t^O»H COvO 00 O N ^f-1^-
N m O O\O0 t^-vo vO lO-^t-cONH mO O\00 S>~ vOvOiOThco NmmOO\ 00 N t^-AO to -"tf-cocONM O O\ O\CX5 t^- vO vO to ^r CO
i_iMmhh ooooo ooooo o oonoo o\<j\Q\tj\o\ o\O\O\ oncxj oooocxjoooo oooocxjoocxj oo nnnn r^-r^t^t^t^
mmmmi-i mmmmm mwhmh mmOOO OOOOO OOOOO OOOOO OOOOO OOOOO OOOOO
66666 66666 66666 66666 66666 66666 66666 66666 66666 66666
w COvO CON COC^>^N"tf" NfON COvO N O H dO> VOVOOOCOO 0O O fi&N OOOtONw cOvC N O O Nt^-CONCO vO'-'OO C~-CO
r^OO On M CO <O C^ O COVO ONCOC^-MIO OtOOtoO vONOOiOm 00 VO fOOOO vOtocoNw O OiOnQnCn 0>0>Oh fl CO tOvO 00 O
NNNCOCO coro^^''*' ^to tOvO VO t^ OiXI 00ON OnOC5mN N rT+fiTi vO r-~O0 CT> O m m N CO ">*• tovO 00 On O M N CO -^-vO
CO N M O O» 00 t^vO iO*i" CONMOOi 00 C>.vO IO ^t" CO CO N M O O>00 C^-vO to ""tf" CO N m m O OnOO O-vO to Tt" CO N N i-i O O>00 t^-
VOVOvOvD >O totOtOtOtO u-jtO'OtO'Sl- -^-t(--<*-^(--^- -<t--<*--^--^->^- COCOCOCOCO COCOCOCOCO CONNNN NNCINN NC-Immm
66666 66666 66666 66666 66666 66666 66666 66666 66666 60666
N ThvO 00 O M "^"VO 00 O N -^vO 00 O N t(-VO 00 O N -^-vO 00 O N ^VO 00 O N T|-vO 00 O N -^O 30 O N ^vO 00 O N "^(-O 00 O
OOOOm mmwmn NNNNCO cocococo^" '^"^(-¦^¦¦^"to iOto>0 toO vOvOvOvOt^- t^O-O. C~-CO WjOOOOCCTi ONOiCriCriO
NNNNN NNNNN NNNNN NNNNN NNNtNN NNNNN NNNNN NNNNN NNNNN NNNNCO
o
I—I
TABLES OF BESSEL FUNCTIONS
Table II. Functions of imaginary argument, and e*
711
X
13*02
I3-O4
i3-o6
13-08
13-10
13-12
13-14
13-16
13-18
13-20
13-22
13-24
13-26
13-28
13-3°
13-32
13-34
13-36
I3-38
13-40
13-42
13-44
13-46
I3-48
13-50
I3-52
13-54
13-56
13-58
13-60
13-62
13-64
13-66
13-68
13-70
13-72
1374
1376
13-78
13-80
13-82
13-84
i3-8§
13-88
13-90
I3'92
13-94
13-90
13.98
14-00
O-III6732
a-IH58.57
O-1H4985
O-m4II4
O-IH324O
O-1I12379
O-I1H5I5
O-IIIO652
O-IIO9792
O-HO8934
O-IIO8O77
O-1IO7223
O-.TIO637O
O-IIO552O
O-IIO467I
O-IIO3825
O-IIO298O
O-IIO2I38
O-IIOI297
O-IIOO458
O-IO9962I
0-1098786
O-IO97953
O-IO97122
O-IO96292
O-1O95465
O-1O94639
O-IO938l6
O-IO92994
O-1O92I74
O-IO9I356
O-1O9O54O
O-1O89725
O-IO889I2
0-1088102
0-1087293
0-1086485
0-1085080
0-1084876
0-1084074
0-1083274
0-1082476
0-1081679
0-1080885
0-1080092
0-1079300
0-1078511
0-1077723
0-1076937
0-1076153
0-1072951
0-1072179
0-1071409
0-1070640
0-1069874
0-1069109
0-1068345
0-1067583
0-1066823
0-1066064
0-1065307
0-1064552
0-1063798
0-1063046
0-1062295
0-1061546
0-1060798
0-1060052
0-1059308
0-1058565
0-1057824
0-1057084
0-1056346
0-1055609
0-1054874
0-1054140
0-1053408
0-1052677
0-1051948
0-1051221
0-1050495
0-1049770
0-1049047
0-1048325
0-1047605
0-1046886
0-1046169
0-1045453
0-1044739
0-1044026
0-1043315
0-1042605
0-1041896
0-1041189
0-1040484
0-1039779
0-1039077
0-1038375
0-1037675
0-1036977
e*K0(x)
0-3441388
O-3438795
0-3436208
0-3433626
0-3431051
0-3428481
O-34259I7
O-3423359
0-3420807
0*3418260
O-34I57I9
0-3413184
0-3410654
0-3408130
0-3405611
0-3403098
0-3400591
0-3398089
0 3395593
O-3393IO2
0-3390616
0-3388137
0-3385662
O-3383I93
0-3380729
0-3378271
o-33758i8
O-337337I
0-3370928
0-3368491
0-3366060
O-3363633
0-3361212
O-3358796
O-3356385
o-3;0398o
O-335I579
0-3349184
O-3346794
0-3344409
0-3342029
O-3339654
O-3337285
O-333492O
o-333256o
0-3330206
0-3327856
O-33255II
0-3323171
0-3320836
ePK^x)
0-3571182
0-3568296
O'35654I7
O-3562544
O-3559679
0-3556820
O-3553968
0-3551123
0-3548285
O-3545454
0-3542629
o-35398ii
o-3537ooo
Q'3534195
O-353I398
0-3528606
0-3525821
0-3523043
0-3520272
o-35i75o6
O-35I4748
0-3511995
0-3509250
0-3506510
O-35O3777
0-3501051
0-3498330
0-3495616
0-3492909
0-3490207
0-3487512
0-3484823
0-3482140
O-3479463
O-3476793
0-3474128
O-347I47O
0-3468818
0-3466172
O-3463532
0-3460897
0-3458269
O-3455647
O-3453O3I
0-3450420
0-3447816
O-34452I7
0-3442624
0-3440037
0-3437456
ex
45I35O-74
460468-63
469770-71
47926071
488942-41
498819-71
508896-53
519176-92
529664-99
540364-94
551281-03
562417-65
573779-24
58537O-35
597195-61
609259-77
621567-63
634124-13
646934-29
660003-22
673336-I7
686938-47
700815-54
714972-96
729416-37
744151-56
759184-42
774520-96
790167-32
806129-76
8224.14-66
839028-54
855978-04
873269-94
890911-17
908908-77
927269-94
946002-04
965112-54
984609-11
1004499-53
1024791-77
IO45493-94
1066614-32
1088161-36
1110143-67
1132570-06
II55449-5O
1178791-12
1202604-28
X
13-02
13-04
13-06
13-08
13-10
13-12
13-14
13-10
13-18
13-20
13-22
13-24
13-26
13-28
X3-3O
I3-32
13-34
13-36
I3-38
13-40
13-42
13-44
13-46
13-48
I3-5O
I3-52
13-54
13-56
I3-58
13-60
13-62
13-64
13-66
13-68
13-70
13-72
13-74
13-76
I3-78
13-80
13-82
13-84
13-86
13-88
13-90
13-92
13-94
13-96
13-98
14-00
712 TABLES OF BESSEL FUNCTIONS
Table II. Functions of imaginary argument, and ex
I4"O2
14-04
I4-o6
14-08
14-10
14-12
14-14
14-16
14-18
14-20
14-22
14-24
14-26
14-28
14-30
14-32
14-34
14-36
I4-38
14-40
14-42
14-44
14-46
14-48
14-50
14-52
14-54
14-56
I4-58
14-60
14-62
14-64
14-66
14-68
14-70
14-72
14-74
14-76
14-78
14-80
14-82
14-84
14-86
14-90
14-92
14-94
14-96
14-98
15-00
0-1075370
0-1074589
0-1073810
0-1073032
0-1072256
0-1071482
0-1070710
0-1069939
0-1069169
0-1068402
0-1067636
0-1066872
0-1066109
0-1065348
O-IO645O9
0-1063831
0-1063075
0-1062321
0-1061568
0-1060817
0-1060067
0-1059319
0-1058572
0-1057827
0-1057084
0-1056342
0-1055602
0-1054863
0-1054126
O-IO5339I
0-1052657
0-1051924
0-1051193
0-1050464
0-1049736
0-1049009
0-1048284
0-1047561
0-1046839
0-1046119
0-1045400
0-1044682
0-1043966
0-1043252
0-1042539
0-1041827
0-1041117
0-1040408
0-1039701
0-1038995
0-1036279 .
0-1035584
0-1034889
0-1034196
0-1033505
0-1032814
0-1032126
0-1031438
0-1030752
0-1030067
0-1029384
0-1028702
0-1028021
0-1027342
0-1026663
0-1025987
0-1025311
0-1024837
0-1023965
0-1023293
0*1022623
0-1021954
0-1021287
0-1020621
0-1019956
0-1019292
0-1018630
0-1017969
0-1017309
0-1016650
0-1015993
0-1015337
0-1014682
0-1014029
0-1013377
0-1012726
0-1012076
0-1011428
0-1010780
0-1010135
0-1009490
0-1008846
0-1008204
0-1007563
o-1006923
0-1006284
0-1005647
0-1005011
0-1004376
0-1003742
0-3318506
0-3316181
0-3313861
0-3311546
0-3309235
0-3306930
0-3304629
O-33O2333
0-3300042
O-3297755
O-3295474
0-3293197
0-3290924
0-3288657
0-3286394
0-3284136
0-3281882
0-3279633
0-3277389
O-3275I49
0-3272914
0-3270684
0-3268458
0-3266236
0-3264019
0-3261807
O-3259599
O-3257396
O-3255I97
0-3253002
0-3250812
0-3248626
0-3246445
0-3244268
0-3242096
0-3239928
0-3237764
0-3235604
O-3233449
0-3231298
0-3229152
0-3227010
0-3224872
0-3222738
0-3220608
0-3218483
0-3216362
0-3214245
0-3212132
0-3210024
e*Kx{x)
o-343488i
0-34323"
O-3429747
0-3427189
0-3424637
0-3422090
o-34J9549
3473
0-3414484
0-3411959
0-3409441
0-3406927
0-3404420
0-3401918
O-339942I
O-339693O
O-3394444
0-3391964
o-3389489
0-3387020
O-3384555
0-3382097
O-3379643
O-3377I95
O-3374752
O-33723I5
0-3369883
O-3367455
0-3365034
0-3362617
0-3360206
O-3357799
O-3355398
0-3353002
6
0-3348226
O-3345845
O-3343469
0-3341098
O-3338733
O-3336372
°-3334OI7
O-333I666
0-3329320
0-3326979
0-3324644
0-33*2313
O-33I9987
0-3317665
O-33I5349
1226898-5
1251683-5
1276969-2
1302765-7
1329083-3
1355932-5
1383324-2
1411269-2
I439778'7
1468864-2
H98537'2
1528809-7
I559693-7
1591201-6
1623346-0
1656139-7
1689596-0
1723728-1
I758549-7
1794074-8
1830317-5
1867292-4
1905014-2
I943498-O
1902759-3
2022813-7
2063677-2
2105366-2
2I47897-5
2191287-9
2235554-8
2280716-0
2326789-6
2373793-8
2421747-6
2470670-2
2520581-0
2571500-1
2623447-9
2676445-1
2730512-8
2785672-8
2841947-2
2899358-3
2957929-2
3017683-4
3078644-6
3140837-4
3204286-5
3269017-4
14-02
14-04
14-06
14-08
14-10
14-12
14-14
14-16
14-18
14-20
14-22
14-24
14-26
14-28
14-30
14-32
I4'34
14-30
14-38
14-40
14-42
14-44
14-46
14-48
I4-5O
14-52
I4'54
14-50
14-58
14-60
14-62
14-64
14-66
14-68
14-70
14-72
*474
14-76
14-78
14-80
14-82
14-84
1486
14-88
14-90
14-92
14-94
14-96
14-98
15-00
TABLES OE BESSEL FUNCTIONS
Table II. Functions of imaginary argument, and ex
713
#„(*)
KX{X)
15-02
15-04
15-06
15-08
1510
15-12
15-14
15-16
15-18
15-20
15-22
15*24
15-20
15-28
1.5-32
I5'34
I5-3O
15-38
15-40
I5-42
15-44
15-46
15-48
15-5O
1.5-52
15-54
15-50
I5-58
15-00
15-62
i5-<>4
15-66
15-68
15-70
15-72
15-74
15-76
15-78
15-80
15-82
15-84
15-86
15-88
15-90
15-92
15-94
15-90
15-98
16-00
0-1038291
0-1037588
0-1036087
0-1036186
0-1035488
0-1034791
0-1034095
0-1033400
0-1032707
0-1032016
0-1031325
0-1030636
0-1029949
0-1029263
0-1028578
0-1027895
0-1027213
0-1026532
0-1025853
0-1025175
0-1024498
0-1023823
0-1023149
0-1022470
0-1021805
O-IO21I35
o* 102046b
O-IOI9799
(VIOI9133
0-1018468
0-1017805
0-1017143
o-1010482
0-1015822
0-101516/)
0-1014507
0-1013851
0-1013197
0-1012544
o-ioi1892
o-ioi1241
0-1010592
0-1009944
0-1009297
0-1008651
0-1008007
0-1007363
0-1006722
o-1006081
0-1005441
0-1003109
0-1002478
0-1001047
0-1001218
0-1000590
0-0999964
0-0999338
0-0998714
0-0998090
0-0997468
0-0996847
0-0996228
0-0995609
0-0994991
O-O994375
0-0993760
0-0993146
0-0992533
0-0991921
0-0991310
0-0990701
0-0990092
0-0989485
0-0988879
0-0988274
0-0987670
0-0987067
0-0986465
0-0985864
0-0985265
0-0984666
0-0984069
0-0983472
0-0982877
0-0982283
00981690
0-0981097
0-0980506
0-0979916
0-0979328
0-0978740
0-0978153
0-0977567
0-0976983
0-0976399
0-0975816
0-0975235
0-0974654
0-0974075
0-0973496
0-3207919
0-3205819
0-3203723
0-3201631
O-3I99543
O-3I97459
O-3I95379
0-3191231
0-3189164
0-3187100
0-3185040
0-3182985
0-3180933
0-3178885
0-3176841
0-3174801
0-3172766
O-3I7O734
0-3168705
0-3166681
0-3164661
0-3162644
0-3160632
0-3158623
0-3156618
0-3154617
0-3152619
0-3150626
0*3148636
0-3146650
0-3144668
0-3142689
0-3140714
8
°-3I3677°
0-3134812
0-3132852
0-3130896
•0-3128943
0-3126994
0-3125049
0-3123107
0-3121169
0-3119235
O-3II73O4
O-3II5370
O-3II3453
0-3111533
0-3109616
O-33I3O37
0-3310731
0-3308429
0-3306132
0-3303839
0-3301552
0-3299269
0-3296990
0-3294717
0-3292448
0-3290184
0-3287924
0-3285670
0-3283419
0-3281174
0-3278933
0-3276696
0-3274464
0-3272237
0-3270014
0-3267796
0-3265582
0-3263372
0-3261168
0-3258967
0-3256771
0-3254580
0-3252392
0-3250210
0-3248031
0-3245857
0-3243687
0-3241522
0-3239361
0-3237204
0-323505?
0-3232903
0-3230759
0-3228620
0-3226484
0-3224353
0-3222226
0-3220103
0-3217985
0-3215870
0-3213760
0-3211654
0-3209552
0-3207454
0-3205360
3335O55-9
3402428-5
3471162-1
3541284-2
3612822-9
3685806-8
3760265-0
3836227-4
39I3724-4
3992786-8
4073446-5
4I55735-6
4239687-0
4325334-3
4412711-9
4501854-6
4592798-1
4685578-8
4780233-7
4876800-9
4975318-8
5075826-9
5178365-4
.5282975-3
5389698-5
549577
5609656-2
5722978-8
58385907
5956538-O
6076868-1
6199628-9
6324869-8
6452640-6
6582992-6
67I5977-9
6851649-6
6990062-1
7131270-7
7275332-0
7422303-4
7572243-9
7725213-4
7881273-0
8040485-3
8202913-9
8368623-7
8537681-1
8710153-7
8886110-5
15-02
15-04
15-06
15-08
15-10
15-12
I5-I4
15-16
15-18
15-20
15-22
15-24
15-26
15-28
I5-3O
I5-32
15-34
15-36
I5-38
15-40
15-42
I5-44
i5-4d
15-48
15-50
15-52
15-54
15-56
15-58
15-60
15-62
15-66
15-68
15-70
15-72
15-74
15-76
15-78
15-80
15-82
15-84
15-86
15-88
15-90
15-92
15-94
I5-96
15-98
16-00
714
TABLES OF BESSEL FUNCTIONS
Table III. Functions of order one-third
X
o
O-O2
O-OA
o-oo
0-08
O-IO
O-I2
0-14
0-16
0-18
O-2O
O-22
0-24
0-26
0-28
0-30
0-32
o-34
0-36
0-38
0-40
0-42
0-44
0-46
0-48
0-50
0-52
o-54
0-56
0-58
o-6o
0-62
0-64
o-66
o-68
0-70
0-72
0-74
076
078
o-8o
0-82
0-84
o-86
o-88
0-90
0-92
0-94
o-gt
0-98
I-00
/1/3W
o-ooooooo
+ 0-2412455
+ 0-3038819
+ 0-3477275
+ 0-3825227
+ 0-4117819
+ 0-4372223
+ 0-4598264
+ 0-4802143
+ 0-4988049
+ 0-5158967
+ 0-5317088
+ 0-5464087
+ 0-5601271
+ 0-5729677
+ 0-5850148
+ °'5963375
+ 0-6069935
+ 0-6170312
+ 0-6264920
+ 0-6354112
+ 0-6438195
+ O-65I7435
+ 0-6592067
+ 0-6662297
+ 0-6728308
+ 0-6790265
+ 0-6848313
+ 0-6902585
+ 0-6953202
+ 0-7000271
+ 07043893
+ 07084159
+ 0-7121152
+ O-7I5495I
+ 07185627
+ 0-7213248
+ 07237876
+ 07259570
+ 07278387
+ 0-7294377
+ 07307591
+ 07318076
+ 07325877
+ 07331037
+ 07333598
+ 0-7333600
+ 0-7331080
+ 0-7326077
+ 0-7318627
+ 0-7308764
- CO
- 3-8181574
- 2-9641628
- 2-5398832
- 2-2665744
- 2-0682560
- 1-9140102
- 17884275
- 1-6828031
- 1-5917752
- 1-5118289
- 1-4405408
- 1-3761797
- 1-3174682
- 1-2634392
- 1-2133449
- 1-1665964
- 1-1227224
- 1-0813409
- 1-0421378
- 1-0048529
- 0-9692681
- 0-9351991
- 0-9024892
- 0-8710041
- 0-8406278
- 0-8112601
- 0-7828134
- 07552112
- O7283861
- 07022788
- 0-6768367
- O-652OI29
- 0-6277661
- 0-6040589
- 0-5808580
" O-558I337
~ O-535859I
- 0-5140100
- 0-4925646
- 0-4715032
- 0-4508080
- 0-4304628
- 0-4104530
- 0-3907653
- 0-3713877
- 0-3523093
- O-33352OI
- 0-3150111
- 0-2967741
- 0-2788016
1 #1/3 M
00
3-8257712
2-9796989
2-5635758
2-2986264
2-1088503
1-9633131
1 -8465950
I7499806
I-668O99I
I-5974279
I-5355364
1-4806867
1-4315952
1-3872889
1-3470145
I-3IOI777
1-2763020
I -2450002
I-2I59537
1-1888973
1-1636083
1-1398978
1-1176047
1 -0965902
1-0767342
I-O5793I9
1-0400917
1-0231329
1 -0069839
0-9915813
0-9768685
0-9627948
O-9493I46
0-9363868
O-9239742
0-9120431
0-9005029
0-8895054
0-8788453
0-8685590
0-8586249
0-8490233
0-8397359
0-8307458
0-8220374
0-8135962
0-8054086
07974623
0789745^
0-7822472
argH1/3(*)
-90°
- 86° 23' 4*72
- 84° 8' 47*63
- 82° 12 I5'4O
- 80° 25' 14*29
- 78° 44' 23*54
- 77° 7'57*21
- 75°34'5i'ii6
- 74 4 23*06
- 72° 30, 3*2i
- 71° 9 29*88
- 69° 44' 26*57
- 68° 20 40*45
- 66° 58' 1*30
- 65° 36'20*81
- 64° 15' 32^17
- 62° 55'29*69
- 61° 36' 8*57
- 60 17'24*70
- 58° 59' 14-57
- 57 41 35-13
- 56° 24' 23*72
- 55° 7'38-oi
- 53° 51 I5"93
- 52° 35 15*65
- 51° 19'35*54
- 50° 4' H'M
- 48° 49 10" 14
- 47° 34' 22*35
- 46° 19' 49*69
- 45° 5'31-20
- 43° 5i' 25^98
- 42° 37'33-23
- 41°23 529
- 40 10' 22*19
- 38° 57' 2?6o
- 37° 43' 52-84
- 36° 30' 52^38
- 35° 18' 0*72
- 34° 5' I7-4O
- 32° 52' 42*00
- 310 40' 14*12
- 30° 27' 53*39
- 29° 15 39/i:47
- 28°' 3'32*02
- 26° 51' 30*76
- 25° 39' 35*39
- 24° 27' 45*66
- 23°16 1*32
- 22° \' 22*12
- 2O° 52' 47*84
*>Kus(x)
00
5-8973367
4-5650965
3-9129445
3-4996127
3-2048056
2-9795927
2-7996089
2-65IIOO3
2-5256038
2-4175728
2-3231916
2-239733I
2-1651865
2-0980307
2-0370894
1-9814363
I-93O33O1
1-8831690
I-8394587
1-7987884
1-7608136
1-7252429
1-6918274
1-6603536
1-6306366
1-6025156
I-57585OI
1-5505163
1-5264049
1-5034188
1-4814718
1-4604863
I-44O393I
1-4211296
1-4026393
1-3848710
1-3677782
I-35I3I86
1-3354533
1-3201469
1-305367°
1-2910835
1-2772690
1-2638979
1-2509467
1-2383936
1-2262184
1-2144022
1-2029275
1-1917780
X
0
O-O2
O-OA
0-06
0-08
o-io
O-I2
0-14
o-io
0-18
O-2O
O-22
0-24
O-2D
0-28
0-30
0-32
o-34
0-36
0-38
0-40
042
O-44
0-46
0-48
0-50
0-52
o-54
0-56
0-58
o-6o
0-62
0-64
o-66
o-68
0-70
0-72
074
0-76
0-78
000
0-82
0-84
o-86
o-88
0-90
0-92
0-94
0-96
0-98
1 00
To compute functions of order -1/3, increase the phase by 6o°.
TABLES OF BESSEL FUNCTIONS
Table III. Functions of order one-third
715
X
I-O2
I-O4
1-06
1-08
I*IO
1*12
i-id
1-18
1-20
1-22
I-24
i-2b
1-28
1-30
1-32
i-34
1-36
1-38
1-40
1-42
1-44
1-46
1-48
1-50
1-52
i-54
1-50
1-58
i-6o
1-62
1-64
1-66
1-68
1-70
1-72
1-74
1-76
178
i-8o
I;82
1-84
i-86
1-88
1 90
1-92
1-94
1-96
1-98
2-OO
7i/a(*)
+ 0-7296524
+ 0-7281940
+ 0-7265045
+ 0-7245872
+ 07224452
+ 07200818
+ 07175000
+ 07147030
+ 0-7116937
+ 0-7084752
+ 0-7050506
+ 07014229
+ 0-6975950
+ 0-6935699
+ 0-6893506
+ 0-6849400
+ 0-6803413
+ °-6755573
+ 0-6705909
+ 0-6654453
+ 0-6601234
+ 0-6546281
+ 0-6409626
+ 0-6431297
+ 0-6371326
+ 0-6309743
+ 0-6246578
+ 0-6181862
+ 0-6115625
+ 0-6047900
+ 0-5978715
+ 0-5908104
+ 0-5836096
+ 0-5762725
+ 0-5688020
+ 0-5612014
+ 0-5534739
+ 0-5450226
+ 0-5376509
+ 0-5295619
+ 0-5213588
+ 0-5130449
+ 0-5046236
+ 0-4960979
+ 0-4874713
+ 0-4787471
+ 0-4699285
+ 0-4610189
+ 0-4520215
+ 0-4429398
- 0-2610869
- 0-2436239
- 0-2264069
- 0-2094308
- 0-1926912
- 0-1761839
- 0-1599051
- 0-1438514
- 0-1280198
- 0-1124076
- 0-0970123
- 0-0818317
- 0-0668639
- 0-0521072
- 0-0375600
- 0-0232209
- 0-0090889
+ 0-0048372
+ 0-0185581
+ 0-0320747
+ 0-0453875
+ 0-0584971
+ 0-0714038
+ 0-084.1081
+ 0-0906101
+ 0-1089100
+ 0-1210079
+ 0-1329039
+ 0-1445980
+ 0-1560900
+ 0-1673799
+ 0-1784075
+ 0-1893528
+ 0-2000354
+ 0-2105152
+ 0-2207919
+ 0-2308653
+ 0-2407351
+ 0-2504011
+ 0-2590629
+ 0-2691204
+ 0-2781733
+ 0-2870212
+ 0-2956640
+ 0-3041014
¦i- 0-3123332
+ 0-3203591
+ 0-3281790
+ O-3357927
+ 0-3432000
i*2<*)i
°7749574
0-7678666
0-7609657
0-7542466
0-7477012
0-7413222
07351026
0-7290360
0-7231162
0-7173372
0-7116936
0-7061802
0-7007921
O-6955245
0-6903730
0-6853336
0-6804020
O-6755746
0-6708477
0-6662179
0-6616819
0-6572366
0-6528790
0-6486062
0-6444156
0-6403046
0-6362706
0-6323113
0-6284245
0-6246079
0-6208594
0-6171771
0-6135590
0-6100034
0-6065083
0-6030722
0-5996933
0-5963702
0-5931013
0-5898852
0-5867204
0-5836056
0-5805395
0-5775209
o-5745485
0-5716212
0-5687379
0-5658974
0-5630987
0-5603409
- 19° 41' i8'<29
- 18° 29' 53*27
- 17° 18' 32*58
- 16° 7' i6?o6
- 14° 56' 34
- 13° 44' 54'<86
- 12° 33' 49'-87
- ii° 22 48'-44
- io° n' 50*43
- 9° o' 55^70
- 7° 50; 4-15
- 6° 39 15'-66
- 50 28' 3o'-n
- 4° 17'47*41
- 3 7 7-45
- i° 56'30*14
- o° 45'55*39
o° 24' 36"88
i°35' 0*76
20 45' 34-33
3° 55' 59''67
50 6' 22 -83
6° 16' 43*91
7° 27' 2'iCj4
8° 37' 20-02
9° 47' 35-18
10° 57 48-50
12° 8' O'-O2
130 18' g'<8i
14° 28' 17*91
15° 38'24*37
16° 48 29-23
17° 58 32<>
19° 8'34-38
200 18' 34*74
21° 28' 33*69
22° 38' 31-2()
23°48'27^48
24° 58'22*40
2(>° 8' 10*05
270 18' 8*47
280 27' 59^)8
290 37' 4()''72
30047'38*62
310 57'26^41
340 ib' 58*77
35 26'43^39
360 36' 27'-ox
37° 46' 95
c*Kll3(x)
1-1809384
I-I7O3945
1-1601329
1-1501411
1-1404073
1-1309205
1-1216703
1-1126469
1-1038412
1-0952444
1-0868482
1-0786451
1-0706275
1-0627885
1-0551215
1-0476204
1-0402790
.1-0330918
1-0260535
1-0191580
1-0124030
1-0057813
0-9992894
0-9929231
0-9866783
0-9805512
O-9745381
0-9686354
0-9628309
0-9571482
O-95I5574'
o-946o<L4
o-94o66(K
o-93536o6
0-9301444
0-9250154
0-9199712
0-91500c) 3
oc>ibi 27A
0-0053239
0-9005961
0-8959423
0-8913605
0-8868489
0-8824057
0-8780291
0-8737176
0-8694694
0-8652,832
0-8611573
X
I-O2
1-04
I-OO
1-08
I-IO
I-I2
I-I4.
I-I6
1-18
I-2O
1-22
1-24
1-26
1-28
1-30
1-32
1-34
1-36
1-38
1-40
1-42
1-44
1-46
1-48
1-50
r-52
i-54
1-56
1-58
i-6o
1-62
1-64
i-6(>
1-68
1-70
1-72
1-74
176
178
1-So
1-82
1-84
i-86
1-88
1-90
1-92
1-94
1-96
1-98
2-OO
J_1/s B-00) =0-5603409 x cos 970 46' 9*65 = -0-0757500.
YZvs B-00) =0-5603409 x sin 970 46' 9^65 = +0-5551971.
716
TABLES OF BESSEL FUNCTIONS
Table III. Functions of order one-third
X
2-O2
2-04
2-06
2-08
2-IO
2-12
2-I4
2-16
2-18
2-20
2-22
2-24
2-26
2-28
2-30
2-32
2'34
2-36
2-38
2-40
2-42
2-44
2-46
2-48
2-50
2-52
2-54
2-56
2-58
2-6o
2-62
2-64
2-66
2-68
2-70
2-72
2-74
2-76
2-78
2-80
2-82
2-84
2-86
2-88
2-90
2-92
2-94
2-96
2-98
3-00
+ O'433777i
+ 0-4245367
+ 0-4152219
+ 0-4058363
+ 0-3963830
+ 0-3868655
+ 0-3772872
+ 0-3676514
+ 0-3579615
+ 0-3482210
+ 0-3384331
+ 0-3286012
+ 0-3187288
+ 0-3088193
+ 0-2988759
+ 0-2889021
+ 0-2789012
+ 0-2688766
+ 0-2588316
+ 0-2487696
+ 0-2386939
+ 0-2286079
+ 0-2185149
+ 0-2084181
+ 0-1983209
+ 0-1882266
+ 0-1781384
+ 0-1680595
+ 0-1579933
+ 0-1479429
+ 0-1379115
+ 0-1279023
+ 0-1179186
+ 0-1079633
+ 0-0980398
+ 0-0881509
+ 0-0783000
+ 0-0684899
+ 0-0587238
+ 0-0490046
+ 0-0393353
+ 0-0297189
+ 0-0201583
+ 0-0106564
+ 00012161
- 0-0081598
- 0-0174685
- 0-0267073
- 0-0358733
- 0-0449638
+ 0-3504008
+ O-3573949
+ 0-3641824
+ 0-3707631
+ 0-3771371
.+ 0-3833043
+ 0-3892647
+ 0-3950185
+ 0-4005657
+. 0-4059065
+ 0-4110411
+ 0-4159096
+ 0-4206923
+ 0-4252096
+ 0-4295216
+ 0-4336280
+ 0-4375318
+ 0-4412307
+ 0-4447262
+ 0-4400187
+ 0-4511090
+ 0-4539975
+ 0-4566849
+ 0-4591720
+ 0-4614595
+ 0-4635482
+ 0-4654389
+ 0-4671325
+ 0-4686300
+ 0-4699324
+ 0-4710406
+ °-47I9557
+ 0-4726788
+ 0-4732111
+ O-4735538
+ 0-4737081
+ O-4736754
+ 0-4734569
+ 0-4730540
+ 0-4724682
+ 0-4717009
+ O-4707537
+ 0-4696281
+ 0-4683256
+ 0-4668480
+ 0-4651970
+ 0-4633741
+ 0-4613813
+ 0-4592203
+ 0-4568930
1 Hi/3W 1
0-5576229
O-5549437
0-5523025
0-5496984
0-5471306
0-5445981
0-5421002
0*5396362
0-5372051
0-5348065
O-5324394
0-5301033
0-5277974
0-5255212
0-5232740
0-5210551
0-5188641
0-5167002
0-5145631
0-5124521
0-5103666
0-5083063
0-5062705
0-5042589
0-5022709
0-5003061
0-4983640
0-4964442
o-4945462
0-4926698
0-4908144
0-4889797
0-4871653
0-4853708
°-4835959
0-4818402
0-4801034
0-4783851
0-4766850
0-4750028
O-4733382
0-4716909
0-4700605
0-4684469
0-4668496
0-4652685
O-4637O33
0-4621537
0-460619/1
0-4591002
ar§ H,Jj (x)
38° 55' 51 -34
400 5' 32"io
410 15' 11*95
420 24' 50^91
43° 34' 29'-oo
440 44' 6'<25
45° 53 427
47° 3' 18*29
48° 12' 53'-I2
490 22' 27*18
500 32' o?49
510 41'33*06
520 51' 4*91
540 o' 36*06
550 10' 6*52
560 19' 36*32
570 29' 5*46
58° 38' 33-95
590 48' i'8i
6o° 57 2g'-o6
62° 6'55''70
630 16' 21^75
64° 25' 47-23
650 35'12-14
66° 44' 36^50
67° 54' o*3i
69° 3'23-59
700 12' 46-35
71 22' 89
720 31'3<>4
730 40' 51 <6o
740 50' 12^38
750 59' 32'-68
77° 8' 52*52
780 18' n"92
790 27' 3o"-86
8o° 36'49''37
81° 46' 7*45
820 55'25*11
84° 4' 42*36
85° 13'59-21
86° 23' 15^66
870 32'3l2
88° 41' 47*39
8g°5i' 2^69
91 ° o' i7'-63
920 9' 32*20
93° 18' 46*41
940 28' 0^28
95° 37' I3*8i
e*Km(x)
0-8570902
0-8530808
0-8491275
0-8452290
0-8413842
O-8375917
0-8338505
0-8301592
0-8265169
0-8229225
0-8193748
0-8158730
O-8124I59
0-8090028
0-8056325
0-8023043
0-7990173
O79577O6
07925634
o-7893949
0-7862643
0-7831710
0-7801140
0-7770928
0-7741066
0-7711547
0-7682366
O-76535I5
0-7624989
07596781
0-7568886
0-7541297
0-7514009
0-7487017
0-7460315
O7433898
07407762
07381900
o-73563o9
0-7330983
0-7305919
0-7281111
O-7256555
07232247
07208183
o-7l84359
07160770
0-7137413
0-7114285
0-7091381
X
2-O2
2-04
2-06
2-08
2-10
2-12
2-14
2-16
2-18
2-2O
2-22
2-24
2-20
2-28
2-30
2-32
2-34
2*36
2-38
2-40
2-42
2-44
2-46
2-48
2-50
2-52
2-54
2-56
2-58
2-OO
2-62
2-64
2-66
2-68
2-70
2-72
274
276
278
2-80
2-82
2-84
2-86
2-88
2-90
2-92
2-94
2-96
2-98
3*oo
To compute functions of order -1/3, increase the phase by 6o°.
TABLES OF BESSEL FUNCTIONS
Table III. Functions of order one-third
717
X
3-O2
3-04
3*o6
3-08
3-io
3'12
3-14
3-16
3-i8
3-20
3*22
3*26
3*28
3-3O
3.32
3-34
3-36
3-38
3-4O
3-42
3-44
3-46
3-48
3-50
3*52
3-54
3-50
3-58
3-60
3-62
3-64
3-66
3-68
3-7°
3-72
3-74
3-76
378
3-8o
3-82
3-84
3J8O
3-88
3*90
3-92
3-94
3-96
3'98
4-00
Ji/sW
- 0-0539763
- 0-0629080
- 0*0717564
- 0-0805188
- 0-0891928
- 0-0977759
- 0-1002656
- 0-114-6595
- 0*1229552
- 0-1311505
- 0-1392429
- 0*1472303
- 0*1551105
- 0*1628813
- 0-1705405
- 0*1780862
- 0-1855162
- 0-1928286
- 0*2000215
- 0-2070929
- 0-2140411
- 0-2208642
- 0-2275605
- 0-2341283
- 0-2405659
- 0-2468718
- 0-2530444
- 0-2590821
- 0-2649836
- 0-2707474
- 0-2763722
- 0-2818568
- 0-2871997
- 0-2924000
- °-2974504
- 0-3023678
- 0-3071333
- 0-3117518
- 0-3162224
- 0-3205442
- 0-3247164
- 0-32^7383
- 0*3326092
- 0-3363283
- 0-3398952
- 0-3433091
- 0-3465698
- 0-3496766
- 0-3526292
- 0-3554274
+ 0-4544013
+ 0-4517471
+ 0-4489323
+ 0-4459590
+ 0-4428292
+ O-4395451
+ 0-4361086
+ 0-4325221
+ 0-4287877
+ 0-4249076
+ 0-4208840
+ 0-4167194
+ 0-4124159
+ 0-4079761
+ 0-4034022
+ 0-3986968
+ 0-3938622
+ 0*3889010
+ 0*3838156
-h 0-3786087
+ o-3732827
+ 0-3678404
+ 0-3622843
+ 0-3566170
'+ 0-3508413
+¦ 0-3449599
+ 0-3389754
-l- 0-3328906
+ 0-3267083
+ 0-3204313
+ 0-3140623
+ 0-3076042
+ 0-3010598
+ 0-2944320
+ 0-2877236
+ 0-2809376
¦l- 0-2740767
-I 0-2671440
+ 0-2001423
•h 0-2530740
1- 0-2459438
+ 0-2387520
-I- 0-2315048
+ 0-2242025
-I- 0-2x08489
+ 0-2094471
•I- O-2O20OOO
¦+• 0-1945106
+ 0-1869819
+¦ 0-1794168
1 **O*) 1
O-4575959
0*4561061
0-4546308
0-4531696
0-4517223
0-4502888
0-4488687
0-4474619
0-4460682
0-4446874
0-4433192
0-4419636
0-4406202
0-4392890
0-4379697
0-4366621
0-4353661
0-4340816
0-4328083
0-4315461
0-4302948
0-4290543
0-4278244
0-4206049
O-4253958
0-4241969
0-4230080
0-4218290
0-4206598
0*4195001
0-4183500
0-4172093
0-4160778
0-4149554
0-4138420
O-4127375
0-4116417
0-4105546
0-4094760
0-4084058
0-4073440
0-400290/1
0-4052448
0*4042073
0-4031770
0-4021558
0*4011410
0-4001351
0-3991361
0-3981444
(i)
96° 46" 26*99
97°55' 39-85
99° 4 52*38
100 14 4''5 9
101° 23 16*49
102° 32'28*08
103° 41' 39*37
104 50 5o'*30
106° 0' 1*05
107° g'11*46
108° 18'21*58
109° 27'31*42
110°36'40*99
ni° 45'50*29
112°54 59-32
IT 4° 4' 8*09
115°13'I6*6l
116° 22' 24*87
117° 3l'32*89
110° 40'40*66
119° 49'48*19
120°58'55*48
122° 8' 2*54
I23° 17' 9*37
124° 26 15*97
125° 35' 22*35
126° 44'28*51
127° 53' 34';4O
129° 2 40*19
130°ii'45*72
131° 20' 51*03
132° 29' 56*15
133° 39' 1*00
134°48 5*78
135° 57 IO?3o
137° 6'14*03
138°15'18*78
139° 24' 22*73
140° 33' 26*51
141° 42' 30*10
142° 5r'33*52
l4< °|3(>;7«>
145° (>' 30*83
14O0 iH' .\i"--j >
147°27'45':45
1480 36' 48*01
140° 4 5' 50*4 r
150° 54' 52-05
152° 3 543
153 12 56*65
0-7068697
0-7046231
0-7023978
07001936
0-6980101
0-6958470
0-6937040
0*6915807
0*6894769
0*6873922
0*6853264
0-6832792
0-6812503
0-6792394
0-6772463
0-6752708
0-6733124
0-6713711
0-6694465
0-6675385
0-6656467
0-6637710
0-6619111
0-6600668
0-6582379
0-6564241
0-6546254
0-6528413
0-6510719
0-6493168
O-0475758
0-6458489
O-044I357
0-6424361
0-6407500
0-6390771
0-6374173
0-0357703
0-6341362
0-632514O
0-0309054
0-6293085
0-0277230
O-(>20l 508
0*6245807
0-6230403
0-6215023
0-6199758
0-6184605
0-6169562
X
3-02
3-04
3-06
3-08
3-10
3-12
3-14
3-16
3'i8
3-20
3-22
3'24
3-26
3-28
330
3-32
3-34
3-3°
3;38
3-42
3-44
3-40
3-48
3-5O
3-52
3-54
3-5O
3-58
3*0o
3-62
3-04
3-()b
3-68
370
3-72
3-74
V7O
¦378
3-80
3*82
^•84
3-80
3-88
3-9o
3-92
.3-94
3-96
3-98
4-00
-vz D-°o) =0-3981444 x cos 213° 12' 56'-65 = -0-3330932.
-1/3 D'°°) =0-3981444 xsin 213° 12' 56'-65;= -0-2181008.
718
TABLES OF BESSEL FUNCTIONS
Table III. Functions of order one-third
X
4-O2
4-O4
4-06
4-08
4-10
4-12
4-ia
4-16
4-18
4-20
4-22
4-24
4-26
4-28
4-30
4-32
4-34
4-36
4-38
4-40
4-42
4-44
4-46
4-48
4-5O
4-52
4-54
4-56
4-58
4-60
4-62
4-64
4-66
4-68
4-70
4-72
4-74
4-76
478
4-80
4-82
4-84
4-86
4-88
4-90
4-92
4-94
4-96
4-98
5-00
- 0-3580707
- 0-3605591
- 0-3628923
- 0-3650702
- 0-3670927
- 0-3689599
- 0-3706718
- 0-3722285
- 0-3736302
- 0-3748770
- 0-3759693
- 0-3769073
- 0-3776914
- 0-3783220
-0-3787997
- 0-3791248
- 0-3792981
- 0-3793201
- 0-3791916
- 0-3789131
- 0-3784856
- 0-3779098
- 0-3771866
- 0-3763170
- 0-3753019
- 0-3741423
- 0-3728394
- 0-3713941
- 0-3698078
- 0-3680815
- 0-3662167
- 0-3642144
- 0-3620702
- 0-3598033
- 0-3573972
- 0-3548595
- 0-3521915
- 0-3493949
- 0-3464712
- 0-3434221
- 0-3402493
- O-3369544
- 0-3335393
- 0-3300057
- 03263554
- 03225903
- 0-3187124
- 0-3147234
- 0-3106254
- 0-3064205
+ 0-1718183
+ 0-1641895
+ 0-1565333
+ 0-1488527
+ 0-1411506
+ 0-1334301
+ 0-1256940
+ 0-1179455
+ 0-1101873
+ 0-1024224
+ 0-0946539
+ 0-0868845
+ 0-0791172
+ 0-0713550
+ 0-0636006
+ 0-0558570
+ 0-0481270
+ 0-0404134
+ 0-0327191
+ 0-0250469
+ 0-0173995
+ 0-0097798
+ 0-0021904
- 0-0053659
- 0-0128864
- 0-0203684
- 0-0278093
- 0-0352065
- 0-0425573
- 0-0498592
- 0-0571096
- 0-0643061
- 0-0714460
- 00785270
- 0-0855466
- 0-0925024
- 0-0993921
- 0-1062133
- 0-1129637
- 0-1196411
- 0-1262432
- 0-1327677
- 0-1392127
- 0-1455758
- 0-1518551
- 0-1580485
- 0-1641539
- 0-1701695
- 0-1760932
- 0-1819232
1 «>) 1
0-3971601
0-3961831
0-3952132
0-3942503
O-3932945
O-3923455
0-3914034
0-3904679
O-389539I
0-3886169
0-3877012
0-3867919
0-3850890
0-3849923
0-3841018
0-3832175
0-3823392
0-3814669
0-3800006
°-37974°o
0-3788853
0-3780363
0-3771930
O-3763553
O-375523I
0-3746963
O-3738750
0-3730591
0-3722485
0-3714431
0-3706429
0-3698478
0-3690578
0-3682729
0-3674929
0-3667178
O-3659476
0-3651822
0-3644216
0-3636657
0-3629145
0-3621679
0-3614258
0-3606883
O-3599553
0-3592267
0-3585026
O-3577827
0-3570672
O-3563559
arg Hllz{x)
154° 21'58*42
155°31 o'<o4
156° 40' 1-51
l57°-49' 2*83
158° 58' 4*00
160° 7' 5*03
161° 16' 5*91
162° 25' 6*66
163° 34' 7*26
164° 43' 7-73
165°52' 8*07
167° 1' 8*27
i68° io' 8V34
169° 19' 8-28
170° 28'. 8''09
171° 37' 7-78
172° 46' 7-34
173° 55' 6-78
175° 4' 6'-io
176° 13' 5*29
177° 22' 4^37
178° 31' 3-33
179° 40 2-18
180° 49' 0*91
181° 57' 59-52
183' 6'58*03
184° 15' 56-43
185° 24' 54*72
186° 33'52*90
187° 42' 50*97
188° 51'48*94
190° q' 46*81
191° 9' 44*58
192° 18' 42*24
193° 27' 39"8i
194° 36' 37-27
195° 45' 34-64
196° 54 3I-9I
198° 3'29*09
199° 12' 26*17
200° 21' 23*16
201 ° 30' 20*06
2O2° 39' l6"87
2O3° 48' 13^58
204 57 IO*2I
206° 6' 6*75
207°15' 3*21
2O8° 23' 59*58
209° 32' 55-86
210 41'52*06
0-6154630
0-6139805
0-6125087
0-6110475
0-6095967
0-6081563
0-6067260
0-6053058
0-6038956
0-6024952
0-6011045
0-5997234
0-5983518
0-5969897
0-5956368
0-5942930
0-5929584
0-5916327
0-5903159
0-5890079
0-5877086
0-5864178
0-5851356
0-5838617
0-5825961
0-5813387
0-5800895
0-5788483
0-5776151
0-5763897
0-5751721
0-5739622
0-5727599
0-5703779
0-5691980
0-5680255
0-5668601
0-5657019
0-5645508
0-5634067
0-5622696
0-5611393
0-5600158
0-5588991
0-5577890
0-5566856
0-5555886
0-5544982
0-5534141
X
4-02
4-04
4-06
4-08
4-10
4-12
4-14
4-ib
4-18
4-20
4-22
4-24
4-26
4-28
4-3O
4-32
4'34
4-36
4-38
4-40
4-42
4-44
4-46
4-48
4'5°
4-52
4-54
456
4-58
4-60
4-62
4-64
4-60
4-68
4-70
472
474
476
4-78
4-80
4-82
4-84
4-86
4-88
4-9O
4-92
4-94
4-96
4-98
5-00
To compute functions of order -1/3, increase the phase by 6o°.
TABLES OF BESSEL FUNCTIONS
Table III. Functions of order one-third
719
X
5-O2
5'O4
5-of)
5*o8
5*io
5-12
5*14
5'i(j
5-18
5*2O
5*22
5*24
5*26
5*28
5*3O
5*32
5*34
5*36
5*38
5*4O
5*42
5*44
5*46
5*48
5*5O
5*52
5*54
5*5<>
5*58
5*6o
5*62
5*64
5*66
5-68
5* 7O
5*72
5*74
5*76
5*78
5-80
5*82
5*84
5*86
5-88
5*9O
5*92
5*94
5*96
5*98
6-oo
- 0-3021105
- 0-2976976
- 0-2031838
- 0-2885714
- 0-2838623
- 0-2790589
- 0-2741632
- 0-2691776
- 0-2641042
- 0-2589454
- 0-2537034
- 0-2483807
- 0-2429794
- 0-2375020
- 0-2319509
- 0-2263285
- 0-2206371
- 0-2148793
- 0-2090575
- 0-2031741
- 0-1972317
- 0-1912327
- 0-1851797
- 0-1790751
- 0-1729216
- 0-1667210
- 0-1004777
- 0-1541924
- 0-1478684
- 0-1415082
- 0-1351143
- 0-1286894
- 0-1222361
- 0-1157509
- 0-1092543
- 0-1027311
- 0-0961898
- 0-0896330
- 0-0830632
- 0-0764830
- 0-0698951
- 0-0633019
- 0-0567061
- 0-0501102
- 0-0435167
- 0-0369283
- 0-0303473
- 0-0237764
- 0-0172181
- 0-0106747
yu.w
- 0-1876576
- 0-1932947
- 0-1988326
- 0-2042696
- 0-2096041
- 0-2148343
- 0-2199588
- 0-2249760
- 0-2298843
- 0-2346822
- 0-2393685
- 0-2439417
- 0-2484004
- 0-2527435
- 0-2569696
- 0-2610776
- 0-2650064
- 0-2689349
- 0-2726820
- 0-2763068
- 0-2798083
- 0-2831855
- 0-2864378
- 02895642
- 0-2925640
- 0-2954366
- 0-2981813
- 0-3007974
- 0-3032845
- 0-3056420
- 0-3078695
- 0-3099667
- 0-3119330
- 0-3137683
- 0-3154723
- 0-3170.-148
- 0-3184857
- 0-3197948
- 0-3209721
- 0-3220176
- 0-3229313
- 0-3237134
- 0*3243639
- 0-3248832
- 0-3252714
- 0-3255288
- 0-3256557.
- 0-3256526
- 0-3255199
- 0-3252580
1 <w 1
0*3556489
o*354946o
o*3542473
O-3535527
0-3528621
0-3521756
0-3514930
0-3508144
0-3501397
o*3494688
0-3488018
0-3481386
o*347479i
0-3468234
0-3461714
0*3455230
0-3448782
0-3442370
O-3435904
0*3429653
0-3423346
0-3417075
0-3410837
o*34O4634
0*3398464
o*3392328
0-3386224
0-3380154
0-3374116
0-3368109
0-3362135
O-3356I93
0-3350282
o*33444Oi
O*3338552
o*3332733
0-3326945
0-3321186
0*33*5457
0*3309758
0-330/1088
0-3298446
03202834
0-3287250
0-3281A04
0-3276166
0-3270667
0-3265104
o*3259749
o*325433i
211° 50' 48*18
212° 59' 44*22
2x4° 8'40*17
215°17'36*05
216° 26'31*84
217° 35' 27*56
210° 44'23*2O
219° 53' 18*76
221° 2' 14*25
222 II 9*67
223° 2O' 5'-OI
224° 29' 0*27
225° 37' 55*46
226° 46' 50*50
227°55'45*64
229° 4'40-62
230° 13'35*53
231°22'30*37
232° 31 25*14
233° 40'19*85
234° 49' 14*49
235° 58' 9-07
2H°o ^ 3''58
238° 15' 58*02
2390 24'52*40
240° 33' 46-72
241° 42'40*97
242° 51'35*16
244° 0' 29*30
245° 9'23-37
246° 18'17*38
247° 27'11*33
248°36' 5*22
249° 44 59-06
2500 53 52-84
252° 2'46*56
253° 11' 40*22
254° 2O' 33*83
255° 20 27*38
250° 38' 2O*88
257°47' M3
2580 5'' 7*72
2(H° 5 1*O()
261° 13'544
Zhz° 22' 47*57
263° 31' 40*75
204° 40 33*88
265° 49' 20*96
266° 58' 19*98
268° ' 7' 12*96
0*5523364
0-5512650
.O-55O ! 998
0-5491408
0-5480878
0-5470410
0-546000!
0-5449651
O*543936o
0-5429127
0-5418952
0-5408834
O*5398773
0-5388767
0-5378818
O-5368923
O-5359O82
O-5349296
O-5339563
0-5329883
0-5320256
0-5310681
O*53OII57
0-5291685
0-5282263
0-5272892
O*526357O
0-5254298
O*5245O74
O-5235899
0-5226772
O-52I7693
0-5208661
0-5199676
°*5I9O737
0-5181844
0-5172997
0-5104195
0-515543°
°*5'467r25
0-5138056
0-5129432
0-5120050
0-51 r 2312
0-5103816
0*5095362
0-5086951
0-5078581
0-5070252
0-5061964
X
5-02
5*O4
5*°6
5-o8
5-10
5-12
5*i4
5*16
5-18
5*2O
5-22
5*24
5-26
5*28
5*3o
5*32
5*34
5-36
5*38
5*4O
5*42
5*44
5*48
5*5O
5*52
5*54
5*56
5*58
5*6o
5*62
5*64
5-00
5*68
5*7o
5*72
5*74
5*76
578
5-80
5-82
5'84
5-80
5-88
5-00
5*02
5*94
5*9°
5*98
600
J_lla F-oo) =0-3254331 x cob 3280 7' 12*96= +0-2763443.
Y_lls F-oo) =0-3254331 x sin 3280 7' 12*96= -0-1718736.
720
TABLES OF BESSEL FUNCTIONS
Table III. Functions of order on^-third
" • x
6-O2
6-O4
6-o6
6-o8
6-io
6-12
6-14
6-16
6-18
6-2O
6-22
6-24
6-26
6-28
6-30
6-32
6-34
6-36
6-38
6-40
6-42
6-44
6-46
6-48
6-50
6-52
6-54
6-56
6-58
6-6o
6-62
6-64
6-66
6-68
6-70
672
6-74
6-76
678
6-8o
6-82
6-84
6-86
6-88
6-90
6-92
6-94
6-96
6-98
7-00
- c
+ (
+ (
+ (
+ (
+ <
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
)-OO4l49O
)-OO23568
3-OO884O2
D-OI52987
3'O2I7298
3-O28I3I3
3-O3450O7
0-0408356
0-O47I337
0-O533927
O-O596IO3
0-0657842
O-O7I9I22
O-O77992O
O-O84O2I3
O-O89998I
O-O9592O2
O-IOI7854
O-IO759I7
O-II3337O
O-II9OI92
0-1246363
O-I3OI863
O-I356673
O-I4IO775
O-I464I47
0-1516774
O-I568635
O-l6l97I4
O-I669992
O-I7I9453
O-I768o80
0-1815856
O-I862766
O-I9O8793
CI953922
O-I998I39
0-2041429
O-2O83778
O-2I25I7I
O-2I65596
O-22O5O4I
O-224349I
O-228O935
O'23I7362
O-235276O
0-2387118
O-242O426
0-2452674
0-2483853
- 0-3248675
- 0-3243490
- 0-3237031 •
- 0-3229304
- 0-3220317
- 0-3210077
- 0-3198593
- 0-3185872
- 0-3171924
- 0-3156758
- 0-3140384
- 0-3122813
- 0-3104053
- 0-3084118
- 0-3063018
- 0-3040764
- 0-3017371
- 0-2992849
- 0-2967212
- 0-2940474
- 0-2912648
- 0-2883748
- 0-2853790
- 0-2822787
- 0-2790756
- 0-2757711
- 0-2723669
- 0-2688647
- 0-2652659
- 0-2615725
- 0-2577860
- 0-2539082
- 0-2499409
- 0-2458860
- 0-2417452
- 0-2375205
- 0-2332136
- 0-2288267
- 0-2243615
- 0-2198201
- 0-2152044
- 0-2105165
- 0-2057584
- 0-2009321
- 0-1960398
- 0-1910836
- 0-1860655
- 0-1809877
- 0-1758524
- 0-1706616
1 #1/3 (*) 1
0-3248940
O-3243576
0-3238238
0-3232926
0-3227640
0-3222380
0-3217146
O-32II936
0-3206753
0-3201594
0-3196460
0-3191350
0-3186265
0-3181204
0-3176167
0-3171154
0-3166164
0-3161198
O-3I56255
0-3146438
0-3141564
0-3136712
0-3131883
0-3127076
0-3122291
0-3117527
0-3112786
0-3108066
0-3103367
0-3098690
O-3O94O33
0-3089398
0-3084783
0-3080189
0-3075615
0-3071062
0-3066528
0-3062015
O-3O57522
0-3053048
0-3048593
0-3044159
O-3O39743
O-3O35347
0-3030969
0-3026610
0-3022271
0-3017949
0-3013646
arg
269°
270°
271°
2720
273°
275°
f6o
2771°
279°
280°
2810
2830
2840
285°
286°
iSy°
288°
2890
2910
292°
293°
294°
295°
296°
297°
3010
3020
303;
3O5c
3°7C
3o8c
3O9c
3ioc
3iic
3I2|
3HC
,j _<
316
3ig
319
320
322
323
324
325
<
16'
24'
33
42
51'
6'
9;
18'
27;
36'
44'
53
2'
II'
20'
29"
38'
46'
55'
4'
13'
22'
31'
40'
49'
57'
6'
15'
24'
33'
42;
0/
17'
26'
35'
44'
53;
1'
3IO'
3 19'
3 28'
3 37
3 46
3 ^s
0 3
0 12
°2I
°3o
5'
58-
51-
44'-
37'
29?
22-
15-
7'-
o-
52"
89
77
60
39
12
81
46
05
60
11
57
44-99
37'-
29'-
21'
IA"-
6'
58"
50'
42'
34'
26'
18'
10
2
46
37
29
21
12
4
56
47
39
3°
22
13
5"
47
38
29
21
12
3
r54
45
36
'27
36
69
98
22
42
58
70
77
80
80
'75
'67
'54
'38
'18
'94
'66
J34
¦'98
•59
•'16
•70
•20
•'66
.'08
'47
'83
il5
'•44
'70
''92
'•11
6
•38
•47
2
5
4
0-5053717
0-5045509
0-5037342
0-5029215
0-5021126
0-5013077
0-5005066
0-4997094
0-4989160
0-4981263
0-4973404
0-4965582
0-4957796
0-4950048
0-4942335
0-4934659
0-4927018
0-4919413
0-4911843
0-4904308
0-4896807
0-4889341
0-4881909
0-4874510
0-4867145
0-4859814
0-4852516
0-4845250
0-4838017
0-4830817
0-4823648
0-4816511
0-4809406
0-4802333
0-4795290
0-4788279
0-4781298
O-4774347
0-4767427
0-4760537
O-4753677
0-4746846
0-4740045
O-4733273
0-4726530
0-4719815
0-4713130
0-4706472
0-4699843
0-4693242
X
6-O2
6-04
6-ob
6-o8
6-io
6-12
6-14
6-16
6-18
6-2O
6-22
6-24
6-26
6-28
6-30
6-32
6-34
6-36
6-38
6-40
6-42
6-44
6-46
6-48
6-50
6-52
6-54
6-56
6-58
6-6o
6-62
6-64
6-66
6-68
6-70
672
6-74
676
678
6-8o
6-82
6-84
6-86
6-88-
6-90
6-92
6-9a
6-96
6-98
7-00
To compute functions of order -1/3, increase the phase by 6o°.
TABLES OF BESSEL FUNCTIONS
Table III. Functions of order one-third
721
X
7-02
7-04
7-06
7-08
7-10
7-12
7-14
7-16
7-i8
7-20
7-22
7-24
7-26
7-28
7-30
7.32
7-34
7-36
7-38
7-40
7-42
7'44
7-46
7-48
7-5O
7-52
7'54
7-56
7-58
7-60
7-62
7-64
7-66
7-68
7-70
772
774
7-76
7.78
7-60
7-82
Th
7-86
7-88
7-90
7-92
7*94
7-96
7-98
8-oo
/173M
+ 0-2513952
+ 0-2542964
+ 0-2570881
+ 0-2597694
+ 0-2623395
+ 0-2647979
4- 0-2671439
+ 0-2693769
+ 0-2714962
+ 0-2735015
+ 0-2753921
+ 0-2771678
+ 0-2788281
+ 0-2803727
+ 0-2818013
+ 0-2831136
+ 0-2843096
+ 0-2853889
+ 0-2863516
+ 0^-2871974
+ 0-2879266
+ 0-2885390
+ 0-2890347
+ 0-2894138
+ 0-2896766
+ 0-2898232
4- 0-2898538
+ 0-2897689
4- 0-28956.86
4- 0-2892534
4- 0-2888237
+ 0-2882799
4- 0-2876227
4- 0-2868525
4- 0-2859699
4- 0-2849756
+ 0-2838702
4- 0-28265^5
4- O-28I3292
4- 0-2798952
4- 0-2783532
4- 0-2767042
4- 0-2749490
4- 0-2730886
4- 0-2711241
4- 0-2690564
4- 0-2668867
4- 0-2646159
4- 0-2622454
4- 0-2597762
^'i/jW
- 0-1654177
- 0-l60I220
- 0-1547791
- 0-1493888
- 0-1439541
- 0-1384774
- 0-1329609
- 0-1274068
- 0-1218174
- 0-1161950
- 0-1105419
- 0-1048604
- 0-0991527
- 0-0934213
- 0-0876683
- 0-0818961
- 0-0761070
- 0-0703033
- 0-0644874
- 0-0586615
- 0-0528279
- 0-0469890
- 0-0411470
- 0-0353042
- 0-0294630
- 0*0236256
- 0-0177943
- 0-0119713
- 0-0061589
- 0-0003594
4- 0-0054250
4- O-OIII92O
4- 0-0169396
4- 0-0226654
+ 0-0283672
4- 0-0340430
4- 0-0396905
+ 0-0453076
4- 0-0508922
4- 0-0564422
4- 0-0619554
4- 0-0674298
4- 0-0728635
4- 0-0782542
4- 0-0836001
4- 0-0888991
4- 0-0941493
4- 0-0993488
4- 0-1044956
4- 0-1095878
0-3009362
0-3005095
0-3000847
0-2996617
0-2992404
0-2988209
0-2984032
0-2979872
0-2975730
0-2971604
0-2967496
0-2963405
0-2959330
0-2955273
0-2951232
0-2947207
0-2943199
0-2939207
0-2935231
0-2931272
0-2927328
0-2923400
0-2919488
0-2915592
0-2911711
0-2907845
0-2903995
0-2900160
0-2896341
0*2892536
0-2888746
0-2884971
0-2881211
0-2877465
0-2873734
0-2870018
0-2866315
0-286262*7
0-2858954
0-2855294
0-2851648
0-2848017
0-2844399
0-2840794
0-2837204
0-2833627
0-2830063
0-2826513
0-2822976
0-2819453
326° 39' 18*50
327° 48' 9^42
328° 57' 0*32
330° 5 5I-I9
331°14'42*03
332°23'32*83
333032'23'-6i
334° 41'I4-36
335°50 5"O7
336° 58' 55*76
338° / 46-42
339° 16 37-O5
340° 25' 27*65
' 341° 34' i»''22
342° 43 8'-77
343°5i'59-28
345° 0'49*77
346° 9 40-23
347° 18' 30*66
348° 27'21''07
349° 36' n-45
350° 45 i''«o
35i°53'52-12
353 2'42*42
354 11'32-70 .
355° 20' 22*95
356° 29' 13'' 17
357° 38' 37
35»° 46'53-54
359 55'43-69
361° 4'33'-8i
362° 13' 23'-91
363° 22' I3'*98
364° 31' 4'-03
365 39 54''05
366° 48'44''05
367° 57' 34-03
369° 6'23'-98
37°° 15' i3?0i
371° 24' 3^82
372°32'53-70
373 41 43-56
374° 50 33''4O
375° 59' 23-22
377 8'!3-oi
378° 17' 2'-78
379 25^52'-53
3»o° 34 ^^25
381°43'31-96
382° 52'21''64
ex f.r 1 v\
e j\.jri(x)
0-4686668
0-4680122
0-4673604
0-4667113
0-4660648
0-4654211
0-4647800
0-4641415
0-4635057
0-4628725
0-4622419
0-4616138
0-4609804
0-4603654
0-459745°
0-4591271
0-4585116
0-4578986
0-4572881
0-4566801
0-4560744
O-455471'2
0-4548703
0-4542718
O-4536757
0-4530819
0-4524905
0-4519013
O-4513I45
0-4507299
0-4501476
0-4495676
0-4489898
0-4484142
0-4478408
0-4472697
0-4467007
O-446I339
0-4455692
0-4450067
0-4444463
0-4438880
o-44333i8
0-4427777
0-4422257
0-4416757
0-4411278
0-4405819
0-4400381
O-4394962
X
7-02
7-04
7-06
7-08
7-10
7-12
7-14
7-16
7-i8
7-20
7-22
7-24
7-26
7-28
7'3o
7-32
7-34
7-36
7-38
7-40
7-42
7-44
7-46
7-48
7'5O
7-52
7-54
7'56
7-58
7-60
7-62
7-64
7-66
7-68
770
7-72
774
7-76
7-78
7-80
7-82
7-84
7-86
7-88
7-90
7-92
7-94
7-96
7-98
8-oo
r_i/3 (8-oo) =0-2819453 x cos 442° 52' 21*64= +0-0349823.
_i/8 (8-oo)=0-2819453 xsin 442° 52' 21*64 = 4-0-2797667.
W. B. F.
722
TABLES OF BESSEL FUNCTIONS
Table III. Functions of order one-third
X
8-02
8-04
8-o6
8-o8
8-io
8-12
8-14.
8-16
8-18
8'2O
8-22
8-26
8-28
8-30
8-32
8-34
8-36
8-38
8-40
8-42
8-44
8-46
8-48
8-50
8-52
8-54
8-56
8-58
8-6o
8-62
8-64
8-66
8-68
8-70
8-72
§"?*
8-76
8-78
8-8o
8-82
8-84
8-86
8-88
8-go
8-92
8-94
8-96
8-98
g-oo
+ 0-2572095
+ 0-2545467
+ 0-2517890
+ 0-2489377
+ 0-2459942
+ 0-2429598
+ 0-2398360
+ 0-2366242
+ 0-2333259
+ 0-2299425
+ 0-2264758
+ 0-2229271
+ 0-2192981
+ 0-2155904
+ 0-2118057
+ 0-2079456
+ 0-2040118
+ 0-2000061
+ 0-1959301
+ 0-1917857
+ 0-18757^7
+ 0-1832989
+ 0-1789600
+ 0-1745601
+ 0-1701008
+ 0-1655842
+ 0-1610121
+ 0-1563865
+ 0-1517093
+ 0-1469824
+ 0-1422079
+ 0-1373878
+ 0-1325240
+ 0-1276185
+ 0-1226734
+ 0-1176907
+ 0-1126725
+ 0-1076208
+ 0-1025377
+ 0-0974252
+ 0-0922855
+ 0-0871206
+ 0-0819327
+ 0-0767237
+ 0-0714958
+ 0-0662512
+ 0-0609918
+ 0-0557199
+ 0-0504375
+ 0-0451467
Ym(*)
+ 0-1146236
+• 0-1196012
+ 0-1245187
+ 0-1293743
+¦ 0-1341604
+• 0-1388931
+ 0-1435528
+ 0-1481438
+ 0-1526645
+ o-i57II33
+ 0-1614886
+• 0-1657888
+ 0-1700125
+ 0-1741581
+ 0-1782243
+ 0-1822096
+ 0-1861127
•+• 0-1899322
+ 0-1936668
+ 0-1973152
+ 0-2008763
+ 0-2043488
+ 0-2077315
+ 0-2110234
+ 0-2142234
+ 0-2x73304
+ 0-2203434
+ 0-2232615
+ 0-2260837
+ 0-2288092
+• 0-2314370
+ 0-2339664
+ 0-2363966
+ 0-2387270
+ 0-2409567
+ 0-2430852
+ 0-2451118
+ 0-2470360
+ 0-2488572
+ 0-2505751
+ 0-2521890
+ 0-2536987
+ 0-2551038
+ 0-2564039
+ 0-2575988
+ 0-2586882
+ 0-2596720
+ 0-2605500
+ 0-2613221
+ 0-2619882
<w 1
0-2815942
0-2812445
0-2808961
0-2805489
0-2802030
0-2798584
0-2795151
0-2791730
0-2788322
0-2784927
0-2781543
0-2778172
0-2774813
0-2771467
0-2768132
0-2764809
0-2761498
0-2758200
0-2754912
0-2751637
0-2748373
0-2745121
0-2741880
0-2738651
0-2735433
0-2732227
0-2729031
0-2725847
0-2722674
0-2719512
0-2716361
0-2713221
0-2710092
0-2706973
0-2703866
0-2700768
0-2697682
0-2694606
0-2691541
0-2688486
0-2685441
0-2682407
0-2679383
0-2676369
0-2673365
0-2670371
0-2667388
0-2664414
0-2661450
0-2658496
arg Hm(x)
384° i'ii'^o
385° 10' o'-94
386° 18' 50^56
387° 27'4o"i6
388° 36'29^74
389° 45' 19^29
390°54 §«83
392° 2'585
.393° 11'47^84
394 20 37*32
395° 29'26*78
396° 38' i6'-2i
397° 47' 5*63
398° 55' 55"O3
400° 4 44-41
401° 13' 33'-76
402° 22' 23'-io
403° 31' I22
404° 40' i«73
405° 48'51*01
406° 57' 40^27
408° 6'29*52
409° 15' i8''74
410° 24' 7^5
4iio32/57'-i4
412° 41' 46*32
413° 5°' 358
414° 59' 24'-6i
416° 8'13^73
417° 17' 2-83
4i8°25'5i^92
4I9° 34' 4O "99
420° 43' 3o'-O4
421° 52'19-08
423° 1' 8-io
424° 9'57?io
425° 18'46-08
426° 27' 35K04
427° 36' 23*99
428° 45' 12^93
429° 54' 1*85
43T° 2 50^75
432°11'39-63
433° 20'28^50
434° 29'I7-36
435°38' 6^20
436° 46' 55^03
437°55 43-83
439° 4'32-'62
440° 13' 21*40
0-4389564
0-4384185
0-4378827
o-4373487
0-4368168
0-4362867
O-4357586
0*4352324
0-4347081
o-434l857
0-4336652
0-4331466
0-4326298
0-4321148
0-4316017
0-4310905
0-4305810
0-4300733
0-4295675
0-4290^34
0-4285611
0-4280605
0-4275617
0-4270646
0-4265693
0-4260757
0-4255838
0-4250936
0-4246051
0-4241183
0-4236331
0-4231496
0-4226678
0-4221876
0-4217090
0-4212321
0-4207568
0-4202831
0-4198109
0-4193404
0-4188715
0-4184041
O-4I79383
0-4174740
0-4170113
0-4165501
0-4160905
0-415632^
o-4x5i757
0-4147206
X
8-O2
5-04
3-oo
8-o8
8-io
8-12
8-14
8-16
8-i8
8-20
8-22
8-24
8-26
8-28
8-30
8-32
8-34
8-38
8-40
8-42
8-44
8-46
8-48
8-50
8-52
8-54
8-5g
8-58
8-6o
8-62
8-64
8-66
8-68
8-70
8-72
f'74
8-76
8-78
8-8o
8-82
8-84
8-86
8-88
8-90
8-92
8-94
8-96
8-98
9-00
To compute functions of order -1/3, increase the phase by 60°.
OOOOO OOOOO OOOOO OOOOO
OOOOO O 00 CO CO 00 OOsl MMM si 6660 O"t/> U1U1U U14w4i.4i.4w ^UWWW W to 10 10 10 M h h h h w O O 6 6
O OOO^ to O O0Gn4* to O 00 O>4* to O 00 OV^ to O 00 O>4». to O COOVP^ 10 O CO O4* W O 00 OM^- to O CoC^4». 10 O CO 0*4*- to
Illll Illll Illll Illl! I I I I I 11111 Illll (III! II+ + + +++ + +
00000 00000 qoooo 00000 00000 oqooo qqqqq qqqqq qqqqq qqqqq
mmmww mmmmm MHHtMM mhimmm hiwooo 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6
00 COM MM On On COi Ui Ui A A W U) tOtOtOMM OOOOCO COM M On Oi UiU4^4^U W 10 10 M H O O O O hi h to WWW
On to O On to O Ui hi M 4w O On to M W O t-n O On hi M to CCW CO W 004*- O 4i O 4i O 4=* CO W COW CCW M tO 10 COW COW O 4^- O
hi GOUi h* Q\ O 4i O^ 00 O OOO CO On 4^ *-i m W 00 tO O» O W Ui M OOnito to hi w O O M On4=* to O M Vi M O W OnO 10 Oi CO
4w 004^ 10 tO »Ui O CCO W OOtOOO 4^ to 4^ O hi MM IO 10 00 O Oi 00 O> hi K> O 4=>- Ul 4^- O W+-W O On O M Ui 4w 4w4w4i.41.4i
Ui 4i 4i Ui O OO CO O\ 10 O M O 0*0 H( Hi W M On O tO-^ Cnh hi 00 10 M W W O W O hi O to W W Ui O hi O W W O to Ui COO
to Ui h 10 O ^o OnvO O tO O ^3 ^^ OnvO hi ^j OJ On >~* OnsI m OnvO CO hi On to si vO vC *Ji On h( m On4^ O*nO^ 4i O nO 10 \O Co O 10 Oi ^*J
+ + + + + + + + + + + -f + + + + + + + + + + + + + ++ + + + + + + + + + + + + + ++ + + + + + + + +
00000 00090 qoooo oqqoq qqqqq qqqqq qqqqq qqqqq qqqqq qqqqq
mmmhihi hhhh)J toioiototo toiototoio tototototo toiotoioio tototoioto tototototo tototototo tototototo
^^J ^^J ^O 00 CO OOvO nO nO O OOhihhhi tOtOtOtO CjJ OJ Co Co 4^ 4^- 4^- 4^ 4^ Oi Oi C-n s^i ^/i Oi Ln Ln On On On On On O^ On On On On On On O"- O*
O-I^sl Mtn OOtOOiOtO (jiOtOOiCO OW O-O hi -b-OiCOOtO 4»> O- OOO M OJ 4^ O>M 00 OOhimiO tOWWWW WWWWI0
to O 00 On 10 CC4* O to G*» 00 O ""i hi hi O M 4*> O t-n O W O>M 00 COM Oi to 00 W M O to W W to O ^3 W CO 10 Oi OnsI M (_n t*i O Oi
O On On O 00 O W O O 10 M Oi C-n *^J »-( M 4^- 4i 411 M C Cri O s! 4i W h O O O OnitotO W 4^ 4*> 4^- 4i 4*> t*^ 10 O 00 O» to O Oi O 4i
hi O* O O W h h hO Oi On to hi hi to ** ^3 O OC O Ui h *<J w SI CCOl OCOl On O 4^ hi 004^ O 4i OnCh hi ^IOOnOnO OtOOtO CO
hi 10 W O On Oi hi O O>W COM 4i On O tO O O O M 10 10 Oi IO H to O*W Oi 10 Cn Co to hi On tO W W OnM to M 00 Hi W W M 4^- W 10
qqqqq qqqqq q o tf o o qqqqq q q q o o qqqqq qqqqq qqqqq qqqqq qqqqq
to to k> to to 10 10 to to to tototototo tototototo totototoio tototototo tototoioto tototototo to to to k> 10 tototototo
Ln Cn '<J\ Ln {j\ Oi Oi %-n t-n Oi Ln Oi ^-n Cji *-n Oi Oi C^i Oi Oi Ln Ln Ln s-n Oi Ln Oi t-n Ln Cn O^ O* On O^ On On On On On On On On On On O*
10 10 10 to W W W 4* 4^ 4^ 4*. {Ji {Ji Oi Ln On On On OnM M M M CO CO COO ^ ^O ^O OOOOhi MwtOtOtO tO W W W 4**
t04wMOtO 4iMOtOtji vl OWU 00 OWOnCOhi 4i CnO tO4i si OWU 00 H+ 0>O 10 Vi 00OW O> OtOUiOOO OJ Q-.^O
tO M W 004w O Oi O On to CC4* O O1 to O Oi to COOi to CCOi to O ^J 4*> hi 00 On 4i hi O M Ln W hi v?) ^3 C^ 4i W to O O COM On
MO to On O Oi K> CC O*'*-n 4^-4^-Ln OC w Ow O^W O CX3M M 00 O tOLntC*^ OsiUWW W4i O^CW 004=*- H\^sJ sjsjifl hiOi
O I0W O C1- OOOOiO 10 to O O> O WW tvO-^ ~-JOOM4i O-f^sl 0000 vj'ji HsJ H 4»>~J OOO O M 0s W O M W CCW CO tO
I
OO COO OOOOGcOO CCCCCCOOCO CC-J MMM slslslsls] (?P<rOW OiOi O>Ui Ui UiUiUiLnUi UiUi4^4^4^
•v) OnUi 4w to 1- O O COM O-4* U Mh O O CC O>'Ji i>W IOho COM OnUi 4=- W to O O CO si O>(-n W tO MOO CCM Oi 4=- W 10 hi
OOOOO OOOOO OCOOO OOOOO OOOOO OOOOO OOOOO OOOOO OOOOO OOOOO
W 10 H Ui 4s.4i.wtO>-, Ui4»-WW tow UL* WtOtOM Ui4»-Wt0Hi Ui4=-W IOhi U1U1 4iWtOM U-I^UU M
W 4* OnM 00 OOtOW-k- Ui C CCO O m i04n'ji O si OCO h to W4»'Jisl 00 C O HUA Ui O>sl OO h 1OWO1 O> si OSO O 10
4wUi >-<w -t-Ui wt0 4»Ui >->tsi WUi wtO W4»- H^tO w^lU h 10 W4^Oi hi W4^Ui m IOWUi M tOW4iUiM
I0A COCO tOWCJiMO m H> ;¦ 00 OHiW4i-ON OCO >- to 4*. CM O O to W Ui On CeO hi to 4^ Oi On OSO M to W Ui O*M 00 O
M O'-nW to 6-«C ~4w ^ OMUi N/ 6" m4^6m^4^ 6siw"o"ui hTsT to" 0CW GC4^ (XW* 00 w"m" hTuVo" W~m" 64^m" 5"w* OnO m"
OoON-J~JtO UsislslUi Ki OCtjJsj O himOMW OOKiUiOnOn OitO COW si O O O M 4^ O 4i O>~J ~J C"W OO to Ui On OM^- Hsl
oqqqo qqqcq qqqqq qqqqq qqqqq qqqqq qqqqq qqqqq qqqqq qqqqq
OJ OJ OJ OJ Co Co C/J Co Co Co o^ Co Co Co Co Co 4^- 4^- 4^ 4^ 4^ 4i 4i 4^ 4- 4^ 4^ 4^ 4i 4^ 4>^ 4^- 4^ 4^ 4^ 4^ 4^- -^ 4i 4i 4^ 4^ 4i 4^ 4w 4^ 4i 4i 4^ 4i
OOOOO ^C \Z •O ^C C^ OOCOC OOOOO OOOOO OOOOO OOOOO OOOOO hiwhimm mmmmm
WA4i-^-U< CnOC OM sjCODCOOO OOOOhi h 10 10 I0W W4^4^UiUi OiO O>M ~J 00 CO OOO O O O M h N K> K> Co Co 4^-
^~ 00 |Os!^ h O OniWMtO CCUi 4s-W-ii. si OOi Hifl CO CCO to On h O3 OnUi On COIOMWhi OOIOOnm
1>J CO O 00 hi OW 10+nsIW m I0U)O CCO 10 CCM COW O hi Ui 10 to C-W 4^-OOOn MWtOCntO WOOOOtOO WOtOCOO
„ ^ . . —
OOOOO OOOOO \C^C -C ^C -O CO OOO OOOOO OOOOO OOOOO OOOOO OOOOO OOOOO
OOOOnO OOCCXSXOG CCM MMM •-) f f J 6 OnUi OiOiUi Ui-^4w4i4w 4wWWWW Ct) to 10 10 10 Nmhhm hiOOOO
O 0OC-4. to O OOCA to O 05 04^ to O CC O-k- to O 00 O4=- to O O0ON4i to O COC4»- 10 O 00On4=- to O COO1-^ to O 00 04^ N
I
o
724
TABLES OF BESSEL FUNCTIONS
Table III. Functions of order one-third
X
10-02
IO-O4
10-06
10-08
10-10
10-12
10-14
10-16
10-18
IO-2O
10-22
10-24
10-26
I0'28
10-30
10-32
10-34
10-36
10-38
10-40
10-42
10-44
10-46
10-48
10-50
10-52
10-54
10-56
10-58
io-6o
10-62
10-64
io-66
10-68
10-70
10-72
1074
io-yf
10-78
io-8o
10-82
10-84
io-8(
io-88
io-yo
io-g
IO-Q/
10-9
10-9
II-O
- 0-1893250
- 0-1924230
- 0-1954380
- 0-1983690
- 0-2012150
- 0-2039750
- 0-2066482
- 0-2092336
- 0-2117305
- 0-2141379
- 0-2164551
- 0-2180814
- 0-2208160
- 0-2228584
- O'2248o78
- 0-2266637
- 0-2284255
- 0-2300928
- 0-2316649
- 0-2331416
- 0-2345224
- 0-2358069.
- 0-2369948
- 0-2380858
- 0-2390797
- 0-2399763
- 0-2407753
- 0-2414768
- 0-2420805
- 0-2425864
- 0-2429945
- 0-2433049
- O'2435i75
- 0-2436325
- 0-2436501
- 0-2435703
- 0-2433934
- 0-2431198
- 0-2427495
- 0-2422830
- 0-2417207
- 0-2410629
- 0-2403100
,- 0-2394626
- 0-2385212
- 0-2374863
- 0-2^6358^
- 0-23-/1382
- 0-2338-264
- O-232423(
+ 0-1662759
+ 0-1622921
+ 0-1582514
+ 0-1541556
+ 0-1500064
+ 0-1458056
+ 0-1415548
+ 0-1372559-
+ 0-1329107
+ 0-1285269
+ 0-1240885
+ 0-1196151
+ 0-1151028
+ O-IIO5533
+ 0-1059685
+ 0-1013503
+ 0-0967006
+ 0-0920212
+ 0-0873142
+ 0-0825814
+ 0-0778247
+ 0-0730460
+ 0-0682473
+ 0-0634306
+ 0-0585977
+ 0-0537506
+ 0-0488913
+ 0-0440217
+ 0-0391437
+ 0-0342593
+ 0-0293704
+ 0-0244790
+ 0-0195870
+ 0-0146963
+ 0-0098090
+ 0-0049268
+ 0-0000518
- 0-0048141
- 0-0096692
- 0-0145113
- 0-0193387
- 0-0241495
- 0-0289417
- 0-0337136
- 0-0384633
- 0-0431888
- 0-0478886
- 0-0525606
- 0-0572030
- 0-0618143
0-2519755
0-2517247
0-2514747
0-2512254
0-2509769
0-2507291
0-2504820
0-2502357
0-2499901
0-2497452
0-2495010'
0-2492576
0-2490148
0-2487728
0-2485314
0-2482908
0-2480509
0-2478116
O'247573i
0-2473352
0-2470980
0-2468615
0-2466257
0-2463905
0-2461560
0-2459222
0-2456891
0-2454566
0-2452248
0-2449936
0-2447631
0-2445332
0-2443040
0-2440754
0-2438474
0-2436201
O2433935
0-243167.=
0-2429420
0-2427172
0-2424930
0-2422695
0-2420466
0-2418242
0-2416025
0-241381^
0-2411610
0-240941
0-2407218
0-240503
4980 42' 3o'-go
4990 51' ig^oo
501 ° 0' 7'-09
5020 8'55^7
5030 17' 43-24
5O4°26' 31 0
505° 35' 19-35
506° 44' 7^39
507 52'55i
5og° 1'43-43
510° io' 31*43
511 19' 19^42
5120 28' 7i
5I3°36' 55'39
5H° 45'43-35
5i50 54' 3i'-3o
517° 3' 19-25
5180 12' 7-18
5i9o2o'55''ii
5200 29' 43^03
5210 38' 30-93 '
5220 47' i8'<82
5230 56' 6^70
525° 4 54-58
5260 13 42>'44
5270 22' 3O'-3O
5280 31' 18-14
529° 40' 5-9»
5300 48' 53^81
531*57'41^62
533° 6'29^43
534°15' 17-23
535 24' 5^02
536° 32' 52-8o
537° 41' 4°-57
5380 56' 28^33
539° 59" i6-o8
541° s; 3-83
542°16 51-56
543 25' 3g'<2g
544° 34' 27-0°
545° 43 14-7^
546°52 2«4i
548° 0 5C10
549 9 37-78
5500 18' 25^4.6
551° 27'13^12
552° 36 ^78
553° 44, 48-43
554 53 36-07
e*Kll3(x)
0-3933263
0-3929393
O-3925534
0-3921687
O-39I7851
0-3914026
0-3910213
0-3906411
0-3902619
0-3898839
0-389507°
0-3891311
0-3887564
0-3883827
0-3880101
0-3876386
0-3872681
0-3868987
0-3865304
0-3861631
0-3857968
0-3854316
0-3850674
0-3847043
0-3843422
0-3839811
0-3836210
0-3832620
0-3829039
0-3825468
0-3821908
0-3818357
0-3814816
0-3811285
0-3807764
0-3804253
0-3800751
o-3797259
0-3793777
0-3790304
0-3786841
0-3783387
O-3779942
O-37765O7
o;3773o82
0-3769665
0-3766258
0-3762860
O-3759472
0-3756092
X
IO-O2
IO-O/j.
io-oo
10-08
io-io
IO-I2
IO-I4.
IO-ID
10-18
IO-20
IO-22
IO-24
IO-26
IO-28
IO-3O
IO-32
10-34
10-36
10-38
10-40
10-42
10-44
10-46
10-48
10-50
10-52
10-54
10-56
10-58
10-60
10-62
10-64
io-6o
io-68
10-70
10-72
10-74
10-76
10-78
io-8o
10-82
10-84
10-86
io-88
10-90
10-92
10-94
10-96
10-98
II-OO
To compute functions of order -1/3, increase the phase by 60°.
TABLES OF BESSEL FUNCTIONS
Table III. Functions of order one-third
725
X
I 1 -O2
1 1 -O.|
I I ¦<>(>
i i -o8
I I'lO
11-12
n-14
I I-M)
l l • I 8
I 1-21)
11-22
11-2.,
I 1-26
1 1 -28
I I -30
11 32
1 1 • 3 4
1 i-jli
t 1-38
I 1 • |O
I I-., 2
l 1 -40
I I •. 18
I ! -50
11-52
1 1 •'=) 1
I 1 46
1 I ¦1I)
I I-(J
I t -04
1 I -Od
I i-()8
I I -70
11-72
1 t -74
1 1-7A
1 1-78
1 i-8()
1 1-82
1 1 -84
1
1 1 -88
1 1 -<)O
I I -<J
1 I *
l l -<)S
I 2-oc
Ju-A-v)
0-230930A
0-2203480
- o-227<O()8
- 0-2250170
0-2240715
- O'2221302
O- 2 2O1 217
- O-2l8(>T<)l)
¦ O-.li583.-l8
- 0-2135075
O-2II2l8<)
0-2087002
O-2O(J82.1
O-2O"^()()(>7
o-. '.0103 4 3
o-10820A3
- o-10548 30
0-1025085
- o- 18004 12
- o- i8()(ii 34
0-1835104
0-18035 1 5
¦ o-177 1 202
¦ 0-17382^8
- o-1 70 |(>3<>
• 0-1A70 \ i 3
• 0-1035582
- (vllii)ol 58
0-1504157
¦ »-i52 7.-,«K
- 0-1400482
¦ o-14 528 Y)
- o- r 4 1 ,i( >81
- o-1 37A024
- 0-1330883
O-12<O2 7(")
0-125721 7
0-121 A725
- o-1 1 758 1 0
- <>-i '34r>°7
- o-io5075(>
«• 1008 350
: o^oo^oo
- 0-087021 2
- 0-0835585
- 0-07.57508
- 0-070321/
vu.W
- 0-0663024
- 0-0709358
— 0-075442A
- 0-O79()T 11
- 0-0843397
- 0-0887266
- 0-0930702
- 0-0973689
- 0-1016210
- 0-1058249
- 0-1099790
- 0-1140819
- 0-1181310
- O-I22T270
- 0-I26O074
- O-I2<H400
- o-i 33773*>
- 0-1375373
- 0-1412303
- 0-1448785
- 0-1484535
- O-I5i0('20
- 0-1554055
- 0-1587801
- 0-1A20853
- 0-1653202
- 0-1684833
- 0-171 5738
- 0-1745004
- 0-1775320
- 0-1803077
- o-1831 805
- 0-1858073
- O-l88-,2(J
- 0-1010814
- 0-1935528
~ 0-1050428
- o-i082505
~ 0-2004750
- 0-2020158
- 0-2040720
- 0-20064 30
- 0-2085282
- 0-2103269
- 0-2 1 2038!)
- 0-21366-27
- 0-2151088
- 0-2 I 6O464
- 0-218005O
- O-2I92744
0-2402850
0-2400675
0-2398506
o-2396342
0-2394185
O-2392O33
0-2389887
0-2387747
0-2385613
0-2383484
0-2381361
0-2379244
O-2377I32
0-2375O26
O-2372O20
0-2370831
0-2368741
0-2366058
o-236457c)
0-236250A
0-2360439
0-2358377
0-2356320
0-23542A0
0-2352223
0-^.350182
0-23481.
7
0-2340117
O-2344O(J
0-2342072
0-2340058
o-.> 338040
0-2336044
0-23 3404A
0-2332052
0-2330063
0-23280711
0-2320101
0-2321127
0-2322159
0-23-20195
0-2318237
0-231A283
"•23'4335
0-2312391
0-2310452
0-2308518
0-2306589
0-230461L
0-2302745
arg
55«°
559°
500°
561 °
5620
5<>4°
5<\5°
5tif)°
5*7°
5680
'5600
57o°o
572°
5^3°
574°
.¦)/.¦)
-6°
-. 0
-T/ / .
578°
58O°
5SI0
5«3°
58 \°
5«5°o
5 86°
5880
5890
59O°
5<)i°
592°
593°
595°
596°
507°
598C
59Oc
6ooc
60 3c
604c
60 5C
0O(>
607
608
609
611
612
<:,(*
2'
11'
19'
28'
37'
46'
55'
12'
21'
30'
39
47'
56'
5
14'
23'
40'
49'
58'
7'
15'
24'
33'
42'
50'
59'
8'
17'
26
34'
43
52
1
10
18
27
45
:>2
IT
20
5 29
' ]l
3 55
-A
23;
46;^
21'-
9-
5^'
44',
19'
69
93
54
72
88
44
55
7 "°9
54'
4^'
29'
17'
4'
52
39
27'
M
2
49
3&
24
T1
59
46
34
21
8
56
43
3i
18
5
53
'40
27
T5
49
',37
'11
\ 5<
'32
' 2C
62
15
67
18
68
17
66
14
61
'08
'53
'98
-
•'86
•'29
• 70
•11
•52
•92
•31
'•09
•°7
4
':8i
'•' 16
'•'.51
;8.5
8
"M
4(y
';° 5
2
>'-'90
>'-i7
exKvz{x)
0-3752722
°-374936°
0-3746008
0-3742665
O-373933O
0-3736005
0-3732688
0-3729380
0-3726081
0-3722791
0-3719509
0-3716236
0-3712972
0-3709716
0-3706469
0-3703230
0-3700000
0-3696779
0-3^935^5
0-3690360
0-3687164
0-3^83975
0-3680795
0-3677623
0-3A74460
o-3f'7i3°4
0-3668157
0-3A65018
0-3661886
0-3658763
0-305 5^48
°'3^'5254T
O'3fM944I
°-3h4^35O
0-3643266
0-3640190
0-3A37122
0-3634062
0-3631009
0-3627964
0-3624027
0-3621897
0-3A18875
0-3015861
0-3612854
0-3609854
0-3003878
0-3600901
O-3597931
X
11-02
II-O4
11 -06
11-08
II-IO
11-12.
11-14
II-IO
11-18
11-20
11-22
11-24
11-26
11-28
II-30
TI'32
n-34
11-36
11-38
IT-4O
11-42
11-44
11 -46
11-48
11-50
11-52
u-54
11-56
11-58
11-Go
TI-62
T 1 -64
11 -66
t -. C Q
11 -uo
I 1 -70
11-72
11-74
11 -76
11 • 10
I 1 -hO
I I-82
11-84
Q /
I l-o6
I T -Oo
11-90
11-92
11-94
I I-9'1
II-O,O
I2-O0
.7 ,,, A2-00) =0-2302745 x cos 6720 i3'8'^7 = +0-1547365-
r_i,3 A2-00) =0-2302745 xsin 6720 i3'8'ii7= -o-i7°5373-
726
TABLES OF BESSEL FUNCTIONS
Table III. Functions of order one-third
12-02
12-04
12-06
12-08
12-10
12-12
12-14
I2-I6
12-18
I2-2O
12-22
12-24
12-26
12-28.
12-30
I2-32
12-34
12-36
I2-3S
12-40
12-42
12-44
12-46
12-48
12-50
12-52
12-54
12-56
12-58
12-60
12-62
12-64
12-66
12-68
12-70
12-72
12-7.
12
12-78
I2-OO
j-74
2-76
12-82
12-84
12-86
12-88
12-90
12-92
12-94
I2'96
I2-98
I3-OO
- 0-0658652
- O-O6I39OI
- 0-0568980
- 0-0523905
- 0-0478696
- O-O43337I
- 0-0387947
- 0-0342443
- 0-0296877
- 0-0251267
- 6-0205632
- 0-0159989
- O-OII4356
- 0-0068753
- 0-0023196
+ 0-0022296
+ 0-0067705
+ 0-0113014
+ 0-0158205
+ O-O2O3259
+ 0-0248159
+ 0-0292889
+ 0-0337429
+ 0-0381763
+ 0-0425874
+ 0-0469744
+ 0-0513356
+ 0-0556694
+ 0-0599741
+ 0-0642479
+ 0-0684894
+ 0-0726967
+ 0-0768684
+ o-oo 10028
+ 0-0850983
+ 0-08915
+ 0-0931665
+ 0-0971361
+ 0-1010607
+ 0-1049388
.+ 0-1087869
+ 0-1125496
+ 0-1162795
+ 0-1199571
+ 0-1235811
+ 0-1271502
+ 0-1306629
+ 0-1341180
+ 0-1375142
+ 0-140850
0-2204540
0-2215437
0-2225430
0-2234519
0-2242700
0-2249971
0-2256333
0-2261782
0-2266320
0-2269945
0-2272658
0-2274458
0-2275347
0-2275326
0-2274397
0-2272560
• 0-2269819
0-2266176
• 0-2261634
• 0-2256196
• 0-2249866
¦ 0-2242647
- 0-2234544
- 0-2225562
- 0-2215705
- 0-2204979
- 0-2193390
- 0-2180943
- 0-2167645
- 0-2153502
- 0-2138521
- 0-2122710
- 0-210607
- 0-208862
- 0-2070373
- 0-2051320
- 0-2031477
- 0-2010854
- 0-1989460
- 0-1967305
- o-i 944399
- 0-192075
- 0-189637
- 0-1871278
- 0-1845472
- 0-1818970
- 0-1791782
- 0-176392
- 0-1735397
- 0-170622
¦2300830
•2298920
•2297015
•2295114
•2293219
0-2291327
0-2289441
0-2287559
0-2285682
0-2283809
0-2281941
0-2280078
0-2278219
0-2276365
0-2274515
0-2272670
0-2270829
0-2268993
0-2267161
0-2265333
0-2263510
0-2261692
0-2259877
0-2258067
0-2256262
0-2254460
0-2252664
0-2250871
0-2249082
0-2247298
0-2245518
0-2243743
0-2241971
0-2240204
0-2238441
0-2236682
0-2234927
0-2233176
0-2231429
0-2229687
0-2227948
0-222621
0-222448
0-2222757
0-2221035
0-221931
0-2217602
0-2215892
0-2214186
O-22I2- ~
13° 21' 55*43
140 30' 42^69
15° 39' 29"93
6° 8' 17-17
4-41
5
6l6
6190 5'514
6200 14' 38*86
6210 23' 25'-o8
6220 32' 13*29
6230 41' o'-5O
6240 49' 47'-7O
625° 58' 34*89
627° 7 22'-o8
6280 16' 9*26
6290 24'56*43
630° 33' 43-6o
631 42 30-76
632 51 17*92
634° 0' 5*07
6350 8'52*21
636° 17'39-35
637° 26' 26*48
638° 35' I3-6I
639 44 o'r73
640 52 47*84
6420 1'34^95
643 10 22*05
644° 19' 9*15
645 27' 56*24
6460 36' 43*33
647° 45' 3O-4I
648 54 I7'49
?5°o K 4;26
651 ° 11 51*62
6520 20' 38*68
654
6
25 "T.
655° 46' 59-82
656° 55' 46"86
658° 4'33-89
6590 13' 20*92
66o° 22' 7^"
66i° 30' 54*96
6620 39' 41 *97
6630 48' 28*97
6640 57' 15-97
666° 6' 2-96
667° 14' 49*95
668° 23' 36*9
6690 32' 23*92
O-3594968
0-3592013
0-3589065
0-3586125
0-3583191
0-3580265
0-3577346
0-3574434
O-357I529
0-3568631
O-3565741
0-3562857
o-355998o
O-3557110
O-3554248
O-355I392
O-3548543
o-35457oo
0-3542865
o-354°°36
O-35372I5
O-35344OO
O-353I59I
0-3528790
O-3525995
0-3523206
0-3520424:
O-35I7649
0-3514881
0-3512118
0-3509363
0-3506614
0-3503871
3535
0-3498405
0-3495681
0-3492964
0-3490254
O-3487549
0-3484851
0-3482159
0-3479473
0-3476794
0-3474120
O-347I453
0-3468792
0-3466137
6
12-02
12-04
12-00
12-08
I2-IO
12-12
I2-I4
I2-ID
12-18
I2-2O
12-22
I2-24
12-20
12-28
I2-3O
12-32
12-34
T2-3D
I2-38
I2-4O
I2-42
12-44
12-46
12-48
12-50
12-52
12-54
12-56
12-58
I2-OO
12-62
12-64
12-66
I2-C8
12-70
12-72
12-74
12-76
12-78
I2-CO
3434
0-3460846
0-3458209
12-82
12-84
12-86
12-88
12-90
12-92
12-94
12-96
12-98
13-00
To compute functions of order -1/3, increase the phase by 6o°.
TABLES OF BESSEL FUNCTIONS
Table III. Functions of order one-third
727
13-02
13-0,1
13-08
13-10
13-20
13-.20
I \-2tt
13W
13-34
i.Vl-*-
*<
13-00
13-70
13-72
*1V74
i3-7<>
I3-7H
13-80
IVH2
H
3
13-88
13-90
13-92
I3-94
13-90
13-98
14-00
0-1441250
0>147337i
-l- 0-1504854
t 0-1535688
f 0-1565861
I- 0-151M303
t 0-1624183
-I- 0-1652310
775
l- 0-1700447
¦»• 0-1732437
h 0-1757606
0-1782214
0-1805084
0-1828095
0-1851244
8'8
77
0-1803.-113
OH) 13H2O
J5
o-198404^
0-20008-22
0-2015875
0-2030101
0-2043496
0-2050054
O-2O(O77'2
8(
0-2088076
0-200.7855
8
O-21 13^58
0-2126278
O-212()O4O
0-2130946
O-2I340O3
O-2I38l8l
O-21/j I98I
0-2142504
\~ 0-2142350
O-2I4I25I
O-2139298
+ 0-2136494
-t- 0-2132840
+ O-2I28339
+ O-2I22994
+ O-2H68O9
- 0-1676415
- 0-1645982
- 0-1614938
- 0-1583297
- 0-1551071
- 0-1518276
- 0-1484923
- 0-1451029
- 0-1416606
- 0-1381670
- 0-1346234
- 0-1310315
- 0-1273926
- 0-1237083
- 0-1199802
- 0-1162097
- 0-1123985
- 0-1085481
- 0-1046001
- 0-1007361
- 0-0967777
- 0-0927806
- 0-0887643
- 0-0847125
- 0-0806329
- 0-0765272
- 0-072*3969
- 0-0682438
- 0-0640696
- 0-0598759
- 0-0556645
- 0-0514370
- 0-0471951
- 0-0429407
- 0-0386752
- 0-0344006
- 0-0301184
- 0-0258305
- 0-02x5384
- 0-0172440
- 0-0129489
- 0-0086548
- 0-0043635
- 0-0000766
+ 0-0042041
+ 0-0084770
+ 0-0127404
+ 0-0169926
+ 0-0212319
+ 0-0254567
0-2210785
0-2209090
0-2207399
0-2205712
0-2204029
0-2202350
0-2200675
0-2199003
O-2I97335
0-2195671
0-2194011
0-2192355
0-2190702
0-2189053
0-2187408
0-2185766
0-2184128
0-2182494
0-2180864
0-2179237
0-2177613
0-2175994
0-2174378
0-2172765
0-2171157
0-2169551
0-2167949
0-2166351
0-2164757
0-2163166
0-2161578
0-2159994
0-2158413
0-2156836
0-2155262
0-2153692
0-2152125
0-2150561
0-2149001
0-2147445
0-2145891
0-2144341
0-2142795
0-2141251
0-2139712
0-2138175
0-2136642
0-2135112
0-2133585
0-2132061
6700 41' io'-89
671° 49'57-36
6720 58' 44^82
674° 7'3i8
675016'18^74
75 56g
677 33'52-63
678° 42 39«57
679 51 26'-50
68i° o' I33
6820 9' o'-35
6830 i7'47«27
6840 26' 34'-i8
6850 35' 21 9
686° 44' 8'-oo
6875254go
6890 1'41'-79
690010'288
691019'15^57
6920 28' 25
693° 36' -19/;33
694 45 36'r2o
6950 54' 23'-o6
697° 3' 9"92
6980 ii' 56'-78
6990 20' 4 3 3
7000 29' 3o'-48
7010 38'17^33
7o2°47 4^17
703 55 5i-oo
706013 24*65
7070 22'II7
7080 30' 589
7O9°39/45/'11
7100 48'3i"Q2
7n°57;i8'i72
713 6' 52
714° 14' 52*31
7i5° 23'39'-io
7160 32' 25^89
7xZo 4I'/12;67
7180 49 59-45
7190 58' 46'-22
721 ° 7'32*99
7220 16' ig'-76
723° 25' 6*52
724 33 53-28
725° 42, 40-03
7260 51' 26*78
O-3455578
°-3452954
O-345O335
O-3447722
O-3445II5
O-34425I4
O-34399I9
O-343733O
0-3434747
0-3432169
0-3429597
0-3427031
0-3424471
0-3421917
0-3419368
0-3416825
0-3414288
0-3411756
0-3409230
0-3406709
0-3404194
0-3401685
8
3399
0-3396683
O-339I702
0-3389221
0-3386744
0-3384273
0-3381808
0-3379347
0-3376892
Q-3374443
o-337I999
66
0-3367126
0-3364698
0-3362275
O-3359857
Q'3357444
O-3355O37
0-3352635
O-335O237
O-3347845
O-3345459
O-3343O77
o-334°7°o
O-3338329
O-3335962
o-33336oo
/ ... A4-00) =0-2132061 x cos. 7860 51' 26*78 = +0-9837943-
r,', A4-00) =0-2132061 xsin 7860 51'26*78= +0-1960494-
728
TABLES OF BESSEL FUNCTIONS
Table III. Functions of order one-third
X
I4'O2
14-04
14-06
14-08
14-10
14-12
14-14
14-16
14-18
14-20
14-22
14-26
14-28
14-30
14-32
14-36
14-38
14-40
14-42
14-44
14-46
14-48
14-50
I4-52
H-54
14-56
I4-58
14-60
14-62
14-64
14-66
14-68
14-70
14-72
14-74
14-76
14-78
14-80
14-82
14-84
14-86
14-88
14-90
14-92
14-94
14-96
14-98
15-00
+ 0-2109787
+ 0-2101933
+ 0-2093250
+ 0-2083743
+ 0-2073417
+ 0-2062277
+ 0-2050330
+ 0-2037580
+ 0-2024.034
+ 0-2009699
+ 0-1994581
+ 0-1978687
+ 0-1962026
+ 0-1944604
+ 0-1926429
+ 0-1907510
+ 0-1887856
+ 0-1867475
+ 0-1846376
+ 0-1824569
+ 0-1802063
+ 0-1778868
+ 0-175.4995
+ 0-1730454
+ 0-1705256
+ 0-1679410
+ 0-1652930
+ 0-162^825
-i- 0-1598109
+ 0-1569792
+ 0-1540886
+ 0-1511404
+ 0-1481359
+ 0-1450763
+ 0-^419629
4- 0-1387970
+ 0-1355800
+ 0-1323131
+ 0-1289979
+ 0-1256355
+ 0-1222275
+ 0-1187753
+ 0-1152803
+ 0-1117439
+ 0-1081677
+ 0-1045530
+ 0-1009014
+ 0-0972143
+ 0-0934933
+ 0-0897400
+ 0-0296652
+ O-0338559
+ 0-0380272
+ 0-0421773
+ 0-0463046
+ 0-0504076
+ 0-0544847
+ 0-0,585342
+ 0-0625547
+ 0-0665445
+ 0-0705021
-1- 0-0734259
+ 0-0783145
+ 0-0821664
+ 0-0859801
+ 0-0897541
+ 0-0934869
+ 0-0971773
+ 0-1008236
-1- 0-1044246
+ 0-1079789
+ 0-1114852
+ 0-1149420
+ 0-1103482
+ 0-1217023
+ 0-1250032
+ 0-1282497
+ 0-1314404
+ 0-1345743
+ 0-1376501
+ 0-1406666
+ 0-1436229
+ 0-1465178
+ 0-1493501
+ 0-1521190
+ 0-1548233
+ 0-1574621
+ 0-1600344
+ 0-1625393
+ o-164975a
+ 0-1673432
+ 0-1696405
+ 0-1718669
+ 0-1740217
+ 0-1761041
+ 0-1781133
+ 0-1800487
+ 0-1819095
4- 0-1836952
+ 0-1854051
1 <(*) 1
0-2130541
0-2129024
0-2127510
0-2126000
0-2124493
0-2122989
0-2121488
0-2119990
0-2118495
0-2117004
0-2115516
0-2114031
0-2112549
0-2111070
0-2109594
O-2I08I2I
O-21O6652
O-2IO5I85
O-2I0372I
O-2I02261
O-2IOO8O4
0-2099349
0-2097898
0-2096449
0-2095004
0-2093562
0-2092122
0-2090686
0-2089252
0-2087822
0-2086394
0-2084969
0-2083548
0-2082129
0-2080713
0-2079300
0-2077089
0-2076482
0-2075077
0-2073676
0-2072277
0-2070881
0-2069488
0-2068097
0-2066710
0-2065325
0-2063943
0-2062564
0*2061187
0-2059813
728° o' 13*52
729° 9' O'-26
730° 17' 47''oo
731° 26 33*73
732° 35 20*46
733° 44' 7-i8
734 52 53v9o
736 1 40-02
737° 10' 27*33
738°19'14*04
739° 28' 0*75
74° 36'47*45
741 45' 34-H
742° 54'20*83
744 3' 7-52
745° 11'54-21
746 20'40*89
747°29'27*57
748° 38' 14*24
749 47 0*91
750° 55'47''58
752° 4 34-24
753 13 20*90
754°22' 7*55
755 30' 54-20
756° 39'40*85
757° 48'27*49
75»° 57 14*13
760 6 o?77
761° 14' 47-4.0
762° 23' 34*03
763° 32' 20*65
764° 41' 7*27
765 49'53-89
766° 58'40*51
768° 7' 27*12
769° 16' 13*73
770°25' 0*33
771° 33' 46*93
772° 42' 33-53
773° 51' 20*12
775° 0' 6*71
776° 8'53*30
777°17 39-88
778 26 26*46
779° 35' 13 4
780° 43' 59*61
781° 52'46*18
783° 1'32*75
784 10' 19*31
0-3331244
0-3328892
0-3326546
0-3324204
0-3321867
O-33I9536
0-3317209
0-3314887
0-3312570
0-3310257
O-33O795O
0-3305648
O-33O335O
0-3301057
0-3298769
0-3296485
0-3294206
0-3291932
0-3289663
0-3287398
0-3285138
0-3282883
0-3280632
0-3278386
0-3276145
0-3273908
0-3271076
0-3269448
0-3267225
0-3265006
0-3262792
0-3260583
0-3258378
0-3256177
0-3253981
0-3251789
0-3249602
0-3247419
0-3245240
0-3243066
0-3240896
O-3238731
0-3236570
°-32344I3
0-3232261
0-3230112
0-3227969
0-3225829
0-3223694
0-3221 =,62
X
14-02
14-04
14-06
14-08
14-10
14-12
14-14
14-16
14-18
14-20
14-22
14-24
14-26
14-28
14-30
14-32
I4-34
14-36
14-38
14-40
14-42
14-44
14-46
14-48
14-50
14*52
M'54
14-56
14-58
14-60
14-62
14-64
14-66
14-68
14-70
14-72
I4-74
14-76
14-78
14-80
14-82
14-84
14-86
14-88
14-90
14-92
14-94
14-96
14-98
15-00
To compute functions of order -1/3, increase the phase by 6o°.
730
TABLES OF BESSEL FUNCTIONS
Table IV. Values of Jn(re)
X
O'l
0'2
o-3
o-4
o-5
o-6
0-7
o«8
o-9
I'O
I-I
1-2
i
• 1*4
i'5
1-6
1-7
i-8
1*9
2'O
2-1
2-2
2-3
2-4
2*5
2-6
2-7
2-8
2-g
3-o
3-1
3'2
3-3
3-4
3*5
3-6
3*7
3'8
3*9
4-o
4-i
4-2
4
4-4
4-5
4-6
4"Z
4-8
4*9
5-o
+ 0-0012490
+ 0-0049834
+ 0-0111659
+ 0-0197347
+ 0-0306040
+ 0-0436651
+ 0-0587869
+ 0-0758178
+ 0-0945863
+ 0-1149035
+ 0-1365642
+ 0-1593490
+ 0-1830267
+ 0-2073559
+ 0-2320877
+ 0-2569678
+ 0-2817389
+ 0-3061435
+ 0-3299257
+ 0-3528340
¦+ 0-3746236
+ O-395O587
+ 0-4139146
+ 0-4309800
+ 0-4460591
+ 0-4589729
+ 0-4695615
+ 0-4776855
+ 0-4832271
+ 0-4860913
+ 0-4862070
+ 0-4835277
+ 0-4780317
+ 0-4697226
+ 0-4586292
+ 0-4448054
+ 0-4283297
+ 0-4093043
+ 0-3878547
+ 0-3641281
+ 0-3382925
+ 0-3105347
+ o-28io<592
+ 0-2500861
+ 0-2178490
+ 0-1845931
+ 0-150573°
+ 0-1160504
+ 0-081291 =
+ 0-0465651
+ 0-0000208
+ 0-0001663
+ 0-0005593
+ 0-0013201
+ 0-0025637
+ 0-0043997
+ 0-0069297
+ 0-0102468
+ 0-0144340
+ 0-0195634
+ 0-0256945
+ 0-0328743
+ 0-0411358
+ 0-0504977
+ 0-0609640
+ 0-0725234
+ 0-0851499
+ 0-0988020
+ 0-1134234
+ 0-1289432
+ 0-1452767
+ 0-1623255
+ 0-1799789
+ 0-1981148
+ 0-2166004
+ 0-2352938
+ 0-2540453
+ 0-2726986
+ 0-2910926
+ 0-3090627
+ 0-3264428
+ 0-3430664
+ 0-3587689
+ 0-3733889
+ 0-3867701
+ 0-3987627
+ 0-4092251
+ 0-4180256
+ 0-4250437
+ 0-4301715
+ 0-4333147
+ 0-4343943
+ O'433347O
+ 0*4301265
+ 0-4247040
+ 0-4170686
+ 0*4072280
+ 0-3952085
+ 0-3810551
+ 0-3648314
JM
+ 0-0000003
+ 0-0000042
+ O-OOOO2IO
+ O-OOOO66I
+ 0-OOOI607
+ O-OOO33I5
+ O'OOOOIOI
+ 0-0010330
+ 0-0016406
+ 0-0024766
+ 0-0035878
+ 0-0050227
+ 0-0068310
+ 0-0090629
+ 0-0117681
+ 0-0149952
+ 0-0187902
+ 0-0231965
+ 0-0282535
+ 0-0339957
+ 0-0404526
+ 0-0476471
+ 0-0555957
+ 0-0643070
+ 0-0737819
+ 0-0840129
+ 0-0949836
+ 0-1006687
+ 0-1190335
+ 0-1320342
+ 0-1456177
+ 0-1597218
+ 0-1742754
+ 0-1891991
+ 0-2044053
+ 0-2197990
+ 0-2352786
+ 0-2507362
+ 0-2660587
+ 0-2811291
+ 0-2958266
+ 0-3100286
+ 0-3236110
+ 0-3364501
+ 0-3484230
+ 0-3594094
+ 0-3692925
+ 0-3779603
+ 0-3853066
+ 0-3912324
AM
__
+ o-ooooooi
+ 0-0000006
+ 0-0000026
+ 0-0000081
+ O-OOOOI99
+ 0-0000429
+ 0-0000831
+ 0-0001487
+ 0-0002498
+ 0-0003987
+ 0-0006101
+ 0-0009008
+ 0-0012901
+ 0-0017994
+ 0-0024524
+ 0-0032746
+ 0-0042936
+ 0-0055385
+ 0-0070396
+ 0-0088284
+ 0-0109369
+ 0-0133973
+ 0-0162417
+ 0-0195016
+ 0-0232073
+ 0-0273876
+ 0-0320690
+ 0-0372756
+ 0-0430284
+ 0-0493448
+ 0-0562380
+ 0-0637169
+ 0-0717854
+ 0-0804420
+ 0-0896796
+ 0-0994854
+ 0-1098400
+ 0-1207178
+ 0-1320867
+ 0-1439079
+ 0-1561363
+ 0-1687200
+ 0-1816009
+ 0-1947147
+ 0-2079912
+ 0-2213550
+ 0-2347252
+ 0-2480168
+ 0-2611405
X
01
O-2
0-3
0-4
o-5
o-6
0-7
o-8
o-g
i-o
i-i
1-2
i-3
i-4
i-5
i-6
1-7
i-8
i-g
2-0
2-1
2-2
2-3
2-4
2-5
2-6
2-7
2-8
2-9
3-0
3*1
3-2
3-3
3-4
3'5
3-6
37
3-8
3'9
4-0
4-i
4-2
4
4-4
4'5
4-6
47
4-8
4-9
5'O
TABLES OP BESSEL FUNCTIONS
Table IV. Values of Jn(x)
731
X
I
2
3
4
5
6
7
8
9
10
ii
12
7o(*)
4- 0-765198
4- 0-223891
- 0-260052
- 0-397150
- 0-177597
4- 0-150645
4- 0-300079
4- 0-171651
- 0-090334
- 0-245936
- 0-171190
4- 0-047689
7iW
4- 0-440051
+ 0-576725
+ 0-339059
- 0-066043
- 0-327579
- 0-276684
- 0-004683
4- 0-234636
4- 0-245312
4- 0-043473
- 0-176785
- 0-223447
M*)
4- 0-114903
+ 0-352834
4- 0-486091
4- 0-364128
4- 0-046565
- 0-242873
- 0-301417
- 0-112992
4- 0-144847
4- 0-254630
4- 0-139048
- 0-084930
7« W
+ 0-019563
4- 0-128943
4- 0-309063
4- 0-430171
+ 0-364831
+ 0-114768
- 0-167556
- 0-291132
- 0-180935
4- 0-058379
4- 0-227348
+ 0-195137
AW
+ 0-002477
4- 0-033996
4- 0-132034
4- 0-281129
+ 0-391232
+ 0-357642
4- 0-157798
- 0-105357
- 0-265471
- 0-219603
- 0-015040
4- 0-182499
JM
4- 0-000250
4- 0-007040
4- 0-043028
4- 0-132087
4- 0-261141
4- 0-362087
4- 0-347896
4- 0-185775
- 0-055039
- 0-234062
- 0-238286
- 0-073471
X
I
2
3
4
5
6
I
9
10
11
12
X
1
2
3
4
5
6
7
8
9
10
11
12
7oW
4- O-00OO2I
-1- O-OOI2O2
4- 0-011394
4- 0-049088
4 0-131049
1 0-245837
4- 0-339197
+ 0-337576
4- 0-204317
- 0-014459
- 0-201584
- 0-243725
4- o-000002
4- 0-000175
+ 0-002547
4- 0-015176
+ 0-053376
+ 0-129587
+ 0-233584
4- 0-320589
+ 0-327461
4- 0-216711
4- 0-018376
- 0-170254
JM
__
+ O-OOOO22
4- 0-000493
4- 0-00^1029
4- 0-018405
4- 0-056532
4- 0-127971
4- 0-223455
4- 0-^05067
+ 0-317854
4- 0-224972
4- 0-045095
,
4- O-O000O2
4- O-OOOO84
4- O-00O939
4- 0-005520
+ O-O2II65
4- 0-058921
4- O-I2632I
4- 0-214881
4- 0-291856
+ 0-308856
4- 0-230381
7ioW
_
—
+ 0-000013
4- 0-000195
4- 0-001408
+ 0-006964
+ 0-023539
4- o-o6o7(>7
+ d-124694
4- 0-207480
4- 0-280428
4- 0-300476
_
4- 0-000002
4- 0-000037
4- O-OOO35I
4- 0-002048
4- 0-008335
+ 0-025597
4- 0-062217
4- 0-123117
-1- O-2OI0I4
4- 0-270412
A'
1
2
3
A
5
6
7
8
9
10
11
12
X
4
I
7
8
9
10
11
12
r t~\
J M\*l
+ 0-000006
4- O-OOOO76
4- O-OOO545
4- 0-002656
4- 0-009624
4- 0-027393
4- 0-063370
4- O-I2I6OO
4- 0-195280
4- o-000001
4- 0-000015
4- O-OOOI33
-\- O-OOO77O
4- 0-003275
4- 0-010836
4- 0-028972
4- 0-064295
4- 0-120148
,
4- O-0000O3
4- 0-00O03O
4- O-OOO2O5
4- 0-00I0I9
4- 0-003895
4- O-OH957
-1- 0-030369
4- 0-065040
—
+ o-ooooof)
4- 0-000051
4- 0-O0O293
4- O-OOI286
4 0-004508
4- 0-013009
4- 0-03*1613
+
4
4-
4-
4-
4
+
—
o-oooooi
O-OOOO12
0-000078
0-000393
0-001567
0-005110
0-013991
4-
4-
4-
4-
4-
4-
7
o-
o-
0
0
0
0
17 W
—
—
000002
000019
000112
000506
001856
005698
X
4
5
(>
7
8
9
10
11
12
732
TABLES OP BESSEL FUNCTIONS
Table IV. Values of Jn{x) and Yn{x)
X
7
s
9
10
it
12
4- O-OOOOOI
4- O-OOOOO5
4- O-OOOO3O
4- 0-OOOI52
+ O-OOO628
+ O-OO2I52
J,.(.v!
+ O-OOOOOI
+ 0-000007
+ 0-000043
+ 0-OOOI99
4- 0-000759
4-
+
H-
4-
/20M
—
O-OOOOO2
0-000012
O-OOOO59
O'OOO25I
X
I
9
10
11
12
X
6
7
8
9
10
11
12
v.W
- 0-2881947
- 0-0259497
4- O-22352I5
•t- 0-2499367
4- 0-0556712
- 0-1688473
- 0-2252373
- 0-1750103
- 0-3026672
- 0-1580605
-t- 0-1043146
4- 0-2490154
4- 0-1637055
- 0-0570992
v.W
4- 0-2298579
- 0-060^266
- 0-2630366
- 0-2207557
- 0-0058681
4- 0-1986120
4- 0-2157208
+ 0-3282489
4- O'268o8o6
4- O-O265422
- O-2O5O949
- 0-2513627
- 0-0914830
4- O-I29OO6I
v.W
4- 0-0983910
4- O-29O3IO0
4- 0-2829432
4- 0-0900258
- 0-1449495
- 0-24851.18
- 0-1512177
X
6
I
y
10
11
12
Ye{x)
Y,(x)
Ya
- 0-1970609
+ 0-0637022
+ 0-2564011
+ 0-2851178
4- 0-1354030
- 0-0892528
8'
- 0-4268259
- 0-1993068
+ 0-0375581
4- 0-2267718
4- 0-2803526
+ 0-1673728
- 0-0402973
- 0-6565908
- 0-4053710
- 0-2000639
4- 0-0172446
4- 0-2OI0200
4- 0-1895207
- 1-1052194
- 0-6114352
- 0-3876699
- 0-1999469
4- 0-0010755
4- 0-1786071
4- 0-2614047
- 2-2906609
- 0-9921953
- 0-5752760
- 0-3727057
- 0-1992993
- O-0I2O492
4- O-I59OI89
9
10
11
12
X
6
7
8
9
10
u
12
YM
- 576fOf»33
- 1-9399240
- 0-9067010
- 0-5454645
- 0-3598142
- 0-1983240
- 0-0228763
Yn(x)
- 16-9318836
- 45°444 7
- 1-A014765
- °-^39437r">
- 0-5203290
- 0-3485399
- 0-1971461
- 56-3168097
- i*-3''4737
- 3-744^-595
- 1-5064942
- 0-7849097
- 0-4987558
- 0-3385583
Yu[x)
- 208-3353554
- 37-83i75O7
- 9-5431OT8
- 3-1778801
- I-3634543
- 0-7396546
- 0-4799704
X
6
I
9
10
TI
12
TABLES OP BESSEL FUNCTIONS
Table IV. Values of Yn(x)
733
X
o-i
O-2
0-3
o-4
°-5
o-6
0-7
o-8
0-9
1-0
i-i
I-2
1*3
1-4
T>5
i-6
1-7
1-8
1-9
2-O
2-1
2-2
2-3
2-4
2-5
2-6
2-7
2-8
2-9
3-o
3-i
3-2
3-3
3-4
3-5
3-6
37
3-8
3-9
4-0
4-1
4-2
4-3
4-4
4-5
4-6
4-0
4-9
- I-5342387
- I-O8IIO53
- 0-8072736
- 0-6060246
- 0-4445187
- 0-3085099
- 0-1906649
- O-O868O23
+ 0-0056283
+ 0-0882570
+ O-I62I632
+ 0-2280835
+ 0-2865354
+ 0-3378951
+ 0-3824489
+ 0-4204269
+ 0-4520270
+ O-47743I7
+ O-49682OO
+ O-5IO3757
+ 0-5182937
+ 0-5207843
+ 0-5180754
+ 0-5104147
+ 0-4980704
+ 0-4813306
+ 0-4605035'
+ 0-4359160
+ 0-4079118
+ 0-3768500
+ O-343IO29
+ 0-3070533
+ O-269O92O
+ O-2296I53
+ O-I8902I9
+ O-I477TOO
+ O-1O6O743
+ 0-064 503 2
+ 0-0233759
- 0-0169407
- 0-0560946
- 0-0937512
- o-i295959
- 0-1633365
- 0-1947050
- O-22346OO
- o-24<K876
- 0-2723038
- 0-2920546
- 0-3085776
YM
- 6-4589511
- 3-3238250
- 2-2931051
- 1-7808720
- i'47I4724
- 1-2603913
- 1-1032499
- 0-9781442
- 0-8731266
- 0-7812128
- 0-6981196
- 0-6211364
- 0-5485197
- 0-4791470
- 0-4123086
- 0-3475780
- 0-2847262
- 0-2236649
- 0-1644058
- 0-1070324
- 0-0516786
+ 0-0014878
+ 0-0522773
+ 0-1004889
+ 0-1459181
+ 0-1883635
+ 0-2276324
+ 0-2635454
+ 0-2959401
+ 0-3246744
+ 0-3496295
+ 0-3707113
+ 0-3878529
+ 0-4010153
+ 0-4101884
+ 0-4153918
¦+¦ 0-4166744
+ 0-4141147
+ 0-4078200
+ 0-3979257
-1- 0-3845940
+ 0-3680128
+ 0-3483938
-1- 0-3259707
+ 0-3009973
+ 0-2737452
+ 0-2445013
-1- 0-2135652
+ 0-1812467
+ 0-1478631
- 127-6447832
- 32-1571446
- 14-4800940
- 8-2983357
- 5'44i37oS
- 3-8927946
- 2-9614776
- 2-3585582
- I-9459O96
- 1-6506826
- I-43I47I5
- 1-2633108
- 1-1304119
- 1 •0223908
- 0-9321938
- 0-8548994
- 0-7869991
- 0-7259482
- 0-6698787
- 0-6174081
- 0-5675115
- 0-5194317
- 0-4726169
- 0-4266740
- O-38I3358
- 0-3364356
- 0-2918869
- 0-2476693
- 0-2038152
- 0-1604004
- o.-1175355
- 0-0753587
- 0-0340296
+ 0-0062760
+ o-°4537T4
+ 0-0830632
+ 0-1191551
+ 0-1534519
+ 0-1857626
+ 0-2159036
+ 0-2437015
+ 0-2689954
-l- 0-2916395
+ 0-3115049
+ 0-3284816
+ 0-3424796
+ O-35343O8
+ 0-3612893
+ 0-3660328
+ 0-3676629
- 5O99-3323786
- 639-8190662
- 190-7748150
- 81-2024845
- 42-0594943
- 24-6915728
- I5-8I9479I
- 10-8146466
- 77753605
- 5-8215176
- 4-5072313
- 3'5898996
- 2-9296706
- 2-4419696
- 2-0735414
- 1-7896705
- 1-5670362
~- I-3895534
- 1-2458651
- 1-1277838
- 1-0292956
- 0-9459092
- 0-8742197
- 0-8116122
- 0-7560555
- 0-7059567
- 0-6600575
- 0-6173586
- 0-5770644
- 0-5385416
- 0-5012882
- 0-4649097
- 0-4291009
- 0-3936317
- 0-3583353
- 0-3230993
- 0-2878581
- 0-2525864
- 0-2172943
- 0-1820221
- 0-1468365
- 0-1118267
- 0-0771012
-' 0-0427844
- 0-0090137
-1- 0-0240631
-1- 0-0562908
-)• 0-0875092
+ 0-1175556
-1- 0-1462672
X
o-i
O-2
0-3
0-4
o-6
0-7
0-8
o-g
I-O
i-i
1-2
1*3
1-4
i-6
1-7
1-8
1-9
2-O
2-1
2-2
2-3
2-4
2-6
2-7
2-8
2-9
3-O
3-1
3-2
33
3-4
3'5
3-6
37
3-8
3*9
4-0
4-i
4-2
4-3
4-4
4-5
4,6
47
4'8
4'9
5'°
-P* CO Co CO Co
CO CO CO CO Co
Cn -pvCO to HI
CO K> to tO tO
K> K> K> K>
Cn-^-CO ti
W M H H H HWM
w O O O O
6o oV-j on
ooooo
tO M
I I I I I
ooooo
m to m toco
O WUi OOHi
tO tO HI HI HI
M 0>OO> O
-?»¦ QOOMO
M-vl M O N
CO tO^J HVO
I I I I I
ooooo
I I I I I
OOOOO
-?cnCnCn On
COtOCn OOtO
OOO tOCn Ht
O O to OCn
I I I I I
OOOOO
O^1J 00
Cn O-f* VOCn
O O 00W
oo to cnooio
1 1 1 1 1
OO O n N
hiO-O^IO
Cn OCn-?. to
On hi toO O\
00 Hi-^. O vO
to hi to-jCn
ooto hi oico
1 1 1
-P» On 6o
CO O O
OCn Cn
*-J On On
Co On tO
1 1
to to
OCO
On*^
ou>
COCO
tOCo
OCO
Cn hi
1
1 1 1 1
N>O*»1 00
\ OA O J^- C71
Cn-P» Cn Co O\
Co
tovDHi O\
tO«vl--4Cn
HI HI M
*~J O tO OnCO
Co ^x co On hi
0N-t»O COCn
HlCO HI OXO
N 0 O
>vj oocnco N
OOVD Ht-f^ tO
J OON O\O
CO OM
I I I I I
OOOOO
I I I I I
ooooo
I I I I I
O O O O hi
I I I I I
I I I I I
I I I I I
I I I I
I I
1 ' ' M HI
Hi hi 10 10 COCn*-4 O On _ _
hhhhh HtOtO lOCO Coji.Cn OnOO O N>Cn C~-J ^l HiCO-^CO OCn
-pt -fx Oi Cn Cn
u cnowa
Co O-vlCnCn
CT O O
D
w tOCOCn On
4O 0 O
o* oc
Cn vD OO 00
Oo-f^ 'OOh
Cn vO VO OM
OOtOC
OCncn
C4^
00N>
tO<J
O0CnJi.Cn O
O vO-|i- CTihi
c O
CvO O>Cn vO
Cn vC *O CTi to
<O hi vOU> hi
OOHi OOCDCn
O 04
vO hi tocn Oo O COO O hi
OOCO hi hi Cn O O0O0-P>.
Co HCnCoco O OOCoCo to
hi Co COCn Co
to o o>o>
M H 00-?>-
w
P
1=1
o
CD
I
I I I I H
4
i i i i i
I I I I I I I I I I I I I I I I I I HI HI iOCoCn CO-(i- Cn ^, ^
1111 i i i • i i I i i i I I l I M H M M MW ^^qohj, jxcncn coon vivDNOOi I I ^**J;
OOOOO O hhhh HiHiMtOtO t0tococo^» Cn O\^J Ow Wvj HviU ONtO-^.-<lCn OCOwOOn OhiOOiO "-" uw-fl
vO O hi toco
Cn CTi OOOCO
OCn-pv CTi hi
O OOtO O^I
^ 4 to CO
Cn VD vO to O\
hi <O tO-J^J
to <O OOW 00
OOtO^I OV--J OCn COCOO
00<J WVO"J HitOHiCnON
^JOtO-P*00 -I^OONtOO
Cn COCn vO O O Co to Co On
HiOOOOOOtO C-4CnOO
JCnco OJ
Oo O CTvOOO*
* O* O
HI CTiCo to OC
Cn O O»-<l-»>-
OOHi COCO 10
Ji. CTiCn CT\ O\
to jto to^j hi
CTiVO O OV-J
I I I
H M HH H
to io to ioco
HHM MtOCOCO-pi.
¦vlC HICO C O-^- O COCO
' ' ' ' H,
tO COCn 00 tO
--J O0^>. O M
hi K>vO-<l--J
wcoCn COCn
OOO O O>00
Co to hi vOco
<i ooao
HICO O
OCO Co Co Co
I I
CO
O tOCn CO to
h5 CTt CTJ
co-vjeo coo
O O to ONCn
oooo ooto
OOO O K> On
J tOj O\
OCn O O CTv
O> to Coto^J
to Ji. vOCn O>
tO-~J CCOM-n
t OC
COCO hi CO tO CO^CnCO 00
Ji Oh'O h CoOOOOCo
OO-P*. O O 00 \DM\OOiS
0O4i OOO to OCnO»-JCo
OnOOOiOJ 4»O-|i.t0Hi
OnCo O COM
to tO*-J wco
O-*- Co-vi O
oooooco o
O O\?
JJ^ to
^I OCo to
to MCOvO
COCn tO tOCn CO 00-^ Cn Cn
• -^J O On On Cn
Yi O tOCoCnCn
tO-<l O C
<O"^ On to Cn
On On Q\ to ^J
60
W 10 K1 @ W
O \C COO Cn
Cn-?1 CO N Hi
6 O
Cn-b-CO tO hi
hoooo
60 co-j a»
ooooo
C-n-^ oj to hi
TABLES OF BESSEL FUNCTIONS
Table IV. Values of Yn(x)
735
o-i
O-2
03
o-4
07
o-8
o-g
10
T-I
12
16
n
20
2-1
2-2
2-3
2-4
2-5
2-6
n
2-g
3*1
3'2
3*3
3-4
3-5
3-6
3-9
4-0
4
4-2
-1-3
4*4
4
4-6
XI
49
- 410842855308
- 1606575569
- 62798159
- 6302655^
- 1060819 [2
- 24768540-5
- 725010o-i
- 2504646-8
- 9821427
- 425674-6
- 200085-33
- 100577-97
~ 53495-91
- 29859-17
- x 7375-13
- 10485-229
- 6533-582
- 4188-852
- 2754-916
- 1853-922
- 1273-8144
- 891-9608
6
460-6465
337-9597
251-67985
189-81514
144-85794
in-77710
- 87-14989
- 68-61497
- 54-52I73
- 4370218
- 35-32025
- 2877095
- 23-612043
- 19-517110
- 16-243027
- 13-607138
- 11-471092
- 9-729277
- 8-300474
- 7-121782
- ^144157
- 5-329114
- 4-646265
- 4-071477
- 3-585472
- 3-172769
- 2-820869
7397
12850308895
- 334788875
- 25192597
- 3390825
- 659430617
- J65354373
- 49949263
- 17396869
- 6780205
- 2894495-9
- 338225-9
103635-01
60684-92
36684-77
22816-93
- I4559-83
- 9508-814
- 6342-471
- 4312-860
- 2985-112
- 2IOO-II2
- I499-96l8
- 1086-4347
- 797-2497
- 592-2137
- 444-9595
- 337-92355
- 259-23861
- 200-77848
- 156-90855
- 123-67548
- 98-27476
- 78-69575
- 63-48271
- 5I-57I68
- 42-17814
- 34/71866
- 2875588
- 23-95941
- 20-07785
- 16-91853
- 14-332870
- 12-205480
- 10-446246
- 8-984362
- 7-763883
335345{5
11563671430I5
- 200810527
- 11330366
- 1219636
197581500
~ 42447194
- 11213538
- 3469552
- 1216180
«24393
004570
- 8993478
- 4318759
- 2183993
1155408-6
6360127
- 362658-9
- 2I34«5-5
129184-5
- 80230-30
- 51000-98
- 33117-32
- 21928-30
- 14782-85
- 10132-671
- 7053-083
- 4980-319
- 3564-032
- 2582-607
- 1893-5218
- I4O3-6955
- 1051-4532
- 795-372O
- 607-2744
- 467-7617
- 363-3271
- 284-4645
- 224-4160
- 178-3306
- 142-69412
- 114-93902
- 93-17343
- 75*99248
- 62-34502
51-42
42-67291
35'58795
29-83101
25-12911
o-i
O-2
0-3
°-4
o-5
o-6
0-7
o-8
0-9
i-o
i-i
1-2
i-3
1-4
1-5
1-6
1-9
2-O
2-1
2-2
2-3
2-4
2-5
2-6
2-7
2-8
2-9
3-0
3
3-2
3-3
3'4
3-5
3-6
37
3-8
3*9
4-0
4-1
4-2
4-3
4-4
4-5
4-6
XI
4-9
The numbers in [ ] are the numbers of digits between the last digits given and the decimal
points. For example, the integral part of F10(o-i) is a number containing 19 digits of which the
first 14 are given.
TABLES OF BESSEL FUNCTIONS
Table TV. Values of e~xIn{x)
X
o-i
0-2
0-3
o-4
o-5
o-6
tl
o-g
1-0
i-i
1-2
1-3
i-4
i-5
1-6
l'l
i-8
1-9
2-0
2-1
2-2
2-3
2-4
2-5
2-6
2-7
2-8
2-9
3-°
3'i
3'2
3'3
3'4
3-5
3-6
37
3-8
3-9
4-o
4-t
4-2
4-3
4-4
4*5
4-6
47
4-8
4-9
5-o
0-0011320
0-0041073
0-0003969
0-0135860
0-0193521
0-0254458
0-0316770
0-0379022
0-0440151
0-0499388
0-0556193
0-0610206
0-0661209.
0-0709088
0-0753811
0-0795406
o-o833947
0-0869539
0-0902306
0-0932390
0-O959939
0-0985103
o-1008034
0-1028881
0-1047787
o-1064892
0-1080327
0-1094217
01106680
0-1117825
0-1127758
0-1136572
0-1144358
0-1151197
0-1157167
0-1162339
0-1166776
0-1170540
0-1173686
0-1176265
0-1178323
0-1179905
0-1181048
0-1181791
0-1182166
0-1182204
0-1181933
0-1181380
0-1180568
o-i,t795T9
0-0000189
0-0001368
0-0004191
0-0009027
0-00x6043
0-0025257
0-0036585
0-0049877
0-0064938
0-0081553
0-0099497
0-0118547
0-0138486
0-0159110
0-0180231
0-0201679
0-0223299
0-0244955
0-0266527
0-0287912
0-0309022
0-0329781
0-0350127
0-0370010
0-0389387
0-0408227
0-0426507
0-0444207
0-0401318
0-0477833
0-0493750
0-0509071
0-0523802
O-O537949
0-0551523
0-0564535
0-0576999
0-0588928
0-0000338
0-0611243
0-0621661
0-0631607
00641096
0-0650147
0-0658774
0-0666994
0-0674822
0-0682274
0*0689364
0-0696107
6~* I k{x)
O-O0OOOO2
O-OOOOO34
O'ooooi57
0-0000450
o-oooiooo
O-OOOI886
0-0003182
0-0004948
0-0007233
0-0010069
0-0013479
0-0017471
0-0022045
0-0027189
0-0032885
0-0039110
0-0045834
0-0053023
0-0060642
0-0068654
0-0077019
0-0085701
0*0094659
0-0103857
0-0113259
0-0122829
0-0132534
0-0142344
0-0152228
0-0162159
O-OI72II2
0-0182063
0-0191910
0-0201876
0-0211700
0-0221447
0-0231102
0-0240654
0-0250090
0-0259400
0*0268576
0*0277610
0*0286495
0-0295227
0-0303800
0-0312212
0-0320458
0-0328538
0-0336449
0*0344190
o-ooooooi
0-0000005
0-0000018
0-0000050
0-0000113
O-OOOO222
0-0000394
0-0000647
0-0000999
0-0001468
0-0002072
0-0002826
0*0003746
0-0004843
0-0006129
0-0007611
0-0009298
0-0011192
0-0013298
0-0015615
0-0018142
0-0020879
0-0023819
0-0026960
0*0030293
0*0033813
0-0037511
0*0041380
0*0045409
0*0049590
0*0053913
0-0058369
0-0062947
0-0067638
0-0072431
0-0077318
0-0082288
0-0087333
0-0092443
0-0097611
0-0102826
0-0108082
0-0113371
0-0118685
0-0124017
0-0129361
0-0134711
0-0140060
0-0145403
X
o-i
O-2
o-3
0-4
o-5
o-6
0-7
o-8
0-9
I-O
I-I
1-2
i-3
I-4
i-5
1-6
1-7
1-8
1-9
2-0
2-1
2-2
2-3
2-4
2-5
2-6
2-7
2-8
2-9
3-0
3-i
3-2
3*3
3-4
3-5
3-6
37
3-8
3-9
40
4-1
4-2
4-3
4.4
4'5
4-6
47
4-8
4-9
5-o
TABLES OF BESSEL FUNCTIONS
Table IV. Values of Kn (x)
73
X
OI
O-2
0-3
o-4
o-5
o-6
O-7
o-8
0-9
i-o
i-i
1-2
1-3
1-4
1-5
1-6
1-7
1-8
i-9
2-O
2-1
2-2
2'3
2-4
2-5
2-0
2-7
2-8
2-9
3'O
3*t
3-2
3'3
3-4
3'5
3;6
3'2
3'9
4-o
4-i
4-2
4-3
4*4
4'5
4-6
47
4-8
4'9
5'°
2-4270690
1-7527039
1-3724601
1-1145291
0-9244191
07775221
0-6605199
0*5653471
0-4867303
0-4210244 ¦
0-3656024
0-3185082
0-2782476
0-2436551
0-2138056
0-1879548
0-1654963
O-I4593I4
0-1288460
0-1138939
0-1007837
0-0892690
0-0791399
0-0702173
0-0623476
0-0553983
0-0492554
0-0438200
0-0390062
0-0347395
0-0309547
0-0275950
0-0246106
0-0219580
0-0195989
0-0174996
0-0156307
0-0139659
0-0124823
0-0111597
0-0099800
0-0089275
0-0079880
0-0071491
0-0063999
0-0057304
0-0051321
0-0045972
0-0041189
0-0036911
Kx (x)
9-8538448
4-7759725
3-o55992O
2-1843544
1-6564411
1-3028349
1-0502835
0-8617816
07165336
0-6019072
0-5097600
O-4345924
o-3725475
0-3208359
0-2773878
0-2406339
0-2093625
0-1826231
o-1596602
0-1398659
0-1227464
0-1078968
0-0949824
0-08372.48
0-0738908
0-0652840
0-0577384
0-0511127
00452864
0-0401564
0-0356341
0-0316429
0-0281169
0-0249990
0-0222394
0-0197950
0-0176280
o-oi 57057
0-0139993
0-0124835
00111363
o-oo9(>382
0-0088722
0-0079233
0-0070781
0-0063250
0-0056538
0-0050552
0-0045212
0-0040446
I99!5O39S46
49-5124293
21-7457403
12-0363013
7-5501836
5-1203052
3-6613300
2-7198012
2-0790271
1-6248389
1-2924388
j -0428289
0-8513976
0-7019921
"•583656o
0-4887471
0-4118051
0-3488460
0-2969093
o^5375(j8
0-2176851
0-1873570
0-1617334
0-1399880
0-1214602
0-1056168
0-0920246
0-0803290
0-0702383
0-0615105
0-0539444
0-0473718
0-0416512
0-0366633
0-0323071
0-0284968
0-0251593
0-0222321
0-0196614
0-017401.}
0-0154123
0-0136599
0-01^146
0-0107506
0-0095457
0-0084804
0-0075380
0-0067036
0-0059643
0-0053089
K3 (x)
7990-0124305
995-0245583
292-9991958
122-5473670
62*0579095
35-4382031
21-9721690
14-4607876
9-9566542
7-1012628
5* -20953 75
3-9106880
2-9922325
2-3265275
1-8338037
1-4625018
1-1783^57
o-95783<->3
0-7847324
0-647385-1
"•5373847
0-4485459
°-3762579
0-3170382
0-2682271
0-2277714
0-1940711
0-1658685
0-1421608
0-122x704
0-1052398
0-0908577
0-0786032
0-0081323
0-0591618
0-0514.581
0-0448273
0-0391079
0-0341649
0-0298849
D-O2()t727
0-0229477
0-02014 iO
0-01701H5
0-0155631
0-0136993
0-0120691
0-0106415
0-0093900
0-0082918
X
0-1
O-2
0-3
0-4
o-5
o-6
0-7
o-8
0-9
i-o
i-i
1-2
i-3
1-4
i-5
1-6
1-7
1-8
1-9
2-U
2-1
2-2
2-3
2-4
2-5
2-0
l-j
2-8
3-0
3-i
3-3
3-4
3-5
3-0
U
3-l»
4-0
'I*1
4-2
4-3
4')
4'5
4-6
4'7
4-8
4-9
5-o
W. B. F.
47
738
TABLES 03? BESSEL FUNCTIONS
Table IV. Values of Kn (as)
o-i
0-2
o-6
0-7
0-8
o-9
i-o
i-i
1-2
i'3
1-4
1-6
1-7
i-8
i-9
2-0
2-1
2-2
2-3
2-4
2-5
2*9
3
3-2
3-3
3-4
3-5
3-6
3'Z
3-8
3-9
4-o
4
4-2
43
4'4
4-5
4-6
47
4-8
4-9
479600-2498
29900-2492
5881-7297
1850-2468
752-2451
359-5O2336
191-994207
111-175708
68-456722
44-232416
29-708098
20-596272
14-661702
ro-672824
7-918871
5-973I29
4-57O567
3-541634
2-775011
2-195916
17530699
1-4106641
1-1432756
0-9325836
0-7652054
0-6312432
0-5232937
°-43576i5
0-3643764
0-3058512
38376010-00
1197004-99
0-2177299
0-1845662
0-1568967
O-I337274
0-1142604
0-0978523
0-0839814
6-0722228
0-0622288
°-°537I39
0-0464423
0-0402191
0-0348822
0-0302965
0-0263491
0-0229453
0-0200054
0-0174623
0-0152591
5739
37127-48
12097-98
4828-8027
2216-1917
1126-2179
618-4609
360-9606
221-26843
141-21917
93-21809
63-31409
44-06778
31-328146
22-686864
16-698431
12-468991
9-431049
7-215746
5-578234
4-352869
3-425650
2716884
2-1700581
17445711
1-4109012
1-1473430
O-9377736
0-7701024
0-6351824
0-5260364
O>4373on
0-3648244
3537
0-2563998
0-2159108
0-1823141
0-1309802
0-1114092
0-0949678
0-0811187
0-0694236
0-0595239
0-0511250
0-0439839
0-0378998
0-0327063
3838080599-8
59880149-8
5243852-5
93OO37-3
242711-8
80839-547
31851-875
14188-899
6940-244
3653-838
2041-2393
1197-4227
73I-7239
462-9164
301-7041
201-77404
138-02271
96-31069
68-40128
49<35II6
36-113765
26766271
20-068791
15-206127
11-632743
8-977621
6-984668
5-474694
4-320732
3-43I763
^•7418356
2-2026750
17786158
1-4430764
1-1760828
0-9625106
07908246
06521676
O6
539949
0-4480852
77
0-3117023
0-2610745
0-2192429
0-1845713
O>I55749O
0-1317219
0-1116385
0-0948088
0-0806716
460608047990
3594OO5995
209911239
27938248
5837182
16-21619-74
548248-34
2I3959-7O
93I55-O5
44207-02
22489-333
12115-446
6847-593
4031-169
2457-700
443
990-964
658-7697
444H77I
3O5-538"
2:13-^8012
151-57608
109-05961
79-45628
58-554O5
43-60523
3278754
24-87388
19-02623
14-66483
11-383660
8-8952x4
6-99373O
5-53O51*
4-397108
3\5/3739
2-821236
7537
1-842914
1-498598
1-2232080
1-0019872
0-8235478
0-6790539
0-5616138
0-4658258
8
4
0-3230800
0-2700847
0-2263181
o-i
02
0-3
0-4
o-5
o-6
0-7
o-8
0-9
i-o
i-i
1-2
i-
I-
i-
!¦•<)
2-O
2-1
2-2
2-3
-'4
2-5
2-1)
3*1
3-3
3
3'5
3
37
3-9
4-0
4-1
4-2
4'3
4'4
4-5
4-6
4-cj
5-o
TABLES OF BESSEL FUNCTIONS
Table IV. Values of Kn (x)
o-i
O-2
0-3
0-4
o-6
07
o-8
0-9
i-o
i-i
1-2
r-8
i-9
2-O
2-1
2-2
2'3
2-4
2-5
2-6
2-7
2-8
2-9
3*1
3-2
3-3
3-4
3-5
36
37
3-8
3 ¦<)
4-0
4-1
4-2
4-3
4-4
4*5
4-6
4-8
4-9
644889647992 [2]
2516402998M
98011017JXI
9787687E2]
1636838C2]
379I8633-59
10996818-69
3758483-72
145601875
622552-12
288269-12
142544-29
74475-O3
40774-60
23240-24
13717-316
8348-321
5220-075
3343-496
2188-117
1459-9812
99I-34I3
683-9099
478-7011
339-5354
243-775OI
176-99414
129-84408
96-17151
71-86762
54-I5I9I
41-11923
31-44899
24-21577
18-76452
14-627050
11-465773
9-035174
7-I55283
5-693I79
4-549986
3-651659
2-379869
1-931814
1-5734796
1-2857868
I-O539552
H794
o-8l
0-7143624
(*)
10318694975920b]
20134817990b]
39l78686f3]
1012785182
251904104
75383634
25977933
10005041
4215494-70
1912706-01
923463-36
470026-62
138717-80
79569-4°
47O59-44
28600-23
17810-48
11337-^47
4866-694
3270-797
2231-581
I543-7592
1081-6417
766-8400
549-6277
397-9588
290-87739
214-49139
T59-47366
119-48709
90-17775
68-52285
52-40296
40-31822
31-19792
24-27131 <
18-979250
14-913071
11-771986
9-333*22
7-430286
5-936798
4-764583
3-836264
3-099405
2-512278
K10 (x)
18574295846304b]
304214741M
2]
i8o7i33[2]
69269092
28833134
12860891
6083974
3027484
1574292-56
850847-84
475814-46
274293-04
162482-40
98636-38
61220-41
387-71-08
25009-68
16406-92
10931-338
73»7939
5O59-53O
35O7-654
2459-620
1743-1174
1247-6333
9OI-3O53
402-5358
2663991
200-0162
151-1457
114-9141
67-56482
52-22047
40-56082
31-65296
24-812255
I9-533I25
I5-439946
12-252049
o-i
O-2
0-3
0-5
o-6
0-7
o-8
I-O
1-1
1-2
1-4
1-6
*7
i-g
2-O
2-1
2-2
2-3
2-4
2'5
2-6
2-7
2-8
2-9
3-Jt
3-2
3-3
3-4
3-5
3-6
37
3-8
3-9
4-0
4-2
4-3
4-4
4-5
4-6
XI
4*9
The numbers in [ ] are the numbers of digits between the last digits given and the decimal
points. For example, the integral part of l?i0 (o-i) is a number containing 19 digits of which the
first 14 are given.
47—2
740
TABLES OF BESSEL FUNCTIONS
Table V. Values of J^n + ^ (x)
X
1
2
3
4
5
6
1
9
10
11
12
13
14
15
i6
17
18
19
2O
21
22
23
24
25
26
11
29
30
31
32
33
34
35
36
32
38
39
40
41
42
43
44
45
46
47
48
49
50
¦ 0-671397
+ 0-513016
+ 0-065008
- 0-301921
- 0-342168
- 0-091016
+ 0-198129
+ 0-279093
I- 0-109608
- 0-137264
- 0-240569
- 0-123589
+ 0-092980
+ 0-211241
+ 0-133968
- 0-057428
- 0-186045
- 0-141233
+ 0-027435
+ 0-162881
-s- 0-145672
- 0-001506
- 0-140786
- 0-147489
- O-O2II2O
+ 0-119324
+ 0-146854
+ 0-040849
- 0-098326
- O-I4393O
- 0-057900
+ 0-077777
+ 0-138882
+ 0-072398
- 0-057748
- 0-131887
- 0-084414
+ 0-038360
+ 0-123138
+ 0-094001
- 0-019766
- 0-112839
- O-IOI2O7
+ O-OO2I2C
+ o-ioi2oi!
+ 0-106088
+ 0-014382
- 0-088476
- 0-108712
- 0-029006
2
1- 0-431099
- 0-234786
- 0-456049
- 0-260766
!- O-IOI2I8
+ 0-312761
t- 0-227356
- 0-041045
- 0-242326
- O-2II7O9
+ 0-001064
+ 0-194364
+ O-2OO8I2
+ 0-029158
- 0-156506
- O-I9IO25
- 0-053248
+ 0-124181
+ 0-180980
+ 0-072807
- 0-095367
- 0-170103
- 0-088648
+ 0-069085
+ 0-158173
+ 0-101229
- 0-044859
- 0-145147
- 0-110835
+ 0-022470
+ 0-131087
+ 0-117665
- 0-001844
- o-ii6iic
- 0-12187?
- 0-017017
+ 0-100400
+ 0-123619
+ 0-034067
- 0-084139
- 0-123031
- 0-049245
+ 0-067544
+ 0-120267
+ 0-06248;
- 0-050842
- 0-115491
- 0-073722
+ 0-034263
+ 0-108885
/, M
+ 0-240298
+ 0-491294
+ 0-477718
+ 0-185286
- 0-169651
- 0-327930
- 0-199052
+ 0-075931
+ 0-254504
+ O'i97983
- 0-022934
- 0-204663
- 0-193660
- 0-014070
+ 0-165437
+ 0-187436
+ 0-042305
- 0-132027
- 0-179536
- 0-064063
-l- 0-102303
+ 0-170034
+ 0-082527
- 0-075230
- 0-159018
- 0-096639
+ 0-050298
+ 0-146606
+ 0-107444
- 0-027202
- 0-132954
- 0-115235
+ 0-006053
+ 0-118244
+ O-I2O22J
+ O-OI3353
- O-I020S2
- O-I226IO
- 0^030910
+ 0-086489
+ 0-122549
+ 0-04655*:
- 0-069898
- O-I2O2I8
- 0-060234
+ 0-053148
+ O-II5797
+ 0-071879
- 0-0.36481
- O-JO9477
V
- 1-102496
- 0-395623
+ 0-087008
+ 0-367112
+ 0-321925
+ 0-038889
- 0-230608
- 0-273962
- 0-082683
+ 0-158435
+ 0-240472
+ 0-107392
- 0-108427
- 0-213323
- 0-123534
+ 0-069367
+ 0-189178
+ O-I34334
- 0-036960
- 0-166521
- 0-141131
+ 0-009238
+ 0-144640
+ 0-144611
+ 0-014793
- 0-123217
- 0-145193
- 0-035665
+ 0-102148
+ 0143181
+ 0-053672
- 0-081454
- 0-138826
- 0-068982
+ 0-061230
+ 0-132360
+ 0-081700
- 0-041613
- 0-124012
- 0-091898
+ 0-022766
+ 0-114011
+ 0-099636
- 0-004863
- 0-102596
- 0-104983
- 0-011925
+ 0-090012
+ 0-108013
+ 0-027428
+ 0-049497
+ 0-223925
+ 0-412710
+ 0-440885
+ 0-240377
- 0-072950
- 0-283437
- 0-250619
- 0-024773
+ 0-196659
+ 0-234314
+ 0-072423
- 0-137671
- 0-214256
- o-100880
+ 0-092573
+ 0-193511
+ 0-119229
- 0-055782
- 0-172580
- 0-131058
-1- 0-024692
+ 0-151550
+ 0-138086
+ 0-002038
- 0-130474
- 0-141266
- 0-025141
+ 0-109441
+ 0-141203
+ 0-045034
- 0-088581
- 0-138331
- 0-061964
+ 0-068053
+ 0-133000
+ 0-076088
- 0-048040
- 0-125516
- 0-087514
+ 0-028733
+ 0-116164
+ 0-096331
- 0-010326
- 0-105223
- 0-102622
- 0-006991
+ 0-092968
+ 0-106479
+ 0-023037
J-% (*)
+ 2-876388
+ 0-828221
+ 0369041
- 0-014568
- 0-294372
- 0-332205
- 0-128524
+ o<I4378i
+ 0-269886
+ 0-164179
- 0-066647
- O-22I2I2
- O-I7579O
+ O-OI6554
-1- O-l8l2I2
+ 0-178019'
+ 0-019864
- 0-146570
- 0-175144
- 0-047829
+ O-II5528
-1- 0-168843
+ 0-069782
- 0-087161
- 0-159948
- O-O87OII
+ O-O6O99I
+ 0-148969
+ O-IOO268
- 0-036788
- 0-136281
- O-IIO029
+ 0-014465
+ O-I222O2
+ 0-116630
+ 0-005987
- O-IO7O25
- O-I2O334
- 0-024528
+ O-O9IO3I
+ OT21365
+ O-O4IIOI
- 0-074495
- O-II9958
- 0-055643
+ 0-057689
+ 0-116253
+ 0-068096
- 0-040876
- O-IIO53O
X
I
2
3
4
5
6
7
8
9
10
11
12
13
14
T5
16
M
T9
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
39
40
41
42
43
44
45
46
47
48
49
TABLES OF BESSEL FUNCTIONS
Table V. Values of «/±(w + i) (%)
X
I
2
3
4
5
6
7
8
9
IO
II
12
13
I4
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
3O
31
32
33
34
35
36
37
38
39
4°
41
42
43
44
45
46
47
48
49
AW
+ 0-007186
+ 0-068518
+ 0-210132
+ 0-365820
+ 0-410029
+ 0-267139
- 0-003403
- 0-232568
- 0-268267
- 0-099653
+ 0-129440
+ 0-234840
+ 0-140709
- 0-002450
- 0-199063
- 0-158507
-I- 0-014610
+ 0-165146
-l- 0-164856
+ 0-021518
- 0-133507
- 0-164423
- 0-049581
-1- 0-103998
-I- 0-159426
-1- 0-071548
- 0-076458
-- 0-151096
- 0-088575
+ 0-050802
+ 0-140218
+ 0-101394
- 0-027012
- 0-127357
- 0-110507
+ 0-005119
+ 0-112964
+ 0-116289
+ 0-014818
- 0-097428
- 0-119045
- 0-032729
+ 0-081099
+ 0-119045
+ 0-048542
- 0-064303
- 0-116541
- 0-062195
+ 0-047346
+ 0-111781
-f-jW
- 13-279444
- 1-674928
- 0-702076
- 0-348902
- 0-027552
+ 0-237949
+ 0-322411
+ 0-184099
- 0-067254
- 0-240524
- 0-210178
- 0-015220
+ 0-176039
+ 0-207411
+ 0-063130
- 0-124998
- 0-195020
- 0-093620
¦+- 0-083050
+ 0-178478
+ 0-113625
- 0-047611
- 0-159810
- 0-126452
+ 0-017196
+ 0-139950
-!- 0-133898
-1 0-009064
- 0-119436
- 0-137049
- 0-031691
-t- 0-098646
1 0-136634
-1- O-O5IOI2
- 0-077891
- 0-133192
- 0-067238
+ 0-057447
+ 0-127156
+ 0-080519
- 0-037567
- 0-118904
- 0-090974
-I- 0-018494
+ 0-108779
+ 0-098712
- 0-000443
- 0-082918
- 0-103842
- 0-016375
+ 0-000807
+ 0-015887
+ 0-077598
+ O-I993OO
+ O-333663
+ 0-384612
+ 0-280034
+ 0-047122
- 0-183879
- 0-266416
- O-I5I943
-1- 0-064567
-1- 0-213437
+ 0-183031
-1- 0-007984
- O-l6ig2O
- 0-187495
- 0-055005
-I O-IIO5I9
•I o-i8oiii
¦1- 0-086555
-- 0-077008
- 0-166640
~ 0-107753
-l- 0-042001
+ 0-149737
1- 0-121443
- 0-012633
- 0-130821
- 0-129349
- 0-013372
-h 0-110760
+ 0-132602
+ 0-035744
- 0-090154
- 0-132005
- 0-054717
+ 0-069461
+ 0-128176
+ 0-070464
- 0-049057
- O-I2l6l<)
- 0-083128
1- 0-029205
4- 0-112774
-1- 0-092836
— 0-010367
- O-IO2O38
- 0-099715
- 0-007388
y-,w
+ 90-079718
+ 5-934028
H- 1-269137
+ 0-625147
+ 0-332945
-(- 0-054598
- 0*193887
- 0-304868
- 0-217577
+ 0-004188
+ 0-200397
+ 0-230091
+ O'OOIOOO
- 0-120260
- 0-210673
- 0-123323
1- 0-060438
-I- 0-182978
-I- 0-144546
- 0-014639
- 0-153403
- o-153094
- 0-021144
1 0-124043
+ 0-155133
-1 0-049333
- 0-095706
- 0-151235
- 0-071438
¦I- 0-068760
+ 0-143437
-I- 0-088450
- 0-043448
- 0-132704
- 0-101062
+ 0-019912
+ 0-119745
+ 0-109751
-h 0-001705
- 0-105122
- o-114951
¦ 0-021284
! 0-089305
1- 0-117016
f- 0-038744
- 0-072710
- 0-116187
- 0-056004
+ 0-055710
+ 0-112833
X
I
2
3
4
5
6
7
8
9
10
ri
12
13
H
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
5O
742
TABLES OF BESSEL FUNCTIONS
Table V. Values of J ±(?1 + ^ {x)
1 I 4- O-OOOO74
2 + O-OO2973
3 + 0-022661
4 + 0-082606
5 + 0-190564
6 I + 0-309779
+ °-363446
+ 0-285580
9 I + 0-084388
10 - 0-140121
11 - 0-253757
12 - 0-186414
13 I 4- O-OO7O55
14 + O-I8OII3
15 I + O-2O3854
16 1 + 0-067428
17 - 0-113872
18 - O-I92649
19 - O-IO9663
20 I + O-O59532
21 I + 0-170603
22 4- 0-132919
23 - 0-015626
24 - 0-144405
25 - 0-144089
26 - O-OI97I6
27 4- O-II6939
28 + 0-147035
29 + 0-047975
30 I - 0-089606
31 t - 0-144100
32 I - 0-070242
33 4- 0-063176
34 + 0-136818
35 I + 0-087324
(*)
36
li
39
40
41
42
43
44
45
- 0-038120
- 0-126274
- 0-099837
+ 0-014761
+ 0-113283
+ 0-108276
+ 0-006668
- 0-098498
- 0-113059
- 0:025987
797-438019
- 20-978200
- 3'i°5334
- 1-057678
46 I + 0-082467
47 + 0-114556
48 + 0-043062
49 - 0-065662
50 - 0-113110
- 0-319846
- 0-073127
+ 0-158877
-!- 0-284832
+ 0-236755
+ 0-04621^
- 0-157348
- O-232II6
- O-I3OIO2
+ 0-063274
+ 0-194373
+¦ O-I63O23
4- O'OO2I3I
- O-I5I52O
- O-I7I89I
- 0-047880
4- O-IIO486
+ 0-168084
4- O-O79936
- O-O73O44
- O-I57O27
- O-IOI996
+ O-O39548
+ 0-I4I6O6
+ O-II64I9
- 0-OO995I
- O-I23523
- O-I24785
- O-OI5?"
+ 0-103879
+ O-I282I4
+ 0-O38II0
- O-O8344O
- O-I2755O
- O'O56866
+¦ O-O628OO
+ O-I2O424
+ O'O72282
- O-O42429
- O-II6528
- 0-084486
+ O-O2269I
+ O-O934I9
+ O-O936O9
- 0-003933
+ 0-000006
+ 0-000467
+ O-OO5493
+ O-O27866
O-O85579
+ O-I833I6
O-29TO96
+ O-34555I
+ O-287O2O
+ O-II2283
- O-IOl8l4
- 0-235447
- 0-207468
- 0-041513
0-141509
+ 0-208276
+ 0-113813
- 0-062725
- 0-180008
- 0-147369
+ 0-002808
4- 0-143468
+ O-I59I67
+ 0-041567
- o-106000
- 0-158079
- O'O738OI
+ 0-070397
4- O-I49OI9
4- 0-096493
- O-O3776O
- O-I349O6
- °-"i543
+ 0-008521
+ 0-120357
+ 0-017176
- 0-098362
- 0-124012
- 0-039312
+ 0-078107
+ 0-123365
+ 0-057931
- 0-119127
- 0-073116
+ 0-037178
+ 0-111907
+ 0-084974
- 0-017496
+ 8681-738496
+ 110-346069
+ 10-117087
+ 2-283448
+ 0-924903
+ 0-308802
+ 0-086412
- 0-130550
- 0-264618
- 0-246614
- 0-005855
+ 0-115406
+ 0-222482
+• 0-164272
- 0-010308
- 0-165924
- 0-184280
- 0-050824
+ 0-109179
+ 0-178483
+ 0-098451
- 0-059244
- o-i6o68t
- 0-122994
+ 0-017102
+ 0-137260
+ 0-135698
+ 0-017726
- 0-111453
- 0-139905
- 0-045989
+ 0-085043
+ 0-137843
+ 0-068414
- 0-059088
- 0-131075
- 0-085598
+ 0-034271
4- 0-120760
•1- 0-098102
- 0-010256
- 0-107796
- 0-106408
- 0-010259
+ 0-092913
+ 0-110876
+ 0-034596
- 0-076725
- 0-111958
9
10
11
12
13
14
15
16
17
18
19
20
21
22
24
25
26
27
28
29
30
31
32
33
34
35
36
32
38
39
40
41
42
43
44
45
46
42
48
49
5O
TABLES OF BESSEL FUNCTIONS
Table V. Values of Jn + j (x)
743
X
2
3
4
5
6
i
9
ro
n
12
13
14
15
16
17
i8
19
2O
+ 0-000063
+ 0-001140
+ 0-007957
+ 0-031941
+ 0-087406
+ 0-177161
+ 0-275940
+ 0-330196
+ 0-286089
+ 0-133432
- 0-068653
- 0-214523
- 0-218661
- 0-081213
+ 0-101797
+ 0-200906
+ °-I47348
- 0-013500
- 0-155322
JlJL (*)
+ O-000008
+ O-OOO2O7
+ O-OOI974
+ O-OIO243
+ O-O35I99
+ 0-088535
+ O-I7I837
+ O-2633O8
+ 0-316850
+ 0-283766
+ O-I4963O
- O-O4OO59
- 0-192766
- O-222722
- O-II2842
+ O-O63457
+ O-1855I5
+ O-I6935O
+ O-O3O877
7?W
+ o-oooooi
+ 0-000034
+ 0-000434
+ 0-002887
+ 0-012324
+ 0-037852
+ 0-089213
+ 0-167162
+ 0-252556
+ 0-305116
+ 0-280630
+ 0-162139
- 0-015412
- 0-171205
- 0-221691
- 0-137449
+ 0-027861
+ 0-165024
+ 0-181568
+ 0-000005
-t- 0-000086
+ 0-000727
+ 0-003827
+ 0-014205
+ 0-040045
+ 0-089590
+ 0-163007
+ 0-243253
+ 0-294700
+ 0-277030
+ 0-171849
-1- 0-005802
- 0-150416
- 0-217076
- 0-156106
- 0-004326
+ 0-141612
_
+ O-OOOOOI
+ O-OOOOI5
+ 0-000165
+ 0-001069
+ 0-004763
+ 0-015904
+ 0-041882
+ 0-089759
+ 0-159277
+ 0-235095
+ 0-285372
+ 0-273106
+ 0-179412
+ 0-024269
- 0-130704
- 0-209985
- 0-169805
- 0-032875
_
—
+ O-OOOOO2
+ O-OOOO34
+ O-OOO272
+ 0-001446
+ 0-005680
+ 0-017442
+ 0-043438
H- 0-089780
+ 0-155899
+ 0-227859
+ 0-276957
+ 0-269236
+ 0-185304
-I- 0-040241
- 0-112207
- O-2OI22O
- 0-179418
X
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
X
5
6
7
8
9
1O
11
12
13
14
15
i5
17
18
19
20
Jag. \x)
+ 0-000007
+ 0-000063
+ O-OOO4O2
+ 0-001846
+ o-oo6i5o8
+ 0-018337
+ 0-044768
+ 0-089695
+ 0-152818
+ 0-221379
+ 0-269315
+ 0-265267
+ 0-189882
+ 0-054141
- 0-094968
- 0-191398
+ o-oooooi
+ 0-000014
+ 0-000103
+ 0-000551
+ 0-002261
+ 0-007421
+ 0-020106
+ 0-045914
+ 0-089532
+ 0-149989
+ 0-215531
+ 0-262335
+ 0-261336
+ 0-193419
+ 0-066273
- 0-078969
./?w
—
+ 0-000003
+ 0-000024
+ 0-000152
+ 0-000718
+ 0-002683
+ 0-008237
+ 0-021263
+ 0-046907
+ 0-089312
+ 0-147378
+ O-2IO2I5
+ 0-255927
+ 0-257478
+ 0-196122
+ 0-076893
—
+ o-oooooi
+ 0-000005
+ 0-000039
+ O-OOO2I2
+ O-OOO898
+ O'OO3IO8
+ O-OO9O17
+ O-O22324
+ 0-047774
+ 0-089050
+ 0-144957
+ O-2O5354
+ O-250OI6
+ 0-253715
+ O-198I53
in. (x)
—
+ o-oooooi
+ 0-000009
-I- 0-000058
+ 0-000280
+ 0-001086
+ 0-003532
+ 0-009760
+ 0-023297
+ 0-048533
+ 0-088758
¦*• 0-142701
+ 0-200884
+ 0-244541
+ 0-250059
—
—
—
+ O-OOOOO2
+ O-OOOOI5
+ O-OOOO82
+ O-OOO355
+ 0-001288
+ 0-003955
+ 0-010469
+ 0-024193
+ 0-049201
+ 0-088443
+ 0-140592
+ 0-196755
+ 0-239451
X
5
6
7
8
9
10
il
12
13
14
15
16
17
l8
19
2O
744
TABLES OF BESSEL FUNCTIONS
Table V. FresneFs integrals
' * h
o-5
r-o
i-5
2-0
2'5
3-°
3-5
4-o
4-5
5'O
5-5
6-o
Oi
(Ji
7-o 1
7-5
8-o
8-5
9-o
9-5
io-o
io-5
IT-0
11-5
12-0
12-5
13-0
13-5
14-0
14-5
i5-o
15-5
i6-o
i6-5
I7-0
17-5
i8-o
i8-5
ig-o
i9-5
2O-O
20-5
2I-O
21-5
22-O
22-5
//-iM*
+ O-55O247
+ 0-721706
+ 0-779084
+ O-7533O2
+ 0-670986
+ O-56IO2O
+ 0-452047
+ O-368I93
+ 0-325249
+ 0-328457
+ 0-372439
+ 0-443274
+ O-522202
+ O-59Ori6
+ 0-631845
+ O-6393OI
+ O-6I2868
+ 0-560804
+ 0-496895
+ 0-436964
+ 0-395087
+ 0-380390
+ 0-395149
+ O-434557
+ 0-488146
+ 0-542511
+ 0-584583
+ 0-604721
+ 0-598871
+ 0-569335
+ 0-524009
+ 0-474310
+ 0-432343
+ 0-407905
+ 0-406589
+ 0-427837
+ 0-465971
1 + 0-511332
+ 0-552774
+ 0-580389
+ 0-58/849
+ 0-57384.2
f- 0-542266
+ 0-501167
+ 0-460707
*f./iM*
+ 0-092366
+ 0-247558
+ 0-415348
+ 0-562849
+ 0-665787
+ 0-711685
+ 0-700180
+ 0-642119
+ 0-556489
+ 0-465942
+ 0-391834
+ 0-349852
+ 0-347099
+ 0-381195
+ 0-441485
+ 0-512010
+ 0*575457
+ 0-617214
+ 0-628573
+ 0-608436
+ 0-563176
+ 0-504784
+ 0-447809
+ 0-405810
+ 0-380217
+ 0-398268
+ 0-432489
+ 0-481770
+ O-533736
+ 0-575803
+ 0-598183
+ 0-596126
+ 0-570890
+.0-529259
+ 0-481750
+ 0-439989
+ 0-413893
+ 0-409336
+ 0-426853
+ 0-461646
+ 0-504875
+ 0-545885
+ 0-574811
+ 0-584939
+ 0-574246
23-0
23-5
24-0
24-5
25-0
+ 0-430662
+ 0-418080
+ 0-425635
+ 0-451078
+ 0-487880
+ 0-545782
+ 0-506824
+ 0-467029
+ 0-436051
+ 0-421217
X
25-5
26-0
26-5
27-0
27.5
28-0
28-5
29-0
29-5
30-0
30-5
31-0
3i-5
32-0
32-5
33'O
33-5
34-o
34-5
35-o
35-5
36-0
36-5
37-o
37-5
38-0
38-5
39-0
39-5
40-0
4°-5
41-0
4i-5
42-0
42-5
43-o
43-5
44-0
44
45-o
45-5
46-0
46-5
47-0
47-5
48-0
48-5
49-0
49-5
50-0
+ 0-526896
+ 0-558628
+ 0-575524
+ 0-573766
+ O-554I27
+ 0-521695
+ 0-484566
+ 0-451832
+ O-43I358
+ 0-427908
+ 0-442034
+ 0-470019
+ 0-504844
+ 0-537944
+ 0-561307
+ 0-569407
+ 0-560508
+ 0-537026
+ 0-504881
+ 0-472012 .
+ 0-446415
+ 0-434212
+ 0-438182
+ 0-457140
+ 0-486272
+ 0-518359
+ 0-545560
+ 0-561321
+ 0-561957
+ 0-547503
+ 0-521665
+ 0-490870
+ 0-462670
+ 0-443897
+ 0-439006
+ 0-449025
+ 0-471341
+ 0*500382
+ 0-529002
+ 0-550239
+ 0-559004
+ 0-553301
+ o-534?76
+ 0-507802
+ 0-479313
+ 0-456160
+ 0-443930
+ 0-445486
+ 0-460311
+ 0-484658
+ 0-425797
+ 0-448300
+ 0-482927
+ 0-521054
+ 0-553369
+ 0-572142
+ 0-573060
+ 0-556212
+ 0-525995
+ 0-489969
+ 0-456974
+ 0-434973
+ 0-429129
+ 0-440605
+ 0-466343
+ 0-499873
+ 0-532930
+ 0-557490
+ 0-567709
+ 0-561313
+ 0-540094
+ 0-509417
+ 0-476871
+ 0-450396
+ 0-436345
+ O-437971
+ 0-454670
+ 0-482187
+ 0-513690
+ 0-541464
+ 0-558799
+ 0-501608
+ 0-549384
+ 0-525282
+ 0-495309
+ 0-466829
+ 0-446755
¦ + 0-439878
+ 0-447720
+ 0-408209
+ 0-496215
+ 0-524837
+ 0-547099
+ o-557°5°
+ 0-554044
+ 0-537309
+ 0-511657
+ 0-483428
+ 0-459523
+ 0-445722
TABLES OF BESSEL FUNCTIONS
Table V. Presnel'a integrals
745
X
O-O2
0-04
O-0()
0-08
o-io
O-I2
0-14
O-IO
0-18
O-2O
O-22
0-24
O-2()
O-28
°'J°
O-32
()• \U
()-3«
O\|O
O-.j-2
O-.J4
O'4(>
04H
0-50
0-52
o-5f>
0-58
<)•(>()
O-0-2
0-64
o-GO
O-08
0-70
0-72
0-74
u-j(>
0-78
o*8o
0-82
0-84
o-86
o-88
0-90
o-y2
0-94
0-96
0-98
T-OO
-1- 0-1128334
+ o-*5(>55i4
+ °-*9537°7
-1- 0-2255314
+ 0-252061r
-l 0-2759976
+ 0-2979565
-l- 0-3183378
+ 0-3374186
+ 0-3554002
+ 0-3724338
+ 0-3886365
-l- 0-4041012
-l- 0-4189028
•1- 0-4331026
-l- o-44(>75i7
+ O-.| 598032
-1- 0*4725635
H 0-48.17941
1- O-,]()(>()I 21
1 0*5080410
1 o-5i()ioi8
-1 o-Jj2()8l25
1 0-5401895
1 0-5502472
1- 0-5599985
1- 0-5094551
-h 0-5786275
-1- 0-5875253
-1- 0-5961571
-1- 0-6045308
1- 0-6126537
-1- 0-6205324
-I- 0-6281731
l- 0-6355815
-1- 0*6427627
+ 0-640,7217
-I- 0-6564631
¦(• 0-6629910
1- 0-6693095
-I- 0-6754224
-I- 0-6813330
-H 0-6870448
-I- 0-6925609
-1- 0-6978843
+ 0-7030179
+ 0-7079643
+ 0-7127261
+ 0-7173059
+ 0-7217059
*jo h{t) dt
+ 0-0007522
1- 0-0021274
+ 0-0039078
-1- 0-0000153
+ 0-0084044
+ 0-0110444
+ 0-0139124
+ 0-0169904
+ 0-0202639
+ 0-0237204
+ 0-0273496
+ 0-0311421
+ 0-0350898
H 0-0391853
+ 0-0434218
+ 0-0477932
+ 0-0522937
-}- 0-0569181
+ 0-0616612
-I- 0-0665185
+ 0-0714853
+ 0-0765575
+ 0-0817309
-1- 0-0870016
-l- 0-0923658
¦1 0-0978198
+ 0-1033602
H- 0-1089835
-I- 0-1146863
•I- 0-1204654
1- 0-1263176
+ 0-1322398
-1- 0-1382290
+ 0-1442820
1- 0-1503961
H- 0-1565683
+ Ol627958
+ 0-1690757
+ 0-1754054
+ 0-1817820
+ 0-1882030
+ 0-1946656
+ 0-2011673
+ 0-2077055
+ 0-2142775
+ O-22O88O9
+ 0-2275131
+ 0-2341717
+ 0-2408543
+ 0-2475583
Maxima and minima
of Fresnel's integrals
x = (n ~ i) t
1-570796
4-712389
7-853982
IO-995574
14-137167
I7«27876o
20-420352
23-561945
26-703538
29-845130
32-986723
36-128316
39-269908
42-411501
45-553O93
48-694686
+ 0-779893
+ 0-321056
+ 0-640807
+ 0-380389
+ 0-605721
+ 0-404260
+ 0-588128
+ 0-417922
+ 0-577121
+ 0-427036
+ 0-569413
+ 0-433666
+ 0/563631
+ 0-438767
+ 0-559088
+ 0-442848
3-141593
6-283185
9-424778
12-566371
15-707963
18-849556
21-991149
25-132741
28-274334
31-415927
34-557519
37-699112
40-840704
43-982297
47-123890
50*265482
+ 0-713972
+ O-343&5
+ 0-628940
+ 0-387969
+ 0-600361
+ 0-408301
+ 0-584942
+ 0-420516
+ O-574957
+ 0-428877
+ 0-567822
+ 0-435059
+ 0-562398
+ 0-439868
+ 0-558096
+ 0-443747
746
TABLES OP BESSEL FUNCTIONS
Table VI. Functions of equal order and argument
n
I O-
2 O
3 o
4 o
Jn (n) I
4400506
3528340
3090627
2811291
5 0-2611405 1
6 0
7 0
8 0
9 0
•2458369
•2335836
•2234550
•2148806
10 0-2074861 1
II C
12 c
13 c
14 c
15 C
16 (
n
18
19
20
21
22
23
24
25
26
27 1
28
29
3O
31
32
33
34
35
36
3l
38
39
40
41
42
43
44
45
46
4Z
48
49
50
•2010140
)• 1952802
>-i9Oi489
>-i855i74
>-i8i3o63
3-1774532
3-1739079
3-1706299
0-1675857
0-1647478
0-1620927
0-1596009
O-I572555
0-1550422
0-1529484
0-1509633
0-1490774
0*1472823
0-1455706
O-I439359
0-1423721
0-1408742
O-I394373
0-1380567
0-1367305
O-I35453I
0-1342222
0-1330349
0-1318885
0-1307805
0-1297089
0-1286716
0-1276667
0-1266925
°*I257473
0-1248297
0-1239383
0-1230719
0-1222291
0-1214090
n* /„ (n)
0-4400506
O-.4445439
O-4457456
0-4462646
0-4465441
0-4467152
0-4468293
0-44691.00
0-4469696
O-4470I53
0-4470512
0-4470800
0-4471036
0-4471233
0-4471399
0-4471540
0-4471662
0-4471768
0-4471861
0-4471943
0-4472015
0-4472080
0-4472138
0-4472191
0-4472239
I 0-4472282
0-4472321
0-4472358
0-4472391
0-4472422
0-4472450
0-4472476
0-4472500
0-4472523
0-4472544
0-4472564
0-4472583
0-4472600
0-4472616
0-4472632
0-4472646
0-4472660
0-4472673
0-4472685
0-4472697
0-4472708
0-4472718
0-4472728
O'4472738
0-4472747
Jn' («)
O-325I47I
0-2238908
0-1770285
0-1490424
O-I3OO9I8
O-II625O2
O-I056I3O
O-O97I34I
0-0901865
0-0843696
0-0794142
O-O75I323
O-07I388O
0'0680806
0-0651336
0-0624879
0-0600969
O-O579234
O'O559374
O-O54II4I
O-O524332
0-0508777
0-0494332
0-0480874
0-0468301
0-0456522
0-0445460
0-0435048
0-0425226
0-0415942
O-O4O7I5I
O-03988I2
0-0390889
"•0383350
0-0376165
0-0369309
0-0362758
0-0356491
0-0350489
0-0344734
0-0339210
0-0333004
0-0328800
0-0323888
0-0319156
0-0314594
0-0310192
0-0305941
0-0301833
0-029786
1
n% Jn' (n)
0-3251471
O-3554045
0-3682342
O-3755633
0-3803908
0-3838497
0-3864704
0-3885364
0-3902143
0-3916089
0-3927897
o-3938°47
0-3946882
O-3954655
O-396I557
O-3967734
o-39733°o
o-397§347
0-3982948
0-3987163
0-3991041
0-3994624
O-399794O
04001035
0-4003917
0-4006614
0-4009143
0-4011521
1 0-4013762
0-4015877
0-4017879
0-4019775
0-4021576
o«402328S
0-4024918
0-4026472
0-4027956
0-4029374
0-4030732
0-4032033
0-4033281
0-4034479
0-4035631
0-403673$
0-4037805
0-403883
0-403982
1 0-404078
0-404170
0-404259
n
1
2
4
5
6
7
8
Q
IO
II
12
13
14
15
16
17
[ 0
19
2O
21
22
23
24
25
26
27
28
29
3°
31
32
33
34
35
36
37
3«
39
40
41
42
43
44
45
46
47
48
49
50
Jn{n)
For values of n exceeding 50, the following approximations may be used with seven-figure
accuracy: ,,. Q-4473Q 73*84 T. 1 0-0058692885
J{) _—[i-2-^j.—-j—
rT, 23 "I 0-0894614637r. 947 1
TABLES OF BESSEL FUNCTIONS
Table VI. Functions of equal order and argument
n
I
2
3
4
5
6
I
9
IO
ii
12
13
14
l5
16
11
19
2O
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
3Z
38
39
40
41
42
43
44
45
46
47
48
49
50
- K (n)
0-7812128
0-6174081
0-5385416
0-4889368
0-4536948
0-4268259
0-4053710
0-3876699
0-3727057
0-3598142
0-3485399
0-3385583
0-3296303
0-3215755
0-3142546
0-^075580
0-3013982
0-2957040
0-2904173
0-2854894
0-2808800
0-2765546
0-2724839
0-2686456
0-2650095
0-2615652
0-2582933
o-2551791
0-2522100
O-2493744
0-2466622
0-2440643
0-2415724
0-2391794
0-2368784
0-2346635
0-2325292
0-2304705
0-2284828
0-2265620
0-2247042
0-2229059
0-2211637
0-2194748
0-2178364
0-2162458
0-2147007
0-2131988
0-2117381
0-2103166
-n* Yn (n)
0-7812128
0-7778855
0-7767114
0-7761387
07758072
07755941
0-7754469
O7753399
O-775259O
0-7751961
O-775I458
O775IO49
0-7750711
0-7750426
0-7750184
0-7749976
0-7749796
O-7749638
O-7749499
o-774937<1
0-7749266
0-7749168
0-7749079
0-7748999
0-7748925
0-7748859
0-7748798
07748742
07748690
07748642
O-7748598
O-7748557
07748519
0-7748483
0-7748450
0-7748419
0-7748389
07748362
o-7748336
0-7748312
0-7748289
0-7748267
0-7748246
07748227
07748208
07748191
07748174
0-7748158
O7748I43
0-7748128
y/ («)
0-8694698
0-5103757
0-3781412
0-3069147
0-2615525
0-2297650
0-2060642
0-1876000
0-1727588
0-1605149
0-1502159
0-1414121
0-1337852
0-1271029
0-1211915
0-1159184
0-1111803
0-1068955
0-1029987
0-0994367
0-0961658
0-0931499
0-0903586
0-0877663
0-0853514
00830953
0-0809819
0-0789973
0-0771293
0-0753678
0-0737029
0-0721267
0-0706318
0-0692116
0-0678605
0-0665732
0-0653451
0-0641718
0-0630496
0-0619751
0-0609450
0-0599565
0-0590071
0-0580942
0-0572157
0-0563695
0-0555539
0-0547671
0-0540074
0-0532735
J Yn' (n)
0-8694698
0-8101709
0-7865654
O-7733765
07647843
0-7586672
0-7540520
0-7504241
0-7474840
0-7450441
0-7429809
07412092
07396683
07383135
0-7371112
07360358
0-7350670
07341890
07333887
07326559
0-7319817
O73I359I
0-7307820
07302453
0-7297446
0-7292763
07288371
07284242
07280352
07276680
0-7273206
07269914
07266790
07263820
07260991
07258295
072557-20
0-7253259
0-7250904
0-7248647
0-7246483
0-7244405
07242407
07240480
07238636
0-7236853
0-7235134
07233475
07231873
0-7230324
n
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
3Z
38
39
40
4i
42
43
AA
45
46
4Z
48
49
5O
For values of n exceeding 50, the following approximations may be used with seven-fi
accuracy: ^ ^ ,077475 90021 r 1 n 0-01016 59059 |~, __ii?3_
L 225n*J+ ft*
0-7116134100 r_
23
" nf L* 14625712
1 . 0-15495 18004 r_ 47
1
'48 TABLES OF BESSEL FUNCTIONS
Table VII. Zeros, jQt n,y0>n, jlt n, ylt n, of Jo (x), Yo (x), Jx (x), Yx (x
)'o,n
Vi, «
9
io
ii
12
13
14
15
16
17
I8
19
20
23
24
25
26
2
2
29
3O
31
3
33
34
35
36
h
39
4'
2-4048256
8-6537279
915344
14-9309177
18-0710640
21-2116366
24-35247I5
27-493479I
30-6346065
33-7758202
36-9170984
40-0584258
43-1997917
46-3411884
49-4826099
52-6240518
55-7655IO8
58-9069839
62-0484692
65-1899648
68-3314693
71-4729816
74-6145006
77-7560256
84-0390908
87-1806298
90-3221726
93-4637188
96-6052680
997468199
102-8883743
106-0299309
109-1714896
112-3130503
115-4546127
118-5961766
I2i-737742i
124-8793089
O-893577O
3-9576784
7-0860511
10-2223450
13-3610975
16-5009224
i9-r
22
>-64i3O97
1-7820280
32-2052041
41-6291645
44-7704866
47-9118963
51-0533286
54-1947794
57-3362457
60-4777252
63-6192158
66-7607160
69-9022246
73-O4374O3
76-1852624
79-3267901
82-4683228
85-6098598
88-7514008
91-8929453
95-0344930
98-1760436
101-3175968
104-4591523
107-6007100
110-7422697
113-8838313
117-0253944
120-1669592
123-3085253
3-8317060
7-0155867
10-1734681
13-3236919
16-4706301
19-6158585
227600844
25-9036721
29-0468285
32-1896799
35-3323O76
38-4747662
41-6170942
44'7593i9O
47-9014609
5I-O435352
54-1855536
57-3275254
60-4694578
63-6113567
66-7532267
69-8950718
73-0368952
76-1786996
79-3204872
82-4622599
85-6040194
88-745767!
91-8875043
95-0292318
98-1709507
101-3126618
104-4543658
107-5960633
1107377548
113-8794408
117-0211219
120-1627983
2-i97I4I3
5-4296811
8-5960059
11-7491548
14-8974421
18-0434023
21-1880689
24-3319426
27-4752950
30-6182865
33-7610178
36-9O35553
40-0459446
43-1882181
46-33O3993
49-4725O57
52-6145508
55-7565449
58-8984962
02-0404111
65-1822951
68-3241522
71-4659861
74-6077996
77-7495953
80-8913753
84-0331412
87-1748947
90-3166370
93-4583692
96-6000923
99-7418072
102-8835147
106-0252153
109-1669097
112-3085985
126-4461387
118-5919607
121-7336349
124-8753051
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
3o
31
32
33
34
35
36
32
38
39
40
TABLES OF BESSEL FUNCTIONS 749
Table VII. Zeros, j% „, y% n, j3< n, yZt n, of J2 (x), Y2 (x), Js (x), Ys (x)
9
io
ii
12
13
14
15
16
17
l8
19
2O
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
Jt,
5-1356223
8-4172441
11-6198412
I479595I8
17-9598195
21-1169971
24-2701123
27-4205736
30-5692045
337165195
36-8628565
40-0084467
43-I534538
46-2979967
49-4421641
52-5860235
55-7296271
58-8730158
62-0162224
68-3021898
71-4449899
74-5876882
77-7302971
80-8728269
84-0152867
87-1576839
90-3000252
93-4423160
96-5845614
99-7267657
102-8689327
106-0110655
109-1531673
112-2952406
115-4372877
118-5793107
121-7213115
124-8632917
128-0052530
3-3842418
67938074
10-0234780
13-2099868
10-3789666
19-5390400
22-6939559
25-8456137
28-9950804
32-1430023
35-2897939
38-4357335
41-5810149
44-7257771
47-8701227
51-0141287
57-3013461
60-4446401
63-5^77658
66-7307471
69-8736034
73-0163509
7f)-i59oo3T
79-3015713
82-4440651
85-5064927
88-72856i2
91-8711766
95-0134441
98-1556685
101-2978536
104-4400031
107:5821201
110-7242073
113-8662672
1x7-0083021
120-1503138
123-2923041
126-4342746
6-3801619
9-7610231
13-0152007
16-2234640
19-4094148
22-5827295
257481667
28-9083508
32-0648524
35-2186707
38-3704724
41-5207197
44-6697431
47-8177857
50-9650299
54-1116156
57-2576516
63-5484022
66-6932417
69-8377884
72-9820804
76-1261492
79-2700214
82-4137195
7006678
91-8439487
94-987II77
98-1301857
101-2731621
104-4160552
107-5588722
110-7016197
113-8443033
116-9869284
120-1294994
123-2720205
120-4144954
129-5569276
4-5270247
8-O975538
11-3964667
14-6230726
17-8184543
20-9972845
24-1662357
30-4869896
33-6420494
36-7947910
39-9457672
43-O953675
46-2438744
49-3914980
55-6846964
58-8304911
61-9758587.
65-1208612
68-2655491
71-4099642
74-554I4O9
77-6981084
80-8418910
83-9855095
87-1289817
90-2723230
93-4I55465
96-5586637
99-7016848
105-9874728
109-1302542
112-2729691
115-4156229
118-5582204
121-7007659
124-8432635
127-9857167
9
10
11
12
14
15
16
17
18
19
20
21
22
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
750 TABLES OF BESSEL FUNCTIONS
Table VII. Zeros, j4, n, yitn,j5, „, y5,n, oi J4 (x), F4 {x), J5 {x), Y5 (x
n
i
2
3
4
5
6
7
8
9
IO
ii
12
13
14
15
16
17
18
19
2O
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
3Z
3»
39
40
7-5883427
11-0647095
I413725367
17-6159660
20-8269330
24-0190195
27-1990878
30-3710077
33-537I377
36-6990011
39-8576273
43-OI37377
46-1678535
49-3203607
52-4715514
55-6216509
58-7708357
61-9192462
.65-0669953
68-2141749
71-3608607
74-5071155
77-6529918
807985341
83-9437799
87-0887615
90-2335065
93-378O39O
96-5223797
99-6665468
1028105563
105-9544223
109-0981571
112-2417718
115-3852762
118-5286792
121-6719886
124-8152114
127-9583541
131-1014225
5-6451479
9-3616206
12-7301445
15-9996271
19-2244290
22-4248106
25-6102671
28-7858937
31-9546867
35-1185295
38-2786681
4 r -4359606
44-5910182
47-7442881
50-8901052
54-0467255
57-1963482
60-3451302
63'493I972
66-6406512
697875753
72-9340384
76-0800980
79-2258022
82-3711919
85-5163019
88-6611620
91-8057980
94-9502321
98-0944839
101-2385704
104-3825064
107-5263053
110-6699788
-8T35372
116-9569899
120-1003451
123-2436104
126-3867924
129-5298972
877M838
12-3386042
15-7001741
18-9801339
22-2177999
25-4303411
28-6266183
31-8117167
34-9887813
38-1598686
41-3263833
44-4893191
47-6493998
50-8071652
53-9630266
57-1173028
60-2702451
63-4220540
66-5728919
69-7228912
72-8721613
76-0207934
79-1688641
82-3164380
85-4635703
88-6103082
91-7566925
94-9027585
98-0485369
101-1940546
1043393353
107-4843998
110-6292667
Ii3'7739523
116-9184713
120-0628368
123-2070606
126-3511534
129-4951246
132-6389830
y*,*
6-7471838
10-5971767
14-0338041
17-3470864
20-6028990
23-8265360
27-0301349
30-2203357
33-4011056
36-5749725
397436277
42-9082482
46-0696791
49-2285437
52-3853121
55-5403458
58-6939271
61-8462803
64-9975855
68-1479890
71-2976113
74-4465520
77-5948946
80-7427095
83-8900562
87-0369859
90-1835423
93-3297633
96-4756819
99-0213268
102-7667232
105-9118934
109-0568569
112-2016312
115-3462317
118-4906725
121-6349657
124-7791228
127-9231536
131-0670674
n
1
2
3
4
5
6
I
9
10
IX
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
3i
32
33
34
35
36
3Z
38
39
40
TABLES OF BESSEL FUNCTIONS
751
Table VII. Zeros, jV3,n, yV3,n* of «/1/3 (*), Yll9 (x); with zeros,
sn,dn, of «/_1/3 (x) + JV3 (x), J_1/3 (a:) - JV3 (x)
[Note. The last two functions are equal to
n/3- {^ j
respectively.]
. \Jva(z) cos 120°- ri/a(a;)s
2-9025862
6-0327471
9-1705067
12-3101938
15-4506490
18-5914863
217325412
24-O7373I4
28-0150117
r
34-2977437
37 4391666
40-5806158
43-7220857
46-8635719
50-0050715
53-1465821
56-2881019
59-4296294
02-5711634
65-7127030
68-8542475
7*-99579°*
75-13734^l
78-2789040
81-4204625
84-5620234
8«6
90-8451519
93-9867101
97-1282878
100-2698581
103-4114297
106-5530025
109-6945765
112-8361516
115-9777275
119-1193044
122-2608821
125-.1024605
I-353OI96
4*4657883
7-6012412
10-7402128
13-8803575
17-0210330
20-1619929
23-3031228
20-4443623
29-5850767
35-8684514
39-0098884
42-15*3485
45-2928269
48-4343202
5I-575825O
547I734XO
57-6588648
61-000395A
64-14^19325
67-2834747
70-4250213
73557
76-7081259
79-8496829
82-9912426
86-1328048
89-2743691
92-4*59353
95-5575O32
98-0990728
101-8406437
104^-9822160
108-1237894
111-2653639
114-4069394
117-5485159
120-6900931
123-8316712
2-3834466
5-6101956
8-6473577
11-7868429
14-9272068
18-0679953
2I-209O210
24-3501925
27-4914601
30-6327941
33-7741762
30-9155941
40-0570394
43-1985061
f8
49-4814874
52-0229964
557645*47
58-9060410
02-0475740
65-1891127
68-3306564
71-4722044
74-6137562
80-8968692
84-0384298
87-1799926
90-3215576
93-4631244
96-6046929
99-7462629
102-8878343
106-0294070
109-1709808
112-3125557
545435
118-5957082
121-7372858
124-8788641
0-8477186
3-9441020
7-0782997
10-2169407
I3-3569532
16-4975630
19-6384856
22-7795923
25-9208165
29-0621201
32-2034801
35-3448813
38-4563138
41-0277704
44-7692461
47-9107371
51-0522406
54"'937545
6
5733579
60-4708067
63-6183427
06-7598840
69-9014299
73-0429798
76-1^45333
79-3260899
82-4676492
85-6092109
88-7507749
91-8923408
5335
98-I754777
101-3170485
10/|-4586205
107-6001938
)-7
H3-8S33435
117-0249197
120-1064969
123-3080748
9
10
II
12
13
M
15
16
ll
18
19
20
21
22
23
24
26
2/
21
29
3°
31
32
33
34
35
3^
ii
39
4°
752
TABLES OF BESSEL FUNCTIONS
Table VIII. Integrals of functions of order zero
Maxima and minima of
and h
a'
O-O2
O-O4
0-06
0-08
O'lO
O-I2
0-14
0-16
0-18
O-2O
O-22
0-24
O-26
O-28
O-3O
0-32
o-34
0-36
0-38
0-40
0-42
0-44
0-46
0-48
0-50
0-52
o-54
0-56
0-58
o-6o
0-62
0-64
o-66
o-68
0-70
0-72
O74
0-76
0-78
o-8o
0-82
0-84
0-86
o-88
0-90
0-92
0-94
0-96
0-98
I-OO
h\X JAt)dt
J n
+ 0-0099997
+ 0-0199973
+ 0-02999x0
+ 0-0399787
+ 0-0499583
+ 0-0599280
+ 0-0698858
+ 0-0798295
+ 0-0897573
+ 0-0996672
+ 0-1095571
+ 0-1194252
+ 0-1292695
+ 0-1390880
+ 0-1488788
+ 0-1586399
+ 0-1683694
-h 0-1780654
-1- o-i8772()O
+ 0-1973493
¦h 0-2069333
H 0-2164763
-,- 0-2259764
+ 0-2354316
+ 0-2448403
¦I- 0-2542004
+ 0-2635103
•1- 0-2727682
+ O-28I9722
1- O-29II2O6
-r O-3OO2II7
+ 0-3092437
+ O-3I82I5O
+ 0-3271238
+ 0-3359684
+ 0-3447472
+ O-3534586
+ 0-362IOIO
+ 0-3706727
+ O-379I722
+ O>3875979
+ 0-3959484
+ 0-4042220
+ 0-412417/
+ 0-4205330
+ 0-4285674
+ 0-4365192
+ °-444387°
+ 0-452169^
+ 0-4598652
j °
- 0-0320078
- 0-0551846
~ 0-0750205
- 0-0926801
- 0-1087153
- 0-1234500
- 0-1370979
- 0-1498103
- 0-1617001
- 0-1728544
- 0-1833430
- 0-1932224
- O-2O25397
- 0-2113348
- 0-2196416
- 0-2274894
¦- 0-2349040
- 0-2419080
- 0-2.(85215
- 0-2547624
- 0-2606471
- 0-2661901
0-2714049
- 0-2763037
- 0-2808977
- 0-2851974
- 0-2892124
- 0-2929516
- 0-2964234
- 0-2996358
- 0-3025960
- 0-3053111
- 0-3077877
- 0-3100319
- 0-3120498
- 0-3138471
- 0-3154290
- 0-3168010
- 0-3179678
- 0-3189344
- 0-3197054
- 0-3202852
- 0-3206781
- 0-3208884
- 0-32092^I
- 0-3207771
- 0-3204634
- 0-3199827
- 0-3193386
- 0-3185347
x = /»,»
2-4048256
5-5200781
8-6537279
i 17915344
14-9309177
18-0710640
21-2116366
24-3524715
27-4934791
30-6346065
33-7758202
36-9170984
40-0584258
43-1997917
46-341x884
49-4826099
+ 0-7352208
-1- 0-3344230
+ 0-6340842
-1- 0-3845594
-1- 0-6028269
-I- 0-4064156
1 0-5864441
-i- 0-5759911
¦: O-4279931
-r 0-5685888
-!- 0-4343856
, O-5629957
"+ O-439333I
"I" 0-5585784
X = )'o, «
0-893577°
3-9576784
7-0860511
10-2223450
13-3610975
16-5009224
19-6413097
22-7820280
25-9229577
29-0640303
32-2052041
35-3464523
38-4877567
41-6291045
44-7704866
47-9118963
l\\\(t)dt
I 0
- 0-3209291
1 o-1920149
- O-X47444 7
-1 0-1237411
-- 0-1085949
+ 0-0978827
0-0898033
+ 0-0834339
- 0-0782474.
-1- 0-0739188
- 0-0702357
-h 0-0670523
- 0-0642652
-\ 0-0617985
- 0-0595953
h 0-0576118
from
For values of x between 0 and 16, the integrals may be calculated with the help of Table I
m the formulae (o.f. § 10-74)
I f
{ Yn(x)H0'(z) +
BIBLIOGRAPHY*
ADAMOFF, A.
On the asymptotic representation of the cylinder functions Jv(z) and Jv'(a) for large
values of the modulus of z. Petersburg, Ann. Inst. polyt. 1906, pp. 239—265. [Jahrbuch
tiber die Fortschritte der Math. 1907, pp. 492—493.]
AICHI, K.
Note on the Function Km{x), the Solution of the Modified BessePs Equation. Proc.
Phys. Math. Soc. of Japan, C) n. A920), pp. 8—19.
AIREY, J. R.
The Roots of the Neumann and Bessel Functions (Dec. 29,1910). Proc. Phys. Soc. xxm.
A911), pp. 219—224.
The Vibrations of Circular Plates and their Relation to Bessel Functions (Feb. 15,1911).
Proc. Phys. Soc. xxm. A911), pp. 225—232.
The Oscillations of Chains and their Relation to Bessel and Neumann Functions.
Phil. Mag. F) xxi. A911), pp. 736—742.
Tables of Neumann Functions On(x) and Yn(x). Phil. Mag. F) xxn. A911), pp. 658—
663.
The Asymptotic expansions of Bessel and other functions. Archiv der Math, und Phys.
C) xx. A913), pp. 240—244.
The Vibrations of Cylinders and Cylindrical Shells. Archiv dor Math, und Phys. C)
xx. A913), pp. 289—294.
Tables of the Neumann functions or Bessel functions of the second kind. Archie der
Math, und Phys. C) xxrr. A914), pp. 30—43.
Bessel and Neumann Functions of Equal Order and Argument. Phil. Mag. F) xxxi.
A916), pp. 520—528.
The Roots of Bessel and Neumann Functions of High Order. Phil. Mag. F) xxxii.
A916), pp. 7—14.
Bessel Functions of Equal Order and Argument. Phil. Mag. F) xxxn. A916), pp. 237—
238.
The Numerical Calculation of the Roots of the Bessel Function Jn{x) and its first
derivative Jn (x). Phil. Mag. F) xxxiv. A917), pp. 189—195.
The Addition Theorem of tho Bcasel Functions of Zero and Unit Orders. Phil. Mag.
F) xxxvi. A918), pp. 234—242.
The Lommel-Weber Q Function and its Application to the Problem of Electric Waves
on a Thin Anchor Ring (Dec. 7, 1917). Proc. Royal Soc. xciv. A A918), pp. 307—314.
Bessel Functions of small Fractional Order anil their application to problems of Elastic
Stability. Phil. Mag. F) xli. A921), pp. 200—205.
AIRY, SIR GEORGE B.
On the Diffraction of an Object-glass with Circular Aperture (Nov. 24, 1834). Trajis.
Camb. Phil. Soc. v. A836), pp. 283—291.
On the Intensity of Light in the neighbourhood of a Caustic (May 2, 1836 ; March 26,
1838). Trans. Camb. Phil. Soc. vi. A838), pp. 379—402.
On the Diffraction of an Annular Ai>crture (Dec. 4, 1840). Phil. Mag. C) xvm. A841),
pp. 1—10.
Supplement to a Paper, On the Intensity of Light in the neighbourhood of a Caustic
(March 24, 1848). Trans. Camb. Phil. Soc. vm. A849), pp. 595—599.
AKIMOFF, M.
Transcendantes de Fourier-Bcssel a plusieurs variables (July 10, 1916 ; June 25, 1917;
Dec. 24, 1917). Comptes llendus, clxiii. A916), pp. 26—29; clxv. A917), pp. 23—25,
1100—1103.
* In the case of a few inaccessible memoirs, references are given to abstracts in the Jahrbxich
iiber die Fortschritte der Math, or elsewhere.
48
754 THEORY OF BESSEL FUNCTIONS
ALDIS, W. S.
Tables for the Solution of the Equation
d2y 1 dy f n«\
+ A J
(June 16, 1898). fVoc. iioyaZ #oc. lxiv. A899), pp. 203—223.
On the numerical computation of the functions O0(<v), Gt(x) and Jn(x*/i) (Juue 15,
1899). Proe. Royal Soc. lxvi. (.1900), pp. 32—43.
ALEXANDER, P.
Expansion of Functions in terms of Linear, Cylindric, Spherical and Allied Functions
(Dec. 20, 1886). Trans. Edinburgh Royal Soc. xxxni. A888), pp. 313—320.
ANDING, E.
Sechs8tellige Tafeln der Besselschen Funktionen imaginaren Arguments (Leipzig, 1911).
ANGER, C. T.*
Untersuchungen iiber die Function Ikh mit Anwendungen auf das Kepler'sche Problem.
Neueste Schriften der Naturforschcnden der Ges. in Danzig, v. A855), pp. 1—29.
ANISIMOV, V. A.
The generalised form of Riccati's equation. Proceedings of Warsaw University, 1896,
pp. 1—33. [Jahrbuch iiber die Fortschritte der Math. 1896, p. 256.]
APPELL, P. E.
Sur l'inversion approche"e de certaines integrates reelles et sur l'extension do l'dquation
de Kepler et des fonctions de Bessel (April 6, 1915). Comptes Rendus, clx. A915),
pp. 419—423.
AUTONNE, L.
Sur la nature des integrates algdbriques de liquation de Riccati (May 7,1883). Comptes
Rendus, xcyi. A883), pp. 1354—1356.
Sur les integrates alge"briques de l'dquation de Riccati (Feb. 13,1899). Comptes Rendus,
cxxvm. A899), pp. 410—412.
BACH, D.
De l'intdgration par les series de liquation
d2y 74—1 dy _
dxl w dx~^'
Ann. sci. de V&cole norm, sup. B) in. A874), pp. 47—68.
BAEHR, G. F. W.
Sur les racines des Equations I cos (# cos <<>)<&<>=0 et I cos (# cos &>) sin2 <<>?&«> =0
Jo Jo
(April, 1872). Archives Neerlandawes, vn. A872), pp. 351—358.
BALL, L. DE.
Ableitung einiger Formeln aus der Theorie der Bessel'schen Functionen (June 6, 1891).
Astr. Nach. cxxvill. A891), col. 1—4.
BARNES, E. W.
On the homogeneous linear difference equation of the second order with linear coeffi-
coefficients. Messenger, xxxiv. A905), pp. 52—71.
On Functions defined by simple types of Hypergeometric Series (March 12, 1906).
Trans. Camb. Phil. Soc. xx. A908), pp. 253—279.
The asymptotic Expansion of Integral Functions defined by generalised Hypergeometric
Series (Dec. 3, 1906). Proc. London Math. Soc. B) v. A907), pp. 59—116.
BASSET, A. B.
On a method of finding the potentials of circular discs by means of Bessel's functions
(May 10, 1886). Proc. Camb. Phil. Soc. v. A886), pp. 425—443.
On the Potentials of the surfaces formed by the revolution of Limacons and Cardioids
about their axes (Oct. 25, 1886). Proc. Camb. Phil Soc. vi. A889), pp. 2—19.
A Treatise on Hydrodynamics B vols.) (Cambridge, 1888).
On the Radial vibrations of a Cylindrical Elastic Shell (Dec. 12, 1889). Proc. London
Math. Soc. xxi. A891), pp. 53—58.
On a Class of Definite Integrals connected with Bessel's Functions (Nov. 13, 1893).
Proc. Camb. Phil. Soc. Tin. A895), pp. 122—128.
* See also under Bourget and Cauehy.
BIBLIOGRAPHY 755
BATEMAN, H.
Certain definite integrals connected Avith the Legeudre and Bessel functions. Messenger
xxxiii. A904), pp. 182—188.
A generalisation of the Legondre polynomial (Jan. 1, 1905). Proc. London Math. Soc.
B) in. A905), pp. 111—123.
The inversion of a definite integral (Nov. 8, 1906). Proc. London Math. Soc. B) IV.
A906), pp. 461—498.
On an expansion of an arbitrary function into a series of Bowsel functions. Messenger,
xxxvi. A907), pp. 31—37.
The Solution of Linear Differential Equations by means of Definite Integrals (Jan. 25,
1909). Trans. Camb. Phil. Soc. xxi. A912), pp. 171—196.
The History and Present State of the Theory of Integral Equations. British Association
Report, 1910, pp. 345—424.
Notes on integral equations. Messenger, xu. A912), pp. 94—101, 180—184.
Some equations of mixed differences occurring in the Theory of Probability and the
related expansions in series of Bessel's functiouw. Proc Int. Congress of Math. I. (Cambridge,
1912), pp. 291—294.
Electrical and Optical Wave-motions (Cambridge, 1915).
BAUER, G.
Von den Coefficienten dor Reihen von Kugelfunctionen einer Variablen. Journal fiir
Math. lvi. A859), pp. 101—121.
Betnerkungen iiber Roihen nach Kugelfunctionen und insbesondere auch uber Reihen,
welche nach Productcn oder Quadraten von Kugelfunctioneu fortschreiten mit Anwendung
auf Cylinderfunctionen (July 3,1875). Miinchener Sitzwigsberichte, v. A875), pp. 247—272.
BECKER, J.
Die Riccatischo Dittcrential-Gleichung. Programm Karlsbad, 1908 B5 pp.). [Jahrbuch
iiber die Fortschritte der Math. 1908, p. 395.]
15ELTRAMI, E.
Intorno ad uu teoroma di Abele e ad alcune sue applicazioni. R. 1st. Lombardo Rendi-
conti, B) xni. A880), pp. 327—337.
Intorno ad alcune serie trigonomctriche (June 17, 1880). R. 1st. Lombardo [tendiconti,
B) xill. A880), pp. 402—413.
Sulle funzioni cilindriche (Jan. 14, 1881). Atti delta R. Accad. delle Sci. di Torino, xvi.
A880—81), pp. 201—205.
Sulla teoria delle funzioni potenziali Htmtnetriohe (April 28, 1881). Bologna Memorie,
D) n. A880), pp. 461—505.
BERNOULLI, DANIEL.
Correspondence with Leibniz 1697—1704. [Published in Lcibnizens Oe«. W<M'kn, Dritte
Folge (Mathematilc), in. (Halle, 1855).]
Notata in praecodena «chcdiasma 111. Co. Jacobi Riccati, Actontm Eruditormn quae
Lipsiae publicantur Supplementa, vm. A724), pp. 73—75.
Solutio problematic Riocatiani propositi in Act. Lipts. Suppl. Tom. vin. p. 73. Acta
Eruditwum publicata Lipsiae, 1725, pp. 473—475.
Exercitationes quaedam mathematieae (Venico, 1724), pp. 77—HO.
Theoremata do oncillationibus eorporum tilo floxili connoxorum et catenae vcrticaliter
suapensae. Co?)im. Acad. Sci. Imp. Petrop. vi. A732—33) [1738], pp. 108—122.
Demonstrationes Thooreniatuni nuoruni do OHuillationiWs corporutn filo flexili connex-
orum et catenae verticaliter suapensae. Comm. Acad. Sci. Imp. Petrop. vn. A734—35)
[1740], pp. 162-179.
BERNOULLI, JOHN.
Methodus genemlia construendi omnes ao<]uatione.s differeutiales priini griuliw. Acta
Eruditorum publicata Lipsiae, 1694, pp. 435—437. [Opera, I. Lau.sjumo and Geneva, 1742,
p. 124.]
BERNOULLI, NICHOLAS (the younger).
Correspondence with Goldbach. See under Fumh.
BESSEL, F. W.
Analytiache Auflosung der Keplcrsuhen Aufgabe (July 2, 1818). Berliner Abh. 1816—17
[1819], pp. 49—55. [Abhandlungen, hurausgegeben von R. Engohnann, i. A875), pp. 17—
20.]
Ueber die Entwickelung der Funotionen zweier Winkel u und u' in Reihen welche naoh
den Cosinuasen und Sinussen der Vielfachen von u und m' fortgehen (June 21, 1821).
Berliner Abh. 1820—21 [1822], pp. 56—60. [Abhandlungen, n. A876), pp. 302—304.]
48—2
756 THEORY OF BESSEL FUNCTIONS
Untersuchung des Theils der planetarischen Storungen welcher aiis der Bewegung der
Sonne entsteht (Jan. 29, 1824). Berliner Abh. 1824 [1826], pp. 1—52. [Abhandlungen, r.
A875), pp. 84—109.]
Beitrag zu den Methoden die Storungen der Kometen zu berechnen (Sept. 24, 1836).
Astr. Bach. XIV. A837), col. 1—48. [Abhandlungen, I. A875), pp. 29—54.]
BINET, J. P. M.
Note sur l'int^grale I yiidye~yi~qy!i prise entre des limites arbitraires (May 24, 1841).
J a
Gomptes Rendus, xn. A841), pp. 958—962.
BOCHER, M.
On Bessel's functions of the second kind (Jan. 1892). Annals of Math. vi. A892), pp.
85—90.
On some applications of Bessel's functions with pure imaginary index (Feb. 11, 1892).
Annals, of Math. vi. A892), pp. 137— It")*.
On certain methods of Sturm and their application to the roots of Bessel's functions
(Feb. 1897). Bulletin American Math. Soc. in. A897), pp. 205—213.
An elementary proof that Bessel's functions of the zeroth order have an infinite number
of real roots (Feb. 25, 1899). Bulletin American Math. Soc. v. A899), pp. 385—388.
Non-oscillatory linear differential equations of the second order (Feb. 4, 1901). Bulletin
American Math. Soc. vn. A901), pp. 333—340.
BOHMER, P. E.
Uber die Zylinderfunktionen (Nov. 26, 1913). Site, der Berliner Math. Oes. xin. A913),
pp. 30—36.
BOHREN, A.
Uber das Airysche Integral t (Oct. 6, 1902). Bern Mittheilungen, 1902, pp. 236—239.
BOOLE, G.
On the transformation of Definite Integrals. Camb. Math. Journal, m. A843), pp. 216—
224.
On a general method in analysis (Jan. 18, 1844). Phil. Trans, of the Royal Soc. 1844,
pp. 225—282.
A Treatise on Differential Equations (London, 1872).
BOURGET, J.
Note sur une formule de M. Anger (Aug. 7, 1854). Gomptes Rendus, xxxix. A854),
p. 283.
Memoire sur les nombres de Cauchy et leur application a divers problemes de ine'caniqu©
celeste. Journal de Math. B) vi. A861), pp. 33—54.
Memoire sur le mouvement vibratoire des membranes circulaires (June 5, 1865). Ann.
sci. de VEcole norm. sup. ill. A866), pp. 55—95.
BRAJTZEW, J. R.
tJber die Fourier-Bcsselschen Funktionen und deren Anwendung zur Auffindung
asymptotischer Darstellungen von Integralen der linearen Differentialgleichungen mit
rationalen Koeffizienten. Warschau Polyt. Inst. Nach. 1902, nos. 1, 2. [Jahrbuch uber die
Fortsckritte der Math. 1903, pp. 575—577.]
BRASSINNE, E.
Sur diverges equations difterentielles du premier ordre analogues a l'dquation de Ricatti
(sic). Mem. de PA cad. R. des Sci. de Toulouse, C) iv. A848), pp. 234—236.
Sur dea equations differentielles qui se rattachent a l'equation de Riccati. Journal de
Math. xvi. A851), pp. 255—256.
BRENKE, W. C.
Summation of a series of Bessel's functions by means of an integral (Nov 27, 1909).
Bull. American Math. Soc. xvi. A910), pp. 225—230.
BRIDGEMAN, P. W.
On a Certain Development in Bessel's Functions (July 22, 1908). Phil. Maq F) xvi
A908), pp. 947—948..
* See also ibid. p. 136.
t This paper, which might have been mentioned in § 6-4, contains the formula § 6-4 A); but
the author does not give the formula § 6*4 B).
BIBLIOGRAPHY 757
BBUNS, H.
Ueber die Beugungsfigur des Hclioincter-Objectives (Oct. 15, 1882). Attr. Nach. civ.
A883), col. 1—8.
BRYAN, G. H.
On the waves on a viscous rotating cylinder (June 4, 1888). Proc. Camb. Phil. Soc. vi.
A889), pp. 248—264.
Wave Motion and Bessel's Functions. Future, lxxx. A909), p. 309.
BURKHARDT, H. F. K. L.
Trigonometrische Rcihen und Integrate (bis etwa 18i3O). Encyklopodie der Math. Wins.
II. 1 (Leipzig, 1904—16), pp. 819—1354.
I3UTTERWORTH, S.
On tbe Evaluation of Certain Combinations of the Ber, Bei aud Allied Functions (May
30, 1913). Proc. Phys. Soc. xxv. A913;, pp. 294—^07.
CAILLER, (.'.
Sur les fonctions de Bessel. Archive* des Sri. (So<: I/eln'tique), (I) xrv. A902), pp. 347—
350.
Note sur une operation analytiquo et son application aux functions de Basnel (March,
1904). Me'm. de la Soc. de phys. et d'hUtoirc mitardlc da Gtmhv., xxxiv. (li)(J—5), pp. 295—
368.
CALLANDREAU, O.
Calcul des transcendantes de Besse!
,;, (Si r go1
HW~l.-2...n\_ l.(w +
pour les grandes valeur.s do a au moyeu de sdrics .semiconvergentes. Bulletin des Sci. Math.
B) xiv. A890), pp. 110—114.
Sur le calcul de« polynomes Xn (cos d) do Lcgondre pour les grandes valeurs do n. Bulletin
de$ Sci. Math. B) xv. A891), pp. 121—124.
CARL1NI, F.
Ricerche sulla convevgenza da!la serie c/te scrva alia soluzione del problenia di Keidero*
(Milan, 1817).
CARS LAW, II. S.
Some Multiform Solutions of the Partial Differential Equations of Physical Mathematics
and their Applications (Nov. 10, 189N). Proc. London Math. Soc. xxx. A899), pp. 121—161.
The Green's function for a wedge- of any angle and other ProbleuiH in tho Conduction
of Heat (Oct. 30, 1909). Proc. London Math. Soc. B) vm. (li>10), pp. 305—374.
The Scattering of Sound Waves by a Cone. Math. Ann. lxxv. A914), pp. 133—147.
The Green's function for the equation V2w. + /t% = 0 (April 28, 1913; March 20, 1916).
Proc. London Math. Soc. B) xni. A914), pp. 236—257; B) xvi. A917), pp. 84—93.
The Theory of the Conduction of Heat (London, 1921).
CATALAN, E. 0.
Note sur l'integrale f°° ^ "*,,.* (Feb. 1840). Journal de Math. v. A840), pp. 110—114.
jo A +x~y
[Reprinted, Min. de la Soc. R. des Sci. de Liega, B) xn. A885), pp. 20—31.]
Sur liquation de Riccati (March 4, 1871). Bulletin de PAcad. It. de Beltjiquo, B) xxxi.
A871), pp. 68—73.
Note sur liquation xi/" + %'-ay/ = O par M. O. Le Paige (Rapport de M. Catalan).
Bulletin de VAcad. R. de Belgique, B) xli. A870), pp. 935—939.
Application d'une formule de Jacobi (Nov. 1808). Mem. de la Soc. R. das Sci. de Lihge,
B) xn. A885), pp. 312—316.
CAUCHY, A. L.
Resume d'un m^moire sur la rndcanique celeste et wur un nouveau caloul appele caleul
des limites (Lu a l'Acad. de Turin, Oct. 11, 1831). Exercices d?Analyse, II. (Paris, 1841),
pp. 48--112. [Oeuvres, B) xn. A916), pp. 48—112.]
Memoire sur la convergence des series (Nov. 11, 1839). Co?nptes Rendus, ix. A839),
pp. 587—588. [Oeuvres, A) iv. A884), pp. 518—520.]
• Translated into German by Jacobi, Astr. Nach. xxx. A850), col. 197—254. [Qes. Math.
Werke, vn. A891), pp. 189—245.]
758 THEOEY OP BESSEL FUNCTIONS
Considerations nouvelles sur la theorie des suites et sur les lois de leur convergence
(April 20, 1840). Comptes Rendus, x. A840), pp. 640—656. [Oeuvres, A) v. A885), pp. 180 —
198.1
Me*thode simple et ge"ne>ale pour la determination numerique des coefficients que ren-
ferme le developpement de la fonction perturbatrice (Sept. 14, 1840). Comptes Rendus, xr.
A840), pp. 453—475. [Oeuvres, A) v. A885), pp. 288—310.1
Note aur le developpement de la fonction perturbatrice (Sept. 21,1840). Comptes Rendus,
XI. A840), pp. 501—5T1. [Oeuvres, A) v. A885), pp. 311—S21.]
Mdthodes propres a simplifier le calcul des inegalites pdriodiques et se"culaires des
mouvements des planetes (Jan. 11, 1841). Comptes Rendus, xn. A841), pp. 84—101.
[Oeuvres, A) vi. A888), pp. 16—34.]
Note sur une transcendante que renferme le developpement de la fonction perturbatrice
relative au systeme planetaire (Oct. 4, 1841). Comptes Rendus, xra. A841), pp. 682—687.
[Oeuvres, A) vi. A888), pp. 341—346.]
Note sur la substitution des anomalies excentriques aux anomalies moyennes, dans le
developpement de la fonction perturbatrice (Oct. 25, 1841). Comptes Rendus, xiii. A841),
pp. 850—854. [Oeuvres, A) VI. A888), pp. 354—359.1
Nouveau Memoire sur le calcul des inegalites des mouvements plane'tairos (April 8*
1844). Comptes Rendus, xvill. A844), pp. 625—643. [Oeuvres, A) vin. A893), pp. 168—
188.
Sur la transformation des fonctions implicites en moyennes isotropiques, ct sur leurs
developpernents en series trigonometriques (May 22, 1854). Comptes liendns, xxxvixi.
A854), pp. 910—913. [Oeuvres, A) xn. A900); pp. 148—151.]
Sur la transformation des variables qui determinent les mouvements d'une planete cm
meme d'une comete en fonction explicite du temps, et sur le developpement de ses fonctions
en series convergentes (June 5, 1854). Comptes Rendus, xxxvin. A854), pp. 990—993.
[Oeuvres, A) xn. A900), pp. 160—164.]
Sur la resolution des equations et sur le doveloppement de leurs racinea en aeries con-
vergentes (June 26, 1854). Comptes Rendus, xxxvin. A854), pp. 1104—1107. [Oeuvres, A)
xn. A900), pp. 167—170.]
Sur une formule de M. Anger et sur d'autres formules analogues (July 15, 1854).
Comptes Rendus, xxxix. A854), pp. 129—135. [Oeuvres, A) xn. A900), pp. 171—177.]
CAYLEY, A.
Sur quelques formules du calcul integral. Journal de Math, xn. A847), pp. 231—240.
[Collected Papers, I. A889), pp. 309—3167]
On Riccati's equation (Sept. 29, 1868). Phil. Mag. D) xxxvi. A868), pp. 348—351.
[Collected Papers, VII. A894), pp. 9—12.]
Note on the integration of certain differential equations by series. Messenger (Old
Series), v. A869), pp. 77—82. [Collected Papers, via. A895), pp. 458—462.]
Proc. London Math. Soc* v. A874), pp. 123—124. [Collected Papers, ix. A896), pp.
19—20.]
CHALLIS, H. W.
Extension of the Solution of Riccati's Equation (Oct. 5, 1864). Quarterly Journal, vii.
A866), pp. 51—53.
CHAPMAN, S.
On the general theory of summability with applications to Fourier's and other series.
Quarterly Journal, xliii. A911), pp. 1—52.
CHESSIN, A. S.
Note on the General Solution of Bessel's Equation. American Journal of Math. xvi.
A894), pp. 186—187.
On the expression of Bessel's Functions in Form of Definite Integrals. Johns Hopkins
Univ. Circulars, xiv. A895), pp. 20—21.
Note on Cauchy's Numbers. Annals of Math. x. A896), pp. 1—2.
On the relation between Cauchy's numbers and Bessel's Functions (July 1, 1898).
Annals of Math. xu. A899), pp. 170—174.
On some relations between Bessel functions of the first and of the second kind (Oct.
20, 1902). Trans. Acad. Sci. of St Louis, xn. A902), pp. 99—108.
Sur l'equation de Bessel avec second membre (Oct. 27, 1902). Comptes Rendtts, exxxv.
A902), pp. 678—679. (
Sur une classe d'equations differentielles redactibles a liquation de Bessel (May 11,
1903). Compies Rendus, cxxxvi. A903), pp. 1124—1126.
* See under Lord Rayleigb.
BIBLIOGRAPHY 759
CHREE, C.
Longitudinal vibrations of a circular bar. Quarterly Journal, xxi. A886), pp. 287—298.
On the CoeflScients in certain Series of Bessel's Functions. Phil. Maq. F) xvn. A909),
pp. 329—331.
CHRISTOFFEL, K B.
Zur Abhandlung: " Ueber die Zahler und Nennor der Naheruugswerte von Ketten-
brlichen" pag. 231 des vorigeu Bandes* (March, 1860). Journal filr Math. LVin. A861),
pp. 90—92.
CINELLI, M.
Diffrazione per aperture fatte sopra superfici curve. II Nuovo Cimento, D) I. A895),
pp. 141—155.
CLEBSCH, II. F. A.
(Jeber die Reflexion an einer Kugelflaehe (Oct. 30,18G1). Journal filr Math. lxi. A863),
pp. 195—262.
CLIFFORD, W. K.
On Bessel's Functions+. Mathematical Papers (London, 1882), pp. 346—349.
COATES, C. V.
Bessel's functions of the Secoud order. Quarterly Journal, XX. A885), pp. 250—260.
Bessel'a functions of the Second order. Quarterly Journal, xxi. A880), pp. 183—192.
COCKLE, SIR JAMES.
On Linear Differential Equations of the Second Order (Dec. 24, 1861 ; Jan. 15, 1862;
May 21, 186-2). Meweni/er (Old Scries), i. A802), pp. 118—124, 164—173, 241—247.
COTTKU, J. R.
A New Method of Solving Legondro'n and Hessel's Equations and others of a similar
type (May 27, 1907). Proc. ji. Irish Antd.% xxvu. A A909), pp. 157—101.
CRAWFORD, L.
n ( 1 d\n~1
A proof of Rodriguos' Theorem55 win v:v=.—--——'-.-- -. I •-.-- -7-1 ain11'1^ and
x b ^ 1.3.5...Bn -1) \nm x dxj
some expansions derived from it (Dec. 13, 1901). Proc. Edinburgh Math. Soc. XX. A902),
pp. 11—15.
CRELIER, L.
Sur quelques propridtt-.s tlo.s fonuLion.s Bea,sdlienucH tirt5ea de la tlu^orio dew fractions
continues (June, 1895). Ann. di Mat. (a) xxiv. A890), pp. 131 — 103. [Dissertation, Bern,
1895.]
Sur la fonction Bessi'lienne de ir cHpiice &n(u:) (Dec. 1890). Bern Mittheilungen, 1897
[1898], pp. 61—90.
Sur les functions hcsadlionncs 0n(x) <\t Sn(x) (Sept. G, 1897; Nov. 29, 1897). Comptes
Rendus, exxv. AH97), pp. 421—423, 8UO—8G3.
CURTIS, A. fl.
On the integration of Linear and Partial Differential KcjuationK (Nov. 24, 1854). Gamb.
and Dublin Math. Journal, IX. A854), pp. 272-290.
CURZON, II. R. J.
GeneraliHations of the Ilermite fiuuttions and their connexion with JJoawel funutious
(Nov. 10, 1913). Proc. London Math. &><>. B) xm. A914), pj>. 417—440.
DATTA, A.
On a generalisation ot' Neumann's Expansion in a Series of Bosrtol Functiou.s (Fob. 29,
1920). Bulletin Calcutta Math. Soe. xi. A921), pp. 23 -34.
On an extension of Sonine's fntegral in HosnuI Fuuctioimil (Jan. 0, liJ1). Bulletin
Calcutta Math. Soc. xi. A921), pp. 221—230.
* See unclev Heine. t Clifford <lied Mun-li :i, 1H79.
J Not Trams. Camb. Phil. Soc. xxi., (is stated in the <lakrbiu-h ilber die P'ortachritte der Math.
1908, p. 363.
§ See footnote t on p. 27.
|| This paper, which deals with the corrected form, givon, in § 13-40 A0), of Nicholson's in-
integral, and with various related integrals, was published after Chapter xm had been paHsed for
Press.
760 THEORY OF BESSEL FUNCTIONS
DEBYE, P.
Nfiherungsformeln fur die Zylinderfunktionen fiir grosse Werte des Arguments und
unbeachrankt veranderlicbe Werte des Index (Dec. 1908). Math. Ann. lxvii. A909),
pp. 535—558.
Semikonvergente Entwickelungen fur die Zylinderfunktionen und ihre Ausdehnung ins
Komplexe (Feb. 5, 1910). Miinchener SitzungsbericMe, xl. A910), no. 5.
DE LA VALLEE POUSSIN, C. J.
Integration de liquation de Bessel sous forme finie (Jan. 26, 1905). Ann. de la Soc.
3d de Bruxelles, xxix. (lbre partie) A905), pp. 140—143.
DENDY, A. AND NICHOLSON, J. W.
On the Influence of Vibrations upon the Form of Certain Sponge Spicules (May 11,
1917). Proo. Royal Soc. lxxxix. B A917), pp. 573—587.
DINT, U.
Serie di Fourier e altere rappresentadoni analitiche delle funzioni di una variahile reale
(Pisa, 1880).
DINNIK, A.
tJber die Darstellung einer willkiirlichen Fuuktion durch Beasel'sche Reihe. Kief Polyt.
Inst. {Engineering Section), 1911, no. 1, pp. 83—85. [Jahrbuch iiber die Fortschritte der
Math. 1911, p. 492.]
Tafeln der Besaelschen Funktionen J±\ und J ±^. Archiv der Math, und Phys. C)
xvm. A911), pp. 337—338.
Tafeln der Besselachen Funktionen J±i, J±%, J±§. Archiv der Math, und Phys. C)
xx. A913), pp. 238—240.
Tafeln der Besselschen Funktionen J±, und J±$' Archiv der Math, und Phys. C)
xxi. A913), pp. 324—326.
Tafeln der Besselschen Funktionen J^ (#0 und J±i (x^)- Archiv der Math, und Phys.
C) xxn. A914), pp. 226—227.
DIXON, A. G,
On a property of Bessel's Functions. Messenger, xxxii. A903), pp. 7—8.
The expansion of xn in Bessel's'Functions. Messenger, xxxii. A903), p. 8.
DONKIN, W. F.
On the Equation of Laplace's Functions, etc. (Dec. 11, 1856). Phil. Trans, of the Royal
Soc. cxlvii. A857), pp. 43—57.
DOUGALL, J.
The determination of Green's function by means of Cylindrical or Spherical Harmonics
(March 9,1900). Proc. Edinburgh Math. Soc. xvm. A900), pp. 33—83.
A Theorem of Sonine in Bessel Functions with two Extensions to Spherical Harmonics
(Dec. 13, 1918). Proc. Edinburgh Math. Soc. xxxvii. A919), pp. 33—47.
DU BOIS REYMOND, P. D. G.
Die Theorie der Fourier'schen Integrate und Formeln (June 26, 1871). Math. Ann. iv.
A871), pp. 362-390.
EARNSHAW, S.
Partial differential equations. An essay towards an entirely new method of integrating
them (London, 1871).
ELLIS, R. L.
On the Integration of certain Differential Equations (Nov. 1840 and Feb. 1841). Camb.
Math. Journal, n. A841), pp. 169—177, 193—201.
On the Method of Least Squares (March 4, 1844). Trans. Camb. Phil. Soc. vm. A849),
pp. 204—219.
EMDE, F.*
Zur Berechnung der reellen Nullstellen der Bessel'schen Zylinderfunktionen. Archiv
der Math, und Phys. C) xxiv. A916), pp. 239—250.
ENNEPER, A.
ITeber ein bestimmtes Integral. Math. Ann. vi. A873), pp. 360—365.
EPSTEIN, S. S.
Die vier Rechnungsoperationen mit Bessel'schen Functionen nebst einer geschichtlichen
Einleitung (Bern, 1894, 58 pp.). [Jahrbuch Uber die Fortschritte der Math. 1893—94, pp.
845—846.]
* See also under Jabnke.
BIBLIOGRAPHY 761
ERMAKOFP, W.
Ueber die Cylittderfunctionen (May, 1872). Math. Ann. v. '1872), pp. 639—640.
ESCHERICH, G. VON.
Zur Besael'schen Differential-Gleichung. Monatshefte fur Math, und Phys. in. A892),
p. 142.
tJber eine Naherungaformel. Monatshefte fitr Math, und Phys. in. A892), p. 234.
EULER, L.
Lettre de M. Euler a M. de la Grange (Jan. 1, 1760). Misc. Taurinensia, n. A760—61),
pp. 1—10.
Recb.ercb.es sur l'inte'gration de liquation
ddz _ ddz b dz c
dtz dxl x dx xx
Misc. Taurinensia, in. A762—65), pp. 60—91.
De integi'atione aequationuin differentialium. Novi Comm. Acad. Petrop. vin. A760—61)
[1763], pp. 154—169.
De resolutione aequationis dy + ayydx-bx^dx. Novi Oomm. Acad. Petrop. ix. A762—
63) [1764], pp. 154—169.
Demotu vibratorio tympanorum. Novi Comm. Acad. Petrop. x. A764) [1766], pp.
243—260.
In&titutionuin Calculi Integralis, n. (Petersburg, 1769).
De oscillationibus minimis funis liberc suspensi. Ada Acad. Petrop. v. pars 1 A781)
[1784], pp. 157—177.
De perturbatione motus chordarum ab earum pondere oriunda. Ada Acad. Petrop. v.
para 1 A781) [1784], pp. 178—190.
Analysis facilis aequationem Eticcatianam per fractionem continuum reaolvendi. Mem.
de VAcad. R. des Sci. de St. Petersbourg, VI. A818), pp. 12—29.
FALKENHAGEN, J. H. M.
Ueber das Verhalten der Integrale einer Riccati'schen Gleichung in dcr Niihe einer
singularen Stelle. Nieuw Archief voor Wis&unde, B) vi. A905), px). 209—248.
PAXEN, H.
Expansion in series of the integral | e~x{t±t~tl) Vdt (April 14,1920). Arkiv for Mat.
J y
Astr. och Fysik, xv. A921), no. 13.
FELDBLUM, M.
The theory of Riccati's equation and applications of the function which satisfies it.
Warsaw University, 1898, nos. 5 and 7; 1899, no. 4. [Jahrbuch ilber die Fortschritte dcr
Math. 1898, pp. 279-280.]
FERIET, K. DE.
Sur les fonctions hypercylindriques (June 13, 1921). Comptes Rendus, clxxii. A921),
pp. 1464—1466.
FIELDS, J. C.
A method of solving Riccati'a Equation (April 8,1886). Johns Hopkins Univ. Circulars
VI. A886—87), p. 29.
dny
Solutions Analogous to Riccati's of Equations of the form -j-^t—^my (May 19, 1886).
Johns Hopki7is Univ. Circulars, vi. A886—87), pp. 29—30.
FILON, L. N. G.
On a New Mode of Expressing Solutions of Laplace's Equation in Terms of Operators
involving Bessel Functions. Phil. Mag. F) vr. A903), pp. 193—213.
On the expansion of polynomials in series of functions (May 10, 1906). Proc. London
Math. Soc. B) iv. A906), pp. 396—430.
FORD, W. B.
On the possibility of differentiating term-by-term the developments for an arbitrary
function of one real variable in terms of Bessel functions (June, 1902). Trans. American
Math. Soc. iv. A903), pp. 178—184.
762 THEORY OF BESSEL FUNCTIONS
FQRSYTH, A. R.
On linear diffei'ential equations: in particular that satisfied by the series
Quarterly Journal, xix. A883), pp. 292—337.
The expression of Bessel functions of positive order as products, and of their inverse
powers as sums of rational fractions. Messenger, l. A921), pp. 129—149.
FOURIEE, J. B. J.
La Theorie aiialytique de la Chaleur (Paris, 1822). [Translated by A. Freeman, Cam-
Cambridge, 1878.1
FREEMAN, A.
Note on the value of the least root of an equation allied to Jo (z) — 0 (April 19, 1880).
Proc. Comb. Phil. Soe. m. A880), pp. 375—377.
FRESNEL, A. J.
Me"moire sur la diffraction de la lumiere [July 29,1818 ; crowned 1819]. Mem. de VAcad.
R. des Sci. v. A821—22), pp. 339—476. [Oeuvres, i. A866), pp. 247—382.]
FRULLANI, G.
Sopra la dipendenza fra i differenziali delle funzioni e gli Tntograli definiti (Feb. 4,
1818). Mem. soc. iial. (Modena), xvm. A820), pp. 458—517.
FUSS, P. H.
C'orrespo7idance matkematiqice et physique de qiielques ce'lebres ge'omkres du xviii*3
siecle*, ii. (Petersburg, 1S43).
GALLOP, E. G.
The distribution of electricity on the circular disc and the spherical bowl. Quarterly
Journal, xxi. A886), pp. 229—256.
GASSER, A.
Ueber die Nullstellen der Besaelschen Fuuktionen (J uly, 1904). MUtlmiungen der Naturf.
Oes. in Bern, 1904, pp. 92—135.
GEGENBAUER, L.
Note iiber die Bessel'schen Functionen zweiter Art (Feb. 8, 1872). Wiener Sitzungs-
berichte, lxv; B) A872), pp. 33—35.
Zur Theorie der Bessel'schen Functionen zweiter Art (July 4, 1872). Wiener Sitzungs-
beriehte, lxvi. B) A872), pp. 220—223.
Note iiber bestimmte Integrale (Feb. 6,1873). Wiener Sitzunqsberichte, lxvii. B) A873),
pp. 202—204.
tfber die Functionen Xnm (June 13, 1873). Wiener Sitzung&herichte, Lxvrn. B) A874),
pp. 357—367.
tfber die Bessel'schen Functionen (March 19, 1874). Wiener Sitzangsberichte, lxx. B)
A875), pp. 6—16.
Uber einige bestimmte Integrale (June 18, 1874). Wiener SitzunqubericMe, lxx. B)
A875), pp. 433—443.
tiber einige beatimmte Integrale (June 17, 1870). Wiener SUzunqsberichte, i.xxii. B)
A876), pp. 343—354.
tiber die Bessel'schen Functionen (June 22, 1876). Wiener Sitzunqsberichte, lxxiv. B)
A877), pp. 124—130.
Zur Theorie der Bessel'schen Functionen (Jan. 18, 1877). Wiener tiitzimysberiehte,
lxxv. B) A877), pp. 218—222.
tiber die Functionen Cnv(x) (April 12,1877). Wiener Sitzunqsberichte, lxxv. B) A877),
pp. 891—905.
Das Additionstheorem derjenigen Funetioneu welche bei der Entwicklung von e"xi nacli
den Nahorunganennern regularer Kettenbriiche auftreten. Wiener Sitzunqsberichte, lxxxv.
B) A882)jpp. 491—502.
tlber die Bessel'schen Functionen (Oct. 11,1883). Wiener Sitzunqsberichte, lxxxviii. B)
A884), pp. 975—1003.
* This work contains a number of letters from Nicholas Bernoulli (the younger) to Goldbaoh,
in which Bernoulli's solution of Riccati's equation is to be found. The reader should notice that, in
Daniel Bernoulli's letters to Goldbach {ibid. pp. 254, 256, 259), the equation described in the table
of contents as Eiccati's equation is really the linear equation; Riccati's equation is mentioned
on p. 260. '
BIBLIOGRAPHY 763
Zur Theorie der Functionen Cnp (x). Wiener Akad. Benksahriften, XLVIII. A884),
pp. 293—316.
tfber die Bessel'schen Functionen (March 10, 1887). Wiener Sitzunqsberichte, xcv. B)
A887), pp. 409—410.
Einige Satze iiber die Functionen Cnv (%). Wiener Akad. Denkschriften, lvii. A890),
pp. 425—480.
tlher die Ringfunctionen (June 4,1891). Wiener Sitzungsberichte, c. B a) A891), pp. 745—
766.
Bemerkung zu der von Herrn Elaas gegebenen Theorie der elektrischen Schwingungen
in cylindrischen Drahten. Monatshefte fur Math, und Phys. iv. A893), pp. 379—380.
tjber die zum elektromagnetischen Potentiale eines Kreisstromes ossociierte Function.
Monatshefte fur Math, und Phys. iv. A893), pp. 393—401.
Eine Integralrelation. Monatshefte filr Math, und Phys. v. A894), pp. 53—61.
Bemerkung iiber die Bessel'schen Functionen. Monatshefte filr Math, und Phys. vm.
A897), pp. 383—384.
Notiz iiber die Besael'schen Functionen crater Art. Monatshefte filr Math, und Phys. x.
A899), pp. 189—192.
Quelquea proprieties nouvelles des raeinea des fonctions de Bessel. Mem. de la Soc R.
des Sci. de Liege, C) ir. A900), no. 3.
[Letter on' a paper by H. M. Macdonald.] Proc. London Math. Soc. xxxn. A901),
pp. 433—436.
Uber eine Relation des Herrn Hobson (May 22,1902). Wiener Sitzungsberichte, cxi. B a)
A902), pp. 5t>3—r>12.
On integrals containing functions of Bcssel. [Letter to Kapteyn.] Proc. Section of Sci.,
K. Akad. can Wet. te Amsterdam, iv. A902), pp. 584—588.
GENOCOHI, A.
Studi in ton to ai oasi d' integrazioue .sotto l'oruni nnita. Mem. dell' Accad. delle Sci. di
Torino, xxiii. (lHfifi), pp. 299—302.
Sur lVquation de Kicoati (Aug. 13, 1877). Comptes liendus, lxxxv. A877), pp. 391—394.
(HBSON, (*. A.
A Proof of the Binomial Theorem with some Applications (Dec. 12, 1919). Proc.
Edinburgh Math. Sue. xxxvm. A920), pp. 6—9.
GILBERT, L. P.
Recherehes aualytiqucs .sur la difllraction de la luniR're. Mi!m. coinvmu's do VAcad. E.
des Sci. de Britxcllcs, xxxi. A863), pp. 1—52.
GIULIANI, O.
Sopra la fuuzione P>1 (cosy) per n infinito. Uiornak di 3f<rt. xxn. A884), pp. 23G—239.
Sopra alcune funzioni analoghe allc funzioni ciliiidriulie. (iioraale di Mat. XXV. A887)
pp. 198—202.
Aluune osHervazidiii sopra le funzujni spheriche di ordino suporiorc al .sccondo e sopra
altre funzioni chc se ne poHwono dedurre (April, 18HB). (liurmdc di Mat. xxvi. A888),
pp. 155—171.
GLALSHKR, .1 W. L.
On Riccati's equation (March 15, 187 1). (Jvmterh/ Journal, XI. AH71), pp. 2G7—273.
On the llolution.s between the particular Integrals in Cay ley's solution of Riccati's
Equation (May 12, 1872). Phil. Mm/. D) xun. AH72), pp. 433—138.
On the Evaluation in Series of certain Definite Integrals. British Association Report,
1872, pp. 15—17.
Notes on definite integrals. Messenger, II. A873), pp. 72 -7i).
On a Differential Equation allied to liiccati's (Oct. 11, 1H72). Quarterly Journal, XII.
A873), pp. 129—137.
Sur une Proprietd de la Function n^'J'. Nouvellr. Cor?: Math. n. A87E), pp. 240—243,
349—350.
On a Formula of Cuuchy's for the Kvaluation of a class-of Ut^liiitti Integrals (Nov. 0,
1876). Proc. Camb. Phil. Son. in. AH8O), pp. 5-12.
On certain Identical Differential Relations (Nov. 9, 187E). Proc. London Math. Soc.
vm. A877), pp. 47—51.
A Generalised Form of Certain Series (May 9, .1878). Proc. London Math. Sue. IX. A878),
pp. 197—202.
On the Solution of a Differential Equation allied to Riceati's. British Association Iteport,
1878, pp. 469—470.
764 THEORY OF BESSEL FUNCTIONS
Example illustrative of a point in the solution of differential equations by series.
Messenger, vin. A879), pp. 20—23.
On a symbolic theorem involving repeated differentiations (May 19,1879). Proe. Camb.
Phil. Soc. ill. A880), pp. 269—271.
On Riccati's Equation and its Transformations and on some Definite Integrals which
satisfy them (June 16, 1881). Phil. Trans, of the Royal Soc. 172 A881), pp. 759—828.
[Proo. Royal Soc xxxil. A881), p. 444.]
GORDAN, P.
See under Herinite.
GRAF, J. H.
Ueber die Addition und Subtraction der Argumente bei Bessel'schen Functionen nebst
einer Anwendung (March, 1893). Math. Ann. xliii. A893), pp. 136—144.
Ueber einige Eigenschaften der Bessel'schen Function erater Art, insbesondere fur ein
grosses Argument. Zeitschrift fur Math, xxxvm. A893), pp. 115—120.
Beitrage zur Auflosungyon linearen Differentialgleichungen zweiter Ordnung mit linearen
Coemcienten so wie von Differentialgleichungen zweiter Ordnung denen gewisse bestimnate
Integrate genugen (March, 1894). Math. Ann. xlv. A894), pp. 235—262.
Relations entre la fonction Beaselienne de lre espece et une fraction continue (May, 1894).
Ann. di Mat. B) xxill. A895), pp. 45—65.
Ableitung der Formeln fur die Bessel'schen Functionen bei welchen das Argument ein
Distanz darstellt (Aug. 4, 1896). Verhandlungen der Schweiz-Naturf. Oes. lxxix. A896),
pp. 59—62.
Einleitung in die Theorie der Besselschen Funktionen. Von J. H. Graf und E. Gubler
B Hefte ; Bern, 1898, 1900).
Beitrag zur Auflo'sung voo Differentialgleichungen zweiter Ordnung denen gewisse be-
stimmte Integrale genugen (May, 1902). Math. Ann. lvi. A903), pp. 423—444.
GRAY, A*
A Treatise on Bessel Functions. By Andrew Gray and G. B. Mathews (London, 1895).
GREEN HILL, SIR A. GEORGE.
On Riccati'a Equation and Beaael's Equation. Quarterly Journal, xvi. A879), pp. 294—298.
On the Differential Equation of the Ellipticities of the Strata in the Theory of the
Figure of the Earth (April 8, 1880). Quarterly Journal, xvn. A880), pp. 203—207.
Determination of the greatest height consistent with stability that a vertical polo or
mast can be made, and of the greatest height to which a tree of given proportions can grow
(Feb. 7, 1881). Proc. Camb. Phil. Soc iv. A883), pp. 65—73.
The Bessel-Clifford Function (March 14, 1919). Engineering, evil. A919), p. 334.
The Bessel-Clifford Function and its applications (Aug. 11,1919). Phil. Mag. F) xxxviii.
A919), pp. 501—528.
GRUNERT, J. A.
(/ilfl _22\J <sin ?V
Beweis der Gleichung ~dj=r— = (-l)il-3...Bz-l)^-- fur s=coa.». Arohiv
der Math, und Phys. iv. A844), pp. 104—109.
GUBLER, E.t
Die Darstellung dev allgemeinen Bessel'schen Function durch bestimmte Integrale
(Sept. 1888). Zurich Vierteljahrsschrift, xxxm. A888), pp. 130—172.
Verwandlung einer hypergeometrischen Reihe im Anachluss an das Integral
I Ja(x)e~bxxe-idx.
Jo
Inaugural-dissertation, Zurich, 1894 C8'pp.). [Graf and Gubler, Einleitung in die Theorie
der Besselschen Funktionen, n. (Bern, 1900), pp. 110—135, 156.]
Ueber ein discontinuierliches Integrale (Dec. 1895). Math. Ann. xlviii. A897), pp. 37—48.
Beweis einer Formel des Herrn Sonine (Dec. 1896). Math. Ann. xlix. A897), pp. 583—f>84.
Ueber bestimmte Integrale mit Bessel'schen Functionen (Oct. 1902). Zurich Viertel-
Vierteljahrsschrift, xlvii. A902), pp. 422—428.
GUNTHER, S.
Bemerkungen viber Cylinderfunctionen. Archiv der Math, und Phys lvi A874)
pp. 292—297.
" See also under Sir Joseph John Thomson.
+ See also under Graf.
BIBLIOGRAPHY 765
GWYTHER, R. F.
The employment of a geometrical construction to prove Schlomilch's series, and to aid
in its development into a definite integral. Messenger, xxxm. A904), pp. 97—107.
HADAMARD, J.
Sur l'expression asymptotique de la fonction de Besael. Bulletin de la iSoc. Math, de
France, xxxvi. A908), pp. 77—85.
HAENTZSCHEL, E.
Ueber die functionentheoretischen Zusammenhang zwischen den Latne'schen, Laplace'-
sclaen und Bessel'schen Functionen. Zeitschrift fur Math. xxxi. A886), pp. 25—33.
Ueber die Fourier BesseFsche Transcondente (Nov. 20, 1887). Zeitschrift fiir Math.
xxxiii. A888), pp. 185—186.
HAFEN, M.
Studien ubereinigeProbleraeder Potentialtheorie. Math. Ann. lxix. A910), pp. 517—537.
HAGUE, B.
A Note on the Graphs of the Beasel Functions of Integral Order. Proc. Phys. Soc.
xxix. A917), pp. 211—214.
HALL, A.
The Besselian Function. The Analyst, I. A874), pp. 81—84.
HAMILTON, SIR WILLIAM ROWAN*.
On Fluctuating Functions (June 22, 1840). Trans. R. Irish Acad. xix. A843), pp. 264—321.
On the Calculation of the Numerical Values of a certain class of Multiple and Definite
Integrals (Sept. 29, 1857). Phil. Mag. D) xiv. A857), pp. 375—382.
HANKEL, H.
Die Cylinderfunctionen erater und zwoiter Art (Dec. 15, 18C8). Math. Ann. I. A869),
pp. 467—501.
Bestimmte Integralc rnit Cylinderfunctionen+. Math. Ann. vm. A875), pp. 4fK—470.
Die Fourier'schen Reihen und Integralo fur Cylinderfunctionen t (May 10, 1869). Math.
Ann. VIII. A875), pp. 471-494.
HANSEN, P. A.
Ermittelung der ubsoluten Storungcn in Ellipsen von bcliebiger Exccntricitat und
Neigung, I. Sckriften der Stermoartc Seeberg (Gotha, 1843). [Mt'inoire mir la determination
des perturbations ab.solues dans les ellipses d'uno oxoentricitu ct d'uno inoliuaison quel-
conques. Par M. Hanson. Traduit do l'AUeniaiul par M. Victor MauvniH (Paris, 184f>).j
Entwickelung des Products einer Potenzdes Radius Vectors mit don Sinus oder Cosinua
eines Vielfachen der wahren Anomalie in Reihen. Leipziger Ablt. n. A855), pp. 181—281.
HANUMANTA RAO, C. V.
On a certain definite integral. Messenger, xlvii. A918), pp. 134—137.
HARDY, G. H.
General theorems in contour integration: with Home applications. Quarterly Journal,
xxxil. A901), pp. 369—384.
Notes on some points in the integral calculus, xvm. Messenger, xxxv. A900), pp. 158—10(i.
Further researches in the Theory of Divergent Heriew and Integrals (May 18, 1908).
Trans. Camb. Phil. Hoc. xxi. A912), pp. 1—48.
On an Integral Equation (Feb. 20, 1909). Proc. London Math. isoc. (-2) vit. A909),
pp. 445—472.
On certain definite integrals whoso values can be expressed in teruiH of BoshoI'h functions.
Messenger, xxxviii. A909), pp. 129—132.
On certain definite integrals considered by Airy and Stokes. (Juartcrh/ Journal, XU.
A910), pp. 226—240.
Notes on some points in the integral calculus, xxvu. Messenger, xu A911), pp. 44—51.
Notes on some points in the integral calculus, xxxv. Messenger, xi.u. A913), pp.
89—93.
On the expression of a number as the .sum of two nquare«. Quarterly Journal, xlvi.
A915), pp. 263—283.
On Dirichlet's divisor problem (April 22, 1915). Proc. London Math. Soc. B) xv. A91G),
pp. 1—25.
Notes on some points in the integral calculus, xlvii. Messenger, xlviii. A918), pp. 81—88.
* A letter by Hamilton on Bessol functions'jH published in Sir G. G. Stokes, Memoir and
Scientific Correspondence, i. (Cambridge, 1<JU7), pp. 131—135.
f Hankel died Aug. 29, 1873. Thoso raemoira were composed from material found among bis
papers.
766 THEORY OF BESSEL FUNCTIONS
HARGREA.VE, C. J.
On the Solution of Linear Differential Equations (June 10, 1847). Phil. Trans, of the
Royal Soc. 1848, pp. 31—54.
On Riccati's Equation (April 4, 1865). Quarterly Journal, vn. A866), pp. 256—258.
HARGREAVES, R.
A Diffraction Problem and an Asymptotic Theorem in Bessel's Series. Phil. Mag. F)
xxxvi. A918), pp. 191—199.
HARNACK, A *
Ueber die Darstellung einer willkurlichen Function durch die Fourier-Bessel'schen
Functionen (Dec. 12, 1887). Leipziger Berichte, xxxix. A887), pp. 191—214; Math. Ann.
xxxv. A889), pp. 41—62.
HARRIS, R. A.
On Harmonic Functions. American Journal of Math, xxxiv. A912), pp. 391—420.
HARTENSTEIN, J. H.
Integration der Differentialgleichung ^4 + ^i—^'2/ ftir elliptiache und parabolische
ox cy
Coordinaten. Arehiv der Math, und Phys. B) xiv. A896), pp. 170—199.
HATTENDORF, K.
See under Riemann.
HAVELOCK, T. H.
Mathematical Analysis of Wave Propagation in Isotropic Space of p Dimensions
(March 16, 1904). Proc. London Math. Soc. B) n. A904), pp. 122—137.
HAYASHI, T.
On a definite integral for Neumann's cylindrical function. JVyt Tidsskrift, xxiu. B
A912), pp. 86—90. [Jahrbuch ilber die Fortschritte der Math. 1912, p. 555.]
On the Integrals I exp (%C?S p8) . qddd (Dec. 1920). T6hoku Math. Journal, xx.
8 Jo L \ mnr /sin2 v ' '
A922), pp. 107—114.
HEAVISIDE, 0.
Electrical Papers, I., n. (London, 1892).
On Operators in Physical Mathematics (Dec. 15,1892 ; June 8, 1893). Proc. Royal Soc.
LIi. A893), pp. 504—529; liv. A893), pp. 105—143.
Electromagnetic Theoryi, n., in. (London, 1899, 1912).
HEINE, H. E.
Ueber die Zahler und Nenner der Naherungswerthe von Kettenbruchen J (Sept. 1859).
Journal fur Math. lvii. A860), pp. 231—247.
Die Fourier-Besselsche Function (June, 1868). Journal far Math. lxix. A809), pp. 128—
141.
Handbuch der Kugelfometionen: Theorie und Anioendunqeu B Biindu) (Borlin, 1878,
1881).
HERMITE, C.
Sur la transceudante En. Ann. di Mat. B) m. A870), p. 83 §.
Extrait d'une lettre de Monsieur Ch. Ilermite a Monsieur Paul (Jordan (June 9, 1873).
• Journal fiir Math, lxxvi. A873), pp. 303—311.
Extrait d'une lettre a M. E. Jahnke (Nov. 25, 1900). Arehiv d<>.r Math, und Phys. C)
I. A901), pp. 20—21.
HERTZ, H.
Tiber die Induktion in rotierenden Kugeln. Dissertation, Berlin, March 15, 1880. [Oes.
Werke, I. (Leipzig, 1895), pp. 37—134.]
Uber das Gleichgewicht schwimmender elasticher Platten. A nn. der Physik und Chemie,
C) xxn. A884), pp. 449—455. [Oes. Werke, I. (Leipzig, 1895), pp. 288—294.]
* Harnack died April 3, 1888.
t This work consists of a series of articles first published in The Electrician, Nature and else-
elsewhere in and after 1894, with numerous additions.
J See also under Christoffel.
§ This note contains a statement of Carlini's formula, which Hormite apparently derived
from Poisson's integral.
BIBLIOGRAPHY 767
HERZ, N.
Bemerkungen zur Theorie der Bessel'achen Functioneu (Sept. 21, 1883). Astr. Nach.
ovn. A884), col. 17—28.
Note, betreffend die Entwicklung der storenden Krafte (Mar. 30, 1884). Astr. Nach.
evil. A884), col. 429—432.
HILB, E.
Zur Theorie der Entwicklungen willkiiiiicher Funktionen nach Eigenfunktionen (Sept.
11, 1917). Math. Zeitsehrift, I. A918), pp. 58—69.
Uber die Laplacesche Reihe (March 15, 1919 j Nov. 17, 1919). Math. Zeitschrift, v.
A919), pp. 17—25 ; vin. A920), pp. 79—90.
HILL, C. J. D.
De radicibus rationalibus aequationis Riccatianae
ubi a, b, c functiones rationales ipsius x (May 24, 1840). Journal filr Math. xxv. A843),
pp. 22—37.
HOBSON, E. W*
Systems of Spherical Harmonics (June 11, 1891). Proo. London Math. Soc. xxil. A891),
pp. 431—449.
On the Evaluation of a certain Surface-Integral, and its application to the Expansion,
in Series, of the Potential of Ellipsoids (Jan. 12, 1893). Proc. London Math. Soc. xxiv.
A893), pp. 80—96.
On Bessel's Functions, and Relations connecting them with Hyper-spherical and
Spherical Harmonics (Dec. 14, 1893). Proc. London Math. Soc. xxv. A894), pp. 49—75.
On the most general solution of given Degree of Laplace's Equation (May 9, 1895).
Proc. London, Math. Soc. xxvi. A895), pp. 492—494.
Note on some properties of Bessel's Functions (Jan.'14, 1897). Proc London Math. Soc.
xxvm. A897), pp. 370—375.
On the representation of a function by series of Besael's functions (Dec. 10, 1908).
Proc. London Math. Soc. B) vn. A909), pp. 359—388.
IIOPF, L. UND SOMMERFELD, A; J. W.
Uber komplexe Integraldarstelluugen der Zylinderfunktionon. Archiv der Math, mid
Phys. C) xvni. A911), pp. 1—16.
HORN, J.
Ueber lineare Difterentialgloichungen mit einem veranderlichon Parameter (Dec. 30,
1898). Math. Ann. Hi. A899), pp. 340—362.
HURWITZ, A.
Ueber die Nullstellen der BesseFschen Function (June 2, 1888). Math. Ann. xxxiii.
A889), pp. 246—266.
Ueber die Wurzeln einiger transcendenteu Gleichungen. Hamburger Mittheiluni/en,
n. A890), pp. 25- 31. [Jahrbuch Uber die Fortschritte der Math. 1890, p. 116.]
HYMERS, J.
Treatise on Differential Equations, and on the Calculus of Finite Differences (Cambridge
1839).
IGNATOWSKY, W. VON.
Uber die Reihenontwicklungen mit Zylinderfunktionen (May 13, 1911). Archil} der
Math, und Phys. C) xvm. A911), pp. 322—327.
Uber Reihen mit Zylinderfunktionen nach dem Vielfachen des Argumcntes (Dec. 1913).
Archiv der Math, und Phys. C) xxm. A915), pp. 193—219.
ISELI, F.
Die Riccati'sche Gloichung. Dissertation, Bern, 1909 D2 pp.). [Jahrbuch Uber die Fort-
Fortschritte der Math. 1909, p. 369.1
ISHERWOOD, J. G.
Tables of the Bessel Functions for pure imaginary values of the argument (April 26,
1904). Manchester Memoirs, xlviii. A903—4), no. 19.
JACKSON, F. IT.
Generalised for.ms of the series of Bessel and Legendre. Proa. Edinburgh Math. Soc.
XXI. A903), pp. 65—72.
On Generalised functions of Legendre and Bessel (Nov-16, 1903). Trans. Edinburgh
Royal Soc. XLI. A905), pp. 1—28.
* See also under Gegenbauer.
768 THEORY OF BESSEL FUNCTIONS
A generalization of Neumann's expansion of an arbitrary function in a aeries of Bessel
functions (Nov. 26, 1903). Proo. London Math. Soc. B) I. A904), pp. 361—366.
Theorems relating to a Generalisation of the Bessel-Function (March 21,1904). Trans.
Edinburgh Royal Soc. xli. A905), pp. 105—118.
Note on a theorem of Lommel (May 13, 1904). Proc. Edinburgh Math. Soc. xxn. A904),
pp. 80—85.
The application of Basic numbers to Bessel's and Legendre'a functions (June 2, 1904;
Dec. 1, 1904; Jan. 18, 1905). Proc. London Math. Soc. B) n. A905), pp. 192—220; B) in.
A905), pp. 1—20, 21—23.
The complete solution of the differential equation for Jw (July 4,1904). Proc Edinbttrgh
Royal Soe. xxv. A904), pp. 273—276.
Theorems relating to a Generalization of Bessel's Function (Feb. 20, 1905). Trans.
Edinburgh Royal Soc. xli. A905), pp. 399—408.
JACKSON, W. H.
On the diffraction of light produced by an opaque prism of finite angle (Nov. 11,1903).
Proc. London Math. Soc. B) i. A904), pp. 393—414.
JACOBI, C. G. J.*
Formula transformationis integralium definitorum (July 9, 1835). Journal filr Math,
xv. A836), pp. 1—26. [Ges.Math.Werke, vi. A891), pp. 86—118.]—Formule pour la trans-
transformation d'une classe d'integrales definies, Journal de Math. i. A836), pp. 195—196.
Verauch einer Berechnuug der grossen Ungleichheit des Saturns nach einer strengen
Entwicklung. Astr. Nach.xxvui. A849), col. 65—80, 81—94. [Ges. Math. Werke, vn. A891),
pp. 145—174.]
Uber die annahernde Besthnmung sehr entfernter Glieder in der Entwickelung der
elliptischen Coordinaten, nebst einer Ausdehnung der Laplace1 achon Methode zur Bestim-
Bestimmung der Functionen grosser Zahlen. Astr. Nach. xxvm. A849), col. 257—270. [Ges. Math.
Werke, vil A891), pp. 175—188.]
JAHNKE, P. R. E.t
Funktionentafeln mit Formeln und Kurven. Von E. Jahnke und F. Emde (Leipzig, 1909).
Uber einige, in der elektromagnetischen Strahlungstheorie auftretende, bestimmte In-
tegrale. Archiv der Math, und Phys. C) xxm. A914), pp. 264—267.
JAMET, E. V.
Sur les Equations anharmoniques (Sept. 13, 1901). Comptes Rendus de VAssoc. Fran-
caise, xxx. (Ajaccio) A901), pp. 207—228.
Sur les Equations anharmoniques. Ann. de la Fac. des Sci. de Marseille, xn. A902),
pp. 1—21.
JEKHOWSKY, B.
Les fonctions de Bessel de plusieurs variables exprimdes par des fonctions de Bessol
d'une variable (Feb. 28, 1916). Oomptes Rendus, cxxil. A916), pp. 318—319.
Sur la fonction generatrice des fonctiona de Bessel a plusieurs variables. Bulletin des
Sci. math. B) xlt. A917), pp. 58—60.
Sur les fonctions de Bessel a deux variables (JVLay 30, 1921). Cornptes Rendus, clxxii.
A921), pp. 1331—1332.
JOHNSON, W. W.
On the Differential Equation
%
Annals of Math. in. A887), pp. 112—115.
JOLLIFFE, A. E.
The expansion of the square of a Bessel function in the form of a series of Bessel
functions. Messenger^ xlv. A916), p. 16.
JULIUS, V. A.
Sur les fonctions de Bessel de deuxieme espece (Dec. 1893). Archives Neerlandaises,
xxviii. A895), pp. 221—225.
Sur les ondes lumineuses sphe'riques et cylindriques (Dec. 1893). Archives Neerlandaises.
xxvili. A895), pp. 226—244.
* See also under Carlini. + See also under Hermite.
BIBLIOGRAPHY 769
KALAHNE, A.
Uber die "Wurzeln einiger Zylinderfunktionen und gewiaaer aus ihnen gebildeter Gleich-
ungen (March 1, 1906). Zdtschrift filr Math, und Phys. liv. A907), pp. 55—86.
KAPTEYN, W.*
Nouvelles formulea pour rdpresenter la fonction Jn ,(x). Bulletin des Sci. Math. B)
xvl. A892), pp. 41—44.
Over Bessel'scIio Function (March 12, 1892). Nieuw Archief voor Wiskunde, x.x. A893),
pp. 116—127. ,
Reohercb.es sur les fonctions de Fourier-Bessol. Ann. sci. de VEcole norm. sup. C) x
A893), pp. 91-120.
Sur quelques integrates definies contenant des fonctions de Beasel. Archives Ne'er-
landuises, B) vi. A901), pp. 103—116.
A definite integral containing Bessel's functions (June 29, 1901). Proc. Section of Set.,
K. Akad. van Wet. te Amsterdam, iv.- A902), pp. 102—103.
Sur un d($veloppement de M. Neumann. Nieuw Archie/ voor Wiskunde, B) vi. A905),
pp. 49—55.
Einige Betnerkungen iiber Bessel'scho Functionen. Monatshefte fur Math, und Phys.
xiv. A903), pp. 275—282.
te Amsterdam, vn. A905), pp. 494—500.
A definite integral of Kummcr (Sept. 30, 1905). Proc. Section of Sci., K. Akad. van
Wet. to Amsterdam, vm. (lijO(>), pp. 350—357.
On an expansion of an arbitrary function in a series of Bessel functions. Messenger,
xxxv. A906), pp. 122—125.
Sur la semination d'une serie infmie. Nieuw Archief roor Wiskunde, B) vii. A907), pp.
20—25.
The quotient of two successive Bessel Functions (Dec. 30, 1905 ; Jan. 27, 1906). Proc.
Section of Sci., K. Akad. van Wet. te Amsterdam, vm. A906), pp. 547—549, 640—042.
Sur le quotient de deux fonctions bessiHienues successives. Archives Ne'erlandaises, B)
XI. A906), pp. 149—168.
kechf.rc.hes sur les fonctions oylindriquea. Mem. de la Koc. It. des Sci. de Libje, C) vi.
A5H0), no. 5.
Sur le calcul munoriquc de la sdric
Mem. dc. la Xoc. II. das Sci. de Lihje, C) vi. A906), no. 9.
On some relations between Bessel's Functions (Feb. 24, 1912). Proc. Section of Sci., K.
Akad. ihui Wet. te Amsterdam, xiv. A912), pp. 962—969.
KKLVIN, LORD.
On the waves produced by a single impulse in water of any depth or in a dispersive
medium (Fob. 3, 1B87). Proc lioi/al So,:, xi.ii. A887), p. 80; Phil. Mag. E) xxni. A887),
pp. 252—255. [Math, and l'/ii/x. 'Papers, iv. A1I0), pp. 303—306.]
Ether, Electricity and Ponderable Matter (.Jan. 10, 1889). Journal of List, of Electrical
Kmjineors, xvjii. A890), pp. 4—37. [Math, and J'k/js. Papers, in. A890), pp. 484 --515.J
KKlMNSlvl, S.
(jber die Difl'orentialgleicliung
O'Z in +1 dz n dz _
Ox- x v.v x dt
(Jan. 1905). Math. Ann. lxi. A906), pp. 397—406.
Integration dor Difi'erontialgleiolnnig
d'JJ _ l 0 _0
Bull. int. de VAcad. des Sci. de Cracooic, 1905, pp. 198—205.
* See also under Gegenbauer.
W. B. F.
49
770 THEORY OF BESSEL FUNCTIONS
KIROHHOFF, G.
Ueber den inducirten Magnetismus eines unbegrenzten Cylinders von weichem Eisen
(June, 1853). Journal filr Math, xlviii. A854), pp. 348—376.
Zur Theorie der Bewegung der Elektricitiit in untcrsjeeischen odor unterirdiachen Tele-
graphendrahten (Oct. 29, 1877). Berliner Monatsberichte, 1877, pp. 508—(ill.
Ueber die Transversalschwingungen eines Stabes von veriuiderlichein Querschnitt
(Oct. 27, 1879). Berliner Monatsberichte, 1879, pp. 815—828; Ann. der Physik und Ckemie,
C) x. A880), pp. 501-512.
Ueber die elektrischen Stromungen in einem Kreiscylinder (April 26, 1883). Berliner
Sitzungsbmchte, 1883, pp. 519—524.
KLUYVER, J. C.
A local probability problem (Sept. 30, 1905). Proc. Section of Sci., K. AL-ad. van Wot.
te Amsterdam, vm. A906), pp. 341—350.
An integral theorem of Gegoubauer (Feb. 27, 1909). Proc. Section of Sci., K. Akad.
van Wet. te Amsterdam, xr. A909), pp. 749—755.
KNESER, J. 0. C. A.
Die Entwicklung willlcurlicher Funktionen in Reiheu die nach Besael\schen Funktionen
forfcschreiten (July, 1903). Arehiv der Math, und Pays. C) vn. A90.3), pp. 123—133.
Die Theorie der Integralgleicluingen und die Darstellung willkurlichcr Funktiouon in
der mathematiachen Phyaik. Math. Ann. lxiii. A907), pp. 477—524.
KNOCKENHAUER, K. W.
Ueber die Oerter der Maxima und Minima dcs gebeugten Lichtes nach den Fronnel'schon
Beobachtungen. Ann. der Physik und Ckemie, (-2) xn. A837), pp. 103—110.
K0NIG, J.
Ueber die Darstellung von Functionen durch uneudlicho Reihen (.Sept. 1871). Math.
Ann. v. A872), pp. 310—340.
Ueber Reihenentwicklung nach Bessel'schen Functiouon A880). Math. Ann. xvti.
A880), pp. 85—86.
KOESTLER, W.
Beitriige zu Reiheneutwickelungen nach Besselsche Zylinderfunktionon. Dissertation,
Bern, 1907 A10 pp.). [Jahrbuch iiber die Forlschritte der Math. 1908, p. f»3f>.]
KOPPE, M.
Die Ausbreitung einer Erschiitterung an der Wollenmaschine dar.stellbar (lurch oinon
neuen Grenzfall der Bessel'schen Functionen. Programm (!)E). Audrms liiudgyinn. Berlin,
1899 B8 pp.). [Jakrbueh iiber die Fortsehritte der Math. 18«.)9, pp. 420—121.]
KUMMER, E. K
Sur l'integration de liquation de Riccati par des inte*gralea d6iini<5.s. Journal filr Math.
XII. A834), pp. 144—147.
Ueber die hypergeometrische Reihe
q.j8 q(a+l)/3(ff + l) . a (a H) (a
"^l ^ l * +'
Journal fiir Math. xv. A836), pp. 39—83, 127—172.
De integralibus quibusdam definitis et seriebus inftnitia (April, IH37). Journal filr
Math. xvii. A837), pp. 228—242.
Note sur l'integration de liquation -~=xm.y. Journal filr Math. xix. A839), pp.
286—288.
Sur l'iutegration de l'equation ~=xm.y. Journal de Math. iv. A839), pp. 390—301.
LAGRANGE, J. L. DE.
Sur le probleme de Kepler (Nov. 1, 1770). Hist, de VAcad. R. das Sci. de Berlin xxv
A769) [1771], pp. 204—233. [Oeuvret, ill. A869), pp. 113—138.]
LAMB, H.
On the Oscillations of a Viscous Spheroid (Nov. 10, 1881). Proa. London Math Sor
xm. A882), pp. 51—66.
On the Vibrations of an Elastic Sphere (May 11, 1882). Proc London Math. Soo xm
A882), pp. 189—212.
BIBLIOGRAPHY 771
On Electrical Motions in a Spherical Conductor (March 14, 1883). Phil. Trans, of the
Royal Soc. clxxiv. A883), pp. 519—549.
On the Induction of Electric Currents in Cylindrical and Spherical Conductors (Jan.
10, 1884). Proc. London Math. Soc. xv. A884), pp. 139—149.
Note on the Induction of Electric Currents in a Cylinder placed across the Lines of
Magnetic Force (June 12,1884). Proc. London Math. Soc. xv. A884), pp. 270—274.
On the Motion of a Viscous Fluid contained in a Spherical Vessel (Nov. 13, 1884).
Proc. London Math. Soc. xvi. A885), pp. 27—43.
A problem in Resonance illustrative of the Theory of Selective Absorption of Light
(Jan. 8, 1900). Proc. London Math. Soc. xxxn. A901), pp. 11—20.
Problems relating to the Impact of Waves on a Spherical Obstacle in an Elasbic Medium
(March, 8, 1900). Proc. London Math. Sac. xxxn. A901), pp. 120—150.
On Boussineaq's Problem (Feb. 13, 1902). Proc. London Math. Soc. xxxiv. A902), pp.
276—284.
On Deep-water Waves (Nov. 10, 1904). Proc. London Math. Soc. B) n. A905), pp. 371—
400. [Presidential Address.]
On the theory of waves propagated vertically in the atmosphere (Dec. 6, 1908). Proc.
London Math. Soc. B) vn. A909), pp. 122—141.
LAMBERT, A.
See Wangerin, A.
LANDAU, E. G. H.
Uber die Gitterpunkte in einem Kreise (May 8, 1915; Jxme 5, 1915; June 4, 1920).
Nachrichten von der K. Qes. der Wiss. zu Qbttingen, 1915, pp. 148—160, 161—171 ; 1920,
pp. 109—134.
Zur analytischen Zahlentheorie der definiten quadratischen Formen (Uber die Gitter-
Gitterpunkte in eiuem niehrdimensionalon Ellipsoid) (May 20, 1915). Berliner Sitzungsberichte
{Math.-phys. Kla&sc), XXXI. A915), pp. 458—476.
Ubor Dirichlots Teilerproblem (July 3, 1915). Miinchener Sitzungsbe)'ichte, 1915, pp.
317—328.
LAPLACE, P. S. DE.
Mdmoiro sur la diminution do la dunSe du jour par lo refroidisaeuient do la terre.
Conn, des Terns, 1823 [published 1820], pp. 245—257.
Traitdde Me'eanique Celeste, v. (Paris, 1825 and 1882).
LAURENT, PAUL MATHI12U HERMANN.
Mdmoire sur les fonctions do Legendro. Journal de Math. C) I. A875), pp. 373—398.
LEBEDEFF, WERA MYLLER.
Uber die Anwendung der Integralgleichnngen in einer paraboliwchen Randwertaufgabe
Math. Ann. lxvi. A909), pp. 326—330.
LEBESGUE, V. A.
+ny*=Q. Jour
LEFORT, F.
Remarques sur liquation /'+ -/+ny*=Q. Journal de Math. XI. A846), pp. 338—340.
Expression numdrique des integrates d<5nnies qui se prcisentent quand on cherche los
terines gene"raux du dEveloppemont dea coordonn6"es d'une planetc, dfans son mouvcinout
elliptique. Journal de Math. XI. A846), pp. 142—152.
LEIBNIZ, G. W.
See Daniel Bernoulli.
LE PAIGE, C*
Note sur liquation xy"+h/-xy=0. Bull, de VAcad. R. de Belgique, B) xli. A876),
pp. 1011—1016.
LERCH, M.
Mittheilungen aus der Integralrechnung. Monatshefte filr Math, und Phy$. I. A890),
pp. 105—112.
Betrachtungen tiber einige Fragen der Integralrechnung. Rozpravy, v. A896), no.,23
A6 pp.). [Jahrbuch Uber Fortschritte der Math. 1896, pp. 233—234.]
* See also under Catalan.
49-2
772 THEOBY OF BESSEL FUNCTIONS
LINDNER, P.
Die Beziehungen der begrenzten Ableitungen mit komplexen Zeiger zu den Besselschen
Funktionen und ihren Nullstellen (Nov. 29, 1911). Sitz. der Berliner Math. Ge$. xi. A911),
pp. 3—5.
LINDSTEDT, A.
Zur Theorie der Fresnel'schen Integrate (Aug. 1882). Ann. der Physik und Chemie, C)
xvir. A882), pp. 720—725.
LIOUVILLE, J.
Sur la classification des transcendantes et sur Tim possibility d'exprimer des racines de
eertaines Equations en fonctions finic3 explicites des coefficients (June 8, 1835). Journal
de Math. n. A837), pp. 56—105; in. A838), pp. 523—547.
Sur ^integration d'une classe d'Equations difierentielles du second ordre en quantity
finies explicites (Oct. 28, 1839). Gomptes Rendus, ix. A839), pp. 527—530; Journal de
Math. IV. A839), pp. 423—456.
Eemarques nouvelles sur liquation de Eiccati (Nov. 9, 1840). Comptes Rendus, xr.
A840), p. 729; Journal de Math. vi. A841), pp. 1—13.
r-ir
Sur l'inte'grale I cos i (u - x sin u) du. Journal de Math. vi. A841), p. 36.
Sur une formule de M. Jacobi (March, 1841). Journal de Math. vi. A841), pp. 69—73.
LIPSCHITZ, E. 0. S.
Ueber ein Integral der Differentialgleichung —s + - 5- + /=0 (July 14, 1858). Journal
OX X OX
far Math. LVI. A859), pp. 189—196.
LOEATTO, E.
Sur l'intcgration des Equations
dxn y ' dxl J
(April, 1837). Journal fiir Math. zvil. A837), pp. 363—371.
LODGE, A.
Note on the Semiconvergcnt Series cf ^n(.r). British Association Report, York, 1906,
pp. 494—498.
LOMMEL, E. C. J. VON.
Beitrage zur Theorie der Beugung des Lichts. Archiv der Math, wiui Phys. xxxvi.
A861), pp. 385—419.
Methode zur Berecbnung ciner Transccndenten. Archiv der Math und Phys. xxxvu.
A861), pp. 349—360.
Zur Integration linearer Dilferentialgleichungen. Archiv der Math, und Phys. xh.
A863), pp. 101—126.
Studien ilber die BesseV&chcn Functioned. (Leipzig, 1868).
?j2m + 1 y
Integration der Gleichung xm+l -- .im + \ +y=0*. Math. Ann. u. A870), pp. 624—635.
Ueber der Anwenduug der Besscl'schcn Functioneu iu der Theorie der Hougiuig. Zeit-
sckrift fiir Math, und P/tys. xv. A870), pp. 141—169.
Zur Theorie der Bewserschen Functionen (Dec. 1870). Math. Ann. in. A871), pp. 475—
487.
Zur Theorie der Besael'achen Functionen (Jan. 1871). Math. Ann. iv. QB71), pp. 103—
116.
Ueber eine rait den BessePschen Functionen verwandte Function (Aug. 1875). Math.
Ann. ix. A876), pp. 425—444.
Zur Theorie der Bessel'schen Functionen (Oct. 1878). Math. Ann. xiv. A879), pp. 510—
536.
Zur Thoorie der Bessel'schen Functioned (Oct. 1879). Math. Ann. xvi. A880), pp. 183—
208.
Die Beugungserscheinungen einer kreisrunden Oeffnung und eines kreisrunden Sohirm-
chens theoi-etisch und cxperiniontell bearhcitet. MuncJiener A bh. xv. A884 —86), pp. 233—328.
Die Beugungserscheinungen geradlinig begrenztcr Schirme. Mihnchener Abh. xv.
A884—86), pp. 531—663.
* The headings of the pages of this paper are •' Zur Theorie der Bessel'achen Functionen."
BIBLIOGRAPHY 773
LORENZ, L.
Sur le deVeloppement des fonctions arbitraires an rnoyeu de fonctions donnees. Tids-
skriftfor Mathematik, 1876, pp. 129—144. [Oeuvres Scientifiques, II. A899), pp. 495—513.]
The'oric de la dispersion. Ann. der Phi/sib und Chemie, C) xx. A883), pp. 1—21. [Oeuvres
Scientifiques, I. A898), pp. 371—396.]
Sur la lumiere refUchie et refractdo par une sphere transparente. K. Danske Videnska-
bernes Sdskabs Skrifter, F) VI. A890), pp. 1—62. [Oeuvret Scientifiques, i. A898), pp. 405—
502.]
LOYE, A. E. H.
Tho Scattering of Electric Wavos by a Dielectric Sphere (Feb. 9, 1899). Proo. London
Math. Soc. xxx. A899), pp. 308—321.
The Transmission of Electric Waves over the Surface of the Earth (Dec. 19, 1914).
Phil. Trans, of the Royal Soc. ccxv. A A915), pp. 105—131.
MACDONALD, H. M.*
Note on Bessel Functions (Nov. 11, 1897). Proo. London Math. Soc. xxix. A898),
pp. 110—115.
Zeroes of the Bessel Functions (April 7, 1898 ; Jan. 12,1899). Proc. London Math. Soc.
xxix. A898), pp. 575—584; xxx. A899), pp. 165—179.
The Addition Theorem for the Bessel Functions (April 5, 1900). Proc. London Math.
Soc. xxxn. A901), pp. 152—157.
Some Applications of Fourier's Theorem (Deo. 11, 1902). Proc. London Math, Soc.
xxxv. A903), pp. 428—443.
The Bending of Electric Waves round a Conducting Obstacle (Jan. 21, 1903; May 12,
1903). Proc. Royal Soc. lxxi. A903), pp. 251—258; lxxii. A904), pp. 59—68.
Note on the evaluation of a certain integral containing Bessel's functions (Dec. 6,1908).
Proc. London Math. Soc. B) vn. A909), pp. 142—149.
The Diffraction of Electric Waves round a Perfectly Reflecting Obstacle (Aug. 13,1909).
Phil. Trans, of the Royal Soc. ccx. A A910), pp. 113—144.
Tho Transmission of Electric Waves around the Earth's Surface (Jan. 10, 1914). Proc.
Royal Soc. xc. A A914), pp. 50—61.
Formulae for the Spherical Harmonic Pn~m(fji) when 1 - fx in a small quantity (Feb. 6,
1914). Proc. London Math. Soc. B) xm. A914), pp. 220—221.
[Extract from a letter to Prof. (Jarslaw, Oct. 17,1912.] Proc. London Math. Soc. B) xnr.
A914), pp. 239—240.
A class of diffraction problems (Jan. 14, 1915). Proc. London Math. Soc. B) xiv. A916),
pp. 410—427.
Tho Transmission of Electric Waves around tho Earth's Surface (May 23, 1916). Proc.
Royal Soc. xcn. A A910), pp. 433—437.
McMAHON, J.
On the Descending Series for Bessel's Functions of Both-Kinds. Annals of Math. vm.
A894), pp. 57—61. ,
On the Roots of the Bessol and certain Related Functions. Annals of Math. ix. A895),
pp. 23—30,
The Expression for a Rational Polynomial in a Scrios of Bessel functions of nth Order
as required in certain Cases of Diriohlet's Problem. Proc. American Assoc. 1900, pp. 42—
43.
MacROBERT, T. M.
Tho Modified Bessel Function Kn (z) (Feb. 13, 1920). Proc. Edinburgh Math. Soc.
xxxviii. (.1920), pp. 10—19.
Asymptotic Expressions for the Bessel Functions and the Fourier-Bessel Expansion
(Jan. 14, 1921). Proc. Edinburgh Math. Soc. xxxix. A1J1), pp. 13—20.
MAGGI, G. A.
Sulla storia clello funzioni cilindriche. Attiddla R. Accad. deiLincei, Ser. 3 (Transunti),
vol. iv. A880), pp. 259—263.
Sopra un problema di olettrostatica (June 3,1880). Rend, del R. 1st. Lombardo, B) xnr.
A880), pp. 384—390.
MALMSTEN, C. J.
Om Integrale f"^ "%?. %¦ Svenska V. Akad. Handlingar, lxii. A841), pp. 66—74.
J o A •\-3>)
* See also under Gegenbauer.
774 THEORY OF BESSEL FUNCTIONS
De l'equation difle"rentielle y^'+^^-Axmy-0 (March 18, 1849). Journal filr Math.
xxxix. A850), pp. 108—115.
Theorenies sur integration de l'Equation ~~ 4- - -4- = ( bxm+ —-A y. Camb. and Dublin
Moih. Journal, v. A850), pp. 180—182.
• MALTEZOS, C.
Sur la chute des corps dans le vide et Bur certaines fonctions trauscendantes. Nouodles
Annales de Math. D) xi. A902), pp. 197—204.
MANFREDIUS, G.
De constructio?ie aequationum diferentialium primi gradus (Bologna, 1707).
MARCH, H. W.
Uber die Ausbreitung der Wellen der drahtlosen Telegraphie auf der Erdkugel (Oct. 21,
1911). Ann. der Physik und Chemie, D) xxxvn. A912), pp. 29—50.
MARC0L0NG0, E.
Alouni teoretni sulle funzioni cilindriche di priina specie (April C, 1889). Napoli Ren-
dkonto, B) ill. A889), pp. 96—99.
MARSHALL, W.
On a New Method of Computing the Roots of Besael's Functions (Oct. 1909). Armah
of Math. B) xi. A910), pp. 153—160.
MATHEWS, G. B.
See under Gray.
MAYALL, R. H. D.
On the Diffraction Pattern near the Focus of a Telescope (Fob. 22, 1897). Proa. Camb.
Phil Soc. IX. A898), pp. 259—269.
MEECH, L. W.
Integration of Riccatr's Equation. Annah of Math. I. A886), pp. 97—103; in. A887),
pp. 47—49.
MEHLER, F. G.
Ueber die Vertheilung der statischen Eloctricitat in einera von zwci kugellcalotten be-
grenzten Korper (July, 1867). Journal fUr Math, lxviii. A868), pp. 134—150.
Ueber eine init deu Kugel- und Cylinderfunctioneu verwandte Function und ihre Ao-
¦wendung in die Theorie der Electricitatsvertheilung. [Elbinq Jahre&lkricht, 1870.] Math.
Ann. xvm. A881), pp. 161—194.
Ueber die Darstellung einer willkurlicheu Function zweior Variablen duroh Cylinder-
function* (Dec. 1, 1871). Math. Ann. v. AK72), pp. 135—140.
Notiz iiber die Dirichlctschen Integralausdriicke fin* die Kugolfunctionon Pn (cosS)
und iiber eine analoge Integralformfiir die Cylinderfunction J{x)\ (Dec. 2, 1871). Math.
Ann. v. A872), pp. 141—144.
ME1SSEL, D. F. E.
Iserlohn Programm, 1862. [Nielseu, Nouvelles Annules de Math. D) n. A902), pp. 396—
410.]
Tafel der Bessel'schen Functionen Ik° und Ikl von k=0 bis /•= 15-5 (Nov. 8, 1888).
Berliner Abh. 1888. {Math. Abh. I.)
Ueber die Besselschen Functionen .4° und Jkl. Programm, Oberrealsch ide, Kiel, 1H90.
[Juhrbuch iiber die Fortschritte der Math. 1890, pp. 521—522.]
Einige Enfrwickeluugen die Be8sel'.schen /-Functionen bctrcffend (May 3, 1891). Astr.
Nach. cxxvn. A891), col. 359—362.
Beitrag zur Theorie der allgemeinen Bessel'schen Function (June 11,1891). Aatr. Nach.
cxxviii. A891), col. 145—154.
Abgekurzte Tafel der Bessel'schen Functionen Ikh (July 10, 1891). Astr. Nach. cxxvni.
A891), col. 154—155.
Beitrag zur Theorie der Bessel'schen Functionen (Oct. 7, 1891). Astr. Nach. cxxvur.
A891), col. 435—438. •
* The headings of the pages of this paper are "Ueber die Cylinderfunction J (.r)."
+ The headings of the pages of this paper are " Notiz iiber die Functionen P" (cos ^) <
uixdJ{x)."
BIBLIOGRAPHY 775
Neue Entwickelungen iiber die BesBel'schen Functionen. (Jan. 25, 1892). Astr. Nach.
cxxix. A892), col. 281—284.
Weitere Entwickelungen iiber die Bessel'schen Functionen (May 2, 1892). Astr. Nach.
cxxx. A892), col. 363—368.
Uber die Absoluten Maxima der Bessel'schen Functionen. Programm, Oherrealsohule,
Kiel, 1892 A1 pp.). [Jahrbuch iiber die Fortschritte dm- Math. 1892, pp. 476—478.]
MELLIN, R. HJ.
Abriss einer einheitlichen Theorie der Gamma und der hypergeometriscben Funktionen
(June, 1909). Math. Ann. lxviii. A910), pp. 305—337.
MICHELL, J. H.
The Wave Resistance of a Ship* (Aug. 9,1897). Phil. Mag. E) xlv. A898), pp. 106—123.
MOLINS, H.
dkv
Sur l'intdgration de liquation diffdrentielle -j4.=axmy (March 6,1876). Mem. de VAcad.
des Sci. de Toulouse, G) vm. A876), pp. 167—189.
MOORE, C. N.
Note on the roots of Bcssel functions. Annals of Math. B) ix. A908), pp. 156—162.
The sumniability of the developments in Beasol functions with applications (Sept. 11,
1908). Tram. American Math. Soc. x. A909), pp. 391—435.
On the uniform convergence of the developments in Bcssel fuuetions (Oct. 30, 1909).
Tram. American Math. Soc. xn. A911), pp. 181—206.
A continuous function whose development in Bessel'a functions in non-snnunable of
certain ordcra (Sept. 4, 1916). Bulletin American Math. Soc. xxiv. A918), pp. 145—149.
On the sumniability of the developments in Bessel'a functionu (Sept. 4, 1917). Trans.
American Math. Soc. xxi. A920), pp. 107—156.
MORTON, VV. B.
The Value of the Cylinder Function of the Second Kind for Small Argument*} (Oct. 25,
1900). Nature, lxiii. A901), p. 29.
MURPHY, E.
On the general properties of definite integrals (May 24, 1830). Trans. Camb. Phil. Soo.
III. A830), pp. 429—443.
MYLLER-LEBEDEFF, W.
See under Lcbedeff.
NAGAOKA, II.
Diffraction Phenomena produced by an Aperture on a Curved Surface. Journal of tlte
Coll. of Sci. Imp. Univ. Japan, iv. A891), pp. 301—322.
NEUMANN, CARL GOTTFRIEDt.
Allgemeine Lo'sung des Problems iiber den stationaren Tanperaturzustand eines homogenen
Korpers, weloher von zwei nicht concentri&chun Kugc.lfla'chen begrenzt vrird (Hallo, 1862).
Ueber dais Gleichgewicht der Warrno und das der Elcetricitiit in cinem Korper, wolcher
von zwei nicht concontrischon Kugclfiiieheii begrenzt wird A862). Journal ftlr Math. lxii.
A863), pp. 36—49.
Ueber die Entvvickelung beliebig gegoboncr Functionou nnch den Besselschan Functionen
(March 28, 1867). Journal fUr Math, i.xvti. A8E7), pp. 310—314.
Theorie der Bessel'schen Functionen. Bin Analogon zur Theorie der Kngelfunctioncn
(Leipzig, 1867).
Ueber die Entwicklungcn einer Function nach Quadraten und Productcn der Fourier-
BeHsel'Bchcn Functionou (Nov. 1869.) Leipziger Berichte, xxi. A869), pp. 221—256. [Math.
Ann. IIL A871), pp. 581—610.]
Ueber Producte und Quadrate der BcHsel'schcn Functionen. Math. Ann. n. A870), p. 192.
tjber die nach Krcis-, Kugel- itnd Cylinder-functionen fortxehreitenden Entwickelungen
(Leipzig, 1881).
Ueber gewi«se particularc Integralc der Difterentialgleichung Ai'T=i?Tin8besondere iibor
die Entwickelung dieser particularcn Integrate nach Kugelfunctionen (March 8, 1886).
Leipziger Berichte, xxxvm. A886), pp. 75—82.
* This paper contains some Tables of Bessel functions which were computed by B. A. Smith,
t See also under Schliifli.
776 THEOBY OP BESSEL FUNCTIONS
NEUMANN, F. E.
Eiue Verallgemeinerung der Zylinderfunktionen. Dissertation, Salberstadt, 1909 B5 pp.).
[Jahrbuch iiber die Fortschritte der Math. 1909, p. 575.]
NICHOLSON, J. W *
The Asymptotic Expansions of Bessel Functions of High Order. Phil. Mag. F) xiv.
A907), pp. 697—707.
On Bessel Functions of Equal Argument and Order. Phil. Mag. F) xvi. A908),
pp. 271—279.
On the Inductance of Two Parallel Wires (June 12, 1908). Phil. Mag. F) xvn. A909),
pp. 255—275.
On the Relation of Airy's Integral to the Bessel Functions. Phil. Mag. F) xvm. A909),
pp. 6—17.
The Asymptotic Expansions of Besael Functions. Phil. Mag. (fi) six. A910), pp. 228—249.
On the Bending of Electric Waves round a Large Sphere, i. Phil. Mag. F) xrx. A910),
pp. 516—537.
The Approximate Calculation of Bessel Functions of Imaginary Argument. Phil. Mag.
F) xx. A910), pp. 938—943.
The Scattering of Light by a Large Conducting Sphere (March 10, 1910). Proo. London
Math. Soc. B) ix. A911), pp. 67—80.
Notes on Bessel Functions. Quarterly Journal, XLii. A911), pp. 216—224.
The products of Bessel functions. Quarterly Journal, xliii. A912), pp. 78—100.
The pressure of radiation on a cylindrical obstacle (Dec. 14, 1911). Proc. London Math.
Soc. B) xi. A913), pp. 104—126.
The Lateral Vibrations of Bars of Variable Section (May 11, 1917). Proo. Royal Soc.
XGin. A A917), pp. 506—519.
Generalisation of a theorem due to Sonine. Quarterly Journal, xlvu i. A920), pp. 321—329.
A Problem in the Theory of Heat Conduction (Sept. 29, 1921). Proc. Royal Soc. c. A
A922), pp. 226—240.
NICOLAS, J.
Etude des fonctions de Fourier (premiere et deuxiemo espece). Ann. sci. de VEcole
norm. sup. B) XT. A882), supplement, pp. 3—90.
NIELSEN, N.t
Sur le produit de deux fonctious cylindriques (July 30, 1898). Math. Ann. lii. A899),
pp. 228—242.
Udviklingor efter Cylinderfunktioner (Aug. 28, 1898): Nyt Tidsskrift, ix. B A898), pp.
73—83.
Sur le deVeloppement de ze*ro en fonctions cylindriques (March 25, 1899). Math. Ann.
ill. A899), pp. 582—587.
Flertydige Udviklinger efter Cylinderfunktioner. Nyt Tidsskrift, x. B A899), pp. 73—81.
Note sur les developpements schloernilchiena en a<5rie de fonctions cylindriques (Nov. 15,
1899). Oversigt K. Danske Videnskabernes Selskabs, 1899, pp. 661—665.
Note supplementaire relative aux developpements BchloemilchionB on .sdrie de fonctions
cylindriques (June 23,1900). Oversigt K. Danske Videnskabernes Selskabs, 1900, pp. 55—60.
Sur une classe de polyndines qui se prcsentent dans la tbiorie dew fonctionn cylin-
cylindriques (Feb. 26, 1900; Jan. 8, 1901). Ann. diMat. C) v. A901), pp. 17—31; C) vi. A901),
pp. 331—340.
Evaluation nouvelle des integrates inde'nnies et des Buries iniinies contenant une fonc-
tion cylindrique (May 23, 1900). Ann. di Mat. C) vi. A901), pp. 43—115.
Sur une clasae de series infinies analogues a cellos de Schlomilch aelon las fonctions
cylindriques (Aug. 17, 1900). Ann. di Mat. C) vi. A901), pp. 301—329.
Recherche sur les series, des fonctions cylindriques dues a MM. 0. Neumann et
W. Kapteyn. Ann. sci. de I'Ecole norm. sup. C) xvm. A901), pp. 39—75.
Note sur la convergence d'une se'rie neumannieune de fonctions cylindriques (Feb. 10,
1901). Math. Ann. lv. A902), pp. 493—496.
Recherches sur une classe de series infinies analogue a celle do M. W. Kapteyn.
(April 13, 1901). Oversigt K. Danske Videnskabernes Selskabs, 1901, pp. 127—146.
Sur les series de factorielles(Jan. 20,1902). Comptes Rendus, oxxxiv. A iH2), pp. 157—160.
Tbiorie nouvelle dea series asymptotiques obtenues pour los fonctions cylindriquea cb
pour les fonctions analogues (March 16, 1902). Oversigt K. Danske Videnskabernes Selskabs.
1902, pp. 117—177.
* See also under Datta and under Dendy. f See also under Sonine.
BIBLIOGRAPHY 777
Equations diffe"rentielles lindaires obtenues pour le produit de deux fonctions cylin-
cylindriques. Nouvelles Annales de Math. D) n. A902), pp. 396—410.
Handbuch der Theorie der Cylinderfunktionen (Leipzig, 1904),
Note sur les series de fonctions bernoulliennes (Deo. 14,1903), Math. Ann. MX. A904),
pp. 103—109.
Sur une inte'grale d&inie (June 5, 1904). Math. Ann. lix. A904), pp. 89—102.
Sur quelques proprie'tes nouvelles des fonotions cylindriques (April 1,1906). Atti della
R. Accad. dei Mncei, E) xv. A906), pp. 490—497.
Recherches sur quelques generalisations d'une identity inte'grale d'Abel (Sept. 17,1906).
K. Danske Videnskabernes Selskabs Skrifter, G) v. A910), pp. 1—37.
Sur les series des fonctions cylindriques. Journ. filr Math, oxxxn. A907), pp. 127—146.
Sur quelques proprie"tes fondaraentales des fonctions sphe'riques (Dec. 20, 1906). Ann.
di Mat. C) xrv. A908), pp. 69—90.
tFber dieVerallgemeinerung einiger von F.und C.Neumann gegebenen nach Kugel- und
Zylinderfunktionen fortschreitenden Reihenentwickelungen (Jan. 26, 1908). Leipziger
Beriohte, lxi. A909), pp. 33—61.
tFber daB Produkt zweier Zylinderfunktionen. Monatshefte filr Math, mid Phys. xix.
A908), pp. 164—170.
tlber den Legendre-Besselschen Kettenbruch (July4, 1908). Milnchener Sitzungsberichte,
xxxviii. A908), pp. 85—88.
NIEMOLLER, F.
Ueber Schwinguugen einer Saite deren Spannung eine stetige Function der Zeit ist.
Zeitsohrift filr Math. xxv. A880), pp. 44—48.
Formeln zur nunierischen Berechnung des allgerneinon Integrals der Bessel'schen
Difterontialgleichufgen. Zeitschrift fiir Math. xxv. A880), pp. 65—71.
OLBR1CHT, R.
Studion iiber die Kugel- und Cylindorfunctionen (Juno 2, 1886). Nova Ada Acad.
Caes. Loop. {Halle), 1888, pp. 1—48.
OLTRAMARE, G.
Note sur l'iutdgrale
'" cos^ dx.
ii + b'ix'i)n
Comptes Randus de I'Assoc. Francaixe, xxiv. A895), part I. p. 182; part n. pp. 167—171.
ONO, A.
On the First Root of Bessel Functions of Fractional Order (April 2, 1921). Phil. Mag.
F) xlii. A921), pp. 1020—1021.
ORR, W. McF.
On Divergent (or Scmiconvergont) Hypcrgoometric Series (May 16, 1898; April 3,
1899). Trans. Camb. Phil. Soc. xvn. A899), pp. 171—199, 283—290.
On the product Jm(jc),/H{x) (May 15, 1899). Proc. Camb. Phil. Soc. x. A900), pp.
93—100.
Extensions of Fourier's and tho Bessel-Fourier Theorems (Dec. 14, 1908). Proc. R. Irish
Acad. xxvn. A A910), pp. 205—248.
OSEEN, C. W.
Neue LoHung dos Nonmiorfcldsohon Dittraktionsproblenis (Jan. 10, 1912). Arkiv for
Mat. Astr. och Fysik, vir. A912), no. 40.
OTTI, JJ.
Eigenschafton BessoVnoher Funktionon ntor Art. Bern Mittheilu?igen, 1898 [1899], pp.
61—90.
PAOLI, P.
Sopra gl' integrali dofhuti (Oct. 8, 1827). Mem. di Mat. e di Fis. della Soc. Italiana delle
So. {Modena), xx. A828), pp. 161—182.
Sull' integrazionc doll' cquaziono
(Oct. 8, 1827). Mem. di Mat. e di Fis. della Soc. Italiana delle Sci. xx. A828), pp. 183—
188.
778 THEORY OF BESSEL FUNCTIONS
PARSEVAL, M. A.
Memoire sur lea series et sur l'integration complete d'une Equation aux diffeYeuces
partielles lineaires du second ordre a eoefficiens constans (Le 16 germinal, an 7—April 5,
1799). Mem. presente's a VInst. par divers savans, I. A805), pp. 639—648.
PEARSON, K,
On the solution of some differential equations by Bessel's functions. Messenger, ix.
A880), pp. 127—131.
The Problem of the Random Walk. Nature^ lxxii. A905), pp. 294, 342.
A mathematical theory of random migration. Drapers Company Research Memoirs,
Biometric Series, in. A906).
PEIRCE, B. 0.
See under Willson. , ,
PERES, J.
Sur lea fractions de Bessel de pluBieurs variables (August 9, 1915). Cotnptus Iiendus,
clxi. A915), pp. 168—170.
PERRON, 0.
Ober die Kettenbruchentwicklung deB Quotienten zweier Bessel'schen Functionen
(Dec. 7, 1907). Munchener Sitzungsberichte, xxxvil. A907), pp. 483—504.
PETZVAL, J.
Integration der linearen Differential-Gleichungen, I. (Vienna, 1851).
PICARD, C. E.
Application de la thcorie des complexes lineaires a l'etude des smrf<§3es et des courbes
gauches. Ann. sci. de VEoole norm. sup. B) vi. A877), pp. 329—366.
PINCHERLE, S.
Sopra alcuni sviluppi in serie per funzioni analitiche (Jan. 12, 1882). Bologna Memorie,
D) in. A881), pp. 151—180.
Alcuni teoreini sopra gli sviluppi in serie per funzioni analiticho (March 23, 1882).
Rend, del R. 1st. Lombardo, B) xv. A882), pp. 224—225.
Delia trasformazione di Laplace e di alcune sue applicazioni (Feb. 27, 1887). Bologna
Memorie, D) vm. A887), pp. 125—143.
PLAN A, G. A. A.
Note sur l'int^gration de l'equation -^L+gai»ly—O (Jan. 20,1822). Mem. della R. Aocad
delle Set. di Torino, XXVI. A821), pp. 519—538.
Recherches analytiques sur la ddcouverte de la loi de pesanteur dos planetes vors lo
Soleil et Bur la theorie de leur mouvemcnt elliptiquc (June 20,1847). Mem. della R. Accdd.
delle Sci di Torino, B) x. A849), pp. 249—332.
POCHHAMMER, L.
Ueber die lineare Differentialgleichung zweiter Ordnung mit linearen Coefncienten.
Math. Ann. xxxvi. A890), pp. 84—96.
Ueber einige beaondere Falle der linearen Differentialgleichung zweitor Ordnung mit
linearen Coefficienten (Sept. 1890). Math. Ann. xxxvin. A891), pp. 225—246.
Ueber eine binomische lineare Differentialgleichung wter Ordnung (Sept. 1890). Math.
Ann. xxxvin. A891), pp. 247—262.
Ueber die Differentialgleichung der allgerueineren i^-Reihe (Jan. 1891). Math. Ann.
xxxvin. A891), pp. 586- 597.
Ueber cine specielle lineare Differeutialgleichung 2tor Ordnung mit linearen Cocffieienten
(May, 1891). Math. Ann. XLI. A893), pp. 174—178.
Ueber die Differentialgleichungen der Reihen JF(p, o-; x) und JF(p, <r, r; x) (June, 1891).
Math. Ann. xli. A893), pp. 197—218.
P01SS0N, S. D.
Memoire sur les integrates d^finies. Journal de Vtcole Poly technique, ix. (cahior 16)
A813), pp. 215—246.
Sur uue nouvelle maniere d'exprimer les coordonnees des planetes dans le mouvement
elliptique. Connaissance des Terns, i825 [1822], pp. 379—385.
Memoire sur Hnt^gration des Equations lineaires aux diff6renc.es partielles. Journal de
VEcole Polytechniqw, xil. (cahier 19) A823), pp. 215—248.
BIBLIOGRAPHY 779
Suite du Mcmoire sur les integrates definies et sur la sommation des series inse're' dans
les pre'cedens volumes de ce Journal. Journal de I'JOcole Poll/technique, xii. (cahier 19)
A823), pp. 404—509.
Memoire svir le calcul des variations (Nov. 10, 1831). Mem. de VAead. It. des Sci. xn.
A833), pp. 223—331.
Sur le developpement des cqordonndes d'une planete dans son mouvemont elliptique et
la fonction perturbatricc de ce mouverncnt. Connaissance des Terns, 1836 [1833], pp. 3—31.
La Theorie de la Chaleur (Paris, 1835).
PORTER, M. B.
Note on the roots of Bessel's Functions. Bulletin American Math. Soc. iv. A898),
pp. 274—270.
On the Roots of the Hypergeometric and Bossel's Functions (June 3, 1897). American
Journal of Math. xx. A898), pp. 193—214.
On the roots of functions connected by a linear recurrent relation of the second order
(Feb. 1901). Annals of Math. B) in. A902), pp. 55—70.
PU1SEUX, V.
Sur la convergence des series qui ho preaontcnt dans la theories du mouvement elliptique
des planetes. Journal de Math. xiv. A849), pp. 33—39.
Seconde note sur la convergence des aeries du mouvement elliptique. Journal de Math.
xiv. A849), pp. 242—246.
PURSER, F.
On the application of Bessel's functions to the elastic equilibrium of a homogeneous
isotropic cylinder (Nov. 11, 1901). Trans. It. Irish Acad. xxxu. A902), pp. 31—00.
Some applications of Beasel's functions to Physics (May 14, 1900). Proc. It. Irish Acad.
XXVI. A A907), pp. 25—66.
1UFFY", L.
Une lecon sur l'oquation do Riccati. Nouv. Ann. de Math. D) n. A902), pp. 529—04ft.
RAMAN LTJAN, S.
A class of definite integrals. Quarterly Journal, xlviii. A920), pp. 294—310.
RAWSON, R.
On Cognate Riccatian Equations AH7G). Messenger, vir. A878), pp. GO—72.
Note on a transformation of Riocati's equation. Masxemjer, xn. A883), pp. 3<J—36.
RAYLEKJH (J. W. NTRUTT), LORI).
On the Vibrations of a Gas contained within a Rigid Spherical Knvclopo (March 14,
1872). Proc. London Math. Soc. iv. A873), pp. 93—103.
Investigation of the Disturbance produced by a Spherical Obstacle on the Waves of
Sound (Nov. 14, 1872). Proc. London Math. Soc. IV. A873), pp. 25:5—283.
Notes on Bessel's Functions. Phil. Mag. D) XUV. A872), pp. 328—314.
Note on the Numerical Calculation or the Roots of Fluctuating Functions (June 11,
1874). Proc. London Math. Sac. v. A874), pp. 1.12—194. [Scientific Papers, I. A899),
pp. 190—195.]
The Theory of'Sound B vols. London, 1877, 1878; 2nd edition, 1894, 189E).
On the Relation between the Functions of Laplaoo and Bossel (Jan. 10, 1878). Proc.
London Math. Hoc. ix. A878), pp. 01— E4. [Scientific Papers, r. A809), pp. 338—341.]
On Images formed without Reflection or Refraction. Phil. Mag. E) xi. A881), pp. 214—
218. [Scientific Papers, I. A8!)9), pp. 513—017.]
On the Electromagnetic Theory of Light. Phil. May. E) xn. A881), pp. 81—101.
[Scientific Papers, i. A899), pp. 518—030.] "
On the Vibrations of a Cylindrical Vessel containing Liquid. Phil. Mag. E) xv. A883),
pp. 380—389. [Scientific Papers, n. A900), pp. 208—211.]
On Point-, Line-, and Plane Sources of Sound (June 14, 1888). Proc. London Math. Soc.
Xix. A889), pp. 004—007. [Scientific Papers, Hi. A902), pp. 44^—46.1
On the Theory of Optical Images, with apodal referonce to the Microscope. Phil. Mag.
E) xlii. A896), pp. 107—195. [Scientific Papers, IV. A904), pp. 230—260.1
On the Passage of Waves through Apertures in Plane Screens, and Allied Problems.
Phil. Mag. E) xun. A897), pp. 259—272. [Scientific Pavers, IV. A904), pp. 283—296.]
On the Bending of Waves round a Spherical Obstacle (May 23, 1903). Proc. Hoy. Soc.
ixxn. A903), pp. 40—41. [Scientific Papers, v. A912), pp. 112—114.]
On the Acoustic Shadow of a Sphere (Jan. 21, 1904). Phil. Trans, of the Royal Soo.
com. A A904), pp. 87-110. [Scientific Papers, v. A912), pp. 149-161.]
780 THEORY OF BESSEL FUNCTIONS
On the Open Organ Pipe Problem in two Dimensions. Phil, Mag. (G) vin. A904),
pp. 481—487. [Scientific Papers, v. A912), pp. 206—211.]
On the Experimental Determination of the Ratio of the Electrical Units. Phil. Mag.
F) XII. A906), pp. 97—108. [Scientific Papers, v. A912), pp. 330—340.]
On the Light dispersed from Fine Lines ruled upon Reflecting Surfaces. Phil. Mag. F)
xiv. A907), pp. 350—359. [Scientific Papers, v. A912), pp. 410—418.]
The Problem of the Whispering Gallery. Phil Mag. F) xx. A910), pp. 1001—1004.
[Scientific Papers, v. A912), pp. 617—620.]
Note on Bessel's Functions as applied to the Vibrations of a Circular Membrane. Phil.
- ~ " —5-] .
Functions. Phil. Mag.
Problems in the Conduction of Heat. Phil. Mag. F) xxn. A911), pp. 381—396.
[Scientific Papers, vi. A920), pp. 51—64.]
,A
A912), pp. 193—202. [Scientific Papers, vi. A920), pp. 111—120.]
Further Applications of BessePs Functions of High Order to the Whispering Gallery
and Allied Problems. Phil. Mag. F) xxvn. A914), pp. 100—109. [Scientific Papers, vi.
A920), pp. 211—219.]
Further roraarks on the Stability of Viscous Fluid Motion. Phil. Mag. ((>) xxvhi. A914),
pp. 609—619'. [Scientific Papers, vi. ( 920), pp. 266—275.]
On the Stability of the simple Shearing Motion of a Viscous Incompressible Fluid.
Phil Mag. F) xxx. A915), pp. 329—338. [Scientific Papers, vi. A920), pp. 341—349.]
On Legendre's Function* Pn(d), when n is great and 8 has any value (April 27, 1916).
Proc. Royal Soc. xcn. A A916), pp. 433—437. [Scientific Papers, vi. A920), pp. 31K—397.]
On Convection Currents iu a horizontal Layer of Fluid, when the higher Temperature
i3 on the under side. Phil Mag. F) xxxn. A916), pp. 529—546. [Scientific Papers, vi.
A920), pp. 432—446.]
On the Problem of Random Vibrations and of Random Flights iu one, two, or three
dimensions. Phil. Mag. F) xxxvn. A919), pp. 321—347. [Scientific Papers, vr. A920),
pp. 604—626.]
REINECK, A.
Die Verwandtschaft zwischen Kugelfunktionen und Besselschen Fuuktionen. Disserta-
Dissertation, Bern (Halle, 1907). G2 pp.) [Jahrhuch iiber die Fortschritte der Math. 1907, p. 495.]
RICCATI, COUNT J. F.
Animadversationes in aequationes differentiates secundi graduw. Actorum Eruditoru?n
quae Lipsiae publicantur Supplementa, viii. A724), pp. 66—73.
Com. Jacobi Riccati Appendix ad Aniinadveraationes in aequationes <Hn"orentialen
secundi gradus, editua in Aotis Eruditorum quao Lipsiae publicantur Tomo vnr. Supple-
mentorum, Sectione n. p. 66. Ada Eruditorum publicata Lipsiae, 1723, pp. 502—510.
RIEMANN, G. F. B.
Zur Theorie der Nobili'achen Farbenringe (March 28, 1855). Aim. der Physik und
Chemie, B) xcv. A855), pp. 130—139.
Partielle Differentialgleichuiu/en uad deren Anwendung auf physikalische Fnupm. Von
Bernhard Riemann. Fur den Drack bearboitet und herausgegebenon von Karl Hattondorf
(Brunswick, 1876).
ROHRS, J. H.
Spherical and Cyliiidric Motion in Viscous Fluid (May 14, 1874). Proc. London Math.
Soc. v. A874), pp. 125—139.
RUDSKI, P.
Ueber eine Klasse transcendenter Gleichungen. Prace Mat. Fiz. in. A892), pp. GO—8!.
[Jahrhuch iiber die Fortschritte der Math. 1892, pp. 107—108.]
Note sur la situation des raies de fti tdt /() O (M LO
, pp 0710.]
Note sur la situation des racines des functions transcendantes /,i+j(.v) = O (May LO,
1891). Mem. de la Soc. R. des Sci. de Lttge, B) xvm. A895), no. 3.
RUSSELL, A.
The Effective Resistance and Inductance of a Concentric Main, and Methods of Com-
Computing the Ber and Bei and Allied Functions (Jan. 22, 1909). Phil. Maq. F) xvil A909),
pp. 524-552. U w *• "
* This is the function which other writers denote by the symbol Pn(eos 0).
BIBLIOGRAPHY 781
KUTGEHS, J. G.
Over die bcpaaldeintegraal I e-"*zv~ldz. Nieuw Archie/ voor Wiskunde, B) vi. A905),
pp. 368—373.
Over eene reeka met Besselsche Functies. Jtiieuw Archie/ voor Wiskunde, B) vir. A907),
pp. 88—90.
Over reokaen van Besaelackc functiosen daarmede samenliangende bepaalde integralen,
waariu Beaselsche functies voorkomon. Niemo Archief voor Wiskunde, B) vii. A907), up.
164—181.
Sur lea functions oylindriqucs de premiere esp6ce. Nieuw Archie/ voor Wiskunda B)
vii. A907), pp. 385—405.
Over eenige toopaasingou der Fourier'sche ontwikkeling -van cen willokcurige functie
naar Besssel'solae functies. JVieuio Archie/ voor Wiskunde, vm. A909), pp. 375—380.
Eft
5, 191
W. VON.
>er die Aunbreituug dor Wellon der drahtlosen Telegraphie auf dor Erdkugel (March
3). Ann. der Physik und Chemie, D) xli. A913), pp. 191—208.
SASAKI, S.
Y (kr) Y' (ka)
On the roots of the equation -v^-r-^—f,n .- = 0. T6hoku Math. Journal, v. A914),
pp. 45—47.
8 A VI DOE, H. G.
Tables of the ber and bci and kor and koi Functions with further formulae for their
Computation (Nov. 12, 1909). Phil. Mag. (G) xix. A910), pp. 49—.08.
SCHAFHEITLIN, P.*
Xlcber die Darstellung der hypergeometriache Roihe (lurch ein bcstiinintea Integral
(Feb. 1887). Math. Ann. xxx. A887), pp. 157—178.
Uebcr cine Integraldanstellung der hypergeometrischen Hcibcn (Jan. 1888). Math.
Ann. xxxi. A888), p. lflfi.
Uober die (itwsn-wshv. nnd /Mwttf-sclio Dinero.ntialgleichung und cino neue Intogralform
der letztoren (Vch. 10, 1894). Journal fur Math. cxiv. AH95), pp. 31 14.
Die Nullstellou der /Av.\W.schen Functionen. Journal fUr Math. exxn. A9(K)), pp. 299—
321.
XT ber die Null.stellen-der Bcsaolfuchen Funktionon zwcitc.r Art (Jan. 10, 1901). Archiv
der Math, und Phy*. C) j. A901), pp. 133—137.
tlber den Verlauf der BoKaeLschen Funktioncn (May 18,15H-1). fferh'nrr Sitzwngsbcrichto,
III. A904), pp. 83-85.
Die Lago der Nallstellen der Heasfil.sclicn Fnnktionen zwciter Art (Juno 27, 1900).
Berliner tiits-itnyslwrichtc, v. A00*5), pp. 8ii—93.
0ber don Vorlauf tier UohsuImcIkmi Funktionon awoitor Art. JahivrfmriclU der J)eut»ehai
Math. VfirnnitriPnq, xvi. A907), pp. 27*2—279.
Die. Thvuric der livsaelschrn Funktiown. Yon Paul Kclmfhnitlin (Leipzig uud Berlin,
1908; Math. Phj/t. Srhri/tvn /iir Ini/cin'citre vnd Mtiuh'oront/e, 4).
Beziohungen zwisdu'ii dcin IntcgnUlogaritlmiuH und don Heanol.si:hen Fuiiktioncn (Fob.
24, 1909). llcrUncr Sitziintisbrrii'hte, vui. A909), pp. E2—E7.
Die Koiuiknnvc.rgcMtou H^ihcn fiir dio JiesHoLsuben Funktionon (Se[)t. 1, 1909). Jahres-
lericht tier Deutsvhen Math. Vi:rcitn';/un<;, xix. A910), pp. 120—129.
SCIIICIMNKII, \V.
On the. asymptotic valiK'.s of tbo coeflicionts in tlio dovolopniont of any power of the
radius vector according to tin1, mean anomaly (March, 185E). doiitds Astronomical Journal,
IV. A8f>(j), pp. 177 18*2. [Math. Ann. XVII. A880), pp. 531—54-1.J
l.Mior di<'. asyniptotischo Wortho der ('ocflicieiitcu in don nacli dor niittleren Anonuilie
vorgoiioimiioiiun Kntwic.ki^luiigtm (May 31, 18.r>0j. Leij>~iqer Berichte, via. A85G), pp. 40—
64. [Math. Ana. xvil. A880), pp. 545—5(H.J
SCHKRK, II. F.
tJber dio Integration dor Gleicbung -;-~ — (a-)r&.v)y. Journal fiir Math. x. A833),
pp. 92—97.
* Sco also under Sonitio.
782 THEORY OE BESSBL FUNCTIONS
SOHLAFLI, L.
Sulle relazioni tra diversi integrali definiti che giovano ad esprimere la soluzione generale
della equazione di Riccati. Ann. di Mat. B) I. A868), pp. 232—242.
Einige Bemerkungen zu Herrn Neumann's Untersuchungen iiber die Bessel'schen
Functioneu (May 4, 1870). Math. Ann. in. A871), pp. 134—149. [With note by C. N.
p. 149.]
Sopra un teorema di Jacobi recato a forma piu generale ed applicata alia funzione
cilindrica (Aug. 1871). Ann. di Mat. B) v. A873), pp. 199—205.
Sull' uso delle linee lungo le quali ii valore aasoluto di una funzione e constitute (Oct. 4,
1872). Ann. di Mat. B) VI. A875), pp. 1—20.
Ueber die Convergenz der Entwicklung einer arbitraren Function f{x) nach den
Besael'schen Functionen Ja (ftvv), J* {fax), /a(/Vr)> ..., wo /3X, C2, fa, •¦• die positiven
Wurzeln der Gleichung J*(fi) vorstellen (Jan. 17,1876). Math. Ann. x. A876), pp. 137—142.
SCHLOMILCH, 0. X.
Note sur la variation des constantes arbitraires d'une integrate de*fmie. Journal fur
Math, xxxni. A846), pp. 268—280.
Analytiscke Studien, n. (Leipzig, 1848).
Ueber die Besael'schen Function. Zeitschrift fiir Math, -and Phys. ir. A857), pp. 137-
165.
SOHONHOLZER, J. J.
Ueber die Auswerthung bestimmte Integrate mit Hiilfevon Veranderungen dos Integra-
tionsweges {Dissertation, Bern, 1877). [Graf and Gubler, Einleitung in die Theorie der
Bessel'schen Funktionen, II. (Bern, 1900).]
SCHOTT, G. A.
Electromagnetic Radiation (Cambridge, 1912).
SCHWARZSCHILD, K.
Die Beugung und Polarisation des Lichts durch einen Spalt. Math. Ann. lv. A902),
pp. 177—247.
SCHWERD, F. M.
Die Beugungserscheinungen au& den Fundamentalgesetzen der Undulationstheorie (Mann-
(Mannheim, 1835).
SEARLE, J. H. C.
On the propagation of waves in an atmosphere of varying density. Quarterly Journal,
xxxix. A908), pp. 51—66.
SEGAR, H. W.
On the roots of certain continuants. Messenger, xxn. A893), pp. 171—181.
SERRET, J. A.
Note sur quelques formules de calcul integral. Journal de Math. vin. (,1843), pp. 1—27.
Memoire sur 1'inWgration d'une equation difl&rentielle a l'aide des dificrentiellcs a indices
quelconqucs (Sept. 4, 1843). Comptes Rendus, xvn. A843), pp. 458—475; Journal do
Math. ix. A844), pp. 193—216.
SHARPE, H. J.
On the Reflection of Sound at the Surface of a Paraboloid (Nov. 1874). (Quarterly
Journal, xv. A877), pp. 1—8.
On a differential equation. Messenger, x. A881), pp. 174—185 ; xi. A882), pp. 41—44.
On a transcendental differential equation. Messenger, xi. A882), pp. 56—63.
On a differential equation. Messenger, xin. A884), pp. 66—79.
Note on Legendre's coefficients. Quarterly Journal, xxiv. A890), pp. 383—386.
On The Reflection of Sound at a Paraboloid (June 20,1899). Proc. Camb. Phil. Soc. x.
A900), pp. 101—136.
SHEPPARD, W. F.
On some expressions of a function of a single variable in terms of Bessel's functions.
Quarterly Journal, xxm. A889), pp. 223—260.
SIACCI, F.
Sulla integrazione di una equazione differenziale e sulla equazione di Riccati (April 13
1901). Napoli Rendiconto, C) vn. A901), pp. 139—143. '
BIBLIOGRAPHY 783
SIBIRANI, F.
Sopra 1' equazione di Riccati. Riv. Jis. mat. xix. A909), pp. 216—220. [Jahrbuch iiber die
FortBchritte der Math. 1909, p. 369.]
SIEMON, P.
Ucber die Integrals einer nioht homogenen Differentialgleiehung zwoitor Ordnung. Pro-
qramm, Luisenschule, Berlin, 1800, 22 pp. [Jahrbuch liber die Fortschritte der Math. 1890,
pp. 340—342.]
SMITH, B. A.*
Table of Bessel's Functions YQ and \\. Messenger, xxvi. A897), pp. 98—101.
Arched <Dams. Proc. American Soc. of Civil Engineers, xlvi. A920), pp. 375—425.
SMITH, CLARA E.
A theorem of Abel and its application to the development of a function in terms of
Bessel's functions (June 8, 1906). Trans. American Math. Soc. vm. A907), pp. 92—10G.
SMITH, O. A.
Quelqnes relationa integrales entrc les fonotions aphdriquea et cylindriques. Giomale di
Mat. B) Xll. A905), pp. 365—373.
SOMMERFELD, A. J. W.f
Die willkiirlichcn Functionon in der mathcrnatisohen Physik. Dissertation, Kiiniy&berg,
1891 G5 pp.). [Jahrbuch iiber die Fortschritte der Math. 1891, pp. -519—523.]
Zur analytiHchen Thcorio der Wiirmeleitung. Math. Ann. xi,v. A894), pp. 263—277.
Mathematisoho Theorie der Diffraction (Summer, 1895). Math. Ann. xlyii. A896), pp.
317—374.
tjl>er die Ausbreitung der Wollen der drahtlosen Telegraphic (Jan. If), 1909). Ann. der
Phi/mh und C/iemie, D) xxvur. A909), pp. 665—736.
])ie Greonsebo Funktion dor Schwitiguugsgleich-ung. Jahresbericht der Devtscher Math.
Vereiniginig, xxi. A912), pp. 309—353.
SON1NE, N. J.
On the rciHolution of functions into inlinito .scries (Jan. 17/29, 1870). Mathematieal
Collection published by the Moscow Math, Soc. [MaTGMaTHSCCKift C<5opinnri>], v. A870),
pp. 271--302, 323—382.
Retihc't'ohes aur h\s foni;tionn irylindriquos et le ddveloppeinont doa fonctions coutinucaeu
aeries (Aug. 1879). Math. Ann. xvi. A880), pp. 1—80.
Sur ]<\s functions cylindriques (Oct. 24, 1887). Math. Ann. xxx. A887), pp. 582—583.
[Note on a paper by Krhafhcitlin.]
Sur Ion fonctions cylindriques. (Extmit d'uno Lettre adre.suc'o a M. Niels Nielsen,
a Coi>enhague, May 6, 1904.) Math. Ann. Lix. A904), pp. 529—552.
Sl'ITZEH, S.
Integral dor Difforontialgloichung xy" — y — 0. Zeitschrift filr Math, und Phys. n. A857),
pp. lCfi—170.
Entwickolung von ekxi'^x in unendlichu Reihen. Zeit&chrift fiir Math, mid Phys. ill.
A858), pp. 244—246.
Darstollung dos unendlichon Kottonbruchcs
--- ¦ -
- ---¦
--- - -
-lx -V 7 -I-...
in goHchlossener Form. Arohiv dor Math, und, I'hys. xxx. A858), pp, 331--334.
Ueber die Integration der Difforcutialgleichung
dn>/
dx" J
A859). Journal fiir Math. lvii. A860), pp. 82—87.
STEARN, H.
On some cases of the Varying Motion of a Viscous Fluid. Quarterly Journal, xvn.
A880), pp. 90—104.
* See ulso undor Micholl. t See also under Hopf.
784 THEORY OF BESSEL FUNCTIONS
STEINER, L.
Intensitats-verhaltnisse der Beugungserscheinung cluroh eine kreisformige Offnung
(June 19, 1893). Math, und Naturwiss. Berichte aus Ungarn, xi. A892—93) [1894], pp
362—373.
STEINTHAL, A. E.
On the Solution of the Equation
a
—>
Quarterly Journal, xvill. A882), pp. 330—345.
STEPHENSON, A.
An extension of the Fourier method of expansion in sine series. Messenger, xxxiii. A904),
pp. 70—77.
A more general case of expansion in sine series. Messenger, xxxiii. A904), pp. 178—
182.
On Expansion inBessel's Functions (June, 1907). Phil. Mag. F) xiv. A907), pp. 547—
549.
STERN, M. A.
Ueber die Anwendung der Sturm'schen Methode auf transcendento Gleichungen.
Journal ftW Math, xxxiii. A846), pp. 363—365.
STIELTJES, T. J. .
Recherches sur quelques series se'iM-convergentes. Ann. sci. de VEcole norm. sup. C)
in. A886), pp. 201—258.
STOKES, SIR GEORGE GABRIEL.
On the numerical Calculation of a Class of Definite Integrals and Itilinitc Scries
(March 11, 1850). Trans. Comb. Phil. »S'oc. ix. A856), pp. 166—187. [Math, and Pkys.
Papers, it. A883), pp. 329—357.]
On the Effect of the Internal Friction of Fluids on the Motion of Pendulums (Dec. 9,
1850). Trans. Camb. Phil. Soc. ix. A856), pp. [8]—[106]. [Math, and Phys. Papers, in.
A901), pp. 1—141.]
On the Discontinuity of Arbitrary Constants which appear in Divergent Developments*
(May 11, 1857). Trans. Camb. Phil. Soc. X. A864), pp. 106—128. [Math, and Phys. Papers,
iv. A904), pp. 77—109.]
Supplement to a paper on the Discontinuity of Arbitrary Constants which appear in
Divergent Developments (May 25, 1868). Trans. Camb. Phil. Soc. XI. A871), pp. 412—426.
[Math, and Phys. Papers, IV. A904), pp. 283—298.1
On the Communication of Vibration from a Vibrating Body to a .surrounding (Jrh*
(June 18, 1868). Phil. Trans, of the Royal Soc. clviii. A808) [1809], pp. 447—463. [Math,
and Phys. Papers, iv. A904), pp. 290-5241
Smith's Prize Examination Papers, Feb. 1853 and Jan. 29, 1807. [Math, and Phys.
Papers, V. A905), pp. 319, 347.]
Note on the Determination of Arbitrary Constants which appear an Multipliers of
Semi-convergent Series (June 3, 1889). Proc. Camb. Phil. Soc. vi. A88!)), pp. 3(is2—MM.
[Math, and Phys. Papers, v. A905), pp. 221-225.]
On the Discontinuity of Arbitrary Constanta that appear as Multipliers of .Sonii-iron-
vergent Seriest (April 23,1902). Ada Math. xxvi. A902), pp. 393—397. [Math, and P/u/s.
Papers, v. A905), pp. 283—287.]
STRUTT, J. W.
See Rayleigh (Lord).
STRUVE, H.
Ueber den Einfluss der Diffraction an Fernrohren auf Lichtachcibcn (May 25, 18H2).
Men. de PA cad. Imp. des Sci. de St. Petersbourg, G) xxx. A882), no. 8.
Beitrag zur Theorie tier Diffraction an Fernrohreu (Aug. 1882). Ami. der 1'hymk und
Ghemie, C) xvxi. A882), pp. 1008—1016.
STURM, J. C. F
Sur les Equations diffe'rentielles lineaires du second ordre (Sept. 28, 1833) Journal da
Math. i. A836), pp. 106—186.
* An abstract will he found in Proc. Royal Soc. xvi. A868), pp. 470—471.
t This, the last published paper which Stokes wrote, contains a summary of 1uh ruBoarclies
composed for the Abel centenary volume.
BIBLIOGRAPHY 785
SUCHAR, P. J.
Sur les equations differentielles lin&iircs re'ciproques du second ordre (Nov. 18, 1903).
Bull, de la Soc. Math, de France, xxxn. A904), pp. 103—116.
SVANBERG, A. F.
De integralibns demiitis disquisitiones. Nova Ada R. Soc. Sci. Upsala, x. A832)
pp. 231—288.
TAKEUCHI, T.
On the integral j">CON^ sin q8, cos qdd6 (May 17, 1920). Tthoku Math. Journal,
xvm. A920), pp. 295—296.
THEISINGER, L.
Beatimmte Tntegrale. Monatshefte fur Math, und Phys. xxiv. A913), pp. 328—346.
THOMAE, J.
Die Brauchbarkeit der Bessel-Fourierschen Reiho. Berichte der Math. Seminar zu Jena,
1912—13, pp. 8—10. [frit. Catalogue of Set. Lit. xin. A913), p. 100.]
THOMSON, SIR JOSEPH JOHN.
/ CON /171
.___ dx. Quarterly Journal, xvur. A882), pp. 377—381.
Recent Researches in Electricity and Magnetism (Oxford, 1893). [Review by A. Gray,
Nature, xux. A894), pp. 357—359.]
THOMSON, W.
Sue. Kolvin (Lord).
T0DHUNTER, I.
Elementary Treatise on Laplace's Functions, Lamp's Functions and BesseVn Functions
(London, 1875).
TURRIERE, E.
Une application goomdtrique do la s6"rie considdriio par Airy dans la diffraction dea
ouvcrtures circulahm Nouvelles Annales de Math. D) IX. A909), pp. 433—441.
UNFERMNGER, F.
t)boi' dio heidon Jntogralo lflBlnaiC!>MGu:-ce)H.i;)f^'' (April 1G, 1808). Wiener Sitzungs-
} sm
berichte, lvh. A808), pp. (ill—620.
VALEWINK, G. 0. A.
Over iiHymptotimjhti ontwikkulingoti (Dissertation, Haarlem, pp. 13H). [Jahrbuch liber
die FortHchritte der Math. llHf>, p. 328.]
VAN VLECK, E. B.
On the RooW of Bcsfiol- and P-fuuotioiiH. American Journal of Math. xix. A897),
pp. 75- -85.
VERDET, E.
Lepo?in d'Optique, Physique, I. (Paris, 1869).
VESSIOT,, E.
Sur (|iielqucH oquatioiiH diffdraitioUos ordinttiroa du Hccond ordro. Aimales dc la Fac.
des Sci dc Toulome, ix. A895), no. <>.
VOLTERRA, V.
Sopra akuuio questioui di invcraione di intograli dofmiti. Ann. di Mat. B) xxv. A897),
pp. 139—178.
VORONOI, G.
Sur une fonction transcendanto ot scs applicationu a la nomination dc quelquos Horiea.
Ann. sci. de PEcoh>. norm. mp. C) xxr. A904), pp. 207—268, 459—534.
Sur le deVeloppement, a l'aide dea fonctions cylindriquiw, dcH Homines doubles
2/ (prri1 + 'iqmn -f rn'*)
oil ?>ma + 2<7??m + rw2 e«t une forme positive a coefficionta en tiers. Verh. des dtritten Int.
Konyresses in Heidelberg A904), pp. 241—24f>.
w. B. F. 60
786 THEORY OF BESSEL FUNCTIONS
WAGNER, C.
Beitrage zur Entwicklung der Bessel'schen Function i. Art. Bern Mittheilungwn, 1894,
pp. 204—266.
Uber die Darstellung einiger bestimmten Integrate durch Bessel'sche Funktionen
(June 12, 1895; Aug. 5, 1895). Bern Mittheilungen, 1895, pp. 115—119; 1896, pp. 53—60.
WALKER, G. T.
Some formulae for transforming the origin of reference of Bessel's functions. Messenger,
xxv. A896), pp. 76—80.
WALKER, G. W.
The scattering of electromagnetic waves by a sphere. Quarterly Journal, xxxr. A900),
pp. 36—49.
WALKER, J.
The Analytical Theory of Light (Cambridge, 1904).
WALLENBURG, G.
Ueber Riccatfsche Differentialglcichungen hohercr Ordnung. Journal fiir Math. cxxi.
A900), pp. 196—199.
Die Difterentialgleichungeu deren allgenieines Integral eine lineare gebrochcno Function
der willkiirlichen Constanten ist. Journal fiir Math. cxxi. A900), pp. 210—217.
Sur l'equation diffeYentielle de Riccati du second ordre (Dec. 14,1903). Gomptes Rendus,
cxxxvn. A903), pp. 1033—1035.
WANGERIN, A.
Cylinderfunktionen oder Bessel'sche Funktionen. Encycloptidie der Math. Wiss. Bd. n.
Teil 1 (Leipzig, 1904—16), pp. 742—757. [Encyclope'die des Sci. Math. Tome n. vol. 5
(Paris et Leipzig, 1914, pp. 209—229), translation by A. Lambert.]
WATSON, G. N.
On a certain difference equation of the second order. Quarterly Journal, xu. A910),
pp. 50—55.
Bessel Functions and Kapteyn Series (April 26, 1916). Proc. London. Math. Soc. B)
XVI. A917), pp. 150—174.
Bessel Functions of Equal Order and Argument (June 17, 1916). Phil. Mag. F) xxxn.
A916), pp. 232—237.
Simple types of Kapteyn Series. Messenger, xlvi. A917), pp. lfH—157.
Bessel functions of equal order and argument (Nov. 13, 1916). Proc. Camb. Phil. Soc.
xix. A918), pp. 42—48.
The limits of applicability of the Principle of Stationary Phase (Nov. 22, 1916). J'ruc.
Camb. Phil. Soc. xix. A918), pp. 49-55.
Bessel functions of large order (June 14, 1917). Proc Camb. Phil. Soc. xix. AOIB),
pp. 96—110.
The Zeros of Bessel Functions (Aug. 17, 1917). Proc. Royal Soc. xoiv. A A1I8), pp.
190-206.
Bessel Functions of Equal Order and Argument. Phil. Mag. F) xxxv. A918), pp. 364—
370.
The Diffraction of Electric Waves by the Earth (May 29, 1918). Proc. Royal Hoc. xciv.
A A919), pp. 83—99.
The Transmission of Electric Waves round the Earth (Jan. 13, 1919). Proc. Royal Soc
xcv. A A919), pp. 546-563.
On Nielsen's functional equations. Messenger, xlviii. A919), pp. 49—53.
The zeros of Lommel's polynomials (May 15, 1919). Proc. London Math. Soc. B) xix.
A921), pp. 266—272.
WEBB, H. A.
The exjjansion of an arbitrary function in a series of Bessel functions. Mesneix/ei- xx xm
A904), pp. 55-58.
On the Convergence of Infinite Series of Analytic Functions (Nov. 10, 1904). Phil.
Trans, of the Royal Soc. cciv. A A904), pp. 481—497.
WEBER, H.
Ueber cinige bestimmte Integrate (Jan. 1868). Journal fiir Math. lxix. A869), pp
222—237. " ll
Ueber die Integration der partiellen Differentialgleichung: ^ + ^ + ?% = 0 (July,
1868). Math. Ann. i. A869), pp. 1—3i>. ** V
BIBLIOGRAPHY 787
Ueber die Besselaohon Functionon und ilire Anweadung auf die Theorio der eloktrischen
KtrSme (May, 1872). Journal far Math. lxxv. A873), pp. 75—105.
Ueber die stationa'ren Strb'mungen der Electrieitat in Oylindern (Sept. 1872). Journal
fur Math, lxxvi. A873), pp.-1—20.
Ucber eiiie Darstellung willkiivlichcr Functionon durch Beasol'scho Functionon (Ocfc.
1872). Math. Ann. vi. A873), pp. 146—161.
Zur Theorie der Bessel'aehen Functionen (July, 1890). Math. Ann. xxxvii. A890),
pp. 404—416.
WEBER, H. F.
Die wahro Theorie der Fresnel'schen Interferonz-Erschoinungcn, Zurich Viarteljahrs-
schrift, xxxv. A879), pp. 33—76; Ann. der Physih und C'hemie, C) viu. A879), pp. 407—444.
WEBSTER, A. G.
Application of a definite integral involving Besaol's futictioii.s to the .self-inductanoe of
solenoids (Dec. 29, 1905). Bulletin American Math. Soc. xiv. A907), pp. 1 -0.
WENDT, CACILIE.
Eino Verallgemeinorung dew Additionsthooroiucs der Bcsael'schcn Functionen eiuter
Art. Monatshefte fur Math, und Phys. xi. A900), pp. 125—131.
WEYL, H.
Singulare Integralgloichungen (April, 1908). Math. Ann. lxvi. A909), pp. 273—324.
WEYR, E.
Zur Integration d«r Diftbrential-Qloiehungen crater Ordnung. Abh. bb'hm. Gcs. Wisx.
(Prog), F) viii. A870—76), Math. Mom. 1.
WHEWELL, W.
Of the Intrinsic Equation of a Curve and ita Application (Fob. 12, 1849). Trans. Camb.
Phil. Sue. vijr. A849), pp. 659—671.
Second Moraoir on the Intrinsic Equation of a Curve and itH Application (April If),
1850). Tram. Camb. Phil. Hoc. ix. A850), pp. lf>0—15(j.
WH1PPLE, F. J. W.
Diffraction by a wedge and kindred problems (Nov. 8, l!Mf>). Proc. London Math. Hoc.
B) xvr. A917), pp. 94—111.
WJ11TE, V. V.
Tlio Diffraction of Plane Electromagnetic VVavas by u Perfoctly Rcllccting Sphcro (Juno
9, 1921). Proc. Royal Soc. c. A A1J2), pp. OOfi -525.
W1JITEHEA1), (!. a.
On the functions ber.e, beia?, kcr.r, kei:f. Quarterly Journal, xi.u. A911), pp. 'MQ—342.
WH1TTAKER, K. T.
On the (Joncral Solution of Laplaco'.s E(piation ami t.ho Equation of Wavo MotioiiH and
on an undulatory explanation of Gravity. Monthly Notices of the Jl. A. S. LXll. A902),
pp. 017—620.
On the partial diflbrential equations of mathematical physics. Math. Ann. lvii. A903),
pp. 333—355.
.On a new Connexion of UeaHel Funotioim with Legnndre Functions (Nov. 13, 1902).
Proc. London Math. Soc. xxxv. A003), pp. 198-20E.
'VV1GEKT, S.
Sur. quelquos functions aritluuctiquea (March, 1913). Ada Math, xxxvii. C1014), pp.
113—140.
WILLIAMSON, 15.
On the Solution of certain Differential Equations (March 5, 18f>(->): Phil. Mac/. D) xi
A856), pp. 364—371.
WILLSON, R. W. AND PEIRCIS, B. 0.
Table of the first forty roots of the BcshoI equation ./„(.»;)=0 with the corresponding
values of J\{x). Bulletin American Math. Soc. in. A897), pp. 153 155.
WILTON, J. It.
A continued fraction Holutiou of the linear differential equation of the second order.
Quarterly Journal, xlvi. A915), pp. 318--334.
50—2
788 THEORY OF BESSEL FUNCTIONS
WIRTINGER, W.
Zwei Bemerkungen zu Airy's Theorie des Regenbogens. Berichte des natur.-med.
Vereins in Innsbruck, xxni. A897), pp. 7—15.
WORMS DE ROMILLY, P.
Note sur l'inte'gration de l'e'quation
da** x dx*
Journal de Math. C) iv. A878), pp. 177—186.
YOUNG, W. H.
On infinite integrals involving a generalisation of the sine and cosine functions (Oct. 6,
1911). Quarterly Journal, xliii. A911), pp. 161—177.
On series of Bessel functions (Dec. 6,1917). Proc. London Math. Soc. B) xvni. A920)
pp. 163—200.
ZELINSKIJ, I. I.
On the integration of Riocati'a equation (Jan. 27, 1890). Proc. Phys. Math. Section,
Naturalists Soc. Imp. Univ. Kazan, vm. A890), pp. 337—342.
790
THEORY OF BESSEL FUNCTIONS
Pn(r; <h, a.,,...,an),420 T_nD 343
Pn (r; a1} a,,..., on \p)} 421 Tn (t, a), 320
P (x, 4 205 Tn (*,#), 582
Tn(*,a;; 5), 602
Tn(t, a:\R\m
(a, b, c,
PU, /3, 7, 4,158
&, 227
&«(*), 166
?,606
?-, 0
), 299
Sn, Sn', 55
5,@,285
/?„(*), 591
5BD 658
, «; #), 598
r|i2), 610
), 152
Sin (a), 320
^o D Sv® (z), 263
SnD
), 345
^,33
Un(z), 71,340
?7-»D 343
Un(w,z), 537
#¦„ (w, 4 537
7n(w, 4 537
Vv (w, z), 538
W, D 339
3», 42
w, 552
F, (^), 64
F("» D 67
F«B» D 70
Yo (z), 59
YnD 58
Y_n D 59
YF(*),63
y^, y/. y", 485
a («), 204
/3D 204
7>60
7 (i;, so), 204
«», 22
&»(*), 56
©, 112
e», 27 ; 291
0, 112
*, 19; 112
\m, 577
/*, 26; 38
/*3, /*2, /*83 ••
vt 38
o-Jr», 502
9, 9r> HI
^,514
^t, 280
nM @,290
iff, 51; 83
(a)n, 100
(v, m), 198
[n], 43
i) ¦m
(«+)
,20
m>0
,1,103
488
LIST OF AUTHORS QUOTED
[The numbers refer to the pages. References are not t/iren to entries in thf bibliography,
pp. 753—788.]
Abel, N. H., 68, 616, 621 Borel, E., 8, 281, 536
Adamotf, A., 196 Bourget, J., 6, 324, 325, 326, 484, 485, 517,
Aichi, K., 80 _ 659, 660
Airey, J. R., 63, 142, 214, 247, 319, 502, 505,' Brajtzew, J. II., 169
516, 659, 660 B'rasainne, E., 91
Airy, Sir George B., 188, 189, 229, 249, 320, Brenke, W. C, 23
321, 322. 654, 659 Bridgeman, P. W., 597
Aldis, W. S., 65, 655, 656, 657, 658, 662, 663, Bromwich, T. J. L'a., 8, 11, 44, 68, 156, 187,
664 189, 191, 202, 203, 214, 230, 231,234, 279,
Alexander, P., 579
Anding, E., 313, 057
302, 349, 360, 385, 391, 393, 399, 574, 575,
E01
Anger, C. T., 21, II, 308, 309, 310, 311, 312 Brims, H., 327
Auisimov, V. A., iJ Bryan, G. H., 127, 480
Appell, P. it, 146, 371 Burkhardt, H. F. K. L., 236, 280
Autonnc, L., 94 Burnsklc, \V. S., 305
Bach, D., 96, 102, 110 Cailler, ('., 44, 14!), 386, 395, 415, 437, 455,
Baehmann, P., 197 530, 537
Baehr, G. F. \V., 470 Callandmui, 0., 19A, 208, 387
Hall, L. dc, ir>7 (.'antor, G. K. L. l\, 037
Barnes, E. \\\, 83, 100, 102, 104, 10"), i:»(>, Cavlini, 1\, (j, 7, 11L, 225, 22(i, 227, 249, 255,
190, 192, 195, 10(8, 220, 221, 340, 351, 357, 2«H, 572
367, 383, 387, 402, 409 (Vir*la\v, II. S., 177, 3(i(i, 395, 499, 500, 507,
Basset, A. B., 7E, 77, 78, 80, 172, 173, 180, 509, 5S3
385, 388, 395, 425, 426, 454 Catalan, K. (-.,21, 22, 27, 96, 173, 188
iijitunian, II., 130, 131, 367, 370, 372, 373, Cauehy, (Baron) A. I,., 7, 15, 16, 21, 150,
376, 379, 380, 38i), 406, 417, 437, 456, 530, 183, 230, -231, 232, 233, 2 47, 249, 259, 309,
533, 535 319, 324, 449, 545, 554, 557, 579
Bauer, (J., 50, 128, 3(>s, 370 Cayley, A., 88, 90, 96, 102, 103, 109, 188,
Beltrami, E., 51, 358, 361, 374, 386, 389, 390, 502
391, 500, 579, 621 Challis, II. W., 9L
Bernoulli, Daniel A700-1782), 2, 3, 4, 9, 85, Chapman, «., 621
86, 87, 88, 111, 123, 478, 576 Chessin, A. S., 135, 175, 325, 346, 382
Bernoulli, Jaiue.s A65-1-1705), 1, 2, 3, 88, 90, Chree, G, 6, 597
92 Chri.sloftel, E. B., 154
Bernoulli, John A667-1748), 1, 2, 3 Chryatal, (,'., 102, 288, 295
Bernoulli, Nicholas, A687-1759), 2 Cinclli, M., E33
Bernoulli, Nicholas, AE95-1726), 2 Clebach, R. F. A., 359, 363
Be.ssel, F. W., 1, 3, 4, 5, 9, 13,14, 15, 18, li), Clifford, W. lv., 90, 91
21, 24, 25, 38, 84, 140, 148, 153, 160, 295, Coatcs, U. V., 173, 180, 313, 622
308, 478, 551, 554, G54 Cotter, J. R., 41
Binet, J. P. M., 183 Crawford, L., 27
B6chor, M., 46, 57, 64, 376, 494, 495, 517 Crelier, L., 28E, 287, 288, 295, 300, 301, 302
Bohmcr, P. E., 142 Curtis, A. li., 96, 110
Boolo, G., 27, 47, 110, 627 Curzon, H. E. J., 395
792
THEORY OF BESSEL FUNCTIONS
D'Alembert, J. le Rbnd, 3
Dandelin, G. P., 503
Darboux, J. G., 233
Darwin, C. G., 437
Debye, P., 225, 235, 237, 240, 241, 247, 249,
250, 251, 255, 262, 263, 268, 513, 516
De la Vallee Poussin, Ch. J., 53, 160, 189
De Morgan, A., 188, 190
Dendy, A., 107
Dini, U., 10, 577, 578, 597, 600, 616, 651
Dinnik,A., 579, 659,660
Dirichlet, P. G. Lejeune, 157, 230, 406, 581,
623
Dixon, A. C, 35, 480, 481, 482
Donkin, W. F., 109
Dougall, J., 65, 411
Du Bois Reymond, P. D. G., 183, 455, 470
Duhamel, J. M. C, 38, 49, 59, 68, 227
Earnahaw, S., 108
Ellis, R. L., 95, 109,110,173
Emde, F., 248
Encke, J. F., 342
Enestrom, G., 92
Enneper, A., 173
Epstein, S. S., 145, 290
Ermakoff, W., 455
Escherich, G. von, 165
Euler, L., 3, 4, 5, 6, 24, 49, 53, 60, 62,87,88,
92, 93, 123, 133, 183, 410, 498, 500, 501,
503, 576, 659
Falkenhagen, J. H. M., 94
Fej&, L., 610
Feldblum, M., 92
Fields, J. C., 110
Filon, L. N. G., 51, 578, 622, 623, 625, 629
Ford, W. B., 578, 605
Forsyth, A. R., 42, 57, 107, 109, 117, 346,
358, 400, 499
Fourier, (Baron) J. B. Joseph, 4, 9,10, 13,
22, 84, 135, 449, 450, 454, 455, 456, 478,
482, 483, 501, 576, 577, 578, 616
Freeman, A., 501
Frenet, F., 27
Fresnel, A. J., 544, 545
Frobenius, F. G., 57
Frullani, G., 14, 19
Gallop, E. G., 405, 421, 422
Gaskin, T., 109
Gasser, A., 509, 517
Gauss, C. F. (Johann Friedrich Carl), 191,506
Gegenbauer, L. von, 50, 51, 129, 138, 151,
274, 283, 284, 290, 293, 351, 362, 363, 365,
366, 367, 368, 369, 370, 373, 378, 379, 383,
384, 385, 386, 389, 390, 391, 393, 395, 396,
398, 406, 407, 413, 414, 415, 418, 426, 430,
438, 439, 480, 508, 517, 522, 524, 525, 579
Genocehi, A., 119
Gibson, G. A., 197
Gifford, E., 662
Gilbert, L. P., 545, 548, 549
Giuliani, G., 155, 156, 324, 326, 327
. Glaisher, J. W. L., 89, 96,102,103,108, 109,
140, 171, 173, 183, 664
Gordan, P. A., 55
Goursat, Edouard J. B., 120
Graeffe, C. H., 502, 503
Graf, J. H., 32, 64, 75, 145, 153, 160, 165,
175, 197, 215, 227, 286, 287, 290, 295, 296,
299, 301, 302, 303, 341, 344, 345, 359, 360,
362, 398, 498, 502, 583
Gray, A, 64, 65, 78, 194, 206, 454, 480, 655
656, 657, 658, 660
Green, G., 124
Greenhill, Sir A. George, 91, 9G
Gregory, Duncan Farquharson, 391
Gregory, Walter, 224
Grunert, J. A., 27
Gubler, K, 32, 64, 145, 160, 165, 177, 197,
215, 227, 286, 287, 301,329, 341, 351, 398,
408, 410, 426, 498, 502, 583
Gunther, S., 153
Gwyther, R. F., 621, 636
Hadamard, J., 204, 205, 527
Haentzschel, E., 71, 96, 159
Hafen, M., 389
Hague, B., 656
Hall, A, 15
Hamilton, Sir William Rowan, 12, 195, 655
Haukel, H., 10, 38, 57, 58, 61, 62, 63, 65, 73,
75, 76, 77, 160, 163, 164, 165, 167, 175,
195, 196, 203, 206, 208, 211," 384, 386, 390,
393, 395, 424, 427, 428, 429, 430, 434, 453,
454, 456, 457, 468, 459, 462, 464, 465, 471,
488, 513, 514, 577, 579, 581, 582, 633
Hansen, P. A., 14, 20, 30, 31, 37, 152, 154,
155, 158, 195, 292, 406, 655, 656
Hanumanta Rao, C. V., 437
Hardy, G. H., 8, 111, 180,183, 188,189, 200,
309, 320, 321, 322, 324, 373, 382, 386, 395,
406, 421, 422, 437, 441, 442, 463, 464, 542,
546, 547, 573, 575, 579, 606, 615, 621
Hargreave, C. J., 88, 170,171
LIST OP AUTHORS QUOTED
793
Hargreaves, R., 538
Haruack, A., 577
Harris, R. A., 15
Havelock, T. H., 125, 171
Hayashi, T., 165
Heaviside, 0., 64, 6.'), 203, 307, 385, 387, 388,
393, 395, 410, 426
Heine, H. E., 4, 50, 05, 66, 84,154, 155, 156,
157, 181, 358, 363, 305
Herrnite, C, 55, 477
Hertz, H., 80, 81
Herz, N., 554, 555
Hill, C. J. D., 94
Hobsou, K. W., 10, 33, 54, 58,125, 128, 120,
149, 172, 174, 280, 353, 363,369, 385, 386,
387, 480, 485, 578, 586, 591, 602
Hopf, L., 178, 406
Horn, J., 225, 526
Hurwitz, A., 9, 297, 302, 303, 304, 305, 306,
307, 483, 484
Ignatowsky, W. von, 365
Iaherwood, J. <}., 057, 658, 604
Jaukson, Dunham, 343
Jackson, Frank Hilton, 43, 44
Jackson, William Hartas, 177
Jaoobi, C. O. .)., (i, H, 14, 21, 22, 25, 20, i>7,
28, 29, 84, ISJ5, 37i), r>f>5, 572
Janict, K. V., 94
Johnson, W. W., 92
Jollifle, A. R, 528, 529
Julius, V. A., 65, 200
Kaliihne, A., 505, 507, 600
Kapteyn, W., 3ft, 1H3, 200, 268, 279, 281,
282, 292, 351, 370, 373, 370, 380, 38E, 404,
413, 498, 499, 531, 032, 533, f>35, 536, 538,
551, 55!), 560, 502, 565, :,(](}, 568, 509,
570
Kelvin (Sir William Thomson), Lord, 81,
124, 203, 225, 229, 230, 233, 21H, 054,
05B
Kepii'ialci, S., 99
Kepler, J., 551, 552
Kirchhoff, G., 107, 196, 203, 389, 578, 016
Kluyvcr, J. U, 367, 41!), 420
Knoser, J. C. O. A., 499, 57H, 583
Knockenhauer, K. W., 545
Konig, J., 354, 523
Koppe, M., 247
Kummor, K. E., 49, 90, 101, 102, 104, 105,
148, 185, 190, 101, 190, 203, 394, 405)
Lacroix, S. F., 27
Lngrange, J. L. de, 6, 27, 28, 551
Lamb, H., 56, 96, 385, 416, 475, 502
Lambert, J. H., 485
Lame", G., 96, 159
Landan, E. G. H., 197
Laplace, P. S. do, 0, 7, 8, 9, 83, 280, 395, 421,
450
Lavgeteau, C. L., 501
Laurent, Paul Mathieu Hermann, 157
Laurent, Pierre Alphonse, 100
Leliedeff, Wera Myller-, 99
Lebesgue, Henri, 457
Lebesgue, Victor Am&liSe, 110, 123
Lefovt, P., 6
Legendre, A. M., 52, 90, 183, 204, 485, 557
THospital, Gr. P. A. (Marquis de St Mesme),
134
Leibniz, G. W., 1, 2, 3
Le Paige, C, 96
Leroh, M., 382, 393, 433, 434, 617
Lindner, P., 484
Lindstedt, A., ^45, 601
Lipnville, J., 27, 28, 87, 111, 112, 116, 117,
119, 120, 123
Lipschitz, R. O. B., 11,12, 195, 200, 206, 331,
339, 3H 1, 386, 390, 633
Lobatsclicvsky, X., 503
Lobalto, R., 49, 90
Lodge, A., 224, 229
Lomniul, K. V, J. von, 13, 21, 23, 25, 30, 34,
38, 43, 45, 40, 47, 49, f>3, 5!), E2, 65, 66,
71, 73, 7E, 77, 96, 07, 9H, 99, 10E, 107,132,
133, 130, 13E, 140, 142, 143, 145, 148, 151,
152, 154, 190, 200, 294, 295, 296, 297, 208,
299, 300, 303, 308, 315, 328, 341, 345, 3-lH,
350, 304, 374, 400, 478, 479, 4H2, 529, 531,
537, 53H, 539, 540, 642, 543, 544, 545, 646,
f>4H, 549, f>50, 576, 654, 655, 050, 658, 0E0,
001, 004
Lorenz, L., 57, 90, 224, 229, 500
Love, A. E. IL, 50, 226, 417, 449, <J54, E62
Macdonald, 11. M., 7K, 79, HO, 158, 170, 171,
225, 229, 233, 305, 377, 385, 38E, 389, 395,
396, 112, 413, 439, 440, 482, 505), 511
Maclean, M., 0;"8
Mi-Mulion, J., 01, ,195, 200, 505, 507, 581
Mac Robert, T. M.J 197
Maggi, G. A., 13
MalniHti5n, C. J., 99, 173, 18.",, 187, L88, 19E,
203
Manftediiw, G., 92
HO—5
794
THEORY OF BESSEL FUNCTIONS
March, H. W., 56, 225, 449
Marcolongo, R., 135
Marshall, W., 505, 506
Mathews, G. B., 64, 65, 78, 194, 206, 454,
480, 655, 656, G57, 658, 660
Maxwell, J. Clerk, 125
Mayall, R. H. U., 550
Mehler, F. G., 65, 155, 157, 169, 170, 180,
183, 425, 431, 455, 475, 476
Meisael, D. F. E., 7, 145, 204, 226, 227, 229,
232, 233, 234, 247, 391, 521, 557, 558, 561,
564, 672, 655, 656, 658, 660, 662
Mellin, R. Hj., 190, 196
Mittag-Leffler, M. G., 83, 497
Molins, H., 106
Moore, C. N., 479, 578, 579, 597, 649
Morton, W. B., 65, 66
Murphy, R., 91, 156, 157
Myller-Lebedeff, W. (see Lebedeff)
Nagaoka, H., 340, 633, 634
Neumann, Carl Gottfried, 16, 19, 22, 23, 30,
31, 32, 33, 34, 36, 37,46, 59, 60, 65, 66, 67,
68, 69, 70, 71; 73, 128, 143, 150,151, 155,
271, 273, 274,276, 277, 278, 280, 281, 284,
286, 290, 291, 292, 345, 358, 359, 361, 363,
365, 386, 418, 424, 440, 441, 453, 455, 456,
470, 471, 473, 474, 475, 476, 522,523, 524,
525
Neumann, Friedrich E., 154
Newman, F. W., 663, 664
Newton, Sir Isaac, 120
Nicholson, J. W., 107, 108, 145, 146, 149,
150,189, 226, 229, 231, 247, 248, 249, 250,
252, 262, 329, 332, 413, 415, 425, 426, 431,
440, 441, 446, 448, 505, 656
Nicolas, J., 77, 84
Nielsen, N., 24, 44, 49, 64, 73, 74, 77, 82, 83,
132, 142,145, 148, 149, 154, 169, 224, 297,
298, 299, 315, 350, 355, 357, 359, 392, 405,
455, 465, 522, 523, 52*5, 526, 527, 528, 571,
572, 574, 597, 622, 629, 636
Niemoller, F., 57, 68, 195
Olbricht, R., 158, 481
Oltramare, G., 173
Orr, W. McF., 145,146,206,224,454,455,579
Otti, H., 71, 274, 286, 341
Panton, A. W., 305
Paoli, P., 53, 95, 186
Parseval, M. A., 9, 21, 24, 68, 105, 229, 358,
359, 384
Pearson, Karl, 98, 99, 419, 421
Peirce, B. O., 501, 660, 664
Perks, J., 44
Perron, 0., 154
Petzval, J., 49
Phragm&i, E., 358
Picard, C. &., 93, 94
Pineherle,S., 190,196, 271, 274, 386, 526, 528
Plana, G. A. A., 10, 38, 42, 45, 49, o3, 95, 96,
99, 195, 554
Plummer, H. C, 270, 552, 555
Pochhamrner, L., 100, 101, 297, 346, 410
Pocklington, H. C, 537
Poincare", J. Henri, 236
Poisson, S. D., 6, 9,10, 11, 12, 13, 24, 25, 38,
47, 49, 52, 67, 68, 69, 73, 95, 96, 160, 173,
183, 185,186,187, 194, 195, 308, 369, 477,
501
Porter, M. B., 299, 477, 480, 485, 515, 517
Preece, C. T., 27
Puiseux, V., 559
Raffy, L., 94
Ram an nj an, S., 382, 449
Rawaon, R., 91
Rayleigh (J. W. Strutt), Lord, 50, 55, 56, 74,
95, 137, 155, 157, 189, 230, 231, 233, 331,
333, 374, 389, 395, 41i), 421, 477, 502, 510,
511, 616, 618, 660
Riccati, (Count) J. 1<\, 1, 2,3, 85,86, 87, 88,94
Riemann, G. F. ?., 80, 158, 172, 203, 229,
235, 427, 457, 486, 623, 637, G49
Riesz, M., 606, 614
Rodrigues, 0., 27
Rohrs, J. R, 10
Rudski, P., 477, 508
Russell, A., 81, 82, 204
Rutgers, J. G., 373, 374, 370, 37E, 380, 579
Rybczynaki, W. von, 56, 225, -149
Sasaki, S., 507
Savidge, H. G., 82, 204, 658
Schafheitlin, P., 64, 137, 142, Ki8, 169, 207,
215, 373, 391, 392, 398, 401, 402, 400, 408,
421, 447, 477, 479, 482, 485, 487, 489, 400,
491, 492, 493, 494, 508, 510, 543
Scheibner, W., 6
Schlafli, L., 10, 14, 27, 28, 30, 32, 33, 63, 04,
65, 67, 72, 79, 90, 91, 143, 145, 151, 160,
171, 174, 175, 176, 178, 179, 181, 185,195,
196, 215, 216, 228, 253,274, 276, 278, 284,
285, 286, 288, 289, 290, 341, 342, 344, 345,
508, 577, 579, 581, 582, 583, 585
LIST OF AUTHOES QUOTED
795
Schlomilch, 0. X., 14, 18, 33, 34, 35, 36,153,
173,183,617,618,619,621,622,628,655,656
Schonholzer, J. J., 145
Schott, G. A., 551, 556, 572, 573
Schwarz, K. H. A., 358, 643
Schvvarzschild, K., 361
Schwerd, F. M., 477, 654
Searle, J. H. C, 199
Segar, H. W., 483
Serret, J. A., 171, 173, 188
Sharpo, H. J., 105, 157
Sheppard, W. F., 199, 454, 579, 595, 615
Siacci, F., 92
Siegel, C. L., 485
Siemon, P., 328, 398
Smith, Bernard A., 655
Smith, Clam E., 621
Smith, Otto Andreas, 50
Sommerfeld, A. J. W., 56, 57, 178, 361, 389,
395, 406, 417, 464, 409 /
Sonine, N. J., 82, 83, 132,137, 139,143,169,
170, 171, 175, 176, 177, 180, 279, 280, 281,
290, 353, 354, 362, 363, 367, 373, 374, 375,
376, 377, 378, 383, 386, 391, 394, 395, 398,
401, til, 415, 417, 118, 431, 432, 433, 434,
439, 454
Kpitzcr, S., 68, 71, 153
Stearn, H., 482, E-21
Steiner, L., 655, 6(>l
Steinthal, A. R, 171, 387
Stephenaon, A., 579
Shorn, TV1. A., 500
Stieltjcs, T. J., 195, 19E, 207, 2OH, 20J), 213,
214, 464
Stirling, Jam on, 7, 8, 214
Stokes, Sir George Gabriel, 8, 12, 53, 55, 68,
<>9, 70, 80, 05, 97, 188, 189, 190, 201, 202,
SWfi, 229, 238, 320, 324, 336, 391, 405, 503,
505, 507, 605, 659
StruU, J. W. (see Raylcigli)
Struvc, U., 328, 329, 333, 337, 392, 396, 397,
417, 661
St.unn, J. 0. F., 304, 477, 479, 517, 518, 521
Sucslmr, P. J., 90
Kvanborg, A. F., 173
Takouuhi, T., 313
Tannery, J., 11, 156, 302
Theisinger, L., 184, 185, 338
Thomson, Sir Joseph John, 65, 173
Thomson, Sir William (see Kelvin)
Tisserand, F., 371
Todhunter, I., 27, 157, 199
Turriere, E., 15
Unferdinger, P., 310
Valewink, 0. 0. A., 196
Vandermondc, A., 102
van Vleck, E. B., 480
Verdet, ft, 477
Vessiot, E., 94
Volterra, V., 579, 621
Voronoi, G., 200
Voas, A., 406
Wagnor, C, 13, 142
Walker, Gilbert Thomas, 360, 361
Walker, James, 328, 331, 333, 537, 544
Wallonburg, G., 94
Waring, E., 503
Watson, O. N., 11, 105, 125, 158, 226, 231,
49, 268, 355, 444, 483, 485, 513, 519, 566,
575
Webb, II. A., 351, 523, 533, 536
Wobor, Hoinrich, 63,64,67,75,165,167,195,
196, 210, 211, 212, 380, 391, 392, 393,394,
39f>, 396, 398, 402, 405, 406, 408, 421, 450,
451, 452, 453, 454, ,455, 408, 469, 470, 495
Wobor, Hoinrich Friedrich, 308,309,310,311,
312, 3L5, 320
WoiorBtriwH, C. T. VV., 358
Wcndt, (Jiicilio, 363
Weyl, II., 189, 454
Weyr, R, 93, 94
Whowcsll, W., 479
Whipple, P. J. W., 177, 313, 387
Whitohead, C. S., 81, 82, 132, 148, 203
Whit,taker, E. T., 44, 50, 124, 126, 173, li>7,
339, 503, 032, 633
WigoH, (!. S., 200
WilliuniHon, 13., 110
WillHon, R. W., 501, 660, 604
Wilton, J. K., 154
Wirtinger, W., 189, 190
Young, W. H., 10, 351, 406, 578, 579, 580,
582, 586, 596, 616, 617
GENERAL INDEX
[The numbers refer to the pages.]
Addition theorems, 358-372 (Chapter xi); for Bessel coefficients of order zero, 128, 359; for Bessel
coefficients of order ?(, 29; for Bessel functions of the first kind (Gegenbauer's type), 362, 367;
for Bessel functions of the first kind (Graf's type), 130,143, 359; for Bessel functions or cylinder
functions of any kind (Gegenbauer's type), 363; for Bessel functions or cylinder functions of any
kind (Graf's type), 143, 361; for hemi-cylmetrical functions, 354; for Lommel's functions of two
variables, 543; for Schlafli's function fn(z), 344; for Schlafli's polynomial, 289; integrals de-
derived from, 367; physical significance of, 128, 130, 361, 363, 366; special and degenerate forms
of, 366, 368
Airy's integral, 188; expressed in terms of Bessel functions of order one-third, 192; generalised by
• Hardy, 320; Hardy's expressions for the generalised integral in terms of the functions of Bessel,
Anger and Weber, 821; references to tables of, 659
Analytic theory of numbers associated with asymptotic expansions of Bessel functions, 200
Anger's function 3V B), 308; connexion with Weber's function, 310; differential equation satisfied
by, 312; integrals expressed in terms of, 312; recurrence formulae for, 311; representation of
Airy's integral (generalised) by, 321; with large argument, asymptotic expansion of, 313; with
large argument and order, asymptotic expansion of, 316
Approximations to Bessel coefficients of order zero with large argument, 10,12; to Bessel functions
of large order (Carlini), 6, 7; (extensions due to Meissel), 226, 227, 232, 247, 521; (in transitional
regions), 248; to functions of large numbers (Darboux), 233; (Laplace), 421; to Legendre func-
functions of large degree. 6-5,155,157,158; to remainders in asymptotic expansions, 213; to the sum
' of a series of positive terms, 8. See also Asymptotic expansions, Method of stationary phase and
Method of steepest descents
Arbitrary functions, expansions of, see Neumann series and Eapteyn series (for complex variables);
Dini series, Fourier-Bessel series, Neumann series and Schlomilch series (for real variables)
Argument of a Bessel function denned, 40
Asymptotic expansions, approximations to remainders in, 213; conversion into convergent series,
204; for Bessel coefficients of order zero with large argument, 10, 12, 194; for Bessci functions
of arbitrary order with large argument, 194-224 (Chapter vn); (functions of the first and second
kinds), 199 ; (functions of the third kind), 196; (functions of the third kind by Barnes' methods),
220 ; (functions of the third kind by Schlafli's methods), 215; (functions with imaginary argu-
argument), 202; for Bessel functions with order and argument both large, 225-270 (Chapter viii);
(order greater than argument), 241; (order less than argument), 244 ; (order nearly equal to argu-
argument), 245 ; (order not nearly equal to argument, both being complex), 262; for combinations of
squares and products of Bessel functions of large argument, 221, 448; for Fresnel's integrals,
545 ; for functions of Anger and Weber (of arbitrary order with large argument), 313; (with order
and argument both large), 316; for Lommel's functions, 351; for Lommel's functions of two
variables, 549; for Struve's function (of arbitrary order with large argument), 332; (with order
and argument both large), 333; for Thomson's functions, ber (z) and bei (z),203; for Whittakor's
function, 340; magnitude of remainders in, 206, 211, 213, 236, 314, 332, 352, 449; sign of
remainders in, 206, 207, 209, 215, 315, 333, 449. See uko Approximations
Basic numbers applied to Bessel functions, 43
Bateman's type of definite integral, 379, 382
Bei B), Ber B). See Thomson's functions
Bemoullian polynomials associated with Poisson's integral, 49
Bernoulli's (Daniel) solution of Biecati's equation, 85, 89, 123
Bessel coefficient of order zero, <70 (z), 3, 4; differential equation satisfied by, 4, 5 ; (gencrul solu-
solution of), 5, 12, 59, 60; expressed as limit of a Legendre function, 65, 155, 157; oscillations of 11
uniform heavy chain and, 3,4; ParsevaPs integral representing, 9; with largo argument, asymp-
asymptotic expansion of, 10, 12, 194; zeros of, 4, 5. See also Bessel coefficients, Bessel functions and
Bessel's differential equation
BeBsel coefficients J,, (z), 5, 6, 13, 14-37 (Chapter 11); addition theorem for, 29; Bessel's integral
for, 19; expansion in power series of, 15; generating function of, 14, 22,23; inequalities satisfied
by, 16, 31, 268; notations for, 13, 14; order of, 14; (negative), 16; recurrence formulae for, 17;
square of, 32; tables of (of orders 0 and 1), 662, 666-G97; (of order m). 664, 730-732; (with equal
order and argument), 664, 746; tables of (references to), 654, 655, 656, 658. See also Beasel
coefficient of order zero, Bessel's differential equation and Bessel functions
Bessel functions, 38-84 (Chapter 111); argument of, denned, 40; differential equations of order
higher than the second satisfied by, 106; expressed as limits of Lame functions, 159; expressed
as limits of JP-functions, 158 ; history of, 1-13 (Chapter 1); (compiled by Maggi and by Wagner),
13; indefinite integrals containing, 132-138 ; order of, defined, 38, 58, 63, 67, 70; rank of, de-
defined, 129 ; relations between the various kinds of, 74; representation of cylinder functions in
terms of, 82; solutions of difference equations in terms of, 83, 355; solutions of Laplace 'si
GENERAL INDEX 797
equation containing, 83,124; solutions of the equation of wave motions containing, 125 ; three-
term relations connecting, 300; with negative argument, 75. Sec also the two "preceding and ten
following entries, and Cylinder functions
Bessel functions of the first kind, Jv (z), 38; addition theorems for, 143, 359, 362, 863, 367,368;
Barnes' type of integral representing, ISO; Bessol's type of integral representing, 176; cut in
plane to render uniform, 46 ; differential equation (Bessel'a) satisfied by, 38 ; expansion of, in
ascending series, 40; expansion of, in descending series, see Asymptotic expansions; expressed
as a generalised hypergeomotric function, 100, 101; expressed as the limit of a hypergeometric
function, 154 ; expressed as the limit of a Legendre function, 156; (physical significance of), 155;
expressed as the limit of a Lommel polynomial, 302; functional properties of, 45; generalisations
of, 43,44,308-3/57; inequalities satisfied by", 49,255, 259,270,406; infinite integrals containing,
Chapter xni, jjaxsivi; of complex order, 46; of order n.+ \, 41; (expressed in finite terms), 52,
55 ; (notations for), 55, 80 ; Poisson's integral representing, 47, 48 ; (modifications of), 161,163,
164, 169, 170; products of, see Products of Bessel functions; quotient of two, expressed as a
continued fraction, 153, 154, 303; recurrence formulae for, 45, 294; relations with Lommel's
polynomial, 297; represented by integrals containing Legendre functions, 173, 174; symbolic
formulae for, 170; tables of (of orders 0 and 1), 662, 666-697; (of order n), 664, 730-782 j (of
order n+^|, 664, 740-745; (of order J), 664, 714-729; (of order - J, method of computing), 664;
(with equal order and argument), 664, 746; (zeros of), 664, 748-751; tables of (references to),
654, 655, 656, 658, 659, 660 ; Weierstrassian product representing, 497 ; with large argument, see
Asymptotic expansions; zeros of, see. Zeros of Beasel functions
Bessel functions of the second kind, Y,, (a) (after Hankel), 57, 63; G7l (z) (after Heine), 65; lr<"> (z)
(after Neumann), 67; Yv(z) (after Weber-Sehliifii, the canonical form), 63; addition theorems
tor, 144, 361, 365, 368; Bessel'a type of integral representing, 177; component parts of, 71, 72,
340; continuity of (qua function of their order), 63; differential equation (Bessel's) satisfied by,
59, 63; expansion of, in ascending series, 59, 60, 61, 69, 72 ; expansion of, in descending series,
see Asymptotic expansions; expressed as an integral containing functions of the first kind, 5,
133, 382, 433 ; infinite integrals containing, 385, 387, 393, 894, 424, 425, 426, 428, 429, 430, 433;
Poisaon's typo of integral representing, 68, 73, 165; (modifications of), 169, 170; products of,
149; (represented by infinite integrals), 221, 441,' 446 ; (asymptotic expansions of), 221, 448;
recurrence formulae for, 06, 71; represented by integralu containing Legendro functions, 174;
symbolic formulae for, 170 ; tables of (of orders 0 and 1), 662, 666-607 ; (of order n), 664, 732-
735 ; (of order J), 0E4, 714-729 ; (ot order - Jj, method of computing), 6E4 ; (with equal order
and argument), 664, 747 ; (zeros of), 748-751; tabloH of, references to, 655, 656, 658 ; with largo
argument, see Asymptotic expansions; with, negative* argument, 75 ; zeros of, see Zeros of
Bessel functions. See also Neumann's polynomial
Bessel functions of the third kind, iV> (z), Jhll} (z), 73; Damon' integrals representing, 192
Befisel's typo of integral representing, 178; PoisHon'R typo of integral representing, 166; (modi-
(modifications of), 108, 169, 170; represented by integrals containing Legendre functions, 174;
symbolic formulae for, 170; tables of (of orders 0'and 1), 662, 066-697; (of order ^), 604, 714-
729; tables of (references to), E57; with largo argument, asymptotic expansions of, 199, 210,
216; with large argument and order, asymptotic oxpanwions of, 244, 245, 262; with negative
argument, 75
Bessel functions whose order and argument are equal, approximations! to, 229, 281,232, 259, 2E0,
448, 515; asymptotic expansions of, 245 ; integrals representing, 258; tables of, 658, 664, 746,
747 ; tables of (references to), 658
Bessel functions whose order is a fraction. Of ordorn ±. ^ rand Airy's integral), 190; (and the
stability of a vortical polo), 9A; tables of, E64, 714-729 ; tables of (references to), 059 ; zeros of,
751- Of orders ±J, tablen of (references to), 659. Of orders -l^, J.-j, tables of (references to),
669. Of small fractional orders, tabloH of zcron of (roforcnccH to), 502, 660. See alto Besael
functions whose order is ±(n + $)
Bessel functions whose order is large, 225 -270 (Chapter vm); HHyinptotic expansions of, 241, 244,
245, 262 ; Carlini's approximation to, 6, 7 ; (extended by MeisHol), 226, 227 ; Horn's /olomontary)
approximation to, 2'2F>; Laplace's approximation to, 7, 8, 9 ; method of stationary phase applied
to, 232; method of HteepCHt descents applied to, 237; miHcelluneouR properties of, 252-261;
tables of (reference to), 6f>8; transitional formulae! for, 248; zeros of, f>13, 516, 617, 518. See
aim Bessel functions whose order and argument are equal
Bessel functions whOBe order is x^n t-J), 10, 52, 80; expressible) in finite terms, 52 ; notations for,
55, 80; tables of, 0E4, 740-745 ; tables of (references to), 658, 659
Bessel functions with imaginary argument, I,.(z), KK(z), K,. (c), 77, 7H; differential equation
natislied by, 77; integrals ropreHonting (of Bessol's typo), 181 ; (of Poifcrnnn's'type), 79, 171,172;
(proof of equivalence of various types), 185-188; monotonic property of, 446 ; of ordor =i (n + 4),
80 ; recurrence formulae, 79 ; tables of (of orders 0 and 1), 6C3, 698-713 ; (of order &), 6C4, 714-
729 ; (of various integral orders), 064, 736, 737-739; tablos of (references to), 657, 658; with liu-ge
argument, asymptotic expansions pf, 202; zeros of, 611; (computation of), 512; (references to),
660
Bessel's differential equation, 1, 19; (generalised), 38 ; for functions of order zero, 5, 12, 59, 60;
for fiinotions with imaginary argument, 77 ; fundamental system of solutions of, 42, 75; has no
GENERAL INDEX 799
Dini series, 577, 580, 596-605, 615-617- (Chapter xvni), 651-653; expansion of an arbitrary func-
function of a real variable into, 580, 600; methods of theory of functions of complex variables applied
to, 596, 602; Riemann-Lebesgue lemma, analogue of, 599 ; Rieinann's theorem, analogue of,
649; summability of, 601, 615 ; uniformity of convergence of, 601, 604 ; uniqueness of, 616, 651;
value at end of range, 602
Dirichlet's discontinuous factor, 406
Discontinuity of arbitrary constants (Stokes1 phenomenon), 201, 203, 238, 336
Discontinuous factor (Dirichlet'a), 406; (Weber's), 405
Discontinuous integrals, 398, 402, 406, 408, 411, 415, 421
Domain K (Kapteyn's), 559; diagram of, 270
Du Bois Reymond's integrals with oscillatory integrands expressed in terms of Beasel functions, 183
Electric waves, 56, 226, 449
Electromagnetic radiation, 551, 556
Elementary transcendants, definition of, 111; order of, 111; solution of differential equations by,
112
Equal order and argument, Bessel functions with, 231, 232, 258, 260; tables of, 746, 747; tables
of (references to), 658, 664
Euler's solution of Kieeati's equation, 87
Exponential function, tablos of, 698-713 ; tables referred to, 663, 664 *
Factors, discontinuous (Dirichlet's), 406; (Weber's), 405; Neumann's en ( = 1 or 2), 22 ; expression
of Bessel functions as products of Woierstrassian, 497
FeJ&r's theorem, analogue of, for Fourier-JBeasel expansions, 610
Finite terms, Bessel functions of order b(n-i-^} expressed in, 52; Bessel functions of other orders
not so expressible, 119 ; solutions of Riccati's equation in, 85, 86, 89; the solution of Riccati's
equation in, not possible except in Daniel Bernoulli's cases and their limit, 128
Flights, problem of random, 4H)
Fourier-Bessel expansion, 580. Sec also Fourier-Bessel series
Fourier-Bessel functions, 4, 84
Fourier-Bessel integrals, see Multiple infinite integrals
Fourier-Bessel series, 576-617 (Chapter xvm), ($49-051 ; expansion of an arbitrary function o? a
real variablo into, 576, 580; Feje'r's theorem, analogue of, 610; KncMor-Somnierfcld expansion
of a combination of Bessol functions into, 499 ; methods of theory of functions of complex vari-
variables applied to, 582, 607 ; order of magnitude of fcorms in (yheppard'si theorem), 55M ; liiematm-
Lebesgue lemma, analogue of, 589 ; lliomann'H theorem, analogue of, (MS); summability of, 57H,
606, 613; tonn-by-terni differentiation of, 578, 005 ; uniformity of convergence of, fiUJJ, 5!>4;
(noar origin), E15 ; uniformity of mnnmability of, 612 ; uniqucncHH of, 016, 649 ; value at end of
range, 594, 008
Fractional differential coefficients, 107, 125
Freanel's integrals, 544; asymptotic expansion of, 545; tables of, 741, 745; tablos of maxima
and minima of, 745; tables of (references to), 6E0, 6E1, 604
Functional equations donning cylinder functions, 82 ; RonoraliHod by Nielsen, 3G5
Functions of large numbers, approximations duo. to Darboux, 233 ; approximations due to Laplace,
8,421. See aim Approximations, Asymptotic expansions. Method of stationary phase and Method
of steepest descents
Fundamental system of solutions of Hossel's differential equation, 42, 75, 7H
Gallop's discontinuous infinite integrals, 121
Gamma functions, reprosontation of UohhoI functions by integrals containing, 190, 192, 221; appli-
applications to determination of asymptotic expansions, 220, 221!; applications to evaluation of infinite
integrals, 383, 434, 43(i
Gamma functions, representation of Iioinmel'H functions by intogralH containing, 351; applications
to determination of asymptotic expansion!*, 352
Gegenbauer's addition theorem for BohhgI functions, 802, 363, 3E7
Gegenbauer's discontinuous infinite Integrals, 415, 418
Oegenbauer's function (,'„" B), 50, 129, 363, 365, 367, .'JOB, 369, 378, 407
Gegenbauer's polynomial An,v[t), 283; contour mtogmlH containing, 284, 524; differential equa-
equation satisfied by, 283; equivalence with special" forma of Lommol'H function, 851; recurrence
formulae for, 283
Gegenbauer's polynomial Hv.n.p @» 29!J, 525
Gegenbauer's representation of J,, B) by a double integral resembling Poisson'd integral, 51
Gegenbauer's type of definite integral, 37H ¦>
Generalised-hypergeometric functions, see Hypergeometrie funotions (generalised)
800 THEORY OF BESSEL FUNCTIONS
Generalised integrals (with implied exponential factor), 1?8, 441, 468, 464
Generating function of Bessel coefficients, 14, 22, 23; of Neumann's polynomials, 281, 282
Gilbert's integrals, 543, 549
Giuliani's function, see Bourget's function
Graeffe's method of calculating zeros, 500, 502
Grafs addition-theorem for Bessel functions, 359, 361
Group velocity, 229
Growth of zeros of Besael functions, 485
Hankel's infinite integrals, 384, 386, 389, 390, 393, 395, 424, 427, 428, 434
Hansen's upper bound for Jn (x), 31; generalised, 406
Hardy's functions Cin[a), Sin{a), Ein(a), (generalisations of Airy's integral), 320; expressed in
terms of functions of Bessel, Anger and Weber, 321, 322
Hardy's integrals representing Lommel's functions of two variables, 546
Hardy's method of evaluating definite integrals, 382
Heat, conduction of, 9, 10, 450, 576, 577, 616
Hemi-cylindrical functions Su(z), denned, 353; expressed in terms of the function of order zero,
353 ; addition theorem for, 354
Hypergeomotric functions, limiting forms expressed as Bessel functions, 154
Hypergeometric functions (generalised), 90,100; Bessel functions expressed in terms of, 100, 101;
notations for, 100; relations between (Kummer's formulae), 101,102; Sharpe's differential equa-
equation solved by, 105
Imaginary argument, Bessel functions with, see Bessel functions with imaginary argument;
Struve's functions with, 329, 332
Indefinite integrals containing Bessel functions under the integral sign, 132-138, 350, 581; tables
of, 744, 745, 752; tables of (references to), 660, 661, 664
Inequalities satisfied by Bessel functions, 16, 31, 49, 255, 259, 268, 406; by Neumann's poly-
polynomial, 273, 282; by Struve's function, 328, 337, 417; by zeros of Bessel functions, 485, 489,
490, 492, 494, 515, 516, 521
Infinite integrals containing Bessel functions under the integral sign, 383-449 (Chapter xin); dis-
discontinuous, 398, 402,406, 408,411, 415, 421; generalised, 441; methods of evaluating, described,
383 ; Eamanujan's type (integrals of Bessel functions with respect to their order), 449. See aim
under the names of various integrals, e.g. Lipschitz-Hankel infinite integral
Infinity of the number of zeros of Bessel functions and cylinder functions, 4, 478, 481, 494, 495
Integrals, expressed in terms of Lommel's functions of two variables, 540; expressed in terms of
the functions of Anger and Weber, 312; Fresnel's, 544, 545, 660, 661, 664, 744, 745; Gilbert's,
548, 549; values of, deduced from addition theorems, 367; with oscillatory integrands, 183;
with the polynomials of Neumann and Gegenbauer under the integral sign, 277, 285. Sec ulxo
Definite integrals and Infinite integrals
Interference, 229
Interlacing of zeros of Bessel functions and of cylinder functions, 479, 480, 481
Irrationality of *¦, 90, 485
Jacotoi's transformation connecting sinnfl with, the (n - l)th differential coefficient of sin2""*? with
respect to cos 0, 26; erroneously attributed to Eodrigues, 27; various proofs of, 27, 28
Kapteyn's domain K, 559; diagram of, 270
Eapteyn aeries, 6,13, 551-575 (Chapter xvn); connexion with Kepler's problem, 551; expansions
into, derived from Kepler's problem, 554, 555; expansion of an arbitrary analytic function into,
570; fundamental expansions into, 557, 559, 661, 564, 566, 568, 571; Kapteyn's domain K, of
convergence of, 559 ; (diagram of), 270; nature of convergence outside and on the boundary of
K, 574 ; second kind of, 572
Kapteyn'B polynomial <©„ (t), 568; expressed in terms of Neumann's polynomial, 569
Kapteyn's type of definite integral, 380
Kepler's problem, 6, 551, 554; Bessel's solution of, 13; Lagrange's solution of, 6
Kinds of Bessel functions, (first) 40; (second) 58, 63, 64, 65, 67; (third) 73
Kneser-Sommerfeld expansion of a combination of Bessel functions as a Fourier-Bessel series, 499
Kummer's formulae connecting generalised hypergeometric functions, 101, 102
Lame* funotions, limiting forms expressed as Bessel functions, 159
Laplace's equation, general solution due to Parseval, 9; general solution due to Whittaker, 124 ;
solutions involving Bessel functions, 83,124; used to obtain addition theorems for Bessel func-
functions, 127
GENERAL INDEX 801
Laplace'a methods of approximating to functions of large numbers, 8, 421
Laplace's transformation, 280, 395
Large numbers, methods of approximation to functions of (Darboux), 233 ; (Laplace), 8, 421. See
also Approximations and Asymptotic expansions
Large order, sec Anger's function, Bessel" functions whose order is large, Struve's function and
Weber's function
Lebesgue's lemma, see Riemann-LebeBgue lemma
Legendre functions, Barnes' notation for, 156; integrals oontaining, 50,173,174, 339, 475; limits
of, expressed as Bessel functions, 65, 165, 157 ; (physical significance of), 155 ; of large degree,
approximations to, 158 ; relation between two kinds of, 174 ; Whipple's transformation of, 387.
Sec also Gegenbauer'a function Gnv (z)
Lipschitz-Hankel infinite integral, 384; generalised, 339
Lommel's functions V," B)> S^y (z), 345, 347 ; eases of expression in finite terms, 350; integrals
representing, 346, 350; recurrence formulae, 4148; special cases expressible by the polynomials
of Gegenbauer, Neumann and Schliifli, 350; special cases with /x±p an odd negative integer,
348; with large argument, asymptotic expansion of, 351
Lommel's functions of two variables, Uv (w, z), Vv [w, z), 537, 538; addition formulae for, 543;
integrals representing, 5-10, 546 ; reciprocation formulae, 542; recurrence formulae, 539; special
case of, 581, 752; tables of, 752; tables referred to, 660; with large argument, asymptotic expan-
expansions of, 549
Lommel's polynomial Rm, v {*), 294, 295; differential equation satisfied by, 297; Hurwitz' notation
9m, v BI 303; limit of, expressed as a Bessol function, 302; of negative order, 11 _Ml) „ (z), 299;
recurrence formulae, 298; recurrence formulae in Hurwitz' notation, 303; relations with Bessel
functions, 295, 297, 302; three-term relations connecting, 300, 301; zeros of, 304, 305, 306
Magnitudes of remainders in asymptotic expansions, 206, 211, 213, 286, 314, 332, 852, 449
Maxima of Beasol functions, 488; of Frosnol's integrals, table of, 745; of integrals of Bossel func-
functions, table of, 752
Mean anomaly, expansions of elements of an orbit in trigonometrical Beriosof, 6, 13, 552, 554, 556
MeWer-Diricalet integral representing Logendro functions, limiting form expressed as Poiason's
integral, 157
Menler-Bonine integrals representing BcshoI funoliouH, 169, 170
Melssel's approximations to BohboI funclionti of largo ordor, 226, 227, 232, 247, 521 ; types of
Kapteyn Borios, 5.r>7, 561, 664, 566
Membrane, vibrations of a circular, 5, 570, (JIB ; vibrations of a Hoctorial, 510
Method of constant phase (Sohlutli's), 216
Method of stationary phase, 225, 229; applied to BohhoI fiiuotioiiB, 231, 233
Method of steepest descents, 235 ; ujipliod to BohhoI functions, 237, 241, 241, 245, 262 ; applied to
functions of Anger andWobor, 316; appliocl to Htruve's function, 338; connexion with Laplace's
method of approximation, 421
Minima of Bessol functions, 488; of I'YcBnol'H integrals, tablo of, 745 ; of integrals of BobboI func-
functions, 752
Motiotonic properties of Jv (vx)lJv (»), 257; of Jv (?) and ./„' (v), 2(H); of A'() (x), t-16
Multiple Infinite Integrals, 450-476 (Chapter xrv); invofitigatod by Noumann, 453, 470; (gonorn,li«od
by Hiuikel), 453, 456, 4E5; (gonoraliwod by Orr), 455; (modifiod by Wobor), 468; Kiomium-
Lobesguo lemmas, analogues of, 457, 471 ; Wobor'n type of, 450
Neumann aeries, 522-537 (Chapter xvi); oxpanmon of nn arbitrary analytic funolion into, 523;
generalised, 525; (apooial hohoh), 30, 31, 3E, E9, 71, lfil ; fiivuront'H expansion, analogue of, 524;
Pincherle'a theorem on llio HiugnlaritioH of, f>2(>; Hpocial 8«ri(!H, 1H, 23, 25, !$!$, 34, 35, 12H, 130,
138,139,140,527,581; Wobb-Kaptoyn (roal variable) theory of, TiiK). Sec <rlxo Addition thoorouiB
and Lommel's functions of two variables
Neumann's factor cn ( = 1 or 2), 22
Neumann's integral for ./„* (z), 32 ; for Nnumann'H polynomial, 278, 2H0
Neumann's polynomial ()n (t), 271, 272, 27i); oonnooknl with Kaptoyn'H polynomial, 569 ; connected
with Neumann's polynomial ilu (t), 292; conndotcd with Hohliifli'H polynomial, 2H5, 2H6; contour
integrals containing, 277; difforontial oquation Hatisfkid l>y, 276; nxpniHHiul in tornw of Loinmol'B
fuuetions, 850; formerly called a BchhoI fuuotion of fcln\ Kc.cond kind, E7, 273; gonomlised by
Gogonbauer, see Ctogenbauor's polynomial An>v{t)\ gonuraUng funclioti of, 2M1, 282; inequali-
inequalities satisfied by, 273, 282; infinite integrals containing, 408 ; Nmimann'ti intogrtil ropresenting,
278, 280; of negative order donnod, 276 ; roourronco formulae for, 274'
Neumann'B polynomial On(t). 290, 291; oxpressod an integral containing Noumann'B polynomial
On (t), 292; Gegenbauor's generalisation of, nee Oegenbauor'a polynomial Hn,i, v (t); recurronoo
formula for, 292
NicholBon's infinite integrals, 431, 441
802 THEORY OF BESSEL FUNCTIONS
Nielaen-Hankel functions, see Bessel functions of the third kind
Null-functions, Lereh's theorem on integrals representing, 382 ; represented by Schlomilch series,
634, 636, 642, 647
Numbers, analytic theory of, associated with asymptotic expansions of Bessel functions, 200
Numbers, Cauehy's, 324; recurrence formulae for, 325
Order of a Bessel function defined, 38, 58, 63, 67, 70; integrals with regard to, 4-19
Ordinary differential equations, see Differential equations
Oscillation of solutions of linear differential equations, 518
Oscillations of membranes, 5, 510, 576, 618; of uniform heavy chains, 3, 4, 576
Oscillatory integrands, Du Bois Reymond's integrals with, expressed in terms of Bessel functions,
183
P-functions, limiting forms expressed as Bessel functions, 158
Parseval's integral representing Jo (z), 9, 21; modifications of, 21
Partial differential equations, see Differential equations
Phase, method of stationary, general principles of, 225, 229; applied to Bessel functions, 231, 233
Phase, Schlafli's method of constant, 216
Pineherle's theorem on singularities of functions denned by Neumann series, 526
Poisson'a integral for Bessel coefficients, 12, 24, 25; for Bessel functions, 47,48,49; (generalised by
Gegenbauer), 50; (symbolic form of), 50; for Bessel functions of imaginary argument, 80; for
Bessel functions of the woiul kind, 68, 73 ; limit of the Mehler-Dirichlet integral for Legondre
functions as, 157; transforn. "tion into contour integrals to represent Bessel functions of any order
(of the first kind), 161,163, 11^; (of the second kind), 165; (of the third kind), 166, 167; (with
imaginary argument), 171, 172; transformations of the contour integrals, 108, 1E9, 170. See
also Parseval's integral and Struve's function
Polar coordinates, change of axes of, used to obtain transformations of integrals, 51, 374, 37E, 37H;
used to express Bessel functions as limits of Legendre functions, 155
Probleme de moments of Stieltjes, 464
Products of Besuel.functions, 30, 31, 32, 82, 146,147,148,149,; Bateman's expansion of, 130, 370 ;
expansions of arbitrary functions into series of, 525, 572; integrals representing, 31,150, 221, 438,
439, 440, 441, 445, 446, 448; series of, 30, 151, 152 ; with large argument, asymptotic expansions
of, 221, 448
Products of Weierstrassian factors, Bessel functions expressed as, 497
Quotient of Bessel functions expressed as a continued fraction, 153, 154, 303
Radius vector of an orbit, expansionos trigonometrical series of the mean anomaly, 6,13,552,553,554
Bamanujan's integrals of Bessel functions with respect to their order, 449
Ramanujan'B method of evaluating definite integrals, 382
Random flights, problem of, 419
Rank of Bessel functions and cylinder functions, 129
Real variables, expansions of arbitrary functions of, nee Dini series, Fourier-Bessel ser4es,
Neumann series (Webb-Kapteyn theory), and Schlomilch series
Reality of zeros of Bessel functions, 482, 483, 511
Reciprocation formulae for Lommel's functions of two variables, 542
Recurrence formulae for Anger's functions, 311; for Bessel coefficients, 17 ; for Bcssel functions
of the first kind, 45 ; for Bessel functions of the second kind, 66, 71; for Beasel functions of the
third kind, 74 ; for Bessel functions with imaginary argument, 79; for Bourget's functions, 326;
for Cauehy's numbers, 325; for cylinder functions, 82; for Gegenbauer's polynomials, 283 ; for
Lommel's functions, 348; for Lommel's functions of two variables, 539; for Lommer.s poly-
polynomials, 298, 303; for Neumann's polynomials O,, (t), 274; for Neumann's polynomials iln (r),
283; for Schldfli's functions, 71, 342, 343; for Schlafli's polynomials, 285; for Htruve's func-
functions, 329; for Weber's functions, 311; for Whittalcer's functions, 339. Sec also Functional
equations, Heml-cyltndrical functions and Three-term relations
Reduced functions, Gailler's, 536
Remainders In asymptotic expansions, magnitudes of, 206, 211, 236, 314, 332, 352; signs of, 20E,
207, 209, 215, 315, 333; Stieltjes' approximations to, 213
Repetition of zeros of Bessel functions and cylinder functions', impossibility of,, 479
Riccati's differential equation, 1, 2, 85-94; connexion with Bessel's equation, 1, 90) equation
cognate to, 91; limiting form of, 86; soluble cases .of (D. Bernoulli's), 85; soluble cases of,
exhausted by D. Bernoulli's formula and its- limit, 123; solutions by various mathematicians
(D. Bernoulli), 2, 85, 89; (Cayley), 88; (Euler), 87; (Schlafli), 90; solved by means of infinite
series by James Bernoulli, 1; transfonnatidns of, 86
Riccati's differential equation generalised, 3, 92, 94; cross-ratio of solutions. 94; equivalence
GENERAL INDEX 803
with the linetn1 equation of the Bocond order, 92 ; singularities of, 94 ; soluble by various num-
numbers (two, we or none) of quadratures, 3, 98
Rlemann-Lebesgue lemma, analogues of the, 457, 471, 589, 599
Kiemann's theorem on trigonometrical series, analogues for Schlo'milch aories, 042, 647; analogues
for series of Fourier-Besscl and Dini, 649
Rodrigues' transformation, see Jacobi's transformation
Schafneitlin's discontinuous infinite integral, 398, 402, 405, 406, 408, 411
Scbafheitlin's integrals representing Bossol functions and cylinder functions, 108,169,490,491,493
Schlafli's functions Tn (z) and Vn(z), 71, 340, 348; addition theorems for, 344, 345; differential
equations satisfied by, 342, 343; of negative order, 343; recurrence formulae for, 71, 342, 343
8chlafli's hypergeometric function, 90
jJchlani'B polynomial Sn(t), 284, '286; addition theorem for, 28(j; connexion with Noumann's
polynomial On (t), 285, 280; Crelier's integral representation of, 288; differential equation
satisfied by, 285; expression by means of Bessel functions, 287; expression in terms of Lommel's
function, 350 ; integrals evaluated in terms of, 350; recurrence formulae for, 285
Schlafli's solution of Biceati'a equation, 90
Schlomilch series, 618-649 (Chapter xix); definition of, 621; definition of generalised, 623 ; ex-
Series containing Besael function, see Dini series, Fourier-Beusel series, Kapteyn series, Neumann
series and Schlo'milch aeries
Series of Besael functions, definition of, 580
Seriea of positive terms, approximation to the sum of (greatest term method), 8
Sharpe's differential equation, 105; Holution by generalised hypergeomotric functions, 105
Sign of remainders in asymptotic expansions, 206, 207, 209, 215, 315, 333, 449 ; of Btruvo's func-
function, 337, 417
Sine-integral expressed as a series of squares of Bessul eoeflie.ionts, 152
Singularities of functions defined by Neumann Hurios (Pincherle's theorem), 526 ; of the generalised
Biccati equation, 04
Smallest zeros of UohhoI functions, 5, 500, 510
Sommerfeld's expansion, see Kneser-Sommerfeld expansion
Sonine-Mehler integrals representing Bussel functions, 160, 170
Sonine'a definite integral, 373; generalised, 3H'2
Sonine's discontinuous infinite integrals, 115
Sonlne's infinite integrals, 432
Spherical geometry used to obtain transformations of integrals, 51, 374, 376, 37R; uacd to express
Bessel functions as limits of Legcndra functions, 155
Sound, Hharpe's dilTorontial equation in the theory of, 1.05
Squares of Bessel functions, are Products of Beasel functlona
Stability of a vortical polo associated with Uosnel functions of order <m<:-lhird, 96
Stationary phase, method of, 225, '229 ; applied to Bessel functions, '231, 233
Steepest descents, method of, 23.r>; applied to Bohh<>1 functions, 237, 241, 244, 245, 262; appliod.
to functions of Anger and Wober, 316; applied to Htmvc's function, 333 ; eonuoxion with
Laplace's method of approximation, 421
StokeB' method of computing zeros of Hessel fuiustionH and cylinder i'unctionn, 503, 505, 507
Stokes' phenomenon of the discontinuity of arbitrary constant)!, '201, 203, 23H, 330
Struve'a function H,, (z), 328 ; connexion with Weber's function, 336 ; difforonlial equation satinllod
by, 329 ; inequalitu'tt coniutctwl with, 32H ; iniinito integrals containing, 392, 31O, 117, 425, 436;
integral representations of, .'B8, 330; occurrence, in gelloralisod He.hloiniloh series, 622, 623, 6!il,
645, 646, 647; of ordov i (;/ I i), 333 ; recurrence, formulae, for, 32'.); iiign of, 337, 417 ; tobies of,
663, 666 697; Theisingcr's integral for, 33H; with imaginary argument, 32!), 332; with lurgu
argument, asymptotic expansions of, 332; with largo argument and order, asymptotic expan-
expansions of, 333 ; zeros of, 471)
Struve's infinite integrals, 396, 397, 121
Sturm's methods appliod to determine, the reality of zeros of Bessel functions, 4H3; of Lomnicl\s
polynomials, 304, 305, 306 ; applied to estimate the value of 1,1m smallest zero of Bossol funotious
and cylinder functions, 517, 518
Symbolic operators in expressions representing BcshcI functions, 50, 170; in expressions ropre-
senting solutions of various difToroutial equations, 41, 51, 1()H; iu the theory of Hchlomilch
series, 627
804 THEORY 01? BESSEL FUNCTIONS
of Bessel coefficients (of orders 0 and 1), 662, 666-697; (of order «), 664, 730-732 ; (vith
[ order and argument),W, 746; of Bessel functions of the hrst kincl! (of oto I- *, -J -4).
Tables
equal order and urg
664
1)
argamcn
order. -J
698-713;
integrals, 664,744-740 ; of integrals of Bessel functions of order ssero, 664, 7o2 , of bliuyo h func-
functions (of orders 0 and 1), 663, 666-697 ; of zeros of Bessel coeihcientu and function* of inlogml
order n and of order -J-, 664, 748-751
Tables- (references to) of Airy's integral, 659 ; of Bessel coefficients and functions derivuhlo from
them, 654, 655, 656,658; of Bessel functions (of orders m + J, - ?i - i), 658, (u>J ; (ot or<lt>rs « :1,
' *.-i ,... * -T. ,v» , • !> 1.1- j. nnAnn. Ul fl/l Kf\!i ftlift 1 »ikW * I'll
Bessel coefficients, functions and associated functions, 659, 660
Theisinger's integral representation of Bessel functions, 184; of Struve's and Wober's functions,
338
Thomson's (Sir William) functions, berz, beiz, 81; connexion with Bessel functions, 81; gemmili-
sations, 81; references to tables of, 658; squares and products of, 82,148 ; with largo argument,
asymptotic expansions of, 203
Tliree-term relations connecting Bessel functions, cylinder functions and Lommol's polynomials,
300, 301
Transcendants, elementary, definition of, 111; order of, 111; solutions of differential equations
by,112
Transitional regions associated with Bessel functions of large order, 248
Uniformity of convergence of Dini series, 601; of Fourier-Bessel series, 593, 594; of Kuntoyn Horics,
575; of Schlomilch series, 632
Uniqueness of Fourier-Bessel and Dini series, 616, 649, 651; of SchlSmiloh Borien, 043, E47
Upper bounds, see Inequalities
Viscous fluid, motion of, associated with Aivy's integral, 189
Wave-motions, equation of, general solutions, 125; generalised to y dimeimionH, 12K; unod to
obtain addition theorems for Bessel functions, 129
Waves, electric, 56, 226, 446 ; on -water, and the method of stationary pliaHO, '2'2i)
Weber's (H.) discontinuous factor, 405
Weber's (H.) infinite integrals, 391, 393, 395, 396; (discontinuous typos of), li'.m, <1()i», Klrt, 40E,
408, 411
Weber's (H. F.) function Ev (z), 308 ; connexion with Anger's function, 310 ; connexion with NtniYo's
function, 336; differential equation satisfied by, 312 ; integrals expreKKod in U;rum of, III'2 ; n\-
currence formulae for, 311; representation of Airy's integral (generalised) by, .TJ1 ; l,al)lcn of, arc
Struve's function ; Theisinger's integral for, 338; with large argument, asymptotic oxpmiKion of,
313; with large argument and order, asymptotic expansion of, 81E
Weierstrassian products, expression for Bessel functions as, 497
Wlaipple's transformation of Legendre functions, 387
Wbittaker's function Vfv(z), 339; differential equation satisfied by, 339 ; recuvrendr. fornuilan for,
339; with large argument, asymptotic expansion of, 340
Wronskian determinant, 42, 76, 77
Zeros of Bessel functions, 477-521 (Chupterxv); computation of (various niothodH of), M'2, 500, 51V2,
503, 516; inequalities connected with, limits of, rates of growth of, 485, 4HS), 4<)u 4SI, .Iim' f,(O
imaginary argument, 511; with unrestrictedly large order, 513,'516
Zeros of Lommel's polynomials (reality of), 304, 305, 306
Zeros of Struve's function, 479
Reprinted by Phoio-offset by Bradford <& Dickens for the University Press Cambridge