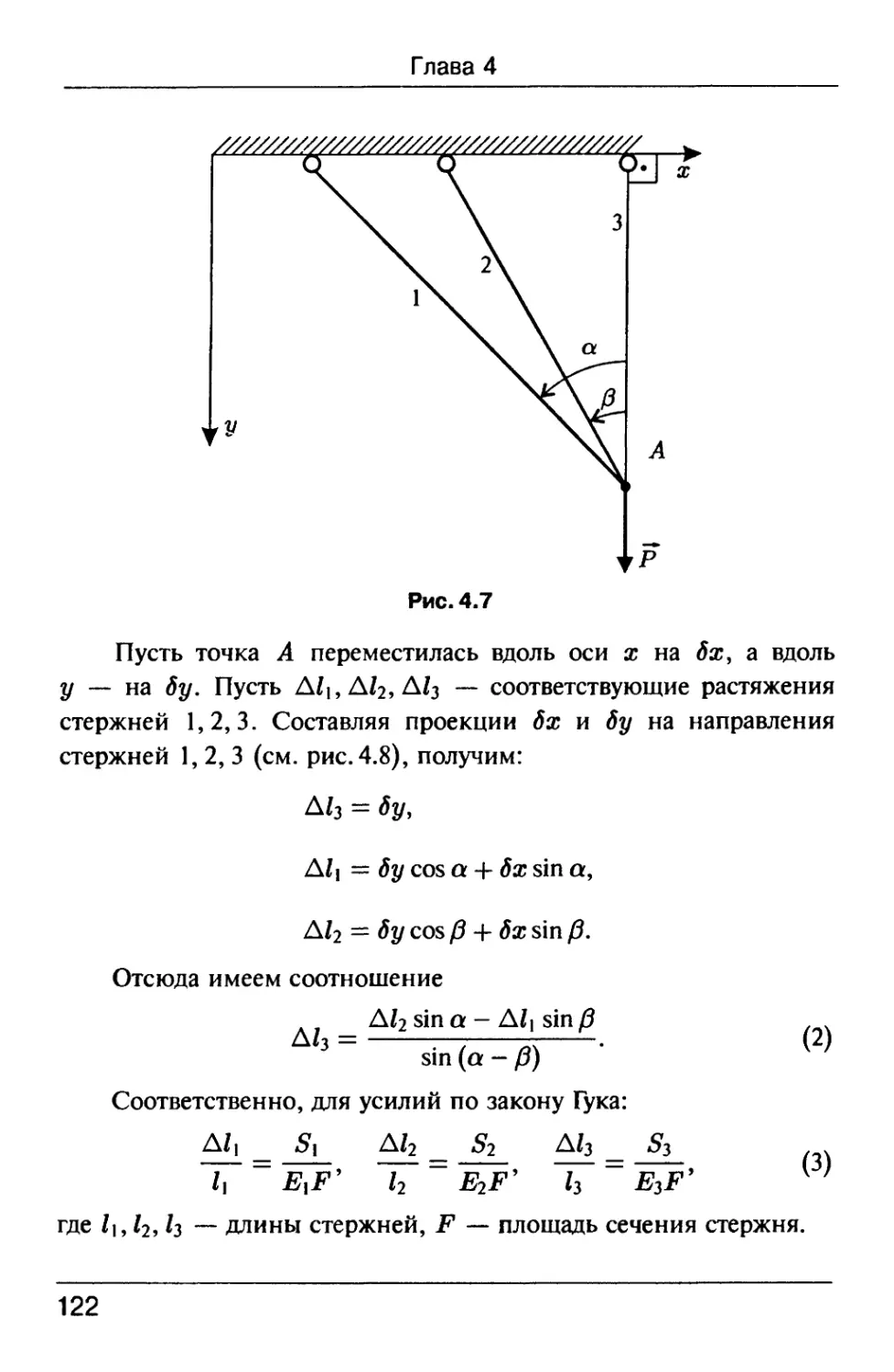
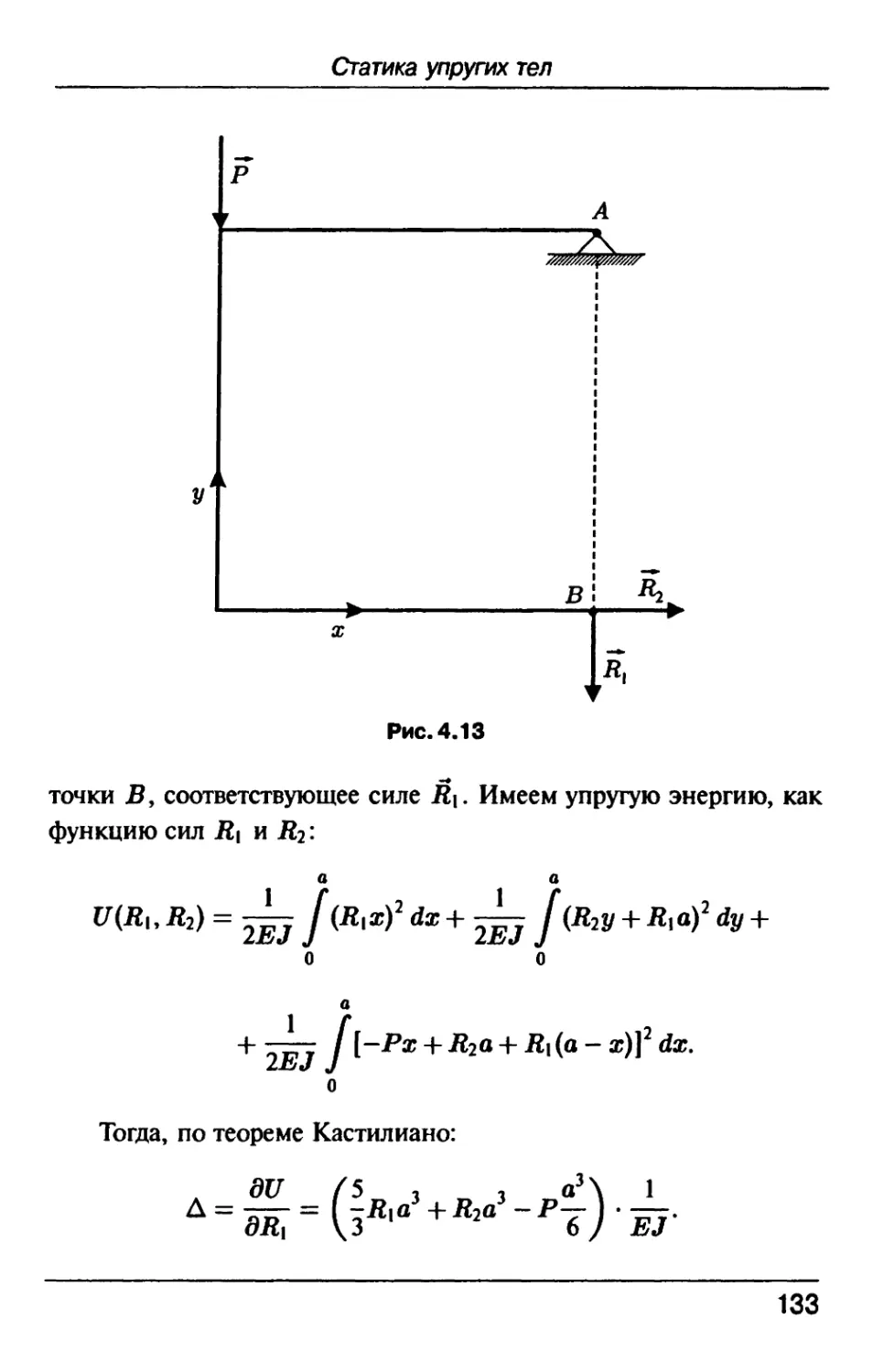
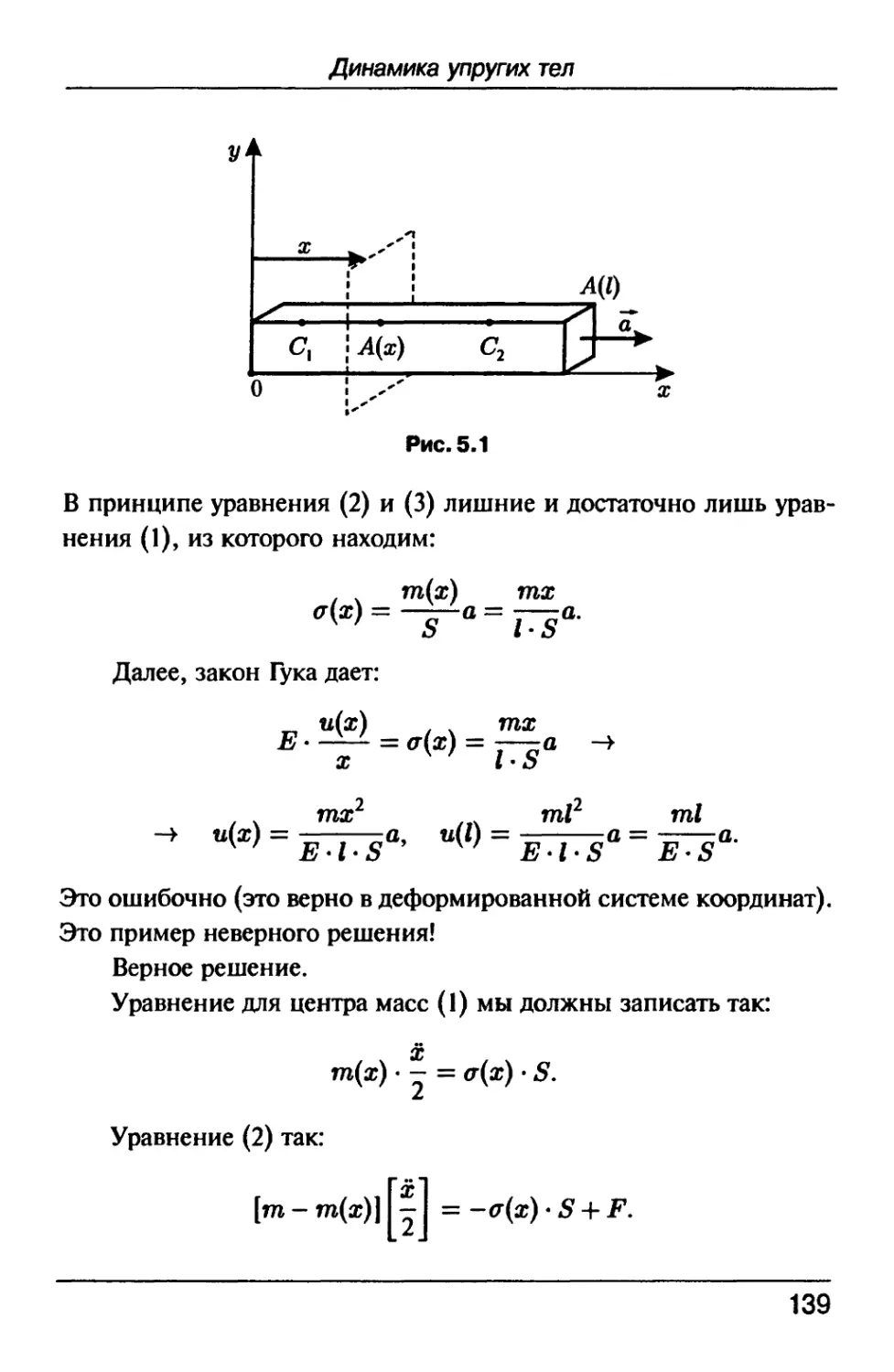
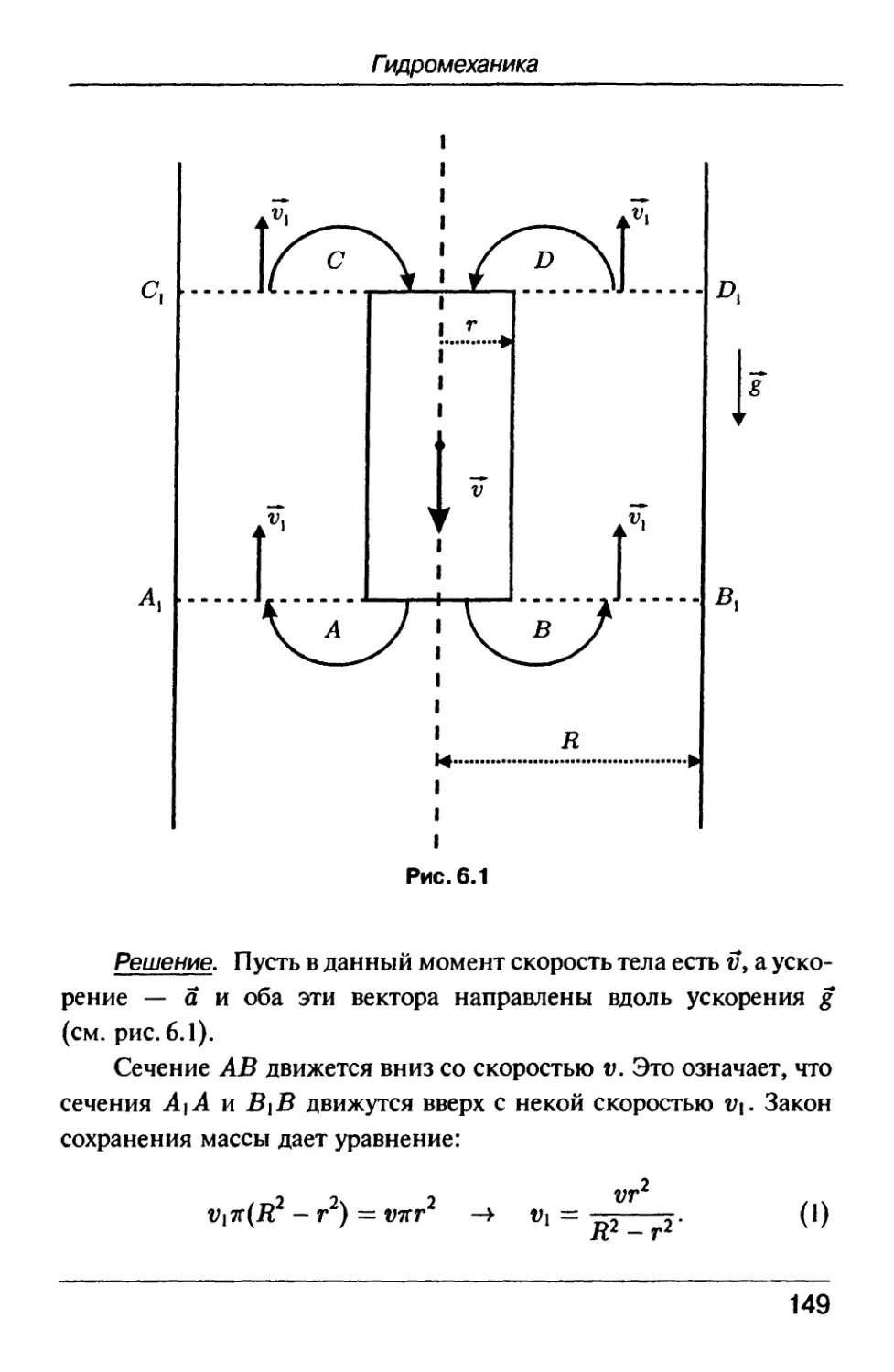
Text
Г.М.Розенблат
МЕХАНИКА
В ЗАДАЧАХ
И РЕШЕНИЯХ
Москва
УРСС
ББК 22.21я73
Розенблат Григорий Маркович
Механика в задачах и решениях. — М.: Едиториал УРСС, 2004. — 160 с.
ISBN 5-354-00727-5
В сборнике представлены задачи из различных областей механики с подроб-
подробными решениями. Все задачи и их решения доступны студентам младших курсов
вузов, овладевшим основами высшей математики и теоретической механики.
Сборник может быть использован для дополнительных занятий со студента-
студентами, интересующимися механикой, для подготовки к студенческим олимпиадам
по механике.
Рецензенты:
академик РАН В. В. Козлов,
доцент кафедры теоретической механики и мехатроники
МГУ им. М. В.Ломоносова К. Е.Якимова
Издательство «Едиториал УРСС». II73I2, г. Москва, пр-т 60-летия Октября, 9.
Лицензия ИД №05175 от 25.06.200! г. Подписано к печати 16.03.2004 г.
Формат 60x90/16. Тираж 1000 экз. Печ. л. 10. Зак. № 90
Отпечатано с готовых диапозитивов в ГП «Облиздат»
248640 г. Калуга, пл Старый торг, 5
ISBN 5-354-00727-5
ИЗДАТЕЛЬСТВО У ± С^ С^
НАУЧНОЙ И УЧЕБНОЙ ЛИТЕРАТУРЫ
E-mail: URSS@URSS.ru
Каталог изданий
в Internet: http://URSS.ru
Тел./факс: 7 @95) 135-^2-16
Тел./факс: 7 @95) 135-^2-46
Г. М. Розенблат, 2004
Едиториал УРСС, 2004
2238 ID 18053
Оглавление
Предисловие 4
Глава 1. Статика 7
Глава 2. Кинематика 21
Глава 3. Динамика 71
Глава 4. Статика упругих тел 113
Глава 5. Динамика упругих тел 137
Глава 6. Гидромеханика 147
Литература 153
Задача состояла в ловле фраз
...Вниманье не дремало.
Вылавливая их, как водолаз,
Я по журналам понырял немало.
Б. Пастернак
«Спекторский»
Предисловие
В настоящем сборнике представлено несколько десятков за-
задач из различных областей механики с подробными решениями.
Большинство задач заимствовано из известных сборников, кото-
которые указаны в списке литературы. Несколько задач придуманы
автором, который однако не претендует на оригинальность. Все
задачи и их решения (или разбор последних) доступны студентам
младших курсов вузов, овладевших основами высшей математики
и теоретической механики.
При подборе задач и изложении их решений автор руко-
руководствовался собственным (давнишним) опытом участия в физи-
физико-математических олимпиадах и нынешним (текущим) опытом
проведения студенческих олимпиад по теоретической механике
в Московском автомобильно-дорожном институте (МАДИ ГТУ),
а также в рамках межвузовских олимпиад московских вузов. По-
Поэтому основные требования к представленным решениям были
следующие: а) решение должно быть достаточно коротким, не-
несложным и подробным, чтобы быть понятным любому желающему
его освоить и применять при решении аналогичных задач; б) лю-
любое утверждение, высказанное в решении, должно быть строго
(по возможности) обосновано в математическом или физическом
смыслах (а лучше и в том и в другом!). Здесь уместно вспомнить
высказывание профессора С. П. Капицы: «Задача — это наука в ми-
Предисловие
ниатюре». Поэтому большинство решений представленных задач
завершается обсуждением и различного рода дополнениями.
Автор выражает глубокую признательность рецензентам: ака-
академику РАН Валерию Васильевичу Козлову и доценту МГУ
им. М.В.Ломоносова Клавдии Евгеньевне Якимовой, доброже-
доброжелательная критика которых способствовала улучшению сборника.
В заключение автору хотелось бы добавить, что большое мно-
множество интересных тем и задач остались «за бортом» настоящего
сборника. Однако это — предмет будущего обсуждения.
L М. Розенблат
Москва, февраль 2004 г.
.Глава 1.
СТАТИКА
Задача 1.1 [1]. Человек массы ть оставаясь на месте,
тянет за веревку груз массы тп2. Коэффициент трения
fi < 1. При какой наименьшей силе натяжения веревки груз
может тронуться? Под каким углом должна быть натянута
веревка?
Решение. Из рис. 1.1 следуют соотношения:
Т cos a ^ Fip' (чтобы груз тронулся),
Т cos а < FTp (чтобы человек не стронулся),
N2 = Р2 - Т sin а ^ О,
N\ = Р, + Г sin а ^ О,
^тр2) ^ pN2, Flp ^ pNx (закон Кулона),
где
Р, = т,?, Р2 =
Статика
Рис. 1.1. Схема сил, действующих на груз и человека
Обозначим tga = т. Тогда получим неравенства:
Т{\ +цт):
ТA-/«-);
Для решения задачи необходимо найти Tmjn, удовлетворяющее
неравенствам (I), причем г 6 0, — . Отметим, что при г > —,
второе из неравенств A) выполнено заведомо, а из первого получим
Pi
Г^учЛ+Я2=Г0.
B)
Ниже будет показано, что при г ^ — ответы для Tmin получа-
получаются заведомо меньше То.
Перепишем неравенства (I) в виде:
1 +
1 - цт
C)
Глава 1
О /* 1//л т
Рис, 1.2. Случай Рх > Р2. Область допустимых Т заштрихована
Беря производные от функций /i(r), /2G") по г заключаем* что
при т € 0, — функция /|(т) строго монотонна, а функция /г(т)
имеет единственный минимум в точке т = fi.
1°. Пусть тп\ > ГП2. Графики функций /i(r) и /г(т) приведены
на рис. 1.2. Из этого рисунка следует, что минимальное Т
достигается при г = ц, т.е. при а = arctg/i, причем
D)
2°. Пусть
Ш2- В этом случае найдем т* — корень уравнения
). Ясно, что
* Pi "" -P| W&2 — Ш| 1
< -,
причем этот корень единственный.
10
2.1.
Статика
Здесь представляются два варианта:
Рг-Р\
т* =
^(Рг+Р) "•
Эта ситуация представлена на рис. 1.3, из которого следует,
что Tmjn также дается формулой D) и а = arctg/i.
2.2.
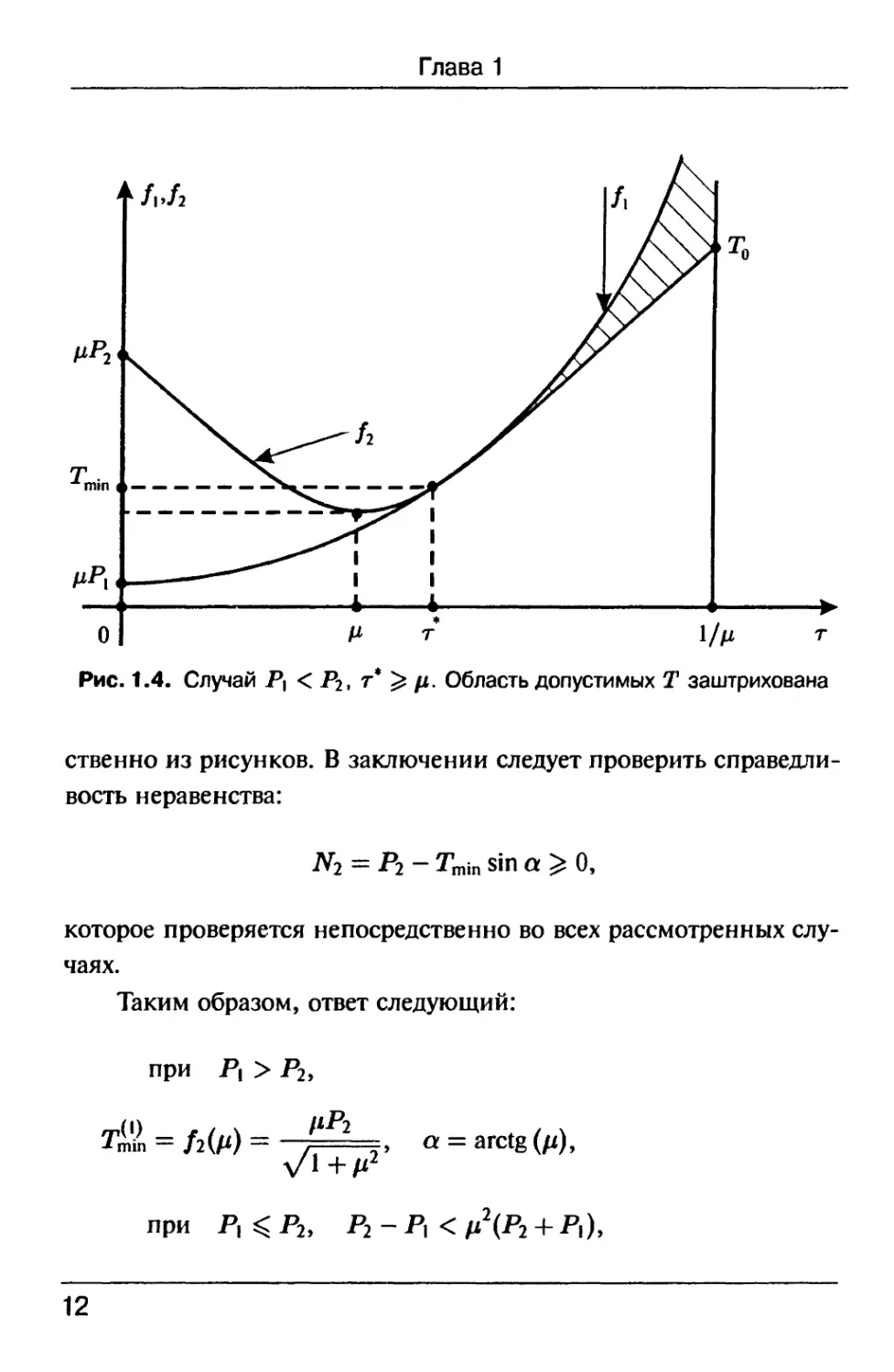
Эта ситуация изображена на рис. 1.4, из которого следует, что
минимальное Г достигается при т = т*, т. е. а = arctgr* причем,
Tmin = f2(T*) = Mr*)=l-
. E)
На этом все возможные ситуации исчерпаны, причем нера-
неравенство rmin < Го (которое дается формулой B)) следует непосред-
0
Рис. 1.3. Случай Р| < P2, r* < /z. Область допустимых Г заштрихована
11
Глава 1
О
Рис. 1.4. Случай Р| < Р2, т* ^ р. Область допустимых Т заштрихована
ственно из рисунков. В заключении следует проверить справедли-
справедливость неравенства:
которое проверяется непосредственно во всех рассмотренных слу-
случаях.
Таким образом, ответ следующий:
при Р, > Р2у
, a = arctg(/i),
1 +//2
при Рх ^ Ръ Р2-Рх< fi2(P2 + Pi),
12
Статика
При
Отметим, что в задачнике НГУ [1] все ответы такие же, кроме
, Для которого дается формула
В сборнике задач Всесоюзных физических олимпиад [6] приве-
приведено некорректное решение, в результате которого получен верный
ОТВеТ ДЛЯ Tmin. О
Задача 1.2 (задача 2.8.4.4 из [1]). На шероховатом гори-
горизонтальном столе лежит брусок (см. рис. 1.5 с видом свер-
сверху). Какую минимальную горизонтальную силу F, перпен-
перпендикулярную бруску, нужно приложить, чтобы его сдвинуть?
Коэффициент трения равен /х, масса бруска га.
Решение. Пусть р — линейная плотность бруска, а его длина
АВ = 21, С — его центр масс. Начальное движение бруска, при
соблюдении перпендикулярности силы F к АВ, будет либо:
1°. поступательное вдоль силы F, либо
2°. мгновенно-вращательное с МЦС, лежащим где-то на линии
АВ (точка Р см. рис. 1.5).
Ясно, что в случае 1° для трогания бруска необходимо
13
Глава 1
Рис-1-5- Вид сверху на горизонтальную плоскость стола
Посмотрим, что будет в случае 2°. Обозначим PC = z. Тогда
уравнение моментов для точки Р с учетом сил трения будет:
l+z 1-х
- J\xpgxdx- J\xpgxdx, ze[0,l]
или так:
Для трогания необходимо неравенство ^J Mp ^ 0, отсюда:
= min
I -f Z
Функция — г- достигает min в точке z = l(y/2 — 1). Таким
(' + «)
образом,
2 — \Pl
= № ¦ 21
v2
- 1).
14
Статика
Ясно, что
Кроме того, можно показать, что силу F выгоднее всегда прикла-
прикладывать в концевых точках А или В.
Случай z ^ I приводит к соотношению
что явно хуже полученного
fimg(V2- 1) « 0,41/img.
Ситуации, когда Р лежит с другой стороны от точки С рассматри-
рассматриваются аналогично и приводят к худшим результатам.
Можно предложить следующее обобщение задачи. Найти ми-
минимальную (по модулю) силу F, способную стронуть брусок,
не накладывая требования перпендикулярности ее к бруску. Оказыва-
Оказывается (доказательство достаточно громоздко), что минимальная сила
обязательно должна быть перпендикулярной бруску, т. е. наличие
составляющей силы F вдоль бруска ухудшает результат (т. е. только
увеличивает модуль силы F способной стронуть брусок!).
Отметим, в заключение, что сформулированная задача рас-
рассматривает процесс перехода силы трения покоя в силу трения
скольжения. Поэтому здесь необходимо учитывать тот факт, что
коэффициент трения /i может, вообще говоря, испытывать скачко-
скачкообразное изменение. Кроме того, сила трения покоя, приложенная
к элементарному куску бруска, направлена против равнодейству-
равнодействующих внешних сил, действующих на этот кусок. А сила тре-
трения скольжения — против скорости, приобретенной этим куском
(как и подразумевается при решении этой задачи!). Учет описанных
обстоятельств существенно усложняет задачу! 1>
15
Глава 1
Рис. 1.6
Рис. 1.7
Задача 1.3. Однородный прямоугольник с основанием а,
высотой Ь и весом Q, лежит на шероховатой горизонтальной
плоскости с коэффициентом трения /. Каким условиям
удовлетворяет величина силы Р (см. рис. 1.6), для которой
прямоугольник находится в равновесии при любом значении
угла а из интервала
Решение. Расчетная схема приведена на рис. 1.7. Для равно-
равновесия необходимо, чтобы
¦F = 0, A)
Fy = P sin a + N - Q = О,
B)
где N — нормальная реакция, F — сила трения (покоя).
Далее, пусть точка приложения силы N есть D. Обозначим
AD = ?. Ясно, что ? 6 @, а). Точное значение ?, оставаясь в рамках
модели абсолютно твердого тела, определить нельзя. Поэтому для
равновесия достаточно исключить возможности поворотов отно-
16
Статика
сительно точки А(? = 0) и точки В(? = а). В результате получаем
неравенства:
а
Р cos а • 6 - Psin а • а 4- Q • - ^ 0, C)
<2 • | - Р cos а • Ь ^ 0, D)
кроме того, еще запишем закон Кулона для силы трения покоя:
F^f-N. E)
Тогда из B) имеем
N = Q-Psma,
поэтому из A) и E) получим неравенство:
рк '•?. ¦ F)
cos a -\- f sin a
Неравенство F) должно выполняться при любых a G ( 0, — 1,
поэтому
Р ^ min | ^— 1 = А.
[cosa-h / sinaj
Чтобы вычислить А, заметим что min дроби соответствует шах
знаменателя. Обозначим
у(а) = cos a + f sin a.
Имеем
у (а) = — sin a + f cos a = 0,
т.е. aextr = arctg / = «о- Кроме того,
у"(а) = - cos а - / sin a < 0,
т. е. это действительно точка max.
3 Зак. 90
17
Глава 1
Следовательно,
max (cos a + / sin a) = cos e*o + / sin e*o = y/l + f2.
fQ
Итак, A = t , и первое условие для силы Р следующее:
Л /2
G)
Далее, из неравенства C) получим
P(sin а - ц cos а) ^ —, где ц = -. (8)
Это неравенство также должно соблюдаться при любых а € 0, - .
Обозначим
Ух (а) = sin a - ц cos a,
тогда
j/i (a) = cos а + fi sin а > 0 при а € 0, ~ ,
Г ^1
т. е. функция у\ (а) монотонно возрастает на отрезке 0, — . По-
Поэтому имеем:
этому имеем:
Объединяя неравенства
Наконец, из D) имеем
-^
(8) и
Р:
(9), приходим к соотношению
'4
< Q
v 2/iCosa'
(9)
A0)
18
Статика
Последнее соотношение (в силу монотонности функции cos a
на интервале ( 0, — 1) будет выполнено при любых a 6 0, — при
условии
условии
Таким образом, мы доказали, что условия A-5), достаточные
для равновесия тела при указанных в задаче условиях, эквива-
эквивалентны неравенствам G), A0), A1), что можно записать более
компактно:
Невыполнение условия A2) влечет нарушение одного из усло-
условий равновесия или же нарушения неравенства Кулона E). Это,
собственно говоря, доказывает и необходимость условия A2) для
равновесия тела. О
Глава 2.
КИНЕМАТИКА
Задача 2.1 [3]. Схват С (см. рис. 2.1) плоского двухзвен-
ного автоматического манипулятора движется с постоянной
скоростью v вдоль прямой ОО\, образующей с осью Ахг
угол а. Найти угловые скорости звеньев АВ и ВС в за-
зависимости от конфигурации манипулятора, т.е. от углов <р\
и ф2, если АВ = 1\, ВС = fe-
Решение. Скорость точки В vb J- Л*1?, г;^ = о;^в -Z|, проекции
скоростей точек В и С на ВС должны быть равны:
cos б
v cos о — Vb cos
\2 /
причем нетрудно подсчитать, что о = a - 7, где у = — - ((р\ + (р2).
Таким образом:
Другой способ:
хСу = h cos <р\ +12 cos (<р\ + <р2)> хс2 = h sin ipx +12 sin (р\ + (p2),
22
Кинематика
?4???^^?Z?4? s~±
Имеем:
x2
Рис. 2.1
, = (sin a, cos a), noox = (cos a, - sin a).
C\ = —'|C«7| sin y?| — /2^2 sin {(p\ 4- y?2)j
cos y?i + /2^2 cos (y?|
Имеем два соотношения:
Vcx cos a = Vc2 sin a, Vc, sin a 4- Vc2 cos a = -w,
(sin2a\
cos a 4- ) = -v,
cos a /
Vc2 = ~v cos a, Vc, = ^^ sin a.
Имеем:
U\[l\ sin y?i 4-^2 sin ((p\ 4-^2)] 4-02 ['2 sin (y? i 4-^2)] = vsina,
u\ [ - /i cos (pi -12 cos (y?, 4- ^2)] + 4>i [ - h cos (<p} + (p2)] = v cos a,
23
Глава 2
cos (<p\ + (fj) — cos (p\ sin (tp\ + ^2)] =
= v [ sin a cos {(f\ -f ^2) + cos a sin (^ + y?2)] 5
-a>|/| sin <P2 = V sin
:
sin
(а в 131 ответ: ш\ = ; -). Интересно отметить, что при
I\sin((p2-(pi)
(р2 -> 0, и)\ -> оо! Аналогично находятся ^2 и о/2. >
Задача 2.2 [3]. Стержень (см. рис. 2.2) движется в плос-
плоскости, опираясь одной из своих точек на вершину угла А.
Конец В стержня скользит по некоторой кривой. Дока-
Доказать, что скорость точки касания стержня направлена вдоль
стержня.
Решение. Простое, но поучительное! точка А угла неподвиж-
неподвижна, т. е. Уд =0. Рассмотрим движение точки А относитель-
относительно системы координат, жестко связанной со стержнем. Тогда
уА = 0 = VAr + Уле- Ясно, что вектор Vat (относительная скорость
точки) направлен вдоль стержня. Отсюда получим Vab — —Vat*
т. е. вектор VAe направлен также вдоль стержня, а это есть скорость
точки касания стержня в рассматриваемый момент времени. >
Задача 2.3 [3]. Два вала (см. рис. 2.3) соединены шарни-
шарниром Кардана—Гука. Найти закон изменения коэффициента
передачи к = —, если угол между валами равен а, а оси
а;,
валов лежат в одной плоскости.
24
Кинематика
At
II II II II II I II I I I I
Рис. 2.2
Решение. Без ограничения общности будем предполагать, что
в начальный момент времени ось крестовины, жестко связанная
с валом 1, перпендикулярна плоскости валов. Ее единичный орт
fci(O) (см. рис. 2.3). Тогда ось крестовины, жестко связанная с ва-
2 Зак. 90
25
Глава 2
лом 2, будет принадлежать плоскости валов. Ее единичный орт
?2@) (см. рис. 2.3). Введем еще единичный орт к^9 который лежит
в плоскости валов и перпендикулярен валу 1 (см. рис. 2.3). В силу
построения угол между ортами к2@) и &з равен 7Г - а, т. е.
(к2(О)-кз) = -cos а.
Кроме того,
(fci@) • ?2@)) = 0, (к\ @) • ?3) = 0 (в силу построения).
Пусть вал 1 повернулся на угол <р\9 а вал 2 при этом —
на угол <р2. Тогда единичный орт к\ нового положения крестовины,
связанной с валом 1, будет иметь разложение:
к\ = fci@) cos v?i +ic^ sin (f\. A)
А единичный орт k2 нового положения крестовины, связанной
с валом 2, будет иметь разложение:
к2 = fc2@) cos y?2 + fci @) sin y?2. B)
Но так как орты крестовин всегда перпендикулярны, то
Перемножая A) и B), получим:
О = (fc, • к2) = (к\ @) • к2@)) cos <p\ cos <р2 + cos y?i sin у?;
+ (&з * ?2@)) sin <p\ cos <p2 + (^3 * ^i(O)) sin V^i s'n V^2
= cos if\ sin y?2 ™~ cos a • sin y?j cos <p2.
Отсюда получаем кинематическую связь:
tg <P) • cos a = tg y?2> v^2 = arctg (cos a • tg y?i),
26
Кинематика
1 1
— - -~5 cos a 2—ф\,
1 + cos2 а • tg2 (p\ cos2 (p\
и2 cos а cos а
cos2 y?i + cos2 a • sin2 y?i 1 - sin2 y?i • sin2 a'
t
о
(точно, как в [3]!).
Эта задача подробно разобрана у Кильчевского [8, с. 138] и в
статье Антонова И. Л., Трушина С. Н., Якимовой К. Е. [33, с. 82]. >
Задача 2.4 [3, с. 183]. В соревнованиях по ориентирова-
ориентированию на местности каждый участник ориентирует свой вектор
скорости по направлению на заранее заданного участника.
Значение скорости выбирается пропорциональным рассто-
расстоянию между ними. В результате решение описывается си-
системой дифференциальных уравнений:
^n = An(fi - fn),
где константы Af > 0, ri — радиусы-векторы участников
(i = 1,п). Доказать, что через конечное время они собе-
соберутся в круге радиуса Го > 0 с центром в точке
2*
27
Глава 2
где fi — начальное положение участников (причем го -> О
при t -> оо!).
Решение. Указанная линейная система дифференциальных
уравнений с постоянными коэффициентами имеет характеристи-
характеристическое уравнение:
Это следует из вида характеристической матрицы:
-А,-
0
А
А,
-А2-
А
0
А2
0 ...
0 ...
0
0
К 0 -Ап-А/
Характеристическое уравнение переписывается в виде:
Отсюда видим, что есть корень А* = О!
Остальные (п - 1) корней имеют отрицательные веществен-
вещественные части (в противном случае будем иметь
Таким образом, решение системы дифференциальных уравне-
уравнений имеет вид:
где Bk(t) — ограниченные функции; Ак
ствующие нулевому корню.
константы, соответ-
соответ28
Кинематика
Ясно, что все Аъ равны между собой, так как собственный
вектор, соответствующий нулевому корню, имеет вид:
(I, 1, •-., О-
Система имеет интеграл:
— = const, A = a
к к
Отсюда следует утверждение задачи.
Задача 2.5 [9, с. 35]. Однородный стержень АВ длины
2а и весом Р опирается одним концом на вертикальную
стену, а другим концом на гладкий неподвижный профиль.
Какова должна быть форма этого профиля, чтобы стержень
АВ в любом положении оставался в равновесии даже
в отсутствие трения?
Решение. Для решения задачи необходимо обеспечить посто-
постоянство координаты ус центра тяжести стороны при любом х
(см. рис. 2.4). Пусть у = f(x) — уравнение профиля. Тогда:
{Уа-У) ,
ус = + у = const = усо-
Кроме того, АВ2 = 4а2 = х2 + (ул - уJ-
Исключая из этих двух соотношений у а - у, получим:
4а2 = х2 + 4(ус0 ~ уJ — Уравнение эллипса.
Если уо = /@) = 0, то очевидно ус0 — а и уравнение эллипса
имеет вид:
. ..
4а2 + а2 '
т. е. эллипс с полуосями 2а, а и центром в точке @, а).
29
Глава 2
g
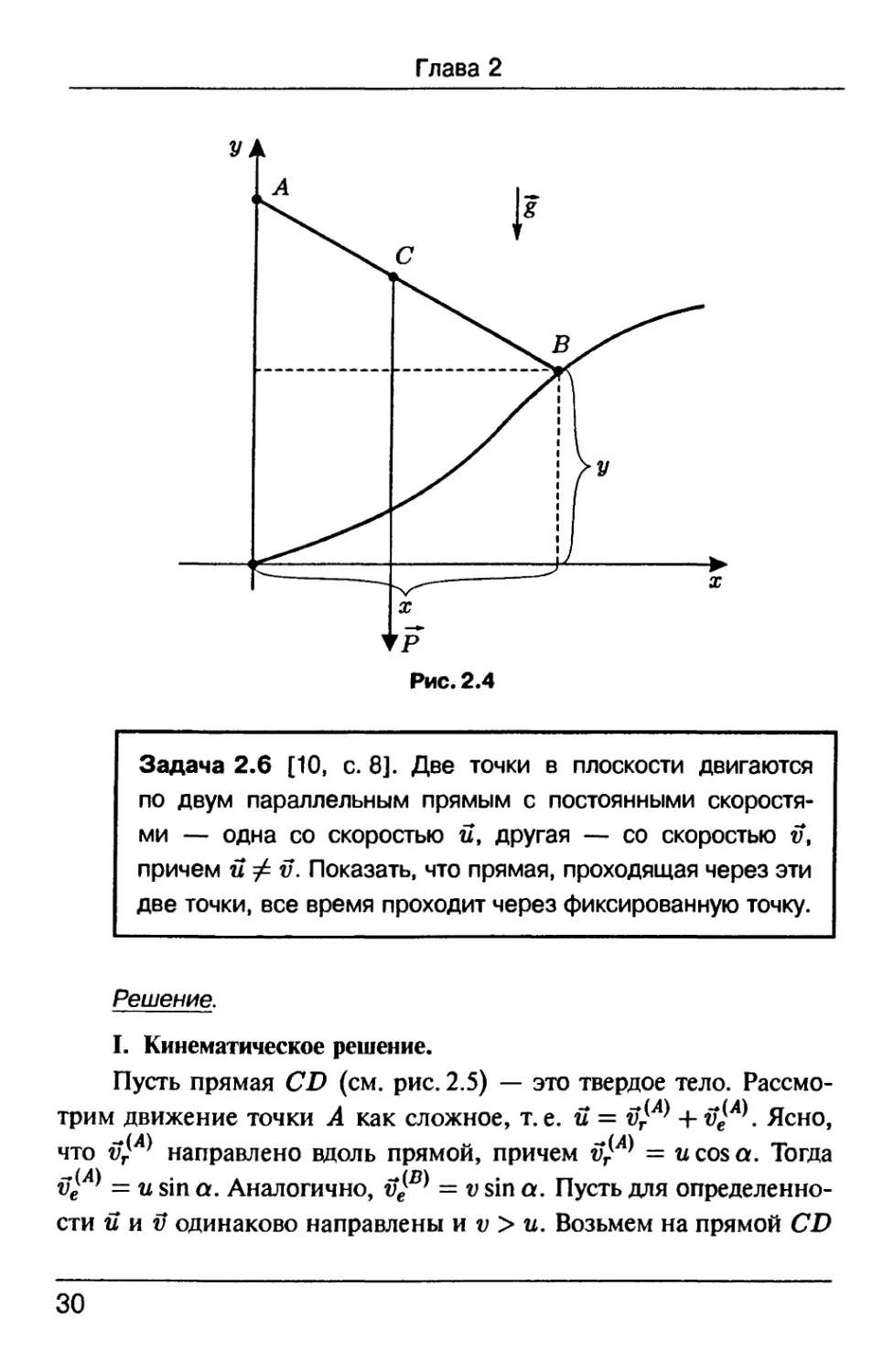
Задача 2.6 [10, с. 8]. Две точки в плоскости двигаются
по двум параллельным прямым с постоянными скоростя-
скоростями — одна со скоростью п, другая — со скоростью v,
причем и Ф v. Показать, что прямая, проходящая через эти
две точки, все время проходит через фиксированную точку.
Решение.
I. Кинематическое решение.
Пусть прямая CD (см. рис. 2.5) — это твердое тело. Рассмо-
Рассмотрим движение точки А как сложное, т.е. u = v}^ + v}A\ Ясно,
что Vr направлено вдоль прямой, причем v}A^ = и cos а. Тогда
v^ = и sin а. Аналогично, tfeB?) = t; sin а. Пусть для определенно-
определенности и и v одинаково направлены и v > и. Возьмем на прямой CD
30
Кинематика
D
Рис. 2.5
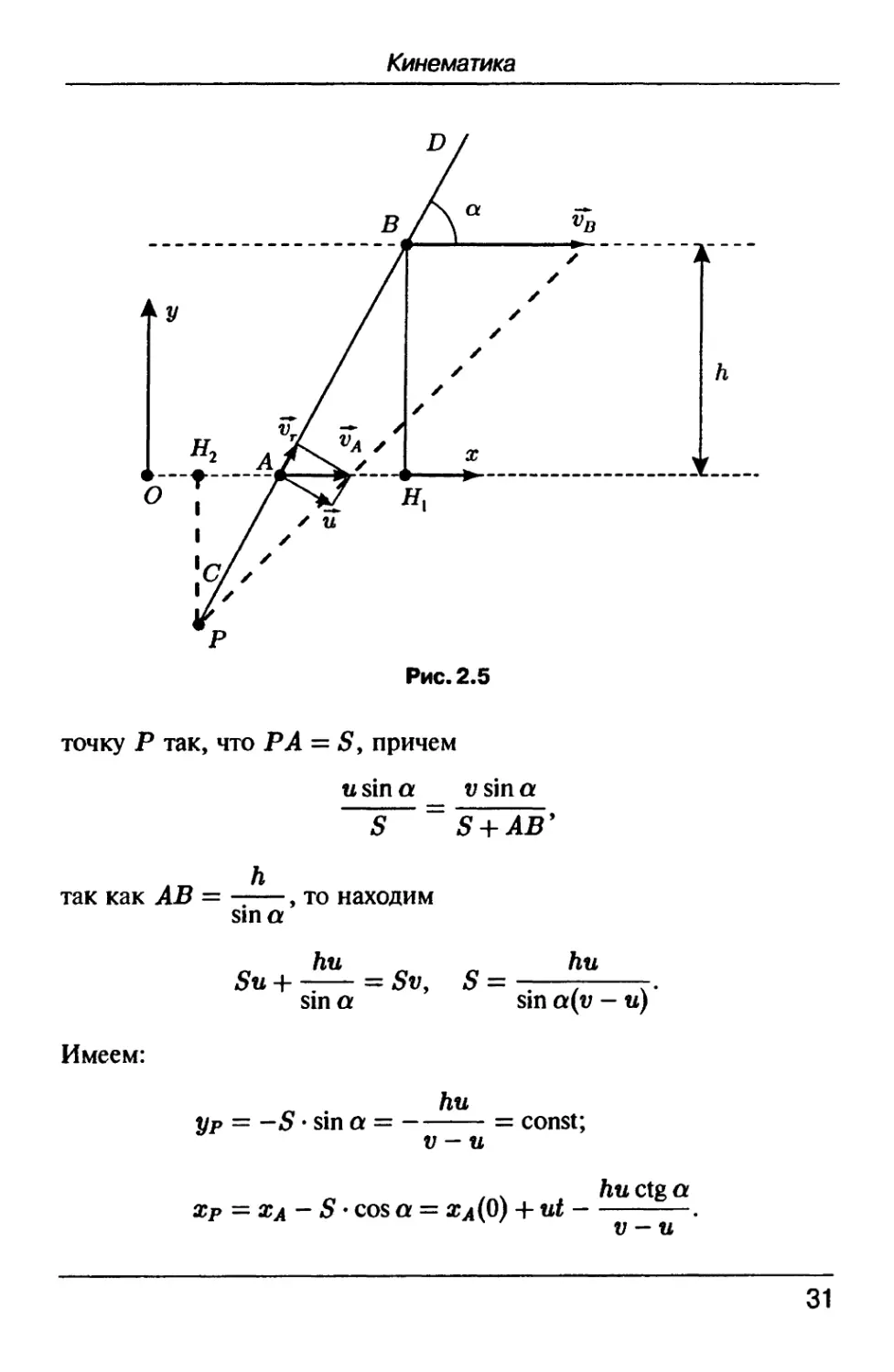
точку Р так, что РА = 5, причем
u sin a v sin a
S S + AB9
так как АВ = , то находим
sin a
Имеем:
Su + -— = Sv, S= -—7 r.
sin a sin a(v - u)
hu
yP = -S • sin a = = const;
= xa- S • cos a = а?л@) + ut —
hu ctg a
31
Глава 2
Но кроме того, учтем соотношение между ж-координатами точек
А и В:
Хв{1) - xA(t) = (v - u)? -ь ^б(О) ~ xA@) = Л ctg a.
Тогда получим:
hu (v-u)t + xD@)-xA@)
v-u h
ut-ut [xB@) - xA@)] = const.
II. Геометрическое решение.
Опустим из Р и В перпендикуляры на ось х: ВН\ и РЯ2.
Из подобия треугольников АЩР и АВН\ находим:
Ы Л
ХВ ~
Дифференцируем это равенство по ?:
-2/рЯв ~ J/p^ + УрЖх + Уръ = hu- hxP.
Подчиним ур условию:
-ypv + yPu = hu, yP = , ур = 0,
V — U
тогда
0 = -h±p9 хР = 0, хР = const
и т.д.
32
Кинематика
веревка
///у//////////,
Рис. 2.6
х
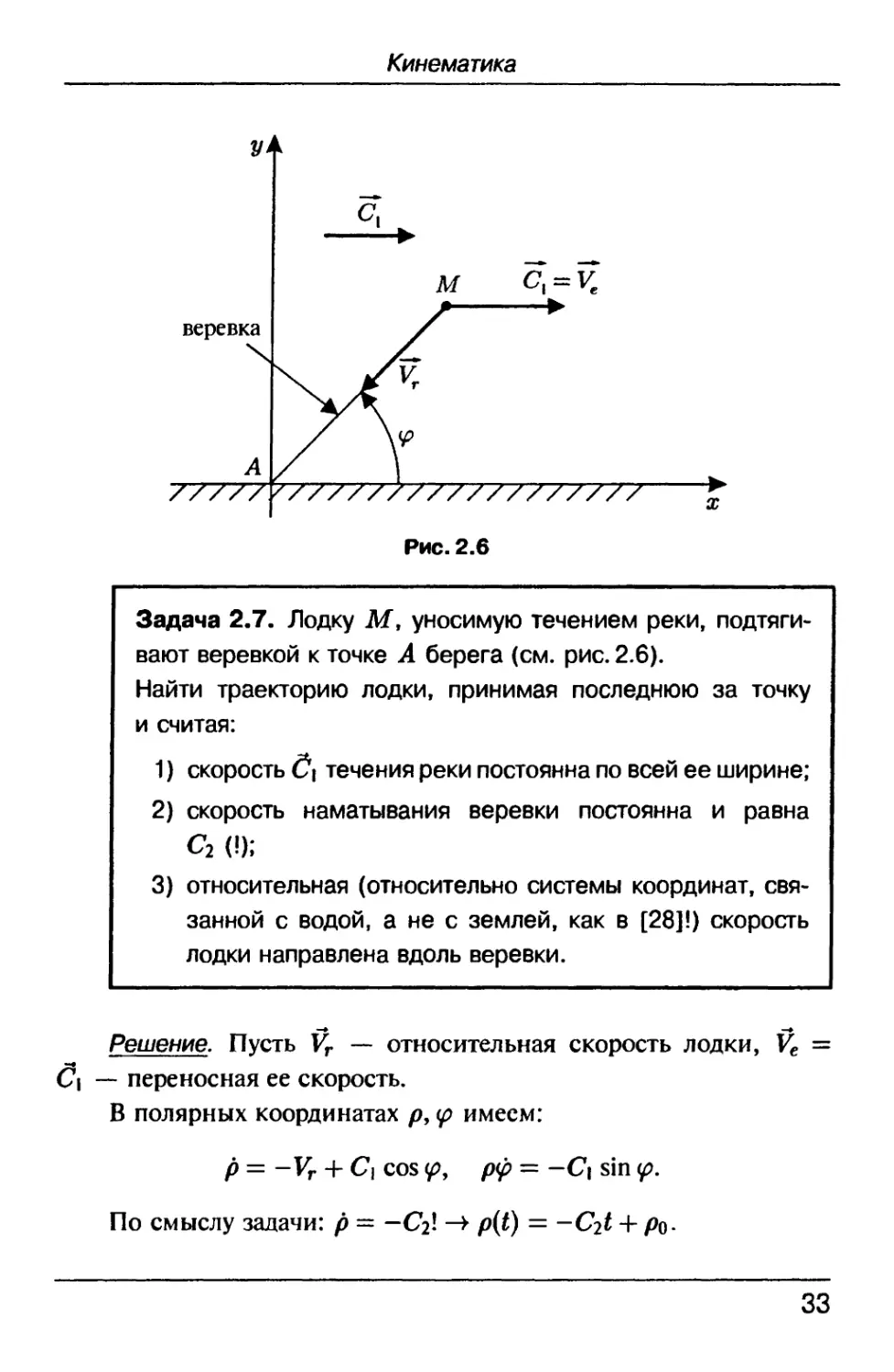
Задача 2.7. Лодку М, уносимую течением реки, подтяги-
подтягивают веревкой к точке А берега (см. рис. 2.6).
Найти траекторию лодки, принимая последнюю за точку
и считая:
1) скорость С\ течения реки постоянна по всей ее ширине;
2) скорость наматывания веревки постоянна и равна
С2 (!);
3) относительная (относительно системы координат, свя-
связанной с водой, а не с землей, как в [28]!) скорость
лодки направлена вдоль веревки.
Решение. Пусть Vr — относительная скорость лодки, V€ =
С\ — переносная ее скорость.
В полярных координатах р9 <р имеем:
р = -Vr + С\ cos <р, рф = -С] sin <р.
По смыслу задачи: р = -Сг! -У p{t) = -Cit + ро-
33
Глава 2
Далее:
dip
sin
1 - cos (p
1 + cos (p
1 - cos y?0
. 1 + cos y?o.
dt_
С- -C2*
7Г«п г
^2 A)
tg^-ctg
C\ p
— in —,
< P
Задача 2.8. Условия предыдущей задачи, но веревки нет,
а гребец все время направляет лодку в точку А берега,
сообщая лодке постоянную относительную скорость С?2 -
Найти траекторию лодки.
Решение. Схема такая же, но здесь Vr = Сг (в предыдущей
задаче Vr = С\ cos у? - Сг!!!).
Уравнение движения в полярных координатах:
р = -Сг + C| cos у?, р^ = -C| sin у?,
р С2 I dp C2 dip cos (p-dip
— _^^ ^_^__ _. nicy /л — ____ ^
^ C| sin у? ' р С\ sin v? sin у?
ln( ~) =7г'п tg-ctg— -
In
Po
sm
sin
к =
С1,'
34
Кинематика
п у
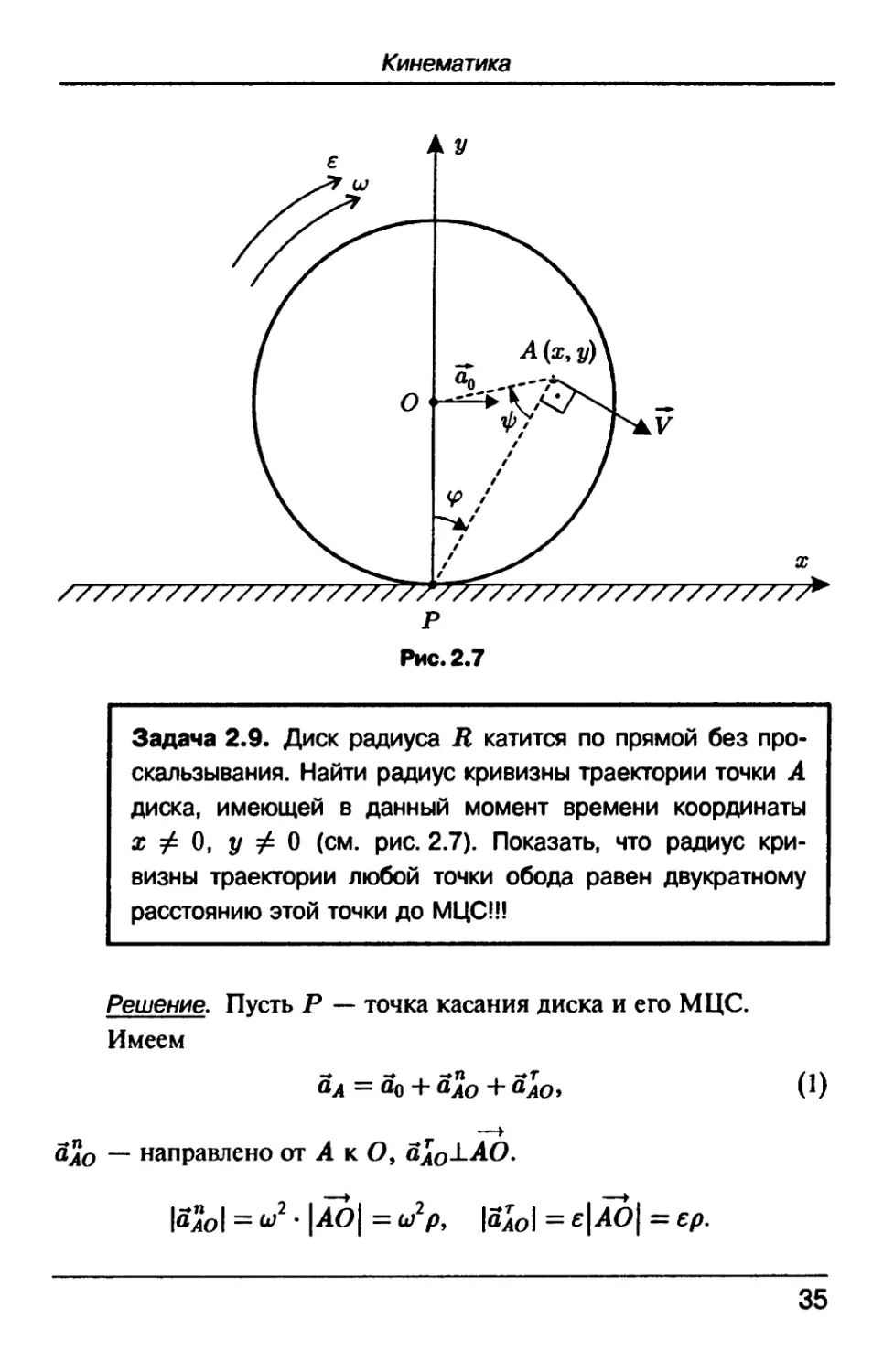
Задача 2.9. Диск радиуса R катится по прямой без про-
проскальзывания. Найти радиус кривизны траектории точки А
диска, имеющей в данный момент времени координаты
х ф О, у Ф 0 (см. рис. 2.7). Показать, что радиус кри-
кривизны траектории любой точки обода равен двукратному
расстоянию этой точки до МЦС!!!
Решение. Пусть Р — точка касания диска и его МЦС.
Имеем
0)
— направлено от А к О9 oJ[o
б=и2р, \aTAO\ = e\AO\=ep.
35
Глава 2
Далее <р — vrcvi OP А, 1р — угол О АР. Тогда
*аох = -ь>2/> • cos I (тг - (V + ф)) - ~ ,
<?АОу = -v2p. sin (тг - (^ + у?)) - ~ ,
o^ = +^/?-sin I(tt-(^ + v?)) -~ ,
^оу = -ер • cos (тг - (^ + р)) - ~ .
= t*)y/x2 + y2 = o;r. Тогда:
V^ = иг cos у?; 1^ = -wr sin у?.
Окончательно:
<йо* = -ш2р • sin (v? + ip), anAOy = -ш2р • cos
*аох = е/> • cos (у? + ДО, <uoj, = -ер • sin (у? + ДО.
Тогда из A) имеем:
пах = eR- ш2р • sin (^ + ДО + ер - cos (<p + ДО,
влу = 0 ~ ^2/> • cos (у? + ДО - ер • sin (у? + ^).
у
Единичный вектор п вектора РА имеет проекции
х у
г * г
36
Кинематика
Тогда:
» *"Ч * ч-» » ^ I / \ I ^Ь ^Ь.
ал = («л • й) = еД и — sin (<p + ф) +ер- cos (<p + if))
г г г
- ш2р- cos (^ + ip) - ер- sin (^ + ф).
кр an
anA eRx - u2p(x sin 7 + у cos 7) + ep(x cos 7 - у sin 7)'
a: = r sin y?, 3/ = r cos p,
r sin if sin7 + r cos p COS7 = r cos ^,
r sin <p cos 7 - r cos p sin 7 = -r sin ip.
Из теоремы синусов для OP A:
R _ р
sin t/> sin cp'
37
Глава 2
Задача 2.10 [3]. Диск радиуса R катится по прямой без
проскальзывания (см. рис. 2.8). Найти геометрическое ме-
место точек диска (в фиксированный момент времени), для
которых нормальное ускорение равно нулю.
Решение. Пусть М(х9 у) — произвольная точка диска в си-
системе координат Рху (Р —- точка касания, М. Ц. С. диска при его
качении).
Имеем:
&мо — направлено от М к О, й^о^-МО. Вектор скорости точки
MLPM.
38
Кинематика
Проецируем обе части равенства A) на направление вектора
РМ:
= eocos--0r-/3-a) - <^мо cos a - arMO sin a
или так:
вм = Q>o sin (p + a) - anMO cos a - aTMO sin a. B)
Далее имеем ao = re, a^o = |М0| • e.
Но из АОМР и теоремы синусов имеем:
ып(р + а) sin a ' ' sin a
Тогда:
sin a
Подставляем полученные равенства в B), получим:
гм = er-sin (р + а) - <РМО cos a-er sin (/? + а) = -апмо cos а.
Так как а^о = о;2 • \МО\ Ф 0 (при качении!), то для соблю-
дения равенства пр -^8м =0 (т. е. равенства нулю нормального
тг
ускорения точки М) необходимо, чтобы cos a = 0, т.е. a = —
Зл-
Злили а = —. Таким образом, угол ОМР всегда для таких точек
прямой!
А это означает, что точка М лежит на окружности с диаметром
ОР, т.е. радиуса -!
Эта задача — упрощение соответствующей задачи из кинема-
кинематики плоского движения твердого тела (точка Р — мгновенный
центр вращения, точка О — центр поворотов, а полученная окруж-
окружность — окружность перегибов, (см. Жуковский [12]). t>
39
Глава 2
ПЛОСКОСТЬ
качения
пластинки
эллиптическая
пластинка
Рис. 2.9
Задача 2.11. Эллиптическая пластинка с полуосями а и Ь
(о > Ъ) катится без проскальзывания по горизонтальной
прямой с постоянной угловой скоростью ш = const. Найти
скорость центра О эллипса в зависимости от времени,
считая, что в начальный момент его большая полуось была
горизонтальна.
Усложнение задачи: найти ускорение точки О, найти законы
изменения координат точки О при произвольном законе
качения эллипса (без проскальзывания).
Решение (см. рис. 2.9).
х = р • cos <р, у = р • sin tp,
p2 cos2 <р p2 sin21
о2 + Ь2"
=1,
40
Кинематика
где р = ОР, а система Оху жестко связана с эллиптической
пластинкой.
х2 у2 _ Bх 2у
at of /ТС \
p— = tg ( - - a) = ctg a = ctg (art).
a
o2 -^ b2
-г tg 9 = ctg (art), tg v = -I ctg a,
o^ a
1 2 , Ь4 2
= 1 + tg Ф — 1 + — Ctg i
cos2 <p a4
b4 ctg2
2 64 ctg^ a
sin ip —
^ ctg2 a a4 + 64 ctg2 a
cos2 ф sin2
+
a2 62
2_ 1 _a4 + b4ctg2a _
P ~ a2 b2 ctg2 a "" a2 + b2 ctg2 a ""
a4 + b4 ctg2 a a4 + b4 ctg2 a
_ a4 sin2 a + b4 cos2 a
a2 sin2 a + b2 cos2 a'
Решение усложненной задачи:
b2
= -т ctg a,
41
Глава 2
пусть хо, Уо — координаты точки О в неподвижной системе
координат AXY (см. рис. 2.9).
уо = р • sin 'ф = р • sin (а + (р) = p(sin а • cos у? + cos а • sin ф)>
р = р(а) — известная функция а.
+ 64 ctg2 a
sir\(p= —
b2 ctg a
/
fl4 + &4 ctg2 a
2 ^
— ctgal,
v> = —
62 a
2b2a
1 + — ctg2 a
a4
a2 sin2 a a4 sin2 a + b4cos2a"
Уо =
a sin
ina-f-6 —
cos2 a
sin a
\/a4 + 64 ctg2 a
Л -:_2
sin
. =(Q sin a + b cos a) =
in ay/a4 + 64 ctg2 a
P
(a2 sin2 a + b2 cos2 a) =
\/a4 sin2 a + b4 cos2 a
= v a2 sin2 a + b2 cos2 a.
ar0 = S - p • cos (a + (p) = 5 - p(cos acosip- sin a sin tp) =
a2 cos a - b2 cos a \Л*4 sin2 a + b4 cos2 a
= о — p—. = S — x
4 4 2 /
V a4 + b4 ctg2 a
y/a2 sin2 a + b2 cos2 a
42
Кинематика
(а2 - ft2) cos а • sin а (а2 - ft2) cos а • sin а
x —. = S —
1 sin2 a + ft4 cos2 а \/а2 sin2 а + ft2 cos2 a
S — длина прокатанной дуги эллипса (S = АР, см. рис. 2.9).
= / y/(dpJ
dx = dp-cosv?- p• sin v?• <fy?,
dj/ = dp • sin v? + p • cos v? • dip,
ab
P(<P) =
sin2 (p + ft2 cos2 v?
dp 1 aft(a2 • 2 sin y? • cos y? - ft2 • 2 cos (p • sin у?) ^
^ 2 (a2 sin2 v? + ft2 cos2 y?) J
aft(a2 - ft ) sin (p • cos y?
(a2 sin2 y? + ft2 cos2 у?) г
aV а2&2(о2 - Ь2J sin2 ip • cos2 p
+
a2 sin2 у?+Ь2 cos2 <p (a2 sin2 (p + b2 cos2 <pK
_ a2b2 Г (o2-b2Jsin2y?-cos2y?1 _
a2 sin2 ip + b2 cos2 y> [ (a2 sin2 (p + b2 cos2 <pJ J
43
Глава 2
a2b2 a4 sin2 <p + b4 cos2 <p
a2 sin2 (p + 62 cos2 y? (a2 sin2 y? + b2 cos2 y?J
a2b2(a4 sin2 y? + 64 cos2 (p)
(a2 sin2 y? + ft2 cos2 y?K
Задача 2.12 [13]. Заяц и лиса. Заяц бежит по прямой
с постоянной скоростью г/, лиса бежит в горизонтальной
плоскости, ее скорость и направлена всегда на зайца.
1) пусть и > v, найти время поимки;
2) пусть и = v, найти уравнение траектории и минималь-
минимальное расстояние, на которое может приблизиться лиса
к зайцу;
3) пусть и, v — произвольны, найти уравнение траектории
(траектория погони).
Решение. На рис. 2.10 представлена система координат Оху,
жестко связанная с зайцем, который находится в точке О и бежит
вправо вдоль оси х со скоростью Vq . Тогда движение лисы (точка А)
в этой системе описывается уравнениями:
? = t/ —tisina, y = -«cosa, A)
где a — угол, образуемый вектором скорости п с осью у.
Обозначим р = \ЛО\. Тогда р = -u + vsina (проекция ско-
скоростей точки А на направление АО). Найдем из этого уравнения
sin a и подставим его в первое из уравнений A), получим:
х = v-u- -
44
Кинематика
Ук
О
Рис. 2.10
Так как v = const и u = const, то это уравнение можно про-
проинтегрировать:
vx(t) + up(t) = (v2 - u2)t + vx0
Мы получили интефал системы A).
1) Пусть и > v. Тогда
up(t) > vp(t) > v\x(t)\
для любых t, правая часть B) обращается в ноль в момент t\:
B)
—72
= 7Т~^ (VXo + иу/х1
т.е. имеем
получим
up(t\) = 0, а так как up(t\) > v\x(t})\9 то
т. е. происходит поимка.
2) Пусть « = v. Тогда из B) получим уравнение траектории
x{t) + \/х2 + у2 = хо + ро = const.
45
Глава 2
Переходя к полярным координатам р и а, получим уравнение
траектории в полярных координатах:
vp sin а + up = vx0 + ир0, p(t) =
М, ЧТ(
p(t)
1 + sin a
Отсюда видим, что
я
и достигается это значение при а = —, т. е. когда лиса и заяц
находятся на одной прямой. Можно показать, что достигается это
значение при t -» оо!
3) uhv произвольны. Перейдем в уравнениях A) к полярным
координатам р и а, получим:
{х = р sin а + pd cos а = t; - и sin а,
у = р cos а + pd sin а = -u cos а.
Отсюда:
I dp v sin a - и
t;cosa
/1 f v sin a - и
-dp= da,
р J vcosa
ро Оо
/v sin a - и ш и f
da = — In cos a — /
t; cos a v J
cos a
и 1 + sin a
= — In cos a In
2v 1 - sin a
= - In (cos a) •
46
Кинематика
Итак, имеем интеграл:
(l + sinaV« „ С /1-sinaV"
:— 1 = С = const -> р = 1 :— )
1-sina/ cosa \1 н-sina/
— это и есть уравнение траектории.
Обозначим
V
и преобразуем, используя cos а = \/1 - sin а • у/1 + sin а:
р = С{\ - sin а) 2 . A + sin а) 2 . >
Замечание. Для наибыстрейшей поимки зайца (при и> v) лиса должна
бежать в упреждающую точку, т. е. в системе Оху вектор и направлять
так, чтобы результирующий вектор скорости точки А (г? = й + (—5))
—>
был направлен в точку О, т.е. w \\ О А (см. рис. 2.11). Однако показать
оптимальность такого управления не просто! Вычислим время при таком
режиме погони и сравним его с полученным в п. 1.
Уравнения в полярных координатах:
{х = р sin а + pa cos а = v - и sin (а и- /?),
г/ = р cos а и- pd sin а = -« cos (а + C).
Отсюда:
{р = v sin а - u cos C,
pa = vcosa-u sin/3,
где Р — управляющий параметр (его выбирает лиса!). Будем вы-
выбирать р по закону:
. vcosa ,
Р = Р = arcsin (при v < и\).
и
Тогда ра = 0, а = ао = const. Имеем:
/ v2 cos2
р = v sin ао - «у 1 2~
47
Глава 2
Рис. 2.11
Отсюда ясно, что поимка, т.е. обращение p(t) в нуль, про-
произойдет через время:
t » = Ро
у/и2 - v2 cos2 по - v sin а0'
при условии, конечно, и> v. Покажем, что t* < t\:
Ро ^ 1
~ v2 cos2 а0 -1; sin a0
т. e.:
n2 - v2 < (v sin Of0 + n) ( \/n2 - v2 cos2 a0 - t; sin aoj,
или так, (после умножения и деления правой части на vsi
у/и2 - v2 cos2 uq):
2 2/ ,
n ~ t; < (v sin a0 + n)
у/и2 - v2 cos2 ao +1; sin ao
\/n2 - v2 cos2 a0 +1; sin a0 < t; sin a0 + ti,
\/ti2 - v2 cos2 Of0 < n,
что верно!
48
Кинематика
Например, при а = О, имеем:
Рои , _ po
t\ U
V V
Если - <& 1, то разница едва ощутима, но ежели — близко к 1, то
и и
разница очень существенна!!!
v 9 *, 10
Например, при - = —, получим —¦ = -т= ~ 2,4, т.е. более
и 10 t у 18
чем в два раза!
Теперь докажем оптимальность прицеливания лисы в упре-
упреждающую указанным образом точку.
Опять напишем уравнения движения точки А:
х = v - u sin 7> У = —« cos 7,
где 7 = с* + Д — управление лисы, причем 7 С [0, 2тг].
Множество всех точек (х,у), куда может попасть точка .А
за время t — это окружность радиуса ut с центром в точке
(х0 - vt9 г/о) (см. рис. 2.12).
Действительно, в системе координат, перемещающейся вдоль
х со скоростью v влево (см. рис. 2.12) начальная скорость у точки
А равна нулю. Точки в этой системе, которые достигаются за время
t при управлении 7 = const, где j G [0, 2тг], образуют, очевидно,
окружность радиуса ut:
x(t) = -
y(t) = -ut cos i,
x2 + y2 = (utJ.
3ак.9О
49
Глава 2
произвольная
траектория
А (х0 - vt, y0)
Рис. 2.12
Покажем, что при любом выборе управления 7 = 7@ точка
к моменту t не выходит за пределы этой окружности. Пусть
противное, т. е.
x2(t) + y2(t)>u2t2,
тогда ввиду непрерывности функции x2(t) + y2(t) существует такое
t\ < t, ЧТО
Точка М с координатами {x(t\), y(t\)} (см. рис. 2.12) принадлежит
окружности радиуса ut. Значит, существует такое 7 = Ъ = const,
что
x(t\) = -ti<sin7i, y(t\) = -trfcos7i,
т. е. точка М достигается движением по прямой AM со скоростью
и за время t. По предположению, точка М достигается движением
по некоторой кривой AM со скоростью и, но за время t\ < t,
что быть не может, так как длина кривой AM больше длины
прямой AMI
Таким образом, область достигаемых точек за время t в ука-
указанной системе координат есть круг радиуса ut с центром в точке
Aq, Точка О (заяц) в этой системе движется со скоростью v
50
Кинематика
Рис. 2.13
вдоль х. Поэтому первый момент времени, когда эта точка коснет-
коснется указанной окружности и будет оптимальным временем поимки
(см. рис. 2.13).
Из ААоОоО* имеем:
(А0О*J = (АоОоJ + (ОоО*J - 2DА)
cos (j
u2t2 = pl + v2t2 + 2p0vt sin a0.
Оптимальное время t = t* есть минимальный положительный
корень этого уравнения, решая которое, получим:
— /¦ —
ро
sin2 a0 + v0 sin a0
in a0)
L
7 7
u2 -v2
что, очевидно, совпадает с выражением для t*, полученным выше.
Ясно, что оптимальная поимка осуществляется прицеливанием
в эту упреждающую точку О*.
5*
51
Глава 2
—V
0
О
Рис. 2.14
Задача 2.13 [14, с. 32]. За лисой, бегущей равномерно
и прямолинейно со скоростью v, гонится собака, скорость
которой п постоянна по модулю и все время направлена
на лису. Когда скорости лисы и собаки оказались взаимно
перпендикулярными, расстояние между ними было равно L.
Определить ускорение собаки в этот момент времени.
Решение. По аналогии с предыдущей задачей: О — лиса, А —
собака, ОА = р — радиус-вектор собаки в системе координат Оху9
связанной с лисой и поступательно с ней перемещающейся, /3 —
полярный угол (см. рис. 2.14). Имеем:
= ^ ~ и cos C; Vav = -u sin C;
'$; aAy = -ucosC-/3;
52
Кинематика
Кроме того,
хл = р • cos/З; Уа=Р- sin/3;
= ±л = /> cos /3 - р/3 sin /3;
= Ул = psin/3 - р/3 cos/3;
Используя вышеприведенные равенства, получим:
v - u cos /3 = р cos C - р$ sin /3
-u sin /3 = /?sin /3 + /?/3 cos /3
- sin/3
+
cos/3
г;
-v sin C = p/3, ^ = — sin /3.
P
Таким образом, ускорение точки А будет:
uv
\aA\ = u\p\ = —anfi.
В частности, при C = — (по условию задачи) имеем
Задача 2.14 [13, с. 16]. Муха заметила на столе каплю ме-
меда, пролетая точно над ней горизонтально со скоростью щ
на высоте Н. Считая, что муха может развивать ускорение 3
в любом направлении, причем \a\ ^ а0» определить, как на-
надо двигаться мухе, чтобы как можно быстрее добраться
до меда? Сколько времени на это понадобится?
53
Глава 2
Рис. 2.15
Решение. Переходим в инерциальную систему координат,
движущуюся со скоростью щ. Тогда в этой системе муха будет
в покое в начальный момент, а капля будет двигаться со скоростью
—г?о вдоль оси Ох (см. рис. 2.15).
Уравнения движения точки А (мухи) суть:
? = asina; у = — a cos а (см. рис. 2.15).
Можно показать, что множество достигаемых мухой к момен-
моменту t точек (я, у) плоскости при \а\ ^ а0, а Е [0,2тг], х@) = 1/@) = 0,
есть круг с центром в точке А (при t = 0) и радиусом
R(t) =
aot2
Ясно, что оптимальное время t будет такое, когда точка В, имею-
имеющая координату Хв(?) = Vot первый раз коснется указанного круга.
Именно на эту точку и нужно прицеливаться мухе своим вектором
54
Кинематика
ускорения ао- А оптимальное t найдется из треугольника
Замечание. Задача существенно усложняется, если дополнительно по-
потребовать «мягкой» посадки мухи на мед, т. е. чтобы ее скорость в момент
достижения меда совпадала со скоростью меда (иначе ей будет сложно
его съесть!). В данном случае
x{t) = v0, У (t) = О,
x(t)=*ot. y(t) = O.
Можно показать, используя принцип максимума Понтрягина, что в этом
случае оптимальное управление а нужно выбирать по закону:
где С\, Сг, С3, С4 — константы. Это — закон дробно-линейного тангенса
(см. [27, с. 103]).
Задача 2.15 (см. [3, с. 24], ответ на с. 239). Мальчик бежит
с постоянной скоростью v и с помощью водила катит перед
собой обод, имеющий форму эллипса с полуосями а и Ь
(а > Ь). Кольцо водила находится на постоянной высоте
h над землей. Найти наименьшую и наибольшую угловые
скорости обода, считая, что он катится без проскальзывания
(см. рис. 2.16).
Замечание. На указанной странице цитированного сборника приведены
ответы:
vb2
va
a2b - h(a2 - b2)'
ab2 + h(a2 - b2)'
55
Глава 2
эллиптический
обод
ведило
Рис. 2.16
которые, как показано ниже, неверны. Нетрудно догадаться, что эти от-
ответы получены для случаев, когда малая или большая полуось эллипса
параллельна дороге. Но это отнюдь не означает экстремальности угловой
скорости обода! Оказывается, что для очень вытянутых эллипсов (а > ft),
минимальная угловая скорость сколь угодно близка к нулю.
Действительно, из нижеприведенных формул B) и C) при
тг
= — получим:
и) =
vb
h =
ab(l - si
ay/a^sm2 T\ + Ь2 cos2 Т\ у/a2 sin2 T\ + b2 cos2 T\
При Л = Ъ = const и а -> оо получим из второго соотношения:
1 - sin Tj I
1 = _^ sin Т| = - и и) -> 0 при а -> оо.
sin T| 2
В то же время из ответов цитированного сборника при h = Ь
получим:
при а -> оо.
П
v
Ъ
п
+ Ьа2 - Ь3
-ь>
тг
Значение тг = — соответствует положению поводка в точке элли-
эллипса с наименьшей его кривизной, при этом при больших а в этом
56
Кинематика
положении большая ось почти параллельна горизонтали и поэто-
поэтому малость ш вполне естественна! Отметим также, что значения
^max получаются из нижеприведенных формул B), C) при
7Г
7Г
т2 = 0и г, = -.
Решение. Пусть А] — произвольная точка эллипса. Проводим
через нее касательную 1\. Затем проводим прямую l\, параллель-
параллельную 1\ на расстоянии h ^ Ь ближе к центру О эллипса. Прямая l\
пересекает эллипс в двух точках: А2 и А2. Эта картина соответству-
соответствует качению эллипса по прямой 1\, причем точка А\ — мгновенный
центр скоростей эллипса, а если качение происходит по часовой
стрелке (как указано на рис. 2.17), то в точке А2 находится по-
поводок мальчика, абсолютная скорость которого v, и направлена
эта скорость вдоль прямой l\, как указано на рисунке. Если ка-
качение эллипса происходит против часовой стрелки, то поводок
находится в точке А2, а скорость его направлена вдоль прямой l\,
но в противоположном направлении. Будем рассматривать движе-
движение поводка (точки Аг) по отношению к системе координат XOY\
жестко связанной с эллипсом. Тогда имеем:
v = vr+v€, A)
где v — абсолютная скорость поводка, vr — скорость поводка
относительно эллипса, направленная по касательной к эллипсу
в точке А2 (прямая 12 на рисунке), ve — переносная скорость
поводка, совпадающая со скоростью точки А2 эллипса при его
качении по прямой 1\ и направленная, следовательно, перпенди-
перпендикулярно к А\А2 в сторону вращения эллипса (см. рис. 2.17).
Теперь производим вычисления в системе координат XOY,
жестко связанной с эллипсом. Уравнение эллипса в параметриче-
параметрической форме
х = a cos т, у = Ъ sin г, 0 ^ г < 2тг, а > Ь.
4 Зак. 90 57
Глава 2
Рис. 2.17
Точка А] имеет координаты:
X] = о cos Т\, j/i = Ь sin т\.
Единичный вектор щ нормали к эллипсу в точке А\\
1 /
й\ = — (bcosrj, osinri), Aj = y/b2cos
Точка i*2 имеет координаты:
Xi = a cos T2, y2 = b sin Г2.
Единичный вектор П2 нормали к эллипсу в точке
+o2sin2T|.
^2 = Т"(Ь cos Т2, о sin Г2), А2 = y/b2 cos2 Г2 + о2 sin2 Т2.
А2
Вектор A \Ai имеет составляющие:
А\А2 = (o(cost2 — costi), 6(sinT2 — sinri)).
Вектор ve = [w x Л1Л2] имеет составляющие:
v€X = o;6(sin T2 - sin т\)9 v€y = -ua(cos Г2 - cos T\).
58
Кинематика
Вектор v имеет составляющие:
vx = -—a sin T], vy = — b cos Tj.
Умножим обе части равенства A) скалярно на вектор п2.
Вектор vr направлен по касательной к эллипсу в точке А2, следо-
следовательно, vr • п2 = 0. Итак имеем равенство:
¦ Vyn2y =
Подставляя вышеприведенные формулы, получим равенство:
v b v a
-—a sin Т\ • — cos r2 + — b cos Т\ • — sin r2 =
А| А2 А| А2
= o;6(sin r2 - sin т{) • — cos r2 - o;a(cos r2 - cos тх) • — sin r2.
А2 А2
Преобразуя, получим:
_ v • ab sin (tj - r2)
a2 sin r2(cos r2 - cos т\) - b2 cos r2(sin r2 - sin rj)
x ' B)
y/a2 sin2 ri + b2 cos2 T|
Теперь отобразим тот факт, что расстояние между прямыми 1\
и l\ равно h ^ Ь < а. Для этого составляем скалярное произведение
вектора А\А2 на единичный вектор нормали п\. Имеем:
6 a
a(cos r2 - cos Г|) • — cos Ту + b(sin r2 — sin Г|) • — sin T|
A A|
*Ъ[1-_их(т1-т2)]
a2 sin2 т\ + Ъ2 cos2 т\
59
Глава 2
Таким образом, наша задача свелась к нахождению max и min
функции <v(t\ , T2) из B) при условии C), т. е. к задаче на условный
экстремум функции со(т\, т2) двух переменных, стесненных огра-
ограничениями 0 ^ т\ < 2тг, 0 < т2 < 27г и равенством C). Принцип
решения может быть таким: сначала находим т2 из C) через т\:
h
тг = Т\ - arccos7, 7 = 1 у/a2 sin2 тх + b2 cos2 Т\.
аи
Затем подставляем найденное тг в формулу B) и задача сводится
к безусловному экстремуму! (по т\ ? [0,27г]). Формула для со(т\)
получается тогда достаточно сложной и необозримой, а задача
может быть решена при помощи компьютерных средств.
Рассмотрим случай малого эксцентриситета эллипса, т. е.:
Ь2 Ъ2
е=1--т«1 -> — = 1-е
а2 а2
(эллипс мало отличается от окружности!).
Зафиксируем величину Ь и разложим выражения из B) и C)
в ряд по е с точностью до малых 1-го порядка по е. Преобразуем B):
v • у/\ — е sin (ti — ту) • у/\ — е
ш — Ц tL х
sin r2(cos r2 - cosT\) - A - e) cosr2(sin r2 - sin r,)
1 v
x —====== = - sin (r, - r2) x
b\/l - ecoszT\ 0
1-е
y/\ - 6rcos2T| • [e • cos r2(sin r2 - sin T\) + sin (т\ - r2)]
Из полученной формулы видно, что при е = 0, получим
о
что можно получить и непосредственно, рассматривая качение
окружности!
60
Кинематика
did
Вычисляем —
de
V
= -sin(r, -т2)х
о
• / \ 1 Г • / 4~COS2T,
-sm(r, -т2)-1 • sin(r, ~r2) »
sin2(r, -т2)
V
-r2)
x -sin2(ri -г2)( 1 т— J -sin(T] ~r2)cosr2(sinr2-sinr,) =
cos2 T\ \ cos r2 (sin Г2 - sin ri)"
sin (r.-r,)
Таким образом, для а/(?) имеем разложение:
cosr2(sinr2-Sinr,)\1
/J w w
2 sin (т,-т2)
Теперь разложим выражение для Л до членов 1-го порядка малости
по е включительно:
h^ b[\ -cos(T|-t2)] _
у/1 — е cos2 T\
= b[\ - cos (т, - т2)] + е —^[1 - cos (г, - г2)] =
= b[\ - cos (r, - r2)] 1 + e^ + O(e). E)
61
Глава 2
Так как т2 входит в D) множителем при е, то мы можем
подставить т2 из E) с точностью до нулевого порядка по е. Имеем
из E):
cos (г, - т2) ~ 1 - - = 7о.
Рассмотрим сначала предельный случай h -> 6.
Тогда 7о = 0 и c
значениях получаем:
7Г
Тогда 7о = 0 и cos (г, - т2) = 0 -> г, - т2 = —. Из D) при этих
^ v Г /l+sin2Tj sinri(-cost,-sinri)\1 _
= - 11 A -sin2Ti - 2sinri costj) =
b[ 2 J
= 7 И "~ «(cos2ri ~ 2sinr! costj) .
bl 2 J
Теперь экстремум легко ищется:
du
О = — = -2 cos T] sin Ti - 2 cos 2tj = 0 -> sin 2rj = -2 cos 2rj,
tg 2r, = -2, cos 2n = ±—р=== = ±-^=, sin 2r, = ±-^=,
/l tg2 2n V 5 V5
l-sin2r, =cos2r, = -(l+cos2ri) = ^Mi-^V
Таким образом, получаем экстремальные значения для си:
62
Кинематика
Достигаются эти экстремальные значения в точках Т\ = ±- arctg 2,
Л 7г Зтг
т. е. отнюдь не в точках т\ = 0, —, 7Г, —, 27г! >
Рассмотрим теперь случай h <b.
Имеем
cos (ti - г2) = 7о <
= Т| - arccos 70,
h
где 70= 1-т-
о
Далее, получим:
sin т2 = sin Т| • 70 - cos Л # л/1 - 7о>
cosr2 = cosГ| • 7о + sinГ| • t/l - 701
sin (т| - r2) =
Подставляем эти формулы в D):
^l-fsin2ri sinri costi B7o-l)
7ov/l -7^(cos2T| -sin2T|)sinr, cost,
\ -
'l-72
+sin2T, sinri COSTi B7o -7o - l) -Toy 1 -7ocos2 T>
+
sin2 т,A-70)^/1-702'
63
Глава 2
Берем производную по т\ и приравниваем ее к нулю.
duj 270 — 'Yo — 1
О = —- = sin т\ cos т\ -f cos 2т\
где
sin 2т\ — — sin 2ti A - 7о) =
A2
г1-7о^
1 . , L 27o2-7o-l
= - sin 2r, +
cos 2т| + sin 2г| B7о - 1) =
= sin2r,f27o--j-
= sin Bri + /5) = О,
2r, + /3 = тг или 2т| + /3 = О,
cos 2ti = 0 =
/? = arctg
270-To-l 2
"То
4То-1|'
кстати, при 7о = 0 имеем C = ± arctg 2, т. е. то что было при h = 6!
А можно и так:
Из уравнения —— = 0 имеем:
ат
tg2T, = —
270-7Q-1
D7о-1)л/1-То2
•2,
64
Кинематика
Рис. 2.18
т\ = —z
] <смрис-218>-
Положим 7о -*¦ ~ » тогда г, * -*
'4
Подставляем в формулу для и:
/
7Г B)
4 4 2
V
Ъ
1-е
3 ±2\ 8/ 2V16
В"
Гб
/ J
65
Глава 2
1 9 1
г, = 0 (или тг/2) при 27о - 7о - 1 = 0, 7о - ^7о - 2 = °>
1 /1 Г 13
7о = 1 (Л = 0!) или 7о = -г (Л не существует, т.к. Л = C/2N > ft),
тг 1 27о - 7о - 1 Л
Т| = — —* 27о — г Н 1 = 0 — обязательно имеет
у 1 ~ 7о корень при 7 G (О, I),
Вот при этом 7* = 1 - т~ >т-е- ПРИ этом Л = Л* наш ответ совпадает
ft
с одним ответом из [3].
Теперь сравниваем с ответами из книги [3] (задача 3.35).
п _ уЪ2 п _ va2
a2b-h(a2-b2Y max аЬ2 + Л(а
Ь2
Выражаем через е = 1 г и ft.
л*
v(\-e) _v 1-е
ft2\ Ъ-he ft Л
ft
66
Кинематика
,,п _ v v v
"max — Ту
1 h h 1 h h 3
2-fr^-1' 2>2 <
Пусть Л = Ь, тогда:
6' ? < 4' Т0ГДа
•МИО-Ш-
а наши:
л/5-П «Л V5+
Ясно, что
и покажем, что
что очевидно!
что
Проверим еще при -¦ = - (т.е. 7о = 1/4).
о 4
Тогда o;extr = г ( • - ^т )» т.е. a;IIjn = итах. Положим - =
Таким образом, полученные нами значения ueXiT более экстре-
экстремальные, чем в [3].
67
Глава 2
Рассмотрим общий случай:
Имеем для —:
а;
w v{l-e) L V
cosT2(sinr2 -si
sin (r, - r2)
cos (rj — ?i) = 1 — — y/l — ecos2 T| =7, r2 = ri - arccos7;
ft
sin (ti - Г2) = \Л - 72,
sin T2 = sin T| • 7 — cos Tj • y/\ - 72,
cos r2 = cos T| • 7 + sin T) • \Л ~ 72;
r_ (cosrj -7+sinri \/1~72) (sinriG-1) -cosri y/l -72) _
cosri sinri [7G- 1) - A ~72)
=cosrisinn
-cos
Имеем
. /272-7-l
inn( — '—
\ v'
inri ( —y } +G- l)-cos2T|G- 1)~
\ vl-72 /
B^2 /y ^ 1 \
—7==r ) +G- l)-cos2nB7- 1).
л/1-72 /
1-е cos2 T\ =
V
A-7J.
68
Кинематика
cos2 г, = - 11 -
sinr, cost, = -W1 - ^—^ • t/21-^ +« - 1.
Подставляя последние формулы в выражение для —, получим
w
функцию F от 7, 7 € [1 - <т, 1 - vl—ё<т], а затем исследуем ее
экстремум. Выражение для F(j) достаточно громоздко.
Глава 3.
ДИНАМИКА
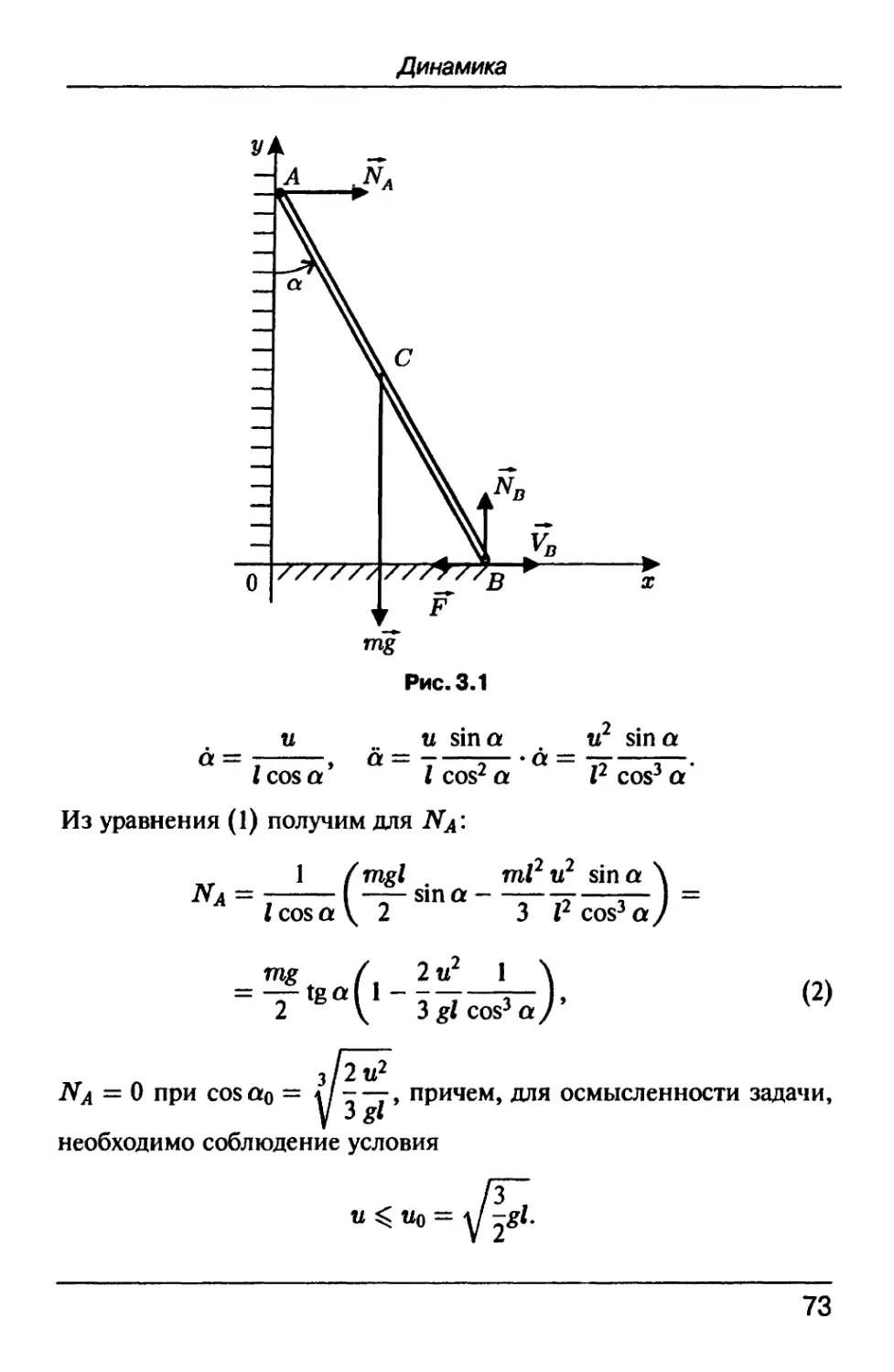
Задача 3.1 ([71, с. 185, пример 34.3). В поле силы тяжести
скользит без трения лестница АВ так, что конец А движется
по вертикали, а конец В-по горизонтали (см рис. 3.1). Дви-
Движение происходит так, что \Vb\ = и = const. Пусть длина
АВ = I, а-угол, образуемый АВ с вертикалью. Определить
угол а, при котором происходит отрыв лестницы от верти-
вертикальной стенки.
Решение. Приведем элегантное решение из [7]. В инерциаль-
ной системе координат, связанной с точкой В, движение лестницы
АВ есть вращение вокруг точки В. Поэтому уравнение моментов
вокруг точки В будет иметь вид:
Jb& = rag- sin a - NaI cos a, A)
где Na — реакция в точке A, JB = -r-.
Далее кинематика:
хв = / sin a, ±в = u = I cos a • a,
72
Динамика
u .. w sma u sin a
I cos a J cos2 a /2 cos3 a
Из уравнения A) получим для
/ cos a \
mg
mgl ml и sin a
sin a —it—;—
2u2l
B)
3/2 «
JV^ = 0 при cosao = */-—г, причем, для осмысленности задачи,
V 3^
необходимо соблюдение условия
73
Глава 3
Отметим, однако, что необходимо скорректировать формули-
формулировку задачи, указав способ, которым осуществляется относитель-
относительное движение Vb = const. Можно, к примеру, приложить в точке В
горизонтальную силу F (см. рис3.1), выбираемую по следующему
закону:
2 V 3 gl cos3 a
хв (xB(Q)
причем sin a = — =
Действительно, в этом случае уравнение для центра масс С
на ось х имеет вид:
= NA-F, хс = -хв, хс = -хв = О,
т. к. Уд = ±в = const. Следовательно, N& = F.
Но более важное обстоятельство заключается в следующем.
Необходимо убедиться в том, что вплоть до того момента, когда
Na = 0, соблюдается условие Nb ^ 0 (т. е. лестница не отрывается
от пола!). Уравнение для центра масс С на ось у имеет вид:
тус = -mg + NB, Ус= ~ cos a,
/ I и и
Ус = -- sin а • а = -- sin а • = -~ tg а,
2 2 «cos а 2
и - w2 J
Ус " 2 cos2 а а ~~ Иcos3 а'
Следовательно,
V 2gl cos3 a) \ Ъ gl cos3 a)
Динамика
Вспоминая выражение для Na из B), получим, что пока Na > О
будет
2 ц2 1
3 gl cos3 a
а потому и Nb > О, т. е. связь в точке В не нарушается!
Посмотрим теперь что будет дальше, т. е. после момента, когда
Na = 0. Опуская выкладки, сформулируем результаты:
1) если скорость и удовлетворяет условиям:
то после отрыва от стены и до падения плашмя (а = тг/2) лестница
также оторвется и от пола.
2) Если скорость и удовлетворяет условию
2
u<-y/gh
то отрыва точки В от пола не произойдет вплоть до падения
плашмя (а = тг/2).
Напомним, что случай
физически не осмыслен, т. е. тогда Na < 0 и точка А отрывается
сразу (т. е. при a = 0!). Можно также сказать, что в этом случае
движение лестницы представляет собой движение обращенного
маятника с равномерно и горизонтально перемещающейся точкой
подвеса.
3) Точка А, оторвавшись от стены, вновь уже не придет
в контакт с ней. Доказательство приведенных фактов основывается
75
Глава 3
на использовании интеграла энергии для обращенного маятника
а2 = <*о + -г (cos ao - cos а),
где ctQ, do — начальные условия.
Тогда для NB получается выражение:
ТТ1Я
NB = — (l + 9 cos a(cos - cos ao)),
где а ^ а0, cosa0 = \1 ~—-
Тогда
= -^ f
- ^ COS2
Кроме того, в системе координат точки В имеем после a
= -—(/sin a) = -Jcosa-d = -Icosaxl a\ + — (cosa0- cosa),
— (Vix) =/2 -2 cos a sin a- f doH- у cosa J + — cos2 a sin a =
= I2 cos a sin a -2 f d2 + — cos a J + —
cos a =
= I2 cos a sin a -2т; z h — cos a | < 0
[ I2 cos2 a0 I
7Г 3 2U2
при a0 < a ^ —, cos ao = ~—r.
2 3«
76
Динамика
Задача 3.2 [7, с. 185]. На двух нерастяжимых невесомых
нитях одинаковой длины горизонтально подвешен в точ-
точке О однородный стержень АВ массой т и длиной 21
(см. рис. 3.2). Нити со стержнем образуют угол а. В неко-
некоторый момент времени нить ОВ обрывается. Найти силу
натяжения Т нити О А непосредственно после момента
обрыва.
Решение. Сначала найдем натяжение нити О А до обрыва.
Проецируем на вертикаль z:
mg - 2Г0 sin a = О
mg
2 sin a'
Послеобрывное состояние стержня характеризуется тем, что
его угловая скорость и = 0, а угловое ускорение е Ф 0! Скорость
точки A: Va = 0, а ее ускорение о не будет равно нулю и напра-
У\
влено ±ОА (т. к. ее нормальное ускорение —- = 0!!). Принимая
ОА
77
Глава 3
эти допущения, получим:
ас = а + ас а ~t
причем а^А = а^д • I = О (так как о;^в = 0), 5^-L^C и а?л = ? • I.
Уравнения движения для центра масс, спроецированные на АО
и перпендикулярно АО суть:
mel • sin a = т# • sin а - Г, A)
т(а + е/ cos а) = mg cos а. B)
И еще уравнение моментов относительно центра масс:
ОЙ-
Г/, sin а. C)
Получим три уравнения для трех неизвестных: Г, 5, а. Из A) и C),
исключая 5, сразу находим:
1 . т гт, . . ™ mgsina
0 = -m^-sina- -- - Г sin a* sin a -* T =
3 3 1 + 3 sin2 a
3 mg sin2 a 3 sin2 a g
e== mn+3sin2a = l + 3sin2a*7' D)
3 sin2 a g cos a
a = g cos a - g cos a • -——-^— = 7;—^ . 0 4;
l+3sin2a A + 3 sin2 a)
Обратим внимание на одно обстоятельство: при a -* 0, Г(а) -> 0!
А в то же самое время до обрыва: Т(а) -у оо при а -у 0. Получа-
Получается, что при малых а натяжение меняет свое значение мгновенно
от бесконечно большого до бесконечно малого. Парадокс обсу-
обсуждается у Пановко [21], где показано, что на самом деле следует
принять натяжение неизменным (!!)
1 + sin2 a
Т - Го = -mg—— . -> -00
2sina(l +3sin2a)
78
Динамика
при a -> 0! (см. Пановко Я. Г. Механика деформируемого твердого
тела, М.: Наука, 1985, с. 238).
Эта задача приведена также в задачнике [22] (задача 702,
с. 120), где дано подробное, более строгое решение, основанное
на непосредственном дифференцировании координат в начальный
момент после обрыва нити. У Виттенбауера рассматривался случай
а = 60°, для которого получен ответ Т = —г-етуг, совпадающий,
очевидно, и с нашим ответом! >
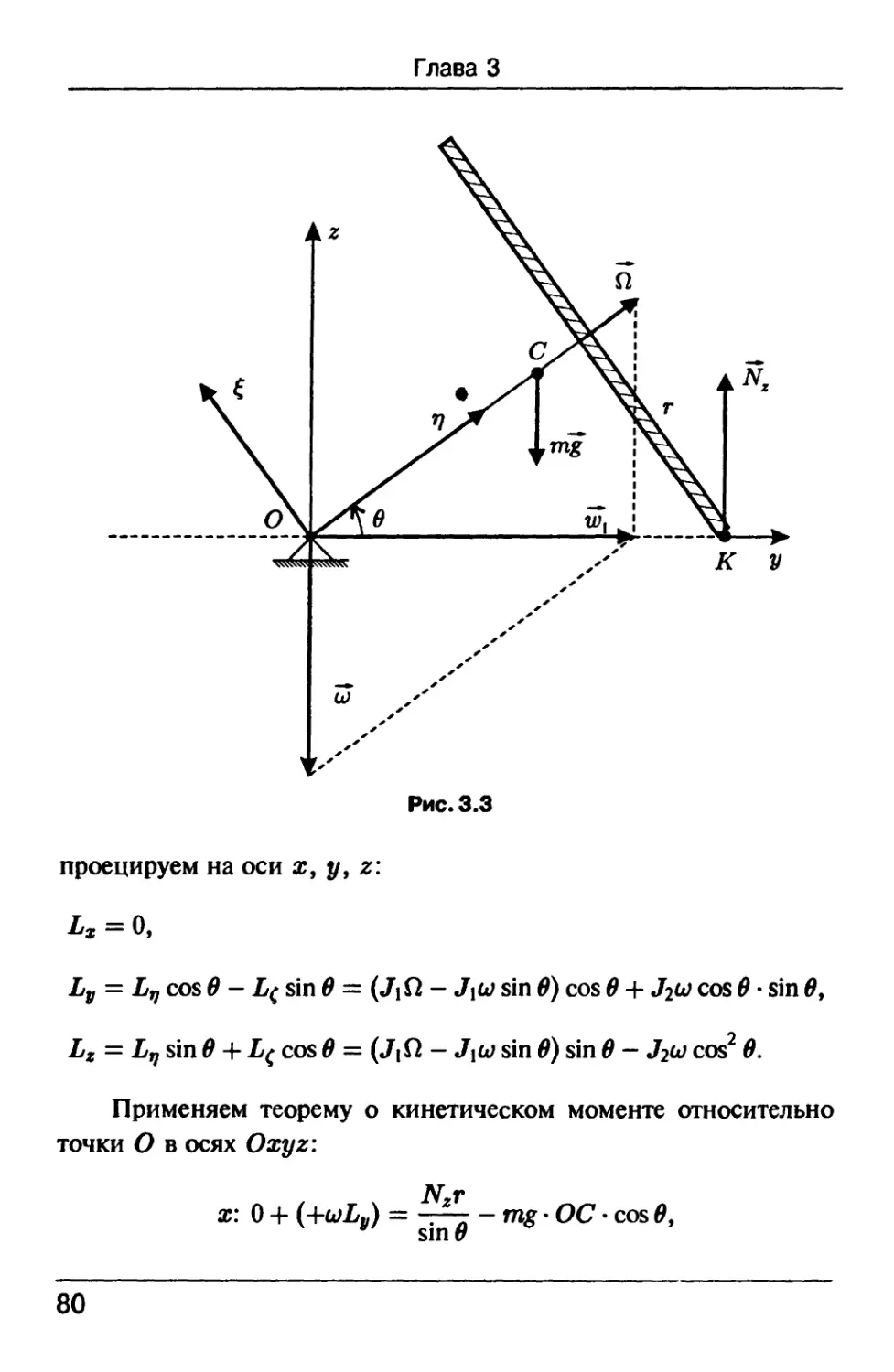
Задача 3.3 [2, с. 47]. Волчок с неподвижной точкой опоры
О, вращавшийся с угловой скоростью по вокруг своей
оси (скорость прецессии « 0), касается горизонтальной
плоскости краем диска (см. рис. 3.3).
Найти угловую скорость волчка, когда проскальзывание дис-
диска прекратится (в момент касания нутаций также не было).
Решение. Ясно, что диск будет катиться по плоскости, про-
проскальзывая при этом. Введем систему Oxyz, ось z — вертикальна,
ось у — по ОК (К — точка касания), ось х — перпендикулярно
z и у. Пусть г — радиус диска, тогда скорость точки К:
иг
V V u
При VK = 0 имеем и = п sin в (и@) = 0!).
В точке касания действуют две (!) силы: Nz (нормальная
реакция) и Nx (сила трения скольжения, направленная против
скорости точки К\). Пусть J\ — осевой момент инерции волч-
волчка, Ji — экваториальный относительно точки О. Кинетический
момент волчка в главных осях
= 0, Lv = J[u- J\U sin в, L^ = -Зг cos в;
79
Глава 3
Рис. 3.3
проецируем на оси х, у, z:
Ly = Lv cos в - L( sin в = (Jifi - Jia; sin ^) cos 0 + J2o> cos 0 • sin в,
Lz = Lv sin 0 + X^ cos в = (Jjfi - J\U sin 0) sin 0 - J2u) cos2 0.
Применяем теорему о кинетическом моменте относительно
точки О в осях Oxyz:
N2r
х: 0 + (+wLy) = -г— - mg • ОС • cos 0,
sin и
80
Динамика
т. к. Lx = 0, то Ly = const = Ly@) = J\ fto cos 0;
В этой задаче для нас важна лишь проекция на у. Имеем:
cos в + u)(J2 - J\) cos 0 - sin 0 = J|fto cos 0 ->
- Ji) sin 0 =
Подставляем сюда и = fi sin 9 при отсутствии скольжения, полу-
получим:
(JJ)us\T?9 Ju П ° !
J\ cos2 в + J2 sin2 в
Угловая скорость й\ волчка направлена по ОК и находится
из параллелограмма Q\ = и + П (см. рис. 3.3):
COS0
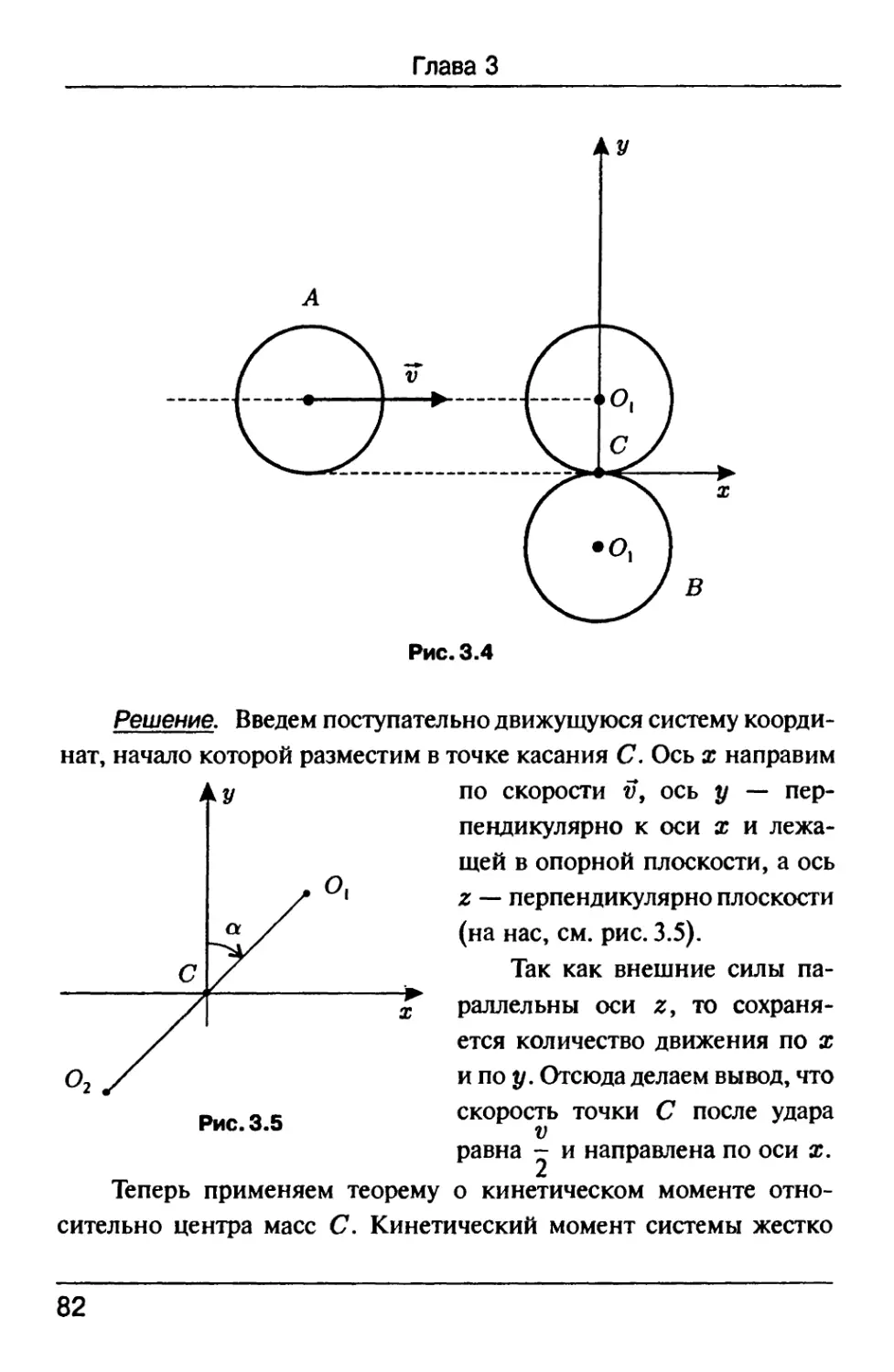
Задача 3.4 [2, с. 47]. Однородный шар А радиуса г и мас-
массы т катится, не проскальзывая, по горизонтальной плос-
плоскости со скоростью центра масс v (см. рис. 3.4). В момент,
когда он касается другого такого же шара Б, лежавшего
неподвижно, шары жестко скрепляются в точке касания С.
Предполагая, что плоскость абсолютно гладкая, определить
силы, с которыми шары действуют на плоскость во время
дальнейшего совместного движения.
7 Зак. 90
81
Глава 3
в
Рис. 3.4
Решение. Введем поступательно движущуюся систему коорди-
координат, начало которой разместим в точке касания С. Ось х направим
по скорости V, ось у — пер-
перпендикулярно к оси х и лежа-
лежащей в опорной плоскости, а ось
z — перпендикулярно плоскости
(на нас, см. рис. 3.5).
Так как внешние силы па-
х раллельны оси z> то сохраня-
сохраняется количество движения по х
и по у. Отсюда делаем вывод, что
скорость точки С после удара
v
равна - и направлена по оси х.
Теперь применяем теорему о кинетическом моменте отно-
относительно центра масс С. Кинетический момент системы жестко
Рис. 3.5
82
Динамика
скрепленных шаров складывается: из вращения (верчения) вокруг
оси z и качения (т.е. вращения) шаров вокруг оси О\СОг- Обо-
Обозначим угловые скорости этих вращений, соответственно, uz и и.
Пусть a — угол, составляемый осью О\О2 с осью у (см. рис. 3.5).
Тогда проекции кинетического момента таковы:
Lx = +2Jw sin a, Ly = +2Ju cos a, Lz = 2(J + mr2)wZy
где J — момент инерции шара относительно оси, проходящей
через его центр масс. Моменты внешних сил /j и /2, приложенных
в точках касания шаров с плоскостью и параллельных оси z9
относительно точки С:
Mx{fx) + Mx(f2) = (fir - f2r) cos a,
Myift+Myfa) = -(/,r - /2r) sin a,
M* = 0!
Тогда имеем уравнения:
{Lx = 2Ju) sin a + 2Ju • a;z cos a = r(f\ - /2) cos a,
Xy = 2Jo; cos a - 2Jo; • uz sin a = -r(/j - /2) sin a,
6JZ = 0, u)z — uzq = const!
Здесь использовано, что a = uz.
Из этих уравнений получим:
и = 0, о; = с^о = const, r(/i - /2) = 2Juuz.
Осталось применить формулы:
1 JV
mvr = 2(J + mr')wzOi — = 2Jw0, /, + /2 = 2mg,
83
Глава 3
получим:
1 / v \ ( mvr
2
Вспоминая, что J = -таг2, получим:
4 2
_ 5>mr v mvr _ 1 mv2
/l - /2 - —^— Tr~^T^2 " 7~7~-
Вспоминая, что f\ + /2 = 2т^, получим:
14r/'
v2
v2
Естественно, что этот ответ корректен при д > ——. Если
скорость v будет достаточно велика, то шар В может отскочить
от плоскости!!!
Кроме того, мы предполагали, что отсутствует начальное вер-
верчение шара, т. е. его собственная угловая скорость по оси zl t>
Задача 3.5. По сторонам прямого угла, расположенного в
горизонтальной плоскости, могут скользить без трения ша-
шарики А и В масс mi \лтп2 соответственно. Шарики связаны
пружиной жесткости к, нейтральная длина которой /. В на-
начальный момент шарики находятся в покое и 2^@) = xq,
Ув@) = г/о (см. рис. 3.6).
Показать, что при yxl -f yl < 21 шарики никогда не столк-
столкнутся, т. е. не придут в точку О одновременно.
84
Динамика
х
Рис. 3.6
Решение. Обозначим угол В АО = а. Тогда уравнения движе-
движения шариков:
Х= -к(у/х2 + у2 -I) -cosа,
У = —fc( у/х1 + у1 - l\ -sinа,
причем cos а =
X
=, sin a =
У
Умножая первое уравнение на ж, второе — на у и складывая,
получаем интеграл энергии:
где h = const = - (xl + yl) -
85
Глава 3
Обозначим х2 + у2 = р2. Тогда имеем:
О ^ —х2 + —у1 = —/Г + Шр + -рЬ - Шро,
причем это неравенство выполнено для любого t.
Предположив, что p(t*) = 0, получим:
к э
0^-ро- klpo -+ 21 < ро,
что противоречит условию задачи B/ > ро\).
Описанная система является консервативной, так как сохра-
сохраняется полная механическая энергия (интеграл энергии). Однако
эта система, по-видимому, неинтегрируема в квадратурах, т. е. у нее
больше не существует интеграла, независимого от интеграла энер-
энергии. Основанием для этого является то, что при / = 0 будем иметь
уравнения
ТП]Х = -кх,
Гк Гк
которые при несоизмеримых частотах и)\ = \ —, со2 = \ —
у ТП\ у 7122
не имеют иных интегралов, кроме интеграла энергии (см. [23]). >
Задача 3.6 [3]. Два одинаковых шарика могут двигаться
без трения по сторонам прямого угла, расположенного
в горизонтальной плоскости. Шарики имеют заряды разных
знаков и начинают движение из состояния покоя. Показать,
что они одновременно окажутся в вершине угла. (Этот
результат верен при любом законе силы притяжения между
шариками!)
86
Динамика
Рис. 3.7
Решение. Уравнения Ньютона для прямолинейных движений
шариков следующие (см. рис. 3.7):
тх = —/ cos а, ту = —/ sin а,
У
cosa =
sin a =
+ у2 у/х2 + у2
Умножим первое уравнение на $/, а второе — на х и вычтем:
- ух) = -
^Ту2
2 j. .-2
^XJ + у
= 0,
—(ху - ух) =0, ху-ух = const = 0 (т. к. х@) = у@) = 0!).
Отсюда
х у d
— = - ->¦ —(In x-lny) =
x у dtx
Xq
х
— = const.
у
Xq
Таким образом, x(t) = y(t) • —, откуда и следует искомый
Уо
результат.
87
Глава 3
Заметим, что этот же результат можно было бы получить, при-
применяя теорему об изменении кинетического момента относительно
точки Р — пересечения перпендикуляров к траекториям точек А
и В\ Центр масс системы и скорость VP \\ Vc и т.д.
См. также: Учайкин В. В. Механика. Основы МСС. Задачи
и упражнения. М.: Ижевск, 2002. Задача 5.37, с. 35; Аппель Я.
Теоретическая механика. Т. 2. С 79. t>
Задача 3.7 [3]. Та же задача, только шарики А и В раз-
разной массы: mi, mi% тп\ Ф гпг. Закон взаимодействия
произволен, но сила направлена по прямой, соединяю-
соединяющей точки. Найти зависимость между координатами хд(?)
и Ув{1)* если в начале шарики покоились и ха@) = хо > 0,
ув{0) = г/о > о.
Решение. В [3] приведен неверный ответ:
Ув{Ь) = Уо
J
Аналогично предыдущей задаче уравнения движения:
где / — закон взаимодействия. В частности, при / = ky/х2 + у2
получим
x(t)=:As\n ( W t + <p{
\ v mi
фигуры Лиссажу и т. д.
88
Динамика
В
1
А,
В
/7777/77777777/
Рис. 3.8
\rn?
Рис. 3.9
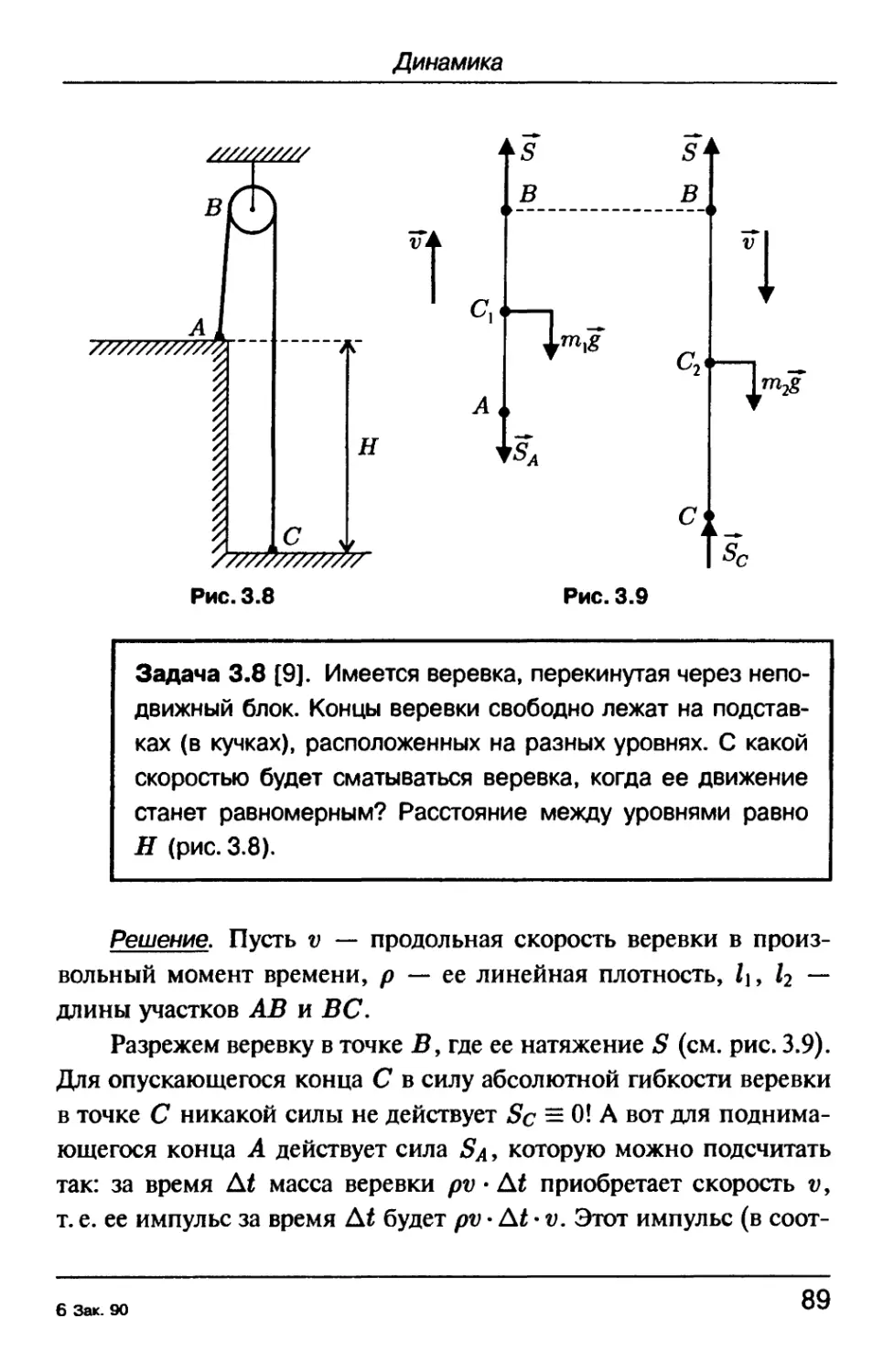
Задача 3.8 [9]. Имеется веревка, перекинутая через непо-
неподвижный блок. Концы веревки свободно лежат на подстав-
подставках (в кучках), расположенных на разных уровнях. С какой
скоростью будет сматываться веревка, когда ее движение
станет равномерным? Расстояние между уровнями равно
Я (рис. 3.8).
Решение. Пусть v — продольная скорость веревки в произ-
произвольный момент времени, р — ее линейная плотность, 1\, fc —
длины участков АВ и ВС.
Разрежем веревку в точке Б, где ее натяжение S (см. рис. 3.9).
Для опускающегося конца С в силу абсолютной гибкости веревки
в точке С никакой силы не действует Sc = О! А вот для поднима-
поднимающегося конца А действует сила 5л, которую можно подсчитать
так: за время At масса веревки pv • At приобретает скорость v9
т. е. ее импульс за время At будет pv-At- v. Этот импульс (в соот-
6 Зак. 90
89
Глава 3
ветствии с законом Ньютона) обеспечивается силой SA&t. Отсюда
SA = pv2. Эта сила приложена к элементу веревки вверх по вер-
вертикали. Тогда со стороны этого элемента на веревку АВ будет
приложена такая же сила, но направленная вертикально вниз.
Теперь составим уравнения для центров масс кусков АВ и ВС
по вертикали:
{mxi) = S - mxg - SA,
77i2t> = —S + Ut2g + 0,
складываем:
(mi + m2)v = (m2 - mx)g - pv2.
7712 —
Отсюда v = const при v = * / g = \JHg.
Задача 3.9 [9, с. 38]. На одном из концов соломинки, ле-
лежащей на гладкой горизонтальной плоскости, сидит жук.
С какой наименьшей скоростью он должен прыгнуть, чтобы
попасть на другой конец соломинки? Длина соломинки 21,
ее масса т, масса жука М. Сопротивлением пренебречь
(см. рис. 3.10, вид сверху).
Решение. Пусть АВ = 21 — соломинка, а жук сидит в точке Б.
Пусть С — центр масс соломинки. Введем систему координат
xyz9 связанную с точкой С, причем ось z — перпендикулярна
плоскости рисунка, ось х — вдоль начального положения АВ9
а у — перпендикулярна АВ (см. рис. 3.10).
Пусть жук прыгает со скоростью v9 проекции которой на вы-
выбранные оси — vx,vy,vz (это абсолютная скорость жука!).
90
Динамика
Точка С приобретает абсолютную скорость vc = (vCX9vcy90)
в соответствии с законом сохранения количества движения:
А л.
м
Vrr. = vx, !
Со
су т у
Кроме того, АВ будет
вращаться с угловой скоро-
скоростью и вокруг неподвижного
центра масс Со, который на-
х
<4г-
ходится на расстоянии
М .
В
Рис. 3.10. Вид на жука с соломинкой
сверху. Ось z и ускорение силы тяже-
тяжести g направлены от читателя
т + М
от точки С на отрезке СВ, причем это вращение происходит
в соответствии с теоремой о сохранении кинетического момента
системы относительно центра масс Со:
Mvy • (/ - Хо) + m\vcy\ • Хо
Используя (I), получим из B):
о; = Mvy(l -
ml2
- 2 и = const = 0.
B)
+ тп—vy • х0 = MVy • I.
Tft
Отсюда находим и:
ЪМ
и = —-vy.
ml y
C)
Рассматриваем процесс в инерциальной системе координат
Cxyz, связанной с точкой С и поступательно с ней перемещаю-
перемещающейся (см. рис. 3.11). В этой системе АВ поворачивается с угловой
91
JL
Глава 3
Ч>
Л
/ ч
Рис. 3.11. ВА\ — проекция траектории жука на плоскость Сху\
В]А] — соответствующее положение стержня
скоростью и из C) вокруг точки С, а жук имеет скорость v*
с компонентами:
vl=vx + \vcx\ = vx (l + — J,
vz = vz.
В этой системе (ввиду отсутствия горизонтальных сил) про-
проекция траектории жука на горизонтальную плоскость — прямая,
проходящая через точку В под углом 7 к оси х, причем
= "T = —
D)
92
Динамика
Стержень АВ вращается вокруг начала координат С с угловой
скоростью и. Условия попадания жука на повернутый конец А\
стержня АВ суть следующие:
(
= (\ + ^
- 2/2 cos (тг - V),
где t — время вертикального полета жука, которое, очевидно,
равно t = —.
g
Кроме того, из равнобедренного треугольника ВСА\ {СА\ =
С В = /) получим
Используя выписанные соотношения, получаем уравнения:
+ М\ ОТ—, 2vz
m )
ЪМ 2vz
ml y g
Учитывая тождество
- (Л
1 +cosy? = 2 cos —,
получим два уравнения:
I l + — ) V w^ +««* — =/• cos [ —-vyvz I,
tg —-vyvz = -i.
E)
93
Глава 3
Таким образом, нужно выбрать vx, vy, vz так, чтобы они удо-
удовлетворяли уравнениям E) и минимизировали функцию v:
v =
min.
Выражая cos а через tg а по формуле cos a =
получим из E) соотношение:
Отсюда мы выражаем vz:
m
л m + M vl+vl
Подставим F) во второе из уравнений системы E):
/ ЗМ т glvxvy \ _ Vy
\mgl m + M vl + vl) vx
F)
или так:
tg
ЗМ
1
m + M Yl + YL
vy vx
Положим — = fi. Тогда fi должно являться корнем уравнения:
V
tg
/ ЗМ ц
\
G)
Предположим, что G) имеет хотя бы один корень // = //о > 0.
Тогда vy = fiovx, а из F) получим:
glvx mgl I
m
vz =
m + M 'vl(l+(i2Q) m + M vx(l+fil)'
94
Динамика
Тогда имеем для функции v :
2 222 2
2-
Нам осталось найти минимум этой функции по vx € [0, со).
Обозначим vl = Z, тогда
! 1
где j4 =
mgl
т + М'
d(v2 (Z))
dZ
= 0
0+/4Г
Подставим это Z в v (Z):
Z =
+ Аг
А А
+
fi+fi
2A
95
Глава 3
Таким образом, имеем:
Осталось разобраться с существованием корня
ния G). Обозначим:
ъм
где а — —, 0 < а < 3.
+ М
т + М
Так как сг < 3, то
о ц 3-1 _ 3 тг f
2 < ТП " 2 < I"
т.е. fhi)e <Ug- при 0</i<oo.
Во-первых, очевидно, /@) = 0, /(оо) = 0.
df _ I
dfi
для уравне-
уравне2J
A+/x2)
->• max/(/i) = /(l) = tg( — J.
Кроме того, /'@) = а. Поэтому ясно, что при а > 1 корень
ЪМ
будет всегда (см. рис. 3.12), т.е. при > 1 ->• 2М > т
т + М
(жук достаточно тяжелый!).
Оптимальные проекции скорости жука суть следующие:
vx =
3 9
I 4
96
Динамика
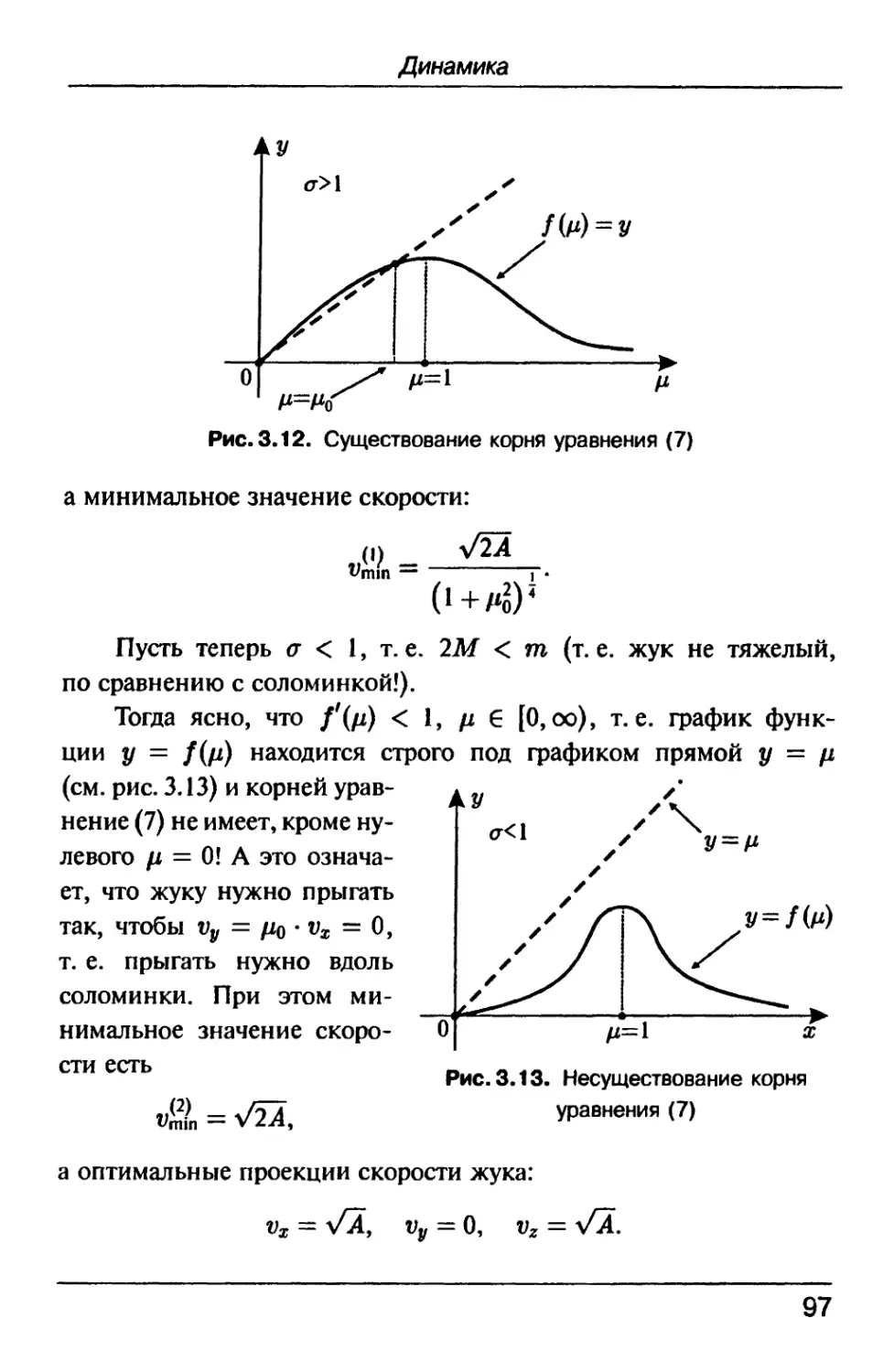
Рис. 3.12. Существование корня уравнения G)
а минимальное значение скорости:
Пусть теперь <т < 1, т. е. 2Af < m (т.е. жук не тяжелый,
по сравнению с соломинкой!).
Тогда ясно, что /'(//) < 1, /х € [0,оо), т.е. график функ-
функции у = /(//) находится строго под графиком прямой у = fi
(см. рис. 3.13) и корней урав-
уравнение G) не имеет, кроме ну-
нулевого fi = О! А это означа-
означает, что жуку нужно прыгать
так, чтобы vy = fiQ • vx = О,
т. е. прыгать нужно вдоль
соломинки. При этом ми-
минимальное значение скоро-
скорости есть
0
= /</*)
Рис. 3.13. Несуществование корня
уравнения G)
а оптимальные проекции скорости жука:
vx = yfAy vy = 0, vz = у/А.
97
Глава 3
В этом случае ответ совпадает с приведенным в книге [9].
Отметим, что из приведенных формул следует неравенство
Vmin, т-е- ПРИ а > 1 жуку выгоднее прыгать так, чтобы vy Ф 0, т. е.
соломинка приобретает вращение! [>
Задача 3.10 [4, с. 17]. В воде покоится лодка. Человек,
находящийся на ней, переходит с кормы на нос. На сколь-
сколько переместится лодка, если сила сопротивления при ее
движении пропорциональна ее скорости.
Решение. Приведем элегантное, но не очень строгое решение
из цитированного сборника задач. На человека со стороны лодки
л / ^ A(mv)
действует сила F (по горизонтали), т. е. F = ———, где m, v —
масса и абсолютная скорость человека (по горизонтали). Такая же
сила, но противоположно направленная, действует на лодку, кроме
того, на лодку действует еще и сила сопротивления, т. е.
где М, и — масса и абсолютная скорость лодки (по горизонтали),
к = const > 0 — коэффициент пропорциональности. Складывая
полученные уравнения, имеем:
-ки • At = тДг/ + М Д и.
Далее, так как все начинается с покоя, а в конце концов лодка и че-
человек остановятся (здесь, возможно, заключается нестрогость)),
то А(Ми) = 0, A(mv) = 0 и тогда uAt = 0 (вообще-то, на-
наверное, подразумевается / uAt), т. е. лодка, в конечном итоге,
не перемещается! (т. е. возвратится на место).
98
Динамика
Приведем более строгое (в математическом смысле) решение.
Используя, те же обозначения, получим из теоремы об изменении
количества движения системы «человек + лодка»:
Мй + mv = -ku9 v = u + w,
здесь w — относительная (в системе лодки) скорость человека.
Интегрируя полученное уравнение при tx(O) = v@) = 0,.имеем:
Ми = -т(и
t
где х = / u(r) dr — абсолютная координата лодки. Таким обра-
о
зом, имеем уравнение:
(М + m)x + kx = -mw.
Из математического анализа известно, что общее решение
такого уравнения дается формулой:
t
x(t) = Сое-М - ае~м f eXrw{r) dr9
о
^ % fc тп „
где Со = const, А = г, а = -. Предполагая в на-
(М + тп) (М + тп)
чальный момент х@) = 0, получим Со = 0, т. е. решение имеет
вид:
t
x(t) = -ae~xt f €Xtw(t) dr. A)
о
К этому уравнению необходимо присоединить условия:
t
/ \ А У Т I I У /О\
99
Глава 3
lim fw(r)dT = L. C)
t-?OQ J
0
Условия B) означают, что перемещение человека и его скорость
ограничены, а условие C) — то, что человек, в конце концов (т. е.
при t -> оо) очутится на носу лодки (т. е. пройдет расстояние L, где
L — длина лодки). Если человек достигает носа лодки за конечное
время t\, (и больше уже не двигается), то из A) имеем:
lim x(t) = -a lim \e~xt f extw(r) dr] = 0.
*-+00 *-+00 [ J J
0
0
Если же человек осуществляет движение к носу за бесконечно
большое время (т. е. при t -> ос), то здесь могут быть две ситуации:
1. lim w(r) = 0. Тогда, применяя к (I) правило Лопиталя
получим:
lim x(t) = lim fJ^. = о.
2. lim w(r) Ф О (человек перемещается к носу импульсами,
общая длительность которых конечна на бесконечном интервале
времени).
Совершим в A) интегрирование по частям, вводя новую функ-
функцию
t
<p(t> г) = / w(t) dr.
т
Тогда получим
t
x(t) = -a e~AV(*, 0) + А / e"A(f"r) • <p(t, r) с
о
100
Динамика
Ясно, что в силу условия B) первое слагаемое в правой части
стремится к нулю при t -> оо. Покажем, что и второе слагаемое
стремится к нулю при t -> оо. Действительно, в силу C) имеем,
что для любого е > О существует такое Т(е), что \<p(t, т)\ ^ е для
всех t, т > Т(е). Тогда при t ^ 2Т(е) имеем:
/¦
Ясно, что последнее выражение при достаточно больших t может
быть сделано сколь угодно малым! Это и означает, что lim xit) = 0.
t-юо
Отметим также следующий факт. Если закон сопротивления
воды является квадратичным по скорости, то можно показать, что
лодка уйдет бесконечно далеко, причем скорость ее будет асим-
асимптотически стремиться к нулю. Доказательство этого факта здесь
не приводится. Этот результат показывает, что на малых скоростях
справедлив закон сопротивления почти линейный по скорости
(например, известная формула Стокса для шара в вязкой среде). О
Задача 3.11 [31, с. 114]. Однородный обруч массы М,
на который намотана невесомая нить с точечной массой т
на конце (см. рис. 3.14) поставлены на шероховатую гори-
горизонтальную прямую с коэффициентом трения скольжения к
(трение качения отсутствует), причем так, что нить висит
вертикально. Покатится он или заскользит?
101
Глава 3
М
Рис. 3.14
Решение. Пусть г —радиус обруча. Положение системы впол-
вполне определяется тремя параметрами: <р — угол собственного пово-
поворота обруча, отсчитываемый против часовой стрелки, х — гори-
горизонтальное смещение центра масс С обруча, а — угол отклонения
прямолинейного участка нити от вертикали, который также отсчи-
тывается против часовой стрелки (см. рис. 3.15).
Введем еще для удобства параметр s — длина прямолинейного
участка нити АВ. Мы предполагаем, что в начальный момент:
х@) = х@) = а@) = 6@) = <р@) = 0@),
@
5@) = So, 5@) = 0.
Из геометрических соображений ясно, что отклонение нити
на угол а от вертикали увеличивает длину ее прямолинейного
участка на га (см. рис. 3.15), а поворот обруча на угол <р (против
часовой стрелки) приводит к уменьшению этой длины на г<р.
Отсюда следует кинематическая связь:
s = $о + та - г<р.
B)
Введем неподвижную систему координат Соху, с началом
в точке Со (исходное положение центра обруча), ось х — по гори-
102
Динамика
Ay
Рис. 3.15
зонтали влево, у — по вертикали вверх. Тогда координаты точки А
суть следующие:
L
хА = х - г cos a - s • sin a,
j/x = г sin a - s • cos a,
C)
где а: — текущая координата центра обруча по оси х.
Далее, пусть F — натяжение нити, Rx,Ry — реакции в точке
касания Р обруча с плоскостью. Запишем уравнения динамики
для центра масс и кинетического момента относительно центра
масс для обруча:
103
Глава 3
Мх = RX-F sin a,
0 = Ry-Mg-Fcosa, D)
Mr2 • ф = -Rx r-Fr.
Далее запишем уравнения Ньютона для груза А:
= -F sin a, my^ = F cos а - mg. E)
Подставим в E) соотношения C) и в полученных равенствах
положим выполненными соотношения A) (т.е. мы рассматриваем
движение сразу же после момента t = О!).
Тогда получим уравнения:
т(х- soa) = 0, m(ra -s) = F- rug. F)
Теперь используем связь B), которую предварительно продиффе-
продифференцируем дважды по t:
s = ra- гф.
В результате получим соотношения:
х = soa, ттф = F - rag, G)
Далее из D) при a = 0, имеем:
F. (8)
Условие непроскальзывания: гф = х.
Пусть это условия выполнено. Найдем соответствующие зна-
значения Rx,Ry. Имеем из G) и (8):
тпх = F - rag, Мх = -Мх - F.
104
Динамика
Складывая эти уравнения, получим:
2Aff тп
Зтп -f 2M
Тогда, чтобы силы трения «хватило» для непроскальзывания,
необходимо выполнения неравенства
т
Зт
Ежели это условие не выполнено, т. е. к < —, то обяза-
обязательно будет скольжение обруча! Доказательство этого факта здесь
не приводится. О
Сделаем несколько замечаний к этой задаче.
Замечание 1. Если масса т жестко прикреплена к обручу в крайнем
положении (несбалансированное колесо), то условие непроскальзывания
таково:
т2 + Mm
k ^ -
Это условие нетрудно получить, заменяя действие массы т на обруч
двумя силами Nx и Ny и записывая уравнения динамики для обруча
и массы аналогично вышеприведенному решению. Отметим, что в кни-
книге [32, с. 303], эта задача решается при помоши метода Лагранжа.
Замечание 2. Если просто прикладывать силу F = mg в крайней точке
горизонтального диаметра обруча, то условие непроскальзывания такое:
m
Этот результат получается просто из записи трех уравнений динамики для
обруча.
105
Глава 3
Замечание 3- В книге Павленко Ю. Г. Задачи по теоретической механике.
М.: Физматлит, 2003. 534 с. (см. с. 268) подобная задача рассмотрена при
помощи уравнений Лагранжа Н-го рода, записанных для двух степеней
свободы ^иа. Найдено частное решение, при котором а — с*о = const,
<p(t) = at2, где а = const, зависящая от а0, причем а0 удовлетворяет
соотношению, зависящему от параметров системы.
Задача 3.12. Диск массы тп, и радиуса г катится без про-
проскальзывания по наклонной плоскости, образующей угол а
с горизонтом. На диск намотана нерастяжимая нить, при
помощи которой он связан с грузом массы тг, имеющим
возможность скользить по гладкой горизонтальной плос-
плоскости (см. рис. 3.16). Пусть в рассматриваемый момент
времени скорости точек системы равны нулю, а нить натя-
натянута и образует угол /? с горизонтом. Определить ускорение
центра О диска в этот момент времени. Сопротивлением
качению пренебречь.
Решение. Для решения задачи необходимо связать ускорения
точек О и В. Обозначим эти ускорения: по, о,в (см. рис. 3.17).
Введем систему координат Вху с началом в точке В, причем ось х
направим по нити В А, а ось у перпендикулярно к ней. Точка А
нити имеет ускорение, совпадающее с ускорением точки А1 диска,
с которой она приходит в касание в рассматриваемый момент,
если нить, конечно, не проскальзывает (этот факт можно показать
и более строго, рассматривая конечные перемещения нити и диска,
а затем устремляя их к нулю).
Пусть АВ = /, o7|, б\ — угловая скорость и угловое ускорение
отрезка АВ нити (который мы считаем твердым телом, так как он
все время натянут!), о^, Si — угловая скорость и угловое ускорение
106
Динамика
Рис. 3.16
диска. Имеем для точки А диска:
алх = «о cos (а - /?) + е2г,
аАу = -ао sin (а - /?) - w^r.
С другой стороны для точки А нити АВ:
а Ах = ав cos/3-и>2{1,
= ав sin /? — €\1.
Из этих соотношений, полагая в рассматриваемый момент
= и>2 = 0, то получим:
ао cos (а - /?) -f Sir = ав cos /?,
-ао sin (а - /?) = а^ sin C - €\1.
107
Глава 3
Рис. 3.17
Осталось теперь вспомнить, что ао = вгг, получим из первого
соотношения:
cos/3
по cos (а -
= ав cos/3
1 + cos (a- P)'
Отметим теперь, что аналогичным образом получается связь
для скоростей точек г;д, €о'.
vax = ^о cos (a — p) -\-0J2r = vb cosp.
Отсюда, так как w2r = vo, получим
cosp
Далее задача решается стандартным образом: либо с помощью
теоремы об изменении кинетической энергии, либо с использо-
использованием теорем о центре масс и кинетического момента для диска
108
Динамика
и груза. Применим второй метод. Обозначим S — натяжение нити.
Тогда для диска теорема о центре масс в проекции на плоскость
качения дает:
т\ао = -Fcll + m\gsina- Scos(a- P), A)
где Fcll — сила сцепления в точке касания Р диска с плоскостью.
Уравнение кинетического момента для диска относительно
его центра масс О дает:
J~=Fcn-S-r9 B)
г
тхг2
где J = — момент инерции диска.
Уравнение для движения центра масс груза В в проекции
на горизонтальную плоскость дает:
Ш2йв = S cos p. C)
Решение уравнений A-3) с использованием полученного соотно-
соотношения для ускорений по и Ор, приводит к следующим результатам.
mj sin a cos2/? .x
ao = g 7 г^ > D)
тп2A + cos 7J + f гп\ + — J cos2 Р
S = m\g
sina
'"*¦ ' -j ) coszp + m\(l + cos7)z
, E)
где обозначено 7 = a - p. Из формулы E) следует, что 5 > 0 (!),
так что связь не нарушается.
В заключение покажем, как рассмотреть кинематику этого
движения более строго, принимая в учет конечные (а не бесконечно
малые!) перемещения.
109
Глава 3
Пусть т] — перемещение груза В вдоль горизонтали (отсчиты-
(отсчитываемое вправо), ? — перемещение центра О диска вдоль наклонной
плоскости (отсчитываемое вниз), /3 — угол, составляемый нитью
АВ с горизонталью (отсчитываемый по часовой стрелке). Примем,
что в начальный момент времени:
Тогда из геометрических соображений следует (подробности
опускаем), что в произвольный момент времени справедливы сле-
следующие соотношения:
г2 + (to - V +1 cos a + г sin>9J + [? sin а + гA - cos/?)]2 =
= (to - V + Z cos aJ + (r + ?sinaJ, F)
(to - V + ? cos a + r sin /3J + [( sin a + r(l - cos/?)] =
-?J. G)
Уравнения F), G) получены в предположении, что нить накру-
накручивается на диск (или раскручивается с него) без проскальзывания,
а сам диск катится по плоскости также без проскальзывания!
Пусть (р — угол собственного поворота диска, отсчитываемый
по часовой стрелке. Тогда качение без проскальзывания соответ-
соответствует условию ф = -, условие накручивания нити:
г
условие раскручивания нити:
. _ ?
г
110
Динамика
Отметим, что уравнение F) может быть приведено к более
простому виду:
гA - cos Р) - ? sin (а - Р) + (/0 - г}) sin /3 = 0, F')
Итак, уравнения F'), G) связывают три функции времени:
T)(t)9f3(t). Исключая из этих уравнений одну (например, /?(?))> мы
получим связь между ?(t) и t](t) (однако это будет достаточно
громоздкое выражение!). Проще найти ?(?) из F') и подставить
в G). Тогда мы получим связь между rj(t) и /?(?).
Если же нас интересует связь между ? и rj для момента времени
t = 0, когда:
Ф) = Ш = 4@) = Ш = /?@) = /3@) = 0, (8)
(как в рассматриваемой задаче, где для простоты будем полагать
Р = 0), то надо продифференцировать по времени дважды соот-
соотношения F'), G) и подставить в них значения из (8). В частности,
применяя эту операцию к уравнению G), получим fj = ?A + cos a),
что совпадает с полученным ранее соотношением
ao[l + cos (a - /?)] = пв - cos/З при /9 = 0!
Аналогичное совпадение может быть получено и при /3 Ф 0,
однако выкладки в этом случае получаются более громоздкими. t>
.Глава 4.
СТАТИКА УПРУГИХ ТЕЛ
Задача 4.1 [15, с. 415]. Стержень поперечного сечения S
растягивается силой F, параллельной его оси (см. рис. 4.1).
Под каким углом а к оси наклонено сечение, в котором
тангенциальное напряжение т максимально? Найти это
напряжение.
Решение. Пусть эта площадка перпендикулярна плоскости zy
и имеет вектор нормали
( \
n= I sin a I (см. рис. 4.1).
- cos a
В предположении равновесия, тензор напряжений а везде
постоянен в теле и совпадает с тензором на торце, где приложена
сила F, и поэтому
ох = 0, cz = 0, а вот ау =
114
Статика упругих тел
с
i w
-у
F
У
п
Рис. 4.1
(Вспомним определение: ах — напряжение, приложенное к пло-
площадке с нормалью, параллельной оси х, и т.д.) Согласно основной
формуле Коши, имеем:
an = axnx + ayny
О
Таким образом, напряжение, приложенное к рассматриваемой
F
площадке, направлено по оси у (!) и равно -~ -sina. По опре-
Ь
делению, касательное напряжение т есть проекция <тп на саму
площадку, т. е.
т = -г sin a • cos a = — sin 2a.
Ь 2Ь
Это выражение максимально при
7Г
а= —
и равно ттах = —.
Более элементарно решение у Тимошенко и Гере [16] (см. рис. 4.2).
115
Глава 4
то
Рис. 4.2
Т = JF, площадь сечения
S
равна , и так как Г равно-
sin a s
мерно распределена на ,
sin a
Т • cos a T
г = ^ = -~ sin а • cos а и т. д.!
& о
sin a
Рис. 4.3
Задача 4.2 [1]. Относительное удлинение стержня равно
е. Найти энергию упругой деформации на единицу его
объема, если модуль Юнга материала стержня равен Е.
Решение. Пусть сила F приложена равномерно по площади
F
торца 5, т. е. с = — = const (по сечению!).
Ь
Тогда закон Гука:
Ах „ Ах
—Е = сг, где — = е\
116
Статика упругих тел
Для того, чтобы удлинить на Ах, сила F (в силу ее прямой
пропорциональности Ах) должна совершить работу
^ Ах „ Ах Ах • Е „ Ах
tAF 8 8
V— объем стержня (а если бы сразу приложить к нему силу F, то
при удлинении на Ах будет 6А* = F • Ах — вторая половина идет
на кинетическую энергию упругих колебаний! (см. [15, с 41]).
Таким образом
zzSA = энергия на единицу объема.
Через а:
~ Ах ^ На а2 _ 1 . <т2
Задача 4.3 [1]. Какую наименьшую работу нужно совер-
совершить, чтобы согнуть в кольцо стержень, имеющий квадрат-
квадратное сечение а х а? Модуль Юнга материала Е, длина
стержня / > о. (См. также [17], задача 13.41!)
Решение. Идея решения достаточно проста: при сгибании
стержня часть волокон его растягивается, а часть сжимается; кроме
того, существует нейтральное волокно (линия), проходящее через
центры симметрии сечений стержня (см. рис. 4.4).
Рассмотрим слой волокон, находящийся на расстоянии х
а а
от нейтрали и заполняющий сечение х ^ ? ^ ж + Ах\ — ^ ц ^ -
117
Глава 4
окружность
[ейтральная
ось
Рис. 4.4
(? — радиальная координата, rj — координата, перпендикулярная
к рисунку). Волокна этого слоя претерпели удлинение
6? = 2тг(Д + х) - I = 2кх (учтено, что 2тгД = И).
Относительное удлинение
Используя предыдущую задачу, получим энергию слоя:
где 6V(x) = о • Дж • 2тг(Д + ж) — объем слоя. Или так:
тр Д~г-2 тр Afir^"
бЕ(х) = — ¦ -р-х2 -a-dx-(l + 2irx) = — • -j-e • (lx2 + 2irx3)dx;
полная энергия
Аналогично и для круглого сечения!
118
Статика упругих тел
Задача 4.4 (о брусе на проволоках, [18, с. 43]). Абсолютно
жесткий брус веса G подвешен на трех параллельных прово-
проволоках, как показано на рис. 4.5. Расстояния между проволо-
проволоками одинаковы. Сечения проволок одинаковы, но материа-
материалы различны и имеют модули Юнга: Е\,Е2,ЕЪ. Определить
усилия, возникающие в проволоках.
Решение. После подвешивания бруса проволоки должны рас-
растянуться, причем так, что точки крепления будут оставаться на од-
одной прямой (так как брус абсолютно жесткий!). Деформированное
состояние (в предположе-
предположении Е\ ^ Е2^ Еъ) пока-
показано на рис. 4.6. Геометри-
Геометрическое свойство трапеции
дает соотношение:
///ЛУ///
2 • А2А'2 = А\А\
Обозначая N\,N2, N3
натяжения в проволоках,
в соответствии с законом
Гука, получим:
дмм&у
G
Рис. 4.5
1? С С " х 7
JLJ2 И/\ JC/$
Присоединяя уравнения статики, записанные для деформиро-
деформированного состояния (уравнение проекций на вертикаль и уравнение
моментов относительно точки А2), получим:
119
Глава 4
Рис. 4.6
Система A), B) легко решается:
4Е\Ез + Е2Е3 + E\Ei
Е2Е3 ^
G,
C)
4Е\Ез + Е2Е3 + E\Ej
Ввиду важности этой задачи в методическом смысле, сделаем
несколько замечаний. >
Замечание 1. Пусть Е\ = Ег = Ej = Е. Тогда из C) получаем
т. е. натяжение нитей не зависит от модуля Юнга I?! Тогда возникает
соблазн распространить указанное решение и на абсолютно жесткие нити.
Однако это некорректно по следующей причине. Уравнения B) — это
уравнения статики, которые не дают решения задачи! А уравнение A)
которое при Е} = Ег = E-i — Е вырождается в равенство 2JV2 = N\ + Ni9
вытекает не из законов статики, а из рассмотрения деформаций системы
(т. е. из кинематики процесса деформирования!).
120
Статика упругих тел
Замечание 2. Из уравнений C) следует, что натяжения NuN2,Ni за-
7? JP 7?
висят лишь от отношений модулей —, —, —. Нетрудно понять, что
Е2 Е$ Е3
этот факт следует также из теории размерностей.
Замечание 3. Следуя Ю. Н. Работнову [18], отметим, что вопрос о том,
что будет, если нити строго математически равны между собой и являются
абсолютно жесткими, принципиально не разрешим и не должен ставить-
ставиться! Действительно, любое, как угодно малое, изменение длины средней
из нитей, приводит к резкому изменению натяжений (натяжение в этой
нити будет равно либо 0, либо G!).
Замечание 4. Задача становится корректной, если нити считать нера-
нерастяжимыми, но брус полагать деформируемым. Тогда задача превращается
в классическую задачу об изгибе балки.
Задача 4.5 (о стержнях, [18, с. 45]). Система из трех стерж-
стержней нагружена силой Р (см. рис. 4.7). Материалы стержней
имеют модули Юнга Е\% Е2, Е^. В остальном стержни
одинаковы и невесомы. Определить усилия в стержнях.
Решение, Представленная система является статически не-
неопределимым пучком. Имеем два уравнения статики:
S\ sin a + S2 sin/3 = 0, P-S\ cos a - S2 cos/3 - S3 = 0, A)
где 5|,52,5з — усилия в стержнях (в предположении, что все
стержни работают на растяжение). Чтобы найти третье допол-
дополнительное уравнение, необходимо рассмотреть кинематику малых
деформаций стержней при указанном способе нагружения. Отме-
Отметим, что уравнения A) составляются для уже деформированного
положения конструкции, но ввиду малости деформаций углы а, /?
в A) незначительно отличаются от исходных (то же касается пер-
перпендикулярности стержня 3 к оси х).
8 3ак. 90
121
Глава 4
Рис. 4.7
Пусть точка А переместилась вдоль оси ж на Eж, а вдоль
у — на 6у. Пусть А/ьА/2, Д/з — соответствующие растяжения
стержней 1,2,3. Составляя проекции 5х и 5у на направления
стержней 1, 2, 3 (см. рис. 4.8), получим:
= 8у,
Al\ = 6у cos a + Sx sin a,
A/2 — Sy cos p + 6x sin /3.
Отсюда имеем соотношение
AJ2sina - A/i sin/3
Д/-, = — ¦ -~
sin (a - /3)
Соответственно, для усилий по закону Гука:
B)
E\F
C)
где l\9l2, h — длины стержней, F — площадь сечения стержня.
122
Статика упругих тел
2\
1 \
6х
6у
Рис. 4.8
Выражая Д(|,ДB,Д(з из C) через Si9S29Si и подставляя
в B), получим
1 ( S2l2 S\li \
= —; г ( —- sin а ——~ sin /3 .
sin (a - Р) \ Е2 Е, V
Деля обе части полученного равенства на /3 и используя
геометрические соотношения
— =cos^8, j- = cos a,
получим:
53 _ 1 /
??з sin (a- p) \
52 sin a 5, si
E2 cos C E\cosa)'
Это и есть искомое третье соотношение.
Вводя параметры
123
Глава 4
получим
1 / sin a sin/?\ . .
sin (a - p) \ cos /3 cos a/
Подставляя формулу D) в уравнения A), придем к системе
двух уравнений относительно S\, Sj, решая которую получим:
с Р с Psina
sin7 ^isin^ ^2 sin" a
i
sin/3 sin 7 cos a sin 7 sin /3 cos /3
где обозначено j = a - C > 0!
Подставляя решение E) в D), получим 5з:
sin/3 sin2 a
Формулы E), F) показывают, что стержни 2, 3 растянуты,
а стержень 1 — сжат (S\ < 0!).
Отметим еще раз, что дополнительное уравнение D) получено
не из законов статики твердых тел, а из, во-первых, законов
кинематики малого деформирования представленной на рис. 4.7
конструкции, и, во-вторых, закона Гука (справедливость которого
для рассматриваемых материалов постулируется!).
В заключение, обратим внимание, что величина усилий S\,
^2»^з существенно зависит лишь от отношений модулей Юнга
материалов:
El El
Ех9 Е2
Впрочем, этот факт следует также из теории размерностей. [>
124
Статика упругих тел
g
vy
Рис. 4.9
Задача 4.6 (определение реакций закрепленной дефор-
деформируемой балки переменной жесткости). Горизонтальная
балка длины /, жестко заделанная на концах, находится под
действием собственного веса. Момент инерции сечения
балки относительно оси изгиба равен 1\ при 0 ^ х < -,
а при - ^ х ^ / он равен fy. Определить силы реакции
и реактивный момент в заделках. Считать, что вес бал-
балки равномерно распределен по всей ее длине и равен q
на единицу длины (см. рис. 4.9).
Решение. Дифференциальное уравнение нейтральной оси
балки имеет вид:
125
Глава 4
где Е — модуль Юнга материала балки, а М (х) — изгибающий
момент в сечении я, I (х) = 1\ при 0 ^ х ^ -, I (x) = h при
- ^ х ^ /. Причем, если мы будем интегрировать A) от А к Б, то
х -»
М (х) = - / qxdx + МА + RAx = —— + МА + RAx.
о
А если будем интегрировать A) от В к А, то меняя на-
направление оси х на противоположное и помещая начало отсчета
в точку Б, будем иметь:
/ах2
qx dx + Mb + Rb% = —— + Мв + Rb%.
о
Задача несимметричная, поэтому, вообще говоря, МА ф Мв,
Решим уравнение (I) от А к В. Граничные условия суть
следующие:
! ~у, B)
у (о) = у' @ = о.
Смысл этих условий такой: концы балки А и Б, во-первых,
не смещаются по у, а, во-вторых, в силу защемления, касательные
к нейтральной линии в точках А и Б имеют нулевой наклон
к оси х.
В результате решения уравнения A) получаются две константы
интегрирования (так как это уравнение второго порядка), которые
вместе с двумя неизвестными МА и RA и использовании усло-
условий B) образуют линейную систему четырех уравнений. Решая
эту систему (промежуточные выкладки опускаем), мы получим
126
Статика упругих тел
следующую систему для реакций Ra и Ма-
' 1 + // 1+3// 11 + 5//
8 "Л^ 2Z ^~*' 48 *
где обозначено у. = —.
Решения системы C) суть следующие:
„ ql3 + 2S(i + n2
2 3 2 ^
ql2 Зц3 + \5\ц2 + $9ц+П
'48 7Г
В силу симметрии системы, для нахождения реакций Rb и Mb
1
нужно в полученных выражениях заменить //на -.
Например,
в
4 1 + 14/Л- (I2 '
Проверка показывает, что Ra + Rb = ql.
Отметим также, что при fi = 1 (балка с постоянным моментом
инерции) получим:
M
Такие же ответы получены для аналогичной задачи (т. е.
балки с постоянным моментом инерции сечения) в задачнике
[19, т. 2, с. 274].
Отметим в заключение, что из формул D) следуют два факта:
127
Глава 4
1. Реакции в заделах зависят лишь от отношения моментов
инерции на участках 0, - и -, IL т. е. от —.
2. В силу монотонности по fi выражений из D) (это проверя-
проверяется непосредственным дифференцированием), можно утверждать,
что при /z G [0, оо) имеем:
причем граничные значения в указанных неравенствах достижимы
(при соответствующих /z). Аналогичные неравенства справедливы
также для Rb и Mb (с заменой знака для Afe!). О
Задача 4.7 (определение реакций опор в статически не-
неопределимой раме). Плоская рама ABCD шарнирно за-
закреплена на концах А и D (см. рис. 4.10). Горизонтальный
элемент рамы имеет длину L и жесткость Е1\ при изги-
изгибе; вертикальные элементы имеют длину Н и жесткость
Е12 при изгибе. Найти реакции опор R\,R2,R3,R4 при
действии силы Р (см. рис. 4.10). Рассматривать только
деформации изгиба!
Решение. Применим теорему Кастилиано (см. [26]). Для этого
подсчитаем упругую энергию стержней фермы при изгибе, как
функцию сил R\, i?2. Имеем следующие формулы для изгибающих
моментов в стержнях:
АВ:
CD: MCD(y) = -R\y-P(L-b)+R2L,
ВС : MCD(x) = -R\H + R2x,
128
Статика упругих тел
Рис. 4.10
MCD(x) = -P(x -b)-R\H + R2x,
Тогда упругая энергия U дается выражением:
(М2АВ
о
о
Ввиду того, что система один раз статически неопределима, то
достаточно получить одно дополнительное соотношение. Согласно
теореме Кастилиано, т.к. перемещение, соответствующее силе R\,
равно 0, то будет выполнено
получаем:
аи
= 0. Проводя вычисления
2Д|Я3 Р (L-b)H2 R2LH2 _
+ ЪЕ12 + ~ЁТ2 2 2EI2 '
129
Глава 4
аи
Мы могли бы выписать соотношение —— = 0 (перемеще-
oR2
ние, соответствующее силе R2y равно 0). Однако этого можно не
делать, т.к. R2 находится из уравнений статики. Беря моменты
относительно точки Dy получим
R2L - P(L - b) = 0, R2 =
Подставл
8U
L
Подставляя найденное выражение для R2 в формулу для
= 0, получим:
(HL 2Н2\_
Rl\EJl+3EI2)~~
Р (L- bJ PL(L-b)
2EI{
Отсюда имеем ответы:
Pb
5t/
Отметим, что использование соотношений —— = 0 пригоди-
uR2
лось бы в этом случае, если бы мы учитывали упругую энергию
также от сжатия стержней. Рассмотрим симметричный случай:
L = Н, Ь = —. Тогда:
Если I\ = I2j то
т.е. вертикальные реакции в семь раз больше горизонтальных. >
130
Статика упругих тел
У\
В
Рис. 4.11
Задача 4.8 (конструктивно статически неопределимая ра-
рама). П-образная рама (см. рис. 4.11) одним концом за-
закреплена шарнирно. На другом конце рамы имеется каток,
опирающийся на жесткую плоскость. Определить реакцию
нижней опоры, считая, что сила Р и жесткость EJ рамы
таковы, что перемещения, возникающие в раме, малы по
сравнению с ее начальными размерами.
Решение. Описанная система является конструктивно (или
кинематически) статически неопределимой! Попытка определить
величину реакции нижней опоры, не учитывая деформации систе-
системы, приводит к абсурдному результату: R = ±оо (для этого нужно
составить уравнение моментов всех сил относительно шарнира А).
Итак, следует учесть горизонтальное смещение катка В. Пусть
131
Глава 4
Рис. 4.12
равновесие системы наступает при угловом повороте рамы на ма-
малый угол <р (см. рис. 4.12). Разложим реакцию R в точке В на две
составляющие R\ и Rj, как показано на рис. 4.12. Ясно, что R\ =
R cos <p « R; Rj = R sin у?« ity?. Уравнение моментов относитель-
относительно точки А, с точностью до малых третьего порядка по <р, дает:
Из рис. 4.12 следует, что увеличение Д отрезка АВ в результате
деформации составляет:
cos y>
cos ^
~~2~"
Теперь попробуем найти это перемещение используя теоре-
теорему Кастилиано. Для схемы рис. 4.13, определим перемещение Д
132
Статика упругих тел
Рис. 4.13
точки Б, соответствующее силе R\. Имеем упругую энергию, как
функцию сил R\ и Ri:
dy +
- ж)]2dx.
Тогда, по теореме Кастилиано:
133
Глава 4
Подставляя в это равенство R\, Ri и Р = R(p, получим, с
точностью до малых третьего порядка по <р, равенство:
EJ Ъ
(p
Пренебрегая — по сравнению с 1, получим:
Заменяя <р
5
3
Ra2
EJ
на
1
= 2
Р
R'
Р2
R2'
Ra2
EJ
получив
3
R =
5
3
i:
3
То
<Р2
2
EJP2
а2
1 iP'EJ
Задача 4.9 (о тяжелом деформируемом стержне). Одно-
Однородный стержень длины L и плотности р поставлен верти-
вертикально на жесткую горизонтальную плоскость (см. рис. 4.14)
предполагая жесткость стержня на растяжение равной EJ,
определить две величины: А\ — смещение центра тяжести
(т.е. центра стержня до деформации!) после деформации;
д2 — расстояние между центрами тяжести до и после
деформации.
Решение. Направим ось х вертикально вверх, причем х = О
соответствует нижнему концу стержня. Пусть и(х) — смещение
сечения х после деформации. Выделим элемент стержня между
х и х + dx (см. рис. 4.15). До деформации длина этого элемента
равна dx, а после деформации
dx\ —dx- u(x + dx) + u(x) &dx~- I — ) dx.
\dxj
134
Статика упругих тел
g
z + dz
z
Рис. 4.14
Рис. 4.15
Изменение длины этого элемента происходит в результате действия
напряжения в сечении ж, которое, очевидно, равно весу части
стержня над сечением х. Согласно закону Гука (для сжатия, которое
в данном случае происходит), получим:
dx - dx\
dx
du 1
Учитывая, что it@) = 0, получим:
u(x) = pg ¦
X-
2
EJ
A)
чим:
Подставляя в формулу A) х = - (для центра тяжести), полу-
-GH
EJ
B)
Теперь определим новое положение центра тяжести дефор-
деформированного стержня в системе Ох. Новые (деформированные)
координаты точек стержня суть х - и(х). Считая плотность р
135
Глава 4
стержня по-прежнему равномерно распределенной, получим:
о
= у / zdz-jj u(z)dz=--j I u(z)dx.
0 0 0
Отсюда, учитывая, что - — координата центра тяжести до
деформации, получим:
Отметим, что из B) и C) следует Дг < Дь Расхождение
получилось потому, что центр тяжести не является фиксированной
точкой стержня в процессе деформации! >
.Глава 5.
ДИНАМИКА УПРУГИХ ТЕЛ
Задача 5.1 [1]. Стержень массы т, длины I и сечения S
тянут за один конец с ускорением а. Модуль Юнга ма-
материала стержня Е. Колебаниями в стержне пренебречь.
На сколько удлинится стержень?
Решение. Возьмем сечение А(х) стержня на расстоянии х
от его начала @ ^ х ^ I) и определим и(х) —- перемещение этого
сечения при движении с ускорением (см. рис. 5.1). Пусть а(х) —
нормальное напряжение в сечении А(х).
Уравнение для центра масс части ОА(х) имеет вид:
т(х) • а = а(х) • S. A)
А для части А(х)АA):
(т - т(х))а = -а(х) -S + F, B)
где F — сила, движущая стержень с ускорением а. Для всего
стержня имеем
та = F. C)
138
Динамика упругих тел
С, \А(х)
Рис. 5.1
В принципе уравнения B) и C) лишние и достаточно лишь урав-
уравнения A), из которого находим:
<т(х) =
Далее, закон Гука дает:
mix)
mx
i(x) mx
mx
EIS
а, «(/) =
ml2
а =
ml
EIS E-S
-а.
Это ошибочно (это верно в деформированной системе координат).
Это пример неверного решения!
Верное решение.
Уравнение для центра масс A) мы должны записать так:
х
т(х) • - = а(х) • S.
Уравнение B) так:
[т - т(х)) Г|1 = -а(х) -S + F.
139
Глава 5
Уравнение C) так: та = F.
х нам не нужно, так что мы его исключаем:
О = а • S[m - т(х)] + aS • т(х) - та • т(х),
. ат(х) ахт
ф)=-s- = -js~-
Разделим теперь стержень на маленькие кусочки
Ах = — (п -> оо).
п
Координата &-й точки
Ы
ее смещение в силу закона Гука:
Ax\ I m a
та kl mal к
~~ SnE 7Г " 5^Е п2"
Тогда общее смещение
(п+ 1)п та/
2
(это верный ответ!).
В этом же круге поучительна такая задача.
140
Динамика упругих тел
Задача 5.2 [17, с. 149]. На гладкую горизонтальную плос-
плоскость положили брусок АВ из однородного материала мас-
массы га, сечения S и длины /, упирающийся одним концом
в выступ (см. рис. 5.2). На другой конец бруска действует
постоянная сила F, равномерно распределенная по сече-
сечению бруска. Согласно закону Гука длина бруска при этом
изменится на величину
где Е — модуль Юнга бруска. На сколько сожмется бру-
брусок, если выступ удалить, а все прочие условия оставить
неизменными?
Решение. Под действием
силы F брусок будет двигать-
F
ся с ускорением a = —. Ис-
m рис 5 2
пользуя результат предыдущей
задачи, получим
Физически это можно объяснить так. В статическом случае все
элементы бруска давят друг на друга с одинаково распределенным
F
давлением с = — (во всех сечениях!) (см. рис. 5.3). А в динами-
динамическом случае для обеспечения элементам одинакового ускорения
F
a = — элементы давят друг на друга с переменным (!) давлением
m
F х
a(x) = 7Г у О^х ^1 (см. рис. 5.4). D>
141
Глава 5
О I x
Рис. 5.3. Статическое распределение напряжений
а(х)
О I х
Рис. 5.4. Динамическое распределение напряжений
Задача 5-3 (жук на жгуте [20, с. 219]). Человек держит
за конец резиновый жгут длиной 1 м, привязанный к дереву.
У другого конца жгута сидит жук. Каждую секунду жук
проползает 1 см по жгуту. Каждую секунду человек, держа
конец жгута, удаляется от дерева на 1 м.
1) Доползет ли жук до человека?
2) Если нет, то почему?
3) Если да, то за какое время?
142
Динамика упругих тел
Решение.
I. Непрерывный вариант.
Рис. 5.5
Пусть точка А жгута О А (см. рис. 5.5) перемещается вдоль
оси Ох со скоростью V\, а жук G двигается со скоростью Т^ вдоль
Ох относительно жгута(!).
Пусть в момент t G находится в точке x(t) оси Ох. Абсолют-
Абсолютная скорость жука G равна х и складывается из относительной Vi
и переносной Vr{x) скоростей:
По определению, Vr(x) -— это скорость точки жгута, име-
имеющей в данный момент координату х. Найдем эту скорость.
Пусть точка А сместилась на Ах&. Если считать жгут невесо-
невесомым и абсолютно упругим (т. е. подчиняющимся закону Гука), то
процесс растяжения будет квазистатическим. Следовательно, от-
относительные деформации любого его куска Ох будут одинаковыми
и не зависящими от х. Таким образом:
Ах
х
АхЛ
ОА
1 Ах
x~At
1
ОА At '
143
Глава 5
Устремляя в последнем равенстве At -* 0, получим:
1 . . 1
где L(t) — текущая длина жгута, равная L(t) = Lq + Vyt, Lq —
начальная длина жгута.
Равенство A) приобретает тогда вид дифференциального урав-
уравнения:
Чтобы решить это уравнение, сделаем подстановку
Тогда:
х = y(LQ + V{t) + y -Vx =
Vy Lq
Так как х@) = j/@) • Lq = 0 (жгут выходит в точности из точ-
точки О, для которой х@) = О!).
Итак, мы имеем следующий закон для координаты жука:
х(<) = (i0 + FiO • — In
V
In .
Vy Lq
Эта формула и дает ответ задачи. Жук достигнет человека в мо-
момент t\: x(ti) = Lo + V\ti. Поэтому 11 является корнем уравнения:
144
Динамика упругих тел
так как для условий задачи — = -—г— = 100.
Too
II. Дискретный вариант (Г. Г. Малинецкий [20]).
Пусть в А;-ю секунду координата жука ж*. Тогда для k -h 1-й
секунды имеем:
где Ак+\ — растяжение точки хк жгута, находимое из закона Гука:
Тогда:
^1 1 1 гт О» 1 1
i * * *^/к+1 Xfc 1 1
" k 100 k + l fc 100 fc+Г
причем при А; = 0 мы полагаем — =0. Отсюда
xk+l 1 /, .1 1 . .1
а так как гармонический ряд расходится, то существует к, что
Хк
1ОЗак.9О
.Глава 6.
ГИДРОМЕХАНИКА
Задача 6.1 [9, с. 39]. Цилиндрический сосуд до краев на-
наполнен водой и плотно закрыт крышкой. В нем находятся три
тела: пробка, кусочек свинца и тело, плотность которого рав-
равна плотности воды. Цилиндр приводится во вращение вокруг
вертикальной оси. Как будут расположены тела в цилиндре?
Решение. При вращении воды каждому ее элементу со сто-
стороны окружающих сообщается сила, обеспечивающая нормальное
ускорение oj2r. Ежели плотность этого элемента равна плотности
воды, то он будет двигаться вместе с водой. Ежели больше (сви-
(свинец), то сила требуется большая и его будет отбрасывать на край
цилиндра. А ежели меньше, то наоборот, к оси! t>
Задача 6.2 ([1], задача 4.3.10). С каким ускорением будет
двигаться длинное цилиндрическое тело плотности р и ра-
радиуса г вдоль оси вертикального высокого цилиндрического
сосуда радиуса R, заполненного жидкостью плотности ро?
Чему равна разность давлений на верхнее и нижнее осно-
основания тела, если его длина равна Л?
148
Гидромеханика
Рис. 6.1
Решение. Пусть в данный момент скорость тела есть гТ, а уско-
ускорение — 3 и оба эти вектора направлены вдоль ускорения g
(см. рис. 6.1).
Сечение АВ движется вниз со скоростью v. Это означает, что
сечения А\А и В\В движутся вверх с некой скоростью v\. Закон
сохранения массы дает уравнение:
-Г2) =
Vi =
vr*
(О
149
Глава 6
Совершенно аналогичное рассуждение справедливо и для се-
сечений CD9CC\yDD\ (см. рис.6Л). Таким образом, если жид-
жидкость несжимаема, то ее часть, заключенная в столбиках АСС\А
и BDD\B> движется вверх со скоростью V\ из A), а ее кинетичес-
кинетическая энергия:
v2ph7r(R2-r2) _\uv2
2 2
где
_ pphirr4
Что касается остальной части жидкости, то ее кинетическая
энергия примерно равна нулю (хотя, строго говоря, это не так!).
Отметим, что коэффициент Ац из B) называется присоединенной
массой в механике жидкости. Применяя теорему об изменении
кинетической энергии к жидкости, получаем:
Т\ = Рдин • t^t2v - АРст • тгг2ь, C)
где РдИН — давление от оснований цилиндрического тела, АРСТ —
перепад статических давлений жидкости, равный
АРСТ = pogh.
Подставляя B) в C) и производя сокращения, получим:
2 / г4 2\
Рот цилиндра = Рдин KR =ж\рфп ^ 2 + Poghr I, U = V. D)
Точно такая же сила, но с обратным знаком, действует от жид-
жидкости на цилиндр, т. е. уравнение центра масс для цилиндра будет
иметь вид:
t 2 171 171
рпТ\Т ' О — -*тяж ~~ -*от цилиндра»
150
Гидромеханика
Подставляя сюда ^тяж = phnr g и выражение D), получим уравне-
уравнение:
г2 (p-po)(R2r2)
(p-po)(R2-r2)
Замечания. 1) Аналогичная задача рассматривается в сборнике Век-
штейна Г.Е. Физика сплошных сред в задачах, М., 2002 г. (с. 133, задача
7-22). Однако, там цилиндр всплывает, причем его плотность р <? />о-
В этих условиях из полученного нами ответа имеем:
г ft"' Д2-гг
а = hm g с г = -g —.
?° р г г
р i
(#-Г*)
2) Рассуждения, приведенные в решении, можно попытаться рас-
распространить на количество движения жидкости, с целью использования
соответствующей теоремы динамики. Однако, результатов это не дает!
Происходит это оттого, что пренебрежение количеством движения жид-
жидкости вне объема A\C{DXB\ неверно. Вообще говоря, в механике жидкости
показывается, что в рассматриваемой ситуации для бесконечного объема
жидкости
Т= / ^-
сходится, а
¦/
pv
расходится (см. [29, с. 190], [30, с. 51]).
3) Зная ускорение из формулы E), можно найти разность давлений
на основаниях цилиндра АР. Имеем:
тг/?Лг2о = irphr2g - 2
-» АР = hp(g -a) =
где АР — гидростатическая разность давлений.
151
Глава 6
Из полученной формулы следует, что: при R -> оо (безграничная
жидкость) имеем АР = ДРс™, при R -» г ЛР = ДРс,*,.- = pgh, т.е.
вес цилиндра на единицу площади!
Далее, из формулы E) для ускорения следует, что при R -» г,
а -> 0, т. е. цилиндр либо не движется, либо сохраняет свое равномерное
движение (жидкости некуда деваться!). Если же R -> оо (безграничная
(Р ~~ Ро)
жидкость), то а = g , а это есть ускорение падения с учетом
архимедовой силы.
Литература
1. Задачи по физике / Под ред. О. Я. Савченко. М.: Наука. 1988. 45 с.
2. Кошкин Г. Л., Сербо В. Г. Сборник задач по классической механике.
Москва—Ижевск: Изд-во РХД, 2001. 346 с.
3. Пятницкий Е. С. и др. Сборник задач по аналитической механике.
М.: Физматлит, 2002. 396 с.
4. Слободецкий И. Ш.у АсламазовЛ. Г. Задачи по физике. М.: Наука, 1980.
174 с.
5. Векштейн Г. Е. Физика сплошных сред в задачах. М.: Институт ком-
компьютерных исследований, 2002. 206 с.
6. Слободецкий И. Ш., Орлов В. А. Всесоюзные олимпиады по физике.
М.: Просвещение, 1982. 256 с.
7. Матвеев А. И. Механика и теория относительности. М.: Высшая шко-
школа, 1986.
8. Кильчевский И. Я. Курс теоретической механики. Т. 2. М: Наука, 1977.
544 с.
9. Савин А. П. у Брук Ю. М. и др. Физико-математические олимпиады.
Сборник. М: Знание, 1977. 160 с.
10. Васильев И. В. и др. Математические соревнования. Геометрия. Би-
Библиотека физ.-мат. школы. М.: Наука, 1974. 80 с.
П. Бухгольц Н. Н.у Воронков И. М., Минаков А. Л. Сборник задач по
теоретической механике М.—Л.: ГИТТЛ, 1949. 275 с.
12. Жуковский Н.Е. Теоретическая механика. Собрание сочинений. Т. 5.
М., 1949.
153
Литература
13. Гельфгат Я. А/., Генденштейн Л. Э.9 Кирик Л. А. 1001 задача по физике
с решениями. Харьков—Москва: Центр «Инновации в науке, технике
и образовании», 1996. 592 с.
14. ГомоноваА. Н. и др. Сборник задач по физике. Ч. I. Механика. М.: МГУ
им. М. В.Ломоносова. Учебно-научный центр довузовского образова-
образования, 1995. 160 с.
15. Сивухин Д. В.. Общий курс физики. Т. 1, Механика. М.: Физматлит,
МФТИ, 2002. 560 с.
16. Тимошенко СП., Гере Дж. Механика материалов. СПб.—М.: Лань,
2002. 672 с.
17. Сборник задач по общему курсу физики / Под ред. В. А. Овчинкина.
4.1. Механика. М.: МФТИ, 1998. 416 с.
18. Работное Ю. И. Сопротивление материалов. М.: Издательство Мо-
Московского университета, 1950, 336 с.
19. Галин Г. Я. и др. Механика сплошных сред в задачах / Под ред.
М.Э.Эглит. Ч. I, И. М.: Московский лицей, 1996. 396, 394 с.
20. Малинецкий Г. Г. Задачи по курсу нелинейной динамики. В сб. Новое в
синергетике. Загадки мира неравновесных структур. М.: Наука, 1996.
263 с.
21. Пановко Я. Г. Механика деформируемого твердого тела. М.: Наука,
1985. 287 с.
22. Виттенбауер Ф. Задачи по механике. М.: Издание Г. К. Боровикова,
1908.306 с.
23. Переломов А. М. Интегрируемые системы классической механики и
алгебры Ли. Москва-Ижевск: РХД, 2002. 237 с.
24. Аппель П. Теоретическая механика. Т. 2. М.: ГИФМЛ, 1960. 487 с.
25. Унайкин В. В. Механика. Основы механики сплошных сред. Задачи
и упражнения. Москва—Ижевск: Институт компьютерных исследова-
исследований, 2002. 196 с.
26. Саусвелл Р. В. Введение в теорию упругости. М.: Изд-во иностранной
литературы, 1948. 674 с.
27. Брайсон А., Хо-Ю-Ши. Прикладная теория оптимального управления.
М.: Мир, 1972. 544 с.
154
Литература
28. Колесников Н. К, Т. В Сальникова, Якимова К. Е. Классическая и ана-
аналитическая механика / Под ред. В. В. Козлова. М.: Изд-во мех.-мат.
ф-та. МГУ им М. В.Ломоносова, 1998. 224 с.
29. Седов Л. И. Механика сплошной среды. Т. 2. М.: Наука, 1984. 560 с.
30. Ландау Л.Л, Лифшиц Е. М Гидродинамика. М.: Наука, 1986. 736 с.
31. Татаринов Я. В. Лекции по классической динамике. М.: Изд-во Мо-
Московского университета, 1984. 295 с.
32. Уиттекер Э. Аналитическая динамика. Редакция журнала «Регулярная
и хаотическая динамика». Издательский дом «Удмуртский универси-
университет», 1999. 584 с.
33. Антонов И. Л., Трушин С. //., Якимова К. Е. Кинематика шарнира
Кардана—Гука. В сб. научно-методических статей по теоретической
механике. Вып. 13, М.: Высшая школа, 1983. 200 с.