ЭНЦИКЛОПЕДИЯ
ЭЛ HVU Л: ГАРНОЙ
МАТЕД\ АТИК И

АКАДЕМИЯ ПЕДАГОГИЧЕСКИХ НАУК РСФСР
ЭНЦИКЛОПЕДИЯ
ЭЛЕМЕНТАРНОЙ
МАТЕМАТИКИ
С
КНИГА ЧЕТВЕРТАЯ
ГЕОМЕТРИЯ
.А.'.'ДТИЧЕСКОГО
'{"ЛЛЕДЖА НМУ
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1963

61
Э68
ГЛАВНАЯ РЕДАКЦИЯ
ЭНЦИКЛОПЕДИИ ЭЛЕМЕНТАРНОЙ
МАТЕМАТИКИ:
П. С. АЛЕКСАНДРОВ,
А. И. МАРКУШЕВИЧ,
| А. Я. ХИНЧИН I
I
РЕДАКТОРЫ КНИГИ ЧЕТВЕРТОЙ J
В. Г. БОЛТЯНСКИЙ,
и. м. яг лом

ОГЛАВЛЕНИЕ
От редакции . . 7
АКСИОМЫ И ОСНОВНЫЕ ПОНЯТИЯ ГЕОМЕТРИИ
(Б. А. Роэенфельд)
§ 1. Возникновение основных понятии геометрии 9
§ 2. «Начала» Евклида ....... 12
§ 3. Появление аксиоматического метода . 18
§ 4. Модели . . . 21
§ 5. Непротиворечивость и полнота аксиоматики 28
§ 6. Аксиоматика геометрии . . 32
6 7- Непротиворечивость и почнота аксиоматики евклидовой геометрии 41
§ 8. Независимость аксиом ... 44
Литература . . . ...... 47
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
(И. М. Яглам, JI. С. Атанасян)
§ 1. Понятие преобразования. Примеры . . 50
§ 2. Применение преобразовании к решению геометрических злдач . 63
§ 3. Аналитическая запись геометрических преобразований 72
§ 4. Произведение отображении и преобразований 80
§ 5. Обратное преобразование . . . 96
§ 6. Общее определение геометрии. Группы геометрических преобра- •¦'„
зований ... . . . . 98 V
§ 7. Группа проективных преобразований .... ""//
§ 8. Неточечные отображения . . ... . 121 «J
§ 9. Принцип перенесения ... . 140
Литература . . 157
ОБЩИЕ ПРИНЦИПЫ ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ
(И. М. Бескин, В. Г. Болтянский, Г. Г. Маслова,
Н. Ф. Четверухин, И. М. Яглпм)
§ 1. Некоторые вопросы практического использования геометрических
построений . . 160
§ 2. О решении задач на построение в зависимости от принятых инстру-
инструментов . . . 167
§ 3. О построениях на ограниченном куске плоскости 177
1*

ОГЛАВЛРНИЕ
4. Общие методы решения задач на построение иа плоскости . 182
Б. Использование геометрических преобразований при решении задач
на построение на плоскости 189
§ 6. Прнближенные методы геометрических построений и их значение
для практики . 193
§7. Геометрические построения в пространстве 200
Литература 203
О РАЗРЕШИМОСТИ ЗАДАЧ НА ПОСТРОЕНИЕ
С ПОМОЩЬЮ ЦИРКУЛЯ И ЛИНЕЙКИ
(Ю. И. Манин)
%
Введение . 205
( 1. Геометрическая часть теории . . . 206
§ 2. Перевод задачи на алгебраический язык 210
§ 3. Классические задачи , . 220
Литература 227
МЕТОДЫ ИЗОБРАЖЕНИЙ
(Н. М. Вескин)
1. Постановка .задачи . . . 229
2. Параллельные проекции . . . 234
3. Параллельная аксонометрия 247
4. Метод Монжа 275
Б. Центральные проекции . 277 ?
§ 6. Построения на изображении . . 288
Литература ' . . ....... 289
ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
(В. Г. Болтянский, И. М. Яглом)
4 1. Определение вектора 292
§ 2. Сложение векторов и умножение вектора на число 298
§ 3. Скалярное произведение векторов . 319
§ 4. Косое произведение векторов плоскости 338
§ 5. Тройное произведение и векторное произведение векторов про-
пространства . 351
§ 6. Применения векторного исчисления к сферической геометрии и
тригонометрии 366
§ 7. Понятие о векторных пространствах 369 ¦
Литература 380-
МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ
(В. Г. Ашкинузе)
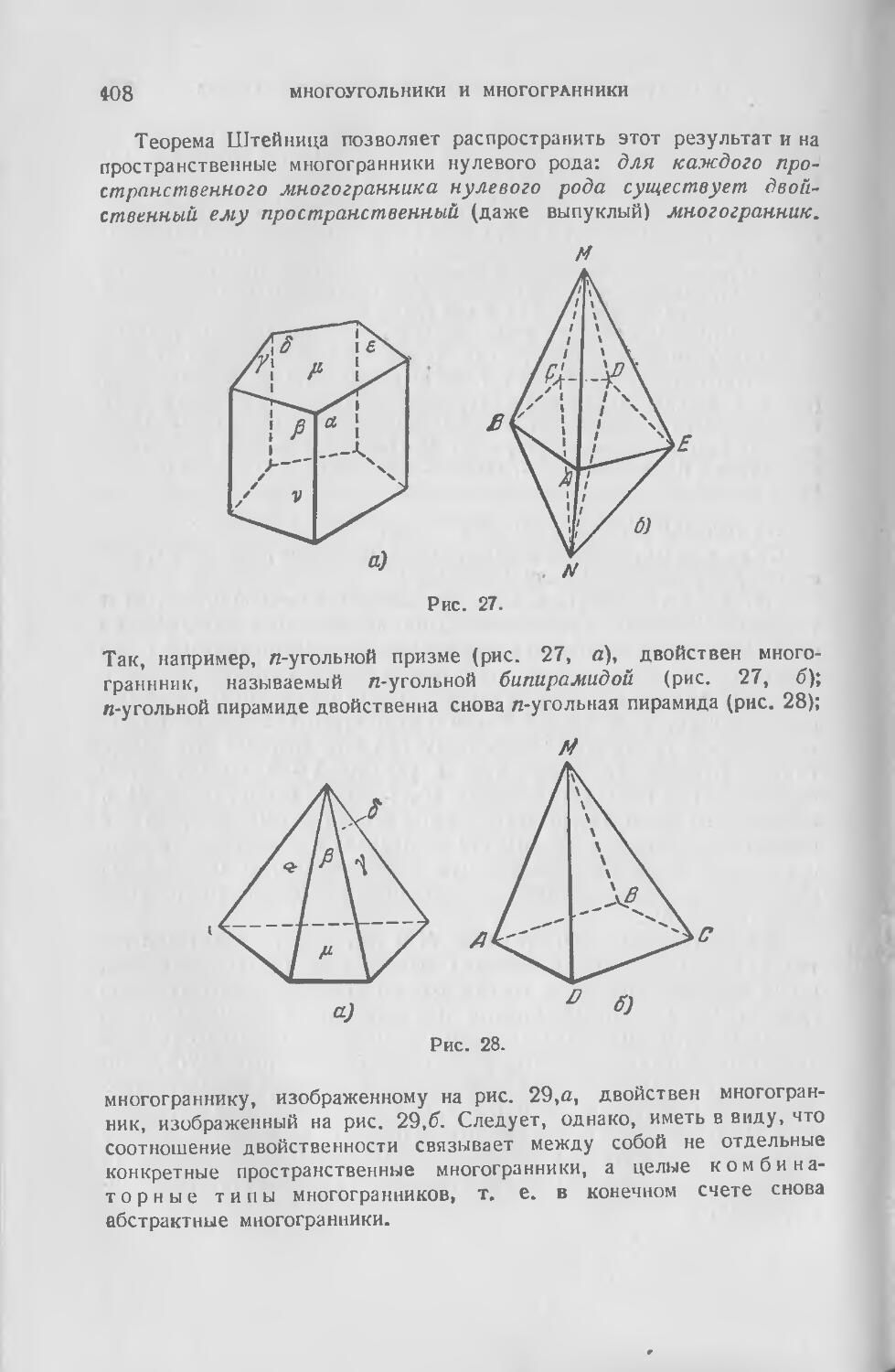
§ 1. Основные определения. Теорема Эйлера 382
§ 2. Комбинаторный (топологический) тип многогранника. Теорема
Штейница . 399
| 3. Развертка многогранника. Теорема Коши 410
Л 4. Правильные многоугольники и многогранники и их обобщения . 420
Литература 446

ОГЛАВЛЕНИЕ 5
ОКРУЖНОСТИ
(И. М. Яглом)
Введение 449
А. Окружность как совокупность точек
§ 1 Обобщение понятия окружности . . 450
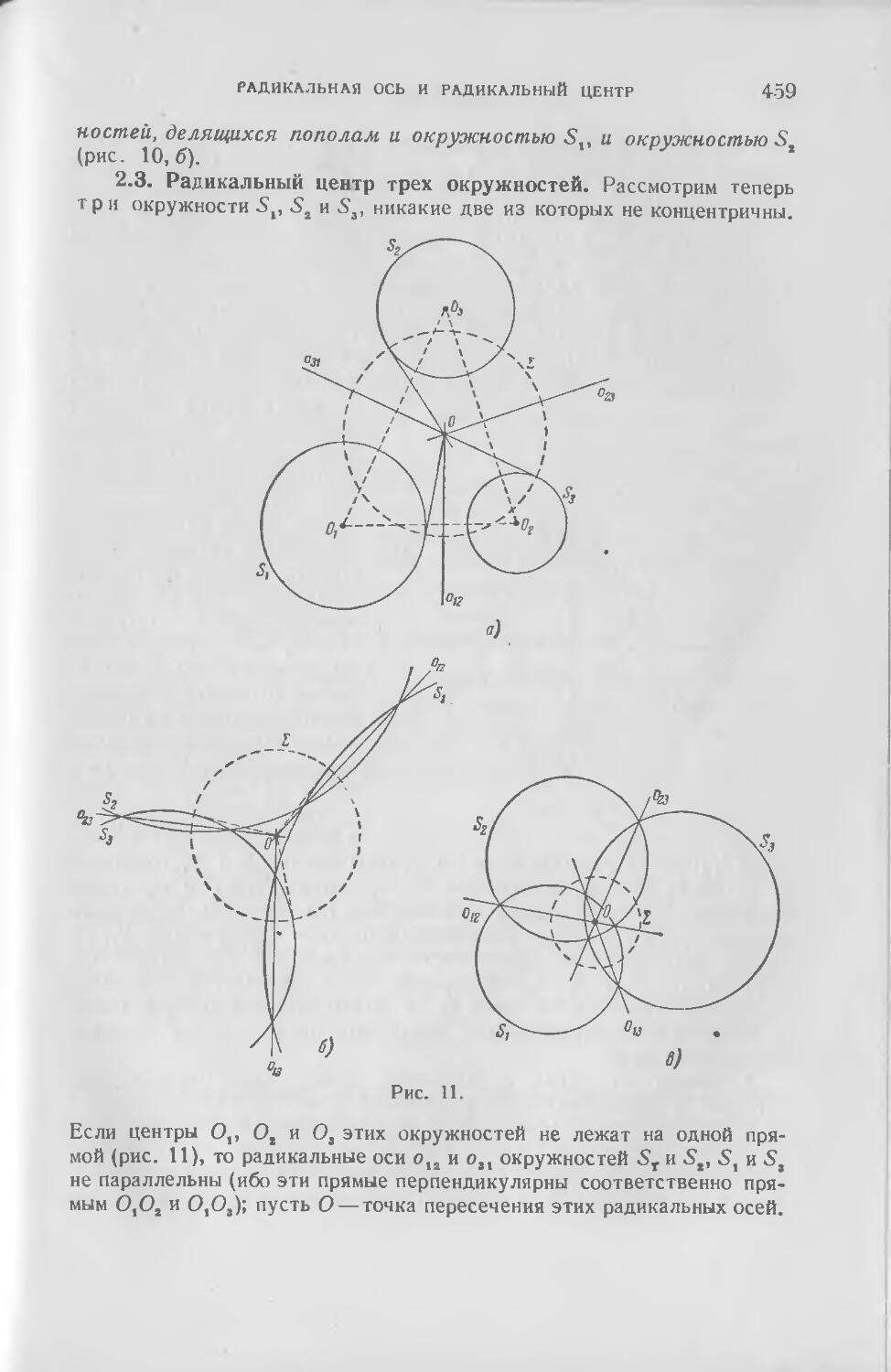
2. Радикальная ось и радикальный центр .... 454
3 Пучки и связки окружностей 461
5 4. Инверсия . . 468
5 Точечная геометрия окружностей 476
Б. Окружность как совокупность прямых
^ 6. Направленные окружности . 479
^ 7. Центр подобия и ось подобия 485
§ 8. Ряды и сети окружностей 490
§ 9. Осевая инверсия 495
5 10. Осевая геометрия окружностей Б04
В. Окружность как совокупность линейных элементов
§ 11. Новый взгляд на окружность . . . . 508
§ 12. Касательная геометрия окружностей . . . . 510
Литература ... 516
ОСНОВНЫЕ ПОНЯТИЯ СФЕРИЧЕСКОЙ ГЕОМЕТРИИ
И ТРИГОНОМЕТРИИ
(Б. А. Роэенфельд)
§ 1. Основные понятия сферической геометрии 518
§ 2. Сферические треугольники . . . ... 530
§ 3. Малые окружности 539
§ 4. Тригонометрические соотношения в сферическом треугольнике Б45
Литература . . 557
Именной указатель . . . . . . . 558
Предметный указатель 659

ОТ РЕДАКЦИИ
Первые три книги «Энциклопедии элементарной математики» (сокра-
(сокращенно ЭЭМ), посвященные арифметике, алгебре и анализу, вышли
свыше десяти лет тому назад. Теперь после долгого перерыва редак-
редакция решила завершить этот труд. За эти годы коллектив сотруд-
сотрудников ЭЭМ понес большие потери. В 1959 г. после продолжитель-
продолжительной болезни скончался Александр Яковлевич Хинчин; еще раньше
мы потеряли Дмитрия Ивановича Перепелкина, участвовавшего в
составлении геометрических книг. То, что издание удалось все же
возобновить, является результатом большой работы, проделанной
Владимиром Григорьевичем Болтянским и Исааком Моисеевичем Ягло-
мом.
Напомним из предисловия к первой книге,'что предлагаемый труд
«не может служить для первоначального изучения предмета. Он
предназначается для людей, изучавших элементарную математику и
уже ставших или готовящихся стать преподавателями элементарной
математики. Он не следует, как правило, ни порядку, ни способу
изложения математики в средней школе, так как то и другое обу-
обусловлено возрастными особенностями учащихся и общеобразователь-
общеобразовательными целями средней школы, т. е. соображениями, которые не играют
роли по отношению к подготовленному читателю-профессионалу.
Логика нашего издания—это логика систематического, по возмож-
возможности простого и доступного изложения тех вопросов математической
науки, из которых строится школьный курс, а также и тех, которые
хотя и не находят в этом курсе прямого выражения, однако необ-
необходимы для правильного и сознательного его понимания и создают
перспективы для дальнейшего развития содержания и методов школь-
школьного курса».
Этот наш первоначальный замысел остается неизменным. Осталось
неизменным и намерение посвятить очередные две книги геометрии.
Что же касается их фактического содержания, то здесь редакция
внесла ряд изменений, продиктованных главным образом желанием
учесть некоторые замечания критики и читательские отклики на
первые три книги. С принятым ныне отбором материала и порядком
его расположения читатель познакомится из оглавлении.

8 ОТ РЕДАКЦИИ
Отметим, что четвертая и питая книги ЭЭМ образуют вместе
самостоятельное целое, так что пользование ими, в известном
смысле, независимо от ранее выпущенных книг, также составляющих
законченный цикл.
В 1951 г., когда вышла в свет первая книга ЭЭМ, никто и не
предполагал, что появятся новые математические профессии (вроде
программиста-вычислителя), подготовка к которым будет возложена
на среднюю школу. В свете новых задач должна быть расширена и
пересмотрена сама концепция «элементарной математики». Соответ-
Соответствующим вопросам редакция предполагает отвести место в послед-
последних книгах (все издание, рассчитано на семь книг), состав которых,
таким образом, будет во многом отличаться от содержания, намечен-
намеченного в предисловии к первой книге.
Если бы пришлось начинать все сначала, мы внесли бы прежде
всего серьезные изменения в структуру и изложение ранее выпущен-
выпущенных книг. Но нам представляется, что в целом они все же оказа-
оказались полезными. Мы надеемся, что эта и следующая книги ЭЭМ
найдут свою читательскую аудиторию и будут полезны и препода-
преподавателям математики средней и высшей школы, и студентам педаго-
педагогических институтов и университетов, а также любителям математи-
математики, не связанным с вопросами ее преподавания.
Редакция

АКСИОМЫ И ОСНОВНЫЕ ПОНЯТИЯ ГЕОМЕТРИИ
СОДЕРЖАНИЕ
{ 1. Возникновение основных понятий геометрии 9
1.1. Понятия геометрии как результат абстракции 9
1.2. Зарождение геометрии в древнем мире . . 11
§ 2. «Начала» Евклида ... .12
2.1. Евклид и его предшественники . 12
2.2. «Постулаты» Евклида 15
2.3. Непрерывность у Евклида и его предшественников .16
2.4. Движения . . 17
§ 3. Появление аксиоматического метода . 18
3.1. Создание неевклидовой геометрии ... 18
3.2. Аксиоматический метод в математике . . ... 19
§ 4. Модели 21
4.1. Модели евклидовой плоскости ... . 21
4.2. Аксиоматические системы в алгебре . 27
§ 5. Непротиворечивость и полнота аксиоматики .28
5.1. Непротиворечивость аксиоматики . 28
5.2 Полнота системы аксиом 30
§ 6. Аксиоматика геометрии . 32
6.1 Основные понятия геометрии Енклида 32
6.2. Аксиомы принадлежности . . 32
6.3. Аксиомы порядка . . .34
6.4. Аксиомы движения .36
6.5. Аксиомы непрерывности . .... 37
6.6. Аксиома параллельности . 40
% 7 Непротиворечивость и полнота аксиоматики евклидовой геометрии 41
7.1. Арифметическая модель геометрии Евклида . 41
7.2. Непротиворечивость и полнота аксиоматики евклидовой пло-
плоскости ... . ... 43
§ 8. Независимость аксиом . . .... 44
8.1- Независимость системы аксиом .... . . 44
8.2. О независимости аксиоматики евклидовой еометрии .... 45
8.3. Заключение ... 46
Литература . . 47
§ 1. Возникновение основных понятий геометрии
1.1. Понятия геометрии как результат абстракции. Геометрия
представляет собой общую науку о пространственных формах.
С пространственными формами человек столкнулся прежде всего

10 АКСИОМЫ И ОСНОВНЫЕ ПОНЯТИЯ ГЕОМЕТРИИ
при измерении участков земли. Греческое слово уecafj-eTQict, or
которого происходит название геометрия, как раз и означает
«землемерие». С другими пространственными формами человек столк-
столкнулся при постройке зданий, выделке сосудов и т. д.
Геометрия, как и вся математика, изучает объекты реального
мира. Однако математические науки существенно отличаются от
«стальных естественных наук, изучающих специфические физические,
химические, биологические, экономические и другие закономерности.
В отличие от этих наук математика изучает объекты реального мира
в наиболее абстрактном виде, существенно отвлекаясь от их кон-
конкретного содержания. В частности, геометрия принимает во внима-
внимание только форму предметов, отвлекаясь от вещества и физических
свойств этих предметов, точно так же как, например, арифметика
принимает во внимание только числа предметов и их отношения.
Этот абстрактный характер математики и позволяет широко приме-
применять в ней дедуктивный метод, т.е. логическое выведение
закономерностей из небольшого числа основных положений (опреде-
(определений, аксиом), в то время как упомянутые выше науки применяют
главным образом индуктивный метод, т.е. установление
общих закономерностей на основе частных эмпирических наблюдений.
Однако эмпирические наблюдения и практический опыт играли
важнейшую роль при возникновении математических понятий и основ-
основных положений математики. Именно потому, что люди миллионы раз
сталкивались с такими арифметическими закономерностями, как не-
независимость результата счета камней или палок от порядка счета,
или с такими геометрическими закономерностями, как единственность
чинии, по которой располагается натянутая веревка, соединяющая
два колышка, смогли выработаться такие основные положения ариф-
арифметики и геометрии, как коммутативный закон сложения и аксиома
о единственности прямой линии, соединяющей две точки. Вся тер-
терминология, применяемая в геометрии, с исключительной наглядностью
свидетельствует о том, что понятия о геометрических образах воз-
возникли путем абстракции от реальных предметов различной формы.
Так, например, слово точка происходит от глагола «ткнуть» и
означает результат мгновенного прикосновения, укола'). Тот же
смысл имеет и латинское слово punctum, от которого произошли
термины Punkt, point (точка) на западно-европейских языках и рус-
русский термин «пункт»: эти слова происходят от латинского глагола
') Это толкование является сейчас общепринятым. Интересно, од-
однако, отметить, что замечательный русский математик Н. И. Лобачевский
придерживался другого взгляда на происхождение термина «точка». Ои
говорил, что точка происходит «от прикосновения пера, откуда заимство-
заимствовано самое название» («точка» — отточенное острие гусиного пера, которым
писали во времена Лобачевского. См. Н. И. Лобачевский, Избранные
труды по геометрии, Изд. АН СССР, Москва, 1956, стр. 108).

ВОЗНИКНОВЕНИЕ ОСНОВНЫХ ПОНЯТИЙ ГЕОМЕТРИИ 11
pungo—«укалываю». Слово линия, от латинского linea, в конечном
счете происходит от латинского слова linum — «лен, льняная нить»;
это показывает, что понятие линии является абстракцией от тонкой
льняной нити. Часто слово «линия» употребляется в значении «пря-
«прямой линии» (откуда, например, термин «линейка»); понятие прямой
линии, очевидно, является абстракцией от натянутой льняной нити.
Такое же конкретное значение имеют и геометрические термины
греческого происхождения: слово сфера происходит от греческого
orpaiQa—-«мяч», куб—от ии|3ос; —«игральная кость», цилиндр—от
KtJXivfiQog — «валик», конус — от Kuvog — «сосновая шишка», приз-
призма— от jiQiojia—«опиленная», ромб—от QGfi|3os— «бубен», трапе-
трапеция— от TQans^iov—«столик». Отсюда видно, что указанные гео-
геометрические фигуры представляют собой понятия, являющиеся аб-
абстракциями от форм мяча, игральной кости, круглого валика, сосно-
сосновой шишки, опиленного бревна, четырехугольного бубна, столика с
раздвинутыми ножками. Слово пирамида, от греческого JfOQafiig,
в конечном счете происходит от древнеегипетского слова ригата,
которым древние египтяне называли свои пирамиды.
Нить, веревка была не только прообразом геометрической линии,
но и первым геометрическим инструментом: натянутая веревка играла
роль линейки; закрепляя один конец веревки, другим ее концом
описывали как циркулем, окружность; деля веревку со связанными
концами на 12 равных частей и придавая этой веревке форму тре-
треугольника, стороны которого соответственно равны 3, 4 и 5 частям,
получали прямоугольный треугольник; таким образом строился
прямой угол. Греки называли древнеегипетских геометров, у кото-
которых они обучались геометрии, aQjiefiwanTai — «натягивателями ве-
веревки»; древнейший индийский геометрический трактат, посвящен-
посвященный правилам построения алтарей, назывался Sulva-sutra-вПравила
веревки». Циркуль и линейка появились раньше всего в Китае:
специальные иероглифы для обозначения циркуля и линейки возникли
в китайской письменности в середине II тысячелетия до н.э. Древние
греки приписывают изобретение этих инструментов Фа л ее у (VI век
до н. э.); во всяком случае египетские «натягиватели веревки», у
которых учился Фалес, по-видимому, не пользовались этими инстру-
инструментами. С циркулем связано появление слова центр — от грече-
греческого слова ksvtqov, обозначающего палку с заостренным концом,
которой подгоняли быков, а позже — ножку циркуля, ставящуюся в
центр описываемого круга.
1.2. Зарождение геометрии в древнем мире. Выработка абст-
абстрактных геометрических понятий являлась результатом длительного
исторического процесса 'накопления геометрических фактов. Перво-
Первоначально установление геометрических фактов происходило экспери-
экспериментальным путем, на огромном числе частных примеров, причем
правила, полученные в этих частных случаях, обобщались на другие

12 АКСИОМЫ И ОСНОВНЫЕ ПОНЯТИЯ ГЕОМЕТРИИ
случаи. Это видно из дошедших до нас правил вычисления площади
четырехугольника у египтян и индийцев, которые точны лишь в
частных случаях, а в общих случаях дают только приближенное
решение задачи: египтяне определяли площадь произвольного четы-
четырехугольника с последовательными сторонами а, Ь, с, d как произ-
а+с b + d
ведение —^— - , что верно только для прямоугольников, а ин-
индийцы определяли площадь произвольного четырехугольника со
сторонами а, Ь, с, d как У (р—а)(р—Ь) (р—с) (р — d), где
р =— (а+ 6 + c-\-d), что верно только для четырехугольников,
вписанных в круг.
Упоминавшемуся нами Фалесу приписываются первые доказа-
доказательства простейших геометрических утверждений; ранее необ-
необходимость «доказывать» геометрические факты, видимо, не осознава-
осознавалась. Доказательства Фалеса до нас не дошли, но" ясно, что эти
доказательства не могли опираться на другие геометрические утверж-
утверждения (аксиомы, ранее доказанные теоремы), как это делается в
современных геометрических доказательствах. Что представляли со-
собой доказательства Фалеса, видно, однако, из формулировок его
теорем: почти во всех теоремах Фалеса требуется доказать равен-
равенство каких-нибудь геометрических фигур—равенство частей кругаг
на которые он делится диаметром; равенство вертикальных углов;
равенство углов при основании равнобедренного треугольника; равен-
равенство двух сторон в треугольнике с двумя равными углами; равенство
двух треугольников, если две стороны и образуемый ими угол в
одном из них равны соответственным элементам другого треуголь-
треугольника. Доказательства этих теорем Фалес производил, несомненно, с
помощью наложения друг на друга тех фигур, равенство которых
требовалось доказать. Известная теорема Фалеса о том, что угол,
вписанный в окружность и опирающийся на ее диаметр,— прямой,
вероятнее всего доказывалась поворотом фигуры на 180°, после чего
возникал четырехугольник, вписанный в круг; далее требовалось
установить, что этот четырехугольник является прямоугольником;
это, вероятно, доказывалось перегибанием четырехугольника по его
средним линиямI.
§ 2. «Начала» Евклида
2.1. Евклид и его предшественники. После формулировки и
доказательства первых геометрических утверждений становится воз-
возможным доказывать одни утверждения (теоремы) с помощью других.
') Вариант такого доказательства приведен в статье «Геометрические
преобразования»; см. стр. 67 этой книги ЭЭМ.

«НАЧАЛА» ЕВКЛИДА 13
Доказательство многих геометрических теорем приписывается П и-
фагору и Демокриту (V в. до н. э.).
Гиппократу Хиосскому (IV в. до н. э.) приписывается
составление первого систематического курса геометрии, основанного
на определениях и аксиомах. Этот курс и его последующие обра-
обработки назывались Uroi/eia — «элементы, стихии», так как здание
геометрии в этих курсах строилось с помощью определений и аксиом
как физическое тело из «элементов» («стихий», т. е. огня, воздуха,
воды и земли). Последующее усовершенствование этих курсов при-
привело к появлению в III в. до н. э. в Александрии знаменитой книги
Евклида с тем же названием (в русском переводе «Начала»), вы-
вытеснившей книгу Гиппократа и остальные ее обработки. Существен-
Существенную роль в создании «Начал» Евклида сыграло создание в IV в.
до н. э. Платоном и особенно Аристотелем теории доказа-
доказательств, а также разработка ими общих принципов дедуктивного
построения науки (т. е. построения науки с помощью выводов, дока-
доказательств). Or латинского названия «Начал» Евклида (Elementa) про-
происходит термин элементарная геометрия, относящийся к сово-
совокупности геометрических результатов, изложенных у Евклида или
получаемых аналогичными методами.
«Начала» Евклида состоят из 13 «книг», из которых I—VI книги
посвящены планиметрии, VII—X книги посвящены арифметике и
несоизмеримым величинам, которые можно построить с помощью
циркуля и линейки, XI—XIII книги посвящены стереометрии. I книга
начинается с изложения 23 определений и 10 аксиом, причем пер-
первые пять из этих аксиом называются «общими понятиями», а осталь-
остальные— «постулатами»; дальнейшие определения содержатся во введе-
введениях к другим книгам.
Несмотря на то, что сочинения предшественников Евклида до
нас не дошли, мы можем составить некоторое представление об этих
сочинениях по «Началам» Евклида: в ««Началах» Евклида имеются
разделы, логически весьма мало связанные с другими разделами;
появление их объясняется только тем, что они внесены по традиции
и копируют «Начала» предшественников Евклида. К таким разделам
относится прежде всего введение к I книге.
Введение к I книге «Начал» Евклида начинается с определения
точки: «Точка—это то, что не имеет частей». Такое определение,
нигде не применяющееся в основном тексте «Начал» Евклида, не-
несомненно фигурировало во всех предыдущих вариантах «Начал».
Смысл этого определения состоит в том, что точка есть неделимая
часть (атом) пространства. Такого представления еще не было у
Фалеса, оно появляется у Пифагора и Демокрита. Понятие о точке
у этих двух мыслителей имеет существенно различный характер:
у Пифагора, идеалиста и мистика, пытающегося объяснить все за-
закономерности мира с помощью числовых соотношений, точки не имеют

14 АКСИОМЫ И ОСНОВНЫЕ ПОНЯТИЯ TFOMETPHH
размеров, а имеют только положение в пространстве; Пифагор
отождествлял точки с числовыми единицами и, в соответствии со
своей философской системой, с душами неродившихся или умерших
людей. У материалиста Демокрита, творца атомистической теории в
физике, точки, напротив, подобно атомам материи, имели конечные,
хотя и «сверхчувственно малые» размеры. Но оба ученых считали,
что в конечном теле имеется конечное, хотя и очень большое число
точек. Измерение площадей и объемов сводилось у Пифагора и Де-
Демокрита к подсчету числа точек в фигуре. Эта точка зрения привела
• • • • пифагорейцев к изучению «фи-
# # # • • • • ГУРНЫХ чисел» — «прямоуголь-
## ••• •••• ных>:>> «квадратных», «треуголь-
«треугольных», «многоугольных» «теле-
I л о 1й сных», «кубических», «пирами-
КВодротные числа дальных» и т д., т. е. чисел
точек, расположенных в виде,
# соответственно, треугольников,
• • • квадратов и других фигур
• • • • • • (рис. 1). «Прямоугольные чи-
в •• ••• •••• ела» — это числа, которые могут
12 6 Ю быть представлены в виде про-
Треугольные числа изведения двух целых множи-
Рис. 1 телей, больших единицы; «те-
«телесные числа» — произведения
трех множителей; «квадратные» и «кубические числа» мы и теперь
называем квадратами и кубами. Суммируя свои конечные атомы в
различных плоских фигурах и телах, Демокрит нашел формулы для
площади круга, объема пирамиды, конуса и шара с помощью свое-
своеобразного приближенного интегрирования.
Следующие определения Евклида: «линия—длина без ширины»,
«поверхность—длина и ширина без глубины» — также восходят к ато-
атомистическим представлениям; линия, которую Пифагор и Демокрит
представляли как цепочку точек, считалась делимой в ее на-
направлении, но неделимой «по ширине», так же как поверхность
считалась делимой в двух направлениях, но неделимой «по глу-
глубине».
Вгсьма древними являются, по-видимому, и определения прямой
линии и плоскости у Евклида: «прямая линия — такая, которая оди-
одинаково расположена по отношению ко всем своим точкам», «плоская
поверхность—такая, которая одинаково расположена по отношению
ко всем прямым линиям на ней». Далее приводятся определения
угла, многоугольника, треугольника и четырехугольника и их видов,
круга и его частей, параллельных линий. Параллельные прямые
определялись как прямые, лежащие в одной плоскости и не пересе-
пересекающиеся между собой.

«НАЧ АЛЛ» ЕВКЛИДА 15
2.2. «Постулаты» Евклида. «Постулаты» Евклида но существу
представляют собой правила построений с помощью идеальной ли-
линейки и идеального циркуля. Первые два постулата «всякие две
точки можно соединить прямой линией» и «ограниченную прямую
линию можно неограниченно продолжать» определяют действия с по-
«иощью идеальной линейки. Третий постулат «из всякого центра вся-
всяким радиусом можно описать окружность» определяют действия с
помощью идеального циркуля'). Четвертый постулат «все прямые
углы равны между собой» является излишним; как было замечено
впоследствии, его нетрудно вывести из остальных аксиом. Послед-
Последний постулат Евклида, его знаменитый V постулат, гласил: «Если
прямая падает на две прямые и образует внутренние односторонние
углы в сумме меньше двух прямых, то при неограниченном продол-
продолжении этих двух прямых они пересекутся с той стороны, где углы
меньше двух прямых».
При формулировке этих постулатов мы встречаемся с равенством
двух углов и со случаем, когда сумма двух углов меньше третьего.
Эти соотношения определяются «общими понятиями» Евклида, по
существу представляющими собой принципы измерения длин, углов,
площадей и объемов. Их также пять: «равные одному и тому же
равны между собой», «если к равным прибавить равные, суммы равны
между собой», «если от равных отнять равные, остатки равны между
собой», «совмещающиеся друг с другом равны между собой», «целое
больше части». Четвертое из этих «общих понятий» дает критерий
равенства прямолинейных отрезков и углов (мы видели, что этот
. критерий равенства применялся еще Фалесом), а также достаточное,
хотя и не необходимое условие равенства площадей более сложных
фигур, т. е. в применении к площадям эту четвертую аксиому сле-
следует понимать так: «совмещающиеся друг с другом фигуры равны
между собой (по площади)». Равенство площадей многоугольников
различной формы доказывалось с помощью присоединения к четвер-
четвертому «общему понятию» первых трех *). Пятое «общее понятие»
вместе с предыдущими дает критерий того, что одна фигура больше
другой; например, чтобы установить, что сумма двух углов больше
третьего, надо убедиться, что третий угол можно наложить на часть
угла, составленного из двух первых углов.
Евклид понимал под решением задачи только построение с по-
помощью идеального циркуля и идеальной линейки. В частности, для
') Полный список «постулатов», на которых основано решение задач
на построение с помощью циркуля и линейки, читатель найдет в статье:
«О разрешимости задач на построение с помощью циркуля и линейки»,
стр. 208—209 настоящей книги ЭЭМ.
г) Полный список «постулатов», на которых основано вычисление пло-
площадей и изложение современного учения о площадях, читатель найдег
в начале статьи «О площадях и объемах» в кн. V ЭЭМ.

16 АКСИОМЫ И ОСНОВНЫЕ ПОНЯТИЯ ГЕОМЕТРИИ
Евклида найти площадь или объем означало построить циркулем и
линейкой квадрат или куб, равный данной фигуре, т. е., как гово-
говорят, произвести «квадратуру» или «кубатуру» этой фигуры. Так как
квадратура круга и кубатура круглых тел с помощью циркуля и
линейки не удавались (и, как впоследствии было доказано Линдема-
ном, невозможны), Евклид не рассматривал ни площади круга, ни
объемов круглых тел. Решение этих задач для многих плоских фигур
и тел было произведено (вскоре после Евклида) Архимедом при
помощи методов, восходящих к Демокриту.
«Начала» Евклида завершались построениями с помощью циркуля
и линейки ребер пяти правильных многогранников, вписанных в сферу
данного радиуса и исследованием полученных несоизмеримых величин.
2.3. Непрерывность у Евклида и его предшественников. Сле-
Следует отметить, что хотя первые определения Евклида и носят следы
атомистических представлений Пифагора и Демокрита, сам Евклид
не разделял этих представлений. Евклид считал, что, например, лю-
любой отрезок можно с помощью его идеальных инструментов делить
пополам неограниченное количество раз. Линии, поверхности и тела
Евклид считал непрерывными и, в частности, неоднократно пользо-
пользовался тем, что две прямые линии или окружности пересекаются,
когда две точки одной из этих линий лежат по разные стороны от
другой. Пифагор и Демокрит не владели понятием непрерывной
величины; для них линии, поверхности и тела были совокупностями
отдельных, дискретных точек. Аристотель определил непрерывную
величину как такую величину, что если разбить ее на две части,
эти части будут иметь общую границу (ср. в связи с этим текст
на стр. 31). У Евклида нет этого замечательного определения, так
как его определения, как мы отмечали, копируют старые, доаристо-
гелевские образцы. Но Евклид, несомненно, считает линии, поверх-
поверхности и тела непрерывными в смысле Аристотеля.
Определив непрерывную величину, Аристотель сделал вывод, что
если дискретную величину можно рассматривать как множество то-
точек, то непрерывную величину ни в коем случае нельзя рассматри-
рассматривать как множество неделимых элементов. Он, по-видимому, исходил
из того, что если точки, как он считал, не имеют размеров, то две
точки, непрерывно прилегающие друг к другу, сливаются в одну
точку и, значит, тоже не имеют размеров; то же происходит и с
тремя и с любым количеством точек, причем это утверждение, вер-
верное для конечного числа точек, Аристотель распространял на беско-
бесконечные множества точек. Поэтому Аристотель представлял себе
линии не как множества точек, как Пифагор и Демокрит, а только
как с места», где могут находиться точки. Отсюда и происходит
наш термин «геометрическое место точек», который мы применяем
к линиям или поверхностям, определенным теми или иными услови-
условиями: Аристотель и последующие математики не могли определить

«НАЧАЛА» ЕВКЛИДА 17
эти линии или поверхности как множества точек, связанных
данными условиями'). Евклид разделял точку зрения Аристотеля
о том, чго непрерывная величина не может состоять из неделимых.
Заметим, что если у Пифагора и Демокрита арифметика была
ели га с геометрией, Евклид всячески подчеркивает, что это прин-
принципиально различные науки и, например, изложив теорию пропорций
непрерывных величин в V книге, доказывает снова те же теоремы
дли целочисленных пропорций в VII книге.
2.4. Движения. Движение (жесткое перемещение фигур) и, в
частности, наложение, бывшее основным методом доказательства у
Фалеса, играет существенную роль и у Евклида. Мы уже видели,
что определение равенства фигур у Евклида основано на совмещении
фигур. Евклид постоянно производит перенос отрезков с помощью
циркуля, да и самое описывание прямых линий и окружностей с по-
помощью линейки и циркуля производится с помощью движения.
В XI книге «Начал» при определении сферы Евклид уже прямо
определяет сферу как результат вращения полуокружности вокруг
ишметра. Однако во всех случаях, когда Евклид может обойтись
бе.! использования движений, он так и поступает. Нет также у
Евклида ни определения общего движения, ни опречеленин враще-
вращения вокру| точки или вокруг оси.
Таким ибра.юм, мы видим, что для одних основных понятий гео-
геометрии — точки, линии, поверхности — Евклид воспроизводит тради-
традиционные определения, но существу, не применяющиеся, так как он
не разделял тех представлений, в связи с которыми возникли эти
определения; для других основных понятий геометрии, таких, как
непрерывность и движение, которыми он постоянно пользуется, он
вовсе не дает определений. Тем не менее в геометрии Евклида уже
имелись совершенно определенные понятия о точке, не имеющей
размеров, но имеющей определенное положение; о линии, являющейся
результатом движения точки и, в частности, о прямой линии и
окружности как о линиях, образуемых движением, производимым
с помощью идеальной линейки или идеального циркуля; наконец,
о поверхностях, получающихся в результате движения линий, и,
в частности, о поверхностях вращения, получающихся в результате
вращения линий.
') Эти ошибочные представления Аристотеля и возникший в связи с
ними бессодержательный термин «геометрическое место точек» до сих пор
лежат тяжелым грузом на методике преподавания математики. В действи-
действительности понятие «геометрическое место точек» полностью совпадает
с понятием «множества точек» (обладающих тем или иным свойством): лю-
любое множество точек является одновременно и «геометрическим местом
точек» (а именно геометрическим местом точек, обладающих свойством
принадлежать этому множеству). См. в связи с этим § 4 статьи «Общие
принципы геометрических построений», стр. 182—183 этой книги ЭЭМ.
2 Энциклопедия, кн. 4

18 ЛкСИОМЫ И ОСНОВНЫЕ ПОНЯТИЯ TROMFTPHH
§ 3. Появление аксиоматического метода
3.1. Создание неевклидовой геометрии. Дальнейшее развитие
геометрии пошли ни пути критики Евклида. Одни математики кри-
критиковали Евклида за то, что он ограничивался рассмотрением только
таких геометрических величин, которые можно построить с помощью
циркуля и линейкн, и поэтому не решал многих арактически важных
задач, как, например, определение площади круга и объемов круг-
круглых тел. Эти пробелы Евклида, как мы знаем, были восполнены
Архимедом. Другие математики критиковали Евклида за то, чго он
разрмвал геометрию и арифметику и понапрасну шказывал для целых
чисел снова то, что он уже доказал раньше для геометрических
величин. Третьи подвергали критике аксиомы Евклида, т. е. его
«постулаты» и «общие понятия» и предлагали исключить некоторые
аксиомы или, наоборот, добавить новые. Особенно большие споры
вызвал наиболее сложный и наименее наглядный постулат Евклида —
его V постулат. Многие математики считали, что этот постулат
является лишним и его можно и непременно нужно доказать как
теорему с помощью остальных аксиом. Другие считали, что следует
заменить постулат Евклида более простым и наглядным постулатом.
Одним из таких более простых постулатов, равносильных V посту-
постулату, является следующий: «Через точку вне прямой можно провести
в их плоскости не более одной прямой, не пересекающей даннук>
прямую».
Критика Евклида, продолжавшаяся свыше двух тысяч лет, при-
привела к двум важнейшим открытиям. Критика того разрыва между
геометрией и арифметикой, который имелся у Евклида, привела
к расширению понятия числа до действительного числа, которым
теперь можно было характеризовать не только отношения соизмери-
соизмеримых геометрических величин, но и отношения несоизмеримых вели-
величин. Действительное число можно непрерывно изменять, вследствие
чего введение действительных чисел в математику было равносиль-
равносильным введению в математику переменных величин. Этот величайший
переворот в математике, связанный в первую очередь с именем Рене
Декарта (XVII в.), непосредственно привел к открытию диффе-
дифференциального и интегрального исчислений, являющихся математиче-
математическим аппаратом механики и классической физики.
Споры по вопросу о V постулате привели к тому, что в начале
XIX века Н. И. Лобачевский, Я. Бойяи и К. Ф. Гаусс
построили новую геометрию1), в которой выполняются все аксиомы
геометрии Евклида, за исключением V постулата, заменяющегося
противоположным утверждением: «В плоскости через точку вне пря-
прямой можно провести более одной прямой, не пересекающей данную.
') См. статью о неевклидовых геометриях в кн. V ЭЭМ.

ПОЯВЛЕНИЕ АКСИОМАТИЧЕСКОГО МЕТОДА 19
прямую».Эта геометрии оказалась столь же непротиворечивой, как
и геометрия Евклида. Открытие неевклидовой геометрии опровергло
мнение многих ученых, уверенных в том, что геометрия Евклида
является единственной мыслимой геометрией, чуть ли не заложен-
заложенной в нашем сознании до всякого знакомства с внешним миром.
Появление новой геометрии поставило вопрос о том, какая геометрия
имеет место в реальном мире: геометрия Евклида или геометрия
Лобачевского. То бесспорное обстоятельство, что геометрия Евклида
является отражением реального мира, не решает вопроса, так как
отражение всегда является лишь приблизительным: так, например,
эксперименты на малых участках земной поверхности согласуются с
предположением о том, что поверхность Земли является плоско-
плоскостью, и нужны эксперименты на больших участках, чтобы доказать,
что более правильно представлять себе эту поверхность сферой.
Аналогично этому, и геометрия Лобачевского в малых участках
почти не отличается от геометрии Евклида, и отличие между ними
проявляется только в больших участках пространства; поэтому сра-
сразу вслед за созданием геометрии Лобачевского возник вопрос о
естественно-научных экспериментах в больших областях реального
пространства, которые уточнили бы геометрическое строение мира,
в котором мы живем1).
3.2. Аксиоматический метод в математике. Если концепция
Декарта привела к переходу от математики постоянных величин
к математике переменных величин, то открытие Лобачевского привело
к переходу от математики постоянных отношений (например, взаимо-
взаимоотношений между точками, прямыми и плоскостями в геометрии
Евклида) к математике переменных отношений; например, эти отно-
отношения могут быть заменены взаимоотношениями между точками,
прямыми и плоскостями другой геометрии — геометрии Лобачевского.
За геометрией Лобачевского возникли и другие непротиворечивые
геометрии. Затем аналогичное изменение привычных отношений стало
производиться и в других математических дисциплинах; например,
наряду с обычной алгеброй появилось много новых алгебр. Возник
целый ряд совершенно новых математических систем, не имеющих
аналогов в классической математике, причем некоторые из этих
систем были использованы в качестве математического аппарата раз-
различных областей' современной физики.
К этим крупнейшим математическим открытиям ученые пришли,
распространяя критику, которой Лобачевский, Бойяи и Гаусс под-
подвергли одну из аксиом Евклида, V постулат, на всю систему аксиом
') Впоследствии, уже в XX веке, вопрос о геометрических свойствах
реального мира привел к появлению теории относительности Эйн-
Эйнштейна, коренным образом ломающей привычные геометрические пред-
представления.
2*

20 АКСИОМЫ II ОСНОВНЫЙ ПОНЯТИЯ ГЕОМКГРИИ
евклидовой геометрии, i .затем, переноси метод научного изло-
изложения с помощью аксиом на другие математические дисциплины.
В результате сложился ют аксиоматический метод в мате-
математике, который ныне является подлинной основой как геометрии, так
и других разделов современной математики.
Для того чтобы понять сущность аксиоматического метода, обра-
обратимся снова к геометрии. До открытия Лобачевского, когда было
распространено мнение о том, что геометрия Евклида — единственно
мыслимая геометрия, считалось, что эта геометрия описывает реаль-
реальное, физическое пространство точно. Поэтому можно было пы-
пытаться определять основные геометрические понятия, указывая реаль-
реальные прообразы этих понятий. Именно так и поступал Евклид и,
по-видимому, его предшественники, начиная с Пифагора и Демокрита.
Правда, мы видели, что представления о точках, линиях, поверхностях
и их взаимоотношениях были совершенно различными у разных уче-
ученых, и даже в одно и то же определение «точка — то, что не имеет
частей», разные ученые вкладывали различный смысл; мы видели
также, что система определений и аксиом Евклида, воспроизводив-
воспроизводившая традиционные образцы, не отражала представлений самого Евк-
Евклида и не охватывала важнейших понятий, которыми он пользовался.
Но после появления геометрии Лобачевского стало ясно, что путь,
которым шел Евклид в своих определениях основных понятий, и
принципиально невозможен. Если мыслимых геометрий много, то
в каждой геометрии должны быть свои основные понятия и поэтому
нельзя дать единые общие определении основных понятий. Иначе
говоря, определения основных понятий должны зависеть от аксиом
геометрической системы. Определения основных понятий той или иной
геометрической системы должны относиться только к данной гео-
геометрической системе и не должны претендовать на определение
основных понятий физического пространства, которое только с раз-
различной степенью точности отражается различными схемами геометри-
геометрических пространств.
Так как единое определение основных понятий для всевозможных
геометрий дать невозможно, то основные понятия геометрии следует
определить как объекты любой природы, удовлетворяющие аксио-
аксиомам этой геометрии. Только такое определение основных поня гий геомет-
геометрии соответствует абстрактному характеру этих понятий. В этом слу-
случае говорят, что геометрическая система определяется системой аксиом.
Таким образом, при аксиоматическом построении некоторой гео-
геометрической системы (или вообще при аксиоматическом построении
некоторой математической теории) мы исходим из некоторой системы
аксиом, или, как говорят, аксиоматики. В этих аксиомах описываются
свойства основных понятий рассматриваемой геометрической системы,
и мы можем представлять себе основные понятия в виде объектов
iiooifi природы, обладающих указанными в аксиомах свойствами.

МОДЕЛИ 21
Относительно самих згих основных понятий (вроде геометрических
понятий «точка», .'.прямая линия» и др.) можно сказать, что они
косвенно определяются аксиомами. Это — пример дескриптив-
дескриптивного определения математического объекта, т. е. определения объекта
описанием его свойств. Никакие другие определения этих основных
понятий геометрической системы невозможны. Из аксиом мы выводим
первые теоремы, из аксиом и уже доказанных теорем выводим вес
новые теоремы, которые и составляют здание рассматриваемой гео-
геометрической системы. Следовательно, аксиомы — это первоначаль-
первоначальные предложения, об основных понятиях геометрии, которые
принимаются в данной геометрической системе без доказатель-
доказательства и на основе которых доказываются все теоремы рассма-
рассматриваемой геометрической системы. Такую же роль играют акси-
аксиомы и в любой другой математической теории.
Евклид и его предшественники примерно гак и понимали роль
аксиом. Поскольку доказательство всякой теоремы геометрии пред-
представляет собой вывод ее из некоторых цругнх (как правило, более
простых) предложений, в результате многовекового развития геомет-
геометрии выкристаллизовались первоначальные предложения, на основании
которых доказывались остальные георемы. Эти первоначальные пред-
предложения («основные понятия» и «постулаты» у Евклида) и были
приняты за аксиомы. Из сказанного ясно, что аксиомы геометрии
имеют сны гное происхождение, г. е. отражают некоторые простые
свойства реального пространства. Из сказанного ясно также, что
в процессе исторического развития геометрии за аксиомы были при-
приняты сравнительно простые, наглядно ясные предложения. Однако
не следует считать, что аксиома — это простая истина, не требующая
аоказательс гва в силу своей очевидности. «Очевидность»—это по-
понятие, чуждое аксиоматическому методу; простота же аксиом—это
результат исторического развития науки и вопрос удобства. К тому
же некоторые теоремы могут показаться «проще» некоторых аксиом.
Например, V постулат Евклида, несомненно «сложнее» для понимания,
чем некоторые перные теоремы геометрии.
§ 4. Модели
4.1. Модели евклидовой плоскости. Предположим, что некото-
некоторая геометрическая система (скажем, геометрия Евклида) задана
с помощью аксиоматики (г. е. системы аксиом). Объекты, удовлетво-
удовлетворяющие аксиомам такой геометрической системы, допускают различ-
различные конкретные истолкования; эти истолкования называются интер-
интерпретациями или моделями рассматриваемой геометрической системы.
Приведем некоторые простые примеры интерпретаций. Предполо-
Предположим, что мы уже имеем некоторую интерпретацию геометрии Евклида,
например понимаем под геометрией Евклица то, что мы узнаем о ней

22
АКСИОМЫ И ОСНОВНЫЕ ПОНЯТИЯ ГЕОМЕТРИИ
в школе. С помощью этой интерпретации мы сейчас построим другие
интерпретации евклидовой геометрии.
Пусть г — некоторый отрезок. Условимся называть «точкой» вся-
всякий шар радиуса г, «прямой» — всякий бесконечный круговой цилиндр
радиуса г и «плоскостью» — всякую полосу толщины 2г, т. е. часть
пространства, заключенную между двумя параллельными плоскостями,
отстоящими друг от друга на расстоянии 2г. Будем, далее, говорить,
что «точка» лежит на «прямой», если соответствующий шар целиком
заключается в цилиндре. Расстоянием между двумя «точками» будем
называть расстояние между цент-
центрами соответствующих шаров.
Очевидным образом можно опре-
аелить теперь «углы», «отрезки»,
(.треугольники», и т. д. Легко
понять, что мы получаем таким
образом новую интерпретацию
евклидовой геометрии: все акси-
аксиомы (а значит, и теоремы) оста-
остаются в этой интерпретации спра-
справедливыми. Например, через
любые две различные «точки»
можно провести «прямую» и при-
притом только одну (рис. 2).
Другую интерпретацию евкли-
евклидовой геометрии1) мы получим с
помощью так называемой стерео-
стереографической проекции. Мы огра-
ограничимся случаем геометрии на плоскости. Пусть П — некоторая
плоскость и 5 — не пересекающая ее сфера. Обозначим через Л'
наиболее удаленную от плоскости П точку сферы S. Если теперь
А—произвольная точка плоскости П, то мы обозначим через А' ту
точку сферы S, в которой отрезок AN пересекает сферу S (рис. 3).
Переход от точек А, В, плоскости П к соответствующим точкам
А', В', ... сферы S и называется стереографической проекцией. При
стереографической проекции плоскость П переходит в множество II',
которое получается, если из сферы S удалить («выколоть») точку N.
Если теперь /— некоторая прямая на плоскости IL то при стерео-
стереографической проекции она переходит в проходящую через точку ./V
окружность /' (из которой удалена точка N). Действительно, если
точка А пробегает прямую /, то все отрезки AN лежат в одной
плоскости (рис. 4), которая в пересечении со сферой S и определяет
окружность /'.
Рис. 2.
") Еще две модели, связанные с начертательной геометрией, читатель
найдет в статье «Методы изображений> (см. стр. 228—290 этой книги ЭЭМ).

молкли
23
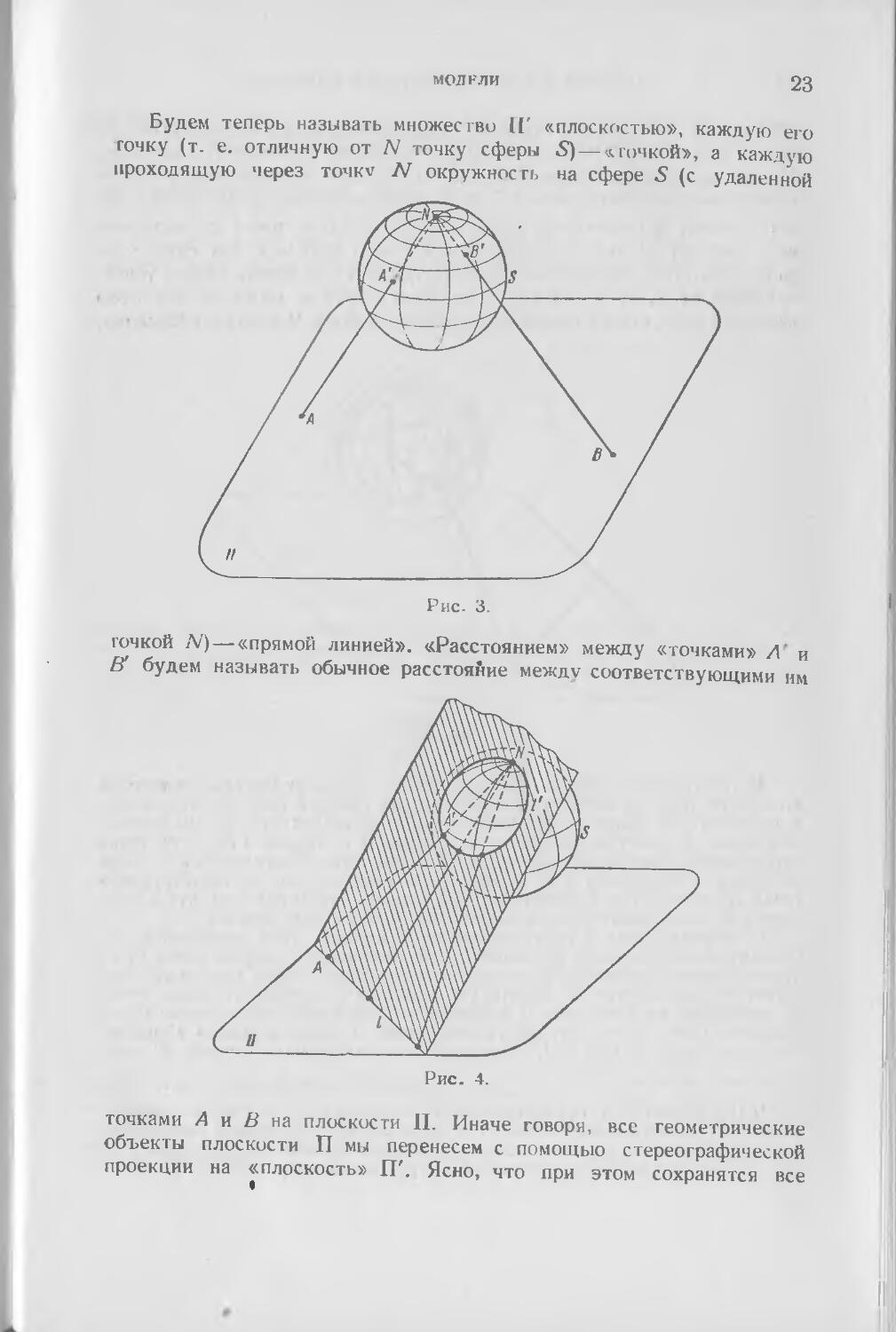
Будем теперь называть множество ГГ «плоскостью», каждую его
точку (т. е. отличную от N точку сферы S) — «точкой», а каждую
проходящую через to4kv ./V окружность на сфере 5 (с удаленной
Рис. 3.
точкой N) — «прямой линией». «Расстоянием» между «точками» /Г и
В будем называть обычное расстояние между соответствующими им
Рис. 4.
точками А и В на плоскости П. Иначе говоря, все геометрические
объекты плоскости П мы перенесем с помощью стереографической
проекции на «плоскость» ГГ. Ясно, что при этом сохранятся все
I

24 АКСИОМЫ И ОСНОВНЫЕ ПОНЯТИЯ ГЕОМЕТРИИ
аксиомы и теоремы евклидовой геометрии, т. е. «плоскость» И'
представляет собой модель (или интерпретацию) евклидовой плоскости.
Можно доказать, что в этой интерпретации «угол» между двумя
пересекающимися «прямыми» /' и /' равен обычному углу между ка-
касательными, проведенными к окружностям 1\ и 1г в точке их пересече-
пересечения (рис. 5). Далее, две «прямые» в том и только в том случае па-
параллельны, если изображающие их окружности не имеют общих точек,
отличных от N, т. е. касаются друг друга в точке N. Из этого
наглядно ясно, что на нашей модели выполняется V постула г Евклида.
Рис. 5.
Из построенной модели легко получить еще одну модель евклидовой
плоскости. Именно, обозначим через Я точку сферы S (рис. 6), ближайшую
к плоскости П. Далее, для любой «точки» А' «плоскости» П' мы обозна-
обозначим через А" точку пересечения плоскости П с прямой РА'. Эта точка
пересечения однозначно определяется, если точка А' отлична от Я. Если
же точка А' совпадает с Я, то мы будем считать, что соответствующая
точка А" «находится в бесконечность», считая таким образом, что к пло-
¦ кости П присоединена одна «бесконечно удаленная» точка1)-
Обозначим через О точку пересечения прямой NP с плоскостью Л.
Обозначим, далее, через П" плоскость П, из которой удалена точка О, но
присоединена «бесконечно удаленная» точка. Далее, когда «точка» А' про-
пробегает на «плоскости» П' некоторую «прямую» /', соответствующая точка
А" описывает на плоскости П некоторую проходящую через точку О <к-
ружность (рис. 6), из которой удалена точка О. Если «прямая» /' прохо-
проходит через точку Я (рис. 7), то окружность, описываемая точкой А", пре-
') Получающийся образ (плоскость с присоединенной к i.ей «беско-
«бесконечно удаленной» точкой) называется расширенной или круговой плоскостью;
она рассматривается в статье «Геометрические преобразования» (см. стр.
57—59 этой книги ЭЭМ) и в статье «Окружности» (стр. 448—517).

МО1КЛ11
вращается r прямую линию, проходящую через точку О (рис. 7; из этой
прямой удалена точка О. но присоединена «бесконечно удаленная»
точка).
Из сказанного ясно, что мы получаем следующею интерпретацию евкли-
евклидовой плоскости. Будем называть «плоскостью» множество П", все его точки
Рис. 6.
(включая «бесконечно удаленную») — «точками», а «прямыми» будем назы-
пать все окружности, проходящие через точку О (из которых удалена точ-
точка О, а также все прямые, проходящие через О (из этих прямых удаляется
Рис. 7.
точке! О, но присоединяется «бесконечно удаленная» течка). На рис. 8
токазаны «прямые» в этой модели. Можно доказать, что в этой модели
«угол» мевду двумя пересекающимися «прямыми» равен обычному углу
между касательными, проведенными к окрхжностям в точке их пересече-
пересечения (рис. 9). Далее, «прямые» в том и только в том случае «параллельны»,

26
АКСИОМЫ И ОСНОВНЫЕ ПОНЯТИЯ ГЕОМЕТРИИ
если изображающие их окружности касаются ь точке О (рис. 10).
Из этого наглядно ясно, что на рассматриваемой модели выполняется
V постулат. Справедливы на этой модели также и другие аксиомы
Рис. 8.
Рис.
и теоремы евклидовой планиметрии. Например, сумма «углов» любого «тре-
«треугольника» (рис. 11) равна 1й (что можно доказать и непосредственно).
Читатель, знакомый с преобразованием, называемым инверсией'), может
легко понять, как связаны между собой модель П" и плоскость П. Инверсия
с центром в точке О переводит прямые линии плоскости П в окружности,
проходящие через точку О, т. е. в «пря-
«прямые на модели П". Этим и устанавли-
устанавливается связь между указанными двумя
моделями.
Рис. 10.
Рнс. И.
Еще две модели евклидовой плоскости можно получить с использова-
использованием комплексных чисел.
Очевидно, что все аксиомы и теоремы евклидовой геометрии на пло-
плоскости выполняются, если считать «точками» комплексные числа («точки
*) См. в этой книге ЭЭМ статьи «Геометрические преобразования»,
стр. 56—59, 74—75, и «Окружности», стр. 468—474.

модели 27
плоскости комплексного переменного»), «прямыми» — множества комплекс-
комплексных чисел вида z=zo + lt, где г0 и /—фиксированные комплексные числа,
a t—действительный параметр (lj=G), а «расстояние» между «точками»,
изображаемыми комплексными числами г и w, положить равным |г—хю\.
Нетрудно проверить также, что все аксиомы и теоремы планиметрии Евклида
выполняются на «плоскости комплексного переменного», расширенной введе-
введением «комплексного числа» со (бесконечность), если считать «точками» все
комплексные числа, кроме числа 0 (но включая «число» оо), а «прямыми» —
все окружности и прямые плоскости комплексного переменного, проходя-
проходящие через точку О. Например, через всякие две «точки» Л и В проходит
единственная «прямая»: если А и В—обычные точки, то эта «прямая» —
окружность, проходящая через точки Л, В и О, а если точка В—беско-
В—бесконечно удаленная, то эта «прямая» — обычная прямая, соединяющая точки
О к А. «Расстояние» между «точками», изображаемыми комплексными чи-
числами г и w, в этом случае равно
существу совпадающая с описанной выше моделью П") получается из
обычной плоскости комплексного переменного, если заменить каждое
комплексное число г числом —.
г
1 11^
. Очевидно, что эта модель (по
г w \
4.2. Аксиоматические системы в алгебре. С примерами аксио-
аксиоматик и их интерпретаций мы встречаемся не только в геометрии,
но и в других разделах математики. В тех областях математики, где
рассматриваются алгебраические операции, одним из важнейших по-
понятий является понятие «группы». Группой называется система объ-
объектов любой природы, называемых «элементами группы», в которой с
каждыми двумя элементами а, Ь, взятыми в определенном порядке, со-
сопоставлен некоторый элемент с = ab, называемый их произведением.
При этом предполагаются выполненными следующие аксиомы:
1°. Операция умножения подчиняется ассоциативному закону, т. е.
a(bc) = (ab)c для любых трех элементов с, Ь, с.
2°. Для любых элементов а, b уравнения ах=Ь, уа = Ь разре-
разрешимы, т. е. существуют такие элементы cud, что ас=Ь и da=b
(закон обратимости).
Таким образом, каждая конкретная группа является интерпрета-
интерпретацией (или моделью) для этой аксиоматики. Группа называется
коммутативной, если выполнена следующая дополнительная
аксиома:
3°. Умножение коммутативно, т.е. ab=ba для любых двух эле-
элементов а, Ь.
В коммутативной группе операцию часто называют не умноже-
умножением, а сложением (т. е. вместо ab пишут а-{-Ь).
Примером группы может служить множество всех целых чисел.
Другими примерами являются: множество всех действительных чисел,
множество всех комплексных чисел, множество всех векторов *). Все
*) См. в этой книге ЭЭМ статью «Векторы и их применения в геомет-
геометрии».

28 лкспоми и основные понятия геометрии
¦) i и группы комму тативны (операции сложение). Дру rue примеры групп,
j также простейшие теоремы о группах (выводимые из перечислен-
перечисленных выше аксиом) читатель может найти в кн. I ЭЭМ (стр. 100—108).
Рациональные, действительные и комплексные числа дают нам
пример более сложной алгебраической системы, — поля. В поле со вся-
всякими двумя элементами а и Ь. взя гыми в опре пленном порядке, сопо-
сопоставлены два элемента с=а-\-Ь и d = ab той же системы, причем
удовлетворяются следующие аксиомы (см. ЭЭМ, кн. I, стр. 113 —120):
1°. Элементы системы образуют коммутативную группу, если
групповой операцией считать сложение.
2°. Элементы системы без нуля ') образуют коммутативную группу,
если групповой операцией считать умножение.
3°. Сложение и умножение элементов связаны дистрибутивным
юконом: a(b-f-с) = ab + ас.
Аксиомы поля также чоиускают большие число самых разно-
разнообразных интерпретаций.
В первых томах настоящего издания читатель может найти и
ряд других аксиоматик: аксиомы натуральных чисел (ЭЭМ, кн. I,
стр. 133 —135), аксиомы метрического пространства (ЭЭМ, кн. III,
стр. 266) и др.
§ 5. Непротиворечивость и полнота аксиоматики
5.1. Непротиворечивость аксиоматики. При рассмотрении аксио-
аксиоматики весьма важным вопросом является выяснение ее непротиворечи-
непротиворечивости. Поясним, что под этим понимается. Пусть мы имеем некоторую
систему аксиом, например аксиомы группы. Из этих аксиом мы можем
ныводить все новые и новые теоремы. Если при этом могут быть
получены две теоремы, противоречащие тру г другу, то аксиоматика
называется противоречивой. Разумеется, аксиоматика только в том
случае может быть положена в основу некоторой содержательной
математической теории, если она не является противоречивой. Воз-
Возникает естественный вопрос: каким образом можно убедиться в том,
что некоторая аксиоматика непротиворечива? Например, является ли
непротиворечивой аксиоматика группы? Тот факт, что аксиомы группы
сформулированы много десятилетий назад и до сих пор не обнару-
обнаружено противоречий, конечно, не может нас убедить в непротиворе-
непротиворечивости этой аксиоматики—-кто знает, может быть такие противоре-
противоречия будут обнаружены через несколько лет! Иначе говоря, сколько
бы мы ни развивали теорию на основе выбранной аксиоматики, мы,
строго говоря, никогда не можем до конца быть уверенными в том,
что выбранная аксиоматика непротиворечива. Внутри самой теории
') Напомним, что нулем коммутативной . руппы называется гакои эле-
элемент 0, что а4-0 = о для любого элемента а.

НЕПРОТИВОРЕЧИВОСТЬ И ПОЛНОТА АКСИОМАТИКИ 29
обнаружить отсутствие в ней «внутренних противоречий» невозможно
(строгое доказательство этого утверждения было дано не так давно
видным американским логиком Куртом Гёделем)
Однако существует прием, позволяющий до некоторой степени
судить о непротиворечивости аксиоматики. Этот прием заключается
в следующем. Предположим, что в нашем распоряжении имеется
некоторая математическая теория — назовем ее «теория Л», — в истин-
истинности которой мы не сомневаемся. Предположим далее, что нам за-
задана некоторая аксиоматика, на основе которой мы должны построить
другую математическую теорию—«теорию ?>». Ясно, что если ми
сможем, пользуясь понятиями, имеющимися в -теории Л>\ построить
некоторую модель, в которой выполняются все заданные аксиомы,
лежащие в основе /.теории Бу>, то тем самым непротиворечивость
лежащей в основе «теории ?>» аксиоматики будет установлена.
Иначе говоря, если мы условимся считать «теорию Л» «истинной»
и если, пользуясь «материалом» «теории А», мы смажем по-
построить модель (интерпретацию) для аксиоматики «теории />»,
то непротиворечивость этой аксиоматики будет тем самым
установлена.
Выше (стр. 19) мы говорили о том, что геометрия Лобачевского «столь
же непротиворечива, как и геометрия Евклида». Какой смысл имеет
это утверждение? Оказывается, что, пользуясь «материалом» геометрии
Евклида, можно построить модель геометрии Лобачевского (впервые
такая модель была построена итальянским геометром Э. Бельтрами
и немецким математиком Ф. Клейном уже после смерти самого
Лобачевского), и наоборот, пользуясь «материалом» геометрии Лоба-
Лобачевского, можно построить модель геометрии Евклида (такая модель
была построена Лобачевским). Следовательно, из непротиворечивости
одной из этих геометрий вытекает непротиворечивость второй, и
обратно').
Из сказанного видно, что непротиворечивость может иметь только
условный смысл: для доказательства непротиворечивости аксиоматики
мы должны построить модель, а для возможности построения модели
нужно иметь какой-то «строительный материал», т. е. нужно иметь
некоторую теорию, в истинности которой мы не сомневаемся. Наи-
Наиболее простой математической теорией является арифметика рацио-
рациональных') чисел (т. е. чисел целых и дробных, положительных и
*) См. статью о неевклидовых геометриях в кн. V ЭЭМ.
г) Непротиворечивость аксиоматики поля рациональных чисел сводится
к непротиворечивости аксиоматики натуральных чисел (так как каждое
т .
положительное рациональное число — изображается парои натуральных
чисел т, /г). Непротиворечивость системы аксиом натуральных чисел уже
нельзя доказать таким же образом. Впрочем, в этой непротиворечивости
нас достаточно убеждает многоьекивой опыт челоречества, постоянно поль-
пользующегося натуральными числами.

3U АКСИОМЫ И OCHUBHblt ПОНЯТИЯ ГЬОМЫ'РИИ
отрицательных). На «истинность» (т. е. непротиворечивость) этой тео-
теории мы будем безоговорочно ссылаться, и с ее помощью будем строить
модели других теорий. Итак, мы будем считать аксиоматику
непротиворечивой, если для нее можно построить модель, исходя
из арифметики рагщоналъных чисел.
Теперь ясно, например, что аксиоматика группы непротиворечива:
множество всех целых чисел представляет собой модель группы.
Другой моделью может служить множество всех рациональных чисел.
Непротиворечивой является и аксиоматика поля: моделью поля может
служить множество всех рациональных чисел.
5.2. Полнота системы аксиом. Весьма важным является и другое
свойство аксиоматики—свойство полноты. Для объяснения того,
чго такое полнота системы аксиом, нужно ввести понятие изомор-
изоморфизма двух моделей. Предположим, что задана некоторая аксиома-
гика, в которой указываются основные понятия и перечисляются их
свойства. Предположим далее, что для этой аксиоматики построены
две модели. Эти модели называются изоморфными, если между
элементами (т. е. основными понятиями) одной модели и элементами
другой модели можно установить такое взаимно однозначное соответ-
соответствие, при котором сохраняются фигурирующие в аксиомах основ-
основные отношения элементов. Например, множество всех целых чисел
и множество всех рациональных чисел представляют собой две мо-
модели группы. Эти модели не изоморфны между собой. Если же
мы возьмем группу всех целых чисел и группу всех целых чисел,
делящихся на 10 (операция — сложение), то эти группы оказы-
оказываются изоморфными между собой. Действительно, ставя в соот-
соответствие каждому числу п число 10 п, мы получаем взаимно одно-
однозначное соответствие между этими моделями, при котором сохраняют-
сохраняются фигурирующие в аксиомах группы отношения (т. е. сумма элементов
переходит в сумму). Изоморфными между собой являются также
приведенные в предыдущем параграфе модели евклидовой плоскости1).
Система аксиом называется полной, если всякие две ее интер-
интерпретации изоморфны между собой. Например, аксиоматика группы не
является полной (так как существуют не изоморфные между собой
группы). Не является полной также и аксиоматика поля.
В качестве примера полной системы аксиом мы приведем аксиома-
аксиоматику поля действит-льных чисел. Именно поле действительных чисел
можно определить как множество объектов любой природы, называемых
«числами» и удовлетворяющих следующим аксиомам:
1° (а к с и о м а поля). Во множестве определены операции сложе-
сложения и умножения чисел, по отношению к которым это множество
является полем.
2° (аксиома порядка). Для всяких двух различных чисел а
и Ь справедливо одно из двух отношений а>Ь, Ь>а, причем если а>Ь
О понятии изоформизма см. также ЭЭМ, кн. I., стр. 120—125.

НЕПРОТИВОРЕЧИВОСТЬ И ПОЛНОТА АКСИОМАТИКИ 31
и 6>с, то а>с (отношение *>» транзитивно), и если а>Ь. то
a~t-c>b-\-c при любом с, а при с>0 имеем aObc.
3° (аксиома непрерывности). Если tee числа разделены
на два класса таким образом, что всякое число II класса больше вся-
всякого числа I класса, то существует или такое число I класса, которое
больше всех остальных чисел этого класса, или такое число II класса,
что все остальные числа этого класса больше его.
Заметим, что приведенная нами аксиома непрерывности является
точной математической формулировкой определения непрерывности
Аристотеля (см. § 1); однако, вопреки запрету Аристотеля, непрерывное
поле действительных чисел состоит из неделимых элементов — чисел,
составляющих бесконечное множество. Аксиома непрерывности в этой
формулировке была предложен.-. Р. Дедекиндом.
Можно было бы доказать, что аксиома Дедекинда может быть заме-
заменена (при наличии первых двух аксиом) аксиомой Архимеда (ЭЭМ,
кн. I, стр. 131) и аксиомой полноты (ЭЭМ. ки. I, стр. 198). Аксиома
непрерывности (в любой форме) делает возможным построение теории
пределов, изучение непрерывных функций и т. д.
Непротиворечивость аксиом поля действительных чисел можно
было бы доказать с помощью модели этого поля, построенной из «мате-
«материала» поля рациональных чисел. Обычно это делается с помощью сече-
сечений в поле рациональных чисел. Мы не будем проводить здесь это
построение, отсылая читателя к курсам математического анализа.
Отметим, что аксиоматика поля действительных чисел является пол-
полной: всякие две модели поля действительных чисел изоморфны между
собой. Именно, всякую модель поля действительных чисел можно поста-
поставить во взаимно однозначное соответствие, например, с бесконечными
десятичными дробями, причем при этом соответствии сохраняются ариф-
арифметические действия, отношение «>» (отношение «больше») и непрерывность.
В самом деле, в произвольной модели поля действительных чисел опре-
определены числа 0 и 1. С помощью сложения мы можем определить все нату-
натуральные числа, а числа, противоположные натуральным, представят со-
собой отрицательные целью числа; определенные нами целые числа попарно
различны. Рассмотрим тепгрь произвольное число х из рассматриваемой
модели. Если число х совпадает с целым числом я0, то мы поставим в
соответствие числу х бесконечную десятичную дробь (я0—1),999 . . . Если
же число х не является целым, то в силу аксиомы 2° и аксиомы Архи-
Архимеда (вытекающей из аксиомы 3°) найдется такое целое число я0, что
/го+1>л:>яо. Далее, деля 1 на 10, мы получим число -= и с помощью
,1 ,2 , 9 с
сложения построим числа «o + Tri' ni> + 77i> ••"о+тя- Если число х не
совпадает ии с одним из этих чисел, то в силу аксиомы 2° найдется такое
._ , л, + 1 я, _,
натуральное число я,<10, что п0 + -^~->х>п0 + -А. Продолжая таким
образом, мы получим, что наше число х либо совпадет с некоторой
конечной десятичной дробью п„, л, п2. . . пк—тогда поставим в соответ-
соответствие числу х бесконечную десятичную дробь
¦¦¦ я*_.(л*-1)999 ....
бесконечная ^сятичная
-1 (ПАТ 1)>*>Я0,И,Л2. . ¦Пь_1Пк,
либо же существует такая бесконечная ^сятичная дробь пв, rt,nartj....,
что при любом k

32 АКСИОМЫ И ОСНОВНЫЕ ПОНЯ ГИЯ ГЕОМЕТРИИ
и этом случае i> силу аксиомы Зг число х должно быть поставлено в
соответствие указанной бесконечной десятичной дроби Это соответствие
устанаиливает изоморфизм рассматриваемой модели и модели, построенной
мз бесконечных десятичных дробен.
§ 6. Аксиоматика геометрии
6.1. Основные понятия геометрии Евклида. Теперь мы можем
дать точное определение «пространству Евклида», т. е. той матема-
математической схемы, которая является отражением реального, физич*_
ского пространства и по существу была разработана в «Началах»
Евклида.
Дать определение пространства Евклиди—это значит, как мы
теперь знаем, дать систему его аксиом, т. е. основных предложе-
предложений, которые справедливы в геометрии Евклида и из которых можно
логически вывести все остальные предложения этой геометрии.
Система этих аксиом должна быть непротиворечивой и полной (т. с
все модели, на которых выполняется эта система аксиом, должны
быть изоморфными между собой).
Пространство Евклида можно определить как совокупность объек-
объектов трех родов, называемых «точками», «прямыми» и «плоскостями».
и преобразований, переводящих совокупность всех точек в себя,
называемых «движениями»; между этими объектами определены со-
соотношения «точка лежит на прямой» (или «прямая проходит через
точку»), «точка лежит на плоскости», «прямая лежит на плоскости»,
«точка лежит между двумя другими точками», причем указанные
объекты и соотношения удовлетворяют перечисленным ниже аксио-
аксиомам. Одновременно с изложением аксиоматики мы будем формули-
формулировать некоторые новые понятия и доказывать простые теоремы —
без этого изложение аксиоматики было бы затруднительным
6.2. Аксиомы принадлежности.
1°. Через каждые две различные точки проходит прямая и
притом только одна.
2°. На каждой прямой, имеются по крайней мере две точки.
3°. Существуют три точки, не лежащие на одной прямой.
4°. Через каждые три точки, не лежащие на одной прямой,
проходит плоскость и притом только одна.
5°. На каждой плоскости имеется по крайней мере одна
точка.
6°. Если две точки лежат на плоскости, то и проходящая
через них прямая лежит на этой плоскости.
7°. Если две плоскости имеют общую точку, они имеют по
крайней мере еще одну общую точку.
8° Существуют четыре точки, не лежащие на одной пло-
плоскости.

АКСИОМАТИКА ГЕОМЕТРИИ 33
В дальнейшем прямая, проходящая через точки А и В, назы-
называется прямой АВ, а плоскость, проходящая через точки 4, В и С,
называется плоскостью ABC.
Из сформулированных аксиом уже вытекают некоторые первые
георемы геометрии. Приведем пример.
Теорема 1. На каждой плоскости можно найти три точки,
не лежащие на одной прямой.
Доказательство. Пусть а — некоторая плоскость и А — ле-
лежащая в этой плоскости точка (аксиома 5°). Пусть, далее, М, N,
Р—три точки, не лежащие на одной прямой (аксиома 3°). Так как
все точки М, N, Р различны, го среди них найдется точка, отлич-
отличная от А. Пусть, например, М=^А. Так как точки М, N, Р не
лежат на одной прямой, то хотя бы одна из точек N, Р не лежит
на прямой МА. Пусть, например, точка N не лежит на прямой МА.
Тогда точки А, М, N не лежат на одной прямой. Действительно,
если бы А, М, N лежали на одной прямой, то этой прямой явля-
являлась бы прямая МА (в силу аксиомы 1°); но точка N не лежит на
этой прямой.
Так как точки А, М, N не лежат на одной прямой, то в силу
аксиомы 4° через них проходит (единственная) плоскость. Если
плоскость AMN совпадает с а, то гем самым в плоскости а найдены
гри точки А, М, N, не лежащие на одной прямой. Если же пло-
плоскость AMN не совпадает с а, го эти плоскости имеют отличную
от А общую точку В (аксиома 7°). Таким образом, в плоскости а
существуют две различные точки А, В.
Пусть теперь Т, U, V, W—четыре точки, не лежащие в одной
плоскости (аксиома 8°). Среди них обязательно найдется точка,
не лежащая на прямой АВ. Действительно, если бы точки Г, (J,
V, W лежали на прямой А В, то все они лежали бы в плоскости а
(аксиома 6°), чего не может быть. Пусть Т не лежит на прямой А В.
Тогда три точки А, В, Т лежат в одной плоскости. Среди точек
U, V, W хотя бы одна не лежит в плоскости АВТ (иначе Т, U, V,
W лежали бы в одной плоскости АВТ). Пусть, например, LJ не лежит
в плоскости АВТ. Тогда точки А, В, Т, U не лежат в одной пло-
плоскости. Действительно, если бы А, В, Т, U лежали в одной плоско-
плоскости, то этой плоскостью могла бы быть только плоскость АВТ
[в силу аксиомы 4°); но точка U не лежит в плоскости АВТ.
Заметим еще, что точки Д, 7", U не лежат на одной прямой.
Действительно, если бы точки А, Т, U лежали на одной прямой,
го эта прямая совпадала бы с прямой AT (аксиома 1°), и потому
точка U льжлла бы в плоскости АВТ (аксиома 6°), что места не
имеет.
Так как точки А, Т, U не лежат на одной прямой, то через них
проходит плоскость (аксиома 4°). Плоскость ATU не может совпа-
совпадать с плоскостью а, так как иначе все четыре точки А. В, 1, U
3 энциклопедии, кн. 4

34 АКСИОМЫ И ОСНОВНЫЕ ПОНЯТИЯ ГЕОМЕТРИИ
лежали бы в одной плоскости а. В силу аксиомы 7° плоскости а
и ATU имеют общую точку, отличную от А. Обозначим эту общую
точку через С. Таким образом, точки А, В, С лежат в плоскости а.
Покажем, что эти точки не лежат на одной прямой. В самом деле,
если бы точки А, В, С лежали на одной прямой, то эта
прямая совпадала бы с АС (аксиома 1°), и потому в силу аксиомы
6° лежала бы в плоскости ATU (ибо эта плоскость содержит точки А
и С), т. е. точка В лежала бы в плоскости ATU. Но это противо-
противоречит тому, что точки А, В, Т, U не лежат в одной плоскости.
Полученное противоречие доказывает, что точки А, В, С не лежат
на одной прямой.
6.3. Аксиомы порядка.
9°. Из любых трех различных точек прямой одна и только
одна лежит между двумя другими.
10°. Для всяких двух точек прямой существует на этой пря-
прямой такая третья точка, что вторая точка лежит между
первой и третьей.
Прежде чем сформулировать третью аксиому порядка (аксиома 11°)
мы введем понятие отрезка. Именно, если А и В—две различные
точки, то отрезком с концами А и В (или, коротко, отрезком АВ)
называется множество, состоящее из точек А, В и всех точек пря-
прямой АВ, расположенных между А и В.
11°. Если прямая Л лежащая в плоскости ABC, не проходит
ни через одну из точек А, В, Си содержит одну точку отрезка
AB. то она имеет общую точку хотя бы с одним из отрезков
AC, ВС.
Эта аксиома называется аксиомой Паша—по имени немецкого
ученого, впервые сформулировавшего эту аксиому.
Пользуясь аксиомами порядка, можно доказать некоторые даль-
дальнейшие теоремы.
Теорема 2. Для всяких двух различных точек А, В суще-
существует точка, лежащая между ними.
Доказательство. Пусть С—точка, не лежащая на прямой
АВ (такая существует в силу аксиомы 3°). В силу аксиомы 10°
существует на прямой АС такая точка D. что С лежит между А
и D. Точка D не совпадает с В, так как иначе две различные пря-
прямые АВ, АС имели две общие точки А, В, что невозможно (аксиома 1°).
В силу аксиомы 10е существует на прямой BD такая точка Е, чтоб
лежит между D и Е. Прямая СЕ не проходит ни через одну из
точек А, В, D. (Если бы, например, прямая СЕ проходила через А,
то она совпадала бы с прямой АС; следовательно, точки А, С, D, Е
лежали бы на одной прямой; на этой же прямой DE лежала бы и
точка В, т. е. точки А, В, С лежали бы на одной прямой, что
невозможно.) Так как прямая СЕ имеет с отрезком AD общую
точку С, то она имеет общую точку с одним из отрезков АВ, BD

АКСИОМАТИКА ГЕОМЕТРИИ 35
(аксиома 11°). Так как точка В лежит между Г) и Е, то точка Е
не лежит на отрезке BD (аксиома 9°). Если мы допустим, что пря-
прямая СЕ имеет сбшую точку F с отрезком BD, то F=^=E (ибо Е не
лежит на отрезке BD), и потому прямые СЕ и BD имеют две общие
точки Е, F. Но тогда прямые CF и BD совпадают (аксиома 1°), что
невозможно. Итак, прямая СЕ не может иметь общие точки с отрез-
отрезком BD, и потому в силу сказанного выше она должна иметь общую
точку И с отрезком АВ. Эта точка И отлична от А и В (так как
прямая СЕ не проходит через точки А, В). Таким образом, на
отрезке АВ существует точка И, отличная от А и В, т. е. сущест-
существует точка Н, лежащая между А и В.
Из приведенных доказательств теорем 1 и 2 ясно видно, что
собой представляют доказательства с помощью аксиом. Эти доказа-
доказательства не нуждаются в пояснительном чертеже и не предполагают,
что мы представляем себе некоторую модель геометрии Евклида.
Это и понятно, ведь в аксиомах перечисляется все, что мы должны
знать об основных понятиях геометрии. Ясно также, что перечень
аксиом у Евклида является далеко не полным (помимо того, что
смысл его первых определений весьма туманный): Евклид существенно
пользовался чертежом при доказательствах, и такое предложение,
как аксиома 11°, для него было очевидным (прямая, входящая
в треугольник через одну его сторону, должна выйти из тре-
треугольника через вторую или третью сторону). Таким образом,
хотя у Евклида имеются начала аксиоматического метода, но при дока-
затечьствах Евклид неявно пользуется «очевидными» свойствами,
не перечисленными в его аксиомах.
Имея в виду, что читатель ясно представил себе характер дока-
доказательств, проводимых на основании аксиом, мы ие будем утруждать
его дальнейшими доказательствами, а ограничимся формулировками
теорем, которые можно доказать с помощью аксиом 1°—11° и уже
доказанных теорем 1 и 2.
Теорема 3. Если прямая I, лежащая в плоскости ABC, не
проходит ни через одну из точек А, В, С, то хотя бы с одним
из отрезков АВ, ВС, АС она не имеет общих точек.
Теорема 4. Любые п различных точек прямой можно так
занумеровать числами 1, 2, 3, ..., п, что если i<Cj<Ck (или
i>y>/j), то j-я точка лежит между i-u и k-h точками.
Для того чтобы сформулировать теорему 5, определим луч. Пусть
О и А — две различные точки. Лучом О А мы будем называть мно-
множество, состоящее из всех точек М прямой ОА, для которых О не
лежит между А и М (точки О и А также принадлежат лучу ОА).
Теорема 5. Всякая точка О, взятая на прямой I, разби-
разбивает эту прямую на два луча. Более подробно: существуют
на прямой I такие точки А .и В, что лучи ОА и ОВ имеют

36 АКСИОМЫ И ОСНОВНЫЕ ПОНЯТИЯ ГЕОМЕТРИИ
единственную общую точку О, а взятые вместе составляют
всю прямую I.
Определим теперь понятие полуплоскости. Пусть /—прямая,
расположенная на плоскости а, и А— точка плоскости а, не лежащая
на прямой /. Полуплоскостью 1А мы будем называть множество,
состоящее из всех точек прямой /, точки А и всех тех точек М плос-
плоскости а, для которых отрезок AM не имеет общих точек с прямой /.
Теорема 6. Всякая прямая i, лежащая на плоскости а,
разбивает эту плоскость на две полуплоскости. Более подробно:
существуют на плоскости а такие точки А и В (не лежащие
на прямой I), что полуплоскости 1А и 1В составляют, вместе
взятые, всю плоскость а, и имеют своим пересечением прямую I
(т. е. точка N в том и только в том случае принадлежит
обеим плоскостям 1А, 1В, если оно лежит на прямой I).
Совершенно аналогично определяется полупространство и уста-
устанавливается, что всякая плоскость ргч;бивает пространство (т. е.
множество всех вообще точек) на два полупространства.
Наконец, введем еще понятие репера (от французского слова
герёге — метка, ориентир), необходимое для формулировки следую-
следующих аксиом. Пусть О — произвольная точка, / — проходящая через
нее прямая и а — плоскость, содержащая прямую /. Выберем один
из двух лучей, определяемых на прямой / точкой О (теорема 5);
обозначим его через /'. Выберем, далее, одну из двух полуплоскос-
полуплоскостей, определяемых на плоскости а прямой / (теорема 6); обозначим
ее через и'. Наконец, выберем одно из двух полупространств, опре-
определяемых плоскостью а; его обозначим через Г". Совокупность
(О, /', а'. Г') мы и будем называть репером.
Легко видеть, что задание упорядоченной четверки точек
(О, А, В, С), не лежащих в одной плоскости, определяет однозначно
некоторый репер. Именно, обозначим через / прямую ОА, а через /' —
луч ОА. Далее обозначим через а плоскость ОАВ, а через а'—полу-
а'—полуплоскость 1В. Наконец, через Г' обозначим го из двух полупрост-
полупространств, определяемых плоскостью а, которое содержит точку С.
Полученный репер (О, /', а', Г') мы будем называть репером, опре-
определяемым упорядоченной четверкой точек (О, А, В, С).
6.4. Аксиомы движения ')•
12°. Всякое движение является взаимно однозначным отобра-
отображением пространства на себя. Более подробно: если f—про-
f—произвольное движение, то любые различные точки переводятся
движением / в различные точки (т. е. если А^=В, то f(A)=^=
zjbf(B)); кроме того, для любой точки М найдется такая точка N,
что f{N) = М.
') О роли движений в геометрии см также статью «Геометрические
преобразования» в этой книге ЭЭМ (стр. 98 и след).

АКСИОМАТИКА TFOMFTPHH 37
13° Пусть f—произвольное движение. Гогда, если точки А,
В, С расположены на одной прямой, причем С лежит между А
и В, то точки /(A), f(B), /(С) также расположены на одной
прямой, причем точка f(Q лежит между /(А) и f[B).
С помощью этих аксиом доказываются следующие теоремы:
Теорема 7. Если /—произвольное движение и А, В, С, D —
четыре произвольные точки, то точки /(А), /(В), /(С), f(D)
в том и только в том случае лежат в одной плоскости, если
точки А, В, С, D лежат в одной плоскости.
Теорема 8. Если f—произвольное движение и А, В, С — три
точки, не лежащие на одной прямой, то точки /{А), /(В), /(С)
не лежат на одной прялюй.
Теорема 9. При всяком движении прямая переходит в пря-
прямую, плоскость — в плоскость, луч — в луч, полуплоскость — в
полуплоскость, полупространство — в полупространство и, сле-
следовательно, репер переходит в репер.
Теперь мы сформулируем еще две аксиомы.
14°. Два движения, произведенные одно за другим, равносильны
некоторому одному движению.
15°. Для всяких двух реперов, взятых в определенном порядке,
существует одно и только одно движение, переводящее первый
репер во второй.
Рассмотрение движений позволяет говорить о «равенстве» гео-
геометрических фигур: две фигуры равны, если одну из них можно
перевести в другую с помощью некоторого движения. Таким обра-
образом, мы получаем возможность говорить о равных отрезках, равных
треугольниках и т. д.
6.5. Аксиомы непрерывности.
16° (аксиома Архимеда). Пусть Ао, Ах, В — три точки.,
лежащие на одной прямой, причем точка At находится между
Ао и В. Пусть, далее, /—движение, переводящее точку At в Аг
и луч А0В—в луч AJB. Положим
Тогда существует такое натуральное число п, что точка В
находится на отрезке Ап_1Ап.
17° (аксиома Кантора). Пусть Ах, Ах, ... и Вх, Вг, ...—
такие две последовательности точек, расположенных на одной
прямой I, что для любого п точки Ап и Вп различны между
собой и находятся на отрезке А„-1Вп_1. Тогда на прямой I су-
существует такая точка С, которая находится на отрезке АпВп
при всех значениях п.
Аксиома 16° (вместе с перечисленными ранее аксиомами) позво-
позволяет доказать следующую важную теорему:

38 АКСИОМЫ И ОСНОВНЫЕ ПОНИ ГИН ГЕОМЕТРИИ
Теорема 10. Пусть MN—произвольный отрезок и О А— про-
произвольный луч. Тогда на луче ОА существует одна и только одна
точка Р, обладающая тем свойством, что отрезок MN равен
отрезку ОР.
Эта теорема позволяет «откладывать» отрезки. Кроме того, она
позволяет ввести понятия «больше» и «меньше» для отрезков, при-
причем для любых двух отрезков АВ и CD выполнено одно и только
одно из соотношений
AB<CD, AB= CD, AB>CD.
Следующую теорему мы назовем теоремой Дедекинда.
Ввиду ее важности мы приведем не только формулировку, но и до-
доказательство этой теоремы.
Теорема 11. Если все точки прямой I разбиты на два (непус-
(непустые) класса таким образом, что между двумя точками одного
и того же класса не лежит ни одной точки другого класса, то
существует точка и притом единственная, принадлежащая лю-
любому отрезку, концы которого принадлежат разным классам.
Доказательство. Пусть Ах и В,—две точки прямой /, при-
принадлежащие разным классам; класс, содержащий точку А,, обозначим
символом 1, а класс, содержащий точку В,— символом II. Пусть С—
произвольная точка, лежащая между Ах и В, (теорема 2). Отложим
на луче В1А1 отрезок BXD, равный отрезку АХС (теорема 10). Так
как АХС<САХВХ, то и BXD<AXBX, и потому точка D лежит на отрез-
отрезке АХВХ. Возможны три случая: точка С совпадает с D, точка С
лежит между Ах и D, точка D лежит между Ах и С. В первом слу-
случае АХС = СВХ, т. е. отрезок АХС два раза откладывается на
отрезке АХВХ. Во втором случае мы имеем: АХС= DBX<CBX, и потому
отрезок АХС не менее чем два раза откладывается на отрезке АХВХ.
В третьем случае отрезок AtD не менее чем два раза откладывается
иа отрезке АХВХ. Итак, в любом случае существует такой отрезок,
который не менее чем два раза откладывается на отрезке АХВХ.
Выберем такой отрезок и будем откладывать на луче АХВЛ от
точки Ах отрезки АХМХ, МхМг, M2Mt, ..., равные этому отрезку. В
силу аксиомы 16° найдется такое число k, что точка Вх лежит на
отрезке Mk_xMk, т. е.
АЛМХ = МхМг = МгМг = ... = Mk_,Mk_, ^ Mk_ XBX.
Каждый из отрезков АХМХ, МХМ2, ..., Mk_tMk_x, а тем более
«остаток» ЖА_,В, откладывается на отрезке АХВХ не менее чем
два раза.
Из условия теоремы легко вытекает, что в последовательности
точек /4,, At,, Ms, ..., Mk_x, ВЛ несколько первых (подряд) принад-
принадлежат классу I, а остальные — классу 11. Пусть, например, точка М{

АКСИОМАТИКА ГЕОМЕТРИИ 39
лежит в классе 1, а точка Mi+l—в классе II; тогда мы обозначим
точку М; через Л2, а точку Mi+i — через В2. (Если точка Ж, при-
принадлежит классу II, то за Ах мы примем точку Л,, а за Вг — точку
Ж,; аналогично, если точка Mk_1 принадлежит классу I, то за Аг
мы примем точку Afft_,, а за В2— точку Ву.)
Итак, мы получили такие две точки А2, В2, лежащие на отрезке
АХВХ, что точка Аг принадлежит классу I, точка В2 принадлежит
классу II и отрезок А2В2 откладывается на отрезке Й,В, не менее
чем 2 раза.
Исходя из точек А2, Вг, мы аналогичным образом сможем по-
построить такие две точки Аг, Bs, лежащие на отрезке АгВ2, что
точка Аг принадлежит классу I, точка Вг принадлежит классу II
и отрезок A2BZ откладывается на отрезке А2В2 не менее чем 2 раза.
Следовательно, отрезок АгВа откладывается на отрезке AxBt не менее
чем 4 раза, т. е. более чем 3 раза.
Продолжая это построение, мы найдем такие точки Ах, Аг, ...
..., Вх, Вг, ...,что при любом п точка Ап принадлежит классу 1,
точка Вп принадлежит классу II; кроме того, точки Ап и Вп распо-
расположены на отрезке Ап_хВп_х, и отрезок АпВп откладывается на от-
отрезке А^ВЛ не менее чем л раз.
В силу аксиомы 17" существует такая точка С, которая принад-
принадлежит отрезку АпВп при любом л. Мы докажем, что точка С является
искомой. Прежде всего докажем, что для любой отличной от С
точки D, взятой на прямой /, найдется такое л, для которого отре-
отрезок АпВп не содержит точки D (а значит, при т^п отрезок АтВт
не содержит точки D). Для этого обозначим через п такое нату-
натуральное число, что отрезок CD откладывается менее п раз на отрезке
AiBI (т. е. при откладывании на отрезке AtB^ отрезков АХРХ =РхРг -=
= Р2Рг= ..., равных отрезку CD, мы получим, что точка В, лежит
между Ал и Рп; существование такого п вытекает из аксиомы 16°).
Если бы теперь отрезок АпВп содержал точку D, то (так как этот
отрезок содержит и точку С) мы получили бы CD<AnBn, и потому
отрезок АпВп не мог бы п раз откладываться на отрезке /4,В,, а это
противоречит выбору точек Ап и Вп. Полученное противоречие пока-
показывает, что точка D не принадлежит отрезку АпВп.
Пусть теперь М — произвольная, отличная от С точка класса 1,
а N — произвольная, отличная от С точка класса II. Выберем на-
настолько большое число л, что ни одна из точек М, N не содержится
на отрезке АпВп. Точка М не расположена между Ап и Вп в силу
выбора числа л. Точка Вп не расположена между Ап и М, так как
обе точки Ап, М принадлежат классу I, а точка Вп — классу 11.
Следовательно, точка Ап расположена между М и Вп (см. аксиому 9°).
Аналогично, точка Вп расположена между Ап и N. Из этого следует,
что обе точки АП, Вп расположены на отрезке МЛ/, и потому точка С
лежит на отрезке MN (см. теорему 4), т. е. С лежит между М и Л'.

40 АКСИОМЫ И ОСНОВНЫЕ ПОНЯТИЯ ГЕОМЕТРИИ
Итак, если М и N — отличные от С точки, принадлежащие раз-
различным классам, то С лежит между М и N. Покажем, наконец, что
С— единственная точка, обладающая этим свойством. Пусть D— точка,
отличная от С. Пусть, далее, М—произвольная точка, лежащая
между Л и С, а N—точка, лежащая не в том классе, в котором
лежит точка М. Так как точка М лежит между D и С, то отрезок
MN не может содержать обе точки С, D. Точку С этот отрезок
содержит (ибо М и N принадлежат различным классам); следова-
следовательно, отрезок MN не содержит точки D: Таким образом, точка D
не обладает указанным свойством.
Итак, существует одна и только одна точка С, обладающая
тем свойством, что всякий отрезок, концы которого принадлежат различ-
различным классам, содержит точку С. Отсюда и вытекает справедливость
теоремы.
Теорему 11 иногда принимают за аксиому вместо аксиом Архи-
Архимеда и Кантора, которые в этом случае выводятся из этой аксиомы
как теоремы; в этом случае эту аксиому называют аксиомой Деде-
кинда, так как она по существу совпадает с предложенной Дедекин-
дом аксиомой непрерывности поля действительных чисел (см. стр. 31).
6.6. Аксиома параллельности.
18е. Через точку А, не лежащую на прямой I, можно прове-
провести в их плоскости не более одной прямой, не пересекающей
прямую I.
Две прямые, лежащие в одной плоскости и не имеющие общих
точек, условимся называть параллельными. С помощью других аксиом
доказывается
Теорема 12. Через точку А, не лежащую на прямой I, всегда
можно провести хотя бы одну прямую, параллельную I.
Поэтому из аксиомы параллельности следует, что через точку,
не лежащую на прямой, можно провести единственную прямую,
параллельную этой прямой.
Аксиома параллельности уже встречалась нам в § 3 как аксиома,
эквивалентная V постулату Евклида.
Аксиомой параллельности и завершается список аксиом евклидо-
евклидовой геометрии. С помощью этих аксиом и сформулированных выше
теорем можно теперь доказывать все теоремы евклидовой геометрии:
признаки равенства треугольников (угол определяется как совокуп-
совокупность двух лучей, исходящих из одной точки), соотношения между
сторонами и углами в треугольнике, теорему о сумме углов тре-
треугольника и т. д., и т. д. Доказательства будут по существу те же,
что и в школьном курсе геометрии, но более последовательно прове-
проведенные (так как школьные доказательства используют не только
аксиомы и указанные выше теоремы, но и нередко 'используют ссылки
на чертеж).

НЕПРОТИВОРЕЧИВОСТЬ И ПОЛНОТА АКСИОМАТИКИ ЕВКЛИДОВОЙ ГЕОМЕТРИИ 41
Изложенная система аксиом пространства Евклида представляет
собой модификацию системы аксиом, предложенной в конце XIX века
немецким математиком Д. Гильбертом. Система Гильберта, за
исключением некоторых частностей, отличается от изложенной сис-
системы тем, что вместо понятия «движение» Гильберт считает основным
понятием «конгруэнтность» («равенство»), т. е. то, что с нашей точки
зрения можно определить как совместимость с помощью движения, а
аксиому Кантора Гильберт формулировал как «аксиому полноты», в
силу которой к пространству нельзя добавить новые точки, так чтобы
продолжали выполняться все аксиомы. Аксиомы движения были пред-
предложены в начале XX века Ф. Шуром.
Таким образом, в изложенной нами системе аксиом основными
понятиями геометрии являются точка, прямая, плоскость и движение,
которые не определяются, но взаимоотношения между которыми
выясняются из аксиом. Возможны и другие системы аксиом простран-
пространства Евклида, в которых за основные понятия принимаются другие
объекты; так, у Гильберта вместо понятия «движение» неопреде-
неопределяемым считалось понятие «конгруэнтности»; в аксиоматике извест-
известного русского геометра В. Ф. Кагана за основу бралось понятие
«расстояния» и т. д. Пример одной из аксиоматик евклидовой геомет-
геометрии, отличной от изложенной здесь, приведен в статье о векторах
в этой книге ЭЭМ (стр. 369 — 370). Разумеется, различные аксиома-
аксиоматики евклидовой геометрии эквивалентны друг другу, т. е., исходя
из одной аксиоматики, можно доказать аксиомы другой аксиома-
гики, как теоремы, и наоборот.
Отметим в заключение, что вычеркивая в приведенном выше
списке аксиом аксиомы 4°—8°, относящиеся к пространству, мы по-
получим систему аксиом евклидовой плоскости (при этом в некоторых
аксиомах надо произвести очевидные изменения; например, следует
изменить понятие «репера», выбросив из него полупространство).
§ 7. Непротиворечивость и полнота аксиоматики
евклидовой геометрии
7.1. Арифметическая модель геометрии Евклида. Теперь, когда
мы имеем полный список аксиом геометрии, можно поставить вопрос
о непротиворечивости геометрии Евклида и о полноте приведенной
аксиоматики. Для доказательства непротиворечивости мы должны
средствами арифметики (ничего другого у нас пока нет) построить
модель евклидовой геометрии; для доказательства полноты следует
установить, что любые две модели евклидовой геометрии изоморфны.
И непротиворечивость, и полнота доказываются с помощью одного
и того же приема — построения системы координат. Для простоты
мы проведем эти построения не в пространстве, а только на евкли-
евклидовой плоскости, и притом очень схематично.

42 АКСИОМЫ И ОСНОВНЫЕ ПОНЯТИЯ ГЕОМЕТРИИ
Прежде всего мы установим взаимно однозначное соответствие
между точками прямой и действительными числами. Пусть О и Л,—
две различные точки прямой. Отложим на луче ОАХ отрезки AtAt,
A2At, ..., равные отрезку ОАХ. На втором луче, определяемом точ-
точкой О на прямой OAt (см. теорему 5) отложим отрезки ОВХ, ВхВг,
В2Вг, ..., равные отрезку ОАХ. Разделив теперь отрезок ОАХ на
10 равных частей1) точками О, С,, С2, , С„, Л,, мы сможем на
каждом из отрезков
...ВД, ВД. Bfi, ОА„ AtAt, Л,Л,... (*)
отложить десять отрезков, равных ОСХ. Затем можно каждую деся-
десятую часть разделить еще на 10 частей и т. д. Точке At- мы поста-
поставим в соответствие целое число /( = 1, 2, ...); точке О поставим
в соответствие число 0, точке B-t поставим в соответствие число
— i(i=\, 2, . . .). Далее, точкам Сх, С2, ..., С9. делящим отрезок
ОА на 10 равных частей, мы поставим в соответствие числа
12 9
— , —. ... -rjr. Деля остальные отрезки (*) на 10 равных частей, мы
получим точки, соответствующие числам ^, где п—любое целое
число. Точно таким же образом мы можем построить точки, соответ-
соответствующие любым дробям вида —^.
Если теперь М— произвольная точка нашей прямой, то при
помощи аксиомы Архимеда мы можем найти такое целое число я,
что точка М находится на отрезке с концами в точках, соответ-
соответствующих числам п. и п-j- 1, но не совпадает с точкой, соответствую-
соответствующей числу я + 1. Затем мы можем найти такое число а, ( = 0,1, 2,..., 9),
что точка М находится на отрезке с концами в точках, соответ-
, а, , а, 4-1 „
ствующих числам « + тд и п~\~ Д . но не совладает с второй из
этих точек. Затем мы найдем такое число а2(=0,1, 2, ..., 9), что
точка М находится на отрезке с концами в точках, соответствующих
числам я + тк + гт! и И + Тп + ^Г - и т- д- Теперь точке М мы
поставим в соответствие действительное число п-f--± -\- r~t -\- -г^ -\- . ..
Построенное соответствие между точками прямой линии и дейст-
действительными числами является взаимно однозначным. Кроме того, оно
обладает следующими двумя важными свойствами: а) если х, у, z—
') Напомним, что для этого используется следующая теорема: если на
одной прямой отложены равные между собой отрезки и через их концы
проведены параллельные между собой прямые «до пересечения с другой
прямой, то на этой прямой при пересечении с параллельными также
образуются равные между cofofl отре-жи. Доказательство этой теоремы
проводится так же, как в школьных учебниках.

НЕПРОТИВОРЕЧИВОСТЬ И ПОЛНОТА АКСИОМАТИКИ ЕВКЛИДОВОЙ ГЕОМЕТРИИ 43
три действительные числа, удовлетворяющие неравенствам x<Zy<Zz
(или х>_у>г), а М, N, Р—точки, соответствующие числам х, у,
z, то точка N находится между М и Р; б) если х — х'=у—у', то
точки М, М', N, N', соответствующие числам х, х', у, у', обладают
тем свойством, что отрезок ММ' равен отрезку MV'. Из существо-
существования этого соответствия ясна аналогия между аксиомами порядка и
непрерывности поля действительных чисел и пространства Евклида.
Мы видим, что если Евклид понимал под «прямой линией» пря-
прямолинейный отрезок, для которого он требовал только возможности
неограниченного продолжения, здесь под «прямой» имеется в виду
сразу вся прямая; аналогично обстоит дело с понятием плоскости.
Введем теперь на плоскости систему координат, т. е. рассмотрим
две взаимно перпендикулярные прямые, пересекающиеся в точке О,
выберем из них равные отрезки ОА1 и ОА, и для каждой из этих пря-
прямых установим указанным выше способом взаимно однозначное соот-
соответствие между точками прямой и действительными числами. Введе-
Введение координатной системы позволяет обычным способом сопоставить
с каждой точкой плоскости пару чисел х, у—координат этой точки.
Таким путем устанавливается взаимно однозначное соответствие
между точками плоскости и парами (х, у) действительных чисел.
Точки, лежащие на одной прямой, удовлетворяют уравнению
первой степени
=0, (**)
в котором хотя бы один из коэффициентов А, В отличен от нуля.
Если три точки М, N, Р лежат на одной прямой, то точка М лежит
между N и Р в том и только в том случае, если она не совпадает
ни с одной из точек N, Р и координаты х этих точек связаны одним
из соотношений
XN^XM^XP ИЛИ XN^XM'^Xp
и аналогично для координат у. Наконец, каждое движение плоскости
изображается преобразованием вида
у' = агх + Ьгу + сг,
для которого векторы (alt аг) и (bv Ьг) являются единичными и
взаимно перпендикулярными (т. е. а\ -\- а\= 1, ^4-^2= 1 а1Ьх-\-агЬг=0).
7.2. Непротиворечивость и полнота аксиоматики евклидовой
плоскости. Изложенные факты позволяют доказать и непротиворечи-
непротиворечивость, и полноту аксиоматики геометрии. В самом деле, все аксиомы
евклидовой плоскости выполняются, как нетрудно проверить, на
арифметической модели, в которой точкой считается каждая пара
(х, у) действительных чисел, прямой называется множество всех
точек, удовлетворяющих некоторому уравнению вида (**), понятие

44 АКСИОМЫ И ОСНОВНЫЕ ПОНЯТИЯ ГЕОМЕТРИИ
«между» и движения определяются указанным выше способом. Мы
не будем проверять выполнение всех аксиом на арифметической мо-
модели. Укажем лишь для примера, что если (xlt ух) и (xt, yt)—две
различные точки, то существует единственная прямая, проходящая
через эти две точки, а именно прямая
(*—*,) (Л —Ух) —(У —Ух) (*• — *i) = 0.
(Заметим, что от умножения всех коэффициентов уравнения (**) на
одно и то же число прямая не меняется.) Этим проверяется аксио-
аксиома 1°. Весьма просто проверяю ich и остальные аксиомы.
Существование арифметической модели показывает непротиворе-
непротиворечивость аксиом евклидовой геометрии. Далее, рассуждения, прове-
проведенные в начале параграфа, доказывают, что любая модель евклидо-
евклидовой плоскости изоморфна арифметической модели (изоморфизм устанав-
устанавливается введением системы координат). Таким образом, любые две мо-
модели евклидовой плоскости изоморфны арифметической модели и потому
изоморфны между собой. Тем самым установлена полнота аксиоматики.
Отметим в заключение, что арифметическая модель простран-
пространства (а не плоское ги) Евклида строится аналогично, только точками
считаются тройки (х, у, z) действительных чисел.
§ 8. Независимость аксиом
8.1. Независимость системы аксиом. Открытие Лобачевского,
приведшее к развитию аксиоматического метода, непосредственно
связано с вопросом о независимости аксиом. Некоторая аксиома
считается независимой от остальных аксиом некоторой аксиоматики,
если ее нельзя доказать, как теорему, исходя из остальных аксиом.
При аксиоматическом построении любой математической теории
естественно стремиться к тому, чтобы среди аксиом не было «лиш-
«лишних», т. е. таких, которые могут быть выведены, как теоремы, из
остальных аксиом. Исторически одним из первых проявлений этого
стремления явилось исключение четвертого постулата Евклида
(о равенстве всех прямых углов, см. стр. 15) из числа аксиом. По-
Последовательное проведение этой точки зрения приводит в конце
концов к построению «минимальной» аксиоматики, т. е. такой, что
каждая из ее аксиом не зависит от остальных. Следует, однако,
иметь в виду, что требование независимости аксиоматики, совершенно
естественное логически и эстетически, совсем не играет сколько-ни-
сколько-нибудь существенной роли. Более того, с точки зрения удобства изло-
изложения аксиоматической теории часто бывает удобно принять за основу
заведомо избыточную аксиоматику, позволяющую проще и быстрее
получать необходимые следствия. *
Для доказательства независимости какой-нибудь аксиомы от
остальных достаточно построить новую систему аксиом, отличаю-

НЕЗАВИСИМОСТЬ АКСИОМ 45
»
щуюся от старой только заменой этой аксиомы на противоположную,
и доказать непротиворечивость полученной системы; непротиворечи-
непротиворечивость системы аксиом, как всегда, доказывается с помощью построе-
построения модели, в которой выполняются все аксиомы системы. Так,
например, аксиоматика группы (аксиомы 1° и 2° на стр. 27)
является независимой. Моделью, в которой выполняется аксиома 1°,
но не выполняется аксиома 2°, может служить, например, множество
всех целых чисел с обычной операцией умножения: уравнение
тх = п, где т и п—целые числа, не всегда имеет целочисленное
решение. Модель, в которой выполняется аксиома 2°, но не выпол-
выполняется аксиома 1°, можно построить, например, из трех элементов
a, h, с со следующей «таблицей умножения»:
aa = bb=cc = a, ab = bc=ca = b, ac = ba = cb = c.
Легко проверить, что в этой модели аксиома 2° действительно вы-
выполняется; например, уравнения
ax = b, уа = Ь
имеют решения х = Ь, у== с. В то же время аксиома 1° не выпол-
выполняется:
(bb) b = ab = b, b (bb) = ba = c.
8.2. О независимости аксиоматики евклидовой геометрии. Ра-
Разумеется, ввиду большого числа аксиом геометрии вопрос о'незави-
о'независимости приведенной выше аксиоматики геометрии весьма сложен.
Существование неевклидовой геометрии Лобачевского доказывает неза-
независимость аксиомы параллельности от остальных аксиом геометрии
Евклида. Системой аксиом геометрии Лобачевского и является та
система аксиом, которая получается из приведенной нами аксиоматики
геометрии Евклида заменой аксиомы 18° аксиомой Лобачевского:
«Через точку вне прямой можно провести в ее плоскости более
одной прямой, не пересекающей данную прямую». Непротиворечивость
геометрии Лобачевского доказывается с помощью моделей, наиболее
важные из которых были построены во второй половине XIX века
Э. Бельтрами, Ф. Клейном и А. Пуанкаре (см. статью о не
евклидовых геометриях в пятой книге ЭЭМ).
Аналогичным приемом можно доказать независимость аксиом не-
непрерывности. Независимость аксиомы Архимеда доказывается при
помощи построения «неархимедовой геометрии», моделью которой
может служить совокупность троек чисел (х, у, z), являющихся уже
не действительными, а комплексными числами, причем соотношение
«больше» в поле комплексных чисел устанавливается следующим
образом: число a-\-bi считается большим числа a'-f ft'i, если b>b',
или в случае, когда b = b', если а>а'. Поэтому, если в поле дей-
действительных чисел для всяких двух чисел а и Ь, из которых а>Ь,

46 АКСИОМЫ И ОСНОВНЫЕ ПОНЯТИЯ ГЕОМЕТРИИ
существует такое натуральное число п, что nb>a (это свойство
действительных чисел и обеспечивает выполнение аксиомы Архимеда
на прямой), то в поле комплексных чисел существуют такие числа
а и р, для которых а>р\ но не существует натурального числа п,
для которого имело бы место неравенство «р>а. Такими числами
являются, например, i и 1, так как при всех п произведение п-\
меньше i. Это свойство комплексных чисел и обеспечивает невыпол-
невыполнение аксиомы Архимеда на прямой в указанной модели неархимедо-
неархимедовой геометрии.
Независимость аксиомы Кантора доказывается при помощи «некан-
торовой геометрии», моделью которой является совокупность троек
чисел х, у, z, являющихся действительными числами, но не произ-
произвольными, а принадлежащими к полю, элементы которого получаются
из единицы применением конечного числа сложений, вычитаний,
умножений, делений и извлечений квадратного корня'). Поэтому,
если на прямой y = z = 0 заданы отрезки AxBv АгВ2, ..., удовлет-
удовлетворяющие условию аксиомы Кантора, причем значения х для точек
/4,, Bt, Аг, В2, ...—рациональные числа, стремящиеся при п—> оо
к действительному числу, не входящему в указанное поле, то точки С,
существование которой утверждается аксиомой Кантора, в этой мо-
модели не существует. По существу сам Евклид рассматривал не то,
что мы называем «пространством Евклида», а именно это неканторово
пространство (см. выше, текст на стр. 15—16).
Особую роль в аксиоматике геометрии играет аксиома 8°, содер-
содержание которой по существу сводится к утверждению, что простран-
пространство имеет три измерения. Независимость этой аксиомы от осталь-
остальных доказывается, например, построением модели четырехмерного
пространства Евклида. В статье «Многомерные пространства»
в книге V ЭЭМ читатель найдет описание и четырехмерного про-
пространства и пространств любого (конечного) числа измерений. В ма-
математике рассматриваются 'также «бесконечномерные» пространства.
Они играют весьма важную роль в современной математике и физике.
8.3. Заключение. Как мы видим, вопрос о независимости системы
аксиом евклидовой геометрии приводит к рассмотрению многих новых
«геометрических пространств», весьма сильно отличающихся по своим
свойствам от привычного нам пространства Евклида.
Весьмз интересно, например, «конечное пространство», которое
получается при замене поля действительных чисел конечным полем,
скажем, полем вычетов целых чисел но простому числу. В «конечном
пространстве» имеется лишь конечное число точек на каждой прямой,
на каждой плоскости и во всем пространстве, а также конечное число
прямых и плоскостей. «Конечные пространства» являются простейшими
') Эта модель тесно связана с геометрическими построениями. См.
в этой книге ЭЭМ статью: «О разрешимости задач на построение с по-
помощью циркуля и линейки», стр. 203—227.

ЛИТЕРАТУРА 47
примерами «дискретных пространств», в которых отсутствуют пре-
предельные точки и непрерывность.
Определенные таким образим абстрактные пространства, которые
можно строить самыми разнообразными способами, позволяют созда-
создавать такие пространственные схемы, с помощью которых мы получаем
возможность более точно отражать реальное, физическое простран-
пространство, чем с помощью схемы пространства Евклида. Кроме того, эти
абстрактные пространства широко применяются в математике,а через
нее имеют новые приложения к реальному миру.
Еще Лобачевский (а также и К. Ф. Гаусс) поставил задачу об экспе-
экспериментальной проверке того, какая геометрия действительно имеет
место в реальном мире: геометрия Евклида или Лобачевского. Как дока-
доказано в общей теории относительности, пространство (и время) реального
мира с весьма большим приближением выражается гак называемой рима-
новой геометрией, открытой в середине XIX века немецким математиком
Б. Р и м а н о м (см. статью о неевклидовых геометриях в книге V ЭЭМ).
Однако и эта пространственная схема является далеко не послед-
последним приближением. Многие физики считают, что целый ряд затруд-
затруднений и противоречий в математическом аппарате современной кван-
квантовой физики объясняется тем, что квантовые, дискретные явления
описываются в непрерывном пространстве, и для преодоления этих
затруднений следует перейти к дискретному, квантованному простран-
пространству. Тот факт, что непрерывное пространство вполне удовлетворяет
требованиям классической физики, нисколько не противоречит этому,
так же как требованиям классической гидродинамики и электродина-
электродинамики удовлетворяет представление о жидкости и электромагнитном
поле как о непрерывных средах, в то время как на самом деле
жидкость состоит из дискретных молекул, а электромагнитное ноле
состоит из дискретных квантов. Таким образом, вполне возможно,
что геометрия вернется к представлениям Демокрита о дискретных
атомах пространства, разумеется, не в столь наивной форме. В этом
случае примут существенно новый вид и основные поня!ия геометрии.
Мы видели, что представления об основных понятиях геометрии и их
взаимоотношениях неоднократно изменялись в ходе развития науки.
Новые научные открытия будущего, несомненно, приведут к даль-
дальнейшим изменениям и в наших геометрических представлениях.
ЛИТЕРАТУРА
[1] Д. Гильберт, Основания геометрии, перев. с нем., М.—Л., Гостех-
издат, 948
Классическое сочинение замечательного немецкого математика,
содержащее одно из первых аксиоматических построений геометрии,
а также тщательный логический анализ предложенной аксиоматики.
В русском издании перевод замечательной книги Гильберта сопровож-
сопровождается комментариями редактора П. К. Рашевского. заметно облег-
облегчающими чтение этого нелегкого сочинения, и содержательной вводной

48 аксиомы и основные понятия геометрии
статьей того же автора, в которой обсуждаются общие вопросы аксиома
тического построения геометрии и разбирается аксиоматика Гильберта
B| П- К. Рашевскпй, Геометрия и ее аксиоматика, Сборник «Матемп
тическое просвещение», вып. 5, М., Физматгиз, 1960, стр. 73—98.
Научно-популярная статья, близкая к вступительному очерку, пред-
предваряющему русское издание (Оснований геометрии» Д. Гильберт.
[3| В. Ф. Каган, Очерки по геометрии. М., Изд. Московского универ-
университета, 1963
Первый раздел этой книги замечательного ученого и популяризатора
математики целиком посвящен вопросам логического обоснования геомет-
геометрии. В конце книги содержится «Приложение», дающее представление
об оригинальной аксиоматике евклидовой геометрии, разработанной
автором.
|1| Н. В. Ефимов. Высшая геометрия, изд 4-е. М., Физматгиз. 1961.
Учебник для студентов университетов по курсу высшей геометрии,
нключающий учение об основаниях геометрии, проективную и неевкли-
неевклидову геометрии. Вопросам, примыкающим к рассматриваемым ь на-
настоящей статье, посвящены главы 1, II и IV книги.
15] В. И. Костин, Основания геометрии, М., Учпедгиз, 1948.
\ч\ Я. Л. Т р а й н и н, Основания геометрии, М., Учпедгиз, 1961.
Книги 5 и 6 представляют собой учебники для студентов педаго-
педагогических институтов по курсу оснований геометрии, включающие уче-
учение об аксиоматическом построении геометрии и элементы неевклидовой
геометрии Лобачевского.
[7] «Начала» Евклида, тт. 1—Ш, перев. с греч.. М., Гостехиздат,
1948—1950
Классическое сочинение, содержащее первый дошедший до нас опыт
дедуктивного построения геометрии.
Б. Л. ваь дер Варден, Пробуждающаяся наука, перев. с голланд..
Физматгиз, 1959.
Историко-математическое сочинение видного голландского матема-
математика, в котором, в частности, прослежено зарождение учения об осно-
основаниях геометрии в древнем мире.
См. также указанный в конце статьи «Геометрические построения»
учебник Д. И. Перепелкина, содержащий полный курс геометрии,
базирующийся на удачно выбранной, заведомо не независимой системе
аксиом.

ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
СОДЕРЖАНИЕ
§ 1. Понятие преобразования. Примеры 50
1.1. Геометрические отображения 50
1.2. Геометрические преобразования 52
1.3 Некоторые типы геометрических преобразований 60
§ 2. Применение преобразований к решению геометрических задач . 63
2.1. Некоторые примеры . ... 63
2.2. Применение симметрии 66
2.3: Использование геометрических преобразований для «симметри-
«симметризации» чертежа 68
§ 3. Аналитическая запись геометрических преобразований 72
3.1. Запись геометрических отображений в координатах 72
3.2. Аналитические методы изучения преобразований 74
3.3. Линейные преобразования 75
3.4. Комплексные координаты точек круговой плоскости .... 77
3.5. Бирациональные преобразования 79
§ 4. Произведение отображений и преобразований ... 80
4.1. Определение произведения отображений; примеры 80
4.2. Некоторые общие свойства произведения преобразований . . 85
4.3. Произведения движен, й; классификация движений .... 86
4.4. Применения ... . . . 89
4.5. Дальнейшие примеры произведения преобразований .... 92
§ 5. Обратное преобразование 96
5.1. Определение обратного преобразования .... 96
5.2. Инволюции 97
§ 6. Общее определение геометрии. Группы геометрических преобразо-
преобразований 98
6.1. Предмет 'еометрии 98
6.2. Геометрия и группы преобразований 101
6.3. Различные геометрии. Аффинная геометрия 102
6.4. Группы преобразований в физике 108
§ 7. Группа проективных преобразований 110
7.1. Гомология 110
7.2. Проективная плоскость . 112
7.3. Применения гомологии к решению задач 114
7.4. Проективные преобразования и проективная геометрия . . . 117
7.5. Координаты в проективной плоскости . . . . ... 117
7.6. Бирациональные преобразования проективной плоскости ... 119
$ 8. Неточечные отображения . . 121
8.1. Примеры неточечных преобразований 121
8.2. Неточечные преобразования в геометрии окружностей .... 124
4 Энциклопедия, кн. 4

50 ГЕОМЕ1РНЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
8.3. Полярное отображение Принцип двойственности в проектив-
проективной геометрии ...... 128
8.4. Подерное преобразование . 134
8.5. Группы неточечных преобразований 136
§ 9. Принцип перенесения .... 14а
9.1. Введение 140
9.2 Принцип перенесения, отвечающий сжатию к прямой .141
9.3. Принцип перенесения, отвечающий инверсии . . . . 143
9.4. Принцип перенесения, отвечающий полярному отображению 146
9.5. Принцип перенесения и модели геометрических систем .156
Литература .157
§ 1. Понятие преобразования. Примеры
1.1. Геометрические отображения. Одним из основных понятий
современной математики является понятие функции1). Переменная
у называется функцией переменной величины х (записывается: у=/(х)),
если каждому значению х, взятому из какого-то допустимого мно-
множества значений (область определения функции) отвечает
единственное значение у. При этом правило, позволяющее определить
у по данному значению х, может быть задано аналитическими фор-
формулами или просто таблицей, в которой перечислены все значения
х и отвечающие им у (этот способ задания функции особенно удобен
в том случае, если х может принимать лишь конечное число значе-
значений), или каким-либо другим способом (например, словесным описа-
описанием, как в случае известной функции Дирихле: каждому
рациональному значению х отвечает значение у = 1, а иррацио-
иррациональному х—значение у = 0).
Заметим, что в определении функции вовсе не требуется, чтобы пе-
переменные х и у обязательно представляли собой действительные числа.
Напротив, в современной математике принимают, что х и у могут быть
элементами совершенно произвольной (возможно различной!) природы—
комплексными числами !), точками плоскости или пространства, какими-
либо геометрическими фигурами, прямыми или произвольными линия-
линиями и т. д. Так можно сказать, что центр, а также радиус окружности
являются функциями этой окружности (здесь область определения
функции состоит из всех окружностей, а ее значения являются точками
или числами). В последнее время большое место в математике заняло
изучение функций y~f{x), где х или даже и х, и у сами являются
функциями в старом смысле этого слова, т. е. числовыми функциями*).
') Ср. ЭЭМ, кн. III, статью «Элементарные функции действительного
переменного Примеры последовательностей функций. Общее понятие
функции», §§ 46 и 54.
*) Функциям комплексного переменного посвящена специальная статья
в кн 111 ЭЭМ («Элементарные функции комплексного переменного»)
3) Изучением функций такого рода занимается в современ ой матема-
математике специальная большая наука—функциональный анализ.
Функции у = 1(х), ,-д. x = x(t) есть функция какого-то переменного I,

ПОНЯТИЕ ПРЕОБРАЗОВАНИЯ. ПРИМЕРЫ 51
В геометрии особо важную роль играют функции у=Ф(х), где
как х, так и у являются точками плоскости или пространства.
В таком случае слово «функция» заменяют обычно выражением
«геометрическое (точечное) отображение». Таким образом, геометри-
геометрическое отображение представляет собой не что иное, как определен-
определенный вид функциональной зависимости у=/(х), где как «аргумент» х,
так и «значение функции» у являются точками.
Итак, для задания геометрического (точечного) отображения
Ф надо указать: 1) некоторую фигуру (точечное множество) А,
называемую областью определения отображения Ф; 2) не-
некоторую фигуру А', называемую областью значений ото-
отображения Ф, и 3) некоторое правило, сопоставляющее с каждой
точкой А области А определенную точку А'=Ф(А) области Л'.
Если данное отображение Ф переводит точку А в точку А' (т. е.
Ф(А)-А'), то точку А' называют образом точки А при отобра-
отображении Ф. Пусть теперь L — некоторая линия (или фигура), целиком
расположенная в области Л. Если точка А пробегает линию (или фи-
фигуру) L, то образ А'=Ф{А) этой точки также пробегает некоторое
множество точек V, расположенное в области Л'. Это множество L'
называется образом множества L при отображении Ф, что запи-
записывается так: L' =Ф(Ь).
Пример 1. Отображение Ф определим следующим образом.
Примем за область определения Л всю плоскость, а за область
значений Л' — некоторую прямую плоскости А. Условимся, наконец,
с каждой точкой А плоскости А сопоставлять точку А', являющуюся
ортогональной проекцией точки А на прямую А' (рис. 1).
Очевидно, что если L — прям'ая, не перпендикулярная А', то ее обраэ
//=Ф(?) совпадает со всей прямой А'; образ Ф(?,) прямой Lv
которая перпендикулярна А', представляет собой одну точку на
прямой А'\ образ Ф{5) любой окружности 5 (или любого треуголь-
треугольника Г, рис. 2) является отрезком.
Пример 2. Введем на плоскости некоторую (прямоугольную)
систему координат XOY. Отображение Ф определим, принимая за
x(t) dt I, называются функционалами,
. /
а функции y=F(x), где и x=x(t) и y=y(t) есть числовые функции
(например, y(t)=x'(t) или y(t)— \ x(t) dt J, называются функцио-
а /
нальными операторами В функциональном инализе функционалы
играют ту же роль, которую в обыкноиенном анализе играют числовые
функции (одного или нескольких переменных); роль функциональных опе-
операторов близка к роли геометрических преобразований.

52
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
область определения и за область значений всю плоскость А
и сопоставляя с произвольной точкой А с координатами (х, у) точку
А'=Ф(А), имеющую координаты (sinx, sin у).
Рис. 1.
Рис. 2.
Пример 3. В качестве последнего примера укажем на вращение
(поворот) плоскости Л вокруг точки О на угол а. Для этого отображения
и область определения, и область значений совпадают со всей
плоскостью Л', образ точки А определяется как такая точка А'
плоскости, что О А' = О А и
//_АОА' = а, причем направле-
направление вращения от О А к О А' на
угол а (по часовой стрелке
или обратное ее движению)
указано заранее (рис. 3).
1.2. Геометрические пре-
преобразования. Между рассмо-
рассмотренными выше примерами 1, 2,
с одной стороны, и приме-
примером 3 — с другой стороны,
имеется существенное разли-
различие. Отображения, рассматри-
 ваемые в примерах 1 и 2,
Рис. 3. таковы, что существуют две
различные точки, образы
которых совпадают, т. е. точки АфВ, для которых Ф(-4) = Ф(?).
Например, если в качестве В взять любую точку прямой АА' (рис. 1),
то для отображения Ф, рассмотренного в примере 1, мы имеем
ф(А) = Ф(В). Аналогично две точки
А(х, у) и В(х + 2л, у — 4л)
переводятся отображением Ф примера 2 в одну и ту же точку.
Кроме того, отображение Ф, рассмотренное в примере 2, таково, что
не каждая точка выбранной нами области значений Л'(^Л) является

ПОНЯТИЕ ПРЕОБРАЗОВАНИЯ. ПРИМЕРЫ 53
образом какой-либо точки при отображении Ф. Например, точка с ко-
координатами B, —-jr-J не является образом никакой точки (ибо не
существует действительного числа х, для которого sinjc = 2). Эти
обстоятельства выражаются следующим образом: отображения, рассмот-
рассмотренные в примерах 1 и 2, не являются взаимно однозначными.
Отображение Ф с областью определения А и областью значе-
значений А' называется взаимно однозначным, если, во-первых,
ни для каких двух различных точек А и В области А их образы
Ф(А) и Ф(В) не совпадают и, во-вторых, каждая точка
области А' является образом некоторой точки при отображении Ф.
Грубо говоря, в}аимно однозначное отображение Ф можно охарак-
охарактеризовать тем, что никакие две различные точки не «склеиваются»
в результ.1те отображения Ф и, кроме того, Ф отображает область
А не на часть области А', а на всю эту область. _
Наибольшую роль в геометрии играют такие взаимно однознач-
однозначные отображения, для которых область определения А совпадает
с областью значений. Такие отображения называются преобразова-
преобразованиями множества А. Само множество А мы будем при этом называть
областью действия преобразования Ф. Итак, преобразованием мно-
множества А (или, иначе, преобразованием с областью действия А)
называется всякое взаимно однозначное отображение Ф, для ко-
которого область определения и область значений совпадают с А-
Отобрчжение Ф, рассмотренное в примере 3 (вращение плоскости
А на угол а вокруг точки О), является, очевидно, примером пре-
преобразования плоскости (т. е. преобразования, областью действия
которого является вся плоскость).
В дальнейшем мы ограничимся в этой статье рассмотрением только
преобразований '), причем таких преобразований, областью действия
которых служит плоскость или «почти плоскость» *). Точнее говоря,
мы вынуждены будем в ряде случаев считать областью действия
преобразования Ф не всю плоскость, а плоскость с «выколотыми»
(т. е. удаленными) точками или линиями. Иногда, напротив, мы будем
присоединять к плоскости новые («несобственные», т. е. не
существующие с точки зрения школьного курса геометрии) точки
или линии. Так как во всех случаях основой для конструирования
области действия преобразования Ф будет служить плоскость, то,
') Отображения, не являющиеся преобразованиями, также играют
в некоторых вопросах геометрии заметную роль. Например, разного вида
проекции трехмерного пространства на плоскость, подробно изученные
в статье «Методы изображений» (стр. 233—234 этой книги ЭЭМ), очевидно,
преобразованиями не являются.
2) В настоящей статье мы почти не будем говорить о преобразованиях
пространства, поскольку более простого случая плоскости достаточно,
для того чтобы осретить все принципиалкные моменты теории геометри-
геометрических преобразований.

64
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
допуская некоторую неточность, мы будем объединять все рассмат-
рассматриваемые преобразования одним общим названием — преобразования
плоскости.
Приведем еще несколько примеров преобразований плоскости.
Пример 4. Выберем на плоскости какое-либо направление ММ'
(его можно задать, например, прямой со стрелкой); зададим также
определенный отрезок а (рис. 4).
Каждой точке А плоскости мы
поставим в соответствие такую
точку А', что отрезок АА' имеет
направление ММ' и длину а.
Построенное преобразование Ф
называется параллельным пе-
переносом плоскости в напра-
направлении ММ' на величину а
(или переносом на вектор
Рис. 4. П р и м е р 5. Выберем на
плоскости определенную точ-
точку О и с каждой точкой А сопоставим такую точку А', что отрезок АА'
проходит через точку О и делится в ней пополам (рис. 5); если
точка А совпадает с О, то и А' не отличается
от О. Определенное таким образом преобразование
Рис. 5.
Рис. 6.
плоскости называется симметрией относительно точки О. Легко ви-
видеть, что симметрия относительно точки О есть частный случай
вращения—она совпадает с вращением вокруг точки О на угол 180°.
') См статью «Векторы н их применения в 1еометрии» (стр. 291—381
•той книги ЭЭМ).

ПОНЯТИЕ ПРЕОБРАЗОВАНИЯ. ПРИМЕРЫ
55
Пример 6. Зададим на плоскости некоторую прямую о и со-
сопоставим с каждой точкой А такую точку А', что отрезок АА' перпен-
перпендикулярен прямой о и делится этой прямой пополам (рис 6); точкам
прямой о мы поставим в соответствие те же самые
точки. Полученное преобразование плоскости на-
называется симметрией относительно прямой о.
Пример 7. Выберем на плоскости точку О
и сопоставим с каждой точкой А такую точку А'
ГЛА ОА' . .
луча ОА, что ттт=*> где "¦ — заданное поло-
DA
жительное число (рис. 7); точке О поставим
в соответствие эту же самую точку. Это пре-
преобразование называется сжатием к точке О') или '
центрально-подобным преобразованием или, на-
наконец, гомотетией2) (с центром О и коэф-
коэффициентом k).
Часто считают, что коэффициент k гомотетии
может быть также и отрицательным числом;
в этом случае за А' принимают такую точ-
ОА'
ку прямой ОА, что /тХ=1^| и направления отрезков О А' и ОА
(от О к А' и от Ок А) противоположны. Если стать на такую
точку зрения, то надо будет считать, что симметрия относительно
точки (пример 5) представляет со-
собой частный случай гомотетии—
это есть не что иное, как гомоте-
гомотетия с коэффициентом k — — 1.
Пример 8. Зададим некото-
некоторую прямую о плоскости и сопо-
сопоставим с каждой точкой А такую
точку А', что точки А и А' лежат
по одну сторону от прямой о, пря-
прямая АА' перпендикулярна о и рас-
расстояния АО и А'О точек А и
У от о связаны соотношением
Рис. 7.
о
Рис. 8.
, /I 7)й~=^' где *—фиксированное
положительное число (рис. 8); если
точка А принадлежит прямой о,
то будем считать, что А' совпадает с А. Преобразование, определен-
определенное таким образом, естественно назвать сжатием к прямой о');
J) Если коэффициент k>\ и, следовательно, ОА'>ОА, то преобразова-
преобразование уместнее было бы назвать растяжением, а не сжатием
*) От греческих слов cjiog — одинаковый (или tjioioc — подобный) и
©etog — расположенный.

56 ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
прямую о называют осью сжатия, а число k—его коэффици-
коэффициентом.
Можно считать, что коэффициент k сжатия может быть и отри-
отрицательным (причем в этом случае отрезки 04' и ОА имеют проти-
противоположное направление, т. е. точки А и А' лежат по разные сторо-
стороны прямой о). Сжатие к прямой о с коэффициентом сжатия k = — 1 пред-
представляет собой, очевидно, симметрию относительно прямой о (пример 6).
Пример 9. Гомотетия с центром О и коэффициентом k (при-
(пример 7) определяется как преобразование, переводящее точку А в та-
такую точку А' прямой ОА, что отношение -щ- равно к. Рассмот-
Рассмотрим теперь преобразование, перево-
переводящее точку А в такую точку А'
луча ОА, что произведение
ОА-ОА' имеет заданную величину:
ОА' ¦ ОА = k, где k— некоторое за-
заданное положительное число (рис. 9).
Это преобразование называется ин-
инверсией') (с центром О и сте-
степенью k). Если k = a2, то точки
окружности 5 с центром О и ра-
радиусом а переходят при инверсии
сами в себя, внешние по отношению
рис g к S точки переходят во внутрен-
внутренние, а внутренние точки — во внеш-
внешние; это обстоятельство оправдывает другое название рассматривае-
рассматриваемого преобразования—симметрия относительно окружности 5.
Симметрию относительно окружности 5 можно также описать геоме-
геометрически: при этом преобразовании внешняя по отношению к S точка А
переходит в точку А' пересечения прямой ОА (где О — центр окруж-
окружности S) с прямой PQ, соединяющей точки Р и Q прикосновения
с 5 проведенных к ней из А касательных, а А' переходит в А; это
следует из того, что в прямоугольном треугольнике ОРА (рис. 9)
РА' есть высота, и потому ОА ¦ ОА' — ОРг = а1 = k.
Можно также считать, что степень k инверсии может быть
и отрицательной, причем в этом последнем случае отрезки ОА'
и О А противоположно направлены и ОА' -OA = \k\.
Заметим теперь, что, строго говоря, мы не дали точного опреде-
определения инверсии, ибо отображение, определенное выше, не определено
в точке О — ей не соответствует при инверсии никакая точка
плоскости. Один из приемов, применяющихся для устранения этой
некорректности,— считать, что область действия инверсии не сов-
') От латинского слова inversiu — обращение.

ПОНЯТИЕ ПРЕОБРАЗОВАНИЯ. ПРИМЕРЫ 57
падает со всей плоскостью; эта область действия Л представлне)
собой плоскость с исключенной («выколотой») точкой О, поскольку
эта точка не имеет образа при инверсии. Ясно, что инверсия пред-
представляет собой взаимно однозначное отображение этой области А
(плоскости с выколотой точкой). Таким образом, мы здесь впервые
встречаемся с преобразованием «плоскости», область действия кото-
которого отличается от всей плоскости. —
Можно встать также на другую точку зрения. Поскольку точка
О не имеет образа при инверсии, можно условно считать, что точка
О переходит при инверсии в «несобственную» (т. е. не существую-
существующую на обычной плоскости) точку Q. Наоборот, точка Q переходит
при инверсии в точку О. При таком соглашении инверсия становится
взаимно однозначным отображением («преобразованием») «расширен-
ной» плоскости Л*, получающейся из обыкновенной плоскости при-
соединением к ней еще одной точки Q. Так как при приближении
точки А к О ее образ А' при инверсии неограниченно удаляется от О
(ибо О А' = тгд ) > то образ Q точки О иногда называют бесконечно ~
удаленной точкой «расширенной» плоскости А*. Плоскость А*, "
полученную присоединением к обыкновенной плоскости одной «беско-
нечно удаленной» точки Q, часто называют расширенной плоскостью1).
Так как мы в дальнейшем встретимся с иными способами «расшире- ^*
ния» обычной плоскости, то нам будет более удобен термин круго-
круговая плоскость. Причины, обусловливающие такое название, будут
раскрыты ниже2).
Итак, мы можем принять за область действия инверсии либо
плоскость с одной выколотой точкой, либо «расширенную» плоскость,
получающуюся добавлением одной «несобственной» точки. Впослед-
Впоследствии мы увидим, что считать областью действия инверсии «расши-
«расширенную» плоскость в ряде отношений значительно удобнее.
Подчеркнем, что утверждение типа «инверсия переводит точку О
в бесконечно удаленную точку Q» не является содержательной тео-
теоремой— оно представляет собой лишь иную формулировку того, что
точка О не имеет образа при инверсии. Однако введение понятия'
круговой плоскости уже выходит за рамки чисто терминологических
соглашений: здесь мы делаем новый шаг по пути математической
абстракции, рассматривая совершенно новое образование — плоскость,
которая, кроме точек, фигурирующих в школьном курсе геометрии,
') Это название принято, например, в теории функций комплексного
переменного.
2) Заметим еще, что «расширенная» (т. е. кругоьая) плоскость ,//*,
являющаяся областью действия инверсии, может быть взаимно однозначно
отображена (при помощи стереографической проекции, см стр 2? и след.
этой книги) на поверхность сферы S, так что поверхность сферы можно
рассматриьать как модель (см. стр 21 и след этой книги) руовой
плоскости. Точка Q переходит при стереографической п, оекциь в «север-

58 ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
содержит еще новую (равноправную с остальными!) «бесконечно
удаленную» точку. При этом круговая плоскость является не менее
законным математическим понятием, чем обычная, «евклидова» пло-
плоскость. Ведь и представление о (безграничной!) плоскости, на кото-
которой каждая прямая может быть неограниченно продолжена в обе
стороны, является лишь математической абстракцией и не имеет
реального смысла; точное описание плоскости доставляется лишь
набором аксиом, характеризующих геометрию на плоскости'). Разное
понимание слова «плоскость» приводит к разным наборам аксиом; так,
на круговой плоскости будет несправедлива аксиома: «через две точки
проходит единственная прямая», поскольку через «обыкновенную»
точку А и «бесконечно удаленную» точку Q проходит бесконечно
много прямых (следует считать, что все прямые круговой плоскости
проходят через «бесконечно удаленную» точку Q, поскольку образы
всех прямых при инверсии проходят через центр инверсии О, являю-
ный полюс» N сферы S. Если при этом радиус сферы S выбран так, что
окружность инверсии переходит при стереографической проекции в экватор
сферы S, го инверсии круговой плоскости JI* будет соответствовать сим-
симметрия сферы S относительно экваториальной плоскости. Иначе говоря,
Рис. Ш
если В и В'—две точки сферы S, симметричные относительно плоскости
экватора, а А, А' — проекции точек 6 и 6' из точки N на плоскость Д*
(рис. 10), то А переходит в А' при инверсии относительно окружности,
в которую проектируется экватор сферы (см. в связи с этим стр. 468—472
этой книги ЭЭ v'i)
') См. в этой книге 33jM статью «.Аксиомы и основные понятия гео-
геометрии».

ПОНЯТИЕ ПРЕОБРАЗОВАНИЯ. ПРИМЕРЫ
59
щийся образом точки Q — см. ниже, стр. 75). Разные подходы к по-
понятию плоскости, характеризуемые разными наборами аксиом, являются
одинаково допустимыми; в одних задачах нам может понадобиться
толковать слово «плоскость» в одном, а в других—в другом смысле.
И, разумеется, совершенно беспредметным явился бы спор, скажем,
о том, имеет ли плоскость одну или много «бесконечно удаленных>
точек: это полностью зависит от принятой точки зрения, диктуемой
теми задачами, которые перед нами стоят. В иных случаях (напри-
(например, в связи с рассмотрением гомологии — см. ниже § 7, или гипер-
гиперболической инверсии—см. пример 10) мы можем прийти к необходи-
необходимости совсем иного пополнения плоскости «идеальными» или «бес-
«бесконечно удаленными» элементами—и полученная на таком пути
«плоскость» будет отличаться от обычной и от круговой плоскости,
но не будет ни «хуже», ни «лучше» их.
Пример 10. Пусть преобразование Ф переводит каждую точку А
в такую точку А', что точки А и А' лежат по одну сторону от прямой о,
прямая АА' перпендикулярна заданной прямой о и OA'-OA = k, гдр О —
точка пересечения прямой
АА' сои k—фиксирован-
k—фиксированное положительное число
(рис. 11). Это преобразова-
\ ие можно назвать гипер-
гиперболической инверсией ') с
осью о и степенью k.
Если k=a*, то точки пря-
прямых I и /,, параллельных о
и удаленных от о к а рас-
расстояние а, псреподят при
нашем преобразовании в
себя, внутренние точки
ограниченной / и /, поло-
полосы переходят ео внешние
точки, а внешние точки
полосы — во внутренние
точки; с этим связано на-
название симметрия относи-
относительно пары параллельных
прямых, которое также
дают иногда рассматрива-
рассматриваемому преобразованию.
Ясно, что преобразование
точек прямой п J_ l при
симметрии относительно па-
пары параллельных прямых
Рис. 11.
I
этой прямой при симметрии
и /, совпадает с преобразованием точек
относительно окружности S с центром
в точке О пересечения л и о и радиусом а; это может быть использовало
для построения образа А' точки А при гиперболической инверсии (рис. 11).
Часто также считают, что степень k гиперболической инверсии может бить
') Причины, обусловливающие такое название, будут объяснены ниже
(см. стр. 75).

60
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
и от р и ц а те л ь н о й; в этом последнем случае ОА'-ОА = \ k\ и направ-
направления отрезков О А' и О А противоположны.
За область действия гиперболической инверсии можно принять пло-
плоскость с выброшенной из нее прямой о, поскольку точки этой прямой не
переходят при нашем преобразовании ни в какие точки плоскости. Можно
также построить и другую область действия гипербо/ ческой инверсии,
не выбрасывая из плоскости «лишние» точки, а наоборот, добавляя к пло-
плоскости новые «несобственные» точки, на чем мы здесь останавливаться
не будем.
Заметим, что все рассмотренные точечные преобразования являются
непрерывными, т. е. обладают следующим свойством: если перемен-
переменная точка Ап, оставаясь все время в области действия преобразования Ф,
стремится к некоторой точке А, также принадлежащей области действия
преобразования (т. е. если расстояние АпА стремится к нулю при неогра-
неограниченном возрастании номера я), то отвечающая точке Ап точка Ап = Ф(Ап)
стремится к точке А' =Ф(А), отвечающей точке А. Легко привести
и сколько угодно примеров не непрерывных преобразований (таким будет,
например, преобразование, при котором все параллельные заданной пря-
прямой / прямые плоскости претерпевают параллельный перенос в направ-
направлении прямой I, но прямые, расстояние которых от / рационально, сдвига-
сдвигаются на величину афЬ, а прямые, расстояние которых от I иррационально,—
на величину 2а). Однако, так как в геометрии используются почти исклю-
исключительно непрерывные преобразования, то мы здесь ограничимся рассмот-
рассмотрением только таких преобразований. Впрочем, свойства непрерывности
рассматриваемых преобразований мы нигде использовать не будем.
1.3. Некоторые типы геометрических преобразований. Нетрудно
видеть, что преобразования, описанные в примерах 3, 4, 5, 6, обладают
следующим замечательным свойством: любые две точки А и В они
переводят в такие точки А' и В',
что расстояние А'В' равно расстоя-
расстоянию АВ (рис. 12—15). Преобразования,
перенес
Вращение
Рнс. 12.
Рис. 13.
сохраняющие расстояния между точками, называются движениями;
таким образом, вращение, параллельный перенос, симметрия отно-
относительно точки и симметрия относительно прямой являются
движениями плоскости.
Преобразование, описанное в примере 7 (гомотетия) обладает тем
свойством, что расстояние между образами А' и В'точек А и В про-

ПОНЯТИЕ ПРЕОБРАЗОВАНИЯ. ПРИМЕРЫ
61
порционально расстоянию между этими точками (где коэффициент
пропорциональности k зависит лишь от преобразования, но не от выбора
точек А и В); это вытекает из подобия треугольников О А' В' и ОАВ
(рис. 16). Преобразования, изменяющие все расстояния между точками
в одном и том же отношении k (иначе говоря, сохраняющие отно-
отношения расстояний между тоЧ- Симметрия
ками: если точки А, В, С и D пе-
переходят в точки А', В', С
А'В' АВ\
и D , TocrD7=='CDj ' называются
А'
Симметрия
Рис. 14.
I
Рис. 15.
преобразованиями подобия (с коэффициентом подобия k);
движения можно также рассматривать как преобразования подобии
с коэффициентом подобия 1. Таким
образом, гомотетия является пре-
преобразованием подобия ').
Преобразование, описанное в при-
примере 8 (сжатие к прямой), обладает
следующим важным свойством —
оно переводит каждую прямую ли-
линию I снова в некоторую прямую
линию V. Это утверждение является
очевидным, если /есть прямая, парал-
параллельная или перпендикулярная оси
сжатия о (в частности, перпендику-
перпендикулярную к оси о прямую сжатие пере-
переводит в себя). Прямая же /, образу-
образующая с о острый угол а, переходит в прямую /', пересекающую ось
сжатия о в той же точке Q, что и /, и образующую с прямой о такой
угол а', что у—=k. В самом деле, если перпендикуляр к прямой
о в точке О пересекает прямую / в точке А и если А' — такая
О
АВ \ DA OBJ
АВ
Рис.
16.
') Нетрудно понять, что гомотетия с (положительным или отрицатель-
отрицательным!) коэффициентом гомотетии k представляет собой' преобразование
подобия с коэффициентом подобия J k |.

62
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
точка этого перпендикуляра, что tg(^A'QO) =
A'QO
то
О А'
' П
— k (рис. 17), откуда и следует, что точка А перехо-
перехоBr
дит в А'. Преобразования плоскости, переводящие каждую прямую
линию снова в прямую, называются аффинными преобразованиями1);
таким образом, сжатие к прямой является аффинным преобразо-
преобразованием. Заметим еще, что сжатие к прямой обладает также следую-
следующими свойствами: оно переводит параллельные прямые в парал-
параллельные и сохраняет отно-
отношение любых двух отрез-
отрезков, принадлежащих ооной
прямой I. Эти свойства
сжатия к прямой нетрудно
вывести из его определения.
Мы, однако, не будем этого
делать, так как впоследст-
впоследствии мы увидим, что этими же
свойствами обладает каж-
каждое аффинное преобразова-
преобразование (ср. ниже, стр. 76—77).
Преобразование, указан-
указанное в примере 9 (инверсия),
не является аффинным; как
мы увидим ниже (см. стр. 75),
о прямую линию оно перево-
переводит в прямую линию или
в окружность; окружность
также переводится инвер-
инверсией в окружность или прямую линию. Преобразование, переводящее
каждую окружность или прямую снова в окружность или в
прямую, называется круговым преобразованием; таким образом,
инверсия есть круговое преобразование2).
Легко понять, что всякое движение и всякое преобразование
подобия переводит каждую прямую линию снова в прямую и каждую
окружность снова в окружность — таким образом, движения и пре-
преобразования подобия являются как аффинными, так и круговыми
Рис. 17.
') От латинского слова affinitas—родство по мужу или жене, свой-
свойство; это название подчеркивает, что аффинные преобразования переводят
каждую фигуру М в фигуру М', достаточно близкую («родстьенную»)
первоначальной (хоть и не столь близкую, как фигура, получающаяся
из М движением или преобразованием подобия).
2) Более подробно теория круговых преобразований излагается в статье
«Окружности», напечатанной в этой книге ЭЭМ, где, в частности, имеется
отличное от приведенного на стр. 74—75 доказательство того, что инверсия
является круговым преобразованием.

ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЙ К РЕШЕНИЮ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ 63
преобразованиями. В самом деле, окружность есть геометрическое
место точек, равноудаленных от одной точки О; прямая же пол-
полиостью характеризуется тем, что для каждых трех ее точек А, В
и С, где В лежит между А и В, имеет место равенство АВ-\~ ВС= АС.
Но так как движения вовсе не меняют расстояний, а преобразования
подобия умножают все расстояния на одно и то же число, то дви-
движение или преобразование подобия переводит окружность в окруж-
окружность, а прямую—в прямую. Можно доказать, что и обратно всякое
преобразование плоскости, переводящее прямую линию снова в пря-
прямую линию и окружность—в окружность, является преобразованием
подобия (в частном случае—движением); на доказательстве этого
мы здесь не остановимся').
§ 2. Применение преобразований к решению
геометрических задач
2.1. Некоторые примеры. Уже перечисленные выше простые
геометрические преобразования могут быть эффективно использованы
для решения содержательных геометрических задач. Широко известны,
например, применения геометрических преобразований к решению
задач на построение. Так, решение задачи о построении отрезка АА',
заключенного между заданными окружностью S и прямой L и имею-
имеющего данные длину а и направление /, непосредственно получается
с помощью параллельного переноса Ф окружности 5 на отрезок а
в направлении /. При таком переносе один конец А искомого отрезка
переходит в другой, откуда ясно, что одним из концов искомого
отрезка является точка пересечения окружности S'—ФE) и прямой
L (рис. 18, а). [Задача может иметь до четырех решений (рис. 18,6),
ибо перенос окружности S можно осуществлять в двух противопо-
противоположных направлениях.] Далее, задача о построении отрезка АА', за-
заключенного между данными прямыми / и /4 и делящегося пополам
в данной точке О, решается с помощью симметрии относительно
точки О (рис. 19; задача имеет, вообще говоря, единственное реше-
решение). Задача о построении в данной окружности S такой хорды АВ,
которая проходит через данную точку А и делится пополам второй
данной окружностью Sv решается с помощью гомотетии с центром А
и коэффициентом -„- (рис. 20; задача может иметь два решения) *).
Но наиболее интересны применения геометрических преобразований
к доказательству теорем.
') См. например, т. II книги И. М. Я г л о м а [2], указанной в
списке литературы в конце статьи.
г) Другие примеры применения геометрических преобразований к ре-
решению задач иа построение читатель может найти в статье «Общие прин-
принципы геометрических построений», стр. 189—193 этой книги.

64
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
Так, из того, что средняя линия C1Ai треугольника ABC гомо-
гомотетична основанию АС с центром гомотетии В и коэффициентом -^¦
Рис. 18.
6)
т. е. С,.4, получается из АС гомотетией с центром В и коэффи-
коэффициентом -д-; рис. 21), следует, что
СХАХ\\АС и СхАх = \
Отсюда, в свою очередь, вытекает, что гомотетия с коэффициен-
коэффициентом— -^-, переводящая А в Av переводит Д ABC в
образованный средними линиями
треугольника ABC; но это ч ^—т—~^й
означает, что прямые AAV
ВВ^ и ССЛ (медианы
Рис. 19. Рис AJ
треугольника) пересекаются в одной точке М ^центре рассматрива.

ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЙ К РЕШЕНИЮ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ 65
емой гомотетии) и делятся в ней в отношении 2:1, считая от вершины.
Далее, при той же гомотетии высоты треугольника ABC переходят
в высоты треугольника A^Bfi^. Но высоты треугольника ABC—это
перпендикуляры, восставленные к сторонам треугольника ABC в их
серединах; поэтому они пересекаются в центре О описанной вокруг ABC
окружности S. Отсюда следует,
что высоты треугольника ABC
пересекаются в одной точке
Н, причем точки Н, О и точка
пересечения медиан М (центр
гомотетии треугольников ABC
и A^Bfi^) лежат на одной
прямой*), и НМ:М0=2.
Можно также заметить, что
окружность ? переходит при
рассматриваемой гомотетии •>
описанную вокруг треуголь-
треугольника AJBXC^ окружность S
(т. е. в окружность, проходя-
проходящую через середины сторон
треугольника ABC), радиус Rl
которой, очевидно, равен поло-
половине радиуса R окружности 5,
а центр О, лежит на прямой
МО, причем 0М:М0х = 2 (ибо
М — центр гомотетии с коэф-
коэффициентом — -g-. переводящей
S в S1,). Отсюда следует, что
точка О, является середи-
серединой отрезка НО, а значит, Рис
окружность 5, гомотетична
окружности 51 также с центром гомотетии Н и коэффициентом гомо-
гомотетии-f--^-; поэтому окружность 5, проходит через середины А'. В'
и С отрезков НА, НВ и НС высот треугольника АВСг).
') Прямая И МО называется прямой Эйлера треугольника ABC.
*) Окружность S, называется окружностью Эйлера треуголь-
треугольника ABC. Часто эту окружность называют также окружностью
девяти точек, поскольку она проходит через 9 «замечательных» точек
треугольника: через середины Л,, В„ С, сторон, через середины Л', В', С
отрезков высот и через основания Р, Q, R высот Последнее вытекает из
того, что точки, скажем, Л, и Л' окружности S, являются диаметрально
противоположными (ибо касательные к S, в точках А, и Л' получаются
из касательной к S в точке А при помощи гомотетии с центром М и коэф-
5 Энциклопедия, кн. 4

66
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
2.2. Применение симметрии. В первую очередь, говоря о при-
применениях геометрических преобразований к доказательству теорем,
следует указать на использование соображений симметрии для вывода
свойств «симметричных» фигур. Чаще всего прилагательное «симме-
«симметричный» указывает на нали-
наличие у геометрической фигуры
оси симметрии, т. е. такой
прямой /, что симметрия отно-
относительно / переводит фигуру
саму в себя (рис. 22). Сим-
Симметричными фигурами являются:
отрезок (у него две оси симмет-
симметрии— перпендикуляр, восста-
восставленный к отрезку в его
Рис. 22. середине, и прямая, на которой
этот отрезок расположен); угол
(ось симметрии —биссектриса угла); равнобедренный треугольник (ось
симметрии—биссектриса угла при вершине); равнобедренная трапеция
(ось симметрии — прямая, делящая пополам основания трапеции); ромб
(оси симметрии—диагонали ромба); прямоугольник (оси симметрии —
средние линии); окружность (оси сим-
симметрии— диаметры окружности) и т. д.
Иногда прилагательное «симметричный»
указывает также на наличие у фигуры
центра симметрии, т. е. точки О,
симметрия относительно которой пере-
переводит фигуру в себя (рис. 23). Цент-
Центрально-симметричными фигурами явля-
являются, например, параллелограмм (центр
симметрии—точка пересечения диаго-
диагоналей) или окружность (центр симмет-
симметрии— центр окружности). Можно также рис 23
заметить, что центральная симметрия с
360°
центром О совпадает с вращением вокруг точки О на угол 180° = —т— .
Это позволяет обобщить понятие центральной симметрии, считая,
что некоторая фигура М обладает симметрией порядка k
с центром О, если она переходит в себя при вращении вокруг
точки О (центра симметрии k-r о порядка) на угол
фициентом —д-, соответственно при помощи гомотетии с центром Н
и коэффициентом +"«¦; значит, эти касательные параллельны между со-
собой). Поэтому прямой угол А1РА'—вписанный в окружность S, и точка
р принадлежит Sx.

Рнс. 24.
ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЙ Ь РЕШЕНИЮ ГЕОМЕТРИЧЕСКИХ .1АДАЧ 67
360°
¦—т— (рис. 24); так, чравильный треугольник обладает симметрией
г?
третьего порядка (относительно центра треугольника), а правильный
я-угольник—симметрией я-го порядка.
Ясно, что известные свойства перпендикуляра, восставленного
к отрезку в его середине, или свойства биссектрисы угла непосред-
непосредственно следуют из того, что рас-
рассматриваемая прямая является осью
симметрии соответствующей фигу-
фигуры. Точно так же все свойства
равнобедренного треугольника выте-
вытекают из его симметричности; из
симметричности окружности сле-
следует, что диаметр, перпендикуляр-
перпендикулярный хорде, делит эту хорду пополам.
Из наличия у окружности S центра
симметрии О вытекает, что вписан-
вписанный угол, опирающийся на диа-
диаметр, можно рассматривать как
угол вписанного в 5 параллелограмма
(рис. 25). С другой стороны, из наличия у окружности 5 осей сим-
симметрии следует, что перпендикуляры, опущенные из центра окруж-
окружности на стороны параллелограмма, являются его осями симметрии,
т. е. что этот параллелограмм пред-
представляет собой прямоугольник; таким
образом, мы приходим к выводу, что
вписанный угол, опирающийся на
диаметр окружности — прямой. Из
того, что линия центров q двух
окружностей 5, и St является осью
симметрии фигуры, образованной эти-
этими двумя окружностями, вытекает,
что точка пересечения общих внеш-
внешних касательных /те, и /ге2 (или общих
внутренних касательных я, и /г,)
окружностей .Sj и Sv принадлежит
прямой q (рис. 26). Центр О пра-
правильного треугольника Т (или квад-
квадрата К) является центром симметрии 3-го (соответственно 4-го) порядка.
Отсюда вытекает, например, что прямые, проведенные через вершины
правильного треугольника Т и отсекающие -^- противоположной сто-
стороны (рис. 27, а), сами образуют правильный треугольник с тем же
центром. Аналогично этому прямые, проходящие через вершины квад-
квадрата К и делящие противоположные стороны пополам (рис. 27, б),
образуют квадрат с тем же центром.
6*
Рис. 25

68
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
Все эти предложения доказываются почти одинаково. Так, из того,
что симметрия относительно линии центров q окружностей 5, и .S,,
изображенных на рис. 26, переводит их в себя, следует, что также
и совокупность общих касательных т1 и т2 окружностей переходит
при этой симметони в себя (точнее тл переходит в тх, а тг — вот,).
Рис. 26.
Но отсюда вытекает, что прямая д является осью симметрии обра-
образованного прямыми т1 и тг угла, т. е. совпадает с биссектрисой
этого угла. Точно так же из того, что вращение вокруг центра О
правильного треугольника Т на угол 120° переводит треугольник Т
в себя, вытекает, что и изображенный на риг 27 а «внутренний»
01
6)
Рис. 27.
треугольник т переходит при этом вращении в себя (прямая а пе-
переходит в b, b — в с, и с—во); поэтому треугольник т также имеет
точку О своим центром вращения 3-го порядка, что возможно
лишь в том случае, если этот треугольник правильный.
2.3. Использование геометрических преобразований для «сим-
«симметризации» чертежа. Употребление преобразований, отличных от
движений и от преобразований подобия, может иногда позволить
использовать простые соображения симметрии в новых, более слож-
сложных условиях. Заметим, например, что сжатие к прямой (пример 8
на стр. 55) позволяет перевести каждый треугольник ABC в равно-

ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЙ К РЕШЕНИЮ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ 69
бедренный треугольник А' ВС,— этого легко добиться с помощью
сжатия к стороне ВС, подобрав коэффициент сжатия так, чтобы
было А'В=ВС (рис. 28; за ВС можно, например, принять ббльшую
из двух сторон АВ, ВС). Отсюда и из того, что параллельные
прямые сжатие переводит в параллельные (стр. 62), вытекает, что
Кс1ждую трапецию ABCD можно сжатием перевести в равно-
равнобедренную трапецию AB'C'D (рис. 29; достаточно перевести
треугольник ABF в равнобедренный треугольник AB'F). А так как
равнобедренная трапеция AB'C'D обладает осью симметрии E'F,
Рис. 28.
Рис. 29.
проходящей через середины основании АВ' и CD, через точку пе-
пересечения диагоналей Е и через точку пересечения продолжений
боковых сторон F, то можно заключить, что и в произвольной, тра-
трапеции ABCD точка пересечения диагоналей, точка пересечения
боковых сторон и середины оснований лежат на одной прямой
(здесь используется то, что сжатие к прямой сохраняет отношение
отрезков одной прямой, стр. 62). Иначе говоря, прямая, соединяющая
точку пересечения диагоналей трапеции и точку пересечения про-
продолжений боковых сторон, делит основания трапеции пополам.
Два сжатия позволяют перевести любой треугольник в равно-
равносторонний. В самом деле, равнобедренный треугольник А'ВС
(рис. 28) можно сжатием к прямой А'С перевести в равносторонний
треугольник А'В'С. Поэтому для доказательства того, что медианы
произвольного треугольника пересекаются в одной точке, достаточно
показать, что пересекаются в одной точке медианы равностороннего
треугольника. Но последнее сразу следует из соображений симметрии
(или из того, что медианы равностороннего треугольника одновременио

70
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
являются его биссектрисами). Отсюда же следует, что если соединить
вершины произвольного треугольника ABC с точками, делящими про-
противоположные стороны в отношении 2:1 (рис. 30), то точка пересечения
медиан образованного проведенными прямыми треугольника совпадает
с точкой пересечения медиан исходного треугольника (ибо совпадают
точки пересечения медиан — центры—изображенных на рис. 27, а
правильных треугольников Т и т);
доказательство этого, не исполь-
использующее соображений симметрии
и свойств сжатия к прямой,
достаточно сложно.
Рис.
где S, касается S2
Аналогичное применение допу-
допускает и инверсия (см. выше, пример
9, стр. 56). Так, например, можно
показать, что каждые две непересе-
непересекающиеся окружности можно неко-
некоторой инверсией перевести в две
равные окружности. Рассмотрим
теперь изображенные ни рис. 31, а
четыре окружности S,, S2, Ss и S4,
S2—S,, S,—S4 и S4—снова S,; точки касания окруж-
C и D. Переведем инверсией две «про-
иостей обозначим через А, В,
тивоположные» окружности S, и S, в равные окружности S, и S,; при
этом рис. 31, а перейдет в симметричный рис. 31, б (осью симметрии ко-
которого является линия центров р окружностей Sz и SJ. Ясно, что пря-
прямая 0ж04 будет являться осью симметрии и образованного точками касания
преобразованных окружностей четырехугольника A'B'C'D', откуда следует,
что этот четырехугольник является равнобочной трапецией. Таким образом,
мы убеждаемся, что точки А', В', С и СУ принадлежат одной окружности ').
А так как инверсия переводит окружность в окружность, то и точки А,
В, С и D принадлежат одной окруж*ости\
Наличие на плоскости «особой» точки О (центра инверсии), переводимой
инверсией в «бесконечно удаленную» (с точки зрения элементарной гео-
геометрии — несуществующую!) точку, открывает новые возможности примене-
применения этого преобразования в элементарной геометрии. Выше мы говорили
о пользе, которую можно извлечь из того, что чертеж геометрической
теоремы часто можно при помощи, скажем, сжатия к прлмой перевести
в «более симметричный» чертеж (ср. стр. 69). Но инверсия значительно
больше изменяет чертежи, чем сжатие к прямой, что делает это преобра-
преобразование еще более ценным Для приложений.
В качестве примера рассмотрим снова теорему: «.если окр жность S,
касается S2, S2 касается Ss, S3 касается S4 и St касается S, (рис. 31,о),
то четыре точки касания принадлежат одной окружности (или прямой)».
Выше мы доказывали эту теорему, преобразовав ее чертеж в более сим-
') Или прямой (см. рис. 31, в). Вообще в вопросах, связанных с ис-
использованием инверсии, мы вынуждены считать окружности и прямые
равноправными (ибо окружность инверсия может перевести в прямую);
поэтому в таких случаях слово «окружность» обычно означает «окружность
или прямая».

ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЙ К РЕШЕНИЮ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ 71
метричный чертеж такого же рода. Но еще сильнее можно изменить этот
чертеж, подвергнув его инверсии с центром в точке А касания окружностей
S, и S2. При этом точка А перейдет в «бесконечно удаленную» точку Q;
к
\
р
1 ,
щ
А
Рис. 31.
окружности S, и S2 перейдут в прямые S, и S2, которые должны быть па-
параллельны, так как они не имеют (отличных от Q) общих точек (ведь S,
и S2 имеют единственную общую точку А\). В результате исходный

72 ГЕПМЕТРИЧЕС.КИР ПРЕОБРАЗОВАНИЯ
чертеж перейдет в совсем иной (см. рис. 32). Но т.к как точки В',
С иО' на рис. 32 принадлежат одной прямой (это следует, например, из
того, что /_ 1 = ?_ 4, как накрест лежащие, и /1 1 = /1 2, ^.4 = ^3; следо-
следовательно, ?_ 2— / 3), то точки В, С и D, образлми которых они^являются,
\ лежат на одной окружности (или
\ на одной прямой) с точкой И
^ _с' (Центром инверсии), что и требо
$г валось доказать.
§ 3. Аналитическая запись
геометрических
преобразований
3.1. Запись геометриче-
геометрических отображений в коорди-
„,. - V натах. Большую пользу при
\ v изучении точечных преобразо-
v \ ваний и отображений может
Р-с. 32. принести метод коорди-
координат. Предположим, что пло-
плоскость отнесена к некоторой системе координат х, у; для простоты
мы будем иметь в виду декаргову систему координат, хотя принципи-
принципиально ничего не изменилось бы при использовании, скажем, полярных
координат. Пусть Ф—некоторое отображение, областью определения
которого служит некоторая область А на плоскости (возможно, вся
плоскость), а областью значений — некоторая область Л' той же
плоскости. Каждая точка А области А характеризуется парой чисел
(х, у), и преобразование Ф сопоставляет с каждой парой чисел
(*, у)(выбранной из некоторой области допустимых значений коор-
координат, характеризующих область А) некоторую новую пару чисел
(х', у') — координаты точки А' = Ф(/4). Другими словами, координаты
(*', у') преобразованной точки А' являются функциями пары чисел х, у:
х' = ц,(х, у), \
у' = Ц(х, у). \ (
Таким образом, задание точечного отображения равносильно зада-
заданию пары числовых функций двух переменных; обратно, каждую
пару функций двух переменных можно представлять себе как
запись определенного отображения'). В частности, формулами ви-
вида A) можно записывать преобразования плоскости.
Выпишем аналитические формулы для некоторых из рассмотренных
выше преобразований. Прежде всего совершенно ясно, что в декар-
•) При этом непрерывным отображениям (см. выше, стр. 60)
отвечают непрерывные функции.

АНАЛИТИЧЕСКАЯ ЗАПИСЬ ГЕОМЕТРИЧЕСКИХ ПРЕОБРАЗОВАНИЙ 73
товой системе координат параллельный перенос записывается сле-
следующим образом:
х =
здесь (х, у)— координаты точки А; (х', у')—координаты преобразо-
преобразованной точки А' и (а, Ь) — координаты постоянного вектора АА' = ММ.'
(вектора переносаI). Далее, симметрия относительно начала коор-
координат О@, 0) записывается формулами:
X '= — X
У—у. I 13>
а симметрия относительно оси х—формулами:
х' = х, \
f—y. i 14)
Обобщением формул C) и D) являются формулы, записывающие
гомотетию с центром О и коэффициентом k:
E>
и формулы, выражающие сжатие к оси х с коэффициентом сжатия А:
при k = — 1 формулы E), F), как и следовало ожичать, переходят
соответственно в формулы C) и D).
Во всех рассмотренных выше случаях функции <р(х, у) и ty{x, у)
(см. A)) имели очень простой вид — они являлись линейными
функциями. В других случаях эти функции оказываются более слож-
сложными; так, например, инверсия с центром в начале координат О и
степенью k записывается формулами:
ky
а гиперболическая инверсия со степенью А (см. стр. 59), осью ко-
которой является ось х,—формулами:
у у
") Ср. ниже, стр. 81.

74 ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
В самом деле, например, формулы G) показывают, что х':у' = х:у,
т. е. что преобразованная точка А' и исходная точка А лежат на
одной прямой с началом координат О и что х'*-\-у'* = г г, т. е.
3.2. Аналитические методы изучения преобразований. Анали-
Аналитическое задание геометрических преобразований позволяет изучать
их свойства методами аналитической геометрии. Докажем, например,
что инверсия переводит каждую окружность или прямую снова
в окружность или прямую. Нетрудно видеть, что уравнение ок-
окружности с центром в начале координат О@, 0) и радиусом г
имеет вид
уравнение окружности с центром в точке Q(a, b) и радиусом г
записывается так:
(х — а)'+(у-Ь)* = г*
или
A(x*+y*) + 2Bx + 2Cy + D = Q, (9)
где
-J- = — а, -?- = — *. ^ = аг+Ь*—гг\ АфО. (9а)
При этом окружность проходит или не проходит через начало коор-
координат в зависимости от того, равен ли коэффициент D уравнения (9)
нулю или отличен от нуля (в первом случае точка с координатами
(О, 0) удовлетворяет уравнению (9), во втором случае — не удовлет-
удовлетворяет). Уравнение (9) охватывает также и прямые линии; прямую
мы получим, положив в эгом уравнении /4 = 0. Если же в уравне-
уравнении (9) и /4=0, и D = 0, то мы будем иметь прямую, проходящую
через начало координат.
Выясним теперь, во что переходит при инверсии геометрическое
место точек, координаты которых удовлетворяют уравнению (9)
(т. е. окружность или прямая). Заметим прежде всего, что форму-
формулы G) можно записать также в следующем виде:
kx >
*" «¦¦+«¦¦' 1
Если подставить в уравнение (9) вместо х и у их выражения из
формул Gа), то получим
Ак2 -+-2Bkx' -t2Lli/ -гL)(x" ±у )—и. (9')

АНАЛИТИЧЕСКАЯ ЗАПИСЬ ГЕОМЕТРИЧЕСКИХ ПРЕОБРАЗОВАНИЙ
75
Отсюда непосредственно следует:
A. Прямая, проходящая через центр инверсии (случай /4 = 0,
D = 0), переходит при инверсии сама в себя;
Б. Прямая, не проходящая через центр инверсии (/4 = 0, пфО),
переходит в окружность, проходящую через центр инверсии;
B. Окружность, проходящая через центр инверсии (А Ф 0,
?> = 0), переходит в прямую, не проходящую через центр инверсии;
Г. Окружность, не проходящая через центр инверсии (АфО,
ВфО), переходит в окружность, также не проходящую через
центр инверсии.
Аналогично этому доказывается, что гиперболическая инверсия (8)
переводит:
A. Прямую у=а, параллельную оси у=0 гиперболической инверсии,— в
прям ю —г = а (или у' = — ), также параллельную оси инверсии;
Б Прямую х=Ь, пер-
перпендикулярную оси инвер-
инверсии,— в ту же прямую;
B. Прямую I с уравне-
уравнением
х = ау-\-Ь (а?ьО), A0)
пересекающую ось у = 0 ин-
инверсии под углом, отличным
от 90°, — в гиперболу
или
, ak
х 7+ь'
(x'—b)y'=ak, AС)
/.'-Ф//1
l'-ФП)
асимптотами которой явля-
являются ось о инверсии и пер-
перпендикуляр q, восставлен-
восставленный ков точке пересечения
прямой I с о (рис. 33; в де-
декартовой системе коорди-
координат с осями о и q уравнение рис 33
A0') записывается в виде
XY = ak\ график этой об-
обратно пропорциональной зависимости является, как известно, гипер-
гиперболой).
Обратно, в прямые линии при гиперболической инверсии переходят пря-
прямые, параллельные и перпеьдикулярные оси о инверсии, и равнобочные
гиперболы A0'), одна из асимптот которых совпадает с осью о инвер-
инверсии; именно этим объясняется прилагательное «гиперболическая» в наз-
названии самого преобразования.
3.3. Линейные преобразования. Иногда аналитическое задание
преобразования кладут в основу его определения. В этих слу-
случаях уже неизбежно приходится выводить геометрические свойства
преобразования из аналитических формул.

76 ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
Рассмотрим следующий пример. Линейными отображениями
плоскости называют отображения, записываемые в какой-либо декар-
декартовой системе координат формулами A), где функции <p(*, у) и
•ф (х, у) линейные:
х = а.
у' = агх + Ь^
:;}
Частными случаями линейных отображений являются, как мы виде-
видели, параллельный перенос B), симметрия относительно точки C)
или относительно прямой D), сжатие к точке (гомотетия) E) или
сжатие к прямой F).
Если в формулах A1) a1 = bl = a2 = fr2 = O, то, очевидно, ото-
отображение переводит все точки плоскости в одну точку (с,, с2). Если
коэффициенты при х и при у в двух уравнениях A1) пропорциональ-
пропорциональны, т. е. a2 = kav bt = Xbl, то при любых х к у имеем
у' = Кх'+с, где с = с,— Kclt A2)
и, значит, все точки плоскости переходят в точки прямой A2) На-
Наконец, если коэффициенты аг; Ь2 не пропорциональны a,, bv т. е.
а,6г — агЬхф0, то уравнения A1) можно переписать в виде
x = alx' + $t/+yl, y=W + P2y'+yt, ЦП
где
а — fcg R _ ~fe» v _ btct—fcgc, \
• а,Ь2-а2Ь, > Р« оЛ-а.Ь. ' Yl 0,6,-0,6,4
1 а,Ь2—a2b, ' Г* щЪг—а2Ъх ' Y* albi—atbl
(для этого достаточно решить уравнения A1) относительно неизвест-
неизвестных х',у'). Таким образом, отображение A1) переводит в каждую точку
(#', у') плоскости единственную точку (*, у) (определенную
по формулам A1')), т. е. является линейным преобразованием.
Покажем, что всякое линейное преобразование переводит каж-
каждую прямую плоскости снова в прямую линию, т. е. является
аффинным преобразованием1). Действительно, для того чтобы найти
линию, в которую преобразование A1) переводит прямую
О, A3)
') Можно доказать, что и, обратно, каждое аффинное преобразование
плоскости является линейным преобразованием, т. е. записывается в коорди-
координатах линейными уравнениями, однако доказательство этого факта довольно
сложно (см., например, Б Н. Делоне и Д. А. Райков, Аналити-
Аналитическая геометрия, ч. I, М.—Л., Гостехиздат, 1948, стр. 152, или И. М. Я г лом
и В. Г. А ш к и н у з е, Идеи и методы аффинной и проективной геометрии,
ч. I, M., Учпедгиз, 1962, стр. 78).

АНАЛИТИЧЕСКАЯ ЗАПИСЬ ГЕОМЕТРИЧЕСКИХ ПРЕОБРАЗОВАНИЙ
77
достаточно подставить в уравнение A3) значения х и у из AГ).
При этом мы получим
(где оба коэффициента /4<
нулю, ибо отображение (И')
тоже является преобразованием
и OjPj — OjPjt^O), т. е. снова
уравнение прямой!
Столь же просто убедиться,
скажем, что линейное преобра-
преобразование сохраняет отношение _
отрезков одной прямой. Дли
этого заметим, что если
.4(х,, уг), В(х2, у2), С(х„ у,),
D(xt, уЛ) — четыре точки од-
одной прямой y = kx-\-b, то
j?~ = — (рис. 64). по точки
дят в точки А'(х[, у[), .... D'(х\, y'J, где
= 0 A3')
и /4C, ' Bft2 не равны одновременно
Ч
Рис. С4.
..., D(xt, yt) nepexo-
a, (*,-
, [ (ft*,+ *) —
= (a,
откуда следует, что
A'B'K2—
AB
C'D'~ Xi-
Предоставляем читателю проверить самостоятельно, что каждое
линейное преобразование плоскости переводит параллельные пря-
прямые снова в параллельные прямые.
3.4. Комплексные координаты точек круговой плоскости.
Поскольку круговая плоскость представляет собой совершенно но-
новое геометрическое понятие, отличное от обычной плоскости, то для
него становятся неприемлемыми принятые способы введения координат,
сопоставляющие с каждой точкой плоскости определенную систему
чисел — координаты этой точки. Тем самым становится невозможным
аналитический подход к инверсии (и другим круговым преобразова-
преобразованиям), рассматриваемой как преобразование круговой плоскости.
Между тем большой интерес, который представляет для геометрии
понятие круговой плоскости, делает весьма важной задачу построения

78 ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
такой системы координат, которая охватывала бы и «бесконечно уда-
удаленную» точку круговой плоскости. Не вдаваясь в детали, мы
наметим здесь один путь решения этой задачи.
Заметим прежде всего, что в качестве координат точки обыкно-
обыкновенной плоскости часто оказывается удобным принимать не пару
чисел х, у, а одно комплексное число z=x± iy («комплексная
координата» точки). В таком случае геометрические преобразования
плоскости будут описываться не парой функций двух переменных
(см. формулы A), стр. 72), а одной, функцией комплексного пере-
переменного1):
z' = F[z). A4)
Расширим теперь область комплексных чисел, присоединив к
«обыкновенным» числам еще одно «идеальное» (несуществующее)
число оо («бесконечность»), определяемое как результат деления
(любого, отличного от нуля) комплексного числа на нуль (невозмож-
(невозможного в области обыкновенных чисел!). Такая «расширенная» ком-
комплексная плоскость по существу совпадает с круговой плоскостью
(причем «идеальное» число оо отвечает «несобственной» точке Q).
Инверсия со степенью k и с центром в точке О, имеющей ком-
комплексную координату 0, аналитически записывается, как мы сейчас
увидим, следующей формулой:
*' = =, A5)
г
где z = x—iy есть комплексное число, сопряженное с числом
z = x-\-iy. Из A5) сразу следует, что центр О инверсии переходит
в «идеальную» точку оо, и наоборот; что же касается отличной от
центра («обыкновенной») точки z = x-\-iy, то она переходит в точку
* ^JLI^j (l5a)
z x + iy .
что и доказывает совпадение преобразования A5) с инверсией (ср.
формулу A5а) с формулами G), стр. 73). Аналогично этому взаимно
однозначными преобразованиями круговой плоскости являются все
преобразования, записываемые дроби о-линейны ми функциями
комплексного переменного
€+^ где ad-ЬсфО, т. е. ± Ф К A6)
cz + d c d
(с, Ь, с, d — комплексные числа). Преобразование A6) переводит
в «бесконечно удаленную» точку Q круговой плоскости точку с ком-
') Ср. ЭЭМ, кн. III, статью «Элементарные функции комплексною
переменного».

АНАЛИТИЧЕСКАЯ ЗАПИСЬ ГЕОМЕТРИЧЕСКИХ ПРЕОБРАЗОВАНИЙ
79
плексной координатой z, определенной равенством cz + d — О, соот-
соответственно cz-\-d = 0 (т. е. с координатой z= или z= 1
и переводит Q в точку z' = — (последнее вытекает из того, что
ь ь
аА а-\- —
г
A6) можно также переписать в виде z' =
или Z =
с+7
2
с+7
«Дробно-линейные преобразования» A6) плоскости комплексного пе-
переменного оказываются тесно связанными с инверсиями1).
3.5. Бирациональные преобразования. С аналитической точки зрения
линейные преобразо ания A1) являются самыми простыми в том
смысле, что здесь функции ф(х, у) и г|) (х, у), фигурирующие в аналитической
записи (I) преобразования, имеют самое
простое строение. Очень удобно также
и то, что в этом случае и координаты
х, у исходной точки ьыражаются через
координаты х', у' преобразованной
точки линейным образом (см. формулы
A1'))- Обобщением таких преобразо-
преобразований являются преобразования, зада-
задаваемые произвольными рациональ-
рациональными (но не обязательно линейными!)
функциями ф и i|) координа1 х и I/
(см. A)), обладающими тем свойством,
что и, обратно, х и у выражаются ч^рез
х' и у' также рационально Прео разо-
вания подобного рода называются бира-
циомальными; в современной геомет-
геометрии они играют весьма важную роль2).
Невырожденные линейные преобразования доставляют простейший пример
бирациональных преобразований. Другими примерами могут служить ин-
инверсия G), гиперболическая инверсия (8) или следующее преобразование:
-IP
\
Рис. S5.
Заметим, что если рассматривать формулы A7) как уравнения с неизвест-
неизвестными х, у и разрешить их, то мы получим в точности такие же формулы,
выражающие хну через к' и у':
У'У+У—1)
' ('
_ г'{х'+у~1)
A7а)
х' (х — 1) + г/ (у -1)
Преобразование A7) имеет любопытный еометрический смысл. Если
соединить произвольную точку А (х, у) плоскости с вершинами 0@, 0),
') Множество преобразозаний A6) круговой плоскости совпадает
с множеством всех круговых пробразований- (ср со статьей «Окружности»,
стр. 478)
!) Понятие бирационального преобразования является основным для
так называ-мой «алгебраической геометрии», выросшей уже в настоящем
столетии в большую и со. .ержательную науку.

80 ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
?i(l, 0), ?2@, 1) «координатного треугольника» О?,?2 и затем симметрично
отразить каждую из прямых АО, АЕХ, Л?2, от биссектрисы соответствую-
соответствующего угла треугольника, то полученные три прямые пересекутся в одной
точке А', координаты х' и у' которой как раз и даются формулами A7)
(рис. 35). Точно так же, если заменить в этом построении треугольник
О?,?2 произвольным треугольником PQR, то мы получим некоторое бира-
циональное преобразование плоскости.
Приведенные примеры указывают, что бирациональные преобразования,
столь важные для высшей геометрии, играют также известную роль и в
геометрии элементарной.
§ 4. Произведение отображений и преобразований
4.1. Определение произведения отображений; примеры. Мы уже
говорили о том, что точечные отображения являются функциями,
отличающимися от привычных нам функций лишь тем, что здесь
и аргумент и само значение функции являются не числом, а точка-
точками. В этом параграфе мы выясним, какой смысл имеет в применении
к отображениям и преобразованиям понятие сложной функции
(функции от функции).
Если у=/(х), a z = g(y), то z также является функцией от
аргумента х:
z = g[f(x)\
(например, если /(х) = а*, g(y)=Y у, ю г=У~ах; если f(x) = sin x,
g(y) — logy, то z = log sin x и т. д.). Аналогично определяется и
«сложное отображение» (отображение от отображения). Именно пусть
Ф — отображение с областью определения Л и областью значений Лх\
пусть, кроме того, задано другое отображение W, областью опреде-
определения которого служит то же точечное множество <АХ, которое
является областью значений для первого отображения. Область
значений отображения W обозначим через Л2. Так как для любой
точки А области Л ее образ А' =Ф(А) принадлежит области At—
области определения преобразования W,—то определена также точка
принадлежащая области А2. Таким образом, с каждой точкой А области
<А сопоставляется точка А" области А2, так что мы получаем неко-
некоторое отображение с областью определения Л и областью значений
Аг. Это отображение, переводящее точку А в А", называют про-
произведением отображений Фи V) и обозначают просто через
(без скобок). Таким образом,
— эта формула является не чем иным, как определением про-
произведения отображений.
*) Иногда также суммой отображений Фи

ПРОИЗВЕДЕНИЕ ОТОБРАЖЕНИЙ И ПРЕОБРАЗОВАНИЙ
81
Если Ф и ^--преобразования с одной и той же областью
действия Л, то их произведение ^Ф также, очевидно, является
преобразованием с той же областью действия А.
Приведем несколько примеров.
1°. Пусть Ф—параллельный перенос на вектор ММ' = а, W —
параллельный перенос на вектор М'М" = Ь, (см. пример 4 на стр.54).
Очевидно, что если АА'#ММ' и А'А"#М'М", то АА"#ММ";
другими словами, если АА'= ММ', А'А" — М'М", то АА"=ММ"
(рис. 36). Таким обрачоч. произведение л?Ф двух параллельных
Рис. 36.
переносов (на вектор ММ' = а и на вектор М'М"=Ь) также пред-
представляет собой параллельный перенос (на вектор ММ" = а-\-Ь)*).
2°. Если Ф есть параллельный перенос на вектор ММ', а !Р —
симметрия относительно точки О, то Ч'Ф представляет собой
симметрию относительно такой точки О,, что 00^=-^ М'М
(рис. 37, а). Это следует из того, что если Ф(А) = А' и ()
=А", то ОО1 есть средняя линия треугольника АА'А", и поэтому
отрезок АА" делится в точке О, пополам (если точки А, А' и О
лежат на одной прямой, то треугольник А А' А" вырождается в отре-
отрезок; проследить, как при этом видоизменяются рассуждения, мы пре-
предоставляем читателю).
Аналогично, если Ф—симметрия относительно точки О, а
W — параллельный перенос на вектор ММ', то WO есть симметрия
относительно такой точки О\, что ОО1 =уЛШ' (рис. 37, б).
') Ср. в этой книге статью «Векторы и их применения в геометрии»,
стр. 295.
6 Энциклопедия, i.f J

82
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ

ПРОИЗВЕДЕНИЕ ОТОБРАЖЕНИЙ И ПРЕОБРАЗОВАНИЙ 83
3°. Пусть Ф—симметрия относительно точки О, a W — сим-
симметрия относительно (другой) точки О, (рис. 38). Ясно, что если
А'—Ф(А), А" = Y(А'), то OOt есть средняя линия треугольника
А А'А" и, следовательно, А А" = 2 00t\ поэтому злегь произведение
Ч'Ф преобразований представляет собой параллельный перенос (на
вектор 2 ОО[).
200,
Рис. 38.
4°. Выясним теперь, что представляет собой произведение двух
симметрии Ф и W относительно прямых I и /,. Здесь следует
различать два случая:
а) Если прямые / и /, параллельны и А' = ф(А), A" = W(A'),
то АА' \J, A'A"\Jt. При этом отрезок АА' делится пополам точ-
точкой Р пересечения его с /; отрезок А'А" делится пополам точкой Q
его пересечения с /,. Отсюда легко усмотреть, что АА" = 2PQ
(рис. 39, а) и, следовательно, произведение УФ есть параллель-
параллельный перенос в направлении, перпендикулярном прямым / и /,, на
расстояние, в два раза большее расстояния между / и /, (вектор
переноса направлен от / к /,).
б) Если прямые / и /, пересекаются в точке О и А'—Ф(А),
A"— W(A'), то, очевидно, ОА' = ОА и ОА" = ОА'; кроме того, лучи
ОА' и ОА образуют равные углы с прямой /, а лучи ОА" и О А' —
с прямой /, (рис. 39, б). Отсюда следует, что ОА" — ОА и что /_АОА"
равен удвоенному углу между прямыми / и /,, т. е. что произведение
УФ npedcmt вляет собой вращение вокруг точки О пересечения
прямых / и /, на угол, равный удвоенному углу между / и /, (на-
(направление вращения — от / к /,).
6*

84
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
>
I
г
С
1
1
I
A*
,—
j
)
o)
Рис. 39

ПРОИЗВЕДЕНИЕ ОТОБРАЖЕНИЙ И ПРЕОБРАЗОВАНИЙ 85
Заметим, что в примерах 3° и 4° мы считали, что центры О и О,
или оси / и /, симметрии Ф и W различны. Можно, однако,
искать и произведение двух симметрии Ф относительно одной и
той же точки О или прямой / (это произведение можно обозначить
через ФФ или через Ф3). Так как симметрия Ф переводит образ А1
каждой точки А обратно в точку Л, то преобразование Ф1 перево-
переводит каждую точку А саму в себя, т. е. не меняет положения ни
одной точки плоскости. Такое «преобразование» I (здесь хотелось
бы говорить об отсутствии всякого преобразования) называется
тождественным преобразованием плоскости; оно анало-
аналогично функции f(x) = x числового переменного х, сопоставляющей
с каждым значением аргумента х то же самое число.
Таким образом, квадрат симметрии относительно точки или
относительно прямой (т. е. произведение двух одинаковых сим-
симметрии) ¦ представляет собой тождественное преобразование (ср.
ниже, стр. 97).
4.2. Некоторые общие свойства произведения преобразований.
Отметим, что, как следует из наших примеров, произведение двух
преобразований (в отличие от произведения чисел), вообще говоря,
существенно зависит от порядка, в котором взяты эти преобра-
преобразования: так, если Ф есть параллельный перенос на вектор ММ' *»= а,
? —симметрия относительно точки О, то WO есть симметрия отно-
сительно такой точки О,, что ООХ = -^- М'М, а ФЧ^—симметрия от-
носительно такой точки Ог, что ООг = -^ММ' (ср. пример 3*, в
частности рис. 37, а, б). Впрочем, это обстоятельство никак не может
нас удивить — ведь произведение преобразований родственно понятию
сложной функции, в которой порядок отдельных функций оказы-
оказывается весьма существенным [совсем не одно и то же, например,
sin2* и sin(x2) или а~х и —ах].
Итак, мы видим, что в отличие от умножения чисел для умно-
умножения геометрических преобразований не выполняется коммута-
коммутативный (переместительный) закон: преобразование Ч?Ф,
вообще говоря, отлично от преобразования ФЧ?. Можно было
бы думать, что также и ассоциативный (сочетательный) закон
обыкновенной арифметики чисел будет нарушаться в «арифметике
преобразований», т. е. что произведения Х(Ч'Ф) и (ХЧ')Ф пре-
преобразований будут различны. Однако легко видеть, что это на самом
деле не так: умножение преобразований всегда ассоциативно.
В самом деле, пусть, скажем, Ф(А)=*АХ, W{Al)=^A1 и
в таком случае, очевидно,

86 ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
с другой стороны,
= А1 и
Таким образом,
для любой точки А. Иначе говоря, каковы бы ни были три пре-
преобразования Ф, f в X, всегда выполнено соотношение
Это последнее преобразование обозначают просто через XWQ) (без
скобок).
4.3. Произведения движений; классификация движений. Рас-
Рассмотренные простые примеры произведений преобразований допускают
интересные и важные приложения. Так, пример 4° может быть исполь-
использован для нахождения произведения параллельного переноса Ф
(на вектор ММ' — а) и вращения W (вокруг точки О на угол а)
или двух вращений Y и х?х (Y,— вращение вокруг точки О, на
угол а,). В самом деле, параллельный перенос Ф можно себе пред-
представить как произведение симметрии 2 и 2, относительно таких
прямых / и /,, перпендикулярных ММ', что расстояние между ними
равно -j MM'; выберем эти прямые так, чтобы /, проходила через
точку О (рис. 40, а). Ан?логично Ч*" представим как произведение
симметрии 2, и 22 относительно пересекающихся в О прямых /, и
/,, угол между которыми равен у а. В таком случае произведе-
произведение WQ сведется к произведению (к последовательному осуществле-
осуществлению) четырех симметрии 2, 2,, 2, и 22 (это можно записать так:
ЧГФ= 2,2,2,2). Воспользовавшись ассоциативностью умножения
преобразований, мы можем записать УФ не в виде B221)B12),
а в виде 22B12,J, отличающемся порядком расстановки скобок.
Но произведение симметрии 2, и 2, представляет собой тождествен-
тождественное преобразование I, не меняющее положения ни одной точки пло-
плоскости; поэтому получаем ЧГФ=222, т. е. WO есть вращение
вокруг точки О, пересечения прямых / и /2 (на угол а).
Аналогично, для того чтобы найти произведение ФЧ*", представим W
в виде произведения двух симметрии 2' и 2, относительно двух
прямых /' и /„ проходящих через О и образующих угол -^-, причем
попрежнему /, _]_ ММ'; далее, Ф представим как произведение двух
симметрии 2, и 22 относительно прямых /, и /2, расстояние между

ПРОИЗВЕДЕНИЕ ОТОБРАЖЕНИЙ И ПРЕОБРАЗОВАНИЙ
87
которыми равно ¦=- ММ' (рис. 40, б). В таком случае мы будем
иметь
и, следовательно, ФЧ*" будет представлять собой вращение вокруг
точки О2 пересечения /' и 1г (на угол а)
Л,
Рис. 40.
Наконец, для того чтобы найти произведение хРгх?1 двух вра-
вращений V, и Чг2 с центрами О, и О, и углами поворота а, и а,,
представим 4х, в виде произведения симметрии относительно двух
прямых, т и Ofit, пересекающихся в точке О, и образующих угол
tj-o,, а W2 — как произведение симметрии относительно прямых Ofi2
и тг, пересекающихся в точке Ot и образующих угол -„-а2. При этом
{?iWl представится как произведение симметрии относительно га,
и т2, откуда следует, что преобразование YjY, совпадает с вра-
вращением вокруг точки Q пересечения /», и тг (на угол а,

88
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗО ВАНИЯ
см. рис. 41, а). Исключение здесь
= А-360°, т. е. ^+^
представляет случай, когда
где k— целие число
(рис. 41, б); в этом случае
+^ = А:-180
сршче т1 и тг будут параллельны и,
следовательно, преобра-
преобразование Ч?^, является
параллельным пе-
переносом.
До сих пор мы гово-
говорили исключительно о
произведениях движе-
движений. Заметим, что из
сказанного выше нетрудно
вывести полную класси-
классификацию всех движений
плоскости. Ясно, что ка-
каждое движение плоскости
полностью характеризу-
характеризуется тем, в какие точки
А', ?', С" перешли какие-
то три точки А, В, С
плоскости, не принадле-
принадлежащие одной прямой: в
самом деле, при этом про-
произвольная точка М пло-
плоскости перейдет в такую
точку М', что расстояния
М'А',М'В' иМ'С соот-
соответственно равны рассто-
расстояниям MA, MB и МС, а
такая точка есть только одна'). Но очевидно, что точки А, В, С
можно совместить с точками А', В', С' при помощи самое большее трех
Рис.
') Условия М'А'^МА, М'В'^МВ определяют на плоскости две
точки ЛГ и М". находящиеся иа рази ых расстояниях от точки С
N - д в'
Рис. 42.
(ибо С ие лежит на прямой А'В'). Поэтому третье условие М'С'--
од но иачио определяет точку М' (pni~ 42).
-МС

ПРОИЗВЕДЕНИЕ ОТОБРАЖЕНИЙ И
___4--4
симметрии относительно некоторых прямых. В самом деле, если точка А
отлична от А', то мы совмещаем эти две точки симметрией 2, относи-
относительно перпендикуляра /,, восставленного к отрезку АА' в его середине;
треугольник ABC перейдет при симметрии 2, в треугольник A'BtCt
(рис. 43). Далее, если точка 5, ==2, (В) не совпадает с В', то мы
совмещаем ее с В' симметрией 2, относительно перпендикуляра lt,
восставленного к ВХВ' в его середине (заметим, что прямая /2 про-
проходит через точку А', ибо ,
А'К = АВ= А'Вх, и, еле- I \ B
довательно, 2, (А') = А').
Если полученный из А'Bfix
с помощью с им ме то ни 22
треугольник А'В'Сг не
совпадает с треугольни-
треугольником А'В'С', то он симмет-
симметричен ему относительн
прямой А 'В' и потому
может быть совмещен с
треугольником А'В'С' при
помощи еще одной сим-
симметрии 25 относительно
прямой А'В'=1, (рис.43). Рис. 43.
Итак, любые два равных
треугольника могут быть совмещены самое большее тремя симмет-
риями относительно прямых, откуда вытекает (см. пример 4°, стр. 83),
что каждое движение плоскости представляет собой либо сим-
симметрию относительно прямой, либо параллельный перенос, либо
вращение вокруг точки (которое, в частности, может оказаться
симметрией относительно точки), либо, наконец, параллельный
перенос или вращение, сопровождаемые еще одной симметрией
относительно прямой г).
4.4. Применения. Полученные результаты могут быть использованы
для решения многочисленных задач на построение и на доказательство.
Рассмотрим, например, задачу о построении многсугольнию А^А2 . . . Ап
по заданным вершинам Qlt Q2,. . . , Qn равш бедренных треугольников с из-
известными углами а,, а2, ..., а„ при вершинах, построенных на его сторо-
сторонах (рис. 44) Эта задача охватывает широко известные задачи о пост-
построении треугольника по центрам построенных на его сторонах квадратов
') Произведение трех симметрии относительно прямой всегда мо-
может быть представлено в виде так называемой скользящей симметрии,
т. е. произведения симметрии относительно некоторой прямой и парал-
параллельного переноса в направлении этой же прямой (см. книги
И. М. Яг л ома [2] и Д. И. П е р е п е л к и н а, [3] указанные б конце
статьи). Итак, каждое движение плоскости является либо параллельным пере-
переносом, либо вращением, либо скользящей симметрией (частным случаем сколь-
вящей симметрии является обычная симметрия относительно прямой).

90
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
(n = 3, а, = а2 = а3 = 90°), или о построении треугольника по вершинам
построенных на его сторонах правильных треугольников (л = 3,
а, = а2=а3 = 60°), или о построении многоугольиика по известным
серединам сторон (л произюльно, а,=а2=... =ап= 180°) . т. д.
Для решения этой задачи заметим, что последовательное применение
вращений В„ В2, .... Вп с центрами Q,, Q8 Qn соответственно на
углы а„ а2, .., ап переводит: сначала точку Ах в Аг, затем в As, ...
и, наконец, Ап обратно в А, (рис. 44). Таким образом, точка At про-
произведением В„ВП_,.. .В2В, рассматриваемых вращений оставляет-
оставляется на месте. Но из доказанных выше теорем следует, что произ-
произведение В = ВП. ..В2В, вращений представляет собой вращение на
угол а, + а2+ ... +а„; центр этого «результирующего» вращения В легко
найти, если последовательно заменить произведение i ращений В, и В2
одним вращением (или парал-
параллельным переносом) В11>; затем
произведение преобразованийВ11'
и В,—одним преобразованием ВA)
и т. д. Но ясно, что единственная
точка, которую оставляет на ме-
месте вращение (на угол, отличный
от k-360°!), есть центр этого вра-
вращения; следовательно, искомая
вершина At многоугольника совпа-
совпадает с центром Q результирующего
вращения В и потому может быть
построена. Далее, ясно, что, зная
точку At (а также точки Q,, Q2,
..., Qn и углы а„ а а„), мы
легко построим и весь л-угольник.
Это рассуждение оказывается
непригодным в одном исключи-
исключительном случае: если сумма
ai +«2+ •-•+ап углов поворота
кратна 360°. В этом случае мы вообще не можем задать произвольным образом
вершины Q,, Q2 Qn построенных на сторонах многоугольника треуголь-
треугольников— ведь произведение вращений В,, В2, ...,В„на углы а,, а2, .. ,ап
(гдеа,+а2+ ... +а„ = А:-360о) является параллельным переносом, который,
вообще говоря (если вектор переноса ?=0), не оставляет на месте ни одной
точки плоскости! Таким образом, как правило, соответствующая задача
на построение при а,+а2+.. .+an = fc-360° не будет иметь решений.
Лишь при некоторых специальных расположениях точек Q,, <22, ..., Qn
результирующее преобразование В = ВП...В2В, явится «паралл. льным пере-
переносом иа нулевое расстояние», т. е. будет тождественным преобразованием
и задача окажется разрешимой. Однако при этом оиа будет иметь даже
«слишком много решений» (т. е. будет неопределенна)—любую точку
плоскости можно будет принять за вершину Л, искомого л-угольника,
ибо тождественное преобразование оставляет на месте все точки плоскости!
Поэтому и здесь задача на построение оказывается неинтересной; содер-
содержательной же является «задача на доказательство», требующая установить
возможный характер конфигурации (расположения на плоскости) то-
точек Q,, Q , Qn, отвечающих реально существующему п-уголь-
нику AtA2...An.
Сказанное хорошо иллюстрируется уже упоминавшейся задачей о по-
построении п-угольника АхАг...Ап по серединам Q,, Qt Qn его сто-
сторон. В условии этой задачи на построение всегда добавляют, что рассмат-
рассматриваемый многоугольник имеет нечетное число n = 2k-\-\ сторон. В этом
Рис. 44.

ПРОИЗВЕДЕНИЕ ОТОБРАЖЕНИЙ И ПРЕОБРАЗОВАНИЙ
91
Рис. 45.
случае а, + а2-^ ... +а„ = BА: + 1)-180° и результирующее преобразование
является вращением на угол BА:+1)-180°, т. е. вращением на 180°, или,
иначе, симметрией относительно некоторой точки; центр Q этой сим-
симметрии (т. е. вершину Л, многоугольника!) легко найти, если воспользо-
воспользоваться содержанием примеров 1°—3°
(стр. 81—83). Если же n = 2k четно,
преобразование В = В„ВП_,.. .В, будет
параллельным переносом (либо тожде-
тождественным преобразованием). Поэтому
середины Q,, Q2, ..., Qn сторон
2&-угольника AxA2...An не могут быть
выбраны произвольно; так. например,
хорошо известно, что при п = 4 эти
точки (середины сторон произвольного
четырехугольника) всегда являются вер-
вершинами параллелограмма') (рис. 45).
Совершенно ясно, с чем это свя-
связано: произведение симметрии 2, и
22 относительно точек Qt и Q2 пред-
представляет собой параллельный перенос П, иа вектор 2Q^Qt (см. пример 3е
на стр. 81—83), а произведение симметрии 2а и 24 относительно точек Q3 и Qt
представляет собой параллельный перенос П2 на вектор 2Q^Qt; поэтому
лишь в случае, если QiQi^=Q1Qt (т. е. если четырехугольник QtQtQaQt—
параллелограмм!), произведение
SjZ^Z, = П2П, четырех симметрии
будет тождественным преобразова-
преобразованием (т. е. задача построения четы-
четырехугольника по серединам его сто-
сторон будет разрешимой.
Вот еще две задачи подобного
рода: что можно сказать о центрах
правильных треугольников, построен-
построенных на сторонах произвольного тре-
угольн 1ка, или о центрах квадратов,
построенных на сторонах произволь-
произвольного четырехугольника (для опреде-
определенности мы считаем, что правильные
треугольники и квадраты построены
вне исходного многоугольника)?
В первом случае искомые три точки
Ri, R2 и /?3 обладают тем свойством,
что произведение вращений В,. В2,
В3 вокруг этих точек на угол 120°
представляет собой тождественное
преобразование (ибо 3-120° = 360°).
Но произведение В2В, первых двух вращений представляет собой вращение В
на угол 240° вокруг точки ft, в которой пересекаются проведенные через ft,
120°
и /?2 прямые, образующие с прямой ft,ft2 углы -—- = 60° (рис. 46; см. выше
стр. 83). Ясно, что произведение вращений В и В, вокруг точек R и
fts на углы 240° и 120° в том и только в том случае явится тождественным
преобразованием, если точка ft, совпадает с ft Таким образом, мы заклю-
6.
Ср. стр. 315 этой книги ЭЭМ.

92
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
чаем, что прямые R,RS и R2RS образуют с R,R2 углы в 60° или что (неза-
(независимо от формы исходного треугольника Л,Л2Ла1) треугольник /?,/?2/?,
правильный.
Во втором случае (рис. 47) центры 7\, Т2, Ta, 71, квадратов должны
быть таковы, что произведение BjB3B2B, вращений вокруг этих точек на
угол 90° представляет собой' тождественное преобразование. Но произве-
произведение В2В, вращений вокруг Т, и Т2 есть не что иное, как симметрия
(вращение на угол 180°) 2, относительно точки U пересечения прямых,
90е
проведенных через 71, и через Тж под углами -^- = 45° к прямой TtTv
Аналогично произведение BiBi вра-
вращений вокруг Т, и 7\ представляет
собой симметрию 22 относительно
такой точки V, что прямые T,V и TtV
образуют углы 45е с прямой T,Tt.
Но ясно, что произведение симмет-
симметрии 222, тогда и только тогда пред-
представляет собой тождественное прео-
преобразование, когда точки U и V совпа-
совпадают. Из совпадения точек U и V в
свою очередь следует, что треуголь-
треугольник 1)ТгТц получается из треуголь-
треугольника UTjTi вращением вокруг точки
U ^ V на 90°, т. е. что отрезки 7\Г, и
ТгТц равны по длине и взаимно перпен-
перпендикулярны. Заметим, что и обратно,
если четыре точки 71,, Т., Тг, ТЛ та-
таковы, что T1T, = TfTi и f,T,±TtTt,
то вершины О и V равнобедренных
прямоугольных треугольниковTlTJJ
и TaTtV совпадут, так что существует
четырехугольник AtA2AsAt, для ко-
которого 71,, Т2, 71,, Т,—центры постро-
построенных иа его сторонах квадратов.
Такимобразом, условия Т,Тг*=Т2ТЛ,
j полностью характеризуют четырехугольники ТГТ2Т3ТЛ, отве-
отвечающие всевозможным четырехугольникам Л,Л2ЛаЛ4.
4.5. Дальнейшие примеры произведения преобразований.
Мы не будем останавливаться здесь столь же подробно на вопросе
о произведении преобразований подобия. Заметим
лишь, что проведенная нами классификация движений
(т. е. перечисление всех возможных типов движений) моментально
приводит и к классификации преобразований подобия,
ибо очевидно, что преобразование подобия П с коэффициентом
подобия k можно представить как произведение (какой угодно!)
гомотетии Г с коэффициентом k и последующего движения А.
В самом деле, если П=ДГ, где А—какое-то преобразование, то
поскольку и гомотетия Г и исходное преобразование подобия П
изменяют все расстоянии в k раз, то преобразование А уже
не меняет расстояний между точками, т. е. является движением.
Таким образом, в определенном смысле все преобразования подобия
Рпс. 47.

ПРОИЗВЕДЕНИЕ ОТОБРАЖЕНИЙ И ПРЕОБРАЗОВАНИЙ 93
сводятся к гомотетии (сжатию к точке). Можно также показать,
что (в аналогичном смысле) все аффинные преобразования сводятся
к сжатию к прямой; более точно, каждое аффинное преобразова-
преобразование А можно представить в виде произведения ПА, где Л есть
сжатие к прямой I, а П — преобразование подобия. Аналогично,
любое круговое преобразование плоскости сводится к инверсии',
каждое круговое преобразование К представляет собой произве-
произведение Пй анверсии Q и преобразования подобия П. Доказатель-
Доказательства этих довольно сложных теорем мы опустим ').
В заключение приведем еще три примера произведений преобра-
преобразований, отличных от движений.
5°. Пусть Ф, есть гомотетия с центром О, и коэффициен-
коэффициентом kv а Ф,—гомотетия с центром 0г и коэффициентом kt.
Выберем на плоскости произвольные точки А и В и положим
Ф1(Л) = /4',Ф2(Л') = /4*, Ф,E) = 5', Ф2 (?')=?". Так как А'В' || АВ
и А В" || А'В', то А'В" || АВ (причем отрезок А"В" направлен в ту же
сторону, что и АВ, если оба числа kl и kt положительны или оба
отрицательны, и направлен противоположно АВ в противном случае);
А'В' А'В" А" В"
так как, далее, -^- = \1гЛ и JrB7=x^k^' то ~Ш==\ kl '* I k* I-
Отсюда следует, что при fe1fe1= 1 преобразование Ф1Ф1 представляет
собой параллельный перенос на вектор АА" (рис. 48, а; в этом
случае для любой точки В имеем ВВ"#АА"); при kxkx=f*\ преобра-
преобразование Ф2Ф, представляет собой гомотетию с коэффициентом ktkt
(рис. 48, б; в этом случае, какова бы ни была точка В, прямая В"В
л'л « о ОА" А"В" ОВ" ,. . \
пересекает А А в такой точке О, что пТ~~Ш'=:ов'==\ l A I '
Заметим еще, что если Ф^1 есть параллельный перенос, то
его направление параллельно прямой Ofij если же Ф2Ф, есть
гомотетия, то ее центр О лежит на прямой Oftt. Это следует
из того, что оба преобразования Ф, и Ф1 переводят прямую Ofix
в себя; следовательно, эту прямую оставляет на месте также преоб-
преобразование (гомотетия или параллельный перенос) Ф2Ф,. Но гомотетия
переводит в себя лишь прямые, проходящие через ее центр, а парал-
параллельный перенос—лишь прямые, направление которых совпадает
с направлением переноса. Отсюда вытекает, в частности, известная
теорема о трех центрах гомотетии: центры гомотетии
трех попарно гомотетичных фигур лежат на одной прямой,
называемой осью гомотетии (рис. 48, б).
Интересно отметить частный случай последнего предложения,
к которому мы приходим, если рассматриваемые фигуры являются
окружностями. Известно, что две (не равные) окружности St, St
') См., например, книги Б. Н. Делоне и Д. А. Райкова или
И. М. Яглома и В. Г. Ашкинузе, указанные в сноске ') на стр. 76,
а также § 5 гл. I статьи «Окружности», стр. 476—478.

94
ГЕОМЕТРИЧЕСКИЙ 11НЕОБРАЗ JBAHHH
имеют два центра гомотетии, совпадающих в случае окружностей,
леж°щих одна вне другой, с точками пересечения их общих внешних
и внутренних касательных \pvc. 49V Отсюда вытек 1ет, в силу дока-
занной выше теоремы, что три точки пересечения общих внешних
касательных (т. е. три внешних центра подобия) трех попарно не-
неравных окружностей лежат на одной прямой. Можно взять и другие
комбинации внешних и внутренних центров подобия: шесть попарных

ПРОИЗВЕДЕНИЕ ОТОБРАЖЕНИЙ И ПРЕОБРАЗОВАНИЙ
95
Рис. 49.

96 ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
центров подобия трех (попарно не равных) окружностей лежат
по три на четырех прямых (осях подобия рассматриваемых
трех окружностей, рис. 49).
6°. Пусть Ф,—инверсия с центром О и степенью kx, Фг — инвер-
инверсия с тем же центром О и (иной) степенью kt. В таком случае,
если Ф1(А) = А' и Ф(А') = А", то точка А" лежит на прямой ОА
{ибо А' лежит на прямой ОА, а А" — на прямой ОА') и ягд-=т*
ибо 0Л' = ^-, а 0А" = {г*п). Отсюда, как может показаться, сле-
сле(
дует, что преобразование Ф,Ф, совпадает с гомотетией Г с цент-
центром О и коэффициентом -?-. Однако надо иметь в виду, что пре-

образование Ф2Ф, хотя и очень близко к гомотетии Г, но отличается
от Г областью действия: областью действия гомотетии Г является
плоскость, а областью действия преобразования Ф2Ф, — либо плоскость
с исключенной точкой О (не входящей в область определения обоих
преобразований ф, и Фг), либо «расширенная» (круговая) плоскость.
Т. Совершенно так же показывается, что произведение YjY, гиперболи-
гиперболических инверсий Y, и Чг с одной и той же осью о и (разными) степенями А,
и kt отличается от сжатия к прямой о с коэффициентом -?¦ лишь тем, что
к,
областью определения преобразования xP2Wl является не вся плоскость,
а плоскость с выброшенной прямой о (или плоскость, надлежащим обра-
образом дополненная «несобственными» элементами).
§ 5. Обратное преобразование
5.1. Определение обратного преобразования. После того как мы
перевели на язык геометрических преобразований понятие сложной
функции, естественно вспомнить и о понятии обратной функ-
функции. Известно, что две функции f(x) и g(x) называются взаимно
обратными, если из того, что f(x) — y, следует g(y) — x; так,
например, взаимно обратными являются функции f(x) = x* и
g(x)=V х, или f(x) = ax и g(x)=logax, или f(x)=sinx и g{x) =
=arcsmje. Иногда для обратной функции употребляется еще сле-
следующее обозначение: функция, обратная для f(x), записывается как
f'1 (х); так, вместо aRSinje в старину зачастую писали sin~\x;,
а в английских учебниках и теперь пишут так. Важно заметить,
что функцию, обратную для функции f(x), можно определить
только в том случае, если ни при каких двух разных значе-
значениях х функция f(x) не принимает одинакового значения у;
именно поэтому при определении функции, обратной функции хг
или sin л; приходится ограничивать область изменения х условиями
соответственно —у^

ОБРАТНОЕ ПРЕОБРАЗОВАНИЕ 97
Заменив теперь х и у в определении обратной функции точ-
точками (при stom роль самой функции будет играть геометрическое
отображение), мы придем к понятию обратного отображения.
Пусть Ф— некоторое взаимно однозначное отображение с областью
определения Л и областью значений Л'. Тогда, как мы знаем, для
любой точки А' области значений Л' найдется ровно одна
точка А области Л, для которой Ф(А) = А' (ого и есть определение
взаимно однозначного отображения). Эту точку А называют
прообразом точки А' при отображении Ф и обозначают симво-
символом Ф~1(А'). Таким образом, с каждой точкой А' области Л' cohoctjb-
ляется определенная точка /4 = ф~'(Л') области Л. Тем самым
мы приходим к новому отображению Ф с обл_1сгью определения Л'
и областью значений Л- Это отображение и называется обратным
для отображения Ф. Так, например, функция у = sinх осуществляет
взаимно однозначное отображение отрезка Л= — у, у действи-
действительной оси на отрезок </?'=[—1, 1]. Поэтому определено обрат-
обратное отображение отрезка А' на отрезок А; это обратное отображе-
отображение обозначается символом arcsin.
В геометрии особенно интересен случай, когда Ф есть преобразо-
преобразование с областью действия Л. Так как Ф взаимно однозначно, го
определено обратное отображение Ф", которое, очевидно, также
является преобразованием с той же областью действия Л. Это пре-
преобразование Ф~' называется обратным преобразованием для пре-
преобразования Ф. Так, например, обратным для параллельного переноса
на вектор ММ' является перенос на (противоположный!) вектор М'М
(ибо если АА'= ММ', то А'А=М'М); обратной для гомотетии
с центром О и коэффициентом k является гомотетия с тем же цент-
центром О и коэффициентом -г- (если —- = /г, то 7ухг — -ь) > обратным
для сжатия к прямой о с коэффициентом k является сжатие к той же
прямой с коэффициентом -j-.
5.2. Инволюции. Особую роль в геометрии играют такие преобразова-
преобразования, которые обрати ы сами себе (другими словами, такие преобра-
преобразования Ф, которые «меняют местами» пары точек: если Ф (Л) = Л\ то
ф (А') = А). Примерами таких преобразований являются' симметрия отно-
относительно точки, симметрия относительно прямой, инверсия (в частности,
симметрия относительно окружности; см. стр. 56), гиперболическая инвер-
инверсия (в частности, симметрия относительно пары параллельных прямых;
см. стр 59). Такие преобразования называют инволютивными преобразова-
преобразованиями или инволюциями ') (ино да их называют также симметриями).
') Латинский термин involutio означает скрученное состояние молодых
листьев. Это — единственный термин, оставшийся в геометрии от замеча-
течьного математика XVII в., создателя проективной геометрии Ж- Д е-
за р га, использовавшего в своем трактате массу новых терминов, как пра-
правило заимствованных из ботаники.
7 Энциклопедия, кн. 4

98 ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
Взаимно обратные преобразования Ф и Ф~* можно определить еще
как такие, произведение которых, взятых в любом порядке, представляет
собой тождественное преобразование (их общей области действия). В част-
частности, тождественным преобразованием является «квадрат» Фг любого инво-
лютивного преобразования Ф. В самом деле, преобразования Ф и ф-1
таковы, что из Ф(А) = А' следует ф-1 (А') = А, и поэтому
Фф-1(А')=Ф{А) = А', Ф-'Ф(/1)=Ф-1(Л') = Л,
т. е. ни преобразование Ф~'Ф, ни преобразование ФФ не меняют поло-
положения точек в их общей области действия Л.
§ 6. Общее определение геометрии.
Группы геометрических преобразований
6.1. Предмет 1еометрии. Учение о геометрических преобразова-
преобразованиях сыграло важную роль в оформлении наших взглядов на сам
предмет геометрии. Оно лежит в основе одного из самых распростра-
распространенных общих определений геометрии, позволяющего разобраться
в сущности сходства и огличий между различными ветвями этой
обширной математической дисциплины. Для того чтобы прийти к по-
подобному определению «геометрии», понимаемой в широком смысле
этого слова, нам надо будет прежде всего остановиться на вопросе
о содержании обычной геометрии Евклида.
В средней школе говорят, что предметом геометрии является
изучение свойств геометрических фигур. При этом «.геометрическую
фигуру» можно описать как какую-то совокупность точек; труднее
ответить на вопрос о «свойствах», которые интересуют геометра.
Ясно, что здесь речь идет не о всех вообще свойствах, какие только
можно придумать; гак, цвет фигуры, вопрос о том, начерчен ли тре-
треугольник белым по черному (мелом на доске) или черным по белому
(карандашом в тетради) вовсе не рассматривается на уроках геомет-
геометрии. Поэтому, для того чтобы уточнить данное выше описание
геометрии, необходимо уяснить себе, чем характеризуются геомет-
геометрические свойства фигур.
Для того чтобы ответить на этот вопрос, обратимся к тем
задачам, которые решаются в геометрии, прежде всего к задачам на
построение, являющимся типичными для этого предмета. Из школь-
школьного курса хорошо известно, что для того, чтобы задача на пост-
построение треугольника имела определенное решение (возможно, не-
несколько решений, скажем, два или четыре), надо задать три незави-
независимых элемента треугольника, например три стороны или две стороны
и угол; два элемента, вообще говоря, определяют бесконечно много
треугольников, а четыре произвольно заданных элемента — ни одного.
Однако утверждение о том, что существует единственный
треугольник с за чанными длинами п, h, с сторон, строго говоря,
не верно: на самом деле таких треугольников можно найти беско-

ГРУППЫ ГЕОМЕТРИЧЕСКИХ ПРЕОБРАЗОВАНИЙ 99
нечно много, но все эти треугольники буду г между собой равны1)
(рис. 50). И когда мы говорим, что задача построения треугольника
по трем сторонам имеет единственное решение, мы только под-
подчеркиваем этим, что все треугольники со сторонами а, Ь, с будут
одинаковыми, равными.
Но что означает в геометрии слово «равные»? Под «равными» фи-
фигурами мы понимаем такие две фигуры Fx и Ft, которые отличаются
друг от друга только положением (не формой и не размерами!), т. е.,
другими словами, равными считаются две фигуры, одна из которых
может быть переведена в другую с помощью некоторого движения
(ср. выше, стр. 60). И если в геометрии треугольники (или другие
фигуры), получающиеся друг из друга движением, считаются одинако-
Рис 50.
выми, т. е. не различаются между собой, то это значит, что и все свой-
свойства у этих треугольников (фигур) будут одними и теми же. Таким
образом, мы видим, что рассматриваемые в геометрии свойства фигур —
э го те свойства, которые не зависят от положения фигуры, т. е.
не изменяются при ее движении: геометрия изучает свойства
фигур, сохраняющиеся при движении фигуры.
Вспомним, что движения мы определили как такие геометрические
преобразования, которые сохраняют расстояния между любыми двумя
точками (см. стр. 60); это соответствует тому, что у равных фигур
отвечающие друг другу отрезки одинаковы *) (так, у равных треуголь-
') Ср текст на стр. 296—297 этой книги ЭЭМ.
2) Более точная формулировка заключается в следующем. Пусть Ft
и F2—две равные фигуры; тогда существует движение Ф, переводящее
фигуру Ft в F2, т. е. F2 — O(Fl). Точку Аг фигуры F2 называют соответ-
соответствующей точке А, фигуры f,, если А2 = Ф{А1). Из определения движения
следует, что расстояние между любыми двумя точками А, и В, фигуры Ft
равно расстоянию между соответствующими им точками А2=Ф(АХ\ и
В„ = Ф(В.) фигуры /v
ЛИЛА

100 ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИИ
ников будут равны не только стороны, но и соответствующие бис-
биссектрисы, медианы, высоты и т. д.). Сформулированное выше опреде-
определение геометрии можно теперь перефразировать так: геометрия изу-
изучает свойства фигур, сохраняющиеся при таких преобразованиях,
которые не меняют расстояний между точками.
Такое определение геометрии создает впечатление, что пер-
первыми, самыми главными свойствами геометрической фигуры, являются
расстояния между ее точками. Но на самом деле это не так — поня-
понятие расстояния между точками (длины отрезка) вообще не фигури-
фигурирует (и не может фигурировать!) ни в одной геометрической теореме.
В самом деле, длина отрезка определяется сравнением его с неко-
некоторым фиксированным раз навсегда отрезком, называемым едини-
единицей длины; поэтому утверждение (в условии или в доказательстве
какой-либо теоремы) о том, что определенный отрезок равен, скажем,
двум, означает, что в этом отрезке два раза -укладывается отрезок,
принятый за единицу длины. Таким образом, это утверждение
привлекает к рассмотрению единичный отрезок, а между тем все
отрезки с точки зрения геометра совершенно равноправны и, оста-
оставаясь в рамках собственно геометрии, нет никакой возможности
отделить какой-нибудь из них для того, чтобы принять его за еди-
единичный! Именно поэтому все определения единицы длины апелируют
к понятиям, которые никак нельзя отнести к геометрии: так, метр
определялся как расстояние между двумя отметками на платиново-
иридиевом эталоне метра, хранящемся в Парижском институте мер
и весов, или, несколько менее точно, как одна 40 000 000-я часть
парижского меридиана Земли (ср. с «чисто геометрическим» опре-
определением прямого угла как такого, который равен своему смежному,
или угла в 1 радиан, определяемого равенством отвечающей ему дуги
окружности радиусу окружности). Поэтому ни в одной геометрической
теореме не может участвовать длина какого-нибудь отрезка, а лишь от-
отношение длин двух отрезков, не зависящее от выбора единицы
длины (например теорема о соотношении между углами и сторонами
треугольника утверждает, что если /_А>/_В. то -т->1, а теорема
т
о прямоугольном треугольнике с углом в 30° — что если в треуголь-
треугольнике ЛЯС мы имеем /_А = 90° и ^5=30°, то | = \
Все эти соображения заставляют нас считать, что правильнее
охарактеризовать (евклидову) геометрию как науку, изучающую
свойства фигур, сохраняющиеся при преобразованиях, не ме-
меняющих отношений расстояний между точками, т. е.
при преобразованиях подобия (см. стр. 61). Но такое опреде-
определение, справедливость которого была мотивирована лишь рассужде-
рассуждениями, относящимися к геометрическим теоремам, перестает быть
верным при переходе к задачам на построение. В самом деле,

ГРУППЫ ГЕОМЕТРИЧЕСКИХ ПРЕОБРАЗОВАНИЙ 101
в этих задачах длина отрезка задается не числом, выражающим
отношение рассматриваемого отрезка к единице длины, а геометри-
геометрически— указанием отрезка, равного интересующему нас (ср. рис. 50).
Поэтому, если в геометрических теоремах подобные фигуры можно
считать «одинаковыми», обладающими одними и теми же геомет-
геометрическими свойствами, то в задаче на построение треуголь-
треугольник i41B1C1, все стороны которого в два раза больше сторон данного
треугольника ABC, будет уж существенно отличаться от ABC—
лишь один из этих двух треугольников может доставлять решение
задачи на построение треугольника, но никак не оба сразу!
Создавшееся положение может первоначально показаться довольно
неожиданным. Нам приходится считать, что при решении задачи на
построение и при доказательстве теоремы мы имеем дело с двумя
разными определениями предмета геометрии и, следовательно,
с двумя разными (хоть и очень близкими одна к другой!) «геомет-
«геометриями». Это положение вынуждает нас дать геометрии новое опре-
определение, которое охватило бы оба определения, к которым мы
пришли выше: лишь имея подобное «общее» определение, мы сможем
считать, что геометрия представляет собой единую науку, а не две раз-
разные науки, которым лишь по ошибке присвоено одинаковое название.
6.2. Геометрия и группы преобразований. Нетрудно понять,
как можно объединить наши два определения геометрии. Вместо
движений или преобразований подобия мы будем говорить о какой-то
совокупности © геометрических преобразований,
не уточняя, о каких именно преобразованиях идет речь; «равными»,
т. е. обладающими одинаковыми свойствами, мы объявим те фигуры,
которые переводятся одна в другую каким-либо преобразованием
из совокупности ©. При этом мы придем к определению геометрии
как науки, изучающей свойства фигур, сохраняющиеся при преоб-
преобразованиях из заданной совокупности © преобразований.
Однако если определение геометрии как науки, изучающей
свойства фигур, сохраняющиеся при движениях, является слишком
узким, то последнее определение геометрии является уже слишком
широким, и в силу этого также неудовлетворительным. В самом деле,
согласно этому определению мы считаем «равными» две такие
фигуры Fx и Ft, что одну из них можно перевести в другую неко-
некоторым преобразованием из совокупности ©. Но для того, чтобы но-
новое понятие «равенства» не расходилось со старым очень уж далеко,
естественно потребовать выполнения следующих трех свойств, кото-
которые выполняются абсолютно для всех типов «равенства», с которыми
мы встречаемся в математике и в жизни ') (равенства чисел, алгеб-
алгебраических выражений, векторов, геометрических фигур, физических
характеристик как сил или скоростей, равенства способностей,
') Ср. текст на стр. 296—297 этой книги ЭЭМ.

102 ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
успехов, художественных достоинств двух произведений искус-
искусства и т. д.):
1 °. Каждая фигура F «равна» сама себе (рефлексивность).
2°. Если фигура F1 «равна» фигуре Ft, то и обратно, Ft
ч.равнаг> Ft (симметричность).
3°. Если фигура Ft «равна» Ft, a Ft «равна» Ft. то и Fl
«равна» Ft (транзитивность).
Ясно, что в случае совершенно произвольной совокупности ®
преобразований «равенство», определенное с помощью этой совокуп-
совокупности, можег и не обладать свойствами 1°—3°. Для того чтобы
обеспечить выполнение этих трех свойств, естественно потребовать,
чтобы:
1°. Совокупность преобразований (Ч содержала тождественное
преобразование 1, переводящее всякую фигуру саму в себя.
2°. Наряду с каждым преобразованием Ф. переводящим
фигуру F, в фигуру Рг, совокупность № содержала и обратное
преобразование Ф~', переводящее фигуру Ft в фигуру Fx.
3°. Наряду с каждыми двумя преобразованиями Фи ?, пере-
переводящими фигуру Fx в фигуру Ft, соответственно фигуру Ft —
в фигуру Рг, совокупность $ содержала и произведение ЧМ> этих
двух преобразований, переводящее Fx в F,.
Совокупность преобразований, удовлетворяющая свойствам 1°—3°,
называется группой преобразований1). Таким образом, мы приходим
к следующему общему определению геометрии, впервые сф >рмули-
рованному известным немецким математиком Феликсом Клейном в лек-
лекции, которую он прочитал при вступлении на профессорскую кафедру
университета в г. ^рлангене (Германия) *) и которая впоследствии
получила название Эрлангенской программы Клейна*):
Геометрия — это наука, изучающая свойства фигур, сохраняю-
сохраняющиеся при преобразованиях некоторой группы ($ преобразований.
6.3. Различные геометрии. Аффинная геометрия. И» приведен-
приведенного выше определения геометрии вытекает, что можно построить очень
') Ср. также стр. 27—28 этой книги ЭЭН.
*) В Германии долгое время существовал обычай, согласно которому
кандидат на замещение профессорской должности должен быт выступить
перед Ученым советом с лекцией на своботнп (ыбтчнную им тему; на осно-
основании этой лекции Ученый совет делал заключение о во;можности допущения
данного лица к профессуре.
В 1854 г. другой выдающийся немецкий математик Бернгард Р и м а н
точно так же выступил перед Ученым советом Гетингенского университета
с лекцией «О гипотезах, лежащих в основании геометрии», в которой изло-
изложил свою концепцию геометрии, явившуюся, по существу, первым общим
определением геометрической науки (отличным от Г.олее позднего опреаеие-
ния Клейна). Взглядов Римана на геометрию, не связанных с понятием
геометрического преобразования, мы здесь коснуться не можем (см. по
втому поводу статью о неевклидовых геометриях в ^ледующеи книге
*) См. работу Ф. Клейна [1J, цитированную в конце статьи.

ГЕОМЕТРИЧЕСКИХ ПРЕОБРАЗОВАНИЙ 103
много разных «геометрий» — столько же, сколько имеется разных
групп преобразований; лишь одной из них является обычная геомет-
геометрия Евклида, изучаемая в средней школе. Мы уже говорили в на-
начале этого параграфа о том, что геометрия (обычная, евклидова)
изучает свойства фигур, сохраняющиеся при движениях. Этот взгляд
на геометрию вполне согласуется с приведенным выше определением
Клейна, ибо совокупность 2) всех движений плоскости является
группой. В самом деле, произведение двух любых движений снова
является движением; преобразование, обратное некоторому движению,
само является движением; движением является также и тождествен-
тождественное преобразование (все это'непосредственно следует из определения
движений). Другой пример группы преобразований мы получим, рас-
рассматривая совокупность ® всех преобразований подобия. Как мы
уже отмечали выше, геометрия, определяемая группой движений 55,
несколько отличается от геометрии, определяемой группой (? преоб-
преобразований подобия, хотя эти геометрии очень близки друг другу.
¦Ложно сказать, что предмет школьного курса геометрии представ-
представляет собой «переплетение» этих двух родственных геометрий: геомет-
геометрии группы 55 и геометрии [руппы (? Выбирая в качестве (У группу
преобразований, отличную от группы движений (или от группы пре-
преобразований подобия), мы придем к иной математической дисцип-
дисциплине к новой, «не евклидовой» геометрии').
Нетрудно понять, что совокупность 3( всех аффинных преобра-
преобразований плоскости (см. стр. 62) образует группу. В самом деле:
1° тождественное преобразование плоскости, очевидно, переводит
каждую прямую линию снова в прямую (в ту же самую!) и, значит,
является аффинным преобразованием; 2° если преобразование Ф
переводит каждую прямую / снова в прямую /', то и обратное пре-
преобразование Ф переводит прямую в прямую (/' в /), т. е. преоб-
преобразование, обратное аффинному, также является аффинным; 3° если
преобразование Ф переводит каждую прямую / в прямую /' и пре-
преобразование Y также переводит прямую в прямую (/' в /"), то и их
произведение ^?Ф снова переводит прямую в прямую (/ в /"), т. е.
произведение двух аффинных преобразований является аффинным
преобразованием. Отсюда следует, что можно рассматривать «геомет-
«геометрию», изучающую «аффинные» свойства фигур, т. е. свойства, сохра-
сохраняющиеся при аффинных преобразованиях (геометрия группы Щ;
соответствующая дисциплина — аффинная геометрия — является в
настоящее время большой самостоятельной наукой.
В аффинной геометрии можно говорить о точках и о прямых, по-
поскольку эти понятия сохраняются при аффинных преобразованиях
1) Очень важную категорию этих «не евклидовых» геометрий состав-
составляют так называемые неевклидовы геометрии (без кавычек) и, в частности,
неевклидова геометрия Лобачевского (см. по этому поводу статью о неевкли-
неевклидовых геометриях в кн. V ЭЭМ).

104 ГЕОМЕТРИЧЕСКИ1; ПРЕОБРАЗОВАНИЯ
(гочка переходит снова в точку и прямая — в прямую). Однако, скажем,
поня гие окружности в аффинн й геометрии отсутствует — ведь аффинные
преобразования могут перевести окружность в линию, не являющуюся
окружностью; поэтому окружность здесь «не имеет геометрического
смысла» (подобно тому как в обычной или евклидовой геометрии
не имеет смысла, скажем, понятие горизонтального направленияI).
Далее, в аффинной геометрии можно говорить о параллельных пря-
прямых, но не о перпендикулярных прямых; об отношении отрезков, при-
принадлежащих одной прямой, но не об отношении отрезков, принадле-
принадлежащих разнчм (не параллельным) прямым (см. свойства аффинных
преобразований, указанные в п. 3.3, стр. 77). Так, типичной аффин-
аффинной теоремой является следующая: три медианы треугольника
пересека отся в одной точке и делятся в ней. в отношении 2:1
считая от вершины; в самом деле, все фигурирующие в этой теореме
понятия имеют аффинный характер. Напротив, скажем, теорема
о точке пересечения высот треугольника связана с понятием перпен-
перпендикулярных прямых, отсутствующим в аффинной геометрии — и в этой
геометрии теорему о точке пересечения высот невозможно сформу-
сформулировать2).
Аналогично аффинным преобразованиям составляют группу и кру-
круговые преобразования (круговой1) плоскости (см. стр. 62); этой
группе преобразований отвечает своя «геометрия», которую можно
было бы назвать круговой геометрией (чаще говорят об ана-
лагматической, или конформной геометрии)'). Приведенные соображе-
соображения доставляют также дополнительную мотивировку целесообразности
введения такого понятия, как круговая плоскость, поскольку лишь
на «расширенной» соответствующим образом плоскости можно говорить
о группе круговых преобразований и, значит, лишь круговая
но не евклидова) плоскость может служить «полем действия» круго-
') Напротив, понятие эллипса (см статью о конических сечениях
и кн. V ЭЭЛ\) принадлежит аффинной геометрии (поскольку каждое аффин-
аффинное преобразование переводит эллипс снова в эллипс)
2) Афринную геометрию можно строить и аксиоматическим путем
(ср. со статьей «Аксиомы и основные понятия геометрии» в этой книге ЭЭМ).
Для этого надо ыорать какие-то основные, неопределяемые понятия
аффинной геометрии и сформулировать в виде аксиом основные их свойства,
из которых все остальные теоремы аффинной геометрии уже можно полу-
получить дедуктивным путем. Аксиоматика аффинной геометрии близка к аксио-
аксиоматике евклидо»О'"| геометрии; только понятие «равенства» отрезков или
углов в ней не имеет смысла и связанные с этим понятием аксиомы
должны быть откинуты или заменены ругими (см., например, указанную
t подстрочном примечании на стр 62 книгу И. М Я г л о м а и В. Г. А ш-
кинузе, целиком посвященную аффинной геометрии). Иной вариант
аксиоматик i аффинной геометрии намечен в статье «Векторы и их приме-
применения геометрии».и напечатанной в этой книге ЭЭМ Сстр. 292—381).
') Некоторое представление о содержании этой интересной геометрии
мо лно получите hj статьи «Окружности» в этой книге ЭЭМ.

ГРУППЫ TFOMFTPHMECKHX ПРЕОБРАЗОВАНИЙ 105
вой (аналагматической) геометрии. Еще одну важную группу преобра-
преобразований (проективные преобразования), приводящую к необхочимости
«расширения» плоскости введением «несобственных» элементов, мы рас-
рассмотрим в следующем параграфе.
Аффинная и круговая (аналагматическая) геометрии представляют
собой обширные разделы геометрии, которым (так же как и рассмат-
рассматриваемой в следующем параграфе проективной геометрии) посвящена
значительная литература и которые имеют важные приложения.
Однако существует и много других «геометрий», отвечающих иным,
группам геометрических преобразований.
В качестве примера отметим здесь чгеометрию», изучающую свойства
фигур, сохраняющиеся при параллельных переносах (т е. «геометрию», в ко-
которой «равными» считаются лишь фигуры, равные в обычном смысле и па-
параллельно расположенные). Нетрудно видеть, что ~овокупность ф всех
параллельных переносов плоскости представляет обой группу; в самом деле:
1Г Тождественное преобразование I можно рассматривать как парал-
параллельный перенос (в любом направлении!) на нулевое расстояние
2°. Преобразование, обратное параллельному переносу, представляет
собой параллельный перенос (см. стр. 97).
Зг. Произведение двух параллельных переносов также есть параллель-
параллельный перенос (см. стр. 81).
Поэтому изучение таких свойств фигур, которые являются общими
для всех фигур, получающихся одна из другой параллельным перенесе-
перенесением, является занятием вполне осмысленным (хоть и не очень интерес-
интересным), и соотгетствующая «геометрия» (геометрия группы 5?) 1 логической
стороны должна считаться столь же законной, как и обыкновенная евкли-
евклидова геометрия (которой она, однако, неизмеримо уступает с точки зрения
важности ее приложений)").
В этой новой «геометрии» теряет смысл целый ряд понятий обыкно-
обыкновенной (евклидовой) геометрии, например длина отрезка (ибо отрезки
разных направлений здесь являются «несравнимыми», поскольку никакие
два такие отрезка нельзя совместить «движением») или величина угла
(по аналогичной причине). Нельзя определить здесь и окружности,
поскольку оба определения окружности — как геометрического места точек,
удаленных от фиксированной точки на постоянное расстояние, и как
геометрического места точек, из которых данный отрезок вилен под постоян-
постоянным (ориентированным) углом — оказываются бессодержательными. В про-
противоположность этому понятие прямой линии, разумеется, полностью
сохраняет свое значение в новой «геометрии»; можно считать даже, что-
оно играет здесь большую роль, чем в евклидовой геометрии, поскольку
теперь прямая является единственной линией, которую можно
«движением» совместить саму с собой. Отсюда вытекает, что в нашей
«геометрии» можно по-прежнему говорить о треугольниках, четырехуголь-
четырехугольниках и т. д. и изучать их свойства. Важную роль играет в рассматривае-
рассматриваемой «геометрии» понятие отношения отрезков о^ной прямой (или
') Эту «геометрию» можно определить тем, что и ней равные фигуры
характеризуются как такие, у которых отрезки, соединяющие соответствую-
соответствующие друг другу пары точек, не только равны в обычном смысле этого
слова, но также параллельны и одинаково направлены (см. т. I книги.
И. М. Яглома [2], указанной в конце статьи, стр. 22—23)

106 ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
параллельных прямых), при определении которого достаточно говорить
о равенстве отре?ков одного направления, «равных» и в старом (евклидовом)
и в новом смысле; мы можем даже ввести для отрезков фиксированного
направления понятие «длины» (не имея, однако, никакой возможности
сравнивать «длины» отрезков разных направлений!). Сохраняет смысл в но-
новой «геометрии» и понятие площади плоской фигуры, поскольку евклидово
определение площади, связанное с рассмотрением сети квадратов и подсче-
подсчетом числа покрываемых фигурой квадратов, использует лишь равенство
квадратов сети, а эти квадраты также «равны» и в смысле рассматри-
рассматриваемой здесь «геометрии»').
Разумеется, все теоремы евклидовой геометрии, которые можно сфор-
сформулировать в терминах «геометрии параллельных переносов», остаются
верными и в этой новой «геометрии»; это вытекает из того, что если все
движения плоскости сохраняют некоторые свойства геометрических фи-
фигур, то, разумеется, эти свойства не нарушаются и при параллельных пере-
переносах. Так, например, мы по прежнему можем утверждать, что медианы
тр'угольнчка пересекаются в одной точке и делятся в ней в отношении 2:1,
считая от вершины (ясно, что все понятия, фигурирующие в этой теореме,
в новой «геометрии» имеют смысл), или что два треугольника ABC и ЛВС,,
для которых СС,\\АВ, равновелики"(рис. 51). В противоположность этому,
скажем, теоремы о том, что пересекаются в одной точке высоты или бис-
биссектрисы треугольника теряют здесь смысл, поскольку мы теперь не можем
говорить о перпендикулярности прямых (и, следовательно, о высотах) и
о равенстве углов с непараллельными сторонами (а значит, и о бис-
биссектрисах).
Теоремы евклидовой геометрии, связанные с понятиями, имеющими
в рассматриваемой здесь «геометрии» новый смысл, могут изменить в этой
«геометрии» свою формулировку. Так, например, из «равенства» двух
треугольников ABC и А'В'С по-прежнему следует «равенство» их соответ-
соответствующих сторон (рис. 52; кавычки, в которые мы берем слово «равенство»,
подчеркивают, что мы понимаем его теперь не так, как в евклидовой
геометрии); однако теперь уже из «равенства» двух пар сторон (напри-
(например, АВ и А'В', АС и А'С) вытекает «равенство» треугольников. Можно
указать еще целый ряд предложений, которые имеют силу в рассматри-
рассматриваемой здесь «геометрии», но не в геометрии Евклида; так, например,
для «равенства» двух треугольников ABC и А'В'С здесь необходимо
<и достаточно) «равенство» трех отрезков АА', ВВ' и СС (см. тот же
рис. 52), а из «равенства» противоположных сторон АВ и DC четырех-
четырехугольника ABCD вытекает, что «равны» и стороны AD и ВС и что диаго-
диагонали АС и BD четырехугольника в точке пересечения челятся пополам
{рис. 53)*).
Видоизменением рассматриваемой «геометрии» (геометрии группы 5р)
является другая «геометрия», изучающая свойства фигур, спхргняющиеся
при всевозможных параллельных переносах и при симметриях относительно
') Ничего не меняет и то обстоятельство, что при таком определении
площади плоской фигуры («Конструктивное определение площади»;
см. в кн. V ЭЭМ статью «Площадь и объем») приходится говорить не
об одной сети квадратов, а о бесконечной последовательности таких сетей
с неограниченно уменьшающимися квадратами сети.
г) К рассматриваемой здесь «геометрии» по существу относится учение
о векторах (см. статью «Векторы и их применения в геометрии»,
в_этой книге ЭЭМ), поскольку равенство векторов^направленных отрезков)
АВ и CD можно определить так: векторы АВ и CD равны, если один из них
можно совместить с другим параллельным переносом (ср. стр. 296).

ГРУППЫ ГЕОМЕТРИЧЕСКИХ ПРЕОБРАЗОВАНИЙ
107
любых точек плоскости. Эти свойства, действительно, составлякт предмет
некоторой «геометрии», поскольку совокупность <2> всех параллельных
переносов и симметрии относительно точек образует группу:
1°. 1 'ждественное преобразование I можно рассматривать как «нуле-
«нулевой» параллельный перенос.
Рис. 51.
Рнс. 53.
2*. Преобразование, обратное параллельному переносу, снова есть
параллельный перенос; преобразование, обратное симметрии относительно
точки, есть снова симметрия относительно точки (та же самая).
3° Произведение двух параллельных переносов снова есть параллель-
параллельный перенос; произведение параллельного переноса и симметрии относи-
относительно точки (взятых в любом порядке) есть симметрия относительно
точки (см. стр. 81—83), произведение двух симметрии относительно двух
точек есть параллельный перенос (см стр. 83; если центры двух
симметрии совпадают, то их
произведение представляет со-
собой «нулевой» параллельный
перенос).
Отекла следует, что сово-
совокупность 3 всех параллельных
перено. ов и всех симметрии от-
относительно точек может быть
положена в оснону определе-
определения своеобразной «геомет-
«геометрии» ') Эга «геометрия» в
известном смысле является
промежуточной между рассматриваемой выше и евклидовой геометриями, по-
поскольку группа © является промежуточной между группой % парал-
параллельных переносов и группой iN движений (группа ©содержит группу ф
и содержится d группе X1) Соответственно этому эта новая «геометрия»
ближе к евклидовой геометрии, чем рассмотренная нами выше «геометрия»
группы ЧД5 Так, например, теперь мы уже можем утверждать, что верти-
вертикальные углы «равны*, ибо два таких угла можно совместить симметрией
относительно их общей вершины (в геометрии группы ф эта теорема
неверна); далее, в новой геометрии «равенства» двух пар сторон тре-
угольнмко ABC и А'В'С недостаточно для того, чтобы утверждать, что
«равны» и сами треугольники (рис. 54), в то время как «равенство» трех
пар сторон уже с неизбежностью влечет за собой «равенство» треуголь-
треугольников Наконец, интересный пример теоремы, сохраняющей силу как
') В этой геометрии «равными» считаются такие фигуры, что отрезки, сое
линяющие соответствующие друг другу пары точек этих фигур, не только
равны ь обычном смысле, но и параллельны, хотя их направления могут
быть и противоположными (ср. т. 1 книги [2J, стр. 22—23 !¦ 27]

108 ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
в евклидовой геометрии, так и в «геометрии» группы 5, но нарушающейся
в «геометрии» группы ^, доставляет так называемая теорема Бойяи —
Гер вина: любые дв i равновеликих многоугольника ривноспставлены, т. е.
могут быть разбиты на соответственно «равные» многоугольные части ')
6.4. Группы преобразований в физи<е. В заключение настоящего
параграфа отметим, что определение геометрии по Клейну, выдвигающее
на первый план понятие о геометрических преобразованиях, которые
сохраняют интересующие нас свойства фигур (т. е. играют роль «движе-
«движений» соответствующей «геометрии»), находит своеобразное отражение и
в физике. Вспомним так называемый принцип относительности
Галилея, играющий фундаментальную роль в механике и утверждаю-
утверждающий, что никакие фчз 1ческие экспер шенты, производимые внутри мех ти-
ческой с /стемы, не могит позволить оэнаружить равномерное и прямолиней-
„ ( f ное движение этой системы.
дя<5—>л'я g силу этого принципа, про-
производя какие угодно опыты,
скажем, на корабле, двигаю-
двигающемся в постоянном направле-
направлении с неизменной скоростью,
мы не сможем обнаружить ни-
никаких эффектов, обязанных
своим происхождением движе-
движению корабля. Из принципа
относительности Галилея сле-
следует, что все изучаемые физи-
физикой свойства сохраняются при
«преобразованиях» физической
системы, состоящих в прида-
придании ей постоянной по величине
и направлению скорости (эти
«преобразования» называются
преобразованиями Галилея). Иными словами, «физические свой-
свойства» тел можно описать как такие свойства, которые не меняются при
преобразованиях Галилея (ср. с определением «геометрических свойств»
как таких, которые сохраняются при движениях, стр. 99).
Принципу относительности Галилея можно придать «геометризирован-
ную» форму, совершенно непосредственно связывающую его с определением
геометрии по Клейну. Предположим, для простоты, что мы ограничиваемся
физическими процессами, которые можно считать происходящими в одной
плоскости, например изучаем движения физических тел на ограниченном
участке земной поверхности, который можно мыслить себе плоским.
Рассматриваемую плоскость мы отнесем к декартовым прямоугольным
координатам (х, у); при этом, скажем, механическое движение материаль-
') См. в кн. V ЭЭМ статью «о равносоставленности многоугольников и
многогранников Тот факт, что эта теорема сохраняет силу !¦ геометрии
группы 5, составляет содержание так называемой теоремы Хадвигера —
Глю ра В «геометрии» группы ^ теорема Бойяи — Гервина заменяется сле-
следующей: для того чтобы два равновеликих многоугольника М и М' были
р^вносистчвлени, неоЗход шо и достаточно, чтобы сумма (ориентированных*.)
дл iH сторон М, параллельных каждой прямой I плоскости, была равна сумме
(ориент 1рованнчх) длш параллельных I сторон М' (см. В. Г. Болтяи
с к и й, Равновеликие и равносоставленные фигуры, М.. Гостехиздат, 1956;
здесь используется то, что в «геометрии» группы $ можно для отрезков
любого фиксированного направления / ввести понятие «длины отрезка»).

ГРУППЫ ГЕОМЕТРИЧЕСКИХ ПРЕОБРАЗОВАНИЙ
109
ной точки будет задаваться формулами,
во времени координат точки
указывающими закон изменения
-в @. I
в @
где /—время. Совершенно ясно, что переход к иной системе координат
никак не может отразиться на содержании физических законов, которые,
следовательно, должны одинаково записываться в координатах (х, у) и
в координатах (х', у1), получающихся при произвольном повороте осей
координат и сдвиге начала координат (рис. 55). Нетрудно убедиться что
переход от координат (х, у) к
координатам
формулами
(х1, у') задается
х' = х cos a—у sin а+о,
у"=х sin а+у cos а + Ь
:\
(*)
Nf
в которых а обозначает угол,
образованный осью х с осью х',
а а, Ь — координаты начала О си-
системы координат (х, у) в системе
(*'. y'Y)'< поэтому любое предло-
предложение, имеющее физический Рис. 55.
смысл, должно сохранять свою
форму при преобразовании^). Принцип же относительности Галилея утверж-
утверждает, что, более того, также и в том случае, если начало и оси системы коор-
координат (х', у') движутся равномерно и прямолинейно по отношению к системе
координат х, у, то и тогда все физические процессы будут записываться
в координатах (х', у') и в координатах (х, у) совершенно одинаково.
Но в том случае, когда начало О' координат (х', у') двигается со скоро-
скоростью v по прямой, образующей с осью х угол |3 (см. тот же рис. 55),
связь между координатами (*', у') и (х, у) будет записываться формулами
jc'=^xcos a—и sin a + cos p • u/+ a,
if = x sin a + у cos a + sin P • vt + b;
(**)
таким образом, все имеющие физический смысл явления должны сохранять
свою форму при преобразованиях (**). Учитывая еще, что в последние
формулы входит также и время / и что выбор того или иного начала
отсчета времени никак не может отразиться на физической сущности
какого-либо процесса, мы можем переписать формулы (**) в следующем
несколько более полном иде:
х' =xcos а—у sin а + cos р-vt +o,
у' — х sin а + у cos а + sin Р ¦ vt + Ь,
t'= t + d;
(***)
здесь d есть время старого начала тсчета времени в новой системе отсчета.
Формулы (***) и описывают математически преобразовлния Галилея; прин-
принцип относительности Галилея утверждает, что физика (точнее — механика),
изучающая лишь движения в плоскости, может "ыть определена как
наука о свойствах трехмерного «мира» (пространства — времени) (х, у, I),
') См. лкхоп куре

110 ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
сохраняющихся при преобразованиях (***). Поскольку преобразования
Галилея (***), как легко показать, образуют группу, то это описание
отождествляет механику плоских движений с некоторой «геометрией» трех-
трехмерного пространства, определенной заданием группы (***) «движений»( ').
Заметим еще, что современная физика заменяет принцип относитель-
относительности Галилея так называемым принципом относительности
Эйнштейна, лежащим ,. основе (специальной) теории относитель-
относительности; это приводит к необходимости заменить преобразования Галилея
(***) более сложными преобразованиями, которые называются преобра-
преобразованиями Лоренца Преобразования Лоренца зависят от некото-
некоторого параметра с (физический смысл которого расшифровывается норией
относительности: с есть скорость света в пустоте); при с—>-со они пере-
переходят в преобразования Галилея. Преобразонания Лоренца также образуют
группу; таким образом, переход от классической механики Галилея и
Ньютона к теории относительности Эйнштейна и Пуанкаре равносилен
изменению взгляда на «геометрию» окружающего нас мира, причем эта
«геометрия», в полном согласии с точкой зрения Клейна, задается ука-
указанием группы преобразований, сохраняющих вид физических законов').
§ 7. Группа проективных преобразований
7.1. Гомология. Наш рассказ о геометрических преобразованиях
был бы неполным, если бы мы не упомянули, хотя бы кратко,
о проективных преобразованиях, совокупность которых составляет
группу проективных преобразований. Эта группа, одна из важней-
важнейших для геометрии, определяет своеобразную «геометрию», носящую
название проективной геометрии и тесно связанную как с евкли-
евклидовой и аффинной геометриями, так и с неевклидовыми геометриями.
Проективной геометрии посвящено много обстоятельных учебных
руководств*); здесь же мы лишь бегло очертим ее преамет.
Знакомство с проективными преобразованиями мы начнем с одного
интересного преобразования — гомологии, определение которого мы
первоначально сформулируем намеренно неточно. Гомологией*)
с осью о и центром О называется преобразование плоскости,
переводящее прямые снова в прямые и оставляющее на месте
') «Геометрия» пространства-времени, в котором мы живем, представ-
представляет собой одну из так называемых неевклидовых геометрий, о которых
упоминалось в подстрочном примечании на стр. 103; эта «геометрия»
(независимо от того, кладутся ли в основу ее построения преобразования
Галилея или преобразования Лореица) отлична как от обычной геометрии
Евклида, так и от неевклидовой геометрии Лобачевского. По этому поводу
см. в кн. V ЭЭМ статью «Неевклидовы геометрии», в которой будет под-
подробнее изложен вопрос о геометрическом истолковании физических законов.
') См., например, Г. Б. Г у р е в и ч. Проективная геометрия, М., Фиэ-
матгиз, 1960; X. С. М. Кокстер, Действительная и проективная плос-
плоскость, М , Физматгиз, 1G60.
*) От греческих слов оцо? — одинаковый и Ял-yog — смысл.

ГРУППА ПРОЕКТИВНЫХ ПРЕОЬРАЭОВАНИЙ 1 1 1
каждую прямую, проходящую через точку О, и каждую точку
принадлежащую прямой о. Отсюда следует что прямую /, пере
секающую ось о в точке Q, гомология Г переводит в прямую /',
пересекающую ось о в той же точке (ибо F(Q — Q), а каждую
парчллельную оси о прямую т гомология переводит в прямую т'
также параллельную прямой о (иб в точку пересечения прямых т
и о мопа бы перейти лишь та же самая точка, а прямая т
не пересекает о).
Для того чтобы построить точку А', в которую гомология Г
переводит произвольную точку А плоскости, достаточно знать
образ М' —Г(/И) какой либо точки М (рис 56; точк 1 ' должнт ле
жать на прямой ОМ, ибо эга прямая при гомолопп переходит в себя)
В самом деле, если пря 0
мая А И пересекает ось /\
гомолог» и о в то 1ке Q, то /gj \
она перейдет в прямую QM' л / ^1 \\
(а если Л.Л1ЦО, то она пе- ? "Г^ч \\
рейдет в параллельную оси , / м^^
о прямую RM , проходящук /? 'р?
через точку /И'). Так как, '' /
далее, искомая точка А' (или '
Ах )лежит, кроме того, на пря- / Р Q
мойО/1(соо ветственно ОАХ), рис_ ^
то она может быть найдена как
точка пересечения прямых ОА и QM' (или ОАХ и RM'). Это построе
ние не проходит в том случае, если исходная точка В лежит на
прямой ОММ', но в таком случае мы можем построить сначала
образ А' Г(А) какой-либо другой точки А и затем построить
образ В' — Г (В) точки В, исходя не из пары точек М, М, а
из пары точек А, А'. Разумеется, следовало бы еще показать,
что наше построение приводит к одному и тому же образу В'
точки В независимо от выбора точки А и что определенное изображен-
изображенным на рис. 56 построением преобразование Г в самом деле обла-
обладает всеми теми свойствами, выполнения которых мы требовали
от гомологии (в частности, что Г переводит прямые в прямые); мы,
однако, примем это на веру, предоставив читателю самостоятельно
провести соответствующие доказательства
М А МО
Заметим, что если -тт7Г= мм> (и только в этом случае), то
треугольники МОА и MM'Q буд>т подобны и прямая QM' \ОА
не пересечет ОА (рис. 57). Таким образом, точке А, принадлежащей
прямой q, гомотетичной о с центром гомотетии Л1 и коэффициентом
гомотетии ..... не отвечает никакая точка плоскости! Иначе говоря,
ММ

112
TE0MFTPH4ECKHE ПРЕОБРАЗОВАНИЯ
за область определения гомологии Г следует принять плос-
плоскость с исключенной прямой q. Прямые, пересекающиеся
в некоторой точке Ау лежащей на прямой q, переводятся гомологией
в непересекающиеся (параллельные!) прямые; при этом совокупность
всех проходящих через точку А прямых переходит в пучок (со-
(совокупность) параллельных между собой прямых (см. рис. 57).
п „, М'В' М'О
С другой стороны, если точка В такова, что -.. = , ^
где R— точка пересечения М'В' с о, то OB'\\RM и, следонагель-
но, не существует точки
М 4 g В, переходящей в точку
'?\ \ I .g В'. Отсюда вытекает, что
область значений
гомологии Г представляет
собой плоскость с исклю-
исключенным из нее геометри-
геометрическим местом всех таких
точек В', т. е. плос-
плоскость с исключен-
исключенной прямой <7i> гомо-
гомотетичной о с центром
гомотетии М' и коэффи-
М'О
циентом гомотетии -rj.-w ¦
Таким образом, гомология не является преобразованием пло-
плоскости, поскольку ее область определения и область значений не совпа-
совпадают (в этом и заключается та нестрогость в определении гомологии,
о которой мы упомянули вначале).
7.2. Проективная плоскость. Затруднения, связанные с тем, что
гомология не является преобразованием, могут быть устранены, если
считать, что каждую точку А прямой q гомология Г переводит
в некоторую «идеальную» или «несобственную» точку А'; при этом
придется считать, что параллельные между собой прямые, в которые
переходят прямые, пересекающиеся в точке А, «сходятся» в этой
фиктивной точке А' (точку А' часто называют также «бесконечно
удаленной» точкой ')). При этом естественно условиться, что все
«несобственные» или «бесконечно удаленные» точки плоскости при-
принадлежат одной «несобственной» или «бесконечно удаленной» пря-
прямой q', в которую переходит при гомологии прямая q. К этим
«несобственным» точкам плоскости надо добавить еще одну «несоб-
«несобственную» точку Z, в которой «сходятся» параллельные между собой
Рис.
') Это связано с тем, что, как легко видеть, при стремлении переменной
точки А к прямой q образ Г (Л) этой точки неограниченно удаляется.

ГРУППА ПРОЕКТИВНЫХ ПРЕОБРАЗОВАНИЙ 113
прямые о и q (а также и все параллельные им прямые); при зтом
естественно считать, что F(Z)=Z.
Плоскость, дополненная фиктивной «бесконечно удаленной» пря-
прямой q , состоящей из всех добавленных к плоскости «несобственных»
точек, называется проективной плоскостью'). Заметим, что каж-
каждой точке проективной плоскости отвечает пучок сходящихся в ней
прямых, пересекающихся в этой точке, если точка «собственная»,
и параллельных между собой, если эта точка «несобственная»
(рис. 58). Отметим еще, что на проективной плоскости любые две
различные прямые имеют ровно одну точку пересечения (собствен-
(собственную или несобственную).
После такого расширения плоскости введением «несобственных»
точек гомология становится преобразованием, областью действия
которого является проектив- f
ная плоскость. Точки пря- Л
мой q переходят при гомоло-
гомологии Г в «бееконечно удален-
удаленные» точки (т. е. T(q) = q')\
аналогично каждая «беско-
нечно удаленная» точка В / \Ыю^ны0
(задаваемая, скажем, пучком / пут
параллельных прямых) пере- '
ходит в некоторую точку В "' '
прямой <7, (т. е. Г(9') = 9,)- Рис- 68-
Разумеется, и произведение
гомологии, взятых в любом числе, и преобразование, обратное гомо-
гомологии, являются преобразованиями проективной плоскости. (Преобра-
(Преобразование Г, обратное гомологии Г, с центром О и осью о, перево-
переводящей точку М в точку М' — Г{Л4), является, очевидно, гомологией
с теми же центром О и осью о, переводящей точку М' в точку
М=Т-Ч,М'); см. рис. 56.)
Можно также рассматривать гомологии, отвечающие случаям, когда
ось гомологии или центр гомологии (или и то и другое вместе) явля-
являются «бесконечно удаленными». Нетрудно, например, убедиться, что
гомология с несобственной осью о и обыкновенным («собственным»)
') Это название связано с тем, что такое же расширение плоскости
введением (несуществующих!) «бесконечно удаленных» точек и прямой
естественно возникает в задачах, связанных с центральным проекти-
проектированием плоскости я на другую плоскость л' из некоторого центра О.
Здесь также на плоскости я найдется прямая q, точки которой не проекти-
проектируются ни в какие точки плоскости я',—это будет линия пересечения
плоскости л с параллельной л' плоскостью, проходящей через центр
проектирования О. С другой стороны, на плоскости я' найдется такая
прямая </,, в точки которой не проектируются никакие точки плос-
плоскости я,—линия пересечения плоскости п' с параллельной п плоскостью,
проходящей через О.
S Энциклопедия, ки. 4

114
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
центром О представляет собой гомотетию с центром О и коэффици-
ОМ' , _„
ентом —т- (рис. 59, а; впрочем, эта гомология несущественно отли-
отличается от гомотетии несколько «большей» областью действия). Да-
Далее, гомология с несобствен-
несобственной осью и несобственным
центром представляет собой
параллельный перенос в на-
направлении прямой, идущей
з центр гомологии, на отре-
отрезок ММ' (т. е. перенос на
вектор ММ'; рис. 59, б).
Сжатие к прямой о также
есть частный вид гомологии
(центр О является несоб-
несобственной точкой, соответ-
соответствующей пучку прямых,
перпендикулярных оси о;
рис. 59, в).
7.3. Применения гомо-
гомологии к решению задач. То
обстоятельство, что гомоло-
гомология переводит пересекаю-
пересекающиеся прямые в параллель-
параллельные, может быть использо-
использовано для решения многих
геометрических задач на
доказательство и построе-
построение. В качестве примера
докажем следующую теоре-
теорему: пусть даны две прямые
/, и 12 и точка Q вне их;
через Q проводятся всевоз-
всевозможные пары прямых а. Ь,
пересекающих 1^и1г в точ-
точках Ал, А2, соответствен-
соответственно Вх, В2 и точки Л,, Вг и
Аг, В, соединяются между
собой (рис. 60, а); геометри-
геометрическое место точек Р пересечения прямых Л,В2 и АгВ1 представ-
представляет собой прямую р. проходящую через точку О пересечения
/, и 12 (параллельную /, и /2, если /, и 12 параллельны). Для доказа-
доказательства произведем гомологию Г, у ко юрой ось, центр и пару то-
«ек М и М' = Г (Ai) подберем так, чтобы роль прямой q рис. 57
играла прямая ОС? (нетрудно убедиться, что так выбрать гомологию

ГРУППА ПРОЕКТИВНЫХ ПРЕОБРАЗОВАНИЙ
11 Г,
всегда возможно). При этом рис. 60, а перейдет в рис. 60, б, на ко-
котором все четырехугольники A,B1B3At являются параллелограммами и
геометрическим местом центров Т* этих параллелограммов является
средняя линия р' — полосы, образованной прямыми /' и /'. А гак как
Q'
гомология переводит прямые в прямые и параллельные прямые (прямые,
пересекающиеся в «несобственной» точке) — в прямые, пересекающиеся
в одной точке, то гомология Г (см. стр. 113) переводит параллель-
параллельные прямые /,, /2 и р' в прямые /,, /г и р, пересекающиеся в од-
одной точке О.
Вот еще один пример: докажем, что если произвольный четырехугольник
ABCD разбит прямей MN, пересекающей его стороны АВи CD на два четырех-
четырехугольника AMND и BMNC, то moiKu P, Q, Я пересечения диагоналей трех

116
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
четырехугольников AMND, BMNC и ABCD лгжат на одной прямой (рис. 61 ,а)').
Элементарное доказательство этой интересной теоремы очень сложно,
однако если использовать преобразование гомологии, то ее доказать легко.
Преобразуем рис. 61,а при помощи гомологии Г, выбранной так, чтобы пря-
прямая PQ играла роль прямой q рис 57 (отметим, что мы пока не знаем.
о)
Р'
Я'
Рис. 61
принадлежит ли точка R той же прямой). При этом мы придем к (совсем
новому!) рис. 61,6, где A'N'\\D'M' (ибо точка Р пересечения AN и DM
переходит в «бесконечно удаленную» точку) и 8'Л/'МС'/И: (ибо переходит
в «бесконечно удаленную» точка Q рис. 61 ,и). А теперь из подобия тре-
треугольников O'A'N' и OM'D', OC'M' и ON'B' (где О—точка пересечения
') Если прямые AD, ВС и MN проходят через одну точку, то наше
утверждение вытекает, очевидно, из доказанной только что теоремы; р этом
частном случае прямая PRQ проходит через точку пересечения прямых
А В .1 CD:

ГРУППА ПРОЕКТИВНЫХ ПРЕОБРАЗОВАНИЙ 1 17
прямых А'В' и CD1 ')) имеем
а/г_ом_ on'_ ос
ON'~OD' ОВ'~бЖ'
Перемножая эти два равенства, получаем
О А' _0С
OB'~OD''
откуда вытекает, что А'С || B'D'. Следовательно, точка R пересечения
прямых АС и BD рис. 61,а переходит в «бесконечно удаленную» точку
рис. 61,6 и, значит принадлежит «прямой о» нашей гомологии—прямой PQ1
7.4. Проективные преобразования и проективная геометрия. Го-
Гомология представляет собой частный случай проективного преобразо-
преобразования— так называют преобразования проективной плоскости,
обладающие тем свойством, что каждую прямую (к числу кото-
которых причисляется и несобственная прямая) они переводят снова в
прямую2). Таким образом, определение проективных преобразований
отличается от определения аффинных преобразований лишь тем, что
их областью действия является не обычная (евклидова), а проек-
проективная плоскость1). Ясно, что совокупность всех проективных
преобразований (проективной!) плоскости составляет группу — до-
доказательство этого фактически не отличается от указанного на стр. 103
доказательства того, что образуют группу аффинные преобразования.
Ветвь геометрии, изучающая свойства фигур, сохраняющиеся при
проективных преобразованиях, называется проективной геометрией.
Примерами теорем проективной геометрии могут служить теоремы,
доказанные нами с помощью гомологии — нетрудно понять, что утверж-
утверждения этих теорем сохраняют свое содержание, если подвергнуть
чертеж теоремы произвольному проективному преобразованию. На этом
обстоятельстве и базировалось выше применение гомологии к дока-
доказательству теорем. Преобразовав чертеж теоремы при помощи
подходящим образом подобранной гомологии, мы существенно упро-
упростим его, сведя тем самым рассматриваемую теорему к более про-
простому частному случаю того же утверждения, причем нам, оказы-
оказывается, достаточно доказать утверждение лишь в этом частном случае.
7.5. Координаты в проективной плоскости. Поскольку проективная
плоскость является совсем иным геометрическим образом, чем обычная
(евклидова) плоскость, то для проективной плоскости оказывается непри-
') Предоставляем читателю самому разобрать случай, когда А'В'\\С'1У
(рис. 61 .в).
2) Можно доказать, что всякое проективное преобразование плоскости
можно осуществить с помощью подходящим образом подобранной гомологии,
сопровождаемой некоторым преобразованием подобия (ср со сказанным на
стр 93 об аффинных преобразованиях)
3) По поводу понятия проективной плоскости можно повторить почти
все, сказанное выше (стр. 58—59) о понятии круговой плоскости

118 ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИИ
менимым обычный способ введения координат. Однако систему коорди-
координат, годную в случае проектисной плоскости, оказывается возможным
получить с помощью небольшого видоизменения обычной конструкции:
достаточно заменить декартовы координаты х, //однородными коор-
координатами х„ х2, х0, связанными с хну соотношениями
При этом, умножив все три координаты х„ хг, х0 на одно и то же число
g^tO, мы получим координаты той же самой точки (ибо декартовы
координаты х к у при этом не изменятся); таким обрагом, однородные коор-
координаты определяются, как говорят, «с точностью до произвольного множи-
множителя g». Если х, не равно нулю, то тройка координат (х,, х2, х,) отвечает
(обыкновенной) точке А плоскости, декартоьы координаты которой определя-
определяются по формулам A8). Если же хп=0, то формулы A8) теряют смысл.
В случае, когда по крайней мере одно из чисел х,, х2 отлично от нуля,
считают, что координаты (х,. х2, 0) отвечают «бесконечно удаленной»
точке А' проективной плоскости (по формулам A8) этой точке приписыва-
приписываются «бесконечно большие» декартовы координаты х и I/, но определенное
отношение — =—— , задающее углоиой коэффициент «проходящих» через
X Х^
эту точку А 'прямых). Наконец, координатам х,=х2 = х„1=0 не отвечает
никакая точка проективной плоскости, т. е. такие значения координат не
допускаются (ибо нельзя говорить и об «угловом коэффициенте» — = —— ,
отвечающем точке @, 0, 0)).
Введение однородных координат позволяет записать любое отображение,
область определения и область значений которого содержатся в проектив-
проективной плоскости, уравнениями 1>ида
*,=ф(*1. *2. *>)
x2 = ij)U.. *,, х„), } A9)
*o = XU,, х2, х0)
(точнее бы было оворить об уравнениях
Q*,=q>(*i, x2, х0),
дх2 = \|)(х„ х2. х0), у A9а)
С^=Х1*„ х2. «о).
где q^O—произвольное число; при этом функции ф(х,, хг, х0), tJ)(x,, х2, х0),
Х(х,. х2, хп) должны оыть таковы, что при замене х„ хг, к,, на ох,, ахг, ох0,
где офО, значения этих функций должны умножаться на некоторое число
хфО, зависящее от о. но одинаковое для всех трех функций)
Особую роль среди всех отображений A9) (или A9а)) играют линей-
линейные отображения проекти ной плоскости
ох, =алх, + b,xs + слх0.
qx2 = а2х, + Ь2хг + с2х,. у B0,

группл проективных преобразований 119
в том случае, когда эти отображения взаимно однозначны (т. е. когда из
формул B0) можно также по х^, х, х„ определить х„ х2, х, с точностью до
общего множителя), они являются проективными преобразова-
преобразованиями. Доказательство этого почти не от.'ичается от доказательства того,
что линейные преобразования оСычной плоскости являются аффинными
преобразованиями (ср. выше, стр. 76 и след.)- Оно использует лишь то
обстоятельство, что каждая прямая проективной плоскости в однородных
координатах записывается линейным уравнением
^О; B1)
так, прямая
Ах + Ву + С = 0 или у=— 4-х — ^г <21а>
с угловым коэффициентом k=—=- в однородных координатах A8) запи-
записывается урарнением B1) (ему удовлетворяет также «бесконечно удален
ная» точка (х,, х2, 0) = (В, —А 0), через которую «проходит» прямая B1а)),
а «бесконечно удаленная» прямая проективной плоскости записывается
простым уравнением х, = 0. М< жно доказать, что и, обратно, каждое про-
проективное преобразование (проеьпи вной) плоскости в однородных координа-
координатах записыесется форл илами типа B0).
7.6. Бирационал>>1ые преобразования проективной плоскости. Идя даль"-
ше по пути, намеченному в коние § 3 можно также определить б и р а-
циональные преобразования проективной плоскости;
эти преобразования характеризуются тем, что фигурирующие в их
аналитической записи A9) функции ф(х,, хг, х,), 1[ (х„ х2, дг„), x(-*i> xi< xo)
суть рациональные функции переменных лс,, хг, х-, и что тем
же свойством обладают и обратные к ним преобрагоиания (ср. выше,
стр. 79). При этом функции ф, if и у. можно даже считать целыми рацио-
рациональными, ибо эти три функции можно одновременно умножить на любое
выражение и таким путем избавиться от знаменателей дробей. Последнее
обстоятельство позволяет классифицировать бирациональные преобразова-
преобразования проективной плоскости по степеням функций (Jj, if, у самыми просты-
простыми бирациональными преобразованиями являются линейные (где функ-
функции (f т)\ х линейны); затем идут квадратичные преобразования
(функции ф ,\|), X второй степени), кубические преобразования (функции
ф, if, х третьей степени) и т. д. ').
О геометрическом смысле линейных (проективных) преобразований мы
уже говорили Примером квадратичною преобра'ова-ния может служить ин-
инверсия G) или гиперболическая инверсия (8) В однородных координатах
можно эти два последних преобразования записать так:
B2)
') Степени функций ф, i|), % не могут быть различными так как необ-
необходимо, чтобы при умножении координат х,, хг, л, на лю он множитель а
все функции умножались на один и тот же множитель т ( =т, о)).

120
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
соответственно
B3)
(ср. эти формулы с G) и (8)) стр. 73) •). Эти примеры являются достаточно
характерными: можно показать, что каждое квадратичное преобразование
проективной плоскости можно представить в виде ЛГ, где Л есть линейное
1}
Рис. 62
') Строго говоря, ии инверсия, ни гиперболическая инверсия ие
являются преобразоваииями проективной плоское ги: инверсия B2)

НЕТОЧЕЧНЫЕ ОТОБРАЖЕНИЯ 121
преобразование (сводящееся, как мы знаем, к гомологии1)), а X—симметрия
относительно окружности (инверсия), или симметрия относительно пары парал-
параллельных прямых (гиперболическая инверсия), или же симметрия относительно
(равнобочной) гиперболы или параболы. При этом симметрия относительис-
гиперболы или относительно параболы определяется в точности так же,
как и симметрия относительно окружности: каждую внешнюю по отиоше
нию к соответствующей криной К точку А она переводит в точку А' пере-
пересечения проходящего через А диаметра кривой К (т. е. прямой, соединяющей
точку А с центром О гиперболы или параллельную оси параболы *)) с
прямой, соединяющей точки Р и Q прикосновения с кривой К проведен-
проведенных к К. из точки А касательных, а точку А' переводит в А; точки кривой К
при симметрии относительно К остаются на месте (ср. рис. 62,а.б с рис. 9 иа
стр. 56). Геометрическое описание всех кубических преобразований плоскости
(а тем более произвольных бирациональных преобразований), аналогичное-
этому описанию квадратичных преобразовании, до сих пор неизвестно.
§ 8. Неточечные отображения
8.1. Примеры неточечных преобразований. К понятию точечного
отображения мы пришли, считая, что аргумент х и значение у функ-
функции y=f(x) являются не числами, как это чаще всего приходится
считать, а точками. Столь же законно, однако, считать, что в обо-
обозначении функции у — f(x) под х и у понимаются не точки, а иные
геометрические объекты, возможно даже объекты разной природы.
На этом пути мы приходим к более общему понятию (не обяза-
обязательно точечного!) геометрического преобразования, например
преобразования а'=Ф(а) в множестве прямых линий, переводящего
каждую прямую а в новую (или ту же самую) прямую а', или пре-
преобразования X' =ФB) в множестве окружностей, переводящего окруж-
окружность 2 в окружность. X'; можно также рассматривать, скажем,
отображения, переводящие окружности в точки (например, 0 = ФE),
где О есть центр окружности S), точки в прямые (ср. ниже стр. 128)
переводит все точки «бесконечно удаленной» прямой х„ = 0 в центр инверсии
0@, 0, 1), а гиперболическая инверсия B3) переводит все точки «беско-
«бесконечно удаленной» прямой х,, = 0 в одну «бесконечно удаленную» точку
/1, A, 0, 0) (отвечающую направлению оси инверсии о), а все точки оси о
инверсии, имеющей уравнение х2 = 0 — в другую «бесконечно удаленную»
точку .4,@, 1, 0) (отвечающую перпендикулярному о направлению) {Мы
отмечали выше, что желание рассматривать инверсию или гиперболическую
инверсию как преобразования плоскости приводит к необходимости
совсем иного пополнения плоскости «идеальными» элементами, отличного
от того, с которым связано понятие проективной плоскости.] Можно дока-
доказать, что единственными бирациональными преобразованиями, областью дей-
действия которых служит вся проективная плоскость, являются линейные
преобразования B0). Аналогично этому единственными преобразованыями
A14), областью действия которых служит круговая плоскость, задаваемыми
рациональными функциями F (г) комплексного переменного г (см. выше, стр. 78),
являются дробно-линейные преобразования A6).
') См сноску*) на стр.117.
г) См. статью о конических сечениях в следующей книге ЭЭМ.

Г22
ГЕОМК 1РИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
или окружности в треугольники. Приведем здесь несколько приме-
примеров таких неточечных преобразований и отображений.
Iе. Ясно, что каждое аффинное преобразование плоскости, пере-
переводящее прямую линию снова в прямую, можно рассматривать
как преобразование в множестве
прямых. Так, сжатие к точке О
(гомотетию) с коэффициентом k
можно рассматривать как пре-
преобразование а' — Ф(а), переводя-
переводящее каждую прямую а в прямую а'
того же направления, расстояние
*ff которой от центра О преобразо-
преобразования равно А-кратному расстоя-
расстоянию прямой а от точки О (рис. 63;
при этом проходящие через О
_t ' прямые переходят в себя). Сжатие
b' и к прямой о с коэффициентом «
можно рассматривать как преобра-
Рис. 63. зование а'=Ф(а), переводящее
параллельную о прямую а, в пря-
прямую а\ того же направления, расстояние которой от о равно fc-кратному
расстоянию прямой а, от о (при этом прямая о переходит в себя), а
прямую а2, пересекающую о,—в прямую а'г, пересекающую о в той же
точке, что и а2 и образующую с о угол, тангенс которого в « раз боль-
больше (т. е. «-кратен) тангенса угла, образованного прямыми а2 и о
<рис. 64). При этом, если о2
раньше мы характеризо- w \
вали аффинные преобразо- "
вания как такие (точеч-
(точечные!) преобразования, ко-
торые переводят прямую
линию (рассматриваемую
как прямолинейный ряд °
точек; рис. 65,а) снова
в прямую, го теперь мы
можем описать их как
такие преобразования в
множестве прямых линий плоскости, которые переводят каждую
точку (под которой мы теперь понимаем пучок пересекающихся в
¦одной точке прямых; рис. 65.6) снова в точку (другими словами,
пучок переводят в пучок).
2е. Также и гомологию Г (см. выше стр. ПО) можно описать
как преобразование в множестве прямых линии плоскости. А имен-
именно гомологию с осью о и центром О, переводящую некоторую пря-
прямую т в прямую т', пересекающую ось о в той же точке, что и
н'\
Рис. 6

НЕТОЧЕЧНЫЕ ОТОБРАЖЕНИЯ
123
т, можно определить как преобразование, которое переводит про-
произвольную прямую а плоскости в прямую а', пересекающую ось
о в той же точке, что и а (параллельную о, если а\\ о) и
проходящую через точку А' пе-
пересечения прямойт' с прямой ОА,
б)
Рис. 65.
где А есть точка пересечения прямых ант (рис. 66; если пря-
прямая b пересекает ось о в той же точке, что и т, то для построения
прямой Ь' = Г {Ь) мы заменим mum' парой прямых а и а', постро-
Рис 66
енных по описанному правилу и пересекающих ось о в иной точке).
При этом гомология Г является преобразованием множества всех пря-
прямых проективной плоскости; изображенную на рис.66 прямую q
она переводит в несобс i венную прямую. Преобразование Г обладает тем
свойством, что пучок прямых, пересекающихся в одной (собственной
или несобственной) точке, оно переводит снони в пучок прямых,
пересекающихся в ооной (собственной или несобственной) точке.

124 ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
8.2. Неточечные преобразования в геометрии окружностей. Аналогична
сказанному относительно аффинных преобразований каждое круговое
преобразование плоскости можно рассматривать как преобразование в мно-
множестве окружностей и прямых линчй, переводящее каждую окружность или
прямую (которую можно также считать «окружностью бесконечно большого
радиуса») снова в окружность или прямую Так из формул (9) и (9') § 3
(стр. 74) следует, что инверсию с центром в начале О (декартовых пря-
прямоугольных) координат и степенью 1 можно описать как преобразование
в множестве окружностей и прямых плоскости, переводящее:
а) прямую ах-\-Ьу = 0, проходящую через начало координат О, в себя;
б) прямую 2ах-\- 2Ьу = 1, не проходящую через О, в окружность
(¦** + {/*)— lax — 2b{/«=0, проходящую через О (центр Q(a, b) этой окруж-
окружности принадлежит перпендикуляру ОР, опущенному из точки О на пря-
1 / 1 \ \
мую, причем OQ = yjj= ; радиус окружности равен QO I =- I I
в) окружность (дг' + У2) — 2ах—2Ьу = 0, проходящую через О, в прямую
2ах-\-2Ьу=\, ие проходящую через О (перпендикуляр ОР, опущенный
из О на эту прямую, принадлежит прямой OQ, где Q (а, Ь) — центр окруж-
окружности; при этом OP--
г)-окружность (х'+у*) — lax—2Ьу-\-с-~= 0, не проходящую через О,
в окружность ** + уг—2-х—2— у-\ = 0, также не проходящую через
С С С
О (центры Q (с, Ь) и (?'(—, —) этих окружностей Z и 2 лежат на
одной прямой с точкой О, причем отношение радиусов г= У аг-{-Ьг—с и
, -,// а\г , ( Ь у Г
г = I/ I —)+( — ) окружностей равно отношению длин отрезков
OQ и OQ', откуда следует, что О является центром гомотетии окружностей
Z и 2 , а степени с и —точки О относительно окружностей ? и ? ')
взаимно обратны). Ясно, что круговые преобразования можно охаракте-
охарактеризовать и как преобразования в множестве точек плоскости, переводящие
каждую окружность (к числу которых здесь причисляются и «окружности
бесконечно большого радиуса» — прямые), понимаемую как совокупность
точек (рис. 67, а), снова в окружность, и, с другой стороны, шк преоб-
преобразования в множестве окружностей (и прямых), переводящие совокупность
окружностей пересекающихся в одной точке (рис. 67,6), снова в такую же
совокупность очсцжностей При этом, разумеется, мы должны рассматри-
рассматривать круговые преобразования как точечные преобразования, действующие
в «расширенной» (круговой) плоскости.
До сих пор мы рассматривали лишь такие иеточечные преобразования,
которые можно трактовать также и как точечные. Однако можно опреде-
определить и такие преобразования в множестве прямых линий или в множестве
окружностей на плоскости, которые не переводят совокупность пере-
пересекающихся в одной точке прямых (пучок прямых) или совокупность
пересекающихся«в одной точке окружностей снова в такую же совокупность
прямых или окружностей и которые поэтому никак нельзя рассматривать,
как преобразования в множестве точек. Содержательные примеры преобра-
преобразований такого рода доставляет теория окружностей2). В втой
См. § 2 статьи «Окружности», стр. 454—461.
См. статью «Окружности».

НЕТОЧЕЧНЫЕ ОТОБРАЖЕНИЯ
125
теории изучаются так называемые осевые круговые преобразования, г. е.
преобразования в множестве прямых линий плоскости, переводящие сово-
совокупность касательных одной окружности 2 снова в совокупность касатель-
касательных одной (вообще говоря, отличной от 21) окружности 2'. Совокупность
пересекающихся в одной точке прямых эти преобразования, как правило,
переводят в совокупность касательных некоторой окружности (таким обра-
образом, эти преобразования «точку переводят в окружность»). Рассматривают-
Рассматриваются теорией окружностей и касательные круговые преобразования, переводя-
переводящие окружность в окружность и сохраняющие касание окружностей. Сово-
Совокупность окружностей, проходящих через одну точку, и совокупность
О
о)
окружнгстей, касающихся одной прямой, они могут переводить в сово-
совокупность окружностей, касакщихся одной окружности (таким образом,
касательны круговые преобразования «точку переводят в окружность» и
«прямую переводят в окружиость>).
Простейшим примером осевого кругового преобразования является
так называемое расширение. Как преобразование в множестве прямых,
расширение Р на величину d определяется следующим образом: каждую
прямую а расширение Р переводит в прямую а', параллельную а и удален-
удаленную от а на расстояние й. Так как это определение не указывает, в ка-
какую именно из двух прямых, параллельных а и удаленных от а на рас-
расстояние d, переходит а, то здесь нужны еще некоторые дополнительные
соглашения. Именно оказывается необходимым считать, что каждая пря-
прямая плоскости является направленной, те. что с обыкновенной
прямой а совпадают по положению две прямые а, и о,, отличающиеся

126 ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
одна от другой направлением (направление на рисунках обычно обозна-
обозначается стрелкой). Прямые о, и аг расширение Р переводит в разные
прямые Qj и а2, сдвигая каждую прямую на расстояние & вправо (если
смотреть в направлении, указанном на преобразуемой прямой; см. рис. 68).
Таким образом, расширение Р приходится рассматривать не как преобразо-
преобразование в множестве обыкновенных прямых плоскости, а как преобра-
преобразование в множестве направленных прямых (осей). Ана-
Аналогично обстоит дело и при рассмотрении более общих осевых круговых
преобразований, с чем и связано прилагательное «осевые> в названии
этих преобразований.
Нетрудно понять, что пучок прямых расширение Р переводит в сово-
совокупность касательных окружности 2 с центром в центре пучка и ра-
радиусом A (pi.c. 69, а); этой окружности
естественно приписать определенное
направление, согласованное с напра-
направлением всех ее касательных (на ри-
рисунках направление окружности также
указывается поставленной на окруж-
^. ~ ч ности стрелкой). Таким образом, есте-
^'¦^ *¦ " -^ ^ Л ственно считать, что расширение на
величину d пер"водит точки в окруж-
окружности радиуса d. Направленную окруж-
окружность 2 на плоскости (задаваемую сово-
совокупностью своих направленных каса-
касательных) расширение Р переводит в
концентрическую с 2 окружность 2',
радиус которой равен r-\-d, или г — d,
или d—г (рис. 69, б—г). Оказывается
рИ1. 68. очень удобным считать, что радиус
окружности может быть и положитель-
положительным и отрицательным, причем первое
означает, что окружность направлена против часовой стрелки, а второе —
что она направлена по часовой стрелке; при этом направленная окруж-
окружность полностью определится указанием своего центра и (положительного
или отрицательного!) радиуса. При таком соглашении расширение пере-
иодит окружность радиуса г в окружность радиуса r + d (см. рис. 69, б—г;
отрицательный радиус имеют окружности 2 и 2' на рис. 69, в и окруж-
окружность 2 на рис. 69, г). Таким образом, расширение Р можно описать как
преобразование в множестве направлгнных прямых плоскости, сдвигающее
каждую прямую вправо на расстояние d. При этом множество всех прямых,
касающихся одной направленной окружности 2 (роль которой может
играть и «окружность нулевого радиуса», так что мы имеем пучок схо-
сходящихся в одной точке прямых), переходит в множество прямых, ка-
касающихся одной окружности 2', т. е. окружность переходит с окруж-
окружность. Но можно также описать расширение и как преобразование в мно-
множестве направленных о ружностей, переводящее окружность (положительного,
нулевого или отрицательного!) радиуса г в концентрическую с исходной
оьружность радиуса r-\-d. Это преобразование переводит совокупность
всех окружностей, касающихся одной направленной прямой /, в совокуп-
совокупность окружностей, касающихся другой прямой V, т. е. прямую оио
переводит в прямую. Однако, как точечное преобразование рассматри-
рассматривать расширение невозможно!
Неточечные преобразования плоскости также довольно часто могут
оказаться полезными для решения конкретных геометрических задач
на построение и на доказательство В качестве первого примера рассмот-
рассмотрим здесь известную задачу о построении общих касательных к овум окруж-

ГШТОЧКЧНЫЕ ОТОБРАЖЕНИЯ
127
ностям 1, и 2, радиусов г, и л,, где г, 5> г2. Применим к чертежу этой
задачи (рис. 70) расширение на величину г2; при этом окружность 22 мы Судем
считать направленной по часовой стрелке (имеющей отрицательный
радиус — гг), так что расширение Р перевидит 22 в точку —центр 2, этой
окружности (именно в этом и заключается смысл применения расшире-
расширения!) Окружность 2, перейдет в окружность ZJ, концентрическую с 2,;
6)
Рис. (i9.
при этом в зависимости от того, считаем ли мы 2, направленной также
по часовой стрелке или против часовой стрелки, окружность 2, будет
иметь радиус ',-г2 (рис. 70, а), ты r. + л, (рис. 70, б). Общие касатель-
касательные окружностей 2, и 22 перейдут в касательные окружности 2,, прохо-
проходящие через точку 2^, их нетрудно построить (построение прямой, каса-
касательной к данной окружности и проходящей через заданную точку, мы

128
ГЕОМЕТРИЧЕСКИ ПРЕОБРАЗОВАНИЯ
считаем известным). Искомая же касательная / окружностей 2, и 2г най-
найдется как прямая, которую расширение Р переводит в проходящую через
St касательную /' окружности S,; она параллельна /' и удалена от /'
на расстояние гг (причем Г расположена справа от направленной пря-
прямой /).
Рис 70
8.3. Полярное отображение. Принцип двойственности в проек-
проективной геометрии. Важным и интересным примером отображения,
переводящего точки в прямые линии, а прямые—в точки, яв-
является так на-ываемое по!ярное отображение Пс центром О. Это
отображение каждую точку А плоскости переводит в прямую а,
перпендикулярную ОА и проходящую через точку А', в кото-
которую точка А переводится инверсией с центром О и степенью 1
(т.е. через такую точку А' луча ОА, что О A' ~~qj)' обратно,
прямую а отображение П переводит в точку А (рис. 71, а).

НЕ ТОЧЕЧНЫЕ ОТОБРАЖЕНИЯ
129
Ясно, что областью действия молярного отображения является
множество всех точек и прямых плоскости. Для наиболее
полного рассмотрения полярного отображения целесообразно счи-
считать, что точки и прямые рассматриваются не на обычной (евклидо-
(евклидовой), а на проективной плоскости. При этом нужно допол-
дополнить определение полярного отображения соглашением, что центру О
соответствует «бесконечно удаленная» (несобственная) прямая проек-
проективной плоскости, а несобственной точке А, определяемой проходя-
проходящей через нее прямой /, соответствует проходящая через О прямая.
А'
б)
Рис. 71.
перпендикулярная /. (В противном случае нам пришлось бы исклю-
исключать из рассмотрения точку О и проходящие через нее прямые, что
также может служить вариантом рассмотрения полярного отображе-
отображения, но менее удобным, чем использование несобственных элемен-
элементов проективной плоскости.)
Ряд замеча тельных свойств полярного отображения П мы укажем
ниже; здесь же отметим лишь следующее его свойство, бесспорно
важнейшее из всех: если Y\(A) = a и В— точка прямой а, то пря-
прямая Ь=П(В) проходит через точку А. Действительно, обозначив
через В' точку пересечения прямой ОВ с прямой ft = Il(fl), мы най-
найдем ОВ-ОВ'=ОА-ОА' (= 1) или
О А'
~ОВ
ОВ'
: О А ¦
Из этого следует, что треугольники О А' В и OR'А подобны; в частности,
^/ ОВ'А = //_ОА'В=90°, и потому точка А лежит на перпендикулярной
9 Энциклопедия, кн. 4

130 TEOMFTPHWECKHE ПРЕОБРАЗОВАНИЯ
к ОВ прямой Ь. Предоставляем читателю проверить, как видоиз-
видоизменится рис. 71, а, если точка А (или В) совпадает с О или является
несобственной.
Это свойство полярного отображения означает, что прямую а,
рассматриваемую как ряд точек, отображение П переводит
в точку А, понимаемую как пучок прямых; обратно, любой пучок
прямых отображение П переводит в прямолинейный ряд точек
(рис. 71,6).
Важнейшим следствием наличия полярного отображения проек-
проективной плоскости является так называемый принцип двойственности
проективной геометрии1). Этот принцип утверждает, что в форму-
формулировке любой теоремы проективной геометрии на плоскости
можно заменить всюду слово «точка-» словом «прямая» и, наоборот;
выражение «.лежит на» выражением «.проходит через», и наоборот;
новая теорема также будет справедлива, если только была
справедлива первоначальная теорема. В самом деле, пусть мы
имеем некоторую теорему проективной геометрии, относящуюся
к расположению точек и прямых. Полярное отображение переводит
выражающий эту теорему чертеж в новый чертеж, в котором роль
точек уже будут играть прямые, а роль прямых точки; при этом
точкам, принадлежащим одной определенной прямой /, будут отве-
отвечать прямые, пересекающиеся в точке Z., отвечающей прямой /. Этот
новый чертеж будет выражать иную теорему, которую можно наз-
назвать «двойственной» первоначальной теореме. Ниже мы поясним эту
общую схему конкретным примером.
Пример применения полярного отображения доставляет нам так
называемая
Теорема Дезарга. Если прямыр ААЛ, ВВг и ССг, соединяющие
соответствующие вершины двух треугольников ABC и И^С,,
пересекаются в одной точке О, то точки К, L и М пересечения
соответствующих сторон этих треугольников лежат на одной
прямой (рис. 72, а). Для доказательства произведем полярное отоб-
отображение П с центром в точке О. При этом точки А и А1
перейдут в прямые а и аг, перпендикулярные прямой ОАА1 и,
следовательно, параллельные между собой; точки В и ??,, С и С,
также перейдут в прямые Ь и bt || b, с и с, || с. Таким образом,
треугольники ABC и А1В1С1 перейдут в новые треугольники с соот-
соответственно параллельными сторонами, образованные прямыми а, Ь, с и
а,, Ьх, сх. Вершины этих новых треугольников мы обозначим через
А', В', С и А,, В\, С[- Так как ГТ (А) = а, П (В) = Ь, то прямая АВ
переходит при полярном отображении в точку пересечения прямых
а и Ь, т.е. П(АВ) = С'. Аналогично 0(^,6,) = С,. Следовательно,
точка К пересечения прямых АВ и AtBt переходит в прямую
') См. учеСники проективной геометрии, укаганные f сьсске2) на стр. 110.

НЕ ТОЧЕЧНЫЕ ОТОБРАЖРНИЯ
131
А,
7
Рис. 72.

132
rF0MFTPH4FCKHE nPF-ОБРАЗОВАНИЯ
CO,, т. e.
Аналогично
П(ЛГ) =?'?,.
Поэтому для доказательства того, что точки К, L, М лежат
на одной прямой, достаточно установить, что прямые А'А[, В'В\,
С'С\ пересекаются в одной точке. Но из параллельности прямых а
и с,, Ь и Ьх, сие, вытекает, что либо треугольники А'В'С' и
А\В[С\ равны и получаются друг из друга параллельным переносом
(рис. 72,6), и тогда прямые А'А\, В'В,, C'Ci параллельны между
собой, т. е. пересекаются в
одной несобственной точке,
либо треугольники А'В'С' и
A'iB,C, гомотетичны, и тогда
прямые A'A'i, B'B'i, C'Ci так-
также пересекаются в одной
точке — центре гомотетии
(рис. 72, е). Следовательно,
в любом случае точки К, L,
М лежат на одной прямой.
Заметим, что одна из точек
К, L, М или даже вся пря-
прямая KLM может оказаться
несобственной (рис. 72, г, д).
Теорема Дезарга явля-
является типичной теоремой
проективной геометрии; сле-
следовательно, к ней применим
принцип двойственности. Эта
теорема утверждает, что
если два треугольника ABC
и AtB1C1 таковы, что пря-
прямые AAt, BBl и CCt пересе-
пересекаются в одной точке О,
то точки пересечения соот-
соответствующих сторон а и с,.
Ъ и hv с и с, двух треугольников лежат на осной прямой
(рис. 73, а). Заменим теперь в формулировке этой теоремы слово
«точка» словом «прямая» и наоборот, в соответствии с принципом
двойственности. Мы получим следующее утверждение: если два
«.трехсторонника» abc и a1bJci таковы, что точки а-а1 (точка
пересечения прямых а и я,), h-bt и c-ct принадлежат одной пря-
прямой о, то прямые, соединяющие соответствующие вершины
трехсторонников, пересекаются в одной точке. Рис. 73, б, выра-
выражающий эту теорему, не отличается от рис. 73, с, выражающего
теорему Дезарга, но само содержание теоремы изменилось—условие
ее заменилось заключением, и наоборот. Таким образом, мы пришли
ь теореме, обратной первоначально сформулированной нами
рис. 73.

HET04E4HbIF ОТОБРАЖЕНИЯ
133
теореме Дезарга (эта пбратная теорема также обычно связывается
с именем Дезарга). При этом полученную таким образом теорему
нам уже не надо доказывать: справедливость ее следует
из (прямой) теоремы Дезарга и принципа двойственности. Разумеется,
имеющее место в нашем случае совпадение теоремы, «двойственной»
исходной теореме, и теоремы, обратной ей, является случайным.
Наконец, приведем еще один пример применения полярного отобра-
отображения к доказательству геометрической теоремы Пусть касательная I к
вписанной окруонности а треугольника ABC пересекает стороны треуголь-
треугольника в точках М, N и Р; прямые ОМ,±ОМ, ONt±ON и ОР^ОР (где
Рис. 74.
О—центр окружности а) пересекают те же стороны в точках /И,, N, и Р,;
докажем, что точки Mt, W, и Р, тоже лежат на одной касательной /,
к окруонности а (рис. 74) Будем считать, что радиус окружности с ра ен 1,
и произведем полярное отображение П с центром О. При этом прямые АВ,
ВС, СА и / перейдут в точки С,, Л,, б, и L, их касания с окружностью а;
точки М, N и Р перейдут в прямые LXC1 }_ ОМ, L1A1\ON и L1B1J_OP;
точки /И,, Nj и Р, перейдут в прямые т, _[ 0Ми n,"j 0Nx и р, _L OP,,
проходящие через точки С,, Л, и В, и, очевидно, параллельные ОМ, ON
и ОР, т.е. перпендикулярные прямым L,C,, LlAl и L,6,. Но отсюда

134
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
следует, что прямые ш„ и, и р, пересекают окружность а в одной точке L,
диаметрально противоположной точке L,; этой точке отвечает (параллель
ная /!) прямая 11г которая касается окружности а в точке L и которой и
принадлежат точки Ми Nx и Р,.
8.4. Подерное преобразование. В качестве последнего примера неточеч-
неточечного преооразования плоскости мы рассмотрим так называемое подерное
преобразование А, переводящее каж-
каждую линию плоскости в другую ли-
линию, но не сохраняющее ни точек,
ни прямых, ни окружностей. Это
преобразование определяется сле-
чующим довольно сложным обра-
образом. Пусть у—некоторая кривая на
плоскости; с каждой точкой А кри-
кривой у сопоставим основание А'
перпендикуляра, опущеннаго из
фиксированной точки О (ц е н т р а
подерного преобразования А) на
касательную с, проведенную к кри-
кривой у в точке А '); когда точка А
пробегает линию у, соответствующая
ей точка А' пробегает новую линию
у', которая и считается образом ли-
Рнс. 75.
нии Y ПРИ преобразовании А (рис. 75). Нетрудно понять, что прямая а
переводится подерным преобразованием в одну точку А — основание пер-
перпендикуляра, опущенного из О на прямую о (рис. 76); точка же А, рас-
рассматриваемая как пучок прямых (которые все играют роль «касательных»
к точке), переходит в окружность 2,
построенную иа отрезке ОА, как на
диаметре (рис. 77). Окружность с
центром О подерное преобразование Д
h
Рис. 76.
Рис. 77.
переводит в себя; если же центр окружности 2 отличен от точки О, то
преобразование А переводит 2 в довольно сложную кривую, называемую
улиткой Паскаля (рис. 78, а—в; изображенная на рис. 70, б «серд-
«сердцевидная» улитка Паскаля называется кардиоидой)- Улитки Паскаля — очень
интересные кривые; они могут быть определены (даже несколькими спосо-
способами) и независимо от подерного преобразования.
') Касательной к кривой у в ее точке А, как обычно, называется
предельное положение секущей АВ, к которому стремится секущая, когда
точка В кривой у стремится к А (см. статью «Производные, интегралы и
ряды», кн. III ЭЭМ, стр. 305).

HETO4E4HHF ОТОБРАЖЕНИЯ
135
Подерное преобразование мы определили как преобразование в множе-
множестве линий плоскости (к числу которых причисляются и прямые линии
и даже точки), переводящее каждую линию у в новую линию у' Вгзмо-
жен, однако, и другой подход к этому преобразованию, в некоторых отно-
отношениях более удобный. Из определения преобразования Л следует, что
о)
6)
Рис. /8.
точка А' преобразованной кривой у', сопоставленная с точкой А кривой у,
полностью определяется заданием точки А и касательной а к кривой у в
точке А — никакие другие данные о кривой у для определения точки А'
Рис. 79.
Рис. 80.
не нужны (А' есть основание перпендикуляра, опущенного из точки О на
прямую о). Но, зная точку А и прямую а, можно определить не только
точку А', но и касательную о'к кривой у' в точке А' В самом деле,
пусть В—другая точка кривой у, и b—касательная к у в этой точке: точ-
точке В отвечает течка В' кривой у', которую можно определить как осно-
основание перпендикуляра, опущенного из точки О на прямую Ь (рис. 79).
Касательную а' кривой у' в точке А' можно определить как предел, к

136
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
которому стремится секущая Л В' когда точка В' стремится к А' иль,
что то же самое, когда В стремится к А. Но когда В стремится к А, точ-
точка Q пересечения прямых о и 6 также стремится к А; отсюда вытекает,
что прямая А'В' — хорда ок-
окружности S,, построенной на
отрезке 0Q, как на диа-
диаметре, — стремится к пря-
прямой о', касательной в точке
А' к окружности 2 (рис. 80),
построенной, как на диаметре,
на отре°ке О А (хорда окруж-
окружности 2, стремится к каса-
касательной окружности 2, ибо
когда В стремится к А, и точ-
точка В' стремится к А').
Из доказанного следует,
что касающиеся между собой
в точке А кривые подерное
преобразование А ереводит
в кривые, касающиеся между
соСой в сопоставленной с А
точке Л'(рис 81, о). Другими
словами можно сказать, что
совокупность точки А и задан-
заданного р ней направления а
преобразование А переводит
• в союкупность точки А' и
заданного в ней направления
а' Точку с проходящей через
нее прямой в геометрии обыч-
обычно называют линейным
элементом. Поэтому можно
сказать, что подерное преобра-
преобразование А есть преобразование
в множестве линейных элемен-
элементов плоскости, переводящее
каждый лин йный элемент
(А, а) в другой линейный эле-
элемент (А', а'). Кривую у. рас-
рассматриваемую как совокуп-
совокупность своих линейных элемен-
элементов (точек у и касательных
к у в этих точках), Л пере-
переводит в другую кривую, обра-
образованную линейными элементами, в которы" переходят составляющие у
линейные элементы (рнс Ы, б). Преобразования такого родл называются
касательными преобразованиями'); таким образом, A ecrnt касательное
преобразование.
8.5. Группы неточечных преобразований. Многое из того, что
было сказано выше о точечных отображениях и преобразованиях пло-
плоскости, может быть перенесено и на произвольные (не обязательно
точечные!) геометрические отображения и преобразования. Так, можно
Рис. 81.
') См. статью «Окружности» в этой книге ЭЭМ, . частности стр 510—513.

МЕТОЧЕЧНЫЕ ОТОБРАЖЕНИЯ
13Т
\
определить произведение ?Ф двух отображений Фи?, пред-
представляющее собой результат последовательного осуществления сначала
огображения Ф, а затем отображения W (разумеется, область зна-
значений отображения Ф должна совпадать с областью определения ото-
отображения ?). В частности, имеет смысл понятие произведения преоб-
преобразований, например двух преобразований, определенных в множестве
прямых линий, или двух преобразований, определенных в множестве
окружностей.
Простой пример произведения двух (неточечных) преобразований до-
доставляет преобразование Р2Р„ где Р, есть расширение на величину d
а Р2—расширение на величину d2. Ясно, что Р2Р, есть тоже расширение на
величину d^d^ ведь Р, переводит (направленную) прямую / в прямую
/,||/ того же, что и I натра- у
вления, лежащую справа от
/ и удаленную от / на рас-
расстояние d,; расширение Р2
переводит /, в прямую I'\\1,
того же направления, лежа-
лежащую справа от /, и удален-
удаленную от /, на расстояние d2; но
ясно, что /' получается из /
расширением на величину
d,-|-d2 (рис. 82; можно также —
рассуждать так: Р, переводиi
произвольную окружность I
радиуса г ч концентрическую
с 2 окружность 2, радиуса —
'•-fd,, а Р2 переводит 2,в кон-
концентрическую с 2, окруж- Рис. 82.
ность 2' радиуса ('• + d1)-f
-fd2 = r-f(J,-|-d2), получающуюся из 2 расширением на величину d,-fd2).
Можно также говорить о произведении ДгА, двух подерных преобра-
преобразований А, и А2: если А, переводит линию у в линию у„ а А2 —линию у.
в линию у\ то преобразование Д2А, переведет у в у' ').
Имеет также смысл понятие произведения П„П, двух полярных ото-
отображений П, и П2; его областью действия будет" множество всех точек
и прямых (проективной) плоскости. При этом ГЦП, будет переводить точки
в точки, а прямые —в прямые, т. е. оно как бы «распадается» на два
отдельных преобразования, одно из которых будет точечным, а дру-
другое—преобразованием в множестве всех прямых проективной плоскости;
первое из них (точечное преобразование), как легко видеть, будет про-
проективным преобразованием «Квадрат» ПП = Пг полярного отображения П
является тождественным преобразованием, ибо переводит каж-
каждую точку и каждую прямую в себя; это означает, что полярное отображение
является инволютивным (см. § 5, стр. 97), т. е. обратным самому себе.
Для неточечных отображений и преобразований имеет смысл также
понятие отображения (или преобразования) ф, обратного
*) Подерные преобразования Д, и Д2 можно также рассматривать как
преобразования в множестве линейных элементов плоскости (см. стр. 136);
в таком случае и произведение А2Д, двух подерных преобразований при-
придется рассматривать как преобразование в множестве линейных элементов.

138 ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
данному отображению (преобразованию) Ф. Это отображение определя-
определяется следующим образом: если Ф переводит геометрический образ а
в геометрический образ а' (а и а' могут являться точками, прямыми,
окружностями или иными геометрическими объектами, возможно раз-
разной природы), то Ф переводит а' в а. Область действия обратного
преобразования Ф совпадает с областью действия преобразования Ф.
Так, скажем, обратной для гомотетии с центром О и коэффициен-
коэффициентом k, рассматриваемой как преобразование в множестве прямых
плоскости, является гомотетия с тем же центром О и коэффициен-
коэффициентом \\k (также рассматриваемая как преобразование в множестве пря-
прямых); преобразование Д, обратное подерному преобразованию А
с центром О, переводит улитки Паскаля в окружности и т. д.
Понятия прои ведения двух (неточечных!) преобразований и обрат-
обратного преобразования позволяют определить группу таких преобра-
преобразований, т. е. такую совокупность On преобразований, которая:
1° содержит тождественное преобразование I; 2° наряду с каждым
преобразованием Ф содержит и обратное ему преобразование Ф;
3е' наряду с каждыми двумя преобразованиями Ф и У содержит и их
произведение ?Ф Ясно, например, что образуют группу аффинные
преобразования, рассматриваемые как преобразования в множестве
прямых линий плоскости, или круговые преобразования, рассматри-
рассматриваемые как преобразования в множестве окружностей.
Более новыми для нас являются группа осевых круговых
преобразований или группа касательных круговых
преобразований; например, все осевые круговые преоОразования
образуют группу, так как I" тождественное преобразование, рассматрива-
рассматриваемое как преобразование в множестве направленных прямых плоскости,
переводит каждую окружность в себя, т. l. является круговым; 2° если
ф есть преобразование в множестве направленных прямых, переводящее
окружности с окружности (круговое преобразование), то и обратное п е-
образование Ф является круговым (если Ф переводит окружность 2
в окружность 2', то Ф переводит 2' в 2); 3° если преобразования ФиТ,
определенные в множестве направленных прямых, переводят окружности
с окружности, то и УФ переводит окружности в окружности (если Ф
переводит окружность 2 в 2,, а V — окружность 2, в 2', то ?Ф перево-
переводит 2 в 2'). Частью группы осевых круговых преобразований является
группа расширений, для построения которой надо определить рас-
расширение на величину нуль (тождественное преосрасование) и расширение на
отрицательную величину — d, сдвигающую каждую (направленную) прямую
на расстояние d в л е во и переводящее (направленную) окружность радиу-
радиуса г в концентрическую с ней окружность радиуса г—d (рис. fc3; ср. выше,
стр. 126). При этом обратным расширению на (положительную или отрица-
отрицательную!) величину d будет расширение на величину —d, а произведение
расширений на величины d, и d2 всегда будет равно расширению на вели-
чин.у d, -\-d2.
Понятие группы (неточечных!) преобразований очень важно потому,
что оно позволяет говорить о геометриях, основным элементом
которых является не точка, а другой геометрический объект —

НЕТОЧНЫЕ ОТОБРАЖЕНИЯ
139
-d
прямая линия, окружность и т. д. Ясно, что приведенное в S 6
общее определение геометрии по Клейну сохраняет силу и в том
случае, если под «геометрической фигурой» понимать не множество
точек, а скажем, множество прямых; в этом случае и «движениями»
соответствующей «геометрии» естественно назвать какие-то преоб-
преобразования в множестве прямых линий плоскости. Однако независимо
от того, играют ли роль «движений», совмещающих между собой
«равные» фигуры, преобразования в множестве точек или какие-то
неточечные преобразования,
определенное с помощью
этих «движений» «равенст-
«равенство» в том и только в том Г, /
случае будет удовлетворять
условиям рефлексивности,
симметричности и транзити-
транзитивности (см. выше, стр. 102),
если совокупность «движе-
«движений» образует группу. Эго
условие очерчивает круг
«неточечных» геометрий, к
числу которых принадлежат
линейчатая геомет-
геометрия (геометрия прямых ли-
линий) и круговая гео-
геометрия (геометрия окруж -
ностей), являющиеся содер-
жательными и хорошо изу-
изученными геометрическими дисциплинами. Ясно, что каждая «геомет-
«геометрия» подобного рода задается указанием группы (неточечных!) пре-
преобразований, играющих в этой «геометрии» роль «движений».
Так, осноиными ветвями геометрии окружностей являются в настоящее
время «точечная геометрия окружностей», базирующаяся на группе точеч-
точечных круговых преобразований, «осевая геометрия окружностей* в основе
которой лежит группа осевых кругоьых преобразований, и «контактная
геометрия окружностей», задаваемая группой касательных круговых пре-
преобразовании ). При этом наша новая (более широкая!) точка зрения на
геометрию приводит к необходимости несколько уточнить изложенную
в предыдущем параграфе концепцию Клейна- теперь нам следует считать
что отдельные «< еометрии» различаются не только группами преобразова-
преобразовании, играющими роль «движений», но и выбором основного элемента «гео-
«геометрии»: так группа аффин ых преобразований может быть положена
в основу «точечной аффинной геометрии» и «линейчатой афЬинной геомет-
геометрии»; группа (точечных) круговых преобразований-—в основу «точечной ана-
аналагматической геометрии» и «круговой аналагматической геометрии» и т д
рис 83
)_
В ЭТОII
")_Этим трем геометриям посвящены гри части статьи «Окружности»
ОН К НИ ГС C/C/i*!. »

140 ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
§ 9. Принцип перенесения
9.1. Введение. Вернемся теперь к определению обычной (евкли-
(евклидовой) геометрии по Клейну. Это определение утверждает, что движе-
движения (или движения и преобразования подобия) не меняют содержания
теорем евклидовой геометрии, т. е. переводят каждый геометрический
чертеж в полностью равноправный ему чертеж, из которого можно
вывести лишь те же самые заключения, что и из первоначального
чертежа.
Последнее обстоятельство связано с тем, что наше преоб-
преобразование сохраняет неизменными все понятия и величины, имеющие
геометрический смысл, —параллельные (или перпендикулярные) прямые
оно переводит в параллельные (перпендикулярные) прямые, равные
отрезки—в равные отрезки, сохраняет величину угла между двумя
прямыми или отношения площадей двух фигур и т. д. Любое же о т л и ч-
ноеот подобия преобразование л уже не будет обладать этим
свойством—оно исказит смысл геометрических понятий и, следова-
следовательно, преобразует исходную геометрическую теорему в какое-то
совершенно новое предложение.
Это утверждение в старину часто формулировали, говоря, что каждо-
каждому (отличному от подобия!) преобразованию Л отвечает свой принцип
перенесения, позволяющий преобразовывать геометрические тео-
теоремы в новые; мы здесь также воспользуемся удобным и выразитель-
выразительным термином: «принцип перенесения». Этот термин имеет следующий
смысл. Преобразование л не сохраняет геометрических понятий,
т. е. оно преобра*ует геометрические образы в новые, с точки зрения
евклидовой геометрии отличные от исходных. Мы можем указать,
как именно преобразует геометрические объекты заданное преобразо-
преобразование л; другими словами, мы можем составить отвечающий рассмат-
рассматриваемому преобразованию «словарь», содержащий «перевод» всех
геометрических понятий, так сказать, на новый «язык», другими
словами,— таблицу, указывающую, во что именно переводит преобра-
преобразование л те или иные геометрические объекты. Этот «словарь»
позволяет преобразовывать («переводить на новый язык») все гео-
геометрические теоремы: в самом деле, из любого предложения, сфор-
сформулированного в терминах обыкновенной евклидовой геометрии, мы
сможем получить новое предложение, заменив все входящие в исходную
теорему геометрические понятия образами, в которые переводит их
преобразование л. Для того чтобы пояснить это последнее утвержде-
утверждение, мы проиллюстрируем его на ряде достаточно разнообразных
примеров; попутно мы увидим, каким богатейшим источником новых
геометрических фактов и теорем могут служить геометрические пре-
преобразования.

ПРИНЦИП ПЕРЕНЕСЕНИЯ
141
9.2. Принцип перенесения, отвечающий сжатию к прямой. Про-
Простейшим из известных нам геометрических преобразований, отличных
от преобразований подобия, является сжатие к прямой; обозна-
обозначим его, скажем, 2 (§ 1, стр. 55). Это преобразование переводит
точку в точку и прямую в прямую; однако окружность Q оно пере-
переводит не в окружность, а в эллипс Е, одна ось которого парлллельна
оси сжатия о, а вторая — перпендикулярна ей, и отношение осей
которого равно коэффициенту сжатие k (рис. 84)'). Все такие эллипсы Е
гомотетичны фиксированному эллипсу Ео с полуосями длины 1 и k,
отвечающему «единичной окружности» (окружности радиуса 1) Qo,
Рис. 84.
или получаются из Ео параллельным переносом. Из того, что сжатие 2
сохраняет отношение отрезков одной прямой (см. стр. 62), следует,
что отрезок АВ длины d это преобразование переводит в отрезок А'В'
длины d-0'К', где О' К' — параллельный А'В' полудиаметр эллипса Ео.
Параллельные прямые преобразование 2 переводит в параллельные
(см. стр. 62); перпендикулярные же прямые 2 переводит в сопря-
сопряженные относительно Е прямые / и т, т. е. такие, что
диаметр эллипса Е, параллельный прямой /, делит пополам все хорды
эллипса Е, параллельные т (рис. 85; это следует из того, что каж-
каждый диаметр окружности Q делит пополам все перпендикулярные
этому диаметру хорды окружности Q).
•) См. в кн. V ЭЭМ статью о конических сечениях.

142
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
Таким образом, преобразованию Z отвечает следующий «словарь»:
Исходное понятие
Точка
Прямая
Окружность Q
Единичная окружность Qo
Параллельные прямые
Перпендикулярные прямые
Длина отрезка АВ
Середина отрезка
Преобразованное понятие
Точка
Прямая
Элчипс Е
«Единичный эллипс» Ео
Параллельные прямые
Сопряженные относительно Е пря-
прямые
Отношение угт?, где ОК—парал-
лельный АВ полудиаметр Ео
Середина отрезка
который можно, разумеется, еще продолжать. Из каждой теоремы евкли-
евклидовой геометрии мы можем получить новую теорему, заменив все
Рис. S6.
Рис. 87.
фигурирующие в исходной теореме понятия с помощью выписанного
«словаря». Это утверждение и составляет содержание «принципа
перенесения», отвечающего сжатию к прямой 2.
Так из теоремы о том, что медиана ра..но5едренного треугольника
служит одновременно и высотой, вытекает, что если стороны АВ и АС
треугольника ABC пропорциональны параллел ным им полудиаметрам эллип-
эллипса Е, то медиана AD треугол >ника сопряжена относительно Е с основанием
ВС треугольника ^рис. об). '1з теоремы о степени точки относительно
окру-кности вытекает, что если череч фиксированную точку М провести
секу-цу.о МАВ эллипса Е (где А и В — точки Е), то произведение МА-МВ

ПРИНЦИП ПЕРЕНЕСЕНИЯ
143
будет пропорционально квадрату 0/<2 параллельного МАВ полудиаметра
_ МА-МВ ,
эллипса Е, т. е. отношение —jyui— будет одним и тем же для исех секу-
секущих (рис. 87); из определения и свойств инверсии (стр. 56 и 75) — что преоб-
преобразован ie 1, сопоставляющее с
каждой точкой А плос осп i такую
точ у А' луча ОА, что ОА-ОА' =
=0К", где К есть точка пересе-
пересечения прямой ОАА' с фиксирован-
фиксированным эллипсом Е с центром О, пе- Ч^д
реводит каждую не проходящую
чергз О прямую плоскости в yr~ ^~—^V^/fNx/1
эллипс, гомот точный Е или полу
чающийся из Е параллельным п? \ О*
реносом (рис. 88) и т. д.
9.3. Принцип перенесения,
отвечающий инверсии. В каче- рис. gs.
стве второго примера естествен-
естественно рассмотреть инверсию I
(§ 1 стр. 56). Это преобразование переводит точку в точку и проходящую
через центр О инверсии прямую в прямую; не проходящую же через О
прямую / инверсия I переводит в проходящую через О окружность Qo,
а окружность Qo—обратно в пря-
прямую /; наконец, окружность Q, не
проходящую через О, преобразова-
преобразование I переводит в другую (может
Рис. 89.
быть, ту же самую!) окружность Q', также не проходящую через О (см.
стр. 75). Параллельные прямые преобразование I переводит в две
окружности (или прямую и окружность), касающиеся в точке О, т. е.
не имеющие отличных от О общих точек (рис. 89, а); перпендику-
перпендикулярные же прямые преобразование I переводит в перпендикулярные
окружности (прямую и окружность), поскольку I сохраняет величину

144
ГТОМЕТРИЧЕСКИР ПРЕОБРАЗОВАНИЯ
угла (рис. 89, бI). Наконец, точки А и В, расстояние между кото-
которыми равно d, инверсия с центром О и степенью k переводит в такие
точки А' и В', что
АЧ!?__ОА' A'R'—H 0A'
(это следует из подобия изображенных на рис. 89, а треугольни-
треугольников ОАВ и ОВ'А' с общим углом О и пропорциональными сторо-
нами: ОА-ОА' = ОВ-ОВ' и, значит, ^ =
то из последней формулы получаем
А'И'—Н k
А так как О А' =
ОА-ОВ'
таким образом, расстояние между преобразованными точками А' и В'
АВ
пропорционально величине ОА-ОВ'
Теперь мы можем выписать «словарь», отвечающий инверсии I:
Исходное понятие
Точка
Проходящая через О прямая
Не проходящая через О прямая
Преобразованное
понятие
Точка
Проходящая через О прямая
Проходящая через О окружность
Проходящая через О окружность Не проходящая через О прямая
Не проходящая через О окруж- Не проходящая через О окруж-
окружность
Параллельные прямые
Перпендикулярные прямые
Угол между прямыми
ность
Касающиеся в точке О окруж-
окружности (или окружность и пря-
прямая)
Перпендикулярные окружности
(или окружность и прямая, или
две прямые)
Угол между окружностями (или
окружностью и прямой, или
двумя прямыми)
АВ
Величина ш-щ
Расстояние между точками А и В
Касающиеся окружности (или Касающиеся окружности (окруж-
окружность и прямая) ность и прямая) или парал-
параллельные прямые
") См. статью «Окружности», стр. 474. [Углом, образованным двумя
окружностями в точке их пересечения, называется угол между их каса-
касательными в этой точке: аналогично угол между прямой и окружностью —
это угол между прямой и касательной к окружности в точке ее пересече-
пересечения с прямой. J

ПРИНЦИП ПЕРЕНЕСЕНИЯ
1+5
и т. д. Этот «словарь» позволяет получать из известных теорем
евклидовой геометрии совершенно новые, зачастую весьма любопыт-
любопытные предложения.
Так, например, из известной теоремы о том, что сумма углов треуголь-
треугольника равна 180°, следует, что если три окружности пересекаются в одной
точке О, то сумма углов ^треугольника», образованного в пересечении этих
окружностей, равна 180° 'рис. 90, а). Из того, что углы при основании
б)
Рис. 90.
равнобедренного треугольника равны следует, что еслч проходящие через
одну точ/.у D окружности nepecet-аются в та<\их трех точ> ах А, В и С, что
корды АВ и АС пропорциональны хордам ОВ и ОС ( т. е. величины .
АС \
и п равны 1, то окружности ОАВ и ОАС образуют одинаковые углы
UA¦ С/С j
окружностью ОВС ( рис. 90, б; обратно, из равенства этих углоь выте-
1_АС\
]~ ОС)'
АВ
ов:
кает, что
Из того, что сумма двух сторон треугольника ье меньше его третьей
стороны, вытекает, что для любых четь,рех точек А, В, С, D плоскости (где
i-очка D играет роль центра О инверсии)
АВ
ВС
_АС_
'DA-DC
или
-CD + BC-AD^AC-BD.
Равенство в последнем соотношении будет иметь место в том и только
в том случае, если точки А, В и С лежат на одной окружности (или пря-
прямой), проходящей через точку D (рис. 91, а; этот случай отвечает тому,
что три исходные точки лежат на одной прямой); таким образом, сумма
произведений противоположных сторон вписанного в окружность четырех-
уолоника ABCD равна произведению его диагоналей — это важная
10 Энциклопедия, ки. 4

14Ь ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИИ
теорема элементарной геометрии, называемая теоремой П т о л е
мея Аналогично этому из теоремы Пифагора вытекает, что если точки А,
В, С и D плоскости таковы, что окружности DAB и DBC перпендику-
перпендикулярны, то
ВС \2 / АС \г
\DADBJ \DB-DCJ \DA-DCJ
Но нетрудно видеть, что условие перпендикулярности окружностей DAB
и DBC равносильно равенству 90е суммы углов В и Л ("пи углов Л и С)
б)
Рис. 91.
четырехугольника ABCD. В самом деле, из рис. 91, б виднп. что
так что сумма /. В + Z. D= Z. UDA + ?_ ADC + {_ CDV как раз равна
углу UDV между окружностями DAB и DBC. Таким образом, последнее
предложение можно сформулировать следующим образом: если сумма про
шит .оложных углов четырехугольника ABCD равна 90°, то сумма квадра-
квадратов произведений его противоположных сторон равна квадрату произведения
диагоналей (ср. с теоремой Птолемея, которую можно сформулировав так:
есл! сумма противоположных ус лов четырехуголънхка равна 180°, mi сумма
про43веден-!й его противоположных сторон равна произведению диагоналей).
Ясно, что число примеров теорем, получаемых из теорем енклидовой
геометрии при помощи «принципа перенесения», отвечающего инверсии I.
можно неограниченно увеличивать.
Не представляет также труда состапить «словарь», соответствующий
гиперболической инверсии (§ 1, стр. 59), в котором, в частности, прямым
будут отвечать гиперболы (см. стр. 75). Применение свяэнного с этим
«словарем» принципа перенесения позволяет получить целый ряд любо
пытнчх теорем, относящихся к гиперболам.
9.4. Принцип перенесения, отвечающий полярному отображе-
отображению. Каждому неточечному отображению, например полярному ото-
отображению П, гакже отвечает свой «принцип перенесении».

ПРИНЦИП ПЕРЕНЕСЕНИЯ
147
Отображение П переводит прямую в точку и точку в прямую;
параллельные прямые оно переводит в точки, лежащие на одной
прямой с центром О отображения, а точки, принадлежащие проходя-
проходящей через О прямой,—в параллельные прямые (рис. 92). Прямые
с и ft, образующие угол а, отображение П переводит в такие точки
А я В. что^ АОВ = а (ибо ОА _[_ с и OB J_ b, так что отмеченные
на рис. 92 углы имеют взаимно перпендикулярные стороны). Точки
А и В, удаленные друг от друга на расстояние d, переходят в такие
прямые а и Ь, что
А'* а°А
где А' и В'—проекции точки О на прямые а и b (рис. 92; это
следует из того, что точки А' и В' получаются из точек А и В
Рис. 92.
Ри„- 93.
инверсией с центром О и степенью 1). Точку А и прямую b (рис. 93),
обладающие гем свойством, что расстояние АР от А до b равно d.
полярное отображение П переводит в прямую а и точку В, причем
расстояние BQ от В до а равно
Для доказательства этого достаточно воспользоваться подобием изо-
изображенных на рис. 93 прямоугольных гранений ОАРВ' и OBQA',
имеющих общий угол ^/ АОВ' = ^/ ВО А' и пропорциональные сто-
рины, заключающие этот угол: ОЛ-ОА' = ОВ-ОВ' и следовательно,
ОА 08 л „ ОА ОВ
тг77 = ггг>'- из подобия этих трапеции следует, чго хё—
ОН'
ОА
АР ~ BQ'

148
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
Остановимся еще на вопросе о том, во что переводит полярное
отображение П окружность 6\ Ясно, что если центр окружности i
совпадает с центром О отображения П, то ? переходит в окруж-
окружность S' с тем же центром О, радиус г которой обратен радиусу г
исходной окружности ( г' =—J; при этом если первая окружность
понимается как совокупность то-
точек, то вторая — как совокупность
прямых (своих касательных), и на-
наоборот (рис. 94). -Пусть теперь
ценгр D окружности ? отличен
от точки О; радиус ее по-преж-
по-прежнему обозначим через г. Окруж-
Окружность 5 мы будем понимать как
совокупность («геометрическое ме-
место») прямых а, удаленных от
точки D на расстояние г. Если
d есть образ точки D при поляр-
полярном отображении, то прямая а пе-
перейдет в точку 4, оасстояние АР
которой от пршой d равно
Рис. 94.
"OD-
Таким образом, окружность ? перейдет в множество всех таких
точек Л, что
АО OD
-Гп =— = const (не зависит от А),
/\ f
т. е. в множество всех точек, отношение расстояний от
которых до данной точки О и до данной прямой d равно посто-
постоянной величине — = е. Но это множество точек представляет со-
собой коническое сечение (эллипс, параболу или гиперболу)
S' с фокусом О и директрисой d; величина е называется эксцент-
эксцентриситетом линии S'1). При этом 5' будет являться эллипсом,
параболой или гиперболой в зависимости от того, меньше ли рас-
расстояние OD, чем г, равно г или больше г, т. е. от того, лежит ли
центр О отображения П внутри 5, на окружности ? или вне 6"
(рис. 95, а —в). ОЗратно, каждая точка окружности 5 (точка, при-
принадлежащая единственной из прямых а) переводится преобразова-
преобразованием П в касательную конического сечения S' (прямую, содержащую
единственную точку А)
') См. в кн. V ЭЭМ uiaroK> о конических сечениях.

\ч
Рис. 95.

150 ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
Таким образом, мы приходим к следующему «словарю»:
Исходное понятие Преобразованное
понятие
Точка А Прямая а
Прямая а Точка А
Точка 4, лежащая на прямой ft Прямая а, проходящая через
точку В
Расстояние ОА от О до точки А Величина ^-р, обратная расстоя-
расстоянию ОА' .от О до прямой а
Параллельные прямые Точки, принадлежащие проходя
щей через О прямой
Угол между прямыми а и ft Угол АОВ
А'В'
Расстояние между точками А и В Величина
57, где А и В
ОА'-ОВ'
проекции точки О на при
мые а и Ь.
Расстояние АР от точки А до Величина
примой b
BQ
-,, где Q и А'—
OBUA'
проекции точек В и А на пря-
прямую a
Окружность с центром О и ра- Окружность с центром О и pj
ДИУСОМ г диусом i
Окружность с отличным от О Коническое сечение с фокусом О,
центром D и радиусом г директрисой d и эксценгриси-
UD
тетом —
г
Касающиеся окружность и прямая Коническое сечение и принадле-
принадлежащая ему точка
Касающиеся окружности Касающиеся конические сечение
и т. д. Этот «словарь» позволяет составить много новых геометрн
ческих теорем, получаемых из известных теорем при помощи поляр-
полярного отображения II.
В качестве примера использовании отвечающего полярному отоб-
отображению II «принципа перенесения» рассмотрим теорему о том, что
высоты треугольника пересекаются в одной точке Н. Нетрудно по
нять, что высоту AXD^ исходного треугольника A1BJC1 полярное отоб-
отображение П переводит в такую точку М стороны ВС преобразованного
треугольника, что угол /МО4 является прямым. Поэтому георема о
точке пересечения высот переходит в следующую теорему: если
через какую-либо точку О в плоскости треугольника ABC провести

ПРИНЦИП ПЕРЕНЕСЕНИЯ
151
три прямые, перпендикулярные прямым О А, ОВ и ОС, то точки
М, N и Р пересечения атих прямых с соответствующими
сторонами треугольника ABC принадлежат одной прямой h
(рис. 96).
Можно применить еще раз полярное отображение (с новым цен
тром Q) к полученной только что теореме; тогда оиа перейдет в более
сложное предложение. В свою очередь и эту последнюю теорему можно
преобразовать при помощи нашего «принципа перенесения» и получить
новое, еще более сложное
предложение. Таким образом,
при помощи нашего приема
из одной теоремы можно по-
получить неограниченно
много новых теорем.
Приведем еще несколько
примеров, показывающих, как
преобразует наш «принцип пе-
перенесения» теоремы, тракту-
трактующие о свойствах окружно-
окружностей.
Начнем с теоремы о том,
что вписанный в окружность S
угол АС В, опирающийся на
диаметр АВ,— прямой. Если
центр полярного отображения
П совпадает с центром О ок-
окружности S, то «принцип пе-
перенесения» переводит эту тео-
теорему в следующую: если а, Ь,
с—три касательные к окружности S, причем а\\Ь (это соответствует тому,
что прямая АВ проходит через О), то отрезок, высекаемый а и b на с, ви-
виден из центра О окружности под прямым углом (рис. 97, а).
Если принять за центр отображения П вершину С прямого угла, то
окружность S перейдет в параболу с фокусом С и директрисой о, полу-
получающейся полярным отображением из центра окружности S; точки А я В
перейдут во взаимно перпендикулярные касательные а и b параболы,
и мы получим теорему: точга пересечения взаимно перпендикулярных каса-
касательных параболы принадлежит ее dupei mpuce (рис. 97, б; эту теорему
можно также сформулировать следующим образом: геометрическое место
вершин описанных вокруг параболы прямых углов есть директриса пара-
параболы). Наконец, приняв за центр отображения П произвольную точку Q
плоскости, мы придем к теореме: две касательные а и Ь произвольного
ко н и чес i ого сечения S', пересекающиеся на его директрисе о (это отвечает
тому, что прямая АВ проходит через О), высекают на произвольной
третьей юсательной с отрезок, видный из фокуса Q кривой S' под прямым
углом (рис. 97, в).
В качестве еще одного примера рассмотрим теорему о том, что каса-
касательная t (круэкности S в ее точье А перпендикулярна радиусу О А; из нее
следует, что отрезок про /звольной касательной а конического сечения S,,
заключенный между директрисой о и точюй юсания Т прял.ой а с S,, виден
из фокуса Q под прямым углом (рис. 98). Любопытные следствия можно
также получить из известной теоремы о прямой Симпсоиа, согласно
которой основания перпендикуляров, опущенных из произвольной точьи Р
окружности S на стороны вписанного в S треугольника ABC, лежат на
Рис. 96.

152
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИИ
одной прямой '). Примем за центр полярного отображения центр О окруж
ности S. При этом окружность S перейдет в другую окружность S, с тем
же центром О (рис.99,а); вписанному в S треугольнику ABC будет отвечать
Рис. 97.
описанный около S, треугольник Afifi^ а точке Р окружности S — касатель-
касательная р окружности S,; основание К перпендикуляра, опущенного из Р на
сторону АВ, перейдет в прямую C,D, где D—такая точка касательной р,
') См., например, первую часть книги Ж- Ад а мара, указанной
в конце статьи, задачу 72.

ПРИНЦИП ПЕРЕНЕСЕНИИ
153
Рис 98.
что ?_ C,OD=90C, т. е. точка пересечения р с прямой OD, параллельной бис-
биссектрисе внешнего угла при вершине С, (ибо ОС, — биссектриса bi утрен-
утреннего угла). Окончательно мы приходим к следующей теореме: прямые,
соединяющие вершины треугольника Afifi, с точками пересечения произ-
произвольной касательной р к вписанной в А,В,С, окружности S, с проведенными
через центр О окружности S, прямыми, параллельными биссектрисам внеш-
внешних углов при тех же вершинах треугольника пересекантся в одной точке
(рис. 99, а). Если принять за центр полярного отображения точку Р. то
окружности S будет соответствовать
парабола S, с фокусом Р, а вписан-
ному в S треугольнику ABC —опи-
—описанный около Si треугольник A,B,Ct,
т. е. треугольник, сторонами которо-
которого являются касательные параболы.
Основания опущенных из Р на сторо-
ы ВС, АС, АВ перпендикуляров пе-
перейдут в перпенцикулярные к РАи
РВ, и PC, прямые, проходящие через
вершины треугольника (заметим, что
точка Р переходит в несобственную
прямую). Таким образом, мы мо-
можем заключить, что три прямые,
проведенные через вершины описан-
описанного около параболы S, пргуголь
ника i4,B,C, перпендикулярно пря-
прямым, соединяющим вершины Al,Bl.Ct
с фокусом Р параболы, пересекаются
в одной точке R (рис. 99, б; отсюда.
в частности, следует, что окружности с диам тром PR проходит через точки
Л,, В, и С,, т. е.что описанная вокруг А,В,С, окружность проходит через фокус
параболы). Наконец, приняв за центр полярного тображения произголь-
ную точку Q. мы придем к теореме' если А,В,С,— произвольный треуголь-
треугольник, описанный вокруг конического сечения S, (т е. треугольник, стороны ко-
которого являются касательными пинии St)uQK. QL, QM — прямые проведен-
ныр через фокус Q кривой S, перпендикулярно QA,, QB, uQCt и пересекавшие
произвольную четвертую касательную р конического сечения S, в точ> ах К,
L и М, то прямые А,'К, B,L и С,М пере екоются в одной то<ке (рис. 99, в).
Вспомним еще теорему о степени точки Р относительно
окружности S, согласно которой произведение РА РВ отрезков любой
проходящей Аерез Р прямой, пересекающей окружность, постоянно (т е за ви-
виси лишь от S и от Р, но не lt секущей РАВ) Приняв точку Р за центр
полярного отображения, мы преобразуем эту теорему в следующую: про-
произведение расстояний от фокуса Р конического сечения S, до параллельных
касательных а и Ь (параллельносп асатсльных а и Ь отвечает тому, что
прямая АВ проходит чепез Р' постоянно, т. с. зависит лишь от S,, но не
от выбора кссатслььых (рис 100)
Иногда, обратно, свойства кон ческих сечений позволяют доказ вать
новые теоремы об окружностях. В качестве примера можно упомянуть
здесь о так назьпаемых фокальных свойствах конических сечений,
согласно которым сумма (разность) расстояний от произвольнпй точки А,
эллипса (гиперболы) S до двух фокусов Р и Q постоянна'); в силу симме-
симметричности кривой S отсю а также следует, что сумма (разность) расстоя-
расстояний от фокуса Р эллипса (гиперболы) до точек Л, и В„ касательные в которых
параллельны, постоянна (т. с. PA, ± PB, = PA,± QA, = ronst; рис. 101, а, б).
') См в кн. V ЭЭМ статью о конических сечениях.

Ч

Рис. 100.

156 ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
Переходя теперь с помощью полярного отображения с центром Р от кони-
конического сечения S к окружности S,, мы получим, что если через внутрен-
внутреннюю (внешнюю) точку Р окружности S, проводить всевозможные секущие АВ,
то сумма (разность) величин, обратных расстояниям точки Р до касатель-
касательных а, и fc, к о\ружности S, в точюх А и В будет постоянна.
Читатель без труда самостоятельно отыщет много других интересных
примеров использования порожденного полярным отображением П «прин-
«принципа перенесения». Содержательные применения имеет также связанный
с подерным преобразованием А «принцип перенесения», исследование ко-
которого мы полностью предоставляем читателю
9.5. Принцип перенесения и модели геометрических систем.
«Принцип перенесения» (точнее, любой из многочисленных «принци-
«принципов перенесения») позволяет сопоставить с каждым геометрическим
предложением другое, совершенно новое предложение. Это новое
предложение может быть проще первоначального, и тогда, доказав
его, мы убедимся тем самым и в справедливости исходного предло-
предложения. Но и б том случае, когда новое предложение доказывается
не более просто, чем исходное, мы не остаемся в проигрыше — ведь
это предложение не надо доказывать самостоятельно, и, сформули-
сформулировав его, мы «даром» получим лишнюю геометрическую теорему.
Однако «принцип перенесения» имеет и иное значение — он проливает
дополнительный свет на самую сущность геометрии (или разных «геомет-
«геометрий», которых, как мы теперь знаем, существует много). В самом деле,
отвечающий «принципу перенесения» «словарь» служит для «перевода
на новый язык» всех геометрических фактов и теорем. Полученное
при таком «переводе» предложение может весьма сильно отличаться
от исходного, однако так как его истинность следует из истинности
исходного предложения автоматически, надо его считать лишь иной
формой того же самого предложения. Если теперь мы приме-
применим наш «принцип перенесения» ко всем геометрическим фактам и
теоремам, то мы получим некоторое видоизменение знакомой нам
геометрии лишь внешне от нее отличающееся, но на самом деле
полностью с ней совпадающее. Мы можем, например, в обычной
геометрии Евклида называть «прямыми» окружности, проходящие
через фиксированную точку О, а под «расстоянием» между двумя
точками А и В понимать выражение -л. __ (см. «словарь» на
стр. 144—145); при этом все геометрические теоремы сохраняют силу,
т. е. мы будем иметь новую «модель»') евклидовой геометрии. Так,
по-прежнему можно будет утверждать, что, скажем, сумма квадра-
квадратов катетов прямоугольного треугольника равна квадрату гипотенузы
или что множество всех точек, равноудаленных от двух данных то-
точек, есть прямая линия, хотя все фигурирующие в этих теоремах
геометрические понятия будут иметь новый, отличный от привычного
нам смысл. Можно также называть «точками» прямые линии, а «пря-
М О понятии модели см. статью «Аксиомы и основные понятия гео-
геометрии» (стр. 21—27 этой книги ЭЭМ).

ЛИТЕРАТУРА 157
мыми»— точки (см. «словарь» на стр. 150)—и все равно все знако-
знакомые нам геометрические теоремы сохранят свою силу, т. е. мы полу-
получим еще одну модель евклидовой геометрии. Этим подтверждается
весьма важный вывод о том, что содержание основных геометричес-
геометрических понятий совершенно несущественно для геометрии, а важны
лишь их свойства '). Именно поэтому возможно, видоизменив подхо-
подходящим образом содержание основных понятий, получить новую модель
исходной геометрической системы, лишь по форме отличающуюся от
ранее имевшейся. При этом все подобные модели следует считать со-
совершенно равноправными, поскольку у нас нет никаких серьезных
оснований предпочесть одну из них всем остальным; в самом деле,
лишь привычка заставляет нас понимать под словом прямая именно
траекторию светового луча, а не иной геометрический образ г).
Оiметим еще, что, разумеется, и для отличных от геометрии
Евклида «геометрий» можно образовать много разных «принципов
перенесения» и с их помощью много разных моделей. Для того
чтобы прийти к какому-то подобному «принципу перенесения», дос-
достаточно лишь преобразовать все понятия этой «геометрии» при
помощи произвольного преобразования л, не принадлежащего группе @
преобразований, играющих в этой «геометрии» роль «движений».
На иллюстрациях, подтверждающих это утверждение, достаточно
ясное после всего сказанного выше, мы здесь не остановимся.
ЛИТЕРАТУРА
|1] Ф. Клейн, Сравнительное обозрение новейших геометрических ис-
исследований («Эрлангенская программа»), перев. с нем., Сб. «Об основа-
основаниях геометрии», М., Гостехиздат, 1956, стр. 399—434.
Основополагающее сочинение знаменитого немецкого математика, в
котором вперви-е были сформулированы принципы теоретико-группо-
теоретико-группового построения геометрии.
[2] И. М. Я г л о м. Геометрические преобразования, тт. I—II, М., Гос-
Гостехиздат, 1955—1956;
Обшир: ое сочинение, рассчитанное на широкий круг читателей, в
котором подробно рассказывается о разных типах геометрических пре-
преобразований и их применениях. В книге освещены также принципиаль-
принципиальные вопросы, связанные с теоретико-групповым определением . еомет-
рии; содержится много задач, иллюстрирующих применения учения
о геометр' ческих преобразованиях. Первый том книги посвящен дви-
движениям и преобразованиям подобия; второй — аффинным, проективным
и круговым преобразованиям.
') Ср. стр. 20—21 этой книги ЭЭМ.
г) С точки зрения приложимости геометрических выводов к вопросам
практической жизни может даже показаться предпочтительным нальиать
«точкой» малый кружок, а «прямой»—узкую полосу; соответствующая
«модель» оСычной геометрии, получающаяся из нее расширением (ср.
стр. 125 и след.), полностью равносильна общепринятой «модели».

158 ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЙ
[3] Д. И. Перепел кин, Курс элементарной геометрии, чч. 1—2, М.—Л.,
Гостехиздат, 1948—1949.
Подробный учебник элементарной геометрии, р котором весьма тща-
тщательно изложены вопросы, связанные с движениями и преобразовани-
преобразованиями подобия, в частности содержится исчерпывающая классификация
движений и преобразований подобия. Наряду с этим в книге рассмат-
рассматриваются и простейшие круговые преобразования — инверсия и рас-
ширсьие. Первая часть книги посвящена планиметрии, а вторая — сте-
стереометрии.
[4| Ж- А д а м а р. Элементарная геометрия, чч. 1—2, перев. с франц., М.,
Учпедгиз, 1957—1С58.
Подробный учебник элементарной геометрии, по охвату материала
близкий к книге Д И. Перепелкина. Среди разделов кни|И. каса-
касающихся геометрических преобразований, можно отметит! изящное по-
построение правильных многогранников, базирующееся i а рассмотрении
конечных групп вращений (см. прибавление И ко второй части). Пер-
Первая часть книги посвящена планиметрии, а вторая — стереометрии.
[5] П. С. Александров, Введение в теорию групп, М., Учпедгиз, 1938.
Популярная книга по теории групп, в которой большое внимание
уделяется группам движений.
[6| А.И Мальцев, Группы и другие алгебраические системы, в книге
«Математика, ее содержание, методы и значение», т. 111. M., Изд-во
Академии наук СССР. 1956, стр. 248—331
Обстоятельная статья посвященная некоторым понятиям современ-
современной алгебры. Основное место в содержании статьи занимает учение о
группах, в частности о группах геометрических преобразований. В
статье подробно рассматривается возрос о дискретных группах дви-
движений, обойденный в настоящем изложении вопроса.
[7] Ф. Клейн, Элементарная математика с точки зрения высшей, т. 11
(геометрия), перев. с нем., М.—Л , ОНТИ, 1954.
Лекции, читавшиеся Ф. Клейном для учителей немецких школ;
вопросам, свя?анным с геометрическими преобразованиями, уделяется
них весьма большое внимание.
[8] Ф Клейн. Высшая геометрия, перев. с нем., М.—Л., ОНТИ, 1939.
Эта книга возникла в результате обработки записей специальных
курсов читавшихся некогда Ф Клейном в Геттингенском университете
Одна из трех частей книги лмеет заголовок «Теория ni еобразованнй»
и весьма широко трактует относящийся сюда круг ьопросов.

ОБЩИЕ ПРИНЦИПЫ ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ
СОДЕРЖАНИЕ
§1. Некоторые вопросы практического использования геометрических
построений . . .160
1.1. Введение 160
1.2. Инструменты для практического осуществления геометриче-
геометрических построений . . . 160
1.3. Точность построения . ... .164
§2. О решении задач на построение в зависимости от принятых ин-
инструментов 167
2.1. Построения линейкой, циркулем, чертежным треугольником и
транспортиром . . - ¦ .... 167
2.2 Построения с помощью одного циркуля (построения Мора—
Маскерони) 168
2.3. Построения с помощью одной линейки (построения Понгеле—
Штейнера) .... . 171
2.4. О построениях с помощью иных наборов инструментов 175
$3. О построениях на ограничен! ом куске плоскости 177
3.1. Построения с помощью линейки ограниченной длины ... 177
3.2. Построение на ограниченном куске плоскости ... 179
§4. Общие методы решения задач на построение на плоскости ... 182
4.1. Метод расчленения условий задачи (метод «геометрических
мест») . ... . ... .182
42 Общая схема решения задачи на построение . . . . . 184
4 3. Алгебраический метод 185
§5 Использование геометрических преобразований при решении задач
на построение на плоскости ... 189
5 1 Общие замечания . . .... 189
5.2 Примеры ... ISO
§6 Приближенные методы геометрических построений и их значение
для практики .193
fi.l. Точные и приближенные решения задач на построение 193
6.2. Задачи на спрямление дуг окр\жности . . . . . 114
6.3. Графоаналитический метод и метод последовательных прибли-
приближений 197
§ 7. Геометрические построения в пространстве *Ю0
7.1. Система постулатов для построений на плоскости 200
7 2. Система постулатов для «воображаемых построений» в про-
пространстве 201
7.3. Пример ... 202
7 4. Заключение . 203
Литература 203

160 ОБЩИЕ ПРИНЦИПЫ ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ
§ 1. Некоторые вопросы практического использования
геометрических построений
1.1. Введение. Решение задач на построение на. плоскости сво-
сводится к выполнению некоторых операции с помощью чертежных ин-
инструментов. Решить задачу на построение — значит по заданным
в условии задачи элементам (точкам, прямым, окружностям и т. д.)
с помощью определенных средств построения (указанных в условии
задачи или выбранных исполнителем) найти искомые элементы,
удовлетворяющие сформулированным в условии задачи требованиям.
Обычно эти требования указывают отношения, в которых должны нахо-
находиться искомые элементы друг с другом или с заданными элементами.
Геометрические построения нашли широкое применение в чертеж-
но-конструкторской и производственной практике. Поэтому нам пред-
представляется целесообразным, прежде чем переходить к математиче-
математическому рассмотрению геометрических построений, уделить внимание
некоторым вопросам, связанным с практическим использованием гео-
геометрических построений, а именно:
общим требованиям к выполнению построений,
выбору инструментов и некоторым приемам решения наиболее
распространенных конструктивных задач,
вопросам точности геометрических построений.
С краткого рассмотрения указанных вопросов мы и начнем первый
параграф.
1. 2. Инструменты для грактического осуществления геометриче-
геометрических построений. Геометрические построения используются в том или
ином виде почти во всех областях народного хозяйства. Выполнение
разнообразных чертежей, вычерчивание графиков, применение графи-
графических методов расчетов, разметка деталей — все это требует гео-
геометрических построений.
Во многих случаях при выполнении геометрических построений
на практике большое, а иногда и решающее значение для оценки
их пригодности имеют простота выполнения построений и получае-
получаемая точность результата. Вследствии этого на производстве, в кон-
конструкторских бюро, всюду, где приходится иметь дело с большим
числом построений, используются инструменты и приемы построений,
обеспечивающие выполнение этих требований.
Так, например, широкое распространение в чертежно-конструктор-
ской практике получила чертежная машина (рис. 1), с помощью ко-
которой проводятся параллельные и перпендикулярные прямые, стро
ятся углы. Чертежная машина заменяет знакомый еще школьникам на-
набор чертежных инструментов: рейсшину, линейку, чертежный треуголь-
треугольник, транспортир. Заметим, что при выполнении построений с помощью
этого набора (с добавлением циркуля) основные построения осущест-
осуществляются наиболее целесообразными приемами. Так, например, иостро-

ВОПРОСЫ ПРАКТИЧЕСКОГО ИСПОЛЬЗОВАНИЯ ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ 161
ение параллельных и перпендикулярных прямых выполняется с по-
помощью чертежного треугольника и линейки (рис. 2, а и б); построение
касательной к окружности при
данной вне окружности точке,
через которую проходит эта
касательная, —с помощью од-
одной линейки (рис. 3) и т. д.
Так как обычный набор
инструментов (циркуль, линей-
линейка, чертежный треугольник,
транспортир и даже чертежная
машина) не всегда может обес-
обеспечить достаточно простое и
точное решение задачи, то для
более сложных построений,
особенно если их приходится
выполнять в большом числе,
используются разнообразные
специализированные инстру-
инструменты и приборы.
Среди них можно указать пантограф для подобного преобразования
фигур, эллипсограф—для вычерчивания эллипсов по заданным осям,
коордиограф — для построения параллельных и взаимно перпендику-
перпендикулярных прямых и нанесения точек по заданным их координатам—и
другие, более специальные приборы.
11 Энциклопедия, кн. 4.

162
ОБЩИЕ ПРИНЦИПЫ ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ
Разнообразен выбор инструментов и при разметке1). Так, например,
разметочные линии наносятся на поверхность металла (часто покры-
покрываемую специальной краской для лучшей их видимости) стальными
чертилками (рис. 4); точки пересечения
проведенных линий (рисок), а иногда и
сами линии, намечаются керном (рис. 5).
Для проведения горизонтальных ли-
линий «а деталях используются специ-
специальные рейсмасы (рис. 6). Для выполне-
выполнения геометрических построений и изме-
Рис. 3. рений используются угольники (рис. 7),
линейки, штангенциркули (рис. 8) и др.
В случае необходимости выполнения построений с большой
точностью применяются мерные плитки, циркули и рейсмасы
Рис. 4.
Рис. 5.
Рис. 6.
Рис. 7.
с микрометрическими винтами. При этом может быть достигнута
точность откладывания и измерения отрезков порядка 0,02 мм.
Покажем, например, как на обработанной плоскости детали выполняются
некоторые построения, применяющиеся в чертежно-конструкторскои прак-
практике, в частности, построение параллельных и перпендикулярных прямых.
') Разметкой называется операция нанесения на заготовку детали
точек и линий, указывающих места последующей механической обработки
в соответствии с данным рабочим чертежом.

ВОПРОСЫ ПРАКТИЧЕСКОГО ИСПОЛЬЗОВАНИЯ ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ 163
HIIHtliHHt
Illllll
J L
! Hit IГ 111 ¦ •
Наиболее простой случай будет, если смежные плоскости (/, 2, 3 на
рис. 9) детали уже обработаны и состаяляют друг с другом прямой угол.
Если деталь тонкая и края ее
неровны, то разметка ведется на
разметочной плите (рис. 10) или
так, как указано на рис. 11.
В некоторых случаях при недо-
недостаточно ровной поверхности
детали параллельные и перпен-
перпендикулярные прямые строятся
обычными приемами с помощью
циркуля и линейки.
Часто при разметке употреб-
употребляются также специализирован-
специализированные комбинированные инструмен-
инструменты. Например, имеется большое
число приспособлений для нахо- рис g
ждения центров отверстий и ци-
цилиндрических выступов, для построения окружностей с недоступным
центром и пр.
Рис. 9.
Рис. 10.
Рис. 11.
В последнее время в разметке используются оптические методы. Так,
например, при выполнении разметки контуров шаблонов в судостроении
вначале с большой тщательностью выполняются на чертежной бумаге
И*

164 ОБЩИЕ ПРИНЦИПЫ ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ
чертежи-шаблоны деталей. Затем эти чертежи фотографируются, и нега-
негативы проектируются на разметочный стол с соответствующим увеличением
Разметчику остается накернить контуры детали. В этом случае точность
разметки существенно зависит не только от правильного влбора масштаба
увеличения и точности накернивания линии, но и от точности выполнения
чертежей для фотосъемки.
1.3. Точность построения. Геометрические построения по требо-
требованиям к точности их выполнения могут быть условно разделены
на две группы:
1) Геометрические построения, не требующие при их выполнения
особой точности; они используются при изготовлении, например,
рабочих чертежей деталей, схем узлов, станков и пр.; на этих чер-
чертежах в случае необходимости проставляются все нужные размеры.
2) Геометрические построения, к точности выполнения которых
предъявляются повышенные требования. Таковы, например, построе-
построения, выполняемые при изготовлении чертежей, по которым ведется об-
обработка деталей на оптико-шлифовальных станках, при разметке
контрольных шаблонов, по которым проверяются контуры изготов-
изготовленных шаблонов и пр. Большая точность построения требуется и
при выполнении численного решения алгебраических или аналити-
аналитических задач графическими методами.
При графическом решении задач могут встретиться случаи, когда
а) точность результата обусловливается исключительно точностью
выполнения построений (например, нахождение с помощью циркуля и
линейки середины данного отрезка), так как решения этих задач тео-
теоретически точные;
б) точность построения не оказывает сколь-нибудь существен-
существенного влияния на точность результата—это будет в тех случаях,
когда в задаче исходные данные заданы приближенно, с точностью,
меньшей той, которую дает само построение (например, графическое
определение толщины угольного пласта, выполняемое при предвари-
предварительной оценке его мощности);
в) точность построения существенно зависит от метода решения
задачи; это важно в тех случаях, когда построение дает заведомо
приближенный результат, ааже если предположить, что исходные
данные заданы точно и идеально точны выполняемые построения
(приближенные построения, например построение отрезка,
равного длине окружности, деление произвольного угла на три
части с помощью линейки и циркуля и др.).
Рассмотрим сначала, какие причины влияют на точность построе-
построения. Вопросам приближенных построений будет посвящен отдель-
отдельный параграф.
Несмотря на то, что графические методы решения задач появи-
появились достаточно давно, вопросами точности таких построений на-
начали заниматься по существу только в последние 50 лет. Это объ-

ВОПРОСЫ ПРАКТИЧЕСКОГО ИСПОЛЬЗОВАНИЯ ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ 165
ясняется тем, что выяснение точности графических построений ранее
не требовалось так настойчиво практикой, как в настоящее время.
В результате теоретического выполнения решения задачи на
построение (рассматривается случай, когда задача имеет решение и
оно выполнено верно) находится фигура, удовлетворяющая всем
требованиям, поставленным в условии задачи. Однако при факти-
фактическом выполнении построения полученная фигура будет, вообще
говоря, отличаться от искомой вследствие неизбежных погрешностей,
возникающих в процессе построения. Эти погрешности могут быть
разделены на три группы:
1. Систематические погрешности, возникающие, например,
вследствие использования приборов с неточной градуировкой, построе-
построений с помощью чертежных треугольников, у которых углы выпол-
выполнены неточно.
Систематические погрешности, естественно, влияют на точность
результата построения и иногда могут быть в той или иной мере
учтены. Для уменьшения их влияния необходимы, например, тща-
тщательная проверка и отбор чертежных инструментов.
2. Случайные погрешности зависят, как видно из самого назва-
названия, от ряда случайных, трудно поддающихся анализу, но всегда
в той или иной мере присутствующих причин. Их величины не
могут быть точно определены, но поддаются оценке *).
Эти погрешности по характеру происхождения могут быть:
а) объективными погрешностями, не зависящими от исполнителя, и
б) субъективными погрешностями.
Объективные погрешности происходят по той причине, что в дей-
действительности не существует идеально точных инструментов, не
существует идеально остро заточенной ножки циркуля, грифеля
карандаша, идеально гладкой бумаги. Поэтому невозможно прово-
проводить на чертеже линии в математическом понимании этого слова
(линии «без ширины»), вместо них получаются полосы, вообще го-
говоря, переменной ширины (из-за неизбежного стирания грифеля),
вместо точки пересечения прямых (в математическом смысле), мы
получаем некоторый криволинейный четырехугольник.
Точно так же при определении точки уколом острия грифеля или
ножки циркуля мы получаем вместо точки «пятно» или отверстие.
При повторных уколах отверстие «разрабатывается», увеличивается
в диаметре, что влияет на увеличение погрешности построения.
Кроме того, на точность построения влияют факторы субъектив-
субъективного характера. Влияние некоторых из них может быть уменьшено
(например, точность построения увеличивается при внимательности
исполнителя), но не может быть полностью исключено.
•) См. таблицу на стр. 166, заимствованную из кандидатской диссер-
диссертации А. А. Мироновича «Анализ точности графических расчете в»
Ленинград, 1950.

166 ОБЩИЕ ПРИНЦИПЫ ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ
Таблица средних значений погрешностей элементарных операции
п. п.
Элементарные операции
Погрешность
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Диаметр «круглой точки» при уколе ножки цир-
циркуля
Диаметр «круглой точки» при уколе карандашом
Средняя толщина тонкой линии
Ошибка укола в данную точку .
Поиторные уколы (от 2 до 9) дают добавочную
ошибку
Ошибка укола циркулем в произвольную течку
прямой
Ошибка укола карандаша r произвольную точку
прямой
Определение точки пересечения прямых . .
Ошибка проведения прямой через точку .
Точность нанесения угла по транспортиру
(г^100 мм)
Точность проведения параллельных и перпендику-
перпендикулярных прямых треугольником и линейкой . .
Точность прикладывания линейки к дьум точкам
Точность прикладыва ия линейки к прямой . . .
Угловая точность прикладывания линейки к двум
точкам
Угловая точность прикладывания линейки к пря-
прямой
0,20 мм
0,25—0,30 мм
0,15 мм
0,08 »
0—0,25 »
0,03 »
0,05 »
0,08 »
0,08 »
16" на 100 мм
0,03 мм
0,002 мм
0,05:2
0.03:1
Рис. 12.
3. Наконец, к третьей группе могут быть отнесены промахи и
ошибки, ведущие к негодности результата, так как при этом полу-
получаются неверные построения.
На основании анализа система-
систематических и случайных погрешнос-
погрешностей можно вывести некоторые эле-
элементарные требования к построе-
построениям, выполнение которых спо-
способствует повышению точности.
Сформулируем некоторые из этих требований. Для увеличения точ-
точности построения необходимо проводить возможно более тонкие
линии. Для уменьшения погрешности следует брать точки, опреде-
определяющие прямую на возможно более далеком расстоянии друг от
друга, так как угловая погрешность (sin а = ' ~\ 2 J уменьшается
при увеличении / (рис. 12). Радиусы вспомогательных окружностей
следует выбирать так, чтобы окружности пересекались под углами,
возможно более близкими к прямым и т. д.

О НЕШ1-НИИ ЗАДАЧ НА ПОСТРОЕНИЕ 167
4. Необходимо также выдерживать принцип однообразия по-
порядка малости отрезков; иными словами, в построении должны
использоваться отрезки приблизительно одной величины *).
§ 2. О решении задач на построение в зависимости от принятых
инструментов
2.1. Построения линейкой, циркулем, чертежным треугольни-
треугольником и транспортиром. Хорошо известно, что не всякая задача на
построение может быть решена конструктивно; иными словами, не
всякая геометрическая фигура, математически вполне определенная,
может быть теоретически точно построена с помощью данного на-
набора инструментов. Так, например, по заданному единичному отрезку
не может быть построен с помощью циркуля и линейки квадрат,
площадь которого равна площади круга единичного радиуса 2). Точно
так же не могут быть выполнены только с помощью этих инстру-
инструментов удвоение куба (см. стр. 220), трисекции произвольного угла
(стр. 221), построение треугольника по его биссектрисам (стр. 223),
построение правильного семиугольника или девятиугольника (стр. 225)
и т. п. Разумеется, одна и та же задача на построение может ока-
оказаться разрешимой при одном выборе набора инструментов и нераз-
неразрешимой при другом.
Мы будем считать, что речь идет о построениях, выполняемых
не циркулем и линейкой, как это обычно делается в работах по
геометрическим построениям, а большим числом инструментов — ли-
линейкой, циркулем, чертежным треугольником и транспортиром. Это
расширение инструментов произведено с целью привести теорети-
теоретическое рассмотрение вопроса о конструктивных элементах в большее
соответствие с чертежной практикой.
Укажем теперь наиболее характерные построения, которые могут
быть осуществлены при однократном использовании приведенных
выше инструментов.
Циркуль. Характерная для циркуля операция заключается в по-
помещении острия циркуля в некоторую (данную или произвольную),
точку и проведения окружности (или дуги окружности) данным или
произвольным радиусом; радиус может быть задан двумя точками.
Линейка. Характерная операция для чертежной линейки — при-
прикладывание края линейки к двум точкам и проведение прямой по
этому краю*).
') Обычно считают, что отношение отрезков не должно превышать 20.
г) См. в этой книге ЭЭМ статью «О разрешимости задач на построе-
построение с помощью циркуля и линейки», стр. 226—227.
') На практике линейкой пользуются также для построения каса-
касательной к данной окружности, проходящей через данную вне ее точку
(см. рис. 3) и для построения общих внешних и внутренних касательных
к двум окружностям.

168 ОБЩИЬ ПРИНЦИПЫ ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ
Поэтому считают, что с помощью линейки могут быть построены
прямая (или луч, или отрезок прямой), проходящая через две дан-
данные (или произвольные) точки.
Чертежный треугольник обладает всеми свойствами односторон-
односторонней линейки и, следовательно, ему свойственны те же характерные
операции, что и для линейки. Кроме того, характерная для тре-
треугольника операция заключается в наложении треугольника на чер-
геж так, чтобы одна из его сторон совместилась с данной прямой,
и проведении прямой по другой стороне угла ').
Следовательно, с помощью чертежного треугольника могут быть
выполнены те же построения, что и с помощью линейки, а также
построение прямой, проходящей через данную точку и образующей
с данной прямой угол, равный одному из углов чертежного тре-
треугольника.
Транспортир. Характерной операцией для транспортира является
прикладывание прямолинейного края «0°—180°» транспортира к дан-
данной прямой, совмещение его нулевой отметки с данной на прямой
точкой и построение точки, находящейся на луче, проходящем че-
через нулевую отметку и образующем заданный угол с данной прямой.
Применение транспортира дает возможность найти точку луча, обра-
образующего некоторый (заданный) угол с данной прямой и исходящего
из данной на ней точки.
Итак, мы получили характеристику выбранных инструментов.
Следует заметить, что все указанные операции могут быть также
выполнены циркулем и линейкой, так что при указанном употреб-
употреблении перечисленных инструментов класс разрешимых задач на
построение совпадает с классом задач, разрешимых циркулем и ли-
линейкой (хотя, конечно, использование большего набора инструмен-
инструментов практически приводит к упрощению самих построений).
Вопрос о том, какие задачи на построение могут быть решены
при помощи выбранного набора инструментов или, что то же самое,
при помощи циркуля и линейки, детально обсуждается в специаль-
специальной статье, помещенной в этой же книге ЭЭМ (стр. 205—227). Там
же обсуждается вопрос о роли произвольных элементов в геометри-
геометрических построениях.
2.2. Построения с помощью одного циркуля (построения
Мора—Маскерони). Укажем теперь некоторые результаты о разре-
разрешимости задач на построение при ином выборе набора инстру-
инструментов.
Здесь следует прежде всего отметить, что набор, состоящий из
циркуля и линейки, эквивалентен в некотором смысле «набору»,
состоящему из одного только циркуля: всякая задача на построе-
') На практике это построение выполняется с использованием л и-
и е й к и и угольника.

О РЕШЕНИИ ЗАДАЧ НА ПОСТРОЕНИЕ
169
ние, разрешимая с помощью циркуля и линейки, разрешима также
с помощью одного циркуля. Однако использование линейки позво-
позволяет фактически провести прямолинейные отрезки, содержащиеся
в искомой фигуре (если задача требует нахождения этих отрезков),
в то время как построения одним циркулем определяют лишь концы
таких отрезков. Следовательно, включение линейки по сути дела
не расширяет числа задач, которые могут быть решены с помощью
одного циркуля. Это положение было впервые высказано в книге
датского математика Георга Мора «Датский Евклид», 1672 г., а
затем в работе итальянского инженера Лоренцо Маскерони «Геомет-
«Геометрия циркуля». 1797 г. Иное доказательство этого же утверждения
было дано в 1890 г. А. Адлером.
Для доказательства теоремы Мора — Маскерони достаточно убедиться,
что с помощью одного циркуля можно определить точку пересечения
двух прямых (каждая из которых за-
задается двумя своими точками), а также g,
течку пересечения заданных прямой
и окружности Мы воспользуемся
Рис. 13.
с этой целью преобразованием инверсии (см стр. 56 этой книги ЭЭМ),
изложив доказательство теоремы Мора—Маскерони в виде решения сле-
следующих шести задач
За д . ч а 1. Даны три точки А, В, С. Найти точку С, симметрич-
симметричную точке С относительно прямой АВ.
Решение непосредственно получается проведением двух окруж-
окружностей (рис. 13).
Задача 2. Даны окружность L, ее центр О и произвольная точка А.
Найти точку М, в которую переходит точка А при инверсии относительно
окружности L.
Решение. Проведем через точку О окружноетъ с центром А, и
пусть В и С—точки пересечения этой окружности с окружностью L
(рис. 14). Далее, проведем через точку О еще две окружности с центрами
В и С. Тогда точка М пересечения двух последних окружностей и будет
искомой.
Доказательство правильности этого построения вытекает из того, что
равнобедренные треугольники ОВМ и ОВА с общим углом О подобны и
потому
OAOMOBF

170
ОБЩИЕ ПРИНЦИПЫ ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ
Рис. 10.
Задача 3. Даны окружность L, ее центр О и две течки А, В. Найти
центр окружности, в которую переходит прямая АВ при инверсии отно-
относительно скружнести L.
Решение. Нзйдем точку С, симметричную точке О относительно
прямой АВ (задача Г1. Тогда точка М, в которую переходит точка С при
инверсии относительно окружности L
(задача 2), является искомой. Для дока-
доказательства правильности построения
обозначим через D основание перпен-
перпендикуляра, опущенного из точки О на
прямую АВ, а через Е — точку пересе-
пересечения прямой OD с окружностью, в ко-
которую при инверсии переходит прямая
АВ (рис. 15). Тогда имеем
j; _ OM-OC=OD-OE (=г2)
Так как, далее, OC=2OD (по определе-
определению точки С), то, очевидно, ОМ=— ОЕ,
и потому М — центр окружности (ибо
ОЕ диаметр).
Задача 4. Даны три точки А, В,
С. Найти центр (кружности, прохо-
проходящей через эти точки.
Решение. Проведем произвольную окружность L с центром в точке
А. Обозначим через М и ,V точки, в которые переходят В и С при инверсии
относительно окружности L (задача 2). Тогда окружность, проходящая
через точки А, В, С, перейдет при инверсии
в прямую MN (рис. 16). Таким образом, нам
остается найти центр окружности, в которую
переходит прямая MN при инверсии относи-
относительно L (задача 3).
Задача 5. Найти точку пересечения
данной окружности L с данной прямой MN.
Решение. Прежде всего заметим, что
на основании задачи 4 мы можем считать
центр окружности L неизвестным. Обозначим
его через А. Найдем теперь целтр О окруж-
окружности, в которую переходит прямая MN при
инверсии относительно окружности L (зада-
(задача 4). Далее проведем окружность с центром
О, проходящую через точку А (т. е. окруж-
окружность, в которую при инверсии переходит
прямая MN). Две точки Р, Q, в которых по-
последняя окружность пересекается с окружностью L, являются искомыми
(рис. 16).
Задача 6. Даны четыре точки А, В, С, D. Найти точку пересечения
прямых АВ и CD.
Решение. Проведем произвольную окружность L с центром в точке А.
При инверсии относительно окружности L прямая АВ перейдет в себя, а
прямая CD—в некоторую окружность V', проходящую через точку А; центр
М этой окружности мы можем найти (задача 3). Найдем теперь точку
Р (отличную от А) пересечения окружности L' и прямой А В (задача 5).
Тогда точка Q, в которую переходит Р при инверсии относительно
Рис. 1С.

О РЕШЕНИИ ЗАДАЧ НА ПОСТРОЕНИЕ
171
окружности L (задача 2), является искомой точкой пересечения прямых
А В к CD (рис. 17).
Очевидно, что из возможности решения задач 5 и 6 с помощью циркуля
и вытекает теорема Мора — Маскерони.
2.3. Построения с помощью одной линейки (построения
Понселе — Штейнера). Швейцарский геометр Якоб Штейнер,
считавший наиболее точным инстру-
инструментом линейку, в 1833 г. пока-
показал, что любая задача на построе-
построение, разрешимая с помощью цирку-
циркуля и линейки, может быть решена с
помощью проведения только прямых
линий, если только в плоскости чер-
чертежа задана окружность и ее центр.
(При этом некоторая окружность счи-
считается построенной, если найдены ее
центр и радиус.) Несколько ранее эта
же теорема была установлена совер-
совершенно другим методом французским
математиком Ж. Понселе.
Для доказательства теоремы Понсе-
Понселе — Штейнера мы решим с помощью
линейки следующие 9 задач на построе-
построение, считая, что в плоскости начерчена
окружность L и задан ее центр О.
Задача 1. Построит^ некоторый прямоугольник
Решение. Через точку О прогедем две произвольные прямые
(рис. 18). Точки А, В, С, D, в которых эти прямые пересекаются с окруж-
окружностью L, являются вершинами прямоугольника.
Рис. 17.
Рис. 18.
Задача 2. Даны две параллельные прямые и две точки А, В на одной
из них. Разделить отрезок А В пополам.
Решение. Обозначим прямую, параллельную АВ, через I. Возьмем
на прямой / произвольную точку С, проведем прямую ВС и на ней выбе-
выберем произвольную точку М (рис. 19). Теперь проведем прямую AM и

172
ОБЩИЕ ПРИНЦИПЫ ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ
обозначим через D точку пересечения этой прямой с прямой Л Наконец,
проведем прям ie АС и BD и обозначим через N их точку пересечения.
Тогда прямая MN проходит через середину отрезка АВ. Доказательство
правильности этого построения легко вытекает из рассмотрения подоб-
подобных треугольников (через Р и Q обозначены точки пересечения прямой
MN с прямыми / и АВ):
AQ_QN _QB
P~C~~NP~D~P'
AQ_QM _QB
DP~~PM~~ PC'
Почленно перемножая подучающиеся равенства
AQ-DP = PC-QB,
AQ-PC = DP-QB
и производя сокращение, получаем AQ2=QB2, т. е. AQ — QB ').
Задача 3. Построить квадрат.
Решение. Построим прямоугольник ABCD, вписанный в окруж-
окружность L (задача 1). Так как АВ || CD, то мы можем разделить отрезки АВ
и CD пополам (задача 2) Точно так же можно разделит- отрезки AD и
ВС пополам (рис. 20). Мы получим четыре
точки М, N, P, Q, являющиеся середи-
серединами сторон прямоугольника ABCD Пря-
Прямые WP и NQ проходят через точку О
(являющуюся центром прямоугольника
и центром окружности I.) и параллельны
сторонам прямоугольника. Следовательно,
,\1Р и NQ—-две взаимно перпендикуляр-
перпендикулярные прямые, проходящие через центр
окружности L. Поэтому точки E,F,G,H,
в которых эти прямые пересекаются с
окружностью L, являются вершинами
квадрата.
Задача 4. Дана прямая I и точка Е
вне ее. Провгсти через точку Е прямую,
параллельную I.
Решение. Построим -прямоуголь-
-прямоугольник ABCD (задача 1) и найдем середины
М, N, P, Q его сторон (задача 2). Далее,
проведем прямые МР и NQ (рис. 21, с). Прямая / не может бьпь парал-
параллельна всем сторонам прямоугольника ABCD. Пусть сторона АВ не
параллельна прямой I. Тогда прямые АВ, NQ и CD пересекаются с прямой
/ в некоторых точках R, S, Т. Так как прямая NQ находится на равных
расстояниях от параллельных ей прямых АВ и CD, то RS—ST. т. е.
S — середина отрезка RT.
Дальнейшее построение по сути дела представляет собой решение за-
задачи, обратной задаче 2. Именно, проведем прямую ТЕ (рис. 21, 6) и на
ней выберем произвольную точку U. Затем проведем прямые US, UR, ER
и обозначим через G точку пересечения прямых ER и US. Наконец, про-
проведем прямую TG и обозначим через F точку пересечения этой прямой с
прямой UR. Тогда EF — искомая параллельная к прямой /
Рис. 20.
') Другое доказательство приведено на стр. 69 этой книги ЭЭМ.

О РЕШЕНИИ ЗАДАЧ НА ПОСТРОЕНИЕ
173
Для доказательства правильности этого построения обозначим через
F' такую точку прямой UR, что EF'\\TR, а через G'— точку пересечения
прямых ER и TF'. Тогда прямая UG' проходит через середину отрезка
TR (ср. задачу 2 и рис. 19), т. е. совпадает с прямой US. Таким
образом, точка О' лежит на прямой US Так как оиа, к, оме того, ле-
6)
Рис. 21.
жит на прямой ER, то точка G' совпадает с точкой пересечения прямых
US и ER, т- е. совпадает с точкой С. Следовательно, прямая TG' совпа-
совпадает с прямой TG, и потому точка F' лежит на прлмой TG Кроме того,
точка F' лежит на прямой UR. Итак, точка F' совпадает с точкой пере-
пересечения прямых TG и UR, т. е. совпадает с точкой F. Но тогда прямая
EF совпадает с EF', т. е. EF\\TR.
Задача 5. Даны прямая I и точка М. Провести через точку М пря-
прямую, перпендикулярную I.
Решение. Построим квадрат EFGH (задача 3). Далее через его центр
О (т. е. через точку пересечения диагоналей EG и FH) проведем прямую,
М
Рис. 22.
параллельную Z (задача 4). Пусть Р — одна из точек пересечения этой
прямой с квадратом (рис. 22). Пусть, для определенности, точка Р лежит
на стороне FG Проведем через точку Р прямую, параллельную EG (зада-
(задача 4) и обозначим через Q точку пересечения этой прямой со стороной EF.

174
ОБЩИЕ ПРИНЦИПЫ ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ
Очевидно, что FP = FQ. Теперь через точку Q проведем прямую, па-
раллетьную FG (задача 4) до пересечения в точке R со стороной GH.
Тогда RG = QF = FP. Теперь из равенства треугольников OPF и ORG (по
сторонам RG = PF, QG=OF и заключенному между ними углу) вытекает,
что ? POF=/_ROG, и потому /_ROP =
= l_ GOF = 90°. Итак, OR — перпендикуляр
к прямой ОР, а значит, и к прямой I.
Остается провести через точку М прямую,
параллельную О/? (задача 4).
Задача 6. Даны отрезок АВ и, кроме
того, прямая I и на ней точка С. Найти
на прямой I такую точку Е, что СЕ = АВ.
Решение. Проведем через точку В
прямую, параллельную АС, а через точку
С — прямую, параллельную АВ (задача 4).
Мы получим параллелограмм ABDC
(рис. 23). Теперь через центр О окруж-
окружности L проведем прямые, параллельные
CD и I (задача 4) и обозначим через D'
и ?' точки пересечения этих прямых с
окружностью L. Тогда треугольник
OD'E' — равнобедренный. Следовательно,
проведя через точку D прямую, парал-
параллельную D'E' (задача 4), до пересечения
в точке ? с прямой /, мы получим равно-
равнобедренный треугольник CDE, и потому
CE = CD=/4B. (Заметим, что, заменив ?'
диаметрально противоположной точкой ?",
мы получили бы на прямой I вторую
точку ?,, находящуюся от С на расстоя-
расстоянии С?, = ЛВ.)
Задача 7. Найти радикальную ось') двух окружностей, если заданы
их центры 0„ 02 и радиусы г,, гг.
Решение. Проведем прямую Ofi2 и в точках О,, 02 восставим к этой
прямой перпендикуляры (задача 5). На этих перпендикулярах отложим
отрезки О1А^=гг и ОгВ = г1 (задача 6).
Теперь проведем прямую АВ (рис. 24) и
разделим отрезок АВ пополам (задачи 2
и 4). Наконец, через середину М отрезка
АВ проведем перпендикуляр к прямог
А В (задача 5) до пересечения в точке D
с прямой Ofi2. Нетрудно видеть, что точ-
точка D лежит на искомой радикальной оси.
Действительно, обозначив через d, и d
Рис. 23.
расстояния
найдем
р ,
от точки D до О, и 0„
',—r\ = dl— r\
Рис. 24.
а это и означает, что точка D лежит на радикальной оси. Остается про-
') Определение и свойства радикальной оси см. в статье «Окружности»,
стр. 455—459 этой книги ЭЭМ.

О РЕШЕНИИ ЗАДАЧ НА ПОСТРОЕНИЕ
175
вести через точку D перпендикуляр к прямой 0,08(задача 5) — это и будет
искомая радикальная ось.
Задача 8. Даны прямая I, точьа М и отрезок г. Найти точки пере-
пересечения прямой I с окружностью, имеющей центр М и радиус г.
Решение. Выберем на прямой / произвольную точку Н и проведем
прямую МН. На прямой МН отложим от точки М отрезок МР = г (зада-
(задача 6). Теперь проведем через центр О окружности L прямую, параллель-
параллельную МН (задача 4) до пересечения в точке Р' с окружностью L. Далее,
проведем прямые МО и РР' и обозначим через А их точку пересечения
(рис. 25). Точку пересечения прямых АН и ОР' обозначим через Н'. На-
Наконец, проведем через точку Н' прямую, параллельную / и, обозначив
через В' и С точки пересечения этой прямой с окружностью L, проведем
прямые АВ' и АС до пересечения в точках В, С с прямой I. Тогда В и
С — искомые точки пересечения прямой и окружности. Для доказательства
правильности этого построения заметим, что из соотношений ОР'\\МРГ
В'С'\\1 вытекает подобие ряда
треугольников с общей верши-
вершиной в точке А. В частности, PJ.
МА НА СА
ОА~Н'А~С'А'
и потому треугольники MAC ^°
и ОАС подобны. Следова-
Следовательно,
МС_МА_МР
~0А
ОС
ОР1'
Рис. 25.
Так как ОС =0Р', то отсюда
вытекает, что МС = МР = г,
т. е. точка С—искомая. Аналогично устанавливается, что MB = г.
Задача 9. Найти точки пересечения двух окружностей, заданных
своими центрами О,, 02 и радиусами /•„ г2.
Решение. Построим радикальную ось I этих окружностей (задача 7),
Если окружности пересекаются, то радикальная ось I является продол-
продолжением их общей хорды, т. е. прямая I проходит через точки пересече-
пересечения окружностей. Поэтому достаточно найти точки пересечения прямой /
с одной из окружностей (задача 8).
Очевидно, что из возможности решения задач 8 и 9 с помощью ли-
линейки (при условии, что в плоскости начерчена окружность L и задан ее
центр О) и вытекает теорема Понселе — Штейнера.
2.4. О построениях с помощью иных наборов инструментов.
В заключение этого параграфа укажем некоторые результаты, каса-
касающиеся применения других наборов инструментов.
В 1890 г. Август Адлер доказал возможность решения всех
задач на построение, разрешимых циркулем и линейкой, при помощи
так называемой двусторонней линейки (т. е. линейки с двумя парал-
параллельными краями), или при помощи прямого или острого угла (а сле-
следовательно, и угольника).
Таким образом, для решения всякой задачи на построение, раз-
разрешимой циркулем и линейкой, достаточно одного из следующих

176 ОБЩИЕ ПРИНЦИПЫ ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ
инструментов: циркуль, двусторонняя линейка, прямой или острый
угол, угольник. Разумеется, комбинируя те или другие из этих ин-
инструментов, можно получить решение, более простое по технике вы-
выполнения.
Существуют также наборы инструментов, с помощью которых
могут быть решены и задачи более высоких степеней (неразрешимые
циркулем и линейкой). Иногда для этого необходимо, чтобы в плос-
плоскости чертежа была задана некоторая фигура. Так, например, каждая
задача на построение третьей и четвертой степени может быть ре-
решена с помощью циркуля и линейки, если в плоскости чертежа
дано отличное от окружности коническое сечение.
Мы приведем для иллюстрации только один пример—решение
задачи трисекции угла при помощи так называемой вставки.
Пусть на рис. 26 AB = BO=OC=OD. Тогда /_ВАО = /_ВОА =а;
далее, угол СВО (внешний
угол треугольника АВО)
равен 2а; точно так же
равен 2а и второй угол
ВСО равнобедренного
треугольника ОВС; нако-
наконец, угол COD (внешний
угол треугольника ОАС)
равен а + 2а = 3а Из
Рис. 26. этого вытекает простой
способ деления на три
равные части произвольного угла с помощью циркуля и вставки, т. е.
линейки с нанесенными на ней двумя делениями А и В. Именно из
вершины О данного угла описываем радиусом, равным АВ, окруж-
окружность. Пусть С и D — точки пересечения этой окружности со сторо-
сторонами угла СОД (рис. 26), который нужно разделить на три рав-
равные части. Будем теперь двигать вставку в плоскости так, чтобы
точка А, отмеченная на вставке, скользила по прямой OD, а край
вставки (т. е. линейки) проходил все время через точку С. Движе-
Движение вставки будем производить до тех пор, пока точка В, отмечен-
отмеченная на вставке, не попадет на окружность. Тогда мы будем иметь
расположение вставки, указанное на рис. 26, и ^_ВАО будет в точ-
точности равен третьей части данного угла COD.
Это описание может создать впечатление, что задача деления
произвольного угла на три равные части решена при помощи цир-
циркуля и линейки—ведь, имея карандаш и линейку, можно сделать
на крае линейки две отметки. Однако когда идет речь о решении
задачи на построение с помощью того или иного набора инструмен-
инструментов, то считаются указанными не физически реализованные инстру-
инструменты, с помощью которых производятся построения, а лишь пере-
перечень тех «элементарных» операций, которые с помощью этих «идеаль-

О ПОСТРОЕНИЯХ НА ОГРАНИЧЕННОМ КУСКЕ ПЛОСКОСТИ 177
ных» инструментов можно выполнять *). Перечисленные же на стр.
167 «элементарные» операции, осуществимые с помощью циркуля
и линейки, не включают такого использования линейки, которое при-
применено в описанном построении. Именно поэтому линейку с отмечен-
отмеченными на ней двумя точками мы назвали «вставкой», чтобы подчерк-
подчеркнуть, что этот инструмент отличен от линейки.
Как же быть с решением так называемых трансцендентных задач?
Классическим примером такой задачи может служить задача о спрям-
спрямлении длины окружности, т. е. о построении отрезка, длина которого
равна 2л/",где г—радиус окружности, а л—отношение длины окруж-
окружности к диаметру, — трансцендентное число. Данная задача не может
быть решена не только с помощью обычного циркуля и линейки, но
и с помощью эллиптического циркуля и вообще инструмента, чертя-
чертящего алгебраическую кривую2).
§ 3. О построениях на ограниченном куске плоскости
3.1. Построения с помощью линейки ограниченной длины. При
решении задач на построение мы всегда так или иначе ограничены
в применяемых средствах построения. Выше мы подробно рассмот-
рассмотрели вопрос о тех ограничениях, которые накладываются выбором
того или другого набора «чертежных инструментов». Однако могут
встречаться и ограничения совершенно другого характера
Ясно, например, что возможность неограниченного проведения
прямых линий и окружностей, постулированная в классической по-
постановке задачи о построениях «циркулем и линейкой», практически
не может быть реализована, так как в нашем распоряжении всегда
имеется лишь «линейка» ограниченной длины, позволяющая соединять
отрезком две точки, находящиеся друг от друга на расстоянии, не
большем /, а также «циркуль» ограниченного раствора, позволяющий
строить окружности не слишком малого и не слишком большого ра-
радиуса (т. е. окружности, радиус г которых удовлетворяет условию
a-^rsg#, где а и b характеризуют возможности «циркуля» — длину
его ножек и т. п.). Поэтому представляет практический интерес
решение вопроса о построениях, которые можно производить «корот-
«короткой» линейкой и циркулем ограниченного раствора.
') Недаром у Евклида, от которого идет постановка вопроса о по
строениях циркулем и линейкой, отсутствуют даже сами слова «циркуль»
и «линейка», а лишь постулируется возможность проводить прямые
линии и окружности (постулаты 1—3 Евклида; см. статью «Аксиомы и ос-
основные понятия геометрии» в этой книге ЭЭМ, стр. 15).
г) Решение ее может быть получено только при помоши инструмента,
чертящего трансцендентные кривые. В частности, для этой цели может
служить прибор для вычерчивания кривых {/=arccosJt, g = o<p (спираль
Архимеда) и др.
12 Энциклопедия, кн. 4

178 OBIUHF ПРИНЦИПЫ ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ
Остановимся здесь для примера на вопросе о возможности по-
построений с помощью линейки ограниченной длины. Именно мы дока-
докажем, что конструктивные возможности линейки ограниченной
длины нисколько не меньше конструктивных возможностей иде-
идеальной линейки неограниченной длины. Иначе говоря, если имеется
набор инструментов, содержащий идеальную неограниченную линейку
(и, возможно, еще другие инструменты, например циркуль), то, за-
заменив в этом наборе идеальную линейку линейкой ограниченной
длины /, мы получим новый набор инструментов, эквивалентный
прежнему, т. е позволяющий решать все задачи, разрешимые »ер-
воначальным набором
инструментов.
Уточним прежде
всего конструктивные
возможности идеаль-
идеальной линейки и линейки
длины /. Именно мы
считаем, что идеальная
. линейка позволяет
' проводить прямую че-
рез две точки, находя-
а) щиеся на произволь-
рис 97 ном (сколь угодно
большом\)расстоянш
друг от друга, i. e. позволяет соединить две точки отрезком и неогра-
неограниченно продолжать этот отрезок за его концы в обе стороны. Что же
можно делать при помощи линейки длины /? Естественно считать,
что с помощью такой линейки можно во-первых соединять отрезком
две точки, расстояние между которыми не превосходит /, и, во-вто-
во-вторых, можно, последовательно перекладывая линейку, неограниченно
продолжать любой отрезок в обе стороны (рис. 27). Объединяя обе
возможности вместе, мы можем сказать, что линейка длины I по-
позволяет проводить прямую лини-о (неограниченную*.) через две за-
заданные точки, расстояние между которыми не превосходит I.
Для того чтобы доказать, что линейка длины / эквивалентна
идеальной (неограниченной) линейке, достаточно убедиться в том,
что с помощью линейки длины I можно провести прямую, соеди-
соединяющую две точки А и В, расстояние между которыми больше I.
Для этого нам понадобится следующая теорема, доказательство ко-
которой читатель может найти в статье «Геометрические преобразо-
преобразования» (стр. 114 этой книги ЭЭМ).
Теорема. Дан угол MAN и точка Q, не лежащая на сто-
сторонах этого угла. Через точку Q проведены три прямые, пере-
пересекающие стороны угла в точках D,, D2, Dt, и соответственно
?,, Е2, Ег (рис. 28). Обозначим через В точку пересечения прямых

О НОС ГНОЕНИЯХ НА ОГРАНИЧЕННОМ КУСКЕ ПЛОСКОСТИ 179
E1Dl и EtDx, а через С — точку пересечения прямых EtDt и E,Dt.
Тогда точки А, В и С лежат на одной прямой.
Из этой теоремы почти непосредственно вытекает требуемое
построение прямой АВ Нужно провести через точку А две прямые
AM и AN, весьма «близко» (т. е. на расстоянии, значительно мень-
меньшем чем /) проходящие от точки В (напомним, что с помощью ли-
линейки длины / можно проводить отрезки сколь угодно большой
длины). Далее через В проведем два отрезка, пересекающие пря-
прямые AM, AN в точках D,, Е2 и D2, ЕЛ. Проведем теперь отрезки
D,f, и D2Et и продолжим их до пересечения в точке Q (рис. 28).
Проведя теперь через Q еще одну прямую, пересекающую AM и
AN в точках D, и ?3, и про-
проводя отрезки D2ES и DaEt.
мы найдем в пересечении
этих отрезков точку С, ле-
лежащую на прямой АВ.
Остается соединить отрез
ком точки В и С и продол
жить отрезок ВС до точки q
А. Для возможности выпол- рис 28
нения этого построения до-
достаточно позаботиться о том, чтобы каждый из отрезков /},?,,
D2E2, D2ES, DJ\ и ВС имел длину, меньшую /, чего легко достичь.
3.2. Построения на ограниченном куске плоскости. Несколько
иного характера ограничения связаны с тем, что практически построе-
построения всегда приходится производить на ограниченном куске плос-
плоскости (скажем, на листе бумаги, на классной доске и т. п.). Эта
жизненная ситуация делает интересными и нужными задачи на
построение с недоступными элементами. Именно, мы будем считать
для простоты, что задан ограниченный кусок плоскости, напри-
например прямоугольник П, внутри которого только и можно производить
построения. Если внутри П заданы два прямолинейных отрезка,
которые при продолжении пересекаются вне П, то точку пересечения
соответствующих прямых называют недоступной точкой. Аналогично
можно говорить о недоступной (т. е. лежащей вне П) точке пересе-
пересечения прямой и окружности (окружность задается, например, неко-
некоторой своей дугой, лежащей внутри П) или двух окружностей. Можно
также рассматривать недоступные прямые (определяемые двумя
недоступными точками), окружности с недоступным центром и из-
известным радиусом (быть может, радиус равен отрезку, соединяющему
две недоступные точки), окружности, проходящие через три недо-
недоступные точки, и т. д.
В качестве примера рассмотрим следующую задачу
Задача 1. Через данную точку В и недоступную точку А
пересечения прямых /, и /, провести прямую.
12*

180
ОБЩИЕ ПРИНЦИПЫ ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ
Решение легко можно получить из теоремы, приведенной на
стр. 178—179. Именно достаточно повторить построение, исполь-
использованное выше при проведении отрезка АВ с помощью «короткой»
линейки (рис. 29; ср. с рис. 28).
Можно также предложить другое решение этой задачи,
основанное на использовании преобразования подобия. Именно выбе-
выберем в прямоугольнике 17 точку О, примем ее за центр подобия и в
качестве коэффициента по-
подобия выберем число It, зна-
значительно меньшее единицы.
Совершим теперь гомоте-
гомотетию1) с центром О и коэф-
коэффициентом 1г. При этой
гомотетии прямые /, и /2
перейдут в некоторые пря-
прямые /, и 4 (рис. 30), а точка
В—в точку В'. Если коэф-
коэффициент гомотетии k доста-
достаточно мал, то прямые /, и
/2 пересекутся внутри пря-
прямоугольника П в некоторой
точке А'. Следовательно,
прямая А'В' является обра-
образом прямой АВ в рассматри-
рассматриваемой гомотетии и, в част-
частности, АВ\\А'В'. Остается
через точку В провести пря-
прямую, параллельную А'В'.
Это второе решение
использует тот факт, что с
помощью гомотетии с доста-
достаточно малым коэффициен-
коэффициентом можно преобразовать
чертеж (состоящий из данных точек и линий, а также тех точек и
линий, которые нужно было бы провести для решения задачи) таким
образом, чтобы он целиком уместился внутри прямоугольника П, что
позволяет «в уменьшенном масштабе» провести все построение. Это
соображение относится, разумеется, не только к данной задаче, но
и вообще к любой задаче на построение, содержащей недоступные
элементы. Иначе говоря, справедливо следующее утверждение, детали
доказательства которого мы предоставляем читателю2): всякая за-
Рис. 30.
') Определение и свойства гомотетии см. на стр. 55 и 60—61.
!) См. также книгу И. М. Я г лом а. Геометрические преобразования,
I, Гостехиздат, М., 1955, стр. 89.

О ПОСТНОЬНИЯХ НА ОГРАНИ IEHHOM КУСКЕ ПЛОСКОСТИ
181
ч
Рис. 31.
дача на построение, разрешимая (циркулем и линейкой) на неог-
неограниченной плоскости, разрешима также и в том случае, если
допускаются лишь построения, производимые внутри заданного
прямоугольника П. (Разумеется, если, например, в задаче требу-
требуется построить некоторую
точку, расположенную
вне прямоугольника П, то
задача считается решен-
решенной, как только указаны
две прямые, проходящие
через эту точку; анало-
аналогично отрезок, не умеща-
умещающийся в П, построен,
если, например, внутри
П найдены три отрезка,
для которых искомый от-
отрезок является четвертым ¦ "*~ "*¦ q
пропорциональным).
Заметим, что первое решение задачи, приведенной на стр. 179,
представляет интерес для геодезии. Если точка пересечения А
двух отмеченных на местности прямых /, и /2 находится в недоступ-
недоступном месте (скажем, в болоте), то для проведения прямой через точку А
и данную точку В можно использовать построение, показанное на
рис. 29 (рис. 31). Оно удобно тем, что для его выполнения требуется
только проведение пря-
прямых линий (что только и можно
делать на больших участках ме-
местности— ведь циркуль с раство-
раствором в пару сотен метров практи-
практически изготовить невозможно!).
Это замечание подчеркивает прак-
практическую ценность построений,
выполняемых на ограниченном
куске плоскости с помощью
одной линейки — здесь наклады-
накладываются сразу два ограничения
различного характера.
Рис. 32.
Сказанное выше делает интересными построения, выполняемые не
только в прямоугольнике, но также на куске плоскости произвольной
формы. Например, может потребоваться выполнить построение, не проводя
никаких линий в нескольких запретных зонах (озера, болота, леса). Не
рассматривая в общей форме вопрос о выполнимости построений на произ-
произвольном куке плоскости, мы ограничимся решением еще одной задачи.
Задача 2. Даны две точки А а В, а также зона Ф, в которой нельзя
проводить построения (рис 32) прич м прямая АВ упирается в зону Ф.
Найти по другую сторону зоны Ф продолжение прямой АВ.

182 ОБЩИЕ ПРИНЦИПЫ ГЕОМЯТРИЧЕСКИХ ПОСТРОЕНИЙ
Зона Ф может быть лесом, не позволяющим произвести визуальное
провешивание прямой, или горой, в которой нужно пробить прямой
туннель и т. д.
Решение. Можно воспользоваться теоремой, сформулированной на
стр. 178—179 (предоставляем это сделать читателю). Можно также прове-
провести через точку А прямую, не задевающую зоны Фив некоторой ее точке
С провести прямую под углом 180° — 2а, где через а обозначен угол ВАС.
Тогда, отмерив на этой прямой отрезок CD=AC, мы получим точку D,
лежащую на продолжении отрезка АВ. Разумеется, можно предложить
множество иных построений.
§ 4. Общие методы решения задач на построение
на плоскости
4.1. Метод расчленения условий задачи (метод «геометриче-
«геометрических мест»). Каждая задача на построение сводится, по существу,
к нахождению по данным в задаче условиям одной или нескольких
точек. Например, построение треугольника (или многоугольника)
сводится к нахождению его вершин; построение окружности — к на-
нахождению ее центра и одной лежащей на окружности точки и т. д.
Между тем, имеющиеся в нашем распоряжении чертежные средства
(линейка, угольник, циркуль, лекала и пр.) приспособлены, как пра-
правило, для вычерчивания линий. Поэтому при решении задачи на
построение каждая точка (кроме непосредственно заданных) обычно
определяется пересечением двух линий. Так, при построе-
построении треугольника ABC по трем сторонам а, Ъ и с мы определяем
вершину С как точку пересечения двух окружностей: окружности
с центром А и радиусом ЛС= Ъ и окружности с центром В и ра-
радиусом ВС=а; при отыскании вписанной в заданный треугольник
окружности центр ее находится как точка пересечения двух бис-
биссектрис треугольника и т. д.
В соответствии с тем, что искомая точка определяется как точка
пересечения двух линий, требования, налагаемые задачей на искомую
точку, обычно можно расчленить на два отдельных условия; назовем
их условие «fi» и условие «v». Ни первое, ни второе из этих
условий, взятое в отдельности, еще не определяет искомой
точки.
Все точки, удовлетворяющие условию «[Х», составляют множе-
множество точек, которое обозначим через М. В школьной практике это
множество принято называть, в соответствии с устаревшей термино-
терминологией Аристотеля'), «геометрическим местом точек», удовлетво-
удовлетворяющих условию «[X»; в дальнейшем мы будем пользоваться более
современным и более коротким термином «множество». Итак, мы
') См. стр. 17 этой книги ЭЭМ.

ОБЩИЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ НА НОСТРОКНИЕ НА ПЛОСКОСТИ 183
обозначили через М множество всех точеь, удовлетворяющих усло-
условию «[X». Точно так же, рассмотрев все точки, удовлетворяющие
условию «v», мы получим некоторое другое множество точек, которое
обозначим через N. Теперь нам остается только найти пересече-
пересечение множеств М и N, т. е. все точки, принадлежащие одновре-
одновременно обоим множествам М, N—это
и будут все точки, удовлетворяющие
Обоим УСЛОВИЯМ <<[Л» И «V».
Проиллюстрируем сказанное не-
несколькими примерами.
Задача 1. Провести окружность,
касательную к сторонам данного
угла {ABC) и притом одной из его
сторон в данной точке (Е).
Для решения задачи достаточно
найти центр искомой окружности S. Так
как окружность 5 должна касаться обеих сторон угла (условие
«[X»), то центр окружности ? должен лежать на биссектрисе
угла ABC (рис. 33, множество М). Так как, кроме того, окруж-
окружность S должна касаться стороны АВ в заданной точке Е (усло-
(условие «v»), тп центр окружности 5 должен также лежать на перпен-
перпендикуляре, проведенном в стороне АВ
угла ABC через точку Е (рис. 33,
множество N).
Таким образом, искомый центр О
шределится как точка пересечения двух
.рямых М и N.
Задача, как видно из сказанного
выше, всегда имеет решение, и притом
единственное.
Задача 2. Пусть на плоскости
рис 34 заданы три точки А, В и С. Тре-
Требуется найти точку, которая нахо-
находилась бы на расстоянии а от точки А и на равных расстояниях
от точек В и С (рис. 34).
В этой задаче искомая точка также должна удовлетворять двум
условиям. Выделим их.
Во-первых, искомая точка должна находиться на расстоянии а от
точки А (условие «[X»). Множество М всех точек, удовлетворяющих
этому условию, является окружностью радиуса а с центром в точке А.
Во-вторых, искомая точка должна находиться на одинаковом расстоя-
расстоянии от точек В и С (условие «v»). Известно, что множество всех
точек, удовлетворяющих этому условию, представляет собой перпен-
перпендикуляр к отрезку ВС, проведенный через его середину (рис. 34,
множество N).

184 ODLUHF ПРИНЦИПЫ ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ
Искомая точка должна принадлежать как первому, так и второму
чножес гву, т. е. является точкой пересечения линий М к N. В за-
зависимости от расположения прямой N и окружности М задача может
иметь два, одно или ни одного решения.
4.2. Общая схема решения задачи на построение. Решение
задачи на построение обычно содержит четыре этапа, которые мы
сейчас и опишем.
1°. Анализ. Расчленение требований задачи на два отдельных
условия «[х» и «v» не всегда производится просто. В сложных
задачах решение начинают с так называемого анализа, в результате
которого устанавливаются соотношения между искомыми и заданными
элементами и определяется план решения задачи.
Анализ задачи заключается в следующем. Мы предполагаем, что
задача уже решена и изготовляем примерный чертеж. С помощью
этого чертежа мы внимательно изучаем требования зааачи. Цель
анализа заключается в том, чтобы выделять два отдельных условия
«[X» и «v», определяющих искомую точку. Иногда сразу выделить
эти условия не удается, и тогда нужно обнаружить цепочку точек,
каждая из которых может быть построена, исходя из данных задачи
л предшествующих точек; завершаться эта цепочка должна искомой
точкой. Для каждой из точек этой цепочки в свою очередь ищутся
два условия «[х» и «v», определяющие ее. При проведении анализа
зачастую приходится проводить на чертеже те или иные вспомога-
вспомогательные линии; во многих случаях именно выбор целесообразных
вспомогательных линий представляет основную трудность решения
задачи. В тех случаях, когда решение не требует проведения вспо-
вспомогательных линий, а искомая цепочка точек (состоящая, быть может,
из одной единственной точки) и условия «[Л» и «v» без труда усмат-
усматриваются непосредственно, стадия анализа может быть опущена.
2°. Построение, в процессе которого в соответствии с пла-
планом решения, найденным в процессе анализа, фактически осущест-
осуществляется (с помощью указанных заранее инструментов, или указанных
заранее элементарных операций) нахождение искомых геометрических
элементов (точек, линий или фигур).
3°. Доказательство того, что построенная фигура является
искомой, т. е. что эта фигура удовлетворяет всем поставленным
в условиях задачи требованиям. Стадия доказательства является
строго необходимой во всех тех случаях, когда в процессе анализа
мы тем или иным способом преобразовывали первоначальные условия
задачи, заменяя их иными, позволяющими, осуществить построение.
Задача, которую мы решаем в процессе доказательства, заключается
в установлении эквивалентности этих новых условий исходным.
В тех случаях, когда анализ задачи не связан с преобразованием
исходных данных задачи, стадия доказательства может быть опу-
опущена.

ОБЩИЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ НА ПОСТРОЕНИЕ НА ПЛОСКОСТИ 185
4°. Исследование, в результате которого выясняется, в ка-
каких случаях решение задачи возможно и какое число решений задача
может иметь в зависимости от заданных элементов (их числа,
взаимного расположения, величин и т. д.)г).
Более подробно мы рассмотрим эти этапы на некоторых из при-
приведенных ниже примеров.
4.3. Алгебраический метод. Условие задачи на построение может
быгь выражено аналитически, если исходить из соотношений между
искомыми и данными элементами.
Пусть, например, дана задача: построить квадрат, площадь
которого в три раза больше плошади данного квадрата.
Обозначив сторону искомого квадрата через х, а сторону данного
через а, получим уравнение
х2 = За2;
его решение
(отрицательное значение корня уравнения не удовлетворяет условию
задачи) дает аналитическое выражение искомого отрезка.
Аналитическое выражение задачи на построение в виде уравне-
уравнения, а его решения в виде корня этого уравнения помогает найти
геометрическое решение, определить, с помощью каких инструментов
оно может быть выполнено (иногда это сразу можно сказать по виду
полученного уравнения), облегчает исследование решения 2).
Эти соображения получили свое полное развитие в аналитической
геометрии, в которой геометрические исследования осуществляются
средствами алгебры.
В самом начале школьного курса геометрии выполняются постро-
построения отрезков, равных алгебраической сумме данных отрезков:
х = а±?; х = а-\-Ь — c + d; x = 3a±2b и т. д.
Позже рассматривается построение четвертого пропорциональ-
пропорционального к трем данным отрезкам, выражаемого формулой
_Ьс _
а
') В качестве примера задачи, исследование которой существенно свя-
связано с числом заданных элементов, укажем известную задачу о построении
п-угольника по заданным на плоскости серединам его сторон (см., напри-
например, И. М. Я г л о м, Геометрические преобразования, т. I, задача 13),
всегда имеющую единственное решение при п нечетном и ни одного реше-
решения или бесконечно много решений при п четном.
2) См. статью «О разрешимости задач на построение с помощью цир-
циркуля и линейкн» в этой книге ЭЭМ стр. 205—227.

186 ОБЩИЕ ПРИНЦИПЫ ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ
построение среднего пропорционального двух данных отрезков:
х = Vab;
построение формулы:
и т. д. Именно к этим построениям во многих случаях сводится приме-
применение алгебраического метода к реше-
решению задач на построение.
Проиллюстрируем сказанное при-
примерами.
Задача 1. Дан треугольник
ABC. Провести прямую, параллель-
параллельную его основанию и делящую попо-
пополам его площадь.
Рис. 35. Решение. Анализ. Пусть
ABC—данный треугольник (рис. 35)
Предположим, что PQ — искомая прямая. Тогда в силу подобия тре-
треугольников PAQ и ВАС имеем
откуда
Это соотношение дает нам очень простое построение: делим
отрезок АВ пополам (точка М) и строим прямоугольный равнобед-
равнобедренный треугольник AMN (^//ШЛ/=90°) Тогда гипотенуза AN
последнего и даст искомый отрезок:
АР™.
АВ
AN= У МЛ/2 + МА2 = ^= .
Откладываем от точки А отрезок AP=AN и проводим PQ\\BC.
Доказательство правильности описанного построения в обрат-
обратном порядке повторяет рассуждения, проведенные в «анализе».
Исследование тоже не представляет труда: решение, оче-
очевидно, всегда имеется, и притом единственное.
Рассмотрим теперь более сложную задачу.
Задача 2. Даны угол LMN (меньший 180°) и точка А на его биссек-
биссектрисе МР. Требиется через данную точки А провести прямую так, чтобы
точки ее пересечения со сторонами данного угла определили отрезок ВС
данной длины а (задача Паппа).
Анализ. Предположим, что задача решена (рис. 36). Опишем
окружность около треугольника МВС. Точку пересечения биссектрисы
с окружностью обозначим через D. Соединим точки В и D. Легко видеть.

ОБЩИН МЕТОДЫ РЕШЕНИИ ЗАДАЧ НА ПОСТРОЕНИЕ НА ПЛОСКОСТИ 187
A BAD.
Из подобия треугольников следует:
BD _РМ
~AD~~~ BD '
или
AD-DM^BD*.
Обозначив МА—т, BD — b, AD*=x, получим, что для решения задачи
достаточно найти отрезок х, определяемый уравнением
При этом отрезок Ь определится как гипотенуза треугольника BDF,
а
один из катетов которого (BF) равен -=-, а прилежащий к нему острый
угол (/_FBD) равен -^-, где п — исходный угол LMN (рис. 36). KD—диаметр
окружности; заметим, что
М ' ^ < 90°. так как а <г 180°.
К
Рис. 37.
Построение. Прежде всего построим вспомогательный отрезок Ь.
После того как отрезок Ь построен, строим отрезок х, пользуясь формулой
Очевидно, отрезок х можно рассматривать как внешнюю часть секущей,
равной х-\-т, проведенной из некоторой точки к окружности диаметра т,
если длина касательной, проведенной из этой же точки к этой окружности,
равна Ь Соответствующее построение приведено на рис. 37.
Положение искомого отрезка ВС найдется теперь следующим образом.
От точки А на продолжении отрезка МА откладываем отрезок AD, рав-
равный х (рис. 36), затем раствором циркуля, равным Ь, на прямой MN
отмечаем точку В. Таким образом, BD = b. Точка В является одним из
концов искомого отрезка ВС. Вторым концом будет точка пересечения
прямых ВА и ML.
Доказательство опять легко вытекает из проведенного выше
анализа.

188
ОБЩИЕ ПРИНЦИПЫ ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ
Проведем исследование решения этой задачи.
Очевидно, что отрезки Ь и х всегда могут быть построены, и притом
однозначно, при любых а, т и а<180°
Решения не будет, если не будет существовать точки пересечения
прямой A1.V и окружности радиуса b с центром в точке D, т. е. если
М (рис. 38)
Ь <. (х + т) sin-jj-
При
. а
Sin-pr
(*)
(*•)
решение будет единственным (окружность
радиуса 4 с центром в точке D касается пря-
прямой MN), а в случае
Ь > (х + т) sin -
(***)
задача будет иметь два решения, причем
отрезки ВС и BiCl будут, как легко видеть,
симметричны относительно биссектрисы МР.
Условия (в)—(***) нетрудно преобразо-
преобразовать так, чтобы они содержали лишь перво-
первоначально данные величины т, а, а. Именно, поскольку x(jc+m) = bl,
т. е.
Рис. 38.
? = __
Ь х+т'
то условие (*) равносильно следующему:
х . а
T<smT-
или
х < Ь sin ~
Подставляя это неравенство в соотношение х(х + т) ~Ьг, получаем
Ь sin -у f b sin -у + т ) > Ь2,
или
6 sin у
sin —
Наконец, так как Ь=- , то окончательно имеем
cos у
а , а

ИСПОЛЬЗОВАНИЕ ГЕОМЕТРИЧР.СКИХ ПРЕОБРАЗОВАНИЙ 189
Это условие эквивалентно соотношению (*), т. е. при его выполнении за-
задача не имеет решений. Аналогично, задача имеет единственно решение
при
а а
и два симметричных решения при
а . а
т<~2 g
§ 5. Использование геометрических преобразований при решении
задач на построение на плоскости
5.1. Общие замечания. В ряде случаев в процессе преобразо-
преобразования исходных данных задачи могут принести пользу те или иные
геометрические преобразования. Наиболее часто употребляются сле-
следующие преобразования:
1) симметрия относительно оси;
2) вращение (в частности, симметрия относительно точки);
3) параллельный перенос;
4) преобразования подобия (в частности, гомотетия);
5) инверсия.
Однако в иных случаях может оказаться полезным также исполь-
использование иных преобразований, например, аффинных или проективных1).
Следует заметить, что применение геометрических преобразований
к решению задач может проводиться двумя принципиально разными
путями.
Один из них заключается в применении геометрического преоб-
преобразования ко всему чертежу (изготовленному в процессе анализа).
Благодаря преобразованию чертеж может упроститься и это облегчит
решение задачи. Например, инверсия может перевести прямую в ок-
окружность или окружность в прямую, и это может оказаться суще-
существенным упрощением в решении задачи; пример такого применения
инверсии читатель найдет в следующем пункте (задача 5). Аналогично
могут применяться и аффинные преобразования; например, произ-
произвольный треугольник может быть с помощью аффинного преобразо-
преобразования превращен в равнобедренный (или даже равносторонний)
треугольник, и это в ряде случаев чрезвычайно упрощает задачу.
Ясно, однако, что применение движений в этом плане бессмыс-
бессмысленно, так как движение преобразует чертеж в равный ему чер-
чертеж и никакого упрощения не произойдет.
Другой путь применения геометрических преобразований (позво-
(позволяющий с успехом использовать и движения) заключается в том,
что мы применяем преобразование не ко всему чертежу в целом,
') По поводу определения и свойств всех упомянутых преобразований
мы можем отослать читателя к помещенной в этой книге ЭЭМ статье «Гео-
«Геометрические преобразования».

190
общик принципы геометрических построений
а лишь к некоторой его части. В ряде случаев это позволяет ка-
каким-то образом сблизить заданные в условии задачи геометрические
элементы, и тем самым найти нить к осуществлению требуемого по-
построения. Примеры, иллюстрирующие такое применение преобразо-
преобразований, читатель также найдет в следующем пункте (задачи 1—4).
5.2. Примеры. Перейдем к рассмотрению задач, иллюстрирую-
иллюстрирующих применение геометрических преобразований.
Задача 1. Построить треугольник ABC no основанию ВС'= а,
высоте AD — h u разности углов при основании, равной ф (т. е
ZbZc)
Рис. 39.
Решение. В этой задаче удобно использовать симметрию
относительно прямой. Предположим, что задача решена, и пусть
точка В' симметрична точ-
точке В относительно прямой
/, проведенной через точку А
параллельно стороне ВС
(рис. 39). Очевидно, чти
^/1=^/5, и потому
=180°— /_ В. Далее,
^/ С и, следователь-
следовательно, /_В'АС = /_Ъ + /_4 =
= 180° + /_ С- /_В =
= 180°—ф. Это и дает ре-
решение задачи. Именно возь-
мем на плоскости отрезок ВС
длины а и на расстоянии h
от прямой ВС проведем параллельную ей прямую /. Построим, далее,
точку В', симметричную точке В относительно прямой /. Тогда
точка А может быть найдена как точка пересечения прямой / и дуги
окружности, стягиваемой хордой В'С и вмещающей вписанный угол
180° —ф.
Задача всегда имеет решение (разумеется, при |ф|<180°), и
притом единственное.
Задача 2. Даны две окружности Sv St и точка А. По-
Построить равнобедренный треугольник АВС(АВ=АС) с данным
углом ф при вершине А так, чтобы точки В и С лежали соот-
соответственно на окружностях S1 и Ss.
Предположим, что задача решена (рис. 4U), и повернем окруж-
окружность Sl вокруг точки А на угол ф. Она займет новое положение St.
При этом вращении точка В окружности 5, перейдет, очевидно,
в точку С окружности .S2. С другой стороны, точка С должна при-
принадлежать преобразованной окружности S,. Таким образом, искомая
точка С является точкой пересечения окружностей 6'2 и 5,. Таким
образом, для решения задачи достаточно построить окружность 5,

ИСПОЛЬЗОВАНИЕ ГЕОМЕТРИЧЕСКИХ ПРЕОБРАЗОВАНИЙ
191
(для нахождения ее центра нужно построить равнобедренный тре-
треугольник АО[О1 с углом ф при вершине А) и найти точки ее пере-
пересечения с окружностью S
Рис. 40.
Так как две различные окружное!и могу г иметь две, одну или
ни одной общей точки и так как окружность .S, можно в любую
сторону (по или против часовой стрелки) поворачивать на угол ф.
то задача может иметь до четырех ре- т
шений. В случае равенства окружностей
5, и 52 задача может иметь и бесчис-
бесчисленное множество решений (если 5, сов-
совпадает с 52).
Задача 3. Даны окружность S.
две ее точки А, В и прямая I. На
данной окружности S найти такую
точку С, чтобы прямые АС и ВС
отсекали на прямой I отрезок PQ
данной длины т.
Анализ. Предположим, что задача
решена и точка С—искомая (рис. 41).
Перенесем параллельно точку А в на-
направлении прямой / на отрезок т.
Полученную точку Ах соединим с точ-
точкой Q. Тогда AA^QP—параллелограмм
(ибо AAt = QP, AAY || QP) и, следова-
следовательно, ^/ AtQB = //_АСВ = а, где а — вписанный в окружность S
угол, опирающийся на хорду АВ.
Отсюда получаем такое
Построение. Перенесем точку А параллельно данной прямой /
на отрезок, равный т. Полученную точку обозначим через А,. На
Рис. 41.

192
ОБЩИЕ ПРИНЦИПЫ ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ
отрезке AtB строим сегмент, вмещающий известный из условия угол а.
Точку пересечения дуги сегмента с данной прямой обозначим через Q.
Точку С мы теперь найдем в пересечении окружности 5 и прямой BQ.
Предоставляя самим читателям провести доказательство и
исследование, укажем лишь, что в зависимости от величины и
Рис. 42.
взаимного положения заданных элементов задача может иметь до
четырех решений (ибо параллельный перенос точки А на отрезок т
можно совершить в двух направлениях; см. рис. 42).
Задача 4. Даны точка А и две пересекающиеся прямые fug.
Через данную точку А провести секущую так. чтобы отрезки
ее AF и AG, заключенные между точ-
точкой А и точками пересечения секу-
секущей, с данными прямыми, имели дан
. AG .
кое отношение k: -—= ft.
Предположим, что прямая АО
(рис. 43) дает решение задачи, т. е.
Применим к прямой / преобразова-
преобразование гомотетии с центром А и коэффи-
коэффициентом k. Прямая / перейдет в прямую
Рис. 43. /' и точке F будет соответствовать
точка G (рис. 43). Точка G принадлежит
одновременно прямым /' и g; следовательно, она является их точкой
пересечения. Отсюда легко получаем необходимое построение. Если
прямые fug непараллельны, то задача имеет единственное решение.
Если же f\\g, то задача либо не имеет ни одного решения (/' не
совпадает с g), либо имеет бесконечно много решений (/' совпа-
совпадает с g).

приближенный методы геометричрских построений
193
Задача 5. Построить окружность, проходящую через две
данные точки А и В и касающуюся данной прямой I (рис. 44).
Анализ. Для решения этой задачи, очевидно, достаточно найти
точку касания искомой окружности и данной прямой.
Пусть окружность S (рис. 44)—искомая. Обозначим через С точку
касания окружности 5 с прямой /. Произведем преобразование ин-
инверсии '), приняв за центр инвер-
инверсии одну из данных точек, напри-
например В, а радиус окружности ин-
инверсии возьмем равным АВ.
При этой инверсии прямая /
перейдет в окружность L, прохо-
проходящую через центр В инверсии,
а окружность 5—в некоторую
прямую т, проходящую через
точку А (точка А переходит в
себя при инверсии) и касающуюся
окружности L в точке Ct, в
которую переходит при инверсии
точка С.
Построение. Проведя из
точки А касательную т к окруж-
окружности L, получим точку касания
С,. Прямая ВС1 пересекает данную прямую / в искомой точке С.
Доказательство правильности построения непосредственно
вытекает из проведенного анализа.
Исследование. В зависимости от расположения точки А
it окружности L задача может иметь два, одно или ни одного ре-
решения.
С
Рис. 44.
§ 6. Приближенные методы геометрических построений
и их значение для практики.
6.1. Точные и приближенные решения задач на построение.
Наряду с теоретически точными решениями задачи в теории задач
на построение рассматриваются и приближенные решения.
Приближенным решением задачи называется результат выполнения
некоторого построения, который мы принимаем за искомое решение,
сознательно допуская при этом некоторую погрешность. Само
построение в этом случае называется приближенным.
Приближенные построения давно уже применяются при выполнении
самых разнообразных графических работ, в том числе и расчетных.
') Определение и свойства инверсии см. в статье «Окружности»,
468—474 этой книги ЭЭМ.
13 Энциклопедия, кн. 4
тр.

194 obiijuf принципы геометрических построкний
Ос'1>1сняется это тем, что замена теоретически точных постро-
построений приближенными во многих случаях значительно упрощает тех-
техническую сторону работы, обеспечивая вместе с тем удовлетвори-
удовлетворительную для практики точность, что особенно важно в тех случаях,
когда требования к практической точности невелики.
Часто приближенные построения используются при решении кон-
конструктивных задач, которые не могут быть точно разрешены при
помощи имеющегося в распоряжении исполнителя набора инстру-
инструментов.
Приближенными графическими способами решаются многие виды
уравнений, для которых точное аналитическое решение или не может
быть получено или его получение сопряжено с большими трудностями
вычислительного характера.
В случае приближенного построения на суммарную погрешность
фактически выполненного построения влияют не только неизбежные
погрешности элементарных операций, но и погрешность выбранного
способа приближенного решения задачи. Поэтому для выяснения
целесообразности применения того или иного приема приближенного
решения задачи необходимо оценить его теоретическую точность.
Теоретически приближенно решить задачу на построение можно
с любой степенью точности. Это вытекает, например, из следующей
теоремы, которую мы здесь приводим без доказательства:
Если среди заданных элементов имеются по крайней мере две
различные точки, то точки, которые могут быть построены
исходя из данных с помощью одного только циркуля, образуют
на плоскости счетное всюду плотное множество.
Отсюда следует, что если искомое точное решение состоит
в определении положения некоторой точки М (или совокупности
точек) по заданным элементам, среди которых имеется по крайней
мере две различные точки, то с помощью одного циркуля (и тем бо-
более с помощью циркуля, линейки и других инструментов) можно
построить точку Mk, либо совпадающую с М, либо как угодно
близкую к ней.
Однако практическое нахождение удобных приближенных приемов
решения задач на построение иногда бывает довольно трудным.
В качестве примеров рассмотрим задачи на спрямление дуг. ок-
окружностей (построение отрезка, длина которого равна длине данной
дуги). Такие задачи часто встречаются в инженерной графике.
6.2. Задачи на спрямление дуг окружностей. Точное их реше-
решение с помощью циркуля и линейки, как известно из теории геомет-
геометрических построений, вообще говоря, невозможно в силу трансцен-
трансцендентности числа л. Поэтому много внимания было направлено на
отыскание достаточно простых и достаточно точных графических
приемов приближенного спрямления дуг окружностей. Много внима-
внимания было уделено также более общей задаче спрямления дуг кривых

ПРИБЛИЖЕННЫЕ МЕТОДЫ ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ
195
второго порядка. Приведем некоторые приемы приближенного решения
этих задач.
1. Требуется графически определить длину дуги АВ (рис. 45).
Пусть С и D—соответственно середины дуги и хорды АВ. Из
точки С проведем перпендикуляр СЕ к хорде АС до пересечения
л
его с хордой АВ (точка ?). Отложим отрезок DF, равный -=- DE.
о
Тогда приближенно длина дуги АВ равна удвоенному отрезку AF.
Найдем погрешность этого
построения. Как легко видеть, С
Длина дуги точно выражается Рис. 45.
формулой AB=aR, где R— ра-
радиус дуги, а а—ее радианная мера. Мы же приближенно принимаем
длину дуги АВ равной
AB^2AF=2Rsm\(l +~ tg'-j).
Абсолютная погрешность Л по определению равна абсолютной
величине разности между истинным и найденным приближенным зна-
значением искомой величины. Следовательно,
Относительная погрешность 6 будет равна
2 . a I л , 2 . , a
Легко проверить, разлагая тригонометрические функции в ряд
по а. что этот способ дает для не очень больших дуг а сравнитель-
сравнительно малую погрешность ^Tqon0*- Для больших дуг погрешность
этого построения велика. Например, при a = я имеем fi = g l=tr 0,061.
2. Другой способ (рис. 46) спрямления обычно применяется для
дуг, меньших 40°. (Для больших дуг погрешность становится значи-
13*

196
ОБЩИЕ ПРИНЦИПЫ ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ
тельной.) В этом случае для спрямления дуги АВ черел центр О ее
проводим прямую, перпендикулярную хорде АВ, и от середины С дуги
АВ на прямой ОС откладываем
отрезок CL = 3/?; через точку С
проводим касательную к дуге
до пересечения ее с прямыми AL
и BL в точках М и N. Длина
отрезка MN и будет прибли-
приближенно равна длине дуги АВ.
Определим погрешность, по-
полученную при этом способе. Так
как AB=aR, AB= 2R sin ^ и
Рис- 46-
/\ABLzn Д MNL, то после несложных выкладок получим:
MN=R-
6sin-|-
2+cos°
абсолютная погрешность
AB\=R
6sin-
относительная погрешность
й =
6sinT
— 1
При малых а эта погрешность примерно равна
3. Для приближенного спрямления полуокружно-
полуокружности могут быть использованы следующие два простых приема.
IS
В,
Рис. 48.
Выполнение построения для первого из них вполне понятно из
рис. 47, на котором аг и at — стороны вписанных в окружность
равностороннего треугольника и квадрата. Длина отрезка ВС прибли-

ПРИБЛИЖЕННЫЕ МЕТОДЫ ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ 197
женио равна длине полуокружности:
ВС = ВО+ОС= аг +ai = R([/~S+V~2)=^R{ 1,732 +1,414) = 3,146#;
относительная погрешность 6=trO, 15%.
Построение по второму способу заключается в следующем: на
диаметре АВ (рис. 48) строим угол СОА, равный 30°. От точки С
в сторону точки А откладываем отрезок CD = 3R. Точки В и D
соединяем. Длина отрезка BD и будет приближенно равна длине
полуокружности. В самом деле, из чертежа следует:
или fi?>=4-Kl20— 18j/3 =s= 3,14/?.
Относительная погрешность 6^:0,002%.
6.3. Графоаналитический метод и метод последовательных
приближений. При решении задач на построение зачастую исполь-
используются также данные, полученные с помощью предварительных рас-
расчетов. Соответствующий метод приближенного решения задач на
построение называют графоаналитическим методом.
Например, задача о делении окружности на п равных частей
может быть решена (а на практике, в частности при разметке, часто
так и решается) при помощи специально составленных таблиц хорд.
На основании предварительных расчетов часто производится вы-
вычерчивание некоторых кривых, построение точек по их координатам,
например при разметке шаблонов, при выполнении чертежей для ко-
копировальных станков и т. д.
Широкое распространение этого метода объясняется тем, что
в ряде случаев он дает возможность осуществить построение более
просто, чем при чисто геометрическом решении; во многих случаях
это — единственно возможный путь решения задачи. Теоретически
погрешность самого метода (точность вычислений) может быть сде-
сделана как угодно малой.
Однако применение графоаналитического метода не всегда удобно,
гак как предварительные расчеты иногда оказываются слишком гро-
громоздкими.
Полезным методом приближенного решения конструктивных задач
является также так называемый метод последовательных прибли-
приближений. Этот метод заключается в многократном повторении некото-
некоторого основного построения, применяемого вначале к заданной сово-
совокупности элементов, а затем к фигурам, получаемым в результате
предшествующих построений.
Если с увеличением порядкового номера построения абсолютные
погрешности результатов неограниченно уменьшаются, то иоследова-

198 ОБЩИЕ ПРИНЦИПЫ ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ
тельность этих результатов будет сходиться к искомому решению,
т. е. тогда теоретически возможна аппроксимация решения с любой
степенью точности.
Оценка точностг построения при методе последовательных при-
приближений обычно затруднена тем, что при построении часто прихо-
приходится выполнять большое число операций. Кроме того, аналитическое
определение погрешности нулевого приближения затрудняется и тем,
что часто нулевое приближение выбирается более или менее произ-
произвольно.
В связи с этим обстоятельством построение обычно выполняется
до тех пор, пока практически совпадут результаты двух последова-
последовательных основных построений.
Число основных построений при решении задач зависит от бы-
быстроты сходимости приближений. При удачно выбранном основном
построении достаточно одного-двух приближений.
Довольно простым примером метода последовательных приближе-
приближений является следующее приближенное решение задачи о трисек-
трисекции угла. Как известно,
или
Следовательно, если дан угол АО В, равный ф, то графически
можно с помощью циркуля и линейки приближенно найти его третью
часть с какой угодно степенью точности, выполняя лишь деление
углов пополам и их сложение.
Для деления угла на 3 части с помощью циркуля и линейки
можно также использовать сумму бесконечно убывающей профессии,
первый член которой равен-к-, а знаменатель равен—-^-. Однако этот
ряд сходится медленнее, чем ряд с общим членом an = jH.
Спрямление дуг окружностей также можно выполнять методом
последовательных приближений. Задача состоит в том, чтобы найти
достаточно простой способ построения последовательностей перимет-
периметров вписанных или описанных ломаных. Мы рассмотрим один изящ-
изящный прием нахождения периметров вписанных ломаных.
Пусть АВ—дуга окружности с центром в точке О, стягивающая
центральный угол а (рис. 49). Примем за нулевое приближение длину
хорды спрямляемой дуги АВ. Затем проведем прямую AN_]_ОЛ, бис-
биссектрису ААЛ угла BAN и ВЬЛ _]_ АВ. Биссектриса ААХ угла BAN
пересечет дугу АВ в ее середине (точка CJ. Итак, BCl = ACl = blCl;

ПРИБЛИЖЕННЫЕ МЕТОДЫ ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ
199
следовательно,
и первое приближение (длина ломаной ЛСгВ) будет
Второе приближение (длина вписанной ломаной, состоящей из четы-
четырех звеньев) находится аналогичным об-
образом: проводим биссектрису ААг угла
AtAN и через точку bs отрезок btbt J_ AA^.
Так как
то
Продолжая процесс, получим последо-
последовательность отрезков АВ, Abv АЬг, .
сходящуюся к отрезку, длина которого Рис 49
равна длине спрямляемой дуги АВ.
Оценим быстроту сходимости процесса. Погрешность ?-го прибли-
приближения равна
следовательно.
Л,Ч
Л'
— У"ж МП
Нетрудно показать, что предел
lim
равен —.
Таким образом, при повторении основного построения погрешность
каждый раз уменьшается примерно в 4 раза.
Из этого построения можно выв'сти одну изящную формулу, впервые
(аналитическим путем) установленную Эйлером. Очевидно, что
i = 2Rsin~.
Далее
BAN = -=-, и потому
-±.

200 СБЩИЬ ПРИНЦИПЫ ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ
Теперь из прямоугольных треугольников ВАЬи 6,Л&2, ЬгАЬг, . . , , находим
. ZR sin -=- .
АВ 2 Я sin а
а а а а
COS -j- COS —- COS -т- COS —
4 4 2 4
ЛЬ, i? sin a
a a a a
COS -5- COS — COS — COS -=-
о 2 4 о
АЪг _ R sin a
Aba = — —
a a a a a
СО8Г6 cos y cos T cos ? cos-
Так как lim Abn равен длине дуги АВ, т. е. равен Ra, то мы приходим
п->со
(сокращая на R) к следующей формуле Эйлера:
sin a
a=
a a a a
COS — COS — COS — COS — . - •
2 4 о lb
§ 7. Геометрические построения в пространстве
7.1. Система постулатов для построений на плоскости. Поста-
Постановка вопроса о геометрических построениях в пространстве отли-
отличается от постановки аналогичного вопроса на плоскости, и мы нач-
начнем с выяснения этого различия.
Геометрические построения на плоскости с помощью циркуля и
линейки основаны на следующей системе постулатов:
1. Через две точки можно провести прямую.
2. Можно построить окружность, имеющую данный центр и дан-
данный радиус.
3. Можно найти точки пересечения двух уже построенных линий.
4. Можно взять произвольную точку на уже построенной линии.
Разумеется, эти постулаты не заменяют каких-либо аксиом гео-
геометрии. Они играют роль аксиом теории геометрических построений ')
и определяют, какие элементы считаются построенными. Например,
первый постулат отличается от аксиомы «существует единственная
прямая, проходящая через две данные точки». Эта аксиома устанав-
устанавливает, что такая прямая существует, а постулат построений добав-
добавляет, что ее можно провести, т. е. что после задания двух точек
ее можно считать построенной.
') Ср. со статьей «О разрешимости задач на построение с помощью
циркуля и линейки», стр. 208—209 этой книги ЭЭМ.

ГЕОМРТРИЧКСКНЕ ПОСТРОЕНИЯ В ПРОСТРАНСТВЕ 201
Перечисленные постулаты отражают практику употребления чер-
чертежных инструментов — циркуля и линейки.
Решение задачи на построение (на плоскости) можно понимать
двояко.
А. Решить задачу на построение — значит свести ее к цепи основ-
основных задач, возможность решения которых постулируется.
Пусть, например, требуется найти середину отрезка АВ. Вот ре-
решение:
1) построить окружность с центром в точке А, имеющую радиус АВ,
2) построить окружность с центром в точке В, имеющую радиус АВ,
3) найти две точки пересечения этих окружностей,
4) провести прямую через эти точки,
5) найти точку пересечения этой прямой с АВ.
Задача решена. Мы не касаемся доказательства и исследования,
j рассматриваем только построение.
Само построение как чертежный процесс мы не производили, за-
заменив его словесным описанием.
Отметим, что способы решения основных задач не требуют объ-
объяснений. Не нужно объяснять, как провести прямую через две точки.
Это — основная задача, решение которой не расчленяется на более
простые шаги. Ее можно решить — это обеспечивается постулатом.
Вопрос, как ее решить, не рассматривается.
Б. Решить задачу на построение—значит выполнить это построе-
построение на бумаге (или на другой материальной плоскости) при помощи
чертежных инструментов.
В геометрии на плоскости между точками зрения А и Б нет
принципиального различия, потому что постулаты точно отражают
свойства чертежных инструментов.
Если учитель задал ученику задачу на построение, то он может
удовлетвориться словесным решением и не требовать вычерчивания').
В самом деле, вся трудность заключается в нахождении цепи основ-
основных задач. Если найдено решение, сформулированное словесно, то
его чертежная реализация не представляет никаких затруднений.
7.2. Система постулатов для «воображаемых построений»
в пространстве. В теории геометрических построений в пространстве
можно предложить систему постулатов, аналогичную приведенной на
стр. 200:
1. Через две точки можно провести прямую.
2. Через три точки, не лежащие на одной прямой, можно про-
провести плоскость.
3. Можно построить сферу, имеющую данный центр и данный
радиус.
') За исключением тех случаев, когда требуется упражнение и про-
процессе черчения.

202 ОБЩИЕ ПРИНЦИПЫ ГЕОМРТРИЧЕСКИХ ПОСТРОЕНИЙ
4. Можно найти линию пересечения двух уже построенных по-
поверхностей (плоскостей или сфер).
5- Можно взять произвольную точку на уже построенной поверх-
поверхности или линии.
6. В уже построенной плоскости можно производить любые по-
построения, допускаемые в геометрии на плоскости.
Эта система постулатов является избыточной. Мы ввели лишние
постулаты (например, 3-й) для усиления аналогии с системой посту-
постулатов для построений на плоскости.
По аналогии с геометрией на плоскости можно под решением за-
задачи на построение в пространстве считать сведение ее к основным
задачам. Но здесь обнаруживается существенная разница с геометрией
на плоскости. Приведенные шесть постулатов составлены по аналогии
с постулатами геометрических построений на плоскости, но в отли-
отличие от последних они не выражают свойств каких-либо инструментов.
На плоскости можно провести прямую карандашом по линейке, а
в пространстве нельзя материальным образом провести плоскость че-
через три точки.
Иначе говоря, на геометрические построения в пространстве не
может быть точек зрения А и Б, а может б:мть только точка зрения А.
Задачу на построение можно решить словесно, но это построение
нельзя реализовать.
Выполняемые таким образом (словесно) построения называются
воображаемыми построениями.
Зачем они нужны?
Во-первых, иногда построения используются для доказательства
существования некоторого объекта.
Во-вторых, воображаемые построения представляют полезное уп-
упражнение и содействуют развитию пространственных представлений.
В то же время ясно, что значение этих построений меньше, чем
значение построений на плоскости. Возможно и иное истолкование
задач на построение в пространстве; оно будет рассмотрено
в статье «Методы изображения» (стр. 288—289 этой книги ЭЭМ).
7.3. Пример. Мы рассмотрим только одну очень простую задачу
для иллюстрации того, что такое воображаемые построения.
Задача. Из данной точки опустить перпендикуляр на дан-
данную плоскость.
Пусть дана плоскость а и точка М вне ее. Возьмем в плоскости а
произвольную точку Р и построим сферу с центром в точке М, про-
проходящую через Р. Если эта сфера не имеет с плоскостью а общих
точек, кроме Р, то МР—искомый перпендикуляр. Если же эта сфера
пересекает плоскость а по окружности, то построим ее центр О;
МО—искомый перпендикуляр.
Мы упоминали выше, что 3-й постулат лишний. Покажем, как
можно решить эту задачу, не пользуясь им.

ЛИТЕРАТУРА 203
В плоскости а возьмем две произвольные точки А к В к прове-
проведем прямую а^АВ. Проведем плоскость |3 МАВ. В плоскости |3
опустим перпендикуляр из М на а; основание этого перпендикуляра
обозначим через N. В плоскости а восставим перпендикуляр к а
в точке N. На этом перпендикуляре возьмем произвольную точку L.
Проведем плоскость \^е LMN. В плоскости у опустим перпендику-
перпендикуляр из точки М на прямую NL: это и есть искомый перпендикуляр
к плоскости.
7.4. Заключение. Теорию построений в пространстве можно раз-
развивать вполне аналогично теории построений на плоскости. Например,
естественно поставить вопрос об общей характеристике всех задач
на построение в пространстве, разрешимых на основе постулатов
1—6. Решение этого вопроса использует основы аналитической гео-
геометрии в пространстве и близко к результатам, изложенным в статье
«О разрешимое ги задач на построение с помощью циркуля и линейки»
(стр. 205 — 227 этой книги ЭЭМ).
Можно также ставить вопросы «о построениях с ограниченными
средствами». Мы уже упоминали выше о том, что постулат 3 на
стр. 201 является излишним и его можно отбросить. С другой сто-
стороны, можно доказать, что всякое воображаемое построение, выпол-
выполняемое на основе постулатов 1—6, можно также осуществить, ис-
используя лишь постулат 3 и возможность пользования циркулем
для нанесения окружностей на сферах (аналог построений Мора —
Маскерони). Все эти вопросы представляют, однако, значительно
меньший интерес, чем соответствующие вопросы теории построений
на плоскости.
ЛИТЕРАТУРА
{1] А. Адлер, Теория геометрических построений, перев. с нем.. Л.,
Учпедгиз, 1940.
Классическое руководство по теории геометрических построений,
рассчитанное на широкий круг читателей и трактующее вопрос весьма
обстоятельно (ограничиваясь, впрочем, лишь случаем построений на
плоскости). Книга содержит много задач.
B] Б. И. Аргунов и М. Б. Б а л к, Геометрические построения на
плоскости, М., Учпедгиз, 1957.
Учебное пособие для студентов педагогических институтов.
C] Д. И. Перепел-кин, Геометрические построения в средней школе,
М., Учпедгиз, 1953.
Небольшая брошюра, рассчитанная на самый широкий круг чита-
читателей; содержит довольно ограниченный материал, разобранный, однако,
весьма тщательно.
[4] Н. Ф. Ч е т в е р у х и н. Методы геометрических построений, М., Уч-
Учпедгиз, 1952.
E] Н. Ф. Четзерухин, Геометрические построения и приближения,
М., Учпедгиз, 1935.
В этой книге обстоятельно разработан вопрос о приближенных
построениях, ь первую очередь о сходящихся приближениях.

204 ОБЩИЕ ПРИНЦИПЫ ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ
|6] И. И. Александров, Сборник геометрических задач на построе-
построение, М., Учпедгиз, 1950.
Весьма обширное собрание геометрических задач на построение,
частично сопровождаемых решениями. Задачи классифицированы по
методам их решения.
|7J Ю. Петер сен, Методы и теории для решения геометрических задач
на построение, М., 1892.
Исторически первый сборник задач на построение, классифициро-
классифицированных по методам их решения. Число задач заметно уступает числу
задач в книге И И Александров.^, однако методы решения охарак
теризованы несколько полнее.
[8] Я. Штейнер, Геометрические построения, выполняемые с помощью
прямой линии и неподвижного круга, перев. с нем., М., Учпедгиз, 1939.
Кл ссическое сочинение, содержащее развернутую теорию по-
построений с помощью одной линейки. Книга содержит также весьма
интересно изложенный теоретический материал (свойства полного че-
четырехсторонника, теория подобия и др.).
[С] П. Ц ю л ь к е. Построения на ограниченном куске плоскости, перев
с нем., М.— Л., ОНТИ, 1935.
Небольшая брошюра, рассчитанная на широкий круг читателей;
содержит много интересных примеров построений, выполняемых на
ограниченном куске плоскости.
[10] Н. В Наумович, Геометрические места в пространстве н задачи
на построение, М., Учпедгиз, 1956; Н. В. Наумович, Простейшие
геометрические преобразования в пространстве и задачи на построение,
М., Учпедгиз, 1959.
Обе книги посвящены геометрическим построениям о трехмерном
пространстве.
ill] L. BKberbach, Theorie der geometrische Konstruktionen, Basel
1952.
Обстоятельный обзор теории геометрических построений на плоско-
плоскости и на поверхности сферы; разобрано весьма большое число разнооб-
разнообразных комплексов инструмен го . и для каждого полностью охарактери-
охарактеризован круг разрешимых этими средствами задач. Изложение доволь-
довольно сжатое, но отчетливое, доступно широкому кругу читателей.

О РАЗРЕШИМОСТИ ЗАДАЧ НА ПОСТРОЕНИЕ С ПОМОЩЬЮ
ЦИРКУЛЯ И ЛИНЕЙКИ
СОДЕРЖАНИЕ
Введение ...... . .... 205
§ 1. Геометрическая часть теории . . 206
1.1. Постановка задачи 206
1.2. Построения циркулем и линейкой . . . 208
§ 2. Перевод задачи на алгебраический язык 210
2.1. Основная лемма ........ . . . . 210
2.2. Выводы 215
2.3. Алгебраические рассмотрения 216
2.4. Случай многочленов третьей степени . . . 218
2.5 Теорема Гаусса . 219
§ 3. Классические задачи 220
3.1. Удвоение куба 220
3.2. Трисекция угла 221
3.3. Построение треугольника по его биссектрисам 223
3.4. Построение правильных многоугольников 225
3.5. Квадратура круга . .... 226
Литература . . . . 227
Введение
Теория геометрических построений с помощью циркуля и линейки
была вызвана к жизни многочисленными безуспешными попытками
решить с помощью такого построения три древние задачи: трисек-
трисекции угла, удвоения куба, квадратуры круга.
Значение этой теории исторически заключается в том, что она
дала одно из первых доказательств невозможности в математике,
выполнив его с помощью точного обозрения совокупности объектов,
которые можно построить, пользуясь только циркулем и линейкой.
Оба математических результата, которые в данной теории получа-
получаются одновременно, но, вообще говоря, могут достигаться разными
средствами, в математике двадцатого века играют особую роль; так,
предметом новой науки — метаматематики—в значительной степени
является изучение вопросов о гом, какие выводы в принципе можно
и какие нельзя получить, пользуясь данными средствами.
Решение основной задачи теории построений циркулем и линей-
линейкой, заключающееся в точном описании совокупности построений,

206 О РАЗРЕШИМОСТИ ЗАДАЧ НА ПОСТРОЕНИЕ
которые можно осуществить, и в описании алгоритма, который даег
возможность решить всякую конкретную задачу или узнать, что эта
задача неразрешима, является по существу алгебраическим; это ре-
решение не могло быть достигнуто до появления необходимых алгебрап
ческих средств. Первое их появление датируется A796 г.) знаменитой
работой юного Гаусса о правильных многоугольниках, которые можно
построить с помощью циркуля и линейки. Эта работа уже содержала
в зачаточном виде основы новой алгебраической теории (позже раз-
развитой замечательным французским математиком Эваристом Галуа, по
имени которого ее называют теорией Галуа) для некоторых полей
частного вида, причем эти алгебраические рассмотрения представляли
собой как раз наиболее глубокую часть работы.
Таким образом, теория построений по существу состоит из трех
частей.
Первая — чисто геометрическая — должна заключать в себе анализ
понятия «построение с помощью циркуля и линейки», с тем чтобы
это понятие было определено четко и недвусмысленно. (Известно,
например, что утверждение о невозможности построения трети за-
заданного угла с помощью циркуля и линейки перестает быть спра-
справедливым, если разрешить некоторые приемы использования линейки ').)
Эта первая часть подготавливает почву для второй, в которой за-
задача переводится на алгебраический язык и ставится в алгебраиче-
алгебраических терминах. Этот перевод не является чисто механической пере-
перефразировкой: он приводит к появлению новых математических объектов,
которые затруднительно или невозможно было бы выразить на гео-
геометрическом языке. С другой стороны, именно появление этих новых
объектов позволяет в конце концов решить задачу. Наконец, третья
часть теории является собственно алгебраической, наиболее глубокой
и наиболее трудной: в ней решается алгебраическая задача, к кото-
которой была приведена соответствующая геометрическая задача — теория
построений.
§ 1. Геометрическая часть теории
1.1. Постановка задачи. При строгом описании понятия «пост-
«построение с помощью циркуля и линейки» следует ясно представить
себе ответ на три вопроса:
а) Что мы хотим построить?
б) Каковы исходные данные?
в) Какими средствами мы можем пользоваться?
Прежде всего будем иметь в виду, что все наши построения
проводятся на выбранной раз навсегда плоскости.
Для ответа на первый вопрос нужно проанализировать имеющиеся
в нашем распоряжении конкретные задачи. Этот анализ показывает,
*) См. выше, стр. 176.

ГЕОМЕТРИЧЕСКАЯ ЧАСТЬ ТЕОРИИ 207
что главной целью решения всегда является построение конечного
числа точек (на плоскости). Сама по себе задача, конечно, не
всегда формулируется так. Однако нетрудно проверить, что любая
задача сводится к такой.
Например, для отыскания некоторой окружности достаточно
построить ее центр и одну из ее точек; для отыскания прямой
достаточно построить какие либо две ее точки; задача трисекции
угла сводится к построению двух точек (Р, Q на рис. 1), через ко-
которые проходят прямые, делящие угол на три равные части. За-
Задача построения треугольника (по каким бы то ни было данным)-
") б)
Рис. 1. Рис. 2.
сводится к задаче построения трех его вершин. Вообще задача по-
построения многоугольника (в частности, квадрата, равновеликого
кругу) сводится к задаче построения его вершин; но дополнительно
нужно указать, какие отрезки, соединяющие пары точек, должны
входить в число сторон многоугольника. (Рис. 2, на котором изо-
изображены два разные многоугольника с одними и теми же
вершинами, показывает, что без этого указания ответ не может
быть определен однозначно.) Задача удвоения куба сводится к
задаче построения двух точек, отстоящих друг от друга на заданное
расстояние (ребро куба, объем которого вдвое больше объема данного
куба). Читатель может сам умножать количество примеров. В прин-
принципе, разумеется, могут быть задачи, для решения которых нужно в
каком-то смысле найти бесконечно много точек (например,
построить эллипс с заданными полуосями). Однако если они не
сводятся к задаче об отыскании конечного числа точек, мы не станем
их рассматривать.
Мы не станем также заниматься вопросом о дополнительных
сведениях, которые нужно получить, когда искомая конечная система
точек построена (например: указать пары точек, являющиеся смеж-
смежными вершинами искомого многоугольника). Обычно эти сведения
получаются прямым геометрическим рассмотрением чертежа.
Итак, мы принимаем следующий ответ на вопрос: а) целы»
любой задачи на построение является указание конечного числа
точек на плоскости.

208 о разрешимости задач иа построение
Теперь ответ на вопрос б) напрашивается сам собой: в качестве
первоначальных данных у нас также должна иметься конечная сово-
совокупность точек на плоскости. В самом деле, для задания угла до-
достаточно задать его вершину и две точки на сторонах; для задания
окружности достаточно задать три ее точки или центр и одну точ-
точку; для задания квадрата достаточно задать его вершины и т. п.').
Итак, мы принимаем следующий ответ на вопрос б): исходными
данными любой задачи на построение является система конечного
числа точек на плоскости.
1.2. Построения циркулем и линейкой. Перейдем теперь к воп-
вопросу в). Ответ на этот вопрос заключается в самом названии статьи:
построение должно осуществляться с помощью циркуля и линейки.
Следует лишь уточнить, что мы имеем право делать с помощью
циркуля и линейки.
Удобно описать процесс построения индуктивно. Мы начинаем
с конечного числа точек на плоскости и хотим получить конечное
число точек на плоскости; процесс построения состоит в том, что
к уже имеющейся системе точек мы добавляем по известным пра-
правилам еще некоторые, а затем отбираем среди всех получившихся
точек те, которые доставляют решение нашей задачи. Вторая часть,
конечно, определяется спецификой задачи; нас интересует сейчас,
по каким правилам добавляются точки.
Назовем шагом построения добавление одной новой точки к уже
имеющимся. Отыскание этой новой точки производится в результате
проведения некоторых операций; по определению, в построе-
построении циркулем и линейкой шаг может состоять только из следующих
операций (причем операции 1 и 2 могут применяться несколько раз,
а операция 3—один раз).
1. Проведение прямой через пару точек имеющейся совокупно-
совокупности. (Эга совокупность является результатом предыдущего шага
или представляет собой первоначально заданную систему точек.)
2. Проведение окружности с центром в одной из точек
имеющейся совокупности и проходящей через некоторую другую
точку этой совокупности.
(Такие прямые и окружности мы назовем построенными на базе
имеющейся совокупности точек.)
3. Выбор одной точки пересечения построенных прямых и
окружностей между собой и добавление этой точки к имеющейся
совокупности.
') Если в качестве данных может быть указано бесконечно много точек,
не сводящихся к точкам конечной совокупности прямых и окружностей,
это резко расширяет область разрешимых задач. Например, задание кри-
кривой, являющейся графиком функции у = хг (и даже любой ее дуги),
позволит затем с помощью циркуля и линейки решить задачу об удвое-
удвоении куба.

ГЕОМЕТРИЧЕСКАЯ ЧАСТЬ ТЕОРИИ 209
Вместо операции 3, которая представляет собой выбор опре-
определенной точки, иногда оказывается необходимым пользоваться
операцией
За. Выбор «.произвольной» точки и добавление ее к имеющейся
совокупности. ,
Следует уточнить здесь употребление слова «произвольный». По
определению это означает, что точку можно «произвольно» выбирать
либо на некотором отрезке прямой, либо на дуге окружности, либо же
в Части плоскости, ограниченной отрезками или дугами, и, возможно,
уходящей в бесконечность. При этом все фигурирующие прямые
и окружности должны быть построены на данном шаге, а концы
отрезков и дуг должны быть точками имеющейся совокупности.
Можно считать, конечно, что «произвольная» точка не должна ле-
лежать на концах отрезков и дуг или на границе упомянутой части
плоскости.
Построением с помощью циркуля и линейки называется после-
последовательность, состоящая из конечного числа onuci-нчых шагов.
Еще раз подчеркнем, что при таком определении часть реального
геометрического содержания данной задачи может остаться в сто-
стороне. Например, останется в стороне вопрос о сведении данной
задачи и желаемого ответа к построению конечного числ) точек
и о выборе из построенной совокупности точек, необходимых для
окончательного решения задачи; останется в стороне также выясне-
выяснение вопросов типа: какие из построенных точек являются смежными
вершинами в искомом многоугольнике, и т. п. Эти вопросы относятся
скорее к «анализу построения», а не к решению проблемы о выпол-
выполнимости требуемого построения.
Итак, пусть задана некоторая конечная совокупность точек на
плоскости; мы считаем, что точку А можно построить (с помощью
циркуля и линейки), если существует такое построение, что (неза-
(независимо от промежуточных «произвольных» выборов точек!) система
точек, полученная в результате этого построения, содержит точку 4.
Задачу на построение мы считаем разрешимой, если совокупность
точек, которые следует найти для решения этой задачи, состоит
только из таких точек, которые можно построить с помощью циркуля
и линейки.
Теперь мы можем сформулировать и «основной вопрос теории
построений с помощью циркуля и линейки». Дано конечное число
точек на плоскости. Какие точки можно построить, исходя из
них?
Мы уже упоминали, что имеется точный ответ на этот вопрос
(т. е. условия, необходимые и достаточные для возможное ги по-
построения точки); существенную роль играет тчкже частичный ответ,
указывающий необходимые условия для того, чтобы точк) можно
было построить.
14 Энциклопедия, кн 1

210 О РАЗРЕШИМОСТИ ЗАДАЧ НА ПОСТРОЕНИЕ
§ 2. Перевод задачи на алгебраический язык
2.1. Основная лемма. Нам понадобятся некоторые сведения из
теории полей: определение числового ноля, конечного расширения и
степени конечного расширения. Все эти сведения можно найти в статье
«Кольцо многочленов и поле рациональных функций» из кн. II ЭЭМ.
Кроме того, мы будем предполагать, что читатель знаком с гео-
геометрическим изображением комплексных чисел точками плоскости,
при котором число а-\-Ы(а, Ь—вещественные числа) изображается
точкой с координатами (а, Ь) в фиксированной раз навсегда прямо-
прямоугольной системе координат.
Это изображение будет играть в дальнейшем основную роль.
Именно мы отождествим плоскость, на которой проводятся все наши
построения, с полем комплексных чисел. Говоря о сложении, умно-
умножении и других алгебраических операциях над точками, мы будем
иметь в виду соответствующие операции над числами, которые изо-
изображаются этими точками. О.шсание всех точек, которые можно по-
получить из данных посредством построения циркулем и линейкой,
равносильно описанию всех отвечающих этим точкам чисел. Мы даже
будем говорить, например, о принадлежности точки к некоторому
полю и т. п.
Итак, пусть в числе данных задачи содержится задание двух
точек на плоскости. Выберем одну из этих точек в качестве начала
координат 0, второй припишем координаты A, 0) (т. е. число 1).
(Кроме этих двух точек, в данные задачи могут входить еще неко-
некоторые другие точки.) Проведем в точке 0 перпендикуляр к прямой,
соединяющей 0 и 1, и отложим единичный отрезок по нему от на-
начала координат. Все эти построения осуществляются с помощью
циркуля и линейки; результатом построения является некоторая
декартова система координат, которую мы и будем использовать для
сопоставления с точками комплексных чисел.
Теперь мы рассмотрим какие-нибудь одно (совершенно произволь-
произвольное) построение циркулем и линейкой. В процессе этого построения
строятся совокупности точек. Символом Ап мы обозначим совокупность
п точек, которая получается на очередном шаге построения. Сле-
Следующий шаг, тем самым, состоит в добавлении к совокупности Ап
еще одной точки, т. е. в переходе к совокупности <4„ + ,. Обозначим
символом Кп наименьшее подполе поля комплексных чисел, содер-
содержащее число i, все числа из совокупности Ап и вместе с каж-
каждым числом содержащее сопряженное к нему число. Первым важ-
важным результатом является следующая основная лемма, устанавлива-
устанавливающая связь между геометрическими операциями над точками и
алгебраическими операциями н-ад соответствующими им числами.
Лемма, а) Любую точку поля Кп можно построить циркулем
и линейкой, исходя из совокупности точек Ап.

ПЕРЕВОД ЗАДАЧИ НА АЛГЕБРАИЧЕСКИЙ ЯЗЫК 211
б) Если переход от совокупности Ап к совокупности Ап + Л состоит
в добавлении точки, полученной пересечением пары прямых, пары
окружностей или прямой с окружностью, построенных на базе точек
Ап, то либо Кп+1 = Кп. либо Kn+l = Kn(Vz), где число z принадлежит
полю Кп и не является в нем полным квадратом. При этом для лю-
любого такого числа z можно построить циркулем и линейкой
число ]/z.
в) Если переход от совокупности Ап к совокупности Ап+1
состоит в добавлении точки, лежащей на данном отрезке пря-
прямой или на данной дуге окружности, или в данной области
плоскости, то эту точку можно выбрать так, чтобы было
К /ж
Рис. 3. Рис. 4.
Доказательство. Начнем с утверждения а). Пусть г,, ... ,zn —
все точки из совокупноеш Ап (которые, как и раньше, мы будем
отождествлять с соответствующими комплексными числами). По опре-
определению ноля Кп любой его элемент получается из чисел i, zx, . .., zn
в результате конечного числа операций сложения, вычитания,
умножения, деления н взятия сопряженного числа. Поэтому доста-
достаточно установить следующий результат: если даны две точки х, у,
то с помощью циркуля и линейки можно построить точки —jc;
х-\~у\ х; х~'\ ху. (Возможность построить число / мы уже отме-
отмечали: напомним, что среди чисел г,, ..., zn содержится единица —
она б.лла выбрана из начальных данных.)
Но этот результат проверяется вполне элементарно. В самом деле,
для построения точки —х нужно провести через О и jc прямую и
циркулем отложить отрезок or О до jc на этой npviMofl по другую
сторону от точки О (рис. 3). Для построения точки х-\-у нужно
провести через точку х прямую, параллельную Оу, а через точку
у — прямую, параллельную Ох (рис. 4). Их пересечение и дастх + _у,
если эти прямые не совпадают, т. е. если точки х, у, О не лежат
на одной прямой. Если же эги три точки лежат на одной прямой,
14*

212 О PA3PFUJHM0CTH ЗАДАЧ НА ПОСГРОННИЕ
ю задача снова сводится к откладыванию (циркулем) данных отрез-
отрезков Hd данной прямой. Для построения точки х'1 достаточно постро-
построить отдельно ее аргумент и модуль. Построение аргумента сводится
к проведению окружности, проходящей через точку х, с центром в
начале координат, отысканию ее точек пересечения с прямой 01 и к от-
откладыванию дуги от одной из этих точек до точки х в другую сторону
по окружности (это даст х, рис. 5). Построение | л: |-1 —это по-
построение четвертого пропорционального к отрезкам |jc|, 1, 1. Хо-
Хорошо известно, как его строить циркулем и линейкой. Затем полу-
полученный отрезок |х|~' нужно отложить по прямой Ох от точки О
в сторону точки v (рис. 6). Наконец, построение точки ху сводится
совершенно аналогичным образом к построению суммы двух углов
(аргументов точек х, у) и к построению отрезка \ху\, т. е. четвер-
четвертого пропорционального к отрезкам 1, |jc|, \y\ (рис. 7).
Мы доказали таким образом, утверждение а) нашей теоремы. Дока-
Доказательство утверждения б) удобно начать со второй его части, т. е.
установить, что если дана точка z (и, разумеется, точка 1), то можно
Лиркулем и линейкой построить (оба значения) У г. Читателю уже
должно быть ясно построение: нужно разделить аргумент точки z попо-
пополам и отложить отрезок длины у \z\ (среднее пропорциональное между
отрезками \z\ и 1; оно строится циркулем и линейкой) от точки О
в обе стороны но прямой, угол наклона которой к действитель-
действительной оси 01 равен половине аргумента числа z (точки М и N
на рис. 8).
Несколько фуднее установить первую часть утверждения б).
Прежде всего мы должны научиться записывать уравнения прямой и
окружностей на комплексной плоскости. Можно, однако, на время
условиться разделять вещественные и мнимые части комплексного
числа, обозначая их символами X, Y. (Это и будут координаты со-

flFPRBOH ЗАДАЧИ НА АЛГЕБРАИЧРСКИЙ ЯЗЫК 213
ответствующеи точки.) Уравнениь прямой, проходящей через
две точки iv,. у,) и (хг, уг) совокупности Ап, запишется в виде
* xl)lyt-yl) — (Y—yl)[xt — x1) = Ot A)
п. е. в виде
где коэффициенты а, Ь, "с легко вычисляются через координаты
точек (jc,, yt), {xt, уг). Далее, уравнение окружности с центром
/ ' x -
О 1
Рис 7. • Рис. 8.
в точке (d, e) из совокупности Ап, проходящей через некоторую
точку (х, у) этой совокупности, можно записать в виде
{X— df + (Y — ef=r\ B)
где r' = (x — d)*-+(y — ef.
Коэффициенты уравнений A) и B) — вещественные числа. Мы
утверждаем прежде всего, что все они прлнадлетат полю Кп. Для
доказательства этого достаточно заметить, что вместе с любым чи-
числом х в поле Кп содержится также его вещественная часть Rex
у I у у у
и мнимая часть Im х, потому что Re х = —~—, Im х = —=— Чи-
/> 2,1
ела же а, Ь, с, d, e, гг в уравнениях A) и B), как мы видели
выше, рационально выражаются через действительные и мнимые
части координат точек из совокупности Ап.

214 О РАЗРЕШИМОСТИ ЗАДАЧ НА ПОСТРОЕНИЕ
Теперь для отыскания точек пересечения мы должны решить
(в вещественных числах!) одну из трех систем уравнений:
| aX + bY+c = 0, I aX+bY+c = 0,
\ a'X+b'Y + c'=0; \ (X-df + (Y-e)% = r\
| (X-d)* + (Y-e)* = r\
\ (X-d'r + (Y-er=r'\
выбрать одно решение этой системы и присоединить полученные числи
X, Y к полю Кп— итогом и будет поле Kn+i. Проверка этого утвержде-
утверждении получается прямо с помощью определений, с использованием того
факта, что если в поле Кп+1 содержатся вещественные числа а, Ь,
то содержатся также и числа а ± Ы.
Но, очевидно, решение первой системы уравнений принадлежит
полю Кп', другими словами, в этом случае kn+i=Kn- Решение же
двух других систем сводится к решению одного квадратного урав-
уравнения с коэффициентами в поле А'/). Присоединение корня этого
уравнения к полю сводится к присоединению корня квадратного из
дискриминанта этого уравнения. Если дискриминант z является пол-
полным квадратом, то Кп+1 = Кп. В противном случае Kn+l = Kn(]/rz)
Утверждение б) доказано1).
Остается теперь проверить утверждение в). Мы покажем даже,
что точки, удовлетворяющие условию в), всюду плотно лежат на
отрезках и дугах.
Пусть дан отрезок прямой, соединяющий две точки х, у из поля Кп-
Тогда середина этого отрезка также принадлежит полю Кп, потому
х I и
что она представляет собой точку ,Г . Применяя это рассуждение
к получившимся двум половинам отрезка, затем к его четвертям и
т. д., мы получаем, что внутри любого отрезка прямой, взятого
между точками х, у, содержится точка из поля К„. Тем самым
установлено, что произвольный выбор точки на отрезке прямой, про-
проходящей через две точки из поля А'„, всегда можно осуществить, не
выходя за пределы этого поля.
Пусть теперь дана окружность С, построенная на базе совокуп-
совокупности точек Ап, и на ней выделена дуга L, концами которой являются
') В случае последней системы полезно предварительно заменить ее
системой, состоящей из первого уравнения и линейного уравнения, полу-
получаемого почленным вычитанием наших двух уравнений.
г) Заметим, что от< утствие вещественных решений у соответствующей
системы уравнений означает, что очередной шаг чанного построения цирку-
циркулем и линейкой не может быть прокеден по некоторой « руСой> причине,
примером которой может служить невозможность построения треугольника,
одна из сторон которого больше суммы двух других.

ПЕРЕВОД ЗАДАЧИ НА АЛГЕБРАИЧЕСКИЙ ЯЗЫК 215
точки, принадлежащие совокупности Ап. Как мы видели выше, урав-
уравнение рассматриваемой окружности С, построенной на базе системы
точек Ап, можно записать в виде B), где d, е и г1 — действитель-
действительные числа, принадлежащие нолю Кп. Далее, любое рациональное
число k принадлежит полю Кп (ибо 1 ? Кп). Будем теперь рассмат-
рассматривать всевозможные точки пересечения окружности С с прямыми,
параллельными оси абсцисс и расположенными на рациональном рас-
расстоянии от этой оси, т. е. с прямыми Y = k, где k — произвольное
рациональное число. Ясно, что эти точки пересечения всюду плотно
расположены на окружности С и, в частности, на дуге L. Но каж-
каждая такая точка пересечения имеет в качестве своих координат X, Y
решение системы
(X-dY + (Y-e)* = r\
Y=k,
и потому, как мы видели выше, эта точка пересечения принадлежит
полю вида Кп (V z), гДе г?Кп- Итак, выбор «произвольной» точки
на дуге L всегда можно осуществить так, чтобы выбранная точка
принадлежала полю Кп{\/z), и потому либо А"п+1 = Кп, либо
К„ + , = М/г), где z e Кп.
Разобрать случай, когда нужно выбирать точку внутри области,
частично ограниченной прямыми и дугами, не представляет труда.
Достаточно, например, заметить, что внутри области всегда можно
найти точку с рациональными координатами, т. е. точку, принадле-
принадлежащую полю Кп.
Таким образом, наша лемма полностью доказана.
2.2. Выводы. Доказанная только что лемма в некотором смысле
решает основной вопрос теории построений с помощью циркуля и
линейки, сформулированный в конце § 1. Для точной формулировки
ответа введем несколько новых понятий.
Обозначим буквой А систему заданных точек, а буквой К —
поле, соответствующее этой системе (напомним, что оно содержит
заданные точки, число / и все сопряженные ко всем своим элементам;
притом это поле является наименьшим с указанными свойствами).
Для любого поля L его квадратичным расширением назовем поле
вида L (|^z), где число z ? L не является полным квадратом в поле L.
Назовем конечное расширение К' поля К допустимым, если оно
получается из поли К в результате конечной цепочки квадратичных
расширений:
К = Кв^Кл<=Кг<= .. с Кп = А";
2^К{ (/ = 0,1, п-\У
Теперь ответ на основной вопрос теории иосфоений можно сфор-
сформулировать так:

216 О РАЗРЕШИМОСТИ ЗАДАЧ НА ПОСТРОЕНИИ
Для того чтобы точку z можно было построить циркулем и
линейкой, исходя из совокупности точек А, необходимо и доста-
достаточно, чтобы точка z содержалась в некотором допустимом
расширении поля К. Этот результат представляет собой простую
перефразировку доказанной выше основной леммы.
Теперь следует разобраться в том, как применять этот резуль-
результат к конкретным геометрическим задачам.
Для возможности такого применения следует прежде всего ре-
решить соответствующую алгебраическую задачу. Это означает, что
мы должны считать искомые точки (т. е. те, которые нужно постро-
построить) неизвестными и составить для них систему уравнений, исходя
из условий задачи (в коэффициенты этих уравнений войдут числа,
соответствующие данным точкам). После этого мы должны либо су-
суметь записать корни уравнений (т. е. искомые точки) в виде неко-
некоторых выражений, содержащих в конечном числе операции сложения,
умножения, деления и извлечения квадратного корня, примененные
к первоначально заданным числам, либо установить, что таких вы-
выражений не может существовать.
В первом случае мы сможем затем геометрически получить ответ
на задачу, строя с помощью циркуля и линейки корни нашей си-
системы уравнений.
Гораздо интереснее второй случай, потому что мы сталкивается
здесь с вопросом нового типа: как установить, что корни данной
системы уравнений не принадлежат допустимому расши-
расширению данного поля?
2.3 Алгебраические рассмотрения '). Ответ на поставленный вопрос
не прост. Больше того, если не накладывать никаких ограничений на
систему уравнений, которая может получиться в результате, то даже не
удастся высказав никаких общих соображений по этому поводу. Мы по-
поэтому наложим следующее условие на рассматриваемый класс задач:
их решение должно сводиться к решению системы уравнений вида
М*. *„)=<>.
F2(x,, ... , х„) = 0, I C)
где X;—неизвестные точки, a F,- — многочлены от переменных х,-, коэффи-
коэффициенты которых входят в поле К, соответствующее заданной первоначаль-
первоначально системе точек. (Задачи трисекции угла и удвоения куба принадле-
принадлежат к этому типу; задача квадратуры круга ге принадлежит Об этом
мы ещг скажем позже )
Если геометрическая задача правильш поставлена, в частности если
начальных i энных достаточно, то она должна допускать только конечное
число ответов В алгебре доказывается, что тогда систему уравнений C)
') Этот пункт рекомендуем при первом чтении стат! и пропустить и
перейти сразу к п 2.4. Ущерба для понимания геометрической части статьи
при этом не произойдет.

ПЕРЕВОД ЗАДАЧИ НА АЛГЬБРАИЧЕСКИЙ ЯЗЫК 217
можно значительно упростить, сведя се методом исключения ь виду
Ф, (*,) = (),
Ф2(дг2)=0,
Ф„(л„)=0,
D)
где на этот раз Ф,-(дг,) — многочлены с коэффициентами в поле К, каждый
из которых зависит лишь от одной переменной Правда, прн этом степени
многочленов Ф, могут значительно вырасти в сравнении с степенями
многочленов F/ н, что еще хуже, у системы D) могут появиться новые
решения Но первое затруднение имеет значение лишь при практическом
счете, а второе мы не будем принимать во внимание, как пргжде, считая,
что если мы разберемся в возможности построения корней системы D),
то отобрать из них решения, дающие ответ геометрической задачи, будет
уже делом доступным.
В свою очередь, построение корней системы D) сводится к построе-
построению корней многочленов от одной переменной с коэффициентами в поле К-
Пуств Ф(»)— такой многочлен. Если нам удастся разложить его на два
множителя ф (дг) = Ф, (дг) Ф2 (х), ни один из которых не является
постоянной величиной, и оба эти множителя имеют коэффициенты нз
поля К, то достаточно будет изучить вопрос о построении корней
каждого из этих множителей в отдельности. Многочлен Ф(<), который
нельзя разложить на множители таким образом, называется не'р во имым
над полем К- (Если ясно, какое поле К имеется в виду, мы будем иногда
для краткости называть такой многочлен просто не ривоОимым.) Следует,
однако, отчетливо понимать, что неприводимгеть мног члена существенно
зависит от поля, над которым этот многочлен рассматривается. Над полем
комплексных чисел, например, люСой многочлен выше первой степени при-
приводим,— этот результат ранее часто называли «основной теоремой алгебры».
Из всего сказанного вытекает, что при принятых ограничениях мы при-
пришли к следующему вопросу. Дан не/ риводимый многочлен с гоэф4ициен-
тами в полг К- Содержатся ли его корни в некотором со,метимом расши-
расширении поля К?
Вопрос не вполне четко поставлен: некоторые корни, казалось бы,
могут содержаться в допустимом расширении, а другие нет. Здесь, однако,
предположение неприводимости позволяет установить следующий важный
результат.
Теорема 1. Если один из юрн й неприводимого многочл:на над по
лем К принадлежит допустимому расш ip наю поля К. то и остальные
ьорни принадлежат допустимому расширению.
(Отсюда, конечно, следует, что если хоть какой-нибудь из корней
этого многочлена не принадлежит допустимому расширению, то и все
остальные обладают этим же свойством.)
Мы не сможем привести здесь доказательства этой теоремы в общем
случае. Оно требует введения довольно трудных алгебраических понятий
и по существу принадлежит к теории Галуа. При разборе конкретных
примеров, однако, нам будут встречаться главным обра.ом неприводимые
многочлены третьей степени. Для этого простейшего случая мы ниже
докажем теорему 1, тем самым оправдав возможность ее последующих
применений.
Читателю следует внимательно отнестись к логической структуре рас-
рассуждений, связанных с этой теоремой. В качестве следствия из нее в п.
2.5 мы получим важный результат, который уже можно будет непосредствен-
непосредственно применять к доказательству неразрешимости геометрических задач.

218 О РАЗРЕШИМОСТИ ЗАДАЧ НА nOCTPOEHHF
2.4. Случай многочленов третьей степени. Пусть Ф(л;) =
= х'-\-рх2-\-qx-\-r— неприводимый многочлен третьей степени с
коэффициентами в поле К, т. е. гакой многочлен, что его нельзя
разложить в произведение двух многочленов с коэффициентами из
поля К, один из которых имеет степень 1, а другой—степень 2.
Мы докажем ниже, что ни один из его корней не может принадле-
принадлежать допустимому расширению К. Но сначала покажем, что спра-
справедлива следующая
Теорема Г Если один из корней многочлена Ф(х) принад-
принадлежит некоторому допустимому расширению поля К. то два
других корня также принадлежат допустимому расширению *).
Доказательство. Пусть цепочка квадратичных расширений
выбрана так, что ее длина (т. е. число п) является наименьшей
возможной из всех длин цепочек, приводящих к допустимым рас-
расширениям поля К, которые содержат какой-нибудь корень много-
многочлена Ф. Из неприводимости многочлена Ф следует, что /z^l.
Соответствующий корень (содержащийся в поле К') обозначим сим-
символом л;, = a + b Yz, где Кп— /("„_, ([/~?); a, ft, z^Kn_x. Так как
х, ? Kn-v т0 Ь=?=0. Имеем теперь
0 = Ф(а-\-Ь\г~г) = Ф1(а, ft, г) + Фг(а, ft, z)\r~z\
Ф{а— ft /~г) = Ф,(а, ft, z)— Ф2{а, ft, z)V~z,
где Ф1 и Фг — некоторые многочлены от трех переменных с коэф-
коэффициентами в поле К. Поэтому числа Ф,(а, b, z) и Фг|о, b, z)
принадлежат полю Kn_t; тогда из первого равенства вытекает, что
Ф, (о. ft, г) = Ф2(а, ft, z) = 0 (потому что j/"z? Лп_,), а из второго вы-
вытекает, что Ф (а—ft |/z) = 0. Тем самым показано, чго число
хг — а—ft У z<^Kn является другим корнем уравнения Ф(х) = 0
(отличным от х,, так как ft ф 0). После этого найти третий корень
уже совсем нетрудно:
х,= —р — (х1+хг) = —р — 2а.
Очевидно, он тоже принадлежит допустимому расширению Кп. Тео-
Теорема доказана.
Заметим, что достаточно добавить к этому доказательству одну
фразу, чтобы установить справедливость следующего предложения.
') В самом простом, но важном случае, огда р = ^ = 0, это совсем
легко доказать. Действительно, тогда х2 = ел:1, х, = егх1, где е = ^—
первообразный корень тр;.тьей степени из единицы. Число е, очевидно,
принадлежит допустимому расширению поля К; следовательно, числа exi
и е2х, также принадлежат допустимому расширению. В общем случав
док а зательство несколько сложнее.

ПЕРЕВОД ЗАДАЧИ НА АЛГЕБРАИЧЕСКИЙ ЯЗЫК 219
Теорема 2'. Если Ф(х)— неприводимый многочлен третьей
степени с коэффициентами из поля К. то ни один его корень
не принадлежит допустимому расширению поля К.
В самом деле, хг = —р — 1а ? /("„_,, что противоречит определению
числа п (напомним, что я 3=1, и потому поле /(„_, определено).
Таким образом, изложенное доказательство теоремы 1' оперирует
с пустым множеством объектов: многочленов третьей сте-
степени, удовлетворяющих условию теоремы Г, вообще не существует!
Тем не менее, конечно, никаких логических несообразностей наши
рассуждения не содержат: «условная» теорема Г сохраняет свою
силу независимо ог отрицательного результата георемы 2' и мы вы-
выделили отдельно эту теорему, поскольку она показывает, какие соо-
соображения применяются для доказательства теоремы 1 в общем слу-
случае. С другой стороны, указанный способ доказательства теоремы 2'
не поддается обобщению на случай произвольной степени, и сама
эта теорема заменяется более сложной по форме теоремой Гаусса
(см. теорему 2, п. 2.5).
2.5. Теорема Гаусса. Мы назовем так следующую теорему, ко-
которую выведем из теоремы 1 п. 2.3.
Теорема 2. Fcju корни неприводимого над полем К много-
многочлена Ф (х) принадлежат допустимому расширению, то степень
этого многочлена равна 2", где п 3* 1 — некоторое целое число.
Из этой теоремы снова следует, что корни неприводимых
многочленов степени 3 вообще не могут принадлежать допустимым
расширениям, потому что 3^=2" ни при каком целом значении п').
Хотя в формулировке теоремы ° участвуют такие понятия, как много-
многочлен и его корпи, появляющиеся в результате непосредственных подсчетов,
в дока ательстне удобно раСотать не с отдельными числами, а с полями.
Дело здесь обстоит так же. как и в доказательстве основ-'ой леммы п. 2.1.
Для переформулировки условия теоремы на языке теории полей возь-
возьмем каком нибудь один корень н многочлена Ф{х) и рассмотрим расшире-
расширение К (й) поля К Ясно, что если 0?/(', то и К (О)ак' Обратное
утвержд(ние тоже, очевидно, справедливо. Поле К (fl) удобно тем, что в
его терминах нетрудно выразить и понятие «степень многочлена Ф(х-)»:
она просто совпадает со степенью конечного расширения (/((в) К). [На-
[Напомним, что это означает. Любое конечное расширение/, поля К является
линейным пространством конечной размерности ') над этим полем. Иначе
говоря, существуют такие п элементов ?„ ... , \n?L, образующие базис
поля L над полем К, что люСой элемент X поля L представляется одно-
значго в виде \ = kI\, + ... +knXn. rie kt, .. . kn?K. Число п называется
степенью расширения и обозначается символом (L.K). В случае, когда
L = /\^il), в качестве элементов X, всегда можно взять просто степени
числа 0, т. е. элементы 1=6°, В б", где п — степень многочле-
многочлена Ф(*).]
') При первом чтении статьи рекомендуем после чтения этого места
обратиться к геометрическим следствиям (§ 31.
Е) См. статью «Векторные пространства и линейные преобразования»
в кн. II ЭЭМ.

220 о резрешимости задач на построение
Теперь мы можем следующим образом переформулировать теорему 2:
если расширение L^dK поля К содержится в допустимом расширении поля К.
то степень (L К) равна 2", где п ^ 1—ц°лое число').
Нам понадобится следующий простой результат. Пусть KcLcM—це-
KcLcM—цепочка конечных расширений Положим I = (L:K), т = (М :К). n — (M:L)
Тогда
т = 1п E)
Доказывают это равенство обычно следующим образом. Пусть X,, ... , X,
— базис поля L над полем К', (J-i, -¦¦ , Цп — базис поля М над полем L.
Т (Х Х Х Х ^)
Тогда элементы (Х,ц,, Х,р.2, ... Х,[1„; ...; Х(р.,, ..., ^р.„), т. е. совокупность
всевозможных попарных произведений X,|iy,. образуют базис поля М над
полем К. Но количество элементов в этом базисе, совпадающее со степенью
(М :К) = т, в точности равно In.
Из равенства E) уже сразу следует теорема 2. В самом деле, пусть
L = K (Y^z) — квадратичное расширение поля Л'. Тогда степень его равна
в точности 2, потому что в качестве базиса расширения L над К можно
взять элементы A, Y^z). Поэтому степень любого допустимого расширения
/<=а:осл:1(=...(=л:Я1=л:', к^ь-лУъ-*). ч
равна (в силу соотношения E)) 2т. Но тогда степень (L:K) любого рас-
расширения L поля К, содержащегося в допустимом расширении К', должна
(снова из-за соотношения E)) делить число 2т. Поэтому (L:K) = 2",
Q^n^m. Теорема 2 доказана.
§ 3. Классические задачи
3.1. Удвоение куба. Теперь мы уже можем применить развитую
общую теорию к ряду геометрических задач. Наша основная цель
состояла в том, чтобы научиться доказывать неразрешимость неко-
некоторых задач, т. е. невозможность построить ряд геометрических
объектов с помощью циркуля и линейки. В соответствии с этим и
подобраны примеры.
Главным нашим инструментом будет теорема 2. Ход исследования
всякой задачи следующий: мы переводим ее на алгебраический язык,
составляем уравнения для искомых точек, выясняем их степень и непри-
неприводимость. Если степень не равна 2", а многочлен неприводим, то
искомую точку (см. теорему 2), нельзя построить с помощью циркуля и
линейки, так что соответствующая задача на построение неразрешима *).
') В такой формулировке этот результат представляется даже более
сильным — заранее совсем неочевидно, что вся/о* конечное расширение
L^K L /C(O) 6Э
р рр
имеет вид L = /C(O), где 6—корень неприводимого многочлена. Это.
однако, можно доказать. Нам это утверждение не понадобится, потому
что из доказательства переформулированной теоремы 2, во всяком случае,
теорема 2 сразу же следует.
г) Читатель, ограничившийся ранее изучением теорем 1' и 2', будет
рассуждать так: если многочлен неприводим, а его степень равна трем,
то искомую точку, как явствует из теоремы 2', нельзя построить с помо-
помощью циркуля и линейки, так что соответствующая задача на построение
неразрешима. Это позволяет полностью понять приведенные в тексте за-
задачи 1, 2, 3.

КЛАССИЧЕСКИЕ ЗАДАЧИ
221
Задача 1. Задан куб (длиной своего ребра). Требуется по-
построить другой куб (т. е. его ребро), объем которого вдвое
больше объема данного куба.
Начало исследования очевидно. Даны две точки (ребро куба).
Как обычно, принимаем их за точки 0 и 1 на комплексной плоскости.
Длина ребра удвоенного куба равна вещественному значению р^2;
для построения точки jX2 мы должны изучить многочлен хг— 2.
Степень его равна трем, и если он неприводим над основным полем
К= Q{i) (Q—поле рациональных чисел), то задача удвоения куба
неразрешима. Докажем, что многочлен х'—2 действительно непри-
неприводим.
Если бы многочлен х' — 2 был приводим над полем Q(i), то
один из множителей обязательно был бы первой степени. Если бы
соответствующий корень не был вещественным, то выделился бы и
другой множитель первой степени с сопряженным корнем, а остав-
оставшийся третий множитель был бы линейным и имел бы уже вещест-
вещественный корень. Это рассуждение применимо к любому многочлену
третьей степени с вещественными коэффициентами: если такой
многочлен приводим над полем Q(i), то один из множителей линеен
и имеет вещественный, а следовательно, даже рациональный
корень.
Но многочлен Xs — 2 не имеет рационального корня, потому что
единственное вещественное значение j/ 2 иррационально.
Напомним доказательство этого факта. Допустим, что
[/2 — p<q, где р, q— взаимно простые целые числа. Тогда p* = 2q',
так что число р должно быть четным; пусть p = 2pt, тогда 4p\ — q*
и, следовательно, число q тоже должно быть четным, а это про-
противоречит тому, что р и q взаимно просты.
Интересно, что на последней стадии решения геометрической
задачи нам пришлось воспользоваться даже чисто арифметическими
соображениями, хотя пока и не очень
сложными!
3.2. Трисекция угла. 3 а д а-
¦1 а 2. Дан 'угол <р; построить
угол-^у.
Задать угол ф — значит задать
три точки: точку 0 — его вершину,
точку 1 на одной из сторон, кото-
которую мы примем за вещественную
ось, и точку z, лежащую на дру- Рис. 9.
гой стороне и имеющую модуль
|z|=l (рис. 9). СЬевидно, z= cosq> + / sin q>. Таким образом,
поле А, соответствующее заданной системе точек, имеет вид

222 о разрешимости задач на построение
К= Q(i, cos<p + /sin<p). Построить угол-^ значит построить число
cos-i--[-f sin-5- или, что равносильно, построить число cos-^- . В сил\
Од О
известных формул тригонометрии,
cos ф = cos ( 2 -|- + -|-J = cos 2 -|- cos —- — sin 2 -у sin -|- =
= Bcos'-|—l)cos-|—2sinfcosfsinf =
= 2 cos' f -cos!- + 2 (l-cos* f) cos |
или
cos ф = 4cos* -5 3 cos ¦— .
О О
Таким образом, число cos ~ является корнем уравнения
о
4х' — Зх — cosq> = 0. Fi
Итак, мы должны построить корень уравнения F).
Перед нами снова многочлен третьей степени; мы должны ра
зобраться, приводим ли он над полем K~Q(i, cos^p -f- i sinq>|. При
некоторых значениях ф он, безусловно, приводим; например, при
<p=-jj-. K=Q(i):
4х' —Зд: —cos i = 4а-' — Зд:= х Dл:1 —3).
Это соответствует хорошо известному обстоятельству: прямой угол
можно разделить на три равные части с помощью циркули и линейки
(при желании читатель может осущестмить «алгебраически» это по-
построение, ретив уравнение 4л — 3 = 0 и построив его корни).
Можно придать точный смысл следующему утверждению, устанав-
устанавливающему в некотором смысле противопеложный результат: при
общем значении ф многочлен 4л:* — Зх — cosy неприводим над полем
К= Q[i, соэф-Н'втф).
Слово «общий» в этой фразе можно определять разными спосо-
способами; обсуждение этих способов и доказательство завели бы нас
слишком далеко. Поэтому ограничимся указанием конкретнаго зна-
значения угла ф, который нельзя циркулем и линейкой разделить на
три равные части. Это — угол ф = — Для доказательства слеаует
о
установить, что при <р = — многочлен, стоящий в левой части урав
нения F), неприводим над полем
-^ + isin-?) =

КЛАССИЧЕСКИЕ ЗАДАЧИ 223
т. е., что левая часть уравнения
8л:' —6л:—1=0 G)
является неприводимым многочленом над полем Q{i, \^3). Если мы
докажем, что многочлен 8v° — 6л:—1 неприводим над полем раци-
рациональных чисел Q, то отсюда будет следовать, что он неприводим и
над полем Q(i, 1^3), потому что любое допустимое расширение поля
Q(i, \^3) является допустимым расширением поля Q.
Решая задачу об удвоении куба, мы уже установили, что для
доказательства неприводимости кубического многочлена над полем
рациональных чисел достаточно установить, что у него нет рациональ-
рациональных корней. Предположим, что такой корень есть; положим 2х= — ,
где р, q— целые взаимно простые числа. Из равенства G) находим
так что q' делится на р и, значит, р=±1. Тогда q удовлетворяет
уравнению q'±3<7* °F I = 0: так как q — целое число, то оно должно
быть делителем свободного члена этого уравнения, так что если це-
целый корень есть, он равен ±1. Но, очевидно, соответствующие
значения x=±-s- не являются решениями уравнения G). Следова-
Следовательно, оно вовсе не имеет рациональных решений.
Итак, циркулем и линейкой нельзя разделить на три равные ча-
части угол -я-=60°, т. е. нельзя построить угол —-— = 20°.
3.3. Построение треугольника по его биссектрисам. Сейчас мы
разберем одну менее традиционную задачу. Треугольник определяется
своими тремя линейными элементами: тремя сторонами, трэмя высо-
высотами, тремя медианами или, наконец, тремя биссектрисами. Постро-
Построить треугольник циркулем и линейкой по заданным сторонам высо-
высотам или медианам сравнительно нетрудно. Не так иб;гоит дело с
биссектрисами. Оказывается, что задача построения треугольника
по заданным отрезкам биссектрис его углов от вершины до
противоположной стороны неразрешима с помощью циркуля и
линейки.
Как и в задаче о трисекции угла, мы не станем разбирать во-
вопрос о неразрешимости «в общем случае» и проведем соответству-
соответствующее рассуждение для частных значений длин биссектрис. Удобно
считать, что две из них равны, потому что тогда удается свести
задачу к исследованию кубического многочлена; если этого предпо-
предположения не делать, пришлось бы рассмотреть уравнение шестнадцатой

224 о разрешимости задач на построение
степени. Мы будем опираться на следующую георему *): если от-
отрезки биссектрис двух углов в треугольнике равны, то эти углы
также равны, так что треугольник равнобедренный. (Доказать
геометрически эту теорему вовсе не легко!)
Задача 3. Построить равнобедренный треугольник по дан-
данным отрезкам биссектрис его углов от вершин до противоле-
противолежащих сторон.
Воспользуемся одной общей формулой, вывод которой предо-
предоставим читателю.
Пусть дан треугольник с полупериметром р и углами а, р, у;
гогда длина биссектрисы угла а равна
В у
sin f- sin -i-
l * I»
COS у COS i-g-!
(Подобные же формулы, конечно, справедливы для /^ и- /г)
В нашем случае р = у; отрезки 1а и /^ заданы. Можно считать,
что /р=1; длину отрезка /а для краткости обозначим просто бук-
буквой /. Если бы мы могли построить циркулем и линейкой искомый
треугольник, то мы могли бы построить также отрезок длины sin -~ .
о
Из формулы (8) мы выведем сейчас, что число sin ~ является кор-
корнем кубического многочлена над полем Q(l) и что при некоторых
рациональных значениях величины / этот многочлен неприводим.
Таким образом, соответствующая задача неразрешима. (Убедитесь,
что тем не менее при всех /, 0 < / < со, искомый треугольник су-
существует!)
Применим формулу (8) к L и отыщем отношение -f- = l, учитывая,
'з
что P = 1Y- Тогда получим
в в а—в е е а—в зв
sin -fj- cos-g- cos—^-t- sin -~- co&-~ cos—^- sin -~-
l if? fif ? - (9)
l
sin -g- cos-^- cos В sin В 2 cos В
(мы снова пользовались тем, что треугольник равнобедренный и,
значит, -п- = -9 PJ- Положим sin-|- = j;; тогда sin ~=3х — 4х';
cos р = 1—2хг. Из равенства (9) вытекает, что х является корнем
уравнения 4х'-Ш2-Зх + 2/ = 0. A0)
') См., например,Д. О. Шклярский, Н. Н. Ченцов, И.М.Я г л о м,
Избранные задати и теоремы элементарной математики, ч 2(М., Гостех-
пздат, 1952), задача 96 и ее решение.

КЛАССИЧЕСКИЕ ЗАДАЧИ 225
Удобно взять / = 3 и произвести замену переменного, положив
у=2х— 2. Число у является тогда корнем уравнения
у»— 15j;— 10 = 0.
Как и прежде, для доказательства неприводимости многочлена
у'—\Ъу—10 достаточно установить, что у него нет рационального
корня. Пусть такой корень есть, и он равен —, где/j, q — взаимно
простые целые числа. Тогда
/>' = 5<7'(Зр + 2«7),
следовательно, р = 5г, где г — целое число, так что
Но последнее равенство невозможно, потому что д не делится на 5.
Наконец, разберем вкратце еще две классические задачи. Для
полного их исследования изложенной выше теории оказывается не-
недостаточно, и некоторые необходимые результаты нам придется при
нять без доказательства.
3.4. Построение правильных многоугольников. Задача 4 Дана ок-
окружность радиуса единица; требуется вписать в нее правильный много-
многоугольник с заданным числом сторон.
Пусть число сторон равно п\ в удобной системе координат задача сво-
сводится к построению корней п-й степени из единицы, т е корней много-
многочлена г"—1 Этот многочлен безусловно приводим: он всегда делится на
п
г—1, и даже на г2 + 1, если п четно. Согласно общему правилу, следует
разложить многочлен г" — 1 на неприводимые множители, однако мы сна-
сначала несколько упростим задачу, пользуясь се геометрическим истолко-
истолкованием
Пусть п = рд, где р, д—взаимно простые целые числа, oia не
равные единице Покажем, что если можно построить циркулем и линей-
линейкой правильный п-угольник, то можно построить также правылин-iie р-уголь-
ник и q-угольник, и наоборот, если можно по/троить правильнее р-уголь-
ник и q-цгольник, то можно построить и правильней ри-игольник. Первое
утверждение очевидно, второе вытекает из того, что если е, (г = 1, . . р),
т|^(/=|, . , д) — Rce корни из едимицм р-й и q-й степени соответственно,
то попарные произведения е,г\/ представляют собой все корни из единицы
pq-й степени. Отсюда следует, что достаточно разобрать вопрос о много-
многоугольниках с р* сторонами, где р — простое число, a k^\—люОое целое
положительное число.
Если р = 2, то при любом k все корни многочлена хг —1 принадле-
принадлежат допустимым расширениям поля Q (i) (и, значит, поля Q\ Читатглю
полезно просерить это утверждение алгебраически; геометрически оно вы-
вытекает из того, что любую дугу можно разделить циркулем и линейкой
иа 2* равных частей.
Пусть теперь р^З.Прежде псегол-" —1 =(*р ~— 1)(х" """"+... + 1).
Корни кердого множителя—это псе непервообразные корни из еди-
единицы р*-й степени. Для построения р*-угольника неооходимо уметь
15 Энциклопедия, ки. 4

226 О РАЗРЕШИМОСТИ ЗАДАЧ НА ПОСТРОЕНИЕ
строить хотя бы один первообразный корень; этого и достаточно, потому
что тогда все остальные корни будут его степенями. Поэтому остается
выяснить, принадлежат ли допустимому расширению поля Q (/) (или, что
все равно, поля Q) корни многочлена х" (p~ll-f-jrp |р"г) + -- +1.
Ответ (по крайней мере, частичный) получить очень легко, если при-
принять без доказательства, что этот многочлен неприводим (существует ряд
докачательств этого факта, и все они используют довольно тонкие ариф-
арифметические соображения,— причиной неразрешимости геометрической задачи
в конечном счете оказываются снова некоторые свойства целых чисел!).
Тогда из теоремы 2 (стр. 219) следует, что если р*~'(р —1) Ф 2", то пра-
правильный р''-угольник нельзя построить циркулем и линейкой.
Тем самым устанавливается, что если р^-угольник можно построить,
то либо р = 2, либо р > 2, и тогда обязательно k = \ и р —1=2". Из того,
что мы доказали, однако, нельзя заключить, что если р = 2" +1 — простое
число, то правильный р-угольник можно построить циркулем и лине кой.
Это утверждение на самом деле справедливо, и оно было впервые доказано
Гауссом. При п — \ получается число р = 2' + 1=3; при л = 2— число р = 5;
при п = 3 получаем не простое число 23+1=9; при п = А получаем /э = 17.
Возможность построить циркулем и линейкой правильный 17-угольник
вообще не была известна до работы Гаусса, и найти такое построение
с помощью только геометрической интуиции очень трудно, если не невоз-
невозможно. В алгебраической формулировке дело сводится к установлению
того, что корни 17-й степени из единицы можно выразить через числа
поля Q (:) с помощью извлечения квадратных корней; это — задача нелег-
нелегкая, но вполне доступная для изложения даже на этих страницах и, по
существу, не требующая никаких дополнительных знаний Мы, однако,
оставим этот вопрос в стороне.
3.5. Квадратура круга. Задача 5. Дан круг; построить квад-
квадрат, равновеликий этому кругу.
Мы уже упоминали, что эта задача тоже неразрешима с помощью
циркуля и линейки. Однако природа этой неразрешимости совер-
совершенно не такая, как у разобранных до сих пор задач.
Как обычно, радиус круга можно считать единичным; дело сво-
сводится тогда к построению квадрата площади я, т. е. отрезка
длины ]/~п. Если бы мы могли построить отрезок длины я, то-мы
могли бы построить и отрезок длины ]/~п, и наоборот. Таким образом,
истинная трудность задачи о квадратуре круга заключается в зада-
задаче о спрямлении (полу)окружности, т. е. в построении отрезка длины п.
Мы пришли к вопросу, принадлежит ли число я допустимому
расширению поля рациональных чисел Q?
В прежних задачах отрицательный ответ на такого рода вопросы
получался так: искомое число было корнем какого-то многочлена
с рациональными коэффициентами, и дальше мы старались применить
к этому многочлену или к его делителю теорему 2' (или теорему 2).
В этом месте стоит напомнить и обратный результат: если число х
принадлежит допустимому расширению поля К, то оно, во всяком
случае, является корнем какого-то многочлена с коэффициентами в
поле К (этот результат справедлив для любых конечных расширений
поля К, а всякое допустимое расширение, по определению, конечно).

ЛИТЕРАТУРА 227
Оказывается, что число л не является корнем вообще ника-
никакого многочлена с рациональными коэффициентами. Принято выра-
выражать это, называя число Л трансцендентным*).
Доказательство трансцендентности числа я использует трудные
аналитические и арифметические средства. Из этого доказательства
и следует невозможность квадратуры круга с помощью циркуля и
линейки, и даже с помощью ряда других чертежных средств (напри-
(например, лекал, ограниченных отрезками алгебраических кривых над
полем рациональных чисел, которые дают возможность удвоить куб
или произвести трисекцию угла).
ЛИТЕРАТУРА
[1] Ф. Клейн, Лекции по избранным вопросам элементарной геометрии,
перев. с нем., Казань, 1898.
Небольшая книжка, содержащая обработку двух лекций, прочитан-
прочитанных знаменитым математиком Ф. Клейном немецким учителям матема-
математики. Первая часть книги содержит изложение вопроса о геометриче-
геометрических построениях, сводящихся к решению алгебраических уравнений,
вторая — учение о трансцендентных числах и элементарное (но совсем
не простое) доказательство неразрешимости задачи квадратуры круга.
[2] Г. Вебер и И. Вельтштейн, Энциклопедия элементарной мате-
математики, перев. с нем., т. 1, Одесса, 1911.
Обширная книга, посвященная вопросам арифметики и алгебры. К
теме настоящей статьи имеют отношение: гл. XVIII Деление окружности
на равные части, гл. XIX Доказательства невозможности (эта глава
начинается с решения вопроса о классе задач на построение, ратре-
шигаых с помощью циркуля и лииейки) и гл XXVI1. Трансцендент-
Трансцендентность чисел е и л.
[3] М. М. Постников, Теория Галуа, М., Физматгиз, 1963.
Книга содержит элементарное изложение алгебраической теории
Галуа, в частности современное решение вопроса "о задачах на по-
построение, разрешимых или неразрешимых циркулем и линейкой
[4] А. Г. Школьник, Задача деления круга, М., Учпедгиз, 1961.
Небольшая брошюра, рассчитанная иа широкий круг читателей.
E] Г. И Дринфельд, Трансцендентность чисел л и е, Харьков, Изд.
Харьковского университета, 1952.
В этой небольшой книге содержится элементарн е решение вопроса
о неразрешимости задачи квадратуры круга.
См. также книги А. Адлера и L. Bieberbac h'a, указанные в списке
литературы к статье «Общие принципы геометрических построений»,
(стр 203 и 204)
') См. статью «Элементы теории чисел» в кн. 1 ЭЭМ, гл. VI, в частно-
частности § 17.

МЕТОДЫ ИЗОБРАЖЕНИЙ
СОДЕРЖАНИЕ
§ I. Постановка задачи 229
1.1 Задача отображения пространства иа плоскость 229
1.2 Циклография 229
1.3 Метод Федорова 230
1.4. Основные требования к методам изображения 231
1 5. Неоднозначность обратного отображения 232
1.6 Проекционные методы изображения 233
§ 2. Параллельные проекции 234
2.1. Свойства параллельной проекции 234
2.2. Метод параллельной проекции на одну плоскость 236
2.3 Жесткие и свободные изображения .... 238
2.4. Изображение плоских фИ|ур 240
2.5. Примеры 244
§ 3. Параллельная аксонометрия 247
3.1. Теорема Польке — Шварца 247
3.2. Полные и неполные изображения 252
3.3. Понятие о параллельной аксонометрии 255
3.4. Условные изображения 258
3.5 Примеры построения аксонометрических изображений .... 2-59
3.6 Общие методы построения аксонометрических изображен-ий 261
3-7 Аксонометризация чертежа 266
3.8. Ортогональная (прямоугольная) аксонометрия 271
§ 4 Метод Моижа . . 275
4.1. Комбинированные изображения 275
4.2. Сущность метода Монжа - 275
$ Б. Центральные проекции 277
5.1 Свойства центральной проекции 277
Б.2 Проективные координаты 279
Б.З Использование проективных координат для построения .изоб-
.изображений 281
5.4. Понятие о центральной аксонометрии 282
§ 6 Построения на изображении . . 288
6.1. Построения н. проекционном чертеже 288
6.2. Примеры . . 288
Литература 289

ПОСТАНОВКА ЗАДАЧИ 229
§ 1. Постановка задачи
1.1. Задача отображения пространства на плоскость. Суще-
Существуют инструменты, оставляющие след на бумаге (например, каран-
карандаш или кисть), но не сущее гвует чертежного инструмента, остав-
оставляющего след при движении в пространстве. Поэтому всякий плоский
предмет можно точно изобразить на бумаге, и здесь не возникает
вопроса о каких-либо методах изображения (кроме только подобного
изменения размеров). Если же требуется изобразить пространствен-
пространственный (трехмерный) предмет, то по упомянутой причине его нельзя
точно скопировать. Мы исключаем из рассмотрения изготовление
моделей, копирующих оригинал. Этот процесс слишком сложен и
может применяться лишь в исключительных случаях. В повседнев-
повседневной же практике мы вынуждены довольствоваться изображением
пространственных предметов на плоскости.
Условимся о следующих терминах.
Предмет, подлежащий воспроизведению, называется ориги-
оригиналом.
Плоская фигура, воспроизводящая или представляющая оригинал,
называется изображением.
Совокупность правил, определяющих, каким образом, зная ориги-
оригинал, получить его изображение, составляет метод изображения.
По причинам, которые будут выяснены ниже,
существует не один, а много различных
методов изображения.
1.2. Циклография. При всяком методе
изображения точки пространства изобража-
изображаются какими-либо объектами на плоскости.
При этом не обязательно, чтобы изображе-
изображение точки было точкой. Существует, напри-
например, метод изображения, называемый ци-
циклографией, дающий изображения* точек
в виде ориентированных окружностей'). рис j
Пусть а—плоскость изображе-
изображения, a М'—произвольная точка пространства (рис. 1). Опустим из М'
перпендикуляр на плоскость а и обозначим основание этого перпенди-
перпендикуляра через Ма. Построим, далее, окружность с центром в М„, радиус
которой равен М' Мй. Наконец, установим на этой окружности такое
направление обхода, которое с точки зрения наблюдателя, находящегося
в точке М', воспринимается как направление против часовой стрелки.
Полученная ориентированная окружность и считается изображением точ-
точки М''. Изображением точки, лежащей в плоскости а, служит она сама.
*) Т. е. окружностей, на которых задано определенное направление
обхода, на рисунках указываемое стрелкой.

230
МЕТОДЫ ИЗОБРАЖЕНИЙ
В этом случае можно считать изображение окружностью нулевого
радиуса.
Циклография осуществляет взаимно однозначное соответствие
между точками пространства и ориен тированными окружностями на
плоскости.
Две точки, симметричные относительно плоскости а, изображаются
одной и той же окружностью, но с разными направлениями обхода.
На рис. 2 показаны изображения прямых. На рис. 2,а изображена
прямая, наклоненная к плоскости а под углом, меньшим 45°, на
рис. 2,6—перпендикуляр к пло-
плоскости а.
1 3. Метод Федорова. Этот
метод заключается в том, что
точки пространства изображаются
на плоскости параллельными век-
векторами. На плоскости а на неко-
некоторой прямой а одно направление
выбирается как положительное;
противоположное направление на
этой прямой считается отрица-
отрицательным. Из двух полупро-
полупространств, определяемых плоско-
плоскостью а, выбирается одно, которое
считается положительным; другое
считается отрицательным. Пусть
теперь /И'—какая-нибудь точка
пространства. Олустим из нее
перпендикуляр на плоскость а и
обозначим основание этого перпен-
перпендикуляра через Мо. Проведем
через /Ио прямую, параллельную а.
Отложим на этой прямой отре-
отрезок М0М, длина которого равна расстоянию точки М' от плоскости а,
т. е. М'М0. При этом будем откладывать отрезок М0М в положи-
положительном (отрицательном) направлении от точки Мо, если точка М'
лежит в положительном (отрицательном) полупространстве. Построен-
Построенный таким образом (связанный!) вектор1) М0М считается изображе-
изображением точки М'. Изображением точки, лежащей в плоскости а, счи-
считается сама эта точка. В этом случае можно считать изображение
нуль-вектором.
На рис. 3 изображена пара точек, симметричных относительно
плоскости с. На рис. 4,а изображена прямая, наклонная к плос-
плоскости а, а на рис. 4,6—прямая, параллельная плоскости а.
б)
Рис. 2.
') Ср. подстрочное примечание на стр. 295 этой книги ЭЭМ.

ПОСТАНОВКА ЗАДАЧИ
231
Итак, изображение точки может быть и не точкой. Однако методы
изображения такого рола не обладают наглядностью и мало распро-
распространены. Поэтому, упомянув о них, мы в дальнейшем будем рас-
рассматривать только те методы, которые точку изображают точкой.
1.4. Основные требования к методам изображения. К методам
ичображения предъявляются два основных требования:
1) наглядность,
2) удобоизмеримость.
Наглядность — это способность изображения вызывать зри-
зрительное впечатление, сходное с тем, какое вызывает оригинал. Изо-
Изображение должно в неко-
некотором смысле заменить
оригинал. Разумеется, мы
V
б)
Рис. 3.
Рис. 4.
имеем в виду только геометрическую форму оригинала. Зрительное
впечатление, вызываемое оригиналом, зависит от многих его свойств,
например от окраски, но окраска не относится к ведению геометрии.
Можно подвергать геометрическому анализу и произведения живо-
живописи, но только с точки зрения рисунка, отвлекаясь от красок,
фактуры и других особенностей.
Наглядность можно понимать и так: всякий человек, рассматри-
рассматривающий изображение, должен понимать, что оно изображает. Для
этого не требуется специальной подготовки или знании каких-нибудь
условностей. Изображения, показанные на рис. 1—4, не обладают
наглядностью. Не зная соглашений, изложенных в тексте, нельзя
понять, что изображено на этих рисунках.
Удобоизмеримость понимается так: по изображению можно,
и притом несложно, восстановить оригинал как твердое тело, т. е.
определить все его размеры. Заметим, что изображение не всегда
определяет оригинал метрически точно. Существуют методы изображе-
изображения, которые определяют оригинал только с точностью до подобия

232
МЕТОДЫ ИЗОБРАЖЕНИЙ
3'
или до аффинного преобразования и т. п.') Однако в этих случаях
достаточно добавления некоторых соглашений, чтобы оригинал опре-
определи ся метрически. Инженерный рисунок обычно определяет ориги-
оригинал, который должен быть изготовлен, например здание, деталь
машины и т. п. Ясно, что такой рисунок должен определять ориги-
оригинал метрически точно.
Изображения на рис. 1—4 обладают удобоизмеримостью.
Требования наглядности и удобоизмеримосги противоречат одно
другому. При построении изображений для художественных целей
предпочтение отдается наглядности. Поэтому
В' В'. художники всегда пользуются методом изобра-
изображения (он называется центральной проек-
проекцией; см. § 5), обеспечивающим наилучшую
наглядность по сравнению с другими методами.
Удобоизмеримость при этом методе не очень
хорошая: определять размеры оригинала хотя и
можно, но для этого требуются сравнительно
сложные построения.
Инженеры-машиностроители и работники
некоторых других специальностей пользуются
методом Монжа (см. ниже). Это — лучший
метод по удобоизмеримости, но наглядность его
мала. Человек, не обладающий специальной
подготовкой, не сможет понять, что на рис. 5
изображен куб.
Самое большое распространение имеют ме-
методы изображения, в которых достигнут неко-
Рис. 5. торый компромисс между требованиями нагляд-
наглядности и удобоизмеримости. Например, метод
параллельной проекции лишь незначительно уступает ло
наглядности методу центральной проекции, зато построения для
определения размеров предмета в этом методе значительно проще.
Метоюм параллельной проекции строятся изображения простран-
пространственных фигур в книгах но геометрии.
1.5. Неоднозначность обратного отображения. Точка в простран-
пространстве определяется тремя координатами, а точка на плоскости — дву-
двумя 2). Можно доказать, что нельзя взаимно однозначно отобразить
пространство (или даже мал^й объгм пространства) на плоскость с со-
сохранением непрерывности; это означает, что обратное отображение
не будет однозначным. Поэтому точка изображения сама по себе
без дополнительных данных не может определять точку оригинала.
') См. в этой книге ЭЭМ статью «Геометрические преобразования»,
стр. 61—62.
2) Иными словами, пространство имеет три измерения, а плоскость —
два (ср. стр. 370 и 377 этой книги ЭЭМ).

ПОСТАНОВКА ЗАДАЧИ
233
д-
-В
Ю
Во всяком методе изображения к точке изображения должен добав-
добавляться еще один параметр, и только тогда точка оригинала будет
вполне определена. Это добавление параметра происходит в разных
методах изображения по-разному.
Например, в проекциях с числовыми отметками из
точки М пространства опускается перпендикуляр на плоскость изо-
изображения а. Пусть Ж—основание этого перпендикуляра. Около
точки М делается числовая отметка, показывающая расстоя-
расстояние точки М' от плоскости а (т. е. длину перпендикуляра М'М);
это расстояние дополнительно снабжается знаком -• или — в зависи-
зависимости от того, в каком полупространстве р
находится точка М'. Точка М вместе с
числовой 'отметкой считается изображе-
изображением точки М''.
При изображении не отдельных точек,
а более сложных оригиналов числовую
отметку не ставят около каждой точки,
а соединяют линией все точки с одина-
одинаковой числовой отметкой и эту общую
отметку надписывают около этой линии.
Линии, состоящие из точек с одинаковыми
числовыми отметками, называются гори-
горизонталями. На рис. 6. изображена
верхняя часть горы. Юго-западный склон
у нее наиболее пологий, а юго-восточ-
юго-восточный— наиболее крутой.
В этом методе числовая отметка и есть
тот параметр, о необходимости которого
говорилось выше. Точка изображения
вместе с числовой отметкой вполне определяет точку оригинала.
В циклографии (см. рис. 1) недостающий параметр задается в виде
радиуса окружности, в методе Федорова (см. рис. 3) — в виде длины
вектора.
1.6. Проекционные методы изображения. В подавляющем боль-
большинстве случаев пользуются проекционными методами изобра-
изображения. Это объясняется тем, что в проекционных методах процесс
построения изображения близок к процессу зрения, т. е. к
процессу образования изображения на сетчатке (разумеется, имея
в виду только геометрическую, а не физиологическую сторону
процесса зрения). Поэтому проекционные методы наиболее наглядны.
В дальнейшем мы будем рассматривать только проекционные
методы изображения.
Проекционными называются все методы, в которых точка
изображения либо служит непосредственной проекцией точки ориги-
оригинала, либо после проектирования производится еще какое-нибудь
Рис. 6.

234 МЕТОДЫ ИЗОБРАЖЕНИЙ
проективное преобразование') (например, подобное преобразование
т. е. изменение масштаба).
Проектирование осуществляется прямыми. В подавляющем боль-
большинстве случаев эти прямые принадлежат связке2). Напомним, что
различают два вида связок: собственные (центральные) связки,
состоящие из всех прямых, проходящих через одну точку (центр
связки), и несобственные связки, состоящие из всех парал-
параллельных между собой прямых (в этом случае говорят, что центр
связки — несобственная, т. е. бесконечно удаленная точка')). Можно
сказать, что связка —это множество всех прямых, проходящих через
одну точку, конечную или «бесконечно удаленную».
Итак, мы будем рассматривать только отображения трех-
трехмерного пространства на плоскость проекционными методами,
в которых проектирование осуществляется связкой, прямых —
центральной связкой или связкой параллельных прямых.
Та область начертательной геометрии — науки об изображениях,—
которая вследствие этих ограничений остается вне нашего поля зре-
зрения, пи своему объему невелика и обслуживает некоторые узко
специальные вопросы (например, в химии многокомпонентных сплавов
иногда используется многомерная начертательная геометрия). Все
технические чертежи и иллюстративные изображения, а также
инженерные рисунки входят в очерченную нами область.
§ 2. Параллельные проекции
2.1. Свойства параллельной проекции. Выберем некоторую
плоскость а за плоскость изображения (т. е. плоскость, на кото-
которой строится изображения). Выберем также в пространстве некото-
некоторую (не параллельную плоскости а) прямую а, указывающую на-
направление проектирования. [Точнее говоря, мы выбираем
не фиксированную прямую (потому что прямая а может быть заме-
заменена любой параллельной ей прямой), а связку параллельных
прямых; прямая а служит представителем этой связки, т. е. при
помощи прямой а мы задаем связку.]
Пусть М' — какая-нибудь точка пространства. Проведем через М'
прямую, параллельную а; она называется проектирующей пря-
прямой. Точка М пересечения этой прямой с плоскостью а считается
изображением точки М'.
') См стр. 110—121 этой книги ЭЭМ,
2) Существуют и такие проекционные методы, в которых для проекти-
проектирования используется не связка, а какое-нибудь другое двухпараметриче-
ское семейство прямых (конгруенция). Мы этих методов рассматривать не
будем
•) Ср. стр. 113 этой книги ЭЭМ.

ПАРАЛЛЕЛЬНЫЕ ПРОЕКЦИИ
235
Сделаем одно замечание, касающееся обозначений. Все обозначе-
обозначения, относящиеся к оригиналу, снабжаются штрихами, а для изобра-
изображений употребляются те же буквы без штрихов. Например,
точка М' имеет изображением точку М,
прямая от'— прямую от.
Такой обычай объясняется тем, что только в начертательной
геометрии, в которой методы изображения представляют предмет
исследования, нам приходится иметь дело одновременно с оригина-
оригиналом и изображением. Во всех других случаях мы имеем дело только
с изображением. Рассматривая рисунки в учебнике геометрии, мы
говорим «это — куб», «это—шар». На самом
деле эти рисунки представляют «изобра-
«изображение куба» и «изображение шара». [Точно
так же и произведения живописи предста-
представляют нам человека через посредство его
изображения.] В начертательной же геометрии
нам приходится одновременно показывать и
оригинал (точка М' на рис. 7) и изображе-
изображение (точка М на том же рисунке). Если бы
мы условились оригинал обозначать буквами
без штрихов, а изображения — буквами со
штрихами, то на всех рисунках нам пришлось
бы пользоваться только буквами со штри-
штрихами и лишь в начертательной геометрии
встречались бы некоторые буквы без штрихов.
Отметим некоторые свойства, характер-
характерные для метода параллельных проекций.
Доказательства мы во всех случаях предоставляем читателю.
1. Каждой точке пространства однозначно соответствует
точка на плоскости а. Разумеется, это соответствие не взаимно
однозначно. Все точки, принадлежащие одной проектирующей прямой,
имеют одно и то же изображение.
При всех методах изображения точки, имеющие одно и то же
изображение, называются конкурирующими точками. В па-
параллельной проекции конкурирующие точки — те, которые лежат на
одной проектирующей прямой.
2. Прямая, если только она не проектирующая, имеет в ка-
качестве своего изображения также прямую линию; проектирующая
прямая изображается точкой.
Поясним, что все геометрические фигуры мы мыслим составлен-
составленными из точек. Поэтому под изображением прямой следует понимать
множество изображений всех ее точек.
3. Параллельные прямые, если только они не проектирующие
и не лежат в одной проектирующей плоскости (т. е. плоскости
Рис. 7.

236 МЕТОДЫ ИЗОБРАЖЕНИЙ
параллельной прямой а), изображаются параллельными прямыми.
Отсюда следует, что изображение параллелограмма—параллелограмм
(который может вырождаться в отрезок).
4. Если точки 4', В', С принадлежат одной прямой (не про-
проектирующей), то
АВ_А'В'
ВС~ В'С "
Точно так же, если А'В' и CD'—отрезки, лежащие на парал-
параллельных (не проектирующих) прямых, то
АВ_А'В-
CD ~ CU ¦
Предложения 2—4 можно также сформулировать несколько иначе.
Оригинал обладает различными свойствами. При параллельном проек-
проектировании некоторые из этих свойств, вообще говоря, теряются,
т. е. не переносятся на изображение, а другие свойства сохраняются.
Последние свойства называются инвариантными относительно
параллельного проектирования '). Всякий параметр, характеризующий
оригинал и не меняющий своего значения ни при каком параллель-
параллельном проектировании, называется инвариантом параллельного
проектирования.
Пользуясь этими понятиями, можно свойства 2—4 сформулиро-
сформулировать так:
2'. Свойство трех (или большего числа) точек «лежать на
одной прямой» инвариантно относительно параллельного проек-
проектирования, т. е. если три точки оригинала обладают этим свойст-
свойством, то их изображения также обладают этим свойством 2).
3'. Свойство двух прямых «быть параллельными» инвариантно
относительно параллельного проектирования.
4'. Простое отношение трех точек, лежащих на одной пря-
прямой, есть инвариант параллельного проектирования. Инвариантом
также является отношение двух отрезков, лежащих на одной
прямой или на параллельных прямых.
Из всего изложенного ясно, что параллельное проектирование
есть аффинное отображение'), но это отображение вырож-
вырожденное, так как оно уменьшает размерность оригинала: точки трех-
трехмерного пространства преобразуются в точки плоскости.
2.2. Метод параллельной проекции на одну плоскость. При
выполнении рисунков мл будем соблюдать следующую условность.
') Ср. стр. 101, 102 этой книги ЭЭМ.
*) Мы не будем каждый раз оговаривать очевидные исключения для про-
проектирующих прямых.
•) Ср. стр. 62 этой
книги ЭЭМ.

ПАРАЛЛЕЛЬНЫЕ ПРОЕКЦИИ
237
/77
Если изображения двух линий пересекаются, то мы будем либо
обозначать эту точку пересечения маленьким кружком (рис. 8а),
либо прерывать одну из линий (рис. 8,6). Первое обозначение будет
применяться в том случае, если оригиналы /' и от' пересекаются;
в этом случае точка А пересечения изображений служит изображе-
изображением точки А' пересечения оригиналов. Второе обозначение приме-
применяется, если оригиналы не пересекаются. Точка пересечения изобра-
изображений не служит в этом случае изображением общей точки
двух линий. Она служит изображением двух различных (конкури-
(конкурирующих) точек: точки А' на линии /' и точки В'—на линии от'. При
этом перерыв линии от (рис. 8,6) значит: точка В' лежит ближе
к плоскости изображения, чем точка А'. Вообразим наблюдателя,
находящегося от плоскости а с той же стороны, с какой и линии
/' и от', и притом весьма
далеко. Если этот на-
наблюдатель смотрит на
.плоскость а вдоль проек-
проектирующих лучей, то его
взгляд встречает сначала
линию /', а затем линию
/я', т. е. для него
линия /' при кажущем-
кажущемся пересечении с лини-
линией от' заслоняет ее1).
При построении изображений встречается много условностей
такого рода. Не следует думать, что цель этих условностей—сти-
условностей—стилизация рисунка или придание ему изя.цества. Они играют важную
геометриче:кую роль, устраняя многозначность в истолковании ри-
рисунка. Например, если бы не ввели только что сформулированного
условия, то как бы мы ответили на вопрос: что изображено на рис. 9,а?
На эгог вопрос возможны, в частности, следующие ответы:
1) На рис. 9,о изображен параллелепипед. Возможно, что мы его
видим сверху и сцраза, а возможно, что снизу и слева.
2) На рис. 9,а изображена плоская фигура.
3) На рис. 9,а изображены двенадцать отрезков, разбросанных
в пространстве и попарно не имеющих общих точек.
На рис. 9,6 эга многозначность устранена. Несомненно, что на
нем изображен параллелепипед, рассматриваемый справа и сверху.
Метрические параметры этого параллелепипеда (углы и ребра) мы
пока определить не можем. К этому вопросу мы вернемся ниже.
Рис. 8.
') Это соглашение, строго говоря, подразумевает, что расстояния от
точек А' и В' до плоскости изображения а считаются ориентированными,
т. е. для точек, находящихся в «положительном» полупространстве (том,
в котором находится наблюдатель), расстояния берутся со знаком +,адля
точек дру.ого, «отрицательного» полупространства—со знаком —.

238
МЕТОДЫ ИЗОБРАЖЕНИЙ
Мы уже говорили, что в проекционных методах кроме проекти-
проектирования допускается еще какое-нибудь проективное преобразование.
Условимся, что в данном случае мы будем допускать подобное пре-
преобразование.
И гак мы приступаем к изучению метода изображения, называю-
называющегося «параллельная проекция на одну плоскост ь».
Этот метод заключается в том, что точка пространства сначала
параллельно проектируются на плоскость, а затем полученное
в этой плоскости изображение подвергается подобному преобра-
преобразованию ').
/
/
А
V
°)
б)
Рис. 9.
Подчеркиваем, что с этого момента читатель, видя на рисунке
точку /И, не должен считать, что она есть непосредственная проек-
проекция точки М'.
Свойства 1—4 (см. стр. 235—236) сохраняют силу при новом
понимании термина «параллельная проекция».
2.3. Жесткие и свободные изображения. При изучении метода
параллельной проекции на одну плоскость, как и при изучении лю-
любого метода изображений, возникают следующие задачи.
1. Как, зная оригинал, построить изображение?
2. Как, имея изображение, судить об оригинале? При этом вовсе
не очевидно, да и не всегда (не при любом мгтоде изображения)
верно, что, имея изображение, можно ответить на любой вопрос,
относящийся к оригиналу.
Приступая к разбору этих задач, заметим, что они допускают
два различных толкования в зависимости от того, имеем ли мы:
а) жесткое изображение или
б) свободное изображение.
') Искажение, которому подвергается оригинал при замене его изобра-
изображением, нисколько не увеличилось бы, если бы мы подвергли полученную
проекцию не подобному, а любому аффинному преобразованию, потому
что само параллельное проектирование есть аффинное отображение. Мы
ограничиваемся подобным преобразованием (для Гольшей элементарности
изложения) именно потому, что эт~ разница несущественна.

ПАРАЛЛЕЛЬНЫЕ ПРОЕКЦИИ 239
Изображение называется жестким, если известны все параметры,
характеризующие метод изображения и положение оригинала.
Пусть, например, требуется построить изображение куба, ребро
которого равно 1 м. Метод параллельной проекции на одну плоскость
характеризуется двумя параметрами, а именно:
1) углом о наклона проектирующих прямых к плоскости изоб-
изображения ');
2) коэффициентом подобия k, т. е. множителем, на который
умножаются все отрезки, полученные в плоскости изображения в ре-
результате проектирования.
Положение куба определяется в случае ортогональной проекции
двумя параметрами. Можно, например, задать углы a, f5, Y проекти-
проектирующего луча с ребрами куба, выходящими из одной вершины. Эти
углы связаны соотношением
cos2 a -f- cos2 p -f- cos2 у = 1,
и потому среди трех углов а, р, у имеется два независимых параметра.
Можно взглянуть на дело и с такой точки зрения. Положение
твердого тела в пространстве определяется шестью napjMerpaMH.
Однако любые параллельные переносы этого тела не влияют на проек-
проекцию (они вызывают только параллельный -перенос этой проекции в
плоскости изображения); эти движения зависят от трех параметров.
Кроме того, повороты тела вокруг оси, совпадающей с проектиру-
проектирующей прямой, в случае ортогональной проекции тоже не влияют
на проекцию, вызывая лишь повороты изображения; эти дви-
движения зависят от одного параметра. Получаем: 6 — 3 — 1=2. Если
проекция косоугольная, то повороты тела вокруг проектирующей
прямой уже меняют вид изображения, и положение тела в этом
случае зависит от трех параметров.
Допустим, что все эти параметры заданы, например:
а = 6Г, & = 0,04;
а = 45°, р = бГ, y = 59°.
При таких параметрах куб с ребром 1 М изобразится так, как по-
показано на рис. 10.
При построении жестких изображений задание оригинала пол-
полностью определяет изображение. Верно и обратное. Зная пара-
параметры, характеризующие проектирующий аппарат и положение
оригинала, мы бы могли определить метрические параметры парал-
параллелепипеда, изображенного на рис. 9,6.
') При о = 90° проекция называется прямоугольной или ортого-
ортогональной, при О 5й 90° — косоугольной.

240
МЕТОДЫ ИЗОБРАЖЕНИЙ
Жесткие изображения находят применение в инженерной практи-
практике. Методы получения таких изображений излагаются в учебниках
начертательной геометрии. Параметры большей частью задаются не
аналитически, а графически, т. е. элементы оригинала и проектирую-
проектирующего аппарата показываются на рисунке. Однако несравненно
большее значение имеют свободные изображения.
Изображение называется свободным, если при его построении
параметры, определяющие проектирующий аппарат и положение
оригинала, неизвестны. Построить свободное изображение куба — зна-
значит изобразить куб, безразлично как расположенный, и безразлично
под каким углом спроектированный на
плоскость, и безразлично с каким после-
последующим изменением размеров.
Разумеется, различие между жесткими
и свободными изображениями заключается
не в виде этих изображений, а в способе
их получения. Так, изображение куба на
рис. 10 построено по заданным парамет-
параметрам, т. е. оно жесткое. Но если бы, желая
как-нибудь изобразить куб, мы начер-
начертили рис. 10, то это было бы для нас сво-
свободное изображение куба.
Методы построения жестких и свобод-
свободных изображений совершенно различны.
Во всех случаях использования изображений с иллюстративной
целью приходится строить свободные изображения. Если учитель
математики для иллюстрации какой-нибудь теоремы чертит на доске
изображение куба с данным ребром, то ему безразлично, как рас-
расположен в пространстве оригинал и под каким углом наклонены к
плоскости доски проектирующие прямые. Ему лишь важно, чтобы
его изображение было «похоже» на куб. Но что это значит? Это
значит, что существует такая система значений параметров a, k и
параметров, характеризующих положение куба, при которой изобра-
изображение куба с данным ребром будет именно таково.
Мы не будем излагать теорию получения жестких изображений
как имеющую узко специальное значение. Отсылаем читателя к
учебникам начертательной геометрии. Зато владение теорией свобод-
свободных изображений совершенно необходимо каждому учителю матема-
математики. Мы изложим эту теорию подробно.
2.4. Изображение плоских ф-шур. В качестве пропедевтики мы
начнем с изображений плоских фигур, расположенных в пространстве.
Можно считать, что плоская фигура входит в состав подлежащей
изображению пространственной фигуры (например, как одна из граней
пирамиды). Если бы требовалось изобразить только одну плоскую
фигуру, то мы могли бы изобразить ее без искажения.
Рис. 10.

ПАРАЛЛЕЛЬНЫЕ ПРОЕКЦИИ
241
Правила изображения плоских фигур основаны на следующей
теореме.
Теорема 1. Любой треугольник ABC может служить изо-
изображением любого треугольника А'В'С.
Прежде всего дадим некоторые пояснения.
Во-первых, говоря об изображениях, мы имеем в виду изображение
по методу «параллельной проекции на одну плоскость».
Во-вторых, дадим более развернутую формулировку. В плоскости
изображения а дан треугольник ARC В пространстве дан треуголь-
треугольник А'В'С. Этот последний треугольник разрешается как угодно
двигать в пространстве. Спрашивается, можно ли придать этому
треугольнику некоторое положе-
положение в пространстве и затем спроек-
спроектировать на плоскость а по неко-
некоторому надлежаще выбранному
направлению так, чтобы проек-
проекцией оказался треугольник, по-
подобный ABC? Если это можно, то
затем подобным преобразованием
полученной проекции можно полу-
получить треугольник, конгруэнтный
ABC, т. е. можно считать, что
треугольник ABC служит мзобра-
жением треугольника А'В'С.
Теорема 1 дает утвердительный ответ на поставленный вопрос.
Доказательство. Построим в плоскости а треугольник А1В^С1,
удовлетворяющий двум условиям:
1) треугольник A1BlCi подобен треугольнику ABC,
2) А^^А'В'.
Затем расположим треугольник А'В'С так, чтобы сторона А'В
совместилась со стороной АгВх, а плоскость треугольника А'В'С
образовала с плоскостью а какой-нибудь угол (рис. 11). Соединим
точки С и С, прямой, и эту прямую примем за проектирующую.
Теперь проекцией треугольника А'В'С служит треугольник АХВХСХ,
подобный ABC. Теорема доказана.
Из приведенного доказательства видно, что задание треугольни-
треугольника-оригинала А'В'С и треугольника-изображения ABL не определяет
полностью проектирующего аппарата. Угол между плоскостями А'В'С
и а остается произвольным, а следовательно, и угол наклона о про-
проектирующей прямой С'С1 к плоскости а не определен. Кроме того,
можно было уравнивать не стороны AtBt и А'В', а #,6, и В'С
или СХАЛ и С А'. Однако, несмотря на неопределенность проектиру-
проектирующего аппарата, положение всех точек изображения вполне опреде-
определенно. Это устанавливается следующей теоремой.
16 Энциклопедия, ки. 4
рис

242 МЬГОДЫ ИЗОБРАЖЕНИЙ
Теорема 2. Если для трех неколлинеарных1) точек А', В',С
плоской фигуры известны их изображения А, В, С, то изображе-
изображения всех точек этой фигуры вполне определены.
Эту теорему можно высказать и так. Пусть А',В',С',М'—четыре
точки оригинала (плоской фигуры). Может ли быть, что при одном
способе эти точки имеют изображения А, В, С, М, а при другом —
А, В, С, М,, где уИ, не совпадает с Ml Теорема 2 отвечает на
этот вопрос отрицательно.
Идея доказательства такова. Четыре точки А', В', С', М'
определяют четырехугольник. Его диагонали точкой пересечения
делятся в определенных отношениях. Эти отношения для четырех-
четырехугольника АВСМ должны быть теми же самыми, откуда следует, что
задание точек А, В, С однозначно определяет точку М.
м
Теперь мы реализуем эту идею подробно.
Доказательство. Соединим точку М' с какой-нибудь из
точек А', В', С, например с А'. Прямая А'М' пересечет сторону
В'С (или ее продолжение) в точке X' (рис. 12, а). Изображение
точки X' однозначно определяется: оно должно лежать на прямой
ВС и делить отрезок ВС в том же отношении, в каком точка А"
1елнт отрезок В' С', т. е.
ВХ _ В'Х'
ХС ~~ Х'С
Построив точку X, мы можем провести прямую АХ (рис. 12, б).
Точка М должна лежать на этой прямой; ее положение определяется
пропорцией
AM _A'M'
~АХ~ А'Х' ¦
(рис. 12, в).
Не лежащих на одной прямой.

ПАРАЛЛЕЛЬНЫЕ ПРОЕКЦИИ
243
Заметим, что если прямая А' М' окажется параллельной В'С',
то прямая AM также должна быть параллельной ВС, и положение
точки М определится из пропорции
AM
Ж
А'М'
~ВГСГ
Изложенный способ нахождения точки М есть не что иное, как
нахождение точки по ее аффинным координатам. Сейчас мы
разовьем эту аналогию подробно.
Как известно, треугольник с упорядоченными вершинами определяет
аффинную систему координат. Иначе говоря, тройка неколли-
неарных точек есть минимальная система точек, обладающая следующим
свойством: всякое аффинное преобразование плоскости, оставля-
оставляющее эти точки на своих ме-
местах, представляет собой то-
тождественное преобрчзгтчпе,
т. е. ohj оспппгяет ни своих
Рис 13.
Рис. 14.
местах все точки плоскости. Это и значит, что всякая точка пло-
плоскости может быть аффинно связана с данной тройкой точек,
т. е. положения разных точек относительно данной тройки аффинно
различимы.
Аффинную систему координат изображают различными способами,
и читатель может не дога ла гься, что во всех случаях мы имеем
треугольник с упорядоченными вершинами, так как его задание
может быть замаскировано другими обэзначениямп или объясняться
с другой точки зрения. На рис. 13 мы видим привычное изображение
аффинной системы координат: оси ОХ и OY, на которых отмечены
единицы масштаба О?", и ОЕг. Эта система вполне определяется
заданием упорядоченной тройки точек О, ?,, Ег. Таким образом,
треугольник ABC может бить превращен в систему рис. 13, если
условиться, что А—начало координат, АВ{в направлении от А к В) —
ось А', АС (в направлении от Л к С) — ось К, отрезки АВ и АС —
единицы масштаба.
Иногда аффинную систему координа г задают двумя неколлииеарными
некторами е1 и е2, выходящими и^ очной точки (рис. 14). Эта фигура
назыкается аффинным репером; в ней ми узнаем греуго 1ышк,
[в*

244 МЕТОДЫ ИЗОБРАЖЕНИЙ
в котором «не проведена» третья сторона. Наконец, весьма удобно
дополнить рис. 13 или 14 до аффинной сетки. Для этого
единицы масштаба по каждой оси повторяются неограниченное число
раз и через их концы проводятся прямые, параллельные осям (рис. 15).
Ясно, что эта сетка из равных параллелограммов вполне определяется
заданием трех точек О, Ev Et.
Теперь вернемся снова к теореме 2 и взглянем на нее с несколько
иной точки зрения. Исходя из треугольника А'В'С (рис. 12, а),
построим аффинную сетку. Точно так же построим аффинную сетку,
исходя из треугольника ABC. Точка М должна занимать на второй
сетке таксе же1) поло-
положение, как точка М' на
первой сетке. Этот способ
особенно удобен, когда
приходится с троить изо-
изображения фигур непра-
неправильной формы.
Все сказанное может
быть выражено так:
Пусть изображения-
. ми трех неколлинеарных
/ точек А', В', С плоской
фигуры служат три
неколлинеарные точки
А, В, С. В таком случае
Рнс. 15. изображением любой
точки М' этой фигуры
служит точка М, которая имеет относительно репера (АВ, АС)
те же самые координаты, какие имеет точка М' относительно
репера (А'В'. А'С).
2.5. Примеры. Рассмотрим теперь примеры на построение изоб-
изображений плоских фигур. Изложенные выше положения (например,
иостроение, показанное на рис. 12) исчерпывают этот вопрос. Однако
иногда бывает удобно вместо применения этих общих способов ис-
исходить из индивидуадьных свойств изображаемых фигур. При этом
всегда следует руководствоваться двумя положениями:
1. Можно выбрать три точки, принадлежащие оригиналу, и изоб-
изобразить их произвольно, т. е. любыми тремя точками. После этого
ничего нельзя изображать произвольно: изображения всех остальных
точек оригинала должны строиться.
2. Надо рассматривать оригинал и искать в нем свойства, инвариант-
инвариантные относительно параллельного проектирования; эти свойства можно
переносить на изображение^
') Предоставляем читателю уточнить смысл этого термина.

ПАРАЛЛЕЛЬНЫЕ ПРОЕКЦИИ
245
Например, если мы обнаруживаем в составе оригинала две
параллельные прямые, то, строя изображения, мы тоже начертим
две параллельные прямые. Если же мы обнаружим в составе ориги-
оригинала две перпендикулярные прямые, то это свойство перенести на
изображение, вообще говэря, нельзя.
Начнем рассмотрение плоских фигур с многоугольников.
Треугольник. Любой треугольник может быть изображен как
угодно. Например, если сказано «изобразить правильный треугольник
со стороною 1 сму>, то можно начертить любой треугольник и
считать его изображением
правильного треугольника
со стороною 1 см.
Пример. Изобра-
Изобразить прямоугольный тре-
треугольник с катетами а
и 2а, в котором из вер-
вершины прямого угла про-
проведены медиана и вы- А
coma.
На рис. 16, а пока-
показан оригинал без иска- Рис 16.
жения. Начертим произ-
произвольный треугольник ABC (рис. 16, б) и будем считать его изоб-
изображением треугольника А'В'С'. Медиана треугольника изображается
медианой, потому что если D'—середина стороны А'В', то и D —
середина стороны АВ. Для изображения высоты сначала проведем
в оригинале «настоящую» высоту А'Е' и определим, в каком отно-
отношении точка Е' делит гипотенузу А'В'. Известно, что отрезки
гипотенузы (на которые она делится высотой) относятся как квадраты
А'Е' 1
катетов, т. е. „,„,—-;-. Следовательно, надо найти на АВ точку ?,
АЕ 1
для которой -рЩ — -т, и тогда СЕ есть изображение высоты.
Важно заметить, что для построения изображения высоты вовсе
не обязательно, чтобы размеры оригинала были заданы аналитически.
Оригинал может быть задан графически. В таком случае мы проводим
в оригинале высоту СЕ', а затем строим точку Е, удовлетворяющую
условию
АЕ^А'Е"
ЕВ ~~ Е'В''
Аналогичные соображения применимы не только к высотам, но также
и к биссектрисам.
Четырехугольник. Из рассуждения, иллюстрированного
рис. 12, ясно, что, изображая четырехугольник A'B'C'D', можно
три точки А, В, С выбрать произвольно, а четвертая точка D должна

246
МЕТОДЫ ИЗОБРАЖЕНИЙ
Рис. 17
быть построена так, чтобы диагонали четырехугольника ABCD делились
точкой пересечения в тех же отношениях, как и в четырехугольник
А'В'С'D'. Верно и обратное. Таким образом, изображением четырех-
четырехугольника может служить любой четырехугольник, у которого
диагонали делятся точ-
точкой пересечения в тех
же отношениях. Напри-
Например, изображением любого
параллелограмма может
служить любой параллело-
параллелограмм.
Пример. Постро-
Построить изображение пра-
правильного шестиугольни-
шестиугольника. На рис. 17, а показан правнльный шестиугольник в натуральном
виде (без искажения). Возьмем произвольный треугольник ABC
(рис. 17, б). Диагональ В'Е' делит диагональ А'С в точке X' пополам.
Поэтому точка X должна быть серединой АС. Проводим прямую ВХ.
Тогда AF\\BX и CD\\BX. Очевидно, В'Е' = Ь-В'Х'; поэтому строим
ВЕ=Ь-ВХ. Далее либо проводим ED\\AB, либо строим CD=2-BX.
Аналогично строим точку Е.
Окружность. Изображением окружности служит эллипс1).
Если эллипс уже был определен каким-нибудь способом, то надо
докага гь, что изображение окруж-
окружности— эллипс. Но можно принять
это свойство за определение: образ
окружности называется эллипсом.
Исходя из этого определении, легко
получить свойства эллипса. Мы в
дальнейшем будем предполагать
свойства эллипса известными.
Рассмотрим в окружности два
взаимно перпендикулярных диаметра
А 'В' и CD' (рис. 18). То свойство
этих диаметров, что они взаимно
перпендикулярны, не инвариантно,
но вот другое их свойство, которое
инвариантно: каждый из них де-
делит пополам хорды, параллельные
другому. Это свойство называется сопряженностью. Мы при-
приходим к следующему выводу:
1) Взаимно перпендикулярные диаметры окружности изоб-
изображаются сопряженными диаметрами эллипса.
') Подробная статья с изложением свойств линий второго поряоиа
(вллипса, гиперболы, параболы) будет помещена в кн. V ЭЭМ.

ПАРАЛЛЕЛЬНАЯ АКСОНОМЕТРИИ
247
Ввиду того, чго метод получения этих свойств однообразен
(на изображение переносятся свойства оригинала, инвариантные от-
относительно параллельного проектирования), сформулируем еще некото-
некоторые свойства, не повторяя выз.ща.
2) Центр окружности изображается центром эллипса.
3) Касательная к окружности в точке А' изображается
касательной к эллипсу в точке А. Эта касательная {изображе-
{изображение) параллельна тому диаметру эллипса, который сопряжен с
диаметром, проходящим через точку касания.
Рис. 19.
4) Квадрат, описанный около окружности, изображается
параллелограммом, описанным около эллипса, причем стороны
этого параллелограмма имеют сопряженные направления; средние
линии этого параллелограмма — сопряженные диаметры эллипса.
Пример. Рассмотрим задачу: изобразить окружность со
вписанным в нее правильным треугольником.
На рис. 19, а показан оригинал.О 1евидно, С'О'_\_А'В', О'Е' = E'D'.
Изобразим окружность прэизвольным эллипсом (рис. 19,6); О —
центр этого эллипса. Примем за С произвольную точку эллипса. Про-
Проведем диаметр CD; пусть Е—середина 0D. Проведем через Е прямую,
направление которой сопряжено CD (для этого надо провести какую-
нибудь хорду, параллельную CD, разделить ее пополам и получен-
полученную середину соединить с О; соединяющая прямая имеет направление,
сопряженное с CD). Точки пересечения этой прямой с эллипсом
суть А и В.
§ 3. Параллельная аксонометрия
3.1. Теорема Польке — Шварца. Изображение пространственных
фигур по методу параллельной проекции на одну плоскость во мно-
многом аналогично изображению плоских фигур.

248
МЕТОДЫ ИЗОБРАЖЕНИЙ
Прежде всего возникает вопрос, может ли пространственный
аффинный репер быть изображен произвольно? Другими словами
имеют ли место теоремы (об изображении пространственных тел),
аналогичные теоремам 1 и 2?
Пространственный аффинный репер это — упорядоченная тройка
векторов (некомпланарных, т. е. не лежащих в одной плоскости),
выходящих из одной точки (рис. 20; сравнить с рис. 14).
Ясно, что задание этого репера равносильно заданию аффинной
системы координат (рис. 21; сравнить с рис. 13), т. е. упорядоченной
тройки осей О'Х', О'У и O'Z', на которых отмечены единицы мас-
масштаба О'Е[, О'Ег и О'Е\.
Рис. 20 или 21 можно дополнить до пространственной аффинной
сетки (рис. 22; сравнить с рис. 15).
Рис. 20.
Рис. Ч\.
Наконец, ясно, что в составе любой из фигур рис. 20, 21 и 22
имеется тетраэдр с упорядоченными вершинами (например, тетраэдр
О'ЕхЕгЕг на рис. 21), который определяет всю фигуру. Таким образом,
тетраэдр A'B'C'D' (рис. 23; сравнить с рис. 12, а) может быть пре-
превращен в систему рис.21, если условиться, что А'— начало коорди-
координат, А'В' (в направлении от А' к В')—ось X' и т. д.
Читатель должен видеть, что рис. 20, 21, 22 и 23 представляют
разные способы задания аффинной системы координат. Например,
аффинный репер рис. 20 можно мыслить как тетраэдр, в котором
«проведены» только ребра, выходящие из одной вершины.
При изображении пространственных фигур, так же как и при
изображении плоских фигур, основной вопрос—это вопрос о том,
как изобразить аффинный репер. Если мы сумеем изобразить его, го
сумеем изобразить и любые фигуры, потому что всякая точка
сверх четырех основных может быть инвариантно связана с этим
репером (она занимает определенное положение в сетке парал-
параллелепипедов, показанной на рис. 22).

ПАРАЛЛЕЛЬНАЯ АКСОНОМЕТРИЯ
249
Аффинный репер, показанный на рис. 20, изображается на плос-
плоскости тремя отрезками, выходящими из одной точки. Поэтому упо-
упомянутый вопрос формулируется так: могут ли произвольные1) три
Рнс. 22.
отрезка на плоскости, выходящие из одной точки, служить изобра-
изображением трех наперед заданных отрезков в пространстве, выходящих,
из одной точки в пространстве?
Если дополнить фигуру рис. 20 до TeTpiSApa, то изображение-
примет вид четырехугольника с диагоналями. Иначе эта фигура
называется полным четырехвершинником
или полным четырехугольником: четыре
точки плоскости общего положения и все шесть
определяемых ими прямых. На рис. 24, а показан
выпуклый, а на рис. 24, б — невыпуклый, четы-
четырехугольник ABCD с диагоналями АС и BD.
Поставленный выше вопрос относительно трех
отрезков можно сформулировать и так: может ли
произвольный полный четырехугольник служить
изображением наперед заданного тетраэдра?
Ответ на поставленный вопрос утвердительный,
следующая теорема, аналогичная теореме 1.
Теорема 3 (теорема Польке — Шварца). Любой полный
четырехугольник ABCD может служить изображением любого
тетраэдра A'B'C'D'.
Интересующая нас теорема впервые была высказана в 1853 г.
немецким геометром Карлом Польке в следующей форме: «три
Рис. 23.
Имеет место
') Т. е. произвольных длин и образующие между собою произвольные-
углы.

250
МЕТОДЫ ИЗОБРАЖЕНИЙ
Рис. 24.
отрезка а х , а у , л z' произвольной длины, лежащие в одной плос-
плоскости, выходящие из одной точки а под произвольными углами друг
к другу, представляют параллельную проекцию трех равных отрезков
ах, ay, az, отложенных на прямоугольных осях координат от начала».
Доказательство Польке было чрезвычайно сложным и неэлементарным.
Оно не было опубликовано, но содержание его до нас дошло
В 1864 г. один из известных математиков того времени Герман
Лмандус I1J в а р ц (ученик Польке1* обнаружил, что перпендикулярность
и равенство отрезков
О'А'. О'В' и О'С несу-
несущественны, т. е. теорему
Польке можно обобщить
следующим образом: если
О'А', О'В' и О'С—три
произвольных отрезка в
пространстве '), выхо-
С дящих из одной точки,
а ОА, ОВ и ОС—три
б) произвольных отрезка на
плоскости, выходящих
из одной точки, то фи-
фигуру (ОА, ОВу ОС) мож-
можно рассматривать как параллельную проекцию фигуры, подобной
{О'А', О'В', О'С). Это значит, что можно фигуру (О'А', О'В', О'С)
1) подобно изменить с надлежащим коэффициентом подобия,
2) надлежащим образом переместить в пространстве,
3) надлежащим образом выбрать направление проектирования,
и тогда проекцией окажется заданная фигура (ОА, ОБ, ОС).
Вместо подобного изменения оригинала можно было бы произво-
производить подобное изменение проекции.
Мы не будем исследовать вопрос о том. определяются ли все
перечисленные шаги однозначно. Скажем только, что первый шаг —
да. а второй и третий — нет.
Только что приведенную теорему можно сформулировать и гак:
Любой полный четырехугольник можно рассматривать как
параллельную проекцию тетраэдра, подобного наперед заданному.
Или
Любой тетраэдр можно параллельно спроектировать на плос-
плоскость так, что получится полный четырехугольник, подобный
наперед заданному.
Эта теорема (в любой из трех приведенных формулировок) назы-
называется теоремой Польке — Шварца. Шварц не только обобщил теорему
') Т е. отрезки любых длин, обгазующие между собой любые углы,
однако не лежащие в одной плоскости.

ПАРАЛЛЕЛЬНАЯ АКСОНОМЕТРИЯ 251
Польке, но и дал простое и элементарное доказательство. Мы не
будем приводить доказательство этой теоремы, потому что оно ши-
широко распространено в учебной литературе по начертательной геомет-
геометрии. Доказа [ельство теоремы Польке — Шварца можно найги, например,
в указанных в конце статьи книгах [1, 2]').
В приведенных формулировках теоремы Польке — Шварца упоми-
упоминается подобие. Это объясняется тем, что непосредственным про-
проектированием данного тетраэдра получить в точности данный пол-
полный четырехугольник, вообще говоря, нельзя: например, из больныги
тетраэдра нельзя получить
маленький четырехугольник.
Однако в той формулировке
теоремы Польке—Шварца, ко-
которую мы выбрали за основную
(теооема 3) подобие не упоми-
упоминается. Эго объясняется тем,
что изучаемый нами метод изо-
изображения включает параллель-
параллельное проектирование и кроме
того подобное преобразование.
Приведем несколько поло-
положений, которыми мы будем рис. 25.
пользоваться при построении
изображений и которые суть разные аспекты теоремы Польке —
Шварца.
1) Изображая любую аффинную систему координат, можно
начертить изображения осей под любыми углами и на каждом
изображении оси принять произвольный отрегок za изображение
масштабной единицы (рис. 25). Напомним, что в аффинной системе
координат масштабы на разных осях могут быть разные.
В частности, рис. 25 может рассматриваться как изображение
декартовой прямоугольной системы координат. Аффинная система
координат называется декартовой прямоугольной, если ее
оси взаимно перпендикулярны и
2) Рис. 9 может рассматриваться как изображение любого
пауаглелепипеда, в частности — как изображение куба с данным
ребром.
3) Рис. 24 может рассматриваться как изображение любого
тетраэдра.
') С историей этой теоремы можно ознакомиться по статье Н. М. Бес-
к и н а, Основное предложение аксонометрии, сб «Вопросы современной
начертательной геометрии», под ред. Н. Ф. Чет1.ерухина, М.—Л., Гостех-
нздат, 1947, стр. 55—126.

252 МЕТОДЫ ИЗОБРАЖЕНИЙ
3.2. Полные и неполные изображения. Изображая любую про-
пространственную фигуру, надо выбрать в составе этой фигуры четыре
точки общего положения (т. е. четыре точки, не лежащие в одной
плоскости) и их изобразить произвольно. Остальные точки этой
фигуры уже не могут изображаться произвольно. Перейдем к воп-
вопросу, как они должны изображаться.
Для изображения плоских фигур аналогичный вопрос решался
теоремой 2 (см. рис 12). При изображении пространственных фигур
дело обстоит иначе, и мы прежде всего выясним, в чем заключается
различие.
Пусть оригинал—плоская фигура. А', В', С — три точки этой
фигуры, а А, В, С—их изображения. Пусть М'—четвертая точка
оригинала. Тогда прямая А'М' пересекает прямую В'С в некоторой
точке X'', и изображение этой точки может быть построено (рис. 12).
Пусть теперь оригинал — пространственная фигура, А', В', С.
D'—четыре точки этой фигуры, а А, В, С, D — их изображения.
Пусть М'—пятая точка оригинала. Тогда прямая А'М', вообще
говоря, не пересекает прямых В'С, CD' и D'B' (в этом различие!),
а пересекает лишь плоскость B'C'D' в некоторой точке X'. Однако
изображение X этой точки не может быть построено, если известны
только точки А, В, С, D.
Более полно, пусть мы имеем некоторый оригинал, т. е. сово-
совокупность точек, прямых, плоскостей, отрезков, треугольников и. т. д.
По всем этим элементам, входящим в оригинал, мы можем одно-
однозначно определить еще некоторые другие элементы, жестко связанные
с оригиналом. Например, имея в оригинале две точки, мы можем
провести соединяющую их прямую, имея три точки, можем опреде-
определить проходящую через них плоскость, имея прямую и плоскость,
можем найти их точку пересечения и т. д. Найдя новые точки,
жестко связанные с оригиналом, мы можем проводить прямые
и плоскости и через них, далее мы можем найти линию пересечения,
скажем, плоскости, входящей в состав оригинала, и уже найденной
плоскости, жестко связанной с ним, и т. п. В;е получающиеся таким
путем новые элементы (прямые, точки и др.) мы будем называть
элементами, связанными с оригиналом. Все они однозначно опреде-
определяются заданием оригинала.
Возникает естественный вопрос, можно ли все эти элементы,
связанные с оригиналом, найти на изображении, точнее говоря, можно
ли однозначно построить изображение элементов, связанных с ори-
оригиналом, имея лишь рисунок (т. е. изображение) самого оригинала?
При этом, конечно, речь будет идти об изображении точек, прямых
и их комбинаций, так как плоскости могут быть заданы на
рисунке лишь находящимися в них точками и прямыми.
Мы сталкиваемся здесь со следующим фактом, имеющим важные
последствия для теории изображений. При изображении плоских

ПАРАЛЛЕЛЬНАЯ АКСОНОМЕТРИЯ 253
фигур всякий элемент (прямая, точка или их комбинация),
связанный с оригиналом, определен однозначно и на изображении
(на рисунке), а для изображения пространственных фигур это,
вообще говоря, не так (ср. рис. 13 и относящийся к нему текст).
Поясним сказанное примерами. Пусть в составе плоской фигуры
имеются две прямые а' и Ь'', а на рисунке — их изображения а и Ь.
Прямые а' и b', если они пересекаются, определяют точку пересе-
пересечения. Их изображения а и Ь, если они пересекаются, тоже опреде-
определяют точку пересечения. Другими словами, если мы уже изобразили
прямые а' и b' прямыми а и Ь, то мы не
можем точку пересечения прямых а' и Ь'
изобразить произвольно; ее изображением
должна служить вполне определенная точка,
а именно точка пересечения прямых а и Ь.
Следующий пример покажет, что для
пространственных фигур дело обстоит иначе.
На рис. 26 легко узнать изображение фигуры,
о которой шла речь на стр. 252: тетраэдр
A'B'C'D' и пятая точка М'\ проведены так-
также отрезки В'М', CM', D'М'. Прямая А'М'
(изображение которой не показано) пересе-
пересекает плоскость B'C'D' в некоторой точке X'.
В оригинале эта точка вполне определена, а ее изображение X на
рисунке не определено. Более того, точку X можно выбрать на пря-
прямой AM произвольно.
Вот еще пример. На рис 27 дано изображение системы координат и,
кроме того, некоторой точки М'. Если через точку М провести пря-
прямую, параллельную оси Z', то она изобразится прямой, параллельной
оси Z. В оригинале эта прямая пересечет плоскость O'X'Y' во вполне
определенной точке, а на рисунке мы не можем построить изо-
изображение этой точки; это изображение может быть отмечено про-
произвольно.
Отмеченное свойство называется неполнотой рисунка (изобра-
(изображения). Изображение называется полным, если всякий элемент
(прямая, точка, их комбинация), связанный с оригиналом, опре-
определен оснозначно и на изображении. Таким образом, рис. 26 и 27
неполные. Мы в дальнейшем будем рассматривать только полные
изображения ').
Изображение четырех (или меньшего числа) точек общего поло-
положения всегда полное. Пусть теперь оригинал содержит более
') Относительно неполных изображений см книгу Н. Ф. Четверу-
х и н а «Изображения пространственных фигур в курсе геометрии», ука-
указанную в конце статьи, и его же статью «Полные и неполные изображе-
изображения» в сборнике, указанном в сноске на стр. 251.

'254
МЕТОДЫ ИЗОБРАЖЕНИЙ
Рис. 27.
четырех точек общего положения и пусть А, В, С, D—изображения
четырех точек А', В', С', D' оригинала, принятых за базис. Для
полноты изображения необходимо и достаточно, чтобы для всех
остальных элементов имеющихся на рисунке, была показана их
жесткая аффинная связь с базисом.
Именно точки А', В', С", D' (изобра-
(изображения А, В, С, D которых заданы), соеди-
соединяющие их прямые А'В', В'D' и т. д.,
а также плоскости А'В'С, A'C'D' и т. д.
у считаются заданными (т.е. имеющими
¦жесткую аффинную связь с базисом). Еслн<
уже известно некоторое количество за-
заданных (т.е. жестко аффинно связанных,
с базисом) точек, прямых и плоскостей,,
то новые точки, прямые и плоскости счита-
считаются жестко аффинно связанными с базисом<
(т. е. заданными) в следующих случаях
Точка считается заданной, если дано ее изображение и указана
проходящая через нее заданная плоскость (или прямая). Точка также
считается заданной, если она указана как точка пересечения двух
заданных прямых или прямой и плоскости, или трех заданных
плоскостей.
Прямая считается заданной, если дано ее изображение и указана
проходящая через нее заданная плоскость. Прямая также счи-
считается заданной, если заданы: две ее точки или одна ее точка и парил
лельная ей прямая, пли
две проходящие через нее
плоскости и т. д.
Наконец. плоскость
считается заданной, если
указаны три лежащие в
ней заданные точки или
лежащие в ней заданные
точка и прямая, или ле-
лежащая в ней заданная
точка и параллельная ей
заданная плоскость и т. д.
Разберем несколько
примеров.
На рис. 28 ABCD — изображение базиса. Прямая Х'У задана,
потому что на рисунке показаны изображения ее следов на плоскостях
D'B'C' и D'C'A' (точки X и К). Точка М' задана, потому что-
дано ее изображение и она лежит на заданной прямой.
Рис. 28 полный. Например, в оригинале существует точка Z'
пересечения прямой X'Y' с плоскостью А'В'С. Изображение этой
Рис. 28.

ПАРАЛЛЕЛЬНАЯ АКСОНОМЕТРИЯ
255
точки тоже однозначно определено. Построение этого изображения Z
показано на рисунке.
На рис. 29 точка М' аффинно привязана к базисному тетраэдру
более простым способом.
На рис. 30 изображена система осей О'Х'. О'У. О'7.'. Единицы
масштаба не изображены, т. е. на этом рисунке нет изображения
базисного тетраэдра. Через точку М' проведены прямые, параллель-
параллельные осям О'Х', O'Y' и О'/"; точки пересечения этих прямых
с плоскостями Z'Y', Z'X' и X'Y' обозначим соответственно чере.<
М\, М'г и М'г. Их изображения Мх, Мг и Мг, т. е. изображении
оснований точки М', в этом случае (т. е. применительно именно
к рис. 30) называются вторичными проекциями точки М'.
М
А В 'X
Рис. 29. Рнс. 30.
Такое название объясняется тем, что в самом оригинале происходит
проектирование точки М' на плоскости V"z', Z'X' и X'Y'. а затем
полученные проекции /Wj, M' и Мз вместе со всем оригиналом
проектируются на плоскость изображения.
Для того чтобы изображение было полным, достаточно задать
кроме М еще одну вторичную проекцию. Остальные две легко
строятся.
Из того, что на рис. 30 нет изображения аффинного базиса, вы-
вытекает некоторый дефект этого рисунка: он не определяет оригинал
метрически (см. 3.7).
3.3. Понятие о параллельной аксонометрии. Назначение всякого
изображения—дать представление об оригинале. В лучшем случае
изображение представляет оригинал исчерпывающим образом, т. е.
имея изображение, можно ответить на любой (геометрический)
вопрос, относящийся к оригиналу. Это значит, что оригинал
определяется метрически, т. е. с точностью до движения в про-
пространстве. Бывают изображения, которые определяют оршинал

256 МЕТОДЫ ИЗОБРАЖЕНИЙ
с меньшей точностью, т. е. позволяют ответить на некоторые,
но не на все геометрические вопросы, относящиеся к оригиналу.
Сейчас мы ответим на вопрос, в какой мере разные методы изо-
изображения позволяют судить об оригинале.
Полное изображение позволяет восстановить оригинал
с точностью до аффинного преобразования, потому что оно позволяет
построить все элементы, аффинно связанные с оригиналом. Другими
словами, полное изображение позволяет ответить на любой относя-
относящийся к оригиналу вопрос, имеющий аффинный характер. Например,
имея на полном чертеже изображение трех точек, лежащих на одной
прямой, мы можем ответить, каково (в оригинале) отношение этих
точек, но мы не можем ответить на вопрос, является ли треугольник,
изображенный на некотором рисунке, правильным (если только нам не
известны еще какие-нибудь свойства изображения, кроме полноты).
Неполные изображения не позволяют судить об оригинале даже
с точностью до аффинного преобразования.
Какие нужны условия, чтобы изображение определяло оригинал
более точно? На рис. 24 показано изображение тетраэдра. Согласно
теореме Польке—Шварца этот рисунок может быть изображением
любого тетраэдра. Значит, имея рис. 24, мы ничего не можем ска-
сказать о тетраэдре-оригинале. С другой стороны, любой тетраэдр
A'B'C'D' может быть переведен в любой другой тетраэдр /4J5JCDJ
аффинным преобразованием. Следовательно, рис. 24 определяет ори-
оригинал лишь с точностью до аффинного преобразования.
Рассмотрим теперь рис. 29. На нем, кроме базисного тетраэдра,
изображена точка М' по правилам, установленным для полного
изображения. Изображение базисного тетраэдра может относиться
к любому тетраэдру, например к A'B'C'D' или к A\B\C\D\. Какой
бы из этих двух тетраэдров мы ни выбрали, в пространстве одно-
однозначно определится некоторая точка, аффинно связанная с этим
тетраэдром так, как это показано на рисунке. В первом случае это будет
точка М', а во втором /Wj. Аффинное преобразование, переводящее
тетраэдр A'B'C'D' в тетраэдр /4jfi]C7/, переводит точку М' в М'г
т. е. система точек A'B'C'D'M' получается из системы A'jB'tC\D'iMt
афинным преобразованием. Это рассуждение может быть проведено
для любого элемента,имеющего жесткую аффинную связь с базисом.
Поэтому справедлива следующая георема (аналогичная теореме 2).
Теорема 4. Если изображение полное и содержит изобра-
изображение базисного тетраэдра, то оно определяет оригинал с точ-
точностью до аффинного преобразования, т. е. позволяет ответить
на всякий evnpoc, касающийся аффинных свойств оригинала.
Как же придать рисунку полную определенность, т. е. сделать
его метрически определенным? В рамках метода «Параллельные

ПАРАЛЛЕЛЬНАЯ АКСОНОМЕТРИЯ 257
проекции на одну плоскость» для этого применяется особая разно-
разновидность этого метода, называющаяся параллельной аксоно-
аксонометрией; для краткости мы пока будем называть ее просто
аксонометрией.
Аксонометрия заключается в том, что к полному изображению,
содержащему изображение базисного тетраэдра, добавляется сло-
словесное примечание, указывающее метрические параметры этого
тетраэдра, т. е. указывается, как принято говорить в начертательной
геометрии, реконструкция этого тетраэдра.
Мы уже говорили что изображение тетраэдра может считаться
изображением любого тетраэдра. Воспользовавшись этой неопреде-
неопределенностью, выберем какой-нибудь тетраэдр и объявим, что имею-
имеющееся на рисунке изображение базисного тетраэдра есть изображе-
изображение именно этого тетраэдра.
Возьмем какой-нибудь, тетраэдр A'B'C'D' указанных размеров.
Всякое аффинное преобразование, оставляющее точки А', В', С", D'
на месте, есть тождественное преобразование, т. е. оно оставляет
на месте все точки пространства. Значит, вместе с точками А', В',
С', D' займут фиксированные положения все лишние элементы ори-
оригинала, т. е. оригинал метрически определен.
Например, рис. 29, дополненный следующей реконструкцией ба-
базисного тетраэдра:
/_ ВАС= 50°, АВ= 52 см,
/_ CAD = 60°, /4С= 40 см,
/_ DAB =90°, AD =58 см,
становится метрически определенным. Он определяет оригинал пол-
полностью, т. е. позволяет ответить на любые вопросы, касающиеся
оригинала, например, каков угол прямой А'М' с плоскостью В'С'D'.
Итак, аксонометрия есть метод изображения, характеризую-
характеризующийся следующими четырьмя признаками:
1) изображение строится по методу параллельной ') проекции
на осну плоскость,
2) оно полное,
3) оно содержит изображение базисного тетраэдра,
4) к изображению дополнительно прилагается реконструкция
базисного тетраэдра.
Аксонометрическое изображение есть изображение метрически
определенное, т. е. оно определяет оригинал полностью.
В учебниках начертательной геометрии аксонометрия рассматри-
рассматривается с несколько иной точки зрения. Оригинал связывается с не-
') Мы пока говорим о параллельной аксонометрии. Суще-
Существует еще центральная аксонометрия, о которой говорится
ниже (стр. 282).
17 Энциклопедия, кн. 4

258
МЕТОПЫ ИЗОБРАЖЕНИЙ
которой системой координа! и затем вместе с этой системой коорди-
координат проектируется на плоскость изображения. При этом на изоб-
изображении должна быть показана аффинная связь всех элементов
оригинала с системой координат. Само слово «аксонометрия» значит
«измерение по осям» (от греческих
слов agcov — ось, jieTQsco — измеряю).
Изображение иа рис.31—аксономе-
рис.31—аксонометрическое, если, например, дано,
что система координат прямоуголь-
прямоугольная, единицы масштаба по всем
осям одинаковые и каждая из них
равна 1 см. Легко узнать длину
отрезка А'В'. Это ясно из того, что
по рисунку можно измерить коорди-
координаты точек А' и В'
Рис 31.
А'B, 2, 2),
fi'D, 5, 4).
Ясно, что такое понимание аксонометрии вполне совпадает с дан-
данным выше определением, потому что задание изображения системы
координат равносильно заданию изображе-
изображения базисного тетраэдра.
Координатная система на аксонометри-
аксонометрических рисунках часто задается не при
помощи осей OX, OY и OZ, а при помощи
изображения разных предметов (большей
частью — куба), размеры которых известны.
Если, например, известно, что нижнее тело,
изображенное на рис. 32, есть куб с ребром 1 м,
то можно утверждать, что на нем стоит
правильная шестиугольная призма (обратить
внимание, в каких отношениях вершины
шестиугольника делят стороны квадрата!) вы-
высота которой равна 50 см, и боковые грани
которой — квадраты.
3.4. Условные изображения. Изображе-
Изображения, для истолкования которых необходимы
некоторые дополнительно сообщаемые условия, называются услов-
условными изображениями1). К ним, следовательно, принадлежат
и аксонометрические изображения.
Рис. 32.
') См. статью Н. Ф. Четверухина «Условные изображения и па-
параметрический метод их пос1роенпя» в сСорнике, указанном в сноске на
стр. 251.

ПАРАЛЛЕЛЬНАЯ АКСОНОМЕТРИЯ
259
Громадное большинство изображений, в том числе художественные
изображения, условные. Эта условность замаскирована тем обстоя-
обстоятельством, что дополнительные условия не формулируются явно,
как это имело место для рис. 31 и 32, а подразумеваются.
Возьмем какое-нибудь произведение живописи '). На нем бывают
изображены предметы, форма и размеры которых нам заранее
известны. Если на картине мы видим человека, то знаем без специ-
специальных примечаний, что его рост 160—180 см, а если видим телеграф-
телеграфные столбы и рельсы, то знаем, что столб перпендикулярен рельсу.
Эго и есть условия, которые не формулируются явно.
Бывают изображения, где одни предметы знакомы, а другие
нет. Незнакомые предметы познаются по связям со знакомыми,
подобно тому как на рис. 32 размеры
и форма шестиугольной призмы опреде-
определяются по ее связям с кубом, на кото-
котором она стоит. Например, изображая
какую-нибудь новую машину, около нее
изображают также людей; это дает нам
представление о размерах машины.
Если вообразить произведение жи-
живописи, на котором не было бы изо-
изображено ни одного знакомого пред-
предмета, то мы не смогли бы понять ни
формы, ни размеров оригиналов.
3.5. Примеры построения аксо-
аксонометрических изображений. Рассмот-
Рассмотрим несколько типичных примеров
построения аксонометрических изобра-
изображений.
Пример 1. Правильная четырех-
четырехугольная пирамида. В основании
пирамиды лежит квадрат. Его можно изобразить любым параллело-
параллелограммом ABCD (рис. 33). Изобразив этот квадрат, мы частично
использовали права, предоставляемые нам теоремой Польке — Шварца,
а именно мы произвольно изобразили два равных взаимно перпен-
перпендикулярных отрезка А'В' и A'D'. Тем самым метрика в плоскости
ABCD вполне определена, и в ней больше ничего нельзя изображать
произвольно. На основании теоремы Польке — Шварца мы можем произ-
произвольно изобразить еще один отрезок, некомпланарный с А'В' и A'D',
например мы можем произвольно изобразить высоту пирамиды (даже
предполагая, что длина высоты задана). Произвол заключается в том,
Рис. 33.
') Разумеется, речь идет о произведении, относящемся к реалистиче-
реалистической живописи, т. е о произведении, претендующем на сравнительно точ-
точное изображение действительных предметов.
17*

260 МЕТОДЫ ИЗОБРАЖЕНИЙ
что мы можем взять изображение высоты любой длины и под любым
углом к АВ. Однако мы не можем произвольно выбирать основание
высоты, потому что в плоскости основания вся метрика определи-
определилась. Основанием высоты должна служить точка пересечения диаго-
диагоналей основания. Нам остается только произвольно взять вершину S.
Мы изобразили высоту параллельно боковым краям страницы. Это
объясняется тем, что обычно высота рассматриваемой пирамиды верти-
вертикальна. Если мы поместим страницу 259-ю
прямо перед собой в вертикальном положении,
то отрезок 50 займет привычное положение.
Пример 2. Прямой круговой конус.
Основание конуса изобразится произвольным
эллипсом (рис. 34). Вершина 5 изображается
произвольно. Контурные образующие (т. е.
входящие в контур изображения; контур
изображения короче называется а б р и с о м)—
касательные к эллипсу, проведенные из точ-
точки S. Разумеется, они касаются эллипса не
в двух вершинах, как это бывает на плохих
рисунках. Осевое сечение получится, если
мы проведем любой диаметр эллипса, но
Рис- 34. отнюдь не соединением точек касания кон-
контурных образующих.
Пример 3. Шар. При параллельном проектировании шара
получается либо окружность, либо эллипс с неравными осями. Это
значит, что в ортогональной проекции абрис шара — окружность, а в
косоугольной — эллипс. Изображение шара в виде эллипса кажется
не наглядным (условия наглядности изображения будут ра1бираться
«а стр. 271—272), поэтому шар целесообразно всегда изображать в
ортогональной проекции.
Итак, сначала начертим окружность, представляющую абрис.
Затем начертим эллипс, изображающий сечение шара по какому-
либо большому кругу (рис. 35); для краткости речи назовем это
сечение экваториальным. Перпендикуляр к плоскости большо-
большого круга, восставленный в центре, пересекает сферу в двух
точках, называемых полюсами, сопряженными с этим большим
кругом. Для краткости будем называть их Северным и Южным по-
полюсами.
Распространенная ошибка — помещать полюсы на абрисе. При таком
изображении экватора, как на рис. 35, ясно, что глаз наблюдателя
находится выше плоскости экватора. Поэтому наблюдатель видит
Северный полюс ниже абриса, а Южный полюс находится на задней,
невидимой для наблюдателя части шара.
Только в том случае, если бы проектирующие прямые были
параллельны плоскости экватора, полюсы помещались бы на абрисе,

ПАРАЛЛЕЛЬНАЯ АКСОНОМЕТРИЯ
261
но в этом случае экватор изображался бы не эллипсом, а отрезком.
Чем шире эллипс, изображающий экватор, тем дальше от абриса
находятся полюсы.
На рис. 35 показано, как построить полюсы, если дано изобра-
изображение экватора; ЛВ — большая ось эллипса. Вообрдзим диаметр шара
А'В' и перпендикуляр к плоскости экватора N'S' {Л/' —Северный
Рис. 35.
полюс, S'— Южный). Вообразим две плоскости—фронтальную (парал-
(параллельную А'В') и профильную (перпендикулярную А'В'). На
рис. 35 слева показана проекция на фронтальную плоскость (вид
спереди), а справа показана проекция"на профильную плоскость(вил
сбоку).
Система «экваториальный круг и диаметр N'S'-» в проекции
на профильную плоскость дает два взаимно перпендикулярных
диаметра круга.
Теперь легко понять следующее построение.
Сносим на правый круг малую ось эллипса. Проводим в круге
соответствую.ций диаметр; этот диаметр —проекция экваториального
круга. Проводим перпендикулярный диаметр; это — проекция диа-
диаметра N'S'. Сносим его концы, как показано, на левый рисунок.
3.6. Общие методы построения аксонометрических изобра-
изображений. Выше мы рассмотрели некоторые отдельные примеры построе-
построения аксон шетрических изображений, а теперь перейдем к общим
методам.
Покажем два из них, наиболее простые по идее:
1) метод координатной сетки и
2) вычислительный.
Метод координатной сетки основан на том, что, имея изображе-
изображение координатной системы, можно построить изображение точки,
если известны ее координаты. Эти координаты без пересчета откла-
откладываются параллельно аксонометрическим осям, причем для каждой
оси употребляется своя аксонометрическая единица.

262
МЕТОДЫ ИЗОБРАЖЕНИЙ
Построим в ортогональной диметрии ') изображение прямой шести-
шестиугольной призмы, из которой вырезан прямой круговой цилиндр. Оси
этих тел совпадают. Сторона основания призмы равна е, радиус
основания цилиндра равен у, высота обоих 1ел равна 2е.
Пусть призма стоит на плоскости X'Y', ось ее расположена на
оси Z' и пара противоположных вершин основания лежит на оси X'.
Тогда вершины основания имеют координаты
A,0,0), (I, У±, о), (-1, ^-. о), (-1, 0,0),
Ч. -Ч- -)• D. - Ч-«)
(здесь положено е= 1).
На рис. 36 эти точки построены по аксонометрической коорди-
координатной сетке. Разумеется, по координатам построены только первые
две точки, а остальные — на основании симметрии. Вершины верхнего
основания должны быть подняты параллельно оси Z на 2е. После
этого получится рис. 37.
Рис. 36.
Рис. 37.
Заметим теперь, что для построения изображения методом коор-
координатной сетки вовсе нет необходимости знать координаты точек
оригинала. Можно копировать оригинал графически. На рис. 38, а
изображена окружность, ее диаметр разделен на десять частей.
На рис. 38, б взят координатный репер, соответствующий рис. 37
(для наглядности он увеличен в три раза); по осям X и К отложены
') Ортогональная диметр ия—вид аксонометрии, в котором
координатная сетка—такая, как изображена на рис. 49. При рассмотрении
этого примера особенности ортогональной диметрии не играют никакой
роли; просто мы должны задаться любой координатной сеткой.

ПАНАЛЛРЛЬНАИ АКСОНОМЕТРИЯ
263
отрезки ~ и -?¦ . Точки окружности переносятся на рис. 38, б
Zi Zi
в такое же положение по новой сетке, какое они занимали на рис. 38, о
по старой сетке. Новую сетку можно было бы сразу нанести
на рис. 37 на верхнее и нижнее основания призмы. Получится рис. 39;
оси координат не обозначены.
/
/
\
/
\
и
\
/
\
\
/
/
Рис. 38.
Метод координатной сетки имеет то неудобство, что приходится
предварительно строить эту сетку. Это загромождает рисунок лиш-
лишними линиями, которые потом приходится стирать, и значительно
уменьшает точность.
От этих недостатков свободен вычислительный мегод, заклю-
заключающийся в вычислении прямоугольных координат точек изобра-
изображения и в нанесении этих точек на миллимет-
миллиметровке.
Изображение есть аффинное отображение ори-
оригинала. Следовательно, координаты точек изобра-
изображения—линейные функции координат точек ори-
оригинала '). Введем на плоскости изображения прямо-
прямоугольную декартову систему координат (|, т]). Тогда
где х', у', z' — координаты точки оригинала, Рис. 39.
а \, т)—координаты ее изображения. Сво-
Свободные члены положены равными нулю. Это значит, что за на-
начало координат системы (|, tj) принято изображение точки
') Ср. § 3 статьи «Геометрические преобра^овапил», стр. 75 — 77 этой
l И 3JM

264
МЕТОДЫ ИЗОБРАЖЕНИЙ
Коэффициенты в формулах A) могут быть определены, если
задаться изчбражением базисного тетраэдра. Возьмем, например,
ортогональную изометрию1). Если
наложить соответствующий репер
на систему (|, r\), to получится
рис. 40. Обозначим размер аксоно-
аксонометрических единиц через
ОЕ, = ОЕг = ОЕг = е.
Тогда точка Ел имеет в системе
(?. 1) координаты |=——^—•
Рис 40 т]=—\. Ее оригинал ?, имеет
координаты х'=\, у' = 0, z' = 0.
Повторяя это сопоставление для точек Et и ?,, заключаем:
точка A, 0, 0) переходит в точку ( — —^—, —-^-J •
* @, 1, 0)
г> @, 0, 1)
@, е).
Подставляя эти координаты в формулы A), мы получим систем)
шести уравнений относительно шести известных aif, из которой
определим все коэффициенты:
е
2" *
Следовательно, формулы A) для ортогональной изометрии примут вид
B)
Изобразим в ортогональной изометрии тело, показанное на рис. 39.
Прежде всего надо выбрать желаемый размер рисунка. Положим,
') См. стр. 273. Ортогональная изометрия имеет аксоно-
аксонометрический репер, показанный на рис. 50.

ПАРАЛЛЕЛЬНАЯ АКСОНОМЕТРИЯ
265
например, е = 25 мм и запишем формулы B) гак:
6 = 21,65@'-*'), \
tl= 12,5 [2*'-(У+0')]. / C>
Формулы C) дают | и rj прямо в миллиметрах. Запишем координаты
вершин призмы (пока только нижнего основания).
точки
1
2
3
4
5
6
1.000
0,500
—0,500
-1,000
—0,500
0,500
0,000
0,866
0,866
0,000
—0,866
—0.866
г'
и
0
0
0
0
0
Подставляя эти координаты в формулы C), получим следующую
таблицу (в ней \ и т) даны до десятых долей миллиметра; эта
максимальная точность, которую может реализовать на глаз опытный
чертежник при работе на миллиметровке).
Nt
точки
1
2
3
-21,7
7,9
29,6
ч
—12.5
— 17,1
— 4,6
точки
4
5
6
21,7
— 7.9
—29,6
12,5
17,1
4.6
Вершины верхнего основания отличаются от вершин нижнего
основания тем, что для них г = 2. Из формул C) ясно, что для
изображений значения \ будут те же, а значения т] увеличатся
на 50 мм. Мы не приводим соответствующих таблиц.
Для изображения выреза возьмем на окружности точки через
каждые 30°. На практике их берут значительно чаще, но мы здесь
только иллюстрируем сущность метода. Координаты точек окружности
(нижней) вычисляются по формулам:
глс 1 у' = sj
*=Т
z'=0.
Таблица справа (на стр. 266) дает координаты точек изображе-
изображения; т), относится к нижнему основанию цилиндра, а т]2—к верхнему^
Величины т), и цг связаны очень просто:
т)г - г,, -г 50.

266
МЕТОДЫ ИЗОБРАЖЕНИЙ
№
точки
1
2
3
4
5
6
7
8
9
10
11
12
х'
0,500
0,433
0,250
О.СОО
—0,250
—0,433
—0,500
-0,433
—0,250
0,000
0,250
0,433
и'
0,000
0,250
0,433
0,500
0,433
0,250
0,000
—0,250
—0,433
—0,500
—0,433
—0,250
г1
0
0
0
0
0
0
0
0
0
0
0
0
№
точки
1
2
3
4
5
6
7
8
9
10
11
12
—10,8
— 4,0
4,0
10,8
14,8
14,8
10,8
4,0
- 4,0
— 10,8
-14,8
-14,8
-6,3
—8,5
—8,5
-6,3
-2,3
2,3
6,3
8,5
3,5
6,3
2,3
—2,3
43,7
41,5
41,5
43,7
41,7
52,3
56,3
58,5
58,5
56,3
52,3
41,7
Теперь остается взять миллиметровку и наносить точки по коор-
координатам (|, ц). Получим рис. 41 ').
Читатель должен иметь в виду, что мы выбрали очень простые
примеры, желая только иллюстрировать метод координатной сетки и
вычислительный метод. Эти методы, особенно
вычислительный, предназначены для сложных
оригиналов. Рассмотренный здесь оригинал
можно изобразить более элементарными спосо-
способами. В частности, когда изображение шестит
угольника уже построено, то можно соединить
его центр с вершинами и соединительные
отрезки разделить пополам. Эллипс проходит
через середины этих отрезков. Кроме того,
можно указать направления, сопряженные по-
построенным относительно этого эллипса. По этим
данным эллипс строится гораздо проще, чем
это сделано в тексте.
3.7. Аксонометризация чертежа. Аксоно-
метризацией чертежа называется добавление
¦к полному чертежу таких условий, относящихся к оригиналу, что
чертеж становится метрически определенным.
Приведем пример. На рис. 42 показаны оси координат и плоскость,
заданная следами. Чертеж этот определяет оригинал только с точ-
точностью до аффинного преобразования. Пусть дано дополнительно,
Рис. 41.
*) Подробности о вычислительном методе читатель может иайти ¦ работе
Н. М Бескина, Вычислительный метод построения изображений, сб.
«Методы начертательной геометрии и ее приложения» под ред. Н. Ф. Чет-
еерухина, М., 1955, стр. 83—99.

ПАРАЛЛЕЛЬНАЯ АКСОНОМЕТРИЯ
267
•что система координат прямоугольная:
/_ Х'О' К= /_ v'°'z' = Z Z'O'X' = 90°.
Это условие еще не делает чертеж аксонометрическим, потому что
неизвестны отрезки О'А', О'В', О'С.
Допустим, что требуется изобразить перпендикуляр, опущенный
из начала координат на плоскость А'В'С. Обозначим основание
этого перпендикуляра через Р". За Р (изображение точки Р1) можно
принять любую точку внутри треугольника ABC, это подтверждает
метрическую неопределенность чертежа. Если бы ребра О'А', О'В'.
О'С были известны, то перпендикуляр ОР нельзя было бы изобра-
изобразить произвольно: положение точки
Р было бы вполне определенным.
Обратно, если мы на рис. 42
изобразим перпендикуляр, т. е.
выберем произвольно точку Р,
то определятся отношения ребер
О'А':О'В':О'С, т. е. чертеж станет
метрически определенным с точно-
точностью до масштаба. Докажем это
утверждение. Для этого покажем,
что, задав любую точку Р внутри
треугольника ABC, можно, и притом
единственным образом, реконстру-
реконструировать, тетраэдр О'А'В'С (с точ-
точностью до масштаба).
Точка Р лежит внутри треугольника ABC потому, что высота
тетраэдра с прямыми плоскими углами при вершине проходит через
точку пересечения высот основания, а последняя точка в данном слу-
случае лежит внутри потому, что треугольник А'В'С остроугольный.
В самом деле, квадраты его сторон суть
Рис. 42.
и сумма любых двух из этих квадратов больше третьего.
На рис. 43, а отдельно изображен треугольник следов ABC
рис. 42 и внутри него произвольно взята точка Р. Через нее
проведены прямые AL, ВМ и CN.
Так как О'Р1—высота тетраэдра О'А'В'С', то, как было сказано
выше, точка Р' есть точка пересечения высот треугольника А'В'С.
Значит, AL, ВМ и CN — изображения высот. Задача, стоящая перед
нами, может быть теперь сформулирована так: дано аффинное изобра-
изображение треугольника с высотами (рис. 43, а) и требуется восстано-
восстановить оригинал (с точностью до размера).

268
МЕТОДЫ ИЗОБРАЖЕНИЙ
Неопределенность размера позволяет нам выбрать один отрезок
произвольно; выберем сторону А'В' (рис. 43,6). Построим точку Л/'
по условию i4'/V' AN
WW=~NB'
Затем восставим в точке N' перпендикуляр к А'В'; точка С должна
лежать на этом перпендикуляре.
в)
Рис. 43.
Построим на А'В', как на диаметре, полуокружность. Точки L'
и М' должны лежать на этой полуокружности, потому что
? A'UВ' = /_ В'М'А' = 90°.

ПАРАЛЛЕЛЬНАЯ АКСОНОМЕТРИЯ 269
Так как точки L' и С должны удовлетворять условию
В'С _ВС
B'L' ~ BL '
то точка С должна лежать на полуокружности, получающейся
из построенной ранее полуокружности при помощи гомотетии *)
п/ л.л. ВС ВС
с центром В и коэффициентом -^j- (отношение -^т нам известно
tiLi LJ Li
из рис. 43, а). Эту полуокружность легко построить, найдя на пря-
прямой А' В' точку -5 из условия
B'S ВС
B'A'~BL
и приняв B'S за диаметр. Значит, точка С' есть точка пересечения
этой полуокружности с перпендикуляром к прямой А 'В' в точке N'.
Тем самым треугольник А'Ь'С' построен.
Чтобы не загромождать чертежа, дальнейшая реконструкция
тетраэдра О'А'В'С продолжена на отдельном рис. 43, в. На этом
рисунке снова воспроизведен только что построенный треугольник
А'В'С с высотами A'L', В'М' и CN'.
Согласно теореме о трех перпендикулярах точка L' служит не
только основанием высоты A'L', но и основанием высоты O'L' боковой
грани О'В'С'. Поэтому, если построить развертку тетраэдра О'А'В'С',
разрезав его по ребрам О'А', О'В' и О'С и совместив боковые
грани с плоскостью основания, то точка О' попадет на продолжение
высоты A'L'. Кроме того, эта точка должна лежать на полуокруж-
полуокружности, построенной на В'С как на диаметре. На рис. 43, в показано
построение точек О,, Ог и Oj> в которые перейдет общая вершина О'
трех боковых граней при развертке.
Если даны некоторые метрические условия, касающиеся оригинала,
недостаточные для того, чтобы чертеж стал метрически определенным,
то получается частичная аксонометризация чертежа.
Например, если известно, что на рис. 44 точки Р' и Q' лежат
соответственно в нижней и верхней гранях параллелепипеда и прямая
P'Q' перпендикулярна этим граням, то рис. 44 частично аксономет-
аксонометризованный. Высоту параллелепипеда, проведенную из точки А',
нельзя изобразить произвольно: ее надо чертить параллельно PQ.
Высоту же грани A'B'C'D', проведенную из точки А', можно изо-
изобразить произвольно.
Частично аксонометризованный чертеж требует большой осторож-
осторожности в обращении с ним, потому что на нем кое-что можно изобра-
изображать произвольно, а кое-что нельзя. Вот поучительный пример воз-
возможных здесь ошибок.
') Определение гомотетии см. на стр. 55 этой книги ЭЭМ.

270
МЕТОДЫ ИЗОБРАЖЕНИЙ
В течение многих веков было принято изображать на рисунке
плоскость в виде параллелограмма. При этом негласно предполагалось,
что этот параллелограмм изображает прямоугольный кусок плоскости.
Тем самым в рисунок вносилась частичная аксонометризация (показаны
два перпендикулярных направления).
Эта частичная аксонометризация огра-
ограничивает свободу изображений в
плоскости. На это обстоятельство
не обращали внимания, что приво-
приводило к ошибкам. Поэтому за послед
ние годы все больше распростра-
распространяется обыкновение изображать ку-
кусок плоскости с оборванными
краями.
Пусть, например, требуется изо-
изобразить правильную четырехуголь-
четырехугольную пирамиду, стоящую на гори-
горизонтальной плоскости. Квадрат, слу-
служащий основанием пирамиды, может быть изображен любым паралле-
параллелограммом, нона рис. 45, а это положение неприменимо ввиду частичной
аксонометризации. Рис. 45, а неправилен, потому что на нем два
различных направления (AD и LO) изображают перпендикуляры,
к одному и тому же направлению (Afi|jZ.M). На рис. 45,6 то же'
А
Рис. 45.
самое изображение правильной четырехугольной пирамиды показано»
на плоскости с оборванными краями; этот рисунок верен.
На рис. 46, а изображен прямой круговой конус. Рис. 46, а не-
неправилен. Его ошибочность обнаруживается, если провести два
сопряженных диаметра эллипса, один из которых параллелен какому-
нибудь «краю» плоскости. На рис. 46, о CD\\LO, a
Рис. 46, б правилен.

ПАРАЛЛЕЛЬНАЯ АКСОНОМЕТРИЯ 271
Предостережем читателя еще от одной возможной ошибки. Каждый
из рис. 45,6 и 46, б в отдельности правилен, но если бы мы исполь-
использовали оба эти изображения, показав правильную четырехугольную
пирамиду и конус, стоящие на одной и той же плоскости, хотя бы
Рис. 46.
и с оборванными краями, то мы получили бы ошибочный рисунок.
Пирамида (рис. 45, б) определяет метрику в плоскости основания,
конус (рис. 46, б) тоже, и эти метрики не совпадают.
3.8. Ортогональная (прямоугольная) аксонометрия. До сих пор
мы рассматривали свободные изображения. В инженерной практике
весьма распространена аксонометрия с заданными параметрами.
Согласно теореме Польке — Шварца куб можно изобразить произ-
произвольно, например так, как на рис. 47. Между тем человек, не изу-
изучавший начертательной геометрии,
не поверит, что это куб, так как
Это изображение не похоже на куб.
Это ставит перед нами вопрос: от
чего зависит наглядность изобра-
изображения, т. е. сходство с оригиналом?
В параллельной проекции изо- Рис 47
бражение показывает оригинал так,
как он виден наблюдателю, смотрящему с очень далекого расстояния
вдоль проектирующих прямых. Самый процесс проектирования близок
к геометрическому процессу зрения. Однако при рассматривании
любого предмета мы всегда помещаемся перед ним. Плоскость изо-
изображения следует вообразить перед предметом или за предметом.
Все лучи зрения (при рассматривании издалека) перпендикулярны
плоскости изображения. Поэтому самое наглядное изображение по-
получается при ортогональном или близком к ортогональному
проектировании.

272
МЕТОДЫ ИЗОБРАЖЕНИЙ
Возвращаясь к рис. 47, скажем, что для того, чтобы изображение
было «похоже» на оригинал, надо, во-первых, чтобы оно было построено
без нарушения геометрических правил (которые аналогичны законам
зрения) и, во-вторых, чтобы оно давало вид оригинала с привычной
точки зрения. Изображение куба на рис. 47 не удовлетворяет второму
условию. Здесь глаз наблюдателя помещается чуть сверху, чуть
впереди и очень далеко влево. Угол проектирующих лучей к пло-
плоскости изображения ач=14о1), т. е. проекция очень далека от орто-
ортогональной.
Кроме угла а, аксонометрия характеризуется следующими пара-
параметрами:
а, р, у — углы проектирующих лучей с натуральными осями.
В аксонометрии принято называть натуральным все, что отно-
относится к оригиналу, а аксонометрическим — все, что относится
к изображению. Например, О'Л",
O'Y', O'Z' — натуральные оси, а ОХ,
OY, OZ — аксонометрические оси.
р, q,r — показатели (коэф-
(коэффициенты) искажения. Так
называются отношения аксонометри-
* ' '—*г ческих единиц el = OEx, ег=ОЕ2,
ег = ОЕг к натуральной единице е
(она предполагается одинаковой по
всем осям):
Рис. 48.
Предостережем читателя от возможного недоразумения. В учеб-
учебниках начертательной геометрии он может встретить утверждение,
что в ортогональной аксонометрии (т. е. аксонометрии с углом а—90°)
коэффициенты искажения связаны формулой
Разъясняем, что эта нормировка имеет силу лишь в том случае,
если изображение есть непосредственная проекция оригинала на
плоскость. Мы же рассматриваем метод изображения, заключающийся
') Здесь мы сталкиваемся с задачей: имея уже выполненное изображе-
изображение в параллельной проекции, найти параметры, "определяющие проекти
руюший аппарат Например, зная, что на рис. 47 изображен куб, узнать
угол а. Графическое решение этой задачи данэ в книге Е. А. Глазунова
и Н.Ф. Чет в ерухина [2] (см. список литературы в конце статьи) в § 9,
а аналитическое — в статье А И Островского «Основные формулы
параллельной аксонометрии» (Труды московского семинара по начерта-
начертательной геометрии и инженерной графике, Москва, 1958, стр. 108—110).

ПАРАЛЛЕЛЬНАЯ АКСОНОМЕТРИЯ
273
в параллельном проектировании и последующем подобном преобразо-
преобразовании. В этом случае все коэффициенты искажения могут быть
заданы произвольно, однако с соблюдением неравенств: квадрат
любого коэффициента искажения не превышает суммы квадратов
двух других.
Углы между аксонометрическими осями (рис. 48) принято обозна-
обозначать так:
= со„
со,
со2
со, = 2я.
Между перечисленными параметрами существуют связи. Выбирая
какую-нибудь ортогональную аксонометрическую проекцию, естест-
естественнее всего задаться коэффициентами искажения. Заметим, что если
все коэффициенты искажения различны, то изображение называется
триметрическим, если два из них одинаковы, а третий отличен
от них, то диметрическим, если все три одинаковы, то изо-
изометрическим.
Если все коэффициенты искажения заданы, то остальные пара-
параметры выражаются гак:
sinu = -
sin p =
sin V =
/Г-
F)
sinco _
^
.in со
Ipq
J
Если проектирующий луч 00' проходит в первом октанте, то
углы ю1?со2 и со, — тупые. Вывод этих формул вполне элементарен,
и мы его не приводим.
Выбирая параметры ортогональной аксонометрии, мы исходим из
того, какие размеры должны иметь изображения ребер базисного
куба, т. е. куба с вершиной О' и ребрами, идущими по осям О'X'',
O'Y', O'Z'- При этом следует различать два случая. Первый — когда
18 Энциклопедия, кн. 4

274
МЕТОДЫ ИЗОБРАЖЕНИЙ
базисный куб имеет определенные размеры. Например, его ребро
е= 1 м, а размеры изображения должны быть е, = 1 см, е2 = ег = 2 ел*.
В этом случае коэффициенты искажения определяются точно
Второй случай — когда размеры базисного куба не указаны, т. е.
„ требуется какой-нибудь
куб (с ребрами, парал-
параллельными координатным
осям) изобразить так,
чтобы было е, = 1 см,
ег = ег = 2 см. В этом
случае коэффициенты
искажения определяются
только с точностью до
множителя, т. е. опреде-
определяются только их отно-
отношения
X p:q:r=\ :2:2.
Рис. 49.
Можно, например, поло-
положить р=\, q = r=2. Выбор множителя несуиц ствен, потому что пра-
правые части формул F) и G) однородны относи 'льно р, д. г.
Полагая р= 1, д = г=2, вычислим, напри ер, со,, со2, со,:
3 \РТ
sinco1 = -
= 0,9922,
Учитывая, что углы со,, со2 и со, тупые, найдем
(рис. 49). Мы видим, что выбор коэффициентов искажения в орто-
ортогональной аксонометрии вполне определяет углы между аксономет-
аксонометрическими осями.
Рассмотрим еще чрезвычайно употребительную систему—орто-
систему—ортогональную изометрию. Полагая p = q = r=\, получим
/
ina= sin p = sin у= у -j ,
sin a
sin со, = sin co2 = sin со, = —g-
В этом случае со, =co2 = cos = 120°. Изображение системы координат
показано на рис. 50. Куб выглядит, как показано на рис. 51. Как

МЕТОД МОНЖА
275
видно, а = р = у, т. е. направление проектирующих прямых совпа-
совпадает с направлением диагонали куба. Все это дает следующую
Рис. 50.
Рис. 51.
геометрическую картину: надо провести плоскость изображения пер-
перпендикулярно диагонали куба и проектировать на нее по направлению,
параллельному этой диагонали. Тогда получится такое изображение,
как на рис. 51. Из двух вершин куба, лежащих на проектирующей,
диагонали, одна заслоняет другую.
§ 4. Метод Монжа
4.1. Комбинированные изображения. Аксонометрия—один из
методов получения метрически определенного изображения. Из других
методов наибольшее распространение имеют так называемые комби-
комбинированные изображения. Как мы говорили выше, плоское точечное
изображение нг может (без дополнительных условий) определять
оригинал из-за нехватки одного параметра. Поэтому иногда задают
несколько разных изображений одного оригинала. Систему несколь-
нескольких изображений одного оригинала называют к омбинированным
изображением или комплексным чертежом.
4.2. Сущность метода Монжа. Примером комбинированного изо-
изображения служит широко известный метод Монжа.
В методе Монжа точка пространства ортогонально проектируется
на две взаимно перпендикулярные плоскости — горизонтальную
П, и фронтальную П2 (рис. 52). Получающиеся точки М', и Мг
называются соответственно горизонтальной и фронтальной
проекциями точки М'. Затем плоскость 1Т2 вращается в направлении,
указанном стрелкой, до совмещения с плоскостью П,. После совме-
совмещения получается рис. 53, называемый эпюром Монжа. На эпюре
Монжа точка М' определяется двумя проекциями /М, и Мг, но эти
проекции не могут задаваться обе вполне произвольно: они должны
лежать на прямой, перпендикулярной оси проекций XX; эта прямая
называется линией связи."
18*

276
МЕТОДЫ ИЗОБРАЖЕНИЙ
/~7ГГ
"О
м,'
Рис. 52.
Точка на плоскости задается двумя координатами. Поэтому задать
одну проекцию точки, например горизонтальную, значит задать две
координаты. Задание фронтальной проекции, которая должна ле-
лежать на уже известной
<* прямой (проходящей че-
через точку /И, перпенди-
перпендикулярно XX), равносильно
заданию еще одной коор-
координаты. Тем самым поло-
положение точки М' в
пространстве полностью
определяется. Если зада-
задана только горизонтальная
проекция, то определяет-
определяется бесконечное множество
конкурирующих точек,
лежащих на одном пер-
перпендикуляре к плоскости П,. Эти конкурирующие точки разли-
различаются своими фронтальными проекциями. Задание фронтальной
проекции эквивалентно также заданию числовой отметки, указы-
указывающей высоту точки над горизонтальной плоскостью.
Бывают исключительные случаи, когда задания двух проекций
недостаточно. Например, если плоскость а перпендикулярна плоско-
плоскостям ITj и П2, то прямые, лежащие ^
в этой пл.ккости, невозможно разли-
различить по своим проекциям. В таких
случаях задается еще третья проек-
проекция — профильная.
Метод Монжа определяет ориги- *
'нал метрически точно, т. е., имея
изображение в виде эпюра Монжа,
можно ответить на любой вопрос,
относящийся к оригиналу.
Мы не вдаемся ни в какие подробности, касающиеся метода
Монжа, потому что он детально излагается во всех учебниках
начертательной геометрии и изучается в средней школе (в курсе
черчения). Заметим, что идея задавать оригинал двумя проекциями при-
принадлежит не Монжу, а является гораздо более старой. Она применя--
лась, например, древнеримским архитектором Витрувием. Монж
вперзые привел этот метод в систему и показал, что можно не
только изобразить любой оригинал, но и, пользуясь этим изображе-
изображением, решить все геометрические задачи, относящиеся к оригиналу ').
М„
рис 53
') См. по этому вопросу вступительную статью Д. И. К а р г и н а
к книге Г. Монжа [3], указанной в конце статьи.

ЦЕНТРАЛЬНЫЕ ПРОЕКЦИИ
277
§ 5. Центральные проекции
5.1. Свойства центральной проекции. Теория центральных про-
проекций сложнее теории параллельных проекций настолько, насколько
проективное преобразование сложнее аффинного. Мы_ изложим неко-
некоторые вопросы, относящиеся к центральным проекциям, исходя из
тех же проблем, которые решались для параллельных проекций, и
указывая, в чем заключается разница в ответах.
Центральная проекция строится следующим образом. Фиксируем
в пространстве це н т р проекции 5 и плоскость проекцииа
(рис. 54). Пусть М'—любая точка пространства, отличная от S.
Проводим прямую SM' (проектирующая пря-
прямая); точка М ее пересечения с плоскостью
а считается изображением точки М*.
Центральную проекцию удобно рассма-
рассматривать только в проективном пространстве
(параллельную проекцию мы изучали в аф-
аффинном пространстве). Если мы не введем
несобственных (бесконечно удаленных) эле-
элементов1), то нельзя будет утверждать, что
всякая точка пространства имеет изображе-
изображение (потому что проектирующая прямая SM'
может оказаться параллельной плоскости а).
В проективном пространстве всякая точка
(кроме S) имеет изображение. При этом
изображение собственной точки может ока-
оказаться несобственной точкой и изображе-
изображение несобственной точки может оказаться собственной точкой.
Центральные проекции обладают следующими свойствами (срав-
(сравните со свойствами 1—4 параллельных проекций, стр. 235—236):
1. Каждой точке пространства, кроме центра проекции, одно-
однозначно соответствует точка на (проективной!) плоскости а.
Конкурирующие точки — те, которые лежат на одной прямой,
проходящей через S.
2. Прямая, если только она не проектирующая, изображается
прямой; проектирующая прямая изображается точкой.
3. Если точки А', В', С', D' принадлежат одной прямой
(не проектирующей), то
АВ_. AD_ А/В^_ . А'Р'
ВС : DC~~ В'С : ТУ С1'
Иначе говоря: сложное отношение четырех точек, лежащих на
одной прямой, есть инвариант центрального проектирования.
*) Ср. § 7 статьи «Геометрические преобразования», стр. 112—113 этой
книги ЭЭМ.
Рис. 54.

278 МЕТОДЫ ИЗОБРАЖЕНИЙ
Условимся теперь, что полученную в плоскости а центральную
проекцию мы еще будем подвергать произвольному аффинному прео-
преобразованию1) (в плоскости а). Таким образом, изображение точки
по методу центральных проекций не есть непосредственная цен-
центральная проекция этой точки.
Теперь, опуская доказательства, сопоставим свойства изображе-
изображений по методу центральной и параллельной проекций.
Изображая плоскую фигуру в параллельной проекции, можно
произвольно изобразить любой треугольник, а в центральной про-
проекции— любой четырехвершинник2) (т. е. четыре точки общего
положения в плоскости).
Если какой-нибудь четырехвершинник, входящий в состав плоской
фигуры, уже изображен, то изображения всех остальных точек этой
фигуры однозначно определяются (в параллельной проекции такую
роль играл треугольник, или, что то же самое, «трехвершинник»).
Пусть A'B'C'D'—оригинал (рис. 55,а), a ABCD— изображение
(рис. 55,6); ?", F', С—диагональные точки четырехугольника
A'B'C'D', E, F, С—соответственные диагональные точки четырех-
четырехугольника ABCD. Пусть М'—еще одна точка оригинала. Прямая
А'М пересекает прямые В'С', CD' и B'D' соответственно в точках
X', У и Z'. Изображения этих точек вполне определены сложными
отношениями, которые должны быть одинаковы в оригинале и в изо-
изображении')
(BCFX) = (B'C'F'X').
Это равенство позволяет найти точку X. Аналогично находятся
точки Y и Z. Впрочем, точки Y и Z можно найти как пересечения
1) Искажение, которому подвергается оригинал при замене его изобра-
изображением, принципиально не увеличилось бы, если бы мы подвергли полу-
полученную проекцию не аффинному, а любому проективному преобразованию,
потому что само центральное проектирование есть проективное пре-
обр'азование. Мы ограничиваемся аффинным преобразованием (для боль-
большой элементарности изложения) именно потому, что эта разница несу-
несущественна.
2) Мы говорим здесь о «четырехвершиннике», а не о четырехугольнике
в сбычном смысле слова (который имеет четыре «стороны» и две «диаго-
«диагонали»), поскольку при центральном проектировании различие между
«сторонами» и «.диагоналями» теряет смысл. Мы считаем, что четырехвер-
четырехвершинник A'B'C'D' имеет три пары противополсжных сторон А'В' и CD1,
А'С и B'D', A'D1 и В'С (всего шесть сторон). Каждая пара противо-
противоположных сторон четырехвсршинника имеет точку пересечения, называе-
называемую его диагональной точкой. Всего, таким образом, у четырехвершинника
есть три диагональных точки.
*) Символ (ABCD) обозначает сложное отношение

ЦЕНТРАЛЬНЫЕ ПРОЕКЦИИ
279
прямой АХ соответственно с прямыми DE и BD (ибо прямые пере-
переходят в прямые, их точки пересечения — в точки пересечения).
Положение точки М на прямой АХ определяется.из условия
) = (A'X'Y'M')
{вместо пары точек X, Y можно пользоваться парами Y, Z или Z, X).
Рис. 55.
5.2. Проективные координаты. Полезно видеть четырехвершин-
«ик и с иной точки зрения. На рис. 56 четырехвершинник
ОЕгЕЕх дополнен двумя диаго-
диагональными точками Fx и Ft.
Задание точки общего поло-
положения Е может быть заменено за-
заданием двух точек Fx и Ft на
прямых ОЕХ и ОЕг. Две оси ОХ и
OY и по две точки на каждой
из них (кроме О) образуют про-
проективную систему коор-
координат. На рис. 57 дано сопоста-
сопоставление аффинной и проективной
систем координат. На рис. 57, а
показаны оси ОХ и OY и на каждой оси — ее единичная точка. Если
М — любая точка плоскости, то для определения ее аффинных
координат следует провести через нее прямые, параллельные осям
X и Y (т. е. прямые, проходящие через несобственные точки этих
осей). Эти прямые определят на осях ОХ и OY точки Рх и Рх.
Рис. 56.

280
Отношения
МЕТОДЫ ИЗОБРАЖЕНИЙ
ОРг
суть аффинные координаты точки М.
На рис. 57,6 показаны оси ОХ и OY и на каждой оси по д в е
точки (кроме О). Если М — любая точка плоскости, то для опреде-
определения ее проективных координат следует провести через нее пря-
прямые /И/7, и
Уже из этого ясно, что точки Fl и Ft играют
a) ff)
Рис. 57
ту же роль, какую в аффинной системе координат играют несобст-
несобственные точки осей. Эти прямые определят на осях ОХ и OY точки
Р, и Рг. Сложные отношения
ОЕг
суть проективные координаты *) точки М (при этом координаты х
и у могут принимать и «значение» оо). Из этих формул видно, что
для точки О х = 0,
» » ?, х = 1,
» » F, х=оо.
Точка ? (рис. 56) имеет координаты д;=1, у— 1; она называется
единичной точкой плоскости.
') Эти координаты называются неоднородными. Они обладают одним
существенным дефектом: точки «бесконечно удаленной» (несобственной)
прямой, не лежащие на осях OX, OY, имеют координаты лг=оо, у=со и
потому не различаются в этих координатах. Для устранения этого дефекта
используются однородные проективные координаты (ср. стр. 118 этой
книги ЭЭМ).

ЦЕНТРАЛЬНЫЕ ПРОЕКЦИИ
28 Г
При удалении точек F\ и Ft соответственно по осям А" и К
в бесконечность проективные координаты превращаются в аффинные.
5.3. Использование проективных коорг/инат для построения
изображений. Прн изображении плоских фигур можно принять че-
тырехвершинник A'B'C'D' за базисный, т. е. считать, что
точка А' — начало координат,
» В'—единичная точка оси X',
» С— » » » Г,
?>'-
плоскости Х'У.
Четырехугольник ABCD тоже примем за базисный четырехугольник
в плоскости изображения. Тогда каждая точка М' оригинала будет
Рис. 58.
изображаться точкой М, которая имеет относительно четырех-
четырехвершинника ABCD те же самые проективные координаты, что
и точка М' относительно четырехвершинника A'B'C'D'.
Так же как и в параллельной проекции, специально строить ко-
координаты каждой точки было бы слишком громоздко. Гораздо удоб-
удобнее построить в плоскости оригинала декартову прямоугольную
сетку, а в плоскости изображения — изображение этой сетки. На
рис. 58, а, показана декартова прямоугольная сетка, т. е. сетка из
равных квадратов. Прямые одного семейства параллельны между со-
собой, т. е. проходят через одну несобственную точку; следовательно,

282 МЕТОДЫ ИЗОБРАЖЕНИЙ
их изображения тоже проходяi через одну точку (вообще говоря,
собственную). Если построить изображения несобственных точек
обоих семейств, то прямая, соединяющая эти изображения, служит
изображением несобственной прямой плоскости оригинала (изобра-
(изображение несобственной прямой называется линией схода).
Пусть 1'2'3'4'—один из квадратов декартовой прямоугольной
сетки. Имея его, можно строить сетку аффинным способом, т. е. не
отмеряя отрезков, а пользуясь проведением параллельных. Построе-
Построение можно производить в такой последовательности:
1) проводим прямую 2'4';
2) через точку 3' проводим прямую, параллельную 2'4'. Она
пересечет прямые \' и Г4' соответственно в точках 5' и 6'; это —
новые два узла сетки;
3) через 5' и 6' проводим прямые, параллельные соответственно
прямым 1'4' и Г2'. Получаем еще три узла: 7', 8' и 9' и т. д.
Теперь ясно, как построить изображение сетки. Первый квадрат
можно изобразить любым четырехугольником; пусть это будет четы-
четырехугольник 1234 (рис. 58,6). Точки1) /=,= 12x34 и /=,= 14x23
суть точки схода прямых сетки; прямая Z7,/7, — линия схода. Прямые,
пересекающиеся на линии схода, изображают параллельные
прямые.
Точка G= F1F1x24 есть точка схода диагоналей, параллельных
2'4'. Через точку 3 проводим прямую 30 и находим точки 5 и 6.
Дальнейшее пос троение не требует объяснений.
Чтобы яснее понять происхождение изображения, показанного
на рис. 58,6, вообразим две прямые, проходящие через 5 и
параллельные прямым декартовой координатной сетки. Они пересе-
пересекают плоскость изображения а в точках Ft и Ft. Линия схода FyFt
есть пересечение плоскости, проходящей через 5 и параллельной
плоскости оригинала, с плоскостью изображения. Рис. 59 снабжен
дополнительной штриховкой и гораздо нагляднее.
Окружность в центральных проекциях может изображаться любой
нераспадающейся кривой второго порядка: эта кривая не должна
пересекать линию схода.
5.4. Понятие о центральной аксонометрии. Вопрос об изобра-
изображении пространственных фигур в центральной проекции разрешается
аналогично такому же вопросу в параллельной проекции: надо изо-
изобразить систему координат и показать жесткую проективную связь
изображаемых элементов фигуры с этой системой координат. Разница
заключается в том, что система отнесения здесь другая.
Проективная система координат в трехмерном пространстве —
это три неколлинеарные оси О'Х, O'Y', O'Z', на каждой из которых
') Символом i2 обозначается прямая, проходящая через точки 1 и 2;
12x34 обозначает точку пересечения прямых 12 и 34.

ЦЕНТРАЛЬНЫЕ ПРОЕКЦИИ
283
даны по две точки (кроме О'). Соединяя между собэй точки ?,, Е2,
Ег, а также Ft, F2, Fa, мы представим эту систему координат так: два
треугольника Е,ЕгЕ, и FxFtFt, лежащие в разных плоскостях, причем
прямые, соединяющие соответственные вершины этих треугольников,
проходят через одну точку (т. е. треугольники перспективны).
Такая фигура (рис. 60) называется «дезарговой конфигурацией». Де-
.«аргова конфигурация в проективном пространстве играет ту же роль,
какую играет тетраэдр в аффинном.
i
\
Рис. 59.
Особый интерес представляет дезаргова конфигурация, для ко-
которой
/_ Х'О' V = /_ Y'O'Z' = /_ Z'O'X' = 90°,
точки Fv Ft, Ft несобственные.
Такую дезаргову конфигурацию мы будем называть прямоуголь-
прямоугольной равнобедренной.
Изображением пространственной дезарговой конфигурации служит
плоская дезаргова конфигурация: у нее оси OX, OY и OZ лежат
в одной плоскости (плоскости рисунка).
Для центральных проекций имеет место теорема, аналогичная
теореме Польке — Шварца для параллельных проекций. Приведем эти
теоремы в сопоставлении.
Вопрос. Можно ли, параллельно проектируя тетраэдр, получить
наперед заданный четырехвершинник?

284
МЕТОДЫ ИЗОБРАЖЕНИЙ
Ответ (теорема Польке—Шварца). Получить в точности
данный четырехвершинник, вообще говоря, нельзя, но всегда можно
получить его с однопараметрическим искажением, а именно: можно по-
получить четырехвершннник, подобный данному.
Если же говорить не о непосредственной параллельной проек-
проекции, а об изображении по методу параллельной проекции, то лю-
любой четырехвершинник может служить изображением любого тет-
тетраэдра.
Вопрос. Можно ли, центрально проектируя пространственную
дезаргову конфигурацию, получить наперед заданную плоскую де-
заргову конфигурацию?
Рис. 60.
Ответ (аналог теоремы Польке — Шварца для цен-
центральной проекции). Получить в точности данную плоскую
дезаргову конфигурацию, вообще говоря, нельзя, но всегда можно
получить ее с двухпараметрическим искажением, а именно: можно
получить плоскую дезаргову конфигурацию, унимодулярно аффиную1)
данной 2).
Если же говорить не о непосредственной центральной проекции,
а об изображении по методу центральной проекции, то любая
плоская дезаргова конфигурация может служить изображением
любой пространственной дезарговой конфигурации.
Чтобы построить изображение пространственной фигуры в сво-
свободной центральной проекции, надо выделить в составе оригинала
>) Унимодулярно-аффинное (иначе: эквиаффинное) пре-
преобразование— аффинное преобразование, сохраняющее неизменными пло-
площади всех фигур.
2) См статью Н. М. Веснина, указанную в сноске на стр. 251.

ЦЕНТРАЛЬНЫЕ ПРОЕКЦИИ 285
пространственную дезаргову конфигурацию^ и изобразить ее произ-
произвольно (т. е. произвольной плоской дезарговой конфигурацией). По-
Построение изображения произвольной точки М' показано на рис. 61.
Прямая О'М' пересечет плоскости Е[ЕгЕг и F^F'tF, соответственно
в точках М[ и М\ Изображение одной из них (например, Мг) должно
быть дано, а изображение другой можно построить (ниже будет
объяснено почему). При реконструкции оригинала по рис. 61 мы
прежде всего должны будем восстановить положение точек М\ и М'г.
Если бы мы имели только треугольник ЕгЕгЕг, то положение точки Ж,
Рис. 61.
в плоскости этого треугольника не могло бы быть фиксировано проекгив-
но жестко, так как треугольник не определяет систему координат
в проективной плоскости. Здесь нам на помощь приходит прямая
пересечения плоскостей EjE^E, и FiFtF, (она называется дезар-
дезарговой прямой). Так как она принадлежит обеим плоскостям, то
в каждой из этих плоскостей мы имеем четыре прямые: стороны тре-
треугольника EiE2E3 (или F,F2Fa) и дезаргова прямая. Четыре прямые
образуют систему координат, и относительно нее можно проективно
жестко фиксировать положение точки M't (а также М'г). Изображе-
Изображением дезарговой прямой служит дезаргова прямая плоской конфигу-
конфигурации, т. е. прямая, на которой лежат точки

286 МЕТОДЫ ИЗОБРАЖЕНИЙ
(согласно теореме Дезарга1) эти три точки лежат на одной
прямой). Точка Мх занимает по отношению к четырем прямым (сто-
(стороны треугольника ЕгЕ^Ег и дезаргова прямая) проекгивно такое же
положение, как точка М[ по отношению к соответствующим четырем
прямым (стороны треугольника ЕгЕгЕ„ и дезаргова прямая).
Теперь можно объяснить, почему задание точки М[ на рис. 61
позволяет построить точку М\ В плоскости E'^E'Jz^ как только что
было показано, мы имеем проективную систему координат. Поэтому
положение точки М относительно этой системы проективно фикси-
фиксировано. Точка М относительно аналогичной системы координат
в плоскости F\F2F, занимает такое же положение, потому что эти
две системы перспективны (центр перспективы — точка О').
Это можно записать так:
{E\,Et,E'v d\ Л*,')?' {F\,F-vF'vd'.M't)
(d'—дезаргова прямая). Отсюда следует
(?„ ?,. ?„ d, Мх) л (Л. ^i. Л. d. Mt)
(d—дезаргова прямая плоской дезарговой конфигурации). Это последнее
соотношение позволяет построить точку Мг, если дана точка /И,. Мы.
ие показываем построения.
Прямая задается своей проекцией с указанием двух уже задан-
заданных точек, например двух следов на плоскостях базисной дезарговой
конфигурации. Плоскость задается следами на двух плоскостях ба-
базисной конфигурации или на любых двух уже заданных плоскостях.
Можно также задавать любой элемент инцидентными ему точками,
прямыми, плоскостями (уже заданными); например, можно задать
плоскость тремя точками.
Рисунок, выполненный с соблюдением указанных правил, опреде-
определяет оригинал лишь с точностью до проективного преобразования.
В самом деле, истолковывая рисунок, можно в качестве оригинала
базисной дезарговой конфигурации подразумевать любую простран-
пространственную дезаргову конфигурацию. Переход же от одной простран-
пространственной дезарговой конфигурации к другой определяет проективное
преобразование пространства.
Если же снабдить рисунок примечанием, дающим реконструк-
реконструкцию базисной конфигурации, то мы получим условное изображение,
определяющее оригинал метрически точно. Этот метод называется
центральной аксонометрией. Центральная аксонометрияг
как и параллельная, представляет собой метод изображения ориги-
См. статью «Геометрические преобразования», стр. 130—133.

ЦЕНТРАЛЬНЫЕ ПРОЕКЦИИ
287
нала вместе с системой координат. Различие между центральной и
параллельной аксонометрией заклюиаетсн в двух пунктах:
1) система координат—не аффинная, а проективная,
2) на изображении должна быть показана проективная (а не
аффинная) связь небазисных элементов с базисом.
Рис. 62 — пример изображении по методу центральной аксономет-
аксонометрии, если известны метрические параметры натуральной системы
координат. Пусть, например, известно, что эта система—прямоуголь-
система—прямоугольная равнобедренная, т. е.
/_X'O'Y' = /_ Y'O'Z' = /_Z'O'X' = 90°. О'Е\ =0'Е'г = О'?"8,
Рис. 62.
точки Ft, F2, F, несобственные; Ж, и Мг — следы прямой г соответ-
соответственно на плоскостих Y'O'Z' и Z'O'X'. ТретпЧ след Ж, можно
построить, и тогда положение точки
М' на прямой проективно жестко
фиксируется сложным отношением
(М М'М М')\ это отношение на изо-
изображении такое же, как в оригинале.
Теория свободных изображений
играет важную роль в аэрофотограм-
аэрофотограмметрии. Имея снимок, сделанный с
самолета, мы обычно не знаем пара-
параметров проектирующего аппарата. Если
бы в момент фотографирования пло-
плоскость фотопленки была параллельна
плоскости земной поверхности, то мы
получили 6а изображение, подобное ори-
оригиналу. Положим теперь, что плоскость фотопленки наклонена к гори-
горизонтальной плоскости, причем угол наклона и другие параметры проек-
проектирующего аппарата неизвестны. Как дешифрировать снимок (т. е. по-
построить по этому искаженному изображению метрически точный план
местности)? Самый простой случай — когда на местности имеются че-
четыре точки об.цего положения, положение которых нам заранее точно
известно. Тогда этот четырехвершинник принимается за базисный, и
снимок превращается в аксонометрическое изображение, по которому
оригинал определяется метрически точно.
Центральной аксонометрией пользуются архитекторы, вычерчивая
проекты зданий (речь идет об общем виде здания в целом). Это
объясняется тем, что мы обычно рассматриваем здание с расстояния,
которое невелико по сравнению с размерами самого здания. Поэтому
изображение в параллельной аксонометрии показалось бы HenpjBAO-
подобним, так как изображение в параллельной проекции есть вид
с очень большого (практически бесконечного) расстояния.

288
МЕТОДЫ ИЗОБРАЖЕНИЙ
§ 6. Построения на изображении
6.1. Построения на проекционном чертеже. Построения на изо-
изображении отличаются от воображаемых построений ') тем, что они
действительно выполняются. Постановка задачи такова: постро-
построить что-либо — значит изобразить это на рисунке.
Так как мы в этой статье рассматриваем только проекционные
методы изображения, то и в этом параграфе мы будем рассматривать
только построения на проекционном чертеже8).
6.2. Примеры. Рассмотрим два примера построений на проекционном
чертеже. Для простоты будем рассматривать только чертежи, постро-
построенные по методу параллельной
(а не центральной) проекции.
Задача 1. Построить пересе-
пересечение параллелепипеда плоско-
плоскостью L'M'\' (рис. 63). Точки V
и Л/ лежат соответственно на верх-
верхней и задней гранях, точка N лежит
на ребре fi'fij.
Решение. Проводим ЛШ, || ААХ.
Теперь Вг и Ж, — изобртжения про-
проекций точек Ы' и М' на верх-
верхнюю грань (направление проекти-
проектирования параллельно боковым реб-
ребрам). Следовательно, МгВ1—изобра-
МгВ1—изображение проекции прямой M'N' на
верхнюю грань. Точка X пересече-
пересечения МЫ и УМ,/?, изображает след прямой М'Ы' на верхней грани.
След секущей плоскости на верхней грани проходит через X'
и L'. Поэтому прямая XL изображает этот след. Отметим ее
отрезок EF, находящийся внутри параллелограмма A^fiJD^.
Теперь /W изображает след секущей плоскости на передней грани.
След секущей плоскости на задней грани изображается прямой ЕМ.
Обозначив точку пересечения этой прямой с СС, через О, найдем,
наконец, и след G/V секущей плоскости на правой грани.
Задача 2. Точка L' лежит в плоскости основания правильной
четырехугольной пирамиды, высота которой равна стороне осно-
основания (рис. 64). Опустить из точки L' перпендикуляр на грань
S'B'C, найти его основание М' и определить длину L'M', если
А'В' = а.
Рис. 63.
') См. стр. 200—203 статьи «Общие принципы геометрических по-
построений».
2) См. книгу Н. Ф. Четверухина [5], указанную в списке лите-
литературы в конце статьи.

ЛИТЕРАТУРА
289
Решение. Возьмем в плоскости основания вместо L' какую-
нибудь другую точку, из которой проведение перпендикуляра к грани
S'B'C не вызывает затруднений.
Такова, например, точка Е'—сере-
Е'—середина A'D'. Перпендикуляр из ?"
на грань S'B'C попадет на высоту
S'F' этой грани. На рис. 65 изо-
изображено сечение S'E'F' пирамиды в
натуральном виде (?'F' = S'Q' = а)
и проведена высота E'G'. Теперь
можно на рис. 64 найти точку G из
условия
F'S'_FS_
f4F~~FG
отрезки F'S' и F'G' даны на
рис. 65, и FS — на рис. 64).
Проведя прямую EG, мы узнаем рИ(. ь4
направление перпендикуляра. Все пер-
перпендикуляры к грани S'B'C' должны изображаться на рис. 64 пря-
прямыми, параллельными EG.
Вообразим плоскость а, проходящую через оба перпендикуляра
(из Е' и из L'). Ее след на плоскости основания изображается пря-
прямой EL. Следы плоскости а на гранях A'B'C'D' и S'B'C должны
пересекаться на прямой В'С. Отсюда вытекает следующее построение.
Находим точку X пересечения EL и ВС.
Проводим XG. Из L проводим прямую, парал-
параллельную EG, до пересечения с прямой GX в
точке Л1 Тогда Z.M и есть изображение перпен-
перпендикуляра, опущенного из V на грань S'B'C.
Определить истинную величину отрезка
L'M' легко, потому что истинная величина
отрезка E'G' известна (рис. 65).
Достаточно определить отрезок L'M' из
пропорции
L'M' _LM
где отрезок EG' берется с рис. 65, а отрезки LM и EG — с рис. 64.
ЛИТЕРАТУРА
[1] Н. А. Глаголев, Начертательная геометрия, М., Гостехиздат, 1953.
Учебник для математических отделеьий университетов, доступный
широкому кругу читателей. Содержит много задач.
[2]Е. А. Глазунов и Н. Ф. Четверухин, Аксонометрия, М., Гос-
Гостехиздат, 1953.
Обстоятельное руководство, весьма подробно трактующее учение о
параллельной аксонометрии.
19 Энциклопедия, кн. 4

290 МЕТОДЫ ИЗОБРАЖЕНИЙ
[3] Г. М о и ж, Начертательная геометрия, перев. с франц., М.—Л., Гос-
техиздат, 1947
Основополагающее сочинение известного французского геометра,
положившее начало начертательной геометрии; в этой книге весьма
обстоятельно разработан метод, называемый сейчас «методом Монжа».
[4| Н. Ф. Четверухнн, Изображения пространственных фигур в курсе
геометрии, М., Учпедгиз, 1958.
Пособие для учителей средних школ. Книга затрагивает многие
упоминавшиеся в статье вопросы.
[5] Н. Ф. Чет веру хин, Стереометрические задачи на проекционном
чертеже, М., Учпедгиз, 1955.
Пособие для учителей средних школ. Разобрано много примеров.
[6| Л. М. Лоповок, Сборник стереометрических задач на построение,
М., Учпедгиз, 1953.
[7] И. Г. Польский, Сборник задач на построение на проекционном
чертеже, М., Учпедгиз, 1958.

ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
СОДЕРЖАНИЕ
§ 1. Определение вектора ......... . 292
1.1 Параллельный перенос . 292
1.2. Вектор 293
1.3. Откладывание вектора от точки . . . . 294
1.4. Векторы и направленные отрезки . . 296
§ 2. Сложение векторов и умножение вектора на число 298
2.1. Сложение векторов 298
2.2. Противоположные векторы, нулевой вектор . . 300
2.3. Свойства суммы векторов ... . . 301
2.4. Вычитание векторов ... . . . 304
2.5. Умножение вектора на число . 305
2.6. Свойства произведения вектора на число . 307
2.7. «Арифметика фигур» . . 308
2.8. Деление отрезка в данном отношении . 310
2.9. Координаты вектора 312
2.10. Линейная зависимость векторов . 314
2.11. Примеры 315
§ 3. Скалярное произведение векторов 319
3.1. Проекция вектора на ось 319
3.2. Свойства проекций . 320
3.3. Связь проекций с координатами . 321
3.4. Связь с тригонометрическими функциями . . . 322
3.5. Примеры -324
3.6. Определение и свойства скалярного произведения . . 328
3.7. Примеры и задачи .331
3.8. Единственность скалярного произведения . 336
§ 4. Косое произведение векторов плоскости . . 338
4.1. Ориентированные площади и косое произведение векторов . 338
4.2. Аналогия между косым и скалярным произведениями . 342
4.3. Дальнейшие свойства косого произведения . 343
4.4. Примеры и задачи . 345
4.5. Вопрос о единственности косого произведения 349
§ 5. Тройное произведение и векторное произведение векторов про-
пространства ....... 351
5.1. Ориентированные объемы и тройное произведение . 351
5.2. Векторное произведение и его связь с тройным произведением 353
5.3. Свойства векторного и тройного произведений . 355
5.4. Двойное векторное произведение . 360
5.5: Примеры . . . 361
5.6. Вопрос о единственности тройного и векторного произведений 364
19»

292
ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
§ 6. Применения векторного исчисления к сферической геометрии и
тригонометрии 366
6.1. Выражение сторон и углов сферического треугольника с по-
помощью векторов . . . 366
6.2. Сферические теоремы косинусов и синусов 368
§ 7. Понятие о векторных пространствах 369
7.1. Аксиоматическое определение векторного пространства . - 369
7.2. Арифметическая модель векторного пространства 370
7.3. Полнота аксиоматики векторного пространства 371
7.4. Аксиоматика элементарной геометрии ... 375
7.5. Некоторые типы многомерных пространств 377
Литература . . 380
§ 1. Определение вектора
1.1. Параллельный перенос. Напомним прежде всего определе-
определение параллельного переноса— геометрического преобразования, тесно
связанного с понятием вектора').
Параллельным переносом плоскости (или пространства) на-
называется преобразование, переводящее каждую точку А плос-
плоскости (пространства) в такую
точку А', что выполнены следу-
следующие три условия:
1°. Отрезок АА' параллелен
заданной прямой I.
2°. Длина отрезка АА' име-
имеет заданную величину а.
3°. Направление отрезка АА'
(от точки А к точке А') сов-
совпадает с заданным на прямой
I направлением.
(Заметим, что на каждой пря-
Рис. 1.
условиями
мой можно выбрать два про-
противоположных направления.) Ха-
1°—3° преобразования ясен из
рактер описываемого
рис. 1.
Сравним определение параллельного переноса с определением раз-
разного рода симметрии — геометрических преобразований, которые из-
издавна изучаются в школе и хорошо известны преподавателям
и учащимся. Центральная симметрия полностью определяется
заданием одной точки — центра симметрии О (каждая точка А пере-
переходит при центральной симметрии в такую точку Л', что отрезок АА'
делится в точке О пополам, рис. 2). Осевая симметрия (рис. 3)
определяется заданием одной прямой—оси симметрии; симметрия
относительно плоскости (в пространстве, рис. 4) также опреде-
') Ср. статью «Геометрические преобразования», стр. 54.

ОПРЕДЕЛЕНИЕ ВЕКТОРА
293
ляется заданием одного геометрического объекта—плоскости сим-
симметрии. Параллельный перенос определяется сложнее, чем симметрии:
для его задания нужно указать прямую, направление на ней и
длину а. Таким образом, геометрический образ, связанный с парал-
Рис. 2.
Рис. 3.
лельным переносом, «сложнее», чем геометрические образы, связан-
связанные с симметриями разного рода. Впрочем, эта «сложность» в зна-
значительной степени субъективная, кажущаяся. Она объясняется тем,
что геометрический образ, связанный с параллельным переносом
(таковым, как мы сейчас
увидим, и является вектор),
непривычен для нас и
в силу этого кажется слож-
сложнее.
1.2- Вектор. Что же та-
такое вектор? Как ни странно,
ответ на этот вопрос пред-
представляет известные затруд-
затруднения. Существуют различ-
различные подходы к определению
понятия вектора; при этом
даже если ограничиться лишь Рис. 4.
наиболее интересным для нас
в этой статье элементарно-геометрическим подходом к понятию вектора,
то и тогда будут существовать различные взгляды на это понятие.
Разумеется, какое бы определение мы ни взяли, вектор с элементарно-
геометрической точки зрения есть геометрический объект, характе-
характеризуемый направлением (т. е. заданной с точностью до параллель-
параллельности прямой и направлением на ней) и длиной. Однако такое
определение является слишком общим, не вызывающим конкретных
геометрических представлений. Согласно этому общему определению

294 векторы и их применения в геометрии
параллельный перенос можно считать вектором, ибо условия 1°—3°
(см. выше) как раз и показывают, что параллельный перенос харак-
характеризуется направлением и длиной. И действительно, можно было
бы принять определение: «вектором называется всякий параллельный
перенос». Это определение логически безупречно, и на его основе
может быть построена вся теория действий над векторами и их
применений. Однако это определение, несмотря на его полную кор-
корректность, также не может нас удовлетво-
удовлетворить, так как представление о векторе как
и геометрическом преобразовании кажется
недостаточно наглядным, далеким от физи-
физических представлений о векторных вели-
величинах.
ГЛы примем следующее определение
вектора: вектором называется семей-
семейство всех параллельных между собой,
Рис. 5. одинаково направленных и имеющих
одинаковую длину отрезков (рис. 5).
Таким образом, вектор представляет собой бесконечное мно-
множество направленных отрезков: из каждой точки плоскости (про-
(пространства) исходит один отрезок, причем все эти отрезки парал-
параллельны, одинаково направлены и имеют одну и ту же длину. Вектор
изображают на чертежах отрезком со стрелкой (т. е. изображают
не все семейство направленных отрезков, представляющее собой
вектор, а лишь один из этих отрезков). Для обозначения
векторов в книгах и статьях применяют жирные латинские буквы
а, Ь, с и т. д., а в тетрадях и на доске — латинские буквы с чер-
черточкой сверху а, Ь, с, ... Той же буквой, но не жирной, а светлой
(а в тетради и на доске — той же буквой без черточки)
обозначают длину вектора. Длину иногда обозначают
также вертикальными черточками — как модуль (абсолют-
(абсолютную величину) числа. Таким образом, длина вектора а
обозначается через а или | с|, а в рукописном тексте длина Рис. 6.
вектора а обозначается через а или \а\. В связи
с изображением векторов в виде отрезков (рис. 6) следует помнить,
что концы отрезка, изображающего вектор, неравноправны:
стрелка (задающая направление вектора) направлена от одного конца
отрезка к другому. Различают начало и конец вектора (точнее,
отрезка, изображающего вектор).
1.3. Откладывание вектора от точки. В связи с тем, что век-
вектор представляет собой семейство всех равных, параллельных и
одинаково направленных отрезков, для любой точки А плоскости
(пространства) найдется в этом семействе отрезок, начинаю-
начинающийся в точке А. Нахождение такого отрезка называют откла-
откладыванием вектора а от данной точки А (рис. 7). Эта операция,

ОПРЕДЕЛЕНИЕ ВЕКТОРА '29Ъ
очевидно, сводится к построению отрезка, равного и параллельного
данному, начинающегося в точке А. Итак, любой вектор а можно
отложить от любой заданной точки А. Если В—конец построенного
таким образом отрезка (рис. 7), то пишут
а^=АВ. A)
Последнее равенство означает, что, откладывая от точки А век-
вектор с, мы получаем отрезок АВ, направленный от точки А к точке В.
В связи с этим иногда бывает удобным обозначать векторы такими
символами, как АВ, ОА, и т. д., где А, В, О—произвольные точки.
При этом следует помнить всегда, что АВ есть не все семейство
отрезков, составляющее вектор, а лишь один отрезок
этого семейства, но такая запись не вызывает недо-
недоразумений, так как этот отрезок полностью опреде-
определяет все семейство.
В целях математической строгости можно были
бы условиться применять обозначение АВ для напра-
направленного отрезка с началом в точке А и концом Рис. 7.
в точке В, сохраняя обозначение а для вектора,
т. е. для всего семейства направленных отрезков1). В таком случае
запись A) была бы некорректной (нельзя приравнять все бесконечное
семейство одному его представителю) и ее было бы более правиль-
правильным заменить записью
^АВ ?а, B)
означающей, что направленный отрезок АВ принадлежит семей-
семейству отрезков (т. е. вектору) с. Однако замена более правильной
записи B) записью A) не будет вызывать недоразумений, в связи
с чем мы всегда в дальнейшем будем пользоваться записью A) при
откладывании векторов.
Теперь мы можем точно и кратко охарактеризовать параллель-
параллельный перенос. Параллельный перенос есть преобразование плоскости,
переводящее точку А в такую точку А', что АА' = а, где а —
заданный вектор. Мы видим, что, подобно тому как симметрия
любого рода определяется одним геометрическим объектом, а именно
центром, осью или плоскостью симметрии, так и параллельный пере-
перенос определяется одним геометрическим объектом, а именно век-
вектором а. Этот вектор называется вектором параллельного пере-
переноса. Однако, для симметрии объект, определяющий преобразование
') Направленный отрезок иногда называют «связанным вектором»
в противоположность «свободному вектору», представляющему собой то
понятие, которое мы здесь обозначаем просто словом «вектор» (семейство
направленных отрезков). Мы, однако, не будем в настоящей статье при-
применять эту терминолоЛию.

296 ВЕКТОРЫ И ИХ ПРИМРНЕНИЯ В ГЕОМЕТРИИ
(точка, прямая или плоскость), является знакомым издавна, а
объект, определяющий параллельный перенос, приходится вводить
в рассмотрение заново.
1.4. Векторы и направленные отрезки. Весьма часто понятию
вектора дается другое определение, а именно следующее: вектором
называется направленный отрезок. При этом векторы (т. е. на-
направленные отрезки), имеющие одинаковую длину и одно и то же
направление (рис. 8), уславливаются считать равными. Конечно,
такое определение страдает математической непоследовательностью,
ибо «равные векторы»—это то же самое, что «один и тот же век-
вектор» (подобно тому как «равные числа»—это
«одно и то же число»), а направленные отрез-
отрезки, изображенные на рис. 8, не совпадают
друг с другом. При таком определении про-
Рис. 8. исходит подмена математических понятий, а
именно подмена понятия равенства понятием
эквивалентности. Равенство двух математических объектов имеет
место тогда и только тогда, когда эти объекты совпадают,
т. е. когда мы дважды рассматриваем один и тот же объект.
Эквивалентностью же считают всякую связь между математиче-
математическими объектами, обладающую следующими тремя свойствами:
I. Всякий объект эквивалентен самому себе («рефлексив-
(«рефлексивность»).
И. Если один объект эквивалентен второму, то и второй
эквивалентен первому («с и м м е т р и ч н о с т ь»).
III. Если один объект эквивалентен второму, а второй-
третьему, то первый объект эквивалентен третьему («т р а н з и-
т и в н о с т ь»).
Например, подобие геометрических форм является эквива-
эквивалентностью (ибо выполнение свойств I—III здесь очевидно). Разу-
Разумеется, равенство является частным случаем эквивалентности, но
эквивалентность отнюдь не всегда сводится к равенству (как пока-
показывает пример подобных фигур). Если мы условимся считать направ-
направленные отрезки, у которых длины и направления совпадают, экви-
эквивалентными, то мы получим отношение эквивалентности (условия
I — III выполняются), но это, конечно, не есть равенство. Таким об-
образом, приведенное выше определение можно счесть некорректным: то,
что в этом определении признается «равенством» направленных отрез-
отрезков (векторов), в действительности является лишь эквивалентностью.
Для устранения некорректности такого вида в математике существует
стандартный прием: все эквивалентные между собой объекты собираются
вместе, в один «класс эквивалентности», и этот класс эквивалентности и
объявляется тем новым объектом, который следует изучать. Именно так
(сознательно или бессознательно) мы поступаем, когда вводим простые
дроби. Отношения 2:3, 4:6, 10:15, 36:54 и т. д. обладают тем свойством.

ОПРЕДЕЛЕНИЕ ВЕКТОРА 297
что любые два из них образуют «верную» пропорцию (в том смысле, что
произведение средних членов в такой пропорции будет равно произведе-
произведению крайних членов); мы признаем такие отношения «эквивалентными»,
и получающийся таким образом класс эквивалентности объявляем одним
B 4 \
или — =—- I
становится «настоящим равенством»; до этого его следовало бы, строго
говоря, понимать именно как эквивалентность, а не как утверждение о
том, что в записи 2:3 = 4:6 в левой и в правой частях равенства написано
«одно и то же».
Аналогично обстоит дело и с «равенством» треугольников (или других
фигур). Изображенные на рис. 9 треугольники, разумеется, не одинаковы,
т. е. не совпадают; поэтому более строгим было бы говорить о них
как об эквивалентных, а не о равных ').
Но в геометрии принято считать два
совпадающих при наложении тре-
треугольника одним и тем же
треугольником, т. е. понимать под
словом «треугольник» сразу весь
класс треугольников, каждые
два из которых можно совместить дви-
движением. Только после этого соглаше-
соглашения приобретают смысл распространен
ные утверждения вроде того, что «зада-
«задача построения треугольника по двум
сторонам а и b и заключенному между
ними углу С имеет единственное рис g
решение» (т. е. что существует лишь
один треугольник с данными сторо-
сторонами а и Ь и углом С) — без этого нового понимания слова «треугольник»
последнее утверждение будет явно неверным2). И лишь это более широкое
понимание слова «треугольник» (не подчеркиваемое в школе явно) делает
законным употребление термина «равные треугольники» г).
То же можно сказати и относительно направленных отрезков. Направ-
Направленные отрезки, изображенные на рис. 8, следует считать лишь «эквива-
«эквивалентными», а не «равными». Если же собрать все эквивалентные направ-
направленные отрезки в один класс направленных отрезков, то такой
класс эквивалентности как рач и будет семейст-ЮМ всех параллельных,
одинаково направленных отрезков одной и той же длины. В результате
мы приходим к принятому нами определению вектора как семейства на-
направленных отрезков. Это определение более корректно, чем определение
вектора kjk одного направленного отрезка.
') Иногда треугольники, изображенные на рис. 9, называют не «рав-
«равными», а «конгруэнтными», т. е. ьводят для эквивалентности фигур, вы-
выражающейся свойством «совпадать при наложении», название конгруэнт-
конгруэнтность. Такая терминология логически безупречна, но сравнительно мало
распространена.
2) Таким образом, строго говоря, сформулированное выше утвержде-
утверждение о задаче построения треугольника по сторонам о иби углу С означает:
существует единственный «класс равных треугольников», такой, что все тре-
треугольники этого класса имеют заданные стороны а, Ь и заданный угол С
(но, конечно, вовсе не единственный треугольник!).
*) Эта точка зрения допускает и дальнейшее развитие. См. по этому
поводу § 6 статьи «Геометрические преобразования», стр. 98—110.

298
ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
§ 2. Сложение векторов и умножение вектора на число1)
2.1. Сложение векторов. Все сказанное пока еще не делает
понятие вектора содержательным и полезным. Большую содер-
содержательность и богатую возможность применений понятие вектора
получает тогда, когда мы вводим своеобразную «геометрическую
арифметику»—арифметику векторов, позволяющую складывать век-
векторы, вычитать их и производить над ними целый ряд других
операций. Отметим в связи
с этим, что ведь и понятие чис-
числа становится интересным
лишь при введении арифметиче-
арифметических действий, а не само по
себе2).
Сумма векторов опреде-
определяется в связи с «суммой»
соответствующих параллельных
переносов, причем сумма парал-
параллельных переносов3) понимается
в том смысле, что эти переносы
выполняются один за другим.
Рис. ю. На рис. 10 показано последо-
последовательное выполнение двух
параллельных переносов. Если первый перенос переводит точку А
в точку В, т. е. характеризуется вектором АВ, а второй переводит
точку В в точку С, т. е. характеризуется вектором ВС, то в ре-
результате выполнения обоих переносов точка А переходит в точку С.
Если взять другие точки А', В', С", перехолящие друг в друга
') Ср. со статьей «Векторные пространства и линейные преобразова-
преобразования» в кн. II ЭЭМ.
2) Сама по себе связь понятия вектора с таким простым преобразо-
преобразованием, как параллельный перенос, еще не создает содержательной «тео-
«теории векторов». Заметим в этой связи, что, скажем, с таким преобразова-
преобразованием, как сжатие к прямой (см. статью «Геометрические преобразования»,
стр. 55), можно сопоставить «геометрический образ», задаваемый прямой
<осью сжатия) и числом (коэффициентом сжатия); однако это будет совер-
совершенно бессодержательной процедурой, поскольку вся теория таких «об-
«образов» ограничится их определением В противоположность этому образ,
сопоставляемый с произвольным аффинным преобразованием (стр. 62), иг-
играет серьезную роль в современной высшей геометрии; это связано с тем,
что для подобных образов (называемых аффинорами) удается опреде-
определить операции сложения и умножения. [Заметим, что возможност! постро-
построить «арифметику векторов» и «арифметику аффиноров» тесно связана с тем,
что геометрические преобразования, с которыми сопоставляются эти новые
понятия,— параллельные переносы и аффинные преобразования — образуют
группы (см. статью «Геометрические преобразования», стр. 102).
*) В статье «Геометрические преобразования» употреблялся термин
«произведение» (преобразований). В научной литературе в одном и том же
смысле используются оба термина — «сумма» и «произведение»

СЛОЖЕНИЕ ВЕКТОРОВ И УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО 299
при этих переносах (так что А'В' АВ и В'С ВС), то точка А'
переходит в результате выполнения обоих переносов в точку С".
Из рис. 10 видно, что Д ABC = Д А'В'С (по двум сторонам и
заключенному между ними углу), так что отрезки АС и А'С равны;
кроме того, эти отрезки параллельны и одинаково направлены, так
как они образуют одинаковые углы с направленными отрезками АВ
и А'В' (или ВС и В'С). Иначе говоря, АС=А'С. т. е. перемеще-
перемещение исходной фигуры в последнее ее положение таково, что все
отрезки, соединяющие соответствующие точки этих фигур, равны и
параллельны. Следовательно, это перемещение также представляет
собой параллельный перенос. Он называется суммой двух последо-
последовательно применявшихся параллельных переносов.
Если мы обозначим через а вектор первого параллельного пере-
НОСЗ у Т. С —рг~ • .
а через Ь — вектор второго параллельного переноса, т. е.
Ь = ВС = В'С.
то результирующий параллельный перенос будет характеризоваться
вектором
Этот вектор с результирующего
параллельного переноса называет-
называется суммой векторов а и Ь, что
выражается записью
с = а + Ь.
Если теперь оставить только
-1— РИС. 11.
векторы а= АВ, b — ВС иС=АС
на рис. 10, то мы приходим к рис. 11, который показывает построе-
построение суммы векторов:
Для построения суммы векторов нужно взять направленные
отрезки, изображающие эти векторы и расположенные таким
образом, что начало второго отрезка совпадает с концом пер-
первого; тогда «.замыкающий-» направленный отрезок, т. е. отрезок,
соединяющий начало первого отрезка с концом второго, будет
изображать сумму двух взятых векторов.
Рис. 11 и данное выше правило сложения векторов приводят нас
также к следующему простому, но важному выводу: для любых
трех точек А, В, С имеет место равенство
ТВ+ВС=АС. C)
Заметим, что это равенство справедливо при любом располо-
расположении точек А, В, С и не требует чертежа, что часто бывает важно.

300
ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
Из соотношения C) и из известных неравенств, связывающих
стороны треугольника, следует, что длина вектора-суммы всегда
не больше суммы длин векторов-слагаемых и не меньше их раз-
разности:
Ясно, что в первом из соотношений D) знак равенства будет иметь
место тогла и только тогда, когда векторы а и b параллельны и
/а+Ь
Рис. 12.
направлены в одну сторону (рис. 12, а): сумма двух параллельных
и одинаково направленных векторов представляет собой вектор,
направленный в ту же сторону, что и слагаемые; длина его
равна сумме длин векторов-слагаемых (рис. 12, а). Во втором из
соотношений D) знак равенства будет иметь место тогда и только
тогда, когда векторы а и b параллельны, но направлены в разные
стороны (причем вектор а имеет большую длину, рис. 12, б): сумма
двух параллельных и противоположно направленных векторов
представляет собой вектор, направлен-
направленный в ту же сторону, что и тот из
слагаемых векторов, длина которого
больше; длина вектора-суммы равна
разности длин слагаемых векторов.
2.2. Противоположные векторы, ну-
нулевой вектор. Остановимся еще на слу-
случае, когда векторы а и b направлены
в противоположные стороны и имеют равные
длины (рис. 13); такие векторы назы-
называются противоположными. Примером противоположных векторов
являются векторы АВ и ВА, где А и В—какие угодно точки. Наше
правило сложения векторов приводит к тому, что сумма АВ-\-ВА
двух противоположных векторов представляет собой «вектор» АА,
имеющий нулевую длину и не имеющий никакого направления; этот
«вектор» изображается «отрезком нулевой длины», т. е. точкой.
Может быть, читателю покажется нежелательным считать, что
Рис. 13.

СЛОЖЕНИЕ ВЕКТОРОВ И УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО 301
АА— тоже вектор, ни мы вынуждены стать на эту точку зрения,
так как иначе оказалось бы, что некоторые два вектора (противо-
(противоположные векторы АВ и ВА) вовсе нельзя сложить.
Итак, АА мы также считаем вектором; этот вектор называется
нулевым вектором и обозначается символом 0:
АА = ВВ=СС—. = 0
{А, В, С—любые точки плоскости или пространства). Для любого
вектора а = АВ мы имеем
АВ + В~В=А~В,
или, иначе,
а + 0 = а. E)
Это равенство, напоминающее знакомое из арифметики равенство
й-)-0 = й; и послужило причиной
того, что вектор АА называется
«нулевым» вектором. Далее, для лю-
любых двух точек А, В мы имеем:
АВ + ВА = АА, т. е.
АВ+ВА = 0. F)
2.3. Свойства суммы векторов.
Установим теперь дальнейшие свой-
свойства операции сложения векторов.
Докажем прежде всего, что сложение
векторов коммутативно (переместительно), т. е. что для любых
двух векторов а и Ь справедливо равенство
G)
Для доказательства этого равенства обратимся к рис. 14, на кото-
котором изображен параллелограмм, сторонами которого служат векторы
а=~ОА = В~С и Ь=ОВ = ~АС. Мы имеем
ОС, ОВ + ВС=ОС,
или, иначе,
— ОС,
откуда и следует равенство G). Заметим, что это доказательство
применимо лишь в случае, когда векторы а и Ь не параллельны.
Если же векторы а и Ь параллельны, го равенство G) непосредст-
непосредственно следует из приведенного на предыдущей странице описания
сумм одинаково направленных и противоположно направленных век-
векторов.

302 ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
В фигуре, изображенной на рис. 14, нетрудно увидеть пра-
правило параллелограмма, применяющееся в физике для опре-
определения суммы векторов («параллелограмм сил»): сумма векторов
ОА и ОВ равна вектору ОС, изображаемому диагональю парал-
параллелограмма ОАСВ (построенного на векторах ОА и ОВ). Сле-
Следует отметить, что «правило параллелограмма» менее удобно для
определения суммы векторов, чем использованное выше определение
суммы векторов на основе равенства C): «правило параллелограмма»
теряет смысл в случае параллельности векторов-слагаемых и нуж-
нуждается в этом случае в дополнительных разъяснениях, в то время
как равенство C) справедливо во всех случаях. В тех же случаях,
когда векторы-слагаемые не параллельны,
правило параллелограмма и принятое выше
определение сложения лишь формой от-
отучаются друг от друга.
Можно еще определить сумму векто-
векторов следующим способом: вектор ОС
называется суммой векторов ОА = а и
ОВ Ь, если середины отрезков ОС и АВ
совпадают (рис. 15). Это правило сло-
сложения, очевидно, эквивалентно данному
Put 15- выше; оно применимо всегда (даже если
векторы а и b параллельны).
Как и в арифметике чисел, в «арифметике» векторов справедлив
ассоциативный (сочетательный) закон сложения векторов, выража-
выражаемый равенством
(8)
Для доказательства мы отложим от произвольной точки О вектор
0А = а, от точки А—вектор АВ = Ь и от точки В — вектор ВС=с.
Тогда мы имеем (см. C))
(а + Ь) + с = (ОА + ~АВ) + ВС-- ОВ+ВС = ОС,
откуда и следует равенство (8). Заметим, что приведенное доказа-
доказательство совсем не использует чертежа. Это характерно (при неко-
некотором навыке) для решения задач и доказательства теорем при по-
помощи векторов. При желании читатель может повторить вывод
соотношения (8), интерпретируя написанные соотношения на рис. 16.
Равенство (8) позволяет записывать сумму трех векторов просто
в виде а-\-Ь + с (без скобок), а вывод соотношения (8) (или рис. 16)
убеждает нас в том, что эта сумме представляет собой замыкаю-

СЛОЖЕНИЕ ВЕКТОРОВ И УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО
303
щую этих трех векторов, отложенных один за другим. Иначе говори
oa+Jb+bc=oc
для любых четырех точек О, А, В, С. То же справедливо
и для любого числа слагаемых: если несколько векторов отло-
отложены таким образом, что начало второго совпадает с концом первого,
0
В
0 (а*Ь)*с=а+(Ь*с)
Рис. 16.
Рис. 17.
начало третьего — с концом второго и т. д., то замыкающая, т. е.
вектор, соединяющий начало первого вектора с концом последне-
последнего, представляет собой сумму всех взятых векторов. Например,
А~В+В~С+СО + Ш= АЁ
(рис. 17).
Из того, что сумма нескольких векторов может быть определена
как замыкающая, непосредственно вытекает следующее условие
замкнутости векторного многоугольника. Пусть а, Ь, с, не-
несколько векторов; отложим
их последовательно один за
другим (т. е. так, чтобы
начало второго совпадало
с концом первого, начало
третьего — с концом вто-
второго и т. д.). Для того что-
чтобы получающаяся ломаная,
составленная из векторов
(она может оказаться не-
невыпуклой и даже пересекаю-
пересекающей себя), была замкнутой
(т. е. чтобы конец последнего вектора совпадал с началом первого,
рис. 18), необходимо и достаточно, чтобы сумма всех этих векторов
была равна нулевому вектору
Рис. 18.

304 ВЕКТОРЫ И .ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
Соотношения G) и (8), т. е. коммутативный и ассоциативный
«коны для сложения векторов, записываются точно так же,
как и аналогичные законы для сложения чисел. Это очень важно и
удобно, так как позволяет, не переучиваясь, производить действия
над равенствами, содержащими векторы, используя навыки, вырабо-
выработанные при изучении действий над числами. Аналогия между чис-
числами и векторами, как мы сейчас увидим, простирается и далее,
при определении вычитания векторов и действиях над равенствами.
2.4. Вычитание векторов. Обратимся к операции вычитания
векторов. Как и в случае чисел, разностью
х = а—Ь (9)
векторов а и Ь назовем такой вектор л:, который в сумме с век-
вектором Ь дает вектор а:
Ь-\-х = а. A0)
Иначе говоря, равенство (9) по определению означает, чго
справедливо соотношение A0). Существует ли вектор д:, который
(при заданных а и Ь) удовлетворяет соотношению A0)? Рис. 19
изображает соотношение A0); на нем векторы а=ОА и Ь = ОВ от-
отложены от одной точки О. Из этого рисунка видно, что разностью
векторов ОА и ОВ является вектор ВА:
0А—~бВ = Ш.
Впрочем, это следует непосредственно и из соотношения C), так как
Итак, для получения разности а—Ъ достаточно отложить
лекторы а и Ь от одной точки и взять вектор, идущий из конца
вектора Ъ к концу вектора а. Таким
образом, операция вычитания векторов
всегда вы пол ни м а. Эта операция,
кроме того, однозначна (т, е. если
Ь-\- х = 6-)-_у, то х=у, в чем предо-
предоставляем убедиться читателю).
Разность а — а двух равных векто-
векторов, очевидно, является нулевым век-
Рис. 19. Т°Р°М а~а = 0. A1)
Далее, век тор 0 — а является вектором, противоположным век-
гору а: находя разность 0 — а по данному выше правилу нахождения
разности, мы видим, что вектор 0 — а изображается тем же отрезком,
что и вектор а, но направлгнным в противоположную сторону:
А~А — АВ=ВА
(ср. F)). Для краткости вектор 0 — а, противоположный вектору а,
обозначают символом—а.

СЛОЖЕНИЕ ВЕКТОРОВ И УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО
Мы уже знаем, что
ЗОГ,
Рис. 20.
(см. формулу F)); без труда проверяется также соотношение
а—Ь = а + (— Ь) A2)
Все эти равенства совершенно аналогичны привычным соотношениям,
выполняющимся для чисел. Формула A2) дает другое определение
операции вычитания: для того чтобы вычесть из некоторого век-
вектора вектор Ь, достаточно
прибавить к нему проти-
противоположный вектор —о.
Соотношения (9) и A0)
показывают справедливость
(для равенств, составленных
из векторов) хорошо изве-
известного правила: слагаемые
из одной части равенства
можно переносить в дру-
другую, меняя знаки на обрат-
обратные. Иначе говоря, при
сложении и вычитании век-
векторов сохраняются все свой-
свойства этих операций, известные из обыкновенной арифметики (ариф-
(арифметики чисел). Ниже мы покажем, что для векторов можно определить
также операции умножения, для которых сохраняются многие законы
обычной арифметики.
2.5. Умножение вектора на число. Введение операций умноже-
умножения для векторов естественно начать с описания процесса умноже-
умножения вектора на число. Положим прежде всего
0-а = 0, 1-а — а; A3)
далее определим произведение вектора на целое положитель-
положительное число п:
па = а + а + .. .-\-а. A4)
п. раз
Учитывая данное на стр. 300 правило сложении параллельных векторов
(см., в частности, рис. 12, а), получаем отсюда, что вектор па имеет
то же направление, что и вектор а, а длина его в п раз больше длины
вектора а: \па\ = п-\а\ (рис. 20, а). Далее, если положить
( — 1)а = — а, A4а)
то из естественного правила a (fta) — ((ф) а мы получим
( —п)а = п [(—!).«] = п-(—а) = — а + ( — а) + ...+(_«),
л раз
20 Энциклопедия, кн

306
ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
и потому направление вектора (—п)а противоположно направлению
вектора а и |( — л)а| = л-|а| (рис^ 20,6). Далее, векторы —аи
а (где т — целое положительное) определим из равенств
т-
— а =1 а = а и т-\ а\=(--1)а = — а A
\ т I m J
Отсюда и из данного выше определения произведения целого поло-
1
жительного числа на вектор заключаем, что вектор — а имеет то же
1
направление, что и вектор а, и в m раз меньшую длину: а
=—-|а|(рис. 21,а); направление вектора —а противоположно
направлению вектора а, а длина его в m раз меньше длины вектора а:
а\ = —-\а\ (рис. 21,6). Наконец, положив
m \ m ' '
п I 1 \ п ( 1 \
— а = п[—а] и а = п[ а
га \ m I m \ m J
A6)
получим, что вектор "Ка, где КфО — любое рациональное чи-
число, имеет то же направление, что и вектор а при Х>0 и про-
противоположное направление
при /,<0, а длина вектора ка
равна произведению абсолют-
абсолютной величины числа Я на длину
вектора а (т. е. |Я,а| = |Я,|-|а|).
С некоторой натяжкой можно
считать, что это правило со-
сохраняет силу и при к = 0 (см.
первую из формул A3); заме-
Рис. 21. тим, что нулевой вектор 0 во-
вообще не имеет направления).
Условимся теперь считать, что выделенное курсивом правило
справедливо для любых вещественных (не только рациональных) чи-
чисел X. Другими словами, будем считать, что произведение К-ОА
представляет собой вектор ОА' определяемый следующими усло-
условиями:
1) точка А' лежит на прямой ОА;
2) отношение ОА':ОА равно \к\, т. е. равно к при к>0 и рав-
равно— к при к<0;
3) точки А и А' лежат (на прямой ОА) по одну сторону от
точки О при к>0 и по разные стороны от точки О при к<0.

СЛОЖЕНИЕ ВИКТОРОВ И УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО
307
Из этого определения видно, что операция умножения вектора на
число тесно связана с преобразованием гомотетии1):
гомотетия с центром О и коэффициентом КфО (рис. 22,я, б)
переводит каждую точку А в такую точку А', что
ОА'=К-ОА.
A7)
2.6. Свойства произведения вектора на число. Указанные выше
свойства A3) — A6) операции умножения вектора на число напоми-
напоминают хорошо известные свойства операции умножения чисел. Следу-
Следующие три свойства также подчерки-
подчеркивают эту аналогию:
A8)
A9)
B0)
Доказательство свойств A8) —
B0) несложно. Рассмотрим, например,
соотношение A8). При а=0 оно оче-
очевидно. Если же а=^0, то из опреде-
определения операции умножения вектора
на число сразу следует, что векторы,
стоящие в обеих частях соотноше-
соотношения A8), параллельны вектору а и
имеют одну и ту же длину (равную
| k | • | /1 ¦ | а |). Поэтому остается толь-
только проверить, что векторы, стоящие в
левой и правой частях соотношения
A8), одинаково направлены; это без труда устанавливается с учетом
знаков чисел k и /. Далее, полное доказательство равенства A9) легко
получить из определения операции умножения вектора на число и
правила сложении векторов, параллельных одной прямой (см. выше,
стр. 300). Наконец, соотношение B0) легко получить, построив па-
параллелограмм со сторонами ОА = а и ОВ=Ь и применяя к этому,
параллелограмму гомотетию с центром О и коэффициентом k; дей-
действительно, учитывая соотношение A7), мы имеем
k (а -+- Ь) = k (ОЛ +1ОВ) = k-OC= ОС' =ОА'
(см. рис. 23, а, б, на которых отдельно изображены случаи &>0 и
). Приведенное доказательство применимо лишь в случае, если
') См. статью «Геометрические преобразования», стр. 55.
20*

308
ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
фигура ОАСВ является параллелограммом, г. е. векторы а и Ъ не
параллельны одной прямой. Рекомендуем читателю самостоятельно
доказать равенство B0) для случая векторов, параллельных одной
прямой.
С
С
Рис. 23.
2.7. «Арифметика фигур». Введенные операции (сложение векторов и
умножение вектора на число) позволяют построить своеобразную «ариф-
«арифметику фигур», имеющую интересные приложения в геометрии. Дл. про-
простоты мы рассмотрим эту «арифметику» только на плоскости.
Выберем на плоскости некоторую точку О и назовем ее нулевой точкой
или началом, отсчета. Если теперь А и В—две произвольные точки пло-
плоскости, то суммой точек А и В мы назовем такую точку С, что
0С=Ш + 0В;
B1)
в этом случае мы будем писать просто С — А + В. (Ясно, что если точки
О, А. В не лежат на одной прямой, то С будет четвертой вершиной па-
параллелограмма, у которого три вер-
вершины расположены в точках О, А, В;
рис. 24.) Точно так же, если А — про-
?^^_ \. извольная точка плоскости и X — дей-
ствительное число, то произведением КА
мы будем считать такую точку ?>,что
мы будем в этом случае писать просто:
Рис. 24.
Из перечисленных выше свойств
сложения векторов и умножения век-
векторов на числа непосредственно вытекают следующие соотношения (А, В —
точки плоскости; % н \i—действительные числа):
(эту точку обозначают просто через А-\-В-\-С);

СЛОЖЕНИЕ ВЕКТОРОВ И УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО
309
Пусть теперь Ф, и Ф2—две плоские фигуры. Рассмотрим всевозможные
суммы Л,+Л2, где Л, и Аг — произвольные точки фигур ф, и Ф2 соответ-
соответственно. Точки А, + А2 заполняют некоторую плоскую фигуру Ф (рис. 25).
которую мы будем называть суммой фигур Ф, и Ф2 и будем обозначать
символом Ф, + Ф2. Если каждая из фигур Ф,, Ф2 состоит из одной точки,
то Ф, + Ф2 будет суммой этих точек; другими словами, сложение
Рис. 25.
фигур является обобщением сложения точек. Аналогично, фигуру %Ф
мы определим как фигуру, образованную всеми точками %А, где А — про-
произвольная точка фигуры Ф (рис. 26). Иначе говоря, фигура КФ получается
из фигуры Ф с помощью гомотетии с центром О и коэффициентом К.
Из свойств сложения точек сразу следуют соотношения
(Ф, + Ф?) + Ф3 = Ф, + (Ф2
(эту сумму мы будем обозначать просто через Ф! + Ф2 + Ф3) и т. д.
Укажем в качестве примера, что если Ф, и Ф2 — непараллельные от-
отрезки, то сумма Ф, + Ф2 является параллелограммом (рис. 27) Суммы
фигур обладают многими интересными
свойствами, делающими плодотворным
употребление в геометрии этогэ поня-
понятия. Так, например, можно доказать,
что если плоские фигуры Ф, и Ф2 выпу-
выпуклые'), то периметр фигуры Ф, + Ф2
равен сумме периметров фигур Ф, и Ф2.
Геометрия изучает свойства фигур,
не зависящие от их распэложения.
Данное же нами определение суммы
фигур, конечно, зависит от положе-
положения слагаемых; сверх того, оно еще
зависит и от выбора начала отсчета.
Это обстоятельство безусловно явля-
является серьезным недостатком определе-
определения. Нетрудно, однако, доказать, что при изменении начала отсчета и при
параллельном переносе слагаемых форма фигуры, являющейся суммой Ф, + Ф2,
не меняется; эта сумма лишь подвергается в результате параллельному
переносу. Вместе с тем поворот слагаемых може- существенно изменить
сумму.Так, на рис. 28,а изображена сумма двух равных между собой треуголь-
Рис. 27.
') Частным случаем выпуклых фигур являются выпуклые многоуголь-
многоугольники (см. в кн. V ЭЭМ статью о выпуклых фигурах и телах).

310
ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
ииков, а иа рис. 28, б—сумма тех же треугольников, один из которых по-
вернут на угол 180°.
Следует отметить, что между «арифметикой фигур» и арифметикой
чисел имеются существенные различия. Так, например, вообще говоря,
не существует «разности».
Ф,—Ф2 двух заданных фи-
фигур Ф, и ф2, т. е. такой
фигуры Ф, что Ф2 + Ф = Ф,;
в частности, можно без тру-
труда доказать, что не суще-
существует разности между тре-
треугольником и кругом.
Отметим, далее, что в
((арифметике фигур», вооб-
вообще говоря, не выполнены
такие соотношения, как
) = 2-Ф,
Рис. 28.
и т. д. Например, если Ф-
окружность радиуса г, то, как нетрудно видеть, фигура Ф + Ф будет кругом
радиуса 1г, а фигура 2Ф представляет собой окружность радиуса 1г.
2,8. Деление отрезка в данном отношении. Нижеследующие три
предложения очень удобны при решении многих задач геометрии
с помощью векторов.
Предложение 1. Если векторы а иЬ параллельны и афО.
то существует такое число k, что b = ka.
Доказательство очевидно.
Предложение 2. Пусть А. В и С—три точки (плоскости
или пространства), причем -„^
АфВ и Q — произвольная чет-
четвертая точка. Точка С тогда
и только тогда лежит на
прямой АВ, когда существует
такое число К. что
QC=7,QA + (l—7,)QB B2)
(рис. 29).
В самом деле, соотношение B2) можно переписать в виде
или, иначе,
или, наконец, в виде
Рис. 29.
QC— QB =
— QB),
ВС=1-ВА,
а это соотношение выполнено тогда и только тогда, когда векторы
ВС и ВА параллельны одной и той же примой, т. е. когда точка С
лежит на прямой АВ.

СЛОЖЕНИЕ ВЕКТОРОВ И УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО
311
Предложение 3. Пусть С—точка, делящая отрезок АВ
в отношении т:п (т. е. АС:СБ = т:п1)), и Q — произвольная точка
плоскости. Тогда
Й ^- <23>
Обратно, если выполнено соотношение B3), то точка С делит
отрезок АВ в отношении т:п.
В самом деле, соотношение B3) можно переписать в виде
QC= QA —
т-\-п
т-\-п
QB,
или, иначе,
QC—QA =
или, наконец, в виде
m + n
(QB—QA),
АВ,
а это и означает, что точка С делит отрезок АВ в отношении т:п
(рис. 30).
Рис. 30.
Рис. 31.
Отметим один важный частный случай предложения 3: точка С
тогда и только тогда является серединой отрезка АВ, когда
QC=^(QA+QB)
B4)
(Q—произвольная точка; рис. 31). Это вытекает из формулы B3)
при т = п (ср. рис. 30). Можно сказать и иначе: для того чтобы
точки А и В были симметричны относительно точки С, необхо-
необходимо и достаточно выполнение соотношения B4).
•) Нижеследующее рассуждение и формула B3) сохраняют силу и в том
случае, если отношение ЛС:Сб = т:п отрицателы о, т. е. отрезки
АС и СВ имеют разное направление (точка С лежит иа прямой АВ вне
отрезка АВ).

312 ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
2.9. Координаты вектора. До сих пор мы говорили лишь о таких
свойствах векторов, которые являются одними и теми же как в слу-
случае плоскости, так и в случае пространства. Теперь мы впервые от-
отметим различие между этими двумя случаями.
Пусть г = О/ и j=OJ — два произвольных вектора плоскости, не
принадлежащие одной прямой (рис. 32, а). Каждый вектор а = ОА
плоскости можно, как легко видеть, разложить на сумму двух век-
векторов а, = 0.4, и а1 = ОА1, направленных по тем же прямым, что и
векторы i, j: для этого достаточно построить параллелограмм OAxAAt,
Рис. 32.
две стороны которого имеют направление векторов i и J, а диаго-
диагональ совпадает с ОА (рис. 32, б; одно из двух слагаемых с, или аг
может и отсутствовать). В силу предложения 1 (стр. 310)
OA1 = x-Ol=xi, OA2 = y-OJ=yj,
где х и у—некоторые действительные числа, и потому
а = ОА = ~ОА, + ОА г = xi + yj.
Итак, если на плоскости фиксированы два ненулевых вектора
i, J, не параллельных одной прямой, то любой вектор а плоско-
плоскости можно представить в виде суммы
a = xi+yj, B5)
где х и у — действительные числа (зависящие, конечно, от вектора а).
Важно отметить, что числа х и у определяются вектором а одно-
однозначно. Действительно, если бы вектор а можно было двумя различ-
различными способами представить в виде суммы B5):
a = xti+yj, a = xj+ yj,

СЛОЖЕНИЕ ВЕКТОРОВ И УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО 313
то йы имели бы
или
(хi — хг) ' = (Уг —J\)/
Так как мы двумя различными способами представили а в виде
суммы B5), то хотя бы одно из равенств x1—xI, yt~yt места не
имеет. Пусть, например, ххфхг. Тогда
xl—x1J'
а это противоречит тому, что векторы i, j не параллельны одной
прямой.
Числа д: и у, однозначно определяемые вектором а по формуле B5),
называются координатами вектора а относительно пары векторов!, У
(или относительно системы коорди-
координат, определяемой векторами i, j).
Говорят также: вектор а имеет в
системе i, j координаты (х, у).
Аналогично этому, если i = Ol.
J= OJ, k = OK— три вектора про-
пространства, не принадлежащие одной
плоскости, то любой вектор а = ОА
можно представить в виде суммы
а = ал-{-аг-{-а,, где векторы ах, а2
и аг принадлежат прямым OJ, OJ и
ОК. Для доказательства достаточно построить параллелепипед
OA^A^^CAD, три ребра OAt, OA2 и СМ, которого направлены по
прямым О/, OJ, ОК. (рис. 33; некоторые из векторов а,, аг и а, могут
превращаться и в нулевой вектор 0). Отсюда следует, что любой
вектор а пространства может быть представлен в виде суммы
a = xi + yj+zk, B6)
где х, у. z — действительные числа. Числа х, у, z к здесь одно-
однозначно определяются вектором а. Они называются координатами
вектора а в системе i, j, k.
Из формул B5) и B6) вытекает:
Если векторы а и Ь имеют координаты (хх, _у,) и (хг> у2) (или,
в пространстве, координаты (х,, yt, zt) и (хг, у2, гг)), то векторы
а + b и У.а имеют координаты (х1-\-хг, yt+yt) и (Kxl, Kyt) (или,
в пространстве, (xt+x2, yx+y2, zt+z2) и (A,*,, Kylt KzJ).
В самом деле, из правил, относящихся к сложению векторов и умно-
умножению вектора на число, сразу следует:
Если a = x1i + yj, a b = xj + yj, то
а + Ъ = (x,i + yj) + (xj + yj) = (хЛ + хг) i + (yt + _у2 )J

314 ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
ка = X (xj+yj) = (Kxj i + (lyjj,
что и доказывает наше утверждение. Разбор случая векторов в про.
странстве (векторов, имеющих три координаты), почти не отличаю
щегося от рассмотренного, мы предоставим читателю.
2.10. Линейная зависимость векторов. Отметим еще важное
понятие линейной зависимости векторов, которое будет использо-
использовано ниже, в § 7. Векторы а,, . .., ak называются линейно зависи-
зависимыми, если существуют такие числа а, ak. среди которых есть
хотя бы одно отличное от нуля, что
Если таких чисел а,, . . ., ak подобрать нельзя, то векторы av . . .,ah
называются линейно независимыми. Имеют место следующие пред-
предложения:
Если два вектора параллельны одной прямой, то они линейно
зависимы. Если три вектора параллельны одной плоскости, то
они линейно зависимы. Любые четыре вектора в пространстве
линейно зависимы.
Справедливость первого предложения вытекает из предложения 1
на стр. 310. Пусть теперь а, Ь, С — три вектора, параллельные одной
плоскости. Если векторы a, b параллельны одной прямой, то между
ними существует линейная зависимость: аа-\- fib — G, и потому между
векторами а, Ь, с имеется линейная зависимость на -f- fib + Ос = 0.
Если же векторы а и Ь не параллельны одной прямой, то, согласно B5).
С = xa-^-yb, где х, у — действительные числа, и потому между век-
векторами а, Ь, с имеется линейная зависимость xa~\-yb-\-(—1)с = 0.
Наконец, пусть а, Ь, с, й — четыре вектора пространства. Если век-
векторы а, Ь, С параллельны одной плоскости, то между ними сущест-
существует линейная зависимость: аа -\- fib -\- ус = 0, и потому между век-
векторами а, Ь, с, d имеется линейная зависимостьаа+ fib 4-ус-\-0d = 0.
Если же векторы а, Ь, с не параллельны одной плоскости, то, со-
согласно B6), d = xa-\-yb-\-zc, где х, у, z — действительные числа, и
потому между векторами а, Ь, С, d и в этом случае имеется линей-
линейная зависимость ха-\-yb-\-zc-f-(—l)d = 0.
Итак, в пространстве существуют три линейно независимых век-
вектора (три вектора, не параллельных одной плоскости), но любые че-
четыре вектора линейно зависимы. Этот факт обычно и имеют в виду,
когда говорят, что пространство имеет три измерения. Плоскость
имеет два измерения, так как на ней можно найти два линейно не-
независимых вектора (два вектора, не параллельных между собой), но
любые три вектора на плоскости линейно зависимы. Наконец, пря-
прямая имеет одно измерение. В математике рассматриваются также
пространства любого (и даже бесконечного) числа измерений. Не-

СЛОЖЕНИЕ ВЕКТОРОВ И УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО 315
сколько слов об этом читатель найдет ниже, в § 7 этой статьи '), а
подробная статья о многомерных пространствах будет помещена
в кн. V ЭЭМ.
2.11. Примеры. В заключение этого параграфа рассмотрим не-
несколько примеров решения задач с помощью векторов. Приводимые
ниже задачи имеют разную степень трудности: некоторые из них
являются вовсе не простыми. Однако, как увидит читатель, исполь-
использование векторов делает все эти задачи вычислительными, т. е. сво-
сводит геометрические рассуждения (с треугольниками, средними лини-
линиями и т. п.) к вычислениям с векто-
векторами, как правило, совсем не сложным.
Приведенные примеры хорошо иллюстри-
иллюстрируют и другие важные достоинства
векторного аппарата: возможность об-
обходиться без чертежей, почти неизбежно
иллюстрирующих лишь один частный слу-
случай разбираемой ситуации и тем самым
оставляющих сомнение в своей универ-
универсальности, параллельное доказательство
родственных (и зачастую разных по фор-
формулировке!) планиметрических и стереоме- Рис. 34.
трических фактов и т. д.
Задача 1. Доказать, что середины сторон произвольного
(не обязательно плоского!) четырехугольника являются вершинами
параллелограмма.
Решение. Пусть М, N, P, Q — середины сторон четырехуголь-
четырехугольника ABCD (рис. 34). Тогда
MN— QP-= MN + PQ={MB+BN) + (PD + DQ) =
= ±A~B + ±-~BC+±CD + ~DA =
Таким образом, MN=QP, т. е. противоположные стороны четы-
четырехугольнику MNPQ равны и параллельны. Следовательно, MNPQ —
параллелограмм.
Задача 2. Даны три тонки О,, О2, О, и еще одна точка М
(все эти точки могут и не лежать в одной плоскости!). Обозначим
через Л1, точку, симметричную М относительно точки О,, через
М2 — точку, симметричную Ж, относительно О2, через Мь — точку,
симметричную М2 относительно О,, через МЛ — точку, симмет-
') См. также статью, указанную в сноске1) на стр. 298.

316
ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
ричную М, относительно О,, через Мъ— точку, симметричную М1
относительно О2 и через Мв — точку, симметричную Мъ относи-
относительно Ог. Доказать, что точка Mt совпадает с исходной точ-
точкой М (рис. 35).
Решение. Пусть Q — какая угодно точка. Используя соотно-
шение_B4) (которое можно также переписать в виде соотношения
QA-{-QB=2QQ, мы можем условие задачи записать в виде следую-
., щей цепочки равенств:
\
Ms 7Ш
рис_ 35 Так как первое и второе из этих
равенств содержат вектор QMt ,
то с их помощью можно исключить этот вектор; второе и третье
равенства позволяют исключить вектор QM2 и т. д. В результате
окажется возможным вычислить вектор QMe. Это можно сделать,
последовательно подставляя значения векторов QMV QMt, ... в по-
последующие равенства, но проще сложить первое, третье и пятое из
выписанных равенств и вычесть из них второе, четвертое и шестое.
Тогда сразу получим
]_ пуй = 0, или Жм = О,
а это и означает, что точки М и М6 совпадают.
«Обычное» решение этой задачи (не использующее векторов) тре-
требует рассмотрения целого ряда треугольников и довольно утомительно.
Задача 3. Доказать, что медианы произвольного треуголь-
треугольника ABC пересекаются в одной точке и делятся в ней в отно-
отношении 2:1, считая от вершины.
Решение. Обозначим медианы треугольника через AD, BE, CF
и выберем еще одну произвольную точку Q (рис. 36). Согласно
формуле B4) мы имеем
Далее, точка Ж,, делящая медиану AD в отношении AM1:MlD= 2: 1
(рис. 37), удовлетворяет соотношению (см B3))
QA+^ QD QA + l A (WQQ)

СЛОЖЕНИЕ ВЕКТОРОВ И УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО 317
Совершенно такой же подсчет показывает, что если М2 и Мг — точки,
делящие медианы BE и CF в отношении 2:1, то
0Жа = QM, = j (QA + QB+ QC).
Таким образом, Ж,, Мг и М, — это одна и та же точка М (через
которую проходят все гри медианы).
Iе/ У
Рис. 36.
Из приведенного решения этой задачи вытекает следующий факт,
который удобно использовать при решении ряда других задач:
Пусть ABC—произвольный треугольник и М—точка пересе-
пересечения его медиан (она называется также центром тяжести
треугольника). Тогда при любой точке Q справедливо соотношение:
QM = -^ {QA + QB+QC). B7)
Задача 4. Медианой «.четырехвершинникаъ ABCD называется
отрезок, соединяющий одну из вершин (скажем А) с центром
тяжести треугольника, образованного тремя другими верши-
вершинами (треугольника BCD). Доказать, что четыре медианы
«.четыре х.вершинникаъ пересекаются в одной точке и делятся
в ней в отношении 3:1, считая от вершины (рис. 38, а, б).
Заметим, что слово «четырехвершинник» может означать как
обыкновенный плоский четырехугольник, так и треугольную пира-
пирамиду (тетраэдр); мы потому и используем этот новый термин, чтобы
подчеркнуть, что рассматриваются одновременно оба случая. Таким
образом, здесь мы имеем одновременно два разных предложения —
одно планиметрическое, а второе стереометрическое,—которые не
различаются по доказательству.

318
ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
Решение. Обозначим медианы «четырехвершинника» ABCD
через АА1У BBt, CCt, DDt и выберем еще одну произвольную
точку Q. Согласно формуле B7) мы имеем
QA1 = ~(QB + ~QC
Далее, точка Mt, делящая медиану АА1 в отношении AAlt :МХА1 = 3:1,
удовлетворяет соотношению (см. B3))
QM, =1 QA + j QAX = 4 QA + А A (QB+ QC+ QD)) =
Е
Совершенно такой же подсчет показывает, что точки М2, М,, Мх,
делящие в отношении 3:1 другие медианы, удовлетворяют тому же
соотношению. Таким образом, Mv Мг,
М„ Мл — эго одна и та же точка М,
через которую проходят все четыре
медианы.
Задача 5- Пусть Е, F; К, L\ M,
N — середины ч-сторонъ АВ и CD, AD
и ВС, АС и BD ^четырехвершинника^
ABCD. Доказать, что отрезки EF,
KL и MN пересекаются в одной точке
и делятся в этой точке пополам
(рис. 39).
Здесь тоже объединены следую-
следующие два с первого взгляда разные
предложения: 1) «.средние линии» EF и KL произвольного (пло-
(плоского) четырехугольника ABCD и отрезок, соединяющий середины
его диагоналей, пересекаются в одной точке и делятся в этой
точке пополам; 2) отрезки, соединяющие середины противопо-
Рис. 39.

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
319
ложных ребер произвольной треугольной пирамиды (тетраэдра),
пересекаются в одной точке и делятся в этой точке пополам.
Решение. Пусть Q—произвольная точка; середины отрезков
EF, KL и MN мы обозначим через Sx, S2 и S, (пока нам еще неиз-
неизвестно, что это — одна точка). С помощью формулы B4) получим:
— ' — QF=1(QC+QD);
~ql=~(QB+QQ;
QN=~(QB+QD).
Отсюда, в свою очередь, вытекает:
QS1=^(QE+QF)=i^"
QB+QC+QD),
, = ±-(QK+'QL) = i(QA+QD + ~QB+~QC),
Последние три формулы и доказывают совпадение точек Slt St
и 5, (ср. формулу G), стр. 301).
§ 3. Скалярное произведение векторов
3.1. Проекция вектора на ось. В этом параграфе мы будем
предполагать, что выбрана единица измерения длин.
Прямая линия, на которой задано некоторое направление (обычно
указываемое стрелкой), называется осью. Пусть/—некоторая ось и АВ—
Рис. 40.
направленный отрезок (рис. 40, а, б). Проекции точек Л и В на пря-
прямую / (т. е. основания перпендикуляров, опущенных из точек А и В
на прямую /; в случае векторов в пространстве это — точки пересечения

320
ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
прямой / с перпендикулярными к / плоскостями, проходящими через
точки А и В) мы обозначим через Л, и ??,. Длину отрезка AtB
взятую со знаком «-f-», если направление AtBt (от А1 к ?,) совпа-
совпадает с заданным на оси / направлением, и со знаком «—» в про-
противном случае, мы будем назы-
называть проекцией направленного от-
отрезка АВ на ось / и будем обозна-
обозначать ее через
пр, АВ= ± (длина ^,5,).
Если отрезок АВ перпендикулярен
оси /, то точки /4j и fit совпа-
совпадают, и пр гАВ оказывается
равной нулю. Легко видеть, что
Рис. 41. если направленные отрезки АВ
и CD определяют один и тот же
вектор, то их проекции на ось / одинаковы (ср. рис. 41, относящийся
к случаю векторов на плоское ги; заштрихованные треугольники,
очевидно, равны между собой). Поэтому можно говорить о проекции
вектора на ось. Проекцию вектора а на ось / мы будем обозна-
обозначать символом пр.га.
Проекцию вектора на ось можно определить еще следующим
образом. Пусть обозначения А, В, Ах, fi, имеют тот же смысл, что и
выше. Обозначим через / вектор длины 1, имеющий направление оси /
(рис. 42). Так как векторы AtBt и / параллельны одной прямой,
причем / ф 0, то в силу предложения
1 на стр. 310 мы можем написать
АхВх = х1, B8)
где х—действительное число. Легко ви-
видеть, что число х как раз равно искомой
проекции: —,
х — пр, АВ.
В самом деле, из соотношения B8) вы- Рис. 42.
текаег, что абсолютная величина числа
X равна длине отрезка AtBt, причем это число положительно,
если векторы AtBt и I одинаково направлены, и отрицательно в про-
противном случае.
3.2. Свойства проекций. Основные свойства проекций выража-
выражаются следующими двумя равенствами, в которых а и Ь—произволь-
Ь—произвольные векторы, а К—действительное число:
npl(a + b) = upla + nplb, B9)
npz (ha) = К - npz a. C0)

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
321
Соотношения B9) и C0) доказываются очень просто. В самом
деле, пусть а = АВ, b — ВС; тогда а-\- Ь = АС. Обозначим через Ах,
fi,, С, проекции точек А, В. С на ось /. Согласно B8) мы можем
написать
где
Но мы имеем
А ,?, = x'l, fi,C, = jc7, А ,С, = xl,
x' = npla, x"=nplb, x = n
xl = Л,С, = -4,5, + fi,C, = x'l+x"l=(x'
откуда х — х' -\- х", и соотношение B9) доказано. Далее, пусть
а=АВ, Ка = АВ'. Спроектируем точки А, В, В' на ось /; мы
б)
Рис. 43.
получим точки /4,, Вл, В\ (рис. 43, а, б—случаи К > 0 и Я. < 0). Из
параллельности прямых AAV BBV В'В, вытекает, что AlBi=KAlB1.
На основании B8) мы можем написать
где
х' = npl(ka).
Таким образом,
V-'/ Л D Tl A D 7 / *-/\ t\ v\ 1
откуда x' = "kx, и соотношение C0) доказано.
3.3. Связь проекций с координатами. Нетрудно усмотреть
связь понятия проекции вектора с его (прямоугольными декарто-
декартовыми) координатами. Пусть ОХ и OY — две взаимно перпендику-
перпендикулярные оси на плоскости (или OX, OY и OZ—три взаимно перпен-
перпендикулярные оси в пространстве), составляющие вместе систему
координат. Обычно ось ОХ (иначе, ось абсцисс) представляют себе
21 Энциклопедия, ки. 4

322 ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
в виде горизонтальной прямой, направленной вправо, а ось OY
(ось ординат) — вертикальной прямой, направленной вверх; в про-
пространстве оси ОХ и OV направляют в горизонтальной плоскости
так, что поворот оси ОХ вокруг О против часовой стрелки
(если наблюдать сверху!) на 90° переводит ее в ось OY (учитывая
направления осей), а ось OZ (ось апликат) направляют верти-
вертикально вверх. Обозначим через i, j единичные векторы осей ОХ
и OF, т. е. векторы длины 1, направления которых совпадают
с направлениями осей (соответственно в пространстве обозначим
через i, j, k единичные векторы осей OX, OY, OZ).
Если теперь а — произвольный вектор на плоскости и (х, у)—
его координаты в системе i, j, то имеют место соотношения
х = проха, y=np0Ya. C1)
Аналогично в пространстве координаты (х, у, z) произвольного
вектора а в системе i, j, k выражаются через проекции по фор-
формулам
х—проха. у=пр0Уа, z=npoZa. C1а)
В самом деле, мы имеем (в случае плоскости)
проха= прох (xi + yj) = ирох (xi) + прад (yj) = х прад i -f ;> npoxj = х.
(так как npoxi— 1, проХ-/=0). Тем самым первая из формул C1)
установлена. Вторая формула и формулы C1а) в пространстве дока-
доказываются совершенно аналогично.
3.4. Связь с тригонометрическими функциями. Укажем еще
связь проекций и координат векторов на плоскости с тригонометри-
тригонометрическими функциями. Пусть XOY — некоторая прямоугольная система
координат на плоскости. Пусть, далее, /—вектор длины 1, обра-
образующий с осью ОХ угол ф. Углы, как обычно, мы уславливаемся
отсчитывать против часовой стрелки (рис. 44); угол, отсчи-
отсчитываемый по часовой стрелке, считается отрицательным. Тогда имеют
место формулы
sincp = проу7, coscp = npOY/, C2)
т. е. вектор / имеет координаты: лг = созф, _у=5'пф- Соотноше-
Соотношения C2) легко проверяются в случае острого угла ф (рис. 45);
в случае же произвольного угла ф их следует рассматривать
как определение величин sin ф и cos ф. Это определение, очевидно,
совершенно эквивалентно определению с помощью тригонометриче-
тригонометрического круга, но, как мы увидим ниже, значительно удобнее.
Пусть а — произвольный вектор. Обозначим его длину через а,
а угол, который он образует с осью ОХ, через ф. Тогда, как легко

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
323
видеть, координаты вектора а имеют следующие значения:
у — asintp. C3)
В самом деле, обозначим через / вектор длины 1, имеющий то же
направление, что и вектор а. Тогда a = al. Так как вектор I имеет
координаты (coscp, sincp), то век гор a = al имеет координаты, указан-
указанные формулой C3).
Из формулы C3) легко вытекает формула для вычисления проек-
проекции произвольного вектора а на любую ось /. Примем ось / за ось
абсцисс и направим ось ординат перпендикулярно к ней. Тогда мы
Рис. 41
Рис 45.
получим систему координат XOY и в этой системе число пр,а
будет в силу C1) абсциссой вектора а. Согласно C3) эта абсцисса
имеет значение ccosq), где а — длина вектора с, а ф — угол, кото-
который он образует с осью абсцисс (т. е. с осью /). Итак,
пр/а =
C4)
Отметим еще, что из данного выше определения синуса и коси-
косинуса (см. C2)) легко вытекают известные формулы приведения:
cos( —ф) = соэф,
sin(— ф) = — sincp, C5)
cos I ф — -^-J =зшф,
sin (ф —тг)= — C0StP-
В самом деле, вектор, образующий угол ф с осью ОХ, и вектор,
образующий угол —ф с осью ОХ, симметричны относительно оси
абсцисс, откуда и следуют первые две формулы C5). Далее, рас-
рассмотрим, кроме системы координат XOV (рис. 46, а), еще систему
координат Х'ОУ, получающуюся из нее поворотом на угол 90° про-
против" часовой стрелки (рис. 46, б). Вектор I длины 1, образующий
21»

324
ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
с осью ОХ угол ф, будет с осью ОХ образовывать угол ф—— t
и потому координаты вектора I в системе XOY будут
.*=СО5ф, у= БШф, C6)
а в системе X'OY' этот же вектор имеет координаты
C7)
Но из расположения систем XOY и X'OY' ясно, что
х'=у, у' = — х C8)
(ибо ось ОХ' совпадает с OY, а ось OY' имеет направление, проти-
противоположное направлению оси ОХ). Из C6), C7), C8) непосредственно
вытекают последние две формулы C5).
»"-*-
ft
Рис. 46.
Из формул C5) легко вытекают все остальные формулы приведе-
приведения. Например, заменяя в последних двух формулах C5) угол ф на
-о- ¦ получим
= ЗШ ( Ф + -7Г ] .
далее,
51п(ф + л)= sin
и т. д.
3.5. Примеры. Вышесказанное позволяет использовать векторы
в решениях, связанных с тригонометрией задач.
Пример 1. Доказать, что в произвольном треугольнике
имеет место соотношение (рис. 47)
а = b cos C-\-c cos В
(это соотношение называется формулой проекций).

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Решение. Положим
825
а="Ж\ Ь = АС, с = ВА
и обозначим через / ось, имеющую направление вектора а (рис. 48).
с
Рис. 47
В с
Рис. 48.
Тогда вектор Ь образует с осью / угол С, вектор с образует с этой
осью угол В, а вектор а образует с осью / угол, равный нулю.
Поэтому (см. C4)) у
пр, а = а, npt Ь = Ь cos С, пр, с = с cos В.
Так как, кроме того, а = с-\-Ь, то из
формулы B9) вытекает требуемое соотно-
соотношение.
Пример 2. Представить выражения
cos a ± cos p и sin а ± sin p в виде произ-
произведений тригонометрических функций неко-
некоторых углов.
Решение. Обозначим через /, вектор
длины 1, образующий с осью ОХ угол
а, а через 1г — вектор длины 1, образую-
образующий с осью ОХ угол р. Тогда вектор lt
имеет координаты (cos a, sin а), вектор 1г имеет координаты
(cosp, sin р) и, следовательно, вектор а = ', + '2 (рис. 49) имеет
координаты
jc=cosct + cosp, 3>=sina+sinp C9)
Рис. 49.
(ср. выше, стр. 320 и 322). А так как вектор а образует с векторами /,
¦ а—В
и 1г углы ± ——-!-, то мы имеем
а — | а | = пра а = пра
.а-р
1-COS-
1 • cos
s) = пра /, + пра 1г =
- = 2-cos-

326
ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
С осью ОХ вектор а образует угол а~? . Следовательно, коорди-
координаты вектора а имеют значения
x = a cos а~Г = 2 cos
а~Всо=а + В
2 cos 2 ,
. а + В а—В . а
— a sin ' = 2 cos -- sin —
D0,
у — a sin = 2 cos -
Из C9) и D0) получаем
cos а + cos p = 2 cos ^=? cos ^±
sin а +- sin P = 2 cos ¦" ¦ sin ^ " .
D1)
Заменяя здесь р на р + л и пользуясь формулами приведения, по-
получаем еще два соотношения
cos а — cos р = — 2 sin ^^ sin ^^,
D2
. с „ . а—В а + В
sin а — sin р — 2 sin —~ cos —^-ь .
Заметим еще, что из D1) и D2), положив а = ф+-'ф, Р=ф—ij),
мы легко сможем выразить cos (ф ± я|)) и sin (ф ± ф) через тригоно-
тригонометрические функции углов
ф и ч]/ (ср. ниже стр. 332).
Приведенный вывод удобен
гем, что пригоден для лю-
/}д„, бых углов а, Р, ф, \р неза-
независимо от их величин и зна-
/ ков.
' Задача 6. Вычислить
суммы
1 + cos ф + cos 2ф -J- - - - + cos пф,
D3а)
sin ф + sin 2ф -J-... -j- sin пф.
D36)
Р е ш е н и е. Построим ло
маную ОАхАг.. -An+t, звенья
которой имеют длину 1, а
внешние углы равны ф (рис.
50). Далее, возьмем систему
координат с началом О и
Рис. 50.
осью ОХ, направленной по вектору ОАи и обозначим:
Тогда вектор 10 образует с осью ОХ угол, равный нулю, вектор /, обра-
образует угол <р. вектор /г угол — 2ф и т. д., вектор /„—угол пф.

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ 327
Следовательно,
вектор /„ имеет координаты (cos 0, sinO) (т. е. I и 0),
« /, « « (cos<p, sin<p),
• 1г « « (cos2<p. sin2<p).
« /„ « « (cos пф, sin яф).
Из этого вытекает, что вектор /„+/, + /2+ • ¦ • +1п имеет абсциссу D3а)
и ординату D36). Но /„+/,+ ... + /n=O4l + I^+ .^1+~A^A~n+i=OAn+u
и нам остается вычислить координаты х, у вектора ОАп+х—это и будут
искомые суммы D3?) и D36).
Пусть М—центр окружности, проходящей через вершины ломаной
OAtAt.. .Ап+1. Опустив из точки М перпендикуляр MN на отрезок OAlt
мы найдем
и потому
2 sin 4-
Вектор ОМ образует г осью ОХ угол -= ^- и потому имеет коорди-
координаты
Ф
Далее, каждый из углов АхМАг, АгМА3, ... равен ф, поэтому ?_ А1МАп+,=
= пф. Следовательно, ?_ NMAn+l = l п-\-~к ) ф. и. значит, вектор МАп+х
образует с осью ОХ угол I п + —)ф—^-. А так как МАп+х=ОМ, то век-
тир VMn+1 имеет координаты
Г/ 1\ я1 / 1\ sln(" + i)(P
х =
Y
2 sin f

328 BFKTOPbl И ИХ ПРИМЕНЕНИЯ В ГЕОМРТРИИ
Наконец, ректор OAn+i=OM +МАп+л имеет координаты
1
2sin-|-
cos-|-
2 sin -|- 2 sin -|- 2 sin -^
Это и есть искомые значения сумм D3а) и D36).
3.6. Определение и свойства скалярного произведения. Пусть
теперь а и ft—два произвольных вектора. Скалярным произведе-
произведением вектора а на вектор ft называется число a-npaft; оно обозна-
обозначается символом ab:
ab = a-npab. D4)
Это определение теряет смысл, если я = 0, так как в этом слу-
случае направление вектора а не определено; однако в этом случае
а = 0, и скалярное произведение ab считается равным нулю.
Из формулы C4) следует, что скалярное произведение можно
также определить формулой
ab = ab cos /_ (a, ft), D5)
где через /_ (a, ft) обозначен угол между векторами а и ft.
Если а = Ь, то скалярное произведение ab принимает вид аа\
его называют скалярным квадратом вектора а и обозначают также
символом аг. Из D5) вытекает, что скалярный квадрат вектора а
равен квадрату его длины:
а* = аг. D6)
Далее, из D5) непосредственно следует, что скалярное умножение
коммутативно (перестановочно):
ab = ba. D7)
Наконец, из D4) легко вытекает также дистрибутивность (распре-
(распределительность) скалярного умножения:
a(b + c) = ab + ac D8)
и его ассоциативность (сочетательность) по отношению к умно-
умножению вектора на число:
D9)

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ 329
В самом деле, в силу B9) и C0) мы имеем
= a- npoft + а прас — ab + ас;
a (Kb) = а • пра Kb = а (К - пра Ь) = К • (а- иро Ь) = К (ab).
Соотношения D6) — D9) выражают свойства скалярного умно-
умножения. Мы добавим к ним еще одно свойство: если а и b—отлич-
b—отличные от нуля векторы, то равенство ab = 0 имеет место тогда
и только тогда, когда векторы а и b перпендикулярны между
собой. Это непосредственно вытекает из формулы D5).
Свойства D7)—D9) скалярного умножения очень похожи на
хорошо знакомые правила действий с числами. Из этих свойств
вытекает, что действия над векторами во многих случаях можно
производить в точности так же, как и действия над числами.
Например,
Bа + Ь) (Зс—d) = Bа + Ь) (Зс) + Bа + Ь) (— d) —
= 6ac + 3bc—lad—bd,
(а—Ь)г = (a — b) (a—b) = аг—2аЬ + Ьг,
(a-\-b)(a—b) = a* — b*
и т. д. В этом, собственно говоря, и заключается ценность скаляр-
скалярного произведения: с одной стороны, оно геометрически инте-
интересно, так как позволяет находить длины отрезков (см. D6))
и величины углов (см. D5) и указанное выше условие перпендику-
перпендикулярности); с другой стороны, скалярное произведение алгебраи-
алгебраически удобно, так как вычисления со скалярными произведе-
произведениями производятся по правилам, хорошо известным из арифметики
и алгебры.
Имеются, однако, и серьезные различия между «арифметикой
векторов» и привычной нам арифметикой чисел. Заметим прежде
всего, что скалярное произведение двух векторов является не век-
вектором, а объектом другой природы — числом («скаляром»). Это
обстоятельство делает невозможным постановку вопроса об определе-
а
нии «векторного деления»—символу -г- нельзя приписать никакого
смысла *). Это же обстоятельство мешает рассматривать произведе-
произведения трех векторов; например, формула
(а + Ь)ш = а' + ЗагЬ + ЗаЬ2
') Можно, правда, определить «частное — от деления числа а на
вектор а» как такой вектор Ь, что скалярное произведение аЬ равно а;
однако и эта операция «деления числа на вектор» не заслуживает серьез-
серьезного внимания (в первую очередь в силу неоднозначности определяемого
таким образом вектора Ь).

.330 ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
на область векторов никак не переносится. Далее, в то время как
в обычной арифметике произведение двух чисел равно нулю только
в том случае, если хотя бы один из сомножителей равен нулю,
в «арифметике векторов» дело обстоит совсем не так: равен-
равенство ab = 0 может выполняться и при а Ф 0, ЬфО (если векторы а
и Ь взаимно перпендикулярны). Последнее замечание влечет за собой
еще одно существенное различие между «.арифметикой векторов»
и обычной арифметикой: векторные равенства нельзя сокращать
на отличный от нуля множитель. В самом деле, если из соотно-
соотношения ас = be для чисел a, b и с фО вытекает, что а = Ь, то из
равенства
ас = Ьс (с фО)
вытекает лишь, что ас—be = 0 или (а — Ь)с — 0 и, следовательно,
вектор а— Ь перпендикулярен вектору с.
Приведем еще формулу вычисления скалярного произведения при
помощи координат.
Пусть в некоторой системе координат XOY вектор а имеет коор-
координаты (дг,, .у,)» а вектор Ь — координаты (xt, yt). Тогда в силу B5)
а = xj,+у J, b = xj + yj,
где i и j—единичные векторы, направленные по осям координат.
Ло 1*=\, У" = 1, у = 0, откуда следует
аЬ = (xj+yj) [x,i+yj) = xxxt? + (xjt
Итак, скалярное произведение двух векторов на плоскости можно
вычислять по формуле
г, E0)
где (*,, J>,) — координаты вектора а, а {х2, уг) — координаты век-
вектора Ь.
Совершенно аналогично устанавливается, что скалярное произведе-
произведение двух векторов в пространстве можно вычислять по формуле
ab=xlxt + ylyt + zlzx, E0а)
где (xv yv г,) — координаты вектора а, а {хг, уг, zt) — координаты
вектора Ь.
Из формул E0), E0а) (которые можно, если угодно, принять за
¦определение скалярного произведения) нетрудно вывести вновь
все его свойства. Так, из них сразу следует, очевидно, что ab = bo\
кроме того, если а = (х1, yj, b = (xt, yt), c = (xa,yt) (мы здесь огра-

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ 331
ничиваемся лишь несколько более простым случаем плоскости), то
a (Kb) = *, (Кхг) + у, (Kyt) = Kxtxt + Kyiyt = К (xtxt + y,yt) = К (ab),
и т. д. (ср. формулы D9) и D8), стр. 328).
3.7. Примеры и задачи. Рассмотрим теперь некоторые задачи,
решаемые с применением скалярного произ- »
ведения.
Пример 3. Доказать, что для любого
треугольника имеет место формула
С;
l — 2abcosC
(теорема косинусов).
Решение. Положим
а = СВ, Ь=СА, с = АВ
(рис. 51). Тогда с = а — Ь и мы имеем (учитывая, что /_(ау Ь) =
с* = с2 = (а —bI-=a1 — 2ab + b2 = a*~2ab cos С±Ь*.
Пример 4. Доказать, что для любого треугольника имеют
место формулы
sin А sin В sin С
а Ь с
(теорема синусов).
Решение. Сохраним те же обозначения, что и в предыдущей
задаче (рис. 51). Тогда
умножая обе части этого равенства на вектор b—с, имеем
. ab—ac — b*—с1,
или
ab cos С— ас cos В= Ь* — сг, т. е. a (b cos С—с cos B) = b% — с2.
Подставляя сюда выражение для а, даваемое формулой проекций (см.
пример 1, стр. 324) имеем
(b cos C-\- с cos В) (b cos С— с cos В) = Ь* — сг,
или
b1 cos2 С— с' cos2 В = Ьг — с».
Поскольку 1 — cos2 C= sin2 С, 1 —cos* fi= sin2 В, мы получаем отсюда
Ьг sin2 C= с2 sin2 В.

332 ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГРОМЕТРИИ
Но так как Ь, с, sin С, sin В положительны, то из последнего равен-
равенства следует, что
bsin С= с sin В,
или
sin В _ sin С
~Ь~~ с ¦
Аналогично доказывается и равенство
sin A sin С
а с
Значит, в самом деле,
sin А sin В sin С
а Ь с
Пример 5. Выразить sin(a±P), cos(a±fl) через тригоно-
тригонометрические функции углов а и р.
Решение. Пусть /, — единичный вектор, образующий с осью ОХ
угол а, а /, — единичный вектор, образующий с осью ОХ угол р.
Тогда векторы /, и /, образуют между собой угол a—р, и потому
(см. D5))
С другой стороны, вектор /, имеет координаты (cos a, sin а), а век-
вектор /, имеет координаты (cos p, sin P). Следовательно, по формуле EU)
/,/, = cos a cos P + sin a sin p.
Сравнивая два найденных выражения для ljt, получаем
cos (a — Р) = cos a cos p + sin a sin p.
Отсюда с помощью формул приведения находятся и остальные
формулы.
Задача 7. Доказать, что если в произвольном «четырехвер-
шинникеу> ABCD противоположные «стороны» АВ и CD, AD и ВС
взаимно перпендикулярны, то перпендикулярны и «.диагонали»
АС и BD.
Здесь мы снова имеем две совершенно разные задачи в зависи-
зависимости от того, лежат ли точки А, В, С, D в одной плоскости или
они расположены в пространстве. В первом случае наше утверждение
гласит: если АВ }_CD, AD J^BC, т. е. CD и AD суть высоты тре-
треугольника ABC (рис. 52), то BD J_ AC есть третья высота треуголь-
треугольника; другими словами, мы приходим к теореме о том, ч го три высоты
треугольника пересекаются в одной точке. Во втором случае мы
утверждаем, что если противоположные ребра АВ и CD, AD и ВС

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
333
треугольной пирамиды (тетраэдра) ABCD перпендикулярны между
собой, то этим свойством обладает и третья пара противополож-
противоположных ребер АС и BD (рис. 53).
В
Рис. 52.
Рис. 53.
Решение. Пусть Q—произвольная точка. По условию имеем
~AB-CD = Q или (QB—~QA)(QD— QQ = 0, т. е.
QB-'QD— QB-QC—'QA-QD+QA-QC=O E\)
и
AD-BC=0, или (QD—QA)(QC—QB) =
т. е.
QD-QC— QD-QB— QA-QC+QA.QB=O.
Сложив равенства E1) и E2), получаем
~Ql;- QD + QA • Qfi— QC- QB— QA ¦ QD = 0,
E2)
или
или, наконец,
(QC-QA)(QD — Qfl) = 0,
что и доказывает теорему.
Задача 8. Доказать, что сумма квадратов «.диагоналей^ АС
и BD произвольного «четырехвершинника» ABCD равна сумме квад-
квадратов его «.сторон» АВ, ВС, CD и DA, уменьшенной на учетверен-
учетверенный квадрат отрезка, соединяющего середины Е и F «.диагоналей»,
т. е.
АС* + BD* = АВ1 + ВС* + CD1 + DA1 — 4EF*.. E3)
Другими словами:
а) Если стороны АВ, ВС, CD и DA (плоского) четырехуголь-
четырехугольника равны а, Ь, с и d, а диагонали АС и BD равны ей/, то
+ c* + d2 = ег

334
ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
где EF— отрезок, соединяющий середины диагоналей четырехуголь-
четырехугольника (рис. 54; ср. с известной теоремой о том, что в параллело-
параллелограмме сумма квадратов сторон равна сумме квадратов диаго-
диагоналей).
Рис. 54.
б) Fcau противоположные ребра АВ и CD, AD и ВС, АС и BD
треугольной пирамиды (тетраэдра) ABCD равны а и о„ Ъ и bv
с и с,, то отрезок EF, соединяющий середины ребер АС и BD
Р (рис. 55), определяется из фор-
формулы
4EF" = а* + а] + Ьг + b\ — сг — с].
Решение. Положим
Afi=o, AD = b, AC=d
(рис. 56). Тогда
BC=d — a, D~C=d—b,
DB=a—b;
далее
Рис. 56. . ,
и, следовательно, получаем, что
EF=A~F—А~Ё=-
Теперь равенство E3) можно переписать в виде
и для его доказательства достаточно раскрыть скобки в левой и пра-
правой частях написанного векторного равенства.

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Рис. 57.
Задача 9. Пусть ABCD—произвольный «четырехвершинник»;
KL и MN—его «средние линии», соединяющие середины «.сторон»
АВ и CD, AD и ВС; ф—угол между «диагоналями» АС и BD
Доказать, что
(АВ2 + CD2)—(AD2 + ВС2) = 2 (KL' — MN2) = 2AC-BD-cos <p.
Другими словами:
а) Если стороны АВ, ВС, CD и DA четырехугольника ABCD равны
а, Ь, с и d, диагонали АС и BD равны е и f и угол между диаго-
диагоналями есть ф, то
а2 — Ьг + с1 — d1 = 2ef cos ф =
= 2(KL2— MN2),
где KL и MN—средние линии че-
четырехугольника (рис. 57). Отсюда,
в частности, вытекает, что следу-
следующие три свойства четырехуголь-
четырехугольника ABCD эквивалентны между
собой (т. е. из выполнения любого
из них следует, что выполнены и
два других свойства):
1) диагонали четырехугольни-
четырехугольника взаимно перпендикулярны;
2) средние линии четырехугольника равны между собой;
3) сумма квадратов двух противоположных сторон четырех-
четырехугольника равна сумме квадратов двух других его сторон.
б) Если противоположные ребра
АВ и CD, AD и ВС, АС и BD тре-
треугольной пирамиды (тетраэдра) рав-
равны а и av Ь и #,, с и с,, а угол
между ребрами АС и BD равен ф,
то
(с2 + а\) — (Ь2 -\- Ь\) = 2сс1 созф =
= 2(KL2— MN2),
где MN и KL — отрезки, соединяющие
середины противоположных ребер АВ
и CD, AD и ВС (рис. 58).
Из этой теоремы, в частности, вы-
Рис. 58. текает эквивалентность следующих
трех свойств тетраэдра ABCD:
1) противоположные ребра АС и BD перпендикулярны между
собой;
2) отрезки MN и KL, соединяющие середины ребер АВ и CD,
AD и ВС, равны между собой;

336 ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
3) суммы квадратов противоположных ребер АС и BD, AD и ВС
равны между собой.
Решение. Сохраним обозначения, введенные при решении пре-
предыдущей задачи. Мы имеем (см. рис. 56, 57)
A~Kb Al ^(a + d) KL ALAK(a
1 1 1
= 77 л, AN = 77 (b + d), MN=AN—AM=W(-
Z Z Z
Следовательно,
(АВг + CD1)—(AD1 + ВС) = [a" + (d—bI]—[b" + (d—a)*] =
= 2ad-2bd =
Остается применить формулу D5).
3.8. Единственность скалярного произведения. В заключение этого
параграфа остановимся еще на следующем вопросе. Определения D4) или
{45) скалярного произведения могут показаться довольно случайными:
естественность их не мотивирована никакими достаточно убедительными
соображениями. Впрочем, простые свойства D7), D3), D9) скалярного про-
произведения убеждают нас в целесообразности изучения этой операции.
Однако заранее не ясно, не существует ли других столь же «хороших»
«произведений векторов», т. е. других способов сопоставить с двумя векто
рами а и b число aob (здесь кружочек символизирует неизвестную нам
пока операцию «умножения векторов»), с тем чтобы выполнялись аналогич-
аналогичные D7) — D9) условия:
E4)
Ь); E5)
E6)
Естественно, что кроме правил E4)—E6) желательно потребовать еще,
чтобы число aob имело геометрический смысл т. е. обладало
тем свойством, что если пара векторов ОА=а и OB = b tpaena» паре векто-
векторов OA, = ai и OBi — bi (т. е. может быть переведена в последнюю движе-
движением) '), то
b b E7)
Покажем, что в случае геометрии в пространстве уже условия E5),
E6) и E7) почти однозначно приводят к скалярному произведению векто-
векторов. На плоскости же дело обстоит иным образом: здесь, для того чтобы
выделить скалярное произведение векторов, существенно необходимы все
четыре условия E4)—E7). В следующем параграфе мы рассмотрим отлич-
отличное от скалярного «произведение» векторов плоскости, удовлетворяющее
условиям E5) — E7), но не условию E4).
') Ср. статью «Геометрические преобразования», п. 6.1.

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
337
Ясно, прежде всего, что если а — аа?, b = bb°, где векторы а" и Ь"
единичные (имеют длину 1), то в силу E5)
aob^(aa0)o(bb°) = ab(a°ob0). E8)
Таким образом, достаточно определить произведение единичных векто-
векторов. Далее, если векторы а" и с" еди ичные и взаимно перпендику-
перпендикулярные я мы рассматриваем геометрию
в пространстве, то пара векторов ОА =а°,
ОС —с" «равна» паре векторов 0А1 = — а0,
Рис. 59.
Рис. 60.
ОС,—с" (одна из них переходит во вторую при вращении вокруг ОС на
угол 180°). Поэтому в этом случае в силу E7) и E5)
а0 о с" = (— а0) о с0 = — (аэ о с°).
и, следовательно.
a» oe° = 0. E9)
Кроме того, в силу того же условия E7) «квадрат» а" о а0 любого единич-
единичного вектора а0 будет иметь одно и то же значение б:
a°oa° = 6. F0)
Пусть теперь ОА— а0 и ОВ = Ь°—два произвольных единичных вектора,
угол между которыми равен /_ (а°, Ь") (рис. 59). Если В, и В2 — проекции
течки В на прямую ОА и иа перпендикулярную ей (и лежащую в плоско-
плоскости ОАВ) прямую ОС, то, очевидно,
Ь°=Ш,+0В2 = cos /_ (a\ &o)-a° + sin ? (а\ Ь°)-с\
где с0—единичный вектор направления ОС. В силу E6), E5), F0) и E9)
получаем
a0ob°=a°o [cos _ (a0, ft")-a° + sin Z (а°, &°)-с°] =
= cos /_ (а0, Ь°) - (а0 о а0) + sin /_ (а0, Ь") ¦ (а0 ос°) = Ь cos /_ (а0, Ь").
Учитывая еще E8), получаем для произвольных векторов а и &
= b-ab cos ?_ (а, Ь).
Таким образом, мы пришли к выражению, отличающемуся от скалярного
произведения D5) двух векторов лишь произвольным (но фиксированным!)
множителем б.
22 Энциклопедия, кн. 4

366 ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
В нашем рассуждении мы нигде не использовали равенства E4). Однако
если рассматриваются векторы не в пространстве, а на плоскости, и соот-
соответственно этому «равными» считаются лишь пары векторов, переводимые
одна в другую движением в плоскости, то заключение о том. что
пары векторов а', с' и —• а\ с" (где а'' — с'—\, a'J_c") «равны» между
собой, будет уже неверно. В этом случае «равны» лишь пары а', с" и
с\ —а° (они получаются одна из другой вращением на 90е вокруг общего
начала О векторов; см. рис. 60). Отсюда следует, что
а" о с• = г" о (— а°) = — (<?° о а0).
и если имеет место также условие E4). то снова получаем
Если же не требовать выполнения условия E4), то доказать равенство E9»
нельзя (см. ниже, стр. 349—350).
§ 4. Косое произведение векторов плоскости
4.1. Ориентированные площади и косое произведение векто-
векторов. До сих нор мы все время рассматривали одновременно векторы
па плоскости и векторы в пространстве; различия между этими двумя
случаями были для нас весьма несущественными. Далее, однако, мы
будг:м рассматривать геометрию на плоскости и геометрию в про-
пространстве раздельно, поскольку в разбираемых
здесь вопросах различие между той и другой
сказывается очень сильно. В этом параграфе
мы будем говорить лишь о векторах на пло-
плоскости.
Вспомним определение скалярного произве-
произведения. Скалярное произведение ab двух векто-
векторов а и Ь есть число, сопоставляемое опре-
деленным образом с этими двумя векторами.
Геометрический смысл этого числа не слишком
прост — он дается формулой D5) или почти
Рис- б1- столь же искусственной формулой D4). Цен-
Ценность скалярного произведения (и уместность
употребления в применении к зтому числу слова «произведение»,
обычно имеющего совсем другой смысл) определяется лишь свой-
свойствами D7), D8), D9) скалярного произведения, весьма похожими
на привычные свойства умножения чисел. Здесь мы определим еще
одно «произведение векторов», обладающее почти столь же простыми
свойствами.
Ясно, что сопоставить число с двумя векторами можно весьма
разнообразными способами.
Так, например, можно объявить этим числом площадь построен-
построенного на векторах а и Ь треугольника ОАВ или параллелограмма
OADB (рис. 61). Однако предложение назвать площадь Ьоаов новым

КОСОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ ПЛОСКОСТИ 339
«произведением» векторов а и Ь представляется с первого взгляда
мало обоснованным.
Проверим все же, не обладает ли величина SoaDB (обозначим ее,
скажем, через Sa ь) свойствами, аналогичными свойствам D7)—D9)
скалярного произведения. Ясно, прежде всего, что
Sa, ft = Sft, a- F1)
Но уже простое свойство D9) скалярного произведения переносится
на величину Sa_ ь лишь в том случае, если множитель Я, является
положительным
S%a. Ь = Sa. \Ь = hSa. ь При К > О, НО Sia? ь = Sa_ и =
¦ =IMSe.6 = — ^а.ь при К<0 F2)
(см. рис. 62).
Для того чтобы исправить это положение, условимся рассматри-
рассматривать площадь ориентированного параллелограмма, построен-
построенного на векторах а и Ь, т. е. считать площадь OADB положи-
положительной, если вектор Ь расположен слева от вектора а (при этом
В
Рис. 62.
мы смотрим в направлении вектора а), и отрицательной в против-
противном случае. Другими словами, можно сказать, что площадь OADB
Рис. 63.
считается положительной, если направление вектора а можно совме-
совместить с направлением вектора Ь вращением вектора а против
часовой стрелки на угол, меньший 180°, (рис. 63, а), и отри-
отрицательной, если направление вектора а переходит в направление
вектора Ь при вращении вектора а по часовой стрелке на
22*

340
ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
угол, меньший 180° (рис. 63, б). Если, наконец, вектор b принадле-
принадлежит той же прямой, что и а, то площадь построенного на а и на ft
«параллелограмма» естественно считать равной нулю. Эту новую вели-
величину мы обозначим пока че-
7 рез S(a,b).
Нетрудно видеть, что
для величины S(a,b) уже
имеет место правило, ана-
логичное свойству D9) ска-
лярного произведения:
а
Пара (а,Ь)
а
пара (Ь,а)
=KS(a,b) при любом К F3)
Рис. 61.
(ибо ориентация построенно-
построенного на векторах Ха, Ь или на
векторах a, Kb параллелограмма при К > 0 будет совпадать с ориен-
ориентацией исходного параллелограмма OADB, а при Я < 0 будет проти-
противоположна ей; см. рис. 62, а — д). Однако теперь уже простое
правило F1) заменяется более сложным
b) F4)
(ибо построенные на векторах a, b
и на векторах Ь, а параллелограммы
имеют противоположную ориентацию;
см. рис. 64).
Обратимся теперь к свойству D8)
скалярного произведения. Мы утверж-
утверждаем, что аналогичное свойство имеет
место и для величины S(a, b):
S(a,b + c)= S (a, b) + S (a, c). F5)
Полное доказательство этого равенст-
равенства мы пока отложим; здесь же мы
лишь проверим его для частного случая, когда все величины
S(a,b), 6(a,c) и S(a, b-\-c) положительны. В самом деле (рис. 65),
5 (о, Ь) + S (о, с) = S0ADB -f- S0AEC = S
= Soadnmb =
= S(a,b-\-c)
(ибо SboBM = S&ADN, поскольку треугольники ОВМ и ADN равны).
Можно было бы доказать соотношение F5), рассмотрев анало-
аналогично случай, когда величины S(a,b), S[a, С) и S(a, b-\-c) имеют
всевозможные знаки, но мы не будем этого делать, а приведем ниже
совершенно другое доказательство.

КОСОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ ПЛОСКОСТИ 341
Равенства F3), F4) и F5) уже дают основания для того, чтобы
присвоить величине S(a, b) название «произведения». Эту величину
называют косым произведением ') векторов а и Ъ и обозначают через
а X &• Равенства F4), F5) и F3) теперь можно переписать так:
аХЬ= —ЬХа; F6)
Хс; F7)
Ь(аХЬ). F8)
Таким образом, косое произведение является ассоциативным по от-
отношению к умножению вектора на число (см. F8)) и дистрибутивным
относительно сложения векторов (см. F7)), но не коммутативным, а ан-
антикоммутативным (так выражают словами равенство F6)). Заметим
также, что известная формула для площади параллелограмма и прави-
правило определения знака произведения axb позволяют утверждать, что
а X b = ab sin /_ (a, b), F9)
где иод /_{а,Ъ) теперь надо понимать ориентированный угол
между векторами а и 6, т. е. угол, знак которого определяется, как
в тригонометрии (угол /_(а, Ь)~ц> положителен, если направление
вектора с совмещается с направлением вектора Ь вращением на
угол ф в направлении против часовой стрелки, и отрицательным, если
вектор а принимает направление вектора Ь при вращении на угол ф
но часовой стрелке). То обстоятельство, что в формуле D5) мы под
/_ (а, Ь) понимали неориентированный угол между а и Ь, т. е. что в двух
соседних формулах мы одним и тем же символом обозначаем разные
величины, не должно нас смущать, ибо можно считать, что и в формуле
D5) угол ^/(а,6) является ориентированным (ибо cos(—a)=cosa).
Из формулы F9) вытекает, в частности, что косое произведение
двух векторов а и b равно нулю в том и только в том случае,
когда один из этих двух векторов нулевой (в этом случае о на-
направлении этого вектора вообще не приходится говорить), или
когда векторы а и Ъ параллельны (и, значит, угол ф равен О
или 180°). В частности, «косой квадрат» вектора всегда равен нулю:
аХа = 0. G0)
Это обстоятельство часто оказывается важным. Отметим еще сле-
следующее простое соотношение, связывающее скалярное и косое про-
произведения двух векторов:
bJ = a*b* ( = a*b2); G1)
это соотношение сразу следует из формул D5) и F9).
Относящиеся к косому произведению правила F6) — F8) позво-
позволяют раскрывать скобки при косом умножении сложных комбинаций
') В литературе употребляется также термин псевдоскалярное произ: едение.

342
ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
векторов. Например,
(а + 26—Зс) X Brf—5e) =
= 2а X d—5с X <? + 46 X ^— 106 X ^—6с X ^+ 15с X е.
Надо только иметь в виду, что замена свойства коммутативности
умножения антикоммутативностью заставляет изменять знак каждый
раз при изменении порядка перемножаемых векторов. Это приводит
к своеобразному искажению знакомых из обычной алгебры формул:
(а—6)х(а + 6) = аха-|-ах6—bxa — bxb — axb—6ха = 2ах6
ибо аха = 6х6 = 0). Рис. 66 иллюстрирует эту последнюю фор-
формулу: площадь параллелограмма OEFG, построенного на диагоналях
ВС=а—6 и AD = a+b параллелограмма ABDC в два раза больше
G
д
Ряс. 66.
площади самого этого параллелограмма. Заметим еще, что условие
равенства нулю косого произведения двух векторов влечет за собой
недопустимость «сокращения» равенств, в которых разные векторы
косо умножаются на один и тот же (векторный) множитель: из ра-
равенства
схс=6хс
следует лишь, что (с—6)хс = 0, т. е. что либо один из «множи-
«множителей» а — 6 и с равен нулю, либо а — 6||с.
4.2. Аналогия между косым и скалярным произведениями. Известный
параллелизм между косым и скалярным произведениями, выражающийся
в близости формул DG) и F7), D9) и F8), а также то, что
если ab = 0, то a_|_ft (и если a_|_ft, то aft = 0);
если aXb = 0, то а\\Ь (и если а\\Ь, то axb = 0),
влечет за собой известный «параллелизм» между понятиями перпендику
лярности и параллельности, позволяющий в некоторых теоремах заменять
слово «перпендикулярный» словом «параллельный» и наоборот без нару-
нарушения истинности теоремы. В качестве примера укажем следующее не-
несложное предложение: если треугольники ABC и Л,В|С, таьопы, что пря-
прямые, проведенные через вершины треугольника А ВС neP"apal^t"m соответ-
соответствующим сторонам треугольника А,В,С, (т. е. через вершину А перпенди-
перпендикулярно или пераллельно стороне В,С, и т. д.), пересекаются в одной

КОСОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ ПЛОСКОСТИ
343
точке О. то и прямые, проведенные через вершины треу ольника А1В1С1
nePnaHa"te''ulo соответствующим сторонам треу ольника ABC, Пересе аются
в одной точке О, (рис. 67, а, б). Для того чтобы не повторять два раза
одни и те же выкладки, мы условимся обозначать через aob скаляр-
скалярное или косое произведение векторов а и ft.
Рис. 67.
Обозначим ОА=а, OB = b, ОС = с, OA1 = al, OBl — bl, OC1 = c1. В та-
таком случае из условия теоремы следует
ао(Ь,—с,) = 0,
т. е.
и, аналогично,
aobl = aocl (a)
b о с, = b о о„ F)
coa, = coft,. (в)
Далее, пусть 00,=г, где О, есть точка пересечения прямых, проведенных
через вершины Л, и В, перПар"лТельн!ГО прямым ВС, соответственно СА;
нам надо доказать, что СО^АВ. Из определения точки О, имеем
(Ь—c)°(«t—г) = 0, т. е. ftoa,—coo,—бог—cor, (г)
(с—а) о (ft,—г) =0, т. е. coft,—aoft, = cor—aor. (д)
Складывая равенства (г) и (д) и используя то, что в силу (а) — (в)
ftoa, = ftoc,, coal=cob1, aobl—aocl, получаем бос,—aoc, = ftor—аог,
или (й—а)о(с,—г) = 0, откуда и вытекает утверждение теоремы.
4.3. Дальнейшие свойства косого произведения. Мы до сих
пор не дали полного доказательства формулы F7). Для того чтобы
сделать это, заметим, что косое произведение векторов можно свести
к скалярному произведению (других!) векторов:
[a]b, G2)

344
ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
где вектор [а]') получается из вектора а поворотом на 90° в поло-
положительном направлении (в направлении, обратном направлению вра-
вращения часовой стрелки; рис. 68). Это сразу следует из формул D5)
и F9): в самом деле, очевидно, что если [а] есть длина вектора [а],
то
[а\=а и /([с], &) = /_ (а, &)— 90°, cos /_ ([а], Ь) = sin ? (а, Ь).
Отсюда следует, что
[а] Ь — [a]bcos /_([d\, b) = absin /_ (a, b) — axb.
А теперь имеем
a x (b -f c) = [a] (b + c) = [a] b + [a] с = a x * + a x c,
что и требовалось доказать
Выведем еще выражение для косого произведения двух векторов
в координатах. Пусть (х, у) и (х%, ул) — координаты векторов а
Рис. 69.
и Ь; при этом единичные векторы i=OEt и J=OE2, направленные
но осям координат, выберем так, чтобы было
iXJ=S(OEl, ОЯ2)=1
(рис. 69; здесь у нас нет необходимости требовать, чтобы оси коор-
координат ОЕг и ОЕг были обязательно взаимно перпендикулярны или
чтобы оба отрезка ОЕг и ОЕг были равны единице длины). В таком
случае, очевидно, имеем
= (xi + yj) X (xj. + ytj) =
= xxx (i x i) + xyt (i хЛ + yxt (Ух i) + yy, (Jxj).
') Обозначение [a] для вектора, получаемого из вектора а поворотом
на 90е, с первого взгляда может показаться несколько вычурным; однако
оно согласуется с обозначениями, введенными ниже, на стр. 354 и 379.

КОСОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ ПЛОСКОСТИ
345
А так как ixi=JXJ=0 и согласно условию ixj'=—Jxi—\, го
получаем
axb = xy,— ухх. G3)
Формулу G3) можно также принять за определение косого
произведения. Из нее сразу получаем:
6X0=^, — ху, = —a
=axb+axc
(здесь вектор с имеет координаты (х2, у2)) и
(ср. выше формулы F6) — F8)).
Равенство G3) можно переписать так:
axb =
X X,
У Ух
G4)
в таком виде оно равносильно известному геометрическому истолко-
истолкованию определителя второго порядка как площади ориентированного
параллелограмма, построенного на векторах, координаты которых
совпадЕют со столбцами определителя '). При эгом свойства F6)—F8)
можно будет истолковать как (хорошо известные) свойства опреде-
определителей
axb= —Ьха,
= "k(ax b),
ибо
ибо
ибо
X
У
X
У
У
1 ~Т
Ух
х*
_
л;
Хх
Ух
X
У
X
У
хг
Уг
%Х X,
ьу у,
_ 1
У Ух
Наконец, формулу G1) можно истолковать как правило возведения
определителя в квадратг):
XX,
У У,
хх,+уу,
Х*1+У*
a2 ab
ab б2
= c2ft2-(c6J.
GГ)
4.4. Примеры и задачи. Приведем теперь несколько примеров на
применение косого произведения векторов.
') См. по этому поводу § 1 статьи «Векторные пространства и линей-
линейные преобразования» в кн. II ЭЭМ.
2) Иоо

346 ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
Пример 6. Вычислить площадь треугольника ABC, зная
длины всех его сторон.
Рис. 70.
Решение. Обозначим СВ = а, СА = Ь, АВ= с. Очевидно, имеем
(рис. 70)
55 ^|СйхСЛ| |ох6|
откуда
Но в силу формулы G1)
(аХ&J = а262 —(aftJ,
и, значит,
С другой стороны,
c = a—b, c* = a*
и, следовательно,
aft = ^ = 2
Таким образом, имеем
J _| =
или, если обозначить а
Это—известная формула Герона для площади треугольника.
Задача 10. Пусть L, М, N — такие точки сторон ВС, СА,
АВ треугольника ABC, что

КОСОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ ПЛОСКОСТИ
347
(рис. 71). Известно, что площадь треугольника ABC равна i>;
требуется определить площадь треугольника LMN.
В
И
Рис. 71.
Рис. 72.
Решение. Сохраним те же обозначения, что и в примере 6.
В силу формулы B3) из § 2 (стр. 311) имеем
см=
Далее из формулы G5) выводим
I
I
S&LMN = \ • INL X NM\ = ¦? | (CL - СЛО х (САГ- C/V) | =
= у | (CZ X CM) + (CM X CN) + (СЛ> X CZ) |.
Следовательно,
a „ K*\, ( Kb ^b + Ka
G6)
К
(axb)-.
Таким образом, окончательно получаем (см. ту же формулу G5))
¦S.
Особенно интересен тот случай, когда точки L, М и N лежат
на одной прямой. Из последней формулы заключаем:
Точки L, /И и N в том и только в том случае лежат на
одной прямой, если
Л1Я.Л=-1 G7)
(теорема Мене лая).
Задача 11. Сохраним те же обозначения, что и в предыду-
предыдущей задаче и обозначим через Р, Q, R точки попарного пере-
пересечения прямых AL, ВМ и CN (рис. 72). Площадь треугольника

348 ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
ABC по-прежнему обозначим через S; требуется определить пло-
площадь треугольника PQR.
Решение. Применим теорему Менелая (см. формулу G7)):
1) к точкам В, Р, М, лежащим на сторонах треугольника ACN:
PN В А МС~ ' PN~ MAW~ *( + •''
2) к точкам A, Q, L, лежащим на сторонах треугольника BCN:
CQAMBZ.__ CQ CZ, ВЛ J_ 1 + Х3 .
QNABLC" ' QN~ LBAN~Kl' X, '
3) к точкам A, R, L, лежащим на сторонах треугольника ВСМ:
RM AC LB~ ' RM~ LC AM~ t( +A*]-
Отсюда, используя формулу B3) и применяя прежние обозначе-
обозначения, получим:
1+Я + ЯЯ ~
Наконец, из формулы G5) имеем (ср. формулу G6))
или, окончательно.
Особенно интересен тот случай, когда прямые AL, ВМ и CN
пересекаются в одной точке. Из последней формулы следует:

КОСОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ ПЛОСКОСТИ 349
Прямые AL, ВМ и CN пересекаются в одной точке в том
и только в том случае, если
V^s=1 G8)
(теорема Ч е в ы)').
4.5. Вопргс о единственности косого произведения. В конце предыду-
предыдущего параграфа мы видели, что скалярное произведение векторов пло-
плоскости однозначно определяется условиями E4), E5). E6) и еще одним
естественным требованием E7), заключавшимся в том, чго две «равные»
(т. е. переводимые одна в другую движением) пары ректоров должны
иметь одинаковое «произведение». В этом параграфе мы отказались от
услония E4) и пришли к косому произведению векторов, горенным образом
отличающемуся от скалярного произведения по своим свойствам. Естест-
Естественно, однако, поставить вопрос о том, нельзя лн найти иные «произве-
«произведения» векторов плоскости, обладающие столь же простыми свойствами
как скалярное и косое произведения, но отличные от них обоих?
Нетрудно покачать, что всякое «произведение» aob векторов плоско-
плоскости, обладающее перечисленными в конце предыдущего параграфа (стр. 336)
свойствами
b), . E5)
( ) c E6)
и свойством
аоЬ = аЛоЬ„ E7)
где пары векторов а, Ь и а,, Ь, «равны» друг другу, сводится к скаляр-
скалярному произведению i косому произведению. В самом деле, из условия E5)
по-прежнему следует
ao& = fl*.(a0o&c), E8)
где векторы а" и b° единичные и
acoa°=6 = const. F0)
Кроме того, если а" и с"—два таких единичных и взаимно перпендику-
перпендикулярных ректора, <гто /_ (а0, с°)= +90°, то произведение а" о с" б\ дет иметь
некоторое постоянное (т. е. одно и то же для всех таких пар векторов
а", с") значение б:
а" о с0 = е = const, G9)
поскольку любые две такие пары а0, с" и а°, с* можно перевести одну
в другую движением.
А теперь, разлагая произвольный единичный вектор b° по векторам а0
и с", где с°=1, /_ (а0, с°)= +90°, получим (ср. стр. 337)
а" о ft" = а" о [cos l_ (a°, b") a" + sin / (о0, Ь°) с"] =
= cos / (ас, ft")-(а0 о а") + sin / (а0, Ь°)¦ (а0 о с0),
откуда в силу E8), F0) и G9) имеем
ао ft = oabcos /_ (a, b) + e afcsin/.(a, b) = 6(ab) + e(axb). (80)
') В нашем рассуждении мы считали, что точки Р, Q и R сущест-
существуют (прямые Al, ВМ и CN не параллельны между собой). Более
точная формулировка теоремы Чевы такова: условие G8) имеет меапо
в том и только в том сл//ча?, если прямые AL, ВМ и СМ пересекаются
в одной точке иш все параллельны между собой.

350
ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
Таким образом, каждое «произведение» векторов, обладающее
свойствами E5) —E7), сводится к комбинации (80) скалярного и ко-
косого произведений с некоторыми постоянными коэффициентами б и б.
Ясно, что из всех таких «произведений» лишь скалярное является
коммутативным (ср. выше, стр 338) и лишь косое является антикоммута-
антикоммутативным.
Отметим еще в заключение, что все наши рассуждения проводились
в предположении, что две пары векторов а, Ь и a,, ft, на плоскости, пере-
переводимые одна в другую движением в пространстве (именно так в кон-
конце § 3 мы переводили друг в друга пары векторов а0, с" и —а0, с0), но ие
переводимые друг в друга движением на плоскости, не считаются
равными. Таким образом, здесь мы рассматриваем еометрию, в которой,
скажем, две симметричные от-
| носительно прямой фигуры
(рис. 73; такие фигуры нель-
нельзя перевзсти одну в другую
движением, оставляющим их
в плоскости) не считаются
одинаковыми. Свое проявле-
проявление этот подход находит в
том, что в рассуждениях мы
свободно пользовались поня-
поняли' тием направления вра-
вращения: угол ?_ (a, ft) мы
считали положительным или
отрицательным в зависимости
| \ / от того, каково направление
1 */ вращения на меньший 180°
угол, переводящего направ-
направление а в направление Ь (см.
стр 339—340). Ясно, что если
не различать между собой
Рис. 73. также и симметричные фигу-
фигуры (и вообще произвольные
фи-уры, переводимые одна
в другую движением в пространстве), то понятии «направление вращения»
становится бессодержательным — ведь при симметрии относительно прямой
направление цращения угла меняется на обратное (рис. 73). Плоскость,
на которой задано определенное направление вращения углов, принимае-
принимаемое за положительное, называется ориентированной плоскостью'). Таким
образом, скалярное произведение векторов определяется на неориентиро-
неориентированной плоскости2); косое же произведение векторов можно определить
лишь на ориентированной плоскости.
') Другими словами, ориентированная плоскость — это поле действия
«геометрии», изучающей свойства фигур, сохраняющиеся при движениях
первого рода (собственных движениях), в то время как обычная, или не-
неориентированная, плоскость рассматрипается как поле действия геометрии,
изучающей свойства фигур, сохраняющиеся при произвольных движе-
движениях (ср. § 6 статьи «Геометрические преобразования», а также
стр. 524—526).
г) Разумеется, ничто не мешает нам и на ориентированной плоскости
рассматривало и скалярное произведение векторов (ср. с замечанием на
стр. 341 о смысле символа /, (a, ft) в определении D5) скалярного произ
ведения).

ТРОЙНОЕ ПРОИЗВЕДЕНИЕ
351
flj
§ 5. Тройное произведение и векторное произведение
векторов пространства
5.1. Ориентированные объемы и тройное произвеление. Перей-
Перейдем теперь к случаю векторов в пространстве. Роль параллело-
параллелограмма в пространственной геометрии играет параллелепипед; поэтому
естественно вместо площади S(a, b) ориентированного па-
параллелограмма, построенного на двух
векторах а и Ь плоскости, рассматри-
рассматривать объем V(a, b, с) ориенти-
ориентированного параллелепипеда
OADBCAfixBx, построенного на
трех векторах ОА = а, ОВ = Ь,
ОС=с пространства (рис. 74). При
этом прилагательное «ориентиро-
«ориентированный» означает, что объем па-
параллелепипеда мы считаем поло-
положительным, если вращение векто-
вектора а на меньший 180° угол, совме-
совмещающее его направление с направлением вектора Ь, наблюдается из
конца вектора с происходящим против часовой стрелки (рис. 75. а;
такие параллелепипеды мы будем называть положительно ори-
ориентированными^; V (а, Ь, с) считается отрицательным, есля вращение
Рис. 74.
Рис. 75.
на меньший 180° угол, совмещающее направление вектора а с на-
направлением вектора Ь, наблюдается из конца вектора с происходя-
происходящим по часовой стрелке (рис. 75, б; такие параллелепипеды мы
будем называть ориентированными отрицательно). Если векторы
а, Ь и с принадлежат одной плоскости, то объем V (а, Ь, с) естест-
естественно считать равным нулю.
Определенную таким образом величину V(а, Ь, с) мы будем
называть тройным произведением векторов а, Ь и с; далее мы

352 ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
всюду будем обозначать ее через (а, Ь, с). Таким образом, здесь
мы впервые встречаемся с весьма своеобразным «произведением»—
в нем фигурируют не два «сомножителя», как обычно, а обязательно
три (векторных) «сомножителя» а, Ь и с. Несмотря на это обстоя-
обстоятельство, за величиной V (а, Ь, с) = (а, Ь, с) оказывается удобным
оставить название тройное произведение — и не только в силу
близости этой величины к косому произведению векторов плоскости,
употребление для которого названия «произведение» мы уже можем
считать привычным, но в первую очередь в силу того, что величина
(а, Ь, с) обладает, как мы увидим несколько ниже, целым рядом
свойств, родственных свойствам обычного произведения чисел (а также
свойствам скалярного и косого произведений векторов).
Нам будет удобнее несколько отложить вывод большинства
свойств тройного произведения. Здесь мы только отметим, что в силу
определения, тройное произведение (ненулевых) векторов а, Ь и
с равно нулю в том и только в том случае, если все векторы
принадлежат одной плоскости (аналогично тому как косое произ-
произведение двух векторов плоскости равно нулю в том и только в том
случае, если эти векторы принадлежат одной прямой). Отметим еще,
что тройное произведение антикоммутативно. т. е. меняет знак
при перестановке любых двух сомножителей:
(а, 6, с) = — (Ь, а, с) = — (а, с, b) = — (c, b, а).
Действительно, по абсолютной величине все выписанные тройные
произведения равны объему одного и того же параллелепипеда и
поэтому одинаковы. Далее (а, Ь, с) =— (Ь, а, с), ибо если враще-
вращение от вектора а к вектору Ь наблюдается из конца вектора с про-
происходящим против часовой стрелки, то вращение от вектора Ь к
вектору а наблюдается из конца с происходящим по часовой стрелке
и наоборот. Менее очевидно соотношение (а, Ь, с) = — (а, с, Ь)\
однако, чтобы его доказать, достаточно проверить, что вращение от
вектора а к вектору С наблюдается из конца вектора Ь происхо-
происходящим по или против часовой стрелки в зависимости от того, имеем
ли мы V(a, b, с) > 0 (черт. 75, а) или V(a, b, с) < 0 (черт. 75, б).
Точно так же проверяется и соотношение (а, Ь, с) — — (с, Ь, а).
Тройные произведения (Ь, с, а) и (с, а, Ь) могут быть получены
из произведения (а, Ь, с) путем двукратной перемены местами
двух «сомножителей»: сначала меняем местами а и Ь, а затем либо
с и а, либо с и Ь. Отсюда следует, что (Ь, с, а) = (а, Ь, с) и
(с, a, b) = (a, b, с). Таким образом, мы приходим к следующему
соотношению, которое является наиболее полным описанием свойства
антикоммутативности — тройного произведения:
(а, Ь, с) = {Ь, с, а) = (с, а, Ь) = — ф, а, с) = — (а, с, b) = —(c, b, а).
(81)

ТРОЙНОЕ ПРОИЗВЕДЕНИЕ
353
ft
О
Рис. 76.
5.2. Векторное произведение и его связь с тройным произве
дением. Прежде чем идти дальше в исследовании свойств тройного
произведения (а, Ь, с), обсудим несколько более тщательно его
строение. До сих пор произведение трех множителей (например, abc,
где а, Ь, с—три числа, или и(а, Ь), где а—число, а а и Ь—век-
Ь—векторы) встречалось у нас лишь как повторное произведение —
сперва перемножались два из наших грех множителей, а затем ре-
результат умножался на третий множитель. Естественно задать себе
вопрос о том, нельзя ли
и тройное произведение
трех векторов предста-
представить как повторное?
Выше мы имели лишь
один вид «произведения»
двух векторов простран-
пространства—скалярное произве-
произведение. Но скалярное про-
произведение сопоставляет
с двумя векторами число;
если это число затем умно-
умножить на вектор, являющийся третьим сомножителем, то мы получим неко-
некоторый вектор, а между тем окончательный результат тройного про-
произведения должен быть числом. Иначе обстояло бы дело, если
бы в результате перемножения двух первых сомножителей мы полу-
получили бы не число (скаляр), а вектор, — тогда, умножив этот вектор
на последний сомножитель скалярно, мы могли бы получить число,
как нам и требуется. Итак, если мы хотим представить тройное про-
произведение векторов в виде повторного произведения, то нам необхо-
необходимо использовать не только скалярное произведение векторов, но
еще и некоторое новое, «векторное» произведение, которое в резуль-
результате «умножения» двух векторов дает снова вектор.
Постараемся сообразить, как может выглядеть такое «векторное
произведение». Объем параллелепипеда OADBCAXDXBX, построенного
на векторах ОА = а, ОВ=Ь и ОС = с, равен произведению площади
его основания OADB на высоту. Но высота параллелепипеда h есть не
что иное, как проекция вектора ОС = С на вектор п, перпендику-
перпендикулярный к плоскости основания (рис. 76). Таким образом, по абсо-
абсолютной величине произведение (о, Ь, с) равно площади построенного
на векторах а и Ь параллелограмма OADB, умноженной на величину
проекции вектора с на вектор п; знак же произведения {а, Ь, с)
будет положительным или отрицательным в зависимости от того, в
какую сторону от плоскости OADB направлен вектор С.
Пусть площадь параллелограмма OADB равна а; в таком случае
мы имеем
\(а, Ь, с)| = а-|пр„е|.
23 Энциклопедия, кн. 4

354 ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
Если мы направим вектор п в такую сторону от плоскости
OADB, что вращение от положительного направления вектора а
к положительному направлению вектора Ь (на угол, меньший
\80°) наблюдается из конца п происходящим против часовой
стрелки, то величина (а, Ь, с) будет положительной или отрица-
отрицательной в зависимости от того, направлены ли векторы с и п в одну
сторону от (перпендикулярной п) плоскости OADB или в разные
стороны. Поэтому при таком выборе вектора п мы можем отбросить
знаки абсолютной величины в последней формуле и написать
(а, Ь, с) = апрпс (82)
(ср. с определением проекции вектора на другой вектор, стр. 320).
Формула (82) очень напоминает по своему строению формулу D4)
из § 3 (стр. 328). Ясно, как перейти от нее к представлению трой-
тройного произведения (а, Ь, с) в виде скалярного произведения двух
векторов. Обозначим через N вектор, направление которого совпа-
совпадает с вектором п, а длина равна o.^=SOADD; в таком случае
a = N, пр^^пр^с и формулу (82) можно будет переписать сле-
следующим образом:
(а. Ь, с) = N- пр^с.
Теперь в силу определения D4) скалярного произведения получаем-
(a, b, c) = Nc.
Условимся теперь называть вектор N векторным произведением
векторов а и Ь; обозначать его мы будем через [а, Ь]. В силу
всего сказанного выше векторное произведение \а, Ь\ векторов а
и Ь определяется следующими тремя условиями:
а) абсолютная величина (длина) вектора [a, b] равна площади
параллелограмма, построенного на векторах аи Ь; если векторы
а и Ь принадлежат одной прямой, то \а, Ь] = 0;
б) вектор [а, Ь] перпендикулярен плоскости, определяемой
векторами а и Ь (т. е. перпендикулярен обоим этим векторам);
в) вектор \а, Ь] направлен в такую сторону, что из его
конца вращение на меньший 180° угол, совмещающее направление
вектора а с направлением вектора Ь, представляется происхо-
происходящим против часовой стрелки.
Таким образом, мы записали тройное произведение (а, Ь, с)
как повторное:
(а, Ь, с) = [а, Ь\с, (83)
или, словами: для того чтобы составить тройное произведение
(а, Ь, с) векторов а, Ь и с, надо прежде всего образовать век-

ТРОЙНОЕ ПРОИЗВЕДЕНИЕ 355
торное произведение \а, Ь\ первых двух векторов, а затем ум-
умножить его скалярно на третий вектор с1)
5.3. Свойства векторного и тройного произведений. Разумеется,
уместность употребления в применении к вектору N = \а, Ь\ названия
«векторное произведение» обусловливается не полученной таким
путем возможностью представлять тройное произведение векторов
как повторное, а сходством свойств «векторного произведения» [а, Ь\
с произведением чисел (а также со скалярным и с косым произве-
произведениями векторов). К выводу этих свойств векторного произведения
мы сейчас и перейдем.
Заметим прежде всего, что в силу формулы (81) и коммутатив-
коммутативности скалярного произведения (см. формулу D7) стр. 328) мы имеем
(а, Ъ, с) = (&. с, a) = [b, c]a = a\b, с]; (84)
таким образом, тройное произведение векторов а, Ь и с равно
также скалярному произведению первого вектора а на вектор-
векторное произведение двух последних векторов Ь и с.
Перейдем теперь к выводу свойств тройного произведения и век-
горного произведения. Мы уже видели, что тройное произведение
(а, Ь, с) антикоммутативно (см. (81)). Отсюда немедленно вытекает,
что векторное произведение \а, Ь] антикоммутативно:
[а, &] = — [&. a]. (85)
В самом деле, из антикоммутативности тройного произведения и
формулы (84) следует
\а. Ь\с = (а. Ь, с) = — F, а, с) =— \Ь. а\с.
Как мы видим, два вектора [a, b] = N и [6, а] = Л1 таковы, что для
любого вектора с имеет место соотношение: Nc = — Me, или, что
то же самое, (Л1 -f- N) с = 0. Таким образом, вектор M-\-N должен
быгь перпендикулярен любому вектору с, что невозможно при
М -f- N ф 0 Следовательно, AI + N=0, т. е. М = —N, а это и есть
соотношение (8з).
Докажем теперь, что тройное произведение (а, Ь, с) ассоциа-
ассоциативно по отношению к умножению любого из векторов-сомно-
векторов-сомножителей на численный множитель:
Ска, 6, с) = (а. ~kb, с) = (а, Ь, 'кс) = 'к-(а, 6, с). (86)
Из формулы (84) и ассоциативности скалярного произведения имеем
(Ка, Ь, с) = (Ы)[Ь, с\ = К(а\Ь, с\) = 1(а. Ь. с).
1) В литературе тройное произведение (а,Ь,с) называется также часто
смешанным произведением. Это последнее название имеет в виду то, что для
образования произведения (а, Ь, с) надо использовать два разных вила
умножения векторов — векторное и скалярное.
л*

356 ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
Формула
(a, Xb, c) = 'K(a, Ь, о
следует отсюда очевидным образом, если использовать антикоммута-
антикоммутативность тройного произведения:
(a. Kb, c) = — (lb, а, с) = — к(Ь, а, с) = К(а, Ь, с).
Аналогично устанавливается соотношение (a, b, 'kc) = 'k{a, b, с).
Установим теперь, что векторное произведение \а, Ь] ассоциа-
ассоциативно по отношению к умножению любого вектора-сомножителя
на численный множитель:
[Ы, b] = [a, Щ = К\а, b]. (87)
В самом деле, имеем
[Я,а, b\c = (ka. b, c)=K(a, b, c) — "k\a. b]c.
Но если векторы [а, b] = N и [ha, b\^=Mt таковы, что при любом
векторе с имеем
Mxc="kNc. т. е. (М, — WV)c = 0.
то, очевидно,
Ml = lN, т. е. \la, b] = l\a. Ь].
Отсюда, используя антикоммутативность векторного произведения,
сразу получаем и равенство [a, Kb] = Х[а, Ь].
Наконец, докажем дистрибутивность тройного произведения:
(а, Ь, с, + с1) = (в, Ь, с,) + (а, Ь, сх) (88)
и аналогично
(а, 6, + 62, с) = (а, 6„ с) + (а, 62, с),
(аЛ-\-аг, b, c) = ial, Ь, с) +(о„ Ь, с). (88а)
В силу дистрибутивности скалярного произведения, очевидно, имеем
(а, 6, с, + сг) = [а. 6](с, + сг) = [а, 6]с,+ [а, Ь\ ct=(a, Ь, с,)+(а, 6, с2).
Формулы (88а) выводятся из формулы (88) с использованием анти-
антикоммутативности тройного произведения; так
1а. Ь, + Ьг, с) = — (а, с, 6, + 62) = —(а, с, 6,) —(а, с, 62) =
= (а, 6,, с) + (а, 62, с).
Докажем также н дистрибутивность векторного произведения:
[а, 6, + 62] = [а, 6,] +[а. 62], Ю. + О,, 6] = [а„ Ь\ + \аш, Ь]. (89)
Ясно, что достаточно доказать лишь первую из формул (89). Но
[а, 6, + 62]с = (а, 6, + 62, с) = (а, bv c) + (a, 62, с) =
= [а, 6,]с+[а, 62]с = ([а, ft,] + [o, Ьш\)с
для любого вектора с. Отсюда: [а, Ь1+Ь1\ = [а, 6J + [а, 62|'

ТРОЙНОЕ ПРОИЗВЕДЕНИЕ
357
Заметим еще, что ассоциативность векторного произведения
для умножения трех векторов места не имеет: вообще говоря,
[[а, Ь\, с] Ф [а, \Ь, с]].
перпендикулярных вектора
Например, если i, j—два взаимно
(рис. 77), то мы имеем
Ш, Л Л = I*. J\= — '• V- U. Л] = И. 01 =0.
Ассоциативность векторного произведения заменяется следующим
своеобразным тождеством:
[а, \Ь,
\Ь, [с,
с, [а, &Ц =
(90)
связывающим «двойные векторные произведения» \а, \Ь, с]], [Ь, \с, а\]
и [с, [а, Ь]\ одних и тех же векторов а, Ь и с взятые с разным
порядком расстановки ско-
скобок. Тождество (90) носит
название тождества
Я ко б и; мы его докажем
ниже.
Нетрудно понять, что
соотношения (85), (86) и
(87) можно довольно просто
вывести из самого определе-
определения тройного и векторно- _
го произведений По-иному
обстоит дело с соотношениями дистрибутивности (88) — (88а) и
(89) — здесь выбранный нами довольно длинный путь доказательства
этих свойств вряд ли можно сократить.
Из доказанных свойств тройного и векторного произведений вы-
вытекают правила перемножения сумм векторов, родственные обычным
правилам раскрытия скобок:
, 2с d — 5е) = 4(а, c,d) — 20(a,c,e) + 6(b, с, d)—30F, с, е)
или
[4а—
= 4[a, c]+\2\a, d] — \b, c] — 3[b, d]
Однако при этом приходится учитывать антикоммутативность трой-
тройного и векторного произведений — в частности то, что векторное
произведение двух одинаковых множителей («векторный квадрат»)
всегда равно нулевому вектору и тройное произведение трех множи-
множителей, по крайней мере два из которых одинаковы, всегда равно
нулю:
[а, а] = 0, (а, а, Ь) = (а, Ь, а) = F, а, а) = (а, а, а) = 0.

358 Вькторы и их применения в геометрии
Учитывая антикоммутативность, имеем, например,
(а -\-Ь, b + с, с + а) = (а, Ь, с) + (Ь, с, а) = 2 (а, Ь, с)
или
[а + 26, 36 —а] = 3[а, 6] — 2 [6, а] =5 [а, 6].
Найдем теперь выражения для тройного и векторного произведе-
произведений в координатах. Пусть векторы а, 6 и с имеют координаты
(х, у, z), (xv ул, zt) и (хх, уг, zt), т. е.
c = xti+yj+ztk.
От векторов i, j, k, направленных по осям координат, мы потребуем
только, чтобы объем построенного на них параллелепипеда был равен
1 и чтобы этот параллелепипед был ориентирован положительно:
(/, /,*)=+ 1.
В таком случае имеем
(а, 6, c) = (xi + yj+zk, xj + yj+zf, xj + yj+ztk) =
= хУ1ггA, j, k) + xz1yt(i, ft, j)+yxxztij, i, ft) +
+ yzlxt(J, k, i) + zxlyi(k, i, fl + zy^^k, J, t),
или, окончательно,
(a, 6, c) = xy1zi+yzlx1 + zxji—xzlyi—yx1z1~zy1xt. (91)
Для того чтобы найти выражение для векторного произведения
векторов а и 6, потребуем, чтобы система координат была декарто-
декартовой прямоугольной и к тому же правой, г. е. чтобы было
[*. /] = *, I/, *l = *. I*. i\=J
(см. рис. 77). При этом получаем
|a, b] = [xi+yj + zk, xj + yj + zfi]^
=**У,[*. f\ + xzx\i, k\+yxx\J, i\+yzjj, k\ + zxxlk, i\ + zyx[k, A
или, окончательно,
[a. b] = {yzl—zyl)i + [zxl—xzl)J+(xyl—yxl)k. (92)
Таким образом, векторное произведение векторов а и b с координа-
координатами (х, _у> 2) и (л;,, у,, zr) имеет координаты
(yzl—zyv zx1—xzl, xyl—yxl).

ТРОЙНОЕ ПРОИЗВЕДЕНИЕ
359
(a.
b.
0 =
X
xx
Хг
У
Ух
Уг
Z
г
z
Формулу (91) можно принять за определение тройного про-
произведения векторов. Если записать ее в виде
(91а)
то мы узнаем в ней известное геометрическое истолкование опреде-
определителей третьего порядка как объемов ориентированных параллеле-
параллелепипедов1). При таком определении антикоммутативность (Ь, а, с) =
= —(а, Ь, с), ассоциативность по отношению к умножению вектора
на число (ка, Ь, с) = Я,(а, Ь, с) и дистрибутивность {al -f- а2, Ь, с) =
= (а,, b, c) + (o2, Ь, с) тройного произведения векторов становятся
следствиями известных свойств определителей третьего порядка:
Xx
Ч
х,
Уг
ч
X
Ч
У,
У
Уг
ь,
Ух
Уг
г«'>4
г
z
zi
г
Ч
Ул
гх
Ч
zB)
= —
=
X
Ч
Ч
X
Ч
ч
Ч
х
У
Ух
Уг
У
Ух
Уг
ут
Ух
Уг
г
Ч
Ч
г
Ч
Ч
г(.)
ч
ч
;
;
+
ХB)
ч
ч
Ут
Ух
Уг
гB)
Ч
Ч
Из известного правила умножения определителей третьего порядка 2)
гB)
получаем также
(a, b,
aa, aft,
Л Ьсх
В частности,
(a, b, cJ =
a* aft ac
a6 62 be
ac be c*
(93)
') См. в кн. И ЭЭМ статью «Векторные пространства и линейные пре-
преобразования»
2) Ср., например, кн. 11 ЭЭМ, стр. 96.

360
ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
Эта формула является «трехмерным аналогом» формулы GГ) преды-
предыдущего параграфа (см. стр. 345).
Формулу (92) также можно записать с использованием определи-
определителей третьего порядка:
i j к
[а, Ь] =
У
Уг
(92а)
Стоящий справа определитель», можно разложить по элементам
первой строки:
J
У
Уг
k
Z
z.
=
У z
Ух *х
i—
X Z
Хх 2,
J +
х у
•х, Ух
к.
(926)
Формулу (92) (или (92а) — (926)) можно принять за определение
векторного произведения; из нее нетрудно вывести все его свойства.
5.4. Двойное векторное произведение. В качестве примера на
использование формулы (92) докажем с ее помощью следующее тож-
тождество:
[с, [a, b]] = (bc)a—(ac)b. (94;
Выберем прямоугольную систему координат так, чтобы направление
оси х совпадало с направлением вектора а; в качестве плоскости
хОу выберем плоскость, содержащую векторы а и Ь; направление
оси z при этом уже определится. В таком случае координаты век-
векторов а, Ь, с будут иметь вид: (х, 0, 0); (хх, yx, 0) и (хг, уг, zt).
Вектор [а, Ь] будет в силу (92) иметь координаты @, 0, хух), а
вектор [с, [а, Ь\\ будет в силу той же формулы (92) иметь коорди-
координаты (yt(xyx),—xt (xyx), 0). Таким образом, мы нашли координаты
вектора, стоящего в левой части соотношения (94). Далее, согласно
E0а) мы имеем
be = хххг + yxyt, ас = xxt,
и потому вектор (be) а имеет координаты (x(xlx1-\- yxyt), 0, 0),
а вектор (ас) b — координаты (хх(хх2), ух(хх2), 0). Отсюда, наконец,
следует, что вектор Fс) а—(ас) b имеет координаты(х(ухуг)—¦д'1(д;л:2),0).
Таким образом, векторы, стоящие в левой и правой частях соотно-
соотношения (94), имеют одни и те же координаты, и потому соотно-
соотношение (94) справедливо.
Заменяя в соотношении (94) обозначения векторов, получим
[а, [Ь, с\\ = (ас)Ь—(аЬ)с,
[Ь, [с, а\\ = (аЬ)с—(Ьс)а.
(94а)
(94б>

ТРОЙНОЕ ПРОИЗВЕДЕНИЕ
361
Складывая теперь все три соотношения (94), (94а), (946), мы полу-
получаем соотношение (90), которое, таким образом, также доказано.
Докажем еще следующие соотношения, которые понадобятся нам
в следующем параграфе:
[[с, Ь], [с, d]] = (a, с, d)b—(b, с, d)a, (95а)
\\а, Ь], \с, d]] = (a, Ъ, d)c—{a, b, c)d, (956)
\а, Ь][с. d] = {ac)(bd)—(ad){bc). (96)
Соотношение (956) легко вытекает из соотношений (94) и (83):
[[с, Ь\, [с, d]] = {la, b]d)-c—([a, b]c)-d = (a, b, d)c — (a, b, c)d.
Далее, из соотношений (956) и (85) вытекает (95а):
[[с, Ь], [С d]] = — llc, d], [a, b]] = — (c, d, b)a + (c, d, a)b =
— {a, c, d)b — (b, c. d)a.
Наконец, формула (96)-вытекает из (83), (81) и (94):
[с, Ь] [с, d] = (с, Ь, [с, d]) = (Ь, [с, й], а) = [6, {с, d]] a =
= {(bd) с — {be) d)a = {bd){ac) — {be) (ad).
5.5. Примеры. Рассмотрим теперь несколько задач, иллюстрирую-
иллюстрирующих применения тройного и векторного произведений в геометрии.
Задача 12. Найти
объем треугольной пирами-
пирамиды (тетраэдра), зная длины
всех его ребер.
Решение. Пусть дан
тетраэдр ОАВС (рис. 78).
Векторы ОА,ОВ,ОС; ~АВ,
ВС, СА обозначим через а,
Ь, с; с', а', Ь'. Дополним
тетраэдр до параллелепи-
параллелепипеда OADBCAfifi^, оче-
очеРис. 78.
видно, что объем этого
параллелепипеда будет в 6 раз больше объема тетраэдра (если
h есть общая высота тетраэдра и параллелепипеда, опущенная из
вершины С, то Vnap = S0ADB
Отсюда получаем
Утетр=А-|(а,&,
Но в силу формулы (93)
(а, Ь, с)г =
-h; Vxexp = g-S
0AB
¦ h и
С)\
аг аЪ ас
аЬ Ьг be
ас be с1

362 ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
С другой стороны, очевидно,
с' — Ь — а, а'=с — Ь, Ь' = а — с.
Поэтому
с'2 = Ь2— 2ab -f- a2, ab = -
и аналогично
ас = g • Ьс =
Таким образом, окончательно имеем
а' + Ь'-с"
(a,
a' + c'—b'1 If + c1—а'г
¦и. следовательно.
2аг
2а1
Ьг-с'
2сг
2сг
Эта формула родственна элементарной формуле Герона (стр. 346),
выражающей площадь треугольника через длины его сторон.
Задача 13. Определить объем параллелепипеда OADBCA'D'В',
зная длины ребер ОА = а, 08=Ь, ОС—с и углы /_АОВ = у,
/_АОС = §, /^ВОС=а между этими ребрами.
Решение. Обозначим по-прежнему ОА =а, ОВ = Ь, ОС—с.
Мы знаем, что
V=Vmv = \{a, Ь, с)|, \Г = (а, Ь, с)г.
В силу формулы (93) и определения D5) скалярного произведения
имеем
V* = (а, Ь, сI =
а2 аЪ ас
аЪ Ьг be
ас be сг
a' ab cos у ас cos p1
ab cos у b1 be cos a
ас cos p be cos a c*
Вынося из 1-й строки определители множитель а, из 2-й строки —
множитель Ь, из 3-й строки — множитель с, затем вынося из 1-го

ТРОЙНОЕ ПРОИЗВЕДЕНА
363
столбца множитель а, из 2-го столбца — множитель Ь, из 3-го сюлбца —
множитель с, окончательно получаем
V2 =
aW
1
cosy
cosp
cosy
1
cos a
cos p
cos a
1
V=abc
1
1
cosy
cosp
cosy
1
cos a
cos p
cos a
1
= abc\f 1 + 2 cos a cos p cos у — cos2 а — cos2 p —
cos*
Задача 14. Дана треугольная пирамида (тетраэдр) ОАВС.
Доказать, что если высоты тетраэдра, опущенные из вершин А
и В, пересекаются между собой, то
При каком условии все высоты тетраэдра пересекаются в одной
точке?
Решение. Обозначим по-прежнему ОА = а, ОВ=Ь, ОС=с;
АВ=с', ВС—а', ~СА = Ь' (рис. 79). Если высоты АР и BQ тетра-
тетраэдра пересекаются, то векторы АР, BQ и АВ лежат в одной пло-
плоскости (и обратно, если эти три век-
вектора лежат в одной плоскости, то
высоты АР и BQ пересекаются). Усло-
Условие нахождения трех векторов АР, BQ,
АВ в одной плоскости имеет вид
(АР, BQ, АВ) = 0.
Но АВ=Ь — с; вектор АР имеет на-
направление перпендикуляра [Ь, с] к пло-
плоскости О??С;векгор BQ имеет направле- Рис. 79
ние перпендикуляра [а, с] к плоскости
ОАС. Поэтому условие пересечения высот АР и BQ принимает вид
([6, с], [а, с], й-а) = 0
[[Ь, с], [а. с]](Ь-а) = О
Но согласно (95 а) вектор \\Ь, с], [а, с]] равен (й, с, с)с (ибо
(с, а, ?#) = 0), т. е. параллелен вектору с (и отличен от нуля).
Таким образом, последнее условие равносильно следующему:
с (Ь — а) = 0, или be = ас.
или (см. (83))

364 ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
Заменяя здесь ОС и ас на ——„ и —!—^ (см. решение за-
задачи 12), получаем
или
что и требовалось доказать.
Этому же равенству равносильно требование, чтобы высоты CR
и 05 пересекались между собой. Требование, чтобы пересекались
высоты АР и CR (а также BQ и 05), равносильно равенству
Высоты BQ и CR (а также АР и 05) пересекаются между собой
тогда и только тогда, когда
Наконец, необходимым и достаточным условием пересечения всех
высот тетраэдра в одной точке является выполнение равенств
5.6. Вопрос о единственности тройного и векторного произведений.
В заключение остановимся на вопросе о том, насколько необходимым
являются именно те определения векторного и тройного произведений,
которые были приняты выше; при этом мы, естественно, требуем, чтобы
эти «произведения» удовлетворяли тем условиям, справедливость кото-
которых и обусловила возможность употребления самого слова «произведение».
Рассмотрим какую либо операцию *, сопоставляющую с каждыми двумя
векторами а и Ь третий вектор а*Ь. Потребуем, чтобы это «произ-
«произведение» обладало свойством ассоциативности по отношению к умножению
вектора на число:
Х(а*Ы (97)
и свойством дистрибутивности
c (98)
Кроме того, потребуем, чтобы наше «произведение» а*Ь имело гео-
геометрический смысл; другими словами, это означает, что если век-
векторы ОА = а и ОВ = Ь могут быть переведены в векторы ОА1^а1 и ОВ1=Ь1
каким-либо движением в пространстве (каким-либо вращением вокруг
точки О), tv и вектор ОС = а*Ь должен переходить при этом движении
в вектор ОС[ = а, *Ь, (ср. стр 336)
Докажем, что в таком случае «произведение» а*Ь с неизбежностью
сводится к векторному произведению [а, Ь\
Положим а = аа°, b = bb°, где а0 и Ь"—единичные векторы Из (97)
вытекает
а*Ь = (аав) * Ffc°> = (ab)(aB*b").
Таким образом, нам достаточно определить «произведение» единичных век-
векторов (ср. выше, стр. 337).

ТРОЙНОЕ ПРОИЗВЕДЕНИЕ
365
Далее, пусть ОР— прямая, перпендикулярная к плоскости единичных
векторов ОА = а", ОВ — Ь° (рис. 80). Вращение вокруг прямой ОР на угол
в 180° переводит векторы а0 и ft0 в векторы — а0 и — ft0; следовательно,
это вращение должно переводить вектор а" * Ь° в вектор (— а0) * (— ft°)=
= а0 * ft0 (см. (97)), т. е. оставлять вектор а" * b° на месте. Но это возможно
лишь в том случае, если вектор а" * ft" принадлежит прямой ОР (т е.
перпендикулярен векторам а" и ft0).
Отсюда вытекает, прежде всего, что «квадрат» а0 * а" любого (единич-
(единичного) вектора равен нуль-вектору 0:
а°*а° = 0.
(99)
В самом деле, если вектор Ь" совпа-
совпадает с вектором а0, то прямую ОР
можно выбирать бесчисленным чи-
числом способов, и вектор а0 * а9, ко-
который должен принадлежать всем
этим прямым, с необходимостью ока-
оказывается нулевым. Далее, пусть
с0 _L о°; тогда «произведение» а0 * с0.
равно Ки°, где и" есть единичный
вектор, перпендикулярный а" и с".
Для определенности мы выберем а"
таким образом, чтобы из его конца
вращение на 90 от вектора а0 к век-
вектору с" наблюдалось проти. часо-
часовой стрелки. Множитель к должен
быть псстоянным, т. е. одним и тем же для любой пары перпен-
перпендикулярных единичных векторов а" и с": в самом деле, если а° и с\ —
два других единичных взаимно перпендикулярных вектора, то вращение,
совмещающее пару а0, е° с парой а°, cj, переводит вектор ка° в вектор
Х,а°, где и° есть единичный вектор, построенный по векторам а\ и с\ в точ-
точности так же, как строится вектор а" по векторам а" и с". Таким образом,
имеем
Рис. 80.
к = const.
A00)
Теперь остается только разложить любой единичный вектор ft0 по ьек-
торам а0 и с", где вектор с0 лежит в плоскости векторов а0 и ft0 и пер-
перпендикулярен вектору а0:
d° = cos /_ (а°, ft°)-a° + sin / (a0, b°)-c"
(ср. выше, стр. 337) Используя теперь (98), (97), (99) и A00), получаем
а0 * ft0=cos / (а°, ft0) (а0 * а0) + sin / (а°. ft0) а0 * с0) = к sin ? (а°, ft0) и".
и, следовательно,
(a, b)-u° — k [а, ft],
где к—постоянная величина.
Аналогично этому решается и вопрос об определении тройного произ-
произведения (а Ь, с) его свойствами ')
Заметим в заключение, что, потребовав от «векторного произведения»
а*Ь выполнения условий ассоциативности по отношению к умножению
") Ср , например. §§ 2—6 напечатанной в кн. II ЗЭМ статьи «Вектор-
«Векторные пространства и линейные преобразования».

366
ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
вектора на число (97) и дистрибутивности (98), мы пришли к произведению
[а, Ь]. Отсюда следует, что если бы мы дополнительно потребовали от
«произведения» а*Ь коммутативности
а*Ь= Ь*а
или ассоциативности в обычном смысле
а * (Ь * с) = (а * Ь) * с.
A01)
A02)
то мы не пришли бы ни к какому «произведению» а*Ь, отличному от
(совершенно неинтересного) «нулевого произведения» а*Ь = 0. Таким об-
образом, требования (97), (98) и хотя бы одно из требонаний A01), A02)
являются несовместимыми (если только еще требовать, чтобы «произведение»
а * Ь имело геометрический смысл)
§ 6. Применения векторного исчисления
к сферической геометрии и тригонометрии
6.1. Выражение сторон и углов сферического треугольника с помощью
векторов. С помощью векторного исчисления можно весьма изящно дока-
доказать многие теорем j сферической геометрии и тригонометрии.
Будем характеризовать каждую точку А сферы радиуса г ее радиусом-
вектором А с началом в центре сферы
(рис. 81). Тогда
\А\ = г (ЮЗ)
Очевидно, что радиусы-векторы двух
диаметрально противоположных точек
противоположны, а ради усы-векторы двух
полярно сопряженных точек1) ортого-
ортогональны, т. е. условие диаметральной проти-
противоположности точек А и В имеет вид
а+в=о,
а условие полярной сопряженности точек А
и В имеет вид
АВ=0.
A04)
Рис 81. Стороны а, Ь, с сферического треуголь
ника ABC связаны с радиусами-векто-
радиусами-векторами А, В, С его вершин очевидными соотношениями
A05)
A06)
ВС=гг cos— , CA = r2cos— АВ=гг cos —
г Т Г
Угол А этого сферического треугольника, т. е. угол между касатель-
касательными к сторонам Ь и с, проведенным в точке А, равен углу между пло-
плоскостями АОВ и АОС (где О —центр сферы), т е. равен углу между пер-
перпендикулярными к этим плоскостям векторами \А. В] и [А, С]. Отсюда
') По поводу используемых здесь понятий сферической геометрии см.
статью «Основные понятия сферической геометрии и тригонометрии» в этой
книге ЭЭМ (стр. 518—557).

применения векторного исчисления 367
следует, что
сосЛ_ [А,В\\А,С\
**А-\[А.В\\А\А.С\\ (Ш7>
и
=1п.4- \\\А. В\. \А. С\\\
SmA- \[А,Ь\\.\[А.С]\ A08>
Из формулы A04) вытекает условие того, что сферический треугольник
А'В'С является полярным по отношению к сферическому треугольнику ABC;
оно имеет вид
АВ' =АС = ВА' = ВС = СА' = СВ' = 0. A09)
Пусть вершины сферического треугольника ABC занумерованы в таком
порядке, что векторы А, В, С составляют правую тройку, т. е. удовлетво
ряют условию {А, В. С)>0. Тогда векторы А', В'. С, идущие к першинам
полярного треугольника А'В'С, выражаются через векторы А. В. С по
формулам
v . [В, С] |С, А\ [А,В\
В С]\ Г- В~\\С.А\\ Г- С - I \А, в] | Т-
Действительно, векторы A10) удовлетворяют условию A09); кроме того-
так как векторы А', В, С, так же как векторы А, В', С к А, В, С', соста"
вляют правые тройки, то точки А', В', С" находятся по ту же сторону от
больших окружностей ВС, СА и АВ, что и соответственно точки А, В, С
Нетрудно проверить (например, воспользовавшись формулами (83) и (95а)),
что тройка векторов А'. В' С также является правой.
Из симметричности формул A09) относительно двух правых троек век-
векторов А, В, С и А'. В', С" видно, что сферический треугольник, полярный
по отношению к треугольнику А В'С. совпадает со сферическим треуголь
ником ABC
Сторона а' полярного треугольника А'В'С определяется соотношением,
аналогичным первому соотношению A05)
В'С = г2 cos — ,
г
о^_ I [С, А\ [А, В] [А,В]\А,С]
cos г _ r2e с _ )[с А]Ы[А ви ,м к||.|[А С]\
откуда в силу A10) и A07) получаем
[С, А\ [А,
= — cos A =cos (л — А).
Аналогично получим
cos — = — cos В = cos (л—В), cos — = — cos f. =cos(ji — С),
откуда видно, что стороны а', Ь', с' сферического треугольника А'В'С
соответств нно равны (л — А) г, (л — В) г и (л — С) г. В силу того, что
сферический треугольник ABC является полярным треугольником для
сферического треугольника А'В'С. таким же образом мы находим, что сто-
стороны а, Ь, с сферического треугольника ABC соответственно равны (л — А') г,
(л — В') г, (л — С) г. Отсюда следует, что углы А', В', С сферическою
треугольника А'В'С соответственно равны ч , л , л . ,

368 ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
6.2. Сферические теоремы косинусов и синусов.
Для доказательств а сферической теоремы косинусов') заметим, что фор-
формулу A07) в силу соотношения (96) можно переписать в в иде
A*-(BC)-(AB)UC)
i-°SA- \[A,B]\-\[A.C]\
Но в силу формул A03), A05) и A06) это соотношение можно перепи-
переписать так:
а Ьс
cos cos — cos —
л Г Г Г
cos А =
. Ь . с
sin — sin —
г г
Отсюда непосредственно вытекает сферическая теорема косинусов:
а Ь с , . Ь . с .
cos —=cos — cos h sin — sin — cos A
r t t r r
Для доказательства сферической теоремы синусов заметим, что формулу
A08) в силу соотношения (95а) можно переписать в виде
\(А,А,С)В-(В, А,С)А\ \А\-\{А,В,С)\
ЦЛ, в] |-| [Л. С]\ ~\[А.В]\\\А.С]\
Но в сил> формул A03) и A06) это соотношение можно переписать
так:
8.пЛ 1 ил. а, о,
г" . Ь . с '
sin — sin —
г г
откуда
sin Л _ 1 | (А, В, С) 1
. а ~ г3 ' . а . Ь . с '
sin — sin — sin — sin —
г г г г
Так как полученное выражение симметрично относительно векторов
А, В. С и сторон A, Ь, с, то этому же выражению равны и отношения
sin б sin С ,
— и , откуда и вытекает сферическая теорема синусов:
О .С
sin — sin —
г г
sin A sin б sin С
.а . Ь .с
sin — sin — sin —
г г г
Применяя сферическую теорему косинусов к полярному треугольнику
А'В'С и выражая а', Ь'. с' чере: А. В С. а А' — через о, ь. с, мы, так же
как на стр 551, получим двой(_тьенную теорему косинусов.
*) См. стр. 547.

ПОНЯТИЕ О ВЕКТОРНЫХ ПРОСТРАНСТВАХ 369
§ 7. Понятие о векторных пространствах
7.1. Аксиоматическое- определение векторного пространства.
В этом параграфе мы приведем аксиоматику, описывающую сово-
совокупность всех векторов (на плоскости или в пространстве). Это, в
частности, позволит нам дать еще одну систему аксиом геометрии,
отличную от аксиоматики, приведенной в статье «Аксиомы и основ-
основные понятия геометрии» (стр. 32—40).
Обозначим через R совокупность всех векторов в пространстве.
В предыдущих параграфах были установлены многие важные свойства
множества R. Некоторые из Этих свойств мы отметим здесь еще раз.
1. Групповые свойства
Для каждых двух векторов а, Ь (т. е. для каждых двух элемен-
элементов множества R) определен вектор а-{-Ь, называемый их суммой.
Эта операция сложения обладает следующими тремя свойствами:
1°. (а-\-Ь)-\-с = а-\-(Ь-\-с) для любых трех векторов а,Ь,с.
2°. a-{-b^=b -f-a для любых двух векторов а, Ь.
3°. Для любых векторов а, Ь уравнение а-{-х = Ь имеет решение
(т. е. существует хотя бы один вектор х, удовлетворяющий соот-
соотношению а-{-х = Ь).
Свойства Iе — 3° показывают, что множество R является коммута-
коммутативной, группой относительно операции сложения векторов (ср. стр. 27).
11. Свойства линейности
Для каждого вектора а и каждого действительного числа X опре-
определен вектор Ха, называемый произведением век-тора а на число X.
Эта операция умножения вектора на число обладает следующими
свойствами:
4°. 1с = а для любого вектора а.
5°. (X + [i)a = Xa + [ia.
6°. X (а + Ь) = Ха + Kb.
Т. X (|ш) = (Кц) а.
(В свойствах 5°, 6°, 7° а и Ь—произвольные векторы, a X, (.1 — дей-
действительные числа.)
111. Метрические свойства
Для каждых двух векторов а, Ь определено действительное число аЬ,
называемое их скалярным произведением. Эта операция скалярного
умножения обладает следующими свойствами:
8°. аЬ = Ьа для любых двух векторов с, Ь.
9°. (с + Ь) с = ас + be для любых трех векторов а, Ь, с.
24 Энциклопедия, кн. 4 *

370 ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
10°. (ка)Ь = К(ab) для любых векторов а, Ь и любого действи-
действительного числа К.
11е. Для любого вектора а число аа неотрицательно и равно нулю
только в случае, если с = 0
[Нулевой вектор 0 определяется равенством с-\-0 = с,
С — произвольный вектор. |
IV. Свойства размерности
12е. Существуют в множестве R три линейно независимых вектора-
13°. Всякие четыре вектора из R линейно зависимы.
Перечисленные аксиомы играют очень важную роль в современ-
современной математике. Как мы знаем, аксиомы Iе—3° вводят весьма важное
понятие группы (см. стр. 27). Аксиомы 1°—7° определяют по-
понятие векторного пространства, также играющее очень важную
роль. Наконец, аксиомы 1°—11° определяют понятие евклидова
векторного пространства, имеющее многие плодотворные примене-
применения в математике. Ниже мы скажем несколько подробнее о векторных
(в частности, евклидовых) пространствах. Сейчас же мы хотим прежде
всего показать, что система аксиом 1°—13° непротиворечива и
полна (см. стр. 28 — 30). Это означает, что, исходя из действи-
действительных чисел, можно построить модель для этой аксиоматики (не-
(непротиворечивость) и что любые две такие модели изоморфны между
собой (полнота).
7.2. Арифметическая модель векторного пространства. Модель
для аксиоматики 1°—13° строится очень просто. Вспомним, что
введение координатной системы позволяет записывать каждый вектор
в виде тройки чисел (х, у, z), причем указанные выше операции
весьма прости выражаются в координатах. Мы установили эти факты,
используя геометрическую модель системы векторов (см. § 1). Те-
Теперь же мы примем координатную запись векторов в качестве исходного
определения. Итак, каждую тройку (х, у, z) действительных
чисел (записанных во вполне определенном порядке) мы условимся
называть «вектором» и обозначим через R совокупность всех таких
«векторов» Далее, сумму двух векторов, произведение вектора на
число и скалярное произведение векторов определим формулами:
Х(х, у, z) = (Kx, Xy,
Остается проверить, что в этой «арифметической» модели системы
векторов выполнены аксиомы 1°—13°. Проверка аксиом 1°—11° не
представляет никакого труда. Укажем кратко, каким образом прове-
проверяются аксиомы 12° и 13Q. Для проверки аксиомы 12° мы установим,

ПОНЯТИЕ О ВЕКТОРНЫХ ПРОСТРАНСТВАХ 371
что векторы
A, 0, 0), @, 1. 0), @, 0, 1)
линейно независимы. В самом деле, линейная комбинация этих век го-
ров с коэффициентами А,, |л, v имеет вид
0, 0) + ц@, 1, 0) + v@, 0, 1) = Ск, |Л, v);
ясно, что эта ^линейная комбинация обращается в нулевой вектор
@, 0, 0) только при A, = n = v = 0, т. е. рассматриваемые три вектора
линейно независимы.
Обратимся, наконец, к аксиоме 13°. Возьмем четыре произвольных
вектора
(с,, Ьл, сл), (с2, Ьх, с2), (с,, Ьг, с,), (а4, Ьл, cj.
Для доказательства того, что эти четыре вектора линейно зависимы,
мы должны найти числа х, у, z, t, среди которых хотя бы одно
отлично от нуля и которые удовлетворяют условию
х(ах1 bx, cx) + y(at, bt, с2) + г(аг, b,, с,) + *(а4, bt, c4) = @,0,0)
Это соотношение, как легко видеть, равносильно выполнению трех
равенств
агу + asz + aj = 0,
Таким образом, для проверки аксиомы 13° достаточно установить,
что написанная система уравнений имеет хотя бы одно ненулевое
решение. Но однородная (т. е. не содержащая свободных членов)
система уравнений первой степени, в которой число неизвестных
больше числа уравнений, всегда имеет ненулевое решение.
Итак, аксиомы 1°—13° в рассматриваемой модели выполняются,
и потому приведенная аксиоматика непротиворечива. Рассмотренную
модель мы будем называть арифметической моделью векторного
пространства.
7.3 Полнота аксиоматики векторного пространства. Прежде
чем переходить к доказательству по л н о ты аксиоматики 1°—13°, мы
выведем из аксиом 1°— 13° некоторые теоремы. Так как эти теоремы
будут доказаны с помощью аксиом, то они справедливы в любой
модели этой аксиоматики.
Теорема 1 Существует единственный вектор 0", обладаю-
обладающий тем свойством, что о-)-0 = а для любого вектора а.
Это вытекает из групповых аксиом 1°—3° (см., например, ЭЭМ, кн. I,
стр. 105—106).
Теорема 2. Для любого вектора р имеет место соотношение
24'

372 ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
Действительно, в силу аксиом 4° и 5° мы имеем
и потому в силу теоремы 1 мы получаем 0-р = 0.
Теорема 3. Если векторы а, Ь, с линейно независимы,
то каждый из них отличен от 0.
В самом деле, если, например, а = 0, то
т. е. векторы а, Ь, С линейно зависимы, а это противоречит предпо-
предположению.
Теорема 4. Пусть а, Ь, с — линейно независимые векторы.
Положим
а' = %а + цЬ + vc.
где %, \х, v — действительные числа, причем КфО. Тогда векторы
а', Ь, с линейно независимы.
Действительно, пусть аа' + C6 + ус — О, т. е.
а (%а + цЬ + \с) + р* + ус = 0.
Пользуясь аксиомами 6°, 7°, 5° (и аксиомой 2°), мы можем это ра-
равенство переписать в виде
Так как векторы а, Ь, с линейно независимы, то отсюда вытекает,
что
Отсюда а = 0 (ибо КфО), и потому C = 0, у = 0- Таким образом,
равенство аа' + fib + ус = 0 имеет место только в случае а = C =
==Y = 0, т. е. векторы а', Ь, с линейно независимы.
Теорема 5. Для любых векторов a, b и любых действитель-
действительных чисел %, [I имеем: (Ка) щЬ) = (fyi) (ab).
Действительно, в силу аксиом 8° и 10° мы имеем
(Ял) (цб) = I (а (цЬ)) = I ( ЦхЬ) а) = Яц фа) = (V) (ab).
Терема 6. Для любого отличного от нуля вектора а можно
найти такое действительное число К, что вектор а* = %а удовле-
удовлетворяет соотношению а*а* = 1.
Достаточно положить % = и применить теорему 5 (число аа
V аа
положительно в силу аксиомы 11°).
Теорема 7. Существуют три вектора а, Ь, с, удовлетво-
удовлетворяющих соотношениям
aa = bb = cc=\, ab = ac = bc — 0.
(Такая тройка векторов называется ортонормированным базисом.)

ПОНЯТИЕ О ВЕКТОРНЫХ ПРОСТРАНСТВАХ 373
Доказательств и. Пусть а', Ь', с'— три произвольных ли-
линейно независимых вектора (аксиома 12°). Тогда вектор а' отличен
от 0 (теорема 3). Выберем такое число А, (очевидно, отличное от
нуля), что вектор а = \а' удовлетворяет соотношению аа=1 (тео-
(теорема 6). В силу теоремы 4 векторы a, b', С' линейно независимы.
Положим b" = b'—(ab')a. Из аксиом 8°, 9°, 10° следует, что
ab" = 0 (непосредственный подсчет). В силу теоремы 4 векторы а,
6", с' линейно независимы. Поэтому вектор 6" отличен от нули (те-
(теорема 3), и значит существует такое число |л, что вектор 6 = |Л&"
удовлетворяет соотношению 66=1 (теорема 6). Из теоремы 5 вы-
вытекает, что аЬ = |Л (аб") = 0. В силу теоремы 4 векторы о, 6, с'
линейно независимы. Положим с" = с'—(ас')а — фс')Ь. Непосред-
Непосредственный подсчет с помощью аксиом 8°,9°, 10° показывает, что ас" = 0,
6с" = 0. Кроме того, векторы а, 6, с" линейно независимы (теорема 4),
и потому с"фО. Поэтому существует такое число v, что век-
вектор C = vc" удовлетворяет соотношению сс= 1. Кроме того, в силу
теоремы 5 мы имеем: ac = v(ac") = 0, bc = v(bc") — 0. Таким обра-
образом, построенные векторы о, 6, с удовлетворяют всем требуемым
условиям.
Теорема 8. Пусть а, 6, С— произвольный ортонормирован-
ортонормированный базис, т. е. тройка векторов, удовлетворяющих условиям
Тогда векторы а, Ь, с линейно независимы.
В самом деле, пусть %, |Л, v — такие числа, что выполнено соот-
соотношение Ка + |л6 + хс = 0. Умножив скалярно обе части этого ра-
равенства на вектор а, мы получим (используя аксиомы 9°, 10°)
K{aa)-\-\x{ab) + v{ac) = 0,
откуда (в силу соотношений, указанных в условии теоремы) К = 0.
Аналогично (умножая на 6, а затем на с) мы найдем, что |л = 0,
v = 0. Таким образом, векторы а, 6, С линейно независимы.
Теорема 9. Пусть а, Ь, с — произвольный ортонормированный
базис и р — произвольный вектор. Тогда существуют такие числа
а, р, у, что
Эти числа а, р, у определены однозначно (они называются коор-
координатами вектора р в базисе а, Ь, с).
Доказательство. Так как любые четыре вектора линейно
зависимы (аксиома 13°), то существуют такие числа и, %, |Х, v, что
кр + Ум + |л6 -f- хс = 0
и среди чисел х, %, ц, v хотя бы одно отлично от нуля. Если бы
число х было равно нулю, то написанное соотношение приняло бы

374 ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
вид Ха + \ib -f- vC = 0, а это противоречит линейной независимости
векторов а, Ъ, С (теорема 8). Таким образом, кфО. Умножив обе
части написанного выше соотношения на — , мы получаем (исполь-
(используя соотношение А,0 = 0, которое доказывается примерно так же,
как теорема 2)
. X . ц . . v n
р -\— ОН—— о-)— с = О,
У. У. У.
откуда
Таким образом, числа
Я. о ц v
а= , 6= -, v =
V.
удовлетворяют требуемому соотношению р = ам-\-$Ь-\-ус.
Если а', р', у'—другие числа, удовлетворяющие соотношению
р — а'а + +Р>'Ь-\-у'с, то, вычитая из одного выражения вектора р
другое, мы получим
Отсюда в силу линейной независимости векторов а, Ь, с (теорема 8)
мы находим
а—а'=0, р — р" = 0, у—у' = 0.
Таким образом, числа а, |3, y определены вектором р однозначно.
Теперь уже нетрудно доказать полноту аксиоматики 1°—13°.
В самом деле, пусть R' — произвольная модель для этой аксиомати-
аксиоматики. Выберем в R' ортонормированный базис о, Ь, С (теорема 7).
Далее, для каждого вектора р (т. е. элемента множества R') мы
выберем такие числа а, р, y- что Р = <ш + $Ь-{-ус (теорема 9), и
затем поставим в соответствие вектору р тройку чисел (а, р, y)- MbI
получаем таким образом взаимно однозначное соответствие между
элементами модели R' и -тройками чисел (а, р, y). t- е- элементами
арифметической модели. Нетрудно показать, что это соответствие
является изоморфизмом. ¦ Действительно, если вектору р соответ-
соответствует тройка (а, р, y)> a вектору р'—тройка (a', P',y')- t- е-
то мы имеем
фЬ + ус) + {а'а + рЬ + у'с) =
у')с,
и потому вектору р+р' соответствует тройка (a-f-a', P+Pi Y + V)-
т. е. сумма векторов (a, p, y) и (а'. Р'. y') b арифметической мо-

ПОНЯТИЕ О ВЕКТОРНЫХ ПРОСТРАНСТВАХ 375
дели. Аналогично, вектору лр соответствует тройка (Ха, А,р, "ку) =
= %(а, р, у). Наконец, скалярное произведение
рр' = (аа + рб + ус) {а а + р + у'с),
как легко подсчитать (используя соотношения аа = ЬЪ = ее = 1,
ab = ac = bc = 0 и аксиомы 8°, 9°, 10°), равно aa'+pp'+YY'. T- е-
равно скалярному произведению векторов (а, |3, у) и (a',fi',y') в
арифметической модели. Итак, построенное соответствие между эле-
менгами множества R' и элементами арифметической модели сохра-
сохраняет сумму векторов, произведение вектора на число и скалярное
произведение, т. е. является изоморфизмом. Таким образом, любая
модель изоморфна арифметической, и потому система аксиом 1° —13°
является полной.
Мы уже знаем две модели этой аксиоматики — арифметическую модель
и геометрическую (т. е. множество всех векторов трехмерного евклидова
пространства, см. § 1). Для сравнения приведем еще две алгебраические
модел1 аксиоматики 1е—13°. Именно будем называть «вектором» каждый
многочлен второй степени с действительными коэффициентами:
Сумму двух «векторов» и умножение «вектора» на число определим как
обычное сложение многочленов и умножение многочлена на число. Оче-
нидно, что при этом аксиомы 1°—7° будут выполнены. Скалярное произве-
произведение «векторов» определим формулой
Ь' +сс'.
Без труда проверяется справедливость аксиом 8°—11°. Проверка аксиом
12е, 13° проводится примерно так же, как в арифметической модели. Та
ким образом, мы получаем ковую модель для аксиоматики Г —13°.
Еще одну, четвертую модель мы получим из этой третьей модели,
по-прежнему считая «векторами» кьадратные многочлены, сохраняя тот
же смысл сложения и умножения на число, но водя скалярное произ-
произведение по-другому:
1
^ dx
^под интегралом стоит обычное произведение многочленов). Это скалярное
произведение также удовлетворяет аксиомам 8°—11° (что легко прове-
проверяется), и потому мы действительно получаем еще одну модель аксиома-
аксиоматики Г —13°.
7.4. Аксиоматика элементарной геометрии. Теперь, пользуясь
аксиоматикой 1°—13°, мы построим новую аксиоматику геометрии,
отличную от той, которая приведена в статье «Аксиомы и основные
'понятия геометрии» (стр. 32—40). В этой аксиоматике основными
понятиями являются, во-первых, векторы и операции над ними
(сложение, умножение на число и скалярное умножение) и, во-вто-
во-вторых, точки и откладывание векторов. Векторы и операции над

376 ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
ними описываются теми же четырьмя группами аксиом, которые рассмот-
рассмотрены выше. Пятая группа аксиом, связанная с откладыванием векто-
векторов, формулируется следующим образом.
V. Точки и откладывание векторов
Кроме множества R, элементы которого называются векторами
и подчиняются аксиомам 1°—13°, вводится в рассмотрение мно-
множество А (пространство), элементы которого называются точками.
Предполагается, что каждой упорядоченной паре точек М, N про-
пространства А поставлен в соответствие некоторый вектор (т. е. эле-
элемент множества R), обозначаемый через MN, причем выполнены
следующие три аксиомы:
14°. Для любой точки М пространства А и любого вектора а
существует такая точка Л/ пространства А, чго MN=a.
15°. Для любых трех (не обязательно различных) точек М, Л/, Р
пространства А выполнено соотношение MN-\-1чР-{- РМ=О.
16°. Если МЛ/ = О, то точки М и Л/ совпадают.
Аксиомами 1°—16° и исчерпывается аксиоматика геометрии.
Как же в этой аксиоматике определяются прямые, плоскости,
отрезки и т. д.? Пусть М и Л/—две различные точки про-
пространства А. Прямой MN мы будем называть множество, состоящее
из всех таких точек Р, что векторы РМ и PN линейно зависимы.
Из приведенных выше аксиом можно вывести, что прямая MN опре-
определяется не только точками М и N, но и любыми двумя своими
различными точками; поэтому мы можем говорить просто о прямых
линиях пространства А. Аналогично определяются плоскости: если
М, Л/, Р—три точки пространства А, не лежащие на одной пря-
прямой, то плоскостью MNP называется множество, состоящее из всех
таких точек Q пространства А, что векторы QM, QN и QP линейно
зависимы. Далее мы будем говорить, что точка Р лежит между
точками М и N (где МфМ), если существует такое число Я, за-
заключенное между нулем и единицей, что МР=К-MN. Наконец,
взаимно однозначное преобразование ф пространства А мы будем
называть движением, если для любых двух точек М, N скалярный
квадрат вектора MN равен скалярному квадрату вектора M'N'', где
Теперь мы имеем все основные понятия геометрии, описанные
в аксиоматике, которая приведена на стр. 32—40. Не очень сложная
проверка позволяет установить, что все аксиомы, указанные на
стр. 32—40, здесь выполняются, так что приведенная здесь система
аксиом 1°.— 16° также доставляет нам аксиоматику геометрии. В свою
очередь из аксиоматики, приведенной на стр. 32 — 40, можно вы-

ПОНЯТИЕ О ВЕКТОРНЫХ ПРОСТРАНСТВАХ , 377
вести все аксиомы 1°—16° (если определить векторы так, как это
указано в § 1). Таким образом, система аксиом геометрии, приве-
приведенная на стр. 32—40, эквивалентна указанной здесь системе
аксиом Г—16°.
7.5. Некоторые типы многомерных пространств. Отметим в за-
заключение, что различные видоизменения аксиоматики 1°—16° при-
приводят к определению других «геометрий», играющих очень важную
роль в современной математике и ее приложениях. Мы уже отмечали
выше, что всякое множество, удовлетворяющее аксиомам 1°—7°,
называется векторным пространством. Аксиоматика 1° — 7° не-
неполна, т. е. существуют различные, не изоморфные между
собой векторные пространства. Если к аксиомам 1° — 7° добавить
сформулированные ниже аксиомы 17°, 18° (представляющие собой
видоизменение аксиом 12°, 13°), то мы получаем п-мерное векторное
пространство. Вот эти аксиомы размерности:
17°. Существуют (в множестве R) п линейно независимых век-
горов.
18°. Всякие л-f-l векторов из R линейно зависимы.
Примером множества, удовлетворяющего аксиомам 1° — 7°, 17°,
18° (т. е. примером л-мерного векторного пространства) может служить
множество всех многочленов степени меньшей п с действительными
коэффициентами (сложение и умножение на число понимаются в обыч-
обычном смысле). Другим примером может служить «арифметическая»
модель, в которой «векторами» считаются всевозможные наборы
(х,, хг, . . ., хп), состоящие из л действительных чисел, а сложение
векторов и умножение вектора на число определяются следующим
образом: если а=(х1, хг, ..., хп) и b = (yl, уг, .., уп)— произ-
произвольные два вектора, а А, — число, то
а + Ь = [х1 + у1, х2+уг, ..., хп+уп),
"ka=(\xv %хл, .., Кхп).
Система аксиом 1° — 7°, 17°, 18° полна, т. е. все л-мерные векторные
пространства изоморфны между собой. В математике рассматриваются
также бесконечномерные векторные пространства (в таком простран-
пространстве для любого л существуют л линейно независимых векторов).
Подробнее о векторных пространствах читатель может прочитать в
статье «Векторные пространства и линейные преобразования», поме-
помещенной в кн. II ЭЭМ.
Всякое множество R, удовлетворяющее аксиомам 1°—11°, 17°,
18°, называется п-мерным евклидовым векторным пространством.
Система аксиом 1°—11°,. 17°, 18° полна, т. е. все л-мерные евклидовы
векторные пространства изоморфны между собой. Например, мно-
множество всех векторов на плоскости представляет собой двумерное

878 ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
евклидово векторное пространство. Моделью «-мерного евклидова
векторного пространства может служить множество всех наборов
(х,, х2, .... хп) п действительных чисел со скалярным произведением,
определенным по формуле
(«.арифметическая модель»). Добавление к аксиомам 1°—11°, 17°,
18° аксиом 14° —16° определяет п-мерное евклидово пространство
<геометрическое)').
Отметим еще п-мерное аффинное пространство, определяемое
аксиомами 1°—7°, 14° —18°. Геометрия этого пространства назы-
называется аффинной геометрией.
В л-мерном евклидовом пространстве можно определить операции
над векторами, аналогичные тем, которые рассматривались в этой
статье. Сложение векторов, умножение вектора на число и скалярное
произведение векторов существенно используются в самом опреде-
определении rz-мерного евклидова пространства; связанные с этими опера-
операциями аксиомы требуют, чтобы свойства всех трех операций остава-
оставались теми же, что и в случае плоскости или (трехмерного) пространства.
Роль тройного произведения векторов в /г-мерном евклидовом про-
пространстве играет так называемое п-кратное произведение векторов,
ставящее в соответствие п векторам
заданным своими координатами в ортонормированием базисе, число
(«,. «а «„)= ' Z
(л) х(п)
1 2
ЛA) XW
Из свойств определителей (см. указанную выше статью в кн. II
ЭЭМ) следует, что
(а,-}-&,. а2, . ... an) = (av аг, ., ап) + (Ьг, а2, ., а„),
(^о,. о2 an) = Xiav a2, ..., о„)
и что /г-кратное произведение векторов меняет знак при перемене
местами любых двух из них
(в,, о2, о3, ..., ап) = — (о2, о„ о„ ...,«„)=...
Роль векторного произведения в /г-мерном евклидовом простран-
пространстве играет так называемое (п—\)-кратное произведение векто-
') См. статью о многомерных пространствах в V кн. ЭЭМ.

878 ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
евклидово векторное пространство. Моделью «-мерного евклидова
векторного пространства может служить множество всех наборов
(х,, х2, .... хп) п действительных чисел со скалярным произведением,
определенным по формуле
(«.арифметическая модель»). Добавление к аксиомам 1°—11°, 17°,
18° аксиом 14° —16° определяет п-мерное евклидово пространство
<геометрическое)').
Отметим еще п-мерное аффинное пространство, определяемое
аксиомами 1°—7°, 14° —18°. Геометрия этого пространства назы-
называется аффинной геометрией.
В л-мерном евклидовом пространстве можно определить операции
над векторами, аналогичные тем, которые рассматривались в этой
статье. Сложение векторов, умножение вектора на число и скалярное
произведение векторов существенно используются в самом опреде-
определении rz-мерного евклидова пространства; связанные с этими опера-
операциями аксиомы требуют, чтобы свойства всех трех операций остава-
оставались теми же, что и в случае плоскости или (трехмерного) пространства.
Роль тройного произведения векторов в /г-мерном евклидовом про-
пространстве играет так называемое п-кратное произведение векторов,
ставящее в соответствие п векторам
заданным своими координатами в ортонормированием базисе, число
*$¦>
хт
ЛA) XW
(«,. «* ап)= ' г
(л) х{п) г(п)
1 2 ¦ ¦ • - „
Из свойств определителей (см. указанную выше статью в кн. II
ЭЭМ) следует, что
(a,-f&,. a2, ... ап) = (а1, аг, ., an) + (bJt a2, ., aj,
(Afl , CL9, . . . , CL ) == Л. \CL , CL9, . ¦ . , CL )
и что /z-кратное произведение векторов меняет знак при перемене
местами любых двух из них
(в,, о2, о3, ..., о„) = — (о2, о„ о„ ...,«„)=...
Роль векторного произведения в /г-мерном евклидовом простран-
пространстве играет так называемое (п—\)-кратное произведение векто-
') См. статью о многомерных пространствах в V кн. ЭЭМ.

380 ВЕКТОРЫ И ИХ ПРИМЕНЕНИЯ В ГЕОМЕТРИИ
Заметим также, что из определения /г-кратиого произведения,
(п— 1)-кратного произведения и скалярного произведения следует, что
(о,, аг, а, . ... аг,) = а1[а11, о„ ..., а„]
(ср. выше, стр. 355).
Все эти операции над векторами могут быть использованы для
вывода теорем, относящихся к я-мерному евклидову пространству.
Наконец, отметим еще одну аксиоматику, также тесно связанную с
понятием вектора и играющую важную роль в современной математике.
Аксиоматика л-мерного евклидова секторного пространства A° —11°, 17°, 18е)
получается из аксиоматики n-мерного векторного пространства A° — 7°. 17°,
18°) добавлением аксиом 8° — 1 1°, вводящих скалярное произведение. Если
же к аксиомам векторного пространства вместо аксиом 6°—11е добавить
нижеследующие аксиомы 8°а — 11°а описывающие вектор ное произведе-
произведение, то мы приходим к важному понятию алгебры Ли. Таким образом,
алгебргй Ли называется множество, удовлетворяющее аксиомам 1°—7е, 17°.
18° и следующим четырем аксиомам.
VI Аксиомы алгебры Ли
Каждой паре векторов а, Ь множества R поставлен в соответствие
вектор с=[а, Ь\, называемый косым произведением векторов аи Ь (иногда
также — коммутатором, этих двух векторов), причем выполнены нижесле-
нижеследующие аксиомы 8°а—11°а (ср. аксиомы 8° а—10°а с аксиомами 8°—10°
на стр. 370; новая аксиома 11са описывает то свойство рассматриваемого
здесь косого умножения, которое заменяет свойство ассоциатив-
ассоциативности обычного умножения чисел)').
8°а. [а, Ь\——\Ь, а\ для любых векторов а, Ь.
9°а. \а + Ь, с] = [а, с] + \Ь, с] для любых векторов а, Ь, с.
10°а. \Ха, b] = X \а, b] для любых векторов а, Ь и действительного
числа Я..
11°а. [а, \Ь, с\\-\-\Ь, [с, а]] + [с, [а. Ь]]=0 для любых трех Еекторов
а, Ь, с.
Таким образом, множество всех векторов трехмерного пространства
является относительно векторного умножения (§ 5) алгеброй Ли.
Мы видим, что описанная в предыдущи? параграфах «арифметика
векторов» находится в центре многих вржных идей современной матема-
математики.
ЛИТЕРАТУРА
[1] Я. С. Дубнов, Основы векторного исчисления, ч. 1, М.. Гостех-
издат, 1950.
Обстоятельная книга, посвященная в основном векторной алгебре и ее
геометрическим и механическим приложен;.ям. Книга снабжена боль
шим числом задач и примеров.
') Ср. с тождеством Якоби, выполняющимся для векторного умножения
векторов обычного пространства (стр. 357).

ЛИТЕРАТУРА 381
B] В. Г. Болтянский и И. М. Яглом, Векторы в курсе геометрии
средней школы, М., Учпедгиз, 1С62.
Пособие для учителей средней школы. Содержит ряд примеров при-
применения векторных методов в планиметрии и стереометрии. В заклю-
заключительном параграфе рассматриваются применения векторного аппарата
в механике.
[3] Н. В. Ефимов, Краткий курс аналитической геометрии, М., Физ-
матгиз, 1962.
[4] А. М. Л о п ш и ц. Аналитическая геометрия, Учпедгиз, М., 1948.
[5] Н. И. М у с хе л и ш в и л и, Курс аналитической геометрии, М., Гос-
техиздат, 1947.
Книги [3] — [5] представляют собой вузовские учебники аналитиче-
аналитической геометрии, рассчитанные на студентов втузов, пединститутов и
университетов; они широко используют векторные методы. Все три
книги содержат изложение векторной алгебры (особенно обстоятель-
обстоятельное в книге [4]).
F] М. Л а г а л л и, Векторное исчисление, перев. с нем.. М., Гостехиздат,
1936.
Серьезный учебник векторного исчисления, содержащий много
приложений.

МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ
СОДЕРЖАНИЕ
§ I. Основные определения. Теорема Эйлера . . . 382
1.1. Плоские многоугольники 382
1.2. Многогранники . . . 384
1.3. Теорема Эйлера . . . 386
1.4. Число вершин, ребер и граней многогранника не! улевого рода 391
1.5. Другое доказательство теоремы Эйлера .... 394
§ 2. Комбинаторный (топологический) тип многогранника. Теорема
Штейница . . . . . 399
2.1. Комбинаторные свойства многогранников. Изоморфизм . . . 399
2.2. Абстрактный многогранник ... 401
2.3. Теорема Штейница ....... 403
2.4. Двойственность . . . .... 407
§ 3. Развертка многогранника. Теорема Коши ... . . . 410
3.1. Развертка многогранника Существование многогранника с
данной разверткой . 410
3.2. Теорема Коши. Основные леммы .412
3.3. Доказательство теоремы Коши . . . 416
3.4. Некоторые обобщения на случай кривых поверхностей . . 419
§ 4. Правильные многоугольники и многогранники и их обобщения 420
4.1 Топологически правильные многогранники . . . 420
4.2. Правильные многоугольники и многогранники . . . 424
4.3 Равноугольно полуправильные многогранники . . 429
4.4 Равногранно полуправильные многогранники . . . 440
4.5 Правильные самопересекающиеся многогранники ... 440
Литература . ... 446
§ 1. Основные определения. Теорема Эйлера
1.1. Плоские многоугольники. Многоугольником (точнее, плос-
плоским многоугольником) называется (плоская) замкнутая ломаная ли-
линия, т.е. совокупность отрезков AXAV АгАг. ..., Ап_лАп, АпАх.
где Ах, Аг, .... Ап — различные точки плоскости, не лежащие все
на одной прямой. Точки Ах, Аг, .... Ап называются вершинами
многоугольника, а перечисленные выше отрезки—сторонами много-
многоугольника. Две стороны, имеющие общую вершину, называются
смежными сторонами, а лве вершины, являющиеся концами одной
и той же стороны, — смежными вершинами многоугольника.

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ. ТЕОРЕМА
383
Очевидно, во всяком многоугольнике число вершин равно числу
сторон. Наименьшее возможное число вершин многоугольника равно
трем. Многоугольник с тремя вершинами называется треугольником,
многоугольник с четырьмя вершинами — четырехугольником и т. д.
Многоугольник называется простым, если никакие две его не
смежные стороны не имеют общих точек (внутренних или концевых);
в противном случае многоугольник называется самопересекающимся.
Так, многоугольники, изображенные на рис. 1, а, б, в, г, простые,
а на рис. 1 д, е, ж—самопересекающиеся. Можно доказать, что
каждый простой многоугольник делит всю плоскость на две об-
области таким образом, что две точки принадлежат одной и той же
области тогда и только тогда, когда их можно соединить непре-
непрерывной линией, не пересекающей данного многоугольника *). Одна из
этих областей характеризуется тем, что она содержит целиком не-
некоторую прямую линию; она называется внешней областью много-
многоугольника. Другая область называется внутренней областью
многоугольника (рис. 2, а, б, внутренние области многоугольников
заштрихованы). Внутреннюю область многоугольника часто называют
тоже многоугольником *).
') См., например, книгу А. Д. Александрова [1], указанную в
списке литературы в конце статьи.
*) Различие между этими двумя определениями многоугольника заклю-
заключается, таким образом, в том, что первое определение рассматривает мно-
многоугольник как линию, а второе—как часть плоскости (т. е. как
«площадь»). Разумеется, бессмысленно говорить о том, какое из этих
двух определений является более «правильным», — все зависит от того,
в связи с решением каких задач рассматривается понятие «миогоуголь-

384
многоугольники и многогранники
Многоугольник называется выпуклым, если для любой его сто-
стороны все прочие стороны расположены по одну сторону от прямой, на
которой лежит данная сторона; так многоугольники, изображенные на
рис. 1, а, б—выпуклые, а на рис. 1, в, г, д, е, ж — невыпуклые.
Легко видеть, что всякий выпуклый многоугольник является про-
простым; обратное, разумеется, неверно: существуют простые невыпук-
невыпуклые многоугольники (см. рис. 1, в, г).
Рис. 2.
1.2. Многогранники. Многогранники представляют собой
простейшие геометрические фигуры в пространстве, подобно тому,
как многоугольники — это простейшие фигуры на плоскости.
Многогранником называется фигура, состоящая из конечного
числа плоских многоугольников (называемых гранями многогранника),
расположенных в пространстве так, что:
1) любая сторона каждой из этих граней является стороной еще
одной и только одной грани (называемой смежной с первой гранью);
2) для любых двух граней а и р можно указать такую цепочку
граней dj, аг, ..., ап, что грань а смежна с а,, грань а, смежна
с аг, .. ., грань аП смежна с C;
3) если грани аир имеют общую вершину А, то выбор граней
<Zj, a2, ..., ап, о которых говорится в предыдущем пункте, можно
осуществить так, чтобы все они имели ту же вершину А1).
Стороны и вершины граней многогранника называются соответ-
соответственно ребрами и вершинами этого многогранника.
Если рассматривать грани многогранника как плоские области
(это возможно в том случае, когда все эти грани являются простыми
ник». В этой статье наиболее целесообразно считать многоугольником замкну-
замкнутую ломаную; в статьях же «Площадь и объем» и «Равносоставленность
многоугольников и многогранников», помещенных в кн. V ЭЭМ, под
многоугольником удобнее понимать часть плоскости.
') Многогранник также можно определять по-разному: можно его
представлять сеСе как «поверхность»; в других задачах (например, в
цитированных выше статьях) его удобнее представлять как «часть про-
пространства» (объем) и т. п.

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ. ТЕОРЕМА ЭЙЛЕРА
385
многоугольниками), то согласно введенному выше определению мно-
многогранник есть некоторая поверхность в пространстве. При этом
первое из содержащихся в определении многогранника требований
говорит о том, что эта поверхность не имеет границы, т. е. является
замкнутой, а второе—о том, что она является связной, т.е.
не распадается на две (замкнутые) поверхности; наконец, третье
требование исключает из числа многогранников поверхности, подоб-
подобные изображенной на рис. 3, у которых при одной вершине имеется
несколько многогранных углов.
Простейшими примерами многогранников могут служить призмы и
пирамиды. Многогранник называется /z-угольной пирамидой, если он
Рис. 3.
Рис. 4.
Рис.
имеет одной своей гранью (основанием) какой-либо л-угольник,
а остальными гранями—треугольники с общей вершиной, не лежа-
лежащей в плоскости основания (рис. 4). Треугольная пирамида называ-
называется также тетраэдром. Многогранник называется л-угольной
призмой, если он имеет двумя своими гранями (основаниями)
равные л-угольники (не лежащие в одной плоскости), получающиеся
друг из друга параллельным переносом, а остальными гранями — па-
параллелограммы, противоположными сторонами которых являются соот-
соответственные стороны оснований (рис. 5).
Многогранник называется простым, если:
1) все его грани являются простыми многоугольниками;
2) никакие две его несмежные грани не имеют общих точек
(внутренних или граничных), за исключением, быть может, одной
общей вершины;
3) две смежные грани имеют только одно общее ребро и не
имеют других общих точек.
25 Энциклопедия, кн. 4

386
многоугольники и многогранники
Подобно простому многоугольнику, поверхность простого много-
многогранника делит все пространство на две области. Одна из этих об-
областей характеризуется тем, что она содержит целиком некоторую
плоскость; она называется внешней областью многогранника. Дру-
Другая область называется внутренней областью многогранника;
часто внутреннюю область, так же как и ограничивающую ее по-
поверхность, называют многогранником.
Многогранник называется выпуклым, если все его вершины,
не принадлежащие произвольной грани этого многогранника, рас-
расположены по одну сторону от плоскости этой грани. Легко дока-
доказать (мы предоставляем это читателю), что всякий выпуклый много-
многогранник является простым и что все его грани являются выпуклыми
многоугольниками ').
1.3. Теорема Эйлера. Перейдем теперь к вопросу о числе вер-
вершин, ребер и граней многогранника. Для многоугольника вопрос о
') Выпуклые многоугольники и многогранники имеют также и другие
определения (эквивалентные приведенному здесь). Например, выпуклый
многогранник можно определить как (ограниченное и содержащее внутрен-
внутренние точки) множество, являющееся пересечением конечного числа полу-
полупространств, или еще как «выпуклую оболочку» конечного числа точек
(вершин). См. по этому поводу статью о выпуклых телах в кн. V ЭЭМ.

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ. ТЕОРЕМА ЭЙЛЕРА
387
числе вершин и сторон решается очень просто: число С сторон
многоугольника всегда равно числу В его вершин:
С=В или С—?=0,
причем существуют многоугольники с любым числом л^З вершин
(и сторон). Для многогранников же, как показывают уже простей-
простейшие примеры (рис. 6, с—д), положение оказывается значительно более
сложным. Обозначая число граней, вершин и ребер многогранника
соответственно через Г, В и Р, получим для многогранников, изоб-
изображенных на рис. 6, следующую таблицу.
Таблица 1
Многогранник
Треугольная пирамида (рис. 6, а) . . . .
Четырехугольная призма (рис. 6, б) ...
Пятиугольная бипирамида (рис. 6, в) ...
Одиннадцатигранник (рис. 6, г)
Двенадцатигранник (рис. 6, д) ...
г
4
6
10
11
12
В
4
8
7
И
18
р
6
12
15
20
28
Чтобы обнаружить какую-либо общую закономерность, связыва-
связывающую число граней, вершин и ребер многогранника, рассмотрим
подробнее, например, произвольные призмы и пирамиды. Для /z-уголь-
ной призмы мы имеем Г=п4-2, В = 2п, Р=3п, а для /z-угольной
пирамиды Г=п-\-\, В=п-{-\, Р=2п. Если увеличить число п на
единицу, то у призмы число граней увеличится на 1, число вершин
на 2, число ребер—на 3, а у пирамиды соответственно на 1, 1 и 2.
Неизменной при этом остается разность (В-{-Г)—Р; при любом п
она равна 2. Таким образом, для призм и пирамид соотношение
между числами Г, В и Р найдено:
Г+В—Р=2.
A)
Читатель без труда проверит, пользуясь приведенной выше таб-
таблицей, что это же соотношение выполняется и для многогранников,
изображенных на рис. 6, в, г, д. Мы покажем сейчас, что на самом
деле оно справедливо для весьма широкого класса многогранников.
Для этого заметим, что вс* более и более сложные многогран-
многогранники можно получать из более простых, «приставляя» эти простые
друг к другу равными гранями (см., например, рис. 7). Выясним,
что будет происходить с величиной Г-\-В—Р, если мы «приставим»
к данному многограннику какой-нибудь другой; ограничимся пока
25*

388
многоугольники и многогранники
случаем, когда этот второй многогранник является простейшим из
всех многогранников — тетраэдром.
Итак, пусть мы некоторую (треугольную) грань многогранника
М совмещаем с равной ей гранью ABC тетраэдра ABCD (рис. 8)
так, что при этом вершина D тетраэдра не совмещается ни с одной
из вершин многогранника М. Тогда число вершин многогранника М
Рис. 7.
Рис. 8.
увеличится на 1 (добавится вершина D), число граней увеличится
«а 2 (добавится три новых грани, но пропадет одна грань, совме-
совмещенная с гранью ABC), число ребер увеличится на 3 (добавятся
ребра AD, BD, CD). Следовательно, величина Г-\-В—Р не изме
нится, так что если соотношение A) выполнялось для исходно-
исходного многогранника М, то оно бу-
будет выполняться и для получен-
полученного.
Наш результат останется в силе
и в том случае, если какая-нибудь
грань тетраэдра окажется в одной
плоскости со смежной гранью много-
многогранника М и будет составлять
вместе с этой гранью одну грань
полученного многогранника (рис. 9).
Тогда в полученном многограннике
будет на одну грань меньше, чем
у указанного выше, но зато пропадет
и одно ребро, так что на значении
величины Г-\-В—Р это не отразится. То же самое может про-
произойти с двумя или даже с тремя гранями тетраэдра.
Подобным же образом легко проверить, что тот же результат
получится, если мы будем тетраэдр прикладывать так, что не одна,
Рис. 9.

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ. ТЕОРЕМА ЭЙЛЕРА
389
а две (рис. 10, а) или три (рис. 10, б) его грани совместятся с
гранями многогранника М.
Наше рассуждение показывает, что соотношение A) выполняется
для достаточно широкого класса многогранников, во всяком случае
Рис. 10.
для всех выпуклых многогранников. В самом деле, взяв внутри
произвольного выпуклого многогранника М любую точку О и соединив
Рис. 11.
ее со всеми вершинами многогранника, мы разобьем этот мно-
многогранник на некоторое число пирамид с общей вершиной О (рис. 11),

390 многоугольники и многогранники
каждую из которых в свою очередь легко разбить на треугольные ¦
пирамиды — тетраэдры (с той же вершиной О). Выберем теперь ка-
какой-нибудь один из полученных тетраэдров и будем последова-
последовательно приставлять к нему остальные '), пока не получим исходного
многогранника М. Так как при каждом шаге величина Г-\-В—Р
не изменяется и так как для начального тетраэдра она равна 2, то
и для многогранника М будет
Г+В—Р=2. (\)
Таким образом, нами доказана следующая
Теорема 1 (теорема Эйлера). Для всякого выпуклого мно-
многогранника
Однако, как видно из приведенного нами доказательства теоремы
Эйлера, она должна оставаться справедливой и для многих невыпук-
невыпуклых многогранников.
Остановимся поэтому подробнее на вопросе о естественных гра-
границах справедливости соотношения A).
Легко понять, что всякий простой многогранник можно разбить
на тетраэдры (так же, как всякий простой многоугольник можно раз-
разбить на треугольники). Тем не менее соотношение A) выполняется
не для всех многогранников. Дело в том, что при составлении мно-
многогранника из тетраэдров для неизменности величины В -{-Г—Р нужно,
чтобы каждый раз, когда тетраэдр приставляется одной гранью, про-
противоположная его вершина не совпадала ни с одной из вершин уже
построенной части многогранника. Однако имеются многогранники,
для которых такого совпадения вершин избежать нельзя; один из
таких многогранников изображен на рис. 12,а (см. также рис. 12 б, в).
Для этого многогранника, как нетрудно подсчитать, будет В-\-Г — Р' =
= 12+12 — 24 = 0.
Теперь кажется наглядно ясным, что (простой) многогранник тогда
и только тогда может быть нужным нам образом составлен из тет-
тетраэдров, когда он не имеет сквозных «дыр», т. е. не является «коль-
«кольцеобразным», как многогранник, изображенный на рис. 12,а, и не
содержит таких «кольцеобразных» частей. Такие многогранники, не
имеющие сквозных «дыр», называются многогранниками нулевого
*) Разумеется, при таком последовательном «приставлении» тетраэдров
надо проявлять некоторую осторожность: нужно следить, чтобы в случае,
когда мы приставляем очередной тетраэдр одной граиью, противополож-
противоположная вершина тетраэдра не принадлежала уже построенному многограннику.
Нетрудно установить, что можно в такой последовательности приставлять
тетраэдры, чтобы это условие каждый раз выполнялось; мы предоставляем
сделать это читателю.

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ. ТЕОРЕМА ЭЙЛЕРА
391
рода. Итак, теореме Эйлера можно придать следующую более об-
общую форму'):
Теорема 2. Для всякого многогранника нулевого рода
Г-\-В—Р=2.
Число Г + В—Р называется эйлеровой характеристикой много-
многогранника. Мы нашли ее для многогранников нулевого рода.
6)
Рис. 12.
1.4. Число вершин, ребер и граней многогранника ненулевого
рода. Перейдем теперь к многогранникам ненулевого рода. Всякий
простой многогранник, не являющийся многогранником нулевого рода,
имеет одну или несколько сквозных «дыр» (замкнутых «колец»). Чи-
Число таких сквозных «дыр» (или замкнутых колец) называется родом
') По сути дела при таком изложении соотношение Г + В—Р = 2 сле-
следовало бы считать определением многогранника нулевого рода (ибо
определения сквозных «дыр» и доказательства соотношения Г + В—Р = 2
для многогранников, не имеющих сквозных дыр, не было дано). Аккурат-
Аккуратное определение «числа сквозных дыр» и доказательства теорем 2 и 3 про-
проводятся средствами специальной математической дисциплины, называемой
топологией.

392
МНОГОУГОЛЬНИКИ II МНОГОГРАННИКИ
многогранника. Многогранники рода 0 уже были рассмотрены выше:
пример многогранника рода 1 также уже встречался нам (см. рис. 12, а);
примеры многогранников рода 2 и 3 изображены на рис. 13, а, б, в.
Многогранник рода 1 можно получить из двух многогранников рода О,
приставив их друг к другу двумя несмежными гранями (рис. 14, а);
многогранник рода 2 можно получить из многогранника рода 1, при-
приставив к нему таким же образом многогранник рода 0 (рис. 14, б);
многогранник рода 3 можно получить таким же образом из многогран-
многогранника рода 2 (рис. 14, в). Вообще, многогранник рода р+1 можно
получить из многогранника рода р, приставив к нему двумя несмеж-
несмежными гранями многогранник нулевого рода. Выясним, как изменяется
при этой операции эйлерова характеристика многогранника.
Пусть к произвольному многограннику Мг, имеющему Г, гра-
граней, fi, вершин и Р1 ребер, приставляется многогранник нулевого
рода /И2, имеющий Г2 граней, В2 вершин и Р2 ребер (см. рис. 14).

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ. ТЕОРЕМА ЭЙЛЕРА
393
Пусть при этом от-угольная грань а, многогранника /И, совмеща-
совмещается с гранью а2 многогранника М2 и л-угольная грань р,— с гра-
гранью Р2. Тогда в полученном многограннике М число граней будет
Г=Г, + Г2-4 B)
(гранями многогранника М будут все грани многогранников Мл и Мг,
кроме граней а,, а2, Р,, Р2). Число вершин многогранника М будет
равно
В= Bi-\- Вг — от—п C)
вершинами многогранника М являются все вершины многогран-
многогранника /И,, а также все вершины многогранника Мг, за исключением
т вершин грани а2 и л вершин грани Р2). Точно так же число ребер
многогранника М будет равно
Р = Р1+Р1—от—п. C'>
Из равенств B), C), C') легко найти эйлерову характеристику
многогранника М
Отсюда, так как многогранник Мг — нулевого рода, в силу тео-
теоремы 2 получаем
Г+В— Р=(Г1 + Б1-Я1)-2.

394 многоугольники и многогранники
Таким образом, увеличение рода многогранника на 1 влечет
уменьшение эйлеровой характеристики на 2. Учитывая, что для мно-
многогранников рода 0 эйлерова характеристика равна 2, мы приходим
к следующему общему выводу.
Теорема 3. Для всякого простого многогранника произволь-
произвольного рода р справедливо соотношение
Г+В—Р=2 — 2р.
В частности, для многогранников рода 1
Г+В—Р=0;
для многогранников рода 2
Г+В— Р= — 2
и т. д.
Теорему 3 нельзя, конечно, считать полностью доказанной нашими
рассуждениями, так как не доказано, что любой многогранник
рода р может быть получен указанным выше способом из некото-
некоторого многогранника родар— 1. Можно показать, что это действительно
так, если допустить некоторую деформацию многогранника, не изме-
изменяющую числа его граней, вершин и ребер; мы, однако, не будем
на этом останавливаться').
1.5. Другое доказательство теоремы Эйлера. В заключение при-
приведем еще одно («топологическое») доказательство теоремы Эйлера.
Эго доказательство приводит также к одному обобщению теоремы
Эйлера (теорема 5 и следствие к ней), которое мы используем -ниже,
при доказательстве теоремы Коши.
Пусть М—выпуклый многогранник. Выберем внутри него произ-
произвольную точку О и проведем сферу S с центром О, целиком заклю-
заключающую многогранник М внутри себя. Теперь мы спроектируем по-
поверхность многогранника М из точки О на сферу S. При этом про-
проектировании каждая вершина А многогранника М перейдет в неко-
некоторую точку А' сферы S; все эти точки на сфере S мы также будем
называть «вершинами». Далее, если АВ—некоторое ребро многогран-
многогранника М, то оно при проектировании из точки О перейдет в дугу А'В'
большой окружности на сфере S, где А' и В'—«вершины», в ко-
которые переходят точки А и В при проектировании. Каждую такую
дугу А'В' мы будем называть «ребром» на сфере S.
Итак, при проектировании многогранника М мы получим на сфере S
¦сетку, состоящую из «ребер» и «вершин», причем, очевидно, число
«ребер» и число «вершин» этой сетки соответственно равны числу
ребер и числу вершин многогранника М. Эта сетка разбивает всю
поверхность сферы S на части (сферические многоугольники), кото-
') Другой подход к определению рода многогранника и доказательству
теоремы Эйлера см. в книге Ж. А д а м а р а[4], указанной в конце статьи.

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ. ТЕОРЕМА ЭЙЛЕРА
395
рые мы будем называть «гранями». Каждая грань многогранника М
проектируется в некоторую «грань» на сфере S, откуда ясно, что
число «граней», определяемых на сфере S сеткой «ребер» и «вер-
«вершин», равно числу граней многогранника М. Итак, на сфере S мы
имеем В «вершин», Р «ребер» и Г «граней», и для доказательства
теоремы Эйлера было бы достаточно установить, что для любой сетки
на сфере справедливо соотношение В—Р-\~Г=2.
Однако это соотношение справедливо не для любой сетки
«ребер» и «вершин», произвольно начерченной на сфере S. Для сетки
же, получающейся при проектировании выпуклого многогранника,
соотношение В—Р-\-Г=2 всегда спра-
справедливо, так как такие сетки обладают
некоторыми специальными свойствами,
обеспечивающими выполнение этого
соотношения.
Прежде всего дадим точное опреде-
определение сетки. Лугой на сфере мы будем
называть незамкнутую ломаную, состав-
составленную из дуг больших окружностей и
не пересекающую саму себя (рис. 15).
Сеткой на сфере мы будем называть
конечную совокупность точек («вер-
(«вершин») и дуг («ребер»), обладающую
следующими свойствами
а) к каждой «вершине» примыкает
хотя бы одно «ребро»;
б) оба конца каждого «ребра» являются «вершинами»;
в) любые два «ребра» либо не имеют общих точек, либо имеют
одну или две общие точки, являющиеся их общими концами.
Ясно, что при проектировании вершин и ребер многогранника М
из точки О на сферу S мы получаем на сфере S сетку. Эта сетка
обладает не только свойствами а), б), в), но и многими другими; на-
например, к каждой «вершине» примыкает не менее трех «ребер».
Наиболее важным для нас свойством сетки, получающейся при проек-
проектировании многогранника, является то, что эта сетка связна. Это
означает, что, двигаясь по «ребрам» сетки, можно пройти от любой «вер-
«вершины» к любой другой «вершине». Сетка, изображенная на рис. 16,
не является связной. Несвязная сетка состоит из нескольких связных
кусков (компонент); например, сетка, изображенная на рис. 16,
состоит из трех компонент. Итак, при проектировании многогран-
многогранника М на сферу S мы получаем на этой сфере связную сетку.
Пусть С—произвольная сетка на сфере S. Обозначим через" В
число ее «вершин», через Р—число «ребер», а через Г — число об-
областей («граней»), на которые сетка С разбивает поверхность сферы.
Число В—Р -f- Г называется эйлеровой характеристикой сетки С.
Рис! 15.

396 МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ
Мы докажем, что справедлива следующая георема, из которой
очевидным образом вытекает теорема Эйлера.
Теорема 4. Любая связная сетка С на сфере имеет эйле-
эйлерову характеристику, равную двум.
Доказательство. Обозначим через /, произвольное ребро
сетки С. Через 1г обозначим какое-либо ребро, имеющее с /, хогя
бы один общий конец (такое ребро существует, так как если бы
к /j не примыкало более ни одно ребро, то сетка С была бы несвяз-
несвязной). Через /а обозначим какое-либо ребро, имеющее общий конец
хотя бы с одним из ребер /,, /2.
Затем выберем ребро /4 (имеющее
общий конец хотя бы с одним из
ребер /,, /г, /,) и т. д. Таким образом
занумеруем все ребра: /,, /2..., /.
Сетку, состоящую из ребер /,,
/2,..., lk (k<^q) и всех вершин, явля-
являющихся концами этих ребер, мы обо-
обозначим через Ck. В результате мы
определим на сфере S сетки С,, С2,...
¦ • •, Cq (причем, очевидно, сетка С со-
совпадает с С). В силу способа нумерации
ребер каждая из этих сеток связна.
Рис 16. Теперь мы докажем методом мате-
математической индукции, что эйлерова
характеристика каждой из сеток С,, С,,..., Cq равна двум. Для
сетки Сх это очевидно: она имеет одно ребро /,, две вершины и одну
грань и потому
В—Р+Г=2— 1 + 1=2.
Пусть уже доказано, что сетка Ck (k<Zg) имеет эйлерову харак-
характеристику, равную двум. Сетка Ck+1 получается из Ck добавлением
одного ребра lk+i. Поэтому, обозначив через Pk число ребер
сетки Ck, а через Pk+l—число ребер сетки Ck+1, мы получим
В силу способа нумерации ребер хотя бы один конец ребра lk+i
является вершиной сетки Ск. Поэтому могут представиться два сле-
следующих случая:
I. Оба конца ребра lk+l являются вершинами сетки Ск.
II. Лишь один конец ребра /ft+1 является вершиной сетки Ск.
Рассмотрим эти случаи раздельно.
Случай I. Так как оба конца ребра lk+l являются вершинами
сетки Ck, то число вершин Bk+i сетки Ck+i равно числу вершин Bh
сетки Ck:

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ. ТЕОРЕМА ЭЙЛЕРА 397
4
Далее, ребро lk+l целиком расположено в одной грани сетки Ch
(ибо это ребро не имеет с Ск других общих точек, кроме концов).
Обозначим эту грань через G. Ясно, что все грани сетки Ck, кроме G,
остаются неизменными при проведении ребра lk+i, т. е. они являются
также гранями и для сетки C/t+1. Число этих граней равно Гк—1,
где Гк — число граней сетки Ch. Мы покажем сейчас, что при проведении
ребра lk + i грань G разбивается на две грани, откуда будет следо-
следовать, что число ГА+1 граней сетки Ck+1 равно (Гк—1) + 2, т. е.
В самом деле, проведем дугу, пересекающую ребро lk+l, и возь-
возьмем на ней две точки Р, Q, лежащие по разные стороны этого
ребра (рис. 17; на этом рисунке грань
G заштрихована). Пусть теперь R—
произвольная точка грани G, не лежа-
лежащая на ребре /ft+1. Проведем в грани
G дугу от точки R до какой-либо
точки N ребра lk+1 и на этой дуге,
не доходя до точки N, возьмем близ-
близкую к ней точку N'. Теперь, идя из
точки N' вблизи ребра lk+i, мы можем
подойти либо к точке Р, либо к точке
Q (рис.17, пунктирная линия). Итак,
любая точка R грани G, не лежащая
на ребре lk+i, может быть соединена
дугой, не пересекающей lk+l, либо с Рис. 17.
точкой Р, либо с Q. Поэтому G разби-
разбивается дугой lk+1 не более чем на две грани (одна, содержащая
точку Р, и другая, содержащая Q).
Однако не может ли получиться, что точки Р и Q также
лежат в одной грани (т. е. могут быть соединены дугой, не
пересекающейся с сеткой С,,+1), так что при проведении ребра
/д,+1 из грани G мы получим только одну грань сетки Cft+1?
Покажем, что этого не может быть. В самом деле, если бы су-
существовала дуга, соединяющая точки Р и Q и не пересекающаяся
с сеткой Ch+l, то эта дуга вместе с дугой PQ образовала бы замкну-
замкнутую линию, не пересекающуюся с сеткой Ck (рис. 18). Эта замкнутая
линия разбивает сферу S на две области1), причем концы ребра l//+i
лежат в разных областях, так как ребро lk+l пересекает один раз
линию Я. Но так как концы ребра /А+1 принадлежат сетке Ck, то
') Здесь мы пользуемся теоремой Жордана: замкнутая линия,
не пересекающая саму себя и расположенная на сфере (или на плоскости),
разбивает поверхность сферы (или плоскость) на две области. Доказательство
теоремы Жордана для случая замкнутой ломаной имеется, например, в
книге А. Д. Александрова [1].

398
МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ
что сетка Ск не пересекается с замкнутой линией Я,
k есть вершины, лежащие по разные стороны
сетки Ск.
получается
но у сетки Ck
линии %. Это, однако, противоречит связности сетки Ск. Итак,
точки Р и Q не могут быть соединены дугой, не пересекающейся
с Ch+l, и потому ребро lk+1 разбивает грань G ровно на две части.
Теперь мы знаем число ребер, вершин и граней сетки Ck+X и
можем найти ее эйлерову характеристику:
Итак, эйлерова характеристика сетки Ск+1 равна эйлеровой харак-
характеристике сетки Ck, т. е., по предположению индукции, равна двум.
Рис. 18.
Рис. 19.
Случай П. Так как лишь один конец ребра lk+J принадлежит
сетке Ch (рис. 19), то при добавлении этого ребра появляется одна
новая вершина, т. е.
Число же граней не меняется:
так как ребро lk+x расположено целиком в одной грани G сетки Ck
и не разбивает эту грань. Таким образом,
в.
(Bk + 1 )-(
= Bk~Ph +Гк =
Итак, индукция проведена, и теорема 4 полностью доказана.
Вместе с тем мы получили еще одно доказательство теоремы Эйлера.
Как же будет обстоять дело для несвязных сегок? Ответ
на этот вопрос дает следующая
Теорема 5. Если сетка С на сфере состоит из т компонент
(/и;з= 1), то ее эйлерова характеристика равна т-\- 1.

КОМБИНАТОРНЫЙ (ТОПОЛОГИЧЕСКИЙ) ТИП МНОГОГРАННИКА 399
Доказательство. Ес^и т-*=\, т. е. сетка С связна, то
утверждение теоремы 5 верно (см. теорему 4). Пусть справедливость
теоремы 5 установлена уже при т < т0. Рассмотрим какую-либо
сетку С, имеющую т0 компонент. Одну из компонент сетки С обо-
обозначим через С', а всю остальную часть сетки С—через С". Тогда
сетка С" имеет /»0—1 компонент, и потому, по предположению
индукции, ее эйлерова характеристика
где В", Р", Г' — числа вершин, ребер
и граней сетки С". Пусть теперь /,,
/г, .. ., lq — все ребра сетки С, зану-
занумерованные таким образом, что при
любом k( = 1, ..., д) ребра l^ /8, ...,
lh образуют связную сетку (ср. дока-
доказательство теоремы 4). Обозначим
через Ck (k= 1, ..., д) сетку, состоя-
состоящую из сетки С и ребер /,, ..., /ft;
ясно, что сетка Сд совпадает с С. Рис 20.*
Индукция, проведенная при доказа-
доказательстве теоремы 4, без всяких изменений проходит и здесь, и мы
получаем, что все сетки С,, ..., С* имеют одну и ту я; е эйлерову
характеристику. Но сетка С, получается из С" добавлением одного
ребра /,, не имеющего с С" общих вершин (рис. 20). Поэтому
при переходе от С к С, число граней не меняется, число ребгр
увеличивается на 1, а число вершин — на 2. Следовательно, эйле-
эйлерова характеристика сетки С,, а значит и сетки Cq = C, равна
" = (В" — Р" -f Г") -f 1 = то+ 1.
Проведенная индукция и доказывает теорему 5.
Следствие. Для любой сетки на сфере справедливо нера-
неравенство
В—
т. е. эйлерова характеристика любой сетки на сфере не меньше двух.
§ 2. Комбинаторный (топологический) тип многогранника.
Теорема Штейница
2.1. Комбинаторные свойства многогранников. Изоморфизм.
Во многих вопросах теории многогранников бывает важно знать
не форму и размеры граней рассматриваемого многогранника, а лишь
число сторон каждой грани и общую схему соединения граней

400
МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ
в поверхность многогранника. К числу таких вопросов относится
и вопрос о связи между числами граней, вершин и ребер многогранника,
рассмотренный в предыдущем параграфе. Свойства многогранника,
связанные лишь с общей схемой соединения его граней, называются
комбинаторными или топологическими свойствами многогранника.
Остальные свойства многогранника называются его метрическими
свойствами; такими свойствами являются, например, величина поверх-
поверхности или объема многогранника, величины его линейных или дву-
двугранных углов.
Более точно комбинаторные свойства многогранника могут быть
охарактеризованы при помощи понятия изоморфизма. Два много-
многогранника называются изоморфными, если между вершинами, ребрами
Рис. 21.
и гранями одного многогранника и соответственно вершинами, ребрами
и гранями другого можно установить такое взаимно однозначное
соответствие, при котором инцидентным между собой вершинам,
ребрам и граням первого многогранника отвечают инцидентные вер-
вершины, ребра и грани второго1). Так, например, треугольная призма,
треугольная усеченная пирамида и «клин» (рис. 21) изоморфны между
собой. О двух изоморфных многогранниках говорят также, что они
являются многогранниками одного комбинаторного (или тополо-
топологического) типа.
Теперь можно сказать, что комбинаторные свойства многогранника —
это те его свойства, которые присущи наряду с этим многогран-
многогранником также любому изоморфному ему, т. е. свойства целого ком-
комбинаторного типа многогранников.
При изучении комбинаторных свойств многогранника мы всегда
можем заменить еги любым изоморфным ему многогранником, т. е. мо-
можем задавать многогранники лишь с точностью до изоморфизма. Чтобы
задать какой-нибудь многогранник с точностью до изоморфизма,
достаточно перечислить все его вершины А, В, С, ..., ребра а, Ь,
*) Вершины, ребра и грани называются инцидентными, если они при-
примыкают друг к другу. Например, ребро и грань инцидентны, если это
ребро является одной из сторон рассматриваемой грани.

КОМБИНАТОРНЫЙ (ТОПОЛОГИЧЕСКИЙ) ТИП МНОГОГРАННИКА 401
с, ... и грани а, р, Y' • • ¦ и указать, какие из них являются
попарно инцидентными. При этом, разумеется, должны выполняться
следующие условия, непосредственно вытекающие из приведенных
в § 1 определений простого многоугольника и простого многогран-
многогранника, а также из геометрического смысла отношения инцидентности
(мы обозначаем далее отношение инцидентности знаком -^.; так
например, запись а^А означает, что грань а инцидентна вер-
вершине А):
I. Отношение инцидентности (грани и ребра, грани и вершины,
ребра и вершины) симметрично, т. е., например, если а-^А, то и А-^-а.
II. Отношение инцидентности транзитивно: если А^а, а-^-а,
то i4-^-a.
III. Если А-^-а, то существуют два и только два ребра, инци-
инцидентных как вершине А, так и грани а.
IV. Если каждая из двух заданных граней инцидентна каждой
из двух вершин, то существует одно и только одно ребро, инциден-
инцидентное обеим этим граням и обеим вершинам.
Va. Каждое ребро инцидентно двум и только двум вершинам.
V6. Каждое ребро инцидентно двум и только двум граням.
Via. Для любых двух вершин А и В можно так выбрать ребра
с,, а2, ..., ап и вершины Л,, Аг, .... Ап_1, чтобы в цепочке
A, a,, At, a2>A2, ..., An_i, an, В каждые два соседних элемента были
взаимно инцидентными; если вершины А и В инцидентны одной и
той же грани а, то все вершины А{ и ребра а,- можно выбрать
так, чтобы они были инцидентными той же грани а.
VI6. Для любых двух граней аир можно так выбрать ребра
с,, а2, ..., ап и грани а,, а2, ..., ап_,, чтобы в цепочке а, а,,
а,, аг, а2, ..., ап_,, ап, р каждые два соседних элемента были
взаимно инцидентны; если грани аир инцидентны одной и той же
вершине А, то и все грани а,- и ребра ai можно выбрать так, чтобы
они были инцидентными той же вершине А.
2.2. Абстрактный многогранник. Желая рассматривать лишь
комбинаторные свойства многогранников, мы, естественно, приходим
к понятию абстрактного многогранника. Абстрактным
многогранником называется (конечная) совокупность произвольных
элементов, называемых вершинами, ребрами и гранями, для которых
каким-то образом определено отношение инцидентности (т. е. ука-
указано, какие вершины, ребра, грани считаются инцидентными), удов-
удовлетворяющее перечисленным выше условиям I—VI. Понятие абстракт-
абстрактного многогранника отражает, таким образом, взятые в чистом виде
свойства инцидентности вершин, ребер и граней конкретных простран-
пространственных многогранников. Мы будем далее без специальных оговорок
пользоваться по отношению к абстрактным многогранникам обычной
геометрической терминологией, называя каждую грань, инцидентную п
вершинам, п-угольником, инцидентные этой грани ребра — ее сторо-
26 Энциклопедия, ки. 4

4П2
МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ
нами и т. п. В отличие от абстрактных многогранников те многогран-
многогранники, о которых говорилось в § 1, мы будем называть простран-
пространственными многогранниками.
Тривиальными примерами абстрактных многогранников являются
одна грань (без ребер и вершин) или одна вершина (без ребер и
граней), а также многогранник, состоящий из одной грани и одной
вершины (не инцидентных между собой).
Столь же тривиальными можно считать абстрактные многогран-
многогранники, определяемые разбиением поверхности сферы на две области
(грани), ограниченные тремя дугами (ребрами), соединяющими по-
попарно три точки (вершины, рис. 22, а), или на три области (грани) —
тремя дугами (ребрами), соединяющими две точки (вершины,
рис. 22, б). Мы будем далее исключать эти случаи из рассмотрения,
предполагая, что каждый
рассматриваемый многогран-
многогранник имеет не менее трех вер-
вершин и не менее трех граней.
Из определения абстракт-
абстрактного многогранника (и приня-
принятого только что условия)
вытекают следующие его
простые свойства.
1°. Две вершины абст-
абстрактного многогранника
могут принадлежать не
более чем одному ребру.
В самом деле, предположим, что вершины А и В принадлежат
двум ребрам а и Ь. По условию V6 каждое из этих ребер должно
принадлежать двум граням; пусть а-^-а,, а~^-а2 ^^Р,, ^""~Pi- Обе
грани а, и а2 не могут совпадать с гранями р, и Р2, так как это
противоречило бы условию IV. Далее, если, например, а, совпадает
с р,, а грани а2 и Р2 различны, то в силу того же условия IV вер-
вершины А и В должны принадлежать еще одному ребру С, общему для
граней а2 и Р2, т. е. мы приходим к абстрактному многограннику,
изображенному на рис. 22,6 и исключенному нами из рассмотрения.
Наконец, если грани а,, а2, р,, |32 все различны, то в силу того же
условия IV через вершину А должны проходить три стороны грани
а, (принадлежащие кроме нее соответственно а2, Р,, Р2), что про-
противоречит условию III.
2°. Две грани абстрактного многогранника не могут иметь
более одного общего ребра.
Доказывается аналогично предыдущему1).
Рис. 22.
') Свойства 2° и 4° можно также получить из свойств I"
с помощью принципа двойственности (см. нвже, стр. 407).
в 3°

КОМБИНАТОРНЫЙ (ТОПОЛОГИЧЕСКИЙ) ТИП МНОГОГРАННИКА 403
3°. Каждая вершина абстрактного многогранника принадле-
принадлежит не менее чем трем граням (а следовательно, и ребрам).
В самом деле, в силу условия Via каждая вершина принадлежит
хотя бы одному ребру, а значит (в силу условий V6 и II), но крайней
мере двум граням. Но если бы некоторая вершина А принадлежала в
тошости двум граням, то эти грани имели бы (по условию 111) два
общих ребра, что противоре шло бы свойству 2°.
4°. Каждая грань абстрактного многогранника имеет не менее
трех вершин (а следовательно, и сторон).
Доказытется аналогично предыдущему.
2.3. Теорема ПИейница. Ясно, что всякий пространственный мно-
многогранник можно рассматривать как некоторый абстрактный многогран-
многогранник. Естественно возникает обратный вопрос: всегда ли существует
пространственный многогранник, изоморфный заранее данному
абстрактному многограннику, т. е. всякий ли абстрактный многогран-
многогранник может быть реализован в виде некоторого пространственного
многогранника. Оказывается, в наиболее важном случае, а именно для
абстрактных многогранников с эйлеровой характеристикой, равной 2, на
этот вопрос можно ответить положительна даже ограничиваясь лишь
выпуклыми пространственными многогранниками. Этот факт был
доказан немецким математиком Э. Штейницем.
Теорема Штейница. Всякий абстрактный многогранник,
эйлерова характеристика которого равна 2, может быть реали-
реализован в виде некоторого выпуклого многогранника."
Доказател.ство теоремы Штейница не может быть проведено
ячшь элементарно-геометрическими методами: оно опирается на
некоторые вспомогательные предложения (см. ниже, леммы 1 и 2),
которые могут быть доказаны лишь с привлечением топологических
соображений.
Не останавливаясь на доказательстве этих вспомогательных предло-
предложении, мы из ожим здесь элементарно геометрическую часть показатель
ства теоремы Штейница, она сама по се е достаточно поучительна
О новную роль в доказательст е теоремы Штейнииа играет одно
преобразование абстрактных многогранников, которое мы сеичас и рас-
рассмотрим
Пу ть а, и а2 — две грани абстракт ого многогранника М, имеющие
общую сторону АВ. Произведем над М с едующ! е операции:
1) иск ючим АВ из числа ре ер мно огранника М;
2) заменим грани а, и а2 одной новой ранью а, считая инцидентными
ей все стороны и вершины гра е а, и а2 (кроме стороны АВ);
3) если после исключения ребра АВ к однои из вершин А и В,
например к А, примыкают только два ребра АА1 и ААг много ран-
ника М, исключим А из числа вершин и заменим эти ребра одним
ребром Л,Л2.
Такое преобразование абстрактного многогранника М назовем о ъеди-
нением его граней а, и а2. Н ример, объединяя две грани куба
(рис 23, а), получим абстрактный многогранник, изоморфный треуголь-
треугольной призме (рис. 23, 6).
26*

404
МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ
Легко видеть, что при объединении двух граней абстрактного много-
многогранника сохраняются все условия, входящие в определение абстрактного
многогранника, за исключением услгви i IV, которое может и нарушиться.
Так, например, если в пирамиде SABCDE (п осматриваемой как абстракт-
абстрактный многогранник) объединить основание AICDE с боковой гранью SAB
(рис. 24), то грань SCD и новая (объединен 1я) грань SCDE будут и\'еть
общие вершины S и D, но не будут, ропр-ки условию IV, иметь общего
ребра, соединяющего эти вершины Таким образом, совокупность вершин,
ребер и гранен, получаемая в результате объед|.нения двух каких-нибудь
граней абстрактного многогранника, может
уже не быть абстрактным многогранником.
Однако имеет место следующая
с 4 г д.
А,А А
l/
/4
/
в,
а)
б)
Рис. 23.
Лемма 1. Во всяком абстрактном многограннике, эйлерова характе-
характеристика которого равна 2 (за исключением многогранника, изоморфного
тетраэдру), можно найти такие све смежные грани, при объединении кото-
которых получается снова абстрактный многогранник.
Отметим попутно, что объединение двух граней абстрактного много-
многогранника не меняет его эйлеровой характеристики. В самом деле, эта
операция, уменьшая число граней на 1, одновременно исключает одно
ребро; если же при этом исключается и какая-нибудь вершина, то число
ребер уменьшается еще на 1. Следовательно, величина В-\-Г — Р остается
во всех случаях неизменной.
Доказательство теоремы Штейница проводится индукцией
по числу и граней многогранника. Рассмотрим сначала абстрактный мно-
многогранник с наименьшим возможным числом граней. Если абстрактный
многогранник им(ет А-угольную грань, то он должен иметь также k
смежных с ней граней, т. е. всего не менее k-\-\ граней. Так как во вся-
всяком сл\чае А^З (свойство 4° абстрактного многогранника), то всякий
абстрактный многогранник имеет не менее четырех граней. Из сказанного
следует также, что многогранник с четырьмя гранями может иметь только
треугольные грани. Но абстрактный многогранник с четырьмя треуголь-
треугольными гранями существует, очевидно, только один: он соответствует извест-
известному нам прострг,- ствеж.ому многограннику — тетраэдру. Таким образом,
для л = 4 теорема Штейнииа справедлива.
Предположим, что эта теорема доказана для некоторого значения п,
т е. что всякий абстрактный многогранник (с эйлеровой характеристикой,
равной 2), имеющий п граней, можно реализовать в виде выпуклого мно-
многогранника.
Рассмотрим произвольный абстрактный многогранник М, имеющий
1 граней. В силу леммы 1 можно объединить некоторые две смежные

КОМБИНАТОРНЫЙ (ТОПОЛОГИЧЕСКИЙ) ТИП МНОГОГРАННИКА
405
грани аир этого многогранника так, чтобы в результате получился снова
некоторый абстрактный многогранник Мо. Пусть А и В — общие вершины
граней а и р, а у — новая грань абстрактного многогранника Мо. Этот
абстрактный многогранник имеет уже п граней; следовательно, по пред-
предположению индукции, существует пространственный выпуклый многогран-
многогранник Мо (рис. 25), изоморфный /Ио. П*сть Y — грань многогранника Мо,
отвечающая абстрактной грани Y> а Л и В — вершины грани у, отве-
отвечающие абстрактным вершинам А к В грани у (если грань y не имеет,
например, вершины А, т. е. если эта вершина сказалась исключенной
при объединении враией а и Р, то в качестве А можно выбрать произволь-
произвольную точку соответствующей стороны многоугольника y)- Отрезок АВ делит
выпуклый многоугольник y на два многоугольника а и р, отвечающих
абстрактным гргням а и р. Рассматривая эти многоугольники а и Р как
новые грани (взамен одной грани y). мы получим из многогранника Mt
Рис. 25.
Рис. 26.
новый пространственный многогранник М,, который, очевидно, будет изо-
изоморфен исходному абстрактному многограннику М. Однако многогранник
М, не является выпуклым, так как две его грани а и р лежат в одной
плоскости. .Деформируем теперь многогранники М, так, чтобы превратить
его в выпуклый.
Чтобы уяснить себе, как это делается, рассмотрим сначала простейший
случай: предположим, что грань а есть треугольник АЬС и что к его
вершине С, кроме ребер АС и ВС, примыкает еще только одно ребро
CD (именно этот случай изображен на рис. 26). Повернем плоскость
грани а вокруг прямой АВ так, чтобы ее новое положение пересекало
отрезок CD в его внутренней точке, и примем эту точку пересече-
пересечения за новое положение вершины С. В результате мы получим выпук-
выпуклый многогранник М (рис. 26), изоморфный многограннику М„ а значит и
абстрактному многограннику М. Этот многогранник М и представляет
собой искомую реализацию абстрактного многогранника М.
Последнее наше рассуждение существенно опирается на то, что вершина
С принадлежит, кроме грани а, еще только двум граням. Если бы
таких граней было хотя_ Сы три, то их плоскости однозначно определяли
бы положение точки С, и никакое вращение грани а вокруг ребра АВ
не было бы возможно (при сохранении неподвижными плоскостей всех
остальных граней) без нарушения изоморфизма с многогранником Mt.

406 МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ
Чтобы завершить доказательство теоремы Штеиница в общем случае, мы
уточним заключительный этап проведенного вьнйе рассуждения: именно,
мы покажем, что всегда можно, не нарушая изоморфизма многогранников
М и М„ повернуть интересующую нас грань а, если при этом смещать
одновременно и плоскости остальных граней. Возможность согласовать
между собой смещения всех граней (а следовательно, и вершин) многогран-
многогранника М, основывается на следующем вспомогательном предложении.
Рассмотрим совершенно произвольную совокупность N граней и вершин
данного абстрактного многогранника; будем всякую такую совокупность
называть для краткости просто набором. Назовем теперь порядком произ-
произвольной грани (или першины), входящей в набор N, число вершин
(соответственно граней), принадлежащих набору N и инцидентных этой
грани (вершине). Для многогранников с эйлеровой характеристикой,
равной 2, имеет место следующая
Л е м м а 2. Во всяком наборе, состоящем более чем из одного элемента,
существует по крайней мере два элемента (т. е. две грани, или две вершины,
или одна грань и одна вершина), порядки которых не превышают 3.
Возвращаясь к доказательству теоремы Штеиница в общем случае, мы
имеем многогранник /И,, изоморфный данному абстрактному многограннику
М, но не являющийся выпуклым из-за того, что две его грани а и р" лежат
В ОДНОЙ ПЛОСКОСТИ.
Пусть т есть общее число вершин и граней многогранника Л1,:
т = В-\-Г. Рассмотрим набор N , состоящий из всех граней и вершин этого
многогранника; в силу доказанной леммы в этом наборе содержится не
менее двух элементов порядка ^3. Обогначим один из таких элементов
через ат, причем выберем его отличным от грани а (если эта грань имеет
порядок 3). Затем рассмотрим новый набор Nv состоящий из всех граней
и вершин многогранника М,, за исключением грани или вершины ат.
В силу той же леммы и в этом наборе имеются хотя бы два элемента
порядка <3; обозначим один из них (отличный от грани а) через am_v
После этого рассмотрим набор Ыг, получаемый из Л\ исключением грани
или вершины ат_х, и обозначим один из его элементов порядка ^3 (от-
(отличный от грани а) через ат_2. Продолжая действовать таким же образом,
мы придем в конце концои к набору Nm_l, состоящему из одной грани а;
обозначим эту грань через а,. В результате все грани и вершины много-
многогранника М, окажутся расположенными в последовательность
а = а„ а2, а,,..., ат_„ ат D)
так, что каждый элемент этой последовательности будет инцидентен не
более чем с тремя из предшествующих элементов.
Повернем теперь плоскость грани а = а, вокруг ребра АВ (общего
ребра граней а и Р) в том направлении, в котором расположены от нее
смежные с ней грани многогранника М„ на достаточно малый угол, после
чего перейдем к элементу аг последовательности D). Если этот элемент
инцидентен а„ т. е. есть одна из вершин грани а, то примем за новое
положение этой вершины какую-нибудь точку, принадлежащую новому
положению плоскости а и достаточно близкую к старому положению вер-
вершины аг (например, точку, наиболее близкую к старому положению а,);
если же элемент аг не инцидентен а,, будем считать его новое положение
совпадающим со старым. Аналогичным образом определим ноаое положение
элемента as, затем—элемента а4 и т. д. Каждый раз, определяя новое

КОМБИНАТОРНЫЙ (ТОПОЛОГИЧЕСКИЙ) ТИП МНОГОГРАННИКА 407
положение элемента ak, мы будем в случае, когда он не инцидентен ии
одному из предшествующих элементов последовательности D), считать это
новое положение совпадающим со старым; если ah инцидентен одному или
двум предшествующим элементам, например пк_г и а/г_1, мы выберем новое
положение ak близким к старому и инцидентным уже определенным ранее
новым положениям элементов а^-\ и ak_2\ наконец, если элемент ak инциден-
инцидентен трем предшествующим элементам, его новое положение однозначно
определится новыми положениями этих трех элементов (плоскость грани
определяется положениями трех вершин этой грани, вершина определяется
положениями трех примыкающих к ней граней).
В результате указанного смещения граней и вершин многогранника
М, мы получим 'новый многогранник М, являющийся выпуклым (в силу
выбранного направления вращения грани а) и изоморфным многограннику М,
(так как взаимно инцидентным вершинам и граням одного из этих
многогранников соответствуют взаимно инцидентные вершины и грани
второго). Таким образом, многогранник М и представляет собой реализацию
абстрактного многогранника М, существование которой утверждает теоре-
теорема Штейница.
Из теоремы Штейница вытекает также
Следствие. Всякий многогранник нулевого рода изоморфен
некоторому выпуклому многограннику.
2.4. Двойственность. С понятием абстрактного многогранника и
теоремой Штейница связан еще один интересный геометрический
факт. Возвращаюсь к определению абстрактного многогранника, легко
заметить, что описываемые этим определением свойства граней в
точности таковы же, как и свойства вершин, т. е. это определение
не изменится, если всюду в нем слово «грань» заменить словом
«вершина» и наоборот; условия I—IV при этом сохранят свое содер-
содержание, условие Va превратится в условие V6 и наоборот. Это
означает, что, имея какой-нибудь абстрактный многогранник М и
называя его грани «вершинами», ребра — по-прежнему «ребрами», а
вершины — «гранями», мы получим совокупность «вершин», «ребер»
и «граней», снива удовлетворяющую всем требованиям определения
абстрактного многогранника, т. е. некоторый новый абстрактный
многогранник М%.
Два абстрактных многогранника М и Мх, между элементами ко-
которых можно установить взаимно однозначное соответствие так,
чтобы вершинам, ребрам и граням одного отвечали соответственно
грани, ребра и вершины второго и чтобы при этом инцидентным
парам элементов одного многогранника отвечали инцидентные пары
элементов второго, называются двойственными друг другу. Это
определение весьма сходно с определением изоморфизма многогран-
многогранников; разница состоит лишь в том, что вершинам одного многогран-
многогранника в случае двойственности должны отвечать не вершины, а грани
второго (и наоборот). Как мы видели, для каждого абстрактного
многогранника существует двойственный ему абстрактный мно-
многогранник.

Ф08
МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ
Теорема Штейница позволяет распространить этот результат и на
пространственные многогранники нулевого рода: для каждого про-
пространственного многогранника нулевого рода существует двой-
двойственный ему пространственный (даже выпуклый) многогранник.
6)
Рис. 27.
Так, например, л-угольной призме (рис. 27, а), двойствен много-
граннник, называемый л-угольной бипирамидой (рис. 27, б);
я-угольной пирамиде двойственна снова л-угольная пирамида (рис. 28);
Рис. 28.
многограннику, изображенному на рис. 29,а, двойствен многогран-
многогранник, изображенный на рис. 29,6. Следует, однако, иметь в виду, что
соотношение двойственности связывает между собой не отдельные
конкретные пространственные многогранники, а целые комбина-
комбинаторные типы многогранников, т. е. в конечном счете снова
абстрактные многогранники.

КОМБИНАТОРНЫЙ (ТОПОЛОГИЧЕСКИЙ) ТИП МНОГОГРАННИКА 409
Двойственные друг другу абстрактные многогранники обладают
сходными комбинаторными свойствами, но только свойства вершин
одного многогранника будут свойствами граней другого. Другими
словами, из всякой теоремы, выражающей комбинаторное свойство
некоторого многогранника Ж, можно получить другую теорему,
относящуюся к многограннику, двойственному М, заменив всюду
в формулировке первой теоремы слово «грань» словом «вершина»
и наоборот. Эта новая теорема называется двойственной первой;
она будет верна или неверна одновременно с первой. В частности,
если какая-нибудь теорема выражает общие свойства многогранников,
т. е. относится к произвольному многограннику, то и двой-
двойственная ей теорема будет относиться к произвольному многограннику
Рис. 29.
Примерами двойственных теорем могут служить установленные
выше (см. стр. 402—403) свойства 1°—4° абстрактных многогранников:
свойство 2° двойственно свойству 1°, а свойство 4°—свойству 3°.
Отсюда ясно, между прочим, каким образом можно получить опущен-
опущенные доказательства свойств 2° и 4°: чтобы доказать, например, свой-
свойство 2°, достаточно провести рассуждение, двойственное доказатель-
доказательству свойства 1°, т. е. заменить всюду в этом доказательстве слово
«грань» словом «вершина» и наоборот. Рекомендуем читателю
самостоятельно выполнить это полезное упражнение. Заметим еще,
что теорема Эйлера, доказанная выше, является примером пред-
предложения, которое двойственно самому себе (для двойственного
многогранника числа Г, В, Р заменяются на В, Г, Р, а алгебраическая
сумма Г-j-B—Р не меняется). В частности, двойственным для много-
многогранника нулевого рода будет снова некоторый многогранник нулевого
рода.
Отмеченное выше положение, связывающее между собой различ
ные комбинаторные теоремы, может быть названо принципом двой-
двойственности (для многогранников). Следует отметить, что этот принцип

410
многоугольники и многогранники
установлен нами лишь по отношению к комбинаторным (топологиче-
(топологическим) свойствам многогранников. Однако, как мы увидим далее,
такая же двойственность распространяется и на некоторые метриче-
метрические свойства многогранников.
§ 3. Развертка многогранника. Теорема Коши
3.1. Развертка многогранника. Существование многогранника
с данной разверткой. Практически, когда хотят изготовить модель
многогранника, ее часто склеивают из плоских многоугольников — граней
многогранника. Для этого нужно не только располагать набором
Ш-
многоугольников, которые должны служить гранями многогранника,
но также знать, какие их стороны следует склеивать между собой.
Совокупность многоугольников, соответственно равных граням неко-
некоторого многогранника, вместе с указанием того, какие их стороны
и вершины представляют собой одни и те же ребра и вершины
многогранника, называется разверткой этого многогранника. Так,
например, развертка многогранника, изображенного на рис. 30,а,
показана на рис. 30, б; здесь часть сторон, подлежащих склейке, уже
совмещены друг с другом, а остальные стороны и вершины, которые
должны быть склеены, обозначены одинаковыми буквами.

РАЗВЕРТКА МНОГОГРАННИКА. ТЕОРЕМА КОШИ
411
Ясно, что имея многогранник, мы всегда можем построить его
развертку. Гораздо менее ясно, можно ли, наоборот, задав заранее
набор многоугольников и схему склеивания их сторон и вершин,
быть уверенным в том, что тем самым определен некоторый много-
многогранник—и если это так, то сколько различных многогранников
мы можем таким образом получить. Иными словами, возникает вопрос
о существовании и единственности многогранника с заранее заданой
разверткой. Мы рассмотрим этот вопрос лишь в отношении выпуклых
многогранников.
Заданная совокупность плоских многоугольников (вместе с задан-
заданной схемой склеивания их сторон и вершин) определяет комбинатор-
комбинаторный тип многогранника, а также форму и размеры его граней. Комби-
Комбинаторный тип согласно теореме Штейница, всегда может быть реализован
некоторым выпуклым много'
гранником, если только вы-
выполняются следующие усло-
условия:
1) должны выполняться
все три требования, фигури-
фигурирующие в определении
многогранника (см. § 1);
2) число вершин, гра-
граней и ребер развертки')
должно удовлетворять тео-
теореме Эйлера:
В+Г— Р=2.
Кроме того, для су-
существования выпуклого мно-
многогранника с данной раз-
разверткой необходимо еще вы-
выполнение следующих метри-
метрических условий:
3) склеиваемые стороны многоугольников должны иметь одинако-
одинаковую длину;
4) сумма плоских углов при каждой из вершин развертки должна
быть меньше 360°.
Условия 1) — 4), необходимость которых очевидна, не явля-
являются еще достаточными для существования искомого многогран-
многогранника. Так, например, совокупность многоугольников, изображенная
на рис. 31, хотя удовлетворяет всем этим условиям, все же не
') При этом, разумеется, стороны (и вершины) многоугольников, подле-
подлежащие склейке, должны считаться одним ребром (одной вершиной) раз-
развертки.

412 МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ
является разверткой никакого многогранника. В самом деле, если
бы существовал многогранник с такой разверткой, то его ребрэ ЕА
было бы перпендикулярно плоскости ABCD (так как ЕА \_ АВ и
ЕА J_ AD), откуда в силу известной теоремы о трех перпендикулярах
следовало бы, что BE ]_ВС, вопреки данной на
развертке величине угла СВЕ.
Оказывается, однако, что перечисленные вы-
выше условия 1) — 4) обеспечивают существование
многогранника (и притом выпуклого), если не
требовать, чтобы этот многогранник имел в точ-
точности данную развертку, а допустить объеди-
объединение некоторых смежных многоугольников дан-
данной развертки в одну грань и, наоборот, раз-
разбиение некоторых многоугольников на несколь-
в ко граней (так, например, на. рис. 31 достаточно
разбить четырехугольник ABCD диагональю BD
на два треугольника, чтобы получить развертку
некоторого выпуклого многогранника; см. рис. 32). Этот факт был до-
доказан в 1942 г. ленинградским математиком А. Д. Александро-
Александровым1).
3.2. Теорема Коши. Основные леммы. Перейдем теперь к во-
вопросу о единственности многогранника, имеющего данную
развертку. Каждому, кто клеил многогранники из разверток, из
опыта известно, что по заданной развертке мы можем получить
только один выпуклый многогранник с точностью до положения в
пространстве8). Этот факт был известен еще Евклиду (жившему в
111 веке до нашей эры), однако первое более или менее строгое
доказательство этого факта было дано лишь в 1813 г. знаменитым фран-
французским математиком О. Коши. Хотя доказательство, данное Коши,
содержало некоторый пробел (который будет указан ниже), замечен-
замеченный и восполненный позже Штейницем, теорема о единственности
многогранника с данной разверткой по праву носит название теоре-
теоремы Коши.
') Доказательство теоремы А. Д. Александрова совсем не элементарно,
и мы не будем его приводить; читатель, желающий ознакомиться с этим
доказательством, сможет найти его в указанной в конце статьи книге
А. Д. Александрова [1].
г) Собственно говоря, из данной развертки можно получить два разных
многогранника, симметричных относительно плоскости; чтобы устранить
эту неопределенность, можно было бы указывать на какой-нибудь грани
развертки, какая сторона ее должна принадлежать внешней, а какая—
внутренней стороне поверхности многогранника. Мы далее не будем раз-
различать таких многогранчиков, считая, что симметричность есть частный
случай равенства многогранников (хотя два таких многогранника, вообще
говоря, не могут быть совмещены друг с другом перемещением в про-
пространстве).

РАЗВЕРТКА МНОГОГРАННИКА. ТЕОРЕМА КОШИ
413
Теорема Кош и. Если все грани одного из двух изоморфных
выпуклых многогранников М и /И, равны соответствующим гра-
граням другого, то эти многогранники равны.
Очевидно, для доказательства равенства многогранников, удов-
удовлетворяющих условию теоремы Коши, достаточно доказать равенство
двугранных углов при всех их соответственных ребрах. Доказатель-
Доказательство основывается на следующих леммах.
Лемма 1. Если, не изменяя длин сторон (плоской) выпуклой
ломаной линии А1А1...Ап, увеличить некоторые из ее углов так,
чтобы полученная лома-
ломаная снова была выпуклой,
то расстояние между кон-
концами этой ломаной увели-
увеличится.
Доказательство.
Для упрощения рассуждений
введем некоторые вспомога-
вспомогательные термины. Будем
называть прямую АхАп (и
любую параллельную ей)
горизонтальной; на-
направление от точки At к
точке Ап будем характери-
характеризовать словами «слева на-
направо»; наконец, направле-
направление, перпендикулярное пря- Рис 33
мой А1Ап и обращенное в
ту сторону от этой примой, с которой расположена данная ло-
ломаная, будем характеризовать словами «сверху вниз» (рис. 33).
Через самую нижнюю вершину Ак данной ломаной проведем
горизонтальную прямую р (таких вершин может оказаться две — Ak
и Ak+l; в этом случае сторона АкАк+Л будет лежать на прямой р). Оче-
Очевидно, вся ломаная AtAx ... Ап будет лежать в полосе, заключенной
между прямыми AtAn и р. Спроектируем вершины Л, и Ап ортогонально
на прямую р и обозначим их проекции соответственно через At и Ап.
Пусть теперь нам нужно увеличить углы ломаной AtAt ... Ап
до некоторых заранее данных величин (меньших 180°, так как полу-
полученная ломаная должна остаться выпуклой). Увеличим сначала (если
2<lft) угол А3 до требуемой величины (если он вообще должен быть
увеличен), повернув для этого сторону АгА1 вокруг точки At (про-
(против часовой стрелки); пусть точка Ах займет при этом положение
А[1\ а ее проекция — положение а[1) (см. рис. 33). Очевидно, обе
точки, А, и А['\ лежат выше точки Аг (ибо отрезок АгА\ъ* должен
лежать внутри угла между лучом АгАх и продолжением отрезка АгАг

414 МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ
за точку Аг); поэтому при указанном повороте проекция точки Л, будет
перемещаться справа налево. Следовательно, точка а[^ будет
лежать левее точки At. Увеличим затем до нужной величины угол
Ах (если 3<А); для этого повернем вокруг точки At как жесткое
целое ломаную А[1)АгАш, или же, что равносильно этому, отрезок
АгА[1\ Так же как и ранее, проекция точки Ал при этом сместится
влево. Поступим таким же образом с углами Ал, ...,Ak_l. Затем
таким же путем увеличим углы An_t. An_t, ..., Ak+t правой поло-
половины данной ломаной; при этом проекция вершины Ап может смес-
сместиться только вправо. Наконец, увеличим угол Ak, поворачивая
вокруг точки Ak обе половины ломаной (левую — против часовой
стрелки, а правую — по часовой стрелке) так, чтобы обе эти поло-
половины оставались выше прямой р.
В результате мы получим новую ломаную AtA2 ... Ап, причем
отрезок Ах Ап^ соединяющий проекции ее концов, будет содержать
внутри себя отрезок АхАп. Таким образом, А1Ап<_А'1А'п. Но А1Ап = А1Ап
(чаккак А.А \\р), аА'А'^А,А„
» Следовательно, АхАп < Л,Л„, и
Т •* лемма 1 доказана.
Отметим, что именно в до-
доказательстве Коши леммы 1
был допущен пробел, лишив-
лишивший необходимой полноты все
^ь___^______^____^__ г данное им доказательство те-
"г 3 оремы. Именно, доказательство
р _ Коши существенным образом
опиралось на тот факт, что,
увеличивая по одному углы
данной ломаной, мы после каждого шага получаем снова
выпуклую ломаную. При этом упускалось из виду, что некоторые
из полученных промежуточных ломаных могут быть и невыпуклыми.
О такой возможности свидетельствует пример ломаной АхАлАгА^,
изображенной на рис. 34: если каждый из ее углов Аг и А3 требу-
требуется увеличить до прямого (в результате чего, очевидно, получится
снова выпуклая ломаная), то, увеличив до нужной величины лишь
один из этих углов, мы придем к невыпуклой ломаной. Приведен-
Приведенное выше доказательство леммы 1 никак не было связано с выпуклостью
промежуточных ломаных.
Лемма 2. Пусть выпуклый многоугольник АгАг ... Ап де-
деформируется в выпуклый же многоугольник так, что длины его
сторон при этом не меняются, а из углов хотя бы один изме-
изменяет свою величину. Отметим знаком «плюс» вершины тех
углов данного многоугольника, которые при этой деформации

РАЗВЕРТКА МНОГОГРАННИКА. ТЕОРЕМА КОШИ 415
увеличиваются, а знаком «.минус» — вершины тех углов, которые
при этой деформации уменьшаются (вершины тех углов, которые
не изменяют своей величины, мы оставляем неотмеченными).
Тогда при последовательном обходе вершин данного многоуюль-
ника мы будем иметь не менее четырех перемен знаков (неотмечен-
(неотмеченные вершины при подсчете перемен знаков не учитываются).
Доказательство. Начав обход вершин многоугольника с
какой-нибудь отмеченной вершины, мы должны, дойдя снова до этой
вершины, вернуться к тому же знаку, с которого начали; следова-
следовательно, число перемен знаков должно быть четным. Оно не может
быть равно нулю, так как в этом случае все отмеченные вершины
имели бы один и тот же знак, например « + », и по лемме 1 одна
из сторон первого многоугольника
должна была бы увеличиться, что
противоречит условию теоремы.
Предположим, что мы имеем всего
две перемены знаков. Это означает,
что при обходе вершин многоугольника
АхАг ... Ап на некотором участке,
скажем, от вершины At до вершины Ak,
все отмеченные вершины буду г иметь
знак е-)-»' а далее—от вершины Ak+1
до вершины Ап — знак «.—» (рис. 35).
Выберем произвольную точку С на сто-
стороне АпАх и произвольную точку D на стороне AkAk+i. Тогда в силу
леммы 1, примененной к ломаной САХ ... AkD, отрезок CD должен
при нашей деформации увеличиться, а в силу той же леммы 1, при-
примененной к ломаной DAk+l ... АпС,— уменьшиться.
Полученное противоречие и показывает, что число перемен зна-
знаков не может равняться 2. Следовательно, это число не менее 4,
что и требовалось доказать.
Замечание. В леммах 1 и 2 мы рассматривали для простоты
лишь плоские многоугольники. Однако эти леммы вместе с их до-
доказательствами (из которых первое требует лишь несущественных изме-
изменений ')) остаются справедливыми и для сферических многоугольни-
многоугольников (т. е. многоугольников на сфере, образованных дугами больших
окружностей). Именно к таким многоугольникам нам придется при-
применять эти леммы.
Лемма 3. Пусть выпуклый многогранный угол деформируется
в выпуклый же многогранный угол так, что его плоские углы
при этом не изменяются, а из двугранных углов хотя бы один
') Именно, большой круг р (вместо прямой р) должен быть выбран так,
чтобы он пересекал большой круг А,Ап в точках О, и 02, лежащих вне
дуги Л,ЛП. Проектирование на р следует осуществлять с помощью окруж-
окружностей, лежащих в плоскостях, перпендикулярных диаметру Ofi2 сферы.

416 МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ
изменяет свою величину. Отметим ребро этого двугранного угла
знаком «.плюс-» или «.минус», смотря по тому, увеличивается или
уменьшается в результате нашей деформации двугранный угол
при этом ребре. Тогда при последовательном обходе ребер много-
многогранного угла мы будем иметь не менее четырех перемен знаков.
Доказательство. Проведем сферу произвольного радиуса
с центром в вершине данного многогранного угла. В пересечении этой
сферы с многогранным углом мы получим сферический многоугольник
(рис. 36), каждая сторона которого будет измеряться соответствую-
соответствующим плоским углом многогранного угла, а каждый угол — двугранным
углом многогранного угла. Деформации много-
многогранного угла будет отвечать деформация
сферического многоугольника; теперь лемма
3 непосредственно вытекает из леммы 2.
3.3. Доказательство теоремы Коши.
Пусть нам даны два изоморфных выпуклых
многогранника М и М', соответствующие
грани которых равны. Мы должны показать,
что все двугранные углы одного из этих
многогранников также равны соответствую-
соответствующим углам другого.
Предположим, что среди соответствующих
Рис. 36. двугранных углов данных многогранников име-
имеются неравные. Отметим каждое ребро много-
многогранника М, двугранный угол при котором больше соответствующего
двугранного угла многогранника М', знаком «плюс», а каждое ребро,
двугранный угол при котором меньше соответствующего двугранного
угла,—знаком «минус»; те ребра, двугранные углы при которых равны
соответствующим им углам, мы оставляем неотмеченными. По нашему
предположению, у многогранника Ж имеются отмеченные ребра; к каждой
вершине, к которой примыкает какое-нибудь отмеченное ребро, в силу
леммы 3 должны примыкать еще по меньшей мере три таких ребра.
Отмеченные ребра образуют на поверхности многогранника М неко-
некоторую сетку С, делящую эту поверхность на несколько областей1).
Ребрами этой сетки будут отмеченные ребра многогранника М, а
вершинами — те из вершин многогранника М, к которым примыкает
хотя бы по одному отмеченному ребру.
Обозначим число вершин, граней и ребер, определяемых сеткой С,
соответственно через В, Г к Р. Подсчитаем общее число х перемен
знаков, которое мы получим, обходя последовательно ребра, примы-
примыкающие к одной вершине сетки С, затем к другой, затем к третьей
и т. д. В силу леммы 3 при каждой вершине будет не менее
') В § 1 мы рассматривали сетки на сфере; рассмотрение сеток на
поверхности выпуклого многогранника ничем не отличается: достаточно
спроектировать поверхность многогранника на сферу.

РАЗВЕРТКА МНОГОГРАННИКА. ТЕОРЕМА КОШИ 417
четырех перемен знаков. Следовательно,
X3s4?. E)
Подсчитаем теперь общее число у перемен знаков, которое мы
получим, обходя последовательно контур каждой грани сетки С.
Число перемен знаков при обходе каждой грани должно быть четным;
кроме того, оно не может превышать числа сторон этой грани. Сле-
Следовательно, для треугольной грани число перемен знаков будет не
более 2, для четырехугольной грани—не более 4, для пятиугольной
грани — снова не более 4, для шестиугольной грани — не более 6,
для семиугольной грани — снова не более 6 и т. д. Таким образом,
если обозначить число треугольных, четырехугольных, пятиугольных
и т. д. граней сетки С соответственно через .Г,, Гл, Fs, ..., то будем
иметь
6Г,+ ... F)
Но, очевидно, общее число перемен знаков не зависит от того,
будем ли мы его подсчитывать по вершинам или по граням сетки С:
два ребра, являющихся соседними при обходе некоторой вершины,
будут соседними также и при обходе некоторой грани, а потому
будут одновременно давать или не давать нам одну перемену знака
при обоих способах подсчета. Таким образом, х=у, и, сравнивая
неравенства E) и F), получаем
6Г7+... G)
Покажем теперь, что это последнее неравенство противоречит
теореме Эйлера. Действительно, согласно следствию из теоремы
Эйлера (стр. 399) мы имеем для сетки С соотношение
В+Г— Pss2,
т. е.
4?Ss8 + 4P— 4Г. (8)
Но, очевидно,
... (9)
Выразим и число Р через числа Гк. Для этого пересчитаем ребра
сетки С, подсчитывая стороны сначала всех треугольных граней,
затем всех четырехугольных граней, затем пятиугольных и т. д.
Всего мы насчитаем таким образом ЗГ, + 4Г4 + 5Г,+... ребер,
однако при этом каждое ребро будет подсчитано дважды (так как
оно принадлежит двум граням). Следовательно,
... A0)
Учитывая соотношения (9) и A0), неравенство (8) можно перепи-
переписать в виде
4Б^8 + 2Г, + 4Г1 + 6/4-)-8Гв-1-... A1)
27 Энциклопедия, кн. 4

418
МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ
Сравнивая неравенство A1) с полученным ранее неравенством G),
мы видим, что они противоречат друг другу, так как правая часть
неравенства A1) заведомо больше правой части неравенства G).
Таким образом, предположение о существовании неравных соот-
соответственных двугранных углов многогранников М и М' привело нас
к противоречию, и теорема Коши пол-
полностью доказана.
Из теоремы Коши следует, что вы-
выпуклый многогранник с жесткими (не-
(неизменяемыми) гранями является жест-
жестким, т. е. не может быть деформирован,
даже если его грани соединены между
собой шарнирно. Заметим, что в этом
отнэшении многогранники резко отлича-
отличаются от плоских многоугольников. Пло-
Плоский многоугольник, вообще говоря,
можно деформировать, не меняя длин
его сторон; например, шарнирный квадрат
деформируется в ромб (рис. 37); исключение здесь составляют лишь
треугольники, которые, как известно, обладают свойством жесткости.
Отметим еще, что в теореме Коши предположение о выпуклости
обоих рассматриваемых многогранников весьма существенно: выпуклый
многогранник может иметь грани, равные соответствующим граням
Рис. 37.
Рис. 38.
изоморфного ему невыпуклого многогранника. (Два таких многогран-
многогранника изображены на рис. 38.) Однако такие многогранники не могут
быть получены один из другого непрерывной деформацией (при кото-
которой не менялись бы форма и размеры граней), так как в процессе
такой деформации выпуклый многогранник еще некоторое время должен
был бы оставаться выпуклым, что невозможно в силу теоремы Коши.

РАЗВЕРТКА МНОГОГРАННИКА. ТЕОРЕМА КОШИ
419
3.4. Некоторые обобщения на случай кривых поверхностей. Вопрос
о существовании и единственности многогранника, имеющего данную раз-
развертку, связан с широким кругом математических вопросов, составляющих
содержание так называемой внутренней геометрии повзрхностей. ЧтоСы
разобраться в постановке этих вопросов, потребуются некоторые дополни-
дополнительные пояснения.
Предположим, что нам дан выпуклый многогранник М и что мы имеем
возможность измерять геометрические величины не вообще в пространстве,
а только на поверхности этого многогранника; в таком положении оказа-
оказались бы, например, «двумерные существа», живущие на поверхности дан-
данного многогранника и ничего не знающие о трехмерном пространстве,
в котором он расположен. Такие существа моглн бы измерять длины
линий, расположенных на поверхности многогранника, а также углы между
ними ') (измерение которых может быть сведено, как легко понять, к изме-
измерению длин), но такие величины, как, например, углы между гранями,
были бы недоступны их измерению (по крайней мере непосредственному).
Запас геометрических сведений, которые могли бы получить эти двумерные
существа о своем многограннике, и составляет содержание внутренней
геометрии этого многогранника. В этот запас сведений входило бы,
например, понятие о вершине многогранника: вымышленные существа
могли бы заметить, что в вершинах, в отличие от других точек поверхно-
поверхности многогранника, полный угол меньше чем 360°.
Два различных (не равных между собой) многогранника могут иметь
одну и ту же внутреннюю геометрию; примерами могут служить хотя бы
многогранники, изображенные на рис. 38. Это будет иметь место в том
случае, когда многогранники изометричны. Два многогранника назы-
называются изометричными, если между точками их поверхностей можно уста-
установить взаимно однозначное соответствие так, что каждой лннни на поверх-
поверхности одного многогранника отвечает на поверхности другого линия такой
же длины; в этом случае говорят также, что два многогранника имеют
одну и ту же внутреннюю метрику. Упоминавшиеся выше двумерные суще-
существа, живущие на поверхностях таких двух многогранников, не могли бы
заметить между ними никакой разницы.
Ясно, что задание развертки многогранника однозначно определяет его
внутреннюю метрику: на развертке многогранника можно непосредственно
выполнять те же измерения, что и на самой его поверхности. Те преобра-
преобразования развертки, которые были указаны в конце п. 3.1 в связи с теоре-
теоремой А. Д. Александрова (объединение смежных граней и, наоборот, разбиение
одной грани иа несколько), очевидно, преобра-
преобразуют данную развертку в изометрическую, т. е.
сохраняют ее внутреннюю метрику. Таким обра-
образом, теорема А. Д. Александрова утверждает
в действительности существование многогран-
многогранника не с данной разверткой, а с данной внут-
r a
') Следует иметь в виду, что величина
угла между двумя линиями, измеренная на
поверхности многогранника, вообще говоря,
отлична от величины того же угла, измеренной
по обычным правилам измерения углов в про-
пространстве. Так, например, изображенный на
рис. 39 угол между прямыми а и Ь, измеренный
на поверхности данного многогранника, следует
считать равным сумме углов а и р\ изображенных там же; ета сумма
больше плоского угла между прямыми а и Ь.
77*

420 многоугольники и многогранники
ренней метрикой. Далее, теорема Коши показывает, что в классе выпуклых
многогранников каждый многогранник однозначно определяется своей
внутренней метрикой.
Понятие изометричности (а значит, и внутренней метрики) без всяких
изменений может быть перенесено на произвольные поверхности (не являю-
являющиеся многогранниками), и по отношению к ним возникают те же вопросы
существования и единственности. Эти вопросы разрабатывались многими
геометрами довольно длительное время и получили окончательное реше-
решение (по отношению к выпуклым поверхностям) лишь в сравнительно недав-
недавнее время. Вопрос о существовании выпуклой поверхности с заданной
внутренней метрикой был решен А. Д. Александровым в 1948 г.: им было
доказано, что требуемая выпуклая поверхность существует тогда и только
тогда, когда данная метрика удовлетворяет деум условиям, которые анало-
аналогичны условиям 2) и 4), сформулированным в п. 3.1 (стр. 411) для много-
многогранников ') Интересно отметить, что для доказательства этой своей тео-
теоремы А. Д. Александров использует теорему о существовании выпуклого
многогранника с данной разверткой: данную метрику он заменяет близки-
близкими к ней развертками многогранников и, построив эти многогранники,
переходит от них к искомой поверхности.
Вопрос о единственности выпуклой поверхности с данной внутренней
метрикой был окончательно р^шен харьковским геометром А. В. П о г о р е-
л о в ы м в 1949 г Им была доказана следующая теорема, существенно обоб-
обобщающая теорему Коши: всякие две изометричные выпуклые поверхности
равны между собой.
§ 4. Правильные многоугольники и многогранники
и их обобщения
4.1. Топологически правильные многогранники. Многогранник
называется топологически правильным, если все его грани имеют
одинаковое число вершин и во всех вершинах сходится одинаковое
число граней2). Ясно, что свойство многогранника быть топологически
правильным есть его топологическое свойство, так что многогранник,
изоморфный топологически правильному многограннику, сам является
топологически правильным. Найдем все комбинаторные типы тополо-
топологически правильных многогранников нулевого рода.
Пусть В, Г к Р — числа вершин, граней и ребер многогранника.
Пусть каждая грань многогранника имеет п вершин и в каждой вер-
вершине сходятся s граней. Так как каждая грань имеет п ребер, то
все Г граней будут иметь пГ ребер; но при этом каждое ребро
многогранника учитывается дважды (потому что оно принадлежит двум
граням). Следовательно,
пГ=2Р. A2)
') Условие 2), требующее, чтобы развертка имела эйлерову харак-
характеристику 2, для поверхностей формулируется как условие гомеоморфности
¦сфере, а условие 4) — как условие положительности кривизны
2) Вводить аналогичное понятие для многоугольников не имеет смысла:
так как каждая сторона многоугольника имеет две вершины и к каждой
вершине примыкают две стороны, то любой многоугольник следовало бы
¦считать топологически правильным.

ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ
421
Аналогично, подсчитывая ребра, примыкающие к каждой вершине,
получаем соотношение
sB=2P. A3)
Но числа В, Г и Р согласно теореме Эйлера связаны соотноше-
соотношением
В+Г — Р=2. A4)
Выражая с помощью равенств A2) и A3) числа В и Г через Р
и подставляя в формулу A4), придем к уравнению
?+?-"-«¦
или, после деления на 2Р:
1 . 1
1 . 1
s + n P + 2 '
A5)
Это уравнение и позволяет найти все возможные (для топологи-
топологически правильного многогранника) значения s, n и Р. В самом деле,
из A5) вытекает неравенство
1.1 1
11.
откуда видно, что хотя бы одно из чисел — и — должно быть
больше j, т. е. хотя бы одно из чисел sun должно быть меньше 4.
Но так как ни одно из чисел s и п по их геометрическому смыслу не
может быть меньше чем 3, то должно быгь либо s = 3, либо л = 3.
-, т. е. п < 6; точно
Далее, так как — sg—, то — >
So /I
—, то — >1Г— -я-
o /I / О
так же находим, что и Кб. Таким образом, мы имеем лишь пять
возможностей: либо л=3, s = 3, 4, 5, либо s = 3, /z = 4, 5. Про-
Проверка ноказывает, что во всех этих случаях число Р, определяемое
равенством A5), а также числа Г и В, определяемые равенствами A2)
и A3), являются целыми. Находя эти числа в каждом из указанных
случаев, мы определим все возможные характеристики топологически
правильных многогранников.
Таблица 2
№ п/п
1
2
3
4
5
п
3
3
3
4
5
S
3
4
5
3
3
р
6
12
30
12
30
в
4
6
12
8
20
г
4
8
20
6
12

422
многоугольники и многогранники
Из наших рассуждений пока не следует, что каждая строка
полученной таблицы определяет в действительности некоторый много-
многогранник. Покажем, что это действительно так, на примере второй
строки.
Согласно содержащимся в этой строке значениям п и s искомый
многогранник должен иметь треугольные грани, сходящиеся по четыре
в каждой вершине. Пусть АхАгА3—одна такая грань. С ней должны
А
Рис. 40.
быть смежными еще три треугольные грани, указанные схематически
на рис. 40, а; при этом вершины At, As, Ав должны быть все раз-
различны, так как в противном случае в одной из вершин сходились бы
не четыре, а только три грани. Далее, к вершинам А1% А2, As должно
примыкать еще по одной грани, как указано на рис. 40, б. Теперь
в вершине Л4 сходятся три грани, причем имеются «свободные» ребра
W и Л4Лв; следовательно, к этой вершине должна примыкать еще
одна грань, имеющая ребра AtAb и Л4Лв (рис. 40, в). Теперь в каж-
каждой вершине Ах, А2, ...,At сходятся по четыре треугольных грани,
причем «свободных» ребер уже не имеется. Схема, изображенная на

ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ
423
рис. 40, в, есть абстрактный многогранник. По теореме Штейница он
может быть реализован в виде выпуклого многогранника (рис. 41);
это и есть искомый топологически правильный многогранник (он пред-
представляет собой четырехугольную бипиримиду, называемую также ок-
октаэдром); в соответствии с данными второй
строки нашей таблицы этот многогранник имеет
12 ребер, 6 вершин и 8 граней.
Как мы видели, схема, изображенная на
рис. 40, в, однозначно определяется значениями
л = 3, s = 4. Следовательно, нами доказано
не только существование требуемого много-
многогранника, но и его единственность (с точ-
точностью до изоморфизма).
Такое же рассуждение может быть проведено
и в отношении любой другой строки таблицы 2.
Первая строка этой таблицы определяет уже
известный нам тэтраэдр, третья — многогранник, называемый ико-
икосаэдром (рис. 42), четвертая — многогранник, изоморфный четырех-
четырехугольной призме и называемый также гексаэдром (рис. 43), пятая —
многогранник, называемый додекаэдром (рис. 44).
Таким образом мы приходим к следующему выводу.
Теорема. Существует пять различных (не изоморфных между
•собой) типов топологически правильных многогранников: тетра-
тетраэдр, гексаэдр, октаэдр, додекаэдр и икосаэдр.
Рис. 41.
Рис. 42.
Рис. 43.
Рис. 44.
Возвращаясь к определению топологически правильного многогран-
многогранника, отметим, что понятия грани и вершины фигурируют в нем
совершенно симметрично; это означает, что многогранник, двойствен-
двойственный (см. выше, п. 2.4) топологически правильному многограннику,
также является топологически правильным. Отсюда следует, что
для каждого топологически правильного многогранника суще-
существует двойственный ему топологически правильный многогран-
многогранник. Из таблицы 2 видно, что октаэдр двойствен гексаэдру,
а додекаэдр — икосаэдру; тетраэдр же двойствен самому себе.

424 многоугольники и многогранники
4.2. Правильные многоугольники и многогранники. Простой
многоугольник называется правильным или метрически правильным,
если все его стороны равны между собой, и все углы равны между
собой (рис. 45). Общеизвестно, что для любого яЗ»3 существует
один и только один (с точностью до подобия) правильный я-уголь-
ник. Чтобы построить его, достаточно разделить какую-нибудь ок-
окружность на п равных частей и соединить последовательно точки
деления.
Многогранный угол называется правильным, если все его линей-
линейные углы равны между собой и все двугранные углы равны между
собой.
Простой многогранник называется правильным (точнее—метри-
(точнее—метрически правильным^, если все его грани являются правильными мно-
многоугольниками, а все многогранные углы —
равными правильными многогранными угла-
углами. Правильные многогранники называют
также Платоновыми многогранни-
многогранниками. Нетрудно показать, что все такие
многогранники являются выпуклыми.
Каждый правильный многогранник
является, очевидно, и топологически пра-
правильным. Поэтому не изоморфных между
собой правильных многогранников, в отли-
Рис 45 чие от многоугольников, может суще-
существовать не больше пяти. Покажем, что
их существует ровно пять (т. е. что в каждом классе топологически
правильных многогранников имеются метрически правильные много-
многогранники) и что любой правильный многогранник будет не только
изоморфен, но даже подобен одному из этих пяти.
Зная топологический тип правильного многогранника, мы можем
построить его схему—так, как сделали это в предыдущем пункте
(см. рис. 40, в) на примере октаэдра. Если в качестве граней на
этой схеме брать равные правильный многоугольники, то эта схема
представит собой развертку искомого многогранника. Таким
образом, развертка правильного многогранника определяется его
топологическим типом однозначно, если не учитывать лишь произ-
произвола при выборе длины ребра. Но при данной длине ребра развертка
в силу теоремы Коши определяет искомый многогранник однозначно
с точностью до положения в пространстве; поэтому, беря ребра
разной длины, мы будем получать подобные между собой многогран-
многогранники. Таким образом, если правильный многогранник данного топо-
топологического типа существует, то он с точностью до подобия един-
единствен.
Остается показать, что метрически правильный многогранник
действительно существует для каждого из пяти топологических

ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ
425
типов, описанных в п. 4.1. Проведем это доказательство снова на
примере октаэдра.
Возьмем четыре равносторонних треугольника и склеим их в пра-
правильный четырехгранный угол PABCD (очевидно, это возможно,
и притом лишь единственным образом,
с точностью до положения этого четы-
четырехгранного угла в пространстве, см.
рис. 46). Это будет один из многогранных
углов требуемого многогранника. Возьмем
теперь другой такой же четырехгран-
четырехгранный угол и приложим его к первому так,
чтобы вершина его совместилась с точкой
А, а две грани совпали с гранями РАВ
и PAD (рис. 47 и 48); это можно сделать
вследствие равенства граней и двугранных
углов. В результате мы получим две новые
грани ABQ и ADQ нашего многогранника.
Рассмотрим теперь четырехгранный угол
с вершиной В, имеющей «свободную» грань
CBQ. Три его плоских угла (лежащих в уже
построенных гранях многогранника) и два двугранных угла (ВР и ВА)
равны соответственно трем плоским и двум двугранным углам исход-
исходного четырехгранного угла PABCD; следовательно, весь четырехгранный
Рис. 46.
Рис. 48.
угол В равен четырехгранному углу PABCD, и мы можем еще один
экземпляр такого же четырехгранного угла приложить к построенной
уже части многогранника так, чтобы его вершина совпала с В,
а три грани — соответственно с треугольниками ВСР, ВРА и BAQ.

426
МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ
После этого мы тем же путем убедимся, что такой же четырехгранный
угол можно приложить вершиной к каждой из точек С, D и Q.
Отсюда непосредственно вытекает, что построенный нами многогран-
многогранник PABCDQ метрически правильный. Он называется правильным
¦октаэдром (рис. 49, в).
Совершенно аналогично может быть доказано существование
¦метрически правильных многогранников в каждом из остальных че-
четырех классов топологически правильных многогранников. Эти
д)
Рис. 49.
метрически правильные многогранники называются соответственно
правильным тетраэдром (рис. 49, а), правильным гексаэдром или
кубом (рис. 49, б), правильным додекаэдром (рис. 45, г), правиль-
правильным икосаэдром (рис. 49, д).
Таким образом, мы получили следующую теорему.
Теорема. Существуют пять различных (с точностью до по-
подобия) метрически правильных многогранников: правильный тет-
тетраэдр, правильный гексаэдр (куб), правильный октаэдр, правиль-
правильный додекаэдр и правильный икосаэдр.
Вместе с тем мы видим также, что для каждого метрически
правильного многогранника существует двойственный ему метрически
правильный многогранник.
Двойственные друг другу правильные многогранники могут быть
получены один из другого следующим простым способом. Пусть дан
правильный многогранник М; рассмотрим центры всех его граней
« примем их за вершины нового многогранника М'. Смежными

Рис. 50.

428
МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ
вершинами многогранника М' будем считать центры смежных граней
многогранника М, а вершинами одной грани М' будем считать центры
граней М, сходящиеся в одной вершине (легко видеть, что эти
центры будут лежать в одной плоскости). Полученный многогранник
М' также будет правильным; кроме того, граням многогранника М
соответствуют вершины многогранника М'', ребрам М—ребра М',
вершинам М — грани М' (причем инцидентным элементам многогран-
многогранника М отвечают инцидентные элементы многогранника М'), т. е.
многогранник М' двойствен многограннику М. Описанное
построение изображено на рис. 50, а — д для каждого из пяти пра-
правильных многогранников.
В указанной выше конструкции многогранники М и М' играют
не равноправную роль (один из них вписан в другой). Иногда удоб-
удобнее пользоваться следующей более симметричной конструкцией.
Построим сферу, касающуюся всех ребер данного правильного мно-
многогранника М (такая сфера обязательно существует и касается каж-
каждого ребра в его середине), проведем в середину каждого из ребер
радиус этой сферы и повернем каждое ребро (точнее — прямую, на
которой лежит ребро) вокруг этого радиуса на 90° (рис. 51). Тогда,
Рис. 51.
как нетрудно показать, ребра, принадлежавшие одной грани, после
поворота будут проходить через одну точку (рис. 51, а), а ребра,
проходившие через одну вершину, расположатся в одной плоскости
(рис. 51, б). Следовательно, ребра многогранника М после поворота
будут определять новый многогранник М' (тоже правильный!), двой-
двойственный М (рис. 52).
Два двойственных друг другу правильных многогранника, имею-
имеющих общие середины соответствующих ребер, взаимно перпендику-
перпендикулярных друг другу, называются взаимными друг другу. Понятие

ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ
429
взаимности, в отличие от понятия двойственности, учитывает не
только топологическую структуру двух многогранников, но также
и соотношение их размеров и их взаимное расположение.
а)
4.3. Равноугольно полуправильные многогранники. Для даль-
дальнейшего нам удобно ввести следующие вспомогательные понятия.
Назовем звездой вершины А данного многогранника совокупность
всех инцидентных ей граней, а также всех вершин и сторон этих
граней. Двойственно этому назовем звездой грани а данного много-
многогранника совокупность всех вершин грани а, а также всех граней
и ребер, инцидентных этим вершинам. По отношению к двум звездам
(двух вершин или двух граней) мы будем говорить об их изомор-
изоморфизме в том же смысле, в каком это было определено выше (см.
п. 2.1) для двух многогранников. Чтобы задать звезду, например,
некоторой вершины с точностью до изоморфизма, достаточно ука-
указать число s граней этой звезды, а также число я, вершин одной
из этих граней а,, число пг вершин смежной с ней грани а,, число ns
вершин смежной с а2 грани а, и т. д.
Топологически правильны^ многогранники можно охарактеризовать
как такие многогранники, у которых звезды всех вершин изоморфны
между собой, а звезды всех граней — между собой. Ограничившись
только первым из этих двух требований, мы придем к более широ-
широкому классу многогранников — к так называемым топологически
равноугольно полуправильным многогранникам. Итак, многогранник
называется топологически равноугольно полуправильным, если
звезды всех его вершин изоморфны между собой.
Поставим своей целью перечислить все такие многогранники,
ограничиваясь снова лишь многогранниками нулевого рода.
При этом мы будем интересоваться лишь многогранниками, не
являющимися топологически правильными, т. е. такими многогран-
многогранниками, к каждой вершине которых примыкает хотя бы две грани,
имеющие различное число вершин.

430 МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ
Для перечисления всех типов топологически равноугольных по-
лупрлвильных многогранников мы будем искать все возможные типы
звезд их вершин. Для каждого найденного типа звезды можно
(и притом однозначно, за исключением одного-единственного случая)
составить схему соответствующего многогранника—так же, как это
было сделано в п. 4.1 на примере октаэдра. Отсюда в силу теоремы
Штейница будет вытекать существование требуемого многогранника
и его единственность с точностью до изоморфизма. Лишь одному
типу звезды, который будет указан ниже, отвечают две различные
схемы, а поэтому и два неизоморфных между собой многогранника')
Мы не будем в каждом случае приводить рассуждений, связанных
с построением схемы многогранника, имеющего известный тип звезды
любой его вершины; читатель при желании сможет выполнить это
самостоятельно, руководствуясь в качестве образца построением
схемы октаэдра, приведенным в п. 4.1.
Введем нужные обозначения Пусть снова В, Г и Р— число вер-
вершин, граней и ребер многогранника, /", — число л,-угольных граней,
Гг—число я2-угольных граней и т. д. Пусть, далее, в каждой вер-
вершине многогранника сходятся s граней, в том числе s, /г,-уголь-
ных граней, s2 я2-угольных и т. д.
Покажем прежде всего, что в каждой вершине многогранника не
может сходиться слишком много граней, т. е. оценим число s сверху.
Так как в каждой вершине сходятся s ребер, то общее число
ребер, подсчитанное по всем вершинам многогранника, будет sB;
так как при этом каждое ребро считается дважды (ибо оно соеди-
соединяет две вершины), то
sB = 2P. A6)
Каждая грань многогранника имеет не менее трех ребер; так
как каждое ребро принадлежит двум граням, то ЗГ=?С2Р, или
в силу A6),
A7)
Из теоремы Эйлера вытекает (так как мы рассматриваем лишь
многогранники нулевого рода), что
В+Г>Р.
Пользуясь соотношениями A6) и A7), получим
^=^- В,
') Интересно отметить, что хотя теория полу правильных многогранников
насчитывает более двух тысяч лет, это нарушение единственности было заме-
замечено лишь недавно.

ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ 431
откуда после простых преобразований находим
Таким образом, s может принимать лишь значения 3, 4, 5.
Постараемся теперь определить все возможные типы звезд вер-
вершин данного многогранника, т. е. найти все возможные значения
чисел nk и sk.
Все л,-угольные грани содержат с одной стороны л,Г, плоских
углов, а с другой- стороны s^ плоских углов. Следовательно,
n.r, = s,B, или Г, = — В. Точно так же Г, = —^? и вообще
111 ¦ п, • nt
Г„ = ^В. A8)
Поэтому общее число граней многогранника будет
.. A9)
Возьмем теперь равенство Эйлера
Г=Р—В+2
и заменим Г и Р их выражениями из равенств A6) и A9):
или *
t+t+---=1^+l- B0)
Для решения поставленной задачи нам предстоит решить урав-
уравнение B0) относительно неизвестных В; s,, s2, ...; л,, л,,... в це-
целых положительных числах.
Рассмотрим раздельно различные возможные значения s.
I. s = 3, т. е. в каждой вершине многогранника сходится по
три грани. Эти грани могут быть либо двух, либо трех различных
типов. В первом случае мы можем положить sl = 2, s2=l, а во
втором будет s, = Sj = s, = 1. Рассмотрим отдельно каждый из этих
случаев.
1) s, = 2, s,= l.
Уравнение B0) принимает в этом случае вид

432 многоугольники и многогранники
Из уравнения B1) вытекает, что
Так как
1 _ 1 2
то —^ тг. а потому —;
п, d п.
1
6 '
т. е.
Далее, из геометрических соображений легко усмотреть, что
число л, должно быть четным. В самом деле, пусть AtAt.. .Аа_1 —
какая-нибудь л,-угольная грань (рис. 53). К вершине А1 должна
примыкать еще одна л,-угольная грань. Пусть, например, к ребру
AtA2 примыкает л,-угольная грань. Тогда в вершине Аг к ребру
АхАг должна примыкать л2-угольная грань и т. д. Продолжая таким
же образом, мы должны, дойдя до вершины Ап, получить л,-угольную
грань при ребре ^„^,; но это
возможно, очевидно, только если
число сторон грани AlAz...Arli чет-
четное.
Итак, л, может иметь лишь зна-
значения 4, 6, 8, 10. Рассмотрим
каждый из этих случаев.
а) л, = 4. Уравнение B1) прини-
принимает в этом случае вид В=2пг и
определяет целое положительное
значение В при любом целом
положительном лг = л. Из равенства
A8) находим: Г1 = п, Гх = 2. Таким
образом, мы пришли к многогран-
многограннику с л четырехугольными и двумя
л-угольными гранями и с 2л верши-
вершинами, в каждой из которых сходятся две четырехугольные и одна
л-угольная грань. Этот многогранник изоморфен п-угольнои призме (рис.
54, а). Итак, мы нашли целую бесконечную серию топологически
полуправильных многогранников; из этой серии следует только исклю-
исключить многогранник, отвечающий значению л = 4, так как он будет
топологически правильным.
1112
б) л. = 6. Уравнение B1) принимает вид -^--l = -^ + -б~. от-
1 б п2 z и
\1п
куда ?=о—— • Следовательно, в этом случае обязательно л,<6.
При л2 = 3 имеем В= 12. Мы приходим к многограннику с
12 вершинами, в каждой hi которых сходятся две шестиугольные
и одна треугольная грань (рис. 54. б).
Значению лг = 4 отвечает многогранник, изображенный на
рис. 54, в, а значению ля = 5 — многогранник, изображенный на
рис. 54, г.
Рис. 53.

правильные многоугольники и многогранники 433
1112
в) л = 8. Уравнение B1) дает -—| = —+ —, откуда ?=
4 /lj *. tS
=.__' , а потому л,<4, т. е. л2 = 3, ?=24. Соответствующий
многогранник изображен на рис. 54, д.
, .„ .. 1,112 о 20я2
г) я, = 10. Имеем: -+_ = -+-, откуда 8=^-^, т. е.
снова л2 = 3. Соответствующий многогранник изображен на рис. 54, е.
2) s, = s2 = s, = 1. Из таких же геометрических соображений,
какие были приведены в случае 1), вытекает, что теперь все числа
л,, л2, л, должны быль четными.
Уравнение B0) принимает в нашем случае вид
Так как в силу этого соотношения —| 1—>-к-, то хотя бы
/1| л2 /lg Л
одно из слагаемых в левой части, пусть, например, первое, должно
быть больше -^-:3 = -g-. Следовательно, п1 < 6, т. е. /г, = 4. Теперь
уравнение B2) можно переписать в виде
i+i-T+i- t i B3)
Как и выше, отсюда вытекает, что, например, — < -^ , т. е.
п2 о
л2 < 8. Следовательно, /г2 = 6 (потому что должно быть п1фп1).
Теперь уравнение B3) сводится к уравнению
1=1 + 2
п, 12^ В'
из которого следует, что пг < 12. Следовательно, имеются только
две возможности: пг = 8 (рис. 54, ж) и пг = 10 (рис. 54, з).
Случай s = 3 полностью исчерпан.
II. s=4. Этот случай также распадается на несколько.
1) В каждой вершине сходятся три грани одного типа и одна
грань другого: sY = 3, s2 = l.
Уравнение B0) принимает в этом случае вид
и из него, так как п2 5= 3, вытекает, что л, ^ 4.
1 2
При /г, = 3 уравнение сводится к уравнению — =—, которое
имеет бесконечно много целых решений: пг = п, В = 2п. Мы полу-
получаем еще одну бесконечную серию топологически полуправильных
многогранников, называемых антипризмами (рис. 54, и). При п = 3
антипризма превращается в топологически правильный многогранник —
октаэдр.
28 Энциклопедия, кн. 4

434
МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ

ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ
435
Рис. 54 (продолжение).
2&*

436
МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ
Значение же п1 = 4 определяет единственное значение п2=3;
этому решению уравнения B4) отвечают два неизоморфных тополо-
топологически полуправильных многогранника (рис. 54, к, л) с изоморф-
изоморфными звездами вершин.
2) 51 = 52==2. В этом случае имеем уравнение
2
я,
_2
"Б
из которого, как и выше, находим, что м1=3, м2 = 4 (рис. 54, м)
или м1=3, А22 = 5 (рис. 54, н).
3) sl = 2, s2 = ss = 1. В этом случае из геометрических сообра-
соображений заключаем, что число пЛ должно быть четным, после чего из
уравнения B0):
4
п.
находим, что пг = 41 /?2 = 3, /23 = 5 (рис. 54, о).
4) sJ = s2 = 5s = 54= 1. В этом случае уравнение B0) принимает
вид
1.1.1.1 , , 2 B5)
и |
/г.
/г,
п.
6 ~~20
.1 Ш V —
Если положить nl<n2< пг < м4, то л} ^3, п2 ^ 4, п8 ^ 5, л4 ^ 6
то противоречит урав-
уравнению B5). Таким обра-
образом, этот случай оказы-
оказывается в действительно-
действительности невозможным.
III. s = 5. Здесь, как
нетрудно убедиться,един-
убедиться,единственный возможный слу-
случай будет Sj = 4, s, = 1.
В этом случае уравне-
уравнение B0) принимает вид
Рис. 55. 4.13
Из этого уравнения находим, что /21 == 3, а м2 = 4 (рис. 54, п)
или А22 = 5 (рис. 54, р).
Итак, мы нашли все топологические типы топологически равно-
равноугольно полу правильных многогранников. Их оказалось всего 14, не
считая двух бесконечных серий (а также пяти типов топологически
правильных многогранников).
Многогранник называется (метрически) равноугольно полупра-
полуправильным или архимедовым, если все его грани — правильные много-

ПРАВИЛЬНЫЕ МН ОГОУГОЛЬНИКИ И МНОГОГРАННИКИ
437
угольники, а все многогранные углы равны между собой. Таким же
образом, как и в п. 4.2, можно показать, что каждый из найденных
нами типов топологически
равноугольно полупра-
полуправильных многогранников
может быть реализован
в виде архимедова много-
многогранника, и притом един-
единственного с точностью
до подобия.
Все эти архимедовы
многогранники были изоб-
изображены на рис. 54 в ка-
качестве представителей
соответствующих тополо-
б)
Рис. 56.
гических типов.
Отметим, что два архимедовых многогранника (рис. 54, мин)
могут быть получены как пересечения взаимных правильных
многогранников (см. также рис. 55 и 56); эти архимедовы много-
многогранники имеют грани двух типов — тех же, что и исходные правиль-
правильные многогранники.
Основные характеристики архимедовых многогранников (за исклю-
исключением правильных) с указанием их названий приведены в таблице.
Таблиц 3
№
пп
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
s
3
3
3
3
3
3
3
3
4
4
4
4
4
4
5
5
Si
2
2
2
2
2
2
1
1
3
3
3
2
2
2
4
4
1
1
1
1
1
1
1
1
1
1
1
2
2
1
1
1
«я
—
—
—
—
—
1
1
—
—
—
—
—-
1
—•
—
л,
4
'6
6
6
8
10
4
4
3
4
4
3
3
4
3
3
п
3
4
5
3
3
6
6
п
3
3
4
5
3
4
5
—
—
—
—
—
—
8
10
—
—
—
—
5
_
п
4
8
20
6
12
12
30
2/г
18
18
8
20
30
32
80
г,
2
4
6
12
8
20
8
20
2
8
8
6
12
20
6
12
—
—
—
—
—
—
6
12
—
—
—
——
—
12
_
—
в
2п
12
24
60
24
60
48
120
2/г
24
24
12
30
60
24
60
г
/г + 2
8
14
32
14
32
26
62
2л+2
26
26
14
32
62
38
92
р
3/г
18
36
'90
36
90
72
180
4/г
48
48
24
60
120
60
150
рис.
54,а
54,6
54,в
54,2
54,д
54,е
54, ж
54,з
54, и
54, ас
54, л
54, м
54,«
54,о
54, л
54, р
Правильная /г-угольная
призма с квадратными
боковыми гранями
(/г=3,5,6,7,...)
Усеченный тетраэдр
Усеченный октаэдр
Усеченный икосаэдр
Усеченный куб
Усеченный додекаэдр
Усеченный кубоктаэдр
Усеченный икосододекаэдр
/г-угольная антипризма
(л=4,5,6,...)
Ромбокубоктаэдр
Кубоктаэдр
Икосододекаэдр
Ромбоикосододекаэдр
Плосконосый куб
Плосконосый додекаэдр

438
МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ
6J
3J
Рис. 57.

ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ
439
Рис. 57 (продолжение).

440 многоугольники и многогранники
4.4. Равногранно полуправильные многогранники. Двойствен-
Двойственным понятию топологически равноугольно полуправильного много-
многогранника является понятие топологически'равногранно полу правильного
многогранника: многогранник называется топологически равногранно
полу правильным, если звезды всех его граней изоморфны между
собой.
Пересчитать все топологически равногранно полуправильные
многогранники можно тем же путем, каким были пересчитаны в
п. 4.3 все топологически равноугольно полуправильные многогранники.
Однако принцип двойственности (см. п. 2.4) позволяет, не повторяя
всех рассуждений предыдущего пункта, сразу воспользоваться их
результатами. Каждому топологически равноугольно полуправильному
многограннику соответствует двойственный ему топологически равно-
равногранно полуправильный многогранник и наоборот. Следовательно,
существует четырнадцать различных (не изоморфных между собой)
топологически равногранно полуправильных многогранников и еще
две бесконечные серии таких многогранников (не считая топологи-
топологически правильных). Основные характеристики этих типов многогран-
многогранников легко получить на основе соображений двойственности из
данных, приведенных в таблице 3 для архимедовых многогранников.
Многогранник называется (метрически) равногранно полупра-
полуправильным, если все его грани равны между собой, а все его много-
многогранные углы правильные. Как и ранее, в каждом из классов топо-
топологически равногранно полуправильных многогранников существуют
метрически равногранно полуправильные многогранники, но в отличие
от предыдущих случаев они, вообще говоря, не подобны между
собой, так как форма их граней не определяется топологическим
типом и требованием метрической полуправильности.
Все равногранно полуправильные многогранники изображены на
рис. 57, а—р в том же порядке, в котором на рис. 54, а—р были
изображены двойственные им архимедовы многогранники.
4.5. Правильные самопересекающиеся многогранники. Если,
говоря о правильных многоугольниках, отказываться от требования,
чтобы они были простыми, то мы получим, кроме уже рассмат-
рассматривавшихся ранее, также самопересекающиеся, или звездчатые пра-
правильные многоугольники. Пример такого многоугольника — правиль-
правильный звездчатый пятиугольник—изображен на рис. 58.
Нетрудно показать (мы не будем на этом останавливаться), что
стороны звездчатого правильного многоугольника М всегда являются
диагоналями некоторого простого правильного многоугольника Ж,,
стягивающими одно и то же число его сторон. Поэтому для по-
построения правильного л-угольника обыкновенно строят простой пра-
правильный л-угольник и проводят все его диагонали, стягивающие по
k сторон, где 1 < k < -=¦. Если число k взаимно просто с п, то при

правильный многоугольники и многогранники
441
Рис. 5ь.
этом получается некоторый правильный звездчатый /г-угольник; если
же k не взаимно просто с /г, то получается несколько отдельных
ломаных — так называемый распадающийся многоугольник (см. рис. 59,
где изображен случай п = 6, k = 2, в котором получаются два тре-
треугольника). Таким образом, для каждого п существует столько раз-
различных (не подобных между собой) правиль-
правильных звездчатых /г-угольников, сколько имеется
целых чисел, заключенных между 1 и -=¦ ,
взаимно простых с л1): правильный звездча-
звездчатый пятиугольник существует только один
(рис. 58), правильных звездачатых семиуголь-
семиугольников— два (рис. 60 а, б), правильных звездча-
звездчатых треугольников, четырехугольников и шести-
шестиугольников не существует вовсе.
Правильные звездчатые многоугольники
можно получить и иначе. Прямые, на которых
лежат стороны любого такого /г-угольника М,
делят всю плоскость на некоторое число частей, одна из которых,
называемая ядром данного /г-угольника М, представляет собой про-
простой правильный /г-угольник Ма. Поэтому любой звездчатый правиль-
правильный /г-угольник М может быть получен из простого правильного
/г-угольника /Ио продолжением каждой его стороны до пересечения
со сторонами, отделяемыми от нее одним и тем же числом k—1
сторон ( 1 < k < ^ ) ; при этом, как и вы-
выше, если k не взаимно просто с п, мы
получаем распадающийся многоугольник.
Перейдем теперь к многогранникам. Если
в определении правильного многогранника
не требовать, чтобы он был простым, мы
получим, кроме уже рассмотренных в п. 4.2
Платоновых многогранников, также самопере-
самопересекающиеся, или звездчатые правильные
многогранники, называемые еще многогран-
многогранниками Пуансо. Укажем' в общих чертах, как можно найти все такие
многогранники 2).
Рис. 59.
•) Таким образом, число различных правильных звездчатых п-уголь-
ников может быть записано в виде -^-ф(п), где ф(п) есть употребляемая
в теории чисел функция Эйлера (см. в кн. I ЭЭМ статью «Элементы
теории чисел», стр. 280—282).
2) С более подробным изложением этого вопроса читатель может озна-
ознакомиться по книге Д. О. Шк л яре кого, Н. Н. Ченцова, И. М.
Яглома[5], указанной в конце статьи.

442
многоугольники и многогранники
Плоскости граней произвольного звездчатого правильного много-
многогранника М делят все пространство на некоторое число частей, из
которых одна, называемая ядром многогранника М, является простым
правильным многогранником Мв. Многогранник Мо имеет столько же
граней, сколько М; поэтому правильный звездчатый многогранник на-
называют так же, как его ядро (тетраэдр, додекаэдр и т. п.).
/\
Рис. 60.
Возможны два случая: 1) смежными в многограннике Мо являются
те же грани, которые смежны в /И; в этом случае каждой грани а
многогранника М (которая обязательно должна быть звездчатой) отве-
отвечает грань а0 многогранника Мо, являющаяся ядром грани а; много-
многогранник М получается в этом случае из своего ядра Ма путем
продолжения его ребер; 2) смежные грани многогранника М не
являются смежными в Мо; в этом случае многогранник М полу-
получается из Ма путем п род о л ж ен и я его граней.
Выясним теперь, какие звездчатые многогранники могут быть
получены указанными способами из известных нам простых правиль-
правильных многогранников.
1°. Тетраэдр. Все грани тетраэдра смежны между собой, по-
поэтому продолжение граней тетраэдра не может вести к цели. Звездчатых
треугольников не существует, поэтому то же самое можно сказать о
продолжении ребер тетраэдра. Поэтому звездчатых тетраэдров не
существует.
2°. Октаэдр. Так как грани правильного октаэдра — треуголь-
треугольники, то продолжение ребер октаэдра не ведет к цели. Продолжение же
граней правильного октаэдра (каждая грань продолжается до пересе-
пересечения с тремя не смежными и не параллельными ей гранями, см.
рис. 61) дает распадающийся многогранник — два пра-
правильных тетраэдра. Следовательно, звездчатых октаэдров также не
существует.
3°. Гексаэдр. Все несмежные ребра и грани правильного
гексаэдра (куба) параллельны между собой. Поэтому и звездчатых
гексаэдров не существует.

ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ
443
4°. Додекаэдр. Продолжение ребер правильного додекаэдра,
т. е. замена каждой его грани а звездчатым пятиугольником с ядром
а (рис. 62, а), приводит к многограннику, называемому малым
звездчатым додекаэдром (рис. 63, а); он имеет 12 звездчатых пяти-
пятиугольных граней, 30 ребер и 12 вершин (выпуклых пятигранных углов).
Рис. 61.
При продолжении граней правильного додекаэдра (каждая грань
продолжается до пересечения с пятью не смежными и не парал-
параллельными ей гранями) возникают две возможности. Рассматривая
в качестве граней нового многогранника получающиеся при этом
простые пятиугольники (рис. 62,6), мы приходим к большому
додекаэдру (рис. 63, б); он имеет 12 выпуклых пятиугольных граней,
30 ребер и 12 вершин (звездчатых пятигранных углов). Рассмат-
Рассматривая же в качестве граней соответствующие звездчатые пяти-
пятиугольники (рис. 62, в), мы получим большой звездчатый додекаэдр
(рис. 63,в); он имеет 12 звездчатых пятиугольных граней, 30 ребер
и 20 вершин (трехгранных углов).
Таким образом мы нашли три типа правильных звездчатых до-
додекаэдров.
5°. Икосаэдр. Так как гранями правильного икосаэдра явля-
являются треугольники, то продолжение ребер икосаэдра не дает нового
многогранника. При продолжении же граней правильного икосаэдра
имеется лишь один случай, приводящий к нераспадающемуся много-
многограннику— случай, когда каждая грань продолжается до пересечения
с тремя гранями, смежными параллельной ей грани (рис. 62, г).

444
МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ
Рис. 62.

ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ
445
Получаемый при этом многогранник называется большим икосаэдром
(рис. 63, г); он имеет 20 треугольных граней, 30 ребер и 12 вершин
{звездчатых пятигранных углов).
6)
Рис. 64.
Рис. 63.
г)
Рис. 65.
Итак, существует всего четыре различных (с точностью до подо-
подобия) звездчатых правильных многогранников. Нетрудно убедиться
в том, что эти многогранники попарно двойственны друг другу:

146 МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ
малый звездчатый додекаэдр двойствен большому додекаэдру, а
большой звездчатый додекаэдр — большому икосаэдру.
Можно рассматривать также аналогично архимедовым многогран-
многогранникам (см. п. 4.3) равноугольно полуправильиые самопересекающиеся
многогранники. Простейшими примерами таких многогранников яв-
являются многогранники, изображенные на рис. 64 и 65 и получаю-
получающиеся в результате пересечения взаимных правильных звездчатых
многогранников. Первый из них—додекаэдрододекаэдр — имеет 24
пятиугольных грани: 12 простых (как у большого додекаэдра) и 12
звездчатых (как у малого звездного додекаэдра). Второй — додека-
эдроикосаэдр — имеет 32 грани: 20 треугольников (как у большого
додекаэдра) и 12 звездчатых пятиугольников (как у большого звезд-
звездного додекаэдра). Всего в настоящее время известен 51 звездчатый
равноугольно полуправильный многогранник, но неизвестно, исчерпы-
исчерпываются ли ими все такие многогранники.
ЛИТЕРАТУРА
[1] А. Д. Александров, Выпуклые многогранники, М.—Л., Гостех-
издат, 1950.
Серьезная, но доступная монография, в значительной степени осно-
основанная на исследованиях автора. Весьма широко освещает круг вопро-
вопросов, связанный с темой настоящей статьи.
[2] Л. А. Люстерник, Выпуклые фигуры и многогранники, М., Гос-
техиздат, 1956.
Научно-популярная книга, имеющая много точек соприкосновения
с темой настоящей статьи.
[3] Д. И. П е р еп е л к и и. Курс элементарной геометрии, ч. 2, М.—Л.,
Гостехиздат, 1949.
Обстоятельный учебник стереометрии. К теме настоящей статьи
примыкает гл. XIX «Теорема Эйлера. Правильные многогранники и
их обобщения».
[4] Ж- А дама р. Элементарная геометрия, ч. 2, перев. с франц., М.,
Учпедгиз, 1958.
Весьма подробный учебник стереометрии. К теме настоящей статьи
примыкает гл. III Дополнений ко второй части «Теорема Эйлера.
Правильные многогранники», Прибавление Е к книге «О правильных
многогранниках и группах движений» и Прибавление F «Теорема Коши
о правильных многогранниках».
[5] Д. О. Шклярский, Н. Н. Чеицов, И. М. Я г л о м, Избран-
Избранные задачи и теоремы элементарной математики, ч. 3, М., Гостехиздат,
1954.
Сборник задач повышенной трудности по стереометрии, сопровож-
сопровождаемых подробными решениями. Второй из четырех циклов задач носит
название «Теория многогранников» и содержит довольно обширный
материал (включая сюда оригинальное доказательство теоремы Коши).
Третий цикл задач называется «Правильные многогранники»; здесь
содержится, в частности, полная теория звездчатых правильных много-
многогранников.

ЛИТЕРАТУРА 447
[6] Цикл статей по геометрии в вып. II журнала Успехи математических
наук, 1936.
К теме настоящей статьи относятся работы: Г. Минковский,
Общие теоремы о выпуклых многогранниках, стр. 55—71 и М. Д е н и,
О жесткости выпуклых многогранников, стр. 72—79.
[7] Цикл статей по наглядной геометрии в вып. X журнала Успехи мате-
математических наук, 1944.
К теме настоящей статьи относятся работы: О. К о ш и, Исследование
о многогранниках, стр. 5—17 и А. Кэлн, О четырех новых правиль-
правильных телах Пуансо, стр. 18—21.
[8] В. Г. А ш к и н у з е, О числе полуправильных многогранников, сб.
«Математическое просвещение», вып. 1, 1957, стр. 107—118; А. Г.
Дорфман, Ромбокубооктаэдры и взаимные им многогранники, там
же, вып. 6, 1961, стр. 207—208.
Эти статьи посвящены вопросу о числе типов полуправильных
многогранников.
[9] Н. S. M. Coxeter, Regular polytops, London, 1948.
Обстоятельная монография видного канадского геометра, содержа-
содержащая исключительно большой материал по теории правильных многогран-
многогранников и их обобщений.

ОКРУЖНОСТИ
СОДЕРЖАНИЕ
Введение 449
А. Окружность как совокупность точек
§ 1. Обобщение понятия окружности . 450
1.1. Направленные отрезки и углы 450
1.2. Разные определения окружности; касание окружностей . . 451
§ 2. Радикальная ось и радикальный центр 154
2.1. Степень точки относительно окружности 454
2.2. Радикальная ось двух окружностей 455
2.3. Радикальный центр трех окружностей 459
§ 3. Пучки и связки окружностей 461
3.1. Пучок окружностей 461
3.2. Связка окружностей .... 466
4 4. Инверсия .... 468
4.1. Определение инверсии ... . 468
4.2. Свойства инверсии . . 471
4.3. Теорема Паскаля . ..... 475
<§ 5. Точечная геометрия окружностей 476
5.1 Круговая плоскость 476
5.2. Круговые преобразования 478
5 3. Понятие о круговой геометрии ...... 478
Б. Окружность как совокупность прямых
§ 6. Направленные окружности 479
6.1. Аналогия между свойствами точек и прямых 479
6.2. Дальнейшее расширение понятия окружности 480
6.3. Касательное расстояние двух окружностей 482
§ 7. Центр подобия и ось подобия 485
7.1. Степень прямой относителоно окружности 485
7.2. Центр подобия двух окружностей 487
7.3. Ось подобия трех окружностей 489
§ 8 Ряды и сети окружностей 490
8.1. Ряд окружностей 490
8.2. Сеть окружностей 492
§ 9 Осевая инверсия 495
9 1. Определение осевой инверсии 495
9.2. Вырожденная инверсия и особая инверсия . . 496
9.3. Свойства осевой инверсии " 498
5.4. Теорема Брианшона 502

ВВЕДЕНИЕ 449
§ 10 Осевая геометрия окружностей 504
10.1. Осевые круговые преобразования 504
10.2. Понятие об осевой круговой геометрии 507
В. Окружность как совокупность линейных элементов
§ 11. Новый взгляд на окружность 508
11.1. Плоскость как множество линейных элементов 508
11.2. Новое определение окружности 509
§ 12. Касательная геометрия окружностей , . . 510
12.1. Касательные круговые преобразования 510
12.2. Задача Аполлония 513
12.3. Понятие о касательной геометрии окружностей 515
Литература 516
ВВЕДЕНИЕ
Учение об окружности занимает в элементарной геометрии весьма
значительное место. Еще со времен Евклида элементарная планимет-
планиметрия рассматривалась как наука, изучающая прямые линии, окружности
и некоторые простейшие фигуры (вроде треугольника или сектора
круга), ограниченные частями прямых и окружностей. Таким образом,
окружность является единственной кривой, рассматриваемой
в курсе элементарной геометрии, что оправдывает большое внимание,
уделяемое изучению свойств этой линии. Значительное число раз-
разнообразных свойств окружности было известно еще древнегреческим
математикам; но особенно велики заслуги ученых XIX века в изу-
изучении этих свойств. В XIX веке был собран богатейший фактиче-
фактический материал, состоящий из многочисленных теорем частного ха-
характера, иногда исключительно красивых и совершенно неожиданных,
и, что значительно важнее, в этом же веке были указаны некоторые
основные общие принципы так называемой «геометрии окружностей».
Цель настоящей статьи и состоит в том, чтобы осветить эти прин-
принципиальные основы теории окружностей, заложенные в первую оче-
очередь немецким математиком Августом Фердинандом Мебиусом
A790—1868) (материал раздела А настоящей статьи), французским
математиком Эдмондом Лагерром A834—1886) (материал разде-
раздела Б) и норвежским математиком Софусом Ли A842—1898) (материал
раздела В). Что же касается разнообразных специальных свойств
окружностей, то на них мы почти не остановимся в нашем, по не-
необходимости довольно сжатом, изложении.
Заметим еще, что все содержание настоящей статьи может быть
без труда перенесено и на геометрию в пространстве; лишь огра-
ограниченность объема заставляет нас отказаться от изложения геомет-
геометрии сфер, не содержащей, впрочем, почти никаких принципиально
новых моментов по сравнению с геометрией окружностей.
29 Энциклопедия, кн. 4

450 окружности
А. ОКРУЖНОСТЬ КАК СОВОКУПНОСТЬ ТОЧЕК
§ 1. Обобщение понятия окружности
1.1. Направленные отрезки и углы. В этой статье значитель-
значительную роль будут играть направленные отрезки и углы. Если на
прямой задать какое-либо направление (оно указывается обычно стрел-
стрелкой), то каждому отрезку этой прямой, кроме абсолютной величины
(длины), можно будет приписать также определенный знак: так на
рис. \,а отрезок АВ положителен, а отрезок CD отрицателей.
В дальнейшем направленные отрезки мы будем обозначать черточкой,
. поставленной над обозначением
i I, > отрезка; так АВ будет обозна-
обозначать обыкновенный (ненаправ-
(ненаправленный) отрезок, а АВ — напра-
направленный отрезок, т. е. отре-
отрезок, взятый с определенным
знаком; таким образом, отрезки
АВ и ВА не отличаются, но
АВ = — ВА. При этом следует
иметь в виду, что, говоря о
произведении (или отношении)
двух отрезков одной прямой,
мы можем считать эти отрезки
направленными, не выбирая за-
рнс> j ранее никакого направления
на самой прямой: если АВ
и CD— два отрезка одной прямой, то независимо от выбора
направления на прямой произведение AB-CD (и отношение —)
V CD)
будет положительным, если направления отрезков АВ и CD (от А
к В и от С к D) совпадают, и отрицательным, если эти направления
различны (как на рис. l.eI).
Аналогично этому, если выбрать какое-либо направление враще-
вращения (определяемое стрелкой, поставленной на некоторой окружности),
то углу между прямыми (ненаправленными!), кроме абсолютной вели-
величины, можно будет приписать также и знак: угол между а и b счи-
считается положительным, если направление вращения от прямой а
к прямой b совпадает с выбранным направлением, и отрицательным
в противном случае (так иа рис. 1,6 угол между прямыми а и b
положителен, а угол между cad отрицателен). В дальнейшем обык-
обыкновенный угол мы будем обозначать знаком ^_, а направленный
угол — знаком -§С; таким образом углы /_(а, Ь) и /_(р, а) не отли-
•) Ср. стр. 55, 56 и 59.

ОБОБЩЕНИЕ ПОНЯТИЯ ОКРУЖНОСТИ 451
чаются, но §; (a, b) = — <?(b, а). При этом направленный угол между
двумя прямыми, так же как и обыкновенный угол, не опоеделяется
однозначно; так на рис. 2 можно считать, что %С {а, Ь) = /_ АОВ
или что $; (а, Ь) = — /_АОС. Нетрудно видеть, что направленный
угол между двумя прямыми определяется с точностью до произволь-
произвольного кратного угла л; так в обозначениях рис. 2 —/ АОС-**
= /_АОВ—л, а указанный стрелкой больший л угол АОС равен
^_АОВ-\-л. Обычно под направленным углом между прямыми а и Ь
понимают наименьший по абсолютной величине угол
между этими прямыми; в случае, если прямые а и Ь перпендикулярны,
считают, что <? (а, Ь) = + -?¦. В дальнейшем у нас символ ¦§; (а, Ь)
будет всюду иметь именно это зна-
значение; в частности, равенство
§; (а, Ь) = ¦§; (с, d) будет означать,
что наименьшие по абсолютной вели-
величине из направленных углов между ¦
а и Ь и между cad совпадают по
абсолютной величине и по знаку.
Заметим, что, говоря об отноше-
отношении или произведении двух углов,
мы также можем считать эти углы
направленными, не задавая заранее
никакого направления вращения: на- ^ис- ^-
пример, отношение -§С(а, b):<?.(c,d)
будет положительно, если направления вращений на наименьший по
абсолютной величине угол, переводящих а в b а с в d, совпадают,
и отрицательно в противном случае. В частности, так как утвержде-
утверждение о равенстве двух углов означает, что отношение этих углов
равно единице, то, говоря о равенстве или неравенстве двух направ-
направленных углов, мы не обязаны задавать заранее какое-то определенное
направление вращения.
1.2. Разные определения окружности; касание окружностей.
Основным предметом изучения в этой статье будут являться окруж-
окружности. Окружность—это множество всех точек плоскости, уда-
удаленных на одно и то же расстояние г от фиксированной точки О;
точка О называется центром окружности, а отрезок г — ее padiiycoM.
В предельном случае можно также считать, что расстояние г — ра-
радиус окружности — равно нулю; в этом случае «окружность» будет
представлять собой одну точку О. В дальнейшем нам часто будет
удобно рассматривать также и точки как окружности, принимая их за
«окружности нулевого радиуса»; в таком случае обыкновенные окруж-
окружности мы будем называть «собственными окружностями». Точки
(«окружности нулевого радиуса») и «собственные окружности» вместе
мы будем называть «окружностями конечного радиуса».
29'

452
ОКРУЖНОСТИ
Данное выше определение окружности не является единственно
возможным. Весьма часто оказывается полезным определение окруж-
окружности как множества всех таких точек М, из которых данный
отрезок АВ виден под постоянным (направленным!) углом а, или,
Рис. 3-
короче, таких точек М, что §; (MA, ЛШ) = а(рис. 3, а). При задан-
заданном отрезке АВ радиус рассматриваемой окружности, естественно,
зависит от величины угла а (из тригонометрии известно, что он
A R \
равен абсолютной величине, отношения |; этот радиус будет
2 sin a) r J }
тем больше, чем меньше (по абсолютной величине) угол а. Если
принять а=0, то мы придем к прямой линии (рис. 3, б), которая,
таким образом, тоже подходит под наше определение и которую
О
6)
В)
Рис 4.
поэтому можно считать предельным случаем окружности. В даль-
дальнейшем нам часто будет удобно причислять прямые линии к числу
окружностей. Ясно, что для таких «окружностей» понятие центра
и радиуса теряет смысл. Мы будем называть прямые «окружностями
бесконечного радиуса»; совокупность обыкновенных окружностей и пря-
прямых— «окружностями ненулевого радиуса»; наконец, под словом просто
«окружности» мы будем часто понимать как обыкновенные окружности,
так и точки («окружности нулевого радиуса») и прямые («окружно-
(«окружности бесконечного радиуса»). Целесообразность этих довольно гро-
громоздких соглашений выяснится в ходе дальнейшего изложения.

ОБОБЩЕНИЕ ПОНЯТИЯ ОКРУЖНОСТИ
453
Понятие касания двух собственных окружностей или собственной
окружности и прямой имеет совершенно ясный смысл (рис. 4, а, б).
В дальнейшем нам будет удобно называть «окружность нулевого
радиуса» 50 и «окружность ненулевого радиуса» St касающимися,
если точка So лежит на окружности или прямой 5, (рис. 4, в, г);
наконец, две «окружности бесконечного радиуса» So и 5, мы будем
называть касающимися, если
прямые So и 5, параллельны
(рис. 4, д). Далее под угло\' ^
между двумя окружностями 0/
ненулевого радиуса So и 5,,
пересекающимися в точке М,
мы будем называть угол между
касательными к So и Sl в этой
точке (рис. 5, а, б; под «каса-
«касательной к прямой» здесь пони- Рис. 5.
мается сама эта прямая). При
этом рассматриваемый угол можно считать ненаправленным или напра-
направленным; заметим только, что направленные углы между 50и 5, в двух
точках пересечения М и N имеют разные знаки (см. тот же рис. 5, о, б).
Особую роль у нас будут играть перпендикулярные (или орто-
ортогональные) окружности, т. е. окружности, образующие в точке пере-
пересечения прямой угол; очевидно, что радиус каждой из двух таких
Рис. Ь.
собственных окружностей, проведенный в точку пересечения, касается
второй окружности (рис. 6,а) и что прямая Su, перпендикулярная
собственной окружности Sv совпадает с ее диаметром (рис. 6, б).
Нам будет удобно еще считать, что «окружность нулевого радиу-
радиуса» Se перпендикулярна «окружности ненулевого радиуса» Sv если
точка So лежит на окружности или прямой St (рис. 6, в). Таким
образом, утверждения «окружность нулевого радиуса So касается
окружности ненулевого радиуса 5,» и «50 перпендикулярна 5,» имеют
одинаковый смысл. Это обстоятельство не должно нас удивлять:
ведь за «касательную к окружности нулевого радиуса 50» можно

454
ОКРУЖНОСТИ
принять любую прямую, проходящую через точку So; поэтому
если точка 50 лежит на окружности или прямой Sv то углу между St
и Sl можно приписать любое значение, в частности можно считать,
что этот угол равен 0 (т. е. что SB и Sl касаются) или что он равен ~
(т. е. что St и 5, перпендикулярны).
§ 2. Радикальная ось и радикальный центр
2.1. Степень точки относительно окружности. Вспомним сле-
следующую теорему, хорошо известную из школьного курса гео-
геометрии:
Если через точку М провести несколько прямых, пересекающих
(собственную) окружность S, то произведение расстояний от
точки М до точек пересечения каждой из этих прямых с окруж-
окружностью (произведение МА • MB на рис. 7, а, б) будет одним и тем
же для всех этих прямых.
Рис. 7.
Эта теорема справедлива как для того случая, когда точка М
лежит вне окружности 5 (рис. 7, а; в этом случае произведение
MA-MB равно квадрату длины касательной, проведенной к окруж-
окружности 5 из точки М), так и для того случая, когда М лежит внутри 5
(рис. 7,6; в этом случае MA-MB равно квадрату половины хорды,
проведенной через точку М перпендикулярно диаметру ОМ окруж-
окружности). Если точка М лежит на окружности 5 (рис. 7, в), то один
из двух отрезков MA, MB равен нулю; таким образом, и в этом
случае произведение МА-МВ не зависит от выбора прямой — оно
равно нулю для всякой прямой. Наконец, если под 5 понимать «окруж-
«окружность нулевого радиуса», т. е. точку (рис. 7, г), то «пересекающая 5»

РАДИКАЛЬНАЯ ОСЬ И РАДИКАЛЬНЫЙ ЦЕНТР 455
прямая, проходящая через не совпадающую с 5 точку М, будет только
одна (и для этой прямой обе точки А и В придется отождествить
с точкой S), так что можно считать, что и в этом предельном слу-
случае наша теорема сохраняет силу.
Заметим еще, что теорема сохраняет силу и в том случае, если
говорить о произведении направленных отрезков МА ¦ ЛШ(см. § 1):
если точка М лежит вне S, то произведение МА • MB всегда будет
положительным, а в противном случае — всегда отрицательным. Таким
образом, и абсолютная величина, и знак произведения МА ¦ MB зави-
зависят лишь от положения точки М и окружности (конечного радиуса) 5,
но не от выбора проходящей через М прямой. Это произведение назы-
называется степенью точки М относительно окружности S. Из
рис. 7, а—г нетрудно вывести, что степень точки М относи-
относительно окружности S конечного радиуса г во всех случаях равна
d* — г", где d—расстояние ОМ от точки М до центра О окруж-
окружности. Для того чтобы это доказать, достаточно принять за пря-
прямую МАВ проходящую через центр окружности S прямую МА0В0.
2.2. Радикальная ось двух окружностей. С введением понятия
степени точки относительно окружности возникает вопрос об отыска-
отыскании целого ряда множеств точек, например множества всех точек,
имеющих относительно данной окружности постоянную степень (это
будет окружность, концентрическая с данной). Из таких множеств
точек особую роль в геометрии играет множество всех точек,
имеющих равные степени относительно двух окружностей S, и
Sz. Это множество точек называется радикальной осью окружностей
5, и St.
Докажем, что радикальной осью двух неконцентрических окруж-
окружностей S, и St конечного радиуса является прямая линия о,
перпендикулярная линии центров этих окружностей; радикальной
оси двух концентрических (не совпадающих) окружностей вовсе
не существует.
Действительно, если точка М принадлежит радикальной оси двух
окружностей 5, и St с центрами О, и О, и радиусами г, и тх (рис. 8),
то в силу сказанного выше должно быть
ОхМг-г\=ОгМг—г\. (•)
Прежде всего, ясно, что это равенство невозможно, если т^фтх
и точки О1 и О2 совпадают,—отсюда вытекает наше утверждение
касающееся концентрических окружностей.
Предположим теперь, что точки О, и О, не совпадают; пусть,
например, О1Ог~1ф0. Покажем, что на прямой Ofit имеется ровно
одна точка Р, принадлежащая радикальной оси. В самом деле,
пусть Р—произвольная точка прямой OtO2 и х — ее расстояние
от О,, которое мы будем считать положительным, если Р и О

456
ОКРУЖНОСТИ
расположены по одну сторону от точки О,, и отрицательным в против-
противном случае. Тогда О1Р=\х\, 02Р=\х— /|, и потому соотношение (*)
принимает вид
хг-г\=(х—W-rl
Это соотношение представляет собой линейное уравнение относи-
относительно неизвестного xv имеющее единственный корень:
х —
2/
Заметим теперь, что точка М в том и только в том случае
принадлежит радикальной оси, если ее проекция Р на прямую 0,0,
о
Рис. 8.
также принадлежит радикальной оси. Это вытекает из очевидного
соотношения
ОХМ' — ОгМ* = О,Р2 — O2/J2

РАДИКАЛЬНАЯ ОСЬ И РАДИКАЛЬНЫЙ ЦЕНТР
457
(см. рис. 8) и соотношения (*). Из этого и следует, что радикаль
ная ось (двух неконцентрических окружностей) представляет собой
прямую, перпендикулярную к линии центров О^.
Можно предложить также следующий векторный» вывод теоремы
о радикальной оси Соотношение (*) можно переписать в виде
где х=О,М 1 — 0fir Раскрывая скобки в этом соотношении, получаем
2xl = t* + r\ — г\
В силу определения скалярного произведения') это соотношение озна
чает что
'* + ''
откуда и вытекает наше утверждение.
Различные случаи расположения радикальной оси двух окружно
стей изображены на рис. В, а — г; анализ этих случаев легко провести
основываясь на формуле (#). Здесь мы отметим только, что если
окружности St и St пересекаются,
то точки их пересечения, очевидно,
принадлежат радикальной оси (ибо
эти точки имеют относительно
обеих окружностей одинаковую сте-
степень, равную нулю) и, следова
тельно, радикальная ось пересекаю
щихся окружностей совпадает с пря
мой, на которой расположена их об
щая хорда (рис. 8, б); если окруж
ности 5, и St касаются, то по ана-
аналогичной причине радикальная ось
проходит через точку касания и,
следовательно, совпадает с общей
касательной (рис. 8, в).
Мы знаем, что если точка М
лежит вне окружности 5, то ее
степень относительно 5 равна квадрату касательной, проведенной
из М к 5. Отсюда вытекает, что радикальная ось двух непересека-
непересекающихся окружностей и часть радикальной оси пересекающихся
окружностей, внешняя по отношению к этим окружностям,
совпадает с множеством всех таких точек М что касательные
проведенные из М к обеим окружностям, равны (рис. 9). Эта
утверждение можно сформулировать еще и по-другому. Пусть окруж-
окружность 2 имеет центр в точке М радикальной оси двух окружностей
Рис. 9.
') См. стр 328.

458
окружности
Sj и 5, и радиус ее равен общей длине касательных MAt и МАг,
проведенных из М к 5, и к S2 (рис. 9). Так как радиус этой окруж-
окружности, проведенный в точку А, (соответственно Аг) пересечения ее
с 5, (с St), является касательной к St (к Sz) и, следовательно, пер-
перпендикулярен радиусу окружности 5, (окружности St), проведенному в
ту же точку, то окружность 2 будет перпендикулярна окруж-
окружностям 5, и St. Обратно, если М есть центр окружности 2, перпен-
перпендикулярной к5, и S2, то касательные, проведенные из М к Sl и к Sf,
будут равны. Таким образом, радикальная ось непересекающихся
окружностей и часть радикальной оси пересекающихся окружно-
окружностей, внешняя по отношению к этим окружностям, совпадают
с множеством центров окружностей, перпендикулярных к двум
данным.
Рис. 10.
Заметим еще, что часть радикальной оси двух пересекающихся
окружностей, внутреннюю по отношению к этим окружностям, также
можно определить геометрически независимо от понятия степени
точки относительно окружности. Условимся говорить, что окруж-
окружность S делит окружность Е пополам (или что 2 делится ок-
окружностью S пополам), если 5 пересекает окружность 2 в ее
диаметрально противоположных точках (рис. Ю,а). Из рис. 10,а видно,
что центр М окружности 2, делящейся окружностью 5 пополам,
расположен внутри 5, а ее радиус равен половине хорды окружности
5, проведенной через точку М перпендикулярно диаметру ОМ этой
окружности, т. е. что квадрат радиуса окружности 2 по абсолютной
величине равен степени точки М относительно окружности 5 (см.
стр. 454). Отсюда вытекает, что часть радикальной оси двух пере-
пересекающихся окружностей St и St, внутренняя по отношению к
этим окружностям, совпадает с множеством центров окруж-

РАДИКАЛЬНАЯ ОСЬ И РАДИКАЛЬНЫЙ ЦЕНТР
459
ностей, делящихся пополам и окружностью 5,, и окружностью St
(рис. 10,6).
2.3. Радикальный центр трех окружностей. Рассмотрим теперь
три окружности .Sp 52 и 53, никакие две из которых не концентричны.
Рис. 11.
Если центры О,, О, и О, этих окружностей не лежат на одной пря-
прямой (рис. 11), то радикальные оси о12 и о,, окружностей Sr и St, St и 5,
не параллельны (ибо эти прямые перпендикулярны соответственно пря-
прямым ОАОг и OtOa); пусть О — точка пересечения этих радикальных осей.

460
ОКРУЖНОСТИ
Так как точка О принадлежит радикальной оси ом, то она имеет одина-
одинаковые степени относительно 5, и St; так как точка О принадлежит
также оси о1г, то она имеет одинаковые степени относительно 5j
и 53. Но отсюда вытекает, что О имеет одинаковые степени отно-
относительно 5г и St, т. е. что О принадлежит также радикальной оси
°гг окружностей St и 5,. Итак, мы видим, что попарные ради-
радикальные оси трех окружностей конечного радиуса Sv St и Sl7
центры которых не лежат на одной прямой, пересекаются
в одной точке О. Эта точка называется радикальным центром
трех окружностей. Поскольку радикальный центр имеет одну и ту
же степень относительно каждой из окружностей A1,, S2, St, то либо
он лежит внутри всех трех
окружностей, либо принад-
принадлежит каждой из них, либо,
наконец, расположен вне всех
трех окружностей.
Из теоремы о радикаль-
радикальном центре вытекает, в ча-
частности, простое построение
радикальной оси о двух не-
непересекающихся окружно-
окружностях 5, и 5, (радикальная
ось пересекающихся окруж-
окружностей совпадает с прямой,
на которой лежит их общая
хирда). Проведем произволь-
произвольную окружность S, центр ко-
которой не лежит на линии
центров окружностей St и 5,
и которая пересекает как 5,,
таки5а (рис. 12). Радикальная ось о, окружностей 5и 5, совпадает
с их общей хордой; радикальная ось о, окружностей S и St также
совпадает с общей хордой этих окружностей. Точка О пересечения
прямых о, и о, является радикальным центром окружностей Sv S2
и 5 и, следовательно, принадлежит также искомой радикальной оси
окружностей St и St. Таким образом, ось о совпадает с перпенди-
перпендикуляром, опущенным из точки О на линию центров (можно также
с помощью иной окружности S' найти еще одну точку О' искомой
радикальной оси).
Очевидно, ч*то если радикальный центр трех окружностей
5,, S2 и 5, лежит вне этих окружностей, то он является цент-
центром единственной окружности 2, перпендикулярной ко всем
трем, данным (рис. \\,а,б). Если радикальный центр О лежит
внутри данных окружностей, то он является центром единст-
единственной окружности 2, делящейся пополам всеми данными окруж-
ог

ПУЧКИ И СВЯЗКИ ОКРУЖНОСТЕЙ 461
костями (рис. 11,в). Если центры трех данных окружностей все
лежат на одной прямой, то единственной «окружностью», перпенди-
перпендикулярной трем данным, является их общая линия центров—«окруж-
центров—«окружность бесконечного радиуса»; «окружности», делящейся пополам
всеми тремя данными окружностями, в этом случае не существует.
Если центры трех окружностей SJt S2 и Ss лежат на одной пря-
прямой, то их попарные радикальные оси о1г, о,, и о2, все перпенди-
перпендикулярны общей линии центров и, следовательно, параллельны между
собой; таким образом, три окружности, центры которых лежат
на одной прямой, не имеют радикального центра. В частном слу-
случае может оказаться, что прямые о,2 и о,, совпадут между собой;
тогда каждая точка этой прямой о будет иметь одина-
одинаковые степени относительно 5, и 58 и относительно S1 и S3. Отсюда
вытекает, что каждая точка прямой о будет иметь одинаковые сте-
степени и относительно окружностей St и 5„, т. е. она совпадает также
с радикальной осью o2S окружностей 52 и 5,. Этот случай, когда
попарные радикальные оси нескольких окружностей все совпа-
совпадают между собой, представляет по ряду причин особый интерес;
мы его рассмотрим подробнее в следующем параграфе.
§ 3. Пучки и связки окружностей
3.1. Пучок окружностей. В аналитической геометрии пучком
прямых называют совокупность всех прямых плоскости, проходящих
через фиксированную точку (рис. 13,а), или совокупность всех па-
параллельных между собой прямых (рис. 13,5)'). Так как мы услови-
условились рассматривать прямые как «окружности», то мы будем считать,
б) В)
Рис. 13.
что рис. \3,а,б определяют пучки окружностей бесконечного радиу-
радиуса. Однако больший интерес будут представлять для нас пучки окруж-
окружностей конечного радиуса. Под таким пучком мы будем понимать
совокупность всех конценфических окружностей («несобственный»
•) Ср. стр. 113.

462 окружности
пучок; рис. 13,в) или совокупность всех окружностей, каждые
две из которых имеют одну и ту же радикальную ось о («собст-
(«собственный» пучок). Прямую о, называемую радикальной осью (собствен-
(собственного) пучка, мы условимся также включать в состав пучка; таким
образом, каждый пучок, отличный от пучка концентрических окруж-
окружностей, содержит хотя бы одну «окружность бесконечного радиуса»
(т. е. прямую). Очевидно, что каждый собственный пучок образует-
образуется прямой о, какой-либо окружностью Sv и всеми такими окруж-
окружностями S, что о есть радикальная ось окружностей So и S (из
сказанного на стр. 461 вытекает, что прямая о явится также ра-
радикальной осью каждых двух из наших окружностей).
Если какая-либо окружность So собственного пучка пересекает
радикальную ось о в точках А к В (рис. 14,а), то любая другая
окружность 5 пучка должна проходить через те же точки А и В
(ибо о есть радикальная ось окружностей So и S); обратно, если 5
проходит через точки А к В, то о есть радикальная ось окружно-
окружностей So и S, и следовательно, 5 принадлежит пучку. Таким образом,
в рассматриваемом случае пучок состоит из всех окружностей, про-
проходящих через две фиксированные точки А к В. Такой пучок на-
называется пучком пересекающихся окружностей. Заметим еще, что
пучок пересекающихся окружностей вовсе не содержит окружностей
нулевого радиуса, т. е. точек.
Предположим теперь, что окружность 50 пучка касается ради-
радикальной оси о в точке А (рис. 14,5). В этом случае любая другая
окружность 5 пучка должна также касаться о в той же точке А,
ибо о есть радикальная ось окружностей SB и 5. Обратно, если S
касается прямой о в точке А, то радикальная ось окружностей So
и 5 совпадает с о. Таким образом, в этом случае пучок состоит из
всех окружностей, касающихся прямой о в данной точке А; такой
пучок называется пучком касающихся окружностей. Пучок касаю-
касающихся окружностей включает одну окружность нулевого радиуса,
а именно точку А: действительно, радикальная ось этой точки
и любой из окружностей пучка совпадает с о. [Заметим, что пучок
концентрических окружностей также содержит одну окружность
нулевого радиуса—общий центр всех окружностей пучка.]
Наконец, если окружность SB пучка не пересекает радикальной
оси о (рис. 14,в), то никакая окружность 5 пучка не может пере-
пересекать о, так как иначе радикальная ось окружностей 50 и 5 не сов-
совпадала бы с о. Далее, никакие две окружности пучка не могут пе-
пересечься, ибо в противном случае радикальная ось этих окружностей —
их общая хорда—отличалась бы от о. Такой пучок называется
пучком непересекающихся окружностей*).
') В литературе перечисленные три типа пучков (изображенные на
рис. 14, а—в) обыкновенно называются эллиптическим пучком, параболиче-
параболическим пучком и гиперболическим пучком.

ПУЧКИ И СВЯЗКИ ОКРУЖНОСТЕЙ
463
Очевидно, что во всех случаях центры всех окружностей собст-
собственного пучка лежат на одной прямой—на перпендикуляре z, опу-
опущенном из центра какой-либо окружности 50 пучка на радикальную
Рис. 14.
ось о; эта прямая z называется линией центров пучка. Заметим
еще, что во всех случаях через каждую точку М плоскости про-
проходит хотя бы одна окружность пучка. Это совершенно очевид-
очевидно для обоих типов «пучков окружностей бесконечного радиуса»,

464 окружности
т. е. для пучков прямых, и для пучков концентрических, пере-
пересекающихся или касающихся окружностей. Покажем, что так же
Зудет обстоять дело и в случае пучка непересекающихся окружно-
окружностей. Прежде всего, ясно, что через каждую точку N линии цент-
центров z проходит окружность пучка: диаметр NN' этой окруж-
окружности определяется равенством ON-ON' = OP-OP', где О и Р, Р' —
точки пересечения линии центров z с радикальной осью и с какой-
либо окружностью 6', пучка (рис. 14,в). В частности, если точка N
такова, что ON2 = ОР-ОР', то N' совпадает с N, и потому 5
явится окружностью нулевого радиуса, т. е. точкой; таким образом,
каждый пучок непересекающихся окружностей содержит две точки Л/,
и Nt (называемые предельными точками пучка), расположенные на
прямой z на одинаковом расстоянии V ОР-ОР' от точки О по раз-
разные стороны от нее. Далее, если точка М не принадлежит линии
центров z, то радикальная ось оу точки М и какой-то окружности 6'0
пучка не параллельна о и, значит, пересекает о в некоторой точке Q,
имеющей равные степени относительно окружности нулевого радиуса М
и окружности SB. Построим теперь окружность 5 с центром на ли-
линии центров z, касающуюся прямой QM в точке М (центром такой
окружности служит точка пересечения прямой z с перпендикуляром,
восставленным к QM в точке М). Очевидно, что точка Q будет
иметь равные степени относительно 5 и SB, т. е. будет принадлежать
радикальной оси этих двух окружностей. Отсюда вытекает, что о —
радикальная ось окружностей 5 и So; следовательно, 5 и есть окруж-
окружность пучка, проходящая через точку М.
Заметим еще, что, поскольку каждая точка Q радикальной оси о
собственного пучка окружностей, лежащая вне окружностей пучка
(т. е. отличная от точки А в случае пучка касающихся окружно-
окружностей и не принадлежащая отрезку АВ в случае пучка пересекаю-
пересекающихся окружностей; см. рис. 14, а,б), имеет одинаковую положитель-
положительную степень а2 относительно всех окружностей пучка, то Q яв-
является центром окружности 2, перпендикулярной всем окружностям
пучка (радиус этой окружности равен а). Таким образом, суще-
существует бесчисленное множество окружностей, одновременно пер-
перпендикулярных всем окружностям пучка. Нетрудно видеть, что
все эти окружности в свою очередь будут образовывать пучок:
действительно, радикальная ось двух таких окружностей совпадает
с линией центров z исходного пучка, поскольку z есть множе-
множество центров окружностей, перпендикулярных этим двум (ср. вы-
выше, стр. 458). Сама прямая z тоже входит в этот новый пучок,
поскольку это есть окружность бесконечного радиуса, перпендику-
перпендикулярная всем окружностям нашего пучка. Два пучка окружностей,
обладающих тем свойством, что каждая из окружностей первого
пучка перпендикулярна всем окружностям второго пучка и, наобо-

ПУЧКИ И СВЯЗКИ ОКРУЖНОСТЕЙ
465
рот, называются перпендикулярными или сопряженными пучками.
Нетрудно видеть, что пучку непересекающихся окружностей будет пер-
перпендикулярен пучок пересекающихся окружностей (ибо все окружности
Рис. 15.
второго пучка должны проходить через предельные точки первого
пучка) и наоборот (рис. 15,а): пучку касающихся окружностей будет
перпендикулярен другой пучок касающихся окружностей (рис. 15,6).
30 Энциклопедия, кн. 4

466
ОКРУЖНОСТИ
Понятие перпендикулярных пучков можно перенести также и на
пучки прямых или концентрических окружностей: очевидно, что все
окружности, перпендикулярные «окружностям бесконечного радиуса»,
составляющим пучок пересекающихся прямых, образуют пучок
концентрических окружностей и, наоборот (рис. 16,а), все окруж-
окружности, перпендикулярные «окружностям бесконечного радиуса», со-
составляющим пучок параллельных прямых, образуют второй пучок
параллельных прямых (рис. 16,5). Это обстоятельство позволяет дать
следующее общее определение всем пучкам окружностей (конечного
б)
Рис. 16.
или бесконечного радиуса): пучок окружностей—это совокупность
всех окружностей плоскости, перпендикулярных двум данным
различным окружностям Sl и S^).
3.2. Связка окружностей. Определим теперь (собственную)
связку окружностей как совокупность всех окружностей конеч-
конечного радиуса, каждые три из которых имеют один и тот же
радикальный центр О (называемый радикальным центром связки),
и всех окружностей бесконечного радиуса (прямых), проходящих
через точку О. Из этого определения следует, что степень точки
О относительно любых трех окружностей конечного радиуса связки
') Если S, и S2 суть две прямые, то мы приходим к пучку концентри-
концентрических окружностей или параллельных прямых; если S, и S2 суть кон-
концентрические окружности — к пучку пересекающихся прямых; во всех
остальных случаях—к собственному пучку окружностей.
Заметим еще, что пучок пересекающихся окружностей можно также
определить как совокупность всех окружностей, делящих пополам две данные
различные окружности S, и S2.

ПУЧКИ И СВЯЗКИ ОКРУЖНОСТЕЙ 467
будет одной и той же; отсюда вытекает, что радикальный центр О
собственной связки окружностей имеет одну и ту же степень относи-
относительно всех окружностей связки. Таким образом, собственную связку
окружностей можно определить также как совокупность всех окруж~
костей плоскости, относительно которых данная тонка О имеет
одну и ту же степень k, и всех прямых, проходящих через О;
точку О иногда называют просто центром связки, а степень k —
степенью связки.
Если при этом k = а2 > 0, то длина касательной, проведенной
из точки О к любой из окружностей конечного радиуса связки, рав-
равна а; отсюда вытекает, что связка состоит из всех окружностей,
перпендикулярных фиксированной окружности ? с центром О и
радиусом а (включая сюда и точки окружности 2 — окружности ну-
нулевого радиуса связки, и проходящие через О прямые—окружности
бесконечного радиуса связки). Если ft = 0, то связка, очевидно, со-
состоит из всех окружностей (конечного или бесконечного радиуса),
проходящих через точку О; такая связка содержит единственную
окружность нулевого радиуса — саму точку О. Наконец, .если
k=—аг<0, то связка состоит из всех окружностей, делящих
пополам окружность 2 с центром О и радиусом а (ср. стр. 458—459),
включая сюда и проходящие через О прямые; такая связка вовсе
не содержит окружностей нулевого радиуса, т. е. точек *).
Кроме собственных связок, к числу связок окружностей причисляют
еще связки всех окружностей, центры 'которых лежат на фик-
фиксированной прямой s, а также прямых, перпендикулярных s
(связки окружностей, перпендикулярных «окружности бесконеч-
бесконечного радиуса-», т. е. прямой s) и связку всех «окружностей бес-
бесконечного радиуса-» (прямых) плоскости.
В заключение заметим, что пересечение двух любых различных
связок (т. е. совокупность окружностей, принадлежащих одновре*
менно двум связкам) всегда образует пучок. Действительно, пере-
пересечение двух связок, одна из которых есть связка прямых, образует
пучок пересекающихся или параллельных прямых; пересечение двух
связок окружностей, перпендикулярных соответственно прямым s, и
s2, образует пучок концентрических окружностей, если s1^s2, и
пучок параллельных прямых, если s, || s2; пересечение двух собствен-
собственных связок окружностей с общим центром и разными степенями
образует пучок пересекающихся прямых. Наконец, во всех осталь-
остальных случаях пересечение двух связок окружностей образует соб-
собственный пучок: если одна из двух связок состоит из окружностей,
перпендикулярных прямой s, а вторая есть собственная связка с цент-
центром О, то пересечение их образует собственный пучок, радикальной
') Собственная связка первого типа называется гиперболической, вто-
второго— параболической и третьего—эллиптической.
ас*

468 окружности
осью которого служит перпендикуляр, опущенный из О на * (это
вытекает из того, что центры всех окружностей конечного радиуса,
принадлежащих пересечению связок, лежат на а, и что точка О
имеет равные степени относительно каждых двух из этих окружно-
окружностей); пересечение же двух собственных связок с разными центрами
О, и О2 образует пучок с радикальной осью Ofi2 (для доказатель-
доказательства достаточно заметить, что, поскольку обе точки О, и О2 имеют
одинаковые степени относительно любых двух окружностей конечного
радиуса, одновременно принадлежащих обеим связкам, то радикаль-
радикальной осью этих двух окружностей является прямая Ofi2).
§ 4. Инверсия
4.1. Определение инверсии. Рассмотрим некоторую фиксирован-
фиксированную связку окружностей и выберем все те окружности этой связки, ко-
которые проходят через определенную точку А плоскости. Эти окружности
принадлежат пересечению двух связок — выбранной связки и связки
окружностей, проходящих через точку А; согласно сказанному выше
(стр. 467) они образуют пучок окружностей (мы здесь исключаем из
рассмотрения тот случай, когда первая связка имеет центр А и
степень 0, и потому все ее окружности проходят через А). Оче-
Очевидно, что если первая связка есть связка всех прямых плоскости
или если точка А совпадает с центром выбранной связки, то полу-
полученный пучок есть пучок пересекающихся прямых; во всех осталь-
остальных случаях это есть пучок окружностей, пересекающихся в двух
точках А и А', или пучок касающихся окружностей (так как все
окружности пучка проходят через одну точку А, то мы не можем
прийти к пучку непересекающихся или концентрических окружно-
окружностей). Таким образом, выбор на плоскости определенной связки
окружностей (отличной от связки всех прямых) позволяет опре-
определить некоторое отображение плоскости, сопоставляющее с каж-
каждой отличной от центра О связки точкой А плоскости вторую
точку А' пересечения окружностей связки, проходящих через
точку А (если все эти окружности касаются в точке А, то мы
будем считать, что наше отображение переводит точку А саму в
себя)'). Это отображение мы будем называть точечной инверсией
или просто инверсией, отвечающей нашей связке. При этом инвер-
инверсия, отвечающая связке окружностей с центрами на прямой * и
перпендикулярных s прямых, называется особой; инверсия, отвечаю-
отвечающая связке пересекающихся в одной точке окружностей, —вырож-
—вырожденной; во всех же остальных случаях мы имеем обыкновенную
') Относительно геометрических отображений см. статью «Геометри-
«Геометрические преобразования» (^последствии эту статью мы будем цитировать
как «Г- П.»), стр. 51.

ИНВЕРСИИ
469
или общую инверсию, причем центр О связки называется центром
этой инверсии., а степень k связки — степенью инверсии.
Очевидно, что вырожденная инверсия переводит любую (отлич-
(отличную от центра О связки) точку плоскости в одну и ту же точку О
(ибо в этом случае совокупность окружностей связки, проходящих
через фиксированную точку А, образует пучок окружностей, пере-
пересекающихся в точках А и О) — это преобразование, разумеется, не
представляет интереса. Далее, особая инверсия представляет со-
собой симметрию относительно прямой s—в самом деле, все окруж-
окружности с центром на прямой s, проходящие через определенную
точку А (а также и перпендикуляр к s, проходящий через А),
Рис. 17.
проходят также и через точку А', симметричную А относительно s
(рис. 17)'). Таким образом, главный интерес представляет обыкно-
обыкновенная или общая инверсия, которую мы в дальнейшем для крат-
краткости часто будем называть просто «инверсией»; в тех случаях,
когда речь будет идти сразу об обыкновенной и об особой инверсии,
мы будем говорить про невырожденную инверсию.
Из данного выше описания собственных связок окружностей выте-
вытекает, что обыкновенную инверсию с положительной степенью а1
можно определить как отображение, сопоставляющее с каждой
точкой А плоскости; отличной от определенной точки О, вторую
точку А' пересечения всех окружностей, проходящих через точку А
и перпендикулярных окружности 2 с центром О и радиусом а
(рис. 18, а); окружность 2, задание которой полностью определяет
инверсию, называется окружностью инверсии. Если считать, что
•) См. «Г. П.», стр. 55.

470
ОКРУЖНОСТИ
6)
Рис. 18.

инверсия 471
окружность 2 может вырождаться в прямую («окружность бесконеч-
бесконечного радиуса»), то последнее определение охватывает также и осо-
особую инверсию—симметрию относительно прямой (рис. 17). Эта
близость между инверсией с положительной степенью и симметрией
относительно прямой находит отражение в том, что инверсию с
положительной степенью часто называют «.симметрией относительно
окружности 2». [Если принять, что окружность инверсии может
также вырождаться в точку (окружность нулевого радиуса), то наше
определение охватит также и вырожденную инверсию.] Аналогично
этому инверсию с отрицательной степенью — а* можно определить
как преобразование, сопоставляющее с каждой точкой А, отличной
от точки О, вторую точку пересечения всех окружностей, про-
проходящих через А и делящих пополам окружность 2 с центром О
и радиусом а (рис. 18,6).
Можно также определить инверсию чисто аналитически. Из того,
что центр О собственной связки имеет относительно всех окружно-
окружностей связки степень k, следует, что каждая окружность связки,
проходящая через определенную (отличную от О) точку А, пересекает
прямую ОА второй раз в такой точке А', что ОА-ОА' =?. Отсюда
видно, что инверсию с центром О и степенью k можно определить
как геометрическое преобразование, переводящее каждую отличную
от О точку А плоскости в такую точку А' прямой О А, что
Это последнее определение инверсии в силу своей простоты явля-
является наиболее распространенным'); мы в дальнейшем также чаще
всего будем пользоваться именно им. В частности, из этого опре-
определения вытекает, что две инверсии с одним центром О и равными
по абсолютной величине степенями k и — k переводят одну и ту же
точку А в две точки А' и А" прямой ОА, удаленные на одно рассто-
I k I
яние тпг от центра инверсии О, но расположенные по разные сто-
роны от него; другими словами можно сказать, что инверсия с отри-
отрицательной степенью — k равносильна инверсии с тем же центром О
и положительной степенью k, сопровождаемой еще симметрией
относительно точки О2).
4.2. Свойства инверсии. Заметим прежде всего, что центр О
не переходит при инверсии ни в какую точку плоскости. Так как,
очевидно, чем ближе расположена точка А к точке О, тем дальше
удален от О образ А' этой точки (причем если только А достаточно
¦) См. «Г. П.», стр. 56.
г) Можно также сказать, что инверсия с центром О и степенью — k
совпадает с произведением инверсии с центром О и степенью k и симметрии
относительно О, ззятых в любом порядке (см. «Г. П.», стр. 80).

472 окружности
близка к О, то расстояние ОА' превзойдет любое наперед заданное
число), то говорят также, что образ центра О инверсии удаляется
в бесконечность или что инверсия переводит точку О в бесконеч-
бесконечность; разумеется, эти выражения следует понимать лишь в том
смысле, что сама точка О при инверсии не переходит никуда, а
близкие к О точки переходят в далекие точки').
Заметим, что невырожденная инверсия «переставляет» между
собой точки плоскости (т. е. если точка А переходит в точку А',
то точка А' переходит обратно в точку АJ). Далее, инверсия с
центром О и степенью k переводит внутренность окружности ?
с центром О и радиусом |^|&| во внешнюю область этой окруж-
окружности и наоборот (аналогично тому, как симметрия относительно
прямой s меняет местами две полуплоскости, на которые s делит
плоскость). Что же касается самой окружности 2, то инверсия пере-
переводит ее в себя; при этом в случае положительного k все точки
окружности 2 переходят в себя (аналогично тому, как при симмет-
симметрии относительно прямой 5 переходят в себя все точки этой пря-
прямой), в то время как в случае отрицательного k каждая точка
окружности 2 переходит в диаметрально противоположную точку.
Отметим теперь два менее очевидных свойства инверсии.
А. Всякая невырожденная инверсия переводит каждую окруж-
окружность ненулевого радиуса снова в окружность ненулевого радиуса
(т. е. каждую окружность или прямую снова в окружность или
прямую).
Так как совершенно очевидно, что симметрия относительно пря-
прямой обладает этим свойством, то надо только доказать, что им
обладает также и обыкновенная инверсия. Прежде всего совершенно
ясно, что инверсия переводит каждую прямую, проходящую через
центр инверсии, саму в себя. Далее, если М и М' суть точки
пересечения проходящей через точку О прямой с окружностью S,
имеющей диаметр ОР, и прямой s, перпендикулярной ОР и пересе-
пересекающей ОР в некоторой точке Р (рис. 19, с), то из подобия пря-
прямоугольных треугольников ОРМ и ОМ'Р' с общим острым углом О
имеем
0Р_ 0М_'
ОМ~ОР' '
откуда следует, что
ОМ-ШТ' =ОР-ОР~.
Последнее равенство показывает, что инверсия с центром О и сте-
степенью k переводит проходящую через О окружность S в прямую s,
') Относительно другого понимания этого утверждения (связанного с
присоединением к плоскости одной «несобственной» точки) см. стр. 58—59.
2) Другими словами, инверсия есть инволютивног преобразование
(см. «Г. П.», стр. 97).

ИНВЕРСИЯ
473
перпендикулярную диаметру ОР окружности и пересекающую
этот диаметр в такой точке Р', что OP- OP = k; обратно, не
проходящую через О прямую s инверсия переводит в проходящую
через О окружность S, диаметром которой служит такой отре-
отрезок ОР перпендикуляра ОР', опущенного из О на s, что
Наконец, пусть 5 — произвольная окружность, не проходящая
через центр О инверсии, и р — степень точки О относительно
окружности S, так что каждая проходящая через О прямая пересе-
пересекает 5 в таких двух точках М и Mlt что ОМ-ОМ, = р. Пусть,
t
Рис. 19.
далее, S' — окружность, центрально-подобная (гомотетичная) S с цент-
центром подобия О и коэффициентом подобия1) —, a Mt и М'— точки
окружности S', отвечающие в рассматриваемом центрально-поюбном
преобразовании точкам М и Ж, окружности 5 (рис. 19, б). В таком
случае имеем
ШЛ' k
ОМ-ОМ^р,
ОМ,
Отсюда следует, что
ОМ-ОМ' =
т. е. что инверсия с центром О и степенью k переводит не проходя-
проходящую через О окружность S в окружность S', центрально-подобную
{гомотетичную) S с центром подобия О и коэффициентом подо-
подобия —, где р есть степень точки О относительно окружности S
») См. «Г. П.», стр. 55.

474 окружности
(причем в центрально-подобном преобразовании точка М окружности 5
отвечает точке М\ окружности 6", а в инверсии точка М отвечает
точке М).
Этим и завершается доказательство свойства А инверсии').
Б. Невырожденная инверсия сохраняет угол между окруж-
окружностями. Точнее, если tx, t2 — касательные к двум окружностям
ненулевого радиуса 5, и S2, пересекающимся в точке А, и t't, t't—-
касательные к окружностям ненулевого радиуса Sj и S't, в которые
переводит 5, и 5, невырожденная инверсия, проведенные в точке А',
отвечающей при инверсии точке А, то
ЗСС,. ',)=?(?. й)
(обратите внимание на порядок касательных!).
Нам опять достаточно показать, что свойством Б обладает обыкно-
обыкновенная инверсия. Из подобия треугольников ОРМ и ОМ'Р (рис. 19, а)
следует, что <? (РО, РМ) = ^.(М'Р', М'О). Но $?(Р0, РМ) =
= ^С(МО, t), где t — касательная к 5 в точке М (оба угла изме-
измеряются половиной дуги МО); следовательно,
0 = §С(*. М'О').
С другой стороны, окружности S и S' (рис. 19, б) образуют
« точках М и Ж, равные углы <? (МО, t) и <? (yW,O, tt) с прямой
ОММ' (это следует из того, что О есть центр подобия окружностей
чЬ' и S'; ср. ниже стр. 489). А так как, кроме того, -§С (М,О, ?,) =
= ^H(t', М'О) (см. стр. 453), то имеем
) = ¦?(*', М'О).
Итак, мы доказали наше утверждение для того случая, когда
одна из двух рассматриваемых окружностей ненулевого радиуса —это
проходящая через О прямая. Пусть теперь S1 и S2 — две произвольные
окружности ненулевого радиуса, пересекающиеся в точке А; 6", и52 —
пересекающиеся в точке А' окружности, в которые переходят .S", и S2
при инверсии. В таком случае имеем (рис. 20)
3; (*,, АО) = §с (а1 о. t[), зс (АО, g = $ (/„ а'О),
откуда
¦что и требовалось доказать.
В частности, из свойства Б инверсии следует, что невырожденная
инверсия переводит любые две касающиеся окружности в касаю-
касающиеся окружности.
1) См. также «Г. П.», стр. 74—75.

ИНВЕРСИЯ
475
4.3. Теорема Паскаля. Преобразование инверсии находит многочислен-
многочисленные применения при доказательстве геометрических теорем. Часто удается
так преобразовать при помощи инверсии чертеж какой-либо относящейся
к окружностям геометрической теоремы, что некоторые из фигурирующих
на этом чертеже окружностей переходят в прямые линии, и чертеж тем
самым упрощается; если же доказать выражаемую преобразованным черте-
чертежом новую, более простую теорему, то отсюда будет вытекать также и
справедливость первоначальной теоремы. Упрощение чертежей с помощью
Рис. 20.
инверсии лежит также в основе многочисленных применений этого пре-
преобразования к решению геометрических задач на построение. Отсылая
читателя по этому поводу, например, к любой из первых четырех книг
приведенного в конце статьи списка литературы1), мы ограничимся здесь
одним простым, но эффектным примером несколько иного рода.
Докажем, что точки Р, Q и R пересечения противоположных сторон
А1А2 и AtAt, АгА, и Л5Л6, A3At и AtAt произвольного (может быть, и само-
самопересекающегося!) вписанного в окружность S шести гольника A1A2AsAiA5At
лежат на одной прямой (теорема Паскаля).
Пусть S, — произвольная окружность, пересекающая S в точках Л, и
А„ S2 — окружность, в которую переводит S, инверсия с центром Р и сте-
степенью k, — PAt-PAs = PAi-PAi (S2 проходит через точки Аг и Аъ); S,—
окружность, в которую переводит S2 инверсия с центром Q и степенью
') См. также «Г. П.», стр. 70—72, 145—146 и статью «Обшие принципы
геометрических построений», стр. 193.

476
ОКРУЖНОСТИ
k2 — QAi-QA3 — QAi-QAt (S, проходит через точки Л3 и Лв); S,—окруж-
S,—окружность, в которую переводит S3 инверсия с центром R и степенью
^3 ^^^в f ) Л I J Л ^^^^ f ) Д f J Д / ^^ rt ж ¦ ^Ч ж*ъ rt
ftg -*— /\/1з " i\/l,j -—i\/lg"i\/l| ^«Jj tnUBd
проходит через точки Л„ и Л,);
наконец, обозначим еще касатель-
u ные к S в точках Л,, Л2, Л3 и Л4
' через tv t2, t} и tit а касательные
к S,, S2, S, и S, в тех же точ-
точках—через и,, ы2, us и п, (рис. 21).
Легко видеть, что при всех трех
инверсиях окружность S перехо-
переходит сама в себя. В силу свой-
свойства Б инверсии имеем
<('i. «.) = <(«.. *,) =
= <(«.. и.) = <(й.. «.)¦
Но равенство -^[ (<„ u,) = <5! (й,, <4)
показывает, что окружности S,
, и S,, пересекающие S в одних и
1 тех же точках Л, и Л4, обра-
образуют в этих точках с окружно-
окружностью S одинаковые (по величине
и по направлению!) углы, откуда
следует, что эти окружности
просто совпадают. Таким обра-
образом, точки Р, Q и R суть центры
инверсий, переводящих S, в S2, S2 в S, и S, в S,, т. е. это суть центры подо-
подобия этих окружностей (см. доказательство свойства А инверсии). Но отсюда
следует, что эти точки лежат на одной прямой (см. ниже стр. 489—490)').
§ 5. Точечная геометрия окружностей
5.1. Круговая плоскость. То обстоятельство, что прямые и окруж-
окружности являются единственными линиями, изучаемыми в элементарной
геометрии, заставляет ограничиться здесь рассмотрением лишь таких
преобразований плоскости, которые переводят прямые и окружности
снова в прямые и окружности. Однако ясно, что никакое (непрерыв-
(непрерывное) преобразование плоскости, переводящее каждую ее точку А
в другую точку А', не может перевести замкнутую линию — окруж-
окружность— в незамкнутую линию—прямую; следовательно, такое преоб-
преобразование должно переводить каждую прямую в прямую и каждую
окружность в окружность *). Тем самым мы приходим к преобразо-
Рис. 21.
•) См. также «Г. П.», стр. 93 и след.
2) Если бы такое преобразование переводило прямую s в окружность
S, то оно должно было бы перевести прямую s,, пересекающую s в точке Л,
в прямую или окружность S,, имеющую с S одну общую точку Л', т. е.
касающуюся S в точке Л'. Это, однако, невозможно, так как прямые s
и s, разбивают плоскость на 4 части (такие, что никакие две точки,
принадлежащие разным частям плоскости, нельзя соединить прямой или

ТОЧЕЧНАЯ ГЕОМЕТРИЯ ОКРУЖНОСТЕЙ 477
ваниям подобия —- единственным преобразованиям плоскости, при ко-
которых любая прямая снова переходит в прямую и каждая окружность
переходит в окружность1),— и действительно эти преобразования
суть единственные, систематически рассматриваемые в курсе элемен-
элементарной геометрии.
Сказанное выше не противоречит тому, что инверсия также пере-
переводит окружности и прямые снова в окружности и прямые: действи-
действительно, инверсия не является преобразованием всей плоскости,
поскольку она не переводит центр инверсии О ни в какую другую
точку плоскости. С другой стороны, именно то обстоятельство, что
совокупность окружностей и прямых переводится инверсией в сово-
совокупность тех же линий, делает весьма желательным включение
этого преобразования в число тех, с которыми оперирует элементар-
элементарная геометрия. Однако для этого прежде всего желательно получить
возможность говорить об инверсии как о преобразовании всей плос-
плоскости, а не плоскости с одной выключенной точкой: ведь иначе нам
придется считать, что инверсия переводит прямую в окружность
без одной точки (ибо центр инверсии мы должны вообще исключить
из рассмотрения), а если нам надо будет прэизвести подряд две
или несколько инверсий, то положение осложнится еще больше.
Выход из создавшегося положения состоит в следующем. Усло-
Условимся говорить, что при инверсии центр О переходит в некоторую
фиктивную «бесконечно удаленную точку» Q плоскости; обратно,
эта «бесконечно удаленная точка» Q переходит в центр инверсии О
(ср. стр. 57). Хотя эта терминология означает только, что инверсия
не переводит О ни в какую реально существующую точку плоскости,
она во многих случаях оказывается чрезвычайно удобной. Так как
прямые при инверсии переходят в окружности, проходящие через
центр инверсии О, то приходится считать, что все прямые плоскости
проходят через «бесконечно удаленную точку»; это соглашение
устраняет различие между прямыми и окружностями, так как прямую
теперь также можно считать замкнутой — она «замыкается в беско-
бесконечности» 2). Плоскость, условно дополненная, таким образом, одной
«бесконечно удаленной точкой», называется круговой плоскостью.
Понятие круговой плоскости является математической абстракцией
в такой же степени, как и понятие обычной (безграничной) плоскости;
в современной математике (в частности, в теории функций комплекс-
комплексного переменного) оно играет весьма важную роль.
окружностью, не пересекающей ни s, ни s,), а касающиеся окружности
(или окружность и прямая) S и S, делят плоскость только на 3 части.
М См. «Г. П.», стр. 62—63. По поводу последующего ср. также «Г. П »
стр. 57—59.
г) Это утверждение означает, что точка А, неограниченно удаляющаяся
по прямой в любом ее направлении, стремится к «бесконечно удаленной
точке» Q (в тодо смысле, что точка А', в которую переводит А инверсия
с центром О, стремится к точке О).

478 окружности
5.2. Круговые преобразования. Преобразования круговой плос-
плоскости, переводящие прямые и окружности снова в прямые и окруж-
окружности (или, другими словами, переводящие в себя совокупность всех
окружностей ненулевого радиуса), уже не исчерпываются одними
преобразованиями подобия — пример другого рода доставляет нам
инверсия. Все такие преобразования называются круговыми преобра-
преобразованиями1). Нетрудно видеть, что каждое круговое преобразова-
преобразование круговой плоскости является или преобразованием подобия
или инверсией, сопровождаемой еще, быть может, преобразова-
преобразованием подобия. Действительно, если круговое преобразование остав-
оставляет на месте «бесконечно удаленную точку» О,, то оно переводит
прямые («окружности бесконечного радиуса» или «окружности, про-
проходящие через бесконечно удаленную точку Q») снова в прямые и
окружности конечного радиуса — в окружности конечного радиуса,
т. е. является преобразованием подобия. Рассмотрим теперь круговое
преобразование К, которое переводит в Q какую-то «конечную»
(т. е. обыкновенную) точку О плоскости. Это преобразование можно
заменить инверсией I с центром О, сопровождаемой еще каким-то
преобразованием П. (П переводит точку Av в которую переводит
произвольную точку А инверсия I, в точку А', в которую переводит
А преобразование К; если <4, всегда совпадает с А', то К совпадает
с инверсией I и никакого дополнительного преобразования рассмат-
рассматривать не нужно.) Очевидно, что П есть тоже круговое преобразо-
преобразование: оно переводит окружность 5,, в которую инверсия I переводит
окружность S, в окружность S', в которую 6'переводит К. С другой
стороны, П переводит прямые снова в прямые (ибо и К и I пере-
переводят в прямые проходящие через О окружности). Поэтому П есть
преобразование подобия, что и доказывает наше утверждение (про-
(произвольное круговое преобразование К совпадает с инверсией I, со-
сопровождаемой преобразованием подобия П).
5.3. Понятие о круговой геометрии. Изучение свойств геомет-
геометрических фигур, общих всем фигурам, получаемым друг из друга
круговыми преобразованиями, составляет предмет круговой геометрии
(или точечной круговой геометрии; смысл прилагательного «точеч-
«точечная» станет ясным из дальнейшего)г). Основную роль в этой геомет-
геометрии играет понятие окружности (ненулевого радиуса); прямая линия
не имеет здесь самостоятельного значения, ибо круговое преобразо--
вание может переводить прямую в окружность. В этой геометрии,
так же как и в обычной геометрии, положение окружности на плос-
плоскости не отражается на ее свойствах (ибо по-разному расположенные
окружности имеют одинаковые свойства); однако здесь уже и вели-
величина радиуса также не помогает различать окружности,"ибо инверсна
') Эти преобразования называются также преобразованиями Мебиуса.
2) Ср. «Г. П », § 6.

НАПРАВЛЕННЫЕ ОКРУЖНОСТИ 479
переводит друг в друга неравные окружности. Напротив, угол между
окружностями играет в круговой геометрии такую же роль, как и в
обычной, поскольку он сохраняется при любом круговом преобразо-
преобразовании (см. стр. 474).
Мы не имеем никакой возможности входить здесь в обсуждение
подробностей круговой геометрии, которой в специальной математи-
математической литературе посвящен целый ряд весьма обстоятельных сочи-
сочинений (из них в списке литературы в конце статьи упомянута лишь
книга Бляшке [8]). Отметим только, что понятия пучка и связки
окружностей играют в круговой геометрии весьма существенную роль;
эти понятия имеют здесь смысл, так как всякое круговое преобра-
преобразование переводит пучок окружностей снова в пучок окружностей
и связку окружностей — в связку1).
Б. ОКРУЖНОСТЬ КАК СОВОКУПНОСТЬ ПРЯМЫХ
§ 6. Направленные окружности
6.1. Аналогия между свойствами точек и прямых. Значительную
роль в геометрии играет то обстоятельство, что свойства точек во
многом напоминают свойства прямых линий г). Так, например, точку
можно задать двумя (проходящими через эту точку) прямыми, а пря-
прямую—двумя (лежащими на этой прямой) точками; точки прямой,
заключенные между двумя данными точками А к В, образуют отрезок
АВ, а проходящие через точку прямые, заключенные между двумя
данными прямыми а и Ь,— угол j/_(a, b) (близость между понятиями
отрезка и угла хорошо иллюстрируется сказанным в п. 1.1); через
три вершины треугольника проходит окружность («описанная» окруж-
окружность треугольника), и трех сторон треугольника касается окруж-
окружность («вписанная» окружность треугольника) и т. д. Цель настоящего
раздела состоит в том, чтобы показать, как далеко заходит этот
параллелизм.
В разделе А мы всюду рассматривали окружность как совокуп-
совокупность точек; такой подход является привычным и для школьного
курса геометрии. В противоположность этому теперь мы будем
смотреть на окружность как на совокупность прямых, касатель-
касательных к этой окружности; другими словами, под окружностью S мы
') Из того, что пучок окружностей можно определить как совокуп-
совокупность всех окружностей, перпендикулярных двум данным, сразу следует,
что инверсия переводит пучок окружностей снова в пучок (ибо перпенди-
перпендикулярные окружности при инверсии переходят в перпендикулярные).
То, что связка при инверсии переходит в свячку, несколько менее оче-
очевидно; доказательство этого составляет несложную, но содержательную
задачу, которую мы предлагаем читателю решить самостоятельно.
2) По этому поводу ср. стр. 130—133.

480
окружности
будем понимать совокупность всех прямых плоскости, удаленных на
одно и то же расстояние г от фиксированной точки О—центра
окружности (рис. 22, а). При этом величина г — радиус окружности —
может равняться нулю; в таком случае мы приходим к точке Sa,
которая здесь рассматривается как совокупность всех прямых, про-
проходящих через <S0 (рис. 22, б). Таким образом, и с принятой в этой
главе точки зрения точка является частным случаем окружности
(«окружность нулевого радиуса»).
6)
Рис. 22.
6.2. Дальнейшее расширение понятия окружности. Заметим,
что сходство между окружностью — множеством точек — и окруж-
окружностью— множеством прямых — нарушается во многих пунктах
Так, например, две окружности могут иметь не больше двух
общих точек, но до четырех общих прямых (т. е. общих каса-
касательных); центры всех окружностей, проходящих через две дан-
данные точки, лежат на определенной прямой (рис. 23, а), в то время
как центры всех окружностей, касающихся двух данных прямых,
заполняют две прямые (рис. 23,6); существует единственная окруж-
окружность, проходящая через три данные точки (рис. 24, а), но целых
четыре окружности, касающиеся трех данных прямых (рис. 24, б)
и т. д. Для того чтобы устранить эти расхождения, мы будем
всюду в этой главе рассматривать направленные окружности и пря-
прямые, т. е. окружности и прямые, на которых выбрано определенное
направление, на рисунках указываемое стрелкой (ср. стр. 450). На-
Направленные окружности называются еще циклами, а направленные
прямые — осями. При этом мы будем считать, что (направленные)
окружности 5, и 6'2 касаются только в том случае, если направления
этих окружностей в общей точке совпадают (рис. 25, а); таким
образом, изображенные на рис. 25, б две окружности теперь не

НАПРАВЛЕННЫЕ ОКРУЖНОСТИ
481
\
Рис. 23.
Рис 24.
11 Энциклопедия, кн. 4

482 .окружности
считаются касающимися. Это же условие мы сохраним и для касания
(направленной) окружности Sx с (направленной) прямой So («окруж-
(«окружностью бесконечного радиуса»). Две (направленные) прямые мы будем
называть параллельными только в том случае, если направления этих
прямых совпадают. Целесообразность введения направленных прямых
и окружностей подтверждается тем, что две (направленные) окруж-
окружности имеют не более двух общих (направленных) касательных
(рис. 26, а); центры всех (направленных) окружностей, касающихся
двух данных (направленных) прямых, лежат на одной прямой (рис. 26,6);
существует единственная (направленная) окружность, касающаяся трех
данных (направленных) прямых ( рис. 26, в) и т. д. В дальнейшем
прилагательное «направленная» мы будем, как правило, опускать.
а) 6)
Рис. 25.
Для того чтобы сохранить в силе приведенное выше определение
окружности, теперь приходится ввести дополнительное соглашение:
ведь прямые, удаленные от точки О на расстояние г, могут касаться
одной или другой из двух окружностей, отличающихся друг от
друга только направлением. Мы будем считать расстояние от точки С
до (направленной) прямой / положительным, если О лежит слева
от / (рис. 27, а), и отрицательным в противном случае. В таком
случае придется считать, что радиус окружности может быть и от-
отрицательным; (направленную) окружность 5 с центром О и (положи-
(положительным, отрицательным или равным нулю) радиусом г можно по-
прежнему определить как «геометрическое место» (направленных)
прямых, удаленны* от О на расстояние г. Очевидно, что все окруж-
окружности, направленные против часовой стрелки, будут иметь положи-
положительный радиус, а направленные по часовой стрелке—отрицательный
(рис. 27,6).
6.3. Касательное расстояние двух окружностей. Под (направ-
(направлении) углом <Г (а, Ь) между двумя (направленными) прямыми а и 1>
мы будем понимать угол между указанными стрелками направле-
направлениями этих прямых (рис. 28, а); при этом <? (а, Ь) определится уже
с точностью до краткого 2я (ср. стр. 451). Под углом ^C(S1.S7i

Рис 26.

484
окружности
между двумя (направленными) окружностями Sx и S, мы буДем пони-
нимать угол между (направленными) касательными к 5, и к S, в точке их
пересечения (рис. 28, б); при этом два угла, образованные окруж-
окружностями S, и 5Ж в гвух точках пересечения, будут отличаться
\ ¦
Рис. 27.
знаками (ср. также стр. 4-53). Как геометрическая фигура, угол между
5, и St представляет собой совокупность всех прямых, проходящих
через общую точку М окружностей S, и S2 и заключенных между
касательными о и b к этим окружностям.

ЦЕНТР ПОДОБИЯ И ОСЬ ПОДОБИЯ 485
Наряду с углом между 5, и 5, мы будем рассматривать также
совокупность точек, принадлежащих общей прямой (общей касатель-
касательной) т окружностей 5, и S, и заключенных между точками А и В
этих окружностей (рис. 28, в)—отрезок АВ, длину которого мы будем
называть касательным расстоянием между S, и St. Так как пря-
прямая т является направленной, то можно считать направленным и
отрезок АВ; отметим только, что касательное расстояние между
двумя окружностями S, и S2 (взятыми в этом именно порядке!),
измеренное по одной или по другой из их общих касательных, имеет
разный знак (ср. направление отрезков АВ и CD на рис. 28, в).
Касательное расстояние между касающимися (и только между касаю-
касающимися) окружностями равно нулю (как и угол между касающимися
окружностями). Если к двум окружностям нельзя провести общих
касательных, то касательное расстояние между ними не существует
вовсе (подобно тому как не существует угла между непересекаю-
непересекающимися окружностями).
Касательное расстояние двух окружностей St и S, обобщает по-
понятие расстояния между точками; оно переходит в это последнее
понятие, если Sx и St суть «окружности нулевого радиуса». В этом
разделе понятие касательного расстояния будет играть большую роль.
§ 7. Центр подобия и ось подобия
7.1. Степень прямой относительно окружности. Рассмотрим
теперь следующую теорему, аналогичную той, которая служила для
определения степени точки относительно окружности (см. § 2, стр. 454):
Если на прямой т взять несколько точек, лежащих вне ок-
окружности S, то произведение тангенсов половин углов, состав-
составленных прямой т с проходящими через каждую из точек каса-
касательными (произведение tg '"'а' ¦ tg * ' на рис. 29, а, б), бу-
будет одним и тем же для всех этих точек.
Для доказательства опустим из центра О окружности .S перпен-
перпендикуляр ОР на прямую т; далее обозначим через А к В точки
соприкосновения с 5 касательных а и Ь, проходящих через точку
М прямой т. Из треугольника ОАР по теореме тангенсов получим
/_РАО—
22 ОР — ОА
t ?РАО+/.ОРА ОР+ОА'
Так как в четырехугольнике ОАМР два противоположных угла пря-
прямые, то вокруг него можно описать окружность; следовательно,
= /_РМО, /_ОРА = /_ОМА (как углы, опирающиеся на

486 окружное in
одну дугу). А так как ,
/_ РМО \- /_ ОМА = /_ РМА I
и
/_ РМО— /_ ОМА = /_ РМО - /_ ОМВ = /_РМВ,
то получаем
>Lg *" 2 OP—О А
^_РМА ОР + ОА
Но на рис. 29, я, б
/_РМВ= +¦§;(/», Ь), /_РМА=*п f •$;(«, а)
обратите внимание на направление углов!); следовательно,
?РМВ_ <$(/л, b) f_PMA _ . <$(т,а)
и, значит,
где г = С*Л^ радиус окружности 6"; d = OP—расстояние от центра
5 до т. Последняя формула остается в силе при любых (по вели-
величине и но знаку; см. выше, стр. 482) г и d'); она и доказывает
требуемую теорему.
п *? (л, а) <1 (т, Ь) ,
Произведение tg =-Ц^—^-tg-^— называется степенью (направ-
(направленной) прямой т относительно (направленной) окружности S.
Очевидно, что степень прямой т относительно окружности 5 (рав-
r—d\
ная отношению . ) положительна, если прямая т пересекает
окружность 5, и отрицательна в пробивном случае (из рис. 29, а, б
видно, что в первом случае углы <2? (т, а) и <?(т, Ь) направлены
одинаково, а во втором — противоположно). Степень т относитель-
относительно 5 равна нулю в том и только в том случае, когда прямая т ка-
касается окружности 5; единице — в том и только в том случае, когда
прямая т проходит через центр окружности S; минус единице—в том
и только в том случае, когда 5 есть точка, через которую прямая т
не проходит. Если т совпадает по положению на плоскости с каса-
касательной к окружности S, но отличается от нее направлением, то сте-
степень прямой т относительно окружности 5 следует считать бесконеч-
бесконечной; наконец, если 5 есть точка и т проходит через S, то степень вооб-
вообще не может быть определена. Отметим еще, что если прямая т пересе-
пересекает окружность S, то степень прямой т относительно 5 равна
квадрату тангенса половины угла, образованного прямой т с S; для
') Рекомендуем читателю самостоятельно рассмотреть ряд представля-
представляющихся случаев (на рис. 29, а, б и г и d положительны).

ЦЕНТР ПОДОБИЯ И ОСЬ ПОДОБИЯ
487
доказательства этого достаточно принять за точку М точку пересе-
пересечения линий т к S (рис. 29, а).
Рис. 29.
7.2. Центр подобия двух окружностей. Рассмотрим теперь две
собственные окружности S, и Sx и найдем все прямые, имеющие
относительно St и 5, одинаковые степени; эта задача аналогична
задаче об отыскании точек, имеющих одинаковые степени относи-
относительно двух данных (ненаправленных) окружностей (см. п. 2.2.).
Если т — такая прямая, d,, dx — расстояния центров О, и О, окруж-
окружностей S, и St от этой прямой, г, и г,—радиусы этих окружностей,
то в силу доказанного выше будем иметь
откуда, составляя производную пропорцию, получим
С—
г. г.
ИЛИ -f = -f- .

488
ОКРУЖНОСТИ
Из последней формулы сразу следует, что если г1—гг, то d, = dJ,
т. е. прямая т параллельна линии центров О,Ог. Если же исклю-
исключить последний случай, то йЛФ dt и прямая т пересечет линию
центров в некоторой точке О; при этом из рис. 30 сразу следует
соотношение
Об, __ dy _ г,
Об2 ~ Ъ~г2 '
чем полностью определяется положение точки О. Обратно, если
6)
Рис. 30.
прямая т проходит через такую точку О на линии центров, что
00,
00,
00,,'
откуда вытекает, что эта прямая имеет одинаковые степени относи-
относительно окружностей St и Бг. Таким образом, мы заключаем, что
если г, Ф rt, то прямые, имеющие относительно окружностей

ЦЕНТР ПОДОБИЯ И ОСЬ ПОДОБИЯ 48У
S, и St одинаковые степени,—это те (и только те) прямые.
которые пересекают линию центров 0t02 в такой точке О, что
00, г. _ „ , ,
=L = —. Эта точка О называется центром подобия окружностей
S, и S, •)¦
Очевидно, что если окружности S, и 6", имеют две общие ка-
касательные (рис. 30, а, б), то их центр подобия совпадает с точкой
пересечения общих касательных; это вытекает из того, что общие
касательные имеют одинаковые (равные нулю) степени относительно
обеих окружностей. Если окружности S, и S2 касаются, то их един-
единственная общая касательная также имеет одинаковые степени отно-
относительно Sl и St, откуда вытекает, что центром подобия этих ок-
окружностей является точка их касания. Равные окружности вообще
не имеют центра подобия, ибо в этом случае прямые, имеющие
относительно обеих окружностей одинаковые степени, не пересека-
пересекаются между собой. Заметим еще, что все прямые, проходящие череа
центр подобия окружностей S, и 5, и пересекающие одну из них,
пересекают и вторую, и притом под тем же углом, что и первую
(ибо степень прямой т относительно пересекающей ее окруж-
окружности 5 полностью определяется углом между линиями т и S);
отсюда снова можно усмотреть, что если окружности 5, и St имеют
две общие касательные, то центр подобия О совпадает с точ-
точкой их пересечения. Важно еще заметить, что если направления
двух окружностей S,, Бг одинаковы (обе направлены по или обе
против часовой стрелки), так что радиусы гЛ и rt имеют оди-
одинаковые знаки, то расстояния d, и dt также имеют одинаковые
знаки (ибо d, :dt =r, :r2), и потому центры О,, О2 окружностей рас-
расположены по одну сторону от любой прямой, проходящей череа
центр подобия. Следовательно, центр подобия расположен вне от-
отрезка OtOt (рис. 30, а). Если же окружности 5, и St имеют противо-
противоположные направления, то их центр подобия расположен на отрезке
ОЛОг (рис. 30", б).
7.3. Ось подобия трех окружностей. Рассмотрим теперь три
окружности S,, St, и Sa. Если центр подобия О,2 окружностей 5,
и Ss не совпадает с центром подобия О1а окружностей 5, и St, то
прямая О1гО1Л имеет равные степени относительно 5, и 5, и отно-
относительно S, и St. Отсюда вытекает, что эта прямая имеет также
одинаковые степени относительно St и 5, и, значит, проходит через
центр подобия О„ последних двух окружностей (рис. 31). Таким
образом, мы видим, что попарные центры подобия трех окруж-
') Ср. «Г. П.», стр. 93—94. (Заметим, что ненаправленные окружности
имеют два центра подобия, в то время каи направленные окружности
имеют один центр подобия—внешний, если окружности направлены одина-
одинаково, и внутренний в противном случае.)

490
окружности
ностеп St, S2 и S3 лежат на одной прямой о '). Эта прямая на-
называется осью подобия трех окружностей; ее можно также опреде-
определить как прямую, имеющую одинаковые степени относительно всех
грех окружностей. Если же центры подобия О12 и О„ совпадают,
ю каждая прямая т, проходящая через общий центр подобия О.
ммеет равные степени относительно 5, и 5, и относительно 5,и 5S.
Рис 31.
Следовательно, т имеет также равные степени относительно S2 и Л'а,
откуда вытекает, что О совпадает и с центром подобия окружностей
St и 5,. Случай, когда попарные центры подобия нескольких окруж-
окружностей все совпадают между собой, аналогичен случаю совпадения
попарных радикальных осей нескольких окружностей (т. е. случаю,
когда все окружности принадлежат одному пучку); мы рассмотрим
его подробнее в следующем параграфе.
§ 8. Ряды и сети окружностей
8.1. Ряд окружностей. Совокупность всех (направленных) ок-
окружностей, каждые две из которых имеют один и тот же центр
подобия О, мы будем называть (собственным) рядом окружностей;
') Ср. «Г. П.», стр. 93.

РЯДЫ И СЕТИ ОКРУЖНОСТЕЙ
491

492 окружности
при этом точку О—центр ряда—мы также будем включать Н сос-
состав ряда («окружность нулевого радиуса» ряда). Кроме тбто к
числу рядов окружностей мы причислим всевозможные совокупности
окружностей фиксированного (по величине и по знаку!) радиуса г,
центры которых лежат на одной прямой z («ряд равных окружностей»;
рис. 32,а); г может быть равно нулю, так что совокупность всех
точек одной прямой тоже будет считаться рядом («ряд окружностей
нулевого радиуса».) Очевидно, что если две окружности ряда имеют
две (пересекающиеся или непересекающиеся) общие касательные m
и п, пересекающиеся в их центре подобия, то все окружности ряда
касаются прямых тип (рис. 32,а, б); в этом случае ряд (состо-
(состоящий из всех окружностей, касающихся тип) называется рядом
окружностей с общими касательными. Если две окружности (соб-
(собственного) ряда касаются в точке О, то все окружности ряда каса-
касаются друг друга в этой точке (рис. 32,в); в таком случае мы при-
приходим к ряду касающихся окружностей (сходному с пучком
касающихся окружностей; см. п. З.1.). Наконец, если какие-то две
окружности ряда не имеют общих касательных, то и никакие две
окружности не имеют общих касательных; в этом случае мы прихо-
приходим к ряду окружностей без общих касательных (рис. 32, г, д) ').
Частным случаем ряда окружностей без общих касательных
является ряд концентрических окружностей, состоящий из всех окруж-
окружностей с центром в фиксированной точке О (рис. 32,д). Во всех
же остальных случаях центры окружностей ряда не совпадают; они
заполняют некоторую прямую z — линию центров ряда (если ряд
имеет центр О, то z есть прямая, соединяющая О с центром какой-
либо окружности S ряда). Очевидно, что при этом каждая точка ли-
линии центров z является центром некоторой (и притом только одной)
окружности ряда.
8.2. Сеть окружностей. Рассмотрим теперь совокупность всех
(направленных) окружностей, каждые три из которых имеют
одну и ту же ось подобия о; такая совокупность окружностей назы-
называется (собственной) сетью окружностей, а прямая о — осью сети.
К числу сетей мы будем причислять также совокупность всех окруж-
окружностей плоскости фиксированного (по величине и по знаку!) радиуса г
(«сеть равных окружностей»); при г 0 мы приходим к совокупности
всех точек плоскости, которая тоже входит в число сетей окружно-
окружностей («сеть окружностей нулевого радиуса»). Очевидно, что собст-
собственную сеть окружностей можно также определить как совокупность
всех окружностей, относительно которых данная прямая т
имеет одну и ту же степень k; эта степень k называется степенью
') Эти три типа рядов окружностей (см. рис. 32, а, б; 32, в и 32, г, д)
называются также эллиптическим рядом окружностей, параболическим
рядом н гиперболическим рядом.

ряды и сети окружностей 493
сети. Отсюда вытекает, что собственную сеть можно также опре-
определить как совокупность всех окружностей, радиус г которых нахо-
находится в постоянном отношении / к расстоянию d от центра окруж-
окружности до оси о сети; эта величина / связана со степенью k сети
\+k / r—d , г \+k\ „
соотношением / = , . ( если —;—; = k, то —г = , . . Если степень k
1—k \ г-\-а а 1 — kj
сети положительна, то сеть можно также определить как совокуп-
совокупность всех окружностей, пересекающих ось о под постоянным углом а
таким, что tg* -jr- = k\ см. рис. 33,a J; если k=0, то сеть состоит
из всех окружностей, касающихся оси о (рис. 33,6); наконец,
если k < О, то нам приводится довольствоваться более сложным
определением сети как совокупности всех таких окружностей S,
что 5 видна под постоянным углом ф из точки Р—проекции центра О
окружности на ось о сети (угол ф связан с числом k соотноше-
нием sin -^- = -г- = . ; см. рис. 66,в ) ).
Докажем теперь, что пересечение двух различных сетей (сово-
(совокупность окружностей, принадлежащих одновременно двум сетям)
образует ряд (если только вообще есть окружности, принадлежащие
этому пересечению). Действительно, пересечение сети окружностей
постоянного радиуса г и собственной сети с осью о и степенью k
образует ряд равных дкружностей, состоящий из окружностей радиу-
са г, расстояние d центра которых до о равно f-ггь I ио° ~Xw = k) '•
пересечения двух различных сетей равных окружностей, так же как и
пересечения двух различных собственных сетей с общей осью вообще
не существует. Далее, окружности, принадлежащие одновременно
двум собственным сетям с непересекающимися осями о, и ог и сте-
степенями kt и k2, удовлетворяют условиям ' = ki и ~ * = k*
г 1 + /г, , г 1 + ?2 ,
или -г- = -.—ri = 'i и 7Г~~1—Г~12< 3Десь г — радиус окружности,
с/, и d2—расстояния от центра окружности до о, и до ог. Но рас-
расстояния dt и rf2 от любой точки плоскости до непересекающихся
прямых о, и о2 (рис. 34) связаны соотношением rf2=±(rf, — а);
здесь а — постоянное (по величине и знаку) расстояние от точек
прямой о2 до прямой о, и знаки «+» и «—» отвечают случаям,
когда прямые о, и о2 параллельны (одинаково направлены) и когда
они противопараллельны (противоположно направлены). Таким обра-
образом, мы приходим к системе уравнений
') Собственная сеть первого типа называется гиперболической, вто-
второго— параболической и третьего—эллиптической.

494
ОКРУЖНОСТИ
Рис. 33.

ОСЕВАЯ ИНВЕРСИЯ
¦Ш5
из которой следует, что
это означает, что пересечение наших двух сетей не существует,
если о, параллельно о2 и /,= /г или о, противопараллельно ог
и /, = — /г, а во всех остальных случаях представляет собой ряд
о)
Рис. 34.
равных окружностей. Наконец, если оси о, и и, двух сетей пересе-
пересекаются в точке О, то пересечение сетей образует ряд с центром О:
действительно, точка О является центром подобия любых двух окружно-
окружностей 5, и St; принадлежащих одновременно обеим сетям, ибо через
зту точку проходят две прямые, имеющие относительно 5,и 5,
одинаковые степени (прямые о, и ог).
§ 9. Осевая инверсия
9.1. Определение осевой инверсии. В полной аналогии с п. 4.1
выберем на плоскости некоторую сеть * окружностей и рассмотрим
все те окружности этой сети, которые касаются данной (направлен-
(направленной) прямой а. Эти окружности принадлежат одновременно как пер-
первой сети, так и сети всех окружностей, касающихся прямой а; со-
согласно сказанному в конце предыдущего параграфа, они образуют
ряд окружностей (мы исключаем здесь случаи, когда ось первона-
первоначальной сети совпадает с с и пересечение двух сетей вовсе не
существует или совпадает с самой сетью, а также когда сеть состоит
из окружностей, касающихся прямой, параллельной а, и пересечения
также не существует). Так как все окружности этого ряда касаются
прямой а, то мы имеем здесь либо ряд окружностей с двумя общими
касательными а и а', либо ряд касающихся окружностей. Таким
образом, выбор на плоскости определенной сети окружностей позво-
позволяет определить своеобразное отображение плоскости, перево-
переводящее каждую отличную от оси о сети (направленную) прямую.а
в новую (направленную) прямую а' (если наш ряд состоит из
окружностей, касающихся прямой а в какой-либо точке, то мы будем

496 окружности
считать, что рассматриваемое преобразование переводит прямую а
саму в себя). Это преобразование мы будем называть осевой инвер-
инверсией, отвечающей рассматриваемой сети '). При этом осевую инвер-
инверсию, отвечающую сети равных окружностей, мы будем называть осо-
особой инверсией; осевую инверсию, отвечающую сети окружностей,
касающихся одной прямой, — вырожденной; во всех же остальных
случаях мы будем иметь обыкновенную или общую осевую инверсию,
причем ось о сети называется осью инверсии, а степень k сети —
степенью инверсии.
9.2. Вырожденная инверсия и особая инверсия. Очевидно, что
вырожденная инверсия переводит каждую прямую плоскости, не
параллельную оси о сети, в одну и ту же прямую о,—это преобра-
преобразование не представляет интереса, и мы в дальнейшем исключим
его из рассмотрения. Более интересна особая осевая инверсия. Пред-
Предположим для начала, что исходная сеть состоит из всех окружностей
радиуса нуль, т. е. из всех точек. Совокупность всех «окружностей
нулевого радиуса», «касающихся» прямой а (т. е. совокупность всех
точек прямой а), представляет собой ряд (равных) окружностей
с общими касательными а и а', где прямая а' отличается от пря-
прямой а только своим направлением. Таким образом, мы видим, что
особая инверсия, отвечающая сети «нулевых» окружностей (точек)
лишь изменяет направление каждой прямой плоскости; такое пре-
преобразование в множестве направленных прямых естественно называть
переориентацией (т. е. «переменой направлений»). Очевидно, что
переориентация переводит каждую окружность S в окружность S',
отличающуюся от S только направлением (в том смысле, что прямые,
касающиеся окружности S, переходят в прямые, касающиеся окруж-
окружности S'); в частности, точки («окружности нулевого радиуса»)
переориентация переводит в себя.
Пусть теперь исходная сеть окружностей состоит из всех окруж-
окружностей радиуса г. Очевидно, что все такие окружности, касающиеся
определенной прямой а, касаются также прямой а', противопарал-
лельной а и удаленной от а на расстояние 2л (величина 2г может
быть и отрицательной—в соответствии со сказанным на стр. 482
это означает, что прямая а' расположена справа от а; на рис. 35
величина 2г положительна). Таким образом, в этом случае особая
инверсия сдвигает каждую прямую на расстояние 2г от его перво-
') Этот термин можно понимать в двояком смысле. Можно считать,
что слово «осевая» подразумевает, что рассматриваемое преобразование
задается не точкой О—«центром» инверсии, как точечная инверсия (кото-
(которую в таком случае лучше было бы назвать «центральной инверсией»),
а направленной прямой о—«осью» преобразования. Можно же рассм три-
вать слово «осевая» как указание на то, что наше преобразгвание перево-
переводит не точки плоскости снова в точки, а направленные прямые («оси»)
в направленные прямые («оси»), т, е. является осевым преобразованием
плоскости (см. ниже, стр. 504).

ОСЕВАЯ ИНВЕРСИЯ
497
начального положения и изменяет направление прямой на обратное.
Преобразование, переводящее каждую (направленную^ прямую а,
в прямую а', параллельную
а и удаленную от а на опре-
определенное расстояние d, назы-
ваетсярасширением на вели-
величину d. Очевидно, что при
расширении на величину d
каждая окружностьс центром
О и радиусом г переходит в Рис. 35.
новую окружность с тем же
центром О, но радиусом г -\- d (рис. 36, а), в частности точки переходят в
окружности радиуса г/(рис. 36, б) —с этим обстоятельством и связано
Рнс. 36.
название «расширение»*). Касающиеся окружности при расширении
') То обстоятельство, что расширение может переводить точки в окруж-
окружности и наоборот, используется в элементарной геометрии: так известное
Рис. 37.
построение общей касательной двух окружностей (рис 37), по существу,
сводится к тому, что две окружности S, и S2 при помощи расширения
переводятся в точку S, и окружность S2.
32 Энциклопедия, кн. 4

498
ОКРУЖНОСТИ
переходят в касающиеся окружности (рис. 38. а); более общо, две
окружности, касательное расстояние которых равно t, переходят при
расширении в новые окружности, касательное расстояние которых также
равно t (рис. 38, б). Итак, мы видим, что особая осевая инверсия,
отвечающая сети окружностей радиуса г, представляет собой
расширение на величину 2г, сопровождаемое переориентацией.
9.3. Свойства осевой инверсии. Перейдем теперь к обыкновен-
обыкновенной осевой инверсии (это преобразование мы часто будем называть
,_- --^ просто осевой инверсией)
с осью о и степенью k.
Очевидно, что каждая
окружность 5 сети, каса-
касающаяся определенной
прямой а, пересекающей о
в точке М, касается также
л прямой а', пересекаю-
пересекающей о в той же точке М
и удовлетворяющей усло-
'"&' "' вию
А'
t
Рис. 38
1С 39); это вытекает
из того, что прямая о
имеет относительно ок-
окружности 6' степень k.
Отсюда вытекает, что
осевая инверсия с осью о
и степенью k переводит
произвольную прямую а
в прямую а', пересекаю-
пересекающую о в той же точке, что и а, и удовлетворяющую соот-
соотношению (*)—это определение осевой инверсии полностью ана-
аналогично аналитическому определению точечной инверсии (см. стр. 471).
Что же касается параллельных оси о инверсии прямых, то каждая
окружность S сети, касающаяся такой прямой Ь, касается также
прямой Ь', противопараллельной Ь и расположенной так, что отно-
отношение расстояний от b и от Ь' до о равно k; это вытекает из того,
о г—d
что степень k прямой о относительно окружности о равна ^
(рис. 39). Поэтому инверсия переводит прямую b в Ь' (и Ь' в Ь).
Это определение осевой инверсии можно несколько «геометризи-
ровать». Условимся задавать определяющую инверсию сеть осью о
и принадлежащей сети окружностью So (т. е. такой окружностью St,
что ее степень относительно о равна k); эту окружность мы будем

осевая инверсия 499
называть направляющей окружностью осевой инверсии. Очевидно,
что осевая инверсия переводит каждую касательную ав окружно-
окружности 50 во вторую касательную а'о той же окружности, проходящую
через точку пересечения а0 с о; касательную Ьс окружности 50, не
пересекающую о, — во вторую не пересекающую о касательную Ь'Л
окружности So; произвольную прямую а, пересекающую ось о и парал-
параллельную касательной а0 окружности So, —в прямую а', пересекающую о
в той же точке, что и а, и параллельную касательной а'й окружно-
окружности 50; произвольную прямую Ь, параллельную не пересекающей о
касательной Ьо окружности SB,—в прямую Ь', параллельную bt и такую,
что отношение расстояний от b и Ь' до о равно отношению рас-
расстояний до о от Ьо и Ьв (рис. 39).
Ри . 39
Очевидно, что всякая невы] ожденная осевая инверсия (т. е. осо-
особая инверсия или обыкновение я инверсия) «переставляет» (направлен-
(направленные) прямые плоскости, т. е. переводит каждую прямую а в ту
прямую а', которая сама переходит в а1). Докажем теперь два
менее очевидных свойства осевой инверсии.
А. Всякая невырожденная осевая инверсия переводит каждую
окружность ограниченного радиуса снова в окружность ограни-
ограниченного радиуса (т. е. кажчую окружность или точку снова в окруж-
окружность или точку).
Так как и расширение и переориентация переводят каждую
окружность ограниченного радиуса снова в окружность ограничен-
ограниченного радиуса, то очевидно, что и особая инверсия обладает этим
свойством. Более сложно показать, что им обладает обыкновенная
осевая инверсия. Обозначим цен^р направляющей окружности S
') Особая инверсия переводит каждую прямую а в противопараллель
ную ей прямую а', удаленную от а на постоянное расстояние 2г и рас-
расположенную справа (или—при отрицательном г—слева) от а. Но в этом
случае и а расположена справа (слева) от а' (прямые сие' противопарал-
лельны!) откуда и вытекает, чт<> а' переходит в а.

500
окружности
нашей осевой инверсии через О0, и пусть а0 и a'Q~две касательные
окружности 50, пересекающиеся в точке Мо оси о и касающиеся
окружности 50 в точках Ао и Ав; #0 и Qo — точки пересечения
хорды /40/4^ с прямой О0М0 и с перпендикуляром О0Ре, опущенным
из О0 на ось о (рис. 40). Из подобия прямоугольных треугольни-
ков O0Qc/?n „ О.М^ O0A0RB и О0МвА0 ^ ^
и то" —/Г
имеем
перемножая почленно эти два равенства, получаем
откуда вытекает, что точка Qo ме зависит от выбора пары ка-
касательных а0, ав (т. е. от выбора точки Мо оси о).
Рис. 40.
Рассмотрим теперь произвольную окружность 5 с центром О и
пусть Q—такая точка перпендикуляра, опущенного из О на о, что
O0Q():OQ = r():r, где г0 и г — (положительные или отрицательные!)
радиусы окружностей So и S; пусть, далее, S' —такая окружность,
что центр подобия окружностей S и S' совпадает с Q,
а радикальная ось окружностей S и S'—со1). Мы утверж-
') Если S есть точка («окружность нулевого раднуса»), то S' — такая
окружность, что о есть радикальная ось окружностей S и S' и OoQ0:O'S =
= rQ:r', где О' и г' — центр и радиус окружности S'; если S—такая соб-
собственная окружность, что радикальная ось окружностей S и Q совпадает
с о, то S' совпадает с точкой Q; если S есть точка оси о инверсии, то S'
совпадает с S.
Для построения окружности S' проще всего построить пару касатель-
касательных ав и с0 окружности So и параллельные им прямые ana' (a0 и а'й,
а а а' пересекаются на оси и). Если S касается прямой а, то из доказан-
доказанного ниже следует, что S' касается с'; это, а также то, что центр подобия
окружностей S и S' нам известен (точку Q можно построить), позволяет
найти S'.

ОСЕВАЯ ИНВЕРСИЯ 501
даем, что рассматриваемая осевая инверсия переводит окружность
S в S'.
Для доказательства заметим, что точка /И, пересечения касательных
я и я, окружности 5, параллельных касательным я0 и я0 направляющей
окружности SB, принадлежит прямой о,, расположенной по отношению
к 5 точно так же, как прямая о — по отношению к So (т. е. такой, что
о, || о и O0Ps>:OP=r0:r, где Р—основание перпендикуляра, опущен-
опущенного из О на о,); это вытекает из того, что фигура, образованная
окружностью 5 и ее касательными я, я,, подобна фигуре, образо-
образованной окружностью So и касательными я0, я0. Далее, прямая ЛЛ,,
соединяющая точки соприкосновения прямых я и я, с окружностью S,
проходит через точку Q (это следует из тех же соображений подо-
подобия). Касательная я' окружности S' в точке Л' пересечения прямой
QAJ с S' параллельна я, (ибо Q есть центр подобия окружностей 5
и S'; рис. 40); далее точка М пересечения прямых ana' лежит
на радикальной оси о окружностей S и S' (ибо МА — МА', так
как треугольники М1АА1 и МАЛ' подобны, а МХА= МХАЛ (рис. 40)).
Но то, что касательные я и я' окружностей 5 и S', параллельные
касательным я0 и я0 окружности So, пересекаются на прямой о, и
доказывает наше утверждение (см. определение осевой инверсии,
стр. 499).
Б. Невырожденная осевая инверсия сохраняет касательное рас-
расстояние окружностей. Точнее, если Л, и Л2—точки соприкосновения
двух окружностей 5, и S2 ограниченного радиуса с их общей каса-
касательной t, и Л,, Л2—точки соприкосновения окружностей S, и S2,
в которые переводит Sf и S3 невырожденная инверсия, с прямой t',
в которую эта инверсия переводит прямую t, то
^1 **2 '*2'Ч -
Прежде всего очевидно, что если особая осевая инверсия пере-
переводит две окружности ограниченного радиуса 5, и 58 в окружности
S, и S2, то касательные расстояния АЛАг и AtAz этих пар окруж-
окружностей таковы, что Л,Л2 = —A,Ai=A2Al (ибо при расширении каса-
касательное расстояние двух окружностей не меняется, а при переори-
ентай.ии оно меняет" знак); таким образом, надо только показать, что
обыкновенная инверсия обладает свойством Б. Заметим далее, что если
МА и МА' суть касательные расстояния точки М оси о инверсии
и двух окружностей S и S', переходящих одна в другую при ин-
инверсии, то
это следует из того, что о есть радикальная ось окружностей S и S'
(рис. 40). Тем самым мы доказали наше утверждение для того слу-
случая, когда одной из двух окружностей является точка М оси о

502
ОКРУЖНОСТИ
инверсии. Если же S, и St — две произвольные окружности, перехо-
переходящие при инверсии в окружности 5, и 58, то точка М пересечения
общих касательных АхАг и /4,Лг к 5, и S, и к S, и 5, лежит на
оси инверсии (рис. 41); поэтому имеем
МА, =
2 = АгМ,
откуда и следует, что
В частности, из свойства Б инверсии следует, что невырожден-
невырожденная осевая инверсия переводит две касающиеся окружности в ка-
касающиеся окружности.
Рис. 41.
9.4. Теорема Брианшона. Осевая инверсия, так же как и точечная
инверсия, может быть использована при доказательстве геометрических
теорем и в решении задач на построение'). В качестве примера приведем
одну теорему, доказываемую с применением свойств осевой инверсии.
Покажем, что прямые р, q и г, соединяющие противоположные вершины
Ау и /44, А2 и Л,, Л, и At произвольного (возможно—самопересекающегося!)
описанного вокруг окружности S шестиугольника Л,/4гЛ^4Л,Л„ пересе-
пересекаются в одной точке или параллельны (теорема Брианшона).
Пусть St—произвольная (направленная) окружность, касающаяся сто-
рои AtA2 и /44Л5 нашего шестиугольника (стороны шестиугольника мы
здесь будем считать направленными, приписав им направление, отвечающее
какому-то произвольно выбранному направлению окружности S); S,—ок-
S,—окружность, в которую переводит S, осевая инверсия с осью q и направ-
направляющей окружностью S (S2 касается сторон А2А, и AbAt); S,—окружность,
в которую переводит S, осевая инверсия с осью г и той же направляющей
окружностью S (S, касается сторон А3АЛ и AeAt); наконец, S,—окруж-
S,—окружность, в которую переводит S, осевая инверсия с осью р и направляющей
окружностью S (S, снова касается сторон Л4Л5 и AtA2; рис. 42). Обозна-
') Много примеров такого рода имеется в указанной в списке лите-
литературы книге И М. Яг лом а [1].

ОСЕВАЯ ИНВЕРСИЯ
503
чая точки касания прямых AtA2, Л,Л„ AsAt и AtAs с окружностью S через
Я,, Рг, Ps и Р4, а точки касания тех же прямых с окружностями S, и S,,
Sj, Ss, снова S, и S, —через Q, и Q,, Q2, Qs, Q4 и Q4, в силу свойства Б
осевой инверсии, имеем (см. также стр. 485):
Но равенство P,Q1 = P,Q, означает, что окружности S, и S, — это одна и
та же окружность. Следовательно, прямые q, г и р являются осями инвер-
Рис 42.
сий, переводящих S, в S2, Sj в S, и, наконец, Ss снова в S,, и значит, совп«-
дают с попарными радикальными осями трех окружностей S,, S^ и S,
(см. доказательство свойства А осевой инверсии). Но отсюда вытекает,
что эти прямые пересекаются в одной точке—в радикальном центре ок-
окружностей S,, S2 и S,—или параллельны (см. п. 2.3).

504 окружности
§ 10. Осевая геометрия окружностей
10.1. Осевые круговые преобразования. В настоящем разделе
точки всюду рассматривались лишь как частный случай окружно-
окружностей— никакого самостоятельного значения они здесь не имели.
Соответственно этому мы здесь уже не будем считать точку основ-
основным геометрическим элементом и откажемся от рассмотрения точеч-
точечных преобразований плоскости, т. е. преобразований, переводящих
каждую точку снова в точку. Роль точечных преобразований будут
теперь играть преобразования множества направленных прямых линий
(осей) плоскости, т. е. преобразования, переводящие каждую направ-
направленную прямую (ось) в новую направленную прямую (ось). Такие
преобразования естественно называть осевыми преобразованиями
Рис. 43.
плоскости. Осевые преобразования, вообще говоря, уже не переводят
точки снова в точки: если понимать под точкой А совокупность
всех проходящих через нее прямых а, Ь, с,... (рис. 43, а), то при-
придется принять, что осевое преобразование переводит точку А в не-
некоторую кривую А', определяемую своими касательными я', />', с', ...
(рис. 43, б); подобно этому точечное преобразование переводит пря-
прямую а, понимаемую как совокупность точек А. В, С в кри-
кривую а', на которой лежат преобразованные точки А', В', С,
Особое место среди всех осевых преобразований занимают осе-
осевые круговые преобразования ')—такие осевые преобразования, кото-
которые переводят каждую (направленную) окружность 5 ограниченного
радиуса в новую окружность S' (т. е. переводят совокупность каса-
касательных произвольной окружности 5 в совокупность касательных
некоторой новой окружности S'). Простейшие примеры осевых кру-
круговых преобразований доставляют уже преобразования подобия:
поскольку эти преобразования переводят каждую прямую снова
в прямую, то их можно рассматривать как осевые, а так как они
') В литературе эти преобразования чаще называются преобразованиями
Лагерра.

ОСЕВАЯ ГЕОМЕТРИЯ ОКР\-ЖНОСТЕЙ 505
переводят также и окружности в окружности, го являются круго-
круговыми преобразованиями1). Более сложным примером может служить
невырожденная осевая инверсия. Нетрудно показать, что последний
пример имеет общий характер, т. е. что каждое осевое круговое
преобразование сводится к невырожденной инверсии; точнее, мы
покажем., что каждое осевое круговое преобразование представ-
представляет собой особую или обыкновенную осевую инверсию, сопровож-
сопровождаемую еще, быть может, преобразованием подобия.
Прежде всего, ясно, что осевое круговое Преобразование, пере-
переводящее каждую точку снова в точку, является преобразованием
подобия; это утверждение лишь по форме отличается от утвержде-
утверждения о том, что все точечные круговые преобразования, переводящие
прямые снова в прямые, исчерпываются преобразованиями подобия
(см. п. 5.1). Далее заметим, что если какое-либо осевое круговое
преобразование переводит какие-либо две точки А и В снова
в точки А' и В', то оно переводит все точки прямой АВ снова
в точки. Действительно, при этом две проходящие через А к В
(направленные) прямые а и Ь, отличающиеся только направлением,
переходят в (направленные) прямые а' и Ь', проходящие через А'
и В' и тоже отличающиеся только направлением, и все точки пря-
прямой АВ, «касающиеся» а и Ь, переходят в точки прямой А'В'',
«касающиеся» а' и Ь'. Поэтому, если осевое круговое преобразо-
преобразование переводит в точки три точки А, В и С плоскости, не ле-
лежащие на одной прямой, то оно переводит в точку каждую
точку М плоскости (точка N пересечения прямых AM и ВС пере-
переходит в точку, ибо она лежит на прямой ВС, и точка М переходит
в точку, так как она лежит на прямой AN; если АМ\\ВС, то нам.
придется только заменить А какой-либо другой вершиной треуголь-
треугольника ABQ и, значит, является преобразованием подобия. Таким,
образом, если осевое круговое преобразование отлично от преобра-
преобразования подобия (а только такие преобразования нас сейчас интере-
интересуют), то имеет место один из следующих трех случаев:
1) преобразование не переводит в точку ни одну точку плоскости;
2) преобразование переводит в точку одну единственную точку
п.юскости (ниже мы покажем, что этот случай на самом деле невоз-
невозможен);
*) Для того чтобы рассматривать преобразование подобия как осевое,
надо еще условиться считать, что оно переводит определенную направлен-
направленную прямую а в другую направленную прямую а' (направления а и а'
могут быть выбраны произвольно) и направленную прямую Ь—в такук>
направленную прямую Ь', что <J(a, 6) = <?(a', b') <J(a, fc) = 0, если b парал-
параллельна a, <$(а, b) = n, если Ь противопараллельна a). Таким образом, од-
одному и тому же преобразованию подобия, понимаемому как точечное
преобразование, могут соответствовать дза различных осевых преобразова-
преобразования (отвечающих двум различным выборам направления оси а').

506
окружности
3) преобразование переводит в точки все точки одной прямой
и только эти точки.
Рассмотрим теперь эти три случая последовательно.
1) Пусть осевое круговое преобразование Л не переводит в точку
я и одну точку плоскости. Рассмотрим две произвольные точки
А' я В' к две проходящие через эти точки прямые а' и Ь', отли-
отличающиеся только направлением; пусть а и b суть прямые, которые
Л переводит в я' и Ь'. В точки прямой А'В' («окружности нуле-
нулевого радиуса, касающиеся прямых а' и b '») переходят окружности,
касающиеся прямых а и Ь. Если бы прямые а и ft пересекались, то
в число последних окружностей входила бы также и точка М пере-
пересечения прямых а и b (ср. рис. 32, б на стр. 492); поэтому в одну
из точек прямой А'В' переходила бы точка М, что противоречит
лашему условию. Отсюда следует, что прямые а и b противопарал-
лельны и все касающиеся их окружности (в частности, и окружно-
окружности А к В, которые Л переводит в точки А' и В') равны (ср. выше
рис. 32, а; прямые а и b не могут быть параллельны, ибо таких
.прямых вообще не касается ни одна окружность). Итак мы видим,
что в любые две точки А' и В' переходят окружности одного ра-
лиуса; следовательно, Л переводит в точки все окружности одного
•определенного радиуса г.
Заменим теперь наше круговое преобразование особой инверсией
(расширением и переориентацией) Г, переводящей в точки окруж-
окружности именно этого радиуса г, сопровождаемой, быть может, еще
некоторым дополнительным преобразованием Р. Это дополнительное
осевое круговое преобразование переводит все точки снова в точки
¦(ибо уже Г переводит окружности радиуса г в точки) и, значит,
является преобразованием подобия; таким образом, наше исходное
преобразование Л является особой инверсией, сопровождаемой пре-
преобразованием подобия.
2) Докажем теперь, что осевое круговое преобразование Л, пере-
переводящее в точку одну единственную точку А, не может сущест-
существовать. Действительно, две отличающиеся только направлением пря-
прямые а и Ь, проходящие через точку А, должны переходить в две
прямые а' и Ь', пересекающиеся в точке А', в которую переходит А.
Рассмотрим еще некоторую, не параллельную а прямую а,; она и
совпадающая с ней по положению (отличающаяся от а1 лишь нап-
направлением!) прямая bl переходят в противопараллельные прямые
а, и bt (ибо ни одна из точек прямой at не переходит в точку;
ср. выше). Заметим теперь, что всегда найдутся такие две окруж-
окружности М', м[, касающиеся соответственно а ц Ь', а, и Ь„ что
одна из них заключается внутри другой (рис. 44, а, б). В эти две
окружности переходят две точки М и Мх прямых а и а,; две отли-
отличающиеся направлением прямые, совпадающие по положению на пло-

ОСЕВАЯ ГЕОМЕТРИЯ ОКРУЖНОСТЕЙ
507
скости с прямой ММХ, должны будут перейти в общие каса1ельные
окружностей М' и /И,; но таких касательных вовсе не существует.
Полученное противоречие и доказывает наше утверждение.
3) Пусть осевое круговое преобразование Л переводит в точки
все точки некоторой прямой о (которую мы здесь будем
считать направленной) и только эти точки; далее пусть Л перево-
переводит в некоторую не лежащую на прямой о точку А' определенную
окружность А. Заменим Л обыкновенной осевой инверсией Г с осью о,
переводящей окружность А в точку А1 (такую, что о есть радикаль-
радикальная ось окружностей А и AJ, сопровождаемой, если это требуется,
¦1'
Ь'
Рис. 44.
каким-то дополнительным осевым круговым преобразованием Р. Пре-
Преобразование Р переводит все точки прямой о снова в точки и, кроме
того, переводит в точку А' точку Ах; поэтому оно переводит все
точки плоскости снова в точки (см. выше стр. 505) и, значит, яв-
является преобразованием подобия. Таким образом, мы видим, что
в этом случае Л представляет собой обыкновенную осевую инвер-
инверсию Т, сопровождаемую преобразованием подобия Р. Этим и завер-
завершается доказательство нашей теоремы.
* 10.2. Понятие об осевой круговой геометрии. Изучение таких
свойств геометрических фигур (в частности, окружностей и различ-
различных систем окружностей), которые не разрушаются осевыми круго-
круговыми преобразованиями, составляет предмет осевой круговой гео-
геометрии, или геометрии Лагерра. Иногда при этом вместо совокуп-
совокупности всех осевых круговых преобразований рассматривают лишь те
из них, которые сохраняют касательное расстояние двух окружностей
(т. е. невырожденные осевые инверсии и движения, а также произ-
произведение осевых инверсий и движений); это позволяет использовать в
осевой круговой геометрии понятие касательного расстояния (в общей

508 окружности
осевой круговой геометрии можно говорить лишь об отношении
касательных расстояний двух пар окружностей1)). Осевая круговая
геометрия представляет собой содержательную геометрическую дис-
дисциплину 2). Большую роль в этой геометрии играют понятия ряда и
сети окружностей; последнее связано с тем, что каждое осевое кру-
круговое преобразование переводит ряд окружностей снова в ряд и сеть
окружностей в сеть (докажите!).
В. ОКРУЖНОСТЬ КАК СОВОКУПНОСТЬ ЛИНЕЙНЫХ ЭЛЕМЕНТОВ
§11. Новый взгляд на окружность
11.1. Плоскость как множество линейных элементов. В первом
разделе настоящей статьи окружность рассматривалась как множе-
множество («геометрическое место») точек. При этом прямая, как правило,
считалась лишь частным случаем окружности, в то время как точки
играли особую роль: они принимались за основной элемент геомет-
геометрии, что находило отражение, например, в том, что в первом разделе
рассматривались исключительно точечные преобразования плоско-
плоскости— преобразования, переводящие точки) к числу которых причис-
причислялась также «бесконечно удаленная точка» Q) снова в точки.
В противоположность этому во втором разделе мы рассматривали ок-
окружность как совокупность прямых линий; соответственно этому
здесь уже точка считалась частным случаем окружности, а прямая
играла особую роль. Теперь мы хотим наметить построение более
общей теории, в которой и прямые и точки совершенно равноправны
с окружностями (представляют собой лишь частные случаи окруж-
окружности). При этом прямые и окружности мы здесь, как и во второй
главе, будем считать направленными, а к числу точек, как и в пер-
первой главе, отнесем также «бесконечно удаленную точку» Q. Под
двумя касающимися окружностями мы теперь будем понимать:
две касающиеся (направленные) окружности или (направленные)
окружность и прямую, имеющие в точке касания одинаковое
направление;
две параллельные (т. е. не пересекающиеся и одинаково направ-
направленные) прямые;
точку и проходящую через эту точку окружность или прямую;
«бесконечно удаленную точку» Q и произвольную прямую.
Поскольку ни точки, ни прямые не будут ничем выделяться из
всего множества окружностей (понимаемых в указанном выше широ-
') Взаимоотношение между совокупностью всех осевых круговых пре-
преобразований и совокупностью осевых круговых преобразований, сохраня-
сохраняющих касательные расстояния между окружностями, аналогично отноше-
отношению между преобразованиями подобия и движениями.
г) Основы которой изложены, например, в указанной в конце статьи
книге В. Бляшке [7].

НОВЫЙ ВЗГЛЯД НА ОКРУЖНОСТЬ
509
ком смысле), то основным элементом геометрии здесь придется счи-
считать какой-то новый геометрический образ. За такой образ удобно
принять так называемый линейный элемент (А, а), т. е. совокун-
Рис. 45.
ность точки А и проходящей через нее (направленной) прямой а
(другими словами, совокупность точки и заданного в этой точке
направления). Окружность мы теперь будем рассматривать как сово-
совокупность всех линейных элементов, зада-
задаваемых точкой окружности и касательной
к окружности в этой точке (рис. 45, а)',
точки, и прямые мы также будем пони-
понимать как совокупности линейных элемен-
элементов (рис. 45, б, в). Заметим еще, что
касание двух окружностей с принятой
здесь точки зрения означает наличие у
них общего линейного элемента (рис. 46);
если уговориться еще, что задание
какого-то направления (указываемого направленной прямой я; две
параллельные прямые задают одно направление) и «бесконечно уда-
удаленной точки» Q определяет «бесконечно удаленный линейный эле-
элемент» (Q, я), то это условие охватит все перечисленные выше
случаи касания окружностей.
Рис. 46.
6)
11.2. Новое определение окружности. При построении геометрии в мно-
множестве элементов каждую кривую \ приходится рассматривать как сово-
совокупность определенных этой кривой линейных элементов (рис. 47, а); при
этом в определении кривой как «геометрического места» линейных

610 ОКРУЖНОСТИ
элементов (Av а,), (Аг, а2), (Л,, а,), . .. надо специально оговаривать, что
точки Аг, Л2, As, ... и прямые а,, а2, а, взятые в отдельности,
определяют одну и ту же кривую, т. е. что не имеет место случай, изо-
изображенный на рис. 47, б (другими словами, надо потребовать, чтобы для
каждого линейного элемента (А, а) рассматриваемой совокупности линейных
элрментов прямая а являлась касательной в точке А к кривой, определенной
всеми точками этих элементов; отсюда
уже будет следовать, что А является точ-
точкой прикосновения прямой а с кривой,
определенной прямыми рассматриваемых
линейных элементов). Окружность как
множество линейных элементов опреде-
определяется как такая кривая, что для двук
произвольных ее линейных элементов (А, а)
и (В, Ь) расстояние АВ полностью опре-
определяется углом Z. (а' Ь) и наоборот (т. е.
если ни расстояние АВ, ни угол /_ (а, Ь)
не равны тождественно нулю для всех
пар линейных элементов кривой, то для
двух пар линейных элементов (А,, а,),
(B1F 6,) и (Аг, а2), (В2, 62) с равными рас-
расстояниями A,B, и Л2В2 равны и углы
?_ (а,, 6,) и /_ (а2, Ьг); рис. 48). При этом
радиус окружности можно определить как
АВ
предел отношения ———j-т- при /_ (а. 6)->-0 или ЛВ-^О1); радиус окруж-
окружности может также равняться нулю (окружность нулевого радиуса пред-
представляет собой точку) или быть бесконечным (окружность бесконечного
радиуса — прямая). Если считать углы направленными (см. § 1 раздела А),
то это определение будет учитывать также и знак радиуса (см. п. 6.2).
§ 12. Касательная геометрия окружностей
12.1. Касательные круговые преобразования. Изучение свойств
окружностей, рассматриваемых как совокупность линейных элементов,
служит предметом весьма содержательной теории, которую можно
было бы развивать аналогично построениям первых двух разделов
статьи. Так, например, здесь можно было бы определить понятие
«степени окружности относительно окружности» и с помощью этого
понятия выделить некоторые специальные системы окружностей, род-
родственные пучкам и рядам или связкам и сетям; далее с помощью
этих систем окружностей можно определять своеобразную «инверсию»,
представляющую собой такое преобразование в множестве линейных
элементов, при котором каждая окружность (понимаемая в принятом
в этой главе широком смысле) переходит в новую окружность и т. д.
') Окружность характеризуется тем, что между расстоянием АВ и уг-
углом /_ (а, Ь) имеется функциональная зависимость: AB = f(?(a, b)); радиус
окружности равен производной возникающей таким образом функции
у = 1(х) при х = 0 (см. ЭЭМ., кн. III, статью «Производные. Интегралы
и ряды»). Угол всюду измеряется в радианной мере.

КАСАТЕЛЬНАЯ ГЕОМЕТРИЯ ОКРУЖНОСТЕЙ 5 И
Однако изложение этой теории требует значительно больше места,
чем допускают рамки настоящей статьи.
Мы здесь ограничимся лишь вопросом о сведении произвольных
касательных круговых преобразований *), т. е. таких преобразований
в множестве линейных элементов,которые переводят каждую окружность
снова в окружность (переводят совокупность линейных элементов произ-
произвольной окружности в совокупность линейных элементов какой-то
другой окружности), к известным нам уже точечным и осевым кру-
круговым преобразованиям. Касающиеся окружности, т. е. окружности,
Рис. 49.
имеющие общий линейный элемент, касательное круговое преобразо-
преобразование переводит снова в касающиеся окружности; с этим обстоятель-
обстоятельством связано и само название «касательное преобразование»2).
Очевидно, что рассмотренные в разделах А и Б точечные кру-
круговые преобразования и осевые круговые преобразования являются
частными случаями касательных круговых преобразований. Действи-
Действительно, поскольку, например, точечное круговое преобразование К
переводит касающиеся окружности снова в касающиеся окружности,
то его можно считать также преобразованием в множестве линейных
элементов: так как совокупность всех окружностей, проходящих через
определенную точку А и касающихся в этой точке друг друга,
переходит в совокупность окружностей, касающихся друг друга
в какой-то другой точке А' (рис. 49), то можно считать, что К
переводит каждый линейный элемент (А, а) в другой линейный
*) В литературе эти пргобразования обыкновенно называются круго-
круговыми преобразованиями Ли.
2) Вообще касательными преобразованиями со ласно Ли называют также
такие преобразования в множестве линейных элементов, которые переоодят
каждую кривую (см. п. 11.2) снова в кривую; такие преобразования пе-
переводят касающиеся кривые (кривые, имеющие общий линейный рлемент)
снова в касающиеся кривые. Касательные круговые преобразования пред-
представляют собой частный случай общих касательных преобразований.

512 окружности
элемент (А', я'I)- С нашей новой точки зрения точечные и осевые
круговые преобразования можно характеризовать как такие касатель-
касательные круговые преобразования, которые переводят точки снова в точки,
соответственно переводят прямые в прямые. Однако существуют
также касательные круговые преобразования, которые не сохраняют
ни точек, ни прямых; к такому преобразованию мы придем, например,
если произведем подряд несколько точечных и осевых круговых
преобразований (скажем, сначала точечную, а затем осевую инверсию).
Оказывается, что этот прием получения касательных круговых пре-
преобразований имеет общий характер, т. е. что всякое касательное
круговое преобразование можно представить в виде последова-
последовательности нескольких точечных и осевых круговых преобразо-
преобразований *).
Сначала предположим, что касательное круговое преобразование М,
переводит в себя некоторую точку А. Произведем теперь последовательно
(точечную) инверсию I с центром А, преобразование М, и еще одну инвер-
инверсию I; полученное таким образом преобразование мы обозначим через Л.
Прямую а инверсия I переводит в окружность S, проходящую через точку
А (окружность, «касающуюся окружности нулевого радиуса А»); преоб-
преобразование М, переводит S в другую окружность S', также проходящую
через А (ибо М„ по предположению, переводит А в себя); наконец, I пе-
переводит S' в другую прямую а'. Таким образом, мы сидим, что преобра-
преобразование Л—последовательность преобразований I, M, и I — переводит каж-
каждую прямую линию снова в прямую линию и, значит, является осевым кру-
круговым преобразованием (обыкновенной или особой осевой инверсией, сопро-
сопровождаемой еще, быть может, преобразованием подобия). Последователь
ность же инверсии I, осевого кругового преобразования Л и снова инвер-
инверсии I совпадает с последовательностью двух преобразований I, исходного
касательного кругового преобразования М, и еще двух инверсий [, т. е.
совпадает с преобразованием М, (ибо две последовательные инверсии I,
очевидно, взаимно уничтожаются); этим и доказывается, что М, можно
представить в виде последовательности трех преобразований I, Л и I.
Рассмотрим теперь произвольное касательное круговое преобразование
М. Если М переводит все точки снова в точки, то оно, как мы уже знаем,
сводится к (точечной) инверсии. Предположим теперь, что М переводит
*) Точечная инверсия с центром О и степенью k представляет собой ка-
касательное круговое преобразование, переводящее каждый линейный эле-
элемент (А, а) в линейный элемент (А^, а'), где А и А' лежат на-одной пря-
прямой т с центром О инверсии, ОА -OA' = k и <$(т, а)=<$(а', т)\ последнее
условие указывает также, как следует направить а', если считать прямую
а направленной. Осевая инв-рсия с осью о и степенью k переводит друг
в друга линейные элементы (А, а) и (А', а'), где а и о' пересекаются в
точке М оси о, tg '—- - tg 9'—- = k и АМ=МА' Столь же просто
указать, как преобразуют произвольный линейный элемент (А, а) особые
точечная и осевая инверсии; мы предоставляем это сделать читателю.
г) Используя терминологию статьи «Г. П.», можно сказать, что каждое
касательное круговое преобразование представляет собой произведение
нескольких точечных и осевых круговых преобразований.

КАСАТЕЛЬНАЯ ГЕОМЕТРИЯ ОКРУЖНОСТЕЙ 513
точку А в окружность S с центром А' и радиусом г1). Обозначим через Т
параллельный перенос на вектор А'А 2) и через Г—особую осевую инвер-
инверсию, определяемую сетью окружностей радиуса г (особую инверсию Г
можно также заменить расширением на величину—г). Преобразование Т пере-
переводит окружность S в окружность S' с центром А и радиусом г; Г переводит
S' в точку А; таким образом, последовательность преобразований М, Т и
Г представляет собой касательное круговое преобразование (обозначим
его через М,), переводящее точку А в себя. Но такое преобразование, как
мы только что показали, можно заменить последовательностью (точечной)
инверсии 1, осевого кругового преобразования Л (обыкновенной или особой
осевой инверсии, сопровождаемой преобразованием подобия) и инверсии I.
С другой стороны, М представляет собой последовательность преобразова-
преобразования М,, особой инверсии Г и параллельного переноса Т на вектор АА'
(последовательность трех преобразований М„ Г и Т не отличается от по-
последовательности пяти преобразований М, Т, Г, Г и Т; но две последо-
последовательные диверсии Г взаимно уничтожаются и два параллельных пере-
переноса Т и Т также взаимно уничтожаются). Таким образом, М совпадает
с последовательностью пяти преобразований I, Л, I, Г u T, что и доказы-
доказывает наше утверждение.
12.2. Задача Аполлония. Касательные круговые преобразования
допускают многочисленные применения к доказательству геометри-
геометрических теорем и к решению задач на построение. Здесь мы огра-
ограничимся одним известным примером такого рода.
Пусть нам требуется построить окружность S, касающуюся
трех заданных окружностей Sx, St и St (рис. 50, а; эта задача
на построение носит название задачи Аполлония). Первона-
Первоначально эта задача кажется очень сложной, поскольку совсем не видно,
как nepefltn от имеющихся ничем не связанных друг с другом ок-
окружностей 5,, 5, и 5, к искомой окружности 5. Можно, однако, так
упростить чертеж задачи, что новая задача будет уже совсем простой.
Прежде всего мы с помощью какого-либо осевого кругового пре-
преобразования Л переведем окружность 5, в точку 5,; окружности 5,
и S, перейдут при этом в новые окружности S2 и 5,. В качестве
преобразования Л можно использовать особую осевую инверсию или
расширение на величину —/",, где гх— радиус окружности 5, (см.
рис. 50, б.) При этом использование осевого кругового преобразо-
преобразования предполагает, разумеется что окружности Sx, S2 и 5, являются
') Если М переводит А в прямую а, то вместо М мы будем рас-
рассматривать последовательность М преобразования М и какой-либо (точеч-
(точечной) инверсии I, переводящей а в окружность S; в свою очередь М будет
получаться, если последовательно произвести преобразования М и I.
(Впрочем, можно доказать, что никакое касательное круговое преобразо-
преобразование не переводит все точки плоскости в прямые, так что наверное най-
найдется точка А, которую М переводит в окружность S ограниченного ра-
радиуса.)
') См. стр. 54.
33 Энциклопедия, кн. 4

514
окружности
S ,'
Рис. 50

КАСАТЕЛЬНАЯ ГЕОМЕТРИЯ ОКРУЖНОСТЕЙ ,) 1!)
направленными. Если зги окружности первоначально были
ненаправленными, го мы зададим их направления произвольно. Раз-
Различный выбор направлений эгих окружностей ааст нам разные реше-
решении задачи Аполлония ').
Искомая окружность S преобразованием А (скажем, расширением)
переводи 1Ся в окружность S', касающуюся окружностей Л'г и .S, и
проходящую через точку 5,. Произведем теперь точечное круговое
преобразование, перево 1шцее точку ?, в «несобственную» точку И,
скажем, инверсию I с центром S-,. При этом окружности 5, и 5,
перейдут в какие-то окружности Л., и Ss, а искомая окружное!i> S' —
в прямую S", касающуюся окружностей S2 и St. Таким образом,
касательное круговое преобразование К, представляющее собой
последовательность авух преобразований — осевого круговою преоб-
преобразования (расширения) А и точечного кругового преобразования
(инверсии) I, — переводит окружности 5,, Ss и 6'3 в «несобственную»
точку Q и в две окружности St и Ss; искомую окружность Л' каса-
касательное круговое преобразование К переводит в прямую Л'", касаю-
касающуюся окружное!ей S2 и .S,. Зная окружности •?. и 5„ .-»ту прямую
S" нетрудно построить; затем от прямой S" легко перейти к окруж-
окружности S' и, наконец, к искомой окружности 6'. В зависимости or
расположения и направлений окружностей St и 53 задача может
иметь два решения (именно зтот случай изображен на рис. 50),
одно решение или ни одного решения.
12.3. Понятие о касательной геометрии окружностей. Изуче-
Изучение таких свойств фигур, которые сохраняются при касательных
круговых преобразованиях, составляет предмет касательной геомет-
геометрии окружностей2). Доказанное выше позволяет утверждать, что
касательная геометрия окружностей изучает свойства фигур,
сохраняющиеся как при точечных, так и при осевых круговых
преобразованиях, и только эти свойства. В этой геометрии уже
не имеет смысла ни понятие угла между окружностями, ни понятие
касательного расстояния; негрут.но показать даже, что здесь нельзя
указать никакого аналога этих понятий, поскольку любую пару ок-
окружностей можно перевести соответственно подобранным касатель-
касательным круговым преобразованием в любую фугую пар\ окружностей.
') Ниже мы \видим, что если окружности S,, S2 и S3 направленные,
то задача Аполлония может иметь до двух решений. Направление трех
ненаправленных окружностен можно выбрать 2-2-2 = 8 разными способами;
это приводит к 16 различным окружностям S. Но эти 16 направленных
окружностей попарно отличаются одна от другой только направлением.
Таким образом, мы заключаем, что в случае ненаправленных окружностей
наибольшее возможное число решений задачи Аполлония равно восьми
2) Элементы эт~й геометрии содержатся в книге Бляшке [7], на кото-
которую мы уже неоднократно ссылались.
33*

516
окружности
Напротив, уже не каждые две тройки окружностей будут обладать
в касательной геометрии окружностей одинаковыми свойствами: так,
легко видеть, что изображенные на рис. 51, а, б две тройки окруж-
окружностей 5,, 5г, 5, и St, S2, Sa нельзя перевести одну в другую (ибо
в противном случае прямая 5 перешла бы в окружность S, «касаю-
«касающуюся» St, St и 5,, а такой окружности вовсе не существует).
Впрочем, можно показать, что все различные (с точки зрения каса-
касательной геометрии окружностей) тройки окружностей, никакие две
Рис. 51.
из которых не касаются между собой, исчерпываются этой парой:
каждую другую тройку окружностей можно перевести касательным
круговым преобразованием в одну из изображенных на рис. 51, а, б.
Более содержательно изучение свойств четверок окружностей; здесь
можно выделить некоторые особо интересные типы четверок и со-
составить некоторые «инварианты» четверок окружностей, т. е. сопо-
сопоставить с четверками окружностей определенные числа, совпадение
которых для двух четверок означает, что в смысле касательной кру-
круговой геометрии эти четверки окружностей «одинаковы», т. е что они
переводятся одна в другую некоторым касательным круговым преоб-
преобразованием. Мы, однако, не имеем никакой возможности остановиться
здесь на этих деталях касательной геометрии окружностей.
ЛИТЕРАТУРА
[1] И. М. Я г л о м, Геометрические преобразования, Гостехиздат, т. I, M.,
1957; т. И, М., 1958.
Книга содержит много частных теорем, касающихся свойств окруж-
окружностей. Второй том состоит из двух глав, последняя из которых специ-
специально посвящена применениям точечной и осевой геометрии окружно-
окружностей к элементарной геометрии.
12] Д. И. П е р е п е л к и н, Курс элементарной геометрии, Гостехиздат,
т. I, М.—Л., 1948, т. И, 1949.
Заключающая т. I гл. X посвящена элементам геометрии окружностей,
включающим понятие о радикальной оси и радикальном центре, о пуч-
пучках окружностей, о точечной инверсии и расширении; имеются также

ЛИТЕРАТУРА 517
много приложений этих понятий к решению элементарно-геометриче-
элементарно-геометрических задач. Заключающая т. II гл XX посвящена стереометрическим
аналогам всех этих понятий.
[3] Ж. Адамар, Элементарная геометрия, перев. с франц., Учпедгиз, ч. 1,
М , 1957, ч. 2, 1958.
Весьма обширный курс элементарной геометрии, содержащий много
задач, сопровождаемых подробными решениями. В т. I, посвященном
планиметрии, имеются понятия радикальной оси и радикального
центра, а также точечной инверсии; в т. II освещены соответствующие
стереометрические понятия. Много приложений.
[4] Б. Н. Д е л о н е и О. К. Ж и то м и р с к i й. Задачник по геометрии, М.,
•Физматгиз, 1959.
Планиметрическая часть книги завершается циклом задач «Начала
геометрии кругов», в котором в форме задач изложены основные по-
понятия (точечной) геометрии окружностей Все задачи сопровождаются
решениями.
[5j Ф. К л е й и, Элементарная математика с точки зрения высшей, т И,
Геометрия, перев. с нем., М.—Л., ОНТИ, 1934.
Весьма содержательный обзор некоторых центральных геометриче-
геометрических понятий и вопросов преподавания геометрии; изложение элементар-
элементарное, но нелегкое в силу сжатости. В части книги, посвященной геомет-
геометрическим преобразованиям, отмечена инверсия и общие касательные
преобразования; в дополнительных замечаниях о некоторых вопросах
элементарной геометрии говорится о расширении.
[6] Ф. Клейн, Высшая геометрия, перев. с нем., М.—Л., ГОНТИ, 1939.
Неэлементарное сочинение, содержащее много материала по геомет-
геометрии окружностей. В частности, в книге говорится о всех трех видах
круговых> преобразований, фигурирующих в настоящей статье.
7] В. Бляшке (W. Blaschke), Vorlesungen fiber Differentialgeometrie,
Bd III, Differentialgeometrie der Kreise und Kugeln, Berlin, 1929- r.
Обширная монография по геометрии окружностей и сфер. Изложе-
Изложение весьма ясное, но неэлементарное

ОСНОВНЫЕ ПОНЯТИЯ СФЕРИЧЕСКОЙ ГЕОМЕТРИИ
И ТРИГОНОМЕТРИИ
СОДЕРЖАНИЕ
§ 1 Основные понятия сферической геометрии 518
1.1. Происхождение сферической геометрии . . 518
1.2. Точки, большие окружности, малые окружности ... 519
1.3. Движение сферы 522
1.4. Предмет сферической геометрии ... ... 524
1.5. Принцип двойственности 526
1.6. Углы на сфере 527
§ 2. Сферические треугольники 530
2.1. Треугольники и двуугольники на сфере . 530
2.2. Полярные треугольники . . 530
2.3. Равенство сферических треугольников .......... 532
2.4. Большая окружность как кратчайшая 534
2.5. Площадь сферического треугольника . . . . 536
§ 3. Малые окружности 539
3.1. Окружности и углы на сфере . 539
3.2. Геодезическая кривизна малой окружности ........ 541
3.3. Формула Гаусса — Бонне .... 543
§ 4. Тригонометрические соотношения в сферическом треугольнике 545
4.1. Сферическая теорема косинусов .... 545
4.2. Сферическая теорема синусов . . . 547
4.3. Формулы пяти элементов . . 549
4.4. Двойственная теорема косинусов 551
4.5. Формулы котангенсов 552
4.6. Случай прямоугольного сферического треугольника 553
4.7. Решение сферических треугольников 555
Литература 557
§ 1. Основные понятия сферической геометрии
1.1. Происхождение сферической геометрии. Геометрия на пло-
плоскости имеет, как известно, существенно «земное» происхождение —
она возникла, как указывает самое слово «геометрия» (YTioiLiETota —
«землемерие»), из измерения земельных участков таких размеров,
которые позволяют рассматривать поверхность земли как плоскость.
Сферическая геометрия, т. е. геометрия на сфере, имеет, на-
притив, «небесное» происхождение: с геометрией на сфере люди
столкнулись впервые в астрономии, при изучении видимой «небесной
сферы». Сферическая геометрия возникла в I—II веках нашей ары,

OCHOBHWF ПОНЯТИЯ СФЕРИЧЕСКОЙ ГГОМ1-ТРИИ
519
когда после римских завоеваний был установлен тесный кон гакi
между греческими н александрийскими геометрами и вавилонскими
aciponoMiiMH. Н I в. появилась .<Сферика» Me не лая. которая тотчас
же была применен.) к астрономии знаменитым Клавдием Птолемее м.
Позже, с развитием мореплавания и географии, сферическую геомет-
геометрик» стали применять и к поверхности земного шара. В настоящее
время как плоская, так и сферическая геометрия широко применя-
применяются в геодезии—на плоской геометрии основана «низшая геоче-
зия»— геодезия небольших участков ?ечли. на сферической геомет-
геометрии основана «высшая геодезия» — геодезия больших участков земли.
Межа.} плоской и сферической геометриями имеется много
общего; это объясняется тем, что сфера облачает такой же «под-
«подвижностью», как и плоскость: вся
кую точку плоскости и выходящее
из нее направление (рис. 1) можно
совместить движением этой пло-
плоскости со всякой чругой ючкой
Рис, 1.
Рис. 2.
плоское ги и выходящим из нее направлением, и точно так же вся-
всякую точку сферы и выходящее из нее направление (рис. 2) можно
совместить вращением этой сферы tv всякой другой точкой сферы
и выходящим из нее направлением*).
1.2. Точки, большие окружности, малые окружности. Если
основными понятиями плоской геометрии являются гонка, прямая и
движение плоскости2), то в сферической 1еометрин такую же роль
играют точка сферы, большая окружность и движение сферы.
Разъясним смысл этих понятий. Сечение сферы венкой плоскостью
представляет собой окружное г ь, так как если опустить из центра
сферы перпендикуляр на эту плоскость и произвести поворот про-
пространства вокруг этою перпендикуляра на любой угол, то при по-
повороте перейдет в себя как сфера, так и плоскость и, спечовательно,
литы их пересечения; поэтому всякая точка этой линии пере-
пересечения нахочится на одном и том же расстоянии от точки пересе-
пересечения плоскости с перпендикуляром, откуда вично, что эта линия
"> См в связи с stum статью о неевклидовых геометриях в кн. V ЭЭМ.
*) См. статью «Аксиомы и основные понятия геометрии», стр. 32.

520 ochobhhf понятия сферической геометрии и тригономктрии
пересечения—окружность. Радиус о этой окружности является ка-
катетом прямоугольного треугольника (рис. 3), гипотенуза которого —
радиус г, а второй катет—перпендикуляр Л, опущенный из центра
сферы на плоскость. Поэтому в силу теоремы Пифагора
Рис. 3.
Эта формула показывает, что величина g принимает максимальное
значение 6 = г при Л=0, т. е. в том случае, когда плоскость проходит
через центр сферы, т. е. является диаметральной плоскостью. В этом
случае окружность на сфере и называется большой окружностью
(иногда —- большим кругом). При
Л>0 мы имеем Q<r; окруж-
окружность на сфере называется в этом
случае малой окружностью.
Так как через всякие три точки
пространства, не лежащие на од-
одной прямой, проходит единствен-
единственная плоскость, то через всякие
две точки сферы, не являющиеся
диаметрально противоположными
(т. е. концами одного диаметра)
проходит единственная диамет-
диаметральная плоскость. Поэтому через
всякие две точки сферы, не явля-
являющиеся диаметрально противо-
противоположными, проходит единственная большая окружность (рис. 4).
Этот факт вполне аналогичен тому, что на плоскости через всякие две
точки проходит единственная прямая. Через две диаметрально про-
противоположные точки сферы, напротив, можно провести бесконечное
множество больших окружностей (рис. 5). Так как всякие две диамет-
диаметральные плоскости сферы пересекаются по ее диаметру, то всякие
две большие окружности пересекаются в двух диаметрально про-
противоположных точках сферы (рис. 6). Здесь мы наблюдаем отли-
отличие сферической геометрии от плоской геометрии, в которой две
прямые пересекаются не более чем в одной точке.
Так как плоскость делит пространство на две области, го боль-
большая окружность делит сферу на две области (рис. 4); эти об-
области называются полусферами. Далее, так как две пересекающиеся
плоскости делят пространство на четыре области, то две большие
окружности делят сферу на четыре области (рис. 6). Наконец,
так как три плоскости, пересекающиеся в одной точке, делят про-
пространство на восемь областей, то три большие окружности, не пе-
пересекающиеся в одной точке, делят сферу на восемь областей
(на рис. 7 изображены восемь областей ABC, ABC, AB'C. А'ВС,

ОСНОВНЫЕ ПОНЯТИЯ СФЕРИЧЕСКОЙ ГЕОМЕТРИИ
521
АВ'С, А'ВС. А'В'С, А'В'С, на которые делят сферу большие ок-
окружности АВ, АС и ВС, причем точки А',В,'С диаметрально про-
противоположны точкам А,В,С и, следовательно, области ABC и А'ВС,
ABC' и А'В'С, АВ'С и А'ВС, А'ВС и АВ'С попарно диаметрально
проти вопо ложны).
Рис. 4.
Рис. 5.
Если первые два из этих свойств аналогичны свойствам прямых
на плоскости, которая делится на две области прямой и на четыре
области двумя пересекающимися прямыми, то третье из указанных
свойств не вполне аналогично соответствующему свойству прямых
Рис. 6.
Рис. 7.
на плоскости, так как три попарно пересекающиеся прямые, не про-
проходящие все три через одну точку, делят плоскость не на восемь,
а на семь частей (рис. 8).
Всякой большой окружности соответствуют две диаметрально
противоположные точки сферы, высекаемые из нее диаметром, пер-
перпендикулярным к плоскости большой окружности (рис. 9). Эти две
точки называются полюсами большой окружности (от греческого
слова я6Я,о2, в латинской форме pulus — «ось», так как перпендикуляр.

522 ОСНОВНЫЕ ПОНЯТИИ СФЕР ИЧ НСКОЙ П-'ОМЕТРИИ И ТРИГОНОМЕТРИИ
восставленный к плоскости окружное in и ее центре, наливается
осью окружности в просфанстве); в частности, полюсами экватора
Земли Являются ее географические полюсы—Северный и Южный.
Очевично, что каждым двум диаметрально противоположным точ-
точкам Л и В на сфере соответствует единственная большая окружность.
Рис. 8.
т. 1я которой точки А и И являются полюсами; эта большая окруж-
окружность называется полярой пары диаметрально противоположных го-
чек А, В (от латинского слова polaris, прилагательного к слову polus).
Каждая точка поляры назыиается полярно сопряженной с кажаым
Рис. 9.
из ее полюсов: иначе говори, точки P. Q сферы являются полярно
сопряженными, если радиусы ОР и OQ перпендикулярны (О—центр
сферы).
1. 3. Движение сферы. Движением сферы называется гакое пре-
преобразование1) сфеоы. при котором сохраняются расстояния между
*) Ср. статьи «Геометрические преобразования», стр. 60, и «Аксиомы и
основные понятия геометрии», стр. 36 -37.

ОСНОВНЫЕ ПОНЯТИЯ СФКРИЧКСКОЙ ГЕОМЕТРИИ
523
точками Иными словами, иреобразовлние ц, сферы является движе-
движением, если для любых точек А, В сферы расстояние между точ-
точками ф {А) и ц> {В) равно расстоянию межчу точками А и В. Так-
как две точки А и В в гом и только в гом случае являются
диаметрально противоположными, если расстояние между ними имеег
наибольшее возможное значение, равное 1г (где г — радиус сферы),
то из определения движения непосредственно следуе i. чго при любом
Рис 10.
Рис. 11.
движении сферы Оиаметрально противоположные точки сферы пе-
переходят в диаметрально противоположные точки. Это свойство
также не имеет аналога в плоской геометрии, так как на плоскости
нет таких пар точек, что шижение одной из этих точек вполне
определяет движение второй. Поэтому, если движение плоскости
является преобразованием множества точек этой плоскости, го дви-
движение сферы по существу является преобразованием множества
нар диаметрально противоположных точек сферы.
В качестве примера движения сферы укажем поворот сферы
вокруг некоторого ее диаметра СС' h;i угол а, при котором каждая
окружность сферы, имеющая линию СС своей осью, поворачиваетси
но себе на угол а (рис. 10; разумеется, все окружности поворачи-
поворачиваются на угол а в саном и том же направлении). Другим примером

524 основные понятия сферичрской геометрии и тригонометрии
движения сферы является симметрия сферы относительно не-
некоторой ее диаметральной плоскости П, при которой каждая точка А
переходит в такую точку А', что плоскость П перпендикулярна от-
отрезку АА' и проходит через его середину (рис. 11). Поворот и сим-
симметрия являются в некотором смысле основными движениями сферы;
именно можно доказать, что всякое (нетождественное) движение
сферы либо является поворотом, либо является симметрией,
либо представляет собой произведение поворота и симметрии
(ср. стр 89).
1.4. Предмет сферической геометрии. Теперь мы можем более
четко очертить содержание сферической геометрии: сферическая гео-
геометрия изучает те свойства фигур на сфере, которые сохраняются
при любых движениях сферы fcp. стр. 99). Фигуры на сфере, ко-
которые могут быть переведены одна в другую некоторым движением
сферы, называются равными фигурами, геометрические свойства рав-
равных фигур одинаковы.
Иногда предмет сферической геометрии определяется иначе. Именно,
вместо движений, определенных выше, рассматриваются только повороты
сферы и изучаются те свойства фигур, которые сохраняются при поворотах.
Фигуры, переходящие друг в друга при некотором повороте, называют
Рис. 12.
в этом случае равными. Фигуры же, которые перехоаят друг в друга
шри движении (в определенном выше смысле), но не могут быть совме-
совмещены поворотом, равными не считают; такие фигуры называют (при
указанном подходе к сферической геометрии) симметричными. Так, на
рис. 12, о изображены равные фигуры (сферические треугольники, см. ниже),
а на рис. 12, б—симметричные фи "уры.
Эти два подхода к сферической геометрии можно сопоставить с двумя
аналогичными подходами к геометрии на плоскости. Именно совокупность
всех движений плоскости можно понимать в смысле, указанном в статье
«Аксиомы и основные понятия геометрии» (т. е. рассматривать все пово-

ОСНОВНЫЕ ПОНЯТИЯ СФЕРИЧЕСКОЙ ГЕОМЕТРИИ
525
роты, параллельные переносы плоскости, а также симметрии относительно
прямой и произведения симметрии и поворотов, симметрии и переносов,
см. стр. 89). С другой стороны, допустимо также построение геометрии
на плоскости, при котором допускаются лишь «движения 1-го рода»—по-
рода»—повороты и параллельные переносы. При такой точке зрения равными счи-
считаются лишь фигуры, переходящие цруг в друга при некотором повороте
или переносе, т. е. фигуры, не только «равные» в обычном понимании
Рис. 13.
этого слова, но имеющие одинаковое направление обхода (по или против
часовой стрелки). Фигуры же, «равные» в обычном смысле, но имеющие
противоположные направления обхода, считают при таком подходе к плос-
плоской геометрии не равными, а лишь «симметричными». На рис. 13, а изо-
изображены равные треугольники, а на рис. 13, б—симметричные.
Если, следуя школьным определениям, понимать под «равными» фи-
фигурами такие, которые могут быть совмещены с помощью «наложения»,
то указанные выше два подхода к плани-
планиметрии будут отвечать двум различным
пониманиям слова «наложение». С одной
стороны, мож,но допускать в качестве «на-
«наложений» любые «механические» переме-
перемещения плоских фигур, не выводящие
их из рассматриваемой пло-
плоскости. Если определить равенство фи-
фигур с помощью таких «наложений» (т. е.
движений 1-го рода), то мы придем ко
второму из указанных выше подходов к
планиметрии; треугольники, изображен-
изображенные на рис. 13, б, в этом случае равными
не будут, так как никакое перемещение
одного из этих треугольников, не выводя-
выводящее его нз плоскости чертежа.не может сов-
совместить его с другим треугольником. С дру-
другой стороны, можно допускать в качестве «наложений» и такие переме-
перемещения фигур, которые выводят их из рассматриваемой плоскости. На-
Например, симметрия относительно прямой при таком подходе также ста-
становится «наложением», ибо ее можно осуществить перемещением в прост-
пространстве (вращением около оси, рис. 14). Такой подход приводит к
обычному пониманию равенства фигур (треугольники, изображенные на
рис. 13, б, в этом случае считаются равными).
Рис. 14.

1/26 основныг поняли сфкричкской гьометрип и ipiiiohomeiphh
Гаким образом, от и -е ie/кчу двумя указанными подходами к пла-
планиметрии заключается н том, что под движениями в одном случае пони-
понимаются «механические» иеремеще шя фнгур в самой рассматриваемой плос-
плоскости, а в другом случае — «механические» перемещения, совершаемые в
объемлющем трехмерном пространстве. Следует заметить, что два указан-
, ны\ подхода к планиметрии мрннодит, строго говори,
к двум раз тичным геометрическим системам. Имен-
Именно в геометрии, основанной только на движениях
1- о рода, существуют понятия, не имеющие смысла в
обычной планиметрии; сюда относятся: направление
обхода фнг\ры, ориентированная площадь фигуры
(площадь, взятая с тем или иным знаком в зависи-
зависимости от направления обхода1)). косое произведение
двух векторов2) и др. Однако в школьном преподавании
эти вопросы обычно оставляются в стороне, в сняэи с
чем становится наиболее естественным рассмотрение
всех гвиженнп. i не топько движений 1-го рода.
В случае геометрии на сфере различие между
указанными двумя подходами кажется на первый
взгляд еще более принципиальным, чем в случае пла-
планиметрии. Ведь никаким «механическим» перемещением
(в трехмерном пространстве) одного из треугольников,
изображенных на рис. 12, б, его нельзя наложить на
второй из этих треугольников (если «вынуть» треуголь-
треугольник ABC из сферы н приложить его к треуго пыш-
пышку А'В'С «фугой стороной», то треугольники не
совместятся метает искривленность сферы, рис. 15).
Однако уго соображение не является принципиальным:
соли сферу с птать расположенной в четырехмерном простран-
пространстве3), то симметричные фигуры (например, треугольники, изображенные
на рис 12,6) могут быть совмещены при помощи «механического» пере-
перемещения в jtom четырехмерном пространстве (т. е. при помощи «движения
1-го рода» в четырехмерном пространстве).
1.5. Принцип двойственности. Мы ви гели, что любое движение
сферы переводит пару диаметрально противоположных точек снова
it пару чиаметра 1ьно противоположных точек. Таким образом, пара
Aиамет]1ально противоположных точек является в сферической
геометрии самостоятельным геометрическим объектом. Отметим
d'iho замеча1ельное свойство этих пар точек: всякой теореме сфе-
сферической геометрии соответствует другая теорема этой геометрии,
получающаяся из первой взаимной заменой слов: пара диаметрально
противоположных точек и бо 1ьиыя окружностью , <лежш на» и чпро-
хоцнт через> соедпникпен и «пересекаются на» и т. д. Например:
Рис.
всякие две большие окружности
на сфере пересекаются в одной
паре диаметрально противополож-
противоположных ючек.
всякие две пары
npoi ивоположных
соединяются одной
ружностью.
диаметрально
ючек- сферы
большой ок-
') См книгу. А. И. Лопшнц, )б
ванных фигур. М. 1956.
) См. ст ть (Векторы и их применения еометрин», стр
3) См статью о многомернь \ ирострчнствач в кн. V ЭЭМ.
измерении площадей ориентиро-
350.

OCHORHWF ПОНЯТИЯ СФВРИЧВСКОЙ ГРОМКГРИИ
Г>'27
Рис. 16.
Это свойство ieopc-м сферической геомефии являйся следствием
того, что венкой большой окружности на сфере взаимно однозначно
соответствует пара ее полюсов, а всякой паре диаметрально противопо-
противоположных точек сферы взаимно однозначно соответствует их шлира,
причем если большая окружное ib прихо-
шт через пару диаметрально противопо-
противоположных точек, то полюсы этой окружности
лежат на поляре этой нары точек (рис. 16).
Это свойство называется принципом
двойственности, а теоремы, получаю-
получающиеся друг из друга указанной заменой,
называются двойственными о'руг другу
теоремами. Если одна из двух двой-
двойственных теорем доказана, то доказатель-
доказательство второй 1еоремы может быть получено
из доказательства первой георемы пере-
переходом от каждой большой окружности к ее
полюсам, а от каждой пары диаметрально
противоположных точек—к ее поляре.
1.6. Углы на сфере. Углом между двумя пересекающимися ли-
линиями в пространстве называется угол между касательными к этим
линиям в точке их пересечения. Частным случаем общего понятии
угла между двумя линиями
является угол между двумя
большими окружностями на
сфере На рис. 17 изображен
у го i ВАС между большими
окружностями \В и АС на
сфере и измеряющий *тог угол
XAY между касательными АХ
и AY к зтим большим окруж-
окружностям.
Если мы проведем большую
окружность, являющуюся по-
полярой вершины А угла на сфере
и пересекающую стороны этого
угла в точках В и С, ю лучи
ОВ и ОС соответственно па-
параллельны лучам \Х и A Y,
касательным к стиронам угла
(рис. 17). Поэтому длина 1уги' большой окружности ВС равна про-
произведению ^_ВАС на радиус еферы, т. е. угол на сфере равен
длине дуги большой окружности между точками сторон угла,
полярно сопряженными с ве\ шиной угли, селенной на радиус
сферы.
Рис. 17.

528 основные понятия сферической геометрии и тригонометрии
Так как оба угла ВАС и ВА'С, образованные двумя полуокруж-
полуокружностями при их различных концах, равны одному и тому же
углу ВОС, то эти углы равны между собой и величина каждого из
них называется углом между двумя большими полуокружностя-
полуокружностями. Две большие окружности определяют четыре угла между двумя
полуокружностями, попарно равные друг другу. Те из этих углов,
обе стороны которых являются продолжениями сторон другого угла,
равны и называются вертикальными углами (рис. 18, а); те из
этих углов, которые имеют одну общую сторону, составляют в
сумме развернутый угол л и называются смежными углами (рис. 18, б).
а)
Рис. 18.
Так как полюсы D и Е больших окружностей АВ и АС пред-
представляют собой точки большой окружности ВС, полученные из .то-
.точек В к С поворотом вокруг прямой АА' на прямой угол, то дуга ВС
равна дуге DE и угол ВАС равен длине дуги DE, деленной на ра-
радиус сферы. Заменяя одну из точек D или Е ее диаметрально про-
противоположной точкой D' или Е' (рис. 19), мы получим угол, смеж-
смежный с углом ВАС. Таким образом, угол между двумя большими
окружностями равен длине дуги, соединяющей их полюсы, делен-
деленной на радиус сферы.
Так как при отражении от диаметральной плоскости полюсы боль-
большой окружности, высекаемой из сферы этой плоскостью, переходят
друг в друга, то большие окружности, проходящие через эти по-
полюсы, при указанном отражении переходят в себя (рис. 20). Поэтому
углы, составляемые этими большими окружностями с большой окруж-
окружностью, высекаемой плоскостью, равны углам, смежным с ними и,
следовательно, являются прямыми углами. Таким образом, большие
окружности, одна из которых проходит через полюс другой,
пересекаются под прямым углом. Будем называть такие большие
окружности перпендикулярными.

ОСНОВНЫЕ ПОНЯТИЯ СФЕРИЧЕСКОЙ ГЕОМЕТРИИ
529
Обратно, отметив на одной из двух перпендикулярных больших
окружностей точку, полярно сопряженную точке пересечения, мы
получим такую точку, что проведенный в нее радиус сферы перпен-
перпендикулярен диаметральной плоскости, высекающей из сферы вторую
Рис. 19.
Рис. 20.
большую окружность (рис. 21), т. е. точку, являющуюся полюсом
этой окружности. Поэтому каждая из двух перпендикулярных
больших окружностей проходит через полюс другой большой
окружности.
Отсюда следует, что большая окружность, являющаяся полярой
точки пересечения двух больших окружностей, перпендикулярна
Рис. 21.
Рис. 22.
обеим большим окружностям, т. е. две большие окружности всегда
обладают единственной большой окружностью, перпендикуляр-
перпендикулярной к ним обеим (рис. 22). Для сравнения заметим, что на плос-
плоскости общими перпендикулярами обладают только параллельные
прямые, причем две параллельные прямые обладают не одним, л
бесконечным множеством общих перпендикуляров.
34 Энцикл педия ки. 4

530 ОСНОВНЫЕ ПОНЯТИЯ СФЕРИЧЕСКОЙ ГЕОМЕТРИИ И ТРИГОНОМЕТРИИ
§ 2. Сферические треугольники
2.1. Треугольники и двуугольники на сфере. В § 1 мы видели,
что три большие окружности на сфере, не пересекающиеся в одной
точке, делят сферу на восемь областей. Каждая из этих областей,
ограниченная дугами трех больших
окружностей, называется сферическим
треугольником (рис. 23). Дуги боль-
больших окружностей, ограничивающие
сферический треугольник, называются
его сторонами, концы этих дуг назы-
называются его вершинами, а углы, обра-
образуемые сторонами сферического тре-
треугольника в его вершинах, называются
углами сферического треугольника.
Ясно, что каждая сторона сферического
треугольника меньше половины боль-
большой окружности.
В отличие от плоскости, где тре-
треугольник является многоугольником
с наименьшим числом сторон, на сфере имеются многоугольники с
числом сторон меньше трех— двуугольники. Двуугольником является
часть сферы, ограниченная двумя половинами больших окружностей
с общими концами; эти общие концы, называемые вершинами
двуугольника, являются диаметрально противоположными точками
сферы. На рис. 24 изображен двуугольник с вершинами А и А'.
Рис. 23
Рис. 24.
Рис. 25.
2.2. Полярные треугольники. Всякому сферическому треуголь-
треугольнику ABC можно поставить в соответствие другой сферический тре-
треугольник А'В'С, вершины которого являются полюсами сторон ВС,
СА, АВ сферического треугольника ABC, лежащими от этих сторон
по ту же сторону, что и соответственно вершины А, В, С (рис. 25).

СФЕРИЧЕСКИЕ ТРЕУГОЛЬНИКИ 531
Будем называть сферический треугольник А'В'С полярным по от-
отношению к сферическому треугольнику ABC.
Если сферический треугольник А'В'С является полярным по
отношению к сферическому треугольнику ABC, то и сферический
треугольник ABC полярен по отношению к сферическому треу-
треугольнику А'В'С. В самом деле, так как точка В' является полю-
полюсом стороны АС, то точка В' полярно сопряжена с точками А а С
(рис. 25). Так как точка С является полюсом стороны АВ, то точка
С' полярно сопряжена с точками А и В. Но так как точка А по-
полярно сопряжена с точками В' и С' стороны В'С, то она явля-
является полюсом стороны В'С При этом, так как точки А и А' ле-
лежат по одну сторону от стороны ВС, то они лежат и по одну сто-
сторону от стороны В'С'. Так же доказывается, что точки В и С тоже
являются полюсами сторон С"А' и А'В' и лежат по ту же сторону
от этих сторон, что и точки В' и С', т. е. сферический треуголь-
треугольник ABC полярен по отношению к сферическому треугольнику А'В'С.
Обозначим точки пересечения больших окружностей АВ и АС со
стороной В'С через L и М, точки пересечения больших окруж-
окружностей ВС и ВА со стороной А'С через /V и Р и точки пересече-
пересечения больших окружностей СА и СВ со стороной А'В' через Q и R
(рис. 25). Тогда, если величины углов CAB, ABC и ВСА обозначить
через А, В и С, а радиус сферы — через г, то дуги больших окруж-
окружностей LM, NP и QR соответственно равны Аг, Вг, Сг. Далее, так
как дуги В'М, LC, С'Р, NA', A'R. QB' соединяют полярно соп-
сопряженные точки, то они равны -к г. Поэтому, если все три угла
4,fi,C=?S |, то дуги B'L и МС, CN и PA', A'Q и RB1, допол-
дополняющие дуги Аг, Вг, Сг до ^гГ, соответственно равны (-^— А \г,
(д— в) г, (j— c\ г. Таким образом, стороны В'С, С А' и А'В'
полярного треугольника в этом случае равны (л.—А)г, (л— В)г,
(л— С)г. Тот же результат совершенно аналогично доказывается и
для случаев, когда углы А,В или С больше -^. Поэтому стороны
треугольника, полярного по отношению к сферическому треу-
треугольнику ABC, соответственно равны (л— А) г, (л — В) г, (л— С) г.
Отсюда, если мы обозначим эти стороны через а', Ъ', с', мы полу-
а' D . Ь' „ с'
чим, что А = л , В=п , С=я , т. е. углы треуголь-
треугольника, полярного по отношению к сферическому треугольнику со сто-
сторонами а', Ь', с', соответственно равны л— —, л , л——.
Сферический треугольник, совпадающий со своим полярным треу-
треугольником, называется автополярным треугольником (от греческого
34*

532 основные понятии сферической геометрии и тригонометрии
«сам» и слова «полярный»). Так как все вершины авто-
автополярного треугольника полярно сопряжены, все стороны этого сфе-
сферического треугольника равны четверти большой окружности, откуда
вытекает, что все три угла этого сферического треугольника пря-
прямые. На рис. 26 изображен автополярный треугольник ABC.
2.3. Равенство сферических треугольников. Согласно сказанному
выше два сферических треугольника называются равными, если их
можно совместить друг с другом движением сферы. Очевидно, что
между вершинами двух равных сферических треугольников можно
установить такое соответствие, при котором и соответственные сто-
стороны, и соответственные углы этих сфе-
сферических треугольников равны: для этого
надо поставить в соответствие каждой
вершине первого сферического треуголь-
треугольника ту вершину второго сферического
треугольника, в которую Он переходит
при совмещении этих сферических тре-
треугольников.
Равенство сферических треугольников,
гак же как равенство плоских треуголь-
треугольников, определяется равенством трех эле-
элементов этих треугольников. Имеются
шесть признаков равенства сферических
треугольников: два сферических тре-
треугольника равны, если:
I) dee стороны одного сферического треугольника равны двум
соответственным сторонам другого сферического треугольника
и равны углы между этими сторонами;
II) два угла одного сферического треугольника равны двум
соответственным углам другого сферического треугольника и
равны стороны между этими углами;
III) все три стороны одного сферического треугольника равны
соответственным сторонам другого сферического треуголь-
треугольника;
IV) две стороны одного сферического треугольника равны двум
соответственным сторонам другого сферического треугольника,
углы, лежащие против двух равных сторон, равны, а углы, ле-
лежащие против двух других равных сторон, одновременно острые
или тупые;
V) два угла одного сферического треугольника равны двум
соответственным углам другого сферического треугольника, сто-
стороны, лежащие против двух равных углов, равны, а стороны, ле-
лежащие против двух других равных углов, одновременно меньше или
, я
больше -д г;
Рис. 26.

C4>EPH4F.CKHF ТРЕУГОЛЬНИКИ 533
VI) все три угла рдного сферического треугольника равны
соответственным углам другого сферического треугольника.
Первые четыре из этих признаков равенства аналогичны приз
накам равенства плоских треугольников и доказываются совершенно
так же, как аналогичные признаки равенства в плоской геометрии.
Далее, V признак равенства сферических треугольников также имеет
аналог в плоской геометрии с той только разницей, что в V приз-
признаке равенства плоских треугольников нет условия, аналогичного
условию, сформулированному в конце V признака равенства сфериче-
сферических треугольников. Доказательство этого признака в плоской гео-
геометрии тривиально: из того, что два угла одного Треугольника со-
соответственно равны двум углам другого треугольника, вытекает, что
и третьи углы треугольников равны между собой. В случае сфери-
сферических треугольников такое доказательство неприменимо, так как
здесь сумма трех углов треугольника не является, как мы уви-
увидим ниже, постоянной величиной (ч. е. эта сумма неодинакова для
различных треугольников). Наконец, VI признак равенства сфериче-
сферических треугольников совсем не имеет аналога в плоской геометрии, где ра-
равенство соответственных углов двух треугольников является приз-
признаком не равенства, а подобия треугольников.
Как же доказываются V и VI признаки равенства сферических
треугольников? Сравнивая I признак равенства со II, III с VI. а IV
с V, мы видим, что если для двух сферических треугольников вы-
выполнен один признак каждой пары, для полярных по отношению
к ним треугольников выполнен второй признак той же пары. Поэ-
Поэтому, так как из равенства двух сферических треугольников, очевидно,
вытекает равенство полярных по отношению к ним треугольников, то
из справедливости одного из признаков каждой пары вытекает
справедливость второго из признаков той же пары. В частности,
справедливость VI признака, не имеющего аналога на плоскости,
вытекает из справедливости III признака, а справедливость V приз-
признака— из справедливости IV признака.
Условия, указанные в конце IV и V признаков равенства сфери-
сферических треугольников, являются существенными. Мы покажем это
сейчас на двух простых примерах.
Пример неравных сферических треугольников, в которых имеют
место равенства двух пар соответственных сторон и углов, лежащих
против двух равных сторон (ср. IV признак), изображен на. рис. 27.
Для построения таких сферических треугольников следует взять
равнобедренный сферический треугольник ABC с основанием ВС и
соединить дугой большой окружности его вершину А с точкой D
основания, не являющейся его серединой. Тогда сферические тре-
треугольники ABD. и ACD имеют общую сторону 4D, равные стороны
АВ и АС и равные yi лы В и С, но их стороны BD и DC не р<звны
по построению.

534 основные понятия сферической геометрии и тригонометрии
Пример неравных сферических треугольников, в которых имеют
место равенства двух пар соответственных углов и сторон, лежащих
против двух равных углов, изображен на рис. 28 (ср. V признак).
Для построения таких сферических треугольников следует построить
Рис. 27.
Рис. 28.
сферический треугольник ABC, у которого углы ABC и АСВ допол-
дополняют друг друга до угла я. Далее на продолжении стороны ВС сле-
следует взять произвольную точку D и соединить ее дугой большой
окружности с точкой А. Сферические треугольники ABD и ACD
имеют общий угол D, равные углы ABD и ACD и общую сторону
AD, но их стороны BD и CD не
равны по построению.
2.4. Большая окружность как
кратчайшая. Во всяком сфериче-
сферическом треугольнике каждая сторона
меньше суммы двух других сторон
и больше их разности. В'самом деле
пусть ЛВС—произвольный сфериче-
сферический треугольник. Допустим, что из
двух сторон АВ, АС сторона АС
• большая. Отложим на стороне АС
дугу АВ', равную дуге АВ (рис. 29).
Проведем какую-нибудь плоскость,
проходящую через точки В, В' и
пересекающую лучи О А и ОС (а не
их продолжения !) в точках А1 и С,.
Треугольники ОАХВ и ОАХВ' равны.
(так как они имеют общую сторону ОАХ, равные стороны ОВ
и ОВ' и равные углы при вершине О). Следовательно, А1В=А1В'.
Так как точки Alt В' и Сх лежат на одной прямой (являющейся ли-
линией пересечения плоскостей ОАС и А^ВС^), причем точка В' лежит
между Л1 и С,, то
B'Cl = AlCl — АуВ' = AlCl~AlB<BC1.
Рис. 2Э.

СФЕРИЧЕСКИЕ ТРЕУГОЛЬНИКИ
535
Рассмотрим теперь треугольники OBCi и ОБ'С1. В этих треуголь-
треугольниках ОСХ—общая сторона и ОВ=ОВ', а третьи стороны связаны
неравенством B'Cl<LBCr Следовательно, углы, лежащие в этих тре-
треугольниках против неравных сторон, связаны неравенством /В'ОС,
/_BOCV Поэтому дуга В'С, стягиваемая углом В'ОС, также
меньше дуги ВС,, стягиваемой углом ВОС1. Иначе говоря,
АС— АВ = АС—АВ' = ВГС<ВС,
т. е. каждая сторона сферического треугольника больше разности
двух других его сторон. Отсюда, в свою очередь, вытекает (после
прибавления слагаемого АВ к обеим частям гюлученного неравенства).
что
АС<АВ + ВС.
Рис. 30.
т.е. каждая сторона сферического треугольника меньше суммы двух
тругих его сторон.
Из доказанной теоремы, гак же как в плоской геометрии, сле-
1ует, что во всяком сферическом треугольнике против большего
угла лежит большая сторона,
а против большей стороны ле-
лежит больший угол.
Далее, из того, что в сфери-
сферическом треугольнике каждая сто-
сторона меньше суммы двух других
сторон, следует, что дуга большой
окружности, меньшая полуок-
полуокружности, короче всякой линии,
состоящей из дуг нескольких больших окружностей, соединяющей
те же точки сферы (рис. 30); это доказывается в точности гак
же, как теорема о том, что прямолинейный отрезок на плоскости ко-
короче всякой ломаной, соединяющей те же точки '). Так как длину
всякой 2) непрерывной линии на
^___- _ сфере можно со сколь угодно малой
') Тот факт, что рассматривается
дуга, меньшая полуокружности,
является существенным, так как
доказательство приведенного утвер-
утверждения (рис. 31) основывается на
рассмотрении цепочки сферических
¦cAB+BC+CD+EE треугольников, а в любом сфериче-
сферическом треугольнике каждая сторона
Рис. 31. меньше полуокружности. Совершен-
Совершенно ясно, что дуга большой окружности, большая полуокружности, не
является кратчайшей.
•) Разумеется, речь идет о «спрямляемых» линиях на сфере (ср. статью
о длине кривой и площади поверхности в кн. V ЭЭМ).

536 основные понятия сферической геометрии и тригонометрии
ошибкой заменить длиной линии, состоящей из дуг больших окруж-
окружностей, соединяющих точки данной линии, то дуга большой окруж-
окружности, меньшая полуокружности, короче всякой непрерывной ли-
линии на сфере, соединяющей те же точки сферы, т. е. эта дуга
большей окружности является кратчайшей линией на сфере.
В этом отношении большая окружность является аналогом прямой ли-
линии на плоскости. Отсюда видно, что та линия на земной поверх-
поверхности (предполагаемой сферической), которая получается на ней
путем провешивания и которую в малых участках принимают за
прямую линию, при достаточном продолжении представляет собой
дугу большой окружности. Так как эти линии проводятся на земной
поверхности геодезистами, то большие окружности называются
также геодезическими линиями на сфере.
Так как кратчайшей линией, соединяющей две точки сферы,
является дуга большой окружности (не превосходящая полуокруж-
полуокружности), то длину этой дуги называют сферическим расстоянием
между двумя точками сферы.
В отличие от плоскости, где невозможны треугольники с двумя
прямыми углами, на сфере возможны такие треугольники: это тре-
треугольники, у которых одна из вершин является полюсом противо-
противоположной стороны; стороны этих треугольников, лежащие против
прямых углов, равны -^ г. Имеются на сфере и треугольники с тремя
прямыми углами: это знакомые нам автополярные треугольники
(рис. 26); у авгополярных треугольников все три стороны равны
-п-т. В том случае, когда сферический треугольник обладает только
одним прямым углом, сторона, лежащая против этого угла, так же
как в случае плоских прямоугольных треугольников, называется ги-
гипотенузой, а остальные две стороны — катетами.
2.5. Площадь сферического треугольника. Будем называть
площадью сферической фигуры, по аналогии с плоладью плоской
фигуры, действительное число, удовлетворяющее следующим четырем
требованиям 1):
1) площадь сферической фигуры является положительным
числом, (свойство позитивности; здесь предполагается, что
сферическая фигура содержит сферический треугольник),
2) площадь сферической фигуры не изменяется при движении
сферы (свойство инвариантности),
3) если сферическая фигура разложена на две сферические
фигуры, то площадь данной фигуры равна сумме площадей двух
фигур, на которые она разложена (свойство аддитивности),
4) площадь всей сферы радиуса г равна 4яг2 (свойство
нормировки).
*) Ср. со статьей о площадях и объемах в кн. V ЭЭМ.

СФРРИЧВСКИЕ ТРЕУГОЛЬНИКИ
537
Прежде всего найдем площадь двуугольника. Из свойства ад-
аддитивности, инвариантности и нормировки следует, что если разде-
разделить сферу на п равных двуугольников (рис. 32), то площадь
каждого из них (т. е. площадь двуугольника с углом —1 равна
—-4лг2. Поэтому площадь двуугольника с углом —— составленного
из т рассмотренных двуугольников, равна —4ЯГ1, а если угол
!—-, то пло-
пло- 2ят
некоторого двуугольника больше и меньше
щадь этого двуугольника заключена между — 4яг* и "Ljl. 4лгг (это
Рис. 32.
Рис. 33.
вытекает из первого и третьего свойств площади). Неограниченно
увеличивая число п, мы можем с помощью предельного перехода
найти .площадь любого двуугольника: площадь двуугольника, углы
при вершинах которого равны а, равна
т. е.
5 (а) = 2гг ¦ а.
Если нам дан сферический треугольник ABC, то пара боль-
больших окружностей, проходящих через две его стороны, определяет
два двуугольника, углы которых равны углу сферического треуголь-
треугольника между этими сторонами (рис. 33). Всего таким образом полу-
получается шесть двуугольников, два с углом А, два — с углом В и
два — с углом С. Треугольник ABC и диаметрально противополож-
противоположный ему треугольник А'В'С (равный треугольнику ЛВС),"входят в
три двуугольника, остальные точки сферы (не лежащие на сторо-
сторонах двуугольников) входят только в один двуугольник. Поэтому

538 ochobhhf понятия сферической геометрии и тригонометрии
сумма площадей шести двуугольников равна сумме площади 5 всей
сферы и учетверенной площади 5(А) треугольника ABC, т. е.
Так как
то мы получаем
4г2 (А + В+ С) = 4яг2 4- 45 (Д),
т. е.
:—Я)- B)
Так каь величины 5(Д) и г2 положительны, то величина
+ B-j-C—я также положительна, откуда следует, что
т. е. сумма углов сферического треугольника больше развернутого
угла. Величина А + В-\- С—я на-
называется угловым избытком сфе-
сферического треугольника.
Рис. 34.
Таким образом, площадь сферического треугольника равна про-
произведению его углового избытка на квадрат радиуса сферы.
Заменяя в последнем неравенстве углы .4, В и С равными им
выражениями я — —, я — —, л — -^- где, а', о', с'—стороны поляр-
полярного треугольника, мы получим неравенство
а' +Ь' Ч-с' <2яг,
показывающее, что сумма сторон сферического треугольника
меньше длины большой окружности.
будем называть сферическим многоугольником часть сферы, ограничен-
ограниченную замкнутой линией (не пересекающей самое себя), состоящей из дуг
больших окружностей. Дуги больших окружностей, ограничивающие сфе-
сферический многоугольник, наэьваются его сторонами, концы этих дур

окружности 539
называются его вершинами, а углы, образуемые сторонами сферического
многоугольника в его вершинах, называются углами сферического много-
многоугольника.
Сферический многоугольник называется выпуклым, если он находится
по одну сторону от каждой большой окружности, проходящей через сто-
сторону многоугольника (рис. 34). Соединяя одну из вершин выпуклого сфе-
сферического л-угольннка дугами больших окружностей со всеми другими
вершинами этого многоугольника, мы разделим его на л—2 сферических
треугольника (рис. 35) Площадь выпуклого сферического л-угольника.
очевидно, равна сумме площадей этих л — 2 сферических треугольников.
Поэтому, так как сумма углов всех л — 2 сферических треугольников равна
сумме 2„ углов сферического л-угольника. площадь Sn выпуклого сфериче-
сферического п-угольника равна
5п = /-г[2п-(л-2)зт], C)
где ?„ — сумма всех его внутренних углов.
Эта теорема остается справедливой и для невыпуклых сфериче-
сферических многоугольников ').
§ 3. Малые окружности
3.1. Окружности и углы на сфере. Как мы видели в § 1,
сечение сферы плоскостью, не проходящей через ее центр, является
малой окружностью. Так как всякие три точки сферы определяют
единственную плоскость, то через всякие
три точки сферы, не лежащие на боль-
большой окружности, можно провести един-
единственную малую окружность (рис. 36).
Так как плоскость делит пространство
на две области, то малая окружность
делит сферу на две области, называ-
называющиеся сферическими сегментами. Та
из этих областей, которая не выходит за
пределы полусферы, называется сфери-
сферическим кругом.
Так как при повороте вокруг диаметра
сферы, перпендикулярного к плоскости. Рис. 36.
высекающей из сферы малую окружность,
эта окружность переходит в себя (ибо этот перпендикуляр является
осью рассматриваемой окружности), то сферическое расстояние точек
окружности от концов перпендикулярного ей диаметра сферы, посто-
постоянно. Обратно, геометрическое место точек сферы, равноотстоящих
от одной ее точки переходит в себя при повороте вокруг диаметра,
проходящего через эту точку, т. е. является малой окружностью
(высекаемой из сферы плоскостью, перпендикулярной этому диаметру).
Таким образом, малая окружность является, геометрическим
') См например, книгу Д. И. Перепелкина 12], указанную в
конце статьи.

540 ОСНОВНЫЕ ПОНЯТИЯ СФЕРИЧЕСКОЙ ГЕОМЕТРИИ И ТРИГОНОМЕТРИИ
местом точек сферы, равноотстоящих от одной точки сферы;
эти точки равноотстоят и от диаметрально противоположной ей
точки. Та из этих точек, для которой сферическое расстояние ее
от точек малой окружности меньше -^- г, называется сферическим
центром малой окружности, а сферическое расстояние точек малой
окружности до ее сферического центра называется сферическим
радиусом малой окружности. Очевидно, что сферический центр
малой окружности принадлежит ограничивающему его сферическому
кругу. Полюсы больших окружностей можно также рассматривать
как сферические центры этих окружностей; сферическим радиусом
большой окружности следует счи-
считать число -^ г.
Так как большие окружности,
проходящие через центр малой окруж-
окружности, перпендикулярны поляре
центра малой окружности, то рас-
расстояние от точек малой окружности
до этой большой окружности (изме-
(измеряемое по «сферическому перпенди-
перпендикуляру») равно дополнению сфери-
сферического радиуса окружности до -д-г.
Обратно, геометрическое место точек
сферы, равноотстоящих от одной ее
большой окружности и расположен-
расположенных по одну сторону от нее, является
геометрическим местом точек, равноотстоящих от одного ее полюса,
т. е. является малой окружностью. Таким образом, малая окружность
является геометрическим местом точек сферы, равноотстоящих
от одной большой окружности и расположенных по одну сто-
сторону от нее. Эта большая окружность называется базой малой
окружности, а расстояние точек малой окружности до базы назы-
называется параметром малой окружности. Очевидно, что сферический
радиус R и параметр Р малой окружности составляют в сумме -g- r.
На рис. 37 изображены центр и база малой окружности.
Пусть центр малой окружности в se плоскости —точка Q, радиус
ее _ЧИсло q, a M—произвольная точка этой окружности (рис. 37),
т. е. OM = r, QM—Q, a /_MOQ—— Тогда из прямоугольного
треугольника OQM мы найдем, что g = rsm —, т. е. длина окруж-
окружности сферического радиуса R равна
C=2nrsin-y. D)
Рис. 37.

малые окружности 541
R Р
С другой стороны, так как sin — = cos — , то длина окружности
параметра Р равна
C=2nrcos~. E)
Так как сферический круг, ограничиваемый окружностью сфери-
сферического радиуса /?, представляет собой сферический сегмент высоты
(R \ R
1—cos —J — 2r sin -=— , а площадь всякого сферического слоя
(в 1астности, сферического сегмента) высоты h равна 2nrh, где г —
радиус сферы, то площадь сферического круга радиуса R равна
S=4TO-2sin'-^- . F)
3.2. Геодезическая кривизна малой окружности. Подобно тому как
окруж'ности на плоскости характеризуются кривизной — величиной, обратной
радиусу, которую можно рассматривать как меру отклонения окружности
от прямой, на сфере окружности также можно характеризовать некоторым
числом, равным нулю для больших окружностей и характеризующим для
малых окружностей степень отклонения этой
окружности ^от большой окружности. Так
как большие окружности называют геодези-
геодезическими линиями, то это число, которое мы
сейчас определим называют геодезической
кривизной малой окружности. Для определе-
определения геодезической кривизны будем рассма-
рассматривать векторы, расположенные ь плоско-
плоскостях и касающиеся сферы в точках данной
окружности, причем начало векторов будем
считать совпадающим с точкой касания
(рис. 38). Для этих векторов следующим
образом можно определить параллельный пере-
перенос вдоль окружности. Касательные пло-
плоскости к сфере в точках окружности явля-
являются в то же время касательными плоскостя- Нис. 38.
ми к прямому круговому конусу в случае
малой окружности (рис. 39) и к прямому круговому цилиндру в случае
большой окружности (рис. 40). Если мы развернем построенный таким
образом конус или цилиндр на плоскость, то наша окружность развер-
развернется на плоскость в виде окружности или прямой. Данный вектор при
нашем развертывании совпадет с некоторым вектором на плоскости. Пере-
Перенесем теперь этот вектор на плоскости параллельно в какую-нибудь дру-
другую точку окружности или прямой, полученной нами при развертывании.
Вектор, полученный в результате этого переноса, перейдет при обратном
накладывании конуса или цилиндра на сферу в некоторый вектор в каса-
касательной плоскости к сфере в соответственной точке окружности Этот
последний вектор мы будем называть вектором, полученным из первоначаль-
первоначального вектора с помощью параллельного переноса вдоль окружности. На рис 39
изображен параллельный перенос вектора вдоль малой окружности.
Рассмотрим теперь такой параллельный перенос, при котором перено-
переносимый вектор, обойдя всю окружность, возвращается в исходную точку.
В случае большой окружности, которая при развертывании цилиндра на

542 ОСНОВНЫЕ ПОНЯТИЯ СФЕРИЧЕСКОЙ ГЕОМЕТРИИ И ТРИГОНОМЕТРИИ
плоскость переходит в прямую линию, в результате такого параллельного
переноса вектор после возвращения совпадает со своим первоначальным
положением (рис. 40). В случае же малой окружности, которая при раз-
развертывании конуса на плоскость пере-
переходит в окружность, в результате такого
параллельного переноса вектор после
возвращения уже не совпадает со своим
первоначальным положением, а повора-
поворачивается на некоторый угол (рис. 41).
Рис. 39.
Нетрудно видеть, что этот угол бучет одним и тем же для любых пере-
переносимых векторов. Будем называть геодезической кривизной окружности на
сфере отношение определенного таким об-
образом угла к длине этой окружности.
Так как в случае большой окружности
вектор при переносе совпадает со своим
первоначальным положением, то геодези-
геодезическая кривизна большой окружности рав-
равна нулю.
В случае малой окружности вектор
при переносе поворачивается на угол,
равный углу при вершине сектора, в виде
которого конус разворачивается на пло-
плоскость (рис. 41). Этот угол равен отношению
Рис. 40
длины дуги этого сектора (равной длине окружности основания конуса) к ра-
радиусу сектора, равному длине прямолинейной образующей конуса. Так как
окружность основания конуса совпадает с данной окружностью, то ее

ОКРУЖНОСТИ
543
длина равна С = 2ял sin—. Прямолинейная образующая / конуса является
катетом прямоугольного треугольника, второй катет которого равен
радиусу г сферы. а противолежащий
R
угол равен отношению —; отсюда
Рис. 41.
R
видно, что l = rtg—'-. Поэтому угол Д поворота вектора при параллельном
переносе вдоль малой окружности радиуса R равен
С " Ц-. G,
а геодезическая кривизна малой окружности радиуса R равна
k=—=—ctg—.
с г s г
(8)
Заметим, что в пределе, когда радиус R малой окружности стремится
к радиусу -=-г большой окружности, геодезическая кривизна k стремится
к нулю.
3.3. Формула Гаусса — Бонне. Параллельный перенос вектора можно
применить к определению площади сферической фигуры, ограниченной
дугами окружностей. Прежде всего рассмотрим параллельный перенос
вектора вдоль контура сферического многоугольника. Так как стороны
сферического многоугольника являются цугами больших окружностей, то
при переносе вектора вдоль стороны сферического многоугольника, он не
изменяет угла, составляемого им с касательными векторами к этой сто-
стороне. Этот угол изменяется Только при переходе через вершину много-
многоугольника. Действительно, если угол в некоторой вершине многоугольника
равен а, то угол между касательными векторами к сторонам этого много-
многоугольника, соответствующими определенному направлению обхода много-
многоугольника, равен я—а (рис. 42). Следовательно, угол переносимого век-
вектора с касательным вектором к стороне многоугольника при переходе
через эту вершину изменяется на то же число л—а (рис 43).
Поэтому при переносе вектора вдоль всего контура сферического
n-угольника вектор поворачивается после возвращения в исходную точку
на угол
Д„ = лл-Х„. (9)

544 ОСНОВНЫЕ ПОНЯТИЯ СФЕРИЧЕСКОЙ ГЕОМЕТРИИ И ТРИГОНОМЕТРИИ
Рассмотрим теперь перенос вектора вдоль контура выпуклого сфери-
сферического многоугольника. Так как площадь Sn выпуклого сферического
я-угольника связана с суммой 2„ его внутренних углов соотношением C),
или, иначе, соотношением
¦^ то мы получаем, что угол Дп и пло-
ча щадь Sn связаны соотношением
Sn=r» Bя-Дп). A0)
Рассмотрим теперь какую-либо
выпуклую сферическую фигуру, ог-
ограниченную дугами окружностей (не
обязательно больших). Если мы впи-
Рис. 42. шем в эту фигуру сферические много-
многоугольники и будем стремить число их
сторон к бесконечности таким образом, чтобы длина наибольшей стороны
многоугольника стремилась к нулю, то площадь Sn вписанного п-угольника
будет стремиться к площади S рассматриваемой фигуры, а угол А„ будет
стремиться к углу Д. на который поворачивается ьектор при параллель-
параллельном переносе вдоль всего контура этой фигуры после возвращения век-
вектора в исходную точку. Поэтому, переходя в равенстве A0) к пределу,
мы получим, что площадь S фигуры и угол Д связаны соотношением
5=ггBл —Д), A1)
составляющим частный случай знаменитой'формулы Гаусса — Бонне.
В качестве примера применим формулу A1) к вычислению плошали
сферического круга. В случае
сферического круга радиуса R
угол Д равен 2л cos— (см. фор-
формулу G)).
случае
Поэтому в этом
\
Рис. 43.
т. е. мы скова получили фор-
формулу F).
В случае сферической фи-
туры, ограниченной произ-
произвольным контуром, состоящим из дуг окружностей, угол Д представляет
собой сумму углов Д,-, смежных с внутренними углами этой фигуры (как
в случае сферического многоугольника) и произведений ft,s,-, где s,-—геоде-
s,-—геодезические кривизны дуг, ограничивающих фигуру, a s,-—длины втих дуг,
т. е. формулу (Ш в этом случае можно переписать в виде
,—}>,«,>¦ A2)
Перенос вектора можно определить и вдоль произвольной глад-
гладкой линии: в этом случае касательные плоскости в точках этой линии
касаются уже не конуса или цилиндра, а поверхности, образованной

ТРИГОНОМЕТРИЧЕСКИЕ СООТНОШЕНИЯ В СФЕРИЧЕСКОМ ТРЕУГОЛЬНИКИ 545
касательными к пространственной линии; гакую поверхность, так же как
конус или цилиндр, можно «развернуть» на плоскость. В этом случае
можно определить геодезическую кривизну линии на сфере в каждой ее точке
как предел отношения поворота вектора при переносе вдоль дуги
линии к длине этой дуги при стягивании этой дуги в данную точку;
в общем случае геодезическая кривизна изменяется от точки к точке
и является постоянной только для окружностей. Площадь сферической
фигуры, ограниченной произвольной гладкой линией, можно определить
по той же формуле A1), что и для рассматриваемых нами фигур, причем
эту формулу можно также переписать в виде, отличающемся от формулы A2)
заменой суммы ^fys,- интегралом V feds от геодезической кривизны контура
С
по длине его дуги. Соответствующая формула и является общей форму-
формулой Гаусса — Бонне для случая сферической поверхности.
§ 4. Тригонометрические соотношения
в сферическом треугольнике')
4.1. Сферическая теорема косинусов. Рассмотрим произвольный
сферический треугольник ABC (напомним, что каждая его сторона
меньше яг).
Прежде всего докажем сферическую теорему косинусов, анало-
аналогичную теореме косинусов плоской тригонометрии; доказательство
сферической теоремы косинусов,
как мы увидим, существенно опи-
опирается на плоскую теорему коси-
косинусов.
Предположим сначала, что ка-
каждая из сторон Ь и с сферического
треугольника ABC меньше -х-г.
Проведем из точки А касательные
AM и AN к сторонам с и Ь и
найдем точки М и N пересечения
этих касательных с продолжения-
продолжениями радиусов ОБ и ОС (рис. 44);
эти точки пересечения сущест-
существуют, так к"ак, по предположению,
каждый из. углов АОС, АОВ меньше -к-. Тогда угол А равен
углу MAN, и для плоского треугольника MAN в силу плоской
георемы косинусов получаем
Рис. 44.
MN* = AN1
— 2AN- AM cos A.
A3)
') См. также п. 6.2 статьи «Векторы и их применение в геометрии»,
стр. 368.
35 Энциклопедия, кн. 4

546 основные понятия сферической геометрии и тригонометрии
С другой стороны, углы ВОС, АОС и АОВ, являющиеся цент-
центральными углами больших окружностей сферы, опирающимися на
дуги а, Ь, с, соответственно равны —, — и —. Поэтому из тре-
треугольника OMN находим
MN* = ОМг + ОЛ/2 — 2OM-ON cos у. A4)
Сравнивая A3) и A4), получаем
ОМг 4- ОЛ/2 — 2ОМ ¦ ON cos -? = AN* + AM* — 2AN- AM cos A. A5)
Из прямоугольного треугольника ОМА находим, что
ОМ*-АМ* = ОА*. g?=cos-i. ^ = sinf, A6)
а из прямоугольного треугольника ON А находим, что
r\ At 0A b AN Ь
OA\ c n
— = cos-, 5F = sinT. A7)
В силу первых формул A6) и A7) равенство A5) можно пере-
переписать в виде
20М • ON cos — = 20Аг + 2AN- AN- AM cos A,
т. е.
ОМ-ON cos у = ОА* +AN-AM cos A. A8)
Разделив A8) на произведение ОМ-ON, получим
а ОА ОА , AN AM .
или, в силу вторых и третьих равенств A6) и A7),
cos — = cos — cos f- sin— sin — cos A. A9)
Если теперь сторона b больше -к-г, а сторона с меньше -^ г,
то продолжим стороны а и b нашего треугольника до пересечения
в точке С, диаметрально противоположной точке С (рис. 45). Тогда
в сферическом треугольнике ABC' стороны АС' и АВ, соответст-
соответственно равные яг — b и с, меньше -к-г, а угол ВАС, смежный с углом А,
равен я—А. Поэтому в силу формулы A9) для треугольника ABC?
cos (я J = cos ( п j cos — 4- sin (л J sin — cos (л—A),

ТРИГОНОМЕТРИЧЕСКИЕ СООТНОШЕНИЯ В СФЕРИЧЕСКОМ ТРЕУГОЛЬНИКЕ 547
т. е.
— cos — = — cos — cos -— sin — sin — cos A,
откуда получаем формулу A9).
Если, наконец, обе стороны b и с больше -=-г, то продолжим
стороны Ь и с нашего тре-
треугольника до пересечения в
точке А' .диаметрально проти-
противоположной точкеЛ(рис. 46).
Тогда в сферическом тре-
треугольнике А'ВС стороны
С А' и ВА', соответственно
равные пг—/> и пг— с,
л Рис. 45.
меньше -к-г, а /_ В A G ра-
равен углу А. Поэтому в силу формулы A9) для треугольника А'ВС
cos y= cos ( n—— Jcos ( я—-?-J + sin (n — — J sin (л—у] cos A,
откуда непосредственно получаем формулу A9).
Формула A9) выражает сферическую теорему косинусов, кото-
которую обычно формулируют в следующем виде (получающемся при
г=1, т. е. для сферы еди-
единичного радиуса): косинус
стороны сферического тре-
треугольника равен сумме
произведения косинусов
двух других сторон и про-
произведения синусов двух
других сторон на косинус
угла между ними.
Заменяя в формуле A9) обозначения сторон а, Ь, с и углов А,
В, С в круговом порядке, мы получим две аналогичные формулы
B0)
Рис. 46.
Ь а с , . а . с п
cos — = cos — cos h sin — sin — cos В
r r r r r
с a b , . a . b
cos — = cos — cos \- sin — sin — cos C.
r r r r r
B1)
4.2. Сферическая теорема синусов. Докажем теперь сферическую
т'еоре'му синусов, аналогичную теореме синусов плоской тригоно-
тригонометрии. Из формулы A9) вытекает равенство
a b с i
cos cos — cos —
r r r
. Ь . с
sin — sin —
r r
35'

548 основные понятия сферической геометрии и тригонометрии
Применяя это равенство, вычислим отношение
. , а . . а а
siir — sin1 — sin* —
г г г
sin* A I— cos1 Я /а Ь с\
' cos cos —cos —
' Г Г
. b . с
sin — sin —
Г г
. . а . , Ь . . с
sin* — siir — sin* —
г г г
. , Ь . . с ( а Ь 'с У ~~
sin —-sin I cos cos — cos— I
r r \ r r r J
sin* — sin2 — sin2 —
r r
T. 2 b\ {, ГМ 7 a b c~V =
I I —cos1 —1A —cos2 — I — ( cos——cos — cos— I
V ' J\ r ) \ r r r )
. , a . , b . , с
sin2 — sin2 — sin* —
r r r
1 —COS2 COS2 COS2 f- 2 COS COS —COS
r r r r r r
Так как полученное выражение симметрично относительно сто
рон а, Ь, с, то оно равно аналогичным выражениям, полученным из
левой части этого равенства заменой сторон, а, Ь, с и углов А, В, С
в круговом порядке. Извлекая квадратный корень из этих выражений,
мы получим три равные выражения:
. а . Ь . с
sin — sin — sin —
sin Л ~sinfi ~sinC ' K
Эта формула и выражает сферическую теорему синусов, которую
обычно формулируют в виде (для г—\): синусы сторон сфериче-
сферического треугольника относятся, как синусы противолежащих
углов. Из формулы B2), в частности, видно, что если в сфериче-
сферическом треугольнике имеет место соотношение 5= п — А, так что
sin В = sin А, то в силу формулы B2) sin—=sin—, т. е. либо а = Ь.
либо Ь = лг—а. Но если а = Ь, то А — Вн в соответствии с соот-
соотношением В=л—А это дает /1 = /?= —. Следовательно, С—полюс
стороны АВ, и потому a=b = -^-r. Таким образом, соотношение
Ь = лг — а справедливо и в этом случае. Итак, если В=п — А, то
стороны а и b связаны соотношением b = nr — а.

ТРИГОНОМВТРИЧЕСКИР СООТНОШКНИЯ В СФЕРИЧЕСКОМ ТРЕУГОЛЬНИКЕ 549
• 4.3. Формулы пяти элементов. Докажем теперь так называе-
называемые формулы пяти элементов. Почленно умножая равенство A9)
на cos— и складывая с равенством B0), получим
Ь а с а с . Ь ? с ,
cos Ь cos — cos — = cos —cos (- cos — cos \-
r ' r r r r r r '
+ sin — sin — cos В + sin — sin — cos — cos A
или, после приведения подобных членов,
Ь „_ Ь _ ,с . . а . с „ , . ь
cos
г. е.
— = cos — cos —f- sin — sin — cos B-j- sin — sin — cos — cos A,
r r r r r r r r
или
b I, »^ . a . с n , . b . с с
cos — A — cos1 — 1 = sin — stn — cos B-\- sin — sin — cos — cos A,
b . , с . a . с „ . b . с с ,
cos — sin — = sin — sin — cos В + sin — sin — cos — cos A.
r r r r r r r
Сокращая обе части этого равенства на sin —, получим
Ь . с .а _ , . Ь с .
cos — sin — = sin — cos В + sin — cos — cos A
r r r ' r r
или, окончательно,
a г, b . с . Ь с .
sin — cos В = cos — sin sin — cos — cos A. B3)
Мы получили одну из формул пяти элементов, которую обычно
формулируют в виде: произведение синуса стороны сферического
треугольника на косинус прилежащего угла равно разности
произведения косинуса стороны, лежащей против этого угла, на
синус третьей стороны и произведения синуса стороны, лежащей
против данного угла, на косинус третьей стороны и косинус
стороны, лежащей против данного угла.
Заменяя в формуле B3) обозначения сторон а, Ь, с и углов А,
В, С в круговом порядке, мы получим две аналогичные формулы:
sin — cos C= cos — sin sin — cos — cos B, B4)
г г г г г v
' . с ш a b . a b y^ ic\r\
sin — cos A = cos — sin sin — cos — cos С. Bо)
Меняя в формуле B3) местами стороны я и с и углы А и С,
¦л затем заменяя обозначения сторон а, Ь, с и углов А, В, С

550 ОСНОВНЫЕ ПОНЯТИЯ СФЕРИЧЕСКОЙ ГЕОМЕТРИИ И ТРИГОНОМЕТРИИ
в круговом порядке, мы получим еще три аналогичные формулы
sin — cos С = cos — sin sin — cos — cos A, B6)
sin — cos A = cos — sin sin — cos — cos B, B7)
r r r r r ' v '
sin — cos В = cos — sin sin — cos — cos C. B8)
Эти формулы аналогичны теоремам проекций плоской тригоно-
тригонометрии.
Заменяя в формуле B3) sin —, sin — и sin — пропорциональными
им величинами sin A, sin В и sin С, мы получим формулу
Ъ с
sin A cos В = cos — sin С— cos — cos A sin В,
или
_os — sin С = cos В sin A + sin В cos A cos —. B9)
Мы получили формулу пяти элементов другого вида, которую
обычно формулируют в виде: произведение косинуса стороны сфе-
сферического треугольника на синус прилежащего угла равно сумме
произведения косинуса угла, лежащего против этой стороны, на
синус третьего угла и произведения синуса угла, лежащего против
данной стороны, на косинус третьего угла и на косинус стороны,
лежащей против данного угла.
Заменяя в формуле B9) обозначения сторон а, Ь, с и 'углов .4,
В, С в круговом порядке, мы получим еще две аналогичные фор-
формулы
С Q
cos — sin A = cos С sin fi + sin С cos В cos —, C0)
cos — sin 5= cos A sin C+ sin A cos Ccos —. C1)
Меняя в формуле B9) местами стороны сиси углы Л и С,
а затем заменяя обозначения сторон а, Ь, с и углов А, В, С в кру-
круговом порядке, мы получим еще три аналогичные формулы:
cos — sin A = cos В sin С + sin В cos С cos —, C2)
cos — sin B= cos Csin A -\- sin С cos A cos —, C3)
cos — sin C— cos A sin В + sin A cos В cos — . C4)
Эти формулы не имеют аналогов в плоской тригонометрии.

ТРИГОНОМЕТРИЧЕСКИЕ СООТНОШЕНИЯ В СФЕРИЧЕСКОМ ТРЕУГОЛЬНИКЕ 551
Формулы пяти элементов B9), CJ). C1), C2), C3) и C4) могут
быть получены также соответственно из формул B8), B6), B7),
B3), B4) и B5), если записать эти формулы для полярного тре-
треугольника и использовать соотношения между углами и сторонами
двух взаимно полярных треугольников.
4.4.-Двойственная теорема косинусов. Докажем теперь двой-
двойственную теорему косинусов, также не имеющую аналога в плоской
тригонометрии. Подставим значение cos — sin .Л из равенства C2)
в равенство C1). Получим
cos —sin 5= cos Л sinC+ (cos В sin C+ sin В cos С cos — J cos C,
или
cos — sin 5= cos A sin C+ cos В sin С cos C+ sin В cos — A — sinz C),
т. e.
cos — sin В sin2 C= cos A sin C+ cos В sin С cos С
или, после сокращения на sin С,
cos A = — cos В cos C-f- sin В sin С cos — . C5)
Формула C5) выражает двойственную сферическую теорему
косинусов, которую обычно формулируют в виде: косинус угла
сферического треугольника равен произведению синусов двух дру-
других углов на косинус стороны между ними без произведения
косинусов двух других углов.
Заменяя в формуле C5) обозначения сторон а, Ь, с и углов А,
В, С в круговом порядке, мы получим две аналогичные формулы:
cosB= — cos С cos A + sin С sin A cos —, C6)
cos C= — cos A cos B+ sin A sin В cos —. C7)
Формулы C5), C6) и C7) двойственной теоремы косинусов
могут быть получены также соответственно из формул A9), B0) и
B1) теоремы косинусов, если записать эти формулы для полярного
треугольника и использовать соотношения между углами и сторо-
сторонами двух взаимно полярных треугольников; этим и объясняется
название этой теоремы.
Заметим, что при малых значениях отношений —, — и — . т. е. при
очень малых длинах сторон а, Ь, с сферического треугольника или при
очень большом радиусе сферы г, сферическая геометрия мало отличается
от плоской геометрии и тригонометрические соотношения в сферическом

552 основные понятия сферической геометрии и тригонометрии
треугольнике можно заменить тригонометрическими соотношениями в пло-
плоском треугольнике. И в самом деле при малых значениях переменного х
можно пренебречь высшими степенями этого переменного и, следовательно,
можно заменить sinx-x—tt + ki на х, a cosx=l — тг+тг— •••
о 5! 2. 4!
хг
на 1—=- или даже на 1. Но при такой замене, как легко проверить,
сферические теоремы косинусов и синусов переходят в одноименные пло-
плоские теоремы, первые шесть формул пяти элементов переходят в теоремы
проекций плоской тригонометрии, а вторые шесть формул пяти элементов
и двойственная теорема косинусов, не имеющие аналогов в плоской три-
тригонометрии, переходят в соотношение А-\-В-\-С=л.
Основные теоремы сферической тригонометрии были открыты
учеными средневекового Востока. Соотношения, выражаемые теоре-
теоремой косинусов, были установлены сирийским Математиком и астро-
астрономом IX века ал-Баттани, выходцем из семьи звездопоклонни-
звездопоклонников—сабиев, у которых в течение многих веков сохранялись
вавилонские астрономические традиции. Сферическая теорема сину-
синусов была открыта почти одновременно среднеазиатскими математи-
математиками и астрономами X века Ибн Ираком из Хорезма, Абу-л-
Вафой из Хорасана и ал-Ходжанди из Ходжента. Соотношения,
выражаемые двойственной теоремой косинусов, были установлены
(с помощью полярного треугольника) в XIII веке работавшим
в Азербайджане Насир-ад-дином ат-Туси, давшим первое
полное изложение всей системы сферической тригонометрии.
4.5. Формулы котангенсов. Деля почленно формулу пяти эле-
элементов B3) на вытекающее из формулы B2) равенство
sin — sin В = sin—sin Л,
мы получим равенство
. b . с с .
ctg— sin cos — cos A
sm A
т. е.
etg В sin A = ctg — sin cos —cos A
или
sin —ctg sin A ctg В = cos— cos A. C8)
Мы получили одну из формул котангенсов, которую обычно
формулируют в виде: произведение синуса одной стороны сфери-
сферического треугольника на котангенс другой без произведения
синуса угла, лежащего против третьей стороны, на котангенс
угла, лежащего против второй стороны, равно произведению
косинуса первой стороны на косинус угла, лежащего против
третьей стороны.

ТРИГОНОМЕТРИЧЕСКИЕ СООТНОШЕНИЯ В СФЕРИЧЕСКОМ ТРЕУГОЛЬНИКЕ 553
Заменяя в формуле C8) обозначения сторон а, Ь, с и углов
в круговом порядке, мы получим две аналогичные формулы:
sin — ctg — — sin Вctg C= «.os — cos В, C9)
sin — ctg у — sin Cctg A = cos ~- cos С D0)
Меняя в формуле C8j местами стороны а и с и углы А и С,
а затем заменяя обозначения сторон а, Ь, с и углов А, В, С в кру-
круговом порядке, мы получим еще три аналогичные формулы:
sin — ctg sin С ctg B= cos— cos С, D1)
sin — ctg sin A ctg C= cos — cos A, D2)
sin— ctg— — sin В ctg A = cos у cos B. D3)
4.6. Случай прямоугольного сферического треугольника. В слу-
случае, когда сферический треугольник ABC—прямоугольный треуголь-
треугольник с прямым углом А, теорема косинусов A9) принимает вид
a he
cos — = cos — cos — D4)
т. е. косинус гипотенузы равен произведению косинусов катетов.
Эта теорема, связывающая гипотенузу и катеты прямоугольного
сферического треугольника, является .аналогом теоремы Пифагора
и называется сферической теоремой Пифагора1).
В случае прямого угла А теорема синусов B2) принимает вид
равенств
sin — = sin ~ sin В D5)
и
sin — = sin у sin С. D6)
Формулы D5) и D6) называются формулами синусов для пря-
прямоугольного сферического треугольника.
В случае прямого угла А формулы пяти элементов B5) и B7)
принимают вид
cos — sin sin — cos — cos C= 0,
•) Записав формулу D4) в виде 1 — ^+ ... = ^ 1 ) )
(ср. стр. 552), можно убедиться, что при г -г- со сферическая теорема Пифа-
Пифагора переходит в плоскую теорему Пифагора: a2 = bs-\-c\
36 Энциклопедия, кн. 4

554 основные понятия сферической геометрии и тригонометрии
и
cos — sin sin — cos — cos B = 0,
откуда находим формулы
D7)
tgf=cos?tg-. D8)
*
Формулы D7) и D8) называются первыми формулами тангенсов
для прямоугольного сферического треугольника
В случае прямого угла А формула C5) двойственной георемы
косинусов принимает вид
— cos В cos C+ sin В sin С cos у = О,
откуда находим формулу
cos — = ctg В ctg С. D9)
Формула D9) называется формулой котангенсов для прямо-
прямоугольного сферического треугольника.
В случае прямого угла А формулы C6) и C7) двойственной
теоремы косинусов принимают вид
cos B= cos С cos — . E0)
и
cosC = sin?cos —. E1)
Формулы E0) и E1) называются формулами косинусов прямо-
прямоугольного сферического треугольника.
В случае прямого угла А формулы котангенсов C8) и D2) при-
принимают вид
SinyCtgy — CtgB^O
и
sin у ctg у— ctg С=0,
откуда находим формулы
tgf=sin-^tgfi, E2)
f E3)

ТРИГОНОМЕТРИЧЕСКИЕ СООТНОШЕНИЯ В СФЕРИЧЕСКОМ ТРЕУГОЛЬНИКЕ 555
Формулы E2) и E3) называются вторыми формулами танген-
тангенсов прямоугольного сферического треугольника.
Сферическая теорема Пифагора, две формулы синусов, две пер-
первые формулы тангенсов, формула котангенсов, две формулы косину-
косинусов и две вторые формулы тангенсов составляют десять формул
прямоугольного сферического треугольника.
•4.7. Решение сферических треугольников. Выведенные нами
тригонометрические соотношения позволяют «решить сферический тре-
треугольник» по любым трем из его элементов (сторон и углов). Если
нам даны три стороны сферического треугольника, то по формуле
A9) теоремы косинусов находим
а Ь с
cos cos— cos—
cos А =
. b . с
sin— sin —
Г Г
и аналогично по формулам B0) и B1) находим cos В и cos С.
Если нам даны две стороны сферического треугольника и угол
между ними, например стороны Ь, с и угол А, то сторону а найдем
по формуле A9) теоремы косинусов. Зная все три стороны сфери-
сферического треугольника, найдем его остальные углы, как указано
выше.
Если нам даны две стороны сферического треугольника и угол,
лежащий против одной из них *), например стороны a, b и угол Л,
то по формуле B2) теоремы синусов находим
sin}
sin В = sin A.
sin —
г
Заметим, что эта формула дает для В два значения, дополняю-
дополняющих друг друга до я; это соответствует тому, что в общем случае
два сферических треугольника с двумя соответственно равными сто-
сторонами н равными углами, лежащими против одной из этих сторон,
не обязательно равны, а возможен случай, когда углы этих треуголь-
треугольников, лежащих против другой стороны, дополняют друг друга до
я, как мы это видели, рассматривая IV признак равенства сфери-
сферических треугольников.
Для определения стороны с и угла С проведем через вершину
С дугу большой окружности, перпендикулярную большой окруж-
') Предполагается, что хотя бы одна из данных сторон отлич-
отличл
на от -г-г
36*

556 ОСНОВНЫЕ ПОНЯТИЯ СФЕРИЧЕСКОЙ ГЕОМЕТРИИ И ТРИГОНОМЕТРИИ
ности АВ '). Если эти большие окружности пересекаются в точке D,
то рассмотрим прямоугольные сферические треугольники ACD и BCD
(рис. 47). В этих треугольниках известны гипотенузы b и а и углы
при вершинах А и В. Второй катет каждого из этих треугольников
определяется по первым формулам тангенсов D7) или D8), а угол
при вершине С определится по формуле котангенсов D9). Сторона с
и угол С сферического треугольника ABC
являются суммами найденных нами сторон
или углов прямоугольных треугольников,
если точка D лежит на егороне АВ, и раз-
разно с т я м и этих сторон или углов, если
точка D лежит на продолжении стороны АВ.
Именно, если оба угла А, В в исходном
треугольнике ABC являются острыми или
оба тупыми, то перпендикулярная к АВ
окружность, проходящая через точку С, пе-
пересекает окружность АВ в двух точках,
одна из которых лежит на дуге АВ; эту точку и следует принять
за D в рассматриваемом случае (рис. 47). Таким образом, углы при
вершинах А и В в прямоугольных треугольниках ACD и BCD сов-
совпадают с углами А и В исходного треугольника ABC, а сторона с и
угол С треугольника ABC являются суммами найденных нами
сторон или углов прямоугольных треугольников ACD и BCD. Если
же в треугольнике ABC один из углов А, В острый, а второй — ту-
тупой, то перпендикулярная к АВ окружность, проходящая через точку С,
пересекает окружность
АВ в двух точках, н и
одна из которых не ле-
лежит на дуге АВ. В этом
случае за D можно при-
принять любую из этих то-
точек, например ту, кото-
которая лежит на продолжении
стороны АВ за точку В
(рис. 48). Таким образом,
угол при вершине А в
треугольнике ACD равен углу А треугольника ABC, а угол при
вершине В в треугольнике BCD равен я—В. При этом сторона с и
угол С треугольника ABC являются разностями сторон AD, BD или
>глов при вершине С треугольников ACD и BCD. Наконец, если
О1ин из углов А, В (например, А) прямой, то треугольник ABC
*) Так как, по предположению, хотя бы одна из сторон а, Ь отлична
от у''.то точка С не является полюсом окружности АВ, и потому через С
проходит единственный перпендикуляр к АВ.

ЛИТЕРАТУРА 557
прямоугольный, и для нахождения стороны с и угла С можно в
этом случае воспользоваться формулами D4), D7).
Если нам даны три угла сферического треугольника, то по фор-
формуле C5) двойственной теоремы косинусов находим
a cos A 4- cos В cos С
cos — =
г sin В sin С
b с
и аналогично по формулам C6) и C7) находим cos— и cos—.
Если нам даны два угла сферического треугольника и сторона
между ними, например сторона а и углы В и С, та угол А найдем
по формуле C5) двойственной теоремы косинусов. Зная все три
угла сферического треугольника, найдем его остальные стороны, как
указано выше.
Если, наконец, нам даны два угла сферического треугольника ')
и сторона, лежащая против одного из них, например углы А и В
и сторона а, то по формуле B2) теоремы синусов находим
. Ь sin В . а
sin — = ——j sin — .
г япЛ г
Заметим, что эта формула дает для Ь два значения, дополняю-
дополняющих друг друга до лг; это соответствует тому, что в общем слу-
случае два сферических треугольника с двумя соответственно равными
углами и равными сторонами, лежащими против одного из этих углов,
не обязательно равны, а возможен случай, когда стороны этих тре-
уюльников, лежащие против другого угла, дополняют друг друга
до т, как мы это видели, рассматривая V признак равенства сфе-
сферических треугольников. Сторону с и угол С по углам А, В и сто-
сторонам a, b мы найдем, как указано выше.
ЛИТЕРАТУРА
[1J Ж- Адам ар, Элементарная геометрия, перев. с франц., ч. 2. М.,
Учпедгиз, 1958
Обширный курс стереометрии; гл. VI и VII пятой книги посвящены
основным понятиям сферической геометрии, а 1 и II дополнения ко
второй части—некоторым дополнительным вопросам сферической гео-
геометрии, в частности определению площадей сферических треугольни-
треугольников и многоугольников. Книга содержит много задач.
[2J Д. И. Перепелкин, Курс элементарной геометрии, т. II, М.—Л.,
Гостехиздат, 1949.
Сферической геометрии посвящена гл. XVI этого обстоятельного
курса стереометрии.
[3J Н Н. Степанов, Сферическая тригонометрия, М.—Л., Гостехиэ-
дат, 194и.
') Предполагается, что хотя бы один из данных углов отличен от-^ .

ИМЕННОЙ УКАЗАТЕЛЬ
Абу-л-Вафа (Абу-л-Вафа Мухаммед ибн Му-
Мухаммед ал-Бузджани) (940—998) -
среднеазиатский математик 552
Адлер (Adler) Август A863—1923) — ав-
австрийский математик 169, 175
ал-Баттани (Абу'Абдалла Мухаммед ибн
Джабйр ал-Баттанй) (850—929)—сирий-
(850—929)—сирийский математик 552 _
ал-Ходжанди (Абу Мухаммед Хамид ибн
ал-Хидр ал-Ходжанди) (ум. ок. 1000) —
среднеазиатский математик 552
Александров Александр Данилович
(р. 1912) — советский математик 412, 420
Аристотель ('AoiototeXtis) C84—322 до
и. s.) — древнегреческий философ 13.
16. 31. 182
Архимед CAOXlMiotiS) (ок. 287-212 до
н. 9.) — древнегреческий математик и ме-
механик 16
Бельтрами (Beltraml) Эудженио A835—
1900) — итальянский геометр 29, 45
Витрувий (Markus Vitruvlus Pollio) B-я
половина 1 в. до и. s.) — римский архи-
архитектор и инженер 276
Галуа (Galois) Эварист A811 — 1832) —
французский математик 206
Гаусс (Gauss) Карл Фридпих A777—1855)—
немецкий математик 47. 206, 226
Гильберт (Hilbert) Давид (I86-—1943) —
немецкий математик 41
Гиппократ Хиосский ('1яяохо4тт)е) B-я по-
половина 5 в. до и. э.) — древнегреческий
геометр 13
Дедекинд (Dedeklnd) Юлиус Вильгельм Ри
хард A831—1916) — немецкий матема-
математик 31, 38. 40
Декарт (Dcscartrs) Рене A596—1650) —
французский философ, физик, математик
18
Демокрит (AthkSxqitoc,) (ок. 460—370 до
н. s.) — древнегреческий философ 13, 14.
16. 17. 47
Евклид <E«xA.ei6t)?) (начало 3 в. до н.э.) —
древнегреческий математик 13, 16. 17,
18, 35. 43. 46, 177. 412
Ибн Ирак (Абу Наср Мансур ибн1 Али ибн'
Ирак) — A0—11 вв.) — среднеазиатский
математик 552
Каган Вениамин Федорович A869 1953)—
советский математик 41
Клейн (Klein) Феликс A 849—1925) — не
мецкий математик 29, 45, 102
Коши (Cauchy) Огюстен Луи A789—1857)—
французский математик 412
Лагерр (Laguerre) Эдмоид A834—1886) —
французский математик 449
Ли (Lie) Софус A842—1 899) — норвежский
математик 449
Лобачевский Николай Иванович A792—
1856) —русский математик 10, 18.47
Маскероии (Maschcroni) Лоренцо A750—
1800)—итальянский геометр 169
Мебиус (Mobius) Август Фердинанд A790-
1Я68) — немецкий математик 449
Менелай (MeviXaog) (I в.) — древнегрече
ский астроном и математик 519
Монж (Monge) Гаспар A746—1818)— фран-
французский геометр 276
Mop (Mohr) Георг A640—1697) — датский
математик 169
Насир-ад-дин ат-Туси (Абу Джа'фар Мухам
мед ибн Мухаммед Насир ад-Дин ат
Туей) A201 —1274) — азербайджанский
математик 552
Паш (Pasch) Мориц A843—1930» — немец-
немецкий математик 34
Пифагор (Ш'юубоас,) (ок. 580—500 до
н. э.) — древнегреческий математик и
философ 13, 14. 16, 17
Платон (ШАтиу) D27—34S до н. э.) —
древнегреческий философ 13
Погорелов Алексей Васильевич (р. 1919) —
советский математик 420
Польке (Pohlke) Карл A810—1876) — не
мецкий геометр 249
Понселе (Poncelet) Жан Виктор A788—
1867) — французский математик и инже-
инженер 171
Птолемей Клавдий (КЯяивюс; ПтоЛедаТод)
B в.) — древнегреческий астроном 519

именной указатель 559
Пуанкаре (Polncare) Аири A854—1912;- Шварц (Schwarz) Герман Амандус AЬ43—
французский математик 45 1921) — немецкий математик 250
Штейнер (Steiner) Якоб A796—1863) —
швейцарский математик 171
Ннман (Rlemann) Георг Фридрих Берихард Штейниц (Steinltz) Эрнст A871 — 1928) —
AS26—1866) — немецкий математик 47. немецкий математик 403
102 ' Шур (Schur) Иссаи A875—194 I) —немец-
—немецкий математик 4 I
Фалес FaXrjg) (конец 7 — начало 6 вв. до Эйлер (Euler) Леонард A707—1783) — ыа-
н. э.) — древнегреческий филосрф II, 17 тематик, механик, физик 190. 390

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абрис 260
Абстрактный многограиннк 401—403, 407
Абсцисс ось 321
Автополярный треугольник 531
Аксиома 20. 21
— Архимеда 37, 45
— движения 36—37, 41
— Дедекиида 40
— Кантора 37, 41, 46
— непрерывности 31, 37
— параллельности 40
— Паша 34
— полноты 41
— поля 30
— порядка 31. 34
— принадлежности 32
Аксиоматика 20, 369
— векторного пространства 369—375
— группы 27, 45
—. независимость 44
—, непротиворечивость 28
—, полнота 30
— поля действительных чисел 30, 31
— элементарной геометрии 375—377
Аксиоматический метод 20
Аксонометризация чертежа 266
Аксонометрическое изображение 259—266
Аксонометрия 257, 258
— параллельная 25?
—, показатели (коэффициенты) искажения
272
— центральная 257. 286. 287
Алгебра Ли 380
Аналагматическая геометрия 104
— — круговая 139
точечная 139
Аитипризма 433. 437
Апликат ось 322
Аполлония задача 513
Арифметика рациональных чисел 29
Архимеда аксиома 37. 45
— спираль 177
Архимедов многогранник 436, 438
Ассоциативности закон 85
Аффинная геометрия 103. 104. 378
линейчатая 139
точечная 139
— сетка 244
— система координат 243, 248
Аффинное отображение 236
— преобразование 62. 76, 93, 103. 104
122, 138. 243, 298
— пространство 378
Аффинный репер 243
— — пространственный 248
Аффинор 298
Аэрофотограмметрия 287
База (малой окружности) 540
Базис ортонорммрованный 372
Бесконечно удалрьная прямая 113
точка 24, 57, [12, 477
Бесконечномерное векторное пространстве
377
випирамида 408
Бирациональное преобразование 79, 119.
Большая окружность 520. 529, 534—536
Большой додекаэдр 443
— звездчатый додекаэдр 443
— икосаэдр 445
— круг 520
Бриаишона теорема 502
Вектор 293, 376
—. длина 294
—. координаты 312—314. 373
— нулевой 301
—, определение 294. 296, 297
—, откладывание от точки 294—296
— параллельного переноса 295
— свободный 295
— связанный 295
Векторное произведение 354
двойное 360. 361
, единственность 364—366
, свойства 355—360
— пространство 370, 377
-, аксиоматическое определение 36S--375
, арифметическая модель 370, 371
бесконечномерное 377
евклидово 370
л-мерное 377, 378
Векторы, векторное произведение 35 4
—. вычитание 304, 305
—, двойное векторное произведение 3S0
36 I
—, косое произведение 338, 341—343. 345
380
— линейно зависимые 314
— — независимые 314
— противоположные 300
— равные 296
—, скалярное произведение 328—331. 342,
350, 369
—, сложение 298—303, 369
—, смешанное произведение 355
—, тройное произведение 351, 352
—. умножение на число 305—308, 369
Вертикальные углы (на сфере) 528
Вершина двуугольника 530
Вершина многогранника 384
— многоугольника 382
— сферического треугольника 530
Взаич(,ьь' мис гогранннки 427

ПРРДМЕТНЫЙ УКАЗАТРЛЬ
56
Внутренняя геометрия поверхностей 4 1
— метрика 4I9
Воображаемые построения 202
Вращение 52. 54 60 83. «6, 87. 89. 90
91 92. 140
Вставка 17
Вторич 1ая пр екция 255
Вторы ф рмулы ai re сов 555
Вып кл и мн гра ник 386 407 418
— мн г угольник 4
Выр жденная ин ер ия 468. 469
осев я инвер ия 4 96
Вычитание вркторов 304, 305
Галилея преобразива! ня 108—110
принцип отно и е ы сти 108. 109
Гаусса те рема 219
Гаусса —Бонне формула 544
Гексаэдр 423
— правильный 426. 442
Геодезическая кривизна 54 1 543. 545
— линия 536
Геомр рические постро ния в пространстве
200 203
иа плоскости сбщая схема решения
81
— —, система постулатов 200
Геометрическое место очек 16, 17, 182
о обряжение 51
еометрия 10, 98—107, 138 155 518
аналагматическая 104
— аффинная 103, 10 . 139. 378
Евклида 18, 19 21 22 41. 45. 47.9
103 140, 156
— конформная 104
— кр говая 104. 139 478
— осевая 507
— Лагерра 507
— ли ейная 13
— Лобачевского 18. 19 45 47 103. НО
— начерта елы ая 234
— неевклидова 03
— окружи стей 139
ка атсльпая 515
— п ективная 105, 110, 117
прямых лннн 139
— риманова 47
ферическая 5Ь8. 524
— элеме a i ая 13 75-377
ерона формул 46
Гиперболическая инверсия 59, 73, 75. 79.
96. 114 21 • 4
, ось 5
— — с еп 1 ь 59
— свя ка 6
— ть кр жии 93
Гиперболиче и пу к 462
— ряд окружи т й 492
ом л гия ПО И, 112 113 114. 115
I 117 121 122
—, обла ть начений 112
—. — опредпе! ия 12
—. ось 110
—. центр lit
Гом тетия 5 , 6 , 61, ЬЗ 64, 65 73 7
5J 9 о 7 П4 22 138 180
192
коэ фици нт 55
—, ось 93
—, центр , 93
Горизонталь 233
Гориз i альная плоскость 275
— проекци 275
грзнь 384
1 руппа 27. 370
аксиоматика 27 4 5
— к ммутативная 369
— преобраз вання 110
138
Движение 17. 36. 41. 60 62. 88 89. 92
9 . 103. 139, 376
— сферы 522—524
Движе! ия ак и ча 36 37 41
Двойн е векторное пр изведение 360. 36
Двойс венная фериче иая орема к снну
с в 551
Двойственности принцип 130, 40
Двойс венные многогр ики 407
— правил ные многогрэ ники 26 427
Дв у ли ик 530
— пл щадь 537
Дед hi да аксиома 40
— те рема 3
Дедуьп вный метод 10
Дезарга еорема 130 132
братьая 132
Дезарг ва конфигурация 283 284
— прямо гольная равнобедре! ная 283
прямая 285
Дейс ви льное чи ло IS
Декар ва прям г льная сие ем коорди
на 251
Дескриптивное определени 1
Диаг нальная то ка 278
Диметрическое из бражеиие 273
Диметрия ортогональная 262
Дирихле функция 5
Ди Ki етн е пр тра! itbo 47
Д дека др 423
— б льш й 443
— звездчатый 4 4 Л
— звездчат й 4 43
— пл к н сый 4 37
правильный 42 442
у еч нный 437
Додекаэдр додека др 4 46
Дод ка д оик са др 44G
Дробно ли ейная функция 78
Дроби линейное преобразование 79 121
Дуг на фере 39
Евклида геометрия 18 19 21 22. 4 45
47 8. 103, 40, 156
— . дель 41 156
— прострш ство 32, 1. 4Ь 47
размерность 46
Евклид ва геометрия — см вклида гео-
мет и я
плоек сть 4 1
— , арифметическая модель 4J
. модель (интерпретация) 21—2
Евклидово п странство п мерное 377 376
Жордава теорем» 397
Звезда вершины 429
— грани 2°
Зв здчатый додека др 443
мног г анннк 14I
Изображение 229
— ак ономе ри еское
диметрич ск 27
— ж сткое 39
— из метрическое ^73
66

562
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Изображение комбинированное 275
~ плоских фигур 240—247
— полное 253. 254, 256
— —. базис 254
— свободное 240
— гриметрическое 273
— условное 258
Изображения метод 229
— —, основные требования 231—233
— — проекционный 233
— плоскость 229
Изометрическое изображение 273
Изометрнчиые многогранники 41©
Изомегрия ортогональная 274
Изоморфизм 30
Икосаэдр 4 23
— больший 445
— правильный 42ь, 442
— усеченный 437
Икосидодекв^др 437
— усеченней 4 37
Инверсии окружность 469
Инверсия 26. 56—58, 62, E«, 73, 74, 78
79, 96, 119, 120, 121. 124, 143. 468
471, 472, 474. 478
— вырожденная 468. 469
— гиперболическая 59. 73. 75, 79. 96,
119 — 121, 146
—. коэффициент 5h
— невырожденная 4 69
— обыкновенная (общая) 469
— осевая 496—502, 505
— — вырожденная 496
направляющая окружность 499
— — невырожденная 499—502
общая (обыкновенная) 496. 498, 505
особая 196—500. 505
. ось 496
, степень 496
— особая 468. 469
—, степень 469
— точечная 468
—, центр 56, 4 69
Инволютивиое преобразование 97, 137
Инволюция 97
Индуктивный метод 10
Интерпретация геометрической системы 21
Инцидентность 401
Искажения поквзатели (коэффициенты) 272
Кап гора аксиома 37 41, 46
Касание 453
Касательная |еометрия окружностей 515
Касательное преобразование 136, 511
круговое 125. 138. 139. 511. 512
— расстояние 485
Квадратичное преобразование 119. 120
Квадратные числа I 4
Квадратура 16
— круга 226, 227
Комбинаторный (топологический) тип
многогранников 400
Комбинированное изображение 275
Коммутативная группа 369
Коммутативности закон 85
Коммутатор 380
Комплексная координата 78
Комплексный чертеж 27Ь
Конгруэнтность 41, 297
Конечное пространство 46
Конкурирующие точки 235
Конус 11
— круговой, аксонометрическое изображе-
изображение 260
Конфигурация дезаргова 283—285
Конформная геометрия 104
Координаты вектора 312—314. 373
Коордиограф 161
Косинусов теорема 331
сферическая 368, 545—54 7
двойственная 551
— формулы 554
Косое произведение 338, 341—343, 345
380
. единственность 349 350
, свойства 343—345
Косоугольная проекция 239
Котангенсов формулы 552—554
Коши теорема 4 13, 4 16, 4 20
Коэффициент гомотетии 55
— инверсии 56
— подобия 61
— сжатия 56
Кривизна 541
— геодезическая 541—543. 545
Круг сферический 539
— —, площадь 54 1, 544
Круговая анала! магическая геометрия 139
— геометрия 104, 139, 4 7ь
— плоскость 24, 57, 58. 7Ь. 79, 121 477
, модель 58
Круговое преобразование 62, 79, 93 104.
124, 125, 138. 139. 478
касательное 125. 138. 139, 511. 512
Ли 511
осевое 125, 138. 139. 504. 505, 512
точечное 512
Куб 11, 426, 442
— плосконосый 437
— усеченный 437
Кубатура 16
Кубические числа I4
Кубическое преобразование 119, 121
Кубоктаэдр 437
— усеченный 4 37
Лагерра (еометрия 507
— преобразование 504
Ли алгебра 380
— круговое преобразование 511
Линейка 161, 167
— ограниченной длины 17»
Линейная геометрия 139
— зависимость векторов 314, 315
— функция 73
Линейное отображение 76
— преобразование 76, 7 7. 79. 119. 121
Линейный элемент 136, 509
Линейчатая аффинная геометрия 139
Линия 11.14
— геодезическая 536
— связи 275
— схода 282
— центров 463. 492
ряда окружностей 492
Лобачевского геометрия 18. 19, 45, 47,
103, 110
Лоренца преобразования 110
Луч 35
Малая окружность 520, 539—545
, база 540
, геодезическая кривизна 543
. параметр 540
, сферический радиус 540
, — центр 540
Мебиусв преобразование 4 78
Медиана 316, 317
Менелая теорема 347

ПРЕДМРТНЫЙ УКАЗАТЕЛЬ
563
Метаматематика 205
Метрически правильный многогранник
424, 426
— — многоугольник 4 24
— равногранно полуправильный много
гранник 440
— равноугольно полуправильный много
граныик 436
Многогранник 384, 386
.— абстрактный 401—403. 407
— архимедов 436, 438
—, вершина 384
— выпуклый 386, 407, 418
—. грань 384
— звездчатый 441
—, комбинаторные (топологические) свой
ства 400
— метрически правильный 424, 426
равиогранно полуправильный 440
равноугольно полуправильный 436
—, метрические свойства 4 00
— нулевого рода 390, 408, 4 29
, топологический тип 420, 423
— Платонов 4 24
— полуправильный 429, 43Ь. 440
— правильный 424
самопере екающийся (звездчатый) 441,
— простой ЗВ5. 424
— пространственный 402
— Пуансо 44 1
—, развертка 410
—, ребро 384
—, род 391
— самопересекающийся 4 41
— топологически правильный 420
¦ раиногранно полуправильный 438
равноугольно полуправильный 429
—, топологические (комбинаторные) свойст
ва 400
Многогранники взаимные 427
— двойственные 407. 426
— изометричиые 4 19
— изоморфные 400
—. комбинаторный (топологический) тип 400
Многогранный угол правильный 424
Многомерное векторное пространство 377
Многоугольник 382. 383
—, вершина 382
—, выпуклый 384
— метрически правильный 424
— правильный 424
— простой 383, 424
— распадающийся 441
— самопересекакщщйся 383
—, смежные вершины 382
—, — стороны 382
—, сторона 382
— сферический 538, 543
—, ядро 4 41
Многоугольные числа 1 4
Модель 21. 29
Монжа метод 232. 275. 276
Мора—Маскероии построения 169—171
теорема 168
Направление проектирования 234
Направленная окружность 480
Направленный отрезок 450
— угол 450
«Начала» Евклида 13
Начертательная геометрия 234
Неархимедова геометрия 4 5
Невырожденная инверсия 469
— осевая инверсия 499—502
Недоступные прямые 179
— точки 1 79
— элементы 179
Неевклидова геометрия 103
Неканторова геометрия 4 6
Неоднородные проективные координаты 280
Непрерывное преобразование 60
Непрерывности аксиома 31. 37
Неприводимый многочлен 217
Непротиворечивая система аксиом 2S
Несобственная связьа 234
— точка 57. 112. 1 13
Неточечное преобразование 121
Нулевой вектор 301
Область действия ?3
— значений 51, 112
— определения 50, 51, 112
Образ 51
Обратная функция 96
Обратное отображение 97. 137
— преобразование 97. 137
Общая инверсия 46 9
— осевая инверсия 49С. 49В. 506
«Общее понятие» 13, 15
Обыкновенная инверсия 4E9
— осевая инверсия 496, 4ii8. 505
Однородные координаты 118
— проективные координаты 280
Окружности, ось подобия 490
— перпендикулярные 453. 528. 529
—. ряд 4С0
—. <еть 492
—, центр подобия 4Й9
Окружность большая 520. 529. 584 - 536
— девяти точек 65
—. изображение 24h
— инверсии 46Ь
— малая 520. 539 — 54.-
— направленная 480
—. определение 451. 452. 479. 480. 510
—, ось о22
—. радиус 451. 510
—, центр 451
— Эйлера 65
Октаэдр 423
— правильный 426. 4 42
— усеченный 437
Ординат ось 322
Оригинал 229
Ориентированная плоскость 350
Ортогональная диметрия 262
— изометрия 274
— проекция 239
Ортонормированный базис 372
Осевая инверсия 496—502, 505
— —. направляющая окружность 49е*
— круговая геометрия 507
— симметрия 292
Осевое круговое преобразование 125. 138,
139, 504. 5U5. 512
— преобразование 496, 504
Основание пирамиды 385
— призмы 385
Особая инверсия 46*. 469
— осевая инверсия 496—500 505
Ось 310
— абсцисс 321 ^
— апликат 322
— гиперболической инверсии 6У
— гомологии 11 0
— гомотетии 93
— окружности 522
— ординат 322

564
ПРЕДМЕТНЫЙ УК<ПАТЕЛЬ
Ось осевой инверсии 4 96
— подобия 9Ь
окружно тей 490
— радикальная 455. 457. 458 462
— сети окружностей 492
— сжатия 56
— симметрии bb
Относительно ти принцип Галилея 108 109
Эйнштейна 110
Отображение (геометрическое, точечное) 51
— ас|финное 236
— взаимно однозначное j3
— линейное 76
—, область значений 51
—, — определения 51
— обратное 97. 137
— полярное 128—133. 137, 14D—148 150
156
Отрезок 34
— направленный 450
Пантограф 1Ы
Паппа задача 186
Параболическая связка 467
— сеть окружностей 493
Параболический пучок 462
— ряд окружностей 492
Параллелограмм сил 302
Параллелограмма правило 302
Параллельная аксонометрия 257
— проекция 232. 234—247
Параллельное проектирование инварнан
2 36
Параллельности аксиома 40
Параллельные прямые 14. 40
Параллельный перенос э4, 60. 63. 16, 76
81, 83. 86. 88, 89 93. 97. 105—107
114. 191. 292. 295, 298, 541, 543
Параметр (малой окружности) э40
Паскаля теорема 475
— улитка 134
Паша аксиома 34
Первые формулы тангенсов 554
Перемесгительно ти закон 85
Перене(ения принцип 14 0, 156. 157
, О1Вечающий инверсии 143—146
— —. — полярному отображению 146—15
— —. — сжатию к прямой 140—143
Переориентация 496
Перпендикулярные пучки окружностей 46Ь
Пирамида I I, 385
— основание 385
— четырехугольная, аксонометрическое изо
бражение 259
Пирамидальные числа 14
Пифагора георема фериче 'кая э53
Платонов многогранник 424
Плоский много гольник 382
Плосконосый додекаэдр 437
— куб 43 7
Плоскость 14, э8. 376
— горизонтальная 75
— евклидова 4 1
— изображения 229
— круговая 24. 57, 58 7Ь. 79. 12 . 477
— проекций 277
— проективная 113. 117
— профильная 276
— расширенная 24, 57. 78
— фронтальная 275
Поверхность 14
Поворот сферы о23, 524
Подериое преобразование 134—137
Подобие —см. Преобразование подобия
Поле 26
Поле действительных чисел 28
, аксиоматика 30, 31
-. допустимое конечное расширение 215
. квадратичное расширение 215
Полная система аксиом 3
Полное изображение 2оЗ. 254, 25t>
П лиоты аксиома 41
Полный четырехвершнйник 249
четырехугольник 248
Полуплоскость 36
Полуправильиый многогранник 4 29, 431»
440
Полупространство 36
Полусфера 520
Польке—Шварца теорем 249. 284
Полюс 521
Поля аксиома 30
Поляра 522
Полярное отображение 128—133. 137
146—14». 150. 156
Полярный сферический треугольник 531
Понселе—Штейнера построения 171 —175
георема 171
Порядка аксиома 31. J4
Построения в пространнее 20U 203
, система постулатов 201, 202
— воображаемые 202
— Мора—Маскерони 109—171
—, общая схема решения 184
— Понселе—Штейнера 1/1 — 17
— приближенные 193—200
— —. графоаналитический метод 197
, метод последова ельиых приблнже
иий 197
—, разрешимость ладач 209
—, система постулатов 200
— циркулем и линейкой 208, 209
Постулат 13. 15, 18. 40. 44
Правильный гексаэдр 426 44
— додекаэдр 426, 442
— икосаэдр 42ь, 442
— многогранник 4 24
самопересекающий я (звездчатый) 4 4
— многогранный угол 424
— многоугольник 4 24
построение 225 /26
— октаэдр 426, 442
— тетраэдр 426, 442
Предельные точки пучка 464
Преобразование 53, 121
— аффинное 62, 76 93. 103 104. 122,
134, 243, 298
— бирациональное 79, 119. 121
— Галилея 108—1 10
—, группа 102—110. 138
— дробно-линейное 79. 12
— инволютивиое 97, 137
— касательное 1 3d. 51 1
круювое 125, 138. 139. 511. 512
— квадратичное 119, 120
— круговое 62, 79 93, 104, 124. 126, 13».
139, 4 78
— кубическое 119, 121
— Лагерра 504
-линейное 76. 77. 79. 119. 121
— Лоренца 1 10
— Мебиуса 4 78
— непрерыв! ое 60
— иеточечное 121
—, область действия 53
— обратное 97 137
— осевое 496, 504
круговое 125. 13В 139, 504, 505, 512
— полерное 134 — 137

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
565
Преобразование подобия 61. t>2, 92. 100
103. 180. 296. 478. 505
— проективное 110, 117. 119
— тождественное 85
— точечное круговое 512
— уиимодулярноаффинное 284
— Центральио-аффииное 55
Призма 11, 385
— основание 385
— правильная 437
Принадлежности аксиома 32
Проективная геометрия 105, 110. 117
— плоскость 113. 117
. бирациональные преобразования 119
, линейные отображения 11 8
— система координат 279
Проективное преобразование 1 10. 117. 119
Проективные координаты 280 / •?
Проектирующая прямая 234
Проекций фирмула 324
Проекция вектора 320
— -вторичная 255
— горизонтальная 275
— косоугольная 239
— на ось 320. 321
, связь с координатами 321, 322
— ортогональная 239
— отрезка 320
— параллельная 232, 234—247
— пр фильная 276
— прямоугольная 239
— с числовыми отметками 233
— стереографическая 22, 57
— фронтальная 275
— центральная 232. 277
Прообраз 97
Простой многогранник 385. 424
— многоугольник 383. 4 24
Пространственный многогранник 402
Пространство 376
— аффинное 378
— векюрное 370, 377
— дискретное 47
— Евклида 32. 41. 46. 47
— конечное 46
— многочерное 377
реальное 4 7
— физическое 47
Противоположные векторы 300
Профильная плоскость 276
— проекций 276
Прямая линия 14, 376
— Симпсона 151
— Эйлера 65
Прямоугольная проекция 23S
Прямоугольные числа 14
Псевдоскалярное произведение 341
Птолемея теорема 146
Пуансо многогранник 441
Пучки окружностей перпендикулярные (со
пряженные) 465
Пучок окружностей 461. 462 466. 467
. предельные точки 464
— прямых 461
Пяти элементов формулы 549—551
Радикальная ось окружностей 455, 457,
458
пучка 462
Радикальный центр окружностей 460, 461
связки 4 66
Радиус 4 51
— сферический 540
Развертка 410
Разрешимые задачи на построение 209
Распадающийся многоугольник 44 1
Расстояние касательное 4 85
— сферическое 536
Растяжение 55
Расширение 125—128, 137. 138. 157. 497
Расширенная плоскость 24, 57, 78
Реальное пространство 4 7
Ребро 384
Реконструкция тетраэдра 257
Репер 36
— аффинный 243
пространственный 248
Рефлексивность 102, 296
Риманова геометрия 47
Род многогранника 391
Ромб 11
Ромбоикосододекаэдр 437
Ромбокубоктаэдр 437
Ряд окружностей 490
— —, линия центров 492
. центр 492
Самопересекающийся многогранник 441
— многоугольник 383
Свободный вектор 295
Связанный вектор 295
Связи линия 275
Связка 234
— окружностей 466, 467
. радикальный центр 466
Сегмент сферический 539
Сетка аффинная 244
— на сфере 395
Сеть окружностей 492
. ось 492
, степень 493
Сжатие к прямой 55. 62, 68, 73. 76, 93
96. 97. 1 14. 122. 141, 298
, коэффициент 56
—. ось 56
— к точке 55. 76
Симметричность 102, 296
Симметрия 66. 9 7. 292
— осевая 292
—. ось 66
— относительно окружности 56, 471
пары параллельных прямых 59
плоскости 292
прямой 55. 56. 60. 73. 76, 85, 89,
190, 469
точки 54, 55, 60. 63, 73. 76, 81. 83,
85. 91. 106, 107
— порядка к 66
— скользящая 89
— сферы 524
— центральная 292
Симпсона прямая 151
Синусов теорема 331
сферическая 368, 547, 548
— формулы 553
Система аксиом 20
— —, независимость 44
. непротиворечивость 28
, полнота 30
— координат 4 3, 321
— — аффинная 243. 248
декартова прямоугольная 251
проективная 278
Скалярное произведение 328—331. 342,
350. 369
— —, единственность 336—338
Скалярный квадрат 328
Скользящая симметрия 89

566
ПРРДМЕТНЫЙ УКАЗАТЕЛЬ
Сложение векторов 298—303. 369
Сложная функция 80
Сложное отношение 278
Смежные вершины 382
— сюроны 382
— углы (на сфере) 528
Смешанное произведение 355
Собственная связка 234
Сопряженные пучки окружностей 465
Сочетательности закон 85
Спираль Архимеда 117
Средства построения 160
Степень гиперболической инверсии 59
— инверсии 4 69
— осевой инверсии 496
— прямой относительно окружности 48ь
— сети окружностей 493
— точки относительно окружности 455
Стереографическая проекция 22. 57
Сторона многоугольника 382
— сферического треугольника 530
Сумма векторов 298. 299. 300 369
. свойства 301—303
— отображений 80
Сфера 11
Сферическая геометрия 518. 524
— теорема косинусов 368. 545—547
двойственная 551
— — Пифагора 553
синусов 368. 547, 648
Сферический круг 539
, площадь 54 1, 544
— многоугольник 538, 543
выпуклый 539
— радиус 54 0
— сегмент 539
— треугольник 36b. J67. 530—639
, вершина 530
, площадь 538
полярный 531
-, решение 555—557
— —, сторона 530
. угловой избыток 538
, угол 530
— центр 540
Сферическое расстояние 536
Схода линия 282
Тангенсов формулы вторые 555
— — первые 554
Телесные числа I4
Теорема 21
Тетраэдр 385, 423
— правильный 4 26, 442
— усеченный 4 37
Тождественное преобразование 85
Топологически правильный многогранник
420
— равиогранно полуправильиый многогран
ник 440
— р 1 вноуг&льио полуправильнын много
гранник 4 29
Топологические типы многогранников 420.
4 23
Топологический (комбинаторный) тип мно
гограниикоа 400
Точечная аналагматическая геометрия 139
— аффинная геометрия 139
— геометрия окружностей 13Р
— инверсия 468
— круговая геометрия 4 7Ь
Точечное круговое преобразование 612
— отображение 51
Точка 10, 13, 376
Точка диагональная 278
Транзитивность 102. 296
Транспортир 168
Трапеция 1I
Треугольник 383
— автополяриый 531
—, изображение 245
—, медиана 316
— сферический 366, 367, 530—530
—, центр тяжести 31 7
Треугольные числа 14
Триметрическое изображение 273
Трисекция угла 176, 221—223
Тройное произведение 351, 352
, единственность 364—366
. свойства 355—360
, связь с векторным произведением 353
Угловой избыток 538
Углы вертикальные (иа сфере) 528
— смежные (на сфере) 528
Угол 4 0. 14 4, 527
— иа сфере 527
— направленный 450
— сферического треугольника 530
Удвоение куба 220, 221
Улитка Паскаля 134
Умножение вектора иа число 305—308. 369
Унимодулярио-аффиниое преобразован не
284
Федорова метод 230. 233
Фигурные числа 1 4
Физическое пространство 47
Фронтвльная плоскость 275
— проекция 275
Функционал 51
Функциональный анализ 50
— оператор 51
Функция 50
— Дирихле 50
— дробно-линейиая 78
— линейная 73
—, область определения 50
— обратная 96
— сложная 80
Центр 11
— гомологии 110
— гомотетии 55, 93
— инверсии 56, 469
— окружности 451
— подерного преобразования 134
— подобия окружностей 489
— проекций 277
— радикальный 460, 461, 466
— ряда окружностей 492
— симметрии 66
кго порядка 66
— сферический 540
Центральная аксонометрия 257. 286. 287
— проекция 232, 277
— симметрия 292
Центрально-подобное преобразование 55
Центров линия 463. 492
Цикл 480
Циклография 229. 233
Цилиндр 1 1
Циркуль 167
Чевы теорема 349
Чертеж комплексный 275
Чертежная машина 160

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
567
Чертежный треугольник 161. 168
Четырехвершинник 278, 279. 281. 283,
284
— полный 24 У
Четырехугольник 383
—. изображение 245, 246
— полный 249
Числовая отметка 233
Шаг построения 208
Шар, аксонометрическое изображение 260
Штейница теорема 403
Эйлера окружность 65
— прямая 65
Эйлера георема 390. 394. 409
Эйлерова характеристика 391. 395
Эйнштейна принцип относительности 110
Эквиаффиниое преобразование 284
эквивалентность 296
Элементарная геометрия 13. 375—377
Эллипсограф 161
Эллиптическая связка 467
Эллиптическая сеть окружностей 493
Эллиптический пучок 462
— ряд окружностей 492
Эрлангеиская программа 102
Ядро многоугольника 441
Якоби тождество 357

энциклопедия
элементарной математики.
книга четвертая — геометрия
М.. Физматгиз, 1663 г., 568 стр. с илл.
Редактор С. А. Широкова.
Техн редактор Н. Я Мурашова.
Корректор О. А. Сигал.
Сдано в няГоп 25'111 1963 г Подписано
к печати 19/ХП 1963 г Бумага СО X 9О'/,в.
Физ. печ л. 35,5. Условн. печ. л. 35.5.
Уч -изд. л. 37.2 1 Тираж 20 000 »кэ.
Т-08843. Цена книги 1 р. 32 к.
Заказ № 2921.
Государственное издательство физико
математической литературы
Москва. В-71, Ленинский проспект, 15.
Гос. типография «Пяргале>. Вильнюс,
ул. Латако, 6