Б. П. Гейдман И. Э. Мишарина Подготовка
к математической олимпиаде

Б. П. Гейдман
И. Э. Мишарина
Подготовка к математической олимпиаде
«ьм шюи
2-4 классы
3-е издание, исправленное
Москва
Айрис-пресс И 2007
УДК [373.3.384:511(072)
ББК 74.200.58+22.1я7-43
Г29
Серийное оформление О. Е. Бауриной, С.С.Коломеец
Гейдман, Б. П.
Г29 Подготовка к математической олимпиаде. Начальная школа. 2-4 классы / Б. П. Гейдман, И. Э. Мишарина. — 3-е изд., испр. — М.: Айрис-пресс, 2007. — 128 с.: ил. — (Школьные олимпиады).
ISBN 978-5-8112-2849-2
Пособие предназначено для подготовки детей к олимпиаде по математике в начальной школе. Представленный материал соответствует определенному году обучения и систематизирован по темам. Предполагается, что вместе с ребенком могут решать эти задачи родители. Учитель и родители имеют возможность разобрать с ребенком любую задачу: к каждой задаче даются ответ и решение.
Учителя найдут в книге также много интересного материала для уроков, занятий математического кружка и для проведения олимпиады в школе.
ISBN 978-5-8112-2849-2	©ООО «Издательство
«АЙРИС-пресс», 2007
Учебное издание
Гейдман Борис Петрович Мишарина Ирина Энгельсовна
ПОДГОТОВКА К МАТЕМАТИЧЕСКОЙ ОЛИМПИАДЕ.
НАЧАЛЬНАЯ ШКОЛА
2—4 классы
Ведущий редактор А Л. Штерн
Редактор В. В. Черноруцкий
Художественный редактор А. М.Драговой
Оформление обложки В. В. Самсонов
Иллюстрации В. А. Артемов
Макет, техническое редактирование Т. В. Исаева
Компьютерная верстка Г. В. Доронина
Корректор З.А. Тихонова
Подписано в печать 21.08.07. Формат 60x90/16. Гарнитура «Школьная». Печать офсетная. Печ. л. 8. Усл.-печ. л. 8. Тираж 7000 экз. Заказ № 1612.
ООО «Издательство «АЙРИС-пресс». 113184, Москва, ул. Б. Полянка, д. 50, стр. 3.
Отпечатано в ОАО «Можайский полиграфический комбинат»
143200, г. Можайск, ул. Мира, 93
Введение
Олимпиады по математике — все более и более распространяющаяся форма математического соревнования для младших школьников.
Как готовиться к таким соревнованиям? Нужно ли проводить специальную подготовку к таким соревнованиям? Отбирать ли школьников для участия в таких соревнованиях? С какого класса можно проводить математические олимпиады? Не давая окончательных инструкций по всем этим вопросам, попробуем поделиться своим опытом работы с учащимися младших классов в этом направлении.
К концу первого года обучения в начальной школе накапливается достаточно материала для проведения олимпиады по математике. Уровень развития учащихся к этому моменту позволяет каждому ученику участвовать в такой олимпиаде, если он этого желает. Повторяем, что любой второклассник может участвовать в олимпиаде по математике, и эту возможность следует ему предоставить.
Содержание олимпиады для каждого года обучения должно соответствовать содержанию программы по математике этого года обучения.
Подготовка к математической олимпиаде начинается с работы на уроке. В содержание практически каждого урока должны входить или арифметические ребусы, или логические и комбинаторные задачи, или задания на разрезание и составление фигур, или другие упражнения на сообразительность.
Работа на уроках математики дополняется занятиями математического кружка. Кружок проводится один раз в неделю, продолжительность занятия от 45 минут до 1 часа. Его посещают все учащиеся, желающие заниматься математикой. На кружке учащиеся обсуждают решения задач и получают на дом задания, которые разбираются на следующем занятии.
В течение учебного года можно проводить в классе, или на параллели нескольких классов, или с учащимися той же
3
параллели других школ различные математические соревнования: математическую карусель, математический бой и т. д.
Мы предлагаем материал для работы на уроке, для занятий математического кружка, для проведения школьных олимпиад по математике. Материал соответствует определенному году обучения, систематизирован по темам. Задания, соответствующие какой-то теме, выстроены в определенной последовательности, даны рекомендации, как их обсуждать с учащимися. В зависимости от уровня подготовки конкретного класса учитель сам определяет, на какой задаче из этой последовательности стоит остановиться на уроке, какие задачи можно дать на кружке, какие — на школьной олимпиаде или на каком-то другом математическом соревновании.
Вся внеурочная работа, направленная на развитие математических способностей учащихся, является естественным дополнением к тому, чем учащиеся занимаются на уроках математики (и не только на них!).
Последний раздел «Задачи для самостоятельного решения» содержит 58 заданий на все разобранные в предыдущих разделах темы.
Авторы долго решали вопрос, разделить задачи для самостоятельного решения по темам и по годам обучения или дать их общим списком. Было решено дать общий список заданий: создать условия, максимально приближенные к олимпиадным. Поскольку задания не требуют специальных знаний по математике (достаточно уметь складывать, вычитать и умножать в пределах тысячи), то их может выполнять любой учащийся, начиная со второго класса.
Авторы учли и то обстоятельство, что вместе с ребенком с большим интересом решают эти задачи родители. Учитель и родители имеют возможность разобрать с ребенком любое задание: к каждому заданию имеется ответ или решение.
Авторы надеются, что, разбирая задания из этой книжки самостоятельно, с учителем на кружке или с родителями дома, дети получают большое удовольствие от занятий математикой.
класс
Подсчет геометрических <
Задача 1. Сколько треугольников изображено на рисунке 1?
на сторонах ал и
Рис. 1
Решение:
Задача 1 (рис. 1, а, б, в) не вызывает затруднений у учащихся. Но даже в этом случае следует ее обсудить.
Начнем со случая 1, а. Дан треугольник АВС. Провели отрезок MN с концами (рис. 2, а).
Сколько новых треугольников добавилось? Один треугольник AMN. Всего стало 2 треугольника: АВС и AMN.
Перейдем к задаче 1, б.
Провели еще один отрезок
KL с концами на сторонах АВ и АС (рис. 2, б).
Сколько новых треугольников добавилось? Еще один треугольник AKL. Всего стало 3 треугольника: ABC, AMN, AKL.
В случае 1, в третий отрезок с концами на сторонах АВ и АС (рис. 2, в) добавит еще один треугольник APQ, и всего станет 4 треугольника: АВС,
AMN, AKL, APQ.	Рис. 2
6
Задача 2. Сколько треугольников изображено на рисунке 3?
Рис. 3
Решение:
Эти задачи немного сложнее.
В треугольнике АВС провели отрезок ВМ, конец М отрезка лежит на стороне АС (рис. 4, а). Добавилось 2 треугольника АВМ и ВМС, и всего стало 3 треугольника: АВС, ABM и СВМ.
В случае 3, б провели еще один отрезок BN, конец N отрезка лежит на стороне АС (рис. 4, б). Добавилось 3 треугольника: ABN, MBN и CBN. Всего стало 6 треугольников: ABC, ABM, CBM, ABN, MBN и CBN.
В случае 3, в третий отрезок ВК, конец К которого ле
жит на стороне АС (рис. 4, в), добавит еще 4 треугольника: АВК, МВК, NBK и СВК, и всего станет 10 тре
угольников.
 При обсуждении задач 1 и 2 можно не вводить буквенных обозначений треугольников и отрезков, а изобра
7
жать стороны данного треугольника одним цветом, каждый новый отрезок своим цветом и подсчет треугольников вести, опираясь на цвет сторон и отрезков. Скажем, если стороны данного треугольника желтые, а отрезок, проведенный из вершины на рисунке 4, а, зеленый, то к желтому треугольнику прибавляем 2 новых треугольника с зеленой стороной.
Если второй отрезок, проведенный из той же вершины на рисунке 4, б красный, то прибавляются еще 3 новых треугольника с красной стороной и т. д.
Задача 3. Сколько четырехугольников изображено на рисунке?
вс	вс
Рис. 5
Решение:
Подсчет четырехугольников на каждом из рисунков 5, а, б, в можно провести так же упорядоченно, как мы делали, считая треугольники в задачах 1 и 2.
Рисунок 5, а. К четырехугольнику ABCD добавляются 2 новых четырехугольника со стороной MN: MNDA и
8
MNCB. Всего на рисунке 5, а изображено 3 четырехугольника.
Рисунок 5, б. С появлением отрезка KL к трем четырехугольникам, изображенным на рисунке 5, а, добавляются 3 новых четырехугольника со стороной KL: KLDA, KLNM, KLCB. Всего на рисунке 5, б изображено 6 четырехугольников.
Рисунок 5, в. Появление отрезка PQ добавляет к шести четырехугольникам, изображенным на рисунке 5, б, еще четыре новых четырехугольника: PQDA, PQNM, PQLK и PQCB. Всего на рисунке 5, в изображено 10 четырехугольников.
Задача 4. Сколько четырехугольников изображено на рисунке 6?
в n к	р	с
			
А М L	Q	D
Рис. 6
Решение:
Устанавливаем порядок счета четырехугольников слева направо. Со стороной АВ четыре четырехугольника: ABNM,ABKL,ABPQ nABCD; три новых четырехугольника со стороной MN: MNKL, MNPQ и MNCD', два новых четырехугольника со стороной KL: KLQP, KLDC и один новый четырехугольник PQDC со стороной PQ.
Всего на рисунке 6 изображено 4 + 3 + 2 + 1 = 10 четырехугольников .
9
Задача 5. Сколько квадратов изображено на рисунке 7?
Рис. 7
Решение:
Подсчет квадратов ведем по числу клеток в квадрате.
Рисунок 7, а. Одноклеточных квадратов — 2 ряда по 2 квадрата в каждом ряду и один четырехклеточный квадрат. Всего 2 • 2 + 1 = 5 квадратов изображено на рисунке 7, а.
Рисунок 7, б. Одноклеточных квадратов — 3 ряда по 3 квадрата в каждом ряду; четырехклеточных квадратов — 2 ряда по 2 квадрата в каждом ряду (один ряд начинается с квадрата со стороной АС, а другой ряд начинается с квадрата со стороной BD, рис. 8); один девятиклеточный квадрат. Всего на рисунке 7, б изображено 3-3 + 2- 2 + 1 = 14 квадратов.
10
Рисунок 7, в. Одноклеточных квадратов — 4 ряда по 4 квадрата в каждом ряду; четырехклеточных квадратов — 3 ряда по 3 квадрата в каждом ряду (первый ряд начинается с квадрата со стороной АС, второй ряд — с квадрата со стороной BD, а третий ряд — с квадрата со стороной СЕ, рис. 9); девятиклеточных квадратов — 2 ряда по 2 квадрата в каждом ряду (один ряд начинается с квадрата со стороной AD, а другой ряд — с квадрата со стороной BE, рис. 9); один — шестнадцатиклеточный квадрат.
Всего на рисунке 7, в изображено 4«4 + 3*3 + + 2 • 2 + 1 = 30 квадратов.
Задача 6. Сколько прямоугольников изображено на рисунке 10?
Рис. 10
11
Решение:
Счет будем вести по числу клеток, из которых состоит прямоугольник.
Рисунок 10, а. Прямоугольники, которые состоят из одной клетки, — это одноклеточные квадраты, их 4; прямоугольников, которые состоят из двух клеток, — тоже 4 (прямоугольник со стороной АВ, прямоугольник со стороной ВС, прямоугольник со стороной CD и прямоугольник со стороной DA, рис. 11); прямоугольник, состоящий из четырех клеток, всего один — данный квадрат.
Рис. 11
Всего на рисунке 10, а изображено 4 4-4 + 1 = 9 прямоугольников.
Рисунок 10, б. Прямоугольников, которые состоят из одной клетки, столько же, сколько одноклеточных квадратов, — 9 штук; прямоугольников, состоящих из двух клеток, — 3 горизонтальных ряда по 2 прямоугольника в каждом ряду (один ряд начинается с прямоугольника со стороной АВ, второй ряд начинается с прямоугольника со стороной ВС, а третий ряд — с прямоугольника со стороной CD, рис. 12) и 3 вертикальных ряда по 2 прямоугольника в каждом ряду (один ряд начинается с прямоугольника со стороной АЕ, второй ряд начинается с прямоугольника со стороной EF, а третий ряд начинается с прямоугольника со стороной FG, рис. 12); прямоугольников, состоящих из трех клеток, — 3 горизонтальных (со сторонами АВ, ВС и CD) и 3 верти
12
кальных (со сторонами АЕ, EF, FG, рис. 12); прямоугольники, состоящие из четырех клеток, — четырехклеточные квадраты, их, как мы уже знаем, 2 ряда по 2 квадрата в каждом ряду; прямоугольников, состоящих из шести клеток (размером 2 клетки на 3 клетки) — 2 горизонтальных (со сторонами АС и BD, рис. 12) и 2 вертикальных (со сторонами AF и EG, рис. 12); и, наконец, один девятиклеточный прямоугольник — данный квадрат.
Всего на рисунке 10, б изображено 9 + (3-2 + 3-2) + + (3 + 3) + 2 • 2 + (2 + 2) + 1 = 36 прямоугольников.
Можно считать число прямоугольников, изображенных на рисунке 10, б немного быстрее, заодно проверить полученный ответ.
Прямоугольников, являющихся квадратами, как мы уже знаем из задачи 5, изображено на рисунке 10, б 14 штук.
Подсчитаем число прямоугольников, не являющихся квадратами.
Горизонтальных прямоугольников: размером 1 клетка на 2 клетки — 3 ряда по 2 прямоугольника в каждом ряду, размером 1 клетка на 3 клетки — 3 ряда по 1 прямоугольнику в каждом ряду, размером 2 клетки на 3 клетки — 2 ряда по 1 прямоугольнику в каждом ряду. Всего 3«2 + 3«1 + 2’1 = 11 прямоугольников.
13
Столько же вертикальных прямоугольников. Таким образом, всего на рисунке 10, б изображено 14 + 11 • 2 = = 36 прямоугольников.
Задача 7. Сколько треугольников и сколько четырехугольников изображено на рисунке 13?
Рис. 13
Решение:
Рисунок 13, а. Шестиугольник ABCDEF состоит из 4 треугольников: ABC, ACD, ADE и AEF. Их на 2 меньше числа сторон данного шестиугольника. Других треугольников нет.
Четырехугольники считаем по часовой стрелке: со стороной АВ — четырехугольник ABCD, со стороной АС — четырехугольник ACDE, со стороной AD — четырехугольник ADEF. Всего 3 четырехугольника.
Рисунок 13, б. Треугольники можно считать в таком порядке: 4 треугольника (АОВ, ВОС, COD, DOA), из которых состоит данный четырехугольник, и 4 треугольника, которые образованы парами соседних треугольников, считаем по часовой стрелке: ABC, BCD, CDA и DAB. Всего 8 треугольников.
14
Четырехугольник всего один — данный четырехугольник ABCD.
Рисунок 13, в. Вначале рассмотрим четырехугольник ABCD без диагонали BD (рис. 14). Треугольников на нем нет, зато четырехугольников (мы их считали в задаче 3) целых 6.
Рис. 14
Теперь проведем диагональ BD. Под диагональю BD получим 3 треугольника и 3 новых четырехугольника и ровно столько же треугольников и четырехугольников над диагональю BD.
Всего на рисунке 13, в изображено 6 треугольников и 12 четырехугольников.
Рисуем картинку, не отрывая карандаш от бумаги
	Предлагается нарисовать фигуру, не отрывая карандаш от бумаги. Проводить линию карандашом можно только один раз. Линия может сама себя пересекать, то есть через какие-то точки линия может проходить несколько раз.
Задача 1. Нарисуй домик, не отрывая карандаш от бумаги (рис. 15).
Решение:
К
Рис. 15
Надо провести линию через точки В, С или О два раза, а через точки А или D надо один раз пройти и один раз выйти или прийти в каждую из этих точек. Точки, из которых выходит четное число путей, будем называть четными, а точки, из которых выходит нечетное число путей, — нечетными. На рисунке 15 точки В, С и О — четные, точки А и В — нечетные. Любая другая точка линии, изображающей домик, — четная (из нее выходит 2 пути).
Для того, чтобы нарисовать домик (рис. 15), надо выйти из одной нечетной точки (А или D) и, рисуя по указанным правилам, прийти в другую нечетную точку (D или А).
	Картинку, в которой нет нечетных точек, можно нарисовать, начиная с любой точки. Разумеется, такую картинку надо правильно рисовать.
Например, если фигуру 16 начнем рисовать из точки А, то, проведя линию до точки В, следует перейти на второй квадрат и провести линию до точки С, затем перей
16
ти на третий квадрат, вернуться в точку С, дорисовать второй квадрат и прийти в точку В, а из точки В вернуться в точку А (рис. 16).
Линия имеет только одно начало и только один конец (у замкнутой линии они совпадают). Нечетная точка требует, чтобы из нее начали рисовать картинку либо в ней закончили рисунок, поэтому линию, в которой ровно 2 нечетные точки, нарисовать, не отрывая карандаш от бумаги, можно (одна из нечетных точек — начало линии, другая— конец линии). Так мы сделали в задаче 1. Линию, в которой более двух нечетных точек, нарисовать, не отрывая карандаш от бумаги, проводя ее только один раз, нельзя.
Задача 2. Можно ли нарисовать конверт (рис. 17), не отрывая карандаш от бумаги, проводя линию только один раз?
Решение:
Невозможно. На этом конверте 4 нечетные точки: А, В, С и D.
Рис. 17
17
	Приведем несколько примеров картинок, которые можно нарисовать, не отрывая карандаш от бумаги, проводя линию только один раз.
Пример 1 (рис. 18). Нечетными точками на этом рисунке являются точки А и В. Причем если выходить из точки А, то сначала надо нарисовать квадрат, вернуться в точку А и нарисовать лист, закончив рисунок в
точке В. И наоборот, если мы выйдем из точки В, то вначале надо нарисовать лист, вернуться в точку В и нарисовать квадрат, закончив рисунок в точке А.
Пример 2 (рис. 19). На картинке с елочками две нечетные точ-
Рис. 19
ки М и N. Вести линию можно из одной из них, тогда при правильном рисовании мы приходим в другую точку.
Пример 3 (рис. 20). Нечетные точки Р и Q находятся на малень-
Рис. 20
ких парусах кораблика.
	В заключении отметим, что такие задания нельзя предлагать учащимся на письменных олимпиадах или на каких-то других соревнованиях, где решения надо представить в письменном виде. Для устных олимпиад, математических боев, математических регат и других подобных соревнований такие задания вполне подходят.
репусы
 Во втором классе можно «разгадывать» ребусы, в которых требуется расставить знаки арифметических действий сложения или вычитания между цифрами так, чтобы получилось верное равенство. Рассмотрим три типа таких задач.
Задача 1. Вставь пропущенные знаки действий «+» или «-»:
а)	5 ... 4 ... 3 ... 2 ... 1 = 3;
6)5 ... 4 ... 3 ... 2 ... 1 = 5.
Решение:
Каждый из этих ребусов имеет два решения. Учащиеся достаточно быстро их находят:
а)5 + 4- 3- 2-1 = 3;
5-4 + 3-24-1 = 3.
6)	5 + 4- 3- 2 + 1 = 5;
5-4 + 3 + 2-1 = 5.
Задача 2. Поставь между некоторыми цифрами знак «+» так, чтобы получилось верное равенство:
1234567 = 100
Решение:
Если поставить знак «+» между всеми цифрами, то в сумме мы не наберем 100. Любое двузначное число в сумме с остальными однозначными числами не дает 100. Следовательно, двузначных чисел в будущей сумме должно быть не меньше двух.
19
Существуют только две пары двузначных чисел 23 и 67, 34 и 56, которые в сумме с остальными однозначными числами дают 100. Три двузначных числа, составленных из цифр в порядке их следования, вместе с остальными однозначными числами не дают в сумме 100, так как 12 + 34 + 56 > 100, а суммы любых других троек двузначных чисел, составленных из цифр в порядке их следования, тем более больше 100.
Таким образом, 1 + 23 + 4 + 5 + 67 = 100 и 1 + 2 + + 34 + 56 + 7 = 100.
Задача 3. Поставь между некоторыми цифрами знак «-» так, чтобы получилось верное равенство:
8 7 6 5 4 3 2 1 = 3
Решение:
Будем двигаться слева направо. Понятно, что первый знак «-» надо поставить между цифрами 7 и 6.
Следующий знак «-» надо поставить между цифрами 6 и 5, так как, поставив его после 5, мы из разности 87 - 65, равной 22, должны вычесть однозначные числа 4, 3, 2 и 1 либо вычесть однозначные числа 4 и 3 и двузначное число 21. В любом из этих случаев число 3 в результате не получится. Итак, знак «-» должен стоять между цифрами 6 и 5.
Рассуждая таким же образом, получим, что знак «-» надо поставить между цифрами 4 и 3. Значение выражения 87-6-54 равно 27, а тогда очевидно, что последний знак «-» должен стоять между цифрами 3 и 2.
Окончательно получаем: 87 - 6 - 54 - 3 - 21 = 3.
Задания с палочками
я Задания с палочками можно использовать для устных соревнований: конкурса капитанов при проведении математического боя, математической карусели, устных олимпиад.
Задания с палочками не требуют методической проработки. Приведем несколько примеров таких заданий.
Фигуры, изображенные на рисунках 21-30, составлены из палочек.
Задача 1. Составь из палочек такую фигуру, как на рисунке 21. Переложи 3 палочки так, чтобы получилось 3 треугольника.
Рис. 21
Задача 2. Составь из палочек такую фигуру, как на рисунке 22. Переложи 3 палочки так, чтобы получилось 3 ромба.
Рис. 22
21
Задача 3. Составь из палочек такую фигуру, как на рисунке 23. Переложи 2 палочки так, чтобы получилось 4 одинаковых квадрата.
Рис. 23
Задача 4. Составь из палочек такую фигуру, как на рисунке 24. Убери 3 палочки так, чтобы получилось 3 квадрата.
Рис. 24
 При выполнении этих заданий нельзя оставлять «лишние» палочки. Например, в задаче 2 (рис. 22) нельзя перекладывать палочки так, как показано на рисунке 25: получится 3 ромба и 3 лишних палочки.
Рис. 25
22
А в задаче 4 (рис. 24) нельзя убрать 3 палочки, указанные на рисунке 26: остаются 3 квадрата и 2 лишних палочки.
Рис. 26
Ответы на задачи 1-4 даны на рисунках 27-30.
Рис. 30
Рис. 29
Логические задачи
 Логические задачи в курсе математики 2 класса требуют от учащихся внимательной работы с текстом. Условие такой задачи можно оформить в виде таблицы, с помощью которой учащиеся быстро приходят к правильному ответу на поставленный в задаче вопрос. Приведем несколько примеров.
Задача 1. Три котенка — Касьянка, Том и Плут — съели плотвичку, окуня и карася. Касьянка не ел ни плотвичку, ни окуня. Том не ел плотвичку. Какую рыбку съел каждый котенок?
Решение:
Составим таблицу, в которой строки обозначены именами персонажей задачи, а столбцы — названиями рыб, которых они съели.
Касьянка не ел ни плотвичку, ни окуня: в соответствующих клетках таблицы ставим «-». Том не ел плотвичку — в соответствующей клетке ставим «-» (табл. 1, а).
Как видно из таблицы 1, а, Касьянка мог съесть только карася, а плотвичку мог съесть только Плут: в соответствующих клетках таблицы ставим «+» (табл. 1, б).
Следовательно, Том съел окуня: в соответствующей клетке таблицы ставим «+» (табл. 1, в).
Таблица 1
	п.	О.	к.
К.	—	—	4-
т.	—	+	
п.	4-		
24
Задача 2. Карлсон, Винни-Пух и Сиропчик участвовали в конкурсе сладкоежек. Карлсон не занял второго места. Винни-Пух не занял ни первого, ни второго места. Какое место занял Карлсон? Винни-Пух? Сиропчик?
Решение:
Составим таблицу, в которой строки обозначены именами персонажей задачи, а столбцы — номерами мест, которые они заняли.
Сделаем пометки в таблице, соответствующие условию задачи (табл. 2, а).
Поскольку каждый персонаж занял какое-то место и каждое из трех первых мест было занято каким-то персонажем, мы можем в строке, в которой стоят два минуса, не задумываясь, поставить в третью клетку плюс и в столбце, в котором стоят два минуса, поставить в третью клетку плюс (табл. 2, б). Винни-Пух занял третье место, а Сиропчик — второе.
Заметим, что если в какой-то клетке стоит плюс, то в остальных клетках строки и столбца, на пересечении которых он стоит, надо поставить минус (табл. 2, в).
Осталась единственная пустая клетка на пересечении строки К. и I столбца. В остальных клетках этой строки и этого столбца стоят минусы, следовательно, в пустую клетку надо поставить плюс — Карлсон занял первое место (табл. 2, г).
Таблица 2
25
Задача 3. Трое друзей учатся в первом, втором и третьем классах. Их фамилии Иванов, Петров и Семенов. У самого младшего из друзей нет братьев и сестер. Семенов учится с сестрой Петрова в одном классе, он самый старший из друзей. Назови фамилии первоклассника, второклассника и третьеклассника.
Решение:
При решении этой задачи не обязательно составлять таблицу. Достаточно внимательно прочитать текст. Семенов самый старший из друзей, следовательно, он учится в третьем классе. У самого младшего из друзей нет братьев и сестер, а у Петрова есть сестра, с которой Семенов учится в одном классе. Следовательно, самый младший из друзей — Иванов. Он учится в первом классе, а, значит, Петров учится во втором классе.

Задачи на разрезание фигуры на одинаковые части
 Фигура представляет собой кусочек сетки с квадратными ячейками, и ее надо разрезать по линиям сетки на несколько одинаковых частей.
Задача 1. Разрежь фигуру по линиям сетки на 3 одинаковые части (рис. 31).
Рис. 31
Решение:
Для решения такого типа задач полезно сосчитать число квадратов, из которых составлена фигура, и найти число квадратов, из которых должна состоять каждая ее часть. Фигура на рисунке 31 состоит из 9 квадратов, ее надо разрезать на 3 одинаковые части, следовательно, каждая часть должна состоять из трех квадратов. Фигурок, состоящих из трех квадратов, 2: полоска и уголок (рис. 32).
Фигуру на рисунке 31 разрезать на полоски невозможно, а на 3 уголка она делится (рис. 33).
Рис. 32
Рис. 33
27
Задача 2. Разрежь фигуру по линиям сетки на 4 одинаковые части (рис. 34) двумя способами.
Рис. 34
Решение:
Фигура на рисунке 34 состоит из 16 квадратов, ее надо разрезать на 4 одинаковые части. Каждая часть будет состоять из четырех квадратов. Имеется 5 фигурок, состоящих из 4 квадратов (рис. 35):
Рис. 35
Фигуру на рисунке 34 можно разрезать двумя способами: на 4 полоски и на 4 уголка (рис. 36).
Задача 3. Разрежь фигуру по линиям сетки на 3 одинаковые части (рис. 37).
Рис. 37
28
Решение:
Фигура на рисунке 37 состоит из 15 квадратов, ее надо разрезать на 3 одинаковые части. Каждая часть будет состоять из 5 квадратов.
Фигура разрезается на 3 пятиклеточные фигурки (рис. 38).
Задача 4. Дана фигура, в которой часть квадратов закрашена. Разрежь фигуру по ———— линиям сетки на 4 одинаковые час- —i----------
ти так, чтобы каждая часть содер- ~~ жала закрашенный квадрат (рис. 39). 3Q
Решение:
Фигура состоит из 12 квадратов. Следовательно, каждая из четырех одинаковых частей должна состоять из трех квадратов. На полоски из трех квадратов, один из которых закрашен, разрезать фигуру нельзя. Следовательно, надо ______
попытаться разрезать на уголки с одним | закрашенным квадратом. Это сделать уда-
/	4л\	Рис-40
ется (рис. 40).
* Фигуры могут быть составлены из одинаковых равносторонних треугольников или одинаковых правильных шестиугольников.
Задача 5. Разрежь фигуру по линиям сетки на 4 одинаковые части (рис. 41).
Рис. 41
29
Решение:
Фигура на рисунке 41 состоит из 12 треугольников, следовательно, каждая часть должна состоять из трех треугольников. Простейшая конструкция из трех равносторонних треугольников — трапеция. Фигура делится на 4 трапеции (рис. 42).
Рис. 42
Задача 6. Разрежь фигуру по линиям сетки на 4 одинаковые части так, чтобы в каждой части был закрашенный шестиугольник (рис. 43).
Рис. 43
Решение:
Фигура на рисунке 43 состоит из 12 одинаковых шестиугольников, четыре из которых закрашены. Надо разделить ее на 4 одинаковые части так, чтобы в каждой части был закрашенный шестиугольник. Каждая часть должна состоять из трех шестиугольников, один из которых закрашен.
Решение показано на рисунке 44.
Рис. 44
 Требуется сосчитать число маршрутов, соединяющих два пункта. Каждый маршрут не должен проходить дважды через одно и то же место.
Задача 1. Сколько маршрутов соединяют пункты А и В? Маршруты проходят по сторонам треугольников (рис. 45).
А ж в
Рис. 45
Решение:
Введем обозначения маленьких треугольников (рис. 46).
Маршруты, соединяющие пункты Ат В, располагаются симметрично: сколько маршрутов содержит отрезок АС, столько же маршрутов содер- А жит отрезок АО.	д
Подсчитаем число маршрутов, про- / \ ходящих через отрезок АС: маршрут Д\ ЛР АСВ состоит из двух сторон маленьких / у \ треугольников, маршруты АСРВ и Р в Q ACDB состоят из трех сторон малень- рыс 4g ких треугольников, и наконец маршрут ACDQB состоит из четырех сторон маленьких треугольников. Всего 4 маршрута. Столько же маршрутов проходит через отрезок AD. Следовательно, всего 8 маршрутов соединяют пункты Ат В.
31
Задача 2. Сколько маршрутов соединяют пункты А и В? Маршруты проходят по сторонам прямоугольников (рис. 47).
Решение:
Введем обозначения маленьких прямоугольников (рис. 48). В этой задаче маршруты, соединяющие пункты А и В, так же как и в задаче 1, располагаются симметрично: сколько маршрутов содержит отрезок AM, столько же маршрутов содержит отрезок AN.
Маршруты, содержащие отрезок AM, могут состоять из 4, би 8 сторон маленьких прямоугольников: 3 маршрута AMDLB, АМОКВ и AMOLB из четырех сторон, 2 маршрута AMDLOKB и AMONCKB из шести сторон и один маршрут AMDLONCKB из восьми сторон. Всего 6 маршрутов.
Столько же маршрутов проходит через отрезок AN. Следовательно, всего 12 маршрутов соединяют пункты А и В.
Задачи
на взвешивание
 Взвешивание происходит на чашечных весах без гирь. На таких весах можно определить, равны ли массы двух совокупностей предметов или масса одной совокупности больше (меньше) массы другой совокупности предметов.
Задача 1. С помощью одного взвешивания на чашечных весах без гирь из 3 одинаковых по виду монет найди одну фальшивую, если известно, что она легче остальных.
Решение:
Кладем на каждую чашу весов по одной монете. Если весы оказались в равновесии, то оставшаяся монета фальшивая. Если весы не в равновесии, то фальшивая монета на чаше, которая будет выше.
Задача 2. С помощью двух взвешиваний на чашечных весах без гирь из 9 одинаковых по виду монет найди одну фальшивую, если известно, что она легче остальных.
Решение:
Разобьем все 9 монет на группы по 3 монеты в каждой группе. Первым взвешиванием узнаем, в какой группе находится фальшивая монета. Для этого кладем на одну чашу весов монеты первой группы, а на Другую — монеты второй группы. Если весы оказались в равновесии, то фальшивая монета осталась в третьей группе. Если же весы оказались не в равновесии, то фальшивая монета оказалась в той группе, которая легче.
33
В любом случае задача свелась к решению задачи 1. Вторым взвешиванием находим из трех монет фальшивую, если известно, что она легче остальных.
Задача 3. Среди четырех монет достоинством в 1 копейку (массой 1 г), 2 копейки (массой 2 г), 3 копейки (массой 3 г) и 5 копеек (массой 5 г) есть одна бракованная, отличающаяся массой от нормальной. Как за два взвешивания на чашечных весах без гирь определить бракованную монету?
Решение:
Первое взвешивание. На одной чаше 2 монеты достоинством в 1 и 2 копейки, на другой чаше монета достоинством 3 копейки. Если весы оказались в равновесии, то монета 5 копеек — бракованная (рис. 49).
' I
—1 =>{о)— бракованная
Рис. 49
Если весы оказались не в равновесии, то монета 5 копеек нормальная. Будем считать, для определенности, что при этом взвешивании монеты достоинством в 1 и 2 копейки, взятые вместе, оказались тяжелей монеты 3 копейки (рис. 50).
нормальная
Рис. 50
Переходим ко второму взвешиванию.
Второе взвешивание. На одну чашу весов кладем монеты достоинством в 2 и 3 копейки, а на другую чашу — нормальную монету 5 копеек.
34
Если весы оказались в равновесии, то монета 1 копейка бракованная (рис. 51).
|@®|
(Т) — бракованная
Рис. 51
Если весы оказались не в равновесии, то монета 1 копейка нормальная, а бракованной монетой является монета достоинством в 2 или 3 копейки.
Если при втором взвешивании монеты 2 и 3 копейки, взятые вместе, оказались тяжелее нормальной монеты 5 копеек, то бракованной монетой будет монета 2 копейки, так как при первом взвешивании она вместе с нормальной монетой 1 копейка оказалась тяжелей монеты 3 копейки (рис. 52).
|_®_|
|®®|	=>@— бракованная
Рис. 52
Если же при втором взвешивании монеты 2 и 3 копейки, взятые вместе, оказались легче монеты 5 копеек, то бракованной монетой будет монета 3 копейки, так как при первом взвешивании она оказалась легче, чем монеты 1 и 2 копейки, взятые вместе (рис. 53).
J => ® — бракованная
Рис. 53
Если после первого взвешивания весы были не в равновесии, то мы рассмотрели случай, когда монеты 1 и 2 копейки, взятые вместе, оказались тяжелей монеты 3 копейки (рис. 50).
35
Рассуждения для случая, когда после первого взвешивания монеты 1 и 2 копейки, взятые вместе, оказались легче монеты 3 копейки, проводятся точно так же. Мы приведем схему этих рассуждений (рис. 54, 55).
Первое взвешивание.
Рис. 54
Второе взвешивание.
@ । ~
□—1 => Q1) — бракованная
=> (3) — бракованная
J => (2) — бракованная
Рис. 55
класс
Магический квадрат
 Квадрат размером 3 клетки на 3 клетки заполняется девятью числами так, что сумма чисел в любой строке, любом столбце, а также по любой из двух его диагоналей одна и та же. Такой квадрат называется «магический».
Например, квадрат на рисунке 56 «магический»: сумма чисел в любой строке, любом столбце и по любой из двух его диагоналей равна 12.
Рассмотрим несколько задач, в которых «магический» квадрат заполняется девятью последовательными числами.
Задача 1. Вставь в пустые клетки квадрата (рис. 57) числа 4, 6, 9, 10, 11, 12 так, чтобы квадрат стал «магическим».
38
Решение:
Квадрат должен быть заполнен всеми натуральными числами от 4 до 12. Найдем их сумму:
4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = 16 • 4 + 8 = 72
I_____4 —............... J
С другой стороны, сумма всех девяти чисел, заполня-
ющих квадрат, должна равняться сумме чисел трех его строк. Сумма чисел в каждой из трех строк одна и та же. Следовательно, сумма чисел в каждой 				
строке должна равняться 72 :3 = 24. Этому же числу равна сумма чисел в каждом столбце и по каждой из двух диагоналей квадрата. Теперь пустые клетки квадрата можно заполнить без особого труда (рис. 58).	5	10	9
	12	8	4
	7	6	11
	Рис. 58		
Задача 2. Вставь в пустые клетки квадрата (рис. 59) числа 4, 5, 6, 8, 9, 10, 11 так, чтобы квадрат стал «магическим».
	3	
	7	
		
Рис. 59
Решение:
Квадрат должен быть заполнен всеми натуральными числами от 3 до 11. Найдем их сумму:
( )
3 + 4 + 5 + 6 + 7 + 8 + 9 + 10+ 11 = 14- 4 + 7 = 63
к______4	'________)
39
Сумма чисел в каждой строке, каждом столбце и по каждой из двух его диагоналей равна 63 : 3 = 21. Следовательно, в пустой клетке среднего столбца должно стоять число 11 (рис. 60, а).
Из оставшихся чисел, которые должны заполнить пустые клетки квадрата, только числа 4 и 6 дают 21 в сумме с числом 11. Из-за симметрии квадрата неважно, как расставить числа 4 и 6 по угловым клеткам нижней строки квадрата (рис. 60, б).
После того, как заполнена нижняя строка квадрата, становится понятно, какие числа должны стоять в оставшихся пустых клетках этого квадрата (рис. 60, в).
	3				3			8	3	10
	7				7			9	7	5
	11			4	11	6		4	11	6
а	б	в
Рис. 60
Задача 3. Вставь в пустые клетки квадрата (рис. 61) числа 2, 3, 4, 5, 7, 8, 9, 10 так, чтобы квадрат стал «магическим».
40
Решение:
Таким же образом, как при решении задач 1 и 2, складывая все натуральные числа от 2 до 10 и деля полученную сумму на 3, находим сумму чисел в каждой строке, каждом столбце и по каждой из двух его диагоналей. Она равна 18.
Заметим, что число, стоящее в угловой клетке «магического» квадрата, участвует в трех наборах чисел, дающих в сумме 18.
Число, стоящее на стороне квадрата в средней клетке, участвует в двух наборах чисел, дающих в сумме 18.
Число 2 участвует только в двух тройках чисел, составленных из чисел данного набора, дающих в сумме 18. Это тройки (2, 6, 10) и (7, 2, 9): 2 + 6 + 10 = = 7 + 2 + 9= 18.
Поэтому число 2 должно стоять на стороне квадрата в средней клетке. В силу симметрии квадрата число 2 можно поставить в среднюю клетку на любой стороне квадрата (рис. 62, а).
Рис. 62
После этого в пустой клетке среднего столбца ставим число 10, а по угловым клеткам верхней строки числа 7 и 9 (рис. 62, б). Теперь квадрат заполняется числами данного набора полностью (рис. 62, в).
41
Задача 4. Заполни квадрат (рис. 63) числами 1, 2, 3, 4, 5, 6, 7, 8, Этак, чтобы квадрат стал «магическим».
		
	5	
		
а
Решение:
Находим, какой должна быть сумма чисел в каждой строке, каждом столбце и по каждой из двух диагоналей квадрата. Эта сумма должна равняться 15, так как (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9): 3 = 15.
В центральной клетке квадрата должно стоять число, которое участвует в четырех тройках чисел, составленных из чисел данного набора, дающих в сумме 15. Таким числом является число 5 — центральное число данного ряда чисел:
( , ) 1+2+3+4+5+6+7+8+9
Таким образом, задача свелась к предыдущей: надо заполнить пустые клетки квадрата, в центральной клетке которого стоит число 5, числами 1, 2, 3, 4, 6, 7, 8, 9 так, чтобы квадрат стал «магическим» (рис. 64, а).
На рисунке 64, б дан ответ.
6	1	8
7	5	3
2	9	4
б
Задачи на разрезание фигуры на одинаковые части
 Во втором классе разбирались такого типа задачи. Приведем несколько примеров более сложных задач, соответствующих третьему году обучения младших школьников.
Задача 1. Фигуры на рисунке 65 надо разрезать по линиям сетки на 4 одинаковые части.
в
Рис. 65
Решение:
Фигура а состоит из 12 клеток, фигура б — из 16, а фигура в — из 20 клеток. Соответственно, фигуру а надо разрезать на части, состоящие из 3 клеток, фигуру б — на части, состоящие из 4 клеток, а фигуру в — на части, состоящие из 5 клеток.
Фигура а разрезается на четыре уголка (рис. 66, а).
Фигура б разрезается на четыре фигурки, похожие на букву Т (рис. 66, б).
43
Фигура в разрезается на четыре фигурки, похожие на печку (рис. 66, в).
Рис. 66
Задача 2. Разрежь фигуру по линиям сетки на 4 одинаковые части двумя способами (рис. 67).
Решение:
Фигура на рисунке 68 состоит из 16 клеток, поэтому фигурки, на которые ее надо разрезать, состоят из четырех клеток. Убрать клетку, выступающую из прямоугольника, можно с помощью фигурки, похожей на букву Г (рис. 68, а), или фигурки, похожей на букву Т (рис. 68, б).
Рис. 68
44
	Следующий цикл — задачи, в которых некоторые клетки фигуры отмечены цветом или картинкой. Фигуру надо разрезать на одинаковые части так, чтобы в каждую часть попала закрашенная клетка или клетка с картинкой.
Задача 3. Разрежь квадрат по линиям сетки на 4 одинаковые части так, чтобы каждая часть содержала по одной закрашенной клетке (рис. 69).
			
			
			
			
Рис. 69
Решение:
Квадрат на рисунке 69 состоит из 16 клеток, следовательно, каждая часть должна содержать 4 клетки, из которых одна закрашена. Такой частью является фигура, похожая на букву Г (рис. 70).
Рис. 70
Задача 4. Разрежь прямоугольник по линиям сетки на 4 одинаковые части так, чтобы каж-
45
Решение:
Прямоугольник отрезком MN делится на два одинаковых прямоугольника, содержащих по 2 клетки с сердечками (рис. 72, а).
Каждый прямоугольник, в свою очередь, делится на две одинаковые ступенчатые фигурки, состоящие из
а	б
Рис. 72
	Рассмотрим задачи, в которых фигуру разрешается разрезать на одинаковые части не только по сторонам, но и по диагоналям клеток.
Задача 5. Разрежь трапецию (рис. 73) на 6 одинаковых частей. Резать можно по сторонам и диагоналям клеток.
Решение:
Трапеция (рис. 73) состоит из 20 квадратов и 8 треугольников. Если из 2 квадратов сделать 4 одинаковых треугольника (разрежем каждый квадрат по диагонали), то оставшиеся 18 квадратов и получившиеся 12 тре-
46
угольников делятся на 6 равных частей. На каждую часть будет приходиться 3 квадрата и 2 треугольника. К тому же надо учесть, что, разрезая на 6 равных частей, надо убрать углы трапеции.
Такой фигурой является маленькая трапеция, состоящая из 3 квадратов и 2 треугольников. Она вырезана по углам данной трапеции (рис. 74, а).
Оставшийся прямоугольник ABCD делится отрезком MN, идущим по диагоналям клеток, на такие же трапеции (рис. 74, б).
Задача 6. Разрежь трапецию (рис. 75) на 4 одинаковые части. Резать можно по сторонам и диагоналям клеток.
Решение:
Рассуждая так же, как при решении задачи 5, получим, что в этом случае каждая часть состоит из 5 квадратов и 2 треугольников (рис. 76).
47
	Проведенные рассуждения можно рассматривать как возможные подходы к решению задачи.
Большинство учащихся обладают богатым воображением и приходят к решению своим путем.
Задача 7. Фигуры а) и б) на рисунке 77 разрежь на 2 одинаковые части. Резать можно по сторонам и диагоналям клеток.
Рис. 77
	Знание числа квадратов и треугольников, которые должна содержать каждая часть, мало что дает. Здесь действительно нужно иметь воображение, чтобы прийти к правильному решению.
Ответ дан на рис. 78.
Рис. 78
Арифметические ребусы

 В 3 классе рассматриваются арифметические ребусы, в которых разрешается поставить между цифрами знаки любых арифметических действий и скобки так, чтобы получилось верное равенство. Разберем несколько таких заданий.
Задача 1. Поставь знаки действий между некоторыми цифрами так, чтобы равенства стали верными:
а)	3	3	3 = 30;
б)	3	3	3	3	= 30;
в)	3	3	3	3	3	= 30;
г)	3	3	3	3	3	3 = 30.
Решение:
В равенстве а) достаточно поставить минус между второй и третьей тройками:
33 - 3 = 30.
В равенстве б) можно перемножить первые три тройки и к полученному результату прибавить четвертую тройку:
3 • 3 • 3 4- 3 = 30.
Равенства в) и г) получаются из равенства а) и б) добавлением четного числа троек. Из четного числа троек можно получить выражение, значение которого равно нулю: 3-3 = 0, 3-34-3-3 = 0, и т.д. Поэтому из любого набора троек, большего двух троек, можно с помощью знаков действий получить выражение, значение которого равно 30:
33 - 3 4- 3 - 3 = 30,
3-3-34-34-3-3 = 30
49
Задача 2. Поставь между всеми цифрами знаки действий так, чтобы равенства стали вер-
ными.
а) 1234567 = 8;
б) 12345678 = 9;
в) 123456789 = 10.
Решение:
Каждый из этих ребусов имеет несколько решений. Приведем одно решение для ребуса а), два — для ребуса б) и три решения для ребуса в):
а)	1 + 2- 3 + 44-5 + 6- 7 = 8;
б)	1 + 23-4 + 5- 6- 7- 8 = 9;
1 + 23 + 4 + 5-6 + 7-8 = 9;
в)	1 • 2 + 3 + 4 + 5 + 6 + 7 - 8 - 9 = 10;
1 + 2- 3 + 4 + 56-7-8-9 = 10;
1-2- 3-4- 5:6 + 7-8-9=10.
Задача 3. С помощью четырех семерок, знаков арифметических действий и скобок составь выражения, значения которых равны 1, 2, 3, 4, 5, 6 и 7.
Решение:
В этом задании знаки арифметических действий можно ставить между некоторыми цифрами. Для некоторых из семи значений можно составить несколько выражений. Приведем по одному выражению для каждого значения от 1 до 7.
77:77=1;
7: 7 +7: 7 = 2;
(7 + 7 + 7): 7 = 3;
77: 7-7 = 4;
50
7 - (7 + 7): 7 = 5;
(7 • 7 - 7): 7 = 6;
7 + (7 - 7) • 7 = 7.
Задача 4. Поставь между цифрами знаки действий так, чтобы равенства стали верными. Можно использовать скобки.
а)	1 2 3 = 5;
б)	1 2 3 4 = 5;
в)	1 2 3 4 5 = 5;
г)	123456 = 5;
д)	1234567 = 5;
е)	12345678 = 5.
Решение:
а)	1 • 2 + 3 = 5;
б)	(1 + 2): 3 + 4 = 5;
в)	(1 - 2 + 3 - 4) • 5 = 5;
г)	(1 + 2 - 3 • 4 + 5): 6 = 5;
д)	(1 • 2 • 3 • 4 + 5 + 6): 7 = 5;
е)	(1 + 2 • 3 + 4 • 5 + 6 + 7): 8 = 5.
Задача 5. С помощью пяти двоек, знаков арифметических действий и скобок составь несколько различных выражений, значение каждого из которых равно 10.
Решение:
2 + 2 + 24-2 + 2 = 10;
22 + 2 + 2 + 2 = 10;
2-2 + 2- 2 + 2 = 10;
51
(2 • 2 + 2 : 2) • 2 = 10;
(2 + 2 + 2 : 2) • 2 = 10;
(2 + 2 + 2) • 2 - 2 = 10;
(2 • 2 + 2) • 2 - 2 - 10;
22:2-2:2 = 10;
(22 + 2): 2 - 2 = 10.
Задачи на переливание
 Рассмотрим задачи двух типов: задачу, в которой требуется разлить поровну с помощью двух сосудов определенное количество жидкости, и задачу, в которой требуется с помощью двух сосудов набрать определенное количество воды из реки (то есть можно в процессе переливания любое количество воды вылить в реку и любое количество воды набрать из реки).
Задача 1. Степашка с Филей приготовили в кастрюле 8 л морса. С помощью трехлитровой и пятилитровой банок они разлили весь морс поровну. Как они смогли это сделать?
Решение:
Каждый шаг переливания фиксируем в таблице 3:
Таблица 3
		1 шаг	2 шаг	3 шаг	4 шаг	5 шаг	6 шаг	7 шаг
Кастрюля 8 л	8	3	3	6	6	1	1	4
Банка 5 л	—	5	2	2	—	5	4	4
Банка 3 л	—	—	3	—	2	2	3	—
После каждого переливания надо следить за тем, чтобы не возвращаться в прежнюю ситуацию. Скажем, если бы на четвертом шаге Степашка с Филей перелили 3 л морса из кастрюли в пятилитровую банку, то они вернулись бы в ситуацию, которая уже была после первого шага: в кастрюле осталось бы 3 л воды, пятилитровая банка была бы полной, а трехлитровая пустой. Поэтому на четвертом шаге надо перелить 2 л морса из пятилитровой банки в трехлитровую.
53
Задача 2. Как набрать из реки 6 л воды, если имеется 2 ведра: одно емкостью 4 л, а другое — 9 л?
Решение:
Решение оформляется в виде таблицы 4:
Таблица 4
	1 шаг	2 шаг	3 шаг	4 шаг	5 шаг	6 шаг	7 шаг	8 шаг
Ведро 4 л	0	4	0	4	0	1	1	4
Ведро 9 л	9	5	5	1	1	0	9	6
Река			4	4	8	8	8	8
Прямоугольник, составленный из квадратов, и квадрат, составленный из прямоугольников
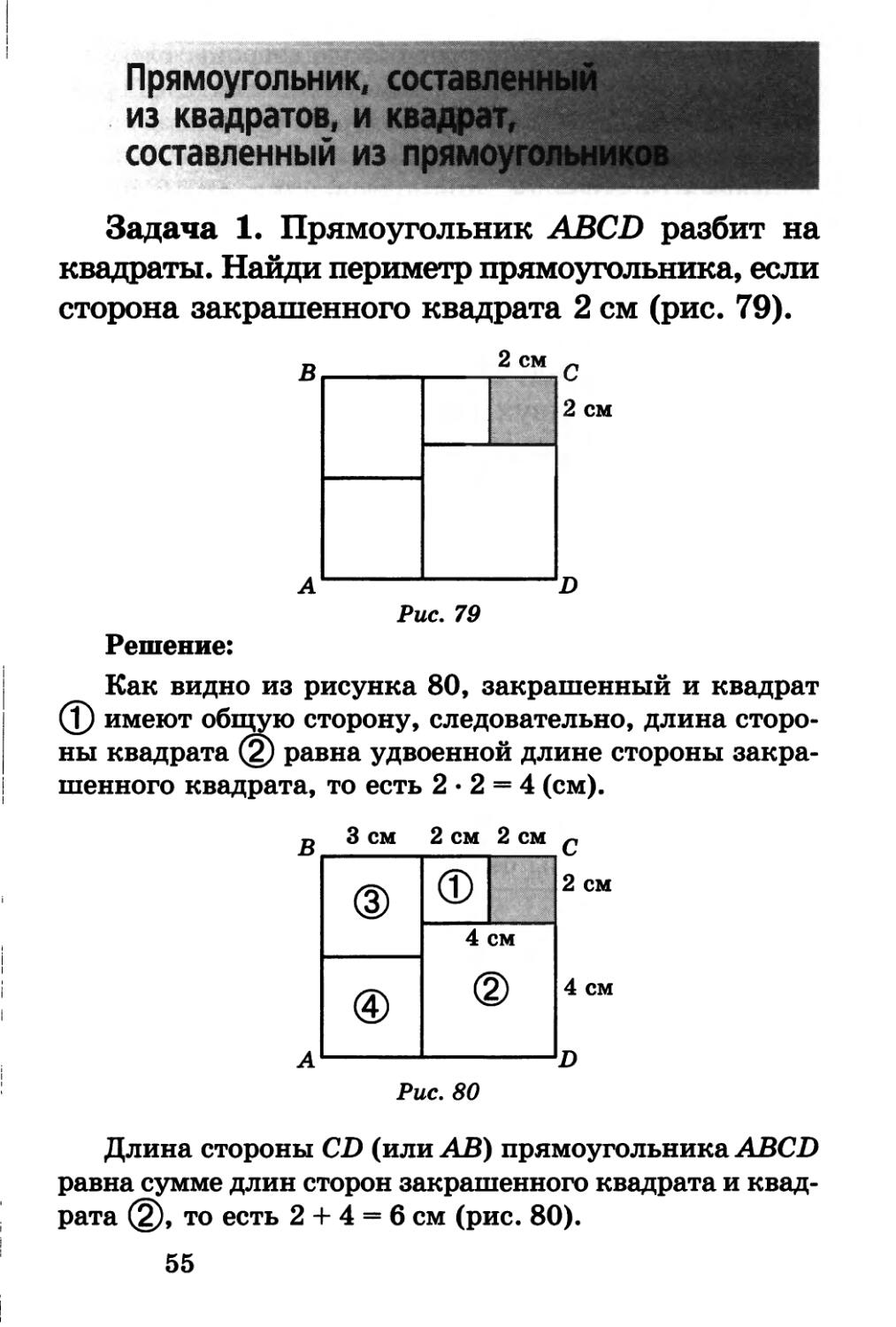
Задача 1. Прямоугольник ABCD разбит на квадраты. Найди периметр прямоугольника, если сторона закрашенного квадрата 2 см (рис. 79).
Решение:
Как видно из рисунка 80, закрашенный и квадрат (1) имеют общую сторону, следовательно, длина стороны квадрата (2) равна удвоенной длине стороны закрашенного квадрата, то есть 2 • 2 = 4 (см).
Длина стороны CD (или АВ) прямоугольника ABCD равна сумме длин сторон закрашенного квадрата и квадрата (2), то есть 2 + 4 = 6 см (рис. 80).
55
Квадраты (3) и @ имеют общую сторону, следовательно, длина стороны АВ прямоугольника ABCD равна удвоенной длине стороны квадрата (3). Отсюда длина стороны (3) квадрата равна 6 : 2 = 3 см (рис. 80).
Длина стороны ВС прямоугольника ABCD равна сумме длин сторон @ и (1) и закрашенного квадрата, то есть 3 + 2 + 2 = 7см (рис. 80), а периметр прямоугольника ABCD равен (6 + 7) • 2 = 26 см.
Задача 2. Квадрат разбит на прямоугольники, периметры двух из них указаны на рисунке 81. Найди длину стороны квадрата.
6 см	
	18 см
Рис. 81
Решение:
Обозначим длины сторон прямоугольников, периметры которых даны через а и Ь, с и d (рис. 82).
Ь с
6 см	
	18 см
Ь с
Рис. 82
56
Противоположные стороны прямоугольника равны, поэтому длины сторон двух других прямоугольников будут равны Ь и d, а и с (рис. 82).Периметр квадрата равен удвоенной сумме длин отрезков а, Ъ, с и d (рис. 82). Но удвоенная сумма отрезков а и Ъ равна 6 см — известному периметру одного из прямоугольников, на которые разбит квадрат, а удвоенная сумма длин отрезков с и d равна 18 см — известному периметру другого прямоугольника. Таким образом, периметр квадрата равен 6 + 18 = 24 (см), а длина его стороны 24 : 4 = 6 (см).
Задача 3. Прямоугольник на рисунке 83 составлен из квадратов. Найди длину стороны самого большого квадрата, если длина стороны самого маленького квадрата равна 1 см.
			
			
			
Рис. 83
Решение:
Квадраты (Т) и (2) (рис. 84) имеют общую сторону, следовательно, длины их сторон равны. Длина стороны квадрата (3) на 1 см больше длины стороны квадрата (2) (или квадрата ф). Длина стороны квадрата (4) на 1 см больше стороны квадрата (3), а длина стороны квадрата (5) на 1 см больше длины стороны квадрата (4) (рис. 84). Следовательно, длина стороны АВ
57
квадрата (5) на 3 см больше длины стороны АС квадрата (1).
Из рисунка 84 видно, что отрезок АВ состоит из отрезков АС и СВ, следовательно, длина отрезка СВ равна 3 см.
Сторона CD квадрата (2), в свою очередь, состоит из отрезков СВ и BD. Отрезок BD — сторона самого маленького квадрата, длина которой 1 см. Следовательно, длина стороны CD квадрата @ равна 3 + 1=4 (см), а длина стороны АВ самого большого квадрата равна 4 + 3 = 7 (см) (рис. 84).
Задача 4. Квадрат ABCD разбит на прямоугольники AM ND и MBCN, периметры которых 14 см и 10 см соответственно. Найди периметр квадрата ABCD (рис. 85).
в
м
А
--------|С
10 см --------N
14 см
--------Ь
Рис. 85
58
Решение:
В периметр прямоугольника AMND входят длины двух сторон квадрата ABCD и длины сторон AM и DN прямоугольника AMND. В периметр прямоугольника MBCN входят длины двух сторон квадрата ABCD и длины сторон МВ и NC прямоугольника MBCN (рис. 85).
Сумма длин каждой пары отрезков AM и MB, DN и NC равна длине стороны квадрата ABCD. Таким образом, сумма периметров прямоугольников AMND и MBCN равна сумме шести длин сторон квадрата ABCD, то есть 10 + 14 = 24 см — сумма длин шести сторон квадрата. Длина стороны квадрата ABCD равна 24 : 6 = 4 см, а его периметр равен 4 • 4 = 16 см.

Сумма трех чисел одна и Та
Задача 1. В ряду из 7 чисел сумма любых трех соседних чисел равна 15. Первое число равно 7. Чему равно последнее число?
Решение:
Сумма первых трех чисел равна 15, первое число равно 7, следовательно, сумма второго и третьего чисел равна 8.
Сумма второго, третьего и четвертого чисел ряда равна 15, сумма второго и третьего чисел ряда равна 8, следовательно, четвертое число равно 7.
Сумма четвертого, пятого и шестого чисел ряда равна 15, четвертое число равно 7, следовательно, сумма пятого и шестого чисел равна 8.
И наконец, сумма пятого, шестого и седьмого чисел ряда равна 15, сумма пятого и шестого чисел ряда равна 8, следовательно, седьмое (последнее) число ряда равно 7 (рис. 86).
Рис. 86
Задача 2. Вставь в квадратики такие числа, чтобы сумма любых трех, взятых подряд, чисел равнялась 20 (рис. 87).
Рис. 87
60
Решение:
В ряду чисел первое число равно 3, а сумма любых трех, взятых подряд, чисел равна 20. Рассуждая так же, как и при решении задачи 1, получим, что четвертое число равно 3 и седьмое число равно 3 (рис. 88).
20
20
3
20
20
Рис. 88
Сумма шестого, седьмого и восьмого чисел равна 20, восьмое число равно 9, седьмое число равно 3, следовательно, шестое число равно 20 - 9 - 3 = 8 (рис. 88).
Сумма пятого, шестого и седьмого чисел равна 20, шестое число равно 8, седьмое число равно 3, следовательно, пятое число равно 20 - 8 - 3 = 9 (рис. 88).
Продолжая рассуждать таким же способом, получим, что третье число ряда равно 8, а второе число ряда равно 9 (рис. 88).
Задача 3. В трех вазах стоят 27 тюльпанов. Когда из первой вазы переставили 5 тюльпанов во вторую, а из второй в третью — 3 тюльпана, то во всех вазах цветов стало поровну. Сколько тюльпанов было первоначально в каждой вазе?
Решение:
Количество всех тюльпанов не менялось в результате их перекладывания из одной вазы в другую, поэтому после всех перекладываний в каждой вазе стало 27:3 = 9 цветков. Следовательно, в третьей вазе первона
61
чально было 9-3 = 6 тюльпанов, во второй 9 + 3 - 5 = = 7 тюльпанов, а в первой 9 + 5 = 14 тюльпанов.
Задача 4. Трем Толстякам принесли 30 пирожных, поровну каждому. Первый Толстяк съел несколько пирожных, второй съел столько, сколько пирожных осталось у первого, а третий съел столько пирожных, сколько съели первый и второй вместе. Сколько всего пирожных осталось у Трех Толстяков?
Решение:
Трем Толстякам принесли 30 пирожных, поровну каждому. Следовательно, каждому Толстяку досталось 30 : 3 = 10 пирожных.
Первый Толстяк съел несколько пирожных, а второй съел столько, сколько пирожных осталось у первого. Следовательно, количество пирожных, которое съели первый и второй Толстяки вместе, равно количеству пирожных, которое досталось первому Толстяку, то есть 10 пирожных.
Третий Толстяк съел столько пирожных, сколько съели первый и второй вместе. Следовательно, третий Толстяк съел тоже 10 пирожных.
Таким образом, Три Толстяка съели всего 10 + 10 = = 20 пирожных, и у них осталось 30 - 20 = 10 пирожных.
Задача 5. Каждый из трех мальчиков имеет некоторое количество яблок. Первый мальчик дает двум другим столько яблок, сколько яблок имеет каждый из них. Затем второй мальчик дает двум другим столько яблок, сколько
62
каждый из них имеет. В свою очередь, и третий мальчик дает каждому из двух других столько яблок, сколько яблок есть у каждого в этот момент. После этого у каждого мальчика оказалось 8 яблок. Сколько яблок было в начале у каждого мальчика?
Решение:
Задачу будем решать с конца. У каждого мальчика оказалось 8 яблок после того, как третий мальчик дал первому и второму столько яблок, сколько у каждого из них было. Следовательно, у первого и второго мальчиков к этому моменту было по 4 яблока, и по 4 яблока они получили от третьего. Третий мальчик к этому моменту имел 8 + 4 + 4 = 16 яблок (3 шаг в таблице 5).
Таблица 5
1 шаг
2 шаг
3 шаг
I м.	13	2	4	8
II м.	7	14	4	8
III м.	4	8	16	8
Когда второй мальчик дал первому и третьему мальчику столько яблок, сколько у каждого из них было, то у первого мальчика оказалось 4 яблока, а у третьего 16 яблок. Следовательно, они получили от второго мальчика 2 яблока и 8 яблок соответственно. У второго мальчика осталось 4 яблока, значит, до этого момента у него было 4 + 2 + 8 = 14 яблок (2 шаг, таблица 5).
Итак, после того как первый мальчик дал второму и третьему мальчику столько яблок, сколько у каждого из них было, у второго мальчика оказалось 14 яблок, а у третьего 8 яблок.
63
Следовательно, они получили от первого мальчика 7 яблок и 4 яблока соответственно. У первого мальчика осталось 2 яблока, значит, до этого момента у него было 2 + 7 + 4=13 яблок (1 шаг, таблица 5).
Таким образом, вначале у первого мальчика было 13 яблок, у второго 7 яблок, а у третьего 4 яблока.
4 ж
Задачи на площади
	Для решения задач, связанных с понятием площади, как правило, достаточно знать основные свойства площади:
	одинаковые фигуры имеют одну и ту же площадь;
	площадь всей фигуры равна сумме площадей частей, из которых она составлена.
Из этих свойств площади следует, что площади фигур, составленных из одних и тех же фигур, равны. На этом выводе основан метод решения трудных (для младших школьников) задач на площади. Для того чтобы найти площадь фигуры или сравнить ее площадь с площадью другой фигуры, полезно разбить фигуру на части, из которых можно составить фигуру, площадь которой дана или легко находится. Или, наоборот, разбить на части фигуру, площадь которой известна, и составить фигуру, площадь которой надо найти. Приведем несколько задач, при решении которых этот метод работает.
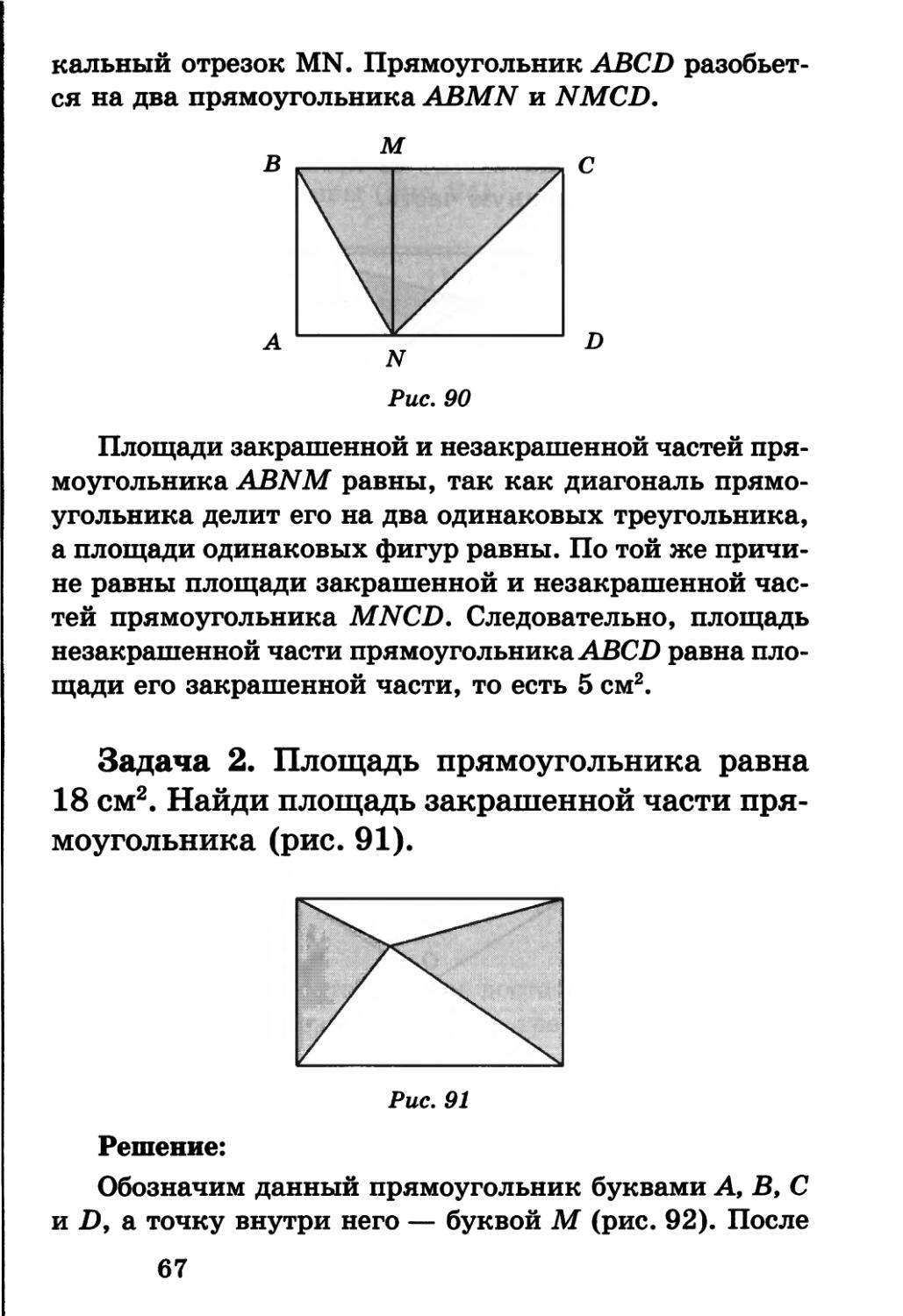
Задача 1. Площадь закрашенной части прямоугольника равна 5 см2. Найди площадь незакрашенной части прямоугольника (рис. 89).
Рис. 89
Решение:
Введем обозначения для данного прямоугольника и закрашенного треугольника (рис. 90). Проведем верти
66
кальный отрезок MN. Прямоугольник ABCD разобьется на два прямоугольника ABMN и NMCD.
Площади закрашенной и незакрашенной частей прямоугольника ABNM равны, так как диагональ прямоугольника делит его на два одинаковых треугольника, а площади одинаковых фигур равны. По той же причине равны площади закрашенной и незакрашенной частей прямоугольника MNCD. Следовательно, площадь незакрашенной части прямоугольника ABCD равна площади его закрашенной части, то есть 5 см2.
Задача 2. Площадь прямоугольника равна 18 см2. Найди площадь закрашенной части прямоугольника (рис. 91).
Решение:
Обозначим данный прямоугольник буквами А, В, С и D, а точку внутри него — буквой М (рис. 92). После
67
решения задачи 1 становится понятно, что достаточно через точку М провести вертикальный и горизонтальный отрезки и закрашенная часть прямоугольника ABCD разобьется на части, из которых можно составить его незакрашенную часть.
Следовательно, площадь закрашенной части данного прямоугольника равна его незакрашенной части, то есть 9 см2 — половине площади самого прямоугольника.
Задача 3. Дан прямоугольник ABCD. В нем проведены диагонали АС и BD, пересекающиеся в точке О. Покажи, что площади всех четырех треугольников АОВ, ВОС, COD и DOA равны (рис. 93).
Рис. 93
Решение:
Проведем те же построения, что и в задаче 2: через точку пересечения диагоналей О данного прямоуголь
68
ника вертикальный и горизонтальный отрезки. Прямоугольник ABCD разобьется на 8 одинаковых треугольников. Каждый из треугольников АОВ, ВОС, COD и DOA состоит из двух таких треугольников. Следовательно, их площади равны (рис. 94).
Рис. 94
Задача 4. Найди площадь закрашенного на рисунке 95 треугольника, если сторона клетки равна 1 см.
Решение:
Заметим, что в этой задаче достаточно просто находятся площади незакрашенных треугольников AMD, BMN, CND. Поэтому площадь закрашенного треугольника DMN можно найти, вычитая из площади квадрата ABCD площади треугольников AMD, BMN, CND.
Площадь квадрата, длина стороны которого 4 см, равна 4 • 4 = 16 (см2).
69
Площадь треугольника AMD равна половине площади прямоугольника, длины сторон которого 2 см и 4 см, то есть (2 • 4): 2 = 4 (см2).
Площадь треугольника BMN равна половине площади прямоугольника, длины сторон которого 2 см и 3 см, то есть (2 • 3): 2 = 3 (см2).
Площадь треугольника CND равна половине площади прямоугольника, длины сторон которого 1 см и 4 см, то есть (1 • 4): 2 = 2 (см2).
Таким образом, площадь закрашенного треугольника MND равна 16-4-3-2 = 7(см2).
Арифметические ребусы
 Требуется расшифровать ребусы, в которых некоторые цифры обозначены звездочками или буквами. Звездочки обозначают любые цифры. Одинаковым буквам соответствуют одинаковые цифры, разным буквам — разные цифры.
Задача 1. Вставь пропущенные цифры:
, * 6 *
+ *7
* * 2 4
Решение:
В разряде единиц верхнего слагаемого ребуса должна стоять цифра 7. При сложении десятков учитываем 1 десяток, получившийся от сложения единиц, поэтому в разряде десятков второго слагаемого ребуса должна быть цифра 5. Для того чтобы сумма трехзначного и двузначного числа равнялась четырехзначному числу, необходимо, чтобы трехзначное число содержало 9 сотен.
Ответ:
,967
+ 57
1024
Задача 2. Расшифруй арифметический ребус:
_**0 3
* 8 * 4с 6
Решение:
Разность четырехзначного и трехзначного числа — двузначное число. Следовательно, уменьшаемое долж
71
но быть четырехзначным числом, меньшим 1100, то есть в разряде тысяч уменьшаемого стоит цифра 1, а в разряде сотен — цифра 0.
Ребус принимает вид:
1003 * 8 *
* 6
В таком виде ребус легко расшифровывается:
1003 “ 987
16
Решим ребус другим способом.
Если разность сложить с вычитаемым, то получится уменьшаемое. Поэтому вместо ребуса на вычитание
_** 0 3 * 8 *
* 6 можно решить ребус на сложение . * 6 * 8 * **0 3
Получившийся ребус решается таким же способом, как ребус в задаче 1. Находится цифра единиц второго слагаемого, она равна 7. При сложении десятков учитывается 1 десяток, получившийся от сложения единиц, поэтому цифра десятков первого слагаемого равна 1.
Сумма двузначного и трехзначного чисел равна четырехзначному числу только тогда, когда трехзначное число содержит 9 сотен.
Решение ребуса получено:
72
16
987
а значит,
1003
987
1003,	16
Задача 3. Расшифруй арифметический ребус:
у 3 *
* *
2 6* + **
**2 6
Решение:
Расшифруем ребус в такой последовательности:
х3*	х3*	3*	у38
* *	* *	* *	2 7
26*	=>	26*	=>	266	=>	266
+ **	+**	"*" * 6	+76
**2 6	1*26	1*26	1026
При первом переходе в разряде тысяч произведения ставим цифру 1, так как при сложении двух трехзначных чисел (второе слагаемое — трехзиачное число, нуль в разряде единиц для краткости при умножении в столбик не пишется) получилось четырехзначное число.
При следующем переходе мы учитываем, что в разряде единиц произведения стоит цифра 6, а в разряде десятков — цифра 2.
Самый трудный последний переход. При сложении 266 со вторым слагаемым в разряде сотен произошел переход через десяток. Следовательно, второе слагаемое должно содержать не менее 7 сотен, а значит, произведение первого множителя на число десятков второ
73
го множителя должно быть двузначным числом, не меньшим 70, и цифрой десятков второго множителя должна быть двойка или тройка.
Если цифра десятков второго множителя — двойка, то цифрой единиц первого множителя должна быть цифра 3 или 8 и число 266 должно делиться на 33 или на 38.
Если цифра десятков второго множителя — тройка, то цифрой единиц первого множителя должна быть цифра 2 и число 266 должно делиться на 32. Но число 266 делится нацело только на 38, и в частном получается 7.
Таким образом, перемножались числа 38 и 27 и ребус расшифровывается полностью.
Задача 4. Вставь пропущенные цифры:
_**0 * 5 » *	2 *
_ 19k 9k
* 4 * 0 Решение:
Расшифруем ребус в такой последовательности:
_** 0	?k 5	_**0	* 5
9k 9k	2 9k	9k 9k	2 9k
_ 19k 9k 9k 4 9k		=>	_140 140	
0		0	
_ 9k 9k 0	35	_840	35
9k 9k	24	70	24
_ 1 40 140		=>	_140 140	
0		0	
74
При первом переходе пользуемся тем, что делимое оканчивается на 0 и что деление выполняется без остатка.
При втором шаге находим, что 35 — единственное двузначное число, оканчивающееся на 5, на которое делится число 140. При делении 140 на 35 в частном получается 4. Таким образом, в ребусе делитель равен 35, а частное 24. После этого нетрудно сделать последний переход, и ребус расшифровывается полностью.
Задача 5. Каждую букву замени цифрой так, чтобы получилось верное арифметическое равенство. Одинаковым буквам соответствуют одинаковые цифры, разным буквам — разные цифры. Известно, что буква Ю обозначает цифру 6.
.ТРЮК ТРЮК ЦИРК
 Для удобства объяснения под суммой цифр мы будем понимать сумму чисел, обозначенных этими цифрами.
Решение:
В ребусе буква Ю по условию обозначает цифру 6.
Букву К можно заменить только на цифру 0, так как сумма двух одинаковых цифр оканчивается на ту же цифру. На этом шаге ребус выглядит так:
 ТР60
ТР60
ЦИРО
75
Далее расшифровка ребуса идет в таком порядке: буква Р обозначает цифру 2, буква И — цифру 5. На этом шаге ребус выглядит так:
. Т260 Т260 Ц520
Очевидно, что буква Т может быть заменена только на цифру 4, и тогда буква Ц обозначает цифру 8. Ребус расшифрован полностью:
.4260 4260 8520
Задача 6. Одно из решений буквенного ребуса
.ПЕСОК	,59068
+ ВОДА такое: + 3 6 4 2
ОАЗИС	62710
Найди другое решение.
Решение:
Посмотрим внимательно на данный ребус и на его решение.
Буквы Е и В встречаются в ребусе только один раз и соответствующие им цифры 9 и 3 стоят в разряде тысяч обоих слагаемых решения. Если поменять эти цифры местами, то равенство не нарушится, а решение ребуса получится новое, так как буква Е теперь обозначает цифру 3, а буква В — цифру 9.
53068 + 9642
62710
76
Задача 7. Реши ребус:
.КУРСК ГОРСК
ГОРОДА
Решение:
В ребусе буква Г обозначает цифру 1, так как при сложении двух пятизначных чисел получается шестизначное число. При этом, чтобы произошел переход через десяток в разряде десятков тысяч, буква К должна обозначать цифру 8 или 9 (меньше 8 буква К обозначать не может, так как буква Г обозначает цифру 1).
Буква К заменяется на цифру 8, если при сложении чисел произойдет переход через десяток в разряде тысяч.
Независимо от того, будет ли буква К заменена на цифру 8 или на 9, буква О должна обозначать цифру О (нуль).
Теперь можно выстроить последовательность замены букв цифрами:
Г=1=>0 = 0=>Р = 5=>У = 4=>К = 9=>А = 8=> С = 3=>Д=7
Ответ:
94539 +10539 105078
Задача 8. Реши ребус:
КОЛЯ ОЛЯ + ля _____я 2222
77
Решение:
В данном ребусе сумма четырех одинаковых цифр, каждая из которых обозначает букву Я, оканчивается двойкой, следовательно, буква Я может обозначать цифру 3 или 8.
Если букву Я заменить на 3, то сумма трех одинаковых цифр, каждую из которых обозначает буква Л, должна оканчиваться на единицу (еще одна единица прибавится в результате перехода через десяток в разряде единиц). Следовательно, буква Л может обозначать только цифру 7. Тогда сумма двух других одинаковых цифр, каждую из которых обозначает буква О, должна оканчиваться на нуль (еще две единицы прибавятся в результате перехода через десяток в разряде десятков). Следовательно, буква О может обозначать только цифру 5, а буква К — цифру 1, которая получается в результате перехода через десяток в разряде сотен.
Если букву Я заменить на 8, то сумма трех одинаковых цифр, каждую из которых обозначает буква Л, должна оканчиваться на девятку (еще три единицы прибавятся в результате перехода через десяток в разряде единиц). Следовательно, буква Л может обозначать только цифру 3. Тогда сумма двух одинаковых цифр, каждую из которых обозначает буква О, должна оканчиваться на единицу (еще одна единица прибавится в результате перехода через десяток в разряде десятков). Но сумма двух одинаковых цифр оканчивается на четную цифру. Следовательно, найти цифру, которую обозначала бы буква О, невозможно, а значит, замена буквы Я на цифру 8 не дает решения ребуса.
Таким образом, ребус имеет единственное решение:
1573
4- 573
73
3
2222
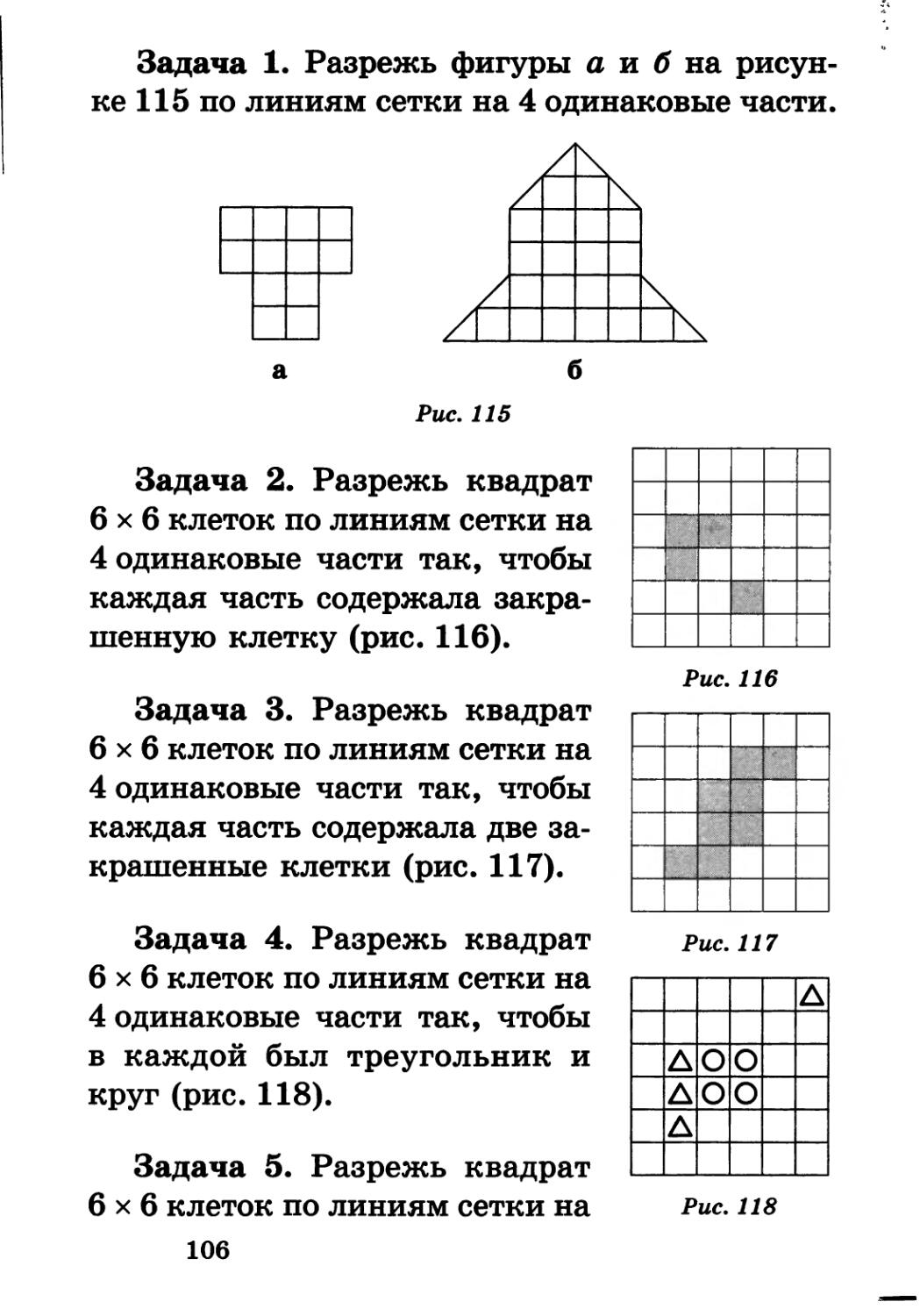
Задача 1. Сколько существует двузначных чисел, в записи которых все цифры нечетные?
Решение:
В разряде десятков может стоять любая из пяти нечетных цифр, и для каждой цифры десятков в разряде единиц может стоять тоже любая из пяти нечетных цифр. Таким образом, всего получается 5 • 5 = 25 чисел.
Задача 2. Сколько существует двузначных чисел, которые записываются различными нечетными цифрами?
Решение:
В разряде десятков может стоять любая из пяти нечетных цифр, и для каждой цифры десятков в разряде единиц может стоять любая из оставшихся четырех нечетных цифр. Всего получается 5 * 4 = 20 чисел.
Можно было сосчитать количество двузначных чисел, которые записываются различными нечетными цифрами, по-другому. Из количества всех двузначных чисел, в записи которых все цифры нечетные (их, как мы уже знаем, 25) вычесть количество двузначных чисел, записанных одинаковыми нечетными цифрами (их 5 — столько, сколько нечетных чисел). Получится тот же результат: 25 - 5 = 20.
Задача 3. Сколько существует трехзначных чисел, в записи которых все цифры четные?
Решение:
В разряде сотен может стоять любая четная цифра, кроме 0, и для каждой из четырех цифр сотен в разря
79
де десятков может стоять любая из пяти четных цифр, получается 4 • 5 = 20 вариантов заполнения четными цифрами разрядов сотен и десятков трехзначного числа. Для каждого такого варианта в разряде единиц может стоять любая из пяти четных цифр. Таким образом, всего получается 4 • 5 • 5 = 100 чисел.
Задача 4. Сколько существует трехзначных чисел, которые записываются различными четными цифрами?
Решение:
В разряде сотен может стоять любая четная цифра, кроме 0, и для каждой из четырех цифр сотен в разряде десятков может стоять любая из оставшихся четырех четных цифр (включая 0). Получается 4 • 4 = 16 вариантов заполнения различными четными цифрами разрядов сотен и десятков. Для каждого такого варианта в разряде единиц может стоять любая из трех оставшихся четных цифр.
Всего получается 4 • 4 • 3 = 48 чисел.
Задача 5. Сколько существует трехзначных чисел, в записи каждого из которых присутствуют цифра 1 и 2 и какая-то цифра, отличная от них?
Решение:
Будем выполнять задание по такому плану:
1)	сосчитаем количество трехзначных чисел, в разряде сотен которых стоит цифра, отличная от 0, 1 и 2, а в разряде десятков и единиц стоят цифры 1 и 2 или 2 и 1;
2)	сосчитаем количество трехзначных чисел, в разряде десятков которых стоит цифра, отличная от 1 и 2, а в разрядах сотен и единиц стоят цифры 1 и 2 или 2 и 1;
80
3)	точно такое же (как в пункте 2) будет количество трехзначных чисел, в разряде единиц которых стоит цифра, отличная от 1 и 2, а в разрядах сотен и десятков стоят цифры 1 и 2 или 2 и 1;
4)	найдем сумму этих трех чисел — искомое количество трехзначных чисел.
Переходим к осуществлению нашего плана.
1)	В разряде сотен трехзначного числа может стоять любая цифра, отличная от 0, 1 и 2, и для каждой цифры сотен в разрядах десятков и единиц могут стоять цифры 1 и 2 или 2 и 1. Получается 7 • 2 = 14 чисел.
2)	В разряде десятков трехзначного числа может стоять любая цифра, отличная от 1 и 2 и для каждой из цифры десятков, в разрядах сотен и единиц могут стоять цифры 1 и 2 или 2 и 1. Получается 8 • 2 = 16 чисел.
3)	Столько же трехзначных чисел получается, когда в разряде единиц стоит любая цифра, отличная от 1 и 2, а в разрядах сотен и десятков стоят цифры 1 и 2 или 2 и 1.
4)	Складывая числа, полученные в пунктах 1)-3), найдем, что всего существует 14 + 16 + 16 = 46 трехзначных чисел, в записи каждого из которых присутствуют цифры 1 и 2 и какая-то цифра, отличная от них.
Задача 6. В 4 «Б» учится 25 детей. Сколькими способами можно назначить двух дежурных по классу?
Решение:
Одного дежурного можно выбрать 25 способами, второго к нему в пару можно выбрать любого из оставшихся 24 учеников. Получается 25*24 = 600 способов. Но при этом каждая пара дежурных была посчитана 2 раза: например, у Волкова был в паре Лисицын, а у
81
R-1A12
Лисицына был в паре Волков. Следовательно, на самом деле, способов составить дежурные пары в 2 раза меньше, то есть 300 способов.
Задача 7. В понедельник у 4 «Б» на пяти уроках пять различных предметов. Сколькими способами можно для 4 «Б» составить расписание на понедельник?
Решение:
На первом уроке может быть любой из пяти предметов, и каждый раз на втором уроке может изучаться любой из четырех оставшихся предметов. Следовательно, расписание на первые 2 урока может быть составлено 5 • 4 = 20 способами, и для каждого такого способа на третьем уроке может быть любой из трех оставшихся предметов. Следовательно, расписание на первые три урока может быть составлено 5 • 4 • 3 = 60 способами, и для каждого такого способа на четвертом уроке может быть любой из двух оставшихся предметов, то есть расписание на первые 4 урока может быть составлено 5 • 4 • 3 • 2 = 120 способами.
На пятом уроке будет изучаться оставшийся пятый предмет.
Таким образом, расписание на понедельник для 4 «Б» можно составить 120 способами.
Разрезаем и составляем
 При решении задач на разрезание и составление фигур полезно сосчитать количество клеток, из которых они состоят, и определить размеры будущей фигуры.
Задача 1. Прямоугольник размером 3x6 клеток, из которого вырезан прямоугольник размером 1x2 клетки, разрежь на две части и составь из них квадрат (рис. 96).
					
					
					
Рис. 96
Решение:
Данная фигура состоит из 16 клеток, следовательно, будущий квадрат должен иметь размеры 4x4 клетки. Теперь не трудно сообразить, что разрез должен пройти так, как показано на рисунке 97.
Из полученных частей составляем квадрат (рис. 98).
Задача 2. Прямоугольник размером 4x9 клеток разрежь на две одинаковые части и составь из них квадрат.
83
Решение:
Прямоугольник размером 4x9 клеток состоит из 36 клеток, следовательно, будущий квадрат будет иметь размеры 6x6 клеток. Можно попытаться разрезать квадрат на две одинаковые части (рис. 99) и из них составить прямоугольник (рис. 100).
Задача 3. Фигуру, изображенную на рисунке 101, разрежь на две части и составь из них квадрат.
Решение:
Фигура на рисунке 101 состоит из 25 клеток. Для ее разрезания и последующего составления квадрата раз-
84
мером 5x5 клеток требуется немного больше воображения, чем для решения предыдущих задач (рис. 102,103).
Рис. 103
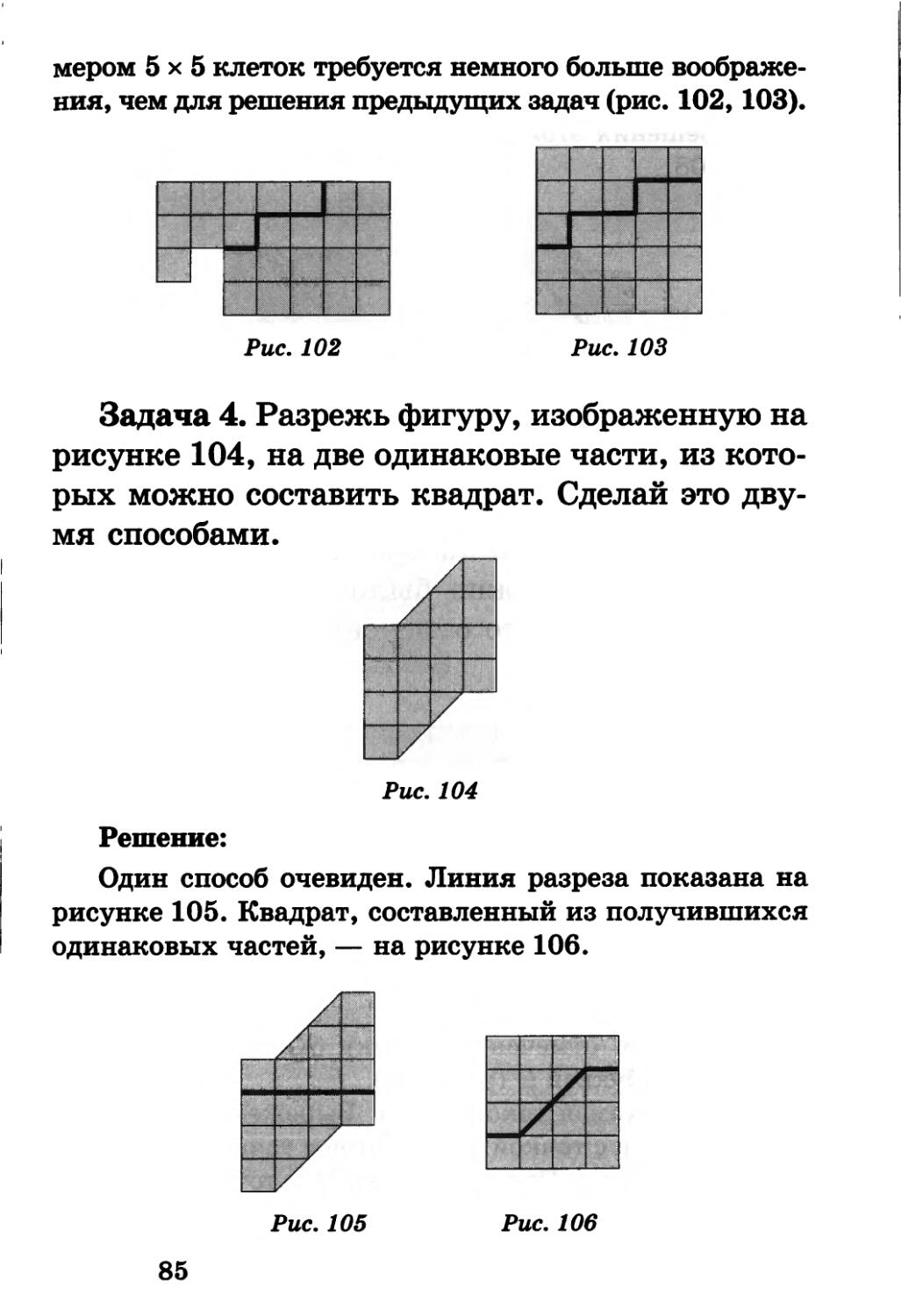
Задача 4. Разрежь фигуру, изображенную на рисунке 104, на две одинаковые части, из которых можно составить квадрат. Сделай это двумя способами.
Рис. 104
Решение:
Один способ очевиден. Линия разреза показана на рисунке 105. Квадрат, составленный из получившихся одинаковых частей, — на рисунке 106.
Рис. 105
Рис. 106
85
Теперь, когда мы знаем, что должен получиться квадрат 4x4 клетки, можно подумать над вторым спо-собом решения этой задачи. Он показан на рисунках 107 и 108.
Рис. 107
Рис. 108
Задача 5. Внутри квадрата отметили точку (рис. 109). Разрежь квадрат на три части так, чтобы из них можно было составить новый квадрат, у которого отмеченная точка будет в центре.
Рис. 109
Решение:
Обозначим отмеченную точку буквой М, а центр квадрата— буквой О (рис. 110).
Воспользуемся такой идеей. Вырежем одинаковые кусочки, один с точкой М, а другой с точкой О, и поменяем их местами. При этом точка М и точка О должны быть одинаково расположены относительно своего кус
86
ка. Проще всего вырезать квадратики 2x2 клетки, один с центром в точке М, а другой с центром в точке О и поменять их местами (рис. 111).
Рис. 111
Логические задачи
 Логические задачи разбирались во втором классе. Их решения удавалось организовать в виде таблицы. В четвертом классе появляются задачи, в которых требуется проверить, какие из высказанных предположений соответствуют действительности. При этом мы сознательно не пользуемся терминологией доказательства от противного.
Задача 1. Рядом сидят мальчик и девочка. «Я мальчик», — говорит черноволосый ребенок. «Я девочка», — говорит рыжий ребенок. Какой цвет волос у мальчика и какой цвет волос у девочки, если известно, что хотя бы кто-то из них солгал?
Решение:
Допустим, что черноволосый ребенок сказал правду: он мальчик. Тогда девочка рыжая. Получается, что рыжий ребенок тоже говорит правду. Но по условию кто-то из них солгал. Следовательно, черноволосый ребенок сказал неправду. На самом деле он девочка, а значит, рыжий ребенок мальчик.
Заметим, что слова «хотя бы кто-то из них солгал» означают, что солгал либо один ребенок, либо солгали оба. В нашей задаче сказали неправду оба ребенка.
Задача 2. Три класса участвовали в туристической эстафете. Один класс занял 1 место, другой — 2 место, а третий — 3 место. Перед началом соревнований болельщики заявили:
1)	4 «А» займет 1 место;
2)	4 «В» не займет 1 место;
88
3)	4 «Б» не будет последним.
Одно из этих предположений оказалось верным, а два других — ошибочными. Какое место занял каждый из четвертых классов?
Решение:
Допустим, что 1-е предположение оказалось верным: 1 место занял 4 «А». Тогда 2-е предположение «4 “В” не займет 1 место» тоже верно. Но по условию задачи оказалось верным только одно предположение. Следовательно, 1-е предположение на самом деле ошибочное: 4 «А» не занял 1 место.
Допустим, что 2-е предположение верно: 4 «В» не занял 1 место. Тогда 1 место остается за 4 «Б» и 3-е предположение «4 “Б” не будет последним» становится тоже верным. Но по условию задачи только одно предположение должно быть верным, значит, 2-е утверждение на самом деле ошибочно.
Таким образом, 1-е и 2-е предположения оказались ошибочными. Следовательно, 3-е предположение верно: 4 «Б» не был последним. На самом деле, 4 «В» занял первое место, 4 «Б» — второе, а 4 «А» досталось третье место.
Задача 3. Четверо друзей соревновались в запуске на дальность бумажных самолетиков. Один из них занял 1 место, другой — 2 место, третий — 3 место и четвертый — 4 место. На вопрос, какое каждый из них занял место, они ответили:
Андрей: Я был вторым, Боря — третьим.
Вася: Я был вторым, Андрей — первым.
Г р и ш а: Я был вторым, Боря — четвертым.
89
При этом известно, что каждый мальчик один раз говорил правду, а один раз — неправду. Кто какое место занял?
Решение:
Допустим, что Андрей первый раз сказал правду: он занял 2 место, а второй раз сказал неправду: Боря не был третьим. Тогда Вася первый раз солгал: он не был вторым, а второй раз сказал правду: Андрей был первым. Но Андрей занять сразу 1 и 2 место не мог, следовательно, Андрей первый раз солгал, а второй раз сказал правду. На самом деле он не занял 2 место, а Боря действительно занял третье место.
Начинаем заполнять таблицу 6, а.
Боря занял, как мы установили, 3 место, поэтому утверждение Гриши «Боря был четвертым» — неправда, а его утверждение «Я был вторым» — правда (табл. 6, б).
Утверждение Васи «Я был вторым» — ложь, а его утверждение «Андрей был первым» — правда. Следовательно, сам Вася был четвертым (табл. 6, в).
Задача 4. Три друга учатся в гимназии. Один из них в математическом, другой — в физиче-90
ском и третий — в биологическом классах. При этом известно:
•	Если Петр математик, то Сергей не физик.
•	Если Роман не физик, то Петр математик.
•	Если Сергей не математик, то Роман биолог.
Определи специальность каждого.
Решение:
Из условия следует такая последовательность утверждений: Петр математик => Сергей не физик => Сергей биолог => Сергей не математик => Роман биолог. Но друзья учатся в разных классах. Следовательно, на самом деле Петр не математик.
Теперь выстраивается такая последовательность верных утверждений: Петр не математик => Роман физик => => Сергей математик => Петр биолог.
задачи
 Для решения текстовых задач учащиеся должны понимать смысл следующих выражений:
«В классе не более 30 учащихся» — это значит, что в классе 30 или меньше 30 учащихся.
«Хотя бы двое учеников отмечают свой день рождения в один день» — это значит, что не менее двух учеников (два или больше двух учащихся) отмечают свой день рождения в один день.
Решив задачу, полезно проверить, удовлетворяет ли найденное решение условию задачи.
Задача 1. Белка спрятала орехи в дуплах трех деревьев. В дуплах первого и второго дерева — 96 орехов, в дуплах второго и третьего — 156, а первого и третьего— 132 ореха. Сколько орехов спрятала белка в дупле каждого дерева?
Решение:
Если мы сложим орехи, спрятанные белкой в дуплах первого и второго, второго и третьего, первого и третьего деревьев, то получим удвоенное количество орехов, спрятанных белкой в дуплах всех трех деревьев. Следовательно, всего белка спрятала (96 + 156 + 132): 2 — = 192 ореха. В дупле первого дерева 192 - 156 = 36 орехов, в дупле второго дерева 192 - 132 = 60 орехов, в дупле третьего дерева 192 - 96 = 96 орехов.
Задача 2. Лена, Рита и Оксана договорились купить к празднику 12 пирожных. Рита купила 5 штук по одной и той же цене, Оксана — 7 штук по той же цене, а Лена вместо своей доли пирожных внесла 24 рубля. Как Рите и Оксане
92
разделить между собой эти деньги, если Лена, Рита и Оксана съели пирожных поровну?
Решение:
Лена, Рита и Оксана съели 12 пирожных поровну, то есть по 4 пирожных каждая. Лена за свои 4 пирожных заплатила 24 рубля, следовательно, одно пирожное стоит 24 : 4 = 6 рублей.
Рита купила 5 пирожных, значит, ей надо вернуть деньги за 1 пирожное, то есть 6 рублей. Оксана купила 7 пирожных, значит, ей надо вернуть деньги за 3 пирожных, то есть 6 • 3 = 18 рублей.
Задача 3. Богатый горожанин оставил два дома в наследство трем сыновьям. Сыновья решили разделить наследство поровну. Каждому из двух старших братьев достался дом, а меньшему выделили деньги: каждый из братьев дал ему 500 динариев. Сколько динариев стоит один дом?
Решение:
Поскольку братья делят наследство поровну, каждый из них должен получить деньгами 1000 динариев. Тогда все наследство оценивается в 3000 динариев, следовательно, дом стоит 1500 динариев.
Задача 4. По двору гуляют козы и гуси. Известно, что всего у них 8 голов и 26 ног. Сколько гусей гуляет по двору?
Решение:
Если бы по двору гуляли одни гуси, то всего было бы 16 ног (8 пар ног). А по условию задачи всего 26 ног 93
(13 пар ног). Следовательно, 5 пар ног могут принадлежать только козам, то есть коз было 5, а гусей — 3.
Задача 5. На площадке молодняка 25 лисят и медвежат катаются на самокатах и велосипедах: лисята по одному на самокате, а медвежата по двое на велосипеде. Сколько лисят катается на самокатах, если самокатов и велосипедов всего 17?
Решение:
Если бы все зверята катались по одному, то понадобилось бы 25 самокатов или велосипедов. А их по условию задачи 17. Следовательно, на 8 средствах для передвижения зверята катаются по двое, то есть велосипедов должно быть 8, а самокатов 9. Таким образом, 9 лисят катались на самокатах.
Задача 6. В коробке лежат 80 фломастеров: красные, синие и зеленые. Какое наименьшее число фломастеров надо взять, не глядя в коробку, чтобы среди них оказалось не меньше 10 фломастеров одного цвета?
Решение:
Если из коробки взять наугад не более 27 фломастеров (27 или меньше фломастеров), то среди них может оказаться не больше 9 красных, 9 синих и 9 зеленых фломастеров, то есть меньше 10 фломастеров каждого цвета.
Если же из коробки взять наугад 28 фломастеров, то среди них обязательно окажется не менее 10 фломастеров одного цвета. Если бы это было не так, то есть среди взятых 28 фломастеров оказалось бы 9 или меньше 9 фло-94
мастеров каждого из трех цветов, то из коробки было бы взято 27 или меньше 27 фломастеров, а не 28.
Задача 7. В корзине лежат одинаковые по величине разноцветные шары: 7 красных, 5 синих, 3 зеленых и 10 белых. Не глядя, мы берем несколько шаров. Сколько шаров достаточно взять, чтобы наверняка 3 из них были разного цвета?
Решение:
Понятно, что 17 или меньше 17 шаров взять недостаточно, так как среди них могут оказаться только белые и красные шары.
Возьмем из корзины, не глядя, 18 шаров. Среди них обязательно будут белые шары, так как красных, синих и зеленых всего 7 + 5 + 3 = 15 шаров. Если среди взятых 18 шаров нет красных, то эти 18 шаров состоят из 10 белых, 5 синих и 3 зеленых шаров. В этом случае шары трех разных цветов присутствуют.
Если среди взятых 18 шаров есть красные, то вместе с белыми их не больше 17, а значит, хотя бы один шар будет синего или зеленого цвета. И в этом случае имеются 3 шара разного цвета.
Таким образом, достаточно, не глядя, взять из корзины 18 шаров, чтобы 3 из них были разного цвета.
Задача 8. В ящике лежит 20 пар красных перчаток и 10 пар синих перчаток в разрозненном виде, то есть для каждой перчатки на правую руку есть перчатка на левую руку, но все перчатки перемешаны. Какое наименьшее количество перчаток надо взять из ящика, не гля-
95
дя, чтобы среди них обязательно нашлась пара перчаток (одна на левую руку, другая на правую руку) одного цвета?
Решение:
Если взять, не глядя, 30 или меньше 30 перчаток, то среди них может оказаться 20 или меньше двадцати красных перчаток на одну руку и 10 или меньше десяти синих перчаток тоже на одну руку, то есть среди 30 или меньше 30 перчаток может не оказаться одной пары одного цвета.
Возьмем, не глядя, 31 перчатку. Тогда среди них наверняка окажется пара одного цвета, так как не может быть больше 20 красных и 10 синих перчаток на одну руку. По меньшей мере одна перчатка (синяя или красная) окажется на другую руку и составит пару.
Задача 9. Три ластика, один карандаш и два блокнота стоят 22 рубля. Один ластик, три карандаша и два блокнота стоят 38 рублей. Сколько стоит комплект из одного ластика, одного карандаша и одного блокнота?
Решение:
Если сложить стоимость 3 ластиков, 1 карандаша и 2 блокнотов со стоимостью 1 ластика, 3 карандашей и 2 блокнотов, то мы получим, что 4 ластика, 4 карандаша и 4 блокнота стоят 22 + 38 = 60 рублей.
Таким образом, 4 комплекта, каждый из которых состоит из 1 ластика, 1 карандаша и 1 блокнота, стоят 60 рублей, а значит, один комплект стоит 60 : 4 = 15 рублей.
Задача 10. Четыре кошки и три котенка весят 15 кг, а три кошки и четыре котенка весят
96
13 кг. Сколько весит каждая кошка и каждый котенок в отдельности?
Решение:
Складываем вес четырех кошек и трех котят с весом трех кошек и четырех котят, получим, что семь кошек и семь котят весят 15 + 13 = 28 (кг). Следовательно, одна кошка и один котенок весят 28 : 7 = 4 (кг).
Три кошки и три котенка весят 4 • 3 = 12 (кг). Вычитая из веса четырех кошек и трех котят вес трех кошек и трех котят, получим вес одной кошки: 15 - 12 = 3 (кг). Вес одного котенка равен 4-3 = 1 (кг).
Задача 11. Из книги выпал кусок. Первая страница куска имеет номер 143, а номер последней страницы куска записан теми же цифрами. Сколько страниц книги выпало?
Решение:
Номер последней страницы выпавшего из книги куска записан цифрами 1, 4, 3, больше числа 143 и оканчивается на четную цифру. Всем этим трем условиям удовлетворяет только число 314. Число выпавших страниц равно 314 - 143 + 1 = 172.
Задача 12. Для нумерации страниц книги понадобилось 688 цифр. Сколько страниц в книге? Нумерация страниц в книге начинается с третьей страницы.
Решение:
Непронумерованных страниц в книге — 2.
Страниц с однозначными номерами — 7 (с третьей по девятую включительно).
97
Страниц с двузначными номерами — 90 (с десятой * по девяносто девятую включительно), для таких страниц понадобилось 90 • 2 = 180 цифр. Остальные страницы книги, очевидно, занумерованы трехзначными числами. На них остается 688 - 180 - 7 = 501 цифра. Следовательно, страниц, занумерованных трехзначными цифрами, 501: 3 = 167.
Таким образом, всего в книге 2 + 7 + 90 + 167 = = 266 страниц.
Задача 13. На дверь квартиры крепится номер, состоящий из отдельных металлических цифр. Сколько всего потребуется таких цифр для нумерации 136 квартир нового дома?
Решение:
Для нумерации квартир с первой по девятую потребуется 9 металлических цифр.
Для нумерации квартир с десятой по девяносто девятую потребуется (99 - 9) • 2 = 180 цифр.
Для нумерации квартир с сотой по сто тридцать шестую потребуется (136 - 99) -3 = 111 цифр.
Таким образом, для нумерации 136 квартир нового дома потребуется 9 + 180 + 111 = 300 металлических цифр.
Задача 14. С верхнего этажа дома двое школьников отправились наперегонки вниз на первый этаж и обратно вверх: один на лифте, а другой пешком. Лифт едет все время с одинаковой скоростью, а спускаться пешком удается вдвое быстрее, зато подниматься — вдвое медленнее, чем на лифте. Кто из школьников раньше вернется обратно?
98
Решение:
Пока первый из школьников будет спускаться пешком и достигнет первого этажа, второй школьник дое-. дет до середины высоты дома (рис. 112, а).
В тот момент, когда школьник в лифте достигает первого этажа, первый школьник поднимется на одну четверть высоты дома (рис. 112, б).
в
Рис. 112
И наконец, когда второй школьник доедет в лифте до верхнего этажа, первый школьник, поднявшись еще на половину высоты дома, окажется на уровне высоты дома (рис. 112, в).
Таким образом, школьник в лифте вернется на верхний этаж раньше.
99
Задача 15. Оля, Коля, Маша и Витя участвовали в олимпиаде. Витя решил 8 задач — больше всех, Оля решила 5 задач — меньше всех. Каждая задача олимпиады была решена ровно тремя из четырех школьников. Сколько задач было на олимпиаде?
Решение:
Коля и Маша могли решить либо по 6 задач, либо один из них решил 6 задач, а другой 7, либо оба решили по 7 задач.
Допустим, что Коля и Маша решили по 6 задач. Тогда, складывая задачи, решенные всеми четырьмя школьниками, получим 8 + 64-6 + 5 = 25 задач. При этом каждую задачу олимпиады мы посчитали 3 раза (каждая задача олимпиады была решена ровно тремя школьниками), поэтому задач на олимпиаде было в 3 раза меньше. Но 25 на 3 не делится, следовательно, Коля и Маша не могли решить по 6 задач.
Такие же рассуждения показывают, что один из них не мог решить 6, а другой 7 задач, но решить по 7 задач Коля и Маша могли. При этом на олимпиаде было (8+7+7 + 5):3 = 9 задач.
Проверим, что 9 задач на олимпиаде решены друзьями так, как сказано в условии.
Например, задачи могли быть решены в порядке, указанном в таблице 7:
Таблица 7
	1	2	3	4	5	в	7	8	9
Витя	+	+	4-	4-	—	4-	+	+	+
Коля	—	4-	—	+	+	+	+	+	+
Маша	+	—	+	—	+	+	+	4-	+
Оля	4-	+	4-	4-	4-	—	—	—	—
100
Задача 16. В школе 400 учеников. Верно ли, что хотя бы два ученика этой школы отмечают свой день рождения в один и тот же день года?
Решение:
В году не более 366 дней. Если даже каждый день года будет днем рождения для какого-нибудь ученика, то не более 366 учеников родились в разные дни года.
В школе 400 учеников, следовательно, хотя бы два ученика отмечают свой день рождения в один и тот же день года.
Задача 17. В школе 880 учеников и 30 классов. Есть ли в такой школе класс, в котором не меньше 30 учеников?
Решение:
Допустим, что такого класса в школе нет, то есть в каждом из 30 классов либо 29, либо меньше 29 учеников. Но тогда во всей школе будет не больше 29*30 = 870 учеников, а по условию их 880. Следовательно, в такой школе есть класс, в котором не меньше 30 учеников.
Задача 18. Банка с медом весит 500 г. Та же банка с керосином весит 350 г. Керосин легче меда в 2 раза. Сколько граммов весит пустая банка?
Решение:
Мед, заполняющий банку, тяжелее керосина, заполняющего такую же банку, на 500 - 350 = 150 граммов. С другой стороны, этот же мед тяжелее керосина в 2 раза, то есть одна банка меда (без самой банки) весит столько же, сколько весят две такие же банки керосина (без самих банок).
Следовательно, керосин, заполняющий банку, весит 150 г, а пустая банка 350 - 150 = 200 граммов.
101
Задача 19. На школьной викторине было * предложено 12 вопросов. За каждый правильный ответ участнику начисляли 10 баллов, а за неправильный ответ отнимали 8 баллов. Сколько правильных ответов дал один из участников викторины, если он набрал 30 баллов?
Решение:
Если бы участник викторины на все 12 вопросов ответил правильно, то он получил бы 10 х 12 - 120 баллов. Теперь поймем главное: за каждый неправильный ответ участник теряет 10 + 8 = 18 баллов (10 баллов он не получает, да еще 8 баллов с него снимают).
Набрав 30 баллов, участник викторины потерял 120 -- 30 = 90 баллов. Следовательно, он дал 90:18 = 5 неправильных ответов, а значит, 12-5 = 7 правильных.
Задача 20. Сошлись два пастуха Иван и Петр.
Иван говорит Петру: «Отдай ты мне одну овцу, тогда у меня будет ровно вдвое больше овец, чем у тебя». А Петр ему отвечает: «Нет! Лучше ты мне отдай одну овцу, тогда у нас овец будет поровну». Сколько же было овец у каждого?
Решение:
Если Иван отдаст Петру одну овцу, то овец у них будет поровну. Значит, у Ивана на самом деле на две овцы больше, чем у
б
Рис. 113
102
Петра (рис. 113, а). Если Петр отдаст одну овцу Ивану, то у Ивана станет на 4 овцы больше, чем у Петра. С другой стороны, по условию, у Ивана тогда будет овец вдвое больше, чем у Петра. Следовательно, у Петра останется 4 овцы, а значит, было у Петра 5 овец. У Ивана же стало 8 овец, а значит, было у Ивана 7 овец (рис. 113, б).
Задача 21. В одной коробке лежат 2 белых шара, в другой — один белый и один черный, а в третьей — 2 черных шара.
№ 1	№2	№ 3
Рис. 114
Рисунок, наклеенный на каждую коробку, неправильно указывает ее содержимое. Из какой коробки нужно достать только один шар, чтобы можно было определить содержимое всех коробок.
Решение:
Возьмем коробку № 2. В ней лежат либо 2 белых шара, либо 2 черных шара.
Достанем шар из этой коробки.
Возможны два варианта:
1) вынут белый шар, тогда в коробке № 2 оба шара белые, в коробке № 3 один шар белый, а другой черный, в коробке № 1 два черных шара;
2) вынут черный шар, тогда в коробке № 2 оба шара черные, в коробке № 1 один шар белый, а другой черный, в коробке № 3 два белых шара.
103
Таким образом, если достать только один шар из коробки Хе 2, то можно определить содержимое всех коробок.
Задача 22. Пять землекопов за пять часов выкапывают пять метров канавы. Сколько землекопов смогут за 100 часов выкопать 100 метров канавы?
Решение:
Если за пять часов пять землекопов выкапывают 5 м канавы, то за 100 ч (за время, в 20 раз большее) те же пять землекопов выкопают канаву в 20 раз длиннее, то есть 100 м канавы.
Ответ: 5 землекопов.
2 34
классы
Задачи
для самостоятельного решения
Задача 1. Разрежь фигуры а и б на рисунке 115 по линиям сетки на 4 одинаковые части.
106
4 одинаковые части так, чтобы в каждой части было три закрашенных клетки (рис. 119).
Задача 6. Разрежь фигурку на 8 одинаковых частей, чтобы в каждой части оказался ровно один кружок (рис. 120).
Задача 7. На рисунке 121, а изображено больше квадратов, чем на рисунке 121, б. На сколько?
Рис. 121
Задача 8. На рисунке 121, а изображено больше прямоугольников, чем на рисунке 121, б. На сколько?
Задача 9. Надо нарисовать чайник, не отрывая карандаш от бумаги и проводя линию только один раз. С какой точки можно начать рисовать чайник: А, В, С, D, Е, F или К (рис. 122)?
107
Задача 10. Составь из па* лочек такую фигуру (рис. 123). Сколько получилось квадратов? Убери 2 палочки, чтобы осталось 4 одинаковых квадрата.
Задача 11. Три подруги вышли в белом, зеленом и си
нем платьях. Туфли подруг были тоже разного цвета: у одной белые, у другой синие, у третьей зеленые. Известно, что только у Вали цвет платья и туфель совпадают. Ни платье, ни туфли Ани не были белыми. Наташа была в зеленых
туфлях. Определи цвет платья и туфель каж-
дой из подруг.
Задача 12. Сколько маршрутов соединяют точки А и В? Каждый маршрут не должен проходить дважды через одно и то же место (рис. 124).
А
В
Рис. 124
Задача 13. На восьми карточках написаны цифры и знаки «+» и «=».
2	3	5	6	7	8
Составьте равенство, используя все указанные карточки.
108
Задача 14. Веревочная сетка с квадратными ячейками поджигается одновременно в точках А и В (рис. 125). Веревка горит равномерно, и кусочек веревки между соседними узлами его------------------
рает за 1 минуту. Сколько времени будет гореть веревка?	д
Рис. 125
Задача 15. Имеется 4 монеты. Из них 3 настоящие и одна фальшивая, отличающаяся от них по массе неизвестно в какую сторону. Как за два взвешивания на чашечных весах найти ее?
Задача 16. Сколько различных четырехзначных чисел можно записать с помощью цифр 1, 2, 3 и 4, если каждую цифру при записи числа использовать:
а)	только один раз;
б)	сколько угодно раз.
Задача 17. В Эрмитаже есть две лестницы: высота первой 13 м, а ее длина (по горизонтали) — 20 м, а второй — соответственно Ими 22 м. На первой лестнице ступенек вдвое меньше, чем на второй. Обе лестницы покрыты ковровыми дорожками. Какая из дорожек длиннее?
Задача 18. Поверхность пруда постепенно покрывается кувшинками. Кувшинки растут
109
столь быстро, что за каждый день закрываемая ими площадь удваивается. Половина поверхности пруда заросла кувшинками за неделю. За сколько дней зарастет вся поверхность пруда?
Задача 19. В темной комнате стоит коробка, в которой лежат 8 синих, 10 серых и 10 черных носков. Сколько носков нужно достать, чтобы среди них наверняка оказались:
а)	хотя бы два носка одного цвета?
б)	хотя бы два серых носка?
в)	хотя бы по два носка каждого цвета?
Задача 20. Однажды в классе число отсут-1
ствующих учеников составило -g- часть от числа присутствующих. Какая часть класса отсутствовала?
Задача 21. Можно ли раздать 52 банана одиннадцати обезьянам так, чтобы любые две получили различное число бананов?
Задача 22. Разбейте числа 1, 2, 9, 25, 49, 64 на две группы так, чтобы сумма чисел одной группы была равна сумме чисел другой группы.
Задача 23. Аня, Таня и Ваня собирали марки о космосе. У Ани и Тани вместе 45 марок о
но
космосе, у Тани и Вани 55 марок. Могли ли собрать вместе Аня и Ваня 75 марок о космосе?
Задача 24. В шоколадном наборе 15 одинаковых по виду конфет с тремя разными начинками, поровну с каждой начинкой. Какое наименьшее число конфет надо взять, чтобы быть уверенным, что среди них есть конфеты с тремя разными начинками?
Задача 25. Игорь и Олег отправились вместе на велосипедах на станцию. Игорь ехал весь путь с одной и той же скоростью. Олег же половину пути ехал со скоростью, в 2 раза большей, а вторую половину со скоростью в 2 раза меньшей, чем скорость, с которой ехал Игорь. Верно ли, что мальчики приедут на станцию в одно и то же время?
Задача 26. Придумай наименьшее двенадцатизначное число, в котором есть все цифры.
Задача 27. На столе лежат три стопки одинаковых по виду монет из 20, 25 и 30 монет. В одной из них есть фальшивая монета, внешне не отличающаяся от остальных. Как при помощи одного взвешивания на чашечных весах без гирь найти стопку, в которой все монеты настоящие?
ill
Задача 28. Найди площадь закрашенной фигуры (рисунки 126, а, б, в), если сторона клет-
Рис. 126
Задача 29. Имеется 2009 одинаковых по виду монет, среди которых либо две фальшивые, либо ни одной. Как за два взвешивания на чашечных весах без гирь узнать, есть среди них фальшивые монеты или нет, если фальшивые монеты имеют одну и ту же массу, отличающуюся от массы настоящей монеты.
Задача 30. Хозяин обещал работнику за 30 дней работы 9 рублей и кафтан. Через 3 дня работник уволился и получил за проработанное время кафтан. Сколько стоил кафтан?
Задача 31. После 7 стирок длина, ширина и высота куска мыла (рис. 127) уменьшились вдвое. На сколько стирок хватит оставшегося куска?
Рис. 127
112
Задача 32. Кирпич весит 2 кг и еще треть собственного веса. Сколько весит кирпич?
Задача 33. В трех ящиках находится крупа, вермишель и сахар. На первом ящике написано «крупа», на втором — «вермишель», на третьем — «крупа или сахар». Что в каком ящике находится, если содержимое каждого из ящиков не соответствует надписи на нем?
Задача 34. На столе в ряд выставлены 9 пакетов с сахаром. Масса первого — 3 кг, а каждый следующий тяжелее предыдущего на 1 кг. Как разложить пакеты в три рюкзака, чтобы количество сахара в каждом из рюкзаков было одинаковым?
Задача 35. Расшифруй ребус:
КНИГА +КНИГА КНИГА НАУКА
Задача 36. Внутри круга отмечена точка, несовпадающая с его центром. Как разрезать круг на 3 части и из этих частей сложить новый круг с центром в отмеченной точке?
Задача 37. На турнире Архимеда каждая школа выставила одну или две команды. Всего из
участвовало 22 команды из 15 школ. Сколько школ выступило двумя командами?
Задача 38. Вася и Петя, поссорившись, разбежались с одинаковыми скоростями в противоположных направлениях. Через 5 минут Вася спохватился, повернул назад и, увеличив скорость, побежал догонять Петю. Во сколько раз увеличил скорость Вася, если он догнал Петю через 5 минут после того, как повернул назад?
Задача 39. Учитель разложил на чашечные весы 16 гирек массами 1, 2, 3,..., 16 граммов так, что одна из чашек перевесила. Пятнадцать учеников по очереди выходили и забирали с собой одну гирьку, причем после выхода каждого ученика перевешивала противоположная чашка весов. Какая гирька осталась на весах?
Задача 40. Из цифр 1, 2, 3, 4, 5, 6 требуется составить два трехзначных числа, сумма которых была бы максимальна (каждую цифру можно использовать по одному разу). Найдите все возможные решения.
Задача 41. В коробке синие, красные и зеленые карандаши. Всего 20 штук. Синих в 6 раз больше, чем зеленых. Красных меньше, чем синих. Сколько в коробке красных карандашей?
Задача 42. Число оканчивается цифрой 9. Если эту цифру отбросить и к полученному чис
114
лу прибавить первое число, то получится 306 216. Найди это число.
Задача 43. Имеется 9 кг сахарного песка. Как с помощью трех взвешиваний на чашечных весах отмерить 2 кг песка с помощью одной гири 200 г?
Задача 44. Квадрат со стороной 1 м разрезали на квадраты со стороной 1 см и выстроили их в один ряд в виде полоски шириной 1 см. Какой длины получилась полоса?
Задача 45. На старом тополе несколько вороньих гнезд, в них живут 20 ворон. Самой старой вороне 38 лет, а самой молодой — 20 лет. Верно ли, что среди ворон есть одногодки?
Задача 46. У кота Матроскина в погребе на двух полках стояло по 15 банок сметаны. С верхней полки он снял несколько банок, а с нижней снял столько, сколько осталось на верхней. Сколько банок сметаны осталось у Кота Матроскина на двух полках?
Задача 47. Митя с Кириллом решили купить футбольный мяч. У Мити не хватило 20 рублей, чтобы его купить, а у Кирилла — 30 рублей. Тогда они сложили свои деньги и купили мяч, причем 60 рублей у них осталось. Сколько стоил футбольный мяч?
115
Задача 48. Если Митя купит 9 тетрадей, то у него останется 9 рублей. А на 12 тетрадей ему не хватает 3 рублей. Сколько денег у Мити?
Задача 49. Таня стоит на берегу речки. У нее есть два кувшина: один на 5 л, а про второй Таня помнит лишь то, что он вмещает то ли Зл, то ли 4 л. Помогите Тане определить емкость второго кувшина.
Задача 50. Одним пакетиком чая можно заварить два или три стакана чая. Денис и Даша разделили коробку чайных пакетиков поровну. Денис заварил 57 стаканов чая, а Даша — 83. Сколько пакетиков чая было в коробке?
Задача 51. Как при помощи чашечных весов без гирь разделить 24 кг гвоздей на две части — 9 кг и 15 кг?
Задача 52. Два охотника отправились одновременно навстречу друг другу из двух деревень, расстояние между которыми 18 км. Первый шел со скоростью 5 км/ч, а второй — 4 км/ч. Первый охотник взял с собой собаку, которая бежала со скоростью 8 км/ч. Собака сразу же побежала навстречу второму охотнику, встретила его, повернула обратно и побежала навстречу первому охотнику и т. д. Так она бегала от одного охотника к другому, пока те не встретились. Сколько километров пробежала собака?
116
Задача 53. Десяти собакам и кошкам скормили 56 галет. Каждой кошке досталось 5 галет, а каждой собаке — 6. Сколько было собак и сколько кошек?
Задача 54. Из пункта А в пункт В выехал велосипедист со скоростью 23 км/ч, и одновременно с ним из пункта В в пункт А выехал велосипедист со скоростью 19 км/ч. Когда первый приехал в пункт В, второму оставалось проехать еще 24 км. Каково расстояние между пунктами?
Задача 55. У мальчика столько же сестер, сколько и братьев. А у его сестры в два раза меньше сестер, чем братьев. Сколько в этой семье мальчиков и сколько девочек?
Задача 56. Сколько существует трехзначных чисел, у которых соседние цифры разные?
Задача 57. Несколько друзей купили арбуз. Петя потратил 12 рублей — четверть суммы, потраченной остальными. Ваня потратил треть суммы, потраченной остальными. Сколько рублей внес Ваня для покупки друзьями арбуза?
Задача 58. С помощью чашечных весов и гири в 1 кг отмерь за семь взвешиваний 100 кг сахарного песка.
Ответы и
Задача 1.
а	б
Рис. 128
118
Задача в.
Задача 7. На рисунке 121, а изображено на 4 квадрата больше, чем на рисунке 121, б. На рисунке 121, б нет одного одноклеточного квадрата, одного квадрата 2x2 клетки, одного квадрата 3x3 клетки и одного квадрата 4x4 клетки.
Задача 8. На рисунке 121, а изображено на 16 прямоугольников больше, чем на рисунке 121, б. На рисунке 121, б нет четырех квадратов, о которых говорилось в решении задачи 7, шести «горизонтальных» прямоугольников размером 1x2, 1x3, 1x4, 2x3, 2x4, 3x4 клетки и столько же «вертикальных» прямоугольников.
Задача 9. На изображении чайника (рис. 122) ровно две нечетные точки: В и С. Нарисовать чайник можно, если начать вести линию из одной из них.
Задача 10. Получилось 7 квадратов. Убери 2 палочки, отмеченные на рисунке 134. Останется 4 одинаковых квадрата.
Рис. 134
119
Задача 11. Нужно составить таблички для цвета платьев и для цвета туфель подруг. Вначале заполни таблицу 8, а для цвета туфель, а затем 8, б — для цвета платьев.
а
Имена подруг	Цвет туфель		
	Б	3	с
Аня	—		+
Валя	+		
Наташа		+	
Таблица 8 б
Имена подруг	Цвет платья		
	Б	3	с
Аня	—	+	—
Валя	+		
Наташа			+
Задача 12. Сосчитаем число маршрутов, содержащих отрезок AM: по 3 маршрута, состоящих из четырех, шести
и восьми сторон маленьких квадратов; 2 маршрута, состоящих из десяти, и 1 маршрут, состоящий из 12 сторон маленьких квадратов. Всего 12 маршрутов (рис. 135).
Столько же маршрутов содержит отрезок AN. Следовательно, всего 24 маршрута соединяют точки Ат В.
Задача 13. 26 + 57 = 83.
Задача 14. На рисунке 136 цифрой 1 отмечены узлы, в которых огонь будет через одну минуту, цифрой 2 — узлы, в которых огонь будет через две минуты. Вся сетка сгорит через две с половиной минуты.
Рис. 135
Рис. 136
Задача 15. Разбиваем 4 монеты на две группы по 2 монеты в каждой.
Первым взвешиванием сравниваем монеты первой группы. Если весы оказались в равновесии, то обе монеты пер
120
вой группы настоящие, а фальшивая находится среди монет второй группы.
Вторым взвешиванием, сравнивая какую-нибудь монету второй группы с настоящей, находим фальшивую монету.
Если же весы при первом взвешивании оказались не в равновесии, то фальшивая монета находится среди монет первой группы, а обе монеты второй группы настоящие.
Вторым взвешиванием, сравнивая какую-нибудь монету первой группы с настоящей, находим фальшивую монету.
Задача 16. а) 24 числа; б) 256 чисел.
Задача 17. Длина ковровой дорожки равна длине ломаной, состоящей из горизонтальных и вертикальных звеньев.
Сумма длин всех вертикальных звеньев равна высоте ле- । стницы, а сумма длин всех го- §
ризонтальных звеньев лома- з ной равна длине лестницы 03 (рис. 137). Каждая дорожка будет иметь длину, равную
сумме высоты и длины лест-
ницы: для первой лестницы	?ис'
13 м + 20 м = 33 м и для второй лестницы 11 м + 22 м = 33 м.
Следовательно, дорожки имеют одну и ту же длину.
Задача 18. Половина поверхности пруда заросла за неделю. На следующий день зарастет весь пруд. Таким образом, вся поверхность пруда зарастает за 8 дней.
Задача 19. а) 4 носка; б) 20 носков; в) 22 носка.
Задача 20. Отсутствовала часть всего класса (рис. 138).
Отсутствующие
Весь класс
Присутствующие
ученики
ученики
Рис. 138
121
Задача 21. Наименьшее число бананов, которое можно раздать одиннадцати обезьянам так, чтобы любые две получили различное число бананов, равно: 0+1+2+3+4+5+ + 6 + 7 + 8 + 94-10 = 55.
Поэтому 52 банана раздать одиннадцати обезьянам так, чтобы любые две получили различное число бананов, нельзя.
Задача 22. Сумма всех данных чисел равна 1 + 2 + 9 + + 25 + 49 + 64 = 150. Следовательно, сумма чисел в каждой группе равна 75, а значит, данные числа разбиваются на такие две группы: 1, 25, 49 и 2, 9, 64.
Действительно, 1 + 25+ 49 = 2 + 9 +64 = 75.
Задача 23. Аня и Ваня не могли собрать вместе 75 марок, так как сумма 45 + 55 + 75, равная удвоенному количеству всех марок, собранных Аней, Таней и Ваней, не делится на 2.
Задача 24. 11 конфет.
Задача 25. Олег вторую половину пути ехал со скоростью, в 2 раза меньшей, чем скорость, с которой ехал Игорь. Следовательно, Олег потратил на вторую половину пути столько же времени, сколько Игорь потратил на весь путь. Но первую половину пути Олег какое-то время ехал, следовательно, он приедет на станцию позже Игоря.
Задача 26. 100 023 456 789.
Задача 27. Пусть в первой стопке 20 монет, во второй — 25, а в третьей — 30. На одну чашу весов кладем все 20 монет первой стопки, а на вторую чашу — 20 монет из второй стопки. Если весы оказались в равновесии, то все монеты первой стопки настоящие. Если же весы окажутся не в равновесии, то все монеты третьей стопки настоящие.
Задача 28. а) 6 см2; б) 3 см2; в) 4 см2.
122
Задача 29. Откладываем одну монету в сторону и делим оставшиеся 2008 монет на две группы по 1004 монеты в каждой. Первым взвешиванием сравниваем монеты этих двух групп. Если весы оказываются не в равновесии, то среди имеющихся 2009 монет есть фальшивые.
Если же весы оказываются в равновесии, то либо все 2009 монет настоящие, либо в каждой группе из 1004 монет есть одна фальшивая. Какой из этих двух случаев имеет место, узнаем из второго взвешивания. Для этого делим 1004 монеты какой-нибудь группы на две равные части по 502 монеты и сравниваем их с помощью второго взвешивания. Если весы оказываются в равновесии, то 1004 монеты этой группы настоящие, а значит, настоящие и все 2009 монет. Если же весы оказываются не в равновесии, то среди имеющихся 2009 монет есть фальшивые.
Задача 30. За проработанные Здня работник получил кафтан, значит, за оставшиеся 27 дней он должен был получить 9 рублей, то есть 1 рубль за каждые 3 дня работы. Следовательно, кафтан стоил 1 рубль.
Задача 31. За 7 стирок кусок мыла уменьшился в 8 раз, 1 то есть осталась-g-часть куска. За 7 стирок израсходовано
-д- частей куска. Следовательно, О
оставшегося куска мыла хватит на одну стирку (рис. 139).
Задача 32. Вес кирпича равен 2 кг и весу одной трети такого же кирпича. Следовательно, 2 кг — вес двух третей кирпича. Одна треть кирпича весит 1 кг, а весь кирпич — 3 кг.
Задача 33. Содержимое каждого из трех ящиков не соответствует надписи на нем. Следовательно, в ящике с надписью «крупа или сахар» содержится вермишель, а значит, в ящике с надписью «крупа» — сахар, а в ящике с надписью «вермишель» — крупа.
123
Задача 34. Масса сахара во всех девяти пакетах равна 3 + 44-5 + 6 + 7 + 8 + 9 +10+ 11 = 63 кг. Следовательно, в каждом из трех рюкзаков должен быть 21 кг сахара. Разложить пакеты с сахаром в три рюкзака можно пятью способами:
4 + 6 + 11	11 + 10	11 + 10	3+7 + 11
3+8+10	9+7+5	9+8+4	4+8+9
5 + 7 + 9,	8 + 6 + 4 +3,	7 + 6 + 5 +3,	5 + 6 + 10
или 11 + 10
8 + 7 + 6
* 9 + 5 + 4 + 3
Задача 35. 28 375 + 28 375 + 28 375 = 85 125.
Задача 36. Вырезать маленький кружок с центром в отмеченной точке и такой же кружок с центром в центре данного круга и поменять эти кружки местами (рис. 140).
Задача 37. 7 школ.
Рис. 140
Задача 38. За первые 5 минут с того момента, как мальчики поссорились, каждый из них пробежал одно и то же расстояние. За следующие 5 минут Петя пробежал такое же расстояние, а Вася — три таких расстояния. Следовательно, Васе пришлось увеличить скорость в 3 раза.
Задача 39. Весы не в равновесии, значит, массы гирек на чашках весов отличаются не менее чем на 1 г.
Если ученик снимет с чашки весов гирьку в 1 г, то либо весы придут в равновесие, либо положение чашек не изменится. Следовательно, для того чтобы стала перевешивать противоположная чашка весов, каждый из 15 учеников должен снять гирьку, масса которой больше 1 г, а значит, на весах останется гирька массой 1 г.
Задача 40. 642 и 531; 641 и 532; 632 и 541; 631 и 542.
124
Задача 41. Если в коробке не менее 3 зеленых карандашей, то в ней не менее 18 синих, то есть в коробке больше 20 карандашей, а по условию в коробке всего 20 карандашей.
Если в коробке 1 зеленый карандаш, то синих в ней 6, а красных 13. Но по условию задачи красных карандашей в коробке меньше, чем синих.
Следовательно, единственный вариант, удовлетворяющий условию задачи, такой: в коробке 2 зеленых, 12 синих и 6 красных карандашей.
Задача 42. 278 379.
Задача 43. Первое взвешивание: на одной чашке 4 кг 600 г сахарного песка, а на другой 4 кг 400 г и гиря 200 г.
Второе взвешивание: на одной чашке 2 кг 400 г сахарного песка, а на другой 2 кг 200 г и гиря 200 г.
Третье взвешивание: из сахарного песка массой 2 кг 200 г отвесить 200 г песка с помощью гири 200 г.
Задача 44. Квадрат со стороной 1 м разрезается на 100 • 100 = 10 000 квадратиков со стороной 1 см. Если все эти квадратики выстроить в ряд, то получится полоса длиной 10 000 см или 100 м.
Задача 45. Если бы среди ворон не было одногодок, то их было бы столько же, сколько различных натуральных чисел от 20 до 38. Чисел от 20 до 38 (20 и 38 включаются) всего 19, а ворон 20. Следовательно, среди ворон есть одногодки.
Задача 46. 15 банок.
Задача 47. Кирилл отдает свои деньги Мите, они покупают мяч, и 60 рублей у них еще остается. Следовательно, Кирилл дает Мите недостающие ему до покупки мяча 20 рублей и еще 60 рублей остается, то есть всего Кирилл отдал Мите 80 рублей — все деньги, которые у него были. Кириллу для покупки мяча не хватало 30 рублей, следовательно, мяч стоил 110 рублей.
Задача 48. У Мити было 45 рублей.
125
Задача 49. Будем наполнять пятилитровый кувшин водой из реки с помощью второго кувшина. Если емкость второго кувшина Зл, то за три раза мы не сможем дважды наполнить пятилитровый кувшин, так как 9 л < 10 л. Если же емкость второго кувшина 4 л, то за три раза пятилитровый кувшин наполнится дважды, так как 12 л > 10 л.
Задача 50. Если бы у Дениса было 29 или больше 29 пакетиков чая, то, заваривая каждым пакетиком 2 стакана чая, он заварил бы 58 или больше 58 стаканов чая. Следовательно, у Дениса было не более 28 пакетиков чая.
Если бы у Даши было 27 или меньше 27 пакетиков чая, то, даже заваривая каждым пакетиком 3 стакана чая, она заварила бы 81 или меньше 81 стакана чая. Следовательно, у Даши было не менее 28 пакетиков чая.
А так как чайных пакетиков у Дениса и Даши было поровну, то у них могло быть только по 28 пакетиков чая.
Всего в коробке было 56 пакетиков чая.
Задача 51. Первым взвешиванием делим 24 кг на две части по 12 кг гвоздей.
Вторым взвешиванием одну часть 12 кг делим на две части по 6 кг гвоздей.
Третьим взвешиванием одну часть 6 кг делим на две части по 3 кг гвоздей.
Из 12 кг и 3 кг составляем часть, равную 15 кг гвоздей, а из 6 кг и 3 кг составляем часть, равную 9 кг гвоздей.
Задача 52. Охотники до встречи шли 18 : (5 + 4) = 2 часа. Столько же времени собака бегала от одного к другому со скоростью 8 км/ч. Следовательно, за это время она пробежала 8-2=16 км.
Задача 53. 6 собак и 4 кошки.
Задача 54. Первый велосипедист за каждый час проезжал на 4 км больше, чем второй. Когда он проехал все расстояние от пункта А до пункта В, то оказалось, что он проехал на 24 км больше, чем второй. Следовательно, все расстояние от пункта А до пункта В первый велосипедист проехал за
126
24 : 4 = 6 часов, а само расстояние между пунктами равно 23 * 6 — 138 км.
Задача 55. У мальчика столько же сестер, сколько и братьев. Следовательно, в семье мальчиков на одного больше, чем девочек, а значит, на два больше, чем сестер у каждой девочки.
По условию у каждой девочки сестер в два раза меньше, чем братьев. Следовательно, сестер у каждой девочки две, всего девочек в семье три, а мальчиков — четыре.
Задача 56. 729.
Задача 57. Петя внес четверть суммы, потраченной остальными на покупку арбуза, то есть пятую часть стоимости арбуза. Следовательно, арбуз стоил 12 • 5 = 60 рублей.
Ваня внес треть суммы, потраченной остальными, то есть четвертую часть стоимости арбуза. Ваня внес 60 : 4 = 15 рублей.
Задача 58. Если шестым взвешиванием будет отмерено 50 кг песка, то седьмым взвешиванием можно на чашечных весах отмерить 100 кг (на каждой чашке весов по 50 кг песка).
Если пятым взвешиванием будет отмерено 25 кг песка, то шестым взвешиванием можно отмерить 50 кг песка (на каждой чашке весов по 25 кг песка).
Если четвертым взвешиванием будет отмерено 12 кг песка, то пятым взвешиванием можно отмерить 25 кг песка (на одной чаше весов 12 кг песка и гиря в 1 кг, на другой чашке 13 кг песка).
Если третьим взвешиванием будет отмерено 6 кг песка, то четвертым взвешиванием можно отмерить 12 кг песка (на каждой чашке весов по 6 кг песка).
Если вторым взвешиванием будет отмерено 3 кг песка, то третьим взвешиванием можно отмерить 6 кг песка (на каждой чашке весов по 3 кг песка).
Если первым взвешиванием отмерить 1 кг песка (это с помощью гири в 1 кг можно сделать), то вторым взвешиванием можно отмерить 3 кг песка (на одной чашке весов 1 кг песка и гипя в 1 кг, на другой чашке весов 2 кг песка).
Список литературы
Баранова Т.А., Блинков А.Д., Кочетков К. IL, Потапова М. Г., Семенов А, В. Олимпиада для 5-6 классов. Весенний турнир Архимеда. М.: МЦНМО, 2003.
Козлова Е. Г. Сказки и подсказки. Задачи для математического кружка. М.: МЦНМО, 2004.
Спивак А. В. Тысяча и одна задача по математике. М.: Просвещение, 2002.
ШарыгинИ.Ф., ШарыгинаТ.Г. Первые шаги в геометрии. М.: Изд-во гимназии «Открытый мир», 1995.
Ященко И. В, Приглашение на математический праздник. М.: МЦНМО, 2005.
Содержание
Введение................................................3
2 класс.....................................................5
Подсчет геометрических фигур............................6
Рисуем картинку, не отрывая карандаш от бумаги.........16
Арифметические ребусы..................................19
Задания с палочками....................................21
Логические задачи......................................24
Задачи на разрезание фигуры на одинаковые части........27
Маршруты...............................................31
Задачи на взвешивание..................................33
3 класс....................................................37
Магический квадрат.....................................38
Задачи на разрезание фигуры на одинаковые части........43
Арифметические ребусы..................................49
Задачи на переливание..................................53
Прямоугольник, составленный из квадратов, и квадрат, составленный из прямоугольников........................55
Сумма трех чисел одна и та же..........................60
4 класс....................................................65
Задачи на площади......................................66
Арифметические ребусы..................................71
Комбинаторика..........................................79
Разрезаем и составляем.................................83
Логические задачи......................................88
Текстовые задачи.......................................92
Задачи для самостоятельного решения.......................105
Ответы и решения..................................... 118
Список литературы.................................... 128
руководителям математических кружков
	Задания для подготовки к олимпиаде
	задачи на подсчет геометрических фигур
	разрезание и составление фигур
	арифметические ребусы и магические квадраты
	задачи на переливание и взвешивание
	площади фигур
	маршруты, комбинаторика, логические задачи и др.
	Подробный разбор типичных задач
	Задачи для самостоятельного решения и ответы к ним