Text
Incl udlng
ixed · t T 0 and
a
Alpha
Science
"-
Qamrul Hasan Ansari
METRIC
SPACES
Including
Fixed Point Theory and
Set-valued Maps
METRIC
SPACES
Incl uding
Fixed Point Theory and
Set-valued Maps
QaInrul Hasan Ansari
a
Alpha Science International Ltd.
Oxford, U.K.
METRIC SPACES
Including Fixed Point Theory and Set-valued Maps
208 pgs.
Qamrul Hasan Anasari
Department of Mathematics
Aligarh Muslim University
,Aligarh
Copyright (g 2010
ALPHA SCIENCE INTERNATIONAL LTD.
7200 The Quorum, Oxford Business Park North
Garsington Road, Oxford OX4 2JZ, U.K.
www.alphasci.com
All rights reserved. No part of this publication may be reproduced, stored
in a retrieval system, or transmitted in any form or by any means, electronic,
mechanical, photocopying, recording or otherwise, without prior written
permission of the publisher.
Printed from the camera-ready copy provided by the Author.
ISBN 978-1-84265-655-6
Printed in India
Dedicated to my wife Shabista Begum
and
our daughters Reem, Warda and Suzan
Preface
This book is based on a course on Metric Spaces that I have been teaching to the
third year B.Sc. (Honours) Mathematics students at the Aligarh Muslim University,
Aligarh, for several years. It is the essence of my lecture notes on the subject as well
as of the several lectures on set-valued maps, Ekeland's variational principle and equi-
librium problems that I have delivered in several workshops and symposia. The course
on metric spaces is the first course leading to the study of functional analysis. It pro-
vides the idea of a distance between any two points on an arbitrary set by generalizing
three basic properties of a distance between two points. These are: (i) the distance be-
tween any two points is always positive, and it vanishes if and only if two points lie
on the same position, (ii) the distance between two points is the same from whichever
point it is measured, and (iii) the distance from one point to another cannot exceed
the sum of the distances from these points to an intermediate point. Numerous books
on metric spaces and topology containing metric spaces are available but in this book,
many definitions and the proof of the results are furnished by providing figures. More
than half of the exercises are supported by the solutions or hints. No existing book
on metric spaces has set-valued maps, Ekeland's variational principle, Caristi's fixed
point theorem, Takahashi's minimization theorem and equilibrium problems. How-
ever, this is the first book in which the equilibrium problem, a unified model of several
problems, namely, optimization problems, saddle point problems, fixed point prob-
lems, complementarity problems, variational inequality problems, Nash equilibrium
problems, etc, is presented in the setting of metric spaces. An elementary treatment
of the set-valued maps is given. The Banach contraction theorem for set-valued maps
(known as Nadler's fixed point theorem), Caristi's fixed point theorem and several
related results for set-valued maps are included. Though the originality of the proofs
is not guaranteed, but the simplicity and clarity of the proofs is definitely ensured.
In Chapter 1, we present the basic definitions, examples and results concerning
metric spaces. The concepts of open spheres, closed spheres and metric subspaces
are also given in this chapter. In Chapter 2, convergence of the sequences, Cauchy
sequences and the completion of metric spaces are discussed. One of the useful re-
sults from functional analysis is Cantor's intersection section theorem which is also
presented in this chapter. Some topological concepts, namely, countability, separa-
bility and Baire's category theorem are given in Chapter 3. Chapter 4 deals with the
concepts of compact spaces, sequentially compact spaces and Bolzano- Weierstrass
property. The equivalence of these three concepts is also discussed. In Chapter 5,
continuity of functions is defined on a metric space to another metric space. Along
with several characterizations of continuity, the image of a compact set under con-
tinuous function is also discussed. The concepts of homeomorphism and equivalent
metrics are included. The uniform convergence of sequences of functions is given.
Vll1
Preface
Chapter 6 deals with the connected metric spaces, components and their properties.
The continuous image of a connected set is also discussed and as a consequence, the
intermediate theorem and a fixed point theorem are derived. Chapter 7 is devoted to
the metric fixed point theory. Banach contraction theorem and several of its gener-
alizations along with their applications are presented. Caristi' s fixed point theorem
and some of its consequences are discussed. An introduction of set-valued analysis,
continuity and fixed point theory of set-valued maps are given in Chapter 8. One of
the most useful and important results from nonlinear analysis is Ekeland's variational
principle. This principle along with several of its equivalent forms and Takahashi's
minimization theorem are given in Chapter 9. Here, an introduction of the theory of
equilibrium problems is presented. The equilibrium version of Ekeland' s variational
principle and several of its equivalent forms are also presented in this last chapter. The
book is intended to be of use to academics and undergraduate students.
I would like to express my profound thanks and gratitude to my friends Prof. S.
AI-Homidan, Saudi Arabia, Prof. M. A. Khamsi, U.S.A. and Prof. J.-C. Yao, Taiwan,
for their kind encouragement at different times during the preparation of this book.
I would also like to express my sincere thanks to my esteemed colleagues Prof. M.
Imdad, Dr. Rais Ahmad, Dr. Shamshad Husain and Dr. S. C. Gupta and our students
Mr. M. Dilshad and Miss Himanshu Gupta for their careful reading of the manuscript.
Also, it is my pleasant duty to thank Mr. N. K. Mehra, Publisher and Managing Direc-
tor, Narosa Publishing House Pvt. Ltd., New Delhi, for taking keen interest in getting
this book published for the benefit of students and workers in the field.
Last, but not the least, I wish to thank my family for their infinite patience, encour-
agement and forbearance. This work would not have seen the light of day had it not
been for their unflinching support during this project. I remain indebted to them.
I welcome any opinions, suggestions, and added information which will improve
the future editions and help readers in future. Benefits for readers will be the best
reward for the author.
Qamrul Hasan Ansari
Notations and Abbreviations
II{
e
N
Z
Q
n
en
+
foo
fP
s
c
B[a, b]
C[a, b]
p(A,B)
5(A)
Sr(x)
Sr[x]
AO
intA
A
cIA
clx A
A C
b(A)
o
(x,y)
-ft
2 x
2 x
2'1
q
the set of all real or complex numbers
the set of all real numbers
the set of all complex numbers
the set of all natural numbers
the set of all integers
the set of all rational numvers
the extended real line
the n-dimensional Euclidean space
the space of ordered n-tuples complex numbers
[0,00)
the space of all bounded sequences of real or complex numbers
the space of all sequences {xn} of real or complex numbers such that
00
L IXnl P < 00 for all p > 1
n=l
the space of all sequences of real or complex numbers
the space of all convergent sequences of real or complex numbers
the space of all bounded real-valued functions defined on [a,b]
the space of all continuous real-valued functions defined on [a, b]
the distance between sets A and B
the diameter of the set A
the open sphere (or open ball) with center on x and radius r
the closed sphere (or closed ball) with center on x and radius r
the interior of the set A
the interior of the set A
the closure of the set A
the closure of the set A
the closure of the set A in X
the complement of the set A
the boundary of the set A
the empty set
the scalar product of x and y
does not converge
the family of all subsets of X
the family of all nonempty closed and bounded subsets of X
the family of all nonempty compact subsets of X
x
Notations and Abbreviations
graph (f) the graph of a single-valued map f
dom(f) the domain of a single-valued map f
Graph(F) the graph of a set-valued map F
Im(F) the image of of a set-valued map F
'Dom(F) the domain of a set-valued map F
Acronyms
EP Equilibrium Problem
EPs Equilibrium Problems
EVP Ekeland's Variational Principle
COP Constrained Optimization Problem
OP Optimization Problem
MP Minimization Problem
SPP Saddle Point Problem
NEP Nash Equilibrium Problem
FPP Fixed Point problem
VIP Variational Inequality Problem
Contents
Preface . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. VII
Notations and Abbreviations ........................................ IX
1 Basic Concepts. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
1.1 Definition and Examples of Metric Spaces. . . . . . . . . . . . . . . . . . . . . . . 1
1.2 Distance between Sets and Diameter of a Set. . . . . . . . . . . . . . . . . . .. 13
1.3 Open Sets and Interior Points. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 15
1.4 Closed Sets and Closure of Sets ............................... 23
1.5 Subspaces . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 29
2 Complete Metric Spaces ......................................... 33
2.1 Convergent Sequences ....................................... 33
2.2 Cauchy Sequences. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 37
2.3 Complete Metric Spaces. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 42
2.4 Completion................................................ 53
3 Separable Spaces. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 55
3.1 Countability................................................ 55
3.2 Dense Sets . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 57
3.3 Nowhere Dense Sets . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 63
4 Compact Spaces ................................................ 67
4.1 Definitions and Basic Concepts. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 67
4.2 Sequentially Compact Spaces ................................. 74
4.3 Totally Bounded Spaces . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 77
5 Continuous Functions ........................................... 87
5.1 Definition and Characterizations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 87
5.2 Continuous Functions and Compact Spaces. . . . . . . . . . . . . . . . . . . . .. 93
5.3 Uniform Continuous Functions. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 94
5.4 Homeomorphism and Equivalent Metrics ....................... 97
5.5 Uniform Convergence of Sequences of Functions. . . . . . . . . . . . . . . .. 103
6 Connected Spaces . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 109
6.1 Separated Sets . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 109
6.2 Connected Sets ............................................. 111
6.3 Continuous Functions and Connected Sets. . . . . . . . . . . . . . . . . . . . . .. 116
6.4 Components................................................ 118
XlI Contents
7 Fixed Point Theorems ........................................... 121
7.1 Banach Contraction Theorem and its Applications. . . . . . . . . . . . . . .. 121
7.1.1 Application to System of Linear Equations . . . . . . . . . . . . . . .. 127
7.1.2 Application to Differential Equations. . . . . . . . . . . . . . . . . . . .. 129
7.1.3 Application to Integral Equations. . . . . . . . . . . . . . . . . . . . . . .. 131
7.2 Further Extension of Banach Contraction Theorem ............... 132
7.3 Caristi' s Fixed Point Theorem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 136
8 Set-Valued Maps . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 139
8.1 Basic Concepts and Definitions. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 140
8.2 Continuity of Set-Valued Maps . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 145
8.3 Nadler's Fixed Point Theorem. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 152
8.4 Some Fixed Point Theorems for Set-Valued Maps ................ 159
9 Ekeland's Variational Principle and its Applications . . . . . . . . . . . . . . .. 161
9.1 Ekeland Variational's Principle in Complete Metric Spaces. . . . . . . .. 161
9.2 Applications to Fixed Point Theorems . . . . . . . . . . . . . . . . . . . . . . . . .. 168
9.3 Applications to Optimization . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 171
9.4 Equilibrium Problems and Extended Ekeland's Variational Principle. 174
9.4.1 EquilibriumProblems................................. 174
9.4.2 Extended Ekeland's Variational Principle . . ". . . . . . . . . . . . .. 175
A Some Basic Inequalities . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 183
B Partial Ordering . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 187
C Nested Interval Property. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 189
References . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. 192
Index .............................................................. 195
Chapter 1
Basic Concepts
In our daily life, we observe that the distance between any two points should always
be positive, it vanishes if and only if two points lie on the same position, the distance
between two points is the same from whichever point it is measured, and the distance
from one point to another cannot exceed sum of the distances from these points to
an intermediate point. By exploiting these fundamental properties of a distance, we
define the distance between two elements of a nonempty set.
1.1 Definition and Examples of Metric Spaces
Definition 1.1. Let X be a nonempty set. A real-valued function d defined on X x X
is said to be a metric on X if it satisfies the following conditions:
(Ml) d(x,y) > 0 for all x,y EX;
(M2) d(x,y) = 0 if and only if x = y;
(M3) d(x,y) = d(y,x) for allx,y EX; (symmetry)
(M4) d(x,y) < d(x,z) + d(z,y) for all x,y,z EX. (triangle inequality)
The set X together with a given metric d on X is called a metric space and it is
denoted by (X, d). If there is no confusion likely to occur we, sometimes, denote the
metric space (X,d) by X.
Since d is the generalization of the distance function, we interpret d (x,y) as the
distance between two elements x and y of the set X. Sometimes d is called a distance
function onX.
The triangle inequality may be interpreted as that "the length of one side of a
triangle can not exceed the sum of the length of the other two sides". Equivalently,
the distance from x to y via any intermediate point z can not be shorter than the direct
distance from x to y.
z
y
x
d(x,y)
2
1 Basic Concepts
The metric d has the following properties:
1. From the triangle inequality (M4), it follows by induction that for any X,y,Zl ,Zz,. . .,
Zn EX,
d(x,y) < d(X,Zl) +d(Zl,Y)
< d(X,Zl) +d(Zl,ZZ) +d(zz,y)
< d(X,Zl) +d(Zl,ZZ) +d(ZZ,Z3) +d(Z3,y)
< d(X,Zl) +d(Zl,ZZ) +... +d(zn,Y).
2. For any x,y,z E X, we have
Id(x,z) - d(y,z) I < d(x,y).
Indeed, it follows from (M3) and (M4) that
d(x,z) < d(x,y) +d(y,z)
and
d(y,z) < d(y,x) +d(x,z) = d(x,y) + d(x,z).
Thus
-d(x,y) < d(x,z) - d(y,z) < d(x,y),
and therefore,
Id(x,z) - d(y,z) I < d(x,y).
Examples of Metric Spaces
Example 1.1. Let X = , the set of all real numbers. For any x,y E X, define
d(x,y) == Ix - yl.
Then (X, d) is a metric space and the metric d is called the usual metric on IR.
Verification. For all x,y,z E X, we have
(M1) d(x,y) > 0;
(M2) d(x,y) == Ix - yl == 0 if and only if x == y;
(M3) d(x,y) == Ix - yl = 1- (x - y)1 = Iy -xl = d(y,x);
(M4) d(x,y) == Ix- yl == I(x-z) + (z- y)1
< Ix-zl+lz-yl
= d(x,z) + d(z,y).
In the verification of (M4) in Example 1.1, we used the fact that la + bl < lal + Ibl for
real numbers a and b. This property is also true for complex numbers a and b. Hence,
we have the following example.
1.1 Definition and Examples of Metric Spaces
3
Example 1.2. Let X = C, the set of all complex numbers. For any x,y EX, define
d(x,y) = Ix-yl.
Then (X, d) is a metric space and the metric d is called the usual metric on C.
Example 1.3. Let X be any nonempty set. For any x,y EX, define
{ 0 if x = y
d (x,y) = 1 if x -I- y.
Then (X, d) is a metric space. The metric d is called discrete metric and the space
(X, d) is called discrete metric space.
Remark 1.1. Example 1.3 shows that on each nonempty set, we can always define at
least one metric that is discrete metric.
Example 1.4. Let X = z, the set of all points in the coordinate plane. For any x =
(Xl ,xz), Y = (Yl,YZ) in X, define
d (x,y) = V (XI - Yl)2 + (X2 - Y2)2.
Then (X,d) is a metric space and d (x,y) is the natural distance between two points in
a plane. d is known as the usual metric on z.
(Xl,XZ)
Xz - Yz
(k
./ .,.k .
<;)
Xl - Yl
Verification. For any x = (Xl,XZ)' Y = (Yl,YZ) and z = (Zl,ZZ) in X. Obviously,
d(x,y) > 0 and so (M1) holds.
(M2)
{:}
{:}
V (XI - Yl)2 + (X2 - Y2)2 = 0
\ Z Z
(Xl - l) = 0 and (xz - yz) = 0
Xl =)'1 and Xz = Yz
d(x,y) = 0
{:}
{:} X = y.
4
1 Basic Concepts
(M3)
d(x,y) = V(XI - Yl)Z + (XZ - YZ)Z
= V (Yl -Xl)Z + (yZ -XZ)Z
= d (y,x) .
(M4)
[d(x,y)]Z = (Xl - YI)Z + (XZ - YZ)Z
= [(Xl - Zl) + (Zl - YI)]Z + [(XZ - ZZ) + (ZZ - YZ)]Z
= (Xl - ZI)Z + (Zl - YI)Z
+2 [ l zy ( )+( )( ) ]
a b c d
+ (XZ - ZZ)Z + (ZZ_YZ)Z
Taking Xl - Zl = a, Zl - YI = b, Xz - Zz = c and Zz - Yz = d, and since
(ab + cd)z < (a z + cZ)(b z + d Z ),
we have
[d (x,y)]z < (Xl - Zl)z + (xz - zz)z
+2 V (XI-Zl)Z+(XZ-zZ)Z V (Zl-Yl)2+(ZZ-YZ)Z
+(Zl - YI)Z + (zz - YZ)z
= [d (x,z)]z + 2d (x,z) d (z,y) + [d (z,y)]z
= [d(x,z)+d(z,y)]z.
Therefore,
d (x,y) < d (x,z) + d (z,y).
Example 1.5. Let X = z. For any X = (XI'XZ)'Y = (YI,YZ) in X, define
d (x,y) = IXI - YII + Ixz - yzi.
Then d is a metric on X and (X, d) is a metric space.
Verification. The conditions (Ml), (M2) and (M3) are obvious. We prove only
condition (M4). For any X = (xt,xz), Y = (YI,YZ) and z = (ZI,ZZ) in X,
d(x,y) = IXI-YII+lxz-yzl
< IXI -zll + IZI - YII + Ixz -zzi + Izz - Yzi
= d(x,z) + d(z,y).
1.1 Definition and Examples of Metric Spaces
5
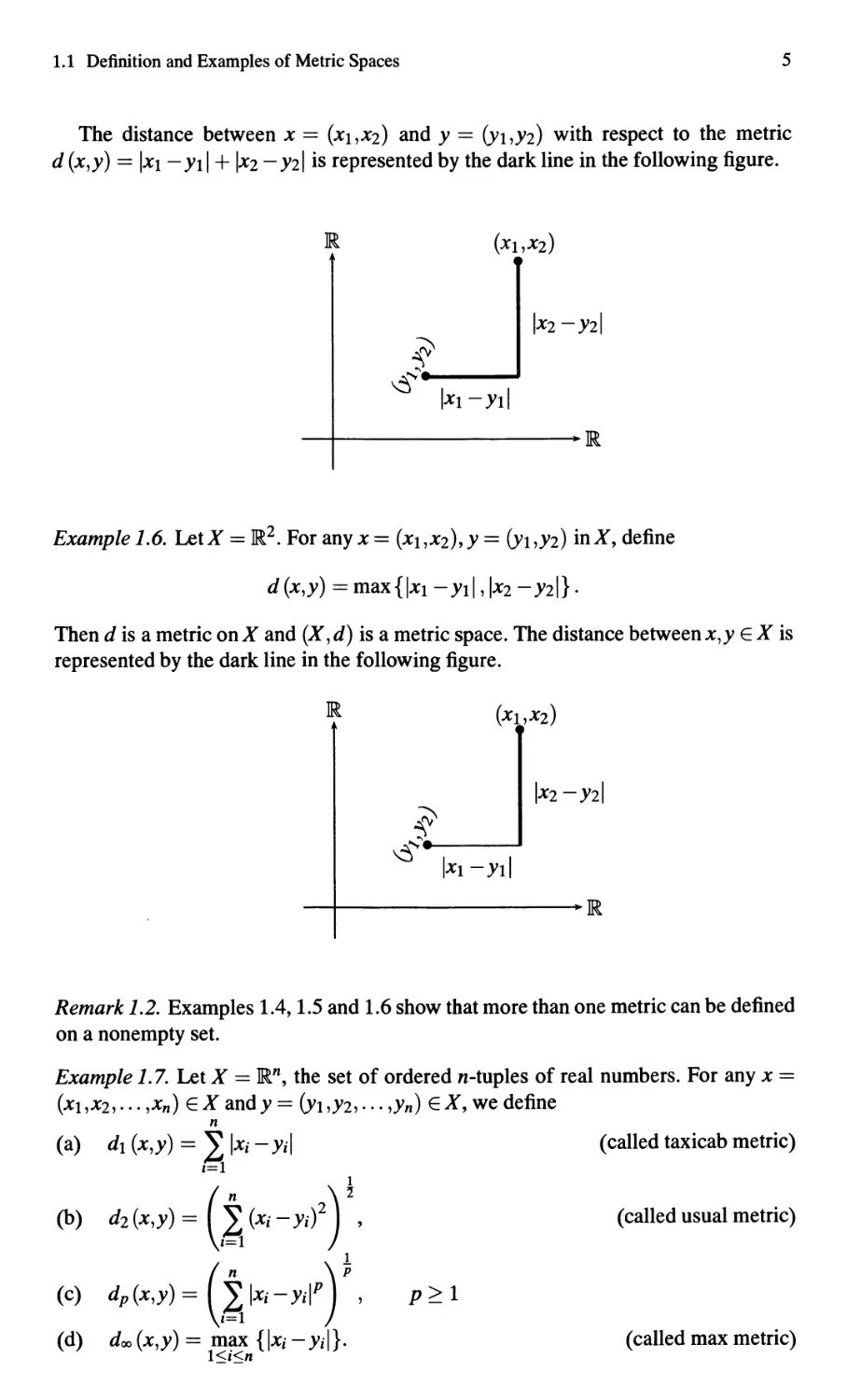
The distance between x = (Xl,XZ) and Y = (Yl,YZ) with respect to the metric
d (x,y) = IXI - Yll + Ixz - yzi is represented by the dark line in the following figure.
(Xl,XZ)
Ixz - yzi
,
"-t
IXI - Yll
Example 1.6. Let X = z. For any x= (Xl,XZ)'Y = (Yl,YZ) in X, define
d (x,y) = max{lxl - Yll, Ixz - Yzl}.
Then d is a metric on X and (X, d) is a metric space. The distance between X,Y E X is
represented by the dark line in the following figure.
(Xl,XZ)
Ixz - Yzi
,
"-t
IXI - Yll
Remark 1.2. Examples 1.4, 1.5 and 1.6 show that more than one metric can be defined
on a nonempty set.
Example 1.7. Let X = n, the set of ordered n-tuples of real numbers. For any X =
(Xl ,Xz,. . . ,x n ) E X and Y = (Yl ,Yz,. . . ,Yn) E X, we define
n
(a) d l (x,y) = IXi - Yil (called taxicab metric)
1=1
1
(b) d2 (x,y) = ( (Xi - Yi)2) 2, (called usual metric)
1
(c) dp(X,Y)=( IXi-YiIP)P, p > l
(d) d oo (x,y) = m x {Ixi - Yil}. (called max metric)
1 l n
6
1 Basic Concepts
Verification. In view of Examples 1.4, 1.5 and 1.6, it is easy to verify that d 1 , d p
and d oo are metrics on X.
The triangular inequality (M4) in the case of d p requires the use of Minkowski
inequality (Theorem A.3)
1 1
dp(X,y) = ( iIXi-YiIP ) P = ( iIXi-Zi+Zi+YiIP ) P
1=1 1=1
1
< ( IXi -zil + IZi - YiIP) P
1 1
< ( IXi -ZiIP) P + ( IZi - YiIP) P
= dp(x,z) + dp(z,y).
Remark 1.3. Let X = cn, the set of ordered n-tuples of complex numbers. We can
define the metrics d 1 , d p and doo on X in the same way as in Example 1.7.
Example 1.8. Let Roo be the space of all bounded sequences of real or complex num-
bers, that is,
ROO = { {xn} C 1R or C: sup IXnl < oo } .
1 n<00
For any x = {xn} E Roo and y = {Yn} E Roo, define
doo (x,y) = sup IXn - Ynl.
1 n<00
Then it is easy to verify that doo is a metric on Roo and (ROO, doo) is a metric space.
Example 1.9. Let s be the space of all sequences of real or complex numbers, that is,
s = {{xn} C or C}.
For any x = {xn} and Y = {Yn} in s, define
d ( ) - IXn - Yn I
X,Y - .LJ I I .
n=12n 1 + X n - Yn
Then (s, d) is a metric space.
Verification. The series 'X i - Ynl I is convergent since its nth term is less
n l 2 n 1 + X n - Yn
than In . The conditions (Ml), (M2) and (M3) can be easily verified.
Let x = {x n }, Y = {Yn} and z = {zn} be in s. Then by the triangular inequality, we
have '
IXn - Ynl < IXn -znl + IZn - Ynl
1.1 Definition and Examples of Metric Spaces
7
and hence 1
IXn - Ynl < IXn - Znl + IZn - Ynl
l+l x n-Ynl - l+lx n -z n l+l z n-Ynl
Ixn-znl IZn-Ynl
+
1 + IXn -Znl + IZn - Ynl 1 + IXn -znl + IZn - Ynl
< IXn - znl IZn - Ynl
l+lx n -z n l + l+l z n-Ynl.
Multiplying both sides by 2 and summing with respect to n, we obtain
d (x,y) < d (x,z) + d (z,y).
Example 1.10. Let 1 < P < 00. Consider the space f,P of all sequences {xn} of real or
00
complex numbers such that IXnlP < 00. Let x = {Xn} and Y = {Yn} E f,P, we define
n=l
1
d (x,y) = C llxn - Ynlp) P .
Then d is a metric on f,P and (f,P, d) is a metric space.
Verification. The conditions (Ml), (M2) and (M3) can be easily verified. Let x =
{x n }, Y = {Yn} and Z = {zn} be sequences in f,p. Then
1
d (x,y) = ( f IXn - Ynl p ) P
1
1
= ( f I xn-zn+zn-YnIP ) P
n=l
1 1
< C l1Xn -znl p ) P + C l1Zn - Ynl p ) P
(by Minkowski's inequality)
= d(x,z) + d(z,y).
Example 1.11. Let B[a, b] be the space of all bounded real-valued functions defined on
[a, b], that is, B[a, b] = {f : [a, b] -+ : f(t) < k for all t E [a, b]}. For f,g E B[a, b],
we define
1 Let 0 :s; a :s; f3. Then a + a f3 :s; f3 + a f3. Dividing both sides by (1 + a) (1 + f3 ), we have
a f3
-<-.
l+a - 1+13
8
1 Basic Concepts
d (I, g) = sup I/(t) - g(t)l.
tE [a,b]
Then (B[a, b], d) is a metric space.
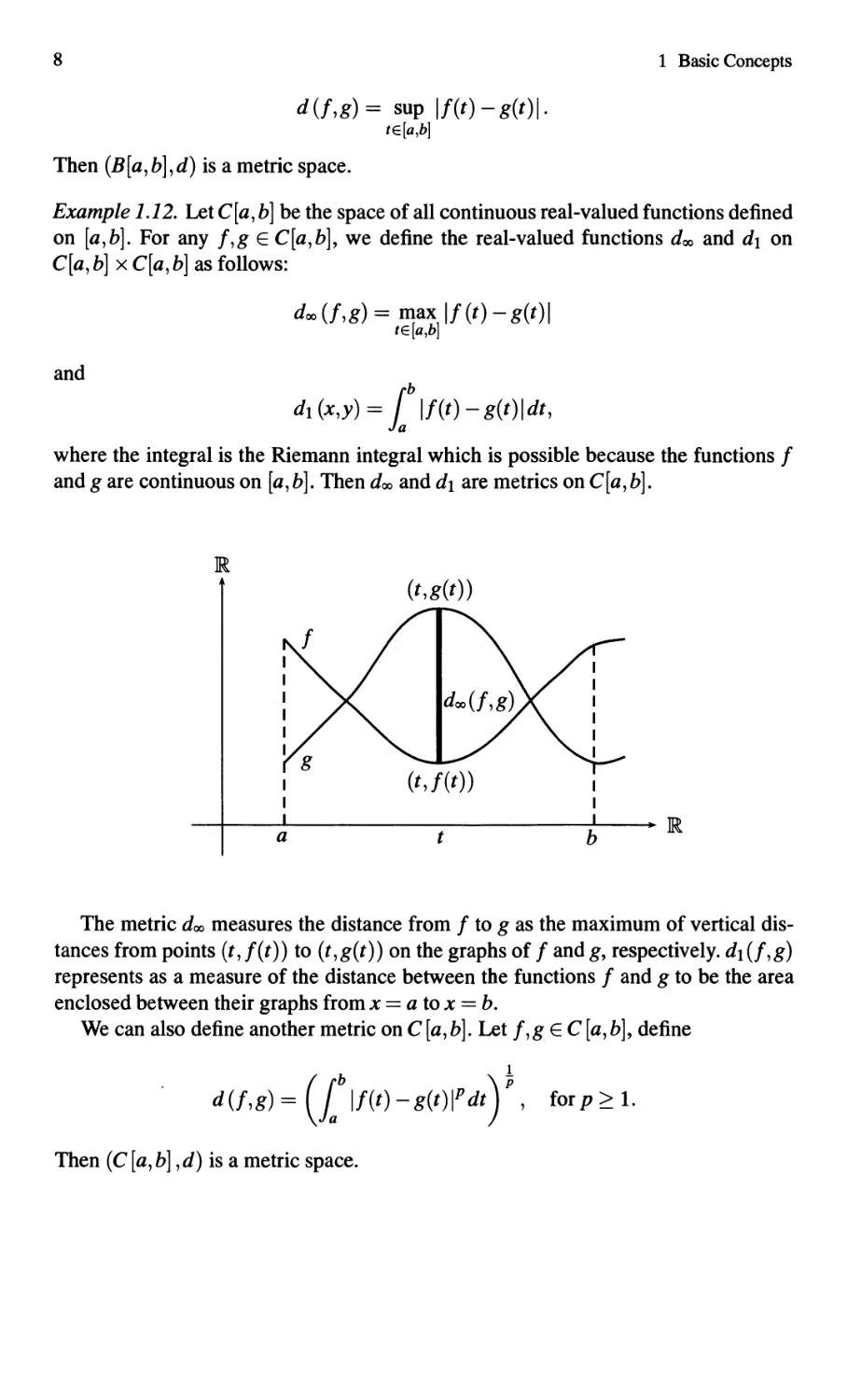
Example 1.12. Let C [a, b] be the space of all continuous real-valued functions defined
on [a,b]. For any I,g E C[a,b], we define the real-valued functions d oo and d 1 on
C[a, b] x C[a, b] as follows:
d oo (/,g) = max II (t) - g(t)1
tE [a,b]
and
dl (x,y) = l b I!(t) - g(t)ldt,
where the integral is the Riemann integral which is possible because the functions I
and g are continuous on [a, b]. Then doo and dl are metrics on C[a, b].
(t,g(t))
a
t
b
The metric doo measures the distance from I to g as the maximum of vertical dis-
tances from points (t, I(t)) to (t,g(t)) on the graphs of I and g, respectively. d 1 (/,g)
represents as a measure of the distance between the functions I and g to be the area
enclosed between their graphs from x = a to x = b.
We can also define another metric on C [a, b]. Let I, g E C [a, b], define
( b ) !
d (f,g) = 1 1 !(t) - g(t) I P dt P, for p > 1.
Then (C [a, b] , d) is a metric space.
1.1 Definition and Examples of Metric Spaces
9
1R
dl (f,g)
a
b
1R
Remark 1.4. Let X be the set of all Riemann integrable functions on [a,b]. For f,g E
X, we define
d(f,g) = l b If(x) - g(x)ldx.
.
Then d is not a metric on X. Indeed, if
f(x) = {
ifx=a
ifa<x < b
and g(x) = 1 for all x E [a,b], then d(f,g) = O. However, f =1= g. It may be noted
that all other properties of a metric do hold. Such real-valued functions are called
pseudometrics on X.
Definition 1.2. Let X be a nonempty set. A real-valued function d : X x X IR+ is
said to be a pseudometric on X if it satisfies the following conditions:
(PM1) d(x,y) > 0 for all x,y EX;
(PM2) d(x,y)=Oifx=y;
(PM3) d(x,y)=d(y,x)forallx,yEX;
(PM4) d(x,y) < d(x,z) + d(z,y) for all x,y,z EX.
(symmetry)
(triangle inequality)
The set X together with a given pseudometric d on X is called a pseudometric space.
Example 1.13. Let X = 2, x = (XI,X2), y = (YI,Y2) E X and d(x,y) = IXI - YII. Then
d is not a metric on X, however, it is a pseudometric on X. Indeed, for x = (0,0),
y = (0,1) EX, we have d(x,y) = 0 but x =1= y. Therefore, it is not a metric onX. It can
be easily checked that d satisfies the conditions (PM1) - (PM4).
Exercise 1.1. Let (X,d) be a metric space. If x,y,z, wE X, then prove that
Id(x,y) - d(z, w)1 < d(x,z) +d(y, w).
Proof. Since
Id(x,z) - d(z,y) I < d(x,y),
we have
10
1 Basic Concepts
Id(x,y) - d(y,z) I < d(x,z)
and
Id(y,z) - d(z, w) I < d(y, w).
Hence
Id(x,y) - d(z, w) I < Id(x,y) - d(y,z) I + Id(y,z) - d(z, w)1 < d(x,z) + d(y, w).
Exercise 1.2. Let X be a nonempty set and d : X x X -+ be a real-valued function
such that the following conditions hold: For all x,y, z EX,
(i) d(x,y) = 0 if and only if x = y;
(ii) d(x,y) = d(y,x) for all x,y EX;
(iii) d(x,y) < d(x,z) + d(z,y) for all x,y,z EX.
Prove that d is a metric on X.
Hint: Put y = x in (iii), we get 0 = d(x,x) < d(x,z) + d(z,x). By (ii), 0 < 2d(x,z) and
so d(x,z) > 0 for all X,z EX.
Exercise 1.3. Let X be a nonempty set and d : X x X -+ be a real-valued function
such that the following conditions hold: For all x,y,z EX,
(i) d(x,y) = 0 if and only if x = y;
(ii) d(x,y) < d(z,x) + d(z,y) for all x,y,z EX.
Prove that d is a metric on X.
Exercise 1.4. Let X be a nonempty set and d : X x X -+ be a real-valued function
such that the following conditions hold: For all x,y,z EX,
(i) d(x,y) = 0 if and only if x = y;
(ii) d(x,y) < d(x,z) + d(z,y) for all x,y,z EX.
Show that these conditions are not sufficient to make the function d a metric on the
set X.
Exercise 1.5. Let X = 2 and x = (0,2), y = (3,6) in X. Find the distance between x
and y by using the metrics of Examples 1.4, 1.5 and 1.6.
Exercise 1.6. Let c be the space of all convergent sequences of real or complex num-
bers. For x = {x n } and y = {Yn} in c, let
d (x,y) = sup IX n - Ynl.
1 ::S;n<oo
Prove that d is a metric on c.
Exercise 1.7. Let JK be the set of all real or complex numbers. Prove that for each
x,y E OC,
dl(X,y) = min{1, Ix-yl}
and
d(x,y) = { I + Iyl
if x = y
if x =1= y
are metrics on JK.
1.1 Definition and Examples of Metric Spaces
11
Exercise 1.8. Let X = [0,1). For eachx,y E X, let
d(x,y) = Ix- yl.
Prove that d is a metric onX.
Exercise 1.9. Let X = Q, the set of all rational numbers. Show that for each x,y EX,
d(x,y) = Ix-yl
is a metric on X.
Exercise 1.10. Let X = {x E IR. : x > O} and d(x,y) = I - I for all x,y EX. Show
that d is a metric on X.
Exercise 1. 11. Let X = and d : X x X -+ be a real-valued function defined by
d(x,y) = v lx - yl for all x,y EX. Show that d is metric on X.
Hint: For any x,y,z E X, we have
[d(x,y)]Z = Ix-yl < Ix-zl+lz-yl
= [d(x,z)]z + [d(z,y)]z
< [d(x,z)+d(z,y)]z.
Exercise 1.12. Let X = Q, the set of all rational numbers, for all , E Q written in
their lowest terms, q,s > 0, and d ( , ) = I - i I. Is d a metric on X?
Hint: Consider j, E Q in their lowest terms. Then d (j, ) = I j - j I = 0 but j =1= .
Exercise 1.13. Show that X = IR. \ Q with d(x,y) = I - 1 is a metric space.
Exercise 1.14. Show that C with
d( ) { min{lzll+lzzl,lzl-11+lzz-11}
Zl,ZZ = 0
if Zl =1= Zz
otherwise
is a metric space.
Exercise 1.15. Determine whether the following real-valued functions defined on x
are metrics on . For all (x,y) E x ,
(a) d 1 (x,y) = [Ix - yl], the greatest integer less than or equal to Ix - yl;
(b) dz(x,y) = In Ix - yl;
(c) d3(X,y) = I sin (x - y)l;
(d) d4 (x,y) = e 1x - Y1 ;
(e) ds(x,y) = I cos(x - y)l;
(f) d6(X,y) = 1x2 - yZI;
(g) d 7 (x,y) = 21x - yl;
(h) dg(x,y) = (x - y)3;
(i) d9(X,y) = Ix - y13.
12
1 Basic Concepts
Exercise 1.16. Let X = and d : X x X -+ be a real-valued function defined by
d(x,y) = { I + Ix-yl + Iyl
if x # Y,
otherwise.
Show that (X, d) is a metric space.
Exercise 1.17. Let X = 2 and for each X = (XI,X2),Y = (YI,Y2) E X, let
d (x ) - { IXI - YII
,Y - IXII + IYll + I X 2-Y21
if X2 = Y2
if X2 #Y2.
Then prove that (X, d) is a metric space.
Exercise 1.18. Let X = 2 and d : X x X -+ be a real-valued function defined by
{ IXI - YII
d(x,y) = d((Xl,X2), (yl,Y2)) = IXII + I X 2 - Y21 + IYII
if X2 = Y2
otherwise.
Show that (X, d) is a metric space.
Hint: Let x = (Xl ,X2), Y = (YI,Y2) and Z = (ZI,Z2) be in X. Observe that d(x,y) >
IXI - YII. If X2 = Y2, then d(x,y) = IXI - Yll < IXI - zll + IZI - YII < d(x,z) + d(z,y).
If X2 # Y2, then Z2 cannot be equal to both X2 and Y2; so assume that Z2 # X2. Then
d(x,y) = IXII + I X 2 -Y21 + IYII < IXII + I X 2 -z21 + I Z 2 -Y21 + IYII
< { (IXII + I X 2 - z21 + IZII) + IZI - YII f Y2 = Z2,
- (lxII + I X 2 - z21 + IZII) + (IZII + I Z 2 - Y21 + IYII) If Y2 # z2
= d(x,z) + d(z,y).
Exercise 1.19. LetX = 2 and for all X = (Xl ,X2),Y = (Yt,Y2) EX, d(x,y) = min{ IXI -
YII, I X 2 - Y21}. Is d a metric onX?
Hint: Choose X = (2,3), Y = (2,4). Then x # Y, but d(x,y) = min{O, 1} = O. Hence d
is not a metric on X.
Exercise 1.20. Show that X = 2 with d(x,y) = d((XI,YI), (X2,Y2)) = IX2 - Y21 is not
a metric space.
Exercise 1.21. Let X = C[O, 1] and doo : X x X -+ be a real-valued function defined
by doo(f,g) = sup If(t) - g(t)1 for all f,g E C[O, 1]. Then calculate the distance be-
tE[O,I]
tween f(t) = t and g(t) = t 2 .
1
Hint: f(t)-g(t)=t-t2=_(!-t)2+ andso sup If(t)-g(t)l= 4 '
tE[O,I]
Exercise 1.22. Let d l and d 2 be metrics on a set X. Is min{ dl, d2} also a metric on
X? Justify your answer.
Exercise 1.23. Let (Xi,di), i = 1,2,... ,n, be metric spaces and X =XI XX2 x ... xXn.
Then prove that for each x = (Xl ,X2,..' ,x n ) E X and Y = (YI ,Y2,... ,Yn) EX,
1.2 Distance between Sets and Diameter of a Set
13
d1 (X,y) = m x di(Xi,Yi)
1 l n
and
n
d2(X,y) = di(Xi,Yi)
1=1
are metrics on X.
Exercise 1.24. Let (X, d) be a metric space. Prove that for each X,Y EX,
d* (x,y) = d(x,y)
1 + d(x,y)
is also a metric on X.
a b a+b
Hint: Use 1 + b > 1 b for all a > 0, b > O.
+a 1+ - +a+
1.2 Distance between Sets and Diameter of a Set
Definition 1.3. Let (X, d) be a metric space and let A and B be nonempty subsets of
X. The distance between the sets A and B, denoted by p (A, B), is given by
P (A,B) = inf {d(x,y) : x E A,y E B}.
Since d(x,y) = d(y,x), we have p (A,B) = P (B,A).
If A consists of a single point x, then
p ({x} ,B) = inf{d(x,y) : y E B}.
It is called the distance of a point x E X from the set B, and is denoted by p (x,B).
Remark 1.5. (i) The equation p (x, B) = 0 does not imply that x belongs to B.
(ii) If P (A, B) = 0, then it does not imply that A and B have common points.
Example 1.14. Let A = {x E : x> O} and B = {x E : x < O} be subsets of with
the usual metric. Then p (A, B) = 0, but A and B have no common point. If x = 0 then
p (x, B) = 0, but x tj B.
Definition 1.4. Let (X, d) be a metric space and A be a nonempty subset of X. The
diameter of A, denoted by fJ (A), is given by
fJ (A) = sup {d(x,y) :x,y EA}.
The set A is called bounded if fJ (A) < k < 00. In other words, A is bounded if its
diameter is finite, otherwise it is called unbounded.
In particular, the metric space (X, d) is bounded if the set X is bounded.
Example 1.15. (a) The real line with the usual metric is an unbounded metric space.
(b) In with the usual metric, the intervals [a, b], (a, b), [a, b) and (a, b] are bounded.
But [a, (0) and (-00, a] are not bounded.
14 .
1 Basic Concepts
(c) The space s of all sequences of real or complex numbers with the metric defined
in Example 1.9 is a bounded space since d(x,y) < f ;n .
n=l
(d) Every set in a discrete metric space (X, d) is bounded and its diameter is 1.
Example 1.16. Consider the set S = {(x,y) E x : 0 < x < 1, 0 < y < I} in z.
With the usual metric d, the diameter of S is J2; with the taxicab metric, its diameter
is 2; with the max metric, its diameter is 1; and with the discrete metric its diameter
is 1.
1
/
/
/
J2//
/
/
/
/
,/
1
Remark 1.6. Let (X, d) be a metric space. We can define other metrics on X with the
help of the metric d in the following manner:
d (x,y)
d1(x,y) = l+d(x,y) and d2(x,y)=min{1,d(x,y)}.
Then d 1 and d z are metrics on X and with these metrics (X,d 1 ) and (X,dz) are
bounded metric spaces irrespective of whether the metric space (X, d) is bounded
or not.
Exercise 1.25. Determine the distance from (3,4) to the set [0,1] x [0,1] in }Rz with
respect to the metrics ( a) usual, (b) taxicab, (c) max, and (d) discrete.
Exercise 1.26. Let A = {x= (Xl,XZ,X3) E 3 :xI+ + < I} be a set in 3. Com-
pute the diameter of A with respect to each of the following metrics: ( a) usual, (b)
taxicab, (c) max, and (d) discrete.
Exercise 1.27. Let A = {x= (Xl,XZ) E z :xI+ < I} andx= (1,1). Find the
distance from x to A for the metrics ( a) usual, (b) taxicab, (c) max, and (d) discrete.
Exercise 1.28. Let A and B be nonempty subsets of a metric space (X, d). Prove that
( a) () (A) = 0 if and only if A is a singleton set;
(b) For each x E A, Y E B, P (A, B) < d (x,y);
(c) If A C B, then () (A) < () (B);
(d) For each x E A, Y E B, d (x,y) < () (A UB);
(e) () (A UB) < () (A) + P (A, B) + {)(B);
(f) If A nB =1= 0, then () (A UB) < () (A) + ()(B);
(g) d(x,A) < d(x,y) +d(y,A) for allx,y EX.
1.3 Open Sets and Interior Points
15
Proof ((e) and (1)). Let a and b be arbitrary elements of A and B, respectively, and
let x,y E A UB. If both x and yare in A, then d(x,y) < 6(A). If both x and yare in B,
then d(x,y) < 6(B).
If x E A and y E B, then by the triangle inequality, we have
d(x,y) < d(x,a)+d(a,y)
< d(x,a) +d(a,b) +d(b,y)
< 6 (A) + d(a,b) + 6(B).
Similarly, if x E Band yEA, we have
d(x,y) < 6(A) +d(a,b) + 6(B).
Thus,
d(x,y) < 6(A) + d(a, b) + 6 (B) for all x,y E A UB.
Therefore,
6(AUB) < 6(A)+d(a,b)+6(B) forallaEA, bEB.
Hence,
6(A UB) < 6(A) + p(A,B) + 6(B).
Now, if A nB =1= 0, we have p(A,B) = 0 and hence 6(A UB) < 6(A) + 6(B).
1.3 Open Sets and Interior Points
Definition 1.5. Let (X, d) be a metric space. Given a point Xo E X and a real number
r > 0, the sets
Sr (xo) = {y EX: d (XO,y) < r}
and
Sr[XO] = {y EX: d (XO,y) < r}
are called open sphere (or open ball) and closed sphere (or closed ball), respectively,
with center x and radius r.
Remark 1.7. (i) The open and closed spheres are always nonempty, since Xo E
Sr (xo) C Sr [xo].
(ii) Every open (respectively, closed) sphere in with the usual metric is an open
(respectively, closed) interval. But the converse is not true; For example, (-00,00)
is an open interval in but not an open sphere.
Example 1.17. ( a) In the metric space with the usual metric, the spheres S r (xo) and
Sr [xo] are intervals
(xo - r,xo + r) and [xo - r,xo + r] ,
respectively.
16
1 Basic Concepts
(b) In the metric space C with the usual metric, the sphere Sr (zo) and Sr [zo] are
circular discs
Iz-zol < rand Iz-zol < r,
respectively, where Zo E C and r > O.
(c) Let X be a nonempty set with the discrete metric d. Then the open sphere Sr (xo)
IS
Sr (XO) = { lxo}
and the closed sphere S r [xo] is
Sr [xo] = { lxo}
if 0 < r < 1,
if r > 1,
if 0 < r < 1,
if r > 1.
(d) Let X = [0,1) be a metric space with the usual metric d (x,y) = Ix - yl for all
x,y EX. Then the open sphere Sr (0) is
S ( 0 ) = { [O,r)
r [0,1)
and the closed sphere Sr [0] is
S [ 0 ] = { [O,r)
r [0,1)
if r < 1,
if r > 1,
if r < 1,
if r > 1.
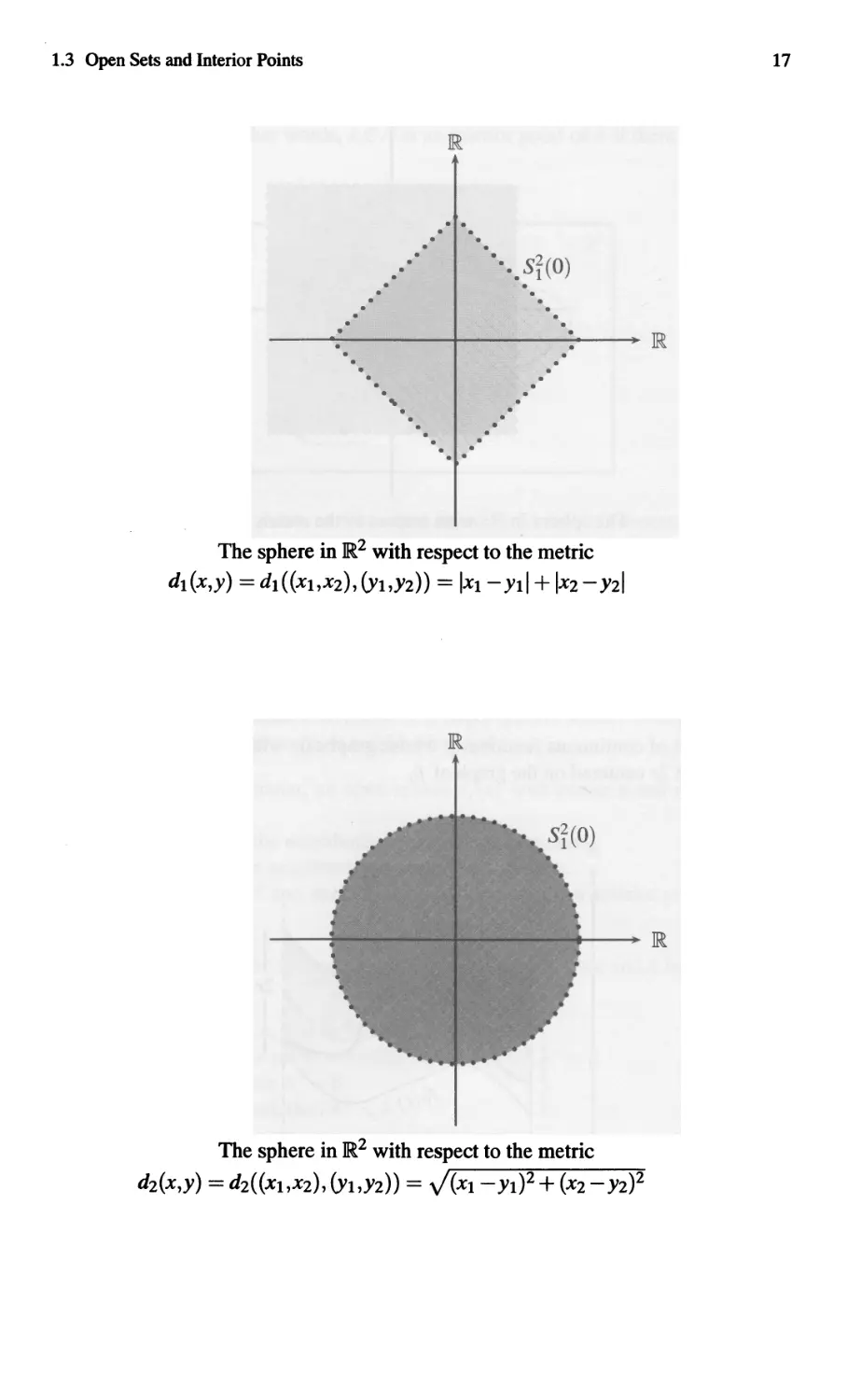
(e) In z, the open sphere with center 0 and radius 1 with respect to the metrics d 1 ,
d z and doo, respectively, (in Example 1.7), are
st (0) = {y = (yt,Yz) E z : IYl l + IYzl < 1 } ,
Si(O) = {Y = (Yt,Yz) E R Z : JY i+ < 1 },
and
Sr (0) = {y E (Yl,YZ) E z: max(IYtl, Iyzl) < I}.
Similarly, we can define the closed spheres.
1.3 Open Sets and Interior Points
IR
. .
. .
. .
. .
.
.
.
.
.
.
.
.
.
.
.
.... si(O)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
. .
,
.
.
.
.
.
The sphere in }R2 with respect to the metric
d l (x,y) = dl ((XI,X2), (YI,Y2)) = IXI - YII + I X 2 - Y21
.
si (0)
.
.
.
.
.
.
.
.
The sphere in }R2 with res pect to the metric
d2(X,y) = d2((XI,X2), (YI,Y2)) = V (XI - YI)2 + (X2 - Y2)2
17
IR
18
1 Basic Concepts
1R
sr (0)
1R
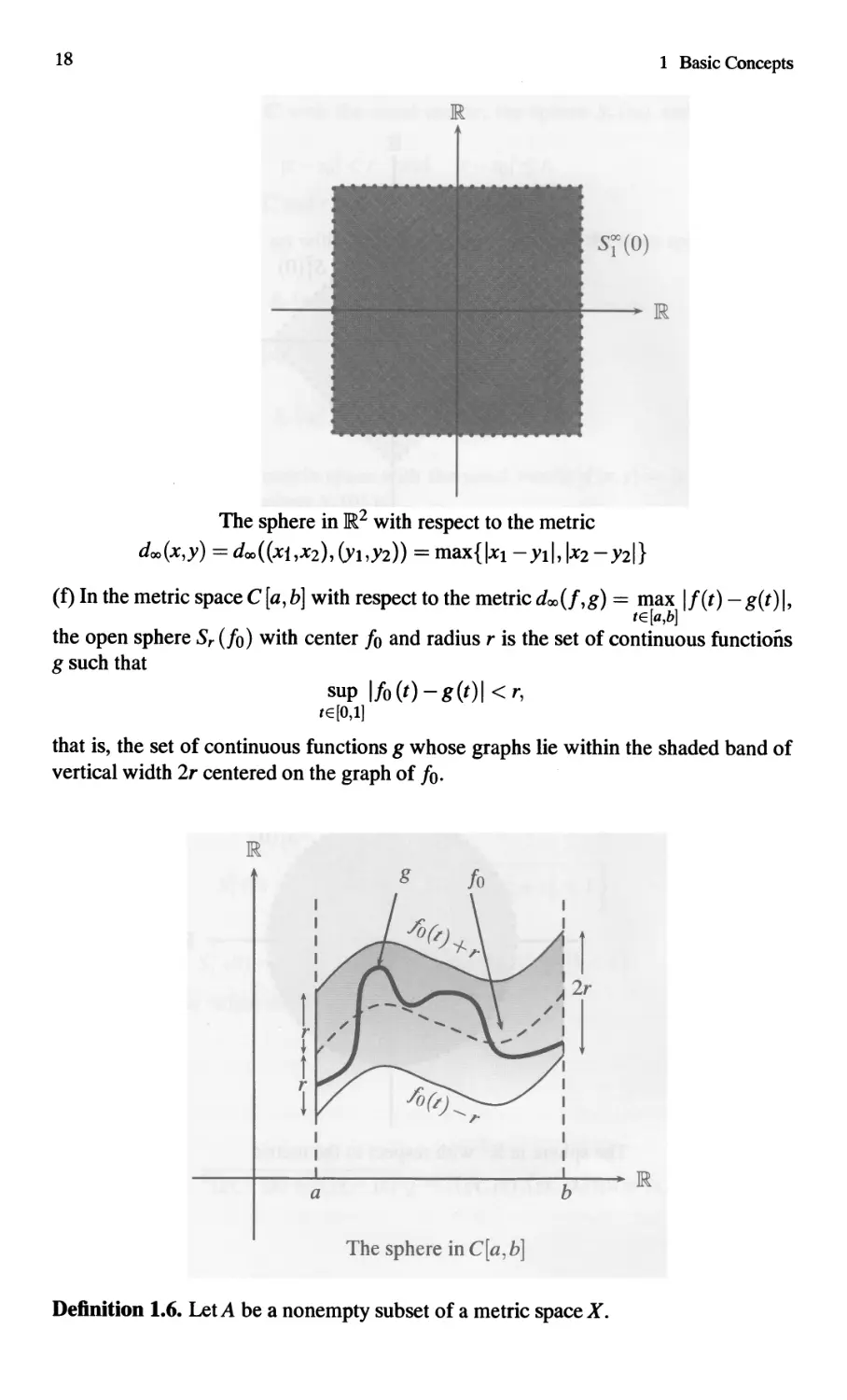
The sphere in z with respect to the metric
doo(x,y) = doo((xl,xz), (Yl,YZ)) = max{l x l - Yll, Ixz - yzl}
(f) In the metric space C [a, b] with respect to the metric doo (I, g) = max I I (t) - g( t ) I,
tE [a,b]
the open sphere Sr (/0) with center 10 and radius r is the set of continuous functions
g such that
sup 1/0 (t) - g(t)1 < r,
tE [0,1]
that is, the set of continuous functions g whose graphs lie within the shaded band of
vertical width 2r centered on the graph of 10.
1R
g 10
f
r
t
r
!
a
b
1R
The sphere in C[a, b]
Definition 1.6. Let A be a nonempty subset of a metric space X.
1.3 Open Sets and Interior Points
19
. A point x E A is said to be an interior point of A if x is the center of some sphere
contained in A. In other words, x E A is an interior point of A if there exists r > 0
such that Sr (x) C A.
x
. The set of all interior points of A is called interior of A and it is denoted by A 0, that
IS,
A ° = {x E A : S r (x) C A for some r > O} .
. The set A is said to be open if each of its points is the center of some open sphere
contained entirely in A; That is to say, A is an open set if for each x E A, there exists
r > 0 such that Sr(X) C A.
. Let x EX. The set A is said to be a neighborhood of x if there exists an open sphere
centered at x and contained in A, that is, if Sr(x) C A for some r > O. In case, A is
an open set, it is called an open neighborhood of x.
Remark 1.8. (i) In particular, an open sphere Sr(x) with center x and radius r is a
neighborhood of x.
(ii) The interior of A is the neighborhood of each of its points.
(iii) Every open set is the neighborhood of each of its points.
(iv) The set A is open if and only if each of its points is an interior point, that is,
A =Ao.
Example 1.18. 1. Let be the metric space with the usual metric and A be a subset of
.
(a) A = (a, b), [a, b), [a,b,], or (a,b], thenAo = (a, b)
(b) If A = N, Z, Q or the set of irrational numbers, then A ° = 0.
(c) If A is a finite set, then A ° = 0.
(d) If A = C the cantor set, then A ° = 0.
00 1
(e) If A = n[-3,-),thenAo=(-3,0).
n=l n
(f) If A = (0,1) nQ, thenAo = 0.
(g) If A = 0, thenAO = 0.
(h) If A = , thenAo = .
2. Let A be a nonempty subset of a discrete metric space X. Then A ° = A.
Example 1.19. 1. In with the usual metric
20
1 Basic Concepts
(a) is an open set;
(b) (a, b) is an open set;
(c) (a,b], [a,b) and [a,b] are not open sets;
(d) The set {1, !, l, .. . } is not open;
( e) A set consists a singleton is not an open set;
(f) The set of all rational numbers Q is not open. But it is open with respect to the
metric d (x,y) = Ix - yl defined on Q;
(g) The cantor set C is not an open set.
2. Let X == [0,1) with the usual metric d(x,y) = Ix-yl for allx,y EX. Then [O,a),
a < 1, is an open set.
3. In the discrete metric space X, every subset of X is an open set.
Remark 1.9. (i) In a metric space X, the empty set 0 and the whole space X are open
sets.
(ii) Whether a set is open or not depends upon the space in which it is considered.
For example, identify the real line with horizontal axis {(x, 0) E z : x E } in
z. is not an open subset of z since does not contain any open sphere in
z. However, in the metric space with the usual metric is an open set.
Theorem 1.1. Let A and B be two subsets of a metric space X. Then
(a) A C B impliesAo C Bo;
(b) (A nB)O =Ao nBo;
(c) (A UB)O :) A ° UBo.
Proof. (a) Let x E AO. Then there exists an open sphere Sr (x) C A for some r > O.
Since A C B, Sr (x) C Band hence x E BO. ThusAo C BO.
(b) Let x E (A nB)o. Then there exists an open sphere Sr (x) C A nB for some r> O.
Therefore, Sr (x) C A and Sr (x) C Band hence x E AO and x E BO. So, x EAo nBo and
thus (AnB)O C AonBo.
To prove the reverse inclusion, let us suppose that yEA ° nBo. Then yEA ° and y E
BO and therefore, there exist open spheres SrI (y) C A and Srz (y) C B for some rl, rz >
O. Set r = min{rl,rz}. Then Sr(y) C AnB and hencey E (AnB)o. Consequently,
AOnBo C (AnB)o.
(c) Let x E A ° U BO. Then either x E A ° or x E BO. This implies that there exists an
open sphere Sr (x) C A or Sr (x) C B for some r > O. So, we have Sr (x) C A UB and
therefore x E (A UB)o. HenceAo UBo C (A UB)o.
Remark 1.10. (A UB)O Cf:. A ° UBo. For example, let X = be the usual metric space
and A = [0,1] and B == [1,2]. Then A UB = [0,2]. Note that A ° == (0,1), BO == (1,2)
and (A UB)O = (0,2). This shows that A ° UBo C (A UB)O but (A UB)O Cf:. AO UBo.
Theorem 1.2. Let (X, d) be a metric space. Then
( a) each open sphere in X is an open set;
(b) a subset A of X is open if and only if it is the union of open spheres.
1.3 Open Sets and Interior Points
21
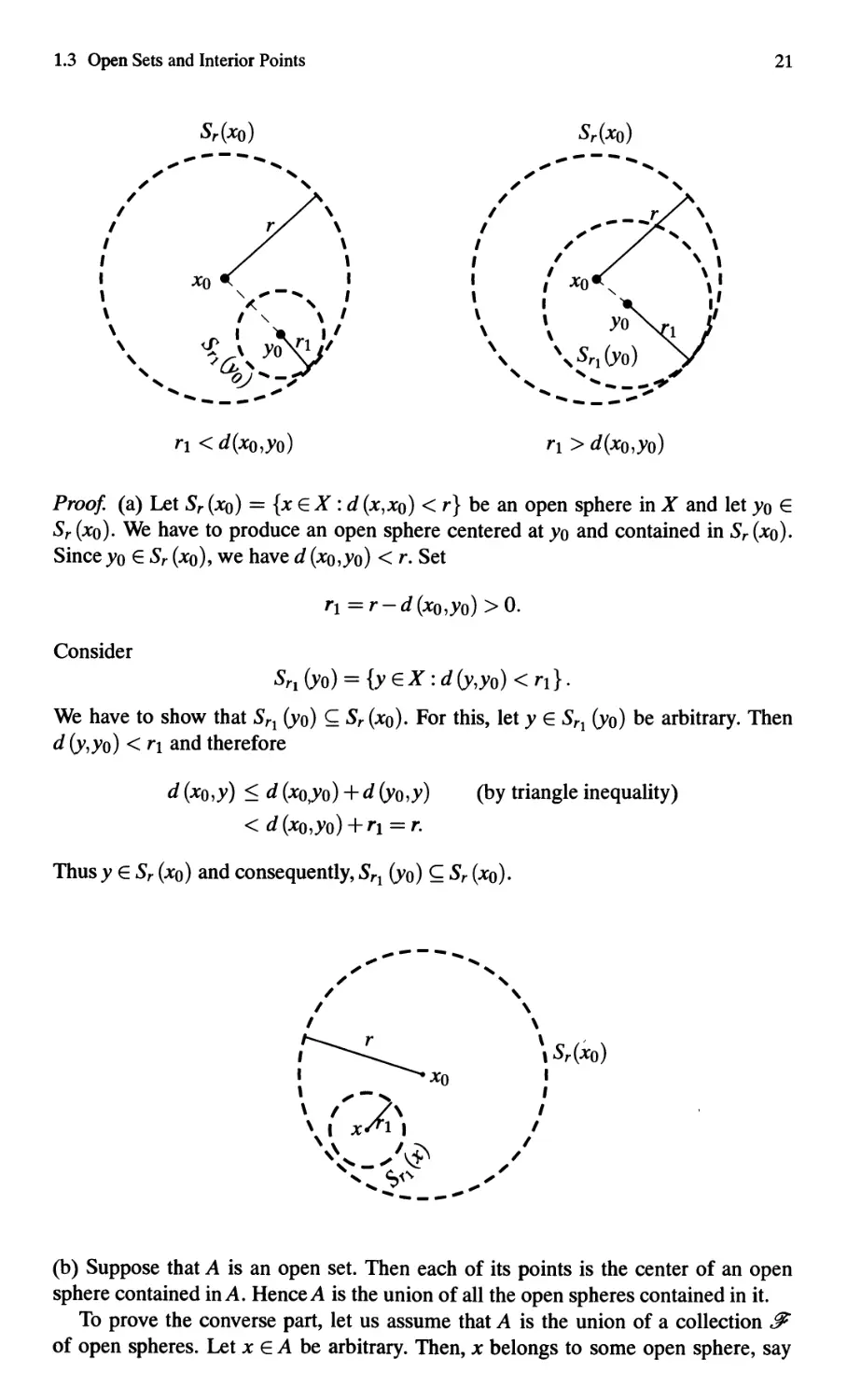
Sr(XO)
Sr(XO)
".,--- ,
;' ,
,
/
, ,
, \
I \
, ,
I Xo I
, '\. -, ,
,
\ ,'\. \ I
\ I I ,
, \ Yo rl ,
, /{i,
" '-"
' ---,'"
".,--- ,
;' ,
,
/
" __ _ _r ,
,, ,\
I , \
',' '\ '
\ {\ XO rl Y
\ ',Sri (YO) Y
, , ,
, ,___fIIJ'
, ".
---'
rl < d(xo,yo)
rl > d(xo,yo)
Proof. (a) Let Sr (xo) = {x EX: d (x,XO) < r} be an open sphere in X and let Yo E
Sr (xo). We have to produce an open sphere centered at Yo and contained in Sr (xo).
Since Yo E Sr (xo), we have d (XO,yo) < r. Set
Tl = r-d (XO,yo) > O.
Consider
SrI (YO) = {y EX: d (y,yo) < rl} .
We have to show that SrI (yO) C Sr (xo). For this, let y E SrI (yO) be arbitrary. Then
d (y,yo) < rl and therefore
d (XO,y) < d (XO,yo) + d (yo,y)
< d (XO,yo) + Tl = T.
Thus y E Sr (xo) and consequently, SrI (yO) C Sr (xo).
(by triangle inequality)
".,--- ,
;' ,
,
/ ,
, ,
, \
\ /
, , Sr(XO)
I Xo I
, ,..-, ,
\ I /\ I
\ I x/tl I ,
, ,
,\ I\ /
" -'"
, '('\, ;'
, ,'"
---
(b) Suppose that A is an open set. Then each of its points is the center of an open
sphere contained in A. Hence A is the union of all the open spheres contained in it.
To prove the converse part, let us assume that A is the union of a collection
of open spheres. Let x E A be arbitrary. Then, x belongs to some open sphere, say
22
1 Basic Concepts
Sr (XO) E . Since each open sphere is an open set, x is the center of an open sphere
SrI (x) such that SrI (x) C Sr(XO)' ButSr(xO) C A and hence SrI (x) C A. Therefore A
.
IS open
Theorem 1.3. Let (X, d) be a metric space. Then
(a) arbitrary union of open sets in X is open;
(b) finite intersection of open sets in X is open.
Proof (a) Let A be any index set, {Aa} aEA be a family of open sets in X and A =
U Aa. Since each Aa is open, it is the union of open spheres for each a E A. Then
aEA
A is the union of unions of open spheres. Hence, by Theorem 1.2, A is open.
n
(b) Let {Ai: i = 1,2,...,n} be the finite family of open sets in X and let A = n Ai.
i=1
Let x EA. Then x is in each Ai. But each Ai is open, hence for each i, there exists
ri > 0 such that Sri (x) C Ai. Set r = min {r1, rz,. . . , r n }. Then
Sr (x) C Sri (x) C Ai for each i = 1,2,... ,n.
n
Therefore, Sr (x) C n Ai =A and hence A is open.
i=1
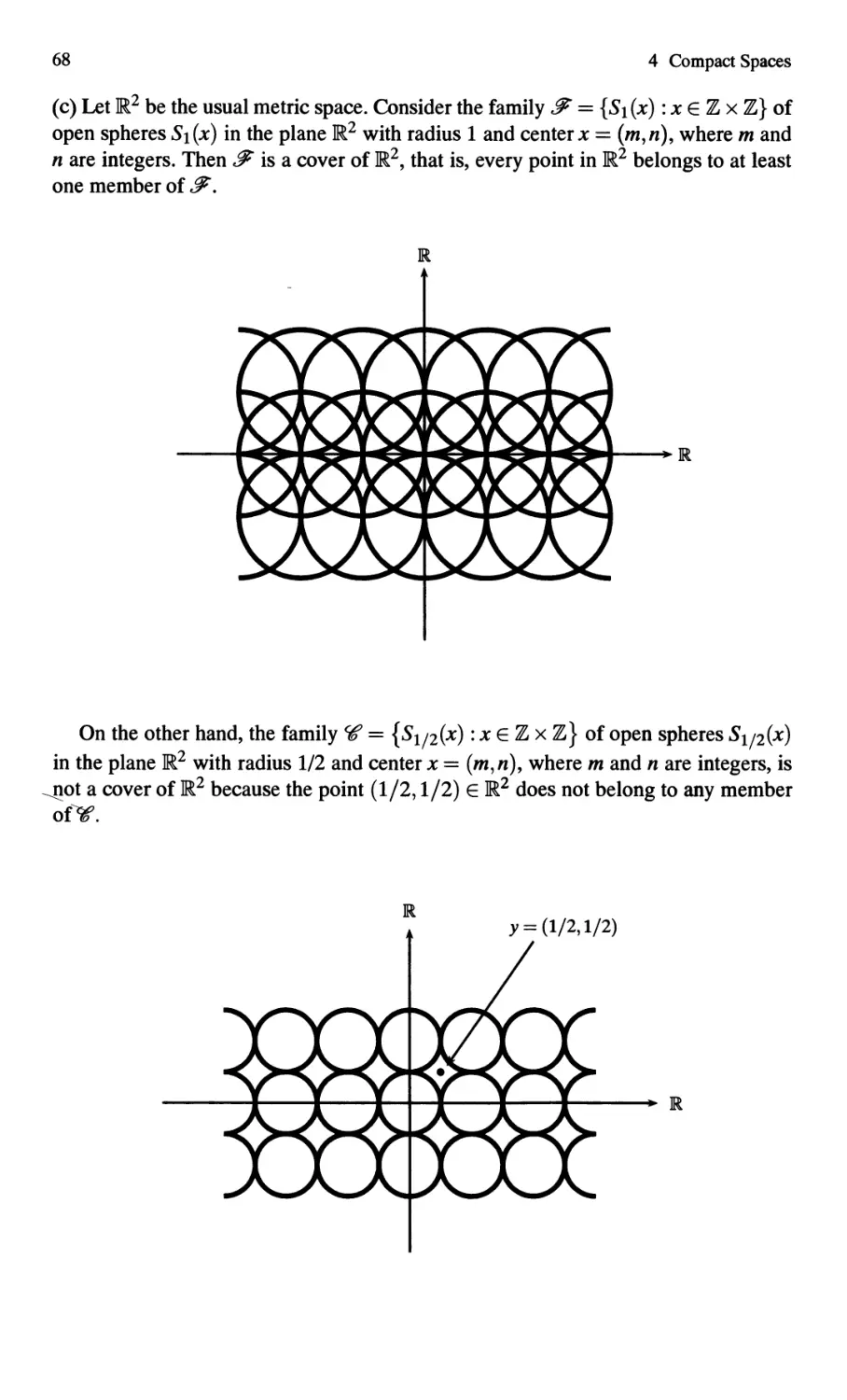
Remark 1.11. Arbitrary intersection of open sets need not be open. For example, let
X = with the usual metric. Consider the family An = {( - , ) : n E N} of open
00
sets. Then n An = {O} is not open.
i=1
Theorem 1.4. Let A be a subset of a metric space X. Then A 0 is the largest open
subset of A.
Proof First of all, we shall prove that A 0 is an open set. For that, let x E A 0 be arbi-
trary. Then, by definition, there exists an open sphere Sr (x) C A for some r > O. But
Sr (x) is an open set, so each of its points is the center of some open sphere contained
in Sr (x). Therefore, each point of Sr (x) is the interior point of A, that is, Sr (x) C A 0 .
Thus, x is the center of an open sphere contained in A o. Hence A 0 is an open set.
Let B C A be an arbitrary open set and let x E B. Then there exists Sr (x) C B C A
for some r > O. This implies that x E A 0 and hence B C A 0 C A. Since A 0 is open, A 0
is the largest open subset of A.
Remark 1.12. A 0 is the union of all open subsets of A.
Exercise 1.29. Find the open spheres with center 0 and radius 1 in the metric spaces
with respect to the metrics defined in Exercises 1.7 and 1.10.
Exercise 1.30. Let A be a subset of a metric space X. Prove that (A 0) 0 = A 0 .
Exercise 1.31. In n, let R denote the set of points having only rational coordinates
and I its complements, that is, the set of points having at least one irrational coordi-
nate. Then prove that R O = 1 0 = 0.
Exercise 1.32. Let (X, d) be a metric space, a E X and 0 < r < r'. Prove that the set
{x EX: r < d(x,a) < r'} is open inX.
1.4 Closed Sets and Closure of Sets
23
Exercise 1.33. Let (X, d) be a metric space and
d * ( ) _ d(x,y)
x,y - .
1 +d(x,y)
Prove that the family of open sets with respect to the metric d is same as the family
of open sets with respect to the metric d* .
Exercise 1.34. Let R be the same as in Exercise 1.31. Prove that
(a) every nonempty open set in n contains a member of R;
(b) every nonempty open set in n contains infinitely many members of R.
Exercise 1.35. Let (X, d) be a metric space and x, y be distinct points of X. Prove that
there exist disjoint open spheres centered on x and y.
Hint: Since x =1= y, d(x,y) > O. Let d(x,y) = 3r for some r > 0, and let Sr(x) and Sr(y)
be open spheres centered on x and y, respectively. Then, clearly Sr(x) n Sr(y) = 0
because the radius of Sr(x) and Sr(y) is r and the distance between x and y is 3r.
1.4 Closed Sets and Closure of Sets
Definition 1.7. Let A be a subset of a metric space X. A point x E X is said to be a
limit point (accumulation point or cluster point) of A if each open sphere centered on
x contains at least one point of A different from x.
In other words, x E X is a limit point of A if
(Sr (x) - {x}) nA =1= 0 for all r > O.
The set of all limit points of A is called derived set and it is denoted by A'.
Example 1.20. 1. In the usual metric space ,
(a) if A = {I,!, ,... }, then A' = {O};
(b) if A = N or Z, then A' = 0;
(c) if A is the set of all rational or irrational numbers, then A' =
(d) every point on the real line is a limit point, and therefore, , = ;
(e) if A is a cantor set C, then A' = C.
2. If A is a subset of a discrete metric space, then A has no limit poi s, since every
open sphere of radius 1 consists only the center. ThusA' = 0.
Remark 1.13. By the definition of a limit point, we follow that any open sphere cen-
tered on a limit point of A must contain infinitely many points of A, that is, to say, a
point x E X is a limit point of A if Sr (x) nA is an infinite set for each r > O.
Let Sr (x) contain a point Xl of A different fromx. If d (x, Xl) = rl, the open sphere
SrI (x) contains a point X2 of A different from x and Xl' And so an indefinitely. It
should be noted that a limit point of A is not necessarily a point ofA. For example, in
Example 1.20 ( a), 0 is the only limit point of the set A = {I, !, , . .. } which is not in
A.
In view of the above remark, we have the following definition.
24
1 Basic Concepts
Definition 1.8. A point x E X is said to be an isolated point of X if there exists an open
sphere centered on x contains no point of A other than x itself, that is, if Sr (x) nA =
{x} for some r > O.
Remark 1.14. If a point x E X is not a limit point of A then it is an isolated point.
Hence every point of a metric space X is either a limit point or an isolated point of X.
Example 1.2t. Consider the metric space X = {O, 1, !, 1, 1, . . . } with the usual metric
given by the absolute value. Then 0 is the only limit point of X while all other points
are the isolated point of X.
Definition 1.9. Let A be a suJ:>set of a metric space X. The closure of A, denoted by A
or cIA, is the union of A and the set of all limit points of A, that is, A =A UA'.
In other words, x E A if every open sphere Sr (x) with center on x and radius r > 0
contains a point of A, that is, x E A if and only if Sr (x) nA =1= 0 for every r > O.
Remark 1.15. Let A and B be subsets of a metric spaceX. Then
(i) 0 = 0
(ii) X X
(iii) (A ) = A
(iv) A <:;; B implies A C B
(v)AUB= A U B
(vi) A = (A )'
(vii)AnB CA n B , butAnB A n B ; For example, in the usual metric space ,
consi der the sets A = (0,1 ) andB = (1,2). Then A n B = [0,1] n [1,2] = {I}, but
AnB=0and nreAnB A n B .
Remark 1.16. In a metr ic pace (X,d), Sr(x) C Sr[x] for any x E X and r > O. By
Rema rk 1.15 (iv), Sr(x) C Sr[x] = Sr[x] because Sr[x] is a closed set. But in general
Sr(x) =1= Sr[x]. For example, let be a discrete metric space. Then Sr(O) = {x E :
d(O,x) < I} = {O} which is open as well closed in X, while Sr[O] = {x E : d(O,x) <
I} = IR. Therefore, Sr(x) =1= Sr[x].
Theorem 1.5. Let (X, d) be a metric space and A be a subset of X. Then x E A if and
only if p (x,A) = O.
Proof. Let x E A . Ifx EA, then obviously we have d(x,A) = O. Assume x A. Then x
is a limit point ofA. Thus for any E > 0, there exists ay E Se(x) nA, that is, d(x,y) < E.
Therefore d(x,A) < E for any E > O. Henre d(x,A) = O.
Conversely, suppose that d(x,A) = O. If x E A, then x E A . Assume x A. Then by
the property of the infimum, for any E > 0, there is ayE A such that d (x,y) < E, that
is, y E Se (x) nA. Since x A, then y =1= x. Therefore, x is a limit point of A, and thus
xEA.
Definition 1.10. Let A be a subset of a metric space X. The set A is said to be closed
if it contains all its limit points, that is, A' C A.
It is obvious that A is closed if and only if A =A.
Example 1.22. In the usual metric space ,
1.4 Closed Sets and Closure of Sets
25
( a) the sets of all rational and irrational numbers are not closed;
(b) the setA = {1,!, 1,'" ,} is not closed, since A' = {O} %A;
00 1 _
(c) if A = n [-3, -), then A = [-3,0];
n=l n
(d) if A = (0,1) nQ, then A = [0,1];
(e) the cantor set C is closed since A' =A C A.
Remark 1.17. In a metric space X, every finite set, empty set and whole space are
closed sets.
Theorem 1.6. Let A be a subset of a metric space X. Then, A is closed if and only if
the complement of A is an open set.
Proof Let A be closed and x E A C be arbitrary. Then x tj A and also x cannot be a
limit point of A since A is closed. Then there exists an open sphere Sr (x) such that
Sr (x) nA = 0. This implies that Sr (x) C A C for some r > O. Since x E A C is arbitrary,
each point of A C is the center of some open sphere which is contained in A c. Hence
A C is open. _____
Conversely, assume that A C is open. Let x E X be a limit point of A. If x E A, then
A contains all its limit points and hence A is closed. If x tj A, then x E A c. Since
A C is open, there exists an open sphere Sr (x) such that Sr (x) C A C . Consequently,
Sr (x) nA = 0 for some r > O. Hence x cannot be a limit point of A which contradicts
to our assumption. Therefore x EA. This proves that A is closed.
Theorem 1.7. In a metric space (X,d), every closed sphere is a closed set.
Proof Let Sr [x] be a closed sphere in X. Then it is sufficient to show that (Sr [x])C,
the complement of Sr [x], is an open set. Let Yl E (Sr [x])C be arbitrary. Then y tj Sr [x]
and therefore d (x,y) > r.
X
d(x,y) > r
---....,
,
' /!
I \
r \
--- 1 I
\ Y "
,Srl (y) z. ,
,
'...._--
Set rl = d (x,y) - r > O. Letz E Srl (y). Then d (z,y) < rl. By the triangle inequality
d(x,y) < d (x,z) +d(z,y)
and we have
26
1 Basic Concepts
d(x,z) > d (x,y) - d(z,y) > d (x,y) - rl = r.
Therefore z Sr [x] and hence z E (Sr [x])c. Thus Srl (y) C (Sr [x])c. But y E (Sr [x])C
being arbitrary, each point of (Sr [x])C is the center of some open sphere contained in
(Sr [x])c. Hence (Sr [x])C is an open set.
By using De Morgan's law
n (A ) = ( U Aa ) C
aEA aEA
and
n ( n ) c
k{Ai = [JAi
and Theorem 1.3, we have the following result.
Theorem 1.8. In a metric space X,
(a) the arbitrary intersection of closed sets in X is closed; and
(b) the finite union of closed sets in X is closed.
Remark 1.18. The arbitrary union of closed sets need not be closed.
Example 1.23. Consider the family {[ , 2J : n E N} of closed sets in the usual metric
space . Then
U{[ ,2] :nEN}=(O,2]
which is not a closed set.
Theorem 1.9. Let (X,d) be a metric space and A be a subset of X. Then A is the
smallest closed subset of X containing A.
Proof We first prove that A is closed. Let x be a limit point of A . Then for a given
E > 0, (Se/2(X) - {x}) n A =1= 0. This implies that there exists y E A such that y E
(Se/2(X) - {x}), that is, d (x,y) < . But since y E A , we have Se/2 (y) nA =1= 0, that
is, there exists z E A such that z ESe /2 (y). This implies that d (y, z) < . By triangle
inequality, we have
d (x,z) < d (x,y) + d (y,z)
E E
< 2 + 2 = E.
This means that, for every E > 0, the open sphere S e (x) contains a point z of A. Hence
x is a limit point of A and therefore x E A . This proves that A is a closed set.
Now, we show that A is the smallest set containing A. Assume that B is any closed
subset of X such that A C B, then it is sufficient to prove that A C B. Let x E A , then
either x E A or x is a limit point of A. If x E A, then x E B and hence A C B. If x is
a limit point of A, then for a given E > 0, (Se(x) - {x}) nA =1= 0, that is, there exists
a point yEA such that y E (Se/2(X) - {x}). Then d (x,y) < E. But since A C Band
yEA, we have y E B. Therefore, p(x,B) = inf d(x,y) = 0 and by Theorem 1.5 x E B .
yEB
Since B is a closed set, x E Band thus A C B.
1.4 Closed Sets and Closure of Sets
27
Definition 1.11. Let A be a subset of a metric space X. A point x E X is called a
boundary point of A if it is neither an interior point of A nor of X \A, that is, x A 0
and x (X\A)o.
In other words, x E X is a boundary point of A if every open sphere centered on x
intersects both A andX\A.
The set of all boundary points of A is called the boundary of A and it is denoted by
b(A).
Remark 1.19. It is clear from the definition that b(A) = A n (X \ A) = A n A C .
Example 1.24. 1. Let be the usual metric space and A C .
(a) If A = [a,b], [a, b), (a,b] or (a, b), then b(A) = {a,b}.
(b) If A = N (respectively Z), then b(A) = N (respectively, Z).
( c) If A = {I, 1, i, .. . , }, then b (A) = {O, 1, 1, i,. .. , }.
(d) If A = Q, then b(A) = .
(e) If A is a set of all irrational numbers, then b(A) = .
2. Let (X, d) be a discrete metric ace and A e x. Then b (A) = 0.
Exercise 1.36. Verify that every subset of the discrete metric space is closed.
Exercise 1.37. Prove that every singlet0l!./set and every finite set in a metric space are
closed.
Exercise 1.38. Let A be a subset of a metric space X. Prove that A is the intersection
of all closed subsets of X containing A.
Hint: LetD = n{B e x: B is closed and A C B}. Then clearly D is the smallest closed
subset of X containingA. From the proof of Theorem 1.9, A = D.
Exercise 1.39. Determine the derive set of the following sets.
(a) A finite setA = {1,2,... ,n}.
(b) R = {(Xt,X2) E 2: Xt,X2 are rational coordinates}.
Exe rcise 1. 40. LetA be a subset of a metric spaceX. Prove that
(i) (X \A) = X \A 0, that is, (AC) = (A O)c.
(ii) (AC)O = (A )C
Exercise 1.41. Let (X, d) be a metric space and A be a closed subset of X. Prove that
x E A if and only if d (x,A) = 0 and hence
x E X\A if and only if d (x,A) > O.
Exercise 1.42. Let (X, d) be a metric space, x E X and A C X be a nonempty set.
Prove that d (x,A) = 0 if and only if every neighborhood of x contains a point ofA.
Exercise 1.430 Let A be a subset of a metric spaceX. Prove that A =X if and only if
(X \A)O = 0, that is, (AC)O = 0.
Exercise 1.44. Let X be a metric space. Prove that every open sphere in X is included
in a closed sphere in X and that every closed sphere in X is included in an open sphere
inX.
28
1 Basic Concepts
Exercise 1.45. Let A be a nonempty subset of a metric space X. Must (A O)C be equal
to cl ( (A )C)?
Hint: Consider Q as a subset of the usual metric space . Then QO = 0 and so (QO) C =
, whereas Q = and (Q) C = 0.
Exercise 1.46. Let (X, d) be a metric space and A C X. Prove that
(a) 6(A) = 6 (A );
(b) b(A) = b(X\A) =A n (X \A);
(c) b(A) = A \A O = (X\A) \ (X\A)O;
(d)X\b(A) =AOU(X\A)O;
(e) A =A o Ub(A);
(f) A =AUb(A);
(g)A O =A \b(A);
(h)AOnb(A) =0;
(i) A is closed if and only if b(A) C A;
(j)A is open if and only ifAnb(A) = 0.
Exercise 1.47. Prove that any closed subset A of a metric space (X,d) is a countable
intersection of open sets.
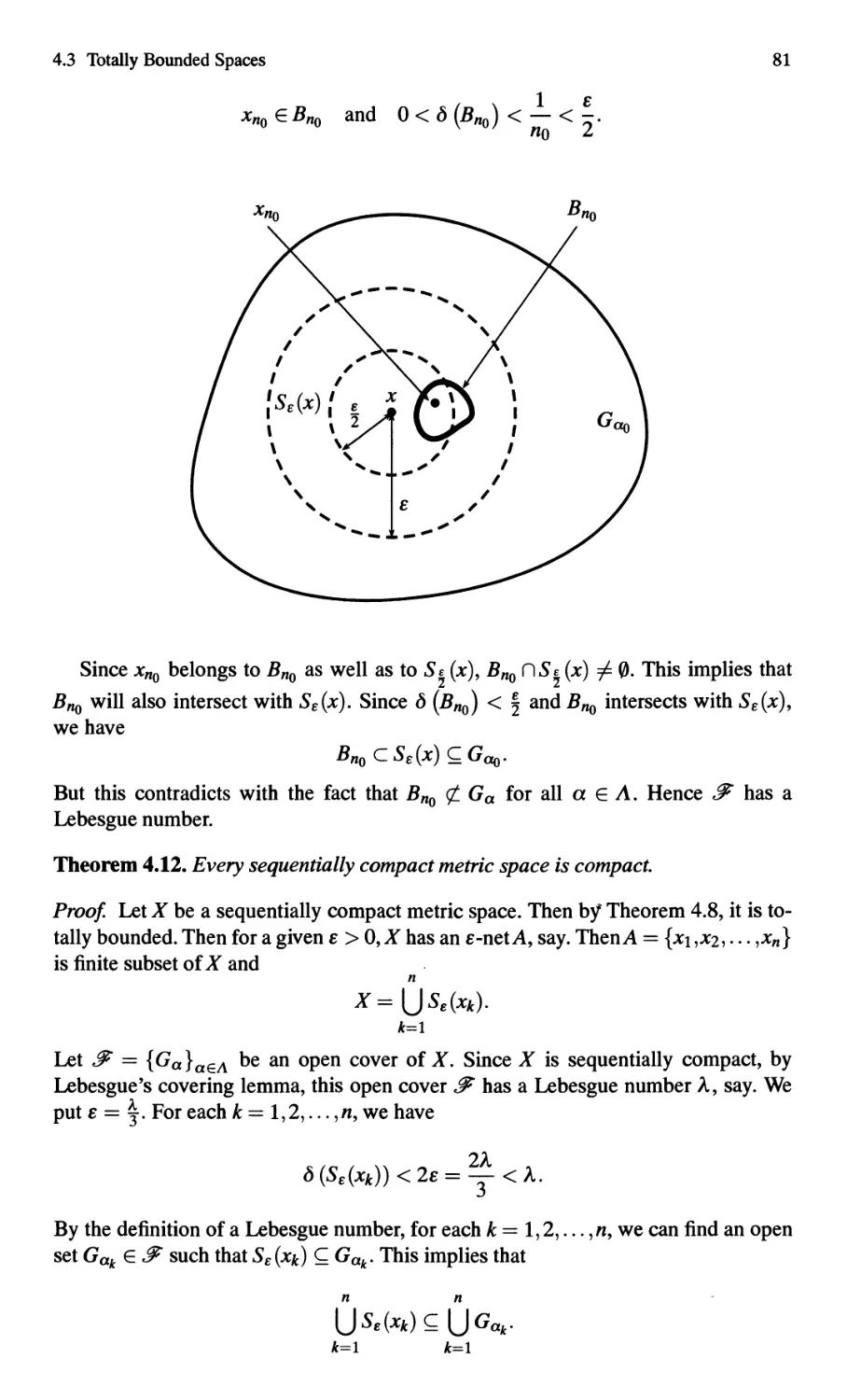
Proof For each n E N, let On = U Sl/n(X). Then On is open and A C On for all
xEA
n E N. Therefore, A C n On. We claim that A = n On. Assume contrary that there
nEN nEN
exists yEn On \A. Since A is closed, A C is open and contains y. Hence there exists
nEN
E > 0 such that Se(y) C Ac. Since E > 0, there exists n E N such that 11n < E. Since
y E On, there exists x E A such that d (x,y) < 1 In < E. SO Se (y) nA =1= 0, which implies
A nA C =1= 0, a contradiction.
Exercise 1.48. Let A be nonempty subset of a metric space X. Prove or answer the
following statements.
(a) b(A) is a closed set.
(b) b(A) = b(X\A).
(c) If x E b(A), does x have to be a limit point?
(d) x E b(A) if and only if for every E > 0, S e (x) contains points of A and of X \ A.
Proof (a) Since. b(A) = A n A C and the intersection of two closed sets is closed, we
have b (A) is a closed set.
(b) This follows from the definition of the boundary and the fact that X \ (X \A) = A.
(c) No. Indeed let A = {O} C IR. Th en A ha s no limit points, but b(A ) = {O }.
(d) Let x E b(A). Since b(A) = A n (X\A), we have x E A and x E (X\A). Then x is
a limit point of A as well as of X \A. Then for any E > 0, we have Se (x) nA =1= 0 and
Se (x) n (X \A) =1= 0.
Conversely let x E X such that for any E > 0, Se(x) contains points of A and of
X \A. It is enough to prove that x E A . If x E A, then we have nothing to prove.
Assume x A. Let E > O. We know that Se (x) nA =1= 0, since x A, then Se (x) nA
contains a point of A other than x. Hence x is a limit point of A, that is, x E A .
1.5 Subspaces
29
1.5 Subs paces
Let (X, d) be a metric space and Y be a subset of X. We may convert Y into a metric
space by restricting the distance function d to Y x Y. In this manner each subset Y of
X can be made a metric space (Y, d lyxY ). On the other hand, we may be given two
metric spaces (X, d) and (Y, d'). If Y is a subset of X, it makes sense to ask whether
or not d' is the restriction of d.
Definition 1.12. Let (X,d) be a metric space and Y be a subset of X. The relative
metric dy on Y is the restriction of the metric function d on Y x Y, that is,
dy (x,y) = d (x,y) for all x,y E Y.
It is easy to see that dy is a metric on Y. The space (Y, dy ) is called the metric subspace
of the metric space (X, d).
In other words, let (X, d) and (Y, d') be metric spaces. We say that (Y, d') is a
subspace of (X, d) if
(i) Y is a subset of X;
(ii) d' = d lyxY restriction of d on Y x Y.
Example 1.25. (a) Let be an usual metric space. If Y = [0,1], (0, 1], [0,1) or (0,1)
and dy (x,y) = Ix - yl = d (x,y) for all x,y E Y. Then (Y,dy) is a subspace of ( ,d).
(b) Let be the usual metric space and Q be the set of rational numbers. Define
dQ : Q x Q -+ by
dQ (x,y) = Ix - yl = d (x,y) for all x,y E Q.
Then (Q,dQ) is a subspace of ( ,d).
(c) Let In (the unit n cube) be the set of all n-tuples (Xl,XZ"" ,x n ) of real numbers
such that 0 < Xi < 1 for i = 1, 2, . .. , n. Define d c : In X In -+ by
d c (x,y) = m x IXi - Yil
l l n
for all x = (Xl ,Xz,. . . ,x n ) E In and y = (Yl ,Yz, .. . ,Yn) E In. Then (In, dc) is a subspace
of ( n , doo), where d oo is the max metric on n, that is, d oo (x,y) = m x IXi - Yi I for all
I l n
x,y E n.
(d) Let sn (the n-sphere) be the set of all n + I-tuples (Xl ,Xz,. .. ,Xn+l) of real numbers
such that xi + .x1 + . . . + X;+ I = 1. Define ds : sn x sn -+ by
n+l
ds (x,y) = }: (Xi - Yi)Z = dz (x,y) ,
1=1
( n+l ) I/Z
where dz is a metric on]Rn defined as dz (x,y) = (Xi - Yi)Z for all X,Y E]Rn.
Then (sn, d s ) is a subspace of ( n+ 1 , dz) .
30
1 Basic Concepts
(e) Let A be the set of all (n + I)-tuples (XI'XZ"" ,Xn+l) of real numbers such that
Xn+l == O. Define dA :A xA by
dA (x,y) == m x IXi - Yil = doo (x,y),
1 ;Z::s; n
for all x = (Xl ,Xz,. . . ,X n , 0) E A and y = (YI ,Yz,. . . ,Yn, 0) E A, where d oo is the max
metric on n+ 1. Then (A, dA) is a subspace of ( n+ I , doo) .
(f) Let P [a, b] be the set of all polynomials defined on [a, b]. Define dp : P [a, b] x
P[a,b] by
dp (f,g) = max If (t) - g(t)1 = d oo (f,g),
tE [a,b]
where d oo is the max metric on C[a,b]. Then (P[a,b] ,dp) is a subspace (C[a,b],doo).
But (P [a, b] ,dp) is not a subspace of (C[a, b], d), where d (f,g) = J: If (t) - g (t)1 dt.
Remark 1.20. If Y is a subspace of a metric space X, then a set which is open (re-
spectively, closed) in Y may not be open (respectively, closed) in X. For example, if
Y = [0, 1] then the set [0, !) is open in Y but not in with the usual metric. Also, if
Y = (0, 1) then the set (0, !] is closed in Y but not in with the usual metric.
Lemma 1.1. Let (Y, dy) be a subspace of a metric space (X, d). If a E Y and r > 0,
then
S (a) =ynSr(a),
where Sr(a) and S (a) are open spheres in (X,d) and (Y, dy), respectively.
Proof We have
Sr(a) nY = {x EX: d(x,a) < r} nY
= {x E Y: d(x,a) < r} because Y e x
= S (a).
Theorem 1.10. Let (Y, dy) be a subspace of a metric space (X, d) and A a subset of
Y. Then
(a) A is open in Y if and only if there exists an open set G in X such that A = G n Y;
(b) A is closed in Y if and only if there exists a closed set F in X such that A = F n Y.
Proof (a) Let Sr (x) and S (x) be the same as in Lemma 1.1. Suppose that A = GnY,
where G is open inX. Let x EA be arbitrary. Then we have to show that x is an interior
point of A, that is, x E A 0 with respect to dy metric.
Since A = G n Y and x E A, we have x E G and x E Y. Since G is open in X, there
exists r > 0 such that Sr (x) e G. Hence, by Lemma 1.1, we have
S (x) = Sr (x) nY e GnY =A.
It follows that x is an interior point of A as a subset of the metric space (Y, dy ). Hence
x EA o with respect to dy metric and hence A is open in Y.
Conversely, assume that A is an open set in Y and let x E A be arbitrary. Then there
exists an open sphere S x (x) such that S x (x) e A. Now, we have
1.5 Subspaces
31
A = US x(x) = U (Srx(x)nY) == ( USrx(x) ) nY
x x x
== GnY, where G = U S x (x).
x
But G being an arbitrary union of open spheres in X is an open set in X. Hence
A = GnY, where G is an open set inX.
(b)A is closed in Y {:} Y\A is open in Y
{:} Y \ A == G nY, (by part (i)) where G is open in X
{:} A = Y \ (G n Y)
{:}A = (Xny) \ (GnY)
{:} A = (X \ G) n Y
{:} A == F nY, where F = X \ G is a closed set in X.
Corollary 1.1. Let (Y, dy) be a subspace of a metric space (X, d) and A be a subset
ofX.
(a) If A is open in Y andY is open inX then A is open in X;
(b) If A is closed in Y and Y is closed in X then A is closed in X.
Theorem 1.11. Let (Y, dy) be a subspace of a metric space (X, d) and A be a subset
ofY. Then
( a) x E Y is a limit point of A in Y if and only if x is a limit point of A in X;
(b) the closure of A in Y, denoted by CIA (Y), is clx (A) nY, where clx (A) is the
closure of A in X. In other words, cly(A) = clx (A) n Y.
Proof (a) Let x E Y be a limit point of A in Y. Then for every open sphere S (x) in
Y, we have (S (x) - {x}) nA =1= 0. For any given r > 0, we have
(Sr (x) - {x}) nA = (S (x) nY - {x}) nA (sinceA C Y)
= (S (x) - {x}) nA =1= 0.
It follows that x is a limit point of A in X.
The converse can be established by retracting the above steps.
(b) Since clx (A) is closed in X, by Theorem 1.10, clx (A) n Y is closed in Y. Since
clx ( A) n Y contains A and since cly (A) is the intersection of all closed subsets of Y
containingA, we must have
cly (A) C clx (A) n Y.
On the other hand, cly (A) is closed in Y, then cly (A) = Fn Y, wtere F is a closed
set in X. Since A C cly (A), F is a closed set in X containingA. Since cly (A) is the
intersection of all closed sets containingA, we have
cly (A) C F.
Hence cly(A) nY C FnY = cly (A).
32
1 Basic Concepts
Exercise 1.49. Let (Y, dy) be a subspace of a metric space (X, d). Then prove that a
subset M of Y is a neighborhood of a point y E Y if and only if there is a neighborhood
N ofy in (X,d) such thatM = YnN.
Proof LetN be a neighborhood of a pointy E Y in (X,d) such thatM = YnN. Then
there exists an open sphere S r (y) such that S r (y) e N. Since S (y) = Y n S r (y), we
have S (y) C Y nN = M. Hence M is a neighborhood of y E Y in (Y, dy).
Conversely, suppose that M is a neighborhood of y in (Y, dy). Then there exists an
open sphere S (y) c M. Let N = M U Sr (y). Then
YnN = Yn (MUS r (y)) = (YnM) U (ynS r (y))
= MUS (y) since M C Y
= M because S (y) e M.
Since Sr (y) e N, N is a neighborhood ofy in (X,d).
Chapter 2
Complete Metric Spaces
The concept of a convergent sequence plays an important role to investigate the
closedness of a set, the continuity of a function and several other properties. In this
chapter, we give an introduction to the convergence of sequences in arbitrary metric
spaces. We investigate the properties under which a sequence is convergent. In real
analysis, Cauchy criteria provides the necessary and sufficient conditions for a se-
quence to be convergent, that is, a sequence is convergent if and only if it is Cauchy.
This Cauchy criteria does not hold for any arbitrary metric space. The metric spaces in
which this Cauchy criteria holds are called complete. Such metric spaces are also con-
sidered and studied. A very important property of a complete metric space is known as
Cantor's intersection theorem. Such theorem and its converse version are presented.
We also consider a metric space which contains an incomplete metric space and some
other points so that every Cauchy sequence is convergent in this larger space. Such
spaces are called completion of an incomplete metric space.
2.1 Convergent Sequences
Definition 2.1. A sequence s in a set X is a mapping from the set of all natural num-
bers N into X. The image under a sequence s of a natural number n is denoted by X n
and is referred as nth term of the sequence s.
Let {xn} nEN be a given sequence and {nk} kEN be a sequence of positive integers
such that nl < nz < .... Then the sequence {X nk } kEN is called a subsequence of the
sequence {x n }.
Definition 2.2. Let {xn} be a sequence in a set X. If there exists a positive integer N
such that X n = x for all n > N, then the sequence {xn} is called eventually constant .
If X n = n for all n E N, then the sequence {xn} is called a constant sequence.
Obviously, a constant sequence is a special case of an eventually constant se-
quence.
Definition 2.3. Let (X, d) be a metric space. A sequence {xn} of points of X is said to
be convergent if there is a point x E X such that for each E > 0, there exists a positive
integer N such that
d (xn,x) < E for all n > N.
The point x E X is called a limit point of the sequence {x n }.
A sequence which is not convergent is said to be divergent.
More preciously, a sequence {xn} in a metric space X converges to a point x EX
if the sequence {d(xn,x)} of real numbers converges to 0 as n 00.
34
2 Complete Metric Spaces
Since d (xn,x) < E is equivalent to X n ESe (x), the definition of convergent sequence
can be restated as follows:
A sequence {xn} in a metric space X converges to a point x E X if and only if for
each E > 0, there exists a positive integer N such that
X n E Se(x) for all n > N.
We use the following symbols to write a convergent sequence
X n -+ X
or
limxn =x
n --+ 00
and we express it by saying that X n approaches x or that X n converges to x.
Remark 2.1. (i) An eventually constant sequence, and hence a constant sequence, is
convergent.
(ii) In a discrete metric space, a sequence can converge to a point only if it is an
eventually constant sequence.
Remark 2.2. The convergence of a sequence in a metric space (X, d) depends on the
space X as well as on the metric d.
Example 2.1. (a) Let {Xn = : n E N} be a sequence in the usual metric space .
Then X n -+ 0 as n -+ 00. However, if we consider the metric space X = (0,1) with
the usual metric, then the sequence {Xn = : n EN} converges to 0 f/:. X. Thus, the
sequence {xn} is not convergent in this case.
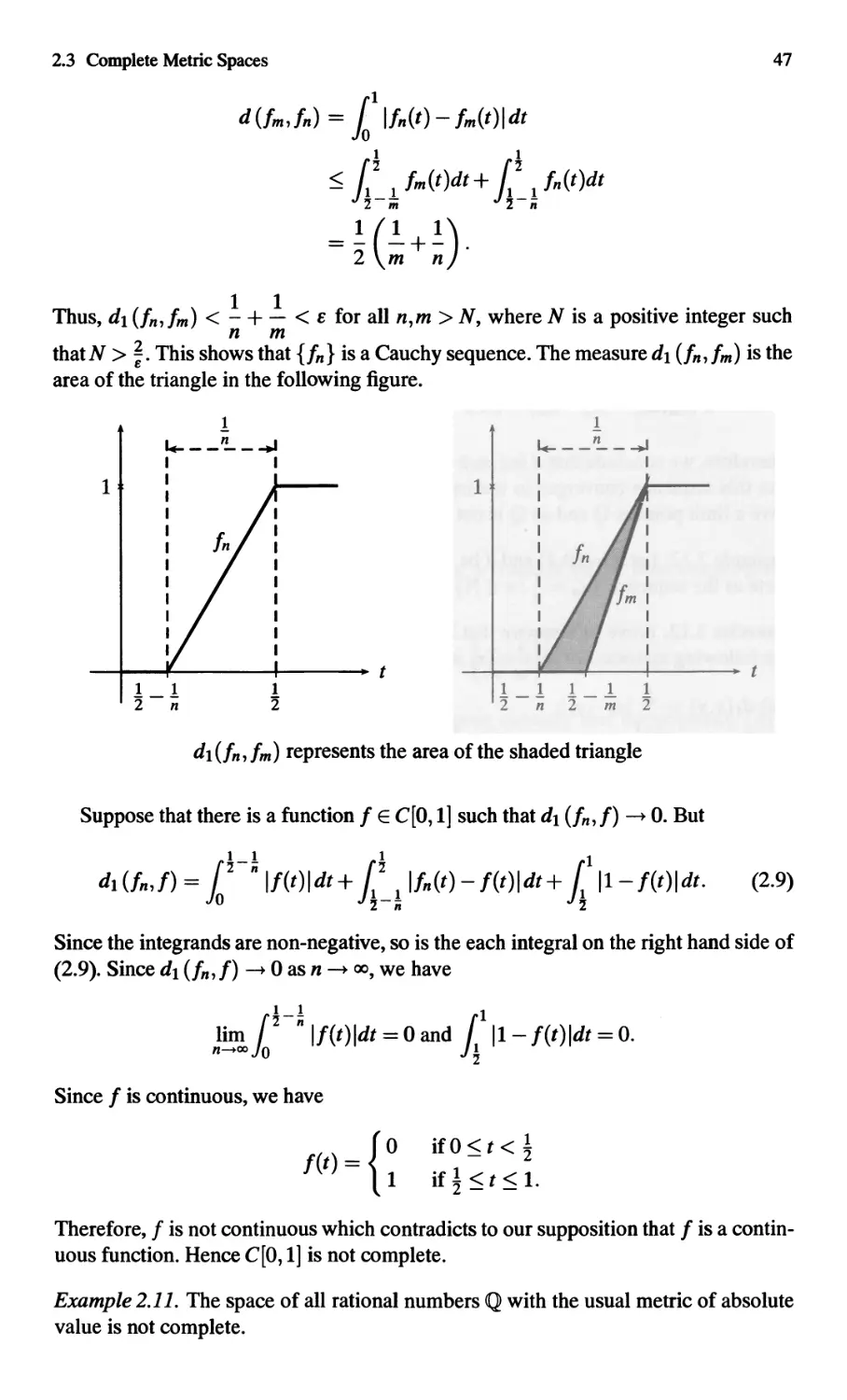
(b) Let {In}nEN be a sequence in the space C[O, 1], where
In(t) = e- nt for all n E N.
Then In -+ 0 with respect to the metric d 1 on C [0, 1] as
1 1 1
d1 (In,O) = e-ntdt = - (1- e- n ) -+ 0 as n -+ 00.
o n
f
On the other hand, the same sequence {In}nEN is not convergent with respect to the
metric doo on C[O, 1] as
doo (In, 0) = max le- nt I = 1 for all n E N.
tE[O,1]
Thus doo (In, 0) -ft 0 as n -+ 00.
Theorem 2.1. A sequence in a metric space cannot converge to more than one limit
point. In other words, in a metric space, every convergent sequence has a unique limit.
Proof. Let (X, d) be a metric space and {xn} be a convergent sequence in X. Suppose
to the contrary that {xn} converges to two distinct points x and y. Then, for each E > 0,
there exist positive integers Nt and Nz such that
E
d (xn,x) < 2 for all n > Nt
2.1 Convergent Sequences
35
and
E
d (xn,Y) < 2 for all n > Nz.
By setting N = max {NI,Nz} and using the triangle inequality, we have
d(x,y) < d (xn,x) + d (xn,Y)
E E
< 2 + 2 = E for all n > N.
It follow,s that x = y. Hence the limit is unique.
Definition 2.4. A sequence in a metric space is said to be bounded if the range set of
the sequence is bounded.
Theorem 2.2. In a metric space, every convergent sequence is bounded.
Proof Let (X, d) be a metric space and {xn} be a sequence in X such that X n x EX
as n 00. Then there exists a positive integer N such that
1
d (xn,x) < 2 for all n > N.
Set r = max {!,d(xn,x) for alII < n < N}. Then
d (xn,X) < r for all n E N.
By the triangle inequality,
d (xn,xm) < d (xn,x) + d (x,xm)
< 2r for all n,m E N.
Hence the diameter of the range set of the sequence {xn} is bounded by 2r. Therefore,
the sequence {xn} is bounded.
Theorem 2.3. Let (X, d) be a metric space and A be a subset of x.
( a) A point x E X is a limit point of A if and only if there exists a sequence {xn} of ,
points of A, none of which equals x, such that {xn} converges to x.
(b) The set A is closed if and only if every convergent sequence of points of A has its
limit in A.
Proof (a) Let x E X be a limit point of A. Construct a sequence {xn} by recursion as
follows:
Since x E X is a limit point of A, we have (SI (x) - {x} ) nA =1= 0. So, we can choose
Xl E (SI(X) - {X}) nA. Likewise the pointsxl,xZ,... ,X n can be chosen such that
Xi E (S + (X) - {X} ) nA fori = 1, 2, . . . , n.
Still ( s 1 (x) - {x} ) nA =1= 0, we can always choose Xn+1 E ( s 1 (x) - {x} ) nA.
n+ 1 n+ 1
By repeating this process infinitely many times, we construct the sequence {xn} by
recursion such that all the points of {xn} are in A and X n =1= x for all n.
36
2 Complete Metric Spaces
Let E > 0 be given and N be a positive integer such that N > . Then
XnES1(X)CSe(X) foralln>N.
n
Hence {xn} converge to x.
Conversely, assume that there is a sequence {xn} of point of A, none of which
equals x, such that {xn} converges to x. Then for every E > 0, there exists a positive
integer N such that
X n E Se(x) for all n > N.
Therefore, (Se(x) - {x}) nA =1= 0 which implies that X is a limit point ofA.
(b) Suppose that A is closed and {xn} is a sequence of points of A which converges to
a point x in X. Then we have to show that x EA.
If the range set of the sequence {xn} is infinite, then it follows from part (i) that x
is a limit point of this set. Since A is closed, we have x EA.
On the other hand, if the range set of the sequence {xn} is finite, then X n = x for all
n > N, since {xn} is a convergent sequence. Since each term of the sequence belongs
to A, so is x.
Conversely, assume that every convergent sequence of points of A converges to a
point ofA. We show that A is closed by showing that it contains all its limits points.
Let x be a limit point of A. Then by part (i), there is a sequence {xn} of points of
A, none of which equals x, such that X n x. By hypothesis x EA. Hence A is closed.
Exercise 2.1. Show that the limit of a convergent sequence of distinct points in a
metric space is a limit of the range set of the sequence.
Proof Let {xn} be a sequence in a metric space such that X n x and let A be the
range set of the sequence {x n }. Then we have to show that x is a limit point ofA.
Suppose that x is not a limit point of A. Then there exists an open sphere Se (x)
such that
(Se(X) - {x}) nA = 0,
that is, Se (x) contains no point of A other than x. Since x is a limit point of the se-
quence, for each E > 0, there exists a positive integer N such that
d(xn,x) < E
or
X n E Se(x) for all n > N
which is a contradiction.
Exercise 2.2. Let (X, d) be a metric space. If {xn} and {Yn} be sequences in X such
that X n x and Yn Y, then prove that d (xn,Yn) d(x,y).
Proof Since X n x and Yn Y, for each E > 0, there exist positive integers Nt and
Nz such that
E
d (xn,x) < 2 for all n > Nt
and
E
d (xm,x) < 2 for all m > Nz.
LetN = max{Nl,N2}' Then, for all n,m > N,
2.2 Cauchy Sequences
37
Id (xn,Yn) - d(x,y) I < Id (xn,Yn) - d (Xn,Y) I + Id (xn,Y) - d(x,y) I
< d(yn,y)+d(xn,x)
E E
< 2 + 2 =E.
Hence d (xn,Yn) -+ d(x,y).
2.2 Cauchy Sequences
Definition 2.5. Let (X, d) be a metric space. A sequence {xn} in X is said to be a
Cauchy sequence if for each E > 0, there exists a positive integer N such that
d (xn,xm) < E for all n, m > N.
Example 2.2. Let X = C[O, 1] be a metric space with the metric d oo defined by
doo(/,g) = sup I/(t) - g(t)1 for all I,g EX.
tE[O,l]
The sequence {In} inX given by
nt
In(t) = - for all t E [0,1],
n+t
is a Cauchy sequence inX. Indeed, for m > n, the function
mt nt
t r---t - -
m+t n+t
(m-n)t 2
(m+t)(n+t)
being continuous on [0,1], assumes its maximum at some point to E [0,1]. So,
d oo (1m, In) = sup Ifm(t) - fn(t)1
tE[O,l]
(m-n)t6
(m + to)(n + to)
t 2 1
< 0 <--+0
(n+to) - n
for large nand m.
Moreover, the sequence {fn} converges to some limit. Indeed, let I(t) = t. Then
nt t 2 1
Ifn(t)-f(t)l= n+t - t =-<--+Oasn-+oo.
n+t - n
Therefore, {In} converges to the limit I, where f(t) = t for all t E [0,1].
Theorem 2.4. Every convergent sequence in a metric space is a Cauchy sequence.
Proof Let (X, d) be a metric space and {xn} be a sequence in X such that X n -+ X as
n -+ 00. Then for each E > 0, there exists a positive integer N such that
38
/
/
2 Complete Metric Spaces
E
d (xn,x) < - for all n > N.
2
By the triangle inequality,
d(xm,xn) < d( m,x)+d(xn,x)
E -E
< 2 +' 2 = E for all n,m > N.
Hence {xn} is a Cauchy Sequence.
Remark 2.3. Every Cauchy sequence in a metric space need not be convergent.
Example 2.3. (a) Consider the sequence {xn} in the usual metric space Q, where
Xl = 1.4
X2 = 1.41
X3 = 1.414
X4 = 1.4142
Xs = 1.41421
Then the sequence {xn} converges to V2. Hence {xn} is a Cauchy sequence. However,
it does not converge to a point of Q.
(b) Let X = (0,1] be a metric space with the usual metric and {xn = : n EN} be a
sequence inX. Then {xn} is a Cauchy sequence since for each E > 0, we have
1 1
d (xm,xn) = - - - < E
m n
1
for all m,n > -.
E
On other hand, X n -+ 0 f/:. X.
Remark 2.4. In Example 2.3 (b), if we consider X = [0,1], then the sequence
{!, 1, 1,'" } is Cauchy as well as convergent.
Theorem 2.5. Let (X, d) be a metric space and {xn} be a convergent sequence in
X such that X n -+ X as n -+ 00. If {x nk } is any subsequence of {x n }, then x nk -+ X as
k -+ 00.
Proof Since X n -+ X as n -+ 00, for each E > 0, there exists a positive integer N such
that d (xn,x) < for all n > N. Also, since every convergent sequence is Cauchy, we
have
d (xnk'X) < d (xnk,x n ) + d (xn,x)
E E
< 2 + 2 for all n,nk > N.
Hence x nk -+ X as k -+ 00.
2.2 Cauchy Sequences
39
Remark 2.5. Theorem 2.5 says that every subsequence of a convergent sequence is
convergent. However, if a subsequence of a sequence in a metric space (X, d) is con-
vergent, then the sequence itself need not be convergent.
Example 2.4. Consider the sequence {x n = ( -1)n : n E N} in with the usual met-
ric. Let {X2n} be a subsequence of the sequence {xn} given by
X2n = 1 for all n.
Then X2n -+ 1 as n -+ 00. However, {xn} is not a convergent sequence.
Theorem 2.6. Let {xn} be a Cauchy sequence in a metric space (X,d). Then the
sequence {xn} is convergent if and only if it has a convergent subsequence.
Proof. Let { x nk } be a convergent subsequence of the sequence {x n }. Suppose that
x nk -+ X as k -+ 00. Then for each E > 0, there exists a positive integer N such that
E
d (Xnk'X) < 2 for all nk > N.
Since {xn} is a Cauchy sequence, we have
E
d (Xnk,X n ) < 2 for all n,nk > N.
By the triangle inequality, we have
d (xn,x) < d (xn,x nk ) + d (Xnk'X)
E E
< - + - == E for all n > N.
2 2
Hence the sequence {xn} is convergent.
The converse part follows from Theorem 2.5.
Exercise 2.3. Consider the sequence {xn} in the usual metric space Q, where
Xl = 0.1, X2 = 0.101, X3 = 0.101001, X4 = 0.1010010001,....
Then prove that the sequence {xn} is Cauchy which does not converge to a point of
Q.
Exercise 2.4. Prove that every Cauchy sequence in a discrete metric space is conver-
gent.
Proof. Let (X, d) be a discrete metric space and {xn} be a Cauchy sequence in X.
Recall that the discrete metric d is defined by
{ 0 ifx=y
d(x,y) = 1 if X of y.
1
Let E = 2 ' Since {xn} is a Cauchy sequence, there exists a positive integer N such
that
40
2 Complete Metric Spaces
1
d (xn,xm) < - for all n, m > N.
2
From the definition of d, we have X n = X m for all n, m > N. In other words, {xn} is of
the form {Xl ,Xz,. . . ,XN ,X, X,.. .}. Hence X n -+ X as n -+ 00.
Exercise 2.5. Prove that every Cauchy sequence in a metric space is bounded.
Exercise 2.6. Let d and d* be two metrics on the same underlying set X and there
exist two real numbers KI , Kz > 0 such that
Kld(x,y) < d*(x,y) < Kzd(x,y) forallx,yEX.
Prove that the sequence {xn} is Cauchy (respectively, convergent) in (X,d) if and only
if it is Cauchy (respectively, convergent) in (X,d*).
Exercise 2.7. Let {xn} be a Cauchy sequence in a metric space (X, d) and {x nk } be a
subsequence of {x n }. Show that lim d (Xn,X nk ) = O.
n-+oo
Proof Let E > O. Since {xn} is a Cauchy sequence in¥, there exists a positive integer
N such that
d (xn,xm) < E for all n,m > N -1.
Now nN > N > N - 1 and therefore
d (XN,X nN ) < E.
In other words lim d (Xn,X nk ) = O.
n-+oo
Exercise 2.8. Let {xn} and {Yn} be sequences in a metric space (X,d) such that {Yn}
is Cauchy and d (Xn,Yn) -+ 0 as n -+ 00. Prove that
(a) {xn} is a Cauchy sequence in X;
(b) {xn} converges to X E X if and only if {Yn} converges to x.
Proof ( a) Let E > O. Since {Yn} is a Cauchy sequence, there exists a positive integer
N I such that
E
d(ym,Yn) < 3 forallm,n>N I .
Since d (Xn,Yn) ---+ 0 as n ---+ 00, there exists a positive integer Nz such that z < ; and
E
d (xn,Yn) < 3 for all n > Nz.
By the triangle inequality, we have
d (xm,xn) < d (xm,Ym) + d (Ym,Yn) + d (yn,xn).
Hence for all n, m > Nz, we have
E E
d (xm,xn) < 3 + d (Ym,Yn) + 3 '
2.2 Cauchy Sequences
41
Let No = max{Nl,Nz}. Then for all n,m > No, we have
E E E
d (xm,xn) < - + - + - = E.
333
Thus {xn} is a Cauchy sequence.
(b) By the triangle inequality, we have
d (yn,x) < d (Yn,x n ) + d (xn,x)
and hence
lim d (yn,x) < lim d (Yn,x n ) + lim d (xn,x).
n-+oo n-+oo n-+oo
But lim d (Yn,x n ) = 0 and if lim d (xn,x) = 0, we have lim d (yn,x) = 0'. Thus,Yn x
n-+oo n-+oo n-+ OO
as n 00.
Exercise 2.9. Let {xn} and {Yn} be Cauchy sequences in a metric space (X,d). Prove
that {d (xn,Yn)} is a Cauchy sequence.
Proof From Exercise 1.1, for any n,m E N we have
Id (Xn,Yn) - d (Xm,Ym) I < d (xn,xm) + d (yn,Ym).
Since {xn} and {Yn} are Cauchy sequences, for any given E > 0, there exist positive
integersN 1 andN z such that for any n,m > Nl we have
E
d (xn,xm) < 2 '
and for any n, m > Nz we have
E
d (Yn,Ym) < 2 '
SetN = max{Nl,N2}' Then for any n,m > N, we have
E E
Id (xn,Yn) - d (xm,Ym) I < d (xn,xm) + d (Yn,Ym) < 2 + 2 = E.
This implies that {d(xn,Yn)} is a Cauchy sequence in .
Exercise 2.10. Let (X, d) be a metric space and d* be another metric on X defined by
d*(x,y) = min{l,d(x,y)}.
Show that {xn} is a Cauchy sequence in (X,d) if and only if it is a Cauchy sequence
in (X,d*).
Exercise 2.11. Let X = C[O, 1] be a metric space with the following metric
[ 1 ] 1/2
d2 (f,g) = 1 1 !(t) - g(t)12
for all f,g E X and for all t E [0,1].
Show that the sequence {In} defined by
42
2 Complete Metric Spaces
fn(t) = { -nt
ifO<t<!
- - n
if < t < 1,
is Cauchy with respect to the metric dz but not Cauchy with respect to the metric d oo .
Hint:
[ 1 1 ] z
d2(fn,fm) = In(n-m)2t 2 dt+ hm(1-mt)2dt
= [ ! ( ! _ 2 + m )]
3 m n n Z
and
m
doo(fn,fm) = sup Ifn(t)-fm(t)I=1--.
O t l n
2.3 Complete Metric Spaces
Definition 2.6. A metric space (X, d) is said to be complete if every Cauchy sequence
in X converges to a point in X.
Remark 2.6. In view of Theorem 2.6, a metric space (X, d) is complete if and only if
every Cauchy sequence in X has a convergent subsequence.
Example 2.5. (a) The usual metric spaces and C are complete.
(b) The set of integer Z with the usual metric is a complete metric space.
Verification. Let {xn} be a Cauchy sequence of integers, that is, each term of the
sequence belongs to Z = {. . . , - 2, -1,0, 1,2, . . .}. Then the sequence must be of the
form {Xl,XZ,X3,..., xn,x,x,x,...}. Indeed, if we choose E = !, then
1
Xn,X m E Z and IXn -xml < 2 implies X n =X m .
Hence the sequence {Xl,XZ"" ,xn,x,x,x,...} converges to x.
(c) The Euclidean space n with the usual metric
1
d(x,y) = ( 1 (Xk - Yk)2)
for all x = (Xl ,Xz,.. . ,x n ) and y = (Y1 ,YZ,. . . ,Yn) in n, is a complete metric space.
Verification. Let {x(m)} be a Cauchy sequence in R n , where x(m) = (xl m ) ,x m) ,
(m) ) . (1) ( (1) (1) (1) ) (Z) ( (Z) (Z) (Z) ) d
. . . ,X n , that IS, x = xl ,Xz ,... ,X n , X = Xl ,Xz ,... ,X n an so on.
Then for each E > 0, there exists a positive integer N such that
2.3 Complete Metric Spaces
43
d(x(m),x(p)) = [ (xim)-xf))2f <£ forallm,p>N.
On squaring both the sides, we get
n 2 2
(xi m ) -xf)) < £2:::} (xi m ) -xf)) < £2:::} Ixim) -xf) 1 < £
for all m,p > N and all k = 1,2,... ,n.
It follows that for each fixed k (1 < k < n), the sequence { xlm) } is a Cauchy
mEN
sequence in the usual metric space . Since is complete, it converges to some point
. 1D> (m) . . (m) (m)
In . Let x k --+ Xk as m --+ 00 for each k = 1,2,..., n, that IS, xl --+ XI,X 2 --+
X2,.. . ,x m) ---+ x n . Then for each k = 1,2,... ,n, Ixim) - Xk 1---+ 0 as m ---+ 00. Let x =
(Xl ,X2,'" ,x n ), then clearly X E n and hence
[ n 2 ]
d(x(m),x)= (Xim)-Xk) ---+0
as m --+ 00.
Therefor, x(m) ---+ X as m ---+ 00, and thus the sequence {x(m) } is convergent. Hence, Rn
is complete.
(d) The unitary space en is a complete metric space.
Example 2.6. By Exercise 2.4, every Cauchy sequence is convergent in a discrete met-
ric space and hence every discrete metric space is complete.
Example 2.7. The space fP (1 < p < 00) of all sequences {xn} of real or complex
00
numbers such that IXklP < 00 with the metric
k=l
1
dp(X,y) = Ct IXk - Ykl P ) P for all x = {xn},y = {Yn} E fP
is a complete metric space.
Verification. Let {x(m)} mEN be a Cauchy sequence in fP, where x(m) = {x m),
x m),... } = { xlm) } , such that I xlm) I p < 00 for all m = 1,2,.... Then for each
kEN k= I
E > 0, there exists a positive integer N such that
1
d p (x(m) ,x(n)) = ( 1 jxim) - xi n ) I P ) P < £ for all m, n > N (2.1)
and thus
jxim) -xi n ) I < £ for all m,n > N and for all k = 1,2,....
44
2 Complete Metric Spaces
This implies that for each fixed k (1 < k < 00), { xim) } is a Cauchy sequence in OC
mEN
(= or C). Since]I{ is complete, it converges in]I{. Let xi m ) Xk as m 00 for all k.
Using these limits, we define x = (Xl ,x2, . . .) and show that X E fP and x(m) x.
From (2.1), we have
I
jxim) -xi n ) I P < £P for all m,n > N and for any I = 1,2,....
Letting n 00, we obtain
lIXim) -xklP < £P for all m > N and for any I = 1,2,....
The sequence { f jxim) -XkIP } is a monotonically increasing sequence which is
k=l 1 1
bounded above and therefore has a finite limit I xim) -xk I P, which is less than or
k=l
equal to E p. Therefore,
ljxim) -XkIP < £P for all m > N.
(2.2)
By Minkowski inequality (Theorem A.4), we have
( 00 ) l/ P ( 00 ) l/ P ( 00 ) l/ P
llxklP < Ixim) -XkI P + jxim)I P .
Thus x E fP. Moreover, from inequality (2.2), we obtain
d p (x(m),x) < £ for all m > N
which implies that x(m) X in fP. Hence fP (1 < P < 00) is complete.
Example 2.8. The space of all bounded sequences r = { {Xk} C l[{ = IR. or C :
sup IXkl < oo} with the metricd(x,y) = sup IXk-Ykl, where X = {Xk},Y= {Yk} E
l k<oo l k<oo
foo, is a complete metric space.
Verification. Let {x(m)} mEN be a Cauchy sequence in r, where x(m) = {x m),
x m),.. . } = { xim) } , such that sup I xim) I p < 00 for all m = 1,2,.... Then for
kEN l k<oo
each E > 0, there exists a positive integer N such that
d (x(m) ,x(n») = sup Ixi m ) -xinr < £ for all m,n > N
1 k< 00
and thus
2.3 Complete Metric Spaces 45
Ixi m ) - xi n ) I < £ for all m,n > N and for all k = 1,2,.... (2.3)
This implies that for each fixed k (1 < k < 00), { xim) } is a Cauchy sequence in
mEN
]I{. Since ]I{ is complete, it converges in ]I{. Let xi m ) xk as m -+ 00 for all k. Using
these limits, we define x = (Xl ,x2, . . .) and show that X E foo and x(m) -+ x.
Letting n -+ 00 in (2.3), we obtain
Ixim) -xkl < £ for all m > N and for any k = 1,2,.... (2.4)
Since x(m) = {xi m ) } kEN E faJ, there is a real number N m such that Ixi m ) I < N m for all
k. Therefore,
IXkl = IXk-xi m ) +xi m ) I < Ixim)-xkl+lxk'i
< E+N m forallm>Nandforallk=1,2,....
This inequality is true for each k and the right hand side is independent of k, it follows
that {Xk} is a bounded sequence of numbers and hence X = {Xk} E f oo .
From (2.4), we obtain
d(x(m),x) = sup jxi m)-xk l < E forallm>N,
1 k < 00
and therefore, x(m) -+ X in f oo . Hence foo is complete.
Example 2.9. The space C[a, b] of all continuous real-valued functions defined on
[a, b] with the metric
doo(/,g) = max I/(t) - g(t)1
tE [a,b]
is a complete metric space.
Verification. Let {/m}mEN be a Cauchy sequence in C[a,b]. Then for each E > 0,
there exists a positive integer N such that
doo (1m, In) = max I/m(t) - In(t)1 < E for all m,n >N. (2.5)
tE [a,b]
Then for any fixed to E [a, b], we have
Ifm(to) - In (to) I < E for all m,n > N.
Therefore, {1m (to) } is a Cauchy sequence in IR. Since IR is complete, this sequence
converges. Let 1m (to) -+ I(to) as m -+ 00. In this way, we can associate to each t E [a, b]
a unique real number f(t). Thus we have defined a function I with domain [a, b]. Now,
we show that f E C[a,b] and 1m -+ f.
From (2.5), we obtain
Ifm(t) - fn(t)1 < E for all m,n > N and for all t E [a,b].
Letting n -+ 00, we obtain
46
2 Complete Metric Spaces
Ifm(t) - f(t)1 < E for all m > N and for all t E [a,b]. (2.6)
To show that f is continuous, we consider any to E [a, b] and any 11 > O. According to
the preceding paragraph, there exists a positive integer Nt ( 11) such that
Ifm(t) - f(t)1 < 11 for all m > Nt (11) and for all t E [a,b].
3
Let n > Nt (11). Then
Ifn(t) - f(t) I < 11 for all t E [a, b].
3
(2.7)
By continuity of fn, we obtain D > 0 such that
11
Ifn(t) - fn(to) I <"3 whenever It - tol < D
Then from (2.7) and (2.8), we have
(2.8)
If(t) - f(to) I < If(t) - fn(t)1 + Ifn(t) - fn(to) I + Ifn(to) - f(to) 1
< 11 + 11 + 11 =11
333
whenever It - to I < D. Therefore, f E C[a, b].
Moreover, from (2.6), we have
max Ifm(t) - f(t)1 < E for all m > N.
tE [a,b]
Thus doo(fm,f) < E for all m > N, and therefore, fm -+ f as m -+ 00. Hence C[a,b] is
a complete metric space.
Example 2.10. The space C[O, 1] is not complete with respect to the metric
d 1 (f,g) = 1 1If (t) - g(t)ldt for all f,g E C[O, 1].
Verification. Let {fn}n 2 be a sequence in C[O, 1], defined by
o
fn(t)= nt-!n+l
1
ifO<t< 1-1
- - 2 n
. f 1 1 < 1
1 ---<t -
2 n - 2
if ! < t < 1.
We claim that {fn}n 2 is a Cauchy sequence but does not converge in (C[O,I],dt).
Indeed,
2.3 Complete Metric Spaces
47
d (fm,!n) = fo 1Ifn (t) - fm(t)ldt
1 1
< h fm(t)dt+ h k fn(t)dt
=! ( !+ 1 ) .
2 m n
Thus, d 1 (fn,!m) < ! + ! < £ for all n,m > N, where N is a positive integer such
n m
thatN > . This shows that {In} is a Cauchy sequence. The measure dl (In, 1m) is the
area of the triangle in the following figure.
1
.... - - '!... - ....
I
1
1
1
...... - - '!.. - ....I
I
J.
I
I
I
I
I
1m I
I
I
I
In
t
t
1 1
2-n
1
2
1 1 1 1 1
2-n 2- m 2
dl (In, 1m) represents the area of the shaded triangle
Suppose that there is a function I E C[O, 1] such that d 1 (In, I) O. But
1 1 1 1
dl (fn,!) = fo'rn If(t)ldt+ h k Ifn(t) - f(t)ldt+ h 11- f(t)ldt. (2.9)
Since the integrands are non-negative, so is the each integral on the right hand side of
(2.9). Since d 1 (In, I) 0 as n 00, we have
1 1
lim ('rn If(t)ldt = 0 and fll1_ f(t)ldt = O.
n ooJo J!
2
Since I is continuous, we have
f(t) = {
ifO < t<!
if ! < t < 1.
Therefore, I is not continuous which contradicts to our supposition that I is a contin-
uous function. Hence C[O, 1] is not complete.
Example 2.11. The space of all rational numbers Q with the usual metric of absolute
value is not complete.
48 2 Complete Metric Spaces
Verification. Let X = Q be the set of all rational numbers and
d(x,y) = Ix-yl forallx,y EX
be the usual metric on X. Choose a sequence {x n }, represented in the decimal system,
such that X n = 1.al a2 . . . an is the largest rational number satisfying < 2. Then we
have the sequence of numbers
Xl = 1.4, X2 = 1.41, X3 = 1.414, X4 = 1.4142, Xs == 1.41421,....
We find that
1
d (xm,xn) = IXn -xml == 0.00.. .Oam+l .. .a n < 10m for all n > m.
Therefore, we conclude that d (xm,xn) 0 as m 00. So, {xn} is a Cauchy sequence.
But this sequence converges to the irrational number V2 Q. Thus {xn} does not
have a limit point in Q and so Q is not complete.
Example 2.12. Let X = (0,1] and d be the usual metric onX. Then (X,d) is not com-
plete as the sequence {Xn = : n E N} C X is Cauchy but X n 0 X.
Exercise 2.12. Prove or disprove that jRn is a complete metric space with respect to
the following metrics: For all x = (Xl ,X2,. .. ,x n ) and y = (Y1 ,Y2,.. . ,Yn) E n,
n
(a) d l (x,y) = IXk - Ykl;
k=l
( n ) l/p
(b) dp(x,y) = k llxk - Ykl P for all p > 1;
(c) doo(x,y) = max IXk - Ykl.
I <.5:k<.5:n
Proof. (c) For any real numbersX1,X2,... ,X n , we have
( ) 1/2 ( ) 1/2
j1 xi < IXkl < n l nlxkl < n xi ·
(2.10)
Indeed, the first inequality follows on squaring both the sides. The second one is
obvious. The third inequality is a consequence of the fact that
( ) 1/2
j1 xi > IXkl
k = 1,2, . . . , n.
Let X = (Xl ,X2,. . . ,x n ) E n and y = (Y1 ,Y2,. .. ,Yn) E n. From inequality (2.10),
we have
( (Xk - Yk)2 ) 1/2 < IXk - Ykl < n l : n IXk - Ykl < n (j1 (Xk _ Yk)2) 1/2 .
(2.11 )
2.3 Complete Metric Spaces
49
From inequality (2.11), we observe that a sequence in n is Cauchy (respectively,
convergent) with respect to one of these metrics if and only if it is Cauchy (respec-
tively, convergent) with respect to the other metric. Since n is complete with respect
to the metric
( ) 1/2
d(x,y) = (Xk - Yk)2 ,
it is also complete with respect to the metric d oo .
Exercise 2.13. Prove that [0, 1) as a subspace of the discrete metric space is com-
plete.
Exercise 2.14. Prove that the space of all natural numbers N with the metric
1 1
d(x,y) = --- forallx,yEN,
x y
is not complete
Proof Let {n}n 1 be a sequence in N. Let E > 0 and N be the least integer greater
than . Ifm,n >N, then
d(m,n)= - < max { !,! } <!<E.
m n mn N
Thus, the sequence {n}n 1 is Cauchy. Suppose contrary that the sequence {n}n 1
converges to some point pEN. Let N 1 De any integer greater than 2p. Then n > N 1
implies that
11 11 1 1 1 1 1
d(p,n)= --- ---->--->-----
p n - p n - p Nl P 2p - 2p .
This shows that the sequence {n}n 1 cannot converge to p, a contradiction of our
supposition. Hence (N, d) is not complete.
Exercise 2.15. Let X = and d : X x X be defined by
d(x,y) = Ix-yl forallx,yEX.
v I +x 2 y' 1 +y2
Show that (X, d) is a metric space but not complete.
Proof We only give the proof of incompleteness. Consider the sequence {n}n 1 of
natural numbers. Observe that
d(n m) = In-ml _ I - I
, v I +n 2 v l +m2 !""1+1 f1+1
V "ii!T V i1i!T
1 1 1 1
< - - - < - + - 0 as n,m 00.
n m n m
50
2 Complete Metric Spaces
Thus {n}n l is a Cauchy sequence in (X,d). Suppose contrary that the sequence
{n }n l converges to some point P E . Then
I n P I 1 1 - E n I
d(n,p) = -
V 1+n 2 v 1+p2 J1+ V 1+p2
1
-+ =1= 0 as n -+ 00.
V I + p2
This shows that the sequence {n} n 1 does not converge to p E IR, a contradiction.
Hence (X, d) is not complete.
Exercise 2.16. Prove that the metric space P[a, b] of all polynomials defined on [a, b]
with the uniform metric
doo(f,g) = max If(t) - g(t)1 for all f,g E P[a,b]
tE [a,b]
is not complete.
Proof Let us take a = 0 and b = 1. Consider the following sequence
n ( t ) k t t n
/n(t) = o 2 =1+ 2 +."+ 2n foralltE[O,1].
Clearly, fn(t) E P[O, 1] for each n E N. We show that the sequence {fn} is Cauchy.
Taking m < n and observe that
d(fn,fm) = max Ifn(t) - fm(t)1
O t l
n ( t ) k m ( t ) k
-max - - -
- 09$1 o 2 o 2
_ max ( ) k
- O t l k=f:+l 2
n 1
<max ): k
- O t l k=m+12
1 1
2 m 2 n
This difference is arbitrarily small for large enough m and n, which implies that {fn} is
a Cauchy sequence in P[O, 1]. However, this sequence does not converge in (P[O, 1], d),
because lim /n(t) = for all 0 < t < 1, is not a polynomial. Therefore, (P[O, 1],d)
n-+oo 2 - t
is not complete.
Theorem 2.7. Let (Y, dy) be a subspace of a metric space (X, d). If Y is complete,
then it is closed.
Proof Suppose that Y is a complete subspace. To prove Y is closed, it is sufficient to
show that Y contains all its limit points.
2.3 Complete Metric Spaces
51
Let x be a limit point of Y. Then by Theorem 2.3, there exists a sequence {x n } of
distinct points of Y which converges to x. Since each convergent sequence is Cauchy,
it is a Cauchy sequence. Also since Y is complete, the limit point x of this sequence
must lie in Y. Thus Y is closed.
Theorem 2.8. Let (X, d) be a complete metric space and (Y, dy) be a subspace of
(X, d). Then Y is complete if and only if it is closed.
Proof IfY is a complete subspace of (X,d), then by Theorem 2.7, it is closed.
Conversely, assume that Y is a closed subspace of a complete metric space X.
Let {x n } be a Cauchy sequence of points of Y. Since X is complete, this sequence
converges to a point x belonging to X. By Theorem 2.3 (ii) and since Y is closed,
x E Y. Thus each Cauchy sequence of point of Y converges to a points of Y. Hence Y
is complete.
Theorem 2.9 (Cantor's Intersection Theorem). Let (X,d) be a complete metric
space and let {Fn} be a decreasing sequence (that is, Fn+l C Fn) of non empty closed
00
subsets of X such that fJ(F n ) -+ 0 as n -+ 00. Then the intersection n Fn contains
n=l
exactly one point.
Proof Construct a sequence {x n } in X by selecting a point X n E Fn for each n E N.
Since Fn+l C Fn for all n, we have X n E Fn C Fm for all n > m. We claim that {xn} is
a Cauchy sequence.
Let E > 0 be given. Since fJ (Fn) -+ 0, there exists a positive integer N such that
fJ(F n ) < E. Since {Fn} is a decreasing sequence, we haveFm, Fn C FN for all m,n > N.
Therefore, X n , X m E F N for all n, m > N and thus, we have
d (xn,xm) < fJ (Fn) < E for all n, m > N.
Hence {Xn} is a Cauchy sequence. Since X is complete, there exists x E X such that
00
X n -+ x. We claim that x E n Fn.
n=l
Let n be fixed. Then the subsequence {X n ,X n +l,"'} of the sequence {xn} is con-
tained is Fn and still converges to x, since every subsequence of a convergent sequence
is convergent. But Fn being a closed subspace of the complete metric space (X,d), it
00
is complete and so x E Fn. This is true for each n E N. Hence x E n Fn, that is,
n=l
00
n Fn # 0.
n=l
00 00
Finally, to establish that x is the only point in the intersection n Fn. Let yEn Fn.
n=l n=l
Then x and y both are in Fn for each n. Therefore,
o < d(x,y) < fJ(F n ) -+ 0 as n -+ 00.
Thus d(x,y) = 0 and hence x = y.
Remark 2.7. The assertion in Theorem 2.9 may not be true if either of the conditions
(i) each Fn is closed
52
2 Complete Metric Spaces
(ii) 6 (Fn) -+ 0 as n -+ 00
is dropped.
Example 2.13. (a) Consider the sequence {Fn}, where Fn = [n,oo) for all n E N, of
nonempty closed subsets of the usual metric space which, of course, is complete.
00
Then 6 (Fn) -ft 0 as n -+ 00 and n Fn = 0.
n=l
(b) Consider the sequence {Fn}, where Fn = (O, ) for all n E N, of non empty subsets
of the usual metric space IR. Then for each n EN, Fn is open but not closed, Fn+ 1 C Fn,
00
6 (Fn) -+ 0 as n -+ 00 and n Fn = 0.
n=l
Now, we have the converse of Theorem 2.9.
Theorem 2.10. Let (X, d) be a metric space. If every decreasing sequence {Fn} of
nonempty closed sets in X with 6(Fn) -+ 0 as n -+ 00 has exactly one point in its
intersection, then (X, d) is complete.
Proof Let {xn} be a Cauchy sequence inX. Let
Gl = {Xl,X2,"'},
G2 = {X2,X3,...},
G n = {X n ,X n +l,"'}.
Then G n +l C G n and so G n +l C G n for all n E N. Therefore, { G n } is a decreasing
sequence of non empty closed sets. Since {xn} is a Cauchy sequence, for a given E > 0,
there exists a positive integer N such that
d (xm,xn) < E for all m,n > N.
Since m,n > N, we have Xm,X n E GN and since d (xm,xn) < E, we have 6 (GN) < E.
For n > N, we have G n C GN and thus 6 (G n ) < 6(GN) < E. Therefore, 6 (G n ) -+ 0 as
n -+ 00.
Since 6(G n ) = 6( G n ), we have 6( G n ) -+ 0 as n -+ 00. Taking Fn = G n , then {Fn}
is a decreasing sequence of nonempty closed sets with 6(Fn) -+ 0 as n -+ 00. Then
00
by hypothesis, there exists an x E X such that x E n Fn. Therefore, d (x,xn) < 6 (Fn)
n=l
for all n and so d(x,xn) < 6 (Fn) -+ 0 as n -+ 00. Hencex n -+x inX. Thus, (X,d) is
complete.
Exercise 2.17. Let (X,d) be a complete metric space and {Gn}nEN be a sequence of
open subsets ofX. Then prove that
int ( n cl Gn ) = int cl ( n Gn ) .
nEN nEN
(2.12)
2.4 Completion
53
Proof Since n cl G n :) cl ( n Gn ) , it is obvious that
nEN nEN
int ( n cl Gn ) :) int cl ( n Gn ) .
nEN nEN
(2.13)
We show the converse of inclusion (2.13). Let x E int ( n cl Gn ) and r > O.
. nEN
Take Xl = x. Then there exists rl E (0, r) such that Sri [Xl] c n cl G n and there-
nEN
fore, Sri [Xl] C cl G n for each n E N. It follows that Sri (Xl) nGl is an open nonempty
set. Therefore, there exist Xz E X and rz E (0, 1-] such that Sr2 [xz] C Sri (Xl) n GI. It
follows that Sr2 [xz] C Sri [Xl] C cl Gz, and so Sr2 (xz) n Gz is an open nonempty set.
Continuing in this way, we find the sequences {Xn}nEN C X and {rn}nEN C (0,00)
such that r n 0 as n 00, and Srn+1 [X n +l] C Srn (xn) n G n for all n. In particular,
Srn+1 [x n + 1] C Sr n [xn] for all . Since X is a complete metric space, by Cantor's Inter-
section Theorem 2.9, n Srn [xn] = {x} for some x EX. It follows that x E G n for all
nEN
n. Since x E Sri [Xl] <;: Sr(X), we have that Sr(x) n ( n Gn ) =1= 0. As r > 0 is arbitrary,
nEN
X E cl ( n Gn ) · Therefore, int ( n cl Gn ) C cl ( n Gn ) ·
nEN nEN nEN
Exercise 2.18. Let (X, d) be a complete metric space and {Fn} nEN be a sequence of
closed subsets of X. Then prove that
cl ( U int Fn ) = cl int ( U Fn ) .
nEN nEN
(2.14 )
Proof It follows directly from Exercise 2.17 by taking G n =X \Fn for all n E N.
2.4 Completion
If a metric space (X, d) is not complete, then it is always possible to construct a
complete metric space which contains this incomplete metric space and some other
points so that every Cauchy sequence in X has a limit point in the larger space. In fact,
we need to adjoin new points to (X, d) and extend d to all these new points in such a
way that the formerly nonconvergent Cauchy sequences find limits auwng these new
points and the new points are limits of sequences in X.
Definition 2.7. Let (X,d) be a metric space. A complete metric space (X* ,d*) is said
to be a completion of the metric space (X, d) if X is a subspace of X* and every point
of X* is the limit of some sequence in X.
54
2 Complete Metric Spaces
Example 2.14. (a) The completion of the space Q of all rational numbers with the
usual metric is the space of all real numbers with the usual metric.
(b) Let X = (0,1), (0,1] or [0,1). The completion of the metric space X with the usual
metric is the metric space [0,1] with the usual metric. '
Definition 2.8. Let (X, d) and (X*, d*) be two metric spaces.
. A mapping f : X -+ X* is said to be an isometry if
d*(f(x), f(y)) = d(x,y) for all x,y EX.
The mapping f-is also called an isometric embedding of X into X* .
. The spaces X and X* are said to be isometric if there exists a bijective isometry
from X to X* .
Remark 2.8. We note that every isometry is always one-to-one.
Theorem 2.11. Every metric space has a completion.
Theorem 2.12. All completions of a metric space are isometric.
Proof Let (X* , d*) and (X**, d**) be any two completions of the metric space (X, d).
Let x* E X* be arbitrary. By the definition of completion, there exists a sequence
{x n } nEN in X such that X n -+ x*. The sequence {x n } nEN may be assumed to belong to
X** . Since X** is complete, {x n } nEN converges in X** to x** , say. Define f : X* -+ X**
by f(x*) = x**. It is clear that the mapping f is one-to-one and does not depend
on the choice of the sequence {x n } nEN converges to x*. Moreover, by construction,
f(x) = x for all x EX. If X n -+ x* E X* and X n -+ x** E X** while Yn -+ y* E X* and
Yn -+ y** E X**, then
d* (x* ,y*) = lim d (xn,Yn) and d** (x** ,y**) = lim d (xn,Yn).
n-+oo n-+oo
Thus
d**(f(x*),f(Y*)) =d(x*,y*) forallx*,y* EX*.
Hence f is an isometry. Thus (X* , d*) and (X**, d**) are isometric.
Chapter 3
Separable Spaces
It is well known that the rational numbers or irrational numbers are densely packed
along the real line. This phenomenon can be characterized in terms of distance by
saying that every point of JR is zero distance from the set of rational numbers Q or
from the/ set of irrational numbers JR \ Q. The c once pt of closure enabled us to write
this density property by the formula Q = or \ Q = . In this chapter, we extend
the idea of density to an arbitrary metric space. We given some other properties of a
metric space, known as topological properties, such as countability, separability and
Baire's category theorem.
3.1 Countability
Definition 3.1. Let 0 be the family of all open subsets of a metric space X. A sub-
family fA C 0 of open subsets of X is said to be a base or basis for 0 if every open
set G E 0 is the union of members of fA.
Further, if the subfamily fA is countable, then it is called countable base or count-
able basis for O.
Before giving the examples of a base for a family of open sets, we mention the
following characterization of a base.
Theorem 3.1. Let 0 be the family of all open subsets of a metric space X. A subfamily
fA C 0 is a base for 0 if and only if for every point x belonging to an open set G,
there exists Bx E fA such that x E Bx C G.
Proof Let fA be a base for 0 and G be any open set in X, that is, G E 0. Then
by definition, G is the union of members of fA. Let x E G. Since G in the union of
members of fA, there exists a set B x in fA such that x E B x C G.
Conversely, let G be any arbitrary open set. Then by hypothesis, for any point
x E G, there exists Bx in fA such that x E Bx C G. Clearly, G = U{Bx E fA : x E G}.
Then every open set is the union of members of fA.
Example3.1. (a) The collection fA = {(a, b) : a,b E JR} of all open intervals forms a
base for the family of all open sets in the usual metric space JR.
If the endpoints a and b are rational, then the collection fA = {(a, b) : a, b E Q} of
all open intervals forms a countable base for the family of all open sets in the usual
metric space JR.
(b) Let X be a metric space. The collection {Srx(x) : x E X and r x > O} of all open
spheres forms a base for the family of all open sets inX.
Indeed, let G be a nonempty open subset of X and let x E G. By the definition of
an open set, there exists r x > 0 (depending on x) such that x E Srx(x) C G.
56
3 Separable Spaces
(c) Let X = jRn be a metric space with the metric
( ) lip
dp(x,y) = IXi - Yil P
for all p > 1,
where x = (Xl ,Xz,. . . ,x n ) and Y = (YI ,Yz,. . . ,Yn) in n. Let r > 0 be a rational number.
The collection {Sr(x) : X = (Xl ,Xz,... ,x n ) where Xi is rational for all i = 1,2,...,n} of
all spheres with rational centers and rational radii is a countable base for the family
of all open sets of X.
(d) Let X be a discrete metric space. Then the collection = {{x} : X E X} forms
a base for the family of all open subsets of X since every subset of a discrete metric
.
space IS open.
If X is countable, then the family is also countable. In this case, is a countable
base for the family of all open subsets of X.
Definition 3.2. A metric space X is said to be a second countable space (or second
axiom space) if there exists a countable base for the family of all open subsets of X.
Example 3.2. (a) In view Of Example 3.1 (a), the collection of all open intervals (a, b)
with a and b as rational points forms a countable base for the family of all open subsets
of . Hence the usual metric space is a second countable space.
(b) Let X = n be a metric space with the metric
( ) lip
dp(x,y) = I IXi - Yil P
for all p > 1,
where x = (Xl ,Xz,. . . ,x n ) and y = (Yl ,Yz,.. . ,Yn) in n. In view of Example 3.1 (c),
(X, d p) is a second countable space.
(c) In view of Example 3.1 (d), the discrete metric space X is second countable if X
is countable.
Definition 3.3. A metric space X is said to be a first countable space (or first ax-
iom space) if for every point X E X, there exists a countable family {Bn(x)} of open
sets containing X such that every open set G containing x also contains a member of
{Bn(x)}, that is, Bn(x) C G for some n.
Example 3.3. The usual metric space is a first countable space. Indeed, we may take
Bn(x) = (x- ,X+ ) for each X E and n E N.
Remark 3.1. Every second countable metric space is first countable but converse is
not true.
Example 3.4. Let X be a discrete metric space, where X is an uncountable set. Then
X is first countable but not second countable.
Indeed, any open sphere Sl/z(x) is a singleton set {x} because X is a discrete metric
space. Therefore, {Sl/n(X)} :=1 is the countable family of open sets containing X such
that every open set G containing x also contains a member of {Sl/n(x) } :=1 because
Sl/n(x) = {x} for all n = 1,2,.... Hence X is a first countable space.
3.2 Dense Sets
57
If X is uncountable, then the singleton sets {x} are also uncountable. Hence every
base is uncountable. Consequently, X is not second countable when it is uncountable.
Theorem 3.2. Every metric space X is a first countable space.
Proof Let x E X and n E N. Set Bn(x) = Sl/n(X). Then {Bn(x)} = {Bl(X),B1/Z(x),
B 1 / 3 (X),...} is a countable collection of open subsets of X such that every member of
this collection contains x. Let G be an open set containing x. Then there exists S e (x)
such that Se(x) C G for some E > O. Therefore, Bn(x) = Sl/n(X) C Se(x) C G for each
n > and hence X is a first countable space.
Exercise 3.1. Let (X, d) be a metric space and Y be a nonempty subset of X. If (X, d)
is second countable, then prove that (Y, dy) is also second countable.
Proof Let fA = {Bn : n E N} be a countable base for the family 0 of all open subsets
of X. Then fA* = {Bn nY: n E N} is countable. We claim that fA* is a base for the
family f# of all open subsets of Y.
Let G be an open set in Y and let x E G. Then there exists an open set 0 in X such
that G = 0 n Y. Also, x EOn Y and so x E 0 and x E Y. Since 0 E 0, there exists a
Bno E fA such that x E Bno C O. Since x E Y, we have x E Bno nY C OnY = G. But
Bno n Y E fA*. Therefore, fA* forms a base for f#. Hence (Y, dy) is second countable.
Exercise 3.2. Let (X, d) be a metric space and Y be a nonempty subset of X. If (X, d)
is first countable, is so (Y, dy)? Justify your answer.
Exercise 3.3. Let X = z be the usual metric space, x = (XI'XZ) E X be any arbitrary
element and GA, (x) = {y = (YI,YZ) E z : (YI -XI)Z + 3(yz -xz)Z < A }, where A >
o. Prove that the family {GA, (x) : A > 0 and x E X} is a base for the family of all open
subsets of X.
Proof Let G be any open set in X and let x E G. Then there exists r > 0 such that
Sr(x) C G. We know that Sr(x) = {y = (Yl,YZ) EX: (YI -XI)Z + (yz - Xz)Z < r}. Let
A = r Z . If Y E GA,(x), then (YI -XI)Z +3(yz -xz)Z < A which implies that (YI-
XI)Z + (yz -xz)Z < A = r Z . Therefore,y E Sr(x) and so y E GA, (x) C Sr(x) C G. Hence
{GA, (x) : A > 0 and x E X} is a base for the family of all open subsets of X.
3.2 Dense Sets
Definition 3.4. A nonempty subset A of a metric space X is said to be dense (or ev-
erywhere dense) in X if A = X, that is, i every point of X is either a point or a limit
point of A.
In other words, a set A is dense /jn X if for any given point x EX, there exists a
sequence of points of A that converges to x.
Before giving the examples of dense sets, we provide a criteria for being dense.
Theorem 3.3. Let A be a nonempty subset of a metric space X. The following state-
ments are equivalent.
58
3 Separable Spaces
(a) For every x EX, p(x,A) = O.
(b) A =X.
(c) A has nonempty intersection with every nonempty open subset of X.
Proof The equivalence of (a) and (b) directly follows from Theorem 1.5. We prove
the equivalence of (b) and (c).
(b) =* (c). Suppose contrary that there exists a nonempty open subset 0 of X such that
A no = 0. Then A C OC and so A C oc = OC because OC is closed. Therefore, A C OC
whence A no = 0 and thus A =1= X, a contradiction of (b). Hence (c) holds.
(c) =* (b). Suppose that (c) holds but (b) does not, that is, A =1= X. Then (A)c =1= 0.
Since A is a closed set, (A ) C is an open set in X and disjoint from A, that is, (A) C n
A = 0. Since (A )C is nonempty open subset of X, by hypothesis, (A )C nA =1= 0, a
contradiction. Hence A =X.
Remark 3.2. It can be easily seen that a subset A of X is dense if and only if A C has
empty interior.
Example 3.5. (a) The set of all rational numbers Q is dense in the usual metric space
since Q = .
(b) Since \ Q = , the set of all irrational numbers \ Q is dense in the usual metric
space .
(c) The setA = {a + ib E C : a,b E Q} is dense in C since A = C.
(d) The set Qn = Q x Q x . . . x Q is dense in n with the usual metric.
"V"
n times
(e) The set
A = {x = (a t , a 2, . . . , an, 0, 0, . . .) : ai E Q for all 1 < i < nand n E N}
is dense in the space fP, 1 < p < 00, with the following metric
( 00 ) l/P
dp(x,y) = IXi - Yil P ,
where x = {Xt,X2,...} andy= {Yt,Y2,...} in fP.
Indeed, we have to show that A = fP. Let x = {Xt,X2,...} E fP be an arbitrary
element and let e > 0 be given. Then there exists a positive integer N such that
00 e P
IXil P < -.
i=tt+ t 2
Since Q is dense in IR, for every real number, there is a rational number which is as
close to it as we wish. Consequently, we can choose an elementy = (at,a2,... ,aN ,0,0,
. ..) E A such that
N e P
}: IXi-ail P < 2'
1=1
Hence
3.2 Dense Sets
59
00
[d(x,y)]P = IXi - ail P
1=1
N 00
= IXi - ail P + i=f+1lxiIP
EP EP
< -+- =E P
22'
and this implies that
d(x,y) < E.
It means that the distance from x E fP to A is zero. By Theorem 3.3, A is dense in fP.
(f) The set P[a, b] of all polynomials defined on [a, b] with rational coefficients is
dense in C[a, b].
Indeed, let f E C[a,b]. By Weierstrass's Theorem (Theorem A.6), there exists a
sequence {Pn} of polynomials with real coefficients that converges uniformly to f on
[a, b], that is, for each E > 0, there exists a positive integer N such that for all t E [a, b]
Ipn(t) - f(t)1 < E whenever n >N
and so doo (Pn, f) < E for all n > N. But any polynomial can be uniformly approx-
imated by a polynomial with rational coefficients since Q is dense in . Therefore,
corresponding to the sequence {Pn}, there exists a sequence { qn} of polynomials with
rational coefficients (that is, {qn} E P[a, b]) such that
1
IPn(t) - qn(t) I < - for all t E [a, b].
n
This implies that
1
doo(pn,qn) = sup IPn(t) - qn(t) I < - for all n = 1,2,....
tE [a,b] n
By the triangle inequality, we have
doo(f,qn) < doo(f,Pn) +doo(pn,qn) -+ 0 as n -+ 00.
Hence qn -+ f E C[a, b] as n -+ 00 and thus P[a, b] = C[a, b].
(g) Let (X, d) be a discrete metric space. Since every subset of X is closed, the only
dense subset of X is itself.
(h) By the definition of a completion, every metric space is dense in its completion.
Theorem 3.4. Let {G n } be a sequence of dense open sets in a complete metric space
00 /
X. Then n G n is also dense in X.
n=l
Proof. Let S be any open sphere in X. In view of Theorem 3.3, it is sufficient to
show that ([1 Gn) ns -I- 0. Since each G n is dense in X, G n =X and G n ns is
60
3 Separable Spaces
nonempty by Theorem 3.3 and open as the intersection of two open sets. In particular,
GI ns is a nonempty open set. Therefore, there exist Xl E GI ns and rl > 0 such that
SrI [Xl] C Srl+e(XI) C GI ns for E > o. Similarly, GznS rl (Xl) is nonempty and open,
so there existxz E GznS rl (Xl) and rz > 0 with rz < 1- such thatS r2 [xz] C GznS rl (Xl).
Continue in this way, we obtain a sequence {xn} such that
Srn [Xn] C G n nS rn _ 1 (Xn-l) for all n = 1,2,...,
with r n < r n 2"1 = Z I 0 as n 00.
------
,,-- ---- Srl+e(XI)
, ,
, ,
,
,
, ,
" " Sr3 [X3]
, ,
. I
:.. Xl I
I E rl I
, .
, ,
, I
, I
, ,
,
, ,
, ,
, "
-- ----
------
Observe that whenever m > n, we have
SrI [Xl] ::> ... ::> Srn [Xn] ::> .. . ::> Srm [x m ].
Note that X is a complete metric space and {Srn [xn]} is a decreasing sequence of
nonempty closed subsets of X such that lJ (Srn [Xn]) 0 as n 00. By Cantor's Inter-
00
section Theorem 2.9, n Srn [Xn] contains exactly one point, say, x. Tl(en
n=l
00
00
{X} = n Srn[xn] C n G n .
n= I n= I
Since X is also in S, we have C l G n ) ns 1=- 0. Hence nOI G n is dense inX.
Definition 3.5. A metric space X is said to be separable if there exists a countable
dense set in X.
A metric space which is not separable is called inseparable.
Example 3.6. (a) The usual metric space IR is separable since the set of all rational
numbers Q is dense in IR.
3.2 Dense Sets
61
(b) The usual metric space C is separable since the set A = {a + ib E C : a, b E Q} is
dense in C.
(c) The Euclidean space n is separable since the set Qn = Q x Q x ... x Q is count-
\....
",
n times
able and dense in n.
(d) The space fP, 1 < p < 00, is separable as the set
A = {x = (al,az,... ,an,O,O,...) : ai E Q, 1 < i < n and for all n E N}
is countable and dense in the space fP.
Indeed, if An denotes the subset of all those elements x = {ai} i 1 such that a j = 0
00
for all j > n + 1, then An is countable and so A = U An. By Example 3.5 (e), A is
n=l
dense in the space f P .
(e) The space C[a,b] is separable since the set P[a,b] of all polynomials defined on
[a, b] with rational coefficients is countable and dense in C[a, b] by Example 3.5 (f).
(f) A discrete metric space X is separable if and only if the set X is countable.
Example 3.7. The space foo of all bounded sequences of real or complex numbers with
the metric
d(x,y) = sup IX n - Ynl
l n<oo
where x = {x n } and y = {Yn} in foo, is not separable.
Consider a subset A = {x = {x n } C foo : X n = 0 or I} of f oo . We claim that A is
uncountable.
If B is any countable subset of A, then the elements of B can be arranged in a
sequence Sl , sz, . . .. We construct a sequence s as follows. If the mth element of Sm is
1, then the mth element of s is 0, and vice versa. Then the element s of X differs from
each Sm in the mth place and is therefore equal to none of them. So, s f/:. B although
sEA. This shows that any countable subset of A must be a proper subset of A. It
follows that A must be uncountable, for if it were to be countable, then it would have
to be a proper subset of itself, which is absurd. We proceed to use the uncountability
of the subset A to argue that foo must be inseparable.
The distance between two distinct elements x andy of A is d(x,y) = sUPl<n<oo Ix n -
Yn I = 1. Suppose contrary that E is a countable dense subset of f oo . Consider the
spheres of radii l whose centers at the points of E. Then their union is the entire space
foo, because E is dense, and in particular contains A. Since the spheres are countable
in numbers while A is not, in at least one sphere there must be two distinct elements x
and y of A. Let Xo denote the center of such a sphere. Then
1 1
1 = d(x,y) < d(x,xo) +d(xo,y) < 3 + 3 < 1,
which is impossible. Hence (f OO , d) is not separable.
Theorem 3.5. Let (X, d) be a metric space and Y be a nonempty subset of X. If X is
separable, then so is Y with respect to the induced metric.
62
3 Separable Spaces
Proof Let S = {X n : n E N} be a countable dense subset of X. If S is contained in Y,
then there is nothing to prove. Otherwise, we construct a countable dense subset of Y
whose points are arbitrary close to those of S. For positive integers m and k, let Sm,k =
S 1 (xm) and choose Ym,k E Sm,k nY whenever this set is nonempty. Then d (Xm,Ym,k) <
l. We claim that the countable subset A = {Ym,k : m and k are positive integers} of Y
is dense in Y.
Let Y E Y and E > 0 be given. Let k be so large that l < and find X m E S 1 (y).
I
Thend(y,x m ) < l andyESm,k nY . Thus
lIE E
d(Y,Ym,k) < d(y,x m ) +d(Xm,Ym,k) < k + k < 2 + 2 = E.
Therefore, Ym,k E Se(y). Since Y E Y and E were arbitrary, it follows that Y E A and
hence A = Y. ThusA is countable dense in Y.
Theorem 3.6. A metric space (X, d) is separable if and only if it is second countable.
Proof Let (X, d) be a separable space andA = {an: n E N} be a countable dense sub-
set ofX. Consider the countable collection of open spheres = {Sl/k(a j) : j,k E N}
with centers at a j, j = 1,2,. . . and radii rk = 1 are rational for all k = 1,2,. . ., that is,
= {Sri (a j) : a j E A for j = 1,2,... and ri is a rational number for i = 1,2, .. . } .
Then we claim that is a base for the family of all open sets in X. Let G be any
open set in X and x E G. Then for some r > 0, Sr(x) C G. Choose a positive integer
m such that < . Since A is dense in X, there exists aj EA such that aj E Sl/m(X),
that is, d (x,aj) < . We now show that Sl/m(aj) C Sr(x). Let Y E Sl/m(aj), then
d (aj,y) < . By the triangle inequality, we have
1 1 2
d(x,y) < d(x,aj) +d(aj,y) < - + - = - < r.
m m m
This implies that Y E Sr(x). Hence Sl/m(aj) C Sr(x) C G. Also, x E Sl/m(aj). Thus,
for every x E G, there exists Sl/m(aj) E containing x and contained in G. Hence
is a countable base for the family of all open sets in X and thus X is a second
countable space.
Conversely, assume that X is a second countable space. Let = {Bn : n E N} be
a countable base for the family of all open subsets of X. For each n EN, we choose a
point b n E Bn. Let A = {b n E Bn : n EN}. Then A is countable. We show that A =X.
Let x E X be arbitrary and G be any open set containing x. Since is a base, there
exists at least one Bno E such that x E Bno C G. From the definition of A, we have
b no E A for all b no E Bno' Ther efo re, G c on tains a point of A other than x and thus, x
is a limit point ofA. Hence x EA and so A =X.
Exercise 3.4. Let A a nonempty subset of a metric space X. Prove that the following
statements are equivalent.
(a) A is dense in X.
(b) The only closed superset of A is X.
(c) The only open set disjoint from A is 0.
3.3 Nowhere Dense Sets
63
( d) A intersects every nonempty open set.
( e ) A intersects every open sphere.
Exercise 3.5. Let {G n } be a sequence of dense open sets in a complete metric space
X. Prove that U G n is dense in X.
nEN
Hint: The proof lies on the lines of the proof of Theorem 3.4.
Exercise 3.6. Let (X, d) be a metric space and Y be a subset of X. If Y is separable
and Y =X, then prove that X is separable.
Proof Let A be a countable dense subset of Y. Let x E X and E > 0 be given. Since
Y = X, there exists y E Y such that d (x,y) < . Also, since A is dense in Y, there exists
z E A such that d(y,z) < . By the triangle inequality, we have
E E
d(x,z) < d(x,y) +d(y,z) < 2 + 2 = E.
It follows that A is dense in X and hence X is separable.
3.3 Nowhere Dense Sets
Definition 3.6. A subset A of a metric space X is said to be nowhere dense in X if
(A ) 0 = 0, that is, A contains no interior point.
Example 3.8. (a) In the usual metric space , any finite set is nowhere dense.
(b) The sets Nand Z are nowhere dense in since N = N and N° = 0.
(c) In the usual metric space 2, the set of points on a line is nowhere dense.
(d) In the discrete metric space, the empty set is the only nowhere dense set.
Remark 3.3. The notion of nowhere dense is not the opposite of everywhere dense,
that is, if a set is not nowhere dense then it does not imply that the set is everywhere
dense. For example, consider the usual metric space and the setA = {x E : 1 <
x < 2}. Since
(A ) 0 = A =1= 0 and (A ) C = {x E : x < 1 or x > 2} = ( -00,1) U (2,00),
A is not nowhere dense as well as not everywhere dense.
Theorem 3.7. Let A be a subset of a metric space X. Then A is nowhere dense in X if
and only if X \ A is dense in X.
Proof. Sin ceX\ A =X\AO, we haveAo =X\ (X\A). Replaci ng A by A , we get
(A )O =X\ (X\ A ). Therefore, (A )O = 0 if and only if X = (X\ A ).
Corollary 3.1. Let A be a closed subset of a metric space X. Then A is nowhere dense
in X if and only if X \ A is dense in X.
64
3 Separable Spaces
Remark3.4. For any subset A of a metric space X, we haveX\ A C X\A. Therefore
from Theorem 3.7, it follows that if A is nowhere dense in X, then X \A is dense in
X. However, the converse is not true. For example, the set of all irrational numbers
\ Q is dense in the usual metric space . However Q is not nowhere dense set in
because Q = .
Definition 3.7. A subset A of a metric space X is said to be of first category if it is a
countable union of nowhere dense subsets. The set A is said to be of second category
if it is not of first category.
Remark 3.5. (i) Every subset of a metric space must be either of first category or of
second category.
(ii) If {An} be a countable family of first category sets, then UAn is of first category
n
because a countable union of countable sets is also countable.
(iii) If X is a metric space of second category and Al C X is of first category such that
X =AI UA2, thenA2 is of second category.
(iv) Since a subset of a nowhere dense set is nowhere dense, and therefore, a subset
of a set of first category is of first category.
Example 3.9. (a) The empty set is of first category.
(b) The set of all rational numbers Q in is of first category.
Indeed, if Xl ,X2,... is an enumeration of the rational numbers, then each singleton
set {Xi} is closed and {Xi}O = 0. It follows that U{Xi}, the set of all rational numbers
in , is of first category.
Theorem 3.8 (Haire's Category Theorem). Every complete metric space is of sec-
ond category.
Proof Let {An} be a sequence of nowhere dense sets in a complete metric space X
00
such that X = U An. Since An is nowhere dense, An has no interior points, so any
n=l
open sphere inX must intersects G n =X \ An for all n = 1,2,.... Therefore, {G n } is a
00 00
family of dense open sets inX. By Theorem 3.4, n G n =1= 0. It follows that UAn =l=X,
n=l n=l
which is a contradiction.
Remark 3.6. Since is complete, by Baire's category theorem, cannot be written
as a countable union of nowhere dense sets.
Exercise 3.7. Let A be a subset of a metric space X. Prove that the following state-
ments are equivalent.
(a) A is nowhere dense inX.
(b) A does not contain any nonempty open set.
(c) Every nonempty open set has a nonempty open subset disjoint from A .
(d) Every nonempty open set contains a nonempty open subset disjoint fromA.
(e) Every nonempty open set contains an open sphere disjoint fromA.
Exercise 3.8. Prove that the Cantor set is nowhere dense.
3.3 Nowhere Dense Sets
65
Exercise 3.9. Let A be an open subset of a metric space X. Prove that A is dense in X
if and only if X \A is nowhere dense in X.
Exercise 3.10. Prove that a finite union of nowhere dense sets in a metric space is a
nowhere dense set.
Proof Let A 1 and Az be nowhere dense subsets of a metric space X and let G be an
arbitrary open set in X. Then by Exercise 3.7 (d), there exists an open set G 1 C G
such that G 1 nAl = 0. Similarly, there exists an open set Gz C Gt C G such that
Gz nAz = 0. Since
Gzn(AtUAz) = (GZnAl)U(GZnAz) =0,
G contains a nonempty open set Gz such that G and At UAz are disjoint. Again, by
Exercise 3.7 (d), At UAz is nowhere dense. By induction, one can easily prove that
the finite union of nowhere dense sets is nowhere dense.
Exercise 3.11. Give an example to show that a countable (infinite) union of nowhere
dense sets in a metric space X need not be a nowhere dense set in X.
Solution. Let X == be a metric space with the usual metric. Consider the set Q of
all rational numbers as a subset ofX. We can write
Q=U{ { : } :PEZ,qEN}.
Then Q has been written as a countable union of nowhere dense sets { } in R. It is
well known that Q is not nowhere dense set in 1R as Q is everywhere dense set in .
Exercise 3.12. If {Fn} is a sequence of closed subsets of the complete metric space X
00
such that X = U Fn, then prove that at least one of Fn's has nonempty interior.
n=t
Hint: Follows from Exercise 2.18.
Exercise 3.13. Prove that the subset 1R \ Q, the set of all irrational numbers, of is of
second category.
Proof Since is a complete metric space, by Baire's category Theorem 3.8, is
of second category. By Example 3.9 (b), the set Q of all rational numbers is of first
category. Since = Q U ( \ Q), by Remark 3.5 (iii), \ Q is of second category.
/
Chapter 4
Compact Spaces
It is well known that every sequence in a closed and bounded subset of has a sub-
sequence converges in it. This result is not true in general metric spaces. The metric
spaces in which every sequence has a convergent subsequence are called sequentially
compact. We present the definition of a compact set in a metric space and its char-
acterizations. The Bolzano- Weierstrass property is given in the setting of a metric
space. We prove that three concepts, namely, compactness, sequentially compactness
and Bolzano- Weierstrass property are equivalent in the setting of a metric space.
4.1 Definitions and Basic Concepts
Definition 4.1. Let X be a metric space and A be any index set.
. A collection = {Ga}aEA of subsets of X is called a cover of X ifUaEA G a =X,
that is, every element of X belongs to at least one member of . If each member
of is an open set in X then it is called an open cover of X.
. A subcollection CC of a cover of X is called a subcover if CC is itself a cover of
X. CC is called a finite subcover if it consists only a finite number of members.
In other words, if there exist Gat' G a2 , . . . , G an E such that Uk= 1 G ak = X, then
the subcollection CC = {Gat' G a2 , . . . , G an} is called a finite subcover of X.
In this case, is said to be reducible to a finite cover or contains a finite subcover.
Definition 4.2. Let X be a metric space and Y be a subset of X. A collection =
{Ga}aEA of subsets of X is said to coverY ifY C UaEA Ga.
Example 4.1. (a) Let be the usual metric space, = {( -n,n) : n E N} and CC =
{( -2n, 2n) : n EN}. Then is an open cover of and CC is a subcover of .
(
-4
(
-3
(
-2
(
-1
IR
o
)
1
}
2
)
3
)
4
(b) Let (0, 1) be a metric space with the usual metric. Let
$={ (0,1- n:l ) :nEN} and ={ (0,1- 4(n I) ) :nEN}.
Then is an open cover of (0, 1) and CC is a subcover of .
68
4 Compact Spaces
(c) Let 2 be the usual metric space. Consider the family = {Sl (x) : x E Z x Z} of
open spheres Sl (x) in the plane 2 with radius 1 and center x = (m,n), where m and
n are integers. Then is a cover of 2, that is, every point in 2 belongs to at least
one member of .
IR
IR
On the other hand, the family CC = {Sl/2(X) : x E Z x Z} of open spheres Sl/2(X)
in the plane 2 with radius 1/2 and center x = (m,n), where m and n are integers, is
--Qot a cover of 2 because the point (1/2,1/2) E 2 does not belong to any member
of'1f .
IR
y = (1/2,1/2)
IR
4.1 Definitions and Basic Concepts
69
Definition 4.3. A metric space X is said to be compact if every open cover of X has a
finite subcover.
A subspace (Y, dy) of a metric space (X, d) is called compact if it is compact as a
metric space in its own right.
A subset Y of a metric space X is called compact if it is compact as a metric
subspace. In other words, a nonempty subset Y of a metric space (X, d) is compact if
it is a compact metric space with the metric induced on it by d.
Example 4.2. (a) The usual metric space is not compact.
Consider an open cover = {( -n, n) : n E N} of JR by open intervals. Let
{(-ni,ni): 1 < i < k} beanyfinitesubcollectionof andletn* =max{nt,nz,...,nk}.
Then n* U =l (-ni,ni). Thus no finite subcollection of covers JR. Hence JR is not
compact.
(b) Any finite subset Y of a metric space X is compact, because in this case every open
cover of Y is finite.
(c) The set of integers Z with the usual metric d (x,y) = Ix - yl for all x,y E Z is not a
compact metric space.
Indeed, {n} = Z n (n - !, n + !) is an open cover of Z. But this open cover does
not have any finite subcover. Thus Z is not compact.
(d) The subspace X = {O} U { : n EN} of is compact.
Indeed, if is a given open cover of X, then there is an element G of containing
O. The set G contains all but finitely many of the points . For each point of X not in
G, choose a member of containing it. The collection consisting of these members
of along with the member G, is a finite subcollection of that coversX.
(e) Let JR be the usual metric space and Y = (0,1) be the subspace of . Then Y is not
compact.
G4
..
.
: G3
. ijI
G2
I "
.
. . .
. . Gt
. . i
"
. .
. .
. .
--., t-H t-
O 1 1 1 1 1 1
6 :5 4 :3 2
Consider the class of open intervals
$= {( ,1), ( , ), ( , ), ( , ) ,...}.
70
4 Compact Spaces
Then Y = U:=1 G n , where G n = ( n Z ' ) for all n E N. Hence is an open cover of
Y. But contains no finite subcover.
Indeed, let * = {( aI, b 1 ) , (az, bz) , .. . , (an, b n )} be any finite subcover of . If
E = min { aI, az, . . . , an}, then E > 0 and (a 1 , bl) U (a z, bz) U .. . U (an, b n ) C (E, 1). But
(0, E] and (E, 1) are disjoint. Hence * is not a cover of Y and so Y is not compact.
(f) Let be the usual metric space and Y = (0, 1] be the subspace of . Then Y is not
compact because the open cover = { ( , 1] : n EN} contains no finite subcover of
(0,1].
On the other hand, the interval [0, 1] is compact.
(g) The open sphere SI (0) with center at origin and radius 1 is not compact.
Indeed, S 1 (0) C U:=z S 1-! (0). However, no finite subcollection of the open cover
n
{ Sl_ k (0) : n = 2,3,.. .} covers Sl (0).
(h) Let (X, d) be a discrete metric space and X be an infinite set. Then X is not com-
pact.
Consider the family = { {x} : x E X} of subsets of X which is an open cover o.f
X since in the discrete metric space, every subset is an open set and so the singleton
set. But there is no finite subcollection of that covers X.
Further, any infinite subset of a discrete metric space is not compact.
Lemma 4.1. Let Y be a subspace of a metric space X. Then Y is compact if and only
if every cover ofY by sets open in X contains a finite subcover ofY.
Proof Suppose that Y is compact and = {Ga}aEA is an open cover ofY, where
each G a is open in X. Then the collection * = {G anY: a E A} is an open cover
of Y by sets G anY open in Y. Since Y is compact, * has a finite subcover CC* of
Y, that is, CC* -. {Gat nY, G a2 nY,... ,G an ny} such that Y = Uk=l (G ak ny). This
implies that Y C U k = 1 G ak and hence CC = {Gat' G a2 , . . . , G an} is a finite subcover of
Y.
Conversely, assume that every cover of Y by sets open in X contains a finite sub-
cover ofY. Then we claim that Y is compact. Let * = {G }aEA be an open cover
of Y, where each G is open in Y. For each a E A, choose a set G a open in X such
that G = G anY. Since * is an open cover of Y, we have
Y = U G = U (G a nY) = ( U Ga ) nY.
aEA aEA aEA
This implies that Y C UaEA G a and hence = {Ga}aEA is an open cover of Y
by sets G a open in X. By hypothesis, some finite subcollection {Gat' G a2 , . . . , G an }
covers Y, that is, Y C U k =l G ak . Thus
( n ) n n
y= UG ak nY= U (GaknY) = UG k'
k=1 k=1 k=1
Therefore, {G t ' G 2 ' . . . , G n} is a finite subcover of Y and hence Y is compact.
Theorem 4.1. Every closed subset of a compact metric space is compact.
4.1 Definitions and Basic Concepts
71
Proof Let Y be a closed subset of a compact metric space X and let = {G a} aEA
be an open cover of Y by sets open in X, that is, Y C UaEA G a, where each G a is open
in X. Then * = U y c is an open cover of X, because y c is open in X. Since X is
compact, * has a finite subcover of X, say CC*. If this finite subcover CC* contains
y c , that is, if
X = Gal UG a2 U... UG an Uy c , where G ak E , k = 1,2,... ,n,
then discard y c since it covers no part of Y; otherwise leave the subcollection alone,
that is, CC* = {Gal' G a2 ,. .. G an }. Then
Y C Gal UG a2 U... UG an , where G ak E , k = 1,2,... ,n.
'\' "
1/ I / \ ,y 1'\ \
I V _ \ I 1 \...... ......
I - -+_1 "
,..\- / \ ?'7 '" v x ,1/ )' , \
/ "XI \/'f*....... I
I ,,_ \ J .A , " / /\ \ ...... -, /
I -, I :>+<
\ ,..-.,..\// /\ ',1/......-....... \
, /)c I \ IX IJ I
"- - , I ""S<.L...... ' \...... / / /
I - +rt - - * - - /
\ A. / I \ /...... .......
" I). I I I
' \ I /
x
,-.......
yc is open
Thus CC* is a finite subcollection of that covers Y. Then by Lemma 4.1, Y is
compact.
Remark 4.1. (i) Any intersection of compact sets is compact.
(ii) The finite union of compact sets is compact.
Definition 4.4. A collection CC = {C 1, Cz, . . .} of subsets of a metric space X is
said to have the finite intersection property if every finite subcollection of CC has
nonempty intersection, that is, for every finite collection {Cl,CZ,'" ,Cn} of CC, we
have ni=l Ci =1= 0.
Example 4.3. (a) Consider the following collection of open intervals
cc = { (0, 1) , (0, ) , ( 0, ) , ( 0, ) ,. . . } .
Then CC has the finite intersection property.
Indeed (O,al) n (O,az) n (0,a3) n... n (O,a m ) = (O,b), where b = min{al,az,...,
am} > O. Therefore, any subclass CC has nonempty intersection even then CC itself has
an empty intersection. Thus CC satisfies the finite intersection property.
72
4 Compact Spaces
(b) Consider the following collection of closed infinite intervals in
cc = {. . . , ( -00, - 2], ( -00, -1], ( -00,0], ( -00, 1], ( -00,2], . . .} .
Then CC has an empty intersection, that is, nnEzCn = 0, where C n = (-oo,n]. But any
finite subclass of CC has a nonempty intersection. So, CC satisfies the finite intersection
property.
Theorem 4.2. A metric space X is compact if and only if every collection of closed
sets in X having finite intersection property has nonempty intersection.
Proof Let X be a compact metric space and CC = {C a } aEA be any collection of
closed sets in X having finite intersection property. Then we claim that naEA C a =1= 0.
Assume contrary that naEA C a = 0. Then by De Morgan's law
U (X\C a ) =X\ ( n Ca ) =X.
aEA aEA
This implies that = {X \ C a } aEA is an open cover of X since each X \ C a is
open. Since X is compact, has a finite subcover CC = {X \ C a ;} 7=1' say. Then
X = Ui=1 (X\C a ;). This implies that X \ (ni=1 C a ;) =X and hence ni=l C a ; = 0. This
shows that CC does not have the finite intersection property, which is a contradiction
of our hypothesis. Hence naEA C a =1= 0.
Conversely, assume that X is not compact. Then there exists an open cover
= {Ga}aEA of X which does not have finite subcover, that is, for every finite
subcollection CC = {Gat' G a2 , . . . , G an} of , we have
Gai IX =} X\ ( Gai) 10 =}
n
n (X\ G a ;) =1= 0.
i=1
For each a E A, let C a = X \ G a , then C a is closed. Since
n n
nCa; = n (X\ G a ;) =1= 0,
i= 1 i= 1
{C a } aEA is a collection of closed sets having finite intersection property. By the hy-
pothesis, naEA C a =1= 0.
On the other hand, since = {G a } aEA is a cover of X, we have UaEA G a = X
and so
n C a = n (X\Ga)=X\ ( u Ga ) =0
aEA aEA aEA
which is a contradiction. Hence X is compact.
Corollary 4.1. A metric space X is compact if and only if every collection CC =
{ Fl , F2, . . . } of subsets of X having finite intersection property, the intersection nF ECC F
of their closures is nonempty.
Proof Let {FI ,F2,". ,Fn} be a finite subcollection of CC such that ni=1 Fi =1= 0. Since
for each i, Fi C F i, we have
4.1 Definitions and Basic Concepts
73
n n
o =1= nFi c n Fi .
i=1 i=1
Therefore, ni= 1 F i =1= 0 and hence CC ' = { F 1 , F 2 , . . .} be a collection of closed sets
having finite intersection property. By Theorem 4.2, nFECC F =1= 0.
Exercise 4.1. ( a) Prove that any intersection of compact sets is compact.
(b) Prove that any finite union of compact sets is compact.
Proof We prove only part (b). Part (a) is left for the readers.
Let {Yk} l be a family of compact sets in a metric spa X. Let = {G a } aEA
be an open cover of U l Yk by sets open in X. Since each Yk is compact, there exists
finite subset Jk of A such that
Yk C U G a ; for each k = 1,2,.. .m.
a; EJ k
Therefore, Uk=1 Yk C Ua;El G a; where J = U 1 Jk is a finite subset of A. Hence every
open cover of U 1 Yk by sets open in X has a finite subcover and thus by Lemma 4.1,
U 1 Yk is compact.
Exercise 4.2. Prove that a metric space X is compact if and only if every family of
closed sets with empty intersection has a finite subfamily with empty intersection.
Proof Let X be a compact metric space and let {C a } aEA be a family of closed sets
in X such that n aEA C a = 0. Taking the complements, we have
X = [0]C = [ n Ca ] C = U ,
aEA aEA
that is, X = UaEA C , where each C is an open set in X since C is the complement
of a closed set Ca. Thus = {C } aEA is an open cover of X. Since X is compact,
there exists a finite subcover CC of cover , that is, there exist C l ' C 2 ' . . . , C n E
such that Ui=l C ; =X. Again, by taking the complement, we have ni=1 C a ; = 0.
Conversely, assume that the hypothesis holds. Then we claim that X is compact.
Let = {Ga}aEA be an open cover ofX. Then UaEA G a =X. Taking the comple-
ments, we have
0= [X]C = [ U Ga ] C = n G ,
aEA aEA
that is, naEA G = 0. Thus, {G } aEA is a family of closed sets with empty intersec-
tion. So, by the given hypothesis, there exists a finite subfamily {G t' G 2 ' . . . , G n }
such that ni=1 G ; = 0. Taking the complements, we have
[ n ] C n
X = [0]C = OG i = k{Gaio
Thus {Gat' G a2 , . . . , G an} is a finite subcover of and hence X is compact.
Exercise 4.3. Let {C n }:=1 be a sequence of nonempty closed subsets of a compact
metric space X such that C n +l C C n for each n E N. Prove that n:=1 C n =1= 0.
74
4 Compact Spaces
Proof Since Cl =:) Cz =:) C3 =:) . . . =:) C n =:) C n + 1 =:) . .. is a nested sequence of nonempty
closed sets in a compact metric space X. Then the collection CC = {C n } :=1 satisfies
the finite intersection property (prove it). By Theorem 4.2, we have n:=1 C n =1= 0.
4.2 Sequentially Compact Spaces
In the real line , we have the following well known result.
Theorem 4.3 (Bolzano- Weierstrass Theorem). If A is a closed and bounded subset
ofJR, then every infinite subset of A has a limit point in A.
This result is no longer valid in the setting of general metric spaces. For example,
consider the metric space (X, d), where X = (0, 1] and d is the usual metric. Then
X itself is closed and bounded. Let A = {1,!, 1, 1, . . .} be an infinite subset of X.
We observe that A has exactly one limit point 0 X. This motivates the following
concept.
Definition 4.5. A metric space X is said to have the Bolzano- Weierstrass property if
every infinite subset of X has a limit point.
Example 4.4. By Bolzano-Weierstrass Theorem 4.3, every closed and bounded inter-
val A = [a, b] has the Bolzano-Weierstrass property.
Theorem 4.4. Every compact metric space has the Bolzano- Weierstrass property.
Proof Let A be an infinite subset of a compact metric spaceX. Assume thatA has no
limit point. Then each point x of X is not a limit point of A, and so, there exists r x > 0
such that Srx(x) does not contain any point of A other than x. Therefore, Srx(x) nA
contains no points of A other than x, that is,
Srx(X) nA = { X}
if x A
if x EA.
(4.1 )
Since at each x EX, we have an open sphere Srx(x) which contains no point of A other
than its center, the family CC = {Srx (x) : x E X} of these open spheres forms an open
cover of X. Since X is compact, there exists a finite subcover of CC, say
{Srx/Xi) : Xi EX and i = 1,2,...,n}
such that X = Ui=l Srx. (Xi). Then
r
A =AnX =An ( 0Srx/Xi) )
1=1
n
= U (AnSrx;(Xi))
i=l
n
C U{Xi} by (4.1)
i=l
= {Xl ,Xz,. ..x n }.
4.2 Sequentially Compact Spaces
75
Consequently, A is a finite set which is a contradiction of our assumption. Hence A
has a limit point.
Definition 4.6. A metric space X is said to be sequentially compact if every sequence
in X has a convergent subsequence.
A subset A of a metric space X is said to be sequentially compact if every sequence
in A contains a subsequence which converges to a point inA.
Example 4.5. (a) Every finite subset of a metric space X is sequentially compact.
Indeed, if A is a finite subset of a metric space X and {XI,X2,... ,x n ,...} is a se-
quence in A, then at least one of the elements in A, say xno must appear in infinite
number of times in the sequence. Hence {Xno ,xno' . . .} is a subsequence of the se-
quence {Xl, X2, . . . , X n , . . .} that converges to the point X no EA.
(b) The open interval A = (0,1) on the real line with the usual metric is not sequen-
tiall y compact.
Consider the sequence {xn} = { !, l, !, . . . } in A. Then X n -+ 0, and therefore, every
subsequence will also converges to O. But 0 f/:. A. In other words, the sequence {xn}
in A does not contain a subsequence that converges to a point in A, that is, A is not
sequentially compact.
In order to prove the following relation
compactness {:} Bolzano- Weierstrass property {:} sequentiall(compactness
we first establish the equivalence between sequentially compactness and Bolzano-
Weierstrass property.
Theorem 4.5. A metric space X is sequentially compact if and only if it has the
Bolzano- Weierstrass property.
Proof Let X be a sequentially compact metric space. Then we claim that every infi-
nite subset of X has a limit point. Let A be an infinite subset ofX. Then we can extract
a sequence {xn} with infinitely many distinct points fromA. Since X is sequentially
compact, the sequence {xn} has a convergent subsequence, say, {x nk }. Letx nk -+ x in
X. Then we prove that x is a limit point ofA.
Let E > 0 be given. Since x nk -+ X as k -+ 00, there exists a positive integer N such
that
x nk E Se(x) for all k > N.
Since {xn} consists infinitely many distinct points from A, we have x nk =1= x for all
k > N. Thus Se(x) contains the element x nk ' for all k > N, of A different from x.
Hence x is a limit point of A. Thus every infinite subset of X has a limit point and
hence X has the Bolzano-Weierstrass property.
Conversely, assume that X has the Bolzano- Weierstrass property. Then every infi-
nite subset of X has a limit point. Let {xn} be an arbitrary sequence in X. Then we
have to prove that {Xn} has a convergent subsequence. Let A be the range set of the
sequence {x n }, that is, A = {Xl ,X2,X3,... ,xn,...} is a set of points Xl ,X2,X3,... ,X n ,....
Then there are two cases:
CASE 1. If A is a finite set, then the sequence {xn} has a point x which appears
infinitely many times in the sequence {xn} (that is, {Xn} = {Xl ,X2," . ,Xn,X,X,.. .}).
76
4 Compact Spaces
Then we have a constant subsequence {x,x,x,...,x...} of {x n } which certainly con-
verges to x.
CASE 2. If A is an infinite set, then the sequence {x n } has infinitely many distinct
points. By our assumption, the set A has a limit point, say, x EX. Then Sl (x) must
have infinitely many points from A. Let us choose one such element, say, xn other
than x. Again Sl/2(X) must have infinitely many points from A and in the same way,
we get x n2 other than x, n2 > nl. Similarly, Sl/3(X) must have infinitely many points
from A and we get x n3 =1= x, n3 > n2, and so on. In this way, we obtain a subsequence
{ x nk } of the sequence {x n } such that
X nk E Sl/k(X) for all k = 1,2, .. . ,
that is,
1
d (xnk'X) < k ---+ 0 as k ---+ 00
and hence x nk x. Thus the sequence {xn} has a convergent subsequence {x nk }, and
therefore, X is sequentially compact.
Corollary 4.2. Every compact metric space is sequentially compact.
Proof It follows from Theorems 4.5 and 4.4.
Theorem 4.6 (Heine-Borel Theorem). A subset of is closed and bounded if and
only if it is compact.
As an application of Corollary 4.2, we present a general form of the Heine-Borel
theorem in the setting of metric spaces.
Theorem 4.7. Every compact subset of a metric space is closed and bounded.
Proof Let (X, d) be a metric space and A be a compact subset of X. If A is finite,
then there is nothing to prove because every finite set is closed and bounded. So, we
assume that A is an infinite set.
Let x E A be arbitrary. Then by Theorem 2.3, there exists a sequence {xn} C A
such that X n x. Since A is compact, by Corollary 4.2, it is sequentially compact,
and therefore, {xn} has a subsequence that converges inA. Let {x nk } be a convergent
subsequence of {x n }. Then x nk x EA and hence A cA. Therefore, A =A and thus
A is a closed set.
Further, letA be unbounded. Then we can find pairs of points of A at arbitrary large
distances apart, that is, there would exist x and y in A such that d (x,y) > M for some
given M > O. Consider the family = {S 1 (x) : x E A} of open spheres with centered
at a point of A and radius 1. Then clearly,
A C USl(X),
xEA
This implies that is an open cover ofA. SinceA is compact, has a finite subcover
CC = {S1 (Xi) : i = 1,2,...,n}, say. Then
n
A C USl(Xi).
i=1
4.3 Totally Bounded Spaces
77
Let k = max {d (Xi,Xj) : i, j = 1,2,... ,n, i =1= j}. Also, let M = k+ 2, then
d(x,y) > k+2.
(4.1 )
Since X andy are inA, there exist Xi andxj such that X E Sl(Xi) andy E Sl(Xj). So,
d(x,y) < d(X,Yi)+d(Xi,Xj)+d(xj,y) <k+2
which contradicts ( 4.1). Hence A is bounded.
Remark 4.2. The converse of the above theorem need not be true. For example, con-
sider an infinite subset A of a discrete metric spaceX. Then A is closed and bounded
because the open sphere Sl (x) is the set {x} alone and d(x,y) < 1 for allx,y EA. But
, 2
the open cover {{x} : x EA} of A has no finite subcover. ThusA is not compact.
In fact, a subset of n with the usual metric is compact if and only if it is closed
and bounded.
4.3 Totally Bounded Spaces
Definition 4.7. Let (X, d) be a metric space and E > 0 be given. A subset A of X is
called an E-net if A is finite and X = UxEA Se (x), that is, if A is finite and its points are
scattered through X in such a way that each point of X is distant by less than E from
at least one point of A.
In other words, a finite subsetA = {Xt,Xz,... ,xn} of X is an E-net for X if for every
point y E X, there exists an Xio E A such that d (y,Xio) < E.
Example 4.6. Let X = {(x,y) E IR x : x2 + yZ < 4}, that is, X is the open sphere
centered at the origin and radius 2. If E = , then the set
A = {(1, -1), (1,0), (1, 1), (0, -1), (0,0), (0, 1), (-1, -1), (-1,0), (-1, I)}
is an E-net for X.
On the other hand, if E = 1/2, then A is not an E-net for X. For example, the point
y = (!, !) belongs to X but the distance between y and any point in A is greater than
1
2'
Definition 4.8. A metric space (X,d) is said to be totally bounded if it has an E-net
for each E > O.
Remark 4.3. Every totally bounded metric space X is bounded but converse is not true
in general.
Since X is totally bounded, it has an E-netA = {Xl,XZ"" ,xn} for each E > O. Then
X = Ui=l Se (Xi)' Since finite union of bounded sets is bounded, it follows that X is
bounded.
Example4.7. Under the usual metric d(x,y) = Ix - yl, tJte real line is neither
bounded nor totally bounded. Under the metric d*(x,y) = min{lx-yl,1}, the real
line IR is bounded but not totally bounded.
78
4 Compact Spaces
IR
2
.... ....
..
.
.
.
.. 1
.. .
.
.
.
-2 : -1
y = (1/2,1/2)
IR
.
.
.
.
.
. .
.
.
.
.
.
...
-1
.
.
.
.
.
. .
.
.
.
.
.
...
. . .
. . .
-2
Theorem 4.8. Every sequentially compact metric space is totally bounded and com-
plete.
Proof. Let (X, d) be a sequentially compact metric space. Assume to the contrary
that X is not totally bounded. Then there exists an E > 0 such that there does not
exist any E -net. Choose a point Xl E X and form the open sphere S e (Xl)' Then, clearly
Se(XI) =1= X for otherwise {Xl} would be an E-net for X. Let X2 E X be an element
such thatx2 Se(XI), that is, d(XI,X2) > E. Form the open sphere Se(X2) and the set
Se(Xl) US e (X2). Then Se(XI) US e (X2) =1= X since in other case {XI,X2} would be an
E-net for X. Letx3 EX be such thatx3 Se(XI) USe (X2), that is,
d(XI,X3) > E and d(x2,x3) > E.
Form an open sphere Se (X3) and a set Se(Xl) USe (X2) USe (X3). Then Se(XI) USe (X2) U
Se(X3) =1= X, otherwise the set {XI,X2,X3} would be an E-net for X.
Continuing in this way, we obtain a sequence {xn} of elements of X such that
n-l
xn USe(Xi) forn=2,3,...,
i=l
that is,
d(Xi,X n ) > E for i = 1,2, . . . , n - 1 and n = 2,3, . .. with n =1= i.
Consequently,
d(xn,xm) > E for all n, m and n =1= m.
Thus {xn} is a sequence with no Cauchy subsequence and hence {xn} cannot have any
convergent subsequence, contradicting our hypothesis that X is sequentially compact.
Hence X is totally bounded.
Now, we prove that X is complete. For that, we have to show that every Cauchy
sequence converges to a point of X.
4.3 Totally Bounded Spaces
79
Let {xn} be a Cauchy sequence. Then for each E > 0, there exists a positive integer
N such that
d (xm,xn) < E whenever m > n > N.
Since X is sequentially compact, every sequence, in particular, a Cauchy sequence,
has a convergent subsequence. Therefore, this Cauchy sequence {xn} contains a sub-
sequence {Xk n }, say, which converges to a point x EX, that is,
lim d (Xk n ,x) = o.
n--+oo
Since {k n } is an increasing sequence of integers, k m > m. We now have
o < d (xn,x) < d (Xn,Xk m ) +d (Xkm,X) < E +d (Xkm,X)
whenever m > n > N. Taking m 00, then we have
o < d(xn,x) < E whenever n > N.
Therefore, the Cauchy sequence {xn} converges to x EX.
Remark 4.4. It is not necessary that a totally bounded metric space is sequentially
compact. For example, consider the metric subspace A = ( -1, 1) of under the usual
metric d(x,y) = Ix - yl for all x,y EA. Then A = (-1,1) is totally bounded but not
sequentially compact. But every totally bounded complete metric space is sequentially
compact.
Theorem 4.9. Every totally bounded complete metric space is sequentially compact.
Proof Let (X,d) be a totally bounded and complete metric space. Let {xn} be any
sequence in X. Since X is totally bounded, it can be covered by a finite number of
open spheres of radius 1, and at least one of these open spheres will contain an infinite
number of members of the sequence {x n }. Let Nt be a such open sphere and let {x n1 }
be a subsequence of the sequence {xn} in Nt.
Since X is covered by a finite number of open spheres and Nt is contained in X,
therefore, Nt can also be covered by a finite number of open spheres of radius !. By
the same argument, there would be an open sphere Nz of radius ! which contains a
subsequence {x n2 } of {x n1 }. Since Nz C Nt, it follows that x n2 E Nt. Continuing in
this way, for any positive integer k, we obtain an open sphere Nk of radius 1 which is
contained in Nk-t and contains a subsequence {x nk } of {Xnk_l }, that is, the diameter
of Nk, fJ (Nk) < i and x nk E Nk, where nk > nk-t. Since x nk , X nk + 1 , . . . all lie in Nk and
the diameter fJ (Nk) < f, it follows that
2
d (xnk,xnk+m) < k '
For any E > 0, choose k > . Then
d (xnk,Xnk+m) < E
and hence {x nk } is a Cauchy sequence of the sequence {x n }. Since X is complete,
this subsequence converges to a point of X. Hence X is sequentially compact.
80
4 Compact Spaces
Corollary 4.3. A closed subspace of a complete metric space is sequentially compact
if and only if it is totally bounded.
Theorem 4.10. Every totally bounded metric space is separable.
Proof Let (X,d) be a totally bounded metric space. Then for each n E N, X has a
-net which is denoted by An. Since each An is a finite set, the set A = U:=l An is
countable. We further prove that A = X, that is, if x E X then we claim that x E A .
Let x E X and r > 0 be given. Choose a positive integer n such Jhat < r. Let
An = {a 1, az, . . . , ak} since each An is finite. Then
k
X=U S 1(aj)
n
j=l
and so xES 1 (a j) for some j = 1,2, .. . , k. Therefore,
n
1
d(x,aj) < - < r
n
and thus aj E Sr(x), that is, Sr(x) nA =1= 0 because aj EAn cA. This implies that x E A
and hence A =X.
Definition 4.9. Let = {G a } aEA be an' open cover of a metric space X. A real
number A > 0 is called a Lebesgue number for the given open cover if for each
subset of X whose diameter is less than A is contained in at least one G a, that is, if
every subset A C X with () (A) < A then A C G a for at least one a EA.
Theorem 4.11 (Lebesgue's Covering Lemma). In a sequentially compact metric
space, every open cover has a Lebesgue number.
Proof Let (X, d) be a sequentially compact metric space and let = {G a} aEA be
an open cover of X. Assume that does not have any Lebesgue number. Then for
each n E N, there exists a subset Bn of X such that
1
o < {)(Bn) < - and Bn ct G a for all a EA.
n
(4.2)
For each n E N, choose a pointx n E Bn. Then {x n } is a sequence of points ofX. Since
X is sequentially compact, {x n } has a subsequence {x nk } converges to a point x EX.
Since x E X and is an open cover of X, x E G ao for some ao EA. But G ao being
an open set containing x, there exists an open sphere S E (x) such that xES E (x) c G ao.
Since {x nk } converges to x, there exists a positive integer N such that for all k > N,
we have
E
d (Xnk'X) < 2 .
Let no > N such that n10 < . Then from above inequality, we have
E
d (Xnk'X) < 2 ' that is, x nk E S 2 (x) for all nk > no.
In particular, xno E S 1 (x). In view of (4.2), we have
4.3 Totally Bounded Spaces
81
Xno E Bno
1 £
and 0<{)(B nO )<-< 2 '
no
",
/
I
I
I I
:Se(X): !-
\ \ 2
\ \
,
\ '.....
,
,
,
,
"
£
\
\
,
I
,
I
I
I
/
",
,."'"
-
Since xno belongs to Bno as well as to S 2 (x), Bno n S 2 (x) =1= 0. This implies that
Bno will also intersect with Se (x). Since () (Bno) < and Bno intersects with Se (x),
we have
Bno C Se(x) C G ao .
But this contradicts with the fact that Bno ct G a for all a E A. Hence has a
Lebesgue number.
Theorem 4.12. Every sequentially compact metric space is compact.
Proof Let X be a sequentially compact metric space. Then b)f Theorem 4.8, it is to-
tally bounded. Then for a given £ > 0, X has an £-netA, say. ThenA = {Xl ,X2,.. . ,xn}
is finite subset of X and
n
X = U Se(Xk).
k=l
Let = {G a} aEA be an open cover of X. Since X is sequentially compact, by
Lebesgue's covering lemma, this open cover has a Lebesgue number A, say. We
put £ = . For each k = 1, 2, . . . , n, we have
2A
() (Se(Xk)) < 2£ = 3 < A.
By the definition of a Lebesgue number, for each k = 1,2, . . . , n, we can find an open
set G ak E such that S e (Xk) C G ak' This implies that
n n
U Se(Xk) C U G ak .
k= I k= I
82
4 Compact Spaces
n n
Since X = U SE(Xk), we have X = U G ak . Hence the class {Gal ,G a2 ,... ,G an } is a
k=l k=l
finite sub cover of X, and therefore, X is compact.
Corollary 4.4. A closed subspace of a complete metric space is compact if and only
if it is totally bounded.
Finally, we have the following relationships.
Compact
.
c
/
o/::
%
'iT
. 'iT
Sequentially Compact
Bolzano- Weierstrass Property
By Theorem 4.5
Exercise 4.4. Let A be a compact subset of a metric space X. Show that the derived
setA' of A is compact.
Exercise 4.5. Which of the following sets are compact? Justify your answer.
(a) A = [0,2) c JR.
(b) A = [0,1] U [2,3] c JR.
(c) A = {x E JR : x > O} c JR.
(d) A = Qn [0,1] = {x E JR: 0 < x < 1 and x is irrational}.
(e) A = {I,!, l, ..., , ...}U{O}.
(f)A = {(x,y) E JR2:y = OJ.
(g) A = {(x,y) E JR2 :x2+y2 < 4}U{(1,2)}.
(h) A = {(x,y) E JR2: a2+y2 = I}.
(i) A = {(x,y) E JR2: 0 < x < 1,0 < y < I}.
Solution. (b) The set A = [0,1] U [2,3] c JR is compact because it is closed and
bounded (Heine-Borel Theorem).
(c) The set A = {x E JR : x > O} c JR is not compact because it is unbounded.
(d) The set A = Qn [0,1] = {x E JR: 0 < x < 1 and x is irrational} is not compact
because x = ! f/:. A, but every interval around it contains irrational numbers which are
inA. Therefore,A c is not open so A is not closed. Therefore, A can not be compact.
4.3 Totally Bounded Spaces
83
(e) Let {G a } be an arbitrary open coverofA. Then the point 0 lies in one of these open
sets. Assume that 0 E G ao for some ao. Since G ao is open and -+ 0, there is an N
such that 1 , N 1 ' . .. all lie in G ao. Since {G a} is an open cover of A, there must exist
Gat' G a2' . . . , G aN (not necessarily all distinct from one another, but we can rename
and give multiple names to the sets as is needed) such that 1,1/2,..., l/N E Gat U
G a2 U . . . U G aN. Then {G ao , Gat' G a2 , . . . , G aN } is a finite subcover of A. Therefore,
every open cover has a finite subcover and so A is compact.
Exercise 4.6. Let A and B be subsets of a metric space X such that A is closed and B
is compact. Prove that A nB is compact.
Proof Let {Ga}aEA be an open cover of A nB by sets open in X. Let Gf3 =X\A.
Then G 13 is open in X since A is closed. Let us denote by J = A U {f3}. We claim that
{ G a} aEJ is an open cover of B. For that, let b E B. Then either bEG 13 (if b A),
or else b E A nB C UaEA Ga. This implies that b E G a for some a E A. In either
case bE G a for some a EJ. Therefore, B C UaEJG a and so {Ga}aEJ is an open
cover of B. Since B is compact, this open cover has a finite subcover, that is, there
exists a finite subset L of J such that B C Ua;EL G a;. The set Lf3 = L - {f3} is a finite
subset ofJ - {f3} = A. Now we show that A nB C Ua;EL G a ;. For this, suppose that
b EA nB. Then b E B C Ua;EL G a ; and so b E G a ; for some ai E L. But b EA and so
b X \A = Gf3' Thus b E G a ; for some ai E Lf3. Thus the open cover {G a } aEA of
A n B has a finite subcover, namely {G a; } a;EL . Hence A n B is compact.
Exercise 4.7. Let {Aa}aEA be any family of compact subsets of a metric space X.
Show thatB = naEAAa is compact, while UaEAAa is not necessarily compact.
Proof Choose a fixed ao E A and put A = na#aoAa and take B =Aao. Since every
compact set is closed, each Aa is closed and so A is closed being an intersection of
closed sets. Since B is compact, by Exercise 4.6, A nB is compact and so isA nB =
nAa.
aEA
Arbitrary union of compact sets need not be compact. For example, consider the
sets An = [-n,n] for all positive integer n, in the usual metric space . Then each An
is compact since it is closed and bounded. But U:=lAn = which is not compact.
Exercise 4.8. Given an example of a metric space X (other than ) having Bolzano-
Weierstrass property.
Exercise 4.9. Show that no finite subcollection of the open cover = {Sl_! (0) : n
n
= 2,3,. . .} of Sl (0) covers Sl (0).
Exercise 4.10. Prove that the real line under the metric d* (x,y) = min {Ix - yl, 1 }
for all x,y E is bounded but not totally bounded.
Exercise 4.11. Let be the usual metric space and Y = (0,1] be a subspace of .
Prove that the open cover = { ( , 1] : n EN} of Y contains no finite subcover.
Exercise 4.12. Prove that a subset A of the usual metric space n is compact if and
only if it is closed and bounded.
84
4 Compact Spaces
Proof Let A be a compact subset of n. Then by Theorem 4.7, it is closed and
bounded.
Conversely, assume that A is closed and bounded. Fix E > O. The set
- { ( Ekl Ek2 Ekn ) . }
C = -;;-' -;;-' .. . , -;;- : ki E Z, 1 < l < n
is an E -net for n. Since A is bounded, there exists r > 0 such that A C S r (0). Then
the set
c=cnsr(o)
is a finite E-net for A. So, A is totally bounded. Then by Theorem 4.9,A is sequentially
compact and Theorem 4.12 implies that A is compact.
Exercise 4.13. t X be a metric space and {Xn} be a sequence in X such that X n x
as n 00. Show that the subset {x} U {x n : n E N} of X is compact.
Proof Let be an open cover for {x} U {x n : n EN}. Then there exists an open set
G E such that x E G. Since X n x and G is open, there exists a positive integer
N such that G contains all points of the set {x n : n E N} for all n > N. For each
i = 1,2,... ,N, let Gi E such that Xi E Gi. Then GUGI U... UGH is finite subcover
of the cover . Hence the set {x} U {x n : n E N} of X is compact.
Exercise 4.14. Let A be a compact subset of a metric space (X,d). Show that for any
subsetB of X, there exists a point X EA such that p(x,B) = p(A,B).
Proof Let p(A,B) = E. Then E = p(A,B) = inf{d(x,y) : x EA,y E B} < d(x,y) for
all x E A and y E B. Therefore, for any positive integer N, there exist X n E A, Yn E B
such that
1
E < d (xn,Yn) < E + - for all n > N.
n
Since A is compact, it is sequentially compact, and therefore, the sequence {xn} C A
has a subsequence {x nk } converges to a point x EA. We claim that p(x,B) =
p(A,B) = E. Suppose contrary that p(x,B) > E. Then for some lJ > 0, E + lJ =
p(x,B) = d(x,y) and so d(x,Yn) > E + for all Yn E B. Since x nk x as k 00,
there exists a positive integer N such that
lJ
d(Xnk'X) < - forallk>N
2
and
1 lJ
d(Xnk,Ynk)<E+-<E+- forallk>N.
nk 2
Then
d (x,x nk ) +d (xnk,ynk) < + E + = E + = p(A,B) < d (X,Ynk) for all nk > N.
But this contradicts the triangle inequality. Hence p(x,B) = p(A,B).
Exercise 4.15. Let A be a compact subset of a metric space (X, d) and let B be a
closed subset of X such that A nB = 0. Show that p(A,B) > O.
4.3 Totally Bounded Spaces
85
Proof Since p(A,B) == inf{ d(x,y) : x E A, Y E B} > 0, it is sufficient to show that
p(A,B) =1= O. Suppose contrary that p(A,B) == O. Then by Exercise 4.14, there exists
x EA such that p(x,B) == p(A,B) == O. By Theorem 1.5,B == B == {x EX: p(x,B) == O}.
Therefore, x E B contradicting to our assumption that A nB == 0.
Chapter 5
Continuous Functions
This chapter deals with the concepts of continuity and uniform continuity of functions
defined on a metric space. Several characterizations and properties are presented. The
concepts of homeomorphism and equivalent metrics are given. The uniform conver-
gence of the sequences of functions defined on a metric space is discussed.
5.1 Definition and Characterizations
Definition 5.1. Let (X, d) and (Y, p) be metric spaces. A function 1 : X -+ Y is said
to be continuous at a point Xo E X if for every E > 0, there exists a fJ > 0 such that for
all x EX,
d (x,xo) < fJ implies p (I (x), I(xo)) < E
that is,
x E S6 (xo) implies I(x) ESe (/(xo)).
In other words, 1 is continuous at a point Xo E X if for every E > 0, there exists a
fJ > 0 such that
1 (S 6 (xo)) C S e (I (xo )) .
The function 1 is said to be continuous on X if it is continuous at every point of X.
f . . ........ .
. . . .
) . .
.
---e .
. .
. f(x) .
.
. x .
. .
.
.
.
. .
. . . .
. xo . . f(xo) .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
.
. . . . . .
. . . . . . .
. .
S (xo) . . . .
. . . . .
. . . . . .
Se (f(xo))
Example 5.1. (a) Let (X,d) be a metric space. The identity function I : X -+ X is
continuous on X.
(b) LetX = be the set of all real numbers with the usual metric. Then every constant
function defined on X is continuous.
(c) Let X be a discrete metric space and Y be a metric space. Then every function
1 : X -+ Y is continuous on X.
88
5 Continuous Functions
(d) Let X = Y = C[.o, 1] with the uniform metric doo(f,g) = sup If(t) - g(t)l. The
tE[O,l]
mapping cp : X -+ Y defined by
(4'(f))(t) = l f(s)ds for all f E qo, 1]
is continuous. In fact,
I (4'(f)) (t) - (4'(g))(t) I = l f(s)ds-l g(s)ds
< llf(S) - g(s)lds
< doo(f,g).
Hence
doo(cp(f),cp(g)) < doo(f,g) for all f,g EC[0,1].
So, the assertion follows if we choose fJ = E.
Theorem 5.1. Let (X, d) and (Y, p ) be metric spaces. A function f : X -+ Y is contin-
uous at a point Xo E X if and only if for every sequence {xn} eX, we have X n -+ Xo
implies f(xn) -+ f(xo).
Proof Let f be continuous at a point Xo EX. Then for a given E > 0, there exists a
fJ > 0 such that for all x EX,
d(x,xo) < fJ implies p(f(x),f(xo)) < E.
Let {x n } C X be a sequence in X such that X n -+ Xo as n -+ 00. Then there exists a
positive integer N such that
d(xn,xo) < fJ for all n > N.
Hence for all n > N, we have
p (f(x n ), f(xo)) < E,
and therefore, f(x n ) -+ f(xo).
Conversely, assume that for every sequence {x n } in X such that X n -+ Xo, we have
f(x n ) -+ f(xo). Suppose that f is not continuous atxo. Then there exists an E > 0 such
that for every fJ > 0, there is an x =1= Xo satisfying
d(x,xo) < fJ but p (f(x), f(xo)) > E.
In particular, for fJ = there is an X n satisfying
1
d(xn,xo) < - but p (f(x n ), f(xo)) > E.
n
Then clearly X n -+ Xo but {f(x n )} does not converge to f(xo). This contradicts to our
hypothesis that f(x n ) -+ f(xo). Hence f is continuous at xo.
5.1 Definition and Characterizations
89
Theorem 5.2. Let (X, d) and (Y, p ) be metric spaces. A function f : X -+ Y is contin-
uous on X if and only if for each x E X and for every sequence {x n } in X, we have
X n -+ X implies f(x n ) -+ f(x).
Remark 5.1. If f : X -+ Y is continuous and f(x n ) -+ f(x) for any sequence {x n } in
X, then the assertion X n -+ X may not be true.
For example, let X = be a metric space with the usual metric and f : X -+ X be
a function defined as
f(x) = for all x EX.
Consider a sequence {x n } in X, where X n = (-l)n for all n E N. Then f(xn) = 1 -+
f ( 1) as n -+ 00 but the sequence X n does not converge to 1 as n -+ 00.
Theorem 5.3. Let X and Y be metric spaces. A function f : X -+ Y is continuous on
X if and only if f-l (G) is open in X whenever G is open in Y.
Proof Assume that f is continuous on X and G is an open set in Y. Then we prove
that f-l (G) is open in X. If f-l (G) = 0, then the result is proved. So, we assume that
f-l(G) =1= 0. Let X E f-l(G), then f(x) E G. Since G is open, Se(f(x)) C G for some
E > O. By the continuity of f, there exists a lJ > 0 such that
f (S" (x)) C Se (f(x)) ,
and since Se (f(x)) C G, it follows that f(S,,(x)) C G. Thus S,,(x) C f-l(G) and
hence f-l (G) is open.
f-l(G)
G
.
f
.
. x
.
.
. .....
. .....
S (x) Se (f(x))
Space X
Space Y
Conversely, assume that f-l (G) is open in X whenever G is open in Y. Let x E X be
arbitrary and E > 0 be given. Then f(x) E Y and Se (f(x)) is an open set. Therefore,
by assumption f-l (Se(f(x))) is open in X and x E f-l (Se (f(x))). Consequently,
there exists a lJ > 0 such that S" (x) C f-l (Se (f(x))) and thus f (S" (x)) C Se (f(x)).
Hence f is continuous at x. Since x E X was arbitrary, f is continuous on X.
Theorem 5.4. Let X and Y be metric spaces. A function f : X -+ Y is continuous on
X if and only if f-l (F) is closed in X whenever F is closed in Y.
90
5 Continuous Functions
Proof Let I be a continuous function and F be a closed in Y. Then Y \ F is open in
Y, and therefore, 1-1 (Y \ F) is open in X. Since
1-1 (F) =X\ (/- 1 (Y\F))
and 1- 1 (Y\F) is open, it follows that 1-1 (F) is closed.
Conversely, assume that 1-1 (F) is closed in X whenever F is closed in Y. Then
we show that I is continuous. Let G be an open subset of Y. Then Y \ G is closed in
Y and by hypothesis 1-1 (Y \ G) is closed in X. Since
1-1 (G) =X\ (/- 1 (y\ G))
and 1-1 (Y \ G) is closed, we have 1-1 (G) is open. Hence I is continuous on X.
Remark 5.2. If I is a continuous function from a metric space X to another metric
space Y, then the image I (G) of an open set G in X need not be open in Y and the
image I(F) of a closed set F in X need not be closed in Y.
For example, consider the function I : defined as I(x) = Xl. Then, of
course, I is continuous on . Let G == ( -1, 1) be an open set in but I( G) = [0,1)
is not open in .
Consider another function I : [1, +(0) IR defined by I (x) = . Then I is contin-
uous on [1,+(0). Let A = [1,+(0), then A is closed as a whole space with the usual
metric but I(A) == (0,1] is not closed in .
Theorem 5.5. Let X and Y be metric spaces. A function I : X Y is continuous il
and only il I (A ) C I (A) for every subset A 01 X.
Proof. Let I be a continuous function. Then 1-1 ( I (A) ) is closed in X, since I (A)
is closed in Y. Now we have
I(A) C I(A) '* A C r 1 (t(A) ) '* A C 1-1 ( /(A) )
and thus A C r 1 ( /(A) ) because r 1 ( /(A) ) is closed. Hence I (A ) C I(A) .
Conversely, let I (A ) C I(A) for every subset A of X. We prove that I is continu-
ous. Let F be any closed set in Y. Then F = F. Now we have
I (/- 1 (F)) C I(f-l(F))= F =F.
This implies that 1-1 (F) C 1-1 (F). But f-l(F) C 1-1 (F), therefore 1-1 (F) =
1-1 (F). Hence 1-1 (F) is closed in X. Thus I is continuous onX.
By combining Theorems 5.2 - 5.5, we have the following result.
Theorem 5.6. Let X and Y be metric spaces and I : X Y be a function. The follow-
ing statements are equivalent:
( a) I is continuous on X.
(b) For each x EX and for every sequence {x n } in X such thatxn x implies f(xn)
I(x).
5.1 Definition and Characterizations
91
(c) f-l(G) is open in X wherever G is open in Y.
(d) f-!JF) is clo sed in X wherever F is closed in Y.
(e) f(A) C f(A) for every subset A ofX.
Theorem 5.7. Let X, Y and Z be metric spaces and f : X Y and g : Y Z be
continuous functions. Then the composite function go f : X Z is continuous on X.
Proof Let G be an open set in Z. Then by continuity of g, g-I(G) is open in Y. The
continuity of f implies that f-l (g-I(G)) is open in X, that is, (f- 1 og-l) (G) =
(g 0 f) -1 (G) is open in X. Hence go f is continuous.
Exercise 5.1. Let f : X Y be a continuous function from a metric space X to another
metric space Y. Give an example to show that f(A O ) C (f(A))O does not hold.
Hint: Consider the function f : defined as f(x) = sinx for all x E and take
A = (0, 31t').
Exercise 5.2. Give an example to show that the following statement does not hold:
f : X Y is continuous if and only if (f(A))O C f (A 0) for all subsets A of X.
Solution. The following function f : defined as
f(x) = {
if x is rational
if x is irrational
is not continuous. However, f(A) C {0,1} for all A C X and (f(A))O = 0. So,
(f(A))O C f(A O ) holds for all subsets A ofX.
For the converse, define a function f : as f(x) = Ixl for all x E and
consider the set
A = ([ - 2, -1] n Q) U ( -1, 1) U ([1, 2] n ( \ Q)) .
Then A O = (-1,1), and therefore, f(A O ) = [0,1). But f(A) = [0,2], and therefore,
(f(A))O = (0,2).
Exercise 5.3. Let X and Y be metric spaces. Prove th at the function f : X Y is
continuous on X if and only if for every subset B ofY, f-l (B) c f-l (B ).
Proof Let f be continuous and A = f-l(B). Then by Theorem 5.5, we have f (A ) C
f(A) and
f(A) C B =* 7(A) CB =* f (A ) CB .
Therefore, A C f- l(li) an d thus f-l(B) C f-l( B ).
Conversely, let f-l (B) C f-l ( B ) for every subset B ofY. Let F be a closed set in
Y. Then F = F and by the hypothesis, we have
f-l(F) C f-l ( F ) = f-l(F).
But f-l(F) C f-l(F), and therefore, f-l(F) = f-l(F). Thus f-l(F) is closed and
hence f is continuous on X.
92
5 Continuous Functions
Exercise 5.4. Let X and Y be metric spaces and I : X Y be a function. Prove that
I is continuous on X if and only if for every subset B ofY, 1- 1 (B O ) c [/- 1 (B) ] o.
Proof Suppose that I is a continuous function on X. Let B be any arbitrary subset
of Y. Then B O is open in Y and by continuity of I, 1-1 (B O ) is open in X. Therefore,
[/- 1 (B O )] 0 = 1-1 (B O ). But
B O C B =* 1-1 (B O ) C 1-1 (B)
and thus,
[/- 1 (B O )] 0 C [/- 1 (B)] 0 .
This implies that 1-1 (B O ) C [/- 1 (B)]0.
Conversely, let G be an open subset ofY. Then GO = G. By the hypothesis
[/- 1 (G)] 0 =:) 1-1 (GO) = 1-1 (G).
But [/- 1 (G) ] 0 C 1-1 (G), therefore, 1-1 (G) = [/- 1 (G) ] 0 and thus 1-1 (G) is open
in X. Hence I is continuous on X.
Exercise 5.5. Let (X, d) be a metric space and for each i = 1, 2, . . . , n, the function
f;, : X IR be continuous. Then prove that the function I : X IRn defined by
I(x) = (11 (x), 12 (x), ..., In (x) ) for all x EX
is continuous.
Proof Let Xo be an arbitrary point in X. Since each f;, is continuous, f9r a given
E > 0, there exists 6; > 0 for each i = 1,2, . . . , n such that for all x E X and for each
i = 1,2,. . . , n
d(x,xo) < i implies l!i(X) - f;(xo)1 < .5n .
Take 6 = min {6 1 , ,"', 6n}. Then d(x,xo) < 6 implies that
{ 2 2 } 1/2
d (/(x),/(xo)) = (11 (x) - 11 (xo)) +... + (In (x) - In (XO)) < E.
Thus I is continuous at Xo EX. Since Xo was arbitrary, I is continuous on X.
Exercise 5.6. Let (X, d) be a metric space and I : X n be a function defined as
I(x) = (11 (x), 12 (x), .. . , In (x) ) for all x EX,
where f;, : X IR is a function for each i = 1,2,. . . , n. If I is continuous on X, then
prove that each f;, is also continuous on X.
Hint: In fact, for each i = 1,2,...,n
If;,(x) - f;,(y) I < d (/(x), l(y)) ,
( ) 1/2
where d (f(x), !(y)) = l.fi(x) - .fi(Y)12 .
5.2 Continuous Functions and Compact Spaces
93
5.2 Continuous Functions and Compact Spaces
Theorem 5.8. Let X and Y be metric spaces and f : X Y be a continuous function.
If A is a compact subset of X, then f(A) is compact in Y.
Proof Let = {Ga}aEA be an open cover of f(A). Then by Theorem 5.3, f-l(G a )
is open in X for each a EA. Hence {A n f-l (G a) } aEA forms an open cover of A.
Since A is compact, there exists a finite set J = {1, 2, . . . , n} of A such that
A= (Anr1(Gk)) =An ( rl(Gk)) =Anr 1 ( Gk).
Thus
A C r 1 ( Gk)
and so
n
f(A) C U Gk.
k=1
Hence {Gl, G2,.. . , G n } is a finite s bcover of . Thus f(A) is compact.
Corollary 5.1. Let X and Y be metric spaces and f : X Y be a continuous function.
If X is compact, then f(X) is bounded.
Proof By Theorem 5.8, f(X) is compact. Since every compact space is sequentially
compact and every sequentially compact space is totally bounded, we have f(X) is
totally bounded and hence it is bounded.
Theorem 5.9. Let X and Y be metric spaces and f : X Y be a continuous function.
If X is compact, then f(F) is closed in Y whenever F is closed in X.
Proof Let F be a closed subset of X. Since every closed subset of a compact set is
compact, by Theorem 5.8, we have f(F) is compact and hence it is closed.
Theorem 5.10. Let X and Y be metric spaces and f : X Y be a continuous function.
If f is bijective and X is compact, then f-l is continuous on Y.
Proof Since f is bijective, f-l : Y X exists and also bijective. Let F be a closed
set in X. Then (f-l) -1 (F) = f(F) and by Theorem 5.9, f(F) is closed in Y. Thus,
the inverse image of a closed set is closed and hence f-l is continuous.
Remark 5.3. In Theorem 5.10, if X is not compact, then f-l need not be continuous.
For example, consider and identity function I : ( , d) ( , all) from IR with the
discrete metric to with the usual metric. Then I is continuous but I-I is not.
Exercise 5.7. Give an example to show that Theorem 5.9 does not hold if X is not
compact.
Exercise 5.8. Prove that a continuous real-valued function defined on a compact set
is bounded and it assumes maximum and minimum values.
94
5 Continuous Functions
Proof Let f:x -+ be continuous and let A be a compact subset of a metric spaceX.
By Theorem 5.8, f(A) is a compact subset of . By Heine-Borel Theorem 4.6, f(A) is
closed and bounded. Thus sup f (A) and inf f (A) exist and belong to f (A). Therefore,
there existx,i EA such that for ally EA, inff(A) = f(x) < f(y) < f(i) = supf(A).
Exercise 5.9. Let (X, d) be a metric space and A be a nonempty compact subset of X.
Prove that for every Xo EX, there exists a Yo E A such that
d(xo,yo) = d(xo,A) = inf d(xo,y).
yEA
Proof Consider the real valued function f : A -+ + defined by f(x) = d(x,xo) for
all x EA. Now If(x) - f(Y)1 = Id(x,xo) -d(Y,xo)1 < d(x,y), so f is continuousonA.
But A is compact, so f has a minimum on A by Exercise 5.8. That is, there exists a
Yo E A such that '
f(yo) = d(xo,yo) = inf d(xo,y) = d(xo,A).
yEA
5.3 Uniform Continuous Functions
Before giving the definition of uniform continuity, we examine the following exam-
ples.
Consider a real-valued function f : [-1,1] -+ defined as f(x) = xl. Let X,Xo be
any points of [-1,1]. Then
d(f(x),f(xo)) = If(x) - f(xo) I = I -x51
= Ix-xol'lx+xol < E
whenever Ix -xol < !E = lJ, where lJ is independent on the choice of x and xo.
Thus for any E > 0, there exists a lJ = ! E such that for any X,Xo E [-1, 1], we have
d (f(x),f(xo)) < E whenever d(x,xo) < lJ.
Now, if we consider the same function f(x) = xl defined on , that is, f : -+
such that f(x) = r-. Then for every real numbers X,Xo, we have
d (f(x),f(xo)) = I -x51 = Ix-xol'lx+xol < E
whenever Ix - xol < lx:xor = lJ, where lJ depends on E and xo.
In this way, we see that lJ may depend not only on E but also on xo. Uniform
continuity is essentially continuity plus the added condition that for each E we can
find a lJ which works uniformly over the entire space, in the sense that it does not
depend on xo.
Definition 5.2. Let (X, d) and (Y, p) be metric spaces. A function f : X -+ Y is said
to be uniformly continuous if for each E > 0, there exists a lJ > 0 (depends only on E)
such that for every x,y EX,
5.3 Uniform Continuous Functions
95
d(x,y) < () implies p (f(x),f(y)) < E.
Remark 5.4. Every uniform continuous function is continuous but converse need not
be true in general. For example, in the first example mentioned above, () is inde-
pendent on the choice of x and xo, and therefore, it is uniformity continuous. But in
the latter example, () depends on E and xo, and hence, it is only continuous but not
uniformly continuous.
Example 5.2. (a) Let X be a discrete metric space and Y be any metric space. Then
any function f : X -+ Y is uniformly continuous.
(b) Let X = (0,1) be a metric space with the metric induced by the usual metric on
and Y = with the usual metric. The function f : X -+ Y defined as f(x) = for all
x EX, is not uniformly continuous.
Let E = ! and () be any positive number. Choose x = and y = n I ' where n is a
positive integer such that n > !. Then
1 1
Ix-yl= --
n n+1
1 1
n(n+l) <;; < D,
but If(x) - f(y) I = In - (n + 1) I = 1 > E. Thus whatever () > 0 may be, there exist x
andy such that Ix- yl < () but If(x) - f(Y)1 > !.
(c) No polynomial function of degree greater than 1 is uniformly continuous on the
usual metric space . Note that any polynomial function is continuous.
(d) The logarithmic function is not uniformly continuous on the usual metric space
X=(O,oo).
Theorem 5.11. Let (X, d) and (Y, p ) be metric spaces and f : X -+ Y be a continuous
function. If X is compact then f is uniformly continuous.
Proof Let E > 0 and x E X be arbitrary. Consider the image f(x) of x and the open
sphere Se(f(x)). Since f is continuous, f-l (Se(f(x))) is an open set inX. Consider
the family = {f- 1 (Se (f(x))) : x EX} of these open sets in X. Then clearly is
an open cover of X. Since X is compact, it is sequentially compact, and therefore, by
Lebesgue's covering lemma (Theorem 4.11) there exists a Lebesgue number () > 0
for . Thus every open sphere of diameter less than () will be contained in at least
one member of and, consequently, we have
S6/2(X) C f-l (Se(f(x))) => f (S6/2(X)) C Se(f(x)).
Hence for each E > 0, there exists a () > 0 (independent of x) such that
() -
d(x,y) < 2 = () => p(f(x),f(y)) < E.
Hence f is uniformly continuous.
Theorem 5.12. Composition of two uniformly continuous functions is a uniformly
conunuousfuncuon.
96
5 Continuous Functions
Theorem 5.13. Let (X, d) and (Y, p ) be metric spaces and f : X Y be an uniformly
continuousfunction. If {xn} is a Cauchy sequence in X, then {f(xn)} is also a Cauchy
sequence in Y.
Proof Since f is uniformly continuous, for each E > 0, there exists a lJ > 0 (only
depends on E) such that for allxt,x2 EX,
d(Xt,X2) < lJ implies p(f(xt),f(X2)) < E.
In particular, we have
d(xn,xm) < lJ implies p (f(xn),f(xm)) < E.
(5.1)
Since {xn} is a Cauchy sequence in X, for a given lJ > 0, there exists a positive integer
N such that
d(xn,xm) < () for all n,m > N.
From (5.1) and (5.2), we obtain
(5.2)
P (f(xn),f(xm)) < E for all n,m > N.
Hence {f(xn)} is a cauchy sequence in Y.
The following example shows that a continuous function may not map a Cauchy
sequence into a Cauchy sequence.
Example 5.3. Let X == (0,00) with the induced usual metric on IR and Y == with the
usual metric. The function f : X Y defined by f (x) == for all x EX, is continuous
onX. Clearly, {Xn : X n == } nEN is a Cauchy sequence inX. But {f ( ) } nEN == {n} :=1
is not a Cauchy sequence in Y. Indeed, the absolute difference of any two distinct
points is at least as large as 1.
Exercise 5.10. Show that the function f(x) == eX defined on the usual metric space
is not uniformly continuous.
Hint: There is no lJ > 0 that guarantees d(x,y) == leX - eYI < 1 for all x,y E with
eY-eX
Ix - yl < lJ. Specially, for all x,y E IR with x < y, we have > t!. Then for any
y-x
y E (0,1), pick X == -lny andy == y -lny, so that eY - if > (y -x)eX == 1.
Exercise 5.11. Let (X,d) be a metric space and A be a subset of X. Prove that the
function f : X defined by
f(x) == d(x,A) for all x EX
is uniformly continuous.
Proof By the triangular inequality
d(x,a) < d(x,y) + d(y,a) for all a E A,x EX.
By taking infimum, we obtain
inf d(x,a) < d(x,y) + inf d(y,a).
aEA aEA
5.4 Homeomorphism and Equivalent Metrics
97
Therefore,
d(x,A) < d(x,y) +d(y,A)
and so
d(x,A) - d(y,A) < d(x,y) for all x,y EX.
By interchanging x and y, we obtain
d(y,A) - d(x,A) < d(y,x) = d(x,y).
Thus
Id(x,A) - d(y,A) I < d(x,y).
Therefore, for a given E > 0, choosing a 6 such that 0 < 6 < E, we have
I I (x) - 1(y)1 = Id(x,A) -d(y,A)1 < d(x,y) < 6 < E,
that is,
I I (x) - f(Y)1 < E whenever d(x,y) < 6.
Hence I is uniformly continuous on X.
5.4 Homeomorphism and Equivalent Metrics
Definition 5.3. Let X and Y be two metric spaces. A function I : X Y is said to be
a homeomorphism if
(i) I is bijective, that is, I is one-to-one and onto
(ii) I and 1-1 both are continuous.
Two metric spaces X and Yare said to be homeomorphic if there exists a homeo-
morphism from X onto Y.
Example5.4. (a) Let [0,1] and [0,2] be metric spaces with the usual metric and
I : [0,1] [0,2] be a function defined as f(x) = 2x for all x E [0,1]. Then f is a
homeomorphism and the spaces [0,1] and [0,2] are homeomorphic.
(b) Let X = (0,00) and Y = be metric spaces such that Y is equipped with the usual
metric and X with the usual metric induced from . Let I : X Y be a function
defined as I(x) = lnx for all x EX. Then f is a homeomorphism between X and Y.
(c) The metric space with the usual metric is not homeomorphic to the metric space
with the discrete metric.
Recall that a mapping I : X Y from a metric space (X, d) to a metric space (Y, p )
is an isometry if
p (/(x), l(y)) = d(x,y) for all x,y EX.
It is obvious that an isometry is one-to-one and uniformly continuous.
Recall also that X and Yare said to be isometric if there exists an isometry between
them that is onto.
An isometry is necessarily a homeomorphism, but the converse need not be true.
In Example 5.4 (a) and (b), the mappings are homeomorphism but not isometry.
98
5 Continuous Functions
Theorem 5.14. Let X and Y be two metric spaces and f : X -+ Y be a bijective func-
tion. Then the following statements are equivalent.
(a) f is a homeomorphism.
(b) The set G c X is open if and only if its image f(G) C Y is open.
(c) The set F C X is closed if and only if its image f(F) C Y is closed.
Proof (a) =* (b). Let (a) hold. Then f and f-l both are continuous. Therefor, for any
open set G eX, we have (f-l) -1 (G) = f (G) is open in Y by using continuity of
f-l.
Conversely, let f(G) C Y be open. Then by continuity of f, f-l (f(G)) = G is
open in X ( f-l (f( G)) = G because f is injective).
(b) =* (c). Let F c X be a closed set. Then X \ F is open in X. By (b), f(X \F) is
open in Y. But f(F) = Y \ f(X \ F). Hence f(F) is closed in Y.
Conversely, let f(F) is closed in Y. Then Y \ f(F) is open in Y. Then f(X \ F) =
Y \ f(F) is open. By (b), X \ F is open and hence F is closed.
(c) =* (a). Let F be a closed subset of X. Then by hypothesis, f (F) is closed in Y.
Since f-l (f(F)) = F, the inverse image of closed set is closed, and therefore, f is
continuous.
Also, since (f-l) -1 (F) = f(F), by hypothesisF is closed in X and f(F) is closed
in Y, we have f-l is continuous on Y. Therefore, f is a homeomorphism.
Remark 5.5. Let X, Y and Z be metric spaces. If X is homeomorphic to Y and Y is
homeomorphic to Z, then X is homeomorphic to Z.
Definition 5.4. Two metrics dl and dz on the same underlying set X are said to be
equivalent if for every sequence {xn} in X and x EX,
lim d 1 (xn,x) = 0 if and only if lim dz(xn,x) = 0,
n oo n OO
that is, a sequence converges to x with respect to the metric d 1 if and only if it con-
verges to x with respect to the metric dz.
The metric spaces (X, d 1) and (X, dz) are said to be equivalent if the metrics d 1
and dz are equivalent.
Remark 5.6. (i) Two metrics d 1 and dz on a nonempty set X are equivalent if and
only if the identity map I : (X, dl) -+ (X, dz) together with its inverse map
1-1 : (X, dz) -+ (X, dl) are continuous, that is, if and only if the identity map
I: (X,dl) -+ (X,dz) is a homeomorphism.
(ii) If two metrics are equivalent then the families of open sets are same in (X,d 1)
and (X,dz).
The following result provides a sufficient condition for two metrics on a set to be
equivalent.
Theorem 5.15. Two metrics d 1 and dz on a nonempty set X are equivalent if there
exists a constant k such that
1
k dz(x,y) < d 1 (x,y) < kdz(x,y) for all x,y EX.
(5.3)
5.4 Homeomorphism and Equivalent Metrics
99
Proof Let {xn} be a sequence in X such that dt(xn,x) 0 as n 00. From the first
inequality in (5.3), we have
1
k dz(xn,x) < dl (xn,x) 0 as n 00
and thus, dz(xn,x) 0 as n 00.
If dz(xn,x) 0 as n 00, then in view of second inequality in (5.3), we have
dl (xn,x) < kdz(xn,x) 0 as n 00
and thus, dt(xn,x) 0 as n 00.
The following example shows that the converse of the above theorem does not
hold, that is, if d t and dz are equivalent metrics then the inequality (5.3) need not be
true.
Example 5.5. Let (X, d) be a metric space and P be anther metric on X defined by
d(x,y)
p(X,y) = l+d(x,y) forallx,yEX.
Then d and P are equivalent metrics on X.
Indeed, let d(xn,x) 0 as n 00. Then obviously p(xn,x) 0 as n 00. On the
other hand, if p(xn,x) 0 as n 00, then for 0 < £ < 1, we have 2 - £ > 1, and also,
there exists a positive integer N such that p(xn,x) < £/2 for all n > N. So
d(xn,x) £
l+d(xn,x) =p(xn,x) < 2 foralln>N
which is equivalent to
£
d(xn,x) < 2- £ < £ for all n >N.
Thus, d(xn,x) 0 as n 00.
On the other hand, we observe that there is no constant k > 0 such that
1
. k d(x,y) < p(x,y) for all x,y E .
This establishes that the condition (5.3) in Theorem 5.15 is not necessary for the
metrics d and p to be equivalent.
This example shows that there always exists an equivalent metric p on a metric
space such that (X, p) is bounded.
Now we present some examples of equivalent and non-equivalent metrics.
Example 5.6. (a) The metrics dl, dz and doo defined on n by
n
dl (x,y) = IXi - Yil
l=t
100
5 Continuous Functions
d2(X,y) = ( (Xi _ Yi)2) 1/2
doo(x,y) = m x IXi - Yil
1 I n
for all x = (Xl" . . ,X n ) E n and y = (YI,. . . ,Yn) E n, are equivalent. In fact, any real
numbers aI, a2, . . . , an, we have
( ) 1/2 ( ) 1/2
al < lail < n.max{lail:l < i < n} < n al .
(b) Let C[O, 1] be a space of all continuous linear functionals defined on [0,1]. Con-
sider the metrics doo and d defined on C[O, 1] by
doo(/,g) = sup I/(x) - g(X) I
XE[O,I]
and
d(l,g) = flf(X) - g(x)ldx
for all I, g E C[O, 1]. Then these metrics d oo and d are not equivalent.
Indeed, let {In} be a sequence in C[O, 1] defined by
In (x) = for all X E [0,1].
Also, let I(x) = 0 for all X E [0,1]. Then d (In, I) 0 as n 00. In fact,
10 1 1
d(ln,/)= dx= O asn oo.
o n+1
However,
doo (In, I) = sup I/n(x) - I (x) I = 1 for all n.
XE[O,I]
SO, lim d oo (In, I) =1= O. Thus the sequence {In} converges to I with respect to the
n--+oo
metric d but not with respect to the metric doo. Therefore, the metrics d oo and d are not
equivalent.
However, for any sequence {In} in C[O, 1] and any I E C[O, 1], when d oo (In, I) 0
as n 00, it does follow that d (In, I) 0 as n 00. Observe that
d (In,!) = r 1 Ifn (x) - f(x) I dx < sup Ifn(x) - f(x) I = dCK> (In,!).
10 XE[O,l]
(c) Let m be the space of all bounded sequences with the following two metrics
d(x,y) = sup IX n - Ynl
l n<oo
and
5.4 Homeomorphism and Equivalent Metrics
101
d ( ) 1 IX n - Ynl
1 X,Y = L.J 2 n 1 + I - I '
n=l X n Yn
where the sequences x = (Xl ,X2,. . .) and Y = (Yl ,Y2,. . .) are elements of m.
Consider the sequence {en} in m whose respective terms are the sequences
el = (1,0,0,. ..),e2 = (0,1,0,. ..),... ,en = (0,0,... ,0, 1,0,.. .),...
where 1 is in the nth place. Let eo = (0,0,0,.. .). Then
d (en, eo) = 1 while dl (en, eo) = 1 = 1 +1 -+ 0 as n -+ 00.
2 n 1 + 1 2 n
Thus the sequence {en} converges with respect to the metric d1 but not with respect
to the metric d. Hence the metrics d and d 1 are not equivalent.
Exercise 5.12. Let X, Y and Z be metric spaces. If X is homeomorphic to Y and Y is
homeomorphic to Z, then prove that X is homeomorphic to z.
Proof Let I : X -+ Y and g : Y -+ Z be homeomorphisms. Then I, g are bijective,
continuous and 1-1 , gl are also continuous. Consider the function go I : X -+ z.
Since composition of two bijective and continuous functions is bijective and
continuous, respectively, go I is bijective and continuous. Also since (g 0 f) -1 =
I-log -1 is continuous. Therefore, go f is a homeomorphism and hence X is home-
omorphic to Z.
Exercise 5.13. Show that the function I : -+ ( -1, 1) defined by
X
f(x) = 1+lxl
for all X E IR
is a homeomorphism. Also, show that I is uniformly continuous on IR.
Hint: The given function f can be restated as
f(x) = { (ltx)
(I-x)
if X > 0,
if x < O.
Observe that the inverse function g : ( -1, 1) -+ of the function I is given by
g(y) = {
(1 +y)
if Y > 0,
if Y < O.
In fact, for x > 0, we have (l x) > 0 and hence,
( x )
(gof)(x)=g 1+ = 1- x =x,
x (1 +x)
whereas, for x < 0, we have (l:'X) < 0 and hence,
x
(gof)(x) =g( 1 x x ) = 1 =x.
102
5 Continuous Functions
Similar computations for log is left for the readers. Since the function 1 and its
inverse g are both continuous, 1 is a homeomorphism.
Now we check the uniform continuity of I. For x,y > 0,
x y Ix-yl
If(x)- f(Y)1 = l+x - l+y = (l+x)(l+y) < Ix-yl.
Similarly, for x < 0 andy < 0, we have I 1 (x) - 1(y)1 < Ix-yl. For x> 0 andy < 0,
x y Ix-y-2xy1
If(x)-f(Y)I= l+x - l+y = (1+x)(l-y)
x-y_2xy+xl+y2
<
- (1 +x)(1- y)
(x-y)(1+x-y)
(1+x)(1-y)
< x-y= Ix-yl.
The case when x or y is 0 is left to the readers.
.
Exercise 5.14. (a) Show that the image of a complete metric space under homeomor-
phism need not be complete.
(b) Show that the image of a complete metric space under a one-to-one uniformly
continuous mapping need not be complete.
Hint: The function 1 in Exercise 5.13 is both homeomorphism and uniformly contin-
uous. is complete but 1 ( ) = ( -1, 1) is not.
Exercise 5.15. A mapping 1 : X -+ Y from a metric space (X,d) to a metric space
(Y, p) is said to be open (respectively, closed) if I( G) is open (respectively, closed) in
Y for every open (respectively, closed) set G in X.
(a) Given an example of a function 1 that is continuous and open, but is not a home-
omorphism.
(b) Given an example of a function 1 that is continuous and closed, but is not a
homeomorphism.
(c) Given an example of a function 1 that is continuous and closed, but is not open.
(d) Given an example of a function 1 that is continuous and open, but is not closed.
Hint: (a) Consider S = {(x,y) E 2 : xl + y2 = 1} and define a map 1 : -+ S as
I(t) = (cos(2Jtt),sin(2Jtt)). Since the components of 1 are continuous, and therefore,
1 is continuous. Observe that it is also open. Indeed, let (a, b) = I and f(I) = b - a.
If f(I) > 1, then 1(1) = S which is open in S. If f(I) < 1, then f(I) is an arc without
endpoints and so is open in S, being the intersection of S with an open disc with the
missing endpoints on its edge. The function is not one-to-one and thus, cannot be a
homeomorphism.
(b) and (c) Consider any constant function 1 : 2 -+ and observe that it is continuous
and closed, but not a homeomorphism, as it is not one-to-one.
(d) Consider the function 1 : 2 -+ defined by I(XI,X2) = Xl for all (XI,X2) E 2
and obs e that it is continuous and open but not closed, as it maps the hyperbola
XtX2 = 1 onto the set \ {O}, which is not closed.
5.5 Uniform Convergence of Sequences of Functions
103
5.5 Uniform Convergence of Sequences of Functions
Definition 5.5. Let {fn} be a sequence of functions from a metric space (X,d) to
another metric space (Y, p) and f : X -+ Y be a function. We say that the sequence
{fn} converges pointwise to the function f if for a given E > 0 and given x EX, there
exists a positive integer N such that
p (fn(x),f(x)) < E for all n > N.
(5.4)
In general, the integer N depends on E as well as on x. It is not always possible to
find an integer N such that (5.4) holds for all x E X simultaneously.
If N depends only on E, then we say that the sequence {fn} converges uniformly
onX.
Definition 5.6. Let {fn} be a sequence of functions from a metric space (X,d) to
another metric space (Y, p) and f : X -+ Y be a function. We say Ithat the sequence
{fn} converges uniformly to the function f if for a given E > 0, there exists a positive
integer N (depending only on E) such that
p (fn(x),f(x)) < E for all n > Nand all x EX.
(5.5)
It is clear that uniform convergence implies pointwise convergence, but converse
need not be true.
Example 5.7. Let X = [0,1] and Y = with the usual metric. Let {fn} be a sequence
of functions fn : X -+ Y defined by
fn(x) = X'.
Then {fn} converges pointwise to the function f : X -+ Y defined by
f(x) = {
ifO < x<1
if x = 1.
Remark 5.7. (i) Observe that the function f is not continuous even though each of
the function fn is continuous.
(ii) Since f is not continuous and {fn} is a sequence of continuous functions, by next
Theorem 5.16, {fn} does not converge unifromly to f.
Example 5.8. Let X = Y = with the usual metric. Let {fn} be a sequence of func-
tions fn : X -+ Y defined by
{ I - ! I x l
fn(x) = 0 n
if Ixl < n
if Ixl > n.
Then {fn} converges pointwise to the function f : X -+ Y defined by
f(x) = 1.
But {fn} does not converge uniformly to f.
104
5 Continuous Functions
Indeed, let E == !. Note that for every n EN, there exists Xo E X with fn (xo) == 0
and so
Ifn(xo) - f(xo) I = 1 > E.
Theorem 5.16. Let (X, d) and (Y, p ) be metric spaces, {fn} be a sequence of continu-
ous functions each defined on X to Y and f : X -+ Y be a function. If fn -+ f uniformly
on X, then f is continuous on X. In other words, an uniform limit of a sequence of
continuous functions is continuous.
Proof Let Xo E X be arbitrary and let E > 0 be given. Since fn -+ f uniformly on X,
there exists a positive integer N (depending on E only) such that for each x EX,
E
P (fn(x), f(x)) < 3 for all n > N.
(5.6)
Let no > N. Since fno is continuous at XO, we can choose 6 > 0 such that for all
x E S6 (xo), that is, d(x,xo) < 6, we have
E
P (tno(X),fno (xo)) < 3 '
(5.7)
Using (5.6) and (5.7), for all x E S6 (xo), we have
p (f(x), f(xo)) < P (f(x), fno (x)) + p (fno (x), fno (xo)) + p (fno (xo), f(xo))
E E E
< 3 + 3 + 3 = E,
and therefore, f is continuous at Xo.
Theorem 5.17 (Cauchy Criterion). Let {fn} be a sequence of functions defined on a
metric space (X, d) to a complete metric space (Y, p). Then there exists a continuous
function f : X -+ Y such that
fn -+ f uniformly on X
if and only if the following condition is satisfied: For every E > 0, there exists a posi-
tive integer N such that
P (fm(x), fn(x)) < E for all m,n > N andfor all x EX.
Proof Suppose that fn -+ f uniformly onX. Then for any given E > 0, there exists a
positive integer N such that
E
p(fn(x),f(x)) < - foralln>NandforallxEX.
2
Thus for all m,n > N and for all x EX,
E E
p(fm(x),f(x)) < 2 and p(fn(x),f(x)) < 2 '
Hence for all m, n > N and for all x EX, we have
E E
p(fm(x),fn(x)) < p(fm(x),f(x))+p(fn(x),f(x)) < 2 + 2 = E.
5.5 Uniform Convergence of Sequences of Functions
105
Conversely, assume that
P (1m (x), fn(x)) < E for all m,n > N and for all x EX.
Then for each x EX, the sequence {fn (x)} is a Cauchy sequence in a complete metric
space Y, and therefore, converges to some point I(x), say. We claim that fn -+ I
uniforml y on X. If E > 0 is given, we can choose N such that for all n > N, we have
E
P (In (x), fn+k(X)) < 2 for all k = 1,2,... and all x EX.
Letting k -+ 00, we obtain
p (fn(x), f(x)) = ! p (fn(x), fn+k(X)) < .
Hence
P (In(x),f(x)) < E fot all n > N and for all x EX,
and so In -+ I uniformly onX.
Exercise 5.16. Let X = Y = IR with the usual metric. Let {In} be a sequence offunc-
tions defined by
0 if x < O
nx ifO<x<!
In(x) = - - n
-nx+2 if!<x<
n- -n
0 if x>
-n
and I(x) = 0 for all x E . Show that In -+ I pointwise on .
IR
(0,1)
(1,0)
IR
1 ( ,O)
(!,O)
Proof If x is close to 0 and positive, then there exists a positive integer N such that
2/N < x and so In (x) = 0 for all n > N. However, there exists no N such that (5.5)
holds for E = !, for all n > N and for all x E IR. For, if such an N were to exist, we
would have
106
5 Continuous Functions
fn(X) < - for ail n > N and for all x E R
We would then have Nx < ! for 0 < x < ; but for x = N, we obtain the contradiction
2 1
3 < 2'
Exercise 5.17. Prove that the sequence {In} defined by
In(x) = tan- 1 (nx) for all x > 0,
is uniformly convergent on [a,oo) when a > 0, but is not uniformly convergent on
[0,00).
Proof. The pointwise limit function is
I(x) = lim In (x) = { !
n oo 0
if x > 0
if x = O.
We show that In -+ I uniformly on [a,oo) when a > O.
For x > 0, we claim that
Ifn(x) - f(x) I = Itan-1(nx) - 1= coC1(nx).
Since 0 < tan- 1 8 < n/2 for any 8 > 0, therefore, when x > 0, we have 0 <
tan- 1 (nx) < n/2 and hence
n 1 n
0< - -tan- (nx) < -.
2 2
(5.8)
Also,
cot( -tan-1(nx)) =nx. (5.9)
It follows from (5.8) and (5.9) that n/2 - tan- 1 (nx) = cot- 1 (nx). The first inequality
in (5.8) implies that
Itan-1(nx)- I = -tan-1(nx) forallx>O.
Thus
Itan-1(nx)- I =coC1(nx).
Let e > 0 be arbitrary. When x > a, the inequality n > c e implies that n > c e ,
so that nx > cot e and hence cot- 1 nx < e in view of the fact that cot- 1 is a decreasing
function. It follows that if N is an integer greater than or equal to c e , then
Ifn(x) - f(x) I = Itan-1(nx) - 1= coC I nx < e
whenever n > N and x > a. However, c e -+ 00 as n -+ 0, so that no integer N exists
for which
I/n(x) - I(x) I < e for all n > N and all x E [0,00).
5.5 Uniform Convergence of Sequences of Functions
107
Actually this proves that the convergence fails to be uniform even on the smaller set
(0,00).
Exercise 5.18. Consider the sequence {In} of functions defined by In (x) = 1 1 for
+x!l,
x E [0, 1]. v
(a) Find I(x) == lim In (x).
n--+oo
(b) Show that for 0 < a < 1, {In} converges uniformly to Ion [O,a].
(c) Show that {In} does not converge uniformly to I on [0,1].
Proof. (a) Since In(l) == 1/2 for all n E N, we obtain 1(1) = 1/2 and
I . 1
1m == 1
n --+00 1 + x"
for 0 < x < 1
which yields I(x) == 1 for 0 < x < 1.
(b) If x E [0, a], then
1 -1
1 +x"
x" an
< .
1+x" - l+a n
Since 0 < a < 1,
an
lim == 0,
n--+oo 1 + an
so {In} converges uniformly to I on [0, a].
(c) Given n E N,let x be such that n0 < X < I, then! < X' < 1. Therefore,
V"2 2
1 x"!
-1 == > 2
1+x" 1+x" 1+1
1
-
4
which implies {In} does not converge uniformly to I on [0, 1].
nx
Exercise 5.19. Let {In} be a sequence of functions defined by In (x) = - for x E
enx
[0,2] .
(a) Show that lim In (x) == 0 for x E (0,2].
n--+ oo
(b) Show that the convergence is not uniform on [0,2].
Proof. (a) Since
In+l (x) (n + 1 )xe nx (n + 1) -x
= == e,
In (x) nxe(n+l)x n
we have lim Ij,+( ( ) = e- x < 1. Thus lim In (x) = 0 for x E (0,2].
n--+ oo n X n--+ oo
(b) Let us find the maximum of In in [0,2]. Since I (x) = nfIIX - n nxnx = 0, we have
(e nx )
1
enx(n - n 2 x) == 0 <=> n 2 x = n <=> x == -.
n
108
5 Continuous Functions
It can be easily seen that is the maximum with In ( ) = . Since
lim sup {l/n(x) - 01: x E [0,2]} = lim In ( ! ) = ,
n oo n oo n e
the convergence is not uniform on [0,2].
Exercise 5.20. Let X = [0, 1] and Y = JR with the usual metric. Let {In} be a sequence
of functions defined by
4n 2 x
In (x) = -4n 2 x+4n
o
ifO < x <2
. f 1 1
1 2n <x<;;
if ! < x < 1.
n - -
Show that the sequence {In} converges pointwise to the constant function I(x) = o.
Chapter 6
Connected Spaces
In this chapter, we discuss the connectedness, components and their properties. The
idea of connected spaces or sets comes from an interval which is in one piece. That
is, an interval cannot be written as a disjoint union of two nonempty open (in it)
subintervals.
6.1 Separated Sets
Definition 6.1. Let X be a metric space. 1Wo nonempty subsets A and B of X are said
to be separated if
An B =0 and A nB=0.
Example 6.1. 1. In the usual metric space ,
(a) the sets A = (1,2) and B = (2,3) are separated;
(b) the sets A = (1,2] and B = (2,3) are not separated.
2. In the discrete metric space IR, the sets A = (1,2] and B = (2,3) are separated, since
in a discrete metric space X, A =A.
Remark 6.1. If A and B are separated sets in a metric space X, then they are disjoint,
since A nB C A n B = 0. But two disjoint sets need not be separated. For example,
A = (1,2] and B = (2,3) are disjoint but not separated in the usual metric space .
Also, the setsA = {x E : x < O} and B = {x E : x > O} are disjoint but not separated
in the usual metric space JR.
Theorem 6.1. Let (X, d) be a metric space and, A and B be nonempty subsets of X. If
d(A,B) > 0, then A andB are separated.
Proof Let d(A,B) = A. Since
d(A,B) = inf{d(x,y):x EA,y EB} = A > 0,
we have
d(x,Y» A forallxEAandyEB.
If x E A, then x cannot be a limit point of B because S A (x) contains no points of B.
"!
Therefore, A n B = 0. Similarly it can be proved that A nB = 0. H;ence A and Bare
separated.
Remark 6.2. The converse of the above theorem is not true in general.
Example 6.2. In the usual metric space JR, the sets
110
6 Connected Spaces
A = {x E : x > O} and B = {x E : x < O}
are separated, while d (A, B) = O.
Theorem 6.2. Let A and B be two nonempty subsets of a metric space X.
(a) If A and B are closed, then they are separated if and only if A and B are disjoint.
(b) If A and B are open, then they are separated if and only if A and B are disjoint.
Proof. Since any two separated sets are disjoint, we only prove one way.
(a) Since A andB are closed, we have
AnB=AnB=AnB.
By the definition of separated sets, we follow the result.
(b) Let A and B be open and disjoint, that is, A n B = 0. Then X \ A and X \ Bare
closed and thus
X\A =X\A, X\B =X\B
and
A C X\B implies A C X\B =X\B.
Similarly, we can show that B C X \A. Therefore,
A nB C (X\B)nB=0 and B nA C (X\A)nA=0.
Hence A and B are separated.
Remark 6.3. Theorem 6.2 says that, in a metric space, any two sets, either both open
or both closed are separated if and if only if they are disjoint.
Theorem 6.3. Let A and B be two separated sets is a metric space X and G = A U B.
Then
(a) A and B are open if G is open;
(b) A and B are closed if G is closed.
Proof. (a) Since B is closed, (B )C is open. Since G =A UB is open, so is (A UB) n
(B )c. Since A andB are separated, A n B = 0 and hence A C ( B) c. Also, B C B implies
( B )C C B C and thusB n (B )C C B nB c = 0. Consequently,
(A UB) n (B )C = [A n (B )C] U [B n (B )C] =A U0 =A.
Hence A is open. Similarly, we can prove that B is ope n.
(b) Since G =AUB is closed, we haveAUB =AUB = A U B . By hypothesis, A and
B are separated and thus A nB = 0. Hence
A = A n (A U B ) = A n(AUB) = (A nA)U (A nB) =AU0=A.
ThusA is closed. Similarly, we can prove that B is closed.
Exercise 6.1. Let C and D be two separated subsets of a metric space X and let A C C
and B C D. Prove that A and B are also separated.
6.2 Connected Sets
111
6.2 Connected Sets
Definition 6.2. A metric space X is said to be connected if it cannot be expressed as
the union of two separated sets.
Furthermore, X is called disconnected if it is not connected, that is, if X can be
expressed as the union of two separated sets. In other words, X is disconnected if
X =AUB where An B = 0 and A nB = 0.
The sets A and B are said to form a separation of X.
Remark 6.4. In view of Theorem 6.2, we have
(i) a metric space X is connected if it cannot be expressed as the union of two
nonempty disjoint closed sets;
(ii) a metric space X is connected if it cannot be expressed as the union of two
nonempty disjoint open sets.
Definition 6.3. A subset Y of a metric space (X, d) is said to be connected if the
subspace (Y, dy) with the metric induced from X is connected.
In other words (Y, dy) is connected if Y =1= A U B, where A and Bare nonempty
disjoint subsets of Y which are open in Y, that is, A = G n Y and B = H nY, where G
and H are open subsets of X.
Example 6.3. Let Y = [-1, 0) U (0, 1] be the subspace of the usual metric space , .
Each of the sets [-1,0) and (0,1] is nonempty and open in Y (although not open in
). Therefore, they form a separation of Y. Alternatively, note that neither of these
sets contains a limit point of the other. (They do have a limit point 0 in common, but
that does not matter). Thus Y is disconnected. It can also be seen in the following
figure.
J.
.:.
.
IR
-1
o
1
Example 6.4. (a) Let Q be the set of all rational numbers with the usual metric
d(x,y) = Ix - yl for all x,y E Q. Then Q is disconnected, because the sets
A = {x E Q : x > J2} and B = {x E Q : x < J2}
are open in Q and non empty disjoint sets such that A n B = 0, A nB = 0 and Q =A UB.
Similarly, the set of all irrational numbers is disconnected.
(b) The space X = {(x,y) E 2 : r- + y2 < 1} U {(x,y) E 2 : (x - 3)2 + (y - 3)2 < 1}
with the usual metric induced from 2 is disconnected.
(c) A singleton set {x} in any metric space X is always connected.