Е. В. ШИКИН
ЛИНЕЙНЫЕ ПРОСТРАНСТВА
И ОТОБРАЖЕНИЯ
Допущено Министерством высшего и среднего
специального образования СССР
в качестве учебного пособия
для студентов вузов, обучающихся
по специальности «Прикладная математика»
ИЗДАТЕЛЬСТВО
МОСКОВСКОГО
УНИВЕРСИТЕТА
1987

УДК 517
Шикин Е. В. Линейные пространства и отображения. — М.:
Изд-во МГУ, 1987. — 3J1 с.
В учебном пособии, в основе которого лежит курс лекций, чи-
таемый автором на факультете вычислительной математики и ки-
бернетики МГУ, излагаются основные понятия и факты теории ко-
нечномерных пространств, действующих на них линейных отобра-
жений и билинейных форм. Рассмотрены свойства линейных отоб-
ражений в евклидовых, унитарных и нормированных пространствах,
элементы тензорной алгебры. Значительное внимание уделено ос-
новам теории выпуклых множеств в конечномерных пространствах,
включая их топологическую классификацию. Изложение доступ-
ное, сопровождается большим количеством примеров как теорети-
ческого, так и прикладного характера.
Для студентов вузов, обучающихся по специальности «При-
кладная математика».
Библйогр. 20 назв. Ил. 118.
Рецензенты:
Кафедра геометрии, топологии и методики
преподавания математики
Белорусского государственного университета им. 9. И. Ленина,
профессор В. Т. Базылев
1702050000—141 ^ „ %м
щ 122—87 © Издательство Московского
077(02)—87 университета, 1987 г.

ОГЛАВЛЕНИЕ
Предисловие . 6
Глава I. Линейные пространства / . &
§ 1. Структура линейных пространств: внешний закон ком-
позиции, определение линейного пространства, простей-
шие свойства, произведение линейных пространств 8
§ 2. Линейные подпространства: определение линейного
подпространства, простейшие свойства, линейная обо-
лочка И
§ 3. Линейная зависимость: линейная зависимость системы
векторов, базис, размерность, линейное пространство
цветов, линейные пространства атомных и молекуляр-
ных составляющих, эквивалентные системы векторов 14
§ 4. Изоморфизм линейных пространств 25
§ 5. Сумма линейных подпространств: размерность суммы
и пересечения, прямая сумма линейных подпространств,
дополнительное подпространство, фактор-пространство 27
§ 6. Линейные аффинные многообразия: параллельные ли-
нейные аффинные многообразия, аффинная оболочка,
аффинная зависимость 32
§ 7. Замена базиса: формулы перехода, ориентация вещест-
~ венного пространства 36
Глава II. Евклидовы и унитарные пространства 39
§* 1. Евклидовы пространства: определение и простейшие
свойства, длина и угол, Ортогональные векторы, матри-
ца Грама, изометрия евклидовых пространств, ортого-
нальное дополнение, расстояние между множествами . 39
§ 2. Унитарные пространства 50
Глава III. Линейные отображения 54
'§ 1. Основные понятия: определение линейного отображе-
ния, .образ линейного отображения, ядро линейного
отображения, теорема о ранге и дефекте линейного
отображения . . ........... 54
§ 2. Операции над линейными отображениями: линейное
пространство линейных отображений, кольцо линейных
операторов, ранг произведения линейных отображений 57
§ 3. Линейные отображения и матрицы: матрица линейного
отображения, размерность пространства линейных отоб-
ражений, преобразование матрицы линейного отображе-
ния при переходе к новым базисам, эквивалентные
матрицы, каноническая пара базисов, матрица линей-
ного оператора 62
§ 4. Инвариантные подпространства: определение и приме-
ры, собственные векторы и собственные значения, ха-
рактеристический многочлен, способ построения соб-
ственного вектора, собственное подпространство, инва-
риантные подпространства минимальной размерности в
* комплексном и вещественном пространствах ... 71
§5. Канонический вид матрицы линейного оператора: мно-
гочлен от линейного оператора, теорема Гамильтона—
3

Кэли, расщепление линейного оператора, треугольный
вид матрицы линейного оператора в комплексном про-
странстве, нильпотентный оператор, жорданова нор-
мальная форма матрицы линейного оператора ... 79
Глава IV. Билинейные и квадратичные формы 92
§ 1. Билинейные формы 92
§ 2. Квадратичные формы 95
§ 3. Приведение квадратичной формы к сумме квадратов:
-метод Лагранжа, метод Якоби 96
§ 4. Квадратичные формы в вещественном пространстве:
/знакоопределенные квадратичные формы, закон инер-
§ 5. Полуторалинейные и эрмитовы формы: полуторалиней-
ные формы, эрмитовы формы 106
Глава V. Линейные отображения унитарных пространств lit
§ 4. Операция сопряжения: сопряженное отображение, свой-
ства операции сопряжения, матрицы взаимно сопря-
женных отображений, ядра и образы взаимно сопря-
женных отображений, нормальный оператор, унитар-
ный оператор, эрмитов оператор, положительный опера-
тор, корень из оператора, сингулярная иара базисов . 111
§ 2. Разложения линейного, оператора: эрмитово разложе-
ние, полярное разложение 125
§ 3. Линейные отображения в евклидовом пространстве:
операция сопряжения в евклидовом пространстве, сим-
метричный оператор, ортогональное преобразование,
простейший вид матрицы ортогонального преобразова-
ния, разложения линейного оператора в евклидовом
пространстве ' . 127
§ 4. Квадратичные формы в евклидовом пространстве: би-
линейная форма в евклидовом пространстве, приведе-
ние квадратичной формы к главным осям . . . 435
§ 5. Гиперповерхности второго порядка в евклидовом то-
чечном пространстве: точечные пространства, приведен-
ные уравнения гиперповерхностей второго порядка,
классификация гиперповерхностей второго порядка в
точечном евклидовом пространстве , 137
Глава VI. Нормированные пространства 144
»§ 1. Норма вектора: определение и примеры, шар и сфера
в конечномерном нормированном пространстве, эквива-
лентные нормы . . 144
§ 2. Норма линейного отображения: согласованные и под-
чиненные нормы, спектральная норма, евклидова норма
матрицы, экстремальные свойства собственных значений
самосопряженного оператора 148
§ 3. Линейные операторные уравнения в унитарном прост-
ранстве: условия разрешимости линейных, уравнений,
нормальное решение, псевдорешение, нормальное псев-
дорешение, квазирешение 154
§ 4. Метод регуляризации отыскания нормального решения:
понятие корректно и некорректно поставленных задач,
сглаживающий функционал, теорема Тихонова . . . 160
Глав а VII. Выпуклые множества , а 166
§ I. Определение и простейшие свойства . . . , „ , 166
§ 2. Операции над выпуклыми множествами . . . . 168
§ 3. Выпуклая оболочка множества . . . . , , . 1/1

§ 4. Три теоремы о выпуклых множествах: теорема Радо-
на, теорема Каратеодори, теорема Хелли . . . . 174
§ 5. Выпуклые многогранники 180
§ 6. Выпуклые конусы: определение и примеры, коническая
оболочка множества, многогранный конус . . . . 184
§ 7. Выпуклые множества в точечных пространствах . . 190
§ 8. Симметризация 192
Глава VIII. Элементы тензорной алгебры 197
§ 1. Понятие тензора: примеры, определение тензора, ал-
гебраические операции над тензорами, примеры тензо-
ров (физические и механические) 197
§ 2. Метрический тензор: метрическая структура простран-
ства, операции опускания и поднятия индексов, псев-
доевклидова метрика, преобразования Лоренца . . 208
Приложение. Опорный материал: матрицы, определители, линейные
системы, принцип индукции, эквивалентность, отобра-
жения, группы, кольца, поля, многочлены, основная
теорема алгебры • 213
Добавление. Выпуклые множества: топологическая структура, диф-
ференциальные свойства, неравенства 242
Введение . . 242
A. Элементы топологии: топология точечного евклидова
пространства, топологическое пространство, подпро-
странство, непрерывное отображение, топологическое
произведение, связность, линейная связность, компакт-
ность . . . 243
Б. Выпуклые множества: простейшие выпуклые множест-
ва, замыкание и внутренность выпуклого множества,
звездность выпуклого множества, звездность й теорема
Хелли, выпуклая оболочка компактного множества,
выпуклое тело, размерность выпуклого множества,
опорные плоскости, выпуклый конус и сферическая
выпуклость, два способа задания выпуклых тел . . 260
B. Топологическая структура: формулировка задачи I,
предельный конус, классификация замкнутых и откры-
тых выпуклых множеств (гомеоморфизм границы, огра-
ниченные выпуклые множества, неограниченные выпук-
лые множества), ответ к задаче I 276
Г. Дифференциальные свойства: формулировка задачи II,
выпуклая гиперповерхность, локальное задание, свой-
ства выпуклой _гиперповерхности, выпуклые кривые,
множество мерьГнуль, гладкость, ответ к задаче II . 283
Д. Некоторые классические неравенства: радиус Юнга,
объем выпуклого тела, неравенство Брунна_—-Минков-
ского, неравенство Бибербаха, экстремальные эллип-
соиды . . 293
Литература ...,.,,.,, 307
Предметный указатель 308
Именной указатель 311

ПРЕДИСЛОВИЕ
Книга написана на основе лекций, которые автор в течение ря-
да лет читал студентам младших курсов факультета вычислитель-
ной математики и кибернетики МГУ как в обязательном курсе
геометрии и алгебры, так и в специальных курсах.
Программой обязательного курса предусмотрено изучение сле-
дующих тем, составляющих основное содержание аналитической
геометрии: геометрические векторы и действия над ними, системы
координат, основные свойства линий и поверхностей первого и вто-
рого порядка на плоскости и в трехмерном пространстве. К эле-
ментам общей алгебры, • включаемым в этот курс, относятся такие
вопросы, как матрицы и операции над ними, определители, свой-
ства линейных систем, а также простейшие факты теории групп,
колец и полей.
Все указанные выше темы излагаются в первом семестре (за
28 лекций).
Материал второго семестра, целиком посвященного непосред-
ственно линейной алгебре, составляет основную часть этой книги
(см. оглавление). Она разбита на 28 лекций. Понятия, факты и
доказательства, включенные в каждую лекцию, реально расска*
зываются в отведенное для лекции время — два академических
часа. Исключения составляют лишь те лекции, в которые при на-
писании книги были включены дополнительные сведения, носящие
иллюстративный или пояснительный характер.
Часть .сведений из первого семестра — элементы общей алгеб-
ры — приводится в Приложении в виде опорного материала. Он
включает в себя определения и формулировки утверждений^ ис-
пользуемых в основной чаёти. И здесь последовательность изло-
жения и разбиение на лекции проводится на основе опыта чтения.
Материал, отнесенный в Добавление, в разные годы читалсч
студентам первого и второго курсов факультета ВМиК. В нем в
доступной для первокурсника форме развиваются основы теории
выпуклых множеств в конечномерных пространствах, затронутые
и в лекциях основного курса. Цель Добавления — путем изложе-
ния ряда классических результатов перекинуть геометрический
мостик в выпуклый анализ.
Мне хочется выразить искреннюю признательность коллегам
как нашего университета, так и некоторых других вузов, многие
беседы и дискуссии с которыми оказали известное влияние на
формирование и курса лекций, и этой книги.
в

Высокая требовательность студенческой аудитории являлась
постоянным стимулом в поиске более простых, доходчивых и яс*
ных, способов изложения. Как уже говорилось, -книга написана на
основе лекций, которые в течение десяти лет автор читал перво-
курсникам факультета ВМиК МГУ. Им она и посвящается.
25 марта 1987 года
Е. В. Шикип

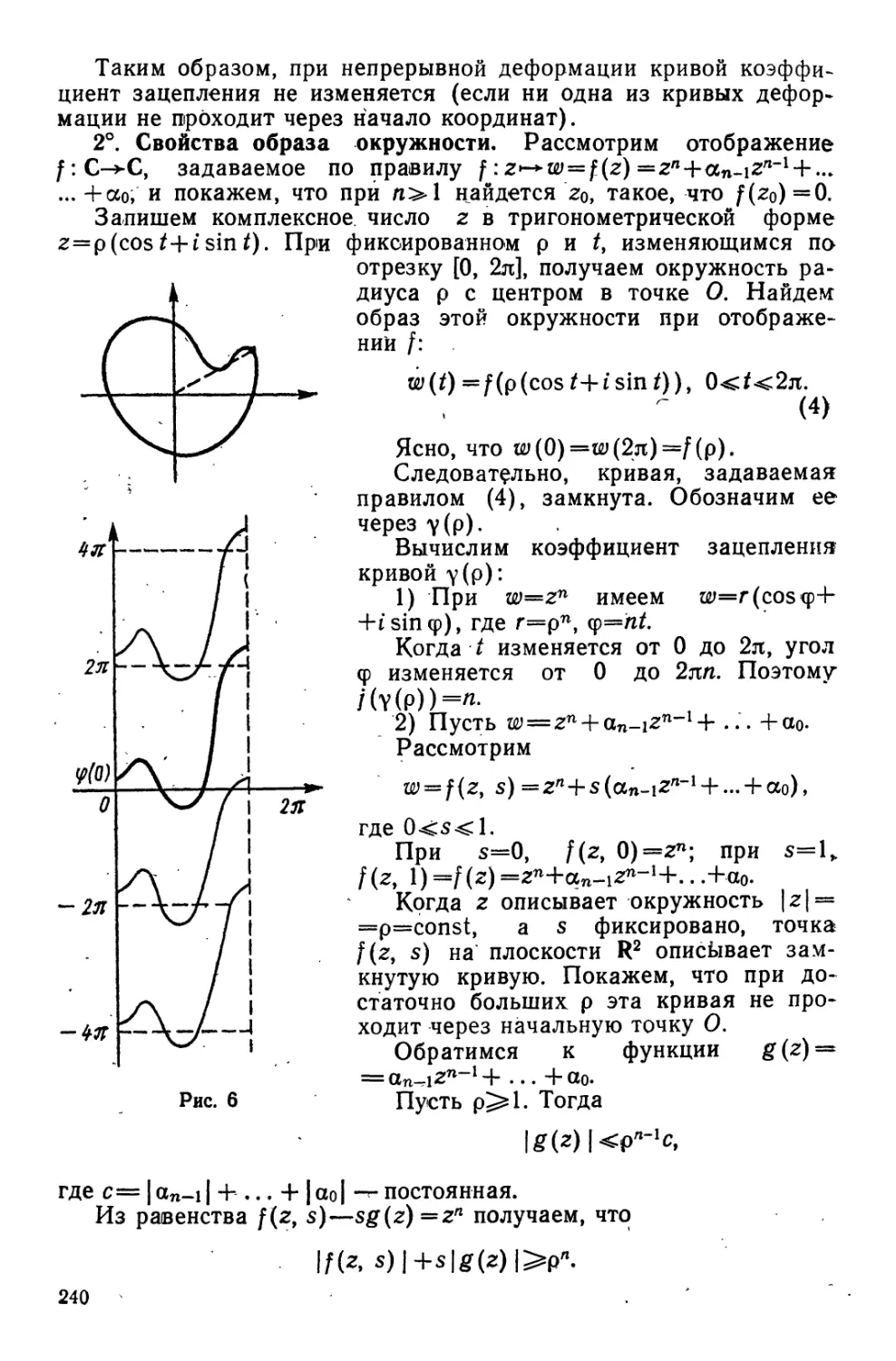
ЛЕКЦИЯ 1
Глава I. ЛИНЕЙНЫЕ ПРОСТРАНСТВА
§ 1. СТРУКТУРА ЛИНЕЙНЫХ ПРОСТРАНСТВ
0°. Внешний закон композиции. Пусть X и У — произвольные
непустые множества.
Определение. Внешним законом композиции (ВнешЗК) у
заданным на множестве Y, называется всякое отображение
cp:XxY^Y.
Пример 1. Пусть X=R, Y=T$ — множество свободных век-
торов в пространстве. Ясно, что отображение RxF3 в У°з, зада-
ваемое правилом
aeR, а^Тг^аа^Тъ
{умножение вектора на число), является ВнешЗК на У%.
Если пара (я, у), где jceX и #еУ, правилом ф отображается
в геУ, то будем писать z=xy.
Пример 2. Внутренний закон композиции (ВнутЗК) являет-
ся частным случаем ВнешЗК (при X=Y).
Г. Определение линейного пространства.
' Определение. Непустое множество V называется линейным
(векторным) пространством над полем Р, если на V заданы два
закона композиции'
ВнутЗК (сложение +) такой, что для любых х, у, 2ЕК выпол-
няются следующие условия:
1) (х+у)+г=х+{у+г)9-
2) х+у=у+х,
3) существует такой элемент 8^V, что для любого x^V
справедливо равенство
x+Q=x,
4) для любого x&V найдется элемент (—x)^V9 для которого
х+ (—х) =6;
ВнешЗК (умножение на элемент поля) со следующими свойст-
вами: для любых x,y^V и любых а, реР
1) а (х+у) =ал;+ш/,
2) (a+$)x=ax+$xt
3) (ар)*-а.(р*)/
4) 1.х=х.
Элементы линейного пространства называются векторами.
Некоторые необходимые понятия и факты из материала первого семестра
отнесены в Приложение.

Примеры линейных пространств
Пример 1. Множество свободных (геометрических) векторов
в пространстве Тз — линейное пространство над полем R:
ВнутЗК — сложение векторов, ВнешЗК — умножение вектора на
число.
Пример 2. Множество вещественнозначных функций С[0, 1],
непрерывных на отрезке [0, 1], — линейное пространство над по-
лем R: ВнутЗК — сложение функций, ВнешЗК — умножение функ*
ции на число.
Пример 3. Поле Р — линейное пространство над полем Р:
ВнутЗК — сложение, ВнешЗК — умножение.
Пример 4. Совокупность прямоугольных тХл-матриц
Ртхп — линейное пространство над полем Р: ВнутЗК — сложе-
ние матриц, ВнешЗК — умножение матрицы на элемент поля Р„
2°. Простейшие свойства.
1+. Нулевой вектор 8 определяется однозначно.
2+. Для каждого вектора х противоположный ему вектор
(—л:) определяется однозначно. < -.
Свойства 1+ и 2+ выполняются вследствие того, что линейное
пространство является абелевой группой (по сложению).
Укажем способы нахождения нулевого вектора, и вектора, про*
тивоположного данному,
3+. Для любого вектора х справедливо равенство 0-х—6.
Доказательство. В силу свойства 2 ВнешЗК ax=(a-f
+ 0)x = ax+0x. Отсюда следует, что Ох=0. В самом, деле, если в
абелевой группе для некоторого элемента а найдется элемент Ь„
такой, что а+Ь=а, то с+Ь = с для произвольного с, т.. е. Ь = 8. О
4+. Для любого х справедлива формула —*= (—\)х.
Доказательство. Из только что доказанного свойства 3**"
и условия 2 ВнешЗК вытекает, что
0=Од:=г(а+(—а))л:=ал:+(—а)х
для любого вектора х и любого aef. В силу того, что у каждо-
го вектора противоположный ему только один, получаем, что
(-а)*—(а-х).
Полагая здесь а=1 и пользуясь свойством 4 ВнешЗК, приходим
к требуемому: (—1)-х=*— (1 -х)—^х. □
5+. Для любого аЕР справедливо равенство а6 = 8. ^
Доказательство. Пользуясь свойством 1 ВнешЗК, полу*
чаем, что . - - * ;
"-• a6=a(;H-(~х))т=:ах+а(-^х)*~'.
В силу доказанного выше свойства 4+ и свойства 3 ВнешЗК
а(—х) =а'( (— 1)х) = (а- (— 1))х= (—cu) ——ах.
Тем самым a6=ax—ax==6* П ■ -_ , ;.
6+. Из равенстве <хл;=6 вытекает, что либо #=0, либо а=0. •
9»

Доказательство. В самом деле, пусть а#0. Тогда сущест-
вует а-1. Умножая на этот элемент обе части равенства ах=8, по-
лучим, что
сг!(а*)—а~!'6.
Выражение слева в силу свойств 3 и 4 ВнешЗК равно х:
arl(ax) = (a,-la)x=\-x=x,
а выражение справа равно Э в силу свойства 5+. Поэтому #=0. П
3°. Произведение линейных пространств. Пусть V\ и V2 — ли-
нейные пространства над полем Р. Рассмотрим их декартово про-
изведение
VxXV2={z=(xu x2)\xx^Vu x2t=V2).
Определение. Произведением линейных пространств V\ и
V2, заданных над полем Р, называется множество V\XV2, наде-
ленное
ВнутЗК: (хи х2) + (хг', x2') = (xi+xi', х2+х2')
и ВнешЗК: а(хи х2) = (ахи алг2).
Утверждение. Произведение ViXV2 линейных пространств V\
и V2 над полем Р также является линейным пространством над
полем Р.
Доказательство. Рассмотрим на множестве ViXV2
ВнутЗК — сложение:
Z=(XUX2)9 Z/=(Xl/,X2/)^Z + Z/^(Xl+Xi/tX2 + X2/).
Выполнение условий 1 и 2 ВнутЗК из основного определения ли-
нейного пространства (см. п. 1°) проверяется непосредственно.
Легко убедиться также и в том, что
е-(еиод
*- нулевой вектор в V=ViXV2, а в качестве вектора из V, про-
тивоположного вектору г= (хи х2), можно взять
-2=(-a:i, -х2)>
Справедливость свойств 1—4 ВнешЗК из основного определения
аеР, 2= (хи х2) -*аг= (а*ь ах2)
очевидна.
Пример 1. Поле комплексных чисел С является линейным
пространством над полем вещественных чисел.
Обобщение. Пусть Vi, .♦♦, Vn — линейные пространства над
полем Р. Тогда множество
ViX...XVn={z*=(xu ..., xn)\xx^Vu ..., xn(=Vn}
Декарт (Descartes) Рене (31.3.1596—11.2.1650) — французский математик
и философ.
Ш

С ВнутЗК Z+Z'= (Xi'+Xu .... Хп+Хп)
и ВнещЗК az=(axu ..ч ахп)
является линейным пространством над полем Р.
Пример 2. Пусть Vi~...= Vrt=P. Тогда линейное пространств
во РХ...ХР=РП называется л-мерным координатным простран*
ством. Его элементами являются упорядоченные наборы из п чи*
сел: ■ m
«-(б1 Бп). Б'еР.
Пример 3* Пусть z={gm} ~ счетная последовательность
£ь • • •, im, ... элементов из Р: Совокупность всех таких последо*
вательностей
С ВнутЗК {W+{WM8m+Sm'}
и ВнешЗК а{|т}={о|т}
является линейным пространством над полем Р.
Совокупность всех сходящихся последовательностей веществен-
ных чисел также является линейным пространством (над полем
вещественных чисел). •
§ 2. ЛИНЕЙНЫЕ ПОДПРОСТРАНСТВА
1°. Определение линейного подпространства. Пусть V — линей»
нре пространство над полем Р.
Определение. Непустое подмножество WczV называется
линейным подпространством линейного пространства V, если для
любых х, y^W и любого аЕР справедливы включения
1. x+yezW и 2. ax&W.
Пример 1. Рассмотрим однородную систему m линейных
уравнений с п неизвестными •
"ml
или, в матричном виде»
АХ=0,
где Л=(а//)бРтхп, ХеРпхи OePmxv. Ранее (см. пример ~4 п, 1°
§ 1) было показано, что PnXi является линейным пространством
над полем Р. Кроме того, из свойств множества решений линей-
ных систем известно, что сумма решений однородной системы и
произведение решения на любое число снова будут решениями
этой системы. Тем самым
{X\X^PnXU ЛХ=0}
линейное подпространство линейного пространства РпХь
Пример 2. В приближенных методах часто функции непре-
рывного аргумента заменяются функциями дискретного аргумент
та — сеточными функциями.
11

Рассмотрим; например, дискретизацию линейного пространст-
ва С°[0, 1] непрерывных на отрезке [0, 1] функций.
Конечное множество точек отрезка [0, 1]
m={Xi=ih\i=0, 1, ..., N; ft=l/N}
назовем (равномерной) сеткой, а сами точки xi — узлами сетки.
Вместо функции f(x)f определенной, на отрезке [0, 1], будем рас-
сматривать сеточную функцию
yt4(xi)-f№
целочисленного аргумента i (i=0, 1, ..,, N) или узла xi сетки он.
Ясно, что сеточную функцию */;=/(#;) можно рассматривать
как вектор у= (у0у\... Ун)т. Тем самым пространство С°[0, 1] за-
меняется конечномерным (размерности N+1) пространством
£2n+i сеточных функций
\ QN+i = ty|* = Of 1, ..., N},
заданных на сетке <ол.
Совокупность сеточных функций, заданных на сетке юл и обра-
щающихся в нуль в граничных узлах сетки,
Q^+i4ftU-0, 1, ..., N; jfo-i/N"-0}t
является. (N—1)-мерным подпространством пространства Qn+i.
2°* Простейшие свойства. Пусть W\ и W2 — линейные подпро-
странства линейного пространства V над полем Р. Тогда
1+. Wi — линейное пространство над полем Р(*=1,2),
Доказательство. Достаточно убедиться в том, что Wi со-
держит нулевой вектор 6eV и что для каждого вектора х из Wi
противоположный ему вектор (— х) также принадлежит Wr.
6=0.*<ee1^, -*-(—1);сеГ* (HI,2)
(в силу требования 2 определения из пункта Г). □
2+. Пересечение
Wif\W2^{x\xeWu xgeW2}
является линейным подпространством линейного пространст-
ва К
Доказательство. Отметим прежде всего, что W\C\W2 всег-
да непусто: содержит нулевой вектор в.
Возьмем в Wifl^2 два произвольных вектора х и у. По опреде-
лению пересечения имеем: х, y^Wi, t=l,2. Из того, что Wi (i=
= 1,2) — линейное подпространство, заключаем, что x+y&Wi
0**1,2) и, значит, x+y<=Wx{\W2.
Включение ax^W\[\W2i где а — любой элемент из Р, доказы-
вается аналогичным рассуждением. □
3+. Сумма
Wx+W2^{xi+x2\Xi^Wh i-l,2}
12

линейных подпространств также является линейным подпростран-
ством пространства V.
Доказательство. Возьмем в Wx+W2 два произвольных
вектора и и v. Тогда по определению суммы найдутся векторы
xu X2, У и У2 такие, что
и=хх+х2 и v=yx+y2>
где xt, yt^Wi (1=5=1,2). Это позволяет представить сумму u+v в
следующем виде:
U+V = (ХХ+Х2) + 0/1 + 1/2) = (Х\+У\) + (Х2+У2) •
Так как Xi+y^Wi (i—1,2), то u+v<=Wx+W2.
Аналогично доказывается включение au^W\+W2. П
4+. Пусть Хи *.., хд — произвольные векторы из подпростран-
ства W и ск, ..., aq — произвольные элементы из поля Р. Тогда
линейная комбинация
а\Х\+.. ,+aqxq&W.
3°. Линейная оболочка. Пусть V — линейное пространство над
нолем Р.
Определение. Линейной оболочкой непустого множества
XczV называется множество L(X)9 определяемое формулой
L(X)^{x^ZU^fxi\xi^Xf a7eP, ?<==#},
т. е. совокупность всевозможных линейных комбинаций векторов
из X. Говорят' также, что линейная оболочка L(/X) порождена
множеством X.
Рассмотрим некоторые свойства линейных оболочек. #
1+. Линейная оболочка L{X) является линейным подпростран-
ством пространства V.
Доказательство. Возьмем в L(X) два любых вектора у1
иУ":
где Xj\ Xk'^X, а/, а/eP. Ясно, что
я
ty ^Zfila'Jx'ffS L(X)9 УЯ<=Р. П
2+. Если XczW,, где W — линейное подпространство простран-
ства V, то L(X)czW.
Доказательство. Возьмем в X произвольные векторы
JC\9 ..., хя. По определению линейной оболочки произвольная ли«
шейная комбинация этих векторов а\Х\+.. ,+aqxq лежит в L{X).
Согласно условию векторы х\, ... ♦ xq лежат также и в W. Послед-
нее означает, что
aiXi+...+aqxqaW
I ' "i ...... 13

(см. свойство 5 пункта -2°). Тем самым каждый вектор из L(X)
принадлежит W. Отсюда вытекает, что L(X)aW. □
Замечание. Из свойств 1+ и 2+ можно заключить, что ли-
нейная оболочка L(X) множества X является наименьшим па
включению линейным подпространством, содержащим X.
Пример. Рассмотрим линейное пространство С(—оо, оо) не-
прерывных вещественнозначных функций. Выберем в нем в каче-
стве X набор одночленов 1, t, ..., tn: Х={1, t9 ..., tn}.
Тогда L(X)=Mn — множество многочленов с вещественными
коэффициентами степени не выше п.
§ 3. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ
0°. Линейная зависимость системы векторов. Пусть V — ли-
нейное пространство над полем' Р и Xi ^ - векторы из V.
Определение 1. Линейная комбинация а\Х\+...+aqxq на-
зывается нетривиальной, если хотя бы один из коэффициентов а/,
/==1, ..., q, отличен от нуля. Если же все а/=0, то эта линейная
комбинация называется тривиальной.
Определение 2. Система векторов хи ..., xq называется ли-
нейно зависимой', если существует нетривиальная линейная комби-
нация этих векторов, равная нулевому вектору 9.
Определение 3. Система векторов называется линейно не-
зависимой, если нулевому вектору в равна лишь тривиальная ли-
нейная комбинация этих"векторов.
ТЕОРЕМА 1. Утв. Система векторов х\9 *.., хд (q>2) из V ли-
нейно зависима в том и толь.ко в том случае, если хотя бы одинг
из этих векторов является линейной комбинацией остальных.
Доказательство. (=^) ,. Пусть а\Х\+.„+aqXg=Q- и, напри-
мер, а^О. Тогда х,~(—-2±Л хг+... + |(—-^^)*«-ь
(-<=)' Из представления
Xq=$\X\+. . t + $q-\Xq-\
вытекает, что
Pl*i+. . , + P^^-i + (—1)Хд^в
и, значит, система векторов хи ..., хя линейно зависима (—\Ф
Ф0). П -
Замечание. Система, состоящая из одного вектора х, ли-
нейно зависима тогда и только тогда, когда x=Q.
ТЕОРЕМА 2. Утв. Система векторов хи ..., хя (<7>1) из V
линейно зависима в том и только в том случае, если существует
вектор,' который можно представить в виде линейной комбинации
векторов Х\, ..., xq по меньшей мере двумя способами.
Доказательство. (=^) Для нулевого вектора в можно ука*-
зать два способа представления: в виде тривиальной линейной
комбинации
6=0*i+.. .+0^
14

и в виде нетривиальной
6=ai*i+.. .+agXq
(последнее возможно в силу линейной зависимости системы векто-
ров Х\9 ..., Xq).
(-*=) Если вектор у допускает два различных представления
y = aiXX + ... + aqXq И y = $iXi + ...+ $qXQ
{зцесъ a/^р/ хотя бы для одного /', 1<г/'<<7)> то линейная зависи-
мость системы векторов Х\, ..., xq обеспечивается наличием сле-
дующей нетривиальной линейной комбинации:
(ai-pi)A:i+...+ (a(7~-^)^=e. □
ТЕОРЕМА 3. Усл. Система векторов Хи ..., хт из V линейно
зависима; векторы *m+i, . •., хя принадлежат V и произвольны.
Утв. Система векторов хи ..., хт, хт+и .... хя линейно зави-
сима. _
Доказательство. От нетривиальной линейной комбинации
а\Х\+.. .+атХт=&
нетрудно перейти к нетривиальной линейной комбинации
ai*i+.. .+атХт+0хт+\+.. .+0^=6. П
ЛЕКЦИЯ 2 ^
1°. Базис. Пусть V — линейное пространство над полем Р, со-
держащее не менее двух различных векторов.
Определение L Будем говорить, что множество XczV по-
рождает пространство Vt если L(X) = V.
Определение 2. Упорядоченное семейство векторов из V
называется базисом V, если оно 1) линейно независимо и 2) по-
рождает пространство V.
Замечание. Упорядоченность означает здесь, что каждому
вектору семейства приписан определенный номер. Из одной си-
стемы векторов (состоящей из q элементов) можно построить q\
различных упорядоченных систем.
Пусть е={ех...еп) — базис пространства V. Тогда для каж-
дого вектора х из V можно указать такие £*, ..., £пеР, что
х =фег + ,..+!% = Ъи1%.
Определение 3. Числа g1, ..., gn называются координата-
ми вектора х в базисе е.
В дальнейшем часто будет удобным следующее обозначение:
13

Утверждение. Вектор-столбец х{е)* однозначно определен для
любого вектора х из V заданием базиса е.
Доказательство легко следует из теоремы 2 пункта 0°. □
Пусть х(е) и у(е) — векторы-столбцы из координат векторов
х и у из V в базисе е.
Утверждение.
(х +U) (е) =х (е) + У (е)> (Кх) (е) = Хх (*)♦
Доказательство легко следует из единственности разложения
вектора по базису. □
ТЕОРЕМА 4. Утв. Система векторов Х\9 ..., хт линейно зави-
сима тогда и только тогда, когда линейно зависимы их координат-
ные столбцы (в каком-нибудь базисе).
Доказательство. Если линейная комбинация векторов
Хи ..., хт равна нулевому вектору:
2?L 1 hxi — 2{LiA,{ (2£= 11 iek) — SJIL i (2/1 i А*&) ek = в,
то в силу единственности разложения вектора по базису
или, что то же, •
Обратное очевидно. D
ТЕОРЕМА 5. Усл. Линейное пространство V имеет базис из
п векторов.
Утв. Всякое семейство, состоящее из т вектороб (т>п), ли-
нейно зависимо.
Доказательство. В силу теоремы 3 предыдущего пунк-
та доказательство достаточно провести лишь для т=л+1.
Пусть а\% -..i Дп+i — произвольные векторы из У. Разложим
каждый из них по базису е= (ех ...еп):
ai=a\lei+..t+ainent
«71+1=0^+1^1+.-. .+ann+ien.
Ранг матрицы. Г /->.,'.- ....
'"• *■•■•■ м---^+л
удовлетворяет неравенству rang Л<л, так как по определении*
ранг матрицы .не: превосходит ни числа ее столбцов, ни числа ее
строк. Это означает, что столбцы матрицы А (их число равно
п+1) линейно зависимы; г
Заметим, что эти столбцы являются координатными столбца-
ми векторов а\9 ..., ап+\ в базисе е.

Из линейной зависимости столбцов матрицы А вследствие тео«
ремы 4 вытекает, что система векторов а\, ..., а>п+\ линейно зави-
сима. П
СЛЕДСТВИЕ. Усл. Линейное пространство имеет базис из
п векторов.
Утв. Любой другой базис этого пространства состоит также
из п векторов.
Доказательство. Пусть базис е состоит из п векторов, а
базис е' — из п' векторов. Ввиду линейной независимости векто-
ров системы е' на основании только что доказанной теоремы за«
ключаем, что п'<п.
. Меняя в приведенном рассуждении базисы е и е' местами, по-
лучаем, что жл' и, значит, п=п'. □
2°. Размерность.
Определение. Линейное пространство V над полем Р на-
зывается
1) n-мерным, если в пространстве V существует базис из п век-
торов, и
2) бесконечномерным, если для любого neN в пространстве
V существует линейно независимая система из п векторов.
В дальнейшем мы ограничимся рассмотрением только конеч*
номерных пространств.
Определение. Число векторов в базисе называется размер-
ностью пространства.
Обозначение: dimpV.
Если V={6}, то dim У=0 по определению.
Пример 1. dim CC=1 (и вообще dim PP=1 для любого по-
ля Р).
В самом деле, каждое комплексное число гФО образует линей-
но независимую систему: для произвольного г'еС справедлива
формула z'=Kz, где X=z'/z.
Пример 2. diiriRC=2.
Пара 1, i образует линейно независимую систему, так как из
равенства
d-l+p-i-O* "■■
где a, p^R, вытекает, что а=р=0.
Пусть zeC произвольно. Записав z в алгебраической форме
z=x-l+y-i, где х, yeR, убеждаемся в том!, что система 1, i по-
рождает С.
Пример 3. Линейное пространство, элементами которого яв-
ляются всевозможные последовательности {£т}, бесконечномерно.
В этом нетрудно убедиться, рассматривая последовательности ви-
да {8mk}> где
*-&
Г7

Пусть neN произвольно. Тогда последовательности
{6i,> К), .... <&}
образуют линейно независимую систему.
Пример 4. dim РР"=я.
Равенство вытекает из разложения
(£', .... 5")—БЧ1. ...,0)+in(0, .... 1)
м невырожденности единичной матрицы /.
ТЕОРЕМА 6 (о неполном базисе). Усл. Система векторов
С\'9 ..., dk из У, где &</i=dim V, линейно независима.
Утв. Найдутся векторы cik+u ..., CLn из V, такие, что система
Ли ..., ап — базис К
Доказательство. Рассмотрим семейство векторов а\% ...
.*.., а*, 6 из V. Если это семейство линейно зависимо, то
так как в нетривиальной линейной комбинации
kiai + ... + kkak + iib = Q
коэффициент \i в силу линейной независимости системы а\9 -.. > я*
обязательно отличен от нуля. Это и позволяет представить Ь в ви-
де линейной комбинации векторов а\, ..., я*'. 6sL(ai, . ..* a*).
Если бы последнее включение было справедливо для любого
вектора Ь из V, то система ai, ...» а* была бы базисом, что невоз-
можно в силу условия k<n.
Таким образом, существует вектор a*+i^V, такой, что система
tu\, ..., a*, afe+i линейно независима.
Если £+1±=л, то эта система — базис V.
Если k+\<n, то рассмотрим семейство аи , а*, Д*-и, 6 и по-
вторим предыдущие рассуждения.
Ясно, что, поступая таким образом, можно достроить данную
линейно независимую систему векторов до базиса пространст-
ва V. □
ТЕОРЕМА 7. Усл. W-* подпространство пространства V над
аюлем Р.
Утв. 1. dim№<dimV.
2. Если dim IP=dim V, то W=V.
Доказательство. Если №={6}, то dim №=0 и, значит,
,dimW<:dimV.
Пусть семейство /ь ..., /т — базис подпространства W. В про-
странстве V эта система также линейно независима. По теореме 5
число векторов в такой системе не может быть больше числа век-
торов в базисе пространства V. Тем самым %
.-dim W=m<cn***dim V.
Если же т=п, то для любого вектора b из V система fu *♦., /m, Ь
38

является линейно зависимой. С учетом линейной независимости
системы векторов /ь ..., \т это можно записать так:
b = aif\ + ... + amfm-
В силу произвольности выбора вектора b последнее означает, что
VcL(/, W-У.
Таким образом, из равенства размерностей dim U?=dim V еле*
дует совпадение пространства W=V. D
Утверждение. В /г-мерном линейном пространстве существуют
линейное подпространства любой промежуточной размерности,
т. е. если dim У=л, то для любого k, 0<.k<n, в V найдется ли*
нейное подпространство Wk, У которого dim №&=£.
" Доказательство. Ясно, что Wox{B}czV.
Пусть е=*(е\...еп) — базис V. Тогда Wk=L(e\t ..., ek). D
3°. Линейное пространство цветов. Основой математического
описания цвета является экспериментально установленный факт,
что любой цвет при некоторых строго стандартизированных уело*
виях его рассмотрения можно представить в виде смеси (суммы)
определенных количеств трех линейно независимых цветов, т. е*
таких цветов, каждый из которых нельзя представить в виде сме-
си каких-либо количеств двух других цветов.
Таких групп из трех цветов бесконечно много. Три выбранных
линейно независимых цвета называются основными, или базисны-
ми, цветами; они определяют цветовую координатную систему
(ЦКС).
Тогда три числа, описывающие данный цвет, являются количе-
ствами основных цветов в смеси, цвет которой зрительно неотли-
чим от данного цвета. Например, цвет Г создается смесью количе-
ства а цвета А, количества б цвета Б и количества в цвета В:
Г=аА+бБ + вВ. ( + >
Числа а, б, в—цветовые координаты (ЦК) данного цвета;
(а, б, в) — цветовой вектор.
Тем самым возникает естественная математическая модель со-
вокупности цветов — трехмерное вещественное пространство, эле-
менты которого суть разнообразные цвета. Это лространство на-
зывается цветовым. Точки, представляющие все реальные цвета,,
заполняют некоторую область цветового пространства. Но мате-
матически все точки трехмерного пространства равноправны, по-
этому удобно считать, что и точки вне области реальных цветов
представляют собой некоторые — нереальные — цвета. Этот под-
ход оказывается чрезвычайно удобным в колориметрии.
Пусть, например, чв качестве основных цветов (базиса) выбра-
ны единичные количества красного, зеленого и синего цветов. Цве-
товые координаты ЦК данного цвета можно искать методом
уравнивания, меняя соотношение между количествами основных
цветов.
1*

Результат уравнивания можно записать в виде цветового
уравнения
Ц=кК+зЗ+сС.
Однако описанная процедура не позволяет уравнять большин-
ство чистых спектральных цветов со смесями трех базисных. В та-
ких случаях некоторое количество одного (или двух) из основных
цветов добавляют к уравниваемому цвету. Цвет получаемой смеси
уравнивают со смесью оставшихся двух базисных цветов (или с
одним). В цветовом уравнении это учитывают переносом соответ-
ствующего слагаемого (или двух) из левой части в правую. Так,
если в поле намеряемого цвета был добавлен красный цвет, то
Ц—кК+зЗ+сС.
При допущении отрицательных значений ЦК все спектральные
цвета можно выразить через тройку базисных цветов.
Качество цвета — его цветность — не зависит от длины цвето-
вого вектора, а определяется его направлением. Пропорциональ-
ное увеличение координат цветового вектора изменяет только его
интенсивность, но не меняет цветности.
Подробнее о цветовых измерениях можно прочитать в книге
-М. М. Гуревича «Цвет и его измерение» (М.—Л., 1950).
4°. Линейное пространства атомных и молекулярных состав-
ляющих. Совокупность веществ, изучаемых в химии, можно рас-
сматривать как множество, элементами которого являются ато-
мы, молекулы, «ионы и тому подобные образования.
Пусть задана конечная совокупность из п различных атомов.
Упорядочим эту совокупность и поставим в соответствие /-му ато-
му вектор
В7. = (0, ..., 1, ..., 0)т, /-1, ..., п.
Рассмотрим множество молекул, построенных из этих атомов.
Вектор молекулы вещества Aif состоящего из атомов Bjf можно
представить в виде
^-SJLipi/B/. (*)
где Pzj^O — число атомов В $ в молекуле А{.
Векторы вида (*) с целочисленными коэффициентами pij на-
зываются молекулярными формами или молекулами. Ясно, что
реальным молекулам соответствуют лишь векторы (*), у которых
Правила сложения
^ + 'i4l-SjLi(p,/ + 'Pi/)B/
и умножения на целое число
вполне естественно вытекают из закона сохранения вещества. Не-
20

трудно убедиться в том, что совокупность молекул {Лг}, состоя-
щих из атомов £i,...,Bn, образует линейное пространство над
кольцом целых чисел Z (модуль) »с естественными операциями
сложения и умножения на целое число (справедливость свойств
1—8 определения Пункта 1° § 1 главы I, лекция 1, проверяется
непосредственно). Его размерность равна числу п векторов Bj.
Совокупность молекул Ль ..., Лт, состоящих из атомов Вь ...
^.., Вп, можно записать в виде
Д — 2/^iPiyBb . 1 = 1, ..., т,
или
Лп1 Vft
'ml
Матрица p=(ptj)GZmXn называется атомной матрицей и
представляет состав молекулярной смеси в терминах атомных со-
ставляющих. Если ранг атомиой матрицы р для молекул вида
\Ai}y i=l,...,m, равен г, то эти 'молекулы лежат в подпростран-
стве 3?г размерности г.
Пример. Для смеси трех веществ С02, Н20 и Н2СОз, обра-
зованных из трех элементов Н, С, О, имеем
С02 \ /0 12
Н20 =12 0 1
^Н2С03/ \2 1 3
Так как rangp=2, то размерность подпространства, в котором
лежат эти вещества, равна двум. Молекулы Н20 и С02 образуют
базис:
СО, Л /0 1
У^шЛ /иЧ/Н20\
Обсудим теперь реакции между молекулами {А{}.
Линейная комбинация
Ф-SZliM,, (**)
где а* — стехиометрические коэффициенты — целые числа, назы-
вается вектором реакции. Если <Хг<0, то t-e вещество является
исходным в реакции, а если^аг>0, то — продуктом реакции. Если
же все <хг- = 0, то имеем тривиальный вектор реакции.
Ясно, что по формуле (**) над данным множеством веществ
{At} можно построить разные векторы реакции. Для химии ос-
новной интерес представляют равенства
2гОгЛг = 0;
21

Произвольный вектор реакции Ф можно записать через атом*
ные составляющие:
Ф - ZZLiS/-ia/M/ - 2JL1Y/B/,
где
Если Yj==0, /=!,..., я, то Ф=0. В этом случае вектор Ф назы-
вают правильной (или простой) реакцией.
Пример. Пусть
Ф=аН2+р02+тН20.
Так как Н2=2Н, 02=20, Н20=2Н + 0, то
Ф=(2а + 2у)Н+(2р+у)0.
Согласно определению реакция будет правильной, если
2а+2у=0, 2р+у=0,
откуда
Ф=а(2Н2+02 —2Н20).
Пусть теперь имеется множество векторов правильных ре-
акций
Ok = lSLiauAt=09 *«1, .... q
(здесь i — номер вещества, участвующего в реакции, а к — номер
реакции). Матрица
a=(ahi)^ZqXm
называется стехиометрической матрицей.
Переходя к атомным составляющим, получаем
2jLiatfft/ = 0f /«I, ...,?; /-1, .... л, ( + )
или
Таким образом, для каждой реакции (с номером k) имеется
линейная однородная система уравнений ( + ) относительно неиз-
вестных ал*. Эта система отвечает хорошо известному правилу
составления уравнений химических реакций: число атомов каж-
дого вида и зарядов -слева в обычной записи химической реакция
должно равняться числу этих же атомов и зарядов справа. При-
влечение для составления уравнений химических реакций мате-
матического аппарата обосновывается следующими соображе-
ниями: 1) данный подход дает весьма простой и стандартный ал-
горитм для определения стехиометрических коэффициентов даже
для систем, где протекает одна реакция, 2) он позволяет, что
наиболее существенно, столь же просто и единообразно опреде-
лять стехиометрические коэффициенты для систем независимых
реакций в любой сложной смеси. По своей сути данный алгоритм
22

отражает обычные законы сохранения числа атомов каждого
вида в реагирующей системе и законы сохранения заряда.
Пример. Рассмотрим, синтез метанола из СО и Н2 в присут-
ствии С02 и Н20. Выпишем атомную матрицу
|СН3ОН
со
н,
со2
( нр j
=
[4 1 1]
0 11
2 0 0
0 1 2
2 0 l|
(av <х2, а3, а4, аб)
Ее ранг равен трем, и три атомных составляющих Н, С и О яв-
ляются базисом подпространства, в котором лежат СН3ОН, СО,
H2i С02 и H2D.
Чтобы найти набор стехиометрических коэффициентов для ре-
акции
сн СНзОН+а2СО+а3Н2+а4С02 + а5Н20=О,
составим систему уравнений
4 11]
0 11-"'.
2 0 0 =0.
0 12
2 0 l]
Фундаментальная система решений этой системы ;.7
(1,-1,-2,0,0), (0, 1,-1,-1, 1)
дает две независимые реакции:
СНзОН — СО — 2Н2=0 или СО+2Н2=СН3ОН
СО —Н2 —С02+Н20=0 или С02+Н2=СО + Н20.
Ранг атомной матрицы Р определяет число независимых ком-
понентов реагирующей смеси, которое весьма существенно яри
изучении равновесий. Ранг стехиометрической матрицы опреде-
ляет максимальное число линейно независимых реакций, кото-
рые, вообще говоря, могут протекать в данной смеси веществ.
При изучении сложных равновесные систем с, большим числом
компонент определение линейно независимых реакций становится
особенно важной задачей. Использование методов линейной ал-
гебры значительно упрощает ее решение. Ранг стехиометриче-
ской матрицы а непосредственно связан с числом реагентов т и
рангом атомной матрицы (J:
rang <х=лг — rang p.
Реагенты, принимающие участие в реакциях, обычно известны
23

либо из экспериментальных данных, либо^ на основании выбран-
ной схемы механизма протекания реакции в системе. Виды ато-
мов из которых образованы реагенты, также известны. Поэтому
можно считать, что число реагентов и атомная матрица известны.
Возникает вопрос, как найти уравнения независимых реакций —
систему базисных реакций, т. е. по атомной матрице р построить
стехиометрическую матрицу а специального вида.
В рассмотренном выше примере стехиометрическая матрица
а имеет следующий вид:
'1 — 1 —2 0 0'
0 1-1—11
Л 0—3—11
Стехиометрическая матрица базисных реакций
СН3ОН СО Н2 С02
1
2
Н20
1 -1—2 0 0
0 1—1-11
полностью определяет стехиометрию зависимых реакций. Напри-
мер, для реакции
СНзОН + ЗН2 —С02+Н20=0
стехиометричеокие коэффициенты получаются путем сложения
соответствующих базисных.
5°. Эквивалентные системы векторов".
Определение 1. Подмножества X и У линейного про-
странства V называются эквивалентными, если их линейные обо-
лочки совпадают (рис. 1):
Рис. I.
Обозначение: X~Y.
Определение 2, Макси-
мальное (по числу векторов) ли-
нейно независимое подсемейство *
векторов из множества X назы-
вается базой X. Число векторов
в базе множества X называется
рангом X.
Обозначение: rang A", * '
Утверждение. Ранги эквивалентных' множеств равны, т. е. ж*
того* что X*rY% вытекает равенство
rang X=rang У,
Доказательство легко следует из того, что
, rangX=dimL{X). О •
24

Замечание. При этом базы X и Y совпадать не обязаны;
это разные базисы L(Ar)=L(У).
Если все векторы множества X линейно выражаются через
векторы множества У, то L(X)(=L(Y) и rangX^rangy.
§ 4. ИЗОМОРФИЗМ ЛИНЕЙНЫХ ПРОСТРАНСТВ
Пусть V и V — линейные пространства над полем Р.
Определение. Линейное пространство V называется изо-
морфным линейному пространству V', если существует взаимно
однозначное^тображение (изоморфизм)
<р:У-*У,
такое, что для любых векторов х и у из V и любого а из Р вы-
полняются соотношения
ф-(*+0)=<р(*)+ф(у). Ф(а*)—скр(х).
л*
Обозначение: V&V (читается: У7 изоморфно V).
Утверждение. ф(6)=6', где в и в' — нулевые векторы V и У
соответственно. .
Доказательство можно провести двумя способами.
1. Пусть jceV—произвольный вектор. Тогда
ф(9)=ф(0-*)=0-ф(л;)=е'.
2. Так «ак V и У—абелевы группы ло сложению, то <р мож-
но рассматривать как изоморфизм групп, и поэтому
Ф(0)=6/. □
Утверждение. Отношение изоморфизма, заданное на множе-
стве всех линейных пространств над полем Р, есть отношение
эквивалентности.
ТЕОРЕМА. Утв. Линейные пространства V и У изоморфны в
том и только в том случае, когда
dimp V=dimp V\
Доказательство. Запишем утверждение теоремы в схе-
матической форме
y~V«=>dimy = dimV
и докажем первую часть теоремы*
(4=) Пусть dim V=^=dim V'=n. Возьмем в каждом из про-
странств V и У по базису: е=(е\....еп)—базис У, е'=(е\...
...еп')—базис У и построим отображение <р :У-+У по следую-
щему правилу.
25

_ Разложим произвольный вектрр х из V по базису е
и 'построим вектор х' из V:
с теми же координатами, но в базисе е'. Покажем, что <р: х*-+
—+х' — изоморфизм.
1. Взаимная однозначность отображения ф легко вытекает иа
того, что разложение по базису единственно.
2. Так как линейные операции над векторами естественно пе-
реносятся на их 'координаты относительно фиксированного бази-
са (теорема 4 § 3), то ясно, что
Ф : х+у>-+х'+у'> ф : а*-* а*'.
Таким образом, V&V.
(=»*) Доказательство будем вести от противного.
Пусть V&V и размерности dim У=л, dim У=л' не равны.
Например, п'>п. Тогда изоморфизм ф:-V-+-V переводит базис е=
= (ei... еп) в систему векторов е\%..., еп\ которая является ли-
нейно зависимой в Y (вследствие теоремы 5 § 3).
Рассмотрим соответствующую нетривиальную линейную ком-
бинацию
SjLiGtye/^ 6'.
Она является образом единственного вектора SjLiocje/, который в
силу взаимной однозначности ф должен быть нулевым
23иаЛ~ 6.
Нетривиальность полученной линейной комбинации и линейная
независимость векторов базиса приводят к противоречию.
Противоречивость допущения п<п' доказывается аналогично.
Тем самым остается лишь одна возможность
п=п'. □
СЛЕДСТВИЕ. Утв. Любое я-мерное линейное пространство
над полем Р изоморфно Рп.
Замечание. Произвольное л-мерное линейное пространство
над полем Р обладает свойствами двух типов:,.
1) индивидуальными (природа элементов, терминология, реа-
лизация законов композиции и т. д.) и
2) общими для всех п-мерных линейных пространств над по-
лем Р (сохраняющимися при изоморфизме).
В теоретических вопросах удобнее рассматривать линейные
пространства с общих позиций, а в примерах—с индивидуаль-
ных.
26

ЛЕКЦИЯ 3
§ 5. СУММА ЛИНЕЙНЫХ ПОДПРОСТРАНСТВ
1°. Размерность суммы и пересечения.
ТЕОРЕМА 1. Усл. V — линейное пространство над полем ~Р,
W\ и W2— его линейные шодпространства.
* Утв. d\m(Wl+W2)+dim(Wl[)W2)=dimWl + dimW2.
Доказательство. Предположим сначала, что
Пусть еи...,ер —базис Wi{]W2. Так как пересечение W\[\W2 яв-
ляется линейным подпространством и пространства W\ и про-
странства W2, то, применив .к системе eu...,ev теорему о непол-
ном базисе (теорема 6 лекции 2), можно построить базисы
ей • • • ,.еР, fu ..., fQ в W{ »и eVi..., ер, gx gr в W2.
Пркажем, что система векторов
0ь • • -, ер, fu..., fQ9 gu -.., gr (1)
является базисом суммы W\+W2:
1. Система (1) .порождает W\+W2.
В самом деле, для любого вектора х из W\ + W2 справедливо
разложение
x=xi + x2=2iaiei + Il^jf]+2kykgkt
2Г Система (1) линейно независима.
Приравняем линейную комбинацию векторов системы (1) х
нулевому вектору
SiOi^+SiPjfj+SfcVtffc^e. (2)
Перенесем третью сумму в правую часть и рассмотрим вектор
Из того, что вектор у можно записать в виде линейной комбина-
ции как векторов из W\t так и векторов из W2, вытекает, что .
Отсюда и в^еялу единственности разложения вектора по базису
ii,..., еР и линейной независимости системы mf\9... ,fq получаем,
что
Pt== ... =р^=0. (3)
Так как система векторов eu...tep, gu*..,gT линейно независи-
ма, то из формулы _ (2) с учетом равенств (3) получаем, лто
ai= ... ==aP=Yi== ... =Yr=0.
В случае, когда
Wl(]W2={Q}9
27

доказательство проводится аналогично, но без системы е\,..+
...,ер. П
2°. Прямая сумма линейных подпространств.
Определение 1. Сумма подпространств Wx и W2 линейно-
го пространства V называется прямой суммой, если для каждого»
вектора х из W\+W2 шара векторов Х\ и х2у для .которой х=хх +
+ х2, где x\eWi, x2^W2, единственна (^Тис, 2).
Обозначение: WX@W2.
ТЕОРЕМА 2. Усл. Пересечение
линейных подпространств W\ и> W2
пространства V тривиально, W\ff
ПГ2={0}, и
dim Wi + dim W2=dim V.
Утв. V=ri©WV
Ясно,'что если V=№i©№2, то и
v=w2ewx.
Доказательство. Согласна
теореме 1
Рис. 2
dimV=dim(Wl + W2).
Тогда из теоремы 7 (утв. 2) лекции 2 можно заключить, что
V=Wi + W2: . -
Тем самым дли любого вектора х из V справедливо разложение
х=х\ + х2, где x\<=WXy x2^W2.
Предполагая, что х=х\+х2'9 где X\^WU x2^W2f получаем
равенство
Х\ — Х\=Х2—X2t
которое в силу условия W\[)W2—{Q} возможно только в том слу-
чае, если *i=Xi/ й х2=х2'.
Значит, V=Wi®W2. П
Определение 2. Линейное пространство V разлагается в
прямую сумму подпространств W\,..., Wmy ' если для каждого
вектора х «из V существует единственный набор векторов хи...
..., xm, такой, что Xj^Wjt j= 1,..., m, и х=х{ + ... +хт.
Обозначение: V = Wx ф... ф Wm> ф/li^/.
3°. Дополнительное подпространство. Пусть № — линейное
подпространство пространства V.
Определение. Линейное подпространство W6 пространства
V называется дополнительным к подпространству W, если
Утверждение. Дополнительное к W подпространство всегда
существует и
28

Доказательство. Бели W={e}, то W*=*V. Если W=V,
т0 W*={Q}.
Пусть
uimW=kt
где 0<k<nt и ei,...,efe — базис HP. Дополним его до базиса все-
го V
ей-- ->ek, fh+u-- -,fn,
рассмотрим L(/h+u • • •»/w) и покажем, что
Раскладывая произвольный, вектор х из V по поствоенному
выше базису
шолучаем, что
дс^ш+а;', ., (4>
где о;=*2*а^еНР и ад'=2,[У^е£(/ь+1, ...,fn), причем разложе-
ние (4) единственно. Поэтому линейную оболочку L(fk+u.. . ,fn)
можно взять в качестве дополнительного подпространства W6.
Легко видеть, что W6 зависит от выбора векторов ffe+ь-••>/>**
и поэтому определено неоднозначно. Тем -не менее всегда
d\mWb=n — k=dimV—dimW.Q
Замечание. Свойство «линейного подпространства быть до-
полнительным является взаимным в следующем смысле: если.
W6 дополняет W до V, то и W дополняет W6 до V.
4°. Фактор-пространство. А. Определение. Пусть V — линейное1
пространство над полем Р и W — «некоторое его подпространство^
Для произвольного вектора х из V построим множество
Wx=x+W={x+w\w(=W}.
Совокупность множеств такого типа обозначим через V/W:
VfW={Wx\xeV).
Пусть Wv=y+W—множество того же типа, что «и Wx.
Определим сумму множеств Wx и Wv по следующему (правилу:
Wx+Wy=Wx+v=(x+y)+W.
Ясно, что Wx+V вновь является множеством того же типа, что и
Wxn Wv (рис.3).
Непосредственно можно убедиться в справедливости следую-
щих соотношений:
(Wx+Wy) + Wz^Wx+(Wy+W2)/
Wx+Wv=Wy+WX9
. wx+w*=wx;
WX+W-X=W:
23

Определим произведение множества Wx на элемент поля а
aWx=Wax.
В справедливости соотношений
a(Wx+Wv)=aWx+aWyt
(a+t)Wx=±aWx+$Wx,
l-Wx=Wx
также можно убедиться непосредственно.
Рис. 3
Тем самым доказано следующее утверждение.
ТЕОРЕМА 3. Утв. Совокупность V/W множеств Wx, где хе
еУ, с введенными выше правилами сложения и умножения на
элемент поля является линейным пространством «ад полем Р.
Определение. Линейное пространство V/W называется
фактор-пространством пространства V по подпространству W.
Замечание. Фактически описанная выше процедура есть
не что иное, как введение на фактор-группе V/W
ВнешЗК:
а<=Р, x+W<=V/W~ax+W<=V/W.
Б. Размерность
ТЕОРЕМА 4. Утв. V/W^W\
Доказательство. Если dim №=0, то W~{Q), W6=V и
v/w=v.
Если dim№=dimV, то W=V, W*={Q) и V/W&{9).
Пусть 0<dim W<dim V.
30

Построим какое-нибудь дополнительное подпространство W6i
Так как V можно представить в виде
то для любого вектора х из V справедливо разложение
x=y+z, (5>
где y&W6 и z^W. Оба слагаемых вектором х определяются од-
нозначно (рис. 4).
Рис. 4
Пусть х — произвольный вектор из Wx: £—x+w.^
С учетом предыдущей формулы получаем, что Jc=y+ (z+w}m
Отсюда в силу единственности разложения вектора на сумму сла-
гаемых из W* и W заключаем, что для всех векторов из wx до*
полнительная ^-составляющая у одна и та же.
Верно я обратное: если х*=у+г*, где z*^Wt то х* лежит
в Wx.
В самом деле, вновь привлекая равенство (5), получаем
Х*;=Х — Z+Z* = X+ (2* — Z).
В силу того, что W—линейное подпространство, 2*.^2e^ и,
значит, x*^Wx.
Это удобно записать в следующем виде:
Wx=*Wy,
где у определяется равенством (5). Тем самым
V/W*={Wy\yeW%
и возникает естественное отображение
описываемое правилом <р:у*-»НРу.
31

Отображение <р является изоморфизмом, так как оно
1) взаимнооднозначно;
2) если <p:yt~Wyg, i^lf 2, то
(f:y1 + y2^Wyl+yi^Wyt + Wy2;
3) если <р : у>-+ Wy и аеР- любое, то
y:ay>~+Way=aWy.
СЛЕДСТВИЕ. Утв. dim V/W=dim V - dim W.
ЛЕКЦИЯ 4
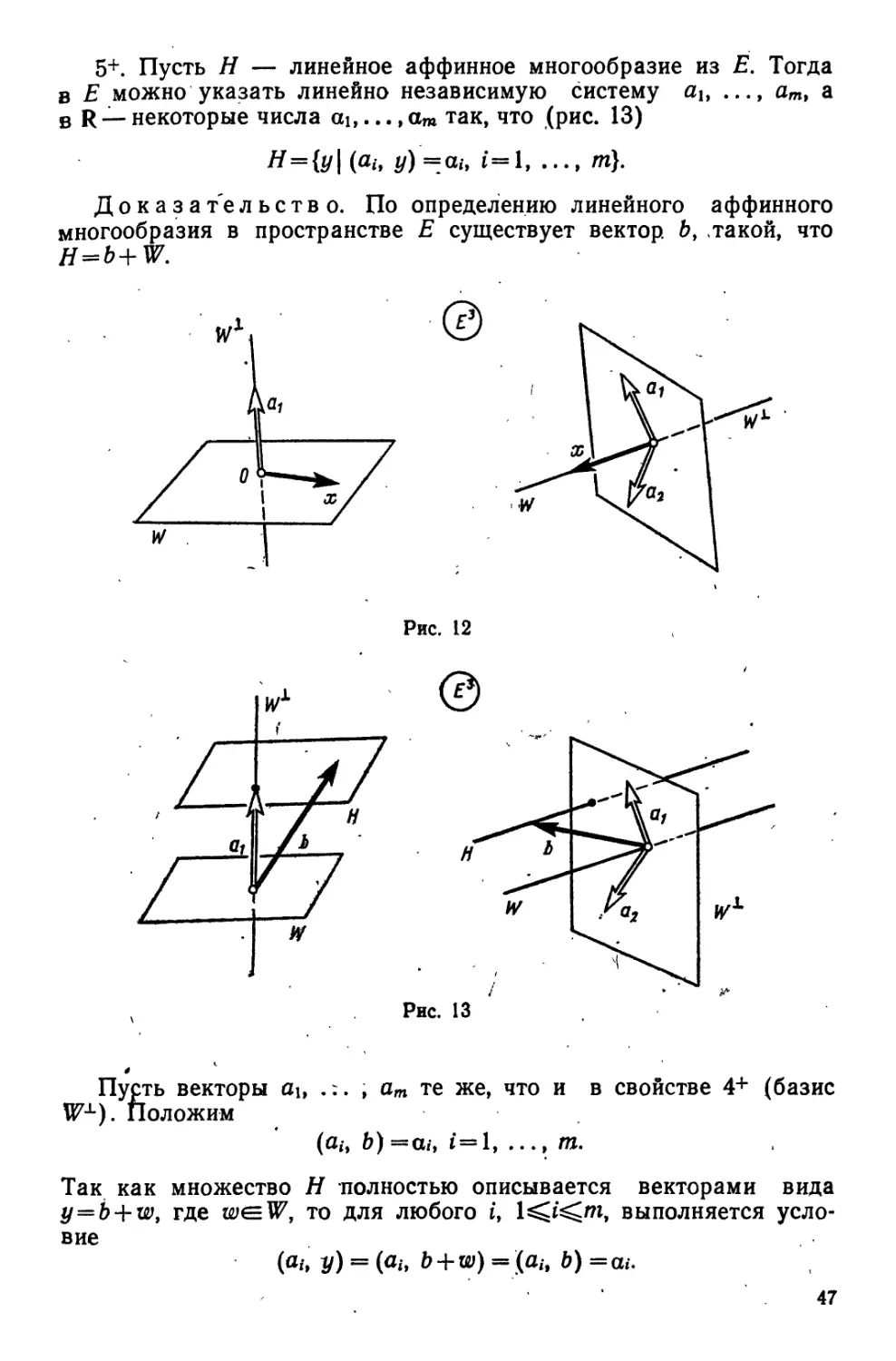
§ 6. ЛИНЕЙНЫЕ АФФИННЫЕ МНОГООБРАЗИЯ
Г. Параллельные линейные аффинные многообразия. Пусть
V — линейное пространство над полем Р и W — некоторое его
подпространство. Зафиксируем в V произвольный вектор х.
Определение 1. Множество Wx—x+ W называется линей-
ным аффинным многообразием (ЛАМ) пространства V; х — век-
тор сдвига.
Определение 2. dim Wx=dimW.
Отметим простейшие свойства векторов из ЛАМ:
1+ a<=Wx<&a — x<=EW.
2+ a, b^WyF^a — bezW.
3+ aeWx4>Wa=Wx.
<по существу они доказаны в предыдущем параграфе).
Пусть W и' W" — линейные подпространства из V, х и у —
произвольные векторы Ш V.
Рис. 5 Рис. б
Определение 3. Будем говорить, что Wx параллельно
Wv", если либо W'aW"y либо W'cW (рис. 5).
Обозначение: Wx'\\Wy".
Утверждение. Из того условия, что два ЛАМ с непустым пе-
ресечением параллельны, вытекает, что одно из них содержится в
32

другом, т. е. WX'WV" и Wx'nWy"¥*0=> либо Wx'.cWv'\ либо
Wv"czWx'.
Доказательство. Пусть для определенности
dim Wx'^dim Wy".
По условию у Wx и Wy" есть общий вектор
zeWx'()Wy".
Тогда вследствие свойства 3+
WX'=WZ\ Wy"=w't".
Так как Wx'\\Wy"9 то W<=W" и, значит,
W/czWz". D
2°. Аффинная оболочка.
Утверждение. Непустое пересечение конечного числа ЛАМ яв-
ляется ЛАМ.
Доказательство достаточно провести для двух ЛАМ.
Пусть Wxf\Wy"^0 (рис. 6). Тогда существует вектор
ZeWx'()Wy".' .
Отсюда следует, что
W'x=z+W'y Wy"=z+W"
и Wx'{)Wv"=z+W'()W". □
Определение. Аффинной оболочкой множества XcziV на-
зываетсЖмножество А(Х)У определяемое формулой
Л(Х)«{0 = 2^/*/|*/€5Х, 2Ув0об/= 1,' ^eNUO}.
Из формулы ao + ai+ ... +aa=l
вытекает, что
a0=l— S^iQ/.
Используя это равенство, преобразуем вектор
(К следующему виду:
У = 2/Loa^ = a0x0 + H}=iajxi = (* — 2/~ia/) *o + 27-i«/*/ =
= x0 + 2^ia;.(xy—x0).
Полученное соотношение позволяет записать множество Л(Х)
так:
^W = {y = ^o + ^eia/(x/—x0);|x0, ^ЕХ, a;GP, ?GN}.
2 Заказ 538 33

Последнее, используя определение линейной оболочки множества
{—Хо)+Х,
L(—x0 + X) =
= {z = 2Ui<x>j(xj—*о)|— *0+ */£(—х0) + Х, a;.GP, ?eN},
можно записать в следующем виде:
A(X)=Xo+L(—Хо+Х).
Подчеркнем, что выделенный вектор х0 выбран в X произвольно
(рис. 7).
Рис. 7 Рис. 8
Свойства аффинной оболочки
1+.ХсА(Х).
2+.АЩ—ПШ.
3+. Пусть ХсЯ, где Я —ЛАМ. Тогда А(Х)<=Н.
Замечание. Свойство 3+ означает, что А(Х)—наименьшее
ЛАМ, содержащее X.
Доказательство. Рассмотрим произвольный вектор Хо из
X. В силу того, что Я— ЛАМ и содержит X, справедлива фор-
мула
H=x0+W,
где W — линейное подпространство. С другой стороны,
A(X)=x0+L(Y),
где X=x0+Y.
Из того, что Хс=Я, или, что то же самое,
34
Xo+Yaxo+W,

©ытекает вкдочение Y<=W. Откуда L(Y)(=W и
A(X)=xo + L(Y)c=xo+W=H. D
4+J(X)cL(I) (рис. 8).
Пример. Рассмотрим в Рп множество решений уравнения
2Г£) —aig4 ... + апБя + Р—0,
где ai, ...,an фиксированы и хотя бы одно из них отлично от
нуля. Как уже отмечалось ранее, множество (решений присоеди-
ненного уравнения
aIg1+...+angn=0
является линейным подпространством Ln-Xal>n.
Множество решений исходного уравнения lo+Ln~\ где go — его
частное решение, есть ЛАМ. Множество решений совместной си*
стемы линейных уравнений
а11^+...+а1п|п + р1=0,
amig1+...+amngn + Pm=0
согласно доказанному выше утверждению также является ЛАМ.
3°. Аффинная зависимость.
Определение 1. Будем говорить, что система векторов
*о, X\9...9xq аффинно зависима, если в поле Р можно указать
элементы Я0, Ль ..., KQy не все равные <нулю и такие, что
k6Xo+faxi+ ....+XQxq=Q, (1)
Л0+Я1+ ...+\=0. (2)
Утверждение. Система векторов x0f X\9...9xQ аффинно зави-
сима в том и только в том случае, когда система векторов х\ —
— jto,...> хд — Хо линейно зависима.
Доказательство. (=*>•) Умножая обе части формулы (2)
на вектор Хо и вычитая полученный результат из равенства (1),
получаем
Kl(Xi— Х0)+ ... + kq(XQ — Х0)=6.
(4=) Переписав нетривиальную линейную .комбинацию
А-1 (Х\ — Хо) + . . . +Xq (Xq — Хо) = в
Несколько по-иному
{—Kl—'... — hq)XQ + hiXi+ ... +kqXq = Q
и полагая Я0=— К\ — ... — Хд, приходим к требуемому. □.
Замечание. Утверждение остается справедливым, если за-
менить вектор хо на любой другой вектор xiy i=\9...9q9 системы.
2* . ' 35

Таким образом, в л-мерном пространстве существуют аффин-
но независимые системы, состоящие самое большее из п+l век-
торов.
Определение 2. ЛАМ Н называется k-плоскостью, если
число векторов в максимальной аффинно независимой системе,
принадлежащей Я, равно k+\\ (п—1)-плоскость называется
гиперплоскостью.
Задача. Доказать, что любую ^-плоскость можно представить
в виде (пересечения не менее п — k гиперплоскостей.
Пример. Множество решений совместной линейной системы
anll + ....+<ai^n + pi = 0,
ранг матрицы которой rang(aij)=r, является (п — г)-плоскостью
в пространстве Rn.
§ 7. ЗАМЕНА БАЗИСА
1°. Формулы перехода. Пусть е=; (е{... еп) и е'= (е\ ... еп') —
базисы линейного пространства V.
Раскладывая векторы системы е' по базису е, получим
ei = HI=ia{ep t = l, ..., п,
или
е1-=а\ег+ ... +а!}еп, i=l, .... п. (1)
Запишем эти соотношения в матричной форме
/ai...a^\
{el...en) = (e1...en)[ (2)
Определение. Матрица
i4=(ai*)e=P„Xn
называется матрицей перехода от базиса е к базису е'.
Отметим, что элементы /-го столбца матрицы А совпадают с
.координатами вектора е{ в базисе е.
Свойства матрицы перехода
1+. е' = еА.
2+. Пусть е — базис пространства V, dim V=n и ЛеРпХп.
Набор векторов ef=eA является базисом V в том и только в том
случае, если det-4=^=0.
Доказательство. Заметим прежде всего, что столбцы
матрицы А являются координатными столбцами векторов систе-
мы е' относительно базиса е. Согласно теореме 4 § 3 необходи-
мым и достаточным условием линейной независимости системы
36

векторов является линейная независимость их координатных
столбцов.
Последнее равносильно невырожденности матрицы Л. D
3+. Пусть
x = $L\Vet. ' (3)
Напомним обозначение: х(е) = (g1... £п)т.
Тогда
х(е)=Ах(е'),
или, подробнее,
гдех = 2?=,|"е;.
Доказательство. С учетом введенного обозначения фор-
мула (3) может быть записана в виде.
m
х = е-х(е) = (е1...еп)\ : .
Аналогичное соотношение имеет место и при разложении вектора
х по базису е': х=е'-х(е').
Тем самым е-х(е)=е'-х(е').
Заменяя в последнем равенстве е' на еЛ, получим, что
ех(е) = (е-А)-х(е').
Умножение матриц ассоциативно вне зависимости от природы
входящих в них элементов (лишь бы имели смысл проводимые
при этом операции). Поэтому
ех(е)=е(Ах(е')).
Отсюда в силу единственности разложения вектора по базису е^
лриходим к требуемому соотношению х(е) =Ах(е'). П
4+. е=е'А-К
Доказательство. Существование матрицы, обратной к
матрице перехода Л, вытекает из невырожденности последней.
Умножая обе части равенства из свойства 1+ «а А~1 справа, по-
лучаем требуемое. □
2°. Ориентация вещественного пространства.
Определение 1. Линейное пространство над полем R назы-
вается вещественным линейным пространством.
Определение 2. Два базиса е и е'=еА вещественного Про-
странства V называются одинаково (противоположно) ориентиро-
ванными, если det Л>0 (сЫЛ<0).
Утверждение. Отношение одинаковой ориентированности, рас-
сматриваемое на множестве всех базисов данного вещественного
пространства V, является отношением эквивалентности.
37

Доказательство!, Рефлексивность бинарного отношения,
введенного в определении 2, следует из того, что
е = е-1 и det/=l>0? .
Из того, что е'=еА9 вытекает формула е = е'А~1 (см. свойство 4+).
Симметричность отношения следует из того, что
&et(A-*) = (detA)-l>0.
Наконец, транзитивность получается из следующих рассуждений.
Пусть е'=еА и е" = е'В. Тогда е" = е(АВ) и det(4B)=deU.
•det5>0. D
Фактор-множество по этому отношению эквивалентности со-
стоит из двух классов, каждый из которых называется ориента-
цией пространства.
Определение 3. Веществен-
ное линейное пространство с вы-
бранной на нем ориентацией назы-
вается ориентированным простран-
ством.
Утверждение. В вещественнохм
линейном пространстве можно- вве-
сти ровно две различные (совершен-
но равноправные) ориентации.
Практически ориентация задается выбором и фиксацией кон-
кретного базиса (который однозначно определяет класс эквива»
лентных ему базисов — ориентацию) (рис. 9).
Рис. 9

ЛЕКЦИЯ .5
Глава II. ЕВКЛИДОВЫ И УНИТАРНЫЕ ПРОСТРАНСТВА
§ 1. ЕВКЛИДОВЫ ПРОСТРАНСТВА
1°. Определение и простейшие свойства.
Определение. Евклидовым пространством называется ве-
> щественное линейное пространство £, в котором определена опе-
рация скалярного умножения
(,):£X£->R, .
т. е. каждой упорядоченной паре векторов ху у^Е ставится в со*
ответствие вещественное число, обозначаемое через (х, у) и назы«г
ваемое скалярныц произведением вектора х на вектор у, такое,
что для любых х, уу z^E и любого числа aeR выполняются со-
отношения:
1- (*. У) = (У> *)•
2. (х*у9 z) = (*, z)+(y, г).
3. (ах, у)=а(х9 у).
4. (х, х)^0, причем равенство нулю возможно в том и только
в том случае, если х =>9.
Примеры евклидовых пространств.
Пример 1. Совокупность геометрических векторов Тъ со
скалярным произведением
(a, ft)-|a|.|6|.cos(a7*).
Пример 2. Для любых двух векторов-
£=(£*, .->Лп) ИТ1=(т11, ..., л") из R"
положим
(6, Л) = 2?=1^¥.
Свойства скалярного произведения проверяются непосредственно.
Пример 3. Линейное подпространство евклидова пространст-
ва само является евклидовым пространством.
Свойства скалярного произведения
1+. (е,х)-0.
2+. (х, ау)=а(ху у).
3+. (х, у+г) = (х9 у) + (х, г). - .
4+. (ULiayct, 2?-i№J) = 2L№i4h(*i' У*)-
Евклид (EvxXei6*n£) (ок. 340 — ок. 287 до н. э.) — математик эпохи эл-
линизма.
39

2°. Длина и угол.
ТЕОРЕМА 1 (неравенство Коши—Буняковского). Утв. {х, у)2^
г^{х> х) {Уу У)> или, в иной форме,
!(*• х) {х, у)
>0.
I (У. х) ({/, у) |
Доказательство. Если (х, х)=0, или, что то же самое,
*=6, то (х, у)=0 для любого вектора у, и требуемая формула
доказана.
Обратимся к случаю, когда хФв. По определению скалярного
произведения неравенство
(tx—у, tx—y)^0
справедливо для любых векторов а: и у из £ и любого teR. Свой-
ство 4+ позволяет записать это неравенство по-иному:
Р(х, х)-Щх9у) + (у, у)>0.
Если считать хФ% и у фиксированными, a t произвольным, то
левую час^ь можно рассматривать как квадратный трехчлен отно-
сительно t. Последний сохраняет свой знак, если его дискриминант
неположителен:
(х,у)2-(х,х)(У> у КО.
Перенося вычитаемое в правую часть, получаем требуемое нера-
венство. □
Задача. Доказать, что (х, у)2=(х, х)(уу у) тогда и только
тогда, когда либо x=tyy либо y = tx.
Определение 1. Длиной вектора х называется число |*|,
вычисляемое по правилу: \х\ = V(x> x).
Ясно, что |х|^0 для любого х m E. Равенство |л:| =0 возмож-
но лишь в случае, если х=9.
Утверждение (неравенство треуголь-
ника) (рис. 10). |*+у|<|х| + М.
Доказательство. Вычислим
квадрат длины вектора х+у:
\х+у\2=(х+у, х+у) = (х, х) +
- +2(Х,У) + (У,У) =
= \х\*+2(х,у) + \у\*.
Заменяя второе слагаемое (л:, у) на | (л:, у) | и применяя неравен-
ство Коши—Буняковского [(л:, y)|<S|*| \y\, получаем, что
\х+у\2^\х\2+2\х\ |f/|+|f/|2=(|A:| + |t/|)2. После извлечения
квадратного корня получаем требуемое неравенство. □
Буняковский Виктор Яковлевич (16.12.1804—12.12.1889) — русский матема-
тик, академик Петербургской. АН (с 1830 года); Коши (Cauchy) Огюстен Луи
(21.8.17-89—23.5.1857) — французский математик, почетный член Петербургской
АН (с 1831 года).
40
Рис. 10

Определение 2. Углом, между ненулевыми векторами х и у
называется число ср, такое, что 0<ф^я и
\x\-\y\
Определение угла' корректно, так как согласно теореме 1
_1<J£lJ£L<i.
\*\-\у\
3°. Ортогональные векторы.
Определение 1. Векторы х и у называются ортогональ-
ными, если (х, у)=0.
Утверждение. Если (х, у)=0 для любого вектора у, то x=Q.
Доказательство. Положим х=у. Тогда (х, х)=0 и, зна-
чит, х=6. D
Определение 2. Система векторов /ь ..., /% называется
ортогональной, если ф, //}=0 при *#/.
Определение 3. Система векторов £ь ..., ^ называется
ортонормированнощ если (е*, e/)=6t/, где б// — символ Кронекера*
Утверждение. Ортонормированная система векторов линейна
независима.
Доказательство. Умножая равенство
скалярно на еи /=1, ..., k, получаем, что а/=0, /=1, .,:, k. D
Определение 4. Базис e=(ei ... еп) евклидова пространст-
ва Е называется ортонормированным, если ~ -
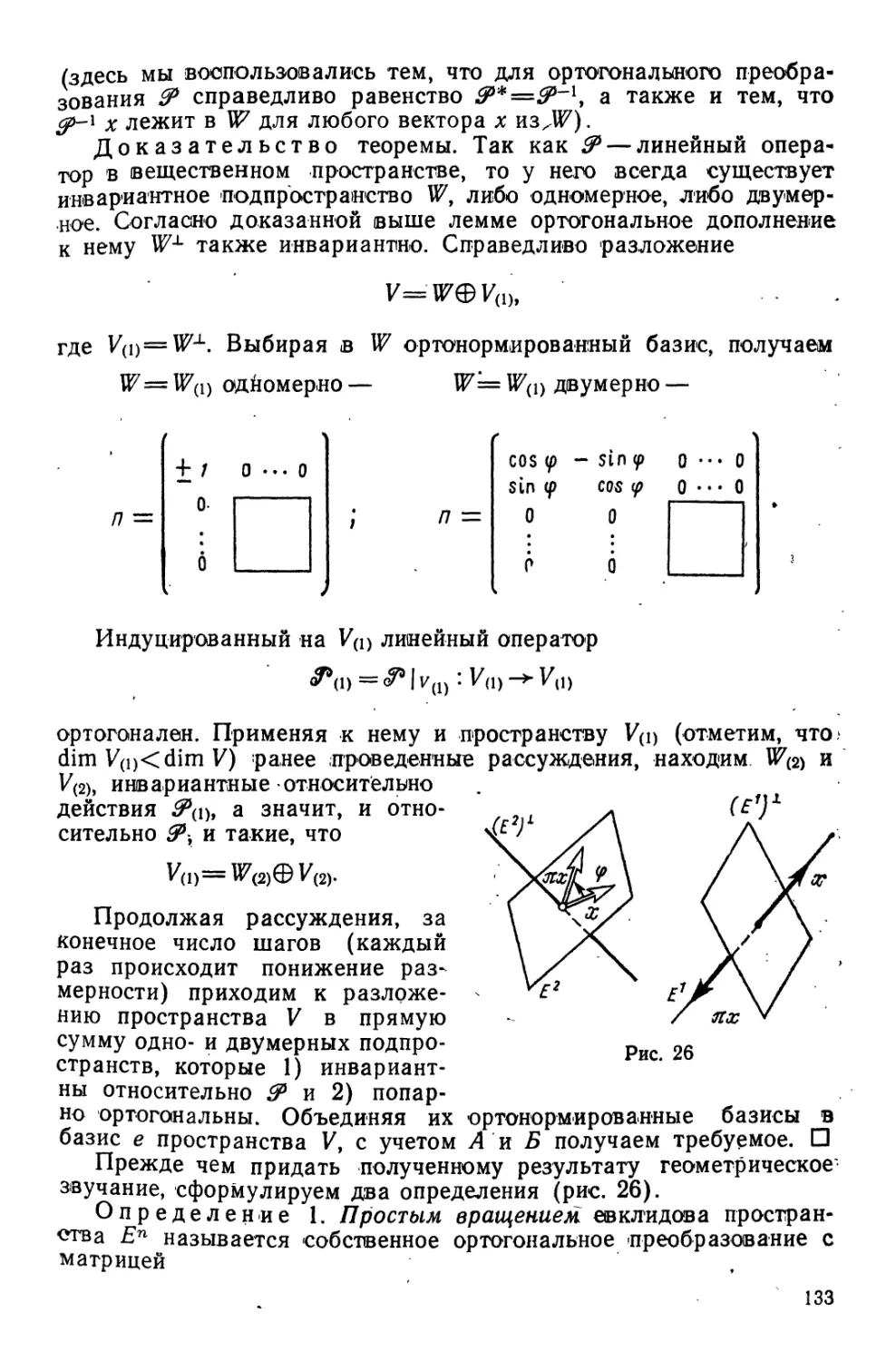
ТЕОРЕМА 2. Утв. В любом конечномерном евклидовом прост*
ранстве существует ортонормированный базис.
Доказательство проведем индукцией по размерности п
пространства.
A. /i=l. Базис пространства образован вектором fi=^=8. Полагая.
получаем ортонормированную систему из одного вектора в\.
Б. Предположим, что в любом (п—1)-мерном евклидовом
пространстве существует ортонормированный базис.
В. Покажем, что ортонормированный базис существует и в лю-
бом /г-мерном пространстве.
Пусть Е — /г-мерное евклидово пространство и /=(/i ... fn) —*
базис Е. Линейная оболочка L(/b ..., fn-\) является (п—1)-мер-
Кронекер (Kronecker) Леопольд (7.12.1823—29.12.1891) — немецкий мате-
матик, почетный член Петербургской АН (с 1872 года),
41

йым евклидовым пространством, в котором ортонормированныи
базис ей •.., вп существует по предположению индукции.
Так как
fn&L(fv ..., /«-О = £(*].; ..., e«-i),
то вектор
gn=fn—ai^i—...—an-iff/i-i
отличен от нулевого при любых a/GR. Выберем коэффициенты
а/, /=1, ..., п—1, из условия
или ai=(fn, et).
Тогда вектор
О ==(?«, <?/) = (/*, */)— а/,
_ g*
lftil
будет обладать следующими свойствами:
1. |е«|=1;2. (ея, */)=0, / = 1, ...,/г— 1.
Таким образом, ей ..., ^«-ь е* — ортонормированныи базис
прфстранства Е. П
Задача конкретного построения ортонормированной системы
векторов ей ..., £т.по заданной линейно независимой системе
/ь • • •, fm решается при помощи метода ортогонализации, по су-
ществу совпадающего с методом доказательства теоремы 2.
Первый шаг. Полагаем g\=fi и находим
„ — &
* Igil
k-й шаг (fc>2). Полагаем
gk=fk—(fk, ei)ex—...— (fk, ek-\)ek-\
(рис. 11) и находим
Рис. 11 Отметим, что
М^ь ••■•» e*)=L(/b ..., /*), Л=1,...., m.
4°. Матрица Грама. ■
Определение. Матрицей Грама для системы векторов / =
= (f\ • • • fm) называется матрица
где
Г«Г(/)=Г(Л ...fm) = (V«7)^Rmxm,
yif = ifi> //)>
тйк.
42
Грам (Gram) Йорген Педерсен (27.6.1850^—29.4.1916) — датский матема-

или, подробнее, ■!
/ifli /l) ...(/l. fm)\
Г(/)= .
\(/«. /i)...(/«. /«)/■
Свойства матрицы Грама \
1+. (удобная форма записи). Рассмотрим произведение столбца
из векторов /ь ..., fm на строку из этих же векторов /т/, в кото-
ром векторные элементы «матриц» /т и / перемножаются скаляр-
но. Ясно, что тогда
Г(/)=Р/.
2+ ГТ = Г.
Два других свойства матрицы Грама менее очевидны.
ТЕОРЕМА 3. Утв. Система векторов /=(fi .., fm) линейно
зависима в том и только в том случае, когда det Г(/) =0.
Доказательство. (=$>•) Пусть система /=(/i ... fm) линей-
но зависима. Последовательно умножая нетривиальную линейную
комбинацию
Ctl/l + . . . + dmfm = 9
скалярно на векторы //, /= 1, ..., т, получаем
ai(/i, fi)+ .,.-+am(fb /m)=0,
Ctl (fm, f\) + . . . +am(/m, fm) = 0, '
или, кратко,
Из существования ненулевого решения полученной линейной сис-
темы вытекает вырождение матрицы ее коэффициентов:
detr(/)=0.
(4=) Пусть detr=0. Тогда столбцы матрицы Г линейно зави-
симы. Тем самым один из них (для определенности m-й) являет.ся
линейной комбинацией остальных:
(//, Ы=М//. /l) + ... + Pm-l(//, f«-l), /=1, ... , /!!.
Полученные равенства можно записать в следующем виде:
(//> fm—Pl/l—. • .—jim-l/m-l) =0, / = 1 /П.
Вектор
ортогонален каждому из векторов /ь ..., /w и, следовательно, лю-
бому вектору из их линейной оболочки L(fu ..., /m).
С другой стороны,
*е=1(/ь ...,/«).
43

Тем самым g = 0, и, значит,
fm = ^Uhfr □
ТЕОРЕМА 4. Усл. Система векторов /=(/i...fm) линейно
независима.
Утв. detr(/)>0.
Доказательство достаточно провести для случая, когда
система / является базисом. Это вытекает из того, что линейно
независимая система f является базисом своей линейной оболочки
L(f).
Пусть / — базис пространства Е nf=fS — другой, пока произ-
вольный, базис Е. Рассмотрим, как связаны между собой матрицы
Грама для / и для J. Имеем
f=T(f) =/Tf = (/S)t/S=St/t/s =
=STr(/)S=STrS.
Здесь мы воспользовались тем, что свойства, доказанные ранее
для матриц, элементами которых являются числа, легко перено-
сятся на рассматриваемый случай (лишь бы имели смысл прово-
димые операции). Итак,
f=sTrs. (*)
Предположим, что f — ортонормированный базис (согласно тео-
реме 2 он всегда существует). Тогда Г==/.
Из равенства
I = (detS)2detr
вытекает, что detr>0. □
Замечания.
(1) Из соотношения (*) вытекает, что если оба базиса / и
?=/S ортонормированы, то
SiS=I.
Верно и обратное: если / — ортонормированный базис и f =/S,
причем матрица S удовлетворяет равенству STS=I9 то система J
является ортонормированным базисом пространства.
Определение. Матрица S= (оц)^Кпхп, для которой выпол-
няется равенство
STS=/, (**)
называется ортогональной.
Свойства ортогональных матриц:
Непосредственно из определения вытекает, что
1+. detS = ±l.
2+. 2/0;/а*/ = 6/*.
3+. ^LiOijOik^&jk*
Кроме того,
4+. Совокупность ортогональных матриц одного порядка обра-
зует группу относительно умножения.
44

В самом деле, для произведения S\S2 ортогональных матриц
Si и S2 выполняется основное равенство
(S1S2)T(S152)=S2T(S1TS1)S2=52TS2=/,
умножение ассоциативно, единичная матрица ортогональна, а
матрица S*"1, обратная к ортогональной матрице S, совпадает
с транспонированной 5Т и, значит, тоже ортогональна.
Определение.
0(/i)={SeR„x«|STS=/}
ортогональная группа.
(2) Доказанное в теоремах 3 и 4 неравенство
detT(/)>0
является обобщением неравенства Коши—Буняковского на сис-
тему, состоящую из произвольного конечного числа векторов.
5°. Изометрия евклидовых пространств.
Определение. Евклидово пространство Е' называется изо-
метричным евклидову пространству £, если существует изомор-
физм линейных пространств ф: Е^Е' такой, что для любых век-
торов х и у из Е выполняется равенство
(ф(*)> ф(#)) = (*,//)•
Само отображение ф называется изометрией.
Таким образом, изометрия — это изоморфизм, сохраняющий
скалярное произведение.
Обозначение: Е'о^Е,
ТЕОРЕМА 5. Утв. Е'^Е^ dim £'=dim E.
Доказательство (=*-) См. доказательство теоремы лек-
ции 2 на с. 26.
(£=) Пусть dim£' = dim£=rt.
Выберем в пространствах Е' и Е ортонормированные базисы
£=(ei ... еп) и e'=(ei' ... еп') соответственно и построим отобра-
жение
Ф: £->£'
ло следующему лравилу:
Ф хх = ULilfet — ULiVe't = x'.
Как и в теореме лекции 2, доказывается, что это отображение
Ф — изоморфизм. Покажем, что ф сохраняет скалярное произве-
дение.
Пусть
Ф; у = 27,14/*, — SjL^e/ = у'.
Вычисляя (х, у) и {х\ у')\
{xi.y) = 2S.1g'4'i (*', y') = 2Lufrf9
убеждаемся в том, что они равны. Тем самым ЕГ2*Е. □
45

ЛЕКЦИЯ 6
6°. Ортогональное дополнение.
Определение. Ортогональным дополнением множества
XczE называется совокупность векторов X-^-czE, определяемая
формулой ' /
■ Хх = {уеЕ\(х9 */) = 0, Vx^X). -
Свойства ортогонального дополнения
1+. X1- — линейное подпространстве Е.
Доказательство. Пусть уи У2^Х\ т. е. (*, t/i)==0 и
(*.» У2) =0 для любого вектора х&Х. Складывая эти равенства»
получим, что для любого вектора х из X
(х, У\) + (х9 У2) = (*> У\+У2).
Тем самым у\+у2^Хх.
Из того, что (Ху */)=0 для любого х из Х9 получаем равенства
(х, ау) = 0, и, следовательно, ау^Хх. П
2+. Если W — линейное подпространство пространства Е9 то
E=W@W\
Доказательство. Будем считать, что W — нетривиальное
подпространство Е. Пусть еи ..., еь. — ортонормированный базис
W, а в*+ь.!..", eq — орионормированный базис W\ Система век-
торов
01, ..., ek, ен+и ея
ортонормирована и, следовательно, является линейно независи-
мой. Если бы она не была базисом, то нашелся бы вектор eq+t
из £, после добавления которого новая система
' ви • • • , вк> в*+1, • • - , eq, eq+\
сохранила бы линейную независимость. Согласно методу ортого-
нализации из предыдущей лекции можно считать, что эта послед-
няя система является ортонормированной.
Тогда вектор eq+\ ортогонален векторам ей ..., £* и, значит,
лежит в W1-. Но так как eq+\ ортогонален базису вк+и • • •» е<г и
этого подпространства, то он может быть только нулевым.
' Тем самым наше допущение, что q<dimEt неверно, и мы по-
лучаем равенство q = dimE. Так как, кроме того, W(]W±={Q}i то-
согласно теореме 2 из лекции 3 Е= W®W\ □
3+. Если W — линейное подпространство, то (W±)±=W.
4+. Если W — линейное подпространство из Е, то в Е найдется
линейно независимая система векторов аи ..., ат, такая, что
(рис. 12)
W={x\(ait x)=09 t = l, .... m}.
Доказательство. Из свойства 3+ вытекает, что в качества-
системы аь ..., ат нужно взять базис ортогонального дополнения.
Тем самым m = dim£— dim W. □
46 ^

5+. Пусть Н — линейное аффинное многообразие из £. Тогда
в Е можно указать линейно независимую систему аи ..., am, a
в R — некоторые числа <ц,..., ат так, что (рис. 13)
H={y\(di, у)=а,-, f=l, .... т}.
Доказательство. По определению линейного аффинного
многообразия в пространстве Е существует вектор Ь, такой, что
H = b+W.
Рис. 12
*
Пусть векторы аи .:. , ат те же, что и в свойстве 4+ (базис
Wx). Положим
(aiy b)==ai, i = l, ...» m.
Так как множество Н полностью описывается векторами вида
#=6 +ад, где w&W, то для любого i, l<t<m, выполняется усло-
вие
(а*, у) = (а/, Ь + ад) = (а,-, Ь) = ш.
47

С другой стороны, если вектор у удовлетворяет равенствам
. (fli. У)=ш, i==l, ...,/п,
то у—b^W. В самом деле,
0=(а/, У) — (а/, 6) = К у—6). '
Это означает, что y^b+W=H. □
Замечание. Вектор сдвига Ь можно выбрать так, чтобы
Ы W.
7°. Расстояние между множествами.
Определение 1. Множество X называется ; метрическим
пространством, если на нем задана метрика
d : Xx*->R0+={aeER|<x>0},
т. е. каждой паре элементов х, у из X поставлено в соответствие
число, называемое расстоянием между х и у и обозначаемое че-
рез d(x, у), такое, что для любых ху у и z из X:
1. d(x, y)=d(y, х)\
2. d(xt у)>0, d(*, у)=(И=^х=у;
3. d(x, z)<d(A:, y) + d(y, z) (неравенство треугольника).
Пример. Нетрудно убедиться в том, что
d(x и)= \ 1, еслихФу,
а(Ху У} . 1 0, если О,
задает метрику на любом множестве X.
Пример 2. Нетрудно убедитуься в том, что правило .
d(*. v)-\x-y\ (l)
задает метрику в евклидовом пространстве.
Замечание. Метрика, введенная в евклидовом пространстве
Е формулой (1), обладает следующим полезным свойством: для
любых векторов х, у и z из Е
d(x+z9 y+z) = d(x, у).
Всюду до конца этого пункта будем рассматривать евклидова
пространство Е и считать, что метрика в нем задана форму-
лой (1).
Определение 2. Расстоянием между множествами X и Y
из евклидова пространства Е называется число d(Xt У), опреде-
ляемое формулой
d(X, У)= inf d(*, у).
х£Х,у£У
В общем случае вычисление расстояния между множествами
является задачей и трудной и трудоемкой. Однако если ограни-
читься рассмотрением линейных аффинных многообразий из
евклидова пространства, то можно указать простые формулы и
несложный способ их вывода.
48

Обратимся к задачам.
Задача 1. Пусть Х = {х} и Y=W — линейное подпространством
По определению расстояния между множествами
d(x, W) = 'inid(xt у).
yew
Так как E=W®W\ то имеет место разложение (рис. 14)
x=yQ+z, (2)
где yo^W, ze№x определены однозначно.
Рис. Г4 % Рис. 15
Покажем, что •
d(x,W)=A(xty0)9
где уо то же, что и в формуле (2). Вычтем из обеих частей равен-
ства (2) произвольный вектор у из W:
х—у=Уо—у+г.
Возводя обе части этого равенства в квадрат, с учетом условия
zLy—у о получим
\х-У\2=\У<г-у\*+\г\*>\г\*.
Из того, что z=x—уо, и из определения d(#, у) вытекает, что
d(x, y)>d(x, уо)
для любого y^W.
Векторы уо и z имеют специальные названия: у0 — ортогональ-
ная проекция вектора х на подпространство Wa a z — ортогональ-
ная составляющая вектора х.
Укажем способ построения ортогональной проекции и ортого-
нальной составляющей (см. формулу (2)).
Пусть ей •.. > ek — ортонормированный базис подпространства
W. Тогда вектор у0 можно представить в следующем виде:
4£

Умножая обе части равенства
х = 2*eia'^ + г
скалярно на векторы в/, /= 1, ..., k, получим
(х, е/)=ц1, / = 1, ..., К
(здесь мы воспользовались тем, что (z, е;) =0).
Таким образом, найден вектор #о, а следовательно, и вектор z
л расстояние d(x, W).
Замечание. В том случае, если базис /ь ..., fk подпрост-
ранства W не является ортонормированным, коэффициент Р/
в разложении вектора у0
вычисляются из линейной системы
(х, M = 2f-iV(f„ U m=l,..., *..
Отметим, что матрицей коэффициентов этой системы является
матрица Грама для базиса fu ..., /*.
Задача 2. Пусть X={x}t Y=Wa=a+W. Тогда d(*, Wa) =
= d(*—a, №).
Справедливость приведенной формулы легко следует из того,
что *
d(x, a + w) = |#— (a + w) | = | (х—а)— до| =d(л:—а, до).
Задача 3. Пусть Х=№' — линейное подпространство и F=
^=WV/==a+№". Из соотношения
&(ц>\ a+w") = |до'—(a+до") | = |w'—a—w"\ =
= \а— w'+w"\ = \а— (до'—до") | =d(a, до'—до") ;
в силу произвольности до'еИР' и до"е№" вытекает, что (рис. 15)
d(W, №fl")=d(a, №'+№").
Задала 4. Пусть Z= №а', У= W. Из того, что
d(a+w',b + w") = \{a+w') — (b + w")\ =
= \(b — a) — {w' — w")\=d(b — afw' — w"),
ж из произвольности выбора до' из W и до" из W" вытекает, что
d(Wa\ Wb")=d(b—a, W'+W").
$ 2. УНИТАРНЫЕ ПРОСТРАНСТВА '
Определение 1. Линейное пространство над полем комп-
лексных чисел называется комплексным линейным пространством.
Ь0

Определение 2. Унитарным пространством называется
комплексное пространство U\ в котором введена операция скаляр-
ного умножения
(,):1/Х£/-С,
т. е. каждой упорядоченной паре векторов х и у из U ставится
в соответствие комплексное число, обозначаемое (ху у) и называ-
емое скалярным произведением вектора х на вектор уу такое, чта
для любых х, у и z из U и любого аеС выполняются следующие
соотношения:
1. (У, х) = (х, у),
2. (*+{/, z) = (*, z) + (y,z),
3. (а*, у)=а(х, у),
4. (*, х)>0; (xt x)=Oox=Q.
Пример. В координатном пространстве Сп скалярное произ-
ведение можно ввести так:
(g, ^) = 2/=i^,
где|=(|1,...,^) и r\=(r\\,.„fr\")h=C\
Для унитарных пространств остаются справедливыми (про*
верьте!) все факты, установленные для евклидовых пространств,
кроме отмеченных ниже. Поэтому основное внимание будет уделе-
но отличиям.
ОТЛИЧИЕ 1. Утв. (х, ау)=а(х, у).
Доказательство.
(*, ау) = (ау9 х) = а(у, х) = а{у, х) = а(х, у). D
ОТЛИЧИЕ 2. (неравенство Коши—Буняковского). Утв.
\(х,у)\*<(х9х)(у;у). (3>
Доказательство. При x=Q обе части в формуле (3) рав-
ны нулю. Неравенство
(tx—t/, tx—*/)>0 (4>
справедливо для любых х, y&U и feC.
Пусть хФв и
(х, х) '
Подставляя выбранное t в тождество
(tx-y9 tx—y) =tt{xy x)—t{x, y)—'t(yt x) + {yy y),
с учетом формулы (4) получаем, что
(х ,у) (x~jj) '
~ (х,х) + (У> У) > °-
Откуда [х, х) (у, у) > 1 {xt у) |2. П
51

Задача. Доказать, что ]{х, у)\2=(х, х) (уу у) в том и только
в том случае, если либо y = tx, либо x=ty.
ОТЛИЧИЕ 3. Нет содержательного аналога понятия угла (од-
нако понятия ортогональности и ортонормированности сохраня-
ются).
ОТЛИЧИЕ 4. Матрица Грама T(f)=fTf системы векторов /
-является эрмитовой Г = Г* (напомним, что матрица А = (ajk)^CnXn
называется эрмитовой, если а/* = а*;; обозначение: А=А*).
Приведем примеры на вычисление расстояний в унитарном
пространстве между некоторыми множествами.
Пусть dim U=n.
Определение. Множество Вп(г)={у\ |у|<>}, где г>0, на-
S*-i{r)=\
зывается замкнутым n-мерным шаром,
(л—1) -мерной сферой радиуса г.
Задача 1. Пусть Х={х}, а y=S"-1(r), хфд. Тогда
-{У\ \У\=г) -
d(x, S"-!(r)) = d х,
1*1
) = И*|-'
■г =
Покажем, что я— ближайщий к вектору х элемент сферы
S*~l{r).
Пусть y^Sn~l(r) произволен. Вычислим длину вектора \у—х\
и построим на обычной двумерной плоскости окружность радиуса
г с центром в точке О и треугольник АОАВ с длинами сторон
\ОА\ = \х\„\ОВ\ = \у\, \АВ\ = \у-х\ (рис. 16).
Нетрудно видеть, что \АВ\^
>МОЛ| — \ОС\\ (или \у—х\>
в s ^ll*l—Л)у причем равенство
возможно лишь в случае, если В=
= С, т. е. \
г
У = X.
1*1
Задача 2. Пусть Х={х} и У=
=5п(г), причем |^1>^. Тогда
(рис. 17)
®'
Рис. 16
d(*,B-(r))-|x|-r.
Рис. 17
Рис. 18
Эрмит (Hermite) Шарль (24.12.1822—14.1.1901) — французский математик.
52

Задача 3. Пусть Х = Вп(г) и Y = Wa, Причем Bn(r){]Wa = 0.
Тогда (рис. 18) , - '
d(B*(r), Wa) = \a±\-r,
где а± — ортогональная составляющая вектора а относительно
подпространства W.
Доказательство проводится так: из центра 6 шара Вп(г) на
ЛАМ Wa опускается перпендикуляр и вычисляется его длина
(«перпендикуляр короче любой наклонной»).

ЛЕКЦИЯ 7
Глава HI. ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ
§ 1. ОСНОВНЫЕ ПОНЯТИЯ
0°. Определение линейного отображения. Пусть V и W — ли-
нейные пространства над полем Р.
Определение. Отображение *
а : V-+W.
называется линейным отображением пространства V в простран-
ство W, если для любых двух векторов х и у из V и любых а и (J
из Р выполняется равенство
«я£ (<x*+ pt/) = cus#x+ p^t/.
Замечание.
(А) Если W=Py то линейное отображение называется линей-
ной формой;
(Б) если W=V, то линейное отображение называется линей-
ным оператором.
Примеры линейных отображений.
(1) Пусть V=Mn, где Мп — пространство многочленов степени
не выше л, a W=Mn-\ (мы рассматриваем здесь вещественный
случай). Тогда
at
линейное отображение: каждому многочлену ставится в соответ-
ствие его производная. >
(2) Пусть V=V\(BV2. Тогда любой вектор х из V можно запи-
сать в виде суммы *х=*Х\ + Х2. Отображение проектирования
&: V-*>VU
задаваемое по правилу &*х=Хи является линейным (рис. 19).
(3) Пусть V=P", W=Pk. При
помощи матрицы ЛеР*х« век-
тор Я=(61...£п)теРп преобра-
зуется в вектор Y= (т|1... Tjfe)Te
ePft, если положить
AX=Y.
Таким образом,
А : Р"->Р*
рис 19 — линейное отображение.
54

Пример. Линейное отображение
А: &o,n->£2o,n -1
действует из пространства сеточных функций
Qo,N={ytH = 0, 1, ..., N}
в пространство сеточных функций
Qo,n-i = №' = 0, 1, ..., N-1}
но правилу
< &yi=yi+\—yi, i = 0, 1, ..., N—1,
(правая разность).
1°. Образ линейного отображения.
Определение 1. Образом линейного отображения st: V-+
-+W называется множество
imst = {y<=W\a*e=V: s&x=y}.
Утверждение, \ms4> — подпространство из W.
Доказательство. Если у и #2^ini.5#, то в V можно ука-
зать векторы Х\ и *2, для которых $4>хх=у\ и st>x2=y2- Так как
jt>(x\ + x2)=s4>X\+$t>X2=y\ + y2> то вектор у\ + у2 лежит в \mst>.
Если yeim j$, то в V найдется вектор х, для которого зФх—у.
Из того, что бФ(ах) =ast>x=ay, получаем, что и вектор ау лежит
в ims&. □
Определение 2. Рангом линейного отображения si> называ-
ется размерность его образа — dim im j#.
Обозначение: rangj^.
ТЕОРЕМА 1. Усл. Семейство векторов Х\, ..., хд из V линейно
зависимо; st>: V-+W — линейное отображение.
Утв. Семейство векторов бФх\, ..., s£xQ из W линейно, зави-
симо. ,
Доказательство. Достаточно рассмотреть нетривиальную
линейную комбинацию
Cti^i + . . . + CLqXq = 9v
и применить линейное отображение s4> к обеим частям этого ра-
венства
a\Mxl + ... + a<fst>Xq = Qw. П
СЛЕДСТВИЕ. Утв. rang^<dim V.
Доказательство. Ясно, что
imst> = L(j6eu ..., sten),
где eu ..., еп — базис V. П
ТЕОРЕМА 2. Усл. е=(е{ ... еп) — базис пространства V; век-
торы /ь ..., fn из W произвольны;
55

Утв. Существует единственное линейное отображение
у которого s£ej=fjt /= 1, ..., п.
Доказательство. Возьмем в пространстве V произволь-
ный вектор х и разложим его по базису е
x = 2nk=ilkek.
Вектор у из W определим по правилу х
Тем самым построено отображение
для которого y=s£x. В том, что оно линейно, легко убедиться не-
посредственно. Ясно, что stek=fkf &= 1, ..., л.
Покажем, что отображение бФ определено однозначно. Пусть
— линейное отображение и S&ek=fk, k=l, ..., я. Вычисляя дей-
ствие отображения <% на произвольный вектор х из V, получаем»
что
Лх =& (2Li£4) = 2*=i£*<*e*== 2Li?fb=Ux.
Это означает, что s4>=3&. Р
2°. Ядро линейного отображения?
Определение 1. Ядром линейного отображения s&:V-+W
называется множество
ker st = {х<= V \ stx=9 w].
Утверждение, кетМ — линейное подпространство V.
Доказательство. Если s£x\ = Qw и 3t>x2=Qw, тои^(хг+
+ x2)=s&Xi + s£x2—Qw. Из того, что *s&x—Qw, вытекает, что
зФ(ах) =as£x = aQw=Qw- □
Определение 2. Дефектом линейного отображения зФ : V-*-
-+W называется размерность его ядра — dim ker s4>.
Обозначение: defects.
СЛЕДСТВИЕ. Утв. defect ^<dim^.
3°. Теорема о ранге и дефекте линейного отображения.
ТЕОРЕМА 3. Утв. defect ^ +rang ^ = dim V (рис. 20).
Доказательство. Обозначим через U = kers& и рассмот-
рим фактор-пространство V/U. Как уже отмечалось, VJU состоит
из множеств вида
Ux±x+U.
Отображение ф : V/U-*-im s& построим по следующему правилу:
Ф : Ux=x+U=x+kers£>-+s&x.
56 4

Это отображение корректно определено, так как любой элемент
х из Ux под действием отображения si переходит в з&х:
Mx=s&{x+u) =s&x + s&u=s£x+Qw=s&x.
Кроме того, оно является и взаимно однозначным: сюръективность
вытекает непосредственно из определения ф, а инъективность сле-
дует из того, что если
Ф(^) = Ф («/?). • v Л
то х=х+й, или, что то же са-
мое, их=итш
Остается доказать линейность.
Пусть
Ф :UXi ~Лхи i = l, 2.
Рис. 20
Так как UXt + UX2=UXt+X2, то ср : UXt + UX2^t4{xl + x2)^=o€x1-f <Лхг.
Из того, что aUx=UaXf вытекает и второе требование
Тем самым
<р : aUx>—s/>(ax) =as£x.
является изоморфизмом. Из того, что V/U£*ims&, получаем
dim V/£/ = dim V—dim U = dim im^=rang зФ. Отсюда, так как
U=kers&, вытекает требуемое равенство: dim V=defect s& +
+ rang^. П
Замечание. Пусть s4>:V-+V—линейный оператор. Тогда и
ker,s# и im^ являются подпространствами линейного простран-
ства V, сумма размерностей которых согласно теореме равна раз-
мерности V. Появляется соблазн доказать, что ker^©im^= V.
Однако, как показывает приводимый ниже пример, это соотноше-
ние в общем случае оказывается неверным.
Пример. Пусть V=M2n-i и
о0 = £п =
dtn
: Л42,1-
-Af:
2/x-l
линейный оператор /г-кратного дифференцирования. Нетрудно
убедиться в том, что в этом примере ker s£ = ims&=Mn-i.
§ 2. ОПЕРАЦИИ НАД ЛИНЕЙНЫМИ ОТОБРАЖЕНИЯМИ
1°. Линейное пространство линейных отображений. Пусть V
и W — линейные пространства над полем Р. Наделим совокуп-
ность всевозможных линейных отображений из V в W:
Hom(V, W)={&\st : V-+W — линейное отображение}
структурой линейного пространства.
57

Сумма линейных отображений.
Определение 1. Для произвольной пары si- и 3S и&
Hom(V, W) определим отображение ^ : V-+W ■ по следующему
правилу:
Фх^&х+Ях, (1>,
где вектор x^V произволен.
, Утверждение. Отображение %?, определенное правилом (1)„
является линейным, т. е. это правило — ВнутЗК на Hom(V, W).
Доказательство, Вычислим, как действует отображение
<& на линейную комбинацию векторов из V:
<&(ах+$у) = <А(ах + $у) + <&(ах + $у)=,*
=а<Ах + §<Ау + affix + $<ffiy =
==а(и£х + тх)+$(<Ау + <Шу)==аЪх + №у. D
Обозначение: <&=,&+3&.
Умножение линейного отображения на элемент поля.
Определение 2. Для любых а из Р и i из Hom(V, Не-
определим отображение 3i : V-+W по правилу
&x = astxt (2)
где вектор х из V произволен.
Утверждение. Отображение Д определенное правилом (2)„
является линейным, т. е. это правило — ВнешЗК на Нот (У, W).
Доказательство. Вычислим, как действует отображение
3& на линейную комбинацию векторов из V:
(Ш (kx + \iy) = аЛ (kx + \iy) = a (kJlx + \itAy) =
= Х(а<Ах)+\1(а,Ау) = Шх + \1<Шу. П
Обозначение: <%=as£f
Утверждение. Множес?во Hom(V, W) с введенными выше
ВнутЗК и ВнешЗК является линейным пространством над по-
лем Р.
Доказательство. Достаточно.проверить все восемь требо-
ваний определения линейного пространства (см. пункт 1° из § 1
главы I, лекция 1), взяв в качестве нулевого отображения
0:V-+W9
такое, что Cx = Qw для любого xeV, а в качестве отображения*
противоположного «я£, (—1),я£. П '
Обозначение: &{V, W).'
Пример. Рассмотрим пространство i?(V, P) линейных форм
на V; его называют пространством, сопряженным V, и обознача-
ют через V*. Покажем, что
dimK* = dimK .
58

Пусть е=(е{ ... еп) — базис V. Зафиксируем в V произвольный
вектор
Линейная форма шеР переводит базисные векторы в элементы
поля: (о(ед;) =afe£P, ft=l, ..., л. Рассмотрим действие со на век-
тор х:
_ со (х) = (о (S!LiE4) = Й-1?© (**) = Я-16Ч.
Нетрудно убедиться, что отображение ф:'У*-ИР*, задаваемое
правилом
корректно определено, взаимно однозначно и линейно, т. е. явля-
ется изоморфизмом. Это означает, что
и, следовательно, dim V* = dim V.
2°. Кольцо линейных операторов. Обратимся теперь к совокуп-
ности всевозможных линейных операторов, действующих на V:
SB{y> У)—{зФ\зФ : V-+V — линейный опердтор}.
Ясно, что определенная в предыдущем пункте сумма является
ВнутЗК и в этом случае. Введем на 3?(Vt V) еще один ВнутЗК.
Умножение линейных операторов.
Определение. Для каждой пары s& и 3& из множества
3?(V, V) определим отображение
V-.V-+V
по правилу
9х=Я(&х), (3)
где вектор х из V произволен.
Утверждение. Отображение 99 определенное правилом (3),
является линейным оператором, т. е. это правило — ВнутЗК на
&{V, V). .
Доказательство. Достаточно рассмотреть действие 9S на
линейную ко»*бинацию векторов из V:
<Щах + fy/) = Л WL {осх + ру)) =
= с& (аЛх + §Лу) = <Ш {а<Ах) + <& (&Ау) =
= к<Ш {<Ах) + рсШ (Лу) = agx + $%у. • О
Обозначение: Ф^ЗИяб.
Утверждение. Множество 9?{V, V) с ВнутЗК (+,) и ВнутЗК
(•) является некоммутативным кольцом с единицей (dimV>l).
Доказательство. Условия, определяющие кольцо, прове-
ряются непосредственно; в качестве единицы следует взять тожде-
59

ственное отображение 2f. Некоммутативность операции умножения
вытекает из следующего простого примера.
Пусть V=R2; операторы s4-: R2->R2 и Jf:R2->R2 определены
следующими правилами:
Л : (l\ Б2) - (Б1, 0), <® : (Б1, Б2) ~ (Б1 + Б2, Б2).
Тогда
ЯгА:($, Б1)-(Б1, 0), сЛМБ1, БЧ — ^ + Б". 0). п
Свойства обратимых элементов кольца 3?(Vy V):
Условия 1+—4+ равносильны.
1+. Линейный оператор $$< обратим.
2+. Линейный оператор $$< взаимно однозначен.
3+. кег^={6}.
4+. im^ = V.
Доказательство. 1ь=^2+. Обратимость $Ф означает, что
существует З&^З?(V, V), для которого
&$=<%&=&. (4)
Инъективность $Ф легко доказывается от противного: пусть Х\Фхъг
но st>X\=s4>x2. Действуя на обе части оператором J?, приходим
к противоречию
X\—2fX\ =$Я£Х1=3!1£бХ2=УХ2 = Х2,
так как (&s&)x=x для любого вектора х. Что же касается сюръ-
ектрвности eS^, то для любого у из V соответствующий вектор х
из V (т. е. такой, что s£x=y) находится так: х=$у. В самом деле„
действуя на обе часта последнего соотношения оператором Ж;
получаем
s£x=(s£$)y=yy=y.
2+=^3+. Из равенства s£x = Q в силу взаимной однозначности sf
получаем, что х=9 и, значит, ker*s£={0}.
3+=^4+. Из того, что кег*я£={0}, вытекает равенство dim V=
=rang^, а так как im*s£—подпространство V, то im*s£=V.
4+=ф-1+. Построим оператор <8, удовлетворяющий соотношению
(4). Так как ims£ = V, то оператор $$> переводит базис в базис:
s£:e=(ei ... en)-+f=(f\ ... /rt). Построим линейный оператор &
так, чтобы
#:/=(/i ... fn)-+e=(ei ... еп).
Согласно теореме 1 § 1 оператор J? определен однозначно.
Остается убедиться в том, что
(Jta£)x=x, (st£)x=x
для любого вектора л: из V.
60

Разложим вектор х по базису е: x=S/g/er/. Тогда
(Л*А)х = &Л (2,^,) = Л {Ъ}У<Ае}) =
= <£ (2 Д//,) = 2,6/Л/, = Х,^, = х.
Аналогично, раскладывая по базису f
x = Zkr\kfk>
получаем, что
(Mi )х=АЯ \^kr\kfk) = JL (2kr)kSfk) -
= Л(Ък^ек)=2кгрь4ек=2к^к = х- □
ЛЕКЦИЯ 8
3°. Ранг произведения линейных отображений. Пусть V9 W ш
Z — линейные пространства над полем Р. Для любых s$>^
&£P(V, W) и <%<=2?(Wy Z) определим отображение
: V-+Z
по следующему правилу:
(Я&)х=Д(&х),
где х — произвольный вектор из V. /
Утверждение. &&<^g (V, Z).
ТЕОРЕМА 1. Усл. MsB&{Vy W)9 &^2?{Wr £).
Утв. 1. rang «Sfa^min (rang st, rang J?).
2. rang st = dim U7=M-ang jfotf = rang 38.
3. rangi?= dim W=^rang^^ = rang j^.
Доказательство. 1. Покажем сначала, что
rang Jta£<rang st>.
Рассмотрим сужение линейного отображения <%: W-*Z Has
imstaW (рис. 21):
Вследствие того, 4Toim^=
= im(Jfe£), ясно, что
dim im .s^dim im J? =
= dimim(J^).
Тем самым rang ,a£>rang Jk#.
Второе неравенство
rang#«rf<rang#
легко следует из того, что
im(^«s0)czim^.
6Р

2. Пусть rang ,$£ = dim W (рис. 22).
Тогда im s£ = W и im(Jf^)=im^.
Откуда rang (3&s£)=rang&.
3. Пусть rang &= dim W.
Тогда fl^im SZaZ.
\mcft~W
w£
' l 1
Ill-Ill 1,1
im$ I
1 ^
Рис. 22
Рассмотрим диаграмму
Ш : IF ^imdS
U U
<S: imc#->im(^o#).
Так как отображение $ — изоморфизм, то оно не изменяет раз-
мерности и, следовательно,
Отсюда получаем требуемое равенство
1 . rang(Jf^) =rang^. □
СЛЕДСТВИЕ. Усл. Ле=Р*хл, BezPw
Утв. 1. rang ВЛ^гшп (rang Л, rang Б).
2. rangi4=fe=^rangBi4 = rangB.
3. rangB=&=и•angBЛ = rangЛ.
Доказательство. При помощи матрицы Л вектор Аг =
— (S1 ••• 1п)т^Рп преобразуется в вектор Y— (ц{ ... цк)т^Рк1
«ели положить AX=Y; вектор Y при помощи матрицы В преобра-
зуется в вектор Z= (^ ... £*)Т€=Р* : 57=Z.
Тем самым построены линейные отображения
А : Р*->Р*, £ : PWP^, ВЛ : Р"-^Р*. П
§ 3. ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ И МАТРИЦЫ
Г. Матрица линейногб отображения. Пусть V и W — линей-
ные пространства над полем Р и dimV=M, dimW=k. Рассмотрим
линейное отображение
62

Пусть е= (е\... еп) — базис V и /= (f\... fk) — базис W. Рас-
кладывая образы базисных векторов е, по базису f, получаем
JLei =S/ela{//, i = 1, ... , я.
Определение. Матрица
(1)
ai
ai
A(e9f) = \
a*
столбцами которой являются координаты образов базисных век-
торов, называется матрицей линейного отображения &: V-+W от-
носительно пары базисов: е в V и f в №.
Пример. Пусть У=№=МП и. 29= -4~:Afn->Afrt. Выберем в
Л1П базис:
£
1, е1 — t, в^ —
2!
[0 10
0 0 1.
poo.'
0
1 *
0
' •. 1
0
0 0
Легко убедиться в том, что
S5e0 = 0, 2Deq±eq-b q=l,...;'n.
Поэтому
D{e9 e)«
Пусть y=stx. Разложим векторы х и у по базисам е и f соот-
ветственно:
* = 2LiE4-, 0=2f.iT|///.4
Подставим полученные разложения в равенство $6х=у. Получим
Привлекая формулы (1), преобразуем левую часть:
Л {tLi&d = Д-гё'A* = SLiP (Sy-iorf//) = 2/=i (2t 1Ы) //-
Из последних двух формул, воспользовавшись тем, что разложе-
ние по базису единственно, получаем, что
ъиЫ=г\*> /=i, ...,£,
6S

или, подробнее,
ai1E1+...+an16n = 41»
(2)
aifegl+ ... +unk%n=r\k.
Применяя введенные ранее обозначения
запишем соотношения (2) в следующем виде:
A{e,f)x(e)=y(f).' . (3)
TEQPEMA 1. Утв. Ранг матрицы А(еу f) не зависит от выбора
«базисов е, f и равен rangs&.
Доказательство. Напомню, что
rang^ = dim im«s#.
Так как
/ imst> = L(s£ei,...,st>en),
то rang^ = r.ang(^£i,...,,я^п). А так как f — базис W, то ранг
этой системы векторов равен максимальному числу линейно не:
зависимых столбцов матрицы А (е, f), т. е.
rang(itei, ..:,<s&en)=rangA(e, f).
В самом деле, так как столбцами матрицы А{е, f) являются
координатные столбцы векторов зФеъ*:.,з4>еп относительно бази-
са f, то сказанное вытекает из теоремы 4 пункта 1° § 3 главы I,
.лекция 2 (система векторов линейно независима тогда и только
тогда, когда линейно независима система их координатных столб-
цов в каком-нибудь базисе). □
2°. Размерность пространства линейных отображений.
ТЕОРЕМА 2. Утв. S(V, !F)~Pdimrxdimv-
Доказательство. Пусть dimV=/z, dim№=&. Зафиксиру-
ем в пространствах V и W базисы е=(р\...еп) и f=(f\...fk) со-
ответственно. Тогда для каждого линейного отображения
лФ : V-+W определена его матрица А (е, f)^Pkxn.
Изучим свойства этой операции
W:st<=2>(Vf W)~A(e, f)e=Pkxn.
1+. Линейность. Пусть y¥\s^^A(ef f) и Ч :31+-+>В(е, f)\ Это
юзначает, что
А{е. f) = №),B(e,f) = W)9
где ш' и {У определяются из соотношений
#
<Аес = 2иМ?р <®ес= 2*=$/,, i = 1 п,
«64

соответственно. Линейное отображение Xs4> + \y£B преобразует век-
торы базиса е по следующему правилу:
(Хо€ + \кЛ)'е1 = hAet + 1и&е( = X^Mfj + V^UMfi =
Тем самым
4?:tet + \rf$~kA{e, f)+\xB(e, f).
2+. Инъективность. Пусть $4>Ф38. Это означает, что найдется
номер i(l<i^n), для которого
(в противном случае s&=&). Отсюда следует, что матрицы
А(е> /) и В(е, f) не равны, так как они различаются t-ми
столбцами.
3+. Сюръективность. Рассмотрим произвольную матрицу
Л=(аг')€=РАхп.
Для (фиксированных) базисов ев пространстве V и / в прост-
ранстве W построим линейное отображение зФ: V-+W так, чтобы
A(e;f)=A.
Рассмотрим следующую диаграмму:
<A:x(=V>-+y(=W
el tf
А:х(е) ~y(f)-Ax(e).
Произвольному вектору х из V ставится в соответствие вектор у
из W по следующему правилу:
e) раскладывая вектор х по базису е
строим столбец л:(в) = (g1... gn)T;
А) умножая столбец х(е) на матрицу А, рассматриваем полу-
ченный столбец Ах(е) высоты k как столбец из координат
У(/)-(Ч1--.т|*)т
некоторого вектора у из W относительно базиса f;
f) строим вектор у:
у- 2/t.V//.
Тем самым построено отображение
Покажем, что отображение si* линейно.
3 Заказ 538 ' 65

В этом нетрудно убедиться, заметив, что каждый из описанных
выше шагов е), A), f) является линейным:
ЛЛх+Х'х' ~Ху + Х'у'
е } t f
А: Хх (е) + Х'х' (е) ~ Ху (/) + Х'у' (/);
здесь Ху (/) + Х'у' (f) = ХАх (е) + Х'Ах' (е) = А (Хх (е) + Х'х' (е)).
Осталось убедиться в том, что матрица А(е, /) построенного*
линейного отображения s4- относительно базисов е и / совпадает
с матрицей А.
Для любого вектора х по построению имеем
Ax(e)=y(f).
Согласно формуле (3)1° матрица А (еу f) линейного отображеция;
s& тот же координатный столбец х(е) преобразует по правилу
A(e,'f)x(e)=y(f).
Отсюда вытекает, что
{A(e,f)-A)x(e)=0
для любого координатного столбца х(е).
Это означает, что матрица А(е, f)—А — нулевая и, следова-
тельно, A (erf) =Л.
Таким образом, отображение
является линейным и взаимно однозначным, т. е. W — изомор-
физм. □
СЛЕДСТВИЕ. Утв. dimS^V, W) -dim V-dim W.
Доказательство. Матрицы
Д*/еPkx n (i= 1, • •.., k\ / = 1,..., n),
все элементы которых, кроме элемента в позиции (i, /) (он ра-
вен единице), равны нулю, образуют базис пространства Рихп-
Число таких матриц равно k-n.
ЛЕКЦИЯ 9
3°. Преобразование матрицы линейного отображения при пе-
реходе к новым базисам.
ТЕОРЕМА 3. Усл. е и e' = eS — базисы V, f и f'=fQ — бази-
сы W\si><=2\y, W).
Утв. A(eff)S = QA(e',f').
Доказательство. Пусть y=s£x. Координатные столбцы
этих векторов х(е) и y(f) относительно пары базисов е и f свя-
заны равенством
y(f)=A(e,f)x(e), (1>
66

,а относительно пары базисов е' и /' соответствующие координат-
ные столбцы х(е') и y(f') — равенством
У(Г)=А(*. П*Ю .(2)
{см. формулу (3) пункта Г). Согласно свойству 3+ матрицы пе-
рехода (см. формулу (4) пункта 1° § 7 главы 1, лекция 4)
• x(e)=Sx(e'),y(f)=Qy(f'). (3)
Подставляя выражения"(3) для х(е) и y(f) в равенство (1), по-
лучаем, что
<}у(П=А1е, f)Sx(e').
Пользуясь далее соотношением (2), получаем отсюда следующее
равенство:
QA(e', f')x(e')=A(e, f)Sx{eT),
которое в силу произвольности вектора х, а значит, и столбца
x(ef) приводит к требуемой формуле
QA(e'f f')=A(e, f)S. D
4°. Эквивалентные матрицы. Пусть матрицы А и ВеР*Жп.
Определение! Будем говорить, что матрицы А и В свя-
заны отношением 91 (обозначение: А91В)У если существуют такие
матрицы
C<=GL(k, Р) и£е=Ш,(/г, P),
что B = CAD.
Утверждение. Отношение 91\ заданное на множестве Р* хп» яв-
ляется отношением эквивалентности.
Доказательство. Бинарное отношение 91, введенное в оп-
ределении, обладает следующими свойствами:
1+. Рефлексивностью, А91А: A=IkAIn, где Ik й 1п — единичные
матрицы &-го и /г-го порядка соответственно.
2+. Симметричностью, A9tB=>B9lA:A = C-lBD-1, так как квад-
ратные матрицы С и D обратимы.
3+. Транзитивностью, A9tB&iB9tE=^A9tE:
Заменяя в равенстве Е=СВВ матрицу В на CAD, получаем,
что Е=(СС) A (DB).
Тем самым 91 — отношение эквивалентности. □
Обозначение: Л~В (читается: А эквивалентна В),
Из теоремы предыдущего пункта вытекает, что две матрицы
одного и того же линейного отображения относительно разных
пар базисов эквивалентны:
А(е\ f')=Q-iA(ey f)S. (4)
Верно и в известном смысле обратное утверждение.
ТЕОРЕМА 4. Усл. Матрицы А и B^PkXn и эквивалентны.
Линейные пространства V(dimP V=n) и №(dimP W=k) произ-
вольны.
** 67

Утв. Существуют базисы е и е' в V и f и f в W п линейное
отображение s4>: V-+W, такие, что
' А-А(е, /), B=A(e',f'). .
Доказательство. Выберем в пространствах V и W бази-
сы е и f соответственно. Построим линейное отображение
считая, как и в лекции 8 (см. доказательство сюръективности в
теореме 2), что А (е, f) =A.
По условию существуют невырожденные квадратные матрицы
С и D, такие, что B = CAD.
Построим новую пару базисов е' и /':
e'-eS, r=fQ.
выбирая в качестве матриц перехода 5=Д Q = C~l. Так как за-
дание пары базисов (в V и W) однозначно определяют матрицу
линейного отображения s&, то
KB = Q-*A(e,f)S-A(er, Г),
(с-м. формулу (4)). П
ТЕОРЕМА 5. Утв. Матрицы А и В эквивалентны в том и
только том случае, если они имеют одинаковые размеры и рав-
ные ранги.
Доказательство. (=ф«) Если Л~В, то B = CAD. Так как
матрицы С и D невырождены, то их ранги совпадает с их поряд-
ками и согласно следствию из пункта 3° § 2 (лекция 8)
rang fi=rang i4D=rangi4.
(^=) Пусть-Л и B^Pkxn и
rang A = rang В=г. (5)
Известно, что при прмощи конечного чцсла основных: элементар-
ных преобразований матрицу А, ранг которой равен г, можно при-
вести к следующему виду:
С л
0 *'
0
L
о •'
0
' J
причем каждое такое преобразование матрицы равносильно ум-
ножению ее на невырожденную матрицу (матрицу одного из ос-
новных элементарных преобразований) слева или справа
Ir = Cm...CxADl...Dq.
68

В силу условия (5) то же справедливо и для матрицы В:
Ir = Ei...ElBfil...Fs.
Полученные равенства можно записать короче: Ir^-A, Ir~B*
Следовательно, Л~ В. О
5°. Каноническая пара базисов.
ТЕОРЕМА 6. Усл. Ранг линейного отображения зФ: V-+W ра~
вен г; dim V=n, dim W=k.
Утв. Существуют базисы е в V и / в Wy относительно которых
'M*,f) =
( р
I7- °
По**?
[ п
г
0
)
А.
(6)
Доказательство. В каждом из пространств V и W
есть линейные подпространства, естественно связанные с задан-
ным линейным отображением зФ\ V-+W. Это kers&cV и im s&cz
czW. Разложим каждое из про-
странств V и W в прямую сумму
их подпространств
(рис. 23) так, что
y2 = ker^, W^imst
К= vt® v2
(для определенности будем счи-
тать, что ядро кег«я£ невырожде-
но). Если базисы е и f прост-
ранств V ъ W получены путем ,
объединения базисов их подпро-
странств V\> У2 и Wu W2 соответственно, то
Г\»£
L^j
\^'
Vi -
у*
[&ИГ
wt
W= W&Wz:
Рис. 23
A (erf) =
, г 1
\о\ О
В самом деле, векторы из W2 в разложении образов векторов
из V не участвуют (входят с нулевыми коэффициентами) — это.
объясняет наличие нулевых элементов в матрице снизу от гори-
зонтальной черты, а все векторы из V2 = ker^ переходят в Qw —•
это объясняет нулевые элементы справа от вертикального от-
резка.
69

Выбрав базис в У2 = кеГо#, занумеруем его так: ег+\,...,еп
(напомним, что dimker.5# = M—г) и достроим до базиса всего V:
»г+1,
. , еп.
Положим Vi = L(e\,..., ет) и рассмотрим сужение линейного ото-
бражения s4>: V-+W на V\\
Так как rang^i = rangs4> и dim Vi = dim Ц7Ь то .s^i: Vi-^Wi
является изоморфизмом.. Всякий изоморфизм переводит линейно
независимую систему векторов в линейно независимую. Поэтому
система fi,...,fr, где fi==Aeiy t=l,.,.,r, линейно независима.До-
полним ее до базиса W: fu ...,/г, /г+ь ... , /Л. Тогда
Л/VJ =
/ Я
КО
|0'-7
1 - л
^
Г
0
так как
<А(е{)
-{
г;
Я. П
Определение. Пара базисов е и /, относительно которой
матрица Л(е, /) линейного отображения s&: V-+W имеет вид (6),
называется канонической парЪй базисов для $&.
6°. Матрица линейного оператора. В случае, если V=W, т. е.
зФ: V-+V — линейный оператор, естественно ограничиваться рас-
смотрением только одного базиса (вместо пары базисов).
Пусть ё= (ех... еп) — базис в V. Тогда
tAei = SjUafc,, г= 1, ... , п.
Определение 1. Матрица
[а} ... а\ ~|
называется матрицей
зиса е.
Если e' = &S — другой базис V, то
A(e')=S~lA(e)S
линейного оператора s& относительно ба-
(7)
{равенство (7) доказывается тем же методом, что и теорема 3
пункта 3°).
Определение 2. Матрицы А и Л'еРпХп называются по-
добными, если существует невырожденная матрица S, для которой
70

Тем самым матрицы линейного оператора относительно раз-
личных базисов подобны.
Свойства подобных матриц А и А'
1+. Для любого линейного "пространства V, dim V=п, найдутся
зФ^9?(У, V) и базисы е и е' в V, для которых А = А(е),
А' = А(е').
2+. deM = deM'.
Доказательств о. det A' = det(S~lAS) =det A. D
3+. det (Л—tI)=det(A'—tl).
Доказательство. Из равенства A'=S~lAS вытекает, что
для любого t
A'—tI=S-*(A—tI)S.n
Так как матрицы линейного оператора относительно разных
базисов подобны, то корректны следующие определения.
Определение 3. Определителем линейного оператора бФ
называется detA(e).
Обозначение: detJ^.
Определение 4. Характеристическим многочленом линей-
ного оператора s& называется det(«s^—tJ), где 3f :V-*V — тож-
дественный оператор,
Утверждение, det (^ — 1У) = (—1)п1п+ (— I)"-1 tr^^-Ч ... +1
-fdetj^.
Определение 5. Уравнение
det(^—^) = 0
называется характеристическим уравнением для линейного опера-
тора s$>. ■ . ; . .
ЛЕКЦИЯ 10
§ 4. ИНВАРИАНТНЫЕ ПОДПРОСТРАНСТВА
0°. Определение и примеры. Пусть V — линейное пространство
над полем Ри^: V-+V — линейный оператор.
Определение. Подпространство W из V называется инва-
риантным относительно линейного оператора s&> если для любого*
вектора х из W зФх также лежит в W, т. е. множество
a(W)={stx\xeW)
лежит в W:st(W)<=W. '
Пример 0. Подпространства {Qv}, V — тривиальные инва-
риантные подпространства для любого s&^£?(V,. V).
Пример 1. Для любого s4-^&{V, V) его ядро kers& и его
образ imj^ являются инвариантными подпространствами.
Задача. Доказать?, что если Wx и W2 — инвариантные подпро-
странства относительно действия s£, то сумма W\ + W2 и пересе-
чение Wi{]W2 также являются инвариантными цодпространствами
относительно s&.
71

Пример 2. Пусть подпространство WczV инвариантно отно-
сительно si. Выберем в W базис еь...,бь и дополним его до ба-
зиса всего пространства V е= (е\...ekek+\ ...en). Тогда
А(е) =
( к
0
А*
Аз
Пример 3. Пусть
V=QV\Wu
причем каждое подпространство Wi, i=l,...,q, инвариантно от^
носительно si. Если базис е пространства V получен путем объ-
единения базисов слагающих его подпространств Wi, то
'*(е) =
А2
0
*•
0
1
Z3
j
1°. Собственные векторы и собственные значения. Пусть V —
линейное пространство над полем Р и ,s&^2?(V, V).
Определение. Ненулевой вектор х из V называется собст-
венным вектором линейного оператора si, если найдется ЯеР,
для которого
six=Xx;
Я называется собственным значением линейного оператора si (от-
вечающим собственному вектору *).
Пример. Собственным вектором оператора дифференциро-
вания
dt
М„-+Мп
является любой многочлен нулевой степени; соответствующее соб-
ственное значение равно нулю.
ТЕОРЕМА 1. Утв. Система собственных векторов линейного
оператора si, отвечающих попарно различным собственным значе-
ниям, линейно независима.
Доказательство. Пусть Яь.-.Д? — попарно различные
собственные значения (А,¥=Я/, 1Ф}) линейного оператора si и
Х\,..*,хд — соответствующие им собственные векторы:
stXi=liXi, i=l,...,q.
72

Доказательство сформулированного утверждения будем вести ин-
дукцией по числу q собственных векторов.
1. Если 9= 1, то Х\Ф&у по определению. *
2. Предположим, что для любого m<q сисуема векторов
Х\>.. • ,Хт линейно- независима.
3. Покажем, что система векторов x\,...,xg также является
линейно независимой.
Предположим противное: существует нетривиальная линейная
комбинация
<zi*i+ ... +>agxq = Qv. (1)
Будем считать для определенности, что сн^О.
Под действием линейного оператора «я£ равенство (1) перехо-
дит в следующее:
Ш^1Х\+ . . . + Q,qkqXq — Qv (2)
Умножая равенство (1) на Хд и вычитая результат из равенства
(2), получим, что
Hi (Arl—kq)X\+ . . . + Щ~\ (А,<7-1—kq)Xq-\ = Qv
Данная линейная комбинация векторов х\,..., хд-х нетриви-
альна, так как коэффициент при х\ cti(Xi — Хд)Ф0.
Это противоречит предположению о том, что система собствен-
ных векторов x\,...fxmt где m<q, линейно независима. □
СЛЕДСТВИЕ. Утв. Число различных собственных значений
линейного оператора si>: V-+V не превосходит размерности К.
Приведем еще одно простое, но полезное свойство собственных
значений и собственных векторов линейного оператора..
Утверждение. Если К — собственное значение оператора s£, то
№ является собственным значением линейного оператора sP (с
тем же собственным вектором).
Доказательство. Действуя на обе части равенства
St>X — \X\
оператором s£, получаем, что '
s&2x=s£(stx)=st(Xx)=Xs£x='k2x.n ^
2°. Характеристический многочлен. Пусть V — линейное про-
странство над полем Р и s&^3?(V, V). Напомним
Определение 1. Характеристическим многочленом линей-
ного оператора зФ называется %(t)=det(M—1&), где f&P.
Пусть е — базис V и А (е) = (а*/). Тогда
%{t) = det(A(e)— */)==
или
a}— t ... оеД
а" ... а„~ t
x(0-SJLdY*<*.
73

Так как %(t) не зависит от выбора базиса пространства V, то
этим же свойством обладают и его коэффициенты:
Yn=(—l)n, Yn-i=(— l)n-1(ai, + ....+ann),...,Yo=det(aI0-
Определение 2. Следом оператора $& называется число
trs4>, вычисляемое по правилу
trey£-=ZJLia£.
ТЕОРЕМА 2. Утв. X является собственным значением линей-
ного оператора $1< в том и только в том случае, когда X— корень
характеристического многочлена, принадлежащий полю Р:
Доказательство. (=^) Пусть X — собственное значение
линейного оператора $$>. Тогда найдется вектор хфв и такой, что
*$&х = Хх. Переписав последнее соотношение в несколько ином виде
(^—ХУ)х=в,
можно утверждать, что ядро оператора s4>—Х& нетривиально:
кег(^—ХУ)ф{в}
и, значит,
defects—Х&)>0.
Так как
defects—ЯД) +rang(j£—XSf) = dim V,
,то в силу последнего неравенства заключаем, что
rang(s&—X3f) <dim V.
Это означает, что det(«s#—ХЭ) =0.
Следовательно, %(Х)=0У и X является корнем характеристиче-
ского многочлена оператора s&.
(<=) Чтобы доказать вторую часть утверждения теоремы, нуж-
но повторить проведенные выше рассуждения, но в обратном по-
рядке. □
3°. Способ построения собственного вектора. Пусть V — линей-
ное пространство над полем Р и s&^3?(V, V).
Покажем, как по известному собственному значению X опера-
тора s£ найти соответствующий ему собственный вектор.
Если е — базис V, то равенство s£x=Xx равносильно матрич-
ному уравнению
А{е)х(е)=Хх(е), (3)
где координатный столбец х(е) = (g1.. .£,п)т составлен из коорди-
нат искомого вектора х в базисе е:
x=2nk=ilkek = ex(e).
Таким образом, задача построения собственного вектора будет
решена, если будет найдено нетривиальное решение системы (3).
74

Эта система — более удобно записать ее несколько иначе: . >
(A(e)—XI)x(e)=Ot=EPnxi
— имеет ненулевое решение, так как в силу теоремы 2
det(A(e)— XI) =0.
Пусть х(е)^Рпх\ — нетривиальное решение системы (3). Тогда
ненулевой вектор
х = ех(е)
является собственным вектором линейного оператора $$> с собст-
венным значением Я.
4°. Собственное подпространство. Пусть, V — линейное прост*
ранство над полем Р, st>^2?(V, V) и Я — собственное значение
оператора зФ.
Утверждение. Множество
является линейным подпространством V, инвариантным относи-
тельно действия линейного оператора *я£.
Доказательство. Вычислим действие оператора s& на
линейную комбинацию векторов из W(xy
<s4> {ах + Pf/) = as4>x + fisty=оХх + $ly=Я (ах+$у).
Тем самым W(k) — подпространство V.
Инвариантность W&) очевидна. D
Определение. W(X) называется собственным подпростран-
ством линейного оператора s4>.
ТЕОРЕМА 3. Усл. Я — корень характеристического много-
члена линейного оператора si (кратности k).
Утв. dim №(*)<&.
Доказательство. Пусть
dim №(„) = /.
Достроим базис fь. • •, ft подпространства W^ до базиса всего
пространства V:f\,..., ft, fi+ь ..., fn.
Матрица линейного оператора s4> относительно базиса f имеет
следующий вид:
i 1
в
О Ц
О | с
i
i
A(f) =
75

а оператору s&—tSf отвечает матрица
A(f) -tl =
0 \c*u-i
(здесь In-i — единичная матрица порядка n—l).
Характеристический многочлен оператора «я£ можно записать
так:
x(0 = (*-0W), (4)
i*e<p(0=det(C—tin-,).
С другой стороны, из того, что % — корень многочлена %(t)
кратности k, вытекает разложение
< X(<H(*-0**W. ; (5)
причем -ф(Я)#0.
Сравнивая формулы. (4) и (5) и замечая, что многочлену
<р(£) обращаться в нуль при £=Я не запрещено, из единственности
канонического разложения многочлена %(t) заключаем,- что / не
может быть больше k. □
Приводимый ниже пример показывает, что I может быть
меньше k.
Пример. Рассмотрим, как действует в пространстве Мп
многочленов степени не выше. п(п>-1) оператор дифференциро-
вания
d
г>=
dt
Мп-*М„
Базисные векторы
**
оператор 2) преобразует по правилу
2>е0=0, 3)ет=ет-х, т=1,
Поэтому
[О 1
О 1
п,
D{e) =
О
О 1
О
Отсюда получаем, что
det(D{e)— tl) = (— 1) n+i^+i.
Тем самым /=0 является корнем характеристического многочле-
76

на оператора &) кратности n+l(k = n+l). В то же время
W(o)=M0 и, значит,
/=dimlF(0)=l.
Таким образом, /=1<п+1 = &.
5°. Инвариантные подпространства минимальной размерности
в комплексном и в вещественном пространствах.
А. Комплексный случай. Пусть V — комплексное линейное
пространство. Тогда у любого s£^2?(y, V) существует инвари-
антное подпространство размерности 1.
Это вытекает из того, что у линейного оператора «я£ в ком-
плексном пространстве всегда есть собственное значение (корень
характеристического многочлена оператора) Я, а значит, и соот-
ветствующий ему собственный вектор x(s£x=Xx). Тогда линейная
оболочка L(x), порожденная этим вектором* является одномер-
ным инвариантным подпространством относительно действия s4>.
Б. Вещественный случай.
ТЕОРЕМА 4. Уел* V — вещественное линейное пространство,
«s# : У-^У — произвольный линейный оператор.
Утв. Существует инвариантное относительно действия линей-
ного оператора s& подпространство, размерность которого не пре-
вышает двух.
Доказательство. 1. У характеристического многочлена
линейного оператора s4- есть вещественный корень А,:%(Я)=0.
В силу теоремы 2 Я являетей собственным значением оператора
зФ. Как и в комплексном случае, линейная оболочка L(x), по-
рожденная соответствующим X собственным вектором х, являет-
ся одномерным инвариантным подпространством.
2..Пусть l=a+i$, $Ф0, — комплексный корень характеристи-
ческого многочлена %{t). Покажем, что у оператора s& существу-,
ет двумерное инвариантное подпространство.
- Пусть е — базис V и А=А(е) — матрица линейного операто-
ра s£ относительно этого базиса. Следуя способу построения соб-
ственного вектора, предложенному в пункте 3°, рассмотрим систе-
му уравнений
(Л-(а+ф)/)а + /т,)=0, (6)
где О, I, rjeRnxi- Эта система имеет нетривиальное решение
£+й), так как
det(A— (a+tp)7)=x(a+tp)=0.
Разделяя в соотношении (6) действительную и мнимую части,
получим, что
Al— all + р/г) = О, Ац—р/£—а/г) = О
или
Л§=<о£— рт], Лг)=р£+1аг). (7)
Прежде чем продолжить доказательство теоремы, сделаем
два важных замечания.
77

Замечание 1. Из соотношений (7) вытекает, что если
1 + [цфО, то и %фО, и -цФО. Предположим,, например, что g = GL
Тогда из первого равенства (7) получаем, что —Рт] = 0, а в силу
условия $фО и г\ = 0.
Замечание 2. Комплексно сопряженный корень Х = а—ф
многочлена %(t) новых решений не приносит: из системы
(i4-(a-tp)/)(C—fe)=0,
описанным выше приемом получаем равенства
Л£ = а£— ре, Ле = Р£ + ае„
отличающиеся от соотношений (7) только обозначениями.
По ненулевым столбцам
^(б'.-.б»)1 и л=(п!--лп>т
построим ненулевые векторы
x = ^=2Li£4 и у = ел=22-1ЛЧ-
Умножая матричные равенства (7) слева на строку е=(^...епЬ
с учетом формулы
(ei...en)A=(&ei...sten)
и равенств
2LnAeklk - ^ (25UE4) = *Лх*
Ъпк=хЛекЧк = ^ (2JLi44) = ^И
получаем два векторных соотношения
«я£х=ои—ру, ,s#y=px + ay..
Рассмотрим линейную оболочку L(*> у). Она обладает следу-
ющими свойствами:
1+. L(x, у) инвариантна относительно действия М:
Л (\ix + vy) = ц<Ах + v<Ay =|i (a*—Ру)+ v (f я + ay) =
= (ац + pv) x + (av— Р|л> у е L (я, y).
2+. dim L(jc,y)=-2.
Равенство |iAr + vy=9 под действием линейного оператора s£
переходит в
(a|i + Pv)x+ (av—p|i)y = 8.
Исключая из этих двух соотношений вектор у, получаем, что»
[— (av—P|i) ji + v (ap,+ Pv) ] x=Q
или p(|i2+v2)* = e.
Так как p#0 и хфд, то |i2 + v2 = 0 и, значит, |i = v = 0.
Следовательно, векторы х и у линейно независимы. Q
78

Замечание. Если у характеристического многочлена нет
вещественных корней, то минимальная (отличная от нуля) раз-
мерность инвариантного подпространства равна двум.
ЛЕКЦИЯ И
.§ 5. КАНОНИЧЕСКИЙ ВИД МАТРИЦЫ ЛИНЕЙНОГО ОПЕРАТОРА
0°. Многочлен от линейного оператора. Расширим понятие много-
члена в следующих двух направлениях.
1. Многочлен от оператора. Пусть V — линейное пространство
лад полем Р, st> : V-+V — линейный оператор и
Q(0 =ia0+>ai*+ ... + a***e=P [t]
некоторый многочлей.
Определение 1. Многочленом от линейного оператора $&
называется линейный оператор 3b\ V-+V, определяемый формулой
&=ъ<&+щя£> + ... + aks£k
(здесь 3f : V-+V — тождественный оператор).
Обозначение: <%— Q (<&).
ЛЕММА. Усл. Q(0 = 2Loa^' и R (0==2/1оР/— многочлены,
операторы^, 3&<==2?(V, V) и «s&#=Jta£.
Утв. Q(st)R(33)=R(<%>)Q(&).
Доказательство. Из условия s£&=&s& легко вытекает,
что
st>&i=&W (1)
для любых i и /eN.
Построим многочлены от линейных операторов «^ и ^:
^ (Л) = 2-LoM'* = Ро^ + М + • • • + Pm^m.
Перемножив их
Q (tf) R (Л) = StoSy-eaiPy^*7,
/?(*)Q(o«) = S/lLoS*eoP^eU/f
•с учетом формулы (1) получим требуемое равенство. П
Определение 2. Линейный оператор s£o'-V->V, удовлет-
воряющий равенству
Q(rfo)=tf,
где 0^3?(V, V) — нулевой оператор, называется корнем много-
члена от линейного оператора.
Iх. Многочлен от матрицы. Пусть Ле
Q(t) =a0+<zi^+ ... +a^eP[/]
-— некоторый многочлен.
79

Определение Г. Многочленом от матрицы А называется
матрица В^РПхп, определяемая формулой
В=и01+щА+ ... +ukAk.
Обозначение: B = Q(A).
2. Многочлен с матричными коэффициентами.
Пусть Л0, Аи ..., Ake=PnXn (АнФО), fe=P.
Определение 3. Матрицу
F (0 = А0 + Axt-v ... + Л^ = iLoAt'
назовем многочленом с матричными коэффициентами (матричный
многочлен).
Определение 4. Будем говорить, что два матричных мно-
гочлена
F(t)**2ti=oAftl и G(t) = 2lLfltt'
равны, F(t)=G(t)9 если k=m и А0=В0,..., Л* = £*.
1°. Теорема Гамильтона — Кэли.
ТЕОРЕМА 1. Утв. Линейный оператор является корнем своего
характеристического многочлена.
Доказательство. Пусть
%(t)=det(st—&) -ao+ai*+ ... + ап-1*п~1 +(—l)ntn
— характеристический многочлен линейного оператора sf>: V-»-V.
Нужно показать, что %(А)=0.
Обозначим через Л=(а^) матрицу линейного оператора s£
относительно (какого-нибудь) базиса е пространства V и постро-
им для матрицы
A-tl-l \ )
присоединенную матрицу ф
B(t)A
\Aln(t)...Ann(t)J
Ее элементами являются алгебраические дополнения матрицы
А—tl, причем алгебраическое дополнение Au(f) элемента, распо-
ложенного в матрице Л—tl на пересечении i'-й строки и /-го столб-
ца, в матрице B(t) располагается в'позиции (/, i).
Гамильтон (Hamilton) Уильям Роуан (4.8.1805—2.9.1865) — ирландский ма-
тематик, член-корреспондент Петербургской АН (с 1837 года); Кэли (Cayley)
Артур (16.8.1821—26.1.1895) — английский математик, член Петербургской АН
(с 1870 года).
80 • '

Каждое алгебраическое дополнение Л,-/(0 представляет собой
многочлен, степень которого не выше п—1, что позволяет запи-
сать матрицу B(t) в следующем виде:
B{t)=Co+dt+...+Cn-it»-1.
Элементы матриц
Cfte=PnXn, *=0, 1,...,л — 1,
суть коэффициенты при k-x степенях многочленов Ац((). Таким
образом, матрица B(t) — многочлен от / с матричными коэффи-
циентами.
Согласно свойствам присоединенных'матриц
(A—tI)B{t) =det {A—tl)l,
или, подробнее,
(A-tl) (С0+ Cit+ ... + Cn-i^-1) =
= (oo+aif+ ... +Un-itn~l + (— l)ntn)I.
Производя необходимые перемножения и приравнивая коэф-
фициенты при одинаковых степенях t, получим матричные равен-
ства:
АС0 =сс0/ , ' [0]
АСг -С0 =04/ , [1]
АС2 -Сг = а2/ , [2]
4СЯ_1 — Crt_2 = art^i/ # [/г—1]
— Сл_1==(—1)«/. ЦЯ]
Умножая [&]-е равенство слева на матрицу Ак, Jfe=0, lf...,/i, и
складывая результаты, приходим к соотношению
O = ao/+aii4+,...+an-i^^1+(— 1)М*=хИ).
Равенство %(«я£) =£? следует из того, что
rangх(<я£) = rangx(st). D
Пример. Пусть V= R2,
Многочлен
\—t—I
%(t).
1 — f
= /2 + l
81

не имеет вещественных корней. Однако
= (? ~o)(?~i)^(o ?) = (_о —?) + (о ?)-(о С)-
2°. Расщепление линейного оператора. Предположим, что ха-
рактеристический многочлен x(t) линейного оператора s£>\V-+V
разложен на взаимнопростые множители:
x(0-xi(')-..»(<).
где
НОД(Хт, х<) = Ь тф1.
Справедливо следующее утверждение.
ТЕОРЕМА 2. Утв. В пространстве V можно указать подпрост-
ранства V\,...,Vk, инвариантные относительно действия линейно-
го оператора s& и такие, что
Доказательство будем вести индукцией по числу взаим-
нопростых сомножителей характеристического многочлена.
А. Проверим справедливость сформулированного утверждения
при & = 2.
Пусть Х(0 =Xi(0X2(0, где НОД(Хь ») = 1.
Обозначим через V\ и V2 ядра линейных операторов xi(st) и
Хг(^) соответственно;
V/«kerx/(J*), /=1, 2.
Покажем, что У/(/=1, 2)' инвариантно относительно линейного
оператора $t>.
Пусть x^Vj, т. е. Xj(«^)*=9- Тогда у=^Фх также лежит в Vf.
1С/(^)У = Х/(^)(^^) = ^Х/(^)^ = ^9=в.
Теперь на V/(/=l, 2) можно ввести индуцированный линейный
оператор
<Af=<A\vf:Vf-+Vf.
(Напомним определение индуцированного оператора: JL\v. оп-
ределен только на векторах из Vj и Л\ч.х~Лх для любого век-
тора из Vj, т. е. для векторов из Vf Л = Л\у--) Ясно, что для
векторов из Vj выполняется равенство
Х/(^)* = Х/(^/)*-
Так как х/(«я£)х — 0-для любого вектора х из Vj (по определению
Vj)> то to(«s*j)=tfj.rae *?/: ^г^У/ — нулевой оператор.
Покажем теперь, что V=Vi®V2-
Я2

Ввиду того, что многочлены %i и Х2 взаимно просты, существу-
ют многочлены u(t) и v (t), такие, что
Xi(t)u(t)+X2(t)v(t) = L
Переходя к многочленам от линейных операторов, получаем, чта
Xi(st)u(st)+&(j*)v(*)=3r. (2)
Поэтому каждый вектор х из V допускает представление
x = xi+x2, где
xi=%2№)v(a)xf x2=%i(st)u(tA)x.
Вычислим ntj(si>)xj, /= 1, 2:
Xi (<А) хг - Хг (Л) %2(o£)v{<A)x =
= t{Jl)v{Jl)x = v(Jl)X{^)x = v{<A)Qx = b
(здесь мы сначала воспользовались леммой пункта 0°, а затем
теоремой 1),
Ч (<Л) х2 = Х2 (о€) \ {Л) и {Л) х = и {Л) X (Л) х = 6.
Полученные равенства xi(^)*i = 9 и Х2(«яО*2=6 означают,, что»
*ieVi, a X2gV2. Тем самым V=Vi+V2-
Остается показать, что 1ЛП^2—{6}-
Пусть x^Vi(]V2. Тогда
Отсюда, пользуясь формулой J1), получаем, что
х = &х = Х1(Л)и(Л)х + Х2(Л)и(Л)х^
= и(Л)Ъг(Л)х + и(Л)К2(Л)х = Ь.
Значит, V= V!0V2.
Б. Предположим, что утверждение теоремы справедливо при
X(0~Xi(0-••»(<). НОД(Хт, Х.) = Ь m#v,
подпространства Vi,...,Vj инвариантны относительно действия
линейного оператора,
Xf{<A\v.) = Oh /=1, ...,/,
и V=Vi®...®Vi.
В. Покажем, что тогда утверждение теоремы справедливо к
при £ = /+1.
Пусть x(0=Xi(0-- -Xi(t)xi+i(t)> НОД(хт, х*) = Ь тфщ.
Многочлены xi==Xi---X^ и Й2 = Хч-1 взаимно просты. Поэтому со-
гласно доказанному в части А найдутся инвариантные относитель-
83

но действия s& подпространства Р^ и V2, причем такие, что
%(Ot\f) = Oi, i=l, 2,
V=Vx®V2. (3)
Так как xi = Xi • • • Х'> то в силу предположения
Б Pi = Fi©... @Vi, где V\,...,Vi инвариантны относительно
индуцированного оператора <АХ — -А\^ или, что то же самое, от-
носительно Ж. Поэтому, полагая V2=Vi+i, из формулы (3) полу-
чаем требуемое разложение
Пример. Рассмотрим оператор проектирования (рис. 24)
£Р: R3-HR3, который каждому вектору х из R3 ставит в соответст-
вие его проекцию х2 на R2: &>х=х2>
Ясно, что R3=R1©R2 и
Вычислим характеристические
многочлены всех трех операторов
x(t)=-t{t-i)\ xx(o =
- .Рис.24 = —f, 5С2(0 = (^—I)2-
Й, далее,
Xi (^)=—Л ker^=R*,
Х2 (**) = (^-^)2, ker (^-^)2 = R2.
3°. Треугольный вид матрицы линейного оператора в комплекс-
ном пространстве. Пусть V — n-мерное комплексное пространртво
m^<=&(V, V).
ТЕОРЕМА 3, Утв. В комплексном пространстве V существует
инвариантное относительно оператора «s£ подпространство W раз-
мерности'л—1.
Доказательство. Пусть Я — собственное значение ли-
нейного оператора s£. Тогда
rang(«s#—13) <п— 1.
Положим im (<&—№) = W.
Ясно, что dim W<cn—L
Рассмотрим подпространство WczV, подчиненное требованиям:
1. W'czW, 2. dimW=n—1, а в остальном произвольное, и пока-
жем, что W инвариантно относительно s£.
&4

По определению W для всякого вектора х из^ V выполняется
соотношение
(j*— №)x={/€=W. ' (4)
Возьмем х из W. Тогда из формулы (4) получаем, что
j&x = hx + y^W (первое слагаемое Хх лежит в W, так как W —
подпространство, а второе у — потому, что W'czW). □
Определение. Будем говорить, что матрица А = (am7) име-
♦ет треугольный вид, если <(W=0 при. m</ (/ — номер строки):
ТЕОРЕМА 4. Утв. В комплексном пространстве существует ба-
зис, относительно которого матрица заданного линейного опера-
тора имеет треугольный вид.
Доказательство. Согласно теореме 3 в пространстве У
найдется подпространство' V7*-1 размерности п—1, инвариантное
относительно st>.
Рассмотрим на V*-i индуцированный оператор
^„-1=^1^-1 : Vn~l -+Vn~l.
По теореме 3 в Vn~~l найдется подпространство Vn~2 размерности
л—2, инвариантное относительно зФп-\ (или, что то же самое, от-
носительно st>)
Рассмотрим на V71"2 индуцированный оператор
ьДп—Ъ = *Ап— 1 I vn—2 == *Л | vn—2
и вновь применим теорему 3.
Продолжая рассуждать подобным образом, после конечного
числа шагов получим цепочку вложенных друг в друга подпро-
странств:
VtFc... <=Vn-*czVn = V,
где dim Vk=k, k=l, ...,n. {
Базис в пространстве V выберем так: (е\) — базис V1) (е^) —
«базис V2; (ехе2...ек) — базис Vk, 3<:k<n.
По построению
&ек=*ш1е1+...+аькек, k=l,...,n.
Поэтому
CCf cCz - • • * ОС1л
Замечание. На главной диагонали матрицы А(е), полу-
ченной в ходе доказательства теоремы 4, располагаются собст-
венные значения линейного оператора st.
85

ЛЕКЦИЯ 12
4°. Нильпотентный оператор. Пусть V — линейное простран-
ство над полем Р и s£^L(V, V).
Определение 1. Линейный оператор $& называется ниль-
потентным, если s4><i=0 для некоторого q^N.
Определение Г. Матрица ЛеРпХ71 называется нильпо-
тентной, если Aq=0 для некоторого ^/eN.
П pji м е р 1. Оператор дифференцирования
ф = ^:Мп.
■Мп
является нильпотентным, так как 2)п+1—0.
Определение 2. Квадратная матрица вида
Jk(%) =
Я 1 0 .
ОЯ 1 .
0 ОЯ .
000 .
0 00.
..00
..00
..00
. Я 1
. 0 Я
называется жордановой клеткой размерности k.
Пример 2. Жорданова клетка /а>(0) является нильпотентной
^матрицей, так как
(/*(0))* = О.
Пример 2'. Матрица
'•МО)
(1)
\№j
нильпотентна, так как Jk = Oy где k— max kf.
Пример 3. Пусть V — .комплексное пространство и линей-
ный оператор st>: V-+V имеет единственное собственное, значение
Я = 0. Тогда s4> является нильпотентным оператором.
В самом деле, по теореме- 4 из -пункта 3° существует базис,
относительно которого матрица ,оператора имеет-треугольный вид.
В силу замечания того же пункта все элементы на главной диаго-
Жордан (Jordan) Мари Эдмон Камиль (5.1.1838—21.1.1922) — француз-
ский математик, член-корреспондент Петербургской АН (с 1895 года).
86

пали этой матрицы равн>1 нулю.. Нетрудно видеть, что
{А{е)У = 0:
и 0
, *'Се) =
о о г—|
>' • t
Верно и обратное: если $Ф — нильпотентный оператор в ком-
плексном пространстве, то все его собственные значения равны
нулю. В самом деле, если х — собственный вектор оператора s&
и К — соответствующее ему собственное значение, то
«С другой. стороны, согласно определению 1 stq=Q и, значит,
Х==0 (так как хф§\.
ТЕОРЕМА 5. Усл. s& : V-+V — нильпотентный оператор.
Утв. В пространстве V существует базис Л, относительно кото-
рого матрица оператора A(h) цмеет вид (1).
Доказательство. Так как оператор s& нильпотентен, то
существует такое meN, что з£т=(У, но Лт фОу если т'<т.
Рассмотрим цепочку операторов
& = Л\ Л=Л\ Л\ ..., Лт~\ Лт^О.
Линейные подпространства l// = kerj#{, /=0, 1,...,т, обладают
следующими свойствами:
1+. Vj-iczVj для любого /= 1,. ..,/п.
В самом деле, если x^Vj-u т. е. ^-1х=в, то x<=Vj, так как
• Л)х = Л (<Af-lx) = ЛЬ = 6.
2+. Vf инвариантно относительно s4>.
Пусть x^Vj, т. е. «s^/jc=8. Из равенства $i>j-l($t>x) =8 вытека-
ет, что
Мх<ее V,-icV, (^ (V,) <= Vj).
Обратимся к цепочке вложенных друг в друга подпространств
{6}- У0с= 1Л<= V2c= ... c=Vm^1c=Vm= V.
Я/аг Л. Рассмотрим .тройку Vm-2c:Vm-ic:Vm.
Из соотношений £$>т=Оу Жт-хФ0 вытекает, что Ут-\ФУт>
Значит, в разложении
Vm = Vm-\ Ф V'm-l,
где через V'm~i обозначено подпространство, дополнительное к
Vm-i в Vm> слагаемые Vm-i и Vm_i нетривиальны.
Пусть (е{... es) — базис Wi.
87

Согласно свойству 1+ векторы st>e\,..., s&es лежат в Vm-x- По-
кажем, что они линейно независимы и
•Lji%Aeu...9steg)()Vmr*={e}.
Пусть ais£ei+ ... +<zs^es = aG
Докажем, что сн= ... =а5—0 и а = 6.
Так как l/m~2=ker^m-2, to ^™-2а=е.
Это означает, что stm~l(a\ei + ... +ases) = 6, или, по-иному,
ai^i+ ... +a5^eVw-i.
Так как векторы е\,..., es лежат в V'm-x, то
а\е{+ ... +a^GWi.
Из того, что Vrn-inVr/m-i = {8}, получаем a^i+...+а^=б.
Отсюда в силу линейной независимости системы (е\... es) заклю-
чаем, что ai= ... =<а5=0 и, значит, арб.
Отметим, что система векторов 2л
Vm-x
Vm-X
ег ... es
линейно независима: подсистемы (е\...е8) и (Ле\...s£es) линей-
но независимы и лежат соответственно в подпространствах V'm-\
и Vm-i, слагающих V:
Vn-x®V'm-x = V. .
1 Шаг Б. Рассмотрим тройку Vm~z<^Vmr-2<^Vm-i-
В силу того, что векторы st>e\,..., stes лежат в Vm-u но не со-
держатся в Vm-2, получаем, что dim Vm-2<6\m Vm^\ и Ут-2ФУт-х*
Значит, Vm-i допускает разложение вида
где через Vfm-2 обозначено подпространство, дополнительное к
Vm-2 в Vm-u причем такое, которое содержит линейно независи-
мую систему векторов s£e\,..., Mes.
Дополним, если необходимо, эту систему векторов до базиса
в V'm-2- Получим (st>ex... st>eses+i ...er) — базис V'™^.
Согласно свойству 1+ векторы
лежат в Vm_2. Покажем, что они линейно независимы и
L(<A%, ..., t42eS9 tAes+u ..., <Aer)()Vm_3 = {6}.
Пусть ^гЛ2ех + ... + kt/£4 + Ps+i^s+i + ... + $rJLer = 4g Vm^.
Докажем, что Pi= ... =рг = 0 и Ь = 6.
Так как Ут-3=кег«5^т~3, то ^т-3Ь = 6.
Это означает, что
88

Отсюда мы заключаем, что
§хзФех + ... +.p*s*e5+p,+i<?5+1+ ... +prereV2.
С другой стороны,
pi«s#ei+ ... +$ss6es+$s+ies+i+ ... +Рг^еУ/т-2
по построению.
Из того, что Vm-2nV'm-2={0}, получаем равенство
$1&е{+... +p^es+p5+ie5+i+... +Рг^г=е.
Отсюда в силу линейной независимости системы (st>e\,..., s&es,
es+\,...#er) заключаем, что pi=...=pr = 0 и, значит, & = 8.
Отметим, что система векторов 2 я 1
V'm-i\ ,ex ...es
Vm-2 iAe±..'. <Aes es+i,*..er
Vm-21 tA2et♦.. <А2е$Ле5+ \ ... <Aer
линейно независима: подсистемы (ev ..., es), (<Aev ..., <AeS9 es+u •••
..., er) и (<A2ev ..., JL\y JU*±u • ••» JUr) линейно независи-
мы и лежат соответственно в подпространствах V'm-u V'm-2 и
Vm-Ъ СЛагаЮЩИХ V: V= Vmr-2®V'mr*(BV'm~l.
Ясен следующий
Шаг В. Рассмотрим тройку Vm-4c: Vm-zCi Vm-2 и т. д.
Число этих шагов конечно по следующей причине. Проделав
очередной шаг (А, Б, В и т. д.), мы получаем линейно независи-
мую систему векторов (2л, 2в, 2я и т. д.),4 причем
2лс=2вс=25с=... .
Так как число векторов линейно независимой системы не пре-
восходит размерности объемлющего пространства (она конечна!),
то в предъявленной цепочке конечное число «звеньев»:
2лс=2Бс:25с:...с:2.
Последнее «звено» 2 является базисом- V.
Подведем итог наших построений: это линейно независимая
система 2 из л—dim V векторов:
\vm-2®vm_2=vmJ
\m=v0
*m—3
\
\e1...es
1 ЛЧ1...кЛ\
\
^s+l • • • er
itAes+t . .}.t/Ler
^Н-1 • • • **
,
\JLm-xe1... Am-lesJLm^2es+1... JLm-4r.. J
■
89

Укажем некоторые свойства векторов из приведенной таблицы^
1+. Каждый вектор из последней строки таблицы под действи-
ем оператора^ бФ переходит в нулевой вектор, т. е. в последней
строке расположены собственные векторы оператора s£ (напом-
ним, что все собственные значения нильпотентного оператора рав-
ны нулю).
2+. Занумеруем элементы произвольного столбца таблицы,
(пусть его номер равен а)
еа, s£eay <А2еау ... 9 Лк~хеа{<Akea = 0),
«
но в обратном порядке (снизу вверх):
hi=s£k-lea, h2=<&k-2ea,...,hk-\=st>ea, ft* = ea.
Тогда
а) система, {hx... hk) линейно независима,
P) sthi = B,stfi2=hl,....,sthk = hk-*i,
у) подпространство W=L(hi,...,hk) инвариантно относи-
тельно s&,
б) матрица индуцированного оператора s£\w относительно ба-
зиса (h\...hu) имеет вид/*(0).
Нумеруя векторы таблицы по столбцам (и снизу вверх в каж-
дом столбце), получаем базис h, относительно которого матрица
нильпотентного оператора s4> имеет вид (1). □
5°. Жорданова нормальная форма матрицы линейного опера-
тора. Пусть V — /г-мерЦое комплексное линейное пространство и.
ste=S?(V, V).
ЛЕММА. Усл. Я — единственное собственное значение линей-
ного оператора st>. . , ..
Утв. В пространстве V существует базис А, относительно кото-
рого матрица оператора s& имеет вид
A(h)
' О
Доказательство. Оператор &=зФ—№ нильпотентен.
Согласно теореме 5 из пункта 4° в пространстве найдется ба-
зис h такой, что матрица B(h) имеет вид (1). Отсюда и из ра-
венства
A(h)=B(h)+ll
следует утверждение леммы. □
ТЕОРЕМА 6. Усл. V — n-мерное линейное пространство,
s4>\V-+V — линейный оператор, характеристический многочлен
которого имеет вид
%(t) = (-i)4t-K)lt-.4t-h)lk>
где Л+ ... +lk = n, /7>l, %5ф\ш(1фт)*
90

Утв. В пространстве V существует базис А, такой, что
Л (А)-
|Ы
1 °
\j%_
1
О
лк\\
11)
квадратные матрицы A\f...,Ak имеют следующий вид:
л =
'•ММ
о
0 КМ.
где i\+ ... +im=li, i=l,...,k; iq>>l\ m = m(i).
Доказательство. Так как сомножители %i = {t—Л*)Ч
/=1, ... , А, взаимно простые, то, применяя теорему о расщепле-
нии из пункта 2°, получаем, что
где подпространства Vi, i= 1,..., k, инвариантны относительно st> и
Ъ(<Л\у£)=0£.
Индуцированный оператор JLi = JL\vi имеет ровно одно соб-
ственное значение Я,- (его характеристический многочлен равен
{—\)li(t—hi)1'). Согласно лемме в подпространстве Vt сущест-
вует базис к1, такой, что матрица оператора s4>i имее? вид
А=Л|(Л') =
fJtt(U)
О
0 'hmiM
где м+ ... + im=/,-, t=l,...,*.
Объединение /i = /i1U^2U • • • U^fe базисов Л1, h2,... ,hk есть иско-
мый базис пространства V. □

ЛЕКЦИЯ 13
Глава IV. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
§ 1. БИЛИНЕЙНЫЕ ФОРМЫ
Пусть V — линейное пространство над полем Р.
Определение 1. Билинейной формой, заданной на Vy на-
зывается отображение
38:VXV-+P,
такое» что для любых векторов х, у и z из V и любого аеР вы-
полняются соотношения:
1. 38{х+уу *)=$(*, z)+48(y, z),
2. &{ах, у)=а&(х,у),
3. 38(х, y+z)=&(xy y)+38{x, z),
4. Я{х, ау)=аЗё{х, у).
Замечание. Билинейная форма 38 (х9 у) линейна по каждо-
му аргументу.
Пример 1. Произведение двух линейных форм s&^3?(Vy P)
и^?е«2?(У, Р) является билинейной формой.
Пусть зФ : jcg^^^gP и 38 : ye=V~&(y)<==P.
Тогда st(x)38{y) — билинейная форма.
Определение 2. Билинейная форма 38 называется симмет-
ричной, если 38 (х, у) =38(у, х) для любых х и у из V.
Пример 2. Скалярное произведение в евклидовом простран-
стве является симметричной билинейной формой.
Определение 3. Билинейная форма 38 называется кососим-
метричной, «ели 38(у, х)=—38(х, у) для любых х и у из V.
Пусть е=(ег ... еп) — базис пространства V. Положим;
£(**/*/) =Р*/- 0>
Определение 4. Матрицей билинейной формы 38 (ху у),
в базисе е называется матрица
B(e) = (p*/)eP«xii.
Утверждение. Для любых х и у из V справедливо представле-
ние
38(ху у)=хЦе)В(е)у(е), ^ (2)
где х(е), у(е) — координатные столбцу векторов ху у соответст-
венно в базисе е.
Доказательство. Разложим векторы л: и у по базису е:
Положим
-w-(D. *(eHD
92

и вычислим 3§(х, у). Имеем <
Л (х, у) = <® (2»в1 &ек, 2»^ r\iej) = 2»/ши1 &4Я(ек,е,).
С учетом формулы (1) получаем, что
Л{х9у) = 2^^гМ^хЦе)В(е)у(е). П
Замечание. Билинейную форму <%(х, у) можно представить
и несколько по-иному:
Я(х,у)=уЧе)В1(е)х(е). (2')
ТЕОРЕМА 1. Усл. В^Рпхп — произвольная матрица и е —
произвольный базис пространства V.
Утв. Существует билинейная форма 3$: VxV-^P, у которой
В(е)=В.
Доказательство. Пусть 5=(р*/). Для произвольно взя-
тых векторов
х = Ц=х1*ек, У = 2^1^/
положим
Л(*|У) = 22§/в1е^рЛ/. (3)
Нетрудно показать, что 3$(х, у) — билинейная форма и
Я(*ъ *у)=Р*/- П
Определение 5. Формулу (3) (а также и формулу (2))
принято называть общим видом билинейной формы.
Утверждение. Билинейная форма 9Ь симметрична в том и толь-
ко в том случае, если матрица В (е) симметрична для любого ба*
зиса е.
Доказательство. (=^) Если билинейная форма J? сим-
метрична, то для любого базиса е=(е\ ... еп) имеем
Р*/=#(**, eft =&{eu ek) = р;*.
(^=) Если В(е)=Вт(е), то формулу (2') можно записать
в следующем виде:
Я(х,у)=Ут(е)В(е)х(е).
Меняя аргументы х и у местами, получаем, что
Л (у, х)=хЦе)В(е)у(е)=Я(х, у), □
Аналогично доказывается
Утверждение, Билинейная форма £8 является кососимметричной
в том и только в том случае, если матрица В{е) кососимметрич-
на, fiT(£)=—в (е) для любого базиса es
ТЕОРЕМА 2. Усл. е, e'=eS — базисы V.
Утв. B(e')=S*B(e)S.
93

Доказательство. Пользуясь формулой (2) для базисов е
и е', получаем, что
Хч\е)В(е)у(е)=х1(е') В(е')у(е')
для любых х и у из V.
Так как х(е) =Sx(e'), y(e)=Sy(e'), то левая часть последнего
соотношения приводится к виду
x?(e)B(e)y(e) = (Sx(e')) *B(e) (Sy(e')) =x?(e') (STB(e)S)y(e').
Сравнивая полученное выражение с правой частью,
х*{еГ) (STB(e)S)y(e') =хЧ(е')В(е')у{е')у
в силу произвольности столбцов х(е') и у{е') получаем, что
S^B(e)S = B(ef). П
Доказанная теорема позволяет сформулировать следующее
определение.
Определение 6. Рангом билинейной формы ЗВ называется
ранг ее матрицы В(е).
Определение ранга билинейной формы корректно, так как
в силу доказанной формулы rang B(e/) =rang B(e).
Обозначение: rang^.
Определение 7. Билинейная форма <%: VXV-+P называет-
ся невырожденной, если для любого ненулевого вектора х из V
можно указать вектор j/eI/, такой, что
. Л(х9 у)ФО. (4)
Билинейная форма 3S называется вырожденной, если для некото-
рого вектора хФд и любого у из V выполняется равенство
Я(х,у)=0. (5)
ТЕОРЕМА 3. Утв. Билинейная форма & : Vx V-*P является
вырожденной в том и только в том случае, если rang iS< dim V.
Доказательство. (=>) Пусть форма <% вырождена. Пола-
гая в равенстве (5) последовательно у равным еи е2, ..., еп, где
е= (ехе2 ... еп) — базис К, получаем п соотношений
3S(xt <?i)=0, ^,e2)=0 ^,е„)=0.
Разложим вектор х по базису е, * = 2£=1£/£*» и пользуясь тем,
что 3B{ei, е}) =р*/, запишем эти п соотношений подробнее
Png1 + ... + P*ign = 0,
. . . (6)
Полученная однородная линейная система обладает следую-
щим рвойством: ненулевой набор I1, ..., 1п (напомним, что вектор
jc, координатами которого являются числа g1, ../, |я, отличен от
94

нуля) обращает каждое из ее уравнений в верное равенство. Это
возможно лишь в случае, если ранг матрицы этой системы мень-
ше числа неизвестных, т. е. если rang В(е)<п и, следовательно,
rang^?<dim V.
(£=) Из того, что rang $j< dim V, вытекает существование не-
тривиального решения системы (6). Рассматривая это решение
как набор координат ненулевого вектора х, получаем, что
&(х, е{)=0у ..., Д(х, еп)=0.
Отсюда для любого вектора # = 2]L1Tl/0/ имеем
Ш (*, у) = Ш (х, SJLj л7*/) = 2jf=1 цШ (х, ej) = ZjL-. v/. 0 = 0.
Значит, форма $ является вырожденной. □
Замечание. Для каждого вектора х из V множество век-
торов {у\&{х, у)=0} является линейным подпространством прост-
ранства V.
§ 2. КВАДРАТИЧНЫЕ ФОРМЫ
Определение 1. Отображение J5 : V->P называется квад-
ратичной формой, заданной на V, если существует симметричная
билинейная форма з4>: VX V->P9 такая, что для любого вектора х
из V выполняется равенство
st(x)=sl(xrx).. (7)
Билинейная форма st(x, у) называется полярной к квадратичной
форме Л (х).
Утверждение. Квадратичная форма однозначно определяет по-
лярную к ней билинейную форму.
Доказательство. Для любой симметричной билинейной
формы s4>{x, у) справедливо тождество
Л (х, у) = — { Л (х + у, х + у) — о€ (х9 х) —Л (у, у)}
(векторы х и у — любые). Если s£(x, у) полярна квадратичное
форме sf(x)9 то с учетом формулы (7) получаем, что
tA(x,y) = -^-{A(x + y) — 3(x)— <Л(у)}*
Тем самым, вычисляя значения квадратичной формы si на векто-
рах х9 у и х+у, мы однозначно определяем число s£(xt у).
Ввиду произвольности векторов х и у отсюда получаем одно-
значную определенность полярной формы si. D
Для квадратичной формы принято следующее
Обозначение: st(x, x); st{x, у) — полярная к st(xt x) били-
нейная форма.
Сформулируем еще несколько определений.
95*

Определение 2. Матрицей квадратичной формы s£(xt х)
в базисе е называется матрица А (е) полярной к ней билинейной
•формы бФ(х, у) в этом же базисе.
Отметим, что матрица А (е) квадратичной формы является
симметричной.
Утверждение. Для любого вектора х из V справедливо разло-
жение
зФ{х9 x)=xi(e)A(e)x(e).
Определение 3. Рангом квадратичной формы называется
ранг ^полярной к ней билинейной формы (или, что то же самое,
ранг ее матрицы в произвольном базисе).
Обозначение: rang «s# (х, х).
Определение 4. Квадратичная форма $4>{х, х) в простран-
стве V называется
невырожденной, если rangiS$(x, x) =dim V,
и вырожденной, если rang .5$ (#, *),<dim V.
$ 3. ПРИВЕДЕНИЕ КВАДРАТИЧНОЙ ФОРМЫ К СУММЕ КВАДРАТОВ
Покажем, как найти базис, в котором матрица квадратичной
формы имеет диагональный вид.
1°. Метод Лагранжа.
ТЕОРЕМА 1. Усл. <s4>(x, #).—-квадратичная форма, заданная
ш V.
Утв. В пространстве V существует базис ft, такой, что
рли A (A) =diag{a,i, ..., А*}.
Доказательство. Пусть е — какой-нибудь базис в прост-
ранстве V. Тогда
а(х, x)=xi(e)A{e)x{e),
или, в иной форме,
Л(х,х) = Ц^хак^у (8)
где
А(е) =
ях(е) = (? ...£*)*.
Если st(x, x) = 0 для любого вектора х, то А (е) =0. Предполо-
жим, что <s4>(x9 х)Ф0.
Лагранж (Lagrange) Жозеф Луи (25.1.1736—10.4.1813) — французский ма-
тематик и механик.
96

Можно считать, что ап^О.
Если это не так, то в матрице А (е):
1) либо существует другой диагональный элемент, отличный
от нуля,
2) либо все диагональные элементы нулевые; но тогда отличен
от нуля некоторый элемент а*/ (1^^</^п).
Обратимся к первой возможности: ацфО> i>\. Переходя к но-
вому базису e'=eS, где
S =
Ч \
0 /.
7
получаем матрицу А(е') =STA(e)S, у которой элемент в позиции
(1, 1) отличен от нуля '(равен аи).
Замечание. Базис е' отличается от базиса е только поряд-
ком векторов: е= {в\в2 ... ег ... еп)-**е' = (е,е2 ••> &\ . •• еп).
Рассмотрим второй случай: а&/=тМ), где l^k<j^.n. Переходя от
базиса е=(е\ ... ek ... в/ ... еп) к базису е'= (ех ... ek + ef ... е\—
—ей ... en)у при помощи матрицы
3 =
... )
... 7
получаем матрицу А (е') =STA (e)Sf у которой элементы в пози-
циях (k, k) и (/, /') отличны от нуля:
o.kk =2а^/, а// =—2а&/.
Тем самым вторая возможность сводится к первой.
Итак, <xi 1=7^=0.
ШАГ А. Перепишем формулу (8), отделяя слагаемые, содер-
жащие координату g1. Имеем
Л (х, х) = а^2 + 2сс12^2 + ... + biy&l* + 2£/-2 *k№>
или, выделяя полный квадрат,
<A(x,x) = *n(ti + ^t* +
\ «п
где affl = aki S^L. (£, / > 2).
4 Заказ 538
+
«in
«11
i")2 + 2£/=2 a(!}!¥,
97

Положим
T|i = gi + 3!V+... + *2.р, тГ = &", m = 2, ...,/г. (9)
Тогда
Л (х, х) = а1Хл12 + Л^ (ху х),
Изменив координаты лроизвольного вектора * (см. формулы
(9)), мы перешли от исходной) базиса е к новому базису f~eS~
Найдем этот базис.
Координаты вектора х должны быть связаны равенством
x(e)=Sx(f) илих(!)=3-1х(е).
Запишем формулы (9) в матричном виде:
. 1ш Z1 a12/an ... a^/a,
\'г\п) \ О
Так как *(<?) = (&1 ... £")т, x(f) = (л1
что
Таким образом,
Если j^(1)(jc, лс)=0; то / — искомый базис. Предположим, что
.tfWfx, *)*е0. ,
Тогда, повторяя предыдущие рассуждения и совершая новый:
шаг (ШАГБ), получим, что
Uil)(x9 х) = аШ2' + <А{2)(х, х),
где Л*>(х9 ^) = SZi/.8ag)C*C/.
В итоге после конечного числа шагов (оно не больше п—1)
мы придем к базису А, обладающему требуемым свойством:
/ /Л о
A(h) = diag{Xlt .... К) = [ '•.
\о к
98

или
<А(х, *) = Яу*+ .,. +knvn\
где A^S'iiv'Tif и Xj = au, .Я2 = а(212), Ав = а$, .... П
Замечание. Предложенный способ может привести к нуж-
ному результату за число шагов, меньшее п—1. Это означает, что
часть коэффициентов Я,- равна нулю; число отличных от нуля
коэффициентов совпадает с рангом квадратичной формы:
rang«s#(x, x)=TangA(h)..
ЛЕКЦИЯ 14
2°. Метод Якоб и. Пусть матрица А{е) = (ац)<^ ■пхп квадратич-
ной формы зФ(х, х) обладает следующим свойством: для любого
k, k*=\, ...,n, определитель
Аь-
aii---^ife
a
П
akk
фО.
Тогда существует базис, в котором матрица квадратичной формы
имеет специальный вид.
ТЕОРЕМА 2. Усл. Д^О, k= 1, ..., п.
Утв. В пространстве V можно указать базис /, такой, что
^(/) = diag{-^
Ав
Ах '
А,
А2' '
А„_.
/
1-
' Ао
Ai
Ai
А2
О
О
Ап—1
Ал ;
где А<>=1.
Доказательство. Рассмотрим систему векторов / =>
«?(fi...M:
fk=yklei + ...+ykkekf Ы,...,я. (1)
Наложим на коэффициенты yk1 А-го вектора /* следующие усло-
вия:
•*(/*.*/)«<), /=1 *„ *(fktek) = l. (2)
Так как
Якоби (Jacobi) Карл Густав Якоб (10.12.1804—18.2.1851) — немецкий ма-
тематик, член Петербургской АН (с 1830 года):
99

то условия (2) можно записать в биде линейной системы
относительно неизвестных у*1,
V*
Из того, что Даг7*=0, вытекает, что эта система имеет единствен-
ное решение у*1,
yuk~\ Y/Л причем
У1
**-i
Л*
(в последнем легко убедиться, например, применив к вычислению
ykk правило Крамера).
Из полученных результатов вытекает, что матрица перехода от
базиса е к системе f имеет треугольный вид, причем на главной
диагонали стоят не равные нулю уцк:
о
г!
Поэтому система /= (f\ ... fn) — базис V.
- Вычислим s£(fk, fm):
1) кфт (в силу симметричности формы sf> можно считать, что
k>m). В силу условий (2)
2) k = m: JL{fky fk) = ykk,A(fk, ek) = yt
Л_А±
A*
§ 4. КВАДРАТИЧНЫЕ ФОРМЫ В ВЕЩЕСТВЕННОМ ПРОСТРАНСТВЕ
1°. Знакоопределенные квадратичные формы. Пусть V —
я-мерное вещественное пространство.
Определение 1. Квадратичная форма <$&(х, х) называется
положительно определенной, если для любого ненулевого вектора
х выполняется неравенство st(xy x)>0.
тик.
100
Крамер (Cramer) Габриель (31.7.1704—4.1.1752) — швейцарский матема-

Пусть А (е) = (a,7)eRnxn — матрица квадратичной формы
s£(xt x) в базисе е и
/au ... alk \
Afe = detI I, k=l, ..., л.
\aftl ... akk)
ТЕОРЕМА 1 (критерий Сильвестра). Утв. Квадратичная фор-
ма s&(xt x) является положительно определенной тогда и только
тогда, когда все A*>0.
Доказательство. (£=) Пусть Ai>0, ..., An>0. Тогда по
теореме Якобисуществует базис /, такой, что
где x = 2*Uti*/a- Так как '
л*=^г->о,- (3)
то ^(д:, *)>0 для любого вектора л:.
Покажем, чтб если хФО, то J#(*, *)>0. Предположим, что для
некоторого вектора х выполняется соотношение
, Л(х% Jc) = 2LiMftl = 0.
Тогда в силу условия (3) т), = ... = т|Л=0 и, значит, х=6.
(=^) Форма «я£(лг, x) является положительно определенной.
Покажем сначала, что все А^О.
Предположим противное: Дл = 0 для некоторого k. Распишем
это условие подробнее:
Л {ev ех)... (Л (<?1( ek)
Л{еь ех)...Л{еь, ek)
Так как строки этого определителя линейно зависимы, то найдутся
числа ць •.. f \ik, не все разные нулю и такие, что
|ii^(«i, */)+...+ |**я*(еЛ, ^/)=0, /= 1 Л.
Отсюда, пользуясь линейностью формы s& по первому аргументу,
получим, что
<s£(\nei + ... + \ikek, <?/)=0, /=1, ..., k.
Умножив /-е равенство на ц/, сложив полученные результаты и
Сильвестр (Sylvester) Джеймс Джозеф (3.9.1814—15.3.1897) — английский
математик, член-корреспондент Петербургской АН (с 1872 года).
101

воспользовавшись линейностью формы s£ по второму аргументу,
приходим к соотношению
Отсюда вытекает, что \x\ei + .. . + р,&е&—0.
Вследствие линейной независимости векторов еи ..., ek полу-
чаем, что \i\ = .. . = р,* = 0. Это противоречит нетривиальности набо-
ра \хи ..., (х*.
Следовательно,
Ai#0, ..., Д«=^0. (4)
Полученное неравенство (4) позволяет вновь воспользоваться
теоремой Якоби: существует базис /, для которого
<А(х, х) = П=хК№?\
где кк=*Ак-\1Ац. Так как ta=«s£(/*, f*)>0 и До — 1, то Д*>0 для
любого Л=1, .... л. □
Определение 2. Квадратичная форма s£(x, х) называется
отрицательно определенной, если s4>(xf x)\<0 для любого ненуле-
вого вектора х.
СЛЕДСТВИЕ 1. Утв. Квадратичная форма <&(х, х) отрица-
тельно определена в том и только в том случае, если A*-i'A*<;0
для любого &=1, ..., п (Д0=1).
Доказательство. Ясно, что отрицательная определенность
формы s£(xt x) равносильна положительной определенности фор-
мы
3&(х, x)=—st(xf х).
Так как при этом В(е)=—А(е), то миноры А* матрицы А(е) и
соответствующие им миноры 6* матрицы В(е) связаны равенст-
вами
8*=(-1)*Д*. (5)
Так как неравенства 8i>0, ..., 6Л>0 являются необходимым и
достаточным условием положительной определенности формы
Я(х9 х), то из формулы (5) получаем, что неравенства
A*-i V
Д* б*
<0
являются необходимым и достаточным условием отрицательной
определенности квадратичной формы $4>(xjx).. □
Определение 3. Минор матрицы называется главным, если
номера его строк ti<...<i* и номера его столбцов /i<...</*
связаны равенствами i'i=/i, ..., ik~jk-
102

СЛЕДСТВИЕ 2. Усл. У симметричной матрицы А=(ац)(
ERnxn миноры
А*М) =
ak\ • • • afefe
>0
для любого А=1, ,.., п.
Утв. Все главные миноры матрицы А положительны.
Доказательство. Выберем в я-мерном вещественном
пространстве V базис е и построим квадратичную форму s£(xy х)ъ
считая, что А(е) =Л :з£>(х, х) =хт(е)Ах(е). В силу критерия
Сильвестра эта форма з&(ху х) является положительно определен-
ной.
Пусть Mq -*■ главный минор порядка q, номера строк и столб-
цов которого равны k\<.. .<kq.
Рассмотрим в пространстве V новый базис е', отличающийся
от базиса е только порядком векторов: первые q векторов е'и • • •
..., ец' базиса е' соответственно равны: е\ = е^, ..., eq — еь.
В новой матрице А(е') квадратичной формы s&{x, x) минор
Мд будет располагаться в левом верхнем углу. Согласно критерию
Сильвестра он должен быть положителен. □
Зафиксируем в вещественном пространстве V симметричную
билинейную форму s£(x, у), полярную положительно определен-
ной квадратичной форме s&(x, x).
Напомним основные свойства формы st>(x, у):
О"*. Любой паре векторов х и у из V ставится в соответствие
вещественное число s£> (x, у).
1+. s£(y, x) =s&(xt у) для любых х, y<=V.
2+. s£(xt y+z)=st>(x, y)+s£(x, z) для любых х, у, z<^V.
3+. <s&(axt у)=аА(х, у) для любых х, j/gF и любого aeR.
4+. s4>(xt x)^0 дляN любого x^V; равенство st(x9 x)=0 воз*
можно лишь для нулевого вектора х.
Сравнивая эти свойства с требованиями, накладываемыми на
скалярное произведение в определении евклидова пространства
(определение I, пункт I0, § I, глава II, лекция 5), приходим к сле-
дующему важному выводу: ♦
Фиксирование в вещественном линейном пространстве симмет-
ричной билинейной формы, полярной положительно определенной
квадратичной форме, наделяет это пространство структурой евк-
лидова пространства.
Замечание. В приложениях интересен также и более общий
случай — фиксирование в вещественном пространстве симметрич-
ной билинейной формы, полярной невырожденной (не обязательно
знакоопределенной) квадратичной форме. Это существенно ис-
пользуется в физических приложениях и при построении эффек-
тивных вычислительных процессов.
юз

2° Закон инерции. Пусть V — вещественное линейное прост-
ранство и h — базис, в котором заданная квадратичная форма
зФ{х, х) имеет вид
Л(ху х) = к^'^ ...+Xnvn\
где * = 2£=iv*Afe, или, что то же,
(К 'о\л*\
<А(х, x)=(v* ...v«)\
О Хп/ \vnj
Пусть r = rangs&(xy x)>0.
Будем считать (перенумерацией векторов базиса этого можно
всегда добиться), что коэффициенты к\9 ..., Кп занумерованы так,
что первыми идут положительные (если они есть), затем отрица-
тельные (если они есть) и нулевые (если они есть):
Я1>0,...Дд>0; Vh<0, ...,Яг<0; Wi=0, ..., кп = 0.
Положим
6*=)С^>, k = q+lt ..., г;
g* = v*, k = r+l, ..., п.
Переходя тем самым от базиса h к базису е,
и л- ( г* * ! * ч 1
б = Л diag |-т==г, . .., —?==-. - /•—, 1 •• м Т7=т=^» Ь
приводим форму ^(х, х) к следующему виду:
где # = 2iUi£*£fc, или, что то же,
.,..].
(6)
(1
Л(х, х) = (Р.;.Г)
О
— 1
— 1
О
о
о
ev
Определение 1. Формулу (6) будем называть нормальным
видом квадратичной формы st(x, x).
104 >

ТЕОРЕМА 2 (закон инерции). Усл. е и / — базисы простран-
ства V, в которых квадратичная форма *я£(х, х) имеет нормаль-
ный в#д.
Утв. A(e)=A(f).
Доказательство. Пусть
Л(ху х) = у\1*+ ...+4S'—t)s+1'— ...— vf\ (7)
где x = SLi4*/ik-
Нужно доказать, что s — qnt = r. #
1. Равенство t = r следует из того, что ранг матрицы квадрат
тичной формы не зависит от выбора базиса (он равен рангу
&(х, х)).
2. Убедимся; что случай q>s невозможен.
Рассмотрим два линейных подпространства
W* = L(eu ..., ея), W~f = L{fs+u ...9fn)
размерностей q и п—s соответственно. В силу предположения
q+n—s>n пересечение We(]Wf нетривиально, т. е. существует не1
нулевой вектор х0, принадлежащий We(]Wf. Это означает,
что вектор х0 можно представить в виде линейной комбина-
ции как векторов ей - - ., е?» так и векторов /5+t> ..., fn:
хо = go1*! + •. • + bqeq = т)о5+1 /•+!+..-+ Лоп/п.
Вычисляя значение квадратичной формы бФ(х, х) при помощи
разложений (6) и (7), получаем, что
ь€(х0, *о) = ^+...+£оа>0
(из условия х0фд вытекает, что хотя бы одно из чисел go1, ...» hq
не равно нулю),
Ж (x0t х0) = -Ло+1'- ... -Ло' <[0.
Полученные неравенства исключают возможность q>s. Анало-
гично отбрасывается возможность q<s. Тем самым q=s. .
Таким образом, нормальный вид квадратичной формы опредег
ляется однозначно. D
Определение 2." Индексом квадратичной формы бФ(х, х)
называется максимальная размерность подпространства W, на
котором зФ{ху х)' отрицательно определена: бФ(х, х)<0 для лю-
бого ненулевого вектора х из W.
Утверждение. Индекс квадратичной формы равен числу отри-
цательных слагаемых в ее нормальном виде.
Обозначение: index si (xt x).
Важный вывод. Ранг rangj^(x, x) и индекс index sl(xy x)
квадратичной формы $£(х, х) однозначно определяют ее нормаль-
ный вид; базис, в котором квадратичная форма имеет нормаль-
ный вид, определяется неоднозначно.
105

ЛЕКЦИЯ 15
I
§ 5. ПОЛУТОРАЛИНЕЙНЫЕ И ЭРМИТОВЫ ФОРМЫ
Пусть V — комплексное линейное пространство.
1°. Полуторалинейные формы.
Определение 1. Полуторалинейной формой, заданной на
пространстве V, называется отображение
^:1/ХК->С,
таире, что для любых векторов х, у и z из V и любого комплекс-
ного числа а выполняются соотношения:
1) &{х+у, z)=st(x, z)+s£(y, z),
2) st>{axy y)=ast>(xt у),
3) st(x, y+z)=st(x, y)+st{xy z),
4) s&(x, ay)=as£{x, y).
Замечание. Полуторалинейная форма si>(x, у) линейна по
первому аргументу и «наполовину» линейна по второму (ср.
с определением билинейной формы, определение 1, пункт 1°, § 1).
Отсюда и название формы — полуторалинейная.
Пример. Примером полуторалинейной формы являете^ опе-
рация скалярного умножения в унитарном пространстве.
Пусть e=(ei ... еп) — базис пространства V. Положим
■**(**. ej)=a,kj.
Определение 2. Матрица А(е) = (а^)еСлхп называется
матрицей полуторалинейной формы st(x, у) в базисе е.
Пусть
•— произвольные векторы из V. Тогда
Л(х, у) = ТК1=хак$\\К
Последнюю формулу можно записать и по-иному (причем дву-
мя способами):
<А{х, у) = хЦе)А(е)^) (1)
и
oZ(x, У) = Ут(е)Ат(е)х(е)9 . (2)
где, как обычно, х(е) = (J-1 ... £")т, у(е) = (г\1 ... Tin)T, а черта
сверху означает переход к комплексно Сопряженным элементам —
Как и для билинейных форм, по матрице ЛеСДХя и базису
пространства е=(ег ... еп) можно построить полуторалинеййую
форму <&(х, у) у у которой А (е) =Л.
Если е и e'=eS — базисы пространства V, то
A(ef)=S^A(e)S.
106

Понятия ранга полуторалинейной формы и ее невырожденнос-
ти также вводятся по аналогии.
Определение 3. Отображение s& : V-+C называется квад-
ратичной формой, заданной на комплексном ♦ пространстве I7,
если существует полуторалинейная форма $4>: VxV->C, такая,
что для любого вектора х из V выполняется равенство
s£(x)=^(x, x). (3)
Полуторалинейная форма А (х9 y)f называется полярной к задан-
ной квадратичной форме А(х).
Утверждение. Квадратичная форма однозначно определяет
полярную к ней полуторалинейную форму:
Доказательство. Для любой полуторалинейной формы
справедливо тождество ;
<Л(х, у) = — {А(х + у, x + y) + iu£(x + iyt x + iy) —
4 t
— JL{x—y, x—y)—itA(x—iy, x—iy)} (4)
(векторы x и у из V — любые). Если s£>(xt у) полярна квадра-
тичной форме <s£(x), то с учетом формулы^ (3) получаем, что
<Л(х, y) = —{Jl(x + y)+iv£(x + iy)—tA{x—y)—i,A(x—iy)}.
4
»
Тем самым, вычисляя значения квадратичной формы s& на векто-
рах х+у9 х—у, x+iy и x—iy,-мы однозначно определяем величину
Ж(х, у).
Обозначение: ЗФ(х, х).
2°. Эрмитовы формы.
Определение 1. Полуторалинейная форма s£(x, у) назы-
вается эрмитовой формой, если
Щу, *)=&(*> У) (5)
для любых векторов х и у из пространства V.
Примером эрмитовой формы может служить скалярное про-
изведение в унитарном пространстве.
Утверждение. Полуторалинейная форма з4>(х, у) является эр-
митовой формой в том и только в том случае, если для произволь-
ного базиса е матрица А (е) этой формы эрмитова, т. е. А (е) =
=А*(е). /
Напомним, что матрица Л* строится по матрице А следующим
образом: А*^(А)'Т.
Доказательство. Меняя местами в формуле (1) векторы
хну
&(У,х)=Ут(е)А(е)7&)
. 107

и применяя к обеим частям равенства (2) операцию комплексного
сопряжения .
A(x,y)=yi(e)A*(e)x(e)t
убеждаемся в справедливости сформулиров.анного результата
непосредственно. □
Утверждение. Полуторалинейная форма s&(x9 у) является эр-
митовой формой тогда и только тогда, когда соответствующая
ей квадратичная форма принимает только вещественные значения.
Доказательство. (=>-) Если форма s£(x, у) эрмитова, то,
полагая в определении (5) х=уу получим, что s£(x, x)=s&(x, x).
(4s3) Пусть st(xt x)gR для любого вектора х из пространства
V, или, что то же,
d (х9 x)=s£(xf х). (6)
Переходя в формуле (4) к комплексно сопряженным величи-
нам, с учётом равенства (6) получаем, что
<Л(х, У)=—{Л(х + у, x + y)—iJl(x + iy, x + iy)—
4 -
—<А(х—у, x—y)+i<A(x—iy, x—iy)}.
Пользуясь тем, что аргументы второго, и четвертого слагаемых
последней формулы можно записать в виде
x+iy r=i (y—ix), x—iy=—i(y+ix),
преобразуем их. Имеем
tA(x+iy, x + iy) = Jl(i(y—ix\ i(y—ix)) =
= i(—i)<A(y—ix, y—ix) = tA(y—ix, y—ix),
<& (x—iy, x—iy) =st>(y+ix9 у+ix).
Тогда
<A(x, у) = — {Л(х+у, x+y)—itA(y—ix, y—ix)—
4
|—<A(x—yt x—y)+itA(y+ix, y + ix)}.
С другой стороны, меняя в формуле (4) векторы х и у местами,
получаем
Л(у, х) = — {*А(у+х, y + x)+itA(y + ix, y + ix)—
4
—Л (у— х, y—x)—io€(y—ix9 y—ix)}.
Легко видеть, что правые части двух последних равенств рав-
ны. Следовательно, Л(у> х) = Л(х, у). □
ТЕОРЕМА. Усл. Квадратичная форма st>(x, x), заданная на
комплексном пространстве V, эрмитова.
№

Утв. В комплексном пространстве V существует базис е=
— (в\... еп), такой, что
(К On
^(e) = diag{Xlt .... К} = \ '•• .
уп/
или, что то же,
JL{xy x)=2nk^%k\lk\\
где x = 2L=i£4; ^eR, *=1, ..., п.
Доказательство. Если \s#(ху х) = 0 для любого вектора я,
nto форма *s£(x, х) имеет нужный вид для произвольного базиса.
Поэтому можно считать, что зФ{х, х)Ф0.
Это означает, что в пространстве V найдется вектор еи Для
которого
*(еи е{)Ф0. (7)
Множество V^l) — {x^V\s^(xt в\)=0} является линейным прост-
ранством размерности п—1.
То, что V(1) — подпространство, вытекает из линейности фор-
мы $Ф{ху у) по первому аргументу. Его размерность равна числу
линейно независимых решений уравнения s&(x> ei)=0, или, под-
робнее,
Л^(/ь *1)+... + Лп^(/«, *i)=0, (8)
где fssz(f\ ... fn) — какой-нибудь базис пространства V и
* = Зл-1Л*/а (чтобы не возникало сомнений в том, что хотя бы
один из коэффициентов уравнения (8) отличен от нуля, можно
считать, что /i = £i).
Положим
Если .я£(1)(х, х)ФО на У<!), то, найдя вектор е2е^[), для которого
^(1)(^2, ^2)=^(^2, ^г) =7^=0, построим линейное подпространство
размерности п — 2 и положим ^(2) = ^(1)| ^ — Л\ (2) и т. д.
Описанный процесс продолжаем до тех пор, пока не придем
к подпространству V^q\ для которого
,A{q) = Jl\v{q) = 0.
Если УЮф{д}9 то, выбрав в нем базис ея+и ..., еп, рассмотрим
систему векторов еи .... ед, ед+и ..., еп.
Покажем, что эта система линейно независима и, значит, обра-
зует базис пространства V.
Пусть
а1г1 + ... + апвл=8. (9)
109

Пользуясь тем, что s£(Q, y)=0 для любого вектора у, в силу ра-
венства (9) получаем, что
<A{2!Li*kek9 ег) = 0.
Преобразуем левую часть этого соотношения с учетом того, что»
s£(ek, ei)=0 для любого &>2. Получаем als&(eu £i)=0. Отсюда
в силу условия (7) вытекает, что а1в=0.
Аналогичными рассуждениями из соотношений
Л {2Ljtfek9 ej) = О, / = 2, ..., q,
последовательно получаем, что аг = .. . = а<7 = 0.
Темв самым формула (9) приобретает вид
a(i+leq+l + ... + anen=Q.
В силу линейной независимости системы ед+и•..., еп получаем,,
что ад+1 = ... = ап = 0 и, значит, линейная комбинация в формуле
(9) может быть только тривиальной.
Таким образом, е\, ...9 еп — базис V.
Найдем вид матрицы формы s£(x,x) в базисе е. По построению
Ж{еи e*)=0, />£.
В силу того что форма эрмитова, также и
<&(ek, e/)=0, />£,
Значит, А (е) = diag{A,b ..., Ля}.
Если x=2k=ilkeky то
Л{х9 ^) = 2Li^f^2LiAfc|^|2. П
Замечание. Нетрудно видеть, что предложенный при дока-
зательстве теоремы способ,приведения матрицы эрмитовой формы
к диагональному виду применим и для симметричных билиней-
ных форм.
В заключение отметим, что для эрмитовых квадратичных форм
справедливы естественные (они и доказываются по той же схеме^
аналоги 1) теоремы Якоби, 2) критерия Сильвестра, 3) закона
инерции. Наконец, фиксированием полуторалинейной формы, по-
лярной к эрмитовой положительно определенной квадратичной
форме, мы задаем в комплексном пространстве структуру унитар-
ного пространства.

Глава V. ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ УНИТАРНЫХ
ПРОСТРАНСТВ
§ 1. ОПЕРАЦИЯ СОПРЯЖЕНИЯ
1°. Сопряженное отображение. Пусть V и W — унитарные прост-
ранства и s£:V->W — линейное отображение.
Определение. Линейное отображение s£*:W->V назы-
вается сопряженным по отношению к линейному отображению
«$Ф.: V-+W, если для любых векторов х из V и у из W выполня-
ется равенство
Замечание. Скалярное произведение в левой части фор-
мулы (1) вычисляется в унитарном пространстве Wt а скаляр-
ное произведение в правой части — в унитарном простран-
стве V.
ТЕОРЕМА 1. Уел, V и W — унитарные пространства,
^e^(V, W).
Утв. Сопряженное отображение s£*^3?(Wt V) всегда су-
ществуете формулой (1) определяется однозначно.
Доказательство. Единственность. Предположим сначала,
что сопряженное отображение s&* существует, и докажем его
единственность.
Пусть y&W — произвольный вектор. Его образ s£*y лежит в
V и, следовательно, может быть разложен по базису е простран-
ства V (который будем считать *ортонормйрованным). Так как
любой вектЪр х из V в ортонормированном базисе е можно запи-
«сать-.в виде
x = 2k=i(xt'ek)ek,
то <А*у = 2Li (*А*у9 ek) eh.
Пользуясь свойствами скалярного произведения в унитарном
пространстве и равенством (1), преобразуем сомножители у век-
торов е*. Имеем
(о€% ek) = (ek, tA*y) = (tAek9 y) = (y, JLek).
Тем самым
JV,y=^U\{y^Jlek)ek
и, значит, образ произвольного вектора у из W при отображении
*я£* однозначно определяется тем, как исходное линейное отобра-
жение si- действует на векторы £1,.,.>ел фиксированного базиса
еу и вектором у*
Ш

Существование. Поставим каждому вектору у из W в соответ-
ствие вектор из V по следующему правилу (будем обозначать
это правило через .я£*):
<А* iyeW~ 2L1 {у, ^,) ^ е= V. (2)
Покажем, что отображение (2) линейно. Имеем
Л* {Ц + Лу) = 2Li (ty + *У, <^) *Л =
= >v2Li (У, о&Л) ^ + VZLi ОЛ о^*) ^ = ^*f/ + А/«у$У.
В справедливости основного равенства (1) можно убедиться
путем сравнения скалярных произведений {st-x, у) и (ху s&*y).
Пользуясь свойствами скалярного произведения в унитарном
пространстве и тем, что базис е ортонормирован, получаем, что
для любых векторов х из V и у из W величины
(<Ах, у) = {Л (2»в1 (х, ек)ек),у) =* Ц^х (х, ek) (Лек, у)
и
(*. Л*у) = (2/=i(*, *,) е7, SLi (J/, o&ft) еЛ) =S*i/ei (х, е}) (у, <Аек) (ef, ek) =
= Ч=[(х,ек)(Лек,у)
равны ^последнее упрощение возможно в силу того, что
(eh ek)=&ik). U
ЛЕКЦИЯ 16
2°. Свойства операции сопряжения. Таким образом, равенство
(1) задает отображение
• :24V, W)-+&(W, V)t
действующее из линейного пространства линейных отображений
из V в W в линейное пространство линейных отображений из W
в V. Укажем некоторые свойства этого отображения *:
1+. (^*)*-^.
2+. (as£) * = as£* (тем самым отображение нелинейно).
' 3+. (^+^)*=^*+^*.
4+. Если ^e^(V, Г) и 4<=&{W9 Z), то (As*)*=„s**#*.
Докажем, например, свойство 2+. Имеем
((осо^) х, у) = а (с^л;, j/) = a (*, ^V) = (*> («с>?*) у),
откуда в силу единственности сопряженного отображения полу-
чаем требуемое {as£)*=as£*. □
Аналогично доказываются оставшиеся свойства.
112

Приведем еще важные для дальнейшего свойства операции
сопряжения * по отношению к пространству ££(V, V) линейных
операторов.
5+. Если detj^^O, то det^*=^0.
Доказательство. Предположим противное: det^* = 0. Это
означает, что в пространстве V найдется ненулевой вектор уу та-
кой, что iS#*f/ = 9. Умножая обе части последнего равенства ска-
лярно на произвольный вектор х9 .получим (х9 s£*y)=Q или
(stx, */)=0.
Пользуясь тем, что оператор s& невырожден и, значит, дей-
ствует на пространстве V сюръективно, можно указать такой век-
тор х, для которого stx=y. Отсюда вытекает, что (у,у)=0. Но
это возможно лишь при #=8. ^
Полученное противоречие позволяет заключить, что сопряжен-
ный оператор «я£* также невырожден. □
6+. Если оператор s4> невырожден, то (j#~1)*= (j^*)"1.
Доказательство. По определению сопряженного опера-
тора
(st-lx9y) = {x9 №~{)*у).
С другой стороны, из очевидного равенства
(оператор *я£* обратим согласно свойству 5+) получаем, что
(<Л~1х9 у) = (Л~1х9 Зу) = (<А~хх9 Л*(Л*)-х у)-
= (Ль€-1х9 (ъ4Г)~1у) = (&к, {Л*)~ХУ) = (х, (ЛТ1У).
Тем самым
\х9 {st~l)*y) = (x9 i&*)-ly).
Отсюда в силу произвольности векторов х и у и единственности
сопряженного отображения заключаем, что (*5^~1)*== (^*)""1. П -
Замечание. Операция сопряжения * для евклидовых прост-
ранств определяется так же, как и для унитарных. Сопряженное
отображение всегда существует и однозначно определяется па
исходному линейному отображению. Для операции * в евклидо-
вых пространствах выполняются свойства 1+, 3+—6+. Отметим, что
вследствие вещественности а в свойстве 2+ операция сопряжения
для евклидовых пространств V и W
. *:&(V9 W)-+S?{W9 V)
является линейной.
Пример (линейная форма в унитарном пространстве). Пусть
V — унитарное пространство и cosS^l/, С). Введем на С ска-
лярное произведение: для а, 0еС положим
(а, P)c=apL
113

Теперь С также является унитарным пространством и (однознач-
но) определено сопряженное отображение
^•^С-2«=1(!/,(о(еЛ))%еУ.
Так как {у,<*л(ек))=у®(ек)9 тр
vf(y) = ySLi<u{ek)ek.
Из основного равенства (а>(х)9 у)с = (х9 <о*(у)) получаем, что
(й(х)у=(х, yh), (1)
где A ==2*Li ©(**)**•
В силу произвольности у из С заключаем, что
о)(лг) = (х, Л).
♦
Таким образом, каждая линейная форма в унитарном прост-
ранстве естественно связывается со скалярным произведением.
3°. Матрицы взаимно сопряженных отображений. Пусть V и
W — унитарные пространства размерностей п и k соответственно.
Рассмотрим пару взаимно сопряженных отображений
а<=2{У9 W) -и st*e&(W9 V).
Выбирая в пространствах V и W базисы е и / соответственно,
строим матрицы этих отображений;
A(e,f)-(ami)9A*(f9e) = (a,"*)9
где
Лет = 2*el ajJJf о«7/ = ^i (*;« е„.
(m = l, ..., л) (/=1, ... ,6)
Если базисы е и / ортонормированы, то из последних собтно-
шеиий находим
ami=(st>em9 fi)9 aj*m=(st*ff9 em)
(m=l,...,n; /=1,...,£)•
Отсюда и из того, что
заключаем: a/*m=am'.
Определение. Матрица 5= (p/m)'eCnXfe называется сопря-
женной матрице Л= (a'm)€C*Xni если
p/w'=a*7f т=1,...,л; /=1,. ..Л
Таким образом, получен следующий результат.
114

Утверждение. Матрицы взаимно сопряженных отображений
относительно любой пары ортонормированных базисов являются
взаимно сопряженными.
Утверждение, rang *я£ = rang «я£*. 1
Доказательство вытекает из того, что операция сопряже-
ния не изменяет ранга матрицы и что ранг матрицы'отображения
равен рангу самого отображения. □
4°. Ядра и образы взаимно сопряженных отображений. Для
любой пары взаимно сопряженных отображений зФ: V-+W и
*я£* : W-+-V тривиальны включения:
ker^c=V, im^*c:V, ker^*c=№, im^c=№.
Утверждение. V=ker^®im<5$*, №=ker.s£*©imj£.
Доказательство. Пусть лгекег^. Это означает, что st>x=
= 6^ и, следовательно, для любого y^W справедливо равенства
{бФх, у)=0 или (х, <s£*y) = 0.
Так как векторы х из кег*я£ и у из W произвольны, то из по-
следнего равенства заключаем, что
ker j£_Lim«s$*.
Пользуясь равенствами
rang «я£ = rang .я£* и defect st + rang «я£ = dim V,
получаем, что линейные подпрбстранства kerj^ и im*s#* прост-
ранства V обладают следующими свойствами:
1) их пересечение состоит только из нулевого вектора Qv>
2) сумма их размерностей равн^ размерности объемлющего
пространства V.
Согласно теореме 2 пункта 2° § 5 главы 1 (лекция 3)
V=ker^®imj^*.
Разложение 1^=кег^*ф1тч5^
доказывается аналогично. □
Замечание. Для линейных операторов $$-щ&{у> V) все
сказанное в последних двух пунктах остается справедливым;
только естественно рассматривать матрицу линейного оператора
для одного ортонормированного базиса (е=/).
5°. Нормальный оператор.
Определение. Линейный оператор s£:V-+V называется
нормальным, если ^**я£ = .5&я£*.
ЛЕММА. Усл. Линейные операторы s4>t&^2?(Vy V) переста-
новочны: $£&=&$&. *
Утв. Существует вектор хоФ%, такой, что ^x0=XxOi 9Sxq=
= [iXQ.
Другими словами, у любой пары перестановочных линейных
операторов, действующих в комплексном пространстве, есть об-
щий собственный вектор.
115

Доказательство. Пусть W=W{k) — собственное под-
пространство линейного оператора s&, отвечающее собственному
'значению X: W(1,) = {x^V\stx=Xx}.
Вычислим действие оператора s£3t на произвольный вектор х
из W. Имеем
Л(Щх) =(<А$)х = (Ш<А)х=<Ш (<Ах) = <Ш (Хх) =Шх.
Это означает, что &x^W. В силу произвольности вектора xelF
отсюда заключаем, что <%(W)czW.
Тем самым подпространство W является инвариантным отно-
сительно действия оператора 33. Это позволяет рассмотреть инду-
цированный оператор
Так как W — комплексное пространство, то у оператора 3$\w су-
ществует собственный вектор xo^W :3§Xo=\iXo.
Из того, что Xo^W, вытекает равенство s£xo=Xxo. ,П
При помощи этой леммы докажем следующий результат. ж
ТЕОРЕМА 2. Утв. Линейный оператор зФ: V-+V является нор-
мальным в том и только в том случае, когда в унитарном прост-
ранстве V существует ортонормированный базис из его собствен-
ных векторов. ,
Доказательство. (=^) Пусть оператор ^является нор-
мальным. Согласно лемме найдется вектор е\ (можно считать, что
| ех | = 1), для которого . *
Ортогональное дополнение Vя"1 вектора ех инвариантно отно-
сительно действия операторов зФ и *я£*. В самом деле, для про-
извольного вектора xeV*"1 имеем
(&х, ex) = (x,si>*el)±(x, уцех) = M*, £i)=0,
(я£*х, ег) = (ху s&ex) = (х, Х\е\) =Х\ (х, ех) = 0.
Тем самым векторы бФх и si>*x ортогональны вектору е{ и также
лежат IB Vn~x.
Согласно лемме в подпространстве Vя"1 найдется вектор
^2, 1^21=1, для которого
Его ортогональное дополнение *Vn~2 в подпространстве Vn~l инва-
риантно относительно действия операторов s&* и $Ф.
Продолжая рассуждать подобным, же образом,, приходим к
ортонормирс[ванной системе векторов еи...,еп, для которой
s4>ek = Xkek, «я£*е* = ц*е*, £=1,...,я.
116

В базисе e=*(e\...en) матрицы операторов $t> и s&* имеют диа-
гональный в'ид. Прежде чем записать соответствующие формулы,
покажем, что lkk = \ik> &=1,...,я.
В самом деле, t*
h=h\ek\2 = h(*k> ek) = (A. A, ek) = (<Аек, ek) = (ek, <A*ek) =
= (**. M*) = Hfe (**» *k) = Hfe I ek 12 = № •
Таким образом,
(4* ) Пусть e=(ei ...£*«) — ортонормированный базис унитар-
ного пространства V и
Определим линейный оператор ^: V-^V посредством следую-
щих формул:
&ек=Хке$, &=1,...,л.
Так как скалярные произведения (^л:, г/) и (х, 3§у):
" (^, у) = WL (2J.J 5Ч)> у) - (2^ E*«yfcfcf 2»в1 tfe,) =
- (2SUi РV*. 2/-i ЧЧ') = S*./-i Л*6*S (е*. ej) = 2^ Я^Чр,
(х, Лу) = (2»в1 ?Ч, Л (2^ туе,)) -
равны для любых векторов х и у из У, то оператор ^ сопряжен
оператору j#. Таким образом,
Убедимся в том, что действия операторов j^*j^ и slst** на
произвольный вектор х из V дает один «и тот же результат. Имеем
JVJU = е>Г о* (2£.i£4) = 2»^ 6**0#о&* = 2^ 5*.>Г (V*) = .
Замечание. Если s4> — нормальный оператор, то s&* также
является нормальным. Кроме того, в унитарном пространстве V
существует ортонормированный базис, векторы которого являют-
ся собственными векторами обоих операторов и^и st*.
6°. Унитарный оператор. Пусть V —. унитарное пространство.
Определение. Линейный оператор °U\V-+V называется
унитарным, если Ш^Ш^З, где Э: V-±V — тождественный опера-
тор. •
117

ТЕОРЕМА 3. Усл. °U — линейный оператор в унитарном прост-
ранстве.
Утв. Следующие высказывания равносильны (рис. 25):
1. ^€=241/, V) — унитарный
оператор.
0ж(~2\ 2: Для любых двух векторов
^ч ,~S^ Vw/ ч^^у~ч х и у из V выполняется равен-
( СО 1 (л) ство <^*- w- (*. у) •
{ 6 ) \U 4* Линейный оператор Ц пе~
реводит любую ортонормирован-
Рис. 25 . ную систему векторов из V а
ортонормированную систему век-
торов.
5. Линейный оператор °U изометричен, т. е. для любого век-
тора а: из У выполняется равенство |<24х| = |х|.
6. Линейный оператор °U нормален и все его собственные зна-
чения, взятые по модулю, равны единице.
Доказательство. 1=^2. Преобразуем произведение (°Uxr
Wy): '
(<Ux% <Uy) = (х, <U*<Uy) = (х, Sfy) = (х, у).
2=^4. Пусть f\>...tfk — ортонормированная система: (//, Ы) =
==б/т. Тогда система Щи...9Щк обладает следующим свой-
ством:
. V (Щи Щт) = (к /«)=*/«
* Vi
и, значит, является ортонормированной.
1=^3. Из того, что °U*°U=2t вытекает, что оператор °U обратим.
Умножая обе части равенства справа на °Urx9 убеждаемся в том,,
что <2/*=^-1.
Откуда легко следует требуемое Ф/^*=(2/^~1=<Зг.
3=^6. Из того, что cU*^cU~lt вытекает, что °Ы — нормальны^
оператор. Пусть к — собственное значение оператора °U ;и х,—
соответствующий собственный вектор. Можно считать, что |je| = L
Тогда
1 = (Xf х) = (<U*<Ux, л:) = (<Ux, <Ux\ =
= (XxM=Xk(xt х) = [*|*.
6=^1. Из того, что <2/*<г/=<2/^*, вытекает, что в пространстве
V существует ортонормированный базис е= (е^... еЛ) из' собствен-
ных векторов оператора 41 и
о \ /КО
U \ ° к
где %ь...Дл — соотв>етствующие собственные значения.
U8

Перемножая эти матрицы в любом порядке, вследствие усло-
вия |Д*| = 1, fe=l,..., /г, получаем, что
' U(e)U*(e) = U*(e)U(e)=L
Это означает, властности, что °и*°и=9.
4=>-1. Пусть e\t...ten и f\=°Ueu... yfn=°Uen — ортонормиро-
ванные баэисы. Возьмем произвольные векторы х и у и разложим
их па базису: v
Ясно, что (A:,t/) = SLiW.
Оператор ^ преобразует векторы х и у по следующему пра-
вилу:
Ux = U (2£., lkek) = 2 «_, £*?#> = 2»=1 £*/*> «^ = 2JL, V//.
Поэтому в силу ортонормированности базиса f
Из последнего соотношения получаем равенство (х, <U*cUy) =
- (*, yl и, далее, (*, (<U*<U—P)y) = 0
В силу произвольности вектора л: имеем (°U*°U—&)y=Q для
любого 1вектора, у из У. Это означает, что °U*°U=2f..
2=ф*5. В справедливости этого утверждения сомнений не возни-
кает: полагая х=у9 получаем, что
\<Ux\2=(<Ux, <Ux) = {x, x) = \x\\
5=ф-2. Воспользуемся* тождеством
ixty) = ±(\x + y\*-\x-y\* + i\x*iy\*--i\x-iy\*).
Заменяя в нем вектор х на Щх, вектор у на °Uy и пользуясь тем,
что °U — изометричный оператор, получаем, что
(UxfUy)^-r(\Ux + Uy\2-\l^-Uy\2 + i\Ux + iUy\2-
-i\Ux-iUy\2) = -^(\U{x + y)\2~\U(x-y)\' + i\U(x+iy)r-
-i\U{x-iy)\*) = \{\x + y\*-\x-y\* + i\x + iy\*-i\x-iy\*) =
= (*,«/)• П
Замечание. Матрица
называется унитарной, если
U*U=UU*=I.
119

Матрица унитарного оператора в ортонормированном базисе
является унитарной (это вытекает из того, что матрицы взаимно
сопряженных операторов в ортонормированном базисе взаимна
сопряженные); отмеченное свойство позволяет от равенств для опе-
раторов <%*<%(=CUCU*=У перейти к равенствам для матриц
U*(e)U(e) = U(e)U*(e)=I
и, далее,
В частности, матрица унитарного оператора в ортонормирован-
ном базисе из собственных векторов имеет следующий вид:
О >„/
ЛЕКЦИЯ 17
(
7°. Эрмитов оператор.
Определение. Линейный оператор st-:V-±V называется
самосопряженным, если .я£*=*я£.
Если V — унитарное пространство, то самосопряженный опе-
ратор называют эрмитовым, а если V — евклидово пространство,,
то — симметричным.
Пусть V — унитарное пространство.
ТЕОРЕМА 4. Утв. Для того чтобы sf>&&'(V9 V) был эрмито-
вым, необходимо и достаточно, чтобы скалярное произведение
№х. У) было эрмитовой формой, или, что то же, чтобы (s£x, х)
было вещественным для любого вектора х из V.
Доказательство. Для всякого линейного оператора st
произведение {s£xyy) является полуторалинейной формой. По-
ложим
Я(х,у) = (&хъу).
Если Л =ь^*, то л (у, х) = (о€у, х) = (уу Лх) = (Лх, у) = <Ш (х, у)
и, значит, $(х,у) — эрмитова форма.
Если же Ш{х,у) = &(у,х), то{Лх,у) = <Ш{х, у) = $(у,х) = (Лу,х) =
= (х,Лу). П
Свойства эрмитова оператора:
1+. Эрмитов оператор является нормальным.
2+. Собственные значения эрмитова оператора вещественны^
Доказательство. Пусть st>x=Xx, где |*| —1. Тогда Х=
=Х-\=:\к(х, х) = (кху х) = {зФх, х) = (х, s£x) = (x, Xx)=iK(xf x) =
=Я-1=Л. □
3+. Собственные векторы эрмитова оператора, отвечающие раз-
личным собственным значениям, ортогональны.
120

Доказательство. • Пусть s£xi=X\X\, $1х2=\къх2, где кхФ%2
и х\Фв> х2фв. Тогда
(з£хи x2)=h\(xu Х2), (хи <я£*2)=М*1> х2).
Вычитая из первого равенства второе и пользуясь тем, что
(«5^*1, х2) = (хи s£x2)t получаем (Х\—К2) (хи *г)=б, откуда легко
вытекает требуемое. О
4+. Матрица эрмитова оператора в ортонормированном базисе
является эрмитовой.
Доказательство. Пусть е — ортонормированный базис и
Умножая обе части этого равенства скалярно на вектор ет, полу-
чаем, что
(<Aek9 ет) = (2/а^у, ет) = 2,a/ (eff em) = a™.
Отсюда
a? = (<Aek, em) = (ел, JLem) = (yfem>^) = a£.
Это означает, что Л(е)=Л*(е). П
Верно и обратное.
Утверждение. Если матрица s^=(akm) линейного оператора Ы
в ортонормированном базисе эрмитова, то эрмитов и с#м опера-
тор «я£. ^
Доказательство. Из того, что a*w = am*, и ортонормиро-
ванности базиса е получаем
(*Аек, ет) = <х£ = ^ = (<Лет, ек) = (ек, <Ает).
Тогда для произвольных векторов '
x=2klkekt у = 2тЦтет
имеем
(<Ах,у) = (Л (2*64). Ъттгет) = 2*,mgV (с^ё*. ет) - *
= 2*Р«5* *Г (**, ^т) - (2*84, 2тлто«^) = (х, Лу). П
8°. Положительный оператор.
Определение. Эрмитов оператор $t> называется положи-
тельным {неотрицательным), если (s&x,дс)>0(>0) для любого
вектора хФд.
Обозначение: s4>>0 (s&>>Q).
Утверждение. Эрмитов оператор s£ является положительным
(неотрицательным) в том и только в том случае, если все его
собственные значения положительны (неотрицательны).
Доказательство. Ограничимся рассмотрением случая,
когда s&>0.
Так как s4> — эрмитов оператор, то в пространстве V сущест-
вует ортонормированный базис из его собственных векторов —
121

(ei...e„) и для любого вектора х=2й|*е* выполняется соотноше-
ние
= ^k.mlklm{Jlek,em) = 2kK\lk\K
Полагая х последовательно равным еь...,еп, получаем, что
Xi>0,...,X»>0.
Hchon доказательство и обратного утверждения. □
Утверждение. Оператор, обратный положительному, положите-
лен.
Доказательство. Так как
defo^nj^X),
то оператор s& обратим. Заменяя в доказанном ранее равенстве
(st*)~l =(&-})* оператор л$* на оператор s&, получаем, что
*s$_1 = («s#-1)* и, значит, оператор s4>~x эрмитов.
Его собственные значения легко определяются по 'собственным
значениям оператора s&:
А так как 1Дь>0, то оператор stf*'1 положителен. □
9°. Корень из оператора.
■ ТЕОРЕМА 5. Усл. ^>0(>0).
Утв. Существует единственный ^f>0(>0), такой, что 3&2=sf>.
Доказательство. Существование. Пусть е — ортонорми-
рованный базис из собственных векторов оператора «я£>0:
<s&ek=kkek, £=1,...,л.
Оператор $ определим посредством следующих формул:,
Яек = ]/%ек9 k = l, ... , п.
Ясно, что Jf — эрмитов оператор. Из того, что А*>0, вытекает,
что ^>0. Кроме того,
&2ек = %кек=я4>ек, £=1,...,я.
Из совпадения действий операторов 38* и s4< на базисные векторы
вытекает требуемое равенство 9&2=$&.
Единственность. Пусть ^Р>0 я ^2=*s^. Покажем, что 97=^.
Так как оператор 92 эрм'итов, то в пространстве V существует
ортонормированный базис f из его собственных векторов. Пусть
jui,..., [in — соответствующие собственные значения.
В силу равенств
*Afl=&if,) --*(|1///) = |#/, /= 1, ; • • . *. '
можно заключить, что f\9...,fn — собственные векторы и опера-
тора ^ с собственными значениями jii2,..., Цл2.
122

Ясно, что {ц!2,..., ц«2}={Л,ь ..., Ы-
Пусть е+ — произвольный собственный вектор оператора
зФ : я£е+=(к+е+. В его разложении по базису f
/=i
отличными от нуля могут быть только коэффициенты при векто-
рах из f, отвечающих тому же собственному значению Х+ относи-
тельно оператора tA{Vk+ относительно <&\.
Запишем это символически так: ^+=2+^// и вычислим 9*е+.
Имеем
Последовательно полагая е+ равным ei,...,ert, получаем, что
%е^^У%кек—^>ек для любого £=1,...,/г. Это означает, что
Определение. Оператор <% называется (арифметическим)
квадратным корнем из оператора s$>.
Обозначение: Y^ ЛХ12.
Замечание. Ясно, что из неотрицательного оператора мож-
но извлечь корень любой целой степени ((корнем /n-й,степени из
оператора ^>0 называется оператор ^>0, такой, что 3&т=$&).
10°. Сингулярная пара базисов. Пусть V и W — унитарные
пространства, si: V-+W — произвольное линейное отображение и ч
<s#* : W-+V{— линейное отображение, сопряженное s£.
Тогда определены два линейных оператора:
Они обладают следующими свойствами.
1+. Операторы s£*s4> и s£s&* эрмитовы.
Доказательство. Пользуясь правилами операции сопря-
жения *, получаем, что
2+. Операторы ,s&*s£ и зФзФ* неотрицательны.
Доказательство. Пусть х — произвольный вектор из V*
Тогда
{JVJLx, x) = (tAx, <Ax)^0.
Аналогично для произвольйого вектора у из W
{ЛЛ*У, у) = {<А% <А*у)^0. D
Ясно, что в пространстве V существует ортонормированный
базис h из собственных векторов оператора s£*$t>y a в простран-
стве W — ортонормированный базис t из собственных векторов
оператора s£s&*.
В дальнейших рассмотрениях большее внимание будет уде-
ляться оператору s4>*$£.
123

3+. Образы базисных векторов /ii,...,An при отображении s£
ортогональны: (s4>hm, st>hj)=Ot тФ\.
Доказательство. Пусть vi2>...>vn2^0— собственные зна-
чения оператора JtJi: JtJLhi =v/A/.
Тогда
(othj, l4h.n) = (b4r*Ahh A«)=vJ(A/f Am). (1)
В силу того что базис h ортонормирован, при тф\ отсюда полу-
чаем требуемое: (sf>hft s£>hm)=0, П '
Из соотношения (1) вытекает, что при т=/
|jtfA/|=V/>0. f
Это означает, что s£hj=frQw в том и только в том случае, если
4+. Вектор ^A/(v/^0) является собственным вектором опера-
тора *5&9£* с собственным значением v/2.
Доказательство,
ТЕОРЕМА 6. Утв. Существуют ортонормированные базисы h=
= (Й1...йя) в пространстве V и /—(fi.../*) в пространстве W, та-
кие, что . - •
tAhi'-
, вг,'/ = г+1, ...1 п;
о*Ъ =
гД-, i=l, ...f г;
6у, i=r+ 1, ... , А.
(2)
Доказательство. Пусть fti,...,ftr, Лг+ь...,Лп — ортонор-
мированный базис пространства V из собственных векторов опе-
pjaTOpa л#*«я£, отвечающих собственным значениям vi2^...^vr2>
>vr+i2=...=vrt2=0.
В пространстве № векторы
., tr-= <Ahr
образуют ортонормированную систему (cut. свойство 3+).
ним ее до ортонормированнаго базиса пространства
Из того, что
Jthf=vfti (/=l,...,r),^/i/ = 9ir (/=г+1,...,л),
вытекает, что '
Допол-
Л,
U
fvi
A(h9 t) =
vr О
О О
124

Согласно свойству матриц взаимно сопряженных отображений
относительно ортонормированных базисов (пункт 3°) имеем
' v,
A*(t9 A) =
vr О
О О
О
Отсюда s£*ti=Vihi (i'=l,...fr), jtf*fc = 6v(i=r+lf ...,А).
Определение. Пара базисов h и ty обладающих свойствами
(2), называется сингулярной парой базисов для линейного отоб-
ражения s£.
ЛЕКЦИЯ 18 ' • '
§ 2. РАЗЛОЖЕНИЯ ЛИНЕЙНОГО ОПЕРАТОРА
1°. Эрмитово разложение.
ТЕОРЕМА 1. Усл. <s£<=:3?(V, V), где V — унитарное простран-
ство.
Утв. Существует и при этом только одна пара эрмитовых опе-
раторов 3Sf <8<=:2!(УУ V), таких, что &=Д+№.
Доказательство. Легко убедиться в том, что операторы
обладают требуемыми свойствами. Например,
Единственность пары вытекает из того, что, допуская разло-
жение вида &=&+№, с учетом равенства s£*=M—iff прихо-
дим к формулам
л=-7(00+***)■ ^ir^-^*)- а ^ (!)
СЛЕДСТВИЕ. Утв. Линейный оператор в унитарном про-
странстве является нормальным в том и только в том случае,
если операторы в его эрмитовом разложении перестановочны.
Доказательство. Из формул (1) лутем прямых вычисле-
ний получаем, что
Наличие этого тождества легко обеспечивает желаемое. □
125

2°. Полярное разложение.
ТЕОРЕМА 2. Усл. $4-^3?{V, V) — произвольный оператор.
Утв. Существуют эрмитов оператор 38^0 и унитарный опера-
тор 01, такие, что s£=$°U.
Доказательство. Из того, что s£*s£^0, вытекает сущест-
вование в пространстве V ортокорм'ировавдюго базиса ей ..., еп
из собственных векторов оператора $&*$&>, отвечающих неотрица-
тельным собственным значениям . '
Vl2> . . . >Vr2>V2r+i= . . . =Vn2=0.
Оператор $& переводит базис ви...%еп в ортогональную систе-
му fx=steu...,fn=si>en.
В самом деле,
(/ь ?т) = (-Лек9 <AeJ = (>A*<Aek, em)^{v2keky em) = v|6te. '
Так ка.к |/ь|=у&, то первые г векторов этой системы fu>>-,ft
отличны от.нулевого.
Полагая
g* = -^-/fc.*=l г,
ч
лолучаем ортонормированную систему gu...,gr, Для векторов ко-
торой выполняются равенства
stek = vhgk,k=lt...tr.
Дополнив эту последнюю систему до ортонормированного базиса
пространства векторами gv+i, • •., gn, добавим к предыдущим г
равенствам еще п — г:
stek=Q=Vkgbt k=r+ 1,..., я.
Построим теперь операторы <U и М\
%lek=gkt Л=1,...,л,
'(так (как оператор °Ы переводит ортонормированный базис е в
ортонормированный, то °Ы — унитарный),
&gk=Vhgk, k=l,...tn, .
{ясно, что оператор $ эрмитов и неотрицателен).
Оператор 3&°U действует на векторы ортонормированного ба-
зиса е так же, как и оператор зФ:
a<Ueh=&gk=\kgk = fk.
Поэтому
sl>=»U. □ (2)
Определение. Разложение вида (2) называется полярным
разложением оператора si.
СЛЕДСТВИЕ 1. Утв. Справедливо разложение вида Л^УФ,
где Т — унитарный, а V — неотрицательный операторы.
126

Доказательство. Рассмотрим сопряженный оператор з&*.
Согласно доказанной теореме имеет место равенство
где ЗВ^О и °U унитарен. Отсюда
Полагая У°=<2/* и <&=ЗВ, получаем требуемое. □
СЛЕДСТВИЕ 2. Усл. Линейный оператор з4> невырожден.
Утв. Операторы 9£ и °U в полярном разложении определены
однозначно, причем J?>0.
Доказательство. Из формул $4>—ЗШу \s&*=<U*<% полу-
чаем,что
JLJL* =<®ииш<® ^&3®> = &\
откуда
§ 3. ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
0°. Операция сопряжения в евклидовом пространстве. Пусть
st^£?(Vy W), где V и W—евклидовы пространства.
Обратимся к § 1 этой главы (лекция 17):
Г) сопряженное отображение *я£* равенством (<s£x, у) = (х, s&*y}
определяется однозначно и всегда существует;
2) операция сопряжения *:2?(Vf W)~+3?(W, V) линейна;
3) матрицы взаимно сопряженных отображений в ортонормиро-
ванных базисах е (из V) и / (из W) связаны равенством
**(f9e) = (st(e;f))*.
1°, Симметричный оператор.
Определение. Линейный оператор s&: V-±V называется
симметричным, если (stx, y)=i{x1 s&y) для любых (Векторов х и
у из V.
ТЕОРЕМА 1. Усл. s£<ElS (V, V) — симметричный оператор.
Утв. Существует ортонормйрованный базис пространства V из
собственных векторов оператора s&.
Доказательство. Покажем сначала, что все собственные
значения симметричного оператора вещественны?
Будем рассуждать от противного. Пусть Х=а+ф, 0=^0,—
корень характеристического многочлена линейного оператора st>.
Тогда существует двумерное (подпространство L(x, у), (инвариант-
ное относительно действия ^. При этом выполняются соотно-
шения
s&x=-ax — p#, s&y=$x + ay.
Умножая первое из них скалярно на вектор у, а второе — на век-
тор х и вычитая одно из полученных равенств из другого, по-
лучим
0=(^*, у) — (х9 s$y) = (ax — pi/, у) — {х, $х + ау) =
=-$((х,х) + (у,у)).
127

Так KaiK хфд и уф®, то последнее соотношение может быть вы-
лолнено лишь в том случае, если {$ = 0, что противоречит предпо-
ложению р=£0. И значит, можно утверждать, что любой корень
характеристического многочлена симметричного оператора з4> —
вещественное число a^R.
Перейдем к построению базиса. Пусть fy — собственное зна-
чение симметричного оператора s& и eh |et'| = l—соответствую-
щий собственный вектор: s^ei — hiei.
Положим L<1>=L(e1). Ортогональное дополнение Vn~l к под-
пространству L*1) инвариантно относительно действия зФ. В са-
мом деле, пусть x^Vn~\ т. е. (х, £i)=0. Тогда
{s4>x, е{) = (х, $£ех)=Хх{х, ei)=0,
или, что то же, ^jceV""1.
' Тем самым V=Vn разлагается в прямую сумму одно- и
(п—1)-мерного подпространств, инвариантных относительно дей-
ствия оператора s£:
Рассмотрим симметричный оператор
Пусть кг — его собственное значение и e2t \е2\ = 1, — соответ-
ствующий собственный вектор: «s^—^n-ies^ta^-
Ортогональное дополнение Vn~2 линейной оболочки IS2) = L(e2) в
пространстве Vn~l (инвариантно относительно оператора «я£п-ь а
значит, и s4>. Тем самым
где V»-*=(LW)\
Продолжая аналогичные рассуждения, .приходим к разло-
жению
V= 1/« = I<D©L<2>© ... ©L<*>,
где L^=L(ek)—линейная оболочка, натянутая на единичный
собственный вектор еъ оператора s4>\ J^ek=Xk6k- ^
По построению векторы ёи...-геп ортонормированы. П
Утверждение. Оператор s4> симметричен в том и только в том
случае, если его матрица А(е) в ортонормированном базисе е
дамметрична.
Доказательство проводится так же, как и в унитарном
случае (эрмитовость оператора и его матрицы в ортонормиро-
ванном базисе равносильны). □
При мер. Разностный оператор
Л :iQo, n -*£2i, N-i
действует из пространства сеточных функций Qo.n =if/iU=0, • ••
...,N}
128

в пространство сеточных функций <Qi,iwi = {f/i| i= 1,
по правилу
Ayi = biyi+i — СгУг + йгУ^и 1=1,..., N—\)
Запишем разностную .краевую задачу
Ауг^—fu 1=1,..., ЛГ — 1, Уо = \1, t/i=V
в матричном виде
,N— 1}
ЛГ = Ф,
(*)
где
< — с
а2 —с2 я2
А = —
»г Ьх
О
а//~1—cN—l
:R(N—1)X(N—1)
— трехдиагональная матрица, Ф=(/г+ацх, /г, — .fN-2, /n-i +
+ &n_iv)t—известный, а У= (yi,.. .,у n-i)t— искомый вектор-
столбец высоты N—1.
Соотношение (*) можно рассматривать как линейное опера-
торное уравнение, где
•Л : Qi, N-i->iQif N-i* —
Введем в пространстве Q\, n-i скалярное произведение
Пусть bi=ai+u i—l>-• •»N— 1.
Тогда матрица Л симметрична и выполняется равенство
(Aytz) = (y9Az).
Последняя формула выражает свойство симметричности опе-
ратора Л, а значит, и разностного оператора Л.
Понятия .положительного оператора, корня из оператора и
сингулярной пары базисов, а также их свойства переносятся на
евклидов случай без изменений.
Перейдем к рассмотрению аналога унитарного преобразова-
ния (преобразованием часто называют невырожденный опера-
тор).
2°. Ортогональное преобразование.
Определение. Оператор &>^S?(Vy V) называется ортого-
нальным, если для любых векторов х и у из V выполняется ра-
венство (!Рх, &у) = (х, у).
ТЕОРЕМА 2. Утв. Следующие высказывания равносильны.
1+. 9* — ортогональный оператор.
2+. 9* — изометричный оператор.
5 Заказ 538 ' 129

3+. Линейный оператор 0> переводит ортонормированный ба-
зис в ортонормированный.
4+. &>*=&>-К
5+. &>3* =&>*&> = &.^
6+. Матрица П(е) оператора 3* в ортонормированном базисе
е ортогональна.
Доказательство. 1=^2. Положив в определении х=у,лег-
ко получаем требуемое
|Лс| =V(&x, <Рх) = K(*> х)= \х\. '
2=ф-1. Из тождества
(*. У) = \{\х+У\%-\*\%-\У\*)
вытекает, что если 3 сохраняет длину (изометричен), то он со-
храняет и скалярное произведение (ортогонален).
1=^3. Очевидно.
3=^1. По условию
(&eh,&em) =(ek, em)=bkm.
Пусть x=2,klkek, f/=2wT)mem — произвольные векторы. Тогда
(<*°*. ^) = 2*.«Е*трт(Л*э £>е,»)=:%к,тЪ*г)т(ек, ет) = (х9 у).
1=^4. Из равенств (оРх, &>у) = (х, &*&*у) = (х, у) «в силу лро-
извольности векторов х и у заключаем, что 3y*3*=2f. Отсюда вы-
текаем что оператор & обратим и равенство д>*=0>-х.
4=>-5. Из последнего соотношения требуемые равенства полу-
чаются без труда.
5=^1. Легко видеть, что (9>х, &*у) = (ху &'Ру) = (х, у).
1=^6. Пусть е — ортонормированный баз»ис и
Рек = 2тп?ем, 9*гщ = 2длрдер.
Тогда (£>ekt &>eq) = 2mn^C
Это означает, что П(е) = (пкт)—ортогональная матрица: П(е)*
.ЛТ(е)=1. *
6=^1. Пусть 17=17(е) —ортогональная матрица. Так как П
ыевырождена, то е'=е17 — базис.
Вычислим матрицу Грама системы е'. Имеем
Г (*') = е'те' = (eUfeU = Пт Г (е) П = ПТП = /. ,
Тем самым базис е' ортонормирован. П
Замечание. Ортогональное преобразование (напомним, что
ортогональный оператор невырожден, и потому мы вправе его
/называть преобразованием) сохраняет углы между векторами,
так как
(х, У)
cos ф = 7 .
. \x\-\y\
130

3°. Простейший вид матрицы ортогонального преобразования.
Из свойства 6+ ортогонального преобразования вытекает, что
det^=±l-
Определение. Ортогональное преобразование называется
собственным (сохраняющим ориентацию)," если det^=l, и не-
собственным, еслиЛе1;^=—1.
А. Одномерный случай. Пусть dimV=l. Тогда для любого
вектора х имеем 0>х=Хх; где X — корень характеристического
многочлена. Откуда (*, х) = (&>х, &>х)=Х2(х, х) и, значит, Х=
= ±1. Тем самым
либо &>+х=х и #+=(1),
либо &-х=—х и П-= (—1).
Б. Двумерный случай. Пусть dim V—2 и е—{е\е2)—ортонор-
мированный базис. Тогда матрица
п-п«-(;!)
ортогональна.
+ ) Пусть аб — р-у= 1. Тогда
Vy «'• и*;
в силу ортогональности матрицы. С другой стороны,
/ар\~» / 6-р \
VY б/ \-Y а /
Тем самым
Так как а2+р2=1, то существует такое ф, 0<др<2я, что
a=oos9, P = sin9.
Всякое собственное ортогональное преобразование двумерного
пространства имеет в произвольном ортонормированном базисе
матрицу вида
/сОБф— БШфХ
\5Шф СОЭф/
(поворот в плоскости на угол ф).
—) Пусть аб — yP=1. Тогда характеристическое уравнение
t2 — (a+6)f— 1=0
имеет вещественный корень. Значит, у оператера 9 существует
собственный вектор /ь |/i| = 1 :&f\ = Xifu Так как ^ — ортого-
нальное преобразование, то Xi = ±l. В силу того, что & не изме-
няет угла между векторами и их длин, единичный вектор /г, ор-
5* 131

тогональный fu под действием преобразования & переходит в
единичный вектор, ортогональный /i, т. е. в вектор ±/2-
Тем самым в базисе (fift) матрица 11(f) ортогонального пре-
образования 9> имеет вид
(*; л-
Так как det^=—1, то это
либо ( ), либо I }
(зеркальное отражение относительно одной из координатных
осей).
ЛЕКЦИЯ 19
В. n-мерный случай.
- ТЕОРЕМА 3. Усл. {P:V-*V — ортогональное преобразование.
Утв. В пространстве V существует ортонормированный базис
е, такой, что
( 1
^
Ще) =
^1
О
•1
COS фх -
sin91
-81Пф1
СОБф!
cosqv
sinq>*
-sintp*
СОБф* )
Докажем сначала вспомогательное утверждение.
ЛЕММА. Усл. !?:V-+V — ортогональное преобразование, Wcz
а V — инвариантное подпространство.
Утв. Ортогональное дополнение W1 также инвариантно отно-
сительно действия #*.
Доказательство. По условию 9i(W)ciWJ но так как
оператор 3> невырожден, то он сохраняет размерность и, значит,
&(W) = W9 или, что то же, &>~l(W) = W.
Пусть вектор у лежит в W1-, т. е. (х> у)—0 для любого векто-
ра х из W.
Чтобы доказать справедливость включения ^yeW\ рассмот-
рим скалярное произведение (9>у, х), где вектор х из W произ-
волен. Имеем
(^</, х)=-(у, F*x) = (yt &-*х) = 0
132

(здесь мы воспользовались тем, что для ортогонального преобра-
зования 9* справедливо равенство ^*=<^~1, а также и тем, что
д>-х х лежит в W для любого вектора х из,№).
Доказательство теоремы. Так как & — линейный опера-
тор в вещественном пространстве, то у него всегда существует
инвариантное подпространство W, либо одномерное, либо двумер-
ное. Согласно доказанной выше лемме ортогональное дополнение
к нему W± также инвариантно. Справедливо разложение
v=w@v(lh -
где V{\)=WX. Выбирая в W ортонормировакный базис, получаем
W— W(i) одйомер.но — W'= W{X) двумерно —
п =
+ /
б
о ... о
/
п =
COS (/)
sin (f
0
0
- sin (p
COS (p
0
0
0 •■
0 ••
4
• 0
■ °
1
J
Индуцированный на V(i> линейный оператор
*H)=P\v{l):Vn)-+V{l)
ортогонален. Применяя к нему и пространству V(i> (отметим, что*
dim V(i)<dim V) ранее проведенные рассуждения, находим W&) и
V(2), инвариантные относительно
действия ^(i), а значит, и отно- , 0tl л (Е1)1
сительно &у и такие, что
V(,)=1F(2)©V(2).
Продолжая рассуждения, за
конечное число шагов (каждый
раз происходит понижение раз-
мерности) приходим к разложе-
нию пространства V в прямую
сумму одно- и двумерных подпро-
странств, которые 1) инвариант-
ны относительно ^ и 2) попар-
но ортогональны. Объединяя их ортонормированные базисы в
базис е пространства V, с учетом А и Б получаем требуемое. □
Прежде чем придать полученному результату геометрическое-
звучание, сформулируем два определения (рис. 26).
Определение 1. Простым вращением евклидова простран-
ства Еп называется собственное ортогональное преобразование с
матрицей
Рис. 26
133

о
1
COSCp—БШф
I ~ sincp costp I
I 'l '
— поворот в двумерной плоскости £2, оставляющий неизменными
векторы из £л~2= (Е2)2-.
Определение 2. Простым отражением евклидова про-
странства Еп называется несобственное ортогональное преобразо-
вание с матрицей
I l I
1 О
( 0 )
которое меняет направление всех векторов прямой Ех яа противо-
положное и оставляет неизменными векторы ш ЕГ*~1=(Е1)±.
ТЕОРЕМА 4. Утв. Всякое ортогональное преобразование мо-
жет быть представлено в виде суперпозиции конечного числа про-
стых вращений и простых отражений.
4°. Разложения линейного оператора в евклидовом простран-
стве.
Определение. Линейный оператор s&: V-+V называется
кососимметричным, - если сопряженный ему и противоположный
совпадают: j^*=—$Ф.
ТЕОРЕМА 5. Усл. s^^3?(V\ ^—произвольный оператор.
Утв. Существует единственная пара операторов & и 9^
&3?(Vt V), таких, что 3& симметричен, Ф кососимметричен и
Доказательство. Легко проверить, что операторы
удовлетворяют утверждению теоремы; единственность вытекает
из того, что разложение st=38+<ff9 где 0& — симметричный, а
V — кососимметричный, операция сопряжения переводит в ,$#*=*
*=J7 — 9. Откуда легко следует, что
ТЕОРЕМА 6. Усл. ste2?(V, ^—произвольный оператор.
134

Утв. 1. Существует неотрицательный оператор <%^0 и ортого-
нальное преобразование ^, такие, что s£=M&> (рис. 27).
2. Если оператор s& невырожден, то указанное разложение един-
ственно; При ЭТОМ <M=Y*A^*> oP — oB^iA-
§ 4. КВАДРАТИЧНЫЕ ФОРМЫ
В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
Пусть V — n-мерное евклидово
пространство.
1°. Билинейная форма.в евкли-
довом пространстве.
ТЕОРЕМА 1. Усл. «$(*, у) —
билинейная форма, заданная на
пространстве V.
Утв. Существует однозначно
определенный линейный оператор *
а: V-+V, такой, что для любых векторов х и у из V выполняется
равенство Щх, у) = (я£х, у).
Доказательство. Существование. Пусть е — ортонормиро-
ванный базис в пространстве V. Вычислим В(е). Имеем В(е)=я
= (P*i), где (pfti)=J7(eft) ej). Тогда
Л(х,у) = 22?/-1рл/6*л/.
Построим линейный оператор s£ : V->V по следующему правилу!
где aftm=pftm, т. е. матрицы оператора s4< и формы $ в базисе е
равны: А (е)=В(е).
Тогда
<Ax = ZklkJlek = 2ktmlkaZem
и
(Лх, у) = Ък,тЛ^<*<к{ет, et) = Sk,/6*T|/ai =
Единственность. Пусть ,$(*, */) = (,я£х, у), где ^:У->У —ли-
нейный оператор. Тогда
{Мх, у) = (ах, у)
для любых векторов х и у m V. Откуда 'получаем, что ((*я£-—
— $&)х, у)=0 для любого вектора у -из V. Полагая у=(М —
— *я£);с, приходим к равенству (J& — s£)x=Q> из^ которого в
силу произвольности вектора х вытекает, что s4>=$t>. П
Замечание 1. Если билинейная форма & 'симметрична, то
^ — симметричный оператор.
135

.' Замечание 2. Теорема справедлива и в случае, если про-
странство V унитарно, а &&{ху у)— полуторалйнейная форма.
Лричем если J? эрмитова, тои^ эрмитов.
2°. Приведение квадратичной формы к главным осям.
ТЕОРЕМА 2. Усл. 38{х, х)—квадратичная форма, заданная
на евклидовом пространстве V.
Утв. В пространстве V существует ортонормированный базис
е< такой, что
Я(<х)=2,А*(£*)2, (1)
где *=2fcgfteft.
Доказательство. По теореме 1 предыдущего пункта би-
линейная форма, полярная &{х, х), допускает представление
Д{х, у) = (<&х, */)Г
где s& — симметричный оператор. Поэтому в пространстве V су-
ществует ортонормированный базис е из собственных векторов
«s£. Тогда для любого вектора х=2ч£кеь справедливо разложение
stx=ZktkKkek.
Отсюда Я{х, x) = (stx, x)=Zkbk(Zh)2- П
Определение. Операция построения ортонорм'ированного
базиса, относительно которого заданная квадратичная форма мо-
жет быть за/писана в-виде (1), называется приведением квадра-
тичной формы к главным осям.
ТЕОРЕМА 3 (о паре квадратичных форм). Усл. V — п-мерное
вещественное пространство, &(х, х) и Ф(х, х) — квадратичные
формы, заданные на V, причем Ф(ху х)>0.
. Утв. В пространстве V существует базис е, такой, что
Я(х, x)=Zkkh(tk)2, V(x, *)=2fe(Eft)2,
где x=2klkek.
Доказательство. Введем в пространстве V скалярное
произведение, положив ло определению
(x,y)^V(x,y).
Теш самым пространство V превращается в евклидово. По преды-
дущей теореме в нем существует ортонормированный базис е, для
«которого Я(х, х) =SfeA,fe(.gfe)2, где x=^hlhek.
Так как е — ортонормированный базис, то
(х"х)—У(х, x)=2ft(P)2. D
Замечание. Аналогичные утверждения справедливы в .ком-
плексном случае для эрмитовых квадратичных форм (схемы до-
казательств те же).
136

§ 5. ГИПЕРПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА В ЕВКЛИДОВОМ
ТОЧЕЧНОМ ПРОСТРАНСТВЕ
1°. Точечные пространства. Пусть V — n-мерное вещественное
линейное пространство.
Рассмотрим непустое множество £2, элементы .которого будем
называть точками и обозначать прописными латинскими буква-'
ми Л, В,... .
Отображение
r:QXQ->V
каждой упорядоченной паре точек из множества Q ставит в со-,
ответствие вектор из пространства V:
(Л, Я)е=ЙХЙ~ r(A, B)e=V.
Обозначение: г (А, В)=ЛВ.
Определение 1. Точка А называется началом вектора,
АВ, а точка В — концом вектора АВ.
Мы ограничимся рассмотрением оюбражений, обладающих
следующими свойствами:
1) Для любой точки А из Q и любого вектора г из V най-
дется точка Б, такая, что АВ'=г.
2) Для любых трех точек Л, Ву С из Q выполняется равенство
AB + BC + CA = Q.
3) Из равенства AB = Q всегда следует совпадение точек
Л и В.
Определение 2. Множество Q, рассматриваемое вместе 'с
отображением r:QXQ-+V, обладающим свойствами 1)—3), на-
зывается n-мерным точечным вещественным пространством; его.
элементы называются точками.
Замечание. Конечно, можно рассматривать точечные про-
странства и над произвольным полем.
Рассмотрим примеры точечных пространств.
Пример 1. Построение в курсе аналитической геометрии
линейного пространства векторов на плоскости — У2— проводится
с одновременным построением отображения г, очевидно обладаю-
щего свойствами 1)—3). В качестве Q здесь выступает плоскость.
Пример 2. Пусть и множество (Q и пространство V совпа-
дают с /г-мерным координатным пространством Rn. Тогда
А=(а1,...,а»), В=(р1,...,р-)-Л1=(р1-а1,...,р--а-).
Полученное точечное пространство называется n-мерным то-
чечным координатным пространством.
Непосредственно из условий 1)—3) и аксиом линейного ,про-)
странства1вытекают следующие утверждения. _
1+. Для любой точки Л из й выполняется равенство AA = Q.
1Э7

Доказательство. Воспользуемся свойством 2). Положив
Л=£ = С, получаем, что ЗЛЛ==6. □
2+. Для любых двух точек А и В ш Q выполняется равенство
АВ=—ВА.
Доказательство. Воспользуемся свойством 2). Положив
J3 = C, с учетом 1+ получаем, что AB+BA=Q. О
3+. Для любых трех точек А, В и С из Q выполняется равен-
ство АВ+ВС = АС.
Доказательство. Требуемое соотношение вытекает из
свойства 2), шереписанного в эквивалентной форме АВ + 5С=
^=—СА и 2+ П
4+. Из равенства векторов АВ и АС вытекает совпадение то-
чек В и С.
Доказательство. Согласно 3+ АС=АВ+ВС. Так как по
условию АВ=АС, то ВС—6. Отсюда в силу свойства 3) полу-
чаем, что В —С. О
Зафиксируем произвольную точку О из iQ. Тогда каждой точ*
ке А из Q можно поставить в соответствие вектор <из V по сле-
дующему правилу:
r:Az=Q*-+OA<=V. (1)
Обозначение: г (А).
5+. Отображение (1) взаимно однозначно.
Доказательство. Инъективность. Из равенства г(А) =
&=г(В), или, что то же, ОА = ОВ, в силу 4+ вытекает, что А=В.
Сюръективность. Пусть г — произвольный вектор из V. Тогда
согласно свойству 1) найдется точка А из Q, такая, что г[А) —
^OA = r. U
Определение 3. Вектор г (А) называется радиус-вектором
точки А с началом в точке О.
Пусть е= (е\... еп) — базис пространства V. Тогда каждой
точке А из множества Q можно поставить во взаимно однознач-
ное соответствие упорядоченный набор чисел (а1,.. .,<хп), кото-
рый определяется из следующего соотношения:
г(А) = бА=Я}-га?е;: (2)
Определение 4. Набор {О; еи...,еп), состоящий из точки
отсчета OsQ и базиса е пространства V, называется (аффинным
координатным) репером точечного пространства.
Определение 5. Числа а1,...,ап, определяемые соотноше-
нием (2), называются (аффинными) координатами точки А отно-
сительно репера {О; ей • • •, £п}.
Обозначение: А (а1,..., а71).
Утверждение. Для любых точек А (а1,..., ап) и В (р1,..., рп)
справедлива следующая формула:
АВ = ОВ—бА = S/-1 (&—of) er
138

Определение 6. Точечное пространство & называется ев*
клидовым, если V — евклидово пространство.
Определение 7. Бели точечное пространство евклидово, а
базис е — ортонормнрованный, то аффинные координаты точки
называются декартовыми координатами.
В евклидовом точечном пространстве 6 естественно рассмат-
ривать декартовы координаты точек.
ЛЕКЦИЯ 20
1°. Приведенные уравнения гиперповерхностей второго поряд-
ка. Пусть 6п — л-мерное точечное евклидово пространство и О —
произвольно выбранная начальная точка. Тогда каждой точке М
из 6п ставится в соответствие вектор х~ОМ.
Если {О; е) — ортонормированный координатный репер, то
М(1\... ,1п), где ОМ=^е{ + ... +Ъ*еп.
Рассмотрим квадратичную форму s£(x, х), не равную тожде-
ственно нулю, и линейную форму 3$(х).
Определение 1. Гиперповерхностью второго порядка в
точечном пространстве 6п называется множество точек, таких,
что
st(xt x)+238(x)+y=Q, (l)
где у — постоянная. "
Пользуясь координатной записью векторов и форм, равенство
(2) можно записать в следующем виде:
я.!-**,?*/+22a.ipme»+y=о, (г>
где
Определение 2. Формула (1) (и формула (Г)) назы-
вается общим уравнением гиперповерхности второго порядка
(в ортонормированием репере).
Замечание. Следует иметь в виду, что множество точек»
координаты которых удовлетворяют уравнению (1'), может Ока-
заться пустым.
Покажем, что для любой гиперповерхности второго порядка в
евклидовом точечном пространстве можно указать такой орто-
нормированный репер, относительно которого уравнение гиперпо-
верхности запишется либо в виде
М|*)2+...+М£02+?=о, (А);
либо в виде
МГ)2+...+МГ)2=2цГ+1 ' (Б)
(здесь (g1, ...,£n)—координаты произвольной точки М гиперпо-
верхности в репере {О; еи ..., еп}).
139

ШАГ 1. Известно, что для любой квадратичной формы
зФ(ху х) можно указать артонормированный базис /, такой, что
для любого вектора *=Е*т|*/ъ справедливо разложение
М(х, х)=2цХк(г)к)2.
-При переходе от репера {О; ё) к реперу {О; f) уравнение гипер-
поверхности (V) преобразуется в уравнение вида
2\=lkk(y\ky+22nk=liik4k+y=0. (2)
Таким образом, первый шаг — это смена базиса:
{О; е}-ЧО; f).
ШАГ 2. Можно считать, что h #0,..., A,r#0, Vh = ... =К—
—0, где r=rangs&(x, x).
Рассмотрим Л^#0, k= 1,..., г. Тогда
,2
МЛ*)2+2^П* = Я*(п* + -g-)' ^
ь*
Преобразуем координаты посредством следующих формул:
^вЧ» + ^_(А= 1, .... г), # = ч*(*=г +1, ..., я).
Это позволяет записать формулу (2) в несколько ином виде:
2*_,Я4 (?)2 + 223-^-Ш*П* + Y = О," (3)
где y = Y—2ft=i-^--
Таким образом, второй шаг — это смена начальной точки:
\ . {О; ПМО, f}.
Подведем некоторые итоги. Возможны два случая:
. (A) \ir+i= ...=Цп=0.
(Б) Среди \ir+u • • •, \*>п есть отличные от нуля.
Случай А дальнейших преобразований координат пространства
не требует (см. формулу (А)).
Обратимся к.случаю Б.
ШАГ 3. Пусть jift^O, где г+1<г<л. Преобразуем координа-
ты ^посредством следующих формул:
5* = ч\ A=l,r..,r;
г*
С=2*1н-1^Ч*. Я = г + 2, ...,п.
440

Здесь числовой множитель ц выбирается из условия
а коэффициенты в выражениях^для £г+2,..., £п следует взять таку
чтобы матрица
(
1 °
I °'ч
0
0
Mih-^niA
I V* I
/
была ортогональной (последнее необходимо для того, чтобы но-
вый базис, соответствующий этому 'преобразованию координат,
был вновь ортонормированным).
Таким образом, третий шаг — это еще одна смена базиса
{6;/} +{О; А}.
В результате проведенных преобразований от формулы (3)
переходим к равенству
^imk)2=wr+l-y- . (4)
В случае, если уФЪ, возникает необходимость, еще одного
шага.
ШАГ 4. Преобразуя координаты посредством формул
приводим равенство (4) к следующему соотношению:
Таким образом, четвертый шаг — ато еще один перенос
{О; А}-*{О; А}.
Замечание. Следует иметь в виду, что при переходе от од-
них координат к другим преобразуется некоторое алгебраическое
выражение, (которое может и не соответствовать ни одному гео-
метрическому объекту.
2°. Классификация гиперповерхностей второго порядка в то-
чечном евклидовом пространстве. В предыдущем пункте было
показано, что в точечном евклидовом пространстве можно вы-
141

брать ортонормированный репер {О; ё) так, что уравнение задан-
ной гиперповерхности Гп-1
st(x> х)+2&{х)+у=0
(приводится к одному из нижеуказанных видов
М^)2+...+МГ)2+Т=0, (А)
h(c,l)2+..-+lr(tr)2=2\itr+l> (Б)
где Кгф 0, ... , Хгф 0, iiф 0; х = ZLi&V
Подвергнем полученные уравнения (А) и (Б) дальнейшим
упрощениям.
Случай А. Положим
а (КТуДГП если y=£Q,
1КТ7|ЯГГ если y = 0.
Тогда соотношение (А) приводится к следующему виду:
(перенумерацией координат, или, что то же самое, базисных век-
торов всегда можно добиться того, чтобы первыми шли положи-
тельные слагаемые (если они есть)). Возможен и /случай, когда
отсутствуют все положительные или все отрицательные сла-
гаемые.
Начнем рассмотрение с невырожденного случая — г=п„
Ц1) р=я — Эп~{— {п— \)-мерный эллипсоид,.
^=0 — мнимый (п — 1) -мерный эллипсоид,
0<р<п — grn-i— (я—,1) .мерные гиперболоиды;
Ц°) р=0, п —мнимый конус,
0<р<п — Жп~1 — (л — \)-мерные конусы второго по-
рядка.
Вырожденный случай — г<п.
Рассмотрим ортонормированный репер {О; ви...9ег} и соот-
ветствующее ему /^мерное точечное евклидово пространство. Для
точек пространства &г уравнения (Ц) описывают невырожден-
ный случай ((г—1)-мерные эллипсоид, гиперболоиды и конусы
второго порядка). Чтобы получить представление о гиперповерх-
ности во всем объемлющем пространстве 6п, необходимо в каж-
дой точке Гг-1 поместить (п—г)-плоскость, параллельную
L(er+\,... ,£n).
Множество точек из 6п, лежащих на всех таких плоскостях,
образует исходную гиперповерхность Гп-1 (рис. 28).
Таким образом, Гп-1 представляет собой цилиндр Гп-1 =
= rr_iX<Sn"r с поверхностью Гг-1 в качестве направляющей (она
определяется уравнением (Ц)) и образующими плоскостями, па-
раллельными 6п~г.
142

Случай Б. Положим
«*=(/ -J-. k=l г.
Тогда соотношение (Б) приводится к следующему виду:
(I1)* , (|Р)* (§рп)1 (Г)2 _otr+» m\
9 9 2 * " " 2 b • \/
al ap ap+l ar
В невырожденном случае — r=n—1 — множество точек про-
странства 6П, описываемого уравнением (П), называется (п —
— I)-мерным параболоидом <рп~х, а в
вырожденном возникает цилиндричес-
кая поверхность. Остановимся на этом
подробнее.
Итак, г</г—1. Рассмотрим орто-
нормированный репер {О; ей . ••> £r+i}
и соответствующее ему (г+1)-мерное
точечное евклидово пространство 6r+l.
В пространстве <Sr+1 гиперповерхность
Тг представляет собой r-мерный пара-
болоид &г. Чтобы получить представ-
ление о строении гиперповерхности
Гя-i во всем пространстве &пу нужно
в каждой точке поверхности &г по-
местить плоскость, параллельную
L(l?r+2,-..., en)=L±(eu ..., er+i). Мно-
жество точек из ёп, лежащих на всех Рис. 28
таких плоскостях, образует исходную
гиперповерхность Гп-ь
Таким образом, Гп_1 представляет собой (параболический)
цилиндр ё*гхбп~г~~1 с направляющей поверхностью ё*т (она
определяется уравнением (П)) <и образующими (п — г — 1)-плос-
костями, параллельными 6п~г-1.
Пример. Рассмотрим в пятимерном пространстве б5 гипер-
поверхность, заданную уравнением £2=2г). Пусть (|о, Ло, *, У,
z)—точка из 65, • координаты которой связаны равенством go2=
^==2tio. Нетрудно видеть, что множество точек {(|о, Ло, х, у, г)} в
пространстве б5, где х, у, ^eR произвольны, представляет собой
трехмерное линейное аффинное многообразие, параллельное
{(О, 0, х, у, z)\xyyy ze=R}.
Объединение 3-плоскостей такого вида и есть искомая гипер-
поверхность.
?М2 = /

Глава VI. НОРМИРОВАННЫЕ ПРОСТРАНСТВА
§ 1. НОРМА ВЕКТОРА
1°. Определение и примеры. Пусть V — линейное пространство
над числовым полем P(Q, R, С).
Определение 1. Пространство V называется нормирован-
ным, если задано отображение
l-hV-R. . .
т. е. каждому вектору х из V ставится в соответствие число
\х\—норма вектора х, со следующими свойствами: 1. |х|^0,
[х\=д**х=в. 2. |а*|==|а||*|, ае=Я. 3. \х+у\^\х\+\у\ (не-
равенство треугольника).
Рассмотрим некоторые примеры.
Пример 1. Пусть V — л-мерное евклидова пространство. По-
кажем, что в нем можно» ввести норму (сделать его нормирован-
ным) многими разными способами.
(а) \х\Е = У(х9 х)—евклвдова норма
(доказательство свойств .нормы см. в пункте 2° § 1 главы П>
лекция 5).
(б) Пусть бФ: V-+V— положительный оператор. Тогда из «его
можно извлечь квадратный корень: бФх/2.
Рассмотрим скалярное произведение (<&х, х).
Нетрудно убедиться в том, что |#|е#= \<А ! х\Е обладает все-
ми свойствами нор/мы.
Определение^. Величина |х\ <& называется энергетиче-
ской нормой вектора х, определяемой оператором $1>. ■
. Отметим два свойства энергетических норм:
.(здесь s& и ^—положительные операторы, а>0).
Пример 2. Пусть х= (^,...,gn) —произвольный вектор лю-
бого из координатных пространств Qn, Rn или Сп. Тогда
• l*|p=(2LilS*lp)I/p,>eN,
— норма. (Доказательство неравенства треугольника в случае
р=2 проводится при .помощи неравенства Коши—Буняковского,
а при р^З при помощи неравенства Гельдера.)
Задача. Доказать, что
|*U=max |6*| .
— норма вектора в координатном пространстве Ck.
144 ,

Пример 3. Рассмотрим комплексное пространство прямо-
угольных матриц размера kXn— С^хп- Тогда
|Л|1= max 2*^1^/1,
\a\^(zU^U\^\2)x/\
|Л|оо= max 2/^1 \<хч\
— нормы матрицы А= (ац)^Скхп-
2°. Шар и сфера в конечномерном нормированном простран-
стве. Пусть V — n-мерное нормированное пространство, х0 —
фиксированный вектор из V, г>0.
Определение 1. Множество векторов из V В0п(хо, г) =
={х\\х — Хо\<г} называется n-мерным открытым шаром радиуса
г с центром в Хо.
Множество векторов из V Sn~l(xo, r)={x\\x — Хо\=г} назы-
вается (п—1) -мерной сферой радиуса г с центром э *о-
Множество векторов из V Вп(хь г)={х\\х — х0|<г} назы-
вается n-мерным замкнутым шаром радиуса г с центром в xq.
Определение 2. Будем говорить, что последовательность
векторов {xk} сходится к вектору а по норме, если
lim \xk—a\ = 0;
вектор а называется пределом последовательности {*&}.
Обозначение: Xh->a. ~
Для дальнейшего нам понадобится следующее свойство шара
(замкнутого) и сферы.
ТЕОРЕМА 1. Усл. {xk} — произвольная * последовательность
векторов из Вп(х0, г) (Sn-l(x0l r)).
Утв. Существует подпоследовательность * {хт} последователь-
ности {Xk}, сходящаяся по норме к вектору
а из Вп(лго, г) (Sn~l (хо, г)).
Доказательство сформулированной теоремы проведем
для случая, когда норма в 'пространстве V является евклидовой
(введенной «а базе скалярного произведения, см. 'пример 1 (а)
из предыдущего пункта)., Кроме того, для простоты выкладок бу-
дем считать, что #о=9-
Выберем в пространстве V ортонормированный базис еь...
...., еп. Тогда для любого вектора
Гёльдер (Holder) Отто Людвиг (22.12.1859—29.8.1937) — немецкий мате-
матик.
145

«з {xk}czBn (г) его норма удовлетворяет соотношению
1**1я = (2?=,||{|2)1/2<г.
Это означает, в частности, что числовые последовательности
Ш>.Щ> {££}
ограничены. Согласно теореме Больцано—Вейерштраоса, извест-
ной из курса математического анализа, у последовательности
{Ik1} существует сходящаяся подпоследовательность {g*1}, g^-^-a1.
Переходя к набору подпоследовательностей
тлщ) а?}.
на основании той же теоремы выделяем из подпоследовательно-
сти fe2} сходящуюся {lq2}: g^-Mi2.
Продолжая эти -рассуждения, в результате получаем набор из
л последовательностей координат
(ёт/> \£т/> • • • > ibm/>
для каждой из которых справедливо 'следующее:
Vm-< &+«2 £-<*».
Положим а = 2jL1a/ey. Тогда для подпоследовательности
{хт}> где ^m = S/LiS^/f исходной последовательности векторов
{xk} выполняется следующее предельное соотношение:
\Xm-a\=(2U\&-*i\2)l/2-+0. -
Таким образом, подпоследовательность {хт} сходится к векто-~
ру а по норме.
Покажем, что а^Вп(г).
Из неравенства треугольника легко следует, что для любых
векторов д: >и у из V выполняется неравенство
\\х\-\у\\<]х-у\.
В рассматриваемом случае | \хт\ — \а\ \^\хт — а|->0.
Отсюда и из того, что |хт|</, получаем, что |а|<г.
Аналогичными рассуждениями для сферы Sn~l(r) получаем
]a\=r. D
ЛЕКЦИЯ 21
3°. Эквивалентные нормы. Пусть V — n-мерное комплексное
линейное пространство, в (котором построены две различные нор-
мы |*|i и \x\2-
Больцано (Bolzano) Бернард (5.9.1781—18.12.1848) — чешский математик;
Вейерштрасс (Weierstrass) Карл Теодор Вильгельм (31.1Q.1815—19.2.1897) —
немецкий математик, член-корреспондент Петербургской АН (с 1864 года).
146

Определение. Будем говорить, что нормы |-|i и |-|2 эк-
вивалентны {обозначение: Ы i~ 1'Ы, если найдутся положи-
тельные постоянные с\ и с2, такие, что для любого вектора х иа
пространства V выполняются неравенства
M2<ci|x|i, |*|i<c2|x|-2.
ТЕОРЕМА 2. Утв. Любые две нормы в пространстве V экви-
валентны.
Доказательство. Выберем в пространстве V базис еи * +
..., еп. Введем скалярное произведение
где x=Ilhlkek и у=?>ъу\кек, и евклидову
норму
WB=(a-ii6*if)1/2.
Пусть | • | — другая норма в прост-
ранстве V. Покажем, что| • |д~ | • | (рис.
29).
1. |x|<CiMje.
Пусть Af=max{|^i|,..., \еп\}. Тогда
для любого вектора х из пространства V
получаем
1*1 = |2tf4l<2* 16*1 \ek\<
<M-2k \%k\-l <МУ2^Т2 V~n
(последняя оценка вытекает из неравенства Коши—Бундовско-
го). Полагая сг = М Vn, получаем требуемое |*Kci|xU.
2. |*U<c8|*|. :
Рассмотрим множество
S«-) = {xs=-V\\x\=\}
i— единичную сферу относительно нормы | • | — и покажем, что
координаты всех векторов из Sn_1 ограничены в совокупности.
Предположим противное: пусть какая-то координата (для
определенности — первая) не ограничена. Это означает,^ что для
любого meN найдется вектор хт, удовлетворяющий условию
| хт | = 1 и такой, что 111т \ > т. Тогда
\*т\в = УЫ&\%> \&\ >т.
Рассмотрим последовательность векторов
* . Хт
Ут ~~! ! »
. ' \*т\Е .
принадлежащих евклидовой единичной сфере SEn~K В силу тео-
147

{ремы 1 (пункта- 2° можно считать, что ут-+Ь по норме |-|я, при
этом |Ь|я=1. Следовательно, Ьфв.
Из сходимости по норме \-\Е в силу доказанного в части 1
неравенства |х\ ^С\ \х\е вытекает, что
\tfai — b\^ci\ym — b\B,
т. е. последовательность ут сходится к вектору Ь по норме | • |.
Так как |хт|=1 и \хт\Е>т, то
\Ут\=^-< — ->0(m-voo).
\хт\Е гп
Следовательно, уш-*® по норме J-|. Отсюда вытекает, что Ь = 9.
Это дает желаемое противоречие.
Таким образом, можно считать, что
A^=sup max |£*f<oo.
Так как для любого вектора х = Ък1£екФ6 выполняется соот-
ношение
— = Zk-2-ekeSr{,
1*1 1*1
то *ло доказанному |lk\^N\x\.
Поэтому
\x\E=V2h\lk\*<VnN*\x\*.
Полагая c2 = \fnN9 -получаем, что Г*|я^сг|х|. Чтобы завершить
доказательство теоремы, заметим, что из | • |я~ | ■ 11 и Ыя~ 1"Ь
следует: | - j i— | - j 2. CD
Замечание. Из доказанной теоремы вытекает, что дока-
занное в пункте 2° свойство замкнутого шара и сферы справед-
ливо для любой, а не только евклидовой нормы, так как из экви-
валентности норм вытекает, что сходимость или расходимость по-
следовательности векторов не зависит от выбора нормы.
§ 2. НОРМА ЛИНЕЙНОГО ОТОБРАЖЕНИЯ
1°. Согласованные и подчиненные нормы. Пусть V и W — ко-
нечномерные комплексные пространства. Линейное пространство
3?{V, W) линейных отображений из V в W «можно сделать нор-
мированным, причем многими способами (как и всякое линейное
пространство).
О п рче д е л е н и е 1. Норма линейного отображения s& назы-
вается согласованной с векторными нормами в пространствах V
и W, если для любого вектора х из V выполняется неравенство
\<Ax\w< \Л\ \x\v.
Отметим одно интересное 'свойство согласованной -нормы ли-
нейного оператора в комплексном пространстве.
148

Утверждение. Пусть Я — собственное значение линейного опе-
ратора s4>, норма которого согласована с нормой в пространстве
V. Тогда |Х|<|^|.
Доказательство. По условию существует вектор Jt, |jc| =
= 1, для которого s£x=hx. Отсюда получаем, что J
|Я| = |Я| \х\ = \Хх\ = \Лх\ < \<А\ \х\ = \Л\. П
Пусть цорма |^| линейного отображения s£ согласована с
нормами V и W. Тогда для любого ненулевого вектора х из про-
странства V справедливо неравенство
\х\
Так как правая часть последнего неравенства не зависит от вы-
бора вектора х, то
sup -—■
хФВу 1*1
< \Л\.
Положим
Ясно, что
ji(t^)= sup
\Лх\
ХФЪу \Х\
(1)
(i^-supl^f-^-)
- x*ev\ \ \х\ )
= sup \,Ay\.
1уЫ
Утверждение. \i(A)—норма в пространстве &{V, W).
Доказательство. 1. Нетрудно видеть, что \x(s£)^0. Из
равенства \i(s&)=0 получаем, что \s£y\=Q для любого вектора
у и, значит, st=C Два других свойства: 2. \i(as&)*=\a\\i(st>) и
3. м,ДО+^Х|л(«я£) +\х(3$) вытекают из свойств точной верхней
храни.
Определение 2. Число \x(st)f определенное формулой (1),
называется нормой линейного отображения s£f подчиненной нор-
мам пространств V и Wr или, коротко, подчиненной нормой.
Таким образом, подчиненная норма является наименьшей из
всех согласованных (с данными векторными) норм.
ТЕОРЕМА 1. Усл. Ж<=2(У, W), &*=&(№, Z).
Утв. ii(&s&)^\x(38)ii(st).
Доказательство. Нетрудно видеть, что
[i(<»^) = sup |^^|=>иР (\т (ттт)\-\Лх\) <
fxM \ \х\=\ \\ \\Лх\ j \ j
< sup \Щ\ sup \Лх\ =ц((Я)(г((^). п
149

Прям е.р. Пусть V=Rn, W=R* и Л e=Rftxn: R"-^Rft. Пока-
жем, что норма
\A\t= max 2JL1 \aif\ (2)
подчинена векторным нормам |x|1 = 2yLi \%'\ и |.(/|1 = 2Li |Л*|.
Имеем
11г(А)= sup \Ах\г =
= sup 2Й.1 IZ^-iaf/^l.
Пусть /о — то значение индекса /, при котором в правой части
формулы (2) достигается равенство. Рассмотрим вектор
Хо=(0,..., l,...,0)e=Rn. Тогда
/•
Н(А)>^1Ы = \А\Х.
С другой стороны,
Ъ(А)< sup 27-4(|6/|2?-i|oi/|)<
< max 2?., \ai}\ = |Л|Г-
Таким образом, \i\ (A) = |Л11.
Аналогично доказывается, что норма
\А\Ф = max 2/Li |а,,|
подчинена векторным нормам | х |«, = max | ^ | и | у |«, = max | ц' |.
2°. Спектральная норма. Пусть V и №— унитарные простран-
ства, s£ : V-^-W — линейное отображение.
Определение. Число .
\<А\ = sup \Лх\Е= sup ]/(t^x, u^x)
называется спектральной нормой линейного отображения ,я£.
ТЕОРЕМА 2. Утв. \ЛI = V^max{v?, ... , v*}, где vi2,..., vn2-
собственные значения оператора *я£*«я£.
150

Доказательство. Выберем в пространстве V ортонорми-
дюванный базис из собственных векторов полуположительного
оператора s&*s£^0. Тогда
• &^
\о£\2 = sup (<Axt rAx)= sup (ху Л*<Ах) =
= - sup S/"eivJ|E/|«<max v),
sJLils'i"-1 1</</г
так как все Vj2 неотрицательны, х = S/Li lje/.
Чтобы убедиться в том, что максимум достигается, достаточно
взять вектор х0 с координата ми £ie = l, gj=0, /=з£/о.
СЛЕДСТВИЕ. Усл. s& — эрмитов оператор.
Утв. |^|=тах|Я(^)1 = sup \(<Лхух)\.
1*1=1
Спектральная >норма обладает еще одним замечательным свой-
ством.
Утверждение. Спектральная норма линейного отображения не
изменяется при унитарных преобразованиях пространств.
Доказательство. Пусть %L\ и % — унитарные преобразо-
вания пространств V и W соответственно. Вычислим 'квадрат
спектральной нормы линейного отображения ,$=%j^2/i.
Имеем
| & |2 = sup (Ях, Ш) = sup (UvAUxXr Ut^Ui*) = -• ■
- sup (U2^(UiX),U2^(Ui^))-^P(U^y,U2^y)^
= sup (<Ay, l£fU*b4y)=sup {<Ay, <Ay)=\<A\2. □
M-i H=i
3°. Евклидова норма матрицы. Пусть Сп и Ск — координатные
пространства и А : СП-*СА. Положим
Г^Ь = (2?-12!7-1 la^l»)172.
где А = (аг-j) eCft Xn.
Нетрудно убедиться в том, что \А\Е является нормой в простран-
стве CftXn-
Отметим некоторые ее свойства.
1+. Пусть ЛеС^хп и BeCjxfe. Тогда
|ВЛ|£<|В|Я |Л|£:
Доказательство.
|A4|£<(ZL2jLi |S?-iftA,|1)1/8<
<(2Li23L,(24.jpto| KI)2)1/2<
<(SLi 2^(25=1 IM2)(2ti |cc,/|2))1/2 =
= ((2L2ti IPfclf)(2li2jLi 1%12))1/2= |5|е-И|£. П
151

2+. Норма \А[Е согласована с векторными нормами 1 л:].2 ==
= (2|^И)'/2-и Ы2=(2М*)'/>.
Доказательство проводится по той же схеме, что и для
свойства 1+. □
3+. | Л11 = tr (Л^4) = tr (ЛЛ*).
Доказательство проводится путем непосредственного вычисле-
ния. D
4\ |i4|£ = SjLiV/, где vi2, ...,vn2 — собственные значения
матрицы А*А.
5\ |Л|| = 2?=1^, где vi2, ...,vfe2 — собственные значения
матрицы ЛЛ*.
Доказательство свойств 4* и 5+ проводится так: сумма
собственных значений равна следу матрицы, далее — свойство
3+ □' '
Пусть s& : V-+W — линейное отображение, переводящее векто-
ры унитарного пространства V в векторы унитарного простран-
ства W. Выберем в пространствах V «и W ортонормированные ба-
зисы е и f соответственно. Вычислим евклидову гаорму матрицы
A (et f) линейного отображения зФ относительно этой пары бази-
сов. Пусть, далее, ег и /' — другая пара ортонор:М1Ированных бази-
сов пространств V и W соответственно. Тогда
6+. \А(е\П\в=\А^П\Е.
Доказательство. В самом деле, пусть & и Г — матрицы
перехода от «пары е, / к паре е\ f':e'=eSy f—fT. Тогда 77Г=
=Л5. Вычисляя \ТА'\2Е и \AS\2E> получаем, что
\AS\2E = tr(ASS*A*) = tr(AA*)= |Л||,
\TA'\\ = ir(A'*T*TAf) = iv(A'*A')=\A'\\. □
ЛЕКЦИЯ 22
4°. Экстремальные свойства собственных значений самосопря-
женного оператора. Будем считать для определенности, что V —
Аимерное евклидово пространство, S&.V-+V — симметричный опе-
ратор. (Случай унитарного пространства и эрмитова оператора
•рассматривается без каких бы то ни было изменений.) Построим
в пространстве V ортонормированный базис газ собственных век-
торов оператора s^:e=(e\...en). Пусть Ai<... <ЯП — соответ-
ствующие собственные значения.
ЛЕММА. Усл. Вектор х из L(et9 •.. ,es)()SnE~~l, где 1</<s<
^п, произволен; SEn~l — евклидова сфера.
Утв. lt^(stx, x)^Ks.
Доказательство. Под действием оператора s4> вектор
x = 2Sk=tlkek переходит в вектор
152

Вследствие того, что векторы еи...,еп ортонюрмированы, имеем
{JLxtx) = ^UtK\lk\^
Учитывая способ нумерации векторов базиса и соответствующих
им собственных значений, а также условие
получаем, что
Равенства достигаются соответственно на векторах et и es. □
Рассмотрим множество векторов
srl=Hel9...9er)f\Sk-1.
Это векторы линейной оболочки £(*ь ...,ег), длины которых рав-
ны единице. В силу леммы для любого вектора из этого множе-
ства, x^Sr-\ выполняется неравенство
(s&x, *XV
Пусть Vn~r+l — произвольное (п — г +1) -мерное подпростран-
ство пространства V и
Sn~r (уп-г+1) = у*~г+1 р| snfl.
Так как r+(n — r+l)=n+
+ 1>п, то существует вектор х0у
общий для Sr~l и Sn~r(Vn-r+l).
Вычисляя ДОлго, #о)> приходим к
заключению (рис. 30):
inf {<Ax, х)<£кг..
Sn~r(Vn-r+1)
С другой стороны, полагая Srt_r = L(er, ... ,en)0Sjrl> в силу
леммы можем записать, что Xr^is&x, x) для любого вектора xg
Отсюда Xr < inf (<Лху х) и, значит,
Sn-r
Рис. 30
sup
inf {JlXy х) = Лг.
Г+Ь СП-Г /т/П-^+Ь
Рассмотрим два симметричных оператора S& и <$, связанных
неравенством ^ — *я£^0.
Пусть ^1<...<ХП и ^1<...<^п —соответствующие наборы
собственных значений этих операторов. Справедливо следующее
утверждение.
Утверждение. А*<ць, &= 1,..., п.
153

Доказательство. По условию
((Я —•*)*,-*) >0,
или, что то же,
№х, х)^(&ху х).
Это означает, что
inf (Лх> х) < inf (<Мх, х)
sn-r sn-r
и, далее,
sup inf (гЛху х)< sup inf (<Шх, х).
' {Sn"r} Sn~r {Sn~r} Sn~r
Отсюда вследствие экстремальных свойств собственных значе-
ний симметричного оператора заключаем, что
§ 3. ЛИНЕЙНЫЕ ОПЕРАТОРНЫЕ УРАВНЕНИЯ В УНИТАРНОМ
ПРОСТРАНСТВЕ
1°. Условия разрешимости линейных уравнений. Рассмотрим
уравнение
$&z=u,
где s£:V-+W — линейное отображение, и из W—известный, а г
•из V—искомый векторы. Пространства V и W унитарные.
Определение. Однородное уравнение
называется сопряженным уравнению s£z—u.
Ранее было доказано, что пространства V и W допускают
представления следующего вида:
V=ker^0im^*, V=im j*©kerjtf*
(см. пункт 4°, § 1 главы V, лекция 16). Воспользуемся этими раз-
ложениями для выяснения условий разрешимости уравнения
s£z=u.
ТЕОРЕМА 1 (альтернатива Фредгольма). Утв. Либо уравне-
ние s£z—u имеет решение для любого вектора и из W; либо со-
пряженное уравнение имеет ненулевое решение.
Доказательство. Пусть уравнение s&z=u имеет решение
для любой правой части и. Это означает, что u€im«s£. Отсюда и
из (разложения пространства W заключаем, что ker^*={9w}.
Пусть сопряженное уравнение M*w=;Qv имеет ненулевое ре-
шение. Это означает, что ядро кег^* нетривиально. Тогда в силу
представления пространства W можно заключить, что в простран-
стве W есть вектор и, не /принадлежащий образу itn^. □
Замечание. Если s4> — линейный оператбр, т. е. если $&:
: V->V, то теорема верна в следующей формулировке: либо урав-
154

нение s$>z=u имеет единственное решение для любого вектора и,
либо сопряженное уравнение s£*w=Q имеет ненулевое решение.
Из разложения W—im££®kers&* вытекает также следующее
утверждение.
ТЕОРЕМА 2. Утв. Операторное уравнение s£z=u разрешимо
тогда и только тогда, когда вектор и ортогонален ядру кег^* со-
пряженного отображения.
2°. Нормальное решение. Пусть операторное уравнение
Жг=щ (1)
где s$>^3?(y, W), u^W, разрешимо.
Обозначим совокупность всех решений уравнения (1) через
H(s&,u):
H(s&iU)={z\stz=u}.
Определение. Нормальным решением уравнения (1) назы-
вается такое его решение, для которого выполняется соотношение
|*ol = inf И-
Другими словами, нормальное решение 2о — это решение наи-
меньшей длины.
ТЕОРЕМА 3. Утв. Нормальное решение всегда существует и
единственно.
Доказательство. Совокупность всех решений уравнения
(1) Н(^Ф, и) является линейным аффинным многообразием. В са-
мом деле, из того, что векторы zr и z" лежат во множестве
<s£z'=u, s&z"=u,
вытекает, что s£ (z" — zp) =6 и, значит, z" — z'eker j£.
С другой стороны, для любого вектора z^z'+ker^, где г'е
еЯ («я£, и) фиксировано, получаем Лл = Л (zr + w) = Лг' + Л® =
= <Az' = u. Тем самым z<=H(s&, и) и, следовательно (рис. 31),
H(s&, w)=2+ker^,
где z — какое-нибудь решение
уравнения (1).
Разложим вектор z в сумму
ортогональной проекции v на
подпространство кег Л и ортого-
нальной составляющей z0: z=
= Zq+V.
Ясно, что z0 — решение урав-
нения (1), ■ • ч
H(st9 u)=zQ+keTSt W^herc/t
и z0-Lkers&. Рис. 31
Фредгольм (Fredholm) Эрик Ивар (7.4.1868—17.8.1927) — шведский мате-
матик.
155

Покажем, что решение z0 имеет наименьшую длину (среди
длин всех решений уравнения (1)).
Пусть z=Zq+v — произвольное решение уравнения (1).. Здесь
иекег^, т. е. z0A-V. По теореме Пифагора
М2-Ы8+М8.
Откуда |г|>|г0| для любого вектора z из H(s£y и). Следова-
тельно, z0— нормальное решение.
Покажем, что нормальное решение определяется однозначно.
Пусть Z\ также нормальное решение уравнения (1): Это означает,
что |zo|=>|2i|. Справедливо равенство Z\=z0+V\.
По теореме Пифагора
|*1|2=Ы8+Ы2.
Откуда следует, что i>i = 6 и Zi=z0. D
Замечание. Нормальное решение ортогонально ядру отоб-
ражения кег.я£. Оно является единственным решением, ортого-
нальным совокупности решений однородного уравнения s&z=Q.
3°. Псевдорешение. Нормальное псевдорешение. Пусть опера-
торное уравнение
stz=u (1)
для заданного вектора u^W неразрешимо.
Прежде чем заняться рассмотрением этого 'случая, целесооб-
разно процитировать часть оживленной дискуссии между завот-
делом линейного счастья Ф. С. Кивриным .и завотделом смысла
жизни К. X. Хунты (А. Стругацкий, Б. Стругацкий. Понедельник
начинается в субботу. М.: Детгиз, 1979, с. 189): «...она не имеет
решения.
— Мы сами знаем, что, она не имеет решения, — сказал Хун-
та, немедленно ощетиниваясь.—Мы хотим знать, как ее решать.
— К-как-то ты странно рассуждаешь, К-кристо... К-как же
искать решение, к-когда его нет? Б-бессмыслица какая-то...
— Извини, Теодор, это ты очень странно рассуждаешь. Бес-
смыслица— искать решение, если оно и так есть. Речь идет о
том, как поступать с задачей, которая решения не имеет. Это глу-
боко 'принципиальный вопрос...»
В попытке ответить «а него введем понятие псевдорешения.
Определение 1. Вектор z° называется псевдорешением
уравнения (1), если
\\Az0—u\=ini \<Az—u\\
zev
другими словами, если вектор z° минимизирует норму невязки
slz — и.
Покажем, что псевдорешение уравнения (1) всегда сущест-
вует.
Пифагор (UiQayopal) (ок. 570 — ок. 500 до н. э.) — древнегреческий мыс-
литель.
156

Запишем последнее соотношение несколько по-иному. Имеем
1^2°— и|= inf \w—u\ =d(u, imtA).
o»gim etf
Это означает (см. главу II, § 1,' 7°, задача 1, лекция 6), что
^2° — ортогональная проекция вектора и на образ отображения
а (рис. 32).
В силу единственности разло-
жения . ^^-—^^^ 1юА.
и=х+у,
где A:^im^, y^kerst*, получаем,
что i5#2°=*x, и, значит, z° яв-
ляется решением уравнения
s&z=x.
(2)
Рис. 32
По аналогии с нормальным ре-
шением совместного операторного
уравнения введем нормальное псев-
дорешение.
Определение 2. Нормальным, псевдорешением уравнения
(1) называется псевдорешение наименьшей длины, или, что то
же, нормальное решение уравнения (2).
Из того, что нормальное псевдорешение уравнения (1) яв-
ляется нормальным решением уравнения (2), вытекает следующее-
утверждение.
ТЕОРЕМА 4. Утв. Нормальное псевдорешение существует ш
единственно.
Определение 3. Уравнение "
s£*s&z=<s&*u
(3>
называется нормальным для уравнения (1).
ТЕОРЕМА 5. Утв. Вектор z° из пространства V является псев-
дорешением уравнения (1) в'том и только в том случае, когда
г° —решение нормального уравнения (3).
Доказательство. Выше было показано, что вектор z° бу-
дет псевдорешением уравнения (1) тогда и только тогда, когда
решение уравнения (2).
Покажем, что уравнение (2) равносильно уравнению
s&*s£z—s&*x.
(4)
Перенося s&*x в левую часть, получаем, что s£*(s£z — x)=Qv, и,
значит, s4>z — x(=kers4>%. Из того, что Жг — х одновременно ле-
жит в irrieS#, и из соотношения ker.s#*_Lim^ вытекает равенство
s£z — x=Qw и, далее,
$£z=x.
Ясно и обратное.
157

Остается показать равносильность уравнений (3) и (4). Она
следует из того, что
s£*u=s£*(x + y)=s&*x. □
4°. Квазирешение. Пусть V и W — евклидовы пространства и
*s4>:V-+W—линейное отображение. Введем на У и IF евклидову
норму \х\ =У"(х, х)у а на S?(Vy W) какую-нибудь норму, согласо-
ванную с нормами пространств V и W.
Рассмотрим операторное уравнение
stz=u. (1)
В практических задачах часто .вместо точного значения пра-
вой части и известно лишь ее приближенное значение, причем
вектор й может и не принадлежать образу линейного отображе-
ния imst.
Одним из путей, позволяющих избежать затруднений, возни-
кающих в связи с отсутствием решения уравнения (1), является
введение понятия квазирешения.
Пусть MczV — заданное множество.
Определение. Вектор z, для которого справедливо соот-
ношение
\JLz—и\ = inf \Лг—и\
м
называется квазирешением операторного уравнения (1) на мно-
жестве М (рис. 33).
<Л[н)
Рис. 33 Рис. 34
Замечание. В случае,* если М= V, вектор z является псев-
дорешением уравнения (1). Тем самым ясно, что в общем случае
квазирешение может быть «и не одно.
Укажем некоторые простые достаточные условия на отображе-
ние ^ и на множество Л1, при которых ювазирешение существует
и единственно (и непрерывно зависит от правой части).
Пусть М — n-мерный замкнутый шар Вп радиуса г с центром
в нуле.
Тогда квазирешение на М существует для любого и из W. Это
вытекает из того, что функция f(z) = \stz— и\\
158

1) непрерывна
l/(2i)-/(22)l = I \Лгх-и\-\Лгг-и\ |< •
<\JL(zx-z^\<\JL\\zx—z2|,
2) достигает минимального значения на некотором векторе из=
ограниченного замкнутого множества Вп, на котором она задана.
Пусть ker^={0y}.
Покажем, что тогда квазирешение z на М—Вп единственно.
Замечание. Если u^s£(M), то квазирешение z совпадает
с обычным (точным) решением.
Положим й = ^5, р=|й — и\.
Пусть г, г=7^=2, также является мвазирешением на множестве
М. Так как ядро тривиально, то
и
|й—и\ = |й—и| =р.
Рассмотрим вектор 2*= —(г+г). Положим .я0г*=ы*, где
и*—(й+й)/2.-
Оценим разность \и* — и\. Имеем (рис. 34)
I ~ ~ 12
= \U — U 2Н И—И 2 — 2- — •- -С05ф =
4 ' ' 4 ' ' 2 2 Т
= p2cosa—<р2.
Тем самым \и* — «|<р, если ф=т*=0.
Неравенство \s£z*— и\<р противоречит тому, что ^
т\ъ\Лг—и\ =р.
м
Таким образом, «вазирешение на л^мерном замкнутом шаре
единственно. □
Замечание. В качестве М можно взять произвольное огра-
ниченное замкнутое выпуклое множество.
ТЕОРЕМА 6. Усл. М — ограниченное замкнутое выпуклое мно-
жество из V, ядро отображения s4> тривиально, вектор и из W
(Произволен.
Утв. Операторное уравнение s4>z—u имеет ровно одно квази-
решение на М.
159

ЛЕКЦИЯ 23
§ 4. МЕТОД РЕГУЛЯРИЗАЦИИ ОТЫСКАНИЯ НОРМАЛЬНОГО РЕШЕНИЯ
Г. Понятие корректно и некорректно поставленных задач.
Пусть V и W — евклидовы пространства, s£:V->W — линейное
отображение. Введем на V <и W евклидовы нормы, а на i?(V, W)
какую-нибудь согласованную операторную \s&\.
Рассмотрим уравнение
stz=u. (I)
Определение 1. Задача отыскания вектора z из простран-
ства V по заданному вектору и из множества X пространства W
так, чтобы выполнялось равенство (1), называется корректно пос-
тавленной, если
1. Для любого вектора и из множества X решение существует.
2. Решение z определяется однозначно.
3. Задача устойчива: для.любого е!>0 можно указать б (е)> О
так, что из неравенств
' \d— ^|<б, \й—и\<6
вытекает, что решения z и г соответствующих уравнений подчи-
няются неравенству \z—г|<Се.
Примером корректно поставленной задачи может служить за-
дача поиска квазирешения уравнения (1) на ограниченном замк-
нутом выпуклом множестве, (рассмотренная в пункте 4° § 3, лек-
ция 22.
Определение 2. Задача, нечудовлетворяющая перечислен-
ным выше требованиям 1—3, называется некорректно поставлен-
ной.
Покажем, что задача поиска нормального решения уравнения
(\) неустойчива и, следовательно, некорректно поставлена.
Пример. Нормальное решение линейной системы
х+у=1
2х+2у
U- НИ)■ ~(J)-
имеет вид z0=(l/2, 1/2)7", |z0|=V2/2 (рис. 35).
Рассмотрим систему
х4-у= 1
2х+2,0004г/ = 2,002
; Л = (М V. и=(1 V
\ 2 2,0004 У \2,002/
Она имеет единственное решение Zo=(—4,5)т.
Нетрудно видеть, что малые изменения исходных данных
\К—А 1=0,0004, |й—ы|=0,002
160

приводят к значительной разнице в нормальных решениях
IV-«ol=yK2". -
Нас будет интересовать следующий вопрос: ка<к строить приб-
лиженные решения уравнения (1), устойчивые к малым измене-
ниям исходных данных?
2°. Сглаживающий функционал.
Рис. 36
Рис. 36
Определение 1. Функция /(г), заданная на пространстве
V, называется выпуклой, если для любых двух векторов z{ и г2 и
любых неотрицательных чисел Х\ и Л2, связанных условием
А,1+Ая=1, выполняется неравенство
t{klZi+h2Z2)<kif(Zi)+X2f(Z2).
Покажем, что функция
f(z) = \Az-u\* , (
является выпуклой на всем пространстве V.
Имеем
f(X1z1 + X2z2)=\A(k1z1+l2z2)—u\2=\X1(Az1—u) + K2(Az2—и)\2 =
, = X1\Az1—u\2 + X2\Az2~u\2—K1K2(Az1—Az2)2<
<K1\Az1—u\2 + X2\Az2—u\2^X1f(z1) + X2f{z2).
Легко заметить, что функция f(z)t кроме того, и непрерывна.
Это вытекает из того, что для любых векторов Z\ и z2 из прост-
ранства V выполняется соотношение
| \Az\—u\ — \Az2—u\ |<
<\Azi—Az2\<\A\ \z\—z2|.
6 Заказ 538
161

Определение 2. Ф/нкция f(z) называется строго выпуклой^
если для любых двух векторов Z\^?z ih любых положительных чи-
сел A,i и А,2, Xi + A,2=l, выполняется неравенство
Нетрудно убедиться в том, что функция f(z) = \z\2 строго вы-
пукл^. В самом деле,
|Я1г1+Я2г2|2=Я?|г1|2 + 2Я1Я2(^1, г2) + х!\г2}^ =
Из того, что сумма выпуклой и строго выпуклой функций
строго выпукла, вытекает, что
F(z) = \stz— u\2 + a\z\2, <x>0,
— строго выпуклая функция (рис. 36). Ясно, что F(z) непре-
рывна.
Покажем, что функция F(z) имеет ровно одну точку мини-
мума.
Пуст> R>0 — некоторое число. Вне шара Bn(R) функция
F(z) оценивается снизу числом aR2 и, значит, F(z)-*<x> при:
Подсчитаем A = iniF(z). '
Выбрав R достаточно большим, можно считать, что A<^nR2^
В силу оценки F(z)>aR2, справедливой вне шара Bn(R), су-
ществует число 7?о, такое, что
A=iniF(z).
Bn{R0)
Так как функция F(z) непрерывна, то в шаре Bn(R0) найдется
вектор z0: F(z0) = А.
Из того, что функция F(z) строго выпукла, вытекает, что та-'
кой вектор^может быть только один. В самом деле, если F{z{)=Ar
где Zi^Bn(R0)> то вектор г = — (^o+z^ также должен лежать
, 2 /
в шаре Bn(R0). Но
Р (-u±fLJ < -L(F(z0)+ F(z1)) = A9
что Противоречит минимальности А.
Определение. Функция
F(z) = \s£z— u\2 + a\z\2, сс>0,
называется сглаживающим функционалом для операторного урав-
нения (1).
Тем самым доказано следующее утверждение.
162

ТЕОРЕМА 1. Утв. Для любого а>0 найдется ровно один век-
тор za из V, минимизирующий сглаживающий функционал F(z),
т е. такой, что F(za) = min F(z).
z€V
Задача отыскания вектора, минимизирующего функционал
F(z), устойчива к малым возмущениям исходных данных {зФу и}9
в то время как задача поиска решения ура1внения (1) свойством
устойчивости, вообще говоря, не обладает.
3°. Теорема Тихонова. Пусть z0 — нормальное решение опера-
торного ура;в нения
s£z=u. (1)
Рассмотрим бнприближение исходных данных ДО, ц}, т. е. па-
ру ДО, й}, такую, что
\s£-*\<6, |й—и|<6, (2)
и оценим \s£z—й\. Имеем
\Лг—и\ = \{^—Л)г— (и—и)\{<Лг—и)|<
<\<А—<А\\г\ + \и—'и\ + \Лл—и\К(\г\ + 1)6+ \Ж—и\. (3)
Неравенство
\&г—и\<(\г\ + \)Ь+\&г—й\ (4)
доказывается аналогичным рассуждением.
В случае, когда z — нормальное решение, z=z0} уравнения
.(1), оценка (3) упрощается
\*г<г-й\<(\го\+Л)6. (5)
Положим F(z) = \stz—й|2+а|г|2.
Вектор; минимизирующий сглаживающий функционал F(z),
обозначим через za. Тогда
а|га|2<|^га-^|2+а|га|2 = ^(2а)<?(г0).
Последнее неравенство получается вследствие того, что га мини-
мизирует функционал F(z).
Пользуясь тем, что
F(za)<F(z0)=\Jz0-Z\*+a\z0\*<(\z0\+l)W + 'a\z0\* (6)
{см. неравенство (5)), получаем
. а|га|2<:(|го| + 1)2б2+а|2о|2.
Тем самым
'|Za|2<|Z0]2+t|20| + l)2— • (7)
a
Тихонов Андрей Николаевич (30.10.1906) — советский математик, академик
АН СССР (с 1966 года).
€* - \ 163

Из того, что
| &za—u | <: (| z* | +1) б + | s£za—u |
(см. формулу (4)), и из оценки
\o€za-Z\2<F(za)<(\z0\ + 1)2б2 -bafz0|
(см. формулу (6)) {вытекает, что
\\m\tAza-u\ = 0.
(8)
Потребуем'дополнительно, чтобы при стремлении а и б к нулю
выполнялось условие
fi2
(9>
и покажем, что тогда za-+z0 по норме, выбранной в пространстве
V (а значит, и по любой другой).
Предположим противное. Пусть для некоторого ео>0 можно
указать числовые последовательности {8k} и {а*} и ^-приближе-
ния {s&k, uk) исходных данных, такие, что
1) 6*->0, ал-*о, в*2/а*-*0;
2) \*ak—Zols^8o> гДе {zak}—последовательность векторов, ко-
торые минимизируют функционалы
FA*)=\<Akz-uk\* + ak\z\\
Обращаясь к оценке (7), можно'заключить, что начиная с не-
которого номера N последовательность {zaJ ограничена па1
норме
\2ak\<c = const.
Выделим из нее сходящуюся подпоследовательность {za„) так,
как это описано в лекции 21.
Пусть
Тогда в силу предельного соотношения
(8) s£z — и = 0 и, значит, г—решение
уравнения (1).
Вследствие оценки (7)
|£|<|20|
и, значит, |z| = |z0|> т. е. г—нормаль-
Рис. 37 ное решение уравнения (1).
164

Ввиду единственности нормального решения получаем, что
i = Z0. ' '
Полученное равенство приводит нас к требуемому противоре-
чию.
Тем самым za-+Zo при <х>-^0, 6->0, а2/б-*0 (рис. 37).
Сформулируем доказанное утверждение.
ТЕОРЕМА 2. ^ Усл. z0 — нормальное решение операторного
уравнения (1), {«s$, и] — б-приближение исходных данных {^, и].
функция а (б) задана на интервале (О, Д), непрерывна и положи-
тельна на нем, и, кроме того, при 6-^0 выполняются предельные
соотношения а(6)-*0, б2/а(б)->0.
Утв. Для любого е>0 можно указать такое бо>0, что для
любых б и а, подчиненных условиям 6< б0, —— <а<а(б0),
вектор zq, минимизирующий функционал F(z) = \iAz — u\2 +a\z\2,
удовлетворяет неравенству \Za—z0|<e.

ЛЕКЦИЯ 24
Глава VII. ВЫПУКЛЫЕ МНОЖЕСТВА
§ 1. ОПРЕДЕЛЕНИЕ И ПРОСТЕЙШИЕ СВОЙСТВА
Пусть V — вещественное линейное пространство.
Возьмем в пространстве V два произвольных вектора х и у.
Определение 1. Всякий вектор 2, определяемый формулой
z = Xx + [iyy где Л>0, [х>0 и Я-4- |х= 1, называется выпуклой комби-
нацией векторов х и у. v
Обозначение:
[х> y]={z\z = Xx + [iyy k>0t \i>0, Я + [х=1}.
Определение 2. Множество X векторов из пространства V
называется выпуклым, если для любых двух векторов х \и у из X
справедливо включение [х, у]<=Х (рис. 38).
Пример 1. Покажем, что линейное аффинное многообразие
(ЛАМ) выпукло.
Возьмем в ЛАМ Я два произвольных вектора х и у. Из того,
что ЛАМ Я допускает представление H=x+L(—х + Н), выте-
кает, что для любого AeR вектор х+Х(у — х) лежит з Н. Зна-
чит, и любой вектор {1—Х)х+Ху из множества [х, у] принадле-
жит Я. Тем самым [х, у]с:Н и, следовательно, Я выпукло.
Рис. 3'8 Рис. 39
Пример 2. Возьмем в качестве V пространство {
Re-ffi=(6l,.:..6,l)IB\...,6,leR} . ,
и рассмотрим линейную функцию
&~(l)=alll + ... + anln+P,
где ai,..., ая> P^R, причем 2/=i |a| > 0.
Покажем, что множество Я+ = {||^(|)>0} выпукло (рис. 39),
166

Возьмем в Я+ два произвольных вектора £ и ц так, что
#"(£)>°> ^(л)^°> и положим
£=Vs+jiti, Я,>0, ц>0, Я+|х= 1.
Оценим #"(£). Имеем
^ (С) = ^ (^ + ИЛ) = 2/=ia;. (А# + |1Ч0 + р = |
= Я SjUa^ + |д 2?в1а;.т|/ + (Я + ц) р =
= М2?=1а^ЧР) + М2^^
Определение 3. Множество Я+ называется замкнутым по-
лупространством.
Аналогично доказывается выпуклость открытого полупростран-
ства #о+ = ЙН#"(£)>0}, а также полупространств Н0~ и #-.
Утверждение. Пересечение выпуклых множеств либо пусто,
либо выпукло.
Доказательство. Пусть Xu...,Xk — выпуклые множест-
ва, пересечение X=[\ki==xXi которых непусто (рис. 40). Возьмем в
X два (произвольных вектора х' и х". Ясно, что векторы х' и *"
принадлежат « всем Х^
№
Г
YX
Г
Рис. 40
Рис. 41
В%г)
В силу выпуклости множеств Х( справедливо включение [х\
x"]cXi, t=l,...,Л. Отсюда вытекает, что [х\ /]сХ П
Замечание. Утверждение справедливо для любого набора
выпуклых множеств.
Пример 3. Множество
/n=ft|€eR"f0<6'<lf /-1 я}
выпукло как пересечение 2п замкнутых полупространств
{Ei6i>o}f...fei6n>o}i{g|g^i}f...ifti6»<i}.
Определение 4. Множество 1п называется n-мерным замк-
нутым единичным кубом (рис. 41).
Замечание. Объединение выпуклых множеств не обязатель-
но выпукло.
167

П р им ер 4. Пусть V — n-мерное евклидово пространство,
1*1 =l/"(xf х) — длина вектора х, г — положительное число,
х0 — вектор из V.
Определение 5. Замкнутым /г-мерным шаром радиуса г с
центром хо называется множество {x\x^Vt \x—Хо|<г}.
Обозначение: Вп(х0, г).
Утверждение. Замкнутый шар — выпуклое множество.
Доказательство. Возьмем в шаре Вп два произвольных
вектора х' и х" и рассмотрим их выпуклую комбинацию х =
= Х'х'+Х"х", Л' + а"=1, Я'>0, Л">0.
Оценим \х—Хо\. Так как*
х—хо =й/ (х'—Хо) +Л" (*"—Хо),
то \х—jcoKVI^—хо\+Х"\х"—jco|-
Из неравенств |л/— хо|^/, \х" — *o|^r вытекает, что \х —
— jc0|<r. □
Определение 6. Открытым «-мерным шаром радиуса г с
центром хо называется множество {лг^У| \х—хо\ <г}.
Обозначение: В0п(хо, г).
Утверждение. Открытый шар — выпуклое множество.
§ 2. ОПЕРАЦИИ НАД ВЫПУКЛЫМИ МНОЖЕСТВАМИ
Рассмотрим некоторые операции над выпуклыми множества-
ми, результатами которых являются также выпуклые множества.
а. Сложение.
Определение 1. Суммой множеств X и Y из V называется
множество Z, определяемое формулой
Z={z=x + y\xe=iX, ye=Y].
Обозначение: X+Y.
Утверждение. Сумма выпуклых множеств — выпуклое мно-
жество.
Доказательство. Пусть X — сумма выпуклых множеств
Хх и Х2: Х=Х{+Х2 (рис. 42).
Возьмем во множестве X два произвольных вектора х и у.
В каждом .из множеств Xk, k=l, 2, можно указать векторы Xk и
yky k=\, 2, такие, что
x=Xi+x2, у=У\ + У*. (1)
Рассмотрим вектор z=Xx+\iy, А,>0, jli>0, X+\i=l.
Используя формулы (1), получим, что
Z = K(Xi + Xi) +^(Ух+у2) = ()JCi + [iyi}+ (}JC2+Iiy2).
В силу выпуклости множеств Xk векторы XXk + Mk принадлежат
Xk (k = \, 2). Поэтому их сумма — вектор z — также принадле-
жит множеству X. □ .
а'. Прямая сумма.
168

Определение 2. Сумма X+Y называется прямой, если для
любого вектора z из множества Х + У разложение х + у, где хеХ,
y^Y, единственно.
Обозначение: X@Y.
Утверждение. Прямая сумма выпук-
лых множеств — выпуклое множество.
б. Вычитание (по Минковскому).
Пусть X — множество векторов из
пространства V; вектор аеУ фиксиро-
ван.
' Обозначение: Ха = а + Х = {а+х\х^Х).
Определение 3. Разностью мно-
жеств X и У из пространства V назы-
вается множество. Z, определяемое фор-
мулой
z=n
уеУЛу.
Рис. 42
Обозначение: X—У.
Утверждение. Если множество X выпукло, то разность X—Y
выпукла (или пуста) (рис. 43).
х*у
Рис. 43
Рис. 44
Доказательство основывается на том, что пересечение
выпуклых множеств либо пусто, либо выпукло (сдвиг лу выпук-
лого множества X на вектор у снова является выпуклым мно-
жеством). □
Свойства вычитания
1+. X—У=У\((У\Х)+У).
2+. Разность X—У состоит из всех векторов г, которые для
произвольного вектора у из множества У допускают представле-
ние в виде разности х—у, где х — соответственно подобранный
вектор из множества X.
3+. (X—Y)—Z=(X—Z) —Y=X— {Y+Z).
(X-Z) + Ya(X + Y)-Z.
(X+Y)\J(X+Z)=X+(Y{)Z). '
(X-Y){](X-Z)=X-(Y[)Z).
(Y-X){](Z-X) = (Y(]Z)-X.
(X+Y){](X + Z)=>X+(Y(]Z).
(X-Y)\j(X-Z)czX-(Yf\Z).
4+.
5+.
6+.
7+.
8+.
9+.
в. Произведение на число.
да

Определение 4. Произведением множества X на число
aeR называется множество У, определяемое формулой У=
= {у = ах\х&Х}.
Обозначение: аХ.
Утверждение. Произведение выпуклого множества на число —
выпуклое множество (рис. 44).
Доказательство. Пусть множество У является произведе-
нием выпуклого множества X на число a : Y=aX.
Возьмем во множестве У два произвольных вектора у\ и у% и
покажем, что вектор
У=иУ\ + Ь2У2, Л,1>0, Я2>0,"&!+**= 1,
также принадлежит У.
Так «как ух = ах\у */2=<х*2, то # = a(A,i*i+A2*2). В силу выпукло*
сти множества X вектор x=X\Xi + X2X2^X и, следовательно, у=
=са<=У. П
г. Декартово произведение.
Определение 5. Декартовым произведением множества X
из V и множества У из U? называется множество Z, определяемое
формулой
Z=(z= (*, у) |хе=Х, y<=Y}aVxW.
Обозначение: XXY.
Утверждение. Декартово произведение выпуклых множеств —
выпуклое множество (рис. 45).
Рис. 45 Рис. 46
Доказательство. Пусть X — декартово произведение вы-
пуклых множеств Х\ и Х2: Х=Х\ХХ2.
Возьмем во множестве Я два произвольных вектора х и у и
покажем, что вектор
z=hx+ixy, X>0, [i>0, Я+м,= 1,
также принадлежит X.
Так как х=(хи х2), У=(Уи f/г)» ГДе **, Ук*=Хк9 k=l> 2, то век-
тор z допускает следующее представление'
z=X(xu x2)+ii(yu У2) =itoi + \iyu Xx2+iiy2h
170

В силу выпуклости множеств Xk; k=\, 2, векторы %Xk + \iyk^Xk и,
следовательно, геХ. П
д. Образ выпуклого множества.
Утверждение. Образ выпуклого множества при линейном отоб-
ражении — выпуклое множество (рис. 46).
Доказательство. Пусть X — выпуклое множество из про-
странства J/и^: V->W — линейное отображение. Покажем, что
множество
st(X)={y=^x\x<=X}
выпукло. . v
Возьмем во множестве $&(Х) два произвольных вектора у\ и
у2 и докажем, что вектор
также принадлежит этому множеству.
В силу определения множества s4>(X) найдутся векторы Х\ и
Х2 из Ху такие, что s4>X\ = y\, 6&Х2=У2- Поэтому вектор у допус-
кает представление y=X\S&X\ +Х2^Фх2 = ^Ф(X\X\Jr'k2X2) и, значит,
принадлежит s£(X), так как k\X\+\k2X2^X. D
§ 3. ВЫПУКЛАЯ ОБОЛОЧКА МНОЖЕСТВА
Пусть X — произвольное непустое множество из простран-
ства V.
Определение 1. Выпуклой оболочкой множества X назы-
вается множество С, которое обладает следующими свойствами:
1) Хс=С, 2) С выпукло, 3) если Хс=У и Y выпукло, то CczY.
Обозначение: convX.
Ясно, что выпуклая оболочка множества, если она существует,
единственна.
Определение 2. Вектор ху определяемый соотношением
х = SLia^,
где S^a, = 1, аг > 0, ... , ak > О,
называется выпуклой комбинацией векторов jti,...,дс*.
Обозначим через С(Х) совокупность всевозможных выпуклых
комбинаций векторов из X:
C(X) = {ZU*txt\xteX9 2^=1, се^О, 4eN},
и покажем, что выпуклая оболочка множества X совпадает с
С(Х).
ТЕОРЕМА (о выпуклой оболочке).
Утв. Выпуклая оболочка произвольного множества совпадает
с совокупностью всевозможных выпуклых комбинаций его векто-
ров.
Доказательство. Покажем, что множество С(Х) обла-
дает свойствами 1—3 определения 1.
17!

1. Чтобы убедиться в справедливости включения XczC(X),
достаточно рассмотреть выпуклые комбинации при k=l.
2. Возьмем во множестве С(Х) два произвольных вектора х и
у и покажем, что вектор
z=Xx + [iyt ^>0, ц>0, Я+ц=1,
также принадлежит С(Х).
По определению множества С(Х) взятые векторы х и у допус-
кают представления
* = 2{иед, * " (1)
где ^ е X, SLiotf =1, а,- > 0, и
y = 2jLiPtf/, (2)
где У/еХ, S/LiP/=l, Р, > 0.
С учетом этих соотношений вектор 2 можно записать в следу-
ющем виде:
г = 2?в1 (И) *, + 2jLi (Цр/) У/.
В силу того что ^еХи У/^У,
2ti (И) + 2?Li (|ip,) = 1, Ясс, ^ 0, цр, ^ 0,
заключаем: z<=C(X).
Это означает, что множество С(Х) выпукло.
3. Пусть У — произвольное выпуклое множество, содержащее
X. Покажем, что С(Х)с=У.
Доказательство будем вести индукцией по числу k слагаемых
в выпуклых комбинациях.
Проверим сначала, что каждая выпуклая комбинация любых
двух точек из X (по определению такая комбинация содержится
в С(Х) при k = 2) принадлежит У.
Возьмем во множестве X два произвольных вектора Х\ и #2.
По условию эти векторы принадлежат также и множеству У.
В силу выпуклости последнего [хи х2]<=У. С другой стороны,
множество [#i, А:г] представляет собой набор всевозможных вы-
пуклых комбинаций
a\Xi + <X2Xb cti+ a2=l, ai>0, аг^О,
каждая из которых принадлежит С(Х).
Предположим теперь, что каждая выпуклая комбинация k = l
векторов из X принадлежит У, и покажем, что в этом предполо-
жении любая выпуклая комбинация k = l+l векторов из X также
Принадлежит У.
Возьмем во множестве X /+1 произвольных векторов Х\у... ,xi,
xi+\ и рассмотрим их выпуклую комбинацию
х = 2Й|сад, 2j£ta= 1,. щ^ 0.
т \

Ясно, что х^С(Х). Возможны два случая.
а а/+1 = 1. Тогда ai = ... = a/ = 0 и вектор х совпадает с вектором
xi+i^X. Так как/по условию XczY, то в этом случае x^Y.
б. a/+i<l. Тогда
a = ai +... + а/ = 1 —a/+i > 0.
С учетом формулы (3) вектор
можно выразить и по-иному:
x = ax'+ai+iXM,
(3)
где
*' = «-:
/ Л*
X/.
(4)
(5)
Комбинация векторов хь...,х/, стоящая в правой^ части фор-
мулы (5), является выпуклой (рис. 47), так как "
2l==i —— = — 2^=1^ = 1,
щ
>0.
Поэтому и по предположению индукции век-
тор /еУ.
Заметим теперь, что вектор х, определяе-
мый формулой (4), есть выпуклая комбина-
ция векторов х' и дгг-f-i из У и потому так-
же принадлежит множеству Y (в силу выпук-
лости последнего). □
Утверждение. Если Xcz У, то С (X) а С (У).
Пример. В вещественном линейном про-
странстве Rnxn квадратных матриц порядка п
рассмотрим набор перестановочных матриц.
(Матрица называется перестановочной, если
ъ каждой ее строке и в каждое столбце есть
ровно один элемент, равный единице, а все
остальные п2 — п элементов нулевые.) Между
перестановочными матрицами я-го порядка и перестановками a^Sn-
имеется следующая связь: каждой перестановке (a(l),...,a(n)}
отвечает перестановочная матрица, элементы ац которой опреде-
ляются правилом
1. ' = *(/).
Рис. 47
«£
0, 1ф0(1).
Рассмотрим выпуклую оболочку множества перестановочных
матриц А,,...,Ащ, где т=п\: о г
bin— С\А\У . . ♦, Am)•
173

Матрицы из выпуклой оболочки Q обладают интересными свой-
ством.
Пусть А= (ai/)EQ«. Тогда
Последнее соотношение, полагая Ак={акц), можно записать к
по-иному:
Нетрудно заметить, что а//>0.
Вычислим S?=iot£/ и SjLi^/. Имеем SLi^/ = ^S^^a*-.
Для 'каждого t под знаком второй суммы только (п—1)! сомно-
жителей ац отличны от нуля (равны единице). Без ограничения
общности можно считать, что матрицы Ль...,Ат занумерованы
так, что в первой-группе из (п—1)! матриц элементы в позиции
(1, /) равны 1, во второй группе из (п— 1)! матриц элементы в
позиции (2, /) . равны 1 и т. д. Это позволяет переписать послед-
нее равенство в следующем'виде:
2j=iat-;- = S^^i^a// + .,. + 2fe=i^a„/ =
k=\Afe + *k=n A>k + . . . + 2jk=n\—n+lA>k = 2,£=iAfc = 1.
Аналогично доказывается, что 2/=iat/==l.
Определение. Матрица А= (aij)^Rnxn называется дважды
стохастической, если ее элементы ац подчинены следующим усло-
виям: / ч
Таким образом, выпуклая оболочка перестановочных матриц
УАи..., Ап\ представляет собой множество дважды стохастиче-
ских матриц Qn> играющих важную роль в приложениях.
ЛЕКЦИЯ 25
§ 4. ТРИ ТЕОРЕМЫ О ВЫПУКЛЫХ МНОЖЕСТВАХ
ТЕОРЕМА 1 (Радона). Усл. Подмножество X /г-мерного веще-
ственного линейного пространства V содержит не менее п+2 век-
торов.
Утв* Множество X можно представить в виде объединения не-
пустых непересекающихся подмножеств, вьшуклые оболочки ко-
торых имеют непустое пересечение (рис. 48).
Доказательство, а. Предпо-
Ъь^ ложим сначала, что множество X со-
° *Ш^ стоит ровно из п+2 векторов:
0 '°^Ш Х = {Хи...9Хп2).
о ° ^Ь*^° Известно, что всякое множество из
п+2 векторов в /г-мерном пространстве
)рис< 48 аффинно зависимо. Поэтому сущест-
174

вует нетривиальная линейная комбинация векторов хи..., хп+2х
такая, что
Xl#l + ... + A.rt+2#rt+2 = 6, (1)
причем
Я1 + ...+Хл+2 = 0. (2)
Так как не все числа ki в равенстве (2) равны нулю, то средц
них обязательно найдутся отрицательные. Это означает, что мно>
:жество индексов
J = {i\h<0}
непусто; но и не исчерпывает всех чисел 1,...,л + 2.
Преобразуем соотношения (1) и (2) к следующему виду:
Поделим обе части равенства (3) на
Нетрудно проверить, что полученный вектор
является выпуклой комбинацией векторов как из подмножества
Xx = {xi\x,s=X9j<$J}%
так и из подмножества
X2={Xi\Xi^X, i^J}.
Это означает, что вектор у принадлежит выпуклым оболочкам
каждого из (подмножеств Х\ и Х2. Тем самым
уеС(Х1)(]С(Х2)
и, следовательно,
С(Хг)Г\С(Х2)Ф0.
Подмножества Х\ и Х2 образуют разбиение множества X: они
непусты, не пересекаются, »и их объединение совпадает с множе-
ством X. - ,
б. В случае, когда cardX>n+2, множество X можно пред-
ставить в следующем виде:
х=х'\)Х'\ } *
где
X'=*{Xu...9Xmd,X" = X\X'.
Радон (Radon) Иоганн (16.12.1887—25.5.1956) — австрийский математик.
,1<75

Способом, указанным в части а, подмножество X' можно раз-
бить на две части Х\ и Х2' так, что пересечение
С(Х1')(]С(Х2')Ф0. (4)
Положим Х\=Х\\ Х2 = Х2\}Х". Из включения X2f(^X2 вытекает,
что
С(Х2')<=С(Х2). (5)
Сопоставляя формулы (4) и (5), получаем, что пересечение
С{Хг)(]С(Х2) непусто. □
ТЕОРЕМА 2 (Каратеодори). Усл. X — непустое множество
векторов /г-мерного пространства V, у — произвольный вектор его
выпуклой оболочки С(Х).
Утв. Во множестве X можно указать векторы х\,...9хт
(т<я+1), одна из выпуклых комбинаций которых совпадает с
вектором j/.
Доказательство. По определению множество С(X) со-
стоит из всевозможных выпуклых комбинаций любых векторов из
X. Поэтому для данного вектора у в X можно найти векторы
Х\у... ,xi, выпуклая комбинация которых равна у:
' y = lLi*tXt, (8J-
где
2Li«,= lf a,>0. Щ
Если /^л+1, то утверждение доказано.
Пусть число / векторов в системе
*о = {*ь ••>*<}
больше л+1. Покажем, что. тогда из множества Х0 можно исклю-
чить часть векторов так, чтобы вектор у допускал представление
вида (6), (7) через оставшиеся векторы.
Из неравенства />л + 2 следует, что система векторов X\9...9xi
аффинно зависима. Это означает, что найдутся числа pi,..., р/,
не все равные нулю и такие, что
2i-iP*=ef (8)
2'=iP; = (b (9)
Среди чисел р, в равенстве (9) есть и отрицательные. По-
этому множество индексов
/={i|P/<0> .
непусто. Рассмотрим отношения
Pt
Каратеодори (Caratheodory) Константин (13.9.1873—2.2.1950) — греческий
математик.
176

и быберем среди них наибольшее:
Yfc = maxYt-. -
j
Умножим обе части соотношений (8) и (9) на yk и вычтем по-
лученные равенства из равенств (6) и (7) соответственно. В ре-
зультате приходим к формулам
y = t=Axi, 2,'.А=1, (10>
где 6,= а, — р^/г-
Определим знаки коэффициентов б*. Возможны три случая.
1
2
3
i = k
U = a*-P<Y*>0 1
•V V/ Л
0 0 0
8i = 0
Л Л\
0 0
Из таблицы видно, что . коэффициенты 6i неотрицательны и по
крайней мере один из них обращается в нуль. Это означает, что
вектор у является выпуклой комбинацией не более чем /— 1 век-
торов из X®.
Уменьшение числа слагаемых в выпуклой комбинации (6)
стало возможным вследствие аффинной зависимости векторов
Обратимся к соотношениям (10), ограничиваясь в дальнейших
рассмотрениях только^еми векторами хи коэффициенты б» при
которых положительны.
Если число этих векторов не превосходит я+1, то утверждение
доказано.
Если же полученная подсистема А^сгЛо содержит большее
(чем /г+1) число векторов, то она аффинно зависима и для нее
вновь, можно повторить (проведенные выше рассуждения. »
Продолжая рассмотрения и соответственно отбрасывая векто-
ры, через конечное число шагов придем к подсистеме xiyy ... ,,
Xi > где m^n+U которая обладает требуемым свойством:
ТЕОРЕМА 3 (Хелли). Усл. Конечное семейство 95 выпуклых
множеств /г-мерного пространства V обладает следующим свой-
ством: пересечение любых п+1 множеств из семейства S6 не-
пусто.
Утв. Найдется вектор, общий для всех множеств семейства @в.
Доказательство. Рассмотрим семейство 95 выпуклых мно-
жеств Xit...9Xs, число s которых удовлетворяет условию 5>л+1_
Хелли (Helly) Эдуард (1.6.1884—1.7.1943) — австрийский математик.
177'

Пусть, кроме того, для любого набора iu..., in+u подчиненного
условию
l<*'i<...<Ort+i<s,
выполняется соотношение
ХиГ\..:Г)ХСп+1ф0. (П)
Нужно показать, что пересечение D/=i^/ непусто.
Доказательство проведем индукцией по числу 5 множеств се-
мейства <%. *
При s==n+1 утверждение теоремы выполняется тривиально.
Предположим, что для любого семейства, которое состоит из
.s = m—1>я+1 выпуклых множеств и удовлетворяет условию
(11), утверждение теоремы доказано.
Рассмотрим семейство из s = m^>n + 2 множеств Х\,...,Хт,
лодчиненных условию (11) .и выпуклых.
По предположению индукции для любого /=1,'. ..,т можно
указать вектор - . •
xtezfljLiX,. (12)
Специально отмелш, что Xi^Xif /=1, ...,m, и Xi^Xj, \Фг.
Множество X={jti,... 1хт} содержит не менее п+2 векторов и
по теореме Радона может быть разбито на два подмножества X'
и Х'\ обладающих следующими свойствами: 1) Х = Х'\}Х"9
2) Х'(\Х"=0, 3) С(Х')()С(Х")Ф0. Перенумерацией множеств
X\,...fXm, если это необходимо, всегда можно добиться того,
чтобы
Х' = {Х\, . . . , Xk} И X" = {Xk+u . . . гХт}.
Из формулы (12) ясно, что множество
X' = {xu...,Xk}czXi9 i=k+l9...,m.
В силу, выпуклости множеств Xi справедливо включение
' С(Х')сХи i=k+\,...ym. (13)
Аналогичными свойствами обладает множество Х"\
Х" = {Хк+и...,Хт}с:Х,; /=1,...,&,
C(X")cXhj=l9...9k. (14)
Из соотношений (13) и (14) вытекает, что
С(Х0ПС(*'')с=Х/,/=1,...,т.
Последнее означает, что
[}?=iXl¥=0. П
178

Пример 1. Рассмотрим в пространстве R" выпуклые мно-
жества
Xt = {t{<=R"№>l}, ZgeeN.
Пересечение любого конечного числа множеств из этого семейства
Х\9.. -yXi,... непусто. Однако в пространстве R* нет ни одного
вектора, который принадлежал бы всем этим множествам однов-
ременно.
Этот пример показывает, что если семейство выпуклых мно-
жеств бесконечно, то утверждение теоремы без дополнительных
предположений перестает быть справедливым (рис. 49).
Рис. 49
Пример 2 (применение теоремы Хелли).
Определение. Общей трансверсалью семейства/ множеств
называется любая прямая, которая пересекает все множества
этого семейства.
Пусть Q — конечное семейство параллельных отрезков на
плоскости, каждые три из которых имеют общую трансверсаль.
Покажем, что тогда существует общая трансверсаль семей-
ства Q.
Решение. Введем на плоскости координаты х, у так, чтобы
отрезки из семейстэа Q были параллельны оси Оу.
Отбросим тривиальный случай, когда все отрезки лежат на
одной прямой (эта прямая и есть общая трансверсаль). Тогда
можно ограничиться рассмотрением прямых вида y = kx+b.
Пусть семейство Q состоит из отрезков
Ъ = {(Х; y)\X = Xi9 ^г~<^<г/г+}.
Рассмотрим в пространстве R2 множества
Xi = Xi(ai)={(k9 6)|, прямая, заданная уравнением y=kx+b„
пересекает отрезок a,}, i= 1,..., m.
1,79

Покажем, что каждое множество Xi выпукло. Обозначим через
(&, Ь) произвольную выпуклую комбинацию inap (k\ bf) и (k"y
Ъ") из Хг.
k=X'k'+'k"k'\ Ь=к'Ь'+к"Ь", ' (15)
где Л' + Г=1, Г>0, Г>0.
Пусть прямые y = k'x+b' и t/=fe"x + 6" пересекают отрезок а\
соответственно в точках (*,-, у/) <и (х/, t//7)- Это означает, что
*/г<у/<*/Л */г<*//'<*л+. (16)
Рассмотрим прямую y = kx+b, где Л и Ь.определены формула-
ми (15). Положим л;=л:;. Тогда
у. = 1щ +b = (X'k' + X"k") xt + (X'b' + X'V) =
= V (*'*, + V) + Л" (k'xi + b") = X'yt+ K'y].
♦ Умножим первое из равенств (16) на А,', второе на \" и сложим
полученные результаты:
УГ^'У1'+%"У"<У1+-
Тем самым доказано, что прямая y = kx+b также пересекает от-
резок^/. Таким образом, множество, Xt выпукло.
Переформулируем условия задачи применительно ж построен-
ным множествам Х(, i=l,...,m.
Наличие общей трановерсали y=kx + b для любых трех отрез-
ков семейства Q равносильно тому, 4fo каждые три из выпуклых
множеств Хи...,Хт пространства R2 ммеют общий элемент (вида
(k, 6)). По теореме Хелли существует пара
Последнее означает наличие общей трансверсали y=k0x+bo се-
мейства Q.
§ 5. ВЫПУКЛЫЕ МНОГОГРАННИКИ
В этом разделе мы изучим некоторые свойства выпуклой обо- *
лочки множества, состоящего из конечного числа векторов.
Рассмотрим конечное множество векторов Х\,...,хт из прост-
ранства V.
Определение 1. Выпуклая оболочка С(хи ... *хт) назы-
вается выпуклым многогранником.
Пример. Множество Qn дважды стохастических матриц яв-
ляется ВЫПУКЛЫМ МНОГОГраННИКОМ В Пространстве R/гхя-
ТЕОРЕМА (о вершинах многогранника). Усл. X — конечное
множество векторов <из V.
Утв. а. Существует подмножество Yc^X, выпуклая оболочка
которого совпадает с выпуклой оболочкой множества X и такое,
что ни один вектор из У не принадлежат выпуклой оболочке ос-
тальных векторов из У.
180

б. Множество У, удовлетворяющее условиям а, единственно.
Доказательство, а. Существование. Если ни один из век-
торов множества X не является выпуклой комбинацией остальных
его векторов, то утверждение справедливо: искомое 'множество У
совпадает с X.
Пусть для определенности
Xl€=C(x2,...,*m). (1)
Покажем, что тогда выпуклые оболочки множеств X и Х\Х\
совпадают:
С \Х\у #2» • • • , Xm) = ^ v#2> • • • » Xm) .
Докажем сначала справедливость включения
С(хи x2,...9xm)czC(x2,...9xm).-
Достаточно рассмотреть векторы вида
tf-X^+SjL^x,, (2)
где Ах + ЕЛгА* = 1, причем Ях > 0, Xt > 0.
Условия (1) можно записать следующим образам:
'x± = l!!L2№* (3)
где 2^=2^=1, № >0.
Подставив выражение (3) для вектора Х\ в формулу (2), по-
лучим, что
Вычислим сумму коэффициентов в этой линейной комбинации.
Имеем
2t=2 (Ах^ + к;) = Хг Sf-r2Mj + 2t--2A* = Лх +• 2t=2At = 1.
Из того, что коэффициенты кцн+Эы, t = 2,...,m, неотрицатель-
ны, можно заключить, что вектор у представляет собой выпук-
лую комбинацию векторов лг2,•'.. ,*т.
Таким образом, у^С(х2>... ,*т).
Обратное включение C(a;i, jc2, ... , хт)1=эС(*2,... yXm) триви-
ально.
Рассмотрим множество Х\ = {*2,..., лгт}.
Если ни один из векторов множества Х\ не является выпуклой
комбинацией остальных, то утверждение справедливо: в качестве
искомого множества У берем множество Хх.
Если же некоторый вектор множества Хх принадлежит выпук-
лой оболочке остальных векторов из Х\у то повторяем проведен-
ные рассуждения.
181

В результате описанного метода «исключения» через конечное
число шагов получим набор У векторов
Ух = Xtt9 .. < ,УР = *ip,
обладающий нужными свойствами:
(а) С(уъ...9ур)=С(хи...,хт),
(б) У1&С{уи...,у1>--->Ур)> *'=1,...,Р (*>
(знак ^ означает, что вектор уг в этой выпуклой оболочке опу-
щен — шапка-невидимка).
б. Единственность. Пусть множество Z={Zif...,zQ} также об-
ладает свойствами (*).
Из совпадения выпуклых оболочек C(Y) = C{Z) вытекает, что»
векторы из множества У можно представить ~в виде выпуклых
комбинаций векторов множества Z:
y^Hl^iarfi, 2Li<x/t= 1, а/, > 0, /= 1, ..., /?, t (4>
а векторы множества Z — в виде выпуклых комбинаций векторов*
из множества У:
2, = 2?в1р,^/? 2^,pl7=i, р,у>0, i=l, ...,?. (5>
Покажем сначала, что YczZ.
Заменяя векторы z, в формулах (4) их выражениями (5) че-
рез векторы г//, получим, что
^ = 2^.(2^^ /=1, ...\р.
Запишем полученный результат, используя следующее обозначен
ние: .
Имеем
yi=2'i=iyiiyi,-l=l,...9p. (6>
Заметим, что
27-17//=^ (SLia«Pii) =
= 2?=,1^(2^ipl7) = 2L1a/t-=l
и, кроме того, 0<у//<1, U /— 1,.•.,р.
Преобразуем формулу (6) к виду
(1—уи)У1 = 21+1УцУ1 (7>
и разберем оба возможных случая: 1) ун<1 и 2) Y"—*-
В первом случае вектор yi можно представить в виде линейной
комбинации остальных векторов множества У. Для этого доста-
точно поделить обе части равенства (7) на 1—ун:
у>=^'-Г^Уг . (8>
1.82

Линейная комбинация в равенстве (8) является выпуклой в силу
неотрицательности коэффициентов
W
1 — у//
и равенства
' 1 —Y// 1-Y// 'ФП) 1-Y//
Полученное включение yi^C{yu..., у и..., уР) противоречит
условию (*), которому множество У должно удовлетворять.
Тем самым доказано, что
Q3L.
~ Y// = l (9)
и, значит,
W = 0. /V* (W)
Запишем формулы (9) и (10) подробнее. Получим соответ-
ственно
2?,ia„p,f = i . (11).
и
v2Lia|£pf/ = 0f /=£/.
Изучим первое из полученных равенств. Из оценки
l=2tLia^pt/< max $u2U&a= max pw
«вытекает, что
рф = тахр„=1. (12)
Так как SjLiPf y = 1, то отсюда следует, что
Р/,/ = 0, }Ф1. (13)
Вернемся к соотношению (5) (при i=ii). В силу равенств (12)
« (13)
**/ = »/. '=Ь ... »Р-
Ввиду произвольности выбора / отсюда вытекает, что YczZ.
Поменяв У и Z ролями и повторив приведенные рассуждения,
получим, что Zc=y.
Таким образом, p = q и Y=Z. П
Определение 2. Векторы уи...,ур, составляющие множест-
во У, называются вершинами выпуклого многогранника С(Х).
Обозначение: М(уи..., уР) (рис. 50).
Пример. Перестановочные матрицы являются (вершинами
многогранника дважды стохастических матриц йл.
183

Пусть множество, векторов х0, X\,...,xk аффинно независимо..
Определение 3. Выпуклый многогранник М (хо, Х\,..., xk)
называется k-мерным симплексом.
Обозначение. ok = ok(x0i Xif...,Xk).
Ясно, что векторы х0у Xi,...,xk суть вершины симплекса <yk.
Рис. 50 Рис. 5>1
Рассмотрим вектор л: из ok:
x = koXo + ...+XkXk, (14)
где Яо + ... + Ял=1, Я/>0.
Утверждение. Для данного вектора x^ak набор Хо,... Дь одно-
значно определен.
Доказательство. Предположим, что вектор х допускает
еще одно разложение вида (14):
x=iioXo+... + iikXk> (15)
где [io+... + |i*=l, (i*>0 (рис. 51).
Тогда
(и-о—А0)л:о+...+ (|i*—Л*)х*5=в
(|Ю—*o)+...+ (|i*—Л*)=0. (16)
Так как семейство векторов *о, ...,#* аффинно независимо, то из
равенства (16) получим, что \ц—Лг=0, i = 0,... Д. О
Определение 4. Числа Аю, ...Дь называются барицентри-
ческими координатами вектора jceo* (х0,..., Xk).
ЛЕКЦИЯ 26
§ 6. ВЫПУКЛЫЕ КОНУСЫ
1°. Определение и примеры. Определение 1. Выпуклым ко-
нусом в линейном пространстве V называется непустое множество
Ki которое содержит
1) сумму х+у любых своих векторов х и у,
2) произведение ах любого своего вектора х на произвольное
неотрицательное число а.
Определение 2. Линейная комбинация 2^Д^ векторов
Xu...,Xm называется неотрицательной, если А^>0, i=l,...,/n.
184

Простейшие свойства:
« 1+. Выпуклый конус содержит нулевой вектор (вытекает из
того, что 6 = 0*).
2+. Выпуклый конус содержит неотрицательную линейную ком-
бинацию любых своих векторов.
3+. Выпуклый конус — выпуклое множество (так как выпук-
лая комбинация — частный случай неотрицательной).
4+. Пересечение выпуклых конусов есть выпуклый конус.
Примеры выпуклых ко-
нусов (рис. 52).
(1) Линейное подпростран-
ство.
(2) Неотрицательный ор-
тант /?"0rt = {I e= R™ 11»>0....
...,£л>0}
(3) Замкнутое полупрост-
ранство Я+ = {|еК/г|а1|1 + ...+
V
(Г)2+(*2)2-Ъ3)2*о
Рис. 52
Рис. 53
(4) K^ii&ww^wr-^vtfrKO, б'>о>.
(5) Множество решений системы линейных неравенств
(*п?+...+*ш?>0,
является пересечением замкнутых полупространств
Hk+^{l<=R*\akiV + ... + aknln>0}, *=1, .
Конус решений системы Ks = П kLflt-
(6) Пусть V — унитарное пространство. Рассмотрим совокуп-
ность полуположительных операторов, заданных на векторах
из V:
т.
{.*€=# (V, V)|^>0}.
185

Покажем, что это множество является выпуклым конусом
в 2?(V, V). Для любых неотрицательных чисел X и \х неравенство
А О^х, х) + |ы {&х, х) >0
выполняется для всех векторов х из V и любых полуположитель-
ных операторов s£ и 3§.
2°. Коническая оболочка множества. Пусть X — произвольное
непустое множество из V.
Определение 1. Совокупность всевозможных неотрицатель-
ных линейных комбинаций векторов из множества X называется
конической оболочкой множества (порожденной множеством) X
(рис. 53).
Обозначение: Con(Ar)={aiX1 + .. . + umxni\XisX9 ш>0, msN}.
Справедливы следующие утверждения.
Утверждение 1. Коническая оболочка — выпуклый конус.
Утверждение 2. Выпуклый конус, содержащий множество X,
содержит и его коническую оболочку.
Это позволяет дать эквивалентное определение конической обо-
лочки множества.
Определение 2. Конической оболочкой множества X назы-
вается йыпуклый конус К(Х)У обладающий следующим свойством:
если XczK, где К — выпуклый конус, то K(X)czK.
3°. Многогранный конус.
Определение L Коническая оболочка конечного множества
векторов называется многогранным конусом.
Определение 2. Конус К называется заостренным, если
из включений х^К и (—х)^К следует, что х — нулевой вектор.
ЛЕММА. Утв. Неотрицательная линейная комбинация ненуле-
вых векторов заостренного конуса равна нулевому вектору тогда
и только тогда, когда она тривиальна.
Доказательство.. (=^) Пусть К ~ заостренный конус и
Хи . -., хт — ненулевые векторы из /С Приравняем к нулевому
вектору некоторую неотрицательную линейную комбинацию этих
векторов: /
2^=1ЯЛ = в, At>0. (1)
Предположим, что коэффициент А,а>>0. Тогда равенство (1) можно
разрешить относительно **:
. xft=-2^-^-*. (2)
Вектор
'- £t* (3)
1Фк
обладает следующими свойствами: у^К (так как линейная ком-
бинация (3) неотрицательна) и (—y)=xk^K (в силу условия
(2)) и, следовательно, совпадает с нулевым вектором. Последнее
противоречит условию ХкФ®. Значит, Xk = 0. □
186

ТЕОРЕМА 1 (о ребрах конуса). Усл. К — многогранный заост-
ренный кон^с, порожденный множеством X.
Утв. а. Найдется подмножество У множества Х9 коническая
оболочка которого совпадает с К, такое, что ни один вектор из
множества У не может быть представлен в виде неотрицательной
линейной комбинации остальных векторов из У.
б. Векторы множества У определены однозначно с точностью
до положительных множителей.
Доказательство, а. Существование. Пусть множество X
состоит из векторов хи .... хт. Укажем способ построения множе-
ства У, которое состоит из векторов уи ..., ур и обладает свойст-
вами:
1) Соп(уи ..., уР) ==Соп{хи .,., хт),
2) yi^Con(yu ..., Уи •-., Ур), /=1,...,р. (*)
Если ни один из векторов xi нельзя представить в виде неотри-
цательной линейной комбинации остальных векторов множества
X, то утверждение справедливо. В качестве множества У можно
взять само X.
Пусть один из векторов множества X принадлежит конической
оболочке остальных векторов из X. Предположим для определен-
ности, что
*1<=С0П(Х2, •♦., Хт), (4)
и покажем, что конические оболочки ' множеств {хи ..., хт) и
{*2, ..., хт) совпадают:
С0П(ЛГЬ ЛГ2, ..., Хт) = СОП (ЛГ2, ..., Хт).
Произвольный вектор yd=.Con(xu „.., хт) можно представить
в виде
у = \1х1 + Ъ«^2Х1х1, А;>0.
Из предположения (4) следует, что вектор
Подставляя эту формулу в предыдущее равенство, получим, что
вектор
y = Sjl2(X1|i, + X?)x,
я, значит, принадлежит Соп(л:2, ..., хт). Этим доказано включе-
ние
С0П(ЛГЬ ЛГ2, ..., Хт)с=С0П(л:2, ..., Хт).
Обратное включение
ч
СОП (XU Х2, ...у Хт) =)С0П (ЛГ2, . . . , Хт)
тривиально.
Рассмотрим множество
^1={^2, • • ., Хт}.
187

Если ни один из векторов множества Х\ нельзя представить в виде
неотрицательной линейной комбинации остальных векторов из Хи
то утверждение доказано: в качестве множества У следует взять
*ь
Если же хотя бы один вектор из Хх принадлежит конической
оболочке остальных, то повторяем проведенные рассуждения.
В итоге (после конечного числа шагов) получим набор У век-
торов
У г =xii> • • • >Ур — х1р>
обладающий нужными свойствами.
б. Единственность. Пусть множество Z={zu ..., zq} также об-
ладает свойствами (*).
Из совпадения конических оболочек Соп(У) =Con(Z) вытека-
ет, что векторы из множества У можно представить в виде неотри-
цательных линейных комбинаций векторов множества Z:
уь= 2f=1 aLizh an ^ 0, / = 1, ... , /?, (5)
а векторы множества Z в виде неотрицательных линейных ком-
бинаций векторов из У:'
2; = 2?=1 Мл Р</ > °> '= 1. - ■ ?• (6)*
Замечание. По крайней мере один коэффициент в каждой
из неотрицательных линейных комбинаций (5) — (6) положителен.
•Заменяя векторы zt в правых частях равенств (5) их выраже-
ниями (6), получим
У1 = 2fel *и &U М/) = 2?=i (2Li «*&/) У'п /= 1,...-, Р.
или
У1 = Ж=1УиУп /=1, ...,р, (7)
где
Y// = 2f=1 а ,р,у ^ 0, 7, / = 1, ... , /7. » (8)
Более того, Y">0> так как yi^Con(yu ■.., 5/, ..., Ур).
Покажем, что.уи = 1.
Предположим сначала, что уи<\. Переписывая равенство (7)
в виде
(1—уи)У1 = 21Ф1УИУ!
и деля обе части на коэффициент при уи получаем, что
В силу неотрицательности коэффициентов этой линейной комби-
нации выполняется соотношение
{/,<=Соп(*/1, ..., г/7, ..., Ур)>
что противоречит условию.
188

Значит, уи>-\. Соотношение (7) удобно переписать так:
1чФ1УиУ1+(уи— l)yt = Q.
Вследствие того, что рассматриваемый конус заостренный, и
в силу леммы последняя линейная комбинация тривиальна:
Y"=1> Уи = 09 \Ф1.
Тогда из формул (8) получаем, что
2?=1 а„р„ = 1, 2*в1 «.#„ = 0, / ф I. (9)
Из соотношений (9) вытекают равенства
а/ф;/ = 0, f=lf ...,f; /=1, ...,р; /V=/.
В силу замечания хотя бы одно из чисел ац положительно.
Пусть, например, а/^>0. Тогда
Pv =0, /=1,...,/>, /9-/. (10)
Вновь в силу замечания хотя бы одно из чисел р,у в разложении
(6) (при i=.i'/)
— положительно. С учетом' соотношения (10) заключаем, что
P,v>0 и *, = ?*,#,.
Положим fi/=l/fy/. Тогда
»i = e^|f б^О, 1=1, ...,/7. (11)
Меняя местами в проведенных выше рассуждениях множества
Y и Z, аналогично получим, что
2t = e#/,i e*>0, i = l, ... ,?. (12)
Из формул (П)~(12) вытекает, в частности, что p = q.
Итак, мы доказали, что умножением векторов множества Z
(соответственно У) на подходящие положительные множители
можно получить все векторы множества Y (соответственно Z).
Это завершает доказательство единственности (рис. 54). □
Задача. Показать, что (рис. 55)
Нп(Х) => aff(X)
U U
con (X) =>conv(X).
ТЕОРЕМА 2. Усл. К — многогранный конус.
Утв. Существуют линейное подпространство W и заостренный
многогранный конус Q, такие, что K = W®Q, причем линейное под-
пространство W определено однозначно (рис. 56).
189

Доказательство. Если конус К заострен, то доказатель*
ство утверждения тривиально. Если же конус К незаостренный,
то он содержит линейное подпространство, размерность которого
,не меньше единицы. Среди линейных
пространств, содержащихся в конусе К,
выберем то, которое имеет максималь-
ную размерность. Ясно, что это подпро-
странство определено однозначно. Обо-
значим его через W и рассмотрим разло-
жение пространства V в прямую сумМу
где W* — какое-нибудь дополнительное
подпространство.
Рис. 54 Множество Q==K(]W6 — многогран-
ный заостренный конус. Ясно, что W®
<BQc=/(. Пусть хе/С. Из разложения x = w+w\ где ©sf, кубе=
^W6, и из того, что (—w) ef, вытекает включение w6 = x—kig
Значит, Kc=W®Qy и, следовательно, K=W®Q. D
Рис. 5,5
Рис. 56
§ 7. ВЫПУКЛЫЕ МНОЖЕСТВА В ТОЧЕЧНЫХ ПРОСТРАНСТВАХ
Пусть О, Аи ..., Ak — точки /г-мерного точечного пространст-
ва s4>n.
Определение 1. Точка Л, определяемая соотношением
ОЛ-ЗЬ^аЛ, , (13)
где 2*в1Я, = '1, Л,>0,
называется выпуклой комбинацией точек Ль ..., Ak.
ТЕОРЕМА 1. Усл. Точка А определена формулой (13); О* —
произвольная точка пространства J&n.
190

Утв.
ОМ = 2?. А, ОМ,. (14)
Замечание. Справедливость теоремы 1 означает, что опре-
деление выпуклой комбинации точек не зависит от выбора точки
отсчета. »
Доказательство. Умножим очевидные равенства
ОМ, = (ГО+ 04, i=l, ...Л
на соответствующие коэффициенты Jw и сложим то, что получится..
С учетом равенства ,
результат можно записать в следующем виде:
В силу условия (13) правая часть последней формулы равна
0^+ОЛ = ОМ.
Сравнивая эти два соотношения, получаем требуемое (14). П
Доказанная теорема позволяет для вычисления выпуклой ком-
бинации точек вместо формулы (13) пользоваться следующей:
4 = Mi+-.- +М*=*2{Ц1М*, 2tA—I, V>0. (15)
Ясно, что при выборе любого координатного репера соответству-
ющие координаты точек А и Ait 4i=l,...,£, будут связаны анало-
гичными соотношениями
<х! = 2*а1Щ, /=1 п.
Пример. Точка А— — Ах -\ А2 -\ А3
О о О
является центром тяжести системы точек Ль Л2, Лз.
Замечай и\е. При доказательстве теоремы 1 неотрицатель-
ность чисел Kt не учитывалась. Поэтому на точечное пространства
можно перенести и понятие аффинной комбинации'точек
Л = 2ЦЯЛ, 2{_Л = 1-
Пусть Л и В"— точки пространства $&п.
Определение 2. Прямой, проходящей, через точки Л и Ву
называется множество точек
LAB = {C=(\—t)A + tB\ts=SL).
Определение 3. Отрезком с концами Л и В называется
множество точек, определяемое формулой
АВ = {С= (l—t)A+ /B|0<*<1}.
191

Определение 4. Множество X из пространства st>n назы-
вается выпуклым, если для любых двух точек Л и В из X отрезок
АВ также принадлежит X.
Доказанная в этом параграфе теорема 1 позволяет переформу-
лировать все утверждения, доказанные для выпуклых множеств
в линейных пространствах, применительно к выпуклым множест-
вам в точечных пространствах. При этом доказательства измене-
ний не претерпевают. Это же относится ко всем рассмотренным
выше операциям над выпуклыми множествами.
Пример. Пусть х1, ..., хп — координаты в я-мерном точеч-
ном пространстве. Если пространство евклидово, то множество
точек; координаты которых удовлетворяют неравенству
где х=(х1 ... х")т, представляет собой я-мерный замкнутый шар
единичного радиуса с центром в.точке О.
Пусть A^Rnxn — невырожденная матрица. Преобразование
у=Ах переводит этот шар в /г-мерный эллипсоид
УтВу^\,
где В—(А-{)ТА~1. Так как это преобразование линейно (преобра-
зуются только векторы координатного репера, начало не изменя-
ется), то эллипсоид — выпуклое множество.
Ясно, что перенос (начала) z=y+a также не нарушает выпук-
лости.
Тем самым произвольный эллипсоид
(г—a)TB(z—a)^l
является выпуклым множеством.
§ 8. СИММЕТРИЗАЦИЯ
Рассмотрим еще одну операцию, которая переводит выпуклое
множество в выпуклое.
Пусть <§ГЛ+1 — (п-Н)-мерное евклидово точечное пространство
и X — ограниченное замкнутое выпуклое множество.
(Множество X называется ограниченным, если существует шар
с центром в начале, содержащий это множество. Замкнутость оз-
начает, что множество содержит все свои предельные точки.)
Пусть Lq — произвольная прямая в пространстве &п+К Выбе-
рем в пространстве ё>п+1 ортонормированный репер {0; еи ..., *Wi}
так, чтобы OeL0, вл+ill^o» и рассмотрим пучок прямых, парал-
лельных оси 0£л+1.
Обозначим через {L} множество тех прямых пучка, которые
пересекают множество X. Пусть L — произвольная прямая из
{Ц. Координаты точек прямой L подчиняются условиям
192

где а1,
ап постоянные. Запишем это так:
Рассмотрим пересечение прямой L и множества X: a = L[\X
Ясно, что а — отрезок (прямой L).
Поставим в соответствие отрезку а отрезок as по следующему
правилу: если
а = {М(Ъ\ ..., e*+i)|6' = a', i=l, ..., /г, a-»+1<g^1<a+ll+1},
то (рис. 57)
г ± *г
а8 = Ш(& e^W-tx'.' = !,....*.
^р
Рис. 57
Рис. 58
При таком преобразовании множество X переходит во множе-
ство XSt обладающее следующими свойствами:
1+. Множество Xs симметрично относительно координатной
гиперплоскости £Л+1 = 0.
Симметричность относительно гиперплоскости g"+1 — 0 понима-
ется в следующем смысле: если точка
то и точка
М&\ ...,¥, Zn+l)<=XSf
Ms (IK ...,§", -6»+i)€=xs.
ции.
2+. Множество Xs выпукло.
Чтобы показать это, введем важное понятие выпуклой функ-
Рассмотрим в гиперплоскости grt+1 = 0 выпуклое множество //.
Пусть
Е^1—/(Б1 БЛ)
Функция, заданная в точках (g1, ..., grt) множества Н.
7 Заказ 538
193

Определение. Функция %n+l=f{V> ..., 1,г) называется вы-
пуклой на выпуклом множестве Я гиперплоскости g"+1 = 0, если
для любых точек 5=(^, ..., %п) и г\=(г\\ ..., г\п) из Я и любых
неотрицательных чисел А, и ц, связанных условием к+\х=1, выпол-
няется неравенство
/(A«+|i4)<A./(6) + |i/(4)f (16)
или, подробнее,
/(Ц1 + ЦЛ1* • • • . Чп+№п) < Я/(Г, ... , Ея) + |1/(л\ • • • , Л").
Функция irt+1=ff(i1, ..., ln), заданная на множестве Я, назы-
вается вогнутой, если (—g) выпукла.
Замечание. Понятие выпуклой функции вводилось ранее
(см. лекцию 23) для векторного аргумента; при этом область оп-
ределения совпадала со всем пространством.
• Утверждение. Если функции /i и /2 выпуклы на множестве
Я, то функция / = ai/i + <X2/2, где ai>0, a2>0, также выпукла на Я.
Доказательство. Достаточно записать неравенство (16)
для обеих функций /i и /2 и затем сложить. □
Заметим, что если / выпукла, а g вогнута, то
— выпуклая функция.
Спроектируем ограниченное замкнутое выпуклое множества
X<z:&n+l на гиперплоскость £л+1=-0. Обозначим проекцию через Я.
Ясно, что множество Я выпукло.
Прямая LMj проходящая через произвольную точку g=(g1,.l»
..., £л) множества Я параллельно оси |л+1, пересекает множество
X по of резку / (может быть и вырожденному). Отрезок / одно-
значно определяется двумя точками, своими концами М~(11, ..,
..., Ъ», £-"+*) и М+(1\ ..., §", g+rt+1), где ^.«+1<6+я+1.
Сопоставляя точке f = (I1, ..., ln) (п+1)-ю координату ниж-
него конца М-, получаем функцию
€я+1=/(6!, ....6я).
заданную на выпуклом множестве Я (рис. 58).
Эта функция выпукла. В самом деле, пусть точка ДО- полу-
чена аналогичным приемом (при помощи проходящей через ^еЯ
параллельно оси 1п+1 прямой LN). Так как точки М- и Лг_ принад-
лежат множеству Ху а X выпукло, то и их выпуклая комбинация
XM-+\xN-(X^0, \x^0y А, + ц = 1) лежит в X. Это означает, что
/(Д+ил)0/(6) + и/(л).
Отсюда, в частности, вытекает, что множество точек МеЙ'""11,
координаты которых удовлетворяют условию
6я+1>/(6?. ....6я)
— «надграфик» функции /(g), выпукло.
194

Аналогично обращаясь с верхним концом отрезка М+, получаем
вогнутую функцию
ln+l=g(V 6").
Таким образом, выпуклое множество X можно записать так:
Х = {(?,...,S",Г+1Ш> • • •.£")sя,/(£, ...,|")<
<in+1<g(i1, ...,s-)}.
Пучок прямых, параллельных оси |n+1, путем описанного" выше
правила преобразует множество X во множество
XS = {G\ ...ЛпЛпН)\(?, ...,Г)еЯ,
4- [/(? rwa1 in)] < in+1 < 4- te^1 5")-
2 ~
■/(б1,....?)]}.
Так как —(f—g).
выпуклая функция, то"^ полученное мно-
жество Xs также выпукло (как и исходное множество X).
Определение. Преобразование X-*XS выпуклого множе-
ства X называется его"симметризацией.
Таким образом, операция симметризации (относительно гипер-
плоскости) не выводит нас из класса выпуклых множеств.
Здесь уместно сказать и о других
видах симметризации, также обла-
дающих указанными свойствами.
Для простоты ограничимся трех-
мерным случаем. Пусть X — выпук-
лое тело в &ъ. Нетривиальное пе:
ресечение тела X с плоскостью 11 =
=c:onst является плоской замкну-
той выпуклой областью. Найдем ее
площадь и построим в этой плоско-
сти равновеликий круг с центром в
точке (g1, 0, 0). Поступая так со
всеми сечениями, получаем тело
вращения (рис. 59). Интересно от-
метить (да и доказать нетрудно),
что и такая симметризация (отно-
сительно оси) не выводит из класса
выпуклых множеств. В многомер-
ном случае можно определить сим-
метризацию относительно плоскости
любой размерности.
Приведем еще два свойства сим-
метризации (без подробных поясне-
ний и доказательств).
7*
Рис. 59
195

3+. Симметризация не изменяет объема тела
\o\(X)=vol(Xs).
4+. Площадь поверхности выпуклого тела не уменьшается
sq(d*)<sq(d*e).

ЛЕКЦИЯ 27
Глава VIII. ЭЛЕМЕНТЫ ТЕНЗОРНОЙ АЛГЕБРЫ
§ 1. ПОНЯТИЕ ТЕНЗОРА
0°. Примеры. Пусть V — n-мерное вещественное линейное про-
странство. В предыдущих лекциях значительное внимание уделя-
лось изучению свойств таких геометрических объектов, как векто-
ры, линейные операторы, линейные и билинейные формы и др.
Фиксируя базис е=(е\ ... еп) пространства V, мы ставили каждо-
му из них (вектору х, линейной форме со : V->R, линейному опе-
ратору s£ : V-+V, билинейной форме 98: VXV-+R) в соответствие
упорядоченный набор чисел — их компоненты.
Таблица 1
Геометрический объект
Вектор
Линейная форма
Линейный оператор
Билинейная форма
ч—'
Компоненты
i'
' щ
а{ ■
е.-/
Число компонент
п
п
п*
п*
При переходе от одного базиса к другому эти числа изменяв
лись. Напомним; как это происходило.
Пусть /=(/1 ... fn) — другой базис пространства У: Тогда
где К=(и;т), Л=(А,,т), т, i==l, ..., я, причем.ЛК=КЛ=/, т. е«
Обозначая для удобства компоненты объектов в новом базисе
теми же буквами, но со штрихов слева вверху/ запишем:
Таблица 2
Вектор
Линейная форма
Линейный оператор
Билинейная форма
' \! = Ъ1*Ц
'Ctj = 2;оЦ
'а* =2. .aWX?
'hm = \i§ijKklm - j
Таким образом, для произвольного базиса каждый из объектов
х> о), ^, д$ задается упорядоченным набором пк (й = 1 или 2)
197

чисел, изменяющимся при переходе к другому базису по опреде-
ленным правилам (единым для объектов одной природы).
Отметим, что некоторые объекты, вычисление которых требует
задания базиса, от выбора базиса вообще не зависят. Например,
ранг, определитель и след линейного оператора, ранг и индекс
билинейной формы.
Попробуем теперь взглянуть на сказанное выше с несколько
иных (более общих) позиций.
1°. Определение тензора.
Определение. Будем говорить, что в пространстве V задан
тензор Т типа (Р\, если
1) в каждом базисе (е) задается упорядоченный набор npV<*
чисел
fx~.ip 1 <h<nf ... , l<ip<n,
'"•V 1</г<я, ... , 1</,<п,
— компонент тензора Т (в базисе е);
2) для набора компонент
,,pkt...kp 1 <^x<Al, . . . , 1 <kp<n,
Zl"V 1<1г<п9 ...,1</,<л,
тензора Т в базисе / справедлива формула
'7£;£«2,, • ••• \ • • • 2/,:.. 2,, г;::;:;^;... *W{;... ^
— закон преобразования компонент тенрора Т (все индексы, по
которым ведется суммирование, независимо изменяются от 1
до п).
Верхние индексы у компонент тензора называются контравари-
антными, а нижние — ковариантными индексами. Тензора
является р раз контравариантным и q раз ковариантным. Его
ранг равен p + q.
Примеры тензоров
(1) Скаляр — тензор типа (JM, вектюр — тензор типа /* ],
линейная форма (ковектор) — тензор типа [У], линейный опера-
тор — тензор типа (\\, билинейная форма (2-форма) — тензор
типа (I).
(2) Символ Кронекера 8/ — тензор типа (|):
'б* = 2, ШЫ = 2Л*х' = tm.
198

Запишем закон преобразования компонент тензрра Т типа
(Р\ более коротко:
'*?:;:}' -2(0.</> г;;;;;^ ... х\Ы\... х{«, (1)
где /=(*i . •• W» /=(/i ••• /V). а символ 2<о,(/) означает, что сум-
мирование проводится по каждому из индексов iu ..., ^, /ь ..., jQ,
независимо изменяющемуся от 1 до п.
Заметим, что выбор букв для обозначения индексов суммиро-
вания в формуле (1) произволен.
Закон преобразования (1) будем называть тензорным законом
типа (Р). Нетрудно заметить, что место каждого индекса у ком-
понент тензора (вверху или внизу) связано с законом преобразо-
вания.
Выразим компоненты Т)1"ЛР тензора Т в базисе, е через его
ъ ъ
компоненты 'Т.1ш",р в базисе f.
Утверждение. Справедлива формула
^:::^=2<*).(|)'^:.-.^^..-х^й...х^ ' (2)
Доказательство. Преобразуем выражение, стоящее
в правой части доказываемой формулы, пользуясь законом (1)
T/;::f; =sWiW ^;:::;;4...tyb•••*!;
и очевидными формулами
2^Я5 щ = 6S, 2/X/X/ = б/.
Имеем
s<*>.«> '^г*Рхй- • • ^А{;.. '.*;* =
=2(*,,(/) (2<.).,от;;:::^*4... я**#...х|*к,... х^... я;<=
=sw.(<) ^:;;Jj(2(*)l(o (яЫ)... (Л^рх^Хх'аЬ • • • (*£*!j» =
=2(s),(0T-::;,6t..6;,6t..6;rr;.;::;;.:. n
Замечание. Так как соотношения (1) можно рассматривать
как систему пр+« линейных уравнений относительно пР+ч неизвест-
ных Т1^'л.р, то доказанное утверждение означает, что эта линейная
система является однозначно разрешимой.
Убедимся в том, что определение тензора корректно.
ТЕОРЕМА 1. Усл. р и ? — произвольные неотрицательные це-
лые числа.
199

Утв. IS пространстве V существует тензор типа ( Р ).
Доказательство. Выберем в пространстве V базис е.
Произвольно взятый набор np+(f чисел Г£"Wl< il9.. .,1Р,]\,...
---JqKn) будем рассматривать как совокупность компонент
тензора типа (Р J относительно этого базиса.
Укажем сначала, как построить компоненты тензора относи-
-тельно любого другого базиса.
Пусть /. — базис пространства V; //=2ix/te/, £r=2/ta'//. Опре-
делим компоненты Т?1'".*" по следующему правилу:
- '^;;;.^ = 2(0д/)т;;;;;;^1;...я*ри^..х^. (1)
Чтобы убедиться в том, что тем самым в пространстве V дей-
ствительно построен тензор типа (Р\, достаточно проверить, яв-
ляется ли тензорным закон преобразования компонент при пере-
ходе от одного произвольно взятого базиса к другому, тоже
, произвольному.
Пусть / и g — два любых базиса пространства V;
gk=\Sfilfh fj=zkvkiek'
Компоненты fT^"'fp относительно базиса / определим по фор-
муле (1), а компоненты "T^'"smp относительно базиса g по следу-
ющему правилу:
; "Г™:;;;^= 2(0,(/) Т^рт^ . >. x^oj;... а'*, . (3)
где gk^^iOk^i, ei = 2kXikgk-
Покажем, что указанный тензорный закон преобразования
(типа [Р]) сохраняется и при переходе от компонент 'T^y/jP
к компонентам ,"7?t,,;m'\
Прежде чем подставлять в правую часть формулы (3) выра-
жение (2) для Т\1,ЛР, заметим, что .
Теперь уже нетрудно видеть, что
f/rpmi...mp
=.2(0,(/) (2(*м/) т£;;*р х£ ... <п£ ... *Л) т? ... т"> а[\... о[* =
200

= 2<».tf> Ttj^.iM^Z1)-• ■("['„•ГфУйо'д---^/sp)-
=S(*,.(o "iz\%< ■ • • W, ■ ■_• иг- □
P
Замечание. На практике для задания тензора, как правило,
используют именно этот прием: относительно выбранного базиса;
(часто естественным образом приспособленного к рассматривае-
мой задаче) задаются компоненты тензора и указывается его тип.
Закон преобразования позволяет найти в случае необходимости
компоненты тензора в любом другом базисе пространства.
Введем понятие равенства тензоров.
Определение. Тензоры Т и S называются равными, если
они имеют один и тот же тип и все их компоненты в каком-нибудь
базисе соответственно равны.
Обозначение: T=S.
Mt...tn и Sjt...i-
в базисе е.
Пусть Т^'У и SJ|;;;Jp— компоненты тензоров Т и S типа
(?)
Равенство T=S означает, что
^...i SH...t
h'--Jq tf-lq
для всех ii,r.'.9ipi /i,...,/g, удовлетворяющих условию l^i'i^
Из закона преобразования тензора вытекает, что указанная
связь между компонентами сохраняется при переходе к любому
другому базису: если 'T^'/fp и 'S*1'.7*р— компоненты равных тен-
зоров Т и S в базисе /, то ,
для любых k\9 •. •, kPt lu ..., Iq, удовлетворяющих условию
Определение. Тензор Т называется противоположным тен-
зору Г, если в некотором базисе е выполняются равенства
rptf.ip rpix...ip
Ясно, что при переходе к другому базису указанное свойство
сохраняется.
2°. Алгебраические операции над тензорами.
1+. Линейная комбинация тензоров. Пусть
г=(г;::::;,) и s=(sj*:;-jp . :
— тензоры типа (Р\, а и (}—произвольные числа. Тогда линей-
ная комбинация
t/ = a7\+pS . ,
201

также есть тензор типа ( ^ с компонентами
(?)
ul;-ip=aTi;-clP + 6Sc;--ilP.
h---1q h-"'q 1i-'>q
Тем самым совокупность тензоров одного типа образует линей-
ное пространство (размерность этого пространства равна числу
компонент).
2+. Умножение тензоров. Пусть Т = (Т1У'лр)—тензор типа (Р\ и
S = (Sl.p+1'"ttP+r) —тензор .типа (г V
Положим
Тогда- U = (Uty'JiP+f)~тензор типа (ptr)>
называемый произведением тензора Т на тензор S.
Обозначение: U = T®S.
Отметим, что в общем случае T®S^S®T. .
3+. Транспонирование тензора. Пусть Г = (Г£'^)—тензор типа
(А где 0[2.
А. Рассмотрим перестановку чисел (1...^) следующего вида:
/i...,.-......,v
\1 ...s...r...qj
а переставляет местами только числа г и s (1^><$^л).
Положим
т1^-лр =Т11'"1р
Тогда Г===(^>;;;^) —тензор типа (*Л.
Будем говорить, что тензор Г получен транспонированием тен-
зора 7 по двум нижним индексам (г-му и s-му).
Б. Операцию транспонирования мажно определить для любого
числа нижних индексов.
Рассмотрим перестановку
1 ...q
ч<х(1)...сг(«7),
На наборе (/) = (/i ... iQ) перестановка а действует по правилу
-с
<*(!)
- (h\
■//J... /, \
\/o(i) ••• /см/
или, что то же, o(/i ... ]ч) = (/«(о ... /о<?)).
202

Будем говорить, что тензор Т — (Т^'лр) получен транспони*
рованием тензора Т по нижним индексам при помощи переста-
новки а, если % ;
В. Операция транспонирования по верхним индексам опреде-
ляется аналогично.
Г. Операция транспонирования тензора при помощи переста-
новки индексов разных типов (верхних и нижних) не определена,
4+. Свертывание тензора. Пусть Т~(Т1У'ЛР) —тензор ranaf^L
где p^l, q^l. Положим
h- -Tm~iq /l* * ,;m-l Wl'' 'lq
Тогда 7 = (Г1,1,' л*-11*+1,лр )— тензор типа к ,], называемый
сверткой тензора Т по двум индексам: &-му верхнему и m-му ниж*
нему.
5+. Симметрирование и альтернирование тензора.
А. Определение. Тензор называется симметричным (па
нижним индексам), если каждый тензор, получаемый из него
транспонированием по любым двум нижним индексам, совпадает
с ним.
Примером симметричного тензора типа f|~ J может служить
симметричная билинейная форма.
Пусть Т = (Г£;;;Jp) —тензортипа (р\ . Положим S^Jp^rJ;;;;^
= —И(о)Г|1!'"1/', (суммирование, ведется , по всевозможным
перестановкам индексов /ь ..., jq). Тогда S = (S^'"^) — тензор ти-
па (Р\ симметричный по нижним индексам.
Б. Определение. Тензор называется кососимметричным
(по нижним индексам), если каждый тензор, получаемый из него
транспонированием по любым двум нижним индексам, противопо-
ложен ему.
Пусть Т = (Т)^\лр)— тензор типа 1Р). Положим A^f^T^;;^ =
=— 2(а) sign a T^yJp{. (суммирование ведется по всевозможным
q\ v\i\'-'iq)
203

перестановкам индексов /ь ..., jq). Тогда А = (А\1"л,р )—тензор
типа у), кососимметричный по нижним индексам.
В. Симметрирование и альтернирование тензора по верхним
индексам определяется аналогично.
Г. Симметрирование и, альтернирование тензора можно прово-
длть и по части индексов.
ЛЕКЦИЯ 28
• На пути совладению техникой обращения с индексами и для
упрощения выкладок полезно правило сокращенного суммирова-
ния.
Рассмотрим, например, следующее выражение
Sj^iA/Bk.
Отметим, что индекс суммирования / в этом выражении встреча-
ется дважды. Опуская знак суммы, запишем его так:
1 _ Л/Я*/.
Условимся_ считать, что повторение индекса указывает на то, что
по этому индексу ведется суммирование (даже при отсутствии
знака суммы). Поэтому последнее выражение нужно понимать
*гэк* ~~
v А№к1=А№к1 + ...+Ая*Вк».'
Сформулируем правило сокращенного суммирования.
Если в некотором выражении какой-то индекс повторяется
(встречается дважды), то по этому индексуvпроводится сумми-
рование; знак суммы при этом опускается.
Пользуясь сформулированным правилом, запишем, например,
закон преобразования (1):
В правой части этой формулы по дважды повторяющимся индек-
сам i*i, ..., ip, /ь ..., jq проводится суммирование.
ТЕОРЕМА 2. Утв. В результате каждой из алгебраических
операций 1+—5+ над тензорами вновь получаются тензоры.
Доказательство. 1+. Компоненты тензоров Т и S изменя-
ется по одному и тому же закону. Запишем этот закон преобра-
зования и для Г, и для 5. Умножим полученные при этом фор-
мулы соответственно на числа а и -0 и, складывая, получим, что
компоненты геометрического объекта U при переходе к новому
базису изменяются по тем же правилам, что и у Г и 5.
204

2+. Перемножая формулы, описывающие законы преобразова-
ния компонент тензоров Т и S, получаем, что компоненты геомет-
рического объекта U изменяются по тензорному закону типа
Доказательство свойств 3+ и 4+ проведем для тензоров типа
Несмотря на то, что это весьма частный случай, по сущест-
ш
ву ограничения общности не возникает, так как в разбираемых
операциях активно участвуют ровно два индекса либо одного типа
(3+), либо разных типов (4+).
3+. Рассмотрим тензор T — (Tlrs) и положим
Ti rpi iqnk frpk
rs — * sr> * lm — * ml.
Компоненты тензора Т преобразуются по правилу
'П»=П*М«. (*)
Пользуясь тем, что выбор букв для обозначения индексов сум-
мирования не влияет на сумму, поменяем в последней формуле
индексы г и s местами. Тогда
lm sr i I m.
Меняя теперь местами / и m, получим
'Tim = 'Tmi = TsД tX^X/ — Trs'k fl£fl<m.
Последнее означает, что Т = {Тп) — тензор типа (*).
4+ Положим Tr = T's, T|=-Tgi.
Вновь прибегая к правилу (*), получим
Отсюда в силу соотношения XimHms^^6i9 вытекает, что f=(fr)—
тензор типа (У).
Важное замечание. Доказательство свойств 3+ и 4+ полезно
провести для тензора Tl}'"bf в общей ситуации. Это позволит
убедиться в спра1ведливости утверждения теоремы и соображений,
высказанных непосредственно перед предложенными доказатель-
ствами этих, свойств. Кроме того, подробные выкладки послужат
хорошим шагом на пути к овладению техникой обращения с ин-
дексами, так называемым индексным формализмом.
5+. Транспонирование не изменяет типа тензора (свойство 3+).
Линейная комбинация тензоров снова есть тензор того же типа
(свойство 1+). Остается убедиться в том, что операция транспо-
нирования либо не изменяет порученного тензора (при симметри-
205

ровании), либо меняет его на противоположный (при альтерниро-
вании).
При транспонировании тензор 5 преобразуется в равный ему
вследствие того, что эта операция изменит только порядок сла-
гающих его тензоров.
При транспонировании тензор А преобразуется в противопо-
ложный вследствие того, что изменится не только порядок слага-
ющих его тензоров, но и знак перед каждым из них.
Примеры. (1) Оператор Jt = (Aty — тензор типа (М. Его
свертка — число tr ,А = А\ = А\+ ... +А% — след оператора —
тензор типа (^) (скаляр).
(2) Введенное ранее (см. главу III) умножение линейных опе-
раторов о€ = (Лр и о§~{Вгт) является сверткой тензорного про-
изведения Л ® <ffi = (Afi'mY-
ЦК-
3°. Примеры тензоров (физические и механические). В этом
пункте все тензоры задаются в трехмерном точечном евклидовом
пространстве ^Г3. Рассматриваются только прямоугольные декар-
товы координатные системы.
(1) Возьмем систему N материальных точек массы mi с коор-
динатами (х\\ хч\ лгзО» i—\, ..., N. Если точки системы жестко
связаны между собой (при движении их взаимное расположение
не изменяется), то мы получаем жесткую систему — «твердое
тело».
В динамике системы материальных точек большое значение
имеет симметричный тензор тица (Jj) ранга 2
'/* = б/* 2£i mi <(*{)" + (4)2 + (4>2>- 2£, m^xi.
Он называется тензорам инерции твердого тела, определяется
свойствами тела и связывает момент количества движения L=
= (Li, L2, L3) с угловой скоростью о= (coi, 0)2, ©3):
(2) Кристаллическое вещество анизотропно — его свойства
в разных направлениях различны. Под действием электрического
поля происходит смещение электрических зарядов в атомных
системах и в частицах кристалла возникает дипольный момент.
Индуцированный дипольный момент зависит от направления при-
ложения поля.
Пусть Е=(Еи Е^ £з) — напряженность электрического поля.
Тогда вектор поляризации Р=(Ри Ръ Ръ) определяется так:
206

где (ац) — тензор поляризуемости, характеризующий диэлектри-
ческие свойства кристалла. Это симметричный тензор второго
ранга типа ^2J.
Работа, затраченная на поляризацию единицы объема от О до
р — плотность энергии и? — вычисляется по следующей формуле:
Поставим вопрос: какие поля Е=(Еи Е2у Е3) отвечают данной
плотности энергии ир = и*?
Так как энергия поля всегда положительна и конечна, то,
считая a«v и w* известными, получаем уравнение эллипсоида
Ili,jaijEiEI=2u*. (*)
Тем самым любой вектор £, необходимый для создания задан-
ной плотности энергии, задается точками, расположенными на
эллипсоиде (*) (рис. 60).
Тензоры, рассмотренные в обоих при-
мерах, симметричны — симметричны мат-
рицы (/,•/) и (а,ц). Это означает, что суще-
ствует координатная система, в которой
эти матрицы имеют диагональный вид. Три
взаимно перпендикулярные оси такой коор-
динатной системы называются главными
осями. Это главные оси эллипсоида энер-
гии.
Вдоль каждой из главных осей имеем:
L||o) (пример 1)—главная ось инерции,
Р\\Е (пример 2) —. главная ось поля-
ризации.
Можно привести и другие примеры
тензоров.
(3) Тензоры второго ранга:
тензор напряжений (5,-/), описывающий внутренние силы в ве-
ществе,
тензор деформаций (Тц) упругого тела.
(4) Тензор третьего ранга.
При напряженном состоянии в кристалле возникает электри-
ческое поле, пропорциональное тензору напряжений:
Пьезоэлектрические коэффициенты Рцн составляют тензор (пьезо-
электрический эффект).
(5) Тензор четвертого ранга.
Для произвольных деформаций упругого тела тензор деформа-
ций Тц связан с тензором напряжений системой линейных соотно-
шений
Tijtsz'ZyijkiSki
Рис. 60

(закон Гука). Тензор yijki в случае, если материал изотропен,
определяется заданием только двух постоянных а и ft:
ytjki=abijbki + ft (SikSji + SitSjk).
§ 2. МЕТРИЧЕСКИЙ ТЕНЗОР
1°. Метрическая структура пространства. Пусть на векторах
л-мерного вещественного линейного пространства V задана невы-
рожденная симметричная билинейная форма g(x, у). Зафиксируем
ее и положим
(х,у)=8(*,У).
В случае, когда g(x, у) — симметричная билинейная 'форма,
полярная положительно определенной квадратичной форме, про-
странство V наделяется, тем самым, структурой евклидова прост-
ранства, а (х, у) представляет собой скалярное произведение^
векторов х и у. ^
Пусть е= \е\ ... еп) — базис пространства V. Рассмотрим cof
вокупность компонент ^
£//-<*/• et). * :;
Ясно, что g^igij) — тензор типа (^j. Назовем его метрическим
тензором или просто метрикой,
Если x=Vet% y=r\ieh то <*, y)=gul4\i.
В главе IV, посвященной билинейным формам, доказано сле-
дующее
Утверждение. Билинейная форма g(x, у) невырождена тогда
и только тогда, когда det(gj/)^0.
Тем самым в любом базисе возможен переход от цц к обрат-
ной матрице. Обозначим компоненты обратной матрицы через glL
Тогда
gihgV=8if, g'kgki=bif.
Утверждение. g*i — тензор типа (j"J, т.е.
Доказательство. Достаточно показать, что матрица 'gst'
определяемая формулой (1), является обратной к матрице
'gst=gtixshtt!. - '
Имеем ч
." '§sm 'gmt=(giJ Щ) tekpfirt)=giJ'gk№ frfO =
Аналогично проверяется равенство 'gtmgms = bts. О
208: ,

2°, Операции опускания и поднятия индексов. Пусть jf=(^/)-
метрика пространства V. Если Т = {Т^'лр) — тензор типа (Р), то
можно построить тензор типа (^Т"!) по следующему правилу:
t. е. сверткой произведения метрического тензора gu и исходного
тензора Т.
Правило (2) называется опусканием верхнего индекса i\.
Аналогично вводится правило поднятия нижнего индекса /ь
(3)
Утверждение. Если опустить индекс, а затем поднять его, та
получится исходный тензор.
Доказательство. Поднимая у тензора, стоящего в левой
части формулы (2), индекс н, получаем
Примеры. (1) Пусть g(x, у) — обычное скалярное произ-
ведение. Компоненты тензора £/ типа (*) можно истолковать
как (контравариантные) координаты вектора * = £>£/.
Опуская индекс, получаем
Рис. 61.
Рис. 62
Таким образом, опускание индекса у координаты £' вектора х
приводит к скалярной проекции этрго вектора на вектор базиса.
Это ковариантная координата вектора х (рис. 61).
Заметим, что /
<*, y)=guZir\I=g4ir\h
209

(2) Тензор Л = {А§ типа П ) можно рассматривать как линей-
ный оператор в пространстве V. Если задана метрика то верхний
индекс можно опустить:
Тем самым получается тензор типа (У), определяющий билиней-
ную форму
st(x, yy=Ai&r\i = ligikAfk4i = (xi sty). (4)
Обратно, поднятием индекса тензора типа {^) можно постро-
ить линейный оператор.
Напомним
Определение. Линейный оператор $Ф называется симмет-
ричным, если
(stx, у) = (ху sty),
л кососимметричным, если
(*&х, у) = —(х, sty).
Из формулы (4) видно, что (косо) симметричность оператора
равносильна (косо) симметричности билинейной формы
Замечание. Если пространство евклидово и координаты
прямоугольные декартовы и, значит, преобразования ортогональ-
ны, то можно не различать верхних и нижних индексов у тензо-
ра — они преобразуются одинаково (напомним, что матрица орто-
гонального преобразования ортогональна и обратная к ней совпа-
дает с транспонированной).
3°. Псевдоевклидова метрика. Пусть g — метрика n-мерного .
вещественного пространства. Квадратичную форму
заменой координат Ё=№г\к можно привести к нормальному виду.
В случае^ если
/= (ч!)2+...+ (л')2-(л'+1)2-., .-(лп)2>
будем говорить, что g^— псевдоевклидова метрика типа
(р, п — р). Пространство с такой метрикой называется псевдоев-
клидовым и обозначается чер^з Rnp,q, q=n—p.
Особенно важен случай RV-ьь
Определение. Пространство К4з,ь используемое в специ-
альной теории относительности, называется пространством Мин-
ковского.
Минковский (Minkowski) Герман (22.6.1864—12.1.1909) — немецкий ма-
тематик.
210

4°. Преобразования Лоренца. В евклидовом пространстве мет-
рика gij в ортонормированном базисе приобретает вид
diag{l, :.., 1}, который сохраняется при ортогональных преобра-
зованиях.
Попытаемся найти преобразования, сохраняющие диагональ-
ный вид псевдоевклидовой метрики
diag{l,;.., 1,-1,..., -1}.
Для простоты органичимся пространством R2i,i.
Рассмотрим преобразование плоскости, оставляющее неизмен-
ным точку О:
x'=ax+by, y'=cx+dy,
и потребуем, чтобы
*2-*/2=*'*-у'\
т. е. чтобы «крест» х2 — у2=0 снова переходил в «крест» х'*—у' =
= 0 (рис. 62).
Из соотношения
{ax+by)2—(cx+dy)2=x2—y2
вытекает, что
а2—с2 = 1, ab—cd=0, b2—d2=~\.
Ясно, что аФО.
Положим a=±cht|), где -ф — угол гиперболического поворота.
Путем простых преобразований можно убедиться в том, что
матрица
н:)
приводится к одной из следующих четырех:
chi|3 shiM /ch\|5—shijA /— ch\f> sh\|A /—chij? —shi|?\
sha|5 _cha|5/ * \sh\|5—ch\|5/ \— sht|) ch\|3/ \ — shij? — сЬ'ф/
Как и в евклидовом случае, полученные преобразования обра-
зуют группу. Эта группа называется группой Лоренца.
Положим
thi|) = —, y~ct.
с
Тогда из матрицы %
/ chi|> —sh г]?\ х
\— sh if chijv ч .
Лоренц (Lorentz) Хендрик Антон (18.7.1853—4.2.1928) — голландский фи-
зик и математик, почетный член АН СССР (с 1925 года).
211

лутем несложных вычислений получаем, что соответствующее пре-
образование плоскости можно записать в виде
Это известные а специальной теории относительности преобразова-
ния, называемые по предложению Пуанкаре преобразованиями
Лоренца.
Пуанкаре (Poincare) Анри (29.4.1854—17.7.1912) — французский математик
а философ, член-корреспондент Петербургской АН (с 1895 года).

ПРИЛОЖЕНИЕ
ЛЕКЦИЯ 1
ОПОРНЫЙ МАТЕРИАЛ
МАТРИЦЫ. ОПРЕДЕЛИТЕЛИ. ЛИНЕЙНЫЕ СИСТЕМЫ
Определение 1. Матрицей А размера гпХп называется
набор m-п чисел ац (/=1, ..., т; /==1, ..., /г) — элементов матри-
цы — записанный в виде прямоугольной таблицы
/ап а12 ... ахп\
Л = | а21а22 • •• а2п 1
\ат1 ат2 * • • агап/
Набор-(ацШ2..:Шп) называется i-й строкой, а набор
(=)
— /-jw столбцом матрицы А (/=1, ..., т\ /=1, ..., п).
Матрица размера \Хп называется строкой, а размера mxl —
столбцом.
Обозначение: Rmxn — множество всевозможных матриц разме-
ра пгХп с вещественными элементами.
Определение 2. Матрицы Л=(ш/) и В=фц) называются
равными, если Л, BsRmXn и ш/=р// для любых i=l m; /«
= 1,...,/г.
Обозначение: А—В.
Определение 3. Суммой матриц Л=(а;/)еКтхп и В=
— {$ij)^Rmxn называется матрица С=(уц)^КтХп, элементы ко-
торой вычисляются по формуле
Уи^аи+Ри (f=l, ..., m; /=1, ..., /г).
Обозначение: А+В.
Определение 4. Произведением матрицы j4=(ar7)eRmXn
на число XeR называется матрица B='(P//)^Rmx*i, элементы ко-
торой вычисляются по формуле
рг;=Яа^ (i=l, ..., m; /=1, ..., п).
Обозначение: ХА.
Определение 5. Произведением матрицы /4=(ai/)eRWXn
на матрицу В=($ц)^КпХ1 называется матрица C=(Yi/)eRmx/,
213

элементы которой вычисляются по формуле
У И = ««А/ + - ■ • + <*(п$п/ = 2£в1 aik$kf
(i=l, ... ,m; /=1,-... ,n).
Обозначение: AB.
Правило суммирования: пусть Л=(ш/)е
Kwxn» тогда;
Свойства операции умножения матриц:
1+. Пусть ЛеКтхп, BeRnx/, CeR^.
Тогда (ЛВ)С-Л(ЯС).
2+ Пусть i4e=R«Xn, B,Ce=RnX/, DeR/xff.
Тогда Л (В+С)=ЛЯ+ЛС, (B+C)D=BD+CD.
Определение 6. Матрица .
а12 a22
a,
'ml ^
a,
m2
: Rn
Xm
a„
^airt a2n
называется транспонированной по отношению к матрице Л=*
= (a//)€=Rmx7i'
Обозначение: Лт.
Свойства операции транспонирования:
1+. (ЛТ)Т=Л. . k
2+ (Л+В)тг=Лт+5т.
3+ (Ы)Т=ЯЛТ
4+. (ЛЯ)Т=ЯТЛТ.
ЛЕКЦИЯ 2
Соглашение об обозначении: Матрицу Л=(a//)eRmX7г
коротко записывать в следующем виде:
будем
Л =
, где ai = (ailt..ain), f=lf ..., т.
Определение 7. Основными элементарными преобразова-
ниями дтрок матрицы называются преобразования следующих
трех типов:
1) перестановка местами двух
строк матрицы
[аГ
...
к
а/
lam
i
1—>
'
axi
... 1
а'
а*
lam;
214

P«ft , РФО;
(аг -
к
\at
Wml
i
r *al ]
<*fe
^+YaJ
i am )
2) умножение строки матрицы
на неравное нулю число
3) прибавление к строке
матрицы другой ее строки,
умноженной на число
Определение 8. Матрица, обладающая следующими двумя
свойствами: (1) если f-я строка — нулевая, то (Н-1).-я также ну-
левая, (2) если первые ненуле-
вые элементы f-й и (£+1)-й строк
располагаются в столбцах с но-
мерами ki и ki+i соответственно,
то ki<ki+u называется ступенча-
той матрицей (рис. 1).
ТЕОРЕМА 1. Утв. Любую
матрицу путем конечного числа
элементарных преобразований
строк (первого и третьего типов)
можно привести к ступенчатой
матрице.
Соглашение об обозначении:
a'=(ai/...am/)T, /=1,
будем записывать ее так: А = (а1... а1... ап).
Определение 9. Основными элементарными преобразова-
ниями столбцов матрицы называются преобразования следующих
трех типов:
1) перестановка местами двух столбцов матрицы
ступенчатая
% матрица
трапециебидная
матрица
Рис. 1
Полагая в матрице А=(ац)(
п,
(al...ak...al...an)^(a\,
.an);
2) умножение столбца матрицы на неравное нулю число
(а1.. .а*.. лп) -> (а1.. .pafe.. лп), р¥0;
3) прибавление к столбцу матрицы другого ее столбца, умно-
женного на число
(а1.. .а*.. .а1.. лп) ►-* (а1.. .ak.. .al+yak.. .an).
ТЕОРЕМА 2. Утв. Любую ненулевую матрицу путем конечно-
го числа элементарных преобразований строк и столбцов можно
привести к матрице вида
о
215

(все элементы матрицы /г, кроме стоящих в позициях (1,1),
(2,2), ..., (г, г), равны нулю).
Определение 10. Правило d:RnXw-*R, согласно которому
каждой матрице A<=RnXn ставится в соответствие число d(A), на-
зываемое определителем матрицы А, называется определителем,
если,оно удовлетворяет следующим условиям:
1) если матрица имеет равные строки, то ее определитель ра-
вен нулю;
2) если некоторая строка матрицы представлена в виде суммы
двух строк, то определитель этой матрицы равен сумме определи-
телей двух матриц, полученных из данной заменой строки, являю-
щейся суммой двух строк,, ее слагаемыми;
3) при умножении строки матрицы на число ее определитель
умножается на это число;
4) определитель единичной матрицы равен единице.
Свойства определителя матрицы:
1+. Матрица А содержит нулевую строку =>- d(A)—0.
2+. Матрица В получена из матрицы А элементарным преоб-
разованием строк 1-го типа =^ d(5)=—d(A).
3+. Матрица В получена из матрицы Л элементарным преоб-
разованием 3-го типа =>- d(5)=d(A).
4+. S=(«a//)'— ступенчатая матрица => d(S)=cn.. >Оп
■>пп*
ЛЕКЦИЯ 3
ПРИНЦИП ИНДУКЦИИ. Усл. Имеется некоторое высказыва-
ние Т(&), где fteN — любое; 7(1) истинно.
Есть правило, руководствуясь которым, можно доказать истин-
ность Т(1) для данного / при условии, что Т(т) истинно для лю-
бого т<1.
Утв. Высказывание Т(к) истинно для любого fteN.
ТЕОРЕМА 3. Утв. Для любого натурального neN существует
ровно одна функция d:Rnxn~^R, удовлетворяющая условиям 1 —
2-3-4.
Определение И. Алгебраическим дополнением элемента
ац в матрице Л=(ш/) называется число Л//=(— l)/+/d(Afr/)
(здесь через Мц обозначена матрица, которая получается из мат-
рицы А удалением элементов i-й строки и /-го столбца).
Свойства определителя матрицы:
1+. Матрица А содержит нулевой столбец =>* d(A)=0.
2+. Матрица В получена из матрицы А элементарным преоб-
разованием столбцов 1-го типа =^ d(B)=—d(A).
3+. Матрица В получена из матрицы А элементарным преоб-
разованием столбцов 3-го типа =>- d(B)=d(A).
4+. Разложение по/-му столбцу*^(Л) = Sfe=iafe)i4fe/, /=1, ..., п.
5+. Транспонирование определителя матрицы: d(AT)=d(A).
6+. Разложение по t-й строке: d(i4) = SLiMtt. * = 1, . •» «•
216

7+. Умножение на «чужие» алгебраические дополнения:
2*riOiH/fc==S»_!atf^k/e0. *Ф1- .
Определение 12. Отображение о:{1, 2 я}-»-{1, 2, ..., «}
называется перестановкой набора (1, .... /г), если а(1)ФаЦ) при
/ 1 2 ... n \
Обозначение: [в{1) а{2) ...в(п)): ■
Определение 13. Перестановки а и т множества {1, 2, ...
. п} называются равными, если o(i)=*x(i) для любого t=
— 1, 2 /».
Определение 14. Перестановки о и т отличаются на транс-
позицию (i, /), если x(k)=a(k) для любого k¥*i9j и т(0=а(/),
т(/)==а(0.
Определение 15. Пара (o(i), o(/)) образует инверсию в
перестановке а, если /</ и а(0 ><?(/)•
Определение 16. Перестановка называется четной, если
общее число инверсий четно, и нечетной, если общее число инвер-
сий нечетно.
Определение 17. Знаком перестановки а называется число
signa=(—1)', где / — общее число инверсий.
Свойства перестановок множества {1, ..., п}\
1+. Если перестановки а и т отличаются на транспозицию, то
sign т=—sign <х.
2+. Общее число перестановок равно п!
3+. Общее число четных перестановок равно общему числу не-
четных.
ТЕОРЕМА 4. Утв. d^)=2{(I)Signorai0(i)...a„(,(n).
ЛЕКЦИЯ 4
г
Пусть Я—(atf)sRmxn> * — целое число, удовлетворяющее не-
равенству l^&^min(m, n). Рассмотрим два набора целых чисел
i\> ..., ik и /ь ..., /*, подчиненных условиям
l<ii<m, ..., l<:ife<m; l</i</i, ..., \<jk<n,
а в остальном произвольных. Построим матрицу &-го порядка
217

располагая в позиции (г, s) элемент aifis матрицы Л, и вычислим
определитель этой матрицы.
Определение 18.
а(Н '"lk) = det(atj).
(h •• • h\
Если l<:i!<...<^<:m, l</i<...</*<«, то А\. . I
называется минором матрицы А порядка k.
ТЕОРЕМА 5. (Бине — Коши). Усл. Л<=Ктхп, Be=RnXm (л>т).
Утв.
/ 1 ... т\ (Цл... qm\
M^=s'<"<^<-A[qi...JB[;...m)
(суммирование ведется по всевозможным упорядоченным наборам
<7=(<7ь ..., Ят)).
Доказательство начнем со вспомогательных рассмот-
рений.
А. Пусть /=(/ь ..., 1т) — произвольный набор целых чисел»
удовлетворяющих условию \<1\<п9 ..., 1</т<:м. Построим из
элементов матрицы В определитель m-го порядка
VI ... т I \ о о
Свойства определителя В I J т 1:
1+. Если среди чисел /ь ..., /т есть совпадающие, то
я I 1=0 как определитель, имеющий равные строки,
д 1'... #/*■ /
2+. Пусть числа /i,..., /m, слагающие набор /= (/i,..., /т)»
попарно не равны: /;¥=// при. t¥=/. Упорядочим набор / по возраста-
нию. Имеем
где l<:^i<.. ,<qm<n. Переставляя строки определителя
В ( * от I в соответствии с предложенной перенумерацией
Бине (Binet) Жак Филипп Мари (2.2.1786—12.5.1856) — французский ма-
тематик.
21,8

учитывая, что при перестановке любых двух строк определи-
тель изменяет знак, получим формулу
D(li---lA . (4i-.-4m\D(4i---
eli...«)-«4i1...J<4i...
ж
- Б. Пусть <7=(<7ь ..., Чт) — некоторый фиксированный упоря-
доченный набор, 1<:<7i<. . ,<qm<n. Рассмотрим следующее выра-
жение:
О)
(?1> • • • > Чт) = Sawlf...,дт) «i/, . . . 0Cm/mB ^ j ^ ]
(2)
(суммирование ведется по всевозможным перестановкам набора
Ч=(Яи •••» Чт), и, значит, в правой части формулы (2) содержат-
ся т\ слагаемых указанного вида).
Так как каждый набор /=(/i> ..., lm) в формуле (2) получен
перестановкой заданного набора <7,,то выражение (2) для (о(ч)
можно, пользуясь формулой (1), записать по-иному:
Замечая, что
. (Ях • • • Чт
1 ...т\
Яг •• -Чт/
окончательно имеем
Ях-'-Ят
^*&\1\...иахк
&ml .
О)
v ' V7i • • • <7m/ V 1 ... m Л
(3)
В. Перейдем к непосредственному доказательству теоремы.
Элементы у</ матрицы С=АВ определяются формулами
Y</-2?-i«uP</. (. /- Ь • • •> т-
Поэтому det С можно записать так:
detC =
Yll • • • Yim
Ymi • • • У mm
2/1==s i a i /tP/t i ... S?1=ia i i$tim
^т=\а™Фт* • • • 2?«-1°ЧА
Воспользуемся свойством 2 определителя. Последовательно при-
меняя его к каждой из т строк det С, получим
detC = 2?1.i...2t-i
219

Любое слагаемое в полученной сумме можно представить в виде
aml3lm\ . . . am/mP/mm
-""•■■-^ :::':)■
Для этого достаточно вынести из i'-й строки (i=l, ..., т) за знак:
определителя общий множитель аць. Тем самым
detc=2?, t-'Ч •••^^('j ;;;'*)■
(4>
Индексы суммирования в формуле (4) независимо изменяются от
1 до л. Поэтому для произвольно взятого упорядоченного набора
Я==(Яи •••> Ят) и любой его перестановки /=(/i, ..., lm) в сумме
(4) можно указать определяемое этой перестановкой / слагаемое
«Ut . . . CLml В
Объединяя все слагаемые, отвечающие набору qy получим, что их
сумма равна (о(д):
(к • • • М
(ср. с формулой (2)). Аналогичным образом поступаем с каждым
упорядоченным набором q.
Учитывая, что все слагаемые суммы (4), соответствующие на-
борам / с совпадающими элементами, равны нулю (свойство 1+)„
окончательно получим . .
detC = 2(0©fa). (5)
Символ 2(a) в формуле (5) означает, что суммирование ведется
по всевозможйвш наборам q=(q\, ..., Ят), подчиненным услови-
ям 1<:<71<...<<7т<:л.
" Переход к более подробной записи формулы (5):
«c=w..<.^(,:;;;I).(?;;.-)
ставит в доказательстве точку. □
СЛЕДСТВИЕ. Усл. А и В — квадратные матрицы.
Утв. det(AB)=detA-detB.
СЛЕДСТВИЕ. Усл. j4e=Rmxn, B<=R„Xm, n<m.
Утв. dtt(AB)=0.
220

Определение, 19. Матрица A^Rnxn называется невырож-
денной, если ее определитель отличен от нуля, deM^O, и вырож-.
денной, если <1еЫ=0.
Матрица ЛеКпХп.
Определение 20. Матрица
В
(Аи ... Лп1\
а" "а')'
где Aji — алгебраическое дополнение элемента ац, называется
присоединенной матрицей для матрицы Л.
Свойство присоединенной матрицы: АВ=ВА=detЛ-/.
' Определение 21. Матрица X^Rnxn, удовлетворяющая со-
отношению
АХ=ХА=1,
называется обратной по отношению к матрице A^Rnxn.
Обозначение: Л"1.
ТЕОРЕМА 6. Утв. Для любой невырожденной матрицы обрат-
ная к ней всегда существует и единственна.
Свойства обратной матрицы:
1+ (Л-^-^Л. 2+ (АВ)-Х-В-ХА~К 3+. det(4-1)e(det^)-1.
Определение 22. Рангом (прямоугольной) матрицы назы-
вается наивысший порядок отличного от нуля минора этой мат-
рицы; такой минор матрицы называется базисным, а строки и
столбцы, которые содержат его элементы, называются базисными,
ТЕОРЕМА 7., Утв. Базисные столбцы матрицы Л линейно не*
зависимы. Всякий столбец матрицы Л можно представить в виде
линейной комбинации ее базисных столбцов.
Замечание. Аналогичное утверждение верно и для строк
матрицы Л.
Обозначение: rang Л.
ЛЕКЦИЯ 5
ТЕОРЕМА 8. Утв. Элементарные преобразования строк к
столбцов матрицы не изменяют ее ранга.
ТЕОРЕМА 9. Утв. Элементарными преобразованиями строк и
столбцов матрицу Л, ранг которой г^гапдЛ^Л, можно привести
к следующему виду:
1 0
\о''ч
0
' ° I
0
221

Определение 23. Квадратные матрицы
°Г '
;... о....
; 9-
называются матрицами элементарных преобразований (элемен-
тарными матрицами); все элементы вне главной диагонали, кро*
ме указанных, равны нулю.
Свойства элементарных матриц:
1+. Элементарные матрицы невырождены.
2+. Умножение матрицы А на элементарную матрицу Р слева
^справа) равносильно элементарному преобразованию строк
{ столбцов) матрицы А 1-го типа.
3+. Умножение матрицы А на элементарную матрицу Q слева
(справа) равносильно элементарному преобразованию строк
^столбцов) матрицы А 2-го типа.
4+. Умножение матрицы А на элементарную матрицу R слева
(на матрицу /?т справа) равносильно элементарному преобразо-
ванию строк (столбцов) матрицы А 3-го типа.
5+. Любая невырожденная матрица разлагается в произведе-
ние элементарных матриц.
ТЕОРЕМА 10. Усл. Ae=RmXn, rangi4 = r>l.
Утв. Существуют невырожденные квадратные матрицы Se
^Rmxm и DeRnxm, такие, что
SAD =
Пусть
/ а11 •... al«pl \
\am1 ... amnpm /
"ml • • • ^mnrm
матрица размера mX{n+l), первые п столбцов которой ненуле-
вые.
Определение 24. Совокупность соотношений
anXi+. ..+ain*n=Ph
(*)
0CmlXi+. . .+Ctmn^ns=:Pm, ♦
222

где числа х\, ••> хп рассматриваются как вел'ичины, подлежащие
определению (неизвестнее), называется системой пг линейных
уравнений с п неизвестными (линейной системой).
Матричная запись линейной системы
ЛХ=5, (*>
где / «и... оь1п \ / Рх \ / х \
* = [ U= •• ,Х= ... .
\ат1...аяи/ \рт/ \хп/
Матрица А называется матрицей системы (*), В — столбцом сво-
бодных членов, X — столбцом неизвестных. Исходная матрица)
А=(А\В) называется расширенной матрицей системы (*).
ЛЕКЦИЯ. 6
Определение 25. Решением линейной системы (*) назы-
вается любая упорядоченная совокупность чисел у\, ..., уп (лю-
бой столбец Г= (yi ... Yn)T), которая (который) при подстановке
в каждое уравнение системы (*) (в (*)) вместо совокупности не-
известных х\9 .♦.., хп (столбца X) обращает его в тождества
(матричное тождество).
Определение 26. Линейная система йазывается совмест-
ной, если у нее существует хотя бы одно решение, и несовмест-
ной, если множество ее решений пусто.
Определение 27. Решения линейной системы <уь --•»JVn и;
Yi'> ...» Yn' называются различными, если нарушается хотя бы од**
но из равенств Yi=Yi'> • • • > Yn^Yn'.
Определение 28. Совместная линейная система называет-
ся определенной, если она имеет ровно одно решение, и неопреде-
ленной,если она имеет не менее двух решений.
ТЕОРЕМА 11 (критерий совместности линейной системы). Утв..
Линейная система совместна тогда и только тогда, когда ранг
матрицы системы равен рангу расширенной матрицы.
Определение 29. Множеством решений линейной системы
называется совокупность всех ее решений.
Обозначение: {*} — множество решений линейной системы *-
Определение 30. Две линейные системы с одинаковым
числом неизвестных называются равносильными, если множества
их решений совпадают.
Обозначение: * ~ *'.
Определение 3.1. Говорят, что линейная система *' полу-
чена из линейной системы * путем элементарных преобразований*
если расширенная матрица А' системы *' получена из расширен-
ной матрицы А системы * элементарными преобразованиями:
строк.
ТЕОРЕМА 12. Усл. Линейная система *' получена из линей-
ной системы * элементарными преобразованиями.
Утв. Линейные системы * и *' равносильны: *~*'.
22$

Определение 32. Говорят, что линейная система имеет
ступенчатый вид, если расширенная Матрица системы имеет сту-
пенчатый вид.
ТЕОРЕМА 13. Утв. Всякая линейная система равносильна ли-
нейной системе ступенчатого вида.
ТЕОРЕМА 14. Утв. Совместная линейная система определена
тогда и только тогда, когда ранг матрицы системы равен числу
неизвестных.
ТЕОРЕМА 15 [правило Крамера). Усл. В матричном уравне-
нии АХ=В квадратная матрица А невырождена.
Утв. Столбец решений определяется по формуле Г=Л"~1В.
Определение 33. Линейная система называется однород-
ной, если столбец свободных членов равен нулевому столбцу:
АХ=0. (*о)
Свойства решений однородной системы:
1+. Однородная линейная система всегда совместна: (0. ..0)те
<е{*0}.
2+. Если число уравнений (*о) меньше числа неизвестных, то
однородная линейная система является неопределенной.
3+. Сумма решений однородной линейной системы снова яв-
ляется решением этой системы.
4+. Произведение решения однородной линейной системы на
число снова является решением этой системы.
Определение 34. Набор решений однородной линейной
системы, удовлетворяющий условиям: 1) решения линейно незави-
симы, 2) любое решение данной системы можно представить в
виде их линейной комбинации, называется фундаментальной си-
стемой решений данной однородной линейной системы.
ТЕОРЕМА 16. Утв. У всякой однородной линейной системы су-
ществует фундаментальная система решений, состоящая из п—г
решений, где п — число неизвестных и г — ранг матрицы системы.
Определение 35. Однородная система АХ=0 называется
приведенной системой для линейной системы АХ=В.
ТЕОРЕМА 17. Утв. Между множествами решений {*} линей-
ной системы АХ=В и множеством решений {*о} приведенной си-
стемы АХ=±0 имеет место следующее соотношение: {*}=Г+{*0},
где Г — какое-либо решение линейной системы АХ=В.
ЛЕКЦИЯ 7
ЭКВИВАЛЕНТНОСТЬ. ОТОБРАЖЕНИЯ.
Определение 1. Декартовым произведением XxY множе-
ства X на множество Y называется совокупность всевозможных
упорядоченных пар вида (х, у)> где х&Х, y&Y.
Если множества X и Y совпадают, то декартово произведение
Х'ХХ называют декартовым квадратом множества X.
224

Определение 2. Говорят, что на множестве X задано би~
парное отношение 91, если в его декартовом квадрате ХхХ вы*
делено непустое подмножество Л. Говорят, что два элемента х и
и кз X связаны бинарным отношением 91, определяемым посред-
ством множества Л, если (х, у)еЛ.
Обозначение: хЯу.
Определение 3. Бинарное отношение 91 называется ре«
флексивным, если х91х справедливо для любого х&Х, т. е. для
любого х^А всегда (х, *)еЛ.
Определение 4. Бинарное отношение 91 называется сим-
метричным, если x9ty=>y9ix,~T. е. если (х, у) еЛ влечет (у, х)еЛ.
Определение 5. Бинарное отношение^ называется тран-
зитивным, если х91у и y9Zz=>x9iz, т. е. если из (х, у)^А и {у, z)e
еЛ следует, что (х, г)еЛ.
Определение 6. Бинарное отношение 91 на множестве X
называется отношением эквивалентности, если оно рефлексивно,
симметрично и транзитивно.
Обозначение: ~.
Определение 7. Множество cl(х) ={у \у^Х, у~х) (читает-
ся: совокупность всевозможных элементов у из множества X, эк*
вивалентных заданному элементу х) называется классом эквива»
лентности элемента х.
ТЕОРЕМА 1. Утв. Два класса эквивалентности либо не пере-
секаются либо совпадают.
Определение 8. Множество всех классов эквивалентности
по данному отношению эквивалентности 91 называется фактор-
множеством множества X по отношению эквивалентности 91.
Обозначение: XJ91, Х/~.
Определение 9. Правило р:Х-+Х\91, относящее каждому
элементу его класс эквивалентности, p;x*-+cl(x), называется ка~
ионической проекцией множества X на фактор-множество Х1Я.
Примеры отношения эквивалентности:
1. Между двумя парами (р, q)% (p\ q') натуральных чисел
устанавливается отношение 91:
(p,q)9t(pf, q')**p+q'~p'-+q.
Это есть отношение эквивалентности. Класс эквивалентности пары
(р, q) — целое число cl(p, q). Тем самым Z=NxN/#!.
2. Между двумя парами (р, q), (pf, qf) целых чисел устанав-
ливается отношение 91:
(p,q)9l(p',q')**pq'=p'q q^0i4'^0.
Это есть отношение эквивалентности. Класс эквивалентности па-
ры (р, q) — рациональное число cl(p, q). Q=ZX (Z\0)/5?.
3. М — множество всевозможных сходящихся последовательно-
стей рациональных чисел {rm}, rm^Q. Между двумя последова-
тельностями {гт}, {гт'} устанавливается отношение 91:
ЫЯЮ« lim Гт = lilT1 С " '
8Ч2 Заказ 538
225

Это отношение эквивалентности. Класс эквивалентности последо,
вательности {гт} -+ вещественное число а. Тем самым Af/52=R.
4. "С1 — совокупность всех вещественнозначных функций, за-
данных на оси и имеющих первую производную. Между двумя
функциями f(x) и g{x) из С1 устанавливается отношение 52:
[существует постоянная с,
lw &v ' [такая, что/(х) — g(x)==c.
Это отношение эквивалентности. Класс эквивалентности функции
/ — неопределенный интеграл от ее производной — f(f(x)dx (f'=
=<р).
5. Между двумя целыми числами х, у устанавливается отноше-
ние Я:
(существует целое число q^Z,
х%у <=> [такое, что x—y = mq,
1 где wgN фиксировано.
Это отношение . эквивалентности. Обозначение: x=y(modm).
Класс эквивалентности целого числа k — совокупность всех целых
чисел, остатокт от деления каждого из которых на натуральное
число m совпадает с остатком от деления, k на это число, — назы«
вается классом вычетов по модулю иг. Фактор-множество
. Z/52=Zm4cl(0),cl(l),...,cl(m-l)}
называется множеством классов вычетов по модулю т. .>.
ЛЕКЦИЯ 8
Определение 10. Отображением множества X во множест-
во Y называется всякое правило /, посредством которого каждому
элементу х из X ставится в соответствие некоторый элемент у из
Y\ элемент у называется образом элемента х при отображении f.
Обозначения: f:X-+Yy f:x-+y, y=f{x).
Определение П. Образом отображения f называется
множество
lmf=f(X)={y\y^Y, a*=X:jf(x)-y}.
Определение 12. Полным прообразом заданного элемента
y^Y называется множество f~l(y)={x\x&X9 f(x)=y).
Определение 13. Отображения f:X-+Y и g:X<-+Y называ-
ются равными, если f(x)=g(x) для любого х^Х.
Определение 14. Отображение f:X-+Y называется сюръек-
тивным если f(X)=Y, т. е. полный прообраз любого элемента у^
.еУ, содержит не менее одного элемента х^Х.
* Опредедение 15. Отображение f:X-^Y называется инъек-
тивным, если из того, что Х\Фх2, следует /(*i)=£/(*2), т. е. полный
прообраз любого элемента уеУ содержит не более одного эле-
мента хеХ
226

Определение 16. Отображение f:X-*Y называется биектив-
ным (или взаимно однозначным), если оно сюръективно и инъек-
тивно, т. е. полный прообраз любого элемента y^Y содержит
ровно один элемент х^Х.
Определение 17. Композицией (суперпозицией или произ-
ведением) отображения f:X-+Y на отображение g:Y-^Z называет-
ся отображение hiX-^Z, задаваемое правилом: h(x)=g(f{x)).
Обозначение: /i=g°/.
Определение 18. Тождественным (или единичным) отобра-
жением называется отображение Ах:Х->-Х, переводящее каждый
элемент х^Х в себя.
- Свойства композиции отображений:
1+. Композиция отображений подчиняется закону ассоциатив-
ности: из того, что f:X-+Y, g:Y->Z, h:Z-+U, следует ho(gof);=
= (hog)of. ~
2+. Для любого отображения f:X->Y "справедливы равенства
1Уо/=/о1х=/.
3+. Композиция сюръективных отображений сюръективна«
4+. Композиция инъективных отображений инъективна.
5+. Композиция биективных отображений биективна.
Определение 19. Отображение f:X-+Y называется обра-
тимым, если существует отображение g:Y*-+Xf такое, что g°f=\x,
/°g=ly; отображение g называется обратным к отображению /.
Обозначение: /~*.
Свойства обратного отображения:
1+. Отображение / обратимо тогда и только тогда, когда / би«
ективно.
2+. Отображение, обратное к данному, единственно.
3+. Композиция обратимых отображений обратима и (g°f)~l—
ЛЕКЦИЯ 9
ГРУППЫ. ЩЛЫДА. ПОЛЯ.
Определение 0. Всякое отображение *:ХхХ-+X называет-
ся внутренним законом композиции (ВнутЗК) на множестве X.
Определение 1. Элемент п^Х называется нейтральным
относительно ВнутЗК * на множестве X, если п*х=х*п=х для
любого х&Х. Говорят в этом случае, что ВнутЗК * обладает
свойством N.
Утверждение. Существует не более одного элемента, нейтраль-
ного относительно заданного ВнутЗК.
Определение 2. Внутренний закон композиции * называ-
ется ассоциативным, если (х*у) *z=x*(#*z)r для любых х> у, -ге
sX Говорят в этом случае, что ВнутЗК * обладает свойством Л.
Определение 3. Говорят, что элемент х^Х имеет симмет-
ричный относительно ВнутЗК, обладающего свойством N, если
существует такой элемент у&Х, что х*у=у*х=п. ВнутЗК *, у ко-
*/••
227

торого для любого элемента х^Х можно указать симметричный
ему элемент j/el, называется обладающим свойством S.
Утверждение. Если ВнутЗК обладает свойствами N и Л, то у
каждого элемента х^Х существует не более одного симметрич-
ного.
Определение 4. ВнутЗК называется коммутативным, если
для любых х, j/eX выполняется соотношение
х*у=у*х.
Будем говорить в этом случае, что ВнутЗК * обладает свойст*
вом С.
Определение 5. Непустое множество G называется груп*
пой, если на G задан ВнутЗК *, обладающий свойствами Л, N, S;
в этом случае ВнутЗК называется групповым законом.
Обозначение: (G, *).
Определение 6. Если групповой закон — умножение •, то
группу (G, •) называют мультипликативной. Если групповой за-
кон — сложение +, то группу называют аддитивной (G, +).
Свойства группы:
Труппа G мультипликативна
1+. Существует единичный элемент e&G.
2+. У любого элемента g&G существует единственный обрат-
ный g~l^G.
3+. Уравнение ax=b (ya=b) имеет единственное решение х~
=аг*Ь (y=ba~l).
Группа G аддитивна
1+. Существует единственный нулевой элемент OeG.
2+. У любого элемента a^G существует единственный проти*
воположный (~-a)^G.
3+. Уравнение a+x=b (y+a=b) имеет единственное решение
*-(-a)+ft(0-ft+(-a)).
Примеры групп:
1. Группа целых чисел (Z, +); групповой закон — сложение.
2. Группа положительных чисел (R+, •) групповой закон —
умножение.
3. Группа прямоугольных матриц одного размера (Rmxn, +).
Групповой закон — сложение.
4. Группа невырожденных квадратных матриц одного поряд-
ка п. Групповой закон — умножение.
Обозначение: GL(/z, R) — общая линейная группа степени п.
5. Множество всех биективных отображений множества X на
себя. Групповой закон — композиция отображений.
4 Обозначение: S(X) — симметрическая группа.
Пусть Х={1, % ..., п}. Тогда S(X)=Sn — симметрическая группа
степени п.
6. Ортогональная группа
0(/г)ЧЛеКпхп|ЛтЛ=ЛЛТ=/}.
228

7. Специальная ортогональная группа
SO(fl)={^€EO(/z)|deM = l}.
8. Унимодулярная группа
{i4e=R»x„|det4-±l}.
Пусть (для определенности) G мультипликативна. -
Определение 7. Непустое множество Я называется под-
группой мультипликативной группы G, если для любых hi,h2y Ле
^Я справедливы соотношения h~l^H, h\-h2^H.
Определение 8. Непустое множество Я называется под-
группой мультипликативной группы G, если для любых hu /i2e
еЯ справедливы соотношения /Н^#, h\-h2^H.
Определение 9. Непустое множество Я называется под-
группой мультипликативной группы G, если Я является группой
относительно группового закона, заданного на G.
ТЕОРЕМА 1. Утв. Определения 7, 8 и 9 равносильны.
Определение 10. Взаимно однозначное отображение
q>: (G, *G)-^(I\ *г)
называется изоморфизмом группы (G, *с) на группу (Г, *г), если
для любых а и Ь из G выполняется соотношение
(p(a*Gb)=<p(a)*r<p(b).
В этом случае говорят, что группа G изоморфна группе Г.
Обозначение: G^T.
ТЕОРЕМА 2. Утв. Отношение изоморфизма есть отношение
эквивалентности на множестве всех групп.
Примеры подгрупп:
1. Множество всех целых чисел, кратных meN:
mZ={m<71 <7eZ)
подгруппа группы целых чисел Z.
2. Множество всех взаимно однозначных отображений множен
ства X на себя, оставляющих неподвижным фиксированный эле-
мент аеХ, _
Sa={f\f<=S(X)ff(a)=a)
— подгруппа симметрической группы S (X) — стабилизатор эле-
мента а.
3. Специальная линейная группа
SL(n, К)={Ле=ОЬ(л, R)|deM=l}
— подгруппа общей линейной группы GL(n9 R).
Определение 11. Левым (правым) смежным классом груп-
пы G по подгруппе Я, определяемым элементом geG, называется
gH={gh\h<=H) (Hg={hg\heEH}).
8 Заказ 538 229

Определение 12. Погруппа Я называется нормальной, ес-
ли gH=Hg для любого g^G.
Замечание. У коммутативной группы (групповбй закон ком-
мутативен) все подгруппы являются нормальными.
Утверждение. Подгруппа Я нормальна в том и только в том
случае, если для любого g^G и любого ЛеЯ выполняется вклю-
чение ghg~l^H.
ТЕОРЕМА 3. Усл. Подгруппа Я нормальна.
Утв. Множество смежных классов {gH\g^G} группы G по
подгруппе Я относительно ВнутЗК
G/H= (aH) (ЬН) ={(ahl) (ah2) \hu Л2€=Я}
является группой. .
Определение 13. G/H — фактор-группа группы G по нор-
мальной подгруппе Я.
Примеры фактор-групп:
1. Группа унимодулярных матриц {A&GL(nf R) |detj4=±l} —
нормальная подгруппа общей линейной группы GL(n> R). Фактор-
группа
GL(/z, R)/{A€EGL(n, R) |deM-±l)
изоморфна мультипликативной группе положительных чисел.
2. Фактор-группа группы целых чисел Z по подгруппе целых
чисел, кратных m, mZ,
Z/mZ=Zm
— группа вычетов по модулю т.
3. Пусть С1(—оо, оо) — множество функций, непрерывных на
всей оси, С01(—оо, оо) — множество функций, непрерывных на
всей оси и равных нулю в нуле. Тогда
СЧ-оо, оо)/С0*(-<*>, oo)^R.
ЛЕКЦИЯ Ю
Определение 14. Отображение <p:G->T называется гомо-
морфизмом группы (G, *о) в группу (Г, *г), если для любых
a, b^G выполняется равенство
ф(а*оЬ)=<р(а)*гф(Ь).
Пример гомоморфизма. Я — нормальная подгруппа группы
G. Отображение n:G-*G/H, определяемое по правилу
n:a<=G*-+a-HeEG/Ht
— гомоморфизм (отображение я называется естественным гомо-
морфизмом).
Свойства гомоморфизма:
1+. Образ гомоморфизма 1тф={аеГ|Заеб, ф(а)=а} — под-
группа группы Г,
230

2+. Ядро гомоморфизма кегq>=s*{g^G\q>(g)=er}. — нормальная
подгруппа группы G. \
3+. Гомоморфизм ф:б-^Г является изоморфизмом в том и
только в том случае, когда ker<p={eo}, 1тф=Г.
ТЕОРЕМА 4. Усл. фгб-^Г — произвольный гомоморфизм.
я: G->G/ker ф — естественный гомоморфизм.
Утв. Существует изоморфизм %:lmq)-*G/ker ф, такой, что
Пример. С[а, Ь] — множество функций, непрерывных на от*
резке [а, Ь]. Гомоморфизм у:0[а, b]-*R задается по правилу
Ф :f(x)~J abf {x)dx.
Ясно, что кегф={/(*) \fabf(x)dx=Q}.
Откуда на основании теоремы заключаем, что
С[а, Ь]/кет ф^К.
Определение 15. Говорят, что группа G имеет порядок п,
если она состоит из п элементов.
Обозначение: card 6=я.
ТЕОРЕМА 5. Усл. card G = n.
Утв. Существует подгруппа симметрической группы Snt та*
кая, что H^G.
ТЕОРЕМА 6. Уся. card G = n, H — подгруппа G и card#=£.
Утв. card (G/#)= л/6.
G — мультипликативная группа, geG, AieN.
Определение 16.
п
gn = g...g, g° = e, g~n = (g-l)n.
Определение 17. Группа G называется циклической, если
найдется элемент a^G, такой, что для любого элемента ?еб
можно указать msZ, обеспечивающее выполнение равенства g=*
=am. При этом говорят, что группа G порождается элементом а:
Определение 18. Порядком циклической группы, порож-
денной элементом а, называется наименьшее натуральное число
п такое, что an=e. Если такого числа нет, то циклическую группу
называют бесконечной.
ЛЕКЦИЯ И
ТЕОРЕМА 7. Утв. Все циклические группы одного порядка
изоморфны. Все бесконечные циклические группы изоморфны.
ТЕОРЕМА 8. Усл. Порядок группы — простое число.
Утв. Группа — циклическая.
Примеры геометрических групп (групп, встречающихся в
геометрии):
8*
23J

1. Гт — правильный m-угольник, Л — вращение вокруг точки
О на угол в ==—2- (рис. 2):
т
'cosO —sine\
^sine cos в/'
В — осевая симметрия с осью L:
В
•и-
Рис. 2
Тогда: 1) Лт=/, 2) В2=/,
3) ЛВЛВ=/, 4) /, Л, В, ..., Л™-\
Ат~хВ — различные преобразова-
ния симметрии многоугольника Тш
и 5) других преобразований сим-
метрии у многоугольника Гт нет.
Определение 19.
.Дл=({1г, Л, В, ЛВ, ..., Л—1, Л—1В}, о)
— группа диэдра степени m\ card Dm=2m. *
2. Пусть на плоскости R2 задана аффинная система коорди-
нат— (|, т]). Предположим, что каждой тбчке с координатами
(£, л) ставится в соответствие точка с координатами (£', т)')> вы-
числяемыми по правилу
тжт
где аб—ру=5^0. Тогда
группа аффинных преобразований плоскости R2.
Определение 20. Непустое множество /С называется коль-
цом, если оно наделено двумя внутренними законами композиции:
сложением + и умножением •, причем
сложение 1) ассоциативно, 2) коммутативно, 3) обладает ней-
тральным элементом (нулем), 4) для каждого элемента существу-
ет противоположный;
умножение 1) ассоциативно и 2) дистрибутивно относительно
сложения, т. е. a(b+c)=ab+ac, (a+b)c=ac+bc для любых а,Ь,се
Если умножение коммутативно, то кольцо называется комму-
тативным. Если умножение обладает нейтральным элементом
(единицей), то говорят, что это кольцо с единицей.
Примеры колец:
1. (Z, +, •) — коммутативное кольцо с единицей.
232

2. (2Z, +,•)—коммутативное кольцо.
3. (Rnxn, +, •) — некоммутативное кольцо с единицей.
4. С[— 1, 1] — коммутативное кольцо с единицей.
ЛЕКЦИЯ 12 - ' .
Свойства кольца: Д
1+. Нулевой элемент единственный.
2+. У каждого элемента ае/С существует единственный проти-
воположный (—а)е/С.
3+. Для любых а, fte/C уравнение а+х=Ь имеет единственное
решение: *=Ь—а.
4+. Для любых а, ft, c^K a(b^-c)=ab—qc, (а—Ь)с=ас — be.
5+. Для любого ае/С а-0=0-а=0.
6+. Для любых а, be/С (—а)Ь=а(—b)=—ab.
7+. Если /С содержит не менее двух элементов и является коль*
цом с единицей 1, то 0¥=1.
8+. В кольце с единицей множество всех обратимых относи-
тельно умножения элементов есть мультипликативная группа.
Определение 21. Ненулевые элементы а и b кольца К
называются делителями нуля, если ab=0.
Примеры колец с делителями нуля:
1. Кольцо матриц R2X2-
Делители нуля (J о)' (о ?)' ■
£. Кольцо непрерывных функций С[— 1, 1].
Делители нуля f(x)=x+\x\, g(x)=*x—\x\.
3. Кольцо классов вычетов Zm по составному модулю m=>nk%
n>\yk>\.
Делители- нуля cl (п), cl (k).
Определение 22. Множество Р, содержащее не менее двух
элементов, называется полем, если оно наделено двумя внутрення*
ми законами композиции: сложением + и умножением •, причем
сложение 1) ассоциативно, 2) коммутативно, 3) обладает ну-
лем, 4) у каждого элемента есть противоположный;
умножение 1) ассоциативно, 2) коммутативно, 3) обладает еди-
ницей, 4) у каждого ненулевого есть обратный и умножение ди-
стрибутивно относительно сложения.
Утверждение. Поле — это коммутативное кольцо с единицей,
которое содержит не менее двух элементов и в котором каждый
отличный от нуля элемент обратим.
Свойства поля (дополнительно к его свойствам как кольца):
1+. В поле нет делителей нуля.
2+. Единица определяется однозначно.
3+. У любого ненулевого существует единственный обратный.
4+. Для любых а и Ь, ЬфО, уравнение Ъх=а имеет единствен-
ное решение x=b~la.
ТЕОРЕМА 9. Утв. Кольцо классов вычетов Zm является полем
тогда и только тогда, когда m — простое число.
233

Определение 23. Натуральное число п называется характе-
ристикой поля, если
1 + ,..+1 = 0
п
и никакое натуральное число, меньшее п, этим свойством не обла-
дает. Если указанное свойство не имеет места ни для какого на-
турального п, то говорят, что поле имеет характеристику 0.
Утверждение. Характеристикой поля может быть либо 0, либо
простое число.
Примеры полей:
1. Поле рациональных чисел Q.
2. Поле вещественных чисел R. __
3. Множество вещественных чисел вида а + |J V^2, где й и Ь
рациональны. ,
4. Поле Галуа GF(4).
•
0
1
а
Р
0
0
0
1 0
0
1
0
1
а
Р
а
0
а
р
1
р
0
р
1
а
'+|
0
1
а
Р
0
0
1
а
Р
1
1
0
Р
а
а
а
Р
0
1
Р
Р
а
1
0
5. Поле комплексных чисел С.
ЛЕКЦИЯ 13
Заметим прежде всего, что множество квадратных матриц вида
(с обычными операциями сложения и умножения матриц) являет-
ся полем, в котором выполняется соотношение
X2+I=Of
Пусть Zi=(*i, yi), z2=(x2, Яг),, где хи *2, уи f/2^R. Определим
два ВнутЗК (+) и (•):
сумму: (хи yi) + (x2t f/2) = (*i+*2, У1+У2),
произведение: (хи ух) (х2, у2) = (*i*2-f/if/2> *i*/2+x2*/i).
Обозначение: С.
Изоморфизм ф устанавливает соответствие
\У х)

между множеством точек плоскости С и полем
({(П)Ь-« }■♦■•>
при этом (+)-*(+), (')-*(•)•
Определение 24. Элементы поля С называются комплекс-
ными числами.
Алгебраическая форма записи комплексного числа z=x+iy.
Определение 25. Комплексное число z=x—iy называется
сопряженным комплексному числу z=x+iy.
Свойства операции сопряжения:
1+. Z\+Z2=Z\+Z2,
2+. Zi-Z2=Zi-Z2.
Тригонометрическая форма записи
«в r(cos<p+tsin<p).
комплексного
модуль,
чисМ z~
<p=arg2 -
где г=\г\=У*2+У*
аргумент комплексного числа (рис. 3).
Свойства модуля и аргумента комплексных чисел (рис. 4):
) л
0
1 г/*+19
/Г
| а ^
07
Z,-Z,
Рис. 3
1+. Ui + ^^l^l + l^l,
* 2+. |Zi-2i|«|ei|.|22|f
3+ arg(2r22)=arg2,+arg22
«(последнее равенство более правильно записать так:
arg (г! • г2) =arg 2i+arg г2 (mod 2я)).
Показательная форма записи комплексного числа: z==relv.
Формула Муавра (cos <р + i sin ср)п=cos щ + i sin я<р.
Корень п-й степени из комплексного числа
rty— пГГТ( Ф + 2/гд ... ф + 2£л \
у 2 =У • Z COS-1—1- htSin -^-^ ,
\ ■ Я Л /
й = 0, 1,
/г—1.
Галуа (Galois) Эварист (26Л0.1811—31.5.1832) — французский математик.
Муавр (Moivre) Абрахам де (26.5.1667—27.11.1754) — английский матема-
тик.
235

Сфера Рицана. Рассмотрим сферу <
s2={(s,n. Ш12+л2+е2=а
лежащую на плоскости (х, у) и касающуюся ее в начальной точ-
ке О. Правило
6 = -
1+Н2
, Л:
1+И2
И2
Рис. 5
1+UI2
где \z\2=x2+y2, устанавливает
взаимно однозначное соответствие
между точками плоскости (xf у)
и сферой с выколотой точкой N
(рис. 5); обратное отображение
записывается так:
х =
1-С
У-
1-S
Обогащая множество С бесконечно удаленной точкой оо—С~
=QJco, устанавливаем взаимно однозначное соответствие между
S2 и С I
ЛЕКЦИЯ 14
МНОГОЧЛЕНЫ. *
Пусть Р — произвольное поле.
Определение 1. Многочленом степени п от переменной t
над полем Р называется выражение вида
f(t) = a» + *xt+ ...+antn = ^*ktk,
где а* — фиксированные элементы поля Рг апфО.
Число п называется степенью многочлена f(t) и обозначается
так: degf. Нулевой многочлен степени не имеет.
Определение 2. Два многочлена называются равными,
если равны их степени и соответствующие коэффициенты при рав-
ных степенях t или они оба нулевые.
Определение 3. Суммой многочленов
называется многочлен
h(t)=2nm=0ymfi»,
коэффициенты которого определяются по правилу Ym = am+|W
0<m</; Ym = (Xm, l<m<n.
Риман (Riemann) Георг Фридрих Бернхард (17.9.1826—20.7.1866)
кий математик.
немец-
236

Обозначение: h(t)=f(t\ + g(t).
Свойство суммы многочленов: deg(/+g)^max(deg/, degg).
Определение 4. Произведением многочленов f(t) и g(t)
называется многочлен
коэффициенты которого вычисляются по правилу ys = 2>k+f=sa>k$i~
Свойство произведения многочленов: deg (/•#) = deg / + deg g.
Утверждение. Совокупность многочленов над полем Я, на ко-
торой введены два описанных выше ВнутЗК, сложение и умноже-
ние, представляет собой коммутативное кольцо с единицей без
делителей нуля.
Обозначение: P[t].
ТЕОРЕМА 1. Усл. /, geP[t]9 g=£0.
Утв. Существует единственная пара A, r^P[t]9 такая, что
О f=gh+r, 2) degr<degg, или г=0.
Определение 5. Многочлен h называется частным от деле-
ния многочлена / на многочлен g, а многочлен г — остатком.
Определение 6. Говорят, что многочлен / делится на мно-
гочлен g, если остаток г равен нулевому многочлену.
Определение 7. Многочлен <р называется наибольшим об-
щим делителем многочленов / и g, если
1Гф является их общим делителем (fug делятся на <р)> .
2) <р делится на любой общий делитель / и g,
Обозначение: НОД(/, g).
Алгоритм Евклида (отыскания НОД):
f=gh\+ru g=r{h2+r2i Г1=г2Лз+г8,...
1 г* = НОД(/, g) J
Утверждение. Наибольший общий делитель двух многочленов
определен с точностью до постоянного множителя.
Определение 8. Многочлены fug называются взаимно
простыми, если НОД (/,£)= с—многочлен нулевой степени (посто-
янная).
ТЕОРЕМА 2. Утв. Для любых /, g^P[t]. Можно указать
такие и, v^P[t]9 что
'fu + gv = HOR(f9g).
Определение 9. Корнем многочлена f(t) называется такое
J0eP94TOf(to)=0.
Утверждение. Если to — корень многочлена f(t)9 то /(0 е
=-(t—t0)h(t)9rneh(t)&P[t].
Определение 10. Многочлен /eP[f] называется неприво-
димым над полем Р, если он делился только на себя и на много-
член нулевой степени.
237

Определение 11. Поле Р называется алгебраически замк-
нутым, если неприводимыми над Р являются лишь многочлены
первой степени. х
ТЕОРЕМА 3 (ОСНОВНАЯ ТЕОРЕМА АЛГЕБРЫ). Утв. Поле
комплексных чисел алгебраически замкнуто.
СЛЕДСТВИЕ. Усл. /е=С[/], degf=/i>l.
Утв. Найдутся <i (леС, такие, что
f{t)=anIlnk~i(t— tk).
СЛЕДСТВИЕ. Усл. f, g<=C|7], deg/<m, degg<m; сущест-
вуют комплексные числа t\9...9tm+\ попарно неравные и такие,
что f(tk) =g{tk) для любого &=1,...,т+1.
Утв. f(t)=g(t)
ЛЕКЦИЯ 15
ТЕОРЕМА 4 (каноническое разложение многочлена над по-
лем С).
Усл. f(t)=ao + a\t+... + antn<^C[t], deg/=n.
Утв. Разложение
/(0 = а|.П)1,(*-*Л
единственно с точностью до порядка сомножителей.
Формулы Виета. Коэффициенты многочлена
f(t)^a0 + ait + ... + a^itn'l + in
выражаются через его корни t\,r..,tn по следующим формулам:
a„_i = — 2^ fy, czn_2 — 2i'^y<ft^rt Vy>
а«-з = —2i^y<£<f^/t /fcfy//, ... , a0 — (— 1)" ^2 • • • *п •
ТЕОРЕМА 5. Усл. /(<)eR[<], <0gC, /0#*o, — корень много-
члена f{t) кратности ko.
Утв. to — корень многочлена f (t) кратности k0.
ТЕОРЕМА 6 (каноническое разложение многочлена над по-
лем R).
Усл. f(t) =а0 +ait+ ... + antn^R[t]f deg/==n.
Утв. Разложение
/ (t) = annU {t-tifi nJUi № +pkt + qk)\
t;<=R, *,#*,(/#/);
A.fcsR, (pk.q^^iPs'Qs) (*#s);
fc,, /*>1, S^ + ^JUi^"'
-единственно с точностью до порядка сомножителей.
Виет (Viete) Франсуа (1540—13.12.1603) — французский математик.
238

Замечание. Если степень многочлена f(t)<^R[t] нечетна, то
у него есть хотя бы один вещественный корень.
ДОКАЗАТЕЛЬСТВО ОСНОВНОЙ ТЕОРЕМЫ АЛГЕБРЫ: у
каждого многочлена с комплексными коэффициентами, степень
которого не меньше единицы, есть комплексный корень.
1°. Коэффициент зацепления замкнутой кривой. Рассмотрим
отображение
Y:[0, 2ji]->R2,
задаваемое формулами
*-*('). У = У(*). 0)
где 0<£<2я; функции x(t) и y(t) предполагаются непрерывными
на отрезке [0, 2я] и таким, что
*(0)г*(2я), £/(0)=r/(2jt). (2)
Множество точек на плоскости R2, определяемое условиями
(1) и (2), будем называть замкнутой кривой у. -
Предположим, что начальная точка О не лежит на у, т. е.
x4t)+y4t)>0.
Введем на плоскости полярные координаты. Тогда для точки
{x(t), y{t)) «кривой у «имеем
r(t) = Vx2(t)+y2(t) >0, cos?(0 = -^f-, sinq>(*)
*(') *5„т/А_ *(')
r(t) r(t)
Из последних двух уравнений угол xp(t) определяется неоднознач-
но (с точностью до слагаемого, кратного 2я). Выберем для ?=0
определенный угол <р(0) (рис. 6). Тогда требованием непрерыв-
ного изменения на отрезке [0, 2я] угол <p(t) определен однознач-
но. Ясно, что разность <р(2я)—ф(0) кратна 2я. Определим коэф-
фициент зацепления кривой у:
. _ ф(2я)-д>(0) у
Рассмотрим пару функций
*(*, s)t y(t, s), (3)
заданных в прямоугольнике П= [0, 2л] X [а, Ь] и таких, что
1) x(t, a)=x(t)y y(t, a)=y(t) для любого £е[0, 2я],
2) *(0, s)=*(2ji, s), у(0, s)—y(2n, s) для любого s^[a, b],
3) x(t, s), y(t, s) непрерывны в прямоугольнике П.
При каждом фиксированном значении s из [а, Ь\ получается
замкнутая кривая ys.
Предположим, что 0^ySt т. е. r(t, s)>0 при любых t и s.
Так как тогда функции <р(0, s) и <р(2я, s) непрерывны, то
непрерывен и коэффициент зацепления кривой j(s). В силу того
что функция J(s) непрерывна на отрезке [а, Ь] и принимает на
нем только целые значения, получаем, что она постоянна, т. е.
для любого s^[a, b] /(s)=/(a)..
239

Таким образом, при непрерывной деформации кривой коэффи-
циент зацепления не изменяется (если ни одна из кривых дефор*
мации не проходит через начало координат).
2°. Свойства образа окружности. Рассмотрим отображение
/:С-^С, задаваемое по правилу f :z>-+w = f(z) = zn+an-\Zn~l + ...
... +ао, и покажем, что при я>1 найдется го, такое, что f(z0)=0.
Запишем комплексное число z в тригонометрической форме
z=p(cost+is'mt). При фиксированном р и /, изменяющимся по
отрезку [0, 2я], получаем окружность ра-
диуса р с центром в точке О. Найдем
образ этой окружности при отображе-
нии /:
w(t)-f(p(cost+isint))9 0<*<2л.
(4)
Ясно, что о;(0)=до(2л;)=/(р).
Следовательно, кривая, задаваемая
правилом (4), замкнута. Обозначим ее
через y(p)-
Вычислим коэффициент зацепления
кривой y(p):
1) При w=zn имеем w=r (cos <p+
+isincp), где г=рп, ф=я£
Когда t изменяется от 0 до 2я, угол
Ф изменяется от 0 до 2лп. Поэтому
j(y(p))=n.
2) Пусть w=zn + an-izn-l+ ... +а0.
Рассмотрим
w = f{z, s)=zn+s(an-\Zn-l + ... + ao),
где 0<5<:1.
При s=0, f(z, 0)=гп; при s=U
f(z, l)4(z)=z"+an-iZ"-l+...+a0.
Когда z описывает окружность |г| =
=p==const, a s фиксировано, точка
/(г, s) на плоскости R2 описывает зам-
кнутую кривую. Покажем, что при до-
статочно больших р эта кривая не про-
ходит через начальную точку О.
Обратимся к функции g(z) =
= an-r\Zn-l+ ... +а0.
Пусть р^1. Тогда
\8(г)\<Р"-1с9
где с= | ап-1| + ... + | ао| -*- постоянная.
Из равенства f{z, s)—sg(z)=zn получаем, что
|/(2, S)\+S\g(z)\>p».
Рис. 6
240

Последние два неравенства позволяют оценить модуль /(г, s)
снизу
\f(z, s)\>pn—cpn-K
Ясно, что р можно выбрать столь большим, чтобы
\f(z,s)\>0
(достаточно взять р>с).
Таким образом, для любого s, 0<s<l, кривая v(p> s) —
— w{z, s)=f(z, s)=f(p(cost+isint), s), 0</<2я, где р=
= const>c, не проходит через точку О.
Значит, коэффициент зацепления кривой у(р, s) не зависит
от 5.
Но при s = 0 этот коэффициент нами вычислен — он равен п.
Следовательно, и для многочлена
w(z, s)=f(zt s)=zn+{an-iZn-l + ... + aCo)s
коэффициент зацепления кривой у(р, s) при s=l также равен п.
3°. Алгебраическая замкнутость поля С. Если свободный член
оо многочлена f(z)
f (Z) = Zn + OLn-\Zn-l + ... + U\Z
равен нулю, то 2о=0 — его корень.
Пусть ао¥=0. Рассмотрим деформацию кривой у(р) при р->0.
Кривая у(р) *в процессе деформации стягивается в точку v(p)~^
Вычисляя коэффициент зацепления полученной вырожденной
кривой ш = ао, убеждаемся в том, что он равен нулю: <р(2я) —
-Ф(0)«0.
Так как коэффициент зацепления «кривой у(р) с началом коор-
динат равен л, то в процессе деформации кривая v(p) при р, из-
меняющемся от с до 0, должна при каком-то значении р0,
Ю<ро<с, пройти через начальную точку О..
Это означает, что при некотором значении to&[0, 2л]
f(po{cost0+isint0))=0.
Таким образом, мы получаем, что^(го) =0, где z0=po(icos£o+
-M'sin/o).
Следовательно, z0=po (cos to + i sin t0) является, корнем много-
члена
w=f(z)=zn+an-\zn-l + ...+ao. □

ДОБАВЛЕНИЕ
ВЫПУКЛЫЕ МНОЖЕСТВА: ТОПОЛОГИЧЕСКАЯ
СТРУКТУРА, ДИФФЕРЕНЦИАЛЬНЫЕ СВОЙСТВА,
НЕРАВЕНСТВА
ВВЕДЕНИЕ
Выпуклость является одним из естественных и хорошо извест-
ных математических понятии. Даже далекий от математики чело-
век имеет в целом правильное наглядное представление о том,
что значат слова «быть выпуклым». Обратившись к такому чело-
веку с просьбой нарисовать что-нибудь выпуклое, можно быть
уверенным в том, что это будет сделано без особого труда и
верно.
Попробуем представить, что же именно будет нарисована
(рис. 1).
К предложенным рисункам можно добавить точку, отрезок,
луч и прямую. Цскушенный рисовальщик прибавит к этому еще и
всю плоскость.
Рис. I Рис. 2
Оказывается, что перечисленными случаями все многообразие
выпуклых множеств на плоскости и исчерпывается.
Естественно задать вопрос: что же я имею в виду, говоря так?
Я хочу сказать, что, нарисовав эти три фигуры, я сумел пол-
ностью описать структуру выпуклых множеств на плоскости.
(Точка, отрезок и луч — выпуклые множества на прямой.) Но
ведь есть же на плоскости и другие выпуклые фигуры. Например,
многоугольник или угол, раствор которого не превышает я: как
быть с ними? Внешнее различие с ранее нарисованными фигура-
ми явно бросается в глаза. Тогда в чем ихч сходство?
Для аргументированного ответа на этот вопрос мы поставим
и попытаемся решить следующую основную задачу.
Задача I. Классификация выпуклых множеств.
Вместе с тем нельзя не заметить, что при всякой попытке вы-
чертить кривую, ограничивающую выпуклую фигуру на плоско-
сти, сохраняется одно непременное обстоятельство: если в некото-
рой точке этой кривой отсутствует касательная к ней, то обяза-
тельно существуют левая и правая полукасательные (рис. 2).
242

Преодолевая в себе желание отнести это к индивидуальным
особенностям манеры исполнения рисунков, естественно задаться
вопросом: существуют ли 'иные причины?
При поиске ответа на этот второй вопрос мы приходим к пос-
тановке другой основной задачи.
Задача П. Исследование особенностей границы выпуклых
множеств.
Чтобы дать математически точную формулировку задач I и II,
следует освежить в памяти некоторые известные факты, а также
познакомиться с рядом новых понятий. Изучая эти лонятия и
связ'и между ними, мы будем тем самым развивать математиче-
ский аппарат, необходимый для решения поставленных задач.
Изложение материала имеет одну особенность: доказательства
формулируемых утверждений по мере продвижения от раздела к
разделу становятся менее подробными. Однако детальный разбор
доказательств весьма желателен. Это вполне доступно и очень по-
лезно. Определенную помощь в разборе доказательств призваны
оказать предлагаемые рисунки, «...and what is the use of a book»,
thought Alice, «without pictures or conversations?» (The Penguin
Complete Lewis Carroll, 1983, p. 15).
А. ЭЛЕМЕНТЫ ТОПОЛОГИИ
Для более четкой формулировки задачи I необходимо ввести
и разъяснить ряд понятий в разной степени известных, подобрать
удобные обозначения. Вводя их по мере надобности, мы ограни-
чимся лишь теми из этих понятий, которые непосредственно свя-
заны с поставленной задачей классификации.
Начать, по-видимому, целесообразно с подходящего примера.
Таковым в данном случае является точечное евклидово простран-
ство. Изучение некоторых свойств этого пространства, проводимое
ниже, сыграет двоякую роль. С одной стороны, через эти свойства
легко объясняется естественность вводимых далее основных поня-
тий. С другой стороны, это позволит глубже познакомиться с из-
вестным объектом, в котором и будут развиваться в дальнейшем
главные события.
1°. Топология точечного евклидова пространства. Пусть &п —
n-мерное точечное евклидово пространство; а «и Ь — точки из &п*
Если в пространстве 6п введены прямоугольные декартовы коор-
динаты х1,...,хп, то а и Ь — точки с координатами а1,..., а* и
Ь\... ,Ьп соответственно. Тогда
|а—*|=/s?ei(a' —б')2
— расстояние от точки а до точки Ъ.
Пусть г — некоторое положительное число.
Множество В0п(а, г) = {х^ё?п\ \х— а\ <г} называется п-мерным
открытым шаром радиуса г с центром в точке а.
243

Множество 5л~!(а, г) ={х^&п\ \х—а\=г) называется (л—I).
мерной сферой радиуса г с центром в точке а.
Множество Вп(ау r)={x^S>n\\x—а|<г} называется п-мерным
замкнутым шаром радиуса г с центром в точке а.
Ясно, что Вп(ау г)=В0п(ау г)US*-1 (а, г).
В тех .случаях, когда конкретные положения центра и величи-
на радиуса не играют существенной роли, будем писать просто:
АЛ S*-1, Вп.
Рассмотрим важный класс подмножеств пространства &п и
^изучим некоторые свойства объектов из этого класса.
Подмножество 0 из пространства &п будем называть откры-
тым множеством, если для каждой точки х из 0 можно указать
положительное число г=г(х) такое, что
В0п(ху r(x))c0t
т. е. каждая точка входит во множество 0 вместе с некоторым
открытым шаром с центром в этой точке.
Ясно, что такие множества существуют. В частности, сформу-
лированным свойством обладает сам открытый шар (рис. 3).
Конечно, есть и множества,
^—^ /* *Х которые не являются открытыми.
/ Hl\ ( \ Например, окружность S1 на пло-
( ^^ ) /С\ * / скости ^2*
В%\ J (y^t^/. Совокупность всех открытых
У ^-^ S1 множеств пространства &п будем
обозначать коротко так: {£?«}.
Рис. Э Пустое множество 0 будем счи-
тать открытым и, следовательно,
ВХОДЯЩИМ В {Оа}.
Построенный класс открытых множеств, естественно, обладает
следующими свойствами: его элементами являются
1+. Пустое множество — 0е{(?„}.
2+. Все пространство — 6п^{0а}.
3+. Пересечение любых двух открытых множеств.
Доказательство. Пусть 0\ и 02 — открытые множества
и 0=0х[\02ф0. Тогда найдется точка ху общая для обоих мно-
жеств 0\ и 02. Вследствие того что множество Oi (i= I, 2) откры-
то, найдется положительное rt-, такое, что
В0я(х, п)<=01, 1=1, 2.
•Положим r=min(ri, г2). Тогда В0п(х, r)cz0i одновременно и для
i=\ и для / = 2.
Отсюда следует, что B0n(xt r)cz0i[\02=0 и, значит, множество
4У — открытое. П
4+. Объединение любой совокупности открытых множеств.
Доказательство. Каждая точка объединения содержится
хотя, бы в одном из слагающих его открытых множеств. Значит,
в объединении содержится и некоторый открытый шар с центром
в этой точке. □
£44

Таким образом, в точечном евклидовом пространстве &п выде-
лен класс подмножеств — открытые множества. Тем самым евк-
лидово пространство обогащается дополнительной структурой, ес-
тественным образом связанной с уже имеющейся функцией рас-
стояния.
Говорят еще, что в пространстве &п задана естественная топо-
логия и что пространство S>nf наделенное навой дополнительной
структурой, является топологическим пространством. (Здесь ничто.
не должно удивлять. Часто случается так, что один и тот же
объект, одно и то же множество несет в себе разную информа-
цию в зависимости от того, что мы уже о 'нем знаем, какую ре-
шаем задачу.)
К этому примеру мы постоянно будем возвращаться, тем более
что сказанного о нем для наших целей уже почти достаточно.
2°. Топологическое пространство. Пусть X — непустое множе-
ство. Обозначим через
семейство его подмножеств, подчиненное следующим условиям:
семейству £Г принадлежат
1) пустое множество 0, .
2) само множество X,
3) пересечение любых двух множеств из семейства #~,
4) объединение любой совокупности множеств из семейства £Г\
Семейство подмножеств такого типа всегда существует (на-
пример, совокупность всех подмножеств множества X) и, как пра-
вило, не одно.
Определение. Семейство W~ подмножеств множества X,
удовлетворяющее условиям 1—4, называется топологией на мно*
жестве X. Множество X вместе с семейством ^ называется топо-
логическим пространством и обозначается через (X, &~)\ часто
просто через X.
Ясно, что семейство открытых множеств [Оа] из предыдущего
пункта задает топологию в пространстве <$п, превращая &п в то-
пологическое пространство. Топология в <Sn, состоящая из таких
открытых множеств, постоянно используется в математическом
анализе и геометрии и именуется естественной топологией.
Множества Ga из семейства 3~ по аналогии со случаем Х=6п
назовем открытыми множествами.
Рассмотрим пример задания в Х=&п другой топологии. Доба-
вим к совокупности шаров с центром в фиксированной точке
^е«8Л—{Впо(х, г)|г>0 — любое} — все пространство <$п и пус-
тое множество, выполняя тем самым требования 1 и 2. Пересече-
нием двух шаров В0п(х, г{) и В0п{х, г2) является шар В0п(х, г),
где r=min(rb г2) (выполнено требование 3). Пусть {В0п(х,
Лх)|аеЛ} — любая система шаров рассматриваемой совокупно-
сти (здесь AcR+ — некоторое множество индексов). Их объеди-
нением будет шар B0n(xf г), где r = supra, иди все простран-
ен
ство 5Л, если supra = oo (выполнено требование 4).
a
245

Выделенное семейство 3" является топологией в <£"> а пара
(<£пу ЗГ) — топологическим пространством. Построенную тополо-
гию в пространстве &п называют концентрической.
Для любого подмножества У топологического пространства X
можно рассмотреть наибольшее из содержащихся в У открытых
о
множеств. Оно обозначается int У (или У) и называется внутрен-
ностью множества У. Иными словами,
inty=Ua«*Get -
где {Ga\a^A} — семейство всех открытых подмножеств, содер-
жащихся в У (здесь А — некоторое множество индексов).
Ясно, что x^intY в том и только в том случае, если найдется
открытое множество GczY, такое, что x^G.
Как показывают примеры шара В0п(х, г) и сферы Sn^l(xy r)
в пространстве 6п с естественной топологией, внутренность 'мно-
жества У может совпадать и со всем У (int B0n=B0n\ и быть
пустой (intS*-1 = 0).
Пример. Рассмотрим в пространстве 6п n-мерный единич-
ный куб
• 1п={х=(х\...9-хп)\0<х1<1, t=l,...,n}.
Покажем, что внутренностью куба 1п является множество
1оп={х= (х\...,хп) 10<л:<"< 1, i = 1,..., л}.
Возьмем лге'ЛЛ Пусть
e = min(l—х\х1).
i
Открытый шар В0п(х, е) радиуса е с центром в точке х содержит-
ся в 10п (рис. 4). Поэтому и вследствие произвольности в выборе
точки х множество 10п открыто. С другой стороны, если Xi равен
О или 1 для некоторого i9 \<i<n, то любой шар В0п(х, г) радиу-
са г с центром в точке х содержит точки, не лежащие в кубе 1пу
как бы ни было мало г. Следовательно, точки: куба J\У которых
х1 равно 0 или 1, не принадлежащего внутренности.
П р и м е р. Рассмотрим в пространстве &п совокупность откры-
тых шаров
(вг(о,-!-)|*ем}.
Пересечение всех таких шаров состоит из одной точки О и не яв-
ляется открытым множеством в естественной топологии &п.
Дополнения открытых множеств имеют -специальное ^название.
Определение. Подмножество У топологического простран-
ства X называется замкнутым, если множество X\Y открыто.
Следующее утверждение непосредственно вытекает из теоре-
тико-множественных результатов о дополнениях пересечений и
объединений множеств:
X\([}tYi)=(]i.(X\Yt)9 X\((]iYi)=[ji(X\Yi).
246

ТЕОРЕМА. Утв. 1. 0 замкнуто.
2. X замкнуто.
3. Объединение двух замкнутых множеств замкнуто.
4. Пересечение любой совокупности замкнутых множеств зам-
кнуто.
Для любого подмножества У топологического пространства
X можно рассмотреть наименьшее из содержащих его замкнутых
Я*1
1
д\
{
Г®!
/
*>
Рис. 4
Рис. 5
множеств, Оно называется замыканием множества У и обознача-
ется через cl У (или F). Иными словами;
с1У = ПаеЛ/\х,
где {Fa\a^A} — семейство всех замкнутых множеств, содержа-
щих У.
Ясно, что для любого множества У выполняются включения
intycycciy.
Определение. Множество дУ=с1У\пйУ называется гра-
ницей множества У.
Утверждение. дУ=?П(Г\7).
Тем 'самым граница любого множества замкнута.
Пример 1. Srt-1 = 5Brt=(?50rt.
Пример 2. Пусть У — открытый круг на плоскости &2 с
центром в точке О, к которому добавлены точки верхней полу-
окружности. Тогда int У — открытый круг, cl У — замкнутый
круг, ЗУ —. окружность (рис. 5).
Пусть У — некоторое подмножество топологического простран-
ства X.
Определение. Точка х^Х называется: :
а) внутренней точкой множества У, если A^int У, .
б) внешней точкой множества У, если xeint(X\y),
'-■ в) точкой прикосновения множества У, если *^с1(У),
• г) граничной точкой множества У, если лгедУ,
д) предельной точкой множества У, если л;ес1(У\л:).
247

Определение. Подмножество Zc=X, содержащее точку
xgX, называется окрестностью этой точки, если существует от-
крытое множество G, такое, что x^GczZ.
Отметим, что всякое открытое множество является окрест-
ностью каждой своей точки.
3 . Подпространство. Пусть X — топологическое пространство
и У — непустое подмножество X Топология пространства X опре-
деляет некоторую топологию на множестве У.
Определение. Топологией на множестве Y, индуцирован-
ной топологией пространства X, называется совокупность мно-
жеств вида UflY, где U — открытое множество в простран-
стве X.
Иными словами, если &~ — совокупность всех открытых мно-
жеств X, то
g~Y={U[\Y\u<=-T)
совокупность всех открытых множеств в У.
Убедимся в том, что семейство 2Ty является топологией на
множестве У.
Ясно, что 0 = 0ПУ и Y=X(]Y (условия 1 и 2). Рассмотрим пе-
ресечение двух произвольных множеств U\(]Y и U2(]Y из совокуп-
ности STy- множество
(Ul[\Y)[\(U2(]Y)^(Ul(]U2)f\Y
также принадлежит семейству 0~Y (условие 3). Если {Ua(]Y\a^
еЛ} — произвольное семейство множеств из совокупности STY>
то
и«ч(*/аПУ)= ({)**AU)f\Y
также принадлежит 9~y (условие 4).
Подмножество YczX, снабженное так построенной (индуци-
рованной) топологией, называется подпространством топологиче-
ского пространства X.
В качестве примера можно взять единичную окружность S1 на
плоскости б2 с топологией, индуцированной естественной тополо-
гией в ^Г2. Тогда открытые множества окружности S1 представ-
ляют собой объединения открытых дуг (дуг без концевых точек).
Сюда же входят и пустое множество, и сама окружность S1.
Вообще, определим на стандартной (п—1)-мерной сфере
S»-i = {* = (**, ...,x")e<HELif*02=l}
топологию, индуцированную естественной топологией простран-
ства.
Строение замкнутых множеств топологического подпростран-
ства разъясняется следующим утверждением.
ТЕОРЕМА. Утв. Множество F замкнуто в подпространстве Y
тогда и только тогда, когда его можно представить в виде пере-
сечения множества У с замкнутым подмножеством из объемлю-
щего пространства X.
248

Доказательство. (=^) Пусть F замкнуто в У. Тогда мно-
жество G = Y\F открыто в У. Поэтому его можно представить
следующим образом: G = Y[}Ga, где Ga открыто в Л". Но
тогда F=Y(]Faf тле Fa = X\Ga> замкнуто в X.
(4=) Пусть F=Y()Hf где множество Н замкнуто в X. Тогда
множество Y{\(X\H) открыто в У, так как Х\Н открыто в X.
Следовательно, множество F замкнуто в У..П
4°. Непрерывное отображение. Непрерывное отображение яв-
ляется естественным обобщением известного из математического
анализа понятия непрерывной функции.
Пусть X и У — топологические пространства и / — отображе-
ние пространства X в пространство У; f:X->Y.
Определение. Отображение f:X-^Y называется непрерыв-
ным в точке хеХ, если для любой окрестности V точки f(x) в
пространстве У найдется такая окрестность U точки х в простран-
стве X, что f(U)aV.
Отображение / называется непрерывным, если оно непрерывно
в каждой точке пространства X.
Пример. Пусть X=Y=S>1 (прямая &х наделена естественной
топологией). Обычное определение непрерывности функции у =
= f(x) в точке х: для любого е>0 найдется 6(e) >0 такое, что
для любого у, подчиненного условию \у—х|<6, выполняется не-
равенство \f(y)—f(x)|<e, — равносильно данному определению.
В последующих разделах добавления будут рассматриваться
отображения /:Х->У, где X и У — подмножества евклидовых
пространств с естественной топологией (определенной через функ-
цию расстояния). Такое отображение будет непрерывным в точке
х^Х, если для любой последовательности точек {xk}, сходящейся
к точке х (\Xk—х|-*0 при &-*оо), соответствующая последова-
тельности точек {f{xk)} сходится к точке f{x) (\f(Xk)—f(x)\-+0
при &->-оо).
ТЕОРЕМА 1. Утв. Отображение f:X-^У непрерывно тогда и
только тогда, когда прообраз любого открытого в У множества
открыт в X.
Доказательство. (=>•) Пусть V — открытое множество в
пространстве У. Рассмотрим его прообраз U=f-{(V). Пусть х —*
произвольная точка множества U. Ясно, что f(x)^V. По опреде-
лению для всякой окрестности Vf(X) точки f(x) можно найти та-
кую окрестность Ux точки х, что
f(Ux)czVf{x)9 или, что то же, Uxczf-l(Vf{x)).
Тем самым UxaU и, значит, точка х входит в множество U вмес-
те с некоторой окрестностью, являясь поэтому внутренней точкой
множества U. В силу произвольности выбора точки х во множест-
ве U отсюда следует, что U открыто.
(4=) Покажем, что отображение f непрерывно, в каждой точ-
ке пространства jceI Пусть V — окрестность точки f(x), где
x^V произвольна. Множество U = f~l(V) открыто и содержит точ-
ку х. Это означает, что U — окрестность точки х и f(U) = V. О
9 Заказ 538
249

Простейшим примером непрерывного отображения топологи-
ческого пространства на себя является тождественное отображе-
ние: 1Х:Х-+Х.
ТЕОРЕМА 2. Утв. Отображение f: X-+Y непрерывно тогда и
только тогда, когда прообраз любого замкнутого в У множества
замкнут в X.
Доказательство. (=^) Если множество F замкнуто в про-
странстве У, то Y\F открыто. Тем самым открыто и f-{(Y\F).
Но f-1 (Y\F)=X\f-l(F)-
Следовательно, множество f~l(F) замкнуто.
(4=) Если множество U открыто в У, то Y\U замкнуто. Тем
самым замкнуто и f-{(Y\U) = X\f~l(U).
Последнее означает, что множество f~l(U) открыто. Отсюда
следует непрерывность /. □ '
ТЕОРЕМА 3. Усл. X, У и Z — топологические пространства;
f: X-+Y и g : Y-+Z — непрерывные отображения.
Утв. Композиция h=gof:X-+Z непрерывна.
Доказательство. Если множество U открыто в простран-
стве Z, то g~l(U) открыто в пространстве У >и f~l (g~l(U)) открыто
в пространстве X. Но
Отсюда следует непрерывность отображения A = g°/.-D
Докажем одно полезное утверждение о свойстве непрерывных
отображений окружности в прямую.
ТЕОРЕМА 4. Утв. Всякое непрерывное отображение окруж-
ности в прямую переводит некоторую пару диаметрально проти-
воположных точек в одну точку.
Доказательство. Пусть f:Sx-+&1 — непрерывное отобра-
жение. Введем на прямой &х координаты. Обозначим через хг
точку окружности 51, диаметрально противоположную точке
xeS1, и положим f(x)=y, f(x) =у', где г/, y'eR.
Функция
Bix)=f(x)-f(x')=y-y'
обладает следующими свойствами:
1) g(x) непрерывна и
2) g{x') =f(x')-f{x) =y'-y= -{у-у') = -g(x).
Таким образом, для данной пары х и х' либо f(x)=f(x') и
все доказано, либо
g(x)-g(x')<0. (*)
Пусть z — произвольная точка на дуге хх' (рис. 6). Ее коор-
динаты и и v определяются соотношениями:
u = costt v = smtt 0<t<n.
Из формулы g(z)=h(t) и неравенства (*) вытекает, что
А(0)-А_(л)<0.
250

Ввиду того что функция h(t) непрерывна на отрезке [0, я], и в
силу последнего неравенства найдется ^о^(0, я), такое, что
д/^0)=0. Отсюда следует равенство g(z0)=0 и, значит, f(z0) —
-f(zo')=0.'
Таким образом, f(z0) = /(z0'),
где z0 и Zq — диаметрально про-
тивоположные точки на окружно-
сти SK □
Особое значение имеют такие
непрерывные отображения, у ко-
торых существуют и непрерывны
обратные отображения.
Пусть X и У — топологиче-
ские пространства и отображение
f:X-+Y обратимо. Это означает,
qTO существует отображение
g: У->Х, такое, что
Рис. 6
£°/=1*, f°g=lr.
Определение. Будем говорить, что топологические прост-
ранства X и У гомеоморфны, если оба отображения fug непре-
рывны. Отображения f и g = f~l называются, гомеоморфизмами
пространств X и У.
. Обозначение: X^Y.
С точки зрения общей топологии гомеоморфные топологиче-
ские пространства не отличаются друг от друга.
Пример 1. Отрезки <[а, р], а#р, и [у, б], уфб, на прямой
8х гомеоморфны. Один из гомеоморфизмов можно задать равен*
ством
f(x) = y+±^L(X-a), xe[oc,p].
р — а
Нетрудно построить обратное отображение /_1 и показать, что
и / и f~l непрерывны.
Рис. 7
Рис. 8
Пример. 2. Рассмотрим окружность и замкнутую ломаную,
ограничивающую квадрат. Покажем, что окружность и эта лома-
лая гомеоморфны (рис. 7).
9* 251

Пусть S1 = {(x, y)\x2 + y*=l} — единичная окружность и L^
= {(*> У)\х= ±U —1<#<1 или у= ±1, — 1<х<1} — ломаная.
Гомеоморфизмы имеют следующий вид:
f:&-+L, f:(Xty)~(JLtJL\.
\ т т J
. f^:L-+S\ f-i:(X9y)~(JLtJLy
где /n = max{|x|, \y\}9 г = Ухг + у2.
Пример 3. Въп^8п.
Соответствующие гомеоморфизмы определяются следующим
образом:
у:Впо-+$п задается формулой у(у)= —^ , а \р:ёп-+Впо задается
формулой г|)(2)~-
1+1г|
Пример 4. Sn\N^en (рис.8).
Соответствующие гомеоморфизмы
Ф : S»\ (0,..., 0, 1) -*#»,!>: g *-*S»\ (0,..., 0,1)
определим соответственно формулами
Ф(лЛ ... ,*»+■) = (—^—, • • Л —-£—V
г|>(*\ ...,*»)= —-^—-(2х\ ...92х», И2-1).
1 + |*12 * -
Пример 5. lntIn^B0n. ,
Пример 6. Из теоремы 4 вытекает, что* соотношения Sl^&l9
S1^/1 и Sx£*Ilo не имеют места.
П р и м е р 7. 1п не гомеоморфно /0П.
Пример 8. Множество {(л;1, л:2, Xs) & £3|jci2 + *22< 1} гомео-
морфно пространству ^Г3:
. (х\ х\ х*) к. ( £ , * , хЛ .
5°. Топологическое произведение. Пусть X и У — топологиче-
ские пространства. Декартово произведение XX У определяется
как совокупность всевозможных упорядоченных пар \ху у)> где
х<=Х и y^Y.
Введем в декартовом произведении топологию, естественно
связанную с топологией в X и в У.
Рассмотрим семейство 3~хуу, которое состоит из всех мно-
жеств, являющихся объединением декартовых произведений от-
крытых подмножеств из пространств X и У. Типичным элементом
семейства ZTxxy служит множество следующего вида:
252

где А — некоторое множество индексов и при любом а из Л
множества Ua и Va открыты в А" и в У соответственно.
Нетрудно проверить, что Тххт — топология.
Действительно, 0 = 0X0, XxY=XxY (условия 1 и 2).
Если.W9 W'seTxxy, to
где А и В — некоторые множества индексов и Ua, £V открыты в
Ху a Va> V/ открыты в У. Тем самым
(а,р)еЛхВ
(U*№)X{Vat)Vp')
(условие 3). Условие 4 выполняется тривиально.
Определение. Декартово произведение ХхУ, наделенное*
описанной выше структурой, называется топологическим произве-
дением пространств X и У.
Пример 1. Если X=Y—&1 — обычная прямая, то XXY=
=S*2 — плоскость с естественной топологией двумерного, евкли-
дова пространства. (Отметим, что открытый круг на плоскости <§2
можно представить в виде объединения счетного (не конечного)
числа прямоугольников — произведений интервалов, открытых
множеств из X и У.) (рис. 9).
Рис. 9
Рис. 10
Пример 2. Топологическое произведение евклидовых прост-
ранств &п и Sm есть евклидово пространство, &nX&m= Sn+m.
Пример 3. Если X — прямая &\ а У — окружность S1, то
8lXSl — цилиндр (рис. 10).
Пример 4. Если X — окружность, а У — круг, то SlXBl —
полноторие. Если и А" и У являются окружностями, то S1X51 =
= Т2 — тор.
253:

Пример 5. Множество *?2\0 гомеоморфно цилиндру &lxSl.
Множество £Гя+1\0 гомеоморфно &lxSn.
6°. Связность. Определение. Топологическое пространство
X называется связным, если единственными его подмножествами,
которые 'и открыты и замкнуты одновременно, являются пустое
множество 0 и все пространство X. Подмножество пространства
X называется связным, если оно связно как пространство с инду-
цированной топологией.
ТЕОРЕМА 1. Утв. Топологическое пространство связно тогда
и только тогда, когда оно не является объединением двух своих
непустых непересекающихся открытых подмножеств.
Доказательство. (=>) Пусть X связно. Предположим, что
X = Xi{JX2i где Ii и 1г — 'непустые непересекающиеся открытые
подмножества пространства X. Тогда Х\Х\ = Х2, так что Х\ от-
крыто и замкнуто одновременно. Отсюда следует, что Хг либо
пусто, либо совпадает со всем X. Соответственно, либо Х2 = ХУ
либо Х2 = 0. В обоих случаях пространство X нельзя представить
в виде объединения двух непустых непересекающихся открытых
множеств.
(£=) Пусть X не является объединением двух непересекаю-
щихся непустых открытых подмножеств. Рассмотрим подмноже-
ство U пространства X, которое одновременно открыто и замкну-
то. Тогда дополнение X\U также одновременно открыто и зам-
кнуто и пространство X является объединением непересекающих-
ся открытых множество f/'и X\U. Поэтому одно из них должно
быть пустым, т. е. либо £/=0, либо U=X. □
Простым примером несвязного множества является объедине-
ние двух непересекающихся кругов на плоскости &*.
Доказав следующее утверждение, мы получим пример связно-
го множества на прямой йГ1.
ТЕОРЕМА 2. Утв. Интервал (0, 1) связен.
Доказательство. Предположим, что интервал (0, 1) мож-
но представить в виде объединения двух его непересекающихся
открытых подмножеств U и V. Поскольку множества U и V не-
пусты, найдутся точка a^U и точка b^V. Пусть для определен-
ности а<Ь.
Рассмотрим c=sup{x^U\x<b}.
Ясно, что с<Ь.
Предположим, что cg[/. Тогда с<Ь. Так как множество U
открыто, то точка с входит в него вместе с некоторым содержа-
щим ее интервалом. Это означает, что справа от с лежат точки
из £/, меньшие Ь. Полученный факт противоречит тому, что с —
верхняя грань. Поэтому точка с не может лежать в U.
Предположение о том, что c^V, также приводит к противоре-
чию. В самом деле, из того, что множество V открыто, вытекает,
что точка с входит в V вместе с некоторым содержащим ее интер-
валом (с—е, с + е), чего не может быть,, та* как с — точная верх-
няя грань.
254

Таким образом, точка с не принадлежит ни U, ни V. Так как,
с другой стороны, с заключена между нулем и единицей, полу-
чаем ожидаемое противоречие. □
Следующее утверждение предоставляет общий метод построен
ния новых связных множеств из уже имеющихся.
ТЕОРЕМА 3. Утв. Образ связного множества при непрерыв-
ном отображении связен.
Доказательство. Пусть X связно и f:X-+Y непрерывное
сюръективное отображение. Если U открыто и замкнуто в У, то
его полный прообраз f~l(U) открыт и замкнут в X.' Но тогда
вследствие связности X либо f~l(U)=0> либо f~1(U)=X. Соответ-
ственно либо £/=0, либо £/=У. Это означает, что множество Y
связно. □
Пример негомеоморфных топологических пространств X и Y
приведен на рис. 11. Замкнутый круг не гомеоморфен замкнуто-
Рис. 11 , Рис. Ш Рис. 13
му кольцу, та!к как при гомеоморфизме граница дХ должна пере-
ходить в границу dY, но граница дХ является связным множест-
вом (как непрерывный образ интервала (0, 1)), а граница dY —■
несвязное множество (его можно представить в виде объединения
двух 'непересекающихся окружностей).
СЛЕДСТВИЕ. Усл. Топологические пространства X и У гомео-
морфны; X связно.
Утв. У связно.
Пример 1. Окружность S1 связна, так как имеется непрерыв-
ное сюръективное отображение
/:(0, l)^S\
задаваемое формулой
f(f) = (cos4nf, sin^tJeES'c:^2.
Пример 2. Отрезок [0, 1] связен. Непрерывное сюръектив-
ное. отображение /:SW[0, 1] задается так, как показано на
рис. 12.
ТЕОРЕМА 4. Усл. Топологические пространства X и У связны.
Утв. Топологическое произведение XXY также связно.

Доказательство. Предположим, что
XxY=U[)V,
где U и V — непересекающиеся открытые множества. Возьмем
точку (#, у) в U. Множество Хх{у) гомеоморфно X и потому
Связно. Отсюда следует, что Хх{у} содержится в [/, так ка«к в
противном случае пересечения Хх{у} с U и V давали бы его
разложение на открытые и непустые непересекающиеся множест-
ва (рис. 13).
Аналогичное рассуждение показывает, что для любого х' из
К слой {x'}xY должен содержаться в U. Значит, все XxY содер*
жится в /У, и, следовательно, V — пустое множество. Поэтому
произведение Хх Y связно. □
Пример 3. Так как отрезок /1=[0, 1] связен, то связен и
Квадрат /2=/1х/1.
Вообще (это просто доказать по индукции), /г-мерный куб
In = In~lXll является связным множеством.
Поскольку прямая &х связна, то связно и /г-мерное точечное
евклидово пространство 8п.
Упражнение. Пусть Y — связное множество в топологическом
пространстве X. Если множество Z подчиняется условию YczZa
czF, то Z связно.
Пример 4. Открытый круг связен как образ плоскости при
непрерывном отображении. Из упражнения вытекает, что связным
будет и множество, полученное добавлением к открытому кругу
всех или только некоторых точек ограничивающей его окруж-
ности.
Пример 5. Множество йРл+1\0 связно при п^\. Отсюда сле-
дует связность сферы Sn: отображение
f :S>n+l\0-+Sn9
задаваемое формулой f(x) — , непрерывно и сюръективно.
1*1
7°. Линейная связность.
Определение. Путем в пространстве X называется непре-
рывное отображение /: [О, 1]->Х
Точка а=/(0) называется началам пути f, а точка Ь = /(1) —
его концом.
Говорят также, что путь f соединяет точки а и Ь.
Образ отображения- / — /([0, 1]) — называется носителем пу-
ти {кривой) в прострьанстве X.
Определение. Пространство X называется линейно связ-
ным, если для любых двух точек а и Ь из X найдется путь, соеди-
няющий их в X.
Пример. Точечное евклидово пространство 8п с естествен-
ной топологией линейно связно, та>к. как для любой пары точек а
и Ъ из ёп отображение /: [0, Х\-+8п, определяемое формулой
f(t) = (l—t)a + tb, является путем, соединяющим эти точки.
256

Вообще^ всякое выпуклое подмножество <£п линейно связно.
ТЕОРЕМА 1. Утв. Образ линейно связного множества при
непрерывном отображении линейно связен.
Доказательство. Пусть пространство X, линейно связно и
g:X-*Y — непрерывное сюръективное отображение. Если а и b —
точки из У, то существуют точки о'и Ь'-в! такие, что g{a')=a>
g(b')=b.
Так как X линейно связно, то найдется путь /, соединяющий в
X точки а' и Ь'. Тогда g°f — путь из а в Ь. □
Пример. Окружность S1 линейно связна. Пользуясь этим,
можно показать, что линейно связны &п+1\0 и Sn. (линейная
связность &п+1\0 следует из того, что любые две точки этого
множества лежат на некоторой окружности, не проходящей через
О; линейная связность сферы Sn вытекает, например, из того, что
она — непрерывный образ 1ГЛ+1\0).
ТЕОРЕМА 2. Утв. Топологическое произведение XxY линейно
связных пространств X и У линейно связно.
Доказательство. Проводится буквально так же, как и
доказательство теоремы 4 предыдущего пункта о связности топо-
логического произведения связных пространств с заменой термина
«связность» на термин «линейная связность». □
ТЕОРЕМА 3. Утв. Линейно связное множество связно.
Доказательство. Пусть X — линейно связное простран-
ство. Докажем, что X связно. Пусть X=U[)V с открытыми й не-
пустыми U и V, U()V = 0. Так как X линейно связно, а множест-
ва U и V непусты, то найдется путь f: [О, 1]->Х, для которого
/(0)е£/, f(l)<=V. Отрезок [0, 1] связен. Поэтому его , образ
f([0> 1]) также связен и, значит, множества Uf\f([0, 1]) и
Vrif([0, 1]) должны пересекаться. Но тогда и множества U и V
пересекаются, что противоречит допущению. Тем самым шростран*
ство X связно. □
Формулируемое ниже утверждение показывает, что для откры-
того подмножества в &п понятия связности и линейной связности
совпадают.
ТЕОРЕМА 4. Утв. Всякое непустое открытое связное подмно-
жество точечного евклидова пространства 6п линейно связно.
Доказательство этой теоремы полезно провести самостоя-
тельно. □ . .
8°. Компактность. Как и в двух предыдущих пунктах, мы рас-
смотрим здесь свойство топологических пространств, сохраняю-
щееся при гомеоморфизме.
Аксиома отделимости. Топологическое пространство
X называется хаусдорфовым (отделимым), если оно обладает сле-
дующим свойством: для любой пары различных точек х и у из X
существуют открытые множества Ux и Uy, содержащие точки х
и у соответственно и такие, что Uxf\Uy = 0.
Пример 1. <£п — хаусдорфово пространство. Любое подмно-
жество из <кп> рассматриваемое как топологическое подпростран-
ство, — хаусдорфово пространство.
257

Пусть У — подмножество хаусдорфова пространства X.
Определение. Покрытием подмножества Y называется се»
мейство подмножеств пространства X — {На\а^А} — такое, что
Уси«еА#«.
Если множество индексов А конечно, то покрытие называется
конечным.
Подпокрытие — это покрытие, все множества которого при-
надлежат исходному покрытию.
Покрытие называется открытым, если каждое его множество
открыто в X.
Определение. Подмножество Y топологического простран-
ства X называется компактным, если всякое открытое покрытие
содержит конечное подпокрытие.
Пример 2. Теорема Бореля—Лебега из математического ана-
лиза показывает, что любое ограниченное замкнутое множество в
евклидовом пространстве 8п компактно. В частности, компактны
замкнутый шар Впу куб /п и сфера Sn~K
Пример 3. Прямая <SX некомпактна: из покрытия {(пг—1,
m+1) |m^Z} нельзя выделить конечного подпокрытия.
Аналогичное рассуждение показывает, что евклидово прост-
ранство &п некомпактно и некомпактно любое ^неограниченное
подмножество евклидова пространства &п\ из покрытия
{{тх— 1, т!+1)Х...Х(тп—1, тп+\) \ти. ..,mneZ}
нельзя выделить конечного подпокрытия.
ТЕОРЕМА 1. Усл. Отображение f :X-+Y непрерывно; ZczX —
компактное подмножество.
Утв. f(Z) компактно.
Доказательство. Пусть {Ga\a^A} — какое-нибудь откры-
тое покрытие множества f{Z). Тогда
{f-l(Ga){a€EA}
— открытое покрытие Z. Так как Z компактно, то найдется конеч-
ное подпокрытие
BczA конечно. Но /(f-^Gp)) = Gp, и потому {GP|[J<=B} — покры-
тие f(Z), являющееся конечным подпокрытием покрытия
{Ga\ae=A}. □
Несложно доказать следующее предложение.
ТЕОРЕМА 2. Утв. Замкнутое подмножества компактного про-
странства компактно.
- Доказательство. Компактные множества обладают сле-
дующим интересным свойством. Пусть X компактно и Y—произ-
вольный бесконечный набор точек из X. Тогда в X найдется точ-
Хаусдорф (Hausdorff) Феликс (8.11.1868—26.1.1942) — немецкий математик;
Борель (Borel) Эмиль (7.1.1871—3.2.1956) — французский математик, член-
корреспондент АН СССР (с 1929года); Лебег (Lebesgue) АнриЛеон (28.6.1875—
26.7.1941) — французский математик, член-корреспондент АН СССР (с 1929 го-
да).
258

ка, в любой открытой окрестности которой содержится бесконеч-
ное число точек из «набора У. Покажем это.
Допустим противное: у каждой точки х из хаусдорфова прост-
ранства X существует открытая окрестность Ux, в которой содер-
жится самое большее конечное число точек из У. Ясно, что
{Ux\x^X} — открытое покрытие. В силу «компактности X из этого
покрытия можно выделить конечное подпокрытие {£/ь..., Uq}.
Каждое из множеств Ut9 /= 1,... ,9, содержит лишь конечное чис-
ло точек >из «абора У. С другой стороны, их объединение
Ui\J...\JUq содержит весь бесконечный набор У. И нужное противо-
речие получено.
Приступим теперь к доказательству сформулированного ут-
верждения непосредственно.
Пусть Z — замкнутое подмножество компактного простран-
ства X. Вновь будем рассуждать от противного: предположим, что
множество Z некомпактно. Тогда существует открытое покрытие
9> множества Z, -из которого нельзя выделить конечнбго подпокры-
тия. Это означает, что в Z можно-указать бесконечный набор то-
тек У, обладающих следующим свойством: каждая из точек набо-
ра У входит в множества из покрытия ^, не содержащие других
точек набора У. Набор У строится так. Пусть х\ — произвольная
точка множества Z. Совокупность элементов покрытия ^, содер-
жащих Х\у не вмещает всего Z. Это означает, что в Z найдется
точка Х2, не попадающая ни в одно из множеств покрытия ^, со-
держащих Х\.
Рассмотрим совокупность элементов покрытия 5^, содержащих
хотя бы одну из точек х\ и #2. На тех же основаниях, что и вы-
ше, находим в Z точку х$9 не попадающую ни в одно из множеств
покрытия ^, содержащих х\ или Хъ
Этот процесс можно продолжить: по набору т точек Xi,...,xm
из Z со свойством — никакие две из этих точек не лежат в одном
и том же множестве из покрытия & — аналогичными рассужде-
ниями в Z находится еще одна точка хт+и добавление которой к
набору х\,...,хт не изменяет его основного свойства, a meN
произвольно.
Рассматривая теперь набор У в объемлющем компактном про-
странстве X и пользуясь доказанным выше свойством компактных
множеств, найдем в X точку х, в любой окрестности которой со-
держится бесконечное число точек из набора У. Найденная точка
х принадлежит множеству Z в силу замкнутости последнего. Но
тогда в покрытии 9* можно указать открытое множество U, со-
держащее ху а значит, и бесконечное число точек набора У. Это
противоречит принципам построения набора У. □
В заключение сформулируем и докажем утверждение, полез-
ное при построении гомеоморфизмов.
ТЕОРЕМА 3. Усл. X — компактное пространство, У — хаус-
дорфово пространство, отображение f:X-*Y взаимно однозначно
и непрерывно.
Утв. f:X^Y (f — гомеоморфизм X на У).
259

Доказательство. Для непрерывности обратного отображе-
ния f~l: Y-+X достаточно показать, что прообраз f(V) произволь-
ного замкнутого в X множества V при отображении f~l замк-
нут в У.
Множество V как замкнутое подмножество компактного прост-
ранства X компактно. В свою очередь компактен и его непрерыв-
ный образ /(V).
Следующее вспомогательное предложение показывает, что
доказательство теоремы можно считать завершенным.
ЛЕММА. Утв. Компактное подмножество W хаусдорфова про-
странства У-замкнуто.
Доказательство. Покажем, что множество Y\W откры-
то. Рассмотрим пару точек x^W и y^Y\W. В силу аксиомы от-
делимости существуют открытые множества Ux и Vx:
Uxr)Vx=0, x<=UXf yezVx.
Семейство {Ux\x^W} покрывает W и вследствие компактности
W содержит конечное подпокрытие {UXl, ... , Ux }. Множество
V =VXl{\ .. .(]VX открыто, содержит точку у и не пересекает-
ся ни с одним из Ux.y i=l,...,g. Поэтому VyczY\W. Значит,
каждая точка у из У\1Г содержится в этом множестве вместе с
некоторой своей открытой окрестностью Vy. Тем самым множест-
во Y\W открыто и W замкнуто. D
Из доказанной теоремы, в частности, вытекает, что образ f(X)
компактного множества X в хаусдорфовом пространстве У при
непрерывном инъективном отображении f:X-+Y гомеомор-
фен X. \
Б. ВЫПУКЛЫЕ МНОЖЕСТВА
1°. Простейшие выпуклые множества. Пусть а и Ь — различ-
ные точки евклидова пространства <Sn.
Точки, представимые в виде (1—t)a+tbf образуют:
прямую L(a, Ь), проходящую через точки а и Ь (при —оо<
</<оо);
луч /[а, Ь), исходящий из точки а и идущий через точку Ь (при
0<:/<о6);
отрезок [а, Ь] с концами а и Ь (при 0</<1);
полуинтервал [а, Ь) с концами а и Ъ (при 0<t<\).
Непустое подмножество X точечного евклидова пространства
&п называется выпуклым, если оно вместе с каждой парой своих
точек Хг и у содержит весь соединяющий их отрезок [х, у].
Эквивалентное алгебраическое условие заключается в том, что
(l—t)x+ty^Xt каковыми бы ни были х^Х, у&Х и te(0, 1).
Приведем некоторые примеры выпуклых множеств в <Sn.
Пример 1. Открытый шар В0п(а, г). Пусть х и у^В0п(а, г),
т. е. \х—а\<г и \.у—а[<Г.. Бели z=(\—t)x+tyY 0<*<1, то
Ш

\z-a\ = \(l-t)(x-a)+t(y-a)\<(l-t)\x-a\+t\y-a\<rt т. е. zee
&Bon(a9rl.
Пример 2. Гиперплоскость Н — сцх1+.. .+anxn=p, где
Так как непустое пересечение выпуклых множеств выпукло, то
отсюда следует выпуклость /г-плоскостей (любая /г-плоскость мо-
жет быть представлена в виде пересечения n-k гиперплоскостей).
Пример 3. Замкнутое полупространство' а\Х1+.. .+<хп#п<Р и,
значит, /г-мерный куб Iй (как пересечение 2п полупространства
j^>0, х*<1, i=l,...,/г).
2°. Замыкание и внутренность выпуклого множества.
ЛЕММА. Усл. а — внутренняя точка выпуклого множества X,
Ь — точка его замыкания X.
Утв. Каждая точка полуинтервала [а, Ь) является внутренней
точкой множества X. '
Доказательство. Для достаточно малого положительного
числа е открытый шар В0п{а, г) целиком лежит во множестве X.
Возьмем на отрезке [а, Ь] точку с=(1—t)a+tb и покажем, что при
0</<1 эта точка является внутренней точкой множества X.
Рассмотрим открытый шар В0п=В0п(с, (1—^)е)* Утверждение
леммы будет доказано, если удастся показать справедливость
включения B0nczX.
. Пусть точка х лежит в шаре В0пу т. е.
|*-с|<(1-0в. (1)
Если точка d принадлежит множеству X, то (рис. 14)
\x-((l-t)a+td)\ = \lx-c)+t(b-d)\<\x-c\+t\b-d\. \ (2)
Рис. 1,4
Так_как Ь — точка прикосновения множества X (напомним, что
Ь^Х)9-то точку d можно выбрать так, чтобы она была достаточ-
но близка к точке Ь. Например, /
(в силу неравенстэа (j) разность, в правой части положительна').

Отсюда получаем, что
\x-c\+tlb-d\<(l-t)e.
Из -соотношения (2) вытекает оценка
|*— ((1 — /)a + W)|<(l — /)e,
или
|<8.
——(x—td)—a
Последнее неравенство означает, что точка
w = —-—(х—td)<=£BnQ(a1z).
Выражая отсюда ху получим, что х=(1—t)w+td. Так как точки w
и d лежат в X, то х также лежит в X вследствие его выпуклости.
В силу произвольности в выборе точки х в шаре В0п заклю-
чаем, что B0nczX и, значит, точка с —внутренняя точка множе-
ства X. □
ТЕОРЕМА 1. Усл. X — выпуклое множество в пространстве
<Sn.
Утв. Множество его внутренних точек int X либо пусто, либо
выпукло.
Доказательство. Пусть ЫХФ0. Если х и у — точки из
int X, то в силу леммы отрезок [х, у] лежит в int X. D
ТЕОРЕМА 2. Утв. Замыкание
/^—«v /*~*\ /—N выпуклого множества выпукло.
( ?) ( У ) [-# ) Доказательство. Пусть
V-^V : Ч-J^., У^ х ~ выпуклое множество и X —
* ,v его замыкание. Возьмем две про-
Рис 15 извольные точки х и у из X к
рассмотрим точку w=(\—t)x+
+ ty, где 0<t<cl (рис. 15).
Так как х и у — точки прикосновения множества X, то для лю-
бого положительного числа е можно указать точки х' и у' из
множества X, такие, что \х'—х\<г и \у'—у\<ъ- В силу выпукло-
сти множества X точка w'=(l—t)x'+ty' принадлежит X. Кроме
того, выполняется соотношение
|ш'-ш| = | (1-0 {x'-xj+t(y'-y)\<e.
Это означает, что в открытом шаре B0n(wy e) найдется точка из
множества X. Отсюда следует включение ше! □
ТЕОРЕМА 3. Усл. X — выпуклое множество; МХФ0.
Утв. Х = ШХ.
Доказательство. Так как intXczX, то включение intXcz
czX тривиально.
Пусть AreintJ и */&?. Так как любая точка отрезка \ху у\ за
исключением, может быть, точки уУл принадлежит intX, то во вся-
262

кой окрестности точки у найдутся точки из intX. Это означает, что
y^lntX. Откуда следует включение XczintX. □
3°. Звездность выпуклого множества.
ТЕОРЕМА 1. Утв. На каждом луче, исходящем из внутренней
точки выпуклого множества, имеется не более одной граничной
точки этого множества.
Доказательство. Пусть внутренность intX множества X
непуста, и xeint X.
Допустим, далее, что на луче, исходящем из точки х, имеются
две граничные точки множества X — у и 2, уФг. Будем считать
для определенности, что у^[х, г]. Тогда на основании леммы пре-
дыдущего пункта точка у должна быть внутренней точкой множе-
ства X, что противоречит допущению.
Таким образом, всякий луч, исходящий из внутренней точки
выпуклого множества X, либо содержится в X, либо пересекает дХ
в единственной точке. □
Определение. Множество X называется звездным относи-
тельно точки д:еХ, если любой луч /, исходящий из точки ху пе-
ресекает границу дХ множества X не более чем в одной точке
Рис. 16 Рис. 17
Поэтому доказанная теорема может быть сформулирована сле-
дующим образом.
ТЕОРЕМА 2. Утв. Выпуклое множество в <8П звездно относи-
тельно любой своей внутренней точки.
4°. Звездность и теорема Хелли. Обобщим введенное в преды-
дущем пункте понятие звездности, ослабив требования на границу
множества.
Пусть и и v — точки множества X из пространства бп. Будем
говорить, что точка и видна из точки v во множестве X, если от-
резок [и, v\ лежит в X. Заметим, что если и видна из v в X, то и
v видна из и : в X.
Множество X называется звездным, если в X найдется точка
иу из которой видны все другие точки этого множества (рис. 16).
Множество U точек и, обладающих указанным выше свойст-
вом, назовем центром множества X. Отметим, что UczX.
Утверждение. Центр звездного множества является выпуклым
множеством.
263

Доказательство.' Пусть и и v — точки центра U. Возь-
мем в X произвольную точку х и рассмотрим Auvx — 2-симплекс
с вершинами и, v и х (рис. 17). Этот треугольник целиком лежит
во множестве X. В самом деле, все его стороны лежат в X по оп-
ределению центра. Если бы некоторая точка z внутри треуголь-
ника не принадлежала X, то лежащая за ней на луче 1[и, г) точ-
ка w отрезка [v, x] была бы не видна из и. Это противоречит то-
му, что w^X и u^U.
Из того, что треугольник Auvx принадлежит X и является вы-
пуклым множеством, получаем, что произвольно взятая точка х
видна из любой точки Xu + \iv, iji^O, V+|i=l, отрезка [и, v]. D
ТЕОРЕМА. Усл. X — компактное подмножество пространства
<Sn. Для любых п+1 точек из X' существует точка, из которой
видны всё эти п+1 точек.
Утв. Множество X звездно.
Доказательство теоремы опирается на несколько простых фак-
тов, к рассмотрению которых мы и переходим.
Факт 1-й. Теорема Хелли, доказанная нами ранее для семей-
ства, состоящего из конечного числа выпуклых множеств, оказы-
вается справедливой и для случая, когда семейство бесконечно
правда, при дополнительном условии, что составляющие его мно-
жества компактны. Доказательство .легко сводится к случаю ко-
нечных семейств.
Факт 2-й. Пусть X и У — компактные множества в 6п. Тогда
существуют точка хо^Х и точка у^У> такие, что
4(*0,Уо)=ВД У).
Напомню, что d(x, у) = \х—у\ и d(X, Y) = iniX£x,yeY<l(x, у).
• Из определения расстояния между множествами' вытекает су-
ществование последовательностей точек {xk} из X и {*/*>} из У, для
которых
d(xki yk)-+d(X, У)
при /гг^оо. В силу компактности множества X из последовательно-
сти \xk) можно выделить подпоследовательность {хт}, для точек
которой й(хт, хо) = | хт~х0 | ->0, где хо^Х, а в силу компактности
У из подпоследовательности {ут} можно выделить новую подпо-
ил едовательность {#/}, для точек которой d(#/, у о) = \ yi—у о I -^0,
где yo^Y.
Так как
d(x0, #o)<d(x0, xi)+d(xif yi)+d{yit y0),
то тем самым
d(x0, */o)<d(X, У).
С другой стороны, d (Xy Y) < d (x0, yo).
Откуда следует, что d(xo, #o)=d(X, У).
Факт 3-й. Если ком'пактные подмножества X и У из 6п не пе-
ресекаются, то d(X, У)>0.
2е4

Это неравенство обосновывается рассуждением от противного.
Из равенства d(X, У)=0 вытекает, что построенные выше точки
Хо^Х и Уо^У должны быть связаны coofношением d(x0, f/o) =0.
Отсюда вытекает равенство л:о=Уо, немедленно приводящее к
нужному противоречию.
Доказательство теоремы. Пусть х. — произвольная
точка из X. Положим
Vx-{yeX\[x9 у]сХ}.
Тем самым Vx — это множество точек, из которых точка х видна
в X. ^
Пусть хи ..., хп+\ — точки из X. Обозначим через у точку мно-
жества Ху из которой они видны. Точка у существует по условик>
и является общей для множеств VXl, ...» Vxn+\-
Нужно показать, что
()xzxVx^0.
Согласно теореме Хелли (факт 1-й) найдется точка
* z&fbexConvV*.
Покажем, что
zs{]xeXVx.
Рис. 1,8
Предположим противное (рис. 18). Тогда 1) либо z не лежит
в X, 2) либо 2gI, но в X найдется точка х, которая не видна из
гвХ
В первом случае в X найдется точка х\ такая, что [г, x')f\X=^
=0.
265.

Во втором случае zel и множество точек [г, х]\Х представ-
ляет собой объединение непересекающихся интервалов. Возьмем
один из них - (г', х'). Ясно, что | — (z'+x')9 х'\()Х = 0. Тем
самым можно утверждать, что на отрезке [г, л:] лежит полуинтер-
вал [и9 *'), такой, что [и9 х'](]Х=х\ но [и9 х')[\Х=0. Поэтому
>" А(и9 X)>0.
На интервале (и9 х') найдется точка v, для которой
|»-V|=-±-d(tt, X)
(вследствие непрерывности функции расстояния |л:—r/1 =d(jc, у)).
Ясно, что
d([u9x]9X)>0.
Так как множества [и9 v] я X компактны, то существует точка
Хо^Х и найдется точка ше[«, v]9 для которых
\xQ-w\=d([u9zi]9X).
Проведем через точку х0 гиперплоскость Я, перпендикулярную
отрезку [w9 xQ] (рис. 19). Так как хо -1 ближайшая к до точка из
Х9 то все точки множества Х9 а значит, и VXo, принадлежат зам-
кнутому полупространству Я+,
примыкающему к гиперплоскости
Я и не содержащему точки w.
Тогда
zeconv VXo<~ Н+ и ^. zxqW > -—-.
Отсюда вытекает, что
0 2
Так как
A(w9 X)<d(v9 x)<\v—x'\=±4(u9 X)<d(u9 X)9
то ясно, что u¥=w.
Из того, что точка и лежит на отрезке [г, w]9 и из неравенства
^х0тг<— вытекает, что на [и9 w] найдется точка w'9 которая
ближе к xq9 чем точка w. Это противоречит выбору точки w. D
5°. Выпуклая оболочка компактного множества. Пусть X —
произвольное непустое подмножество пространства 6п.
Выпуклой оболочкой множества X называется наименьшее из
содержащих его выпуклых множеств. Известно, что выпуклая обо-
лочка множества слагается из всевозможных выпуклых комбина-
566

ций его точек (напомним, что точка х называется выпуклой ком-
бинацией точек Хи...,хт, если ее можно представить в следую-
щем виде:
X—h\X\\. ..TAm^m,
где К\+. ..+Ят=1 и Xi>0, ..., Ят>0).
ТЕОРЕМА 1 (Каратеодори). Усл. X — подмножество про-
странства <8П.
Утв. Каждая точка из выпуклой оболочки множества X может
быть представлена выпуклой комбинацией не более п+1 точки из
множества X.
Доказательство для точечного пространства проводится
совершенно аналогично тому, как это делается для линейных про-
странств (см. лекцию 25). П
Опираясь на классический результат Каратеодори, докажем
следующее утверждение.
ТЕОРЕМА 2. Усл. X — компактное множество в пространст-
ве 6П.
Утв. Выпуклая оболочка множества X компактна.
Доказательство. Обозначим через А множество веек то-
чек я=(ао, он, ..., <Хп), для которых 2?=оа/ = 1 и а;>0, 1=0, ...
..., п.
Множество А ограничено (содержится в кубе /n+1) и замкнута
(как пересечение п+2 замкнутых полупространств), следователь-
но, компактно. Поэтому множество
W = AxXx...xX = AxXn+l
также компактно.
Пусть ау=(а0, ..., ап; *о, • • - > xn)^W. Положим
/(w) = 2jL<№*?.
Построенное отображение
f:W-+6n
непрерывно (в силу линейности), a W компактно. Поэтому его об-
раз f(W) компактен.
По теореме Каратеодори f(W) совпадает с выпуклой оболоч-
кой множества X. О '
6°. Выпуклое тело.
Определение. Выпуклым телом в пространстве <8П назы-
вается компактное выпуклое множество, внутренность которого
непуста.
ТЕОРЕМА 1. Утв. На каждом луче, исходящем из внутренней
точки выпуклого тела, имеется ровно одна граничная точка.
Доказательство. Пусть X — выпуклое тело, x^XniX и
1Х — луч, исходящийиз точки х. Пересечение lxf]Xt будучи ком-
пактным и выпуклым, представляет собой отрезок [xt y]czX. Лю-
267

бая точка z^'lXl отстоящая от точки х дальше, чем точка у, не
принадлежит X. Поэтому у — граничная точка множества Л".
По теореме 1 пункта 3° иных граничных точек множества X луч
1Х не содержит. □
Рассмотрим точки Хо, х\у ..., хп из пространства 6Л, не лежа-
щие в одной гиперплоскости. Их выпуклая оболочка называется
симплексом (точнее, я-симплексом), а сами точки x0i X\, ..., хп —
вершинами симплекса (рис. 20).
Рис. 20
Рис. 21
ТЕОРЕМА 2. Утв. /г-симплекс в пространстве &п — выпуклое
тело.
Доказательство. Пусть о — я-симплекс с вершинами
ХоУ ... t хп. Из определения симплекса непосредственно вытекает,
что о компактно.
Определим отображение /:<Sn-><Sn по следующему правилу:
/: w = (Xv ..., ХЛ)~х = (1 —2?=ih) x0 + SjLiV*.
Если Л — множество всех точек w=(X\, ..., Хп), таких, что Xi>
>0, Х\+. ..+Хп—1, то отображение / является гомеоморфизмом Л
на о (на этих множествах отображение взаимно однозначно и не-
прерывно в обе стороны).
Покажем, что точка
ауЛ =
/г + 1
п+\
является внутренней точкой Л. Выберем в &п открытый куб /0П,
такой, что
где 8 = .
п (п+ 1)
тельны и
\h 1— <е, 1=1, ..., пу
I п + 11
Координаты Хи ••> 'Хп точек w<=I0n положи-
Значит, /0П — открытая окрестность точки .Wq&A, целиком лежа-
щая во множестве Л. Ее образ f(Ion) является открытой окрест-
268

ностью точки xo=f(w0), полностью лежащей в симплексе <т. Сле-
довательно, Xo^intio. D
7°. Размерность выпуклого множества. Пусть X — выпуклое
множество. Среди ^-плоскостей пространства <Sn, содержащих
множество X, найдется (единственная) ^-плоскость наименьшей
размерности. Эта ^-плоскость называется аффинной оболочкой
множества X.
По определению число k называется размерностью выпуклого
множества X
Обозначение: длтХ.
Напомню, что k-симплексом называется выпуклая оболочка
точек Хо, . -., Xk из ёп (k^n) при условии, что эти точки не лежат
в одной (£—1) -плоскости.
Пример. Размерность ^-симплекса равна k.
Утверждение. Всякий ^-симплекс является выпуклым телом в
своей аффинной оболочке (в индуцированной топологии).
Отсюда вытекает простое, но важное для дальнейшего утверж-
дение.
ТЕОРЕМА. Утв. Выпуклое множество, рассматриваемое в сво-
ей аффинной оболочке содержит внутренние точки (в индуци-
рованной топологии).
Доказательство. Если размерность выпуклого множества
X равна ky то в нем найдутся точки Хо, Хи . • •, **, не лежащие в
<7-плоскости размерности, меньшей k. Применив к ^-симплексу с
вершинами хо, *ь ..., Xk теорему 2 предыдущего пункта, получим
утверждение этой. П -
8\ Опорные плоскости. Пусть X — n-мерное выпуклое мно-
жество в пространстве &п.
Определение. Опорной k-плоскостью множества X будем
называть ^-плоскость, которая содержит точки замыкания X мно-
жества X, но не содержит его внутренних точек.
Опорные 0-плоскости — это точки границы дХ\ опорные
(лг— 1) -плоскости — это гиперплоскости, которые содержат точки
замыкания Ху но не разделяют никакие две точки ^самого множе-
ства X. (Последнее свойство можно использовать как определение
опорных плоскостей для выпуклых множеств без внутренних, то-
чек.)
ТЕОРЕМА 1. Усл. Опорные ^-плоскости П^, П2*,_... множест-
ва X сходятся к /г-плоскости П*, содержащей точки X (когда мно-
жество X ограничено, ^-плоскость ПА автоматически содержит
точки замыкания).
Утв. П* также является опорной ^-плоскостью множества X
(рис. 21).
Доказательство. Сходимость ^-плоскостей понимается в
следующем смысле: для любой точки аеП* существует последо-
вательность точек {аи ai^IJik}, сходящаяся к точке а {\щ—а|-*-0
при i~^oo), и угол между ^-плоскостями П** и П* стремится
к нулю.
269

Согласно определению опорной ^-плоскости достаточно пока-
зать, что ГР не содержит внутренних точек множества X.
Предположим противное: x^intXf]Tlk.
Тогда начиная с некоторого номера т все точки ^еПД- схо-
дящиеся к тозке л;, попадут в шар В0п(ху е). Это противоречит ус-
ловию, наложенному на /г-плоскости ПД П
ТЕОРЕМА 2. Усл. Х\ — ограниченное выпуклое множество;
Х2 — произвольное выпуклое множество; Х\[\Х2=0.
Утв. а. Существуют точки Х\^Х\ и х2^Х2, такие, что
d(%, 4) = d(Xv X8) = infyi€Xliy.6X,d(y1, y2).
(1>
б. Если гиперплоскости П\у П2 и П проходят через точки хи х2
и —(хг+х2) соответственно и перпендикулярны прямой L(xi,x2)>
то Пг, i=l, 2 — опорная гиперплоскость множества Xi и П отде-
ляет Х\ от Х2.
в. Если множество Х\ состоит из одной точки х\, то точка х2
единственна.
Доказательство, а. Существование точек х\ и х2 следует
из ограниченности множества "Х\. (Напомним, что разобранный
ранее (см. пункт 4°) факт 2-й относился к случаю, когда оба мно-,
жества Х\ и Х2 ограничены; рассматриваемый здесь случай легка
к нему сводится.) Покажем сначала, что в множестве Х\ есть точ-
ка хи ближайшая к множеству Х2. Пусть точки у\ и у2 принад-
лежат соответственно Х\ и Х2. Расстояние от трчки у\ до множест-
ва Х2 определяется формулой
<%р X2) = mfyisXid(yv y2).
Ближайшей точкой к множеству
Х2 будет та, для которой функция
d(y\)=d(yu X2) имеет минимум.
Нетрудно доказать, что d(y\) — не-
прерывная функция точки у\. Тог-
да из замкнутости и ограниченности
множества Хи вытекает, что в
Х\ существует точка хи в которой
функция d(j/i) имеет минимум.
Во множестве Х2 есть точка х2+
ближайшая к точке Х\ (рис. 22).
б. Если бы, например, гипер-
плоскость П2 не была бы опорной
для множества Х2, то нашлась бы
точка у^Х2 с той же стороны от
П2, что и х\. Тогда угол Z.yx2X\ был
бы острым и для малых t>0 имело»
бы место неравенство
Рис.22 |*i-(l-0*2-fy|<l*i-*2|.
270

Ho z=(l—t)x2-\-ty<^X2, что противоречит условию (1).
Легко видеть, что гиперплоскость П отделяет множество Х\ от
множества Х2 и проходит от каждого из них на расстоянии
-5-1*1—*il-
Ясно, что слой между гиперплоскостями П\ и П2 не содержит
точек ни из Х\, ни из Х2 и разделяет эти множества.
в. Если Х\={х\}, то точка х2 называется проекцией точки Х\ на
множество Х2. Предположение о существовании второй проекции
z приводит к противоречию: — (х2 +г) е X и
Ui— \(*2 + г)
Как показывает рис. 23, для существования,точек х\ и х2у удов-
летворяющих условию (1), ограниченность множества Х\ сущест-
венна. . ч
ТЕОРЕМА 3. Усл. X' — произвольное выпуклое множество в
пространстве 6П, X — я-мерное выпуклое множество^ множество
X' не содержит внутренних точек множества Х\ x^Xf\X\
Рис. 23 . Рис. 24
Утв. Множества X и X' имеют в точке х общую опорную гипер-
плоскость (рис. 24).
Доказательство. Зафиксируем какую-нибудь внутреннюю
точку z множества X. Обозначим через Хт множество, получае-
мое из X растяжением в [1 ) раз с центром подобия г.
Пусть
Х'т=Х'()Вп(х, т) (рис. 25).
Тогда Хт()Хт'=0 и, согласно предыдущей теореме, существует
гиперплоскость Пт, которая отделяет Хт' от Хт и содержит точку
Xi —• #2
Xi — г
< l*i—*il = \xx—z\. П
271

отрезка [х, хт]у соединяющего точку л: с ее образом хт при рас-
тяжении:
Так как \х—хт\~ — \х—z\9 то в последовательности гипер-
т
плоскостей {Пт} найдется подпоследовательность {П6}, которая
сходится к некоторой гиперплоскости П, содержащей точку х.
Ясно, что гиперплоскость П не может разделять точки у\ и #2 из
X, потому что в противном случае нашлись бы точки yis^XSy cxo-
Рис. 25
дящиеся к уь 1=1,2, и гиперплоскости ns при больших s разделя-
ли бы y\s и f/25.* Аналогично обосновывается свойство гиперплос-
кости П не разделять никакие два точки у\ и у2 из X': у{^Хт\
/=1,2, при достаточно большом т, и Us не может разделять точ-
ки у\ и у2 при s>m. □
СЛЕДСТВИЕ. Утв. Каждая опорная' ^-плоскость множества
X, в частности каждая точка границы дХ, лежит в некоторой
опорной для X гиперплоскости.
Определение. Опорным полупространством выпуклого мно-
жества X называется содержащее А замкнутое полупространство,,
опирающееся на опорную гиперплоскость множества X.
ТЕОРЕМА 4. Усл. X — выпуклое множество, не совпадающее
с 6п.
Утв. Замыкание X совпадает, с пересечением всевозможных
опорных полупространств множества X.
272

Доказательство. Ясно, что это пересечение содержит мно-
жество X. Если окажется, что некоторая точка xq из пересечения
не попадает в X, то ввиду замкнутости X найдется шар Воп{х0, г),
для которого
В0"(хо, г)()Х=0.
По предыдущей теореме найдется гиперплоскость, разделяющая
Хо и X. Одно из ограниченных ею полупространств не будет со-
держать точку jto, содержа точки из X. Полученное противоречие
завершает доказательство. □
ТЕОРЕМА 5. Усл. X — м-мерное выпуклое множество в про-
странстве <Sn; пары различных точек а& и bk границы дХу &eN,
сходятся к точке х.
Утв. Предел L всякой сходящейся последовательности прямых
L(aky bk) лежит в опорной гиперплоскости множества X в точке х
{рис, 26).
Рис. 26
Рис. 27
Доказательство. L есть опорная прямая множества X,
так как все попавшие на L{ak, bk) внутренние точки множества X
могут лежать только на отрезке [aky bk]. □
9°. Выпуклый конус и сферическая выпуклость. Выпуклое мно-
жество, которое можно представить в виде объединения лучей,
исходящих из одной точки, называется выпуклым конусом. Общая
точка всех лучей называется вершиной конуса.
Простейшими примерами выпуклых конусов являются:' луч,
^-плоскость, все пространство, полупространство (замкнутое мно-
жество, ограниченное гиперплоскостью).
Пусть Sn~l — сфера в пространстве &п. Возьмем на S71-1 две
произвольные точки а и b и проведем через них и центр О сферы
Sn~l двумерную плоскость П2.
Пересечение плоскости П2 со сферой Sn_1 представляет собой
окружность, лежащую на Sn_1; радиус этой окружности равен ра-
диусу сферы Sn_1. Такая окружность называется большой окруж-
ностью, проходящей через точки а и Ь.
Если точки а и b являются концами одного диаметра сферы
«S71-1 (центр О — середина отрезка [а, Ь]), то через эти точки мож-
но провести бесконечно много больших окружностей; каждую из
этих окружностей точки а и Ь делят на две дуги равной длины.
273

Если же точки а и ft не лежат на одном диаметре сферы Sn~\
то через эти точки проходит единственная большая окружность;
точки а и ft разбивают эту окружность на дуги разной длины.
Определение. Множество X на сфере 591-1 называется
сферически выпуклым, если для каждой пары точек аи ft множе-
ства X меньшая из дуг большой окружности, проходящей через
точки а и ft, содержится в X.
В случае, когда точки а и ft диаметрально противоположны,
это условие следует понимать так: множеству X принадлежит хо-
тя бы одна из полуокружностей большой окружности, проходящей
через точки а и ft (рис. 27).
. Между выпуклыми конусами и сферически выпуклыми множе-
ствами существует тесная связь.
Пусть К — выпуклый конус с вершиной в точке О, Sn_1 — сфе-
ра с центром в этой же точке О.
Утверждение. Множество X=Kf]Sn-1 сферически выпукло.
Верно и обратное.
Утверждение. Множество К= \]x^xlXt где 1Х — луч, идущий
из точки О через точку х> есть выпуклый конус.
В справедливости этих утверждений легко убедиться непо-
средственно (рис. 28).
Рис. 28 Рис. 29
ТЕОРЕМА. Утв. Выпуклое множество М.на сфере Sn~lx либо
содержится в некоторой замкнутой полусфере сферы Sn~\ либо
совпадает со всей сферой Sn_1.
Доказательство. Пусть множество MczSn~l сферически
выпукло. Тогда совокупность лучей, исходящих из центра а сфе-
ры Sn_1 и идущих через точки множества М, заполняет выпуклый
конус Кавп.
Если а — внутренняя точка конуса /С, то К совпадает со всем
пространством <Sn, а множество М — со сферой S71-1. Если же а —
граничная точка конуса /С, то К имеет в точке а опорную гипер-
274 ■

плоскость, пересечение которой со сферой Sn~l ограничивает зам-
кнутую полусферу, содержащую множество М. □
10°. Два способа задания выпуклых тел. С выпуклым телом X
связана его опорная функция
/i:<Sn->R,
определяемая формулой
h (и) =тах {(и, х) \ х^Х}у
где (иу х) — скалярное произведение.
Ясно, что максимум в определении опорной функции h(u) до-
стигается (скалярное произведение {и, х) непрерывно по аргу-
менту х, выпуклое тело X компактно). Для заданного и обозна-
чим через х(и) элемент множества X, на котором достигается
максимум. Тогда (и, х) = (и, х(и)) — уравнение гиперплоскости,
опорной к множеству X в направлении, определяемом вектором и.
Тело X лежит в отрицательном полупространстве относительно
вектора и (рис. 29).
Если и— единичный вектор, то h(u)—расстояние от начала
координат до гиперплоскости Н(и), взятое с соответствующим
знаком.
Свойства опорной функции:
1+. й(и>>0 (если 0<=Х).
2+. h(ku)*=lh(u), где ?^>0.
3+. h(u+v)<hiu)+h(v).
Из свойств 2+ и 3+ вытекает, что опорная функция выпукла.
Справедливо следующее утверждение (приводим только фор-
мулировку).
ТЕОРЕМА. Утв. Любая функция h(u) со свойствами 1+—3+
является опорной функцией для некоторого (причем единственно-
го) выпуклого тела.
Задание опорной функции является одним из основных спосо-
бов задания выпуклых тел.
Приведем еще два свойства опорной функции, показывающие
ее связь со сложением множеств и умножением множества на
число.
4+. h{X+Y, u)=h(Xy u)+h(Yy и).
5+. h(XX, u)=Xh(Xt и), k>0.
Пример. Вычислим опорную функцию сферы Sn-l(at r).
Имеем
1) A(S»-'(0, 1),м)-|и|,
2) S»~l(a, r)=a+rSn-x(0, 1),
3) h(S"-i(a,r))-(a,u)+r\U\.
При размещении начала координат О внутри выпуклого тела
вводят функцию расстояния (функция Минковского)
Z):<S"-*R,
275

определяемую формулой
jinffaUeX], ифО,
D(u) = \ I I a J
I 0,
Свойства функции расстояния:
1+ D(u)>0.
2+. D (Ли) =XZ) (u), где Я>0.
3+. D(m+u)<D(m)+D(i>).
Определение. Два выпуклых тела называются полярными
(или двойственными) друг другу, если опорная функция одного
есть функция расстояния для другого.
В. ТОПОЛОГИЧЕСКАЯ СТРУКТУРА
1°. Формулировка задачи I. Если X — выпуклое множество,
то множество его внутренних точек intX (если оно непусто) и его
замыкание с\Х также выпуклы. Заметим, что замыкание с\Х по-
лучается из внутренности intX присоединением всех точек грани-
«ГУ
_х,
од
Рис. 30
Рис. 31
цы дХ. Если же довольствоваться присоединением к intX только
части граничных точек, то как показывает следующий пример,
свойство быть выпуклым можно нарушить.
Добавив к открытому квадрату только его вершины, мы полу-
чим, что некоторые из выпуклых комбинаций новых точек уже
не принадлежат множеству (рис. 30):
^ у {хг + х2)е£В;
С другой стороны, присоединение к открытому кругу любого
подмножества точек ограничивающей его окружности выпуклость
сохраняет.
Обратимся к множествам на прямой. Интервал (0, 1) и сег-
мент [0, 1] являются выпуклыми множествами. Таким же свой-
ством обладает и полуинтервал (0, 1], получающийся из интерва-
276

ла (О, 1) присоединением граничной точки 1. Однако никакие два
из этих промежутков не гомеоморфны: интервал — открытое мно-
жество на прямой, сегмент — замкнутое, а полуинтервал ни от-
крыт, ни замкнут.
В плоском случае положение намного сложнее. Например, при-
соединение к открытому кругу k и /, кФ1, точек ограничивающей
его окружности приводит к множествам, которые негомеоморфньк
Пусть X — произвольное "выпуклое множество в пространстве
$п. Если его размерность равна k, то множество X, рассматривае-
мое как подмножество содержащей его ^-плоскости (аффинной
оболочки множества X), является выпуклым множеством с внут-
ренними точками (рис. 31).
Подведем итоги. Вид всех выпуклых множеств в точечных ев-
клидовых пространствах был бы известен, если бы мы знали все
возможные виды /г-мерных выпуклых множеств в пространстве &п.
Чтобы не усложнять интересующую нас классификацию второ-
степенными деталями, мы будем рассматривать /г-мерные выпук-
лые множества только двух типов — открытые и замкнутые, т. е.
либо отбрасывая границу, либо присоединяя ее целиком.
Задача I. Дать топологическую классификацию n-мерных вы-
пуклых множеств в пространстве 6П: а) замкнутых, б) открытых.
2°. Предельный конус. Пусть X — выпуклое множество в &п.
Возьмем в X произвольную точку * и рассмотрим исходящие из
этой точки лучи /*, целиком принадлежащие исходному множест-
ву X.
Обозначим через К(Х, х) множество точек, расположенных на
построенных лучах.
ТЕОРЕМА 1. Усл. К{Х9 х)Ф0.
Утв. К(Х9 х) — выпуклый конус.
Доказательство. Пусть у\ и {/2 — точки множества
К(ХУ х). Покажем, что любая точка z=(l—t)y\+ty2,>де 0</<1,
лежит в К(ХУ х) (рис. 32).
Рис. 32 Рис. 33
Точка уи *в1, 2, располагается на луче li^K(Xt x), проходя-
щем через некоторую точку Zi из X. Поэтому возможна запись
yi=*x+li(Zi-x), где Ki>G, i=l, 2.
Это позволяет представить точку z в следующем виде:
2= (1—0 (x+h (Zi—X) ) +t (х+Х2 (*2—Х) ) =X+\\ ( (\X\Zi + li2Z2) —*)", .
277-

где
fX [X
Отметим, что ц>0, m,i>0, |U2>0, |ii+|yt2—1.
Вследствие выпуклости множества X точка f/=jLii2i + fi222 лежит
в X, а точка z=#+|w(#—x) принадлежит лучу, исходящему из точ-
ки х и идущему через точку у. Следовательно, z^K(X, x). Это
означает, что множество К(Х, х) выпукло. □
ЛЕММА. Усл. X — замкнутое выпуклое множество в про-
странстве &п\ луч 1Х с началом в точке х лежит во множестве Х\
луч 1Уу у^Х, сонаправлен лучу 1Х.
- Утв. Луч 1У лежит в X.
Доказательство. В силу выпуклости множества X для
любой точки z луча 1Х отрезок [у, z] содержится в X. Произволь-
но выбранная точка а луча 1У является пределом последовательно-
сти точек cik, лежащих на отрезках [у, zk], где Zk^lx (рис. 33). Так
как множество X замкнуто, то ае!
СЛЕДСТВИЕ 1. Усл. X — замкнутое выпуклое множество.
Утв. Выпуклый конус К(Х, у) можно получить из выпуклого
конуса К(Х, х) параллельным переносом (рис. 34).
Фис. 34
СЛЕДСТВИЕ 2. Усл. X — замкнутое выпуклое множество, со-
держащее прямую L.
Утв. Множество X представляется в виде совокупности точек,
лежащих на прямых, параллельных прямой L и пересекающих
множество Х(]Н, где Н — гиперплоскость, перпендикулярная L.
Доказательство вытекает из того, что пересечение Х(]Н —
выпуклое множество. □
ЛЕММА. Усл. К(Х,х)=0.'
Утв. Множество X ограничено.
278

Доказательство. Можно считать, что выпуклое множест-
во X замкнуто. Если это не так, то следует перейти к замыканию.
Предположим, что множество X неограничено. Тогда найдется
такая последовательность точек {хт}у что \хт—х\-*оо при т-^оо.
Из отрезков [ху хт] можно выбрать подпоследовательность, сходя-
щуюся к лучу /. Так как все отрезки [х> хт] лежат во множестве
X, то и луч / также лежит в X (в силу замкнутости последнего).
Но тогда К(ХУ х) должно содержать /. Таким образом, предполо-
жение о неограниченности множества X привело нас к противо-
речию. □
ТЕОРЕМА 2. Усл. Множество X замкнуто.
Утв. К(ХУ х) замкнуто.
Доказательство. Пусть х0 — точка прикосновения множе-
ства К(ХУ х). Ясно, что хо^Х. Если луч 1=1 [х, х0) целиком не со-
держится в X, то на нем можно указать граничную точку у0^дХ.
Пусть точки Xk из К(Х9 х) сходятся к точке х0. Тогда и лучи /* =
=/[*, Xk)<=K(X, x) сходятся к лучу /. Это, в частности,, означает,
что последовательность' точек .{xk,m^lk}, таких, что \Хк>т—х\=тг
сходится к точке jc0,m^/, |*o,m—х\=т. Еслц взять число т доста-
точно большим, то предельная точка хо,т последовательности
{Xk,m} будет лежать на продолжении отрезка [ху у0] за точку у^
т. е. вне множества^. Это противоречит замкнутости множества
X. Значит, х0€ЕК(Х, jc). □
Если множество X неограничено, то К(ХУ- х) называется era
предельным конусом. Из доказанного выше вытекает, что пре-
дельный конус однозначно определяется заданием вершины.
3°. Классификация замкнутых и открытых выпуклых множеств.
Пусть X — замкнутое /г-мерное выпуклое множество. Зафиксируем
во множестве X произвольную внутреннюю точку а и рассмотрим
лучи, исходящие из этой точки.
Возможны три случая:
1. Ни один из лучей, исходящих из точки а, не пересекает гра*
ницы дХ множества X.
2. Всякий луч, исходящий из точки а, пересекает границу дХ
множества X.
3. Не все лучи, исходящие из точки а, пересекают границу дХ
множества X.
Ясно, что в случае 1 множество X совпадает со всем простран-
ством ёп и вследствие этого не имеет границы.
а. Гомеоморфизм границы. Сосредоточим внимание на случаях
2 и 3. Следовательно, можно считать, что граница множества X
непуста: дХ¥=0.
Согласно теореме 1 пункта 3° раздела Б луч /, исходящий из
точки а, может пересекать границу выпуклого множества только
в одной точке. Построим единичную сферу Sn_1 с центром в точ-
ке а и сопоставим каждой точке х границы дХ точку у сферы
Sn-\ которая лежит на том же луче /. Тем самым получено вза-
имно однозначное отображение h границы дХ на сферу Sn~x {слу-
чай 2) либо на часть сферы Sn~l (случай 3).
279

so-;
Отображение h непрерывно, поскольку оно является проекти-
рованием точек границы дХ на сферу Sn_1 посредством лучей, ис-
ходящих из ее центра а: сходящейся последовательности точек
{yk} границы дХ соответствует сходящаяся последовательность то-
чек {Zk} на сфере Sn_1 (рис. 35).
Покажем, что обратное отображение h~l также непрерывно.
Пусть точки zk сферы Sn_1 соответствуют точкам yk на границе
дХ и сходятся к некоторой точке z на S71-1, соответствующей точ-
ке у границы дХ. Докажем, что по-
следовательность {yk} сходится к у.
Предположим противное: последо-
вательность точек {yk} — расходя-
щаяся.
Тогда либо из последовательно-
сти {уи} можно выбрать подпосле-
довательность {ут}, сходящуюся к
точке у\ отличной от у, либо из
последовательности {#*} можно вы-
брать подцоследовательность {ут},
расходящуюся к бесконечности
(неограниченно удаляющуюся от
точки а).
Первая возможность. В силу
замкнутости границы дХ точка у'-
как предельная для точек границы
сама принадлежит дХ. С другой
стороны, лучи 1[а, ут) сходятся к
лучу 1[а, у) вследствие того, что они
проходят через точки zm сферы Sn~\
сходящиеся к точке z (соответству-
ющей точке у). Это означает, что
точка у' должна лежать на том же луче t[a, у). Но так как луч,
исходящий из точки а, может пересекать границу дХ выпуклого
множества X только в одной точке, то точки у к у' должны сов-
падать. .
Вторая возможность. Точки уш неограниченно удаляются от
точки а. В силу выпуклости множества X каждый отрезок [а, ут]
целиком леждт в X. Вместе с тем эти отрезки сходятся к лучу
Ла> у) у потому что соответствующие точки zm на сфере S71-1 схо-
дятся к точке z (соответствующей точке у). В силу замкнутости
множества X весь луч /[а, у) содержится в X. Но тогда этот луч
не может содержать точек границы множества X. А это противо-
речит тому, что такая точка на луче /[а, у) "есть. Полученное про-
тиворечие исключает и вторую возможность.
Таким образом, построенное отображение проектирования h
границы выпуклого множества на сферу или в сферу — гомео-
морфизм.
б. Ограниченные выпуклые множества. Случай 2.
Рис. 33
280

ТЕОРЕМА. Усл. Всякий луч, исходящий из внутренней точки
а замкнутого /г-мерного выпуклого множества X пересекает его
границу дХ. .
Утв. Множество X гомеоморфно /г-мерному шару Вп. Граница
дХ гомеоморфна (гс—1) -мерной сфере Sn-K
Доказательство. В рассматриваемом случае построен-
ное выше отображение h представляет собой гомеоморфизм гра-
ницы дХ на сферу Sn~K
Пусть х — точка множества Ху а у — точка его границы, лежа-
щая на луче /, идущем из точки а через точку х. Сопоставим
точке х точку z в единичном шаре Вп так, что
и z лежит на луче / (рис. 36).
Этим определяется гомеоморфизм множества X на замкнутый
шар Вп. •□
Рис. 36 Рис. 37
Важное замечание. Ясно, что при этом множество
mtX гомеоморфно В0п.
в. Неограниченные выпуклые множества. Случай 3, когда мно-
жество X содержит только часть лучей, исходящих из точки а, до-
пускает две возможности:
множество X не содержит ни одной прямой,
множество X. содержит хотя бы одну прямую (рис. 37).
Первая возможность. Множество точек, расположенных на лу-
чах, исходящих из точки а и не пересекающих границу дХ мно-
жества X, образует выпуклый конус К{ХУ а). Конус К(Х, а) пере-
секает сферу Sn_1 по сферически выпуклой области М. Эта об-
ласть обладает следующими свойствами:
10 Заказ 538
281

1) М содержится в замкнутой полусфере (отсекаемой от Sn-*
гиперплоскостью Я),
2) М — замкнутое множество на сфере Sn~l (в силу замкну-
тости предельного конуса К{Х, а)).
3) М гомеоморфна m-мерному (0<т</г— 1) шару Вт (про-
екция области М на гиперплоскость Н представляет собой огра-
ниченное замкнутое m-мерное выпуклое множество, гомеоморфное*
как уже доказано выше, шару Вт\ с другой стороны, ортогональ-
ное проектирование есть гомеоморфизм М на N).
Дополнение G=Sn-l\M представляет собой область, гомео-
морфную открытому (п— 1) -мерному шару В0п~\ или, что то же
самое, пространству 6п~К Поэтому определенное выше отображе-
ние h (проектирование из точки а на сферу Sn_1) устанавливает
гомеоморфизм границы дХ и области G. Тем самым доказано, что
в случае 3 граница дХ гомеоморфна ёп~\
Множество Q, которое получается из шара Вп после удаления
точек множества М, гомеоморфно полупространству ё+п.
Построим гомеоморфизм f:X-*Q.
Пусть х — точка из множества X. Если луч /, идущий из точ-
ки а через точку х, пересекает границу дХ в точке у, то сопоста-
вим точке х точку z на / так, что
\г—а\ = ! - .
\У — а\
Если же луч /, идущий из а через х9 не пересекает границы дХ»
то сопоставим точке х точку z на луче / так, что
Определенное таким образом отображение / представляет со-
бой гомеоморфизм множества X на множество Q. Тем самым мно-
жество X гомеоморфно полупространству 6+Л.
Важное замечание. Из построения / видно, что множе-
ство intX гомеоморфно ёп.
Вторая возможность. Пусть множество X содержит пол-
ную прямую. Обозначим через Пг содержащуюся в X г-плоскость.
Ясно, что ее размерность г подчинена условию 1<г</г—'1.
Пусть П±п~г — (л—г) -плоскость, ортогональная Пг. Тогда
xn-r=x(]iiTr
является (я—г)-мерным выпуклым множеством, лежащим в П±п-Г
и не содержащим полной прямой. По доказанному ранее его гра-
ница дХп~г гомеоморфна либо Sn~r-\ либо б*-'-1, а само множе-
ство Хп~г гомеоморфно либо (/г—г) -мерному шару Вп~г, либа
(л—г) -полупространству 6+п~г.
В силу следствия 2 из предыдущего пункта множество X вме-
сте с каждой точкой ^*е1п_г содержит r-плоскость, идущую через
282

х* параллельно r-плоскости Пг. Это означает, что граница дХ
складывается из точек, лежащих на r-плоскостях, параллельных
j]r и проходящих через точки множества дХп~г.
Тем самым граница дХ множества X гомеоморфна либо
5n-r-1X<Sr (это произведение следует понимать как цилиндр с
г-мерными образующими), либо <Sn~r-1XSr=<Sn~I.
Соответственно само множество X гомеоморфно или Bn-rxSr,
или <S+n-rX<Sr=<S+n.
Важное замечание. Легко видеть, что множество intX
гомеоморфно ёп.
4°. Ответ к задаче I. Произвольное замкнутое n-мерное вы-
луклое множество гомеоморфно
либо замкнутому /г-мерному шару £п,
либо полупространству ё+п,
либо одному из цилиндров Bn~rXSry 2<гкп—\.
Доказательство того, что никакие два из перечисленных здесь
цилиндров между собой негомеоморфны, представляет значитель-
ные трудности, намного превосходящие рамки пособия.
К представленному перечню следует добавить еще две «возмож-
ности: замкнутое я-мерное выпуклое множество может совпадать
либо со всем пространством <Sn,
либо со слоем (произвольной ширины) между двумя парал-
лельными гиперплоскостями.
Все открытые /г-мерные выпуклые множества гомеоморфны
вмещающему их пространству ёп.
Г. ДИФФЕРЕНЦИАЛЬНЫЕ СВОЙСТВА
1°. Формулировка задачи II. Приведенные выше рисунки прос-
тейших выпуклых множеств на плоскости и~в пространстве пока*
зывают, что на границе таких множеств (кривых или поверхно-
стях соответственно) могут возникать различные особенности.
Теперь постараемся дать ответ на вопрос о том, каковы эти
особенности и как велико их число. Или, более точно:
Задача II. Исследовать характер особенностей, возникающих
ла границе /г-мерного выпуклого множества в пространстве, и
оценить множество точек, несущих эти особенности.
2°. Выпуклая гиперповерхность.
Определение. Выпуклой гиперповерхностью в пространстве
<Вп называется граница /г-мерного выпуклого множества Xcz£?n
при условии, что она непуста и связна.
Для п = 2 и я = 3 вместо термина «гиперповерхность» исполь-
зуются термины кривая и поверхность соответственно.
Отметим, что граница выпуклого множества является выпук-
лой гиперповерхностью во всех случаях, кроме тех, когда выпук-
лое множество есть слой между двумя параллельными гиперплос-
костями или все пространство.
Переформулируем основной результат предыдущего раздела
£ удобной для последующего форме.

ТЕОРЕМА 1. Утв. Выпуклая гиперповерхность гомеоморфна
или Sn~\ или <$п~х, или Sn-k-lX&k, 1<&<>1—2 (она называется
соответственно замкнутой, открытой или цилиндрической).
Так как в дальнейшем мы будем изучать локальные свойства,
то термин «выпуклая гиперповерхность» будет употребляться
также для связных подмножеств полной выпуклой гиперповерхно-
сти, открытых относительно самой гиперповерхности.
Пусть 2Г — выпуклая гиперповерхность, ограничивающая вы-
пуклое множество X. Множество X вполне определяется гиперпо-
верхностью #~, за исключением тривиального случая, когда Ф —
гиперплоскость. Опорные гиперплос-
кости и внутренность множества X
называются также опорными гипер-
плоскостями и областью, лежащей
внутри гиперповерхности.
Пересечение всех опорных полу-
пространств множества Л", которые
ограничены опорными гиперплоско-*
стями в фиксированной точке хе^,
представляет собой выпуклый ко-
нус К с внутренними точками. Его
граница Ж называется касательным
конусом множества X или гипер-
поверхности & в точке х (рис. 38).
Если УС —■ гиперплоскость, та
это единственная опорная гипер-
плоскость к & в точке х<>. В этом случае мы будем говорить»
что Ж есть касательная гиперплоскость к гиперповерхности &*
в точке х, и называть У гладкой в точке х.
ТЕОРЕМА 2. Усл. Выпуклая гиперповерхность У является
гладкой в точках х некоторого множества Та@~.
Утв. На множестве Т касательная гиперповерхность непрерыв-
но зависит от точки х.
Доказательство сформулированного утверждения легко
следует из теоремы 1 пункта 8° раздела Б. □
3°. Локальное задание.
ТЕОРЕМА. Утв. Выпуклая гиперповерхность #" в окрестности
каждой своей точки представима в форме
x*=f(x\ ..., х"~ь),
где х1, ...., хл-1, хп — прямоугольные декартовы координаты в
пространстве <Sn.
Доказательство. Если довольствоваться косоугольными
координатами, то достаточно взять за координатную гиперплос-
кость хп=0 произвольную опорную гиперплоскость к У в точке
х и направить ось хп по лучу /, исходящему из точки х во внут-
реннюю область гиперповерхности У (обозначим ее через L).
Из теоремы 5 пункта 8° раздела Б вытекает, что каждая близ-
кая к L прямая, параллельная. L, пересекает ST вблизи х ровна
.284

в одной точке (простым рассуждением от противного). Чтобы убе-
диться в существовании прямоугольных декартовых координат
с требуемым свойством, возьмем конус Jjf*, полярный конусу Ж:
он состоит из лучей, которые перпендикулярны опорным гипер-
плоскостям конуса Ж и идут из точки х во внешнюю для Ж об-
ласть. Если «Ж3—гиперплоскость, то Ж* состоит из одного лу-
ча, перпендикулярного Ж и идущего в полупространство, где
нет ЗГ.
Нетрудно видеть, что конус Ж* выпуклый. Поскольку Ж<^К9
то конус Ж* имеет в точке х опорную гиперплоскость Я, не со-
держащую в себе иных точек Ж* (рис. 39).
Рис. 39
Так как луч I, перпендикулярный Я, проходит через внутрен-
ние точки конуса К, то, взяв Я за координатную гиперплоскость
хп = 0 и направив ось хп вдоль I внутрь /С, мы построим прямо-
угольную декартову систему координат с нужным нам свойством.
Итак, каждая точка х на выпуклой гиперповерхности £Г имеет
на ней окрестность £FX, которая в некоторой прямоугольной декар-
товой системе координат х1у ..., хп~\ хп с началом в точке х=0
может быть представлена в следующем виде:
x*=f{x\ ...,x"-l)>0, /(О, ...,0)=0,
где
2?-/ (*<)2 < Ь\ 6>0. □
4°. Свойства выпуклой гиперповерхности.
1+. Функция xn=f(x\ ..., хп~х) — выпуклая.
Напомним, что функция xn=f(x\ ..., хп~х)> определенная на
выпуклом множестве Y пространства S>n~1=={\x\ ..., хп~1)}, назы-
вается выпуклой, если из того, что точки
*={х\...9х*-*)9 у=(у\ .... 0*-1')еУ,
следует неравенство
f[(l-t)x+ty]^(l-t)f(x)+if(y),
гДеО<*<1 _ любое.
285

Выпуклость функции xn = f(x) вытекает из выпуклости в про-
странстве 8п множества
(надграфика функции f(x))
2+. Разностные отношения
l/(*i, ...t S-^-fjyi, ..., yn~l)\
VyzUv-y1)*
, хфу,
ограничены (рис. 40).
Рис. 40
Ограниченность разностных отношений выпуклой функции вы-
текает из теоремы 5 пункта 8° раздела Б и из того, что ось хп идет
внутрь конуса /С.
3+. Выпуклая гиперповерхность в пространстве 8п является
(п—1)-кубируемой.
Существование (п—1)-мерного объема выпуклой гиперповерх-
ности вытекает из ограниченности разностных отношений (в отли-
чие от всех других свойств выпуклых гиперповерхностей, отмечен-
ных в этом пункте, доказательство свойства 3+ совсем непростое;
так как сформулированный факт не используется нигде дальше,
его доказательство целесообразно спустить).
4+. Если хп = 0 — касательная гиперплоскость к выпуклой ги-
перповерхности в точке О, то из теоремы 5 пункта 8° раздела Б
вытекает, что для любого е>0 можно указать такое б>0, что
\f(*)-f(y)\
\х-у\
<е
при И<8, \у\ <б.
286

Это означает, что у функции f(x) в точке х=0 есть дифферен-
циал.
5°. Выпуклые кривые. Если y = f(x) — выпуклая кривая, то при
Х\<Х2, Х\' <Х2\ Х\^.Х\\ Д^2^^2
выполняется неравенство
/(*i)-/(*2) ^ f(xl)-f(x2)
——— ^ ; ;
Xi — Х2
(1)
Для левой и правой производных функции y=f(x) будем поль-
зоваться следующими обозначениями:
Положим в неравенстве (1) .
x2=xl'=x, Xi=x+t(t<0), x2'=x+tf(t'>0).
Тогда
f(x + t)-f(x) f(X + t')-f(x)
Отсюда вытекает существование в точке х производных f-'(x) и
/+'(#); при этом
fj(x)^f+'(x):
Если fa'(x)—угловой коэффициент
произвольной опорной прямой в
точке ху то (рис. 41)
/-'(*)</.'(*)<f+'(*)
, fa'[Xi)^fa'(X2)
при х{<х2.
Утверждение. Число точек, где рис 41
производная f'(x) не существует, не
более чем счетно.
Доказательство. Покажем, что множество точек, где
/-' (х) </+' (х), не более чем счетно.
Занумеруем все рациональные числа: ги ..., гт, ••• . Пусть
в некоторой точке х выполняется неравенство
fJ{x)<f+'(x). (2)
Тогда найдется рациональное число rm, такое, что
f-'(x)<rm<f+'[x) (3)
(среди всех рациональных чисел, удовлетворяющих этому нера-
венству, выбираем то, которое имеет наименьший номер).
287

Из определения правой производной вытекает, что для всех |,
больших х и достаточно близких к х,
г '<, ПЪ)-Н*)
или
rm(Z-X)<f(t)-f(x). (4)
Среди рациональных чисел, больших х, выберем то, которое имеет
наименьший номер — г*, причем так, чтобы неравенство (4) вы-
полнялось для всех |, подчиненных условию x<l<rk.
Таким образом,
МБ-i) </(£)-/(*).
если x<l<rk.
Аналогичными рассуждениями получаем, что для всех т), мень-
ших х и достаточно близких к х, выполняется неравенство
f(r\)-f(x)
или
П1\)Ч{*)>Гт(1\-Х). . . (5)
Найдется рациональное число гд, обладающее следующими свой-
ствами:
1) /><*,
2) /(л)— f(*)>rm(n—*) Для всех т), таких, что rq<r\<x,
3) q — минимальный из номеров.
Покажем, что отображение л;»-»*(/л, ky q) множества точек х%
в которых выполняется неравенство (2), на множество троек це-
лых чисел является взаимно однозначным.
Предположим противное: X\*-*-(mf k, q) и х2>~* (jn, kt q)9 причем
Xi<X2.
Тогда rq<xx<x2<rk.
В соотношении (4) положим *=*i, g=*2 (это можно сделать,
так как X\<x2<rk). Имеем
/(*2>— f(Xi)>rm(x2—xi).
Полагая в формуле (5) г\=хи х=х2, получаем, что
f(xl)—f(x2)>rm(xl—x2).
Складывая последние два неравенства, приходим к противоре-
чию. □
6°. Множество меры нуль. Для оценки множества точек выпук-
лой гиперповерхности, несущего на себе особенности, введем одно
интересное понятие.
Рассмотрим в пространстве ё>п n-мерный куб с ребром дли-
ны а:
1п=1п(а)={(х\ ..., х^е^ЦХ*'—&'<a, j=l, ..., п)
288

(здесь b={b\ ..., Ьп) — фиксированная точка пространства &п).
£го объем
vo\In(a)=an.
Определение. Множество Xcz&n имеет меру нуль, если
для любого е>0 существует последовательность кубов {/^с^Г*},
такая, что
XcUw/?, 5S«-ivol/?<e.
Справедливо следующее утверждение.
ЛЕММА. Утв. Объединение счетного числа множества меры
нуль имеет меру нуль.
Доказательство. Пусть Хи Х2, ... — множества меры
нуль в пространстве &п. Для заданного е>0 каждое множество Xk
можно покрыт^ кубами, суммарной объем которых меньше е/2*:
X*eL£i/w. 2lLivol/t<-5-.
Тогда
X = U*—Л *- \Jk,i=\lkti\
2&-i vol /2t, < 2£-i -~ = e. D
2*
Замечание. Из доказанной леммы вытекает, что для опре-
деления множества меры нуль подходят как замкнутые, так и
открытые кубы, а также шары, параллелепипеды и т. п.
Введем следующее вспомогательное обозначение:
<r>-i=={(xi, ..,, x»)e&n\xn=t)f te=R.
ТЕОРЕМА. Усл. X — компактное множество в пространстве
<8п\ для любого teR множество X[\<gtn~x имеет меру нуль
в gt*-\
Утв. Множество X имеет меру нуль в пространстве &п.
Доказательство сформулированного утверждения опира-
ется на один простой факт:
Покрытие отрезка [а, Ь] интервалами (аи Ь\), ..., (ат> Ът)
назовем минимальным, если при удалении любого из них остав-
шиеся интервалы не покрывают отрезка [а, Ь].
Утверждение. Сумма длин интервалов минимального покрытия
меньше, чем (b—a) + (bm—ах).
Доказательство. Перенумеруем интервалы так, чтобы
а\<а2<.. .<ат. Это возможно, так как, допуская равенство at=
= ^+1, получаем лишний интервал {(aiy bi), если, Ь^&и-ь или
(Д/+ь bi+i), если bi+\<bt).
Из минимальности покрытия следует, что
ai+\<bi<bi+i
289

(иначе либо нарушалось свойство покрытия (при b^a^i), либо
получался лишний интервал (ai+u Ьж) (при bt+i^bt)). Наконец,
[в цротивном случае получалось бы
(аж, 6/+1)d(ar-, bi)\]{ai+2y bi+2);
лишний интервал— (ян-ь &ж))-
Таким образом,
r^m-l
STLi (bt- at) = 2S1 (aw-a,) + (b,-am) + 2Г=7' (b~ai+l) <
r.m—2 ,
= bm—a1 + bm-i—a2 < bm—ax + b—a. D
В силу ограниченности множества X достаточно считать, что
/е [а, Ь] и, значит,
X^g"-*X[a, b].
Положим Xt=X{\<gtn~x (рис. 42) и зафиксируем е>0. Так как
множество Xt имеет меру нуль, то существует покрытие Xt откры-
тыми кубами 1\с
XtczWt = (Jr-i/w. SZ-i vol lb < e.
Рис. 42
Рис. 4а
При фиксированном t функция \хп—1\ непрерывна на множестве
X к обращается в нуль только на Xt.
Множество X\(WtX[at b]) компактнб. Поэтому на этом мно-
жестве функция \хп—1\ достигает своего минимума a<&—a.
290

Отсюда вытекает, что
ХГ\{хе#п\ \xn—t\<a)<^WtX(t—ai t+a).
Семейство интервалов {Jt,a=(t—a, f+а)} покрывает отрезок
\а> Ь]. Переходя к минимальному подпокрытию {Jt.a\j= 1,... ; m}>
применим доказанное выше предложение:
2/Li leng th Л.,а < 2 {b—a) + 2а < 4(6—а).
Параллелепипеды
{Ц.1 X Jtjta\j= 1, ..., m; ie N}
покрывают множество X; сумма их объемов меньше 4 [Ь—а) г. П
Определение. Будем говорить, что свойство Т выполнено
почти всюду, если множество точек,, в которых это свойство нару-
шается, имеет меру нуль.
Пример. Множество точек на прямой, в которых выпуклая
функция y=f{x) не имеет производной, является множеством ну-
левой меры. В самом деле, как доказано в предыдущем пункте,
это множество не более чем счетно. Занумеровав его элементы
аь ..., ak> ..., построим покрытие
сумма длин слагающих интервалов которого меньше, чем е.
7°. Гладкость.
ТЕОРЕМА. Утв. Выпуклая гиперповерхность почти всюду диф-
ференцируема.
Доказательство сформулированного утверждения прове-
дем индукцией по размерности гиперповерхности.
В конце предыдущего пункта была доказана справедливость
утверждения для кривых, т. е. в &2.
Предположив утверждение верным для &п~1, гС^Ъ, докажем
его справедливость для случая <£п.
Пользуясь тем, что дифференцируемость — локальное свойст-
во, будем рассматривать гиперповерхность в малой окрестности ее
точки.
Без ограничения общности можно считать, что гиперповерх-
ность задана следующим образом:
x*=f(x\ ,.., я""1),
где 2Й (*02 < б2.
Рассмотрим сечение гиперповерхности гиперплоскостью
*'*=a, |a|<6.
291

Полученное множество
ixn = f(x\ ...,x»-*)t
i.v'=a
представляет собой зависящую от i (/=1, ..., п—1) и от а вы-
пуклую гиперповерхность &~а* в пространстве &п^.
Множество точек области x' = a, xn = 0t отвечающих точкам,
в которых гиперповерхность ЗГа1 не дифференцируема,, имеет по
предположению нулевую (п—2)-меру. Кроме того, оно ограничено
и замкнуто, а значит, компактно. Поэтому множество Q точек
[х\... ,хп-\ 0), где не дифференцируемые^ или ^«2, имеет
нулевую (я— 1)-меру. Если точка (х\ ..., хп~\ 0) не принадлежит
множеству Q, то касательный конус гиперповерхности SF в точке
(х\ ..., хп~\ f(x\ ..., хп~1)) содержит (п—2)-плоскости, которые
в этой точке касаются гиперповерхностей 3^ и &%* (рис. 43).
Эти (п—2)-плоскости не могут совпадать. Поэтому содержащий
их касательный конус Ж сводится к гиперплоскости. Значит, ги-
перповерхность SF дифференцируема во всех точках (х1, ..., хп~К
!(х\...,х"-1)).при (х\ ...,*"-V0)eEQ.
Для завершения доказательства теоремы достаточно убедиться
в том, что множеству Q на гиперповерхности &" соответствует
множество нулевой меры.
8°. Ответ к задаче II. В каждой точке выпуклой гиперповерх-
ности существует опорный конус. Мера множества точек на гипер-
поверхности, в которых опорный конус не сводится к гиперплос-
кости, равна нулю. И почти каждая точка выпуклой гиперповерх-
ности является гладкой.
Несколько слое в заключение.
В определении выпуклого множества евклидова структура объ-
емлющего пространства (т. е. наличие в точечном вещественном
пространстве скалярного произведения) не используется. Однако
в процессе поиска ответа на вопросы задач I и II мы проводили
многие рассмотрения в /г-мерном точечном евклидовом простран-
стве <$п.
Это делалось совершенно сознательно для того, чтобы упрос-
тить ряд рассуждений и выкладок.
На самом деле установленные свойства выпуклых множеств и
ограничивающих их выпуклых гиперповерхностей остаются спра-
ведливыми при любом способе введения скалярного произведения,
т. е. от выбора скалярного произведения в точечном пространстве
не зависят.
Сказанное позволяет сделать следующий важный вывод: ре-
зультаты задач I и II справедливы в любом конечномерном то-
чечном вещественном пространстве.
292

Д. НЕКОТОРЫЕ КЛАССИЧЕСКИЕ НЕРАВЕНСТВА
1°. Радиус Юнга.
ТЕОРЕМА. Усл. X — множество в 8п, diam Я<2. .
Утв. Существует n-мерный замкнутый шар Вп(г) радиуса
r = K2n/(n + 1) , такой, что X<z:Bn(r).
Если множество X не принадлежит никакому меньшему шару,
то X содержит вершины правильного n-симплекса с ребром дли-
ны 2.
Прежде чем переходить к доказательству теоремы Юнга, вновь
отметим, что утзерждение теоремы Хелли верно и для бесконеч-
ного семейства выпуклых множеств при условии, что все они ком-
пактны. Соответствующее доказательство проводится простым све-
дением к случаю конечных семейств (см. пункт 4° раздела Б).
Кроме того, в формулировке теоремы и в ее доказательстве
содержится ряд понятий и фактов, требующих пояснения.
1. Диаметр diamX множества X определяется так:
diamX= sup d(xt у).
х,уЬХ
2. я-симплекс а{хь>..,хп) называется правильным,если длины
всех его ребер равны, т. е.
d(xi9 */) = const, \Ф\.
3. Пусть X={x0i ..., Хт}> т^п — множество точек. Тогда су-
ществует наименьший шар Вп, содержащий X; центр этого шара
принадлежит выпуклой оболочке множества.
Покажем, что такой шар всегда существует.
Функция
r(*)= max d(xf X:)
задана во всем пространстве <$пу непрерывна (функция расстоя-
ния d(x, Xj) непрерывна, максимум непрерывных функций непре-
рывен) и вне шара достаточно большого радиуса R с центром
в начале координат удовлетворяет неравенству
r(*)>Jf.
Поэтому в замкнутом шаре радиуса R найдется точка у, такая,
что г(у)^.г(х) для любой точки х из 8п.
Убедимся теперь в том, что точка у принадлежит выпуклой
оболочке множества X.
Предположим, что это. не так. Тогда существует гиперплоскость
Я, разделяющая точку у и множество X. Опустим из точки у на
гиперплоскость Я перпендикуляр. Его основание z к каждой точке
из множества X находится ближе, чем у. Это вытекает из того,
что в треугольнике AyzXj угол Zyzxj тупой (рис. 44).
Юнг (Young) Уильям Генри (29.4.1863—7.7.1942) — английский математик.
293

Покажем (хотя это и не нужно для доказательства теоремы
Юнга), что шар наименьшего радиуса определен однозначно.
Пусть шары Вп(у\, г) и Bn(y2f г) равных минимальных радиу-
сов содержат множество X. Но тогда множество X содержит и их
пересечение Вп(у\, г) f\Bn(y2f r). Последнее в свою очередь по-
падает в шар
Вп
( У1 + У* л[г2 \yi~y*\2 \,
радиус которого меньше минимального.
Доказательство теоремы. Предположим сначала, что
множество X конечно и состоит из т элементов, т^п:
X = {%()> . . . , Хщ}'
X Обозначим через t/=0 центр наимень-
шего шара Вп, содержащего множество
X, а через г его радиус.
Из того, что Geconv X, вытекает:
Положим
dij = d(xir Xj) = \xi—*/|<2.
Отсюда получаем, что d*/2 = 2r2—2(xif Xj).
Для каждого j выполняется соотноше-
ние
л2
Рис. 44
1 —Ху = 2^/^ ^ 2t=o^i
ли
4 2
Суммируя по / от 0 до т, получаем, что
— (2Л0^Л, Xj) = —
т^(т + 1) —.
Откуда
2т
Случай равенства
г2 =
т+ 1
2п
<-
2п
п + 1
влечет за собой т=п и йц = 2
для всех хФ], что и завершает доказательство первой части.
Рассмотрим теперь множество X из пространства <fTn, у которо-
го card X^n+ 1.
Для каждой точки х из множества X возьмём шар
*,-{*! 1*-*1</^}-
294

Согласно доказанному выше для множеств, состоящих из п+1
(или менее) точек, каждые п+1 из шаров Вх имеют общую точку.
Отсюда на основании теоремы Хелли вытекает, что пересечение
(\х*хВх непусто. □
2°. Объем выпуклого тела. Естественным и далеко идущим
обобщением понятия длины отрезка и площади простейших гео-
метрических фигур в планиметрии является понятие /г-мерного
объема.
n-мерный объем есть функция vol", определенная на некоторых
подмножествах я-мерного точечного евклидова пространства <$п и
принимающая неотрицательные вещественные значения.
Мы ограничимся перечислением некоторых основных свойств
и приведем формулы для вычисления объемов простейших выпук-
лых тел.
Объемы множеств в точечном евклидовом пространстве <8п>
для которых они определены, обладают следующими свойствами.
Объемы:
1+. Неотрицательны.
2+. Аддитивны: если для двух множеств X и У из пространства
$*", не имеющих общих внутренних точек, определены объемы
vol" (Я) и vol" (У), то
vo\n(X()Y) = уо1я(Х)+уо1я(У).
3+. Инвариантны относительно преобразований вида
y=Sx+a,
где 5 — ортогональная матрица: если для множеств X и У из
пространства &п определены объемы vol"(Я) и vol"(У) и одно из
них может быть совмещено с другим путем параллельного пере-
носа и вращения, то vol* (Я) = уо1л(У).
4+. Объем единичного куба 1п равен 1: vo\n{In) = 1.
Из этих свойств вытекает:
А. Монотонность объема: если для множеств X и У, связанных
условием ХсУ, определены объемы vol"(Л) и vol"(У), то
vo\n(X)^vo\»(Y).
Б. Если зФ : 8п-+&п — линейное отображение (аффинное пре-
образование, сохраняющее начальную точку) и для множества X
определен объем vol"(Л"), то
vol" (Л (X)) = | det Ж | vol" (X).
На множестве всех многогранников существует, и притом един-
ственная, неотрицательная функция, удовлетворяющая свойствам
1+—4+.
При помощи предельного перехода понятие объема распрост-
раняется с сохранением свойств 1+—4+ с класса многогранников
на более широкие классы множеств, в . частности на выпуклые
тела.
295

Объем выпуклого тела Q определяется следующим образом;
Рассматриваются всевозможные многогранники Ху лежащие в
выпуклом теле Q, и всевозможные многогранники У, содержащие
выпуклое тело Q:XczQ<ziY (рис. 45).
Рис. 45
Тогда справедливо равенство
supvoln(^)=infvolrt(y).
XdQ QcY
Это общее значение указанных нижней и верхней граней и назы-
вается я-мерным объемом volrt(Q) выпуклого тела Q.
Примеры.
(1) Куб- Согласно свойству 4+ л-объем единичного куба 1п
равен 1. Куб со стороной длины а является образом единичногр
куба 1п относительно умножения на число a; i4 = diag{ab ,.., а} —
матрица соответствующего преобразования. Поэтому его объем
равен ап. - \
(2) Параллелепипед. Это множество определяется так. Пусть
О — начальная точка и /ь ..., ln — линейно независимые векто-
ры в пространстве <§п. Множество точек
P*4*i/i + ... + Wn|0</*<lf * = 1,...,л}
называется параллелепипедом, натянутым на векторы 1\% ..., 1п~
Пусть {О; ей • ••> еп} — ортонормированный репер в простран-
стве <£п и «я£ — линейное отображение, переводящее векторы ei
в векторы lu i=l, ..., я. Если Л=(а/') — матрица этого отобра-
жения в базисе е :A=A(e), то
(1и .... 1п) = (еи ..., еп)А. (*)
Вычислим матрицу Грама Г(/) полученной системы векторов
/=(/i .../«):
Г(/)=ЛЛТ.
296

Следовательно,
Vdet Г (/) = Kdet (ААТ) = | det A | .
С другой стороны, detst> = detA и отображение si* переводит
единичный куб в параллелепипед Рп.
Поэтому объем параллелепипеда Рп равен |det*s#|.
Формулу (*) можно записать и так:
Тогда *
'- vol«(/i /я) - | det (a/0 |.
Величина det (a/) называется ориентированным объемом паралле-
лепипеда Рп относительно выбранного базиса е. • .
(3) Шар. Если (х\ ..., хп) — прямоугольные декартовы ко-
ординаты в пространстве &п, то n-мерный шар Вп(г) радиуса г
с центром в fo4Ke О определяется формулой
В»(г) = {(х\ ...,*") |Я-1 (*02< г2}-
Так как шар Вп(г) получается из единичного шара Вп(\) рас-
тяжением (или сжатием) в г раз, то
\о\пВ"{г)*=гп\о\пВ»(\).
Постоянную
©Я = У01ЯВЯ(1)
можно вычислить при помощи следующей индуктивной формулы:
©„ = ©„_! ^(l-n^dt, л>£.
Приведем некоторые значения со*:
о 4 1 2
о)х = 2, о)2 = я, (о3 = — я, о)4 = — п*. ^
о 2
Вообще,
Г(л/2+1)
где Г(/) — гамма-функция Эйлера.
(4) Эллипсоид
получается из шара
2?=i(x02<l
растяжением в а' раз вдоль i'-й координатной оси, т. е. путем ум-
ножения на матрицу diagfa1, .,., ап}. Поэтому его объем равен
<опа1 ...ап.
3°. Неравенство Брунна—Минковского.
. - 297

ТЕОРЕМА. Усл. Хо и Х\ —- выпуклые тела в пространстве 8п,
*(0<*<1) — любое.
Утв.
J. -L _L
КЛ((1-/)Х0+«1)>(1-/)КЛ(Х0)+^'1(Х1), (1)
где V(*)=vol»(X).
Равенство в формуле (1) возможно в том и только в том слу-
чае, когда тела Хо и Х\ гомотетичны. Иными словами, функция
f(t) = Vn((l-t)X0 + tX1)
является вогнутой функцией переменной t, Q^l^l (рис. 46); она
J
тл
у
1 Ht)
t
>fd)
1
Рис. 46 Рис. 47
сводится к линейной лишь в том случае, когда тела Х0 и Х\ гомо-
тетичны (т. е. подобны и подобно расположены).
Прежде чем переходить к подробным рассмотрениям, разъяс-
ним ряд понятий, которые встречаются по ходу доказательства.
1. Будем говорить, что выпуклые тела равны, Х=У, если одно
из них может быть совмещено с другим движением (т. е. преоб-
разованием вида y = Sx+at где S — ортогональная матрица).
2. Равные тела X и Y называются параллельно расположен-
ными, если их можно совместить параллельным переносом (т. е.
преобразованием вида у=х+а).
3. Преобразование, которое при некотором фиксированном
<а^8п из пространства &п и некотором положительном числе а
лереводит произвольную точку х из пространства 8п ъ а + аху
называется гомотетией (рис. 47). • '
Говорят, что тела X и Y гомотетичны, если существует гомоте-
тия, переводящая одно из них в другое.
4. Если S(x) — площадь сечения тела X плоскостью, перпен-
дикулярной оси абсцисс и пересекающей ее в точке (х, 0, 0), то
Эйлер (Euler) Леонард (15.4.1707—18.9.1783) — швейцарский математик,
академик Петербургской АН (с 1726 по 1741 год и с 1766 года); Брунн (Brunn)
Карл Герман (1.8.1862—20.9.1939) — немецкий математик.
298

объем тела X вычисляется по следующей формуле (рис. 48):
V(X)= lbaS(x)dx,
а абсцисса хц центра тяжести тела X по следующей:
[baxS{x)dx.
V(X)
Для я-мерного случая указанные формулы несут ту же инфор-
мацию.
Рис. 48
Рис. 49
Доказательство сформулированного утверждения будем
вести индукцией по числу измерений объемлющего пространст-
ва <ff*.
На прямой 8х утверждение теоремы выполняется тривиально:
Х0 и Х{ — отрезки и неравенство (1) сводится к равенству.
Допустим, что утверждение теоремы верно в пространстве
<$п~х, и докажем, что оно справедливо и в пространстве 8п.
Сформулируем сначала одно вспомогательное утверждение и
покажем, как из него следует требуемый, более общий результат.
ЛЕММА. Усл. Выпуклые тела Х0 и Х\ имеют равные объемы;
t, 0<t<l — любое.
Утв. Тело Xt= {l—t)Xo+tX\ имеет больший объем, кроме тога
случая, когда тела Ло и Х\ равны и параллельно расположены,
так что Xt также равно им.
Пусть Х0 и Х\ — произвольные выпуклые тела. Тогда тела
У° vl'n(X0
Т" ^0» М. —
Vl/n(X1)
Хг
имеют объем, равный единице.
299

Поэтому из леммы следует, что
V(Ys)>l, (2)
где 0<5<1. Положим
s = . tv^ix,)
W -t)Vl/n (X0) + fVl'n (Xx)
Вычислим объем тела
у (l-t)X0 + txx
(i—t)V]/n(X0) + tVl/n(X1) / .
и, пользуясь неравенством (2), получим
V(Xi)^l(l-i)V^(X0)+tV^(X1)]a. (3)
Извлекая корень п-й степени из обеих частей, приходим к требу-
емому соотношению (1).
*л Знак равенства в формуле (3) стоит только тогда, когда он
стоит в формуле (2), т. е. когда тела Y0 и Y\ равны и параллель-
ны, а значит, Х0 и Х\ гомотетичны. □
Таким образом, теорема будет доказана, как только мы убе-
димся в справедливости сформулированной выше леммы.
Допустим, что теорема верна jb пространстве 8ПштХъ и докажем,
что, лемма справедлива для я-мерных выпуклых тел.
Для простоты /г-мерный объем , будем называть просто
объемом, а (п—1)-мерный — площадью.
Пусть Хо и Х\ — выпуклые тела в пространстве, имеющие рав-
ные объемы: Будем считать эти объемы равными единице. Про-
ведем какую-нибудь гиперплоскость Я и перенесем (параллельно)
тела Х0 и Х\ так, чтобы гиперплоскость Я стала опорной к ним
обоим. Отметим, что это не изменяет объема тела Xt=(l—t)X0+
+txx.
Рассечем тело Хь 1=0, 1, гиперплоскостью Я,, t=0, 1, парал-
лельной Я, так, чтобы часть тела Хц лежащая в слое между Я и
Н^ имела объем, равный v, 0<и<1. Ширину слоя обозначим че-
рез xi. Ясно, что Xi=Xi(v) (рис. 49).
Пусть Si(v). — площадь сечения Zi=Xi(]Hi(v). Ясно, что
dv=SidXiy i = 0, 1, (4)
и, далее,
. V (Xt) = # StdXi = J JSi (v) х{ (v) dv, ,
где Ы — ширина тела Xi в направлении, перпендикулярном гипер-
плоскости Я.
Из формулы (4) вытекает, что
%—h'-*'• (5)
Линейная комбинация сечений
Zt=(t — t)Z0+tZl
300

содержится в теле Xt и лежит в гиперплоскости, параллельной Я,
яа расстоянии
xt(v) = (l—t)x0(v) + txx(v) (6)
ют нее. Если St(v) —- площадь множества Zt, то для объема тела
Xt справедливо неравенство
V(Xt)^ll0St(v)dxt(v)= lloSt{v)x't(v)dv. (7)
По предположению индукции неравенство (1) применимо к се-
чениям Z0 и Z\. Поэтому
st (v) > l(i -t) srl (v)+tsr\v)]^.
Кроме того, из формул (5) и (6) следует, что
x't(v)=(l-l)-±r+t-^. •■
«bo oi
Пользуясь последними двумя соотношениями, заменим St(v) и
JCt'(v) в формуле (7). Получим
1 1
Оценим подынтегральную функцию в правой части неравенст-
ва (8). Положим g = Si/50. Тогда эту функцию можно представить
в следующем виде:
1
/(S)=Ki-Q+fc№"lP+l O-'+y)-
Функция /(£) определена на луче (0, оо), положительна и
непрерывна на нем. Так как
lim/(6)=lim/(S)=+oo,
то на (0, с») найдется точка, в которой /(g) достигает минимума.
Производная
1 п
/'(6)=-ш^(1-*+^~1Г:а(Г"1-1)
* £
обращается в нуль лишь при g=l. Это и есть точка минимума.
Соответствующее значение функции /(1) = 1. Поэтому /(g)"^l,
причем /(g) = 1 лишь в случае, когда g = l.
- Таким образом, подынтегральная функция в неравенстве (8)
не меньше единицы.
Отсюда и из неравенства (8) получаем,, что
V(Xt)>l. (9)
301

Покажем теперь, что V(Xt) = l лиый> тогда, когда тела Х0 и Хх
равны и параллельно расположены.
Проследим цепочку неравенств, которая привела нас к оценке
(9). Если V(X*) = 1, то в каждом из них должен стоять энак ра-
венства. Поэтому должно быть f(g) = lf т. е. 6=1, или, иными сло-
вами, ,
S0{v)=Si(v).
Но тогда из формулы (5) и из условия *0(0) =*i(0) =0 (тела Х0
и Х\ опираются на одну и ту же гиперплоскость Н) вытекает, что
x0(v)=xi(v): 710}
Это означает, что гиперплоскости, отсекающие от тел Х0 и Хг
части равных объемов, совпадают.
Из равенства (8) и формулы для вычисления координаты цен-
тра тяжести тела
1
х=—— [tS(t)dt
V(X)t
вытекает, что центры тяжести обоих тел Х0 и Х\ находятся на
одинаковом расстоянии от гиперплоскости Н. Поэтому если па-
раллельным переносом тела Х0 (или Х\) совместить их центры
тяжести, то опорная гиперплоскость Н останется общей.
Но гиперплоскость Н была выбрана произвольно. Поэтому,
когда совпадают центры тяжести тел Х0 и Х\, должны совпадать
и все соответствующие опорные гиперплоскости.
Это означает, что совпадают и сами тела.
Следовательно, до параллельного переноса они были равны
и параллельно расположены. □
♦4°. Неравенство Бибербаха.
ТЕОРЕМА. Усл. X — выпуклое тело в пространстве &п, (ort —
объем /г-мерного единичного шара.
Утв.
voln(X)<-^(diamX)n.
Доказательство. Без ограничения общности можно счи-
тать, что
diamX<l.
Обозначим через~ У тело, симметричное X (рис.
50) относительно начальной точки О, и положим
Z = ±(X + Y). (*>
Функция Vn(iX+(l — t)Y) вогнутая, так что
Рис.50 V(Z)^V(X)=V(Y)y
302

причем равенство возможно лишь в том случае, если тело X гомо-
тетично телу У, т. е. если тело X является центрально симметрич-
ным.
Пусть diamZ=|jc—у\, где х\ у — точки из множества Z.
Из формулы (*) вытекает, что
где х', у'ЕХ, *", у"е=К. Тогда
\х-У\=\\* + *-У'-?\<\\*'-У'\ +
+ ±|x''_/|<^diamX+^r<l.
Следовательно, diamZ<!l.
Из проведенных рассуждений вытекает, что достаточно ограни-
читься рассмотрением центрально симметричных тел.
Итак, пусть X — центрально симметричное выпуклое тело.
Тогда из условия
_ diamX^l (**)
вытекает, что тело X содержится в я-шаре единичного диаметра.
Из того, что объем такого шара равен —^-, и из неравенства
(**) получаем требуемое. □,
5°. Экстремальные эллипсоиды.
ТЕОРЕМА. Усл. X — выпуклое тело в пространстве <Sny ae
^ё'п — фиксированная точка.
Утв. Существует, и притом ровно один, n-мерный эллипсоид
1) с центром в заданной точке а,
2) содержащий тело X и
3) имеющий минимальный объем среди всех эллипсоидов, об-
ладающих свойствами 1) и 2).
Определение. Эллипсоид, удовлетворяющий требованиям
1), 2) и 3), называется описанным (вокруг тела X) эллипсоидом
с заданным центром а.
Доказательство. Единственность будем доказывать от
противного: предположив наличие двух различных эллипсоидов
со свойствами 1), 2) и 3), построим третий эллипсоид, удовлетво-
ряющий требованиям i) и 2) и имеющий меньший объем.
В утверждении теоремы речь идет об эллипсоидах вида
(х—а)тЛ(х—а)<1,
где х= (х1.. ,хп)т и а=(а1...ап)т — координатные столбцы.
Будем считать, что
Бибербах (Bieberbach) Людвиг Георг (4.12.1886) — немецкий математик.
303

а) точка а совпадает с начальной точкой О (преобразованием,
не изменяющим объемов — переносом у=х—а — этого всегда
можно добиться),
б) один из эллипсоидов является шаром.
В самом деле, пусть 3i и Э2 — два описанных эллипсоида
с заданным центром а:
хтЛ1*<1, лгтЛ2х<1.
Существует преобразование вида у=38х, сохраняющее объемы и
переводящее эллипсоид Э\ в шар Вп. (Это преобразование стро-
ится в два этапа: сначала преобразованием 2=Sx, где S — орто-
гональная матрица, приводим эллипсоид Э\ к главным осям
2тСг<1, где C=diag{ai, .♦., aw}, затем путем подходящих сжатий
и растяжений вдоль главных осей получаем шар yTDy^.ly где
Z) = diag{a,...,a}.
При этом конечно, det Л=Па1 = а/г.)
Преобразование у—Six переводит эллипсоид Э2 в эллипсоид
Э, а тело X в тело У, не изменяя их объемов.
Рассмотрим шар В и эллипсоид Э с центрами в О, содержа-
щие выпуклое тело У и имеющие равный минимальный объем.
Выбрав подходящим образом координаты в пространстве <$\
можно считать, что шар В и эллипсоид Э задаются неравенст-
вами
«,(■£)'< 1.Д, (£)'<. ,.)
соответственно. Так как шар В и эллипсоид Э содержат тело X,
то неравенства (*) выполняются для всех точек х из тела X. От-
сюда следует, что эллипсоид Э*,
2 V а2 (Щ* J
содержит тело X. Вычислим его объем i л
_ J_
vol,(3*J = (DlinLiVTa^(a2+(*01) 2<
< со„П?=1 (abt)2 = /vol (5). vol (Э) = vol {В).
В силу минимальности vol (В) в последнем'соотношении дол-
жен стоять знак равенства. Откуда вытекает, что а2+ (Ь«)2=2аЬ*
и, значит, a = bl для любого L Тем самым В = 3 и требуемое про-
тиворечие получено.
Существование описанного эллипсоида с заданным центром
определяется наличием следующих фактов:
1) уо1л(-У)>0 (так как X — тело),
2) vol*(3)>vol"(X),
304 ,

3) в описание эллипсоида входит конечное число параметров—
п(п+\)/2 элементов его матрицы Л,
4) voln(9)^—^=r.
' v ' /deM
Доказательство проводится обычным способом с использованием
теоремы о свойствах функции, не-
прерывной на компактном множе-
стве. □
Замечание. Результат оста-
ется верным, если искать описан-
ный эллипсоид, не фиксируя зара-
нее.его центр, т. е. среди всех эл-
липсоидов, содержащих данное те-
ло, существует, и притом ровно
один, эллипсоид минимального объ-
ема.
Аналогично вводится понятие и Рис. 51
другого экстремального эллипсои-
да— вписанного (рис. 51).
ТЕОРЕМА. Утв. Среди всех эллипсоидов, содержащихся в дан-
ном выпуклом теле, существует, и притом ровно один, эллипсоид
наибольшего объема.
Задача построения для заданного выпуклого тела описанного
и вписанного эллипсоидов часто встречается в приложениях. По-
кажем, как эту задачу можно свести к задаче выпуклого про-
граммирования.
Ограничимся рассмотрением случая,, когда ищется эллипсоид,
описанный вокруг многогранника.
Пусть М — выпуклый многогранник с / вершинами x\9...,xi
и OeintAf. Тогда для любого эллипсоида.
(х — а)тА(х — а)<1,
содержащего многогранник М, выполняется условие
.. 6=1 — атЛа>0.
Это позволяет преобразовать неравенство (1) к
виду:
хтВх+2x4^1,
где В=6-1Л, &=— 8~1Аа.
' Нетрудно убедиться в том, что при такой способе задания эл-
липсоида его объем V можно найти по формуле
(о
следующему
(2)
V =
(D„
Уф(в>ь)
где
Ф(в, ь)= (det*r
(— detB)"
в =
в ь
Ьт —1
(3)
Рассмотрим пространство RV q=n(n+3)/2, точки р которого
строятся по матрице B=($i5) и столбцу b=(61f...,6n)T так:
Р=(Рп> Pi2,...,Pm; P22,...,p2n;'...;Pnn; ь\...,ьп).
305

Множество точек <Q<=R4, первые л(/г+1)/2 координат которых
суть элементы симметричной положительной матрицы, выпукло.
Покажем, что функция Ф(р)=Ф(5, Ь), определяемая прави-
лом (3), обладает следующим свойством: множество
{реО|Ф(Р)>*}
выпукло при любом t (такие функции называются квазивыпук-
лыми) .
Пусть pi, р2 и p==A,ipi + X2M^i+A.2=l, A,i>0, Х2>0)— точки
из (Q, а Э\\ Эч и Э — соответствующие им эллипсоиды. Линейным
преобразованием пространстэа <£пу сохраняющим объем, матри-
цы Ви В2 и B=XiBi+X2B2 этих эллипсоидов можно одновремен-
но привести к диагональному виду.
Если B = diag{plb...,pnn}, то Ф(Р)=/(р)^-п(Р), где
./(Р) = П7.1р„, Fcpj^i + SLt-^.
Ра
Легко проверить, что
hF(M+^F(h)>F(n- (4>
Пусть Ф(рт)^(/п=1, 2) или, что то же,
f(M>Fn(Mt, m=l, 2. (5)
Тогда, воспользовавшись известным неравенством
' п,"=1(^+г,)'/">щ=1^/п+п^г,
из соотношений (4) и (5) получим, что
/(P)>(^i(f(Pi))1/"+^2(f(p2))1/-)-^(X1F(p1)+^JF(p2))-^^
>Fn($)t. '
Тем самым, Ф(р)^/.
Для того чтобы искомый эллипсоид Зоп вида (2) содержал
многогранник М, необходимо и достаточно выполнение нера-
венств
XiTBxi+2xiTb^\, i=l,...,Z. (6>
Это позволяет свести поставленную задачу к следующей: най-
ти симметричную положительную матрицу B^Rnxn и столбец.
b= (61,.. . ,ЬП)Т, подчиненные условиям (6) и такие, что
Ф(Я, Ь)-ипах.
Ограниченность множества точек пространства R^, удовлетво-
ряющих поставленным условиям, вытекает из невырожденности
многогранника М и следующего простого факта: выпуклое мно-
жество X ограничено, если К(Х, л:)=0 для любой точки jce!
.(с. 278).
Таким образом, задача построения эллипсоида, описанного
вокруг заданного выпуклого многогранника, свелась к поиску
максимума квазивыпуклой функции на ограниченном выпуклом
множестве.

ЛИТЕРАТУРА
1. Воеводин В. В. Линейная алгебра. М.: Наука, 1980.
2. Ильин В. А., Поз ня к Э. Г. Линейная алгебра. М.: Наука, 1974.
3. Кострикин А. И. Введение в алгебру. М.: Наука, 1977.
4. Мищенко А. С., Ф о м е н к о А. Т. Курс дифференциальной геометрии и
топологии. М.: Изд-во МГУ, 1980.
5. Понтрягин Л. С. Метод координат. М.: Наука, 1977.
6. Пшеничный Б. Н. Выпуклый анализ и экстремальные задачи. М.: На-
ука, 1980.
7. Скорняков Л. А. Элементы алгебры. М.: Наука, 1980.
8. Степанов Н. Ф., Ерлыкина М. Е., Филиппов Г. Г. Методы ли-
нейной алгебры в физической химии. М.: Изд-во МГУ, 1976.
9. Т и х о н о в А. Н., А р с е н и н В. Я. Методы решения некорректных задач.
М.: Наука, 1974.
10. Тышкевич Р. И., Ф е д е н к о А. С. Линейная алгебра и аналитическая
геометрия. Минск: Вышэйща школа, 1976.
11 Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по фи-
зике. М.: Мир, 1976 (выпуски 3 и 4), 1977 (выпуск 7).
12. Чар и н В. С. Линейные преобразования и выпуклые множества. Киев:
В ища школа, 1978.
Литература к Добавлению
1. Александров А. Д. Выпуклые многогранники. М.—Л.: ГИТТЛ, 1950.
2. Бляшке В. Круг и шар. М.: Мир, 1967.
3. Буземан Г. Выпуклые поверхности. М.: Наука, 1964.
4. Б у р а г о Ю. Д., 3 а л г а л л е р В. А. Геометрические неравенства. Л.: На-
ука, Ш80.
5. Д а н ц е р Л., Г р ю н б а у м Б., К л и В. Теорема Хёлли. М.: Мир, 1968.
6. Келли Дж. Л. Общая топология. М.: Наука, 198L.
7. К о с т р и к и н А. И., М а н и н Ю. И. Линейная алгебра »и геометрия. М.:
Изд-во МГУ, 1980.
8. Лейхтвейс К. Выпуклые множества. М.: Наука, Ш85.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Альтернатива Фредгольма 154
Альтернирование 203
База системы векторов 24
Базис 15
— ортонормированный 41
Вектор 8
v- реакции 21
— сдвига 32
— собственный 72
Вершина многогранника 183
Внутренность множества 246
Вращение простое 133
Вычитание множеств 169
Гиперплоскость 36
Гиперповерхность выпуклая 283
— второго порядка 139
Гомеоморфизм 251
Гомотетия 298
Граница множества 247
Группа Лоренца 211
Дефект линейного отображения 56
Длина вектора 40
Дополнение ортогональное 46
Зависимость аффинная 36
— линейная 14
Закон инерции 104
— композиции внешний (ВнешЗК) 8
— тензорный 199
Замыкание множества 247
Значение собственное 72
Изометрия 45
Изоморфизм 25
Индекс квадратичной формы 105
Квазирешение 158
Клетка жорданова 86
Комбинация выпуклая 166, 171, 190
Компоненты тензора 198
- ковариантные 198
контравариантные 198
Конус выпуклый 184, 273
— многогранный 186
— предельный 279
Координаты барицентрические 184
— вектора 15
— декартовы 139
— точки 138
Корень из оператора 1,23
Коэффициенты стехиометрические 21
^-плоскость 36
— опорная 269
Матрица атомная 21
— Грама 42
— линейного оператора 70
отображения 63
— нильпотентная 86
— ортогональная 44
— перехода 36
— сопряженная 114
— формы билинейной 92
— — квадратичной 96
——.полуторалинейной 106
— унитарная 119
— эрмитова 52
Матрицы подобные 70
— эквивалентные 67
Метрика 48
— псевдоевклидова 210
Минор матрицы главный 1,02
Многогранник выпуклый 180
Многообразие линейное аффинное
(ЛАМ) 32
Многочлен матричный 80
— от матрицы 80
оператора 79
— характеристический 71, 73
Множество выпуклое 166, 192, 260
— замкнутое 246
— звездное 263
— компактное 258
— линейно связное 256
— меры нуль 289
— ограниченное 192
— открытое 245
— связное 254
Неравенство треугольника 4Q
Норма 144
— подчиненная 149
— согласованная 148
— спектральная 150
— энергетическая 144
Оболочка аффинная 33
— выпуклая 171
— коническая 1.86
—линейная 13
308

Образ линейного отображения 55
Объем 295
Окрестность точки 248
Оператор индуцированный 82
— кососимметричный 134
— линейный 54
— неотрицательный 121
— нильпотентный 86
— нормальный 115
— ортогональный 129
— положительный 121
— самосопряженный 120
— симметричный 120
— унитарный 117
— эрмитов 120
Определитель линейного оператора
71
Ориентация 38
Отображение линейное 54
— непрерывное 249
— сопряженное 11,1
Отражение 132
— простое 134
Пара базисов каноническая 70
сингулярная 125
Поворот 131
Подпространство' дополнительное 28
— инвариантное 71.
— линейное 11
— собственное 75
— топологическое 248
Покрытие множества 258
Полупространство опорное 272
Преобразование Лоренца 212
— ортогональное несобственное 131
собственное 131
Проекция ортогональная 49
Произведение декартово 170
— линейных пространств 10
— скалярное 39, 51
— топологическое 253
Пространство бесконечномерное, 17
— евклидово 39
— линейное 8
вещественное 37
комплексное 50
— метрическое 48
Пространство нормированное 144
— ориентированное 36
— псевдоевклидово 210
— топологическое 245
.— точечное 1.37
— унитарное 51
— хаусдорфово 257
— га-мерное 17
Прямая 191
Псевдорешение 156
— нормальное 157
Путь 256
Радиус-вектор 138
Разложение полярное 126
— эрмитово 125
Размерность выпуклого множества
269
— линейного пространства 17
Ранг линейного отображения 55
— системы векторов 24
— формы билинейной 94
квадратичной 96
Расстояние между множествами 48
Репер координатный 138
Решение нормальное 155
Свертка 203
Симметризация 195
Симметрирование тензора 203
Симплекс 184, 268
Система векторов ортогональная 41
—— ортонормированная 41
След оператора 74
Составляющая ортогональная 49
Сумма множеств 168
— прямдя 28, 169 »
Сфера 52, 145, 168, 243
Тело выпуклое 267
Тензор 198
— метрический 208
Топология 245
— естественная 245
Трансверсаль общая 179
Транспонирование тензора 202
Угол между векторами 41
Уравнение нормальное 157
— сопряженное 154
— характеристическое 71!
Фактор-пространство 30
Форма билинейная 92
вырожденная 94
невырожденная 94
— линейная 54
— квадратичная 95, 107
вырожденная 96
невырожденная 96
отрицательно определенная 102
положительно определенная^
100
—г кососимметричная 92
— молекулярная 20
— невырожденная 94
— полуторалинейная 106
— полярная квадратичной 95
— симметричная 92
— эрмитова 107
Функционал сглаживающий 162
Функция выпуклая 161, 285
строго 162
— опорная 275
309»

Центр множества 263 Эллипсоид вписанный 305
— описанный 303
Шар 5% 145, 168, 243
э Ядро линейного отображения, 56

ИМЕННОЙ УКАЗАТЕЛЬ
Бибербах 303
Бине 218
Борель 259
Брунн 298
Буняковский 40
Виет 238
Галуа 235
Гамильтон 80
Гёльдер 145
Грам 42
Декарт 10
Евклид 39
Жордан 86
Каратеодори 176"
Коши 40
Крамер 100
Кронекер 41*
Кэли 80
Лагранж 96
Лебег 258
Лоренц 211.
Минковский 210-
Муавр 235
Пифагор 156
Пуанкаре 212
Радон 1,75
Риман 236
Сильвестр 101
Тихонов 163
Фредгольм 155?
Хаусдорф 25&
Хелли 177
Эйлер 298
Эрмит 52
Юнг 293
Якоби 99?

УЧЕБНОЕ ПОСОБИЕ
Евгений Викторович Шикин
ЛИНЕЙНЫЕ ПРОСТРАНСТВА И ОТОБРАЖЕНИЯ
Зав. редакцией С. И. Зеленский
Редактор Р. Д. С о л о д
Художественный редактор Ю. М. Добрянская
Переплет художника Н. Н. Сенько
Технический редактор К. С. Чистякова
Корректоры Н. В. Картышева, Н. И. Коновалова
ИБ № 2619
Сдано в набор 17.11.86. Подписано в печать 25.06.87. Л-62186.
Формат 60X90/16. Бумага тип. № 3. Гарнитура литературная.
Высокая печать. Усл. печ. л. 19,5. Уч.-изд. л. 20,06. Тираж 4720 экз.
-Заказ 538, Изд. № 4335. Цена 1 руб.
Ордена «Знак Почета» издательство Московского университета.
103009, Москва, ул. Герцена, 5/7.
Типография ордена «Знак Почета» изд-ва МГУ.
119899, Москва, Ленинские горы