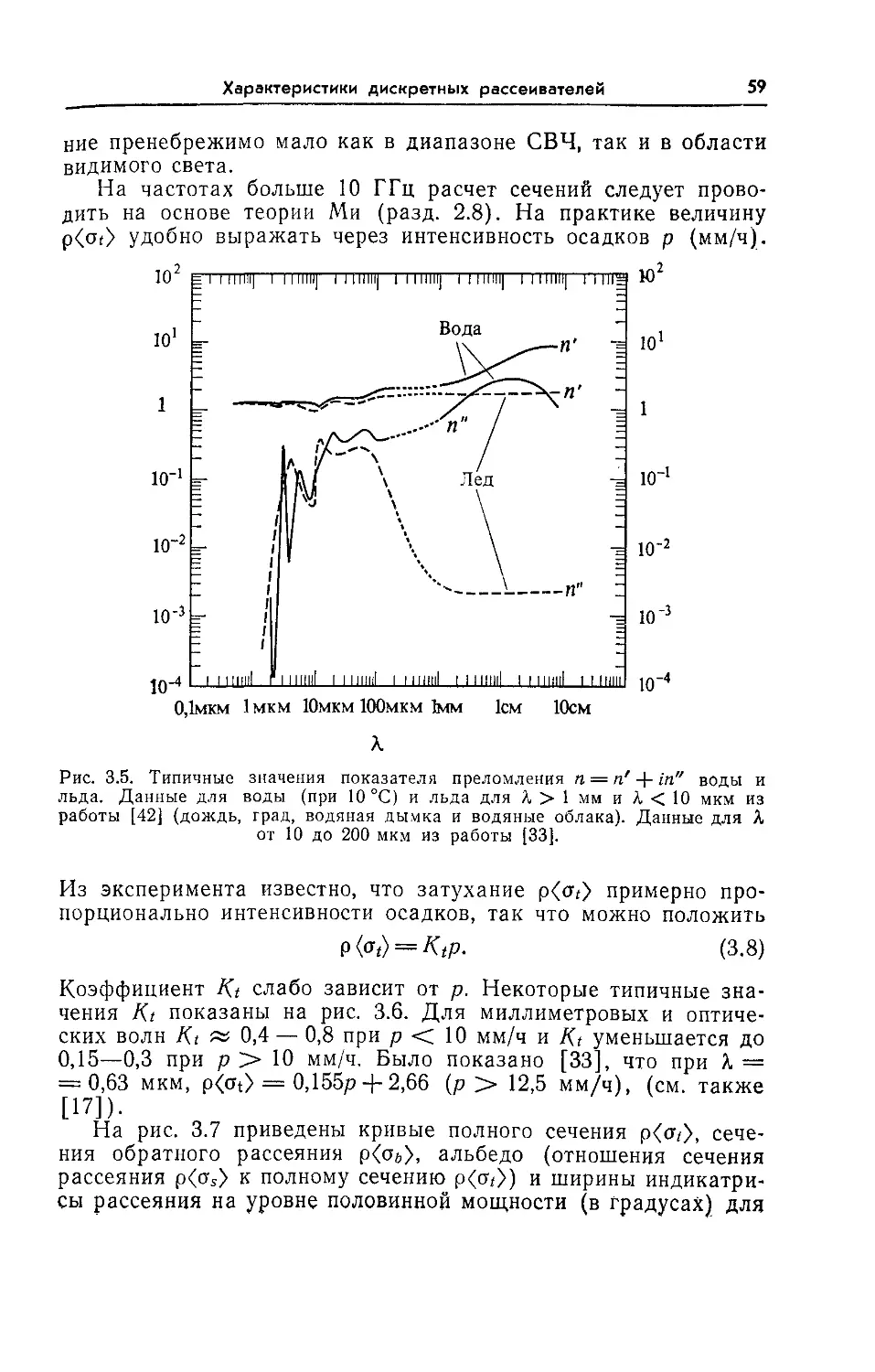
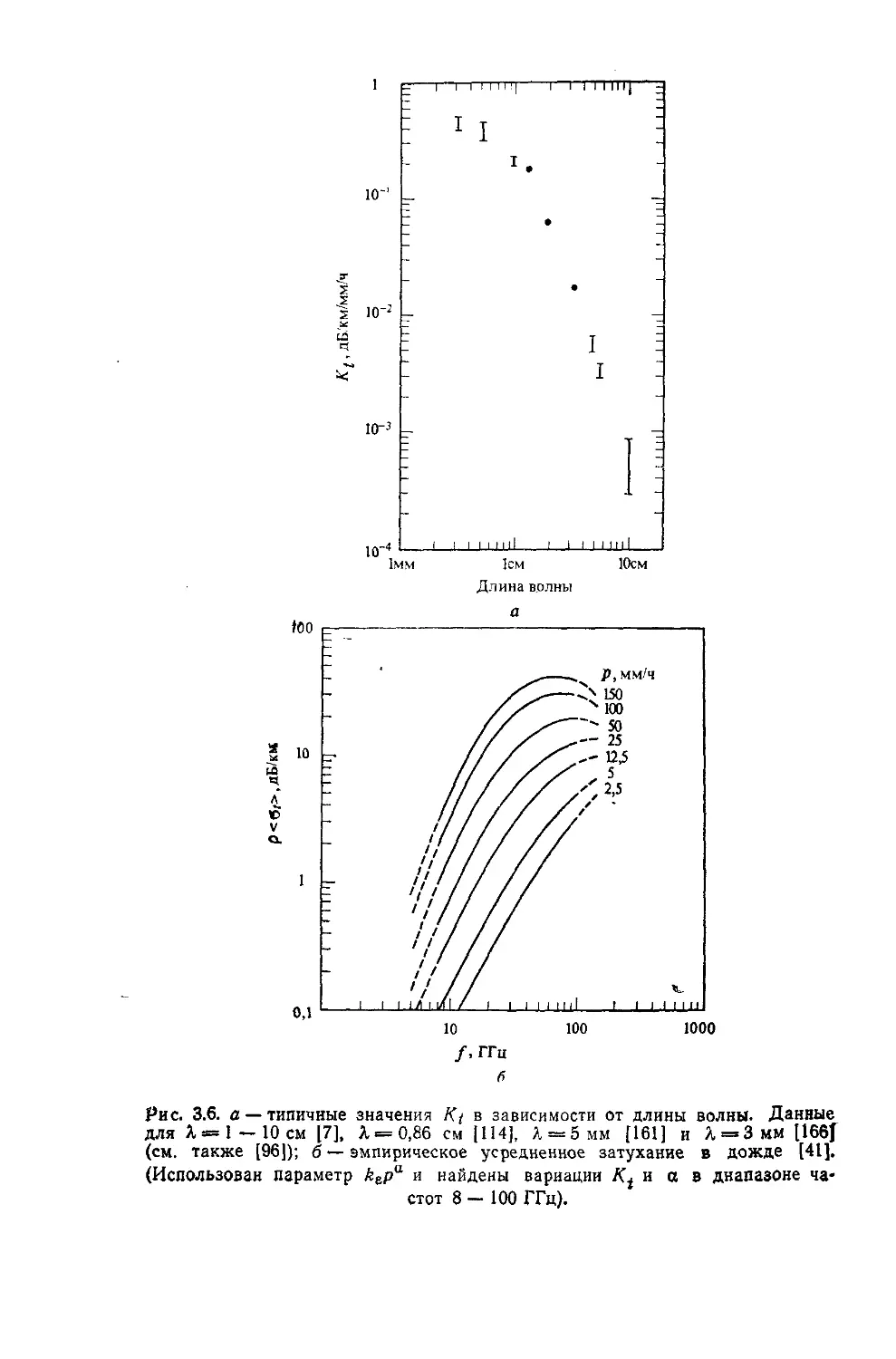
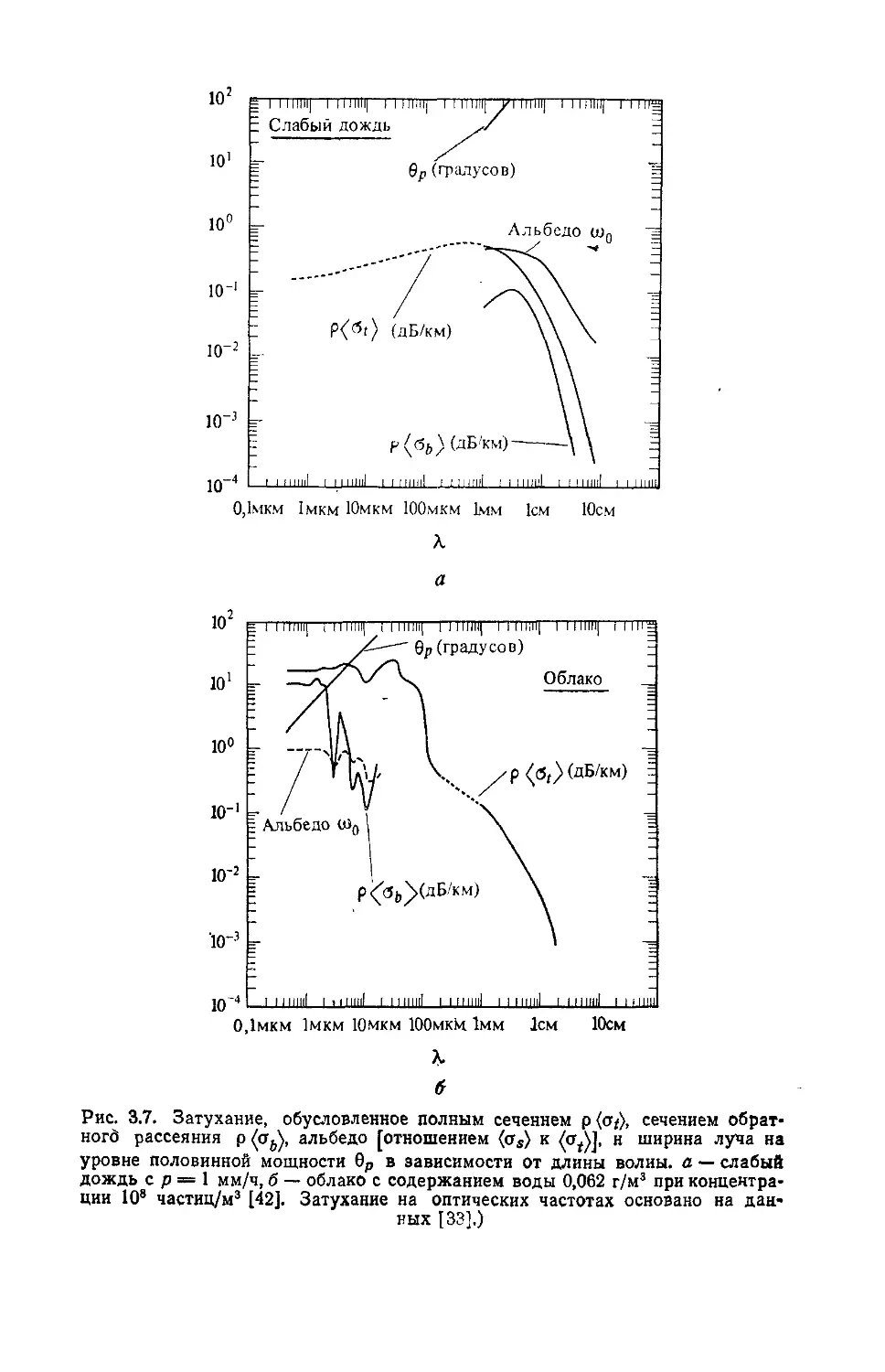
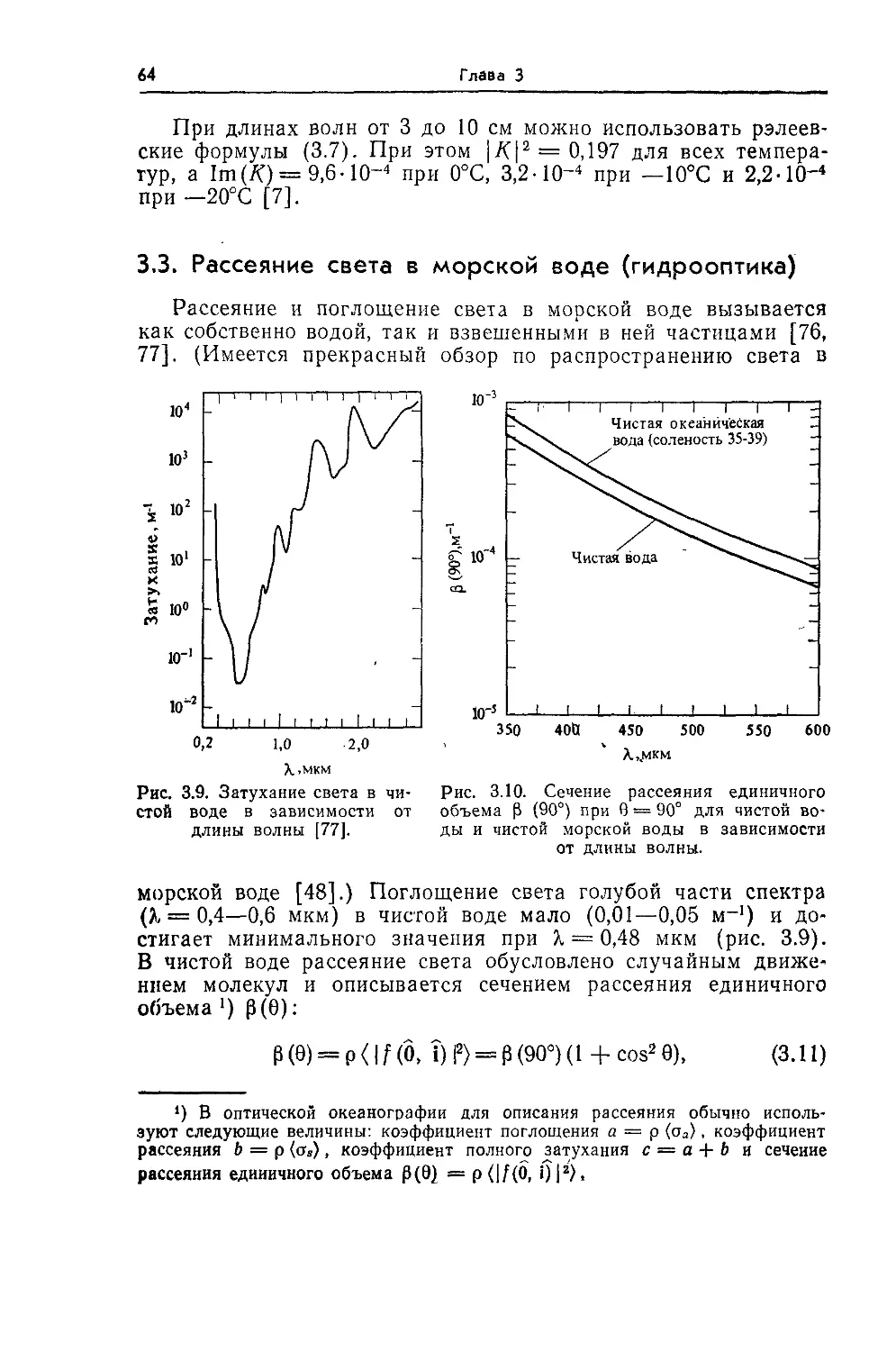
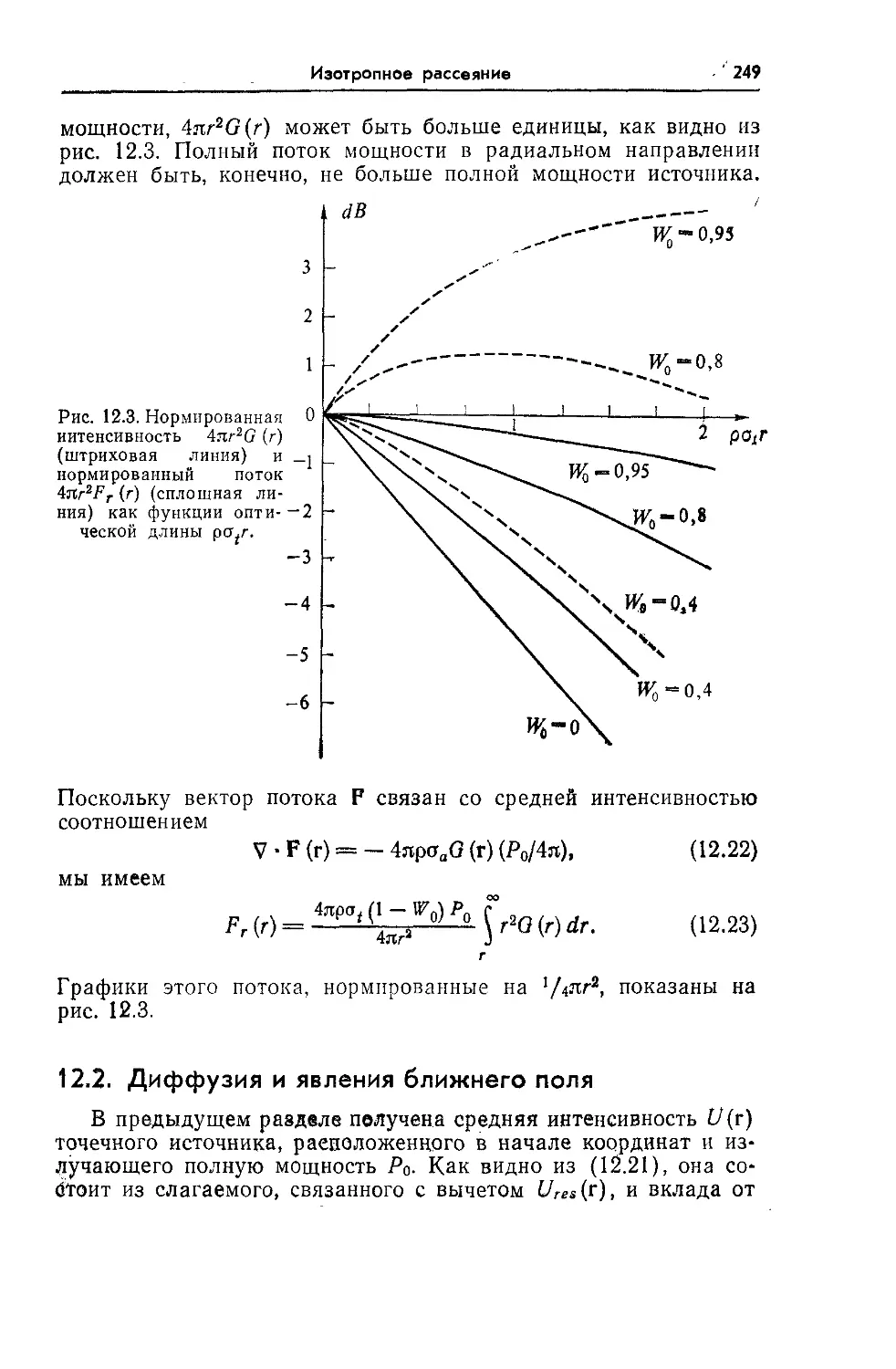
Text
А.Исимару
РАСПРОСТРАНЕНИЕ И РАССЕЯНИЕ ВОЛН В СЛУЧАЙНО-
НЕОДНОРОДНЫХ СРЕДАХ, т. 1
Двухтомная монография А. Исимару представляет собой подробное и полное
введение в статистическую теорию распространения волн — один из важнейших
разделов современной оптики, радиофизики, "акустики.
В первом томе рассматриваются теория однократного рассеяния и
распространение волн в облаке случайно распределенных рассеивателей, а также
феноменологическая теория переноса излучения.
Книга рассчитана на научных работников в области атмосферной оптики,
локации, связи, радиоастрономии и акустики. Она может служить учебным
пособием для аспирантов и студентов старших курсов.
Содержание
Предисловие к русскому изданию 5
Предисловие 6
От автора 9
Глава 1. Введение 11
ЧАСТЬ I. РАССЕЯНИЕ И РАСПРОСТРАНЕНИЕ ВОЛН В
РАЗРЕЖЕННЫХ ОБЛАКАХ ДИСКРЕТНЫХ РАССЕИВАТЕЛЕЙ.
ПРИБЛИЖЕНИЕ ОДНОКРАТНОГО РАССЕЯНИЯ
Глава 2. Рассеяние и поглощение волны отдельной частицей 17
2.1. Сечение рассеяния и амплитуда рассеяния 17
2.2. Общие свойства сечений 20
2.3. Оптическая теорема 23
2.4. Интегральные представления амплитуды рассеяния и сечения 23
поглощения
2.5. Рэлеевское рассеяние 27
2.6. Борновское приближение (рассеяние Рэлея — Дебая) 31
2.7. ВКБ-приближение для поля внутри частицы 34
2.8. Решение Ми ЗУ
2.9. Эллиптически-поляризованные волны и параметры Стокса 40
2.10. Частичная поляризация и естественный свет 42
2.11. Сложение независимых волн 43
2.12. Матрица рассеяния и матрица Стокса 43
2.13. Преобразование параметров Стокса при повороте системы координат 45
2.14. Распределение частиц по размерам 47
2.15. Акустические волны 48
2.16. Рассеяние акустических волн 50
Глава 3. Характеристики дискретных рассеивателей в атмосфере, 52
океане и биологических средах
3.1. Метеорологические радиолокаторы, шумы и помехи 52
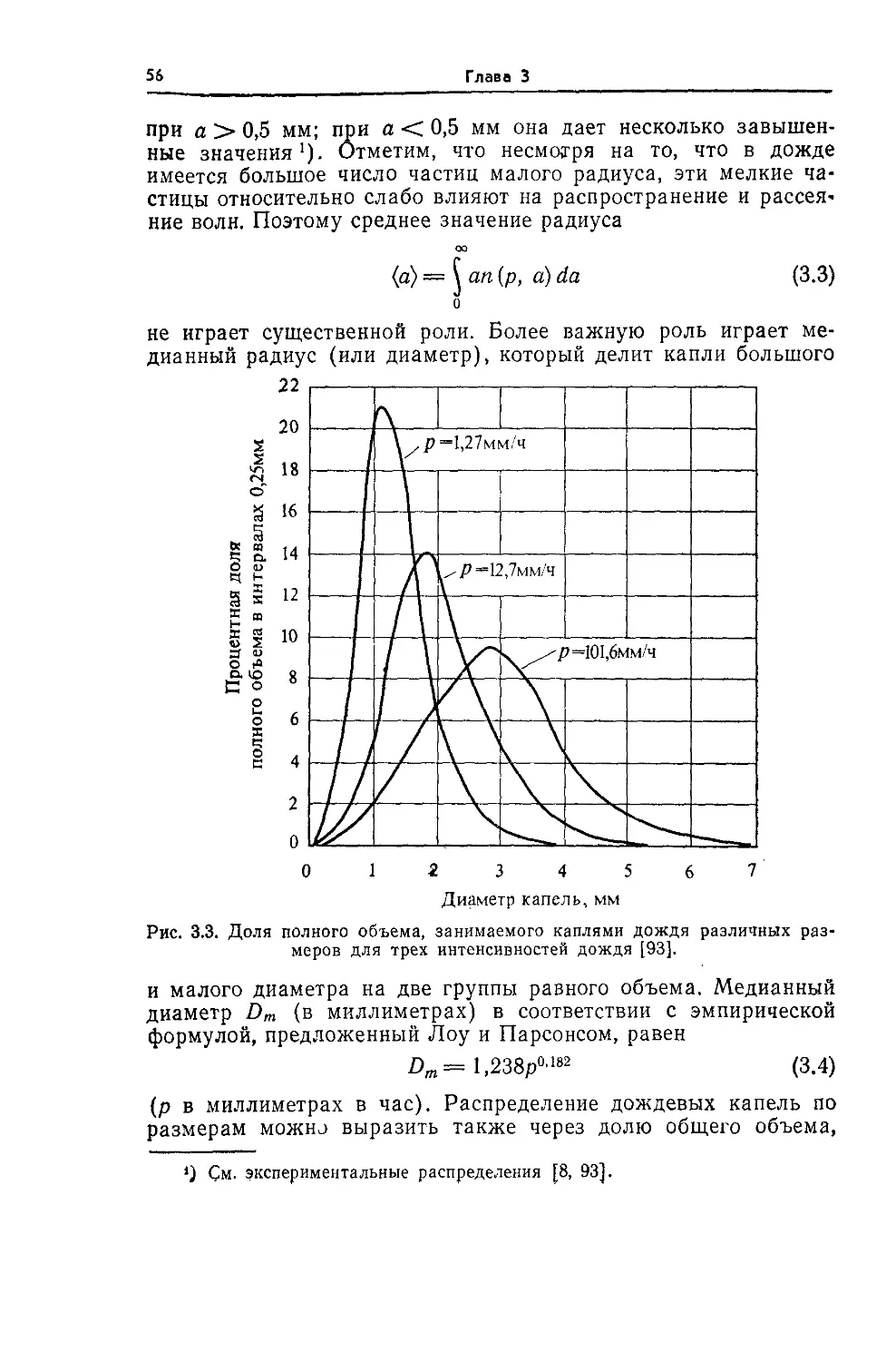
3.2. Аэрозоль и гидрометеоры 54
3.3. Рассеяние света в морской воде (гидрооптика) 64
3.4. Рассеяние звука в воде (гидроакустика) 66
3.5. Рассеяние на биологических средах 74
Глава 4. Рассеяние волн в разреженных облаках частиц 82
4.1. Средняя мощность рассеянного поля в приближении однократного 84
рассеяния
4.2. Мощность рассеянного поля в первом порядке теории многократного 86
рассеяния
4.3. Случай узкой диаграммы направленности 88
4.4. Когерентное и некогерентное поле 91
4.5. Сечение рассеяния движущейся частицы с учетом временной 94
корреляции
4.6. Временная корреляционная функция и частотный спектр рассеянного 99
поля
4.7. Пространственная корреляция рассеянного поля 101
4.8. Коррлеяция поля, принимаемого движущимся приемником 103
4.9. Распределение вероятности рассеянного поля 104
Глава 5. Рассеяние импульсных волн в случайном облаке частиц 108
5.1. Общая формулировка проблемы распространения и рассеяния 108
импульсов в нестационарной случайной среде
5.2. Двухчастотная функция когерентности и смешанной момент 111
выходного импульса
5.3. Время когерентности и полоса когерентности 113
5.4. Рассеяние узкополосного импульса 114
5.5. Обратное рассеяние импульса, излучаемого остронаправленным 118
излучателем
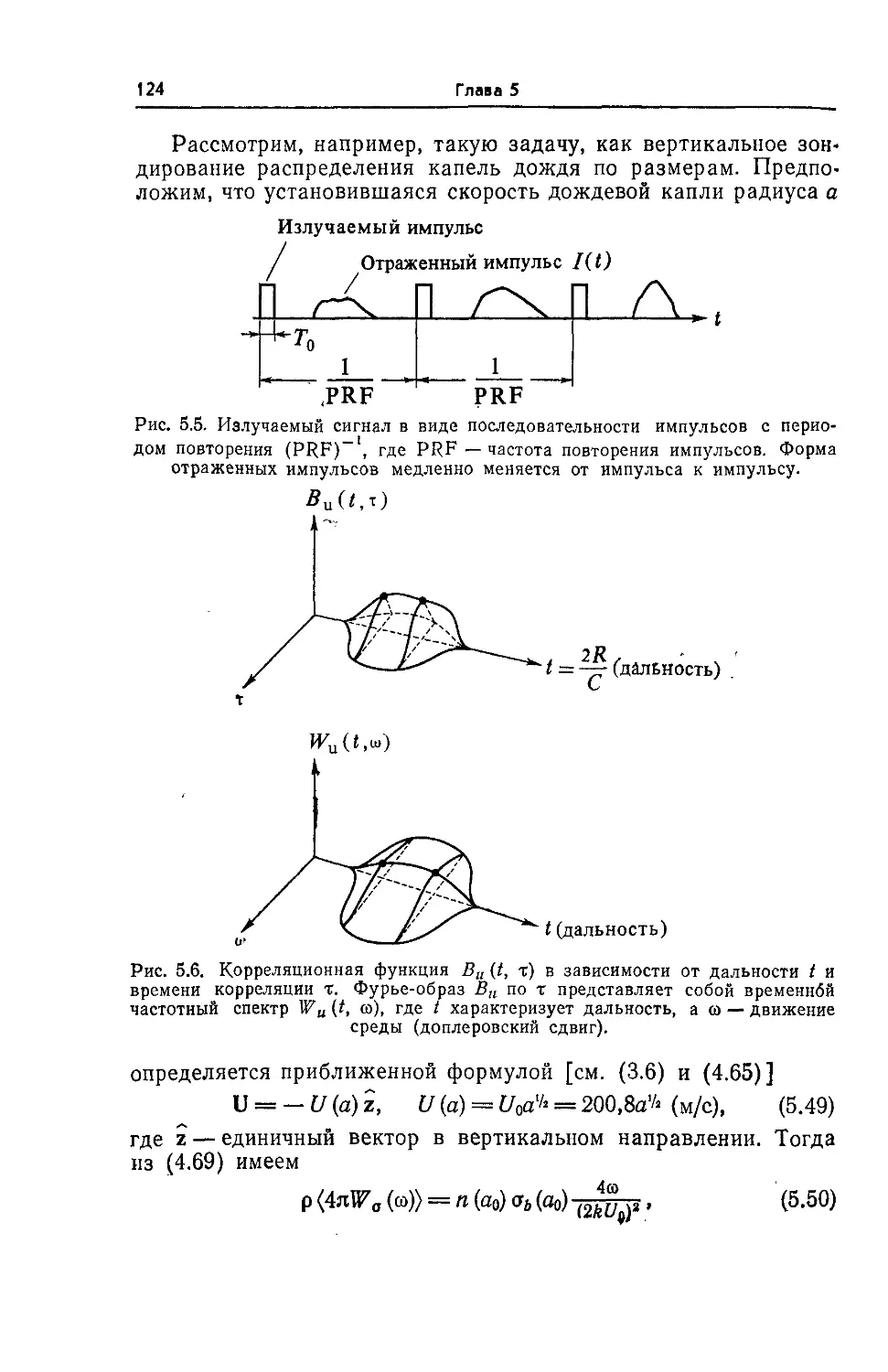
5.6. Обратное рассеяние последовательности коротких импульсов 123
5.7. Обратное рассеяние импульса, излучаемого передатчиком с широкой 125
диаграммой направленности
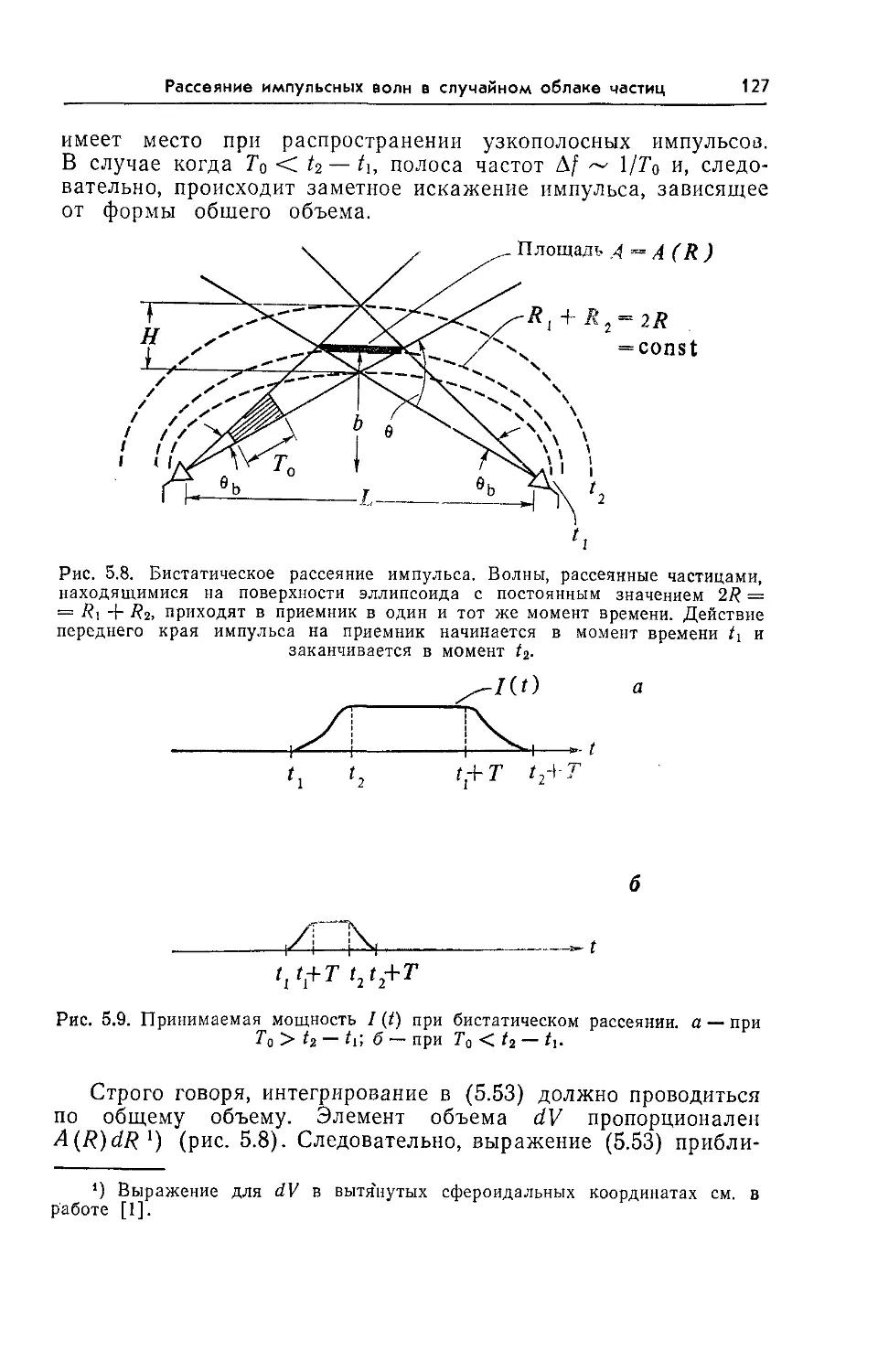
5.8. Бистатическое рассеяние импульса 126
5.9. Представление через функцию неопределенности 128
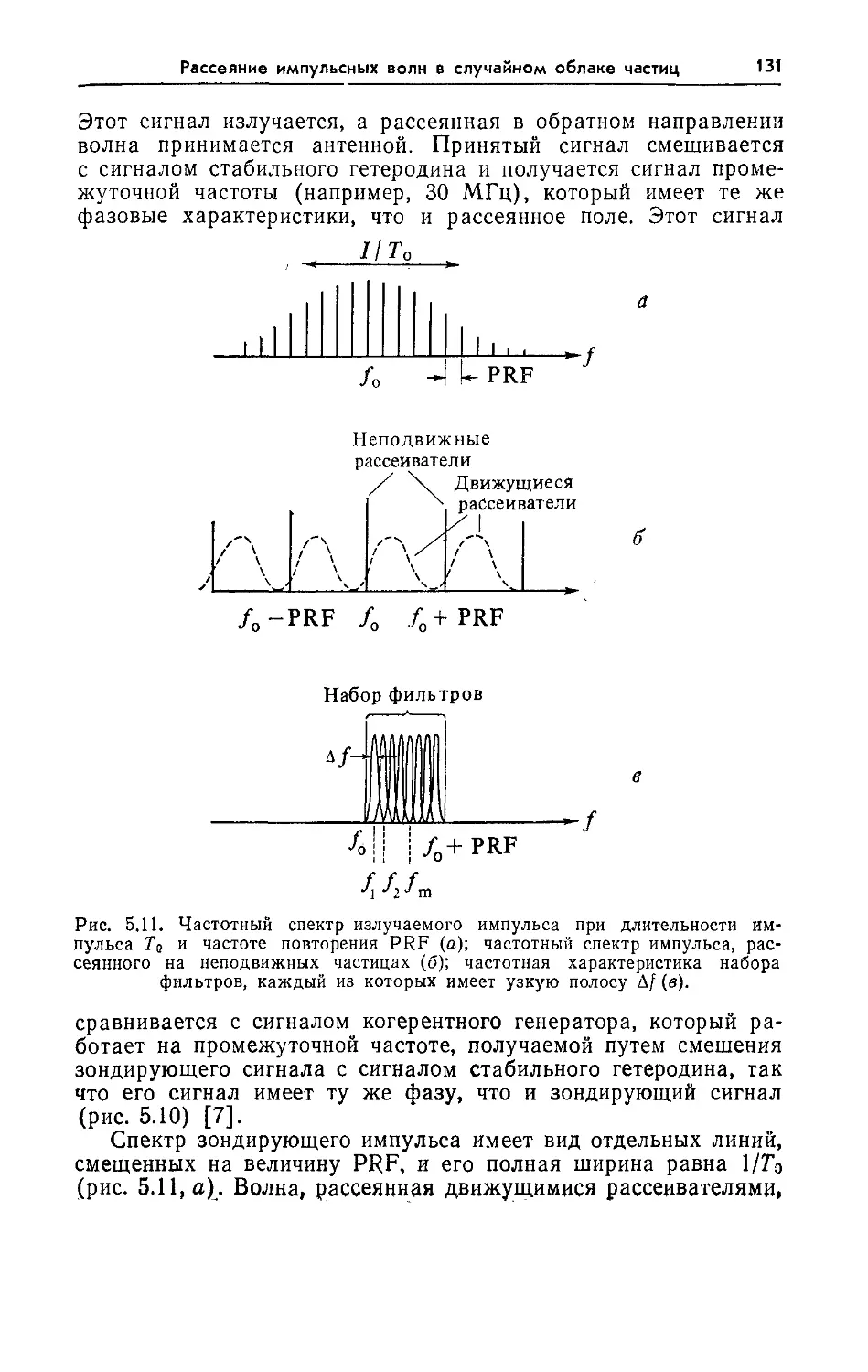
5.10. Импульсно доплеровский радиолокатор 130
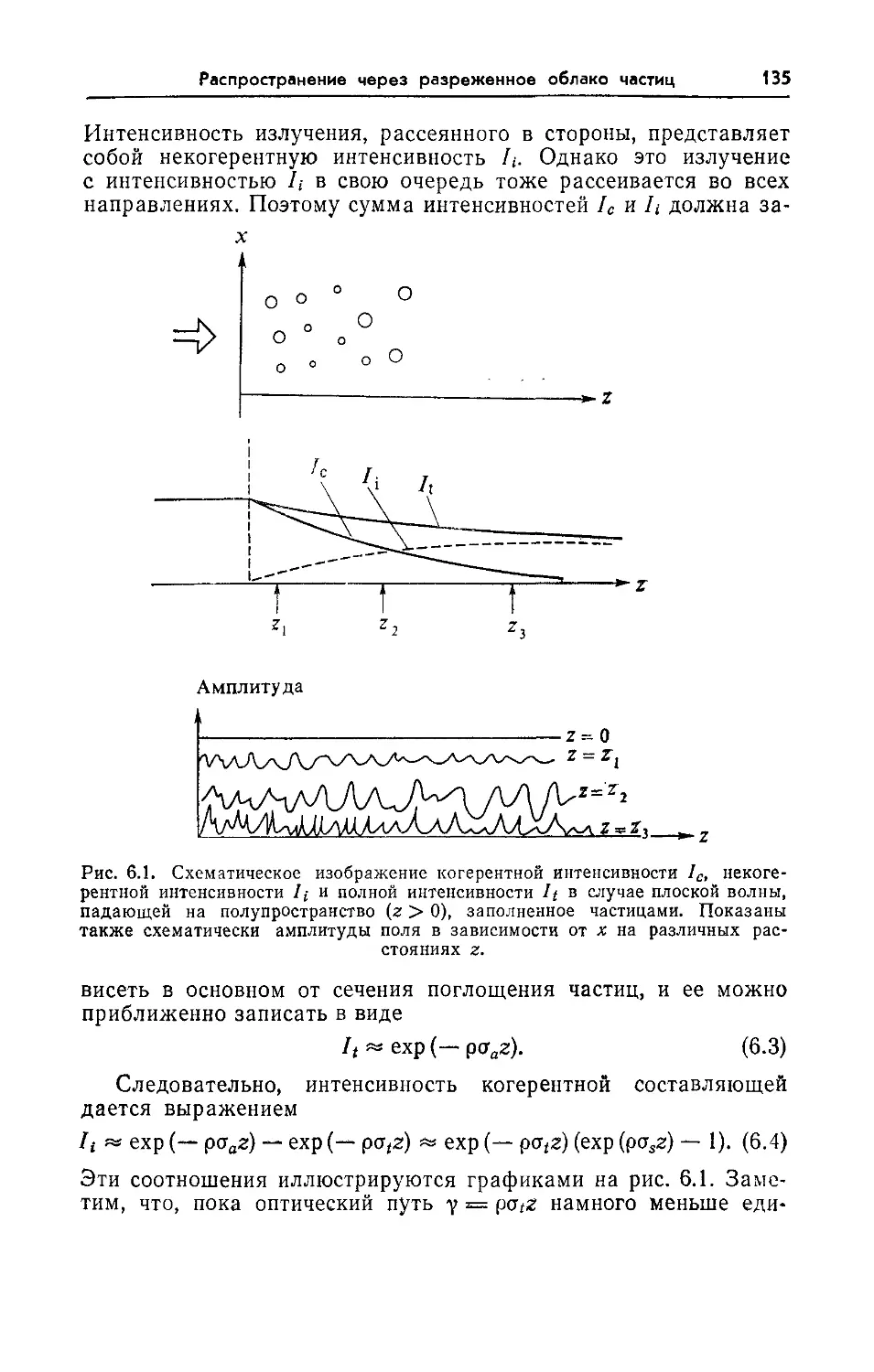
Глава 6. Распространение в пределах прямой видимости через 184
разреженное облако частиц
6.1. Когерентная и некогерентная интенсивности и пространственная 136
корреляция флуктуации в плоской волне
6.2 Временная корреляция и частотный спектр плоской войны 141
6.3. Распространение плоской импульсной волны в пределах прямой 143
видимости
6.4. Распространение между излучателем и приемником в пределах 145
прямой видимости
6.5. Распространение импульса между излучателем и приемником 151
6.6. Приближение Рытова для флуктуации амплитуды и фазы 153
6.7. Приближение Рытова для плоской волны 155
6.8. Временная корреляция и частотные спектры флуктуации уровня и 159
фазы плоской волны
6.9. Приближение Рытова с учетом направленных свойств излучателя и 161
приемника
ЧАСТЬ II. ТЕОРИЯ ПЕРЕНОСА ИЗЛУЧЕНИЯ В СЛУЧАЙНОМ
ОБЛАКЕ РАССЕИВАТЕЛЕЙ
Глава 7. Теория переноса излучения в случайном облаке частиц 163
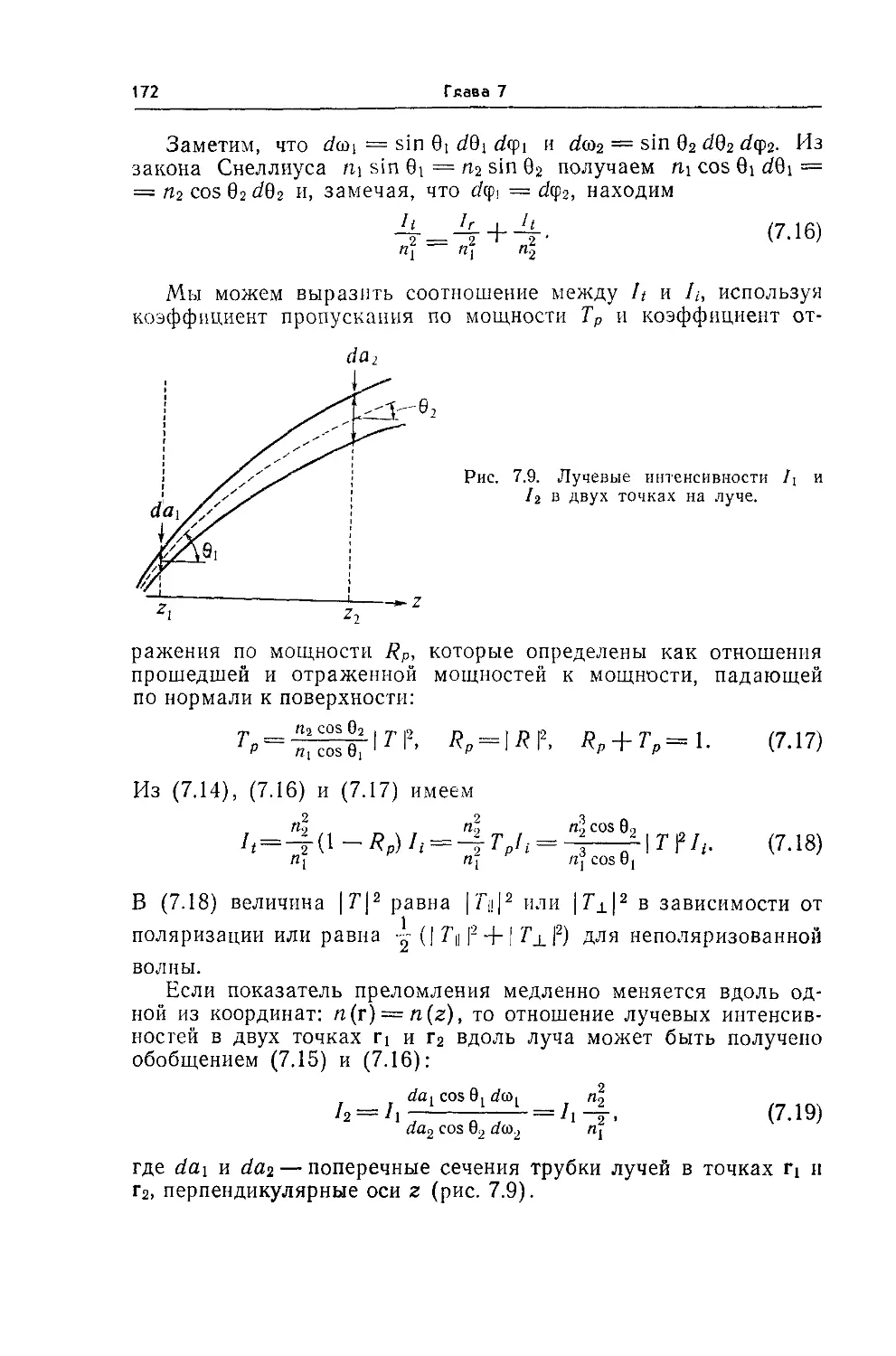
7.1. Лучевая интенсивность, поток и плотность энергии 165
7.2. Лучевая интенсивность в свободном пространстве и на границах 169
раздела однородных сред
7.3. Дифференциальное уравнение для лучевой интенсивности 173
7.4. Ослабленная падающая интенсивность, диффузная интенсивность, 176
граничное условие и функция источника
7.5. Интегральная форма уравнения переноса 178
7.6. Эффективная площадь антенны и принимаемая мощность 181
7.7. Уравнение переноса для частично поляризованной электромагнитной 183
волны
7.8. Связь лучевой: интенсивности с вектором Пойнтинга 185
Глава 8. Приближенные решения для разреженной среды 187
8.1. Лучевая интенсивность в приближении первого порядка теории 188
многократного рассеяния
8.2. Падение плоской волны на плоскопараллельную среду 189
8.3. Падение коллимированного пучка на плоскопараллельную среду 192
Глава 9. Диффузионное приближение 195
9.1. Вывод диффузионного уравнения 195
9.2. Граничные условия 199
9.3. Падение коллимированного пучка на слой рассеивающих частиц 201
9.4. Решение для случая плоской волны, падающей на слой рассеивающих 202
частиц
9.5. Решение для случая коллимированного пучка конечной ширины, 204
падающего на слой рассеивающих частиц
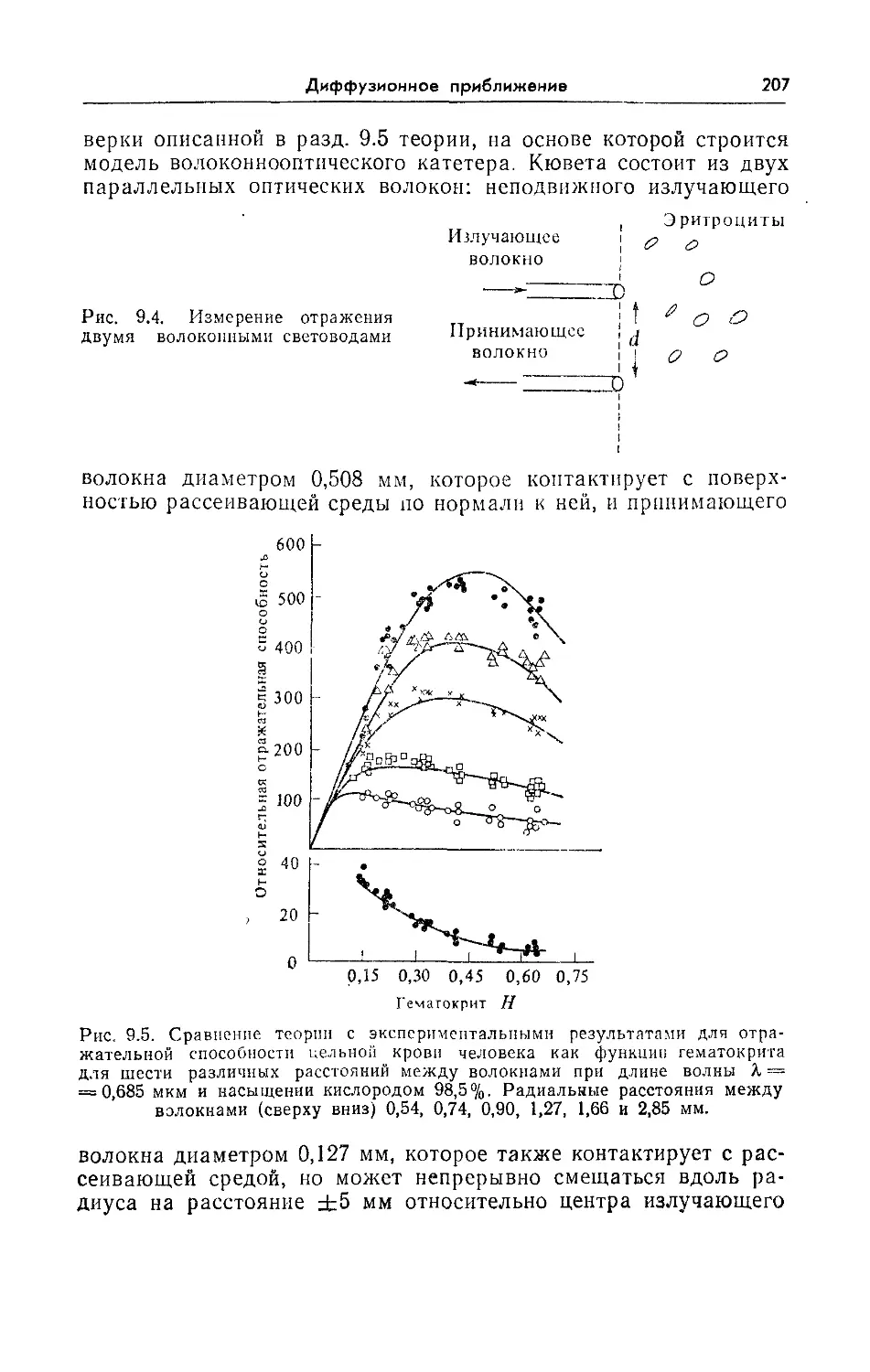
9.6. Диффузия от точечного источника 206
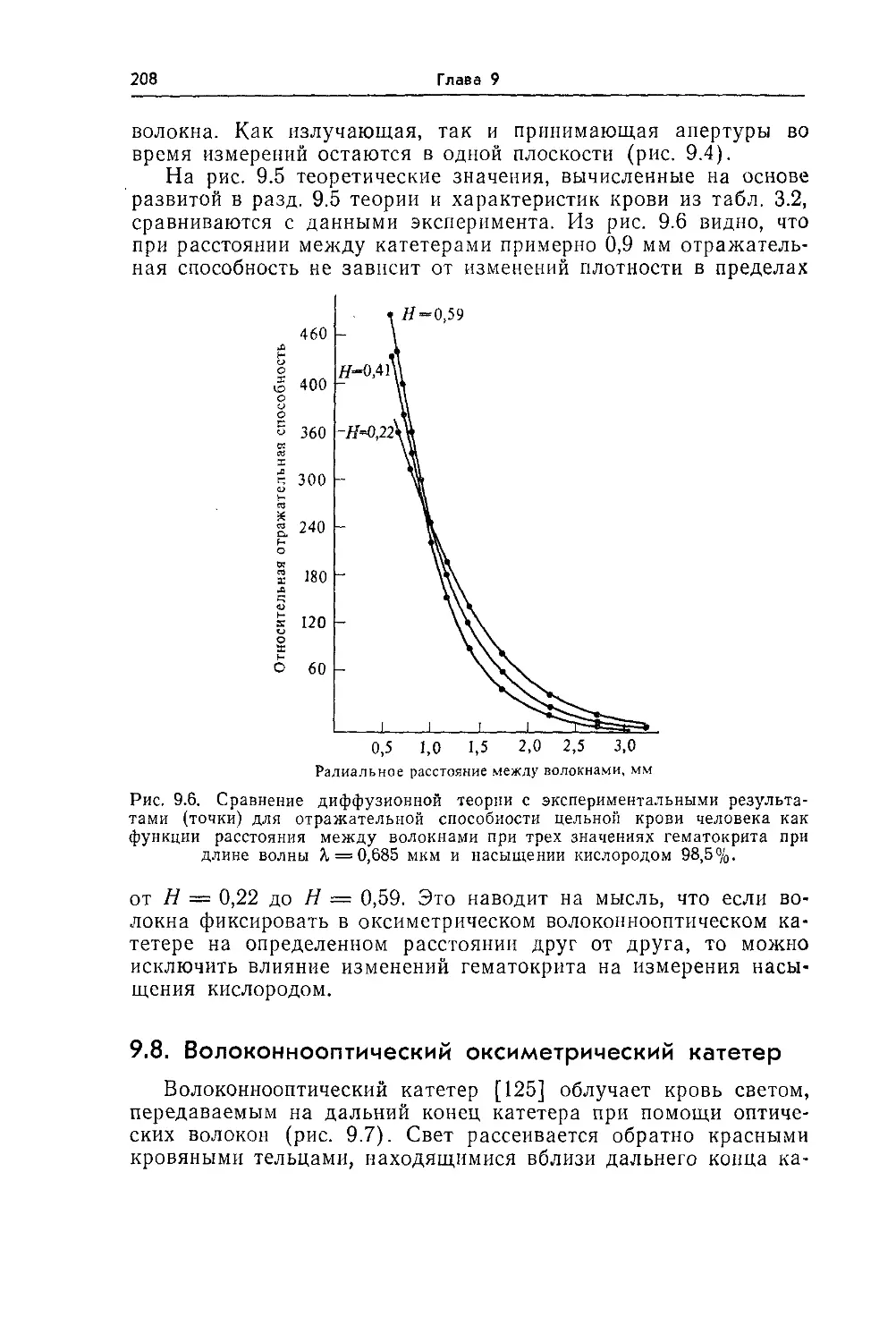
9.7. Измерение отражения с помощью двух волоконных световодов 206
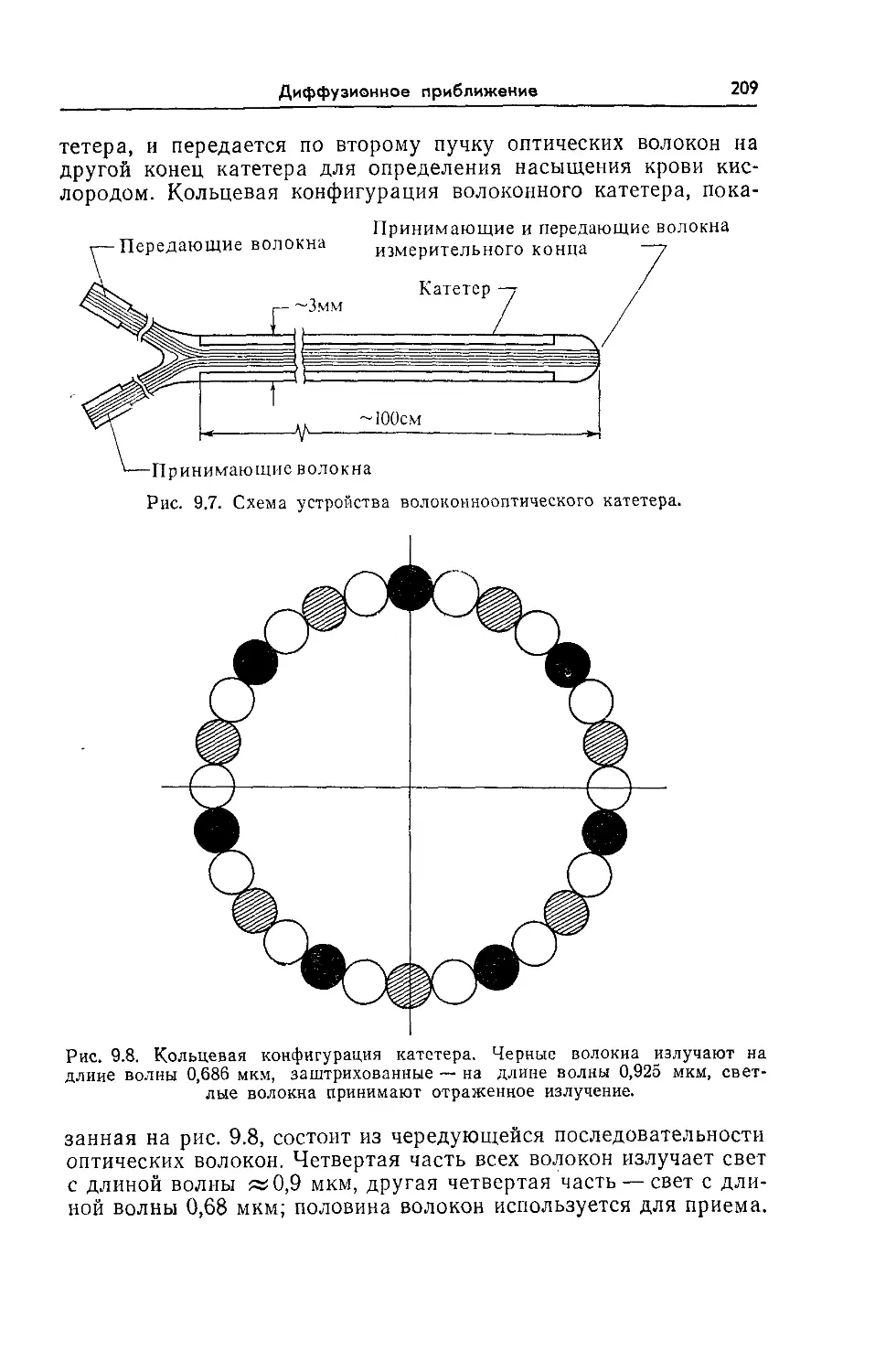
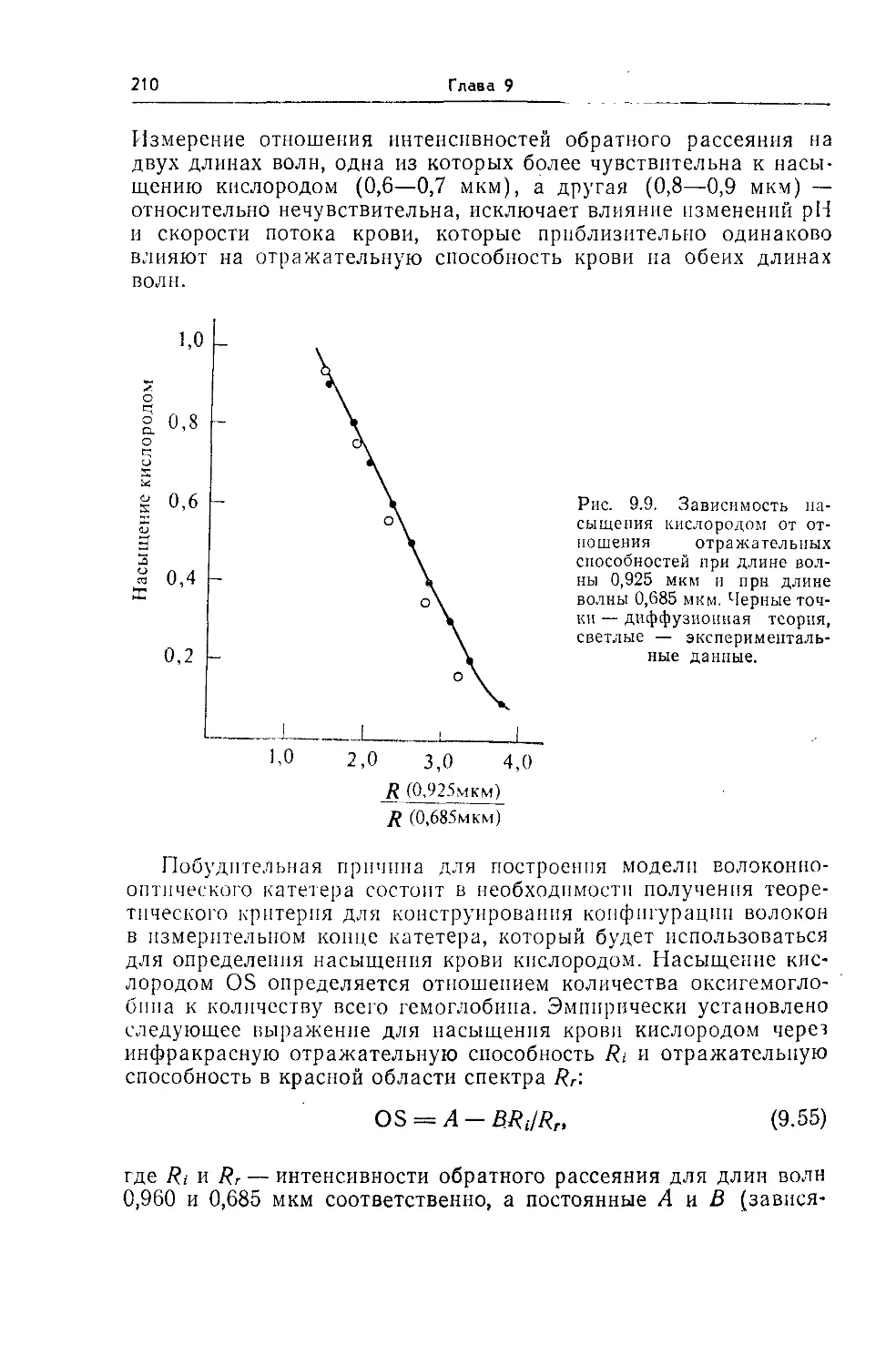
9.8. Волоконнооптический оксиметрический катетер 208
Глава 10. Двухпотоковая и четырехпотоковая теории 212
10.1 Двухпотоковая теория Кубелки и Мунка 212
10.2. Коэффициенты К и S в двухпотоковой теории 216
10.3. Четырехпотоковая теория 217
Приложение 10А 220
Глава 11. Плоскопараллельная задача 224
11.1 Нормальное падение плоской волны на плоскопараллельный слой 225
11.2. Типичные фазовые функции 227
11.3. Квадратурная формула Гаусса 228
11.4. Общее решение 231
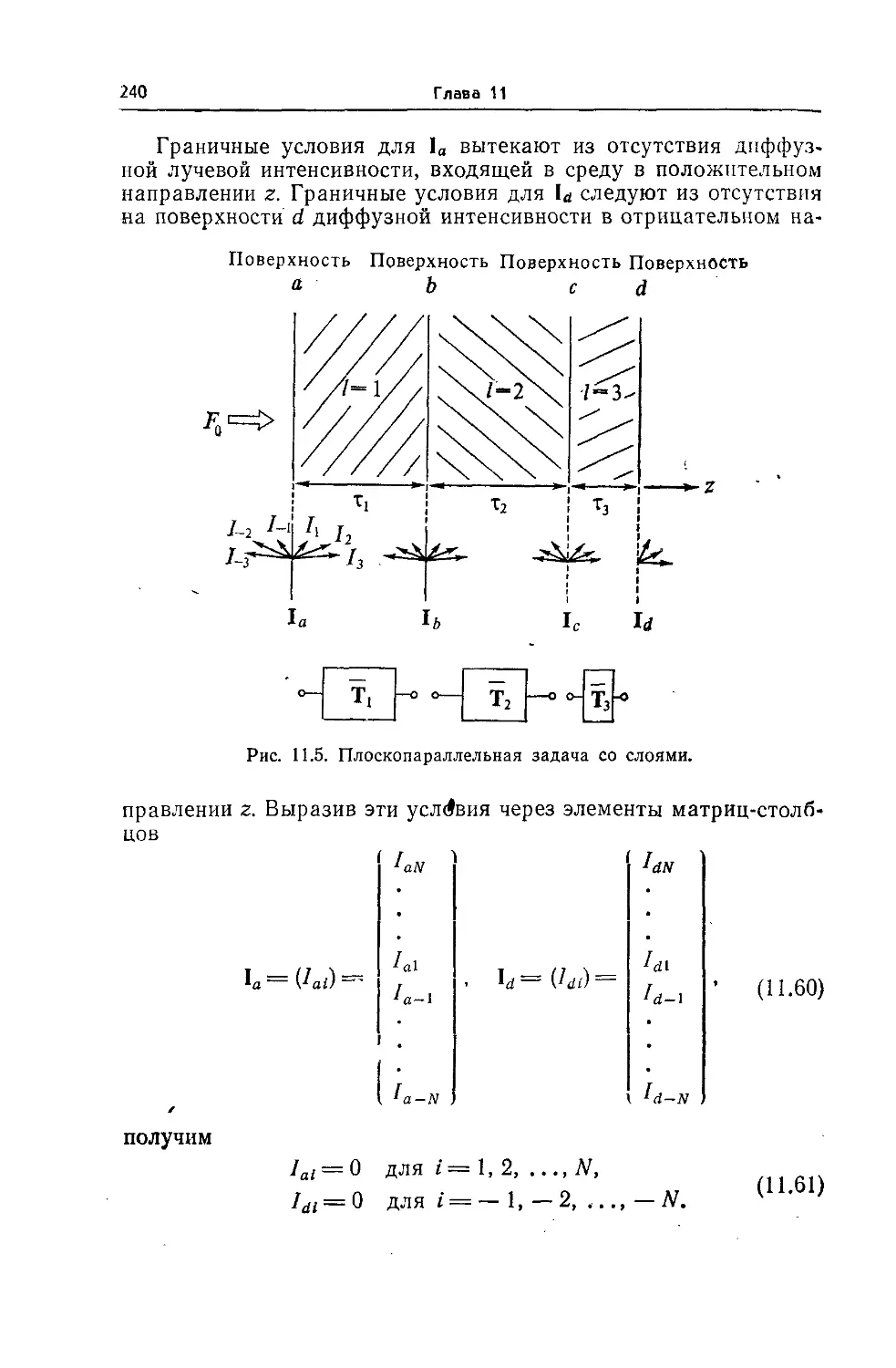
11.5. Полубесконечная среда 238
11.6. Наклонное падение и другие методы. 238
11.7. Слоистая плоскопараллельная среда 239
11.8. Некоторые смежные проблемы 242
Глава 12. Изотропное рассеяние 243
12.1. Метод преобразования Фурье для изотропного рассеяния 244
12.2. Диффузия и явления ближнего поля 249
12.3. Излучение при произвольной падающей интенсивности 251
12.4. Излучение в случае направленной сферической падающей волны 252
12.6. Излучение при произвольном распределении источников 254
12.6. Изотропное рассеяние в конечном объеме и проблема Милна 256
Глава 18. Приближение для больших частиц 258
13.1. Вывод дифференциального уравнения в малоугловом приближении 258
13.2. Общее решение 260
13.3. Приближенное решение для случая медленного углового изменения 263
диффузной интенсивности
Литература 268
Предметный указатель 274
Предметный
Альбедо поверхности и дна океана
192
— частицы 20, 174, 189
Аэрозоль 54
Биоакустика 79
Биооптика 75
Биоэлектродинамика 62
Ближнего поля явления 249
Видимость 62
— оптическая 62
ВКБ-приближение 34
Волна неполяризованная 43
— плоская импульсная 143
— сферическая падающая 252
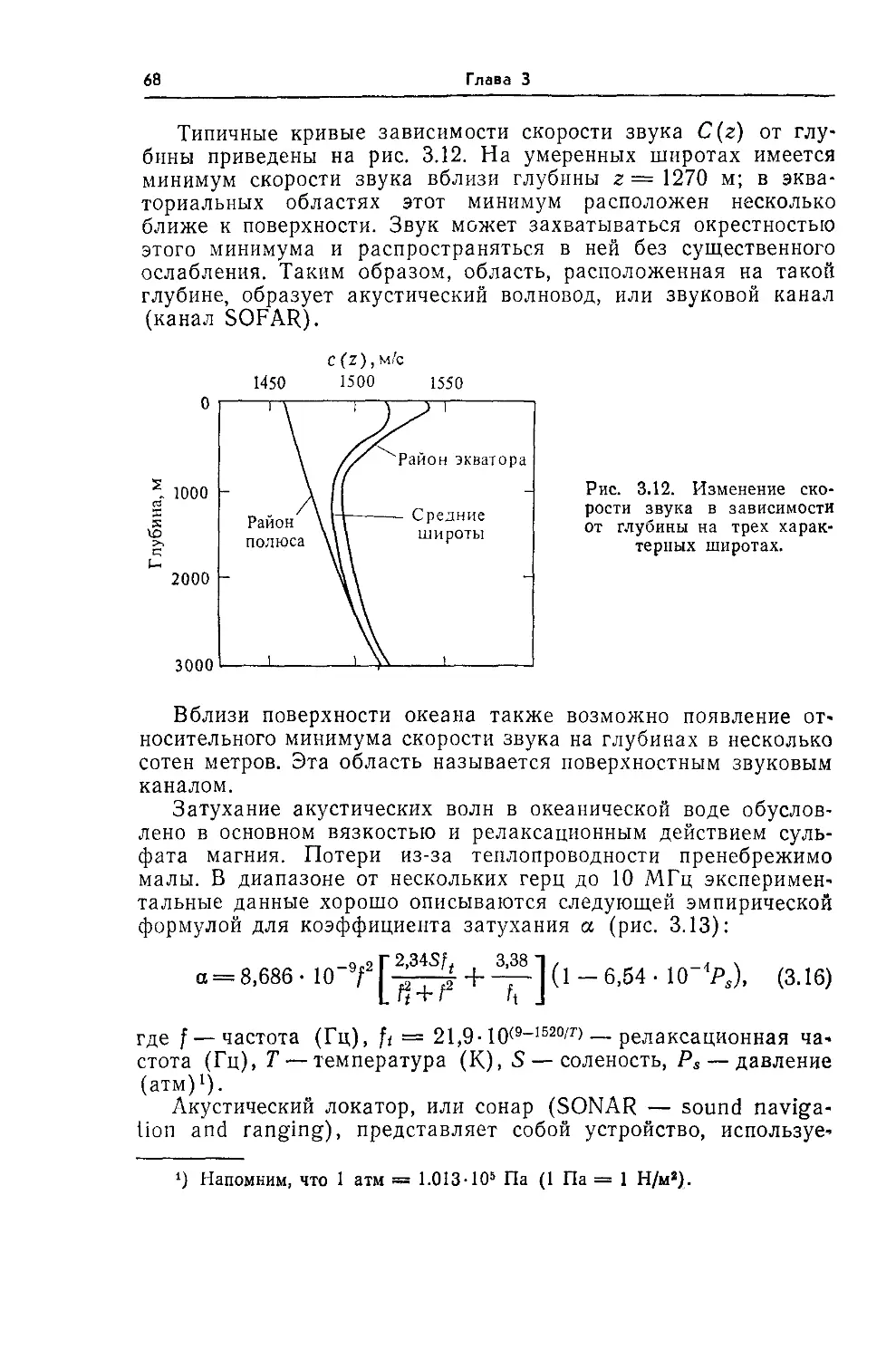
Волновод акустический 68
Волны акустические 48
— частично поляризованные 183
Время когерентности 113, 150
Гамма-распределение
модифицированное 57
Гематокрит 76, 79, 207
Герца вектор 24
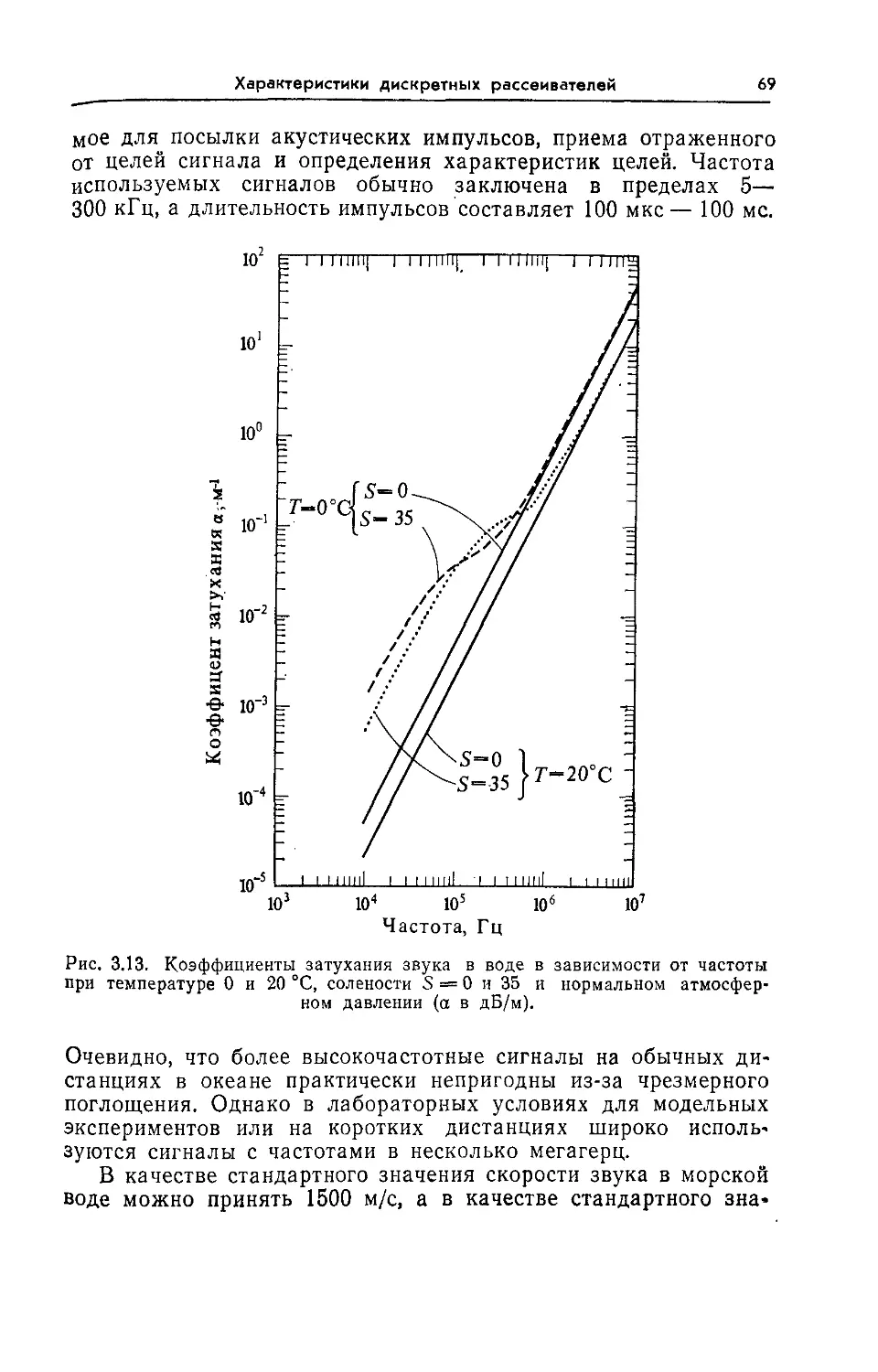
Гидроакустика 66
Гидрометеоры 54
Гидрооптика 64
Град, оптические и СВЧ-свойства 63
указатель
Граничные условия для
двухпотоковой теории 214
диффузной интенсивности
176, 199
лучевых интенсивностей на
границе однородных сред 171
четырехпотоковой теории
219
Двухпотоковая теория 212
Диаграмма направленности по
мощности 84
— неопределенности 129
Диаграммы ширина на уровне
половинной мощности 89
Диаметр медианный дождевых
капель 56
Диатермия 74
Дисперсия флуктуации
интенсивности 93
Диффузии длина 246
Диффузия от точечного источника
206
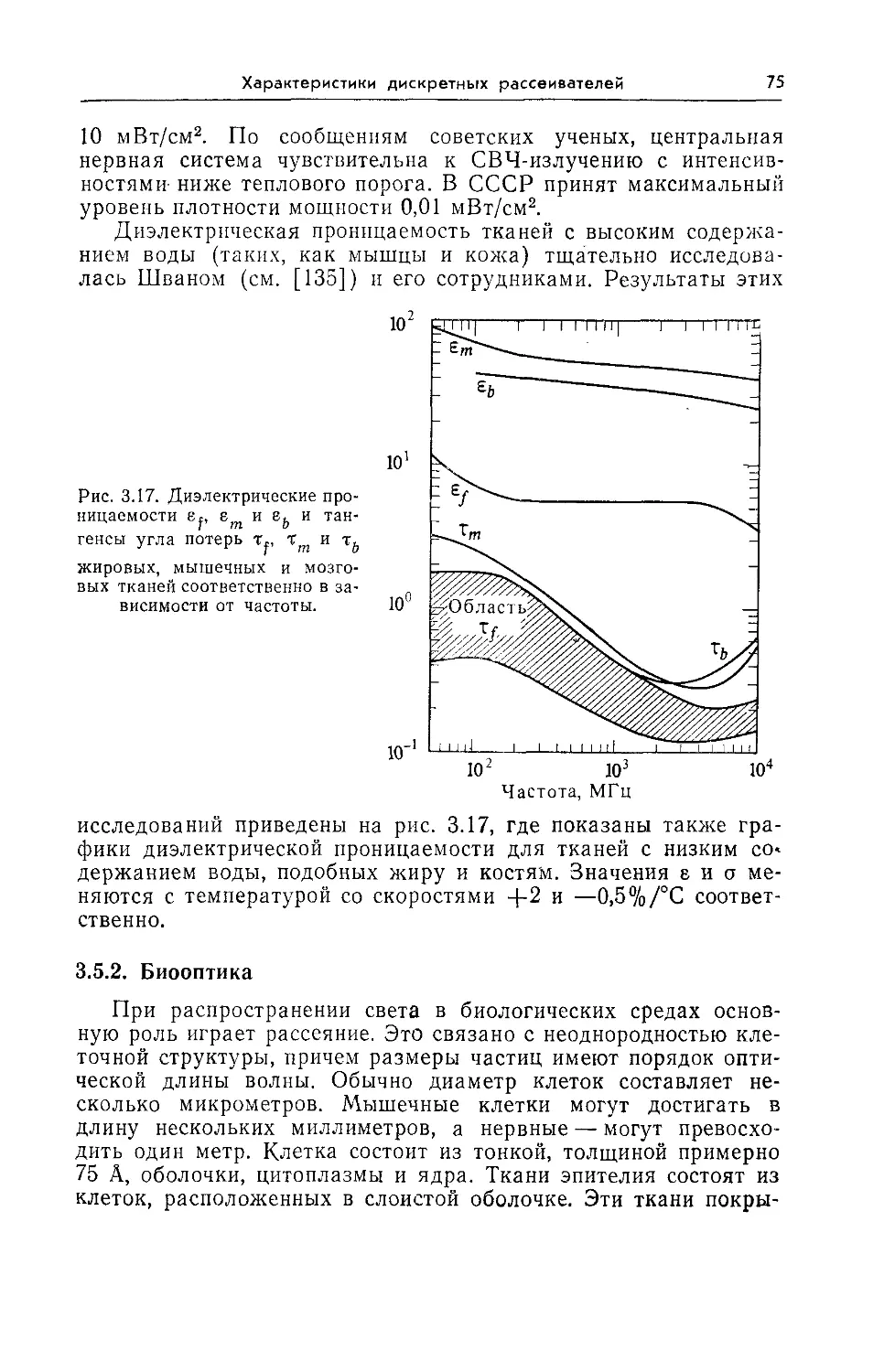
Диэлектрическая проницаемость
жировой, мышечной и мозговой
тканей 75
Длина свободного пробега для
изотропного рассеяния 247
Доплеровский сдвиг 97
Дымка, оптические и СВЧ-свойства
62
Естественный свет 42
Закон диффузного отражения 191
— затенения 225
— Кирхгофа излучения черного тела
178
— Ламберта 169
— Ламберта — Вира 76
— Юнга 65
Затухание в дожде 59
Зона Френеля 157
Излучатель остронаправленный 118
Излучение диска 255
— изотропное 169
Измерение отражения 207
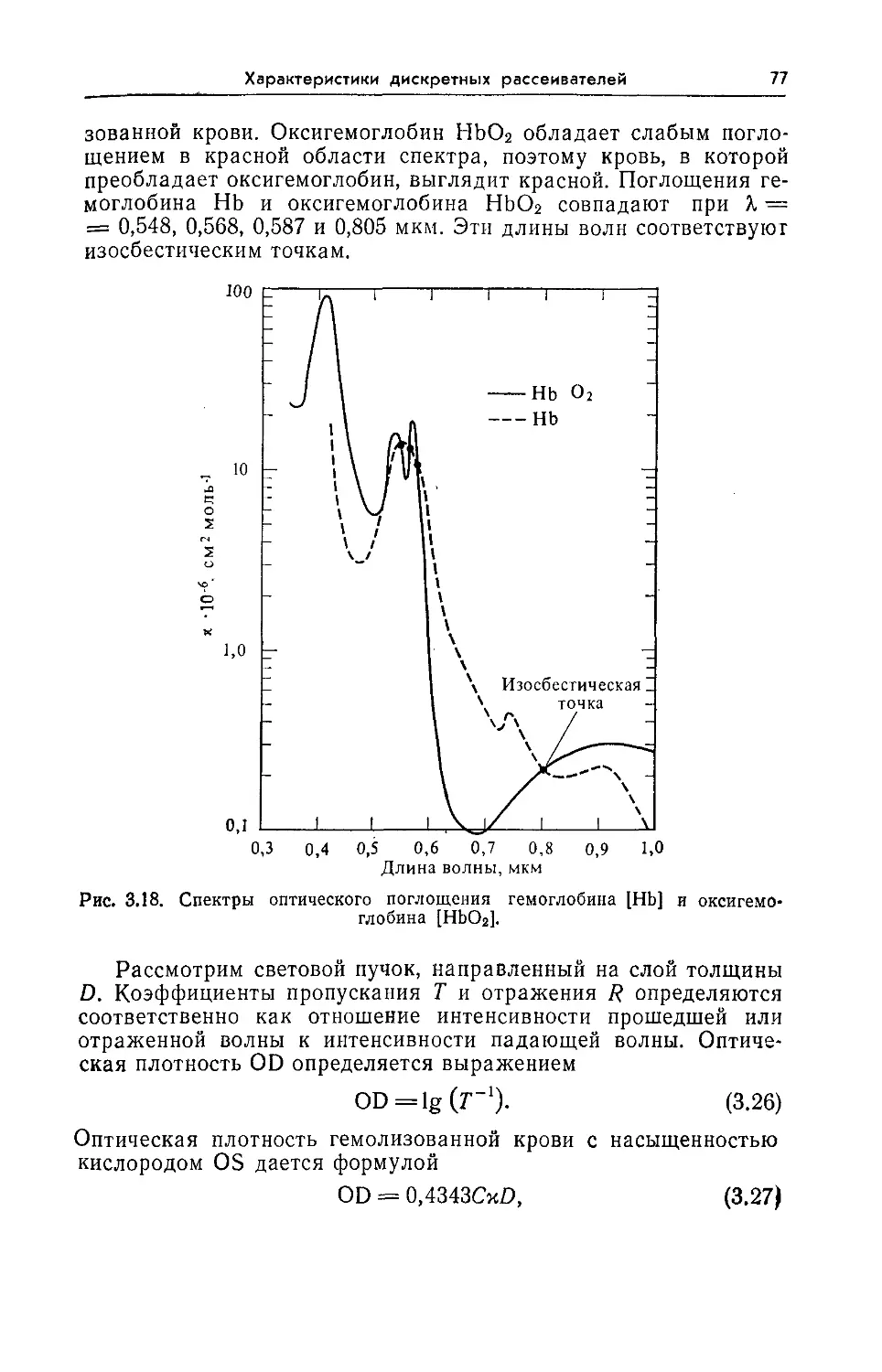
Изосбестические точки 77
Импеданс акустический
характеристический 51
Импульс, распространение и
рассеяние 108
между передатчиком и
приемником 151
— узкополосный 109
— уширение 113
Инвариантное погружение 239
Индикатор дальность—высота (ИДВ)
53
— движущихся целей (ИДЦ) 133
— кругового обзора (ИКО) 53
— типа А 53
Интенсивность диффузная 176, 188
—. когерентная 92, 137
— коллимированная 177
— некогерентная 92
— падающая ослабленная 179,188
— поверхностная 166
— поля 165
— средняя 169
Канал звуковой 68
— с некоррелированным рассеянием
114
— стационарный 114
— — с некоррелированным
рассеянием 114, 117, 129
— SOFAR 68
Катетер волоконнооптический 206,
209
— оксиметрический 208
Кирхгофа закон 178
Когерентности полоса
113
Концентрация 84
— бактерий 192, 194
Корреляционная функция временная
99, 141, 159
Корреляция рассеянного поля
пространственная 101
Косинус угла рассеяния средний 197
Коэффициент использования
апертуры 90
— поглощения 64
— полного затухания 64
— усиления 90
Красные кровяные тельца 76
Кровь гемолизованная 76
— ультразвуковые свойства 80
— характеристики и сечения 78
Лагранжев подход, описание
акустических волн 48
Локатор акустический 52, 68
— лазерный 52
Лучевая интенсивность 165
измерение 167
коллимированного пучка 193
на плоской границе 171
— — постоянство в свободном
пространстве 169
Малоугловое приближение 258
Метод перевала 150
Ми решение 37
Милна проблема 201, 256
Многократного рассеяния теория 181
Тверского 163, 181
Многократное рассеяние 84, 163
Насыщенность кислородом 76, 78,
207
Нефть, акустические свойства 70
Облака, оптические и СВЧ-
характеристики 62
Огибающая комплексная
модулированного сигнала ПО
Океаническое дно, альбедо 192
площадь 67
Оксиметрия 78
Оптическая плотность 77
— теорема 23
Оптический путь 86, 135, 179
Осадки, интенсивность выпадения 55
Освещенность 168
Отражение диффузное 191
и прохождение 224
— от облаков при оптической
локации 121
Первый порядок теории
многократного рассеяния 82,
86, 187
Плоскопараллельная среда 189, 224
Плотность потока,
распространяющегося назад 167
вперед 167
— энергии 165, 168
Площадь эффективная приемной
апертуры 85
Поглощение света в чистой воде 64
Пойнтинга вектор 185
Показатель преломления воды и льда
59
Поле когерентное 92
— некогерентное 92
— среднее 92,137
— флуктуационное 92, 137
Поляризация частичная 42
— эллиптическая 40
Поперечное сечение пучка
среднеквадратичное 267
Потенциал скоростей 49
Поток в теории переноса 165
Приближение борцовское 31, 86
— диффузионное 83
— однократного рассеяния 82, 84
Приемник движущийся 103
Принцип инвариантности 239
Пуанкаре сфера 42
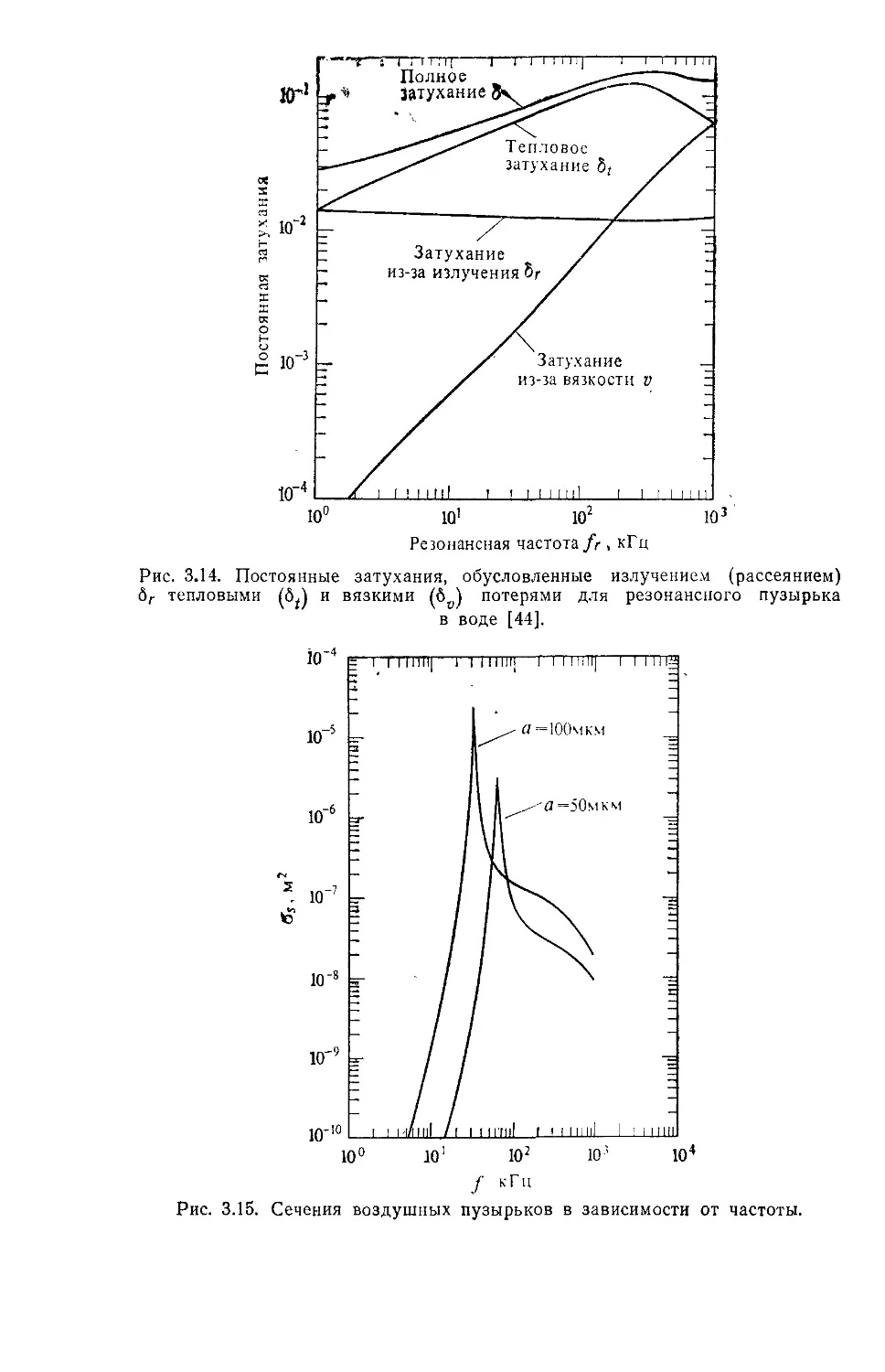
Пузырьки воздушные 70
Пучок коллимированный 192, 201,
204, 217
— оптический, флуктуации в дожде
160
— размер 193
Радиолокатор доплеровский 130
импульсный 53, 130, 133
— когерентный 53, 130
— метеорологический 52
— некогерентный 53
— обычный 53
— однопозиционный 86
Разреженная среда 187
Распределение вероятностей
рассеянного поля 104
— дождевых капель по размерам 55,
123
— Лоу и Парсонса 56
— Маршалла и Палмера 55, 160
— по размерам 47, 55, 123
— Рэлея 105
— угловое 263
— частиц по размерам 47
Распространение волн в облаке
больших частиц 258
пределах прямой видимости
134
Рассеиватели в атмосфере 32
биологических средах 54
океане 52
Рассеяние акустических волн 50
— звука в воде 66
— изотропное 243
— импульса бистатическое 126
обратное 118
для передатчика с широкой
диаграммой направленности \2о
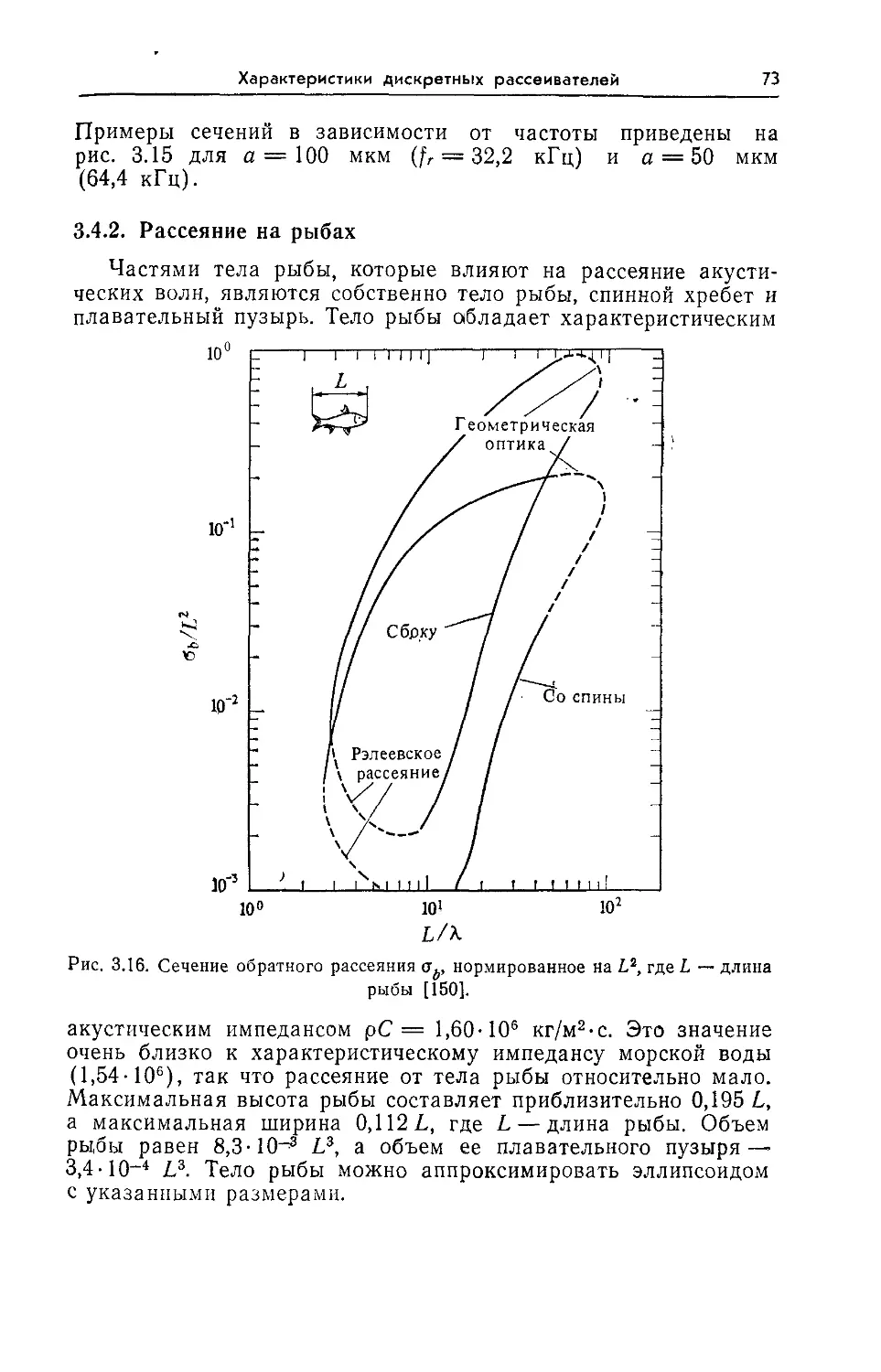
— на биологических средах 74—81
воздушных пузырьках 70
круглом диске 33
однородной сфере 32
— — случайно ориентированной
частице 34
— обратное от дождя 91
— рэлеевское 27, 28
— — на сфероидальном
диэлекрическом теле 30
— Рэлея —Дебая 31
Рассеяния амплитуда 18, 25
большой сферы 140
— коэффициент 64
Расходимость угловая 266
Рытова приближение 153
Светимость энергетическая 168
СВЧ-излучение, максимальная
безопасная плотность
мощности 74, 75
обратное рассеяние от дождя 91
— нагреватель 74
Сечение 17
— геометрическое 20
— дифференциальное рассеяния 19
— крови 78
— обратного рассеяния частицы 19
слоя 91
— поглощения 20, 26
— полное 19
— рассеяния 17
бистатическое 85
единичного объема морской
воды (свет) 65
зависящее от времени 94
Сжимаемость 49
Скорость звука в воде, воздухе и
нефти 67, 70
— «слепая» доплеровского
радиолокатора 132
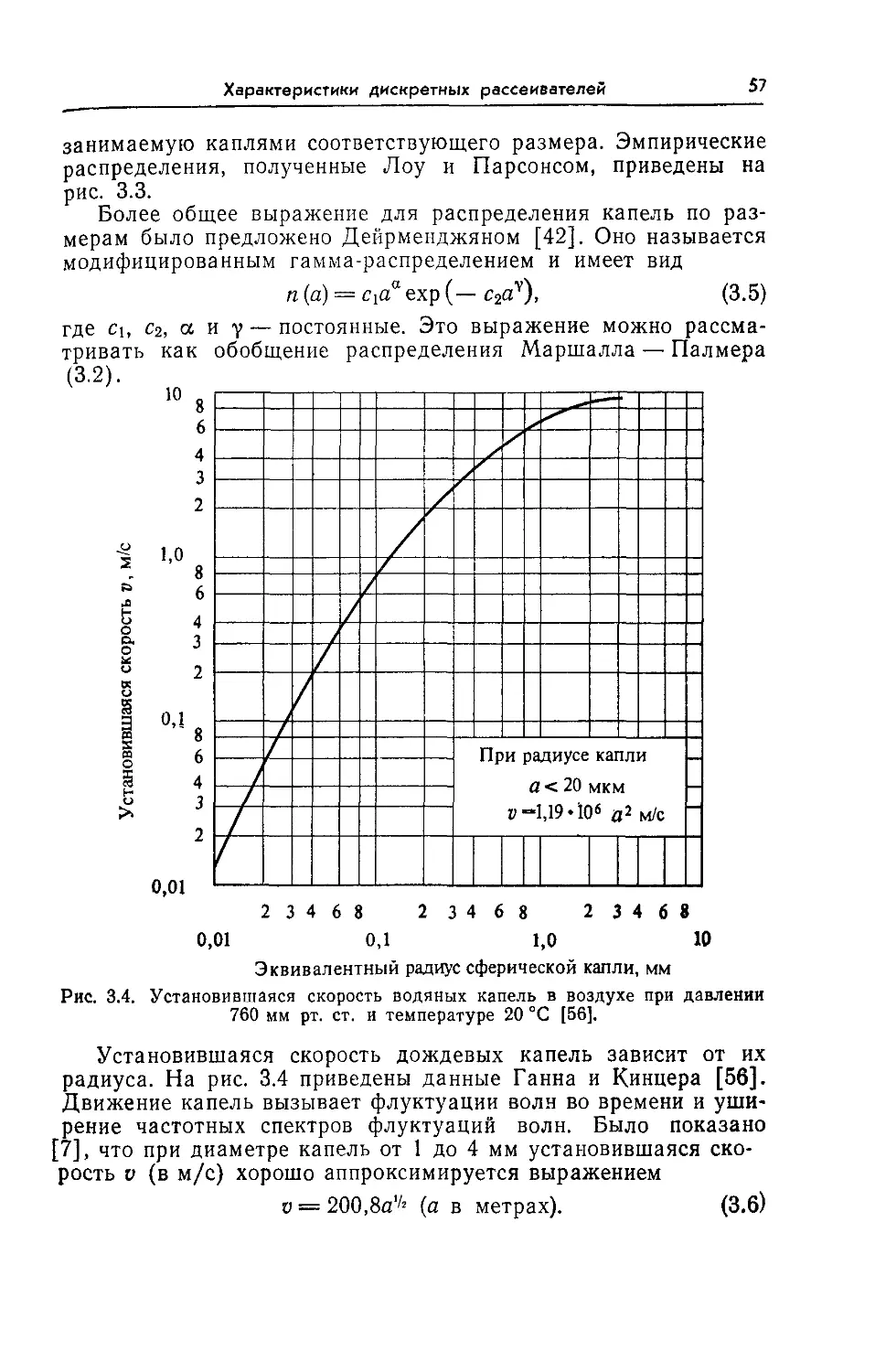
— установившаяся дождевых капель
57
— частицы 95
Среда слоистая плоскопараллельная
239
— случайная нестационарная 108
Смешанный момент, двухчастотный
111
Смог 62
Снег 63
Собственное значение 233
Собственный вектор 233
Сохранение энергии 175
Спектр угловой 263
— уширение 113
— частотный 93, 99, 142
волны, распространяющейся в
дожде 143, 160
флуктуации волн 159
Среда полубесконечная 238
Стационарная случайная функция 93
Стокса матрица 43, 184
параметры 40, 183
преобразование при повороте
системы координат 45
Теория двухпотоковая Кубелки и
Мунка 212
— переноса излучения 164, 173
нейтронов 164
— четырехпотоковая 217
Тепловое излучение 242
Термоклин 67
Ткани мышечные, диэлектрическая
проницаемость 75
Туман, оптические и СВЧ-свойства
62
Угол ориентационный дождевой
капли 55
Узкая диаграмма направленности 88
Уравнение Больцмана 164, 173
— волновое акустическое 49
— диффузионное 199, 250
— интегральное Шварцшильда—
Милна 257
— Максвелла — Больцмана со
столкновениями 164
— переноса 164,173
интегральная форма 178
— радиолокации 85
бистатическое 85
—Дайсона и Бете — Солпитера 181
Фаза комплексная в методе Рытова
153
Фазовая матрица 184
Флуктуации интенсивности 93
— фазы 153
Формула интерполяционная
Лагранжа 229
— квадратурная 229
Гаусса 228, 230
—Хени — Гринстейна 198
Функция взаимной когерентности
164
двухчастотная 111
— источника 175
— корреляционная 93
Функция неопределенности 128, 129
— передачи ПО
нестационарная 110
— фазовая 19, 174, 227
Рэлея 223
— фильтрующая по углам 157
— характеристическая флуктуации
скорости 96
Характеристики рассеяния и
поглощения дождя 55
Центральная предельная теорема 104
Частицы в морской воде 64, 65
— вращательное движение 98
— движущиеся 94
Частота повторения импульсов 53,
124
— резонансная воздушных
пузырьков в воде 71
Число Кристофеля 229
Ширина луча передающей антенны
89
Эйлерово описание акустических
волн 48
Экстинкции парадокс 20
Эритроциты 76
Ядра Айткена 54
Предисловие к русскому изданию
Исследование флуктуационных явлений при распростране-
распространении волн в случайно-неоднородных средах привлекает все боль-
большее внимание специалистов самых разных областей современ-
современной науки и техники, таких как оптика, акустика, радиофизика,
.астрономия, техника связи, радиолокация и радионавигация,
биология. Поэтому в настоящее время ощущается острая по-
потребность в таком пособии по распространению и рассеянию
волн в случайно-неоднородных средах, которое с одной стороны
было бы доступно для неспециалистов в этой области, а с дру-
другой — давало бы достаточно полное и строгое представление
о предмете.
Двухтомная монография А. Исимару, на наш взгляд, вполне
удовлетворяет этим требованиям. В ней рассматриваются все
основные понятия теории, подробно анализируются все наибо-
наиболее полезные с точки зрения приложений теоретические методы
и детально описываются эффекты, возникающие при распро-
распространении электромагнитных и акустических волн в случайно-
неоднородных средах и при рассеянии на шероховатых поверх-
поверхностях. Существенным достоинством монографии является то,
что наряду с традиционными вопросами в ней затронуты и по-
последние достижения в этой области, в частности теория силь-
сильных флуктуации. В целом монография Исимару является осно-
основательным и квалифицированным введением в статистическую
теорию распространения и рассеяния волн и охватывает все
основные разделы этой теории.
В отличие от большинства книг подобного рода автор уде-
уделяет большое внимание практическим приложениям. Так, весь-
весьма подробно анализируется распространение и рассеяние на-
направленных волновых пучков и импульсных сигналов, изла-
излагаются принципы дистанционного зондирования в биологии и
геофизике, рассматриваются вопросы адаптивной оптики и т. д.
Единый подход к изложению материала делает монографию
методически стройной и удобной для эффективного изучения
предмета. В немалой степени этому способствует и весьма пол-
полная библиография, включающая большое число работ как за-
зарубежных, так и советских авторов.
Предлагаемый перевод монографии Исимару на русский
язык, по нашему мнению, будет полезным для научных работ-
работников и инженеров, а также для аспирантов и студентов таких
специальностей, как атмосферная оптика, астрономия, геофи-
геофизика, радиолокация, связь, метеорология, океанология и др.
Член-корр. АН СССР В. И. Татарский
Предисловие
Проблема распространения и рассеяния волн в атмосфере,
океане и биологических средах в последние годы становится все
более важной, особенно в таких областях науки и техники как
связь, дистанционное зондирование и обнаружение. Свойства
указанных сред, вообще говоря, подвержены случайным изме-
изменениям в пространстве и времени, в результате чего амплитуда
и фаза распространяющихся в них волн также могут претер-
претерпевать пространственно-временные флуктуации. Эти флуктуации
и рассеяние волн играют важную роль во многих проблемах,
представляющих практический интерес. При рассмотрении во-
вопросов связи приходится сталкиваться с амплитудно-фазовыми
флуктуациями волн, распространяющихся в турбулентной ат-
атмосфере и турбулентном океане, а также с такими понятиями,
как время когерентности и полоса когерентности волн в среде.
Рассеянные' турбулентной средой волны можно использовать
для установления загоризонтной связи. Диагностика турбулент-
турбулентности прозрачного воздуха, основанная на рассеянии волн, даег
существенный вклад в решение вопроса о безопасной навигации.
Геофизики интересуются флуктуациями волн, возникающими
при их распространении через атмосферы планет, и таким спо-
способом получают информацию о турбулентности и динамических
характеристиках этих атмосфер. Биологи могут использовать
флуктуации и рассеяние акустических волн с диагностическими
целями. В радиолокации могут возникать мешающие эхо-сиг-
эхо-сигналы от ураганов, дождя, снега или града. Зондирование гео-
геологических сред с помощью электромагнитных и акустических
волн требует знания характеристик, рассеяния случайно распре-
распределенных в пространстве неоднородностей. Упомянем, наконец,
недавно возникшую область океанографии — радиоокеаногра-
радиоокеанографию (исследование свойств океана по рассеянию радиоволн).
Центральным пунктом этой методики является знание характе-
характеристик волн, рассеянных на шероховатой поверхности.
Все перечисленные проблемы отличаются статистическим
описанием волн и сред распространения. Эта характерная черта
позволяет ввести основные понятия, общие для всех указанных
проблем. В данной книге мы намерены дать единое и система-
систематическое изложение основных вопросов распространения и рас-
рассеяния волн в случайных средах. Это непростая задача, но мы
надеемся, что читатели смогут уловить общие идеи, несмотря на
Предисловие
различие формулировок и обилие областей, охваченных в этой
книге. Следует подчеркнуть, что в связи с различием природы
проблем для получения полезных результатов приходится ис-
использовать разные приближенные методы. Поэтому мы дадим
систематическое описание используемых приближенных мето-
методов, применимых для широкого класса задач.
Дистанционное зондирование геофизических и метеорологи-
метеорологических параметров методами, основанными на распространении
и рассеянии волн, стало чрезвычайно важным и полезным сред-
средством изучения структуры и динамики атмосферы. Получаемые
таким образом сведения используются для улучшения качества
прогноза погоды, для разработки методов искусственного воз-
действия на погоду, для исследования загрязнений атмосферы
и для повышения безопасности воздушного сообщения. Обзор
современного состояния исследований в этой области служит
введением для последующего* изучения более общих методов
дистанционного зондирования.
Таким образом, предлагаемая книга предназначена для ин-
инженеров и научных работников, интересующихся вопросами
распространения и рассеяния оптического, акустического и СВЧ
излучения в атмосферах планет, в океанах и в биологических
средах, особенно для тех из них, кто занимается проблемами
связи в таких средах и вопросами дистанционного зондирования
свойств этих сред. Данную книгу можно рассматривать как вве-
дение в круг основных понятий и результатов статистической тео-
теории распространения волн. Включенное в книгу систематическое
описание теории переноса излучения и теории многократного
рассеяния представляет интерес также для химиков, гео-
геофизиков и специалистов в области ядерной физики. Предвари-
Предварительная подготовка, необходимая для понимания книги, пред-
предполагает некоторое знакомство с методами решения волновых
уравнений, уравнений Максвелла, с векторным исчислением,
рядами и интегралами Фурье.
Рассматриваемые в книге вопросы можно разбить на три
группы: волны в случайных облаках дискретных рассеивателеи,
волны в сплошных случайных средах и рассеяние волн на ше-
шероховатой поверхности. Случайные облака дискретных рассей*
вателей представляют собой случайное распределение в про-
пространстве множества частиц. Их примерами являются дождь,
туман, смог, град, частицы в океане, красные кровяные тельца
в крови, молекулы полимеров и другие частицы, совершающие
броуновское движение. Сплошные случайные среды — это сре-
среды, свойства которых меняются случайно и непрерывно во вре-
времени и в пространстве. В качестве примеров приведем турбу*
лентность чистого воздуха, выхлопные струи двигателей, тропо-
тропосферную и ионосферную турбулентность, турбулентность океана
Предисловие
и биологические среды, такие как биологические ткани и мышцы.
Примерами шероховатых поверхностей являются поверхность
океана, поверхности планет, границы раздела между различ-
различными биологическими средами и негладкие поверхности свето-
световодов.
В первом томе монографии (части I и II) рассматриваются
теория однократного рассеяния и теория переноса излучения.
Теория однократного рассеяния применима для описания рас-
рассеяния волн в разреженных облаках рассеивателей. Она охва-
охватывает большое число встречающихся на практике ситуаций,
включая радиолокацию, а также лазерную и акустическую ло-
локацию в различных средах. Относительная математическая про-
простота этой теории позволяет без излишних трудностей ввести
большинство фундаментальных понятий, таких как полоса ко-
когерентности, время когерентности, временная частота, и рас-
рассмотреть движение рассеивателей и распространение импуль-
импульсов. Мы приводим также некоторые оценочные значения харак-
характеристик частиц в атмосфере, океане и в .биологических средах.
Теория переноса излучения, которую также называют кратко
теорией переноса, имеет дело с изменением интенсивности вол-
волны, распространяющейся через случайное облако рассеивате-
рассеивателей. Эта теория используется при решении многих задач рас-
рассеяния оптического и СВЧ излучения в атмосфере и биологиче-
биологических средах. В книге описываются различные приближенные
способы решения, включая диффузионное приближение, метод
Кубелки — Мунка, плоскослоистое приближение, приближение
изотропного рассеяния и малоугловое приближение.
Во втором томе (части III, IV и V) приводится большое ко-
количество новых результатов, полученных в последнее время в
теории распространения и рассеяния волн в случайных средах.
Часть III посвящена теории многократного рассеяния волн в
случайных облаках рассеивателей. Часть IV охватывает теорию
слабых и сильных флуктуации волн в сплошных случайных
средах и в турбулентности. В части V даны основы теории рас-
рассеяния волн на шероховатой поверхности и дистанционного зон-
зондирования свойств случайных сред, включая некоторые важные
вопросы решения обратных задач.
От автора
В основу этой книги положен курс лекций, подготовленный
автором для аспирантов первого года обучения по специаль-
специальности «Волны в случайных средах» и читавшийся им на элек-
электротехническом факультете Вашингтонского университета на
протяжении нескольких последних лет. Материалы этой книги
использовались также при чтении в 1973 и 1974 г. недельного
курса лекций по теории волн в случайных средах и ее приме-
нениям в Университетском колледже Лос-Анджелеса.
Автор выражает признательность своим коллегам и аспи-
аспирантам, сделавшим много полезных замечаний. Особую благо-
благодарность он приносит Зигельману и Карлсону из Вашингтон-
Вашингтонского университета, Ричарду. By из Лаборатории реактивного
движения, Кавуру Йе из Университетского колледжа Лос-Анд-
Лос-Анджелеса, Курту Джонсону из Университета штата Юта, Виктору
Тверскому из Иллинойсского университета (Чикагское отделе-
отделение), Маркувицу из Нью-Йоркского политехнического инсти-
института и Келлеру из Нью-Йоркского университета (Курантовский
институт) за полезные обсуждения, советы и поддержку. Зна-
Значительная часть работы над. этой книгой выполнялась при под-
поддержке Электротехнического общества (ранее Кембриджская
исследовательская лаборатория ВВС), Национального научного
фонда и Национального института здоровья. Автор признателен
также миссис Эйлин Флюэллинг за оказанную помощь при под-
подготовке рукописи и квалифицированную перепечатку.
Глава 1
Введение
Во многих задачах распространения- и рассеяния волн среду,
в которой проходит волна, можно рассматривать либо как де-
детерминированную, либо как случайную. По детерминированным
задачам проведено большое количество исследований; сюда от-
относятся, например, теория антенн различного типа, теория ди-
дифракции и рассеяния, направленные волны. В -отличие от этих
задач многие природные и биологические среды испытывают
случайные изменения во времени и в пространстве. Поэтому
волны в таких средах претерпевают случайные изменения ам-
амплитуды и фазы, так что их описание должно проводиться на
языке статистических средних величин и распределений вероят-
вероятности. В данной книге мы обращаемся к следующим вопросам:
как волна взаимодействует со случайной средой, как эти взаи-
взаимодействия формулируются и выражаются математически и как
получить решения большого класса практически важных задач.
Монография разделена на пять частей. Первый том содер-
содержит части I и II. В части I (гл. 2—6) рассматривается рас-
рассеяние и распространение волн в разреженных случайных об-
облаках рассеивателей. Здесь для объяснения фундаментальных
понятий теории флуктуации волн в случайных средах исполь-
используется теория однократного рассеяния и ее незначительное об-
обобщение, что позволяет избежать излишних математических
сложностей. Кроме того, эта теория охватывает широкий круг
важных для практики задач распространения и рассеяния волн
в атмосфере, океане и других случайных средах. Часть II
(гл. 7—13) посвящена теории переноса излучения. Второй том
включает части III—V. В части III (гл. 14 и 15) рассматри-
рассматривается теория многократного рассеяния волн в случайных обла*
ках рассеивателей. Часть IV (гл. 16—20) охватывает теорию
слабых и сильных флуктуации в сплошной случайной среде и
в турбулентности. В части V (гл. 21 и 22) описаны рассеяние
на шероховатой поверхности и дистанционное зондирование слу-
случайных сред.
Случайные среды можно разбить на три группы: случайные
облака дискретных рассеивателей, сплошные случайные среды
и шероховатые поверхности. Случайные облака дискретных рас«
сеивателей представляют собой случайное распределение в про*
отранстве множества частиц. Примерами могут служить дождь,
12 Глава 1
туман, смог, град, аэрозоль, частицы в океане, красные кровя-
кровяные тельца, молекулы полимеров, молекулы. Анализ распростра-
распространения и рассеяния волн в таких случайных средах может быть
осуществлен в два этапа. Сначала мы рассматриваем харак-
характеристики рассеяния и поглощения отдельной частицы, а затем
переходим к рассмотрению характеристик волны при наличии
большого числа случайно распределенных рассеивателей.
Первый этап обсуждается в гл. 2. Она начинается с опреде-
определения амплитуды рассеяния и сечений рассеяния и поглощения.
Кратко описаны рэлеевское рассеяние, приближение Рэлея —
Дебая (борновское), приближение ВКБ и теория Ми. Включено
также обсуждение поляризационных эффектов и параметров
Стокса. Дано краткое описанде всех определений для случая
акустических волн.
В гл. 3 приведены примеры характеристик рассеяния и по-
поглощения для некоторых практических задач. Обсуждаются
свойства частиц в атмосфере и океане, к которым относятся
аэрозоль, гидрометеоры, воздушные пузырьки и рыбы. Кроме
того, рассматриваются оптические и акустические свойства
красных кровяных телец в крови.
При низкой плотности частиц, когда эффектами многократ-
многократного рассеяния можно пренебречь, применима теория однократ-
однократного рассеяния. В гл. 4—6 на основе теории однократного
рассеяния даны решения некоторых прикладных задач. Задача
рассеяния рассматривается в гл. 4, а гл. 5 посвящена распростра-
распространению и рассеянию импульсного излучения. Здесь дано общее
описание распространения и рассеяния импульса в случайной
среде с изменяющимися во времени свойствами. Гл. 6 посвя-
посвящена флуктуациям волны в облаке дискретных рассеивателей
применительно к задаче распространения в пределах прямой
видимости.
В гл. 7—13 излагается теория переноса излучения, а в гл. 14
и 15—теория многократного рассеяния. Исторически задача
распространения волн в облаке случайных рассеивателей иссле-
исследовалась с двух различных точек зрения. Одна из них — тео-
теория переноса излучения, или просто теория переноса, другая —
теория многократного рассеяния. Теория переноса имеет дело
с интенсивностями распространяющихся волн. Она опирается
на феноменологические и эвристические закономерности пове-
поведения интенсивности волны при распространении и впервые
была предложена Шустером в 1905 г.') в его работе по распро-
распространению излучения в загрязненной атмосфере. Основное диф-
*) Уравнение переноса излучения ранее было предложено известным рус-
русским физиком О. Д. Хвольсоном (см. Известия Петербургской Академии наук,
т. 33, с. 221, 1890 г.). —Прим. перев.
Введение 13
ференциальное уравнение этой теории называется уравнением
переноса, оно эквивалентно уравнению Больцмана в кинетиче-
кинетической теории газов и уравнению переноса нейтронов. Это уравне-
уравнение успешно применялось при исследовании видимости в ат-
атмосфере и под водой, в морской биологии, при разработке фо-
фотографических эмульсий и при исследовании распространения
лучистой энергии в атмосферах планет, звезд и в галактиках.
В гл. 7 даются определения таких фундаментальных величин,
как лучевая интенсивность, поток и плотность энергии. Выво-
Выводятся дифференциальные и интегральные уравнения, которым
подчиняются эти величины, и приводятся граничные условия
общего вида и соотношения, выражающие закон сохранения
энергии.
Точных общих решений уравнений, выведенных в гл. 7, до
сих пор не найдено. Тем не менее имеется ряд частных случаев,
для которых удается получить простые и полезные приближен-
приближенные решения. В гл. 8 и 9 рассматриваются два таких предель-
предельных случая: разреженное и плотное облака дискретных рассеи-
вателей. Для разреженных облаков может быть использовано
первое приближение теории многократного рассеяния, а для
плотных — диффузионное приближение. Эти два метода при-
применимы для решения широкого круга прикладных задач. При-
Примерами могут служить распространение и рассеяние СВЧ и
оптических волн в аэрозолях и гидрометеорах, рассеяние
оптического излучения на бактериях и диффузия света в
крови.
В гл. 10 и 11 обсуждается распространение волн в среде,
ограниченной, параллельными плоскостями. Такая простая гео-
геометрия отвечает большому числу физических ситуаций (атмо-
(атмосферы планет, слои в океане, слой крови или тонкий слой
краски) и допускает довольно простые решения. В гл. 10 рас-
рассматриваются двух- и четырехпотоковая теории, которые широко
использовались до последнего времени. Этот метод был развит
эвристически Кубелкой и Мунком в 1931 г. В гл. 10 мы вклю-
включили его вывод на основе теории переноса излучения, обеспечи-
обеспечивающий новое теоретическое обоснование двух- и четырехпо-
токовой теорий. Гл. 11 посвящена описанию многопотоковой
теории, удобной для численных расчетов на ЭВМ, в ней также
дается общий формализм решения задач для многослойных
сред.
В гл. 12 и 13 рассматриваются два других предельных слу-
случая малых и больших частиц. Если размер частицы мал по
сравнению с длиной волны, то рассеяние почти изотропно (рав-
(равномерно во всех направлениях), за исключением дипольного
рассеяния в электромагнитном случае. При изотропном рас-
рассеянии амплитуда рассеяния постоянна, и это приводит
14 Глава 1
к существенным математическим упрощениям. Эти упрощения
рассматриваются в гл. 12; они указывают на ясную связь с диф-
диффузионным приближением, обсуждаемым в гл. 9. В гл. 13 пред-
представлено приближение для больших частиц. Если размер час-
частицы велик по сравнению с длиной волны, то рассеяние проис-
происходит в основном вперед, и уравнение переноса может быть ре-
решено точно методом преобразования Фурье. Это приближение
применимо во многих задачах распространения оптических пуч-
пучков в воде и атмосфере.
В отличие от теории переноса в аналитической теории (или
теории многократного рассеяния) исходят из волнового уравне-
уравнения, получают решения для отдельной частицы, вводят эффекты
взаимодействия многих частиц и уже затем рассматривают ста-
статистически усредненные величины. Один из наиболее употреби-
употребительных вариантов теории многократного рассеяния был развит
Тверским. Детальное изложение его теории дано в гл. 14. Там
же рассматривается связь теории переноса с теорией многократ-
многократного рассеяния Тверского.
В гл. 15 рассматривается задача о флуктуациях волн и рас-
распространении импульсного излучения в облаке случайных рас-
сеивателей, которая важна с точки зрения проблем связи и ди-
дистанционного зондирования. Однако ввиду математических
трудностей в этом направлении было получено очень мало ре-
результатов. В данной главе делается попытка ввести читателя
в круг основных понятий, описывающих флуктуации волн и
распространение импульсного излучения в облаке случайных
рассеивателей, включая влияние рассеивателей на по-
полосу когерентности, форму импульса и разрешение изобра-
изображений.
Термин «сплошная случайная среда» обозначает среду, по-
показатель преломления которой меняется случайно и непрерывно
во времени и в пространстве. Примерами могут служить тропо-
тропосферная и ионосферная турбулентность, атмосферы планет, сол-
солнечная корона, турбулентность жидкости, турбулентные следы
и факелы самолетов и ракет, турбулентность чистого воздуха
и биологические среды. Если в данной точке случайной среды
флуктуации ее свойств ниже определенного уровня, то флук-
флуктуации волны малы. В этом случае обычно говорят о «слабы/1
флуктуациях». Если же флуктуации свойств среды велики, то
этот случай относится к так называемым «сильным флуктуа-
циям». Для слабых флуктуации возможен ряд упрощений и
приближений. Этому случаю посвящены гл. 16—19.
В гл. 16 рассматривается рассеяние монохроматических волн
и импульсов на объеме сплошной случайной среды. Здесь учи-
учитывается влияние движения среды и вводятся такие характери-
характеристики, как двухчастотные корреляционные функции, полоса ко-
Введение 15
герентности и время когерентности, которые приобретают все
большее значение в теории связи.
Гл. 17 посвящена задаче распространения волн в случайной
среде в пределах прямой видимости. Эта задача находит приме-
применение при анализе распространения СВЧ и оптических волн в
атмосфере. Изложение этих вопросов ведется на основе спек-
спектрального представления флуктуационных характеристик волн
и показателя преломления среды. Вводятся понятия спектраль-
спектральной и пространственной фильтрующих функций; учитывается
влияние изменения свойств случайной среды вдоль пути распро-
распространения.
В гл. 18 рассматривается распространение сферической вол-
волны и волнового пучка. Понятие сферической волны используется
в большинстве задач распространения СВЧ-излучения. Поня-
Понятие волнового пучка необходимо при анализе распространения
в случайных средах волн оптического и миллиметрового диапа-
диапазона. В гл. 19 обсуждаются временные флуктуации и спектры
волны, распространяющейся в случайной среде с меняющимися
во времени свойствами. Эти характеристики находят применение
в дистанционном зондировании атмосфер планет и солнечной
короны, а также полезны при дистанционном определении ско-
скорости ветра.
Гл. 20 посвящена сложной проблеме сильных флуктуации.
Интенсивные исследования в этом направлении проводятся в
США, СССР/Японии, Нидерландах и других странах. В данной
главе предпринята попытка дать введение в теорию сильных
флуктуации и общий обзор этой теории. Подробно рассматри-
рассматриваются взаимная функция когерентности в случайной среде,
временные частотные спектры и двухчастотные корреляционные
функции. Затрагиваются также вопросы флуктуации интенсив-
интенсивности, теория тонкого экрана, модуляционная передаточная
функция случайной среды и адаптивная оптика.
В гл. 21 дается введение в теорию рассеяния волн на шеро-
шероховатых поверхностях. Обсуждаются два основных подхода —
метод малых возмущений и метод Кирхгофа, а также кратко
перечисляются последние достижения в области рассеяния волн
на поверхности океана. Для указанных двух приближений вво-
вводится понятие сечения рассеяния единичной площадки шерохо-
шероховатой поверхности. Рассматриваются когерентная и некогерент-
некогерентная (диффузная) составляющие интенсивности и их временные
частотные спектры с учетом движения шероховатой поверхно-
поверхности.
В последние годы заметно возрос интерес к дистанционному
зондированию таких метеорологических параметров, как ско-
скорость ветра и интенсивность турбулентности методами, осно-
основанными на распространении и рассеянии волн. Недавно было
'R' Глава 1
предложено несколько новых методов дистанционного зондиро-
зондирования. Гл. 22 посвящена описанию современного состояния ис-
исследований в этой интересной и важной области. Рассматри-
Рассматриваются три общих метода решения обратных задач: метод
регуляризации, метод статистического обращения и метод обра-
обращения Бакуса — Гильберта.
В приложениях дана сводка полезных формул для спек-
спектральных представлений случайных функций. Включены также
краткие сведения о параметрах турбулентности и о флуктуа-
циях показателя преломления.
I
Рассеяние и распространение
волн в разреженных облаках
дискретных рассеивателей.
Приближение однократного
рассеяния
Глава 2
Рассеяние и поглощение волны
отдельной частицей
Основной интерес для нас представляют характеристики про
хождения и рассеяния волны при наличии облака случайно
распределенных частиц. Анализ этой задачи мы проведем в два
этапа. Сначала рассмотрим отдельную чартицу и изучим ее ха-
характеристики рассеяния и поглощения. На втором этапе мы
учтем вклады большого числа частиц и выведем общие соотно-
шения для волны, распространяющейся в облаке случайно рас'
пределенных частиц. В данной главе описывается первый из
этих этапов — анализ характеристик отдельной частицы. Этот
вопрос исчерпывающе освещен в ряде книг1), поэтому здесь
приводится лишь краткая сводка основных результатов.
2.1. Сечение рассеяния и амплитуда рассеяния
При освещении частицы волной часть падающей мощности
рассеивается, а часть поглощается. Эти два явления — рассея-
рассеяние и поглощение — удобнее всего описывать, предположив, что
частица освещается плоской падающей волной.
') Подробный анализ дан в работах [87, 162] (см. также [86, 127]).
В работе [42] приведены таблицы характеристик рассеяния частиц в атмо-
атмосфере и "распределение частиц по размерам. Проводящие тела и акустически
твердые и мягкие объекты описаны в работе [22]. См. также работу [128],
где приведено много примеров сечений рассеяния, и обзор по рассеянию света
в химии [90]. Более полная теория рассеяния изложена в работах [55, 94,
18 Глава 2
Рассмотрим линейно-поляризованную плоскую электромаг-
нитную волну, распространяющуюся в среде с диэлектрической
проницаемостью ео и магнитной проницаемостью цо; электри-
электрическое поле такой волны имеет вид
2Г). ' B.1)
Здесь амплитуда поля | Е,-| выбрана равной 1 В/м, k =©
= 2я/Я — волновое число, % — длина волны в среде, i — единич-
ный вектор в направлении распространения, а е,- — единичный
вектор, задающий направление поляризации.
Частица
T
W
Рис. 2.1. Плоская волна Е; (г) падает на диэлектрический рассеиватель; рас-
рассеянная волна Es (г) наблюдается на расстоянии R в направлении 0.
Эта волна падает на частицу (рис. 2.1) с диэлектрической
проницаемостью
•Mr)==-ir=e;(f)+<(r), B-2)
которая, вообще говоря, является комплексной и зависит от
координат, так как частица может обладать поглощением и
быть неоднородной. Поле на расстоянии R, отсчитываемом от
некоторой точки внутри частицы в направлении единичного
вектора 0, равно сумме поля падающей волны Е; и поля рас-
рассеянной на частице волны Es. На расстояниях R < D2/% (D —
характерный размер частицы, например ее диаметр) вследствие
интерференции волн от различных точек частицы амплитуда и
фаза поля Es меняются сложным образом. В этом случае гово-
говорят, что точка наблюдения г находится в ближней зоне ча-
стицы. При R > D2/X рассеянное поле Es ведет себя как сфе-
сферическая волна и может быть представлено в виде
E,(r) = f(O,T)-^-, R>D%, B.3)
где амплитуда рассеяния fF, i) описывает амплитуду, фазу и
поляризацию рассеянной волны в дальней зоне в направлении
Рассеяние и поглощение волны отдельной частицей 19
6 при условии, что на частицу падает плоская волна, распро-
распространяющаяся в направлении i. Следует отметить, что даже в
случае линейной поляризации падающей волны рассеянная вол-
волна, вообще говоря, имеет эллиптическую поляризацию.
Рассмотрим плотность потока мощности Ss рассеянной в на-
направлении 6 волны на расстоянии R от частицы при падении на
нее волны с плотностью потока мощности S,-. Дифференциаль-
Дифференциальное сечение рассеяния частицы определяется следующим обра-
образом:
ad (б, i) = lim K&SJSt)] = | f (б, T) I2 = (at/An) p F, T), B.4)
где Si я Ss — амплитуды векторов плотности потока мощности
падающей и рассеянной волн:
i-(EsXH;)==-^f6, B.5)
а г|0 = (\х,о/ео)'Ь — характеристический импеданс среды. Видно,
что Od имеет размерность площади, деленной на телесный угол.
Сечение рассеяния а& имеет следующий физический смысл.
Предположим, что в пределах телесного угла 1 стерадиан
вблизи направления 0 плотность потока мощности рассеянной
волны постоянна и равна значению для направления 0. Тогда
поперечное сечение частицы, от которой рассеивается такая
мощность, равно ад отсюда ясно, что а<* меняется в зависимости
от 0. Безразмерная величина р@, i) в B.4) называется фазовой
функцией и широко используется в теории переноса лучистой
энергии1). Величина at— это полное сечение, которое опреде-
определено ниже [формула B.9)].
В радиолокационных приложениях часто используются би-
стажческое радиолокационное сечение рассеяния аы и сечение
обратного рассеяния аь. Они связаны с аа соотношениями
аы F, 0 = 4n<yd (б, Т), аь = Anad (- Г, Г). B.6)
Величину аь называют также радиолокационным сечением рас-
рассеяния. Физический смысл аы можно выяснить аналогично тому,
как это сделано для ад Предположим, что в пределах полного
телесного угла 4я плотность потока мощности постоянна и рав-
равна значению плотности для направления 0. Тогда поперечное
сечение площадки, от которой рассеивается такая мощность,
равно значению ал для направления 0 умноженному на An.
') Фазовая функция описывает рассеянную мощность и не имеет ника:
кого отношения к фазе волны. Название «фазовая функция» возникло в
астрономии и связано с фазами Луны.
20 Глава 2
Рассмотрим теперь полный поток мощности, рассеянный ча-
частицей во всех направлениях. Сечение частицы, дающей такое
количество рассеянной мощности, называется сечением рассея-
ния as', оно определяется формулой
J|fF, f)pd<D = -g- J p (б, Т) rfco, B.7)
as = J
4я 4я 4я
где da — элемент телесного угла. Отношение Wo сечения рас-
рассеяния к полному сечению называется альбедо отдельной ча-
стицы и определяется выражением
4
\pF,i)da>. B.8)
4я 4я
Рассмотрим далее полную мощность, поглощаемую части-
частицей. Поперечное сечение частицы, отвечающее этому количе-
количеству мощности, называется сечением поглощения оа.
Сумма сечений рассеяния и поглощения называется полным
сечением at:
Ot = os + aa. B.9)
2.2. Общие свойства сечений
Прежде чем перейти к детальному математическому описа-
нию определенных выше сечений, целесообразно, по-видимому,
дать общее представление о том, как эти сечения связаны с гео-
метрическим сечением частицы, длиной волны и диэлектриче-
ской проницаемостью.
Если размер частицы во много раз превосходит длину вол-
волны, полное сечение at с увеличением размера частицы прибли-
приближается к удвоенному геометрическому сечению частицы agl).
Для объяснения этого факта рассмотрим падающую волну
с плотностью потока мощности S,- (рис. 2.2). Полный поток
мощности в пределах геометрического сечения ag, равный Siag,
либо рассеивается, либо поглощается частицей. Позади частицы
имеется область тени, где поля практически нет. В области тени
рассеянная частицей волна по амплитуде в точности равна па-
падающей, но фаза ее отличается на 180°, так что амплитуда по-
потока рассеянной волны равна Siag. Таким образом, общий по-
поток, рассеянный и поглощенный частицей, приближается к
5,-ffg -f- Siag, так что полное сечение at стремится к
at -> 2Siag/St = 2аg. B.10а)
') Это явление называется парадоксом экстинкции (см. [162]).
Рассеяние и поглощение волны отдельной частицей 21
Видно также, что полная мощность, поглощаемая очень боль-
большой частицей, не может превосходить значения 5,ag, так что
сечение поглощения аа стремится к некоторому постоянному
значению, несколько меньшему, чем геометрическое сечение:
Oa^Og. B.106)
Если размер частицы много меньше длинььволны, то сечение
рассеяния as обратно пропорционально четвертой степени длины
волны и прямо пропорционально квадрату объема частицы.
Чтобы продемонстрировать это [87] (см. также разд. 2.5), за-
Рис. 2.2. Связь полного сечения большой частицы с ее геометрическим се-
сечением.
метим, что рассеянное поле Es порождается полем внутри ча-
частицы, так что поле Es на расстоянии i? пропорционально па-
падающему полю Ei и объему V рассеивателя:
\ES\ = \E,\[(const) V/R].
Константа в этом уравнении должна иметь размерность (дли-
на)~2, а поскольку она зависит только от длины волны, она
должна быть пропорциональна %г2. Сопоставляя этот результат
с B.3), получаем "
I F I I F I V \ F i I f & П I
\bs\~\hi |-щт~1?Л ? •
Таким образом, as ~ |f@, i) |2 ~ У2Д4- Рассеяние на малой
частице, обладающее указанным свойством, обычно, называют
рэлеевским рассеянием. Сечение поглощения аа малого рассеи-
рассеивателя обратно пропорционально длине волны и прямо пропор-
пропорционально его объему. Сравнивая с геометрическим сечением
[см. B.21) и B.32-)], имеем
<Уа8~(размерЛГ[(е;- lJ + ef], B.11a)
ojog~ (размер/К) *?. B.116)
Кривые таких нормированных сечений в зависимости от от*
носительного размера частицы приведены на рис. 2,3.
22
Глава 2
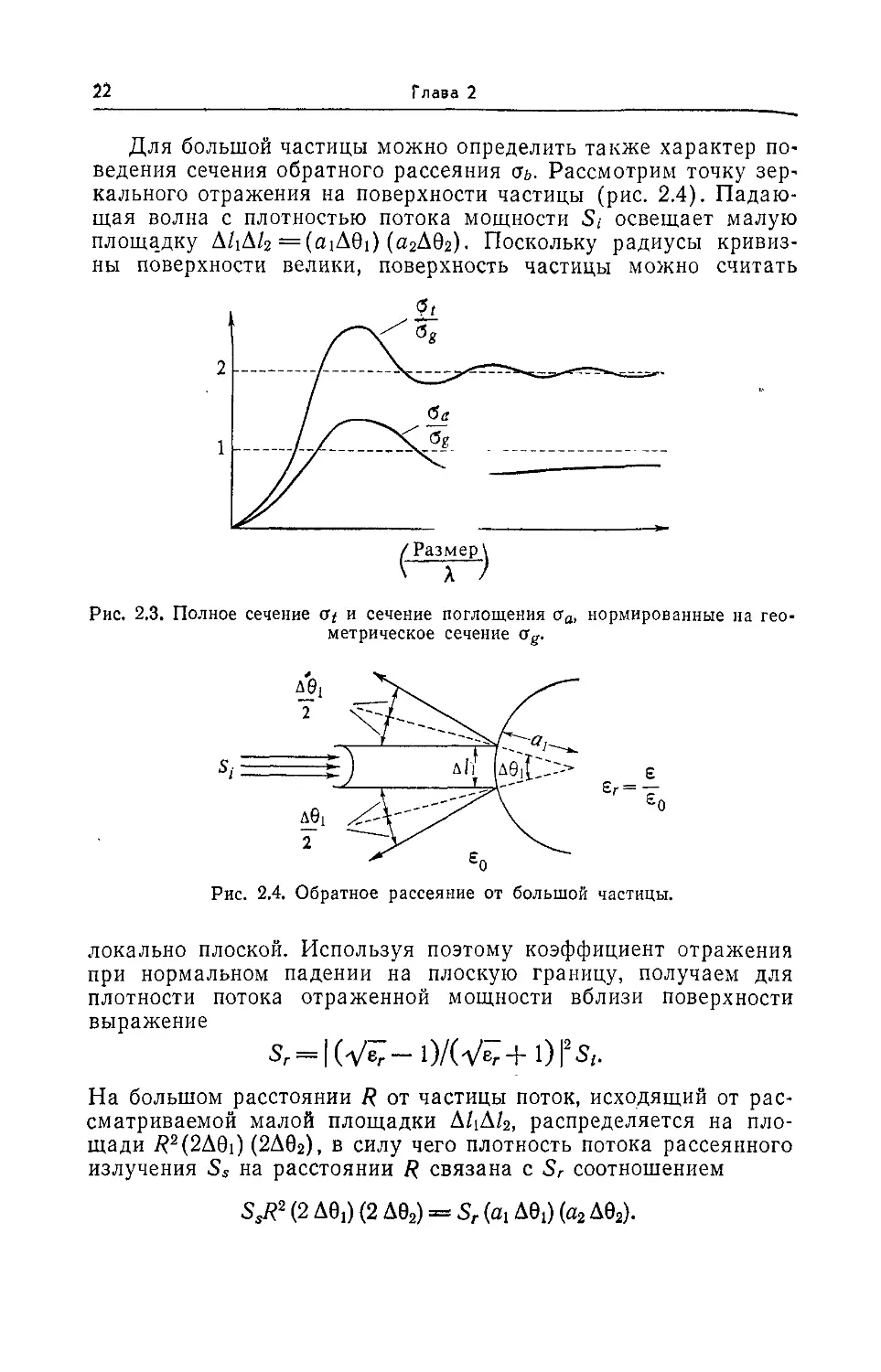
Для большой частицы можно определить также характер по-
поведения сечения обратного рассеяния оь- Рассмотрим точку зер-
зеркального отражения на поверхности частицы (рис. 2.4). Падаю-
Падающая волна с плотностью потока мощности 5,- освещает малую
площадку A/iA/г =(aiA8i) (агАбг). Поскольку радиусы кривиз-
кривизны поверхности велики, поверхность частицы можно считать
Рис. 2.3. Полное сечение at и сечение поглощения аа, нормированные на гео-
геометрическое сечение Og.
Рис. 2.4. Обратное рассеяние от большой частицы.
локально плоской. Используя поэтому коэффициент отражения
при нормальном падении на плоскую границу, получаем для
плотности потока отраженной мощности вблизи поверхности
выражение
На большом расстоянии R от частицы поток, исходящий от рас-
рассматриваемой малой площадки A/iA/2, распределяется на пло-
площади 7?2BA8i) BA02), в силу чего плотность потока рассеянного
излучения 5S на расстоянии R связана с Sr соотношением
B де,) B де2) = sr {ax део (а2 де2).
Рассеяние и поглощение волны отдельной частицей 23
Отсюда получаем для сечения обратного рассеяния Оь выра-
выражение
= 4гот4(-?, 0= li
R<*>
|(V^)/(V^+0|2. B.12)
Полученное выражение представляет собой предельное значе-
значение вь при стремлении размера частицы к бесконечности, по-
поэтому при любом конечном размере частицы сечение аь может
иметь значение, существенно отличающееся от B.12) [42].
2.3. Оптическая теорема
Полное сечение at описывает полные потери мощности в па-
падающей волне, обусловленные рассеянием и поглощением вол-
волны в частице. Эти потери тесно связаны с поведением рассеян-
рассеянной волны в направлении вперед, и соответствующее общее со-
соотношение является содержанием оптической теоремы, или тео-
теоремы о рассеянии вперед.
Оптическая теорема утверждает, что полное сечение at свя-
связано с мнимой частью амплитуды рассеяния в направлении
вперед f (i, i), и эта связь имеет вид
o< = Dn/A!)Im[f(T,T)]-e/, B.13)
где Im означает «мнимая часть», а е,- — единичный вектор, ха-
характеризующий направление поляризации падающей волны (до-
(доказательство этой теоремы приведено в работе [21]).
Эта теорема используется для расчета полного сечения в
тех случаях, когда амплитуда рассеяния известна. Она исполь-
используется также при определении ослабления когерентного поля.
2.4. Интегральные представления
амплитуды рассеяния и сечения поглощения
Математическое описание амплитуды рассеяния и сечений
рассеяния и поглощения можно осуществить одним из двух спо-
способов. Для тел простой формы, подобных сфере или бесконеч-
бесконечному цилиндру, удается найти точные выражения для этих ве-
величин. Точное решение для сферы из диэлектрика, которое на-
называют решением Ми, рассмотрено в разд. 2.8. Однако в боль-
большинстве практически важных случаев форма частиц не яв-
является простой. Поэтому нужен метод определения приближен-
приближенных значений сечений рассеяния и поглощения, пригодный для
24 Глава 2
частиц сложной формы (рассеяние на телах произвольной фор-
формы рассмотрено в работе [100]). Такой метод можно разрабо-
разработать, исходя из интегральных представлений амплитуды рас-
сеяния. Простота вычислений делает этот метод полезным и для
частиц простой формы.
Рассмотрим диэлектрическое тело, относительная диэлек-
диэлектрическая проницаемость которого является функцией прост-
пространственных координат:
ег (г) = ±?L = е; (г) + < (г) в объеме V. B.14)
Тело занимает объем V и окружено средой с диэлектрической
проницаемостью ео.
Запишем уравнения Максвелла
УХЕ = и»ЦоН, B.15а)
VXH = -«fl»(r)E. B.156)
Здесь принимается, что магнитная проницаемость ц0 постоянна
и одинакова как внутри, так и вне тела. Если уравнение B.156)
записать в виде
V X Н = - /©воЕ + Jeq, B.15в)
где
( — шеб [ег (г) — 1] Е в объеме V,
eq \ 0 , вне объема V,
то слагаемое ieq можно рассматривать как эквивалентный источ-
источник тока, порождающий рассеянную волну. Решение уравнений
B.15а) и B.15в) имеет вид
. Е(г) = ЕЛг)+ЕЛО, H(r)=IMr) + He(r), B.16)
где Е,- и Hi — электрическое и магнитное поля первичной (или
падающей) волны, которые существовали бы в отсутствие ча-
частицы, a Ej, и Hs — электрическое и магнитное поля рассеян-
рассеянной этим телом волны. Используя вектор Герца Ш, запишем ')
ns(r), B.17a)
= J [ег (г') - 1] Е (г') Go (r, г') dV, B.176)
v
где G0(r, г') = ехр(/&|г —-г'|)/Dя|г —-г'|) — функция Грина
свободного пространства.
'} Уравнение B.176) справедлвдо только при 1\#.г'. .
Рассеяние и поглощение волны отдельной частицей 25
Для нахождения амплитуды рассеяния рассмотрим поле
Ej(r) в дальней зоне частицы. Из рис. 2.5 видно, что г = R0,
так что в дальней зоне амплитудный множитель 1/|г — г'| функ-
функции Грина можно приближенно заменить на 1/R. В фазе вели-
величину |г — г') заменить на R нельзя, так как эта разность может
Рис. 2.5. Геометрическое положение точки внутри частицы г' и точки наблю-
наблюдения г.
значительно превосходить длину волны. Разлагая |г — г'| и
биномиальный ряд и ограничиваясь первым членом разложения,
получаем
| г - г' | = (Я2 + г'2 - 2Rr' • 6)'/2 ~ R - г' • 6.
В результате при больших R функция Грина принимает вид
С л. -Л _ exp UkR — ikr'-O) @ < R*
wo (r> r ) — 4nR~ ' ' '
Отметим также, что в дальней зоне
V (e'**/#) ^ (eikR/R) (ikVR) = (ikO) (e'^/R), B.19)
и, следовательно, оператор V эквивалентен ikO. Подставляя
B.18) и B.19) в B.17), находим ')
Es(r) = f(O, T) ехР^, B.20)
f F, Т) - -^ \ {- б X [б X Е (г')]} {гг (г') - 1} exp (- ikr' ¦ О) dV.
v
Это точное выражение для амплитуды рассеяния fF, i) через
полное электрическое поле Е-(г') внутри частицы. Поле Е(г')(
•) Отметим, что {—~0Х [0 X Е]} = Е — 0@-Е), где 0@-Ё) — компонен-
ta Е вдоль 0. Поэтому {0Х["ХЕ]} представляет собой компоненту Е, пер-
перпендикулярную к 0.
26 Глава 1
вообще говоря, неизвестно, поэтому выражение B.20) не дает
замкнутого описания амплитуды рассеяния через известные
величины. Однако во многих практически важных случаях поле
Е(г') можно приближенно заменить некоторой известной функ*
цией и, таким образом, получить полезное приближенное выра^
жение для f@, i). Это будет осуществлено в разд. 2.5—2.7.
Сечение поглощения аа диэлектрического тела представляет
собой объемный интеграл от потерь внутри частицы:
аа=
-о*-
Если амплитуда падающей волны выбрана равной единице
(\Ei\ = 1), то сечение поглощения равно
B.22)
Выражения B.20) и B.22) являются точными интегральными
выражениями для амплитуды рассеяния и сечения поглощения
через неизвестное полное поле Е(г') внутри частицы.
Заметим здесь же [130], что можно вывести другое инте-
интегральное уравнение — не для электрического поля Е(г), а для
магнитного поля Н(г). Из уравнений Максвелла для электри-
электрического поля Е находим векторное волновое' уравнение вида
V X V X Е (г) - со^оеоЕ (г) = ш^ое0 [ег (г) - 1] Е (г). B.23)
Для магнитного поля Н получается волновое уравнение, содер*
жащее член с градиентом er(r):
V X V X Н (г) - со2ц0е0Н (г) = coWo[е/(г) - 1] Н (г) -
-i(oe0[V8r(r)XE(r)]. B.24)
Поэтому интегральное уравнение для Н содержит два слагае-
слагаемых:
Н (г) = Н, (г) + Hs (г) - Н, (г) + V X V X Hms (r),
nms (г) «= J [е, (Г') - 1] Go (г, г') Н (г') dV -
v
- -jjL- [ Go (f, г') V\ (г') X E (O dV', B.25)
"где Yzr(r') — градиент по переменной г'. Второе слагаемое в
выражении для Hms описывает влияние деполяризации волн и
неоднородности диэлектрической проницаемости тела. В случае
Рассеяние и поглощение волны отдельной частицей
27
однородного шара V'er(r') равен дельта-функции, сосредоточен-
сосредоточенной на его поверхности, и второе слагаемое превращается в по-
поверхностный интеграл.
2.5. Рэлеевское рассеяние')
В разд. 2.2 мы уже отмечали О\бщие свойства рассеяния на
малых частицах. Рассеяние на малых частицах обычно назы-
называют рэлеевским рассеянием. В данном разделе мы приводим
подробный анализ рассеяния на некоторых телах простой формы.
Рис. 2.6. Электростатическое поле
внутри диэлектрического шара.
Рассмотрим диэлектрический шар, размер которого много
меньше длины волны. Из-за малости размера шара электриче-
электрическое поле внутри него и вблизи от его поверхности должно быть
практически гаким же, как в электростатике. Из электроста-
электростатики известно, что поле внутри диэлектрического шара, поме-
помещенного в постоянное электрическое поле Е,, однородно и равно
[153] (рис. 2.6)
где е, — единичный вектор в направлении поляризации па-
падающей волны. Подставляя B.26) в B.20), находим
f (б, Т) = — [3 (вг - 1)/(вг + 2)] V [- 6 X (б X е,)]. B.27)
Отметим, что | [—6 X @ X е<) ] | = sin %, где х — угол между
%i и б (рис. 2.7).
') Cta. [49, 80], где приведены решения для сферических тел в низкоча-
низкочастотном приближении.
28
Глава 2
Указанная угловая зависимость рассеянного поля совпадает
с угловой зависимостью поля электрического диполя, ориенти-
ориентированного в направлении Е в диэлектрике. Этого следовало ожи-
ожидать, поскольку рассеянное поле возбуждается эквивалентным
источником тока
Je<? = -/coe0(8r-l)E, B.28)
который можно рассматривать как набор электрических дипо-
диполей с дипольным моментом ео(ег— 1)Е. Выражение B.27) спра-
справедливо даже в том случае, когда частица обладает поглоще-
Диаграмма
Рис! 2.7. Диаграмма направлен-
направленности диполя при рэлеевском
рассеянии.
нием и ее относительная диэлектрическая проницаемость ег ком-
плексна.-
Дифференциальное сечение рассеяния а<*@, i) равно1)
k*
3(er-l)
V2 sin2
B.29)
где sin2x= 1 — @-e,J.
Отметим, что сечение рассеяния обратно пропорционально
четвертой степени длины волны и прямо пропорционально квад-
квадрату объема рассеивателя. Эти два свойства малых расЬелвате-
лей были получены Рэлеем из теории размерностей (каКэто
показано в разд. 2.1). I ^"^
Голубой цвет неба может быть объяснен тем, что голубая
часть спектра белого света рассеивается сильнее красной из-за
наличия зависимости типа Аг~4. Далее, как видно из рис. 2.7, из-
излучение неба под прямым углом к направлению на Солнце
должно быть линейно-поляризованным. Эти два свойства — го-
голубой цвет неба и поляризация излучения — в прошлом веке
представляли собой большую научную за/ аду и были оконча-
окончательно объяснены Рэлеем2). Рэлей обра!ил внимание на то,
что рассеивателями не обязательно должны быть капли воды
J) Заметим, что [—О Х@ X е,)] = е, — 0@е().
2) Ньютон полагал, что голубой цвет неба обусловлен интерференцией
лучей, отраженных от передней и задней поверхностей водяных капель,.по-
капель,.подобно тому как это происходит при отражении от тонких пленок и при на-
наблюдении интерференционной картины ньютоновых колец, но он не смог дать
удовлетворительного объяснения цвета и поляризации [87].
Рассеяние и поглощение волны отдельной частицей
29
или льдинки, как это обычно предполагалось; он указал, что
сами молекулы воздуха могут давать вклад в это рассеяние.
Рассмотрим теперь сечение рассеяния as малой диэлектри-
диэлектрической частицы:
1
4я
= -JS" ) °ы d® —
4л
к2
(AnJ
г
Л4
Мвг-1)
д .1, 2
„ I
о ¦ 1 О
Or ^~ 6
2
Л 2я
F2 \ sin х d% \ d^ sin2 x =
о
128я5а6
ЗЯ4
о
ег-1
B.30)
Часто бывает желательно сравнить сечение рассеяния с реаль-
реальным геометрическим сечением па2. Отсюда мы получаем урав-
уравнение Рэлея
-Ш?=—3— 17+2 ' B'31)
Уравнение Рэлея. справедливо только при малых значениях
ka. Обычно в качестве верхнего предела радиуса частицы при-
принимают значение а = 0.05Л. При этом значении уравнение Рэ-
Рэлея B.31) приводит к ошибке, меньшей 4% [87].
Сечение поглощения аа получается из выражения B.22),
если подставить в него B.26):
аа=-
ег
V, -^_ =
2 ^
3 '
B.32)
Полное сечение at равно сумме B.31) и B.32). Отметим,
что значение at не может быть получено из B.27) с помощью
оптической теоремы, поскольку из B.27) следует, что при
е" = 0 at = 0. И вообще при любой заданной аппроксимации
Е(г') внутри частицы сумма сечения рассеяния, получаемого
интегрированием |/|2 в B.20) по всему телесному углу 4я, и
сечения поглощения B.22) дает значительно более точное зна-
значение полного сечения, чем значение, получаемое при непосред-
непосредственном применении оптической теоремы к B.20).
Если частица представляет собой эллипсоид
х'2/а2 + У2/Ь2 + z2/c2 = 1, B.33)
а падающее поле Е,- имеет компоненты Eix, Ely и Eiz в направ-
направлениях х, у и г,. то компоненты псля внутри частицы равны
[153, 162]
l[ ((-l)Ax], B.34)
оо
где Ах = \(s + а2)"' [(s + а2) (s + b2) (s + с2)\~ щ ds.
30 Глава 2
(Компоненты Еу и Ег получаются соответствующей эаменой а,
b и с.) Подставив B.34) в B.20) и"Х2\22), легко найдем сече*
ния рассеяния и поглощения. Нетрудно видеть, что функции
Ь\ = -каЬсАх, L2 — i?abcAu и ^3=4=-^- abcA, зависят только от
отношений b/а и с/а и не зависят ©т-абсолютных значений а,
Ь и с. Известно также, что Li + L2 + L3=l. Для вытянутого
сфероида (а > Ь = с)
а для сплюснутого сфероида (а <С Ъ — с)
7 arctg 0 • B<35б)
В качестве примера рассмотрим плоскую волну единичной
амплитуды (\Ei\ = 1), поляризованную в направлении х и рас-
распространяющуюся в направлении г. Пусть эта волна падает на
малую диэлектрическую сферу радиуса а. В дальней зоне по от-
отношению к этой сфере компоненты электрического поля даются
формулами
Замечая, что
[-0-Х @ X е,)] = - [0 F • е,) - е,],
ег = х, в-6 = ^-0== 0, в •x = cos6cos^>1 ^-x= —sin0,
находим
Ев — Ео (cos 0 cos ф) exp (ikR), Еф = Ео (— sin <j>) exp (ikR),
где
¦3(sr-l)lV_
R '
— k* Г
~ 4я L
Отметим, что sin2 %= I — sin2 G cos2 <f>.
В качестве другого примера рассмотрим сфероидальное ди-
диэлектрическое тело, форма которого описывается уравнением
B.33), где а<Ь = с. Предположим, что падающая волна по-
поляризована в направлении х и распространяется в направле-
направлении z. Тогда множитель 3/(ег + 2) в формуле для сферы мы
Рассеяние и поглощение волны отдельной частицей 31
должны заменить на [1 + Li(er — I)]. В результате найдем
ЗА4
1+1, (ег-
V,
где/-1 определено формулой B.356), а V = */зяаЬ2.
2.6. Борновское приближение
(рассеяние Рэлея—Дебая)
Рассмотрим теперь характеристики рассеивателя, относи-
относительная диэлектрическая проницаемость ег которого близка к
единице. В этом случае приближенно можно считать, что поле
внутри рассеивателя совпадает с полем падающей волны:
Е (г) « Е; (г) = ег exp {ikr • 1).
Подставляя это выражение в B.20), получаем
i (б, !) = -?- [-6 X F X it)] VS (К),
5(ke) = y \ [вГ (г7) - 1] ехр (/к, • г') dV,
B.36)
B.37а)
B.376)
где ks == ^is = Л;(Г— 0), \\s\ = 2sin(8/2), а 8 — угол между Т и
0 (рис. 2.8).
Рис. 2.8. Связь между векто-
вектором ls и углом 6.
Такое приближение справедливо при
(er- 1ND< 1,
B. 38)
где D — характерный размер частицы, например ее диаметр.
Заметим, что B.376) представляет собой фурье-образ от
ег(г')—1 в направлении is. Поэтому, амплитуда рассеяния
f@, i) пропорциональна фурье-образу от ег(г') — 1 при значе-
значении волнового числа ks. Если разность ег(г')— 1 отлична от нуля
лишь в малой по сравнению с длиной волны области, то сече-
сечение рассеяния слабо зависит от ks и потому практически изо-
изотропно по углу 6. Если размер частицы во много раз превосхо-
32
Глава 2
дит длину волны, то рассеяние в основном сконцентрировано
в узком телесном угле в направлении^ вперед, 0 « 0. Это явле-
ние аналогично соотношению между Протяженностью функции
во времени и шириной ее спектра: есля—протяженность функ-
функции равна Т, то ее спектр перекрывает частотный диапазон ши-
шириной 1/Г.
Сечение поглощения в борновском приближении получается
из выражения B.22):
ca = k )B?(r)dV.
V
B.39)
Рассмотрим несколько примеров.
г'
Л 2П ЗП 4ТС
kG 2 sin i
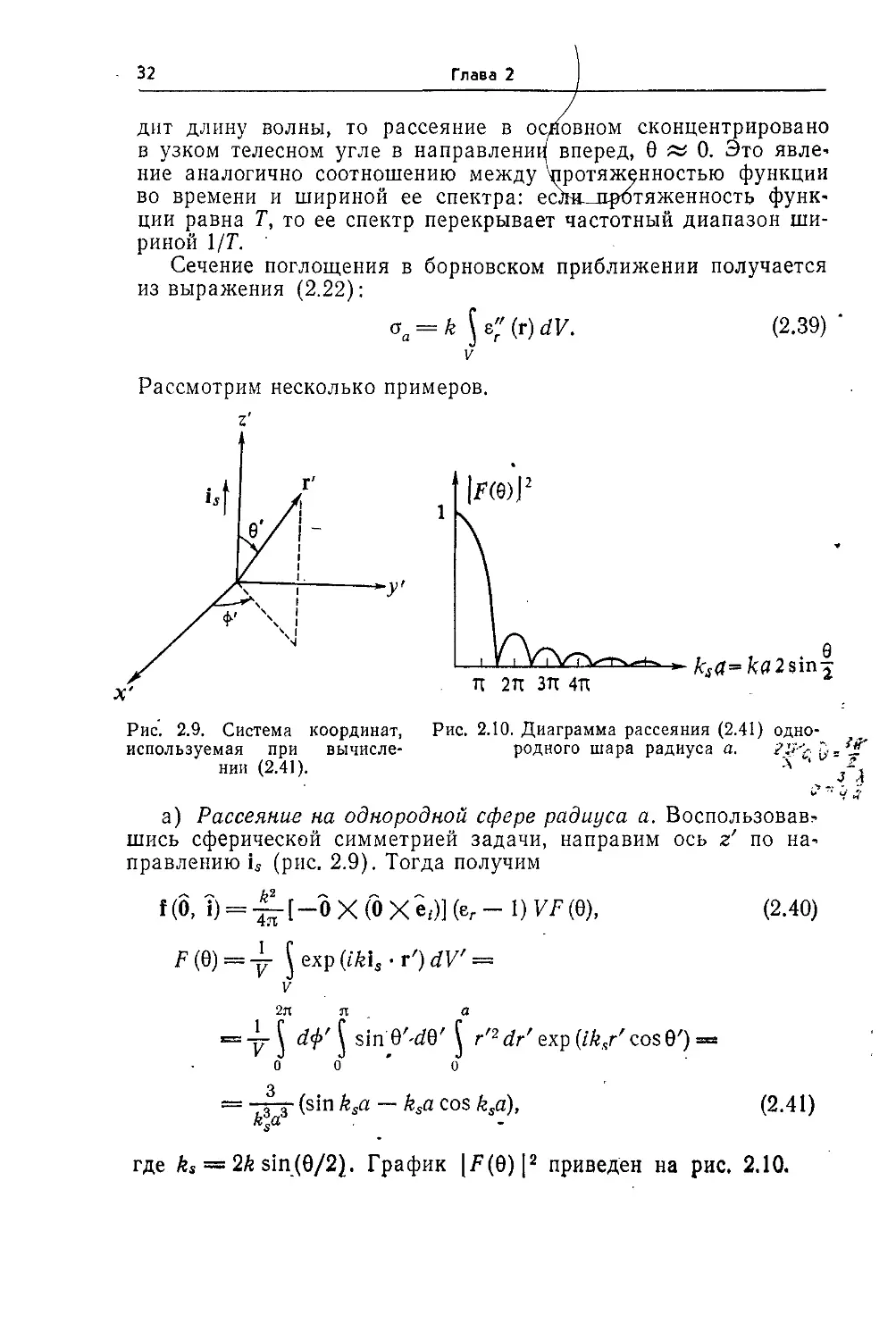
Рис. 2.9. Система координат, Рис. 2.10. Диаграмма рассеяния B.41) одно-
используемая при вычисле- родного шара радиуса а. ?1У^ \
нии B.41). S '
3 Л
""" " Ч Л
а) Рассеяние на однородной сфере радиуса а. Воспользовав^
шись сферической симметрией задачи, направим ось г' по на-
направлению и (рис. 2.9). Тогда получим
i(б, Т) = — [-0 X @ X е,)] (ег - 1) VF @),
B.40)
F @) = -L J exp (ik\, • г') dV =
2л
= —r-o-(sin^a — ksa cos ksa), B.41)
ksa
где ks — 2k sin@/2). График [/^F) [2 приведен на рис. 2.10.
Рассеяние и поглощение волны отдельной частицей
33
б) Рассеяние на круглом диске. Рассмотрим диск радиуса а
и толщины d (рис. 2.11).
Выразив декартовы компоненты векторов направления рас-
распространения падающей волны i и рассеянной волны б через
Рис. 2.11. Диск радиуса а и толщины d и направления i и 0 в B.42).
сферические координаты, найдем
ks — kslx + ks2y -
ksi = k (sin 0; cos <j>{ — sin 0O cos ф0]
kS2 — k (sin Qt sin ф( — sin 90 sin ^>o]
&s3 = k (cos Qt — cos 0o).
Используя замену переменных интегрирования
у' = p'sin^', получаем1)
F = jr
B.42)
= p'cos^/ и
2л a d/2
-i- \ df J p' dp' 5 dz' ехр [/ (Ляр' cos ф' + k2p' sin ф'
d/2
B.43)
') Пусть А,
2л
\ + Щ cos0[ и к2 = Л^к\ + fe| sin^j. Тогда имеют место
формулы \ йФ' ехр [/ 'у fej + k\ р' cos @' — 0j)J = 2я/0 y\k\ + ?2 Р у я
л
34 Глава 2
где k\, ki и fa равны соответственно ks\, kS2 и ksz- Отметим
также, что
kli + k\i = k* [sin2 Qi + sin2 eo ~ 2 sin Qtsin eocos (^ - f\,)]. B-44)
Если волна падает перпендикулярно поверхности диска
(9, = 0),то
р _ 2/, (feg sin e0) sin [kd sin2 F0/2)] . ,„ .-.
?asin60 Arfsin2(e0/2) " ^ ¦*
Характеристики рассеяния произвольной частицы с аксиаль-
аксиальной симметрией можно найти из B.43), выбрав соответствую-
соответствующим образом пределы интегрирования.
в) Рассеяние на случайно ориентированной частице с ак-
аксиальной симметрией [160, 162]. О|братим внимание, что в вы-
выражении B.43) *Jk\ + k\ и къ представляют собой соответ-
соответственно поперечную и продольную компоненты (по отношению
к оси г) вектора kis = k{\ — 0). Обозначив через р угол между
и и осью z, запишем ^Jk\ + k\ = ks sin P и k3 = ks cos p.
Для случайно ориентированной частицы интенсивность рас-
рассеянной волны нужно усреднить по всем возможным ориента-
циям частицы. Из-за стохастичности необходимо усреднять не
поле, а интенсивность:
B.46)
-i
В частном случае диска выражение B.43) для F дает
2 ^ Г th г, ~Ы Й\ Si" lfes (rf/2) C0S P]
Подставив это выражение в B.46), найдем характеристики рас-
рассеяния случайно ориентированного диска (см. также [142]).
2.7. ВКБ-приближение для поля внутри частицы
Оптическая теорема применима для рассеивателя произволь-
произвольной формы и размера. Однако мы отмечали, что в рэлеевском
и борновском приближениях, рассмотренных выше, применение
оптической теоремы не дает правильного значения полного се-
сечения рассеяния. Действительно, в указанных приближениях
амплитуда рассеяния f@, i) непоглощающей частицы вещест-
• Рассеяние и поглощение волны отдельной частицей 35
венна. Это связано с тем, что амплитуда рассеяния f @, i) прак-
практически вещественна, и эта вещественная функция описывает
общие угловые характеристики рассеяния. С другой стороны,
мнимая часть f (б, I) в этих приближениях мала, а именно она
описывает полную убыль мощности, обусловленную как рассея-
рассеянием, так и поглощением, и потому связана с сечением экстинк-
ции. В связи с этим рэлеевское и борновское приближения хо-
хороню описывают угловые характеристики рассеяния, но недо-
недостаточно точно определяют мнимую часть амплитуды рассеяния.
Тем не менее полное сечение рассеяния в этих приближениях
можно получить, проинтегрировав амплитуду рассеяния по пол-
полному телесному углу, подобно тому как это делалось в преды-
предыдущем разделе.
Если бы мы располагали более точным решением, то для
вычисления сечения экстинкции можно было бы использовать
оптическую теорему. Кроме того, такое решение лучше описы-
описывало бы характеристики рассеяния. Такое улучшенное прибли-
приближение можно найти, используя для нахождения поля внутри ча-
частицы метод ВКБ1). Отметим, что приближение Рэлея пригодно
для малых частиц {kD «С 1), а борновское приближение спра-
справедливо при (er-l)^Z)<C 1. В последнем случае величина kD
может быть большой. В противоположность этому, ВКБ-при-
ВКБ-приближение справедливо при
(ег-1N?>>1, ег-1<1. B.48)
Таким образом, ВКБ-приближение дает решение в тех случаях,
когда рэлеевское и борновское приближения становятся непри-
непригодными.
В ВКБ-приближении поле Е(г) внутри частицы аппрокси-
аппроксимируется распространяющейся волной с волновым вектором, со-
соответствующим веществу частицы. Кроме того, предполагается,
что, поскольку ег— 1 < 1, угол преломления равен углу паде-
падения, так что волна внутри частицы движется в том же направ-
направлении, что и падающая волна. Коэффициент пропускания Т че-
через поверхность частицы заменяется коэффициентом пропуска-
пропускания при нормальном падении на плоскую границу раздела. Та-
Таким образом, если падающая волна имеет вид
ге„ B.49)
то поле Е(г) в точке В (рис. 2.12) принимается равным
Е (г) = ТЕ{ exp [ikzi + Ikn (г — zO] e,, гх < г < z2. B.50)
') ВКБ — первые буквы фамилий авторов этого метода — Вентцеля, Кра-
мерса и Бриллюэна [130, 133].
Глава 2
Здесь п= ¦yf&r — показатель преломления частицы, а Т — ко-
коэффициент пропускания, который принимается равным
Г = 2/(«+1). B.51)
Подставляя B.50) в B.20), находим
f (°-')=ir [~°х <°х
vs
где
S (б, z) = у jj 2 [п (г') - 1 ] ехр \ikzx + i*/* (/- zx) - ikr' • б] dV.
v
Полное сечение рассеяния at дается оптической теоремой
= k Im J 2 (я - 1) ехр [- Ik (n - 1) *i + Ik (n — 1) z] dV. B.53)
v
Сечение поглощения аа определяется выражением B.22). Ис-
Используя B.50), получаем
= J
B.54)
где kn = k (n, + ш
Рис. 2.12. Пределы интегриро-
интегрирования при использовании ВКБ-
приближения B.52).
В качестве примера рассмотрим однородную сферическую
частицу радиуса а. Замечая, что zx = — *\]а2 — р'2 и dV =
= dz'p'dp'dj»', получаем
A2Z) 1
?а
.2
па
где
2 ехр (- У)
— 1)с, У =
B.55а)
B.556)
Рассеяние и поглощение волны отдельной частицей
37
Следует отметить, что, вообще говоря, ВКБ-приближение
дает значения, несколько превышающие истинные сечения. При
малых значениях k(n—\)а получаемые значения неточны, и
в этой области следует использовать рэлеевское или борновское
приближение.
2.8. Решение Ми
Точное решение задачи рассеяния плоской электромагнитной
волны на изотропном однородном шаре было получено в 1908 г.
Ми, и обычно о нем говорят как о решении или о теории Ми.
В этом разделе мы приведем краткое описание решения Ми.
Более подробное изложение можно найти в большинстве учеб-
учебников (см., например, [87]). В работах [173, 174] рассмотрены
случаи сфероидальных частиц и тел произвольной формы.
Рис. 2.13. Геометрия зада-
задачи Ми.
Рассмотрим шар с относительной диэлектрической проницае-
проницаемостью гг = е/ео, на который падает распространяющаяся вдоль
оси z волна, поляризованная в направлении оси х (рис. 2.13):
Ei = e-ikzx. B.56)
Любое электромагнитное поле можно выразить в сфериче-
сферической системе координат через две скалярные функции Пх и П2 —
радиальные компоненты электрического и магнитного векторов
Герца:
B.57)
Функция III описывает все ТМ-моды, когда Нг = 0, а функция
П2 все ТЕ-моды с Е, = 0. Как Пь так и Щ удовлетворяют ска->
лярным волновым уравнениям
(V2 + k2m2) П = 0
вне сферы,
внутри сферы.
B.58)
38 Глава 2
Электрическое и магнитное поля определяются через IIi и П2
выражениями
Е = V X V X (гП,г) + /co^oV X (rU2r),
Н = - /coeV X (гП,г) + V X V X (гЩт)
где е = ео вне среды и е = егео внутри ее.
Падающее поле B.56) можно описать двумя скалярными
функциями Щ и П|, которые выражаются через сферические
гармоники следующим образом:
I ^'ЙУ *»м р»<cos 8)cos*.
B.60)
ЙТГ ¦„ (Ar) P' (cos 8)sin ^,
где 1|зя (ж) = x/n (л;) = V^/2 /n+I/l (x), a T) = Vm-o/eo. Эти
жения можно получить [153], сравнивая выражения для сфе-
сферических гармоник с радиальными компонентами Е« и Е, полу-
получаемыми из П{ и П|.
Запишем общие выражения для рассеянных полей при г > а,
используя два набора произвольных констант ап и Ь„:
Г' , B.61)
где ^п(х) = хк^Цх) = л/пх/2 Н^+уз(х). Для полей внутри сферы
при г < а, используя наборы констант сп и dn, запишем
оо
г 1 \"™* i^~ B/z ~ 1^ 1
/"П. = -гт—\2 / —<——-• -———«- с i]) \hftif)Р (cos 8) cos Ф7
n"J B.62)
n-l
Граничные условия представляют собой требование непре-
рывности компонент Ев, Еф, Не и Нф на границе г = а. Гранич-
Граничные условия в таком виде содержат как Пь так и Пг, и для их
разделения нужно выбирать подходящие линейные комбинации
Рассеяние и поглощение волны отдельной частицей
39
полей. Например, комбинация sin Q(d/dQ) Ев-\-(д/дф)Еф дает не-
непрерывность (д/дг) (rlli). Такие соображения приводят к гра-
граничным условиям для IIi и ГЬ, которые формулируются в виде
требования непрерывности т2Пь (д/дг) (rlli), Ш и (д/дг) (гЩ).
Используя эти условия, находим
С„ (а) < (Р) - т% (Р) ? (а)
B.63)
mln (а) ф„ (р) - % (P) ln (a)
где a = ka и C = kma. Рассеянные поля Еф и Ев вдали от сферы
имеют вид
leikr ieikr
Еф= г- 5, (9) sin ф, ?9 = —г—>"
оо
2п+1
[а"я«(cos е) + 6*т»(cos е)]>
B.64)
Здесь
Р1„ (cos Э) d ,
я„ (cos 0) = s.n6 , т„ (cos 9) = __ />я (cos 6).
Полное сечение рассеяния at получается из оптической тео-
теоремы
=
n-l
Сечение обратного рассеяния as дается формулой
ге-1
B.66)
а сечение рассеяния os — формулой
B.67)
n-l
40
Глава 2
2.9. Эллиптически-поляризованные волны
и параметры Стокса
В предыдущих разделах мы рассматривали линейно-поляри-
линейно-поляризованные волны. Однако в общем случае необходимо проанали-
проанализировать ситуацию, когда падающая волна имеет эллиптическую
поляризацию (см. [21, 31, 117]). Рассмотрим распространяю-
распространяющуюся в направлении оси z плоскую волну, у которой компо-
компоненты электрического поля зависят от времени по закону
Ех = Re {Ехе~ш) = Re [at exp (— /б, + ikz — по/)] = a, cos (т + б,),
Еу = Re (Е2е~ ш) = Re [а2 ехр (— /б2 + ikz — до/)] = а2 cos (т + б2),
B.68)
где т = со/ — kz, a E\ и ?2 комплексные амплитуды ?* и Еу.
При эллиптической поляризации общего вида конец вектора
Рис. 2.14. Правая эллиптиче-
эллиптическая поляризация.
электрического поля Е = Ехх + Еуу описывает эллипс. Уравне-
Уравнение этого эллипса можно получить, исключив переменную т из
системы B.68):
(Ex/aiJ + (Еу/а2J - 2 (ExEyla{a2) cos б = sin2 б,
B.69)
где б = бг — 6i — разность фаз. Из уравнений B.68) видно, что
при sin б > 0 имеет место левая поляризация, а при sin б < 0 —
правая. Как показано на рис. 2.14, поляризацию называют пра-
правой, если электрический вектор поворачивается в ту сторону,
куда нужно поворачивать бурав с правосторонней резьбой,
чтобы он завинчивался в направлении распространения волны.
Для описания эллиптически-поляризованнои волны B.68)
необходимо три параметра. Ими могут быть, например, ai, a2
и б. Однако более удобно использовать параметры одинаковой
размерности. В 1852 г. Стоке ввел параметры, которые сейчас
Рассеяние и поглощение волны отдельной частицей 41
носят его имя. Это следующие величины:
U = 2аха2 cos б = 2 Re (ЕХЕ*2), V = 2аха2 sin б = 2 Im (EXE'2), ^>70^
где Е\ = а\ ехр (—ib\ + ikz) и Е2 — а2 ехр (—гб2 + i&z)' — ком-
комплексные амплитуды компонент Ех и Еу электрического поля.
Эти четыре параметра связаны между собой соотношением
P = Q2 + U2+V2, B.71)
которое следует из B.70). Уравнения B.70) и B.71) опреде-
определяют три независимые величины, с помощью которых можно
описать любую эллиптически-поляризованную волну.
Например, для линейно-поляризованной волны, плоскость
поляризации которой составляет угол гро с осью х, имеем а\ =
= Ео cos -фо, ач = Ео sin -фо и б = 0. В этом случае параметры
Стокса равны
/ = ?§, Q = El cos 2i|H, I/= ?§ sin 2i|j0, V = 0. B.72)
Для волны с правой круговой поляризацией а\ = а2 = ?о, б =
= -л/2, так что
/ = 2?* Q==0, U=0, У= — Щ. B.73)
В теории переноса излучения чаще используют так называе-
называемые модифицированные параметры Стокса, которые опреде-
определяются следующим образом:
/i = |?ir\ h = \E2f, I/ = 2Re(?i?S), V = 2lm(ElE*2). B.74)
С другой стороны, эллипс, изображенный на рис. 2.14, можно
описать, задав его большую а и малую Ъ полуоси и угол t|). Вы-
Выразив параметры Стокса через /, b/а и i|), получим
Q = I cos 2% cos 2ф, 6r = /cos2%sin 2ф, V = Isin2%, B.75)
где tg% = ±6/fl, причем знак плюс отвечает левой, а знак
минус — правой поляризации.
Из выражений B.75) видно, что параметры I я V зависят
только от полной интенсивности и от отношения осей и не за-
зависят от ориентации эллипса (угла i|j). Напротив, параметры Q
и U зависят от выбора системы координат. Этот факт окажется
полезным в дальнейшем, когда мы будем исследовать вопрос
об аддитивности параметров Стокса.
Выражениям B.75) можно поставить в соответствие декар-
декартовы координаты {X, Y, Z) точки (г, 6, ф) на сфере радиуса
42
Глава 2
г = I с угловыми координатами 6 = л/2 — 2% и ф = 2я|?: X =
= г sin 8 cos ф, Y — г sin 6 sin ф и Z = rcos6. Эта сфера назы-
называется сферой Пуанкаре; ее полюсы отвечают круговым поляри-
поляризациям волны: северный полюс отвечает левой поляризации,
Рис. 2.15, Сфера Пуанкаре.
а южный — правой. Северная и южная полусферы отвечают ле-
левой и правой эллиптической поляризации, а экватор — линейной
поляризации (рис. 2.15).
2.10. Частичная поляризация и естественный свет
В эллиптически-поляризованной волне, рассмотренной в пре-
предыдущем разделе, отношение амплитуд а,\ и а2 и разность фаз
б = 62 — 6i постоянны. Это имеет место в случае чисто моно-
монохроматической волны (имеющей единственную частоту). В бо-
более О|бщем случае немонохроматической волны, характеризуе-
характеризуемой спектром ширины Да, амплитуды и разность фаз претер-
претерпевают непрерывные изменения в пределах полосы Аа и, сле-
следовательно, а\, dj и 6 являются медленно меняющимися функ-
функциями времени. Поэтому параметры Стокса, вообще говоря,
должны выражаться через усредненные величины. Обозначая
усреднение по времени угловыми скобками < >, получаем
U = 2 (а{а2 cos б) = 2 Re <ЭД),
V = 2 (aia2 sin б) = 2 Im (Е,Е'2).
( '
Для модифицированных параметров Стокса (Л, /2l U, V) имеем
/l = <|?'i|2>, I2 = (\E2\2). В этом случае условие B.71) долж-
Рассеяние и поглощение волны отдельной частицей 43
но быть заменено на
+ U2+ V2. B.77)
«Естественный свет» характеризуется тем, что его интенсив-
интенсивность постоянна в любом направлении, перпендикулярном к на-
направлению луча, а также тем, что ортогональные компоненты
его поля некоррелированны. Следовательно, для естественного
света должны выполняться необходимые и достаточные условия
/ = 2<|?|2>, Q = U=V = 0. B.78)
В общем случае волна может быть частично поляризован-
поляризованной. Степень поляризации т определяется отношением
m = (Q2 + ?/2+V2№ B.79)
так что для эллиптической поляризации т = 1, для частичной
поляризации 0 < т < 1 и для неполяризованной волны (есте-
(естественного света) т = 0.
2.11. Сложение независимых волн
Наиболее важным свойством параметров Стокса с точки зре-
зрения их применения в задачах распространения волн в случай-
случайных средах является «аддитивность» этих параметров для не-
независимых волн (см. [31], разд. 14.7).
Если частицы в объеме распределены случайно, то интенсив-
интенсивности волн, рассеянных разными частицами, некоррелированны
между собой. Поэтому рассеянные в случайной среде волны счи-
считают «независимыми» или «некогерентными».
Можно показать, что при сложении независимых волн пара-
параметры Стокса суммарной волны представляют собой соответ-
соответствующие суммы параметров Стокса отдельных независимых
слагаемых. Этот факт используется в дальнейшем при выводе
общего уравнения переноса излучения.
Следует отметить, что параметры Стокса — это не что иное,
как лучевые интенсивности, которые рассматриваются в разд. 7.7,
и только что упомянутая «аддитивность» может быть объяснена
более удовлетворительно. Такое объяснение дается в гл. 14.
2.12. Матрица рассеяния и матрица Стокса
рассеяния f@, i) опред|
= f F, !)(«'*«/*) B.80)
В разд. 2.1 амплитуда рассеяния fF, i) определяется соот-
соотношением
44
Глава 2
при условии, что на рассеиватель падает линейно-поляризован-
линейно-поляризованная волна
B.81)
г (г) = exp (iki - г) е{.
Чтобы получить более общее описание рассеянной волны, при-
пригодное для эллиптически-поляризованных, частично поляризо-
поляризованных и неполяризованных волн, удобно перейти к следующей
системе координат.
Частица
Eiy-Ещ
Рис. 2.16. К определению амплитуды рассеяния. Плоскости yz и YZ совпа-
совпадают с плоскостью рассеяния.
Выберем в качестве оси г направление распространения па-
падающей волны; ось у выберем так, чтобы плоскость yz была
«плоскостью рассеяния», т. е. плоскостью, в которой лежат еди-
единичные векторы i и 0 направлений распространения падающей
и рассеянной волн (рис. 2.16). Электрическое поле падающей
волны имеет две компоненты: Е,х — Eix и E-w = Ещ — перпенди-
перпендикулярную к плоскости рассеяния и параллельную ей. Аналогич-
Аналогично этому рассеянная волна тоже имеет две компоненты Esx =
= Esx и Esy = Es\\.
Ясно, что Es± и Es\\ линейно связаны с Ец и Ещ, так что
можно записать [162]
B.82)
Поля Eix и Et\\ вычисляются в начале координат х = у =
= z = 0, a ?sj. и Es\\ — на расстоянии R от него. Функции /ц,
/i2, /21 и /22 зависят от угла 8 и связаны с функциями рассеяния
Si, S2, S3 и 54, фигурирующими у Ван де Хюлста [162] и в
Рассеяние и поглощение волны отдельной частицей
45
решении Ми для сферы, соотношениями
fu = (i/k)Su fl2 = (i/k)St, f2i =
= (i/k)S2. B.83)
В этом случае оптическая теорема принимает вид
at = Dnjk) Im fu @) = Dn/k) Im /22 @).
B.84)
Возникает вопрос, каковы будут параметры Стокса рассеян-
рассеянной волны /is, hs, Us и Vs, если известны функции рассеяния и
если падающая волна имеет произвольную поляризацию, а ее
параметры Стокса равны lu, I2i, Ui и Vi. Такую связь можно
найти, используя уравнения B.74) и B.82). Она выражается
с помощью матрицы Стокса а размера 4X4 [42]:
Is = (\/R2)al{, B.85а)
где h и It — векторы-столбцы 4 X 1» а о — матрица 4X4:
/,=
hs
us
- V, -
B.856)
a —
I Ail2 I/.212
|U2 |f 22 Г
2Re(/u/21) 2Re(/12/22) Re
_2Im(/u/21) 2Im(/12Q Im
- Im (fuf22 -
Такое представление в виде матриц используется ниже при вы-
выводе уравнения переноса излучения с учетом поляризации. От-
Отметим, что для сферически-симметричных частиц /i2 = /2i = 0,
и матрица а зависит лишь от
Re (fиГ22) и Im (fnfl2).
четырех величин | /n |2, |/22|
2.13. Преобразование параметров Стокса
при повороте системы координат
В этом разделе мы рассмотрим преобразование параметров
Стокса при повороте системы координат (х, у, z) на угол ф во-
вокруг оси z (рис. 2.17). Полученные здесь формулы будут затем
использованы в гл. 7 при выводе уравнения переноса излуче-
излучения для частично поляризованных волн.
46
Глава 2
Обозначим через 1\, /2, U и V параметры Стокса в системе
координат х, у, г, а через /{, Г2, U' и V — в системе х', у', г'.
Компоненты электрического поля Ех = Е\ и Еу = Е2 связаны
с компонентами ЕХ' = Е'х, ЕУ' = Е2 линейным преобразова-
преобразованием
Е'х = Ex cos ф + Е2 sin ф, Е2= — Ex sin Ф + Е-г cos ф. B.86)
В соответствии с определением B.76) имеем
= (\Ех |2) cos2 ф + < | Е212) sin2 ¦/- + 2 Re (ExE*2) sin ф cos ^ =
= Л cos2 ^ + /2 sin2-/" + j (sin 2^) t/.
Аналогичным образом /<>, t/' и К' можно представить в виде
линейного преобразования l\, I2, U и V вида
I (z, х') = I (^ I (z, х), B.87)
где I (z, х') — вектор-столбец (/'ь /г, С/', I/')- Единичный век-
вектор г указывает направление распространения волны, а единич-
4)
Чу
у
Рис. 2.17. Вращение вокруг оси z.
ный вектор х' — направление поляризации Е[. Через I(z, x)
обозначен вектор-столбец (/ь /2, U, V), a L(^) представляет
собой 4 X 4-матрицу
cos2</>
0
sin2 ф cos2^ — -~ sin 2</> 0
— sin
0
sin
cos
B.88)
Рассеяние и поглощение волны отдельной частицей 47
2.14. Распределение частиц по размерам
До сих пор мы рассматривали характеристики отдельной
частицы. Однако основная задача состоит в определении взаимо-
взаимодействия волны с большим числом случайно расположенных
частиц. Частицы, с которыми приходится иметь дело, не обяза-
обязательно имеют одинаковый размер, обычно их размеры распре-
распределены в некотором диапазоне. Поэтому весьма важно учесть
распределение частиц по размерам.
Пусть n(D)dD — число частиц в единичном объеме с раз-
размером (например, диаметром) от D до D + dD. Тогда полное
число частиц в единичном объеме равно
оо
р = J n(D)dD B.89)
о
и называется концентрацией или плотностью частиц.
Можно также определить плотность вероятности частиц с
размерами от D до D -f- dD:
оо
\l. B.90)
Полное сечение частицы at зависит от ее размера, поэтому сред-
среднее значение <сг<> и дисперсия полного сечения равны
оо
{at)=\ot(D)W(D)dD, B.91)
var (at) = J [at (D) - (ot)f W (D) dD. B.92)
Аналогично можно получить выражения для среднего размера
частиц <?>> и для дисперсии:
(D) = J DW (D) dD, var (D) = J (D ~ {D)f W (D) dD. B.93)
о о
Всюду в этой книге при использовании at или какого-либо
другого сечения подразумевается, что это определенные выше
средние значения.
Например, если распределение частиц по размерам дается
формулой
n(D) = ADexp(—D/B),
где А я В — постоянные, то средний размер равен </)> = 2В,
а плотность р = АВ2,
48 Глава 2
2.15. Акустические волны
Для акустических волн переменное давление p(r, t) играет
ту роль, которую в предыдущих разделах играло электрическое,
поле E(r, t). В этом разделе мы даем краткое описание рас-
распространения акустических волн в упругих средах (см., напри-
например, [88, 102, 109, 123]).
Упругие среды можно разделить на жидкие и твердые.
К жидким средам относятся как собственно жидкости, так и
газы; они могут быть подразделены на вязкие и идеальные (не
обладающие вязкостью) жидкости. Вязкие и идеальные жидко-
жидкости можно подразделить далее на сжимаемые и несжимаемые.
Распространение акустических волн возможно в трех типах
сред: в упругих твердых телах, в вязкой сжимаемой жидкости
и в идеальной сжимаемой жидкости. В этом разделе мы дадим
краткое описание распространения волн в таких идеальных сжи-
сжимаемых жидких средах, как газы и собственно жидкости. При-
Примерами могут служить капельки тумана в воздухе и воздушные
пузырьки в воде.
Поведение жидкости описывается двумя фундаментальными
уравнениями: уравнением движения и уравнением сохранения
массы. Уравнение движения имеет вид
P = 4r + gradP = 0' <2-94>
где р — плотность (кг/м3), V — скорость (м/с), а р — давление
(Н/м2). Производная d/dt описывает скорость изменения во
времени в системе координат, движущейся вместе с некоторой
частицей жидкости. Такой подход называют лагранжевым. В от-
отличие от этого в эйлеровом подходе используется производная
d/dt, описывающая скорость изменения во времени в фиксиро-
фиксированной точке пространства, через которую протекает жидкость.
Эти производные связаны соотношением
d/dt = d/dt + (V • grad). B.95)
Сохранение массы описывается уравнением
V .(pV) + dp/d/ = 0. B.96)
Представим р, р и V в виде суммы средних значений ро, ро и
Vo и малых осциллирующих слагаемых р\, pi и Vi, описываю-
описывающих акустическую волну.
Предположим сначала, что жидкость покоится (Vo = O),
а амплитуды акустического давления pi и плотности pi малы по
сравнению со средними значениями ро и р0. Тогда уравнения
Рассеяние и поглощение волны отдельной частицей 49
B.94) и B.96) примут вид
PoaV,/d/ + gradp, = O, B.97)
PoV • Vi + dpi/dt = 0. B.98)
Давление p, вообще говоря, является функцией плотности р.
Поэтому для малых р\ и pi можно написать
)pPu B.99)
следовательно, р\ линейно связано с рг.
Р1 = с*ри с2 = (др/др)р, B.100)
Постоянная с зависит от рассматриваемого вещества и пред-
представляет собой скорость распространения в нем акустической
волны. Используя соотношение B.100),' выразим в уравнении
B.98) pi через р\\
Применяя к уравнению B.97) оператор дивергенции и исполь-
используя затем B.101), получаем
)^—0, B.102)
где % =(с2ро)~1 — сжимаемость жидкости.
Уравнение B.102) является основным уравнением распро-
распространения акустических волн в неподвижной среде. Отметим,
что множитель 1/р0 стоит под знаком дивергенции. В случае
однородной среды его можно вынести за знак дивергенции:
-^4^ = 0. B-103)
Однако если в среде имеются границы или если плотность сре-
среды меняется в пространстве, то множитель 1/р0 в уравнении
B.102) выносить за знак дивергенции нельзя.
В однородной среде, как это видно из уравнения B.97),
rot Vi = 0. Поэтому Vi можно представить в виде градиента
скалярной функции Ф:
Vi = — grad<D. B.104)
Функция Ф называется потенциалом скоростей; она удовле-
удовлетворяет волновому уравнению
^^р = 0; B.105а)
50 Глава 2
давление pi и плотность pi выражаются через нее посредством
соотношений
Р. = И?. Р. = -?-?•¦ BЛ056)
Граничные условия на поверхности раздела двух сред вклю-
включают: а) непрерывность давления р\ и б) непрерывность нор-
нормальной компоненты скорости \\.
Для потенциала скоростей Ф эти граничные условия требуют:
а) непрерывности р0 <ЗФ/д/ и б) непрерывности дФ(дп.
Для монохроматических волн, зависимость которых от вре-
мени определяется множителем ехр(—mt), имеем
(У2 + /г2)Ф = 0, /г = со/с, V: = — gradQ, р1 = — тр0Ф.
B.106а)
Вектор плотности потока мощности S дается выражением
s^l-^v;. B.Ш66)
2.16. Рассеяние акустических волн
В этом разделе мы кратко опишем характеристики рассея-
рассеяния и поглощения волны давления, возникающей при падении
Рис. 2.18. Рассеяние акустических волн на частице.
на частицу акустической волны единичной амплитуды!)
(рис. 2.18)
г). B.107)
Амплитуда рассеяния /@^, i) в акустическом случае — ска-
скалярная функция, так что рассеянное акустическое поле имеет
вид
Р, (г) = / (б, 1) (eikR/R), Я > D%. B.108)
') В этом разделе для краткости индекс 1 для акустических величин
опускается. Так, например, вместо ри мы будем писать р<.
Рассеяние и поглощение волны отдельной частицей 51
Векторы плотности потока мощности падающей и рассеянной
волн равны
St = (\рс 172%)!, S, = (| ps 172%) б, B.109)
где т]о = роСо — характеристический импеданс, а р0 и с0 — плот-
плотность покоящейся среды и скорость звука в ней. Дифференци-
Дифференциальное сечение рассеяния аа, сечение рассеяния as, сечение по-
поглощения оа и полное сечение at в этом случае также выра-
выражаются формулами, приведенными в разд. 2.1. Оптическая тео-
теорема здесь принимает вид
at = Dл//г2) Im / (Г, Г). B.110)
Интегральное представление амплитуды рассеяния /(б, i)
несколько отличается от электромагнитного случая из-за нали-
наличия в уравнении B.102) множителя 1/р0 под знаком диверген-
дивергенции.
В случае монохроматических волн уравнение B.102) прини-
принимает вид
V2p -f k2p = - k2yKp + div [y0 grad p], B.111)
где yK — (xe — x) /x, Yp — (Pe — p) /pe, k2 = co2/c2 = и2хр, причем
x и p — сжимаемость и плотность среды, окружающей частицу,
а хе и ре — сжимаемость и плотность частицы.
Члены в правой части уравнения B.111) являются источни-
источниками рассеянной волны, поэтому амплитуда рассеяния ДО, i)
имеет вид
/ @, Т) = ? \ (укр - /Yp{ Гр) ехр(- ikO- r') dV. B.112)
v
Следует отметить, что для малой частицы первое слагаемое
под знаком интеграла в B.112), как и в электромагнитном слу-
случае, дает изотропное рассеяние, а второе слагаемое описывает
рассеяние с индикатрисой, пропорциональной 0-i = cos 6.
Из выражения B.112) можно получить формулы для рэлеев-
ского, /Зорновского и ВКБ-приближений.
Глава 3
Характеристики дискретных рассеивателей
в атмосфере, океане
и биологических средах
В гл. 2 мы рассмотрели математическое описание и привели
общие характеристики поглощения и рассеяния волн отдельной
частицей. В данной главе мы дадим ряд численных примеров
таких характеристик для частиц, с которыми чаще всего прихо-
приходится иметь дело на практике. К ним относятся аэрозоли и гид-
гидрометеоры в атмосфере, различные частицы в океане, воздуш-
воздушные пузырьки и рыбы в воде, а также эритроциты в крови. Этот
перечень примеров не является исчерпывающим; его цель со-
состоит в том,'чтобы дать общее представление о численных зна-
значениях величин, встречающихся в практических приложениях.
Кроме того, эти примеры используются в последующих главах
для иллюстрации различных теоретических методов.
3.1. Метеорологические радиолокаторы, шумы
и помехи
Метеорологические радио-, лазерные и акустические лока-
локаторы являются важными средствами дистанционного зондиро-
зондирования атмосферы. В этом разделе мы приведем краткое описа-
описание метеорологических радиолокаторов. Более подробное опи-
описание можно найти в работах [7, 43, 95, 147]. По поводу ис-
использования оптического диапазона см. [45, 158].
На частотах ниже 1 ГГц влияние метеорологических явле-
явлений на работу радиолокаторов, вообще говоря, пренебрежимо
мало. Однако на более высоких частотах становятся существен-
существенными отражения от различных частиц, например от дождя, сне-
снега или града. Такие радиоотражения от метеорологических об-
образований обычно называют шумами, поскольку они «зашум-
ляют» экран радиолокатора и мешают оператору, который дол-
должен выделить на их фоне самолет или какую-ли,бо другую цель.
Примерами зашумляющих отражений являются отражения от
метеорологических образований, отражения от деревьев и дру-
другой растительности, от различных сооружений и от морской по-
поверхности. В некоторых случаях волна, излученная одним ра-
радиолокатором и рассеянная на атмосферных частицах, может
быть принята другими радиолокаторами. Такой нежелательный
сигнал называется помехой.
Характеристики дискретных рассеивателей
53
Шумы и помехи нежелательны для нормальной работы ра-
радиолокатора, но те же самые явления имеют значительный ин-
интерес для метеорологических исследований и предсказания по-
погоды. Метеорологические радиолокаторы используются для оп-
определения и изучения областей, занятых осадками, для изуче-
изучения гроз, торнадо и ураганов.
Обычно метеорологические радиолокаторы имеют пиковую
мощность порядка 25—500 кВт и могут принимать сигналы
мощностью порядка 1СН2— Ю-14 Вт. Мощность принято выра-
выражать в децибелах по отношению к уровню 1 мВт, и такая ве-
величина , обозначается дБм. Например, 100 кВт соответствует
Рис. 3.1. Индикатор типа А (а), индикатор кругового обзора (ИКО) (б),
индикатор дальность — высота (ИДВ) (в).
80 дБм, а 10~13 Вт— 100 дБм. Длина волны метеорологических
радиолокаторов колеблется от 1 до 20 см (частота 30—1,5 ГГц)
[7]. В большинстве радиолокаторов передаваемый сигнал имеет
форму импульсов длительностью порядка 1 мкс с частотой по-
повторения импульсов PRF порядка 1000 Гц.
Большинство метеорологических радиолокаторов исполь-
используется для измерения интенсивности отраженного сигнала. По-
Поскольку в них не учитывается информация, заключенная в фазе
принимаемого сигнала; такие радиолокаторы называют некоге-
некогерентными, или обычными. В противоположность этому радио-
радиолокатор, с помощью которого можно измерять фазу принимае-
принимаемого сигнала (по отношению к фазе излученного сигнала), на-
называется когерентным, или импульсно-доплеровским (разд. 5.10).
На практике широко используются радиолокационные инди-
индикаторы трех типов. Это индикатор типа А, индикатор кругового
обзора (ИКО) и индикатор дальность — высота (ИДВ). В ин-
индикаторе типа А горизонтальное отклонение луча пропорцио-
пропорционально времени распространения импульса, т. е. дальности. Вер-
Вертикальное отклонение пропорционально интенсивности приня-
принятого сигнала (рис. 3.1, а). ИКО дает изображение принятого
54
Глава 3
сигнала в полярной системе координат. Сканирование антенны
производится с постоянной скоростью по азимуту. Радиус про-
пропорционален дальности, а яркость точки на экране пропорцио-
пропорциональна интенсивности принятого сигнала. Индикаторы такого
типа широко используются на метеорологических станциях
(рис. 3.1,6). В ИДВ используется сканирование антенны в вер-
вертикальном направлении. Этот индикатор отображает принимае-
принимаемый сигнал в системе координат, абсциссой которой является
дальность, а ординатой — высота (рис. 3.1, в).
3.2. Аэрозоль и гидрометеоры
Для метеорологических радиолокаторов важную роль играют
размеры частиц аэрозоля и гидрометеоров, их состав, форма и
ориентация. Мы приведем здесь краткую сводку характеристик
аэрозоля и гидрометеоров.
Ядра Айткена
Дым, смог —
-«-Мгла-»-
Аэрозоль—
Пыль—*-
Туман Дымка Дождь
Облака Изморось "^
Водяная пыль
над океаном
i Гидрометеоры -
¦Град-i
1_
нм
мкм
мм
см
Размер часищ _ —>~
Рис. 3.2. Размеры различных частиц в атмосфере.
Аэрозоль представляет собой взвесь частиц вещества в ат-
атмосфере [43, 54]. В качестве примеров упомянем смог, дым, ту-
туман, облака, дымку и пыль. Размеры частиц обычно меньше
1 мкм. Гидрометеорами в атмосфере называют частицы воды в
жидком или в твердом состоянии. Примерами могут служить
частицы дымки, дождя, снега, града, вдояной пыли у поверх-
поверхности океана, облаков и тумана, размеры которых превышают
1 мкм.
Аэрозоль образуется в результате химических реакций ме-
между различными газами воздуха и в результате процессов го-
горения— лесных пожаров, извержений вулканов и сжигания
Характеристики дискретных рассеивателей 55
топлива. Для формирования гидрометеоров обычно требуется,
чтобы воздух был немного перенасыщен водяными парами и в
нем имелись малые частички, известные под названием ядер
Айткена, на которых начинается процесс конденсации. Пример-
Примерные размеры аэрозоля и гидрометеоров приведены на рис. 3.2
[43, 165].
Чтобы изучать влияние этих частиц на распространение волн,
важно знать их распределение по размерам, плотность, сечения
рассеяния и поглощения и зависимость этих параметров от ча-
частоты волны. Ниже мы приводим краткое описание типичных
характеристик.
3.2.1. Дождь1»
Распределение капель дождя по размерам зависит от интен-
интенсивности выпадения осадков р, которая обычно выражается в
миллиметрах в час. Разумно предположить, что капли дождя
имеют сферическую форму. Лишь в очень сильном дожде капли
имеют форму сплющенного эллипсоида (фигуры, получаемой
вращением эллипса вокруг малой оси) и падают под опреде-
определенным ориентационным углом 2) (углом между малой осью
эллипсоида и вертикалью). Сферическая капля данного диа-
диаметра 2а падает с определенной установившейся скоростью
v(a). Пусть п(р, а)—число капель в единичном объеме с ра-
радиусом от а до a -f- da при интенсивности осадков р. Тогда ин-
интенсивность осадков р (в миллиметрах в час) равна
оо
р = 1,51 • 104J v(a)n(p, a) a3da, C.1)
о
где v измеряется в метрах в секунду, п — в обратных кубиче-
кубических метрах, а — в метрах, 1,51 • 104 = 3600-4л/3. Типичные зна-
значения р: 0,25 мм/ч (моросящий дождь), 1 мм/ч (слабый дождь),
4 мм/ч (умеренный дождь), 16 мм/ч (сильный дождь), 100 мм/ч
(сильный ливень).
Распределение по размерам капель п можно выразить эм-
эмпирической формулой, полученной Маршаллом и Палмером
[7, 103],
п(р, а) = пое-аа, C.2)
где «о = 8-106 м~4, а = 8200 р~0-21 (м-1), a p измеряется в мил*
лиметрах в час. Эта формула хорошо описывает распределение
1) Исчерпывающие сведения по поглощению в дожде имеются в работе
[104]; см. также [20, 50, 59, 63, 69, 112—114, 138, 139, 152].
*) Ориентационный угол приводит к деполяризации волны, вызывая связь
между волнами с ортогональными поляризациями (см. [32, 113, 137]).
Глава 3
при а > 0,5 мм; при а < 0,5 мм она дает несколько завышен-
завышенные значения1). Отметим, что несмотря на то, что в дожде
имеется большое число частиц малого радиуса, эти мелкие ча-
частицы относительно слабо влияют на распространение и рассея-
рассеяние волн. Поэтому среднее значение радиуса
(а) —\ап(р, a)da
C.3)
не играет существенной роли. Более важную роль играет ме-
медианный радиус (или диаметр), который делит капли большого
22
5 о-
О о
X а
Я ю
Я
о.
20
18
16
14
12
10
8
б
4
2
0
к
ЦТ
II
ZT
IE
if
\ .р—1,27мм/ч
_L
^р-12,7мм/ч
\
/ FA
77 /К ^
^ ^/Р =101,6мм/ч
х
X
—¦—
Диаметр капель, мм
Рис. 3.3. Доля полного объема, занимаемого каплями дождя различных раз-
размеров для трех интенсивностей дождя [93].
и малого диаметра на две группы равного объема. Медианный
диаметр Dm (в миллиметрах) в соответствии с эмпирической
формулой, предложенный Лоу и Парсонсом, равен
Z)m=l,238p0'182 C.4)
(р в миллиметрах в час). Распределение дождевых капель по
размерам можно выразить также через долю общего объема,
') См. экспериментальные распределения [8, 93].
Характеристики дискретных рассеивателей
57
занимаемую каплями соответствующего размера. Эмпирические
распределения, полученные Лоу и Парсонсом, приведены на
рис. 3.3.
Более общее выражение для распределения капель по раз-
размерам было предложено Дейрменджяном [42]. Оно называется
модифицированным гамма-распределением и имеет вид
п(а)~ сiaaexp(—с2ау), C.5)
где С\, с2, а и у — постоянные. Это выражение можно рассма-
рассматривать как обобщение распределения Маршалла — Палмера
,3.2).
I
1,0
0,1
8
6
4
3
2
о
6
4
3
2
К
6
4
3
2
/
/
/
/
1
/
/
/
/
/
/
/
/
При радиусе капли
а < 20 мкм
»-Ц9'106 а2 „/с
-
0,01
23468 23468 23468
0,01 0,1 1,0 10
Эквивалентный радиус сферической капли, мм
Рис. 3.4. Установившаяся скорость водяных капель в воздухе при давлении
760 мм рт. ст. и температуре 20 °С [56].
Установившаяся скорость дождевых капель зависит от их
радиуса. На рис. 3.4 приведены данные Ганна и Кинцера [56].
Движение капель вызывает флуктуации волн во времени и уши-
рение частотных спектров флуктуации волн. Было показано
[7], что при диаметре капель от 1 до 4 мм установившаяся ско-
скорость v (в м/с) хорошо аппроксимируется выражением
v = 200,8а''! (а в метрах). (З.б)
58 Глава 3
Сечения рассеяния и поглощения дождевых капель зависят
от длины волны. Заметим, что характеристики распространения
волн определяются не самими сечениями частиц, а полной сум-
суммой сечений всех частиц из единичного объема, т. е. величинами
p(ot}, p(os} и р(оаУ- Ниже мы изучим поведение этих величин
в диапазонах СВЧ, миллиметровых и оптических волн.
На частотах ниже 6 ГГц (Я = 5 см) большая часть дожде-
дождевых капель удовлетворяет условию ka <<С 0,1, так что в этом
случае применима теория рэлеевского рассеяния. Даже на ча-
частоте 10 ГГц (Я = 3 см) ka много меньше единицы (за исклю-
исключением сильного дождя), и рэлеевское рассеяние является
хорошим приближением. В рэлеевском приближении имеем
(разд. 2.5)
оо
^^\6п{а)йа, C.7а)
оо
Р (°а) = "Г" Im (К) \ а3п (a) da, C.76)
о
Р (<*д = Р {<*,) + Р {<Уа), C.7в )
n{a)da, C.7г)
где К *= (ег— 1)/(ег + 2), а угловые скобки < > означают усред-
нение по всем размерам частиц.
Величина К. зависит от длины волны и температуры. В диа-
диапазоне длин волн Я от 3 до 10 см \К\2 почти не меняется при
температуре от 0 до 20°С и равно 0,93. Мнимая часть Im(/C)
меняется при Я = 10 см от 0,0074 (при 20°С) до 0,00688 (при
10°С), а при А, = 3,21 см — от 0,01883 (при 20°С) до 0,0247
(при 10°С). Эти значения можно вычислить, зная показатель
преломления воды п = п' + in" = (er) '!к Некоторые типичные
значения п' и п" приведены на рис. 3.5 (более подробные све-
сведения о показателе преломления воды и льда в оптическом диа-
диапазоне имеются в работах [62, 116, 132], см. также [66, 131] и
великолепный обзор по поглощению в дожде [70]). Отметим,
что мнимая часть показателя преломления воды п" начинает
играть существенную роль при Я больше нескольких микроме-
микрометров. Она вызывает значительное поглощение волн диапазона
СВЧ, миллиметрового и инфракрасного излучения, но практи-
практически не играет роли для видимого света. Для льда мнимой
частью п" можно пренебречь при % больше 100 мкм и при Я
меньше нескольких микрометров, откуда следует, что поглоще-
Характеристики дискретных рассеивателей
59
ние пренебрежимо мало как в диапазоне СВЧ, так и в области
видимого света.
На частотах больше 10 ГГц расчет сечений следует прово-
проводить на основе теории Ми (разд. 2.8). На практике величину
' v удобно выражать через интенсивность осадков р (мм/ч).
Е I N ! И!1| I I I II1111 ГТТТПШ Г I I N111] I I 11МИ| I I 11М11| 1 i IMir
10'
10
i-i
,-2
10
10"
ю-4
Вода
п' -=
10
10"
I Ilinil I I liiiiil jq-4
101
10
,-1
-2
0,1мкм 1мкм Юмкм 100мкм 1мм 1см 10см
X
Рис. 3.5. Типичные значения показателя преломления п = п' + in" воды и
льда. Данные для воды (при 10 °С) и льда для Л > 1 мм и Я < 10 мкм из
работы [42] (дождь, град, водяная дымка и водяные облака). Данные для А,
от 10 до 200 мкм из работы [33].
Из эксперимента известно, что затухание р<сг<> примерно про-
пропорционально интенсивности осадков, так что можно положить
p(ot) = Ktp. C.8)
Коэффициент Kt слабо зависит от р. Некоторые типичные зна-
значения Kt показаны на рис. 3.6. Для миллиметровых и оптиче-
оптических волн Kt « 0,4 — 0,8 при р < 10 мм/ч и Kt уменьшается до
0,15—0,3 при р > 10 мм/ч. Было показано [33], что при % —
= 0,63 мкм, p<crt> = 0,155р +2,66 (р > 12,5 мм/ч), (см. также
[17])-
На рис. 3.7 приведены кривые полного сечения p(ctt), сече-
сечения обратного рассеяния р<а6>, альбедо (отношения сечения
рассеяния p<as> к полному сечению р<а<>) и ширины индикатри-
индикатрисы рассеяния на уровне половинной мощности (в градусах) для
1000
Рис. З.6. а — типичные значения /С/ в зависимости от длины волны. Данные
для Л ¦= 1 — 10 см 17], Л = 0,86 см [114], Л = 5мм [161] и Я = Змм[16бГ
(см, также [96]); б — эмпирическое усредненное затухание в дожде [41].
(Использован параметр kepa и найдены вариации Kt и а в диапазоне ча-
частот 8—100 ГГц).
1OZ
101
10°
ю-1
10
10"
-3
i 11 iiiiij i 11 miii| i 11 iiiitj пи iiiij /\ niHij i 11 jiinj ГТТ
Слабый дождь
Qp (градусов)
Альбедо
(дБ/км)
р(бй)(дБ'км)
I IN Mill I I I I Illll I I Mlllll I I I I I III! I I II Mill I M I Illl! 1 I Nllll
0,1mkm Imkm Юмкм ЮОмкм 1mm 1cm 10cm
A,
a
Bill IMIIJ ГПЬПЦ
10'
10°
1С"'
ю-2
io-3
N III Illllj 1 ) 1 ltill|
Qp (градусов)
Облако _
р(б,)(дБ/км) Е
I Альбедо W,
Г4 | | | null 111 Mlllf M III Illl I I II Illll I i 111 Illl III I Illll I I I Illll
ОДмкм Imkm Юмкм ЮОмкм 1мм 1cm 10cm
Рис. 3.7. Затухание, обусловленное полным сеченнем р {о*<), сечением обрат-
ногд рассеяния р (аь}, альбедо [отношением (as) к (оЛ], н ширина луча на
уровне половинной мощности 8Р в зависимости от длины волны, а — слабый
дождь с р = 1 мм/ч, б — облако с содержанием воды 0,062 г/м3 при концентра-
концентрации 108 частиц/м3 [42]. Затухание на оптических частотах основано на дан-
ных [33].)
62 Глава 3
случая слабого дождя с содержанием воды 0,1167 г/м3, что при-
примерно соответствует интенсивности дождя 1 мм/ч. Отметим, что
на оптических частотах затухание несколько меньше. Кроме того,
на рис. 3.7 приведены графики всех указанных величин для
облака с содержанием воды 0,062 г/м3. Обратим внимание, что
в оптическом диапазоне имеется значительное затухание. Оно
связано в основном с рассеянием, так как поглощение мало
(альбедо примерно равно единице). Отметим также, что в диа-
диапазоне СВЧ при распространении волн в облаках или в тумане
сильно сказывается как поглощение, так и затухание, связанное
с рассеянием.
Угловые характеристики рассеяния на дождевых каплях вы-
вычислены для нескольких типичных случаев [42]. Полуширина
индикатрисы рассеяния 0Р оказывается пропорциональной от-
отношению длины волны к размеру капли. Типичный пример при-
веден на рис. 3.7.
На высоких частотах длина волны может быть во много раз
меньше медианного размера частиц, в результате чего рассеян-
рассеянная энергия концентрируется вблизи направления распростра-
распространения падающей волны. В этом случае часто удобно описывать
индикатрису рассеяния гауссовой функцией
< I f @, i) I2) = (y/я) (°s) exp (- уО2), C.9)
где 6 = arccos @ • i), a Y = D1n2)/82. Выражение C.9) норми-
нормировано так, что интеграл от него по всем углам равен <а*>:
оо
Ю= 5<|f@, f)P>rfa«2*j<|fF, f) I2) G cfG. C.10)
4л
3.2.2. Облака1), туман, дымка и смог
Частицы, из которых состоят облака и туман, представляют
собой капли воды или льдинки, размеры которых, как правило,
не превосходят 100 мкм. Медианный радиус обычно равен 2,5—
5 мкм, а концентрация р может меняться от 106 до 109 м~3, при-
причем типичным значением является 108 м~3. Содержание жидкой
воды может колебаться от 0,03 г/м3 в слабом тумане до 2 г/м3 —
в плотном, а оптическая видимость (p(ot})~1 может меняться
от 1 км до 30 м. Типичные численные значения p(at), p<cr&>,
альбедо и полуширины индикатрисы рассеяния 6Р показаны на
рис. 3.7 для случая кучевого облака с концентрацией частиц
108 м~3 и содержанием воды 0,062 г/м3.
Типичные значения медианного радиуса частиц дымки лежат
в пределах 0,05—0,5 мкм, а концентрация может достигать зна-
См. исторический обзор по физике облаков [19].
Характеристики дискретных рассеивателей
63
чения 108 м~3. На рис. 3.8 показаны типичные значения р<о(>,
p<as>, р(оьУ и 8Р в зависимости от длины волны для дымки с со-
содержанием воды 49 мкг/м3 и концентрацией 108 м~3.
Краткое изложение результатов различных экспериментов
по распространению волн через туман, облака и дымку имеется
101
10° г
Ю" г
1-2
10
ИГ1* Г
10"
\ /<
1 1Ш|
¦ ^
1 II Illlll 1 III
/"'I ' ' 1 ' ' lllll!i ' ' '" =
- Qp (градусов)
Мгла ;
Альбедо Шо _
\ ^ \
№ 1
У/— р<(бь>(дБ/км) |
nil ! 1 iui|il 1 1 1 mill i i i iiiij
0,1мкм Imkm 10 мкм IOOmkm 1mm 1cm
К
ю'
ю1
10°
ю-1
ю-2
Юк
40"
I 11IIIIK I III IIIII I
^вр (градусов) -
: рад
Альбедо и)п
г р<б,)>(дБ/км)
i р/дЛ(дБ/км)
i i mill i I 11тnil i i hhirf i t Mini!
Юмкм IOOmkm 1mm
К
1cm 10cm
Рис. 3.8. Полное сечение р (а^, сечение обратного рассеяния р (<т6), альбедо
((as)/(Gf)) и ширина пучка на уровне половинной мощности 0Р; а — дымка
с содержанием воды 49 мкг/м3 и концентрацией 10 частиц/м3, б — град с со-
содержанием воды 0,3 г/м3 и концентрацией 10 частиц/м3 [42].
в работе [28]. Опубликован также ряд экспериментальных дан-
данных по атмосферным аэрозолям и загрязнениям [27, 68, 96, 164].
3.2.3. Снег и град
Снег, вообще говоря, вызывает значительно меньшие потери,
чем вода такого же веса (рис. 3.5), так что затуханием волн
диапазона СВЧ в сухом снеге можно пренебречь. Однако в слу-
случае мокрого снега затухание существенно возрастает. Известно,
что ледяная сфера, покрытая тонким слоем воды, имеет сече-
сечение рассеяния, сравнимое с сечением рассеяния сферы, состоя«
щей целиком из воды.
Некоторые типичные значения характеристик рассеяния и
поглощения для града с содержанием воды 0,3 г/м3 и концен-
концентрацией частиц 10 м~3 приведены на рис. 3.8.
64
Глава 3
При длинах волн от 3 до 10 см можно использовать рэлеев-
ские формулы C.7). При этом |/(|2 = 0,197 для всех темпера-
температур, a Im(tf) = 9,6-10-4 при 0°С, 3,2-10~4 при —10°С и 2,2-Ю-4
при — 20°С [7].
3.3. Рассеяние света в морской воде (гидрооптика)
Рассеяние и поглощение света в морской воде вызывается
как собственно водой, так и взвешенными в ней частицами [76,
77]. (Имеется прекрасный обзор по распространению света в
1-5
I I I I I I -
Чистая океаническая
вода (соленость 35-39)
I
I
1,0 2,0
А.,мкм
Рис. 3.9. Затухание света в чи
350 400
450 500
Х,,мкм
550
600
Рис. 3.10. Сечение рассеяния единичного
б |3 (90°) 8 9° й
у р
стой воде в зависимости от объема |3 (90°) при 8 = 90° для чистой во-
[7] й й
длины волны [77].
) р
ды и чистой морской воды в зависимости
от длины волны.
морской воде [48].) Поглощение света голубой части спектра
(>, = 0,4—0,6 мкм) в чистой воде мало @,01—0,05 м-1) и до-
достигает минимального значения при J\, = 0,48 мкм (рис. 3.9).
В чистой воде рассеяние света обусловлено случайным движе-
движением молекул и описывается сечением рассеяния единичного
объема ') рF):
Р (в) = р < I / @, Т) Р> = Р (90°) A + cos2 8),
C.11)
') В оптической океанографии для описания рассеяния обычно исполь-
используют следующие величины: коэффициент поглощения а = р (аа>, коэффициент
рассеяния Ь = р (as) , коэффициент полного затухания с = а + b и сечение
рассеяния единичного объема 0(9) = р(|/@, i)|2),
Характеристики дискретных рассеивателей 65
где 0 = arccos(O, i). Это выражение применимо для неполяри-
зованного (естественного) света (рассеяние поляризованного
света рассматривается в работе [77]). Коэффициент рассеяния Ъ
определяется выражением
6 = p<(rs>==A6n/3)P(90°). C.12)
Характерные значения сечения рассеяния единичного объема
При 8 = 90° в зависимости от длины волны показаны на
рис. 3.10.
Частицы, взвешенные в морской воде, включают в себя:
а) желтое вещество (продукты гниения, возникающие в резуль-
результате разложения растений и веществ животного происхождения)
с размером частиц порядка микрометра или миллиметра и
б) дискретное вещество (неорганическое вещество, возникаю-
возникающее при дренировании почвы и при выветривании, а также ор-
органическое вещество — планктон и разрушенные клетки с раз-
размерами больше нескольких микрометров).
Количество взвешенного вещества в океанической воде ко-
колеблется от 0,04 до 18 мг/л. Распределение его по размерам су-
существенно сказывается на характеристиках рассеяния света.
Вообще говоря, размеры этих частиц заключены в интервале от
0,01 мкм до нескольких сотен микрометров. Распределение ча-
частиц по размерам, по-видимому, хорошо описывается законом
Юнга
п(а) = Аа-а, C.13)
где А и а — постоянные. Обычно а принимают значения между
Таблица 3.1
Типичные значения р <(Т^>, p<(Ts> и р<сга> для взвешенных частиц
в океане [76] 1)
Место Длина^волны, Р<°*>'м-' P<°s>. м-1 Р<оа>, м-1
Карибское море 0,44 0,09 0,06 0,03
0,655 0,06 0,06
Океан у берегов Кали- 0,522 0,08 0,01 0,07
форнии
Южная часть Балтийско- 0,380 1,15 0,21 0,94
го моря 0,655 0,27 0,20 0,07
' Приведенные здесь значения описывают только влияние взвешенных частиц. Для
нахождения полного затухания к этим значениям необходимо добавить затухание в чистой
воде.
66
Глава 3
2,25 и 4,5. Показатель преломления, обусловленный наличием
различных взвешенных частиц, в 1,02—1,25 раза больше пока-
показателя преломления мор-
морской воды [176] (см. ре-
результаты измерений [26]).
Некоторые типичные зна-
значения р<оч>, p<as> и р<стд>
приведены в табл. 3.1 ¦).
На рис. 3.11 показана ти-
типичная индикатриса рассея-
рассеяния <ad(9)> = <|f(e, i)|2>, нор-
нормированная на ad(90°). На
рассеяние вперед сильно
влияют крупные частицы.
Поскольку распределение по
размерам крупных частиц
A0—100 мкм) зачастую не-
неизвестно, расчет и измере-
измерение индикатрисы рассеяния
вблизи 9 = 0 сталкивается
с трудностями. Однако
обычно большая часть из-
Рис. 3.11. Типичная индикатриса
20 40 60 80 100 120 140 160 180 рассеяния дискретных частиц в
Угол рассеяния б град
морской воде [77].
мерений указывает на отличие примерно в 50 дБ между значе-
значениями при 8 = 0 и 8 = 90°.
Было найдено, что отношение <Od D5°) > к полному сечению
рассеяния (as} для океанической воды примерно постоянно и
колеблется от 2-10~2 до 3,5-10~2.
3.4. Рассеяние звука в воде (гидроакустика)
Случайные флуктуации акустических волн (это явление на-
называют также реверберацией) в океане обусловлены рассеянием
а) на воздушных пузырьках, рыбах, морских животных, орга-
органических и неорганических частицах, б) на турбулентных и
слоистых нерегулярностях распределений температуры и плот-
') Приведенные в таблице значения учитывают только взвешенное веще-
вещество. Чтобы получить полное затухание, к приведенным значениям нужно до-
добавить затухание, обусловленное чистой водой.
Характеристики дискретных рассеивателей 67
ности и в) на нерегулярностях поверхности и дна океана [88,
109, 115, 150, 157]. В данном разделе мы сначала приведем крат-
краткое описание типичных акустических свойств океана. Затем мы
рассмотрим характеристики двух основных видов рассеивателей
в воде — воздушных пузырьков и рыб. Турбулентность и харак-
характеристики неровных поверхностей рассматриваются в гл. 16—21.
Дно океана [150, 157] условно делится на три части: шельф,
склон и абисс. Шельф представляет собой мелководную часть
океана, расположенную в прибрежной области в виде полосы,
ширина которой колеблется от нескольких километров до 100 км.
Наклон дна в этой области мал, так что глубина на границе
шельфа может достигать 100 м. Склон характеризуется боль-
большими значениями наклона дна A к 20 или 30), и глубина здесь
достигает нескольких километров; имеются долины и ущелья,
которые называют каньонами. Абисс характеризуется меньшими
наклонами дна и занимает примерно 80% площади океаниче-
океанического дна. В абиссе обнаружены большие подводные горы и
трещины.
Температура верхнего 200-метрового слоя воды в океане от-
относительно постоянна (изотермична), если не принимать во вни-
внимание флуктуации температуры, обусловленные турбулентно-
турбулентностью. Ниже этого слоя появляется значительный вертикальный
градиент температуры, которая примерно на глубине 1000 м до-
достигает своего минимального значения около 4 С. Эта область
называется термоклином. Далее температура равномерно воз-
возрастает вплоть до дна океана.
Скорость звука С (м/с) при атмосферном давлений на по-
поверхности описывается эмпирической формулой [150, 157]
С =1449,2 + 4,6237: - 0.0546Г2+ 1,391E-35), C.14)
где Т — температура в градусах Цельсия, a S — соленость в ты-
тысячных долях (по весу). Обычно соленость S имеет значение
около 35. Скорость звука возрастает с температурой, соленостью
и глубиной со скоростями
АС/А7 = 2,7 м/с°С, C.15а)
AC/AS =1,2 м/с, C.156)
АС/ЛЯ = 0,017 с, C.15в)
где Н — глубина в метрах.
Скорость звука в воде, содержащей несколько объемных про-
процентов воздушных пузырьков, существенно меньше скорости
звука в воде без пузырьков и имеет значение порядка 40 м/с.
Она уменьшается до 20 м/с в воде с содержанием воздуха
50 объемн. % [150].
68
Глава 3
Типичные кривые зависимости скорости звука С (г) от глу-
глубины приведены на рис. 3.12. На умеренных широтах имеется
минимум скорости звука вблизи глубины z = 1270 м; в эква-
экваториальных областях этот минимум расположен несколько
ближе к поверхности. Звук может захватываться окрестностью
этого минимума и распространяться в ней без существенного
ослабления. Таким образом, область, расположенная на такой
глубине, образует акустический волновод, или звуковой канал
(канал SOFAR).
X
Я
Ю
>
0
1000
2000
яппп
1450
'\
Район
полюса
i
с(г),
1500
I
\
м/с
1550
Район экватора
Средние
широты
Рис. 3.12. Изменение ско-
скорости звука в зависимости
от глубины на трех харак-
характерных широтах.
Вблизи поверхности океана также возможно появление от-
носительного минимума скорости звука на глубинах в несколько
сотен метров. Эта область называется поверхностным звуковым
каналом.
Затухание акустических волн в океанической воде обуслов-
обусловлено в основном вязкостью и релаксационным действием суль-
сульфата магния. Потери из-за теплопроводности пренебрежимо
малы. В диапазоне от нескольких герц до 10 МГц эксперимен-
тальные данные хорошо описываются следующей эмпирической
формулой для коэффициента затухания а (рис. 3.13):
3,38
- A-6,54-10-4), C.16)
t J
где f — частота (Гц), ft = 21,9-10(9-I520/:r>— релаксационная ча-
частота (Гц), Т — температура (К), S — соленость, Ps — давление
(атмI).
Акустический локатор, или сонар (SONAR — sound naviga-
navigation and ranging), представляет собой устройство, используе-
') Напомним, что 1 атм = 1.013-105 Па A Па = 1 Н/ма).
Характеристики дискретных рассеивателей
69
мое для посылки акустических импульсов, приема отраженного
от целей сигнала и определения характеристик целей. Частота
используемых сигналов обычно заключена в пределах 5—
300 кГц, а длительность импульсов составляет 100 мкс — 100 мс.
10 Э I I I пи 1| ГТТТТТП] ГТТТТТТТ] 1
I Ml Mill I I I I Illl
104 Ю5 106 1rt7
Частота, Гц
10'
Рис. 3.13. Коэффициенты затухания звука в воде в зависимости от частоты
при температуре 0 и 20 °С, солености S = 0 и 35 и нормальном атмосфер-
атмосферном давлении (а в дБ/м).
Очевидно, что более высокочастотные сигналы на обычных ди-
дистанциях в океане практически непригодны из-за чрезмерного
поглощения. Однако в лабораторных условиях для модельных
экспериментов или на коротких дистанциях широко исполь-
используются сигналы с частотами в несколько мегагерц.
В качестве стандартного значения скорости звука в морской
воде можно принять 1500 м/с, а в качестве стандартного зна-
70 Глава 3
чения характеристического импеданса ') р0С = 1,54• 106 кг/м2-с.
Эти значения отвечают поверхностному слою воды с темпера-
температурой 13°С, соленостью 35 и плотностью р0 = 1026 кг/м3. В от-
отличие от этого в воздухе при температуре 20°С и нормальном
атмосферном давлении A атм = 1,013-105 Па) плотность ро ==
= 1,21 кг/м3, скорость звука С = 343 м/с, характеристический
импеданс роС = 415 райлов. Из-за столь большого различия
характеристических импедансов воздуха и воды сигнал, падаю-
падающий на границу раздела вода — воздух, практически полностью
отражается. Нефть имеет плотность «900 кг/м3, скорость звука
порядка 1300 м/с и характеристический импеданс 1,117-106 рай-
лов.
Уровень акустического давления обычно выражают в деци-
децибелах по отношению к опорному уровню2) 0,1 Па = 1 мкбар.
Если акустическое давление равно 1 Па, то это означает, что
его уровень на 201g( 1/0,1)= 20 дБ превышает уровень 1 мкбар.
3.4.1. Рассеяние на воздушных пузырьках
Мы описали некоторые общие характеристики акустических
волн в океанической воде. Обратимся теперь к описанию двух
основных видов рассеивателей в океане — воздушных пузырь-
пузырьков и рыб.
Воздушные пузырьки присутствуют главным образом вблизи
поверхности, на глубинах в несколько метров. Их возникновение
обусловлено опрокидыванием волн, следами кораблей и подвод-
подводных лодок, падением снежинок и дождевых капель, а также
жизнедеятельностью морских животных, например сифонофор.
Размеры пузырьков могут меняться от нескольких микрометров
до нескольких сотен микрометров, а их концентрация состав-
составляет от нескольких пузырьков в одном литре, до сотен пузырь-
пузырьков в одном кубическом сантиметре.
В поле акустической волны воздушный пузырек начинает
пульсировать и его радиус осциллирует около среднего значе-
значения с частотой падающей волны. На некоторой частоте эти ос-
осцилляции становятся резонансными и амплитуда осцилляции
достигает максимума. Мощность, рассеиваемая таким пульси-
пульсирующим пузырьком, довольно значительна, а сечение рассеяния
') Единица характеристического импеданса в системе СИ называется рай-
лом A райл = I кг/м2-с).
2) Приведем связь единиц СИ и СГС, широко используемых в акустике.
Давление: 1 Па = 10 дин/см2 = 10 мкбар; сила: 1 Н = 105 дин; мощность:
1 Вт = 107 эрг/с; энергия 1 Дж = 107 эрг. Используется также другой опор-
опорный уровень 2-10~4 мкбар = 2-10~5 Па. Этот опорный уровень обычно ис-
используется в воздухе и отвечает пределу слышимости человеком сигнала ча-
частоты 1 кГц. Интенсивность соответствующей плоской волны в воздухе при-
приблизительно равна B-IQ-6J/400= 10 Бт/м2 [87, 101].
Характеристики дискретных рассеивателей 71
на резонансной частоте очень велико по сравнению с сечением
рассеяния пузырька в нерезонансной области. Отношение этих
сечений может достигать 103.
В предположении адиабатичности процесса пульсаций резо-
резонансная частота приближенно равна
/г = Bяа)~1Л/Зу^/ро, C.17)
где а — радиус пузырька, у — отношение удельных теплоемко-
стей газа в пузырьке, Ра — гидростатическое давление в окру-
окружающей среде, а ро —• плотность окружающей среды. Для воз-
воздушных пузырьков на уровне моря, приняв у = 1,4, Ро = 105 Па
и ро = 1025 кг/м3 B5°С), получим
fr = 3,22/а (м). C.18)
Если размер воздушного пузырька много меньше длины
волны в воде, рассеяние акустической волны на нем почти изо-
изотропно. В этом случае сечение рассеяния as воздушного пузырь-
пузырька приближенно равно [102, 109, 135, 150]
Ana2.„ 1Q.
"*~ [(шг/шJ-112-
где о»/- = 2nfr, а б = 8r + dt -f- 8V — постоянная затухания коле-
колебаний пузырька, связанная с переизлучением (рассеянием), теп-
тепловыми и вязкими потерями.
Постоянная затухания бг, обусловленная рассеянием, дается
формулой бг = k,a — 0,013, где kr = (ar/C, С — скорость звука
в воде. Тепловые и вязкие потери приближенно пропорциональ-
пропорциональны fr' и fr соответственно. Зависимости этих постоянных зату-
затухания от fr приведены на рис. 3.14. Из C.19) видно, что при
резонансе os значительно превосходит геометрическое сече-
сечение па2.
Ширина резонансной области на уровне половинной мощно-
мощности Af определяется выражением
^- = 6 = 6А + 6( + 60. C.20)
'г
Сечение обратного рассеяния оь, сечение поглощения оа и пол-
полное сечение at резонансного пузырька приближенно равны
б, + л б
г Г
Для частот, существенно отличающихся от резонансной, при-
приближенно имеем
Оь = <*л = at. C.22)
«г1
s
X
Iff
н
'-—'-г с 1 ; и : i| 1
Полное
-Г* Затухание J
Т1 1 1 1 1 II] ! 1 1 1 1 1 II
Тепловое / -
затухание 5( /
; Затухание / ;
из-за излучения 5/- /
- у/
/ II 1 Mil 1
Затухание -
из-за вязкости v E
i i i i i м1 i i i м 11
10° lQi Ю2
Резонансная частота ft, кГц
103
Рис. 3.14. Постоянные затухания, обусловленные излучением (рассеянием)
дг тепловыми FЛ и вязкими (ба) потерями для резонансного пузырька
в воде [44].
10"'
2 ю-7
10'
10'
= гттпттт] I I Iiniij I I 11inij ГТТТП5
а~Ю0мкм
а—50м км
I М-1Л III! / I I M I'Hll I I I I 11 III I [MM
10° 101 102 10' 104
Рис. 3.15. Сечения воздушных пузырьков в зависимости от частоты.
Характеристики дискретных рассеивателей
73
Примеры сечений в зависимости от частоты приведены на
рис. 3.15 для а = 100 мкм (/, = 32,2 кГц) и а = 50 мкм
F4,4 кГц).
3.4.2. Рассеяние на рыбах
Частями тела рыбы, которые влияют на рассеяние акусти-
акустических волн, являются собственно тело рыбы, спинной хребет и
плавательный пузырь. Тело рыбы обладает характеристическим
10°
Ю -
ю-
1 1
: .z
iiii i
-
[ A
- \
i
\
\
\
t i
i i i j 11 j
-4
/
// Сбр.ку-
1
Рэлеевское
рассеяние/
/
ч
1 N. 1 1 1 1 1
| ] | 1 J.4.^1 |
1 IT
Геометрическая
! 1 1 | 1 1 1
/ /-Go спины
/ / =
/
/
/ i t t i i i i 11
10°
10!
L/K
102
Рис. 3.16. Сечение обратного рассеяния ob, нормированное на L2, где L — длина
рыбы [150].
акустическим импедансом рС = 1,60-106 кг/м2-с. Это значение
очень близко к характеристическому импедансу морской воды
A,54-106), так что рассеяние от тела рыбы относительно мало.
Максимальная высота рыбы составляет приблизительно 0,195 L,
а максимальная ширина 0,112 L, где L — длина рыбы. Объем
ры,бы равен 8,3-Ю^3 L3, а объем ее плавательного пузыря —
3,4-Ю-4 L3. Тело рыбы можно аппроксимировать эллипсоидом
с указанными размерами.
74 Глава 3
Акустический импеданс спинного хребта составляет 2,5-
-106 кг/м2с, поэтому он дает больший вклад в рассеяние. Спин-
Спинной хребет можно аппроксимировать цилиндром длины 0,65 L
и диаметра 0,012 L. Наиболее существенным для рассеяния аку-
акустических волн является плавательный пузырь, так как нахо-
находящийся внутри него воздух почти полностью отражает звук.
Плавательный пузырь можно аппроксимировать цилиндром
длины 0,24 L и радиуса 0,0245 L. На рис. 3.16 приведен прибли-
приблизительный диапазон экспериментальных значений сечения об-
обратного рассеяния по данным работы Хаслетта (см. [150]). Эти
данные ограничиваются диапазоном 3 < L/X <C 60, но можно
ожидать, что при L/X > 60 преобладают геометрооптические
эффекты и a/L2 должно быть пропорционально (L/X)p, где р
меняется от 0 (эллипсоидальная форма) до 1 (цилиндрическая
форма) и далее до 2 (плоская форма). При L/X < 3 должно
быть применимо рэлеевское приближение. В этом случае р = 4.
3,5. Рассеяние на биологических средах
3.5.1. Биоэлектродинамика
Электромагнитные поля в диапазоне частот от 1 МГц до
100 ГГц могут распространяться в биологических средах, испы-
испытывая при этом в различной степени поглощение, отражение я
рассеяние. Отражение возникает на границах тканей, а рассея-
рассеяние вызывается неоднородностями с размером порядка длины
волны в тканях [79, 81].
Излучение на частотах 27, 12, 915 и 2450 МГц используется
для диатермии в США; в Европе для этой цели используется
излучение на частоте 433 МГц. Среди других медицинских при-
приложений СВЧ-излучения упомянем нагревание охлажденной
крови до температуры человеческого тела перед переливанием
и селективное нагревание раковых или доброкачественных опу-
опухолей для управления действием противораковых препаратов.
В СВЧ-нагревателях обычно используется частота 2450 МГц,
их обычная мощность около 2 кВт, а максимальная — 5,25 кВт.
Влияние СВЧ-излучения на биологические системы может
носить как тепловой, так и нетепловой характер. Поглощаемая
тканями мощность вызывает повышение температуры, которое
зависит от диффузионных механизмов нагревания и охлаждения
тканей. Если способность системы к терморегулированию ока*
жется недостаточной, чтобы справиться с подводимым количе-
количеством тепла, ткани разрушаются, и может наступить смерть.
В США при долговременном облучении человека в качестве
безопасной плотности мощности рекомендуется значение
Характеристики дискретных рассеивателей
75
10 мВт/см2. По сообщениям советских ученых, центральная
нервная система чувствительна к СВЧ-излучению с интенсив-
ностями- ниже теплового порога. В СССР принят максимальный
уровень плотности мощности 0,01 мВт/см2.
Диэлектрическая проницаемость тканей с высоким содержа-
содержанием воды (таких, как мышцы и кожа) тщательно исследова-
исследовалась Шваном (см. [135]) и его сотрудниками. Результаты этих
Рис. 3.17. Диэлектрические про-
прогенсы угла потерь %,, %т и т6
жировых, мышечных и мозго-
мозговых тканей соответственно в за-
зависимости от частоты.
103
Частота, МГц
104
исследований приведены на рис. 3.17, где показаны также гра-
графики диэлектрической проницаемости для тканей с низким со«
держанием воды, подобных жиру и костям. Значения е и а ме-
меняются с температурой со скоростями +2 и —0,5%/°С соответ-
соответственно.
3.5.2. Биооптика
При распространении света в биологических средах основ-
основную роль играет рассеяние. Это связано с неоднородностью кле-
клеточной структуры, причем размеры частиц имеют порядок опти-
оптической длины волны. Обычно диаметр клеток составляет не-
несколько микрометров. Мышечные клетки могут достигать в
длину нескольких миллиметров, а нервные — могут превосхо-
превосходить один метр. Клетка состоит из тонкой, толщиной примерно
75 А, оболочки, цитоплазмы и ядра. Ткани эпителия состоят из
клеток, расположенных в слоистой оболочке. Эти ткани покры-
76 Глава 3
вают поверхность тела или выстраиваются вдоль нее и осуще-
осуществляют функции защиты и регулирования секреции. Соедини-
Соединительные ткани поддерживают и связывают клеточные ткани со
скелетом. Мышечные ткани состоят из клеток длиной 1—40 мм
и диаметром до 40 мкм. Нервные ткани состоят из нервных кле-
клеток, называемых нейронами, которые осуществляют передачу
информации между центральной нервной системой и мышцами,
органами, железами и т. д. [79]. (Рассеяние света на бактериях
описано в работе [37]; применение лазеров в медицине рассмо-
рассмотрено в работе [169].)
Свет использовался для определения содержания кислорода
в крови. Красные кровяные тельца (эритроциты) имеют форму
двояковогнутых дисков с максимальным диаметром около 7 мкм
и толщиной около 1 мкм в центре и 2 мкм на краях. Эритроциты
непрерывно образуются в костном мозге, переносятся потоком
крови и поглощаются и восстанавливаются в печени. Обычно
имеется примерно 5-Ю6 эритроцитов в 1 мм3. Эритроциты со-
составляют примерно 40% всего объема крови. Объемная доля
эритроцитов в крови называется гематокритом Я. В нормаль-
нормальной крови Я = 0,4. Остальные 60% объема крови составляет
практически прозрачный водный раствор солей, называемый
плазмой.
В красных кровяных тельцах имеются молекулы гемоглобина
НЬ, которые легко окисляются в молекулы оксигемоглобина
НЬО2. Насыщенность кислородом OS определяется как отноше-
отношение количества оксигемоглобина [НЬОг] к полному количеству
гемоглобина [НЬО2] + [НЬ]. Чтобы найти характеристики по-
поглощения света в самом гемоглобине, оболочку эритроцитов раз-
разрушают; при этом гемоглобин находится в растворе. Такой рас-
раствор называют гемолизованной кровью. Он представляет собой
однородную поглощающую среду. Уменьшение интенсивности
света dl в этой среде пропорционально интенсивности / и эле-
элементу пути dz:
dl = — al dz. C.23)
Таким образом, интенсивность света уменьшается по экспонен-
экспоненциальному закону
/ (г) = I @) ехр (- аг), C.24)
который называется законом Ламберта — Бира. Постоянная по-
поглощения а зависит от концентрации молекул С (моль/см3) и
от удельного коэффициента поглощения х (см2/моль):
а = Си. C.25)
На рис. 3.18 приведены кривые удельных коэффициентов погло-
поглощения у.н и но гемоглобина НЬ и оксигемоглобина НЬО2 гемоли-
Характеристики дискретных рассеивателей
77
зованной крови. Оксигемоглобин НЬО2 обладает слабым погло-
поглощением в красной области спектра, поэтому кровь, в которой
преобладает оксигемоглобин, выглядит красной. Поглощения ге-
гемоглобина Hb и оксигемоглобина НЬОг совпадают при % =
= 0,548, 0,568, 0,587 и 0,805 мкм. Эти длины волн соответствуют
изосбестическим точкам.
iOO
10
1,0
O.I
1 1 1 1 1 1
,\
1 \
- и
: i
i
\
\
\
\
-
-
z
-
-
i
i
л А
\ IV
\ V
V
1
1
1
1
1
\
I
\
\
\
\
\
\
\
\
\
\ \
\
\
\
\
HbOj
--Hb
_
-
-
—
—
_
_
Изосбестическая I
точка
A /
ч/^—5
/ \
/ \
/ \
' \ i \
0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
Длина волны, мкм
Рис. 3.18. Спектры оптического поглощения гемоглобина [НЬ] и оксигемо-
оксигемоглобина [НЬО2].
Рассмотрим световой пучок, направленный на слой толщины
D. Коэффициенты пропускания Т и отражения R определяются
соответственно как отношение интенсивности прошедшей или
отраженной волны к интенсивности падающей волны. Оптиче-
Оптическая плотность OD определяется выражением
OD = lg(r-'). C.26)
Оптическая плотность гемолизованной крови с насыщенностью
кислородом OS дается формулой
OD = 0,4343CxD, C.27)
78
Глава 3
где Ск = СоХо + ChKh — среднее взвешенное от хо и %h. Через
Со и Сн обозначены концентрации [НЬО2] и [НЬ] соответственно,
а через к0 и хл — удельные коэффициенты поглощения [НЬО2] и
[НЬ]. Замечая, что OS = Со/(Со -\- Ch), можно также написать
C = Co + Cft, x = xh + OS{x0-xk). C.28)
Проведя измерение оптической плотности OD гемолизован-
ной крови на двух длинах волн и зная из рис. 3.18 значения хо
и хн на этих частотах, можно найти насыщенность кислородом
OS (см. [81], где описан спектрофотометр для оксиметрии in
vivo). Если выбрать две длины волны, одна из которых прихо-
приходится на красную часть спектра (например, A,i = 0,66 мкм,
xoi = 0,10-106 и %h\ = 0,80- 10s), а другая совпадает с изосбе^
стической (к2 = 0,805 мкм, хО2 = хм = 0,20-106), то получим
C-29)
где ODi и OD2 — оптические плотности при Х\ = 0,66 мкм и
%2 = 0,805 мкм соответственно.
Оптическая плотность обычной крови существенно отличается
от оптической плотности гемолизованной крови из-за того, что
в обычной крови гемоглобин находится в эритроцитах, и имеет
место значительное рассеяние света. Характеристики рассеяния
и поглощения эритроцитов (красных кровяных телец) наиболее
удобно описывать сечениями рассеяния и поглощения. Типичные
значения этих сечений приведены в табл. 3.2.
Таблица 3.2
Типичные значения сечения рассеяния as, сечения поглощения аа,
показателя преломления п — п' + м" п0 отношению к плазме,
среднего косинуса угла рассеяния р, одного красного кровяного тельца,
коэффициента переноса ро>г [разд. 9.5, 9.7 и 9.8] для цельной крови
с гематокритом Я = 0,41 [125]
Насыще-
Насыщение
кислоро-
кислородом
100%
0%
к
мкм
0,665
0,675
0,685
0,955
0,960
0,965
0,665
0,675
0,685
0,955
0,960
0,965
п
1,036
1,036
1,036
1,036
1,036
1,036
1,036
1,036
1,036
1,036
1,036
1,036
п"
(Х10Ч
0,240
0,244
0,248
0,111
0,109
0,109
2,203
2,207
2,023
0,052
0,049
0,047
о* * мкм2
S'
57,20
56,14
55,09
33,47
33,18
32,90
56,58
55,53
54,56
33,54
33,27
32,98
О . МКМ2
СЕ
0,060
0,060
0,059
0,191
0,187
0,185
0,542
0,535
0,484
0,090
0,085
0,080
0,9951
0,9950
0,9949
0,9925
0,9924
0,9924
0,9951
0,9950
0,9949
0,9925
0,9924
0,9924
МКМ2
0,283
0,281
0,281
0,251
0,251
0,251
0,279
0,278
0,278
0,252
0,252
0,252
мм—1
0,747
0,744
0,739
0,666
0,666
0,665
0,738
0,735
0,731
0,668
0,667
0,666
Характеристики дискретных рассеивателей 79
Гематокрит Я связан с концентрацией эритроцитов р и объе-
объемом одного эритроцита Ve соотношением
p = H/Ve. C.30)
Поэтому коэффициент поглощения роа равен
poa = HoJVe. C.31)
При достаточно малых значениях Н(Н << 0,2) коэффициент рас-
рассеяния pos дается аналогичной формулой
pas = Has/Ve. C.32)
При Я > 0,5 частицы становятся тесно упакованными, а среда
становится почти однородной. В этом случае всю кровь можно
рассматривать как однородную среду, состоящую из гемогло-
гемоглобина, в которую вкраплены рассеивающие частицы из плазмы,
окружающей красные кровяные тельца. В пределе #-> 1 «плаз-
«плазменные частицы» исчезают и коэффициент рассеяния pos дол-
должен стремиться к нулю. Это приводит к следующей приближен-
приближенной формуле для pos:
pas = H(l-H)as/Ve, C.33)
где множитель A—Я) учитывает исчезновение рассеяния при
#->-1. Зачастую плотная упаковка (Я = 1) недостижима, и
влияние упаковки нельзя описать простой функцией A — Я).
Например, если частицы представляют собой твердые сферы, Н
не может превосходить значения 0,64. Тогда следует принять
[9]
pos = (Hos/Ve)f(H), C.34)
где функция f(H) должна монотонно уменьшаться от 1 при
U = о до 0 при некотором определенном значении Н.
3.5.3. Биоакустика'>
Акустический коэффициент затухания а на единицу длины
пути в тканях, как правило, меняется по закону /", где f — ча-
частота, а п лежит в пределах от 1 до 2. Коэффициенты затуха-
затухания а для мышц, печени, почек, мозга и жира примерно про-
пропорциональны частоте f и лежат в интервале от 0,5-10~6 до
2• 10~6 f дБ/см. Типичные значения коэффициента затухания а,
скорости звука с и плотности ро приведены в табл. 3.3.
Влияние ультразвука на свойства крови подробно исследова-
исследовалось. Обычно в биологических средах используются частоты в
]) См. [135]. Использование ультразвука в медицине описано в работах
[1Б4, 167].
80 Глава 3
Таблица 3.3
Типичные значения коэффициента затухания а,
скорости звука С и плотности р0 биологических тканей [135, 167]
Тип тканн Частота, МГц а, см С, см/с ро" г/см3
Жир
Мышцы
Кости
Мозг
Почки
Печень
диапазоне от нескольких сотен килогерц до 10 МГц, так что
длина волны во много раз больше размера красных кровяных
телец. Поэтому рэлеевская формула для сферы того же объема,
что и у красного кровяного тельца, должна давать хорошее при*
ближение для характеристик рассеяния и поглощения. Ампли-
Амплитуда рассеяния f @, i) дается формулой
1,0
1,0
1,2
1,0
2,0
2,0
0,08
0,13
1,7
0,1
0,04
0,19
1,44-105
1,57-105
3,36 • 105
1,54- 105
1,56 • 106
1,55-105
0,97
1,07
1,7
k2a3 / к — х Зр — Зр
(V- + ifc+fcos e
) •
где k = 2п/Х, К — длина волны в окружающей среде (плазме),
а — радиус эквивалентной сферы, ке и ре — адиабатическая
сжимаемость и плотность красных кровяных телец, х и р — со-
соответствующие характеристики плазмы, а 9 — угол между б и Т.
Объем обычного кровяного тельца равен 0,87 мкм3, а эквива-
эквивалентный радиус а составляет 2,75 мкм. Сжимаемость и плот-
плотность красного кровяного тельца равны ке = 34,1 • 10~12 см2/дин,
ре = 1,092 г/см3, те же параметры для плазмы составляют к =
= 40,9- Ю-12 см2/дин, р = 1,021 г/см3.
Сечение рассеяния os дается формулой
па*
4(ka)* \
9 1
'I x — к
1 s
+
1
3
зре
-3p
+ P
]•
C.36)
Используя приведенные выше численные значения ке, ре, к, р
и а, находим
as=l,l -Ю-16/4 см2, C.37)
где / — частота в мегагерцах.
Сечение поглощения аа пропорционально частоте и равно
Вп Aka / % — у. Зр — Зр ,
Характеристики дискретных рассеивателей 81
где Im означает «мнимая часть выражения». Мнимые части ке,
ре, % и р неизвестны. Известно однако, что в диапазоне от 0,1
до 10 МГц сечение поглощения аа во много раз больше сечения
рассеяния as, откуда следует, что затухание в крови обуслов-
обусловлено главным образом поглощением, а не рассеянием. Известно
также, что затухание плоской волны в облаке случайных рас-
рассеивателей равно роа Нп/см. Постоянная затухания пропорцио-
пропорциональна гематокриту Н и частоте / (в мегагерцах) и приближен-
приближенно равна
о = E + 7) • 10~2#f Нп/см = 0,ЗЯ/ дБ/см. C.39)
Поскольку а = раа =z{H/Ve)oa, сечение поглощения отдельного
эритроцита равно
сга = б. 10~12/ см2,
где / измеряется в мегагерцах. Характеристики рассеяния и по-
поглощения могут существенно зависеть от вязкости плазмы и
эритроцита [3].
Глава 4
Рассеяние волн в разреженных
облаках частиц
В гл. 2 и 3 представлены характеристики отдельного рассеи-
вателя и приведены некоторые примеры, с которыми чаще всего
приходится иметь дело на практике. Обратимся теперь к глав-
главной цели данной книги, а именно к изучению характеристик
волны, распространяющейся через облако случайно распреде-
распределенных рассеивателей. Укажем сразу, что, имея дело с волной
в облаке из множества частиц, как правило, рассматривают два
предельных случая: разреженные и плотные облака. Если плот-
плотность частиц мала, можно использовать приближение однократ-
однократного рассеяния (рис. 4.1, а). В этом приближении предполагает-
предполагается, что излученная волна приходит к приемному устройству,
встретившись лишь с очень небольшим числом частиц. При этом
считается, что рассеянная волна порождается однократным рас-
рассеянием на какой-либо частице, а рассеяния более высоких крат-
ностей считаются пренебрежимо малыми. Результаты такого
приближения чрезвычайно просты и широко используются в
приложениях, включая метеорологические радиолокаторы [7] и
акустику океана [157]. (Общая теория рассеяния света изло-
изложена в работах [16, 36].)
При увеличении концентрации частиц уже нельзя считать,
что распространяющаяся в прямом направлении волна не от-
отличается от падающей,, и возникает необходимость учитывать
затухание волны из-за рассеяния и поглощения вдоль пути рас-
распространения (рис. 4.1,6). В таком приближении по-прежнему
считается, что рассеянная волна обусловлена однократным рас-
рассеянием на частице, но здесь уже учитывается затухание из-за
рассеяния и поглощения как падающей, так и рассеянной волн
при их распространении. Такой подход частично учитывает мно-
многократное рассеяние, и поэтому мы его будем называть первым
приближением теории многократного рассеяния. Это приближе-
приближение широко используется при изучении поглощения в дожде.
Слова «разреженный», «малая плотность частиц» и т. п. ис-
использовались выше без соответствующей строгости. Вообще го-
говоря, разграничение различных приближений должно зависеть
от таких величин, как оптический путь и альбедо, которые за*
висят от длины волны, размера частиц и их характеристик рас-
рассеяния, а также от. свойств излучателя и приемника. Эти во-
вопросы рассматриваются в последующих разделах, посвященных
соответствующим приближениям.
Рассеяние волн в разреженных облаках частиц 83
Указанные выше два приближения — однократное рассеяние
и первое приближение многократного рассеяния — пригодны для
описания большинства встречающихся на практике задач. От-
Относительная простота этих методов обусловила их чрезвычайно
широкое использование. Однако оба этих приближения пригод-
пригодны лишь для разреженных облаков частиц. В противоположном
a
Излучатель Приемник
,^-" -'%,
Затухание
Рис. 4.1. Однократное рассеяние (а), первое приближение многократного рас-
рассеяния (б), многократное рассеяние (в) и диффузионное приближение (г).
случае, когда плотность частиц велика, оказывается полезным
другой метод, который называется диффузионным приближе-
приближением (рис. 4.1, г). Этот метод подробно рассматривается в гл. 9.
Существует еще промежуточная область концентраций ча-
частиц, лежащая между областями малых плотностей (когда при-
применимо однократное рассеяние и первое приближение теории
многократного рассеяния) и больших плотностей (когда спра-
справедливо диффузионное приближение), где многократное рассея-
рассеяние играет важную роль (рис. 4.1, в). В последующих главах мы
рассмотрим некоторые методы, разработанные для описания
волн в этой сложной для расчетов области. Здесь же мы оста-
84 Глава 4
новимся на однократном рассеянии и на первом приближении
теории многократного рассеяния.
Вообще говоря, при исследовании волн в случайных средах
все задачи можно разделить на два типа: а) рассеяние волны
в случайной среде и б) распространение волны в случайной
среде в пределах прямой видимости. Среди примеров задач рас*
сеяния можно назвать изучение аэрозолей и гидрометеоров с по-
помощью радиолокаторов, лазерных и акустических локаторов,
а также рассеяние света и звука в йоде. Примеры задач рас-
распространения в пределах прямой видимости включают опреде-
определение флуктуации амплитуды и фазы волны, вызванных слу-
случайной средой, и влияния этих флуктуации на системы связи.
Каждый из этих двух типов задач (рассеяние и распростране-
распространение) в свою очередь можно разбить на два вида в зависимости
от того, является ли излученная волна монохроматической или
импульсной.
Данная глава посвящена рассеянию монохроматической вол-
волны в случайной среде. Рассеяние импульсных волн рассматри-
рассматривается в гл. 5, а задачи распространения в пределах прямой ви-
видимости изучаются в гл. 6. Первые три раздела данной главы
посвящены анализу средней мощности рассеянной волны. В ос-
остальной части главы обсуждаются флуктуации рассеянной вол-
волны, корреляционные функции, спектры и распределения вероят-
ности.
4.1. Средняя мощность рассеянного поля
в приближении однократного рассеяния
Рассмотрим объем V со случайно распределенными части-
частицами, на который падает монохроматическая волна от излуча-
излучателя с диаграммой направленности по мощности G/(i). Требуется
определить среднюю мощность, которую примет приемник с эф-
эффективной площадью апертуры АГ(Ь) (рис. 4.2). Возьмем ма-
малый объем dV, содержащий р dV частиц, где р — концентрация
частиц, т. е. число частиц в единичном объеме. Предполагается,
что этот объем достаточно удален как от излучателя, так и от
приемника. Пусть Ri и R2— расстояния от dV до излучателя и
приемника соответственно, a i и 0 — единичные векторы в на-
направлении распространения падающей и рассеянной объемом
dV волн.
Плотность падающей мощности Si на элементе объема dV
можно выразить через мощность излучателя Pt и его диаграмму
направленности по мощности Gt{\) в направлении i:
l D.1)
Рассеяние волн в разреженных облаках частиц 85
Тогда плотность мощности, рассеянной одной частицей, в месте
расположения приемника Sr равна ( |/(б, i) f/Rl)Si. Поскольку
частицы расположены в объеме dV случайным образом, интер-
интерференцией волн, рассеянных разными частицами можно прене-
пренебречь и просто сложить мощности волн, однократно рассеянных
всеми частицами из dV. В результате получим плотность мощ-
1
Приемник
Рис. 4.2. Приближение однократного рассеяния.
ности, рассеянной частицами из dV, в точке расположения
приемника Sr:
где Gб; = 4я|/@, i) [2 = агр(О, i)—бистатическое сечение рас-
рассеяния отдельной частицы.
Принимаемая мощность Рг равна Ar@)Sr, где Лг@)—эф-
Лг@)—эффективная площадь приемной апертуры для волн, приходящих
в направлении 0.
Таким образом, полная принимаемая мощность Рг опреде*
ляется бистатическим уравнением радиолокации
. D.3)
\R\
Здесь использовано соотношение Ar@) = (W/4n)GrF), справед-
справедливое при использовании согласованного по входному импе-
импедансу и поляризации приемника [145]; G,@) — диаграмма на-
направленности по мощности приемной антенны, К — длина волны.
86 Глава 4
В случае однопозиционного радиолокатора, когда передат-
передатчик является также и приемником, получаем обычное уравне-
уравнение радиолокации
D <* \2[Gt(l)fpa
—/д^з Р4—^F, D.4)
где оь — сечение обратного рассеяния частицы, a Ri = R2 = R.
Для практического использования уравнения радиолокации D.3)
и D.4) должны быть видоизменены с учетом рассогласования
по импедансу и поляризации и других потерь [146].
Границы применимости приближения однократного рассея-
рассеяния зависят от глубины проникновения падающей волны в
объем V. Наиболее удобно глубину проникновения измерять
с помощью оптического пути 7- Приближение однократного рас-
рассеяния справедливо, если
L
у = J pcrt ds r* pcr^L < 1, D.5)
о
где интегрирование проводится вдоль произвольной прямой вну-
три объема V, a L — линейный размер объема V (рис. 4.2). Од-
Однократное рассеяние аналогично борцовскому приближению, в
котором падающее на частицу поле аппроксимируется полем
первичной волны (разд. 2.6).
Используя приближение однократного рассеяния и прибли-
приближение первого порядка теории многократного рассеяния, кото-
которое рассматривается в следующем разделе, можно получить
важные формулы, описывающие флуктуации волн, распростра-
распространение узкополосных и широкополосных импульсов, а также
учесть движение частиц. Эти вопросы представляют особый ин-
интерес для специалистов, занимающихся проблемами связи, по-
поэтому они подробно рассматриваются в этой и в последующих
главах.
4.2. Мощность рассеянного поля в первом порядке
теории многократного рассеяния
Как видно на рис. 4.1, б, в первом порядке теории многократ-
многократного рассеяния учитывается затухание волны, вызванное ее рас-
рассеянием и поглощением вдоль пути распространения. Этот ме-
метод находит широкое применение при исследовании распростра-
распространения волн миллиметрового и оптического диапазонов в дожде,
тумане, смоге и снеге. Он используется также и при анализе
распространения света и акустических волн в воде.
Рассеяние волн в разреженных облаках частиц 87
В предыдущем разделе мы обсудили уравнение радиолока-
радиолокации в приближении однократного рассеяния. Рассмотрим теперь
это уравнение в первом порядке теории многократного рассея-
рассеяния. При этом необходимо учесть уменьшение плотности падаю-
падающей мощности Si в dV (рис. 4.2), которое характеризуется пол-
полным сечением. Таким образом,
где Yi — оптический путь от передатчика до элемента объема
dV, который равен
л.
Yi = \ pot ds. D.7)
о
В этом выражении плотность p(s) и полное сечение Ot{s) могут
зависеть от положения рассеивателя на прямой, соединяющей
передатчик с элементом dV.
Аналогичным образом в выражение D.2) для плотности рас-
рассеянной мощности Sr в приближении однократного рассеяния
теперь нужно ввести множитель ехр(—у2), где у2 — оптический
путь от элемента dV до приемника:
«2
уг=\ рсг(ds. D.8)
о
Используя D.7) и D.8), находим, что принятая мощность Рг
определяется уравнением радиолокации
Я2О, A) G F) -. ~
' г - @, i)exp(-Yl-Y2)d7. D.9)
В случае однопозиционной локации имеем
D.10)
где Ri = R2 = R и yi == Y2 = Y-
Выше мы считали, что все частицы имеют одинаковые раз-
размеры. Распределение частиц по размерам можно учесть, если в
D.9) и D.10) использовать среднее полное сечение {at} и сред-
среднее бистатическое сечение рассеяния <сг&;>, которые опреде-
определяются следующим образом. Пусть n(D, r)dD — число частиц
с размером от D до D + dD в единичном объеме около точки г.
88 Глава 4
Тогда yi и 7г определяются выражениями
и V2 = \ Р (сг<) ds, D.11а)
о oJ
где
00 ОО
= \п (Д г) at (D) dD, р (г) = \ п (Д г) dD,
а рсгь((О, i) и роь нужно заменить на
оо
Р(оы) =\n(D, г)о»(D)dD, D.11 б)
О
оо
р (сг6) = ( п (D, г) оь (D) dD. D.11 в)
о
Часто удобно сравнивать рассеянную мощность Рг, опреде-
определяемую выражением D.9), с мощностью сигнала излучателя,
принимаемого на расстоянии R от него. Эта мощность опреде-
определяется выражением
рс V QtG)GrCi)
Pt ~ DлJ R2 е ' К*Лг>
где i — единичный вектор, направленный от передатчика к
приемнику, а у дается формулой
D.13)
4.3. Случай узкой диаграммы направленности
Во многих практических приложениях диаграммы направ-
направленности излучателя и приемника сосредоточены внутри узких
телесных углов. В этом случае параметры среды (концентра-
(концентрацию частиц р и сечение а) в пределах общего объема Vc, обра-
образуемого пересечением диаграмм (рис. 4.3, а), можно считать по-
постоянными, что позволяет значительно упростить формулу D.9).
Будем считать, что диаграмма направленности по мощности
излучателя Gt(\) приближенно описывается гауссовой функцией
Gt (I) - Ot (То) ехр {- (In 2) [B9/8!)* + WfaW], D.14)
Рассеяние волн в разреженных облаках частиц
89
где Ь — единичный вектор, направленный от излучателя в не-
некоторую характерную точку общего объема Vc, 0 и ф — углы,
отсчитываемые от i0 в вертикальном и горизонтальном направ-
направлениях, а углы 0i и $i определяют ширину луча в вертикальном
и горизонтальном направлениях на уровне половинной мощно-
Общий объем Vo \/Vi\
'в,,*:
Излучатель
Приемник
'Излучатель
Рис. 4.3. а — двухпозиционный (бистатический) радиолокатор с узким лучом;
б — однопозиционный радиолокатор с узким лучом. Через 0i и Ф1 обозначены
ширины лучей на уровне половинной мощности в вертикальном и горизон-
горизонтальном направлениях соответственно.
сти. Аналогичным приближением мы воспользуемся и для дна*
граммы направленности приемной антенны Gr{0):
Gr (б) = Gr (бь) exp {- (In 2) [B0/02J + Bф/Ф№), D-15)
где 02 и ф2 — ширина приемной диаграммы направленности на
уровне половинной мощности в вертикальном и горизонтальном
направлениях соответственно.
Подставляя D.14) и D.15) в D.9) и выполняя интегрировав
ние, найдем выражение для принимаемой мощности
Pr X2Gt(h)Gr@a)
— = —
(Oo, i0) exp (- Yi - Y2) Vc. D.16)
Явное выражение для общего объема Vc можно получить, по-
положив Q = y/Ri и ф = г/^ в D.14), Q = y'/R2 и ф = г'/Я2 в
D.15) и используя связи y' = ycosQs — х sin 0S и z' = z. Тогда
интегрирование в D.9) легко выполняется (dV = dx dy dz), и
для общего объема Vc получаем
Vc= 1,206-
sin es
D.17)
90 Глава 4
где 1,206 = я У л /8 (In 2Iг. Это выражение справедливо, если
Qs значительно превышает сумму 9i -\- 9г.
Для однопозиционной локации [уравнение D.10)] получаем
(рис. 4.3, б)
V(R%fll8\n2)dR. D.18)
Тогда уравнение D.10) можно записать в виде
со
-?- = B,855- 1<Г4)Л,2[ВД)]2 9,& $ ^-e^dR, D.19)
о
где 2,855- Ю-4 = я/DяK(8 In 2).
Диаграммы направленности Gt(io) и Gr@0) связаны с эффек-
эффективными площадями At и Аг передающей и приемной апертур
соотношениями
Gt(iQ) = 4t4nAt/k2, Gr@0) = 4r4nAr/l\ D.20)
где r\t и т)г — коэффициенты использования передающей и при-
приемной апертур, имеющие обычно значения 0,5—0,6. Ширины
пучков 01, <pi и 02, >р2 связаны с размерами апертур. Например,
9] определяется размером апертуры D\ в направлении 0 соот-
соотношением
Qi = alX/Dl рад, D.21)
где константа щ обычно принимает значения от 1,3 до 1,6 в за-
зависимости от распределения токов в пределах апертуры. Комби-
Комбинируя D.20) и D.21), можно получить следующую формулу
для коэффициента усиления:
Gt = (т^ацха) (я2/0^,) « я2/8,*,. D.22)
Пример А. Рассеяние света в воде. Рассмотрим рассеяние
светового пучка в морской воде. Ширина пучка 0i = 2°, а длина
волны К — 0,655 мкм. Ширина диаграммы направленности при-
приемника 02 = 2°. Расстояния до общего о.бъема R\ — R2 = I м,
а угол рассеяния 0S = 20°. Предположим, что коэффициент по-
поглощения воды (рис. 3.9 и табл. 3.1) aw — 0,05 м, а величины
Р<0(>, p(os} и р<оа>, обусловленные наличием взвешенных ча-
частиц, равны соответственно 0,27, 0,20 и 0,07 м^1 при к =
= 0,655 мкм.
Для вычисления Pr/Pt воспользуемся уравнением D.16). Из
D.22) находим Gt = Gr = л2/в1 = 8100. Параметры yi и Уг
равны Yi = (aw + p(ot})Ri = 72 = 0,32. Предполагая, что
Od{45o)/os = 3-10-2 и crdB0°)/crdD5o) ~ 25, получаем рвы =
«= Ащоа B0°) = 4л • 0,2 • 3 • 10-2 • 25 = 1,885. Из D.17) находим
Vc = 0,000106 м3. Таким образом, мы получаем
Pr/Pt = 1,495 • 10~п = - 108 дБ.
Рассеяние волн в разреженных облаках частиц 91
Принимаемая мощность Рс в случае, когда луч передатчика на-
направлен на расположенный на расстоянии 1 м от него прием-
приемник, определяется формулой D.12). Подставляя значения % =
= 0,655 мкм, Gt = Gr = 8100, R = 1 м и у = 0,32, получаем
Pc/Pt = 1,29-10. Рассеянная мощность, отнесенная к Рс, со-
составляет Рг/Рс = 1,16- Ю-4 = —39 дБ.
Пример Б. Обратное рассеяние СВЧ-излучения от дождя.
Рассмотрим мощность обратного рассеяния от слабого дождя
A мм/ч) на расстоянии 5 км при использовании трехфутовой
(«si м) параболической антенны на длине волны К = 1 см.
Отношение принимаемой мощности к излучаемой определяется
по формуле D.19). Предположим, что эффективность использо-
использования апертуры t\t = 0,55. Учитывая, что At = n,D2/4, D =
= 3-12-0,0254 м и % = 0,01 м, находим из D.20) Gt =
= 4,538-Ю4. Полагая еще а\ = 1,5, находим из D.21) 8i =
= ф1 = 1,64-10~2 рад. Из рис. 3.7 определяем р(оьУ = 0,035 и
р(сг<> = 0,075. Подставляя эти значения в D.19) и вспоминая,
что у = р<сгг> (R — Ro), a Ro = 5 км, имеем
•^ = 5,53-Ю-4 pp[-°y~*o)W=l,37 -10-'° = -98,6 дБ.
Пример В. Сечение обратного рассеяния единичной площадки
слоя толщины d. Рассмотрим слой толщины d со случайно рас-
распределенными частицами. Предположим, что этот слой осве-
освещается излучателем, расположенным на большом расстоянии
Ro ~S> d. Тогда в D.19) под знаком интеграла можно заменить У?
на Ro. В результате получим
d
¦^ = B,855- 10~4)A,2G?9if \, Л6= \ рсгй ехр (- 2Y) dR.
pt ' Ro о
Здесь Аь — сечение обратного рассеяния единичной площадки
слоя толщины d. Если концентрация частиц постоянна, то
Аь = (РМ) {1 - ехр (- 2р)]/2р}, р = 9otd.
Величина Аь удобна для описания характеристик обратного
рассеяния и часто используется для анализа обратного рассея-
рассеяния от тумана и облаков при исследованиях с помощью лазер-
лазерных локаторов (разд. 5.5).
4.4. Когерентное и некогерентное поле
В предыдущих разделах мы обсуждали связь рассеянной
мощности с характеристиками частиц. Поскольку частицы рас-
распределены случайным образом и обычно находятся в непрерыв*
92 Глава 4
ном движении, рассеянное поле не постоянно: его амплитуда и
фаза испытывают случайные флуктуации. Мощность рассеян-
рассеянного поля, рассмотренная в предыдущих разделах, представляет
собой «среднюю» мощность и не учитывает флуктуации.
В данном разделе мы поясним понятия среднего и флуктуа-
флуктуационного поля, а также средней и флуктуационной мощности.
Существуют различные способы описания флуктуационных ха-
характеристик поля. Наиболее важными характеристиками яв-
являются: дисперсии, корреляционные функции, функции когерент-
когерентности, моменты высших порядков, энергетические спектры и
функции плотности вероятности. Мы дадим здесь определения
этих величин и опишем их взаимосвязь. В дальнейшем эти све-
сведения будут использоваться при решении задачи рассеяния на
облаке случайно распределенных частиц.
Рассмотрим квазимонохроматическую волну с несущей ча-
частотой о)О. При распространении этой волны в случайно неодно-
неоднородной среде ее амплитуда и фаза испытывают случайные флук-
флуктуации во времени и в пространстве. Ее поле v(r, t) —вещест-
—вещественная функция времени t и координаты г. Это поле можно вы-
выразить через комплексную амплитуду и (г, t), амплитуду А (г, t)
и фазу ф(г, t):
v (г, 0 = Re [и (г, () ехр (- 1щЦ], «(г, t) = A (r, t) exp [1ф (г, /)],
D.23)
причем А (г, t) и ф(г, /) —медленные функции времени.
Поле и {г, t) является случайной функцией координаты г и
времени t, поэтому его можно представить в виде суммы сред-
среднего поля <«> и флуктуационного поля Uf\
u{t,t) = (u(r,t)) + uf{t,t), D.24)
> = 0. D.25)
Угловыми скобками обозначено усреднение по статистическому
ансамблю [39].
Среднее поле <«> называют еще когерентным, а флуктуа-
ционное — и; — иекогерентным полем. Квадрат амплитуды ко-
когерентного поля называют когерентной интенсивностью, а сред-
среднее значение квадрата некогерентного поля — некогерентной ин-
интенсивностью; эти величины обозначаются 1С и U соответствен-
соответственно. Средняя интенсивность </> равна сумме 1С и /;:
), D.26)
Функция когерентности Г(гь t\\ r2, h) поля в точке п в мо-
момент времени t\ и поля в точке Гг в момент времени t2 опреде-
определяется следующим образом:
Г (г„ h; r2, i2) = (и (гь *,) и* (r2, t2)). D.27)
Рассеяние волн в разреженных облаках частиц 93
Используя D.24) и D.25), находим
Г = Гс + Г/; D.28а)
Гв = <и(г,,/,)><«* (г2, *2)>, D.286)
где Ff описывает корреляцию флуктуации поля щ = и — <«> и
называется корреляционной функцией. Функцию когерентности Г
называют иногда вторым нецентральным моментом, или кова-
риацией поля. Она играет важную роль в задачах распростра-
распространения волн в случайно-неоднородных средах.
Интенсивность / можно представить в виде суммы средней
интенсивности </> и флуктуации интенсивности //:
/ = |«Р = </> + /,. D.29)
Дисперсия сг2. флуктуации интенсивности If равна
<т/2 = </2?> = </2>-</>2, D.30)
где </2> = <|«|4> = <«2и*2>. Очевидно, что </2> выражается че-
через четвертый момент поля и.
Второй момент интенсивности (hh} равен
</1/2) = <и1«>2н*2). D-31)
где
Il = ulu*, I2 = u2u*2, ul=u(rl,tl), u2 = u(r2,t2).
Во многих задачах, с которыми приходится иметь дело на
практике, поле u(r, t) для конечных интервалов времени можно
считать стационарной случайной функцией времени. Например,
флуктуации волн в турбулентной атмосфере и в гидрометеорах
приближенно можно считать стационарными в пределах не-
нескольких минут. Рассмотрим корреляционную функцию Г;, оп-
определенную выражением D.28в) в точке п = г2 = г и U = t2 +
-f- т. Если поле стационарно, Г; зависит только от г и т:
Г, = Г>(г,т). D.32)
Частотный спектр Wf(r, со) флуктуационного поля щ в этом слу-
случае определяется фурье-образом корреляционной функции Г/ '):
Wf (г, со) = 2 J Tf (r, т) еш dx, D.33)
— оо
оо
Г,(г, t) = -L \ Wf(r,<a)e-t°*de>. D.34)
') Данный выбор коэффициентов в преобразовании Фурье приводит к
обычному спектральному представлению D.37) корреляционной функции [14,
15, 156].
94 Глава 4
Отметим, что формула D.33) описывает поведение частотного
спектра вблизи несущей частоты соо, так что истинная частота
гармоник равна соо + со. Вообще говоря, корреляционная функ-
функция Г7(г, т) комплексна и удовлетворяет соотношению
Г, (г, т) = г;(г,-т). D.35)
Спектр Wf(r, со) является вещественной положительной функ-
функцией [155, 172].
Если корреляционная функция Tf вещественна, то она яв-
является четной функцией т, вследствие чего Wf(r, со) также яв-
является четной функцией со. В этом случае приходим к следую-
следующим соотношениям:
Wf (r, со) = 4 J Tf (r, т) cos (сот) dx, D.36)
о
оо оо
Tf (r, x) = ~\wf (r, со) cos (сот) rfco = J Wf (r, /) cos Bя/т) df. D.37)
о о
В последующих разделах мы будем исследовать поведение
дисперсий, корреляционных функций и функций когерентности,
частотных спектров и функций распределения вероятности поля,
рассеянного случайным облаком частиц.
В задаче рассеяния волны, рассеянные случайным облаком
частиц, можно считать почти полностью некогерентными, а ко-
когерентное поле — практически равным нулю. Однако, если среда
не полностью случайна, рассеянное поле включает в себя неко-
некоторую когерентную составляющую. Например, отражение СВЧ-
излучения от слоя теплого или холодного воздуха в атмосфере
часто происходит когерентно, тогда как рассеяние СВЧ-излуче-
ния на слое турбулентного воздуха практически полностью не-
некогерентно.
В задаче распространения в области прямой видимости поле
на малых расстояниях от излучателя практически когерентно.
При увеличении расстояния когерентная часть поля уменьшает-
уменьшается, а некогерентная возрастает. На больших расстояниях поле
становится полностью некогерентным. Этот вопрос более под^
робно рассматривается в гл. 6.
4.5. Сечение рассеяния движущейся частицы
с учетом временной корреляции
В разделах 4.1—4.3 мы нашли выражения для средней мощ-
мощности поля, рассеянного на случайном облаке частиц. Здесь мы
рассмотрим влияние движения частиц на рассеянное поле. При
Рассеяние волн в разреженных облаках частиц
95
перемещении частицы от точки к точке фаза рассеянного на этой
частице поля изменяется во времени, что в свою очередь при-
приводит к флуктуациям рассеянного поля. Корреляционная функ-
функция полей, рассеянных на множестве случайно распределенных
частиц, определяется суммой вкладов от всех частиц.
Чтобы учесть движение частиц, удобно рассмотреть сначала
рассеяние на отдельной движущейся частице. Движение части-
частицы можно подразделить на поступательное перемещение центра
Рис. 4.4. Направления падаю-
падающей i и рассеянной Ъ волн и
движение частицы от положе-
положения г2 в момент времени t2 до
положения Г| в момент t, со
скоростью V.
тяжести частицы и на вращательное движение частицы вокруг
этого центра. Рассмотрим сначала частицу, движущуюся без
вращения со скоростью V. Предположим, что скорость V на-
намного меньше скорости распространения волны, так что можно
ограничиться рассмотрением только нерелятивистских эффек-
эффектов.
Рассмотрим монохроматическую падающую волну
Е{ (г) = exp (kr ¦ Т), D.38)
где k = 2яД = соо/с — волновое число, i — единичный вектор
в направлении распространения и /о = о)о/2л — частота. Рас-
Рассеянное поле Es в момент времени t\ на расстоянии Ro в на-
направлении 0 вдали от частицы равно
-exp[/?(i— б)
D.39)
где ri — положение частицы в запаздывающий момент времени
t[ = tl — RJc. Аналогично рассеянное поле в момент времени /2
равно (рис. 4.4)
exp [ik (\ - 0) • r2 + ikRo],
D.40)
96 Глава 4
где r2 — положение частицы в момент времени t'2 = t2 — R2jc.
Положения частицы т\ и г2 связаны с ее скоростью и моментами
времени /[ и t2:
г,-г2= \ Vdt, D.41)
где скорость V, вообще говоря, зависит от времени: V = V(t).
Однако в большинстве встречающихся на практике случаев ско-
скорость V можно считать постоянной в пределах интервала вре-
временной корреляции поля. Заметим также, что
^-^ = 11~^-с-1{^-Я2)- D-42)
Поскольку Ri — R2 порядка V A[ — /?), последнее слагаемое в
D.42) при V «С с пренебрежимо мало, и приближенно можно
положить
*\-*2***1- *2- D-43)
Поэтому D.41) приближенно можно представить в >более удоб-
удобном виде
г, — r2 = Vt, x = U — t2. D.44)
Определим теперь дифференциальное сечение рассеяния с
учетом временной корреляции crd(O, i, т) посредством соотно-
соотношения
ad F, Т, г) = lim (Я20 (Е, (/,) Е*а (/2))]. D.45)
Ra -> °°
Используя D.39), D.40) и D.44), получаем
ad@.1,T) = crd@)T)<exp(/ks.VT)), k, = ft A-0), D.46)
где crd(O, i)—дифференциальное сечение рассеяния неподвиж-
неподвижной частицы (V = 0).
Вообще говоря, скорость V частицы складывается из средней
скорости <V> = U и флуктуационнои скорости V/:
V = (V) + Vf = U + Vf! D.47)
так что D.46) можно представить в следующем виде:
ad (б, Т, т) = od @, Т) x(ksr) exp (iks ¦ Ut). D.48)
Здесь %(ks%) — характеристическая функция флуктуации ско-
скорости
) = <exp^-VlfT)>. D.49)
Рассеяние волн в разреженных облаках частиц
97
Выражение D.48) представляет собой фундаментальное вы-
выражение для дифференциального сечения рассеяния движущейся
без вращения частицы с учетом временной корреляции. Если
частица вращается вокруг своего центра тяжести, то нужно про-
проводить дополнительное усреднение по вращательному движе-
движению. Обозначив такое среднее через (оа{0, 0>л получим вместо
Рис. 4.5. Доплеровский сдвиг ча-
частоты D.54), обусловленный движе-
движением частицы.
D.48) следующее выражение для сечения рассеяния с учетом
временной корреляции:
ad (О, X т) = (ad @,1 )>, % (ksx) exp (&, • Ux).
D.50)
Тогда частотный спектр Wa@, i, т) этого сечения в соответ-
соответствии с D.33) будет равен
ш
O@,i,o)) = 2 \ ad@, i,x)emTdx.
D.51)
Рассмотрим пример. Если частица движется с постоянной
скоростью U (Vf = 0) без вращения, то
о* @, i, x) = ad @, i) exp (iks • Ux),
Wa @, f, со) = 2ad @, f) б (со + ks - U).
D.52)
D.53)
Вспоминая, что ks = ft(i — 0) и k = ®o/c, видим, что из D.53)
следует формула для доплеровского сдвига частоты (рис. 4.5)
ш/ша= — (Т— б) • (U/c). D.54)
Напомним, что в D.51) через со обозначено отклонение частоты
от несущей частоты ©о, так что частота рассеянной волны опре-
определяется выражением
m + ojo = oj0[l —(f—OMU/c). D.55)
Доплеровский сдвиг D.54) можно представить также в виде
ев/т,, = - 2 sin F/2) (Ud/c), D.56^
98
Глава 4
где Ud — компонента скорости U в направлении is = i — 0.
Если флуктуации скорости Vf распределены по нормальному
закону с дисперсией <j9j каждой из ортогональных компонент,
то, используя функцию плотности вероятности
p(\f) = Bnof)-'''exP(-\y2&*), D.57)
получаем
) ^о|т72). D.58)
Тогда частотный спектр Wa будет иметь вид
Wa @, С, со) = 2ad (б, Т) [2n/kyff> ехр [- (со + ks ¦ )/()
D.59)
Эта формула дает явное описание уширения спектра, обуслов-
обусловленного флуктуациями скорости, и доплеровского сдвига ча-
частоты (рис. 4.6).
k,-U>0
ks; U < 0
-ks-U
Рис. 4.6. Доплеровский сдвиг — ks ¦ U и уширение спектра Дсо = I 2k о Л.
Рассмотрим теперь случай вращающейся частицы D.50).
Примером может служить доплеровский сдвиг, обусловленный
вращательным движением молекулы полимера [16, 118]. Пред-
Предположим, что частица представляет собой тонкий стержень, на-
направление оси которого задается единичным вектором s и не-
непрерывно меняется во времени. Сечение рассеяния тогда яв-
является функцией 0, i и s. Полагая, что вектор s в моменты вре-
времени t\ и ti принимает значения Si и s2 соответственно, запишем
tfd = tfd FД sb s2). D.60)
Обозначим через p2(s2)ds2 вероятность того, что в момент вре-
времени t2 вектор s ориентирован в пределах телесного угла ds2
около направления s2, а через pi(su s2)dsi — условную вероят-
ность того, что в момент времени ^i он ориентирован в телес-
Рассеяние волн в разреженных облаках частиц 99
ном угле ds\ около направления si при условии, что в момент
времени t2 он был ориентирован в направлении s2. Тогда полу-
получим
d @, i, sb s2) pi (sb s2) p2 (s2) dsi ds2. D.61)
Мы здесь не будем вдаваться в подробности расчета р\ и р2
для частных случаев. Отметим лишь, что общая формула D.61)
может быть использована при анализе влияния наклонного па-
падения дождевых капель на распространение СВЧ излучения и
при анализе рассеяния света на полимерах. Отметим также,
что при полностью хаотической ориентации частиц р\ = р2 =
= 1/4я и D.61) сводится к случаю, рассмотренному в примере
«в» раздела 2.6.
В этом разделе мы обсудили эффекты, вызываемые движе-
движением отдельной частицы. Вообще говоря, необходимо учитывать
взаимодействие частиц, и статистическое усреднение, которое
мы проводили в данном разделе, должно учитывать совместную
плотность вероятности, т. е. вероятность того, что одна частица
в момент времени t2 находится в точке г2, а другая в момент
времени t\ находится в точке Гь Поскольку решение этой задачи
дает мало полезной информации при существенном усложнении
математических выкладок, мы не рассматриваем здесь этот во-
вопрос [118, 119].
4.6. Временная корреляционная функция
и частотный спектр рассеянного поля"
Временную корреляционную функцию рассеянного поля лег-
легко найти, зная сечение рассеяния с учетом временной корре-
корреляции, о котором шла речь в предыдущем разделе. Мы пред-
предполагаем, что корреляция полей, рассеянных различными ча-
частицами, пренебрежимо мала, так что можно просто суммиро-
суммировать вклады отдельных частиц. Такой подход должен привести
к простому обобщению соотношения D.9). Обозначая через
V{t) выходное напряжение приемника, пропорциональное рас-
рассеянному полю Es{t), для корреляционной функции Bv(%) имеем
= с \ к7л1($?Т Ра" <°> f' T) ехР (~ Yi - Y2) dV, D.62)
jJ (in) KiH2
где t = *i — t2, c = (V2}/(Pr-Pt), a o«(S, T, т) = 4гат^@, Г, т) и
определяется формулой D.48) или D.50).
*) Измерения энергетических спектров описаны в работе [18].
10Э Глава 4
Частотный спектр №V(©) выходного напряжения V(t) дается
выражением D.62) с заменой аы на 4я№0(б, i, со), где Wa опре-
определяется формулой D.51).
В D.62) легко учесть влияние распределения частиц по раз-
размерам; для этого достаточно воспользоваться формулами, ана-
аналогичными D.11). При этом для оптических путей у\ и у2 можно
по-прежнему использовать выражение D.11а). Что же касается
величины роы, то для расчета необходимо дополнительно учесть
тот факт, что частицы разного размера могут перемещаться
с разными скоростями. Такое явление определенно имеет место
в дожде, установившиеся скорости капель которого зависят от
их диаметра. Поэтому следует принять
оо
р <<ти> = \ п (?>) аы F, I, т, D) dD, D.63)
о
где должна учитываться зависимость скорости частицы от ее
размера D.
В качестве примера рассмотрим бистатическое рассеяние на
дожде в случае, когда излучатель и приемник обладают узкими
диаграммами направленности и справедлива формула D.16).
Имеем
Bv W = TllZi P <<*" (Oo, io, т)> ехр (Yl - y2) Vc. D.64)
Выбрав ось z в вертикальном направлении, запишем установив-
установившуюся скорость дождевой капли диаметра D в виде
U = — U(D)z. D.65)
Тогда из D.52) имеем
Р {оы) =]n(D) abl @, 1, D) ехр (- /ks • zU (?>) т) dD. D.66)
о
При этом частотный спектр определяется равенством
00
р DnWa (б, Т, ©)> = 2 J n (D) вЬ{ (б, i, D) б [ее - ks • zV (D)] dD,
о
D.67)
интеграл в котором можно вычислить, используя формулу [162]
Рассеяние волн в разреженных облаках частиц 101
где через хп обозначены корни функции f(x). В результате по-
получим
ks ¦
D.69)
где Do удовлетворяет уравнению со = ks-zU(Do).
Из выражения D.69) следует, что спектр на некоторой ча-
стоте со прямо пропорционален распределению частиц по раз-
размерам n(D) при D = Do, поэтому измерения спектра можно ис-
использовать для нахождения распределения частиц по разме-
размерам n(D) при условии, что известны скорости V(D) частиц и
их бистатическое сечение рассеяния аы(®, •, D).
4.7. Пространственная корреляция рассеянного поля
Корреляция значений рассеянного поля в двух различных
точках важна для анализа реверберации звука в океане [115].
В данном разделе мы рассмотрим этот вопрос на примере, гео-
геометрия которого изображена на рис. 4.7, где показан излуча-
излучатель, освещающий случайную среду, и два приемника, располо-
расположенные в точках P\(d/2, 0, 0) и Р2(—d/2, 0, 0). Задача состоит
в определении корреляции сигналов в точках Pi и Р2.
Рассмотрим поле, рассеянное элементом объема dV, окру-
окружающим точку (R2, Э, ф). Разность фаз поля в точках Р\ и Р2
равна т|э = k (R2 — RT). Предполагая, что объем dV достаточно
удален от приемника, приближенно можно написать
ф == k (R'2 - R2) ~ - kd @ • х) = kd sin 6 cos f. D.70)
Тогда пространственная корреляционная функция напряже-
напряжений V\ и V2 в точках Pi и Р2 принимает вид
yl-y2 + i^dV. D.71)
Если излучатель расположен в начале координат (рис. 4.7), то
Г= —0 и
= с J ^(Sff~Vu exP I- Y. - Y2 + ikd (Т ¦ х")] dV. D.72)
Отметим, что dV = R2dR dQ, где dQ — элемент телесного угла,
так что при заданном расстоянии R корреляционная функция
(V1V2} пропорциональна фурье-образу от G<(!)Gr(—i) рсгь по уг*
ловой координате с ядром преобразования ехр[/Ы(Т-х)].
102
Глава 4
Указанную связь корреляционной функции (l^iVsi} с диаграм-
мами направленности антенн Gt(\), Gr(—i), основанную на пре-
образовании Фурье, можно сравнить с аналогичной связью ме-
между функцией взаимной когерентности и распределением в про-
пространстве некогерентных источников [21]. По существу, случай-
случайные частицы, освещаемые антеннами с диаграммами направ-
направленности Gt и Gr, можно рассматривать как совокупность неко-
некогерентных источников.
dV
л
¦ X
Излучатель
Излучатель
Рис. 4.7. К вычислению простран- Рис. 4.8. Корреляция полей в точках Pi
ственной корреляционной функции и Рг, обусловленная тонким слоем
рассеянных полей в точках Рх и Р2. частиц на расстоянии Ro.
В качестве примера рассмотрим корреляцию полей в точках
Pi и Р2, лежащих в плоскости хг. Угол между линией, соеди-
соединяющей точки Pi и Р2, и осью х обозначим через ср и будем счи-
считать, что рассеивающие частицы сосредоточены в тонком слое
толщины Аг на расстоянии Ro (рис. 4.8), а излучатель с диа-
граммой направленности
расположен в начале координат. Предположим также, что диа-
диаграмма направленности приемника имеет такой же вид.
Тогда имеем
¦ф = kd (sin 0 cos Ф cos ф + cos 0 sin ф),
2л я
~ со \ d* $ 6 dQ ехР [~ B92/ео) + '¦].
Рассеяние волн в разреженных облаках частиц 103
где с0 «* (cX2Glpob/Dnf Щ) Az. Замечая, что |0| <С 1, имеем
п
\ dj> exp {ikd sin 9 cos j> cos ф) = 2nJ0 (kd sin 9 cos ф) «*
о
«* 2я/0 (/г gTO cos ф).
В результате приближенно получаем ')
a) = (nco/A) exp [ikd sin ф - (kdJ/4A\, D.74)
где
2 Ы sin Ф
—
При ф = 0 корреляционная функция (V1V2) пропорциональна
ехр[—(kdQ0J/8], откуда следует, что корреляция уменьшается
при увеличении расстояния между точками d и при увеличении
ширины пучка 90.
4.8. Корреляция поля,
принимаемого движущимся приемником
Рассмотрим приемник, перемещающийся со скоростью Vr из
точки Г2 в момент времени t2 в точку ri = r2 + V,t в момент вре-
времени t\ = t2 + т. Корреляция принятых в моменты t\ и t2 сигна-
сигналов совпадает с корреляцией сигналов в моменты t\ и t2, при-
принятых покоящимся приемником при условии, что вся среда
вместе с излучателем перемещается со скоростью —Vr. Поэтому
можно использовать выражение
(V (*,) V* (t2)) = с \ V°t{y°rf роы @, I т) exp (- yi - y2) dV,
D.75)
куда нужно подставить сечение оы@, i, т) для частиц, движу-
движущихся со скоростью —\г- Если |V,t| много меньше Ri и R2, то
изменением остальных величин (Ri, R2, Gt и Gr), как правило,
можно пренебречь.
Задача о корреляции сигналов, принимаемых движущимся
приемником, играет важную роль в акустике океана; имеется
ряд экспериментальных и теоретических исследований этой
задачи ([115], разд. 31).
') При вычислениях использована формула Вебера и Сонина, приведен-
приведенная в книге [101].
104 Глава 4
4.9. Распределение вероятности рассеянного поля
Рассмотрим сначала распределения вероятности амплитуды
А и фазы ф рассеянного поля Es. Представим Es в виде «квад-
«квадратурных компонент» поля X и Y:
ES = A ехр (#) = X + iY, D.76)
где X = A cos ^>, a Y = A sin ^>. Поле ?$ является суммой полей,
рассеянных множеством различных частиц, так что можно за-
записать
Е, = Е Ая ехр (#„) = Е (Хп + »У„). D.77)
п=-1 п=1
Далее, «центральная предельная теорема» [10, 39] утверждает,
что распределение вероятности суммы N независимых случай-
случайных величин при N->-оо стремится к нормальному распределе-
распределению независимо от того, каково распределение вероятностей
каждой из этих случайных величин.
Естественно предположить, что каждое слагаемое Хп и Yn
является независимой случайной величиной. Поэтому, применяя
центральную предельную теорему к D.77), приходим к выводу,
что величины X и Y распределены по нормальному закону.
Предположим также, что фаза_ ф распределена равномерно
в интервале @,2я). Это предположение естественно, поскольку
фаза фп каждого слагаемого Л„ехр(/0„) случайна и можно при-
принять, что она равномерно распределена в интервале @, 2л), так
что сумма D.77) не должна иметь выделенного значения фазы ').
В этих рассуждениях неявно заключено утверждение о стати-
статистической независимости фазы ф и амплитуды А. Поэтому плот-
плотность вероятности р(А, ф) амплитуды А и фазы ф можно пред-
представить в виде
р(А,ф) = р(А)р(ф), р(ф)=1/2п, 0<ф<2л. D.78)
На основании D.78) можно легко доказать следующие соотно-
соотношения:
со 2я
(X) == (A cos Ф) = J dA J йфА cos фр (А, ф) = 0,
о о
{у) = (Азтф) = 0, D.79)
(XY) = (A2 sin ф cos ф) = 0, (X2) = (У2) = а2 = j J A2p (A) dA.
') Это предположение неверно при наличии когерентной составляющей
поля (разд. 21.12).
Рассеяние волн в разреженных облаках частиц ' 105
Поскольку X и У распределены нормально и некоррелированны,
они независимы [39], и их совместная плотность вероятности
р(Х, У) равна
р (X, Y) = p (X) р (Y) = BЖТ2)-1 ехр [- (X2 + У2)/2а2]. D.80)
Замечая, что
р (X, У) dXdY = p (А, ф) dA d<f>,
=\ p{A, D81)
получаем
p (A) = (A/a2) ехр (- Л2/2а2). D.82)
Полученное распределение называется распределением Рэлея.
Отметим, что оно характеризуется единственным параметром а.
Таким образом, мы делаем вывод, что амплитуда и фаза рас-
рассеянной волны статистически независимы, причем амплитуда А
подчиняется распределению Рэлея, а фаза распределена равно-
равномерно.
Средняя амплитуда <Л> равна [39]
оо
(А) = J Ар (A) dA = [(я/2) а2]4'. D.83)
о
Аналогично для интенсивности / = А2 имеем
</> = 2а2, <(/-</»2> = 4а4 = </>2. D.84)
Отметим, что дисперсия флуктуации интенсивности (/ — <1>)
равна квадрату средней интенсивности, откуда следует флук-
туационный характер всей рассеянной мощности.
Дальнейшее обобщение D.84) приводит к результату
= {Г)" N\ D.85)
с помощью которого можно проверить, распределена ли ампли-
амплитуда А по рэлеевскому закону или нет.
Рассмотрим далее совместную плотность вероятности ам-
амплитуд А\ и А2 рассеянных полей Е\ = Es{t\, U) = Л1 ехр(i^>i)
и Е2 = Es(f2, t2) = Л2ехрA02). Прежде всего запишем
Ех = Хх + (Ги ?2 = Х2 + /У2. D.86)
Совместная плотность вероятности р{А\, Л2) дается формулой
р(Аи Л2)= J dh \ d4>2p(Alt A3, фи ф2). D.87)
106 Глава 4
Отметим, что в силу равенства
р(Аъ Аа, фи ф2)с1А1аА2с1ф1сгф2 = Р(Х1, У,, Х2, Y2)dXldYldX2dY2
D.88)
имеет место связь
Р Мь А2, фи ф2) = р{Хи Yu X2, Y2) А,А2. D.89)
Вспоминая, что Х\, Y\, X2 я Y2 — гауссовы случайные вели*
чины, запишем р(Х\, Y\, X2, Y2) в виде [39]
р(Хи Yu Xa, Y2) = BяJ|й;; J , D.90)
где а/у — алгебраическое дополнение к элементу kij корреля-
корреляционной матрицы k = ({ZiZj}) размера 4 X 4, Z\ = Х\, Z2 = Yu
Zz = X2, Z4 = Y2, a | k | — детерминант матрицы к.
Предположим, что рассеянные поля Е\ и Е2 наблюдаются
вдали от рассеивающей области, что расстояние между точ-
точками п и Г2 много больше радиуса корреляции поля и что вре-
временной интервал между t\ и t2 не превосходит по порядку вели-
величины временного радиуса корреляции поля. Именно этот случай
наиболее часто встречается в практических приложениях. Тогда
можно принять, что
<*,*,> = <У,У,> = (Х2Х2) = (Y2Y2) = a2. D.91)
Кроме того, из D.79) следует '
<Х,У1> = <^2У2> = 0. D.92)
Наконец, можно показать, что приближенно
(XiX2) = (Y1Y2) = a, <^2У,> = -<^1У2> = Р. D.93)
Доказательство D.93) основывается на том факте, что величина
(EiE2} представляет собой сумму вкладов от множества частиц,
причем фазы этих вкладов пропорциональны полной длине
траектории. При суммировании всех этих вкладов от большого
объема, содержащего множество рассеивателей, они стремятся
погасить друг друга. Поэтому можно утверждать [156], что
<ВД = <(*, + /У,) (Х2 + iY2)) « 0. D.94)
Равенства D.93) следуют непосредственно из D.94).
С учетом D.91), D.92) и D.93) получаем следующее выра^
жение для корреляционной матрицы k:
k =
- a2
0
a
- -6
0
a2
P
a
a
P
a2
0
-P -
a
0
a2J
D.95)
Рассеяние волн в разреженных облаках частиц 107
Отсюда находим
«И = «22 = «33 = «44 = °6 A ¦— Ро)>
а1з = аз1 = а24 = «42 == - аа4 A - р$),
а12 = <z2i == а34 = а43 = 0, D.96)
«14 = ~ К23 = а41 = - К32 = РСТ4 A - pi),
Подставляя D.96) в D.90), получаем следующее выражение
для р(Аи А2, фи ф2):
ехр {- B | к | Г1 [аи (А\ + Л2) + 2alzAlA2 cos @, - Ф2) -
Из D.97), D.89) и D.87) находим окончательное выражение
для совместной плотности вероятности р(А\, А2):
- D'98)
где /о — модифицированная функция Бесселя нулевого порядка.
На основании D.98) найдем смешанный момент амплитуд
Ai и А2
со оо
\ J И2РИ1. Л^АМЛа. D.99)
о о
Входящий сюда интеграл можно выразить через эллиптические
интегралы. Используя разложения этих интегралов в ряды, для
коэффициента корреляции амплитуд ЪА получаем
ЬА (гь h; г2, к) = «Л,Л> - (ЛJ)/«Л2) - (ЛJ) =
= 0,915р2+0,058Л4+ .... D.100)
где pi = (а2 + Р2)/^4. Из D.93) замечаем, что
<?i?5> = 2(а + ip), (|Ei f) = ([E2f) = ([E |2> = 2а2,
Из D.100) и D.101) заключаем, что коэффициент корреля-
корреляции Ьа амплитуд А\ и Л2 представляется в виде ряда по пара-
параметру р\, равному квадрату амплитуды корреляционной функ-
функции (ЕуЕ*^. Отметим еще, что при малых значениях р\ коэф-
коэффициент корреляции Ьа приближенно равен 0,915 р2.
Глава 5
Рассеяние импульсных волн
в случайном облаке частиц
В предыдущей главе было рассмотрено рассеяние непрерыв-
непрерывной волны в случайном облаке рассеивателей. Здесь мы изучим
вопрос о рассеянии импульсной волны в случайном облаке ча-
частиц. Характеристики рассеяния импульсного излучения важны
для ряда приложений. Например, работа радиолокаторов, ла-
лазерных и акустических локаторов может быть подвержена влия-
влиянию со стороны хаотических отражений и реверберации, обус-
обусловленных случайными частицами. Кроме того, характеристики
рассеянного импульса могут использоваться для дистанционного
зондирования плотности частиц и их распределения по разме-
размерам.
В этой главе мы дадим сначала введение в общую теорию
распространения и рассеяния импульсного излучения в случай-
случайных средах. Затем |будут рассмотрены результаты, получаю-
получающиеся в первом приближении теории многократного рассеяния.
При этом мы учтем влияние движения частиц в предположе-
предположении, что скорости рассеивателей малы по сравнению со ско-
скоростью распространения волны. Кроме того, мы будем считать,
что ширина полосы импульса мала по сравнению с несущей ча-
частотой. Эти предположения справедливы для большинства прак-
практических приложений. В гл. 15 и 20 рассматриваются более
сложные задачи, относящиеся к сильным флуктуациям импульс-
импульсного излучения, обусловленным многократным рассеянием, а
также к распространению и рассеянию широкополосных импуль-
импульсов.
5.1. Общая формулировка
проблемы распространения
и рассеяния импульсов в нестационарной
случайной среде
Рассмотрим линейную случайную среду, которая может быть
нестационарной и диспергирующей. Примером такой среды мо-
может служить случайное облако движущихся рассеивателей. Ха-
Характеристики распространения и рассеяния импульса в такой
среде удобно описывать, используя двухчастотную функцию
взаимной когерентности. Такое представление позволяет также
Рассеяние импульсных волн в случайном облаке частиц 109
выяснить смысл таких понятий, как полоса когерентности и
время когерентности. В данном разделе мы рассмотрим эти об-
общие понятия и представления [13, 73, 85, 175].
Рассмотрим поле Оо@ в приемнике, отвечающее входному
импульсу Vi(t), излучаемому передатчиком. Функции Vo(t) и
Vi(t) являются вещественными функциями времени. Обычно
входной импульс Vi(t) представляет собой заданную функцию
времени. Однако в некоторых приложениях в качестве входного
сигнала используются шум или случайный сигнал, так что Vi(()
может быть и случайной функцией времени. Поскольку среда
нестационарна и линейна, в общем случае можно записать
t
= J
E.1)
где h(t, f) — импульсный отклик приемника в момент времени /
на входной импульс передатчика, излучаемый в момент вре-
времени if. Заметим, что если Vi{t) =8{t — t'), то vQ(t) = h(t, t').
Импульсный отклик h(t, t'), вообще говоря, является веще-
вещественной функцией двух переменных t и /'. Только в случае ста-
стационарной среды h становится функцией разности t — t'. Им-
Импульсный отклик h является характеристикой случайной среды
и поэтому представляет собой случайную функцию времени.
Запишем функцию Vi(t) в виде интеграла Фурье1) через ее
спектр У; (со):
Vi{a)e-latda. E.2)
Подставляя это выражение в E.1), получаем
оо
оо @ = S Vi (со) Н (со, t)e~ш d®, E.3)
— оо
где Я(о), t) определяется выражением
оо
Н (со, t) = J h (/, / — f) еш dtf. E.4)
Поскольку vo{t) и vi[t)' — вещественные функции временя,
имеем
Vi (со) = V\ (- со), Я (со, /) = Н* (- со, /). E.5)
') Это возможно только для детерминированных Vi(t). О спектральном
представлении случайных функций см. [155].
110 Глава 5
Чтобы понять физический смысл функции Я (со, t), положим
vi (() = cos (ио( = Re [exp (— /со0/)]. E.6)
Тогда получим
v0 (() = Re[H (<o0, t) exp (- iaQt)]. E.7)
Поэтому функция Я (ю, /)ехр(—Ш) представляет собой выход-
выходной сигнал в том случае, когда на входе действует гармониче-
гармоническая функция времени ехр(—Ш). Функция Я (a, t), вообще го-
говоря, является комплексной случайной функцией со и t и назы-
называется нестационарной функцией передачи. Заметим, что если
среда стационарна, то функция Я не зависит от времени.
Во многих практических задачах входной импульс представ-
представляет собой модулированный сигнал с несущей частотой со0, ко-
который может быть записан в виде
vt (t) = Re [щ (t) exp (- too/)], E.8)
где f0 = шо/2л — несущая частота. Функция Ui{t) комплексна и
называется комплексной огибающей сигнала vi. Мы можем
также записать
М0 = Л,@ехр[#<@], E.9)
где Ai и <pi — меняющиеся во времени амплитуда и фаза соот-
соответственно. Для узкополосного входного импульса Ai и <?,• яв*
ляются медленно меняющимися функциями времени.
Выходной импульс vo{t) может быть представлен в анало-
аналогичном виде
v0 (() = Re [но (() exp (- Ш)], щ (() = Ао (/) exp [if0 (()], E.10)
где Но — комплексная огибающая выходного импульса, а Ло и
фо — меняющиеся во времени амплитуда и фаза соответственно.
Запишем теперь общее соотношение E.3) через комплексные
огибающие. Представим комплексную огибающую входного сиг-
сигнала Ui(t) через ее спектр ?/;(©) в виде интеграла Фурье
E.11)
Тогда спектр входного сигнала У«(©) для Vi(t) дается выраже-
выражением
Vt (со) = 1 [Ut (со - соо) + Щ(- со - соо)]. E.12)
Подставляя выражение E.12) в формулу E.3) и используя со-
соотношения E.5), можно представить vo(t) в виде E.10) с функ-
Рассеяние импульсных волн в случайном облаке частиц 111
цией uo(t), определяемой выражением
оо
«о @ = \ Ut (©) Н (©о + со, /)е- '»' rfco. E.13)
Это общее выражение связывает комплексную огибающую вы-
выходного сигнала uo{t) со спектром (У,(со) комплексной огибаю-
огибающей входного сигнала и,(/).
Флуктуационные свойства выходного импульса часто описы-
описывают при помощи смешанного момента его комплексной оги-
огибающей
Он используется в задачах распространения СВЧ и оптического
излучения, в которых обычно измеряется комплексная огибаю-
огибающая (или флуктуации амплитуды и фазы). В задачах акустики
океана часто может наблюдаться экспериментально смешанный
момент самого выходного импульса, определяемый как
В Ah, ti = (vo(tl)vo(t2)). E.15)
Моменты Ви и By связаны с входной функцией через нестацио-
нестационарную функцию передачи Я. Эта связь рассматривается ниже.
5.2. Двухчастотная функция когерентности
и смешанный момент выходного импульса
Предположим сначала, что входной импульс является детер-
детерминированной функцией. Тогда смешанный момент комплексной
огибающей E.14) есть
Ви {(и t2) = \ dm \ d&2Ui fa) W fa) Г ехР (—
— оо —¦ оо
где
Г = Г (©о + «!, со0 + со2, /,, /2) = (Н (©о + «ь /i) Я* (©о + м2) 4)>-
Это общее выражение для смешанного момента комплексной
огибающей является основным для дальнейшего анализа в этой
главе. Функция Г описывает корреляцию выходных полей, от-
отвечающих двум падающим монохроматическим волнам с двумя
различными частотами ©о + «i и со0 + «2, и называется двухча-
стотным смешанным моментом, или двухчастотной функцией
взаимной когерентности. Из формулы E.16) видно, что решение
задач распространения и рассеяния импульсов сводится к на-
нахождению двухчастотной функции когерентности Г.
112 Глава 5
Интенсивность I(t) выходного импульса пропорциональна
<|и@ |2> и дается выражением
/(/) = \ don \ d&2Ui (©О Щ (со2) Го ехр [— / (©i — ©2) t], E.17)
— 00 — 00
где Го — значение функции Г при t\ = ti = /:
Го = (Я (©о + ©ьО Н* (щ + ©2, 0>.
Смешанный момент выходного импульса Bv в E.15) опреде-
определяется выражением
Bv{t\, t2)= \ d(o[ \ dviWi(©1) V\{®2)Гехр(— ш'/i + tofo), E.18)
—00 —00
где
Г = Г @Эь СЙ2, Л, ^2)==(Я(сй1, t\) Н (кJ, ^г)),
©1 = СОо " 01 И 02 == ©0 ~\~ 02.
Выражение для Во можно представить через огибающую,
если учесть, что
^о = з" [«о ехр (— г©о0 + Щ ехр (ш0/)]. E.19)
В результате имеем
Bv (ti, t2) = -j Re {Bu (i\, t2) exp [— ia>Q (t\ — t2)]} -f-
+ ^ Re {Cu (/,, t2) ехр [- ги0 (^ + Щ, E.20)
где функция Cu(ti, t2) = <wo(^i)«o(^)> дается формулой
оо оо
Си (tu t2) = ^ rf©i J rfco2t/i (©i) f// (©2) Г\ ехр (— гсох/х — /
— 00 —00
Г1 = (Я (©о + ©1, /1) Я (©о + ©2. /2)>. E.21)
Первый член в E.20) медленно меняется в зависимости от сред-
среднего времени /= 2-^1 + ^2) и является осциллирующей функ-
функцией разностного времени % = t\ — t2 с частотой со0. С другой
стороны, второй член представляет собой осциллирующую функ-
функцию t с частотой 2соо и поэтому может быть легко отфильтрован.
Тогда получим
Bv (tu k) ~ \ Re {Bu (/,, /j) ехр [- ш0(/, - Щ. E.22)
Рассеяние импульсных волн в случайном облаке частиц 113
На практике обычно несущую частоту понижают до некоторой
промежуточной частоты путем смешивания выходного сигнала
с сигналом постоянной частоты от местного гетеродина и выде-
выделения разностной частоты, так что ©о в экспоненте E.22) мо-
может быть такой промежуточной частотой.
5.3. Время когерентности и полоса когерентности
В задачах связи влияние случайной среды на распростране-
распространение волн часто оказывается удобным описывать с использова-
использованием понятий время когерентности и полоса когерентности.
Рассмотрим понятие время когерентности. При прохождении
волны с частотой со через случайную среду волна на выходе,
вообще говоря, испытывает флуктуации во времени. Корреля-
Корреляция выходной волны в два различных момента времени t\ и t2
убывает с увеличением т = U — t2. Разность времен At, при ко-
которой корреляция практически исчезает или спадает до неко-
некоторого заданного уровня, называется временем когерентности.
Оно характеризует временную корреляцию волны с частотой со.
Величина, обратная времени когерентности, есть уширение
спектра волны, обусловленное случайной средой. Как показано
в разд. 4.6, фурье-образ функции взаимной когерентности по
разности времен т представляет собой временной частотный
спектр волны.
С другой стороны, можно посылать две волны на различных
частотах coi и ©2 и наблюдать флуктуационные поля в один мо-
момент времени. При увеличении разности частот корреляция этих
двух флуктуационных полей уменьшается. Разность частот А/ —
= fd = (coi — со2)/2п, при которой корреляция почти исчезает
или спадает до некоторого заданного уровня, называется поло-
полосой когерентности и является мерой коррелированности волн на
двух различных частотах в один момент времени. Величина, об-
обратная полосе когерентности, представляет едбой уширение им-
импульса, обусловленное случайной средой.
Эти понятия легко проиллюстрировать при помощи двухча-
стотной функции когерентности, характеризующей корреляцию
между волной с частотой wi в момент времени t\ и волной с ча-
частотой ©2 в момент времени t2. Чтобы наглядно изобразить
время когерентности и полосу когерентности, нужно построить
график двухчастотной функции когерентности Г(©о + «ь ©о+
+ ©2, U, t2) в пространстве переменных fd и т для фиксирован-
фиксированных среднего времени ^ = у (А + 4) и центральной частоты
©о + «с где ©с = 2"(©i + ©2) (рис 5.1). Время когерентности A.t
и полоса когерентности А/ показаны на этом рисунке.
114
Глава 5
Во многих практических ситуациях двухчастотная функция
когерентности Г является почти стационарной во времени и,
следовательно, ее можно считать не зависящей от t. Этот слу-
случай отвечает так называемому стационарному в широком смысле
каналу. С другой стороны, если Г не зависит от сос, то это соот-
соответствует каналу с некоррелированным рассеянием. Если же
двухчастотная функция когерентности не зависит ни от ©с, ни
от t, то говорят о стационарном в широком смысле канале с не-
некоррелированным рассеянием.
Рис. 5.1. График двухчастотной функции когерентности в зависимости от раз-
разностной частоты f. = /j—f2 и разностного времени t = <j — t2; показаны
время когерентности Ы и полоса когерентности Af.
До сих пор мы рассматривали общие выражения для флук-
туационных характеристик выходного импульса, в которые свой-
свойства среды входят через двухчастотную функцию когерентности.
В последующих разделах эти общие выражения используются
для анализа задачи рассеяния.
5.4. Рассеяние узкополосного импульса.
Выражения, приведенные в предыдущих разделах, носят об-
общий характер и применимы как в случае широкополосных, так
и в случае узкополосных входных сигналов. В этом разделе мы
рассмотрим рассеяние узкополосного входного сигнала.
Пусть на входе имеется сигнал с комплексной огибающей
ut(t) вида E.9) и со спектром ?/,(©) вида E.11). Этот сигнал
посылается излучателем в направлении облака случайно рас-
Рассеяние импульсных волн в случайном облаке частиц
115
пределенных частиц, а рассеянный импульс регистрируется
приемником (рис. 5.2). Предположим, что частицы располо-
расположены в дальней зоне по отношению к излучателю и приемнику,
работающим на несущей частоте. Нас будут интересовать флук-
туационные характеристики принимаемого импульса, описывае-
описываемого его комплексной огибающей uQ(t). Поскольку среда флук-
флуктуирует, выходной импульс «о@ является случайной функцией
времени. Поэтому мы рассмотрим интенсивность выходного им-
импульса /(/), даваемую выражением E.17), и смешанный мо-
момент Ви, определяемый формулой E.16).
Рис. 5.2. Взаимное располо-
расположение излучателя, излучаю-
излучающего импульс в направле-
направлении случайного облака ча-
частиц, и приемника, регистри-
регистрирующего рассеянный им-
импульс.
Приемник
Как обсуждалось в разд. 5.2, выходной импульс ио(О вы-
выражается через функцию передачи #(co0 + o), t) формулой
E.13). Чтобы найти функцию передачи для рассматриваемой
задачи рассеяния, заметим, что #(©, t) является выходным сиг-
сигналом в случае, когда входной сигнал имеет вид ехр(—Ш).
Для определения H(m,t) рассмотрим отдельную частицу,
расположенную на расстояниях Ri от излучателя и R2 от прием-
приемника. Сначала будем считать, что частицы неподвижны. Поле
в месте расположения частицы при входном сигнале вида
ехр(—imt) определяется выражением
, л.
л. exp
E.23)
где ft(l) —диаграмма направленности излучателя по полю, свя-
связанная с диаграммой направленности по мощности Gt(i) соот-
соотношением
4я|МГ)Р = <М0. E.24)
Это соотношение получается из того условия, что квадрат поля
в E.23) должен совпадать с плотностью мощности, определяе-
определяемой выражением Gt/4ixRi. С учетом затухания, обусловленного
1 f 6 Глава 5
поглощением и рассеянием другими частицами, лежащими на
пути от излучателя до данной частицы, выражение E.23) при-
принимает вид
где Yi=== \ 9°tdR— оптический путь, р — плотность частиц,
о
a at — полное сечение частицы, расположенной в точке R
(разд. 4.2).
Поле E.25) падает на частицу. Пусть амплитуда рассеяния
этой частицы есть fp@, i). Введем также приемную диаграмму
направленности по полю />@) такую, что |)>F)|2 характеризует
эффективную площадь Аг@) приемной антенны. Она связана
с приемной диаграммой направленности по мощности б>@) со-
соотношением
6GrF). E.26)
В результате для функции передачи #(со) имеем
Н (со) = ft (?) /р F, Т) U@) «p[tt(*1 + jW-v./2-v./2] , E.27)
где Yi и V2 — оптические пути, определяемые формулой D.11а).
Запишем теперь двухчастотную функцию когерентности Г
E.16) для случайного распределения частиц, находящихся в
элементе объема dV. Заметим, что поля, рассеянные различ-
различными частицами, можно считать некоррелированными, вслед-
вследствие чего вклады от всех частиц просто складываются. Тогда
получим
Г = (Я(соо + со,) Я*(соо + со2)) =
- Р (соо + со,) Г (соо + со2) еХР ^ <*^Н*' + ^ р dV. E.28)
где с — скорость распространения волны, а
F (со) = U (T) fp @, Т) fr (б) ехр [- Y./2 - Y«/2].
В случае узкополосного входного сигнала |coij <C coo и |со2| <С
<С ©о, поэтому приближенно мы имеем
F (соо + со,) « F (со0 + со2) « F (со0). E.29)
В результате находим
=ШУЬ±М E.30)
Рассеяние импульсных волн в случайном облаке частиц 117
Укажем, что узкополосное приближение E.30) соответствует
стационарному в широком смысле каналу с некоррелированным
рассеянием. Подставим теперь формулу E.30) в E.16). По-
Поскольку со] и со2 в экспоненту E.30) входят только в виде раз-
разности cod = (oi — @2, нетрудно выполнить в E.16) интегрирова-
интегрирование по coi и иг, которое дает
Ви «и h) = \ ^)G/J0) obi @,1) ехр (- y, - Ya) Bi9 dV, E.31)
где
Bi = И| (/, - (*, + R2)/c) и* (/, - (*, + R2)/c).
Интенсивность I(t) определяется тем же выражением E.31),
но в котором необходимо заменить В, на Л:
Ii = \ui(t-(Rl + R2)/c)\\ E.32)
Формулы E.31) и E.32) представляют собой общие выраже-
выражения для функции когерентности и интенсивности выходного им-
импульса «о @ в случае узкополосного сигнала, получающиеся в
первом приближении теории многократного рассеяния для не-
неподвижных частиц. Отметим, что окончательное выражение
E.31) может быть получено и как обобщение уравнения радио-
радиолокации ,без привлечения двухчастотной функции когерентно-
когерентности. Однако приведенный в этом разделе вывод является более
строгим, поскольку предположение об узости полосы было ис-
использовано нами, только начиная с формулы E.29). На самом
деле E.31) легко обобщить на случай широкой полосы, для ко-
которого имеем
где
oo
G{t)= J daF (<do + со) U, (со) е~ ш.
До сих пор мы предполагали, что частицы неподвижны. Если
частицы движутся, то бистатическое сечение оы@, i) следует
заменить на сечение рассеяния с учетом временной корреляции
<зы@, 1, т), определяемое формулой D.48). В соответствии с
предположением, обсуждавшимся в разд. 4.5, разность времен х
есть г = ti — h.
Заметим также, что мы рассматривали случай частиц одного
размера. Между тем легко учесть распределение частиц по раз-
1(8
Глава 5
мерам, для чего нужно заменить pebi и pat следующими вели-
величинами:
Р<*ы
(D) n (D) dD, pot -> \ ot Ф) п (D) dD, E.34)
где n(D)dD — число частиц размера (например, диаметра) D
в интервале (?), D + dD).
5.5. Обратное рассеяние импульса, излучаемого
остронаправленным излучателем
Рассмотрим теперь на основе общих выражений E.31) и
E.32) обратное рассеяние импульса от облака случайно рас-
распределенных частиц (обратное рассеяние ультразвука см. в ра-
работах [143, 144]).
Излучатель
и приемник
Рис. 5.3. Излучение импульса длительности То остронаправленной передаю-
передающей антенной с шириной луча по уровню половинной мощности 0^ и прием
рассеянного импульса той же антенной.
Будем считать, что для приема сигнала используется пере-
передающая антенна, которая имеет ширину луча на уровне поло-
половинной мощности 8й Fй «С 1) (рис. 5.3). Тогда, используя фор-
формулу D.19), получаем
E.35)
где
DлK
V 8 In 2 / •
Заметим, что пока речь идет рб интенсивности I(t), движение
частиц можно не учитывать, поскольку разность времен t\— t2=
= т равна нулю и сечения рассеяния с учетом временной кор-
корреляции сводятся к обычным сечениям.
Рассеяние импульсных волн а случайном облаке частиц
119
Полагая f = 2R/c и записывая E.35) в виде свертки, для
импульса произвольной формы получаем
7@= J f(f)\u,{l-n?df,
E.36)
f(t') =
Ap(R)a,(R)e-^ (с
R2
D)' Y=
где R = (c/2)t\ Ri = (c/2)t\ и R2 = (c/2)ti Заметим, что здесь
мы включили вариации плотности p(R) и характеристики рас-
рассеяния частиц оь (R) и at (R) вдоль трассы распространения.
/(О
Излучаемый импульс
/ (огибающая)
Рассеянный
импульс
7@ ,
*то>тг
Рис. 5.4. Интенсивность обратного рассеяния / (t) от слоя толщины /?2 — R\>
показанного на рис. 5.3. Время распространения в слое туда и обратно равно
Tt =2 (R2 — Ri)/c, длительность импульса То; а — характеристика среды
как функции расстояния R — ct/2, б — рассеянный импульс при To<Tt,
в — рассеянный импульс при Го > ?Y
Из формулы E.36) видно, что если длительность импульса
То меньше, чем время распространения через слой и обратно
Тх = 2(R2 — R\)/c, то времена нарастания и спада отраженного
импульса приблизительно равны То; если же Го больше, чем
Т\ = 2(/?2 — R\)/c, то времена нарастания и спада определяют-
определяются величиной Т\ = 2(R2 — R\)/c (рис. 5.4). Отсюда также сле-
следует, что при очень малой длительности импульса форма при*
нимаемого импульса приближенно совпадает с функцией f{t\.
120 Глава 5
В самом деле, если падающий импульс имеет вид дельта-функ-
дельта-функции:
\ut(t)? = E<A((), E.37)
где Ео — полная энергия, то
I(t) = Eof(t) = EofBR/c). E.38)
Поскольку интенсивность в момент времени t пропорциональна
функции /, вычисленной на расстоянии R — ct/2, интенсивность
E.38) может быть использована для нахождения характери-
характеристик частиц, расположенных на расстоянии R. Например, при
известных сечениях по измерениям интенсивности I(t) может
быть найдена плотность p(R). Этот метод применим в таких
прикладных задачах, как акустическое обнаружение косяков
рыб, а также определение плотности аэрозоля и гидрометеоров.
В более реальном случае, когда импульс имеет прямоуголь-
прямоугольную форму:
0/Г° ПРИ 0<i<T0' ,-om
0 при /<0 и />Г0, E'39)
имеем
t-Tt R-bR
где AR = сТо/2 и R — ct/2. Из E.40) видно, что в некоторый
момент времени г интенсивность I(t) представляет собой усред-
усредненное по интервалу (R — AR, R) значение величины, стоящей
под интегралом. Расстояние AR равно половине длины импульса
сТ0, поэтому в любой момент времени t интенсивность дает ин-
информацию о свойствах среды внутри объема, глубина которого
равна сТ0/2, а поперечные размеры определяются шириной пе-
передающего луча. Этот объем называется радиолокационным
объемом, или объемом разрешения радиолокатора.
Из рис. 5.4 ясно также, что если время прохождения Т\ че-
через среду меньше длительности импульса То, то форма рассеян-
рассеянного импульса в основном повторяет форму входного импульса,
за исключением переднего края и хвостовой части. Заметим
также, что в этом случае G\ < Го) в промежутке между /{+
+ Т\ = 2R2/C и t[ + Го = 2Ri/c+ To рассеянная интенсивность та-
такая же, как в монохроматическом случае.
Вообще говоря, в случае обратного рассеяния от слоя слу-
случайной среды толщиной d = R2 — R\ полоса когерентности при-
приближенно равна \/Т\ = c/2d. Поскольку спектр излучаемого им-
импульса длительностью Тй>Т\ сосредоточен в области |со| <
< 1/Г0 < 1/Гь изменение формы импульса несущественно. Од-
Рассеяние импульсных волн в случайном облаке частиц 121
нако, если То < Т\, рассеянный импульс имеет форму, сильно
отличающуюся от формы излучаемого импульса.
В качестве примера рассмотрим слой толщины d, содержа-
содержащий случайное облако частиц с равномерным распределением
в пространстве. (Отражение от облаков при оптической локации
рассматривается в работах [5, 25, 34, 106]; см. также обшир-
обширный обзор [35]. Деполяризационные эффекты рассматриваются
в работах [99, 129].) Этот слой расположен на большом рас-
расстоянии Ro(Ro !Э> d) от передатчика. Входной импульс имеет
прямоугольную форму E.39). Из формулы E.40) имеем
R
/(/) = у^ \ pab[U(R~Ro)-U(R-Ro-d)]exp(-2y)dR,
Hi
где Ri = \{d — cT0), Ri = &{ct), y = pat{R-RQ), U(R-R0)-
единичная ступенчатая функция, так что U(R — R0) —
—U(R — Ro — d) представляет собой ступеньку ширины d. Этот
интеграл легко вычислить. Например, если Т\ = 2d/c больше,
чем То, то
(ра ) ехр (~ patct) texp
2pCTt
при '—~ + T0<i
/ (*-( АЕ° \ (пп \ (ехр [~ рУ (^ - ГоI - ехр (~
при
Рассмотрим корреляционную функцию Bu(t\, /2) рассеянного
импульса. Поскольку мы рассматриваем два различных мо-
момента времени, необходимо привлечь сечение рассеяния с уче-
учетом временной корреляции. Здесь удобно вместо ^ и ^ исполь-
использовать среднее время i = -z{t\-\-l2) и разностное время т =
= U — h- Используя обратное сечение рассеяния с учетом вре-
временной корреляции <7й(т) = 4жх<*(—i, i, т), где оа определяется
формулой D.48), и следуя процедуре получения формулы E.35)
122 Глава 5
для узкого луча, перепишем E.31) в виде
Bu(t, ч) = А \ -^^—м;(^-^)«:(/2-^)^. E.41)
д.
Вводя обозначение t' = 2R/c, получаем
Ви (/, т) = \ f (Г, т) иt (/, - f) u\ {t2 - f) dt', E.42)
где
/ it', t) = — V
а другие величины определены в E.36). Формула E.42) дает
общее выражение для корреляционной функции выходного им-
импульса, рассеянного в обратном направлении средой, показан-
показанной на рис. 5.3.
Из E.42) следует, что корреляционные свойства выходного
импульса определяются корреляционной характеристикой ча-
частиц Оь(Я, т), учитывающей их движение, и произведением оги-
огибающих входного импульса и. G, — t')u*t(t2 — /'). Интервал кор-
корреляции Тр, связанный с движением частиц, приближенно равен
Bk\ V]) = с/Dя/о| V\), где V — скорость частиц. Обычно этот
интервал корреляции велик по сравнению с длительностью им-
импульса. Предположим, что ширина импульса То намного меньше,
чем время распространения Т\, и наблюдение рассеянного им-
импульса осуществляется в период времени между 1[-\-Тй и Ц
Такая ситуация обычно встречается в акустических локационных
и радиолокационных исследованиях атмосферы. Предположим
также, что ширина импульса То мала по сравнению с интерва-
интервалом корреляции Тр, связанным с движением частиц. Тогда вид
корреляционной функции определяется только формой входного
импульса, и она приближенно оказывается равной
Bu (t, t) = / (/, т) ^ мг (/j -1') u\ Q2 - f) dt'. E.43)
В случае прямоугольного импульса
Uo при 0 <: / < То,
щ{-1) ' 0 при /<0 и 1>Т0
получаем
Ви (t, т) ==/(/, т) A -1 т (/Го) Ео, |т|< Го, E.44)
где I Uq 12 = Eo/Tq.
Рассеяние импульсных волн в случайном облаке частиц 123
5.6. Обратное рассеяние последовательности
коротких импульсов
В радиолокации и в звуковой локации излучаемая мощность
обычно имеет вид последовательности коротких импульсов, дли-
длительность которых Го намного меньше времени распростране-
распространения Т\. Свойства среды могут медленно меняться во времени, и
отраженный сигнал принимает вид, показанный на рис. 5.5.
Кроме того, движение частиц может быть выявлено по корре-
корреляционной функции, зависящей от разности времен т = U — U,
или, что то же самое, по спектру с доплеровским сдвигом ча-
частоты. В этом случае отраженный сигнал можно рассматривать
как случайную функцию аргументов t и % (i описывает измене-
изменение в зависимости от расстояния R = ct/2, а т — изменение во
времени среды в фиксированной точке R; рис. 5.6).
Рассмотрим корреляционную функцию Bu{t\, t2) отраженного
импульса. Как уже отмечалось выше, имеются две корреляцион-
корреляционные функции — одна по t, другая по т. Поскольку корреляция
по t описывает временную корреляцию между импульсами, она
не отличается от корреляционной функции одного импульса,
рассмотренной в предыдущем разделе. Корреляция по т в фикси-
фиксированный момент времени t (или при фиксированной дальности)
представляет интерес для многих приложений, включая импульс-
импульсные доплеровские системы.
При фиксированном t корреляционная функция по т опреде-
определяется формулой E.42), взятой при t\ = t2 = t:
Ви (/, т) = \ f (f, т) щ (t -1') u\ (t - П df. E.45)
В случае короткого импульса длительности То имеем
ВЯ (/, т) ~ / (/, г) Е0 = 'Р(«>М**>« (Т) Eq> E.46)
где R = ct/2. Тогда временной частотный спектр Wu(t, со) имеет
вид
Wu (/, tt) = ^'^y^V (|) Ео, E.47)
где R = ct/2, a W0(R, a) — спектр сечения D.51).
Если включить в рассмотрение распределение частиц по раз-
размерам, то необходимо заменить p4nWa на <4W>
р DnWa) = J n {D)'4nWa (со, D) dD. E.48)
124
Глава 5
Рассмотрим, например, такую задачу, как вертикальное зон-
зондирование распределения капель дождя по размерам. Предпо-
Предположим, что установившаяся скорость дождевой капли радиуса а
Излучаемый импульс
Отраженный импульс 1@
1
1
,PRF PRF
Рис. 5.5. Излучаемый сигнал в виде последовательности импульсов с перио-
периодом повторения (PRF)~ , где PRF — частота повторения импульсов. Форма
отраженных импульсов медленно меняется от импульса к импульсу.
2 d
t = — (дальность)
t(дальность)
Рис. 5.6. Корреляционная функция Ви (t, т) в зависимости от дальности t и
времени корреляции т. Фурье-образ Вп по т представляет собой временной
частотный спектр Wu {t, ш), где / характеризует дальность, а о — движение
среды (доплеровский сдвиг).
определяется приближенной формулой [см. C.6) и D.65)]
U = - U (a) z, U (а) = U^ = 200,8а1/. (м/с), E.49)
где z — единичный вектор в вертикальном направлении. Тогда
из D.69) имеем
E.50)
Рассеяние импульсных волн в случайном облаке частиц
125
где ао = <xJ/BkUoJ и Uq = 200,8. Если мы измеряем частотный
спектр Wu(t, со) при фиксированной дальности R = ct/2, то в
соответствии с E.47) получаем (yDnWa(R, со)> как функцию со.
Из формулы E.50) видно, что каждому размеру а0 отвечает оп-
определенная частота со. Следовательно, зная сечение обратного
рассеяния Оь(ао) как функцию ао, из спектральных измерений
можно определить распределение частиц по размерам п(ао).
5.7. Обратное рассеяние импульса, излучаемого
передатчиком с широкой диаграммой
направленности
В предыдущих разделах мы исследовали характеристики рас-
рассеянного импульса в случае остронаправленного излучателя.
Если же диаграмма направленности излучателя широкая, то не-
необходимо исходить из общего выражения E.31). В качестве
у///////////-
Рис. 5.7. Обратное рассеяние импульса:
излучаемого слабонаправленным из-
излучателем. Частицы сосредоточены
в тонком слое толщины Дг.
i
'?/2////////////////, ' 4z
7
T Излучатель
примера рассмотрим обратное рассеяние импульса от тонкого
слоя рассеивателей. Для простоты будем считать, что излуча-
излучатель изотропен (Gt = const; рис. 5.7). Тогда, замечая, что dV =
= rdrd<f> dz, получаем
ft Bn) Л2
DяK
R
3 ' dR.
E.51)
В случае когда входной импульс имеет вид б-функции E.37),
интенсивность I(t) равна
DяK
\2j'
E-52)
126 Глава 5
Заметим, что в случае тонкого слоя рассеянная интенсивность
I(t) убывает как R~3 ~ t~3, тогда как при объемном рассеянии,
рассмотренном в предыдущем разделе, /(/) пропорциональна
R-2 » t~2. Отсюда следует, что временная зависимость рассеян-
рассеянной интенсивности позволяет выявить характер пространствен-
пространственного распределения частиц.
5.8 Бистатическое рассеяние импульса
Общее выражение для случая бистатического рассеяния дано
в E.31). Поэтому интенсивность I(t) равна
E.53)
Из E.53) видно, что все волны, рассеянные из точек, для ко-
которых величина Ri + R2 постоянна, приходят в приемник в один
и тот же момент времени. Эти точки расположены на поверхно-
поверхности эллипсоида вращения, фокусы которого совпадают с точ-
точками расположения излучателя и приемника [156]. Этот эллип-
эллипсоид быстро расширяется во времени. Например, скорость рас-
расширения Vb = db/dt в средней точке (Rt = R2 = R) может быть
получена из условия R2 = b2 -\-(L/2J:
дЬ R dBR)
_ _ (R) _ _Я_ _
Vb ~~ dt ~ 26 dt 26 С ~
dt ~ 26 dt 26 С ~ 2 sin F/2) '
Если ширина передающего и приемного лучей Qb мала
(рис. 5.8), а длительность импульса велика, так что То >
> (^2 — ^i) = H/vb, где Н — высота общего объема передаю-
передающего и приемного лучей, то передний край импульса начинает
давать вклад в рассеянную мощность в момент времени t = t\.
Хвост импульса достигает общего объема в момент ti -f- T и
выходит из него при t% -+- Т. Поведение принимаемой мощности
во времени показано на рис. 5.9, а. Если длительность импульса
Го меньше, чем t2 — t\, то принимаемая мощность ведет себя,
как показано на рис. 5.9, б.
Время нарастания в случае То> U — U равно t2 — ti — H/vb,
а скорость Vb примерно равна с/2 sin F/2). Такому времени на-
нарастания отвечает полоса частот
А/ « -j~t: ~ m sin (э/2) • <5-55)
Если Af велико по сравнению с полосой излучаемого импуль-
импульса, то искажение формы импульса несущественно. Это обычно
Рассеяние импульсных волн а случайном облаке частиц
127
имеет место при распространении узкополосных импульсов.
В случае когда То < t2 — U, полоса частот А/ ~ 1/Г0 и, следо-
следовательно, происходит заметное искажение импульса, зависящее
от формы общего объема.
_ Площадь 4 = A (R )
Рис. 5.8. Бистатическое рассеяние импульса. Волны, рассеянные частицами,
находящимися на поверхности эллипсоида с постоянным значением 2R =
= R\ + /?2, приходят в приемник в один и тот же момент времени. Действие
переднего края импульса на приемник начинается в момент времени t\ и
заканчивается в момент tt.
-»-1
t2-\-T
_ t
tltl+Tt2t2+T
Рис. 5.9. Принимаемая мощность / (t) при бистатическом рассеянии, а — при
То> t2 — tu б — при То < t2 — t\.
Строго говоря, интегрирование в E.53) должно проводиться
по общему объему. Элемент объема dV пропорционален
Л(/?)с//?') (рис. 5.8). Следовательно, выражение E.53) прибли-
') Выражение для dV в вытянутых сфероидальных координатах см. в
работе [1].
128 Глава 5
женно представляет собой свертку мощности входного импульса
I/ @ = I Ui @ |2 с функцией A (R):
Ро @ - J Л (R) Pt (t - Л/с) dR. E.56)
5,9. Представление через функцию неопределенности
В предыдущем разделе мы получили выражение для корре-
корреляционной функции выходного импульса. Другая форма записи
статистических характеристик импульса основана на использо-
использовании функции неопределенности [170]. Перепишем формулу
E.16), введя среднее время t — -~(t\-\-t^j, разностное время
т — h — t2, центральную частоту сос = у («i + «2) и разностную
частоту cod = coi — @2. Замечая, что
cod/ + <»ст, cfcoi da>2 = dd)d d(oc, E.57)
запишем
Bu (tu t2) = Bu (t, т) = ^ W„ (ad, coc, /, t) exp (— /cod/ — гсос0 dcod ^coc,
E.58)
где Wu — зависящая от времени спектральная плотность выход-
выходного импульса, определяемая выражением
Wu = Ui (coi) Ut (ca2) Г (coo + ffli, co0 + co2, /1, /2). E.59)
Функцию неопределенности %i(a)d,t) входного импульса оп-
определим как
/ К )\i Oi) и\ Ы ехР (- Чт) d®c-
Поскольку
и* (^i) «i (Q = S S ^ (^i) ^ ы ехр (- чт - чо <ч ^>
функцию неопределенности можно представить как фурье-об-
раз:
т) —ST J««СО "*. W ехР КО
В общем случае входной импульс ut(t) может быть случайной
функцией времени. Тогда функция неопределенности выражает-
Рассеяние импульсных волн в случайном облаке частиц 129
Xi (®d, r) = — J Bt (t, т) ехр (mdt) dt, E.63)
ся через фурье-образ корреляционной функции Bi(th t2):
1
2я
где Bt{t, i) = (ul(tl)ui{t2)). Из E.63) следует
\\\%i Ы т) I2 Л»„ dr = ~ \ J | В( (/, т) |2 Л й?т. E.64)
Поскольку |В;(/, т)|2 = ([«( (^)и*(^)|2)' интеграл в правой ча-
части E.64) можно выразить в виде Ео/2л, где Ей — полная энер-
энергия входного импульса
EQ = ^\ut{f)fdt. E.65)
Таким образом, имеем
E.66)
Из уравнения E.66) следует, что для импульса с заданной пол-
полной энергией весь объем, ограниченный поверхностью |%,|2 и
плоскостью время (т)—частота ((о<*), остается постоянным не-
независимо от формы импульса. Этот вывод называется принципом
неопределенности. Это означает, например, что сжатие функ-
функции %i{(Hd, т) в направлении т или cod сопровождается соответ-
соответствующим расширением в направлении другой координаты.
Функцию неопределенности часто представляют графически
в виде диаграммы неопределенности. Она представляет собой
линию Со в плоскости cod, т, на которой значение |%г|2 принимает
некоторое постоянное значение. Это значение может быть взято
таким, что
4
Перепишем E-. 16) через введенную функцию неопределенно-
неопределенности для случая стационарного в широком смысле канала с не-
некоррелированным рассеянием. Тогда двухчастотная функция ко-
когерентности Г является функцией ш и т и не зависит от (оо
и t. В результате имеем
Ви(t, t)=\%i(а* т)Г(cod, т)ехр(-mdt)dad. E.68)
Сравнивая это выражение с формулой E.63), находим, что
функция неопределенности выходного импульса равна произве-
произведению функции неопределенности входного импульса и двухча-
стотной функции когерентности Г.
130
Глава 5
5.10. Импульсно-доплеровский радиолокатор1)
В предыдущих разделах мы исследовали среднее значение
рассеянной мощности, а также корреляционные свойства и
спектр рассеянного поля. Среднюю рассеянную мощность I(t)
можно регистрировать при помощи традиционного, или некоге-
некогерентного радиолокатора. Но функцию когерентности и спектр
можно измерить только в системе, которая осуществляет реги-
регистрацию фазы рассеянного поля по отношению к фазе зондирую-
Переключатель
So
Г~А - *¦ Г —" So (импульсное)
fo+fd ] fo+fd
~fo +fd
Пере-
Передатчик
Смеситель
приемника
Усилитель
ПЧ
fo
Смеси-
Смеситель син-
хрониза-
хронизации
fs
fs
Гетеродин
Синхрони-
Синхронизируемый
генератор
ПЧ
ПЧ+/,
Фазовый
детектор
Рис. 5.10. Блок-схема импульсно-доплеровской системы.
щего сигнала. Такая система называется когерентным радиоло-
радиолокатором. Радиолокатор, измеряющий сдвиг частоты, обуслов-
обусловленный движением рассеивателей, называется доплеровскич.
Доплеровский радиолокатор с непрерывным сигналом может
быть использован для измерения доплеровского сдвига частоты,
но он не дает информации о дальности. Импульсно-доплеров-
Импульсно-доплеровский радиолокатор позволяет получать информацию как о ско-
скорости, так и о дальности рассеивателей. В этом разделе мы даем
краткое описание импульсно-доплеровской системы.
В импульсном радиолокаторе передатчик генерирует после-
последовательность коротких импульсов. Пусть /о — несущая частота,
Го — длительность импульса и PRF — частота повторения им-
импульсов (например, fQ = 3 ГГц, То = 10 мкс и PRF =* 1000).
') Применение импульсно-доплеровских систем в медицине рассматри-
рассматривается в работе [6]. См. также прекрасный обзор по использованию ультразву-
ультразвука в медицине [52].
Рассеяние импульсных волн а случайном облаке частиц
131
Этот сигнал излучается, а рассеянная в обратном направлении
волна принимается антенной. Принятый сигнал смешивается
с сигналом стабильного гетеродина и получается сигнал проме-
промежуточной частоты (например, 30 МГц), который имеет те же
фазовые характеристики, что и рассеянное поле. Этот сигнал
^ И То ^
л±
/о
t-PRF
Неподвижные
рассеиватели
/ ^\ Движущиеся
рассеиватели
/0-PRF /0 /0+PRF
Набор фильтров
¦411 I Уо+PRF
Рис. 5.11. Частотный спектр излучаемого импульса при длительности им-
импульса Tq и частоте повторения PRF (а); частотный спектр импульса, рас-
рассеянного на неподвижных частицах (б); частотная характеристика набора
фильтров, каждый из которых имеет узкую полосу Д/ (в).
сравнивается с сигналом когерентного генератора, который ра-
работает на промежуточной частоте, получаемой путем смешения
зондирующего сигнала с сигналом стабильного гетеродина, гак
что его сигнал имеет ту же фазу, что и зондирующий сигнал
(рис. 5.10) [7].
Спектр зондирующего импульса имеет вид отдельных линий,
смещенных на величину PRF, и его полная ширина равна 1/Гэ
(рис. 5.11, а). Волна, рассеянная движущимися рассеивателями,
132
Глава 5
имеет частотный спектр, сдвинутый на доплеровскую частоту и
уширенный (рис. 5.11,6).
Чтобы измерить спектр сигнала от движущихся рассеивате*
лей, в импульсно-доплеровской системе используется набор
фильтров, каждый из которых имеет узкую полосу (например,
100 Гц) (рис. 5.11, в). Измерение скорости осуществляется по
Стробы
дальности
Записывающее*
¦*- устройство
Рис. 5.12. Импульсно-доплеровская система со стробированием по дальности
и набором фильтров.
фильтру, на выходе которого сигнал имеет максимальную вели-
величину. Доплеровский спектр может быть получен также путем
цифровой обработки. Для получения информации о дальности
осуществляется стробирование сигнала (рис. 5.12).
Из рис. 5.11,в видно, что если доплеровская частота стано-
становится равной частоте повторения импульсов PRF, то доплероа*
екая линия совпадает со спектральной линией неподвижных рас-
сеивателей, и они становятся неразличимыми. Скорость рассей-
вателей V, отвечающая этому условию, называется «слепой»
скоростью. .Поскольку доплеровская частота волны, рассеянной
Рассеяние импульсных волн в случайном облаке частиц 133
в обратном направлении рассеивателем, движущимся со ско-
скоростью V, есть 2Vfk, то «слепая» скорость равна
/2. E.69)
Вторая «слепая» скорость равна удвоенному значению, опреде-
определяемому формулой E.69).
Импульсно-доплеровская система используется для наблюде-
наблюдения движений снега, дождя, града и т. п. [7]. Упомянем здесь
также систему, называемую индикатором движущихся целей
(ИДЦ), которая аналогична импульсно-доплеровскои. Эта си-
система обнаруживает движущуюся цель путем сравнения рас-
рассеянных волн для различных импульсов и подавления сигналов
от неподвижных целей. Это может быть сделано с использова-
использованием линий задержки или цифровой обработки. ИДЦ обычно
приводит к неопределенности по дальности, тогда как информа-
информация по доплеровскому сдвигу однозначна (подробно об ИДЦ и
импульсно-доплеровскои системе см. в книге [146]).
Глава 6
Распространение в пределах
прямой видимости
через разреженное облако частиц
В гл. 4 и 5 мы рассмотрели характеристики непрерывных и
импульсных волн, рассеянных на облаке случайно распределен-
распределенных частиц. В этой главе мы исследуем распространение волн
через случайную среду в пределах прямой видимости. Задача
распространения в пределах прямой видимости представляет
особый практический интерес. Например, характеристики мил-
миллиметрового и оптического каналов связи через земную атмо-
атмосферу часто подвержены влиянию дождя, тумана и снега, а на-
наличие различных частиц и рассеивателей оказывает влияние на
распространение оптических и акустических волн в воде.
Задачи рассеяния и распространения в пределах прямой ви-
видимости удобно рассматривать отдельно, так как поведение вол»
в этих двух случаях носит совершенно различный характер.
В задаче рассеяния волна является почти полностью некогерент-
некогерентной, причем в отсутствие среды рассеянная волна вообще отсут-
отсутствует. В задаче распространения в пределах прямой видимости
исследуемая волна содержит как когерентную, так и некогерент-
некогерентную составляющие, причем в отсутствие среды она переходит
в падающую волну.
Прежде чем перейти к детальному анализу характеристик
волн, полезно дать приближенное описание поведения волны в
задаче распространения в пределах прямой видимости. Рассмо-
Рассмотрим пример нормального падения плоской волны на полубес-
полубесконечную среду, содержащую случайные частицы (рис. 6.1). Как
уже говорилось в разд. 4.4, интенсивность когерентной состав-
составляющей поля 1с есть квадрат амплитуды когерентного поля <и>,
интенсивность некогерентной составляющей /,¦ представляет со-
собой средний квадрат амплитуды некогерентного поля «/, а пол-
полная интенсивность h есть сумма /с и 1с
It = (I) = (\u?) = Ic + l{,
/с=1<и>Р. It = (\u,f), u = (u) + uf. ( 6Л)
Интенсивность когерентной составляющей 1С уменьшается из-за
рассеяния и поглощения, поэтому она должна убывать (разд. 4.2)
с ростом коэффициента затухания, равного произведению плот-
плотности р и полного сечения ot = os + °a'.
F.2)
Распространение через разреженное облако частиц
135
Интенсивность излучения, рассеянного в стороны, представляет
собой некогерентную интенсивность /;. Однако это излучение
с интенсивностью /,• в свою очередь тоже рассеивается во всех
направлениях. Поэтому сумма интенсивностей 1С и h должна за-
о
о
0
О
0
0
0
0
о
о
О
О
h
Амплитуда
Рис. 6.1. Схематическое изображение когерентной интенсивности 1С, некоге-
некогерентной интенсивности /,¦ и полной интенсивности It в случае плоской волны,
падающей на полупространство (г > 0), заполненное частицами. Показаны
также схематически амплитуды поля в зависимости от х на различных рас-
расстояниях z.
висеть в основном от сечения поглощения частиц, и ее можно
приближенно записать в виде
It~exp(-9aaz). F.3)
Следовательно, интенсивность когерентной составляющей
дается выражением
U «* ехр (— paaz) — ехр (— patz) & ехр (— patz) (exp (pasz) — 1). F.4)
Эти соотношения иллюстрируются графиками на рис. 6.1. Заме-
Заметим, что, пока оптический путь у = potZ намного меньше еди-
136 Глава 6
ницы, преобладает когерентная составляющая поля (z = z{).
При значениях у, близких к единице, когерентная интенсивность
1с и некогерентная интенсивность /,¦ сравнимы по величине
(z = z2), а при у >• 1 1с практически обращается в нуль, и пол-
полная интенсивность I* содержит только некогерентную состав-
составляющую (z = z3). Для иллюстрации этого на рис. 6.1 показано
поведение флуктуации амплитуды. Следует заметить, что фор-
формулы F.2) — F.4) не учитывают эффектов обратного рассеяния,
размеров частиц, характеристик приемника и т. д. и поэтому
являются приближенными. Тем не менее они дают представле-
представление о некоторых общих характеристиках поля в задаче распро-
распространения в пределах прямой видимости.
В этой главе мы исследуем поведение поля в области слабых
флуктуации. Это та область, где поле в основном когерентно,
так что амплитуда некогерентной составляющей поля намного
меньше амплитуды когерентной составляющей. В случае пло-
плоской волны, показанном на рис. 6.1, это соответствует малому
по сравнению с единицей оптическому пути у = patz (z = zi).
На рис. 6.1 видно также, что если рассеяние намного меньше
поглощения (т. е. альбедо os/ot < 1), то некогерентное поле
мало по сравнению с когерентным даже при оптическом пути
порядка или больше единицы. Поэтому данный случай также
может быть отнесен к области слабых флуктуации. Другой ча-
часто встречающийся на практике случай слабых флуктуации
имеет место, когда прием излучения осуществляется в узком
конусе. В этом случае количество рассеянной энергии, попадаю-
попадающей в приемник, мало по сравнению с энергией когерентного
поля и, следовательно, принимаемое поле в основном когерент-
когерентно. Примером такой ситуации является прохождение СВЧ-излу-
чения через дождь, когда при большом оптическом пути флук-
флуктуации могут быть слабыми из-за узости диаграммы направлен-
направленности приемной антенны.
В этой главе мы рассмотрим как монохроматические, так и
импульсные волны. Анализ будет проведен с использованием
первого приближения теории многократного рассеяния, обсуж-
обсуждавшегося в гл. 4, и приближения Рытова. Более строгий анализ
для случая сильных флуктуации дается в гл. 15.
6.1. Когерентная и некогерентная интенсивности
и пространственная корреляция флуктуации
в плоской волне
В этой главе мы рассматриваем два метода исследования
флуктуационных характеристик волны, распространяющейся в
пределах прямой видимости, а именно первое приближение тео*
Распространение через разреженное облако частиц
137
рии многократного рассеяния и метод Рытова. Первый из них
удобен при решении задач рассеяния. Что касается распростра-
распространения в пределах прямой видимости, то здесь метод Рытова при-
применим в более широкой области флуктуации волны, чем первое
приближение теории многократного рассеяния. В то же время
последний метод оказывается более удобным при анализе им-
импульсных задач, а также в тех случаях, когда необходимо учи-
учитывать направленные свойства приемной и передающей антенн.
точке {x\y\z')
Падение
плоской
волны
г2(х2,0,Ю
Рис. 6.2. Падение плоской волны на полупространство, заполненное случай-
случайными частицами. Точки наблюдения (х\. О, L) и [хг, О, L), где Х\ = — *2 =>
rf/2
По этой причине в данном разделе мы воспользуемся первым
приближением теории многократного рассеяния. Метод Рытова
будет рассмотрен в разд. 6.6.
Рассмотрим плоскую волну, падающую на полубесконечную
среду, содержащую большое число случайно распределенных
частиц (рис. 6.2). Поле и(п) в точке ri=(xi, О, L) состоит из
среднего (когерентного) поля <и> и флуктуационного поля щ\
и (п) = (« (г,)} + uf (r,).
F.5)
Среднее поле <м> и когерентная интенсивность /с определяются
выражениями
= I <и (г,)) I2 = ехр (
= \ pot dz.
F>6)
138 Главе 6
Флуктуационное поле Uf представляет собой сумму полей, рас-
рассеянных всеми частицами, находящимися в слое 0 ^ z ^ L.
Вкладом обратного рассеяния из области z> L мы пренебре-
пренебрегаем.
-Запишем сначала поле, рассеянное одной частицей из эле-
элемента объема dV, расположенной в точке (х', у', z'):
uf (г,) = Щ& exp (ikz' + ikRi -1 -1) .
* F-7)
Yo= ] patdz и Yi=j P^tdR,
о о
где f@, z) — амплитуда рассеяния частицы, у0 и vi — оптиче-
оптические пути, a Ri — расстояние от точки (л/, у', z') до точки
(хь О, L). Суммируя вклады от всех частиц, получаем
(г,) = \ Щ%- exp (ikz' + ikR, -%.-2f)pdV. F.8)
v
Щ
Аналогичным образом можно записать флуктуационное поле
«f(r2) в точке Г2=(х2, О, L); для этого нужно лишь заменить
в F.8) Ri, yi и 6i на R2, 72 и 02:
ut (г8) = \ Щ^- exp (ikz' + ikR2 -f-^)pdV. F.9)
v
Корреляционная функция полей Uf{r{) и Uf(r2) находится пу-
путем усреднения по ансамблю произведения этих двух интегралов.
Заметим однако, что поля, рассеянные различными частицами,
некоррелированны между собой, вследствие чего двукратные ин-
интегралы сводятся к однократному интегралу:
)\ F.10)
Таким образом, имеем
F.11)
где fi = fF1, z) и f2 = fF2, z). Заметим, что точки п и г2 вы-
выбраны в плоскости xz при z = L, а, поскольку падающая волна
является плоской, корреляционная функция Bu(ri, т2) должна
быть функцией Jd| = fri — r2| = \х\ — дг2|.
Распространение через разреженное облако частиц
139
Укажем, что значение |d| может быть ограничено величиной
порядка радиуса корреляции, так как вне радиуса корреля-
корреляции Ви практически обращается в нуль. Кроме того, почти во
всем объеме V расстояния Ri и R2 намного превышают радиус
Рис. 6.3. Углы рассеяния 6 и Ф.
корреляции. Поэтому можно воспользоваться следующими при-
приближениями (рис. 6.3):
k{Rx — R2) ~kd sine cos Ф, d = x{—x2, F.12)
0 = x sin 9 cosф + У sin Э sin <f> + zcosЭ,
где единичный вектор 0 записан в сферической системе коорди-
координат (8, ф). Заметим также, что dV = R2dR sin 8rf8t?^>. Интегри-
Интегрирование по ф можно провести, воспользовавшись формулой
\ exp (ikd sin Э cos ф) dф = 2я/0 (kd sin Э). F.13)
В результате имеем
я/2 L/cos 6
Bu(d) = 2я$ J
F.14)
где y'=\p(jtdR и f@)=fF, ])". Если среда однородна
о
(?' = P<*tR и уо = potL — potR cos 8), легко провести интегри-
140 Глава 6
рование по R. В этом случае имеем
я/2
Ви (d) = 2я \ sin Э dQ |f(9)|2 /0 (kd sin 6) g (у, Q),
о *< F.15)
где ji == cos 8 и у = pa^L.
Рассмотрим несколько частных случаев. Предположим, что
рассеяние изотропно. Тогда
F.16)
В этом случае получаем
Я/2
ви (d) = -g- J sin е с?е/0 (йй sin e) g (y, e). F.17)
При изменении 8 от 0 до л/2 множитель ^(у, Э) меняется от
уехр(—у) Д° ехР(—У)- Поскольку основной вклад в интеграл
дает область вблизи 6 = 0, этот множитель приближенно можно
положить равным 7ехР(—У)- Воспользовавшись формулой
п/2
jj sin6d6/0(zsin6) = ^-, F.18)
о
в этом приближении находим
^g|^-Y). F.19)
Рассмотрим теперь случай, когда размеры частиц намного
больше длины волны и, следовательно, рассеянное излучение
сосредоточено внутри малого угла Э. В этом случае квадрат
модуля амплитуды рассеяния можно записать в виде
I / (б) Р = (Vя) Ъ ехр (- ар62), F.20)
где ар = 2,77/GL, а 6Р6 — ширина (в радианах) индикатрисы
рассеяния частицы по уровню половинной мощности [формула
C.9)]. Заметим, что амплитуда рассеяния большой сферы ра-
радиуса а определяется выражением ') [162]
-?o-Ji(kasmQ). F.21)
Следовательно, ширина индикатрисы рассеяния равна
ерЬ==1,02Л/О, D = 2a. F.22)
!) Отметим, что / = iS*/k.
Распространение через разреженное облако частиц 141
Подставляя F.20) в F.14) и учитывая, что |6| < 1, получаем
Ви (d) = pffsiLe-Y J Э dQ2ap exp (- ap62) /0 (k dQ), F.23)
J p exp (- ap6
о
где интегрирование по 8 распространено на область от 0 до оо,
поскольку область G ^ 1 дает малый вклад в интеграл. Этот ин-
интеграл может быть вычислен с использованием-формулы
со
\ ехр (- рЭ2) /о (гВ) Э dQ = -L. ехр (_ -|L) . F.24)
о
В результате находим
Su (rf) = poreL ехр [- y - (kdf/4ap]. F.25)
Некогерентная интенсивность /,¦ определяется выражением
/(=Bu@) = posLexp(-Y). F.26)
Заметим, что если /,• в формуле F.4) разложить в ряд по
степеням posz, то первый его член совпадет с выражением F.26).
Из формул F.19) и F.25) видно, что если размеры частиц
малы по сравнению с длиной волны, то радиус корреляции по-
порядка длины волны; в противоположном предельном случае он
порядка размера частиц D (укажем, что (ap)ll2/k ~ D). При-
Приведенные значения радиуса корреляции применимы в случае
приемника, имеющего изотропную диаграмму направленности
(точечный приемник). Ниже мы покажем, что диаграммы на-
направленности приемника и излучателя оказывают значительное
влияние на радиус корреляции принимаемой волны.
6.2. Временная корреляция
и частотный спектр плоской волны
Временная корреляционная функция Ви{т) флуктуационного
поля щ в точке г = @, 0, L) для двух различных моментов вре-
времени U и ^ получается из формулы F.11), если положить
Ci = Г2 и использовать для fj*2 в случае движущихся частиц
выражение
fJl = \f?%(k.t)exp(ik, • Ik), F.27)
где |f|2 = ad@, i)—дифференциальное сечение рассеяния,
X(kst)—характеристическая функция флуктуации скорости V/,
142 Глава 6
определяемая формулой D.49), ks = k(i — 0), U — средняя ско-
скорость частицы, at = li — t2. В результате находим
г f/,
Ви (т) = (uf (r, /j) и) (г, /2) = \ -^f- ехр (— y0 — y') P dV, F.28)
v
где yo и y' определены в F.7) и F.14) соответственно.
Рассмотрим сначала случай, когда флуктуации скорости V/
пренебрежимо малы по сравнению со средней скоростью U, так
что %(ksx)= 1. Используя сферическую систему координат F.12),
получаем
я/2 ]
SI f ffli I2
sin 0 dQ 'n >] /0 (kUtx sin 0) X
X exp [ikbzr A - cos 9)] g (Y, 9), F.29)
где средняя скорость U записана в виде суммы поперечной ско-
скорости Ut{Ut— |Uf|) и продольной скорости Uzz, a ^(y, 6) оп-
определяется формулой F.15).
Рассмотрим случай частиц с размерами, намного превышаю-
превышающими длину волны. Тогда, пользуясь формулой F.20) и прибли-
приближенными равенствами
ехр [ikUzj A - cos 0)] » ехр [ikUz% (92/2)], g (Y, 0) « у ехр (- у),
F.30)
получаем
где А = 1 — i(kUzx/2ap).
Заметим, что если скорость U перпендикулярна оси z
(Uz = 0), то формула F.31) совпадает с формулой F.25), если
в последней d заменить на Utx. Такого соответствия между дли-
длиной корреляции и временем корреляции в случае поперечной
скорости следовало ожидать, поскольку поле в точке г в мо-
момент t совпадает с полем в точке г + 1Ьт в момент t -f- x ввиду
того, что частицы за время т смещаются на расстояние U<t.
Рассмотрим теперь временной частотный спектр \Vu(a>) при
U 0
Г° Г па Т'/а Г а и
Wu (со) = 2 \ Ви (т) e'«« dx = DposL) [-щ^\ ехр [- Y - -щ
F.32)
Мы видим, что при со = со/ = kUt/{a.pI12 частотный спектр спа>
дает в е раз по отношению к своему значению в точке со = 0.
Распространение через разреженное облако частиц 143
Используя F.20) и F.22), получаем
со, == 5,29Ut/D. F.33)
Отсюда следует, что уширение спектра приближенно равно
Ut/D, и время когерентности совпадает со временем, за кото-
которое частица проходит расстояние порядка своего размера. На-
Например, капли дождя при интенсивности выпадения 12,7 мм/ч
имеют диаметр 2 мм (рис. 3.3) и установившуюся скорость 6 м/с
(рис. 3.4). Поэтому уширение спектра составляет примерно
3 кГц.
В некоторых случаях, например при распространении волны
в дожде, капли имеют распределение по размерам n(D) и их
конечная скорость зависит от размера. Это можно учесть, поло-
положив в формуле F.32) os = os(D), ар = ap(D) = 2,77/A,02X/DJ
и [/(= Ut{D). Тогда получим
Wu (со) = \ п (D) dD4as (D) L [-щ^\ ехр [- Y - ^щщг\.
F.34)
где v = р(at)L=\ n(D)ot(?>)LdD.
о
6.3. Распространение плоской импульсной волны
в пределах прямой видимости
Рассмотрим характеристики плоской импульсной волны, па-
падающей на полупространство, заполненное частицами. Предпо-
Предположим, что излучаемый импульс имеет узкую полосу, сосредо-
сосредоточенную вблизи несущей частоты «о. В этом случае среднее
поле в точке наблюдения г = @, 0, L) дается формулой
{и (г, /)) = «,(/- L/co) ехр (- у/2), F.35)
где Ut(t) —поле падающей волны в плоскости z = 0, у — опти-
оптический путь, а Со — скорость распространения волны.
Следовательно, корреляционная функция Bc(tu ^2) когерент-
когерентного поля в точке г и интенсивность когерентной составляющей
144
Глава 6
lc(t) равны
Вс (h, t2) = (и (г, /,)) (и (г, 4)) = ut (/, - -?) щ (t2 - ?) ехр (- у),
F.36)
Ic (t) = | <ц (г, 0> Р =
и*
- -^) f ехр (- у).
F.37)
Корреляционная функция некогерентной составляющей поля
х,У
Рис. 6.4. Импульсные вол-
волны, рассеянные частицами,
лежащими на параболоиде
вращения F.41), которые
приходят в точку наблюде-
ния (О, О, L) в один и тот же
момент времени.
щ'(г, t) находится с использованием процедуры, изложенной в
разделе 5.5 (рис. 6.4):
Некогерентная интенсивность If(t) дается формулой
F.38)
. F.39)
Из формулы F.39) видно, что импульсные волны, рассеянные
на поверхности, где
г' + R = U = const, F.40)
приходят в точку наблюдения г в один и тот же момент вре-
времени. Учитывая, что R =[х2 + у2 -{-(L — гJ]1'2, можно пока-
показать, что эта поверхность является параболоидом вращения с
фокусом, расположенным в точке наблюдения (рис. 6.4):
jc2 + f/2 = 4/o[fo+?-z], F.41)
где fo = -j (^<o — L) — фокусное расстояние. Этот параболоид
быстро расширяется со временем. Например, при 2 = 0 скорость
Распространение через разреженное облако частиц 145
расширения Ve = dx/dt дается формулой *)
V дХ (*-2 + *2)'/а . /R,04
Рассмотрим случай, когда начальный импульс имеет виц
дельта-функции:
F.43)
Подставляя это выражение в F.39) и используя формулу для
элемента объема dV == R2dR sin Ы Qd ф, получаем
я/2 L/cos 9
IfЦ) = 2п\ sinQdQ J dRp\f(Q)fX
6i О
^^^) F.44)
где уо = pvtz', у' = potR и z' = L — R cos 0. Предел интегриро-
интегрирования 0i определяется из того условия, что в момент времени
t = Lo/co cos 8i должен быть равен L/Lo (рис. 6.4). Проводя
интегрирование по R, находим
п/2
If (t) = 2я J sin 9 dQp | f F) p Eoco [eXi_Co?e ] • F-45)
e,
Если |/(e) |2 = const (=os/4n), то
при t>±,
L F-46)
Заметим, что в рассматриваемом приближении некогерентная
интенсивность /f(/) имеет логарифмическую особенность при
t = L/Cq. Однако полная энергия, получаемая интегрированием
выражения F.46) по времени, конечна.
6.4. Распространение между излучателем
и приемником в пределах прямой видимости
Выше мы рассматривали распространение монохроматиче-
монохроматической и импульсной плоских волн, падающих на полупростран-
полупространство. Теперь мы исследуем распространение волн с учетом на-
направленных свойств излучателя и приемника.
') Эта формула получается путем дифференцирования F.41) по времени
С учетом того, что dLq/dt == с».
146
Глава 6
Рассмотрим излучатель с диаграммой направленности по
мощности Gt(i), расположенный в начале координат @, 0, 0),
и приемник с диаграммой направленности по мощности Gr{0),
расположенный в точке г = @, 0, L) (рис. 6.5).
h
распро-
распространения в пределах пря-
прямой видимости; показаны
диаграммы направленности
излучателя и приемника и
частица, расположенная
в точке г'.
Напряжение V(t) на выходе приемника состоит из среднего
значения <V(^)> и флуктуационной составляющей V;(t):
V (t) — (V (/)) + Vf (I). F.47)
Тогда смешанный момент Bv(ti,t2) определяется выражением
BB(ti, t2) = (V(tl)V*(t2)) = (V(ti))(V*(t2)) +Bf(tu t2),
В (t i) = (V O)V'(t)) F-48)
Поле у приемника состоит из поля, пришедшего прямо от из-
излучателя, и поля, рассеянного частицами. Поскольку рассеянное
поле имеет случайные амплитуду и фазу, среднее значение его
равно нулю, тогда как среднее значение поля прямой волны
постоянно. Отсюда ясно, что прямая волна дает вклад в среднее
выходное напряжение <F>, а рассеянное поле — в его флуктуа-
ционную составляющую Vf (t).
Следовательно, величина <F><F*> в F.48), представляющая
собой когерентную мощность, равна мощности прямой волны
Рс, вычисленной уже в D.12):
Я2 Gt (z) Gr (z)
Pt
F.49)
где Pt — излучаемая мощность и у — оптический путь, опреде-
определяемый по формуле (разд. 4.2)
F.50)
Корреляционная функция Bj(ti,t2) флуктуационного поля
найдена в разд. 4.6:
Bf{tu t2) = Pt \
, F.51)
Распространение через разреженное облако частиц 147
где т = t\ — t2 и напряжение нормировано таким образом, что
величина Bf(t, t)= <| Vf {t) |2> = Ps представляет собой рас-
рассеянную мощность.
Во многих приложениях ширина излучаемого и приемного
лучей мала (доля радиана) и интеграл в F.51) можно прибли-
приближенно вычислить следующим образом. Воспользуемся гауссо-
гауссовым представлением для диаграммы направленности, рассмо-
рассмотренным в разд. 4.3:
G,(i) = G,(z)exp(-a,e?), Gr@) = Gr(z)exp(-a,62), F.52)
где af = D1n2)/e2b = 2,77/e2b, a, = D In 2Щ„ = 2,77/е2й, а Btb и
Qrb — ширина (в радианах) передающего и приемного лучей на
уровне половинной мощности соответственно. Поскольку основ-
основной вклад в некогерентное поле дает рассеяние на частицах
вблизи направления вперед, для характеристик рассеяния ча-
частиц можно использовать также малоугловое приближение. Се-
Сечение рассеяния оы@, i, т) движущихся частиц определено фор-
формулой D.48). Предположим, что флуктуации скорости распре-
распределены по нормальному закону, описываемому формулами D.57)
и D.58). Тогда вы@, i, т) имеет вид
ан (О, X т) = ab. (z, z) ехр[- (ар + й2а^/2) 62р + ikUx],
abi (z, z) = 4apas,
где os — сечение рассеяния [формула C.9)],ap = 2,77/926, 0pb —
ширина (в радианах) индикатрисы рассеяния частицы на уровне
половинной мощности, а2. — дисперсия флуктуации скорости
частиц, а U=l)-(\ — 0). Здесь мы положили ks=k2 sin@p/2) «
« kQp, так как 8Р мало.
Если U выразить в компонентах (Ux, Uy, Uz), то U запи-
запишется в виде
U = (sin Qt + sin 9r) (Ux cos Ф + Uу sin f) + Uz (cos Qt — cos 0r),
F.54)
где (R\, Qt, Ф) — сферические координаты частицы, находящейся
в точке г' (рис. 6.5). При U = Uxx приближенно имеем
, F.55)
где мы положили sin 0; й Bf и sin 9Г « Эг. Заметим также, что
при |вл| < 1, |8/| < 1 имеем
F6)
148 Главе 6
Подставляя F.52), F.53), F.55) и F.56) в формулу F.51),
получаем
Вf{x) WGt(z)Gr(z) f Л/2 2П
~р~г— шг з
о
L — z'
' °Г F.57)
zf L
> <> ) \ л i 1
О z'~
i .9
Y ===
и
Рассмотрим частный случай, когда плотность частиц и их
распределение по размерам постоянны вдоль пути распростра-
распространения волны. Тогда имеем
р = (L/z'f [a + b (z'/L) + с (z'/Lf], F.58)
где а = ар -\- at, р = pOtL/2 — 2at и с = at + а, — pOtL/2.
Вычислим сначала рассеянную мощность Ps = Bf@). Для
этого положим в F.57) т = 0. Кроме того, так как подынте-
подынтегральное выражение содержит множитель ехр(—Р®г)> верхний
предел интегрирования по 8гя/2 можно заменить на оо, не
внося существенной погрешности. Тогда получим ')
Р, РС y-pr-s-, ,.„._, " , ._.,_, - ,, F59а)
где А = Аас — Ь2 и А > 0. Если А < 0, то
pt pt V—А
Было показано [74], что если at = ar ~ 0 и у = potL <g. I,
то формула F.596) принимает вид
^- = A (pa,L), P = Pc + Ps~Pt [Щ&фЩ еХр (- paeL).
F.60)
') Заметим, что \ (а + Ьх + ел:2) йл: == arctg ( b+^_cx\ д > 0.
См. также [60].
Распространение через разреженное облако частиц 149
Эти формулы согласуются с выражениями F.2) и F.3). В более
общих случаях вычисления нужно проводить по формулам
F.59). При этом необходимо помнить, что формулы F.59) по-
получены в первом приближении теории многократного рассеяния,
вследствие чего они применимы лишь в тех случаях, когда вели-
величина Ps мала по сравнению с Рс.
Рассмотрим теперь временную корреляционную функцию
Bf(x), определяемую формулой F.57), для случая, когда харак-
характеристики частиц постоянны вдоль пути распространения волны.
Для простоты будем считать, что флуктуации скорости частиц
пренебрежимо малы (of = 0), так что в F.57) можно положить
q\ = 0. Предположим также, что средняя скорость U равна
Uxx, как в формуле F.55). Тогда, пользуясь соотношениями
2я
exp (ix cos ф) йф = 2л/0 (х),
F.61)
из формулы F.57) получаем
Bf(x)
f(x) _ Рс г , apposL
ехр ч
где р определяется выражением F.58), а А2 = {kUxJ(L/z'J.
Временной частотный спектр Wf(o) определяется выраже-
выражением
= Рс )
0
Интеграл в F.63) можно вычислить при co-vO. При с > 0 и
А > 0 имеем [60]
4P.aDpa,L Гп V /2с + Ь\ / Ь \~\
w<@)=-щ- Л/т [Ar sh (гж-) ~ Ar sh (ж)] • F-64)
где А = 4ас—Ь2. Аналогичное выражение может быть получено
для А < 0 и с < 0.
150 Глава 6
При больших о можно воспользоваться методом перевала,
который дает следующее значение интеграла [21]:
А (г) ехр [- f (г)] dz « A (zs) exp [- f (z.)] [j^f. F.65)
где zs — седловая точка, определяемая из условия
= 0.
' ^«' дг
Тогда при Д/4с > 0 получаем
4Рм„оа„Ь 2я
Из формулы F.66) видно, что время когерентности Тс прибли-
приближенно равно
Если ширина передающего и приемного лучей Э« и 0,6 и опти-
оптический путь pa<Z- малы, то имеем
щ ~ ar » ap, а^ ^ а,. > pof/L. F.68)
В результате получаем приближенное выражение
„ / 2,77 \'/i 1 ,„ ап.
Те ~ ( д2 1Й2 ) 7Т77Т- F'69)
е
Поскольку 9<б ~ 1,5Л/О< и 0Гй ~ \,5K/Dr, где Z); и Dr — раз-
размеры передающей и приемной антенн, имеем
Отсюда следует, что в случае остронаправленной антенны
время когерентности примерно равно времени перемещения ча-
частицы на расстояние порядка размера апертуры. Этот результат
существенно отличается от полученного выше результата F.33),
согласно которому время когерентности в случае точечного
приемника по порядку величины совпадает с временем прохож-
прохождения частицей расстояния, равного ее размеру. Точечный
приемник регистрирует рассеянные волны, приходящие из всего
рассеивающего объема, так что время когерентности зависит
только от характеристик частиц, тогда как остронаправленная
антенна принимает рассеянные волны из узкой конической об-
области, и потому время когерентности зависит главным образом
от характеристик антенн и значительно превышает время коге-
когерентности в случае точечного приемника.
Распространение через разреженное облако частиц 151
6.5. Распространение импульса между излучателем
и приемником
В предыдущем разделе были рассмотрены флуктуационные
характеристики непрерывной (монохроматической) волны, рас-
распространяющейся через случайное облако рассеивателей. Здесь
мы исследуем распространение импульса в такой среде в первом
приближении теории многократного рассеяния. Будем предпо-
предполагать, что излучаемая волна имеет узкий спектр, сосредоточен-
сосредоточенный вблизи несущей частоты ш0, так что справедливо прибли-
приближение E.29).
Рассмотрим прямую волну (среднюю волну), задаваемую
(V(t)y в формуле F.47). В предположении узкой полосы имеем
(V С)) (V* &)> = (W) «, ft ~ L/c0) и] (t2 - L/c0), F.71)
где Рс определяется выражением F.49), а «,-(/)—комплексная
огибающая излучаемого импульса E.9). Ясно, что форма им-
импульса прямой волны не отличается от формы падающего им-
импульса и,-.
Рассмотрим теперь корреляционную функцию флуктуации
выходного импульса. Общее выражение для нее, обсуждавшееся
в разд. 5.5, имеет вид E.31)
) = Pt \ ^ffS'JJV» F, I -с) ехр (- у, - V*) Bt dV,
V DЛ) ^#2
c0
где Со — скорость распространения волны. [В этом разделе ско-
скорость волны мы обозначаем с0, чтобы отличить ее от величины с
в формуле F.58).]
Как уже говорилось в разд. 5.5, импульсы, рассеянные сфе-
сфероидальной поверхностью с фокусами в точках расположения
излучателя и приемника, для которых Ri + R2 = const, прихо-
приходят в приемник в один момент времени.
Если излучатель и приемник имеют узкую полосу, можно
воспользоваться упрощениями, сделанными в формуле F.57).
Тогда получим
(z) Gr (z) f rf Г g & $
Pi—^(taj1
0 0 0
F.73)
где г|з определяется формулой F.57), а величина Ri -4- ^2, вхо-
входящая в Bi, определяется выражением
^$. F.74)
152 Главе 6
Интенсивность I(t) состоит из интенсивности прямой волны
/с@ и некогерентной интенсивности Is(t):
I(t) = IAt) + If(t), Ic(t) = (Pc/Pt)Ii(t-L/c0), F.75)
где Ji(t — L/co) = \ui(t — L/co)\2. Из формул F.73) и F.74)
находим некогерентную интенсивность If(t):
// W = т; Bappcr,L2) \ dz' \ 8, ddr 6XP(-~/ r) It (t, z'), F.76)
о о
где р определяется формулой F.58), а
В качестве примера рассмотрим входной импульс вида
F.77)
где Eq — полная энергия импульса. Подставляя F.77) в F.76)
и интегрируя по б,, получаем
F.78)
при t>±.
при t<±-.
где р дается формулой F.58), а Q =[(L — г')/2с0] {L/z').
Из формулы F.78) видно, что входной импульс содержит ко-
когерентную интенсивность lc{t), которая тоже имеет вид 6-им-
пульса, и некогерентную интенсивность //@, затухающую во
времени по экспоненциальному закону. Это затухание обуслов-
обусловлено рассеянием на различных частицах всего рассеивающего
объема.
Приближенное вычисление интеграла в F.78) при больших
t — L/co можно осуществить методом перевала.
В качестве примера рассмотрим случай широких диаграмм
направленности излучателя и приемника, когда at — <хг да 0. При
этом имеем
^ {Llz'f [ap + (pcr(jL/2) (z'/L) (I - z'/L)}, F,79)
Распространение через разреженное облако частиц 153
Вычисление интеграла методом перевала дает
~-BapposE0cо) Vяехр [— j- (( — —) (8ар — potL)\
при /»-?. F.80)
0 при /<-?.
Это выражение справедливо только при условии 8ар — potL > 0.
Из выражения F.80) видно, что если оптический путь pad.
мал, то скорость экспоненциального затухания интенсивности
lf(t) зависит от характеристик рассеяния частицы. Так, напри-
например, в случае больших по сравнению с длиной волны размеров
частиц (D) величина ар приближенно равна [(nD)/2X]2, по-
поэтому постоянная времени затухания Та дается приближенной
формулой
Td=(L/c0)(X2/2n2D2). F.81)
Полная энергия некогерентной составляющей получается инте-
интегрированием выражения F.78) по времени; по порядку вели-
величины она равна (Pc/Pt)EoposL.
6.6. Приближение Рытова
для флуктуации амплитуды и фазы
Выше для описания флуктуационных характеристик моно-
монохроматической и импульсной волн мы использовали первое при-
приближение теории многократного рассеяния. В этом приближении
поле у приемника и (г, t) представляет собой сумму когерентного
<м(г, 0) и некогерентного Uf(r, t) полей:
и (г, 0 = <и(г, 0> + и,(г. t). F.82)
Это соответствует теории слабых флуктуации, применимой лишь
в случае, когда некогерентная интенсивность <|uf|2> мала по
сравнению с когерентной интенсивностью |<«>|2.
В этом разделе мы даем другое возможное представление
поля через флуктуации комплексной фазы т|з. Запишем поле в
виде
и (г, 0 = ио(г, /)е*'г-«, F.83)
где «о (г, t) —некоторое исходное поле с определенными ампли-
амплитудой и фазой.
В качестве и0 можно выбрать поле волны в свободном про-
пространстве, т. е. в отсутствие случайной среды, или какое-либо
154 Глава 6
другое поле, например среднее поле <и(г, /)>. В этом разделе
мы используем
¦ ио(г, 0 = <«(г- Ф. F.84)
Функция г|)(г, t), вообще говоря, комплексна:
¦Ф (г, /) = х(г, /) + /S,(r, /). F.85)
Если и и но записать через амплитуды Л и Ло и фазы S и So, то
мы получим
и (г, /) = Л (г, t) exp [IS (г, 0], «о (г, 0 = Ло (г, f) exp [/So (r, /)].
F.86)
При этом функции х и Si в F.85) принимают вид
t(r,t) = \n(A/A0), S,(r, /) = S(r, 0~So(r, 0- F.87)
Из формулы F.87) видно, что вещественная часть х(г> О ком-
комплексной фазы г|) представляет флуктуации логарифма ампли-
амплитуды А, или уровня, а мнимая часть Si — флуктуации фазы.
Оказывается, что выражение F.83) удобно при исследовании
распространения в пределах прямой видимости, тогда как вы-
выражение F.82) более пригодно при анализе рассеяния. Это
можно пояснить путем следующих рассуждений. В задаче рас-
распространения в пределах прямой видимости волна при прохож-
прохождении через один тонкий слой испытывает флуктуации ампли-
амплитуды и фазы. Тогда поле можно записать в виде «0«i, где и0 —
поле падающей волны, а и\ описывает флуктуации. Поле «o"i
представляет собой поле "волны, падающей на второй слой, на
выходе которого поле волны имеет вид «0М1Н2. Таким обра-
образом, полное поле на выходе равно произведению u0ulU2U3 ...
(рис. 6,6, а). Если каждый флуктуационный сомножитель ип
представить в виде экспоненты exp tyn, то полное поле будет
равно и = «оехр(я)з1 + ^2 + ^з + ¦ • •)¦ Это означает, что пока-
показатель экспоненты ф в F.83) есть результат сложения всех
флуктуации tyn вдоль трассы распространения. Поскольку поле
на выходе является произведением многих сомножителей, его
удобно записать в экспоненциальной форме F.83).
При анализе рассеяния удобнее рассматривать рассеянное
поле как сумму вкладов различных участков рассеивающей
среды (рис. 6.6,6). Поэтому в задаче рассеяния обычно исполь-
используется запись F.82).
В данном разделе мы рассмотрим флуктуации уровня % и
фазы Si в случае распространения в пределах прямой видимо-
видимости, используя метод Рытова. Этот метод основан на переходе
от волнового уравнения для поля и к нелинейному уравнению
Риккати для ijp, которое решается методом интегрального урав-
уравнения. Подробное изложение метода Рытова дано в гл. 17. Здесь
мы приведем без вывода выражение для первой итерации, имею-
Распространение через разреженное облако частиц
155
щее вид
и (г, /) = <«(г, /)>ехр[и,(г, t)/(u(r,
F.88)
где Uf(r, t) —решение, отвечающее первому приближению тео-
теории многократного рассеяния. Заметим, что если величина
= U0U, U2 U,
u= ut+u2 + u3 +
Рис. 6.6. Перемножение вкладов от всех слоев в задачах распространения
в пределах прямой видимости (а) и сложение вкладов от различных участков
среды в задачах рассеяния (б).
Uf/(u} мала по сравнению с единицей, то экспоненту можно раз-
разложить в ряд:
и = <и>[1+ «,/<">+ •••]• F.89)
Если в этом ряде мы удержим первые два члена, то придем к ре~
шению, соответствующему первому приближению теории много-
многократного рассеяния F.82).
6.7. Приближение Рытова для плоской волны
Рассмотрим комплексную фазу в выражении F.88):
* = % + iSi = uf (r, /)/<« (г, /)>. F.90)
Для случая плоской волны мы используем выражение F.8) для
щ:
~cos
dV-
156 Главе 6
Амплитуда рассеяния /F, z), вообще говоря, комплексна и имеет
вид f@, г)— |f|exp(ip). Как было отмечено в F.21), с увели-
увеличением размера частиц 6 стремится к я/2. Воспользовавшись
также приближениями, сделанными в F.12), запишем F.91)
в виде
Ф (г,) = J lf(%z)l ехр (/6, - б2 + Из) р dV, F.92)
v
cosB) 6 kdX
где 6, = ^(l-cos9) + p, ba = potR(l cosB), 63 =
X sin 6 cos фу dV = R2dR sin Q dQ йф, ri={d/2, 0, L). Тогда
флуктуации уровня и фазы можно представить в виде
Комплексно-сопряженная функция я|з* равна
/(°^z)l exP(-i6i ~62-i63)рdV. F.94)
Введя переменную ф' = я + Ф, ее можно переписать в форме,
содержащей множитель ехр(-Н'бз):
¦' (г.) = J 11^11 ехр (- /б, - 62 + /б3) р rfF. F.95)
v
Из формул F.92) и F.95) находим
%(г,) = J IM%Z)I cos б, ехр (- 62 + /б3) рdV,
Vntra~u F>96)
5i (г,) = ) lt(yU sin б, ехр (- б2 + /бе) Р dV.
v
Аналогично в точке г2 =(-—б(/2, 0, L) имеем
% (rj) = J 1(У cos б! ехр (- б2 - гб3) р d V,
v
Si (Га) = J lf(|z)l sin б, ехр (- б2 - /б3) р dV.
v
Следовательно, корреляционная функция флуктуации уровня
в точках ri и г2 есть
F.98)
Распространение через разреженное облако частиц 157
После интегрирования по ф находим
л/2
Вг (d) = 2яр J sin QdQ \f @) р gx (L, 0) Уо (M sin 9), F.99)
о
L/cos 9
где gx (L, 0) = \ cos26jexp(—2b2) dR. Таким образом, мы
о
пришли к общему выражению для корреляционной функции
Bx(d). Функцию gx{L, 6) можно вычислить точно. Поскольку
основной вклад во флуктуации дает область малых 0, разложим
функцию gx (L, 0) в ряд по 0. В результате получим прибли-
приближенное выражение
Sx.(L, 0)=4[! + e4,(-Ve»/2),M*L9» + 2P)-rin
Выясним смысл функции gx(L, 0). Как видно из формулы
F.99), корреляционная функция получается перемножением под
знаком интеграла индикатрисы рассеяния частицы |f(9)|2 и
функции gx(L, 0). Это означает, что функция gx{L, 0) выре-
вырезает некоторую часть углового распределения (углового спектра)
рассеянной мощности. Поэтому ее можно назвать фильтрующей
функцией по углам.
Из выражения F.100) следует, что функция gx (L, 0) при
6 = 0 равна (L/2) A-f cos2p), а при 0>(X/LI/2 она практи-
практически совпадает с L/2. Ширина индикатрисы рассеяния |f@)|2
примерно равна X/D, где D — размер частицы. Поэтому если D
намного меньше, чем радиус зоны Френеля (ILI/2, то ширина
индикатрисы рассеяния частицы k/D велика по сравнению с
(X/LI12, и следовательно, gx(L, 0) в области углов от 8 = 0 до
0= (X/LI12 мало влияет на флуктуации. В этом случае можно
приближенно принять gx(L, 0) » L/2. В противоположном пре-
предельном случае, когда D велико по сравнению с радиусом зоны
Френеля {XLI12, функцию gx можно аппроксимировать выраже-
выражением (L/2)(t +cos2p).
Рассмотрим часто встречающийся в приложениях случай,
когда D <C {%L) '/2. Тогда приближенно имеем
л/2
Вх (d) = яр! J sin Э db | / (9) |2 /о (Ы sin 6). F.101)
о
При малых по сравнению с длиной волны размерах частиц
|f(8)|2 приближенно можно заменить на а$/4я и провести ин-
интегрирование [101]. В результате получим
В% (d) = (posL/2) [(sip kd)/kd]. F.102)
158 Глава 6
Отсюда видно, что радиус корреляции d « X. Если размер ча-
частиц велик по сравнению с длиной волны, используем выраже-
выражение
| / F) р = (aoajn) exp (- ар62). F.103)
Тогда пределы интегрирования можно распространить на об-
область от 0 до оо, что дает
Вх (d) = (pasL/2) exp (- (ЫJ/4ар). F.104)
Отсюда следует, что радиус корреляции порядка размера ча-
частиц D.
Дисперсия <х2> флуктуации уровня определяется выраже-
выражением
л/2
(X2) = 2яр J sin 6 dQ | / F) |2 g% (L, 6). F.105)
о
Как следует из формул F.102) и F.104), при D <^(XL)l>2 при-
приближенно находим
<X2> = per,Z,/2. F.106)
Полезно выяснить смысл формулы F.106). Для этого рассмо-
рассмотрим интенсивность / = <|ы|2>. Из выражений F.88) и F.90)
получаем
/ = | (и) f <ехр 2х> = ехр (- potL) <exp 2%). F.107)
Среднее значение <ехр 2х> связано с дисперсией <%2>. Если пред-
предположить, что уровень х имеет нормальное распределение, то
получим
(ехр 2Х> = ехр [2 <х> + 2 <(х - (х)J)]. F.108)
Поскольку (Uf) = (%) + KS\} = 0, имеем
/ = ехр (— potL) ехр B (х2)) = ехр (— patL + posL) = exp (— paaL).
F.109)
Заметим, что выражение F.26), отвечающее первому приближе-
приближению теории многократного рассеяния, соответствует первому
члену разложения F.4). С другой стороны, приближение Ры-
това F.109) приводит к формулам F.3) и F.4) и потому его
можно считать более точным, чем первое приближение теории
многократного рассеяния.
Заметим, что здесь мы пользовались приближенной форму-
формулой F.106). Чтобы найти более точное решение, следует исхо-
исходить из формулы F.105). Укажем также, что формула F.109)
основана на предположении о нормальном распределении флук-
флуктуации логарифма амплитуды. Имеется довольно много экспе*
Распространение через разреженное облако частиц 159
риментальных и теоретических подтверждений этого предполо-
предположения, поэтому его можно считать вполне оправданным.
Рассмотрим теперь фазовые флуктуации. Корреляционная
функция Bs определяется выражением
л/2
Bs (d) = 2яр J sin 6 dQ | / F) |2 gs (L, 6) /0 (kd sin 6), F.110)
о
L/cos 9
где gs(L, 8)= \ sin26!exp(— 262) dR. Фильтрующая функция
о
по углам gs(L, 0) для фазы при 6 = 0 равна (L/2) A—cos2|3),
а при 6 > (X/LI/2 практически совпадает с L/2. Мы не даем
здесь детального анализа фазовых флуктуации. Укажем лишь,
что при D <C (XL)i/2 флуктуации фазы и уровня примерно равны:
Bs{d)~Bt(d), <S?)~<x2). F.111)
/
6.8. Временная корреляция и частотные спектры
флуктуации уровня и фазы плоской волны
Временная корреляционная функция В% (т) флуктуации
уровня в точке г = @, 0, L) в два различных момента времени ti
и t2 получается из формулы F.98), если положить в ней бз = 0
и заменить |/|2 выражением F.27) для fj*2 с учетом движения
частиц:
f f*
Вх(т)= J -A cos2 fl, ехр (- 2б2) р dK. F.112)
v
Если флуктуационная скорость Vf пренебрежимо мала по
сравнению со средней скоростью U, то, следуя процедуре, ис-
использованной при получении формулы F.29), находим
л/2
В% (х) = 2лр \ sin 6 dQ | / F) |2 ?х (L, 6) /0 (kUtr sin 6) X
Хехр[/ШгтA -cos 6)], F.113)
где Ut — поперечная составляющая U и Uz — составляющая
вдоль оси z.
В частном случае Сг = 0 и D < {XLI12 имеем
L sin(kUft)
(
kUtr
140 Глава 6
Частотные спектры для этих двух случаев находятся путем пре-
преобразования Фурье:
Wx (со) = 2 J В (т) еш dr. F.115)
о
При D < К получаем [60]
( 2posL/kUt при о < | kUt |,
W Л©) = < ' ^ ' F.116)
х ' (. 0 при о > | Ш* |. '
При D > Я находим
F.117)
Резкий скачок в F.116) связан, конечно, с приближением,
использованным при нахождении Вх (т); более точный расчет
должен давать плавный переход. Во всяком случае, ширина
спектра приблизительно равна |?Л|Д при D <§; К и \Ut\/D при
В полученных формулах нетрудно учесть распределение ча-
частиц по размерам n(D). Так, при D <C i имеем
где Z?o определяется из условия а = kU(DQ). При D >¦ Я, нахо-
находим
° f яа„(О) V/2 f an(D)a>2
2n(D)as(D)L{1Mfmw\ exp { - 1^щщг
F.119)
В качестве примера рассмотрим флуктуации в оптическом
пучке, распространяющемся в дожде. Как видно из рис. 3.5, вода
практически не поглощает в видимом диапазоне, а размеры ча-
частиц дождя велики по сравнению с длиной волны. Поэтому при-
приближенно можно считать, что полное сечение at и сечение рас-
рассеяния as равны at « as ~ 2na2. Кроме того, в соответствии
с C.6) установившаяся скорость Ut(D) дождевой капли радиуса
a=D/2 приблизительно равна 200,8а1/2 м/с. Воспользуемся
также формулой ар = 2,77/A,02X/DJ. Распределение частиц по
размерам аппроксимируем распределением Маршалла — Пал-
мера C.2) я(а)=гаоехр(—аа), где гао = 8-1О6 м-4, а =»
= 8200р-°-21 м-1, a p — интенсивность дождя в миллиметрах в
час. Подставляя эти значения в F.119), получаем
Г1)
F.120)
Распространение через разреженное облако частиц 161
где ap/(kUtJ = Аа и А = 6,7-Ю-6. При интенсивности дождя р
порядка 1 мм/ч спектр Wx(a>) при со = [@,2а)/А]1/2 спадает в
два раза по сравнению с его значением в точке со = 0. Это со-
соответствует примерно 2,5 кГц.
6.9. Приближение Рытова с учетом направленных
свойств излучателя и приемника
Рассмотрим задачу о распространении в пределах прямой ви-
видимости между излучателем, расположенным в начале коорди-
координат @, 0, 0), и приемником, расположенным в точке @, 9, L)
(рис. 6.5). Среднее напряжение (V} на выходе приемника, ко-
которое пропорционально когерентному полю <м(г, /)>, опреде-
определяется выражением
^^(l ) F.121)
где gt(z) и gr(z) —диаграммы направленности по полю излуча-
излучателя и приемника, а у — оптический путь, определяемый форму-
формулой F.8). Заметим, что \gt\2 и \gr\2— диаграммы направлен-
направленности по мощности Gt и Gr, а |<У>|2 — когерентная мощность,
даваемая формулой F.7):
I /т/\ |2 _ Рс _ Д2 Gt (z) Gr (z) ,
Флуктуации выходного напряжения Vf пропорциональны
флуктуационному полю щ и равны
't~2+ik (Ri + ^J dV' F> 123>
где /@, i, /')—амплитуда рассеяния частицы, расположенной
в точке г', в момент времени t — Яч/с (рис. 6.5). Из формул
F.123) и F.121) находим комплексную фазу
>^2 ' — ехр (ц) dV,
*L + ik(Rl + R2 — L), F.124)
fi,
162 Глава 6
Выражение F.124) можно упростить, если использовать при-
приближения F.52) и F.56). Поскольку gtn(i) и grn@)—норми-
grn@)—нормированные диаграммы направленности, имеем
F.125)
где предполагается, что фазы этих диаграмм постоянны. Кроме
того,
г' L
Ъ + \2 — Y = —2z'2 \ 9<*t dz + у \ Р^( dz,
о ZJ F.126)
0 л. 0 / — L (L ~ z'] fl2
Л-, + Л-2 - L — g? Ur-
Амплитуда рассеяния fF, i) для неподвижных рассеивателей
может быть записана в виде
/ (б, Т) = V^F1 ехР (~ "Г"8
где р — фаза, а амплитуда выбрана таким образом, что
F.128)
Фаза р меняется от нуля для частиц, малых по сравнению с дли-
длиной волны, до яД для частиц, больших по сравнению с длиной
волны [162] '). Рассматривая поведение / вблизи 6Р = 0, при-
приближенно получаем
ар » 2,66 (?>/АJ. F.129)
В случае движущихся частиц из F.53) находим
- (ар + —5^-J 6^ + /й?/тJ ,
F.130)
где т = /{— /г «* Л — /2.
Подставляя формулы F.125) —F.127) и F.130) в F.124),
можно найти флуктуации уровня % и фазы Si. Детального ана-
анализа мы здесь не проводим, поскольку он совершенно анало-
аналогичен случаю плоской волны. Следует отметить, что подобно
тому, как обсуждалось в разд. 6.4, существенное влияние на
флуктуации могут оказывать направленные свойства излучателя
и приемника.
') Заметим, что / = iS*/k, и учтем выражение F.21).
II
Теория переноса излучения
в случайном облаке
рассеивателей
Глава 7
Теория переноса излучения
в случайном облаке частиц
В гл. 4—6 мы обсудили характеристики рассеяния и распро-
распространения монохроматических и импульсных волн в разрежен-
разреженном облаке частиц. В этом случае можно было использовать
либо приближение однократного рассеяния, либо первое при-
приближение теории многократного рассеяния, либо приближение
Рытова. Эти приближения становятся неприменимыми при уве-
увеличении плотности числа частиц, когда когерентная интенсив-
интенсивность становится сравнимой с некогерентной интенсивностью
или меньше нее. В этих условиях доминирующую роль в опре-
определении флуктуационных характеристик волны начинают играть
эффекты многократного рассеяния. Исторически в теории много-
многократного рассеяния были развиты два различных подхода. Один
из них можно назвать строгой, или аналитической теорией, а
другой — теорией переноса.
В строгой теории (см. ссылки на литературу в гл. 14 и 15)
исходят из основных дифференциальных уравнений — уравнений
Максвелла или волнового уравнения, вводят характеристики
рассеяния и поглощения частиц и получают соответствующие
дифференциальные или интегральные уравнения для таких ста-
статистических величин, как дисперсии и корреляционные функции.
Такой подход является математически строгим в том смысле, что
при этом в принципе можно учесть как эффекты многократного
рассеяния, так и влияние дифракции и интерференции. Однако
построить теорию, которая полностью учитывала бы все эти
эффекты, практически невозможно, поэтому все теории, дающие
приемлемые решения, являются приближенными и справедливы
лишь в определенной области значений параметров. Теория
Тверского, диаграммный метод и уравнения Дайсона и Бете —
164 Глава 7
Солпитера представляют собой разновидности строгой теории.
Мы опишем эти теории в гл. 14 и 15.
С другой стороны, теория переноса [31, 105, 122, 148] не ис-
исходит из волнового уравнения. Эта теория оперирует непосред-
непосредственно с переносом энергии в среде, содержащей частицы. Та-
Такая теория строится эвристически и не является строгой в мате-
математическом отношении. Даже если эффекты дифракции и ин-
интерференции и учитываются при описании характеристик рас-
рассеяния и поглощения одиночной частицы, теория переноса сама
по себе не включает дифракционных эффектов. В теории пере-
переноса предполагается, что при сложении полей отсутствует кор-
корреляция между ними, так что складываются интенсивности, а не
сами поля.
Теория переноса, называемая также теорией переноса излу-
излучения, берет свое начало с работы Шустера 1903 г. Основное
дифференциальное уравнение этой теории называется уравне-
уравнением переноса и эквивалентно уравнению Больцмана (называе-
(называемому также уравнением Максвелла — Больцмана со столкнове-
столкновениями), используемому в кинетической теории газов [149] и
в теории переноса нейтронов1). Такая формулировка является
гибкой и способна описывать многие физические явления. Она
с успехом применялась в задачах атмосферной и подводной ви-
видимости, морской биологии, оптики бумаг и фотографических
эмульсий, а также при анализе распространения излучения в
атмосферах планет, звезд и галактик.
Несмотря на различие исходных предпосылок этих двух под-
подходов, они имеют дело с одними и теми же явлениями, поэтому
можно ожидать наличия некоторой фундаментальной связи ме-
между ними. Такая связь действительно имеет место, и мы пока-
покажем ниже, что лучевая интенсивность, используемая в теории
переноса, и функция взаимной когерентности, используемая в
строгой теории, связаны преобразованием Фурье. Это означает
также, что, хотя теория переноса строится на основе сложения
интенсивностей, она содержит информацию о корреляции полей
[71,72].
В теории переноса можно учесть поляризационные эффекты,
введя матрицу Стокса. Однако в большинстве случаев из сооб-
соображений математического удобства поляризацией пренебрегают.
В этой главе всюду, за исключением разд. 7.7, поляризационные
эффекты не рассматриваются. Об этом нужно помнить, в осо-
особенности при интерпретации экспериментальных данных.
В данной главе мы дадим определения- важных величин и по-
поясним их свойства для свободного пространства, а также одно-
') Благодаря этой экивалентности теория переноса нейтронов непосред-
непосредственно применима к теории переноса излучения. По теории переноса ней-
нейтронов см. работы [11, 29, 40, 168].
Теория переноса излучения в случайном облаке частиц 165
родных и неоднородных сред, содержащих частицы. Затем мы
выведем основное дифференциальное уравнение, называемое
уравнением переноса для интенсивности в случайном облаке рас-
сеивателей, обсудим закон сохранения энергии в такой среде и
поясним граничные условия. Мы выведем также общие инте-
интегральные уравнения и дадим их физическую интерпретацию.
Анализ частично поляризованных волн на основе уравнения пе-
переноса осуществляется путем введения параметров Стокса.
В последнем разделе мы рассмотрим связь лучевой интенсив-
интенсивности в теории переноса с вектором Пойнтинга в теории Макс-
Максвелла.
7.1. Лучевая интенсивность, поток
и плотность энергии
Начнем с определений основных величин, используемых в
теории переноса. К ним относятся лучевая интенсивность, по-
поток, плотность энергии и средняя интенсивность. Наиболее важ-
важной является лучевая интенсивность.
Рассмотрим поток волновой энергии в точке г в хаотически-
неоднородной среде. Частота, фаза и амплитуда волны случайно
меняются во времени, поэтому величина и направление связан-
связанной с ними плотности потока также непрерывно меняются. Для
данного направления, определяемого единичным вектором s,
можно записать среднюю плотность потока энергии, заключен-
заключенную в единичном интервале частот вблизи частоты v и в еди-
единичном телесном угле. Эта величина /(г, s) называется лучевой
интенсивностью, а также яркостью или энергетической яркостью,
и измеряется в единицах Вт-м^-стерад-1- Гц. Она является од-
одной из фундаментальных величин в теории переноса излучения.
Связь лучевой интенсивности с вектором Пойнтинга и функцией
взаимной когерентности рассматривается в разд. 7.8 и 14.7.
Мощность dP, протекающая в единичный телесный угол da>
через элемент поверхности da, ориентированный в направлении
единичного вектора s0 в частотном интервале (v, v + dv), дается
выражением (рис. 7.1)
dP = / (г, s) cos 6 da dm dv (Вт). G.1)
Лучевая интенсивность описывает характеристики поля, из-
излучаемого поверхностью (рис. 7.2, а). Однако можно также вы-
выбрать точку г на воображаемой поверхности А в пространстве и
рассматривать поток мощности I-da da> dv, падающий на эле-
элемент поверхности da. Этот поток должен быть равен потоку
I+da da dv, исходящему из элемента da в противоположном на-
166
Глава 7
правлении s (рис. 7.2,6). Аналогично мы можем рассмотреть
поток, падающий на поверхность извне (рис. 7.2, в).
Лучевая интенсивность /+(г, s) описывает излучение, испу-
испускаемое поверхностью, независимо от того, является ли эта по-
Рис. 7.1. К определению луче-
лучевой интенсивности / (г, s) и
мощности dP согласно G.1).
вирхность действительно излучающей или воображаемой, и на-
называется поверхностной интенсивностью. Интенсивность излу-
излучения /-(г, s), падающая на поверхность, которая может быть
Л
Л
Излучающая
поверхность
Поверхность
приемника
Рис. 7.2. Поверхностная интенсивность /+ и интенсивность поля /_.
как реальной, так и воображаемой, называется интенсивностью
поля. Эти две величины представляют различные понятия, но
численно они тождественны, поэтому нет необходимости разли-
различать их математически.
Измерение лучевой интенсивности в Точке г в направлении s
можно осуществить следующим образом. Возьмем приемник
с малой апертурой Да, принимающий излучение из телесного
угла Дсо, и ориентируем его в направлении — s (рис. 7.3). Пусть
фильтр приемника пропускает волны в частотном диапазоне
Теория переноса излучения в случайном облаке частиц
167
(v, v + dv). Тогда лучевая интенсивность будет равна принятой
мощности Рг, деленной на Аа Асо Av, где Аа, Асо и Av выбираются
достаточно малыми.
Фильтр (v.v+iv,)
ДШ
Рнс. 7.3. Измерение лучевой интенсивности.
Рассмотрим полный поток, проходящий через элемент da
на поверхности А. Пусть So — единичный вектор, нормальный
к поверхности da (рис. 7.4). Тогда поток получается в резуль-
результате интегрирования G.1) по телесному углу 2л в направлении
вперед @^6^ л/2) и может быть записан как F+ da, где
Рис. 7.4. Поток через элемент da поверхности А.
F+ — плотность потока, распространяющегося вперед, опреде-
определяемая выражением
F+ (г, so) = \ / (г, s) s • s0 da, s • s0 = cos 6. G.2)
Bл) +
Аналогично можно определить плотность потока в обратном на-
направлении F- для потока, протекающего через da в направле-
направлении —so. Такая плотность дается выражением
/r_(r,s0)= \ /(г, s)s • (— s0)da, G.3)
I2n)~
где интегрирование по телесному углу 2л проводится в интер-
интервале л/2 ^ 6 ^ л. Как F+, так и F- измеряются в единицах
168 Глава 7
Вт-м~2-Гц. Для излучающих поверхностей плотность потока F+
часто называют энергетической светимостью (рис. 7.5, а). В слу-
случае падения излучения на поверхность поток F- называют осве-
освещенностью. В произвольной точке г можно рассматривать плот-
плотность потока F+ в направлении so, перпендикулярном некоторой
воображаемой поверхности А, и плотность потока F- в направ-
направлении —So (рис. 7.5, б). Полная плотность потока в направле-
направлении So есть векторная сумма F+ и F-.
Светимость Освещенность \л
а б в
Рис. 7.5. Энергетическая светимость F+ и освещенность F
Полную плотность потока можно выразить как компоненту
вектора плотности потока F(r) вдоль So:
F+ (г, s0) - F_ (r, s) = F (r) • i0, F (г) = [l (r, I) s da, G.4)
где интегрирование проводится по полному телесному углу 4я.
Вектор F(r) дает величину и направление полного потока мощ-
мощности. Он используется в разд. 7.3 в связи с законом сохране-
сохранения энергии.
Рассмотрим плотность энергии и (г) в точке г. Количество
энергии, покидающее за единицу времени dt малый элемент по-
поверхности da по нормали к нему в телесном угле da и частот-
частотном интервале (v, v + dv), равно / da dm dv dt. Эха энергия зай-
займет объем da cdt, где с — скорость распространения волн. По-
Поэтому плотность энергии du(r) в единичном интервале частот
равна
, , . I da dot dv dt I (r, s) da ,„ r4
du^^ dacdtd, = с • <7'5)
Складывая энергию, приходящую со всех направлений, полу-
получаем плотность энергии
= 1 5/(г, s)fife. G.6)
4л
Теория переноса излучения в случайном облаке частиц 169
В некоторых случаях удобно рассматривать среднюю интенсив-
интенсивность
\(r,l)dta. G.7)
4л
Средняя интенсивность, вообще говоря, не представляет собой
поток мощности; она пропорциональна плотности энергии.
Если лучевая интенсивность /(г, s) не зависит от направле-
направления s, то излучение называют изотропным. Если лучевая интен-
интенсивность излучения от элемента поверхности da изотропна, то
мощность Р, излученная этим элементом в направлении s, дается
выражением
Р(Вт-стерад~' • Гц-1) = (Ida) cos G = P0cos6, G.8)
где 6 — угол между направлением s и нормалью к поверхности
da. Соотношение G.8) называют законом Ламберта [21].
7.2. Лучевая интенсивность в свободном пространстве
и на границах раздела однородных сред
Хотя мы рассматриваем распространение волн в случайно-
неоднородных средах, тем не менее полезно исследовать поведе-
поведение введенных в предыдущем разделе величин в свободном про-
пространстве и в однородной среде. Прежде всего мы покажем, что
лучевая интенсивность в свободном пространстве постоянна
вдоль луча. На первый взгляд это утверждение противоречит
обычному представлению о потоке мощности, распространяю-
распространяющемся в свободном пространстве, но на самом деле оно вполне
естественно. Докажем это.
Рассмотрим лучевые интенсивности 1\ и 12 в двух точках п
и г2, разделенных расстоянием г вдоль направления s, и два
малых элемента поверхности da\ и da2, перпендикулярные s
(рис. 7.6). Выразим двумя способами мощность, падающую на
da2. Согласно G.1), эта мощность равна I\da.\d(sn- С другой
стороны, она должна быть равна I2 da2 d®2. Но dax du>i = da2 d<a2,
поскольку da\ = r2 da>2 и da% = r2 rfcoi, что и доказывает постоян-
постоянство лучевой интенсивности вдоль луча в свободном простран-
пространстве. (Более удовлетворительное доказательство см. в разд. 14.7.)
В качестве примера рассмотрим излучение, исходящее в ок-
окружающее пространство от сферы радиуса а (рис. 7.7). Пред-
Предположим, что излучение с поверхности сферы не зависит от на-
направления, т. е. при r = a /(r, s)=/0 = const, где вектор s на-
направлен в произвольном направлении наружу, и /(г, s) = 0 при
170
Глава 7
s, направленном внутрь сферы. Вычислим лучевую интенсив-
интенсивность на расстоянии г от центра сферы. Вследствие постоянства
лучевой интенсивности в свободном пространстве имеем /(г, s) =
=/о при углах 0 ^ 6 ^ во, где 60 = arcsin -у. Плотность по-
Рис. 7.6. Доказательство инвариантности лучевой интенсивности в свобод-
свободном пространстве-
Рис. 7.7. Излучение сферы.
гока в радиальном направлении дается выражением
Fr (г) = F(r) • г = ^ / (г, s) s ¦ fcfco =
2л 6j
dq> ^ sin 9 dQ/0 cos 0 -= я/0 (уJ . G.9)
Заметим, что, хотя величина / постоянна, /v(r) уменьшается как
г~2, что и следовало ожидать на основании закона сохранения
энергии. Полная излучаемая мощность равна
Pt = Fr4nr2 = 4n2a2h G.10)
и, конечно, не зависит от расстояния г. Плотность энергии а(г)
дается выражением
2я e,i
Л (Г) =4 $ *ф$81пе<«)/ое=^[1- Yl-(i)8]; G.11)
Теория переноса излучения в случайном облаке частиц
171
средняя интенсивность равна
G.12)
Рассмотрим теперь условие, которому должна удовлетворять
лучевая интенсивность на границе раздела двух сред с показа-
показателями преломления щ и Пг (рис. 7.8).
Рис. 7.8. Лучевые интенсивности на
плоской границе двух однородных сред.
Для плоской волны, падающей на плоскую границу, коэффи-
коэффициент отражения R = Er/Ei и коэффициент пропускания Т ==
= Et/Ei даются выражениями
„
n.\ cos 6г — яг cos 6[
П] COS 02 + Яг COS 8| '
Я] cos 8, — tit cos 82
rti COS 81 + П2 COS 82 '
1п\ cos
T =
Я2 COS 81 + Я, COS 82 '
2rt, cos 81
tl\ COS8| + П2 COS 62 '
(/.10)
где /?u и Гц соответствуют электрическим полям, поляризован-
поляризованным в плоскости падения, a /?j. и Т± — электрическим полям,
поляризованным перпендикулярно плоскости падения.
Очевидно, что отраженная лучевая интенсивность I, связана
с /,• соотношением
/г=тч-, G.14)
, где R есть либо /?ц, либо Я\, в зависимости от поляризации.
Если волна не поляризована, то |Л!|2 переходит в — (| /?ц f +
+1 R± I2).
Теперь нужно определить, чему равно отношение /<//,-. Из
рис. 7.8 видно, что для того, чтобы связать /( и А, нужно учесть
связь da>\ и doJ- Поток мощности, падающий на малый элемент
поверхности da на границе раздела, должен быть равен сумме
отраженного и прошедшего потоков:
It da cos 61 rfcoi = Ir da cos 0j
/* da cos 62
G.15)
172
Гкавв 7
Заметим, что da>\ = sin 8t dBi dq>i и da>2 = sin 62 сЮ2 с?ф2. Из
закона Снеллиуса щ sin 81 = n2 sin в2 получаем ni cos 81 d8i =
== «2 cos 62^62 и, замечая, что d(f\ = dq>2, находим
я?
G.16)
Мы можем выразить соотношение между It и /,-, используя
коэффициент пропускания по мощности Тр и коэффициент от-
Рис. 7.9. Лучевые интенсивности
/2 в двух точках на луче.
*-Z
ражения по мощности i?p, которые определены как отношения
прошедшей и отраженной мощностей к мощности, падающей
по нормали к поверхности:
^ __ пг cos 62 , j р
' р я, cose, '' "
Из G.14), G.16) и G.17) имеем
2 2
__ | г. р
— 1
1.
G.17)
«2 COS 82
nj cos 0!
Tflt. G.18)
В G.18) величина \Т\2 равна |Гц|2 или \Т±\2 в зависимости от
поляризации или равна ¦-- (| Гц р + | Т± |2) для неполяризованной
волны.
Если показатель преломления медленно меняется вдоль од-
одной из координат: п(г) = n(z), то отношение лучевых интенсив-
носгей в двух точках п и г2 вдоль луча может быть получено
обобщением G.15) и G.16):
da{ cos8t
, — ц
da2 cos 62
G.19)
где da\ и da.2 — поперечные сечения трубки лучей в точках п и
г2, перпендикулярные оси г (рис. 7.9).
Теория переноса излучения & случайном облаке частиц 1?5
7.3. Дифференциальное уравнение
для лучевой интенсивности
В предыдущем разделе мы определили лучевую интенсив-
интенсивность и другие фундаментальные величины. Мы рассмотрели
также характеристики лучевой интенсивности в свободном про-
пространстве и на границе двух однородных сред. В данном разделе
мы изучим основные характеристики лучевой интенсивности в
среде, содержащей случайные частицы. Такие частицы рассеи-
рассеивают и поглощают энергию волны, и эти характеристики должны
учитываться в дифференциальном уравнении, которому удовле-
Рис. 7.10. Расстояние лучевой интенсив-
интенсивности, падающей на объем ds, с напра-
направления s' на направление s.
творяет лучевая интенсивность. В теории переноса излучения это
уравнение называют уравнением переноса. Оно тождественно
уравнению Больцмана, используемому в теории переноса ней-
нейтронов.
Рассмотрим лучевую интенсивность /(г, s), падающую на
цилиндрический элементарный объем с единичным поперечным
сечением и длиной ds. Объем ds содержит pds частиц, где р —
число частиц в единице объема, называемое плотностью числа
частиц. Каждая частица поглощает мощность оа1 и рассеивает
мощность osl, поэтому уменьшение лучевой интенсивности
dl{r, s) в объеме ds выражается в виде
dl (г, s) = — р ds (аа + as) Г = — р dsatl. G.20)
В то же время лучевая интенсивность должна возрастать вслед-
вследствие рассеяния в направлении s части лучевой интенсивности
/(г, s), падающей на данный объем с других направлений s' и
добавляющейся к интенсивности /(г, s) (рис. 7.10). Чтобы опре-
определить этот вклад, рассмотрим волну, которая падает на ча-
частицу в направлении s'. Плотнасть падающего в малом телесном
угле dw' потока S, = /(г, s')du>'. Этот поток падает на частицы
174 Глава 7
в объеме ds. Плотность потока мощности Sr для волны, рассеян-
рассеянной единичной частицей в направлении s на расстоянии jR от
частицы, дается выражением Sr=[|/(s, s') \2/R2]Si, где f(s, s')—¦
амплитуда рассеяния, определенная в разд. 2.1. Поэтому обус-
обусловленная Si лучевая интенсивность рассеянной в направлении s
волны равна
Srtf- = |/E, ar) I2 S, = | / (S, S') |2 / (г, V) Ло'.
вой интенсивности, рассеянной в направлении s частицами из
объема ds, получим
Добавив падающий поток со всех направлений s', для луче-
рассеянной в направлении s частицами из
]pds}f(l,s')\4(r, s')d<o', G.21)
4л
где интегрирование выполняется по всем телесным углам со',
чтобы учесть вклады со всех направлений s'. Мы можем выра-
выразить G.21), используя фазовую функцию1) p(s, s'):
р(s, l') = ~\f (s, ?) I2, ± \ p (s, s') rfco = Wo = -^ , G.22)
4jt
где IFo — альбедо одиночной частицы.
Лучевая интенсивность может возрастать также вследствие
излучения из объема ds. Если обозначить через e(r, s) мощ-
мощность излучения единицы объема в единичный телесный угол
в направлении s, то указанное увеличение интенсивности выра-
выразится как
ds e (r, s). G.23)
Объединяя вклады G.20), G.21) и G.23), получаем уравнение
переноса:
Опт р
= - petl (r,s) + ^j-\p (I, s') / (г, s') rf<o' + e (r, s). G.24)
4я
Левую часть этого уравнения можно выразить также с по-
помощью оператора градиента или дивергенции:
dI(J;s) = sv/ (r, i) = div [/ (r, s) s], G.25)
где мы воспользовались тем, что s — постоянный вектор, так что
divs = 0.
') Название «фазовая функция» берет свое начало в астрономии, где оно
относится к лунным фазам. Оно не имеет никакого отношения к фазе волны.
См. разд. 2.1, а также [162].
Теория переноса излучения в случайном облаке частиц 175
В этом уравнении размеры частиц, а также плотность числа
частиц могут быть различны в разных точках, поэтому pat и р
могут быть функциями г. Расстояние иногда удобно выражать
через безразмерный оптический путь т, определенный как ')
i=\petds. G.26)
Оптический путь т = 1 означает, что вдоль данного участка
пути поток мощности уменьшается из-за рассеяния н поглоще-
поглощения, согласно G.20), до значения, равного ехр(—1) от падаю-
падающего потока. Учитывая G.26), можно записать G.24) в виде
dI% S) = - / (т, s) + -^ \р (s, ?) / (т, ?) dco' + / (т, s), G.27)
4я
где функция 7(r, s) =e(r, s)/pa* называется функцией источ-
источника.
Рассмотрим теперь закон сохранения энергии. Запишем ле-
левую часть уравнения G.24) с помощью дивергенции в виде
G.25), после чего проинтегрируем обе части G.24) по полному
телесному углу 4л. Вспоминая определения вектора потока F
G.4) и средней интенсивности U (г) G.6) и используя G.22),
получаем
div F (г) = — рва \ I (г, s) da + \е (г, s) da, G.28а)
4л 4я
где
?(r)= J в (г, s)afco G.286)
4я
— мощность, излучаемая единицей объема в единичном интер-
интервале частот (Вт-м-3-Гц-1), а
Еа (г) = Рва \ I (г. s) rfco = 4npaaf/ (г) G.28в)
— полная мощность, поглощаемая единицей объема в единичном
интервале частот. Заметим, что в G.28в) оа1 есть мощность, по-
поглощаемая одиночной частицей при облучении с интенсивно-
интенсивностью /, а полная поглощенная мощность дается суммированием
аа1 по телесному углу 4л и всем частицам независимо от на-
направления /.
1) В гл. 4—6 мы использовали обозначения у для оптического пути и т —
для разностей времени. В данной главе, следуя Чандрасекару [31], мы обоз-
обозначаем оптический путь через т.
176 Глава 7
Физически G.28а) означает, что выходящий из единичного
объема поток F равен мощности, излучаемой единицей объема,
минус мощность, поглощаемая единицей объема. В случае среды
без потерь аа = 0 и в отсутствие источников выполняется закон
сохранения потока мощности:
V • F (г) = 0. G.28г)
7.4. Ослабленная падающая интенсивность,
диффузная интенсивность, граничное условие
и функция источника
Полную интенсивность') часто бывает удобно разделить на
две части: ослабленную падающую интенсивность hi и диффуз-
диффузную интенсивность la-
При прохождении волны через объем V, содержащий рассеи-
рассеивающие частицы, падающий поток уменьшается в соответствии
с G.20) и возрастает в соответствии с G.21). Та часть потока,
которая уменьшается из-за рассеяния и поглощения, согласно
G.20), называется ослабленной падающей интенсивностью и
удовлетворяет уравнению
Л1т1}1Л) =-9°tIrdr,*). G.29)
Другая часть, которая порождается в среде в результате рассея-
рассеяния, называется диффузной интенсивностью (рис. 7.11). По-
Поскольку полная интенсивность /(г, s) = /M-(r, s)-\-Id(r, s) удо-
удовлетворяет уравнению G.24), диффузная интенсивность удовле-
удовлетворяет уравнению
d'd' S>
= - ?atld (r, I) + -g- J p (s, V) Id (г, V) da' +
4я
+ ег,(г, s) + e(r, s), G.30)
где eri — функция эквивалентного источника:
Srt (Г, 8) = -g- \ р (S, S') 1т1 (Г, s"') do»', G.31)
4я
порожденная ослабленной падающей интенсивностью.
Граничное условие на поверхности S среды, содержащей
много частиц (рис. 7.11), можно получить, заметив, что диффуз-
') В этой книге /(г, s) всюду обозначает лучевую итенсивность, иногда
называемую просто интенсивностью,
Теория переноса излучения в случайном облаке частиц 177
ная интенсивность порождается только внутри среды. Поэтому
нужно потребовать, чтобы на поверхности среды S отсутство-
отсутствовало диффузное излучение, входящее в среду, так что диффуз-
диффузная интенсивность на S всюду должна быть направлена на-
наружу1). Математически это граничное условие выражается в
виде
/d(r, s) = 0 на S при s, направленном внутрь S. G.32)
Для неограниченной среды нужно потребовать, чтобы диффуз-
диффузная интенсивность на бесконечности обращалась в нуль. Это
S
Рис. 7.11. Падающая интенсивность /,-,
ослабленная падаюшая интенсивность /г;
и диффузная интенсивность /rf.
условие обсуждается в гл. 11 на нескольких примерах. Уравне-
Уравнение G.30) вместе с граничным условием G.32) составляют пол-
полное математическое описание задачи.
Ослабленная падающая интенсивность может быть коллими-
рованной или диффузной. Например, падающая волна можег
быть сильно коллимирована в направлении So, как в случае ла-
лазерного пучка или плоской волны. Такую интенсивность назы-
называют коллимированной падающей интенсивностью /с,-. Для из-
излучения, падающего в направлении So, величину /с,(г, s) можно
выразить с помощью дельта-функции:
1с1 (г, s) = Рф (& - шо), G.33)
где Fq — плотность потока (Вт-м~2-Гц-1), 6(й> — шо)—дельта-
функция по телесному углу (стерад), а ш и шо — единичные
векторы, представляющие телесные углы в направлениях s и So.
Например, в сферической системе координат
а / - - ч б (8 - 80) б (Ф - 0О) Г . , А ...
б (со — шо) = ^-д , ^ б (со — щ)йи= 1,
da = sin 6 dQ df. G.34)
В противоположность коллимированной падающей интенсив-
интенсивности диффузная падающая интенсивность приходит с разных
направлений и ее величина различна для разных направлений.
В качестве примера рассмотрим падение рассеянного облаком
') Строго говоря, это относится только к выпуклым областям, для ко-
которых выходящее из рассеивающего объема излучение не может попасть в
него снова.
178 Глава 7
излучения на поверхность океана. В этом случае падающая вол-
волна будет не коллимированной, а диффузной. Соответствующую
ей интенсивность мы назовем диффузной падающей интенсив-
интенсивностью.
Рассмотрим теперь функцию источника /(г, s) = e(r, s)/pa*.
Для точечного источника мощности Ро (Вт/Гц), находящегося
в точке Го и излучающего изотропно во всех направлениях, имеем
е (г) = А б (г -г0) (Вт • м~3 • стерад-1 • Гц). G.35)
Если среда находится в локальном термодинамическом равно-
равновесии при температуре Т (в Кельвинах), то закон Кирхгофа для
излучения черного тела дает разумное приближение для излу-
излучаемой энергии ([89], гл. 1). При этом можно приближенно за-
записать
), В(Т)= *"^ -, G.36)
где /( и Л — постоянные Больцмана и Планка.
7.5. Интегральная форма уравнения переноса
В общем случае существуют два подхода к рассматриваемой
задаче. При одном из них исходят из дифференциального урав-
уравнения, получают общее решение с неизвестными коэффициен-
коэффициентами, а затем с помощью соответствующих граничных условий
находят эти коэффициенты. Другой подход состоит в переходе
от дифференциальных уравнений с заданными граничными ус-
условиями к интегральным уравнениям для некоторых неизвест-
неизвестных функций. В случае задач с простой геометрией (например,
плоскопараллельная атмосфера) широко использовался подход
на основе дифференциальных уравнений. Для задач с более
сложной геометрией часто удобнее исходить из интегральных
уравнений и получать их приближенные решения. Мы рассмо-
рассмотрим здесь общую интегральную постановку задачи.
Пусть имеется объем V, содержащий случайные частицы
(рис. 7.12). Будем исходить из дифференциального уравнения
= - per,/(м)т^(рE, s')/(г, ?)da' + е(г, s). G.37)
4л
Это дифференциальное уравнение первого порядка по аргу-
аргументу s. Замечая, что уравнение G.37) имеет вид
f Q> • G.38а)
Теория переноса излучения в случайном облаке частиц
179
получаем общее решение
/ (г, s) = се~х + е-* J Q (s,) е* rfs,, G.386)
где т = \ рсг( cfs — оптический путь, с — константа, а
Q (s) = -^ \ р (s, s') / (г, s') da/ + е (г, s). G.38b )
4л
Теперь используем граничное условие, согласно которому в
точке падения г = г о диффузная интенсивность Id обращается
Рис. 7.12. Ослабленная падающая
интенсивность /Г!- и диффузная ин-
интенсивность / ..
в нуль, так что полная интенсивность при этом равна падающей
интенсивности Л(г0, s). Измеряя расстояние s от точки г = Го,
получаем
/ (г, s) = lrl (r, s) + Id (r, s), Irl (r, s) = /; (r0, s) exp (— т),
Id (r, s) = \ exp [- (т - тО] f(^) \ p (s, s') / (г„ s') rf«.'+ G.39)
+ e(rb
где Iri — ослабленная падающая интенсивность, /d — диффузная
S Si
интенсивность, т = \ pat ds, a x{ = \ pcrf ds. Если объем V, co-
0 0
держащий рассеиватели, характеризуется показателем прелом-
преломления п, отличным от показателя преломления среды, то падаю-
падающую интенсивность /i(r0, s) нужно заменить на прошедшую ин-
интенсивность /f(r0, s), причем s есть единичный вектор направле-
направления распространения прошедшего поля, рассмотренный в
разд. 7.2.
Уравнение G.39) представляет собой интегральное уравне-
уравнение для лучевой интенсивности /(г, s) вдоль луча с направле-
направлением s. Однако, поскольку входящий в него интегральный член
180
Глава 1
содержит вклады от интенсивностей, которые приходят с раз-
разных направлений s', это уравнение, очевидно, неполно. Более
полное описание должно включать вклады от всех точек объе-
объема V.
Чтобы получить такое интегральное уравнение, проинтегри-
проинтегрируем G.39) по полному телесному углу и разделим обе части
Рис. 7.13. Физический смысл интеграль-
интегрального уравнения G.41).
полученного соотношения на 4л. При этом левая часть G.39)
перейдет в среднюю интенсивность 0(г):
-^ J / (г, s) fifco = f/ (г).
G.40а)
4л
Ослабленная интенсивность даст величину
-^ \ Irl (r, s) da = 4г \ /, (го, si в"* da = Uft (г). G.406)
4л
Для вычисления интеграла от диффузной интенсивности заме-
заметим, что d® = da/\r — п|2 и da ds\ = dV\. Учитывая это, окон-
окончательно получаем
р s, s')I(rlts')d(D'
4л
exp [— (t--T
4я | r - r, |2
G.41)
Физический смысл G.41) можно пояснить, рассмотрев рис. 7.13.
Первый член в правой части Uri{r) есть средняя интенсивность,
связанная с приходящей со всех направлений ослабленной па-
падающей интенсивностью. Для интерпретации второго члена за-
заметим, что 1(т\, s') есть интенсивность, падающая на объем dV\
с направления s', поэтому первое слагаемое в интегральном
члене есть вклад от /(ri, s') в направлении s, ослабленный сфе-
сферической расходимостью |г — г11 —2 и поглощением ехр[—(т — х\)];
Теория переноса излучения в случайном облаке частиц 181
этот вклад интегрируется по всем телесным углам ©' и по всему
объему V. Второе слагаемое в интегральном члене есть вклад
з поле в точке г от функции источника в точке п.
Уравнение G.41) выражает среднюю интенсивность U(r),
которая пропорциональна плотности энергии. Вполне аналогично
можно получить и уравнение для вектора потока F(r):
F (г) = Fri (г) + J № J p (I, s') I (г,, V) da' +
L 4я
где F (г) = \ /(г, s)sdco. В гл. 14 будет показано, что эти урав-
4я
нения фактически согласуются с теорией многократного рассея-
рассеяния Тверского и с уравнениями Дайсона и Бете — Солпитера.
7.6. Эффективная площадь антенны
и принимаемая мощность
В предыдущем разделе мы обсудили общие соотношения для
лучевой интенсивности, имеющие вид дифференциальных и ин-
интегральных уравнений. Однако при практическом измерении лу-
лучевой интенсивности нужно принимать во внимание характери-
Рис. 7.14. Эффективная поверхность приемника Аг (s"r> s) и принимаемая
мощность Рг.
стики приемника. Эти характеристики наиболее удобно выразить
через эффективную площадь приемной антенны Ar(sr,s). При
падении на приемник с направления s волны с плотностью по-
потока мощности Si(s) (Вт/м2) для приемника, ориентированного
в направлении —sr (рис. 7.14), эффективная площадь поверх-
поверхности антенны определяется как отношение принятой мощности
Рг (Вт) к плотности падающего потока S;(s):'
Pr=A,(Sn*)St(l). G.43)
182 Глава 7
Величина А, имеет размерность площади и зависит от на-
направления падающей волны s и ориентации приемника s,. Ис-
Используя падающую на приемник лучевую интенсивность /(г, s),
получаем
Рг = \ Ar (sr, s) / (r, s) dm (Вт/Гц), G.44)
Q
где интегрирование производится по телесному углу, содержа-
содержащему все падающие на приемник волны. Например, для случая,
изображенного на рис. 7.14, интегрирование должно проводиться
по области 0^0^ я/2. В общем случае эффективная площадь
приемной антенны может соответствовать узкому (малые 6) и
широкому углу приема. В частном случае, когда приемник оди-
одинаково чувствителен к мощности, приходящей со всех направ-
направлений, мы имеем A,($r, s) = Ao cos 9. Такие характеристики при-
приемника можно учесть в общих интегральных выражениях преды-
предыдущего раздела. Мощность PR, принимаемая в точке г приемни-
приемником, ориентированным в направлении —sr, полностью анало-
аналогично G.41) дается выражением
PR (г, sr) = PRrl (г, sr) + PRd (г, I). G.45)
Здесь Р/?п(г, sr)—принимаемая мощность, обусловленная ос-
ослабленной падающей интенсивностью:
Prh (г. sr) = \ Аг (sr, s) /„ (г, s) da, G.46)
а
a PRd(f, sr)—принимаемая мощность, связанная с диффузной
интенсивностью:
РцАг, sr) = J Ат (s, 1Г) Г-^- \ р (s, s') / (г„ s^) rf<D7 +
V L
V
i]ap\*X)] G.47)
В большинстве практических приложений эффективную пло-
площадь антенны можно считать такой же, как в случае свободного
пространства. Однако, строго говоря, все характеристики приема
могут зависеть от случайно распределенных рассеивающих ча-
частиц. В общем случае флуктуации падающей на приемник волны
вызывают уширение средней диаграммы направленности и па-
падение коэффициента усиления антенны. Этот эффект иногда на-
называют потерями, обусловленными связью среда — антенна
[140].
Теория переноса излучения в случайном облаке частиц
183
7.7. Уравнение переноса для частично поляризованной
электромагнитной волны
До сих пор мы не учитывали никаких поляризационных эф-
эффектов, что оправдано только для акустических волн. Для элек-
электромагнитных волн такое описание может служить лишь неко-
некоторым приближением. В данном разделе мы дадим общую фор-
формулировку теории переноса электромагнитных волн с учетом по-
поляризации. Электромагнитные волны в случайно-неоднородных
средах фактически всегда являются частично поляризованными,
поскольку даже для линейно-поляризованной падающей волны
Рис. 7.15. Преобразование па-
параметров Стокса при повороте
на угол Фи рассеянии с на-
направления s' на направление s
и повороте на угол Ф2.
рассеянная волна будет, вообще говоря, эллиптически-поляри-
зованной, причем ее поляризация будет меняться хаотически
из-за случайных неоднородностей среды.
При рассмотрении частично поляризованных волн лучевую
интенсивность /(г, s) нужно заменить вектором I(r, s, t), ком-
компонентами которого являются параметры Стокса (Л, /2, U, V)
для лучевой интенсивности (Вт-м^-стерад-'-Гц-1). Параметры
Стокса определяются в прямоугольной системе координат, где
ось z совпадает с направлением распространения, а 1\ и h —
средние интенсивности компонент х и у электрического поля
(разд. 2.9 и 2.10). В соответствии с принятыми в этой главе
обозначениями единичные векторы в направлениях х и z обо-
обозначим t и s (рис. 7.15). Аналогично G.24) запишем
d\ (r s, t)
ds
1 / 2\ i
= - pot\ (г, s, t) +
+ •*?/-$ Р (s, t; s', P) I (r, s', P) do' + е (г, s, f). G.48)
in
Здесь мы использовали принцип аддитивности параметров Сток-
Стокса для независимых волн. Вектор I выражается матрицей-столб-
матрицей-столбцом из четырех элементов (/j, /j, U, V), а Р — матрица размера
184 Глава 7
4X4, называемая фазовой матрицей и связывающая параметры
Стокса падающей волны I(r, s', t') с параметрами Стокса рас-
рассеянной волны, определенными для направлений s и t Через
е(г, s, t) обозначены параметры Стокса источника, которые опи-
описывают излучение в единичном телесном угле вблизи направ-
направления s.
Фазовую матрицу P(s, t; s', t') можно выразить следующим
образом. В разд. 2.12 мы ввели матрицу Стокса o(s, x; s', x),
связывающую параметры Стокса рассеянной волны L(s, x)
с параметрами Стокса падающей волны L(s', x), причем пло-
плоскость, определяемая векторами s и s', называется плоскостью
рассеяния, а ось х перпендикулярна этой плоскости. Для моно-
монохроматической волны эти величины сводятся к плотностям энер-
энергии рассеянной и падающей волн (Вт/м2). Мы можем опреде-
определить параметры Стокса для лучевой интенсивности (Вт-м~2-сте-
рад-'-Гц-1) для цилиндрического объема с единичным сечением
и длиной ds, содержащего pds частиц. При этом можно запи-
записать
\s (s, x) = р dsa{s, х; s', x) \t (s', х), G.49)
где Ь и L — параметры Стокса для лучевой интенсивности. Те-
Теперь нам нужно связать I,(s', x) с I(s', t'). Такая связь сводится
просто к преобразованию параметров Стокса при вращении осей:
Это преобразование обсуждалось в разд. 2.13:
l<(8/.x) = L(^1)Ks/,f/). G.50)
Аналогично имеем
I(M) = L(-q>2)I(s,?). G.51)
Отсюда следует, что фазовая матрица Р имеет вид
Р (s, t; s', t') = I (- ф2)Ъ (s, x; s', x) L (</>,), G.52)
что соответствует повороту от t' к х, рассеянию с направления s'
на s и повороту от х к t.
Мы не будем здесь останавливаться на дальнейших деталях,
поскольку они достаточно подробно описаны в других учебниках.
(См., например, [31, 136] о представлении матрицы рассеяния
для плоскопараллельной среды с вертикальными и горизонталь-
горизонтальными осями отсчета.)
Теория переноса излучения в случайном облаке частиц 185
7.8. Связь лучевой интенсивности
с вектором Пойнтинга
В разд. 7.1 мы определили лучевую интенсивность как плот-
плотность потока мощности, распространяющейся внутри единичного
телесного угла в диапазоне частот (v, v-f-dv). В данном раз-
разделе мы дадим другое определение, которое связывает лучевую
интенсивность с полями, удовлетворяющими уравнениям Макс-
Максвелла.
Рассмотрим вектор Пойнтинга S для волны в диапазоне ча-
частот (v, v + dv):
S(r, 0 = Е(г, 0ХН(г,0. G.53)
В каждой точке г этот вектор есть случайная функция времени,
и, поскольку каждая компонента S меняется со временем, коней
вектора S движется случайно. Рассмотрим трехмерное про-
пространство, в котором ортогональные координаты есть компо-
компоненты S, а именно Sx, Sy и Sz. Пусть W(SX, Sy, Sz)dSxdSydSz —
вероятность того, что конец вектора S находится в элементе
объема dSxdSydSz. Используя сферические координаты E, 9, ф),
где Sx = S sin 0 cos ф, Sy = S sin 0 sin ф и Sz = S cos 9, мы мо-
можем записать эту вероятность в виде
W (Sx, Sy, Sz) dSx dSy dSz = W (S, 9, ф) S2 dS dm, G.54)
где d<a = sin 0 cfO dф. Функция плотности вероятности W удовле-
удовлетворяет условию нормировки
W (S, 0, ф) S2 dS da> = 1. G.55)
4n б
Теперь мы можем определить лучевую интенсивность /(г, s) как
/ (г, s) = J SW (S, 0, ф) S2 dS. G.56)
о
Это означает, что / есть сумма всех векторов Пойнтинга, кон-
концы которых локализованы в единичном телесном угле в направ-
направлении S, определяемом координатами (9, </>).
Средняя интенсивность U дается выражением
°°
U = -~ \ da \ SW (S, 9, ^)S2cf5, G.57)
4п О
а вектор потока F равен
оо
F = Jj dm jj SsW {S, 0, ф) S2 dS. G.58)
4л
186 Глава 7
Для акустических волн вектор Пойнтинга нужно заменить на
S = pV и воспользоваться приведенными выше соображениями.
Определение G.56) выражает лучевую интенсивность как
статистическое среднее от случайно меняющегося вектора Пойн-
Пойнтинга и дает некоторое представление о физической природе лу-
лучевой интенсивности.
Лучевая интенсивность в том виде, в котором она определена
в данной главе, представляет собой средний поток мощности.
При этом флуктуации волны, связанной с этим потоком, не рас-
рассматриваются. Возникает вопрос, имеется ли какая-нибудь связь
между лучевой интенсивностью и волновыми характеристиками
поля?
Поскольку уравнение переноса выведено эвристически на ос-
основе энергетических соображений, волновые характеристики
поля, по-видимому, не входят в эту эвристическую картину, за
исключением разве что характеристик рассеяния и поглощения
частиц. Однако, поскольку при вычислении сечений и амплитуд
рассеяния использовалось волновое уравнение, лучевая интен-
интенсивность не может быть найдена без знания взаимодействия по-
полей со средой. В ряде последних работ рассматривалась связь
теории переноса со строгой аналитической теорией; некоторые
аспекты этих интересных разработок обсуждаются в гл. 14. Там
показано, что соотношение G.57) можно обобщить, выразив
функцию взаимной когерентности как фурье-образ лучевой ин-
интенсивности.
Глава 8
Приближенные решения для разреженной
среды
В гл. 7 мы развили общую теорию переноса для, распростра-
распространения волн в присутствии случайных частиц и получили уравне-
уравнение переноса и интегральные уравнения для лучевой интенсив-
интенсивности. Однако точные решения этих уравнений получены лишь
для небольшого числа частных случаев. Примерами такого рода,
для которых решения найдены и записываются в приемлемой
для расчетов форме, являются плоскопараллельные задачи и за-
задачи с изотропным рассеянием, которые рассматриваются в
гл. 11 и 12. В большинстве практических случаев уравнение пе-
переноса не удается решить точно и возникает необходимость об-
обратиться к приближенным решениям. Даже в тех случаях, когда
точные решения известны, соответствующие выражения часто
оказываются настолько сложными, что желательно иметь более
простые приближенные решения.
Как уже указывалось в начале гл. 4, имеется два предельных
случая — разреженное и плотное распределения, — для которых
могут быть получены относительно простые решения. Для раз-
разреженного распределения рассеивателей мы можем использо-
использовать обобщение уравнения радиолокации и получить решение
в первом порядке теории многократного рассеяния. Это сделано
в гл. 4—6 и дало полезные результаты, касающиеся флуктуации
и корреляционных характеристик. Можно также исходить из из-
изложенной в гл. 7 теории переноса и получить решение в первом
порядке теории многократного рассеяния для разреженного рас-
распределения рассеивателей. Эти два подхода эквивалентны и для
заданной случайной среды дают одну и ту же принимаемую
мощность. Однако теория переноса дает решение, выраженное
через лучевую интенсивность, что оказывается удобным для не-
некоторых приложений.
В данной главе мы рассмотрим решение в первом порядке
теории многократного рассеяния на основе изложенной в гл. 7
теории переноса. Такой подход дает простые решения для лу-
лучевой интенсивности в случаях плоской волны и пучка волн.
Приложения этой теории включают оптическое рассеяние в
океане и в биологических средах.
188 Глава 8
8.1. Лучевая интенсивность в приближении первого
порядка теории многократного рассеяния
В гл. 4—6 для получения приближения первого порядка мы
использовали подход, основанный на уравнении радиолокации,
учитывая при этом характеристики излучателя и приемника.
В данной главе мы дадим альтернативное представление при-
приближения первого порядка на основе развитой в гл. 7 теории
переноса.
Полная лучевая интенсивность в точке г состоит из ослаблен-
ослабленной падающей интенсивности /,-<¦ и диффузной интенсивности 1Л.
Как показано в G.39), диффузная интенсивность равна сумме
всех интенсивностей, рассеянных частицами при облучении пол-
полной интенсивностью. Последняя, вообще говоря, неизвестна. Од-
Однако в приближении первого порядка мы полагаем, что полная
интенсивность, падающая на частицы, приближенно равна ос-
ослабленной падающей интенсивности, которая известна. Отсюда
получаем решение в приближении первого порядка
/(г, 8) = /г,(г, в) + /Лг, s), (8.1)
s
U (r, s)=J ехр [- (х-тх)\ Г^ \ р E, I') Iri (n, s') rfa' + е (г„ s)l dsx.
О L 4л J
(8.2)
Интегральное представление для принимаемой мощности, со-
соответствующее соотношениям G.45) — G.47), в приближении пер-
первого порядка выражается как
Р* = Р*г1 + Ря* (8.3)
РЯг1=\аг(ь>Iг1(г, (o)d(o, (8.4)
у
|Г _г'|
х р§ \ р & *">!" (*'> *')d&f +е (г'> *I dV'>
L 4 J
\
где приемник находится в точке г, а Аг(а>) — эффективная пло-
площадь приемной апертуры (рис. 8.1).
Это приближение первого порядка применимо к большому
числу практических задач и очень полезно из-за своей относи-
относительной математической простоты. Однако оно пригодно только
в том случае, когда плотность рассеивателей настолько мала,
что некогерентная мощность существенно меньше когерентной.
Приближенные решения для разреженной среды
189
Это условие обычно выполняется в следующих двух ситуациях:
а. Для плоской волны, падающей на среду, которая содер-
содержит случайные частицы, приближение первого порядка приме-
применимо, когда оптическая длина меньше примерно 0,4 (т с< 0,4) и
частицы в основном поглощают (альбедо Wo;<O,5). Этот слу-
случай рассматривается в следующем разделе.
б. Для волны, ограниченной малой областью углов, как в
случае передатчика с узким лучом, это приближение применимо
Рис. 8.1. Приближение первого поряд-
порядка для принимаемой мощности Р^ (8.3).
Мощность Р^ содержит вклад от ослаб-
ослабленной интенсивности Iri и вклад от
диффузной мощности, просуммирован-
просуммированный по всем точкам объема г''
на значительно больших дистанциях, в особенности когда ча-
частицы поглощают (Wo c< 0,9). Этот случай встречается при рас-
распространении микроволнового и оптического излучения в атмо-
атмосфере.
В следующих разделах мы дадим несколько примеров ис-
использования приближения первого порядка для лучевой интен-
интенсивности.
8.2. Падение плоской волны
на плоскопараллельную среду
Рассмотрим слой толщины d, содержащий случайные частицы
(рис. 8.2). Пусть плоская волна с плотностью потока Fi падает
на слой под углом 0,-, а ось х выбрана так, что плоскость паде-
падения совпадает с плоскостью хг. Показатели преломления среды
в областях г < 0, 0 < г < rf и г > if есть пи п2 и пъ соответ-
соответственно. Типичная задача, соответствующая этому случаю, —
определение интенсивности света в толще океана при облучении
сверху. Тогда z = 0 соответствует поверхности океана, a z = d —
дну океана [76].
Для плоскопараллельной задачи часто удобнее использовать
оптическую длину т = potz в направлении г, а не оптическую
длину в направлении распространения волны pafzsec0. Удобно
также вместо угла 9 использовать параметр \i = cos 9.
190
Глава 8
В этих обозначениях ослабленную падающую интенсивность
можно записать в виде
(8.6)
. Iх. Ф) = Л) ехр (— -^-) б (© — ю0),
где т = poiZ, цо — cos 0q, a Fo = T^Fr, Т\г — коэффициент про-
пропускания для лучевой интенсивности из среды 1 в среду 2, ко-
который дается выражением G.18). Через ю и «о обозначены еди-
Среда
Рис. 8.2. Падение плоской волны на плоскопараллельную среду толщины d>
содержащую случайно распределенные частицы.
ничные векторы в направлениях @, ф) и @О, фо) соответственно,
а через б(ш —оH)—дельта-функция по телесному углу, опре-
определяемая выражениями
б (о — ©о) ==
6 (9 - 8„) 6 (Ф -.
б (ю — ш0) d®—\
sinG
б (9 - е0) б @ - фа)
sin 0 dQ йф =
(8.7)
Вычислим теперь диффузную интенсивность внутри среды,
используя описанное в разд. 8.1 приближение первого поряд-
порядка. Из рис. 8.2 видно, что интенсивность 1а+ для 0 ^ 0 <
< п/2A ^ ц > 0) состоит из вкладов ослабленной падающей
интенсивности от области @,2), тогда как 1й- для л/2<6^.
Приближенные решения для разреженной среды 191
^ п@ > ц ^г — 1) — из вкладов от области (z, d). Подставляя
(8.6) в (8.2) и полагая е(гь s) = 0, получаем
_ р (tt 0; цо, 0)
S
ехр V но У еХр I ц J
т_\ _ Г _ _то_ , Тр—т1
Цо / 6ХР1 Цо й '
р (р., 0; Но 0) 6
= Тп 1z_n0F0> 1<ц
(8.9)
где т — рст<2, то = potd, (х = cos 0, цо = cos 0o.
Диффузная интенсивность, рассеянная вперед, ld+ равна нулю
при 2 = 0, увеличивается с ростом z и достигает максимума при
_ In и — in цо /й , m
Т-- 1/цо-1/ц (8Л0)
независимо от индикатрисы рассеяния р(ц, ф; ц0, фо). При 6 =
= бо величина Ц+ равна
и достигает максимума при т = ро-
Диффузная интенсивность вне среды может быть легко по-
получена с помощью соотношений (8.8) и (8.9). Для z > d диф-
диффузная интенсивность la равна T23h+(d, 0, ф), а для 2 <; 0 диф-
диффузная интенсивность есть T2ild-(O, 0, ^), где Г2з и Т2\—опре-
Т2\—определенные в разд. 7.2 коэффициенты пропускания лучевой ин-
интенсивности из среды 2 в 3 и из 2 в 1 соответственно.
Часто особый интерес представляет диффузная интенсивность
для случая, когда содержащая частицы среда является полу-
полупространством z < 0. Соотношение, выражающее угловую за-
зависимость отраженной диффузной интенсивности, называют за-
законом диффузного отражения. Эту угловую зависимость обычно
выражают через угол отражения Qr = я — Э. Используя cos Qr =
= цг = — ц, получаем
U (V-r) 4S
o + Mr
что дает приближение первого порядка ([31], разд. 47.1) для
закона диффузного отражения.
192 Глава 8
В данном анализе мы пренебрегли вкладом от отражения на
задней поверхности z = d. Если эта поверхность сильно отра-
отражающая и гладкая с коэффициентом зеркального отражения /?,
то к правой части (8.9) нужно добавить следующую диффузную
интенсивность:
р (ц, Ф; — цо, 0) ехр [(т0 — т)/ц] — ехр [— (т0 — т)/цо] np exD f !!
(8.13)
- 1 < ,u < 0.
Если поверхность г — d сильно диффузна, так что отражен-
отраженная интенсивность почти равномерно распределена в пределах
телесного угла 2я, то к (8.9) нужно добавить диффузную интен-
интенсивность
-1<ц<0, (8.14)
где Rd — альбедо поверхности, определяемое отношением
nl'd/noFo. Эта ситуация часто встречается в случае песчаного
дна океана [76]. Заметим, что полная отраженная мощность
равна nl'd (интеграл от цГа по телесному углу 2я).
Рассмотрим теперь мощность, получаемую приемником с те-
телесным углом приема Дш = Д;г Д<?, где |До| «С 1. Если лучевую
интенсивность записать в виде
+ /d0i, ф), (8.15)
то принимаемая мощность Pr будет равна
ц,#, (8.16)
где ци^ ограничены интервалами
Но - Дц/2 < |1 < цо + Дц/2, ^ - А^/2 <Ф<фо + Д</>/2. (8.17)
При значениях ц и ф, лежащих вне интервалов (8.17), прини-
принимаемая мощность Pr равна Дю/Дц, ф).
8.3. Падение коллимированного пучка
на плоскопараллельную среду
В некоторых практических ситуациях падающую волну мож-
можно представить в виде узкого коллимированного пучка. Приме-
Примером может служить определение концентрации бактерий в жид-
жидкости с помощью лазерного луча [107, 141, 171]. Другой при-
пример—лазерный или высокочастотный ультразвуковой пучок в
океанской воде, содержащей органические и неорганические ча-
частицы [76].
Приближенные решения для разреженной среды
193
Рассмотрим коллимированный пучок с гауссовым изменением
интенсивности в плоскости, перпендикулярной к направлению
распространения. Предположим, что такой пучок падает нор-
нормально на плоскопараллельную среду (рис. 8.3).
Рис. 8.3. Падение гауссова
пучка на случайно распре-
распределенные частицы в слое
толщины d.
л
(x.O.z)
At
Лучевая интенсивность при 2 = 0 равна
(8.18)
где Wo — размер пучка1), a Fo — его интенсивность. Угловая
зависимость в (8.18) аппроксимируется дельта-функцией 8(ю).
Ниже будет показано2), что лучевая интенсивность есть фурье-
образ функции взаимной когерентности, и точная лучевая ин-
интенсивность коллимированного пучка дается выражением
(8Л9)
где 0 = arc cos s-z, a k = 2лД — волновое число. Более полный
анализ выражения (8.19) будет дан ниже. Однако на малых
расстояниях при z<nWo/X выражение (8.18) дает хорошее
приближение к (8.19), поэтому в данном разделе мы используем
(8.18).
Используя выражение (8.18), получаем следующее выраже-
выражение для ослабленной падающей интенсивности /г,-:
]н (г, s) = ^0 ехр (- ^ -
Й-
(8.20)
') Обозначение Wo для размера пучка не следует путать с альбедо оди-
одиночной частицы в G.22).
2) См. A3.8в) и разд. 14.7. Заметим, что W\ в (8.19) равно 2W2 в
A3. 8в).
194 Глава 8
Полная проходящая мощность при 2 = 0 дается выражением
оо оо
J dx 5 dy \d®Ir{(t, s) = jnWlF0. (8.21)
— оо — оо
Диффузную интенсивность легко вычислить, подставляя
(8.20) в (8.2). Например, величина ld+, показанная па рис. 8.3,
для точки (х,0,г) и направления @, 0) равна
U+ = \ ехр [- рог, (г - zi) sec В] (ig-) p @, 0; 0, 0) ^0 X
о
Xexpl-—l-po/Zllrfzisece, (8.22)
\ w0 /
где х\ = Хо + г1! tg 8. Этот интеграл можно выразить через функ-
функцию ошибок.
Это решение использовалось при определении концентрации
бактерий методом оптического рассеяния [107, 141].
Глава 9
Диффузионное приближение1)
В.гл. 8 мы рассмотрели приближение первого порядка теории
многократного рассеяния, применимое в случае разреженной
среды. В общем случае это приближение справедливо только
тогда, когда объемная плотность, равная отношению объема, за-
занятого частицами, к полному объему среды, значительно меньше
0,1%. Если же объемная плотность много больше 1%, то отно-
относительно простые п хорошие результаты даются диффузионным
приближением. При объемной плотности порядка 1% ни прибли-
приближение первого порядка, ни диффузионное приближение не мо-
могут быть справедливы, и нужно решать полное уравнение пере-
переноса. В данной главе мы рассмотрим вывод диффузионного урав-
уравнения из уравнения переноса, а также некоторые решения для
плоскопараллельной задачи. Диффузионное приближение с ус-
успехом использовалось для анализа волоконнооптических окси-
метров при исследовании крови [78, 79, 126].
9.1. Вывод диффузионного уравнения
Как мы уже указывали в разд. 7.4, интенсивность излуче-
излучения в случайно-неоднородной среде можно разделить на две ча-
части: ослабленную падающую интенсивность Iri и диффузную ин-
интенсивность Id. Для заданной падающей волны Л-,- легко вычис-
вычислить. Диффузная же интенсивность должна удовлетворять урав-
уравнению переноса [уравнение G.30)]
<11л(т, s) , i '\ . per/ Г /" "/\ , , ~/ч , , ,
— ds = — potld(r, s) + -~ ]p(s, s )/d(r, s')dco' +
4л
+ er/(r,s) + e(r, sO, (9.1)
где Zri — эквивалентная функция источников, связанная с ос-
ослабленной падающей интенсивностью 1,с.
гг1 (г, s) = Jg- \ р (I ?') 1ы (г, s') do/, (9.2)
4л
a e(r, s) —функция источников.
') Более подробное обсуждение диффузионного приближения см. в книгах
[11, 108].
196
Глава 9
В диффузионном приближении предполагается, что диффуз-
диффузная интенсивность встречает много частиц и рассеивается на них
почти равномерно во всех направлениях, поэтому его угловое
распределение почти изотропно (рис. 9.1). Но угловая зависи-
зависимость не может сводиться к константе, так как при этом поток
Fd обращается в нуль и распространение мощности отсутствует.
Поэтому диффузная интенсивность должна быть немного больше
Рис. 9.1. Диффузная интенсивность
ld (г, ?) в диффузионном приближении.
для направления полного потока, чем для обратного направле-
направления. Математически мы выразим это, предположив, что /<*(г, s)
аппроксимируется выражением
/Лг, i) « ?/Лг) + cFd(r) • i, (9.3)
где с — константа, Fd(r) —вектор диффузного потока, ориенти-
ориентированный вдоль единичного вектора S/ и определяемый выраже-
выражением
(9.4)
4л
а ?Лг(г)—средняя диффузная интенсивность, которая пропор-
пропорциональна плотности энергии G.7):
d(r,s)dc*. (9.5)
4л
Представление /<*(г, s) в виде (9.3) схематически изображено
на рис. 9.1. Константу с в (9.3) легко найти, заметив, что
Fa (r) = Fd (r) sf=\ld (r, s) s • sf rf©. (9.6)
4л
Подставляя (9.3) в (9.6), получаем с = 3/4л, поэтому диффу-
диффузионное приближение для диффузной интенсивности дается вы-
ражением
Ia(T,s) = Ud(r) + ~Fd(T)-s. (9.7)
Диффузионное приближение 197
Правую часть (9.7) можно рассматривать, как первые два члена
разложения /<* в ряд Тейлора по степеням s-s/, поэтому второй
член в (9.7) должен быть много меньше первого: Ua^> j F"d | -
Приступим теперь к выводу диффузионного уравнения, кото-
которое основано на приближении (9.7). Прежде всего проинтегри-
проинтегрируем (9.1) по всему телесному углу 4л и получим общее соотно-
соотношение, выражающее сохранение мощности G.28а):
div Fd (г) = - 4npoaUd (г) + 4npasUrt + Е (г), (9.8)
где Uri (г) = — \ 1Н (г, s) da и Е (г) = \ е (г, s) dco. Затем под-
ставим (9.7) в (9.1). В предположении, что фазовая функция
p(s, s') зависит лишь от угла между s и s', получим
s • grad Ud + j^s- grad (Fd ¦ s) ==
= — patUd — -^ patFd ¦ s + pasUd + -—¦ pat?d ¦ spi + eri + e, (9.9)
где е то же, что в (9.1), a pi дается выражением
p(s,sf)s-i'd<of (9.10)
4л
и описывает усредненное рассеяние вперед (s-s' > 0) за выче-
вычетом обратного рассеяния (s-s'-<0) для отдельной частицы.
Часто бывает удобно записывать р\ в виде р\ = W0\x; здесь
Wn — альбедо единичной частицы, ар, — средний косинус угла
рассеяния 8, даваемый выражением
Д - ( \ р (s, s') ц d^'\j( \ р E, I') йа'Л, (9.11)
где \i = cos 0 = s-s'. Заметим, что, поскольку фазовая функция
p(s, s') зависит лишь от угла рассеяния у, мы можем разложить
эту функцию в ряд по функциям Лежандра:
оо
р(в, s0= HwnPn(cosy), cosy = s-s', (9.12a)
причем pi выражается в виде
Р! = ^-, Д = р1/Го = Г1/ЗГо. (9.126)
Фазовую функцию часто можно аппроксимировать следую-
следующим выражением, включающим только Wo иД:
р (ц)=Г0A-Д2)A+Д2
198 Глава 9
Это формула Хени — Гринстейна, которая часто используется
при описании рассеяния на кровяных тельцах [125] и облаках
[38,65].
Умножим обе части (9.9) на s и проинтегрируем полученный
результат по полному телесному углу 4л ')
grad Ud = — -^ pa, (I — Pi) Fd +
+ A J ert (r, i) S dco + A J e (r, s) s rfco. (9.13)
4л 4л
Величина at A—Pi) называется транспортным сечением at,
[11]. Оно показывает, что если рассеяние анизотропно, то эк-
эквивалентное полное сечение уменьшается на множитель 1 — р\
по сравнению с изотропным случаем. Транспортное сечение
можно записать также в виде
a,r = a,(l-pi) = as(l-A) + ora. (9.14)
Как показано в C.33), с ростом плотности числа частиц экви-
эквивалентное сечение рассеяния уменьшается на множитель 1 — Я,
где Я— отношение объема, занимаемого рассеивателями, к пол-
полному объему. Это отношение, выраженное через плотность числа
частиц р и объем единичного рассеивателя Ve, равно величине
pVe, так что
as->as(l-H). (9.15а)
При этом транспортное сечение atr для среды с высокой плот-
плотностью определяется выражением
atr^as(l-H)(l-ix) + aa. (9.156)
Уравнение (9.8) выражает div Fd через Ud, а уравнение
(9.13)— grad Ud через Fd. Исключим Fd из этих двух уравнений,
выразив Fd из (9.13) и подставив его в (9.8). В результате по-
получим следующее дифференциальное уравнение для Ud-
(r) - Y?dUd (r) = - 39as9otrUrt (r) - ± 9atrE (r)
\ e(r,s)srfG), (9.16)
4л 4л
где %d = 3poapair При высокой плотности среды as и atr в
(9.16) определяются выражениями (9.15а) и (9.156). Уравнение
') Для любого вектора А имеем
s (s-A) doo = —- А и \ s [s • grad (,A-s)] с/со = 0.
4я 4я
Диффузионное приближение 199
(9.16) есть основное диффузионное уравнение в стационарном
случае ') для средней диффузной интенсивности Gd(r) и вместе
с граничным условием, которое мы рассмотрим в следующем
разделе, дает полное математическое описание диффузионного
приближения. Если диффузная интенсивность найдена, то поток
Fa можно вычислить с помощью (9.13).
9.2. Граничные условия
Точное граничное условие для диффузной интенсивности 1,<
состоит в том, что на поверхности рассеивающей среды диффуз-
диффузная интенсивность, входящая в среду снаружи, должна быть
равна нулю G.32):
/d(r, s) = 0 при s, направленном внуть среды. (9.17)
Но, согласно диффузионному приближению, /d(r, s) имеет
простую угловую зависимость, определяемую выражением (9.7),
Рис. 9.2. Направления п и s для гра-
граничного условия (9.18).
а в диффузионное уравнение входит единственная скалярная
функция Ud{r). Вследствие такого приближенного представле-
представления граничное условие (9.17) не может удовлетворяться точно,
и нужно рассмотреть некоторое приближенное граничное усло-
условие. Одним из таких приближений является условие, что на по-
поверхности среды полный диффузный поток, направленный
внутрь, должен обращаться в нуль:
Id (г, s) (s • п) da = 0, (9.18)
2л
где п — единичный вектор нормали к поверхности, направлен-
направленный внутрь среды, а интегрирование проводится по полусфере
sn > 0 (рис. 9.2).
Условие (9.18) может быть выражено через одну лишь сред-
среднюю интенсивность Ud- Для этого запишем сначала Yd в виде
') Уравнение диффузии, зависящее от времени, имеет вид DV2u — аи —
= du/dt, где D — коэффициент диффузии, а а описывает абсорбцию ([108],
разд. 2.4).
200 Глава 9
суммы нормальной (Fan) и тангенциальной (Fat) к поверхности
компонент:
р с п 4- f i ^Q ! Q^
4 a l dn i * at • \ • *-v
Подставим теперь (9.7) и (9.19) в (9.18) и выполним интегри-
интегрирование, используя сферическую систему координат с z = n и
х = t:
2л л/2
(Fdti • s) (s • n) da = Fdt^ ^ sin 9 cos ф cos 6 sin QdЪdф = 0,
: 0 0 /g 20)
2л л/2
{Fdnn • s) (s • n) dco == Fdn \ \ cos2 0 sin 0 fi?9 d^> = -^- F^.
2л 0 0
Тогда граничное условие (9.18) примет вид
-2^d(rs)-\ dl\ =0 на поверхности г = г5. (9.21)
Далее, выразим Fdn в (9.21) через Ud, используя (9.13):
Fdn = n-Fd = - ~- n • grad Ud (r) + п ¦ Q, (г), (9.22)
где
Qi (г) = —— \ [ег1 (г, s) + е (г, s)] s da.
tr 4л
В отсутствие источников e(r, s) =0, используя (9.2), запишем
Q, (г) = -р- [ da' \~ [p(s, s') s da lH (г, s'). (9.23)
ir 4л *- 4jt J
Заметим, что если рассеиватели изотропны, то p(s, s') = const,
и СЬ = 0. Поэтому Qi описывает влияние анизотропии на кар-
картину рассеяния.
Подставив (9.22) в (9.21), получим граничное условие, вы-
выраженное через Ud:
ЦАТ) - -UAr)+ 2"-Ql(r*} =Q (924)
где д/дп — нормальная производная по направлению внутрь
среды.
Следует подчеркнуть, что граничное условие (9.24) является
лишь приближенным. Фактически диффузионное приближение,
как известно, само по себе справедливо лишь для области, до-
достаточно удаленной от границ и источников. Можно получить
некоторое представление о том, насколько приближенным яв-
Диффузионное приближение 201
ляется граничное условие (9.24), сравнив его с точным гранич-
граничным условием для частного случая. Такое сравнение можно про-
провести для задачи изотропных рассеивателей, для которой в слу-
случае полубесконечного слоя известно точное решение. Эта задача
известна под названием проблемы Милна. Точное решение ее
¦ можно разделить на две части, одна из которых удовлетворяет
диффузионному уравнению (разд. 12.2 и 12.6). Эта часть удо-
удовлетворяет граничному условию
справедливому с точностью до 0,7% в случае, когда альбедо
Wq — os/ot заключено в интервале 0,6 ^ Wo ^ 1. Заметим, что
для изотропных рассеивателей Q, = 0, а константа 2/3patr в
(9.24) сводится к 2/Зра*. Эту константу нужно сравнить с вели-
величиной 0,7104/pcr(W0 в (9.25). Ясно, что множитель 2/3 в (9.24)
нужно рассматривать лишь как некоторое приближение и что
решение в диффузионном приближении должно быть справед-
справедливо, только когда альбедо Wo близко к единице и частицы в
основном рассеивают, а не поглощают.
9.3. Падение коллимированного пучка на слой
рассеивающих частиц
В качестве примера применения диффузионного уравнения
рассмотрим случай коллимированного пучка, падающего нор-
нормально на слой со случайными частицами (рис. 9.3).
Падающий
пучок-
Рис. 9.3. Падение коллимирован- *
ного пучка на слой со случайно ~7
распределенными рассеивателями. ~7
о о
о
Рассмотрим прежде всего диффузионное уравнение (9.16).
Ослабленная падающая интенсивность для коллимированного
пучка, изображенного на рис. 9.3, дается выражением (разд. 8.3)
Irl (r, s) = Fo (Р) ехр (- patz) б (« - ю,), (9.26)
где Fo(p) — плотность потока G.33), р = хх -4- уу, © и ©2 — еди-
единичные векторы в направлениях s и г соответственно, а
202 Глава 9
8 (to—©г)—дельта-функция по телесному углу. При этом дру-
другие источники излучения в среде отсутствуют. Поэтому ?(г)= О
и e(r, s) =0. Подставив (9.26) в (9.2) и (9.8), можно выразить
член с источниками в правой части (9.16) через Fa. Заметим,
что
p
(9.27)
V- ^eri(r,s)sd(a ¦=]—- \p(s, z)sdoA ¦ V[F0(p)exp(— patz)\ =
= — (patJ piF0 (p) exp (— patz),
где учтено, что вектор \ р (s, г) s dec направлен вдоль оси г.
Подставив (9.27) в (9.16), получим следующее диффузион-
диффузионное уравнение, применимое к случаю коллимированного падаю-
падающего пучка:
\Юй (г) - **Ud (г) = - Q (г), «| = 3 (pcrfl) (9atr),
Q (г) = [3paspotr + 3pospotii] -~- exp (— patz).
Граничные условия для слоя, показанного на рис. 9.3, даются
выражением (9.24), которое можно записать в форме
Ud(r)-h-^Ud(r)+^ = 0 при 2 = 0,
(9 29)
Ud(r) + h~Ud(r)-\^-^0 при z==d,
где h = 2/3patr и Qi (r) = (ст5р./а/г) Fo (p) ехр(—ра<г).
Если средняя диффузная интенсивность Ud(r) найдена, то
поток и диффузную интенсивность можно найти из (9.13) п
(9.7):
Fd (г) = ^Р^(Р) ехр (- р аг2) z - ^- grad Ud (r). (9.30)
Для среды с высокой плотностью as и а<г в (9.28) — (9.30) нужно
заменить на соответствующие величины, согласно (9.15а) и
(9.156).
9.4. Решение для случая плоской волны,
падающей на слой рассеивающих частиц
Случай плоской волны, падающей на слой рассеивающих ча-
частиц, можно проанализировать в рамках теории, развитой в пре-
предыдущем разделе. Для плоской волны Fo(p) в (9.26) переходит
Диффузионное приближение 203
в константу Fo, a (9.28) дает
^ patz), (9.31)
где Qq = [3pGspotr + 3pcspatfi]Fo/4n. Граничные условия (9.29)
принимают вид
Ud(z)-h^7Ud(z) + ~~ = 0 при 2 = 0,
а п i \ (9-32)
Ud(z) + h-gUd(z)-±^ = 0 при z = d,
где Qi (г) = (os\\/oir)F0exp{—potz) и А = 2/Зра/г. Общее решение
(9.31) есть сумма частного решения Уф и решения однородного
уравнения Udc- Для того чтобы найти частное решение, поло-
положим
-patz). (9.33)
Подставляя (9.33) в (9.31), находим
А = — Q0/[(pc>;J — %й\ (9.34)
Величина Ujc удовлетворяет однородному уравнению
" TJ „111 Л (Q 'ЗГЛ
дг2 dc Kdudc~v' {У.оО)
так что
Udc (z) = С\ exp bidz) + С2 exp (— y-dz), (9.36)
где С\ и C2 — неизвестные постоянные, которые определяются
с помощью граничных условий (9.32). Подставляя Ua{z) =
= Udp(z)+ Udc(z) в (9.32), получаем два уравнения для двух
неизвестных С\ и С^.
С, A - %dh) + С2 A + Kdh) = - Л A + ра;Л) - -^ ,
(9 37)
Cj A + Kdh) exp (xdrf) + C2 A — xdA) exp (— %dd) =
= - A (j - pcrtA) exp (- potd) + ^- exp (- patd).
Отсюда легко найти Ci и С2.
Можно показать, что в случае полубесконечной среды
(d->oo) выполняются соотношения
Ud {z) = Л exp (— patz) + C2 exp (— %dz).
204 Глава 9
Поток Fd(z) можно вычислить из (9.30). Более того, если рас-
сеиватели не поглощают, то аа -> 0 и
Fd (г) =—F0 exp (- potz) z. (9.39)
Это показывает, что в непоглощающей полубесконечной среде
диффузный поток Fd равен по величине и противоположен по
направлению ослабленному падающему потоку Fri(z) =
= Foexp(—potz)z. Физически это означает, что, хотя падающий
поток Fo и диффундирует в среде, в конечном итоге весь поток
Fo рассеивается обратно и возвращается в направлении —г.
В случае полного отсутствия потерь ка = 0, и (9.35) пере-
переходит в уравнение Лапласа
-^Udc = 0. (9.40)
При этом вместо (9.36) решение можно записать в виде
(9.41)
Используя граничные условия (9.32), легко найти отсюда реше-
решение для непоглощающих рассеивателей.
9.5. Решение для случая коллимированного пучка
конечной ширины, падающего на слой
рассеивающих частиц
Общее решение (9.28) и (9.29) может быть получено с по-
помощью функции Грина G(r, г'), удовлетворяющей условиям
V2G(r, r')-%dG(r, г') = -в(г, г'),
G(г, r')-h~G(г, г') = 0 при 2 = 0, (9.42)
G (г, г') + h -r— G (г, г') — 0 при z = d.
Используя вторую формулу Грина
а, (9.43)
где д/дп — производная в направлении внешней нормали, можно
получить полное решение ?/<*:
(г) = J G (г, г') Q (г') dV + \ G(r'2hl{rr) da'>
V
Ud
где объем V ограничивается условиями 0 ^ z ^ d и
— со ^ х, у ^ + °°- Функция Грина в цилиндрической системе
Диффузионное приближение 205
координат с г и г', выраженными через (р, ф, z) и (р', ф', г') со-
соответственно, имеет вид [101]
оо оо
Q (г, г0 = ? ?
«Р [/«(«-«01 J
^ ^ (яр) ^ (яр)
m--con.l Л п (945)
для р > р'. Для р < р' нужно поменять местами р и р' в (9.45).
Здесь Km и /т — модифицированные функции Бесселя [75],
a ZnB)—собственная функция, удовлетворяющая граничному
условию (9.42) и имеющая вид
' Zn(z) = sm(knz + yn), (9.46)
где собственное значение kn удовлетворяет уравнению
tgknd = 2hkj[(hkn)*-l], (9.47)
а уп = arctg (hkn) ¦ Нормировочный множитель N2n равен
d
Nl=\(Zn(z)fdz, (9.48)
о
а Хп связано с kn соотношением
К = % + *1- О-49)
Подставив теперь (9.45) в (9.44), мы получим окончательное
решение. Если коллимированный пучок симметричен относитель-
относительно оси z, то Fo (p) становится функцией только от модуля р. При
этом Ud не зависит от ф, так что
Ud (p, z) = 2я \ р' dp' \ dz'Gu (p, z; p', z') Q (р', г') +
о о
оо
+ \ \ р' ф'Со (р, г; р', 0) Q, (р', 0), (9.50)
где
Go(p, 2; р', /) = ? Z*(fy
при р > р'; при р <С р' нужно поменять местами р и р'.
Решение, кратко описанное в данном разделе, использова-
использовалось при определении диффузионных характеристик крови [78,
79, 126] (об отражении света от крови см. [4]). На основе этой
206 Глава 9
теории была построена модель волоконнооптического катетера,
используемого для спектрофотометрических измерений содер-
содержания кислорода (насыщения кислородом) в крови. Теория
сравнивалась с данными по отражению в катетерах при физио-
физиологических вариациях в крови НЬСО, НЬО2 и гематокрита. При
этом наблюдалось превосходное согласие предсказаний теории
с результатами эксперимента, подтверждающее правильность
теоретического подхода, развитого в данной главе [125].
9.6. Диффузия от точечного источника
Рассмотрим диффузию мощности от точечпою источника,
локализованного в начале координат в неограниченном про-
пространстве, содержащем случайные рассеиватели, и излучающего
полную мощность Л), которая распределяется равномерно по
всем направлениям. Соответствующий такой постановке задачи
источник, согласно G.35), описывается функцией
е(г, s) = -g-e(r). (9.51)
Диффузионное уравнение (9.16) принимает вид
Wd (г) - *lUd (r) = -~ рст,гР0* (г), (9.52)
а решение дается выражениями
[^4 (9.53)
(9.54)
Заметим, что в случае непоглощающих рассеивателей %а = 0,
и полный поток 4nr2Fd через сферическую поверхность радиуса г
не зависит от г и равен Ро, как это и должно быть в соответствии
с законом сохранения энергии.
9.7. Измерение отражения с помощью
двух волоконных световодов
Для измерения относительной отражательной способности в
случае однородной среды с дискретными рассеивателями была
сконструирована двухволоконная кювета ([125], см. также
табл. 3.2, где приведены некоторые характеристики крови). Та-
Такая кювета использовалась с целью получения данных для про-
Диффузионное приближение
207
верки описанной в разд. 9.5 теории, на основе которой строится
модель волоконнооптического катетера. Кювета состоит из двух
параллельных оптических волокон: неподвижного излучающего
Излучающее
волокно
Эритроциты
IP О
О
Рис. 9.4. Измерение отражения
двумя волоконными световодами
Принимающее
волокно
О О
О
волокна диаметром 0,508 мм, которое контактирует с поверх-
поверхностью рассеивающей среды по нормали к ней, и принимающего
600
Л
Н
О
I 500
О
и
о
5 400
I зоо
н
X
S.200
с
к
= 100
о 40
20 -
ч
—1—1 i I- * i
0,15 0,30 0,45 0,60 0,75
Гематокрит Н
Рис. 9.5. Сравнение теории с экспериментальными результатами для отра-
отражательной способности цельной крови человека как функции гематокрита
для шести различных расстояний между волокнами при длине волны Я =
= 0,685 мкм и насыщении кислородом 98,5%. Радиальные расстояния между
волокнами (сверху вниз) 0,54, 0,74, 0,90, 1,27, 1,66 и 2,85 мм.
волокна диаметром 0,127 мм, которое также контактирует с рас-
рассеивающей средой, но может непрерывно смещаться вдоль ра-
радиуса на расстояние ±5 мм относительно центра излучающего
208
Глава 9
волокна. Как излучающая, так и принимающая апертуры во
время измерений остаются в одной плоскости (рис. 9.4).
На рис. 9.5 теоретические значения, вычисленные на основе
развитой в разд. 9.5 теории и характеристик крови из табл. 3.2,
сравниваются с данными эксперимента. Из рис. 9.6 видно, что
при расстоянии между катетерами примерно 0,9 мм отражатель-
отражательная способность не зависит от изменений плотности в пределах
460
400
360
300
240
180
120
О 60
0,59
0,5 1,0 1,5 2,0 2,5 3,0
Радиальное расстояние между волокнами, мм
Рис. 9.6. Сравнение диффузионной теории с экспериментальными результа-
результатами (точки) для отражательной способности цельной крови человека как
функции расстояния между волокнами при трех значениях гематокрита при
длине волны X = 0,685 мкм и насыщении кислородом 98,5%.
от Н = 0,22 до Н = 0,59. Это наводит на мысль, что если во-
волокна фиксировать в оксиметрическом волоконнооптическом ка-
катетере на определенном расстоянии друг от друга, то можно
исключить влияние изменений гематокрита на измерения насы-
насыщения кислородом.
9.8. Волоконнооптический оксиметрический катетер
Волоконнооптический катетер [125] облучает кровь светом,
передаваемым на дальний конец катетера при помощи оптиче-
оптических волокон (рис. 9.7). Свет рассеивается обратно красными
кровяными тельцами, находящимися вблизи дальнего конца ка-
Диффузионное приближение
209
тетера, и передается по второму пучку оптических волокон на
другой конец катетера для определения насыщения крови кис-
кислородом. Кольцевая конфигурация волоконного катетера, пока-
- Передающие волокна
Принимающие и передающие волокна
измерительного конца
-Принимающие волокна
Рис. 9.7. Схема устройства волоконнооптического катетера.
Рис. 9.8. Кольцевая конфигурация катетера. Черные волокна излучают на
длине волны 0,686 мкм, заштрихованные — на длине волны 0,925 мкм, свет-
светлые волокна принимают отраженное излучение.
занная на рис. 9.8, состоит из чередующейся последовательности
оптических волокон. Четвертая часть всех волокон излучает свет
с длиной волны «0,9 мкм, другая четвертая часть — свет с дли-
длиной волны 0,68 мкм; половина волокон используется для приема.
210
Глава 9
Измерение отношения интенсивностей обратного рассеяния на
двух длинах волн, одна из которых более чувствительна к насы-
насыщению кислородом @,6—0,7 мкм), а другая @,8—0,9 мкм) —
относительно нечувствительна, исключает влияние изменений рН
и скорости потока крови, которые приблизительно одинаково
влияют на отражательную способность крови на обеих длинах
волн.
1,0
0,8
0,6
0,4
0,2
1,0
2,0 3,0 4,0
R @,925мкм)
R @,685мкм)
Рис. 9.9. Зависимость на-
насыщения кислородом от от-
отношения отражательных
способностей при длине вол-
волны 0,925 мкм и при длине
волны 0,685 мкм. Черные точ-
точки — диффузионная теория,
светлые — эксперименталь-
экспериментальные данные.
Побудительная причина для построения модели волоконно-
оптического катетера состоит в необходимости получения теоре-
теоретического критерия для конструирования конфигурации волокон
в измерительном конце катетера, который будет использоваться
для определения насыщения крови кислородом. Насыщение кис-
кислородом OS определяется отношением количества оксигемогло-
бпна к количеству всего гемоглобина. Эмпирически установлено
следующее выражение для насыщения крови кислородом через
инфракрасную отражательную способность Ri и отражательную
способность в красной области спектра Rr:
OS = A-
(9.55)
где Ri и Rr — интенсивности обратного рассеяния для длин волн
0,960 и 0,685 мкм соответственно, а постоянные А и В (завися-
Диффузионное приближение 211
щие от геометрии пучка волокон) и параметры крови могут быть
определены эмпирически. Таким образом, для различных кон-
конфигураций постоянные А и В различны, и для точной клиниче-
клинической проверки in vivo работоспособности волоконнооптического
оксиметра при каждой конфигурации волокон необходима ка-
калибровочная кривая. Такая кривая изучалась многими исследо-
исследователями. На рис. 9.9 сплошной линией показана' калибровочная
кривая, полученная теоретически для модели катетера, а точки
соответствуют экспериментальной калибровке катетера.
Глава 10
Двухпотоковая и четырехпотоковая теории
В теории переноса волна, распространяющаяся в облаке слу-
случайных частиц, описывается лучевой интенсивностью /(г, s),
которая в общем случае зависит от положения г и направления s
в трехмерном пространстве. Однако в задачах, связанных с нор-
нормальным падением плоской волны на плоскослоистую случайно-
неоднородную среду, лучевая интенсивность является функцией
одной пространственной переменной z и угла 0 : / = f(z, 0). Об-
Общее замкнутое решение при произвольной фазовой функции
даже в этом простом случае не найдено. Как описано в гл. 11,
для решения общей задачи с успехом используется метод раз-
разложения в ряд, и этот метод дает результат, сходящийся к точ-
точному решению при увеличении числа членов разложения. Од-
Однако такой подход при достаточно большом числе членов раз-
разложения требует значительных затрат машинного времени. Вме-
Вместо метода разложения в ряд ранее широко использовались ме-
методы, известные под названием двух- и четырехпотоковой теорий.
Они не требуют ничего, кроме простых алгебраических операций,
и, как было показано, дают сравнительно хорошее согласие с
экспериментом. Недостатки этих методов состоят в том, что
некоторые коэффициенты приходится определять эмпирически,
границы применимости недостаточно хорошо установлены и нет
полного теоретического обоснования [25, 58, 91, 92, ПО, 124].
10.1. Двухпотоковая теория Кубелки и Мунка
В 1931 г. Кубелка и Мунк разработали теорию, основанную
на модели двух световых потоков, распространяющихся в пря-
прямом и обратном направлениях. Впоследствии многие авторы
улучшали эту теорию и сравнивали ее выводы с данными экспе-
эксперимента. Было найдено, что двухпотоковая теория хорошо опи-
описывает экспериментальные результаты, если освещение диффуз-
но и среда достаточно замутнена, так что свет рассеивается
диффузно. Двухпотоковая теория неприменима для описания
падающего на среду коллимированного пучка. В этом случае
следует использовать четырехпотоковую теорию (разд. 10.3).
Рассмотрим диффузные потоки F+(z) и F-(z), распростра-
распространяющиеся в положительном и отрицательном направлениях оси г
Двухпотоковая и четырехпотоковая теории
213
соответственно. Внутри бесконечно малого элемента dz поток п
положительном направлении F+ уменьшается вследствие погло-
поглощения и рассеяния в обратном направлении (рис. 10.1):
dF+ = -(K + S) F+pat dz=-(K + S) F+ dx, A0.1)
где p — число частиц в единице объема, at — полное сечение для
отдельной частицы, Kot — эффективное сечение поглощения для
F+, К — безразмерный коэффициент поглощения, а т = patz —
оптическая длина. На первый взгляд можно подумать, что Kot
равно сечению поглощения частицы оа. Однако это не так, по-
поскольку Kot описывает поглощение диффузного потока F+ и от-
отличается от сечения поглощения аа, определенного для случая
Рис. 10.1. Потоки в прямом и
обратном направлениях Р+ и F_,
Коэффициенты К и S описывают
поглощение и рассеяние.
F++dF+
ft-O)
(Т) (X + dT) (Т-Т0)
падения плоской волны. В действительности, как будет показано
ниже, Kot приближенно равно 2оа. Можно также было бы поду-
подумать, что Sat равно сечению обратного рассеяния as_, которое
представляет собой интеграл от дифференциального сечения по
телесному углу 2я в обратном направлении. Хотя произведение
Sot каким-то образом связано с as~, его величина зависит еще и
от того, что F+ есть диффузный поток. Как видно из приведен-
приведенных соображений, величины К и S не связаны явно с физиче-
физическими параметрами отдельной частицы, и в этом состоит одна
из слабостей рассматриваемой теории. В разд. 10.2 мы попы-
попытаемся связать эти коэффициенты на основе точной формули-
формулировки уравнения переноса излучения. Однако в данном разделе
мы будем трактовать К и S как коэффициенты поглощения и
рассеяния, которые нужно определять экспериментально.
Поток F+ уменьшается согласно A0.1), но одновременно его
величина возрастает из-за вклада от обратного рассеяния по-
потока F- (рис. 10.1). Поскольку этот вклад описывается тем же
коэффициентом обратного рассеяния S, имеем
dF+ = SF_patdz = SF_dx. A0.2)
Аналогично F- уменьшается на величину
dF_ = -(K + S) F_pat (- dz) = (K + S) F_ dx
и возрастает на величину
dF = SF+pot (— dz) = — SF+ dx.
214 Глава 10
Отсюда получаем два связанных дифференциальных уравнения:.
+ SF_, ^ = (K + S)F_-SF+. A0.3)
Решения уравнений A0.3) получаются ') в предположении
экспоненциальной зависимости от т(-~ехр(ат)) потоков F+ и
F... Тогда d/dx = а, и из A0.3) мы получаем
[а + (К + S)} F + - SF_ = 0, SF+ + [a-(K + S)]F_ = 0. A0.4)
Для получения ненулевых решений F+ и F_ нужно приравнять
нулю определитель, составленный из коэффициентов уравне-
уравнений A0.4):
а + (К + S) -S
S a-iK +
откуда получаются два значения а:
а± = ± VК (К + 25) = ± ао. A0.6)
При каждом значении а отношение F-/F+ дается одним из урав-
уравнений A0.4):
л ^ F~ .--
+ F+ "
для а+, A0.7)
А_=-~ = ~з— для а_.
F+ А+
Полные выражения для F+ и F- являются линейными комбина-
комбинациями двух решений для а+ = ао и а_ = — «о:
F+(x) = Clea+x + C2ea-\ F_ (т) = С,Л+еа+т + С2А_еа-\ A0.8)
где d и С2 — неизвестные коэффициенты, которые определяются
из граничных условий.
Простейшие граничные условия следующие: при т = 0 по-
поток в положительном направлении F+ равен падающему потоку
/•"о, а при т = то падающий на слой поток в обратном направле-
направлении Т7- отсутствует:
F+@) = F0, /г_(то) = О. A0.9)
Подставляя A0.8) в эти два граничных условия, получаем
С[ А- ехр (а-Тр) С2 А+ ехр (а+т0)
Fo~ Д ' F0 ~ Д ' A0Л0)
А= Л_ехр(а_т0) — Л+ехр(а+т0).
') Общая методика, использующая собственные значения и собственные
векторы, изложена в разд. 11.4.
Двухпотоковая и четырехпотоковая теории
215
Коэффициент отражения R при т = 0 дается выражением
1 — ехр (— 2аит0) ~|
A0.11)
а коэффициент пропускания Т при т = то — выражением
F, (т0) (l — A2J\ ехр (— аото)
Т _ — — = d ехр (аото) + С2 ехр (— аото) = -2 — ,
Fo 1-л_ ехр(-2а0т0)
A0.12)
где А- определяется из A0.7):
Л_ = SftK + S + ао). A0.13)
Если среда полубесконечна (то-> °°), то С\ = 0, С2 == Fq и
Отсюда видно, что поток в положительном направлении F+
уменьшается с увеличением г, а поток в отрицательном направ-
Рис. 10.2. Потоки в прямом р \—N
и обратном направлениях +
для случая иолубесконечной
среды.
лении F- возрастает с уменьшением г. Полный поток в поло-
положительном направлении есть F+(x)—F-{%) (рис. 10.2).
Граничные условия A0.9) не учитывают отражения на гра-
границах при т = 0 и т = то. Отражение можно учесть следующим
Рис. 10.3. Отражение и прохождение
на границах.
R2F+
т=0 т=т0
образом. Пусть- /?,¦ — коэффициент отражения падающей волны
при т = 0, Ri — коэффициент отражения для потока F-, падаю-
падающего справа на поверхность т = 0, a R2 — коэффициент отра-
отражения для потока F+, падающего слева на поверхность т = то
(рис. 10.3). Тогда граничные условия имеют вид
F @) = A— RiJFq-t- R{F_@) при т = 0,
_„ A0.15)
216 Глава 10
Подставляя A0.8) в A0.15), получаем
С, _ (А- - R2) exp (а-т0)
(l — Rt)Fa A
Сг _ (А+ - Ri) exp (а+то) A0.16)
(l-Ri)Fo Д
Д = A - Я, А+) (Л_ - Я2) exp (а_т0) - A -Я, Л_) (Л+ - Я2) exp (а+т0).
Коэффициент отражения при т = 0 равен
Rs= t (ШЛ7)
а коэффициент пропускания при т = to равен "
T = (l-R2)F+(r0). A0.18)
10.2. Коэффициенты К и 5 в двухпотоковой теории
Формулировки, приведенные в предыдущем разделе, осно-
основаны на упрощенной модели, которая предполагает наличие
лишь двух потоков F+ и f_, связанных посредством коэффи-
коэффициентов К и S. Предпринимались попытки экспериментально
связать эти коэффициенты с характеристиками отдельной ча-
частицы. Оказалось [110], что произведение Kot всегда близко
к удвоенному сечению поглощения оа, a Sat близко к
z/iWo— XI\W\, где Wo — альбедо, a W\ — первый коэффициент
разложения фазовой функции р(ц, ф; \i, <f>'):
2я 2я
n=0
где Pn(v) —функции Лежандра степени п.
Как показано в приложении 10. А, двухпотоковые уравнения
A0.3) можно вывести из уравнения переноса. Однако коэффи-
коэффициенты в получаемых таким образом уравнениях непостоянны,
а зависят от угловых характеристик лучевых интенсивностей.
Более того, коэффициенты К и S первого уравнения A0.3) ока-
оказываются отличными от коэффициентов К и S второго урав-
уравнения. Эти коэффициенты становятся постоянными, если пред-
предположить, что лучевые интенсивности полностью диффузны и
Двухпотоковая и четырехпотоковая теории 217
почти изотропны (не зависят от направления). В этом случае
имеем
A0.20)
= W0- Z WaCl, A0.21)
п нечетно
где величины Сп равны 1/4, 1/64, 1/256, .. . для п = 1, 3, 5, ...
(приложение 10А). Выражение A0.20) согласуется с экспери-
экспериментальными данными [ПО] и с теоретическими предсказа-
предсказаниями Кубелки [91], однако A0.21) слегка отличается от экс-
экспериментального значения 3/41^о — l/iWi [НО].
Поучительно сравнить постоянную поглощения ао, даваемую
выражением A0.6), с постоянной поглощения Xd в диффузион-
диффузионной теории (9.16):
A0.22)
Заметив, что Д = W\/3Wo, получим
^]}*. A0.23)
Экспериментальное значение 3/^W0 — XI*W\ [ПО] дает
«о = {(ajat) [3 Wo - W, + 4ajat] }''\ A0.24)
Если использовать S = Wo — 'A^i из (Ю.21), то мы получим
«о - (ojot) \4W0 - Wl + 4aa/at] }Vl. A0.25)
Выражения A0.23) — A0.25) близки, но не тождественны. Это
указывает на то, что двухпотоковая теория оказывается близкой
к диффузионной теории, если лучевые интенсивности почти пол-
полностью диффузны, однако связать коэффициенты из этой теории
-с характеристиками отдельной частицы сложно, и их необхо-
необходимо определять экспериментально. Отсюда следует также, что,
даже если эти коэффициенты измерены для некоторого опреде-
определенного значения плотности рассеивателей, они оказываются не-
непостоянными, и их значения могут быть различными для разных
плотностей.
10.3. Четырехпотоковая теория
Описанная в предыдущих разделах двухпотоковая теория
применима только к распространению диффузных интенсивно-
стей. Но во многих современных приложениях источники излу-
излучают коллимированные пучки света с узкой спектральной поло-
218 Глава 10
сой. Если падающая волна коллимирована, то вследствие силь-
сильного различия характеристик диффузного и коллимированпого
излучения распространение света нельзя уже описывать только
двумя диффузными потоками. Интенсивность коллимированного
пучка ослабляется из-за рассеяния и поглощения частиц в среде
(она называется «ослабленной падающей интенсивностью»).
Часть мощности коллимированного пучка, рассеянная частицами,
распространяется но всех направлениях п соответствии с харак-
характером индикатрисы рассеяния частицы (она называется «диф-
«диффузной интенсивностью»). В четырехпотоковои теории перенос
интенсивности описывается прямым и обратным коллпмпровап-
нымп потоками и прямым и обратным диффузными потоками.
Коллимпрованные потоки, характеризуемые ослабленными пп-
тепсивностямн, затухают из-за поглощения и рассеяния и, не-
непрерывно рассеиваясь, преобразуются в диффузные. С другой
стороны, диффузные потоки ослабляются из-за рассеяния и по-
поглощения, но увеличиваются из-за трансформации коллимиро-
коллимированного потока в диффузный. Очевидно, что диффузные потоки
не могут преобразовываться в коллнмироваппые.
Основываясь на высказанных соображениях, получим диф-
дифференциальные уравнения четырехпотаковой теории. Пусть Fc+
и Fc-—прямой п обратный коллимированные потоки соответ-
соответственно, a F+ и F- — прямой и обратный диффузные потоки.
Коэффициенты К и S для диффузной интенсивности определены
в предыдущих разделах. Введем еще коэффициент поглощения
коллимированных пучков k, коэффициент рассеяния коллимн-
рованного пучка в диффузное излучение того же направления
Si и коэффициент рассеяния коллимированного пучка в диффуз-
диффузное излучение обратного направления S2. Пользуясь этими оп-
определениями, нетрудно записать систему связанных уравнений
для четырех потоков (рис. 10.4):
-^^= — (a +b)t+ + bt_ + i1/*c+ + 52rc_, A0.26)
Решение этой системы находится так же, как в двухпотоковой
теории, и имеет вид
, A0.27)
С2А2е-а * + С3Л3еал + С4В4е^,
Двухпотоковая и четырехпотоковая теории
219
где С\, Сг, С3 и С4 — неизвестные постоянные, а
К = k + Si + S2, ao = [K(K + 2S)]%,
А =В = ¦S<Sa+ (К + -S+ Я) St д =в = 55, + (K + .S-A)S2
. 1 К + 2S - а0
Л2 Л3 ~ К + 2S + а0 •
Граничные условия в четырехпотоковой теории можно сфор-
сформулировать аналогично A0.15). В результате получим
Fc+ @) = TtF0 + №- @),
F+ @) = T2F0 + R2FC_ @) -f R3F_ @) (т = 0), A0.28)
^с_ (т0) = #4^+ (то), /*"_ (t0) = R5FC+ (tu) -f /?6/7+ (t0) (t = T0).
Смысл постоянных Tl,T2,Ri, ..., /^ понятен из рис. 10.5. Че-
Четыре условия A0.28) необходимы и достаточны для определения
четырех неизвестных коэффициентов С\, С2, С$ и С4 в A0.27).
Г,
R
т = о
¦к
Рис. 10.4. Четырехпотоковая теория. Рис. 10.5. Граничные условия в четы-
четырехпотоковой теории.
Четырехпотоковую теорию можно сравнить с теорией пере-
переноса излучения следующим образом. Разделим лучевую интен-
интенсивность / на коллимированную интенсивность /с и диффузную
интенсивность Id- Коллимированная интенсивность имеет вид
1С (т, ц) = Fe+ (т) б (ii - 1) + Fe_ (т) б (ii + 1) A0.29)
и удовлетворяет уравнению
Подставляя A0.29) в уравнение переноса и учитывая A0.30),
получаем
die г 1 1
A0.31)
220 Глава 10
Уравнения A0.30) и A0.31) можно записать в виде A0.26) и
идентифицировать коэффициенты так же, как показано в прило-
приложении 10А. Если принять, что /+ и /_ не зависят от \х, то о коэф-
коэффициентах Л и S можно сделать те же выводы, что и в A0А.7)
и A0А.8). Можно также записать
о
(х, 1), S2 = y \ d\x,pQ{\i, 1), A0.32)
о -1
Si + S2 = Wo и k + Si + Si = 1. Таким образом, k = 1 — Wo
и kot = Oa- Используя разложение A0.19), можно записать
/t нечетно /г нечетно
где Сп дается выражением A0А.9).
Двух- и четырехпотоковая теории нашли широкое примене-
применение в лакокрасочной и бумажной промышленности [110] и при
оптическом определении содержания кислорода в крови [79].
Приложение 10А
В данном приложении мы выведем коэффициенты К и 5 из
теории переноса излучения. При этом полученные результаты
будут иметь интегральный вид и включать неизвестную угловую
зависимость лучевых интенсивностей. Поэтому их нелегко ис-
использовать для вычисления коэффициентов /( и S, однако они
поясняют смысл этих коэффициентов.
Запишем уравнение переноса для плоскопараллельной гео-
геометрии (разд. 11.1) с учетом того, что Fo = 0:
-1
Рассмотрим теперь лучевую интенсивность в положительном на-
направлении /+(т, ц) и лучевую интенсивность в отрицательном
направлении /_(т, (д.):
/(т, [л,) для ц > 0,
0 для (х < 0,
.0 для ц >0,
! (т, ц) для ц < 0.
Двухпотоковая и четырехпотоковая теории 221
Запишем A0А.1), используя /+ и /_, в виде двух уравнений:
1
= - /+"+ j S Ро (I*. 1*0 /+ (т, ц') ф'
о
о
(И, ц') /_ (т, ц7) й?ц' (ц > 0), A0А.З)
+ J
-1
1
И1 IP
-^г = — /- + г- j Ро (ц. ц') '+ (*> м-') 4".' + ¦
о
о
j\po (ц, цО /_ (т, ц') <V (и > 0). A0А.4)
Для того чтобы преобразовать A0А.З) и A0А.4) в уравнения
для потоков, проинтегрируем A0А.З) по \i от 0 до 1, а A0А.4) —
от —1 до 0. Замечая, что поток F+ в положительном направле-
направлении и ноток F- в отрицательном направлении определяются вы-
выражениями
1 0
/7+ = 2я\/+(т, ix)\i,dyi, F- — -—2n \ /_ (т, \х)\лй\и, (ЮА.5)
о -1
преобразуем A0А.З) и A0А.4) к виду, соответствующему двух-
потоковой теории:
Ц±- = - (К + S'), F+ + S[F_, ^~ = (К + S')a F- - 52F+,
A0А.6)
где
1 1 1
Sir г
/+ (т, ц) йц — — \ d\i. \ rffi'po (ti. i1') 1+ (т, W)
1
0
0
I \ d
— 1
\
H'Po
1+
(M
(т.
x')
/-(T,
- J /- (T, |i) I* <
222 Глава 10
О 0 0
\ /- d\i — — I rffi \ rff-i'po (И. И') I-
(К + 5'J = о ,
— \ /_Ми
-1
о 1
I f , f ,, ,
¦Tj- \ ац \ d\i р0 (ц, (i ) / f
р/ -1 0
\ /+ц dpi
о
Очевидно, что эти коэффициенты непостоянны и зависят от
угловых характеристик /+ и /_. Более того, в общем случае в
A0А.6) (K + S')i и Si не равны (K + S'J и 52. Однако эти
коэффициенты становятся постоянными, если волна полностью
диффузна. В этом случае /+ и /_ становятся функциями только
от т и не зависят от угла ц, причем (/C + S')i= (/( + S'J и
Si = S2 и выполняются соотношения
/ JS _|_ О/\ О/ Z^* О /1 TW" \ /1 Л Д у\
0 1
с с
S'i = S2 — S= \ d\i \ dix'po (\и, (д.7). A0А.8)
Соотношение A0А.7) было выведено Кубелкой [91]. Оно экви-
эквивалентно условию Кох = 2оа и подтверждает известный экспе-
экспериментальный результат для диффузного света. Соотношение
A0А.8) при учете разложения A0.19) принимает вид [101]
оо
S=W0~ Z WnCl
ra=l
п нечетно
„ (ц) dy, = (~'} ,(Tw ''' /~ " t2) для л^З, A0А.9)
Сп = j Для " = } •
Величины Ct равны 1/4, 1/64, 1/256, ... для п= 1, 3, 5, ... .
Величина S в A0А.9) несколько отличается от эксперименталь-
экспериментального значения 3/iWo— l/*Wi [109]. Это различие частичгю обус-
обусловлено членами с п > 1, которые могут объяснять отличие Wo
от 3/\Wo. Другая причина этого различия состоит в предположе-
предположении о независимости /+ и /_ от ц, использованном при выводе
Двухпотоковая и четырехпотоксзая теории 223
A0А.7) и A0А.8). Следует заметить, что для полностью диф-
диффузной волны это предположение не справедливо. Как уже ука-
указывалось в гл. 9, диффузная лучевая интенсивность должна
иметь несколько большее значение в направлении вперед, чем
в обратном направлении. В обозначениях данной главы более
точное выражение для лучевой интенсивности можно записать
в виде
7(т, ц) = /о(т) + ^г[/?+(т)-^_(т)]ц. (ЮА.10)
Между тем соотношения A0А.7) и A0А.9) основаны на пред-
предположении, ЧТО /(Т, ц) =/+(т) ДЛЯ |1 > О И 7(Т, р) -= /-(х) ДЛЯ
0
Глава 11
Плоскопараллельная задача
Задача о распространении волн в среде, ограниченной парал-
параллельными плоскостями, широко изучалась в последнее время
[31, 110, 148], поскольку она описывает множество физических
ситуаций. Например, в виде плоскопараллельной среды можно
представить атмосферы планет, облака и океан при освещении
их солнцем или другими источниками излучения. Другими при-
примерами являются биологические эксперименты, связанные с от-
Падающий
поток хл
Полный поток —|s
Рис. 11.1. Диффузное отражение и
прохождение (а) и закон затенения (б)
для плоскопараллельной среды.
б
ражением при прохождении света через мазки крови и биологи-
биологические ткани. В этих задачах представляет интерес нахождение
энергетических характеристик отражения и прохождения
(рис. 11.1, а). Если же энергия излучается внутри среды вдали
от ее границы, то можно интересоваться угловой зависимостью
выходящего из среды излучения (рис. 11.1,6), называемой зако-
законом затенения.
Задачу о плоской волне, падающей на плоскопараллельную
среду со случайным распределением частиц, можно описать ма-
математически с помощью уравнения переноса, используя только
две переменные — расстояние г и угол 0. В противоположность
этому общая задача с произвольным возбуждением и произволь-
произвольной средой требует для своего описания уравнения, зависящего
Плоскопараллельная задача
225
от пяти переменных: х, у, г, в и f Точное решение, выраженное
через известные функции в замкнутом виде, не найдено даже
для задачи с двумя переменными.
В данной главе мы опишем метод, основанный на квадратур-
квадратурной формуле Гаусса ([31], гл. II и III), который позволяет легка
получить численные решения на ЭВМ. При этом решение дается
в виде ряда, точность которого возрастает с ростом числа его
членов. Другое решение в виде ряда, использующее полиномы
Лежандра, обсуждается кратко в разд. 11.6. Рассматриваемую
задачу можно также сформулировать в виде интегрального урав-
уравнения, основываясь на «принципе инвариантности» и «инвариант-
«инвариантном погружении». Эти вопросы изложены в превосходных учеб-
учебниках [2, 12] и здесь не рассматриваются.
11.1. Нормальное падение плоской волны
на плоскопараллельный слой
Рассмотрим плоскую волну с потоком мощности Fq, падаю-
падающую нормально на слой толщины d (оптическая толщина то =
= potd; рис. 11.2).
Падающий
поток
х
/
т=о
d
Рис. 11.2. Геометрия плоскопараллельной задачи и углы (Э, Ф) для лучевой
интенсивности.
Будем исходить из уравнения переноса
dl (г, s)
ds
¦ J/7E, 8')/(Г,
4л
A1.1)
Заметим прежде всего, что, поскольку геометрия задачи и па-
падающая волна не зависят от к и у, интенсивность /(г, s) есть
функция только от г и 0. Уравнение A1.1) удобно переписать,
используя оптический путь т = potz в направлении г. Разделим
также лучевую интенсивность на ослабленную интенсивность Irt
226 Глава 11
и диффузную интенсивность 1а- Ослабленная интенсивность для
коллимированного падающего потока Fo равна
lri(r, I) = Foe-* 6(s9i)n6B@) = Foe-Ч(ц - 1) Д (ф), A1.2)
где jx = cos 0, элемент телесного угла равен da = sin 0 dQ d<$> =
= — d\y,d<\>, а дельта-функции определяются условиями
"л
<J6(9)d0=l, б (9)== 0 при 0=^0,
о
6(ц — 1)й?ц= 1, 6 (p. — 1) = 0 при (х ^ 1,
о
1
-1
6 (^) d$ == 1, б(^.) = 0 при
о
Подставляя I = l,i-\-Id в A1.1) и используя A1.2), получаем
дифференциальное уравнение для Л*(г, s)=/d(T, ц):
-1 0
A1.3)
где d% = p0(ds cos 0. Для того чтобы исключить отсюда зависи-
зависимость от ф, проинтегрируем A1.3) по ф от нуля до 2я, что дает
1
= -r- \ d\i pa ((x, \x ) /d (t, ix ) -|—-—p0 (fx, \)F{,e~x, A1.4)
-l
где
2л -2л
1 Г If
ц') = — \ dф — \ dф'р (ц Ф' \х' ф/)
2л J 2я J ' г 1Г ' г ' ' '*
О О
Дифференциальное уравнение A1.4) является основным
уравнением, определяющим /Дт., |х), и вместе с граничными ус-
условиями составляет полную математическую постановку задачи.
Если среда, содержащая частицы, представляет собой вакуум
или свойства этой среды совпадают со свойствами окружающих
Плоскопараллельная задача 227"
сред (г < 0 и z>d), то граничное условие при т = 0 заклю-
заключается в отсутствии диффузного излучения, распространяюще-
распространяющегося в положительном направлении:
Л,@, ц) = 0 для 0<ц<1, A1.5а)
а при х = то — в отсутствии диффузного излучения в отрица-
отрицательном направлении г:
Мто, Ц) = О для — 1<}г<0. A1.56)
При наличии на границах т = 0 и т = то отражения условия
A1.5а) а A1.56) нужно .модифицировать, включив коэффи-
коэффициенты отражения и пропускания. Но в данной главе мы огра-
ограничимся случаем простых граничных условий A1.5а) и A1.56).
11.2. Типичные фазовые функции
Прежде чем приступить к решению плоскопараллельной за-
задачи, полезно описать некоторые типичные фазовые функции.
Простейшая фазовая функция отвечает изотропному рассеянию:
р {ц, ф; ц', ф') = р0 (ц, и') = !F0 = -^- = альбедо. A1.6)
Для непоглощающих частиц, размеры которых малы по срав-
сравнению с длиной волны, в случае неполяризованной падающей
волны применима фазовая функция Рэлея
/>(И, Ф: и'. ^/) = -|(l+cos2v), (П-7а)
где у — угол между направлениями (^, ф) и (\х,г, ф'), определяе-
определяемый условием
cos y = cos б cos 9' + sin б sin б' cos (Ф — ф').
Интегрируя A1.7а) по ф и ф', получаем
р0 Ох, /) = j [\ + vY2 + 1 A - ц2) A - ^'2)]. A1.76)
Полезное и общее выражение для фазовых функций дается
разложением в ряд по полиномам Лежандра /5«(ц)= Л, (cos 0).
Если рассеяние симметрично относительно направления падаю-
падающей волны, то фазовая функция зависит только от у, и ее можно
выразить в виде ряда по функциям Лежандра:
оо
р (]х, ф; »', ф') = р (cos y) = I WnPn (cos у). A1.8а>
228
Глава If
Используя известное разложение [75]
Рп (cos у) = Рп (Ц) Рп (!*') + 2
j-=^ P™ (ц) PJT (ц') cos /л (* - Я
и интегрируя A1.8а) по ф и </>', получаем [см. (9.12а) и A0.19)]
Ро (|*. |*0 = Z ^Л (и) Яя (ц'). A1 -86)
п-0
где Wo — альбедо частицы.
Отметим, что во всех рассмотренных только что примерах
выполняется соотношение симметрии
А>(И, V>') = Po(li', M-) = Ро(— Р-, — и') = Ро(—И'. — И)- (П.9)
11,3. Квадратурная формула Гаусса
Общее решение интегро-дифференциального уравнения A1.4),
выраженное через известные функции в замкнутом виде, не най-
найдено. Рассмотрим поэтому решение, основанное на приближен-
приближенном представлении интеграла в A1.4). Это представление на-
называют квадратурной формулой Гаусса [1]. Мы обсудим его
кратко в данном разделе, прежде чем приступить к решению
уравнения A1.4).
/(х)
Рис. 11.3. Приближенное предста-
представление интеграла A1.10).
xm b
Попытаемся представить интеграл от функции f(x) в виде
ряда, включающего значения f(xj) в конечном числе т точек
х = xh } == 1, ..., т (рис. 11.3):
(х) dx
A1.10)
где со (л:)—весовая функция. Вопрос состоит в том, как выбрать
точки Xj и определить а,, чтобы получить наилучшую аппрокси-
аппроксимацию интеграла при наименьшем числе членов т. Этот вопрос
Плоскопараллельная задача 229
можно сформулировать математически, введя погрешность е:
Ь т
A1.11)
Покажем прежде всего, что если функция f(x) аппроксимируется
полиномом степени т — 1, то даже при произвольном выборе X/
можно полностью устранить погрешность. Для этого выразим
f(x) в следующем виде, включающем произвольные Xj:
т
где F (х) = П (х — Xj) = (х — xi) (х — х2) ... (х — хт) и F' (х) =
= dF(x)jdx. Заметим, что, поскольку F{x) есть полином сте-
степени т, правая часть A1.12) есть полином степени т—1. За-
Заметим также, что F(x)/[(x— Xj)F'(xj)] становится равной еди-
единице при x->Xj и обращается в нуль при x-*-Xi 1ф\. Поэтому
A1.12) представляет f(x) в виде полинома степени m— 1, давая
точные значения /(#/) при х = х,-. Соотношение A1.12) назы-
называется интерполяционной формулой Лагранжа. Подставляя
A1.12) в A1.10), получаем
Эту величину называют числом Кристофеля, связанным с F(x)\
Ясно, что если f(x) есть полином степени т— 1, то погрешность
е тождественно обращается в нуль; причем это верно при про-
произвольном выборе X/.
Если изменения функции f(x) таковы, что полином степени
т—1 недостаточен и для адекватного описания f(x) требуется
полином более высокой степени, то погрешность A1.11), вообще
говоря, отлична от нуля. Возникает вопрос, можно ли даже и
в этом случае устранить погрешность, выбрав точки х\ не произ-
произвольно, а некоторым надлежащим образом? Это достигается
с помощью описанной ниже «квадратурной формул»». Такая
формула дает значение интеграла от функции, представленной.
в виде полинома степени 2т— 1, согласно A1.10), с нулевой по-
погрешностью. Для получения этой формулы запишем f(x) в виде
следующего полинома степени 2т— 1:
т га —1
1-0
230 Глава 11
где Ci — постоянные. Поскольку F(x) есть полином степени т,
второе слагаемое в A1.14) есть полином степени 2т—1. Вся-
Всякую функцию, представленную в виде полинома степени 2т — 1,
можно записать в виде A1.14), выбрав соответствующим обра-
образом постоянные Си Подставим теперь A1.14) в левую часть
A1.10). В результате, помимо ряда, стоящего в правой части
A1.10) и возникающего из первой суммы A1.14), мы получим
также дополнительный ряд, который возникает из второй суммы
в A1.14). Если соответствующим выбором Xf дополнительный
ряд окажется возможным обратить в нуль, то тем самым мы
достигнем цели, представив интеграл от полинома степени
2т—1 в виде суммы т членов, как и в формуле A1.10). Это
можно сделать, выбрав X/, а следовательно, F(x) так, что
ъ
F{x)xla>{x).dx = 0 для / = 0, 1, ..., т— 1. A1.15)
Это означает, что полином F(x) должен быть ортогонален к1
с весовой функцией в>(х). Формула A1.10) с коэффициентами
A1.13) и полиномом F(x), удовлетворяющим условиям A1.15),
называется квадратурной формулой.
Для плоскопараллельной задачи имеем а(х)=\, а = — 1,
6 = +1. В этом случае, учитывая, что полином Лежандра
Рт(х) ортогонален всем х1, / = 0,1, ... ,т — 1, можно выбрать
F(x) = Pm(x), A1.16)
причем Xj должны быть нулями полинома Лежандра Рт(х). Та-
Таким образом, можно записать
-1 /-1
где
«,-
m(i) _, (/)
и Xj выбраны так, что Pm(xj) — Q. Это квадратурная формула
Гаусса.
Для рассматриваемой плоскопараллельной задачи т удобно
выбрать четным: т = 2N. Используя р, вместо х, запишем
1 N N
\ ffo)^= ? ау/Ы-ЕаЛ/Ы + М-ц,)], A1.18)
-1 J — N 1-1
где
Плоскопараллвльная задача 231
и мы использовали тот факт, что Аглг есть четная функция
ц, а;- = a-j и [x,j = —(л_/. Первые члены последовательностей ц/
и а/ имеют вид
7V = 2, (ц = 0,3399, а, = 0,6521, (П.19)
(х2== 0,8611, а., = 0,3479.
Значения для N ^ 3 приведены в книгах [1, 31].
11.4. Общее решение
Вернемся к плоскопараллельной задаче, заданной уравне-
уравнениями A1.4), A1.5а) и A1.56). Требуется решить уравнение
1
^а1"(ау] +ыт, |*>—4- S ^'tpo(n, но/л*, иО]+
-1
(П.20а)
с граничными условиями
Аг(О, М-) = 0 при
/Лто> М') = 0 при —
Прежде всего, используя формулу Гаусса A1.18), выразим
интеграл из A1.20а) в виде ряда
1 N
-1 /—JV
где \ji-i = — щ (рис. 11.4). Подставим A1.21) в A1.20а) и по-
положим в полученном соотношении ц = [и, i = ± 1, ±2 ±N:
ИГ
dld (%, (лг) 1
* /—л/
+ -r~ PoilK \)Fue~x. A1.22)
Уравнение A1.22) можно записать в более компактной мат-
матричной форме
4rld(r) + Sld(r) = Be-\ A1.23)
232
Глава 11
где Мт) = [//(т)] — матрица-столбец, 2NX 1, Л(т)=Л*(т, ц,-),
S =[5,/] — квадратная матрица 2# X 2N, В = [В«] — матрица-
столбец 2N X 1, а элементы 5,-/ и В; определяются выражениями
при i = 1, Bt = ; ' Fo,
ц.
2ц.
при i Ф).
Строки и столбцы этих матриц расположены так, что индекс i
меняется как (+N, ..., +1, —1, ..., —N) сверху вниз, а ин-
х,у
М-1
Рис. 11.4. Направления, соответствую-
соответствующие ц. = cos0.. Отметим, что ц_» =
= — ц^ при / = 1, 2 Л/1.
деке / — как (-\-N, ..., +1, —1, ..., —N) слева направо [что
видно в A1.26)]. Вследствие соотношения симметрии для
poili, (д.') A1.9) элементы Si/, расположенные симметрично отно-
относительно центра матрицы S, одинаковы по величине и противо-
противоположны по знаку:
С С С (Л 1 ОК\
И — — ^ — i, —i> ^ij '— J — I, —!• v1 l.4Of
В качестве примера запишем A1.23) для случая N = 2:
ш- I 1т\ -л г- Ч Ч Ч 9 "
5,2 5ц —5_ц —5_i2
5-12 5_ц —5ц —5i2
d
dx
Л(т)
L/_2(t)-
- 5_22 5_2i —
— О
22
В,
L/_2(t)-
A1.26)
где учтено соотношение симметрии A1.25).
Общее решение линейного дифференциального уравнения
первого порядка A1.23) дается суммой частного решения 1р(т)
и решения однородного уравнения 1с(т). Частное решение полу-
получается подстановкой
1р(х) = ае-\ ' A1.27)
Плоскопараллельная задача 233
где а = (а)—матрица-столбец 2N X 1 с постоянными элемен-
элементами а,-. Подставив A1.27) в A1.23), получим
lp(x) = ae"t = (S—V)~lBe"t, A1.28)
где U — единичная матрица 2JV X 2iV.
Для решения однородного уравнения
¦^-Ie(*) + SIe(T) = 0 (Ц.29)
положим
1е(т) = Р?А*. A1.30)
где Я, — неизвестная постоянная. Подставляя это выражение в
A1.29), получим
0. A1.31)
Это матричное уравнение задачи на собственные значения. Для
получения ненулевого решения р определитель матрицы XV + S
нужно приравнять нулю:
|HJ-fS| = 0. A1.32)
Этот определитель есть полином от Я, степени 2N, так что имеет-
имеется 2N значений Х — К, п= ±1, ±2, ..., ±N, удовлетворяющих
уравнению A1.31). Для каждого Я.л матрица-столбец р = р„ =
= [Р„г] определяется из A1.31). Это уравнение определяет
только относительные значения элементов pn/, i = ±\, ±2, ...
..., ±N. Величины Я,л и рга называются соответственно собствен-
собственными значениями и собственными векторами матрицы S. Вслед-
Вследствие соотношения симметрии A1.25) Я§^1 Рш удовлетворяют
условиям.
К = -Ь-п, Р„1 = Р-».-|. A1-33)
Формальное доказательство условий A1.33) здесь не дается, но
их легко проверить для примера A1.26).
Общее решение однородного уравнения 1С дается линейной
комбинацией собственных векторов р„ с произвольными коэффи-
коэффициентами Сп:
I» = Z CfiIVV = Z фЄЛТ + ? C.JUe-Ч A1.34)
где элементы р_л связаны с ря посредством A1.33). Полное ре-
решение Id(t) равно
W, (П.35)
где 1Р(т) определяется согласно A1.28), а 1с(т)—в соответствии
с A1.34). Имеется 2N неизвестных постоянных Сп, п =
234
Глава 11
= ±1, ±2, ..., ±N, которые определяются граничными усло-
условиями A1.206). Подставляя в A1.206) ^ = щ, получаем сле-
следующие 2N условий:
= 0,- / = —1, —2, ...,-N.
A1.36a)
A1.366)
Решение 1<* A1.35) есть матрица-столбец 2N X 1- Интенсив-
Интенсивность часто бывает удобно представлять не как матрицу, а как
непрерывную функцию /<*(т, \л), зависящую от т и ц. Это можно
сделать, записав I{%, \i) в виде интеграла:
/ (т, ц) = Iri (т, ц) + Id (т, ц) =
-^- дляц>0,
A1.37)
^ дляц<0,
где
/ (т, ц) = 1
(Ц, ц') /„ (т, цО +
-1
Выражая интеграл в /(т, (д.) по формуле Гаусса и подставляя
в A1.37), получаем для ц > 0
h (т, ii)=т~ («-' - е-
h (т, ii)=т~
п-1
n-l
И ДЛЯ |Л < 0
п-1
п-1
(H.39)
Плоскопараллельная задача ' 235
где
N
А (и) = -^4^— Fo + yYj UiPQ ^' •*') а']
I N
N N
i N I N
Поток в положительном направлении F+(x) дается выражением
A1.40)
которое можно записать в виде ряда:
N N
1 «• t
где-
t-i
N
i-l
Аналогично поток в отрицательном направлении F_'(t) дается
выражением
о
-1
N
= В-е~" + ^СпВ-пех^ + ?с_„В:„е-Ч A1.42)
n-l
где
N
i-l
Выражения A1.37) — A1.42) дают лучевую интенсивность и
прямой и обратный потоки в точке т.- Из тшх легко вычислить
отраженные и -прошедшие лучевые интенсивности и потоки при
236
Глава 11
т = 0 и т = ю- При х = О диффузная отраженная лучевая ин-
интенсивность есть 1@, ц) в A1.39) для ц < 0, а отраженный по-
поток F-@) определяется согласно A1.42). При т = то прошедшая
лучевая интенсивность равна Irt (то) + Id (to, \i), где Id опреде-
определяется согласно A1.38), а поток дается выражением A1.41).
Проиллюстрируем рассмотренную процедуру для простого
случая N=1 и изотропного рассеяния pa{\i, ц') = Wo. Для
N = 1 формула Гаусса имеет простой вид:
_[
~,
(П.43)
й
dx
AM
И.
2
— 1
2ц 1
_ _ t-V-x
(I—?)__/-iW_
-Foe-\ A1.44)
Частное решение A1.28) дается выражением
e~x,
A1.45)
причем
(i-^)-«. -
2ц,
а,
¦Fo,
откуда находим
1 +
«
_
l
4я
l - Wo - ni
Для получения решения соответствующего однородного уравне-
уравнения вычислим сначала собственное значение Хп из A1.32):
-Го
= 0. A1.46)
Из этого уравнения получаем Х\ = —
Собственные векторы р„ даются выражениями
Плоскопараллельная задача 237
для которых соотношения симметрии A1.33) очевидны. Таким
образом, полное решение A1.35) имеет вид
С_1в-Ч ( ' }
где Ci и С_1 — неизвестные постоянные. Используем теперь гра-
граничные условия A1.36):
- С_! ехр (- Я,,т0) = 0, A1.48)
из которых легко определить С\ и С-\\
— cij ехр (— ^i^q) + 6а_ j ехр (— т0)
1 ~~ ехр (—
С-' ехр (—Я1Т0) — б2 ехр (Я^о)
Таким образом, для \х > 0 получаем
/ (т, (I) = Irt (х, ц) + /d (т, (i), /г/ (т, ц) = Рое-^б (ц —
A1.50)
Wo Г a, + a , + FJIn
а для (j, < 0 имеем
№n f a, + a , + FJ2n
[*Xp
Заметим, что члены, содержащие Fo в первых слагаемых в
A1.51) и A1.52), дают решение первого порядка, рассмотренное
в гл. 8 [выражения (8.8) и (8.9), где нужно положить ц0 = 1)],
а остальные члены описывают эффекты многократного рассея-
рассеяния.
Этот пример иллюстрирует методику, описанную в данном
разделе, однако полученные при этом численные значения нужно
рассматривать как очень приближенные, поскольку формула
Гаусса A1.43) дает очень грубую аппроксимацию. Фактически
238 Глава 11
известно, что Ki должно быть меньше единицы, если N достаточ-
достаточно велико. Поэтому очевидно, что полученные формулы нельзя
использовать при Wo > 2/з. так как при этом Ki > 1.
11.5. Полубесконечная среда
Задачу о нормальном падении плоской волны на полубеско-
полубесконечную среду можно решить, полагая просто т0 —* оо в ре-
результатах предыдущего раздела. При другом подходе можно
использовать граничное условие при х~*-°°, когда должна быть
только уходящая волна. Это означает, что в общем выражении
для \с A1.34) решение с ехр(^„т) недопустимо, поскольку оно
неограниченно возрастает при т-»-оо. Таким образом, все Сп,
п == 1, 2, ..., N, должны быть равны нулю, и 1С должно иметь
вид
lc=ZC_nfi_ne-bn\ A1.53)
Входящие сюда N постоянных С_„ определяются из N условий
A1.36а) прит = 0.
Рассмотрим теперь задачу об излучении полубесконечной
среды, занимающей область т < 0. Решение этой задачи назы-
называют законом затенения. В этом случае падающая волна по-
порождается при х-*-— оо. Если рассмотреть все собственные зна-
значения Кп, то можно заметить, что для больших N только одно из
них, Хи меньше единицы, а все другие больше единицы. Поэтому
все члены ехр(—т) и ехр(—%пх), кроме ехр(—^it), при боль-
больших х обращаются в нуль, так что решение дается выражением
I = C_fi_ie-b" + 2 С„Р,АТ. A1.54)
Входящие сюда N + 1 постоянные С-\ и Сп определяются из N
граничных условий при т = 0:
1.@, И*) = 0, /=-1,-2, ...,-N, A1.55)
и условия, что полный поток Fo при х = 0 считается известным.
11.6. Наклонное падение и другие методы
Если исходная волна падает на среду наклонно в направле-
направлении (цо, ^о), то лучевая интенсивность /(г, s) есть функция т,
цп ф; поэтому ее можно разложить в ряд Фурье
м
I(т,-ц, ф) = S /„(т, ц)cosт(ф-ф0). A1.56)
го-0
Плоскопараллельная задача 239"
Подставляя этот ряд в уравнение переноса (детали этого ме-
метода даны в работе [31]), можно получить М + 1 уравнение
для /т.
Описанный в данной главе метод основан на квадратурной
формуле Гаусса. Имеются и другие методы, которые оказались
также эффективны при решении рассматриваемой задачи. Так,
например, лучевую интенсивность можно разложить в ряд по
полиномам Лежандра с неизвестными коэффициентами ([11],
гл. 3). Можно также рассмотреть общие соотношения между от-
отражением и прохождением, для конечного слоя и составить со-
соответствующие интегральные уравнения. Такой метод оказался
достаточно эффективным ([31], гл. 7, а также [2, 12]). Основную
идею этого метода называют принципом инвариантности и ин-
инвариантным погружением. В следующем разделе мы опишем
аналогичную методику, применимую к случаю слоистой плоско-
плоскопараллельной среды.
11.7. Слоистая плоскопараллельная среда
Обобщим теперь результаты предыдущих разделов на случай
слоистой структуры, содержащей рассеивающие частицы. Пред-
Предположим, что частицы в 1-м слое характеризуются плотностью
pi, полным сечением oti и фазовой функцией poi(n, ц') (рис. 11.5).
Расстояния внутри каждого слоя мы будем измерять в единицах
собственной оптической толщины xi = piOttz и предположим, что
на первый слой падает плоская волна с потоком мощности Fo-
Пусть 1„ — матрица-столбец 2N~X,l, состоящая из диффуз-
диффузных лучевых интенсивностей на поверхности а в направлениях
р, = ц;, i = N, ..., 1, —1, .... —N [см. пояснения к A1.23)].
Пусть \ь — матрица-столбец 2N X 1 из диффузных интенсивно-
интенсивностей на поверхности Ь.щ
Если найти 2N X 2N-матрицу Ti и 2N X 1 -матрицу Fi для
первого слоя между поверхностями а и Ъ, которые связывают 1„
и \ь следующим образом:
Ii = FI+f,Ie, A1.57)
и аналогично для второго и третьего слоев
Л = Ра + ТаЬ, Id = F3 + f3Ic, A1.58)
.то, рассмотрев последовательность слоев, нетрудно получить со-
соотношение, связывающее 10 и Id'.
li = F + fle,- (П.59)
где
240
Глава 11
Граничные условия для 1„ вытекают из отсутствия диффуз-
диффузной лучевой интенсивности, входящей в среду в положительном
направлении z. Граничные условия для Id следуют из отсутствия
на поверхности d диффузной интенсивности в отрицательном на-
Поверхность Поверхность Поверхность Поверхность
а Ъ с d
7-3-
Irf
т,
-oo-
т2
О О-
Тз
Рис. 11.5. Плоскопараллельная задача со слоями.
правлении z. Выразив эти условия через элементы матриц-столб-
матриц-столбцов
IaN л Ion
'а V at)
/«I
la-N
= (hi) —
h-x
I ld-fi
получим
для /=1,2 N,
для г = — 1, — 2 —N.
A1.60)
A1.61)
Плоскопараллельная задача 241
Подставляя A1.61) в A1.59), можно записать 2N уравнений
для 2N неизвестных, 1Ш- для i = —1, —2, ..., —N и /^ для
i= I, 2, ..., N при условии, что F и Т известны.
Таким образом, задача о слоистой среде, изображенной на
рис. 11.5, может быть полностью решена, если мы можем найти
F/ и Т/ для каждого слоя.
Опишем теперь, как получить матрицы F; и Т/. Рассмотрим
первый слой (/=1). Полное общее решение для слоя A1.35)
было получено выше. Запишем его в матричной форме1):
где а — матрица-столбец 2N X 1 из A1.28), р — матрица 2N X
X 2N с элементами р„/, а Е, — матрица 27VX 2N, определяемая
соотношениями
Ёх = (Ец), I, j = N, ..., 1, — 1, .. ., — N,
Матрица С есть-матрица-столбец 2N X 1 с элементами С«
из A1.34).
В A1.62) I (т) должно быть равно \а при т = 0 и I» при т =
= ть Поэтому имеем
Исключая С из этих двух уравнений, получаем
В этих выражениях р и Et представляют собственные векторы и
собственные значения для слоя; а описывает источники и про-
пропорционально Fo. Эти величины можно получить, зная Si,- и В;
в A1.24).
Для второго слоя (/ = 2) можно аналогично найти F2 и Т2
по Sij и Bi, характеризующим этот слой. В этом случае Fo в вы-
выражении для Bi нужно, конечно, заменить на Foe~Xl.
Таким образом, в общем случае матрицы F; и Т/ можно за-
записать в виде
Эти величины вычисляются, если известны плотности р;, полные
сечения аи и фазовые функции ро/(ц> &') Для каждого слоя.
]) Диффузная интенсивность Id из A1.35) обозначена в A1.62) через I...
чтобы избежать путаницы с la на поверхности d в A1.58) и A1.59).
242 Глава 11
11.8. Некоторые смежные проблемы
Решения уравнения переноса излучения для плоскопарал-
.лельных задач рассматривались в связи с самыми разнообраз-
разнообразными проблемами. Например, с помощью уравнения переноса
изучалось излучение слоев тумана и рассеяние света на обла-
облаках [83, 84, 120, 121]. Рассматривалось также рассеяние опти-
оптического излучения в океане и прилегающих слоях воздуха [57,
82]. Плоскопараллельная задача с тепловой функцией источни-
источников применялась для описания микроволнового теплового излу-
излучения ледников и других приповерхностных образований [51, 61,
151, 159].
Глава 12
Изотропное рассеяние
В предыдущей главе теория переноса излучения использова-
использовалась главным образом для решения таких задач, как определе-
определение законов затенения, диффузного отражения и прохождения
при облучении плоскопараллельной среды плоской волной. Од-
Однако во многих приложениях, относящихся к распространению
оптических, миллиметровых и акустических волн в атмосфере,
океане и биологических средах, необходимо рассматривать ха-
характеристики распространения сферических волн и волновых
пучков. При этом нужно решать трехмерную задачу в более об-
общей постановке. Она, конечно, значительно сложнее задачи
о падении плоской волны на плоскопараллельную среду, и ее
точное решение, по существу, еще не найдено. В связи с этим
возникает необходимость нахождения приближенных решений.
Два таких решения рассматриваются в этой и следующей гла-
главах.
Первое решение может использоваться, когда размеры частиц
много меньше длины волны, а второе — в противоположном пре-
предельном случае. В этих двух случаях математическое описание
задачи существенно упрощается, что позволяет относительно
легко найти полезные решения. Если размеры частиц много
меньше длины волны, то индикатриса рассеяния практически не
зависит от угла рассеяния, за исключением случая дипольного
рассеяния электромагнитных волн. При этом можно считать, что
фазовая функция р( s, s) постоянна и равна альбедо Wo = as/ot-
Этот случай называют случаем изотропного рассеяния [11, 30,
31, 40, 98, 105]. Общий случай, когда фазовая функция p(s, s)
непостоянна, называют случаем анизотропного рассеяния. Для
изотропного рассеяния можно получить некоторые точные реше-
решения, выявляющие многие общие характерные черты распростра-
распространения волн, которые трудно выделить в более общем случае ани-
анизотропного рассеяния. Кроме того, имеется возможность прове-
проверить приближенные решения, полученные для анизотропного
рассеяния, сравнивая их с точными решениями для изотропного
случая. Изотропное рассеяние служит также хорошим приближе-
приближением для многих практических ситуаций, когда размеры частиц
много меньше длины волны.
С другой стороны, когда размеры частиц велики по сравне-
сравнению с длиной волны, рассеяние ограничивается областью малых
244 Глава 12
углов вблизи направления вперед и поэтому возникает возмож-
возможность упростить уравнение переноса, используя малоугловое
приближение. Этот вопрос будет рассмотрен в следующей главе.
12.1. Метод преобразования Фурье
для изотропного рассеяния
Для изотропного рассеяния фазовая функция p(s, s') по-
постоянна и интегральное уравнение G.41) для средней интенсив-
интенсивности U (г) принимает вид
U(r) = Urt(r) + J Go (r - г') [pasU (г') + е (г', s)] dV, A2.1)
v
где G0(r) = [exp(—рыг)]/4лг2. Уравнение A2.1) применимо как
к случаю конечного объема V, так и к случаю неограниченной
среды.
¦ Рассмотрим сначала случай точечного источника, располо-
расположенного в точке г' и излучающего полную мощность Pq. Функ-
Функция источника в этом случае дается выражением [см. G.35) ]
е(г) = (Р0/4яN(г-г'), A2.2)
и A2.1) принимает вид
\0(r-r')U(r')dV. A2.3)
Обозначим через G(r) интенсивность U(r) в случае источника,
помещенного в начало координат и излучающего полную мощ-
мощность Ро/4я = 1. Тогда можно записать
G(r) = Go(r) + P<rs \ Go (r - гО G (r') dV. A2.4)
v
Входящая сюда функция G(r) представляет собой среднюю ин-
интенсивность излучения точечного источника из точки г = 0 и
является функцией Грина. Если функция G(r) найдена, то через
нее можно выразить решение для случая произвольной ослаб-
ослабленной падающей интенсивности С/г/(г). Поэтому в данном раз-
разделе мы подробно остановимся на характеристиках G(r).
Если объем V не ограничен, то точное аналитическое выра-
выражение для функции Грина G(r) можно получить с помощью пре-
преобразования Фурье следующим образом. Возьмем фурье-образ
от A2.4) Г
G (К) = J G (г) ехр (- /К • г) dV, G (г) = -~ J G (К) ехр (Л(
A2.5)
Изотропное рассеяние 245
Замечая, что фурье-образ от свертки есть произведение фурье-
образов, получаем
G(K) = G0(K) + porsG0(K)G(K), A2.6)
откуда находим G(K)= GO(K)/[1 — pasG0(K)]. Заметим теперь,
что, поскольку Go (г) есть функция только от модуля г и не за-
зависит от его направления, G0(K) зависит только от модуля К
и имеет вид
Gu (К) = Go (К) = dVG0 (г) ехр (- /К • г) =
2л и оо
— \ d<j> \ sin В dQ \ г2 dr -.—«—^— ехр (IKr cos 8) =
J J J 4ЯГ
0 0 0
J P0^ + i/fn ~" T~2f ln 1 - ((K/pot) = IT аГС tg \~po^) '
A2.7)
Возьмем теперь обратное преобразование от A2.6). Это трех-
трехмерное обратное преобразование Фурье можно упростить, заме-
заметив следующее, Поскольку G(K) есть функция только от мо-
модуля К и не зависит от направления К, мы имеем
оо
S4.TT Г
G(K)exp(iK-r)dK = —\G(K) sin (Кг)КdK. A2.8)
о
Далее, так как G(K)—четная функция К, интегрирование в
A2.8) можно распространить на область (— оо, -j-co):
^f- J G(K)eiKrKdK. A2.9)
— ОО
Такой переход оказывается целесообразным, поскольку контур
интегрирования теперь можно замкнуть на бесконечности и ис-
использовать для вычисления интеграла метод вычетов.
Запишем
°M=W7 \ ТГщ4(Щ)* A2Л0)
Чтобы в этом выражении контур интегрирования замкнуть на
бесконечности и свести интегрирование к вычислению вычетов м
вкладов от разреза, как показано на рис. 12.1, нужно, чтобы
подынтегральное выражение обращалось в нуль при \К\ -*¦ оо.
Но в интеграле A2.10) arctg(/(/pOf) стремится к it/2 при
246
Глава 12
¦*- оо, поэтому подынтегральное выражение не обращается
в нуль на бесконечности.
Чтобы обойти эту трудность, запишем
G ^ = ~ ~&tfT~d7 ) \-(paJKarctg(K/pat)dK- A2Л1>
Контур интегрирования теперь можно деформировать, как пока-
показано на рис. 12.1. В A2.11) имеются два вида особенностей: по-
полюсы в точках, где 1 —(pcrs//C)arc tg(/</pa() = 0, и точки ветвле-
ветвления, связанные с арктангенсом.
В D
Комплексная
плоскость К
Q
o-ipo,a0
f-ipo.
Рис. 12.1. Контур интегрирования в комплексной плоскости А"; локализация
полюсов при ±/рст(а и точек ветвления при ±ро\.
Рассмотрим сначала местоположение полюсов К = КР. За-
Заметим, что, поскольку tg(Kp/pcrs)= KP/pot и at ^ as, полюсы не
могут быть вещественными. Однако корни Кр могут быть чисто
мнимыми. Действительно, полагая КР = ± ipotao, имеем
1 — (Wo/ao) ar th а0 = О,
A2.12)
где Wo — отношение сечения рассеяния к полному сечению, на-
называемое альбедо. Уравнение A2.12) можно записать в виде
A2.13)
Решение этого уравнения ао как функция альбедо Wo изоб-
изображено на рис. 12.2. Как будет показано ниже, величина ао имеет
простой физический смысл. Удобно записать patao=\/L, где
L — расстояние, на котором связанное с вычетом слагаемое
уменьшается в е раз, называемое длиной диффузии.
Изотропное рассеяние
247
Точки ветвления можно определить из соотношения
A2.14)
откуда видно, что arc tg Z имеет точки ветвления при Z = ± L
Таким образом, точки ветвления К = Кы определяются усло-
условием
Kbr/pot = ±i. A2.15)
Найденные полюсы и точки ветвления показаны на рис. 12.1.
Рассмотрим теперь интеграл в A2.11). Поскольку г > О,
€хр(г'Л>) обращается в нуль при |/С|->оо в верхней полупло-
полуплоскости комплексного переменного К, так что интеграл оказы-
Рис. 12.2. Решение уравне-
уравнения A2.13) (зависимость а0 от
Wo).
еается равным сумме произведения 2лг на вычет в точке КР
= ipota0 и вклада от разреза (рис. 12.1):
Слагаемое Gres(r), связанное с вычетом, равно
Gres (г) = -±~ Ра ехр (— pataor),
d _ 2ag(l-gg) 2/2(L2-/2)
A2.16)
П2.17)
где
d Го (a2 + Wo - 1) W0L2 {p\VQ +l2- L2) "
В этом выражении / — полная длина свободного пробега, опре-
определяемая из равенства pat = 1//, а L — введенная выше длина
диффузии.
Рассмотрим теперь вклад от разреза Gbr{r). Заметим, что,
полагая К = ipott'). Для контура CD, показанного на рис. 12.1,
мент
) Определение арктангенса см., например, в книге [1]. Заметим, что аргуг
величины К — ipot есть я/2 для CD и —Зл/2 для ВС.
248 Глава 12
имеем
1 . Я ~
Т + Т = Г" П2.18а)
а для контура ВС —
1п
1218б>
поэтому интегрирование вдоль разреза дает
П2 ехР (— P<*trt) r° 7",exp(— pay/)
¦ — Bя)* г М l+t (WJt) Т2 "' ' ) \+l (WJt) Г, '
оо
= -р- [ 9 U, Wo) exp (- рог^г/) Л, A2.19)
где
Вычисление интеграла можно еще более упростить, положив
и = lit. Тогда
^\(-^f)^-- A2.20)
Таким образом, полное выражение для средней интенсивности
U(г) излучения изотропного источника с полной мощностью Ро
имеет вид
¦ftrv" A2.21)
оо
4^ ехр (~ paiCtor) + S $ 8 (t, wo) exp (- patrt) dt.
Графики нормированной интенсивности 4nr2G(r) приведены
на рис. 12.3, где параметром является Wq. Заметим, что, по-
поскольку G(r) представляет собой плотность энергии, а не поток
Изотропное рассеяние
' 249
мощности, 4nr2G(r) может быть больше единицы, как видно из
рис. 12.3. Полный поток мощности в радиальном направлении
должен быть, конечно, не больше полной мощности источника.
3 -
2 -
Рис. 12.3. Нормированная 0
интенсивность 4nr2G (r)
(штриховая линия) и _j
нормированный поток
4nr2Fr (г) (сплошная ли-
линия) как функции опт и- — 2
ческой длины potr.
-3
Поскольку вектор потока F связан со средней интенсивностью
соотношением
V • F (г) = - 4jxporaG (r) (РоМ, A2.22)
мы имеем
A2.23)
Графики этого потока, нормированные на 1/цпг2, показаны на
рис. 12.3.
12.2. Диффузия и явления ближнего поля
В предыдущем разделе получена средняя интенсивность V (г)
точечного источника, расположенного в начале координат и из-
излучающего полную мощность Л). Как видно из A2.21), она со-
йтоит из слагаемого, связанного с вычетом Ures(r), и вклада от
250 Глава 12
разреза Ubr(r). В данном разделе мы рассмотрим физический
смысл этих слагаемых.
Слагаемое Gres (г), связанное с вычетом, дается выражением
A2.17). Поскольку а0 всегда меньше единицы и Gres(r) содер-
содержит множитель 1/г, этот член спадает медленнее, чем ослаблен-
ослабленная интенсивность, которая изменяется как A/г2)ехр(—potr).
Если поглощение мало (Wo близко к единице), то параметр ао
близок к нулю и Gres спадает очень медленно. Поведение Gres
тождественно диффузионному процессу, и Gres удовлетворяет
диффузионному уравнению
[V2 - (pcW] Gres (г) = - рст^б (г). A2.24)
Это уравнение можно сравнить с уравнением диффузии (9.16)
при е(г) = 6(г):
(V2 - Kd) Ud (г) = - Зра, A - „,) б (г), A2.25)
где /С! = Зрсг(рсгД1 — Р[). Можно показать, что с уменьшением
поглощения (W0^-l) величины (potaoJ и Р^ в A2.24) прибли-
приближаются соответственно к 3potQeafWQ и З/tt?2,. Эти величины от-
отличаются от соответствующих постоянных в A2.25) при pi = 0
(изотропное рассеяние) на Wu и W2V
Чтобы показать это, заметим, что при Wq -*-1 «о -*¦ 0, поэтому
A2.13) можно разложить в ряд:
откуда при Wo -*¦ 1 получаем Pd = З/Wl и
. A2.27)
В общем случае, если частицы в основном рассеивают
(№о-»-1)> то на больших расстояниях, когда оптическая длина
больше единицы, слагаемое от вычета больше слагаемого, обус-
обусловленного разрезом. Вблизи источника (когда оптическая дли*
на меньше единицы) нужно учитывать оба слагаемых в пол-
полной интенсивности. Таким образом, диффузионный процесс ока-
оказывается доминирующим при оптических длинах, превышающих
единицу.
С другой стороны, если частицы в основном поглощают
(Wo < 1), то при оптических длинах больше единицы вклад от
вычета много меньше вклада от разреза, причем вклад от раз-
разреза приближается к A/г2)ехр(—)
Изотропное рассеяние 251
12.3. Излучение при произвольной падающей
интенсивности
Используя функцию G(r) для излучения точечного изотроп-
изотропного источника, можно описать излучение в неограниченной
среде при произвольной падающей интенсивности. Рассмотрим
A2.1) при е ==0:
U (г) = Uri (г) + pas J Go (г - г') U (г') dV. A2.28)
v
Взяв фурье-образ от этого интегрального уравнения, получим
т4да)- A2-29)
Обратное преобразование Фурье этого выражения дает решение
задачи. С другой стороны, можно записать
U (К) = Urt (К) + pa, !_p^(K) Urt (K)=Uri (К) + P<rsG (К) Url (К)
и, проведя обратное преобразование Фурье, получить
(r-Tf)Utl(rf)dV/, A2.30)
где G (г) описывает излучение точечного источника в неограни-
неограниченной среде, как это было показано в предыдущем разделе.
Первый член в A2.30) дает ослабленную интенсивность, вто-
второй — диффузную интенсивность.
Выражение A2.30) можно еще упростить, заметив, что б(г)(
имеет вид A2.21). Запишем это выражение в форме
G (г) = 9atPd Gd (p,r) + pa, $ g (t, Wo) Gd (p2, r) dt, A2.31)
где Gd(P, r\= e-$r/4nr, Pi = pata0 и p2 =
Используя теперь интеграл
\ еХР1я|г-^ГП U«(f/)dV'> A2-32^
V
запишем решение в виде
U (г) = Url (г) + (P<rs) (pert) \PaI (Pi. r) + J g V. Wo) I (fe. г) dt\.
{12.33)
252 Глава 12
Здесь второй член соответствует диффузии, а последний — вкла-
вкладу от разреза. Интеграл в A2.33) иногда бывает удобно выра-
выразить через оптическую длину, а не через обычную длину. Так,
обозначая через т вектор оптической длины т = patr, получаем
[ -I
РЛ(«о. i)+\g(i, Wo) IN(t, r)dl\, A2.34)
i J
где
In {a> r) = J exp(-«[t-p) Urt {%f) dV,^
Заметим, что задача о нахождении излучения при произволь-
произвольной ослабленной падающей интенсивности Uri(r') в неограни-
неограниченной среде теперь сводится к вычислению интеграла /(Р,г)
или 1дг(а, г), которые выражаются через е~ат/4ят.
12.4. Излучение в случае направленной сферической
падающей волны
Сферическая волна, ограниченная определенным телесным
углом, представляет большой практический интерес, поскольку
миллиметровые, оптические и акустические волны часто направ*
Излучатель
Рис. 12.4. Средняя интенсивность U (т, 9) для направленной сферической
волны с угловой зависимостью / F).
ляются большими отражателями, линзами и преобразователями
и распространяются в пределах малого конуса (рис. 12.4).
Рассмотрим ослабленную падающую интенсивность
e, ф), A2.35)
где х = patr — радиальная оптическая длина, а /F, 0) описы-
описывает угловую зависимость. Для иллюстрации методики без из-
излишних усложнений будем считать функцию / не зависящей от
Вычислим теперь величину In (oi.), определяемую выраже-
выражением A2.34). Для этого разложим Uri(r) и Dя|т — t'|)r'X'
Изотропное рассеяние 253
X ехр(—а|т — т'|) по сферическим гармоникам, используя свой-
свойство ортогональности последних:
я-0
ехр(-а|т-т'|) _ 1 у У Bп I 1) {п ~m)l X
4я | т — т' | 4я Zj Zj (я + m)!
X Рп (cos В) P? (cos 6') Rn (a, т, т') ехр [im (ф - ф% A2.36)
где т и т' — векторы, направленные от начала координат к точ-
точкам (т, 6, ф) и (т/, 6', ф') в сферических координатах. Функция
Rn дается равенствами
Г — а}п (tax) /гп" (lax') при т < х',
т.,х,х') = \ „; /;„_ллпи;„_ч при т>т/) A2.37)
где /п и /г^1' — сферические функции Бесселя и Ганкеля соот-
соответственно.
Прежде всего выполним интегрирование по 6' и ф''. Заметим,
что dV'x = xr2dx' sin 8' dB' йф' и интегрирование по ф' исключает
все т Ф 0. Заметим также, что
я ,
\ Рп (cos 6) Р'п (cos 9') sin 9' dV = \
о I
О при п ф п',
О
при п = п'.
2п+
Учитывая это, получаем
IN (а, х, В) == — ^ 6„ (а, т) а„Р„ (cos 0),
00
Ьа(а, т)=5
— ^
° х A2.38)
оо
/ЯО«M h^(iax')e-* dx>\.
254 ,. Глава 12
Окончательно решение дается выражением
А(ао'т) +
00 / /
п-о I
g (Л У о) 6„ (Л *) л] } <*Л (cos 6). A2.39)
Выражение A2.39) является точным, однако в случае узкого
пучка сходимость ряда оказывается медленной и нужно исполь-
использовать какие-либо другие методы. Принимая во внимание, что
как т, так и т/ в A2.34) находятся вблизи оси (8 = 0), для ап-
аппроксимации в A2.35) воспользуемся приближениями
To
f@)-f(O)exp^--^V 6 =
ехр(-т) вЧ,[-(та + т?/2т3)] <12'40>
4ят 4ЯТ,
где б| равно ширине пучка по уровню половинной мощности,
деленной на 4 In 2. Аналогично можно аппроксимировать вели-
величину ехр(—а|т — т'|)/4л|т —т'|, что упрощает интегрирование
в A2.34).
12.5. Излучение при произвольном распределении
источников
Предположим, что источник e(r, s) в A2.1) излучает мощ-
мощность изотропно во всех направлениях, т. е. e(r, s) зависит
только от г. Пусть Р(т)—мощность, генерируемая в единице
объема в точке г. Тогда из A2.1) можно получить следующее
интегральное уравнение для средней интенсивности U(r);
U(r)=\ Go (r - г') -^ dV + pas J Go (г — г') U (r') dV. A2.41)
V V
Выполнив преобразование Фурье, получим
U (К) = Go (К) ^- + 9osGo (К) U (К),
откуда находим [см. A2.6)]
г//кл Gp (К) А1 (К) г ,„ Р (К)
Изотропное рассеяние
255
Таким образом, решение U(r) выражается через функцию Гри-
Грина G(r) как
A2.43)
U(r) = \ G(t-r')^dV.
Используя A2.31), получаем
= pot\
U(г) = pot\pdlt(рь г) + J g(/, Wo) 1,фъ т)dt\, A2.44)
где
•Используя среднюю интенсивность на единицу сечения, выра-
выраженную в оптических длинах, U(х) = U(г)/(potJ и мощность
Рис. 12.5. Излучение диска радиуса а.
Р(%) = Я(г)/(ра(K, генерируемую в единице объема, также вы-
выраженную в оптических длинах, формулу A2.44) можно запи-
записать через вектор оптической длины т = pew:
U (г) = PdIt (a, т) + \g (t, Wo) h (t, т) dt, A2.45)
где
(c r\— [ exp(-a|T-T'|) Р(т') ,
В качестве примера рассмотрим случай, когда источники рас-
расположены на диске радиуса а (рис. 12.5). Ось диска совпадает
с осью г цилиндрической системы координат. Пусть Ра — мощ-
мощность, излучаемая единицей поверхности диска, измеренной а
единицах оптической длины. Заметив, что
ipv A2.46)
256 Глава 12
получим
ОО
U (а, т) = Ц*- \ /о (Лр,) /, (Кха) ехр (- Zx
о
dX
1 ' ^\2+a? '
A2.47)
где %a — pota, а координаты т равны (рт, Zx).
12.6. Изотропное рассеяние в конечном объзме
и проблема Милна
В предыдущих разделах мы рассматривали излучение в не-
неограниченной среде. Если же рассеивающий объем конечен, го
можно сначала рассмотреть излучение в неограниченной среде,
используя функцию Грина G(r), а затем ввести распределение
воображаемых источников на поверхности объема так, чтобы
излучение этих поверхностных источников вместе с излучением
в неограниченной среде удовлетворяло граничным условиям на
поверхности ([11], разд. 2.5).
При другом подходе исходят из основного интегрального
уравнения A2.1). Проиллюстрируем этот подход на следующей
задаче. Пусть среда занимает полупространство z > 0, а излу-
излучение порождается на бесконечности при z^-+°°. Требуется
найти угловую зависимость выходящего из среды при 2 = 0 из-
излучения. Эта задача впервые изучалась Милном [31] и обычно
называется проблемой Милна.
Уравнение A2.1) для этой задачи принимает вид
U (г) = 9as [ Go (r - г') U (г') dV, A2.48)
где V — полупространство z > 0. Замечая, что U(r) есть функ-
функция только от z, мы можем проинтегрировать Go no x и у. По-
Полагая далее |г — г'[ =7? и замечая, что dx' dyr ~2nRdR, полу-
получаем
ОО О©
dxf \ dy'G,{x-x')^\ \
|
| г-г' |
^ A2.49)
00
где Ei(y)=\ (e~xy/x)dx~ интегральная показательная функ-
функция.
Изотропное рассеяние 257
Используя A2.49) и оптическую длину т = potz, из A2.48)
находим
оо
?/(т) = -^5 E{{\t-t'\)U{t')ut'. A2.50)
о
Это уравнение называют уравнением Шварцшильда — Милна.
Мы не станем подробно останавливаться на этой проблеме, так
как она детально описана в литературе [31, 40] и, хотя и пред-
представляет значительный исторический и теоретический интерес,
является лишь частной проблемой, практические приложения
которой ограниченны. Следует отметить, что точное решение этой
проблемы можно разделить на две части, причем одна из них
подчиняется диффузионному уравнению и удовлетворяет тому
же граничному условию, которое использовалось в диффузион-
диффузионном приближении. Этот вопрос рассматривается в гл. 9.
Глава 13
Приближение для больших частиц
Во введении к гл. 12 описаны два предельных случая, допу-
допускающих относительно простые решения. Один из них, когда
размеры частиц много меньше длины волны, называется случаем
изотропного рассеяния; он рассмотрен в гл. 12. В данной главе
мы обсудим другое приближение, соответствующее случаю ча-
частиц с размерами, много большими длины волны. Такое прибли-
приближение оказывается полезным при изучении распространения оп-
оптических и акустических пучков в воде и атмосфере, где раз-
размеры частиц часто значительно больше длины волны.
Задача о распространении волн в случайном облаке больших
частиц тесно связана с задачей о распространении волн в сплош-
сплошной случайной среде с большим радиусом корреляции. По су-
существу, распространение оптического излучения в турбулентной
атмосфере можно описывать аналогично тому, как это делается
в данной главе. Мы обсудим эту аналогию ниже (см. также
[71]).
13.1. Вывод дифференциального уравнения
в малоугловом приближении
Если размеры частиц много больше длины волны, то волна
рассеивается частицами главным образом в пределах малого
угла вблизи направления вперед, поэтому возникает возмож-
возможность упрощения уравнения переноса. Уравнение переноса G.24)
вместе с G.25) можно записать в виде
s • grad / (г, s) = — patl (г, s) +
+ ^-\р(*. s') / (г, 50 da>' + е (г, s). A3.1)
Запишем A3.1) в декартовых координатах, используя обозна-
обозначение г = хх + t/y -f- гг, где х, у и z — единичные векторы соот-
соответствующих направлений. Единичный вектор s выражается че-
через направляющие косинусы /, т, п:
z, A3.2)
Приближение для больших частиц 259
где I2 + т2 -f- п2 = 1, причем в сферических координатах F, ф)
/ = sin8cos</>, m = sin 9 sin </>, « = cos6,
а дифференциал dl dm, который мы обозначим через ds, связан
с дифференциалом телесного угла da> соотношением
ds = dldm = cos 9 sin 9 d9 d<? = я d®. A3.3)
Выберем ось z так, чтобы излучатель и приемник были лока-
локализованы вблизи точек (х = 0, у = О, z = 0) и (х = 0, у = 0,
z = L) соответственно. Поскольку рассеяние ограничивается об-
областью малых углов вблизи направления вперед, приходящая
к приемнику рассеянная волна направлена в основном вдоль
оси г. Это означает, что угол 9 должен быть всегда малым. По-
Поэтому можно использовать следующее приближение. Так как
угол 8 мал, положим я = cos 8 да 1. Далее, хотя пределы ин-
интегрирования по / и т ограничены условием /2 + /п2^1, без
существенной ошибки их можно распространить до ±оо:
оо оо
jj dl J dm= Jds, A3.4)
поскольку основной вклад в лучевую интенсивность соответст-
соответствует области малых |/| и \т\, а вклад от больших |/| и \т\
пренебрежимо мал. Кроме того, будем считать, что фазовая
функция p(s, s') зависит только от разности s — s'.
Используя эти приближения, запишем A3.1) в виде
¦§j/B, Р, s) + s- VtI(z, р, s) =
= - pn<TtI B, p, s) + -^ 5 J p (S - SO / (Z, P> SO ds' + 6 (Z, p, S),
A3.5)
где
Здесь плотность числа частиц мы обозначили через ря, чтобы из-
избежать путаницы с радиальным вектором р.
Граничное условие можно выбрать вблизи излучателя при
2 = 0:
/@, р, 8) = /„(р, s). A3.6)
Уравнение A3.5) вместе с граничным условием A3.6) дает пол-
полную математическую постановку задачи.
260 _ Глава 13
В качестве примера рассмотрим коллимированный пучок с
гауссовой амплитудой и поперечным размером W. Лучевую ин-
интенсивность при 2 = 0 можно получить следующим образом. Как
будет показано в гл. 14, функция взаимной когерентности
Г(рь рг) есть фурье-образ от лучевой интенсивности /(р, s):
Г(Рь р2) = Г(р, pd)=<u(pl)
1(9, s) = -щг jj Г (р, gd) exp (— iks ¦ gd) dpd, A3.8a)
где р = 'A(pi+ Рг), Pd = pi — Р2, a u(pi) и и(р2) — значения
поля в точках pi и р2 соответственно. Используя это и замечая,
что для коллимированного пучка при г = О
A3.86)
получаем следующее выражение для лучевой интенсивности кол-
коллимированного пучка при 2 = 0:
/0 (Р> s) = {k2W2I0/n) exp (- p2/W2 - k2W2s2), A3.8в)
где полная мощность Pi есть
Я, = \ I и (Р) I2 dp = J J /о (р, s) rfs dp = nW2Ia, /о = | «о Р. A3.8г)
13.2. Общее решение
Общее решение уравнения A3.5) можно получить с помощью
преобразования Фурье1). Применим к A3.5) преобразование
Фурье по аргументу р. Обозначим через А фурье-образ от /
по р:
со
h(z, и, s)= ^ I(z, p, s)exp (in ¦ р)dp, A3.9a)
2, р, s) = -^jf ^ 7! B> z- s) ехР (—/х • Р)rfx- A3.96)
В результате получим
> z' s')rfs'~?B, х, 8) = 0, A3.10)
') Вместо этого можно использовать метод характеристик для линейных
дифференциальных уравнений с частными производными [156].
Приближение для больших частиц 261
где Е — фурье-образ по р от e(z, p, s). Прежде всего упростим
первый член A3.10), полагая
Л (z, х, s) = /2(z, х, s) exp {(is • х — pnat) z). A3.11)
Тогда A3.10) примет вид
оо
¦gj h {г, и, s)—Р-~ J Jp(s - s')exp{-ix ¦ (s-s')z}/2(z, и, s')rfs'—
— CO
— E(z, x, s) exp {— is • x + pnat) z) = 0. A3.12)
Далее, преобразуя по Фурье второй член, представляющий собой
интеграл типа свертки, получаем произведение двух функций.
Используя соотношения
P(q)= ^ p (s) exp (is • q) ds, A3.13a)
— oo
oo
F(z, v., q)=^/2(z, x, s) exp (is • q) ds, A3.136)
— oo
CO
Eq(z, x, q)=^?(z, x, s)exp(is -q)ds, A3.13b)
находим
-^F{z, x,q)--^rP(q-*z)F(z, x, q)-
— EQ (z, x, q — nz) exp (pnatz) = 0. A3.14)
Это линейное дифференциальное уравнение первого порядка для
F, которое легко решить.
В отсутствие источников e(z, p, s) в среде имеем
F (z, x,q) = F @, х, q) exp Г J -^- P (q - «zO dz'l.
A3.15)
Окончательное решение I(z, p, s) получается из A3.96), A3.11)
и A3.15):
, p, s) = ^)J
x\dqexp(-is-q)F(z, к, q). A3.16)
262 Глава 13
При z = 0 f(z, р, s) должно.быть равно /0(р, s) из A3.6), так
что
Л) (и, q) = F @, и, Q) = ^ S /о ^Р> S^ехр ("* • Р + /s • Я) rfP ^5-
A3.17)
Окончательное выражение можно записать в несколько более
простой форме, заменив переменную q на q' = q — хг и опустив
затем штрих у q'. Это дает
/ (г, р, s) = —^ ^dx^dq ехр (— Ы • р — is ¦ q) FQ (и, q + кг) X
XK(z, *, q), A3.18)
где
К (z, к, q) = exp|- Jp«a*{l - ^ P (q + * {z - z'))} dz'\
Выражение A3.18) представляет собой общее решение урав-
уравнения A3.5) в отсутствие источников в (z, p, s). При наличии
источников уравнение A3.15) нужно модифицировать так, чтобы
удовлетворить уравнению A3.14)
Интегралы, входящие в найденное решение, трудно оценить,
и в настоящее время в общем случае произвольной функции рас-
рассеяния p'(s — s') удобное выражение для /, по-видимому, otcvt-
ствует. Однако поучительно рассмотреть частный случай, когда
функция рассеяния аппроксимируется дельта-функцией для на-
направления вперед:
p(s_s') = 4nr06(s-s'), A3.19)
где Wo — альбедо отдельной частицы, a 4nWo выбрано так, что
Wo = 47Г S р (^ ~ ?) d&' ~ ^Г S p (s ~ s'} ds'- A3-20)
Подставляя A3.19) в A3.18), получаем
I(z, p, s) = /@, p — sz, s)exp(— pnaaz), A3.21)
где ва — сечение поглощения частицы. Отсюда видно, что луче-
лучевая интенсивность распространяется без изменения направле-
направления s, испытывая ослабление, определяемое сечением поглоще-
поглощения частицы.
Рассмотрим другой пример (разд. 15.2 и 15.3). Пусть падаю-
падающая волна — плоская:
/о (P. s) = /ofi(s), A3.22)
так что A3.17) принимает вид
F0(q, *) =Bп)Ч0Ь(х). A3.23)
Приближение для больших частиц 263
Фазовую функцию будем считать гауссовой:
p(s) = 4apr0exp(-aps2)> A3.24)
где ар пропорционально (D/XJ (D — диаметр частицы, А, — дли-
длина волны). Используя A3.24), для К(z, и, q) в A3.18) получаем
выражение
/C(z, x,q) = exp |-$ Рпаф-Гоexp(-^)]rf*'J. A3.25)
Если оптическая длина pnotz много больше единицы, то A3.25)
можно аппроксимировать выражением
К (г, к, q) = expf-\Pnot[l-Wo+ ^-q?]dz'\. A3.26)
Подставляя A3.23) и A3.26) в A3.18), находим
W] A3-27)
Заметим, что в этом приближении угловое распределение, часто
называемое угловым спектром, уширяется, и ширина пучка на
уровне половинной мощности растет как z1'2. Заметим также, что
поток F(z, p) дается выражением
F(z, p)= J/(Z, p, s)rfs = /oexp(-Pn(Taz). A3.28)
Это показывает, что уширение углового спектра сопровождается
уменьшением амплитуды, причем ослабление полного потока
просто пропорционально сечению поглощения.
13.3. Приближенное решение для случая медленного
углового изменения диффузной интенсивности
Как показано в предыдущем разделе, несмотря на то, что
общее решение уравнения A3.5) известно и в отсутствие в среде
источников имеет вид A3.18), интеграл в A3.18) для произволь-
произвольной фазовой функции вычислить не удается. В некоторых прак-
практических ситуациях, таких, как распространение оптических пуч-
пучков в воде и атмосфере, ослабленная падающая интенсивность
сильно коллимированна, тогда как диффузная интенсивность
имеет широкий угловой спектр и медленно меняется при изме-
изменении угла рассеяния. В этих условиях можно получить более
простое решение следующим способом [46, 53J.
264 Глава 13 . .-
Рассмотрим случай, когда в уравнении A3.5) источник
e(z, p, s) отсутствует. Запишем лучевую интенсивность в виде
суммы ослабленной падающей интенсивности hi и диффузной
интенсивности Id-
Тогда имеем
-^ Irl (z, р, s) + s • VtIrl (z, p, s) = — pnatlri (z, p, s), A3.29)
•¦jjh{z, p, s) + s • VtId(z, p, s) = — р„ст^ (z, 9, s) +
<(s — sr)Id(z, p, s')ds' -\-Qd(z, 9, s), A3.30)
— oo
где
oo
Qd(z, 9, s) = ~^-\\p(s — s')Iri(z, 9, s')ds\ A3.31)
— oo
Решение A3.29) легко получить в виде интеграла Фурье, если
заметить, что A3.29) совпадает с A3.5), за исключением равен-
равенства нулю фазовой функции р и функции источников е. Поэтому,
полагая в A3.18) Р = 0, получаем
1Н B, Р, s) = -тк-тг \ d% \ dq ехр (— Ы • р — is • q) FQ (z, q + иг) X
Xexp(-Pnfftz), A3.32)
где Fq(k, q + v,z) — фурье-образ от падающей лучевой интенсив-
интенсивности при г = 0, даваемый выражением A3.17).
Подставив A3.32) в A3.31), получим
Qa (г, 9, s) = (^-) (^J \dx J dq ехр (- йе • р - is • q) P (q) X
X /=¦(> (и. q + «г) ехр (- р„ст,2). A3.33)
Рассмотрим теперь A3.30). Если диффузную интенсивность Id
можно считать медленной функцией углов (т. е. медленной функ-
функцией /' и т') и если фазовая функция зависит лишь от угла ме-
между направлением падения s' и направлением рассеяния s [т.е.
от |s — s'|2=(/—/'J+ {т — т'J], то приближенное решение
A3.30) можно получить, разлагая подынтегральное выражение
в ряд Тейлора и удерживая первый член этого ряда. Заметим,
что
P. s')ds'=$$p(s')A,(z, P, s' + s)ds', A3.34)
—оо
Id(z, p, &' + s) — Ia(z, p, s) + s'VsId(z, 9, s) +
...,
Приближение для больших частиц 265
где Vs = {d/dl)x + (dldm)y, s = /х + Щ- a s' = I'x + tn'y. Под-
Подставляя A3.34) в A3.30) и замечая, что p(s') есть функция от
V2 + т'2, и что I' = sin 6' cos f, tn' = sin Q' sin ^', J J p (| s' |2) X
Xl'dl'dtn' = Q, a
2л я
(I s' P) I'2dV dm' = J rf^' J sin 9' d6'p (sin2 6') sin2 0' cos2f --=-
О О
получаем')
~ Id {z, p, s) + s • VtId B, p, s) =
= — PnOjd (z, p, s) -f pnGtWo -^- \\U {z, p, s)-\-Qd{z, p, s),
A3.35)
где
оо
r r
(s') (I'2 + m'2) dl' dm'
\\p (s') rfr dm'
и мы использовали соотношение
оа = <у* — (То=сгЛ1—Wo), Wo = -7— \ \ p(s') dl'dm'. A3.37)
Уравнение A3.35) можно решить точно с помощью преобразо-
преобразований Фурье A3.9а) и A3.96), где
Л (г, х, s) = /2 (z, х, s) exp {{is ¦ x — pnaa) z). A3.38)
Ч результате получаем решение 2)
l( P. s) = -^yrjc?x Jdqexp(-m.p-/s-q)FdB, x, q + zz),
A3.39)
') Полное разложение в ряд приведено в работе [23].
2j Это решение совпадает с полученным работе [53]. j
266 Глава 13
где
X ехрГ- Pnotz' - J Кdz"\dz',
фр„ета)
a Fo"(»t, q)—фурье-образ лучевой интенсивности /0(р, s) при
2 = 0, определяемый выражением A3.17).
Полная лучевая интенсивность l(z, р, s) есть сумма Iri(z, p, s)
A3.32) и Id(z, p, s) A3.39).
Рассмотрим теперь мощность, принимаемую апертурой. Если
Ar(p, s)—нормированная эффективная поверхность приемной
апертуры, то полная принимаемая мощность в точке z есть
р, s) =
«rK Ч)^(г, х, q). A3.40)
где аг и Fr — фурье-образы от Л, и /:
/> (г, х, q) == ( dp \ ds ехр (/и • р + is • q) / (z, p, s),
r ; A3.41)
ar (и, q) = \ rfp \ ds exp (— ix • p — is • q) Ar (p, s).
Угловая расходимость пучка вблизи аксиального направления
есть
[ ds | s |2 / (г, 0, s)
<S2)= J . A3.42)
\ ds/ (z, 0, s)
Среднеквадратичное поперечное сечение пучка равно
[ dp \ ds (яр2) / (г, р, s)
(яр2) = J J . A3.43)
\ dp \ ds/ (z, p, s)
Выражения A3.30), A3.42) и A3.43) оценивались [47, 53] для
случая падающего пучка A3.8) и эффективной поверхности
апертуры Ar (p, s) = ехр (— p2/W?) при гауссовой форме фазо-
фазовой функции.
Приближение для больших частиц 267
Приведем окончательные выражения для этого частного слу-
случая, опуская детальные выкладки работ [47, 53]. Пусть фазо-
фазовая функция имеет вид
i^(^±fl) A3.44)
причем мы использовали соотношение
ldm. A3.45)
Падающая интенсивность при 2 = 0 дается выражением
A3.8в). Тогда для P(z) из A3.40) получаем
d A346)
P @) С + 3Вт2 ' J С + Звт2 + Зг/2 + г/3 '
о
где
и Ро = nW2/0 — полная излучаемая мощность. Угловая зависи-
зависимость A3.42) имеет вид
eVdy
4, A3.47)
L '
где
(Л f ft 1 .,\ //^ 1 Ой
Я (Г/, Т) ==
<e2)' u
+ P + У) (Сз + ЗРт2 + 3j/2 + j/3) - 3 (Рт+ j/ + У2/2)
(C3 + Зрт2 + 3(/2 + г/3J
Следовательно, среднеквадратичное поперечное сечение пучка
A3.43) равно
(^l g) A3.48)
Литература
1. Abramowitz M., Stegun I. A., Handbook of Mathematical Functions, U. S.
Govt. Printing Office, Washington, D. C, 1964.
2. Adams R. N., Dentnan E. D., Wave Propagation and Turbulent Media, Else-
vier, Amsterdam, 1966.
3. Ahuja A. S. JASA, 51, 182 A970).
4 Anderson N., Sekelj P., Phys. Med. Biol., 12, 185 A967).
5. Anderson R. S., Browell E. V., Appl. Opt. 11, 6, 1345 A973).
6. Baker D. W., IEEE Trans. Sonics Ultrasonics, SU-17, 170 A970).
7. Battan L. /., Radar Observation of the Atmosphere, Univ. of Chicago
Press, Chicago, Illinois, 1973.
8. Bean B. R., button E. ]., Radio Meteorology, Dover, New York, 1968.
(Имеется перевод: Вин Б., Даттон Е. Радиометеорология, Пер. с англ. —
Л.: Гидрометеоиздат, 1971.)
9. Beard С. /., Kays Т. Н., Twersky V., IEEE Trans. Ant. Prop., AP-15, 1, 99
A967),
10. Beckmann P., Spizzichino A., The Scattering of Electromagnetic Waves
from Rough Surface, Pergamon, Oxford, 1963.
11. Bell 0. /., Qlasstone S., Nuclear Reactor Theory, Van Nostrand-Reinhold,
Princeton, New Jersey, 1970.
12. Bellman R., Wing G. M., An Introduction to Invariant Imbedding, Wiley,
New York, 1975.
13. Bello P. A., IEEE Trans. Commun. Syst., 11, 360 A963).
14. Bendat J. S., Piersol A. O., Measurement and Analysis of Random Data,
Wiley, New York, 1966.
15. Bendat J. S., Piersol A. O., Random Data, Wiley (Interscience), New York,
1971.
16. Berne B. J., Pecora R., Dynamic Light Scattering, Wiley, New York, 1976.
17. Biggs A. W., ed., AGARD Tonf. Proc. no. 107. Telecommunication aspects
on frequencies between 10 and 100 GHz, Technical Editing and Reproduc-
Reproduction, Ltd., Harford House, London, 1973.
18. Blackman R. В., Tukey I. W., The Measurement of Power Spectra, Dover,
New York, 1958.
19. Blanchard D. C, Bentley and Lenard: Pioneers in cloud physics, Am. Sci.,
60, 746 A972).
20 Blevis B. C, Dohoo R. M., McCormick K. S., IEEE Trans,, AP-15, 394
A957).
21. Born M., Wolf E., Principles of Optics, Macmillan, New York, 1964. (Име-
(Имеется перевод: Борн М., Вольф Э. Основы оптики, Пер. с англ. — М:
Наука, 1973.)
22. Bowman I. J., Senior Т. В. A., Uslenghi P. L. E., Electromagnetic and
Acoustic Scattering, North-Holland Publ., Amsterdam, 1969.
23. Bremmer H., J. Res. Nat. Bur. Std., 68D, 967 A964).
24. Brinkworth B. I., Appl. Opt, 11, 1434 A972).
25. Brinkworth B. J., Appl. Opt., 12, 2, 427 A973).
26. Brown О. В., Gordon H. R., Appl. Opt., 13, 2874 A974).
27. Byer R. L, Qarbuny M., Appl. Opt., 12, 1497 A973).
28. Cantor I., Appl. Opt., 12, 1482 A973).
29. Case К. М., Zweifel P. F., Linear Transport Theory, Addison-Wesley,
Reading, Massachussetts, 1969.
Литература 269
30. Case К. М., Hoffman F. D., Placzek G., Introduction to the Theory of
Neutron Diffusion. Vol. 1, Los Alamos Scientific Lab., Los Alamos, New
Mexico, 1953.
31. Chandrosekhar S., Radiative Transfer, Oxford Univ. Press, London and
New York, and Dover, New York, 1950. (Имеется перевод: Чандрасекар С.
Перенос лучистой энергии. Пер. с англ. — М.: ИЛ, 1953.)
32. Chu Т. S., Bell Syst. Techn. J., 53, 8, 1557 A974).
33. Chu Т. S., Hogg D. C, Bell Syst. Techn. J., 47, 723 A968).
34. Cohen A., Appl. Opt., 14, 12, 2873 A975).
35. Coulson K-, Fraser R., Rev. Geophys. Spase Phys., 13, 732, 826 A975).
36. Crosignani В., DiPorto P., Bertolotti M., Statistical Properties of Scattered
Light, Academic Press, New York, 1975.
37. Cross D. A., Latimer P., Appl. Opt,, 11, 5, 1225 A972).
38. Danielson R. E., Moor D. R., van de Must H. C, J. Atmos. Sci., 26, 1078
A969).
39 Davenport W. В., Root W. L., Random Signals and Noise, McGraw-Hill,
New York, 1958. (Имеется перевод: Давенпорт В. Б., Рут В. Л. Введе-
Введение в теорию случайных сигналов и шумов. Пер. с англ. — М.: ИЛ, 1960.)
40. Davison В., Neutron Transport Theory, Oxford Univ. Press, London and
New York, 1958.
41. de Buttencourt I. Т., J. Reprints Raytheon Co., 12, 1, 2 A975).
42. Deirmendjlan D., Electromagnetic Scattering on Spherical Polydispersions,
American Elsevier, New York, 1969.
43. Derr V. E., Remote Sensing of the Troposphere, U. S. Govt. Pn'nting
Office, Washington, D. C, 1972.
44 Devin C, Jr., JASA, 31, 12, 1654 A959).
45. Divari N. В., ed., Atmospheric Optics, Consultant Bureau, New York, 1970.
46. Долин Л. С.— Изв. ВУЗов (Радиофизика), 1964, 7, № 2, с. 380.
47. Долин Л. С.— Изв. ВУЗов (Радиофизика) 1966, 9, № 1, с 61.
48. Duntley S. Q., J. Opt. Soc. Am., 53, 214 A963).
49. Durney С H., Johnson С. С, Massoudi H., IEEE Trans. MTT, 23, 2, 246
A975).
50. Easterbrook B. J., Turner D., Proc. IEE (London), 114, 557 A967).
51. England A. W., Radio Sci., 9, 447 A974).
52. Erickson K. R., Fay F. /., Jones J. P., IEEE Trans. Sonics Ultrasonics,
SU-21, 144 A974).
53. Fante R. L, IEEE Trans., AP-21, 750 A973).
54. Fedoseev V. Л., Advances in Aerosol Physics, Israel Program for Scientific
Translation, Ltd., 1971.
55. Felsen L. В., Marcuvitz N., Radiation and Scattering of Waves, Prentice-
Hall, Englewood Cliffs, New Jersey, 1973. (Имеется перевод: Фелсен Л.,
Маркувиц Н. Излучение и рассеяние волн: Пео. с англ. — М.: Мир, 1978.)
56. Fletcher N. Н., The Physics of Rain Clouds, Cambridge Univ. Press, Lon-
London and New York, 1962.
57. Funk C. J., Appl. Opt., 12, 301 A973).
58. Gate L. F., Appl. Opt, 13, 2, 236 A974).
59. Godard S. L, IEEE Trans., AP-18, 4, 530 A970).
60. Градштейн И. С, Рыжик И. М. Таблицы интегралов, сумм, рядов и
произведений. — М.: Наука, {971.
61. Гурвич А. С, Калинин В. И., Матвеев Д. Т. — Изв. АН СССР, Физика
атмосферы и океана, 1973, 9, с. 712.
62. Hale G M., Querry M. R., Appl. Opt. 12, 555 A973).
63. Harrold Т. W., Proc IEE (London), 114, 201 A967).
64 Hemenger R. P.. J Opt., Soc. Am., 64, 4. 503 A974).
65 Heney L, Greenstem J.. Astrophys. J., 93, 70 A941).
66. Hermann B. M., Browning S. R., Baltan L. /., Tables of Radar Cross
Sections of Water Spheres, Univ. of Arizona, TR No. 9, 1961.
270 Литература
67. Hildebrand F. В., Introduction to Numerical Analysis, McGraw-Hill, New
York, 1956.
68. Hodgeson 7. A., McClenny W. A., Hanst P. L., Science, 182, 248 A973).
69. Hogg D. C, Bell Syst. Techn, J., 48, 2949 A969).
70. Hogg D. C, Chu T. S., Proc. IEEE, 63, 1308 A975). (Имеется перевод:
Хогг, Чжу, ТИИЭР, 1975, 65, с. 52.)
71. Ishimaru A., Radio Sci., 10, 1, 45 A975).
72. Ishimaru A., Proc. IEEE, 65, 1030 A977). (Имеется перевод: Исимару А.,
ТИИЭР, 1977, 65. с. 46.)
73. Ishimaru A., Hong S. Т., Radio Sci., 10, 6, 637 A975).
74. Ishimaru A, Lin J. C, AGARD Conf. Proc. № 107, Telecommunication
aspects on frequencies between 10 and 100 GHz, Technical Editing and
Reproduction, Ltd., Harford House, London, 1973.
75. Jahnke E., Emde F., Losch F., Tables of Higher Functions, McGraw-Hill,
New York, 1960. (Имеется перевод: Янке Е., Эмде Ф., Леш Ф. Специаль-
Специальные функции: формулы, графики, таблицы. Пер. с нем, — М.: Наука,
1977.)
76. Jerlov N. G., Optical Oceanography, Elsevier, Amsterdam, 1968.
77. Jerlov N. G., Nielsen E. S., Optical Aspects of Okeanography, Academic
Press, New York, 1974.
78. Johnson С. С, IEEE Trans., BME-17, 129 A970).
79. Johnson С. С, Guy A. W., Proc. IEEE, 60, 6, 692 A972). (Имеется пере-
перевод: Джонсон, Гай, ТИИЭР, 1972, 60, с. 49.)
80. Johnson С. С, Durney С. Н., Messoudi H. IEEE Trans., MTT-23, 9 739
A975).
81. Карапу N. R., Fiber Optics, Academic Press, New York, 1967.
82. Kattawar G. W., Humphreys T. J., Appl. Opt., 15, 1, 273 A976).
83. Kattawar G. W., Plass G. N., Catchings F. E., Appl. Opt., 12, 1071
A973).
84. Kattawar G. W., Plass G. H., Hitzfelder S. J., Appl. Opt., 15, 632 A976).
85. Kennedy R. S., Karp S., Proc. of MIT-NASA Workshop, NASA SP-217,
US. Govt. Printing Office, Washington, D. C, 1969.
86. Kerker M., ed., ICES Electromagnetic Scattering, Pergamon, Oxford, 1963.
87. Kerker M., The Scattering of Light, Academic Press, New York, 1969.
88. Kinsler L. E., Frey A. R., Fundamentals of Acoustics, John Wiley, New
York, 1962.
89. Кондратьев К. Я- Лучистый теплообмен в атмосфере. — М. — Л.: Гидро-
метеоиздат, 1956.
90. Kratohvil J. P., Annal. Chem., 38, 517 A966).
91. Kubelka P., J. Opt. Soc. Amer., 38, 448 A948).
92. Kubelka P., Munk F., Zs. Tech. Phys., 12, 593 A931).
93. Laws J. O., Parsons D. A., Am. Geophys. Un. Trans., 24, 452 A943).
94. Lax P. D., Phillips R. S., Scattering Theory, Academic Press, New York,
1967.
95. Lhermitte R., Science, 182, 258 A973).
96. Lin С I., Baker M., Charlson R. J., Appl. Opt., 12, 1356 A973).
97. Lin J. C, Ishimary A., Propagation of Millimeter Waves in Rain, Dept. of
Elec. Eng., TR No. 144, Univ. of Washington, Seattle, Washington, 1971.
98. Lin J. C, Ishimary A., JASA, 56, 6, 1695 A974).
99 Llou K., Lahore H.t J. Appl. Meteorol., 13, 257 A974).
100. Livesay D. E., Chen K. M., IEEE Trans. MTT, 22, 12, 1273 A974).
101. Megnus F. W., Oberhettinger F., Formulas and Theorems for the Functions
of Mathematical Physics, Chelsea, New York. 1954.
102. Malecki I., Physical Foundations of Technical Acoustics, Oxford Univ.
Press (Pergamon), London and New York, 1968.
103. Marshall J. S. Palmer W. M. K., J. Meteorol., 5, 165 A948).
104. Medhurst R. S., IEEE Trans., AP-13, 550 A965).
Литература 271
105. Menzel D. #., ed., Selected Papers on the Transfer of Radiations, Dover,
New York, 1966.
106. Milton J. ?., Anderson R. C. Browell E. V., Appl. Opt, 11, 3, 697 A972).
107. Molcho I., Estimation of the Macroscopic Optical Scattering Parameters
of Tenuous Solutions, Ph. D. Thesis, Elec Eng. Dept., Univ. of Washing-
Washington, Seattle, Washington, 1975.
108. Morse P M., Feshbach H., Methods of Theoretical Physics, McGraw-Hill,
New York, 1953. (Имеется перевод: Моос Ф. М., Фешбах Г. Методы ма-
математической физики Пер с англ.— М.: ИЛ, 1960.)
109 Morse P. M., Ingard К. О., Theoretical Acoustics, McGraw-Hill, New York,
1968.
110. Mudgett P. S., Richards L. W., Appl. Opt., 10, 1485 A971).
111. Newton R. G., Scattering Theory of Waves and Particles, McGraw-Hill,
New York, 1966.
112. Oguchi Т., J. Radio Res. Labs., 13, 141 A966).
113. Oguchi Т., Radio Sci., 8, 1, 31 A973).
114. Okamura S. et al., J. Radio Res. Lab., 6, 255 A959).
115. Ольшевский В. В. Статистические свойства морской реверберации. — М.:
Наука, 1966.
116 Palmor К F., Williams D., JOSA, 64. 8, 1107 A974).
117. Papas С. Н., Theory of Electromagnetic Wave Propagation, Plenum
Press, New York, 1965
118. Pecora R., J. Chem Phys., 40, 6, 1604 A964).
119. Pecora R., J. Chem. Phys., 48, 9, 4126 A968).
120. Plass G. N., Kattawar G W., Appl. Opt., 7, 3, 415 A968).
121. Ptass G. N., Kattawar С W., Catchings F. E., Appl. Opt., 12, 314
A973).
122. Preisendorfer R. W., Radiative Transfer on Discreet Spaces, Oxford Univ.
Press (Pergamon), London and New York, 1965.
123. Redwood M. R., Mechanical Waveguides, Oxford Univ. Press (Pergamon),
London and New York, 1960.
124. Reichman J., Appl. Opt., 12, 1811 A973).
125. Reynolds L., Optical Diffuse Reflectance and Transmittance from an Ani-
sotropically Scattering Finite Blood Medium, Ph. D. Dissertation, Elec.
Eng., Univ. of Washington Seattle, 1975.
126. Reynolds L, Johnson С С. Ishimaru A., Appl. Opt., 15, 2059 A976).
127. Rowell R. L, Stein R. S., eds., Electromagnetic Scattering, Gordon and
Breach, New York, 1967.
128. Ruck G. T. et al., Radar Cross Section Handbook, Vols. I and II, Plenum
Press, New York 1970.
129. Sassen K-, J. Appl. Meteorol, 13, 923 A974).
130. Saxon D. S., Lectures on the Scattering of Light, UCLA Dept. of Meteorol.
Sci. Rep. № 9, 1955.
131. Saxton J. A., Meteorological Factors in Radio Wave Propagation pp. 292—
306, Phys. Soc. London. 1946.
132. Schaaf J W, Williams D., JOSA, 63, 726 A973).
133. Schiff L. /., Quantum Mechanics, McGraw-Hill, New York, 1955. (Имеется
перевод: III и ф ф Л. И. Квантовая механика. Пер. с англ. — М.: ИЛ,
1959.)
134. Schuster A., Astrophys. J.. 21, 1 A905).
135 Schwan H. P., Biological Engineering McGraw-Hill, New York, 1969.
136. Sekera Z., JOSA 56, 12, 1732 A966).
137 Semplak R A.. Radio Sci, 5, 559 A970)
138 Semplak R A., Bell Syst Tech. J., 50, 8 2599 A971).
139. Semplak R. A., Turrin R. H., Bell Syst Tech. J., 48, 1767 A969).
140. Шифрин Я. С. Вопросы статистической теории антенн. — М.: Сов. радио,
1970. Г Г
272 Литература
141. Shimizu K-, Species Identification and Descriminative Concentration Esti-
Estimation of Microbial Particles by Laser Scattering, M. S. Thesis, Elec. Eng.
Dept., Univ. of Washington, Seattle, Washington, 1976.
142. Shimizu K., Ishimary A., Opt. Eng., 16 A978).
143. Shung K. K., Sigelmann R. A., Reid I. M., IEEE Trans. Biomed. Eng.,
BME-23,6, 460 A976).
144. Sigelmann R. A., Reid J. M., JASA, 53, 1351 A973).
145. Silver S., Microwave Antenna Theory and Design, McGraw-Hill, New York,
1949.
146. Skolnik M. I., Radar Systems, McGraw-Hill, New York, 1962. (Имеется
перевод: Сколник М. Введение в технику радиолокационных систем. Пер.
с англ. — М.: Наука, 1966.)
147. Skolnik M. /., Radar Handbook, McGraw-Hill, New York, 1970. (Имеется
перевод: Сколник М. И. Справочник по радиолокации. Пер. с англ. —
М.: Сов. радио, 1976.)
148. Соболев В. В. Перенос лучистой энергии в атмосферах звезд и планет. —
М.: Гостехиздат, 1956.
149. Sommerfeld A., Thermodynamics and Statistical Mechanics, Academic Press,
New York, 1956. (Имеется перевод: Зоммерфельд А. Термодинамика и
статистическая физика. Пер. с нем. — М.: ИЛ, 1955.)
150. Stephens R. W. В., Underwater Acoustics, Wiley (Interscience), New York,
1970.
151. Stogryn A., Radio Sci., 5, 509 A974).
152. Stratton J. A., Proc. IRE, 18, 1064 A930).
153. Stratton J., Electromagnetic Theory, McGraw-Hill, New York, 1941. (Име-
(Имеется перевод: Стрэттон Д. А. Теория электромагнетизма. Пер. с англ.—
М. — Л.: Гостехиздат, 1948.)
154. Stroke G. W. et al., Ultrasonic Imaging and Holography, Plenum Press,
New York, 1974.
155. Татарский В. И. Теория флюктуационных явлений при распространении
волн в турбулентной атмосфере. — М.: изд-во АН СССР, 1959.
156. Татарский В. И. Распространение волн в турбулентной атмосфере. — М.:
Наука, 1967.
157. Tolstoy /., Clay С. S., Ocean Acoustics, McGraw-Hill, New York,
1966.
158. Tricker R. A. R., Introduction to Meteorological Optics, American Elsevier,
New York, 1970.
159. Tsang L, Kong I. A., Radio Sci., 10, 1025 A975).
160. Turner L, Appl. Opt., 12, 1085 A973).
161. Ушков О. Я-, Герман В. Л., Ваксер И. X. — Укр. физ. журн., 1961, 6,
с. 618.
162. Van de Hulst H. С, Light Scattering by Small Particles, Wiley, New York,
1957. (Имеется перевод: Ван де Хюлст Г. Рассеяние света малыми части-
частицами. — М.: ИЛ, 1961.)
163. Van der Pol В., Bremmer #., Operational Calkulus, Cambridge Univ.
Press, London, 1959.
164. Ward Q. et al., Appl. Opt., 12, 2585 A973).
165. Weast R. C, ed., CRC Handbook of Chemistry and Physics, Chemical Rub-
Rubber Co., Cleveland, Ohio, 1970.
166. Weibel O. E., Dressel H. O., Proc. IEEE, 55, 497 A967). (Имеется пере-
перевод: Вейбел, Дрессел, ТИИЭР, 1967, 55, с. 22.)
167. Wells P. N. Т., Physical Principles of Ultrasonics Diagnosis, Academic
Press, New York, 1969.
168. Williams M. M. R., Mathematical Methods in Particle Transport Theory,
Wiley, New York, 1971.
169. Wolbarshi M. L., Laser Application in Medicine and Biology, Vol, I, Ple-
Plenum Press, New York, 1971,
Литература 273
170. Woodward P. M., Probability and Information Theory with Application to
Radar, Oxford Univ. Press (Pergamon), London and New York, 1964.
(Имеется перевод: Вудворд Ф. Ai. Теория вероятностей и теория инфор-
информации с применениями в радиолокации. Пер. с нем. — М.: Сов. радио,
1955.)
171. Wyatt P. /., Appl. Opt, 7, 1879 A968).
172. Яглом А. М. — УМН, 1952, № 5, с. 51.
173. Yeh С. Phys Rev,, 135, А1193 A964).
174. Yeh С, JASA, 46, 797 A969).
175. Zadeh L. A., Proc. IRE, 38, 291 A950).
176. Zaneveld J. R. V., Pak H., JOSA, 63, 3, 321 A973).
Предметный указатель
Альбедо поверхности и дна океана
192
— частицы 20, 174, 189
Аэрозоль 54
Биоакустика 79
Биооптика 75
Биоэлектродинамика 62
Ближнего поля явления 249
Видимость 62
— оптическая 62
ВКБ-приближение 34
Волна неполяризованная 43
— плоская импульсная 143
— сферическая падающая 252
Волновод акустический 68
Во.^иь; акустические 48
— частично поляризованные 183
Время когерентности 113, 150
Гамма-распределение модифицирован-
модифицированное 57
Гематокрит 76, 79, 207
Герца вектор 24
Гидроакустика 66
Гидрометеоры 54
Гидрооптика 64
Град, оптические и СВЧ-свойства 63
Граничные условия для двухпотоко-
вой теории 214
диффузной интенсивности
176, 199
лучевых интепсивностей на
границе однородных сред 171
четырехпотоковой теории 219
Двухпотоковая теория 212
Диаграмма направленности по мощ-
мощности 84
— неопределенности 129
Диаграммы ширина на уровне поло-
половинной мощности 89
Диаметр медианный дождевых ка-
капель 56
Диатермия 74
Дисперсия флуктуации интенсивности
93
Диффузии длина 246
Диффузия от точечного источника 206
Диэлектрическая проницаемость жи-
жировой, мышечной и мозговой
тканей 75
Длина свободного пробега для изо-
изотропного рассеяния 247
Доплеровский сдвиг 97
Дымка, оптические и СВЧ-свойства
62
Естественный свет 42
Закон диффузного отражения 191
— затенения 225
— Кирхгофа излучения черного тела
178
— Ламберта 169
— Ламберта — Вира 76
— Юнга 65
Затухание в дожде 59
Зона Френеля 157
Излучатель остронаправленный 118
Излучение диска 255
— изотропное 169
Измерение отражения 207
Изосбестические точки 77
Импеданс акустический характеристи-
характеристический 51
Импульс, распространение и рассея-
рассеяние 108
между передатчиком и
приемником 151
— узкополосный 109
— уширение 113
Инвариантное погружение 239
Индикатор дальность—высота (ИДВ)
53
— движущихся целей (ИДЦ) 133
— кругового обзора (ИКО) 53
. — типа А 53
Предметный указатель
275
Интенсивность диффузная 176, 188
— когерентная 92, 137
— коллимированная 177
— некогерентная 92
— падающая ослабленная 179, 188
— поверхностная 166
— поля 165
— средняя 169
Многократного рассеяния теория 181
Тверского 163, 181
Многократное рассеяние 84, 163
Насыщенность кислородом 76, 78, 207
Нефть, акустические свойства 70
Канал звуковой 68
— с некоррелированным рассеянием
114
— стационарный 114
с некоррелированным рассея-
рассеянием 114, 117, 129
— SOFAR 68
Катетер волоконнооптический 206,
209
— оксиметрический 208
Кирхгофа закон 178
Когерентности полоса 113
Концентрация 84
— бактерий 192, 194
Корреляционная функция временная
99, 141, 159
Корреляция рассеянного поля про-
пространственная 101
Косинус угла рассеяния средний 197
Коэффициент использования аперту-
апертуры 90
— поглощения 64
— полного затухания 64
— усиления 90
Красные кровяные тельца 76
Кровь гемолизованная 76
— ультразвуковые свойства 80
— характеристики и сечения 78
Лагранжев подход, описание акусти-
акустических волн 48
Локатор акустический 52, 68
— лазерный 52
Лучевая интенсивность 165
— — измерение 167
коллимированного пучка 193
— — на плоской границе 171
постоянство в свободном про-
пространстве 169
Малоугловое приближение 258
Метод перевала 150
Ми решение 37
Милна проблема 201, 256
Облака, оптические и СВЧ-характери-
стики 62
Огибающая комплексная модулиро-
модулированного сигнала ПО
Океаническое дно, альбедо 192
площадь 67
Оксиметрия 78
Оптическая плотность 77
— теорема 23
Оптический путь 86, 135, 179
Осадки, интенсивность выпадения 55
Освещенность 168
Отражение диффузное 191
и прохождение 224
— от облаков при оптической лока-
локации 121
Первый порядок теории многократно-
многократного рассеяния 82, 86, 187
Плоскопараллельная среда 189, 224
Плотность потока, распространяюще-
распространяющегося назад 167
вперед 167
— энергии 165, 168
Площадь эффективная приемной апер-
апертуры 85
Поглощение света в чистой воде 64
Пойнтинга вектор 185
Показатель преломления воды и льда
59
Поле когерентное 92
— некогерентное 92
— среднее 92, 137
— флуктуационное 92, 137
Поляризация частичная 42
— эллиптическая 40 .
Поперечное сечение пучка среднеквад-
среднеквадратичное 267
Потенциал скоростей 49
Поток в теории переноса 165
Приближение борновское 31, 86.
— диффузионное 83
— однократного рассеяния 82, 84
Приемник движущийся 103
Принцип инвариантности 239
Пуанкаре сфера 42
276
Предметный указатель
Пузырьки воздушные 70
Пучок коллимированный 192, 201,
204, 217
— оптический, флуктуации в дожде
160
— размер 193
Радиолокатор доплеровский 130
импульсный 53, 130, 133
— когерентный 53, 130
— метеорологический 52
— некогерентный 53
— обычный 53
— одпопозиционный 86
Разреженная среда 187
Распределение вероятностей рассеян-
рассеянного поля 104
— дождевых капель по размерам 55,
123
— Лоу и Парсонса 56
— Маршалла и Палмера 55, 160
— по размерам 47, 55, 123
— Рэлея 105
— угловое 263
— частиц по размерам 47
Распространение волн в облаке боль-
больших частиц 258
пределах прямой видимости
134
Рассеиватели в атмосфере 32
биологических средах 54
океане 52
Рассеяние акустических волн 50
— звука в воде 66
— изотропное 243
— импульса бистатическое 126
Обратное 118
— Для передатчика с широкой
диаграммой направленности
— на биологических средах 74—81
воздушных пузырьках 70
круглом диске 33
• однородной сфере 32
случайно ориентированной ча-
частице 34
— обратное от дождя 91
— рэлеевское 27, 28
на сфероидальном диэлекриче-
ском теле 30
— Рэ лея — Дебая 31
Рассеяния амплитуда 18, 25
— — большой сферы 140
— коэффициент 64
Расходимость угловая 266
Рытова приближение 153
Светимость энергетическая 168
СВЧ-излучение, максимальная безо-
безопасная плотность мощности 74,
75
обратное рассеяние от дождя
91
— нагреватель 74
Сечение 17
— геометрическое 20
— дифференциальное рассеяния 19
— крови 78
— обратного рассеяния частицы 19
слоя 91
— поглощения 20, 26
— полное 19
— рассеяния 17
— — бистатическое 85
единичного объема морской
воды (свет) 65
зависящее от времени 94
Сжимаемость 49
Скорость звука в воде, воздухе и
нефти 67, 70
— «слепая» доплеровского радиолока^
тора 132
— установившаяся дождевых капель
57
— частицы 95
Среда слоистая плоскоиараллельная
239
— случайная нестационарная 108
Смешанный момент, двухчастотный
111
Смог 62
Снег 63
Собственное значение 233
Собственный вектор 233
Сохранение энергии 175
Спектр угловой 263
— уширение 113
— частотный 93, 99, 142
волны, распространяющейся в
дожде 143, 160
флуктуации волн 159
Среда полубесконечная 238
Стационарная случайная функция 93
Стокса матрица 43, 184
параметры 40, 183
преобразование при повороте
системы координат 45
Теория двухпотоковая Кубелки и
Мунка 212 •
— переноса излучения 164, 173
нейтронов 164
— четырехпотоковая 217
Предметный указатель
277
Тепловое излучение 242
Термоклин 67
Ткани мышечные, диэлектрическая
проницаемость 75
Туман, оптические и СВЧ-свойства 62
Угол ориентационный дождевой кап-
капли 55
Узкая диаграмма направленности 88
Уравнение Больцмана 164, 173
— волновое акустическое 49
— диффузионное 199, 250
— интегральное Шварцшильда—Мил-
Шварцшильда—Милна 257
— Максвелла — Больцмана со столк-
столкновениями 164
— переноса 164, 173
интегральная форма 178
— радиолокации 85
— — бистатическое 85
— Дайсона и Бете — Солпитера 181
Фаза комплексная в методе Рытова
153
Фазовая матрица 184
Флуктуации интенсивности 93
— фазы 153
Формула интерполяционная Лагран-
жа 229
— квадратурная 229
Гаусса 228, 230
— Хени — Гринстейна 198
Функция взаимной когерентности 164
двухчастотная 111
—- источника 175
— корреляционная 93
Функция неопределенности 128, 129
— передачи 110
нестационарная 110
— фазовая 19, 174, 227
— — Рэлея 223
— фильтрующая по углам 157
— характеристическая флуктуации
скорости 96
Характеристики рассеяния и поглоще-
поглощения дождя 55
Центральная предельная теорема 104
Частицы в морской воде 64, 65
— вращательное движение 98
— движущиеся 94
Частота повторения импульсов 53, 124
— резонансная воздушных пузырь-
пузырьков в воде 71
Число Кристофеля 229
Ширина луча передающей антенны 89
Эйлерово описание акустических волн
48
Экстинкции парадокс 20
Эритроциты 76
Ядра Айткена 54
Оглавление
Предисловие к русскому изданию 5
Предисловие 6
От автора . , 9
Глава 1. Введение 11
ЧАСТЬ I. РАССЕЯНИЕ И РАСПРОСТРАНЕНИЕ ВОЛН
В РАЗРЕЖЕННЫХ ОБЛАКАХ ДИСКРЕТНЫХ РАССЕИВАТЕЛЕЙ.
ПРИБЛИЖЕНИЕ ОДНОКРАТНОГО РАССЕЯНИЯ
Глава 2. Рассеяние и поглощение волны отдельной частицей .... 17
2.1. Сечение рассеяния и амплитуда рассеяния 17
2.2. Общие свойства сечений 20
2.3. Оптическая теорема 23
2.4. Интегральные представления амплитуды рассеяния и сечения
поглощения 23
2.5. Рэлеевское рассеяние 27
2.6. Борновское приближение (рассеяние Рэлея — Дебая) ... 31
2.7. ВКБ-приближение для поля внутри частицы 34
2.8. Решение Ми 37
2.9. Эллиптически-поляризованные волны и параметры Стокса . 40
2.10. Частичная поляризация и естественный свет 42
2.11. Сложение независимых волн 43
2.12. Матрица рассеяния и матрица Стокса 43
2.13. Преобразование параметров Стокса при повороте системы
координат 45
2.14. Распределение частиц по размерам 47
2.15. Акустические волны 48
2.16. Рассеяние акустических волн , 50
Глава 3. Характеристики дискретных рассеивателей в атмосфере, оке-
океане и биологических средах 52
3.1. Метеорологические радиолокаторы, шумы и помехи . . . . 52
3.2. Аэрозоль и гидрометеоры 54
3.3. Рассеяние света в морской воде (гидрооптика) 64
3.4. Рассеяние звука в воде гидроакустика) 66
3.5. Рассеяние на биологических средах 74
Глава 4. Рассеяние волн в разреженных облаках частиц 82
4.1. Средняя мощность рассеянного поля в приближении одно-
однократного рассеяния 84
4.2. Мощность рассеянного поля в первом порядке теории много-
многократного рассеяния 86
4.3. Случай узкой диаграммы направленности 88
4.4. Когерентное и некогерентное поле 91
4.5. Сечение рассеяния движущейся частицы с учетом времен-
нбй корреляции . , 94
Оглавление 279
4.6. Временная корреляционная функция и частотный спектр рас-
рассеянного поля 99
4.7. Пространственная корреляция рассеянного поля 101
4.8. Коррлеяция поля, принимаемого движущимся примеником . 103
4.9. Распределение вероятности рассеянного поля 104
Глава 5. Рассеяние импульсных волн в случайном облаке частиц . .108
5.1. Общая формулировка проблемы распространения и рассеяния
импульсов в нестационарной случайной среде 108
5.2. Двухчастотная функция когерентности и смешанной момент
выходного импульса 111
5.3. Время когерентности и полоса когерентности ....... 113
5.4. Рассеяние узкополосного импульса 114
5.5. Обратное рассеяние импульса, излучаемого остронаправленным
излучателем 118
5.6. Обратное рассеяние последовательности коротких импульсов . 123
5.7. Обратное рассеяние импульса, излучаемого передатчиком с
широкой диаграммой направленности 125
5.8. Бистатическое рассеяние импульса 126
5.9. Представление через функцию неопределенности 128
5.10. Импульсно доплеровский радиолокатор 130
Глава 6. Распространение в пределах прямой видимости через разре-
разреженное облако частиц 184
6.1. Когерентная и некогерентная интенсивности и пространствен-
пространственная корреляция флуктуации в плоской волне 136
6.2 Временная коррелрция и частотный спектр плоской войны . 141
6-3. Распространение плоской импульсной волны в пределах пря-
прямой видимости 143
6.4. Распространение между излучателем и приемником в пределах
прямой видимости 145
6.5. Распространение импульса между излучателем и приемником 151
6.6. Приближение Рытова для флуктуации амплитуды и фазы 153
6.7. Приближение Рытова для плоской волны 155
6.8. Времени корреляция и частотные спектры флуктуации уров-
уровня и фазы плоской волны 159
6.9. Приближение Рытова С учетом направленных свойств излуча-
* теля и приемника 161
ЧАСТЬ II. ТЕОРИЯ ПЕРЕНОСА ИЗЛУЧЕНИЯ
В СЛУЧАЙНОМ ОБЛАКЕ РАССЕИВАТЕЛЕЙ
Глава 7. Теория переноса излучения в случайном облаке частиц, . . . 163
7.1. Лучевая интенсивность, поток и плотность энергии . . . .165
7.2. Лучевая интенсивность в свободном пространстве и на гра-
границах раздела однородных сред 169
7.3. Дифференциальное уравнение для лучевой интенсивности . . 173
7.4. Ослабленная падающая интенсивность, диффузная интенсив-
интенсивность, граничное условие и функция источника 176
7.5. Интегральная форма уравнения переноса 178
7.6. Эффективная площадь антенны и принимаемая мощность . . 181
7.7. Уравнение переноса для частично поляризованной электро-маг
нитной волны 183
7.8. Связь лучевой, интенсивности с вектором Пойнтинга ... ,185
280 . Оглавление
Глава 8. Приближенные решения для разреженной среды 187
8.1. Лучевая интенсивность в приближении первого порядка тео-
теории многократного рассеяния 188
8.2. Падение плоской волны на плоскопараллельпуго среду . . . 189
8.3. Падение коллимированного пучка на плоскопараллельную
среду 192
Глава 9. Диффузионное приближение 195
9.1. Вывод диффузионного уравнения 195
9.2. Граничные условия 199
9.3. Падение коллимирванного пучка на слои рассеивающих частиц 201
9.4. Решение для случая плоской волны, падающей на слой рас-
рассеивающих частиц 202
9.5. Решение для случая коллимированного пучка конечной шири-
ширины, падающего на слой рассеивающих частиц 204
9.6. Диффузия от точечного источника 206
9.7. Измерение отражения с помощью двух волоконных световодов 206
9.8. Волокошюоптический оксиметрический катетер 208
Глава 10. Двухпотоковая и четырехпотоковая теории 212
10.1 Двухпотоковая теория Кубелки и Мунка 212
10.2. Коэффициенты К и S в двухпотоковой теории 216
10.3. Четырехпотоковая теория 217
Приложение ЮЛ 220
1ава 11. Плоскопараллельная задача 224
11.1 Нормальное падение плоской волны на плоскопараллельный
слой 226
11.2. Типичные фазовые функции 227
11.8. Квадратурная формула Гаусса 228
11.4. Общее решение 231
11.5. Полу бесконечная среда 238
11.6. Наклонное падение и другие методы 238
11.7. Слоистая плоскопараллельная среда 239
11.8. Некоторые смежные проблемы 242
Глава 12. Изотропное рассеяние 243
12.1. Метод преобразования Фурье для изотропного расселения . ii44
12.2. Диффузия и явления ближнего поля 249
12.3. Излучение при произвольной падающей интенсивности . . .261
12.4. Излучение в случае направленной сферической падающей
волны 252
12.6. Излучение при произвольном распределении источников . . 254
12.6. Изотропное рассеяние в конечном обйеме и проблема Милна 256
Глава 18. Приближение для больших частиц 258
13.1. Вывод дифференциального уравнения в малоугловом прибли-
приближении 268
13.2. Общее решение 260
13.3. Приближенноерешение для Случая Медленного углового изме-
изменения диффузной интенсивности 263
Литература 268
Предметный указатель 274
Страница
4
Строка
10 сн.
ОПЕЧАТКА
Напечатано Сладу»
1 р. 30 к. 2 р. 60 к.
По
чьей
Изд-
вине
ва
Зак. 763