Author: Попов Ю.П. Самарский А.А.
Tags: вычислительная математика численный анализ математика решение задач газовая динамика
ISBN: 5-02-014377-7
Year: 1992
Text
А, А, САМАРСКИЙ, 10, П. ПОПОВ
РАЗНОСТНЫЕ МЕТОДЫ
РЕШЕНИЯ ЗАДАЧ
ГАЗОВОЙ ДИНАМИКИ
тдлштг, трктьк. дополнкннок
Динуш'но Государственным комитетом СССР
но народному образованию в качество
учебного подобия для студентов вузов.
обучающихгя но сп<:цит.лъности «Прикладная математика»
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЛИКО-МАТЕМАТИЧЕСКОП ЛИТКРАТУРЬГ
1 ii P J
KCK 22.103
С17
УДК 510.G2 @75,8)
Самарский Л. Л., II о и о в 10. II. Разностные методы решения з;<
дач ганокий динамики: Учеб. пособие: Для вузов.— 'Л-с илд., доп.— М.: На\
к». Гл. ред. фии.-мят. лит.. 1902.- -124 с— ISBN fi-f^-nl/,377-7.
Дано систематическое пзло.коппе методов построения, исследования ;
реализации разностных схем для численного решения нестационарных з;
дач газовой динамики и магнитной гидродинамики. Третье издави
B-е н:!Д.— 1980 г.) значительно расширено за счет повой главы, посвящсб
пой исследованию внутренних диссипатпвпых и дисперсионных свопст
ралпостпых схем для уравнений гиперболического типа.
Для студентов старших курсов и аспирантов по специальности «При
кладная математика». Может представлять интерес для научных работай
коп п области прикладной математики, фп.чикн ц м. дапики.
'iafci. 2. Ил. V.V1. НнОлпогр. 108 назв.
С 053(U2)-n2 37'91 Г "' : ¦•¦' т
ISBN 0-02-01-4Г,77-7
ОГЛАВЛЕНИЕ
Предисловие к третьему изданию J
Предисловие 7
Введение И
Глава I. Элементы газовой динамики 16
§ 1. Математическая модель газовой динамики 10
$ 2. Интегральная форма уравнений газовой динамики ... 25
§ 3. Уравнения газовой динамики в дифференциальной форме . . 31
S А. Гиперопличпость системы одномерных нестационарных урав-
уравнений газовой динамики 47
§ 5. Разрывные решения 5й
$ й. Структура фронта ударной волны 63
S 7. Задача о поршне 72
5 8. Распад произвольного разрыва 81
Г лава II. Некоторые принципы построения разностных схем газовой
динамики 94
5 I. Оспоиные понятия ц обозначения теории разностных схем 94
5 2. Анализ некоторых разностных схем газовой динамики. Поня-
Понятие консервативности схемы 10Я
§ 3. Полностью консервативные разностные схемы .... 11<>
$ А. Однородные разностные схемы. Искусственная вязкость . . 124
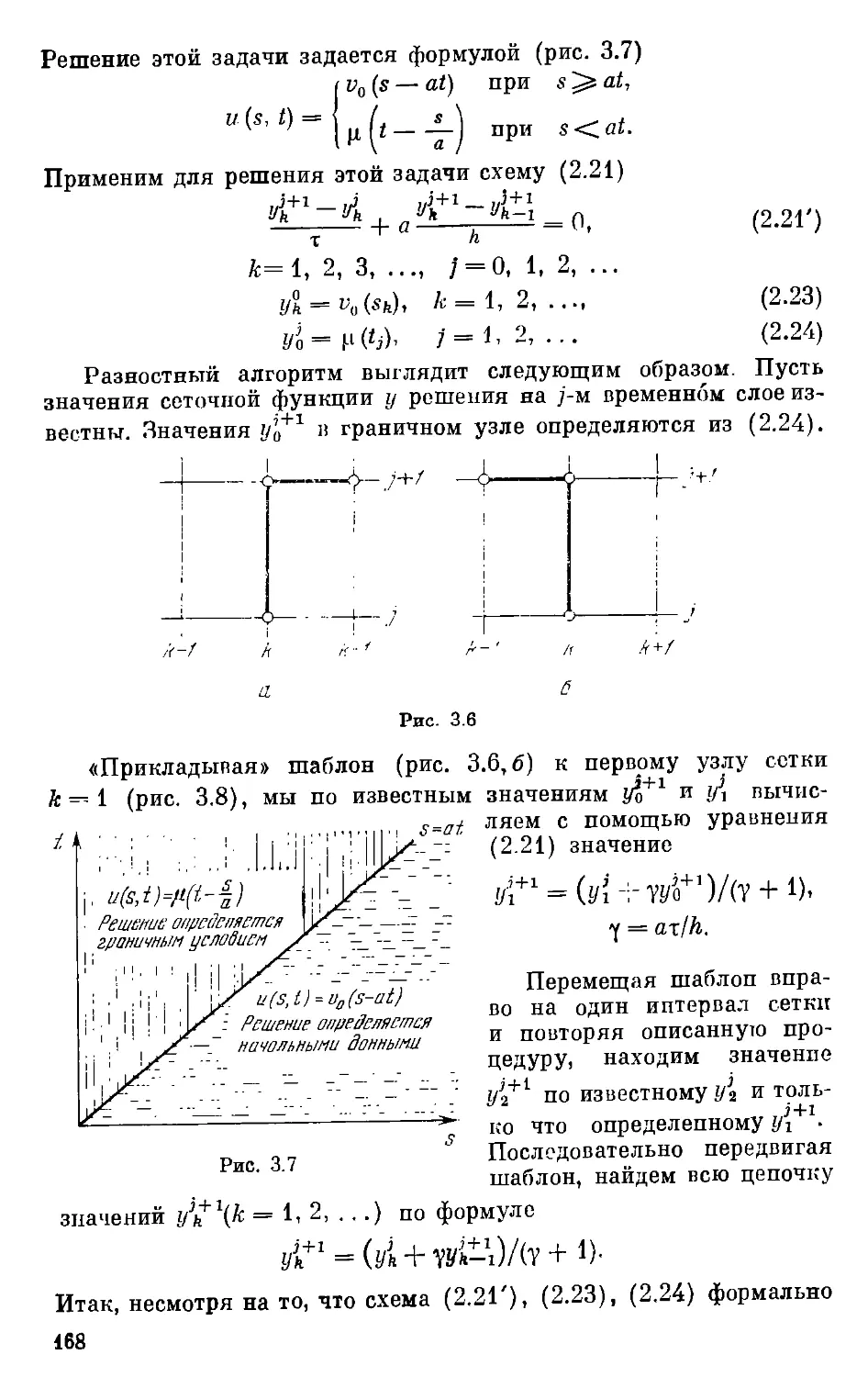
S 5. Результаты численных расчетов 132
§ 6. Разностные схемы для уравнения теплопроводности . . . 143
Глава III. Устойчивость разностных схем газовом динамики . . 152
§ 1. Понятие устойчивости разностной схемы 152
§ 2. Устойчивость разпостпых схем для уравнения переноса. Спек-
Спектральный метод и принцип максимума 159
§ 3. Энергетический метод исследования устойчивости разностных
схем 171
5 Л. Устсшчшюсть схом для системы двух уравнений цорного по-
порядка 175
•) 5. Влияние вязкое гп па устойчивость разностных схем . . . 182
§ 6. Устойчивость рлппостпых схем для уравнения теплопровод-
теплопроводности 180
Глава IVr. Реализации разностных схем газовой динамики . . 192
§ 1. Явные методы 192
S 2. Метод Ньютона. Метод прогонки 197
$ 3. Применение метода Ньютона к решению разностных уравне-
уравнений газовой динамики 200
§ 4. Метод раздельных прогонок 222
jj 5. Граничные усчппия 228
§ 6. Практические рекомендации -'34
1* ч
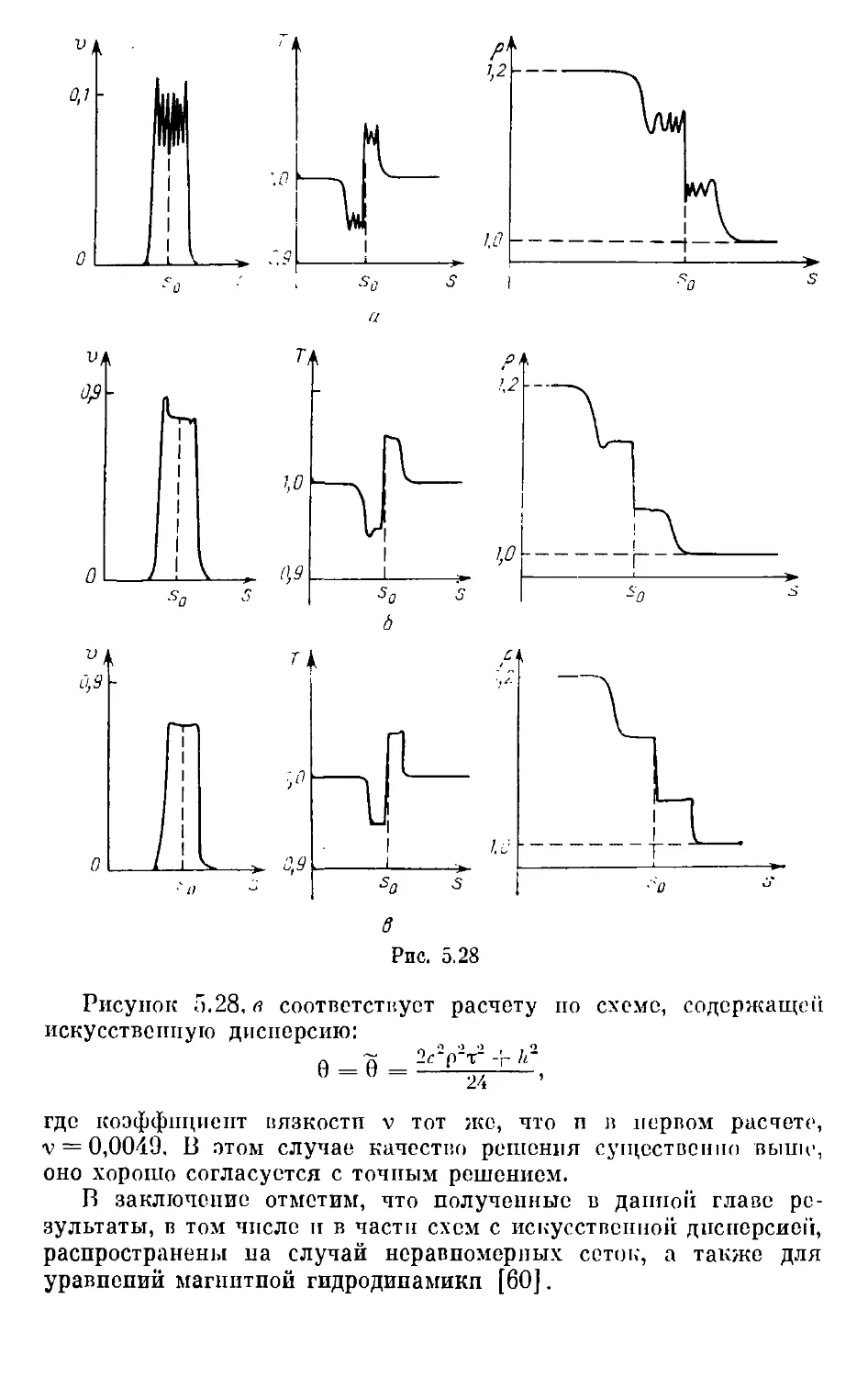
Глава V. Разностные схемы с искусственной дисперсией . . . 242
§ 1 Квазилинейное уравнение переноса и некоторые свойства его
решения 242
$ 2. Метод дифференциального приближения 253
5 Л. Искусственная дисперспя 267
§ /1. Разностные схемы с искусственной ;iiic[iopnwii для уравнений
газошш динамики 279
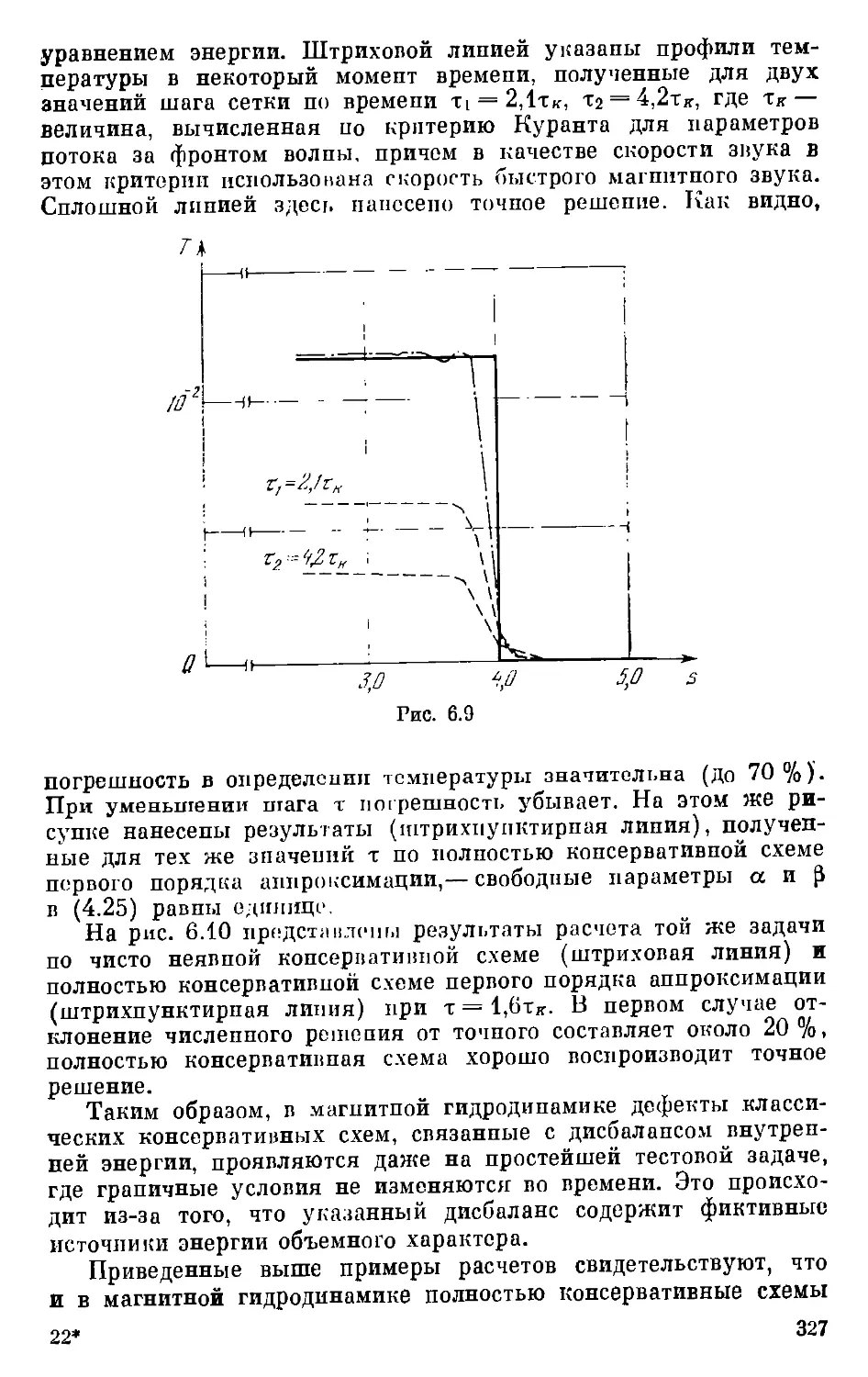
Г л а л а VI. Разностные схемы магнитном гидродинамики . . . 291
§ 1. Приближения магяитпой гидродинамики. Осповные уравнения 29*
§ 2. Уравпепия одпомерного нестационарного магпитогидродина-
мического течения 300
§ Л. Некоторые особенности магнитной гидродинамики . . . 3GS
§ А. Полностью копсерпятивпьгп разностные схемы для уравнений
магнитной гидродинамики 32.1
§ Г). Решение разностных уравнений электромагнитного поля . . 330
§ (!. Расчет электрических цепей в задачах магнитной гидродина-
гидродинамики 338
§ 7. Расчет задач магнитной гидродинамики с учетом фазового пе-
перехода 350
Г л ana VII. Полностью консервативные разностные схемы для дву-
двумерных уравнений газовой динамики ЗСО
§ 1. Система дифференциальных уравнений в лаграпжевых пере-
меппых; ее свойства 361
§ 2. Семейство несимметричных схем 3G3
§ 3- Полностью консервативная разностная схема для двумерных
задач газовой динамики 372
§ Л. Вариацпонно-разностный подход к построению полностью кон-
консервативных схем 3S2
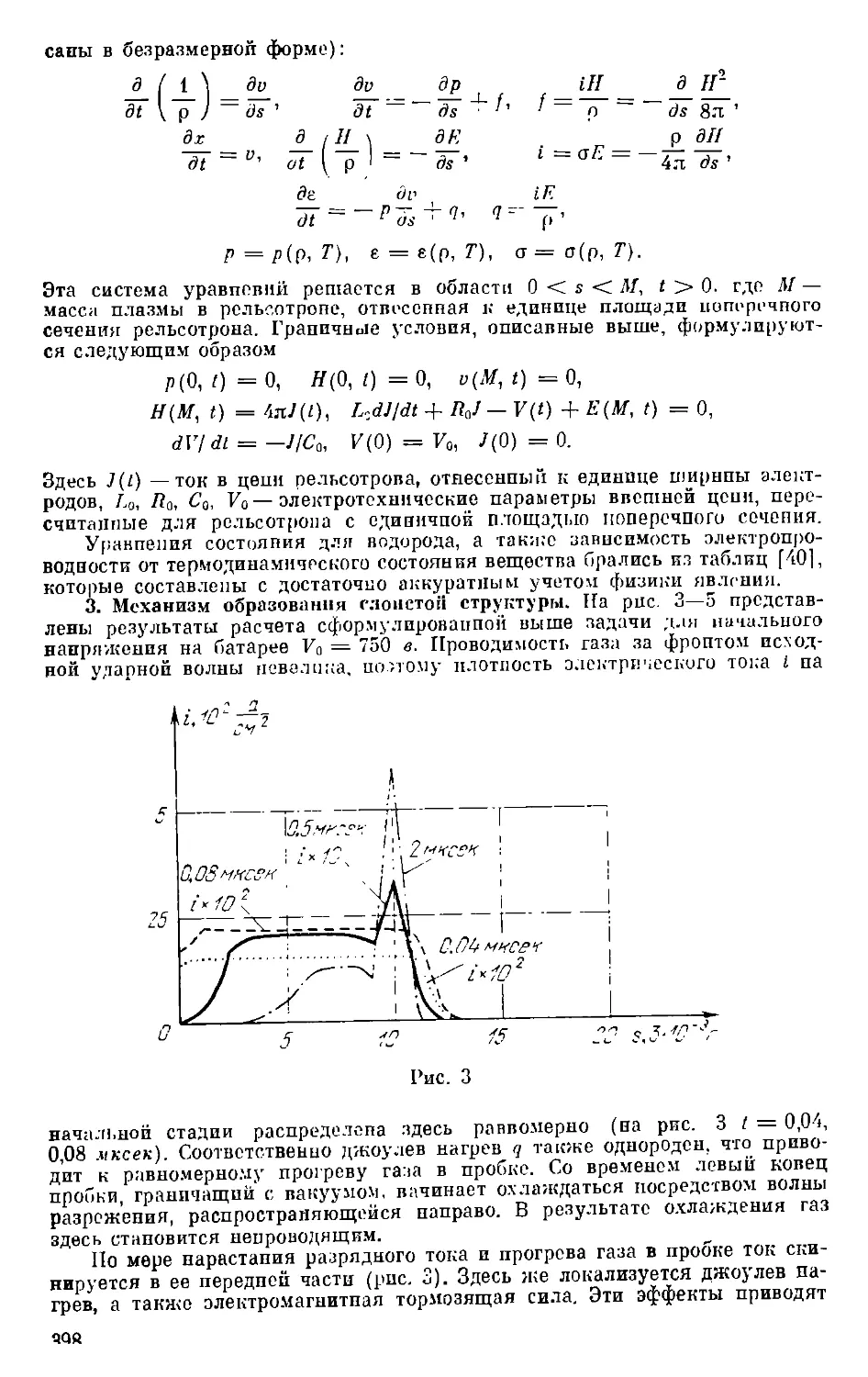
П ;> и л I) ,1, с if н е. Примеры постановки п решения некоторых задач
магнитной гидродинамики 3f:'i
§ I. ('ч.'шмод'-нстнне плазмы с магнитным полем в 1:;>нале рельсо-
T|Kiiia •'^'0
§ 2. CiubiiOTO4Hiiii"i раярнд с учетом эффекта гторпчиого пробоя 40 1
§ -1 Мигинтогндродипамичесь'ин модель цепышки ев- рхиовой . . 4i S
Cuiicof,- литературы 417
Предметный указатель 42-
ПРЕДИСЛОВИЕ К ТРЕТЬЕМУ ИЗДАНИЮ
•°>а время, прошедшее с момента опубликования предыдущего
издания книги, теория численных методов решения уравнении
газовой дипамикт и практика их применения для расчета при-
прикладных задач получила дальнейшее развитие.
Характерным стало рассмотрение пространственно многомер-
многомерных: (главным образом двумерных) течений га.ча, осложненное
учетом дополнительных физических янлеппп, таких как химиче-
химические реакции, фазовые переходы, перенос излучения и т. д.
Повышение сложпостп задач требует применения более со-
совершенных ir, прежде всего, более экономичных вычислительных
алгоритмов с тем, чтобы обеспечить получение решения на ЭВМ
:ia приемлемое машинное время. В свою очередь построение эф-
эффективных численных методов невозможно бе.! разнития теории.
Поэтому оправдано то внимание, которое уделяется во всем ми-
мире специалистами и области вычислительной газодинамики раз-
различным теоретическим п методическим аспектам этой проблемы.
К сожалению, в силу нелинейности уравнений строгие мате-
математические исследования разностных схем и .методов их реали-
реализации в газовой динамике затруднены. .'{десь широко использу-
используются различные эмпирические соображения н аналогии, «техно-
«технологические» приемы и пр., целесообразность которых оправдыва-
оправдывается вычислительной практикой и, прежде всего, анализом те-
стопых расчетом модельных задач, имеющих точные решения.
Одни из серьезных вопросов, возникающих при расчете задач
газомоп динамики, состоит в правильном поспропзведепин реше-
решения в областях, где оно претерпевает сильные изменения во вре-
времени п пространстме. Заметим, что такого сорта решения типич-
типичны для современных прикладных задач науки, техники, техноло-
технологии. IJtot ион рос связан не только с соблюдением основных за-
копон сохранения и других соотношений физического характера,
что обсуждается и главах, посвященных построен ню полностью
коисериатннпых схем. Практика расчетов показывает, например,
что в окрестности таких газодинамических особенностей, как
фронт ударней но гпы. наблюдаются резкие осцилляции сеточно-
сеточного решения, н..н, напротив, его аномальное размазывание, не
отражающие физическом реальности. Для борьбы с отмеченными
явлениями различными авторами предлагаются и используются
различт.ге приемы, п 1;о.гшчестпо раЛот на :>ту тему постояппо
увеличивается.
В настоящее издание включена глава, в которой укапанный
круг проблем рассматривается с «ра;шостно-фнзнческой» точки
зрения. Ураткчшя разностной схемы трактуются как законы
эволюции некоторой днскретпой среды, элементарными «квапта-
ми» которой являются пространственные ячейки сетки. Эта дис-
дискретная среда не адекватна исходной непрерывной среде, описы-
описываемой системой дифференциальными уравнениями. Оказывает-
Оказывается, в частности, что дискретная среда обладает впутреппей или
так называемой схемной диссипацией и дисперсией, которые
обусловливают различия между сеточным решенном и решением
дифференциальной задачи.
В главе V, включенной и настоящее издание, для анализа
диссипатпвпых п дисперсионных снойетв разностных; схем прн-
меияетсн известный метод дифференциального приближения.
Выясняется механизм появления :>тих факторов н их зависимость
от шагои сетки, споеоПа аппроксимации отдельных членов урав-
уравнений гг т. д. II результате удается построит!, разностные схемы
нового типа — с\еми с искусственной дисперсией.— г. которых
действие указанных факторов ослаолено, что повышает качество
разностного решения.
Понятия схемной диссипации и дисперсии позволяют также
с помощью метода дифференциального приближения а пал нзи ро-
ропать с единой позиции и другие схемы, применяемые для расче-
расчета Пыстронеремеииых газодинамических течений.
В данном издании в первую главу включен дополнительно
параграф, посвященный решению классической задачи о распаде
произвольного разрыва. Это решение использовано в дальнейшем
is качестве теста.
Внесены также исправления замеченных опечаток и петоч-
ностей.
Авторы выражают искреннюю благодарность С. И. Мухину,
оказавшему большую помощь при раооте над настоящим изда-
изданием, особенно при подготовке материалов питой главы.
Л. Л. Самарский, Ю. П. Пипов
ПРЕДИСЛОВИЕ
По многих областях современной науки но.шикают задачи,
включающие в качестве существенного элемента уравпения га-
газовой динамики. Уравнения газовой динамики нелинейны, по-
поэтому единственным эффективным и универсальным способом их
решения в настоящей время являются численные .методы, осно-
основанные па использовании быстродействующих электронпых вы-
вычислительных машин (ОПМ).
Количество научных работников, в тел'! пли пион мере свя-
связанных с решением падач газодинамики, постоянно увеличивает-
увеличивается, чем объясняется растущий интерес к соответствующим раз-
разделам вычислительной математики. Отсюда также нытекает пе-
обходимисть it пособиях с систематическим изложением основ
данного вопроса. К этой категории и относится настоящая кпига.
При численном решепип задач газовой динамики методом ко-
конечных разностей непрерывная среда заменяется некоторой дис-
кретпоп моделью, а дифференциальные уравнения, описывающие
исходную задачу,— копечпой системой алгебраических соотпоше-
nnii (разностной схемой). Разностная схема, аппроксимирующая
дифференциальную задачу, может быть построена пеединствеп-
ным образом. Поэтому возникает проблема конструирования оп-
оптимальных в определенном смысле разностных схе.м.
15 книге изложены пекоторые общие принципы (консерватив-
(консервативность, однородность п т. д.), позволяющие получать разностные
схемы газовой динамики, которые обладают хорошими количест-
количественными характеристиками. В частности, сформулирован прин-
принцип полной коисерпатпшшетп, который дает возможность строить
схемы, правильно передающие быстро изменяющиеся решения
даже иа грубых сотках, когда фактически теряется аппроксима-
аппроксимации. Эти качественные принципы имеют теоретическое обоспо-
iiiinne для линейного случая н подтверждены практическими
расчетами дли нелинейных задач. При изложении основные во-
вопросы теории иллюстрируются простыми наглядными примерами.
Следует отметить, что болынинстно описанных принципов но-
носит эвристический характер и отражает общие физические зако-
закономерности изучаемого явления. По-видимому, ото обстоятельст-
обстоятельство носит общин характер: на современном этане решать числен-
но сложную iie/iuueimyio задачу математической физики как аб-
абстрактно математическую пецелееообразпо. Эффективные раз-
разностные схемы и алгоритмы могут быть построены лишь при
соответствующем учете физического содержания исследуемого
объекта.
При паписаипи книги авторы стремились познакомить чита-
читателя с приемами построении и анализа разностных схем газовой
динамики, указать схемы и алгоритмы, надежность и эффектив-
эффективность которых проверена на практике при решении больших
сложных задач, описать ряд «технологических» вопросов, пеиз-
Гожпо возникающих при реализации численных алгоритмов на
Г)НМ и составляющих «кухпю» исследователя — вычислителя,—
одпим словом, передать в какой-то степени многолетний опыт
решения задач газовой динамики и магнитной гидродипамики,
накопленный большим коллективом, в который входят и авторы.
Авторы полагают, что подробно познакомившись с материа-
материалом книги, читатель сможет самостоятельно проводить числеп-
HOL1 решение одномерных нестационарных задач радиациоппой
газовой динамики и магнитпой гидродипамики.
Математическое моделирование явлений, процессов и конст-
конструкций является эффективным средством теоретического анали-
анализа задач, выдвигаемых наукой и техппкой. Прямой расчет па
!)|?М — практически едипствеппый способ решепия сложпых си-
систем пелннсГшых уравнений, описывающих многие актуальные
проблемы физики, химии, биологии и т, д, В то же время только
(прямой расчет может обеспечить те высокие требования, кото-
которые предъявляет практика к точности результатов теоретических
исследований, недь полученная в них информация является ос-
основной при проектировании сложпых устройсти современной
техники.
13 настоящее время все более употребительным, п особенпо-
гти применительно к математическому апалпзу задач физики,
становится термин ((вычислительный эксперимент» [79]. Суть
:/юго метода организации теоретического исследования сложпых
прикладных проблем состоит в том, что па основе математиче-
математической модели путем непосредственного численного решепия соот-
соответствующих уравнений количественно определяется поведение
изучаемого объекта в тех или иных условиях. Сопоставление ре-
результатом расчетои с имеющимися данными наблюдений, натур-
натурных экспериментов позволяет оцепить эффективность исходной
математической модели и в случае необходимости модпфициро-
пать ее с тем, чтобы добиться большей ее адекватности рассмат-
ринаемому явлению. На осиове прошедшей такую проверку мо-
модели появляется позможность прогнозировать поведепне иссле-
исследуемого объекта и условиях, пока недостижимых п натурном
эксперименте, иыясинть оптимальные параметры н режимы ра-
работы действующих или проектируемых конструкций. В этом
смысле создание численных методов и программных комплексов,
реализующих их на ЭВМ, в определенном смысле эквивалентно
создаиию крупных эксперимепталышх установок, а деятельность
lio проведению расчетов, обработке и интерпретации нх резуль-
результатов и т. д. можно рассматривать как апалог реального физиче-
физического эксперимента в лаборатории.
Очевидно, что при решешш сложных иаучпо-техничеекпх
проблем вычислительный эксперимент по сравнению с экспери-
экспериментом натурным .чпачителыш дешевле и достуипее, его подго-
подготовка и проведение требует меньшего времени, оп дает болео
подробную информацию и т. д. Однако альтернативное противо-
противопоставление эксперимента вычислительного и натурного было бы
неверным. П современных исследованиях, обеспечивающих пауч-
но-технпческнй прогресс, оба эти метода должны использоваться
в разумном сочетании.
Пм'шслптелмши лкспоримопт носит птерацпоппый миогова-
рнантным характер, так как в процессе его проведения уточня-
уточняется математическая модель, модифицируется иычпелнтельпьш
алгоритм, соиершеистнуется организация вычислительного процес-
процесса и обработка результатов расчета. Это вынуждает предъявлять
достаточно жесткие требования к эффективности и экономично-
экономичности численных алгоритмов, к иозможпости их реализации за ми-
минимальное машинное время при сохранении достаточной
точности.
С точки лре.чпм программирования вычислительный экспери-
эксперимент характерен тем, что для каждой модели необходимо решать
'ютьшоо число вариантов (варьируя определяющие параметры
задачи п, кролк> того, как говорилось выше, саму математиче-
математическую модель). Ота особенпость («многовариантность» п «мпого-
моделыюсть») вычислительного эксперимента проявляется в
многократных изменениях программы, реализующей алгоритм,
причем эти измепеипя касаются как структуры программы в Ц(>-
Л1ш, так и отдельных ее частей. Новая технология программиро-
программирования строится па оспове модульной (блочной) структуры мате-
математической мо/к-лн и алгоритма. Построенные но этому принципу
проблемно-ориентированные программные комплексы и системы
принято называть пакетами прикладных программ. Их ха-
характерная черта заключается в возможпостп постоянного ра.чии-
тпя, расширении ла счет включепия повых модулей, реализую-
реализующих новые возможности.
В приложении в качестве примеров вычислительного экспе-
эксперимента приведены постаповки и решения трех задач; «взаимо-
«взаимодействие плазмы с магнптпым полем в канале рельсотропа»,
«сильноточный разряд с учетом эффекта вторичного пробоя» п
«магпнтогпдродппампческаи модель вспышки сверхпоноп». .г)тп
задачи, относящиеся к актуальным направлениям физики плаз-
плазмы и астрофизики, позволяют паглядно продемонстрировать эф-
эффективность численных алгоритмов, описанных в кнпге.
Исследования, выполненные различпымп авторами в послед-
последние годы, показали, что направление, связанпое с конструирова-
конструированием и применением полностью коисерватпвпык разностных
схем для решепия различных задач математической физики, яв-
является весьма плодотворным. Сформулированный первоначально
для одномерных задач газовой динамики и магнитной гидроди-
памики в лаграткевых массовых переменных принцип полпой
копсерватшшостп был патом распространен па другие классы за-
задач. Так в работах [22, 23, 97] предложеп вариацноппо-разпост-
ный подход к построению двумерных полностью консервативных
схем для ypaniioniEii газодинамики п магнитной гидродинамики.
Эти схемы были использовапы для расчета ряда практически
важных задач и продемонстрировали свою высокую эффектив-
эффективность [6, 18, 19, 25].
Полпостью консервативные схемы Пыли построепы также для
задач, описываемых кинетическими уравнениями, и также хоро-
хорошо себя зарекомендовали в практических расчетах [12, 74].
При чтении кппги желательно знакомство с элемептарпыми
сводепиямн из теории галодипамичеекпх течений (по любому си-
систематическому курсу газовой динамики), с особенностями по-
стаповки задач математической физики (например, по книге
А. Н. Тихонова. Л. Л. Самарского [93]), а также с основными
вопросами теории ра;шостпы\- схем (см., например, кпигу
Л. Л. Самарского [78|). Однако для цельности изложения и
кпиге предусмотрены специальные разделы, содержащие все пе-
обходимыо справочные сведения.
Следует отметить методическое и идейное единство итого по-
пособия с кпигами: «Введеппе в теорию разпостных схем» [77] и
«Теория разностных схем» [78] Л. Л. Самарского, «Устойчи-
«Устойчивость разпостпых схем» Л. Л. Самарского и Л. В. Гулина [80],
«Разностные методы для эллиптических уравпепий» Л. Л. Са-
Самарского и В. Б. Андреева (М.: Наука, 1976), «Методы решения
сеточпых уравнешш» Л. А, Самарского и Е С. Николаева
(М.: Наука. 1978).
Книга возникла на основе лекций, которые авторы и течение
пескольких лет читали в Московском государственном универси-
университете для студептов и асипраптов физического факультета и фа-
факультета вычислительной математики и киберпетики. Она иред-
пазпачепа для широкого круга читателей, связапных с примене-
пиом разпостпых методов к решению задач газодинамики н маг-
магнитной гидродипамики.
Авторы считают своим приятным долгом выразить большую
благодарпость II. И. Волосевцчу, В. Я. Гольдину, А. В. Гулину.
Н. II. Калиткипу, С. И. Курдюмову, Л. II. Фаворскому и другим
сотрудпикам Института прикладпон математики АН СССР, сов-
местпая работа с которыми пад решением различных задач га-
газодинамики и магнитной гидродинамики нашла отражение и
этой книге.
А. А. Самарский, 10. П. Попов
ВВЕДЕНИЕ
Многие вопросы современной науки п техники в той или
nnoii мере связаны с решепием уравнении газовой дипамики.
В качестве примера можпо пазвать аэродинамику летательных
аппаратов н задачи астрофизики, прогноз погоды п проектирова-
проектирование магнитогидроднпамических геператоров электрической энер-
энергии, теорию реактивпых двигателей, управляемый термоядерный
синтез и многие другие актуальпые проблемы.
Отдельные ра.чделы газовой динамики развиваются достаточ-
достаточно давно и письма интенсивно. Получено много важных, инте-
интересных и «изящпых» результатов, и тем не мепее общих методов
jjuuiuuuH газодинамических задач до сих пор не существует. Бо-
Более того, следует отметить, что здесь в общем случае пока нет
;;аже доказательств существования п одпнетпенпости решения.
Это объясняется сложностью уравнений газовой динамики и
прежде всего их нелинейностью. В то же время именно нели-
нелинейность порождает такие эффекты, как, например, ударные
волны, не имеющие аналога в линейном случае п представляю-
представляющие большой теоретический и практический интерес.
Уравнения газовой динамики описывают движение сплошной
сжимаемой среды. В последнее время практика все чаще выдви-
выдвигает задачи, где на газодипампчеекпе течения воздействуют раз-
различные дополнительные факторы такие, как электромагнитные
и гравитационные поля, процессы тепло- и электропроводности,
химические реакции и т. д. Учет подобпых явлений усложняет
математическую постановку задач и порождает самостоятельные
проблемы при их решении. Однако и здесь основу задачи по-
прежнему составляют классические уравнения газодинамики.
Поэтому разработка эффективных методов решения этих уравне-
уравнений представляет один из важных вопросов для многих разделов
современной наукп.
Отметим, что в газовой динамике хорошо разнит и широко
применяется аппарат автомодельных решений. С помощью тако-
такого подхода осуществлена постановка и проведен анализ многих
важных задач. Автомодельные методы позволяют детально ис-
исследовать отдельные качественные сторопы явлении, получать
количественные оценки, выяснять влияние различных парамет-
параметров. Однако построение автомодельных решений, как правило,
11
позможно лишь для некоторых частных, упрощенных вариантов
исходной задачи.
В общем случае фактически единственным эффективным спо-
способом решения задач газовой диыамикп являются численные ме-
методы, основанные ла использовании быстродействующих элект-
электронных вычислительных машин. Эти методы получили свое раз-
развитие сравнительно недавно, примерно и точение последних трех
десятилетий. В отличие от аналитических методов, где зачастую
для каждой задачи разрабатываются скои самостоятельные прие-
приемы решения, численные методы отличаются большой универ-
универсальностью и применимы для исследования широкого класса
Ш1Л0ПИЙ.
Конструирование вычислительного алгоритма подразумевает
два этапа: иервый — построение разностной схемы для матема-
математической модели, т. е. аппроксимация исходной системы диффе-
дифференциальных и интегральных уравнении системой разностных
(алгебраических) уравнении, и второй — построение эффектив-
эффективного метода д-m решения этих разностных уравпений.
Построение разностном схемы в задачах гидродинамики мож-
можно рассматривать как замену непрерывной среды, описываемой
дифференциальными уравнениями, пекоторым дпекретпым" ее
аналогом, эволюция которого происходит по законам, выражае-
выражаемым разностными уравнениями. При такой замене возникают
новые параметры — шаги (по времени и пространству) разност-
разностной сетки, которая вводится вместо области непрерывного изме-
изменения аргумента. Представляется естественным с точки зрепня
создапия экономичного алгоритма использовать так называемые
грубые сетки с большими шагами (с малым числом узлов), в си-
силу того что машинное время, необходимое для решения разност-
разностных уравнений, возрастает с уменьшением шагов (ростом числа
узлов). Однако разностная схема «близка» к исходной системе
дифференциальных ураънений лишь асимптотически при неогра-
неограниченном измольчеппп тагов сетки. При конечных шагах сетки,
используемых на практике, дискретная модель среды, описывае-
описываемая разностными уравнениями, может заметно отличаться от не-
непрерывной среды. Это различие зачастую порождает в расчетах
паразитические эффекты разностного происхождения, снижаю-
снижающие ценность разностного решения. Поэтому важно строить та-
такие схемы, которые сохраняли бы свои «хорошие» качества на
сетках, применяемых в реальных расчетах (как говорят, на
«грубых» сетках).
Для линейных уравнений математической физики существует
хорошо развитая теория разностных схем, опирающаяся на три
фундаментальных понятия: аппроксимацию, устойчивость и сле-
следующую из них сходимость.
Изучение аппроксимации разностной схемы для гладких
функций не представляет труда как в линейном, так и в пели-
нейном случаях. Доказательство устойчивости схемы фактически
сводится к получению некоторых априорных оценок, выражаю-
12
щих непрерывную зависимость разностного решения от входных
данных задачи. В отличие от линейного случая построение по-
подобных оценок для нелинейных уравнений сопряжено с больши-
большими трудностями, а для уравнений газодинамики такие оценки
вообще отсутствуют. Поэтому проверку устойчивости схем обыч-
обычно проводят на некоторых линейных аналогах исходной задачи,
например, в акустическом приближении.
Поскольку получить достаточно общие количественные апри-
априорные характеристики разностных схем газовой динамики не
удается, приходится использовать различного рода качественные
соображения. Естественно, например, требовать, чтобы дискрет-
ыая модель была адекватна непрерывной модели, т. и. правиль-
правильно передавала физические особенности научаемых процессов.
Уравнения газодинамики — это математическое выражение
основных законов сохранения (массы, импульса и эпергин). По-
Поэтому разумно строить разностную схему так, чтобы в пей так-
также выполнялись аналоги этих законов. Схемы такого тина назы-
называются консервативными. В важности этого требования можно
убедиться уже па примере линейных задач, где консерватив-
консервативность является необходимым условием сходимости схемы.
Дальнейшее развитие принципа консервативности привело к
понятию полной консервативности. Полностью консервативные
схемы для уравнений газовой динамики характеризуются тем,
что в них выполняются не только разностные аналоги основных
законов сохранеипя, но также и дополнительные соотношения,
зыражающпе баланс отдельных видов эпергпи. Примеры показы-
показывают, что применение таких схем особенно эффективно при ис-
лоль.'шваын:! «грубых» сеток" для задач, которые описываются
фуикциямн, резко изменяющимися во времени и пространстве.
Помимо физических требований к схемам предъявляются
также требования алгоритмическою характера. Например, весь-
весьма важпым является свойство однородности схемы. Оно заклю-
заключается в том, что формулы, по которым ведется расчет, должны
записываться едпнообраяпо во всех узлах сетки, без явного вы-
выделения вояможпых «нерегулярностен» решепия, например, то-
точек разрыва. Свойство однородности существенно упрощает ор-
организацию программы для реализации алгоритма па ЭВМ.
Свойства того пли иного алгорптма для расчета задач газоди-
газодинамики, как правило, трудно оцепить теоретически. Поэтому при
анализе качества схемы, помимо различных априорпых сужде-
суждений, большую роль играют апостериорные исследования. Сюда
в первую очередь следует отнести опробование схем н алгорит-
алгоритмов на специальных «точных» регнепиях — тестах. Для этого
проводится расчет некоторых упрощенных вариаптов исходной
задачи, которые быть может не дают полную физическую карти-
картину процесса, но допускают простое (например, аналитическое)
решение.
Сопоставление результатов расчетов с известными решения-
решениями позволяет судить о точности схемы, скорости сходимости
13
и т. д. Поэтому построение точных тестовых решений, в частно-
частности автомодельных, представляет собой необходимый элемент в
общей лрограмме конструирования численных алгоритмов.
На практике, в зависимости от типа рассматриваемой задачи,
от особенностей изучаемого процесса, используются различные
формы записи системы уравнепий газовой динамики (стациопар-
пые или нестационарные уравнения, одномерное и многомерное
приближение, эйлеровы координаты или переменные Лагран-
жа и т. д.).
В этой книге подробно описаны алгоритмы численного реше-
решения одномерных нестационарных уравнешш газовой динамики и
магпитпой гидродинамики в лаграпжевых .массовых координатах.
Однако многие прнпципы построения и решения разностных
схем естественным образом обобщаются и для других задач ма-
математической физики. В главе VI такое обобщение проведено
для днумерпых задач газовой динамики в лаграижевых пере-
переменных.
Следует отметить, что для рассматриваемого класса одномер-
одномерных нестационарных задач газодинамики существуют и другие
методы численного решения такие, как, например, метод харак-
характеристик, метод «распада разрывов», метод «крупных частиц»
и т. д. Их подробное описание можно найти в соответствующих
публикациях. Не ставя перед собой цель дать обзор всевозмож-
всевозможных методов (подобный об:юр можно паггпг в главе III книги
Б. Л. Рождественского и Н. Н. Янеико [70]), мы ограничили
ил.тожешге достаточно иодробыым и стгетоматичоекпм отгисятшем
одного класса разностных схем, которые в течение длительного
времени применялись для решения разнообразных задач газовой
динамики и магнитной гидродинамики. Описываемые схемы про-
прошли многолетнюю проверку па практике и показали высокую
надежность.
В первой главе книги пзложеиы некоторые физические и ма-
математические основы газовой динамики в форме, удобиой для
использования в дальнейших главах. Однако эта глава не пре-
претендует на полноту и, коиечпо, не может заменить систематиче-
систематический курс газодинамики. Поэтому у читателя предполагается оп-
определенная степень знакомства с теорией газодинамических
течений.
Точно так же § 1 главы II, который посвящен описанию ос-
основных понятий теории численных методов, носит справочный
характер. Детальпое пзложепие затронутых здесь вопросов мож-
можно найти, например, в [78]. Остальные параграфы второй главы
посвящены принципам построения разностных схем радиацион-
радиационной газовой динамики, таким как консервативность, полная кон-
консервативность, однородность. Приведены примеры, подтверждаю-
подтверждающие эффективность этих принципов.
Основным требованием, которому должна удовлетворять лю-
любая разностная схема, является свойство сходимости, обеспечи-
обеспечивающее близость разностного решения к решению дифференци-
и
альпой задачи. Схэдцмость схемы вытекает из ее аппроксимации
п устойчивости. Анализ устойчивости разностных схем газодина-
газодинамики содержится в главе III. При этом используются липейпые
модели уравнений газовой дппаммтш — уравнения акустики и
уравнение переноса. В последнем параграфе главы III рассмот-
рассмотрены вопросы, связанные с устойчивостью разностных схем для
уравнения теплопроводности.
Содержание главы IV составляют методы решения разност-
разностных схем, представляющих собой системы алгебраических урав-
уравнений. Неявные схемы решаются с помощью итерационных ме-
методов. Подробно рассмотрено применение метода Ньютона,
который позволяет свести разностную схему к системе линейных
«трехточечных» уравнений, решаемых с помощью прогонки.
Описан также метод раздельных прогонок. Его применение це-
целесообразно в тех случаях, когда исходная система уравнении
газодинамики усложнена учетом дополнительных факторов, та-
ки\ как теплопроводность, электромагнитные поля и т. д. Следу-
Следует отметить, что в главе IV получены оценки сходимости итера-
итерационных процессов решения уравнений газовой динамики, что
является новым результатом.
Описанные в главах II—IV методы построения и решения
разностных схем газодинамики обобщаются к главе VI mi случай
системы одномерных нестационарных уравнений магнитной гид-
гидродинамики. Изложены вопросы, связанные с решением уравне-
уравнений электромагнитного поля для случая сильномепяющегося ко-
коэффициента электропроводности. Рассмотрен метод расчета
электротехнических цепей, которые являются важным элементом
многих задач магнитной гидродинамики. В первом параграфе
глаиы VI рассмотрены некоторые общие вопросы теории магнито-
гидродинамических течений и, в частности, отмечен ряд специ-
специфических эффектов, которые порождает учет в уравнениях газо-
зоп динамики электромагнитного поля.
В VII главе рассмотрены двумерные уравнения газовой дина-
динамики в переменных Лаграпжа. Построена разностная схема, об-
обладающая свойством полной консервативности. Заключительный
параграф главы посвящен краткому описанию вариационно-раз-
вариационно-разностного подхода к построению полностью копсервативпых схем.
ГЛЛВЛ I
ЭЛЕМЕНТЫ ГАЗОВОЙ ДИНЧМИКИ
В этой главе изложены некоторые сведения по теории газо-
газодинамических течений. Объем п форма изложения продиктова-
продиктованы потребностями последующих глав.
В §§ 1—3 рассматриваются основные приближения матема-
математической модели газовой динамики, дается представление о пе-
переменных Эйлера и Лаграпжа, приводятся различные формы
записи системы уравнений газодипамикп с теплопроводностью.
В § 4 анализируются некоторые математические свойства систе-
системы одномерных нестационарных уравнений газодинамики, пока-
показана ее гиперболичность, рассмотрено линейное приближение —
акустика. § 5 посвящеп разрывным газодинамическим регпетш-
ям — контактным разрывам и ударным волнам. В § 6 изучается
структура фронта ударной волны в дпееппатпвпой среде, обла-
обладающей вязкостью и теплопроводностью. В § 7 содержится ре-
решение классической задачи о равномерно движущемся поршне,
где в зависимости от направления движения поршпя в газе воз-
возникает либо волна разрежения, либо ударная волна. Здесь тис
рассмотрено автомодельное решение задачи о поршне, движу-
движущемся ускореппо.
§ 1. Математическая модель газовой динамики
1. Приближение сплошной среды. В газовой дипамике изуча-
изучается движение сжимаемых жидких п газообразных сред.
Для теоретического анализа газодинамических явлений ис-
используется широко распространенный прием — математическое
моделирование. При этом вместо реального процесса рассматри-
рассматривается пекоторып упрощеппый, идеальный процесс — как гово-
говорят, «модель явления»,— который выбирается так, чтобы он,
с одной стороны, отражал осповпые качественные стороны явле-
явления и, с другой стороны, допускал достаточно простое математи-
математическое описание. По мере углубления исследования строятся но-
новые модели, более детально описывающие явление. Факторы,
которые считаются второстепенными на данном этапе построе-
построения математической модели, отбрасываются. Однако на следую-
следующих этапах исследования, по мере усложнения модели, они мо-
могут быть включены в рассмотрение. В зависимости от цели ис-
исследования один и тот же фактор может являться основным или
второстепенным.
16
Принятие допущения или, как говорят, приближения, опре-
определяют рамки применимости модели. Только п этих рамках, во-
вообще говоря, будут справедливы все введоипые понятия и все
полученные результаты. Обоснованном разумности и аффектив-
ностн модели является сравнение розультатол. полученных с по-
помощью этой модели, с экспериментальными данными.
В основе газодинамической модели лежит фундаментальное
предположение о «сплошности» среды. Как известно, любая сре-
среда дискретна — она состоит из отдельных микрочастиц (атомов,
молекул, ионов, электронов и т. д.), расстояние .между которыми
во много раз превышает их собственные размеры. Эти частицы
хаотически движутся, сталкиваясь друг с другом. Расстояние,
пройденное частицей за время между двумя столкновениями, на-
называют длипой свободного пробега. Эта длина тем меньше, чем
больше частиц заключено в единице объема среды, т. е. чем
больше ее плотность. В газовой динамике рассматриваются до-
достаточно плотные среды, содержащие в единице объема громад-
громадное количество частиц. Представление1 об этой величине может
дать число Лвогадро, т. о. число частиц в одной грамм-молекуле
вещества Л/Л = E • КJ3 1/г -моль. В таких объемах влияние час-
частиц сказывается усреднению. Поэтому можно рассматривать
лпшь некоторые средние характеристики объема, пе интересу-
интересуясь поведением отдельных микрочастиц.
Н этом и заключается смысл перехода к модели сплошной
среды, заполпяющеп пространство непрерывным образом. Конеч-
Конечно, такой переход можно осуществить не во г.сех случаях. Коли-
Количественным критерием применимости приближения сплошной
среды может служить перавепство
///,«1, A.1)
где I — длина свободного пробега, L — .характерный размер
задачи.
Степень малости отношения 1/L в A.1) в конкретных зада-
задачах может быть различной. Например, в газах при обычных ус-
условиях / ~ 10~г'—Ю~6 см. Поэтому условие A.1) для тел с ха-
характерным размером L порядка сантиметра и выше выполпено
с хорошей точностью.
Условие A.1) может выполняться пе только за счет «мало-
«малости» /. Так, например, в межзвездном газе длина свободного
пробега велика по сравнепию с привычными размерами. Однако
если изучаются явления коемпческнх масштабов — обтекание
Земли солнечным ветром или эволюция Галактики, то характер-
пый размер задачи велик, критерий A.1) выполнен, и разре-
жеппую межзвездную среду можно рассматривать как сплошную.
В то же время, если речь идет об исследовании полета кос-
космического корабля в этой межзвездной среде, то характерный
размер задачи (размер корабля) уже пе может обеспечить вы-
выполнение неравепства A.1), и здесь использование приближения
сплошной среды неправомерно
2 А, А. Самарский; Ю", ГГ. -Попов 17
Гипотеза сплошности, которая представляется сейчас совер-
совершенно очевидной, в слой время завоевывала тхмщии. конкури-
конкурируя с другими теориями. Например. Ньютон считал, что воздух
состоит из отдельных-, не связанных друг с другом частиц. При
обтекании тела эти частицы, налетая па него, отдают свой им-
импульс. П этом, в частности, Ньютон, впдел механизм возникпове-
иия подъемно» силы.
Предположение о сплошности в газовой динамике ведет свое
начало от Эйлера, который впервые стал рассматривать газ как
непрерывную, легко деформируемую материю.
В математическом отношении предположение о сплошности,
непрерывности среды позволяет взять па вооружение достаточио
хорошо разработанный аппарат непрерывных функций, диффе-
дифференциальное и интегральное исчисление.
В газовой динамиг;е бесконечно малым принято называть
объем, малый r геометрическом отношении, т. е. ооъем, измере-
измерения которого малы по сравнению с характерными размерами за-
задачи. В то же время этот объем достаточно велик, так что в
нем заключено оо.чыпоо число микрочастиц, п ого можно рас-
рассматривать как .момент сплошной среды. О движении такого
ныделенпого .малого элемента говорят как о движении частицы
среды (газа, жидкости).
Приближение сплошности является основным, но не единст-
единственным в модели газовой дпнамикп. Помимо него, делается ряд
общих предположений об евклидовости пространства, о малости
скорости движения среды но сравнению со скоростью света, аб-
абсолютности премепп и пр.. а также принимаются определенные
допущешш о свойствах самой среды (наличие или отсутствие
вязкости, теплопроводности, гравитационных сил и г. д.).
2. Характеристики сплошной среды. Элементы термодинамики.
Для количественного описания процессов л газе вводятся раз-
личпые характеристики.
Положение частицы среды характеризуется ее радиус-векто-
радиус-вектором г в некоторой системе координат. Изменение положения ча-
частицы в пространстве со временем определяется ее скоростью:
y = dr(t)ldl; A.2)
здесь t — время. \) процессе движения взаимпое расположение
частиц среды изменяется. Изучение движения газа состоит в па-
хожденип движения лсе\ его частиц.
Состояние газа характеризуется еще рядом параметров, назы-
называемых термодинамическими.
Под плотностью газа р понимают массу вещества, заключен-
заключенного в единице иГн.ома. Сила, дейстнующая в среде на единичную
площадку нормально к ее поверхности, назынается дапленнем р.
К термодинамическим параметрам относятся также темпе-
температура Т, удельный объем т) = 1/р, энтропия .S' и др. Аккурат-
Аккуратное определение этих понятий, установление соотношений меж-
между ними составляют предмет термодинамики (см., например,
18
1'ис. 1.1
внешними источниками,
[55]). Мы ограничимся кратким напоминанием фактов, которые
окажутся необходимыми в дальнейшем.
В термодинамике вводится понятие внешних параметров, ха-
характеризующих положение внешних но отношению к газу тел,
с которыми газ взаимодействует в процессе движения.
Рассмотрим для определенности однородный газ, заключеп-
ный в цилиндрический сосуд, закрытый с одного конца непо-
неподвижной стенкой, а с другого— riV
поршнем (рис. 1.1). В данпом
случае внешним телом явля-
являются стопки сосуда и поверх-
поверхности поршня, граничащая с с
газом. Они ограни чипа ют заня-
занятый газом объем V, который \ \х —
является внешним параметром.
В общем случае в число внеш-
внешних параметров включаются и
различные силовые поля, созданные
например электромагнитные поля.
В процессе взаимодействия газа с внешними телами внешние
параметры изменяются — газ совершает работу (или над газом
совершается работа). В нашем примере (рис. 1.1) при бесконеч-
бесконечно малом изменении внешнего параметра — объема dV, вызван-
вызванного бесконечно малым перемещением поршня, газ совершает
работу
dA = —pd\\ A.3)
или, в пересчете на едпппцу массы газа,
da = —р dr],
где 1] =• 1/р — удельный объем, т. е. объем единицы массы газа.
Заметим, что эта работа отлична от пуля только при перемеще-
перемещении внешних тел. Тщи, при истечении газа в вакуум из сосуда,
перемещения внешних тел не происходит, и работа, вычислен-
вычисленная по формуле (J.3), равна нулю в силу того, что давление на
границе газ — вакуум обращается в пуль. Совершая работу, газ
изменяет свою энергию. Изменение аиергпн газа может проис-
происходить также за счет обмена теплом с внешними телами.
Связь между энергией газа, совершенной им работой и под-
подведенным теплом в термодинамике устанавливает первое начало,
являющееся частным случаем общего закона сохранения энер-
энергии. Для единицы массы газа эта связь выглядит следующим
образом
с/е =¦ dQ — р di], A-4)
где е — удельная внутренняя энергия газа, Q — количество теп-
тепла, подведенного к единице массы газа.
Соотношение A.4) справедливо не только для рассмотренно-
рассмотренного нами примера (рис. 1.1), по вообще для любых равновесных
2* 19
процессов в газе. Напомппм, что термодинамически р-лшовеспым
называется процесс, протекающий бесконечно медленно, причем
его любое промежуточное состояние является равновесным.
В свою очередь равновесным термодинамическим состоянием си-
системы называется состояние, не изменяющееся со временем при
фиксированных внешних параметрах п отсутствии теплообмена
с внешними толами.
Реальные процессы, естественно, протекают с конечными ско-
скоростями и. строго говоря, ые япляются равновесными. Однако
идеализация, свя.чаппая с введением равновесности, достаточно
хорошо описывает широкий круг лв.мчнш, и поэтому ее введение
оправдано.
Из первого начала термодинамики шлтекаот. что внутренняя
энергия в является однозначной функцией состояпия газа. Ве-
Величины же Qua накисит не только от состояния системы, но и
от ее предыстории, т. е. от процесса, в результате которого сис-
система пришла в ото состояние. Инылш словами, величина d& —
полный дифференциал, в отличие от dQ и da, не представляю-
представляющих, вообще гопоря, полных дифференциалов каких-либо выра-
выражений.
Существование еще одного полного дифференциала тг, следо-
следовательно, однозначной функции состояния (:штропии S) посту-
постулирует второе начало термодинамики:
dS = dQ/T или TdS = <l& + [>di]. A.5)
Введенный в рапс'нстве A,5) «интегрирующий делитель» Г, на-
называется температурой. Температура является внутренним пара-
параметром, характеризующим состояние гапа. Со статистической
точки зрения температура определяется средней кинетической
энергией теплового хаотического движения молекул га;;а.
Очевидно, величина энтропии определяется с точностью до
произвольной постоянной. Значение этой постоянной устанавли-
устанавливает третье начало термодинамики (теорема Нерпста). из кото-
которого следует, что при абсолютном пуле температуры энтропии
системы равна нулю:
5^0 при Т -»0.
Заметим, что в общем случае для процессов, не являющихся
равновесными, но допускающих введение функции температуры,
энтропии и т. д., формулировка вторит начала приобретает вид
dS > dQ/T,
причем знак равенства относится к равполеспым процессам.
1.5 частности, для теплоизолированных систем с dQ = 0 (адиаба-
(адиабатических систем) второе начало записывается в виде
dS>0. A.6)
Как показывает неравенство A.6), процессы в системе идут так,
что энтропия системы не уменьшается.
20
Для равновесных процессов среди термодинамических- функ-
функций р, р, е, r\, T, S п т. д. имеются только дво независимые.
Если в качестве таких независимых параметров принять темпе-
температуру Т и плотность р, то остальные функции могут быть вы-
выражены через них:
/;=/;(р, Г), е = е(р, Т)
и т. д. Такие равенства носят название уравнений состояния.
В простейшем случае идеального газа эти уравнения име-
имеют вид
е = е(Г), A.7)
глр R — газовая постоянная. Кечи внутренняя .-шортя газа лн-
HL'iino зависит от температуры, второе из равенств A.7) может
¦Пыть записано и виде
г^ПТЦч — 1), A.8)
где у — безразмерная величина, равная отношению тенлоемко-
cTcii газа при постоянном давлении и постоянном объеме.
3. Подход Лагранжа и подход ёЖлера к изучению движения
сплошной среды. Для описания двнлачши сплошном среди ис-
используют два подхода, связанных с выбором системы координат.
При использовании подхода Лагранжа наблюдение ведется
за фиксироваппои частицей среды, прослеживается изменение во
времени ее параметров. Зная судьбу всех частиц, мы имеем ис-
исчерпывающую информацию об изучаемом процессе. Очевидно,
независимыми переменными, помимо времени, в этом случае
должны являться некоторые призпаки, позволяющие отличать
одну частицу от другой (так называемые переменные Лагран-
/¦''/). Например, если число частиц конечно, то их можно пере-
перенумеровать, н за лагранжеву координату частицы принять ее
номер.
Часто в качестве переменных Лагранжа выбирают координа-
координаты начального положения частицы. В этом случае закон движе-
движения сплошной среды, т. е. движение любой ее частицы, выража-
выражается формулами
xi-gtW, А, А О- » = i, 2, ;). A.9)
где xt — текущие координаты частицы, а л\ — координаты ее на-
начального положения при t — 0, т. е. лагранжевы переменные:
Зафиксировав в ([.д)х°г, х%, ха3, мы получаем закон движения
отдельной частицы, иными словами, ее траекторию. Фиксируя t
и рассматривая g, как функции переменных х\, х% хя, мы полу-
получаем распределение всех частиц по пространству на данный мо-
момент времени.
21
Формулы A.9) устанавливают взаимно однозначное соответ-
соответствие между Xi их\ ). Поэтому, разрешая лх относительно х^г
можно получить
х<[ =hi(x1, т.. .г,. /). A.10)
При этом нкобпап преобразоваиин
fli = [)(x1,ri,xa)/f)(a». A -'I;) A-11)
предполагается отличным от нуля во все моменты времени.
В подходе Уплера наблюдение ведется аи точками фиднческо-
го' пространства. Переменными Эйлера являются координаты
точки паблюдспнн х\, Х2, хз. Чере.ч точку пространства с тече-
течением времени проходят различные частицы среды. Зпачение, на-
например, скорости, и дапной точке физического пространства в
данный момент времепи отождествляется со значением скорости
тон частицы среды, которая в даппый .момент проходит через
точку.
Во избежапно возможных недоразумении при определении
скорости формулой v = dr/dL укажем, что здесь г не является
радиус-вектором точки наблюдения в физическом пространстве,
т. е. независимой переменной Эйлера, ('(.гласно определению
A.2) г есть зависящий от времени раднуг-нектор некоторой фик-
фиксированной частицы среды.
Существо подходов Лаграпжа и Эйлера хорошо отражает, как
нам представляется, удачпое сравпепие, заимствоваппое из [87].
Изучение движения воды в реке можно вести, либо плывя па
лодке от истоков реки до ее устья и наблюдая за судьбой от-
отдельных частиц жидкости (подход Лаграижа), либо паблюдая
за течением с берега в определенных .местах (подход Эйлера).
А. Связь между подходами Эйлера и Лаграижа. И подход .')fi-
лорл, и подход Лаграижа дают полную картину движения среды
и в ;)том смысле они лквивалептпы друг другу, .'{пая закоп A.У)
движения частиц и зависимость произвольного параметра / от
начальпого положения частиц и времени: / = f{x\, х\. j", t), т. е.
имен описание движения среды по Лагранжу, мы всегда можем,
воспользовавшись формулами A.10), получить представление
этого движения в переменных Эйлера: 1 = j[h\{xx, x2, x3j t),
Ii2(x\, Х2, хз, L), /гз(^ь Х2, хз, L), t]. Здесь мы учли предположе-
пие о том, что во всех системах отсчета время течет одппаково
(абсолютпость времепи).
Аналогично осуществляется переход от перемепных Эйлера к
перемоппым Лагранжа. Для этого нужно предварительно проин-
проинтегрировать уравпеиия
dxijdl = vt(xi, х2, хз, t), i = 1, 2, 3,
*) Если в течепин со временем образуются пустоты, то для точек фи-
физического пространства xt, соответствующих птим пустотам, по существует
образов в проагранстве начальных состояний а^. Поэтому в дальнейшем этот
случай не рассматривается.
21
з результате чего булут получены формулы
Xi-nirt 4 4 t). (I.I2)
Пояспим сказаппое гта простом примере. Пусть пзнестна зависи-
зависимость для скорости в форме
и; = Ua = const, v-2 = v3 = 0
{одпородпое поступательное движение). Интегрирование соот-
соответствующей системы уравнении
dxjdt = U о, dx2/dt = 0, dx3/tU = О
даст
где постоянные интегрирования определены нз начальных уе-
уело пий.
Имея формулы перехода A.12), нетрудно построить зависи-
зависимость любого параметра / от переменных Лаграпжа. ис.ш и i-
зостно его представление по Пп.черу 1{х\, ,rj, .гз, I). ДеИстии-
Т.'Л [.ПО,
A-13)
Из последней формулы, в частности, можно получить связь меж-
между ойлеровой и лагранженой производными по времени. Заме-
Заметим, что, дифференцируя / по времени при фиксированных
.С]. Х2, Хз, мы вычисляем частную производную по времени п
фиксированной точке физического пространства (эйлерова про-
ншодная). Фиксируя лагранжевы координаты х°л, х°2, .г[{ и прово-
проводя дифференцирование по времени, мы получаем так называе-
называемую полную или субстанциональную производную, характери-
характеризующую изменения, происходящие с иыделенпои частицей среды
вдоль ее траектории (лаграижева производная).
Итак, продифференцируем A.13) по /, фиксируя г?. Л, а1":
df of ill t!r, i)l <lc., Of d*->
dt ot ' n.rl dt n c/.r., dt "* ox.t dt * \l-li)
Здесь df/dt и df/dt — производные Лаграпжа и Эйлера соответст-
dx-
веппо. Учитывая, чго производная -~ (а^. з", х\, l) прп фикси-
фиксированных х\, х2, хЛ есть i-я компонента скорости выделенной
частицы, перепишем A.14);
23
Проиллюстрируем особенности подходов Уйлсра и Лаграпжа
и, в частности, различия между производными по времени в
этих подходах двумя примерами.
Рассмотрим одномерное (т. е. зависящее лишь от одной про-
пространственной переменной, например х\) движение среды. Пусть
это течение является стационарным по Эйлеру djdt = 0, по неод-
неоднородным по пространству 0/дх1^к0 (рнс. 1.2).
Так как течение стационарно по Эйлеру, то значение любо-
любого параметра / в каждой точке пространства не изменяется со
временем: f(x\)=f = const, f(,X\) = { = cou?t. Однако в силу не-
одпородпости течения /^/. Поэтому в любой частице среды, пе-
переместившейся из сечения х\ в сечеппо .г-., значение параметра
/ изменяется па величину А/ = / — /. Если Д.г; ='Х\—Х\ доста-
достаточно мало, это изменение можно представить в виде
Отсюда лаграпжева производная по времени для такого течения
есть
iL
dt
^O) точеши:. В силу
течения любая его ха-
хаl-сть функция только
т- е- 1!0 исех точках
ii::Mencinre / происхо-
происхоII
Рис 12
что, естественно, согласуется с oonjeii формулой A.15).
Другой пример. Рассмотрим одномерное однородное (д/дх\
= 0), но нестационарное по Пйлсру (d/d В
однородности
рактеристика
ирсмонн /(/)
нространстг.а
дит по одному II тому же закону.
Поэтому ii.iMciieiine параметра / в
частице, сместиншоися ini положения
— =
х\ и положение .г. (см. рис. 1.2),
_ _ будет II точноегц таким же, что и в
самих точках х\, Х\. Иными словами, djjdl = djjdt, т. о. эйлерова
и лаграпжепа произподные но времени и лтом случае совпадают.
Таким образом, можно сделать заключение, что лагранжева
производная по времени определяется как нестациопарностью
процесса, так и неоднородностью распределения параметров в
пространстве, где перемещаются частицы среды.
Несмотря па отмеченную выше эквивалентность подходов
Эйлера и Лаграпжа для описания мехапнческого движения сре-
среды, использование одного из пих может оказаться предпочти-
предпочтительнее при постановке и решении конкретных задач (си.
пиже § 3).
24
§ 2. Интегральная форма уравнении газовой динамики
1. Общий случай. Переменные Эйлера. Уравнения газовой ди-
динамики представляют собой выражение общих законов сохране-
сохранении массы. импульса ir энергии. Запишем их, пользуясь пере-
переменными Эйлера.
Пусть V—некоторый фиксированный объем физического
пространства, в котором происходит течение газа, Б—гладкая
замкнутая поверхность, огра- __
пичивающая отот объем
(рис 1.3). Масса газа, заклю-
заключенная в этом объеме в неко-
некоторый момент времени I, выра-
выражается интегралом
fp(r, t)dY,
V
где г = {.ri, x-i, ги — радиус-
вектор элемента об-ьема dV =
= dxidx2dx3, p — плотность га-
tj в ном. Частнцм среды в 1'ис. 1.3
споем движении входят и вы-
выходят из объема \\ пересекая его границу 2. Количество газа,
покидающего объем Г за единицу времени, составляет величину
¦ o(vn)d2, где п — единичный вектор внешней нормали к эле-
элементу поверхности dl (рнс. 1.4), (vn) — скалярное произведение.
Составим
--= h — l\:
Гис. 1.4
вощества за промежуток времени At
f[p(r, *,¦ — (> (г. t,)]dV + \ f p(vn)d2A = 0. B.1)
V < г
J^ равнение B.1) выражает закон сохранения массы в объеме F
па интервале времени Af и носит название уравнения нераз-
неразрывности.
Прп выводе второго уравнения газовой динамики — уравне-
уравнения движения — предположим, что в среде действует некоторая
внешняя сила с объемной плотностью F(r, /). Примерами такой
силы могут служить: сила тяжести, электромагнитная сила Ло-
Лоренца, действующая на про-
подяншн газ, движущийся и
магнит нем ноле, и т. д.
Гал, находящийся в объ-
объеме Г, обладает количеством
движения, равным \ pvr/V.
V
11.ЧЛ1П1С111Н' этой величины
со нремемем происходит :)<<
счет пых» кания газа, поки-
покидающего объем V, причем
л единицу времени теряется
Рис.
— ) p(vn) xdZ.
а также :?a счет действия инешпнх сил. Помимо объемной
ипешней силы F(r, t), на га:?, заключенный л выделенном
о'ъеме V, действует сила со стороны остальной массы газа. Это
взаимодействие носит поверхностный характер, и в общем слу-
случае сила взаимодействия Р в каждой точке поверхности 2 на-
направлена иод некоторым углом к внешней нормали (рис. 1.5).
Касательная составляющая силы Рт связана с наличием в
среде вязкостп; это сила трения, возникающая при относительном
движении слоев газа, которые соприкасаются по поверхности Г.
Если мы ограничимся рассмотрением певязких сред, то сила по-
поверхностного изапмодекствпя сиедстся к нормальной составляю-
составляющей, которую можно представить в виде
Р„ = — рп,
где р—газокипотнческоо давление. Полпый пмпульс этой сстлп
за промежуток времени AL = L2— t\ составит
— \ j рп dZ dl.
'lis
Учитывая все сказанное, запишем закон сохранения импуль-
импульса в объеме V *):
\ !р (г, t2) v (г, /,) — р (г, «,) v (г, L{)\ dV + \ [' (vii) v dl dt =
= — I pndldi ¦+ \ FdVdl. B.2)
*) В B.2) в интегралах по времени все фут:':г;ии зависят от г и
26
Ото выражение естг, интегральная форма урапнонии движопия
среды. В отличие ог B.1), это уравнение — нокторпоо.
Чтобы получить третье уравнение, следует записать для объ-
объема V закон сохранения энергии. Полная опоргпя газа (внутрен-
(внутренняя плюс кинетическая) л объеме V вычисляется по формуле
р (f + \) dV.
V
Ее изменение происходит за счет переноса через ноперхпость I,
работы внешних сил (объемных и поверхностных), а также за
счет действия инешштх источников, если таконые имеются:
[ {(> (г, U) [у (г, /,) + Ц^] - о (г, /,) [f. (г, г,) + и-^-Щ) dV +
h л '-2
+ f f p(e + 4f) (vn) di! dt ==-[("/> (vn) dl dt +
\(Fv)dVdt + \ \ QdVdl- \ \ (Wn)dSd/, B.3)
') — мощность объеипг.г^ источпшсои энергии, расиродолспных л
пространстве, паприм -р пптонс1гвпость джоулова нагрева электри-
электрическими токами, текущими is проводящем гане. Последний член в
B..'!) oiriici.riiaer при-, ш; rmeprini чере:» поверхность ohiiOMa il .'ia
счет процессом тепли^^шодностп, VV— иектор плотности теило-
пого потока. Эта неличггпа определяется через остальные пара-
параметры следующим образом (закон Фурье):
W = —х grac! T
(Т — температура). Если среда изотропна, то х — скаляр, назы-
называемый коэффициент¦;.!( iеплопроводпасти. .")тот коэффициент яп-
ляется, вообще гонорл. функцией термодинамического состояния
иреды: х =х(р, 7').
Уравнение B.3) г, газодинамике называют уравнением
энергии.
Полученные уравне-шш ra:$onoir динамики B.1) — B.3) прод-
стаиляют собой интегральную форму законов сохранения массы,
ндшульса и энергии, "hri ураннепия -чаппсапы в переменных
Эйлера, так как объем газа V, фигурирующий п формулах, фик-
фиксирован по отношению к эйлеровым координатам.
2. Интегральные уравнения в переменных Лагранжа. Нетруд-
Нетрудно получить лагран;ко:н) представление тех же законоп сохра-
сохранения. Рассмотрим 1.ч'т,ем, образованный фиксированными части-
частицами среды, которыл перемещается вместе со средой, изменяя
свою конфигурации (так называемый ежпдкнй объем»)
27
(рис. 1.6). Повторим для этого жидкого объема V(t) рассужде-
рассуждения, проведенные выше для неподвижного объема. За промежу-
промежуток времени At = h — ^i частицы газа переместятся в новое поло-
положение, объем V(t) деформируется.
Однако при ;>том количество час-
1тпц и объеме Пи изменится, и мас-
ea газа осгапется прежней:
\' о(г. Л,)г.'Г =
vfll)
Ото соотношение представляет со-
собой лакоп сохранения массы в ин-
рпс 1 g тегралыюй ферме, записанный
для жидкого объема, т. е. в
форме Лагрянжа. Существенным отличием от :ч'!лерова нида OTor.j
же уравнения B.1) является зависимость от времени объема, по
которому проводится интегрирование.
Рассмотрим далее уравнение движения. Так как » процессе
дпнжепня частицы среды но поступают и объем и не покидак>г
его, то в балансе пмпульса так же, как в законе сохранения мас-
массы B.4) будет отсутствовать член, связанный с потоком пмпулг.-
са через поверхность Т(?) объема. Изменение количества движе-
движения в этом случае происходит лишь за счет внешних (объемных
и поверхностных) сил:
\ р(г, /,)v(r, L)dV — \ p(r,*,)v (г, *,)??!" =
= — f f
j f FdVdt. B.3)
Аналогичные изменения претерпевает и ураппение эпергпи. Оно
припимает вид
I
= - \ [ р (vn) dl dt + J' j (Fv) c-V dl
? , ?
+ j j QdV dl - j j (Wn) dXdt.
1, Vit) t, 2@
28
Три уравнения газовой динамики B.1) — (--¦'') (или аналогич-
аналогичные уравнения в форме Лаграпжа) содержат пять подлежащих
определению функции р, р, е, Т, v. (Векторное уравнение B.2)
мы рассматриваем как одно уравнение, а вектор v как одну не-
неизвестную функцию.) В связи с этим вводят дополнительные со-
соотношения, намывающие систему уравнений газодинамики. Таки-
Такими соотношениями яиляются термодинамические уравнения со-
состоянии
Р=Р(р. Л. е = е(р, Т).
Если уравнении, выражающие законы сохраш пня массы, им-
импульса, iiiii'pniii носят достаточно общий .характер, то уравнения
состояния несут информацию о конкретной мидели газовой ди-
памикп, о конкретных свойствах среды. Так для модели идеаль-
идеального газа уравнения состояния имеют вид A.7).
Отметим, что при использовании подхода Лаграпжа количе-
количество неизвестных увеличивается: дополнительно приходится ис-
искать на каждый момент времени положение и пространство ча-
частиц среды. В этом случае к системе уравнений добавляется
соотношение
dtldt = v,
являющееся фактическим определением скорости.
Три закона сохранения и уравнения состояния (а п лаграп-
жевом случае и уравнение для г) составляют замкнутую систему
уравнений газовой динамики.
3. Интегральные уравнения одномерного течения газа. В даль-
дальнейшем при построении разностных схем для задач газовой ди-
пампки мы будем рассматривать одномерные нестационарные
точения газа, т. с. течения, в которых все параметры среды зави-
зависят лишь от одной пространственной координаты и времени. По-
Получим для этого случая уравнения в интегральном виде.
Обычно рассматривают три тина одномерных движений —
цлоские, ососимметричныо н сферически симметричные движении.
В этом параграфе мы ограничимся лишь плоскими одномерными
течениями *).
Пусть х\ — единственная пространственная переметшая, от ко-
которой зависят все параметры среды (далее для одномерных те-
течений мы опустим у координаты нижний индекс xj^x). Общие
интегральные выражения законов сохранения B.1) — B.3) спра-
справедливы и для частного случая одномерных течений газа. Выбе-
Выберем и качестве объема V, фигурирующего в этих формулах, пря-
прямой параллелепипед, основания которого—квадраты единичной:
площади, лежащие » некоторых плоскостях II' и П", проведен-
проведенных через х и х" перпендикулярно оси х (сечения х' и х"
произвольны) (рпс. 1.7). 1J дальнейшем таком параллелепипед
*) Осе- и сферически симметричные случаи рассматриваются анало-
аналогично.
24-
мы будем называть единичным. Нам достаточно изучить поведе-
поведение га;т п таком объеме. В силу плоской симметрии процессы
и любом другом таком же
параллелепипеде оудут про-
протекать аналогично. Элемент
объема единичного паралле-
параллелепипеда выражается так:
4V *= 1 ¦ 1 -<1х, где единицы
имеют размерность длины, и
их произиедсчше выражает
площадь поперечиого сече-
сечения параллелепипеда. Далее
л выкладках ото пропзпеде-
ние опущено.
Предположим для про-
простоты, что лектор скорости
имеет лишь одну компонен-
компоненту, направленную по оси
абсцисс, v\ t=i v,
Учнтыпая dcj скапанное,
перепишем для одномерного
Т
х
о
п
1
1 !
т ,
с
»-
х
О
Гис. 1.
Гис. 1.8
случая уравнение неразрывности B.1):
\[р(х,1?)—р(л, l,)lds+ \[p(x",t)a(/',t) - j) {У, t) r (x', Л| dt =0.
B.0)
Так как через боковые грани параллелепипеда поток вещестиа
«тсутстпует, от интеграла по поперхности S в нашем случае оста-
остались лишь нпп гр<1.и,1 но основаниям параллелепипеда, площади
которых равны едпинце. Перед интегралом по торцу х стоит :шак
ыинус, так как .чдесь иапранлепие скорости газа и ппошпей пор-
.мали к поверхности нротшюноложны (м иыкладках скорость при-
принимается иоложнтрлг.пон).
Преобразуем соотношение B.G). Выберем и фазоном плоскости
х, t контур С — прямоугольник со сторонами, параллельными
осям коордипат; размеры стороп указапы па рис. 1.8, п.
'10
Рассмотрим выражение
=¦(' (f« rfar — рг di) = О, B.7)
Нетрудно убедиться в том, что вдоль указанного контура С ураи-
псппя B.П) и B.7) равносильны.
То як: самое справедливо для случая, к<гда контур С со-
состоит из любого конечного числа отрезком, параллельных осям
координат (рис. 1.8,6). Действительно, мы можем разбить область
Т па песколько прямоугольников и для каждого записать соотпо-
шепнс B.7). Суммируя контурные интегралы, мы получим, что
слагаемые, относящиеся к внутрспппм границам, взаимно унич-
уничтожаются, так как каждый отрезок внутренней границы прохо-
проходится дважды в противоположных направлениях. В результате
ьновь приводим v формуле B.7), но для контура более сложном
конфигурации.
13 случае произвольного контура покроем плоскость .г. t сет-
коп, образованной линиями, параллельпымп осям координат
(рис. 18, в). Выберем минимальную область Г* с контуром 6'*,
образованную ячейками сетки, в которой целиком лежит псходешя
область Т с контуром С. Для С* формула B.7) справедлива. При
измельчении ячеек сетки, С* -*¦ С. Не останавливаясь па обосно-
обосновании предельного перехода, заключаем, что в пределе формула
B.7) оказывается справедливой для любого замкнутого кусочно-
гладкого контура С в плоскости (х, I), При лтом предполагается,
что подынтегральные функции ограничены, кусочпо-непрерывш.т
и па контуре С могут терпеть разрыв лишь в отдельных точках.
К виду, аналогичному B.7), можпо преобразовать и дна дру-
других уравнения — закопы сохранения импульса и :>пергии:
(n>
clr — (/>-(-ft/'-) dt = [ [ F (Lr dt, B.8)
+ 4 + t) + w]d>=
= [ j Fv dx dl -!- f j Q dx dt. B.9)
lt 'r
Здес1> F и W — компоненты по х вектороп ппешпей силы и теп-
теплового потока.
§ 3. Уравнения газовой динамики в дифференциальной форме
1. Дифференциальные уравнения в переменных. Эйлера. Инте-
Интегральные соотношения B.1)—B.8) являются наиболее общей
формой уравнений газовой динамики. В них п<- содержатся про-
производные от функций, характеризующих состояние среды, и по-
потому не предполагается больших ограничении на гладкость этих
функций. Более того, выведенные уравнения допускают суще-
ствонание разрывных решений (см. § 5).
3t
Однако па практике при решении задач удобнее пользоваться
уравнениями галопом дипамики в дифференциальной форме, ко-
которые могут быть получены на оснопе пнтегральпых уравнений.
Переход к дифферепциальным уравнениям сужает класс допусти-
ыых решений. 13 частности, дифференциальные уравнения не со-
содержат важный случай разрывных уравнении.
Обратимся к закону сохранения массы B.1). Преобразуем в
соответствии с известной формулой векторного анализа новерх-
ностпый интеграл к объемному:
f p(vn)d2 = f dlv'(f)\)dV.
Разделим далее обе части уравнения B.1) па At = t2 — t\ и
устремим At к nyjno. Предполагая, что соответствующие произ-
иодпыо существуют, получим
l^r +
V
Отсюда в силу произвольности объема V следует:
до 1. (. ,л ji
—~- + divpv — (I. C.1)
Дифференциальное уравнение неразрывности C.1) по-преж-
по-прежнему выражает тот же физический факт, что и соотпошепие
'B.1),— закоп сохрапепия массы. Из процесса вывода уравпепия
C.1) ясно, что производная по времени в нем является эйлеро-
эйлеровой, и само уравнение записало в перемепных Эйлера.
Векторное уравнение движения B.2) предварительно спроек-
спроектируем па координатное паправлепис xh и затем проделаем пре-
преобразования, аналогичные тем, которые привели нас от уравнения
B.1) к C.1). В результате получим
Левая часть этого равенства с учетом уравпения перазрывпости
C.1) преобразуется к виду
—- ~ lUvpmv = р (^— + (vV) Vij.
Оператор (vV) у, к о рассматривался и § 1 при определении суб-
станцнопальной производпой (см. A.15)).
Итак, дифференциальная запись закона сохрапепия импульса
та копа
или в р.екторпоп форме
-^ + (vV)"v = - — grsul /) + —.
Так ;ке выводит»1» п дифференциальное уравпение эперпги.
22
Система дифференциальных уравнений газовой динамики в пе-
переменных Эйлера выглядит следующим образом
i? + divpv = O, C.2)
_g+(vV)v L grad л +-?-, C.3)
C.4)
p = p(p,T), e = e(p, T). C.5)
2. Дифференциальные уравнения в переменных Лагранжа.
Дифференциальные уравнения газодинамики можно получить и
иа интегральных уравнений в форме Лагранжа B.4), B.5). Раз-
Разделим уравнение B.4) на At = ti — 11 и устремим At к нулю.
В пределе имеем
j O. C.6)
V(O
Заметим, что здесь дифференцирование ведется вдоль траекторий
частиц газа, составляющих движущийся жидкий объем V(t),
и таким образом, в C.6) входит лагранжева производная по вре-
времени. В силу того, что объем, по которому ведется интегрирова-
интегрирование, изменяется во времени, дифференцирование в C.6) следует
проводить по изпестной формуле
-? \" Ф{с1У) = \ fe + div((Pv)]dF, C.7)
v(o v(o
где Ф(г, /) — пекоторая скалярная функция.
Применяя формулу C.7) к C.6) и учитывая произвольность
объема Vit). получим ураинение неразрывности в переменных
Эйлера
совпадаю'.цее с C.2).
Однако можно применить к урапнению C.6) некоторый дру-
другой прием, который иршюдит к дифференциальному ураппепию
неразрывности в форме Лагранжа.
Интегрирование в C.6) ведется в переменных Эйлера, т. е.
dV = d.r;(!r-jd.t3- Сделаем замену переменных: перейдем от пере-
переменных Пйлера х\, Х2, х?, к переменным Лагранжа х\, х\. г\, пони-
понимая иод ними, как и и § 1, начальное иоложеыие частиц среды.
Известие, что при такой замене элемент объема преобразуется
3 А. А. Самарский, Ю. П. Попов 33
по формуле
dV = dxx dx2 diz = A dxj dx°2dx°3 = A dV°, C.8)
где A — якобиап преобразопаппя A.11)—предполагается поло-
положительным. Переменный объем V(t) в пространстве переменных
Эйлера, по которому ведется интегрирование, перейдет в некото-
некоторый объем Vй в пространстве начальных состояний х\, х%, хл.
Этот объем У0 уже не зависит от времени. Поэтому
IT
v v
И далее
4i (PA) = U. C.9)
Полученное уравпенпе представляет собой дифференциальное
уравнение неразрывности и переменных Лагранжа.
Уравнение движения B.5) можно преобразовать к виду
jpvdV= j (— grad p + F) dV. C.10)
А
dt
V(t) V(t)
Если применить к лоной частп C.10) формулу C.7), граау жп
получится уравнение движения в форме Эйлера. Использование
описанной выше замены переменных позволяет следующим об-
образом преобразовать левую часть C.10)
A § j j
V°
Jg ^9§dV. C.11)
y V(t)
Здесь мы учли, что, согласно C.9), произведение р\ ест', вели-
величина постоянная и может быть вынесена из-под знака дифферен-
дифференцирования. Кроме того, в конце цепочки преобразований C.11)
сделана обратная замена переменных. Подставляя C.11) к C.10),
имеем
р ¦? - - grad/> + F. C.12)
Аналогично C.12) строится п уравнение энергии.
Выпишем получающуюся таким образом спетому дифферен-
дифференциальных уравпепий:
Т), е = е(р, Т).
34
Строго говоря, система C.13) не полностью записана в лагран-
жевых переменных — в левых частях уравнении стоят лагранже-
лагранжевы производные по времени, однако в их правых частях диффе-
дифференцирование проводится по эйлеровым координатам.
Система уравнений C.13) весьма похожа на уравнения
C.2) — C.5), что лишний раз демонстрирует эквивалентность под-
подходов Эйлера и Лагранжа. Более того, уравнения движения и
энергии в C.13) получаются непосредственно из C.3) и C.4):
достаточно воспользоваться выведенной в § 1 связью A.13) между
лагранжевой и эйлеровой производными по времени. Однако мы
предпочли вывести уравнения C.13) непосредственно, так как
сам процесс их вывода позволяет ярче проиллюстрировать раз-
различия между переменными Эйлера и Лагранжа.
3. Дифференциальные уравнения одномерного неустановивше-
неустановившегося движения газа. Лагранжевы массовые переменные. Чтобы
получить дифференциальные уравнения одномерного нестационар-
нестационарного течения, можно воспользоваться интегральными уравнениями
одномерного движения из § 1. Однако проще обратиться к общим
дифференциальным уравнениям C.2) — C.5). Для одномерного
неустановившегося плоского течения газа (д/дх2 = <
д/дх[ ^ д\дх Ф 0) из них сразу следует:
др д . „ dv dv
р = р(р, Т), е = е(р, Т).
В C.14) под v и W понимаются проекции векторов скорости
и теплового потока на ось х, а члены с внешними силами F и
источниками энергии Q опущены, так как их учет в данном па-
параграфе не является принципиальным.
Введем в рассмотрение так называемые лагранжевы массовые
координаты. Поясним их смысл на конкретном примере — пло-
плоской одномерной нестационарной задаче об истечении газа в ва-
вакуум.
Эта задача формулируется следующим образом. Рассмотрим
две параллельные плоскости, пространство между которыми за-
заполнено газом (рис. 1.9). Левая плоскость — неподвижная степ-
ка, ее эйлерова коордипата в течение всего процесса постоянна
и равна xq. Правая плоскость, которая отделяет газ от вакуума,
в начальный момент t = 0 мгновенно убирается (физически это
отвечает, например, разрыву некоторой диафрагмы), и начинает-
начинается, как говорят, процесс истечения газа в вакуум. Мы предпола-
предполагаем, что процесс истечения будет одномерным. В частности, это
означает, что граница газа с вакуумом будет оставаться плос-
плоскостью во все моменты времени (ее координата xa(t)); кроме
того, траектории всех частиц—прямые, параллельные оси х.
Рассмотрим поведение газа в единичном параллелепипеде
хо<х<хъA) (см. рис. 1.9,а,б, а также § 1). Заметим, что хотя
3* 35
объем этого параллелепипеда изменяется со временем, частицы
газа не покидают его и не приходят извне, так что масса газа в
параллелепипеде остается неизменной. Обозначим ее через М.
Проведем в начальный момент в параллелепипеде сечение не-
некоторой плоскостью А, параллельной его основаниям. Очевидно,
все частицы газа, находившиеся в этом сечении в начальный мо-
момент, будут двигаться одинаково и образовывать в любой момент
? > 0 плоское сечение (его можно назвать «жидким сечением»).
Эйлерова координата этого сечения т.АA) изменяется со временем
в соответствии с законом движения частиц газа. Частицы среды,
находившиеся в параллелепипеде левее жидкого сечения А,
в процессе движения не могут оказаться прайсе его, так как r
противном случае в газе началось бы перемешивание и наруши-
нарушилась бы одномерность течения. Поэтому масса вещества, нахо-
находящаяся в параллелепипеде слева от сечения А, в течение всего
процесса будет оставаться постоянной и равной ее начальному
количеству:
xA(t) xA@)
sA= j p(y,t)l-ldy= ] p(y,Q)l-ldy. C.15)
Произведение единиц здесь, как и в § 1, соответствует единич-
единичной площади поперечного сечения параллелепипеда. В дальней-
дальнейшем мы также опустим в формулах это произведение.
Чтобы при этом не возникло недорааумений с размерностями,
будем считать, что в задачах с плоской симметрией s выражает
массу, приходящуюся на единицу площади поперечного сечения,
и имеет размерность г/см2.
Рассмотрим общее выражение
C.16)
устанавливающее соответствие между величинами х и s. Когда х
изменяется от ха до xB(t), s пробегает значения от 0 до М. Если
в C.16) зафиксировать верхний предел интегрирования х, то
определенная таким образом функция s(t) будет выражать мас-
оу, находящуюся в единичном параллелепипеде левее сечения
х = const. Если же зафиксировать в C.16) зпачеште s@=s;s=s M),
то верхпий предел будет функцией времепи x(t), причем полу-
полученная зависимость соответствует траектории дпижопия частиц,
левее которых в единичном параллелепипеде заключена масса s.
Итак, величина s обладает характерным свойством — для каж-
каждой частицы среды в рассматриваемом одномерном течении она
имеет снос значение, по изменяющееся в процессе движения.
Поэтому величина я может быть выбрана в качестве переменной
Лагранжа. Учитывая, что s имеет размерность массы, такую пе-
переменную называют лагранжеаой массовой координатой.
36
Равенство C.16) устанавливает взаимно однозначную Ц
между лагранжевой массовой координатой и переменными Эйле-
Эйлера х, t. Очевидно, одной такой связи недостаточно для того, чтобы
выполнить замену переменных. Необходимо еще определить вто-
вторую переменную Лагранжа — время. Это делается посредством
равенства
t. = t, C.17)
которое выражает тот факт, что в лагранжевых и эйлеровых ко-
координатах время течет одинаково. Чтобы избежать путаницы,
Вакуум
Вакуум
X
в формулах этого параграфа мы будем помечать время в пере-
переменных Лагранжа буквой t с индексом л; буквой t без индекса
обозначается время в системе переменных Эйлера.
4. Уравнения газодинамики в лагранжевых массовых перемен-
переменных. Формулы C.16) и C.17) реализуют переход от переменных
Эйлера к лагранжевым массовым координатам. Преобразуем
уравнения C.14) в соответствии с этими формулами от перемен-
переменных Эйлера х, t v. переменным Лагранжа s, ta. Выведем предва-
предварительно соотношения для преобразования производных. Как в
при всякой замене переменных, имеем
d a ds д dtn d д ds a dtn .„ ,Q.
""ГТ" — -5 TT" "T T7~ ~o7i *"o~" ^ ~o ^T" "T" 7 ~X~ • I O. lo)
at os ot at- ot ox ds ox dt ox
Из C.17)' следует
dtjdt = i, dtJdx = 0, C.19)
а из C.16) —
ds/dx = p(x, t). C.20)
Несколько сложнее вычисляется произкодггая ds/dt:
= - И*, t)v(x. t) - р(х0, t) v (x0, О]. C.21)
Здесь производная dp/dt заменена с помощью уравнения нераз-
неразрывности из C.14). Так как в рассматриваемой нами задаче ле-
левая граница неподвижна: v(xq, t) = 0, то
ds/dt =—p(x, t)v(x, t). C.22)
Если же левая граница движется по некоторому заданному
закону xo = xo(t), то вместо C.16) имеем
х
s (х, t) = j p 0/, /) dy.
j
При вычислении ds/dt в преобразовании, аналогичном C.21), не-
необходимо провести дифференцировапне по переменному нижпому
пределу интегрирования. В результате вновь приходим к форму-
формуле C.22). Подставляя C.19), C.20) и C.22) в C.18), получим
Возвратимся к прежнему обозначению для лаграпгкепой произ-
производной по времени d/dtn *= d/dt и перепишем C.23) п несколько
иной форме:
d д^ ^д_ д _1 д_ -о п/\
~dt ~ It + li' ~дТ ~ ~р~ ~di'• @.^.1)
Первая из формул C.24) совпадает с определением субстацио-
нальпой производной, которое было получено в § 1 для случая,
когда лагранжевыми переменными являются координаты началь-
начального положения частицы. Это можно было предвидеть заранее,
если учесть, что функция s также характеризует начальное по-
ложепие частицы. Особенно наглядна эта связь между s и началь-
начальной координатой частицы х° в случае, когда исходная плотность
газа постоянна: р(х, 0) = ро=- const, и хо = 0. Действительно,
для фикспропанной частицы имеем •.
s= [ Р О/. О dy = \ р0 dy = рох°.
*в °
Преобразуем теперь уравнения C.14) с помощью C.24); при
этом будем считать, что все величины являются функциями х
и t. Рассмотрим для примера уравнения неразрывности:
df> д , ч / пи ос) \ dv (!(¦ „ bv*
Остальные уравнения преобразуются аналогично. Система уравне-
пий газовой динамики для одномерного плоского нестационарного
течения и лагранжеиых массовых координатах приобретает вид
d I 1 ^ Зу dv dp dx
~J ~ Us* ~dl ~ 57' ~~di=V'
d
= е(р, Т).
К трем законам сохранения и уравнениям состояния здесь
добавлено уравнение для нахождения траектории частицы x(t).
Прямые производные по времени в C.25) означают, что здесь
дифференцирование ведется вдоль траектории частицы (субстацио-
нальная производная). Однако с точки зрения лагранжевых пере-
переменных s и t = tл — это обычные частные производные по времени.
Имея в виду сделанное замечание, в дальнейшем при записи
уравнений газодинамики в лагранжевых массовых координатах
мы будем использовать там, где это не вызовет недоразумений,
частные производные по времени:
д I { \ dv dv dp dx
~оГу~р~1 ^7' ^дТ ~ i/7' ~ьг '~ '
ir' C'25)
Р = р(р, Г), е = е(р, Л-
о. Особенности постановки задач газовоп динамики в лагранже-
лагранжевых массовых переменных. Выше мы подробно разбирали особен-
особенности подхода Лаграпжа к изучению движения газа, свойства
лагранжевых неременных. Естествечшо, нояппкает вопрос, в чем
заключаются преимущестпа переменных Лагранжа, когда они
проявляются п в каких случаях ими следует пользоваться на
практике. Отметим нреждо всего, что система уравнений газоди-
газодинамики для одномерного нестационарного случая в лагранжевых
массовых координатах (Я.25) выглядит более просто и компактно,
39
нежели система C.14). Однако главное состоит не в этом. Целе-
Целесообразность использования массовых переменных Лагранжа оп-
определяется особенностями изучаемого течения газа. Для широкого
круга явлений математическая формулировка задачи в лагранже-
вых массовых координатах оказывается существенно проще, чем
в переменных Эйлера. Связано это в основном с постановкой
краевых условий.
Р
t=0
хв(О}
о
к ^
/V
х„
Рис. 1.10
Обратимся вновь к описанной в п. 3 этого параграфа задаче
об истечении газа в вакуум. Представим качественное поведение
решения как в переменных Эйлера, так и в лагранжевых массо-
массовых координатах. На рис. 1.10 указаны распределения плотности
гааа в координатах х и s на три последовательных момента вре-
времени 0 < 11 < t2.
Область определения переменной s (рис. 1.10,6) заранее из-
известна @ < s < М) и не изменяется со временем. В эйлеровых
координатах правая граница области определения решения xB(t)
переменна (рис. 1.10,а), причем закон ее зависимости от времени
подлежит определению в процессе самого решения задачи. Поэто->
40
му краевые условия, формулировка которых является неотъемле-
неотъемлемой частью постановки задачи, в переменных s выглядят так
17@, 0-0, р(М, t) = 0. C.26)
В то же время в эйлеровых координатах имеем
17@, <) = 0, p[xB(t), «1=0. C.27)
Задание режима на границе, положение которой определяется
искомым решением, приводит при решении задачи к дополнитель-
дополнительным трудностям. Поэтому разобранную задачу об истечении в ва-
вакуум и вообще одномерные зада-
задачи о течении конечной и неизмен-
неизменной во времени массы газа, удоб-
удобно формулировать и решать в ла-
гранжевых массовых переменных.
Отметим, что в лагранжевых
массовых координатах удобно ре-
решать также задачи с контактны-
контактными разрывами. Контактный раз-
разрыв есть образование, локалпзо- рис \ц
ванное по массе, т. е. связан- \
ное с фиксированными частицами среды (см. § 5). При рассмот-
рассмотрении в переменных Эйлера такой разрыв перемещается в про-
пространстве, что в численных расчетах приводит' к его «размазыва-
«размазыванию» по координатной сетке. В лагранжевых массовых перемен-
переменных координата контактного разрыва остается неизменной во /Все
время процесса. Поэтому никакого «размазывания» здесь не про-
происходит.
Часто приходится иметь дело с задачами, где рассматриваются
газы различных сортов, отличающиеся друг от друга физическими
свойствами, такими, как уравнения состояния, коэффициенты теп-
теплопроводности и т. д. Подобные задачи, если они допускают одно-
одномерную интерпретацию, удобно также решать в массовых пере-
переменных. В этом случае границы областей, занятых различными
газами, находятся при фиксировапых значениях массовой пере-
переменной. При использовании подхода Эйлера эти границы дви-
движутся в пространстве, и за ними необходимо специально
следить.
Конечно, использование подхода Лагранжа оправдано не
всегда. В этом убеждает простейший пример течения газа в трубе
между двумя сечениями I и II (рис. 1.11). Решать такую задачу
в переменных Лагранжа неудобно, так как в этом случае масса
газа между сечениями / и // переменна во времени, и краевые
условия приходится задавать на границах изменяющейся во^ вре-
времени области в массовых координатах. В то же время в эйлеро-
эйлеровых переменных сечения I и II пеподвижны, что делает при-
привлекательным рассмотрение задачи в координатах Эйлера.
Следует иметь в виду, однако, что избежать задания краевых
условий на движущихся границах удается не всегда. Пусть в рао*
41
смотренном выше примере истечения газа в вакуум левая стенка
выполнена из легкоиспаряющегося вещества, которое иослс испа-
испарения вовлекается в процесс истечения. Такая ситуация часто
встречается, например, в электродинамических ускорителях плаз-
плазмы. В этом случае при использовании лагранжеиых массовых
координат, левое краевое условие приходится ставить па перемен-
переменной границе, причем закон движения этой границы (т. е. масса
испаренного вещества) зависит от самого
решения (в частности, от температуры
газа) и поэтому не может быть указан
заранее.
При рассмотрении этой задачи в пе-
переменных Эйлера аналогичная трудрюсть,
как указывалось выше, возникает при
формулировке граничного условия на гра-
границе газ — вакуум.
6. Лаграпжевы массовые леремепные
для задач с цилиндрической и сферической
симметрией. До спх пор мы обсуждали
способ шюдония. лагранжечн.гх массовых
коордипат и копкретпой задаче об исте-
истечении газа и иакуум. Очевидно, что точ-
точно так жо можно определить массовые
переменные в любой одномерной плоской
задаче.
В случае цилиндрической симметрии
вместо C.16) следует использовать фор-
формулу
сс=/раашш
L .л. ^
L
К
i
i
У
s = 1 р(у, t)i/dy.
C.28)
По физическому смыслу здесь s — масса газа, заключенная » ци-
цилиндрическом секторе единичной высоты с п.-шмуталглшм углом
в один радиан (см. рис. 1.12,а). Этот сектор играет ту же роль,
что и «единичный параллелепипед» л плоском случае. Нормиров-
Нормировка лагранжевой переменной на один радиап удобна тем, что п
системе уравнений не появляется дополнительных множителей
2л. В цилиндрическом случае s — масса, приходящаяся па едини-
единицу высоты,— имеет размерность г/см.
Заметим также, что нижний предел интегрирования в C.28)
не обязательно должен быть нулевым. Если рассматривается ци-
цилиндрический слой газа, то в качестве этого предела следует
ваять координату внутренней границы слоя.
Для сферически симметричных течений лаграпжева массопан
яоордината вводится следующим образом:
= J P</2 dy.
C.29)
142
В этом случае она соответствует массе, заключенной в телесном
угле в один стерадиан (рис. 1.12, б). Здесь s имеет размерность
грамм (г). Формулы C.16), C.28) и C.29) можно объединить
в одну:
Г
« = j P О/, I) Уп dy, C.30)
о
где параметр п = 0, 1, 2 соответственно для случаев плоской, ци-
цилиндрической и сферической симметрии.
Не останавливаясь на деталях вывода, который в точности
повторяет рассуждения, проведенные выше для плоского случая,
приведем систему одномерных нестационарных уравнепий газовой
динамики в лагранжевых массовых координатах C.30), описы-
описывающую случаи плоской, цилиндрической и сферической сим-
симметрии:
d (rnv) av n op dr
ds ' dt os ' dt
д ( , v*\ д i n \ d{rnW) /Q Q,4
-r-r 8 + -7T = — (prnv) i- '-, C.31)
dt \ 2 / os v ' ds v '
7. Закон изменения объема. Система уравнений C.31) записа-
записана в так называемой дивергентной форме. Она выражает основ-
основные закопы сохранения. В самом деле, достаточно проинтегриро-
проинтегрировать, например, уравнение энергии по времени и массовой коорди-
координате, т. е. выполнить процедуру, обратную той, которая прпвела
нас от интегрального уравнения B.9) к дифференциальному,
чтобы получить закон сохранения энергии для фиксированной
массы газа на некотором промежутке времени.
Однако C.31) — не единственная форма записи уравнений га-
газодинамики в переменных Лаграпжа.
Для простоты вновь ограничимся уравнениями одномерного
плоского движения C.25) или, что то же, C.31) при и = 0,
а также положим, что потоки тепла в среде отсутствуют: W = 0
(адиабатический случай). Обратимся к уравнению перазрывности
и подставим в него вместо скорости v = dx/dt:
д I \ \ d
Проинтегрировав это равенство по t и s, приходим к соотно-
соотношению
м
\ ds/p = х (М, t) — х (О, I). C.32)
о
Здесь М — масса газа в «единичном параллелепипеде», а х(М, t)
и х@, t)— эйлеровы координаты правой и левой границ этой
43
массы. Равенство C.32) можно назвать законом изменения объ-
объема. В самом деле, подынтегральная величина ds/p есть объем,
который занимает масса ds, и, следовательно, интеграл выражает
полный объем единичного параллелепипеда. Справа в C.32) сто-
стоит тот же объем, но вычисленный непосредственно (х(М, t) —
¦^-х@, t) — высота параллелепипеда, а множитель, отвечающий
единичной площади основания, опущеи).
Итак, уравнение неразрывности в форме C.25) дает не закон
сохранения массы, а некоторый иной физический факт, который
мы определили как закон изменения объема. В этом нет ничего
удивительного, так как при использовании лагранжевых массо-
массовых координат закон сохранения массы ныполняется автомати-
автоматически.
Вместо уравнения неразрывности в C.25) можно использовать
соотношение
dx = ds/p. C.33)
Это равенство является частным случаем общей формулы C.8);
величины dx и ds — элементарные объемы в соответствующих
пространствах, а величина l/p — dx/ds = Д (см. C.20)) — яко-
якобиан соответствующего преобразования переменных. Отметим, что
при численном решении кадач формула C.33) часто оказывается
удобнее, нежели само уравнение неразрывности.
8. Различные формы записи уравнения энергии. Рассмотрим
далее уравнение энергии. Умножин предварительно уравнение
движения на v, получим соотношение
которое определяет измененпе по времени кинетической энергии
единицы массы газа. Вычитая C.34) из уравнения энергии
C.25), где W = 0, придем к равенству
или, учитывая уравнепие неразрывности,
-гг -- — р -тг ¦ •• C.36)
Урапненпл C.35) и C.36) гмоют непосредственный физиче-
физический смысл: они показыиагот, что пзмепеипе ныутрепией тепло-
тепловой энергии газа происходит за счет работы сил данлепия. Срав-
Сравнивая C.36) и A.4), можно убедиться, что это уравпение фак-
фактически выражает первое начало термодинамики для адиабати-
адиабатического случая.
^¦¦•С^гласно нторому началу термодипамики A.5) имеем, о учо-
^6м C.36),
) C7)
rjtfi S (p,'f) —э-нтропия единицы массм газа.
Отсюда для гладких адиабатических течении получаем еще
одну возможную формулировку уравнения энергии
dS/dt = O. C.38)
Все сказанпое выше справедливо прп любых ураипепнях со-
состояния.
Обратимся теперь к идеальному газу. Выразим для пего из
уравнений состояния A.7) и A.8) заииспмость нпутренпен энер-
энергии от давления и плотности:
e =
V-l P '
Используя полученное соотношение и формулу C.36), придем
после несложпых преобразований к выражению
1- Р -г- \ —• — —, -гт — = 0. C.39)
ot ' f at \ p / v - 1 of ^ pV I v '
Таким образом, для адиабатических раннопесных течепи!! идеаль-
идеального газа для каждой частицы газа остается неизменным во вре-
времени отношение р/р7:
р/рт = const. C.40)
Сопоставляя C.39) с C.37), можно получить, используя A.8),
явное выражение для энтропии идеального гала через остальные
термодинамические параметры
В C.41) опущена произвольнан постоянная, с точностью до ко-
которой определяется энтропия каждой частицы газа.
Если в какоп-то момент времени пп; частицы газа и.мелп оди-
одинаковую энтропию, то в соответствии с C.38) этот факт будет
наблюдаться по псе последующи^ момопты времопи. Такие тече-
течения, в которых энтропия всех частип; газа но все моменты вре-
времени одинакова, па.чьшагот изоэнтропическими.
Получеппыо выше различные формулировки уравнения опер-
оперши относятся к случаю, когда и среде отсутствуют дпесшгатип-
ныо процессы. При наличнп, например, теплопроводности пптро-
пия частиц уже не остается ностоянпой,— ее измепегшо оппсыпа-
ется уравнением
Реальные вещества всегда и той или иной мере обладают свой-
свойством теплопроводности. Поэтому адиабатическое точение можно
рассматривать как некоторый предельный случай, когда коэффи-
коэффициент теплопроводности среды х печезающе мал.
Возможен и противоположный предельный случай: а ->¦ °°.
Так как величина теплового потока W при этом остается конеч-
45
ной, то температура должпа оыть однородной по прострапстпу:
dT/ds ->- 0. Физически этот факт очевиден — за счет сильного про-
процесса теплопроводности псоднородпостп температуры интенсивно
разглаживаются. На практике подобная ситуация встречается при
изучепии явлепий, происходящих при очень высоких температу-
температурах, ибо коэффициент теплопроводпостп х(р, Т) здесь является
резко возрастающей функцией температуры.
В указанном предельном случае, который называют изотерми-
изотермическим, роль ураппепия эпергии выполняет соотношение
Т = const.
Копкретпое зпачепие температуры определяется внешними тела-
телами, с которыми взаимодействует рассматриваемый газ.
Уравпение состояния для идеального газа п изотермическом
случае приобретает вид липейпой связи между давленном и плот-
плотностью: /? = Лр, Л = const или
р/р = А.
Сраппииая последнее раненстно с C.40), можно заключить,
что пекоторые результаты для изотермических течений идеаль-
идеального газа могут быть формально получены ил соответствующих
формул для адиабатического случая, если в них подставить f = 1.
При этом, как следует из уравнений состояпня, теплоемкость
идеальпого газа становится бесконечной, что и обеспечивает не-
неизменность температуры.
Итак, мы получили несколько видов записи уравнения энер-
энергии для газодинамических течений. Мы убедились, что псе они
для гладких решений, эквивалентны в том смысле, что посред-
посредством равносильных преобразований сводятся друг к другу. По-
Поэтому при постановке п решении задач можно пользоваться лю-
любым ir;i этих ипдов. D то же время физическая суть различных
формулировок одного л того же уравнения может быть неодина-
копа — каждая формулировка отражает определенную физиче-
физическую закономерность процесса.
9. Интегральные уравнения в лаграижевых массовых перемен-
переменных. Заключая этот параграф, приведем без вывода систему урав-
уравнений газовой динамики в интегральной форме для одномерного
нестационарного случая в лаграижевых массовых переменных:
e + JilJ ds — pv dt = 0. C.44)
Эта система аналогична соответствующей системе из § 1 (см.
уравпепия A.7) — A.9)) и может быть получепа из общих инте-
интегральных уравпепий газовой динамики в форме Лаграпжа. Коп-
тур, по которому здесь ведется иптегрировапие, лежит в плоско-
46
сти (s, /); требования к ггсму аналогичны соответствующим тре-
бопаншш пз § I.
Система C.42)—C.44) потребуется нам при построении раз-
еостпых схем.
§ 4. Гиперболичность системы одномерных нестационарных
уравнении газовой динамики
\. Акустическое приближение. Уравнении газовой динамики
являются нелинейными (квазилинейными) и это обстоятельств
порождает основные трудности при их исследовании и решепии
конкретных задач. До сих нор и достаточно общем случае для
уравнепип газодинамики не дока.чапы утверждения о сущестно-
вапии решения и его единственности. Поэтому при изучении
свойств атих уравнений часто обращаются к различным упрощен-
упрощенным частным случаям, пыяспяя па их примере качественные за-
закономерности газодинамических точении. Например, таким ши-
широко распространенным мастным случаем является акустическое
приближение. В акустике рассматриваются «слаоые» движения
газа, т. е. такие движения, когда пор параметры гала мало откло-
отклоняются от некоторых исходных значений. -)то позволяет линеари-
линеаризовать общую систему уравнений, что существенно упрощает
задачу.
Рассмотрим неограниченное пространство, заполненное покоя-
покоящимся одпородпым газом. Начальник значения ого параметров
обозпачим через ра, ро, Уо = 0. В газ пносится малое возмущение.
Задача состоит в изучении дальнейшей судьбы атого возмущепия.
Естественно ожидать, что возмущение, малое в начальный мо-
мепт, остапется малым во все моменты кремеnir. Ото означает, что
решение можно искать в виде малого отклонения от начального
состояпия:
р=ро + р, р = ро+р, D.1)
причем условие малости выражается неравенствами
\plpo\ « 1, Ip/pol « 1. D.2)
Неравенства, аналогичные D.2), предполагаются выполненными
пе только для самих фупкций, по и для их производных.
Анализ акустического приближения можно проводить как в
эйлеровых, так и в лаграпжевых переменных. Мы воспользуемся
массовыми переменными Лаграпжа и ограничимся одномерным
плоским случаем,— основные качествеппые закономерности аку-
акустики отчетливо просматриваются и па атом простом примере.
Напомпим также, что мы рассматриваем среду без диссипации —
вязкость и теплопроводность отсутствуют.
Подставим D.1) в уравпепия C.25') и пренебрежем членами
второго порядка малости. Уравпенне неразрывпости
47
с учетом того, что скорость v = v является малой первого поряд-
порядка, дает
# + Pof = 0. D.3)
Рассматривая далее давлепие как фупкцию двух термодипамиче-
ских параметров (плотпости и аптропии) р = р(р, S), запишем
следующее соотпошение
др_ _ /_?р\ _?р 1др\ as 2 dp
at ~ [ dp Js ot + [ ds)p at ~ c at'
где с2 = (др1др)е. Как припято в термодипамике, пижпий индекс
S или р у производной показывает, что при ее вычислепии эптро-
пия или соответственно плотпость предполагаются постояппыми.
Второй член справа опущен, так как движепие газа в акустике
адиабатичпо, и в качестве уравпепия энергии можно использо-
использовать форму C.38), которая гласит: dS/dt = O. Перепишем с уче-
учетом этого D.3)
Эр о 2 <?У // /\
^^. D-4)
Здесь ипдексом «О», как и всюду в этом параграфе, помечены
параметры, вычислеппые для пачальпого фопа, по которому рас-
распространяются малые возмущепия.
Липеаризация уравпепия движения в C.25') дает
dv/dt = —dp/ds. D.5)
Уравпення D.4), D.5) п образуют систему уравнении аку-
акустики: исключая из псе одну из пеизвестпых функций, например
v, получим для описания возмущения давления иростеншое урав-
уравнение гиперболического типа — уравнепие колебаний струны
Остальные функции (плотпость, скорость и т. д.) также удовлет-
удовлетворяют аналогичному уравпепию.
2. Скорость звука. Решение уравнения D.6) ищется в виде
P(s, 0 = /i(s — CopoO+Ms + CopoO D.7)
в соответствии с методом распространяющихся волп. Вид функ-
функций /i и /2 определяется формой пачальпых возмущепий. Физи-
Физический смысл решепия D.7) таков: малые возмущепня распро-
распространяются без искажепия вправо и влево по пространству со
скоростью Соро (бегущие волпы). В газовой дипамике по опреде-
определению скорость распрострапепия малых возмущепий пазывается
скоростью звука. Так как мы используем лагранжевы массовые
координаты, то скорость а = соро является «массовой скоростью
звука», т. е. скоростью распространения малого возмущения по
массе от частицы к частице.
48
При использовании эйлеровых координат, т. е. в обычном фи-
физическом прострапстве роль скорости звука играет величипа со.
Для адиабатического течения идеальпого газа эту величину пе-
трудпо вычислить. Достаточпо воспользоваться полученпым для
этого случая в предыдущем параграфе соотпошепием C.40):
P/J Ло/Ро = const.
Отсюда вытекает
с = 1 (др/др) Б = Ьр[р =
Все полученпые результаты оказываются справедливыми и для
изотермического случая, который рассматривался в копце § 3,
достаточпо лишь всюду положить "у = 1. При этом, в отличие от
адиабатической скорости звука D.8), величипу
Ct = 1~pIq = 1RT~ D.9)
пазмвают изотермической скоростью звука.
Из формулы D.7) следует, что но крайпей мере для плоского
случая, который мы рассматрилаем, возмущепия по амплитуде со
времепем пе нарастают. Это оправдывает сделапное выше пред-
иоложепие о малости решопия во все момепты времепи, если
только пачальпое возмущепие было мало.
Прямые
s = ±соро? + const D.10)
па плоскости (.?,/), вдоль которых распространяются возмущепия.
пазымагатся характеристиками (рис. 1.13).
При расирострапепии плоской звуковой волпы частицы газа
остаются пеподвижпыми до тех пор, пока пришедшее возмущепие
пе вовлечет их в движепие. После того как возмущепие прошло,
частица останавливается. Направление смещепия частиц можпо
вычислить из D.7), D.5). Так, для возмущепия, распространяю-
распространяющегося вправо, имеем
и = ¦?¦ р. D.11)
f о
Ипыми словами, в волпе сжатия частицы смещаются в па-
правлении распространения волпы; в волне разрежения — в про-
противоположную сторопу. Апалогичпый факт имеет место и для
«левой» волпы. Из D.11) следует также оцепка малости для
скорости:
Iw/col = Ip/pol «: 1,
т. е. акустическое приближение применимо, если возмущение ско-
скорости частиц мало по сравнению со скоростью звука в газе.
3. Справочные данные. Как было показано в предыдущем пара-
параграфе, уравнения газодинамики в частном случае акустического
4 А. А. Самарской, Ю. П. Попов 49
приближения имеют гиперболический тип. Выясним, как обстоит
дело в более общем случае.
Напомним предварительно некоторые определения для систем
квазилинейных уравнений первого порядка:
iu + 4^u=b, D.12)
dt ox '
где u(ar, t) = {ii\(x, t), ..., un(x, t)) — пепгишстная вектор-функ-
вектор-функция, образопаппая п искомыми функциями, А = {ац{х, t, u)},
/1 иоласть возмущенного
Т течения
Характеристики
S---Sa/>at+Ct№St
Хараятерисгт/h и
Рис. 1.13
i, j = \, 2, ..., п,— матрица порядка и, а Ъ = {Ь\(х, t, u), ...
..., Ъп{х, t, и)} — вектор правой части. Квазилипейность системы
D.12) проявляется в том, что матрица А и вектор Ь, вообще го-
говоря, зависят от решепия и. Число к(х, t, u) называется соб-
собственным значением, а вектор 1 — {1и .. ., IJ — левым собствен-
собственным вектором матрицы А, если вьшолпено равепство
Ь4=Д D.13)
причем предполагается, что хотя бы одна из компонент вектора 1
отлична от пуля. Из D.13) следует, что для нахождения всех
собственных значений к необходимо решить уравнение п-й
степени:
= 0, D.14)
где Е — единичная матрица.
50
Система уравнений D.12) называется гиперболической в пе-
которои области пространства х, t, и, если всюду в этой области
собствеппые значения Ki, ..., Хп матрицы А вещественны и раз-
личпы*).
Пусть система D.12) гииерболичпа. Умпожим ее слева на к-й
собственный вектор Г*1, отвечающий собственному значению Кк,
и учтем равенство D.13):
к = 1, 2, .... п.
Выражение в скобках в D.15) есть производная вдоль линии,
которая задастся уравнением
dx/dt = Xk(x, t, u), к = 1, 2, ..., п. D.16)
Отразим это обстоятельство при помощи следующего обозначения
(d/dt)k. D.17)
С частными случаями формулы D.17) мы уже встречались.
Так, если X = dx/dt = 0, то дифференцирование D.17) недется
вдоль линии х = хо = const на плоскости (х, t) и djdt = d/dt сов-
совпадает с пйлеровой производпой по времени, вычисляемой в фик-
еиропаппой точке физического пространства хо.
Другой пример:
dxldt = v D.18)
(обозначения соответствуют § 1). В этом случае получаем вы-
выражение
d/dl = д/dt + vd/дх,
определяющее субстанциональную производную; здесь линией,
вдоль которой ведется дифференцирование, является траектория
частицы D.18).
Линии, определяемые уравнениями D.10), для гиперболиче-
гиперболической системы уравнений первого порядка D.12) называются ха-
характеристиками. Уравнения D.15), полученные в результате
преобразования исходной системы, с учетом D.17) можно запи-
записать в виде
"Й) -1. 2 и. D.19)
Соотношения D.19) называются характеристической формой си-
системы уравнений D.12). Их особенность состоит в том, что в
каждом уравнении D.19) дифференцирование проводится только
вдоль одной характеристики.
*) Требования, предъявляемые к собственным значениям К в опреде-
определении гиперболичности, могут быть несколько ослаблены (см., например,
[73]). Однако для наших целей такое определение достаточно.
4» 51
4. Характеристическая форма уравнении газодинамики. Ис-
Используя приведенные справочные данные, обратимся к системе
уравнений газодинамики для одномерного нестационарного слу-
случая в лагранжевых массовых координатах C.25).
Заменим в уравнении движения производную от давлепия:
др / др\ др I др \ 3S о о д I 1 \ as ,. om
{i)? + [J C"P-() + а *' (ь20)
ITSJP17 = -CP17
где с = У {др/др)8 — скорость звука, a={dpldSH. Перепишем те-
теперь основпые уравпеппя системы C.25) с учетом D.20), пола-
полагая W = 0:
jL(_M_i^ = 0, D.21)
at \ р ) он ^ '
*L _ cV -^(±) + ад4 = 0, D.22)
dt * us у р J Os K '
В качество уравпепия эпергии мы выбрали одну из эквива-
эквивалентных форм C.38).
После вледения обозначений
A/Р
и = \ v
S
D.24)
система уравнений газодинамики D.21) — D.23) приобретает вид
D.12), где х заменяется на s, а вектор цравой части Ь тожде-
тождественно ранен нулю*). Решая уравнение D.14)
del{A - IE) = -Щ2 - cV) - 0,
находим собственные зпачепия:
Л.1 = 0, К2 = ср, Я,3 = — ср. D.25)
Они вещестнеины и различны прп условип (dpfdp)s > 0, которое
оказывается липолненпым для большппства практически иптерес-
ных сред. Таким образом, система одпоморпых пестацпопарцых
уравпепий газовой дипампки имеет гпперболический тип.
Равенства
ds „ i/.я ds , . „,,.
определяют характерист[гкп системы уравнепий газовой динами-
динамики. Заметим, что второе и третье из уравнений D.26) обобщают
на случаи «немалых» двияееппй результаты, полученные пышо
для акустического приближения (см. формулы D.10)). Харак-
*) Последнее обстоятельство 6 = 0 имеет место только в плоском йлу-
чае, рассмотрением которого мы и ограничиваемся здесь в целях простоты.
52
теристика же, определяемая первым из уравнений D.2Р>), совпа-
совпадает с траекторией частицы. Действительно, лагранжева массовая
координата s частицы при ее движении вдоль траектории со вре-
временем не изменяется.
Следует сказать, что если бы мы проводили рассмотрение в
переменных Эйлера х, t, то уравнения для характеристик выгля-
выглядели бы следующим образом
dx dx . dx ., о_.
Решая уравнение D.13) для всех трех значений %, найдем
собственные векторы:
ср 1
1
-«/(cp)
(
= о
ll lcc/(cp)
Далее построим с их помощью характеристическую форму
системы уравнений газовой динамики:
% = 0, D.28)
D.29)
D.30)
Нетрудно видеть, что в каждом из ураннений D.28) — D.30) диф-
дифференцирование недется вдоль одпои из характеристик D.26).
Характеристика, соответствующая собственному зпачепию X = 0,
совпадает с траекторией частицы. Вдоль нее остается пеизменным
значение энтропии (см. D.28)). Поэтому характеристику ds/dt =
— 0 называют ипогда энтропийной.
Г). Инварианты Римана. Особенпо просто выглядят уравнения
D.28) — D.30) для изоэнтроштческпх течений 5 = const, рассмот-
рассмотрением которых мы ограничимся в этом параграфе:
= 0, D.29)
^0- (ь30)
Ураинение D.28) выполпено автоматическп.
Введем функцию
53
Функция ф зависит только от одного аргумента — плотности.
В общем случае любая термодинамическая характеристика среды,
в том числе и скорость звука с, может быть представлена как
функция двух любых термодинамических параметров, например
плотности р и эптропии S. Но в рассматриваемом случае пнтропия
постоянна: S — So = const. Поэтому с(р, S)=c(p, So)-c(p), <p =
= ф(р); с помощью ф(р) сделаем замепу: лместо пеизпестнмх
функций v п 1/р введем две новые функции
р
-j-dp, D.31)
Фупкцпи г+ и г~ называют инвариантами Римапа. Их изеде-
ние придает системе D.29), D.30) еще более компактный иид:
_.(ср---=0, D.33)
0- D-34>
_.(ср---
дг~ дг
Это и есть система уравнений газовой динамики в инвариантах
Рима на. Правда, для полной законченности сюда следует подста-
иить вместо сир их пыражепнн через г+ и г~, что несложно
сделать.
Можно заметить, что в уравнениях D.33) и D.34) дифферен-
дифференцирование проводится соответственно пдоль второй и третьей ха-
характеристик D.26), которые обычно называют С+ и С~-.тарак-
теристиками системы уравнений газодинамики. Это дает возмож-
возможность получить еще один вид записи:
r+ = const вдоль С+- -jf = + ср, D.33')
r~ = const вдоль С : — = — ср. D.34')
Инварианты определяются с точностью до произвольной постоян-
постоянной. Поэтому в формулах D.31), D.32) в качестве нижнего
предела интегрирования ро можно выбрать значение плотности в
произвольной фиксированной частице среды.
Пойдем на дальнейшие упрощения и рассмотрим идеальный
газ. Опираясь на формулы A.7), A.8), C.40), D.8), после не-
несложных выкладок получим
r+ = v + —j с, r- = v— ^—^ с. D.35)
Произвольные постоянные, с точностью до которых определяются
г+ и г~, здесь опущены.
54
Инварианты Римана и уравнения в инвариантах, построенные
на первый взгляд совершенно формально, имеют наглядную ин-
интерпретацию. Пусть рассматривается задача о течении газа, на-
начальное состояние которого задано. Это означает, что при t = О
(рис. 1.14) известны распределения по пространству веек фпзп-
С -характеристики
характеристики
ческих характеристик, в том
числе скорости ra:ia u(s, 0)
и скорости звука c(s, 0).
Пользуясь формулами D.3Л),
можно вычислить и началь-
начальные значения пипарпантов
г+ и г~ (напомним, что мы
считаем газ идеальпым,
а течение изознтропнчсским).
На плоскости s, t существу-
существует сетка и;! С+ и С~-харак-
терпстик, так как через лю-
любую точку плоскости (а, I)
проходят две характеристики
из этих семейств (рис. 1.1-1).
Вдоль характеристик переносятся без изменения значения соот-
соответствующих инвариантов: по С+-характерпстикс Л А' — инвари-
инвариант г+, по {^-характеристике — /¦". Р> гплу мтого можно записать
равенства
f , 2
Рис.
Гр = Up +
Гр = Vp
V-1
Ср
- о
2
С А,
Ср = ГВ = VB —
(',.36)
где нижний индекс указывает, в какой точке на рис. 1.14 вычис-
вычисляется данная функция. Выразим состояние в произвольной точ-
точке Р через начальные данные, используя соотношения ('г.ЯВ).
Имеем
(i-37)
0,Г) (сА + сп).
Зная скорость газа иР и скорость звука сР, можно вычислить
в точке Р все остальные параметры.
Имея формулу D.37), нельзя, однако, утверждать, что со-
состояние газа в точке Р целиком определяется заданием началь-
начального состояния при t = 0 лишь п двух точках Л и В. Дело в том,
что Р есть точка пересечения двух характеристик, которые, как
отмечалось пыгпе, зависят от решения и заранее неизвестны. Ход
характеристики, т. е. ее наклон в каждой точке (например, на-
наклон характеристики ВВ' в точке D) определяется состоянием
газа в этой точке (см. D.26)). В свою очередь состояние газа
определяется значением инвариантов Римана г+ и г~, приноси-
55
мых в эту точку соответственно из точек М и В. В конечном
счете положение точки Р на плоскости (s, t) и значение пара-
параметров среды в ней определяются начальными условиями на
отрезке АВ и не зависят от состояния газа пне этого отрезка.
В этом смысле отрезок АВ называется областью зависимости
точки Р. Заштрихованный на рис. 1.14 «криволинейный угол» есть
область влияния точки М, т. е. та зона, где решение зависит от
состояния газа в точке М (но не определяется им полностью).
§ 5. Разрывные решения
1. Соотношения на разрыве. В § 3. переходя от интегральных
уравнений газодинамики к более простым дифференциальным
уравнениям, мы отмечали, что при этом класс допустимых реше-
решений сужается — из рассмотрения выпадают разрывные решения.
Поэтому, приступая к анализу решений с разрывами, играющих
важную роль в приложениях, мы должны внонь обратиться к
уравнениям газовой динамики в интегральной форме.
Предположим, что течение среды, в котором ее параметры
терпят разрыв, является одномерным и плоским. При этом по-
поверхность разрыва, т. е. поверхность, где характеристики изме-
изменяют свое значение скачком, есть плоскость, перемещающаяся в
пространстве с некоторой скоростью &(t).
Для описания такого течения мы можем использовать интег-
интегральные уравнения B.7) — B.9). Если опустить члены, соответ-
соответствующие внешним силам, источникам энергии и тепловым по-
потокам, эти уравнения имеют ннд
($adx — prdt = (i.
|. pv dx — (p -i - pi'-) dt = 0. E.1)
p (e + 4-) dx - py (e + -j -;--?) dt = 0,
где интегрирование ведется по некоторому контуру, свойства ко-
которого обсуждались и § 2. Заметим, что и E.1) напрапление
скорости газа v нормально к плоскости разрыва. Выберем п каче-
качестве контура С контур ABB'А' (рис. 1.15). Линия РР' есть тра-
траектория разрыва x(t), поэтому вдоль нее
Значения параметров среды, вычисленные справа и слева от раз-
разрыва, снабдим соответственно индексами 0 и 1. Наша цель полу-
получить соотношения, связывающие эти значения. Для этого, запи-
записав уравнения E.1) для контура С, будем неограниченно сбли-
сближать боковые стороны криволинейного четырехугольника ABB'А'
так, чтобы они оставались по разные стороны от линии разры-
разрыва x(t).
56
Интегралы по верхнему и нпншему основаниям ВВ' и АА'
при этом стремятся к нулю, так что, например, первое из урав-
уравнений E.1) переходит в пределе в соотношение
Г Р'
f (p! dx — PjVj, dt) + )(podx — povodt) = O. E.2)
Г' P
Учитывая, что вдоль линии разрыва РР'
dz = g) dt,
перепишем E.2):
- J (Pl2> - plVl) dt + J (po0 - poco) Л = 0.
Отсюда в силу произвольности ti и i2 следует
pi(«i —2>) = po(wo —2>). E.3)
Поступая аналогично с остальными уравнениями E.1), по-
получим также
p^vy-^y + pi =po(va-@J + po, E.4)
Pl ((-Ч-
Уравнения E.3) — E.5) представляют собой общую форму со-
соотношений, связывающих параметры
по обе стороны от поверхности газоди-
газодинамического разрыва и скорость ее
распространения. Эти соотношения, t?^~~'
называемые соотношениями Гюгопио,
выражают законы сохранения потоков
массы, импульса и энергии через по-
поверхность разрыва.
Часто соотношения Гюгонио записы-
записывают в системе координат, движущейся
вместе с разрывом со скоростью 0.
В птом случае все скорости преобразу-
преобразуются согласно формуле рпс {\§
u = v-3> (П.б)
и тогда рамепстиа E.3) — E.5) приобретают следующий пнд:
Pi"i + Pi =
Pi"i
Pi ul\
, Ро , "о
+ 7Г + —!•
E.5')
57
2. Контактный разрыв. Величина m«*poMo = piMi представляет
собой поток массы вещества через разрыв. В зависимости от ве-
величины этого потока разрывы в газовой динамике делятся на две
группы.
Разрывы с
т = 0 E.7)
называются контактными. Соотношепие E.7) означает, что через
поверхность такого разрыва отсутствует поток вещества. Так как
по физическому смыслу pi и ро не раины пулю, равенство E.7)
может быть выполнено лишь при и\ = uq = 0, а ото, согласно
(Л.6), дает
V{ = VQ = &>.
Линия контактного разрыва па фазовой плоскости совпадает с
траекторией частицы. Таким образом, контактный разрыв есть
образование, не перемещающееся но массе, связанное во все вре-
время процесса с одними и теми же частицами среды и движущееся
вместе с ними. Именно поэтому контактные разрывы удобно рас-
рассматривать в лагранжевых массовых координатах (разумеется,
если течение одномерно). В этом случае не нужно вести наблю-
наблюдение за перемещениями разрыва,— его массовая координата ос-
остается неизменной.
Н силу (Г).7) первое и последнее из соотпотпспий Гюгонио вы-
выполняются автоматически, а оставшееся соотношение (о.4') дает
р\ = рч. E.8)
Итак, на поверхности коптактного разрыва должны быть непре-
непрерывны нормальная составляющая скорости газа и давление.
Остальные функции, например температура и плотность, изменя-
изменяются скачком.
Отметпм, что если л газодинамическом течеппи присутствуют
различные среды, отличающиеся уравнениями состояния, то гра-
границы их раздела являются контактными разрывами.
3. Ударные волны. Адиабата Гюгонио. Обратимся теперь к раз-
разрывам с. m ?= 0, которые лосят название ударных воли. Вопрос, о
знаке тп здесь существенной роли не играет,— этот знак указы-
указывает, лишь и какую сторону направлен поток массы через разрыв.
Перепишем соотношения Ггогонио для ударной полны, сокра-
сократим в уравнении (•")..!') обе части па m — piit\ = poUo и введя удоб-
удобную для проведения дальнейших иыкладок функцию л = 1/р:
-!2-= -% (Г).9)
^--^ = />.-/V E-Ю)
E.Н)
Из соотношения E.9) выразим щ и исключим эту величину из
E.10). Получим
и\ = тй (Pi - Ро)/(Ч> - Tli)- E-12)
Аналогично
—Ро)/(Ло —ill)- (М3)
Комбинация полученных формул дает возможность выразить ска-
скачок кинетической энергии единицы массы газа на разрыве:
—
= —(Pi-
В сиою очередь ота формула в сочоташш с E.11) позволяет за-
записать соотношение
gi (Pi' Tli) — *"'o(/V "По) = ~Y~ (^1 "'" Ро) (^о — Tli)' E.14)
которое называют уравнешгем адиабаты Гюгппио. Это уравнение
связывает параметры термодинамического состояния газа (давле-
(давление и удельный объем) но обе стороны от разрыва. Если ударная
волна распространяется по газу с заданным состоянием (пара-
(параметры ро и т|о известны), то, чтобы определить состояние га.ча за
фронтом волны, необходимо, согласно E.14), задать значение од-
одного из параметров р\ или ц\.
4. Ударные волны в идеальном газе. До сих пор мы анализи-
анализировали свойства газодинамических разрывов в общем случае, не
делая никаких конкретных предположений относительно уран-
нений состояния. Далее мы продолжим рассмотрение ударных
волн для идеального газа. Подставляя выражение для внутрен-
внутренней энергии идеального газа е = рг\/(у — 1) в E.14), можно пре-
преобразовать уравнение адиабаты Гюгопио к одному из пидов
Pt (V+1) ч0 —(V —1) ч,
Ра (V -1I1, -(V-
либо
Чо (V + 1) />! + (V - 1)
E.15)
E.10)
Для дальнейшего нам потребуются формулы для сравнения
относительной скорости газа и (скорости газа относительно си-
системы координат, связанной с фронтом ударной волны) п спо-
спорости звука с. Напомним, что для идеального газа с~ = "fpi] (см.
D.8)). Воспользуемся равенством E.1-) п вычислим отношение
квадратои этих скоростей для начальных значении параметром,
т. е., как говорят, на «фоне» перед фронтом ударной волны:
"о ^(Р.-Ро) Pi-P0
59
Точно так же выводится и равенство
Отношение удельных объемов, стоящее в знаменателе, исключим
с помощью E.16) и после преобразований получим
л Г Т
E.17)
E.18)
Имея набор формул E.12) — E.18), приступим к описанию
свойств ударных волн в идеальном газе. Интенсивность ударной
волны определяется ее
амплитудой, т. е. величи-
величиной скачка, который пре-
претерпевают параметры газа
при переходе через фронт
волны. Будем считать, что
начальное состояние газа
задано параметрами ро, г\о.
Тогда графическое изобра-
изображение адиабаты Гюгонио
E.15) на плоскости тер-
термодинамических состоя-
состояний р, х\ (линия 36 на
рис. 1.16) есть геометри-
геометрическое место точек, в ко-
которые можно перевести
газ из исходного состояния
ро, "По, «пуская» по нему
ударную волну. Задавая
значение удельного объе-
Гис. 1.16 ма r|i за фронтом ударной
волны (тем самым задает-
задается интенсивность ударной волны х\о — Tli), мы но адиабате Гю-
Гюгонио сразу определяем величину данления р\ за волной, и затем
значение любого параметра газа.
Адиабата дё на плоскости р, х\ имеет горизонтальную и вер-
вертикальную асимптоты. Действительно, как следует ил E.15), при
Ц\/Цо ~* °° отношение давлений стремится к значению р\1ро -*¦
-+¦—(ч — 1)/(ч + 1). Аналогично из E,16) при pi/po^-°° выте-
вытекает, что отношение удельных объемов стремится к конечной
величине
1цЛ1о = (Т — 1)/(Т + !)¦ E.19)
Физически это означает, что в ударной волне нельзя сжать
газ больше чем в (Y~M)/(Y—1) раз. Для одноатомного газа с
f = 5/3 эта величина равна четырем, для двухатомного с *[ =
= 7/5 — шести.
60
Остановимся на предельном случае pilpo -*- 1. В соответствии
с E.16) t]i/t]o-*1, и, следовательно, состояние газа за фронтом
такой волны мало отличается от исходного: ро, т]о. В частности,
Со -*¦ С\ и формулы E.17) и E.18) для этого случая дают
Таким образом, ударная волна бесконечно малой интенсивно-
интенсивности (т]о—т][-»-0) распространяется относительно газа со ско-
скоростью звука, т. е. фактически вырождается в звуковое возмуще-
возмущение, правда, в отличие от § 4, разрывного характера. Физически
этот результат достаточно очевиден. Разобранному предельному
случаю на рис. 1.16 соответствует точка О.
5. Теорема Цемплена. Адиабата Гюгонио Ж состоит из двух
ветвей: О А при т] < щ и О А' при т] > щ. Знаки приращений
Ар = р\ — ра и Дт] = т]| — т]о вдоль адиабаты протвоположны. По-
Поэтому формально ветвь ОА отвечает ударным волнам повышения
давления (Ар > 0) и сжатия (Ат]<0, Др>0), а ветвь ОА' —
ударным волнам понижения давления (Ар < 0) и раширения
(Ат]>0, Ар<О).Для ударных волн сжатия (р\/ро > 1), согласно
E.17) и E.18), имеем
т. е. фронт такой ударной волны распространяется относительно
фона со сверхзвуковой скоростью, а относительно газа за вол-
волной — с дозвуковой.
Для ударных волн разрежения имеют место обратные нера-
неравенства
UoAo<l, и\/с\>1.
Выясним, как обстоит дело с измененном энтропии в ударпых
волнах. Приращение энтропии при движении вдоль адиабаты Гю-
гонип можно было бы вычислить непосредственно но формуле
C.41). Однако мы воспользуемся несколько иными соображения-
соображениями. Проведем на плоскости (р, т]) через точку (р«. цп) линию,
вдоль которой энтропия остается неизменной п ря:шои So, т. е.
значепию в точке (рп, 1}о). Такая линия называется адиабатой
Пуассона; ее уравнение в соответствии с C.40) есть
Рм1=рА E.20)
(линия 5s на рис. 1.16).
Адиабата Пуассона — это геометрическое место точек на плос-
плоскости (р, т]), в которые можно перенести газ из начального со-
состояния ро, т]о адиабатическим путем без изменения энтропии.
Итак, ;1'>ль !/*: AS—Si — Sq^O; иышо .У3 (область, покрытая
горизонтальной штриховкой) Д^>0; иод адиабатой (вертикаль-
(вертикальная штриховка) AS<0.
Взаимное расположение адиабаты Гюгонио и адиабаты Пуас-
Пуассона такоио, что при т](<т]о адиабата Пуассона проходит ниже
61
адиабаты Гюгонио. В этой нетрудно убедиться следующим об-
образом: из E.20) видно, что для адиабаты Пуассона при pi -*¦
-*¦ то t]i -*¦ 0, в то вреия как адиабата Гюгонио целиком располо-
расположена правее асимптоты г^ =|-тгтт1о > 0- Поэтому для ветви ОА
адиабаты Гюгонио AS > 0, т. е. в ударных волнах сжатия энтро-
энтропия газа возрастает по сравнению со значением на фоне.
Кривые ZP и Ж в точке О имеют касание второго порядка.
Ветвь адиабаты Гюгонио ОА' при T)i>T)o расположена под
адиабатой Пуассона, поэтому для ударных волн разрежения эн-
энтропия убывает. Однако такое заключение находится в противо-
противоречии со вторым началом термодинамики: dS 3* 0. Поэтому удар-
ударные волпы разрежения, формально содержащиеся в соотношениях
Гюгонио, существовать не могут. Такой вывод мы сделали для
идеального газа, однако он справедлив и в общем случае при
сравнительно слабых ограничениях на вид уравиений состояния
и носит назианио теоремы Цемплепа.
6. Приближение «сильной волны». Выше мы уже выделяли
случай ударной полны сжатия предельной амплитуды:
А=оо, ть-^I^-Jv E.21)
:)тот случай носит название приближения «сильной волны» и
реализуется тогда, когда давленном на фоне можно пренебречь
по сравнению с давлением за ударной волной. Например, это
можно сделать для ударной волны, распространяющейся по хо-
лодпому фону с pa ~ 0. Получим для этого случая явные фор-
формулы, выражающие значения параметров газа за фронтом волны
череп параметры па фоне и скоростт. волпы. Подставим вторую
н.1 формул E.21) в E.Я). Учитывая определение скорости и =
-- v — 2D, а также предполагая, что газ, по которому движется
рассматриваемая пами ударпая волна, покоится (vQ = 0), получим
Давление р\ за фронтом выразим из E.10):
2 9г
л температуру—из уравнений состояния: '
Т = 2(у —1)^2
1 (Y+lJ R'
Подытожим результаты. Если по идеальному покоящемуся (z>o =
= 0) холодному (ро = О, То = 0) газу, плотность которого ро,
движется ударная волна со скоростью iZ), то за ее фронтом гаэ
принимает следующие значения параметров:
_ у — i _ у f
у~Т~1 'lo' Pi-Y-lPo' Pl^V+tM0' E.22)
1
1
Тт1
l
В более общем случае ирп р ?= 0 формулы иесколько услож-
усложняются. Опуская выкладки, приведем лишь результаты, следую-
следующие в этом случае пз соотпошепий Гюгонио:
у —
1 Y г 1 % Y -г 1 °
- _г_ «л ^L ^о1^ т _ pi
» -
§ 6. Структура фронта ударной волны
1. Постановка задачи. В предыдущих параграфах, анализируя
разрывные решения, мы рассматривали уравнения газовой дина-
динамики без учета диссипативпых процессов. Однако наличие дисси-
диссипации (вязкости, теплопроводности и т. п.) присуще всем реаль-
реальным газодинамическим явлениям. Наиболее заметпо опа проявля-
проявляется в тех зонах течений, где параметры газа испытывают резкие
изменения по нространстпопной координат!!. Именно такие усло-
условия осуществляются, например, во фронте ударной полны. Из-
Известно, что диссипатшшые процессы приводят к псадиабатичпости
течения, к термодинамически необратимому превращению анергии
в ее пизшуго форму — тепло. Диссипация япляется причиной уве-
увеличения энтропии во фронте ударной полны.
Таким образом, рассмотренные иышс ра.чрыипме решения яв-
являются своего рода идеализацией для газа с печезающе малыми
коэффициентами теплопроводности, вязкости и т. д. Строгий ана-
анализ этих решений должен проводиться с учетом диссипатикпых
факторов. При этом вместо разрыва иолпикает некоторая узкая
переходная область, в которой параметры газа изменяются уже
непрерывно.
Рассмотрим структуру фронта ударной волны в газе, обладаю-
обладающем вязкостью и теплопроводностью. Что касается процессов теп-
теплопроводности, то они были приняты во внимание при выводе
уравнений газодинамики C.25). Вязкость в этих уравнениях учте-
учтена не была. Не вдаваясь в подробности, мы укажем лишь, что
наличие в среде вязкости приводит к дополнительному негазоди-
негазодинамическому переносу импульса и энергии. Математически в про-
простейшем одномерном случае это можно выразить посредством
63
некоторой «добавки* <d («вязкого давления*) к газодинамическо-
газодинамическому давлению р, имеющей вид
й = _v dvldx, F.1)
где v — коэффициент вязкости.
Мы будем анализировать структуру плоской ударной волны,
считая течение газа одномерным. Соответствующая система урав-
уравнений в лагранжевых массовых координатах выглядит следую-
следующим образом *):
( F'2)
до dg ,R qv
v2
dW
Здесь g — сумма газокинетического и «вязкого» давлепий: g =
= /? + (о. С учетом C.23) перепишем F.1):
со = —vp dv/da. F.5)
Поток тепла имеет вид
W = —хр dT/ds. F.6)
Коэффициенты v пязкости и у. теплопроводности для простоты
положим постоянными, хотя реалт.по это некоторые функции
термодинамического состояния газа. Кроме того, газ будем счи-
считать идеальным.
Пусть ударная волна движется с постоянной скоростью Ф по
газу с известными параметрами pa, pa, vq — «фону», который про-
простирается в положительном направлении оси s до +°°. Г.'-м^етвсш-
но считать этот газ покоящимся: i>o = O. Пусть такжр емгтояние
газа, возникающее за фронтом волны и пока неизвеп м^и>. про-
простирается по s до —°°. Положим при этом, что на «оГк-м-. "ч;ско-
нечностях» режимы установились, т. е. параметры газа приняли
соответствующие значения и производные по прострииг.тву от
любой величины / равны нулю:
Такая идеализовапная постановка задачи в бесконечной области
—°°<s<+oo связана, с одной стороны, с тем, что заранее ши-
ширина фронта неизвестна, и, с другой стороны, с желанием от-
отвлечься от конкретного вида краевых условий в pea.и.пых за-
задачах.
Профиль изменения параметров гаэа в волне также «-читаем
установившимся; он распространяется по массе с постоянной
¦) Анализ структуры фронта ударной волны можно вести в « перемен-
переменных Эйлера; конечные результаты, естественно, от этого ш- шмепятся.
64
скоростью D. Массовая скорость волны D связана с эйлеровой
скоростью распространения волны 2) соотношениеи
D=(S> — v)p. F.8)
Будем искать решение поставленной задачи, т. е. псе функ-
функции, описывающие течение газа, в виде (/—любой параметр)
/(я, 0 =f(D, l=*-Dt. F.9)
Функция /(|) дает профиль параметра / по переменной я в
фиксированный момент времени (t = const) либо закон изменения
со временем этого параметра в фиксированной частице среды
(s = const).
2. Диффереициальиое уравнение для структуры. Замена пере-
переменных F.9)*) эквивалентна переходу в систему координат, свя-
связанную с волной, где профили всех параметров стационарны.
Эта замена позволяет выразить производные по я и t через про-
производную по |:
djds = d/dl, д/dt = —Ddld%
и тем самым свести систему уравнений в частных производных
F.2)—F.4) к системе обыкновенных дифференциальных уран-
пений:
F.10)
v di> тж/ у. dT
Равенство F.7), играющее роль граничных условий, преобразу-
преобразуется к виду
= 0. (fi.ll)
В частности, тепловой поток Wo и вязкое давление too на фоне
при s =+оо в силу F.11) обращаются в нуль:
Проинтегрируем уравнения F.10) по % от фона % = +°° до не-
некоторого текущего значения:
-D(j\-j\o)=v, F.13)
Dv = g-Po, F.14)
D(e-eo + vV2) = gv + W. @.15)
Здесь учтены условия F.12), а также то обстоятельство, что газ
на фоне покоится (уо = О). Исключая из системы уравнений
*) Такую замену называют введением автомодельности типа «бегущей
волны».
5 А А Г.штП'п! тл тт тт„и„- ""
F.13) —F.15) все известные, кроме ц, а также диссипативных
членов со и W, получим для случая идеального газа
Заметим, что обе части этого равенства обращаются в нуль на
фоне при т] = т]о(!-*¦+°°) в полном соответствии с F.11). Ана-
Аналогично левая, а следовательно, и правая части должны обратить-
обратиться в нуль и при |-+¦ —оо. Поэтому значение удельного объема y\it
которое устанавливается при % -*¦—°°, должно быть равно
у — 1 , 2у Р„
11i-q7-11o+—-
Сравнивая этот результат с E.23), убеждаемся, что он совпа-
совпадает с тем, что дают в этом случае соотношения Гюгонио для
ударного перехода. Итак, дифферопциальпоо уравнение F.16)
(а :>то действительно диффереп-
циальное уравнение, так как и со
и W пропорциональны нроизвод-
пой dr\ld\) в самом деле описы-
описывает структуру фронта ударной
полны, «размазанной» пязкостьзо
и теплопроводностью. Оно опро-
деляет кривую Ц = 1Ц{\) Ц\ «S
*? Ц ^ Ло- где Tio и ni связа-
связаны соотношениями Гюгонио
(рис. 1.17). Зная ц{\), можно по-
построить профили всех остальных
параметров.
Важно отметить, что значения г\а и t)i, которые соединяет
интегральная кривая уравнения F.16), не зависят от конкрет-
конкретного вида диссипации. Тот или иной вид вязкости и теплопровод-
теплопроводности определяет лишь характер «размазывания» параметров,
ширину фронта и т. д., но отнюдь не интенсивность газодинами-
газодинамической ударной волны.
3. Структура фронта ударной волны в вязкой среде. Квадра-
Квадратичная вязкость. Рассмотрим подробно структуру ударной волны,
возникающую в результате действия одной только вязкости (Ж =
езО). Преобразовав в этом случае со с помощью (G.13) к виду
й>=—^, получим из F.16) обыкновенное дифференциальное
уравнение первого порядка
е!т) (у--
2v
—лИл —л,)-
Оно легко интегрируется:
о =
2v
(Г,. 17)
¦>0. F.18)
Произвольная постоянная К определяет однопараметрическое се-
семейство решений. Это и естественно, так как, формулируя зада-
задачу, мы не «привязали» начало отсчета координаты s (соответст-
(соответственно |) ни к одной характерной точке профиля полны. Сде-
Сделаем это.
Продифференцируем F.17) по | и, приравняй вторую произ-
производную нулю, найдем значение удельного объема t]i<t]<t]o,
при котором все кривые семейства F.18) имеют точку перегиба:
т] =(t]0+t]i)/2.
Теперь пыберем из семейства крипых F.18) ту, у которой абс-
абсцисса точки перегиба равна нулю. Подставив \=0 и т]=т] в
(R.18), получим уравнение для К:
F.19)
откуда К= 1. Итак, мы выделили кривую
т), + V
fll
1
,аЬ
(жирная линия на рис. 1.18), которую и будем анализировать
далее.
Формально ширина фронта ударной волны, размазанного вяз-
вязкостью, бесконечна. Но основное изменение лсех величин проис-
происходит в некоторой конечной области. Определим характерный раз-
размер этой зоны, т. е. эффективную ширину фронта. Это можпо
1
Рис, 1.18
сделать различными способами, но все они дают качественно оди-
одинаковые результаты. Мы поступим следующим образом. Проведем
к кривой F.19) касательную в точке перегиба 5 = 0. Точки пере-
пересечения этой касательной с прямыми т] = щ и 11 = 1]! и дадут
искомую ширину фронта Д.
Наклон касательной найдем из уравнения F.17), в правую
часть которого нужно подставить т] = т] =(т]о + Ц\I2:
5*
Эффективная ширина фронта ударной волны выражается следую-
следующим образом
8v
А =
(Y+ 1) Л (Чо-П,)"
F.20)
Видно, что эта ширина определяется интенсивностью волны (ее
скоростью и амплитудой) и коэффициентом вязкости. При умень-
уменьшении коэффициента вязкости v аффективная ширина фронта
сокращается (рис. 1.19), так что в пределе при v = 0 имеем раз-
разрывное решение, рассмотренное в предыдущем параграфе.
Выясним теперь, какую структуру фронта ударной волны по-
порождает так называемая квадратичная вязкость
F.21)
пропорциональная, в отличие от «линейной вязкости» (8.1), квад-
квадрату производной скорости. Очевидно, все рассуждения, нрипед-
шие нас к уравнению F.16), сохраняют силу и в этом случае.
Выразив со через | и т] и подставив полученное выражение в
F.16), получим дифференциальное уравнение
(л.- л) (л-л,)-
Его интегрирование дает
Л E) - Ц±
со,
Ш
g + к),
F.22)
@.23)
К — постоянная интегрирования, которая, как и в F.18), задаст
однопараметрическое семейство решений уравнения F.22). Поло-
Положи» К = л/2, выделим из :т>го
В В' семейства интегральную кримую,
у которой точка перегиба ц = ц =
{ Ц\I2 совмещена с пача-
А'
Ч лом отсчета S, = 0 (рис. 1.20).
\ Для нас предстанляет интерес
_\w-t лишь участок кривой т](g), рас-
расположенный на рис. 1.20 между
точками А и В. Именно эта часть
*? крнпой Ti(g) в сочетании с луча-
лучами Л = 1]о И Ц = Ц\ (ЛИНИЯ
В'ВАА') дает решение задачи о
структуре фронта ударной пол-
полны. Характерная черта, отличающая полученное решение от разо-
разобранного выше случая линейной иязкости,— конечная ширила
фронта волны Л. Из F.23) без труда определяется ее величина
Рис. 1.20
F.24)
Примечательно, что здесь ширина размазывания не зависит от
интенсивности волны. При стремлении коэффициента вязкости и,
к нулю гладкое решение вырождается в разрывное и в этом
случае.
4. Структура фронта волны в теплопроводной среде. Рассмот-
Рассмотрим случай, когда вязкость в среде отсутствует и структура фрон-
фронта ударной волны формируется под влиянием процесса теплопро-
теплопроводности. Уравнение F.16) по-прежнему справедливо, только в
нем отсутствует вязкость (со = О). Для простоты будем считать,
что коэффициент теплопроводности постоянен у. (р, Т) = хо = const.
Тогда поток тепла в автомодельных переменных имеет пид
W = - -Л. ?±-.
F.25)
Наша задача — получить связь между производными dTjd\
и d-x\ld\; тогда F.16) вновь сведется к обыкновенному дифферен-
дифференциальному уравнению для функции
т](|). Из соотношений F.13) и F.14),
с учетом того, что со = 0, а следова-
следовательно, g = p, иыразим давление:
р = р0.-О2(т) — тH). F.26)
Из уравнения состояния теперь сле-
следует формула для температуры:
'2 ft -
О
F.27)
Рис. 1.21
Графическая зависимость F.27) представлена на рис. 1.21. Диф-
Дифференцируя F.27) по т), получим
\-1I\ @-28)
Первое слагаемое в скобках есть квадрат изотермической мас-
массовой скорости звука (см. D.9)):
Таким образом, выражение в скобках в F.28) обращается в нуль
в той точке течения, где скорость волны становится равной ме-
местной изотермической скорости звука.
Если в F.28) подставить р из F.26), то это равенство можно
записать в виде
^ = -^ft-»!*)' <6-28')
где
Учитывая сказанное выше, отметим, что в точке, где т] = т],,.,
скорость ударной волны совпадает с местной изотермической ско-
скоростью звука.
Подставляя выражение для потока тепла F.25) в F.16) и
учитывая, что dT/d%=(dT/dr\) (di]/db,), приходим к уравнению
dr\
4xo(v —1)
F.29)
которое и определяет «теплопроводную» структуру фронта удар-
ударной волны.
Проанализируем качественно поле интегральных кривых этого
уравнения. Прежде всего отметим, что, в отличие от предыдуще-
предыдущего случая с вязкостью F.17), в F.29) знаменатель обращается
Па
Рис. 1.22
в нуль при т] = т]*. Физическое содержапие этой особенности
решения было выяснено выше — в этой точке осуществляется
переход через изотермическую скорость звука. Ясно, что поведе-
поведение интегральных кривых ураннепия F.29) существенно запи-
сит от взаимного расположения характерных значении удельного
объема т)о, т][ и т)+.
При условии
T]*<Th, F.30)
которое справедливо для достаточно слабых ударных полн, удов-
удовлетворяющих неравенству
-1 Ро
F.31)
картина интегральных кривых имеет ппд, указанный на
рис. 1.22,о. Здесь дана одна интегральная криная, которую мож-
можно выделить из общего семейства так же, как в «вязком» случае.
В силу условия F.30) в диапазоне tii<t]<t]o правая часть
уравнения F.29) положительна и особенность, связанная с Л*'
отсутствует. Ветвь интегральной кривой, заключенная в указан-
указанном диапазоне изменения т|, и представляет собой решение задачи
о структуре фронта полны, удовлетворяющей условию F.31).
Как видно, это решение непрерывно. Соответствующая диаграм-
диаграмма (Г, т]) представлена на рис. 1.22,6.
Ширина «размазывания» здесь бесконечна, однако если ввести
эффективную ширину фронта так, как это делалось выше для
случая вязкости, то можно показать, что она пропорциональна
величине коэффициента теплопроводности хо.
5. Изотермический скачок. Перейдем к анализу структуры
сильных ударных волн с
3V-1 ро
Д2-
-v V
Здесь уже Л1 < Л* < Ло' и потому поле интегральных кривых
уравнения F.29) имеет иной вид (рис. 1.23,о).
Рис. 1.23
Ветвь интегральной кривой, расположенной в диапазоне rii <
< Л < Ло. уже не может целиком описать решение задачи о струк-
структуре. При переходе через л* интегральная кривая поворачивает
обратно, и далее движение вдоль нее осуществляется в положи-
положительном направлении оси |. Это не имеет физического смысла,
в соответствии с определением F.9),
означало бы для D > О при фиксированном s движение «против
времени». При фиксированном t это же обстоятельство приводит
к неоднозначности параметром среды и пространстве по коорди-
координате s.
Выход из этой ситуации заключается в постановке разрыпа
в решении, где удельный объем скачком изменяет значение от
некоторого т)с до величины г\\. В силу того, что среда обладает
теплопроводностью, температура на разрыве должна оставаться
непрерывной, так как в противном случае здесь вешшклп бы
бесконечно большие потоки тепла. Условие «изотермичностн»
позволяет определить значение tic: г\с =
>т|1.
71
Поведение температуры на плоскости (Г, ц) для этого слу-
случая указано на рис. 1.23, б. Заметим, что описанный изотермиче-
изотермический разрыв не подчиняется условиям Гюгонио, выведенным в
§ 5 для среды без диссипативных процессов. В нашем случае
течение в существенной степени определяется потоком тепла, ко-
который на разрыве претерпевает ска-
скачок.
Характерные профили парамет-
параметром во фронте сильной ударной вол-
волны по координате s па некоторый
момент времени представлены на
рис. 1.24. Здесь, в отличие от слабых
ноли, теплопроводность не в состоя-
состоянии полностью «разгладить» ско-
скорость, давление и удельный объем,
и в структуре сохраняется скачок
dtiix неличин. Температура при птом
непрерывна, правда, ее производные
терпят разрыв. Передний фронт волны (на рис. 1.24 волна
движется в положительном направлении оси s) находится в бес-
конечости, однако задний фронт (разрыв) расположен в конеч-
конечной точке.
Итак, в отличие от вязкости, теплопроводность сохраняет раз-
разрывы плотности, скорости, давлепия и т. д. в структуре фронта
сильной ударной волны.
§ 7. Задача о поршне
1. Постановка задачи. Классическая задача о поршне в одно-
одномерном плоском случае формулируется так. Однородный покоя-
покоящийся газ занимает полупространство, ограниченное слева плос-
плоскостью— поршнем (рис. 1.25).
В начальный момент времени t—
= 0 поршень под действием неко-
некоторых внешних сил пачинаот дви-
двигаться со скоростью, закон изме-
изменения которой во времени Г/ =
= U(t.) задай. Знак U(t.) может
быть любым и зависимости от
того, вдвигается поршень is газ
или выдвигается из пего. В газе
начинается движение в виде вол-
волны, фронт которой распрострапя- Рис ^ 25
ется от поршня, захватывая но-
новые частицы среды. Исследование возникающего газодинамиче-
газодинамического течения н состапляет существо задачи о поршне.
Особенно просто решение задачи о поршне выглядит н том
случае, когда скорость поршня во все моменты времени t > 0
постоянна. При этом, как следует из общей теории размерности,
79.
задача допускает автомодельное решение [87]. Этот случай мы и
рассмотрим ниже. Газ будем считать идеальным, влиянием дис-
сипативных процессов пренебрежем.
Сформулируем математическую постановку задачи. Систему
уравнений запишем в лагранжевых массовых координатах*):
1+Р2^-0, G.1)
% + 4? = <>, G-2>
р/рч = const. G.3)
Начальные данные однородны:
p(s, 0)=р0, рE, 0) = р0, v(s, О)=ио = О. G.4)
Заметим, что уравнение G.3) выражает изоэнтропичггость
процесса. Переход от адиабатичности к изоэнтропичности здесь
оправдан благодаря тому, что начальные данные однородны. За-
Задача решается в области t > О, s > 0. Мы полагаем, что частицы
газа с координатой s = 0 все время прилегают к поршню и имеют
ту же скорость. Поэтому краевое условие имеет вид
v@,t)=U, G.5)
где скорость поршня U = const задана.
С помощью приема, который уже использовался в § 4, преоб-
преобразуем производную от давления, входящую в G.2):
0р_ _ / др\ до _ о др_
ds ~ \ dp Js ds — ds '
Уравнение G.2) приобретает следующий вид
¦г+<21 = 0. G.2')
2. Автомодельное решение. Будем искать автомодельное реше-
решение поставленной задачи, т. е. такое решение, в которое незави-
независимые переменные s и t входят не произвольным образом, а лишь
в комбинации
l = s/t, f(s, t) = f(t), G.6)
g— аптомодольпая переменная, /— любая из функций р, р, и.
Выразив производные
_^/_ = |_ _df_ ?1 _ j__rf/
01 t tfi; ' ris ~ t rfS '
заменим дифференциальные урапнения G.1), G.2) системой
обыкноиенпых уравнений (система «автомодельных уравнений»)
_ I *1 !- о2 — - О
2
dp pdv__0 G.7)
*) Совершенно аналогично решение строится и в переменных Эйлера.
73
Краевое условие G.5) при ?>0 в автомодельных переменных
примет вид
v@)=U, G.8)
так как поршню соответствует автомодельная координата % = 0.
Отметим прежде всего, что уравнения G.7) допускают тривиаль-
тривиальные решения, где все функции постоянны. В частности, таким
решением является «фон»: р = ро, v = vo = 0. Очевидно однако,
что непрорывное решение задачи о поршне (а мы ищем именно
непрерывное решение) не может быть целиком построено из три-
тривиальных участков, где все параметры постоянны. Решение долж-
должно содержать области, в которых параметры газа изменяются.
Для того чтобы однородная система уравнений G.7) имела
нетривиальаое решение, ее определитель должен равняться нулю:
Т. е. Ь, = ±ср. Из G.6) следует, что | > 0, так как величины s и
t по физическому смыслу положительны. Поэтому из двух воз-
возможностей выбираем:
\ = с9. G.9)
Уравнения G.7) при этом становятся зависимыми, и оба при-
приводятся к виду
Скорость звука с является функцией одной лишь плотности р.
Так как все частицы газа в начальный момент времени имели
параметры р0, ро, то уравнение G.3) может быть записано как
/>/pv = Р/Р
Выражая отсюда р через р и подставляя результат в формулу
для скорости звука, имеем
) 711)
IT I n
где Со = l/'ifolpo — скорость звука на фоне.
Подставим G.11) в G.10) и проинтегрируем полученное урав-
уравнение от пекоторой точки ?о. и которой, как мы предполагаем,
происходит непрерывная «стыковка» рагематрпиаомого нетри-
нетривиального решения с триииальпым решением — фопом: рAо) =
= Ро, с(?о) = со, и(|о) = О. Имеем
u=i^ffjLyv-1)/2_1
Последнюю формулу с учетом G.11) можно переписать следую-
следующим образом
v — 2c/(f — 1) = 2со/(ч — 1) = const. G.12)
74
Левая часть G.12) есть инвариант Римана г~ (см. D.35)), вы-
вычисленный для идеального газа. Равенство G.12) устанавливает,
что во всем нашем непрерывном решении (если оно существует)
инвариант Римана г" постоянен.
Отметим, что подобные газодинамические непрерывные изо-
энтропические течения, в которых один из инвариантов Римана
постоянен, посят название волн Римана или простых волн.
Итак, нетривиальное решение, которое мы ищем, является
простой волной.
Подставим G.11) в G.9) и заметим, что \о = соро. Это позво-
позволяет получить явную зависимость плотности в автомодельном
решении от переменной g:
РШ = ро(ё7Ы2/(т+|>- G.13)
Остальные функции выражаются без труда:
СП:\ __ с fg/g \(v—1)/(V+1) П 14)
^Ш-^^^Г1'^1'-!!- G-15)
Нетриниальное автомодельное решение получено.
3. Решение задачи о поршне, выдвигаемом из газа. Будем
строить решение задачи о поршне, комбинируя это нетривиаль-
нетривиальное решение с тривиальными постоянными течениями.
Рассмотрим сначала случай, когда скорость поршня отрица-
отрицательна (поршень выдвигается из газа):
и=—и0, ио>о.
Диапазон изменения автомодельной переменной такоп: 0 ¦<
< | < °°, причем в точке g = О паходится поршень. Точка |0 со-
соответствует фронту полны, рас-
раси, jo к
пространяющейся от поршня.
Поэтому правее |о решение три-
тривиальное — невозмущенш.тй фоп
(рис. 120):
Леиее точки go построим в со-
ответстипи с формулами G.13)
и G.15) нетривиальное автомо-
автомодельное ретенпе p(g) и v(%),
пеирерыппо примыкающее к
фону. Однако эти формулы
нельзя использовать по псом
иптеркале @, go). Дейстинтель- [1цс х 26
но, из G.15) следует, что
V(Q)~ —2Ы{Ч — 1), а ОТО В общем случае не согласуется с гра-
ничпым условием G.8). Поэтому решение G.13), G.15) имеет
смысл рассматривать лишь до точки |i, где
v(ti)=—h\ G.16)'
и далее (для 0<?<?i) непрерывным образом продолжить его
тривиальным решением: v = Vi=*—С/о, P = pi==p(?i)- Значение
координаты gi определяется из формулы G.15) после подстанов-
подстановки в нее i>(li)= —Uq:
Значение pi дает соотношение G.13):
Pol'l-:
._ i I/oyv+i)«v-D
Решение задачи о поршне в автомодельном виде построено.
Чтобы получить теперь распределение скорости газа, его плотно-
плотности и прочих функций по массовой переменной s в некоторый
иН
О
Рис. 1.27
фиксированный момент нремеип ?>(), нужно «растянуть» про-
профили этих параметров и(|), р(%) (рис. 1.20) п направлении ко-
ордипаты \ v, t раз. В самом дело, согласно G.6), s = gf. В птом
и проявллотся свойство автомодслыюсти решения,— изменяясь
со временем, оно тем не менее сохраняет основные качестпепные
черты, остается «самоподобным»*). Зависимость плотности от
*) Это слово является Пуквальпьш переводом термина «elfsimilnrity,
распространенного в американской литературе и являющегося .швивален-
том понятия «автомодельный)).
7ft
массовой координаты на два момента времени t\ и ti приведена
на рис. 1.27,о. Здесь же дана соответствующая картинка на фа-
фазовой плоскости (s, t). Физический смысл величины ? — местная
«корость звука (массовая) (см. G.9)); в частности, |о = соро—
массовая скорость звука на фоне, gi = cipi— в газе, примыкаю-
примыкающем к поршню. Поэтому оба фронта волны — передний (точка А
на рис. 1.26 и рис. 1.27, о) и задний (точка В) движутся с мест-
местными скоростями звука. Их траектории на плоскости (s, t) —
прямые ОА (s = copoi) и ОВ (s = cipi?). Сопоставляя этот резуль-
результат с D.33'), убеждаемся, что эти прямые являются С^-характе-
ристиками.
В точках А и В, где «сшиваются» нетривиальное решение с
тривиальным, производные всех параметров течения терпят раз-
рып, в то время как сами эти параметры непрерывны. Разрывы
такого типа называют слабыми, в отличие от рассмотренных выше
сильных разрывов (контактных разрывов и ударных волн), на
которых испытывают скачки значения самих параметров.
Факт, установленный нами выше, справедлив и в общем слу-
случае — слабые разрыиы движутся вдоль характеристик; скорость
их распространения совпадает с местной скоростью звука.
Область между точками А и В есть волна разрежения, плот-
плотность здесь падает, а частицы газа приобретают отрицательную
скорость, изменяющуюся от нуля до величины —Uq. Ширина
этой области пропорциональна времени (соро — cipi)i. У поршня
образуется зона газа с параметрами pi, с\, v\ = —Uq. Ее размер
также возрастает пропорционально времени.
На рис. 1.27,6 для сравнения приведены картинки в перемен-
переменных Эйлера. Здесь луч 00'— траектория поршня. На фазовой
плоскости в зоне полны разрежения (между линиями ОА и ОВ)
^-характеристики являются лучами, расходящимися веером из
точки О. Течения такого типа называются центрированными про-
простыми волнами. В остальных зонах фазовой плоскости (^-харак-
(^-характеристики параллельны соответственно прямым ОА или ОВ.
Итак, построенное нами решение задачи о поршне, выдпигато-
щемся ия газа, является центрированной простой волной разре-
жегшя.
Как видно из рис. 1.20, такое решение можно построить толь-
только тогда, когда скорость поршня заключена п диапазоне 0 <
< Г/о «S 2со/(Т—!)¦ Если скорость превышает критическое зна-
значение Uo>2co/('f—1), поршень отрывается от газа; между
поршнем п газом возникает зона вакуума. Возникающее тсчопие
газа называется истечением в вакуум. Частицы с координатой
s = 0 движутся со скоростью у@, t) = —2со/(ч — 1)' так называе-
называемой скоростью истечения в вакуум, плотность этих частиц
р@, *)=0.
4. Решение задачи о поршие, вдвигаемом в гаэ. Рассмотрим
другой случай — поршень вдвигается в газ:
v @, t)=U0> 0.
77
Попытка сконструировать решение так, как это было сделано
выше, формально приводит к следующей картине (рис. 1.28).
В области между ?о и |j решение получается трехзначным. Это
не имеет физического смысла и свидетельствует о том, что в
данном случае непрерывного решения не существует.
Решением задачи о поршне, вдвигаемом в газ с постоянной
скоростью, является разрыв — ударная волна. Ее параметры мож-
можно определить с помощью соотношений E.23), воспользовавшись
тем фактом, что скорость газа за фронтом волны известна и рав-
равна скорости поршня Ui = С/о. Тогда скорость распространения
фронта ударной волны есть
¦и,
О
Значения остальных параметров теперь определяются по общим
формулам E.23).
Мы разобрали сравнительно простой вариант задачи о порш-
поршне, когда скорость поршня постоянна во все моменты времени
t > 0. Такая постановка содер-
содержит определенные черты идеа-
идеализации. Действительно, пор-
поршень, который в начальный мо-
момент покоился, не может мгно-
лснпо приобрести коночную ско-
скорость, так как это спязано с
действием бесконечно больших
сил. Реально, поршень в тече-
течение определенного времени раз-
разгоняется, прежде чем достичь
заданного значения скорости.
В общем случае при произ-
произвольном законе движения порш-
поршня задача уже не автомодельна,— в ее формулировке появляются
дополнительные размерные параметры такие, как, например, вре-
время выхода поршня на режим постоянной скорости. Однако при
некоторых специальных законах движения поршня автомодель-
автомодельные решения возможны и здесь.
5. Задача об ускоряющемся поршне. Рассмотрим задачу об ус-
ускоряющемся поршне, скорость которого изменяется по закону
v(O,t)=Vot", G.17)
п > 0, Fo — размерная постоянная. Поршень вдвигается в газ,
образуются ударные волны, и теперь в системе уравнений газо-
газодинамики уже нельзя использовать уравнение изоэнтропичности
G.3). Запишем систему уравнений газовой динамики в виде
C.25')
dv_
dt
dp
ds1
дг
dv
dt ~ P ds '
е =
,, G.18)
dt ds' dt ds' dt ^ ds ' 7—1'
где по-прежнему r\ = 1/p. Относительно печального состояния-
78
газа для простоты предположим, что
Л = Ло, v = vQ = 0, р = ро = 0, е = е0 = 0, G.19),
т. е. газ «на фоне» холодный или, что то же, его давление пре-
пренебрежимо мало по сравнению с давлением, возникающим в воз-
возмущенной области.
В качестве автомодельной переменной здесь удобно выбрать
G.20)
¦а все параметры течения газа, входящие в G.18), искать в виде
v(s, i) = Foa(|)i", ti(*iO-Vi®,
^ n, G.21)
V2
Размерные множители, а также показатели степени у времен-
временных множителей в G.21) выбраны иэ соображений размерно-
размерности. Кроме того, приняты во
внимание краевые условия:
формула для скорости в смыс-
смысле явной зависимости от вре-
мени должна «стыковаться» с
G.17). Отсутствие зависимости
от времени в формуле для
удельного объема л диктуется
тем обстоятельством, что удель-
ный объем на фоне не изменя-
Рис. 1.29
ется со временем. Остальные
параметры фона: давление, ско-
рость, внутренняя энергия рав-
вы нулю, и для них подобное
условие ш.шолнимо автоматически при любой зависимости от t
в G.21). С помощью G.20) и G.21) система уравнений G.18)
приводится к «автомодельному виду»:
. , .. «. dh da. n
G.22)
Краевые условия для полученной системы обыкновенных диф-
ференциальпых ураипепий дают формулы G.17)
а@)=1, G.23)
79
ибо точка ? = 0 при t>0 соответствует поршню, и G.19)
=1. «(&>)¦= °. РAо)=О, вAо) = О. G.24)
Значение автомодельной переменной go, где происходит «сшива-
«сшивание» решения системы G.22) со значениями на фоне G.24),
заранее неизвестно. Это «сшивание» происходит разрывным об-
образом через ударную волну. Положение фронта волны по массе
на любой момент времени определяется величиной |0 в соответ-
соответствии с G.20)
'о
Отсюда легко вычисляется массовая скорость фронта ударной
волны
и ее эйлерова скорость, т. е. скорость распространения в физи-
физическом пространстве:
2) = Di\o = (n+\)Volotn. G.25)
Параметры газа за фронтом ударной волны при 1 = 1о—0 свя-
связаны со значениями параметров на фоне при 1 = |о + 0 посред-
посредством соотношений Гюгонио E.22) (рис. 1.29). Подставим
u(s,t)k
?.7
Рис. 1.30
h=O Ur
формулы G.21) при | = |о + О в E.22); учитывая выражение
для скорости G.25), получим
^ (п-М) So-
= а (^-0) =
G.20)
у-1
*» (n + 1)- Й-
(v-i-ir
Таким образом, построение автомодельного решепия задачи
об ускоряющемся поршне свелось к исследованию системы обык-
обыкновенных дифференциальных уравнепий G.22) в области 0 <
<|<|0 —0 при условиях G.23) и G.26). Аналитическое ре-
решение здесь получить не удается. Тем не менее провести чис-
80
ленное интегрирование не представляет труда. Удобно решать.
задачу справа налево от точки | = §о — 0, где значения всех
функций известны G.26). Левое условие G.23) «пристреливает-
«пристреливается»; «параметр пристрелки»—положение фронта волны |0, ко-
которое пока осталось неопределенной величиной. Типичное по-
поведение кривых решения в автомодельных переменных и в фи-
физических переменных s, / представлено на рис. 1.30, а, б (сплош-
(сплошные линии).
Мы рассмотрели систему уравнений G.18) без диссипатив-
ных членов. В принципе можно было бы провести рассуждения
с учетом, например, вязкости F.5) (штриховые линии на
рис. 1.30, а, б). Правда, в этом случае, для того чтобы задача
осталась автомодельной, приходится вводить явную зависимость
коэффициента вязкости от времени. Это снижает ценность та-
такого решения с точки зрения его физического смысла. Однако
такое решение может быть использовано в качестве теста при
оценке свойств того или иного численного метода расчета урав-
уравнений газодинамики.
§ 8. Распад произвольного разрыва
1. Постановка задачи. Проведенный в § 5 анализ показал,
что не любой разрыв газодинамических параметров течения яв-
является разрывным решением уравнений газовой динамики. Для
этого требуется, чтобы на поверхности разрыва выполнялись оп-
определенные соотношения (соотношения Гюгонио), связывающие
значения параметров газа по обе стороны от разрыва и выра-
выражающие непрерывность потоков массы, импульса и энергии. Яс-
Ясно, что если за счет каких-либо внешних воздействий в средо
будет создан разрыв, не удовлетворяющий соотношениям Гюго-
Гюгонио (произвольный разрыв), то далее в таком виде он суще-
существовать не сможет,— возникнет некоторое газодинамическое те-
течение, подчиняющееся уравнениям газовой динамики. Если в ма-
математической модели среды отсутствуют дпссипативные факторы,
то развивающееся решение
может содержать разрывы —
ударные волны и контакт-
контактные разрывы, удовлетворяю-
удовлетворяющие соотношениям Гюгонио.
Описанный эффект и состав-
составляет существо явления, на- 1>ис- 1-31
зываемого распадом произ-
произвольного разрыва. Задача о распаде произвольного разрыва пред-
представляет не только теоретический интерес, результаты ее ре-
шепия имеют многочисленные практические приложения. Так,
на рис. 1.31 изображена схема «ударной трубы»— установки,
используемой в лабораториях для со.чдания ударных волн, бы-
быстро движущихся газовых потоков и т. д. В части трубы (а),
отделенной диафрагмой (с), каким-либо способом создается газ
С> ".. Л. С ч.фскиП, Ю. II. Попив 81
¦p,,fi,,v.-O.
¦ ¦ a . ¦ ¦
1 r ' Ъ ¦'¦'¦'¦'¦¦ ¦
с повышенным давлением (р\ > ра, ла счет взрыва, нагнетания
компрессором и т. д.). В начальный момент диафрагма, отделя-
отделяющая этот газ от «фона» (Ь) (газа при обычных условиях),
прорывается, и в этом месте возникает разрыв, не удовлетво-
удовлетворяющий условиям Гюгонпо. В результате его распада по «фо-
«фоновому» газу вправо будет распространяться ударная
волна, интенсивность которой, как следует из общих соображе-
соображений, определяется разностью давлений р\ — р0. Однако про-
провести детальный расчет характеристик этой ударной волны и
тем самым построить «теорию ударной трубы» можно лишь на
основе решения задачи о распаде разрыва.
Переходя к математической постановке задачи о распаде про-
произвольного разрыва, условимся считать ее одномерной в прибли-
приближении плоской геометрии. Такое предположение справедливо для
ядра возникающего точения, ведь все влияния в газе распро-
распространяются со скоростями порядка скорости звука, и, следова-
следовательно, воздействие стенок трубы, ее торцов и т. д. проявится
в ядре потока спустя некоторое время. В течение этого про-
промежутка времени мы можем пренебречь граничными условиями
и рассматривать идеализированную постановку задачи в неогра-
неограниченном пространстве, считая параметры среды слева и справа
от разрыва постоянными: pt, pi, z^i = 0 и ро, ро, 1>о = О
(рис. 1.32, а). Равенство нулю скоростей в этой постановке есть
t--o
5
Ра,Ро,иа
Рис. 132
отражение особенностей частной задачи об ударной трубе. В об-
общей постановке задача о распаде произвольного разрыва форму-
формулируется следующим образом: в начальный момент i*-0 в не-
неограниченном пространстве вдоль плоскости s= О все параметры
га.ча испытывают произвольный разрыв. В каждом из полупро-
полупространств (х > 0, s < 0) газ однороден, значения всех его пара-
параметром постоянные. В классической постановке предполагается,
что диссипативные процессы в среде отсутствуют. Газ по обе
стороны от разрыва в общем случае может обладать разными
термодинамическими свойствами, например разными постоянны-
постоянными в уравнениях состояния.
Решение задачи о распаде произвольного разрыва состоит
в определении газодинамического течепия, возникающего при
/ > 0. Другими словами, речь идет о решении задачи Коши для
82
уравнений газовой динамики, в которой начальные условия за-
заданы в виде описанного выше произвольного разрыва.
2. Структура решения. Нетрудно видеть, что во входных дан-
данных сформулированной задачи о распаде произвольного разрыва
отсутствуют параметры, имеющие размерность длины и времени.
Исходя из этого обстоятельства и основываясь на общих ре-
результатах, можно утверждать, что решение задачи о распаде
произвольного разрыва является автомодельным, а автомодель-
автомодельная переменная, как и в задаче о поршне, имеет вид | = sit.
Как известно (см. гл. I, § 7), класс такого типа амтомодель-
ных решений для уравнений газовой динамики исчерпывается
постоянными решениями, в том числе соединенными через раз-
разрыв (контактный или ударную волну), а также центрированны-
центрированными простыми волнами разрежения. Таким образом, в результате
распада разрыва в каждую сторону от места его первоначаль-
первоначального расположения будут распространяться ударные волны и
простые волны разрежения, причем в силу свойства автомодель-
ности структура решения во все моменты времени / > О будет
оставаться одной и той же.
Несложные рассуждения показынают, что в каждую сторону
от разрыва может распространяться не более одной волны, удар-
ударной или центрированной волны разрежения. Действительно, как
известно (см. гл. I, § 7), фронт ударной волны распространяет-
распространяется относительно газа перед волной со сверхзвуковой скоростью
и с дозвуковой относительно состояния газа, образующегося за
волной. В волнах разрежопия любая точка профиля, в том числе
и фронты (передний и задниц), движется с местном скоростью
звука. Имея в виду эти факты, рассмотрим некоторые гипоте-
гипотетические ситуации.
Пусть в результате распада разрыпа возникло течение, в ко-
котором вслед за ударной волной движется центрированная волна
разрежопия. В силу отмеченных выше соотношений между ско-
скоростями фронтон, через определенное время волна разрежения
нагопит фронт ударной волны. Тем более это произошло бы, если
пслод за первой ударной волной двигалась бы вторая ударная
иолпа. В тот момепт, когда вторая полна (разрежении пли удар-
ударная) догонит фронт первой ударной полпы, изменится каче-
качественная структура решения: число нолп каждого сорта, их ско-
скорости и т. д., что противоречит условию автомодельности.
Поэтому, если it результате распада разрыва образовалась удар-
ударная волна движущаяся направо или налево, за ней никакие
другие волны распространяться не могут. Аналогично за волной
разрежения не может распространяться ударная волна.
Ситуация, когда за волной разрежения следует вторая волна
разрежения (рис. 1.33) в задаче о распаде разрыва также воз-
возникнуть не может. Дело в том, что задний фронт перпой волны
разрежения (точка В) и передний фронт второй волны (точ-
(точка С) движутся с одной и той же скоростью, равной скорости
зпука л состоянии 1. Поэтому рясстояппе между ними остается
<"¦* 8:5
постоянным (I = const). В силу автомодельности конструкция
решения и, в частности картина, изображенная на рис. 1.33,
должна оставаться подобной во все моменты времени / > 0. В то
же время при малых / -*¦ 0 формирующееся решение занимает
исчезающе малую пространственную область. Это приводит к
выводу, что величина I должна быть равна нулю (/ = 0), а в
ш
т
В Е A s
Рис. 1.33
этом случае две движущиеся друг за другом волны разрежения
фактически вырождаются в одну простую центрированную вол-
волну разрежения.
Итак, искомое автомодельное решение задачи о распаде про-
произвольного разрыва представляет собой одну из трех возможных
комбинаций волн, расходящихся от места первоначального рас-
расположения разрыва: в каждом направлении движется по одной
ударной волне (УВ), по одной волне разрежения {ВР); в одну
Рис. 1.34
сторону распространяется ударная волна, в другую волна раз-
разрежения (см. рис. 1.34).
Состояния газа, возникающие па правой и левой волнами,
должны быть либо одинаковыми, либо стыковаться через кон-
контактный разрыв {К), который образуется в той массовой точке
(частице), где разрыв находился в начальный момент. Напом-
Напомним, что на коптактном разрыве непрерывны нормальпая к пло-
плоскости разрыла компонента скорости н давление, остальные тер-
термодинамические фупкции могут претерпевать разрып.
Заметим, что вариант решения задачи о распаде разрыва,
когда направо распространяется волна разрежения, а налепо —
ударная волна, принципиально не отличается от случая, пред-
S4
•ставленного на рис. 1.34, б, и потому отдельно не рассматрива-
рассматривается.
3. Адиабата Пуассона и адиабата Гюгонио на фазовой пло-
•скости. Анализ решения задачи о распаде произвольного разрыва"
графически удобно проводить на фазовой плоскости состояний
(у, р). В этих переменных, в отличие, например, от плоскости
(г|, р), контактный разрыв, позникающий в решении этой задачи,
точнее два состояния среды, стыкующиеся через контактный раз-
разрыв, представляют собой точку. Выведем в переменных и, р
для случая идеального газа уравнения для адиабат Пуассона
и Гюгонио, которые необходимы для количественного решения
задачи.
Обратимся сначала к уравнению для адиабаты Пуассона.
Рассмотрим простую центрированную волну разрежения, распро-
распространяющуюся в положительном направлении оси s по фоновому
состоянию газа с параметрами у0, ро. Интегрируя выведенное для
этого случая уравнение G.10) с учетом соотношения для иде-
идеального газа G.11), получим
где v и р отвечают значениям скорости и давления, возникаю-
возникающим в газе после прохождения волны разрежения, со, ро—ско-
ро—скорость звука и плотность на фоне. С учетом условия постоянства
энтропии в каждой частице газа
соотношение (8.1) можно преобразовать к интересующему нас
виду:
2?
Очевидно, в (8-2) показатель степени больше единицы:
2^/G —1)>1. 1'анонстпо (8.2) представляет собой уравнение
адиабаты Пуассона, записанной для центрированной простой
волны разрежения, распространяющейся по фону i>o, Ро направо
(у<Уо). Характерные особенности поведения этой кривой на
плоскости (у, р) представляет рис. 1..Ч5, а. Точка с координа-
координатами Уо, ро отвечает фоновому состоянию газа (состоянию 0)
и называется центром адиабаты. Сама адиабата расположена м
диапазоне О^р<ро и пересекает ось у п точке Уо —2со/(т — 1)
(напомним, что величина 2co/("f— 1) равна скорости истечения
газа в вакуум). Нетрудно вычислить наклон этой кривой в точ-
точке, являющейся центром адиабаты:
#1 (8.3)
85
Он определяется массовой скоростью звука на фоне. Символ &0
рядом с кривой на рис. 1.35, а следует расшифровывать следу-
следующим образом: речь идет об адиабате Пуассона, отвечающей
простым центрированным волнам разрежения, распространяю-
распространяющимся по фону 0 (нижний индекс) направо (стрелка над бук-
буквой). Построенная адиабата представляет собой геометрическое
Рис. 1.35
место точек на плоскости состояний, в которые газ может быть
переведен из фонового состояния 0 посредством простой волны
разрежения.
На рис. 1.35, б изображена адиабата Пуассона &а, для цент-
центрированных простых волн разрежения, распространяющихся по
состояпию 0 налево. Эта кривая является зеркальным отраже-
отражением рассмотренной выше адиабаты ^о. Ее уравнение имеет
вид (v > vQ):
27
(8.4)
Объединяя (8.2) и (8.4), запишем
Р = Ра И —
V—г
, U = v — va.
Перейдем к построению адиабаты Гюгопио, отвечающей удар-
ударным полнам. В качестве исходных соотношений возьмем равен-
равенства E.9), E.10) и E.16) из гл. I:
,,2 2
^-y = P-/V (8-6)
~ D -4- h.D
(8.7)
86
где u = v — 2), UQ = vo — ?fr,h= \+\> & ~ скорость фронта удар-
ударной волны. Рассматриваются ударные волны, распространяющие-
-ся по фону Vq, po\ v, p — состояние, возникающее за фронтом
волны. Подставляя функцию г\, выраженную из (8.5), в (8.6),
получим
и\ + ии0 = г\0(р — р0),
и далее, учтя выражение для и и ыо, имеем
Отсюда выводим соотношение для скорости фронта волны:
(8.8)
Из (8.5) и (8.7) следует равенство
подставив в которое (8.8), приходим к квадратному уравнению:
A _ h) р1 — Г 2 A — К) р0 + Щ- ] р — Г h ?— р0 — A — h) pi = 0
Здесь, как и ранее,
U = v — vQ,
(8.9)
(8.10)
Решение уравнения (8,9) дает искомую формулу для адиабаты
Гюгонио:
(8.11)
Знак «+» перед корнем выбран из тех
соображений, чтобы при U = 0 (v =
= vq) давление р равнялось фоновому:
р = р0. На основании теоремы Цемиле-
на (см. гл. I, § 5) существуют только
ударные волны сжатия и повышения
давления, поэтому в (8.11) р^ро. На
плоскости (у, р) (см. рис. 1.3б)адиабата
изображается критюй, имеющей две ветви, иетнь Зёй (?/>0,
v > Vq) отвечает ударным «олнам, распространяющимся по фоно-
фоновому состоянию 0 направо, ветвь Жо (f/<0, v < v0)— «олнам,
движущимся налево. Эти ветки расположены симметрично
87
Рис. 1.36
относительно вертикальной прямой v — v0. Угол наклона иетвей
в центре адиабаты (i>o, po) составляет
dp
dv
,=1) =±соРо,
(8.12)
где знак «+» соответствует ветви Жа, а знак «—»— ветви
Объединяя адиабату Пуассона ^о и адиабату Гюгонио
получим кривую (рис. 1.37), представляющую собой геометри-
геометрическое место точек на плоскости состояний (у, р), в которые
можно перевести газ из фонового состояния (i>o, po) с помощью
простой центрированной волны разрежения или ударной волны,.
Л",
Рис. 1.37
Рис. 1.38
т. е. газодинамических течений, допускающих автомодельное
представление с переменной | = sit. Разным точкам этой кривой
соответствуют волны разной интенсивности, причем построен-
построенная кривая отвечает волнам, распространяющимся относительно
фона направо. Заметим, что, в силу условий (8.3) и (8.12),
адиабаты ZPQ и <5^о имеют в точке (i>o, po) общую касательную.
Будем обозначать построенную гладкую кривую через slo.
Аналогичную кривую можно построить и для волн, распро-
распространяющихся палено, комбинируя адиабаты ^о и Mq.
4. Построение решения. Приступим к решению задачи о рас-
распаде произвольного ра.чрына, принимая за исходные данные кар-
картину, изображенную на рис. 1.32, б. На плоскости (v, p) со-
состояния среды справа и слева от первоначального разрыва да-
даются точками 0 и 1 (рис. 1.38). Построим кривую s&o, соответ-
соответствующую волнам (разрежения и ударным), движущимся по
состоянию 0 направо, и кривую s?\ — для волн, распространяю-
распространяющихся по состоянию 1 налево. Как обсуждалось выше, только
такие волны могут возникать в интересующем нас решении за-
задачи о распаде разрыва. Очевидно, состояние газа, возникающее
эа волной, идущей направо, будет лежать на кривой ^о, а за
волной, движущейся по состоянию 1 налево,— на кривой sf-i.
Возникающие состояния, как говорилось в п. 2, должны быть
либо одинаковыми, либо стыковаться через контактный разрыв.
В любом случае эти состояния изображаются одной и той же
точкой на плоскости (и, р). Очевидно, такой точкой может быть
единственная точка пересечения кривых s?0 и s?\,— точка К.
Эта точка лежит на ветвях Зёо и Зё\ кривых s&o и si-\. Поэтому
при указанном взаимном расположении начальных состояний О
л'
<J
Рк
ф.
Рис. 1.39
и 1 (рис. 1.38) в результате распада разрыва направо и налево
пойдут дно ударный полны {УВ0 и УИ[) (см. рис. 1.39), а в ме-
месте расположения первоначального разрыва образуется контакт-
контактный раарыи К с параметрами рк, Vk. Как видно, такой картине
соотиотствует следующее соотношение между значениями дав-
давления рк>ро, Pk>Pi. Плотность и температура на контактном
pa.tpi.ino могут претерпевать разрыи (Pot^Pi. ТофТ{, см.
рис. I..49,а). Траектории фронтон ударных волн, а также контакт-
контактного ра.чрыиа в лаграпжевых массовых и в эйлероных коорди-
координатах схематически указаны на рис. 1.39, б и в. Для количе-
количественного расчета параметров, возникающего в результате рас-
распада точения, следует в данном случае приравнять правые части
соотношения (8.11), записанного для правой и левой ударной
нолпы:
Р„ +
* L Г|«> *
+ 16Т рп ,г _
(y + if \ K
- я. '- -Ч-
j_
1('>V
¦('•'к— У]J
iii (т ,-1)"
(8.13)
Величина скорости vK, определяемая из этого уравнения, дает
по;)мо;кпость иычислить с помощью (8.11) давление на контакт-
контактном разрыве рк, и далее все остальные параметры течения,
включая скорости ударных волн SDо иЙ|.
89
Изменяя взаимное расположение на плоскости (и, р) точек
О и 1, отвечающих начальным данным задачи, можно получить
и другие разновидности распада разрыва. Используем для этой
цели следующий прием: зафиксируем состояние газа 0 справа
от первоначального разрыва, а в качестве состояния 1 рассмот-
рассмотрим поочередно точки А, В, С, D, F, расположенные при одном
и том же значении давления р = Р\ (рис. 1.40).
\
V V
\
Рис. 1.40
Для случая С поведение адиабат s&o и sl\ указано на
рис. 1.41, а. Точка их пересечения К лежит на ветви 2/ва адиа-
адиабаты J^o и на ветви 9>\ адиабаты s&\. Следовательно, результа-
результатом распада будет ударная волна, идущая направо, и волна раз-
разрежения, движущаяся по состоянию 1 налево. Характерно, что
в этом случае Pi>Pk, ра<рк. Для количественного решения
задачи необходимо из уравнения
=- Pi |l —
2V
V-l
(8.14)
получающегося приравниванием правых частей равенств (8.11)
и (8.4), определить величину скорости на контактном разрыве
Vk. Далее аналогично выше рассмотренному случаю вычисляет-
вычисляется рк, например, с помощью (8.4), и все остальные параметры
течения. Точке D на рис. 1.40 соответствует расположение адиа-
адиабат зФъ и «5^1, изображенное на рис. 1.41,6. В этом случае в обе
стороны от разрыва расходятся волны разрежения. Отметим, что
здесь р\ > рк, р0 > рк. Количественно решение определяется с
помощью формул (8.2) и (8.4).
Итак, мы рассмотрели три основных типа распада газодина-
газодинамического разрыва, которые качественно были предсказаны
в п. 2.
90
Остановимся еще на двух частных случаях. Первый соответ-
соответствует точке F на рис. 1.40. Картина расположения адиабат
представлена на рис. 1.41, в. Как видно, адиабаты s&o и \s?\ не
ямеют общих точек. В этой случае в среде в результате рас-
распада разрыва возникает пустота, а решение представляет собой
дне простых центрированных волны разрежения, посредством
которых осуществляется истечение газа в образовавшуюся зону
вакуума. Условием возникновения такого течения является вы-
лолнение неравенства
2
Другой частный случай представляет точка Б на рис. 1.40.
Здесь состояние 1 лежит непосредственно на адиабате s?o, и,
следовательно, точна пересечения адиабат К совпадает с точкой
В, соответствующей состоянию 1. Это означает, что в рассматри-
рассматриваемой ситуации начальный разрыв не является произвольным,—
состояния 0 ж 1 связаны соотношениями Гюгонио, а исходный
разрыв представляет собой ударную волну. При t > 0 фронт этой
91
волны будет двигаться со скоростью, определяемой соотношени-
соотношением (8.8).
4. Примеры задач о распаде разрыва. Применим изложенную
выше технику решения задачи о распаде разрыва для анализа
конкретных примеров.
Рассмотрим сформулированную в п. 1 задачу о течении, воз-
возникающем в ударной трубе (см. рис. 1.Л1 и 1.32, а). Точки (У
и 1, отвечающие исходным состояниям
газа, которые разделены в начальный мо-
момент диафрагмой, расположены fi птом
случае па оси р: vo = V\ = О, р\ > р0.
Рис. 1.42 дает представление о располо-
расположении адиабат .я?0 и s?\, а также точки
их пересечения К. Как видно, решение
задачи будет содержать ударную волну,
распространяющуюся по фону направо,
и волну разрежения, идущую в противо-
противоположную сторону. Параметры ударной
волны несложно вычислить так, как эта
и было описано выше. Однако и без рас-
расчетов нетрудно убедиться в том, что ин-
интенсивность ударной волны определяется
перепадом давлений р\ — р0. Так, при дав-
давлении рг — /уточка К' расположена дальше от точки 0, нежели
А'. При этом амплитуда волны будет больше: рк — Ро>Рк—Ро.
и скорость распространения выше.
В качестве второго примера рассмотрим задачу о столкнове-
столкновении двух одинаковых ударных волн. Пусть по однородному по-
покоящемуся газу (фону) с параметрами Уо = О, р0 нанстречу друг
и t --0 jl-дм ; -О
О*
О и
Рис. 1.42
р*
и*
р
и
F*
и
т
и,- С
Рис, 1.43
другу движутся две ударные волны одинаковой интенсивности
причем давление за их фронтами известно р = р% (см.
рис. 1.43, а). В момент времени t = () фронты ударных волн
соприкасаются в точке s = 0 (рис. 1.43,6). Возникает газодина-
газодинамический разрыв, причем параметры справа и слева от него
62
условиям Гюгонио не удовлетворяют: р0 = />„,, у0 = — у*, px =
= /V «1 = и*- Задача состоит в нахождении картины течения,
которое будет формироваться при t > 0.
Для построения решения используем плоскость (у, р). Фоно-
Фоновому состоянию газа здесь соответстиует точка Ф (рис. 1.44),
лежащая на оси р. Ударная полна, движущаяся по фону налево,
переводит газ в состояние б, лежащее на адиабате Гюгонио <ЖФ
при значении данления р =- л*. Значение скорости газа в этом
состоянии v = — v* определяется как абсцисса точки 0. Анало-
Аналогично находится состояние 1, возникающее за фронтом ударной
волны, распространяющейся па-
право. Параметры газа в этом
состоянии в силу симметрии за-
задачи таковы: v = у*, р = р%.
Построенные состояния 0 и 1
являются исходными для решения
задачи о распаде разрыва с на-
начальными данными, изображен-
изображенными на рис. 1.43, б. Далее для
нахождения решения использует-
используется алгоритм, описанный в преды-
предыдущем пункте: строятся адиабаты
st-o и s4-\ и анализируется поло-
положение точки их пересечения К.
В данном случае в силу симмет-
симметрии задачи она лежит на оси р
(ук = 0) на ветвях Жо и Ж\. Сле-
Следовательно, после столкновения исходных волн возникнут две
расходящиеся ударные волны одинаковой амплитуды. Газ между
их фронтами покоится (vK — 0, а давление равно р = рк) (см.
рис. 1.43, в). Числовые значения всех параметров возникающего
течения без труда определяются с помощью формулы (8.11) для
адиабаты Гюгонио.
Заметим, что «полоиипу» построенного решения (например,
область s > 0) можно рассматривать как решение задачи об от-
отражении ударной волны от жесткой стенки, находящейся в точ-
точке s — 0.
В заключение параграфа укажем, что задача о распаде раз-
разрыва, решение которой строится аналитическими методами, ши-
широко используется в качестве теста при апробации вычислитель-
вычислительных алгоритмов.
ГЛАВА II
НЕКОТОРЫЕ ПРИНЦИПЫ ПОСТРОЕНИЯ
РАЗНОСТНЫХ СХЕМ ГАЗОВОЙ ДИНАМИКИ
В этой главе некоторые общие принципы теории разностных
¦схем — однородность, консервативность и др.— применяются для
построения полностью консервативных схем одномерной неста-
нестационарной газодинамики. С помощью численных расчетов про-
продемонстрировано, что такие схемы обладают рядом преимуществ
по сравнению с другими схемами того же порядка аппроксима-
аппроксимации. Вводный первый параграф содержит основные понятия и
обозначения теории разностных схем. В § 2 обсуждается поня-
понятие консервативности разностной схемы, которое получило даль-
дальнейшее развитие и принципе полной консервативности (§ 3).
Из общего многоиараметрического семейства схем на основе
сформулироиашгого в § 3 критерия выделепо одпопараметриче-
ское множество полностью консервативных схем первого поряд-
порядка аппроксимации по премени и единственная схема второго по-
порядка. § 4 посвящен однородным разностным схемам газодина-
газодинамики, рассмотрен, в частности, метод сквозного расчета ударных
ноли с помощью искусстненной вязкости. В § 5 путем непо-
непосредственных расчетом некоторых тестовых задач проводится со-
сопоставление разностных схем различных типов. В § 0 обсужда-
обсуждаются способы построения разностных схем для уравнения теп-
теплопроводности.
§ 1. Основные понятия и обозначения теории разностных схем
1. Общие замечания. Решение многих задач газовой динамики
представляет практический интерес для различных областей нау-
науки и техпики. Однако уравнения газодинамики даже в простом
одномерном нестационарном случае весьма сложны, и сложность
эта заключена прежде всего в их нелинейности. Поэтому, не-
несмотря на то, что аналитические методы решения задач газовой
динамики достаточно давно и весьма интенсивно развиваются,
существует ограниченное число проблем, решение которых уда-
удалось построить в якном виде.
Большой прогресс и решении задач математической физики
вообще и газовой динамики в частности вызвало широкое внед-
внедрение численных методов па основе применения быстродейству-
быстродействующих электронных вычислительных машин (ЭВМ). Эти методы
обладают большей универсальностью по сраыгепию с классиче-
94
сними аналитическими методами и позволяют «вычислять» ре-
решение с заданной степенью точности.
Не следует, однако, думать, что численные методы целиком
вытеснят традиционные аналитические методы решения. «Точ-
«Точные» аналитические решения, полученные для некоторых упро-
упрощенных «предельных» вариантов исходной задачи, позволяют
полнее представить механизм изучаемого явления, его зависи-
зависимость от характерных параметров. Это в свою очередь дает воз-
возможность лучше отработать численный алгоритм. Кроме того,
точные решения выполняют, как правило, роль тестов, которые
используются при отладке программ для ЭВМ, а также для
контроля точности расчетов. Таким образом, численные и анали-
аналитические методы должны разумным образом сочетаться при ис-
исследовании задач. Следует отметить, что возможности современ-
современной вычислительной техники не беспредельны, и это ограничи-
ограничивает класс задач, которые могут быть решены численно. Так,
если способы расчета пространственно одномерных нестационар-
нестационарных задач газовой динамики в настоящее время достаточно хо-
хорошо разработаны и широко применяются, то двумерные и тем
более трехмерные расчеты больших практически важных задач
нона немногочисленны.
И все же. несмотря на все оговорки, численные методы яв-
являются сейчас наиболее эффективным и перспективным сред-
средством исследования задач газовой динамики.
Среди всевозможных численных методов наиболее разрабо-
разработанным представляется метод конечных разностей. Часто даже
отождествляют эти понятия, хотя существуют и прочие числен-
численные методы такие, как, например, вариационные методы (Рит-
ца, Бубнова— Галёркина и др.).
Существо метода конечных разностей состоит в следующем.
В рассматриваемой области пространства вместо непрерывной
среды, состояние которой описывается функциями непрерывного
аргумента, вводится ее разностный аналог. Эта дискретная мо-
модель среды описывается функциями дискретного аргумента, ко-
которые определены в конечном числе точек на сетке. Дифферен-
Дифференциальные уравнения, т. е. законы, и соответствии с которыми
эволюционирует непрерывная среда, заменяются соответствую-
соответствующими алгебраическими конечно-разностными соотношениями.
В итоге дифференциальная задача заменяется (аппроксимирует-
(аппроксимируется) системой разностных ураппоний — разностной схемой.
В дальнейших пунктах этого параграфа мы напомним ос-
основные понятия теории разностных схем (подробнее см. [77]).
2. Сетки. Исходным пунктом прп построении разностной схемы
являете» яамеиа области непрерывного изменения аргумента не-
некоторым конечным множеством точек, лежащих в этой области.
Это мпожестно есть область определения функций дискретного
аргумента; оно называется разностной сеткой. Соответственно
функции дискретного аргумента, определенные на этой сетке,
носят название сеточных функций.
95
Для одномерной задачи простейшим примером пространствен-
пространственной разностной сетки является равномерное разбиение отрезка
[О, М] на N равных частей, длина которых есть h = M/N (рав-
(равномерная разностная сетка). Отрезок [О, М] можно рассматри-
рассматривать, например, как область изменения лагранжевой массовой
переменной в пространственно одномерной задаче, М — рассмат-
рассматриваемая масса газа. Точки деления st отрезка (на рис. 2.1 от-
отмечены кружками), число которых в данном случае составляет
% <Cfh M S
N-: N
N + 1 @<i<.N), называют узлами сетки. Расстояние между
узлами si+\ — Si^h есть шаг сетки (по массе), величина h име-
именуется часто массовым интервалом. Совокупность узлов состав-
составляет множество точек он, где определяются сеточные функции:
Ы), — ist = ih, i = 0. . . ., N).
Наряду с узлами, которые называют целыми точками, часто
рассматривают так называемые «.полуцелые точки» si+i/2 —s, +
+ U,.r)A (па рис. 2.1 они отмечены крестиками). Множество полу-
полуцелых точек также можно использовать в качестпс области оп-
определения сеточных функций.
Несмотря на кажущуюся простоту, «опрос о рациональном
ныборе сетки заслуживает внимания. С одной стороны, количе-
количество узлоп сетки желательно брать большим, т. е. пользоваться
мелкими, подробными сотками. Точнее переданая при этом об-
область изменения дискретного аргумента, мы интуитивно рассчи-
тыиаем лучше аппроксимировать непрерывное решение сеточны-
сеточными функциями. К тому же известные теоретические суждения
о кнчестие разностных схем (аппроксимация, сходимость и т. д.)
применимы, как правило, лишь для достаточно мелких сеток.
С другой стороны, практические соображения, и в первую
очередь ограниченность быстродействия и объема памяти 1ШМ,
заставляют обращаться г; сеткам со сравнительно небольшим ко-
количеством узлов. В дальнейшем такие сетки мы будем называть
«грубыми» или «реальпммп».
Подобная конфликтная ситуация типична для разностных
мегодои, и выбор разумного компромисса зачастую определяется
не рекомендациями теории, а опытом и интуицией исследовате-
исследователя. Например, при выборе сеток часто используют неравномер-
неравномерные сотни*). Если имеется априорпая информация о решении,
например известно расположение некоторых его особенностей,
для «разрешения» которых необходима мелкая сетка, то есте-
*) См. также п. 9 настоящего параграфа.
¦96
ственно, не увеличивая общего числа узлов, сгустить сетку в
окрестности особенностей; в областях гладкости решения сетку
можно сделать редкой. На рис. 2.2 представлен пример нерав-
неравномерной сетки — ее шаг hi = s;+1 — s; [Zih[ = M\ выбран пере-
переменным с тем, чтобы наилучшим образом передать пик реше-
решения u(s).
Однако и такой прием не универсален,— достаточно обра-
обратиться к случаю, когда особенность решения перемещается по
сетке, причем закон ее движения, как это чаще всего бывает
на практике, заранее неизнестен.
Аналогично разностной сетке в пространстве определяется
сетка по временной переменной:
шг = Ui, j = О, I, 2, . . .; /j+.i — tj — г/»;
t, — шаг сетки по времени, в общем случае зависящий от номе-
номера шага. Произведение сеток
«и = (О/, X (ot = {(i,-, tj), si+i = j \
г = 0, 1, 2, ..., /V, /-О, 1,
2, ..., so = 0, sN = М, to = 0}
дает пространственно-вре-
пространственно-временную разностную сетку
для численного решения од-
одномерной нестационарной Рис. 2.2
задачи (рис. 2.3). Набор уз-
узлов (s,, tj) при 0 =S i =S N и фиксированном / называют
j-м с ременным слоем сетки ы. Иногда рассматривают «полуце-
«полуцелые» слои, отвечающие сначению tj+i/2 = t}• + 0.5т,-. Узлы, распо-
расположенные на вертикальных прямых i = 0 и г = iV, называют
граничными.
Значение сеточной функции I/ в некотором узле сетки (s,, fj)
будем обозначать через ц[ илтг у:
Соответственно
2/ (Si Li' 'j) = -'/i_i = .'/ (± 1) и У ('s'b ';+i) = y\+l = .'/¦
3. Сеточные функции. Нормы в сеточном пространстве. Раз-
Разностная задача строится с целью нахождения сеточной функ-
функции у. определенной на введенной сетке и близкой к решению
и соответствующей дифференциальной задачи. Сеточная функ-
функция у есть функция дискретного аргумента, решение дифферен-
дифференциальной задачи и — функция непрерывного аргумента. Они
принадлежат разным функциональным пространствам. Поэтому
возникает вопрос, как судить о степени близости этих функций.
Обычно поступают следующим образом. Рассматривают зна-
значения и в узлах сетки, что дает некоторую сеточную функцию
А. А. Самарский, Ю. П. Попов 97
uh, являющуюся, как говорят, проекцией решения и на простран-
пространство сеточных функций, и близость функций ути характеризу-
характеризуют величиной Wy — uh\\, где 11-11 — некоторая норма в пространстве-
сеточных функций. Естественно брать в качестве такой нормы
некоторый сеточный ана-
аналог нормы п обычном про-
странстпо. В теории раз-
разностных схом широко ис-
используется, например, се-
сеточный аналог нормы в
пространстве непрерыв-
непрерывных функций С (на фик-
сироианпом временном
слое)
ty>\ = max \y\\,
а также сеточный аналог1
НОрМЫ В Z/2
JV-1 \1/2
Рис. 2.3 О близости решений раз-
разностной и дифференциаль-
дифференциальной задач можно говорить в том случае, когда величина \\у — uh\\
неограниченно уменьшается при бесконечном дроблении сетки.
4. Разностная аппроксимация дифференциальных операторов.
Основной момент в постановке разностной задачи состоит в пе-
переходе от дифференциальных уравнений, описывающих эволю-
эволюцию сплошной среды, к соответствующим соотношениям для се-
сеточных функций.
В классическом анализе производпая от функции непрерыв-
непрерывного аргумента определяется следующим образом:
'——SjLTl—^-^-. A.1)
Для функции дискретного аргумента на фиксированной сетке
понятие подобного предельного перехода теряет смысл. При оп-
определении разностной производной вместо отношения бесконечно
малых ограничиваются отношением конечных разностей. Пусть
Si-\, S{, si+i — три последовательных узла равномерной разно-
разностной сетки по пространству с шагом h = si+\ — «,¦ = s,¦ — si-\
(рис. 2.4). Для аппроксимации производной A.1) в узле s; (на
/-м временном слое) можно использовать следующие соотно-
соотношения
_ V('i+V У-У (*<.',) W+i - ~ W у(+1)- у ,, 0.
У*— *. . —.9. — к h ' ^-2)
у-,=
У (si> <}) - У (si~v У _У\~ У\-г » - » (- - 1)
Выражения A.2), A.3) называют односторонними разно-
разностными производными, у, — правая производная (или производ-
производная вперед),у^ — левая (или производная назад).
Очевидно, правая производная в узле г является левой в уз-
узле 1 + 1, т. е. у. = у-(+ !)• Аналогично у- = У,{— 1)-
Помимо соотношений A.2), A.3), используют также цент-
центральную, или двустороннюю разностную производную
y{si+v tj)-v('i-v li) yUi - И-1 yH-l)-y(-l) (i »
« si + l—si_1 Ih Ih v '
Нетрудно проперить, что симметричное выражение A.4) явля-
является полусуммой односторонних производных A.2) и A.3):
у. =0,5 (у, +(/-).
Аналогично определяется разностная производная по времени
Вторая разностная производная определяется следующим об-
образом:
1 ГУ; + 1 — У; Уг-Уг-Л У; + 1 ~ 2уг + gj-i _у (+ 1) - 2у + у(-1).
*"~ A L A A J ' А2 да
Эта ианись представляет собой разностную производную от пер-
первой разностной производной. Отметим,
что для ратшомерпой сетки и-= у-
5. Погрешность аппроксимации. За- —А
менял дифференциальный оператор L i-f i t+/
некоторым разностным оператором Lh, Рис. 2.4
мы допускаем ошибку — погрешность
аппроксимации, от величины которой будет зависеть точность ре-
решения разностной задачи.
Выясним величину погрешности аппроксимации дифференци-
дифференциального оператора разностным для случая первых производных,
используя разложение в ряд Тейлора некоторой гладкой
функции:
u(si.v tj) = u(si ±h, lj) =
= и (8il h) ± h -g- (st, tj) + 4 S <««' Ь) + О (ha).
Исходя из определений A.2) — A-4), получим для погрешности
аппроксимации г|э = Lhuh — (Lu)h в каждом конкретном случае
следующие выражения
- |f (*„ fj) = A § (*i.г;)
99
¦Фо («О = ; ^
Эти соотношения справедливы для достаточно гладкой функции
u(s, t) непрерывного аргумента.
Говорят, что разностный оператор Lh аппроксимирует на
классе функций дифференциальный оператор L с порядком п > О
(п — порядок аппроксимации) в точке st, если для погрешности
аппроксимации имеет место
"Фж — "Ф (Si) = Lhuh - (Lu)h \s^5i --= О (/г").
В соответствии с этим определением односторонние разно-
разностные производные A.2), (l.ii) аппроксимируют производную
A.1) с первым порядком, а центральная производная—со
вторым.
Замечание. Производная у, является правой относительно
узла Si п в то же время левой относительно узла si+]. Очевидно,
относительно полуцелой точки si+]/2 = s( + 0,5/г эта же произ-
производная
является центральной. Таким образом, разностная производная
у* аппроксимирует производную A.1) с первым порядком в уз-
узлах i и I + 1 и со вторым порядком в нолуцелой точке I + 1/2,
Аналогичное утверждение справедливо и для разностной про-
производной по времени: выражение и, аппроксимирует произнод-
пую du/dt с первым порядком О(х) па слоях ) и ] + 1, и со вто-
вторым О(х2)— на полуцелом слое j+ 1/2.
Вторая разностная производная u-s аппроксимирует произиод-
ную д-u/ds2 со вторым порядком:
и- = —о (Si, tj) + -го —i (*"» li) + ° (ll ) = ~2 (v*< 'i) + ^ 'ft )•
Как видно из структуры приведенных выше формул, вели-
величина погрешности аппроксимации представляет собой произве-
произведение шага сетки (k или т) в некоторой положительной степени
на соответствующую производную от решения. Поэтому на гру-
грубых сетках, где шаги h и т нелики, а также для решений, пре-
претерпевающих резкие изменения но времени и пространстве,
величина погрешности аппроксимации i|; может стать не малой,
так что само понятие аппроксимация теряет смысл.
6. Разностная аппроксимация дифференциальных уравнении.
Возможные способы аппроксимации дифференциальных уравне-
шш мы рассмотрим на примере одного ил ураипопий газовой
100
динамики — уравнения движения
—
dt
ds
A.G)
Функции непрерывного аргумента — скорость v и давление р
заменим на сетке со сеточными функциями, сохраняя для них
обозначения и и р. Нулем пока считать, что эти сеточные функ-
функции вычисляются в узлах сетки (s^, tj). Используя введенные
выше обозначения, мы можем предложить для аппроксимации
(Ц) (Hi) (Hi)
Рис. 2.5.
IHJJ (Ц) (Hj)
Рис. 2.6
дифференциального уравнения A.6) следующие конечно-разно-
конечно-разностные соотношения:
vt + pl = 01 A.7')
vt + P-s = 0. A.7")
Участвующие и этих записях наборы узлов называются шаб-
шаблонами (рис. 2.5).
Погрешность аппроксимации уравнения A.6) разностными
уравнениями A.7'), A.7") в узле (s,, t,) имеет первый порядок
по времени и пространству О(т + /г). Разностное уравнение с
центральной производной по пространству
vt + р. -=0, A.7'")
записанное на четырехточечном шаблоне (рис. 2.6), имеет в уз-
узле (Sj, lj) второй порядок аппроксимации по пространству: г[' ==
= 0(т + /г2). Однако, кат» это будет показано в гл. III, такая
аппроксимация через точку приводит к неустойчивым схемам.
Существует еще один подход к аппроксимации уравнения
A.6). Будем относить значение сеточной функции давления на
каждом временном слое к полуцелым точкам (яц-1/2, tj), а скоро-
скорости — к целым (,V(, tj). Тогда разностное уравнение днижения на
шаблоне, изображенном на рис. 2.7, примет вид (в индексных
обозначениях)
°i+l-* + pj+1/,-p{-1/a_Om (L8)
Здесь разностная производная от давления симметрична отно-
относительно точки (si, tj) и имеет в ней второй порядок аппрокси-
аппроксимации O(h2). Разностная производная по времени от v имеет в
этой точке первый порядок аппроксимации 0{х), т. е. уравнение
101
A.8) аппроксимирует дифференциальное уравнение A.6) в точ-
точке (*\, lj) с порядком i[i = О(х + /г2).
Л отличпо от A.7'"), где центральная производная вычисля-
вычисляется «через точку» \р\ не участвует в записи разностного урав-
уравнения), в соотношении A.8) производная от давления опреде-
определяется по соседним точкам, что позволяет избежать неустойчиво-
неустойчивости схемы (см. гл. III). Для упрощения записи разностных со-
соотношений введем еще одно безындексное обозначение
yi+i/2 -=у1 = У-
Теперь соотношение A.8) можно переписать в компактном, так
называемом, безындексном виде
vt+p-t = 0. A.8')
До сих пор для рагшостной аппроксимации пространственной
производной в A.0) мы использовали /-й временной слой. Раз-
Разностные уравнения, построенные по такому принципу, называ-
называются явными. В такое уравнение входит лишь одпа величина
Рис 2.8
с (/ + 1)-го или, как говорят, с «верхнего» слоя и\+л--= и. Если
значения сеточных функций fj, p\ на /-м слое известны, то зна-
значение v выражается явным образом, например, из A.8'):
v = v — хр-.
Очевидно, при записи разностных уравнений можно пользовать-
пользоваться и «верхним» временным слоем. Тогда на шаблоне с полуце-
полуцелыми точками (рис. 2.8) получим аналогично A.8')
ut+?; = 0. A.9)
Напомним, что крышка над р означает, что эта леличипа вычис-
вычисляется па (/+ 1)-м слое (р= pi+1 = Pi+\/2).
Погрешность аппроксимации уравнения A.6) уравнением
A.0) в узле (t, /+1) равна г|з = О(т + /г2).
Разностные уравнения A.9) называются неявными,— здесь
на верхнем слое оказываются «завязанными» несколько различ-
различных неизвестных величин, и получить явную формулу для их
выражения через значения функций на /-м слое не удается.
102
Методы решения неявных разностных уравнений представляют
большой самостоятельный вопрос (см. гл. IV).
Для разностной аппроксимации уравнения A.6) можно ис-
использовать линейную комбинацию соотношений A.8') и A.9)
vt + ap-s + (l — a)p- = 0 A.10)
на шеститочечном шаблоне (рис. 2.9).
В дальнейшем для сокращения записи будет использоваться
обозначение
где а — так называемый весовой множитель.
С помощью этого обозначения можно переписать A.10)
в виде
у,+ р^> = 0. A.10')
При частном значении а = 0,5 соотношение A.10') имеет от-
относительно точки (si, tj+\/2) порядок аппроксимации O(x2+h2).
В остальных случаях аппроксимация
¦ф = О(т+/г2) (t-!/zJ+fJ
7. Постановка разностной задачи. -1 ж fc
Постановка дифференциальной за-
задачи в газовой динамике, помимо
самих уравнений, включает форму-
формулировку краевых условий и началь-
начальных данных, которые обеспечивают
выделение из совокупности всех воз-
возможных решений единственного. Те
же элементы должна содержать и
разностная постановка задачи. Способы аппроксимации некото-
некоторых дифференциальных уравнений разностными были разобра-
разобраны в предыдущем пункте. Характер разностной аппроксимации
граничных и начальных условий зависит от конкретного вида
задачи.
В качестве иллюстрации рассмотрим задачу об истечении газа
в вакуум^ постановка которой для дифференциального случая
была сформулирована в § 3 гл. I. Напомним, что в этой задаче
слева газ граничит с неподвижной стенкой, поэтому левое крае-
краевое условие выглядит следующим образом
Правое краевое условие на границе газа с вакуумом имеет вид
где М — масса газа, заключенная в единичном параллелепипеде.
Начальные условия таковы: газ однороден и покоится, так что
v(s, 0)=i>0 = 0, p(s, O)=po, p(s, 0) = р0, 0<s<M.
103
В этсш простейшей ладаче ралностпая аппроксимация краевых
и начальных условии записывается без труда:
yJ = O, /Ж = 0, ; = 1. 2
г,° = 0, />? = />„, р? = р0, i = l. 2 Л'-l.
Здесь для простоты рассмотреп случай, когда все сеточные функ-
функции вычисляются в целых точках сетки.
Разностные уравнения в совокупности с разностной аппрокси-
аппроксимацией граничных п начальных условий составляют разностную
схему. Ралностпая схема есть система алгебраических соотноше-
соотношений, методы решения которых представляют самостоятельную
проблему.
В дальнейшем иногда для краткости мы будем называть так-
также рапностпой схемой одну лишь систему разностных уравнений,
подразумевай при атом, что в конкретной задаче к ней добавля-
добавляется ра.нюстпал лапнсь начальных и краевых условий.
8. Сходимость и устойчивость разностных схем. Пусть у — се-
сеточная функция, являющаяся решением разностной задачи,
a Uh — проекция в пространство сеточных функций решения со-
соответствующей дифференциальной задачи. Если в пекоторой се-
сеточной норме для любого фиксированного t -= t^ = jnT имеет
место условие
j!(/o — i/V|->() при //->0, т->0 (/0->оо).
то говорят, что решение разностной задачи сходится к решению
дифференциальной задачи (разностная схема сходится). Если
при этом
то говорят, что разностная схема сходится со скоростью О(hn' +
Ч- т."") пли имеет порядок точности пл по пространству и ni — по
времени.
Сходимость считается одним из основных критериев качества
разностной схемы, обеспечивающим правильное воспроизведепие
искомого решения па сетке. К сожалению, это свойство схемы,
как1 правило, трудно проверить теоретически, в особенности для
11О.1Пнег'шых ладач. Обычно для доказательстпя сходимости про-
проверяют другое свойство схемы, называемое устойчивостью. Под
устойчивостью понимают непрерывную зависимость решения раз-
разностной задачи от входных данных (в нашем случае от началь-
начальные п граничных условий).
•Запишем символически разностную схему, аппроксимирующую
дифференциальную задачу Ln == /, в виде
Uy = (f. A.11)
Это представление включает печальные п краевые услошш (ф —
аппроксимация входных данных /). Пусть у — решение разностной
104
задачи с измененными входными данными <р
?*1/ = ф. A.12)
Разностная схема устойчива, если существует постоянная К > О,
не зависящая от шагов сетки /гит (при достаточно малых значе-
значениях Лит) и от выбора ф, ф и такая, что имеет место нера-
неравенство
||р-у||<л:11ф-ф||. A.13)
Заметим, что сеточные нормы в левой и правой частях этого не-
неравенства могут быть различными.
Из устойчивости и аппроксимации схемы вытекает ее схо-
сходимость.
Для доказательства этого факта рассмотрим невязку
¦ф = Lhuh — Lhy = Lhuh — ф. A.14)"
Выразим отсюда
Lhuh — я|э + ф = ф. A.15I
В силу определения устойчивости A.13) имеем, исходя из A.11)
и A.15),
Ни* - у\\ «= Ккр - фИ = КЦ\\.
Чтобы выразить величину повязки г|э, добавим к правой части ра-
равенства A.14) слагаемое (I — Lu),,, которое тождественно равно
нулю. Получим
ty = (Lhuh — ф) + (/ — Luh) = (fh — q>) + (Lhuh — (Lu)h).
Теперь условно устойчивости приобретает вид
\\у - uh\\ s? К{Ц - fj + WLhuh - (Lu)hH}. A.16)'
Таким образом, при наличии аппроксимации, когда Нф — Д11 -*¦
-* 0 п WLhiin — (Lu)h\l -*¦ 0, при дроблеппп шагов сетки условие
устойчивости A.16) обеспечивает сходимость схемы \\у — ик\\ -* 0.
Для общего случая теоретические доказательства устойчивости
разностных схем галодинампкн, т. е. априорные оценки вида
A.13), в настоящее время отсутствуют. Рассмотрение проводится
обычно для простейшего случая акустического приближения (см.
подробнее гл. III). Явные схемы обладают устойчивостью лшш.
при достаточно малом шаге сетки по времени т, удовлетворяю-
удовлетворяющем неравенству типа т ^ тк, где тк — некоторая критическая
величина временного шага,
rK = h/(pc), A.17)
с — скорость звука.
Неявные схемы формально обладают большей устойчивостью,
однако их реализация с помощью итерационных процессов по-
порождает дополнительные ограпичепия па шаг т того же порядка,
что и A.17).
105
9. Неравномерные сетки. Выше, вычисляя погрешность ап-
аппроксимации, мы предполагали, что сетка является равномерной.
В п. 2 этого параграфа указывалось, что встречаются ситуации,
когда целесообразно использовать неравномерные сетки. В этом
случае вычисление погрешности аппроксимации приводит к неко-
некоторым осложнениям. Для иллюстрации обратимся к разностному
оператору второй производной. На неравномерной сетке его вы-
выражение выглядит следующим образом
Функция у здесь отнесена к полуцелым точкам. Как будет видно
в дальнейшем, именно так аппроксимируется в уравнении энер-
энергии член, соответствующий процессам теплопроводности. Символ
УаТ "УДем использовать для обозначения разностной производной
второго порядка па неравномерной сетке. Погрешность аппрок-
аппроксимации указанного оператора выглядит так
° «¦
где h — некоторая средняя величина шага сетки.
Для неравномерной сетки
Д. , . ¦—¦ 2й« —\- К: -
л* = t+l 4fe; '-1 - о A).
Это означает, что фактически аппроксимация в точке (локальная
аппроксимация) отсутствует. Таким образом, сильная неравно-
неравномерность сетки, когда соседние интервалы резко отличаются друг
от друга по величине, вредна.
Остановимся на одном способе построения перавномерпых се-
сеток. Пусть hi+i ¦= qhi, т. е. укрупнение (д>1) или дробление
(<7<1) сетки осуществляется по закону геометрической прогрес-
прогрессии со знаменателем q (вообще говоря, q может зависеть от но-
номера интервала <). Тогда
7- -2-1-1/7 (?-D2
Л =
4 h<\ '
и, например, для q> \. имеем: при q = 1,1 Л ¦-= 0.002. при q ¦= 1,2
А =0,008, при q — \.?) А = 0,015 и т. д. Видно, что если q не
сильно отличается от единицы (</<il,3), то и локальная погреш-
погрешность будет невелика. Подобные сетки широко используются па
практике.
Отметим еще. что в задачах, где получить теоретические до-
доказательства сходимости схемы не удается, часто используется
следующий прием. Проводят несколько расчетов задачи, тгосле-
доиптелыю сгущая сетку, т. е. увеличивая число узлов сетки и
соответственно уменьшая шаг. На осповании поведения решений,
полученных таким образом, судят о сходимости схемы, о порядке
ее точности. В случае равномерных сеток их сгущение произво-
производится тривиальным образом, например путем деления шага по-
нолам. Если же специфика задачи требует использования нерав-
неравномерных сеток, то сгущение следует проводить достаточно акку-
аккуратно с тем, чтобы обеспечить одинаковую степень неравномер-
неравномерности для всех сеток. Для этого можно воспользоваться так
называемыми квазиравномерными сетками, которые обладают
следующими свойствами. Пусть h\ , к = 1, 2, ...,— последова-
последовательность сеток. Тогда требование квазиравномерности состоит
в том, что выполнено условие
где а > О — может зависеть от номера г, но не зависит от к, либо
существует такая постоянная Л/о, что а <L Л/о для всех к.
10. Справочные данные. В заключение этого параграфа пере-
перечислим введенные в нем обозначения для сеточных функций, так
как они будут широко использоваться в дальнейшем:
У (st, *,-) = у\=у, у (Si ± h, tj) = y3i±1 = y(± 1),
У (Si, t}+1) = г/;,+1 = У,
y[si +-^-h,f.}J =yi+l/2 = y\ = y, ^щ
_ У (+ 1) — У У — У (— 1) = У—У
Ниже при проведении выкладок нам потребуется формула пе-
перехода от одного веса к другому
y(a)=ym + (a-?,)xyt. A.19)!
Справедливость ее нетрудно проверить, раскрыв безындексные
обозначения в соответствии с A.18).
Будут использоваться также формулы для разностного диф-
дифференцирования произведения сеточных функций
(yv)s-y(+i)vs-'-vys, A.20)
(yv)-s= y(-l)v-.-\-vy-r A-20')
Докажем первую из этих формул:
Так же доказывается и формула A.20').
Аналогичная формула справедлива и для разностного диффе-
дифференцирования по времепи:
=*ijvt + vyt. A.21)
107
§ 2. Анализ некоторых разностных схем газовой динамике.
Понятие консервативности схемы
1. Прнмер построения разностной схемы газовой динамики.
В предыдущем параграфе описаны некоторые способы аппрокси-
аппроксимации одного из дифференциальных уравнений газовой динами-
динамики — уравнения движения конечно-разпостпыми соотношениями.
Распространив один из этих способов на остальные уравнепия,
мы получим некоторую разностную схему численного решения
одномерных нестационарных задач газовой динамики.
Как отмечалось в гл. I, дифференциальные уравнения газоди-
газодинамики допускают различные формы записи, выражающие опре-
определенные самостоятельные физические аспекты явления, эквива-
эквивалентные с математической точки зрения, т. е. сводящиеся друг
к другу посредством равносильных преобразований. При построе-
построении разностной схемы на первый взгляд все эти формы пред-
представляются равноправными, и поэтому для аппроксимации может
быть выбрана любая из них.
Выберем, например, следующий тшд системы дифференциаль-
дифференциальных уравнений газовой динамики в переменных Лагранжа:
дг dv ,о /v
р = рПТ, * = ^rj- B-5)
В данном случае уравнепия состояния B.Г)) описынают идеаль-
идеальный газ, однако с точки .чрония построения разностных схем это
не является принципиальным. Полтпму в дальнейшем при записи
ра:пюстиой схемы уравнения состояния будут часто опускаться.
Система уравнений B.1) — B.Г>) решается в области Q =
= {0<s<Af, f>0); граничные п начальные условия, н соответ-
соответствии со сказанным в п. 7 § 1, не рассматриваем.
В области Q введем равномерную сетку
(О = { (.«(, tj) , (S, и/2, h) , Si+l ¦-= Si + k,
s(-m.,2 = .^ + 0,.r)ft, i = 0, 1. ..., .V - 1. яо = 0. .?v ¦ - M,
Ш = M, tM = t, + т, j = 0, 1, ...}. B.6)
К у:1лам сетки (s,, l;) будем относить сеточные функции ско-
скорости v[ и эйлеровой переменной х[, к «полуцелым» точкам
(Sf+i/2, ^j)—сеточные функции давления, плотности, внутренней
108
= Pb ?i
энергии _и температуры: t
TI+112 = Т\ (рис. 2.10). Аппроксимируя по образцу A.8) диффе-
дифференциальные уравнения газодинамики B.1) — B.5), можно по-
получить следующую (одну из возможных) разностную схему:
B.7)
B.8)
B.9)
B.10)
B.11)
1
•°i+l/2
v\+1 — 4
Т
xi+1 — xi
X
1 "\
Pi+l/2 /
,J+1 __ „j+1
_ „i+l Vi+l Vi
Pi+l/2 1 i
/;i4-l/2 = И+1/2/1/ i+l/2i
R
= ^h ПХ/Л.
Локальная погрешность аппроксимации отдельных дифферен-
дифференциальных уравнений системы B.1) — B.5) разностными соотно-
соотношениями B.7) — B.11) — О(т + №). Заметим, что при записи
¦у-7
Рис. 2.10
лтой cxcmf.i но пригалогл. пользо.чатт.ся какими-либо пространст-
пространственными интерполяциями сеточпых фупкций, так как дипамичс-
gkiio и, х и термодинамические функции отнесены к различным
(целым и «полуцелым») точкам сетки. Схемы, подобные B.7) —
B.11), описаны в литературе п достаточно шпроко применяются
на практике (см., например, [73, 7П, 1071). Они ведут свое на-
начало от известной схемы «крест», предложенной первоначально
для уравнении акустики. Следует указать, что в отличие от
B.7) — B.11) в классическом «кресте» «полуцелые» точки сетки,
к которым относятся термодинамические функции, сдвинуты от-
посителыго узлов (.ч,-, t,) на половипу шага не только по про-
страистпу, но и по времени. Однако ото обстоятельств с точки
зрения наших рассмотрений пе является существенным.
Одна из привлекательных черт схемы B.7) — B.11) состоит
в том, что хотя правые части всех уравнений, кроме B.7), отно-
109
сятся к верхнему (;+1)-му временнбму слою (неявность), тем
не менее схема без труда разрешается явным образом. Для этого
следует рассматривать уравнения схемы в указанном порядке;
тогда из B.7) по известному с предыдущего ;-го слоя профилю
давления pi+t/2 вычисляются значения скорости v\ . из B.8)
и B.9) по найденной скорости v{ определяются х{ ' и pi+i/2>
далее уравнение B.10) в сочетании с B.11) дает 71+J/2. еШ/а
и р&\,ш.
Используя обозначения A.18), перепишем построенную раз-
разностную схему B.7) — B.11) в безьшдексной форме:
vt = — />-, B.7')
xt = v, B.8')
A/ph = v,, B.9')
ё«=—/ю„ B.10')
p = Rjif, E = Rf/(y-i). B.11')
Чтобы в дальнейшем избежать громоздких обозначений, мы
всюду, где это не вызовет недоразумений, опустим черту над
функциями р, р, е, Т, имея по-прежнему в виду, что они отно-
относятся к полуцелым точкам сетки. С учетом этого замечания схе-
схема B.7') —B.11') примет вид
vt = -P;, B.7")
xt = v, B.8")
= vt, B.9")
= —pv,, B-10")
e=_R77(f-l). B.11")
2. Анализ разностной схемы. В дифференциальном случае
уравнение B.4), выражающее закон изменения внутренней
энергии газа, может быть преобразовано с использованием других
уравнений системы к дивергентному виду
е+ -TJ = -
Уравнение B.4') представляет собой закон сохранения энергии.
Выясним, как обстоит дело с законом сохранения энергии в
разностной схеме B.7") — B.11"). Попытаемся преобразовать
аналогично дифференциальному случаю разностное уравнение
энергии B.10") к дивергентной форме. Умножим уравнение дви-
движения B.7") на г/0'51 = 0,5(у + v). Учитывая, что
Л( = ^^~=0,5D B-12)
НО
получим уравнение
О,5(У2)< = -У(о.5^-_ B.13)
Воспользовавшись формулой A.19), преобразуем правую часть
уравнения B.10"):
pv, = (р + xPi) (^°-в> + 0,5xi;t). = M°lB) - №, B-14)
где ___ Щ
" B.15)
Подставим B.14) в B.10") и сложим полученное выражение
«с B.13). Эта операция дает
(е + 0,5v*)t = - pv[0<b) — уСв.»^ -f bg.
Первые два члена в правой части «сворачиваются» в соответствии
« формулой разностного дифференцирования произведения A.20).
Окончательно получаем
= -(/>(-1)у@'5'). + 6<!Г. B.16)
Ото соотношение является разностным аналогом дивергентного
уравнения анергии B.4'). Оно представляет действующий в рас-
рассматриваемой схеме сеточный закон сохранения энергии, записан-
записанный для одного массового интервала h на промежутке времени т.
Суммирование соотношений B.16) на сетке по i и j @<i<iV,
h^i^h) Дает сеточный аналог интегрального закона сохране-
сохранения энергии.
Итак, в схеме B.7") — B.11") разностный закон сохранения
энергии оказывается невыполненным. Изменение энергии здесь
определяется не только работой сил давления, но и дополнитель-
дополнительными источниками 8S", имеющими чисто разностное происхож-
происхождение.
Дисбаланс энергии, порожденный этими не обладающими фи-
физическим смыслом фиктивными источниками, накапливается со
временем. Мощность источников на гладких решениях составляет
О(х) и уменьшается при использовании мелкой сетки по времен-
временной пороменшш. С другой стороны, иеличипа Ь<% практически пе
зависит от шага сетки по массе h и потому не может быть суще-
существенно уменьшена аа счет дробления пространственной сетки
(см. B.1Г,)).
Мы можом получпт|| несколько иную модификацию соотноше-
соотношения B.10), если сложим уравпение B.10") с уравнением B.13),
записанным в (/+ 1)-м уллс сетки
B.13')
13 атом случае имоом
(е + 0,5у2(+1)), = -(ру@5')8 + 6^. B.17)
Взяп полусумму уравнений B.16) и B.17), получим третью
111
симметричную форму
(е + v2 + vl{+i))t « - (p*v<°.% + 6<Г, B.18)
где
Pt = 0.5 (р + р(- 1)) = 0,Г) (pi+1/a + р!_1/2) B.19)
— линейная интерполяция на равномерной сетке сеточной функ-
функции давления в целую точку. Интересно отметить, что в B.16) —
B.18) дисбалансные члены 6S" одинаковы.
Три различных вида разностного дивергентного уравнения
энергии B.16) — B.18) отвечают трем различным определениям
в схеме кинетической энергии,— в первом случао кинетическая
энергия массового интервала определяется по скорости его левого
конца 0,5/г.1'2, во втором — по скорости правого 0,!5/гу2( + 1), в по-
последнем случае используется полусумма 0,5@,5hv2 +
+ 0,5fei?2 (+1) ) = 0,25 (у2 + у2( + 1)). Соответственно в каждом слу-
случае определяется и разностный вид работы сил давления.
Однако ни при одном определении не удается избежать нару-
нарушения в схеме закона сохранения энергии, что является суще-
существенным дефектом схемы.
3. Консервативные разностные схемы. Пример влияния некон-
неконсервативности. Разностная схема должна отражать основные свой-
свойства непрерывной среды. Поэтому естественно требовать, чтобы
в схеме прежде всего выполнялись разностные аналоги основных
законов сохранения. Разностные схпмы, обладающие этим свой-
свойством, называются консервативными. На важность требования
консервативности схемы обратили внимание в начале 50-х годов
А. Н. Тихонов и Л. А. Самарский [89]. Ими был предложен пн-
тегро-иптерполяциопиый метод для конструирования консерва-
консервативных разностных схем и построен пример, когда неконсерва-
неконсервативная разностная схема, обеспечивающая второй порядок точно-
точности в классе достаточно гладких коэффициентов, расходится в
классе разрывных коэффициентов [90].
Изложим один из примеров такого типа. Для наглядности
рассмотрим простейшую модель — задачу для стационарного
уравнения теплопроводности:
в@)=1, вA) = 0,
k{x)-[k2, ?<*<i.
Коэффициент теплопроводности k(x) терпит разрыв в точке
х ¦= g. Поэтому дифференциальное уравнение рассматривается
лишь в областях гладкости 0<.r<g и с,<х<\. На разрыве
должны выполняться дополнительные условия, необходимые с
112
физической точки зрения и выражающие непрерывность темпе-
температуры и теплового потока:
Г, du 1 , du
\k -j— = к -r-
L dx J dx
х=\~й
= 0.
Эти условия в совокупности с граничными условиями выделяют
единственное решение,— функция и(х) кусочно линейна и имеет
вид (рис. 2.11)
— ах,
Заметим, что исходное дифференциальное уравпение может быть
записано в педивергентной форме:
, d2u dk du ,.
iC , -т- —:— ~~: — U.
(l/- dx dx
В области 0 ^ x ^ 1 введем равномерную сетку мЛ = {х{ = ih, i —
= О, 1, ..., TV, h--=\IN). Пусть точка разрыва х = g коэффициен-
коэффициента k(x) ноиала и интервал между гс-м
и (ге + 1)-м узлами:
Заменим дифференциальную задачу
разностной схемой, причем будем
аппроксимировать недивергентную
форму уравнения
ч —¦ -
Рис. 2.11
+ 2h 2h '
i = i, 2, ..., TV-1, уо=Л, yN =0.
(В безындекспой форме: ку-хх-\-
+ коуо =0Л
X*X )
Преобразуем разностное уравнение к следующему виду:
1 г. /
— ["I (yi+i — уи — а\ (yi — yi-i)] = 0,
, 1 .. , 1
где а; = /,-j >-(*«ti — '^-1)' "i = *i + -j-(frifi — 'ч-i)- Очевидно,
что построенная разностная схема не является консервативной.
Условием консервативности является равенство ai+l = bt, при
выполнении которого выписанное разностное уравнение
8 А А. Сяморокий. Ю. П. Попов ИЗ
приводится к дивергентному виду
свидетельствующему о выполнении закона сохранения. Однако
условие ai+i — b( при ki Ф к2 нарушено в ближайших к точке раз-
разрыва х—% узлах (х = х„ и х = хп+у).
Члены, нарушающие консервативность схемы, можно тракто-
трактовать как некоторые фиктивные источники тепла, помещенные
в эти узлы. Их мощность прямо пропорциональна разности коэф-
•фициептов теплопроводности к\— к2 и обратно пропорциональна
величине шага сотки h.
Решение системы разностных уравнений находится в явном
виде. При измельчении сетки h -*¦ 0 оно стремится к некоторой
функции п(х), удовлетворяющей следующей дифференциальной
задаче:
ц@) = 1, иA) = 0
и дополнительным соотношениям в точке х ¦= |
[й] = 0, [kdu/dx] = -q,
где q = q(c>, к\, к?, К) — фиктивный источник тепла в точке раз-
разрыва коэффициента к (х).
Величина q может изменяться в пределах от — °о до +°°;
в частности, q = 0(й(х) = и(х)) только при к\ •= 1B- Па рис. 2.11
даны кривые и(х) и и(х) для случая ki = 10, &2 = 1, 1^=0,5.
Приведенный пример показывает, что некопсервативпая разпост-
пая схема, вообще говоря, расходится.
Заметим, что любая консервативная схема для данной задачи
сходится. Для широкого класса задач свойство консервативности
является необходимым условием сходимости.
А. Интегро-интерноляционньгй метод. Сущность иптегро-иптер-
полнциошюго метода состоит в tout, что разпостпые уравнения
строятся па основе интегральных соотпошепий, выражающих за-
законы сохранения для элементарной ячейки сетки. При этом па
сотке плодится оиредсленшая интерполяция искомого решения
и коэффициенте') уравнения, измепяя которую можно получать
различные разностные схемы.
Поясним сказанное па примере уравнения энергии. Запишем
разностное уравнение, аппроксимирующее интегральное уравне-
уравнение оперши (см. (З.^Л) гл. I):
¦)'()-¦ \-r-/2)ds- pndl -:Q,
для контура С, изображенного на рис. 2.12. Примем следующую
аппроксимацию отдельных контурных интегралов, входящих в
это уравнение:
j e (s, tj) ds = 8i+1/2/i,
H + i
vlY] h,
B.20)<
-j-i-i
J p (Si, t) V (Si, t) dt = 4" Ы+1/2 + pi-l/2) Vl+1T.
4
Тогда интегральное уравнение энергии порождает следующее-
разностное дивергентное уравнение:
или, с учетом обозначений A.18) и B.19) и замечания на с. 110
[е + 0,25(»*(+ 1) + i>2)h = -(Р* ^- B.21)
Поступая так же с остальными уравнениями газодинамики,
можно построить, например, следующую разностную схему:
= vs,
B.22)
vt = — p-s, xt = v,
le + 0,25 (v* (+1) +
Изменяя характер интерполяции B.20), мы получим семейство
схем, причем все они будут консервативными, т. е. для них вы-
выполнены сеточные аналоги законов сохранения массы, импульса
и энергии. Действительпо, например, в схеме B.22) уравнение
энергии, имеющее дивергентный вид, фактически выражает раз-
разностный закон сохранения энергии для одного массового интер-
8* Н5
вала h за одип шаг т по времени. Суммирование этого уравнения
по сетке даст интогралышп сеточный закон сохранения энергии.
5. Анализ консервативной схемы для уравнений газовой дина-
динамики. Остановимся подробно на схеме B.22) и выясним, как из-
изменяется в ней внутренняя энергия. Вычтем из уравнения энер-
энергии B.21) полусумму равенств B.1Я) и B.13'), предварительно
преобразовав правую часть B.21) следующим образом
Ср-Л = К/>* + т (/>*)*) (<;(°'5) + 0Jnvt)]s = (р^°'% - &g, B.23)
где
Ь8 = -х @,5ptvt + »(/>*)<).. B.2-1)
В результате приходим к уравнению
ef = — /w<0-5) + tig. B.25)
Таким образом, в схеме B.22) внутренняя энергия газа изменя-
изменяется но только за счет работы сил давления, как это предписыва-
предписывается физическим содержанием процесса. Дополнительный вклад
ппонь вносят фиктивные источники 8S", причина появления кото-
которых имеет ра;шостную природу и состоит в песогласоваппости
отдел I.пых уравнений разностной схемы. Величина дисбаланса
ЬЖ имеет порядок О(т), практически не зависит от шага сетки
по массе h и, таким образом, может быть уменьшена в данной
схеме лишь за счет измельчения временного шага сетки. В схеме
B.22) соблюдается закон сохранения полной энергии (внутрен-
(внутренней плюс кинетической), однако нарушен баланс тепловой энер-
энергии. Такой дефект схемы способен исказить внутреннюю энергию,
температуру и другие функции. Он не менее опасен, чем наруше-
нарушение закона сохранения энергии в некопсервативпых схемах,
особенно в задачах, где рассматриваются явления, сильно зави-
зависящие от температуры, такие, как электропроводность, теплопро-
теплопроводность и т. д.
§ 3. Полностью консервативные разностные схемы
1. Постановка задачи. Схемы с недивергентным уравнением
эне pi ни. Мы убедились, что рассмотренные » предыдущем пара-
параграфе разностные схемы адекватно описывают поведепне непре-
непрерывной газодинамической модели лишь в пределе при бесконеч-
бесконечном измельчении шага разностной сотни по времени, когда влия-
влияние дпсбалапсных членов становится исче.зающе малым. На
реп/н.ш.ту сетках при iii;na\ конечной иоличииы и яадачах, реше-
решение которых представляется функциями, быстро ляменятощггмп-
ся но времени и пространстве, такие ра.чностпые схемы из-за
наличии в них фиктиппых источников энергии могут существенно
исказить изучаемое явление.
С то же время вычислительная практика выпуждаст прово-
проводить расчеты на грубых сетках. (Под такими сетками мы пони-
116
маем сетки, у которых шаги не малы, например, шаг по времени
сравним с величиной тк, фигурирующей в условии устойчивости
A.17).) При зтом все же желательно, чтобы точность расчетов
была не слитком малой.
Таким образом, возникает проблема построения разностных
схем, обеспечивающих заданную точность па реальных грубых
сетках.
Поиск таких схем будем вести в некотором исходном семействе
разностных схем, заданных па сетке: ш = isi = ih, i = 0, 1, ..., N;
s,+]/2-(i + ll2) h, i = 0, 1, ..., TV— 1; U = jt, / = 0, 1, ...}. Сеточ-
Сеточные функции v\ = v, x\ = x, как и ранее, относятся к узлам
(s,Litt), фуПКЦИП же Pi + l/2 ¦-= Pi = />< Pi + l/2 = Pi = P» ei + l/2 =
= г\ = e — к полуцелым точкам (s^(/2, tj). Здесь черта пад функ-
функциями означает сдвиг па полшага по пространственному индексу.
Итак, рассмотрим многопараметрическое семейство разпост-
цых схем, аппроксимирующих систему уравнений газовой дина-
динамики в виде B.1) — B.4) с педивергентпым уравнением энергии
yf = —p(.°i>. C.1)
xt = у(°«\ C.2)
A/р), = у(°з), C.3)
(О.) {О \ /О / \
е, = — рУ t)v( »). C.4)
Веса 0 < ак <. 1, к = 1, 2, ..., 5, являются параметрами схемы.
Варьируя их, можно получить различные схемы от чисто явной
(оь = 0) до чисто неявной (ak = 1).
Отберем из семейства схем C.1) — C.4) те, которые правиль-
правильно передают необходимые энергетические соотношения даже па
грубых сетках.
Выясним, как обстоит дело is схемах C.1) — C.4) с законом
сохранения энергии. Проделаем уже использовавишеся в § 2 вы-
выкладки. Умножим C.1) па у@5) и сложим получающееся при
этом соотношение
0,Г) (i;-)t = — i/o,f,)p{ai) C.5)
с уравпепием :шергни C.4), правую часть которого представим
с помощью формулы A.19) в виде
+ (а, - 0,5) тог), =
= р vs ' ~ Ь'<5¦, (•'¦G)
bff - — т! (ст- — 0,5) p(aih>ts — (о-! — о-!) PiV(°^ .
Окончательно приходим к равенству
(г -\- 0,5у2)( = — (р'' (— 1) v )г + &<%• (•^•7)
117
Это уравнение является разностным аналогом закона сохране-
сохранения энергии на сетке для одного интервала h за шаг т. Как вид-
видно, в общем случае в схемах с педивергептпым уравнением энер-
энергии этот закон нарушен за счет фиктивных источников энергии
Ь<%', имеющих чисто разностное происхождение. Мощность этих
источников имеет па гладких решениях первый порядок по г
(величину О (т.)) и практически не зависит от шага сетки по-
массе h.
2. Условия полной консервативности. Из структуры дисбаланса
C.6) следует, что в частном случае при
о, =о4 = а, 05 = 0,5 C.8)
(а — параметр) оп тождественно обращается в пуль.
Таким образом, при выполнении условий C.8) разностная
схема C.1) — C.4) обладает замечательным свойством, аналогич-
аналогичным дифференциальному случаю,— педивергептпое уравнение
энергии C.4) посредством тождественных алгебраических пре-
преобразований сводится к дивергентному виду
(е + О.йу2) , = - (р<«> (-1) у<°-«).. C.9)
Очевидно, в этом случае в схеме выполнены как закон сохране-
сохранения полной энергии, так и балансы по отдельным видам энергии
(внутренней и кинетической). Причем это свойство по зависит
от величины шагов разностной сетки.
Любопытно отметить, что при условии C.8) уравнение C.4)
эквивалентно еще одной дивергентной форме
(е + 0,Гш2(+1)), = - (р«"у<0-5») „ C.10)
которую можно получить, сложив уравнение C.1) с уравнением
(З.Г>), записанным в (г + 1)-м узле сетки.
Полусумма C.9) и C.10) дает еще один вид
= - (t^V0'5»),. C.11)
В рассматриваемой схеме справедливы три разновидности ди-
дивергентного уравнения энергии, и тем самым три различные фор-
формы закона сохранения полной энергии. Они отличаются способом
записи кинетической энергии и работы сил давления. Таким обра-
образом, каждая из них определяет свою дискретную модель явления.
Отметим, что уравнения C.8) и C.10) в силу эквивалентно-
эквивалентности уравнению C.4) имеют второй порядок аппроксимации по
пространству. В то же время отдельные члены этих уравнений
аппроксимированы с первым порядком. При дополнительном
условии
03 = 05 C.12)
уравнение энергии с учотом уравнения неразрывности C.3) сво-
сводится к следующему педивергептпому соотношению:
е,+р«"A/р), = 0, C.13)
118
которое аппроксимирует дифференциальное «энтропийное» урав-
де , д ( 1 \ Л
нение энергии -г- + р -jr (-jr I = 0.
Итак, при сформулированных условиях C.8), C.12) схема
C.1) — C.4) одновременно аппроксимирует различные виды диф-
4>ерепциальпых уравнений энергии, каждое из которых имеет пе-
лосредствеппый физический смысл.
В схеме выполнен и закон сохранения импульса, что следует
из дивергентпости уравнения движения C.1), которое фактически
выражает это для одного интервала сетки h за шаг по времени т
Обратимся теперь к уравнению неразрывности. В гл. I пока-
показано, что в дифференциальном случае оно допускает различные
формы записи, эквивалентные математически, по имеющие раз-
различную физическую интерпретацию. Проанализируем с этой точки
зрепия дискретный случай. Преобразуем правую часть уравнения
C.3) с помощью формулы A.19) и уравнения C.2):
y(°i) = (y(°l) + (о3 — О2) XV-t)t = (Xt + (О3 — О2) TVt), = Xt, + 6F,
Отсюда следует, Что лишь при условии
о3 = о2, C.14)
когда bV тождествеппо обращается в пуль, в схеме C.1) — C.4)
выполнено соотпошепие
1/р = ж., C.15)
или в индексной форме
А/р{+1/2 = х{+1 - 4- C.15')
Равенство C.15) аппроксимирует дифференциальное уравнение
неразрывности в форме C.33) гл. I, которое мы назвали «зако-
«законом изменения объема». Соотношение C.1Г/) наглядно иллю-
стрпрует смысл этого закона применительно к массовому интер-
интервалу сотки. Оно часто используется в расчетах вместо уравнения
неразрывности C.3). При нособлюдопии условия C.14) указан-
указанное разностное соотпошепие для объема нарушается. Заметим
еще, что закон сохранения массы в схеме C.1) — C.4), записан-
записанной в лаграпжевых массовых координатах, выполняется триви-
тривиальным образом. Сформулированные памп условия C.8), C.12),
C.14), которые мы перепишем еще раз в виде
О|=04 = а, П2 = О;) = Ог, = 0.Г), C.16)
выделяют из общего семейства схем C.1) — C.4) одпопарлметри-
одпопарлметрическое семейство (свободный параметр а)
Vi = -pf\ Xt = i*™>. (!/(,), = г[ал)- ^-//"Vi0-81. C.17)
119
Как было показано выше, уравнение энергии в этой схеме пу-
путем равносильных алгебраических преобразований может быть,
сведено к педивергептпому виду
8i + p(«'(l/p)i = O, C.18)
или к дивергентному виду (симметричная форма)
(е + -f (v2 + v*{ + i)))t = - (Pfv^b))a, C.19>
а уравнение неразрывности — к соотношению
Щ = х.. C.20)
Для построенного семейства схем выполнены не только раз-
разностные аналоги основных законов сохранения (массы, импульса-
и полной энергии), как для классических консервативных схем,
но также ряд дополнительных сеточпых соотношепий, пеобходи-
мость выполнения которых диктуется физическими соображе-
соображениями. Схемы такого типа были названы полностью кон-
консервативными [67]. Нарушение условий полной консервативно-
консервативности C.16) порождает различные дисбалансы, которые па грубых
сетках для негладких решений достигают значительной величи-
величины, и приводит к тому, что разностная схема плохо моделирует в
дискретном случае процессы, протекающие в непрерывной среде.
3. Анализ семейства консервативных схем. Мы построили пол-
полностью консервативную схему C.17), исходя из семейства схем1
C.1) — C.4) с педивергептпым уравнением энергии.
Подобные построения мы можем осуществить и па оспове
схем с дивергентным уравнением энергии (консервативных схем).
Возникает вопрос, не получается лгг в этом случае другой тип
полностью консервативных схем.
Рассмотрим следующее мпогопараметрическое семейство:
vt = - /;1Ч C.21)
xt = y(°a), C.22)
A/Р)« - у<Ч C.23)
(е -J- ± (,?- + у«(+ \)))i = - (ply№)B. C.24)
Опо отличается от семейства C.1) — C.4) уравнением энергии,
которое в данном случае обеспечивает выполнение закона сохра-
сохранения энергии.
Выясним, при каких условиях в этой схеме соблюдается ба-
баланс внутренней энергии, для чего сведем уравнение C.24) к пе-
педивергептпому виду. Вычитая из C.24) полусумму уравнения
C.5) и уравнения C.5), записанного в (?+1)-м узле, получим
е, = - p(°iV30'5) + 6#, C.25)
& = _ т [(о5 - 0,5) p^)vt - (а, - о4) (/,*), уС.)].. C.26)
120
Отсюда следует, что в копсервативпой схеме C.21) — C.24)
при соблюдепии закопа сохрапепия полпой эпергии парушеп ба-
баланс впутреппей энергии. Тепловая эпергия газа е здесь измепя-
ется пе только за счет работ сил давления, но также из-за фик-
фиктивных источников энергии. Дисбаланс hS, возникающий за счет
рассогласоваппости отделышх уравпепий схемы, имеет па глад-
гладких решепнях порядок О(т). Его структура аналогична структу-
структуре дисбаланспого члепа &S" C.6), за исключенном одпого обстоя-
обстоятельства: величина Ь<% и отличие от b<S нмеот дивергентный ха-
характер, являясь разностной производной некоторого выражеппя.
Условия, при которых б^Г обращается и нуль, совпадают с
условиями C.8), обеспечивающими равенство пулю члепа Ь<§ в
C.7). При этом, как нетрудно проверить, дивергептное уравнение
C.24) эквивалентно недивергентпому уравнению C.17).
Дальнейшие преобразования па пути выделения из семейства
C.21) — C.24) полностью консервативных схем, аналогичны тем,
которые были проведены в предыдущем пункте. Они вновь при-
приводят к условиям C.16) и той же схеме C.17).
Таким образом, одпопараметрическое семейство схем C.17)
включает все возможные полностью консервативные разпостпые
схемы, аппроксимирующие на заданном шаблоне спетому одно-
одномерных нестационарных уравнении газовой динамики в лаграп-
жевых массовых координатах. На практике, как правило, удобнее
пользоваться полностью консервативными схемами с педивергепт-
пммн уравнениями.
Полностью консервативные схемы представляют собой суже-
сужение класса обычных консервативных схем. Очевидно, для полу-
получения полностью консервативных схем можно использовать те
же приемы, что и при построении консервативных схем, напри-
например, описанный в § 2, п. 4 нптегро-пптерполяциопнын метод.
При :)том дополнительно следует соблюдать некоторое формаль-
формальное правило отбора: разностная схема должна одновременно
аппроксимировать различные виды записи исходной дифферен-
дифференциальной системы уравнении, имеющие непосредственный физи-
физический смысл. Другими словами, отдельпьге разпостпые уравне-
уравнения схемы должны быть сформулированы таким образом, чтобы
они допускали преобразования, аналогичные дифференциальному
с i у чаю.
Построенное одпопараметрпческое семейство полностью коп-
оерпнтивпых схем па гладких решениях имеет порядок аппрок-
аппроксимации (9(А2+т). П частном случае при
а = 0,Г» (.4.27)
получается едпнетпепиян полностью консервативная разностная
схема второго порядка аппроксимации*).
*) Подробная схема построена в [25] на основе других соображений.
121
Итак, устрапив пеопределеппость в исходпом мпогопараметри-
ческом семействе схем, мы указали такие зпачепия свободных
параметров (весов ак), при которых схема па произвольной сетке-
удовлетворяет некоторому комплексу разумпых с физической
точки зрения требований.
Отметим, что при построении полпостью копсервативпых схем
мы пеявпо ввели ряд ограпичепий, сузивших исходпое семейство,,
из которого выбиралась схема, обладающая пужпыми свойствами.
Прежде всего рассматривался класс двухслоипых схем, что, впро-
впрочем, естествеппо для системы уравпепий B.1) — B.5), которые
содержат лишь первую производпую по времепи.
Для того чтобы пояспить характер още одпого ограшгченияг
проведем предварительно апализ следующей схемы [95]
Vt = —p-, Xt = v, (l/p)t = vt. e,= -p<°.%s. C.28)
Это также схема типа «крест»; опа отличается от B.7") —
B.11") лишь весом у давлепия в уравпепий эпергии. Взяв полу-
полусумму уравпений движепия па (/ + 1)-м и (; + 2)-м слоях и ум-
пожив ее па v, получим
0,5v(vt + vt) = - vp^b). C.29>
Нетрудно показать, что левая часть этого равепства может быть
приведепа к виду
-- . 1
vt)=-T
Суммируя C.29) с уравпепием эпергии в C.28), приходим окоп-
чательпо к следующему результату
(-1Н,- C-зо>
При желапии равепство C.30) можпо симметризовать апало-
гичпо C.11). Таким образом, в схеме C.28) педивергептпо&
уравнение эпергии оказывается возможпым свести к дивергепт-
пому уравпепию C.30), которое формальпо можпо рассматривать-
как закон сохрапепия полпой эпергии. Однако при этом кипети-
ческая эпергия е\ должна определяться формулой
неприемлемой с физической точки зрения. Действительно, со-
гласпо C.31) оказывается певозможпым определить эту величи-
величину по зпачепиям скорости в пекоторый фиксироваппый момепт
времепи, папример в начальпый, так как в C.31) входят величи-
величины с двух временных слоев. Кроме того, кинетическая энергия по
своему смыслу величипа неотрицательная, в то время как фор-
122
мула C.31) может дать для е\ отрицательное зпачепие, если
скорость в ?-м узле измепит зпак за шаг т.
Поэтому мы исключим из рассмотрения схемы, в которых раз-
ностпая аппроксимация кипетической энергии содержит два или
¦более иремепных слоев.
4. Полностью консервативная схема для пространственно од-
яомерпого случая с произвольной симметрией. Построепня, вы-
полненпые выше, легко обобщаются для одпомерпых цилипдри-
чески и сферически симметричпых задач. Соответствующая си-
система дифферепциальпых уравпепий, получеппая в гл. I, имеет
вид
at ~ r ar dt ~v' at \ 9 I- ds v l>' at p dS v v>>
где п = 0, 1, 2 для плоского, цилипдрического и сферического
случаев соответствеппо.
В рассматриваемой области {0 ^ я < М, t>0} введем перав-
номерпую сетку
<0 = {(Si, tj), (si+i/2, tj), S,+ x=Si + hi1 Si+1/2--=S,+ 0,o/li,
Ь+1=Ь + т„ i = 0, 1, ..., TV— 1,
so = 0, sN = M, to = O, / = 0, 1, 2, ...}.
К целым точкам сетки (st, tj) будем отпосить сеточпые фупкции
радиуса г} = г_и скорости o\ = v, к нолуцелым (s1+1/2, tj) — дав-
давления pS+i/2 = р\ = Р. плотности Pi+j/2 = р| = р и впутреппей
энергии е;+1/2 = el = е, причем, как и выше, черту над фупкция-
ми, относящимися к полуцелым точкам, опустим.
Система разпостпых уравпепий записывается следующим об-
ра.чом:
vt = - Rpf, C.32)
г, = гА°'Ь\ C.33)
(l/p)t = (Л1/о.8))„ C.34)
е, = — р^ (Rv^))sl C.35)
где
II — для плоского случая,
г<0-5' —дли случая цилиндрической симметрии,
г г -\- г2)/3 — дли случая сферической симметрии,
—свободпый параметр.
В формуле C.32) через у~ обозначена производная пазад
на неравномерной сетке от сеточной функции, определенной
123
в полуцелых точках:
Разпостная схема C.32)— C.35) аппроксимирует систему
уравпепий газовой дипамики C.31) гл. I с порядком (9(т + й2),
при а = 0,5 порядок есть О(т2+А2).
В схеме C.32) — C.35) выполпепы следующие локальные за-
копы сохрапения. Закоп сохрапепия объема (закоп сохрапепия'
массы выполпеп автоматически):
j r\+1 — г{ — плоский случай,
[(WJ—('tJ]/2—цилиндрический случай,
= [(W+i)—('t)]/2—цилиндрический случ
1+1/2 I [('i+iK — ('iK]/3 — сферический случай.
Напомпим, что масса отнесена к одному радиану в цилиндриче-
цилиндрическом случае и к едипице телесного угла — в сферическом.
Закоп сохранения энергии соблюдается в виде
(е + 4 (^2 + V* (+ 1)) )( = - №№-*)„ C.37>
hiP)-l/2+ hi-i['U 1/2 • г
vj\ep.Jf= '-—— интерполяция ситочной функции дав-
Н "+" i—1
лепия в целую точку для пераипомерпой сетки.
§ 4. Однородные разностные схемы. Искусственная вязкость
1. Вводные замечания. Одним из важных требований, предъ-
предъявляемых к разпостпым схемам, является требование одпородпо-
стн схемы [91], [92]. В это понятие икладынается следующий
смысл.
Как отмечалось в гл. I, при решении задач газовой дипамики
могут встречаться различпые особеппости, папример ра.чрывы ре-
решения — ударпые волпы и контактные разрывы. К последним
отпосятся и грапицы раздела двух сред с различными физиче-
физическими свойствами. Помимо этих физических особенностей, в про-
процессе решепия задачи копечпо-разпостпымп методами приходится
иметь дело с нерегулярпостями разностного происхождения.
К ним следует отнести, например, граничные точки сетки. Нали-
Наличие в задаче подобных «пеоднородностен» вынуждает в окрест-
окрестности каждой особом точки видоизменить алгоритм численного
счета, приспосабливал его к каждой индивидуальной особенности.
Такой путь весьма неудобен,— он громоздок и приводит к боль-
большим сложностям при реализации логической структуры алгорит-
алгоритма, lioo, как правило, заранее положение нерегулярных точек
неизвестно.
Естественно пытаться строить такие разностные схемы, кото-
которые реализуются по одним и тем же формулам во всех узлах
124
сетки, независимо от того, совпадает данный узел с точкой нере-
нерегулярности решения или пет. Схемы такого типа и называются
однородными или схемами сквозного счета.
2. Расчет разрывных решений. Обратимся к способам расчета
разрывных газодинамических решений — контактных разрывов и
ударных воля. Как отмечалось в гл. I, контактный разрыв пере-
перемещается в пространстве вместе с частицами вещества, т. е. не-
неподвижен по массе. Отнесем контактный разрыв, существовавший
в течении в пачальньш момент или образовавшийся позднее,
к ближайшему узлу сетки. Тогда во все последующие момепты
времепи разрыв будет оставаться в этом же узле. Нормальпая
компонента скорости, относящаяся к целым точкам, в силу этого
оказывается непрерывной па контактном разрыве, что соответ-
соответствует физической сущности явления. В то же время зпачепия
сеточных функций плотпости и температуры, измеряемые в бли-
ближайших полуцелых точках слева п справа от разрыва, могут
претерпевать скачок, величина которого такова, что давление
остается пепрерывпым.
Итак, благодаря использованию массовых коордипат и сетки
с целыми и полуцолыми точками, не возникает проблем (в одно-
одномерном случае) для «сквозного» расчета контактных разрывов.
В переменных же Эйлера .,
для решения апалогичпой ]
задачи приходится пред- /> Тпчшт ,u/w
принимать дополнитель- ¦• ч' ' (
пые усилия, ибо здесь по-
положение в пространстве
контактпого разрыва, во-
вообще говоря, заранее не-
известпо.
Сложнее обстоит дело
с построением однородных
разностных схем для рас-
расчета задач с ударпыми
волнами. Напомпим, что
фронт ударпой волпы пе-
перемещается по массе, а Рис. 2.13
параметры течения по
обе стороны от разрыва снязапы условиями Гюгопио (E.9) —
E.11) гл. I). Попытки осуществить расчет движепия удар-
ударпой волпы пепосредствеппо по разпостпым схемам типа C.1) —
C.4) или C.21)—C.24) оказываются неудачными. На рис. 2.13
представлены результаты такого расчета. За фронтом удар-
пой полны сеточные функции испытывают резкие колебания,
не позволяющие установить истиппые значения параметров. Не-
верно передается и скорость распространения фронта волны.
Важно отметить, что паблюдаемая «болтапка» не является след-
следствием вычислительной неустойчивости схемы. При измельчении
шага сетки по времени расчеты дают похожие результаты. Полу-
125
чеппая резко колеблющаяся кривая, неприемлемая в качестве
решения физической задачи, представляет тем пе менее решение
соответствующих разпостпых уравпепий. Механизму возпикпове-
пия таких колебапий может быть дана паглядпая интерпретация.
Дпскретпую модель среды, описываемую разностной схемой,
можпо в целях паглядпости иптерпретировать как систему, скон-
сконструированную из сосредоточеппых масс (топких пластипок с
массой, равпой массе интервалов сетки), которые взаимодейству-
взаимодействуют друг с другом без трения через упругую среду, заполняющую
пространство между пими. В мехапическом отпошешш такая си-
система эквивалептпа набору шариков, соедипеппых пружипками
с перемеппой жесткостью (шарики могут смещаться только в
продольпом паправлепии, см. рис. 2.14). При распрострапопии
сильпого возмущения (аналога ударпой волпы) шарики приходят
в движение, которое посит колебательпый характер и пе затухает
в силу отсутствия в системе трепия.
3. Искусственная вязкость. Для расчета ударпой волпы без
явного выделения па сетке ее фронта применяется метод «раз-
мазывапия» фропта за счет введепия в систему разпостпых урав-
уравпепий пекоторых диссипативпых членов (так называемой псевдо-
псевдовязкости или искусственной вязкости). Опи моделируют действие
реальпой вязкости, т. е. преобразуют кипетическую эпергию ко-
колебательного движепия в тепловую эпергию [75, 107]. Очевидпо,
диссипативпый мехапизм теплопроводности для этой цели мепее
удобеп, так как при этом разрывы в решении для достаточно
сильпых ударпых волп сохраняются, в то время как вязкость
«разглаживает» ударпые волпы любой интенсивности (см.
гл. I, § 6).
Для пепрерывпой среды влияпие вязкости па структуру фроп-
фропта ударпой волпы подробпо рассматривалось в § G гл, I. Уравпе-
пия газодипамики в этом случае записываются следующим об-
образом
О I 1 \ ди ди 0 , де. , . д»
где со — вязкость. Наиболее часто рассматриваются линейпая вяз-
вязкость
со = —vp dv/ds
¦и квадратичная вязкость
со = \ip(dv/dsJ.
В результате действия вязкости все параметры во фропте удар-
ударной волпы измепяются пепрерывпо.
126
В разпостпой схеме псевдовязкость вводится как добавок к
давлепию, аппроксимирующий соответствующее дифферепщгаль-
пое выражепие. Как и сеточпая фупкция давлепия, псевдовяз-
псевдовязкость относится к полуцелым точкам сетки.
Для случая липейной вязкости имеем
со/
+ 1/2 '
О, \A+i>v\.
Псевдовязкость предпазпачепа «работать» лишь па фропте
ударпой волны, поэтому па волнах разрежепия, которым соответ-
соответствует положительпый зпак производпой от скорости, вязкость
в разпостпом счете полагается равпой пулю.
Используя безыпдекспые соотпошепия A.18), перепишем ещ&
раз определение искусственной вязкости:
—vpi-,, w.<0,
0, vt>0. DЛ>
Здесь черта над фупкциями мир, «измеряемыми» в полуцелых
точках сетки, опущена.
Коэффициент вязкости v па практике подбирают так, чтобы
«размазать» фропт ударпой волпы па 3—4 массовых иптервала
сетки. Однако для линейной вязкости это сделать трудпо, ибо-
эффективная ширина «размазывапия» зависит от иптепсивности
волпы: для слабых волн она велика, для сильпых — стремится
к нулю (см. F.20) гл. I).
Этого педостатка лишепа «квадратичпая вязкость» (ипогда е»
называют вязкостью Неймана):
Здесь ширина фронта ударной волны конечна, не зависит от си-
силы волпы и равна (см. F.24) гл. I)
А =
Отсюда получаем оценку для коэффициента вязкости
2 я
где к = 3 -i- 4 — количество массовых интервалов, на которое мы
хотим размазать фропт ударпой волпы, h — величина иптервала.
При 1 = Г>/3 эта оцепка дает
D.3')
Формулу D.2) можно записать также в виде
1(и.-1и.1). D.4)
127
Часто в расчетах используют комбинацию линейной и квадра-
тичпой вязкости.
Следует отметить, что весь анализ структуры фропта ударпой
волпы, па результаты которого мы здесь опираемся, выполпеп
в гл. I для дифференциальных уравнений. Строго говоря, подоб-
пое рассмотрение следует провести и для разностных уравпепий.
Пример такого подхода дан в работе [83]. Исследованы различ-
различные типы вязкостий и показапо, что решение типа «разпостпой
бегущей волпы» сходится к соответствующему решению системы
дифференциальных уравнепий.
Таким образом, псевдовязкость есть искусственный механизм,
позволяющий осуществить сквозной расчет ударных волп без
явпого их выделепия па сетке, а разпостпая схема газовой дипа-
мпки с нееидоиязкостыо янляотся однородной. Под областью
фропта в этом случае понимается зона резкого изменения пара-
метро» течения.
Заметим, что ширина ударного перехода, обусловленная дей-
действием псевдовязкости, не имеет никакого отношения к реальной
ширине фронта волны, которая составляет несколько длин сво-
свободного пробега молекул.
С точки зрения построения полностью консервативных схем
добавление нсеидовязкостп но вызывает трудностей. Достаточно
всюду в схемах вместо газокинетического давления р использо-
использовать полное давление g, представляющее собой сумму обычного
и «вязкого» давлений: ?=р + й>. Например, для плоского случая
такая схема имеет вид
Vl == - nf\ A/[>)( ^ г<°'5). .г, = 1*>.-Ч Pt = -*г«Ыол\ е=р-\а.
Существуют н другие способы для расчета разрывных газоди-
газодинамических решении. Так, в принципе можпо решать разностные
уравнения газодинамики без дисенпатпвпых членов в области
гладкости, «сшивая» решения па разрыве с помощью разностно-
разностного аналога соотношений Гюгонпо. Однако такай схема не явля-
является однородной, опа подразумевает постоянный контроль яа
перемещением разрыиа и выполнение в ею окрестности специаль-
специальных операций по «сшиванию» решении. Ото вызывает дополни-
те.п.пые трудности, которые усугубляются еще и тем. что разры-
разрывы и газовой динамике могут образоваться с течением времени
даже при гладких начальпых и граничных условиях.
А. Разностные уравнения и граничных узлах сетки. Рассмот-
Рассмотрим способы записи разностных уранпеппп схемы и граничных
точках сетки. Обратимся для примера к схеме C.1) — (З/i) из
предыдущего параграфа. Очевидно, что уравнение двнжепия
Xt --= Г( ='
во всех целых точках сотки г = 0. 1, 2, .... N п уракшчши нераз-
неразрывности и энергии
128
во всех полуцелых точках i + Чг (i = 0, 1, ..., N— 1) записывают
одинаковым образом.
Иначе обстоит дело с уравнением движения
vt = —p{ail D.5)
Во внутренних узлах сетки i = 1, 2, ..., /V — 1 это уравнение
имеет вид (индексная форма, неравномерная сетка, для простоты
Oi=0)
i i "i-fl/2 ' i —i/2 // n\
—;— = — -пгглг^лг—7- D-b)
Соответствующий шаблон указан на рис. 2.15, а. В граничных
же точках, например в нулевом узле i = 0, запись этого уравне-
уравнении такова
„i+i. „i „') . п)
"°P/ P (A 7
P0
(см. шаблон на рис. 2.15,6). Центральная производная от сеточ-
сеточной функции давления в точке ? = 0 заменена односторонней.
—<!>—х—<>-
Рис. 2.15
Кроме того, в D.7) присутствует значение давления в целой точ-
точке ро, и то время, как но всех других формулах эта сеточная
функция относится к полуцелым точкам.
Схема, в которой во тшутренних точках сетки расчет ведется
по формуле D.5), а в граничных используется уравнение D.7),
является неоднородной — численный алгоритм оказывается зави-
зависящим от помора узла сетки. Аналогично обстоит дело и с днвер-
гчнтпым уравнением энергии в семействе консервативных схем
C.21) —C.24).
Избавиться от неоднородности в данном случае позволяет сле-
следующий несложный прием. Расширим формально разностную сет-
КУ: добавив к ней слева и справа по одному фиктивному массо-
массовому интервалу, величину которых положим равной нулю Л_, =
¦= hs = 0 (рис. 2.16). Так же формально введем значения сеточ-
9 А. А. Самарский. Ю. П. Попов 129
ной функции давления, отнесенные к серединам этих фиктивных
интервалов:
?-1/2= P-i, Pn+\i2= P~N. D.8)
(Здесь мы вновь используем черту, обозначающую, что соответ-
соответствующая сеточная функция вы-
вычисляется в полуцелой точке сет-
-yiV ки.) По существу эти значения
совпадают со значениями давле-
давления в граничных узлах
Теперь на новой сетке уравнение
D.5) автоматически обращается
в D.6) во внутренних узлах сет-
сетки и в D.7) — в граничном
узле.
То нее самое справедливо и для уравнения энергии C.24)
в семействе C.21)— C.24), причем здесь (р*)п= Р-\ = /V
5. Интегральные соотношения на сетке. Выше неоднократно
отмечалось, что разностные уравнения являются сеточными ана-
аналогами некоторых физических законов и носят локальный харак-
характер. Так, например, дивергентное разностное уравнение энергии
выражает закон сохранения энергии для одного массового ин-
интервала сетки за один шаг по времени. Чтобы получить инте-
интегральные соотношения дли всей рассматриваемой в задаче массы
газа, следует просуммировать соответствующее разностное урав-
уравнение по сетке. Это удобно сделать па введенной в предыдущем
пункте «расширенной» сетке, включающей фиктивные интервалы
й_,=й„-=О.
Так, для семейства схем C.1) — C.4) с педивергептным урав-
уравнением энергии на промежутке времени ?,, <i t < ?,, интегральный
баланс внутренней энергии для всей массы газа выполнен в виде
"S1 tyi = - 2 V (o4/4+1 + A - о,) p{) X
i=0 i-jj i = 0
(„5 + 1 „j+l „3
° J±
Это соотношение получено суммированием уравнений C.4).
Для записи сеточных сумм применяются обозначения
2 UiVihi =(y, v), 2 UiVihi = \y, v), 2 yivihi = \lh v\- (/(-10)
1=1 i=0 i=0
Используя эти обозначения, мы можем переписать интегральный
13*
баланс D.9):
[е,
D.9')
где, как обычно, у *-2 = у'* — у^.
Разностный аналог интегрального баланса полной энергии
в схеме C.1) — C.4) получается суммированием по сетке урав-
уравнений C.7) или аналогичных уравнений, где кинетическая энер-
энергия массового интервала вычисляется как полусумма 0,25(v2 +
+ v2(+l))k. Для последнего случая имеем
h h '* (os)
где
N-l
— полная энергия всей массы газа на /-м временном слое, а
= - S t(<J. - 0,5) [p(CTi), y4.) - (c, - c4) [Pt, y(ff.))} т? D.12)
— суммарный дисбаланс полной энергии. Для полностью консер-
консервативной схемы R = 0.
Для семейства консервативных схем C.21) — C.24) инте-
интегральный баланс полной энергии получается суммированием по
сетке уравнений C.24)
Это и есть запись закона сохранения энергии для всей
массы газа.
В то же время интегральный разностный баланс внутренней
лпоргии имоот пид (см. C.25), C.26))
[е,
D.14)
2 2 i Aitj = - 2 ((a6 - 0,й) (pfr) (vN)t - p[_V (yo)«) -
iJ
- (°i - ot) ((pN)t wf») - (P-x)* vfr)) 1 t?. D.15)
131
В силу дивергентной структуры дисбалапсного члена Ь& в
C.26) при суммировании по i слагаемые, относящиеся ко внут-
внутренним точкам сетки, взаимно уничтожаются.
Замечание. При введении в схему псевдовязкости поря-
порядок уравнений повышается,— в уравнении движения фактически
присутствует вторая производная по пространству от скорости.
Это вынуждает ставить дополнительные граничные условия.
Обычно в крайних фиктивных интервалах сетки h-\ и h-N псев-
псевдовязкость полагают равной нулю. В противном случае искус-
искусственная вязкость может нарушать интегральный баланс энергии
системы.
Р. принципе вычисление балансных соотношений можно про-
проводить и на основании исходных интегральных уравнений
C.42) — C.44) гл. I, записанных для полной массы газа. Однако-
при этом следует использовать тот же вид аппроксимации функ-
функций, что и в самих разностных уравнениях. Другими словами,
балансные соотношения должны являться следствиями конкрет-
конкретной рассматриваемой схемы. В противном случае эти балансные
соотношения окажутся нарушенными даже для полностью кон-
консервативных схем.
§ 5. Результаты численных расчетов
1. Выбор тестовой задачи. В этом параграфе будут изложены
результаты численной проверки теоретического анализа разност-
разностных схем газодинамики, который был выполнен в предыдущих
параграфах и привел к формулировке полиостью консервативных
схем. Эти схемы, как отмечалось, более эффективны, чем прочие
схемы, при расчете на грубых временных сетках решений, пре-
претерпевающих сильные изменения во времени и пространстве.
В качестве простейшей задачи, имеющей решение такого типа,
можно указать классическую задачу о поршне (см. гл. I, § 7),
где возникает ударная волна, во фронте которой параметры те-
течения испытывают резкие изменения.
Рассмотрим случай, когда поршень вдвигается в газ с посто-
постоянной скоростью Uq. Газ в начальном состоянии будем полагать
однородным (p(s, O)=po), покоящимся (v(s, 0)=0) и холодным
{T(s, 0) = 0). В качестве уравнения состояния используем урав-
уравнения состояния идеального газа
Тогда, как нзвестпо, от поргапя в глубь газа пойдет ударная
волна со скоростью (см. гл. I, § 7)
Of) - L±J [Г
Параметры газа за фронтом волны вычисляются по формулам
132
E.22) гл. I:
v+ У ! - (v + t)* Я =^T IT'
При значениях f = 5/з (одноатомный газ) С/о = 2/("f + 1) = 0,75,
po = 1, /? = 1 они составляют &) = 1, yi = 0,75, pt = 0,7Г), Tt =
= 0.187Г,, р,=4.
Расчеты проводились для конечной массы газа М (O^s^M).
На левой границе — поршне(s = 0)— задавалась скорость v@, l)=*
= С/о, или, в разностном виде, v'a = С'„, ;= 1, 2, . . . Правая гра-
граница s = M считалась неподвижной creiiKoii: v(M, t) = 0 или
vn = 0, 7 = 1,2, ... Расчет продолжался до тех пор, пока удар-
ударная волна не достигала правой границы, которая располагалась
достаточно далеко (М — велико), чтобы дать возможность раз-
разностному решению полностью сформироваться. В качестве на-
начальных данных Пралось исходное состояние газа:
р?= 1, 7"?= 0, г = 0, 1, ..-, -V- 1,
г"=0, i = 0, 1, ..., N.
Для оПоспечения возможности сгевозпого расчета ударной вол-
пы в схему вводилась псевдовя.чкость. Разностная сетка Оралась
равномерной, шаг по массе составлял h —0,1, шаг но времени
варьировался.
2. Результаты расчетов по неконсервативным схемам. Обра-
Обратимся сначала к семейству схем с недивергентным уравненном
энергии C.1) — C.4). На рис. 2,17,я представлены результаты
расчета сформулированной задачи о поршне по одной из схем
этого семейства — чисто неявной схеме, где ak= 1, к=> 1, 2, ..,, 5.
Здесь даны графики температуры по массовой координате на по-
последовательные моменты времепи для трех расчетов с различны-
различными значениями шага сетки по времени:
т, = 0,22т*, т2 = 1,33т*, т3 = 2,66т*,
где величина т* вычислена по условию A.17) для параметров
за фронтом волны (подробнее см. гл. III). Ьл\ числовое значение
тл- = 0,04.г).
На рис. 2,17, я нанесено также точное решепие задачи для
системы уравнений газовой динамики без диссипаций. Как вид-
видно, при больших значениях шага сетки по времепи т>т^ пара-
параметры течения газа за фронтом волны, полученные в результате
расчетов, заметно отличаются от точного решения, а скорость
движения ее фронта не равна единице, С увеличением т это рас-
расхождение усиливается.
На рис. 2.17,6 изображены результаты аналогичного расчета,
проведенного по полностью консервативной схеме, выделенной из
того же семейства C.1) — C.4): Ст|=а4 = а = 1, Стг = 0"з = сгб = 0,5.
133
Эта неявная схема, формально имеющая первый порядок аппрок-
аппроксимации О(т), такой же, как и рассмотренная выше чисто неяв-
неявная схема. При всех тех же значениях т, которые использовались
Точное решение
Точное решение
и в предыдущем примере, наблюдается хорошее совпадение реше-
решения разностной задачи с точным решением.
3. Оценка дисбалапсного члепа в пеявной пеконсерватнвной
схеме. Оценим количественно роль дисбаланса полной энергии
в иеявной схеме, использованной в первом примере. Обратимся
к точному решению для структуры фронта ударной волны (см.
гл. I, § 0). Правда, это решение построено для дифференциаль-
дифференциальных уравнений, однако оно может быть использовано для про-
проведения оценок и в разностном случае.
134
С учетом псевдовязкости дисбаланс полной энергии C.6) для
чисто неявной схемы имеет вид
6& = —0,5zgv,.. E.1)
В гл. I, § 6 показано, что дифференциальное уравнение, оп-
определяющее «вязкую» структуру фронта, имеет вид
Кроме того, из соотношений F.13), F.14) гл. I для нашего слу-
случая следует
2 )
Эти формулы позволяют вычислить дифференциальный ана-
аналог дисбаланса (">.!) на рассматриваемом автомодельном реше-
решении типа бегущей волны:
= -:0,5т* ^ = -
(rH - т|)« (г, - г,,) (г, _ ц), E.2)
г] =- 0,5(т]0 Н- rii)-
Отсюда, в частности, видно, что дисбаланс энергии возрастает
на ударной волне с уменьшением коэффициента вязкости v, так
как в этом случае решение становится «круче».
Аналогично можно получить оценку для члена работы сил
давления в правой части уравнения энергии C.7):
A = -(g(-l)
E-3)
Таким образом, отношение двух членов, стоящих в правой
части уравпепия C.7) и определяющих в схеме изменение пол-
полной энергии, составляет (рис. 2.18)
6& _ _ (у -'-1
А ~ г 4v
-(¦П — ¦
EУ')
Эта величина достигает максималь-
максимального по модулю значения вблизи
переднего и заднего фронтов волны
при т) = т]0 и т] = т)(:
а= max
= х-
8v
E.5)
Рис. 2.18
Здесь дисбалансные члены вно-
вносят наибольший относительный
вклад. При уменьшении шага сетки
по времени относительное влияние фиктивных разностных ис-
источников энергии уменьшается.
Выясним, при каких ограничениях на шаг сетки т неявная
схема дает «пе слишком искаженное» решение. Потребуем, что-
135
бы максимальный вклад дисбаланспого члена составлял не более
10 % от работы сил давления
а ?=0,1. E.6)
Напомним, что эффективная ширина фронта ударной волны
в случае линейной вязкости выражается формулой
Л =
(V i-l)^»!,,-»!,)
В расчетах она составляет 3—4 массовых интервала, т. е. Л = kh,
где к = 3-^4. Учитывая это, мы получаем ил E.6) н (о.5) нера-
неравенство
х <0,1Л- -jy = 0,1/c— \-jr) = 0,1/пгка, E.7)
где т к определяется формулой A.17), a = cm/D, ст = рс — мас-
массовая скорость звука.
Для задачи об ударной волне, результаты расчета которой
представлены на рис. 2.1E, к = 3 -г- 4, а a « 0,5, и полученное
неравенство приобретает вид
т< @,15 -*- 0,2) Tfl,
Итак-, при ньшолнепии условия E.7) влияние дисбаланса энергии
практически не скапывается на характере разностного решения;
когда условие E.7) нарушено, использование неявной схемы с
недцвергентпым уравнением энергии C.1) — C.4) на грубой вре-
временной сетке становится неэффективным, что подтверждают рас-
расчеты, результаты которых приведены выше.
Л а м е ч а н и е. Рассмотренная нами неявная схема имеет по-
порядок аппроксимации по времени 0{т). Погрешность аппрокси-
аппроксимации нединергентного уравнения энергии ралностным уравне-
уравнением C.4), вычисленная формально на автомодельном решении
задачи о структуре фронта ударной волны, имеет по величине
тот же порядок, что и дисбалансный член E.2). Поэтому, если
дисбаланс велик (сравним с основными членами уравнения энер-
энергии), то столь же велика и погрешность аппроксимации. Однако
в этом случае само понятие аппроксимации уже теряет смысл.
Проанали.шронапный пример убеждает и том, что полностью
консервативные схемы являются более пффектпвпыми но срав-
пешно с прочими схемами на грубых сетках, когда отсутствует
аппроксимации ра.чпостноп схемой системы уравнений галоди-
намнкп.
\. Пример расчета по консервативным схемам. Обратимся те-
теперь к семейству консервативных схем C.21) — C.24). Повторим
расчет задачи о поршно, описанной ш.ине, по одной из схем
этого семейства, например по чисто неявной схеме ок ~ 1, к =
= 1, ..., 5. Результат оказывается аналогичным нредставленпо-
му на рис. 2.17, б,— независимо от шага сетки по времени раз-
136
ностное решение близко к точному. Чтобы осмыслить этот факт,
проанализируем структуры дисбаланеных энергетических членов
в схемах C.1) —C.4) и C.21) —C.24).
В семействе схем C.1) — C.4) с недииергентным уравнением
энергии фиктивные источники Ь&', порождающие дисбаланс пол-
нон оперши, имеют объемный характер (см. C.6), C.7)). Их
дейстние н интегральпом дисбалансе D.12) суммируется по от-
отдельным интервалам сетки.
В семейстне консервативных схем C.21) — C.24) дисбаланс
внутренней энергии 6df C.26J имеет дивергентный вид. Фиктив-
Фиктивные источники энергии в этом случае носят «поверхностный ха-
характер»— они «работаjot» лишь в граничных интервалах сетки
«о и /2,v-i, а внутрь области эта фиктивная энергия, порожден-
порожденная дефектами разпостпой схемы, распространяется в виде свое-
своеобразного потока. Мощность поверхностных источников энергии
в D.14) определяется производными по времени от сеточных
функций давления и скорости в граничных узлах. Если эти ве-
величины слабо изменяются во времени, соответствующие дисба-
лапеные члены малы. Именно такой и является используемая
нами и качестве теста задача о поршне — в ней граничные ре-
режимы постоянны, и, следовательно, дисбаланс энергии равен
нулю.
5. Сравнение консервативных и полностью консервативных
схем. Итак, в качестве теста для сравнения классических кон-
консервативных и полностью консервативных схем следует взять
задачу с неременными но времени краевыми условиями. Приме-
Примером может служить задача об ускоряющемся поршне, который
вдвигается и газ с нарастающей во времени скоростью:
у @, t)= УоГ, и>0, E.8)'
или в разностной форме
li-Vtf, 7 = 1,2. ... E.8')
Как показано в гл. I, § 7, эта задача допускает автомодель-
автомодельное решение при всех / > 0, которое определяется решением си-
системы обыкновенных дифференциальных уравнений G.22).
На рис. 2.19, а и б в автомодельных неременных даны ре-
результаты расчета задачи об ускоряющемся поршне при п = 0,5
но двум схемам одного порядка аппроксимации О(т)—консер-
О(т)—консервативной о"| = 0,5, а.? = аз = 04 = о = 1 (рис. 2.19, а) и полностью
консервативной oi=O4 = l, 02 = 03 = 05 = 0,5 (рис. 2.19,6). Ре-
Результаты приведены на три последовательных временных слоя,
одесь же нанесено точное решение (сплошная линия).
Хотя точное решение задачи антомодельно нри всех t > О,
численное решение, полученное но консервативной схеме, этим
свойством не обладает: значения температуры 8(?) в области
О < ? < 0,4 на различные моменты времени заметно отличаются
друг от друга (рис. 2.19, а). При 0,5К ? значения 0(?) накла-
накладываются приблизительно на одну линию, что свидетельствует
137
об автомодельности численного решения в этой области. Однако
эта линия не совпадает с точным решением.
Аналогичный расчет по полностью консерватипнои схеме да-
дает хорошие результаты (рис. 2.19,6).
Пользуясь формулами для точного решения (см. гл. I, G.21))
где 3@)—числовое значение «автомодельной функции давле-
давления» 3A) ПРИ 1 = 0, можно оценить мощность фиктивного
а-Ц5
источника энергии, локализованного у границы с поршнем.
В соответствии с D.15) имеем для рассмотренной консерватив-
консервативной схемы
= V
* [р0 (гп)(
E.9)
Эта величина положительна, чем и объясняется тот факт, что
температура, полученная и расчетах (рис. 2.19, а), пренышает
истинные значения. С увеличением п вли/пше дисбаланса ра-
растет. Расчеты это подтверждают: па рис. 2.20, а даны результаты
для консервативной схемы (а\ = а2 = а3 = or, = 1, а4 = 0,5) для
значения п — 3 (темные треугольники). Видно, что относитель-
относительная величина отклонения от точного решения возросла но срав-
сравнению со случаем п = 0,5 (рис. 2.19, а). На рис. 2.20, а нане-
нанесено также решение, полученное но другой консервативной схе-
схеме: 04 = 0,5, Oi = Ог = аз = as = 1 (светлые треугольники). Для
этой схемы оценка дисбаланса, аналогичная E.9), дает
1
R = - -i- тр @) Vfcy
E.10)
4ЯЯ
Отметим, что этот дисбаланс отрицателен, и потому значения
температуры, которые дает разностная схема, здесь меньше
истинных. По абсолютной величине E.10) в полтора раза мень-
меньше, чем E.9), и это также согласуется с расчетами (ср., на-
например, значения 0A) вблизи максимума). Для сравнения на
этом же графике приведены результаты расчета по полностью
консервативной схеме: ai=a4=l, a2 = a3 = a5 = 0,5 (кружки).
О
Как следует из структуры E.9), E.10), влияние дисбаланса
внутренней энергии должно убывать при уменьшении шага сет-
сетки по времени. Это демонстрирует рис. 2.20, б, на котором при-
приведены расчеты по консервативной (треугольники) и полностью
консервативной (кружки) схемам при п = 5 для двух значений
т (для ti •— темные, для ti/2 — светлые).
Суммируя результаты теоретического анализа и численных
расчетов, мы можем заключить, что при расчете задач газовой
динамики полностью консервативные разностные схемы дают
определенные количественные преимущества по сравнению с
другими схемами того же порядка аппроксимации, в том числе
и классическими консервативными схемами. Эти преимущества
проявляются при расчете быстропеременных во времени и про-
страпстпо решений па грубых «роменпых разностных сетках,
когда фактически неприменимо понятие аппроксимации.
6. Полностью консервативные разностные схемы для уравне-
уравнений гравитационной газовой динамики. В приближении гравита-
гравитационной газовой динамики и магнитной гидродинамики описы-
139
ваются различные практически интересные задачи астрофизики,
такие как процессы в атмосфере Солнца, эволюция звезд и т. д.
[8, 11, 39, 46, 47]. В простейшем случае плоской одномерной
геометрии уравнения газодинамики с учетом гравитации имеют
вид
E.12)
E.13)
E.14)
р = &(р, Г), г = &(р. Т). E.15)
Отличие от рассматривавшейся выше системы уравнений газо-
газовой динамики состоит здесь и наличии в уравнении движения
E.11) ускорения силы тяжести G, которое в данном простейшем
случае считается постоянным. В задачах гравитационной газо-
газодинамики начальные значения термодинамических функций оп-
определяются заданием некоторого распределения температуры
T(s, 0) = T0(s) и при v(s, 0) = 0 уравнением гидростатического
равновесия, следующим из E.11):
dS3 (e,O). T(s.())). E.16)
w
i
p
de
W
= V,
дх
~ Is'
= — P
dv
17'
Дивергентная форма уравнения лпергии, к которой приво-
приводится в данном случае соотношение E.14). такова:
Слагаемое Gx в левой части E.17) выражает потенциальную
(гравитационную) энергию.
В гравитационном газодинамике показано, что консерватив-
консервативные1 разностные с\емы обладают преимуществами перед пекон-
сериатшшыми схемами. 'Гак. и [100] отпт копрос рассмотрен на
примере задачи о распространении ударной волны и неоднород-
неоднородном среде с экспоненциально изменяющейся плотностью. При
построении конссриатниных разностных схем для гравитацион-
гравитационной газодинамики в качестве уравнения энергии используется
разностная аппроксимация дивергентного соотношения E.17).
Однако это не всегда удобно. Например, при численном моде-
моделировании процессов в атмосфере звезды, где плотность неве-
невелика, вклад тепловой энергии е в полную энергию е + v2/2 + Gx
может оказаться весьма малым. В такой ситуации вычисление
температуры с помощью разностного дивергентного уравнения
энергии, аналогичного E.17). приводит к заметным ошибкам
140
172. 101]. Это обстоятельство заставляет использовать разно-
разностные схемы с недивергентным уравнением энергии. Проанали-
Проанализируем, к каким последствиям это может привести [48].
Обратимся к следующему семейству схем, аппроксимирую-
аппроксимирующих систему уравнений E.11) — E.14):
Vt=-p<f>-G, E.18)
xt = irf«, E.19)
1,'р = х„ E.20)
[°ъ). E.21)
Заметим, что при G = 0 значение параметра р = 0,5 выделяет
из семейств E.18) — E.21) построенную выше полностью кон-
консервативную схему C.17). При G^O и значении Р = 1 получа-
получается схема, широко используемая в астрофизических приложе-
приложениях (см., например, [101]). Суммируя, как это делалось выше,
уравнение энергии E.21) с уравнением движения E.19), умно-
умноженным на у@5), можно получить соотношение
( + ^ + ^(+D + с,
где
8#! = 0,5(р - 0,5) [vt + (v(+l))t]. E.22)
Видно, что в общем случае закон сохранения полной энер-
энергии в семействе схем E.18) — E.21) не выполнен. Исключение
•составляет схема с [3 = 0.5, которую естественно назвать пол-
полностью консерпатитшой схемой для уравнений гравитационной
газодинамики E.11) — E.14).
Принцип полной консервативности позволяет установить раз-
разностное выражение для аппроксимации гранитацшшной силы и
л более сложном случае, когда имеется зависимость от коорди-
координаты. Например, соответствующее сферически симметричному
случаю выражение GM/r2 следует аппроксимировать соотношени-
соотношением GM/(rr).
Приведем краткое описание расчетом задачи о распростране-
распространении ударной волны и плоской атмосфере звезды, которые демон-
демонстрируют отрицательную роль дисбаланса E.22) и тем самым
подтверждают преимуществ полностью консернативных разно-
разностных схем. (Подробное изложение этих результатов дано в [46,
48|.) Ьудем рассматршшть задачу в области 0 ^ s =Si M, где s =
= 0 соотпотстпуот основанию атмосферы, a s = M — внешней ее
границе. Плотность атмосферы спадает к границе s = М в со-
отпетстпии с условием гидростатического равновесия E.16). При
.V = 0 поршень, дпигаясь с постоянной скоростью внутрь газа
(протип направления действия гравитационной силы), порожда-
порождает распространяющуюся в атмосфере ударную волну. Проходя
по среде с убывающей плотностью, ударная волна увеличивает
свою амплитуду. Течение газа за фронтом ударной волны тор-
141
мозится силой тяжести, в результате чего за фронтом форми-
формируется зона разрежения.
Указанные особенности распространения ударной волны в ат-
атмосфере звезды видны на рис. 2.21, где на два последователь-
последовательных момента времени представлены графики по скорости газа и
приращения температуры в ударной волне Т — То- В расчетах
,, V, км/сек
10
¦ К км/сек
100 сек
0,5
. . \\\ >
1,0 х,10*см
Рис. 2.21
А,...
10 х,Ю см
принято а — 1, сплошная линия на графиках отвечает значению
fl = 0,5, штриховая — j} = 0, штрихпунктирная—[} = 1. Значения
физических параметров, таких как G, То и т. д. соответствуют
атмосфере Солнца. Для расчета ударных волн введена искус-
142
«твенная вязкость. Рис. 2.21 показывает, что расчеты с разными
значениями [} заметно различаются. В случае Р = 1 газ за фрон-
фронтом ударной волны имеет большую энергию, а в случае Р = 0 —
меньшую чем при Р = 0,5. Это следствие того, что в первом слу-
случае фиктивный источник E.22) положителен, а во втором —
отрицателен. В расчетах, представленных на рис. 2.21, шаг сетки
по времени выбран достаточно большим, с тем чтобы проявилось
влияние дисбаланса б^Гь При измельчении т результаты расче-
расчетов с [3 = 0 и (} = 1 приближаются к результатам расчетов с
Р = 0.5.
§ 6. Разностные схемы для уравнения теплопроводности
1. Консервативная схема для уравнения теплопроводности.
Выше были рассмотрены некоторые способы построения разно-
разностных схем, аппроксимирующих систему одномерных нестацио-
нестационарных уравнений газодинамики без учета реальных диссипа-
тивных процессов. Обратимся теперь к случаю, когда в задаче
присутствуют процессы теплопроводности. Изменится лишь урав-
уравнение энергии, которое для одномерного плоского случая имеет
вид
где е(Г)—удельная внутренняя (тепловая) энергия, W =
=—xpdT/ds — поток тепла. Введем обозначение к = рк(р, Т).
С учетом сказанного имеем
де dW IR 0,
W = -k%. F.3)
Здесь / = — р dv/ds — источник энергии газодинамического проис-
происхождения (в этом параграфе его мощность мы будем считать
известной)- Квазилинейное (коэффициент к, вообще говоря, есть
функция температуры) уравнение параболического типа F.2) и
является уравнением теплопроводности. В интегральной форме
это урамноние выглядит следующим образом
;, ds -W dt -.-. \ 1 / (.?, /) ds dt, F.4)
где С—замкнутый кусочно-гладкий контур, ограничивающий на
плоскости (.?. t) облает?. G.
В соответствии с идеей интегро-интерполяционпого метода
(см. § 2, п. 4) используем интегральное уравнение F.4) для
построения консервативной схемы. Введем в рассматриваемой
части плоскости (s, t) сотку
(О = { (St. t}). (Si+1/2, tj), Si+l = Si + hh Si+i/2 = Si + 0,ohi,
i-0, 1 N-i, ts+i = ti + T,,j = O, 1, .-.}
143
Сеточную функцию потока тепла W\ будем относить к узлам
сетки (su tj), а к полуцелым точкам (s(+i/2, tj)—температуру
T'i+i/2 = Т\, внутреннюю энергию fij+i/a = &{, коэффициент тепло-
теплопроводности /4+1/2= к\, который определяется значениями темпе-
температуры Т\, и плотности р1!, и источник газодинамической энергии
/i+i/2 = 7i (см. рис. 2.22). Далее черточки над функциями к, /,
е, Т и т. д. мы опусим.
Применим интегральное уравнение F.4) к контуру С, охва-
охватывающему элементарную ячейку разностной сетки (рис. 2.22).
При этом испольнуем следующий способ вычисления интегралов,
входящих в F.4):
Ч+i
j W (Si, t) ds'as [aWi+1 + A - a) W{] T,-
4
f{s,t)dsdt^]ihixj.
Здесь 0 ^ a < 1 — свободный параметр, позволяющий варьиро-
варьировать интерполяцию сеточной функции W. Способ вычисления
газодинамического источника ]{ подробно описан в предыдущих
i+¦'/?. /+/
Рис. 2.22
параграфах. Учитывая все сказанное, приходим к следующему
разностному уравнению, аппроксимирующему дифференциальное
уравнение F.2):
\-A—О) т- + /г+1/2-
'J L I
или в безындексной форме
144
@.5)
F.5')
Построим теперь разностное уравнение для теплового потока
F.3). Проинтегрируем для этого на временном слое t, по отрезку
st-i,2 < s < S.+1/2 уравнение дТ/ds = —Wjk, вытекающее из F.3).
Получим
г K,
ii-u% = j k ^ j.j as.
ai—1/2
Считая, что функция W в промежутке Si-i/2< s < si+i,2 имеет
постоянное значение, равное W\i имеем
i+i/2 - TU1/2 = - W\
и далее
(G-0)
Напомним, что безындексное обозначение уу соответствует раз-
разностной левой производной, вычисленной на перанномерной сет-
сетке. Здесь
" -1
ds
а\
0,5 (Aj-r
! f
"Г "i_i) J
*(*,«.)
(fi.7)
Величину j ds/k называют тепловым сопротивлением отрезка
2. Аппроксимация коэффициента теплопроводности. Интеграл
в выражении F.7), аппроксимирующем коэффициент теплопро-
теплопроводности, можно заменить различными разностными соотноше-
соотношениями, например:
4+1/2
f EL = _
si+l/2
Л л Л
ds_= ds^ ds^
J к J A ' J Л
•{+1/2
«i-l/2 «i-l/2
ГДе ai±l/2 == A (p(±i/2) li±\[2)-
10 Л. Л. CnMipcritrt, TO. П. Попов
145
Соответственно коэффициент а\ будет иметь вид
а1- = №- d- = kj-
г.;
F.8)
где к =
— интерполяция коэффициента те-
плопроводности в целую точку на неравномерной сетке. Заметим,
что приведенные формулы F.8) для вычисления коэффициента
теплопроводности а\ в некоторых условиях могут оказаться не-
неэффективными. Действительно, пусть / = 0, а коэффициент теп-
теплопроводности к зависит от температуры так, что при Т = О об-
обращается в нуль (к = 0). Рассмотрим задачу о распространении
температурной волны по холодно-
холодному фону (Г = 0). Она имеет в этом
случае конечный фронт (см. подробнее
в п. 4). Предположим, что в некоторый
момент времени фронт тепловой (тем-
(температурной) волны, распространяющей-
распространяющейся направо, совпадает с г-м узлом сет-
сетки, так что Г.+1/2 = 0, a TVi^^O
(рис. 2.23). В этом случае разностный
коэффициент теплопроводности к\, вы-
вычисленный по второй и третьей фор-
формулам F.8), тождественно равен нулю,
ибо ki+l/2 = k(T{+i/2) = 0. Поэтому по-
поток тепла W\ в узле i также будет ну-
что тепло никогда не проникнет в
интервал hi сетки и температура
i-f
i+f
Рис. 2.23
левым. Это означает,
следующий массовый
TVi/2 здесь так и останется нулевой. Такая картина, полученная
в рамках дискретной модели, противоречит физическому смыслу.
Очевидно, перная и третья формулы F.8) приведут к аналогич-
аналогичному результату при расчете тепловой волны, распространяю-
распространяющейся налево.
Избежать подобных недостаткон можно, воспользовавшись
для вычисления а\. например, формулой, представляющей собой
полусумму первых двух соотношений на равномерной сетке в
F.8):
4 = {Н-1/*+к{+1/2)/2. @.0)
В силу того, что коэффициент теплопроводности записит от тем-
температуры и плотности ki+[/2 = k(Ti+l/2, pi+i/2)= k(Ti, p;), коэф-
коэффициент a\ разпостпого уравпепия n г-м улле п F.9) будет оп-
определяться значениями температуры и плотности в соседних
полуцелых точках и\ — а{Т\, ~Т\_Л, р]. p;_i).
146
Сводя вместе разностные уравнения F.5) и F.6), имеем
е< = — W[a) + /, W = — аТ~ (ОАО)
или, после исключения функции W,
Использование интегро-интерполяционного метода позволило
построить консервативную схему для уравнения теплопроводно-
теплопроводности F.2), F.3), имеющую второй порядок аппроксимации по
пространству О(h2) на равномерной сетке. Значению о = 0 в
F.10), F.11) отвечает явная схема, а значению о = 1 — чисто
неявная схема; обе они имеют порядок аппроксимации О(т).
При а = 0,5 получаем схему второго порядка аппроксимации по
времени 0(т2); ее называют симметричной схемой или схемой
К ранка — Николъсона.
Заметим, что разностные уравнения F.10) и F.11) записы-
записываются одинаково во всех точках сетки, даже если коэффициент
теплопроводности разрывен. Поэтому сформулированная схема
является однородной.
3. Формулировка краевых условий. Постановка задач для
уравнения теплопроводности в ограниченной пространственной
области включает формулировку краевых и начальных условий.
В качестве начальных данных обычно задается распределение
температуры среды
T(s, 0)=q>(«), 0<s<M,
или, в разностной форме,
T°i+i/2 = Ф (*+i/a), i = 0, 1, ..., N - 1. F.12)
Краевые условия в зависимости от конкретных физических
особенностей задачи могут иметь различный вид.
Весьма распространенными являются задачи, где на границах
рассматриваемой области заданы режимы изменения со временем
температуры (I краевая задача):
Г@, t)=B*(t), T(M, t) = Q**{t), F.13)
или теплового потока (II краевая задача):
W@, t)=w*(t), W(M, t)=w**(t). F.14)
Встречаются и более сложные случаи, когда на границе за-
задается связь между тепловым потоком и температурой:
W@, t)=w*[T@, I), t], W(M, t)=w**[T(M, t), t]. F.15)
Функции w* и w**, вообще говоря, являются нелинейными.
Примером может служить задача, в которой масса газа излучает
с границы как абсолютно черное тело:
W@, t)=—aoT*{O, t), W(M, t)~o0T*(M, t),
где (To — постоянная Стефана — Больцмана.
10* 147
Возможны также комбинации условий F.13) — F.15) на пра-
правой и левой границах.
Обратимся к способам записи краевых условий в разностной
задаче. Уравнение F.10), или F.11), записанное, как и исходное
уравнение энергии, в полуцелой точке, рассматривается на рас-
расширенной сетке, включающей фиктивные крайние интервалы
/i_i =0 и йу — 0. Значения температуры в этих интервалах фак-
фактически совпадают со значениями температуры в граничных уз-
узлах сетки (рис. 2.2/i): Т3_г — Т}й. f3N ¦¦= T3N. Поэтому краевые
о—ж—о—к—о—х--о
N-1 N N+f
Рис. 2.24
условия F.13) в разностном виде выглядят следующим образом
TU == е* (/,-), fit = е** ц,). F.16)
Условия F.15), включающие как частный случай F.14), при-
приобретают форму
Wj0 = w* (fU, /,-). WjN = U;** (fjN, t}). @.17)
Способы решения разностных уравнений F.10) при краевых
условиях F.16), F.17) будут изложены ниже з § 5 гл. IV.
4. Некоторые аналитические решения. Выяснение эффективно-
эффективности выбранного численною алгорима, особенно для случая не-
нелинейных уравнений, обычно проводят на примере расчета не-
некоторых тестовых задач, допускающих точные аналитические
решения. Для уравнения теплопроводпости таким тестом может,
в частности, служить задача о прогреве среды, заполняющей
полуограниченное пространстио s > 0, потоком тепла, поступаю-
поступающим через левую границу — неподпижпую степку s = 0. В силу
того, что движение здесь не принимается во внимание, различие
между эйлеровой и лагранжевой массовой координатами несу-
щестнеппо.
Предварительно укажем некоторые частные решения уранне-
niiii (В.2), (G.3). Пусть для простони е(Т) = Т, а коэффициент
теплопронодпости янляется степенпой функцией температуры:
к = коТа. Тогда для урагшения
dt ds \ " ds
можно искать аптомодельпое решепие типа «бегущей полны» в
виде T(s, t)=T(c,), где c,=s-Dl (см. подробнее гл. I, § 6, где
подобное автомодельное решение строится для уравнепий газо-
дипямики). Выполнив указанную зямепу переменных и проведя
148
несложное интегрирование, получаем функцию
11/а
F.19)
которая удовлетворяет уравнению F.18). Здесь si— произволь-
произвольная постоянная.
Другое частное решение уравнения F.18) можно построить
методом разделения переменных. Положим T(s, t)=v(s)Q(t) и
подставим этот предполагаемый вид решения в F.18). После
стандартных операций приходим к двум обыкновенным диффе-
дифференциальным уравнениям
Л. (к v" —\-Xv — - Я01+« F 20)
ds \ ° ds ) dt ч '
где ?»— параметр разделения. Интегрирование уравнений F.20)
приводит к выражению
Г a(s — s\2 11/<х
где S| и с — постоянные интегрирования. Заметим, что частным
решением F.18) является также тривиальное решение
T(s, 0=0. F.22)
Из построенных частных решений при соответствующем под-
подборе начальных и граничных условий можно сконструировать
решение указанной выше задачи о прогреве среды. Так, напри-
например, функция, скомбинированная из частных решений F.19)
и F.22),
[~2р (дг .ц .5. _ ,s.)j1/a „piI о < s < Sl + Dt,
0 при s > s, + Dl
Г
A5.23)
представляет собой решение следующей задачи
/в4т ¦ *>0,
at
Г @,0 =
7-(я.0) =
(fi.24)
?) . . li/а
о,
Начальные данные и ь-раопое услоние заданы, исходя из конк-
конкретного вида решения (В.23). Решение (В,23) представляет со-
собой температурную волну, распространяющуюся от стенки, гре-
romeii среду, паправо. Заметим, что эта температурная полна
имеет, как говорят, конечный фронт,— точка, где температура
149
обращается в нуль, движется с постоянной скоростью D. При-
Причина того, что скорость распространения тепла в рассмотренной
задаче конечна, кроется в нелинейной зависимости коэффициен-
коэффициента теплопроводности от температуры. Как известно [93], в клас-
классическом линейном случае скорость распространения тепла бес-
бесконечна.
Аналогично функция
F.25)
12*в(а+2)(;-0] ПРИ ^
О при s
является решением задачи
Г<*'^2*. («+"') (с-
F.2C>
T(s,0) =
2*n (« + 2)
0
Решение F.25) описывает остановившуюся температурную
волну. Несмотря на то, что в среду через границу s = 0 со вре-
временем поступает тепло, температура в области s > si остается
нулевой.
Т
0,5 s
Рис. 2.25
Решения F.23) и F.25) приведены в [86]. Оттуда же взяты
рис. 2.25, а и б, на которых эти аналитические решения Сопо-
Сопоставлены с результатами численного решения задач F.24) и
150
F.26) соответственно. Параметры задачи имеют здесь следую-
следующие значения: для задачи F.24) (рис. 2.25а): а = 2, ка = 0,5,
^4=0, D = b\ для задачи F.26) (рис. 2.25,6): а = 2, /с0 = 0,5,
*i=0,5, с = 0,1125.
Тот факт, что коэффициент теплопроводности, зависящий от
температуры, обращается в нуль на фронте температурной волны,
вынуждает использовать в расчетах для вычисления коэффици-
коэффициента а\ формулу F.9) или же определять значение а\ по сред-
пеп температуре
(т w hlTl-\l2 ~~ Аг-1Г/+1/2
nt т^ пг — 1
Результаты, полученные в гл. II, относятся к одномерным
нестационарным уравнениям газовой динамики, записанным в
лагранжевых массовых координатах. Однако высказанные идеи
и принципы могут быть использованы и для других случаев.
Так, например, в [68] рассмотрены вопросы, связанные с по-
построением полностью консервативных разностных схем для од-
одномерных нестационарных уравнений газодинамики, записанных
в переменных Эйлера.
Однако, попытка построить такие схемы в рамках семейства
двухслойных (по времени) разностных схем не привела к ус-
успеху. Более того, в [49] показано, что весьма широкое семей-
стно двухслойных разностных схем для уравнений газовой
динамики в переменных Эйлера не содержит полностью консер-
консервативных схем. В [50] построена явная трехслойная схема, об-
обладающая свойством полной консервативности. Однако примене-
применение на практике подобных схем для решения газодинамических
уравпешш, содержащих лишь первые произйодные по времени,
порождает, как известно, определенные трудности.
Построить двухслойные полностью консервативные разно-
разностные схемы для уравнений газодинамики в переменных Эйлера
удается с помощью специального подхода [43]. Он основан на
использовании в разностных уравнениях у членов, которые со-
содержат пространственные производные, временных весов, явля-
являющихся функциями решения. Указанный подход легко обобща-
обобщается на многомерный случай.
ГЛАВА III
УСТОЙЧИВОСТЬ РАЗНОСТНЫХ СХЕМ
ГАЗОВОЙ ДИНАМИКИ
В глапе III на примере линейной модели уравнений газоди-
газодинамики выполнен анализ устойчивости различных разностных
схем. § 1 посвящен общим вопросам и определениям. Примени-
Применительно к одному линейному уравнению переноса продемонстри-
продемонстрированы особенности различных приемов исследования устойчи-
устойчивости разностных схем,— спектрального метода, принципа мак-
максимума (§ 2) и энергетического метода (§3). В § 4 рассмот-
рассмотрена устойчивость разностных схем для уравнений акустики.
В § 5 даны примеры влияния вязкости на устойчивость схемы.
В § 6 получены условия устойчивости для уравнения теплопро-
теплопроводности, отмечены вопросы, связанные с асимптотической ус-
устойчивостью.
§ \. Понятие устойчивости разностной схемы
1. Сходимость схемы. Метод конечных разностей представляет
собой способ «вычисления» приближенного решения дифферен-
дифференциальной задачи. Естественно, что такое приближенное разно-
разностное решение должно быть близко к точному решению, причем
различие между ними должно уменьшаться по мере дробления
сетки. Такое свойство разностной схемы, с помощью которой по-
получено приближенное решение, называется сходимостью схемы.
Строго понятие сходимости формулируется следующим обра-
образом. Пусть в области G пространства х = (х\, ..., хР) с грани-
границей Г требуется найти решение дифференциального уравнения
и(х, I)
i? = Lu-'r f(x,t), xseG, 0<г<7', A.1)
удонлетпоряющее некоторым краевым
1и = ц(х, t), х^Т, 0«5?«5Г, A.2)
и начальным условиям
и(х, 0) = щ(х), x^G, A.3)
где L и I — дифференциальные операторы по переменной х;
f(x, t), \i(x, t) и uq(x)— заданные функции («входные данные»
задачи).
Область G + T непрерывного изменения аргумента заменяет-
заменяется дискретным множеством точек — сеткой «л = (О;, + fj,, («л —
множество внутренних узлов сетки х{, ^ — совокупность точек
сетки, принадлежащих границе Г). Отрезок времени 0 ^ t < Т,
ыа котором рассматривается решение задачи, также разбивается
на конечное число интерпалов — вводится сетка по временной
переменной t: ыг = {?,-, / = О, 1, .. .}. Пусть h—шаг сетки по
пространству, т. е. параметр, характеризующий плотность рас-
расположения узлоп сетки шл п G + Г, т — шаг сетки по времени:
LjV\ — ij = т. В общем случае шаги сетки переменны, т. е. сетка
неравномерна. Исходную дифференциальную задачу на сетке
<а = «л X й)г аппроксимируем, например, разностной схемой (см.
A.18) гл. II):
у, = LhyM+<{:, Х;^Шь, ^еиг, A.1'У
Ly = \, Xi^tb, tj<^a)r, A.2')
y° = vOi x,eb)hi y = o, A.3')
tj\o yi — сеточная функция, аппроксимирующая решение диффе-
дифференциальной ладами и, Lh, и lh—некоторая разностная аппрок-
ошация операторов L и /, ф, v, v0—заданные сеточные функ-
функции, аппроксимирующие «входные данные» дифференциальной
ля дачи /, ц, ио.
Очевидно, рассматримаемие niiMH одномерные нестационар-
нестационарные задачи газовой динамики и разностные схемы их решения
укладываются в приведенные общие операторные формулировки.
Говорят, что решение разностной задачи A.1') — A.3') схо-
сходится в некоторой сеточной норме к решению дифферепциаль-
пой задачи A1) — A-3), если для любого tj (О <С tj <C ij =7")
имеет место
|! и (хи tj) — y\l -v 0 при /г->0, т->0, (l/i)
т. е. п.'шельчепие сетки, и тем самым увеличение количества уз-
узлоп сотки (например, числа временных слоев /о), приводит к
ноограничснному сближению разностного и дифференциального
pemeHiiii. Если при ато.м
то говорят, что схема A.1') — A-3') имеет точность m по вре-
времени и п — по пространству.
Как правило, и нелинейных задачах математической физики,
конфыо п представляют практический интерес, обосновать схо-
сходимость схемы, т. е. доказать справедливость условия A.4), ока-
оказывается затруднительным.
Иногда ни практике наполнение лого условия пытаются про-
проверить экспериментально, проводя серию расчетов задачи по
одной и топ же схеме и последовательно сгущая пространствен-
пространственную сетку, дробя шаг сетки h в 2, 4, 8 и т. д. раз. Оценивая
153
количественные различия в полученной последовательности раз-
разностных решений, делают выводы о сходимости схемы, и порой
даже о ее точности. Однако если говорить строго, вряд ли та-
такой путь может дать ответ. Действительно, в § 2 гл. II был
приведен пример, когда разностное решение при дроблении шага
стремится к функции, не имеющей ничего общего с решением
исходной дифференциальной задачи. Указанный выше «экспери-
«экспериментальный» способ проверки сходимости в этом случае зафик-
зафиксирует сближение последовательных разностпых решений, одна-
однако принять этот факт за подтверждение сходимости схемы было
бы опрометчиво.
С другой стороны, как будет показано ниже, условно устой-
устойчивости многих схем требует при дроблении пространственной
сетки соответствующего измельчения шага по времени. В про-
противном случае сходимость схемы может быть нарушена. Воз-
Возможность же «уловить» экспериментально указанную связь меж-
между шагами сетки по нремеип и пространству представляется
весьма проблематичной, тем более в задачах с сильно неодно-
неоднородными профилями параметров.
2. Корректность и устойчивость схемы. Принятым методом
проверки сходимости разностной схемы является теоретическое
исследование ее свойств аппроксимации и устойчивости, нали-
наличие которых оказывается необходимым и достаточным условием
сходимости.
Проверка аппроксимации разностной схемы достаточно про-
проста и сводится фактически к разложению решения в ряд Тей-
Тейлора.
Основной интерес и основную трудность представляет иссле-
исследование устойчивости схем. Понятие устойчивости разностной
схемы является составной частью определения корректности раз-
разностной схемы. Напомним содержание определения корректно-
корректности применительно к задачам математической физики для не-
непрерывного случая.
Задача A-1) — A-3) считается поставленной корректно, если
выполнены два условия:
1) задача однозначно разрешима при любых входных данных,
из некоторого класса,
2) решение задачи непрерывно зависит от входных данных.
По аналогии определяется и корректность разностной задачи.
Ра.чностная задача A.1') — A-3') поставлена корректно, если при
любых достаточно малых шагах сетки:
1) решение у существует и единственно при всех входных
данных из некоторого допустимого семейства,
2) решение у непрерывно зависит от входных данных, при-
причем ата зависимость равномерна относительно величины шагов
сетки.
Второе условие означает, что существуют такие постоянные
Mi > 0, Mi > 0, Л/з > 0, не зависящие от h, x и от выбора вход-
входных данных (при достаточно малых h и т: \h\ < ho, т<То), что
154
справедливо неравенство
\y(t)-y (t) ||A) < My I v0 - v0 [A) + M2 max J ф (Г) - cp (t') |B) +
+ M3 max |v(O-v(f')l. * = *i- A-5)
Здесь г/ и у — решения разностной задачи A.1') — A.3') с вход-
входными данными соответственно vo, cp, v и i>o, ф, v; II-II<i>, И-Nf2> —
некоторые нормы в пространстве сеточных функций. Свойство
разностной схемы, выраженное неравенством A.5), и называется
устойчивостью схемы A.1') — A.3') по входным данным или про-
просто устойчивостью.
Неравенство
Н0(ONi, <ВДо-ио11м) A.6)"
выражает устойчивость схемы по начальным данным (ф = фэ
= 0, v = v = 0).
Неравенство
l?@-tf@llci)<Ms max 1ф(О-Ф(«'I(« A-7)
означает устойчивость по правой части (v = vo=O, v=v = 0).
Неравенства типа A.5) — A.7) называют также априорными
оценками для схемы A.1) — A.3). Построению подобных апри-
априорных оценок и посвящена в оснопном теория устойчивости раз-
разностных схем *).
В этой глапе в основном будет рассматринаться задача Коши.
В общей теории устойчивости доказывается, что для линейных
задач схемы, устойчипые по начальным данным, устойчивы и
по правой части [80]. Поэтому и дальнейшем мы ограничимся
глатшым образом исследованием устойчивости разностных схем
по начальным данным.
Заметим, что в случае линейных операторов Lh и lh оценка
устойчивости по начальным данным может быть записана в виде
lly'll «S МХЦЧ. A.6')
Для задач гиперболического типа и, в частности, для задач
газовой динамики без учета диссипативных процессов, постоян-
постоянная в A.6') равна единице:
\\у3\\ «S ЦЧ. A-6")
Если справедлшю неравенство тппа
ll!/J+1ll S? ll^ll. A.8)
то гопорят, что схема равномерно устойчива но начальным дан-
данным; действительно из A.8) сразу же следует 11г/)+1Н < \\уЧ. Од-
*) Вопросы устойчивости разностных схем подробно рассмотрены в кни-
книгах [77, 78, 80].
155
нако соотношение A.8) гарантирует нечто большее: ненараста-
ненарастание не только начальных ошибок, но и погрешностей, внесен-
внесенных на любом промежуточном временном слое.
Существуют и другие типы устойчивости. Например, в даль-
дальнейшем мы встретимся с оценкой устойчивости вида (р — устой-
устойчивость)
\\yi+[\\ < plly'W, A.8')
где р = ес°х, т — шаг сетки по времени, Со > 0 — постоянная,
не зависящая от шагов сетки. И хотя р > 1, оценка A.8') обес-
обеспечивает выполнение неравенства A.С) с константой М\, оп-
определяемой из следующего условия pj <^ecoJl = ег'»т =-- \[1, где
Т — промежуток времени 0 < t, «S Т, на котором рассматривается,
решение.
3. Акустика — линейная модель газодинамики. В общем слу-
случае исследовать устойчивость ра.чностных схем газовой динами-
динамики не удается в силу больших трудностей, порождаемых нели-
нелинейностью уравнений. Это обстоятельство вынуждает ограничить-
ограничиться рассмотрением линейного приближения газовой динамики —
акустикой (см. § 4 гл. I). Таким образом, о сходимости разно-
разностной схемы газовой динамики приходится судить по тому, как
эта схема «работает» в частном случае акустики, т. е. насколь-
насколько хорошо схема воспроизводит процесс распространения малых
возмущений.
В акустическом приближении уравнения газовой динамики
сводятся к одному уравнению гиперболического типа второго
порядка (уравнению струны, D.A) гл. I) для возмущеиия лю-
любого из газодинамических параметров. Решение этого уравнения
представляет собоГг две волнг.1 с неизменным профилем, которые
распространяются в противоположные стороны со скоростью'
звука.
Уравнения акустики могут быть записаны также в виде си-
системы двух уравпений первого порядка
аи да да . чп oi> .. ,-..
77 =-17' ^f=-(coPo)--^- A.9)
Здесь v и р — амплитуды возмущения скорости и давления в
акустической волне, распространяющейся по однородному газу
с параметрами ро, vq".
v(s, t)=-vo + v(s, t), p(s, t)=po + p(s, t).
Co = T'lfpo/po — адиабатическая скорость звука, a = copo — массо-
массовая скорость апука, т. е. скорость, с которой возмущение ла-
хватывает новые массы газа, перемещаясь от частицы к частице.
Малость возмущения характеризуют неравенства типа
\р/ро\<1. A.10)
Обычно, изучая устойчивость разностных схем газодинамики
на модельном примере — акустике, аппроксимируют диффе-
156
ренциальные уравнения A.9) разностными схемами, например
семейством схем вида
Zt = -y.*\ pt = -a*Z<*\ A.11)
где a. fJ — свободные параметры.
Однако аппроксимация линейных дифференциальных уравне-
уравнений акустики конечно-разностными соотношениями — операция
не вполне законная. В самом деле, как дифференциальные урав-
уравнения газодинамики, так и разностная схема являются некото-
некоторыми самостоятельными математическими моделями сплошной
среды и протекающих в пей процоссоп. Несмотря на то, что обо
эти модели описывают одну и ту же физическую реальность,
разностные схемы, определяющие дискретную модель, имеют
свои специфические особенности. Так, в гл. II показано, что
различные возможные разностные схемы не эквивалентны, мно-
многие из них порождают своеобразные эффекты разностного про-
происхождения, не имеющие аналога в реальном случае, например
фиктивные источники энергии. На грубых сетках, которые и
используются на практике, такая «разностная физика» может
заметно исказить изучаемое явление.
Неустойчивость разностной схемы есть также проявление ео
внутренних свойств, отражающих дискретный характер модели
и заключающихся в том, что различные погрешности, неизбеж-
неизбежно сопровождающие процесс вычисления решения, имеют тен-
тенденцию к неограниченному нарастанию.
Уравнения акустики A.9) получены линеаризацией общих
дифференциальных уравнений газовой динамики и описывают
процесс распространения малых возмущении при использовании
непрерывной модели среды. Рассматривая тот же физический
процесс в рамках дискретной среды, мы должны в предположе-
предположении о малости амплитуды возмущенна линеаризовать систему
разностных уравнений газодинамики и полученную линейную
разностную схему считать дискретным аналогом акустики. Ана-
Анализ покапывает, что полученная таким образом схема эквива-
эквивалентна A.11) лишь при достаточно малом шаге сетки т, причем
характер малости определяется условием A.10): т ~ О(р/ро)*).
В дальпойшем мы будем рассматрнпать устойчивость семей-
семейства разностных схем A.11). Для удобства переобозначим се-
сеточные функции
v = — v, u = /5/a, a = const > 0. A-12)
Теперь система разностных уравнений акустики принимает сим-
симметричный вид
Отметим, что мы рассматриваем простейшим случай: устой-
устойчивость по отношению к возмущениям однородного состояния
*) Отметим, что для полностью консервативных схем такая оквива-
лептпость имеет место и для грубых сеток (при любых т).
157
газа, т. е. устойчивость постоянного решения. Возможно иссле-
исследование устойчивости и для других случаев, например на изве-
известном решении задачи о структуре фронта ударной волны. При
этом существенно усложняется техническая часть анализа,—
в системе линейных уравнений A.13) появятся дополнительные
члены, связанные с дифференцированием исходного решения;
кроме того, коэффициенты уравнений становятся функциями
пространства и времени.
Л. Линейное уравнение переноса. Для того чтобы нагляднее
вскрыть существо вопроса и продемонстрировать особенности
различных методов исследования устойчивости разностных схем
газонон динамики, часто обращаготся к простейшему случаю,—
линейному однородному уравнению переноса:
A.14)
да
ди
а 17 =
Для этого уравнения в области— °° <s < °°, t > О рассматри-
рассматривается задача Коши: при L = О решение удовлетворяет некото-
некоторым начальным данным
в (я, О)=ио(«). A.15)
Коэффициент а, который для простоты мы будем полагать по-
постоянным, может иметь любой знак.
Решение задачи A.14) — A.15) представляет собой волну
u(s, t)=-vo(s -at), A.16)
распространяющуюся со скоростью а. Профиль волны задан на-
начальными данными A.15). Линии s — at = const, вдоль которых
Рис. 3.1
переносятся постоянные значения решения, являются характери-
характеристиками (рис. 3.1). Для вычисления решения A.16), Еюнечно,
но нужно строить разностные алгоритмы и писать программы
для ОВМ. Однако изучение разностных схем, аппроксимирую-
аппроксимирующих задачу A.14) —A.15), имеет определенный методический
интерес. Исследованию уравнения переноса — отой простейшей
модели уравнений газовой динамики — посвящена обширная ли-
литература.
158
§ 2. Устойчивость разностных схем для уравнения переноса.
Спектральный метод и принцип максимума
1. Разностные схемы для уравнения переноса. Рассмотрим раз-
постные схемы решения задачи Коши для уравнения переноса
да ди „
-^-+а— =0, — oo
oo,
B.1)
u(s, 0) = vo(s).
В области G = {—°о < s < °°, t > 0} введем равномерную сет-
сетку 0) = (Ол X СО г,
соЛ = {.<?* = М, к = 0, ±1, ±2, ...},
сох = и, = /т, у = 0, 1, 2, ...}.
Сеточпую функцию у, аппроксимирующую решепие и дифферен-
дифференциальной задачи, отнесем к узлам (sk, tj) сетки: y = y(f>k, Ь) —
к-1
— Ук = У*)- Сформулируем две янпые разностные схемы решения
задачи B.1). Первая схема
J+1 _ J J —vi
УЛЛ* + а Ук+\ Ук
+ а
\
= О, к = 0, ± 1, ± 2, ..., У = 0, 1, ...,
B.2)
4 л = о, ±1, ±2,...
Опа определена па шаблоне, изображенном па рис. 3.2, а. В бе-
зыпдекспой записи схема B.2) имеет вид
yt + ay. = O. B.2')
Вторая схема
у*+1~у* + ау*~ЛУ*-1=я0, А = 0, ±1,..,, / = 0, 1, ..., B.3)
S = uo(*n). /ь = 0, ±1, ±2, ...
*) Далее в отой главе нижнпй пространственный индекс у сеточных
функций будем обозначать через к, оставив символ i для обозначения мпи-
ыой единицы.
1S9
В безындексной форме
yi + ау-=0. B.3')
Эта схема определена па шаблоне (рис. 3.2.6). Обе схемы име-
имеют первый порядок аппроксимации O(h + r), и формальное раз-
различие между ними состоит лишь п способе записи разностной
производной по пространству,— в одном случае это правая про-
пгнюдная (схема B.2)), в другом - леная B,3). Тем не менее
и смысле устойчивости эти схемы отличаются радикально: при
я >0 первая из них всегда неустойчива (абсолютно неустойчивая
схема), вторая — устойчина при определенном соотношении на
шаги сетки /гит (услопно устойчииая схема).
2. Метод гармоник. Решение дифференциальной задачи Коши
B.1) при некоторых предположениях относительно его гладко-
гладкости можно цредстанить и инде интеграла Фурье
u(s. /)=—?=- С »-(Н. /)eio*d0. B.4)
— ос
Функция и;@, t) удовлетворяет уравнению
dw @. t) , . „ . ,о _,
—-—¦ -- iaQw @. t) = 0, B,;.j)
at'
которое получается после подстанош.и B.4) в исходное урап-
иенне B.1). Решая B.5), найдем:
гг(О, 0= w(Q, 0)e-'"9(,
где г^@, 0) определяется по начальным условиям. Окончатель-
Окончательно решение заиисыиастся следующим образом
и (s. I) = —^= \ и
Kai; гонорят, решение линейной задачи B.1) представимо в ви-
виде супернолпции монохроматических бегущих воли пли гармоник
и; @, О)в;в(>-0|). B.6)
Поэтому и линейном случае о спопстиах решепня часто судят
по понедению совокуииости гармоник* B.(i).
Метод изучения устойчивости ра.аюстпмх схем, носящий па-
зиапие метода гармоник, оснопяп па нспол^.'шнашш аналогичных
иредстанлепий для дискретного случая. Об устойчивости схемы,
т. е. об ;жолюции но нремепи полученного с помони>ю этой схе-
мм parmocTiioro решения, судят по поведению частных сеточных
решении, имеющих вид ра.чпострюй гарлгоншеи:
г/?, = V (ц)е{^е1кч> = \'ц^\ ц = е'^. с -- е'"<. B.7)
Для простоты можно считать V = 1. Здесь г — мнимая единица,
160
к и / (пространственный и временной номера узла сетки) яв-
являются показателями степени q и § в правой части B.7), <р —
произвольное действительное число. Сеточная функция у явля-
является периодической по пространству. Величина i|)(<p) и тем са-
самым <?(ф)—комплексное число, которое подбирается так, чтобы
гармоника B.7) действительно была решением, т. е. удовлетво-
удовлетворяла разностному уравнению.
Заметим, что | = cos <р + i sin<p и lgl=l. В то же время
величина Igl может принимать любое значение (положитель-
(положительное). Если окажется, что для некоторых cpU/(cp)|>l, то соот-
соответствующие гармоники со временем будут неограниченно на-
нарастать. Это означает нарушение неравенства A.6') и свиде-
свидетельствует о неустойчивости схемы на решениях частного вида.
Неустойчивость схемы в частном случае порождает неустойчи-
неустойчивость н общем случае,— ведь общее решение может содержать
«неустойчивые гармоники» с \д\ > 1.
Если при любых значениях <р имеем |д|<1, то все гармо-
гармоники B.7) ограничены. Однако отюда еще не следует ограни-
ограниченность общего решения. Поэтому условие lgl>l представля-
представляет достаточное условие неустойчивости (l^l^l— необходимое
условие устойчивости), а метод гармоник позволяет устанавли-
устанавливать неустойчивость схем.
3. Анализ устойчивости схемы yt + aya = 0. Воспользуемся
описанным выше методом гармоник для анализа устойчивости
разностных схем для уравнения переноса. Рассмотрим схему
B.2), использующую правую разностную производную по про-
пространству:
!А+1->А Vk+i-Vk = 0
т А
Пусть для определенности a > 0. Подставим в разностное урав-
уравнение частное решение — гармонику у& = qi?,':
т А
Сокращая па qj%k Ф 0, получим q = 1 + 7 A — §) = A + 7 —
— 7 cos ф) — if sin ф, где 7 = aj/h — параметр, характеризующий
схему. Итак, гармоники, в которых для каждого ф значение q
определяется по указанной формуле, являются частными реше-
решениями исходного разностного уравнения. Вычислим квадрат аб-
абсолютной ьелнчипы ц:
1г/12 = A + 7 — 7 COS фJ + 7281П2ф = 1 + 47G + 1)з1п2(ф/2).
В силу того, что a > 0, параметр 7 также положителен; это оз-
означает, что независимо от соотношения шагов сетки /гит при
всех ф таких, что sin(<p/2):?t0) имеет место неравенство |gl>l.
Необходимое условие устойчивости не выполнено, схема B.2)
всегда неустойчива. Неустойчивость такого типа называется аб-
11 А. А. Самарский, Ю. П. Попов 161
солютпой неустойчивостью,— ее не удается избежать никаким
дроблением сетки.
4. Спектральный метод. Предложенные разностные схемы
B.2) и B.3) для численного решения уравнения переноса фор-
формально могут быть записаны в операторном виде:
Л+1 = SyK у> = [yl р = к - и„ ..., к, ....к + п2]. B.8)
Числа П\ и п2 определяются шаблоном, на котором построена
конкретная разностная схема. Оператор S, называемый операто-
оператором перехода с одного временного слоя па следующий, позво-
позволяет в результате последовательного применения трансформиро-
трансформировать начальные данные в разностное решение па любом шаге
по времени. Для линейных схем оператор S липееп.
Очевидно, разностная схема, операторную запись которой
представляет равенство B.8), будет устойчива по начальным
данным, если оператор S по норме ограничен единицей:
Ш s= 1. B.9)
Действительно, в этом случае имеем
s IIуЦ\.
Таким образом, условие B.9) обеспечивает равномерную устой-
устойчивость схемы по начальным данным: Hj/J+1ll < Wy'W < ... ^ \\у°\\.
Если же вместо B.9) выполнено соотношение II5H < 1 + сот
(со>О — постоянная, по зависящая от h и т), то оценка устой-
устойчивости изменится:
I y'3+1 IK A + сот) I1, у' | < есох |! у' |<...< ec°(j+1 'J if К ес<>ТЦ уа \\.
Здесь 0 ^ tj ^ Т — промежуток времени, па котором ищется ре-
решение.
Рассмотрим уравнение B.8) па сеточных решениях частного
вида
yi = qit = v{h)qK B.10)
После подстановки B.10) в B.8) с учетом линейности опера-
оператора S получаем qv = Sv, откуда |д|НЫ! = 115у11 ^ Il5!l!lyll и
1<?(ф) I ^ H5II. Поэтому необходимое условие устойчивости схемы
состоит в выполнении (для всех ср) .неравенства
1?(ФI<1 B.11)
(или |д(ф) I ^? 1 + сот). Здесь v(k)=vk—сеточтгые собстпенпые
функции разностной краевой задачи: они удовлетворяют уравне-
уравнению qv = Su и граничным условиям задачи. Величина q явля~
ется, таким образом, соответствующим собственным значением.
Условие устойчивости в этом случае выглядит так
gKl, B.12}
где максимум берется по всем собствеппым зпачепиям.
162
Собственные значения q образуют спектр оператора S, по-
поэтому неравенство B.12) называют также спектральным крите-
критерием устойчивости. Как уже говорилось, этот признак дает не-
необходимое условие устойчивости. Доказательство достаточности
подразумевает полноту системы собственных сеточных функций,
что имеет место не всегда. Однако спектральный критерий часто
используют как практическое достаточное условие устойчивости.
Сказанное в этом пункте убеждает, что по существу метод
гармоник является частным случаем спектрального метода для
задачи Коши.
5. Анализ устойчивости схемы yt + ay- = 0. Исследуем
схему
>А+1-у{ auj-yL1_Q B.13)
X h
с помощью метода гармоник. Подставим в разностное уравнение
сеточную функцию
A \
определим q n вычислим квадрат модуля этой величины. В ре-
результате получим
откуда следует
lg(cp)l <1 при -у<1, ^14j
\q((f) I > 1 при f > 1.
Последпее из приведенных неравенств показывает, что при
^ > 1 необходимое условие устойчивости не выполнено. Следова-
Следовательно, в этом случае рассматриваемая схема является неустой-
неустойчивой.
Информация, содержащаяся в первом из неравенств B.14),
не позволяет сделать заключение об устойчивости схемы при
f s? 1. Для этого мы должны воспользоваться каким-либо дру-
другим методом анализа устойчивости схем, дающим достаточные
условия.
6. Принцип максимума. Вповь рассмотрим схему yt + ay- = 0
при условии
0<<у<1. B.15)
Перепишем разностное уравнение B.13) в следующем виде
В силу условия B.15) коэффициенты правой части этого равен-
равенства положительны. Поэтому из пего следует оценка
Взяв максимум по к от обеих частей неравенства па соответ-
соответствующем временном слое, получим \iyi+lh ^ Wy'h, где \у'^}с —
= max | г/11 — сеточный аналог нормы в пространстве непрерыв-
к
а* 163
ных функций. Полученное неравенство означает равномерную
устойчивость схемы по начальным даппым:
Последнее неравенство называют также принципом максимума
для разностной схемы: максимальное значение модуля разно-
разностного решения достигается на границе области. Для задачи Ко-
ши, которую мы рассматриваем, это имеет место в начальный
момент па прямой t = 0. Таким образом, выполнение принципа
максимума фактически является достаточным условием устойчи-
устойчивости разностной схемы.
Суммируя результаты исследования схемы с левой производ-
производной для уравнения переноса у% + аг/^=О, полученные с помощью
метода гармоник и принципа максимума, можно сделать вывод
о том, что необходимым и достаточным условием ее устойчи-
устойчивости является выполнение неравенства B.15). Перепишем его
в виде
t<h/a, а>0. B.16)
Итак, рассмотренная разностная схема условно устойчива при
определенном ограничении на величину шагов разностной сетки.
Условие B.16) называют критерием Куранта; это условие часто
встречается при исследовании устойчивости разностных схем для
задач гиперболического типа.
Отметим, что в случае неравномерной сетки и непостоянного
коэффициента a = a(s, t)>0, для обеспечения устойчивости схе-
схемы B.3) условие Куранта должно соблюдаться во всех точках
сетки:
х}^ hJa(Si, t,),i = 0, ±1, ±2, ...;/ = 0, 1, ...
7. Геометрическая интерпретация. Полученные результаты,
касающиеся устойчивости разностных схем для уравнения пере-
переноса, могут быть проиллюстрированы с помощью наглядных гео-
геометрических представлений.
Обратимся сначала к схеме B.3) (yt + ay- = 0, а = const> 0)
Перепишем разностное уравнение в виде
ui+1=-(i-y)'A + yyi-i- B-17)
Это соотношение может быть истолковано следующим образом:
значение разностного решения в узел (sK, ti+\) приносится по
характеристике АА' (рис. 3.3) с нижнего временного слоя t-t из
некоторой точки .у*:
Точка (s*, tj) не совпадает, вообще говоря, пи с одним из уз-
узлов (sp, tj), p = Q, ±1, ±2, ..., и значение решения и пей ут
определяется по значениям в соседних узлах. При f < 1 точка
(s*> У попадает в промежуток между узлами (sk-u tj) и (sk, tj)
и определение в ней значения y*m сводится к интерполяции се-
164
точной функции по значениям y{-i и у{ (рис. 3.3, а). Если же
If > 1 (рис. 3.3,6), то s = s+ находится вне интервала (sh-i, sk)t
и значение у1^, определяемое правой частью B.17), находится
с помощью экстраполяции, которая, как известно, приводит к
большим погрешностям.
Заметим, что областью зависимости решения исходной задачи
B.1) для точки (s^ ti+i) на слое t = tj (если его принимать за
начальный) является точка (s*, tj). Для разностной схемы B.3J
Рис. 3.3
область зависимости включает два узла (s*-i, tj) и (sk, tj). Если
критерий Куранта B.16) не выполнен, то область зависимости
решения u = u(s, t) находится вне области зависимости разно-
разностного решения у = у\- В этом случае наблюдается неустойчи-
неустойчивость, сходимость схемы отсутствует. В самом деле, примем слой
tj за начальный и будем изменять данные на этом слое вблизи
точки s*. Тогда решение u(s, t) в точке (sk, tj+\) будет изме-
изменяться. В то же время решение разностной задачи yi «не
заметит» этих изменений.
Точно так же можно проиллюстрировать абсолютную неус-
неустойчивость схемы B.2) (рис. 3.4). Область зависимости диффе-
дифференциальной задачи — точка (s*, tj), из которой осуществляется
Рис. 3.5
перенос решения по характеристике АЛ' в узел (sA, tj+l), при
любых соотношениях между шагами сетки Лит лежит вне об-
области зависимости разностной задачи, состоящей из узлов (sh, tj),
До сих пор рассматривался случай, когда коэффициент урав-
уравнения B.1)—а, имеющий смысл скорости, был положителен.
Если этот коэффициент отрицателен, то наклон характеристик
отрицателен и результат исследования устойчивости схем B.2)
и B.3) изменится.
Нетрудно проверить, что схема B.2) при а < 0 становится
условно устойчивой, причем необходимое и достаточное условие
ее устойчивости выражает критерий Куранта
-1 s? -у <0 или |fl =? 1.
Схема же B.3) будет абсолютно неустойчивой (рис. 3.5).
Если в исходном уравнении переноса скорость переменна —
a — a(s, t) может наменять знак, то целесообразно использо-
использовать следующую комбинированную ра;шостную схиму
lit + а-у, + а+у-$ = 0, B.18)
где
а- =
— (а - | а |) =
0,
a,
a,
0,
a <
a 5
a <
CO,
CO.
я+ = " (я + |я|)
Эта схема автоматически обращается в схему B.3) при а 5= 0
и B.2) при а < 0 и потому условно устойчива при выполнении
критерия Куранта т =S /г/1 а I.
8. Схема с центральной разностью. Наряду с проанализиро-
проанализированными схемами, содержащими односторонние разностные про-
производные, для уравнения переноса может быть предложена схе-
схема с центральной разностью:
V y »y = a BЛ9)
А--О, ±1, ±2, ...; / = 0, 1, ...,
или в безындексноц записи
Ук =
,/(л ауо =0. B.19')
S
Эта схема, п отличие от предыдущих схем, имеет второй поря-
порядок аппроксимации по пространству.
В § 1 гл. II указывалось, что такой способ аппроксимации
прои.шодной по пространству порождает неустойчивость схемы.
Покажем, что схема B.19) является абсолютно неустойчивой.
Используем для этого метод гармоник, который дает необходи-
необходимые условия устойчивости. Подставим в уравнение B.19) ча-
частное решение J/'L = (/:'ё'• Получим
|-J — 1 — V '——Г— = 1 — »Y sin Ф-
И далее Igl2 = 1 + f2sin2<p. Итак, при всех Т и ф таких, что
sin <р =7^0, имеем 1д(фI>1. Следовательно, схема B.19) неус-
неустойчива при любых соотношениях между шагами сетки и любом
знаке а.
Полученный факт можно прокомментировать следующим об-
образом: формально схема B.19) представляет собой полусумму
ехем B.2) и B.3) (г/° = 0,5 (г/3 + г/-)), одна ил которых (в за-
зависимости от знака а) всегда абсолютно неустойчива в смысле
ныполнения неравенства A.6").
Заметим, что IgP^Sl + f2. Предположим, что существует
такая постоянная со>О, что f2 = (axfhJ < сох. Тогда |?|2<С
< 1 + спт,<^ес°х и соответственно j д\ <?0'5CcjT- Поэтому для
расслтатриваемого частного решения — разностной гармоники —
имеет место оценка
которая означает, что при введенном ограничении на шаги сетки
a2xjh2 < со, погрешности в решении могут нарастать со време-
временем, однако скорость этого роста ограничена экспонентой.
9. Неявные схемы. Исследованные выше схемы для линейного
уравнения переноса были явными,— при записи разностных про-
производных по пространству в этих схемах использовались зна-
значения разностного решения с предыдущего (нижнего) временно-
временного слоя.
Перейдем теперь к анализу неявных схем. По аналогии с
B.2) и B.3) рассмотрим две схемы с односторонними разно-
разностными производными:
й+1-у{ , у{%\-у'к+1 п
г н а h - и'
к = 0, ±lLdb2, ..., / = 0,1,... B.20)
(lit + ays = О), ijk = vo(sh)\
{ a
4 = 0, ±^±2, ..., у = 07 1, ... B.21)
(yt + ayi = O), yh = vo(sh).
Соответствующие шаблоны представлены на рис. 3.6, а и б.
Использование подобных неявных схем особенно удобно при
численном решении краевых задач. Рассмотрим уравнение пере-
переноса в полубескопечной области 0 < s < оо при заданном крае-
краевом условии (а > 0)
^.Ьй^ = 0, 0<s<oo,
u{s, O)=vo(s), 0^s<°°, 0
u@, t)=ii(t), t>0, v0@)=\i{0).
167
Решение этой задачи задается формулой (рис. 3.7)
vo(s — at) при s ^ at,
и (s, t) = '
-—j при
Применим для решения этой задачи схему B.21)
Л k + а — ^—^ = 0.
х h '
fc=l, 2, 3, ..., / = 0, 1, 2, ...
j/fe = vu (s/i), /с = 1, _, ...,
B.21')
B.23)
Уо« H(*i)- / = 1, 2, ... B.24)
Разностный алгоритм выглядит следующим образом. Пусть
значения сеточной функции у решения на ;-м временном слое из-
известны. Значения у\ х и граничном узле определяются из B.24).
Рис. 3.6
«Прикладыпая» шаблон (рис. 3.6,6) к первому узлу сетки
к — 1 (рис. 3.8), мы по известным значениям г/?+1 и у\ пычис-
ляем с помощью уравнения
B.21) значение
Решение определяется
граничным условием
s,tj = ue(s-at)
Решение определяется
начальными донными
Рис з 7
1 = ar/h.
Перемещая шаблон впра-
вправо на один иптервал сетки
и повторяя описанную про-
процедуру, находим значение
'. . у\ по известному у\ и толь-
¦*Г ко что определенному у[ г-
Последовательно передвигая
шаблон, найдем всю цепочку
значений гД+1(А; = 1, 2, . . .) по формуле
Итак, несмотря на то, что схема B.21'), B.23), B.24) формально
168
является неявной, она легко разрешается явным образом. Подоб-
Подобные алгоритмы называют схемами бегущего счета.
Исследуем устойчивость схемы B.21'), B.23), B.24) при
к = 1, 2, ... Перепишем разностное уравнение в виде
(l + V)yi+1 = Vy{±\+yik- B-25)
Учитывая, что равенство рассматривается лишь при к = 1, 2,
3, ..., имеем
A + у) max | y{+1 \ < у max | у>?\ \ + max | ifh |,
к h h
где к = 1, 2, 3,... Определим сеточную порму следующим образом
|, к = 1, 2, 3, ...,
где максимум берется ио внутренним точкам кФО. Тогда из
уа Т
у1;1
м/
предыдущего соотношения следует
A + У)IIyj+1\\c<:Vmax [jyi+i\\c, |yo+11 1 + \yi ||c
Существует две возможности: либо максимум сеточной функ-
функции на (у'+1)-м временном слое достигается в граничной точке
bi+1|<ko+1l = M';+i)b A=l, 2, ...,
либо во внутренней, и тогда из B.25) следует
Объединяя два последних неравенства, можно записать
Последовательно применяя это неравенство, получим
<max{|(xi+1l, \nj\, ..., Ifi'l,
или
max
169
Полученное неравенство означает, что для разностной схемы
B.21'), B.23), B.24) справедлив принцип максимума — реше-
решение у достигает максимального по абсолютной величине значения
либо на границе (& = 0), либо в начальный момент (/ = 0). Это
обеспечивает устойчивость схе-
схемы по начальным данным и
краевому условию. Геометриче-
Геометрическая иллюстрация для разо-
разобранного случая дана па
рис. 3.9. Формула B.25) пока-
показывает, что значение разност-
разностного решения приносится в узел
(sk, t1+i) по характеристике АА'
,¦ ^._t/ из некоторой точки L, где оно
D „ Q вычисляется с помощью линей-
хгИС. О.У 14-1 1
ной интерполяции по Ук-i и г/й
Точка L, область зависимости дифференциальной задачи, попада-
попадает внутрь области зависимости разностного решения (отрезок
к-/ к кЧ А-/ к / /И/
У*1
Рис. 3.10
MN) при любом значении параметра у, т. о. при любом соотно-
соотношении шагов сетки. Итак, неявная схема с левой разностью
B.21'), B.23), B.24) при д > 0 является безусловно ус-
устойчивой.
Для неявной схемы B.20) с правой ра;шостью соотнотствую-
щий чертеж дан па рис. 3.10. Искомое значение разностного ре-
решения, приносимое в узел (sk+i, tj+\) по характеристике АА',
вычисляется посредством интерполяции между <Д " Цк п случае
f >1 и экстраполяции — при f < 1. Можно ожидать, что рассмат-
рассматриваемая схема будет устойчива, если f 3s 1, и неустойчива в
противном случае. Строгие выкладки, связанные с исполыюпапи-
ем метода гармоник и принципа максимума, аналогичные тем,
которые были проведены выше, подтверждают это.
§ 3. Энергетический метод исследования
устойчивости разностных схем
1. Некоторые определения. Метод, указанный в названии пара-
параграфа, оказывается весьма эффективным при исследовании устой-
устойчивости разностных схем.
Предварительно поясним идейную сторону вопроса на простом
примере одного линейного уравнения переноса с постоянным ко-
коэффициентом. Результаты анализа устойчивости разностных схеи
для этого уравнения, полученные здесь с помощью энергетиче-
энергетического метода, будут сопоставлены с условиями устойчивости этих
же схем из предыдущего параграфа, где применялся метод гар-
гармоник и принцип максимума. В дальнейшем в § 4 энергетический
метод будет использован для анализа системы разностных урав-
уравнений.
Сделаем некоторые замечания, уточняющие постановку диф-
дифференциальной задачи Коши для уравнения переноса. Ищется
решение уравнения
-^+л^=0, —oo<s<oo, />0,
удовлетворяющее начальному условию
ll(s, O)=Vq(s), —oo<s<oo.
Будем дополнительно считать, что функция vo(s) является фи-
финитной, т. е. обращается в нуль вне некоторого конечного про-
промежутка: vq(s) = 0 при Isi 5= I.
Тогда решение задачи u(s, t) в
любой конечный момент времени
t\ также обращается г. пуль при
достаточно большом значении isi
(рис. П.И): u(s, t\) = 0 при isi >
Если в рассматриваемой обла-
области плоскости (.s, t) ппести с.етку
со = он X ок.:
; Гис. 3.11
то сеточпая функция /м, аппрокси-
аппроксимирующая решение, также будет финитпон — она обращается и
нуль в узлах с достаточно большими номерами Ny.
Ill = 0 при | /.- | > N3:
Определим скалярное произведение сеточных функций у и
Ь=-оо
C.1)
C.2)
171
Если сеточные функции у и v являются финитными, т. е. удов-
удовлетворяют условию C.1), то сумма C.2) фактически берется по
конечному числу точек (—Nj<.k^Nj).
Скалярное произведение C.2) порождает норму
Ц1-Ш1)- C.3)
В пространстве сеточных функций, заданных на ал, определим
разностный оператор дифференцирования (назад)
(Ay% = a l*-_J?z? = a * \ " = (<4/;)i C.4)
k = 0, ±1, ±2, ...
Результат применения этого оператора к сеточной функции вновь
является сеточной функцией.
2. Сопряженный оператор. Вычислим скалярное произведение
(Лу, v) = 2 (ay-)kuhh,
Л
где у и v — две сеточные финитные функции. В гл. II была по-
получена формула A.20') для разностного дифференцирования
произведения сеточных функций: {yv)- = y(—i)v- +vy-.Выразии
отсюда vy- и после суммирования по к на конечном интервале
\к\ <п получим
п п
¦^ / \ Ъ ^ / \ h t*\ c»\
Л=—п Л=—п
Пусть п > Nj, где Nj — величина, фигурирующая в определении
C.1) финитности. Тогда первые два слагаемых в правой части
C.5) обратятся в нуль. Перепишем C.5) еще раз, «сдвинуп» в
последней сумме индекс суммирования на единицу и учтя ра-
равенство (v;)k = (y,)*_i:
п п—!
Л. Vb(i/-'\.h=— ?\ HbirAbh.
Возвращаясь к обозначениям C.2), имеем
(,'/s, '") -- — (//. rs). C.6)
По определению опоратор А* япляотся сопряженным и опера-
оператору Л, осли выполнено рапепстпо
(Ay, v) = (y, A*v). C.7)
Соотношение C.6) дает пояможпость заключить, что ПAтфяя?е1г-
ным к разностному оператору Ау = а;/-ч я:!ляетгя оператор
(А*у)„ = -(ау.)к = -а(/А+, - yk)/h. C.8)
Заметим, что оператор Л не япляетгя гнмпг^пряиампп^и: А* Ф
ФА.
172
Построим еще одну разностную формулу, полезную для даль-
дальнейшего:
УУ-. = у ^^ =*=?=* + (yV)) = [<А +
Отсюда после суммирования на сетке с учетом финитности сеточ-
сеточной функции у (см. C.1)), получим (у-г, У) = hjy-^/2 или в
операторной записи
(Ay, y)-h\\AyPj{2a). C.9)
3. Примеры исследования устойчивости схем энергетическим
методом. Рассмотрим разностную задачу
Vt + ау-з = О, а > 0, yl = u0 (sk), к = 0, ±1, ± 2, ... C.10)
Эта схема, аппроксимирующая исходную дифференциальную за-
задачу, была проанализирована в § 2. Схема устойчива при а > 0,
если выполнен критерий Куранта
/a. C.11)
Продемонстрируем на ее примере особенности применения
энергетического метода исследования устойчивости разностных
-схем. Перепишем C.10) в виде
умножим на г/<0'5) и просуммируем по сетке. В результате получим
\ 1
Учитывая, что г/@'5) = у + -^ i)it = у ^ Г/*У' запишем
Окончательно, используя формулу C.9), имеем
-g-('//,-)« ==~ (т — — 'АУ
1
Если прапая часть итого рапепстпа неположительна, что itmoot
место при условии
r<h/a (a>0), C.12)
то отсюда следует пераиепстпо ll?/j+ll! <: Il;/Jll, означающее раштомер-
ную устойчивость схемы C.10) по пачальным данпым. Ппергс-
тнчеслсий метод устапаилгшает достаточные услопгтя устойтп'".ости.
В рассмотрешюм случае татсттм угломпом яг.ляется nepaiirTTcTEo
C.12), совпадающее с критерием Курапта, получегншм ранее.
Однако метод ппергетичеекпх шфапопгт'1. может датт. и боль-
большую информацию, пежоли та. которую догтапляют мстпд гармо-
пик и принцип максимума. Так, п предыдущем параграфе была
173
рассмотрена схема с центральной разностью
г/, + аг/с=О. C.13)
Метод гармоник показал ее абсолютную неустойчивость. Проана-
Проанализируем теперь эту же схему с помощью энергетического метода.
Перепишем C.13) в операторном виде
О, C.14)
где
(Ay)k=(ay.)k=a(yk+1 — yh-l)/Bh), к = 0, ± 1, ± 2, . . .
C.15)
Полезно заметить, что
° 1 1
Ау = ау. = — а (у-г + y*) = ~j- (АУ — А*У)-
Тогда в соответствии с определением сопряженного оператора
C.7)
(Ау, у) = 4" КАу.. У) - (Л*у, у)\ = 0. C.1G)
Проделаем теперь цепочку стандартных операций. Домножпм
C.14) на г/(а5) и просуммируем по сетке:
Преобразуем правую часть с помощью C.14) и C.16):
- {Ау, у<0М) = - (А/а у) + -—) Аи«" = -J-1| Ау||2.
Итак, производная по времени от квадрата пормы неотрица-
неотрицательна:
(ilz/H2), = TllAz/i!2>0, C.17)
следовательно, норма сеточной функции у при переходе со слоя
на слой может увеличиваться. Однако рост этой величины огра-
ограничен. Чтобы доказать это, оценим предварительно входящую в
C.17) норму НАг/И:
II Ay f = a? 2, (У* )lЛ = ^ 2 (У*+1 - ^-iJ ;i <
/Hi+yti)'K4lUf- C-18)
Подставляя полученный результат в C.17), имеем возможность
записать
174
При условии a2ilh2 ^ c0 = const справедлива мажорантная оценка
1 + (a2x/ti?) т < eV.
Таким образом, мы пришли к неравенству
Это неравенство приводит к условию устойчивости по начальным
данным следующего вида:
где Т — граница интервала времени, на котором рассматринается
решение @<t'<T). Схема с центральной разностью C.14)
является устойчивой с константой, большей единицы, при вы-
выполнении условия x<coh2/a2 (р-устойчивость).
Заметим, что подобное условие устойчивости не является есте-
естественным для уравнений гиперболического типа. Оно напоминает
условия устойчивости схем для параболических уравнений.
§ 4. Устойчивость схем для системы двух уравнений
первого порядка
1. Анализ схемы «крест» методом гармоник. Задача Коши для
ураннений акустики ставится следующим образом. В области
— оо<5<оо, t> О ищется решение системы двух дифференциаль-
дифференциальных уравнений первого порядка
ди ди ди ди // «.
dt ds dt ds v '
удовлетворяющее начальным условиям
V(S, 0) = V0(s), u(s, 0)=U0(s), —oo<s<oo.
Семейство ра;нюстных схем, аппроксимирующих эту дифференци-
дифференциальную задачу, было указано выше (см. A.13)):
vt = auf\ щ = avf\
v°h = v0 (sh), u°h = u0 (sk), /,¦ = 0, ± 1, ± 2, . .., D-2)
a, (i — свободные параметры.
Продемонстрируем применение метода гармоник для анализа
устойчивости схем такого тина. Обратимся к конкретному слу-
случаю а = 0, (i = l. Эта схема аналогична известной схеме «крест».
Правда, в классической схеме «крест» сеточная функция v, ран-
ранная скорости с точностью до знака, относится к узлам сетки
(s{, tj), а функция и, которая пропорциональна давлению— к точ-
точкам (л',+ 1/2, ij+i/2). Поотому шаблоны, на которых определены
уравнения схемы, имеют крестообразную форму (см. рис. 3.12),
что н послужило причиной названия схемы.
175
Перепишем схему D.2) при а, = О, р = 1 в индексной форме:
D.3)
ик~1
т ~" h т -"¦
Рассмотрим частные разностные решения вида
и{ =
D.4)
I
где ? = е'ф, V, U — амплитуды гармоник, i — мнимая единица, ср —
произвольное действительное число, <?(ф)—комплексное число,
подлежащее определению. Сеточные функции D.4) периодичны
по пространству: это связано с тем, что рассматривается задача
Кошн. В случае краепой
. , задачи необходимо рас-
~J+ ' сматривать соответствую-
соответствующие сеточные собственные
_ / + / функции.
После подстановки
D.4) в D.3) получаем
-у+л> систему алгебраических
уравнепий
,,J*'/2
и;
k-l
к-ф.
i
к к < f/г
Рис. 3.12
(q-\)V-V(i-±)U = O,
q^(l-\)V-(q-\)U=O,
у = ar/h.
Для того чтобы эта система имела нетривиальные решения, ее
детерминант должен обращаться в нуль. Это дает уравнение
д2 — 2A —2f sin2 (ф/2) )q + t = O,
корни которого
q± = i — 2^ sin (ф/2) [^ sin (ф/2) ±
йш2(ф/2)-1]. D.5)
Рассмотрим случай, когда критерий Куранта нарушен: ^>^-
Тогда существуют значения <р, при которых подкоренное выраже-
выражение в D.5) положительно. Корни q+ и ?_ вещественны, причем
абсолютная величина q+ превышает единицу. Этого достаточно,
чтобы сделать заключение о неустойчивости схемы «крест» при
невыполнении условия Куранта. По аналогии с одпим уравнени-
уравнением переноса, рассмотренным ранее, можно ожидать, что при
7^1 будет наблюдаться устойчивость. Далее мы докажем это
строго.
2. Энергетические соотношения для дифференциальной задачи.
Энергетический метод особеппо удобен при анализе устойчипости
разностных схем для систем уравнений. Прежде чем применить
его к схеме D.2), сделаем некоторые замечания, относящиеся к
дифференциальной задаче D.1).
176
Умножая первое из уравнений D.1) на v, а второе — на и ж
складывая результаты, получим
±?(и' + и>)-ш±(и»). D.6>
Предположим, что функции и и v являются финитными, т. е.
обращаются в нуль при достаточно большом Isl. Чтобы обеспе-
обеспечить финитность и ж v в любой конечный момент времени, до-
достаточно потребовать наличие этого свойстиа и начальный мо-
момент, т. е. финитность функций uo(s) и vQ(s).
Интегрирование равенства D.6) по s дает
O, D.7)
+ °°
где .?(?) = 0,5 J (ц2 + it) da—так называемая «энергия» системы.
— 00
Из D.7) следует энергетическое тождество
= E(O), D.8)
выражающее закон сохранения энергии.
С помощью D.8) в теоретических исследованиях доказывает-
доказывается, в частности, единственность решения задачи Коши D.1). Дей-
Действительно, для разности двух решений, соипадающих и началь-
начальный момент времени, энергия тождественно равна нулю в любой
момент времени. Это и означает совпадение решений.
3. Энергетические соотношения для разностной схемы. Полу-
Получим разностный аналог закона сохранения D.8). Будем анализи-
анализировать сразу все семейство схем D.2), не выделяя пока конкрет-
конкретных случаев. Используя введенные в предыдущем параграфе обо-
обозначения для операторов
АУ = аУ-3 и А*У = — аУ*>
запишем систему разностных уравнений акустики D.2) в виде-
vt=Auia), ut = —A*vi*K D.9)
Умножим первое из этих уравнений на vii} = vi0-5} + ({} — 0,5)tv,,
а второе — на и(а) =ulQ-5) +(<t—0,5) тиг и просуммируем полу-
полученные соотпошения на сетке:
0,5(M2), + (p-0,5)Tllz;,ll2 = (;lu(a\ vw), D.10)
0,5(Ы12)( + (а-0,5)т1!и(Н2 = -(Л*1;(е), u(a))- D.11)
Складывая эти равенства, имеем после несложных преобразо-
преобразований
Jt = Q, J = J + xQ, D.12)
где
/ = 0,5 (Hull2 + 1Ы12), D.13)
<? = -T[(a-0,5)llu(ll2 + (p-0,5)lb,ll2]. D.14)
12 А. А. Самарский, Ю. П. Попов 177
Если для какой-либо конкретной схемы (т. е. конкретных зна-
значений параметров а и [}) будет доказана знакоопределенность
выражения
то это будет означать устойчивость данной схемы в энергетиче-
энергетической норме D.13):
Ji+l </0_
4. Устойчивость полностью консервативных схем. Используем
полученные ныше энергетические ра.чностные соотношепия для
исследонания устойчивости семейства полностью консернатинных
схем, которые были построены и гл. II. Наномпим, что в се-
семействе D.2), представляющем разностный аналог уравнений
акустики, этим схемам соответствуют значения C = 0,5, а — сво-
свободный параметр. Очевидно при этом из D.11) следует
<У — —т(сс — 0,5) HwJ!2,
и для выполнения неравенства Q =5 0, обеспечивающего устойчи-
устойчивость схемы, нужно потребовать
сс>0,5. D.15)
Итак, для устойчивости полностью консервативных схем (в
акустическом приближении) достаточно выполнения условия
D.15). В частности, полностью консервативгтая схема со вторым
порядком аппроксимации а = 0,5 устойчива. Она обладает также
замечательным свойством: для нее Q ^ 0 и, следовательно, раз-
разностный закон сохранения энергии в схеме имеет форму, анало-
аналогичную дифференциальному случаю D.8):
Если же в схеме 0,5<а<1, то Q =? 0 и энергия в разностной
схеме убывает в результате действия собственных диссипативных
свойств схемы
Скорость убыпапия раяпостной энергии тем выше, чем грубее
сотка по времени, ибо Q имеет порядок О (г).
Рассмотрим теперь подробнее япную полностью консеркатш!-
ную схему с а = 0, ,3 = 0,5:
vt = аи-, ut = av[°'b\
Применяя метод гармоник, т. е. рассматривая частпые разност-
разностные решения пида t'l - Fr/'| . u{ = Uif^\ приходим аналогично
D.5) к следующему выражению для q
<7+ = * — VSin 9~
178
Ф . / ¦. ¦ О ф /
Если у2 sin2 -у < 4, то под корнем стоит отрицательная величина,.
д+ ж q- — комплексно-сопряженные величины и
При y sin2 -—¦ ~^\величины q+ и q~ — вещественны, и нетрудно
видеть, что одна из них по модулю превышает единицу. Итак,
метод гармоник указывает, что явная полностью консервативная
схема абсолютно неустойчива в смысле пынолпения неравенства
A.8).
Обратимся теперь к энергетическому методу. Величина Q с
учетом второго из уравнений D.9) может быть записана в виде
^v + v)f,
используя который нетрудно получить следующую оценку
^^-l-li^^^+^^-fii^iiM^lf + IU'f). DЛ0)
Здесь использованы известные неравенства 1Ы*у11 <i \\A*l\ \\y\\ и
(У + §J ^ 2(у2 + g2). Подставляя D.16) в основное соотношение
D.12), получаем неравенство
7 D.17)
Пусть сетка такова, что выполнено условие
0,5t!U*II2<cq, D.18)
где со > 0 — некоторая постоянная величина, не зависящая от т
и h. Тогда из D.17) можно заключить, что
7- О,5сот1Й1 < /+ О,5сот1Ы12.
Неравенство только усилится, если из левой его части вычесть
неотрицательную величину O,5coTlluli2, а к правой добавить
О,5сот1Ы12. Учитывая определение / (см. D.16)), можно записать
/A — сот)< /A + сот) или
7<р/, р = A + Сот)/A-сот) при 1-сот>О. D.19)
Очевидно, р>1. Поэтому разностное решение со временем на-
нарастает. Оценим скорость его роста. Предварительно докажем
справедливость вспомогательного неравенства
1/A -х)<еаох, ао>1. D.20)
Рассмотрим функцию ](х) = ea°x(i — х) — \. Ее производная
/' (х) = еа°х (а0 — 1 — аох) полозкительна в интервале
0 < х < 1 — 1/а0 < 1 при ао > {. D.21)
12* 179
Так как /@) = 0, то функция f(x) положительна, по крайней
мере в интервале D.21), и, следовательно, здесь выполнено
D.20).
Если положить ао = 2, x = cot, то D.20) дает соотношение
1/A - сот)
справедливое при 0 < сот < 0,5. Кроме того, имеет место уже ис-
использованное нами неравенство 1 + сот ^ ес° . Объединяя эти
неравенства, получим оценку
р = (\+сот)/(\-сот)<езс°\ D.22)
Возвращаясь к D.19), запишем
}+ J\ сг = Зс0,
и, продолжая далее, получим
где О «? t} <, Т — конечный отрезок времени, на котором рассмат-
рассматривается решение исходной задачи.
Итак, явная полностью консервативная разностная схема с
а = 0, E = 0,5 условно устойчива; характер устойчивости допус-
допускает нарастание погрешности со временем, но этот рост ограни-
ограничен экспонентой. В расчетах это явление может привести к по-
потере точности. Условие устойчивости D.18) накладывает ограни-
ограничение на шаг сетки по времени т < 2co/IU*il2. Ввиду того, что
|! =
4г
у/0 Witt
D.23)
(это соотношение доказывается аналогично C.18)), достаточное
условие устойчивости можно нредстаипть в виде
Как пидпо, условие устойчивости и сам тип устойчивости явной
полностью консернатипной схемы для уравнений акустики те же,
что и для схемы с центральной разностью в случае уравнения
переноса (см. п. 3 § 3).
Напомним, что, нмбпряя нише пелмчииу an = 2 п псфаиопстве
(^.20), mi.i уже ввели ограничение па т:
а-,, = г„т < 1 - ~-- -у-
Таким образом, шаг по т должен удоплотнорять дчум мсрлиен-
стиам, и irpanyio чаетт. которых иходит пока неопределенная по-
постоя нпая Со
- 1 ^ г„ h"
(I "
Оптимальным п смысле наименее жестких ограпитений на т яв-
180
ляется случай, когда правые части обоих неравенств совпадают,
что позволяет указать величину со = a/h. Таким образом, неравен-
неравенство, выражающее условие устойчивости явной полностью консер-
консервативной схемы, приобретает вид т =? 0,5/i/a, с точностью до коэф-
коэффициента 0,5 совпадающий с условием Куранта.
5. Достаточное условие устойчивости схемы «крест». Вернемся
к анализу схемы «крест», неустойчивость которой при нарушении
условия Куранта была показана в начале § 4. Применим к этой
схеме (а = 0, |5 = 1) энергетический метод. Для величины Q (см.
D.14)) с учетом исходных уравнений D.9) и формулы разно-
разностного дифференцирования произведения имеем
= — 0,5т[(Л*гГ, и,) + (Ли, »,)] = —0,5т(Ли, у),.
Соотношение D.12) в этом случае может быть преобразовано
к виду
Jt = [0,5(Hull2 + Ы2)+ 0,5т(Ли, v) ] , = 0.
Если будет доказано, что величина / = 0,5[Hull2 + Ilyll2+ х(Ли, v)]
неотрицательна G 3^0), то это будет означать устойчивость схе-
схемы «крест» в некоторой сложной сеточной норме, в качестве ко-
которой следует выбрать 7. Выполним несложную оценку:
7 32 0,5 (Hull2 + toll* - т11ЛП Hall Ы).
Теперь для обеспечения неотрицательности J ^ 0 достаточно
потребовать выполнения неравенства т11ЛН <i 2, тогда J' S5
^0,5(Hull — Ну11J5з0. С учетом D.23) получаем достаточное ус-
условие устойчивости схемы «крест»:
т=? h/\a\ или |"fl s? 1,
т. е. критерий Куранта. Это обстоятельство в сочетании с резуль-
результатом, полученным в п. 1 данного параграфа, дает возможпость
утверждать, что необходимым и достаточным условием устойчи-
устойчивости схемы «крест» для уравнений акустики является критерий
Курапта.
Получепшлй факт допускает столь же наглядную геометри-
геометрическую иптерпретацию, что и условно устойчивости для одного
линейпого ураппепия переноса. При расчетах по схеме «крест»
vt — OAj-. u, = av, значения r'h+1 и г',{\\ сеточной функции па
(/ + 1)-м нременпбм слое определяются по значепиям предыду-
предыдущего слоя"?,_,. и'ц п «л+1, и\ соотпстстиснпо с помощью первого
уранпения. Второе из уравнений ехчшы дает позможпость чыч^с-
лить значепие функции?./» по найдепным значениям г'1 ' и i'h+\.
Таким образом, если исключить промежуточные зпаченпя с, то
сеточная функция и в узле (.s1, l^\) определяется по значениям
этой же функции па предыдущем слое it точках (sft_i, /,j), (.<;,,, 1}),
(si,4.i, lj), которые и образуют для \злл (¦-¦„, t-,>\) область зависи-
зависимости разностного решения. Область заипсимог.ти точки (skl ^4.1)
181
в дифференциальной задаче представляет отрезок
Он выделяется точками пересечения характеристик А А' и ВВ',
которых в акустике две, с линией t = tj (рис. 3.13). Если отрезок
[s*> s**] попадает в область зависимости разностной задачи, что
имеет место при выполнении условия Куранта, то схема устойчи-
устойчива. В противном случае наблюдается неустойчивость и отсутствие
сходимости.
Рассмотренные выше примеры исследования устойчивости раз-
различных разностных схем для уравнения переноса и системы
уравнений акустики подтверждают
общий принцип: неявные схемы-
обладают большим запасом устой-
устойчивости, который возрастает с уве-
увеличением степени неявности, па-
пример с увеличением параметров
а и ,3 в общем семейстин схем
D.1). Однако решение неявных
разпостных уравнений представ-
представляет, как правило, значительные
алгоритмические трудности.
Замечание. Используя энер-
энергетический метод, мы, в част-
частности, показали, что для устойчивости схемы «крест» необходи-
необходимым и достаточным условием является критерий Курапта: т <
<h/\a\. Анализ полного двухпараметрического семейства схем
D.2) приводит к следующему необходимому и достаточному ус-
условию устойчивости [3]:
Гис. 3.13
§ 5. Влияние вязкости на устойчивость разностных схем
1. Модельное уравнение переноса с вязкостью. В гл. II ука-
указывалось, что для обеспечения возможности сквозного расчета
ударных волн используются однородные разностные схемы с псев-
псевдовязкостью. Наличие «вязких» членом в разностных урамнениях
может изменить условия устойчивости, которые были получены
выше без учета диссипации.
Возникающие здесь возможности рассмотрим на простом при-
примере одного линейного уравнения переноса. При наличии члена,
моделирующего действие псевдовязкости, дифференциальное урав-
уравнение выглядит следующим образом
ди . ди д'и
E.1)
Для него в области — °° < s < °°, t > 0 решается задача Коши
с начальными данными
u(s,Q)=vo(s). E.2)
182
Как отмечалось выше, вторая разностная производная опре-
определяется разностью первых производных в соседних узлах сетки
Производная вычислена в узле к, относительно которого она
симметрична. Можно определить вторую производную несколько
иначе:
На равномерной сетке эти выражения совпадают: y-s = y-s.
Итак, разностный аналог дифференциального уравнения с вяз-
вязкостью E.1) выглядит следующим образом (явная схема):
Vi -г ay-t = vy-s.
Возможны и другие аппроксимации, различающиеся способом
записи первой разностной производной по пространству.
2. Устойчивость схемы yt + ay- = v«/-s. Рассмотрим разност-
разностную задачу Коши для уравнения переноса с вязкостью
yt + ay- = vyh, E.3)
yb = vo(sk), k = 0, ±1, ±2, ... E.4)
Пусть для определенности а > 0. При v = 0 отсюда получается
схема B.3'), необходимое и достаточное условие устойчивости
которой даот критерий Куранта
а. E.5)
Проанализируем устойчивость схемы E.3) при v Ф 0. Используя
метод гармоник, ищем частные разностные решения вида
у{ = r/J?\ | = е'ч», E.6)
ср—произвольное действительное число, ^г(ф)—комплексное чис-
число. Подставив jik в E.3), получим урамнение
откуда определяется q:
q = [\ — 2("f + 2со)з1п2(ф/2)] — i-y sin ф, E.7)
где if = ax/h, оэ = vr/h2.
При отсутствии вязкости (о>=0) гюмыполнепие условия Ку-
Куранта ("f > 1) влечет за собой неустойчивость схемы (l^l^l).
При (аФО схема может оказаться неустойчивой, даже если усло-
условие Куранта выполнено. R самом деле, пусть 0 < ^ ^ 1. Рассмот-
183
рим частный случай сеточной гармоники E.6): зш2(ф/2)=1.
Тогда sin<p = 0 и q=l — 2(^ + 2@). Чтобы рассматриваемая схе-
схема оказалась неустойчивой, достаточно потребовать, чтобы вы-
выполнялось неравенство |^г|>1. При фиксированном f это воз-
возможно, если
со < — 0,5f или со > 0,5A—7).
Таким образом, неудачный выбор коэффициента вязкости приво-
приводит к неустойчивости схемы даже при выполнении критерия Ку-
Куранта. Другими словами, «вязкие» члены могут ухудшать устой-
устойчивость разностной схемы по сравнению со случаем, когда дис-
диссипация отсутствует.
3. Устойчивость схемы «крест» с вязкостью. Система уравне-
уравнений акустики с учетом вязкости имеет вид
dv ди d"v ди dv
В акустическом приближении в уравнении энергии вязкостью,
которая имеет первый порядок малости, можно пренебречь по
сравнению с давлением, так что движение газа по-прежнему
можно считать изоэнтропическим.
Разностная схема, обобщающая на случай учета вязкости
обычную схему «крест», записывается следующим образом:
vi = аи- + [iv-s, ut = avt. E.8)
Вновь используем метод гармоник. Рассмотрим частные реше-
решения системы разностных уравнений E.8)
ui=Uq%\ vjh=Vq^\ l = e^. E.9)
Как обычно, ф — здесь произвольное действительное число,
?(ф) — комплексное число, которое подбирается так, чтобы гар-
гармоники E.9) удовлетворяли системе E.8).
Подставляя E.9) в E.8), получим однородную систему ал-
алгебраических уравнений
где f = ax/h, ш = цт/h2. Равенство нулю определителя этой си-
системы дает уравнение для q
g2 - 2[1 - 2 (и + 72)sin2(9/2)] g+ I - 4ш sin2((p/2)= О,
корнями которого являются выражения
<7± = 1 — 2(ш + f2)sii
E.10)
Рассмотрим случай, когда подкоренное выражение в E.10) отри-
отрицательно и корни q+ и <?_ являются комплексно-сопряженными.
184
.Для этого должно выполняться неравенство
(oj + fJsin2(<p/2)<f. E.11)
Это неравенство в свою очередь возможно, если параметр ш до-
достаточно мал
а < 1/4, E.12)
а параметр f лежит в интервале
0,5-У1/4-ш<ч<0,5 + У1/4-ш. E.13)
При условии E.11) квадрат модуля q± равен 1 — 4a>sm2(<p/2).
С учетом E.12) и ш > 0 получим \д±\ < 1. В частном случае
отсутствия вязкости (ш = 0) имеем lg±l = l. Итак, гармоники
E.9) при выполнении условия E.11) в обычной схеме «крест»
не затухают, в то время как вязкость приводит к затуханию ука-
указанных колебаний.
Присутствие вязкости в рассматриваемой схеме порождает
€олее жесткие условия устойчивости. Действительно, пусть пара-
параметр f таков, что условие Куранта выполнено, а нераненства
E.13) и, следомательно, E.11) нарушены:
0,5 + У1/4 —<а<т<1.
Тогда, как следует из E.10), |д-|>1, что п означает неустой-
неустойчивость схемы.
4. Вязкость в схеме с центральной разностью для уравнения
переноса. Рассмотрим устойчивость еще одной схемы для уравне-
уравнения переноса при учете вязкости
\lt -•- aijo = vy-s. EЛ4)
Ранее с помощью метода гармоник было показано, что это
схема при отсутствии вязкости (v = 0) неустойчива в том смысле,
что не выполняется неравенство liy)+1ll ^ Wy'W и амплитуда гармо-
гармоник со временем может нарастать. Исследование с помощью энер-
энергетического метода позволило установить характер этого роста,—
оказалось, что гармоники нарастают но быстрое некоторой экспо-
экспоненциальной функции.
Проанализируем теперь устойчивость схемы E.14) при
Переписав E.14) в индексной форме
2h
_
выразим отсюда значение сеточной функции решения на нерхпем
временном слое:
i/l+1 = A - 2ш) y>h + (со - 0.5y) ul+i + (й ¦!- 0.5y) y'k-v
Предполагая неотрицательность коэффициентов правой части это-
этого соотношения
1-2а 5*0, ю-0,5-^0, <а + 0,5-^^0. E.15)
185
получим
II yj+1 lie < fA — 2ш) + (ш — 0,5v) + (a + 0,5y)] §y> J]c = || i
где \\уЦс = max|z/i|.
Это неравенство, выражающее принцип максимума для схемы
E.14), является достаточным условием устойчивости.
Итак, для рассматриваемой схемы имеет место равномерная
устойчивость по начальным данным, если выполнены неравен-
неравенства E.15). Эти неравенства выполняются, если коэффициент
вязкости лежит в диапазоне
;v<AVBr), E.10).
что в свою очередь возможно лишь при условии Куранта т <
<й|а|. Содержание неравенства E.16) понятно: с одной сторо-
стороны, для того чтобы вязкость оказала влияние на устойчивость
схемы, ее коэффициент не должен быть слишком малым. В то
же время он не должен превышать величину, за которой начи-
начинается неустойчивость разностного ураннения E.14) как явного*
уравнения параболического типа.
Как следует из E.16), минимальное допустимое значепие ко-
коэффициента вязкости v=\a\h/2. При этом вязкий член в урав-
уравнении E.14) имеет порядок 0(h).
§ 6. Устойчивость разностных схем
для уравнения теплопроводности
1. Необходимые условия устойчивости. В предыдущей главе-
было построено семейство разностных схем, аппроксимирующих
уравнение теплопроводности (см. F.11) гл. II)
где 0 < о < 1 — свободный параметр. Напомним, что через у у
здесь обозначена производная назад на неравномерной сетке (см.
C.32) гл. II).
Пусть для простоты / ег 0, а = const, а удельная внутренняя1
энергия пропорциональна температуре: & = cvT, как это имеет
место для идеального газа. Тогда на равномерной сетке эта схе-
схема приобретает вид
%\ (C.1).
(—o)T.
Как и в предыдущих параграфах, будем считать, что реше-
решения уравнения F.1) рассматриваются на сетке {sk = kh, tj=jx,.
к = 0, ±1, ±2, .... 7 = 0, 1, 2, ...}. Применим для исследования
устойчивости схемы F.1) метод гармоник, т. е. рассмотрим пове-
поведение во времени частных решений вида
П = ч%\
186
где | = е'", ф — любое действительное число. Множитель перехода
со слоя на слой д((р) определяется в результате подстановки
этой гармоники в уравнение F,1), После несложных преобразо-
преобразований получим
= 1-4хA-о)а1Па«р/2) х _ Л< F<2)
' 1 -г 4хо sin" (ф/2) h~
Потребуем, чтобы выполнялось неравенство —1 «? g =С 1. Пра-
Правая часть его выполнена всегда, лопая — при условии
- 4х sin" (ср/2)
которое заведомо справедливо, если
Соблюдение неравенства F.3) является необходимым условием
устойчивости. Если оно по выполнено, то можно указать такие
гармоники (такие значения ф), для которых \q\ > 1, что и озна-
означает неустойчивость схемы.
2. Достаточные условна устойчивости. Метод гармоник, исполь-
использованный в предыдущем пункте, позволил установить необходи-
необходимое условие устойчивости F,3), Оказывается, что это же условие
является и достаточным. Для доказательства указанного утверж-
утверждения применим энергетический метод. По-прежнему будем вести
рассмотрение в неограниченной по s областп.
Как и ранее, рассмотрим скалярное произведение
и порождаемую им норму
ll^li —V Су, у). F.5)
Умножим разностное уравнение теплопроводности
Tt = a-f-^J F.6)
па Tt и результат просуммируем по сотке. Получим
%\ Tt). F.7)
Выше в § 3 была доказана формула (см. C.6)) (//.,. г) = — (у, i>).
Полагая в атом раиепстпе у = T-f и v = Tt, имеем
Используя далее формулу A,19) гл II для перехода от веса о
к весу 0,5, можно записать v<-a)vt = vl0'5ivt + (o — 0,5)т(г'(J =
= 0,5(у2)( +(о — 0,5)т(у(J. Подставляя сюда в качестве v = Т~
187
и суммируя получающееся соотношение по сетке, приходим к
формуле
G*°. *й) = 0,5 ( | Т-) f )t + (c- 0,5) т| Tv f. F.9)
С учетом выведенных соотношений F,8), F.9) уравнение F,7)
преобразуется к виду
| Tt Р + 0,5сс2 ( | T-f )t + ос2 (а - 0,5) т | T-t |;« = 0. F.10>
Для проведения дальнейших рассуждений нам потребуется
неравенство
||y;|f<AH|2, (б.ц>
Докажем его справедливость. Обращаясь к известному неравен-
неравенству (а+ ЬJ < 2(а2+ Ь2), получаем соотношение
суммирование которого по сетке и дает нужный результат F.11).
Полагая в F.11) v = Tt, перепишем это неравенство в форме
В соответствии с этой формулой заменим в F,10) первое сла-
слагаемое меньшей величиной. После приведения подобных членов
получим
4- + «2 (а - 0,5) т] | T-at \* + 0,5а2 ( | Т-\* )t
Если в F.12) выражение в квадратных скобках неотрицатель-
неотрицательно, т. е.
/12/4 + а2(о-0,5)т^0, F.13).
то, отбрасывая первое слагаемое, имеем
а*(||Г-||'),<0 или ||71+1||2<И|2.
Таким образом, при соблюдении условия
о>о0 = ^--К-, F.14)
которое следует из F,13), справедливо неравенство
где S11 = а2||7^|а. Величину S называют энергией оператора
Л: Ay = a2y-t (см. правую часть исходного уравнения F.6))
S1 = — (AT1, T1). Поэтому F,15) означает устойчивость рассмат-
рассматриваемой схемы по начальным данным в энергетической норме
, Р), 4 =-Л.
188
Достаточное условие устойчивости выражено неравенством
F.14). Сопоставляя этот результат с F.3), убеждаемся, что не-
неравенство
i k /О ЛП\
является необходимым и достаточным условием устойчивости по
начальным данным разностной схемы F.6),
Необходимое и достаточное условие устойчивости явной схемы
(о = 0) выглядит следующим образом
аат/Аа<1/2. F.17)
Чисто неявная схема (о = 1) и симметричная схема (о = 0,5)
являются абсолютно устойчивыми.
Сформулированные выше условия устойчивости построены
для простейшего случая, когда коэффициент уравнения а2 по-
постоянен. Аналогичные условия могут быть получены и в боле©
общем случае для линейного уравнения параболического типа с
переменными коэффициентами (см., например, [80]).
3. Асимптотическая устойчивость. Для уравнения теплопровод-
теплопроводности с постоянным коэффициентом
в области 0 < s < I, t>0 рассмотрим краевую задачу с однород-
однородными граничными условиями
Г@, t) = 0, ГA, 0=0. *>0. F-19)
и некоторыми начальными данными
T{s, 0) = <p(s), 0<ssSl. F.20)
Как известно (см., например [93]), решение этой задачи мо-
может быть построено с помощью метода разделения переменных.
Оно имеет вид
Т{и, 0= 2 спе-^оп(з), F.21)
П = 1
где Я„ = а2я2га2— собственные числа, a vn(s)= V2sin nns — соб-
собственные функции задачи. Коэффициенты сп определяются рас-
распределением температуры в начальный момент
1
сп = ] Ф (s) vn (s) ds.
о
Так как собственные значения Хп = а2я2га2 с увеличением номе-
номера п резко возрастают, то при больших значениях t влияние стар-
старших гармоник быстро затухает и решение в основном определя-
189
ется первым членом ряда F.21) (регулярный режим)
ГМ^с^'уЛя). F-22)
Определим норму функции u(s, t) следующим образом
1
•| и (t) \- = J и2 (.v, t) ds.
о
Учитывая, что для всех п имеет место е х~^е п , а также при-
принимая но внимание ортонормированность системы собственных
функций (yn(s)}, имеем из F.21)
I Т @ f = f Г- (л, 0
6
(, 0 ^ ^ J\& =,
6 " я
Отсюда следует априорная оценка для решения дифференциаль-
дифференциальной задачи
Разностная
F.18)-@.20),
]T[t)l^e ijnO),!.
схема, аппроксимирующая
выглядит так:
"'it = i)D /.'=-0, 1, 2. ...
красную
2
, Л'.
@.23)
задачу
F.24)
@.25)
F.20)
Если решение ;)той разностной задачи рассматривается на до-
достаточно большом промежутке мремопи, то разумно потребовать,
чтобы его поведение было аналогично поведению решения диф-
дифференциальной задачи F.18) — F.20). Например, естественно
требопать, чтобы при t -*¦ °° разностное решение было близко к
регулярному режиму F.22). Построим некоторое частное реше-
решение уравнения F.24) вида
Ti = q'smfik, k = 0, \, ...,N. F.27)
Чтобы пта сеточная функция удовлетворяла краевым условиям
F.25), достаточно положить {5 = a/N, где N=i/h — число ин-
интервалом равномерной сетки, введенной на отрезке 0 «S s < 1.
Итак, 3 = л/г и
Ti = qJ*u\nhk. @.27')
Множитель q. определяющий характер изменения разностного
решения со временем, определяется в результате подстановки
@.27') в уравнение F.24). По аналогии с F.2) пмстм
1-4хA-а)8ш2(лА/2)> x = crz F.2S)
190
При достаточно малой величине шагов сотки выражение для
q можно преобразовать к виду
q = e-aVx -f О [т (т + h-)].
Таким образом, при некоторых ограничениях на шаги сетки
поведение во времени найденного решения F.27') при больших
tj = ;т описывается множителем
Разностное решение в этом смысле близко к регулярному ре-
режиму F.22). Схемы, решение которых обладает указанным свой-
свойством, называются асимптотически устойчивыми.
В [80], в частности, показано, что для рассмотренной выше
разностной схемы F.24) — F.26) справедливы следующие утвер-
утверждения. Явная схема (о = 0) асимптотически устойчива при не-
некотором ограничении па шаг сетки т, которое практически сов-
совпадает с условием обычной устойчивости F.17). При о = 0,5
схема F.24) — F.26) абсолютно устойчииа, однако асимптотиче-
асимптотическая устойчивость имеет место лишь при условии т < то, то < h/л.
Схема с о = 1 (абсолютно устойчивая) асимптотически устойчииа
при любых т. Асимптотическую точность схемы F.24)—F.26)
может характеризовать отношение
где q определено соотношением F.28).
Пусть а = 1, h = 1/30, f, = 0,4, т = х0 = h/n. Тогда
1,204 при о = 1,
1,(КМ при о = 0,5.
Итак, ошибка в главном члене для чисто неявной схемы (о =
= 1) достигает 20%, в то время как для симметричпой схемы
(о = 0,5) эта ошибка составляет всего 0,4%, т. е. в 50 раз
меньше.
ГЛАВА IV
РЕАЛИЗАЦИЯ РАЗНОСТНЫХ СХЕМ ГАЗОВОЙ ДИНАМИКИ
В главе описаны некоторые методы решения систем алгебраи-
алгебраических уравнений, к которым сводятся разностные схемы газовой
динамики, построенные выше. В § 1 рассматриваются явные
схемы и простейшие итерационные процессы; показано, что при
этом возникают жесткие ограничения на шаги сетки. § 2 содер-
содержит изложение метода Ньютона и метода прогонки, которые при-
применяются в § 3 для решения разностных уравнений газодинами-
газодинамики. Доказана сходимость возникающего при этом итерационного
процесса. Проведепо сопоставление различпых методов регаешш
разностных схем гаиоиой днпампки на примере расчета тестовой
задачи о портпе. Обсуждаются особенности расчета задач на
грубых времепных сетках. В § 4 описано применение метода
раздельных прогонок к решепию разностных уравнений газопой
динамики с теплопронодностыо. В § 5 даны формулировки ра.ч-
личного типа краевых условий для разностпых задач газодинами-
газодинамики и обсуждаются соответствующие алгоритмические вопросы.
В § 6 указаны некоторые практические рекомендации по реше-
решению задач газодинамики разностпымн методами.
§ 1. Явные методы
1. Явная полностью консервативная схема. Разностная схема,
аппроксимирующая дифференциальные уравнения газовой дина-
динамики, представляет собой систему алгебраических' уравнений от-
относительно значений сеточных функций. Такие системы уранне-
пий, являющиеся, как правило, пелипейпыми, приходится решать
на каждом временном слое сетки. Число уравпепий системы оп-
определяется количестиом узлоп сетки по пространству (обычпо
оно составляет 30 -н 200). Таким образом, вопрос о практической
реализации разпостпой схемы в общем случае является доста-
достаточно сложной самостоятельной проблемой.
В гл. II были получены полностью консернатипные разностные
схемы для уравнений газовой динамики, обладающие определен-
определенными преимуществами по сранненпю с другими схемами того же
порядка аппроксимации. Напомним нид этой схемы для случая
плоской симметрии без учета диссипативных процессов:
192
Чтобы проанализировать принципиальную сторону вопроса,
ограничимся в целях большей наглядности рассмотрением изо-
изотермического приближения (см. гл. I п. 8). В этом случае урав-
непие энергии заменяется соотношением Т = То = const, что за-
заметно упрощает выкладки. Заметим таюте, что при использова-
использовании метода раздельных прогонок (см. ниже), полная система
уравнений расщепляется на части, решаемые отдельно; при этом
в части, описывающей движение, возни кают уравнения, аналогич-
аналогичные изотермическому случаю.
Полностью консервативная схема A.1) для изотермического
приближения может быть записана г. виде
О -^ — /¦';"'• xi -= '•" °">'- l.'P = •*"«. Р = ¦?'({>)¦ (Ь2)
Здесь использовано свойство полностью копсервативпнк схем,
в соответствии с которым уравнение неразрывности можно запи-
записать в форме «закона сохранения объема», удобной в практи-
практических вычислениях для определения плотности. В качестве
уравнения состояния будем расематрниать уравнение состояния
идеального газа:
р = с2р.
где с = const > 0 — изотермическая с к фость звука.
В схеме A.2) о —свободный пара.метр. При частном значении
о — 0 получается так называемая «янпая» полностью консерва-
консервативная схема с порядком аппроксимации O(x + h-), имеющая в
ипдекспой записи вид
A.3)
(l.'O
r' + l —г
X' — X
Отдельные разностные уравнения отой с\емы являются пепипы-
ми: в правые части равенств A.4)—A-(>) входят значения се-
сеточных функции с верхнего временного слоя. Однако несмотря
на это укапанная схема без труда разрешается яыпим оПрааом
(отсюда и название—«явная» полностью копсернатшшал схема).
В самом деле, первое уравнепие схемы дп'.-т воимоя.'ность по
сеточной функции давления р\, известной па предыдущем слое,
определить значения скорости па (/ -i I) м слое '4 ¦ Ннндеипые
зпачеппя скорости в соответствии с уравнением AА) определя-
определяют сеточную функцию л] *, по которой с помощью A.5) вычис-
вычисляется плотпость pi1 и далее из A.6)— давление р[ х-
13 а. А. Самарский, Ю. П. Попов 193
Простота описанного алгоритма делает его привлекательным
с точки зрения практической реализации. Однако запас устой-
устойчивости схемы A.3) — A.6) невелик, и это порождает достаточно
жесткие ограничения на шаг сетки по времени. Действительно,
как отмечалось r гл. III, устойчивость газодинамической схемы
исследуют на основе ее акустического аналога, который для
A.3) — A.6) имеет впд
vt = auv ul = ai>(.°'t). A.7)
Здесь функция v с точностью до знака есть возмущение скорости,
a it—11о::мупк'нпг давления, отнесенное к а—массовой изотер-
изотермической скорости зиуиа.
В гл. III показано, что схема A.7) р-устоичина при р = <?с°
(<?о > 0—постоянная, независящая от шагов сеткп, 0 < tt < Т —
интервал времени, па котором рассматривается решение) в сеточ-
сеточпой норме
j
При этом устойчивость носит условный характер и имеет место
при ограничении на шаг:
Таким образом, «явная» полностью консервативная схема с о =
= 0 условно устойчива, прпчем устойчивость носит «параболиче-
«параболический» характер (в правой части A.8) фигурирует квадрлт шага
h) п допускает иарастанпе погрешности со временем. Отметим,
что условие A.8) накладывает па шаг сетки т довольпо жесткие
ограничении.
2. Пример итерационного процесса для неявной схемы. Неяв-
Неявные полностью консервативные схемы A.2) с о S* О.о безусловно
устойчивы. Однако п этом случае разрешить получающуюся си-
систему уравнений явным образом уже не удается. Разностные
уравнения являются здесь нелинейными, поэтому для их решения
приходится прибегать к различным итерационным процессам.
Приведем пример простейшего итерационного процесса, поло-
положив для определенности о=1. Тогда схема A.2) принимает г.ид
;+1 j n7+i nj+i
- h ' K "'
i h '
j + I '}
¦TJ__fi = n.5(i;!+1-riU A.10)
р{+1 = Ы+\ A.12)
Значение каждой сеточпой функции на верхнем (/+ 1)-м времен-
194
ном слое будем определять с помощью итерационного процесса
h
ft -тс
где к — помер итерации.
Заменим п A.9)—A.12) искомые функции на (/+1)-м слое
их .шачениямп па (к+1)-п и A'-ii итерациях. Это можно сделать
различными способами, например так:
ft-t I . ft h
ft-я n+j
ft = rc, (I -12')
Очепидпо, если итерационный процесс сходится, то при к -*¦ °°
реализуется исходная схема (l.'J) — A.12). 15 качостпо нулсион
итерации, как праиило, берутся зна'кчшя функции с нредмду-
щего слоя ^i — у\. Решение системы урапнешш A.Я') — A.12')
не предстаг.ляет труда: для итого на каждой итерации иукпилыю
повторяется последовательность операций, описанная и рассмот-
рассмотренной выше процедуре решешгя «ягшои» схемы A.3) — A.0).
л
Имеппо по пзпестпой па к-п итерация функции давления Pi из
ft + i
уравнения A.9') находится скорость /';. из A.10') определяется
Г;, далее из A.11') — плотность р; п из A.12') — данлопио
ft+I Используя полученное зиачепне давления на номой итера-
итерации ft + I можно приступить к вычислению (/,-1 2)-ii итерации
Рг->
и т. д. Итерационный процесс прекращается при пыполпенни ка-
какого-либо услоппя сходимости, которое спндетольстпует о том, что
различие между сеточными функциями па соседних итерациях
стало меньше некоторой заданной Ж'лпчпны, мыопрае.мои ни
соображении точности. Значения функции, полученные1 на послед-
последней итерации к=К, объяпляются значениями на (/+1)-м слоо
к i+i
по времени i/i = yi- Так, с помощью итерационного процесса
осуществляется последовательный переход с одного временного
слоя на другой. Найденные сеточные функции удомлетпоряют ис-
исходным разностным уравнениям лишь приближенно с некоторой
точностью.
U* 195
Исслсдуелс сходимость описанного итерационного процесса ре-
решения уравнений газодинамики (в дальнейшем будем пазыпать
его «зейделевскпм», ибо он относится к итерационным процессам
этого типа). Так же, как и при изучении устойчивости «явной»
полностью консерватиппой схемы, ограничимся рассмотрением ли-
линейного приближения газодинамики — акустики. II :>том случае
апалогпчно A.7) имеем схему
vt = au-. ut=.av{s°'b), A.13)
пли и индекспоп форме
A-11)
. _ (, -
«Зейделевскнй» итерационный процесс в применении к A.14)
дает
A.15)
ft+I
т
3
= 0
"i~
.5a
ft
- U
h
I
i—T
Введем следующие обозначения
k к . , ft h . .
А,н^,Н-ы\+\ br,~Vi—ri+1. (lie)
Вычитая из уравнепий A.15) соотметствующпе уравнения A.14),
получим
А иг = vl Auj — Au?_! I, A u; ¦¦= О.Г>7 1A fi+, — A ^ J,
где
h-\-\ й+1
Исключив из второго уравнения Aci+1 и A Cj с помощью пер-
первого уравнения, приходим к равенству
ft+i /ft k ^\
откуда
; А и c «^ 27- An i|c,
196
Таким образом, для сходимости итерационного процесса до-
достаточно потребовать выполнения нерапенстпа 2"B<1, т. е.
0<4<l/V2. A.17)
Можно показать, что нерапепстно A.17) является и пеобхо-
дпмым условием сходимости итераций: существуют примеры, ког-
когда при невыполнении услопия A.17) итерационный процесс рас-
расходится.
В предыдущей глапе было показано, что схема с о = 1 из се-
семейства A.1) безусловно устойчива (см. § А, п. А). Однако рас-
рассмотренный способ решеппя нелинейных разпостпых уравнений
этой схемы приподпт к ограничению па шаги сетки A.17), кото-
которое является даже более жестким, чем услоппе Куранта v-<i.
Качественно волннкпошмше ограничений типа A.17) понятно —
использование любого итерационного процесса для решения си-
системы пеявных ураипенпй фактически связано с введением опре-
определенной степепи «явности», что пквивалептпо ухудшению устой-
устойчивости вычислительного процесса. Очевидно, условия сходимо-
сходимости для разных итерационных процессов различпы.
§ 2. Метод Ньютона. Метод прогонки
1. Метод Ньютона для решения нелинейных уравнений. Неяв-
Неявные разностные уравнения газодинамики являются нелиней-
нелинейными.
Для численного решения нелинейных уравнений применяются
разлпчпые методы, одппм пз которых является метод Ньютона.
Напомним вкратце его содержание. Рассматривается задача о
нахождении корня хо уравпеипя
/(*) = 0. B.1)
Предполагается, что в некоторой окрестности корня функция
f(x) вместе со своими производными f (х) и /" (х) пепрерыпиа,
а /' (х) л }" (х) и птой окрестности не обращаются в пуль. Пред-
Представим значепне фупкции / в точке х = Хо с помощью разложения
в ряд Тейлора, ограничиваясь лппейпым членом:
О = Нхо)*Пх)+Г(х)(хо-х). B.2)
Выразим отсюда зд хо « х — f(x)lf'(x).
Последиее соотпотеппе порождает итерационный процесс для
вычисления значения хо:
h
Здесь k—помер итерации, х-*-ха при /;-*¦<». Начальное прибли-
приближение, т. о. зпачепне па нулевой итерации целесообразно вы-
выбирать так, чтобы выполнялось перавопстпо [7]
!&Г\
0\
х)>0.
197
По существу метод Ньютоиа состоит в построении системы каса-
к
тельных к кривой y = f(x) в точках х = х (рис. 4.1). Касатель-
h
ная, проведенная в точке х. пересекаясь с осью абсцисс, дает
значение следующего приближения х. Поэтому метод Ньютона
часто называют методом касательных. Последовательные ирибли-
h
жепия х сходятся к корпго xq монотонно. Для частного случая,
когда f(x) янляется линейной функцией, метод Ньютона дает
точное значение корня xq за одпу итерацию. В общем случае
этот итерационный метод имеет высокую скорость сходимости.
Заметим, что итерационная
формула B.'Л) может быть за-
записана в виде линейного урав-
к !- 1
иония относительно л:
Л /ft+1 fe\ к
¦'г г — ! A А\
k /ftx
где у = у\х).
Рассмотрим теперь систему
нелинейных уравнений
}[(xi, .... ха) = 0,
Применешге метода Ньютона для отыскания корпя :тш си-
системы приводит к итерационному процессу решения системы ли-
линейных уравнении, которые строятся аналогично B.4);
dx.
ih+l И ()f ih + 1 k \ h
Л xl 'rlJ • • • ~Г , \ Xn Xnj = /j,
B-0)
df /fc + l И 0/ /h+I k \ ft
— { Xl — JTt) +...+ — [ Xn — Xn\ = — /„.
Производные dfmldxp, m, p = 1, ..., и, нычисляются па ггредыду-
щей итерации.
2. Метод прогонки. Использование пеяпных разностных схем
приводит к необходимости решать системы алгебраических урав-
уравнений. Важным частным случаем являются системы так назы-
называемых <<трехточечпых)> разностных уравнений, которые связы-
связывают неизвестные значения сеточных функций в трех соседних
узлах сетки. Решать такие системы позволяет извествый метод
прогонки [21, 78, 81], который мы здесь кратко напомним.
198
Система трехточечпых линейных уравнений для сеточной
функции у в общем случае может быть записана в виде
Aiyi-l-Cty, + Biyi+l = -Ft, B.6)
где i=l, -.., N— 1 — номер узла сетки, А,-, 23,-, С, F* — извест-
известные коэффициенты.
Граничные условия для достаточно широкого класса задач
могут быть приведены к форме
—Соуо + Воух = —Fo, i4.vy.v-i - Сяу* = —Fs, B.7)
где Со, So, Fo, а также An. CiV, FN заданы. После незначительных
упрощений лрп Со Ф 0, Су Ф 0 эти условия приводятся к виду
?/0 = tti!/i+V|, I/w = Xs#.v-!+V2, B.8)
гдо v.) = Во/Со, vi = Fo/Со и Иг = А к/С х, vo = Fw/Cw-
При использовании метода прогонки предполагается, что па-
параметры сформулированной задаяи удовлетворяют исравспстиам
Л,-> 0, 5,>0, Ci>At + Bi, 0<y.[, "X2ssl,
-х, + "Х2<2, »«1, 2, ..., JV-1, B9)
которые обеспечивают разрешимость задачи B.G), B.8) и устой-
устойчивость метода прогонки.
Для решения системы уравнений B.G), вообще говоря, можно
использовать различные методы линейной алгебры. Метод про-
прогонки учитывает специальный вид системы — трехдиагоналыюсть
ее матрицы.
Решение задачи B.G), B.8) в методе прогонки ищется п мпдо
0i = a,+ 1jf,+ 1 + B,+t, / = 0, 1, ..., N— 1, B.10)
где oti+i, Pi+i — неизвестные пока коэффициенты прогонки. Исклю-
Исключая с помощью B.10) пз B.6) последовательно значения у,-\ и
Уи приходим к равенству
[ (AiOi - C,)a1+i + Bt] yi+i + [ (i4,a, - С.) p,+ I +(Afr + F,)] = 0.
Это равенство, а следовательно, п уравнепие B.G), пз которого
оно [солучепо, автоматически удовлетворяется, если выражения
в квадратных скобках тождественно раппы пулю:
{Ам - C,)ai+! + Bt = 0, (А& - С) Э,+1 + {А& +F,) = 0.
Из послрдних двух равенств следуют рекуррентные формулы для
коэффициентов прогонки
г = 1, 2, ..., 7V-1.
Чтобы вычислить по этим формулам значения as n ^ во всех
узлах сетки, т. е., как говорят, выполнить прямую прогонку, нуж-
нужно знать значения ai и ^ь Эти числа определяются с помощью
левого краевого условия B.8):
ai-xi, pi = vi. B.12)
109
Обратная прогонка проводится по формуле B.10)—по найден-
найденным значениям а,, р, определяются искомые значения сеточной
функции г/,-, I = N — 1, ..., 0. Исходное значение yN, с которого
начинается обратная прогонка, определяется на основании сов-
совместного решения правого краевого условия в B.8) и соотноше-
соотношения B.10), записанного в-точке i = N:
г/jv-i = aNyN + Pjv
(аЛ- и р\- уже вычислены в ходе прямой прогонки). В результа-
результате получим
У*--=(\* + х2?*)/A - *&¦*)¦ B.13)
Условия B.9) обеспечивают выполнение неравенств
0<а,^ 1, ? — 1, 2, .-., Лг, B.14)
которые в свою очередь гарантируют устойчивость счета по фор-
формуле B.10), а также необращепие в нуль знаменателя (в 2.13),
так как "X2&jv < 1.
Метод прогонки широко применяется па практике и имеет
ряд модификации. Одна us таких модификации, известная под
названием потокового варианта метода прогонки, описана
в гл. VI.
§ 3. Применение метода Ньютона к решению
разностных уравнении газовой динамики
1. Изотермический случай. Неявная разностная схема для за-
задач газодинамики представляет coooii систему нелинейных ал-
алгебраических уравнении. Применим для се решения итерацион-
итерационный метод Ньютона.
Для большей наглядности вповь обратимся к простому изо-
изотермическому случаю:
vt = — /4°\ xt = 1'@'Г)), 1/Р = я.н Р = & (Р)- C-1)
Перепишем ;>ту схему в виде системы уравнений следующим
образом
r _L 1 — '-n l 1 о
s ~ p )i ~ л pi+i ~ '
C.2)
200
Применение к соотношениям C.2) метода Ньютона приводит
к следующей системе разностных уравнении:
b + l A \ /А + 1 h
Pi ~Pi)-[ Р1_л - pi
*+l A /A+l h\ A
Xi — Xi — 0,5t { Vt — Vi) = — /2,<,
h+1
(Pi)
M /i! /A \ /A + l A
i - fi - ?' \Рг) { Pi - pi
h
Правые части jn.i зтих равенств (п = 1, 2, 3, 4) получаются из
соответствующих выражений C.2) путем замены индекса / + 1
на номер итерации /с.
Отметим, что фупкции f\\il и /г,г1 липейны по всем своим ар-
аргументам. Поэтому, как отмечалось в п. 1 § 2 пастоящей главы,
па всех итерациях, начиная с первой, будут иметь место соотно-
соотношения:
А А
В справедливости этого утверждения можно убедиться и не-
непосредственно, анализируя формулы C.3). Обратимся, например,
ко второму из соотношений C.3) и нодставим в него вместо
А А А
функции /2,i ее выражение через xt, V{ и т. д. Получим
А+1 А /А-М А \ А А /АЛ 1
Xi — Jci —0,5т [ Vi — Vi) = — /2>г = — Xi — x\ — 0,5t \Vi + vl) \,
к = 0, 1, 2, ...
Перенося все слагаемые в одну часть и приводя подобные
члены, приходим к равенству
А+1 . /А+1
А+1
Полученное соотношение означает, что /oj^O, к = (), 1, ...
к
Функция /з нелинейна, поэтому /3,гФ0, к = 1, 2, ... Что касает-
касается функции /4, то здесь все определяется видом уравнения сос-
состояния,—если функция ^"(р) в C.2) линейна, как это имеет
место для идеального газа (р = с2р, с — const — скорость звука),
А А
то /4,i = ^ />• = 1, 2, . .., в противном случае /,,,,^0. Введем
обозначение
ft+1 A+l A
Заметим, что оно отличается от подобного же обозначения
к
A.16), использованного выше. В A.16) под приращением Ау
Щ
понималась разность между значением сеточной функции на
к-ш итерации и точным решением. В C.4) разность берется
между двумя соседними итерациями.
С учетом C.4) система C.3) перепишется в виде
*+1 от / а+1 а+1 \ а
6 Щ + Т ^б Pi ~ б Р*-1' = ~ /i.i'
h+1 ft + 1 A
6 Х{ — О,Г)тб V{ = — /2,i, C.5)
I ft+1 h+1\l h+1 I lh V k
[6 xi+l — 6xijjh + f) pi j [pij = — /3ib
A+l /ft \ A+l ft
б Лг — .^' IPiJ 6 pj = — /4i;.
fc-i 1
Всо искомые приращения ftfe y\ имеют здесь номер итерации
/л \ ;<
/с+ 1, а сеточные функции /«,г(» -^ 1- 2, .'!, 4), 5*' \pij, Pi, поме-
помеченные номером /с, считаются известными. В дальнейшем для
сокращения записи мы будем опускать номер итерации. Кроме
того, распространим безындсксные обозначения для разностных
производных A.18) гл. II на приращения Ьу и сеточные функ-
функции /(, pi, 5й' (р;). Все сказанное позволяет модифицировать за-
запись уравнений C.5):
8и + ахбр- — — /,, б.г — О,Г)тб|1 = — /,,
Ьха -г бр/р- = - /,, 6/j — 5"' (р) б|> = — /4, C.5')
На основе C.5') приращения всех функции без труда выража-
выражаются через приращение скорости 6у
Ьх = 0,5т6у — /2, бр = —0,5тр2буа — Y,
C.6)
бр = -0,5тр3^'бУз - ^'F - /4, F =¦ р2(/3 _ (/2).).
Подставляя выражение для 8р в первое уравнение системы
C.5'), приходим к уравнению для би:
6у - 0,5ат- (р2.^'б1'3)- = - п Л- от (/4 + 0")')-.
В индексной форме это равенство сводится к трехточечному
уравнению
A^ui-[-CSvi + BSvi+l=--Fi, i = l, 2, ..., iV-1. C.7)
Коэффициенты зависят от номера итерации к а вычисляются по
формулам
А _ 4- И' р?-A.,, I-1 (i)! ,»й - А«.
Ci = 1 + Т ("Г] Vpf-l^f-X + Pf^i ) = 1 + ^i + йг, C,8)
к к. (к к, к
A ft ft
Напомним, что /i,i = О, /2i; = 0, ]3ii Ф 0. к —= 1, 2, ... Для
А
идеального газа также и /4,г = 0, к = 1, 2, ... Поэтому па регу-
регулярной итерации i^l в этом случае правая часть C.7) вычис-
вычисляется по несложной формуле
А ГА ft /Aft
Уравнение C.7) на каждой итерации может быть решено с по-
помощью описанного в предыдущем параграфе метода нрогопки.
Отметим, что условия B.9), гараптнрущие устойчивость нрогон-
ки, для уравнения C.7) выполнены,— из C.8) следует: Ai>0,
Bt>0, C\=l + Ai + Bi>Ai + Bi, i=. 1, 2, ..., TV —1. Здесь уч-
учтено, что &' = dfP/др > 0 (см. § 4 гл. I).
Формулировка граничных условии для уравнепия C.7) и
способы решения соответствующих краевых задач будут изложе-
изложены в § Л.
Решив уравнение C.7) и найдя во всех узлах сетки прира-
к + \"
щепие 6 i'i ¦ можно по формулам C.6) вычислить приращения
ft-! I ft+1 Al 1
остальных функции 6 а",, 6 р;, 6 р\. .'Ьтем по общей формуле
ft+l h ft+1
\Н = Vi + б Hi определяются значения всех сеточных функций
на (/с+1)-й итерации. Далее процедура повторяется: по форму-
формулам C.8) находятся зпачепия коэффициентов трехточечпого
/ft + 1 fc + 1 *+1 A+1\
уравнения на новой (/l+1)-h итерации \А\,1}{, 6'j, h\ J, и
A+o
путем решения уравпепия C.7) вычисляется значение б v-L . За-
Затем определяются приращения для всех остальных функций и
далее значения самих функций па (А- + 2) -й итерации.
Итерационный процесс продолжается до тех пор, пока не бу-
будет совершено ладанное число итераций или выполнено некото-
некоторое условие сходимости, например, условие вида
А+1
N. C.9)
Здесь ei, е.2 — малые величины, причем параметр ?\ характери-
характеризует точность, с которой реализуется исходная разностная схе-
схема; слагаемое ег добавлено для того, чтобы критерий сходимости
А / h \
C.9) иравилыю срабатывал в случае, когда уг (.например v-i) об-
обращается в пуль.
В качестве пулевого приближения обычно используют зпаче-
цпя сеточпых функций с предыдущего шага
к = yi. (З.Ю)
Заметим, что при этом (см. C.2))
L Ф 0, L Ф 0, L = 0, /4ii - 0. . C^1)
гоз
При построении трехточечного уравнения C.7) мы исключи-
исключили из системы C.5') црыращения всех сеточных функций, кроме
скорости 6t>. Конечыо, это не единственная возможность. Напри-
Например, исключив все функции, кроме давления, можно получить
трехточечное уравнение относительно б/».
Отметим также, что нри построении разностной схемы можио
ввести функцию удельного объема ri = 1/р. В этом случае систе-
система уравнений A.1') примет вид
где последнее соотношение есть уравнение состояния. Заметим,
что и отличие от A.1') здесь первые три урапнегшн линейны;
нелинейность содержится в уравнении состо.чшт. Так, для иде-
идеального газа (изотермический случай) имеот место \> = с21ц.
После линеаризации A.1') получим вместо C.5') следую-
следующую систему разностных соотношении:
6т) — 6х, == — /3, 6р — Ф'бм = — /4,
где /i='/2 = /3 = 0 при А: 3* 1. Исключая отсюда все функции,
кроме бг), приходим к трехточечному уравнешпо для бт|.
Каждый способ ностроепия трехточечного уравнения порож-
порождает спой итерационный алгоритм.
2. Сходимость итерационного процесса. Выясним условия схо-
сходимости итерационного процесса, описанного в предыдущем
пункте. Для простоты ограничим рассмотрение случаем идеаль-
идеального газа
^() с2р, с = const.
Перепишем исходную систему линеаризованных уравнепий
C.3), подставив вместо правых частей /„ их выражения.
Получим
ft+l . _ /h+l ft+l
Vi ~v\ + oT{ Pi - pi_
xt —xl—0,5x[vi -\-vl) ¦¦=(), C.12)
1 /fc+1 h+l\ j /h+l h \ .
\ - Xi ) 4- jj- { Pi — pi) __
Pi 14
k+l h+l
Pi -r2 Pi =0, & = 0, 1,2, ...
Испольауем обозначение
ft+l ft+l .,, Л + 1 -.
Ai/ = » -j/J+1= у -у- C.13)
Вычтем последовательно иа каждого уравнения C.12) соот-
соответствующее уравнение C.2). Результат запишем, используя
204
введенное обозначение C.13):
h+l k+i fc+l h+i
A v -,-отАр- = 0, A x — 0,5тД v = (I,
==0.
Первое, второе и четвертое уравнения здесь отличаются от
соответствующих уравнений системы C.5') лишь отсутствием
правых частей. Нелинейное третье уравиеиие более существенно
отличается от соответствующего уравнения C.5'). Посредством
несложных выкладок ого можно преобразовать к виду
fc+l h+\ Ik j k\2i h _
Axt +Д p /p2 - - Up)/(pap). C.15)
Из соотношений C.14) следует
fc+l h + l h+l A+l
Д xs - 0,5тД c.s = — О,5ат;Др-з = — О.оаЛ^Др-^.
Подставляя отот результат в (З.'1'i), имеем
А+1 к Л-( I A „
// - a* yh ~ - у*/р, C.10)
/?+1 ft+l ft ft
где /у = Д <) , aJ = 0,5ат2с2р-. 1.5 индексной форме C.10) можно
привести к виду
k
11 + -idi/ii*) !п - -4 ( т-х + //i+iJ = - yi/pi- C-17)
Заметим, что если рассматривать задачи, где в граничных
точках г = —1, i == N заданы режимы изменения со временем
давления Р^1 = Р* (tj+1), P3n1= P**(tj+1), то, полагая в гранич-
fc h
ных точках для всех к ==0, 1,2. ... />_i= /** @-м)» PN=P**(tj+i),
к h h к
имеем Д/j-i = 0, Арм = 0 и, следовательно, Др_1 = 0, Арм= 0- Это
дает граничные условия для уравнения C.17)
A+l h+l
//_1=0, un-0. C.18)
К неоднородному уравнению C.17) с одпородпыми краевыми
условиями C.18) применим принцип максимума [77]. Напом-
Напомним формулировку некоторых его следствий.
Рассматривается задача: найти сеточную функцию у(х), удов-
удовлетворяющую во внутренних узлах сетки сол уравнению
Я (*,?)?(?) = *¦(*), C.19)
а в граничных точках сетки ^Л краевому условию
у(х)=р(х). C.20);
205
Здесь х — регулярный узел сетки, Ш'(т)—множество соседпих
с х узлов с, ^ х, А(х), В(х, g)—заданные коэффициенты урав-
уравнения. Относительно нпх предполагаются выполненными следу-
следующие неравенства
А(х)>0, Д (*,?)> О, .2)И = Л(а)- V В (х, I) > 0. C.21)
В этих' условиях имеют место следующие теоремы.
Теорема 1. Пусть функция у{х), определенная на
неположительна на границе: у(х)^0 на ^п, и всюду на (Ол вы-
выполнено неравенство 5f[//j^0; тогда у(х) неположительна всю-
всюду па со„ + in.
Теорема 2. Если 2)(х)>0 всюду на 05л, то для решения
уравнения C.19) с р.(х)—0 верна оценка
We. C.22)
Оченмдно. уравнении C.17) является частным случаем C.10)
с коэффициентами
Нетрудно видеть, что Л, > 0, #;_, > 0. В,.., > 0, 20 > 0.
Граничные условия, т;ак поиа.чыппет равенство C.18), п дап-
ном случае нулевые. Так как
то применение теоремы 1 дает
ft+l Л+1 h+l
yi+l = Л (ч = (н - pi41 < 0, к = 0, 1, 2, .. .
Таким образом, в процессе итерации приближенно к корню pi 1
происходит снизу. Использование теоремы 2 приводит к следую-
следующему результату
!; // 1,<:;г/2/рцс<"ч!и1г/|1, C.23)
где 1] -= 1/р — удельный оПъем, 3)=\. Видно, что рассматривае-
мый пторацпопный процесс является квадратичным, как это и
должно быть для метода Ныотопа.
Обозначим через
/?-'|Л1И'|Я>1Ь C.24)
Тогда из C.23) следует
(Ь ,2 Ih-l 22 /0X2*+! /0\2Л+'-1°
\
/ /.' — 1 , 2 z l<)\2 /0\2
Учитывая обозначение C.24), имеем
206
Отсюда видно, что если начальное приближение таково, что
li*\ 14У 1с = IhlkllP - Pile = q < 1. C.25)
то итерационный процесс сходится.
Если в качестве нулевой итерации используются значения
сеточных функций на предыдущем шаге, то для q получаем
выражение
q = II llp'+lK ilpJ — p^'ll,. = xlil/p^'li,. llp.ii,.. C.26)
Эта величина зависит от характера рассчитываемого процесса
и, в частности, определяется скоростью изменения функции во
времени. Однако за счет выбора шага сетки по времени всегда
можно обеспечить выполнение неравенства C.25), т. е. сходи-
сходимость итерационного процесса.
3. Оценки для расчета иаотер.чической ударной волны. В ка-
качестве иллюстрации рассмотрим, к каким ограничениям приво-
приводит условие сходимости итерации C.25) для конкретного при-
примера — расчета движения ударной волны, возникающей в задаче-
о поршне. Однородные разностные схемы, обеспечивающие
екпо.шоп расчет ударных волн i'c:i явного выделения фронта
волны, предполагают введение вязкости. Точное решение задачи
о «вязкой» структуре фронта ударной волны построено в § 6
гл. Г. Однако там оно получено для адиабатического случая, в то
время как оценка C.25) построена п предположении об изотер-
мп'шистп течения. Поэтому предварительно получим результаты
для структуры изотермической ударной волны в идеальном газе.
Система дифференциальных уравнений в этом случае имеет вид
til] ov dv _ iig _ ,
at Os' at Os' C27)
v dv с
C0 = -,T37' P = T]'
где с > 0 — изотермическая скорость звука.
Так же как в § 6 гл. I, введем автомодельную переменную
| = ,v — //', где I) = const > 0 — массовая скорость движении
фронта ударной волны. Переход к автомодельной переменной
позволяет привести систему уравнений в частных производных
C.27) к обыкновенному дифференциальному уравнению
t|=-?-O1o-t,)(ti-ti,)- C.28)
Здесь г)о и r)i=a2r)o — значения удельного объема перед фрон-
фронтом ударной волны и за ним, а = а/1) — параметр, характеризу-
характеризующий интенсивность ударной волпы, а = c/rjo — массовая изотер-
изотермическая скорость звука. Так как D>a, то 0 < а < 1.
Уравнение C.28) формально можно получить из уравнения
F.17) гл. I для адиабатического случая, если положить в нем
Tf-1.
207
Точно так же из общей формулы для эффективной ширины
фронта ударной полны F.20) гл. I
при f — 1 получается значение этой величины для изотермиче-
изотермического случая
Л = 4v/(Z>(tio— Л|))- C.29)
Точное решение уравнения C.28) позволяет вычислить зна-
значения норм, входящих в C.20):
-„ .Л , лЧ1„-ч,)я
Поэтому согласно C.26) имеем
4v Ч|
Учитывая выражение для эффективной ширины размазывания
фронта ударной волны вязкостью C.20) и полагая, что эта ши-
ф(а. 1 рина составляет п массовых интервалов
cct-icii Л = •?/.' (ооычпо коэффициент вяз-
вязкости v подбирается так, чтобы п —
-;ti-4), преобразуем условие сходимо-
сходимости итерационного процесса к виду
- v ^ '' ^
1 -а'
C.30)
Здесг,
1 а
= h'(cot) — величина, вычислен-
вычисленная но условию устойчивости Куранта
для параметров за фронтом ударной вол-
волны. Тдиим образом, величина максималь-
максимального шага т, допустимого в расчетах за-
задачи об ударной волне, зависит от ее ин-
интенсивности (величины параметра а: 0 <
<а<1). Расчет сильных ударных волц
(а ->- 0) требует использования мелкого шага т; при расче-
расчете слабых воли, близких к акустическим (а-1- 1), ограничения
практически отсутствуют (рис. 4.2).
Итак, применение итерационного метода Ньютона для реше-
решения даже абсолютно устойчивых разностпых схем приводят к
ограппчениям на шаги сетки. Однако эти ограничения заметно
слабее, нежели условие A.17), полученное в п. 3 § 1 для про-
простейшего явного итерационного процесса.
\. Учет пеевдовязкостн. Как отмечалось в гл. П, для обеспе-
обеспечения возможности сквозного расчета ударных волн в разност-
разностную схему вводится нсевдовязкость. В простейшем изотермиче-
изотермическом случае система разностных уравнений с псевдовязкостью
208
принимает вид
vt = - g(;\ 8 = Р 4- а. ^ = i'(OlS)- л. = 1/Р, Р = ^ (р). C.31)
Искусственная вязкость
o)i = Q(pi, i'i, yi+i), C.32)
или в безындекспой записи
co = Q(p, v, v(+l)) C.32')
может иметь различную форму. Обычно используются либо «ли-
«линейная вязкость»
(,),- = —0,5vpi((i;,-+i— у()//г- I (vi+l — vt)lh\), C.33)
й) = —0,.r)vp(i>,—I(w.)l), C.33')
либо «квадратичная вязкость»
со,- = -0,5цр,| A7,+ , — v,)/h\ ((y,+ i - v,)/h - I (»«+, - vt)lh\), C.34)
,;)\ip\v.\(v.— \v.\), (o.o4 )
либо их линейная комбинация.
Проанализируем, как повлияет присутствие в схеме нсевдо-
вязкости на процесс ропюппя разностных уравнений с помощью
итерационного метода Ньютона.
Исходную разностную схему можно записать в виде системы
¦}{У -- = т (''( -г А'-1') "-= °. /аТ;1 = т (от, — i'@l5)) = О,
/' + 1 — А '/I II /.'1 + 1 г, <& 1г.\ Л /Ч Чг>\
_/^~х = со — И (р. г, г ( f 1)), /e^i1 = a' — (л + со) = 0.
Проводом лпполрп.чацию этих урапнепий методом Ньютона.
В результате аналогично C.5') получим
бг; + ot8<;- = — /,. их — OJwbr /.,,
8х, -\- 6р/Р" = — /л- й/> — 5^'о'р = — /4,
0@ — — 00 0V-- ОУD 1) = — /г, @.0())
<^n — F/J "Г б@) = — /в.
Заметим, что функция /Й1{ равна пулю па всех итерациях: на
нулевой (/с = 0) в силу выбора начального приближения:
о .о .о ....
па остальных (к > 1) вследствие линейности функции /Je+1 в
C.35).
14 А. А. Самарский, Ю. П. Попов 2Q9
Исключая из C.36) все функции, кроме 6г, приходим к ли-
линейному уравнению
|yj, C.37)
где К = р2[/з-(/2),]
Это уравнение является трехточечным относительно сеточной
функции 6у и вновь может быть приведено к индексной фор-
форме C.7)
В&и<+1 = —Ft.
Однако, в отличие от C.8), коэффициенты вычисляются здесь
ио формулам
(oil
T
C.38)
Входящие в эти формулы производные от псевдовязкости вычис-
вычисляются на основании конкретного вида функции Q в C.32). На-
Например, для линейной вязкости C.33)
h \ /ft ft\ ftft
О/Др'{ = - О.Г)у [vt ~\vt\h = ©i/pi, C.39)
f—vpf//i при v,<0,
*V{.+ I)ji \duji ft
О при v,
В остальпом учет псевдовязкости не вносит никаких допол-
дополнительных изменений по сравнению с предыдущим пунктом.
При Q = 0 формулы C.38) вырождаются в полученные ранее
выражения C.8).
Нетрудно видеть, что как для линейной, так и для квадра-
квадратичной вязкости справедливы неравенства
210
h k
которые обеспечивают положительность коэффициентов Л,-, В{
в C.38). Для вязкостей указанных типов выполнено также со-
соотношение
i = — \du!dv)i,
k
позволяющее преобразовать коэффициент С\ в C.38) к виду
h h k
Ct = 1 + Л{ + Щ.
Указанные факты в соответствии с общей теорией обеспечи-
обеспечивают устойчивость прогонки.
5. Адиабатический случай. Распространим метод, описанный
в н. 1 для изотермического случая, на уравнения адиабатиче-
адиабатического течения газа. Сиитвитстнующая разностная схема такова
>t == — p. , jct = v . xs = l/p,
A
e, = _ p^v<»'-'\ p = g> (Pi 7'), e = «¦ (p, T).
Чтс'ы uo иагромиждать изложение, ми внонь опустили псевдо-
псевдовязкость, ее учет производится в точности так же, как это было
проделано в предыдущем пункте. Перепишем разностную схему
в виде
!\У = т (vt + р^) = 0. /Й1 = т (xt - v^) = 0.
А'л -*s- 1/p = о, /i;,1 = T(p« + p<040>5)) = o,
/Й1 = P - ^ (P, ?') = 0, fi? = t-& (p, Г) = 0.
Но сравнению с C.2) сюда дополнительно вошло иелинейпоо
уравнение энергии; нелинейными, вообще говоря, являются и
уравнения состояния.
Применение метода Ньютона нршюдит к линейной системе
ураппешш
6у ¦':- отЬр- = — /,, Ьх — 0.5т6у = — /2,
bxs + 6р/р2 = - /,, бе + 0,отр1%с,-г от1.
'(¦+ f «¦) = -/
Все сеточные функции, кроме приращений Ьу, вычисляются
здесь па предыдущей А--й итерации. Например, линеаризованное
уравнение энергии фактически выглядит так:
бь 4 О.Г)т//0Nу, -f- от уD°'5) б /) = - /4-
Входлщие в последние два уравнения производные при
14* 211
постоянной темнературе
C.41)
и постоянной плотности
dSP\dT = {д^дТ)р, dgjdT = (<3<Г/<ЗГ)Р C.42)
также вычисляются на /с-й итерации и относятся к иолуцелым
точкам сетки. В дальнейшем для сокращения мы опустим у этих
производных нижние символы Г и р. Для идеального газа с
уравнениями состояния
p = pRT, е=Д77(ч-1)
производные C.41) и C.42) выглядят так
{д.У:до I; =---¦ П Г ¦, hjf '<) Т); == П(ц,
\ (ЗУ3)
Заметим, что для идеального газа уравнение состояния для е
линейно, и нотому /в==0на всех итерациях А: = 0, 1, ....
Рассматривая изотермический случай, мы исключили из сис-
системы линеаризованных уравнений все неизвестные сеточные
функции, кроме приращения скорости, и таким образом свели
задачу к трехточечному уравнению для 6и, которое решалось
далее прогонкой. Т,очно так же можно преобразовать и систему
C.40). Однако, как было отмечено выше, аналогичоое уравоенно
можно получить для приращения любой функции. Например,
исключая из C.40) все функции, кроме бр, получим
fcft+i ftft+i л ft ¦¦ k k i
abp — o-c'jJ) S/ь = — (b a = dtf UlT -{¦ ^0"
S
S
, ft ft
A .-
, /-"I
5[Ы A l> 1j Ь
В индексной форме соотношение C.44) эквивалентно трехто-
трехточечному уравнению
Aibpi-i — dbpi Л- Bi8pi+i = — Fi,
для коэффициентов которого справедливы формулы
ft ftftftftftfth
А-х = а (т//*)а pi, lh = Au Ci = Ai + Bi + cLi
Для идеального газа в обычных условиях
ft п I hk, \ ft n2 ft
л л / ft л
р = 0,5Л(
212
-г ft
Поэтому коэффициенты Л;, Hi положительны. Соответствую-
Соответствующее неравенство
ft ft ft
которое обеспечивает устойчивость прогонки, выполнено, если
20 что, как можно показать, имеет место при условии
. h ft-i\ Ik
л л — Л" J/л
<l/(a(v-1)), Л = Vf»
(относительное изменение удельного объема за один шаг не
должно быть большим).
Итак, для адиабатического случая принципиальная сторона
вопроса не изменилась,— разностная схема по-прежнему сводит-
сводится к трехточечтшу уравнению, которое решается методом про-
прогонки с итерациями.
6. Исследование сходимости для адиабатического случая с уче-
учетом вязкости. Проведем обобщение условия сходимости метода
Ньютона C.2о) для адиабатического случая с учетом линейной
вязкости [77]. Полностью консервативная разностная схема для
идеального ra.ja может быть записана следующим образом
tt=-—gwr\, C.46)
t-= ——рц, я = р + со, со ¦¦= — ~va. C-/|7)
i 1 Ч
Последние три уравнения C.47) могут быть заменены одним
B-=-bgr\ + bw., C.48)
где
Применение старгдартной процедуры метода Ньютона к снс-
темо C.4Г>) — C.47) при а > 0 приводит аналогично (З.п') на
каждой итерации к системе лпнепных уравнений
бг + oibg- — — /р Ьх — 0,5тбг ¦-= — /.,,
бл:.-6л = -/з, бе + я(о)бл + атт1,бя =-А, C.49)
бе — br\6g — bg6i\ — bvbv, = —/5,
где /m, m ¦¦=• 1, 2, ..., 5, вычисляются по формулам аналогичным
C.2), а коэффициенты при неизвестных 6у отнесены к к-й ите-
итерации, папример Л'=(л'1 — лО/т- Исключая из C.49) прираще-
приращения всех функций кроме 6i', можно вновь прийти к трехточечно-
трехточечному уравиению типа C.7), которое решается методом прогонки.
Итак, метод решения схемы C.45) —C.47) буквально повторяет
алгоритм, описанный выше.
213
Обратимся теперь к анализу сходимости этого метода. Вычи-
Вычитая из каждого уравнения системы C.49) соответствующее урав-
уравнение схемы C.45) — C.47), придем досле некоторых преобразо-
преобразований к системе уравпений, подобной C.14):
ft + l fe+l ft+l ft+l ft + l k+l
A v + отД g- = О, Л x — 0,5тД v =0, Л xs — Л х\ =0,
k+l ft ft+l ft ft+l ft ft ft+l ft+l
Л e + ацА g + og/S. r\ — aAr\Ag + ат\А g -\- A — а) ^Д т] = 0,
C.50)
ft+I к h-'rl k ft + l k ft ii + 1
А г — br\A g — bgA r\ ¦{- bAr\Ag — bxA v, = 0»
ft+i Ji+i
Исключив из C.50) приращения всех функций кроме у\ = Д gu
придем к уравнению
h ft-f-i h /Ml k + l \ ft
.4; yt - Hi [ yi:l r .VJ.J = Fit i = 0, 1 N- I, C.51)
где
A k ft
Hj = (b + a) in — ОТЦ + 2flj,
/5{ - a-l [n.r,-J- ((b + o)f, + A - o)^) -|- 6v].
к k ft
о) Д
Очевидно, что Bi >0. Потребуем, чтобы выполпялось неравенство
I)i =-- Ai — 2IU = (b + о) rii — ащ > 0. C.52)
Заметим, что при атом также выполнено поравоиство М > 0.
Такилг образом, выполнение неравенства C.52) обеспечивает
примешчше ппппципа максимума [77, 78].
Если опять огратшчиться рассмотрением граничных условий
по давлению:
и принять во внимание, что в гранитных точках i = —1, N —
принято «запулять» псевдовязкость coL'i = соУ" = 0, имеем для
уравнения C.51) однородные краевые условия:
k+i ft+i ft+i ft+i
Примененио принципа максимума к C.51) дает
ftft || k
C.53)
Id
214
(b -f a) t| — ar\ !'c
где
:! h -
[ (Ь-1-д)(т|-т|)
11- n
F i- a) T) — ar\ \c
j-a
Очевидно, сходимость итерационного процесса Ньютона име-
имеет место, если гу*<1, а также выполнено условие C.52), кото-
которое можно записать в виде
k
а
6 4-a
Т].
C.52')
Неравенство q,_< \ выполнено, если при всех i = 0, 1, ..., N—1
справедливо
-К
C.54)
Рассмотрим дне возможности. Первая отвечает процессу раз-
разрежения газа, когда т); > ц,. Тогда в C.54) правое неравенство
выполнено, а левое приводит к условию
Ч > 0,5 11] -J- -jfr-a т]), C.55)
выполнение которого одновременно гарантирует справедливость
C.52').
В противоположном случае (Tii<Tl;)i отвечающем сжатию
гана, условие C.54) оказывается нмиолпенпым, если ипог.ь
справедливо (.')..").")), а также перавопство C.56):
причем условие C.j2') при этом будет выполнено. Разумно
предположить, и это подтверждается расчетами, что для выпол-
пения перавеиства C.55) при любом к достаточно потребовать
его выполнения па нулевой итерации к = 0. Условие C.55) при
о
к = 0 (п = л) может быть преобразовано к виду
" <г Ь
b -\- с
откуда, после деления на т. а также учета формулы разностного
дифференцирования р, =¦ —i)i/t)ti, t) =¦ 1/р имеем
>-1. C.57)
Заметим, что для случая сжатия имеем р( > 0, и тем самым
условие C.57) выполнено. Неравенство C.56) после несложных
215
преобразований приводится к виду
1 + -г) Т1]Р; ¦< I. (о.оо)
Об7.едипяя C.57) и C.58), приходим к условию
:1лрЛ<1- C-59)
Для изотермического случая G = 1, b — ¦<») C.59) переходит в
ыеравепство
с<1, C.60)
которое имеет тот же тип, что и долучеыпое выше для случая,
когда по учитывается поевдовязкость; условие C.25), однако,
является менее «жестким».
Следует указать, что полученное для адиабатических течений
услоиие сходимости итераций C.59) пакладывает Полое сильные
ограничения па шаг т, чем в изотермическом случае.
Отметим также, что одна и та же разностная схема, к кото-
которой применяется итерационный процесс, может быть записана в
несколько отличающихся формах, папример с использованием
сеточной функции плотности или удельного объема. Ото может
лесколько изменить характер нелинейности схемы и тем самым
повлиять на условия сходимости итераций.
7. Результаты численных расчетов. Полученные оценки макси-
максимального шага т, использование которого допускают различные
описанные выше алгоритмы, подтверждаются численными расче-
расчетами. В качестве теста рассматривается классическая задача о
поршне, вдвигаемом в газ с постоянной скоростью [70].
Все рассмотрения будут проведены для изотермического слу-
случая при уравнении состояния р = с2р. Исходпое состояние газа
имеет вид
p(s, 0) = ро =¦ 1, л («, 0) = ло = 1, p(s, 0)- по = 0,25, C.61)
v(s, 0)= уо = О.
Значение и.чотормической скорости звука с = 0,5. Сравнитель-
Сравнительный анализ алгоритмов проводится на примере варианта задачи,
где скорость поршня равна Fo = y(O, 2)= 0,75. При этом, как
следует из соотношений Гюгонно, скорость фронта ударной вол-
волны D = 1, а параметры газа за фронтом имеют следующие
значения
р, =4, л. = 0,25, /;, =-- 1, у, = 0,75. C.62)
При расчетах в рассматриваемой пространственпой области вво-
вводилась равпомерыая сетка с шагом h = 0,1. Шаг сетки по вре-
времени варьировался, параметр о =¦ I.
Для обеспечения возможности сквозного расчета ударной вол-
волны в схему вводилась линейная вязкость со = — \pva с коэффи-
коэффициентом v, так что фронт волны размазывался на п интервалов
216
сетки (см. гл. I, F.20) при 1=1), при этом
4v
n =
C.G3)
При значении коэффициента v = 0,05, которое использовалось в
расчетах, и значении D = 1 имеем п « 2,7.
Расчет сформулированной задачи был осуществлен с по-
помощью трех алгоритмов: по явной полностью консервативной
схеме A.3) — A.6), но чисто неявной полностью консервативней
схеме с использованием .итерационного процесса зейделонского
типа A.9')—A.12'), а также с применением метода Ньютона
(см. п. 1). На рис. 4.3 представлены результаты расчета (про-
(профили скорости на последовательные моменты времени) задачи
о поршпе по явной схеме для различных значений т. При
т = 0,03 (| = т/ть = 0,0) решение передается хорошо (рис. 4.3, а).
2,0
Рис. 4.3
При т-=-0,04 (% = 0,8) профиль скорости за фроптом волпы ста-
становится <(нилообразпым» (рис. 4.3, б). При еще больших шагах
т ~ 0,05 (?~1) развивающаяся болтапка полностью искажает
решение (рис. 4.3, в). Интересно сопоставить этот результат
с теоретической оценкой A.8). Хотя неравенство A-8) и накла-
накладывает па т весьма жесткое ограничение «параболического» ти-
типа, одпако содержащаяся в пем произвольная постоянная со
приводит к тому, что рассматриваемая схема оказывается эффек-
тивпой на практике при X =€ 1.
На рис. 4.4 дапы результаты расчета тоii же задача по чис-
чисто пеявпой схеме с нрилюненпем зейде.ленского итерационного
процесса. При т —0.015 (| = 0.3) решение передается удовлет-
удовлет0 0 (
рц р (| ) р р
ворительно (рис. 4.4, а), при т = 0.017,1 (% — 0,ЗГ>) (рис.
6)
профиль скорости приобретает ярко выраженный «пилообразный»
характер. Заметим, что уже при этих значениях т итерационный
процесс сходится медленно. В расчетах чпело итераций было ог-
217
рапичепо величиной /со = 30 при т = 0,015 и ко = 100 при т =
= 0,0175. Тем не менее этого количества итераций оказалось не-
недостаточно для того, чтобы удовлетворить условию сходимости
C.9) с относительной точностью ?; = 10~4. При дальнейшем
увеличении шага, панример при т = 0,02 (| = 0,4) (рис. 4.4, в),
°\
I
1,0 2,0 S
Рис. 4.4
воспроизвести решение с помощью указанного алгоритма не
удается.
Итак, экспериментально нолучеппор ограничение на шаг сет-
сетки имеет вид
При невыполнении этого условия алгоритм в рассматриваемой
задаче работает плохо. Это согласуется с теоретической оценкой,
лилученпой в § 1 для акустики A.17), которая имеет вид
т<
0,7).
На рис. 4.5 приведепы результаты расчетов, выполненных по
чисто пеявной схеме (о = 1) с примепепием метода Ньютона для
следующих зпачепий шага: т = 0,01 (? = 0,12) (рис. 4.5, а),
т = 0,2 (| = 4) (рис. 4.5, б), т = 0.6 (?=12) (рис. 4.5, в).
Заметим, что шаг т = 0,6 является для данной задачи весьма
крупным: фропт волпы при этом за одип шаг по времени прохо-
проходит шесть массовых иптервалов сетки. Тем пе менее решение
воспроизводится удовлетворительно и итерационный процесс
сходится сравнительно быстро: при т = 0,01 количество итера-
итераций А: = 2, при т = 0,2 — к = 3, при т = 0,6 — к = 4.
Совместный апализ теоретических результатов и результатов
расчетов приводит к важному выводу об эффективности приме-
применения для численного решения задач газовой динамики пол-
полностью консервативных схем в сочетании с итерационным мето-
218
дом Ньютона. Построенные на этом принципе алгоритмы допус-
допускают использование грубых сеток с большими т, не теряя при
этом свойства адекватности физическому явлению, что дает воз-
возможность сокращать машинное время, необходимое для решения
задач.
8. Особенности расчета задач газовой динамики на грубых сет-
сетках. Как отмечалось выше, численный алгоритм, сочетающий пс-
пользовапие пеявиых полностью коисервативлых схем с итера-
итерационным методом Ныотопа, позволяет вести расчеты при шагах
v
\
7,0 2,0 3,0 S
в
т, заметно превышающих xk. с то время как обычпо па практи-
практике т ^ Ть. Переход к таким грубым сеткам порождает ряд новых
явлений, непосредственно связанных с дискретностью той моде-
модели среды, каковой является разпостная схема. Укаже.и пекото-
рые подобпые эффекты, которые необходимо учитывать при фи-
лической интерпретации результатов расчетов. Так, в частности,
анализируя результаты, представлеппые на рис. 4.5, в, следует
отметить колебания, которые претерпевают разностное решение
в окрестности порпшя. Ути колебания наблюдаются лишь при
достаточной величине шага сетки по времени т ^ 0,03 (s^6),
причем они возрастают с ростом т. Колебания происходят во
времепи от шага к шагу с медленно убывающей амплитудой.
Указанные колебания есть следствие <(удара», который наносит
поршень но грапнцо среды во время первого шага но пременн,
разгоняясь с большим ускорением из состояния покоя при / = 0
до конечной скорости Vo при / = т. Убедиться в этом позволяют
результаты расчета, нредставленпые на рис. 4.6. Значения всех
параметров .{дрсь те же, что и для расчета па рис. 4.5, в Яа иск-
исключением начальных данных: для рис. 4.5, в они задаются ра-
равенствами C.61), для рнс. 4.6 —это гладкие распределения, со-
соответствующие «размазанной» ударной волне, продвинувшейся
219
внутрь области на 10 массовых интервалов. Как видно на
рис. 4.6, дальнейшее движение ударной волны при ?>0 уже не
сопровождается колебаниями функций у поршня. Тот же ре-
результат получается, если поршень набирает скорость ностенеп-
по. а не приобретает ее за один шаг.
Другой тип колебаний, которые наблюдаются в расчетах с
крупными шагами т,— это волнообразное распределение пара-
параметров на ударным фронтом (рис. 4.G). Амплитуда этой волпы
0,5:
0\
Рис. 4.G
увеличивается с ростом т, в то же иремн волна затухает по мере
удаления от фронта к поршню. Расстояние мезкду максимумом
и минимумом в профиле, формирующемся за фронтом (полоипна
длины волны), приблизительно равно числу массовых интерва-
интервалов сетки, которое, проходит фронт за один шаг по времени (для
рис. 4.5, в и рис. 4.E это число равно шести интервалам).
п и
/,'71 0,?.
п п\. п t
D О
/
'' 7
/ К
}¦ ¦ \
¦ -\
/ (-
Рис. 4.7
Причина возникновения этих колебаний заключается в диск-
дискретном характере среды (разностной сетки), по которой движет-
движется ударная волна.
Еще одна специфическая деталь серпп расчетоп, представ-
представленной па рис. 4.Г), состоит п особенностях размазывания фрон-
фронта ударной полны. JJри малых т эффективная ширина фронта
ударной волны совпадает со значением C.G3), полученным для
точного решения и равного для рассматриваемого случая п = 2,7.
Однако но мер!1 увеличения т эта ширина растет, хотя значение
коэффициента вязкости v остается неизменным (см. рис. 4.7, где
представлены профили удельного объема т) и вязкости со в уста-
установившемся профиле волны, полученным в расчетах с различ-
различными т).
220
С целью выяснить причину указанного явления запишем
первое дифференциальное приблпжепие для исходного семейства
схем A.2), где учтена искусственная вязкость [98, 99]:
1 ах
о ~~ ds'
Здесь чертой сверху отмочены функции, вычисленные в точке
(si+i/2, fj+i/2). Член порядка 0{х) в первом уравпенпи C.64)
можно трактовать как некоторую дополнительную вязкость
со = — (а —п.5)т^-. C.1M)
Коэффициент этой вязкости зависит от параметров дискретной
среды о и т, причем при т -> 0 дополнительная вязкость стано-
становится исчезающе малой. При больших т вязкость со может стать
заметной и повлиять па решепие.
Вязкость ы представляет собой часть сооствеппоп (аппрокси-
мационной) вязкости схемы, имеющую порядок О (т.).
Для схемы с о = 1, которая рассматривалась выше в расче-
расчетах, представленных па рис. 4.Г). 4.7, имеем (о = —O.ot—. В за-
задаче о структуре фропта изотермической ударной волны, где о>
порождает дополнительное размазывание волпы, вязкие члены
со п со можпо представить с помощью точпого решения C.28)
в впде
о) I) -iJ-, 0) = — V -т±.
Таким образом, для рассматрпваемо11 задачи фупкцню Q — со + о>
можпо рассматривать как некоторую суммарную вязкость
О -^ v *-0,Г)тЛ2Т1 D г/Т]
являющуюся линейной и обладающую коэффициентом v = v +
+ 0,5т/Jт). Этот коэффициент зависит от решения т)(|), однако
для оценок можио пользоваться эффективной величипой vn4 =
= v + 0,5tD2t), где т)| s= т) s? тH — пекоторое среднее значение
удельпого объема. Ширина ралмазынання фронта полны сум-
марпой вязкостью Q, j;ai; это следует из формулы C.63), будет
определяться формулой
Отсюда видно, что при т -> 0 велпчппа ;"г(т) совпадает с класси-
классическим значением C.63), которое следует из точпого решения
221
дифференциальной задачи о структуре фронта ударной волны.
С ростом т ширина размазывания увеличивается по линейному
закону. Расчеты подтверждают этот вывод. На рис. 4.8 дана за-
зависимость п(т), полученная экспериментально в результате об-
обработки серии расчетов, часть которых представлена на рис. 4.7.
Значения параметров здесь таковы:
D = i, v = 0,0r,, h = 0,1, т)о = 1, ть =
= 0.25. Экспериментальные точтш хо-
хорошо ложатся на прямую с ц = 0,5.
Это естественно, так как расчеты по-
казынают, что при различных т дейст-
действие вязкости максимально в районе с
11 ~ 0,5 (см. рис. 4.7).
,fr / Заметим, что из-за наличия аппро-
кснмациониой вязкости в условии схо-
сходимости итераций C.30) вместо фик-
| сированной величины п должна стоять
| L ;. _:___ иелпчппа п(т), увеличивающаяся С
0 0.5 7,0 г ростом т. Это обстоятельство, а также
Рис. 4.8 тот факт, что условие сходимости
C.30) носит достаточный характер,
позволяет на практике пользоваться сетками с шагами т, замет-
заметно превышающими максимальное зпачепие, предписываемое не-
неравенством C.30).
При малых зпаченнях шага т влияпие собственной вязкости
схемы повелпко и, как известно, расчет ударной волны без ис-
искусственной диссипации (со = 0) практически невозможен. Одна-
Однако при больших т ^ Tjii действие аппроксимационной вязкости
схемы становится достаточным для обеспечения необходимого
«размазывания» фронта ударной волны.
§ 4. Метод раздельных прогонок
1. Общин случай с учетом вязкости и теплопроводности. Учет
теплопроводности в ра.шостнон газодинамической схеме заметно
усложняет алгоритм ее решения.
Рассмотрим общее семейство полностью консервативных схем
газовой динамики, включающих псевдовязкость и процессы теп-
теплопроводности:
vi = - U&\ xt = v(a'b\ xt = 1/р, g = р -!¦ и,
„ = _ /ЛЧ.'0-" - и'1Ч w = - ктт, (/i.1)
р=.?(р,Т), 8 = й"(р, Т),
к = К(9, р(-1), Т, Г(-1)), oj=Q(P, v, v(+i)).
Для большей общности будем предполагать, что схема D.1)
222
записана на неравномерноп сетке:
где
й, — 0,n(Af + Л*_,)-
Свободные параметры oi н О2 в D.1) отличны от нуля, так что
эта разностная схема не может быть разрешена явным образом.
Перепишем систему разностных уравнений D.1) в виде
f[? = т (vt + 4-Ol)) = 0, /ft1 = т (*, - i,<°'«) = О,
/# = Xt- i/p = I), /iy = т (e, + *(Ч<0'5) + Wi°a)) = 0,
Я+1 = W + kTv = О, /Й1 = /j - .? (p. Г) = 0,
/ft1 - e - ff (p, Г) = 0.
^У = Л - ЛГ (p. p (- 1), rj(-l)) = 0,
Используя стандартные безыпдексные обозначения и технику,
развитую в настоящей главе, применим к решению этой системы
метод Ньютона. Линеаризованные уравнения для разности сеточ-
сеточных функций на двух соседпих итерациях записываются следую-
следующим образом
bv + то! fig- = — /15 fix — Сотбу = — /2, 6.rs + бр;р2 = — /3,
бе J-0,5t»(OiN!;s -!- za^&g - то2вИ^. = - /4. D.2)
6j? =-6/) + бм.
Система D.2) весьма громоздка, что сказывается на дальней-
дальнейших формулах. Исключая из D.2) приращения всех функций,
кроме скорости ц температуры, можно свести эту систему к
двум линейным уравнениям
223
0,5x4 [(Jjf p«to. + g^ p' (- 1) to-.) T7\ +
to + _?_ to (+ 1)) - xo2
/7 + то2 (h - T7h)s -
f Г + ^ V( ») 1 + (f + ™,»6»' |) Г. 0.4,
где F = p2[/3 — (/2),]. Первое есть следствие уравттепия движе-
движения, второе — уравнения энергии.
(; пеполь.юваынем иидоксиой зап;!С!1 соотношения (^.З), D.4)
можпо представить в форме
Atfoi-i — C&vi + Bibvi+1 + Di&Ti-i — Е{ЬТ{ = — t\, A.3')
+ D'fiT^ - E\&Ti~+ G\bTi+l = - I'l D.4')
Выражения для коэффициентов Ai, A{, B^, B{ и т. д. без тру-
труда получаются из D.3), D.4). Однако они слишком громоздки,
и мы их здесь не приводим.
Особенностью системы D.3'), D.4') является то, что второе
уравнение содержит значения искомой функции bv в четырех
точках i — 1, i, i+i, i + 2, и потому для его решепия метод
обычной прогонки неприменим.
2. Случаи дК/др = 0. Ксли коэффициент теплопроводности
среды не зависит от плотности, ситуация заметно упрощается.
При дК/др = дК/др(— J)=0 из уравнения D.4') выпадают зна-
значения 6гл_1 и 6гл+2. В результате вместо D.3'), D.4') имеем
Лгдгг^ - dbvi + n,8ri+l ~ DibTi _! - I-UbTi =-- - Ft, D.Г,)
- C'ibVi + B[8vi+1 + D'fiT^ - !ф\ |. C\&Ti+l = - F\. A6)
Коэффициенты первого уравнении вычисляются uo формулам,
следующим из D.3):
224
где
А
я;
Для коэффициентов уравнения D.6) соотношение D.4) дает
формулы
= о,т ! 0,?>r p2^r + T- ) - *> = CTiT I 0,5 -г-pa -^ —
1 \ к ' dp * 'i * \ Л rdp
ft, Г Л А, /Л fc \ * /ft ft ft
[ ?л) l ) /7 + то, (/5 - Гт/
где
ч
Вводя сеточные вектор-фупкции
перепишем систему D.5), D.E) в матричной форме
(At Di\ (Ct ЕЛ. (Вг 0 \
, бщ-х - , 6щ + I 6u,-+I = - I-Y D.9)
Для решения D.9) на каждой итерации может быть использова-
использована матричная прогонка [66, 81]. По ходу вычислений придется
обращать матрицы второго порядка, две ил которых (при 6u,-i и
6iii+i) являются треугольными.
Очевидно, что к системе D.9) задача сведется и в том слу-
случае, если отказаться от строгого применения метода Ньютона и
пренебречь вариацией плотности бр в приращении коэффициен-
коэффициента теплопроводности Ьк. Оправданием этому может служить тот
физический факт, что коэффициент теплопроводности, как пра-
правило, в гораздо большей степени определяется значением темпе-
температуры среды, нежели ее плотностью.
3. Раздельные прогонки. Итак, разностную схему для одномер-
одномерных нестационарных уравнений газовой динамики с теплопро-
водпостью свести в общем случае к трехточечным уравнениям,
для решопия которых годятся формулы обычной прогонки, не
удается. Избежать такого рода трудностей позволяет так назы-
называемый метод раздельных, или последовательных прогонок [84].
Суть его заключается в следующем.
Разностные уравнения схемы D.1) делятся па две группы.
Группа I—«динамическая», включающая ураппепия движения,
неразрывности и одно из уравнений состояния:
Vt = -g~l)' Xt = V{°A\ Хг = 1/р, ? = /> + Ю,
р = ^(р, Г), co = Q(p, v, y( + l))
Группа II («тепловая») состоит из уравнения энергии, опреде-
определения теплового потока и второго уравнения состояния:
)
e = <ff(p, Г), Л = Я(р, р(-1), Т, Т{-{)).
Уравнения каждой группы решаются итерационным методом
Ньютона самостоятельно, с последующими дополнительными
итерациями между группами. В группе I определяются сеточ-
сеточные функции v, р, х, в группе II — Т, W. При решении уравне-
уравнений одной группы величины, которые вычисляются в другой
группе, считаются неизменными, «замороженными». Поэтому
группа уравнений I весьма похожа на рассмотренный в § 3 слу-
случай изотермической газодинамики. Отличие состоит в том, что
здесь температура по пространству не является постоянной, од-
однако распределение ее задано.
Группа II фактически есть уравнение теплопроводности с
известным распределением источников газодинамического проис-
происхождения.
Расчет динамической группы уравнений D.10) сводится с
помощью метода Ньютона к решению трехточечного уравнения
h h+1 k ft + l h h+1 U
AS v i_x - db vi + B& vi+i = - F{, D.12)
коэффициенты которого вычисляются по формулам D.7).
Аналогично тепловая часть D.11) приводится к уравнению
i ,i+i i, i+i i, i+i i,
/Wi-i - ?iS 'I\ + G'i8 Ti+1 = - F{. D.13)
1 , l, l,
Для коэффициентов Z)j, Ei. Gi справедливы формулы D.8),
соотношение для /¦' несколько упрощается:
i, г i i .г i n i i
ft = [-h + ™.<4°'0)/« + и + то2(/5 - 7Y/
Номера итераций в уравнениях D.12) и D.13) обозначены
разными символами к и /, так как каждое из этих уравнений ре-
решается с помощью своего итерационного процесса.
Алгоритм решения задачи с помощью метода последователь-
последовательных прогонок выглядит как показано на рис. 4.9.
Уравнение группы I D.12) решается на каждой итерации А; ме-
методом прогонки. Температура в процессе этих итераций не изме-
изменяется, ее значение пока берется с предыдущего /-го слоя, так
с j-га-
j-гасло*
\
1
1
1 '
1 '
1
1
I
!
1
1
К
Внешни/1 итгаеиш
, Внутренни? ?-."п,:ечн
, итврации(Н': /.пхрииии
L
, ¦ А Г ,
Группа I j ryr/;a
PjC4f!,V ]+1-2Э
СЛОЯ
A.1
Т
'"' \
—\А
i
! ^./^Л
!
1
Рис. 4.9
что уравнение состояния в группе I фактически имеет вид
р=-^(р, Р).
Количество итераций К подбирается так, чтобы обеспечить нуж-
нужную точность. Для этого можно использовать, например, крите-
критерий сходимости итераций вида
k
max
+
б г,
(/i.14)
После окончания итераций полученные значения сеточных
к к к
функций pj, Vi, xi передаются и группу II и используются здесь
для вычисления коэффиципнтов уравнения D.13). Уравнение
D.13) решается на каждой итерации I методом прогонки. В про-
процессе этих итерации изменяется сеточная функция температуры,
значения же плотности, скорости и эйлеровой координаты фик-
фиксированы. Итерации заканчиваются на некотором номере I = L
при выполнении условия сходимости для 8Ти аналогичного кри-
критерию D.14). В результате определяется сеточная фупкция тем-
L
пературы Т\.
Заметим, что при больших значениях коэффициента тепло-
теплопроводности, когда обычная прогонка нриводпт к потере точно-
точности, для решения уравнения теплопроводности в части II может
быть применен потоковый вариант метода прогонки [3">], кото-
который позволяет избежать указанных трудностей.
Оба упомянутых итерационных процесса можно назвать вну-
внутренними, ибо они проводятся изолированно в рамках каждой
группы. Помимо них существуют внешние итерации между груп-
группами I и II. В процессе этих итераций описанная последователь-
15* 997
ность действий, включающая два внутренних итерационных цик-
цикла, повторяется. При этом в группе I в качестве заданного про-
профиля температуры используется результат, полученный в части
II \7'J па последней внешней итерации.
Как показывает практика, внешний итерационный процесс
достаточно быстро сходится, т. е. здесь можно ограничиться дву-
двумя — четырьмя итерациями. Значения сеточных функций, полу-
полученные па последнем"! внешней итерации, отождествляются с ре-
результатом (/'+ 1)-П1 временного слоя.
Порядок', в котором рассматриваются части I и II в методе
последовательныv прогонок, может быть любым.
Метод последовательных прогонок, состоящий н) серии пов-
повторяющихся итерационных циклон, требует для реализации
большого машинного времени, нежели матричная прогонка,
к которой сводится задача, если положить ОК/др = 0 (см. п. 2).
Однако этот метод имеет и ряд преимуществ. Они связаны преж-
прежде всего с меньшим объемом информации, которую при выпол-
выполнении расчетов необходимо хранить в оперативной памяти Э1Ш.
Это обстоятельство особенно ощутимо, когда решаются задачи
газовой динамики, осложненные дополнительными процессами:
электромагнитными полями, излучением, химической кинетикой
и т. д. В этом случае соответствующая система уравнений может
быть разбита на большее количество групп, которые «итериру-
«итерируются)) самостоятельно. Поэтому метод последовательных прого-
прогонок оказывается весьма эффективным, особенно при решении
сложных задач па вычислительных машинах со сравнительно
небольшой оперативной памятью.
Кроме того, метод последовательных прогонок удобен в алго-
алгоритмическом отношении, в частности, он допускает отладку со-
соответствующей программы па ЭВМ но частям.
§ 5. Граничные условия
1. Вводные замечапия. Выше были рассмотрены некоторые
итерационные способы решения неявных разностных схем. Они
приводили к Трехточечпым уравнениям, к которым применим
метод прогонки. Чтобы использовать для расчета рекуррентные
формулы прогонки, необходимо, исходя из краевых условий, за-
задать исходные значения коэффициентов прогонки в одной из
граничных точек сетки и значение искомой сеточной функции
на другой границе. Укажем, как ото делается для разностных
схем газодинамики.
Изложение начнем с более наглядного случая изотермиче-
изотермической газодинамики. Напомним, что именно к этому случаю сво-
сводятся уравнения группы I в методе последовательных прогонок.
Для простоты опустим пока псевдовязкость. Тогда соответствую-
соответствующая разностная схема в результате применения метода Ньютона
сводится к трехточечному уравнению для сеточной функции
ЙУ( — разности скоростей на двух соседних итерациях:
k h+l ft fe+i ft h+i ft
Л;6 Vi-i — СгЬ vi + B^ Vi±i=—Fi. E.1)
Коэффициенты отого уравнения вычисляются по формулам C.8).
Уравнение E.1) на каждой итерации к решается методом
прогонки, причем в процессе «прямой прогонки» по рекуррент-
пым формулам вычисляются коэффициенты прогонки (см.
B.11))
k A h h
-i, E.2)
а в ходе «обратпеш прогонки» находятся значения сеточной
функции
Л + 1 Л ft-t-i к
б vi =- ai+l5 vi+1 + р1+1, г ==- Л' — 1, N-2, ...,0. E.3)
ft- ft h+l
Значения коэффициентов ccj, p! и значение б uN определяются
из краевых условий.
2. Граничные условия для скорости. Рассмотрим класс задач,
где на обеих границах области (.? = 0, s = М) задапы законы из-
изменения со временем скорости
v(O,t)=V*(t), v(M,t)=V**(t);
фупкции V* и V** известны.
При формулировке разностной задачи эти условия аппрокси-
аппроксимируются естественным образом:
v{+1 = V* (t}+1), vtf1 = V** (ti+t). (Г,Л)
Рошонио разностной задачи на (/+1)-м временном слое оп-
определяется в результате итерационного процесса
Й-.0О
Учитывая E.4), положим, что в граничных точках на всех ите-
итерациях, включая пулевую, выполнены условия
*о = v* C;+i). »n = v** (h+i)- A- = о, 1,...
h+l ft+i
Отсюда следует: 5 г0 = 0, б vy = 0, А- — 0,1, ... Но тогда в соот-
соответствии с общими формулами B.8), B.12), B.13) получим
^ = 0,^ = 0,6^ = 0. /,- = 0,1,2, ... E.5)
Теперь в нашем распоряжении имеется вся необходимая ин-
информация для того, чтобы осуществить численное решение
задачи.
3. Граничные условия для давления. Обратимся теперь к за-1
дачам, где па границах заданы режимы давления
р@, t) = P*(t), p(M,t) = P**(t).
В разностной записи
i+ RV Л+1 ?+ E.6)
(рис. 4.10, а также п. 4 § 4 гл. II).
Уравнение C.1) получено и.ч системы разностных уравнений
C.2), первое уравнение которой (уравнение движения) имеет
вид
= *4+1-(;j + |(pi-/>i_1)(a) = 0. E.7)
Выше в задачах, где в качестве краевых условий задавались
законы изменения скоростей, уравнение E.7) рассматривалось
Рис. 4.10
лишь во внутренних узлах сетки i = 1, 2, ..., N — 1. Теперь,
когда па границах задано давление, использование уравнения
E.7) в граничных узлах сетки (? = 0, i = N) позволяет получить
два дополнительных соотношения, которые учитывают гранич-
граничные режимы E.6).
Так, при i — 0 с учетом E.6) имеем
""i+1 - ""* + ш 1° С^о+1 - р* (*i+0) + A - °) U - ^* @))]=о.
Примепенне к этому равенству метода Ньютона дает
h+i T k+l k
6 ^ E8
(^+l) ~ A - О) Р* (^1 ПрИ к = °'
0 при к ^ 1.
+
Для приращения б р0 в соответствии с формулами C.6) справед-
ливо равенство
ft+l ft ft / к ft \ / ft,ft ft
б Po = — 0,5тр0^0 [Sv! — 6voj jh — S'qYq — /4i0.
Окончательно, из E.8) получаем
ft ft+i ft ft+i ft
— 6'06 v0 + Bob Vl = — /'„, E.9)
где
\2 ft. A . ft ft
C'o = 1 + Bo, E.10)
Соотношения E.9), E.10) можно было бы получить и как
следствие общих формул C.7), C.8) при i = 0, если дополни-
дополнительно положить, что в фиктивном интервале h-\
Р'-г=0, р_! = 0, А-=0,1, ..., E.11)
h
и учесть новое выражение E.8) для /ll0. Точно так же при i = N
и формальных условиях
&>'N = 0, pN = 0, A = 0,1,..., E.12)
из общих формул C.7) и C.8) имеем
ft ft + l h ft + l ft
AN6 vn-i - CN6 vN =-FN, к = 0,1, ..., E.13)
ft ft а
где коэффициенты Ля, Cn, Fh вычисляются аналогично E.10).
Соотношения E.9), E.13), полученные с учетом краевых ус-
условий E.6), позволяют с помощью формул B.8), B.12), B.13)
выразить необходимые значения коэффициентов прогонки
ft ft /ft ft ft I ft
oj = BojCo, px = F0JC0, /г = 0,1, ..., E.14)
и сеточной функции
ft+i /л ft ft \i(k л ft \
б ь-w ={FN + f>NAN)l\CN-aNAN), % = 0,l, ... E.15)
h h
Значения коэффициентов avv, Ptv в E.15) вычисляются в ходе
«прямой прогонки» E.2). Заметим, что в E.14) знаменатель
С0ф0, в чем легко убедиться по виду формул E.10). Не равен
нулю также и знаменатель в E.15).
Итак, формулы E.14), E.15) делают задачу полностью оп-
определенной в случае, когда на границах задано давление.
Очевидно, в задачах с граничными условиями смешанного
типа, где на одной границе задана скорость, а на другой — дав-
давление, анализ краевых режимов приводит к комбинации формул
E.5) и E.14), E.15).
Мы рассмотрели схему, в которой отсутствовала псевдовяз-
псевдовязкость. Ее учет не вызывает принципиальных усложнений. Сле-
Следует лишь пользоваться более громоздкими формулами C.18),
где дополнительно к E.И) и E.12) нужно положить равными
нулю псевдовязкость Q и ее производные в фиктивных интерва-
интервалах h-i и Кц.
4. Граничные условия для температуры. Если в системе урав-
уравнений газовой динамики учтена теплопроводность, то на грани-
границах области должны быть предусмотрены условия для тепловых
функций. Как правило, в граничных точках считаются известны-
ми законы изменения со временем температуры
Г@, 0=0*@. Т{М, 0=0**@ E.16)
либо теплового потока
W@, t)=w*(t), W{M, t)=w**{t). E.17)
Возможны и более сложные случаи, когда на границе зада-
задается соотношение между температурой и потоком:
W@,t)=w*[T@,t),t], W(M,t)=w**[T(M, t),t\. E.18)
Обратимся теперь к разностной задаче. Если для решения
схемы используется метод последовательных прогонок, то урав-
уравнение энергии D.11), которое рассматривается в «тепловой»
группе II, сводится к трехточечному итерационному уравне-
уравнению D.13)
г , г-ri i. i+i i, г+1 г,
Dib 7\_i — Е$ Ti + G;67'i+1 = — Fi, i = 0,1, .. ., Лг — 1. E.19)
Применение метода прогонки к этому уравнению предполагает
вычисление сначала коэффициентов прогонки
i , i ,i i ,
I G; I Д;Т1, f F;
(+i (+i I i+\
и далее определение сеточной функции б Ti'.bTi --= |i+i6 Ti+l +
+ T)i+n i = Лг — 1, Лг — 2, . ..,(). Чтооы начать счет, следует за-
; i
дать коэффициенты |о, щ и значение функции в крайней точке
Уравнение E.19), как и уравнение энергии D.11), из кото-
которого оно получается, следует рассматривать на расширенной сет-
сетке, включающей фиктивные интервалы h-\ = 0 и hN = 0
(Й-i =О,5йо, fin --= 0,5'fc.v-i) (рис. 4.11). Значения температуры в
фиктивных интервалах Т~\ и TN, а следовательно, и приращении
6Т_1, ЬТп, относятся фактически к граничным узлам i — 0,г = ЛГ:
rpi + i rpi+i 7^;+i т1''*
Для задач E.16), где на границах задана температура, раз-
разностная форма краевых условий с учетом сделанных замечаний
такова:
Значения сеточной функции температуры на любой итерации
(/+1)-го шага естественно задать в граничных точках следую-
следующим образом:
i i
f_x = Q*(tj+1), Tn = 6** (tj+1). E.20)
о
Напомним, что во внутренних точках при I = 0 имеем: Ti = Т\,
i = 0,l, ...,N — 1.
'-! а о 1 ,v-2 '//-/ 'n н
с^-Х-о—*—о—х—о о—И—о—К—о-х-о
h rff h'O
Iff f 2 . . . N-t N N+f
Рис. 4.11
Соотношения E.20) порождают граничные условия б Т-г = 0,
б Tn = 0,1 = 0,1, ..., которые в свою очередь дают
?о = 0, т|0 - 0, 6 Гк =¦_ О, I - 0,1, ... E.21)
5. Граничные условия для теплового потока. Рассмотрим соот-
соотношения E.18), которые, очевидно, включают условия E.17)
как частный случай. При формулиромке разностной задачи эти
соотношения принимают вид
W^+1 — in* (T'+1 t- Л Wif1 -- ni** ('fit1 f-, "i (^ 99\
Используем разностное выражение для потока тепла через
температуру:
W\+x = — кг(Т3-±\,т1±\)(т{+1 — T{±l)/hi, i = 0; N. E.23)
Равенства E.22) и E.23) образуют две системы уравнений, от-
относящиеся к граничным точкам / — 0, i = N. Линеаризуя эти
системы уравнений с помощью метода Ныотопа, получим, на-
например, прп i = 0
i , i+i i, i+i i,
— Е_^Т_Х +G-JS То =—/_!, E.24)
где
Е'-г = A-o/6-i — (дк/дТ(— 1)) (тг) - дю*/дТ{- 1),
E.24')
2i3.
Точпо так же в точке / = iV имеем
i.i+i 1,1+1 i,
DN6 TN-X - EN6 TN = - FN. E.25)
Коэффициенты E.25) вычисляются аналогично E.24').
Сравнивая E.24), E.25) с общими формулами B.8), B.12),
B.13), заключаем
i, i, i,ii,
110 = 77-' b!N=-
60=77 р
E-i E -i en~Indn
Эти формулы завершают анализ класса задач, где условия
для тепловых функций на границах заданы по тепловым потокам.
§ 6. Практические рекомендации
Выше были изложены некоторые принципы построения раз-
разностных схем для одномерных нестационарных задач газовой
динамики и описаны алгоритмы для их численной реализации.
Однако каждый, кому приходилось иметь дело с реализацией
на ЭВМ достаточно сложных вычислительных алгоритмов, неиз-
неизбежно сталкивался с различными трудностями технологического
характера. Даже при полной ясности алгоритма, как правило,
возникают некоторые «сопутствующие» трудности, для преодоле-
преодоления которых вычислителю-прикладнику приходится изобретать
специальные приемы. Совокупность такого рода приемов, накоп-
накопленных со временем и проверенных практикой, составляет свое-
своеобразную «кухню» исследователя. К сожалению, такой опыт
редко обнародуется, так что фактически каждому вычислителю
приходится приобретать его самостоятельно, обучаясь на соб-
собственных ошибках.
В атом параграфе описаны некоторые приемы работы, которые
оказываются полезными при численных расчетах задач (причем
не обязательно газодинамических).
1. Приведение задачи к безразмерному виду. Один и:) первых
вопросов, возникающих при численном решении какой-лыПи прак-
практически интересной задачи, это вопрос о выборе системы единиц,
в которой будут измеряться все физические параметры. Обойтп
связанные с этим трудности позволяет так называемое обезраз-
меривание задачи, т. е. приведение системы уравнений, гранич-
граничных условий и т. д. к безразмерному виду. Для этого каждую
функцию, фигурирующую в формулировке задачи, представляют
следующим образом:
F = FoF, F.1)
где F — безразмерная функция, a Fo — некоторый постоянный
размерный множитель, представляющий характерный масштаб
для измерения величины F. Часто в качестве масштабпых мпо-
жителей выбирают параметры, непосредственно входящие в усло-
234
вия задачи: коэффициенты вязкости, теплопроводности, газовую
постоянную, скорость ударной волны, скорость поршня и т. д.
При этом в системе уравнений, приведенных к безразмерному
виду, появляется ряд безразмерных постоянных коэффициентов,
таких, как число Рейнольдса, число Прандтля и т. п. Обычно
каждый класс физических задач характеризуется своим набором
подобных безразмерных параметров.
Если предполагается, что программа для ЭВМ, по которой
будут осуществляться расчеты, должны быть универсальной, тан
что с ее помощью возможно численное исследование задач раз-
различных классов, то может оказаться целесообразным другой под-
подход к обезразмериванию задачи.
Пусть все функции, входящие в систему уравнений газоди-
газодинамики, обезразмерены согласно формуле F.1)*)
t = tot, S = S0S, X = XqX, V = V0V,
p =-- pop, p = pop, T = Tof, v = vov и т. д.
Из общей теории размерности известно, что среди всех раз-
размерных постоянных to, So, xo, vo, Та, vo и т. д. только четыре
имеют независимую размерность. Например, в качестве таких
независимых постоянных можно выбрать величины
?о, хо, ро. ^о. F.3)
Размерности всех остальных величин выражаются через них.
Подставим F.2) в дифференциальные уравнения газовой ди-
динамики C.25') гл. I. Тогда, например, из уравнения
dx/dt=v F.4)
получим -r—^ = vov. Выберем масштаб скорости v0 следующим
образом:
F.5)
Тогда уравнение F.4) в безразмерной форме выглядит так:
dxldt = v. Аналогично рассмотрим уравнение неразрывности
д_ 1\\ _ ди
dt\pj~ds'
Имеем
J ^
Выберем масштаб массовой координаты so следующим образом:
«о = pozo. F.6)'
*) Договоримся, что нижний индекс 0 в F.2) и далее в этом пункте не
является сеточным обозначением, это — символ размерного масштабного
множителя.
235
Для рассматриваемых задач с плоской симметрией s имеем раз-
размерность г/см2.
С учетом F.5) и F.6) уравнение неразрывности преобразу-
преобразуется к безразмерному виду
Si \ Р/ dY
Поступая так же с остальными уравнениями, можно полу-
получить следующую безразмерную форму системы уравнений газо-
газовой динамики:
d I I \ dv (Гх ~ до д^ ~
— — = -=, -тс- = Г, — = —-?:, U = р + СО.
dt\p ) ds dt dt ds
~* ~ ,~ ~ ~ @.7)
CJ = — V p тс, -s; = — ff ^^ ^ , И = — li —,
ds dt ds ds ds
где обезразмеривание выполнено в соответствии с формулами
.1 — 1 2 2i—2
ио — хо'о I *о — Рп-'п' во — Со — шо — Ро' о — Р(го'о '
v = р x2t~x г = v2 = х'11~г W = о и3 = о х3<~3
Аналогично приводятся к безразмерному виду и уравнения
состояпия.
Нетрудно видеть, что если в полученной системе безразмер-
безразмерных уравпений F.7) опустить волну над всеми функциями, то
она в точности совпадет с системой уравнений в размерном виде.
Поэтому в расчетах можно использовать обычную систему урав-
уравнений, рассматривая ее как безразмерную. Числовые значения
параметров, определяющих конкретное решении задачи (коэф-
(коэффициенты уравнений, значения функций в начальный момент
и т. д.), следует предварительпо преобразовать к безразмерному
виду по формулам F.2). Значения же определяющих размерных
параметров t0, х0, ро, То выбираются, исходя из специфических
особенностей рассматриваемой задачи так, чтобы безразмерные
функции по величине были порядка единицы.
Результаты решения задачи преобразуются к размерному ви-
виду также с помощью соотношений F.2).
При таком способе обезразмеривания переход к расчету задач
иного класса связан лишь с изменением величины масштабов
'о, хо, ро, То и никак не отражается па расчетных формулах.
2. Блочная структура программы. В реальных задачах уравне-
уравнения состояния, зависимость коэффициента теплопроводности от
термодинамического состояпия и другие свойства среды могут
иметь достаточно сложный вид, причем этот вид может изме-
изменяться при переходе от одного класса задач к другому. Различ-
Различную форму для разных задач может иметь и псевдовязкость.
В то же время в расчетные формулы, описанные выше, вхо-
входят как сами эти величины, так и производные от них (д^/др,
236
дК/дТ, dQ/ди и пр.). В связи с этим ых вычисление целесообраз-
целесообразно производить в специальных подпрограммах-блоках, обращение
К которым предусматривается в соответствующих местах общей
программы (рис. 4.12). Такая блочная структура программы при-
придает ей большую универсальность: замена того или иного изо-
изолированного блока обеспечивает возможность перехода к расчету
задач для сред с другими физическими свойствами.
Внешние иглериции
Внутренние итерацт
[pynna I
L
Влах
О)
Блик '
уриВнеь:?
актин..-* \
на j+2 -?•
слаС
Рис. 1.Г2
Блочная структура программы облегчает также численное ре-
решение таких задач, где пространственная область 0 < s < Л/ со-
состоит ии нескольких подобластей (Mn < s < Л/п-и, га = 0, 1, ...
.-.., R — 1, Л/о = 0, Ма = М) с различными свойствами (несколь-
(несколько различных; газон). .'!десь основные расчетные формулы оста-
остаются одними н теми же, нужно лишь при вычислении характе-
характеристик газа в данной подобласти обращаться к соответствующе-
соответствующему блоку.
«{. Использование точных решении для отладки программ. Соз-
Создание программы для ЭВМ, как правило, включает так назынае-
мып этап отладки, который позволяет убедиться и том, что па-
писаппая программа не содержит ошибок. Обычно для этой цели
используют некоторые упрощенные варианты задачи, решение
которых известно или может быть получено сравнительно не-
несложными методами. Если результаты, полученные путем чис-
численного расчета по «отлаживаемой» программе некоторой систе-
системы таких тестовых вариантов, близки к точным решениям, то
это дает определенную гарантию правильности работы програм-
программы. Конечно, система тестов должна быть подобрана так, чтобы
обеспечить проверку всех узлов программы. Блочная структура
программы дает возможность сделать это по частям, что позво-
позволяет быстрее локализовать возможные ошибки.
Отметим, что расчет тестовых задач, имеющих точное реше-
решение, может преследовать и другие цели, такие, как выяснение
237
точности схемы, определение экспериментальным путем реаль-
реальных условий сходимости алгоритма и т. д. Примеры расчетов
такого рода приведены в § 5 гл. II, где они использовались для
сравнения разностных схем различных типов.
Опишем ряд типичных тестов, которые используются при от-
отладке программ, предназначенных для расчетов одномерных не-
нестационарных задач газовой динамики в лагранжевых массовых
координатах.
Здесь прежде всего следует назвать задачу о поршне, вдви-
вдвигаемом в газ с постоянной скоростью и порождающем в нем
ударную волну. Постановка этой задачи и ее решение были опи-
описаны в § 7 гл. I. Остановимся на особенностях ее численного
расчета.
Рассмотрим некоторую конечную область изменения массовой
переменной 0 < s < М и введем в ней равномерную разностную
сетку с шагом h = M/N (s, = ih, i = 0, 1, ..., N). Пусть слева
(s = 0) находится поршень, скорость движения которого задана
и равна U. Соответствующее граничное условие для разностной
задачи при г = 0 имеет вид: 1>30+* ^ U. Условие па правой грапи-
це при s ¦= М, i = N зададим в форме vff1 = 0. Эту границу мы
считаем неподвижной, расчет будем продолжать до тех пор, пока
ударная волна не достигнет ее. В качестве уравнений состояпия
возьмем соотношения для идеального газа
Для простоты газ в исходном состоянии («фон») можно счи-
считать холодным р -= Т = е = 0, покоящимся v -= 0 и однородным
р = Ро. В соответствии с содержанием п. 1 этого параграфа мож-
можно считать, что задача сформулирована в безразмерном виде.
Предположим также, что определяющие безразмерные парамет-
параметры выбраны так, что R — 1, ро=1, V ¦= 2/(v + 1). Тогда скорость
ударной волны ЗУ = 1, а параметры газа за ее фронтом таковы
(см. формулы E.22) гл. I):
Р] м TJlf, щ = 2 , pi _ 2 Ti = 2(T-1). F.8)
и V —1 T-tl1 V-Ы ' (V+1)
При V = 5/3 они принимают следующие числовые значения:
р, =4, и, = 0,75, pi-0,7."), Г, = 0,1875. F.8')
Шаг разностной сетки но времени т для отладок обычно вы-
выбирают следующим образом:
т = атК1 F.9)'
где а = 0,2 н- 0,3, а величина тк вычисляется из условия Куран-
Куранта по параметрам газа за фронтом ударной волны
При y =¦ 5/3 имеем xK = hlllb.
238
Шаг сетки по пространству h можно выбрать, например,
следующим образом: М = 3-М, N = 30-^40, так что /г ^ 0,1.
Заметим, что если при А = 0,1 шаг по времени взять равным
т = 0,01, то это будет соответствовать в условии F.9) значению
««0,22.
В силу того, что скорость фронта волны 3) равна единице,
время расчета можно ограничить величиной 1% = М/2) = 3 н- 4.
О,?.:
0,5
0,2:
О
Энтропийный след
1..=!/
г
и /а
м
V
,75
0е
,'¦
0,25
у
-^ 1
— 1
i =0
'и
j
/
\
\
Энтропи,
\
\
ч \
fb'l
\t.
след
\
\
Т
и
\
\
\
\
\
1 ,.,
-1 U.u
t '.
\ '
О
б
Рис. 4.13
М s
Начальные данные в этом случае задают обычно одним из
двух способов. Первая возможность: весь газ в начальный мо-
иент ?=0 имеет «фоновые» значения параметров, т. е. покоится,
имеет нулевую температуру и давление, и плотность, равную
единице (рис. 4.13, а):
0,
» = 1, 2, ...,
(G.10)
При использовании второй возможности предполагается, что
ударная волна, порожденная поршнем, к моменту t = Q уже про-
прошла некоторое расстояние m @ < m < М, 0 < i < i# < Л^). По-
239
этому начальные данные задаются в виде (рис. 4.13, б)
|2/(v + l), 0<;<ц,
|2(y
'~1 О, /*<*<# — 1.
Результаты расчетов, представленные па рис. 4.13, й и б и
соответствующие разным способам .чадания начальных данных
(С).10) и ((>.11), имеют общую характерную деталь. Н окрест-
окрестности ^ила сотки, где начальные данные испытывают скачок
(точка г^О и ((i.10) и /= /„. л ((>. 11)), решение, полученное
численно, аамстпо отличается or точного. Температура здесь
имеет UTiK, плотности—(«пропал», так что давление н скорость
остаются гладкими.
Птот эффект п.чвостеп в литературе1 под названием энтропий-
энтропийного следа. Происхождение его обч.гепнется причинами разност-
разностного характера. Дело и том, что формулы точного решения
(•г).22) гл. 1, описывающие скачкообразное изменение параметров
ш> ([роите ударисл"! полны, справедливы лишь при отсутствии в
среде диссиннтивпых процессов. I! противном случае, как из-
кестпо, скачок «размазывается» и возникает некоторая структу-
структура фронта волны.
Для дискретной модели среды, которая описывается ра.чпост-
пой схеме!'! с нссвдовязиостыо, скачкообразные начальные дан-
данные ((>.'()) или ((>. 11) не соотве.тстн; ют, таким оГ>ра:юм, профи-
профилям параметрои л ударной волне. Поэтому пачнпаотсл пере-
перестройка npo(|)HJiei'i (сгнюооралпый распад разрыва и дискретной
диссиплтпвпоп среде.)- и в результате? решение асимптотически
выходит па нужный режим ударной полны с «вя.чкон» структу-
структурой. Как следствие указанной перестройки профилей, л точно
начального разрыва остается «энтропийный след». Давление и
скорость в :m>i"i области достаточно гладкие, так что «рассосать-
«рассосаться» за счет газодинамических факторов этот след не может.
Гели в качестве начальных данных выбрать профили пара-
параметров, соответствующие лязкой ударной волне н дискретной
среде, то л разностном решении энтропийный след не возникает.
Так же, как тест с ударной волной, осуществляется расчет
волны разрежения в задаче о поршне, который выдвигаете;! из
газа (см. § 7 гл. 1).
Для ми дач с тсчиюнроподпостыо испольнуются дополнитель-
дополнительные тесты. Простейший состоит в расчете уравнения оперши при
«отключенных» газодинамических процессах. Если предположить
еще, что коэффициент теплопроводности постоянен и плотность
среды всюду равна единице (р = 1), то уравнение энергии вы-'
240
рождается в линейное уравнение теплопроводности
cvdTldt = kd2T/ds2, 0<s<M, t>0.
При заданных краевых условиях I, II или III рода соответ-
соответствующая задача для этого уравнения без труда решается мето-
методом разделения переменных (см., например, [93]). Реализация
получающегося точного решения по общей программе также не
вызывает затруднений. Достаточно взять уравнения состояния
в виде
задать нулевые граничные условия для скорости
и начальные даттпые
ti = 0. ( = 0, 1 ,/V —1,
чтобы «отключить» влияние газодинамических аффектов.
В более общем случае, когда необходимо проворить функцио-
функционирование всех чаете» программы при расчетах задач газовой
динамики с теплопроводностью, в качестве теста можно исполь-
использовать точное решение для ударной полны в среде с теплопро-
теплопроводностью (см. § 0 гл. 1).
Постановка разностной задачи в том случае повторяет все
сказанное выше для случая обычной ударной волны, возникаю-
возникающей б среде иод действием поршня. Дополнительно следует ла-
дать граничные условия для тепловых функции. В соответствии
с уравнением @.20) гл. I нужно потребовать, чтобы обе границы
были теплоизолированными:
H'jfl = HV1-d. @.12)
Если начальные данные имеют разрыппын вид. то п разност-
разностном решении также возникает гштроппиньш след. Однако при
наличии теплопроводности пик температуры is районе :>птро;шй-
иого следа со временем начинает разглаживаться. Этот процесс
оказывает влияние па большую пространственную зону, нежели
в адиабатической газодинамике. В результате разностное реше-
решение выходит па нужный режим заметно позже. Избежать этого
в некоторой степени можно за счет изменения вида левого крае-
краевого условия в @.12): Т3п+г = Т*, где Т* соответствует значе-
значению температуры в точном решении за фронтом ударной волны.
Заметим, что всюду в атом главе мы ограничились рассмот-
рассмотренном одномерных ураппеппн гааопой динамики для случая
плоской симметрии. Обобщение полученных результатов на за-
задачи с. цилиндрической пли сферической симметрией не вызы-
вызывает принципиальных трудностей и связано лишь с более гро-
громоздкими формулами,
241
ГЛАВА V
РАЗНОСТНЫЕ СХЕМЫ С ИСКУССТВЕННОЙ ДИСПЕРСИЕЙ
В главе изложен метод исследования диссипативпых и дис-
дисперсионных свойств разностных схем, основанный иа анализе
их дифференциального приближения. Построены схемы с искус-
искусственной дисперсией, обладающие большей эффективностью при
расчете быстроизмепяющпхея или разрывных решений. В § 1
описаны свойства решения дифференциального квазилинейного
уравнения переноса, которое является хорошей моделью урав-
цений газовой динамики. В § 2 да примере уравнения переноса,
как липейпого. так и квазилипейпого, рассмотрены основные
особеппостп метода дифференциального приближения. Описаны
свойства решешш уравпепня Бюргерса и уравнения Кортепега —
де Bprirsa ц па этой основе проапализировапы дифференциальные
приближения различных схем. Теоретические выводы сопровож-
сопровождаются данными расчетов. В § 3 для уравнения переноса по-
построены схемы с искусственной дисперсией п приведено их
подробное исследование. Полученные результаты обобщаются в
§ 4 для случая уравнений газовой динамики. Приводятся при-
примеры расчета тестовых задач.
Заключительный § 8 посвящен описанию постановки и ре-
решения задачи о распаде произвольного разрыва.
§ 1. Квазилинейное уравнение переноса
и некоторые свойства его решения
1. Постановка задачи. В предыдущих главах подробно обсуж-
обсуждались некоторые принципы, такие, как консервативность, пол-
пая консервативность, однородность, устойчивость п т. д., из ко-
которых следует исходить при построепии разностных схем и алго-
алгоритмов для численного решения широкого круга задач газовой
динамики. Однако вычислительная практика показывает, что
даже при соблюдении указанных требований качество разност-
разностного решения в ряде случаев может оказаться неудовлетвори-
неудовлетворительным. В особенности это касается задач, решение которых
описывается функциями, быстроизмепяющимися по простран-
пространству или содержащими разрывы. В окрестности таких особен-
особенностей численное решение может испытывать осцилляции или
интенсивное «размазывание», не отражающее физической реаль-
реальности. Для интерпретации подобных явлеппй, а также для раз-
242
работки эффективных методов их устранения могут быть ис-
использованы представления о внутренних диссипативных и дис-
дисперсионных свойствах дискретной среды, законы поведения
которой задаются уравнениями разностной схемы.
Предварительно для наглядности рассмотрим возникающие
здесь вопросы на модельном примере — квазилинейном уравне-
уравнении переноса. С одной стороны, это уравнение достаточно просто
и его точное решение нетрудно сконструировать. С другой — оно
нелинейно и хорошо моделирует основные свойства системы
уравнений газодинамики, например, возможность возникновения
в решении в некоторый момент времени сильного разрыва при
гладких начальных данных. Поэтому квазилинейное уравнение
переноса является классическим объектом, широко используе-
используемым для апробации и отработки кап методов теоретического
исследования систем нелинейных гиперболических уравнений,
так и методов их численного расчета [73, 102]. Напомним, что
этот прием мы уже применяли в гл. III, демонстрируя па при-
примере линейного уравнения переноса методы исследования устой-
устойчивости разностных схем.
Итак, задача Коши для простейшего квазилинейного уравпе-
пия гиперболического типа формулируется следующим образом:
и (.v, 0) = t'o (s), — оо < я< + оо. A.2)
Характеристики С для этого случая определяются соотношением
(см. гл. II, § 4)
С: -? = «/(.<.'). A.3)
а характеристическая форма записи уравнения A.1) имеет вид
*!-„. (!/»)
где дифференцирование проводится вдоль характеристики. Ра-
Равенство A.4) означает, что решение идоль характеристики
постонпно. Величину этой постоянной г/0 можно вычислить по на-
начальным данным в той точке so, из которой выходит данная ха-
характеристика Но = Vo(Sn) .
Таким образом, в силу A.3) наклон каждой характеристики
па всем ее протяжении одинаков, и, следовательно, характери-
характеристика па плоскости (s, t) есть прямая линия. Если начальные
данные не постоянны (i>o(s)?z const), то характеристики в отли-
отличие от линейного случая не являются семейством параллельных
прямых (рис. 5.1).
Подчеркнем, что поведение характеристик A.3) зависит от
решения, которое в свою очередь определяется начальными дан-
данными. Поэтому следует говорить не о характеристиках уравне-
уравнения A.1), а о характеристиках задачи A.1), A.2).
16* 243
Вводя автомодельную переменную l = s — u(s, t)t, можно
представить решение исходной задачи в неявном инде [73]:
u(s, t)=*u(%)=vo(s-u(st t)t). A.5)
2. Свойства некоторых точных решений. Исходя из описан -
ных свойств решения задачи A.1), A.2), нетрудно построить ее
точное решение. Проделаем это для случая, когда начальные
данные A.2) задаются ку-
сочпо-линейпой функцией.
При этом будем рассмат-
рассматривать два варианта зада-
задачи с dvo(s)fds^O (вари-
(вариант I) и с dvo(s)fds<l)
(вариант II)(см. рис. 5.2),
решетшя которых имеют
различный тип.
Вариапт I:
Aи
аи
и (*. 0) = v0 (s) =
0, s<0,
и.
Рис. S.1
0<s<^, (l.G)
He выписывая решение задачи A.6) явно (что несложно
сделать), проапализируем его поведение с помощью рис. Г>.3.
Здесь на фазовой плоскости (s, t) представлено семейство ха-
характеристик задачи A.6). В зонах I и III характеристики есть
Рис. 5.2
параллельные прямые с наклоном ds/dt = и0 и dsfdt = 0 соответ-
соответственно. Значения решения в этих зонах равны Мо и нулю соот-
соответственно. В зоне II имеем расходящийся веер прямых харак-
характеристик, вдоль которых решение из начальных данных перено-
переносится без изменения. Ширина этой зоны со временем растет;
244
О < s s? d + uQl, решение здесь остается линейным по s:
«(«,*) =
d+%t
¦s.
Сопоставляя отмеченпые факты с результатами исследования
вадачи о поршпе (гл. II, § 7), видим, что описанное решение
Рис. 5.3
задачи г, неянгкш инде A.5) аналогично простой волне разреже-
разрежения и гадиной динамике.
Обратимся теперь к варианту задачи с dvo(s)Ids < 0.
Вариант II:
ди. ди
¦JJ- + и — = 0, и (s, 0) = v, (s) =
«п.
-y). U<s<d, (l.G')
0
Система характеристик па фазовой плоскости и решенио
вадачи A.6') формально строятся, как и в предыдущем случае
(рис. 5.4). Вновь в каждой из зон I и III решение имеет по-
постоянное значение (нуль и и0 соответственно), а характеристики
245
параллельны. В зоне И, ширина которой со временем сокра-
сокращается, характеристики образуют сходящийся веер, а решение
остается линейным по пространственной переменной. Нетрудно
показать, что все характеристики в зоне II пересекаются в мо-
момент времени <* = d/uQ в точке s = d, производная решения
при этом становится бесконечно большой. Такую ситуацию в
Рис 5.4
теории гиперболических уравнений принято называть «градиент-
«градиентной катастрофой».
Отметим, что в отличие от задачи A-6) здесь на фазовой пло-
плоскости появляется зона IV, которая трижды покрыта характе-
характеристиками, приходящими сюда из зон I, II и III. Формально
решение в этой области становится трехзначным (см. рис. 5.4).
Учитывая, что с помощью A.6') мы моделируем описание газо-
газодинамических течений, следует сделать вывод, что неоднознач-
неоднозначность решения неприемлема с физической точки зрения. С целью
246
ее устранения в решение, начиная с момента Ц, вводится раз-
разрыв, являющийся аналогом газодинамической ударной волны
Правила, в соответствии с которыми проводится постановка раз-
разрыва, будут обсуждены ниже.
Особенности поведения построенных решений можно проком-
прокомментировать следующим образом. Множитель и во втором сла-
слагаемом в исходном уравнении A.1), определяющий наклон ха-
характеристики на фазовой плоскости, есть скорость распростране-
распространения в пространстве данного значения решения. В отличие от
линейного случая эта скорость зависит от решения — точки про-
профиля u(s, t), отвечающие большим значениям, движутся быст-
быстрее, мепытш — медленнее. Почому в задаче A.6') ладпий фронт
волны, соответствующий наи-
наибольшему нгачгниго решения
и0. нагоняет нередгаш стоящий
фронт с u = U. li задаче A.C) —
наоборот: передний фронт вол-
волны движется направо со ско-
скоростью щ, а ладпий стоит.
Таким оЛралом, решения
рассмотренных нами задачA.6)
и A.6') для квазилинейного
уравнения переноса достаточно
хорошо отражают свойства
двух наиболее характерных ре-
решений уравнении газопой дина-
динамики — простой полны разре-
разрежения и ударной волны.
3. Тестовые варианты. Сопо-
Сопоставление известных решений
задачи A.1), A.2) с результа-
результатами численных расчетов по
тем или иным разностным схе-
Рис. 5.5
мам открывает возможность непосредственного изучения каче-
качества этих схем, роли отдельных входящих в них параметров
уточним с этих позиций постановку задачи, конкретизируя вид
начальных данных A.2). Будем считать, что функция vots)
удовлетворяет следующим условиям-
(''« (s) — Ь) ds = М > 0, Ъ = const
0,
*>v A'7)
Такие начальные данные представляют собой профиль типа «ша-
«шапочки», возвышающейся над фоном и = Ь (рис. 5.5). Точки
247
профиля, где решение имеет большую величину, будут двигаться,
как было сказано выше, быстрее, чем основание «шапочки».
Со временем форма профиля u(s, t) будет изменяться, и в кон-
конце концов произойдет «градиентная катастрофа»—в решении
возникнет разрыв. Момент «градиентной катастрофы» можно
рассчитать по начальным данным i>o(s). Действительно, рассмот-
рассмотрим две характеристики, выходящие при t = 0 из некоторых то-
точек с близкими координатами s = s и s = .s + 6 (рис. 5.5). На-
Наклон характеристик определяется величинами решения на них
Vo(s) и vo(s + ?), а момент пересечения t равенством
s + Vo(s)t=s + 6+ Vo('s + б) г.
Отсюда паходим
= _
или, переходя к пределу при б -*¦ О (в предположении достаточ-
достаточной гладкости фупкции Vo(s)),
г — KG)]-1- A-8)
Для определения момента «градиентной катастрофы» из всех
значений A.8) нужно выбрать наимепыпее:
U= min \--^—1 A.9)
Очепидпо, возникновение разрыва происходит па спадающей вет-
ветви решения, где его производная по s отрицательна.
Рассмотрим вопрос о правилах постановки в решении разры-
разрыва при l^>-t^. Мамитим, что уравнение A-1) может быть пере-
ппсапо в так называемом дивергентном виде:
Ot
JL (-?} = о. (l.io)
Учитывая вытекающее пепосредствепно из начальных дан-
данных свойство решения
lim ы(л,/)= Л, <>0, A.11)
8-> ' ОС
получим после интегрирования A.10) по s соотпошение
¦i-j (u(8,t)-b)d?=0. A.12)
—ос
Получсааое соотношение естественно трактовать как закон
сохранения, справедливый для задачи A.1), A.7). С геометри-
геометрической точки зрения это означает, что площадь фигуры, ограни-
ограниченной сверху кривой u(s, t), а снизу прямой u(s, t)=b
248
(рис. 5.6), остается со временем неизменной:
[u(s,t) — j
A.13)
Очевидно, вводить разрыв в многозначное решение необходимо
так, чтобы закон сохранения A.13) не был нарушен. Для этого
t -о
-р
Рис. 5.6
координату разрыва sf в каждый момент времени следует выои-
рать из условия равенства площадей криволинейных фигур А
и В на рис. 5.6: SA = SB.
В дальнейшем в тестовых расчетах мы будем использовать
конкретный вид начальных данных, удовлетворяющих условиям
A.7):
ди , ди А /а л /\
u(s, O) = vo(s) = Ac\r2{s)+b.
Картина решения задачи A.14), на последовательные моменты
времени при значениях параметров Л = 0,2, b = 1,0, представ-
представлена на рис 5.7. Момент «градиентной катастрофы», вычислен-
вычисленный по формуле A.9), в этом случае равен D s 11,49, Можно
показать, что с течением времени при '•>'•* профиль возмуще-
возмущения над фоном асимптотически стремится к прямоугольному
треугольнику, основание которого увеличивается как 1/t, а высо-
высота уменьшается по такому же закону.
Аналогично газодинамическому случаю можно рассматривать
точное решепие типа «ступеньки», которое возникает в задаче
Коши A.6') после момента градиентной катастрофы и постанов-
постановки разрыва в соответствии с правилами, изложенными выше.
Для большей общности будем считать, что значения решения
455 s/h
слева и справа от разрыва равны соответственно но и щ (uo<ui),
а скорость перемещения разрыва — D.
Описанпое решение, очевидно, является автомодельным с
автомодельной неременной c, = s — Dt (автомодельиость бегущей
волны) (см. гл. I, § 6). Учитывая связь между производными
_д_ = _d_ J>_ n_d_
ds ~~ dc,' at ~ dc, '
Получим из уравнения A.10)
-D— +±^! = Л
После интегрирования этого соотношения по | от — °о до +°°
для нашего решения имеем
~D{uv-u0) +|(^_U2)= 0.
Это равенство можно рассматривать как апалог газодинами-
газодинамических соотношений Гюгонио на разрыве. Опо устанавливает
связь между значением решения по обе стороны от разрыва и
скоростью разрыва
и -I- и
250
Заметим, что рассмотренное решение может быть реализовано
в задаче на полуограниченной прямой, моделирующей газодина-
газодинамическую задачу о поршне:
*L + U^L = O, 0<s<
t>0,
u(s,0) = uo, 0<s<
и @, t) = ult t > 0,
А. Результаты численных расчетов. Для численных расчетов
сформулироваыцой выше тестовой задачи A.14) будем исполь-
использовать две схемы, представляющие собой развитие схем для ли-
линейного уравнения, исследованных на устойчивость в гл. III.
Схема А:
0, у'к = v0 (sh).
Схема В:
A.15)
A.16)
Разностные уравнения A.15), A.16) рассматривались на конеч-
конечном промежутке 0 < s < L, где величина L выбиралась достаточ-
S'fl
но большой. На границах области задавались естественные гра-
граничные условия
yi = УЬ = Ь. A.17)
Использовалась равномерная сетка с шагами А = 0,1 ПО прост-
пространственной координате и т = 0,08 « xk по времени (тк = hjum^% —
характерная величина, фигурирующая в критерии устойчивости
Куранта (см. гл. III, § 2\).
251
Заметим, что обе схемы являются в линейном приближении
абсолютно устойчивыми и имеют погрешность аппроксимации
О (т 4- h) и О (т + h9) соответственно.
Задача A.15), A.17) решалась с помощью метода бегущего
счета, задача A.16), A.17)—методом прогонки. Результаты ра-
расчетов приведены па рис. 5.8 и 5.0. здесь же штриховыми линия-
линиями изображены точные решения A-14). Решепие, полученное по
Чк
176 193
Ф
i.2
V
1.0
855
86с
Рис. 5.9
956 s/h
схеме A-15) (рис. 5.8), является сильно размазанным. Осповпые
особенности точного решении, в частности наличие разрыва, пе-
переданы плохо. Это наводит на мысль, что в дискретной среде,
описываемой разностной схемой A.1')), действуют мощные дцеси-
патнвные факторы, хотя в исходной дифференциальной задаче
252
A.14) члепы. отвечающие таким процессам, в явном виде от-
отсутствуют.
Графики, приведенные па рнс. 5.9 для схемы A.16), показы-
показывают, что в этом случае при ?>/* за фронтом разрыва в чис-
численном решении возникают сильные колебания, существенно его
искажающие. На асимптотической стадии при 1^>1% численное
решепие распадается на отдельные возмущения, распространяю-
распространяющиеся друг за другом с различными скоростями. Такая картина
пе имеет ничего общего с точным решением. Это дает основание
предположить, что в случае использования схемы A.16) соответ-
соответствующая дискретная среда является сильно диспергирующей.
Отмеченные факты подтверждают вывод о том, что дискрет-
дискретная модель процесса, реализованная с помощью тог! или иной
разностной схемы, является самостоятельным объектом, облада-
обладающим собственными с<разностпо-физнческими>> свойствами, кото-
которые могут заметно отличаться от свойств исходной дифференци-
дифференциальной задачи. Так", схемы A.15), A.10) обладают внутренней
диссипацией и дисперсией, что и приводит к искажению решения.
Эффекты, проанализированные на примере модельной задачи
(l.l-i), наблюдаются и п газодинамических расчетах. Выяснение
природы этих явлений и разработка методов их устранения явля-
является актуальной проблемой теории разпостпых схем. Настоящая
глава и посвящена указанпым вопросам применительно к зада-
задачам для системы гиперболических уравпений.
§ 2. Метод дифференциального приближения
1. Идея метода. Актнвпое развитие теории разностпых схем
пачалось значительно позднее, чем таких классических математи-
математических дисциплин, как анализ и теория дифференциальных урав-
уравпений. Поэтому естественно желание исследователей привлечь
хорошо разработанпый аппарат этих разделов математики для
изучепия разностных схем. Одним из направлений такой деятель-
деятельности является разработка и применение метода дифференциаль-
дифференциального приближения [30, 31, 98, 99, 38, 59].
При построении разпостпон схемы, аппроксимирующей пеко-
торую дифференциальную задачи, бесконечномерное пространство
функций непрерывного аргумента заменяется конечномерным
пространством сеточных функций, а дифференциальное уравне-
уравнение— системой алгебраических соотношений. Тот факт, что реше-
нпе дифференциальной задачи и сеточное решение принадлежат
разным функциональным пространствам, порождает определен-
определенные трудности при теоретическом анализе снойств разностных
схем. Поэтому зачастую рассматривают разностные операторы в
том же фушщиопалыюм пространстве, что н аппроксимируемые
дифференциальные операторы, считая, что разностные схемы
удовлетворяются функциями непрерывного аргумента в каждой
точке рассматриваемой области, а пе только в узлах сетки. Это
253
предположение лежит в основе метода дифференциального
приближения.
Продемонстрируем идею этого метода и технику построения
дифференциальных приближений на примере разностной схемы
для линейного уравнения переноса:
-g- + a-^=0, -oo<s< + oo, *>0, а>0. B.1)
Аппроксимируем B.1) на равномерной сетке с помощью одной
из рассмотренных ранее (гл. III, § 2) разностных схем:
^ ^ Уг +аУг /'-1 = 0, B.2)
i = 0, ±1, ...; 7 = 0, 1, ...,
(yt~ay-t = Q). B.2')
Вояьмем достаточно гладкую функцию v(s, t) и выразим ее зна-
значения в узлах сетки (su t1+l), (s,-i, i,-) с помощью разложения
в ряд Тейлора в узле (s,-, ts):
= v
)' 7Г17
Подставляя эти значения в разностную схему B.2) вместо соот-
соответствующих значений сеточной функции у, получим соотноше-
соотношение, записанное в узле (s,-, tj}:
i? + a dv -
Формально мы выполнили операции, которые совершают при
определении локальной погрешности аппроксимации уравнения
B.1) разностной схемой B.2) на классе функций v(s, t). Пра-
Правая часть B.3) и представляет co6oii выражение для этой по-
погрешности. Ее величина определяется старшими по т и h чле-
пами суммы и пмоет в данном случае; первый порядок O(x+h).
Если анализ погрешпости аппроксимации закапчивается этим
выводом, то метод дифференциального приближения состоит в
более глубоком изучепии структуры правой части B.3). При
этом, как отмечалось выше, будем рассматривать соотпошеиие
B.3) пе только в узлах сетки, по и в любой точке области
g(oo<.S<+°°, t>0).
Уравпеппс B.3) пазывают дифферепциальпым представле-
представлением разпостноп схемы B.2), записапным в так называемой
Т-форме (гиперболической форме). Если ряд в правой части
B.3) сходится, то решепие дпфферепциальпого уравпения B.3)
254
эквивалептпо решению разпостпого уравпения B.2) в том смыо
ле, что зпачепия пепрерывпой фупкции v(s, t) в узлах сетки
(Si, tj) совпадают со значепиями разпостпого решепия у\. Схо-
Сходимость ряда в правой части B.3) зависит от шагов сетки т и h,
а также от характера решепия, н се исследование представляет
собой самостоятельную проблему [98].
Из сопоставления уравпения B.3) для u(s, t) и уравнения
B.1) для u(s, t) впдпо, что различно между этими фупкциями
обусловлепо паличием в B.3) правой части, отличпой от нуля.
Следовательно, по той же причппо решение у\ разпостпого урав-
непия будет отличаться от искомого решопия u(s, t). Таким
оГфазом, оказывается возможным свести изучение свойств раи-
ностпого решения, и тем самым, качеств разпостпон схемы к
анализу дифференциальпого соотпошепия B.3).
Довольпо очевидпо, что указапные различия сильнее прояв-
проявляются па грубых сетках, а также па решениях, сильно меняю-
меняющихся во времепи и прострапстве. Это подтверждает структура
правой части B.3),
2. Дифференциальное приближение для линейного уравнения
переноса. Уравпепие B.3) содержит полпую информацию о раз-
ностпом решении и, исследовав его, можпо сделать исчерпываю-
исчерпывающие выводы о достоипствах и недостатках рассматриваемой
разностной схемы. Однако из-за пеогранпченности количества
членов ряда в B.3) выполпить такое исследование оказывается
затруднительным. Поэтому обычно ограничиваются апализом
уравнения B.3), в правой части которого оставлено лишь конеч-
конечное число слагаемых. Наиболее распространенным является,
случай, когда в B.3) сохрапяют лишь старшие члепы разложе-
разложения по т и h, порядок которых совпадает с порядком погреш-
погрешности аппроксимации схемы. Получающееся при этом из B.3)
уравнепие пазывают первым дифференциальным приближением
схемы. Конечно, это дифференциальное приближение уже пе
эквивалентно полностью исходпоп разпостпой схеме, однако при
определенных условиях из пего можпо получить достаточно
содержательпую нпформацию о свойствах схемы.
Первое дифференциальное прпплижепие схемы B.2) име-
имеет вид
(W . dv т <Гг ah д v /О /ч
+a + {2Л)
Это так называемая Г-форма дифференциальпого при-
приближения, опа содержит в правой части дифференцирование
Как по пространствеппой, так и по времеппой перемеипой. Для
практических целей оказывается удобпым перейти к П-форме
(параболической) записи первого дифференциального приближе-
приближения, которая содержит в правой части только производные по s.
Для этого необходимо исключить из правой части B.4) произ-
производные по времени, что можно сделать с помощью самого же
255
соотношения B.4). С целью продемонстрировать технику полу»
чения П-формы дифференциального приближения
проведем подробные выкладки для рассматриваемого здесь слу-
случая явной схемы для линейного уравнения переноса. Продиф-
Продифференцируем B.4) по s, выразим вторую производную:
Л a%v т Л , ah д3и
*~--amt-?iJT-2
at osoi *¦ at
и подставим результат в правую часть B.4):
ду . ду ах д"\> ah д'у . т2 д3у axh d3v ,r>
~дТ ~ds ~2 dsdt + ~T~ ~~&? * ~T~ ~^з 4~ d/ dt' ' ^
Учитывая, что мы рассматриваем первое дифференциальное при-
приближение, можно отбросить в правой части B.5) последпие два
слагаемых, которые имеют порядок O(i- + ih):
dv dv ax <9J» ah й2» .„ „.
Теперь в правой части B.6) в смешанной производной необхо-
необходимо заменить дифференцирование по t на дифференцированно
по s. Продифференцируем B.6) по s, выразим d^v/dsdt и под-
подставим результат в B.6):
ду dv a'x d2v . ah д2у а2х2 д3у axh д3у
Виовь отбрасывая члепы, имеющие порядок малости выше, чем
О(т + h), получим
dv dv ah .. . d'v ax .r, ^
Уравнение B.7) является первым дифференциальным прибли-
приближением разностной схемы B.2), записанным в П-форме. Про-
Проанализируем его. Правую часть в B.7), которая и составляет
отличие дифференциального прнблнжепия схемы от исходпого
дифференциального уравнения B.1), можно трактовать при
1 — 1 > 0 как присутствие в схеме некоторой диссипации тина
линейной вязкости (см. гл. III, § Г>). Происхождение этой дис-
диссипации имеет чисто разностпую природу и поэтому естественно
называть ее внутренней, собственной диссипацией схемы или
схемной вязкостью. Очевидно, что выражепие в правой части
B.7) представляет собой лишь главную часть полной схемной
вязкости (аппроксимационной вязкости), имеющую порядок
O(h). Остальные «диссинативпые» слагаемые, имеющие более
высокий порядок малости и лависящие от Гюлее высоких четных
производпых но s, были отброшены при выводе первого диффе-
дифференциального приближения.
Наличие в схеме B.2) внутренней вязкости проявляется в
расчетах в виде размазывания разностного решения, причем ин-
интенсивность этого размазывания возрастает с увеличением шага h.
Заметим, что при нарушении условия Куранта, т. е. при
Y>1, B.8)
коэффициент схемной вязкости в B.7) становится отрицатель-
отрицательным. В этом случае можно формально рассматривать B.7) как
уравнение теплопроводности с отрицательным коэффициентом
теплопроводности. Как известно, задача Кожи для такого урав-
уравнения является некорректной, что свидетельствует о дефектах
рассматриваемой явной схемы, которые проявляются в виде ее
неустойчивости.
Изложенные результаты подтверждают, что метод дифферен-
дифференциального приближения является эффективным инструментом
анализа качества разпостпых схем.
Отметим, что способы построения дифференциального пред-
представления разностных схем и приемы преобразования дифферен-
дифференциальных приближений от одной формы к другой весьма разно-
разнообразны и подробно описаны в литературе [59, 98]. В силу
громоздкости соотиетствующнх выкладок мы не будем их в даль-
дальнейшем приводить, ограничиваясь формулировкой окончатель-
окончательных результатов.
Применим метод дифференциального приближения для иссле-
исследования еще двух схем, аппроксимирующих линейное уравнение
переноса,
Uf\-ay? = " B-9)
и
iJt + aiJV = 0, B.10)
S
отличающихся способом аппроксимации пространственной про-
производи ой.
Первое дифференциальное приближенно в I[-форме имеет вид
для схемы B.0)
\-а—= —г 0.-х (с — (',;>) —г. B.41)
и для схемы B.10) —
ill) , i)v .у i ., -i ii'v /o i .-Ц
— -\. a— = а-г (a— (),.>)—-. (-•!-)
at ' os v ' ds- x '
Уравпения B.11), B.12) однотипны п отличаются лишь коэф-
([шциептом вязкости (коэффициентом при второй производной
d2v/ds'2). Потому, как и в случае схемы B.2), можно сделать
вывод о том, что схемы B.9) и B.10) также обладают внутрен-
внутренними днссипатшшыми свойствами. Коэффициенты схемной вяз-
вязкости в B.11) и B.12) зависят от веса а у пространственной
производпон, н. следовательно, с помощью итого параметра мож-
можно управлять дисснпативпыми свойствами схемы. Для чисто
17 А. А. Снмпгч- .nit. 10. II. Поной 257
неявных схем с G=1 при прочих рапных условиях влияние
схемной вязкости паибольшее. Для явной схемы B.10) с а = 0
коэффициент cxeMnoii вязкости отрицателен и сама схема не-
неустойчива. Схема B.9) при а = 0 совпадает с явной схемой B.2),
которая пеустойчнва при нарушении условия Куранта.
При а = 0,7\ дли симметричной схемы B.10) коэффициент
вязкости в B.12) обращается и пучь, порядок аппроксимации
схемы повышается п становится рапным (){v -V li ). Соотпет-
стпешю попытается и порядок перпого дпфферепцпальпого при-
приближения схемы. Теперь при его построении нужно удерживать
члены с т.2, 1г2 и т/г. Можно ожидать, что и лтом случае «ралма-
.•шваппе» разностного решения будет ослаблено. Для схемы B.Я)
при а = 0,Г> коэффициент внутренней вязкости н нуль не обра-
обращается и имеет порядок ОAг).
Итак, анализ семейства схем для линейного уравнения пере-
переноса с помощью метода дифференциального приближения пока-
показывает, что эти схемы обладают внутренними диссипативными
свойствами. Ото приподпт к размазыванию, искажению разност-
разностного решения. Пелпчнпа коэффициента схемной визкостп зависит
пе только от шагов сотки, по п определяется способом аппрок-
аппроксимации производных. При этом спммотрнчпые аппроксимации
порождают более слабую схемную диссипацию.
Я. Уравнение Бюргереа и уравнение Кортеиега — Дс Bpn;tn.
Как мы видели выше, дифференциальное приближение схемы
является более сложным, чем исходное дпфферепциальпое ураи-
испи1'. С.пойстнамн этого приближения определяются особепттоетн
разностного [Н'пимшя. Полому прежде, чем строить и апалнзн-
рммпть дифференциальные приближения для кнаиплнисм'пюпг
случая, мрипеде.м спеденпя си{.аноч пого характера о типичных
1!<>:шпК!МО1Ц11Х' .чдесь ураинеппя1..
Нажным обобщением кпалнлпшм'шого уравнения переноса пй
случай н>1:и;п.\ сред является уравнение Лп>ргерса [0(>] :
1Г|)аная части моделирует депстине газодинамической нязкоечн
peau.iioi'i или искусственной, которая пепо.п.луется для сквозно-
сквозного расчета решении, содержащих ударные полны. Ламетим, что
nepitoe дифференциальное нриближеппе ра.чиостных схем д/ш
линейного уравнения переноса, рассмотренное выше, также пред-
представляет собой ураипе.ппе Пюргерса.
Сформулируем дли ураипеппя ].лоргерса задачу К'ошн, анало
гичиую A.7):
IIII 1111 (I'll -
lit ' О.ч ' gs-
и (к, 0) =-- L',, (s), — оо < s < + ею,
258
lim vo(s) = b, lim^^=O, г„ (.v)>0, B.11)
+00
f (i'0(s)-ft)ds = .lf><>.
—00
Решение этой задачи может быть получено и аналитическом
ннде [П4]:
u(s,t) = h —2ц-^ hi ч,A,1), i = s—bt, B.15)
О
Из этих формул следует асимптотика иопсдсния решения при
больших значениях /:
При выводе B.1C) использовано соотношение, справедливое
при больших з > 1:
z
<?~z°' « 2 /яг [ I — Ф (г)], Ф (г) = —^- Г е1" rfi].
Т/л J
и
Выражение B.1П) свидетельствует о том, что при достаточно
малом коэффициенте вязкости и больших временах разность
[u(s, t)—b], являясь гладкой функцией, близка по форме к
прямоугольному треугольпику с высотой T/2M/t и оспопапнем
l/2Mt. Именно такую форму, как отмечалось в § 1, имеет на
асимптотической стадии решепие задачи Кошн для квазилиней-
квазилинейного уравнения A.1), A.2), A.7), которая получается из B.14)
при ц = 0.
Таким образом, при больших I решение задачи Конш B.14)
для уравнения Бюргерса представляет собой «размазанное» вяз-
вязкостью разрывное решение задачи Кошн A.1), A.2), A.7), что
естественно с физической точки зрения (см. рис. ,1.10).
Еще одпим обобщением квазилинейного уравнения переноса
па случай диспергирующих сред является уравнение Кортеве-
га де В риза:
17* 25')
Опо является модельным для описания воли малой, по ко-
конечной амплитуды в средах, обладающих дисперсией, и впервые
было выведено для задачи о длинных волпах на мелкой во-
де [ЮЗ].
Изучению уравнения Кортевега — де Вриза посвящена об-
обширная литература, достаточно подробная библиография по это-
этому вопросу содержится, например, в [9, 41]. Для ого исследо-
исследования и решения используются различные методы, такие, как,
Рис. 5.10
например, сведшие к пбратпон задаче рассеивания для уравне-
уравнения Шредпнгора, построение стационарных решений и т. п.
15 частности, покапано, что уравнение B.17) при ? > 0 имеет н
.чапнспмостгг от величины i дин тина решении инда u(s, t) —-
-¦¦¦¦ U{s — Dt) — солптопм и периодические волны.
Со.ттоны \\:;\\ \ едшпчшыо волны описываются формулой
!/(.•¦•. 0 = -leli"
- мгл
B.18)
Пдесь Л — амплитуда силнтона, l—S\2$IA—эффективная ши-
ширина его осн()пан1М1. Солптон движется относительно фона со
скоростью П ~- Л''Л. П общем случае в решении одновременно
могут присутствовать несколько солптонов, причем солитоны
с большей амплитудой являются более узкими и движутся
быстрее,
260
Решение типа периодической волны также имеет аналитиче-
аналитическое представление:
-Т. ' B-19)
где dn а — эллиптическая функция Якоон с модулем (XS^l,
я, у — некоторые постоянные.
Удобно рассмотреть уравнение B.17) в безразмерном виде.
Введем безразмерные величины следующим образом:
— и - .1 - At
и = X' & = Т' L = 1~'
где Л — амплитуда возмущения, а / — некоторый характерный
размер, например полуширина печального возмущения. В этом
случае задача Кошп для безразмерного уравнения Кортевега —
де Вриза выглядит следующим образом:
- _ .,- ;1я- _ ._ . _ ...
ut
ds
ds
Очевидно, размерные решения, соответствующие одной и той же
безразмерпой функции начальных данных. /Tq(.v) и одинаковому
1'ис. 5.11
значению параметра б, будут подобны. Параметр б играет паж-
пую роль в теории диспергирующих сред и характеризует отно-
отношение нелинейного конвективного члена к дисперсионному. Для
решений солптонпого тина существует характеристическое зна-
значение параметра подобия 6* = l/l2|!)|. При фиксированные
начальных данных значениям параметра 6<Сб* п Й ^> 6Ф соот-
соответствуют качестпеппо различные решения.
В случае б^>б* («малые» р) решение представляет собой
цуг солптопои. причем с увеличением fi пх количество будет уве-
личииаться, амплитуды возрастать п зффеи'тнвная ширина умень-
уменьшаться (рис. П.И).
При б^о'з, («большие» i) решение B.20) есть осциллиру-
осциллирующий волпоноп пакет (рис. Г>. 12).
При 6 ~ б+ имеет место решение смешанного тина, состоя-
состоящее из волнового пакета и системы солнтонов (рис. 5.13). По-
201
скольку скорость сол in ста пропорциональна его амплитуде, со-
литопы п решении с течением времени располагаются в порядке
убывания амплитуд. Впереди движется солитон с максимальной
амплитудой, расстояние между последовательно расположенны-
расположенными солитоиамц увеличивается. Волшиюп пакет имеет отрицатель-
отрицательную групповую скорость, пропорциональную коэффициенту $
['не. П. 12 Рис. 5.i:S
и B.17), и движется п сторону, противоположную распростра-
распространению CO.'IIITOUOB.
Число солптопоп п их амплитуды определяются величиной
параметра подобия б п формой начальных данных vo(s) ¦ На-
Например, покачано, что условно распада исходного возмущении
па два солитопа имеет вид
где
Нижняя граница параметра подобия й=5[ отделяет класс
начальных данных, распадающихся па несколько солитопчв, от
иоамущешш ?о(лг), эволюционирующих с образованием одного
солитопа и волнового пакета.
Формулы для определения числа солитопоп Л' и их ампли-
амплитуд ап выглядят особой по просто для начальных данных специ-
специального вида A.14):
y.i(s)^ A clr2(s - ,s0) + ft, B.21)
.s\, — координата положения середины начального возмущения.
15 этом случае
п = 1,2, ...,.Y, B.22)
где А2 = Д/j}.
Определенной моделью, одновременно учитывающей иаличие
к среде диссипации и дпеперсии, может служить уравнение Кор-
тевега — де В риза — Бюргерса:
~пГ и ТТ ^' Р —з" = И —Г- {2.26)
262
Степень проявлешш тех или пных эффектов в его решетит
зависит от соотношения коэффициентов (} и ц.
4. Дифференциальное приближение для квазилинейного слу-
случая. Применим метод дпфферепциалыюго приближения для апл-
лиза схем A.15) и A.10). Результаты расчетов но пнм были
приведены в конце предыдущего параграфа и оказались неудов-
неудовлетворительными. Ради большой общности выводов рассмотрим
вместо A.15) п A.16) следующие разностные уравнения:
B.2
21)
//; ¦ yy^-v!,\"l\ B.25)
Прежние схемы A.15), A.16) следуют отсюда при значениях
параметров а — 0.5, v = 0. Пялкость и правые части уравнений
B.24), B.25) введена для того, чтобы, как и в газодинамике,
обеспечить возможность сквозного расчета разрывов, и возник-
возникновении которых даже iu гладких начальных данных мы убе-
убедились выше.
1 [-форма дифференциального приближении для рассматривае-
рассматриваемого квазнлпнойпого случая выглядит следующим образом:
at
(is ¦ ' ()s-
Коэффициенты в этом уравнении имеют значения:
для схемы B.24) —
[¦1 -> -I
—^—| 4 tv (ст 4 <т.) -| Inva 4 т'-'г-ст ,
rh ,
[I = v + и, u = -т + тс-а,
К = vx (?,а1 — 0.5) Ь T-v- (la2 + 0.5 - 2d) — ^f- A
// _ TL- (ст _ (i,.-,), G = -TV- (Гт — 0,5) A — a);
для схемы B.25) —
— 'id),
ii == v + a, a = xv-a,
E = vx Cdx — 0,5) + x-l-- Dd2 + 0,5 — 2a),
/' = Tr (CT — 0.5), С .-= т-r (a — 0,5) A — o),
B.2<S)
где a = (a- 0,5), oi = (ar - 0,5).
Соотношение B.26) не является первым дифференциальным
приближением, помимо членов порядка O(z + h) здесь оставлены
для целей дальнейшего исследования слагаемые порядка
203
+ /iJ). Уравнение B,20) весьма сложно, однако, если огра-
ограничиться рассмотрением решении с малой амплитудой, нослед-
лими тремя слагаемыми в правой части можно пренебречь.
В этом случаи дифференциальное приближенно B,2A) сводится
к уравнению Кортевега -- до Врпла--Нюргерса:
Т7Г
ИГ .-, II Г ~ II Г
i' Ь | —т- = .и —-
«¦•>' о.Г as-
B.29)
При сделанных допущениях обратимся к анализу конкретных
схем (l.l-i) и (l.l(i). Для них коэффициенты уравнения B.2'.))
принимают значения:
1L
Г,
и
12
ТТ
[i -- 0 для схемы A .Id).
1>о втором случае нрп и =0 мы имеем чистое уравнение Корте-
нсга — до Мрпиа л, используя результаты предыдущего пункта,
можем оценить характер решения уравнения B.29) с началь-
начальными данными т1.ч A.-1Л). Оценим д.чя итого величину коэффи-
коэффициента ,5 для yc.ronnii реального расчета, результаты которого
приведены на рис. П,',), Параметры итого расчета имели значе-
значения: й = 1, Л==П.2, /-ПО, h -0.1, т = (),08. Коэффициенты
уравнения B.29) являются функциями решения y(s, /), что
есть следстшк1 нелинейности рассматриваемой схемы. Однако
М.-тод
Формула B.2J)
Расчет A.1A)
С/ L
0,21)
0,1.-|
0.14
Таб
0,04
л и г; а 1
о t
0,005
учитывая, что мы рассматриваем в качество решения возмуще-
возмущения небольшой амплитуды (А<.1>), Пудом принимать для оце-
оценок .'паченпн коэффициентов, линеаризированных вблизи фона
v(s, t)=-^h. Таким образом, ^ = ^о ~ 0.0022, и для параметра
подобия ft—¦ \ Л121$ имеем б яь A1.V) ^§> Л^= у 12. Следовательно,
решение задачи будет носить солнтоппып характер, и, применял
формулы B.22), можно определить число солитопоп N и их
амплитуды а„ (и == 1, 2. ..., N). Для рассматриваемого расчета
Л^ = 4, а значения амплитуд указаны в табл. 1. Для сравнения
здесь же приведены амплитуды со.'штонон, полученные в
расчете по схеме A.10) па момент времени ?=К)о,4. Ампли-
Амплитуда четвертого солитопа находится за пределами точности
расчета.
2A4
Таким образом, результаты, полученные путем теоретического
исследования схемы A.10) с помощью метода дифференциаль-
дифференциального приближения, не только качественно, но и количественно
хорошо совпадают с результатами численного расчета. Проведен-
Проведенный анализ позволяет сделать вывод: в разностной среде, опи-
описываемой схемой A.10), преобладают дисперсионные свойства,
что является причиной дефектов разностного решения.
Для схемы A.1Г)) с несимметричной пространственной про-
производной, так же как и в линейном случае B.9), и дифферен-
дифференциальном приближении присутствует схемная вязкость, которую
нельзя устранить с помощью подбора веса а. Коэффициент няа-
костн ц, вычисленный вблизи фона v(s, [)=¦-!), ранен п. ==0,0.1.
')та величина окалывается столь значительной, что диссипация
в схеме преобладает над дисперсией. Указанное обстоятельство
проявляется, как показывает рис. 1.8, в сильном «размытии»
решения в зонах его сильного изменения но пространственной
переменной. Так, например, разрыв окалывается размазанным
настолько, что изменяется качественный характер решения.
Обсуждаемое разностное решение весьма близко и решению
уравнении Пюргерса B.1.1) при соответствующих -тчелиях
параметров. Так1, координата максимального значении амплиту-
амплитуды и (я, /) —b решения задачи B.14) па момент времени
/« 'il.f. — 2.1.0 равна s,,,..,, =: i!7,7 = 377Л, а само значение ампли-
амплитуды, как следует из асимптотических формул B.10), состав-
составляет 0,072. Численное решение па тот же момент времени имеет
максимальную амплитуду, рапную 0,074, и этот максимум рас-
расположен при значении координаты s =-- 37.ЧА.
Заметим, что из-за наличия большой внутренней вязкости
схема A.Ы) дает возможность без введения искусственном вяз-
вязкости вести сквозной расчет решения с разрывом, правда, суще-
существенно его искажай.
Анализ выражении B.27) показывает, что использование
значении весов а п а\. отличных от 0,.1, в диапазоне 0,1 < с, с: '-'¦
^' 1, обеспечивающем устойчивость схемы, приводит к увеличе-
увеличению коэффициента ji п тем самым к усилению схемной .ис-
синацип.
Изложенные результаты свидетельствуют, что в смысле ')ис-
сипативных к дисперсионных свойств схемы A.1.1) ji A.10)
противоположны друг другу и в то н»е время пи одна из них
не может обеспечить достаточную точность разностного решении.
Рассмотрим, какую роль может сыграть введение в укапан-
укапанные схемы искусственной вязкости с коэффициентом v > 0. Для
схемы A.1-1) эта процедура, как следует из_B.27), ведег к
увеличению и оез того большого коэффициента и,.
На вопрос, как влияет искусственная вязкость па свойства
схемы A.16), дают ответ расчеты задачи A.14) по схеме B.2.1),
результаты которых представлены на рис, 5,14, а. Ндесь на по-
последовательные моменты времени даны профили разностного
265
решения, полученные при уже использовавшемся выше наборе
параметров A, b, h, т для четырех значении коэффициента v = 0;
0,00008; 0,00125; 0,0Гь Штриховой линией указано точное реше-
решение задачи A.14). Как показывает сравнение рис. Л. 14, а и
V--G
ф
Г).14, б, отвечающих значениям v = 0 л v -- 0,00008, малые зпа-
чепия коэффициента мягкости практически не влияют па карти-
картину нозпикпонепия в рашюстпом решении солитопов. Напротив,
рис. 5.14, г показывает, что использование iicivyccTiiuimoii вязко-
вязкости с большим коэффициентом v сильно размазывает решение
и существенно ею искажает. Пелпчпиа v здесь выбрана числен-
численно равной коэффициенту схемном визкости yi в расчете, выпол-
выполненном но несимметричной схеме A.15) и представленном па
рис. 5.8. Как видно, результаты обоих расчетов близки, что есть
отражение близости их дифферепциальпых приближений.
266
Лпачеппе коэффициента вязкости па рис. 5.1'*, в v--0,0012.1
янляотся и пзностном смысле граничным: в расчетах с меньши-
меньшими значениями v преобладают дисперсионные аффекты, прояв-
проявляющиеся и виде колебаний решения за разрывом, при больших:
коэффициентах размазывание решения становится неприемлемым.
Итак, введение и схемы A.1 Г»), A.1E) искусственной пя.чко-
стп не может существенно улучшить качество разностного ре-
шения. }{ то же время отметим, что, изменяя соотношение меж-
между коэффициентами ц п C в дифференциальном приближении
схемы, мы получаем возможность воздействовать па качество
ра.'птостного решения.
Как отмечалось в § 1, для рассматриваемой задачи Кошн
A.1), A.2), A.7) справедлив .чакон сохранения (см. A.12),
A.13)). Для схем A.1 Г»), A.10) разностные аналоги этого .чако-
.чакона не выполняются, и, следовательно, лти схемы не япляются
консервативными. Возникает вопрос, не избавит ли свойство
консервативности схему от дефектов, которые Пыли подробно
описаны иьппо.
Общий вид консервативной схемы, аппроксимирующей квазн-
линейпое уравнение переноса в форме A.10), но аналогии с
B.24). B.2о), запишем следующим образом:
у, 1 (:гГ - v//^- B.30)
Закон сохрапепия па сетке состоит в выполнении равенства:
.V
Ц \j\li = con.st, B.31)
которое справедливо для B..'!()) при условии ,</,', -- //jv, что н
предполагалось в описанных выше расчетах.
§ 3. Искусственная дисперсия
I. Разностные схемы с искусственном дисперсией для квази-
квазилинейного уравнения переноса. Проведенный в предыдущем па-
параграфе с помощью метода дифференциального iipiifonr.vnim
анализ некоторых разностных; схем для квазилинейного уравне-
уравнения переноса щптел к следующим выводам «разиостпо-фп/.п ie-
ского» характс[)а.*) Дискретная модель с.[)еды. оппс.ываелгая roil
пли liiioii |.;:::п,)С1 ::.*Г. cxcMoii, обладает <>niji pmiitt.vtt Ottct ttnai tttutht-
Mn и Ottciicprr.iiiiiu.'.in cnuUci (шли, имеющими чисто разнос] nm) про-
происхождение. Наличие такой схемной ии.итеги и Oncncpci,:; !>г;п:т
К иекп'.кенн;.') ра-пюстпого решения по <¦ ]»;11:111¦ if111(i i рс-шсппем
*) Замечание при корректуре. Jlcriufniui' сооорп/.'лчпш выска-
высказаны в кппге (['.1 с т ч с р 1\. Вычислительные мсголы и ;iiiii;niiii;ii n;ir;i;"-
CTcit. Т. 1.— М.: Мир. 1001.
¦_»И7
исходной дифференциальной задачи. Коэффициенты схемной вяз-
вязкости и дисперсии зависят от шагов сетки, типа аппроксимации
отдельных членом уравнения и т. д., и потому существует прин-
принципиальная возможность управлять с помощью этих параметров
качеством разностного решения.
С такой позиции, т. е. с «разностно-фнзпческой» точки зре-
зрения, введение в схему искусственной вязкости есть споено явного
плияпия на структуру и коэффициенты дифференциального при-
приближения схемы и тем самым па ео дпееппатпвпые свойства. Ие-
кусственпая вязкость, в случае недостаточности собственной дис-
диссипации схемы, помогает подавить внутреннюю дисперсию и по-
порождаемые ею осцилляции и области сильных изменений ре-
решении.
С целью расширения возможностей влияния на свойства схе-
схемы рассмотрим способ, связанный с непосредственным воздейст-
воздействием па схемную дисперсию путем явного введения в разностное
уравнение слагаемого, содержащего третью производную по про-
пространственной переменной.
Видоизмененные таким образом схемы B.25) и B.30) примут
соответственно вид:
(yj + ,/,/f)_0^) = v?/a'), (.4.1)
Рассматривать аналогичные модификации схемы {2.2А) иг пред
ставляотея целесообразным из-за ее большой и неустранимой
внутренней вязкости.
Слагаемые !•&¦_<; • призванные уменьшить искажающее влия-
влияние схемной дисперсии, естественно назвать по аналогии с пс-
кусствеппой вязкостью искусственной дисперсией. Будем считать,
что коэффициент пскусствеппой дисперсии 0 имеет порядок*
O(r2 + h2) (см. B.20) — B.28)). Таким образом, введение в eve
му дополнительного члена формально не изменяет порядна ее
аппроксимации. Так же обстояло дело и с искусственной нян-
костью, коэффициент которой имел порядок v = O(/i) и соответ-
соответствии с результатами, изложенными в § 4 гл. II.
Схемы C.1), C.2) записаны па пятиточечном шаблоне, для
их решения может быть использовал алгоритм пятиточечной про-
прогонки [81]. В связи с расширением шаблопа нозпикает вопрос о
дополнительных граничных условиях. В данном случае, когдл
задача Копш A.1), A-2) реализуется на большом, по конечном
иптервале 0 < s <¦ L, зададим на границах области в дополнение
к A.17) (г/о = ij'n = b) естественные условии
Используя общие приемы исследования устойчивости (см.
гл. III), петрудио показать, что схемы C.1), C.2) в линейном
208
приближении устойчивы црп условиях:
о 3* 0,5, о, 3* 0,5, а2 3* 0,5.
Параболическая форма дифференциального приближения схем
C.1), C.2), заппсапная аналогично B.20) с точностью до члешж
иторого порядка малости, при о = 0,5 пмеет ппд
_.hI,_ + (p_O)-ir = v-r-A_-7-^
C/.)
где
а остальные коэффициенты равны:
для схемы C.1) —
Г. =¦¦ :Jtv (а, - 4) + ±f . F = - 0,Гш-,
для схемы C.2) —
Из структуры дифференциального приближения C.4) следует,
что, варьируя коэффициент искусственной дисперсии 0, можно
воздействовать на свойства схемы, изменяя соотношение между ее
дисперсионными п днссипативнымп факторами. Выясним, к чему
•.1Т0 ведет на практике. В расчетах, как н ранее, будем нсноль-
:швать те же значения шагов сетки (к — 0,1, т = 0,08) и нарамет-
ро», характеризующих начальные данные A.14) (Ь=Л, Л =0,2).
Для определенности положим oi = 02 = 0.5. Коэффициент В вы-
выберем равпын зпачепню коэффициента схемной дисперсии ?>, вы-
вычисленному па «фоне» {v{s, t) = b):
* 0,0022.
На рпс. 5.15 представлены результаты соответствующих рас-
расчетов по схемам C.1), C.2) при отсутствии искусстиепной вяз-
вязкости v = 0. Как видно, качестио разностного решения пе улуч-
улучшилось: за разрыном по-прежпему паблюдаются колебания, при-
причем количество осцилляции — солнтонов — возросло. Этот факт
имеет простое объяснение. Дпфферонциальпое приближенно C.4)
в предположении малости амплитуды решения, когда можпо пре-
пренебречь последпими тремя слагаемыми, сводится к уравпеиию
Кортевега — де Вриза. При этом коэффициент при третьей про-
производной р — 0 —Р — Ро пе равен нулю, хотя п имеет малое по
сравнению с Ро значение. Как следует из свойств уравнения Кор-
Кортевега — де Криза, при уменьшении Р (с ростом коэффициента
269
подобия о) количество солитонои увеличивается, а их ширина
сокращается. Именно ато мы и наблюдаем к расчетах. Заметим,
что если бы мы выбрали коэффициент так, чтобы и точности
скомпенсировать схемную дисперсию 0 = ^(т, h, v), картина ре-
решения принципиально но измепилас.ь: и игру иступили бы дис-
дисперсионные слагаемые более высокого порядка, описываемые чле-
членами с нечетными произиоднымп по пространству.
У/
1,2
10
'у
1,2
г г
>,?¦
-
l-
41*
176
191
ц
72'!
387
-0, 9-/30
о
1а,!Л1пшя м ра.шостпых решениях па рис. 5.15 обусловлены
ноконсернатинпостыо схемы C.2) —для нее не сохраняется «ин-
«интеграл» B..-М). Поэтому и дальнеГнпем будем рассматрпиать
лини, копсерватт-.иую схему C.2).
Па рнс. 5.10, а даны результаты расчета по с\еме (.Я.2) той
же лядачн при наличии искусстпсппон мя.жостн v = 0,00015
UlTpuxoBoii лнпиен, как н па пред!,1дущн\- рпсупклч-, отменено
точное решение. Несмотря па пекчторче .-/-фокты (характерные
искажения в виде провала у заднего фронта волны, небольшие
осцилляции перед передним фронтом) в целом полученное реше-
решение заметно ближе к точному, чем результаты расчета по схемам
бел искуестиепноп дисперсии.
Па рис 5.10, 6 представлен расчет с v - 0,0075. Отмеченные
па рлс. 5.10, rt погрешности сгладились, прпндл, несколько возрос-
возросло размалыиаппе фронта разрыва.
Таким образом, мы приходим к выводу: пнрдение искусствен-
искусственной дисперсии позволяет уменьшить суммарную схемную дис-
270
Персию и тем самым устранить низкочастотные колебании
г. разностном решении. Оставшиеся высокочастотные осцилляции
могут быть подавлены искусственной вязкостью с меньшим
12
10
У,
V
1,0
\
r--4Z*
I/O
yj^
195
•
у')
У1
s/h
\
Л*- *¦
334 387
v=u,C0015, 3-/3.,
s/h
'С r'4
s/h
.-.У-
Рис, 5.10
коэффициентом. И результате иачосгио разностного решения
улучшается, в частности, сокращается хараггтериая ширина раз-
размазывания разрыва,
271
2. Различные виды искусственной дисперсии. Использован-
Использованная в C.1), C.2) искусственная дисперсия Пыла лнгтейна отно-
относительно третьей проплводной, ее коэффициент мы положили рав-
пым постоянной 0 = ^0- Для более точной компенсации схемной
дисперсии следовало бы, согласно C.5), сдолать коэффициент
0 зависящим от решения 0 = [}(т, h, v). Однако это порождает
дополнительные трудности с точки прения реализации схемы,
а результат, как отмечено иыше, практически не улучшает.
Достичь некоторого прогресса здесь позволяет другой вид ис-
искусственной дисперсии'.
П — форма дифференциального приближения :>топ схемы в глав-
главных членах — совпадает с (ЗЛ). Слагаемые с коэффициентами Е,
F и G несколько отличаются от рассмотренного иыше случая,
влияние :ithx отличий можно усмотреть из результатов расчетов
по схеме C.6), приведенные на рис. Г>. 17,а, Пдесъ вновь о = О| —
= 02 = 0,5. На рис. 5.17, а показано решен но ирн л=0, 0 = ро =
= 0,0022. Решение вновь имеет ярко вырагкоипый солитонпый
характер, причем солптоны формируются быстрее, их число боль-
больше, амплитуды выше, чем в соответствующих расчетах по схеме
C.2). Г)то свидетельствует о более точной компенсации суммар-
noi'r схемной дисперсии с помощью искусственной дисперсии.
На рис. Г».17, 6 даны результаты расчета при наличии искус-
искусственной вяпкостп с v = 0,0075, 0 = Рп = 0,0022. Несмотря на
имеющееся небольшое искажение заднего фронта полны, умень-
уменьшающееся со временем, профиль решения, полученный численно,
весьма близок к точному. Ширина размазывания фронта разрыва
на момент времени t = \1^ составляет всего 7 — 8 разностных ин-
интервала.
Недостаток рассмотренных выше форм записи искусственной
дисперсии состоит в необходимости использовать для аппрокси-
аппроксимации третьей производной пятнточечный шаблон. Такое расши-
расширение шаблона вызывает дополнительные неудобства при чис-
численном решении соответствующего разцостного уравнения. По-
Поэтому рассмотрим способ введения искусственной дисперсии, не
требующий расширения шаблона.
Дифференцируя исходное уравнение переноса, записанное к
дивергентной форме A.10), получим равенство:
Ot dg-
аппроксимируя которое на сетке, имеем
Таким образом, возможно предложить еще один вид разност-
разностной схемы с искусственной дисперсией для аппроксимации
272
1.2 -
У
it2
;./
-
~ *
it
J
/-
f
i/
'(
\
\
\;
n
'.17
_
-
¦ 70 '89
' h
?
•2? 386 335 s-.i
•j-0,00'75, B-J30
Рис. 5.17
18 А. А Самарский, Ю, IT, Попов
исходной задачи A.1). A.2):
\h т тг(#")(°'
C.7)
Отметим, что схема C.7) записана на трехточечном шаблоне.
На рис. 5.18 указано решение, полученное но отой схеме при
v = 0,005, 0 = ^0 = 0,0022, а = аг = 0,Г>. Нидно, что разностное ре-
решение практически соипадает с точным за исключением узкой
л
ПЧ
>90
s/b
12
Г. 41
\0\
324 3S6 393 s/h
v-0,0Of-. 0-J30
I'iic. Г).18
окрестности фронта разрына. Шпрпна разма.чьпшнпя на момент
нремепи l—'\Lb егк-таиляст А П шагов сотки про нространстну.
Таким образом, 1!а[)ьпруя вид пскусстиениой дисперсии, могкпо
добиться улучшения начостиа узазпостиого решения. Среди рас-
рассмотренных иыигс схем с пскусстленпон дисперсией схема C.7)
показала паплучнпи; результаты для аадачн A.1), A.2) и классе
решений, порождаемых начальными данными A.14).
3. Исследование свойств разностных схем на решениях типа
ударно"! нолим. 1'ымн: с помощью .метода дифференциалмшго
приближения дли кпазилннсипого урашкчшя переноса были ио-
строепы схемы с iicuyctvruoniioii дненернснеп, которые оказались,
более оффектпшымп. чем обычные, при иоспроп.чнедепш! реше-
ииii с разрымамгг. Практическая проперка теоретических ныподои
проподилась путем расчета задачи Ь'шпн A.1), A.2) при одних
и тех же начальных данных A.14). Профиль решения нредстаи-
ляет собой «шапочку» над постоянным фоном, ^г.олюцпонпрую
щую с образованием разрыпа и на асимптотической стадии, при-
приближающуюся к прямоугольному треугольнику.
274
В то же время из-за нелинейности уравнения коэффициенты
дифференциального приближения зависят от решения. Поэтому
все рассуждения и выводы, сделанные ныше по результатам рас-
расчетов, несут на себе в определенной мере отпечаток конкретного
решения. В силу этого возникает необходимость пронерить полу-
полученные результаты па примере других классов решений задачи
A.1), A.2).
Обратимся с этой целью к разрывному решению—«ступень-
решению—«ступеньке», которое возникает в задаче Копш для кпазилииеГшого урав-
уравнения переноса, при начальных данных вида A.()'). Если значе-
значение решения па фоне перед разрывом рашю »о, а значение ре-
решения за разрывом равно и\, uq<iu, скорость распространении
фропта разрыва, кок отмечалось и § 1, и. 3. будет равна D =
= O,5(mo + mi), а само решение является автомодельным, с аито-
моделыюй переменной. ? = я — Dt.
И в этом случае сеточное решение, полученное по любой рас-
рассмотренной в § 1 разностной схеме, будет описываться с извест-
известной точностью дифференциальным приближением, имеющим вид
уравнения Кортевога — де Врнза — Бюргсрса B.23). На его ос-
основе с помощью указанной автомоделыюетп «бегущей волны»
определим структуру рассматриваемого ступенчатого решения, ко-
которая будет формпропаться лод влиянием схемной вязкости и
дисперсии. Выполнив выкладки аналогично тому, как это было
сделано в гл. I, § G, получим с учетом граничных условий
Inn и (s, t) = (/„, 11ш -^— --= 0 (•'•o)
S --}-oo s • — oo f S
следующее обыкновенное дифференциальное уравнение:
Второе из условии C.8) дает, что при 5 -v —°е разность
— (и(|)— «о)/2 должна обратиться и пуль, т. с. и(Х)-* и
\-у «о как' и и разрывном решении
D -
((|) ) д р у, Х) и\ при
\-у —«о, как' и и разрывном решении.
Если коэффициент [5=0 и среда является чисто днееппатпп-
iioii, уравнение C.0) без труда интегрируется:
"A)=
t [-Ac •¦
где a =(«i - - Hi))I Bii). а К—произвольная постоянная интегри-
интегрирования (ср. Гл. I ((i.lM)). Решение- -гладкая монотонная кри-
кривая, предстапляюгцан р.-1змазаппьп пя::костыо разрыв. Пффектпн-
пая ширина {(азмак.шаппя, оп])еделяемая нгислоиом к'асателыкп'г
и точке перегиба d['u/d%9 = 0, составляет А —(На)/(и\ - г/о).
При Ji ^ 0, [1=^0 ограп][Ч1шся исследованием поведения реше-
решения вблизи фронтов волны. Проведем, например, линеаризацию
уравнения C.У)вблизи заднего фронта, положив и(с)== ii\ + и (|),
18* 275
где |ul <». 13 этом случае из C.9) следует
Поведение решеппя урапнепия C.10) определяется знаком дис-
криминапта: di = ц2 — 2fJ(«i — w0).
Возможны три случая:
1) дискрпмпнапт положителен <У|>0; общее решение опре-
определяется формулой
где A.i.2 = ^jj
2) дискриминант ранен нулю, d\ = 0; общее решение имеет
ЛИД
где ti = |(p
3) дискриминант отрицателен, d\ < 0; общее решепие записы-
записывается следующим образом:
и (|) = е"<(Ci sin Qg + C2 cos Qg),
где декремент затухания г| и частота колебании Q падаются ра-
пепствами
11==JL o = iE) он)
ч 2р, - ^р . ij-iu
Гю всех формулах С\, С2— нроизвольиыо постоянные.
Итак, при d\ < 0 решение вблизи задпего фронта имеет осцил-
осциллирующий характер, и условие появления осцилляции спязапо с
«преобладанием» дисперсии пад вязкостью:
В противном случае решение имеет монотонный характер.
Диалогично можпо показать, что условие позникпонения ос-
осцилляции вблизи переднего фронта полны имеет нид
Очевидпо, что ;т> нераоепство может пыполняться лишь при от-
отрицательном коэффициенте р < 0. Дисперсия такого вида носит
назвапие аномальной.
Проведенные теоретические рассмотрения иосят общий харак-
характер. При анализе результатов расчетов по конкретным схемам
следует прпшшать по внимаиие соотноШеПИЯ коэффициентов,
шшяпие члепов более высоких порядков в дифференциальпых
приближениях и т. д. Чтобы оцепить роль этих факторов, обра-
обратимся к расчету задачи A.1) для квазилипейпого уравпения
276
переноса с «размазанными» начальными данными:
1.2. л-^м.
1,2 — П.2л/(л0Л), п <.*<«„/,,
C.13)
Задача решалась па достаточио большом промежутке —L < s < L,
73 8?
^r;,co:-: 6=0
¦'—чЛ
7J 8"
*° 26:
1,0
¦j = с. /Г'л;; о п
70 9П
175 s/h
1'iic. 5.19
па концах которого задавались граничные услоппя u( — L, t) = Ui,
u(L, t) = uo. Шагн разпостиои сетки, как и всюду и глаие, состав-
составляли т = 0,08; h = 0,1. Параметр и0 был выбран рапным «о = 8,
277
т. е. момент «градиентной катастрофы» определяется следующим
образом: t# = nJi/U.2 = A.
На рис. П.19 даны расчеты сформулированной задачи по кон-
консервативной схеме (.''>.7) при а = О|=0,5, 0 = 0 для следующих
значении коэффициента искусственной вязкости: v 0
(рис. П. 19, а), \=0,00Г) (рис. o.ii), о), v = 0,02.1 (рис. 5.19, «)•
Как видно на первых двух' рисунках, решение заметно осцилли-
осциллирует за фронтом волны, при v — ¦0,012.") решение, сделан одно-два
колебания, выходит па нужный режим.
Попытаемся применить для объяснения наблюдаемых фак-
фактов развитые выше теоретические1 представления. Дифференци-
Дифференциальное приближение схемы A5.7), как указывалось выше, совпа-
совпадает с (.'5.И), так как членами высших порядком в B.2A) можно
пренебречь is силу выбора начальных данных (.'5.1.')). Здесь ц. — г.
а коэффициент $ вычисляется по формуле
/Г т-
Т'ассматрпкал v как napbnpyoMi.ii'i параметр, убеждаемся, чти,
согласно (Н.12), осцилляции у .чадпего фронта волны прекратятся
при
> лч =
(),о:У|.
Здесь коэффициент ji вычислен по значениям решении за полной:
^ ~ 0,002!). |)тот результат весьма бллзок i; даппьтм расчета. До-
Достаточно хорошо соответстиуют расчетам н теоретические значе-
значения таких величин, как декремент затухания ц = v/B^(«i)),
и полунернид колебании Т -¦¦-- n/i}(ii\), (см. (i5.ll)). Г)тп данные
приведены в табл. 2, здесь же указаны средние значения ;>тпх
пелпчин, получеппкк1 в расчетах но схеме (•'!.7). (Осреднение
выполнено по нескольким максимальным оецнлляцпям.)
Т я б л и ц а 2
II
0,A0')
0,005
0.007
0.0::.!
(
1
,„„
.000
,«()
.20
.2.4
1
1
пел
.00
'''¦г
0
0
О
о
54
,¦"'¦'*
,.¦>;>
.71!
' '11КЛ
0/ii)
0.51
0,52
(!,7- 0,8
Таким обритом, изложенные pe.'iy.ibTai'i.i иодич'ршдшот :»|)
фектпвность теоретических представлении, опирающихся па ана-
анализ дифференциального приближении, для объяснения енонггп
разностных схем п для решений типа ударной иол им. Поэтому
278
ость основания ожидать, что схемы с искусственной дисперсией
проявят свои положительные качества и и атом случае.
1.2
86 9?
252 257 s/h
•j.-_,005, 6-р0
Рис. 5.20
На рис. ij.20 представлены результаты расчета тип и.с :s<i/u<4ii
по схеме C.7) при а = о, =0,5, О = ^0-= 0,0022, v = 0,00Г>. Дей-
етпителыю, численное решение иоеьма близко к точному, разма-
:!Ь[иание согтаплнет четыре шгториала сетки,
¦а топ и.т задачи
§ А. Разностные схемы с искусственной дисперсией
для уравнений газовой динамики
1. Дифференциальное приближение. Ныше па примере квази-
квазилинейного ураипоппя переноса был продемонстрирован метод
теоретического исследования диссииатпиных и дисперсионных
(¦iioi'icTii разностных схем, ос.понапнып па пспользонанпп диф-
({кфенциалыюго приближения. Он позволил дать «раз[к)стио-ф|г-
зпческую» трактовку дефектом схем, наблюдаемых при расчете
разрышп.1\ и О1>1стро1геременных решении и естестпепным образом
irpiiisojt к построению схем нопого типа (схем с искусстпонной
диспорсио1'(). и которых охи дефекты it значительной степени ос-
ослаблены. I) настоящем параграфе развитые предстаилипия обоб-
обобщаются па газодинамический случаи.
Для простоты рассмотрим систему уравнении газовой динами-
динамики и изотермическом приближении:
dp
Tit' \~n ) ' iTJT'
7O = ~7Г, ' Р = r"i'-
('..1)
пли, исключая даиленпе р,
ill
<Jv (Jv ., rjp
Us ' (Л ' r>s
Аппрокспмируем D.1') на рапномерной сетке разностной схе-
схемой, полученной путем редукции общего семейства полностью
279
консервативных схем (см. гл. IV, § 1)
S.°\ ц=р-ии
« (/(.2)
р = с-{\ (л -=—\рг3, O^a^l.
Для обеспечения свойства однородности при расчете ударных
воли и схему введена лппеппан искусственная нязиость <о.
Построим для схемы A.2) дифференциальное приближенно.
Не воспроизводя здегь громоздкие выкладки, проведение которых
целиком основано на технике, продемонстрированной ii § 2, при-
приведем окончательный результат, 11-форму дифференциального
приближения семейства схем (Л.2). и папнеп которой учтены чло-
ны до нторого порядка малости 0{т~ -г h2) включительно:
р'— ст Г *' !°1><"Л , '¦!> ""
, -3)
"с ,. Он (№) ..'^ ^Зр ''Q . (/(I О'о
•л д, .'« ¦ (/iS.J t)s ¦ о.-- dl!-
где
[>> == Bt-V'-(.- + Л-) 21. р = р vt (а - ().Г>) (..
Z = _ vo — О = п(.- f—
[ он ¦ ¦ ' yds
v == v ; v,, v, — it - i'a — A,Г>) о. н == vt (а — (i.'ij - T.'-pV- /6.
Полагая, как ооычпо, v = G(/г), имеем
? = О(т2+/г2), ? = 6>(т2 + /г2), лГ=6>(т+/0. ц = ^(т2 + /г2).
И:! впда днфферепцпалыюго приближения следует, что помимо
hisho iine;U'inioii ncKyccTHOHuoii .'ишсГиюн ия.чкогти с коэффициен-
коэффициентом v, схема обладает собственной линейной вянкостыо с коэф-
коэффициентом Vi = TC2fi(o — 0..")), а также собствен чай квадратичной
вязкостью Q с коэффициентом ц. Копффиценты ;irn\ д|гс.сппати1>-
иых фактором достигают мишшалг.мых лнячеппм uniT о = 0,Г):
vi=0, [1 = тас2р2/6. (Напомним, что схема (i.2) и линейном
приближении устойчива при а>0,5.) Видно также, что при уве-
увеличении степени неявности схемы внутренние диесинатинные
спойстиа схемы усиливаются.
15 дифференциальном прнблп;кешш D.3) присутствуют также
члены, содержащие третьи нропикодиыо d3u/ds3. cfip/ds'*, которые,
как следует из результатов предыдущих параграфов, характери-
характеризуют дисперсионные свойства схемы.
Итак, по сравнению со случаем квазилинейного уравнения пе-
ропоса, для изотермической газодинамики дифференциальное
приближение является заметпо более громоздким, однако сохра-
сохраняет характерные черты, позволяющие рассматривать свойства
280
разностных схем в терминах внутренней днссинацнп. внутренней
дисперсии.
2. Тестовое решение. Результаты численных расчетов. Система
дифференциальных ураттений D.3), представляющая собой диф-
дифференциальное приближение схемы D.2), слишком сложна для
непосредственного исследования, поэтому проанализируем шшя-
лие внутренних диссипатгпшых п дисперсионных свойств путем
численных расчетом. В качестве нериого теста рассмотрим авто-
автомодельное решение системы D.1) тпиа простой волны. Для
адиабатического случая такое- решение было построено в гл. I,
§ 7. При этом окапалось, что в решении нее искомые вели-
величины являются функцией одной из ппх, например плотности р:
v = v(p), /)=/»(р) и т. д.
Положим по аналогии и Gь1') у == г(р). После ннтегриро-
пания имеем
v(s, t)= v(())= ±cli)(p)+coii.«t. D,5)
При этом плотность р удовлетворяет уравнению
^-ucn^ = () (Щ
ill ' Hi v '
интегрирование которого даот
p(s, t)==q{s + cD), (АЛ)
где вид функции ф определяется им дополпнтс.-п.ных условий
конкретной задачп. Знаки «±» n (I")), D.(i) и (it» n D.7) от-
отвечают иолпам, распространяющимся соответственно направо и
палево вдоль осп я. В дальнейшем будем рассматривать лишь
волны, распространяющиеся направо:
(.(.•>¦, t) = $(s — cpt), v(s, 0 == с lnp +const. D.8)
Как видно, построенное решение уравнений (^.l) де^к'тнптсльпо
является автомодельным: оно описывается функциями, завися-
зависящими от одного аргумента — автомодельной переменной s — cpt.
Учитывая формулы D.8), сформулируем задачу Копт для
уравнений и '.отермическсиЧ газовой динамики:
—, —=— с2—, — oo<,v<+oo, t>(),
(/,9)
где po — фоновое значение плотности, а функция <|(.v), обладаю-
обладающая необходимой гладкостью, удовлетворяет условиям, анало-
аналогичным A.7):
lim ф() (s) = О, f ([„ (.%¦) as = M < оо. A.10)
Н силу специального выбора начальных данных задача D.9) об-
обладает решением типа D.8), где вид функции ф и значение
2S1
постоянной и v (s, t) определяются без труда:
Это решение обладает темп же свойствами, что и решение типа
простой волны для квазилинейного уравнения в § 1. Оно пред-
представляет собой полиу, распространяющуюся в положительном па-
пранления оси s, профиль которой искажается со временем и силу
нелинейности задачи. И дальнейшем в расчетах ограничимся рас-
рассмотрением функции ((и, имеющих вид «шапочки»:
| (),Г)/1 [i — ео.ч — , ()<.s'<2.\,
О, Л<П, 1>\<.ч.
При этом и решении п момент времени /* = n)in 1 —|rft|-() (.v)/t?.v| |
иозннкает разрмг,. Условном постановки разрыва, как п в § I,
является сохранение интеграла D.10). На асимптотической ста
дин профиль решения приближается к прямоугольному тре-
треугольнику. Па рис. Г».21, а изображены профили плотности па д;;а
момента иремепн i = 2/i и t — 40, полученные в расчетах задачи
D.9) при следующих значениях параметров: А = 0,1; т — 0,08;
с = 0,Г>; ро=1; Л = 1,Г); /1=0,2, v=0. При :>том .момент «гра-
«градиентной катастрофы» составляет /-ф = 9.П4.
(Сплошные линии соответствуют значению веса а = 0,5; штри-
штриховые лпппн — а—1, пунктиром отмечено точное решение зада-
задачи. Для схемы второго порядка аппроксимации (а = 0,Г)) при
отсутствии искусственной вязкости v = О внутренняя диссипация,
как отмечалось выше, невелика. Педущут роль it otovt случае
играют дисперсионные факторы, что п проявляется is обрапона
пни солптонов. В пеикпой схеме (а=1) преобладает днссина
цин— разрыв сильно размазан, решение гладкое.
Рисунки Г).21, б и в демонстрируют влияние искусственное!
вязкости в схеме с а — ОД По мере увеличения коэффициента v
осцилляции решения за фронтом становятся слабее, однако ши-
ширина фропта размазыпаппя разрыпа позрастает. Так, при v = 0,01
(рис. Г).21, в) пта ширина па момент времени /. = 40 « •/i,2/si.
составляет двенадцать интервалов сетки. Этим данное решение
похоже па расчет по иеянноп схеме (а=1) (рис. Я.21,а). ТакоГг
результат становится понятным, если принять во внимание, что
суммарный копффпцепт линейной вязкости v в D.Я), D.4) у
обеих схем примерно одппакои. Дсйстннтелыю, для схемы с а = 0
имеем v = 0,01, vi=0, так что v = v + V| = 0,01. Для неявной
схемы (а=1): v = 0, vi = тс2(а — О,Г>)р « 0,01, v = v + v, « 0,01.
3. Спектральные свойства решения. Итак, для газовой дина-
динамики характерные особенности разностных решений и соответ-
соответственно «разностно-физическая» трактовка свойстп разностных
схем остаются такими же, что и для уравнения переноса. Полто-
282
му представляется естественпым обобщить развитые ранее пред-
представления о схемах с искусственной: дисперсной на случай газо-
пой динамики.
Однако предварительно отметим па следующий возможный
«опрос. Нужно ли, усложняя схему, бороться с со внутренней
Г-Л; 6^,1,5
/./ -
1,0
160 17 г
Рис. 5.21
диссипацией и дисперсией, стараясь поаккуратнее передать реше-
решение в зоне разрыва? Ведь к под я искусственную иялкость (гл. II,
§ 4), мы ставили задачу: подавить колебания решении за фрон-
фронтом разрыва, понимая, что возникающее при :>том его размазы-
папие физического смысла, ш.1текаюии.то ни существа исходной
ладачи, не имеет. И поэтому будет :>то размазывание несколько
больше или меньше,— этот факт с прикладной точки зрения ма-
малосуществен.
Сформулированная так постановка правомочна не для всех
классов задач. Например, в [10, 47, 48] с помощью численных
283
расчетов исследуется распространенно мапштогидродипамических
волн в атмосфере звезд. В силу нелинейной трансформации фронт
волны становится круче, формируется кназистацпонариый спектр
решения, устанавливается «перекачка» энергии из длипнополпо-
иой части спектра и коротковолновую. Описанные процессы об-
обсуждаются как иозможпып механизм передачи :шоргип из инут-
ренпих областей знезды на ее периферию, объясняющий высокую
температуру хромосферы.
При расчете этой ладачп размазынаппе фронтон, кап за счет
искусстнеппой, так и за счет схемной вязкости, может заметно
исказить фпяпческии смысл результатом. Объясняется это том,
что иптспеттнпость дпесипатшшого фактора влияет на соотнотне-
ние высокочастотных и низкочастотных составляющих спектра
репгенпя и другие его топкие особенности. Для решения подоб-
подобных задач часто применяют более точные численные методы,
такие, как спектральный метод Галершша, псевдоспектралытьш
метод «точных пространствепных пропзнодных» и т. д. [10, 64].
Однако указаппые методы являются более громоздкими, менее
универсальными п требуют для реализации большего машпппого
времени. Поэтому актуальной задачей является построение pa:s-
постных методов, обеспечивающих хорошее качество решения и
для задач указанного класса.
Рассмотрим более подробно вопрос о спектральных свойствах
решения. Пусть у{ = у (Sh- ';)— сеточная функции решения.
(Здесь для обозпаченпя прострапстиеппого ппдекса ипопь, как к
гл. III, используем к, оставляя i для обозпачепия мнимой еди-
пицы i=V—1.) В фиксироваппый момепт времени t, разложим
на сетке 0 ^5 к ^ N yi, как функцию нрострапствеплого индекса к
в дискретный ряд Фурье [81]:
1/л= i YtLe л,
где коэффициент У„ (шределяется (формулой
N-1 . h
1 ^71 ¦ — 2.12I-J-.
П = }2^ N- D.13)
Под спектром численного решения па момепт времени t3 будем
понимать набор zn = YJY0 (n = 0, 1, ..., N—i), т. е. отнорми-
роваипый набор амплитуд гармоник D.13). На рис. 5.22 пред-
представлены па момепт иремени t = 40 спектры числшпых решений
(фупкция плотности), обсуждавшпхея выше (рис. Г).21). Спект-
Спектральные характеристики изображены в виде графика, где по го-
ризоптальпои осп отложен номер гармоники п, я но вертикаль
пой — модуль соответствующего коэффициента разложения lznl.
Для сравнения штриховой линией указан на тот же момент при-
примени спектр решения исходной задачи D.9) с вязкостью при
284
•v = 0,005, полученный псеъдоспектральным методом [10, 64], ко-
который мы будем рассматривать как эталонный.
Сплошная линия соответствует расчету по схеме D.2) с а =
= 0,5, v = 0. Хорошо видно, что спектр в этом случае является
v-D, 6=0,5
v-o,oob.a=u.b
пееВдрспектра/п-.гч
,-етод, v=0,005
немонотонным и сильно отличается от аталоппого. Максималь-
Максимальные различия относятся к области волновых чисел n ~ 26 -г- 30.
что связано с характерпым размером первого из формирующихся
в решении солитонов.
Расчет с о = 0,5 v = 0,005 дает лучший спектр, однако нали-
наличие осцилляции за фронтом разрыва заметно проявляется и л
атом случае.
285
Неявная схема <j = 1, v = 0 (штрнхнунктнрпая линия), обла-
обладающая значительной ттутрепией вязкостью (v«0.01), разгла-
разглаживая решепие, «обрезает» коротковолновую часть спектра, Та-
Таким образом, в ряде случаен сопоставление спектра числепного
решения со спектром эталонного может дать более точный кри-
критерий качества решеппя, пежелн визуалышп контроль,
4. Схемы с искусственной дисперсией. Вид разностной схемы
с искусственной дисперсией для уравнений газодннакнми D,1)
нетрудно усмотреть нл дифференциального приближения D.3):
/7 = Р + 0), /' = <"-[>. 0) = Vp!'«.
Присутствие в схеме третьих производных, которые н пред-
представляют искусственную дисперсию, порождает определенные ал-
алгоритмические трудности, связанные с расширением шаПлопа.
Поэтому, учитывал вытекающие h:i ('i.i) ргнюнетпа
t?-J-(A.\ ^ .,__!__«!'¦_.,
<5s3 tit1 nt \ P 1' (;.«3 f- 0.1- >>t
рассмотрим другой вариант схемы:
g = р + (о, ^ = c2f), (о = —л
Дифференциальные приближения схем D.14) и D.1.1) совпада-
совпадают с точпостыо O(x2 + h2) и в главных члепах имеют нид
D.16)
Здесь но сравпепню с D.3) отброшен ряд членов квадратичного
порядка малости. Как видно, за счет выбора коэффициентов ис-
искусственной дисперсии 0 п 0 появляется возможность воздейст-
воздействовать па внутреннюю дисперсию схемы. В частности, как и для
квазилинейного уравнения переноса, можно положить их рапны-
рапными зпачештямп коэффициентов 3 л 3- вычисленным на фоне при
() = ро:
.> 2 '1 о , , ¦>
2т с р„ -:- h
о Р(Ы Р ?
О - Р ([)„) - ff0 = ^Ц^— ' vt (а - О.Г)) р„.
Па рис. 5.23 даны результаты расчетов задачи D.П) но схеме
D.15) при значениях параметров а = 0,5, v = 0,005 и 0 = ро,
0 = 0 (рис. 5.23, а), а также 0 = 0, 0 = ^0 (рис. 5.23,6). Заметим,
280
что в иыбрапных параметрах Ро = Ро ~ 0,ОООГ)Ь. Отметим, что ре-
результаты этих расчетов практически совпали. 1)то подтпорждает
теоретический иыоод [60], доказательство которого мы здесь по
ojrjb. Ь- г. ft 2,~.г :.
. ',8 1-*-!¦'¦ 5//;
,:.ОИГ>, Я в,-, О- .'.6 .'•¦•¦
162 !69
'4<Ч 256 ф
Рис. 5.23
приводим, о том, что на формнронание решения плняет лишь сум
марная искусственная дисперсия, где каждый коэффициент рав-
равноправен.
По сравнению с расчетами Ge:? искусственной дисперсии
(рис. 5.21) результаты оказались ближе к точному решению,
однако осцилляции за фронтом разрьша псе же заметны.
Па рис. 5.24, а представлены результаты расчетои при 0 —
= 0 = Зо. Здесь же на рис. 5.24,6, где указан спектр, для cpais-
пения приведены спектральные характеристики решения, полу
ченного нсевдоснектральным методом (штриховая линия). Видпи,
что решение воспроизводится удовлетворительно,— па разиитиг'г
стадии его профиль близок к прямоугольному треугольнику, ши-
ширина размазывания разрыва составляет к моменту ? = 40 при-
примерно четыре сеточных интерпала. Хорошее качостпо решения
подтверждается и близостью его спектра к эталонному. Таким
образом, в данном расчете искусственная дисперсия в достаточной
стеиени скомпенсировала схемную дисперсию, и выбранной ис-
искусственной вязкости (v = 0,005) оказалось достаточно для того,
287
чтобы погасить колебания в решении и в то же время не сильно
размазать разрыв.
Рис. 5.25 соответствует расчетам, выполненным при О = 2[5О,
0 = 0, и 0 = 0, 0 = 2Eо соответственно. Полученные результаты
& = {j--j30,v--0,0u5,0=0,5
псрЦЯаспб^трагвнтп
метод, v-u,QC5
U40
130 163 168 210
a
249 254 sjh
10
20
30 40
5
Рис. 5.24
50
60
близки друг к другу! а также к результатам предыдущего рас-
чота с 0 = 0 = [Jo. Это вновь подтверждает упоминавшийся выше
факт, что действие искусственной дисиерспи в схеме D.2) опре-
определяется суммой коэффициентов 0 + 0. Отметим, что этот вывод
теоретически обоснован в [59] для случая, когда решение пред-
представляет небольшое возмущение фона, типа тех, которые мы рас-
рассматриваем в расчетах.
1'88
Результаты расчетов, изображенные на рис. 5.2Л, имеют и
практическое значение. Они свидетельствуют, что искусственную
дисперсию, правда с удвоенным коэффициентом, можно вводить
лишь в одно уравнение. Это позволяет заметно упростить алго-
алгоритм расчета. ^
Действительно, при О Ф О, О Ф 0 нелинейная разностная схема
D.15) с помощью метода Ньютона сводится па каждой итерации
:.2У
v-o,oob,-a-2BB,a--o, 0-0.5
:53 168
2*9 255 S/7i
v--0,005, в-О, ё-2ро,С=Э,5
/62/67
5
Рис. 5.25
246 255 s/ti
к системе диух трехточечных уравнений, для решения которой
используется матричная прогонка. В случае если член искусст-
искусственной дисперсии входит лишь в одно уравнение @ = 0, 0^0
либо 0 Ф 0, 0 = 0), задача сводится к одному трехточечному урав-
уравнению, которое решается с помощью скалярной прогонки, что
заметно проще.
Анализ устойчивости схемы D.15) в общем виде достаточно
громоздок. Говоря о результатах этого анализа, укажем лишь,
что при 0 = 0 условия устойчивости схемы D.15) в линейном
приближении совпадают с условиями устойчивости схемы D.2):
о 5= 0,5. При 0 Ф 0 возможно появление ограничений на шаги
сотки.
5. Схема с искусственной дисперсией в задаче о поршне. Ис-
Исследуя разностные схемы с искусственной дисперсией для ypais-
нспия переноса, мы не ограничились рассмотрением тестон лишь
13 Л. Л. Самарский, 10 II II.,,,ив 289
одного типа. Помимо простой волны, разностная схема была
опробована и на решениях типа ударной волны, что позволило с
большей надежностью подтвердить результаты теоретического
анализа. Поступим аналогичным образом п в случае уравнений
газовой динамики. Обратимся с этой целью к классической задаче
о поршне,
Пусть в исходном состоянии при ? = 0 покоящийся (v(s, 0) =
= i>o = 0) однородный (p(s, 0) = po) газ, заполняет полупростран-
полупространство s > 0, ограниченное слева поршнем. При t > 0 поршень
вдвигается в газ с постоянной скоростью i>@, t)=U. При отсут-
отсутствии диссипации решением задачи, которая описывается ураи-
пенняып D.1), яиляется разрывной профиль — ударная волна,
фронт которой движется от поршня с иостояпиой скоростью D.
Для рассматриваемого изотермического случая соотношения меж-
между значепиямн параметров газа по обе стороны от разрыва могут
быть получепы из E.23) гл. I, где нужно положить ^ = 1. На-
Например, при конкретных значениях ро=1, U = 0,1, с = 0,5 для
скорости волны и параметров газа за ее фронтом пмеем D « О,Г)Г>,
Vi = U = 0,l; pi =(Z)/cpoJpo « 1,22. На рис. fi.2G даны результаты
расчета этого конкретного варианта задачи о поршне на сенсе
с шагами h — 0,1; т = 0,08 по схеме D.2) с о = 0,5. Коэффициент
искусственной вязкости варьируется. Наблюдается стандартная
картина: при малых коэффициентах v за фронтом волны наблю-
наблюдаются колебания, вязкость с большим коэффициентом их по-
подавляет, приводя одновременно к большому размазыванию фрон-
фронта разрыва. Так, прп л> = 0,01 па момент временп г = 40 ширппа
:>того размазьжашш составляет 10 —11 интервалов сетки,
Анализ линеаризованного вблизи заднего фронта тшлны диф-
дифференциального приближения D.3), мыполнеппьш в автомодель-
автомодельных переменных аналогично § 3 и. 3, позволяет установить кри-
критическое значение коэффициента вязкости:
(/,.18)
где (} = (} + (} (см. (/i.4)). При v>v;1. колебания за фронтом пил-
ггы и линейном приближении отсутствуют. При значениях пара-
параметром, использованных в расчете, пеличнпа критического коэффи-
коэффициента составляет v^ да 0,010. Результаты, представленные иа
рис. Г).20, хорошо с этим согласуются.
Па рис. 5.27 даны результаты расчета той же задачи по схеме
с искусственной дисперсией D.15) при о = 0,5, v = 0,005, 9 = 0,
0 = 2^0 = 0,0011. Как мидпо, осцилляции за фронтом отсутствуют,
ширина размазывания разрыва составляет 3—4 пптервала.
Таким образом, расчеты задачи о поршне подтверждают сде-
ланпые ранее выводы о свойствах газодинамических разностных
схем с искусственной дисперсией.
6. Адиабатический случай. В этом параграфе рассмотрение
разпостпых схем для уравнений газоион динамики проводи-
290
лось на примере сравпптельно простого изотермического прибли-
приближения. Отметим, что все полученные результаты переносятся и
на случай адиабатической газовой динамики. Приведем для
t-24
F
1.2
1.0
T = :_C
= O,()nS; 6-0,5
121 130
a
; 6=0,''
123 133
\i
209 217 s/h
i-40
IV,
211 221 s/h
p
7 1
1,0
-
v-0,1/
t -24
\
\
Vj
123 135
212 223 s/h
Рис. 5.20
примера вид разностное схемы с искусственной дисперсией для
адиабатического случая:
Г.. 19)
f (=
= P + (-¦). 0) --• — V[K'a.
If'*
201
Здесь обозначения и смысл входящих параметров 0 и 0 те же,
что и в D.15). Продемонстрируем свойства схемы D.19) на при-
примере численных расчетов. В качестве тестовой возьмем задачу о
распаде произвольного разрыва (гл. I § 8). Будем для опреде-
определенности считать, что па исходном разрыве (ого массовая коор-
координата so) температура непрерывна, а скачок испытывают лишь
t-?--
1?3129
Гис. 5.27
плотность и, соответственно, давление. В начальный момент среда
справа и слева от разрыва покоится. В качестве уравнений со-
состояния используются обычные соотношения для идеального газа
(A.7), A.8) гл. I) с показателем адиабаты f = 5/3 и газовой
постоянной Я = 0,831.
Па рис. 5.28 представлены результаты расчета этой задачи
при следующих значениях начальных данных:
Точное решение, которое здесь без труда строится с помощью
формул, указанных в § 8 гл. I, содержит ударную волну, распро-
распространяющуюся направо, простую иолну разрежения, идущую и
противоположную сторону, и контактный разрыв в точке .%.
Графики на рис. 5.28 приведены на момент времени t = 0.4,
отношение шага сетки по премени к шагу т,., следующему i'.t
условия устойчивости Куранта, составляет т/т/,«1, параметр
а = 0.5, значения параметров v, 0, 0 варьировались.
Расчет, результаты которого даны па рис. 5.28, а ныполпеп по
оиычнеш схеме 0 = 0 = 0 с. коэффициентом искусственной линей-
линейной вязкости v = 0,0049. Как видно, за ударной полной и волной
разрежения возникает интенсивная «болтанка», природа которой
обсуждалась вышо в этом параграфе.
Увеличив коэффициент иязкости до v = О, I (рис. 5.28,6), мож-
можно подавить эти осцилляции, заметно «размазав» при этом фронт
ударной волны.
292
P1
12
1,0
Q\ I I V , 0,9
-.0
0,9
Рис. 5.28
Рисунок Г).28, в соответствует расчету по схеме, содержащем!
искусственную дисперсию:
где коэффициент иязкостп v тот гке, что п п нервом расчете,
v = 0,0049, В этом случае качество решения существенно выше,
оно хорошо согласуется с точным решением.
В заключение отмстим, что полученные в данной главе ре-
результаты, в том числе и в части схем с искусственной дисперсией,
распространены на случай неравномерных сеток, а также для
уравнений магнитной гидродинамики [60].
ГЛАВА VI
РАЗНОСТНЫЕ СХЕМЫ МАГНИТНОЙ ГИДРОДИНАМИКИ
В этой главе принципы построении и реализации разностных
схем газодинамики, изложенные выше, обобщены на случаи од-
одномерных нестационарных задач магнитной гидродинамики. Пер-
т.ая половина гланы содергкит необходимые сведения по теории
машитогидродинамических течении. 15 §§ 1, 2 выводятся уравне-
ппя магнитной гидродинамики л обсу;кдаютсн различные формы
их записи. В § 3 ошгеаны некоторые специфические особенности
магнитной гидродинамики, такие, как «вморожечшость» п диффу-
лия магнитного поля, наличие нескольких скоростей звука н т. д.
В § 4 для уравнении магнитной гидродинамики построены пол-
полностью консернатшшые разностные схемы. § Г> содергкит изложе-
изложение методов расчета разностных урпииешш электромагнитного
поля, в том числе и для случая малой проводимости. § 6 посвя-
посвящен методам расчета электрических цепей в задачах магнитпой
гидродинамики. § 7 посвящен описанию двух методов расчета
задач магнитной гидродинамики с учетом фазового перехода.
Изложение ведется па примере задачи об импульсном ускорении
плазмы в электромагнитном ускорителе эрозионного типа.
§ 1. Приближения магнитной гидродинамики. 'I
Основные уравнения : ' |
1. Уравнения Максвелла. Газ, нагретый до высокой темпера-
температуры, становится электропроводным, При дншкепии проводящей
среды п плектромагпптном поле п ней возникают электрические
токи, появляются обусловленные этими токамп силы и источники
тепла. Все это влияет на движение и термодинамическое состоя-
состояние среды. Электрические токи порождают также магнитное поле,
которое, складыпаясь с исходным полем, изменяет его. В резуль-
результате возникает сложная, как правило, нелинейная картина взаи-
взаимодействия движущейся электропроводной среды с электромаг-
электромагнитным полем.
Явления такого тина в последнее десятилетие все чаще ста-
становятся объектом изучения как в фундаментальных плазменных
исследованиях, так и в сняли с конкретными техническими при-
приложениями. В теоретическом отношении широкий круг вопросов
и этой области может быть рассмотрен в рамках магнитной гид-
гидродинамики.
2<V.
Уравнения магнитной гидродинамики объединяют уравнепия
газодинамики, в которых учтены эффекты, связапные с влиянием
электромагнитных нолей, и уравнения Максвелла, описывающие
электродинамические процессы.
В дифференциальной форме уравнения Макспелла обычно за-
записывают следующим образом [42, 44, 45]:
го1Н__1+__, A.1)
rotE=_±°ni A.2)
с tit '
divE = 4.-10,, A.Л)
divH = (i. A.4)
Здесь Е и II — векторы напряженности электрического п магнит-
магнитного полей, i — плотность электрических токов, ре—плотность
электрических зарядов, с — скорость света в пустоте. Уравнения
A.1)—A4) яаппсапы и переменных Эйлера, псиолкюинпн абсо-
абсолютная гауссова система единиц. Изменение электрического за-
заряда со променом описывается дифференциальным уравнением
dpe/dt + divi = O, A.5)
которое выражает закон сохранаенпя заряда и по аналогии с со-
соответствующим уравнением газодинамики часто называется урав-
уравнением перазрынпостп.
В общем случае в систему A.1) — (Li), помимо Е и II, входя г
векторы D и В — электрическая н магнитная индукции соответ-
соответственно. Для изотропных срод справедливы линейные соотноше-
соотношении I) = еЕ, В = и.1Г, где безразмерные коэффициенты е и и,, на-
называемые диэлектрической н магнитной проницаемостью, опре-
определяются свойствами конкретной среды. В магнитной гидродина-
гидродинамике обычно рассматривают такие среды, где е и ц мало отли-
отличаются от единицы. Поэтому в дальнейшем будем считать е = 1,
ц=1 и использовать уравнения в форме A.1) — A.4).
Уравнения A.3), A.4), вообще говоря, являются следствиями
уравнений A.1), A.2) п том смысле, что если соотношения A.Л),
A.4) выполнены в начальный момент времени, то они будут
справедливы п и любой другой момент. Действительно, применяв
операцию div к урапноппю A.2), получим
clivH O,
откуда п следует одно из сформулированных утверждений. Вто-
рое утверждеппе получается из уравнения A.1) после примене-
применения к нему операции div п учета соотношения A.5). Одпако,
несмотря па то, что уравнения A.3) и A.4) ис являются неза-
независимыми, их иногда используют при решении задач вместо од-
одной из проекций уравнений A.1) п A.2) соответственно.
295
2. Соотношения на разрыве для электромагнитных величин.
Дифференциальные уравнения Максвелла справедливы в тех
областях, где решение обладает достаточной гладкостью. Если же
в среде существуют поверхности, на которых функции, входящие;
в дифференциальные уравнения A.1) — A-г)), терпят разрыв, то
необходимо пеполыювать дополнительные соотношения, связываю-
связывающие электродинамические параметры на разрыве. Получаются
они из интегральных уравнений Максмелла, которые мы здесь не
приводим, и п системе координат, где поверхность разрыва по-
покоится, выглядят следующим образом (рнс. 0.1):
(Ех)„ -
= 0.
Лдесь Еп, Я„ — нормальные, a Er. Ht — касательные к поверхно-
поверхности ра:)рмпа S компоненты векторов
напряженности электрического и маг-
магнитного нолей, i — плотность поверх-
поверхностного тока, д — поверхностная плот-
плотность электрических нарядов, п—век-
п—вектор единичной нормали к поверхности
2. Таким образом, нормальная компо-
компонента вектора напряженности магнит-
магнитного поля н тангенциальная — электри-
электрического поля непрерывны. Разрыв нор-
нормальной компоненты электрического
поля определяется поверхностной плот-
плотностью электрических зарядов, а разрыв тангенциальной состав-
составляющей магнитного ноля — плотностью поверхностного тока.
3. Приближения магнитной гидродинамики. Рл.нпе уже отме-
отмечалось, что в магнитной гидродинамике часто рассматриваются
среды, для которых с хорошей точностью диэлектрическая и маг-
магнитная проницаемости равны единице.
Кроме того, считается, чти среда является ипааипентралыюй,
т. е. суммарный электрический заряд в любом элементарном объе-
объеме равен нулю: р„ *= 0.
В магнитной гидродинамике предполагается также, что про-
проводимость среды достаточно велика, а рассматриваемые процессы
протекают так медленно, что членом A/с) 3E/3f (током смеще-
смещения) в уравнении A.1) можно пренебречь но сравнению с током
проводимости i. Энергия электрического поля при этом оказыва-
оказывается малой по сравнению с энергией магнитного поля
Е2«Н2. A.7)
Конечно, отбрасывание токов смещения упрощает уравнения Мак-
Максвелла, однако следует иметь в нпду, что при этом изменяется
их структура. Поэтому применение упрощенных уравнений для
анализа явлений, где не выполнены сделанные предположения,
может привести к искаженному оппсашпо этих явлений. Так
290
электромагнитные волны в пустоте распространяются со ско-
скоростью с. Уравнения же магнитной гидродинамики, где токи сме-
смещения опущены, дают в этом случае бесконечную скорость рас-
распространения электромагнитного ноля.
С учетом указанных приближений система уравнений Макс-
Максвелла приобретает нид
i = -?- rol H, —'-ТГ = — rotE, div H = 0. A.8)
Уравнения A.8) записаны в покоящейся системе коордипат.
При переходе к системе коордипат, движущейся относительно ис-
исходной с некоторой скоростью v, электродинамические параметры
изменяются. Если пренебречь релятивистскими эффектами, что
возможно при условии
\с/< 1,
которое в магнитной гидродинамике предполагается выполпен-
пым, то формулы перехода к движущейся системе координат (па-
(параметры в пен помечены штрихами) выглядят так:
И - И. i' = i, E'= E-;~[vX "I- A-9)
Таким образом, уравнения Максвелла в движущейся систем.1 ко-
ордпнат записываются следующим образом [V)'\\
i=^rotH. -i^-'i ==-L rot fvXH|—rotE, ilivH=0. A.10)
Уравнения A.10), среди которых лишь шесть независимых
скалярных соотношении, содержат девять неизвестных функций
(компоненты вектором i, E и II). Чтобы замкнуть систему
A.10), обычно используют дополнительное уравнение вида
i=/(E, II, v, ...), связывающее различные электро-, гало- и тер-
термодинамические характеристики среды. В простейшем случае, это
соотношение таково:
i=aE, A.11)
где скаляр а есть электропроводность среды. Уравнение A.11)
записано в системе коордипат, где рассматриваемый элемент ве-
вещества покоптся. Оно носит название закона Ома. 13 более общем
случае в закопе Ома присутствуют слагаемые, которые зависит
от напряженности магнитного поля и описывают анизотропию
проводимости, слагаемые, связанные с градиентом электронного
давления, и т. д.
\. Уравнении магнитном гидродинамики в векторной форме.
Уравнения A.10), A.11) описывают электродинамическую часть
задачи. Влияние газодипамичеекпх процессов проявляется здесь
через скорость движения среды v в A.10), а также электропро-
подпость а (см. A.11)), которая определяется термодинамическим
состояпием вещества: а = а(р, Т).
Обратимся к газодинамической части задачи. Соответствующая
система дифференциальных уравнений была приведена в гл. I
(см., например, C.2) — C.5)). Влияние электромагнитного поля
297
здесь скажется следующим образом: и уравиепия диижения C.3)
п эпергин C.4) войдет объемная электромагнитная сила, плот-
плотность которой равна
F=~ ИХ И]- A-12)
с
Кроме того, и уравнении энергии полнятся объемпыс источни-
источники тепла Q, связанные с нагревом проводящей среды электриче-
электрическими токами (так называемое джоулево тепло).
Мощность этих источников вычисляется по формуле
D=(iE). A.13)
Принимая во внимание пакоп Ома A.11), выражение для джоу-
лева тепла можно представить также л виде
Таким образом, полная система уравнений магнитной гидро-
гидродинамики в переменных Эйлера имеет кпд
-^- -|- (Uvpv = 0, (l.i'i)
Ш +(vV)v»__L grail p + f, I^-Ltiii-Ш, (иг,)
at p 6* p
i=^rotH, (I.Hi)
*—- = rot |vXHj — с rot E, ftiv H = 0, A.17)
i = oE, A.18)
+ -^-j = fliv /pv + g —- (fv) <liv W,
= 1!^, W = — и grail 7', (I. HI)
71), e = e(p, T), A.2A)
х = и(р, Г), о = о(р, Г). A.21)
Здесь i и ^ — плотность силы и мощность тепловых nrni'iiini.Ois
в пересчете па едипицу массы.
К уравнению A.17), которое носит название уравнения индук-
индукции, добавлено соотношение divH = 0. Как ул;е отмечалось, ото
соотношение не является независимым (см. п. 1), по иногда ис-
используется вместо одной из проекций уравнения индукции. Со-
Соотношения A.21) выражают физические свойства среды — тепло-
и электропроводность. Построение этих зависимостей для коыкрот-
пых веществ к широком диапазоне изменения термодинамических
параметров р и Т представляет самостоятельную серьезную
проблему.
Уравнение индукции A.17) можно преобразовать к несколько
ипому виду. Используя правила векторного исчисления, запишем
Учтем, что tliv II == 0, и выразим из уравнении неразрывности
A.14) divv:
Подставляя все это в A.17), получим уравнение индукции в виде
й
5. Уравнении магнитной гидродинамики в безразмерной форме.
Выше, в гл. IV, отмечалось, что при численном решении конкрет-
пых задач соответствующую систему уравнении удобно тгривсстп
к безразмерному виду, выбран и качестве основных размерных
масштабов некоторые характерные параметры. Любая функция
при этом представляется в виде F = FqF, где /•' и F — соответ-
соответственно размерная и безразмерная величины, Fa— масштаб из-
измерения.
Обезразмерпм систему уравнении магнитной гидродинамики
A.14) — A.21), приняв за основные размерные параметры вели-
величины
хо, to, po, То. A.23)
Масштабы измерения остальпых величии выражаются через па-
параметры A.23) следующим образом:
— 1 2 2, — 2 щ •! 2, — 2
'"(¦ — -г(''й ' Ри = fVo = Ро^'о'о ' Ь'и = го = 'го'о 1
t • — 2 1 г/ п
/О "~ О 0 ч 0 "^ го 0 ~
С учетом сделанного выбора масштабов система уравнении
магпптноп гидродинамики преобразуется к безразмерному виду
(тильда — символ безразмерной фуикции — опущепа)
U -I- div pv =-- 0, -^ + (vV) v = - -L grad p + f,
f = [IXHj/p, i = ^rrotH, i = oE,
^ = rof[v X H] — rot E, divH = 0, A.25)
= div p\ -f Q + (fv) div W,
, = ill), W = - v. grad T, p = p (p, 7'),
= e(p, T), x = x(p, T), o = o(p, Л,
299
Как видно, за исключением размерного множителя с в уравне-
уравнениях полн и в выражении для электромагнитной силы, система
A.25) совпадает с системой A.14) — A.21). В дальнейшем мы
будем использовать уравнения магнитной гидродинамики в форме
A.25), предполагая, что обезразмерииание нынолнсио.
Основные масштабы A.23) выбираются в соответствии с кон-
конкретными особенностями рассматриваемой задачи. Если величины
этих параметров взять в виде
хо=Ютсм, /о = 10" сек, ро=1Ок г/см3, То = 1О"эв,
где пг, га, k, p — некоторые числа, то остальные масштабы будут
иметь значения
Уо = Ют-П си/сек,
Ро = 1020"-")+" дн/см- » Ю2(т-")+"-6 атм,
ео = ю2("-«) Эрг1г, Но = iom-n+ft/2 a,
Ео = Ю2(т-»:+*/2-8 e/CMi io =.-= ю*/2-»+| aicM2,
ao^lO9*"-^ \/ом-см = 9-\020+п-2т 1/сек,
r/0= 102-3'1 эрг!г -сек, /0-=10'"-2п дн/г,
Wo -= 103(m-n)+'1 дрг/ейк • cmq,
v.o = Ю4-3"-1-"-11 эрг/сек ¦ см ¦ эв.
§ 2. Уравнения одномерного нестационарного
магнитогидродинамического течения
1. Особенности одномерных задач в магнитной гидродинамике.
Прежде чем формулировать спетому ураппопий для одномерных
магпитогпдродпнамнчиских течешш, когда все фупкции записях
лишь от одпой ирострапстиенноп координаты, проапалтпруем
структуру, которую имеет в атом случае магпптпое поле. Оори-
тимся к уравпепию divH = O. Для одномерных задач оно приоб-
приобретает вид
-LJL{r4r,)^Q, B.1)
где г—эйлерова координата (радиус), II,— компопента вектора
напряженности магнитного поля вдоль радиальпого направления;
значения параметра га = О, 1, 2 отвечают соотиетствепно плоской,
цилиндрической и сферической симметрии задачи.
Для плоского случая (ге?=О) из B.1) следует
# г = НТа = const, B.2)
причем, используя ураинение индукции, можпо убедиться, что по-
постоянная Яг не зависит и от времени.
Для случая цилиндрической симметрии (га = 1) уравнение
B.1) дает
НА1 B.3)
где постоянная Л также не зависит от времени. Заметим, что
^сли в задаче область изменения пространственной переменной г
включает ось симметрии г = 0, то А ^ 0, и тем самым радиаль-
радиальная компонента магнитного поля отсутствует:
Яг = 0. B.4)
Полюс
В противном случае у оси системы напряженность магнитного
ноля принимает бесконечно большие значения, что лишепо фи-
физического смысла.
Аналогично в случае сферической симметрии (п = 2) получаем
Нг = А/г°-. B.5)
Однако остальные компоненты магнитного (а также и элект-
электрического) поля здесь оказываются тождественно равными пулю.
Пояснить это обстоятельство мож-
можно с помощью следующих нагляд-
наглядных рассуждений. Рассмотрим не-
некоторую сферу радиуса Rq, центр
которой совпадает с центром сим-
симметрии задачи (рис. 0.2). На этой
сфере в силу симметрии задач»
любая компонента магнитного по-
поля при всех значеппяхугловфиб
должна иметь одну и ту же велп-
чппу, например //Ф(/?о, ф, 0)=йг<ро-
Очеиидно, однако, что это воз-
возможно не на всех широтах 0.
Исключение составляют полю-
полюсы 0 = 0, я, где функция //„ ста-
становится многозпачной. Поэтому
необходимо положить Яф() = 0. Так как радиус рассмотренной
сферы произволен, то /7Ф(г, t)*=-Q. Аналогично получим, что
//о (г, 0 = 0.
Если к тому же область изменения пространственной перемен-
переменной содержит центр системы (г = 0), то в B.5) Л = о, и, следова-
следовательно, в этом случае ;)лектромагпитное поле тождественно равно
пулю. Если же задача решается и области, не содержащей точку
>¦ = 0, то возможно радиальное магинтное ноле, неизменное во
времени и спадающее по радиусу в соответствии с законом
B.5)*). Однако и в этом случае оно не оказывает влияния на
дипжепие среды. Поэтому одномерные задачи магнитной гидроди-
гидродинамики имеет смысл рассматривать лишь для плоской и цилинд-
цилиндрической симметрии.
*) Аналогичный факт имеет место и в газовой динамике: в задачах, об-
обладающих сферической симметрией, возможно лишь радиальное движение.
301
2. Одномерный плоский случай. Пусть вес компоненты векто-
векторов скорости и напряженности магнитного ноля отличны от пуля
v = {y, ц, и;}, Н = {//,,, //,„ //,}
и зависят только от х и t.
Как отмечалось в предыдущем пункте (см. B.2)), продоль-
продольная компонента магнитного поля постоянна
Нх = Ил = const. B.G)
Из A.25) следует, что вектор напряженности электрического по-
поля и плотность электрического тока имеют лишь поперечные
компоненты
i = {0, f,, U, Е = {0, Еу, EJ,
i ли, . i он B.7)
Компоненты вектора плотности электромагнитной силы f =
= p"'[iXH] вычисляются следующим образом:
/ L а тт _ / н \ f _ 'г//-гП / _ 1уН*° /о я\
1х — — {'упг Lzlly), /у— — 1 ]г— р • 1-W
Эти ныражения с учетом B.7) можно представить также п виде
р f ^± fOiJb BS)
7ж - ~~ р Ох \ 8л )' 7у ~ 4лр 0х ' /z ~ 4лр Ох • ^-° '
Джоулево тепло в уравнении энергии представляется в несколь-
нескольких формах
= '•/•„+',*, = _О_ (?2 ?2) = ^+А B 9)
i р р V у ' 2У Ор V /
Принимая во внимание все сказанное, запишем систему уравне-
уравнений магнитной гидродинамики для одпомерных плоских течений
в переменных Эйлера
Зр , ар до ,.
дх — ~
Ж "Г" дх ~ ~~^~дх~ ' '*' 1Х р" to" V 8jx '»
ди . ди
_
/!/ ~ 4лр Ох '
дю дш ,
5t ^ р; + v
302
dt { p ) ' V dx \ p / ~ p dx p Oxy
= z B.10)
I p dx p Ox '
1 дНг
—, iz —
7 = -y(lvEv + izEz),
p = p{p,T), e = e(p, Г), a = a(p, Г).
Уравнение индукции здесь записано в форме A.22). Поток теп-
тепла в уравнении энергии для простоты опущен. Введя лагран-
жевы массовые координаты s, / (см. § 3 гл. I), систему B.10)
можно переписать так
0t
Op д ("I + Hi \ dx
д" -t { - If*° 0Hi> dlJ
dm 'ЛтП дН, dz
ttx = //«o, B.15)
JT ди . дЕ
dt \ p I "*» a* ' л, ' B.16)
я til
pf^L, i1 = aA.2 = 7P_^2i, B.18)
4л as ' 'til as v '
B.19)
p-p(p, T), e = e(p, Г), o = o(p, Г). B.20)
3. Различные формы уравнении анергии. В § 3 гл. I, где рас-
рассматривались уравнения газодинамики, отмечалось, что уравне-
уравнение энергии может быть представлено в нескольких формах,
выражающих различные физические аспекты явлепия. В мате-
математическом отношении эти формы эквивалентны и сводятся друг
к другу посредством равносильных преобразований. В дальней-
шем это послужило отправным пунктом при построении пол-
полностью консерватшшых разностных схем газодинамики. В маг-
магнитной гидродинамике, громимо внутренней и кинетической энер-
энергии газа, имеется третий вид энергии — энергия электромагнит-
электромагнитного поля. Соответственно увеличивается и число различных
форм записи уравнения энергии. Действительно, умножим урап-
пения B.12)—B.14) соответственно на v, а и w и вычтем по-
лучепныо соотпошепия из B.19). Это прпиодит к недивергепт-
пому уравнению
В отличие от обычной газодипамики, здесь внутренняя эпер-
гия газа изменяется со временем не только за счет работы сил
газокинетического давления, но и в результате нагрева электри-
электрическими токами. Используя уравнение неразрывности B.11),
можно указать несколько видоизмененную форму недивергонт-
ного соотношения B.21):
де , О I 1 \ /О ,-.,-..
+ P <2-22>
Получим теперь дивергентное уравнение энергии. Обратимся
предпарптольпо к проекции уравнения индукции B.16). Его
лепуго часть с помощью уравнения пералрывности B.11) можно
представить в виде
at \ p ; p ot ' •" Os'
Подстапляя это выражение в B.16), получаем возможность вы-
выразить пропзподпую:
1 д11у тт Ои „ ди и 0Kz
Умножим полученное уравнение, а также уравнепио B.16) на
Hv/(8л,) и результаты сложим. Это даст уравнение
Ot \&пр) 8я ds + 4л ds + 4л Os '
которое описывает изменение со временем удельпой магнитной
энергии, связанной с г/-компопентой магнитного поля. Рассмат-
Рассматривая аналогичным образом другую проекцию B.17) уравнения
индукции, имеем
Ot \8кр ) 8л ds "" 4л ds 4л ds
Складывая B.23) и B.24) с уравнением энергии B.19), где
величины q и / выражены через функции Н и Е с помощью
остальных уравнений системы, получим после несложных
304
преобразований
Это и есть дивергентная форма уравнения энергии*), указыва-
указывающая закон изменения полной энергии. Выражение для полной
энергии, стоящей под знаком производной п левой части B.25),
складывается из тепловой, кинетической и магнитной энергий.
Напомним, что в приближении магнитной гидродинамики энер-
энергией электрического поля пренебрегают (см. A.7)). В правой
части помимо члена —d(pv)/ds, связанного с работой газодина-
газодинамических сил, присутствуют члены
выражающие работу магнитных сил. Заметим, что первый из
этих членоп аналогичен работе сил газокинотического давления,
в снязи с чем величину (Ну -j- Hl)/(8n) называют магнитным дав-
давлением.
Выражение ПХ = (ЕУН, — ?2//„)/Dя), входящее в правую
часть B.25), является проекцией на радиальное направление
вектора II — [Е X Н]/Dл), который имеет смысл плотности по-
потока электромагнитной энергии (вектор Умова — Пошьтипга).
4. Случай цилиндрической симметрии (Нг = 0). Рассмотрим
сначала задачи такого типа, когда пространстпеппая область со-
содержит ось симметрии. Согласно B.4) в этом случае радиальная
компонента магнитного поля отсутствует: II = {0, //«, #Л. Элек-
Электрическое поле и ток также имеют лишь азимутальные и осевые
составляющие:
Е = @, ЯФ, ЯЛ, i = @, U, О,
Электромагнитпая сила напраплепа вдоль радиуса:
/ -'а п щ\- ' д ("'А ' з(г//фJ
в («l + и'Л ш%
(
р дг \ 8л ) 4лрг *
Движепие газа из-за отсутствия компонент силы /ф и /2 имеет
чисто радиальный характер: v = {v, 0, 0).
*) Уравнение B.19) пазывают иногда полудивергентной формой урав-
уравнения энергии,— газодинамические члены в B.19) входят дивергентным об-
образом, электромагнитные — нет.
20 А. А. Самарекий, Ю. П. Попов 395-
Соответствующая система уравнении и лагракженых массо-
массовых координатах может быть приведена к ииду
d? Os ' ds 8 Л- /' ds
dt \ j) j ()/¦ T 3* ' ot \ j)
0(rv) , '«>E
= - р —j-1 + q, q -= ±-
P 5(г//ф)
р
P = P(V,T), e = e(p, Г), о=о(р, Г).
Уравиепио ипдуь'цпн для азимутальной составляющей магнит-
магнитною поля //ф » B.20) носло несложных выкладок можно прс-
<|брязонаТ1.
dt \pr I ds '
Уравпепие энер!ии в системе B.26) записапо в недпнергент-
пой форме. Используя уравнение движения, можно представить
это уравпение в полудивергентной форме:
Н].1разив с помощью уравнения индукции закон изменения со
ироменем энергии магпитного поля, перейдем далее к дивергент-
дивергентному уравнению энергии, аналогичному B.25):
а ( „я III--И:
I 2 '
Оно показывает, что полная энергия гала изменяется в резуль-
результате работы сил газокипетического и магнитного давления, а так-
такте потока электромагнитной энергии.
5. Случай цилиндрической симметрии (Нг^ 0). 1-х л и область
изменепия пространственной переменной пе содержит точку г =
= 0 (например, задача решается вне некоторого цилиндра, ось
которого совпадает с осью симметрии), то радиальная компонен-
компонента магнитного поля может быть отлична от пуля (см. п. 1 § 2).
В этом случае электромагнитная сила, помимо радиальной, име-
имеет и другие составляющие. Движение перестает быть чисто ра-
радиальным, появляются осевая и угловая компоненты скорости.
Выпишем систему уравнений для магпитогидродинампческих те-
306
тгешш такого типа. Чтобы избежать чрезмерной громоздкости,
положим, что осевая компонента магнитного поля равна нулю:
Н = {//,, //„, 0). При этом в силу B.3) Нг = Л/г, где А — посто-
постоянная, являющаяся параметром задачи. Векторы плотности элек-
электрического тока и напряженности электрического поля имеют
в этом случае лишь осевую составляющую ,
z Anr дг 2
Электромагнитная сила и скорость газа обладают двумя компо-
компонентами
Jr pr- иг 8л ' 7ф ~ 4лрг дг Угп^
? f "г
pr- иг 8л ' 7ф ~ 4лрг
\ = {v, и, 0).
Система уравнений и лаграпжевых массовых координатах выгля-
выглядит следующим образом
JL(A
[
0t [ р ) ~~ ds ' dt ~ '•''
9о и- _ ,др 1 /Г(гДф)'
at ~ Т ~ "~ 7h + -'г' }г г 0.1 8л '
Ои , ни , , "г
at + T ~/(Р' /•р-й
+ , Д (Я,0 + rffi ,-
^ + , Д. (Я,0 + rffi, ,- = ? ^ = а^2, B.27)
pr ris х ' 0s г Ал да г v '
(УК Й (/'У) ,
p '
р = р(р, Г), е = е(р, Г), о-о(р, 21)-
Заметим, что уравнение движения для азимутальной компо-
компоненты скорости может быть преобразовано к форме
д{ги) rIIr а . гт n л а . ,. , ,„ 9Я.
описывающей изменеппе момента количества движения.
Уравнение индукции также приводится к более компактному
виду
Уравнение энергии, записанное в системе B.27) недивергент-
недивергентным образом, сводится к полудивергентной и дивергентной
20* 307
формам
<п
Аналогично формулируются уравнения для случая, когда маг-
литиое поле имеет и осевую компоненту.
§ 3. Некоторые особенности магнитной гидродинамики
1. Явление «вморожеииости». Рассмотрим случаи, когда про-
лодимость вещества близка к идеальной, т. о. а -- *>. Обращаясь
к выражению для джоулепа тепла A.13')
Q = 12/0 = аЕ=,
которое при всех условиях должно оставаться коночным, можно
сделать вывод о том, что электрическое поле и идеальном про-
иоднике отсутствует
Е-0. C.1)
Плотность токов при этом может быть отлична от нуля.
С! учетом C.1) уравнение индукции A.^2) упрощается
Лдесь djdt = d/dt + (\V)—нолпая производная по времени (см.
гл. 1).
Сформулируем теперь уравнение, которое определяет эволю-
эволюцию «жидкой лшпш», т. е. линии, образованной в каждый мо-
Ss $ мент времени одними и теми
.___B«zizi^ »_ же частицами среды. Пусть
¦-'¦[ \rt6x х 61 = {fij:, fit/, 6z} — элемент
I j. * Д2 длины этой линии в момент
—*i «' ^- *Н времени t, (x, у, z) и (х +
j + z + 6z)—коор-
j , / /, )р
Sx" j t'=t+At динаты концов этого элемен-
^Т^ *" та> Рассмотрим тот же эле-
х мент ЖИдКой липни спустя
Рис. 6.3 промежуток времени At в
момент t' = t + At. Вычис-
Вычислим, как изменилась его длина. В проекции на ось х имеем
(рис. 6.3)
8х' = 8х+А2~А>. C.3)
Предполагая, что 8х и Д? малы, запишем
\ = v (x) At, A2 = v(x + 6x) At = \v (x) + g 6x1 At.
308
Подставляя эти соотношения в C.3), получим
&х' — 8хс до
дх'
At дх
откуда при At -*¦ 0 следует соотношение
d ? ? до
—- ОХ = ОХ —.
dt дх
Аналогичные уравнения справедливы и вдоль направлений у
и z. Переходя к векторной форме записи, получаем уравнение,
описывающее изменение во времени элемента жидкой липни:
i-
(Л/,)
По структура ,)го уранпонно в точности совпадает с ураипе-
лиом индукции для идеально проводящей среды C.2). Это даот
возможность утперждать, что если векторы 61 и Н/р в некоторый
.момент времени совпадали по направлению, то они будут иметь
одинаковое напрамлепне н и любой другой момент времени, а нх
длины будут изменяться пропорционально.
Другими словами, частицы, находившиеся в начальный мо-
момент на некоторой магнитной силовой линии (т. е. на линии,
касательная к которой в каждой точке совпадает с папранлсинем
лектора Н), л дальнейшем будут перемещаться вместе с этой
линией. Магнитный силовые линии оказываются накрепко спя-
данными с веществом, как бы «вмороженными» в пего.
Эффект вмороженное™ магнитных силовых линий обуслонли-
иает один из механизмов генерации магнитного поля. Пусть жпд-
кис линии идеально проводящей среды растягиваются со вре-
временем, например, вследствие турбулентности. Тогда соответствен-
соответственно должна увеличиваться длина вектора Н/р, а это (в несжимае-
несжимаемой среде) п означает рост напряженности магнитного поля.
2. Диффузия магнитного поля. Если проводимость среды ко-
конечна, то второй член в правой части уравнения индукции
d /Н \ ,/Н „\ 1 .„
"(тГГрТ—rotE
отличен от нуля. Чтобы выяснить его физический смысл, рас-
рассмотрим случай, когда среда покоится (v = 0). Первое слагаемое
справа при этом обращается в нуль, а субстанциональная про-
производная слева совпадает с эйлеровой производной по времени
(d/dt= d/dt). Используя закон Ома A.11) и первое из уравне-
уравнений Максвелла A.10), преобразуем C.5) к виду
<зл'>
Для простоты положим, что проводимость среды постоянна о = Go.
Плотность среды р в силу отсутствия движения не зависит
от времени, так что обе части уравнения C.5') можно сократить
309
на мпожитоль 1/р. Тогда формулы векторного исчисления в со-
сочетании с уравнением Максвелла div Н = О позволяют записать
C.5') в виде
^ !дн, (Я.г.)
at
и
где Д — оператор Лапласа.
Соотношение C.6) указывает, что для каждой компоненты
магпитного поля справедливо уравнение параболического типа,
описывающее процесс диффузии поля через проводящую среду.
Коэффициент диффузии, равпьш 1/Dлоо), обратно пропорцио-
пален электропроводности. Это означает, что проникновение маг-
магнитного поля в сравнительно холодную, слабо проводящую среду
происходит весьма интенсивно, и нанротнв, проводники, близкие
к идеальным, задерживают поле.
В общем случае, когда среда движется и проводимость ее
конечпа, имеют место оба рассмотроппых выше конкурирующих
цроцесса: магшгтпое поле увлекается веществом н п то же лре-
мя как бы «просачивается» сквозь него. Спяль поля и вещества
по является столь жесткой, как в случае вмороженности.
3. Гиперболичность уравнений магнитной гидродинамики для
случая идеально проводящей среды. Обратимся к системе уравне-
уравнении магнитной гидродинамики для одномерного плоского случая
B.11)—B.20). Как отмечалось выше, п идеально проводящей
среде (о = °°) электрическое поле отсутствует, и джоулепо тепло
тождоствонпо равно пулю. Недивергонтпое уравнение эпергпп
здесь имеет вид (для плоского случая)
который пичем не отличается от соответствующего уравнения
энергии в обычной газодинамике. Поэтому оно может быть при-
приведено к энтропийному виду OS/dt = O, показывающему, что те-
течение идеально проводящей среды является адиабатическим.
Выберолг и качестве независимых термодинамических функ-
функций удельный объем 1/р и энтропию S. Тогда производную от
давления в уравнении движения B.12) можпо преобразовать
точно так же, как это было сделано с D.20) гл. I:
эр „ , о I 1 \ , а?
где с = V (dpidp), — газодинамическая скорость звука,
/5
Производную по времени в уравнении индукции B.16) рас-
раскроем с помощью уравнения неразрывности B.11)
д 'п-
Аналогично поступим с уравнением B.17). Учитывая все сказан-
310
ное, перепишем систему уравнений B.11) —B.20) в следующем
виде
4л its
2^
4л й
dw
Это система семи квазилинейных уравнении первого порядка
содержит семь неизвестных функций. Введя вектор-функцию
U = И/р, v, и, w, НУ1 111, S)
и матрицу
А =
0
0 »
¦ с~р~
0
0
0
0
0
— 1
0
(J
0
Р11и
пПг
0
0
A
0
0
-рнх0
0
0
0
0
0
0
0
0
0
— Пх0/(Ля)
0
0
0 0
0
0
7/2/Dл)
0
0
о
О
A1
г/.
0
0 °
'1
О
•о!
перепишем систему C.7) в стандартном виде
dV/dt + A dV/ds = 0.
Рассмотрим уравнение
Н" 772 I Г/2 I 77*
= 1*хО + Л у + IIz
(см. § 4 гл. I). Решая его, найдем собственные числа
И
V=0. Я2Д = ± тгтА-Р =
311
При II Ф О эти значения к вещественны и различны, что ови-
детельствует о гиперболичности рассматриваемой системы магни-
тогидродинамическнх уравнений C.7). На плоскости (.?, t) су-
существуют семейства характеристик четырех ттшон:
ds/dt = О, (.4.8)
ds/dt = ±ал, C.9>
ds/dt = ±а+, C.10)
ds/dt = ±а-. C.11)
4. Скорости звука в магнитной гидродинамике. Характеристи-
Характеристика C.8), отвечающая собственному значению }. = 0, как и в слу-
случае обычной газовой динамики, является «энтропийной» и сон-
падает с траекторией частиц.
Наклон осталышх характеристик в каждой ючке плоскости
($, I) определяется величинами ал, а+, а.-, которые являются
маггштогидродинамимескими скоростями звука (массовыми). Ана-
Анализ линейною приближения уравнений магнитной гидродинами-
гидродинамики, аналогичный тому, который был выполнен для акустики в
§ 4 гл. Т, показывает, что малые возмущения распространяются
в среде с одной нз скоростей ал, at, а_ и ланмснмостп от харак-
характера изменения и них- параметров течения.
Величина
а л = р#хо/У4яр
называется альфвеповской скоростью, а палые ьозмущопия, рас-
распространяющиеся с этой скоростью и виде ио.чн,— алр.фнопопсктг-
ми. В звуковых волнах такого типа давление, плотность и про-
продольная компопепта скорости остаются неизменными, а возму-
возмущение претерпевают поперечные составляющие скорости и
напряженности магнитного поля. Таким образом, альфвеиовские
звуковые полны япляются поперечными,— частицы газа п них
испытывают смещения в направлеппп, перпендикулярном к на-
направлению распространения волны. Заметим, что звуковые вол-
волны в газодинамике являются продольными.
Величины
4лр V \L ^ 4.1.1,;
P"
/1 Г о Н2 1 / / 11- N2 c2'24 1
называются быстрой и медленной магнитными скоростями звука,
а соответствующие им малые возмущения — быстрой и медлен-
медленной магнитозвуковыми волнами. В волнах этого типа наряду
с поперечными компонентами поля и скорости изменение пре-
претерпевают также плотность, давление и продольная компонента
скорости. Продольная же составляющая вектора напряженности
магнитного поля постоянна в силу предположения об одномер-
одномерности течения.
Можно показать, что магнитные скорости звука находятся в
следующем соотношении
а-^ал^а,. C.12)
Указанные скорости являются массовыми. Соответствующие ско-
скорости распространения малых возмущении п физическом про-
пространстве вычисляются так
= Дл/р =
=а±/р= У± [с1 + Н2/Dяр) ±
Если компонент,! поля в направлении распространения волны
раина нулю {Нх = О), то скорости а-(с-) и ал(сА) также равны
нулю. В отом случае в среде могут существовать лишь быстрые
магнитные звуковые полны, скорость которых равна
Непрерывнее
решен/с ff
cpeite
р^шемие
Н2/Dлр).
5. Магиитогидродннамические ударные волны. Вращательный
разрыв. R магнитной гидродинамике без учета днеенпативных про-
процессов (в частности, о = °°), как н в обычной газодинамике,
возможны решения разрыв- г .
ного типа. Их строгий ана- '. ^
лиз следует проподитъ па ос-
нопе интегральных уравне-
уравнений магнитной гидродинами-
гидродинамики. Мы преследуем иллюст-
иллюстративные гюли и поэтому
поепользуемся другим прие-
приемом.
Наибольший интерес
представляют разрывпые ре-
шепия типа ударных волн,
перемещающиеся по массе.
Как мы видели, и чистой газодинамике можно получить доста-
точпо полное представление об ударных волнах, анализируя их
структуру в диссипативной среде. Решение в этом случае явля-
является непрерывным и гладко соединяет значения параметров те-
течения перед фронтом полны и за ним (рис. 6.4), причем сами
эти значения остаются теми же, что и в разрывном решении.
Гладкое решение уже можно анализировать с помощью диф-
дифференциальных уравнений. Удобно использовать при этом ав-
томоделыюсть тина «бегущей волны», т. е. искать решение
313
Ряс. 6.4
«размазанной» ударной волны в виде;
/(*, t) = f(l), t = s-Dt, C.13)
где I) = const — массовая скорость фронта волны *).
Обратимся к системе уравнений магнитной гидродинамики
для одномерного плоского случая B.11) —B.20), предположив
для простоты, что векторы скорости и папряжоппости магппт-
ного поля пмеют лишь по две компоненты:
\ = {и; и, 0}, Н - [//хо, //, 0].
Таким образом, мы рассматриваем течения частного типа, ког-
;i;i векторы напряженности магнптпого ноля перед фронтом вол-
волны и за ним лежат в одной плоскости. Запишем систему урав-
уравнений в виде
Лт) Пи <9у д/> Он _ л''1 <•]!
at, ~ ()s ' dt Os 01 4 Л (Is '
О . TT . TT (hi , П"
— (Пц) = #*<>—, ^-/'-ги-!--^,
P = RT/r\, г =
Для удобства дальнейших иыкладок здесь введен удельный
объем т] = 1/р. По аналогии со случаем чистой газодипамикн в
уравпепия движения п энергии введена вязкость со, так что пол-
полное давление g складынается из газокипетического, магпитпого
и вязкого. Вязкость со яиляется в C.14) тем самым диссипатпв-
ным механизмом, который обеснечпнает «разглаживание» раз-
разрывных решений. Далее мы используем линейную вязкость
C.15)
Из C.13) следует связь между производными
df/ds = djldl, df/dt = -D (df/d*),
с помощью которой система в частпых производных сводится
к системе обыкпопеппых дифференциальных уравнепий
„ dr\ dv j-. dv tig
и
du xv dit T4 d / тг \ TT d,u yq i -i.
*) Подробно постаповка задачи о структуре фронта ударной волны из-
излагалась в § 6 гл. I.
314
Проиптегрируем эти уравпеппя по 1 от фопа (s = °°, 1 = °°),
где все параметры имеют певозмущенные зиачепия щ, Vo, «о, Но,
во, ро и т. д. Получим
r\0) = v-vQ, C.17)
vo) = g-gQ, C.18)
uo) = ^-(H-Ho), C.19)
-П(НЦ- ПЛ) = #,„(и - ы0), C.20)
= (^ - govo) 5F <ffu - 7/o"o)- C'21)
Заметим, что если в C.17) — C.21) вязкость отсутстпует
(о) = 0), т. е. g = p + H2/(8n), то эти уравнения можпо рассмат-
рассматривать как соотношения на поверхности сильного разрыва, дру-
другими слопами, как обобщеппе соотпошепи]'! Гюгонно па случай
магнитпой гидродипа\1ики.
Будем считать, что газ перед ударной полной покоится: г0 =
= !to = 0. Естественно также положить, что соо = 0. Выразим из
C.17) — C.20) все функции через удельпый объем ц:
v = -D(r\-r\o), g = go-D2(y\-r\o),
C.22)
D ; II Т. Д.
Д--//»/D)
4 л
Заметим, что формулы для Н и и имеют смысл, если зпамена-
тель D2y\ — #|0/Dя) не обращается и нуль. Подставляя C.22)
и уравнение опергин C.21), учитывая вид уравнопий состояния
и ныражепие для вязиости C.15), придем к дифференциальному
уравнепию
. . А.
ц —
\
т] (До !¦ Д) ¦!-(V—1) (ч — ч0) Д
Это уравнение описывает структуру фронта магнитогидроди-
намической ударной волны в вязкой среде. Определив из C.23)
') i г.
i( и подставив эту функцию в C.22), можно найти характер
изменения поперек фронта волны н других функций.
Правая часть C.23), а следовательно, и производная, стоя-
стоящая в левой части, обращаются в нуль на фоне перед волной
при 11 = г\0. Другое значение удельного объема ц = ци при ко-
котором производная равна нулю, отвечает течению, устанавливаю-
устанавливающемуся за фроптом ударпой волпы.
Величипа Ц\ определяется из кубического уравнения, которое
получается в результате приравнивания к пулю выражения и
фигурных скобках в правой части C.23).
В общем случае при 1\Ф0 пронптегрпропатт. уравнение C.23)
не столь просто, как в газодинамике. Однако определенную ин-
информацию можно получить, и не проводя интегрирование, а лишь
анализируя поведение решения в окрестности передпего и зад-
заднего фронтон полны при ц = Цо и Ц = Ц\, которые при исполь-
использовании линейной вязкости C.15) находятся в бесконечно уда-
удаленных точках (при | = ±°°). При этом даже не обязательно
знать точное значепие r|i, достаточно того факта, что dr\/d% -»- О
При 1] - Т],.
Рассмотрим сначала о1фестиость переднего фропта волпы г) =
= i]o- Положим
Ц = ца+Ц, C.24)
где г] — малая величина, |г||/г|о"^ 1. После подстановки C.24)
в C.23) с точностью до малых первого порядка получаем
# = - — Л. C-2Г.)
dl vtH " v >
где постояппая А'о может быть преобразована к «иду
а'о = (з>\ - 4..) (а>; - г1л)/(а>0* - «?,„)•
Величины с+ о, с_ о—соответственно быстрая и медленная маг-
нитпые скорости звука, сл,о — скорость Альфиеиа, вычисленные
по значениям параметров перед фронтом ударной волны; 2)о —
эйлерова скорость фронта ударпой полпы относительно газа пе-
перед волной: 2Do = Dr\0.
Рассмотрим ударные волны сжатия, для которых г\ < О
(рис. 6.5). Производная dr\/d% положительна, поэтому постоян-
постоянная А'о в C.25) должна быть больше нуля, что с учетом нера-
неравенства C.12)
С-о *? Сл.О < С+ о
возможно лишь в дпух случаях:
либо с%,0<2>1 либо clM<2>l<c2At0. C.2G)
Для того чтобы проанализировать поведегшо решения пблилп
заднего фронта волны, следует положить в C.23) r\ = r\i + т|,
где r|i — есть корепь правой части этого уравнения, а т] — малое
316
приращение. В результате получится соотношение, аналогичное
C.25). Однако это соотношение можно построить и более про-
простым путем.
Воспользуемся следующими соображениями. Уравнения
C.17) — C.21) и псе дальнейшие формулы, включая C.25), по-
получены в результате интегриро-
интегрирования обыкновенных диффе-
ренциальпых уравнений C.16).
При этом интегрирование ве-
велось от значений параметров
перед волной щ, vo, щ, ро, Но
и т. д.
Очевидно, проинтегрировать
уравнения C.16) можно и в
обратном направлении от зна-
значений Г|,, V\, Щ, ри Н\ И Т. Д.,
которые достигаются в потоке
за фронтом ударпой волпы.
Результат такого интегрирова-
интегрирования в точности совпадает с Со-
Соотношениями C.17) — C.20),
если только нижний индекс
«0» здесь заменить на «1». Все последующие выкладки также
сохраняют силу, так что аналогично C.25) будем иметь вблизп
заднего фронта г\\
I
Гис, 6.5
J2L
dl
C.27)
где ^ = (?1- с\л)(®\- с*_лI(Ф\- с*АЛ). Здесь с±А, еАЛ~
магнитные скорости звука в потоке за фронтом ударной волпы,
2D\=Dx\\ — эйлерова скорость волны относительно газа за ее
фронтом.
Приращение ц в C.27), а также производная dv\jd\ положи-
положительны (см. рис. 6.6), поэтому К\ < 0, что возможно, если вы-
выполнено одно из двух условий:
c2A,1<3>l<cl.1,S>21<cL,,, C.2S)
Выше отмечалось, что разность D2r\ — //жо|(/|^) не обращается
п нуль, следопательно, ни в одной точке структуры волны от-
относительная скорость фронта не совпадает с местной альфвеноп-
ской скоростью (Dr\)" =7^= с\ — Н% т)/Dл,). Учитывая это обстоятель-
обстоятельство, можно сделать въпюд, что нерапсистна (Л.26) п C.28)
одновременно могут выполняться лишь в следующих двух со-
четапиях:
C.29)
C.30)
Условия C.29), C.30) выделяют два возможпых типа ударпых
волн — соответствепио быстрые и медленпые магнитогидродина-
мпчоские ударпые волны
сжатия (рис. 6.6).
Этот факт апалогнчен
результату, который дает
теорема Цемплепа в слу-
случае газовой динамики. От-
Отметим, что обычно усло-
условия C.29), C.30) полу-
получают па оспове апализа
эволюцпоппости магпито-
гидродинамических удар-
ударных иолп (см. [51]).
Сопоставляя неравен-
неравенства C.29), C.30) с фор-
формулой C.22) для магнит-
магнитного поля //, можно сде-
сделать вывод, что в быстрых
ударпых волнах сжатия напряженность поля возрастает, а в мед-
медленных— падает (рис. 6.7).
В случае, если продольная компонента магшгтпого поля отсут-
отсутствует (#ж0=0), то с-=0, Са = 0 и возможны лишь быстрые
, /
з ¦
\
1
Mahj4-j" МГД
удя/мыг: вечны
Быстрые Mfj.
ydnpHbis волнь
Ш:
''///У/////,
О
['-¦о
ьа.о
Рис. б.0
С+,в
Рис. G.7
магпитогидродипамнческие ударпые полны, удовлетворяющие
условию
Я2
II2
Л л = с\ + -цЛг
318
Обратимся теперь к случаю, когда разность D2r\—#L
в C.22) равна пулю, т. е. скорость движения волны относительно
газа па фоне совпадает с альфвеповской: D" = а\л. При этом
оказывается, что соотношения C.19) и C.20) совместны лишь
при условии
т| = По- C.31)
Формулы C.17), C.18) с учетом C.31) дают v = vq, g = go- Ил
уравнения энергии C.21) следует Т = Тй. Таким образом, нес
термодинамические параметры в потоке постояппы. Неизменна п
продольная компонента скорости v, так что вязкость тождествен-
тождественно равна пулю (<а = 0). Для магнитного поли и поперечной со-
составляющей скорости получаем
ill //2
C.32)
Отбрасытш тривиальное решепне // = II q, и = uq, имеем
Hi = ~Но,
2#oVr|o/ (
Построенное решение является разрывным (функции II и и —
изменяются скачком, остальпые параметры — непрерывны) н
представляет собой волпу,
распространяющуюся со ско-
скоростью Лльфвепа:
D'o = al,o = a'A.i = Dl-
Напомним, что мы рас-
рассматриваем случай, когда
вектор папряжеппости маг-
магпитпого поля все время ос-
остается в одпоп плоскости. -На
При этом оказалось, что па
разрыве этот вектор повер- Рис G.8
пулся па угол 180° (рис.
6.8). В общем случае угол поворота вектора II, может быть лю-
любым. Разрывы указаппого типа пазывают вращательными, па
рис. 6.6 им соответствует точка Л.
Рассмотренные выше решепия разрывного типа перемещают-
перемещаются по массе. Наряду с пими в магпитпой гндродипамике суще-
существуют разрывы, через которые поток пещества отсутствует. Если
при этом компопепта магпитпого поля в паправлепии, перпепди-
кулярпом поверхности разрыва, пе равна пулю, то па таком
разрыве скорость, давлепие и напряженность магпитпого поля
пепрерывпы, скачки могут претерпевать плотность и темпера-
температура. По аналогии с газодинамикой эти разрывы называют кон-
контактными. Если же векторы напряженности магнитого поля но
обе сторопы от разрыва параллельны поверхности разрыва, то
здесь могут измепиться скачком касательпая составляющая ско-
310
рости и магпитпое поле. Испытывают скачок и термодипамиче-
ские фупкции, причем величипа перепада газокипетического
давлепия такова, что полное давление р + Н2/ (8л) остается пе-
прерывпым. Разрывы этого типа .пазываются тангенциальными.
§ 4. Полностью консервативные разностные схемы
для уравнений магнитной гидродинамики
1. Вводные замечания. Особенность полностью консерватив-
консервативных разностпых схем (см. гл. II) состоит в том, что такие
-схемы одновременно аппроксимируют различные виды запи-
записи системы днфферепцпальпых ураппеннй, каждый из кото-
которых отражает определеппый физический аспект явлепия. Благо-
Благодаря этому такие схемы правильно передают, например, с.оот-
иошепия между разпыми формами эпергип (в газодинамике
между впутреппен и кипетической), в то время как схемы дру-
других типов порождают фиктивные источники анергии, которые
на грубых сетках могут заметпо исказить решение.
В этом параграфе мы получим нолпостыо копсервативпые
схемы для системы одпомерпых нестационарных уравиепий маг-
иитпоп гидродипамнки [69]. Обратимся к случаю плоской сим-
симметрии и для простоты положим спачала, что продольпая компо-
попта магпитпого поля отсутствует. Тогда можпо выбрать си-
систему коордипат так, чтобы поперечное магнитпое поле имело
лишь одпу составляющую, папример, Н = (О, Н, 0).
Электрический ток и электрическое поле также будут иметь
но одпой компоненте:
1 = {0f0,f}. Е-={0,0,?'}, 1~оЕ=.-^°?..
Электромагнитная сила дебетует и продольном напраилопни:
i = {/, 0, 0}, / = -iff/p,
так что движение среди происходит лишь в направлении оси х:
\ = lv. 0, 0}.
Уравпенпя, описывающие магпптогидродинамические течепия
такого типа в лаграпжевых массовых коордипатах, получаются
из системы B.11)-B.20):
( 1
dv/dl = -др/ds + /, / = -ill/p, дх/dt = v, D.2)
^' (b3)
де/dt = -p dv/ds + q, q = iE/p. D.5)
Уравнение анергии D.5) записано в недпвергептпоц форме.
Как отмечалось п § 2, оно может быть преобразовало к полу-
320
дивергентному и дивергентному видам. Действительно, суммируя
D.5) с уравнением движения D.2), умноженным на v, получим
-?W + fv + V- D.6)
Ото соотношение описывает изменение со временем газодинами-
газодинамической энергии, т. е. внутренней и кинетической.
Уравнение индукции D.3) позволяет вычислить, как изменя-
изменяется со временем энергия магнитного поля:
) 8л Os + 4л да ' *•J'''
Суммируя D.7) с уравнением D.6), имеем
2 Иг \ д Г/ И*
) " Ц* +
о I и , И \ д Г/ И
^(Ё + Т + tat) " - «ГЦ* + 1л
Это дивергентное соотношение показывает, что полная энергия
(внутренняя, кинетическая и магнитная) изменяется за счет ра-
работы сил газокинетического н магнитного давления и потока
электромагнитной энергии.
Заметим также, что электромагнитная сила / = — ?#/р пред-
ставима в дивергентной форме / — (Н-/(8л)). Поэтому уран-
пение движения может быть записано в виде
ди О I , II-
который наглядно выражает закон: количество движения неко-
некоторой массы газа изменяется иод действием газодинамического
и магнитного давления, приложенного к границам этой массы.
2. Случай плоской симметрии. Кгтогтшчшо иотребовап,, чтобы
в разностной схеме, аппроксимирующей спетому дифференциаль-
дифференциальных уравнений магнитной гидродинамики D.1)—D.5), выполня-
выполнялись разностные аналоги соотношений D.6), D.8) и т. д. И этом
случае разностная схема будет адэкватно моделировать реальные
физические процессы, протекающие в непрерывной среде, неза-
независимо от характера сетки.
Введем в рассматриваемой области пространства (s, t) равно-
равномерную сетку <d = {(s,,, t3), /c = 0, 1, ..., N, / = 0, 1, . ..} с шага-
шагами h и т: sk+l = sk-\- h, tj+l = tj + x_. К узлам сетки (sb t,), по-
помимо газодинамических величин x}h и vJh, будем относить также
сеточные функции Е\. i{, /i, аппроксимирующие напряженность
электрического поля, плотность тока п электромагнитную силу.
В иол у целых точках (sA+l/2, ^) будем «намерять» наряду с функ-
функциями Efc+i/21 Ph+i/2' Ph+i/2 сеточную функцию напряженности
магнитного поля #h+i/a- На сетке м рассмотрим следующую раз-
разностную схему, аппроксимирующую систему уравнений D.1) —
21 А. А. Самарский. Ю П. Попов 221
D.5) (использованы безыпдексные обозначения)
(у) - ^5\ D.9)
(',.12)
Здесь Oi, 02, Оз — параметры, значения которых иредстонт ni.i-
CpaTii, исходя n;i cooGpaJitciinii liojuioii i;oiicepii;mii!HocTii. Jieca
у функции p, p, v и D.9) — D.1M) выбраны так, чтобы при
// - 0 ;)та схема обращалась в газодинамическую полностмо кон-
сернатшшую разностную схему, построенную и гл. II. Напомним,
что 0<asSl — свободный параметр. Инд разностной аппрокси-
аппроксимации электромагнитной силы / будет получен ниже.
Ураннепие D.12) записано в целой точке сетки. В то же вре-
время сеточные функции плотности р и электропроводности о отно-
относятся к иолуцелым точкам. Потому и D.12) иснользотша ли-
иеппая нптерноляция атнх величин из нолул,елых точек и целую:
Р* = 0,5 (р + р (- 1)), а* = 0,5 (а + а(- 1)).
15 уравнении энергии (АЛо), которое относится к полуцелой
точке, разностный аналог джоулеиа тепла q записан в целой
точке, что снижает порядок аппроксимации по прострапстну до
О (It). В дальнейшем мы укажем, как следует симметршюна'п.
выражение для q, чтобы нолучигь итороп порядок аппрокси-
аппроксимации.
Проанализируем, как в схеме D.9) — D.13) прообразуется
уришкмше энергии. Умножим уравнение дипжения D.10) па vVJ<5)
п сложим результат с педииергентиым уравнением энер-
энергии D.13).
Получим
(e. + vi/2)t= — {p<a){—i)v'0-r>!),+fvl0-S) + q. {AM)
Это соотношение аппроксимирует нолудинергептпый вид урав-
уравнения энергии (^.(i).
Преобразуем несколько ра.чностпоо иыраииипк: дли джоулеиа
тепла q. Учитыная уранпеппе D.12), имеем
Перейдем здесь с помощмо формулы A.19) гл. II от восон
и о3 соответственно и 0,5 и щ:
](о')Н т(а,-а,)/:',] =
322
где
dt = х\(а, - a,) TI^Et + (о2 - 0,Г>) Н-^}. D.16)
Обратимся теперь к уравнению индукции D,11). Используя
формулу для разностного дифференцирования произведения
-4 *-!¦
которая следует ип A.21) гл. IT, а также уравпепие неразрыв-
неразрывности D-9), можно преобразовать (^. 11) к ниду
Умножим иолученпое выражение на ///(8л), а уравнение ин-
индукции D.11) на ///(8л) и возьмем их полусумму. Вновь нри-
меняя формулу D.17), где у — ///(8л), a ]/z = ///p, приходим
к результату
Пто равепстпо аппроксимирует дифференциальное уравнение
D.7). Сложим его с D.14), где джоулево тепло преобразовано
в соответствии с формулой D.15):
*>¦
Предпоследнее слагаемое в правой пасти итого равенства с
помощью формулы A.21) гл. II можпо представить в виде
пи .. . .. „,„....
8л ' \ 8л
TaiciiM образом опопчательпо получим
,+*
('..20)
D.21)
Полученное соотношение аппроксимирует дивергентное урав-
уравнение энергии D.8). Как" видим, в общем случае па изменение
полной энергии п с\еме оказывают влияние фиктивные источни-
источники d. Как и в газодинамике, они возникают из-за рассогласован-
рассогласованности отдельных разностных уравнений схемы, и на грубых сет-
21* 323
ках могут достигать значительной нсличпны, искажая картину
исследуемого явления.
Если положить
0,-0,-р, оа-0,5, / = - (ЯЯДвл))-, (\.22)
то дисбаланс энергии d = d\ + d2 будет тождественно ранен нулю
(см. D.16), D.21)). Получающаяся при этом из D.9) — D.13)
схема является полностью консервативной,— уравнение анергии
в ней с помощью алгебраических преобразований сводится от
недивергептного вида к полудивергентиому и дивергентному.
Наметим, что условия полной консервативности D.22) уста-
устанавливают для электромагнитной силы / дипергентпую форму,
обеспечивающую выполнение разностного аналога закона сохра-
сохранения импульса. Однако, используя уравнение D.12), ей можно
придать и недивергептный вид
/ = _ 0,5 [ ГЯ„/р„ + Ш*/р,], D.23)
аппроксимирующий соответствующее дифференциальное ш.тра-
жепие.
Построенное семейство полностью консервативных схем со-
содержит два свободных параметра: вес у газокипотнчесиого дав-
давления а, и р — вес (в уравнениях индукции и энергии) у на-
напряженности электрического поля Е.
Как говорилось выше, член, описывающий джоулеп ил рев q,
в уравнение энергии входит несимметричным образом, что л спою
очередь порождает несимметрию дивергентного уравнения энер-
энергии D.20) и дает первый порядок аппроксимации O(h). От это-
этого можно избавиться, если использовать симметричное выраже-
выражение для q в D.13):
q - 0,5 [(//p,)@'«?(W + (i(+ 1)/р,( + 1))fOi:i)?(p)( !- 1)].
В этом случае нодявергентное уравнение энергии приводится к
следующему дивергентному виду:
г
„@.5)
v
Заметим еще, что закон «сохранения объема» 1/р = х. в рас-
рассматриваемой схеме выполнен. Это соотношение зависит лишь
от способа разностной записи газодинамических членов, а они
взяты из гл. II, где построены полностью консерватинпые схемы
для газодинамики, обладающие таким свойством.
Мы построили полностью консервативные разностные схемы
для системы уравнений магнитной гидродинамики на основе се-
семейства схем с недивергентным уравнением энергии. Естествен-
Естественно, Ч1о аналогичные построения можно повторить, исходя из
324
семейства с полудивергентным или дивергентный уравнением
энергии. В последнем случае исходное семейство схем будет
консервативный.
Анализ показывает, что получающиеся при этом схемы тож-
тождественны полностью консервативной схеме, построенной выше.
Напомним, что аналогичный факт имел место и в обычной газо-
газодинамике. Однако здесь существуют и некоторые различия.
В консервативных газодинамических схемах дисбаланс внутрен-
внутренней энергии имеет дивергентный вид, так что фиктивные источ-
источники носят поверхностный характер. В магнитной гидродинамике
дисбаланс внутренней энергии произвольной консервативной схе-
схемы содержит, вообще говоря, фиктивные источники объемного
характера.
В заключение этого пункта выпишем полученное семейство
полностью консервативных разностных схем для системы одно-
одномерных плоских уравнений магнитной гидродинамики в случае,
когда продольная компонента магнитного поля отсутствует:
f = - ( FHI/{8л))- = - 0,5 [ Tlljpt + itf ,/p J, D.25)
(///p), - Е?\ i = о*Е = р*#-/Dл),
Pl = - р<а?°*> + q,
q = 0,5 [(ijpj^l^ -;-(»(+ l)/p*(+ l))@'5)?(P)(+ 1)].
Уравнение энергии, представленное здесь в недивергентной
форме, с помощью равносильных алгебраических преобразований
приводится к одному и.! трех нидов:
При значениях свободных параметров а = $ = 0,5 получается
единственная полностью консервативная схема второго порядка
аппроксимации. В остяльпых случаях порядок аппроксимации
ранен О(х + /г2). Мы рассмотрели простейший вариант, когда
вектор напряженности магнитного поля ортогонален оси х. Все
сказанное без труда обобщается и на случай отличной от нуля
продольной компопенты магнитного ноля. Система соответству-
соответствующих дифферепциальпых уравнений приведена в § 2 (см. фор-
22 а. А. Самарский, Ю. П, Попов 325
мулы B.11) — B.20)). Полностью консервативная разностная
схема здесь выглядит так
v xt = v vt = -p-
(/ь26)
Для простоты мы ограничились случаем, когда магнитное поле
и скорость имеют лишь по одной поперечной состан.ииощей:
II = {//о, //, 0}, v={u, и, 0>.
Учет z-компопент поля и скорости проводится точно так же.
Уравнение энергии в схеме D.26) алгебраическим путем можно
свести к дивергентному виду
8лр/г
D.27)
3. Результаты численных расчетов. Численные расчеты под-
подтверждают выводы, полученные в результате теоретического ана-
анализа разностных схем для уравнений магнитной гидродинами-
гидродинамики [58].
15 качество тоста рассмотрим задачу о поршне, который вдви-
вдвигается в газ с постоянной скоростью и порождает в нем быструю
магнитогидродииамическую ударную волну.
Газ идеально проводящий (о — °°, Е = 0), нетеплопроводпг.ш,
подчиняется уранненинм состояния: р=ЯрТ, е = ДТ/(ч — 1)
(Я = 1, f = 5/3), и в пачалмши момент покоится (v(s, 0)^0,
u(s, 0) = 0). Остальные параметры при ? = 0 имеют следующие
значения
p(s,O)=l, T(s, 0) = 0. Но = 2,507, Я(s, 0)= 1,401.
Скорость поршня ладана, ее компоненты ранни
v{0, t) = 0,25, и @, /) = -0,2735.
Значения параметром течения, которые устапнилнпаются за
фронтом возникающей полны, иычиелнштся по соотношениям
Гюгопио:
v = 0,25, и 0,27:15, Т = 0,0117, р = 1,3."{. // — 2,802.
На рис. 6.9 приведены результаты расчета oniicaiinoii задачи
о поршне на чисто неявной разностной схеме с недпиергентпым
32fi
уравнением энергии. Штриховой линией указаны профили тем-
дературы в некоторый момент времени, полученные для двух
значений шага сетки по времени xt = 2,1т*, тг = 4,2тя, где т.*—
величина, вычисленная ио критерию Куранта для параметров
потока за фронтом волны, причем в качестве скорости зиука в
этом критерии иснользонана скорость быстрого магнитного звука.
Сплошной линией здесг. нанесено точное решение. Как видно,
10 х (I —
а
\
\
\
\ \
\
—1
3,0 *,0 5,0 s
Рис. 6.9
погрешность в определении температуры значительна (до 70%).
При уменьшении шага т погрешность убывает. На этом же ри-
супке нанесены результаты (штрихпунктирпая линия), получен-
полученные для тех же значений т по полностью консервативной схеме
первого порядка аппроксимации,— свободные параметры а и [J
в D.25) равны единице.
На рис. 6.10 нродстянлоиы результаты расчета той же задачи
по чисто неявной копсерпатинпой схеме (штриховая линия) и
полностью консервативной схеме первого порядка аппроксимации
(штрихпунктирпая линия) при т = 1,6тя. В первом случае от-
отклонение численного решения от точного составляет около 20%,
полностью консерватинпая схема хорошо воспроизводит точное
решение.
Таким образом, в магнитной гидродинамике дефекты класси-
классических консервативных схем, связанные с дисбалансом внутрен-
внутренней энергии, проявляются даже на простейшей тестовой задаче,
где граничные условия не изменяются во времени. Это происхо-
происходит из-за того, что указанный дисбаланс содержит фиктивные
источники энергии объемного характера.
Приведенные выше примеры расчетов свидетельствуют, что
и в магнитной гидродинамике полностью консервативные схемы
22* 327
обладают определенными количественными преимуществами по
сравнению с прочими схемами того же порядка аппроксимации.
4. Случай цилиндрической симметрии. Не останавливаясь на
подробностях вывода, который аналогичен плоскому случаю, при-
приведем некоторые результаты, касающиеся разностных схем для
w
и i
Рис. 6.10
случая цилиндрической симметрии. Пусть продольная компонен-
компонента магнитного ноля отсутствует: //г = 0. Система соответствую-
соответствующих дифференциальных уравнений и лаграюкевых массовых ко-
координатах приведена в п. 4 § 2 B.26)). Аппроксимирующее ее
семейство полностью копсерватшшых разностных схем выглядит
следующим образом:
1
/ i-@,.M —1L ! I, _У !r -U_ I =:
/'' \ Й-т /- 1Ч.л) \ Я-г I-' \ п I
— —.— 111 U j, *
4л « * r
D.28)
= _ //(«) (r(o,:,)t,,o,5))s
9 = ~ W
(О,Г))
328
Здесь использованы обозначения для сеточных функций
йф = (г#ф)н1/а, Е = (is1*)!,
а = г* (+ 1) = (г + г (+ 1))/2,
Ь = г(О'5)г(О'5)(+1)/аа.
В пыражении для электромагнитной силы fr фигурирует безраз-
безразмерный множитель Ь. На гладких решениях он равен единице
с точностью до O(x2 + h2). Введение этого множителя обеспечи-
обеспечивает алгебраическую эквивалентность недивергентного уравнения
энергии в D.28) дивергентному соотношению
8л
L\ /*r'J«L J*
Это выражение аппроксимирует дивергентное уравнение энергии
(см. с. 306) п выражает разностный закон сохранения энер-
энергии в применении к одному массовому интервалу сетки за один
шаг по времени. Нетрудно получить и интегральный закон со-
сохранения энергии для всей массы газа на произвольном проме-
промежутке времени. Для этого следует просуммировать соотношение
D.29) по 7=7i, /i + l, .. ., 72, где )\ и ]ч некоторые временные
слои, и по к = 0, 1, . .., N— 1. Нужно иметь в виду, что для
крайних фиктивных интервалов сетки (см. п. 4, § 4, гл. Щ
справедливы соотношения для левого интервала: h-\ = 0, р(—IK1
залогично. В результате пол*
3) приобретает вид
! — А — П, D.30)
и для правого интервала hN = 0 аналогично. В результате пол*
ный баланс энергии для схемы D.28) приобретает вид
где
— полная энергия газа на /-м временном слое сетки;
— работа внешних газодинамических сил;
@,в)„@,5) 7/-17/-1 ,.@,5)„@,6)
+ о_ Ф
320
— работа внешних магнитных сил;
— электромагнитная энергия, поступившая в область, занятую
газом, через границу в виде потока Умова — Пойнтинга. Заме-
Заметим, что интегральный баланс D.30), так же как и дифферен-
дифференциальные уравнения D.28), D.29), записан для массы газа,
приходящейся на единицу высоты и один радиан азимутального
угла.
§ 5. Решение разностных уравнений электромагнитного ноля
1. Метод раздельных прогонок для разностных схем магнитной
гидродинамики. По сравнению с газовой динамикой система урав-
уравнений магнитной гидродинамики с теплопроводностью является
более сложной,— здесь появляются дополнительные уравнения,
Внешние итерации
CJ-2O
СЛОИ
г;
Промежуточные итерации
Внутренние Внутренние
итерации(Н)
Группа I
(динами-
чесная)
итерации(т)
1±
Группа R
(магнит-
(магнитная)
Блок
со
Блок
урабненип
состоя-
состояния
Внутренние
итерации (L)
Группа Ж
(теп но-
новая)
I
I
| но j+2-п
| L.1OU
Блок
б
олик
Расчет j+f-го -
слоя
Рис. 6.11
описывающие электромагнитное поле; кроме того, и прежних
уравнениях появляются дополнительные члены. Поэтому для
решения разностных схем в магнитной гидродинамике целесооб-
целесообразно использовать метод раздельных прогонок, изложенный в
§ 4 гл. IV. Естественно выделить уравнения электромагнитного
поля в отдельную группу (магнитную часть) и рассматривать
ее наряду с динамической и тепловой группами уравнений.
330
Схема метода раздельных прогонок для этого случая пред*
ставлена па рис. 6.11. Кроме внутренних итераций, в каждой
из отдельных групп — динамической, магнитной и тепловой^
а также внешних итераций, предусмотрены промежуточные ите-
итерации между группами уравнений (па рис. 6.11 такие проме-
промежуточные итерации указаны между магнитной и тепловой груп-
группами). Комбинируя в зависимости от характера задачи число
внутренних, промежуточных и внешних итераций, можно достичь
заданной точности за минимальное время.
Электромагнитная сила, входящая в уравнение движения,
и джоулев нагрев в уравнении энергии вычисляются в магнит-
магнитной части и во внутренних итерациях в группах I и III не уча-
участвуют. Точно так же скорость, плотность и электропроводность
(зависящая от температуры и плотности), фигурирующие в
уравнениях электромагнитного поля, во внутренних итерациях
в части II считаются неизменными.
Заметим, что уравнения электромагнитного поля линейны.
Поэтому при их численном решении необходимость в итераци-
итерационном процессе может возникнуть лишь в случае, когда элек-
электропроводность зависит от напряженности магнитного поля, мо-
моделируя апияотропию среды, или граничные условия имеют ка-
какой-либо специальный (нелинейный) вид.
2. Особенности расчета уравнений электромагнитного поля нрн
малых значениях электропроводности. Разностные уравнения
электромагнитного поля, которые решаются в магнитной группе
II, в простом случае плоской симметрии при отсутствии про-
продольной компоненты магнитного поля выглядят следующим об-
образом (см. 4.25)):
Они записаны для сеточных функций Я, Е, i, параметры
р, стф считаются известными. Исключая из E.1) функции i и
Е, приходим к уравнению для напряженности магнитного
поля Н:
Это разпостпое уравнение второго порядка аналогично уравне-
уравнению теплопроводности (см. F.11) гл. II); роль коэффициента
тсплопронодпости играет выражение l/^ina^) (так называемая
магнитная вязкость).
При р = 0 уравнение E.2) стапонится явным, его устойчи-
ность имеет место лишь при ограничении па шаги сетки (см.
§ В гл. Ill):
В задачах низкотемпературной плазмы, где проводимость сре-
среды мала, а па отдельных участках может даже обращаться в
331
нуль, условие E.3) приводит к слишком жесткому ограничению
на шаг сетки т. Использование явных схем для практических
расчетов оказывается в этом случае неэффективным.
Обратимся к неявным схемам, которые, как отмечалось в § б
гл. III, являются формально безусловно устойчивыми. При [5 > О
соотношение E.2) может быть переписано в виде трехточечпого
уравнения относительно значений магнитного поля Н па
() + 1)-м слое:
AhHit\ - CJfi+l + BkWk\\ = - П, E.4)
гдо
A=l, 2, ...,ЛГ-
Величины р, р^ и а^ считаются здесь известными.
Уравнение E.4) при добавлении краевых условий (например,
первого рода) легко решается с помощью метода прогонки (см.
§ 2 гл. IV).
Однако такой алгоритм становится неприемлемым в случае,
когда электропроводность среды становится малой (а->-0). Ко-
Коэффициенты уравнения E.4) при этом неограниченно возраста-
возрастают, и в процессе вычисления решения происходит потеря точ-
точности. Большие трудности возникают при определении напря-
напряженности электрического поля
H-* E>5)
Когда проводимость о становится малой, производная от напря-
напряженности магнитного поля также стремится к нулю: //-->0
В то же время электрическое поле Е, как следует из физиче-
физических соображений, должно оставаться конечным. Определение
его значения в численном расчете по формуле E.5) фактически
приводит к вычислению отношения двух малых величин, что и
дает плохие результаты.
3. Потоковый вариант метода прогонки. Избежать трудностей,
возникающих при расчете уравнений электромагнитного поля
в случае малой проводимости среды, позволяет предложенный
в [35, 36] потоковый вариант метода прогонки. Изложим содер-
содержание этого метода в применении к уравнениям E.1). Иск-
Исключив плотность тока ?, перепишем E.1) в виде двух разно-
разностных уравнений
(Ц&\ ^ E.6)
В индексной форме эти соотношения выглядят так:
Е&\ - Е{+1 - 4+1//{+1 = - Bl E.7)
с[++\е{\\ - #?i + н{+1 = о, E.8)
332
где
^+1 _ 2" K+1 +
* pi+
Равенство E.8), соответствующее второму из уравнений E.6),
записано в (/с + 1)-м узле.
Для решения системы разностных уравнений E.7), E.8) вве-
введем линейную связь между сеточными функциями напряжен-
напряженности электрического и магнитного полей:
аМ+1 + Р*4+1 = V*. E.9)
Коэффициенты ак, [5*, fk пока неизвестны.
Выразим из последнего соотношения при ос* "^ О
#i+1 = (Vft-pV?{+1)/aft E.10)
и подставим в E.7), E.8). В результате получим (верхние ин-
индексы у if*, Ek, A\+1, C'h'1, B{ здесь и далее опущены)
ah
\- 1>к =
a
_ii*fc_//fc+1+*=o. <5Л1>
ah k+1 T ah
Заметим, что коэффициенты ah, pA, fh в формуле E.9) опре-
определены с точностью до множителя, так что можно ввести неко-
некоторую нормировку этих коэффициентов. Сделаем это с помощью
соотношения
сс*-М* = 1- E.12)
Исключая теперь из E.11) величину Ек, имеем
II i_ /о /^ \ ТГ ** ft D /С л Q V
¦/'*+l T"(Ph ~ (-*к+\)Ик+1 — Ifft. — pkDk. (O.lO)
Сопоставляя полученное выражение с исходным равенством
E.9), записанным в Gс + 1)-й точке, можно сделать вывод о про-
пропорциональности коэффициентов:
Это равенство позполяет построить рекуррентные формулы
для вычисления коэффициентов прогонки. Йри этом в зависи-
зависимости от характера краевых условий можно использовать одну
из двух возможностей: либо проводить прямую прогонку (т. е.
вычисление коэффициентов ah, [5ft, fk) слева направо в порядке
возрастания номера узла сетки к, а обратную (вычисление. фуик«
ций Eh, Hk) справа налево, либо наоборот. Остановимся здесь
на первом варианте. Из E.14) следует, что
Условие нормировки E.12), переписанное для (А: + 1)-й
точки:
а*и - $k+iAh+\ = 1. E.16)
дает возможность. вычислять ал+1- После подстановки первого
из соотношений E.15) в E.16) получаем
l-.^)A+l]-1. E.17)
Окончательный вид рекуррентных формул для вычисления
остальных коэффициептов прогопки Taicon:
Ун-Мн ,. ,, . ,v , (--..18)
Построим теперь формулы для оиределепия сеточных функ-
функций Eh, Ifh по пайдегшым значениям коэффициентов. Первое из
соотношении E.11) с учетом условия пормировки E.12) дает
Ек = A + МО (Я*и + BJ - -ihAh, к = N - 1, N - 2, .... 1, 0.
E.19)
Для вычисления //,, воспользуемся равенством E.10), кото-
которое с учетом E.12) и E.19) можно перекисать в виде
ЯА = Ч*-МЯ*+1+Я*Ь k = N-U Л'-2, ..., 1, 0. E.20)
Заметим, что с помощью условии нормировки E.12) мы иск-
исключили из псох формул коэффицш-чп- прогопки ос,,. Таким обра-
образом, в процессе расчетов этот коэффициент можпо вообще не
вычислять, уменьшив том самым объем информации, которую
пужпо держать в оперативпой памяти ЭВМ.
Вычислительный процесс, описываемый рекурреитпыми фор-
формулами E.18) — E.20), представляет собой алгоритм решения
разпостпых уравнений электромагпитного ноля E.6) с помощью
потокового вариапта метода прогонки. Для реализации этого
алгоритма необходимо задать зпачепия коэффициептов прогопки
слева ро, Jo и зпачепие фупкции EN справа. Эти величины опре-
определяются па осповапии грапичпых условий задачи.
4. Граничные условия. В магнитпой части решается краевая
задача для дифференциальных уравпепий электромагпитного
доля
J_!H\_ dji г- Р дН
!н~\(Г) ~ ds' '" ~ 4ла ds
в области: 0 <:* < М, t > 0. •;
Граничные условия, описывающие достаточно широкий класс
физических задач, формулируются в виде
хA)Я@, t)-Vl)E@, *) = v(l),
хE)Я(Л/, t) + %B)E(M, t) = vB\ t>0, E.21)
x<«>>0, кш>0, x(e) + Я(в) Ф О, а =1,2.
Коэффициенты хA), х(г), КA), кB), л>A), \l2) могут являться
функциями времени.
При постановке разностной задачи граничные условия аппрок-
аппроксимируются следующим образом
E.22)
+ Х^Е^1 = v<«. E.23)
Здесь учтено, что разпостпая задача рассматривается на рас-
расширенной сетке (см. § 4 гл. ^1), где в силу условий fe_i = О,
/ij7 = 0 имеет место: Я_1 = Яо, НЯ = НЯ (рис. 6.12).
X о—X—о о
-/ О 1 ?..* М-2 JV-/ Л Л+/
Рис. 6.12
Преобразуем несколько левое краевое условие E.22). Вос-
Воспользуемся для этого разностным уравнением E.8) в точке
А 1
где Со = 2лао^о/ро, так как естественно считать, что в фиктивном
интервале см = 0 и p_i = 0. Выразим отсюда Н-\ и подставим
в E.21):
хA)Яо-(АA) + иA)Со)Яо = уA>. E.24)
Сравним это равенство с линейной связью E.9), записанной
при к = 0 _
+ Ео = to- E-25>
Принимая во внимание условие нормировки E.12), согласно ко-
которому
«о = 1+ Mo* Л = -j- ^т J-*
получим, что
335
Значения этих коэффициентов позволяют начать прямую про-
прогонку E.18).
Правое краевое условие E.23) в сочетании с соотношениями
(AN = 0 в силу условия hN = 0), дает
Определив EN, мы имеем возможность совершить обратную про-
прогонку E.19), E.20).
о. Замечание об устойчивости потоковой прогопки. Для коэф-
коэффициентов исходных разностных уравнений E.7), E.8) в точке
к = 0 справедливы неравенства Ло > 0, Со 5= 0. Кроме того, по
условию E.21) х<1)^0 и А/" 2*0. Поэтому коэффициент прогоп-
прогопки Ро, который вычисляется по формуле E,26), неположителен
Ро<О, причем знак равенства здесь имеет место лишь при
Я,A) = 0, С0 = 0 (о0 = 0).
Структура коэффициентов ЛА, СК и формулах E.7), (.18) та-
такова, что при любом к = 0, \, ...
Лк>0, Ch>0.
Это обстоятельство с учетом условия- ^о 5^ 0 позволяет заключить
на основании рекуррентной формулы (о.18), что коэффициент
прогонки [3А всюду неположителоп: ^ «^ 0, к = 0, 1, . .., N. Но
тогда в силу E.17) имеем
<1, А=1, 2, ..., 7V.
Получепное неравенство и формулы для коэффициентов прогон-
прогонки E.15) гарантируют устойчивость описанного вычислительного
процесса по отношению к случайной ошибке.
Неположительность коэффициента jl,v и условия E.21) обес-
обеспечивают необращение в нуль знаменателя в формулах E.27).
Непосредственный анализ формул потоковой прогонки
E.18) — E.20), E.26), E.27) показывает, что построенный алго-
алгоритм решения разностных уравнений электромагнитного поля
применим и для задач, где проводимость мала пли равна нулю.
Если в некоторых точках сетки проводимость обращается в
нуль, то в соответствующих узлах коэффициент Ch также равен
нулю (см. формулы E.7), E.8)). Однако это не препятствует
использованию указанных формул.
Более того, алгоритм легко перепосится и на другой пре-
предельный случай/ когда проводимость среды приближается к иде-
идеальной а -*¦ оо. Здесь вместо коэффициента Ch, который неограни-
неограниченно возрастает, следует вычислять обратную величину
Dh=*Ck = g. +~—г— - —
33(i
Коэффициенты прогонки теперь будут вычисляться по формулам,
следующим из E.18) после умножения числителя и знаменателя
на Dk+i:
E.28)
Соответствующие видоизменения претерпевают и соотношения
E.26) для коэффициентов [Jo, fo-
Таким образом, сочетание формул E.18) и E.28) дает одпо-
родную разностную схему, позволяющую осуществлять расчет
уравнений электромагнитного поля при любых значениях элек-
электропроводности среды о без явного выделения границ непрово-
непроводящих и идеально проводящих областей.
Описанный потоковый вариант метода прогонки применим и
Для расчета разностного уравнения энергии л тепловой группе
уравнений. Это целесообразно делать для задач, где коэффициент
теплопроводности велик и течение газа имеет изотермический
характер.
6. Пример численного расчета. Убедиться в преимуществе
потокового варианта метода прогонки по сравнению с обычной
и
10
0,1
ко -10s
ог
Рис. 6.13
прогонкой позволяет пример, приведенный в [36]. Рассматрива-
Рассматривается задача
дЛ — М. F — 1 I \дН
dt дх ' J ^ ' дх ' ' '
1, 0 < Ж 0,1,
0, 0,2<х<0,3,
Я@, 0 = 5, //@,3, 0=1°,
5, 0 < Ж 0,1,
#(а;,0)= 1,0, 0,1<ж<0,2,
10, 0,2<х<0,3.
В терминах электродинамики третья область @,2 < х < 0,3)
является идеально проводящей, дак как о ~ 1/к. На рис. 6.13
337
указаны (на два момента времени и = 0,005 и tz — 0,015) реше-
решения сформулированной задачи, полученные методом потоковой
прогонки (сплошные линии) и с помощью обычной прогонки
(штриховые линии). Рис. 6.13, а соответствует значению ко —
= 105, рис. 6.13, б— значению /со=1О6. Такие значения к отве-
отвечают малой проводимости среды. На рис. 6.14, а и б приведены
соответствующие графики для величины Е.
Рис. 6.14
Рис. 6.13 и G.14 показывают, что увеличение коэффициента ко
(уменьшение проводимости) при больших значениях ко не влия-
влияет на результаты, полученные методом потоковой прогонки. В то
же время обычная прогонка приводит в этом случае к полной
потере точности. При этом более «чувствительной» функцией
является Е.
§ 6. Расчет электрических цепей в задачах
магнитной гидродинамики
1. Постановка задачи о з-пинче. При решении различных за-
задач магнитпой гидродинамики (течения в МГД-каналах, элек-
электродинамическое ускорение плазмы, сильноточные разряды
и т. д.) одним из существенных элементов является учет внеш-
внешних электрических цепей. Например, в электрических разрядах
практически вся энергия в начальный момепт заключена в бата-
батарее конденсаторов внешней цепи.
С математической точки зрения учет цепи означает введение
в систему уравнений магнитпой гидродинамики дополнительного
соотношения — электротехнического уравнения цепи,— которое
играет роль грапичного условия для электромагнитной части за-
задачи. Конкретный вид этого соотношения зависит от конструк-
конструктивных особенностей элементов цепи в той или иной задаче. Од-
Однако принципиальные моменты, связанные с постановкой задачи
и построением разностной схемы для ее решения в одномерном
случае являются общими для цепей различных типов. Они могут
338
иГПЕНна
разрнд/wu -i-
быть достаточно подробно проиллюстрированы на примере зада-
задачи об электрическом разряде в геометрии z-тшича [63].
?хема такого разряда представлена на рис. 6.15. Батарея
конденсаторов С с начальным напряжением Uq разряжается че-
через формирующийся в разрядной камере плазменный шнур ци-
цилиндрической формы. Радиус шпура R(t) изменяется со време-
временем. R и L — параметры внешней цепи,— активное сопротивление
и индуктивность. Элементом конст-
конструкции цепи являются так называе-
называемые, «обратные провода», замыкаю-
замыкающие цепь. Они могут быть выполне-
пы как в виде системы отдельных
проводников — шли, так и в форме
сплошного металлического цилинд-
цилиндра, ось которого совпадает с осью
плазменного шнура. В последнем
случае «обратные провода» обеспе-
обеспечивают осевую симметрию гранич-
граничных условии задачи по электромаг-
электромагнитному полю. Пренебрегая краевы-
краевыми эффектами на торцах плазменно-
плазменного шнура, можно рассматривать за-
задачу в одномерном приближении,
считая, что все параметры плазмы
зависят от единственной простран-
пространственной переменной — радиуса.
Разрядный ток, текущий но плаз-
плазме, разогревает ее, возникающие
электромагнитные силы вызывают
движепие плазмы к оси, так что в результате газ, первоначально
заполняющий разрядную камеру, может «оторваться» от ее сте-
стенок. Электротехнические параметры плазмы резко изменяются
со временем. Все ото порождает сложное м а гпитогидр о динамиче-
динамическое течение, сопровождающееся переходом энергии из внешней
цепи в нла.чму п обратно.
Считывая осевую симметрию, а также то, что электрическое
и магнитное поля имеют здесь лишь по одной компоненте (Л\
и //<р), можно из общей системы B.20) выделить следующие
уравнепия, описывающие электромагнитную часть задачи:
Рис. 6.15
at \or
dEz
17'
д
их
@.1)
Плотпость среды р п ее электропроводность а определяются
в процессе решении остальных уравнений магнитной гидро-
гидродинамики.
Уравпепия @.1) рассматриваются в области 0 «? s =S М, ?>0,
где М — масса, приходящаяся па единицу длины разряда и ази-
азимутальный угол в один радиап. Краевые условия формулируются
339
так: в центре при s = 0 (г = 0)— условие симметрии
Я,@, 0-0. F.2)
Справа на границе плазменного шнура при s = M (r = R(t))
Н,(М, t) = 2J(t)/B(t). F.3)
Здесь J(t) — полный разрядный ток, R(t) — радиус плазменного
цилиндра, его значение определяется при решении уравнений
движения. Закон изменения разрядного тока со временем, вооб-
вообще говоря, неизвестен. Правда, если расчет проводится для кон-
конкретного эксперимнта, то этот закон можно задать, исходя из
экспериментальных данных. Однако расчеты показывают, что
такой способ не всегда является удовлетворительным, так как
при этом теряет смысл баланс энергии системы, искажается
динамика процесса. Действительно, при нарастающем со време-
временем разрядном токе плазменный шнур сжимается, площадь его
поперечного сечения уменьшается, электрическое сопротивление
растет. Реально это сразу же должно сказаться на разрядном
токе — характер его роста должен соответственно измениться.
В расчетах же с заданным законом J(t) этого не происходит.
Из-за отсутствия указанной обратной связи, разрядный ток про-
продолжает расти, увеличивается сжатие плазмы, ее температура,
что уже противоречит реально наблюдаемой картине разряда.
Таким образом, закон J(t), зависящий от характера развиваю-
развивающихся процессов, нельзя «навязывать» системе, его следует опре-
определять с помощью уравнения для внешней электрической цепи,
которое должно решаться совместно с остальными уравнениями
магнитной гидродинамики.
2. Электротехническое уравнение цепи. Обратимся к одному
из уравнений Максвелла, уравнению индукции A.2), которое
запишем в иптегральпой форме:
ф Е dl = — d<$jdt, F.4)
с
где Ф = | (Hn) dZ — поток магнитного поля через поверхность 2,
V
натянутую на замкнутый контур С. Для рассматриваемой задачи
о z-пипче выберем в качестве контура С контур АА'В'В
(рис. 6.15), проходящий по поверхности плазменного цилиндра
АА', далее по внешней цепи и образующей В'В цилиндра, игра-
играющего роль «обратных проводов». Учитывая, что магнитное поле
вне плазменного шнура с током 1 (t) на расстоянии г от оси
определяется формулой
Я<р(г, *) = 2/(f)/r, Д(f)<г<Д,
(R*— радиус «обратного провода»), вычислим магнитный поток
Ф через контур АА'В'В:
R*
ф-jJ
Я(О
340
Таким образом, уравнение F.4) для выбранного контура дает
lE,(M,t) = -2l-± (j(t)ln^). F.5)
Выражение в квадратных скобках в левой части этого соотноше-
соотношения есть падение напряжения во внешней цепи, Et (Л/, t) — на-
напряженность электрического поля на границе плазменного шну-
шнура, U(t) — текущее значение напряжения на емкости С, которое
вычисляется с помощью уравнения
dU J (t)
В начальный момент напряжение на емкости задано (U@) = Uo),
ток в цепи отсутствует (У@) = 0). Поделив уравнения F.5),
F.6) на Z, перепишем их в виде
?(^y F.7)
-J/C0, F@)=Fo,
где Lo = L/lt Bo = B/l, CQ = Cl, V= UHt Vo = UJl — параметры
цепи, отнесенные к единице длины плазменного шнура.
Электротехнические соотношения F.7) определяют закон из-
изменения разрядного тока J(t) в граничном условии F.3) и тем
самым замыкают электромагнитную группу уравнений. С физи-
физической точки зрения первое уравнение F.7) выражает закон
Кирхгофа, который гласит, что сумма падений напряжений в
замкнутом контуре электрической цепи равна действующей в
контуре электродвижущей силе, в данном случае индукционного
происхождепия.
Если умножить первое соотношение F.7) на J, т. е. на заряд,
протекающий по цепи в единицу времени, и проинтегрировать
затем полученное равенство по t, то получим уравнение
= 0. F.8)
Здесь е (t) = 0,5 (Lo + 2 In (BjB («)) J2 (t) + 0,5C0F2 (t) — текущее
значение электромагнитной энергии, заключенной в емкости и ин-
индуктивности (в пересчете на единицу длины плазменного шну-
шнура), Q= \fR0J2dt — потери энергии на джоулев нагрев сопротив-
о
t
ления внешней цепи, П j (В (t) Ег {М, t) Я,, (М, *)/Dя)) dt —
о
электромагнитная энергия, поступившая в цепь или вы-
вышедшая из нее в виде потока Умова — Пойнтинга, А =
= \ R (t) v (М, t) . Ф8я ' dt— работа магнитных сил над плазмой,
о
23 а, А. Самарский, Ю, П. Попов 341
ее знак зависит от направления движения границы плазменпого
шнура; так, например, при v(M, t)<0 цепь совершает работу
над плазмой и в результате теряет энергию. Таким образом, ра-
равенство F.8) выражает закон сохранения электромагнитной энер-
энергии цепи.
Сведем вместе все соотношения, описывающие краевую зада-
задачу о z-динче для уравнений электромагнитного поля:
* (?*)_??', Ег = ^ * (,#„), @.9)
dt \ pr J ds 4по ds v *' v '
//,@, t) = 0, R(t)II9(M; t) = 2J(t), F.10)
J ~V(t) + ЕЛА1, 0 = - 2-^ (J(t) In ^), @.11)
5 ^ JФ)=? Jo- F-12)
3. Полностью консервативная разностная схема для уравнений
цени. При использовании метода раздельных прогонок задача
F.9) — (G.12) для уравнении электромагнитного поля с внешней
электротехнической цепью решается изолированно от динамиче-
динамических уравнений и уравнения энергии. Разностные соотношения,
аппроксимирующие ураппеннн ло.чя (fi.fl), ((j.10), оы.гп построе-
построены выше,— они входят в полностью консервативную разностную
схему D.28) для задач магнитной гидродинамики с осевой сим-
симметрией и имеют вид
' =4^( ф);> (
A^У-\1 - (Av)i+1 == 0. (Т'Лу1 - (/'ф)^ = 2-Я к. (G.1/.)
Здесь фигурируют сеточные функции: //Ф — (''^рИ-м/г- l'*—(l'<ifu
а — ''* (+1) =-- ('' + '¦(+ О)/-' параметр ji произволен.
Сформулируем теперь разностный аналог уравпепий цени
F.11), @.12) в ннде следующих соитпонгеппй, содержащих че-
четыре параметра
;«,) _ y(»a) ..;. y^n) _- _ 2 // In ^i) , @.15)
Vt=-±-J^), /°^-<i, Ги=У0. @.10)
Неизвестные пока значения параметров 0m, m = 1, 2, 3, 4,
определим с помощью принципа полной консервативности. Вы-
Выясним, как в разностной схеме @.13) — F.16) обстоит дело с за-
законом сохранения электромагнитной энергии. Умножим уравне-
уравнение F.IT)) на /@'5) и npGofipa.'iyGM отдельные его члены. Первое
слагаемое:
^ F.17)
342
Третье слагаемое с помощью формулы A.19) гл. II представим
в виде
@2 _ о,5) Tvt] [j(**) + @,5 - е4) tjt]
где
0 = т[@,5 - 64) У'0'5'/, + (G2 - 0,5)У@-5)У,]. F.18)
Выразив /(е«) из разностного уравнения F.16), получим
Проанализируем правую часть:
Обратимся теперь к разностному уравнению движения в схеме
D.28), которое рассмотрим в последнем узле сетки {грг—rN)Ji.=
)
),
= Улг'5)- С его помощью получим, что
@,5) 2 /,,@.6)\2
^(^-1 +О(*). F.20)
Можно получить и другое выражение
. F.20')
23* 343
Взяв полусумму выражений F.20) и F.20'), окончательно
имеем
In ^ = — т Гд'1 "N' + О (т3). F.21)
rN rNrN
Собирая все результаты F.19) — F.21) п принимая во внимание
соотношение (/г(ф0'8)),у = 2Ji0'°\ вытекающее из краевого условия
F.14), получим после суммирования по j=ji, /i + 1, ..., /2 раз-
разностный баланс энергии, аппроксимирующий дифференциальное
выражение F.8)
е'г _ еЧ — 2л (Л I- II) -\- Q + Л. F.22)
Входящие сюда функции записываются так:
е> .-= о,п \r.a + 2 in 5* I (У3J + о,г»г:о (V1J,
г, II = _ 2 7~ /';л':')(/'(ф0'5)),ут. ((>-23)
Вообще говоря, при лаппси баланса F.22) отброшены члены
порядка О(т3), входящие в F.21). Несложный анализ показы-
показывает, что эти члены могут стать заметными лишь при условии
TVN/rN ~ 1, т. е. если сетка настолько груба, что граница плаз-
плазменного шпура за один шаг по времени перемещается па рас-
расстояние, сравнимое с радиусом шнура. На практике подобная
ситуация не реализуется, так что отброшенными членами всегда
можно пренебречь.
Как видно, разностный закон сохранения электромагнитной
энергии в общем случае нарушен за счет дисбаланса Д в правой
части F.22). Избежать этого можно, положив
92 = 94 = 0,5. F.24)
При этом условии в силу F.18) дисбаланс энергии тождествен-
тождественно равен нулю.
Чтобы симметризовать выражение для джоулевых потерь па
внешнем сопротивлении Q в F.23), естественно положить также
61 = 0,5. F.25)
Оставшийся пока свободным параметр 8з выберем из следую-
следующих соображений. Запишем интегральный баланс энергии плаз-
плазмы D.30) применительно к рассматриваемой здесь задаче об
электрическом разряде в геометрии z-пинча
Q't -&1 = -&-А-П. F.26)
344
Учитывая, что в этом случае электрическое поле имеет лишь
осевую, а магнитное — азимутальную компоненты, и принимая
во внимание граничное условие (h9)-\ = 0, перепишем выраже-
выражения для А и П в F.26)
9 У^)У)^х. F.27)
X 8nrwrw X
Заметим, что выражение для работы газодинамических сил 31
в F.26) равно пулю, так как па оси в силу условия симметрии
равна пулю радиальная компонента скорости Vq, а па грапице
плазменного шпура с вакуумом pN = 0; если же плазма запол-
заполняет разрядную камеру целиком, то уЛ- = 0.
Сопоставим соотношение F.26) с балапсом энергии цепи
F.22), отпормироваппым иа азимутальный угол в одип радиан:
и-?¦
F.28)
Дисбаланс энергии А отсутствует, ибо мы считаем условия
F.24) выполненными. Члепы Л и П и F.26) н F.28) выражают
обмен энергией между цепью и нла.-шотт. Поэтому при суммиро-
суммировании уравнений F.26) и F.28) они должны взаимно уничто-
уничтожиться. Следовательно, разностная запись работы магнитных
сил А и потока энергии П в F.23) и F.27) должна быть оди-
одинакова. Это имеет место, если выполнено условие
93=р. F.29)
В этом случае сумма соотношений F.26) и F.28) дает
=-()/B:i). F-30)
Формула F.30) показывает, что электромагнитная энергия цепи
переходит в энергию газа Q (тепловую, кинетическую и магнит-
магнитную), а также частичпо расходуется па нагрев Q сопротивления
во внешней цепи. Если в задаче учесть процессы теплоперепоса,
то в правую часть F.30) войдут члепы, связанные с потерями
на излучение эпергии.
Невыполнение условия F.29) ведет к тому, что в разностной
схеме энергия, ушедшая из цепи, не будет равна энергии, посту-
поступившей в плалму. Это, естественно, нарушает общий закон со-
сохранения энергии.
Условия F.24), F.25), F.29) «отбирают» из семейства схем
F.13) — F.16) полностью консервативную схему, которая пра-
правильно передает энергетические соотношения в дискретной моде-
модели. Эта схема имеет вид
(Аф)'-,= 0, (й,)* = 2/,
345
LJt -(- RnJi0'a) - У(о-5) + 1-W = -2(j In Щ , F.32)
V, = -J^S)/C0, /° = 0, V°=V0.
4. Решение разностных уравнений поля совместно с электро-
электротехническим уравнением цепи. Сформулированная выше разност-
разностная задача F.31), F.32) решается при использовании метода
раздельных прогонок в магнитпой части. Перепишем эту задачу
в индексной форме. Уравнения F.31) принимают вид
F.33)
ья+1 — ("<р)я+1
где
4+l = 4 -^ ,J+i Л+п2' «i+1 = 'i'1(+i) =
}
Как видно, уравнения F.33) с точностью до формул для вы-
вычисления коэффициентов Ah и Bh совпадают с уравнениями E.7)
и E.8), метод решения которых с помощью потоковой прогопки
был рассмотрен в предыдущем параграфе. Приведем граничные
условия F.32) к стандартной форме E.22), E.23).
Очевидно, левое краевое условие (Лф)_1 = 0 следует из общей
формулы
x^WlV-^M4-^ F.34)
при
= 0, vcl) =
Рассмотрим условие на правой границе. Перепишем уравне-
уравнения цепи F.32) в виде
Выразив из второго уравнения величину V+1, подставим в пер-
первое и учтем, что J = 0,5(h,t)K. Приведя подобные члены, получим
гB), F.35)
348
где
X = тг
„B)
= J1l-f—f-irQ+Tlnir
' - A -
?3
Заметим, что хС2) > 0, ^.B' > 0.
Таким образом задача F.31), F.32) сведена к случаю, под-
подробно рассмотренному в предыдущем параграфе. Решение ее
строится методом потоковой прогонки. Следует отметить, что в
силу линейности уравнений необходимости в итерационном про-
процессе в этом случае не возникает.
5. Электрическая цепь в задаче о 6-пинче. Выше рассмотрен
случай задачи о я-пинче, когда плазма является одним из эле-
элементов электрической цепи, ,
О; Разрядная
! —^камера
по которому протекает раз-
разрядный тон. Цепь такого ти-
типа называют копдукциоппоп.
Существует класс задач,
где плазма связана с птгелп-
ней цепью индукционным
образом. Примером может
служить задача об электри-
электрическом разряде, в геометрии
так пазыиаемого 0-пинча, ти-
типичная схема которого пред-
станлена на рис. fi.lfi. Элек-
Электрическая емкость С с на-
начальным напряжением на
пей Vo разряжается па ви-
виток — металлический круго-
круговой цилиндр, разрезанный по
образующей. Длина нитка /, радиус /<\.:. Внутри витка поме-
помещается разрядная камера, заполненная газом. A3 некоторых
вариантах камора в начальный момент заполняется горячей про-
проводящей плазмой.) Процесс разряда сопровождается возникнове-
возникновением мощного индукционного электрического поля ?,'„, под дей-
действием которого происходит электрический пробой в газе и па-
чипают течь азимутальные токи, образующие замкпутые петли.
Эти токи в свою очередь порождают осевое магнитное поле Нг,
которое складывается с магнитным полем разрядного тока в вит-
витке. Электромагпитпые силы сжимают плазму к оси системы.
Если длина плазменного шпура достаточно велика, так что мож-
можно пренебречь торцевыми эффектами, и во все время процесса
сохраняется осевая симметрия шнура, то задача допускает рас-
рассмотрение в одномерном нестационарном приближепии*). Един-
Р|1С- 6.16
*) Предполагается, что пространственпая поуспшчивость шнура отсут-
отсутствует.
347
ствонная пространственная переменная здесь, как и в задаче
о z-пинче,— радиус.
Дифференциальные уравнения для электромагнитного поля
в этом случае имеют вид (см. B.26))
Левое граничное условие на оси симметрии при г = 0 (s = 0)
таково:
Е,@, t) = 0. F.37)
Остановимся подробно на выводе правого краевого условия.
Заметим, что у внутренней границы витка (при г = В^) имеет
место соотношение
Нг(Л„ t) = 4nJ/l = 4яг, F.38)
где i = J/l — погонная плотность токов, текущих по витку (пред-
(предполагается, что ток равномерно распределен по длине). Запишем
теперь интегральное уравнение индукции
для контура, проходящего по витку (штриховая линия А'ВА на
рис. 6.17) и далее по внешней цепи
\b -g- + RJ — V (t)] + Я„ = - d<bttdt. F.39)
Выражение в квадратных скобках — падение напряжения на
внешней цепи, RB — электрическое сопротивление единицы дли-
длины витка, V(t) — текущее напряжение на емкости, определяемое
из уравнения
dV/dt = -J/C. F.40)
я*
Величина Ф* = 2л J Hz(r,t)rdr— есть магнитный поток через
о
контур А'ВА радиуса /?*. Используя первое из уравнений F.36),
представим производную от потока в виде
dd\ldt глЛфЛ'ф (Я*, 0- F.41)
Запишем соотношение, аналогичное F.41), для замкнутого
контура, проходящего по поверхности плазменного шнура радиу-
радиуса R(t) (см. рис. 6.17):
t) = -2nR(t)E,(M, t), F.42)
где Ф — поток магнитного поля через поперечное сечение плаз-
менного шнура, М — масса плазмы, приходящаяся на единицу
длины разряда и азимутальный угол в один радиан. Сложим
348
уравнения F.39) и F.42) и учтем, что
/. Получим
F.43)
Кроме того, имеем
dV/dt = -i/C0, i@) = 0, 7@)= Vo, F.44)
где Lo = LI, Ro = Rl, Co = C/l — электротехнические параметры
внешней цепи, отнесенные к единице длины разряда, Vo — на-
начальное напряжение на емкости.
В правой части соотношения F.43) стоит производная от маг-
магнитного потока Ф* — Ф, вычисленного по кольцевой области
между плазмой и витком (см. рис. 6.17). Положим, что прово-
проводимость в этой области равна нулю, в частности, будем считать,
1'.тпшя разрядив.!
п внешней
F7 цени
,,
V/
Плазмтный
шнур
Рис. 6.17
что материал, из которого выполнепы стенки разрядпой камеры,
является неэлектропроводным. Тогда магпитное поле здесь по-
постоянно по пространству, так что можпо записать следующую
формулу для магнитного потока:
ф^ — ф = я (Rl — Н- (t)) Нг {М, t) =-- 4я2 (Rl — R~ (t)) I (t).
Учитывая все сказанное, перепишем еще раз соотношепия, опи-
описывающие краевую задачу для уравнений электромагнитного по-
поля в геометрии Э-пинча:
i'-!] ^ (;¦/<¦„), /:ф = - ^ °^-, (G./i5)
di
E,@, 0 = 0, fh(M, /) = /1л
-V(t)~ 2nR(t) /:-ф(.1Л l) =
], @.46)
dt
= 0, V@) =
349
Заметим, что по аналогии с задачей о z-пипче (см. F.8))%
лз электротехнических уравнений следует закон сохранения
электромагнитной энергии цепи:
где е (t) = 0,5 [Lo + 4я2 (/?' - В- («))] г + 0,5C0F- (t)— электромаг-
t
нитная эпергия, Q = j (Ло + Ль) i3 dt— эпергия, пошедшая на
о
джоулев пагрев внешнего сопротивления и витка,
— эпергия, поступившая в цепь или вышедшая из нее в ниде
потока Умова — Пойнтинга,
А^ \n(t)v(M,t)'l2z<"'t]dt
—раоота магпитпых сил над плазмой.
Полностью консервативная разностная схема для задачи
F.45) — F.46) строится аналогично разобраппому выше случаю
2-пипча и выглядит следующим образом
() 4\ у,
1 Р /1 4ло« «'
е0 = 0, IIN = 4:и,
Loit + (/?0 + Лъ) /@'5) - К@'5) - 2n4v) = - ^2 [(/?;- /"S,)i]t, («/18)
Vi _ _j@.5./C()) f0 = 0) l/°=F0.
В схеме выполнен разностный аналог яакопа сохранения элек-
тромагпитпой энергии F.47).
Решение системы разпостпых уравпепий (G.48) осуществля-
осуществляется методом потоковой прогонки так же, как это описано в пре-
предыдущем пункте.
§ 7. Расчет задач магнитно» гидродинамики
с учетом фазового перехода
1. Постановка задачи об электромагнитном ускорении плазмы
при учете фанового перехода. Необходимость учета явления пере-
перехода вещества из одного фазового состояния в другое возникает
при решении многих прикладных задач газовой дипамики и маг-
miTiioii гидродинамики таких, как, например, электрический
взрыв проволочек, взаимодействие лазерного излучения с веще-
веществом, фазовые превращения в сплошных средах и т. д. В на-
настоящем параграфе особенности постановки задач такого сорта
350
и некоторые методы их численного решения рассмотрены на
примере математического моделирования процессов в импульс-
импульсных электромагнитных плазменных ускорителях эрозионного
типа. Схема такого устройства приведена на рис. 6.18. Электри-
Электрический ток, возникающий при разряде батареи кондепсаторов Со,
течет по плазме и разогревает ее, а электромагнитная сила уско-
ускоряет плазму в направлении оси х, В результате воздействия по-
потока тепла из горячей плазмы диэлектрик разрушается, переходя
^Электроды
¦-• •¦"¦['¦*.
Дуялентрии Ллазма
Рис. 6.IS
из твердого состояния (кондепсиролаппая фаза) в газообразное.
Этот процесс известен под названием ;>розии или абляции ди-
диэлектрика. Возникшая в результате абляшш диэлектрика плаз-
плазма вовлекается в процесс электромагнитного ускорения. Описан-
Описанные эрозионные ускорители могут использоваться как двигатели
малой тяги, например для управления космическим кораблем на
орбите. В этом случае плазмообразующий диэлектрик является
рабочим веществом двигателя.
Большинство работ по расчету ускорепия плазмы в импульс-
импульсных электромагнитных ускорителях эрозионного типа выполпено
при использовании либо различпых полуэмпирических зависимо-
зависимостей величины ускоряемой массы от параметров разряда, либо
данпых эксперимента, на осповании которых определяется масса
испаренного вещества [15, 44, 79]. Это делает соответствующую
математическую задачу внутренпе несамосогласованпой.
Аккуратпое рассмотрение задачи должно проводиться п рам-
рамках «замкнутой» постановки, в которой математическое описание
процесса фазового перехода диэлектрика в плазму является
частью общей системы уравнении [28, 2'.)].
Рассмотрим процесс ускорения пла.чмы в рамках одномерных
нестационарных уравнений магнитной шдродипамики для случая
плоской симметрии, которые могут быть получены из общей
системы B.11)-B.20):
71
Ни
(IV
71
ill
I) I I \ (W (IV _1_ _L t I - — —
"П I ~7T" I 7Г7' 777 ,.«. ' i' n fiK
Hill
8л '
dt
4 л Os '
351
дг ди , dW .- ..
Tt = -PTt + 4-i;' {7Л)
_ iE
Ч~ Р '
= P(P.
= x(p,
w
T),
T),
dT
ds
e = e(p, T),
a = a(o, T).
Система уравпений решается в области / 3* 0, 0 *? s =? Л/ = М„ ф +
+ Мап, где М — масса вещества в ускорителе, отнесенная к еди-
единице площади поперечного сечения (так пазываемый единичный
ускоритель). Величина массы М пеизменна во времени, в то
время как составляющие ее масса конденсированной фазы (ди-
(диэлектрика) Л/,(,ф и масса плазмы Мпя изменяются в процессе фа-
фазового перехода. Указанное обстоятельство делает целесообраз-
целесообразным использование в задаче лагранжевой массовой перемепной s,
ибо в этом случае границы пространственной области 0<s^M
оказываются неподвижными по массе. Если же систему уравне-
уравнений G.1) решать лишь в области, занятой плазмой 0=^5=5
^ МплA), то возникает дополнительная задача определения на
каждый момент времени положения границы области Maji(t).
Кроме того, лагранжевы массовые переменные удобны при ана-
анализе процессов вблизи границы плазмы с диэлектриком, где в
узкой пространственной зоне происходит резкое (на несколько
порядков) изменение плотности. Использование в этом случае
эйлеровых переменных привело бы к значительным трудностям
при выборе в этой зоне разностной сетки. Будем считать, что
левая грапица области 0 < s ^ М — точка s = 0 — соответствует
левой границе диэлектрика, а координата s = М — границе плаз-
плазмы с вакуумом. Подобласть 0^5<Мкф(г) отвечает конденсиро-
конденсированной фазе (диэлектрику), a MKli,(t)^s < М (М — Мкф(г) =
= МПЛ) — зопе, занятой плазмой. Точка я* (t) = Мк.ф@ есть по-
ложопие поверхности, где осуществляется фазовый переход.
В процессе расчетов она явпо не выделяется, благодаря исполь-
использованию одпородиых разностных схем расчет осуществляется
сквозным образом. При s = 0 и s = M ставятся следующие крае-
краевые условия
2)
p(M,t)=O, W(M,t) = 0, Н(М, 0 = 0.
Здесь I(t) — ток, протекающий через единичный ускоритель, т. е.
ускоритель с электродами единичной ширины и единичным рас-
расстоянием между ними. Величина I(t) определяется из электро-
техпического уравнения для внешней цепи (см. § 6):
§=-^ U@) = U0, 7@) = 0, G.3)
352
где Lq, Rq, Co, Uo — электротехнические параметры внешней цепи
единичного ускорителя, соответственно индуктивность, активное
сопротивление, емкость и начальное напряжение на ней.
В начальный момент рассматриваемая система характеризу-
характеризуется следующими значениями величин:
v(s, 0)'=0, H($, 0) = 0, p(s, 0) = />0 = const при
p(s, О) = (ркф) = ро, T(s, О) = (Гк.ф)о при
@),
= (рпл)о, T{s, 0) = (ГплH при Л/к(О)<5<Л/
Ниже изложены два метода численного решения задачи
с учетом фазового перехода, к разряду которых относится и
сформулированная задача об эрозионном импульсном электро-
электромагнитном ускорителе плазмы. Оба метода основаны на приме-
применении однородных полностью консервативных разностных схем
для уравнений магнитной гидродинамики. Использование едино-
единого выражения для уравнений состояния и других физических
свойств вещества в различных фазах позволяет явно не выде-
выделять границу раздела фаз. Методы отличаются формой записи
уравнений состояния. Отметим, что описываемая методика про-
продолжает идеи, содержащиеся, например, в [26, 27, 52, 61], кото-
которые связапы с использованием уравнений состояния для описа-
иия фазовых переходов.
2. Описание метода I. В более простом методе I в интервалах
разностной сетки, соответствующих диэлектрику, вещество опи-
описывается уравнением состояния конденсированной фазы. Если в
ходе расчета значение температуры в каком-либо из интервалов
достигает критического 7'*, известного из эксперимента, то в
этом интервале осуществляется переход к уравнениям состояния
газообразной фазы, которые сохраняются до конца расчета. Этот
способ описания фазового перехода является весьма наглядным
и отражает тот факт, что обычно используемые нлазмообразую-
щие диэлектрики (например, фторопласты) иптеисшшо разлага-
разлагаются при достижении некоторой температуры Т* н этот процесс
носит необратимый характер.
Уравнения состояния и выражения для транспортных коэф-
коэффициентов в этом случае записываются, например, в виде
Чс*,
G-7)
353
где верхняя строчка в каждой формуле отпосится к конденсиро-
конденсированной фазе, а нижняя — к плазме. В G.5) — G.8) с есть адиа-
адиабатическая скорость звука в конденсированной фазе, р0 — плот-
плотность конденсированной фазы, R — газовая постоянная,
сКф, спл — теплоемкости, с* — константа, учитывающая измене-
изменение внутренней энергии при переходе из одного фазового состоя-
состояния в другое, остальные обозначения те же, что и в предыдущих
главах.
В G.5)—G.8) использованы простейшие зависимости (на-
(например, уравнения состояния идеального газа в G.5), закон
Спитцера в G.8) и т. д.), однако яспо, что они без какого-либо
принципиального влияния па метод расчета могут быть замене-
заменены формулами, более реальпо отражающими физику явления.
В разностной схеме, построенной с нривлечепим соотношений
G.Г>) — G.8) н являющейся дискретным аналогом среды, вещест-
вещество может находиться или в конденсированном, пли в газообраз-
газообразном состоянии. При этом переход нз конденсированной фазы в
газовую осуществляется конечнымп порциями, равными по вели-
величине интервалам сетки.
3. Описание метода IT. В методе I Г, кроме чисто конденсиро-
конденсированной и газообразной фаз, рассматривается также зона смеси
фаз. В этой зоне будем различать плотности конденсированной и
газовой фаз. Обозначим их через р„.ф(8, t) и рал(«, t) соответст-
венпо. Общая плотность среды p(.v, t), очевидно, вычисляется
следующим образом
p(s, /) = apK.4(s, 0 + A — «)РплE, t), G.9);
где a(s, () — объемное содержание копденсированной фазы,
(A — а) — соответственно объемное содержание газовой фазы).
Величина а определяется из условия, что обе фазы имеют оди-
одинаковое давление [61]:
Р = Рп„(рпл, Т)-- ЯклЛркф, Т), G.10)
где для /»,. ф и /)„., используются такие же выражения, как в фор-
формуле G.5).
Плотности газа и конденсированной фазы находятся из урав-
уравнений, описывающих закон сохранения массы для среды, в кото-
которой происходит химическая реакция. Эти уравнения в одно-
одномерном случае в лагранжевых массовых переменных имеют вид
у, (Сфк.ф) "I- (Сфк.ф) Р J = — /,
д до GЛ1)
щ (A — а) рпл) + (A — а) ррл) P-? = J,
где / — масса вещества, перешедшая из конденсированной фазы
в газовую в единице объема в единицу времени. Сумма уравне-
уравнений G.11) дает уравнение неразрывности в обычной форме, ис-
используя которое можно преобразовать первое из соотношеиий
354
G.11) к виду
Величину / можно определить, обратившись к уравнению Арре-
ниуса, описывающего кинетику пиролиза диэлектрика
GЛЗ)
где Е — энергия активизации, Л —газовая постоянная, Z — мно-
множитель, характеризующий материал. Подставив G.13) в G.12),
приходим к уравнению
lncp
где
(p(s, O=ap«<i./P, 0<ф<1, G.15)
— относительное содержание конденсированной фазы. Исключив
а, рКф, РпЛ из уравнений G.9), G.10) и G.15), получим квад-
квадратное уравнение для давления:
Так как в газовой фазе давление неотрицательно, то согласно
G.10) давление смеси фаз также неотрицательно, и потому для
р выбираем лишь одно значение корня
р = 0,5 {с2(рФ - ро) + A - <f)RpT +
2>- G.10)
Заметим, что при ф = 1 уравнение G.1G) переходит в уравнение
состояния конденсировапппой фазы, а при ф^О—в уравнение
состояния идеального газа, т. е. при крайних значениях ф G.16)
соответствует формуле G.5).
Учитывая, что внутренняя энергия является аддитивной
фупкцней массы, для удельной энергии имеем выражение
е(р, Г)=фе1<ф+A-ф)К„„ G.17)
где екф, е„л те же, что и в G.G). Соотношения G.15) — G.17)
дают уравнения состояния, используемые в методе 11. Коэффи-
Коэффициенты тепло- и электропроводности в методе 11 вычисляются
по формулам тииа G.17), либо по упрощенным формулам:
|х„.ф ПРИ q>0.5,
у (р. 7 ) =
х„7 ' при ([ < ().;),
1 ° F ' G.18)
О при ([ > 0,5,
СГП/ ТтрТГ ([ •< О.,).
В отличие от метода I, где каждый пнтерпал массовой сетки
соответствует либо конденсированной, либо газовой фазе, в ме-
Я5.г>
тоде II интервал сетки может содержать одновременно обе фа-
фазы. Границей фаз (это принято, например, в G.18)) условно
можно считать точку, где ф = 0,5. Расчеты показывают, что зо-
зона, в которой осуществляется переход от ф = 0 к <р = 1, оказы-
оказывается весьма узкой в массовых координатах. Таким образом,
учет испарения диэлектрика в методе II не носит дискретного
характера, а граница фазового перехода «размазана» в простран-
пространстве термодинамических переменных.
4. Сопоставление двух методов при расчете реальпой задачи.
Опишем результаты некоторых методических расчетов, выпол-
выполненных по методам I и II, которые позволяют выяснить качест-
качество этих методов, а также сопостанить их друг с другом. Сравне-
Сравнение проведем на примере сформулированной в начале параграфа
задачи G.1) — G.4). Как отмечалось выше, в методе I переход
вещества н,ч конденсированной фалы в газовую происходит пор-
порциями, которые не могут быть по величине меньше массового
Т,эВ
0,12
-0,08
Хонде.'нсированная Фаза \ Газ
Кзн&еха/ребачная фс/за_
1'ис. 6.10
Рис. 6.20
интервала сетки:. Это обстоятельство отрицательно сказывается
на результатах расчета. Действительно, в испарившейся порции
вещества давление в соответствии с G.5) резко возрастает и на-
начинается интенсивное расширение вещества, с результате чего
температура в «испарившемся» массовом интервале резко падает
и может даже принимать значения, меньшие, чем температура,
установившаяся к этому моменту в диэлектрике. При этом ока-
оказывается, что расширяющаяся масса газа прогревается потоками
тепла не только со стороны горячей плазмы, но рг со стороны
диэлектрика, что физически не оправдано. Сказанное иллюстри-
иллюстрирует рис. G.19, на которой для метода I приведены профили
температуры и теплового потока на три последовательных мо-
356
мента времени непосредственно перед испарением очередной
порции вещества (для i = 0,587 мкс (кривая 1)), сразу после
«испарения» (для t = 0,590 мкс B)) и через несколько шагов
по времени после «испарения» (для f = 0,G15 мкс C)) (положе-
(положение границы раздела фаз в соответствующие моменты указано
вертикальными линиями).
После того как испарившееся вещество прогреется до темпе-
температуры, превышающей Т *, происходит нагрев и испарение но-
новых порций вещества. Вследствие этого выход массы носит
скачкообразный характер (рис. G.20, штриховая линия). Таким
образом, модель, используемая в методе I, «загрубляет» картину
процессов в районе границы раздела фаз.
Разностное решение той же задачи, полученное по методу II
оказалось свободным от подобных недостатков (рис. G.21, для
t = Q,75 мкс (кривая 1), для t = 0,76 мкс B), для t = 0,79 мкс
C)). Видно, что температура ведет себя монотонно, тепло посту-
поступает в диэлектрик со стороны пагретого газа. Наблюдаемое в
-0,08 -
Газ
Рис. 6.21
расчетах резкое уменьшение по абсолютной величине теплового
потока в массовых интервалах, где произошел фазовый переход,
объясняется тем, что в данных расчетах использовался разрыв-
разрывный коэффициент теплопроводности (см. G.18)), причем в газе
при низких температурах (порядка Т*) он лгтачительно меньше,
чем в конденсированной фазе. Этого недостатка можно избежать,
если воспользоваться для коэффициента х формулой, аналогич-
аналогичной G.17).
357
R данной модслп фазоппго перехода выход массы носит плав-
плавный характер (рис. (>.2О, сплошная линии). График той же за-
зависимости в методе I колеблется около этой линии. В среднем
же выход массы и обоих подходах достаточно бли:юк.
Другие интегральные характеристики, такие, как полный ток
в разряде, напряжение па батарее конденсаторов, электромагнит-
электромагнитная оперши, поступившая в ускоритель, баланс энергии по ви-
видам, омический нагрев и т, д., в обеих моделях оказываются
близкими,
358
Не сильно отличаются и распределения параметров плазмы
по длине ускорителя. Так на рис. 6.22 и 6.23 показаны профиля
плотности тока /, скорости v, температуры Т и плотности р па
два момента времени: рис. 6.22 соответствует начальной стадии
процесса, рис. E.23 отвечает моменту максимума разрядного то-
тока (штриховые липни — метод I. сплошные — метод II). Видно,
что с течением времени решения в опои\: вариантах выходят
практически на одни и тот же режим.
Следует отметп-п., что в методе II фазовый переход рассчиты-
рассчитывается с учетом кинетики разложения дпалоктрпкн. Температура
па границе раздела фаз в :пом случае определяется в процессе
расчета и составляет п данном случае 0,07—0,072 о». Ото хоро-
хорошо согласуется с экспериментальными результатами и соответ-
соответствует величине 7'*, которая задавалась в методе I и качестве
температуры фазового перехода (Т* = 0.07 эв).
Заметим, что хотя для большей наглядности изложение в па-
параграфе пелось применительно к системе одномерных уравнении
магнитной гидродинамики, описанная методика расчета фазового
перехода без труда переносится п па другие задачи, в том чис-
числе и многомерные. Эта методика пыла использована для числен-
численного моделирования процесса олоитромагпптпого ускорения плаз-
плазмы в зрозиошюм ускорителе и показала свою высокую оффек-
тшшость.
ГЛАВА VII
ПОЛНОСТЬЮ КОНСЕРВАТИВНЫЕ РАЗНОСТНЫЕ СХЕМЫ
ДЛЯ ДВУМЕРНЫХ УРАВНЕНИЙ ГАЗОВОЙ ДИНАМИКИ
В главе обобщается принцип полной консервативности на
случай двумерных уравнений газовой динамики в переменных
Лагранжа. В § 1 из общих уравнений выводятся уравнения дву-
двумерной газодинамики в переменных Лагранжа и подробно ана-
анализируются соотношения эквивалентности, которым они удовлет-
удовлетворяют. § 2 посиящеи анализу семейства четырех разностных
схем, определенных на несимметричных пространственных шаб-
шаблонах. В § 3 с помощью отнх несимметричных схем строится
симметричная схема. Показано, что она обладает свопстпом пол-
полной консервативности. § 4 посвящен краткому описанию вариа-
вариационно-разностного подхода к построению полностью консерва-
консервативных схем.
§ 1. Система дифференциальных уравнений
в лагранжсвых переменных; ее свойства
1. Исходный вид системы уравнений. Полученная в гл. I об-
общая система уравнении газодинамики и отсутствии диссипатив-
ных лроцсссоп, внешних сил п источников может быть записана
в видо
°i \ pcHvv-O, A.1)
PJ7=— gradp, A.2)
р^=—pclivv, A.3)
/> = ^(р, Г), e=#(p, T). A.4)
В уравнениях A.1) — A.4) производная по времени лагранжева.
В настоящей главе мы ограничимся рассмотрением двумерных
плоских течений в декартовых переменных х, у. Будем также
считать, что вектор скорости имеет две компоненты и ж V.
В этом случае уравнения A.1) — A-3) перепишутся следующим
образом
360
Как и в предыдущих главах, полностью консервативные раз-
разностные схемы для двумерного случая будем строить б лагран-
жевых переменных. Однако в отличие от одномерного случая
.здесь ввести лагранжевы массовые коордипаты уже не удается
(см. гл. I, § 3), поэтому в качестве лаграижевых неременных
выберем эйлеровы коордипаты начального положения частиц
при t = 0:
а = х@), Ь = у(О). A.9):
Чтобы записать систему уравнений A.Г>) — A-8) в лагранжевых
переменных, необходимо выразить производные д/дх и д/ду че-
через д/да и д/db. Это делается по стандартным формулам
df d(f,y) _ i d{f,y) ,Mm
дх дух, у) Л д(а,Ь)' К1-^)
df д (х, f) _ i д (x, f) . ...
ду 6(x,y) A d(a,b) » ^ ;
где использовано ооозначение
а (/. g) ='Ц?К _?!_??
d (li ч) ^5 ''Ч ^11 ^S '
а А — якобиан преобразования пространственных перемеппых
х, у к а, Ь:
A.12)
~д(а,Ь)~6ао1> db 6а ^ ' '''
С учетом сказанного система A.Г>) — A-8) приобретает следую-
следующую форму:
др _
ot
р
Л
л"
д (и, у) д (х, и)] .. .,.
2. Свойства эквивалентности системы дифференциальных урав-
уравнений. Выше для одномерного случая было показано, что пол-
полностью консервативные схемы формально удовлетворяют преоб-
преобразованиям эквивалентности, аналогичным тем, которые имеют
место для дифференциального случая. Поэтому предварительно
изучим, какие соотношения эквивалентности имеют место в дву-
двумерном случае для системы уравнении A.14) — A.17).
24 Л. Л. CaM:ipci;n>). IO II. Попов 301
Непосредственной проверкой можно убедиться в справедливо-
справедливости равенства
д (и, у) д(х, у) _ ЗД Л 1Я\
д(а,Ь) "*" <Э(я,6)~ а«' К '
сопоставление которого с уравнением пералрьпшостн A.16) дает
±^Р J_?A (А Л,П
Р at ~ \ of V'-'-v
откуда следует равенство
рА = роАо = const, A-2A)
где ро. Ао — .шачеппи величин р п А в пачальный момепт вре-
времени / = 0.
Принимая во внимание полученпып результат, можно пере-
переписать уравнения движения A.14), A.15) и энергии A.17)
в пи до
п \ — = — д(р'^ - _ \'lR дЛ _ °JL (Ui\
1 '• ° ot 0 (а, Ъ) [да 01, <П> оа\'
. (lv _ д (.г, р) \др_дх_,1^(Гг_'\
1 ° " tit ~ д (а, Ь) = [да db Ob <>а \'
п Л °± _ ,, Г'7 <"¦ У)
»оао at — — Р [а (Л> Ь)
д;
Ifl.r dv дх dp j | ,. оо,
оТ Оа) \0а 7ф 7Ш~да)\'^ '""'
Кроме того, дли ;гги\ же. уравнении существует дииергентнн.ч
запись выражений, стоящих к квадратных счгоПках к прапык
частях A.21)—A.23):
\ 3 I <h\ til <>.r\~\\ ,. „.
Интегрирование уравнений движении по лаграпжевым пере-
переменным а, Л непосредственно приводит к интегральному закону
сохранении импульса. Комбинируя соотношении A.19) и A.20),
можно переписать уравнение неразрывности в форме
Как известно, якоонан преооралопапия А НМООТ СМЫСЛ СООТНОШб-
ния элементов площадей па плоскостях, связанных этим преоб-
преобразованием. Поэтому уравнение A.24) можно рассматривать как
обобщение «закона изменения объема» (см. гл. I, § 3, ц. 7) для
362
случая двух церемонных. После пптегрироваппн по I и перемен-
пым a, b A.24) даот интегральное выражение этого закона.
Заметим также, что, сопоставляя A.17), A.18), A.20) и
A.24), можпо переписать уравпешю энергии в одной из форм:
в 0А ,. ог.
r> (L25>
ИЛИ
Кроме того, иеднвергеитиое уравнение энергии A.2.3), выражаю-
выражающее баланс внутреннем энергии, после суммирования с уравне-
уравнениями движения A.21'), A.22'), предварительно умноженными
на составляющие скорости и и и соответственно, может быть
приведено к виду
а
2
Это дивергентное уравнение представляет собой запись закона
•сохранения полной энергии.
К системе уравнений движения, неразрывности и энергии,
в какой бы форме каждое из них не было записано, следует при-
присоединить также уравнения, определяющие траектории частиц,
?,—¦ ?— <••*»
Приведеипые выше различные формы записи двумерных-
дифференциальных уравнений газодинамики эквивалентны и
сводится друг к другу с помощью простых равносильных преоб-
преобразовании, точно также, как это имело место в одномерном слу-
случае. Наша цель состоит в определении класса разностных схем
для двумерных нестационарных уравнений газовой динамики в
лаграпжевых переменных, для которых бы выполнялись анало-
аналогичные соотношении эквивалентности. Очевидно это обеспечит
для искомого класса схем выполнение свойства полпой консер-
консервативности.
§ 2. Семейство несимметричных схем
1. Разностная сетка и некоторые обозначения. Будем рассмат-
рассматривать решение сформулированной выше системы уравнений в
прямоугольной пространственной области D: @ ==? a sS L, 0^6=5
^ lb] при / > 0. Введем в D сетку, для простоты равномерную
по каждому направлению:
он = {(a,, b,); at =fl(-i + ha, а0 = 0, / = 1, .... Na,
bj = 6j_i + Ль, йо = 0, у = 1, ..., Nb).
24* 303
Сетку по временной переменной t определим обычным
образом:
<а, = {/*; /А+, = tk + T,t0 = О, к = 0, 1. ...!.
Систему дифференциальиых уравнении газодинамики будем ап-
аппроксимировать на пространственно-временной сетке со = со,, X соt.
Сеточные функции компонент скорости и эйлеровых переменных
будем относить к узлам сетки (i, /). x'lj, ly/j, щ), щ)-а сеточные тер-
термодинамические функции к «полуцелым» точкам (/+'/2, У+'/г),
представляющим собой пересечение диагоналей прямоугольных
ячеек на плоскости (a,b): />?+i/2j + 1/2, Рн-1/2 .;+].¦:¦ Fi+i/2;4-j/2.
Ti+i/2j+i/2 (см, рис. 7.1, a).
Отметим, что разностная сетка м введена в плоскости лаграп-
жевых переменных а, Ъ (начальных положении частиц). Со вре-
временем из-за перемещения частпц среды картина расположения
Гнс. 7.1
узлов сетки в эплеролом (физическом) пространстве искажается
(рис. 7.1, б). Однако в переменных Лаграижа, где строится раз-
разностная схема, сетка не изменяет свою конфигурацию.
Н дальнейшем подобно одномерному случаю будем использо-
патг» для сеточных функций компактные Пегшидекспые обо-
обозначения:
у {аи lij, th) =- у*} = у,
У («i: 1/2- /'; 1/-2- lh) = .'/'Vi/2 i+i/2 = .V.
// (й;, hj, th+1) --= т/?/1 = l/,
B.1)
364
Для разиостпого дифференцирования будем также применять
безыпдекспые обозначения
B 2)
Аналогично определяются производные по переменной Ь: уь и г/^.
2. Несимметричные схемы и их свойства. Построение пол-
полностью консервативных схем для одномерного случая, проведен-
проведенное в гл. II, выполнено па основе «метода весов», с помощью
которого подбиралась пужная интерполяция но времепи правых-
частей разностных уравнений газодинамики, содержащих прост-
пространственные производные. 13 двумерном случае помимо этого
большую роль играет такжо правильный подбор пространствен-
пространственной интерполяции сеточных функции.
Опустим подробные иыкладкп, снизанные с конструированием
двумерных схем, которые являются весьма громоздкими, и обра-
обратимся непосредственно к анализу свойств уже построенных схем
[56]. При этом для большей наглядности мы положим пока рав-
равной пулю одну из компонент скорости и = 0; большинство прин-
принципиальных попросов может быть выяснено н на этом упрощен-
упрощенном примере. Разностная схема для и Ф 0 будет приведена да-
далее. Заметим, что и качество одного ил принципов построения
схем, обсуждаемых ниже, принято следующее требование: дву-
мсриая схема для частного случая одномерного точения (по пе-
переменной х или у) должна обращаться в известные полностью
консервативные одномерные схемы.
Рассмотрим систему дифференциальных ураппешш г- .oBoii
динамики при v = 0 и следующей форме:
in, _\0р31_др_ Оу] 9 .,
'" "at [да db ol> да]' ^'' >
\ -1 (J-\ — \ди д!1 а» ду~\ /9 /ч
''" " d't \t> ) ~~ [да ob —пЬд~а[ ^ 1>
Исполь.чуя виедепиые выше обозначения, аппроксимируем урав-
псш1Я B.Л) — B.Г>) следующей ралностпои схомоЛ (схема 1)
(здесь и в дальнейшем, как и в гл. II, черту над термодинами-
термодинамическими сеточпымн функциями />, р, г и Т будем опускать):
mut =LX (W*) = - l^y™ ~ *№>]. B-0)
365
±\ - Л,
1,) - и\
B.7)
B.8)
Шаблоны для разностных оиераторок L{ и Л( указаны на
рис. 7.2. Величины 0<оь Ог < 1 — параметры схемы. Как ука-
указывалось выше, для одномерных течении, когда все функции
зависят лишь от одной пространственной nopoMeuiioii х (тогда
(Ц)
m
т
i-f i
Шаблон Lf
i-f
Шаблон Л f
Рис. 7.2
у = й) или у (тогда х = а) разностная счема B.E)--B.8) долж-
должна вырождаться в одномерную полностью консериатнвпую схему
C.17) гл. П. В соответствии с этим вес oi у давления р в урав-
уравнениях B.G) п B.8) взят одинаковым, а вес у скорости и в опе-
операторе Л| взят равным 0,5. Вес аг у сеточпой функции у пока
оставлен свободным.
Величина т аппроксимирует произведение роЛо. Г)та величи-
величина имеет смысл массы разностной ячейки, отнесенной к ее пло-
площади в начальный момент. В соответствии с A.20) мы считаем,
мто масса ра.-шпе.тпыу ячеек сетки со временем не изменяется.
Поэтому закон сохранения массы в дискретной модели, описы-
описываемой разностной схемой 1, выполняется автоматически. Заме-
Заметим, что величина гп в случае неравномерной сотки зависит от
номера узла Шц. Проведем пекоторые выкладки с целью убе-
убедиться в том, что уравнения схемы I удовлетворяют определен-
определенным соотношениям эквивалентности, о которых говорилось выше.
Добавляя и вычитая из правой части B.G) слагаемое р ' Уа^
п воспользовавшись одной из формул разностного дифференци-
дифференцировании произведения
(fg)a = /(+!,)*„ + gfa, (/.;')- = / (- 10 ff- + gf-, B.9)
можно преобразовать это уравнен по к дивергентной форме
B.10)
Полученное соотноигение является разностным аналогом A.21')
п обеспечивает выполнение в схеме I закона сохранения импуль-
импульса (в проекции на ось х).
Нетрудно убедиться в том, что уравпешю энергии B.8) так-
также приводится к виду
являющемуся раяггостпым аналогом A.23') при v = 0. Анало-
гичпое преобразование можно совершить и в правой части урав-
пепия иеразрывпости B.7). Умпожим теперь уравпение движе-
движения B.0) на и105) =0,')(и + и). Получим разиостпый аналог ба-
баланса кинетической анергии
т („*/2)t = {u^p&W - „(o.^.)^.)]. B.12)
Суммируя полученное равенство с уравнением энергии B.8) и
используя формулы разностного дифференцирования произведе-
произведения B.9), приходим к уравнению
Ш (8+^/2)! = -[(Л
{^HW^i"^] B.13)
Это урапнепие аппроксимирует дпвергентпое дифференциальное
уравнение A.27) и выражает разностный аналог .чакона сохра-
сохранения полпой энергии для рассматрипаемой дискретпой модели.
Заметим еще, что из B.7) и B.8) очевидным образом выте-
вытекает равенство
аппроксимирующее ш'дпт'ргсптноо диффоренцнальнос уравпеппо
энергии A.2(>).
Итак, в схеме 1 пространственные и временные интерполяции
отдел 1.пых чл(мюв разностных уравнений подобраны так, что для
этой схемы выполняются законы сохранения импульса л полной
энергии (закон сохранения массы, как гопорилось выше, выпол-
выполняется автоматически), а также баланс внутренней энергии в
формулах B.8), B.11) п B.14).
Как видно, схема 1 яилиотся несимметричной и имеет первый
порядок аппроксимации но времени н пространству О(т+'/га +
+ /г,,). I) частности, при определении полпой энергии разностной
ячейки в утоп схеме е + и2/2 (см. B.13)) кипетическая энергия
вычисляется по скорости лишь одного из четырех узлов (углов
ячейки), а именно нижнего левого (?', j) (см. рис. 7.1).
Подобно схеме 1 можно построить еще три схемы, последова-
последовательно проворачивал шаблон па угол и ПО0. Псе :mi схемы так-
также являются несимметричными, кинетическая опергин ячейки
сетки и них определяется но скорости одного из четырех угло-
угловых узлов. Указанные схемы есть двумерные аналоги несиммет-
несимметричных одномерных схем, в которых точно также кинетическая
энергия одномерной ячейки сетки — массового интервала, опре-
367
деляется по скорости одного ил ого копцоп (см. гл. II, § 3, п. 2).
Если предположить, что рассматрикасмое течение является од-
померпым, то несимметричные диумерные схемы для этого сли-
сличая вырождаются в соответствующие одномерные полностью
консервативные схемы.
•¦¦-/ -
*¦---
Шо/fr/m /,
•¦'¦¦ /
Рис. 7.'!
Выпишем упомянутые несимметрп'шьк1 схемы, а также соот-
соответствующие им дивергентные виды иаписи уравнения энергии,
считая по-прежнему для простоты !' = ().
Схема II (см. шаблон на рис. 7.3):
„, (-
_ L,
Д1П!ер1ентаыи вид уранпепни энергии:
¦I It
= - [(p{(!i) (- и ЛЧ*(М) (+1,)), -
Слема 111 (см. шаблон на рнс. 7.4):
m(-1r -!..)«« =
.A) - Ля(к. /
(i) t Г (
Дивергентньп! вид уравнении энергии:
= - [(р(ЧАЧ@-5)(+i,)), -
ЗЙ8
Схема IV (см. шаблон на рнс. 7.5):
т
L) = л4 (в, УЫ) = [
Дивергентпый вид уравнешш энергии:
Отметим, что для каждой н.ч схем 11 — IV имеет место запись
уравнений движения и энергии в форме, подобной B 10) и
V////у/.:'//,
тН,,-72)
1-7
Гис. 7/i
Шаблон /j
B.11) для схемы I с дивергентной правой частью. Кроме того,
для всех этих схем уравнение энергии записывается также в
форме B.14). Укажем еще, что в каждой из схем I—IV уравне-
уравнение дшгження записано для скорости и в узле (г, j). Поэтому
J - ¦•"
X
Шаблон А,
Гис. 7.5
величина и/, входящая в это ураппепие, в каждой из схем отне-
сепа к соответствующей ячейке, примыкающей к узлу (?, /).
3. Анализ закоиа сохранения объема для несимметричных схем.
В общем случае при наличии второй компоненты скорости v Ф 0
семейство несимметричных разностных схем для уравнений
369
газодинамики может Сыть записано следующим образом:
Xt =
= у@-5\
= #((>, Г),
B.17)
B.18)
B.19)
B.20)
где и, / = 1, 2, 3, 4, причем допускаются произвольные сочета-
сочетания значений п и /, a 0=Soi, 02, аз *S 1 — параметры схемы. При
записи схемы B.15)—B.20) сделано предположение о равно-
равномерности сетки m — const. 1$ силу того, что в уравнения дниже-
пия, неразрывности и оперши члены с компонентами скорости и
н v входят в виде отдельных слагаемых, свойства схемы при лю-
любых п а I аналогичны свойствам схом I — IV. Так в nroii схемо
пыполнепы закон сохранения полной энергии, а неднпергентпое
уравпеште B.18) можно привести к соответствующей дшюртепт
пой форме записи.
Выясним, как обстоит дело в схеме B.15)—B.20) с законом
сохранения объема. Рассмотрим отот вопрос па примере конкрет-
конкретной схемы:
п=\, / = 3, о2=
=-0.
Анализ других схем проводится точно также п прпнодпт к
аналогичному результату. Преобразуем для ныбрапшш схемы
правую часть уравнения перазрьпшостн, поспользоваишпоь урав-
уравнением B.19) и правилом разностного дпфферепциромапнн и1)
времени произведения:
Имеем
-- Л3(у, х) =--
= dj, B.21)
где
B.22)
Таким образом, уравпеиие перазрывиости B.17) при выбрашшх
значениях параметров п, I, Ог, Оз преобразуется к виду
m(±]=dt, B.23)
который является разностным апалогом днффсренцнальпого
уравнения A.24). Поэтому функция d должна аппроксимировать
якооиап Д=
)
Я (т, у)
...
- пеличнпа якоииана преооразовапия, как из-
-г,
вестпо, представляет соиой отношепне элементов площадей па
плоскостях (х, у) и (а, Ь). Естественно требовать, чтобы раз-
разностная аппроксимация якооиана равнялась отношению площа-
площади ячейки S(t) (см. рис. 7.G) к ее площади б начальпый момепт
S@)= liJh,- Рассматривая стороны ячейки ABCD как вектора
Рис. 7.G
(например, сторону АН как вектор с проекциями (кьх,,, h,,y,,),
сторону ВС как нскт(>р с проекциями (haxa(+l2), haya(+12)
п т. д.) и используя формулы векторного ана.чп.ча, можно выра-
выразить площадь ячейки S с помощью одной из следующих формул
(см. рис. 7.G):
S =
S, =
- хь
U)у,,-
kh,
B.25)
Как видно из сопоставления B.22) с этими формулами, имеет
место соотношение
s
S @)
какь
B.2E)
означающее, что закон сохрапепия объема в схеме B.1Л) — B.20)
нарушен. Таким обра:кш, для рассмотренного семейстна песим-
метрпчпых схем с порядком аппроксимации O(x + ha + hb) вы-
выполнены основные законы сохрапения (массы, импульса, энер-
энергии), а также соотношение, выражающее баланс внутренней
эпергии, но нарушен закоп сохрапепия объема.
371
§ 3. Полностью консервативная разностная схема
для двумерных задач газовой динамики
1. Симметричная схема. Помимо проанализированных выше
несимметричных по пространству схом можно построить симмет-
симметричные схемы, определенные с помощью сумм введеппые выше
операторов Lu и Л,.
Обратимся в качестве примера к следующей схеме (по-преж-
(по-прежнему сетка ранпомерпа т. = const):
+
let \ \
. (:;.1)
|- Л3(,л ,(я-))]|-
-[Л1(,,^))+Л,(И,х(в»))]Ь C.4)
I, = ц@-51, C.5).
г/, = у@-5\ C.G)
2'), е = гГ(р, Г). C.7)
Шаблон для этой системы указан на рис. 7.7. Как видно, он яв-
является симметричным по пространству (па равпомерпой сетке),
и потому схема C.1) — C.7) имеет второй порядок аппроксима-
аппроксимации О (h* + hi).
372
Проанализируем вопрос о выполпепии в схеме C.1) — C.7)
.чакона сохрапепня объема, например при копкретпых зпачепиях
параметров 02=1, оз = 0.
i ;
Рис. 7.7
Преобразуя с помощью C.6) правую часть уравиепия nepa.i-
рывности C.3) аналогично B.21), получим
тЦЛЛ", у) + Л.,(», У)] - [At(/;, x) + A3(v, .r)]} =
—ХЬ
-Ш,
C-8)
где 5 — площадь ячейки сетки, которая определяется формулой
B.24). Полученное равенство свидетельствует о том, что в рас-
рассматриваемой симметричной схеме закон сохранения объема
.чыполпеп.
Для этой схемы выполпепы также закоп сохрапепия импуль-
импульса и различпые формы оалапса впутреппой эпергии.
Заметим, что используя вместо полусумм операторов
(^ + ^3) н '/2(Ai + Лз) выражения '/2(^2 + ^4) и 'ЫЛг + Л^,
можпо построить еще одну симметричпую схему, которая будет
иметь свойства эквивалоптиостп, аналогичные схеме C.1) — C.7).
Приведем еще одпу симметричпую разностную схему. Опа
определяется с помощью суммы лссх четырех разностных опера-
операторов Ln и А::
= 5s(p, T), ? = ff(p, T),
4
где
1=1
C.9)
C.10)
373
С помощью непосредственной проверки можно убедиться в
справедливости следующих операторных равенств:
L\ + U = L2 + LA, А, ЬА3 = А2 +А4, C.11)
в силу которых все три прпведеппых выше симметричные схемы
совпадают. Наметим, впрочем, что с точки зрения реализации па
практике одна и.) форм записи симметричной схемы может ока-
оказаться предпочтительнее. Итак, фактически существует единст-
единственное трехнараметрпческое семейство симметричных схем, где
пространственные отношения фиксированы, а 0 г? О), оа. Оз2^',
как и в одномерном случае, «регулируют» интерполяцию но ври-
мепп сеточных фупкций в правых частях уравпепий схемы. От-
Отметим, что если параметр О\ — произволен, то параметры 02 и Оз
связаны между сооон. Действительно, анализируя закон сохра-
сохранения объема и преобразуя правую часть уравнения неразрыв-
неразрывности C.3) в симметричной схеме C.1) — C.7), мы выбрали сле-
следующие значения параметров: о2=1, Оз = 0. Аналогично мы по-
поступили и при анализе песимметричпои схемы B.15) — B.20).
Это было сделано для того, чтобы в процессе выкладок C.8) и
B.21) воспользоваться формулой разностного дифференцирова-
ппя произведипия
-7g. + gf., C-12)
где роль jug играли соответственно функции у и х. Формулу
C.12) можно записать в более общем виде. Перепишем еще раз
C.12), поменян мостами / и g:
Ue)t = Jg. + gh- C.12')
Просуммируем теперь C.12) н C.12'), предварительно умножив
C.12) на а, а C.12) па A -ос). Получим
Используя формулу C.13) вместо C.12) и нреоора.чонанпнх ти-
типа C.8) п B.21), можно убедиться, что параметры Ог и Оз долж-
должны оыть связаны соотношением
02+03-1. C.14)
Таким ооразом, семейство схем C.10) фактически является
двухпараметрическнм.
Для этого семейства справедливы разностные апалоги зако-
законов сохранения объема, импульса, а также различные формы
баланса внутреппеп энергии и, кроме того, имеют .место дивер-
гептпые и недивергептные виды записи правых частей в уравпе-
пиях движения п иеразрывпости.
Рассмотрим теперь вопрос о выиолпеипп в этой схеме закопа
сохранения энергии.
2. Аналогия с одномерным случаем. Напомним предварительно
пекоторые сведепия отпосительпо свойств иолпостью копсерва-
тивпых разпостпых схем для одпомерпого случая (см. гл. II,
374
§ 3). Недивергентиое уравпеппе эпсргии в этой схеме
е, = _ р< V» C.15)
с помощью равпосильпых преобразований приводится к дивер-
гептпому виду, что и свадстельствует о выполиспии в схеме раз-
разностного апалога .чакона сохранения эпергип. Эти преобразова-
преобразования выполняются следующим образом: уравпепие движепия
vt = -Pf C.10)
умножается па г !) 5', что дает уравпепно
(v*/2)t = -vl0A)plf). C.17)
Соотношение, аналогичное C.17), имеет место и в соседпем
(г + 1)-м узле:
(»- ( + 1)/2), = - viOfi) ( + 1) р'°\ C.17')
Складывая теперь C.15) с полусуммой равепств C.17), C.17'),
получаем дивергентное уравпение энергии
C-18)
где р% = 0,5 (р + /;(— 1)) для рамиомерпой сетки и
(P*)i = ' l~1')]i '-1 ' ' ^» = 0,5 (hi + Л^)
для перавпомерпоп сетки. Уравпепие C.18) выражает закоп со-
храпепия эпергпи, причем в качестве объекта, для которого за-
писап этот закон, фигурирует массовый ипторвал сетки h-t
0,5 (Л^Ь^)
i i+1 \i-r i/ ЛУ1
6
Рис. 7.8
(рис. 7.8). Для ООЛ011 наглядпоп демонстрации этого факта пере-
перепишем C.18) в виде
Полная эпергия массового иптервала ht складывается из его
впутреппей эпергип hiEi и кипетической 0,25 (и?+ yi+i)i которая
определяется по сЕСОростям копцов интервала (см. рис. 7.8, а).
375
Величины (/'*)i и (/'*)i + i есть интерполяции давления в узлы i
и ( + 1, являющиеся границами интервала /(.. Однако возможен
и другой подход к анализу закона сохранения полной эпергии в
полностью консервативной схеме. .Запишем уравнение для внут-
внутренней энергии C.15) для (('—¦ 1)-го интервала
Сложив теперь C.1G) с полусуммой уравнении C.13) и C.13'),
получим
C.19)
для равномерной сетки. Это соотношение также можно рассмат-
рассматривать как выражение закона сохранения полной энергии для
области, являющейся полусуммой соседних массовых иптерва-
лов. Более наглядным этот факт представляется, если C.19) пе-
переписать на неравномерной сетке в виде (см. рис. 7.К, б)
J+l
М
i—1
T.
C.19')
полная энергия области
aiieprnii составляющих ее
Л, определяется cyMMoii
полуинтервалов 0,3/t,- и
2 вычисленной ио ско-
скоКак видно,
внутренних
0,3/ii-1 u кппетической энергии 0,5//?(у;J,
ростп i-го узла.
3. Особенности вычисления балансных соотношений в двумер-
двумерном случае. Построив симметричную схему C.10). мы избавились
от основпого недостатка, которым обладали песпмметричпые схе-
схемы I—IV,—парушепия закона сохранения объема. Однако для
симметричных схем остался пока невыясненным вопрос о выпол-
выполнении закона сохранения эперпш.
Ныкладкп, проведенные в [37],
которые мы здесь пе воспроизво-
воспроизводим из-за их громоздкости, пока-
показывают, что для двумерпой лаг-
рапжевой ячейки сетки закоп со-
храпепия полпоп энергии в сим-
мотрнчпой схеме пе выполпеп.
Дисбаланс нолной эпергии имеет
днвергептпую структуру и пе за-
зависит от шага сетки по времепи
т, па гладких решепиях его поря-
док О (kl + hi).
Используем другой способ вычислештя баланса энергии, по-
подобный тому, который был описан выше для одпомерпого слу-
случая. С этой целью разобьем каждую осповпую лаграпжеву ячей-
ячейку массы М на четыре части, массы которых одинаковы; Мп —
376
= 0,25 М, п = 1, 2, 3, 4 (см. рис. 7.9), а значения удольпой
внутренней эпоргии е„, вообще говоря, различны. С каждой та-
такой «малой» ячойкой сляжем некоторую скорость, в качестве
которой выбором скорость и„ того узла, который является общим
у малой и осповпой ячеек (па рис. 7.9 эти узлы отмочепы круж-
кружком). Эволюцию каждой малой ячейки будем описывать с по-
помощью соответствующей несимметричной схемы из § 2. Напри-
Например, па равпомерпой сетке будем иметь следующие урав^епия
движения и внутренней энергии:
w(un)t=Ln(p^\y^l C.20).
,,t(Kri), = -//4\n(,,,/^). C.21)
Здесь давление р предполагается одинаковым во всех частях ос-
новпон ячейки п для простоты вторая компонента скорости от-
отсутствует (у = 0). Нетрудно нпдетъ, что суммирование уравпо-
пия C.21) по всем четырем частям осповной ячейки приводит
к разпостпому уравпепию симметричной схемы C.10), выражаю-
выражающему балапс впутроппей энергии этой ячейки:
'»*=- //П]Ч 2 л»(«. № - - №(„. №,
П 1
4
1 V
где е = -jr 2ii ?n-
n = l
Суммирование уравнения C.20) но малым ячейкам, приле-
прилегающим к узлу (', j) (см. рис. 7.10), дает разностное уравпепие
движения симметричной схемы C.10)
4
( (°l) (ai)\ Г I (°l) (°2Л
оннсывающее закон сохранения импульса для вспомогательной
лаграпжевой ячойкп, сконструпроваппой ип малых ячеек так,
как покааапо на рис. 7.10.
Просуммируем теперь но четырем малым ячейкам, составляю-
составляющим вспомогательную ячейку, уравнения C.21) п уравпепия
C.20), умноженные предварительно па ^п0'5'- После довольно
громоздких выкладок можно преобразовать результат к соот-
соотношению
m 10,25(ег -|- е2(- 12) + «-а(_ 1„ - 12) -и е4(- it)) + u-/2]t =
C.22)
25 А. Л. Самарсний, Ю. П. Попов 377
которое является выражением .чакона сохранения энергии для
вспомогательной лаграпжевой ячейки сетки. Впрочем, уравнение
C.22) можно получить п без громоздких выкладок, ведь оно
представляет собой сумму законов сохранения энергии для четы-
четырех частей вспомогательной ячейки, а эти законы, как показапо
hrr ^ в § 2, справедливы для всех
четырех несимметричных схем.
у+/ Таким образом, па лагран-
женоп плоскости можно рас-
Vi ТТГ77ГТ" ~ Т сматривать две системы раз-
.j постных ячеек (основных и
вспомогательных), сдвинутых
относительно друг друга по
^. * каждому направлению на по-
лышпу шага. При использова-
использовании для построения дискрет-
Рис. 7.10 пой модели среды симметрич-
симметричной схемы, для системы основ-
основных ячеек выполнены лакоя сохранения ои'ьоыа п различные
формы баланса внутренней энергии, а для системы вспомога-
вспомогательных ячеек — законы сохранения импульса и полной энергии.
Л .чтом смысле симметричная схема является полностью копсер-
дативпой.
ri
<
\
-
у//-'///,
м
mi И i Г | ¦ ¦ | i
¦.
L-!
I
Рис. 7.11
Все рассуждения, которые Пы.тн проведены для равномерных
сеток, очевидным образом переносятся и на случаи неравномер-
неравномерных сеток (см. рис. 7.11).
4. Результаты тестовых расчетов. Разностная схема, аппрок-
аппроксимирующая двумерные дифференциальные уравнения газовой
динамики, представляет собой нелинейную систему алгебраиче-
алгебраических уравнений высокого порядка относительно значений сеточ-
сеточных функций на верхнем временном слое. Для простоты рас-
рассмотрим вопросы, связанные с реализацией таких схем на при-
примере уравнений газовой динамики в изотермическом прибли-
приближении.
378
В этом случае схема может быть записана следующим
образом
тщ = L (/)(ai), t/a*)), mvt = -L (/><Ч №). р = M/S. (Л.Г.)
Здесь,для нахождения плотности вместо уравнения неразрывпо-
сти использовано соотношение pS—M, являющееся следствием
закона сохранения объема, который выполнен в схеме в силу
свойства полной консервативности. Семейство схем C.23) явля-
является двухпараметрическим (О «G аи Ог, оз =S 1, 02 + 03 = 1).
При oi=O2 = 0, оз =¦ 1 имеем так называемую явную пол-
полностью консервативную схему. .'Здесь аналогично одномерному
случаю значения сеточных' функции на верхнем слое определя-
определяются без каких-либо алгоритмических сложностей. Действитель-
Действительно, перепишем для этого случая уравнения си.-мы C.23) в сле-
следующем виде
mut = L(P,y), x, = uio-s\ mvt = -L(P,x), yt = у'0-5', C.24)
.1/
Решая уравнения схемы C.24) и указанной последовательности,
получим явный алгоритм построения решения па верхнем
(А:+1)-м временном слое: из первого уравнения, в правую часть
которого входят сеточные футл^ин лишь с /;-го слоя, находим
значение ком1К)непты скорости и. из второго, используя получен-
полученное значение и, вычисляем х и т. д.
Однако нетрудно показать, что как и в одномерном случае
схема C.24) обладает плохой устойчивостью, что порождает до-
довольно жесткие ограничения па шаг т и делает применение утой
схемы в практических расчетах сравнительно малоэффективным.
При 0| ^ О,Г) полностью консервативная счема C.23) стано-
становится безусловно устойчивой, но для ее решения приходится
привлекать какие-либо итерационные процессы. Использование
простейшего явного итерационного процесса, как1 и в одномерном,
случае, приводит к ограничениям па шаг сетки по времени, ко-
которые являются даже более жесткими, чем условие Куранта.
Анализ показывает, что весьма эффективным итерационным ме-
методом решения неявных разностных схем газодинамики являет-
является метод Ньютона. Мы опустим здесь достаточно громоздкие вы-
выкладки, связанные с применением метода Ньютона к схеме
C.23), которые можно найти в [37], и ограничимся изложением
соображений общего характера.
В одномерном случае использование метода Ньютона приво-
приводит на каждой итерации к системе линейных алгебраических
уравнений с трехдиагопальпои матрицей, которая легко решает-
решается с помощью прогонки (см. гл. IV). В двумерном случае соот-
соответствующая система линейных уравнений имеет существенно
25* 379
оолее сложную структуру и се решение представляет лначuto.il-
пыо трудности. .'{десь возникает необходимость и еще одном ите-
итерационном процессе для решпння собственно системы линейных
уравнений, и от качества этого «внутреннего» итерационного
процесса в большой степени зависит эффективность всего алго-
алгоритма в целом. 13 примере численного расчета тестовой задачи,
описаппом пил;!.1, для решения линейной системы использован
метод блочных итерации [4."}, Г>7]. Этот метод в нашем случае
Рис. 7.13
сходится, кпк1 можно показать, при любом значении величины
шага по времени, однако число итерации быстро нарастает с
увеличением т.
Для тестовых расчетов в качестве примера выберем классиче-
классическую задачу о поршне, который вдвигается в газ и порождает в
нем ударную нолну. Рассмотрим изотермический вариант этой
задачи, описание которого укладывается в схему C.23). В ка-
качестве исходной пространственной области нрнмем квадрат
ARCD : @ < a <i /,, 0 <. Ъ <. L), стороны которого со временем мо-
гут переметплться в плоскости (х, у), играя роль поргапеп
(рис. 7.12). И начальном состоянии гл.ч однороден и покоится:
р(а, Ь, О)=ро=1. "(й, Ь, 0)=0, у (а, Ь, 0)=0. Скорость звука
с = 0,5.
В первых вариантах расчета в качестве граничного режима
задавалось движение одной из сторон квадрата внутрь области
с постоянной скоростью: либо левой
C.2Г.)
u(O,b,l)=Uo, v@,b,t)=O, U0>0,
лиоо нижнеп
к(а, 0,/)=0, v{a,O,t)=VQ, К„>0.
C.2G)
На остальных частях границы обе компоненты скорости задава-
задавались пулевыми.
При укапанных краевых условиях возникает одномерпое те-
течение газа с ударной волной, распространяющейся от степки —
норшпя вдоль одного из координатных направлений. Такие ва-
варианты задачи позволяют сопоставить оцисаппый выше алго-
алгоритм решения двумерных уравнений газодинамики с апалогич-
пой одномерной методикой. Расчеты показали, что результаты,
380
полученные по обеим методикам, сог.падают ка:; и отношении
нрофилей сеточных функции, так и в отношении количества ите-
итераций в иыотоиовском процессе, а также ширины размазывания
фронта волпы в зависимости от шага т и других методических
параметров счета.
В качестве примера существенно двумерного течения рас-
рассматривался вариант задачи, когда ударная волна распространя-
распространяется вдоль диагонали АС квадрата ABCD (см. рис. 7.12). Чтобы
реализонать \ казаипое течение, па сторонах квадрата ЛВ и AD
.шдавалси граничный режим специального типа для компонент
скорости, паираиленпых внутрь области. Этот режим представля-
представляет собой «размазанную ступеньку» (см. рис. 7.1!'). которая со
временем перемещается вдоль стороны ьиадрата со скоростью
\'LD, где П — скорость фронта ударной полны. 11 расчетах при-
принималось ?/'о = U.7.1 и I) = 1. Продольная компонента скорости на
сторонах ЛВ и AD задавалась раплоп uy.no.
На рис. 7.14 п 7.15 нредстанлены результаты расчета рас-
распространения такой «косой» ударной попил. L'nc. 7.14 демонст-
демонстрирует вид разностной сетки в переменных Uii.iepa и начальный
—^
¦ Ц
/- -
i
§:
1
\
—
1
_
1—
1
.
v
j
-
Ц
\4-
1
—
L
1-
\
—|-
—
—
П. i
0,8 /,2
Рис. 7.14
момопт (лагранжева сетка) и на шаг по времени А: = 6. Расчет
проведен для значения т = 0,213, превышающего величину тк,
следующую из условия Куранта, в 4—5 раз. Число итераций по
Ньютону равно семи.
На рис. 7.15 на шаг /: = G дапы линии уровня давления.
Расчеты выполнены по пеявпой схеме О[ = 1. сь = Оз = 0,о
на сетке 20 X 20. Расчеты показали, что решение тестовой зада-
381
чи об ударной волне воспроизводится удовлетворительно даже
при крупных шагах т. значительно превышающих тк.
Анализ проведенных в настоящей главе теоретических рас-
рассмотрений и численных расчетов позволяет подтвердить для дву-
двумерных уравнений газовой динамики тот ж и вывод, который был
Рис. 7.15
сделан для одномерного случая: сочетание неявных полностью
консервативных схем ir итерационного метода Ньютона дает воз-
возможность построить аффективный алгоритм, допускающий ис-
использование грубых соток по времени.
Двумерные расчеты, up и веде иные выше, носят иллюстратив-
иллюстративный характер. В работах [0, l(i. 19, 20. 23] полностью консерва-
консервативные схемы были применены для расчета сложных задач маг-
магнитной гидродинамики, имеющих практический интерес, и также
продемонстрировали спою эффективность.
§ 4. Вариациоппо-разпостпмн подход
к построению полностью консервативных схем
1. Принцип наименьшего действия. Вариационные нрипцины
являются одним нз наиболее общих способов описания и иссле-
исследования физических явлении и процессов.
В [23, 97J предложено использовать вариационный подход
для построения полностью консервативных разностных схем дву-
двумерной газодинамики и магнитной гидродинамики. В настоящем
параграфе на примере газодинамики кратко описаны особенно-
особенности применения этого подхода, а результаты, полученные с его
помощью, сопоставлены с полностью консервативными схемами,
построенными выше в § 3.
382
Напомним предварительно основные понятия, спя-иппые с ва-
вариационными принципами. Как известно, каждая механическая
система может быть охарактеризовала некоторой функцией, на-
называемой функцией Лаграижа;
L (Х[. Х-2. . . ., Z.Y. X]. i'2 Хх, t),
где Xi хх — обобщенные координаты системы, полностью
опредемяющпе ее положение, N— число степеней споГюды сис-
системы, /—время, xk—(ljrjdl — обобщенная скорость. Функция
Лаграижа содержит только хк и хк, /г = 1, .. „ N, it не зависит от
производных более иысокого порядка, и :»то отражает то обстоя-
обстоятельство, что механическое состояние системы целиком опреде-
определяется заданием координат и скоростей.
Пусть н споем движении система и моменты мремепн t\ и 1-2
проходит некоторые фиксированные положения, задаваемые яа-
оорамп ипачсппи .Ti", ...д^из;1/1, ..., .r'v'. Тогда и соответствии
с принципом наименьшего действия Гамильтона движение систе-
системы между этими положениями происходит таким образом, чтобы
интеграл (Оействие по Гамильтону)
N= f A(J-.. ••- з-лг. ¦'! rs,t)dt A-1)
иmi'.'I нацменi.iiii'c i!(i,4M(i".i;iioo лначешш.
Принцип наименьшего доПствпя понколяет иывистк уравис-
пия движения MexanitnecKoii системы. Продемонстрируем ато на
простейшем примере, когда механическая система характеризу-
характеризуется лишь одной степенью свободы: Л/•— 1.
Пусть ./¦(/) траектория дпнжеиия системы, для которой S
имсот минимум iS —¦ 5о. Ото означает, что дли любой другой
траектории
x(l)+8x(t) D.2)
действие имеет ,ч паче и не, превышающее; Л'о (8хA)— вариация
.?(/)). Поскольку все сравниваемые траектории D.2) должны в
моменты времени 1\ и /г проходить через фиксированные поло-
положения х(П и хB\ имеем
8х(/,)=бх(/2)==0. D.3)
Истинная траектория хA), точнее уравпеипе, ее описываю-
описывающее, определяется из условия минимальности S, т. е. из условия
равенства пулю первой вариации действия:
65 = 6 JL(z, x, t)dt = O. D.4)
¦I
383
Производя операцию нарьнронаппя по o'lL
приходим к равенству
uiiv:.: правилам,
.Г.)
d
Учитывая, что Ьх = -^Ьх. проинтегрируем вклч.е слагаемое в
левой части D.5) по частям:
d с \ ,, f)L „
l' / d iiL „ \ ,,
В сплу ('(.Л) первый члел в этом выражопнн р;>;¦;* -л нулю. Т,аким
образом, D.5) дает равенство
Отсюда, учитывая произвольность варнацтпг ?•.¦•, иколчателтлю
приходим к уравнению
которое и sie.vainiico ллзынпстся уравнением Лаграпжа. Еслп
функция Лаграпжа для рассматрлпаемоп мечанлческой системы
известна, то ураинение D.0), устанаплппаюиио спяль между
ускорением, скоростью н координатой, нредстаиляет собой диффе-
репциальпое ураиненпе дипжешш.
Если система обладает несколькими стапелями свободы, то
при использовании принципа наименьшего действия необходимо
проводить варьирование независимо по каждой координате хк.
Это дает систему уравнений:
V.
4^ ()
Для простейшей замкнутой механической системы, т. е. для
системы N материальных точек с массой тк, взаимодействующих
только друг с другом и не взаимодействующих пи с какими
внешними телами, функция Лаграпжа имеет вид
L = Ет„ - U, D.7)
JV N ¦
V1 1:к V Xh
где дкин =7. 'Пд -у- = 7. '"fc-т" — кинетическая энергия системы
uA = ift и U — ее потенциальная энергия, описывающая взаимо-
взаимодействие материальных точек между собой.
384
Если для замкнутой системы функция Лагранжа явно не за-
зависит от времени (однородность времен»), энергия системы со-
сохраняется. Действительно, пусть L = L(x, x). Вычислим полную
производную от функции L по времени:
dL v? / dL ¦ dL ¦¦ \
Заменим здесь производную dfj/dxk в соответствии с уравнением
D.6'). Имеем
N • К
dL V? I _d_ I дГ.\ ¦ , OL dxh\ V1 d , ui. v
A=i \ \dxh' dxh
Таким образом, можно записать
И;) D.8) си\дует, что п рассматриваемой михаушчсской систе-
системе величипа
остается пеизи^ннои со временем. (Эта величина называется
энергией системы.) Действительно, обращаясь к D.7), видим, что
N X
2
л=1 uxk k=i
и, следовательно, величина D.9)
N
представляет couoii полпую энергию системы, состоящую из ки-
кинетической и потенциальной.
В общем случае, когда система не является замкнутой, ео
энергии можег 1именяться п результате взаимодействия с внеш-
внешними телами.
Заметим также, что однородность функции Лагранжа по про-
страпствоппьш координатам приводит к тому, что в замкнутой
системе материальных точек выполнен и закон сохранения
импульса.
2. Вариационный приниии и уравнения ГЛЗОВО" ДИНЭМПКП.
Рассмотрим, какие результаты дает применение описанпого ва-
вариационного принципа в газово» динамике. В целях большей
наглядности ограничимся случаем одномерного плоского адиаба-
383
тического течения газа. Будем также использовать лагранжевы
массовые координаты.
Функция Лагранжа для фиксированной массы газа может
быть записана в виде [87]
/ = ?кин ?н
г v2 У
где ?КИ1| = —ds — кинетическая энергия, а /-Mi = \ е dx— вну-
о "
тренияя тепловая энергия газа.
Мы воспользовались, как и в предыдущих главах, лаграпже-
пымн массовыми переменными. Как ооычно, здесь М—масса га-
иа в единичном параллелепипеде (см. гл. 1, § 3).
Функционал действия по Гамильтону в ;>том случае припима-
ет форму
'2 м
xdl. D.10)
При движении рассматриваемой среды как механической систе-
системы действие ? должпо быть минимальным. Заметим, что в слу-
случае сплошпой среды варьирование действия S следует проводить
с учетом дополнительных соотношений — уравнений связи, в ка-
качестве которых в даппом случае выступают закоп сохрапеппя
объема (закон сохранения массы выполнен автоматически):
и первое начало термодинамики:
dt; = - pdr] = Л dp. D.12)
Р"
Необходимо также принять во внимание уравнение движения
лаграижевых частиц:
¦I = v. D.1.J)
Итак, принцип наименьшего действии в применении к D.11)
дает
6.S' = [ j (vf>v — Sf) dsdt = ti. D.14)
Рассмотрим первое слагаемое этого уравнения, используя D.13)
и правило интегрирования по частям:
'2 м '2 л( м К {г м
ЯГ Г d Г Г Г dv
vdvdsdt = I i i1—— ox as at = \ voxds — 1 \ —r- ox as at.
J J dt J J J dt
to 1 Q 0 t 1 Q
11 11
38C
В силу того, что состояние газа в моменты /| и to фиксиро-
фиксировано, имеем бдг(^|) = бх(^)= 0, и следовательно, первое слагае-
слагаемое в последнем выражении равно нулю. Таким образом, для
первого слагаемого п D.14) имеем
I., М <i ЛГ
j J v bv ds dt = — j j -J 6a; ds dt. D.15)
Обратимся ко второму слагаемому. В соответствии с D.12)
имеем
бе = -^- 6р,
п варьирование уравнения связи D.11) дает
р2" Р ~ "<""
Сводя эти соотношения вместе, получим
42 М '.. .11 1г ЛГ
Г Г Г Г р Г Г <>
— I \ ое ds dt = — I I —г op ds dt = \ \ n — ox ds dt =
4,0 /l0 ' 4,0
= J p 6a: d/ - j j ^bxdxdt. D.16)
Здесь к интегралу по s было применено правило интегрирования
по частям.
Считая для простоты, что движение границ области, занятой
газом, задано для всех варьируемых траекторий хA.)+ 8x(t)
одинаковым образом: и@, t)=v*(t), v(M, t)=v**(t) (как, на-
например, в задаче о поршне), имеем в граничных точках
6х@, t)=bx(M, 0 = 0. D.17)
В противном случае в D.16) войдут граничные условия по
давлению и экстремальное значение функционала действия
D.10) будет достигаться на истинных траекториях движения
частиц среды, удовлетворяющих не только уравнениям гидроди-
гидродинамики, но и граничным условиям.
С учетом D.17) подстановка D.15) и D,10) в D.14) даст
*2 М
откуда в силу произвольности вариацпц Ьх приходим к известно-
известному уравнению движения:
387
Уравнение непрерывности следует нз закона сохранения объ-
объема D.12). Действительно, после дпфференцпрппапия D.11) по
времени с уметом D.1.4) получим
_d_ I I
<lt \ р
Изменение внутренней энергии определяется х:~. ?н< пнем сия-
зп D.11):
(!е_ _ j_ _rfp _ _^_
dt ~ ~ (,- <lt ~ ~ P dt
Можно также показать, что отсутствие явной зависимости
лагранжиана L от времени аналогично D.8) автоматически обес-
обеспечивает выполнение закона сохранения энергии.
К перечисленным уравнениям необходимо добавить еще за-
замыкающее систему уравнение состояния.
3. Построение полностью консервативной схемы вариационно-
разностным методом для одномерного случая. Применим вариаци-
вариационный подход к построению разностных схем. Обратимся вновь
к одномерному случаю. Будем рассматривать некоторую диск-
дискретную модель среды, задаваемую прострапстпешюй сеткой
он = (•*/, S.-+I = Si+ ht, i = 0, 1, ..., Л),
как мехаппческуго систему, эволюция которой во времени проис-
происходит непрерывным образом, Система состоит нз Л' массовых ин-
интервалов hi, I = 0, 1, ..., Л'—1, каждый из которых обладает
удельной внутренней энергией е(, а скорости концов пптерпа-
ла—V; и vi+\. Координатами, определяющими положение систе-
системы, являются координаты узлов ci'ti.ti х,; i = 0. 1 IV. Сеточ-
Сеточные функции, оштсыиающие систему, зависят <<т дискретного
аргумента ,s\ и ненрерышюго t, т. с. дискретизация среды выпол-
выполнена лишь но пространству. Лагранжиан такой системы можно
записать в виде
л1 о лг—1 h , }
i —0 i=0
Первое слагаемое есть кипетическая энергия системы (как
оиычпо h-[ = hs=0 — фиктивные интервалы (см. гл. 1, § 4)).
второе — ее тепловая энергия. В принципе, для построения урав-
пепий, описывающих эволюцию рассматриваемой системы, нуж-
нужно определить разностный апалог действия по Гамильтопу S>,,
вычислить его первую вариацию, ириравпять ее нулю и т. д. Од-
Однако можно непосредственно воспользоваться общими формула-
формулами, полученными в п. 1, и в частности, уравнениями Лаграп-
жа D.6'):
dt - ' dJck
388
В качестве уравнений связи возьмем разностные аналоги за-
закона сохранения объема D.12):
термодинамическое соотношение D.12), выражающее первое па-
чало термодинамики для интервалов сетки, и уравпепие для
траектории D.J3), написанное в узлах сетки.
Вычислим пермое слагаемое и уравиепии D.20):
Л'
,1 dL,, ,i ,1 жгу • л • dfi, do и
-jT — = ln—l r'iXi = IT fift-r« = 'г*7Г = h« ИГ- <42>
О.тк f.^i-,-0
Обратимся ко второму мл он у в D.20), имея в виду, что урав-
пеппе состоя пи я для адиабатического случая может быть нред-
ставлепо с учетом D.21) как сложная функция е,-=
[ )]
°±h _ J_ 'v1 / Г i °3: drlu , , Oek~i <hh-i I _
= hhPh гг + hk~iPk~i —rr^ = — Pk~ Pk-i- D.23)
k ft
Здесь использованы соотношения, полученные дифферепцирова-
ннем D.21):
Свод» D.22) к (-1.23) в D.20), получим во внутренних точ-
точках сетки разпостпо-дифферепциалыюе уравнение движения:
"¦b~jT = —\Рь—Pk-ii- D.Z4;
Заметим, что это уравнение фактически выражает закоп со-
хранепия количества движеппя для области Л„ составлеппой из
половипок массовых интервалов сетки, примыкающих к i-му уз-
ЛУ- Суммнровапие D.24) по сетке дает иптегра.и.нып закоп со-
сохранения количества движения.
Разделив D.24) на Л», приведем разпостно-днффоренцналыюе
ураипсние движения к форме
Напомним, pj = —:—- есть производная назад па неравпомер-
пой сетке.
Дифферонциальпо-разпостное уравнение неразрывности сле-
следует из закона сохранения объема D.21) н формулы D.13):
Уравпепие энергии и «энтропийной форме» для каждого интер-
интерпала вытекает из ураипепия связи D.12):
-^=_РкА(±\ D.2G)
Используя D.2Г)). имеем также
^ = - Ph{vs)k. D.20')
Закоп сохранения полной энергии для рассматриваемой си-
ст(!мы пыпо.чкястся лнтоматпчоскн и силу тог», что функция
Лаграижа системы /.,, (см. D.19)) по зависит явно от времепи.
Птот факт можно установить и с помощью непосредственных
НЫ'ШСЛСШШ.
Перепишем функцию Лаграижа D,19) в виде
IV-1
Тмк как эта функция обладает свопстном аадптнвности, рассмот-
рассмотрим ее для некоторой подобласти i\ «? i sS U:
„2 I „2
Продифференцируем лагранжиан Tjh по времени:
а/,, • ь},. ¦¦
Ох, Ох ,
1 i
Заметим, что для внутренних узлов подобласти i|
¦- h — 1 имеют место равенства
of if, aL. «//уд oi.lt
и поэтому в этих точках для ГЛ справедливы уравнения Лагран-
>ка D.20). С ттх помощью можно преобразовать выражение,
300
стоящее в D.28) под злаком суммы так, как ото было сделано
при выводе соотношения D.8):
R узлах /i и !2 соотношения D.29) не выполняются. Введем п
рассмотрение вспомогательные лаграпжианы
,.? .1-й?
U1} = //j -i'1/' '' — hi _,f; _,. D.31)
Нетрудно видеть, что для лагранжиана Д, + ?л + -^л соот-
шиненни D.29) выполняются и в узлах U, i2- Добавим в правую
часть D.28) тождества, полученные дифференцированием D.31)
и D.31'):
: ?2
2
_^-Wi —-2 + //; -!i», =0.
3
Так как в узлах U " '2 также справедливы уравнения Лагранжа
D.20), то можно свернуть в получающемся равенстве члены, от-
отвечающие дифференцированию по х{ , д:4 , л\ ,.г: по формулам,
апалогичпым D.30). После несложных преобразований получим
Xi\ +
дт
Здесь использованы уже встречавшиеся рапее формулы:
391
Левую часть D.32) можно преобразовать к виду
[¦
^-2-('V'-^
Ч -i
vli\ , Ч d К
1 J " 111 i liiL _j? —
2 dJ\2/~t~2djl2/~
= +i
i ,— 1
'i-1
- 2 2 '" 2 V1 - - К ~f
1,-1 d b"»i
'v
dE
ГДО
2 Л 2 T ^rfl 2 rfi '
'.,-1
(',.33)
— полная энергия газа, заключенного в подооласти i\ ^ i ^ 12-
Таким обпи-чои, окончательно приходим к равенству
7Г" = — (РКи1 — Р1 -ir» )' D.34)
которое и н{»едстаиляет собой дифференцпальпо-разностную
формулировку закона сохранения энергии.
Построенная система дифференциально-разностных уравне-
уравнений D.24), D.2-1), D.26) обладает свойством полной консерва-
консервативности в том смысле, что для нее выполняются необходимые
преобразования эквивалентности. На заключительном этапе по-
построения разностной схемы нужно осуществить дискретизацию
но времени. Для этого пропзподные по времени в левых частях
указанных уравнении следует заменить разностными выраже-
выражениями, а разностные производные по пространству «разнести» с
некоторым весом на два времеппых слон сетки—у'-й и (/ + 1)-й.
При этом веса подбираются так, чтобы получающаяся в резуль-
результате разностная схема сохранила свойство полной консерватив-
консервативности, которым обладала дифференциалыю-ра.-шостная система
уравнений, R результате мы придем к схеме
\i4t * \р h )'
302
которая совпадает с полностью консервативно» схемой, построен-
построенной в гл. II.
Мы подробно остановились на одномерном случае, чтобы на
простом примере наглядно продемонстрировать особенности при-
применения вариационно-разностного метода для построения пол-
полностью консервативных; схем.
Однако следует указать, что в одномерном случае достоинст-
достоинства вариационного подхода не проявились в полной мере.
А. Двумерный случай. При использовании вариационного под-
подхода для построения полностью консервативных схем отправным
цунктом являются построение разностной функции Лаграпжа и
формулировка дополнительных соотношений — уравнений связи.
После этого построение; системы дифференциально-ра.чност-
пых уравнений, а затем и полностью консервативной схемы сво-
сводится к пыполнешпо формализованных процедур.
Рассмотрим двумерное плоское течение газа в ооластп D:
{О «;«=?/„, 0< fr^Zj; а = х@). Ь = у(О)—лагранжовы коорди-
координаты. И D введем сетку так, как ото было описано в § 2. Тогда
по аналогии с одномерным случаем функцию Лаграпжа молит
записать в следующем виде;
Na Nh a , Na-1 JV2-1
22^ 1 2
i—Oj—0 i- 0 }-—0
Здесь тпц—масса основной ячейки сетки,
Ми = 4 (тИ +"';- ij + тц-i -г ini-ij:-i)
—масса вспомогательной ячейки, построенной вокруг узла (i, j).
Мы опускаем подробности, связанные с рассмотрением грашг-i-
пых узлов сетки, введепием фиктивных слоев ячеек вдоль гра-
границ п т. д. Эти вопросы обсуждаются в [20, 22].
В качестве дополнительных соотпошешш (уравнений связи)
рассмотрим закон сохранения объема:
где Б0 = 5{х,ъ xt+li, x,uh л-г+ij+i, J/.-j, Уи-i « Уа^\, [/,+ i j+i) — пло-
площадь ячейки сетки. Для ее определения можпо воспользоваться
формулами B.24) или B.25).
Кроме того, считаем, что в каждой ячейке выиолпено соотно-
соотношение, выражающее второе пачало термодинамики: ch = —rdp,
о"
а в узлах сетки справедливы динамические уравиеипя
26 а. А. Самарский, Ю. П. Попов 393
Заметим также, что внутренняя энергия ячейки ец является
сложной функцией координат узлов ячейки
e.j = e и,.:(л-1., xi+\ j, xij+u xt+-.J+[, yiU j/.+u, J/ij+i,
D.38)
Принцип наименьшего действия в случае двух независимых
пространственных переменных приводит к системе уравнений
Лагранжа:
СН^'-' "'T>J ' (/,..49)
dt
Подставляя сюда лагранжиан D.35), имеем для внутренних уз-
узлов сетки:
dur
м^ =
Ox..
dy;-
- Pii -^7 ~ fli-i j -jr + Pi-ii-i Oyi + A-j-i -^ и т-«'
('..41)
OS.. dS'. dS._.- OS•
Входяшио сюда производные т~> тр^' —j j" '' t)'~ ' и т' ^'
вычисляются для площади ячейки (см. D.24), D.25)).
Подставив значение этих производных в D.40), D.41) и про-
проведя громоздкие, но несложные выкладки, можно показать, что
правые части дифференциально-разностных уравнений D.40),
D.41) совпадают с правыми частями уравнении симметричной
схемы (см. C.1), C.2)).
Аналогично одномерному случаю строятся и другие диффе-
дифференциально-разностные двумерные уравнения, к которым потом
применяется операция дискретизации по времепи. В результате
получим двухмерную полностью консервативпую схему, которая
совпадает с симметричной схемой из § 3.
С помощью вариационно-разностного подхода в [16, 17, 19]
построены полностью консервативные разностные схемы для
уравнений магнитной гидродинамики и выполнены расчеты ряда
практически важных задач, связанных с исследованием устойчи-
устойчивости процесса сжатия лазерных термоядерных мишеп.мг, «схло-
нывания» тяжелого лайнера, Релей — Тейлоровской неустойчи-
394
вости и т. д. Результаты этих расчетов подтвердили высокую эф-
эффективность полностью консервативных схем.
Касаясь сравнения двух методов построения двумерных пол-
полностью консервативных схем, следует отметить, что вариацион-
вариационно-разностный подход имеет более формализованную структуру.
В то же время метод, использованный в §§ 2, 3, обладает боль-
большей наглядностью и легко обобщается на случай учета диссица-
тивных факторов, таких как теплопроводпость, копечная прово-
проводимость и т. д. На наш взгляд, па практике при построении пол-
постыо консервативных схем следует разумно сочетать оба
метода.
26*
ПРИЛОЖЕНИЕ
ПРИМЕРЫ ПОСТАНОВКИ И РЕШЕНИЯ
НЕКОТОРЫХ ЗАДАЧ МАГНИТНОЙ ГИДРОДИНАМИКИ
§ I. Взаимодействие плазмы с магнитным полем
в канале рельсотрона *)
I. Описание эксперимента. В работах [37, 108] описан эксперимент по
торможению плазменного сгустка магнитным полом в канале рельсотропа.
Схема эксперимента iibiroii устаповии представлена па рпс. 1, п. Плазменный
сгусток, полученный путем сжатия газа (подорода) п в-пинче, инжектиро-
инжектировался в рельсотрон, представляющий собой дпа параллельных электрода,
подключенных к батарее конденсаторов. В начальный момент пространство
между электродами однородно заполнено холодным непроводящим водоро-
водородом при давлении 0,3 тор. В некоторый момент времени электрическая цепь
Источник
'Лпзменньп;
:¦
'
Покоящийся
газ
3
Рис. 1
замыкается через горячий плазменный сгусток, вошедший в межэлектрод-
межэлектродный промежуток. Возникающее магнитное поле, направленное перпенди-
перпендикулярно к плоскости рисунка, тормозит движение сгустка.
В эксперимепто изучались особенности динамики торможения сгустка,
в частности зпвисимость от начального папряжения па батарее копдепса-
*) Эта работа выполнена авторами совместно с Г. 15. Даниловой,
В. А. Дородницыным, С. П. Курдюмовым и Л. С. Царелой. Подробное ее
изложение содержится в [34, 85].
396
торов. Фиксировались СФР-граммы (пространственно-временные диаграм-
диаграммы) движения плазмы в межрельсовом промежутке (рис. 2), а также ре-
регистрировалось пространственное распределение температуры в плазме
вдоль электродов па последовательные моменты времени.
При определепных значениях параметров в эксперименте наблюдается
сложная слоистая структура, возникающая в плазме за фронтом ударной
волны (рис. 2). Анализ распределения температуры показывает, что эта
структура образована чередующимися зонами сравнительного горячего (тем-
(температура Т ~ 2 -s- 5 яв) и холодного (Т ~ 0.2 4-0,5 зв) газа. Светящиеся
¦Г, СМ
1в -
л 10 <?
Рис. 2
слои, отделенные от фропта ударной волны томным промежутком, движут-
движутся в обратном направлении, кэличестно последонательно рождающихся
слоев, наблюдаемых в эксперименте, около десяти (па рис. 2—шесть). При
этом одповремеппо в канале рельсотропа находятся не более одного —двух
слоеп. Важной особенностью слоистой картины течения является порого-
пороговый характер условии ее появления: она шмлтдается лишь при достаточно
большом начальном напряжении на батарее конденсаторов, превышающем
величину Г* = 400—50п й.
2. Постановка задачи. В численном эксперименте задача о торможопии
плазменного сгустка магнитным полем рассматривается в рамках, уравне-
уравнений магнитной гидродинамики в одномерном (плоском) нестационарном
приближении в лаграпжевых массовых неремеппых. Расчет начинается с
момента, когда плазменный сгусток входит в мел;рсльсовое пространство
и замыкает внешнюю электрическую цепь (рис. I, 6). Плазменный сгусток
моделируется ударной волной, распространяющейся по покоящемуся хо-
холодному газу, заполняющему рельсотроп. Скорость движения фронта удар-
ударной волны, размер сгустка, т. е. длина «плазменной пройми :;а фронтом вол-
волны и другие параметры уудачи согласованы с :м;счгерт;ептальпы.\ш даппыми.
В эксперименте плазменный сгусток, двигаясь от источника плазмы к
электродам, увлекает за собой газ, так что ;ia пим образуется разреженное
пространство, где давление мало. В расчетах это обстоятельство моделиро-
моделировалось с помощью лелого краевого условия по газодинамическим функциям:
на левой границе во все время процесса поддерживалось пулепоо дапление.
Правая граница — неподвижная стенка. На вей задается .-течение папря-
женности магнитного поли, закон изменении которого во времени вычисля-
вычисляется из электротехнического урапнения для гвешпей цепи. Слева магнит-
магнитное поле поддерживается раввым нулю. Такое условие означает, что ток,
текущий в цепи рельсотрона, целиком замыкается через плазму.
В расчетах пе учитывались процессы теплоперепоса. Как показывают
оценки, в рассматриваемом диапазоне изменения параметров влиянием теп-
теплопроводности и излучения можно пропебречь,
Соответствующая система уравиешш ;; ручается из общей системы
B.11) — B.20) в приведенной гл. VI (обозначения те же, уравнештя запи-
397
сапы в безразмерной форме):
— ( — ) — dv
dt \~p ) = ds ' ЪТ ^ '
dJL
dx_
dt
d_
of
de
ill
Г) ~
d
~~ d~s
P
II-
8 я
dll
IF.
P=p(p,T), e = e(p, Г), а=о(р, 71).
Эта система уравпппий решается в области 0 < s < Л/, г > 0. гдп Л/ —
массн плазмы в рельсотропе, отвосеппая и единице площади иопоречпого
сечения рельсотрона. Граничные условия, описавные выше, формулируют-
формулируются следующим образом
/>@, 0 =0, Я@, 0 =0, v(M, t) =0,
Я (AT, t) = lnJ(l), L-dJ/dt + R0/ — V(t) + E(M, t) = 0,
dV/di = —.//С, F@) = Fo, У@) = 0.
Здесь J(t) —ток в цеин рельсотрова, отнесенный к единице ширины элект-
электродов, Lo, Па, Со, Vo—электротехнические параметры введшей цени, пере-
пересчитанные для рельсотрона с единичной площадью поперечпоги сочепия.
У|)ннпепня состояния для водорода, а так;ке аависимость элег»троп|>о-
водности от термодинамического состояния вещества брались ил таблиц [401,
которые составлены с достаточно аккуратным учетом физики явлении.
3. Механизм образования монетой структуры. На рис. 3—5 представ-
представлены результаты расчета сформулированной выше задачи ;иш начального
напряжения на Патарее Vo = 750 в. Проводимость газа за фронтом ncNод-
ncNодной ударной волны невелика, истому плотность электрического тока i па
1>ис. 3
нача.и.ной стадии распределена лдесь равпомерно (на рис. 3 t = 0,04,
0,08 мксек). Соответствеыцо джоулев нагрев q также однороден, что приво-
приводит к равномерному прогреву ra:ia в пробке. Со временем левый ковец
прооки, граничащий с вакуумом, вачинает охлаждаться посредством волны
разрежения, распространяющейся направо. В результате охлаждения газ
здесь становится непроводящим.
По мере нарастания разрядного тока и прогрева газа в пробке ток ски-
нируется в ее передней части (рпс. 3). Здесь же локализуется джоулев на-
нагрев, а также электромагнитная тормозящая сила. Эти эффекты приводят
к вояникновеиию Г-слоя [33, 85] — области в газе с относительно высокой
температурой, которая поддерживается текущими здесь токами. Бурное,
взрывоподобное выделение джоулева тепла в зоне Г-слоя вызывает разброс
газа пз этой области, что, в частности, усиливает начальную ударную вол-
волну. С ростом полного тока электромагнитная сила, действующая в основном
в районе Г-слоя, увеличивается, что приводит к торможению Г-слоя и да-
далее к его остановке и движению в обратпом паправлетши. Это, в свою очередь,
порождает мощную ударную волну, идущую налево вниз по потоку. Од-
Одновременно образуется и волна разрежения, распространяющаяся направо
7 -
Рис. 4
вслед за исходной ударной волной. Поэтому газ в этой зопе справа от Г-слоя
охлаждается, а электрический ток и джоулев пагрев вытесняются в paiiou
фронта волпы. В результате возникает пторой Г-слой (см. рис. 4). Описан-
Описанные выше процессы, сопровождающие развитие Г-слоя, повторяются. Одна-
Однако интенсивность ударпоп волны, распрострпняющейся ваправо от второго
Г-слоп, мала, так что па пей следующий З^-слой уже по возникает. Рис. 4
позволяет проследить изменение температуры в течение всего процесса.
Таким образом, в потоке формируются неоднородности — горячие
Г-слои, разделенные золами .холодного газа. Характерный вид имеет и про-
профиль плотности. В районе Т-слоов плотность мала: при возпиквовении слоя,
сопровождающемся бурным выделением тепла, здесь происходит резкое
разрежевпе газа вследствие разлета. В процессе обратвого дишкевия Т-слои,
кап поршни, «сгребают» газ перед собой, уплотняя его.
На рис. 5 ва плоскости (х, t) изображены траектории движевил обра-
образовавшихся Г-слоев и фронта ударной волны. Сопоставление этого графика
с СФР-граммой рис. 2 укалывает на большое число общих черт.
R расчете фронт ударной волны движется, замедляясь, со скоростью
12—14 км/сск. Ото хорошо соответствует экспериментальной картине. <По-
лосатый» участок па СФР-грамме легко отождествляется с Г-слоями, раз-
разделенными промежутками холодного газа. Характерна «крючкообразная»
форма полос, наблюдаемая в эксперименте. Она соответствует форме тра-
траектории Г-слоев, полученной в расчете. Начальная часть траектории до
момента остановки слоя в эксперименте не регистрируется, поскольку тем-
температура в Т-слое на этой стадии еще невелика.
399
В расчетах, так же как и в эксперименте, варьировалось начальное на-
пряжеиие па батарее конденсаторов. Если напряженно ниже иекоторого
критического лпачепин V» D00 < [¦'„ <450 к), щ i,яртина течения принци-
uiiajii.iio изменяется: Г-слои
пи во.шнкают, слоистая струк-
структура исчезает. Таким образом,
порогового паппя-
,'щеииыи '
х,с»
30
и окспери-
значения
жишя в расчете
менте близки.
4. Влияние начальных, не-
одпородаостен плазменного
i'i-устка. Первоначально дела-
. mod попытки объяснить
слоистую структуру потока и
эксперименте как развитие
начальных пеодпородпостей,
исегда присутствующих и
пс\сд1:ом плаумеипом сгуст-
сгустке. Для проверки таком воз-
возможности был проведеп сле-
следующим численный акспери-
меит. I! начальны:! профиле
температуры за фронтом вол-
:<ы Ггллм гшесеиы во.чмущепкя,
[К'.импша которых составляла
5 %от самого значения темпе-
температуры. 1'асчет показал, что
iiepm.ni 7-СЛО11 возникает па
11(>:1мущ(!пчи, расположешю.м
бли-л.-С! всего к фронту иолпы,
<1 .'(атсм, расширяясь, .чахваты-
б
I'ilOT
:!V ei'(
1'пс.
описанные иыше
ту массу, где он обра-
и соотиетсгп> ющем ва-
рпс.'ота без тчальпых
i lice ха|>актерт1ыо
динамики процесса,
с возмущениями, в том
в п. 3, присутствуют п в расчете
числе наблюдается возникновение второго Т-слоя,
Остальные начальные воамутцения не ра.шмвагатси, ибо образопавшпп-
ся первый, а затем и втором У'-слоп за счет высокой илектропроводпостл
газа в них «экранируют» магнитное поле. Таким образом, модуляция
начальной температуры к плазменном сгустке с амплитудой. 5 % и ниже
но может явиться причиной вогшикповеппя. «полосатого» течения в рель-
сотроне в условиях рассматриваемого эксперимента.
В цоло.м сопог.тннлопие акенпрнмептяльных дпггных я результатов рас-
четои позволяет утпор;кдить, что в [7, 108] пкеиеримепталыю зарегистри-
зарегистрировано явление Г-слоя, открытое ранее теоретически [85].
§ 2. Сильноточный разряд с учетом эффекта
вторичного пробоя*)
1, Янлепие пторичного пр'.шоя в сильноточных разрядах. В эксперимен-
экспериментах но сильноточным импульсный галоимм разрядом в z-пппчах (рис, 6)
при определенных условиях наблюдается так назыпас.мая «особеппость» в
законе изменении со временем раарядного тока. Эта особенность возпикает
в перпом полупериоде колебания тока — в некоторый момент времени паде-
*) Эта работа выполнена авторами совместно с Г. В, Даниловой,
С. И, Курдюмовым п Л. С. Царевой. Подробное изложение работы можно
найти в [34].
400
япе разрядпого тока сменяется резким его иарастапием (рис. 7). Появле-
Появление особенности в токе сопровождается рядом дополнительных эффектов:
загрязнением илагшы примесями вещества, из которого вынолпепы стенки
разрядной камеры, и, как следствие, измененном ггллучательнмх свойств
плазмы, возникновением п плазме электрических токов, текущих в обрат-
обратном направлении но отношению к освовпому току, резким изменением
! jl :¦
!! I
Л i
Рис. 6
гипчм'рофплнчра.'пх характеристик разряда (нпдуктивности, сопротивле-
сопротивления) и т. д.
В свое нремя появление в разрядах подобных особенностей пытались
объяснить еще одним видом неустойчивости плазмы, в результате з:оторой
ила.тменпип шпур, изгибаясь, касается стенок разрядпой каморы [51. Испа-
реппов при этом вощвство стенок попадает в разряд, загрязняет плазму,
изменяя ее сипГютпа. Однако работы пос-
последних лет, а также переосмысливанпе ¦
старых :)|;спср11мс!гталы1ых данных заг.тан-
jijiiht отк;)латься от таког"| точки зрения.
Сейчас можно считать установленным, что
неустойчивость, по крайней мере п течение
первого нолупернода разряда, отсутствует,
так что нлазменпый шпур сохраняет осо-
ную симметрию [1.4, 1(M|.
13 [101, 11M1 предложена иная модель
для объяснения лилепнп, сопровождаю-
сопровождающих Бозпикппиепне особенности в разряде.
И пен сущестненпую роль играют процес-
процессы дт1С('.1'.1].чцпз1 :I10|)г;ш и, в частности, спетовое излучение, которое испаряет
вещество стопок разрядном камеры. В газе, образовавшемся в пристеночной
облпетн, п релул1.тате испарения происходит электрический пробой (так
пиликаемое «пторпчпое ia;itiirairne разряда»), пачипают течг. токи. Как по-
казынашт пкеперн.монты, эти периферийные токи могут стать сравнимыми
по величине с нолпым разрядным током.
R .жепериментах \А2] отмечался также мощный кратковременный пик
плектрпчесяого напряжения в разряде и наблюдалось появление частиц
с ныеоьой. энергией, ускоренных, по-видимому, возникающей большой раз-
разностью потенциалов.
После возникновения особенпости ток в центральном шнуре может
«отключиться» от внешней цепи. Тогда в плазме возникнет впутренний
Рас. 7
электрический контур, замыкающийся при помощи обратных токои, теку-
текущих по впутронпой части слоя испаренного вещества, Электромагнитная
энергия этого контура со временем дпссипируется.
Следует указать, что эксперименты по z-нинчам с вторичным пробоем
проводились для различных веществ (водород, аргон, гелии и т. д.). Ока-
аалось, что качественные и многие количественные характеристики процес-
процесса сравнительно слабо зависят от сорта газа.
2. Постановка задачи. В численных экспериментах задача о сильнотот-
ном разряде в гоомотрии z-пинч рассматривалась в рамках одномерных не-
нестационарных уравнений магнитной гидродинамики:
dv dp ill dr
!n=Vj
dt \ fi i
д (ту)
OS
az
dt ~~
a i ii \ _
dt \ ()/' ,'
f)(ru)
os
cis
ail'
OS
4д f/s
B.1)
p = p(p, Г), e = e(p, Г), о = а(р, Г),
Пдесь Я—азимутальная компонента наиряжеииостп магтштного иолн, /.',
i—ог.гяые сортавляЮ1г;ие алектридсч кого поля и и;км, W—поток энергии
светового излучении. Длп расчета <>тоа величины испольлугтгя урп
перекоса
юде
vft+i
T ,-1,2 т.
d 1
Г
W = 2 V Г /
гдо in — число групп по частоте [v^, va+i 1 ¦• иа которое разбивается спектр
излучения, (J., у — косинусы углов между направлением полета фотона и
осями г a z соответственно, /*(ц, у, г, t) — осроднонная интенсивность из-
излучения, а У.к — осредненный коэффициент поглощоцпя излучения в к-&
спектральной группе, /Vp — равновесная спектральная интенсивность из-
лучечпгн.
Решение системы B.1), B.2) ищется в области t > 0, 0 < s < М, где
М — масса плазмы, приходмщаяся на единицу длины разряда и один ра-
диап по азимутальному углу.
Граничные условия в цецтре на оси симметрии при s — 0 (г = 0):
о@, t) = 0, Я@, t) = 0, IV(O, t) = 0.
Предполагалось, что на правой грапице при s = М излучение иззшп отсут-
отсутствует, а движение плазмы ограничено неподвижной стенкой разрядной
камеры, радиус которой r(M, t) — гК: у (Л/, () = 0. Граничный режим пз-
мененин магнитного иолп оиределяегся соотношением
И(М, I) = 2J{t)lrK.
Разрядный ток J(t) в свою очередь определяется из электротехнического
уравнения для внешней цепи, которое для рассматриваемого случая,
где внешняя граница плазменного шнура неизменна во времени
R (t) = r(M, t) = гк, может быть записано в виде
dV_
dt
о'
/(О)- 0,
A~icn
Из-за отсутствия аккуратного математического описания явление элект-
рического пробоя, который происходит на рапней стадии разряда в при-
пристеночной зоне, в системе B.1), B.2) не учтеио. Чтобы аффективно смоде-
смоделировать последствия пробоя, начальное состояние газа выбиралось спе-
специальным образом (]>ис. 8). Холодный (Т ~ 300 СК) покоящийся газ при за-
дашю.м давлении />о равномерно заполняет разрядную камеру. Исключение
составляет пристеночная область Д <— 1 см
(гк = К) см), где температура составляет
1 за. Начальное распределение плотиости
p(s, 0) подбиралось так, чтобы давление всю-
всюду в камере было одинаковым и равным />,. т
Это предотвращает возникновение в па чаль-
ной стадии разряда искусственного движе- \
пня среды. |
И качестве вещества разрядной плазмы в |
расчета1: рассматривался литий. Данные по I
ураплешпо состояния и проводимости для не- |
го брались из таблиц [401, при их вычисле- О rK r
пшг прггпята во впимапце ионизация и ряд
других эффектов. Способ расчета коэффиц»- Рис. 8
ентов поглощения излучения света, учиты-
учитывающий процессы фотопоиизации и тормозного поглощения, описан в [62].
В расчетах использовалась перавпомерпая разпостная сетка, сгущаю-
сгущающаяся к оси и к краю плазменного шнура. Чтобы в процессе сжатия маг-
магнитным полем плазменный шнур мог «оторваться» от сетки разрядной ка-
-lu ры, последний массопый интервал геткп был «паделен» свойствами ва-
вакуума (я - 0, х».==0). Тяним образом, остллыпш часть плазмы, которая
является элоктропроводпом и модолируот иипч, может в процессе разряда
U.iMCIIfiTI, СВОЙ ]l,i:(.ML'|l.
При числсишом рршшшп задачи методом раздельных прогопок урав-
ноние '.шергин решалось совместно с мвогогрупиовым уравнением переноса
излучения С2.2| с помощью методов, описаниях в [62J.
Отмртим, что особенноегмо задач рассмотренного типа является нали-
наличие двух рс.чко различающихся масштабов времени. Один масштаб зада-
етсп полупериодом разрядного тока и определяется плсктротех'пическими
свойствами ралрида и впешпей цепи. Другой—связан с динамическими
пульсациями плазменного шнура: их характерное время, особенно на ста-
стадии максимального сжатия плазмы, и сотгш рал меньше полупериода раз-
разряда. Необходимость нккурпгпо обсчитывать псе стадии разряда, в том
числе н эти быстрые пульсации, приводит и весьма малым шагам сетки
по времени. Полтому количество шагов по времепи в отдельных вириаптах
расчетов, где сжатия плазменного шнура велики, доходит до нескольких де-
десятков тысяч. В силу того что на каждом шаге приходится решать итера-
итерационны мн методами сложную систему нелинейных уравнений, общие за-
затраты машинного времепи оказываются значительными.
3. Расчет разряда без учета испарении стенок. Чтобы получить исход-
исходный материал для построения модели «вторичного пробоя», которая будет
иснользоиапа далее и вычислительных экспериментах, предварительно бы-
была проведена серия расчетов без учета эффекта испарения стенок. Значения
электротехнических и геометрических параметров в расчетах выбраны в
соответствии с описанием реальной установки [42]; радиус разрядной ка-
камеры г к = Ю см со длина 2 = 50 см, радиус «обратных проводов» /¦«=14 ем,
индуктивность внешней цепи L = 100 см, активное сопротивление R =
= 5 • 10~3 ом, емкость батареи С = 48 мкф, начальное напряжение на ней
403
V<j = 20 ка, что соответствует :)не])гии около 10 кдж, начальное давлепио
газа г, камере pj ~ 0,1—0,05 мм рт. ст.
На рис. 9, а представлен график разрндпого тока J{1) для варианта I,
в котором начальное давление газа ро равно 0,015 ат (.масса плазмы М =
¦= 1,6 X 10"s г). Эта цифра па два порядка превышает значепие давления в
t, MKCSK
Рис. 9
эксперименте, где наблюдалась особеппостъ тока. Кривая J[t) на рис. 9, а
имеет гладкую форму, полупсрнод разряда составляет около 8,5 мксг.к.
На рис. 9, б указано изменение во времени радиуса плазменного шпура
(проводящей части плазмы), на рис. 9, а — его активного сопротивления
Лр('). Разрядный ток, пе превышающий в максимуме 300 к л, оказывается
J, ка г
200
здесь недостаточным для того, чтобы заметно сжать плазменный шнур, ми-
инмальный радиус которого составляет 8 см, В силу того что площадь по-
поперечного сечения шнура значительна, сопротивление Rp невелико. Неболь-
Небольшой максимум па графико Rp при t ~ 3 мкеек связан с сокращением разме-
размера шнура, а дальнейшее падение — с прогревом плазмы и увеличением ео
проводимости.
На рис. 10, а и б дапы аналогичные графики для варианта II с /;о =
•= 0,0015 ат (М = 0,16 • 10~3г). Количество плазмы здесь умепыпено на по-
порядок по сравнению с вариантом I, так что магнитное поле разрядного тока
уже сильнее сжимает плазму: минимальный радус шнура сократился до
2 ем. К моменту максимального сжатия (( ~ &мксек) сопротивление плазмы
возрастает, что отражается на графике J(t) в виде некоторого провала.
404
Однако этот провал, находящийся на спадающей ветви, нельзя отождеств-
отождествлять с особенностью тока, типичный пид которой дан на рис. 7.
Рис. 11, я и й повторяют те же кривые для варианта III, где ро =
= 0,00015 ат (М = 0,016 • 10~3 г). Эти значения параметров уже близки к
условиям экспериментов, где наблюдается особенность в токе. Величина
разрядного тока здесь по сравнению с предыдущими вариантами I и II
меньше. Однако количество разрядной плазмы настолько мало, что магнит-
нос поле тока весьма интенсивно сжимает плазменный шпур, так что его
радиус в момент максимального сжатия (t ~ 2,8 мкеек) сокращается до
Рис. И
нескольких .миллиметров. Импеданс плазмы при этом резко возрастает.
Сильны]) скачок испытывает и напряженность электрического поля. Так, на
границе плазмы с вакуумом она достигает 1,5 кв/см. Характерная «ширина»
пиков /¦.'(() и Itp(t) составляет 0,3 н- 0,5 мкеек.
После момента максимального сжатия плазма начинает расширяться —
радиус плазменного шнура растет, сопротивление и электрическое поле спа-
спадают. Однако магнитное ноли разрядного тока оказывается достаточно боль-
большим, чтобы удержать плазмевпый шпур на радиусе около 1 см. Разряд
выходит па так называемый кпазистационарныы режим, когда параметры
срашштолы.'о слабо изменяются со временем. Разрядный ток при этом ста-
стабилизируется на уровне примерно 120 ка. На квазистациоиарной стадии
разряда электромагнитная энергия, поступающая в плазму из внешней
цепи, почти целиком упосится световым излучением. Этот факт демонстри-
демонстрирует рис. 12, па котором предстачлен энергетический баланс разряда. Видно,
что энергия излучения, вышедшая из плазмы к моменту t — 7,5 мкеек,
составляет почти три четверти от полной энергии, запасенной в начальный
момент в батарее конденсаторов. При этом основную часть световой энер-
энергии разряд излучает в момент максимального сжатия и далее во премя
квазистацпоиарпоп стадии. Таким образом излучение—существенный фак-
фактор, определяющий энергетику и динамику разряда. Этим, в частности,
рассматриваемая модель z-пинча отличается от модели в работе [14], где
излучение не принималось во внимание. Поэтому в [14] диссипация энер-
энергии в разряде происходит медленнее, ы это сказывается па «упругости»
плазменного шнура, радиальные пульсации которого затухают медлеппо.
Расчеты показывают, что в процессе сжатия плазменного шнура в
плазме под действием электромагнитных сил возникает ударная волна, схо-
сходящаяся к оси симметрии. В момент кумуляции волны на ось температура
плазмы достигает 10 ов, а в центральной зоне шпура возникают больгапе
значения плотности (до 10~3 г/см3) н электрического тока (до 1 мга/с.ч2).
Правда, зона, в которой локализованы эти токи, имеет небольшой размер:
ее радиус составляет доли миллиметра. По мере сжатия плазмы величина
тока здесь нарастает.
Описанные расчеты, проведенные без учета испарения стенок камеры,
по своим результатам качественно отличаются от соответствующих экспе-
405
римептов. В частности, эти расчеты не содержат экспериментально наблю-
наблюдаемую особенность в законе изменепия со временем разрядного тока. Это
делает необходимый внесение в расче-
расчеты дополнительных элементов.
ri. Расчет разряда с учетом эффек-
эффекта вторичного пробоя. Предыдущие
расчеты показывают, что излучение
плазмы играет существенную роль в
формировании разряда. Величина пото-
потока светового излучения достаточна для
того, чтобы испарить заметное количе-
количество вещества со степок разрядном ка-
камеры. Наиболее интенсивное излуче-
излучение наблюдается па стадии максималь-
максимальные сжатия плазмы. К атому же мо-
моменту, как свидетельствуют расчеты,
j-ersKo возрастает и напряженность
электрического поли в разряде. В ре-
'.y.ii.iiiTe no образовавшимся у стенки
парны может вновь произойти электри-
электрически'! пробои («повторное нажигание
разряда»).
''. вычгслптелышх экспериментах
:.:от . ффепт моделпрог.идся следующим
ойрл.мм. .'.а оспону брался нариапт III
п.ч предыдущего пункта с давлением р0,
6.!ii;i; iiM к аксперииеиталымму. Резуль-
Результаты, полученные п утом варианте, на
некоторый момент (%, предшествующий
максимальному сжатпю шнура, исполь-
:obii.i:tci, в качестве исходных данных
для дальнейшего расчета, где помимо
прежней массы плазмы М в рассмотре-
рассмотрение^ включалась дополнительная мас-
са .17, соответствующая испаренному ве-
распределялась вблизи степкн камеры в виде
.. чкеек
Рис. 12
ществу стопок. Эта масса
слеш толщины Л (рис. 13).
Пространство между атой массой и центральным плазменным шнуром
(зона В па рис. 13) есть вакуум. Параметры испаренного вещества (рас-
(распределение плотности, толщина оболочки Л1 варьировались, причем ока-
оказалось, что они слабо влияют на результаты. Температура паров задавалась
-' тг' : i
* "' -
1
«а
а
"(Г/
Гнс. 13
достаточно большей A-^5 эв), чтобы аффективно имитировать послед-
последствия происшедшего здесь вторичного электрического пробоя, В качестве
испаренного вещества в расчетах для простоты рассматривался также
литий. Однако параметры, определяющие численные значения клектропро-
200
водности и коэффициентов поглощения излучения в этой зоне, варьирова-
варьировались в широких пределах. Расчеты показали устойчивость результатов
относительно этих вариаций.
Варьировалось и начальное магнитное поле, В частности, расчеты про-
проводились для двух предельных случаев: с магнитным полем, напряженность
которого распределена п зонах В, С, D по закону
Я (г, «») = 2/(«»)/г,
а также с нулевым магнитным полем в зоне С. В силу того, что область С
находится па сравнительно большом расстоянии от центра G—10 см),
различие в исходной магнитной .зпергии между обоими вариантами неве-
невелико. Качественно :>тп варианты отличаются друг от друга тем, что в ва-
варианте с пулевым магнитным нолем в зоне С на внутренней ее поверхности
в расчетах паплгодаютск обратные токи, мялянные с проникновением сюда
магнитного поля ил центральной области. Пока магнитное иоле не успело
еще проникнуть и лону С и здесь сохраняется линия, вдоль которой напря-
напряженность магнитного unaed ыиоп нулю
(«нулевая линия магнитного поля»),
суммарный обратный ток по величине
равен центральному. Такую ситуации
можно трактовать как существование
в плазме замкнутого внутреннего элекг-
рцческого контура.
В расчетах время существования
такого контура составляет 0,5 -.-
-ь 1 миген. По мере «заполнении» зо-
зовы С магнитным полем обратные токи
уменьшаются, что эквивалентно «под-
«подключен пю» центрального тока к внеш-
iie.i :i,e::if.
('формулированная задача описыва-
описывает реальные, процессы, сопровождаю-
сопровождающие нтирлчпын нроГюп, упрощенно.
Фактически зде.с, предполагается, что
испарение р.ещества со стенок происхо-
происходит .МП1О1ШППО, в момент 1^., в то вре-
время как па самом деле этот процесс про-
продолжается в течение некоторого про-
промежутка времени па стадии интенсив-
интенсивного сжатии плазмы. В расчетах качест-
качественное влнлиие этого фактора оценивалось с помощью вариации момента
испарен Hit и вторичного пробоя, т. е. параметра t,.
Другим важным параметром задачи, значении которого заранее неиз-
неизвестно, .<ii-.-i!ii-fe,f и, личина массы испаренного вещества М. На рис. 14 при-
приведены .liii.ijiauuu pa 1Г1ЯДНОГО тока для различных значений Л/ (варианты
IV- -VI). Для мрианта IV М составляет 4 % от массы центрального плаз-
плазменного шпура. Результаты в этом случае практически не отличаются от
расчета парн.ття Ш. Оболочка из исиарепппго вещег.тва {С) разогнанная
магнитными силами до больших скоростей, быстро «падает» па централь-
центральный плазменный шпур,
В варнапте V (Л/ = М) разрядный ток при 2>г„ испытывает некоторые
колебания и затем выходит на режим, близкий к вариантам III, IV.
В варианте VI дооавленная в рашяд масса почти на порядок превы-
превышает массу шнура. Полученный в этом расчете график разрядного тока J(t)
качественно и количественно близок к ;>ксиериментальньш кривым с «осо-
«особенностью». Проанализировав серию расчетов, делаем вывод о том, что
принятая в расчетах модель эффективно описывает реальное явление
лпшь при достаточно больших значениях пепаронной массы, в несколько
раз превышающих величину массы центрального плазменного шнура,
407
- %М
бариангг 7 М=М
вариант W
t»=2,7S
Рис. 14
Сопоставляя результаты расчетов задачи о снлыготочпом разряде при
учете повторного пробоя с данными экспериментов, можио заключить, что
они в целом соответствуют экспериментальной картине и содержат ряд
«топких» качественных аффектов, наблюдаемых реально.
§ 3. Магпитогидродииамическая модель вспышки
сверхновой *)
1. Математические модели шшшкп сверхповой. Выяснение механизма
вспышки сверхновой, построение и исследование математических моделей
итого явления составляют собой одну п-ч важных астрофизических проб-
проблем. Имеются два типа моделей пс.пышкп: согласно одной из них" вспышка
есть следствие гидродинамической неустойчивости, согласно другой—теп-
другой—тепло кои неустойчивости.
Результаты, полученный к настоящему времени в рамках указанных
моделей, не ино.тпп енпжмегпуют данным наблюдении. Кроме того, в :>тих
моделях нитрируются г;п по важнейшие характеристики звезды, как вра-
вращение и магнитное по.,41. Между чем скорость вращения :;и>-:-.д на сланной
последовав литости до.чод.пт до величин -00 >,-,»/<ч->: на :)ku«it(i|)c [IOfi|.
Наблюдения п\ :ы;|ров \''-] П'';;а я.шают также наличие па н\ понерх-
пости сильного магнитного под;!. I'lTii'.'TpnpyPMaH ci;opocTi. прапюпии пуль-
пульсаров значительно меньше продельного яычеегп;, мри котором цонтробоя!-
лая сила па акпаторе рапп.ч гравитационной. Так как- ii[iii сжатии с сохра-
сохранением полного момента вращения .пн'.дл главной пос.н.'Доп.милыгостн до-
стпглст предельного пращегшя при плотности, значительно меньшей, чем
и нейтронной звезде, то т.-пмн звезда п процессе оволюцип дол;кпа терять
момент прашеппя. При :>-;о\г но -.mis,1.ч.> выделение значительной опергии
вращения, соответствующе и по ппоя.мл величины зпертетике взрыва
Pi рабою [8] нрелтг,!;.'па М"Де п. пенышкп сг.ерхпопой, происходящей
:'.а счет тгергпп вращеин;;. I! к тесгве механизма, способного обеспечить
быструю передачу момента вращения ядиа периферийным частям апозды,
раее.матрпкается маппггтЮ" плапмодепствпе.
2. Ностапопка задачи. 13 чпедеппыч расчетах взрыв cnepvuonoii рассмат-
рпг.ается и одномерном (осевая симметрии) нестационарном магпнтогпдро-
дипамг,чее|;ол| ирпблпи^чпщ. ,'!не!да представляется в виде вращающе-
вращающеюся гравптмрующего бесконечного цилиндра
*''' .'рис. М). Центральная часть иплпндра, соответ-
' ." т ствующая устойчивой нейтронной звезде, пред-
, -у'/'"-'¦""¦ полагается несжимаемой, ее радиус со временем
по изменяете!. 1'нешпяя газообразная оболочка
моделирует ат.мсеферу звезды. Реально подобная
i.-.'i; мша мо;кег нчзнпкпуть на определенно!"! ста-
.i:i:i :>;;од|оц>п; ззеиды. когда и результате потери
у(;¦'¦¦!;'¦¦! '¦ п;-т-: и последующего коллапса обра-
образую 1ся тт*]-.-|;>гслыю ирпща!ощоегч ядро (устоя-
¦¦ш,!,1я не. I ронная звезда) и вращающаяся нок-
руг iici к ,' I мое фора.
P. .la i;i =!•.' рпесматряваются днить процессы,
I'm1, la ;lp()iic\ii.;;ii;iiie и оболочке При г > /!'. (ем.
:.iic. [.")¦ lii'1'1 1ГОМ полнеть нзметчизц прострал-
С.1СТРМЫ, что iio.UiijiiH'T внести ра-
спн;ппон
;[на.'|Ы1\'ю
п'ремепяоп не co;ii'p;;;ii :¦ ,it-.i
папряигецпогч я м.пямтпого зюля. которая- в против-
противном случае тождественно равнялась бы нулю (см. п. 1
Вешестпо ободочки ечнтаотен нимл.мо проводящим (п
тенле peiioi'a отсутствуют, учи ii.m.i-i;ri-i- .шить потери ка
лучоппе. Физическая нязкос'п, in ii<m-/.м н-рпвастся,
5
та!
2 гл. VI).
нейтринное п.1-
по eiKi.'i. ме;кду
*) Подробно .iTii модель ir i.i'i'.'a'ii : ;; ! '. 'i. И].
слоями атмосферы в процессе вращения осуществляется лишь за счет маг-
магнитных сил.
Внешняя граница звезды есть граница с вакуумом, начальное распре-
распределение плотности моделирует резкий переход от плотных внутренних сло-
слоев к разреженным внешним.
Полный момент вращения системы (центральное ядро и оболочка) ос-
остается неизменным во времени, однако в процессе эволюции может про-
происходить «перекачка» момента из ядра в оболочку и обратно. Естестествен-
но считать, что скорости вращения внутренних слоев оболочки и внешней
границы ядра совпадают, т. е. оболочка вращается относительно ядра без
проскальзывания.
Предполагается, что в начальный момент времени на стационарно вра-
вращающуюся систему (твердотелмго вращающееся гравитирующее ядро и
дифференциально вращающаяся оболочка) пакладынаотся магнитное поле,
сил оные линии которого радлальны. В процессе дальнейшего вращения
в силу «вморои>снпости» магнитные силовые липни искривляются, появля-
появляется азимутальная компонента магнитного поля и связанные с ней осевые
электрические токи.
Ил (Ьпаических соображен ни следует, что полный ток через поперечное
сеченпе. рассматриваемой цилиндрической звезды должен быть равен нулю
п, следовательно, ашшутальпор магнитное поле па поверхности оболочки
должно обращаться в пуль. Такуо ситуацию можно трактовать как за-
мыкапио мектрпческну токов на «бесконечности», т. е. существование зам-
кпутых петель тока. Это соответствует реальпой картинг, наблюдаемой для
сферических звезд.
Система урашгошш для описанной задачи может быть получена из
системы {2.21) гл. VI (см. также B.28), B.29)) при о = оо:
-lf-L'j= '''("'I, ±=v, гОЧ-=и, C.1)
(It \ (i / (Is Ot ot
ill - Г. .: - Г _^ - J -?- Lr"*l. -L g, C.2)
ot r os r ds 8 Л
" (''"'> — '_ r_ " (' <p) C 3\
~'rt 4H oi K '
- ['--¦'-) -r/IrJL(l), ,//,.-.. A - const, (Vi)
at. \ ;w ; r (h ¦¦ r ! '
''*{¦=— p—~—-\ /(f. T), C.5)
/; = p(p, T), e = F.(p, T). C.6)
П допплщ ii не т: принятым v, r.i. VI обозначениям здесь g =
— 1n-V/Af. '-;,¦) •• гряиптацпон,!,::! iii.i.i, G — гравнтацношнш постоян-
постоянная, .If,, - масса я.Ч;',"|. прн^одннишегт на ечппицу длины цилиндра и угол
и один р:паап. f - - пот'рп oiicfirini па [i:iiTpnnnne пзл\гчгнне, ср — азпму-
Tiuii.ni.iii ,\ т.ч.
Система уравпопнИ решается в оплаггп ( > 0, 0 < s < .If (/?,, < г< R(t)),
где 3/ - масса оболочки, отнесенная и (¦.•пптппе длппы и \тлу в однп радн-
»п. Ii-,. IHD соотпетстпепно внутр'пппп ti впешппп т'йдпусы оболочеи.
Крагвы'1 vcnniMiii. физическое си ii ir.i.-.-nnie которых обсуждалось выше,
::аш1гыи:1 in'1'ii г.нмуюлпш образом
.;.!/. /) --= 0 // I !/. ¦) = 0, C.8)
где и(') \ ишная скорость вркшсиим ;i им. Условие ппотопнетпа момента
21 а. А Г,|\мс>. | mi У) П Попоп *^9
вращепия системы fimглядит так
м
-1 MaRQu (О, t) + I r (s, t) и (s, i) ds = const. C.9)
о
Заметим, что дифференцируя условие C.3) но времепи и используя урав-
вепие C.3) в сочетании со вторым условием C.8), можно привести C.0)
к виду
М dh
Уравпепия состояния C.6), а также вид фупкции для пейтринпых по-
потерь /(р, Т) задавались с помощью снецпальпых апнроксимациоппых фор-
формул, учитынающпх различные физические аффекты (подробнее см. fill).
Начальпое распределение плотности p(s, 0) подбиралось так, чтобы смо-
смоделировать ро.1кое ее падении в оболочке от ядра к внешнему краю. Длп
этого использовались зависимости типа
p(s, 0) ~ 1/г" C.10)
или
р(«, 0) ~ехр[-а(г-Д0J], (ЗЛО')
где парамет[1Ы п. а подбирались в соответствии с конкретными физическими
особенностями задачи.
Предполагается, что в начальный момент радиальное движение отсут-
отсутствует (r(s, О) = 0). Начальная скорость вращения частпц u(s, 0) но кен-
леровским орбитам определялась из уравпепия
u-(s, 0)/(r(s, 0) —r(s, O)dp(s, 0)/3s + ?C, 0) = 0,
которое елг-дурт из уравнепия движения C.2) при t = 0. Походное распре-
распределение давлешш p(s, 0) вычисляется по заданным профилям p(s, 0) и
T(s. 0).
Чтобы полностью определить начальное состояние системы, необходимо
также зядать начальпую угловую скорость вращепии ядра: п@) = (о0.
3. Результаты расчетов. Основными безразмерными параметрами, ощ'О-
делмгощими peuieiiuo сформулированной выше задачи о взрыве сверхиошш,
являются отпошсиия
'^ = л3/1.-.л/:-0!(|-, \'^7Si), Р ~ л/о/л/.
Параметр а характеризует отношение начальной магнитной цнергии систе-
системы к киЕ1Стичос!;ой (или гравитационной), параметр р равен отношению
масс нейтрального ядра и оболочки.
В расчетах', описанных пиже., параметр [1 = 1, что соответствует реаль-
реально наблюдаемой ситуации, когда масса ядра звезды и масса атмосферы с.рмп-
нимм. Параметр ос варьировался в днапаюпе Ю~' с' с. sj 10" 8. Отметим, что
велпчнпи наиряженпости млгаитиого ноля па новерхпости нейтроппы*
зпепд-пульсаров, онределенпая на основе их замедления, не превышает по-
поличины 5 • 1013 гс, что соответствует значениям а ^ 10 8 (характерный ра-
радиус нейтронной звезды в расчетах принят Ro — 10е см, масса на единицу
длины 2лД/0 = 0,5 • 10~5Д/с. Мс — масса Солпца). Следует, впрочем, hwi'ii.
ввиду, что паблюдаетс» только полоидальпая компопента магнитного поля
нейтроппых ,чг,е:(л. Bo:iMo;r:iio, что тороидальпые поля внутри neiiTpoiniofi
звезды па 2—3 порядка сильнее, так же как магпитное ноле солнечного пит-
ва заметно сильнее среднего поли Солпца, П птом случае величина а будет
составлять 10"—Ю~5. Укажем, что основную трудность для математиче-
математического моделирования представляют варианты задачи с малыми зпачепия-
ми а, требующие для расчета большого машинного врр.мепи, пропорцио-
пропорционального 1/Уя, Поэтому для выяснепия общих закономерностей процесса
410
-10 \-
Рис. 16, a
-ю\
Рис. 16, б
расчеты были начаты с более «легких» вариантов, отвечающих значениям
о « Ю-1—10~2. Начальная температура в расчетах была принята нулевой:
T(s, 0) = 0. Так как характерной время задачи проиорциоьально 1/1'сс, удоб-
удобно при анализе п сопоставлении результатов расчетов с разными а вос-
воспользоваться некоторыми новыми переменными функциями:
ta=Vat, va = -
t = T7=- C-11)
Остальные функции остаются без изменения.
На рис. 16 дана полученная в расчете картина процесса для значения
а = 10~2. Здесь на последовательные моменты времени ta = 0,5, 2, 10
представлены профили функций ра, va, Ta, га, (йф)а и угловой скорости
Рис. 16, в
соа = и/г по переменной s, отпормированной на единицу. (На рисунках пы-
декс а у функций опущен.) Рис. 16, а, вьшолиеппьш для ta = 0,5, соответ-
соответствует начальной стадии, Видно, что за счет вращения и «вмороженностн»
возникает азимутальная компонента магнитного поля kv. Положение di.ct-
ремума функции Аф = г//ф определяет точку, где происходит смена зпака
возникающей радиальной компоненты скорости v (точка М на рис. 16, а).
Часть оболочки, расположенная слева от этой точки, «падает» на ядро и.
уплотняясь, «палппарт» на него. Вещество справа от точки М движется на
периферию, образуя разлетающуюся часть оболочки. Как следствие, в ок-
окрестности точки М паблюдастся провал плотности. Со временем точка М,
где имеет место изменение знака радиальной скорости и, перемещается
по массе к внешпей границе оболочки, приблизительно «отслеживая» поло-
положение экстремума функции Лф (см. рис. 16, б, в). Исходное положение кри-
критической точки М определяется начальными данными, в частности, рас-
распределением плотности p(s, 0). При вариации атого профиля положение
412
точки Л/ нссколi,i;o изменяется, однако оощая картина процессов остается
прежней.
Вследствие пращепия ядра в оболочке формируется магнитогидродпна-
мическая ударная волна, фронт которой движется по радиусу вслед за точ-
точкой М. Возникающая ударная волна является медлепной магнитогидроди-
намической, скорость ее фронта меньше альфвеновской: при переходе через
фронт волны функции р, Т, v возрастают, а функции и и /гф — убывают.
Фронт ударной волны хорошо разрешен на рис. 16, бив.
На рис. 17 представлены на последовательные моменты времени про-
профили температуры (цифрами у кривых указано соответствующее значе-
значение ta). Видно, что за фронтом ударной волны температура имеет довольно
Г,
V
V
3
1
I
Гис. 17
Рис. 18
резкий пик, откуда в основном наблюдается нейтринное излучение. Источ-
Источник нейтрино / в C.5) резко зависит от температуры (/ ~ Г6), поэтому из
области, расположенной ближе к ядру, где температура становится ниже,
нейтринное излучение несущественно.
Рис. 16, а — в показывают, что за фронтом ударной волны образуется зо-
зова, примыкающая к ядру и твердотельно вращающаяся вместе с ним (угловая
413
скорость со здесь практически постоянна по радиусу). Радиальное движение
в зтой области отсутствует, температура и функция Лф распределены одно-
однородно, толщина этой зоны сравнительно невелика (см. график '(«)). Фак-
Фактически возникает новое ядро, масса которого со временем возрастает по
мере продвижения фронта ударной волны и дополнительного «налипания»
на центральное ядро вещества оболочки.
Рис. 18 демонстрирует эволюцию во времени пространствешшго распре-
распределения угловой скорости вращения ш (цифры указывают апачеиие ta). Хо-
Хорошо видно движение ударной волны, во фронте которой со терпит разрыв,
и твердотельпо вращающаяся (<о ж const) часть оболочки, «налипающая»
Рис, 10
па ядро. К моменту ta = 6 цептра.и.пап часть ооолочки вместо с ядром
изменяют папраплепнг1 вращения. Максимальное значение угловой скоро-
скорости, достигаемое при обратном вращения, составляет одну треть от началь-
noii скорости вращения ядра.
Рис. 19 отпечает расчету, выполненному для значения параметра а =
= 10~4. Сопоставлеппе ятих графиков с piic. ifi, б, относящимся к тому же
МОМСПТу BpeAItMIIf ta = -, ПО ДЛЯ а = l'.i 2, ПОЗМОЛЯСТ СДРЛЭТЬ ВЫВОД О ТОМ,
что решения задачи ирл различных а являются качественно сходны-
сходными. При различии в величине а на два порядка функции ра, Та, а>а,
1>а{Ю* и т. д. (см. C.11)) отличаются незначительно. В то же время
сами фупкц:гп, например, г, hv для атпх значепиГг а отличаются па
порядок. Таким оорачом, расчеты ног;азывают, что решение рассматри-
рассматриваемой задачи о взрыве сверкяовоп обладает своеобразным «квазипо-
добием» относительно изл(енепия параметра а. Это факт подтверждает и
рис. 20, на котором представлепы па момент /а = 2 результаты расчета для
значения а = 10~3.
Отмеченное обстоятельство является весьма важным как для понима-
понимания природы явления в целом, так и для экстраполяции количественных
414
результатов расчетов в область малых а, где проведение прямых расчетов
затруднено требованием болыпого .машшшиго времени.
При малых а начальное магнитное поле является слишком слабым для
того, чтобы вызвать заметное радиальное движение в оболочке. Со време-
временем в процессе вращения звезды происходит «намотка» магнитных силовых
линий па ядро, в релультате чего возрастает напряженность магнитного по-
поля и усиливается .магпитогидродинамическое взаимодействие. Процесс ока-
оказывается как бы патяпутым ло времени в 1/а раз. Сравнительно медленное
выделение эперпш в вариантах с малыми а хорошо соответствует требо-
вания.м, следующим из паблюдении кривых блеска сверхновых.
Рис. 20
На рис. 21 изображена Сорма м.ичшпюп nuioBoii липни па попоит
промоин tn = ~ для двух вмриаптов расчета: а = 10 2 (шгрпловая линия)
и а= 10~4 (силошная линии). Количество оборотов силовой линии отлича-
отличается примерно н \а pu;i. В процессе нюлюцип знезды ео вращение замед-
замедляется, а ;шерп:>1 вращения переходит главным образом в магнитную и
тепловую элештио, которая в свою опередь частично превращается в энер-
энергию нентрпиыого излучения. На поздней стадии потери на нейтринное из-
излучение составляют уже более ноловппы всей лнергии. Величина кинети-
кинетической .шергин радиального движения нарастает со временем, однако в
общем балансе ее ролг. ненолика, например при а = 10~2 лта энергия со-
стаиляет около пяти процентов от всей энергии. По .мере уменьшения а
эначегше кипотнчоской оперши радиального движения еще более падает.
Следует одпако иметь в виду, что к концу процесса практическп вся кнпети-
ческая энергия оказывается сосредоточенной в разлетающейся части обо-
оболочки, которая имеет сравнительно малую массу. Поэтому величина удель-
удельной кинетической энергии здесь значительна.
415
Как показывают распеты, ири больших временах (ta ~ 40) продолжа-
продолжается разлет около трех процентов массы оболочки. Внутренняя же часть
оболочки, твердотельпо вращающаяся вместе с ядром, совершает враща-
тельпыо колебания около пулевого значения со, причем максимальная ско-
скорость вращения составляет около одпой десятой от начальной величины шо.
Очевидно, что в силу принятой в задаче одномерной цилиндрической
геометрии и соответствующего гравитационного потенциала в конечном ито-
итоге разлет внешней части оболочки прекращается и ее вещество начнет па-
падать па ядро. В этом состоит один из недостатков одномерной постановки.
Рис. 21
Однако полученные для случая цилиндрической симметрии результаты да-
дают возможность пронести оценки еорошеппоп массы для сферического слу-
случая [2|. -On опепки приводят i; выводу, что пеличпгга сброшешшй массы
составляет о'.'оло 13 % массы пболичкп независимо от значения а, а кпгге-
тпческая ;-.иет)п1я cfiponiennoii массы составляет порядка З.Т> % от пачальпой
лнерпеп сш'.тсчщ для а = 10~4 и около 8 % для а = 10. Если припнть
17о = 1• 10~'-6';1/с п оценит!, лпергпю вращения в 1053 прг. то 1;инетическая
энергия сорошеипои части оболочки, составляющая Я • 10"' эрг, вполне со-
соответствует ¦.шоргетпке взрыва све[>\!юпы>:.
Оцеиивая в целом результаты численного модслироваппп мапшторота-
HiioiFiioro n.'ipFiinii сперхповой, следует сказать следующее. 11сслг>довапие,
п[)опедениое и рамках одномерной цилиндрической модели, можпо счптать
достаточно полиым. Оно аозиоляет выявить принципиальные черты явле-
явления: расслоение оболочки, возникновение медленной МГД — ударно1'г волны,
обра'юпапне центрального ндра. увеличивающего свою м.цту в процессе
лволюции. вылет на иолыиое расстояние от ядра некотором части m-iccfi
оГюлочии, несущей .iffhhiiтельную величину кинетической -шергнп и i* д.
Количественные оценки сделанные иьпне па основе расчетов, так:м'. удон-
летворителыю сопоставляются с нш'людаемыми фактами. Поэтому успеш-
успешное научение одггомерноГг модели mo;i;iio [>пссматривать как nepBF.iii лтап
исследования, обосновывающий целегооираапость дальпейпмто усоверп.".;пст-
вовапия модели и. в частности, переход к двумерной постановке а.чдачи.
СПИСОК ЛИТЕРАТУРЫ
1. Андрианов A.M., Б а з и л е в с к а я О. А., Прохоров Ю. Г. Ц
Физика плазмы it проблема управляемых термоядерпых реакций. Т. II.—
М.: Изд-по АН СССР, 1958.
2. Л р д е л я п II. В., Б и с п о в а т ы й - К о г а п Г. С, Попов Ю. П.
Исследование магпиторотацшшного взрыва сверхновой в цилиндрической
модели / Астрономический журнал.—1979.—Т. 56, № 6.—С. 1244—1256.
3. Ар делян П. В., Гулин А. В. К обоснованию устойчивости раз-
ногтгп.гх- г\ем для уравнений акустики.—Пренршгт/ИПМ АН СССР.—М.,
1978,— № !)Г).
4. Лрделяп П. В., Попои Ю. П. Особенностп прпмепепип числен-
численных методов в задача* о мгииторотациоииом взрыве сверхповой.—- Пре-
припт/ИПМ АН СССР.-1970,-Л» 107.
5. А рцимовип Л А. Управляемые термоядорпыо реакции.— М.: Физ-
матги:1. -1003.
В. Афанасьев Ю. В., Басов П. Г., Г а м а л и й Е. Г. и др. Нагрев
и сн.-атио лазерных- лишенец — Преприпт/ФИЛН СССР.—М., 1977.— № 167.
7. Вере .тин И. С, Жидков II. П. Методы вычислений: В 2 т.—
М.: Физматгиз, 1i)fi2.
8. Бисноватый-Koran Г. С. О механизме взрыва вращающейся
звезды как свермювон // Астрономический журнал — 1970.— Т. 47, № 4.—
С. 813.
9. R о р е л и н К). А. Численное исследование нелинейных волн в раз-
разреженной плазме.—Новосибирск: Наука, 1977,
10. Б и с и о в а т ы й - К о г п н Г. С, Попов СБ., Попов 10. П. Пе-
лшн'йпая трансформация МГД-полп в изотермической среде — П|)еприпт/
ИПМ АИ СССР — М., 1080.—№ 90.
11. Б и с н о в а т ы й - К о г я п Г. С, Попов 10. П., С а м о х и н А. А.
Магнитогидродиннмнческая модель взрыва сверхповой.— Преприпт/ИПМ АН
СССР.—М., 1975.— № 16.
12. П о б ы л е в А. В., Ч у я п о в В. А. О полностью консерпатпвпых
разностных схемах для кипетического уравнения Ландау.— Преприпт/ИПМ
АН СССР.— М., 107Л,— М 28.
13. Б о р з у н о в II. А„ О р л и н с к и и Д. В., Осовец С. М. Исследо-
Исследование, .мощного импульсного разряда в газах с помощью скоростной фото-
фоторазвертки II Атомная оперта.— 1958.— Т. 4, А» 2.—С. 149—153.
14. Б р а г и и с к н й С. И., Г е л ь ф а н д И. М., Федор ен ко Р. П. //
Физика плазмы и проблема управляемых терлюядерпых реакций. Т. IV.—
М.: Изд-по АН СССР, 1958.
1Г). П и х р е в В. В., Г! е м с к о в А. И., Прут В. В., X р а и р о в В. А.
Моделирование процесса рачряда на ЭВМ / Вопросы фпзш;и гшзкотемпе-
ратуппой плазмы.— Минск: Наука и техника, 1970.— С. 276—282.
16. Волкова Р. А., Головизиин В. М.. У л и ir ц ч Ф. Р., Фавор-
Фаворский А. П. Числшшоп моделнровапис обжатия магпптпого ноля куму-
лирующим лайнером.—11репринт/ИНМ АН СССР.—М., 1976.— № 111.
17. В о л о с с в и ч П. П., Г а м а л и й Е. Г., Г у л и н А. В. и др. Дву-
Двумерные эффекты при лазерном сжатии стеклянных оболочек // Письма в
ЖЭТФ.— 1976.— Т. 24, № 5.— С. 283—286.
417
18. В о л о с е в п ч П. П., Го л ь д и п R. Я.. Калиг к и и II. П. И др.
Некоторые стадии сильноточпого разряда в плалме.— Преиринт/ИПМ АН
CCCI1.- - М., 1071.-- Л: 40.
1М. Г а с и л он В. Л., Го л овил пин В. М.. Т а р а п М. Д. и др.
О численной моделировании Релей — Теилеровскоп неустойчивости в несжи-
несжимаемой жидкости.— Препритгт/ППМ ЛИ СССР.—М., 197!).—ЛЬ 70.
20. Гаси лов В. Л., Куртмулаев Р. X., Голов из нив В. М.
и др. Численное моделирование компрессии тороидальной плазмы квазисфе-
рпческим лайнером.—Нрепршгг/ППМ АН СССР.—М.. 1979.— Д» 71.
21. Г о д у п о в С. К., Р и б с и г. к и й К. С. Разноствые схемы.— М.: Нау-
];а, 1A77.
22. Г о л о п н з п и н В. М., К о р ш и я Т. К., Самарский Л. Л., Ф а-
в о р г к и й Л. II. О вариацпопно-разноепшх схемах двумерной магнитной
гидродинамики.--Пренрипт/ИПМ ЛИ СССР.— М., 1977.— Л« 57.
23. Г о л о в и '1 пин В. М., Самарски ii Л. Л., Фаво р с к и й Л. П.
П.фиациопный подход к построению копечно-рпяпострых моделей в гидро-
гидродинамике // ДЛИ СССР.— (977,—Т. 23.", X 6.—С. 1285—1288.
2'i. Г о л i> л ii и В. Я. и др. Исследование задач магнитной радиацион-
радиационной гидродинамики численными методами пи ЭВМ.— Пренриит/ИПМ АН
СССР.—М., 1971.— „V: 36.
25. Голь дин В. Я., И о п к м п Н. П., Калиткнп Н. Н. Об пптро-
пинной схеме расчета газодинамики Ц ЖВМ и МФ.— I960.— Т. 9, As 6.—
С. 1/A1-1413.
26. Гольдип В. Я., Калиткип И. II. Электрический взрыв прово-
проволочки.— Пргпринт/ИПМ АН СССР.— М., 1970.
27. Г о л ь д и п В. Я., Калиткип II. Н., Л о в п т а п Ю. Л., Р о ж-
д е с т в с и с к и ii Б. Л Расчет двуыерпых течешш с детонацией / ЖВМ
и МФ.— 1972.—Т. 12, № 6.—С. 1606—1611.
28. Гущин II. С, Попов 10. II. К расчету аадач магнитной гидро-
д;:|'<шпки с учетом фазового перехода / ЖВМ п МФ.— 1977.— Т. 17,Л» 5.—
С. 1248-1255.
29. Гущип II. С. Попов 10. П.. С. а в и ч е в В. В. Расчет песта-
:.:юпарпого ускорения плазмы с учетом абляции диэлектрика / Физика
плазмы.— 1976.— Т. 2, JV» 5.— С. 742—749.
30. Давыдов 10. М. Применение метода диффереициальных прибли-
приближений для исследования и построоппя пелипеншлх разпостпых схем //
ЧММСС." Новосибирск: 1980.—Т. 11, JV» А.— С. 41—59.
31. Давыдов Ю. М., Скотников В. П. Дифференциальные при-
б.чнжепия разностных схем.— М.: ВЦ АН СССР, 1978.
32. Да iic он Ф., Тер-Хаар Д. Нейтронные звезды и пульсары.—
М.: Мир. 1973.
33. Данилова Г. В., Дородницын В. А., Курдюмов С. П.
и др. Взаимодействие сгустка плазмы с магпитпым полем в канале рель-
сотропя.— Препринт/ИПМ АН СССР.— М., 1973.—№62.
34. Д а п и л о в а Г. В., Курдюмов С. П., Попов Ю. П. и др.
Рлгчет сплыюточпых разрядов с упетом пффекта вторичпого пробоя.— Пре-
нрпит/ИПМ АН СССР.—М., 1974.— Х° 6.
35. Дегтярев Л. М., Фаворский А. П. Потоковый вариант ме-
метола прогопки дли ра.шостиых ладач с сильно меняющимися коэффициен-
коэффициентами Л ЖВМ и МФ. - 1П60.— Т. 9, Л« 2.—С. 211—218.
36. Дегтярев Л, М„ Фаворский А. П. Потоковый вариант ме-
метода прогопки // ЖВМ и МФ.— 1968 —Т. 8, № 3.—С. 670—684.
37. Захаров А. И., Клавдиев В. В., Письменный В. Д. и др.
Экспериментальное наблюдение Г-слоев в движущейся плазме, взаимодей-
взаимодействующей с магпитпым нолем // ДАН СССР.— 1973.— Т. 212, N> 5.—С. 1092—
1095.
38. II в а и о в М. Я., К о р е д к и й В. В., К у р О ч к и н а Н. Я. Иссле-
Исследование свойств разностных схем сквозного счета второго порядка аппрок-
аппроксимации // ЧМСС-Новосибирск: 1930.- Т. И, № 2.-С. 41-63.
39. Иванова Л. II., И м ш е н н и к В. С,, Ч е ч е т к и н В. М. Пуль-
418
сацпонный режим термоядерного взрыва плотного углеродного ядра авеа-
ды,— Препринт/ИПМ ЛИ СССР,—М., 1973,—№ 69.
40. Калит кип Н. Н., Кузьмина Л. В., Рогов В. С. ТаилицЫ
термодинамических функций и транспортных коэффициентов плазмы.— Пре-
принт/ИГЩ ЛН СССР,— М., 1972.
41. Карпман В. И, Нелинейные волны в диспергирующих средах.—
М.: Наука, 1973.
42. К в а р ц х а в а И. Ф., Матвеев 10. В., Р е ш е т п я к Н, Г. К во-
вопросу о ме^'апилме ускорения заряженных частиц в динамическом с-пин-
че // Письма в ЖЭТФ,— 1972.— Т. 15, .№ 10.—С. 619—622.
43, Ко л до Па Л. В., Новещенко Ю. Л„ Попов 10. П. Двухслой-
Двухслойные полностью коисепвлтптшо разностные схемы для уравнений газовой
динамики в переменных Эйлера / ЖВМ и МФ,— 1987.— Т. 27, Л» 5,
44, Колесников П. М. Электродинамическое ускорение плазмы,—
М,: Лтомиэдат, 1!O1.
45, Коллатц Л. Функциональный анализ и вычислительная мате-
математика. - М.: Мир. 1969.
40, Ко со в и ч е в Л. Г., Попов 10. П. Некоторые особенности рас-
распространении ударных воли в атмосфере Солнца.— Преприпт/ИПМ ЛН
СССР,— М„ 1978.— Ki 73.
47. Ко с о в и че в Л. Г., Попов 10. П. К вопросу о квазипериодиче-
квазипериодических колебаниях в атмосфере Солнц:!.- М.: ИПМ АН СССР, 1979.
48. К о с о в и ч е в Л. Г., П о п о в Ю. П. К расчету одпомерпых неста-
нестационарных задач гравитационной газодинамики Ц ЖВМ и МФ, 1979.—
Т. 19, Ki 5.
49. Кузьмин Л. В., Макаров В. Л. Об одном алгоритме построе-
построения полностью коисервативпых р\;шостных схем / ЖВМ п МФ.— 1982.—
Т. 22. № 1.
50. Кузьмин Л. В., Макаров В. Л., Меладзе Г. В. Об одной
полностью консервативной ралпосгной схеме для уравнений газовой дина-
динамики в переменных Эйлера // ЖВМ и МФ.— 1980.— Т. 20, JVa 1.
51. Куликовский А, Г., Л ю б и м о в Г. А. Магпитаая гидродинами-
гидродинамика.— М.: Фияматгия, 1962.
52. К у р о п а т е н к о В. Ф., С а п о я; п и и о в А. Т. Расчет неустано-
неустановившихся движений сжимаемых сред с фазовыми перехода.\ги / Числен-
Численные методы мехапикп сплошной среды.— Новосибирск: Наука 1971.—
Т. 2. № 5.
53. Ландау Л. Д.. Лифшиц Е. М. Теория поля.—М.: 1962.
54. Ландау Л. Д., Лифшнц Е. М. Электродинамика сплошных
сред.—М.—Л : Гостехиздат, 1937.
53. Лоотовип М. А. Введение в термодинамику.— М.— Л.: Гос-
Гостехиздат. 1952.
50. М а ж о р о в а О. С, Попов 10. П. О полностью консервативных
схемах для двумерных уравнений газовой динамики / Дифференц. уравне-
уравнения.— 1979.—Т. 15. Л» 1.— С. 1318-1331.
ГO. М а ж о ]) о п а О. С, Попов 10. П. К расчету двумерных уравне-
уравнений газовой динамики.—Препринт/ИПМ АН СССР.— 1VI., 1977.— № 55.
58. Маламуд В. Г., Попов 10. П., Ш а и и р о В. С. Примопеппо
полпостью консервативных схем к расчету задач гидродинамики и магнит-
магнитной гидродинамики.— Препрянг/ИПМ АН СССР. — М., 1970.— №28.
59. Мухин С. II., Попои С. Б, Попов 10. П. О разностных схе-
схемах с искусственной дисперсией // ЖВМ и МФ.— Т. 23, Л» 6.
00. Мухин С. П., Попов СБ., Попов Ю. ГТ. Рааиостпыв схемы
с искугхтвеппой дисперсией для уравнений магнитной газодинамики.— Пре-
Преприпт/ИПМ АН СССР.—М., 19S5. — Л» 19.
01. Нпгматулип Р. П. Модель движения и ударные волны в двух-
двухфазных твердых телах с фазовыми переходами // ПМТФ.— 1970.—Т. 1, № 1.
G2. Никифоров А. Ф. Уваров В. Б. Коэффициенты поглощения
счета в плазме,- Пропринт/ППМ АН СССР,— М,, I960.- Лг 36.
63, Попов Ю, П. Расчот электротехнических цепей в задачах маг-
магнитной гидродинамики // ЖВМ и МФ,—1971,—Т. 11, № 2,—С, 449—461.
419
6'i. Попов С. Б., Попов Ю. П. Особенности решения задач газовой
динамики копечно-разностными методами.— Проприет/ИПМ АН СССР.— М.,
1978.—Л1» 98.
65. Попов Ю. П., Самарская Е. Л. О сходимости итерационного
процесса Ньютопа для решения рамностпьгх уравпонпй газовой динамики Ц
ЖИМ и МФ.— 1977.— Т. 17, Кг 1.
fi6. Попов Ю. П.. Самарская Е. Л. Особенности численного реше-
решения уравпеппп газовой динамики на грубых сетках.— Препринт/ИПМ АН
СССР.— М., 1979.— Л» 103.
07. Попов Ю. П., С а м а р с к п й А. А. Полпостыо ковсервативные
разностные схемы // ЖВМ и МФ.—1969.—Т. 9. Ла 4.—С. 953—958.
68. Попов Ю. П., Самарский Л. Л. Полностью копсервативные
разиостпые схемы для уравнепнп газодинамики в nopevnrabix Эйлера //
ЖВМ н МФ.- 1970.-Т.'Ю, № З.-С. 773-779.
09. П о и о ь Ю. П., Сампрский Л. А. Полностью консервативные
ра.шостпые схемы для уранпеннп магпитпоп гидроцппамнкп // ЖВМ и
МФ.— 1970.—Т. 1П. Д1 ',.—С. !190—0J1S.
70. Попон Ю. II., С а и я р с к nil А. Л. О методах пислешюго реше-
решения одиоморпых нестационарных залач газовой дипамики // ЖВМ и МФ.—
1976.-Т. 16, Ai 6.-С. ШЗ-1518.
71. Потапенко И. Ф., Чуяпов В. А. О полностью консерватив-
консервативных схемах для системы уравнений Ландау // ЖВМ и МФ.—1979.—¦
Т. 19. Кг 2.
72. П о т т е р Д. Вычислительные методы в физике.— М.: Мир, 1975.
73. Рождественский Б. Л., Япенко Н. II. Системы квазили-
квазилинейных уравнений.— М.: Наука, 1978.
74. Р о з а п о в В. Б., Р у х а д з о А. А. Излучение, линэмика и устой-
устойчивость плотной плазмы сильпоточвых разрядов.— М.: ФИАП СССР, 1969.
75. Рихт майор Р., Нортон К. Разностные методы решения крае-
пых :;адач.— М.: Мпр, 1972.
76. С а в и ч е в 15. 13. К расчету скорости упоса массы диэлектрика в
нмпульспом разряде / Вопросы физики низкотемпературной плазмы.—
Мпп'ск: Наука и техника. 1970.— С. 287—291.
77. Самаре г; и п А. А. ТЗведепие в теорию разпостных схем.— М.:
Паука, 1971.
78. Самарский А. А. Теория раппостпых схем.—М.: Наука, 1977.
79. Самарский А. А. Математическое моделирование и математиче-
математический гжеперпмепт / Вестпик АН СССР.— 1979.— Кг 5.
^0. Самарски н А. А., Г у л и п А. В. Устойчивость разностных
схем.— М.: Паука, 1973.
81. Самарский А. А., Николаев Е. С. Методы решения сеточ-
пых уравнений.—М.: Наука, 1978.
82. Самарски й А. А., П о п о в 10. П. Разностпые схемы газовой ди-
дипамики.— М.: Наука, 1075.
83. С а м а р с к и й А. А., А р с е н и н В. Я. О численном решении урав-
пепнй газодинамики с различными типами вязкости ,/ ЖВМ и МФ.—
1961.-Т. 1.
S4. С а м а р с к и й А. А., В о л о с е в и ч П. И., В о л ч и п с к а я М. И.,
К у р д ю м о в СП. Метод конечных разностей для решения одномершлх
пестациопарпых задач магнитной гидродинамики // ЖВМ и МФ.—
1968.— Т. 8.
85. Самарский А. А., Д о ]> о д п и цы н В. А., Курдгомов С. П.,
Попов 10. П Образование Г-слоеп при торможении плазмы магнитным по-
полем // ДАН СССР.— 1974.—Т. 216, А1» 6.—С. 1254—1257.
(S6. Самарский А. А., Соболь И. М. Примеры численного расче-
расчета температурных волн // ЖВМ и МФ.—1963,—Т. 3, Л: 4—С, 702—719.
S7. Седов Л. II. Механика сплошной среды, т. I, II.— М.: Наука, 1973.
88. С е д о в Л. И. Методы подобия и размерности в механике.— М.:
Физматгиз, 1962.
89. Т и х о н о в А. Н., Самарский А. А. О сходимости разностных
схем в классе разрывных коэффициентов // ДАН СССР.— 1959.—Т. 124, К° 3.
420
90. Тихонов А. Н.. Самарский Л. А. Об ояпородвых разностных
схемах // ЖВМ и МФ.— 1961,—Т. 1, Л1 1.— С. 5—63.
91. Тихонов А. П., Самарский А. А. О разностных схемах для
уравнений с разрывными коэффициентами Ц ДАН СССР.— 1956.—
Т. 108. № 3.
92. Тихонов А. Н.. С а м а р с т; \т А. Л. Об однородных разностных
схемах // ДАН СССР.— 1958.—Т. 122. № 4.— С. 562—566.
93. Т и х о н о в А, П., Самарский А. А. Уравпеппя математической
физики,— М.: Наука, 1977.
94. Тихонов А. Н., Самарским А. Л., За к л язь минский Л. А.
и др. Нелинейный эффект образования самоподдерживающеюся высокотем-
высокотемпературного слоя газа в нистационарвых пропессах магвптной гидродинами-
гидродинамики // ДАН СССР,— 1967.—Т, 173, Л» 4.—С. 808—811.
95. Трощиев В. Е. О дивергентпости схемы «крест» численного ре-
шеппя уравнении газовой динамикп ,'/ Чис иппыс методы механики сплош-
сплошной среды.—Новосибирск: Наука.— 1970.— Т. 1, JY» 5.—С, 87—9G.
Я6. У из ем Дж, Линейныо и пелппейпые волны.—М,: Мир, 1977.
97. Фаворский А. П. Варпациопно-дпскретпмо модели уравнений
гидродинамики.—Препринт/ИПМ АН СССР,— М., 1979.—Л? 159.
98. Ш о к и н Ю. И. Первое дифференциальное приближение.— Ново-
Новосибирск: Наука, 1979.
99. Яненко Н, Н,, Шокип Ю, И. On аппроксимациоппой вязкости
разностных схем // ДАН СССР.— 19G8,—Т. 182, № 7.—С. 776—778.
100. С о 1 о rn b a n t D. G,, Gardner Y. II. Shock waves propagation
in a inhomogeneons medium using finite differences // J. Comp, Phys.— 1976.—
V. 22,- P. 389.
101. Crist, у R. F. Computational methods in stellar pulsation // Methods
in computational physics.—V. 7.: Astrophysics,—New York — London: Academ.
Press, 1907,—P. 191.
102. II о p f E, The partial differential equation ut + uux = \iuxx // Comm.
Pure and Appl. Math.— 1950.—V. 3, N 4,
103. Korteweg D. J., de Vries O. On the change of form of long
waves advancing in a restangular channel, and on a now lype of long. Statio-
Stationary waves II Phyl. Mag.— 1895.— V. 39, N 5.
104. Kvartskhava I. F., Malveev Yu. V., Khautiev E. Yu.
Plasma losses in high — current plasma configuration due to the inverse skin
effect II Nuclear Fusion.—1971.—V. 11.— P. .'149—355.
105. Kvartskhava 1. F., Matveev Yu. V. Role of recurring dis-
discharge ignition in a dynamic z-pinch ,/ Nuclear Fusion.— 1971.— V. 11.—
P. 385—387.
106. Slettebak A. Observed rotational velocities of single stars //
Stellar rotation. Dordrecht..— 1970.—P. Л.
107. Von Neumann J,, Richtmyor R. П. A method for numerical
calculation of hydrodynamics shocks // J. Appl, Phys.— 1949.— V. 21.
108. Zakharov A. I., Klaldiev V. V., Pismenny V. D. etc.
The experimental observation of T-Iayers in moving plasma interacting with
tbe magnetic field // Physics letters,— 1973,— V. 43A, № 2,
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автомодельное решение 73
Автомодельность типа «бегущей вол-
волны.) В5, 31.1
Адиабата Гюговио 59, 87
— Пуассона 61, 85
Акустическое приближение 47, 156
Априорные оценки 155
Ассимнтотическая устойчивость 191
Безыидекеиые обозначения 107
Вектор Умова-Пойнтиига 305, 341
Вморожеиность м.шштпых силовых ли-
линий 308
Волна простая 75
центрированная 77
разрежения 77
— Ричапа 75
— ударная 58, 381
— — магнитогидродинамическая 313
Вязкое давление С1
Бнзык-ть еа
— аштрокеимационная 256
— искусстЕ1енн<(н 126
— квадратичная GS. 127
— линейная 127
— схемная 256
Г-фирма дифференциального приближе-
приближения 254
Гиперболичность системы уравнений 51
газовой динамики 52
—¦ магнитной гидродинамики 310
Градиентная катастрофа 246
Давление магнитное 305
Джоулево тепло 295
Дисперсия 260
— искусственная 26S
— схемная 267
— аномальная 27<3
Дисперсионные свойства схемы 280
Диссипация схемы собстпеииая 256
Диесипативные и дисперсионные свой-
свойства схемы 205, 267
Диспергирующие среды 261
Единичный параллелепипед 30, 35
Задача о поршне 72, 238
ускоряющемся 78
Закон изменения объема 44
— Ома 297
— сохранения полной энергии 390
— — электромагнитной анергии цепи
342, 350
422
Инварианты Римана 54
Интегро-иитерполяциоиный метод 114,
143
Интерпал массопый 96
— фиктивный 129, 335
Истечение в вакуум 77
Корректность разностной задачи 154
Критерий устойчивости Куранта 164
Метод гармоник 160
— дифференциального приближения 253,
254
— Ньютона 197
— прогонки 198
— раздельных прогонок 226, 330
— спектральный 162
— энергетический 171
Ненизка 105
Обезразмериваиие задачи 299
Область влияния 56
— зависимости 56
Однородная разностная схема 125
П-форма дифференциального приближе-
приближения 255
Псриое дифференциальное приближение
255
уравнений изотермической га-
зоной динамики 2SU
Перемсчшые Лаграижа 21, 23
— массовые 35, 36
— Эйлера 22
Линч 2-LLLI114 ;!.;и
— (I пинч 347
Погрешность аппроксимации 99
Полная производная по времени 23
Полудивергеитыая форма уравнения
энергии 305
Полуцелые точки сетки 9G
Порадок точности 104
Потоковый вариант метода прогонки
332
Приближение сильной волны 62
Принцип максимума 163
Принцип наименьшего действия 382
Прогонка обратная 200
— прямая 199
Прогонки метод 198
Псепдовнзкость 120
Разностная производная вторая 99
— — леиая 99
правая 99
— — центральная 9J
— схема 104
для уравнении теплопроводноещ
— — консервативная 112
— — однородная 125
полностью консервативная дл;1
диумерных задач газовой динамики
372
— — — — — одномерных уравнении
газовой дпнамшш 120, 123
— — — — — магнитной гидродинамики
325, 328
— — — — — уравнения цепи 342, 350
Гаирыв ирлщательный 319
— изотермический 71
— контактный 41, 319
— 1-пльпый 77
— слабый 77
— танп-нцпалпный :'2И
Распад ироилюльппго разрыва 81
Сетка разностная 95
— — неравномерна)! 106
равномерная 96
Сеточная функция 95
Скорость альфвеновская 312
— звука 48
изотермическая 49
мапштогндродпнамическая 312
— истечения в вакуум 77
— сходимости 194
— ударной волны 61
Слой сетки временийй 97
СоОстнениая линейная вязкость 280
— квадратичная вязкость 280
Собственное значение 50
Собственный вектор левый 50
Солитон 200
Соотношения Гюгоипо 57
Сопротивление тепловое 145
Спектр численного решении 284, 287
Структура фронта ударной полны 03
— — — — в теплопроводной среде 69
— — при наличии пязкостц 06
Субстанциональная производная 23
Схема несимметричная ,402
— нелвнал 102
— симметричная 372
— с искусственной дисперсией 272, 2Pti
— склонного счета 125
— пиная 102
Теорема Цечплеиа 62
Течение изотермическое 45
— 1г;аг>нтро11Пчегкие i5
У.'.ел сетки !Ui
Уравнение Г)юргерса 25S
— движения 20
— индукции 2ЯЗ
— Коргевега-де Приза 231)
— — — Оюргсреа 202
— нера.фыппости 25
— переноса 158
квазилинейное 2-1.1
— оперши 27
Уравнении газовой динамики в инва-
инвариантах 1'имана 54
— — -- дифференциальные 31
— — - - — в лаграна.ч'вых массовых пе-
переменных .'1ч
- — — — п переменных Эйлера 33
— — - - интегральные 25
в „таграшкевых массовых пе-
переменных 23, 4A
— -- — одномерного т.^нчшя газа 29
— магнитной гидродинамики в вектор-
векторной форме 24S, 2У'.1
— в лаграшкевых массовых пере-
переменных 302, 306, 307
— Максвелла 295
— состоянии 21
Устойчивость разностной схемы 104, 105,
155
— для уравнения теплопроводно-
теплопроводности 186
Функция Лагранша механической си-
системы 383
Характеристика энтропийная 53
Характеристики 49, 51
— гигтелш уравнений глг.обой дипами-
1'Н 5У
— — — магнитной гидродинамики 311
Характеристический форма системы
уравнений 51
— — газодинамики 53
Целые точки геткп 9G
Шлг сеткп 96
Ширина фронта ударной волны 67
Электротехническое уравнение цепи 338,
С'Птрсчшйнып след 2'уО
Учебное издание
САМАРСКИЙ Александр Андреевич
ПОПОВ Юрий Петрович
РАЗНОСТНЫЕ МЕТОДЫ РЕШЕНИЯ
ЗАДАЧ ГАЗОВОЙ ДИНАМИКИ
Заведующий редакцией Е. Ю. Ходан
Редакторы С. И. Мухин, Т. И. Пташник
Художественный редактор Г. М. Коровина
Технический редактор И. III. Аксельрод
Корректор И. Я. Нриштиль
ИГ, N8 41210
Сдано в найор 20.12.90. Подписано к печати 13.03.92.
Формат 60x90/16. Бумага типографская JJ4 1. Гар-
i [ [ г г у 11. i обыкнпнепн.'ш. 1Геч.чгь высокая. Усл.
неч. л 26,3. Усл. кр.-отт. 2й,."р. Уч.-изд. л. 27,54.
Тираж li'wii ju.i. Заказ Л» 606. С-027,
Издательсио-произвпдственпое
и [Шиготорговое оиъедчнение «Наука».
Главная редагция
Aшлш.о-матем:1ти'1есг<ой литературы
117071 Москва B-7I, Лсшшсьнй проспект, 15
Чстнертап типография издательства «Наука»
C:i ]П77 г. Новосибирск, ", Стиниславсчого, 25